Квантовая механика. Том I - Коэн-Таннуджи К., Диу Б., Лалоэ Ф.

Важное предупреждение: как работать с книгой
Глава I. Волны и частицы. Введение основных идей квантовой механики
C. Квантовое описание частицы. Волновой пакет
D. Частица в поле скалярного потенциала, не зависящего от времени
B. Ограничения, налагаемые соотношением неопределенностей
С. Соотношение неопределенностей и атомные параметры
D. Соотношение неопределенностей и дополнительность
Е. Простое исследование двумерного волнового пакета
F. Связь между одномерной и трехмерной задачами
G. Одномерный гауссов волновой пакет. Расплывание волнового пакета
Н. Стационарные состояния частицы в поле прямоугольного одномерного потенциала
J. Поведение волнового пакета на скачке потенциала
Глава II. Математический аппарат квантовой механики
B. Пространство состояний. Обозначения Дирака
C. Представления в пространстве состояний
D. Уравнения на собственные значения. Наблюдаемые
E. Два важных примера представлений и наблюдаемых
F. Тензорное произведение пространств состояний
В. Некоторые полезные свойства линейных операторов
D. Детальное рассмотрение представлений {|r>} и {|p>}
$Е. Несколько общих свойств двух наблюдаемых Q и Р, коммутатор которых равен $i\hbar$$
G. Применение свойств тензорного произведения: двумерная потенциальная яма бесконечной глубины
C. Физическая интерпретация постулатов о наблюдаемых и их измерении
D. Физический смысл уравнения Шредингера
E. Принцип суперпозиции и физические предсказания
В. Изучение тока вероятности в некоторых частных случаях
С. Среднеквадратичные отклонения двух сопряженных наблюдаемых
D. Измерения, выполняемые в части физической системы
G. Представления Шредингера и Гейзенберга
М. Связанные состояния частицы в потенциальной яме произвольной формы
N. Несвязанные состояния частицы в присутствии потенциальной ямы или потенциального барьера произвольной формы
О. Квантовые свойства частицы в одномерной периодической структуре
Глава IV. Применение постулатов к простым случаям: спин 1/2 и двухуровневые системы
B. Иллюстрация постулатов в случае спина 1/2
C. Фиктивный спин 1/2 в двухуровневой системе
F. Спин 1/2 в статическом и вращающемся магнитных полях: магнитный резонанс
G. Исследование молекулы аммиака с помощью простой модели
H. Влияние связи между стабильным и нестабильным состояниями
Глава V. Одномерный гармонический осциллятор
С. Решение уравнения на собственные значения гармонического осциллятора методом полиномов
D. Анализ стационарных состояний в представлении {|p>}
Е. Трехмерный изотропный гармонический осциллятор
F. Гармонический осциллятор с зарядом в однородном электрическом поле
G. «Квазиклассические» когерентные состояния гармонического осциллятора
B. Стационарные состояния в представлении {|х>}. Полиномы Эрмита
Н. Собственные моды колебаний двух связанных гармонических осцилляторов
J. Моды колебаний бесконечной линейной цепочки связанных гармонических осцилляторов. Фононы
К. Моды колебаний непрерывной физической системы. Применение к излучению. Фотоны
L. Одномерный гармонический осциллятор в термодинамическом равновесии при температуре Т
Глава VI. Общие свойства угловых моментов в квантовой механике
B. Соотношения коммутации операторов угловых моментов
D. Применение к орбитальному угловому моменту
D. Угловой момент стационарных состояний двумерного гармонического осциллятора
E. Заряженная частица в магнитном поле. Уровни Ландау
$Е. Несколько общих свойств двух наблюдаемых Q и Р, коммутатор которых равен $i\hbar$$
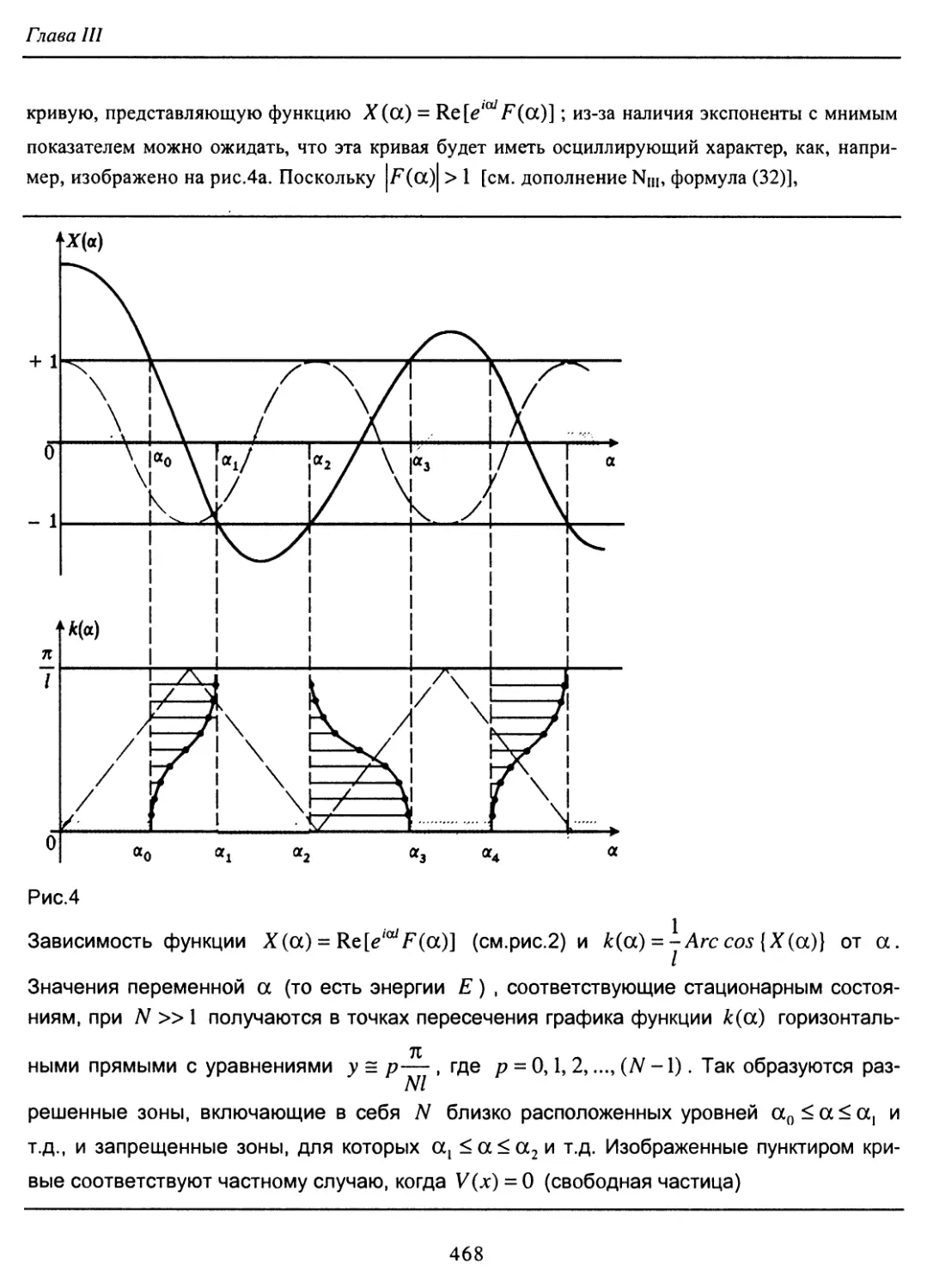
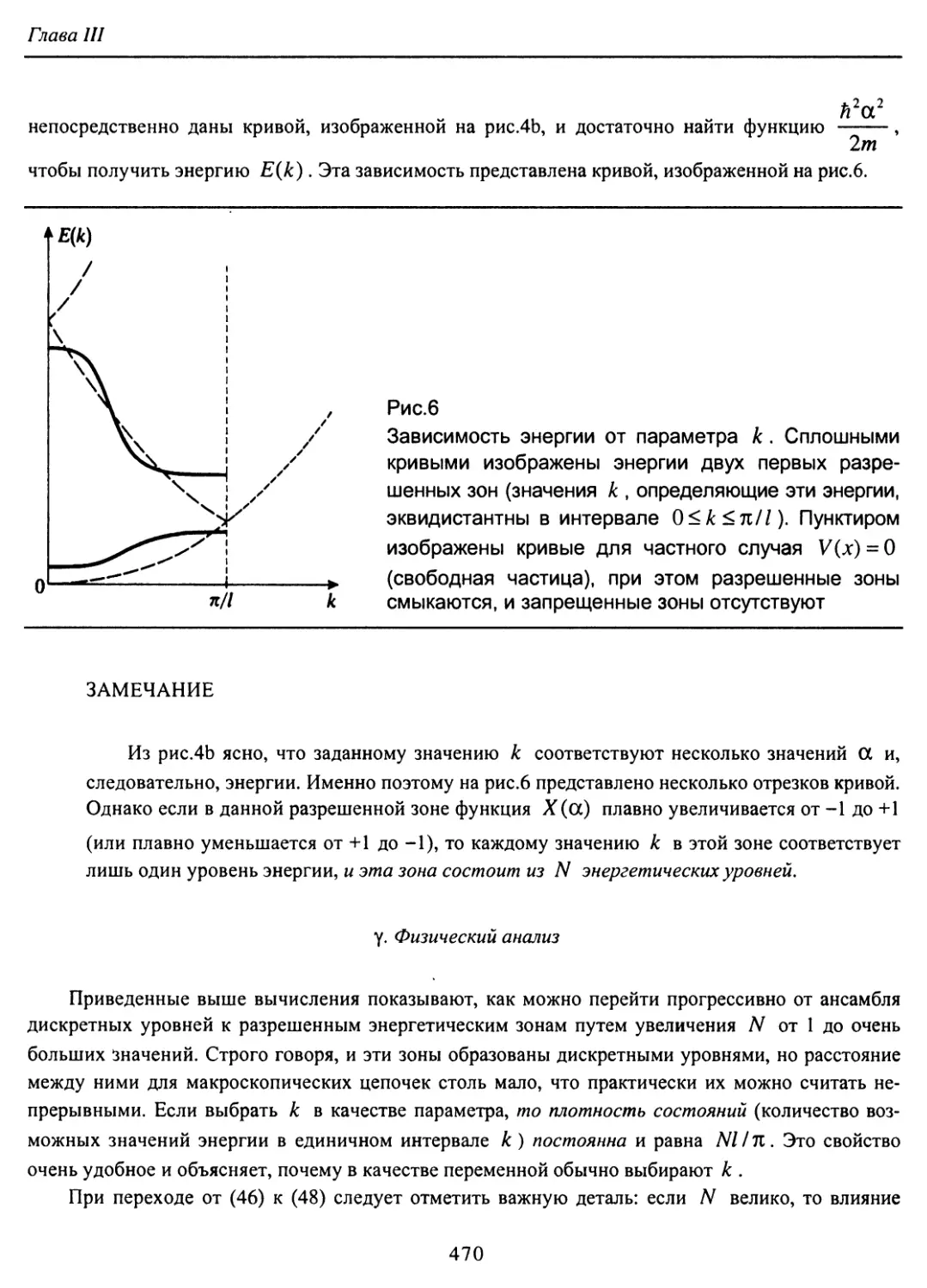
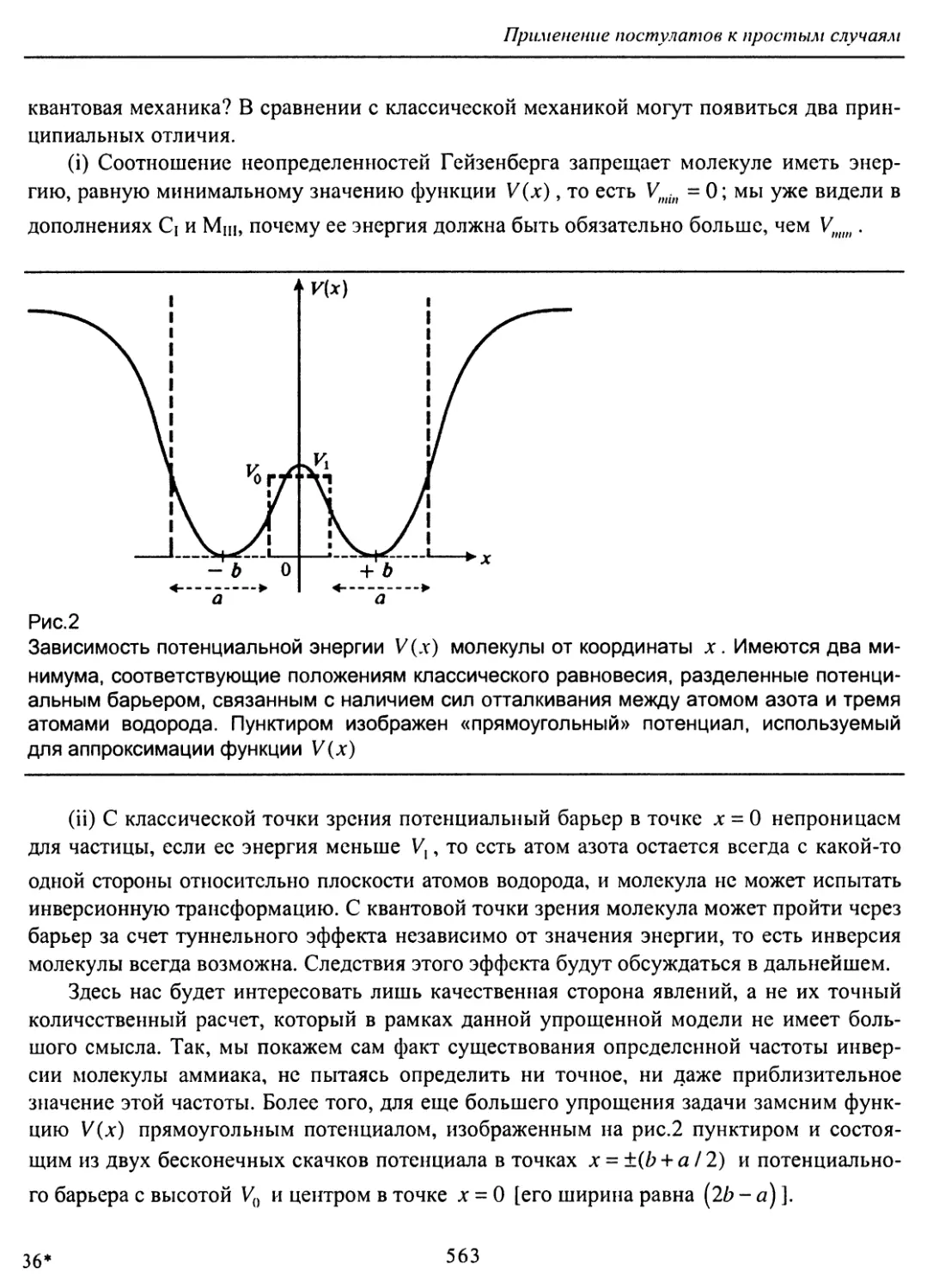
Author: Коэн-Таннуджи К. Диу Б. Лалоэ Ф.
Tags: энергетика физика механика квантовая механика
ISBN: 5-7525-1131-3
Year: 2000
Similar
Квантовая механика. Том II
Квантовая механика для математиков
Квантовая механика
Text
                    КЛОД КОЭН-ТАННУДЖИ
БЕРНАР ДИУ
ФРАНК ЛАЛОЭ
КВАНТОВАЯ
МЕХАНИКА
Перевод с французского
Л.Н.НОВИКОВА
Том I
Екатеринбург
Издательство Уральского университета
2000

CLAUDE COHEN-TANNOUD Л
BERNARD DIU
FRANCK LALOE
MECANIQUE
QUANTIQUE
Paris
Hermann
1973

КЛОД КОЭН-ТАННУДЖИ
БЕРНАР ДИУ
ФРАНК ЛАЛОЭ
КВАНТОВАЯ
МЕХАНИКА
Перевод с французского
Л.Н.НОВИКОВА
Том I
Екатеринбург
Издательство Уральского университета
2000

УДК530.145@75.8Ь
ББК Й:314я73-Г
К767
Издание осуществлено в рамках программы «Пушкин»
при поддержке Министерства иностранных дел Франции
и Посольства Франции в России
Ouvrage realise dans le cadre du programme d'aide a la publication Pouchkine
avec le soutien du Ministere des Affaires Etrangeres Fran^ais
et de l'Ambassade de France en Russie
© Л. Н. Новиков, 2000
(перевод)
© Hermann, Paris, 1973
ISBN 5-7525-1131-3 (T. I) © Издательство Уральско
ISBN 5-7525-1085-6 университета, 2000

Памяти сына моего Бориса посвящаю
ПРЕДИСЛОВИЕ ПЕРЕВОДЧИКА
Вниманию читателя предлагается многолетний труд французских физиков, известных
не только своим вкладом в современную атомную физику и спектроскопию, но и плодотворной
педагогической деятельностью в ведущих высших учебных заведениях Франции. Положив
в основу книги традиционный курс нерелятивистской квантовой механики, авторы
преследовали главную цель — изложить квантовый формализм в его наиболее понятной форме на
базе богатейшего экспериментального материала по атомной и молекулярной спектроскопии,
и это несомненно следует приветствовать не только с чисто научных позиций, но и по
педагогическим соображениям.
Квантовую механику в нашей стране преподают не только студентам
физико-математических специальностей, но и в виде части курса общей физики, и в этом смысле книга Клода
Коэна-Таннуджи, Бернара Диу и Франка Лалоэ является универсальным учебным пособием
для студентов и аспирантов всех уровней обучения, так как по широте охвата излагаемого
материала и детализации математического аппарата она не имеет себе равных среди всех
известных публикаций.
Оригинально и интересно написанная книга французских ученых будет с интересом
встречена широким кругом читателей. Она окажет несомненную пользу студентам всех
физико-математических специальностей и всем тем, кто серьезно интересуется современной
квантовой механикой.
Издание русского перевода книги встретило немало трудностей, но благодаря поддержке
ряда предприятий Уральского региона оно все же смогло выйти в свет. Прежде всего следует
отметить решающий вклад Уральского электрохимического комбината (г. Новоуральск) и его
генерального директора А.П. Кнутарева, оказавшего безусловную поддержку этого издания.
В качестве спонсора книги выступило также ОАО «Екатеринбургский завод по обработке
цветных металлов». Его генеральный директор, академик РИА Н.И. Тимофеев вместе с
переводчиком посвящают данный труд светлой памяти Валентина Фадеева, друга и однокурсника,
безвременно ушедшего из жизни.
Значительная помощь была оказана известным предприятием ЗАО «Уралвестком»,
генеральный директор которого В.Ю. Молчанов с полным пониманием поддержал реализацию
данного проекта.
И, конечно, нельзя не упомянуть реальную помощь Посольства Франции в Москве,
включившего издание книги в программу «Пушкин» и оказавшего финансовое содействие.
Всем указанным организациям и их руководителям переводчик выражает свою глубокую
благодарность.
Следует также искренне поблагодарить авторов книги Клода Коэна-Таннуджи, Бернара
Диу и Франка Лалоэ за постоянное внимание к работе над русским переводом и поддержку в
течение многих лет подготовки этого издания.
Наука определяла и будет определять будущее России, и хочется надеяться, что эта
книга станет заметным вкладом в дело подготовки кадров высшей квалификации и символом
дружбы и сотрудничества между Францией и Россией.
Л.Н. Новиков,
кадидат физико-математических наук,
доцент кафедры теоретической физики УГТУ-УПИ

ПРЕДИСЛОВИЕ
К РУССКОМУ ИЗДАНИЮ
Мы были очень рады выходу в свет перевода нашей книги по
квантовой механике на глубокий и прекрасный русский язык, на котором
говорило и писало так много выдающихся мыслителей — писателей,
философов и ученых. Безусловно, для нас, физиков, в памяти возникает
прежде всего имя Льва Ландау, являющегося символом этой великой
традиции. Всем известен его решающий вклад в физику и его
замечательные книги, до сих пор успешно служащие делу подготовки новых
поколений физиков благодаря оригинальности и компактности
изложения. И он был не одинок. Великолепная школа русских физиков,
имена которых знают все и все их уважают, ими восхищаются,
слишком велика, чтобы можно было перечислить их поименно. Именно
поэтому мы считаем для себя особой честью представить этот перевод
вниманию столь престижного научного сообщества.
Мы отчетливо понимаем те трудности, с которыми пришлось
столкнуться при подготовке этого издания. Только наш друг Леонид
Новиков, с которым мы имели удовольствие сотрудничать в прошлом
во время его визита во Францию, был способен преодолеть их. Именно
он предложил идею этого перевода много лет тому назад и смог с
замечательной настойчивостью претворить ее в жизнь в весьма сложных
условиях. Он выполнил огромную работу по переводу объемного
научного издания, которая могла быть реализована лишь специалистом
его уровня. От глубины души искренне благодарим его за то, что он
смог добиться исполнения этой идеи и доставил нам глубочайшее
удовлетворение увидеть наш труд на русском языке.
Клод КОЭН-ТАННУДЖИ
БернарДИУ
Франк Л АЛОЭ

ВАЖНОЕ ПРЕДУПРЕЖДЕНИЕ:
КАК РАБОТАТЬ С КНИГОЙ
Содержание книги состоит из двух отдельных, хотя и
неразрывно связанных частей: глав и дополнений.
Главы содержат основные теоретические положения
темы и соответствуют, за небольшим исключением,
реальным лекционным занятиям.
Таких глав в книге 14, и в принципе их можно изучать
независимо от дополнений.
Дополнения следуют в конце каждой главы; они
обозначены буквами с цифровыми индексами,
соответствующими главе (например, Av, Bv, Cv и т.д.). В конце каждой
главы имеется список дополнений, количество их может
меняться от 2 до 14 в зависимости от главы.
Дополнения могут быть различных типов: некоторые из них
предназначены для облегчения усвоения материала главы или
для уточнения некоторых положений; в других могут быть
рассмотрены конкретные физические задачи, открывающие
перспективу в различных областях физики; одно из дополнений, как
правило последнее, содержит простые упражнения.
Уровень дополнений также различен: обычно они могут
быть поняты на базе изложенного в главе материала, но
некоторые могут оказаться существенно сложнее других.
Не рекомендуется изучать всю совокупность дополнений в
том порядке, в котором они представлены. Лучше, если
читатель выберет себе небольшое их количество (например, 2 или 3),
а также несколько упражнений; все остальные могут быть
рассмотрены позднее.
Отметим, наконец, что в тексте глав и дополнений при
первом чтении некоторые абзацы могут быть просто пропущены:
они напечатаны мелким шрифтом.

ВВЕДЕНИЕ
СТРУКТУРА И УРОВЕНЬ КНИГИ
Нет необходимости напоминать о фундаментальной роли квантовой механики в
современных физике и химии. Ее важность отражается, конечно, и в постановке высшего
образования: так, например, в действующих французских программах предусмотрено
знакомство с основными идеями квантовой физики уже на втором году обучения в
университете, а детальное изучение основ квантовой механики и ее наиболее важных
приложений производится на третьем году обучения.
Эта книга является прямым результатом многолетнего опыта преподавания
квантовой механики на факультете естественных наук Парижского университета и затем в
университетах Париж-V и Париж-VI. Нам казалось весьма важным четко выделить даже
в самой структуре книги два разных, но взаимодополняющих аспекта преподавания
(лекции и практические занятия). Именно этим объясняется разбиение книги на две
составляющие, отмеченные выше в «Важном предупреждении». С одной стороны, в главах
сосредоточен материал, накопленный при чтении лекций в указанных выше учебных
заведениях, и он нами серьезно обсуждался и уточнялся до написания книги. С другой
стороны, для дополнений мы использовали опыт проведения практических занятий и
упражнений, а также ряд проблем и задач, предлагавшихся студентам для
самостоятельного решения, для докладов, курсовых работ и выпускных работ третьего цикла. Как мы
уже отмечали выше, совокупность глав составляет в нашем представлении с точностью
до нескольких уточнений содержание тех лекций, которые авторы читали на четвертом
курсе университета. Конечно, не может быть и речи о том, чтобы за один учебный год
изучить все дополнения, материал которых накапливался в течение многих лет: читатель —
преподаватель или студент — должен сам выбирать те из них, которые наиболее
соответствуют роду его занятий, вкусу или преследуемой цели. В ходе создания этой книги
мы постоянно имели в виду, что нашим читателем является студент — будущий физик,
с которым мы работали много лет, поэтому мы стремились не переступать порог
трудности, определяемый сложностью усвоения и понимания квантовой механики и
следующий из вопросов, задаваемых студентами. Конечно же, мы надеемся, что эта книга
окажется полезной и другим категориям читателей (аспирантам, молодым ученым,
преподавателям среднего звена образования и т.д.).

Чтобы начать чтение книги, не обязательно иметь уже некоторую начальную
подготовку в области квантовой механики: действительно, за редким исключением, студенты
не имеют такой подготовки. И, напротив, нам кажется необходимым дополнить
предлагаемый нами курс квантовой механики курсом атомной физики (в широком смысле
слова), который был бы более тесно связан с экспериментом и носил бы описательный
характер.
ОБЩИЕ ПРИНЦИПЫ ИЗЛОЖЕНИЯ МАТЕРИАЛА
Нам кажется, что наилучшим способом освоения квантовой механики является ее
использование для решения конкретных задач. Именно поэтому мы вводим как можно
раньше (с главы III) постулаты квантовой механики, чтобы применять их в дальнейшем
изложении. Действительно, наш опыт преподавания показал, что лучше сгруппировать
все постулаты в начале курса, чем вводить их в несколько приемов. Кроме того, нам
кажется более предпочтительным сразу же использовать пространство состояний и
обозначения Дирака: если развивать сначала волновую механику, применяя только
волновые функции, и лишь потом вводить более общий формализм кет- и бра-векторов,
приходится неизбежно прибегать к повторениям. Более того, запоздалое введение этих
обозначений может сбить студента с толку и породить сомнения в понятиях, которые он
только что получил и еще не успел полностью усвоить.
После вводной главы, в которой на качественном уровне излагаются квантовые
идеи с помощью простых оптических аналогий, мы синтетическим образом представим
математический аппарат (глава II) и постулаты (глава III) квантовой механики. В главе III
попытка синтеза делается не только в отношении формулировки постулатов, но также и
при обсуждении их физического содержания, что позволяет читателю с самого начала
познакомиться с общими физическими следствиями новых постулатов. Начиная с
главы IV (а точнее, с дополнений к главе III), мы переходим к приложениям, сначала к
самым простым (двухуровневые системы, гармонический осциллятор и т. д.), а затем
постепенно и к более сложным (атом водорода, методы аппроксимации и т. д.). Мы все
время стремимся к тому, чтобы изложение квантовой механики иллюстрировалось
многочисленными примерами, взятыми из различных областей (атомная физика,
молекулярная физика, физика твердого тела и т. д.). Конечно, во всех этих примерах нас
прежде всего интересует квантовый аспект явлений, и мы не имеем возможности детального
исследования всех частных вопросов, которые вытекают из их анализа и являются
предметом рассмотрения в специальной литературе. При каждом удобном случае
квантовые результаты сопоставляются с классическими, чтобы явно выделить их сходство
или различие и выработать у читателя интуитивный подход к квантовым эффектам.
Такая существенно дедуктивная точка зрения побудила нас отказаться от
исторического введения квантовых идей, то есть от представления и обсуждения
экспериментальных фактов, которые поставили под сомнение классические идеи. Таким образом,
мы намеренно отказались от индуктивного подхода, который кажется необходимым для
придания физике истинного лица, как науки, всегда имеющей дело с эксперименталь-

ными фактами, являющимися ее движущей силой. Этот подход кажется более уместным
для книги по атомной физике или для вводных лекций по квантовой физике на самом
элементарном уровне (например, первый цикл обучения).
Аналогично, мы умышленно избегали любой дискуссии по философским вопросам
квантовой механики и любых попыток ее интерпретации. Подобная дискуссия, несмотря
на ее несомненный интерес, должна, по нашему мнению, проходить совсем на другом
уровне: нам кажется,, что для плодотворного обсуждения этих вопросов необходимо
сначала овладеть «ортодоксальной» квантовой теорией, которая заслужила всеобщее
признание благодаря замечательным успехам во всех областях физики и химии.
Преподавание квантовой механики, которое легло в основу этой книги, было
результатом многолетней совместной работы всей нашей группы. Мы хотели бы
поблагодарить всех тех, кто в разное время работал в ее составе, и особенно Жака Дюпон-Рока и
Сержа Ароша за их дружеское сотрудничество, за плодотворные дискуссии, которые мы
вместе вели во время наших еженедельных собраний, за идеи задач и упражнений,
предложенные ими. Без их энтузиазма и неоценимой помощи мы никогда не смогли бы
предпринять и довести до конца написание этой книги.
Мы не можем, конечно, забыть, что двое из нас всем обязаны господам Альфреду
Кастлеру и Жану Бросселю, а третий — господину Морису Леви. Именно в
стимулирующей обстановке их лабораторий мы открыли для себя красоту и мощь квантовой
механики. Мы не забудем также то значение, которое имело для нас обучение
современной физике на лекциях господ Альбера Мессиа, Клода Блоха и Анатоля Абрагама в те
годы, когда третий цикл обучения не был еще введен в систему французского высшего
образования.
Подготовка рукописи к печати не могла бы быть выполнена без помощи многих
людей и, в частности, мадам и мадемуазель Оше, Бодри, Буа, Броджи, Эмо, Эваэр, Лемир и
Тузо. Мы хотим выразить им свою глубокую благодарность.

Глава I
ВОЛНЫ И ЧАСТИЦЫ.
ВВЕДЕНИЕ ОСНОВНЫХ ИДЕЙ
КВАНТОВОЙ МЕХАНИКИ

ПЛАН ГЛАВЫ I
А. ЭЛЕКТРОМАГНИТНЫЕ
ВОЛНЫ И ФОТОНЫ.
1. Кванты света и соотношения Планка—Эйнштейна.
2. Корпускулярно-волновой дуализм.
a. Анализ эксперимента Юнга.
b. Квантовое единство двух аспектов света.
3. Принцип спектрального разложения.
В. МАТЕРИАЛЬНЫЕ
ЧАСТИЦЫ
И ВОЛНЫ МАТЕРИИ.
1. Соотношения Луи де Бройля.
2. Волновая функция. Уравнение Шредингера.
С. КВАНТОВОЕ ОПИСАНИЕ
ЧАСТИЦЫ. ВОЛНОВОЙ
ПАКЕТ.
1. Свободная частица.
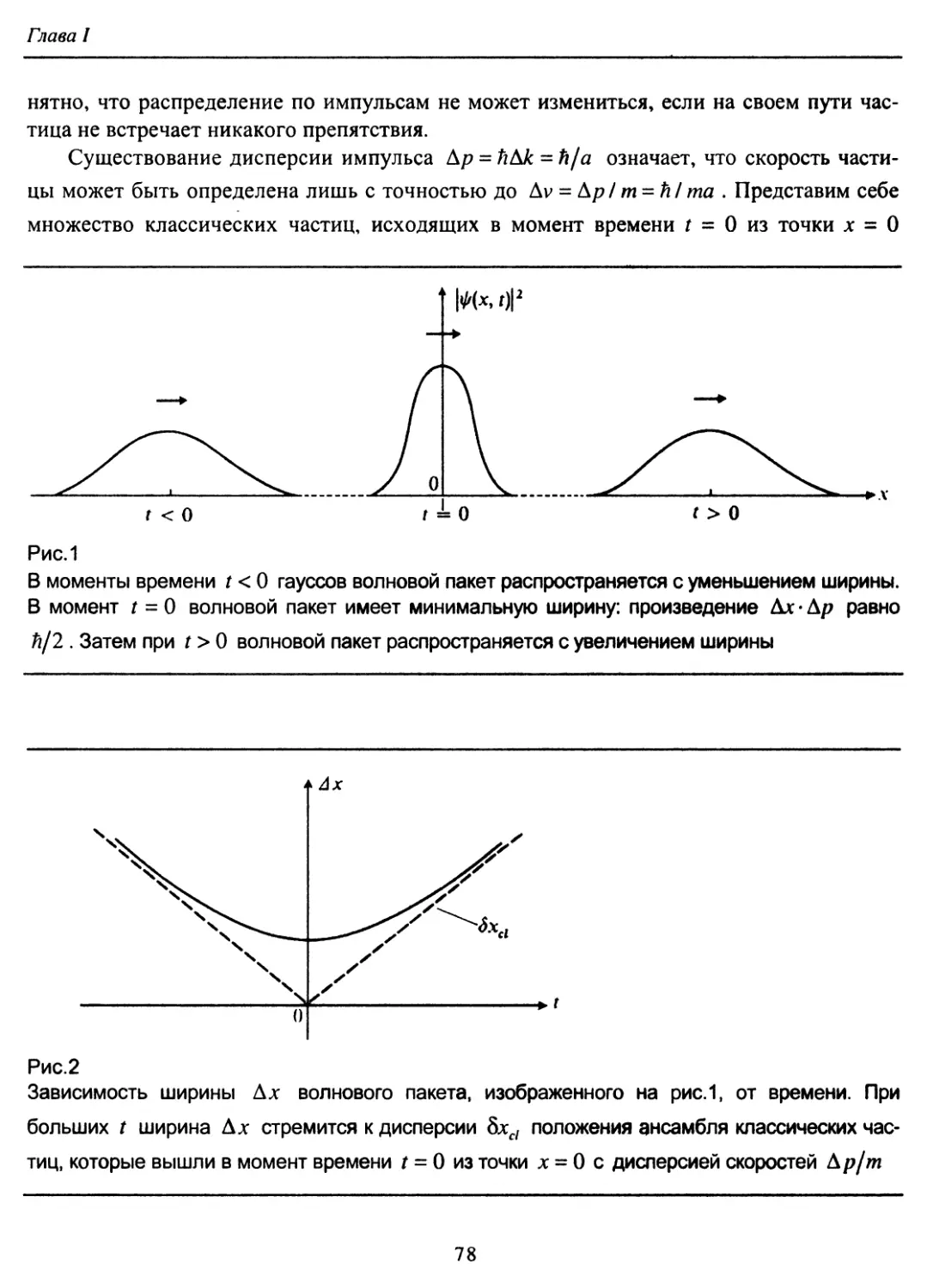
2. Форма волнового пакета в заданный момент времени.
3. Соотношение неопределенностей Гейзенберга.
4. Эволюция свободного волнового пакета во времени.
D. ЧАСТИЦА В ПОЛЕ
СКАЛЯРНОГО
ПОТЕНЦИАЛА,
НЕ ЗАВИСЯЩЕГО
ОТ ВРЕМЕНИ.
1. Разделение переменных. Стационарные состояния.
a. Определение стационарных состояний.
b. Суперпозиция стационарных состояний.
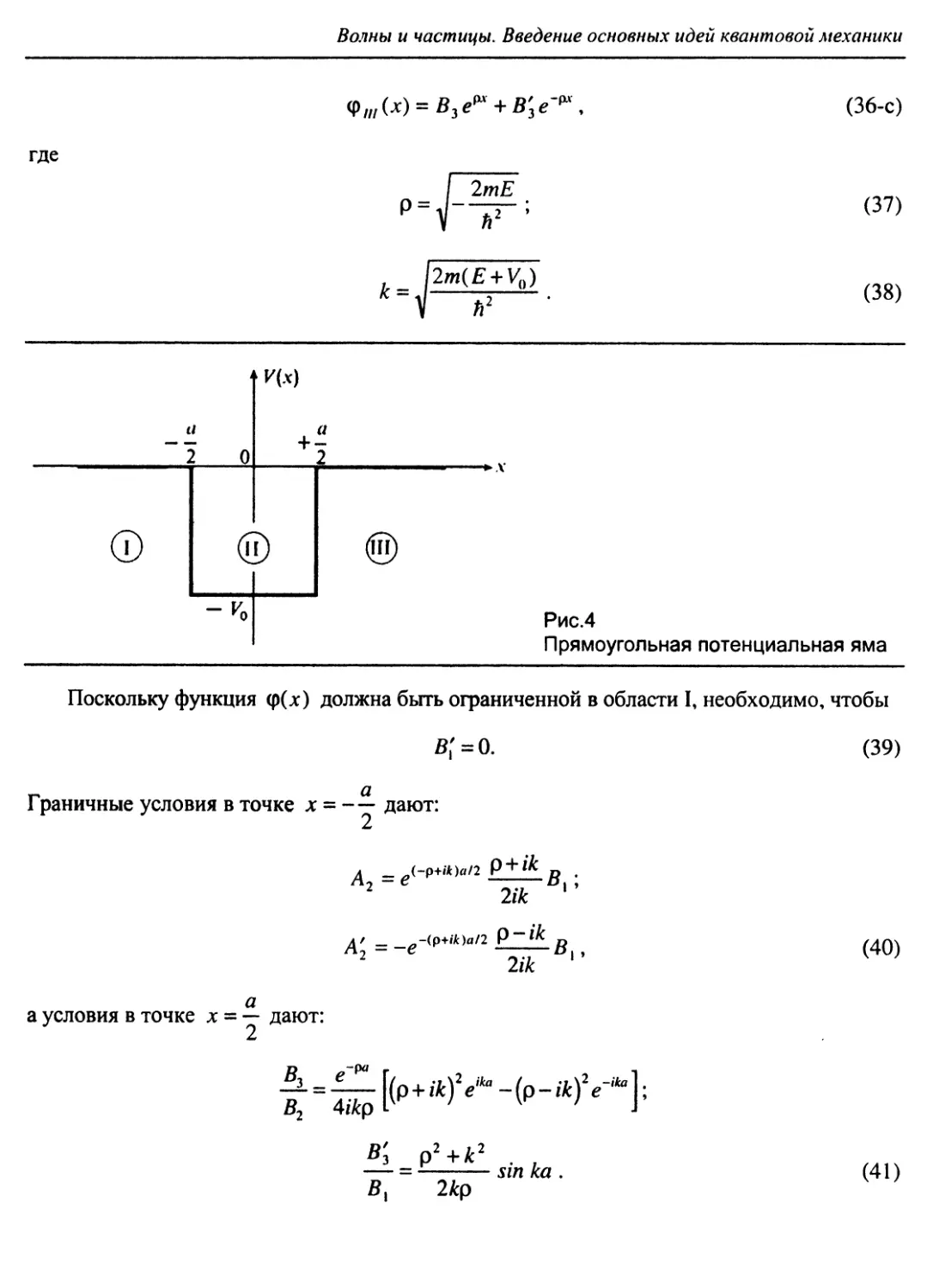
2. «Прямоугольные» одномерные потенциалы. Качествен
ный анализ.
a. Физический смысл прямоугольного потенциала.
b. Аналогия с оптикой.
c. Примеры.

На современном уровне научного познания квантовая механика играет
фундаментальную роль для понимания и описания явлений природы. Действительно, как только
эти явления происходят в атомном или субатомном масштабах, их можно объяснить лишь
в рамках квантовой физики. Так, например, само существование атомов и их свойства,
химическая связь, прохождение электрона через кристалл и т. д. не могут быть поняты
на основе классической механики. Даже в тех случаях, когда нас интересуют
макроскопические физические объекты (то есть имеющие размеры, характерные для повседневной
жизни), для их полного научного описания исследование нужно начинать с изучения
поведения отдельных атомов, входящих в их состав. Именно в этом смысле квантовая
механика является основой нашего понимания природных явлений, включая и те, которые
традиционно относятся к химии, биологии и т. д.
С исторической точки зрения квантовые идеи, объединив свойства материальных
частиц и излучения, внесли неоценимый вклад в фундаментальные понятия физики.
Действительно, к концу XIX века все физические явления связывали с двумя, как
казалось, различными категориями: веществом и полем излучения, для которых были
установлены различные законы. Для описания движения материальных тел использовалась
механика Ньютона (см. приложение III), успехи развития которой были в свое время
замечательными. В том, что касается поля излучения, теория электромагнетизма,
благодаря введению уравнений Максвелла, позволила полностью понять целую совокупность
явлений, которые относили к различным областям: электричество, магнетизм и оптика;
так, в частности, электромагнитная теория излучения получила блестящее
экспериментальное подтверждение после открытия радиоволн. И, наконец, взаимодействие излучения
с веществом прекрасно описывалось с помощью силы Лоренца. Перечисленная
совокупность законов с учетом имевшихся экспериментальных данных обеспечивала физике
состояние, которое можно было считать удовлетворительным.
Однако в начале XX века физика испытала глубокие потрясения, в ходе которых
родились релятивистская механика и квантовая механика. Релятивистская и квантовая
«революции» были в значительной степени независимыми, так как ставили под вопрос
справедливость классической физики с разных точек зрения: классические законы не
выполнялись как в случае материальных тел, двигающихся с очень большими
скоростями, сравнимыми со скоростью света (релятивистская область), так и для процессов в
атомном или субатомном масштабах (квантовая область). Важно подчеркнуть, однако,
что в обоих случаях классическая физика являлась следствием новых теорий как при-
13

Глава I
ближение, справедливое для большинства явлений в привычных масштабах. Так,
например, механика Ньютона позволяет правильно предсказать движение твердого тела,
если это движение является нерелятивистским (скорость мала по сравнению со
скоростью света) и макроскопическим (размеры тела велики по сравнению с размерами
атомов). С фундаментальной точки зрения квантовая теория всегда остается необходимой:
только она может объяснить само существование твердого тела и значение его
макроскопических параметров (плотность, теплоемкость, упругость и т. д.). На самом деле
вплоть до настоящего времени мы еще не располагаем теорией, которая бы
удовлетворяла нас, будучи одновременно квантовой и релятивистской, ибо трудности на пути ее
создания весьма велики. Большинство же атомных и молекулярных явлений могут быть
хорошо описаны в рамках нерелятивистской квантовой механики, которая и предлагается
вниманию читателей этой книги.
Настоящая глава является вступительной, в ней лишь вводятся основные понятия и
идеи квантовой механики, и не следует требовать от нее ни полноты, ни строгости
описания. Ее главная цель — пробудить любопытство читателя, указав на явления,
несовместимые с такими прочно закрепленными в нашем интуитивном сознании понятиями,
как, например, траектория, и сделать «приемлемой» для него квантовую теорию,
продемонстрировав простыми, но количественными расчетами ее способность решать сложные
проблемы, встречающиеся в атомных масштабах. Впоследствии мы вернемся к введенным
в этой главе понятиям, уточнив их как с математической (глава II), так и с физической
(глава III) точек зрения.
В § А мы прежде всего введем основные идеи квантовой механики (дуализм
«волна—частица», механизм измерения), опираясь на хорошо известные оптические
эксперименты. Затем в § В укажем, как можно эти идеи распространить на материальные
частицы (волновая функция, уравнение Шредингера). Далее детально исследуем свойства
«волнового пакета», связанного с частицей, и введем соотношения неопределенностей
Гейзенберга (§ С). И, наконец, в § D обсудим несколько простых, но типично квантовых
эффектов.
А. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ И ФОТОНЫ
1. Кванты света и соотношения Планка—Эйнштейна
Ньютон считал свет потоком частиц, упруго отскакивающих, например, при
отражении от зеркала. В первой половине XIX века были выполнены эксперименты,
демонстрирующие волновую природу света (интерференция, дифракция), после чего оптические
явления получили объяснение в рамках электромагнитной теории. Скорость света с
была связана с электрическими и магнитными константами, а поляризация света
интерпретировалась как проявление векторного характера электрического поля.
Однако при исследовании излучения абсолютно черного тела электромагнитная
14

Волны и частицы. Введение основных идей квантовой механики
теория оказалась бессильной, и это побудило Планка в 1900 году выдвинуть гипотезу
квантования энергии: электромагнитная волна с частотой v может обладать лишь такой
энергией, которая будет кратна кванту энергии /?v, где h — новая фундаментальная
константа. Позже Эйнштейн, придав этой гипотезе значительно более общий смысл,
предложил вернуться к корпускулярной теории A905): свет состоит из потока фотонов,
каждый из которых обладает энергией hv. Эйнштейн показал, как введение понятия
фотона позволило бы очень просто описать непонятные до того времени свойства
фотоэффекта. Тем не менее потребовалось почти двадцать лет, чтобы непосредственно доказать
существование фотона как независимой частицы в эффекте Комптона A924).
Эти результаты привели к следующему заключению: взаимодействие
электромагнитной волны с веществом осуществляется при помощи нераздельных элементарных
процессов, в которых излучение ведет себя как поток частиц — фотонов. Корпускулярные
(энергия Е и импульс р фотона) и волновые (частота со = 2tiv и волновой вектор к,
где |к| = 2я / X , v — частота и X — длина волны) параметры связаны
фундаментальными соотношениями:
Е = hv = йсо (соотношения Планка—Эйнштейна);
p = fik, (A-1)
где ft = h 12я определяется через постоянную Планка h :
h = 6,62 • I О4 джоуль х секунда. (А-2)
В любом из элементарных процессов полные энергия и импульс должны сохраняться.
2. Корпускулярно-волновой дуализм
Итак, мы вернулись к корпускулярной концепции света. Значит ли это, что волновая
теория должна быть отброшена? Конечно, нет: мы увидим сейчас, что типично
волновые явления, наблюдаемые в экспериментах по интерференции и дифракции света,
невозможно объяснить в рамках чисто корпускулярных представлений. Анализируя
известный эксперимент Юнга, мы придем к следующему заключению: полное его
объяснение можно получить, лишь сохраняя одновременно и волновой и корпускулярный
аспекты света (кажущиеся априори несовместимыми). Затем мы покажем, как этот
парадокс может быть разрешен путем введения основных квантовых понятий.
а. АНАЛИЗ ЭКСПЕРИМЕНТА ЮНГА
Схема этого эксперимента приведена на рис.1. Монохроматический свет,
испущенный источником У, падает на непрозрачную пластинку, в которой проделаны две узкие
щели F! и F2, освещающие экран наблюдения # (например, фотографическую пластинку).
15

Глава 1
Если щель F2 закрыта, на экране # формируется изображение щели Fi в виде
дифракционного распределения интенсивности света /,(*); аналогично при закрытой щели Ft
дифракционное изображение щели F2 описывается распределением 12{х). Если же обе
щели остаются открытыми одновременно, то на экране наблюдается система
интерференционных полос. В частности, легко установить, что соответствующее им
распределение интенсивности 1(х) не равно сумме интенсивностеи, полученных при открытых
щелях Fi и F2 в отдельности:
/(*)*/,(*)+/,(*)
(А-3)
Л
8
Рис.1
Л + л v
Схема эксперимента Юнга по интерференции света (а). На экране % каждая из щелей
FL и F2 образует дифракционное изображение с интенсивностями /,(*) и 12{х)
(сплошные кривые на рис. (Ь). Если одновременно открыты обе щели, интенсивность 1(х) на
экране не равна /,(*) +/2(jc) (пунктирная линия) и осциллирует вследствие
интерференции электрических полей, испущенных щелями F, и F2 (сплошная кривая на рис. (с)
Можно ли с помощью корпускулярной теории, необходимость которой была
показана в предыдущем параграфе, объяснить описанный результат эксперимента? Наличие
дифракционной картины при открытии лишь одной из щелей можно было бы попытаться
объяснить, например, путем учета влияния соударений фотонов о край щели; конечно,
необходимо было бы уточнить подобное объяснение, и подробный анализ показал бы,
16

Волны и частицы. Введение основных идей квантовой механики
что оно не может быть признано достаточным. Пока же мы сосредоточим внимание на
явлении интерференции. Можно попытаться объяснить ее, включив в рассмотрение
взаимодействие фотонов, прошедших через щель Fb с фотонами, прошедшими через
щель F2; этот анализ привел бы нас к следующему заключению: при уменьшении
интенсивности источника if (т.е. количества фотонов, испущенных в 1 сек.) вплоть до того,
что фотоны падают на пластинку и затем на экран по одному, взаимодействие между
ними должно уменьшаться и в пределе стать равным нулю, вследствие чего полосы
интерференции должны исчезнуть.
Прежде чем указать на результат эксперимента, вспомним волновую теорию которая
объясняет наличие полос совершенно естественным образом. Интенсивность света в
любой точке экрана tf пропорциональна квадрату амплитуды электрического поля в этой
точке. Если Ех(х) и Е2(х) представляют в комплексной форме электрические поля,
созданные в точке х щелями Fi и F2 соответственно (щели ведут себя как вторичные
источники света), то полное поле в этой точке от двух щелей, открытых одновременно, равно:
£(х) = £,(*)+£2(;с). (А-4)
Используя комплексную форму записи, получим*:
I(x)oc\El(x) + E2(x)\\ (A-5)
Поскольку, с другой стороны, интенсивности /,(jc) и 12(х) пропорциональны соот-
II2 | |2
Е1(х)\ и |£2(*)| » из формулы (А-5) следует, что 1(х) отличается от
1{(х)+ 12(х) интерференционным членом, зависящим от разности фаз между Ех и Е2,
наличие которого и объясняет интерференционные полосы. Таким образом, как
предсказывает волновая теория, при уменьшении интенсивности источника У> полосы
сохраняются, и лишь их интенсивность уменьшается.
Что же происходит в действительности, если источник испускает фотоны
практически по одному? Ни предсказания волновой теории, ни предсказания корпускулярной
теории не подтверждаются экспериментом:
(i) если вместо экрана # поставить фотопластинку и сделать достаточно большую
выдержку, чтобы зафиксировать большое количество фотонов, то приходится
констатировать, что интерференционные полосы не исчезли, и, следовательно, нужно отказаться
от чисто корпускулярной интерпретации, согласно которой полосы появляются
вследствие взаимодействия между фотонами;
* Поскольку описываемый здесь эксперимент выполнялся с неполяризованным светом,
векторный характер электрического пвйя не играет существенной роли. Для простоты в этом
параграфе мы не будем его учитывать.
2 Квантовая механика
17

Глава 1
(ii) если, напротив, сделать выдержку столь малой, что на фотопластинку упадет
всего лишь несколько фотонов, то мы увидим, что место падения каждого фотона
окажется четко локализованным и даже очень слабая картина интерференции не появится,
то есть нужно также отвергнуть чисто волновую интерпретацию явления.
В реальности происходит следующее: по мере того, как фотоны попадают по одному
на фотопластинку, точки попадания фотонов распределяются случайным образом, и
только при очень большом их количестве характер распределения приобретает
непрерывный вид, образуя интерференционные полосы; там, где плотность точек попадания
выше, появляется яркая полоса, а там, где эта плотность ниже, — темная полоса. Таким
образом, можно сказать, что интерференционная картина образуется постепенно по мере
накопления большого числа соударений фотонов о пластинку.
Итак, результат этого эксперимента приводит к кажущемуся парадоксу, который
может быть сформулирован в рамках корпускулярной теории следующим образом.
Поскольку взаимодействие между фотонами исключается, нужно рассматривать каждый
фотон в отдельности. Но понять, почему ситуация резко меняется в зависимости от того,
открывается одна или две щели, невозможно: как объяснить, что прохождение фотона
через одну из щелей существенно зависит от того, открыта или закрыта вторая щель.
Прежде чем приступить к обсуждению этого вопроса, уместно отметить, что в
описанном эксперименте мы не пытались конкретизировать, через какую именно щель
прошел попавший на экран фотон. Чтобы получить эту информацию, можно поместить за
каждой из щелей Fi и F2 какой-либо детектор (например, фотоумножитель). При этом,
если фотоны проходят на экран по одному, можно установить, через какую именно щель
прошел тот или иной фотон, ибо сигнал от детекторов может быть получен только от
одного из них, но никак от двух сразу. Очевидно, что обнаруженные таким образом фотоны
окажутся поглощенными и не смогут попасть на экран. Удалим, например,
фотоумножитель, стоящий за щелью Fi. Детектор, стоящий за щелью F2, покажет нам, что из большого
числа фотонов около половины пройдет через щель F2. Можно заключить, что остальные
фотоны, двигающиеся к экрану, пройдут через щель Fb но изображение, создаваемое ими
на экране, никоим образом не похоже на интерференционную картину, ибо вторая щель
оказывается закрытой, и наблюдается лишь дифракционное изображение щели Fi.
b. КВАНТОВОЕ ЕДИНСТВО ДВУХ АСПЕКТОВ СВЕТА
Выполненный выше анализ показывает, что все описанные явления невозможно
описать, если оставаться в рамках только одного аспекта света — корпускулярного или
волнового. На первый взгляд кажется, что они исключают друг друга. Чтобы преодолеть
это затруднение, необходимо критически пересмотреть концепции классической физики
и допустить, что они не могут быть сохранены в новой области явлений (ее принято
называть микроскопической), несмотря на то, что повседневный опыт говорит нам об их
справедливости. Так, например, одной из важных особенностей этой области является

Волны и частицы. Введение основных идей квантовой механики
та, которая проявилась в эксперименте Юнга, когда мы ставили счетчики фотонов
позади щелей: любое измерение в микроскопической системе вносит в нее существенное
возмущение, причем это свойство нужно рассматривать как новое, ибо привычный опыт
говорит нам, что измерительный прибор практически не влияет на изучаемую систему.
Такой критический пересмотр классической физики навязан нам экспериментом, и мы
обязаны, конечно, руководствоваться экспериментальными данными.
Вернемся сначала к «парадоксу», о котором говорилось выше: поведение фотона,
проходящего через одну из щелей, зависит от того, закрыта или открыта вторая щель. Мы
видели, что любая попытка регистрации прохождения фотона через конкретную щель
мешает ему попасть на экран. Обобщая подробный анализ описанных экспериментов, можно
утверждать, что нельзя одновременно наблюдать интерференционную картину и знать,
через какую именно щель проходит каждый фотон (см. дополнение DO. Таким образом,
чтобы разрешить парадокс, необходимо отказаться от мысли, что каждый данный фотон
проходит обязательно через какую-то определенную щель. Тем самым ставится под
сомнение понятие траектории частицы, являющееся фундаментальным в классической физике.
С другой стороны, когда фотоны падают по одному, точки их соударений с экраном
постепенно образуют интерференционную картину. Это означает, что заранее нельзя
определить, в какую точку экрана попадет тот или иной конкретный фотон. Тем не менее
все фотоны испускаются источником в равных условиях. Следовательно, классическая
идея о том, что начальные условия полностью определяют последующее движение
частицы, оказывается разрушенной. Можно лишь констатировать, что вероятность попадания
испущенного фотона в определенную точку х экрана пропорциональна
интенсивности 1{х), вычисленной с помощью волновой теории и равной \Е(х) | .
В результате многочисленных пробных попыток, описывать которые здесь не имеет
смысла, было введено понятие корпускулярно-волнового дуализма, основные положения
которого можно схематически резюмировать следующим образом*:
(i) корпускулярный и волновой аспекты света неразделимы; свет ведет себя
одновременно и как волна и как поток частиц, причем волна помогает вычислить
вероятность обнаружения частицы;
(и) предсказать поведение фотона можно лишь вероятностным образом;
(Hi) информация о фотоне в заданный момент времени / дается волной £(г, г),
являющейся решением уравнений Максвелла; мы будем говорить, что эта волна
характеризует состояние фотонов в момент /. Функция £(r, t) интерпретируется как амплитуда
вероятности нахождения фотона в точке г в момент времени /: это означает, что
соответствующая вероятность равна |£(r, t) | .
* Уместно отметить, что такая интерпретация физических явлений рассматривается в
настоящее время как «ортодоксальная» и вызывает возражения некоторых физиков.
2*
19

Глава 1
ЗАМЕЧАНИЯ
(i) Уравнения Максвелла, будучи линейными и однородными, допускают
применение принципа суперпозиции: если Ех и Е2 являются их решениями, то сумма
Е = Х1Е1 +А2£2, где А,, и Х2 — постоянные, также является решением. Именно
принцип суперпозиции позволяет объяснить в рамках классической оптики
явления волнового типа (интерференция, дифракция). В квантовой физике
интерпретация £(г, О как амплитуды вероятности необходима для того, чтобы такие явления
могли быть описаны.
(ii) Теория позволяет лишь получить вероятность того, что то или иное явление может
иметь место. Поэтому экспериментальная проверка должна быть основана на
повторении большого количества одинаковых опытов (в описанном выше
эксперименте нужно послать большое число одинаковых фотонов, чтобы получить картину
интерференции, являющуюся материализацией вычисленных вероятностей).
(iii) Здесь мы говорим о «состоянии фотона» для того, чтобы в § В иметь возможность
ввести аналогию между £(r, t) и волновой функцией \|/(г, г), характеризующей
квантовое состояние материальной частицы. Эта «оптическая аналогия»
оказывается очень плодотворной и позволяет, в частности, как мы увидим в § D,
практически без вычислений просто объяснить многие квантовые свойства материальных
частиц. Однако не следует увлекаться этой аналогией и думать, что можно со всей
строгостью считать £(r, t) квантовым состоянием фотона.
Мы скоро увидим, впрочем, что тот факт, что функция \|/(r, t) является
комплексной, в квантовой механике существенно важен, тогда как комплексное
обозначение для функции £(г, О в оптике введено скорее из соображений удобства,
поскольку лишь ее вещественная часть имеет физический смысл. Точное
определение квантового состояния (комплексного) поля излучения может быть дано
только в рамках квантовой электродинамики — теории одновременно и квантовой
и релятивистской. Обсуждение этих вопросов здесь было бы преждевременным, и
мы ограничимся лишь кратким обзором в дополнении Kv.
3. Принцип спектрального разложения
Основываясь на введенных в § 2 понятиях, обсудим другой простой оптический
опыт, интересуясь теперь поляризационными характеристиками света. Это позволит
понять фундаментальные концепции, касающиеся измерения физических величин.
Опыт состоит в том, что плоская монохроматическая поляризованная световая
волна направляется на анализатор А. Если направление распространения волны совпадает с
осью Oz, а единичный вектор ер определяет ее поляризацию (рис. 2), то анализатор А
пропустит лишь поляризацию, параллельную оси Ох, и поглотит поляризацию,
параллельную оси Оу.
20

Волны и частицы. Введение основных идей квантовой механики
Классическое описание этого эксперимента, верное для достаточно больших интен-
сивностей падающего света, состоит в следующем. Плоская поляризованная волна
характеризуется электрическим полем вида:
Е(г,0=Е0е/{к^'\ (А-6)
i г
где Е{) — константа, причем интенсивность / света пропорциональна \Е0\ . После
прохождения света через анализатор А образуется плоская волна, поляризованная вдоль
оси Ох:
E'(r,0=^e^/a:-w/), (A-7)
интенсивность которой /', пропорциональная \Е{}\2, определяется законом Малюса:
/'=/соу29, (А-8)
где 0 = (еж, е/;) — угол между единичными векторами оси Ох и поляризации.
Что же будет происходить на квантовом уровне, то есть при столь малых интен-
сивностях /, что можно считать, что фотоны попадают на анализатор по одному?
(При этом подразумевается, что за анализатором помещается детектор фотонов.)
Заметим прежде всего, что невозможно зарегистрировать «часть фотона» — или фотон
прошел через анализатор, или был им поглощен. Затем (за исключением частных
случаев, которые мы скоро обсудим) признаем, что знать с полной уверенностью заранее,
будет ли данный фотон поглощен анализатором или пройдет через него, нельзя, можно
лишь определить соответствующие вероятности. И, наконец, если посылать один за
другим большое число фотонов, то в результате получится классическая картина, то есть
после анализатора получим практически закон распределения N cos2 0 .
Из вышеприведенного описания отметим следующие положения.
(i) Измерительный прибор (в данном случае анализатор) может дать лишь
некоторые избранные результаты, которые мы будем называть собственными результатами*.
В описываемом эксперименте имеется только два возможных результата измерения:
фотон проходит через анализатор или задерживается им. Говорят, что имеет место
квантование результата измерения в отличие от классического случая [формула (А -8)], где
интенсивность /' могла изменяться непрерывным образом между 0 и / в зависимости
от угла 0.
* Причина такого названия станет ясна в главе III.
21

Глава 1
Рис.2
Схема простого эксперимента с поляризованной световой волной. Луч света
распространяется в направлении Oz и проходит последовательно через поляризатор Р и
анализатор А; 0 — угол между осью Ох и электрическим полем волны, прошедшей через Р;
колебания, проходящие через А, параллельны оси Ох
(и) Каждому из собственных результатов соответствует собственное состояние. В
нашем случае собственные состояния характеризуются векторами:
е = е
р х
или
е = е ,
Р У '
(А-9)
где е — единичный вектор оси Оу . Если ер = ех, с достоверностью известно, что
фотон прошел через анализатор; если ер = е^, он с достоверностью будет задержан.
Таким образом, имеет место следующее соответствие между собственными результатами
и собственными состояниями: если перед измерением частица находится в одном из
собственных состояний, то результат измерения точно определен и не может быть ничем
иным, как соответствующим собственным результатом.
(iii) Если перед измерением состояние было произвольным, заранее можно
определить только вероятности получить различные собственные результаты. Чтобы найти эти
вероятности, состояние частицы представляется в виде линейной комбинации
различных собственных состояний; в нашем случае, если ер — вектор произвольной
поляризации, можно записать:
■ excos Q + eysin 0.
(А-10)
22

Волны и частицы. Введение основных идей квантовой механики
Вероятность получить такой собственный результат пропорциональна квадрату модуля
коэффициента, с которым входит соответствующее собственное состояние (постоянный
множитель определяется условием равенства единице суммы всех вероятностей). Из (А-10)
следует, что каждый фотон имеет вероятность cos2Q пройти через анализатор и sin2d
быть поглощенным анализатором (действительно, cos2 в + sin2Q = 1), как и
предполагалось выше. Это правило названо в квантовой механике принципом спектрального
разложения. Следует отметить, что конкретный вид разложения зависит от типа
рассматриваемого измерительного прибора, ибо нужно использовать те собственные состояния,
которые ему присущи: в формуле (А-10) выбор осей Ох и Оу определен анализатором.
(iv) После прохождения через анализатор свет полностью поляризован вдоль оси Ох.
Если теперь поставить после первого еще один анализатор А', имеющий ту же ось, то
все фотоны, прошедшие через А, пройдут и через А'. Согласно пункту (ii) это значит,
что после прохождения анализатора А состояние фотонов является собственным
состоянием ед . Таким образом, состояние частиц резко изменилось: до измерения оно
определялось вектором E(r, t), коллинеарным с е;,, а после измерения, давшего
дополнительную информацию (фотон прошел через анализатор), его состояние
характеризуется другим вектором, коллинеарным с е х. В этом проявляется высказанное ранее в § А-2
утверждение о том, что измерение фундаментальным образом возмущает
микроскопическую систему (здесь фотон).
ЗАМЕЧАНИЕ
Определенность результата при е = ел. или е = еу является лишь частным
случаем. Действительно, вероятность одного из этих возможных событий равна 1; но чтобы
подтвердить это предсказание, необходимо выполнить большое количество экспериментов:
ведь нужно убедиться, что все фотоны проходят (или не проходят) через анализатор, ибо
факт прохождения (или поглощения) одного отдельного фотона не может служить
характеристикой того, что е = ev или е = е .
В. МАТЕРИАЛЬНЫЕ ЧАСТИЦЫ И ВОЛНЫ МАТЕРИИ
1. Соотношения Луи де Бройля
Одновременно с открытием фотонов исследование спектров испускания и
поглощения атомов выявило фундаментальное их свойство, которое невозможно было понять в
рамках классической физики: спектры состояли из тонких дискретных линий. Иными
словами, данный атом может излучать или поглощать лишь фотоны со строго
определенными частотами (т. е. энергиями). Это свойство легко объяснить, если допустить, что
23

Глава I
энергия атома квантуется, то есть может принимать только определенные дискретные
значения Et, где i = 1, 2, ..., п, ... . Испускание и поглощение фотона сопровождается
«скачком» энергии атома от одного разрешенного значения Ei до другого значения Е},
причем закон сохранения энергии требует, чтобы фотон имел частоту Etj,
удовлетворяющую соотношению:
/zv/7=|£,.-£y.|. (В-1)
Только те частоты, которые подчиняются формуле (В-1), могут испускаться или
поглощаться атомом.
Существование дискретных уровней энергии было подтверждено независимо
опытом Франка—Герца. Бор интерпретировал его, используя понятие избранных
электронных орбит и, совместно с Зоммерфельдом, ввел эмпирическое правило, позволяющее
вычислить эти орбиты в случае атома водорода. Но фундаментальная природа этих
правил квантования оставалась загадкой.
И вот в 1923 году Луи де Бройль выдвинул следующую гипотезу: все материальные
частицы могут обладать, как и фотоны, волновым аспектом. И он вывел правила
квантования Бора—Зоммерфельда как следствие этой гипотезы, причем разрешенные
уровни энергии находились аналогично тому, как собственные моды колебаний натянутой
струны или резонатора. Эксперименты по дифракции электронов (Дэвиссон и Гермер,
1927) блестяще подтвердили существование волнового аспекта материальных частиц,
продемонстрировав, что интерференционная картина может быть получена с такими
частицами, как электроны.
Таким образом, любой материальной частице с энергией Е и моментом импульса р
ставилась в соответствие волна с частотой со = 2nv и волновым вектором к, причем
соотношения между этими величинами оставались теми же, что и для фотонов:
E-hv- йю;
(В)
р = Ш.
Другими словами, частице сопоставлялась волна с длиной
X = у-т = гт (соотношение Луи де Бройля). (В-3)
1к1 N
ЗАМЕЧАНИЕ
Очень малая величина постоянной Планка h объясняет, почему волновой характер
материи так трудно обнаружить в макроскопических масштабах; в дополнении Aj к данной
главе будет дана оценка порядков величины длин волн де Бройля для различных
материальных частиц.

Волны и частицы. Введение основных идей квантовой механики
2. Волновая функция. Уравнение Шредингера
В соответствии с гипотезой Луи де Бройля мы распространим понятия, введенные в
§А для фотона, на все материальные частицы. Пересмотрев каждое из заключений этого
параграфа, мы придем к следующим формулировкам.
(i) Понятие классической траектории следует заменить понятием состояния;
квантовое состояние частицы (например, электрона*) характеризуется волновой функцией
\j/(r, t), которая содержит всю возможную информацию о частице.
(и) Функция i|/(r, t) интерпретируется как амплитуда вероятности нахождения
частицы в момент времени t в точке г. Поскольку допустимые значения координат
частицы образуют континуум, вероятность нахождения частицы в момент t в элементе
объема dV = dx dy dz, расположенном в точке г, должна быть пропорциональна d3r и,
следовательно, является бесконечно малой величиной й^(г, /). Тогда |\|/(г, г)| следует
интерпретировать как плотность вероятности, записав:
^7(r,0 = C|\|/(r,0|Vr, (B-4)
где С — нормирующая константа (см. замечание (i) в конце § В-2).
(Hi) Принцип спектрального разложения применим к измерению любой физической
величины ,с/:
— полученный результат относится неизбежно к ансамблю собственных
результатов {а};
— каждому собственному значению а соответствует собственное состояние,
то есть собственная функция \|/(г); эта функция такова, что если \|/(г, /0) = \уа (г), где
/0 — момент времени измерения, то измерение с достоверностью даст значение а ;
— если \|/(г, 0 — произвольное состояние, то вероятность ,°?а получить при
измерении в момент времени /0 собственное значение а можно вычислить, разлагая
\|/(г, г0)в ряд по функциям \|/„(г):
V(r,f0) = 2>e4/e(r)- (B-5)
а
Тогда
* Мы здесь не учитываем существование спина электрона (см. главу IX).
25

Глава 1
a
(наличие знаменателя обеспечивает равенство 1 полной вероятности: £.^ =1).
а
Если в результате измерения действительно получено значение а, то волновая
функция частицы сразу же после измерения становится равной :
i1/,(r,r0) = \|/a(r). (B-7)
(iv) Остается записать уравнение, которому подчиняется функция \|/(r, t). Его
можно ввести совершенно естественным образом, исходя из соотношений Планка и Луи
де Бройля. Однако, мы не ставим себе цель обоснования такого фундаментального
уравнения и просто его запишем, а затем обсудим некоторые его следствия, экспериментальная
проверка которых подтверждает справедливость уравнения. Впрочем, мы вернемся к
этому вопросу в главе III.
Если частица с массой т подвержена действию потенциала V(r, t)\ ее волновая
функция \|/(r, t) подчиняется уравнению Шредингера:
(В-8)
Сразу же видно, что это уравнение является линейным и однородным по \|/; таким
образом, для материальных частиц справедлив принцип суперпозиции, который, будучи
объединенным с интерпретацией функции \|/ как амплитуды вероятности, дает
возможность объяснить эффекты волнового типа. С другой стороны, заметим, что
дифференциальное уравнение (В-8) является уравнением первого порядка по времени; это условие
необходимо для того, чтобы состояние частицы в момент времени t{), характеризуемое
функцией \|/(г, г{)), определяло его последующую эволюцию.
Итак, имеется глубокая аналогия между веществом и полем излучения: в обоих
случаях правильное описание явлений требует введения квантовых концепций и, в
частности, понятия корпускулярно-волнового дуализма.
т— i|/(r, o = -
ut
п2
A\|/(r, t) + V(r4 OV(r, t)
2m
* Здесь V(r, t) обозначает потенциальную энергию. Это, например, произведение
электрического потенциала и заряда частицы. В квантовой механике принято называть функцию V(r, t)
потенциалом.
26

Волны и частицы. Введение основных идей квантовой механики
ЗАМЕЧАНИЯ
(i) Для системы, состоящей из одной частицы, полная вероятность найти частицу в
любой точке пространства в момент времени t равна 1:
Jd04rf 0 = 1, (в"9)
где, поскольку d^(r, t) определяется формулой (В-4), следует заключить, что
волновая функция V(r, t) должна быть квадратично интегрируемой, то есть
интеграл
J|v(r,o|V
(В-10)
должен быть сходящимся. Константа нормировки С , стоящая в выражении (В-4),
определяется выражением:
^ = J|v(r,0|Vr
С (В-11)
(мы увидим позже, что форма уравнения Шредингера требует, чтобы величина С
не зависела от времени). Часто используют нормированные волновые функции,
для которых
J|\|/(r,»|Vr = l. (B-12)
В этом случае С = 1.
(ii) Отметим существенное различие между понятиями классического и квантового
состояний. Состояние классической частицы в момент времени / определено
шестью параметрами, характеризующими ее положение и скорость, то есть
х, у, z, vv, v , v. Состояние квантовой частицы определяется бесконечным
набором параметров — значениями волновой функции \|/(г, /) в различных точках
пространства. Классическое понятие траектории, как последовательность различных
состояний классической частицы во времени, должно быть заменено понятием
распространения волны, связанной с частицей. Вернемся, например, к описанию
эксперимента Юнга, приведенному ранее для фотонов, но пригодному в принципе
для таких материальных частиц, как электроны; при наблюдении
интерференционной картины бессмысленно ставить вопрос, через какую щель прошла каждая из
частиц, поскольку связанная с ними волна проходит одновременно через обе щели,
(iii) Уместно отметить, что в отличие от фотонов, которые могут быть испущены или
поглощены в ходе эксперимента, материальные частицы не могут быть созданы
27

Глава I
или уничтожены: когда нагретая нить накала испускает электроны, они не
возникают, а существуют и ранее в теле нити. Аналогично, поглощенный счетчиком
электрон не исчезает, а остается в атоме или участвует в образовании
электрического тока. На самом деле релятивистская теория предусматривает возможность
создания и уничтожения материальных частиц: так, например, фотон с достаточно
большой энергией, проходя близко от атома, может породить электронно-
позитронную пару, и, наоборот, позитрон, столкнувшись с электроном,
аннигилирует с ним, порождая фотоны. Однако мы уже указали в начале этой главы, что
здесь ограничиваемся нерелятивистской теорией и асимметрично трактуем время
и пространственные координаты. В рамках нерелятивистской квантовой механики
материальные частицы не могут быть ни созданы, ни уничтожены. Этот закон
сохранения, как мы увидим, играет первостепенную роль; необходимость отказа от
него является одним из серьезных затруднений при построении релятивистской
квантовой механики.
С. КВАНТОВОЕ ОПИСАНИЕ ЧАСТИЦЫ. ВОЛНОВОЙ ПАКЕТ
В предыдущем параграфе мы ввели основные концепции, необходимые для
квантового описания частицы. В этом параграфе рассмотрим их подробнее и установим
несколько очень важных свойств. Начнем с простейшего случая свободной частицы.
1. Свободная частица
Рассмотрим частицу, потенциальная энергия которой равна нулю (или постоянна) в
любой точке пространства. Это значит, что частица не подвержена действию какой-либо
силы, то есть является свободной.
При V(r, 0 = 0 уравнение Шредингера имеет вид:
Э П2 (С-1)
ih— \|/(г, 0 = -—-A\|/(r, t).
at 2m
Это дифференциальное уравнение имеет очевидные решения вида:
y(r9t) = Aeiikt
где А — константа, а к и 0) связаны соотношением:
М2
оо = — . (С-3)
2т
Заметим, что в соответствии с соотношениями Луи де Бройля [см. (В-2)] условие (С-3)
_ д /(кг-шо (С-2)
28

Волны и частицы. Введение основных идей квантовой механики
выражает, что энергия Е и импульс р свободной частицы связаны хорошо известным
из классической механики равенством:
£ = !-• (С-4)
2т
Позже (в § С-3) мы вернемся к физической интерпретации состояния вида (С-2);
уже сейчас видно, что поскольку
|\|/(г, г)|2 =|А|2, (С-5)
плоская волна этого вида представляет частицу, вероятность найти которую в любой
точке пространства одинакова (см. замечание, приведенное ниже).
Принцип суперпозиции позволяет утверждать, что любая линейная комбинация
плоских волн, удовлетворяющих условию (С-3), также будет решением уравнения (С-1).
Такую суперпозицию можно записать в виде:
V(r.O = ^J«(k)e'«kM>"rfJ* (C.6)
(здесь d3k по определению является бесконечно малым элементом объема в
пространстве k: dkxdkydkz)\ функция g(k), которая может быть комплексной, должна быть
достаточно регулярной, чтобы ее можно было дифференцировать под знаком
суммирования. Впрочем, можно показать, что любое квадратично-интегрируемое решение может
быть записано в виде формулы (С-6).
Волновая функция в виде суперпозиции плоских волн типа (С-6) называется
трехмерным «волновым пакетом». Для простоты мы часто будем рассматривать случай
одномерного волнового пакета*, полученного путем суперпозиции плоских волн,
распространяющихся вдоль оси Ох . В этом случае волновая функция зависит только от х и /:
V(jc, 0 = -fL Jg(k)ei[kx-*ik)lldk . (С-7)
л/2я -со
В следующем параграфе нас будет интересовать форма волнового пакета в заданный
момент времени; если мы выберем его за начало отсчета времени, то волновая функция
примет вид:
* Простая модель двумерного волнового пакета приведена в дополнении Е|. В дополнении F|
исследованы некоторые общие свойства трехмерного волнового пакета, там показано также, что в
некоторых случаях можно перейти от трехмерной задачи к нескольким одномерным.
29

Глава I
\|/(х, 0) = -tLt\g(k)eikxdk . (С-8)
л/2я
Видно, что g(k) есть Фурье-образ (см. приложение I) функции \}/(х, 0):
g(k)=-j=lv(x,0)e-ikxdx. (C-9)
Таким образом, справедливость формулы (С-8) не ограничивается лишь случаем
свободной частицы: действительно, каким бы ни был потенциал, всегда можно записать
функцию \|/(х, 0) в этой форме, и выводы, которые последуют ниже в § 2 и § 3, являются
вполне общими. К свободной частице мы еще вернемся в § 4.
ЗАМЕЧАНИЕ
Плоская волна вида (С-2), модуль которой остается постоянным во всем
пространстве [см. (С-5)], не является квадратично-интегрируемой; строго говоря, она
не может представлять физическое состояние частицы (аналогично в оптике
плоская монохроматическая волна не может быть реализована физически). И, напротив,
суперпозиция плоских вида (С-7) может быть квадратично интегрируемой.
2. Форма волнового пакета в заданный момент времени
Форма волнового пакета определяется зависимостью функции 1|/(jc,0) от х,
определяемой равенством (С-8). Допустим, что \g(k)\ имеет форму, представленную на рис.3,
то есть характеризуется явным максимумом в точке к = &0, ширина которого на
половине высоты равна Ак .
\Ф)\
Рис.3
Ход функции \g(k)\ — модуля
преобразования Фурье от функции \|/(х, 0)
(предполагается, что эта функция характеризуется
максимумом с шириной Ак и центром в
точке к = к0)
30

Волны и частицы. Введение основных идей квантовой механики
Попытаемся сначала понять качественно поведение функции \|/(x, 0), рассмотрев
простейший случай: функция \у(х, 0) является не бесконечной суперпозицией плоских
волн е±х, как в формуле (С-8), а всего лишь суммой трех плоских волн с волновыми
векторами к0, к0 , к0 +— и амплитудами, пропорциональными 1, 1/2 и 1/2. Тогда имеем:
\|/(*) =
*(*о)
л/2я
1кх [ '(*о~)^
е"+-е 2
1 Цк0Ах
+ -е 2
2
42п
(Ак ^
1 + cos —х
{ 2
(С-10)
Видно, что модуль | \|/(jc) | максимален при х - 0; это происходит потому, что при х = 0
все три волны находятся в фазе и интерферируют конструктивно, как показано на рис.4.
Ак
*. *f-WVWW¥
Рис.4
Вещественные части трех волн, сумма которых дает функцию, \|/(х) описываемую
формулой (С-10). В точке х = 0 три волны находятся в фазе и интерферируют конструктивно;
при отклонении от х = 0 между ними появляется разность фаз, и интерференция
становится деструктивной в точке х = ± -
Ах
На нижнем графике рисунка представлена
Re{ij/(x)}. Пунктирная кривая соответствует функции [\ + cos(Ak-x/2)]t модуль
которой дает | \|/(jc) | (то есть форму волнового пакета)
31

Глава 1
По мере отклонения от этого значения х волны испытывают сдвиг по фазе друг
относительно друга, и величина |\|/(*)| уменьшается. Интерференция становится полностью
деструктивной, когда сдвиг фазы между волнами е1к°х и е1<<к^Ш2)х равен ±п : действи-
Ах
тельно, \\1(х) становится равной нулю, если jc = ±—, где Ах определяется равенством:
Ах • Ак = An .
(С-11)
Это равенство указывает, что ширина Ах функции |\}/(;с)| (расстояние между двумя
нулями этой функции) тем больше, чем меньше ширина Ак функции \g(k)\.
ЗАМЕЧАНИЕ
Формула (С-10) показывает, что |vj/(x)| является периодической функцией от х, и,
следовательно, имеет набор максимумов и минимумов. Это происходит потому, что \\f(x)
представляет собой суперпозицию конечного числа волн (здесь трех); если бы имела место
суперпозиция непрерывной бесконечности волн, как в формуле (С-8), периодичность
отсутствовала бы, и функция \\f(x, 0) могла бы иметь только один максимум.
Вернемся теперь к общей формуле (С-8), описывающей волновой пакет. Ее форма
также является результатом явлений интерференции: модуль | \j/(jc, 0) | максимален,
когда различные плоские волны интерферируют конструктивным образом.
Действительно, пусть а(к) —аргумент функции g(k):
g(k) = \g(k)\eiaW.
Предположим, что а(к) изменяется регулярным образом в интервале
Ак'
(С-12)
Ак
0 2
, где функция | g(k) \ существенно отлична от нуля; тогда, если интервал Ак
достаточно мал, можно разложить а (к) вблизи к = к0:
da'
а(к) =a(kQ)+(k-k0)
что позволяет переписать формулу (С-8) в виде:
dk
(С-13)
32

Волны и частицы. Введение основных идей квантовой механики
/IV + cxU'o)!
VU0)=-
л/2я
\\g{k)\el{k-k^x-^dk,
(С-14)
где
*п = -
da
~dk
(С-15)
J*=*o
Форма выражения (С-14) удобна для изучения зависимости I V|/(jc, 0) | от х\ при
большом значении разности
подынтегральная функция от к многократно
осциллирует в интервале Ак; при этом видно (см. рис.5а, где представлена в качестве
примера вещественная часть этой функции), что вклады последовательных осцилляции
аннулируют друг друга, и интеграл по к оказывается ничтожно малым. Иначе говоря,
если х отстоит достаточно далеко от х0, фазы различных волн, образующих ij/(jc, 0),
быстро меняются в области А к , и эти волны взаимно уничтожаются в результате
интерференции. Напротив, если х = х{), подынтегральная функция от к практически
не осциллирует (см.рис.56), и модуль | V|/(jc, 0) | максимален.
^Кс{\д{к)\с11к-^){х-^\
/L#)|
fRc{ lyik)]^-^1*-**]
/Ш
I* - *о|
Рис.5
Зависимость от к подынтегральной функции в формуле для \|/(jc, 0). На рис.(а) х имеет
такое значение, что |х-*0|>1/Д£ , и функция многократно осциллирует в интервале Ак .
На рис.(Ь) х имеет такое значение, что |jc — jc0| <c 1 / Ак , и функция практически не
осциллирует, вследствие чего интеграл от нее по к достигает заметного значения. Центр
волнового пакета [точка, в которой модуль | \j/(jc, 0) | максимален] расположен в точке х = х0
3 Квантовая механика
33

Глава I
Таким образом, положение центра волнового пакета равно:
(С-16)
Мы получили его при условии, что фазы различных волн, составляющих i|/(jc, 0), очень
мало меняются в области А к (условие «стационарной фазы»).
Если х отличается от х0, функция | \j/(jc, 0) | уменьшается, причем это уменьшение
становится наиболее выраженным, когда комплексная экспонента е,{к'к°Пх~Хо)
осциллирует примерно один раз при изменении к в области А к , то есть когда
Ак-(х-х0) = \. (С-17)
Если Ах — приблизительная ширина волнового пакета, то
Ак-Ах>\. (С-18)
Таким образом, мы получили классическое соотношение между ширинами двух
функций, которые являются Фурье-образами друг друга. Наиболее важным является то,
что произведение Ак • Ах ограничено снизу, а точное значение этой границы зависит,
конечно, от точного определения Ах и Ак .
Таким образом, волновой пакет вида (С-7) описывает состояние частицы,
вероятность нахождения которой в момент времени t = 0 ничтожна вне интервала с шириной
Ах с центром в точке х0.
ЗАМЕЧАНИЕ
Выполненные выше рассуждения могли создать впечатление, что
произведение Ак • Аде должно быть всегда порядка 1 [см. (С-17)]. Обратим внимание, что
здесь речь идет лишь о нижней границе: невозможно образовать волновой пакет,
если произведение Ак • Ах мало по сравнению с 1, но это вполне возможно для
любых больших значений этого произведения [см., например, дополнение Еь в
частности, замечание (и) в § 3-в]. Именно поэтому формула (С-18) записана в виде
неравенства.
3. Соотношение неопределенностей Гейзенберга
Неравенство (С-18) имеет в квантовой механике исключительно важные следствия.
Мы сейчас обсудим их, оставаясь для простоты в рамках одномерной модели.
Мы видели, что плоская волна е'(*о*-@°,) соответствует постоянной по оси х плот-
•*лД0) = *о=-
da
Ik
34

Волны и частицы. Введение основных идей квантовой механики
ности вероятности при любом значении t; иначе говоря, это можно выразить, считая
бесконечно большой ширину Аг . Напротив, в эту волну входит лишь одна частота ш0 и
единственный волновой вектор к0 ; согласно соотношениям де Бройля это означает, что
энергия и импульс частицы точно определены: Е = /ШH и р = М0. Такая плоская волна
может, впрочем, рассматриваться как частный случай выражения (С-7), в котором g(k)
записывается в виде дельта-функции:
*(*) = 8(*-*0). (С-19)
Тогда соответствующее значение А к равно нулю.
Это же свойство можно интерпретировать иначе в рамках принципа спектрального
разложения (см. § А-3 и § В-2). Сказать, что частица, описываемая в момент времени
/ = 0 волновой функцией \|/(*,0) = Ае1кх, обладает строго определенным импульсом,
означает, что в результате измерения импульса в этот момент времени будет получено
значение p = hk со стопроцентной вероятностью. Отсюда следует, что функция е,кх
характеризует собственное состояние, соответствующее импульсу р-Ьк . С другой
стороны, поскольку для любого вещественного значения к существует плоская волна,
являющаяся решением уравнения Шредингера, все собственные значения, которые априори
могут быть получены при измерении импульса в произвольном состоянии, должны быть
вещественными числами (в этом случае квантование возможных результатов отсутствует;
как и в классической механике, все значения импульса разрешены).
Рассмотрим формулу (С-8). Она описывает функцию \[/(лг, 0) как линейную
суперпозицию собственных функций импульса е1кх с весовыми коэффициентами g(k). Поэтому
с точностью до постоянного множителя величину | g(k) |2 следует интерпретировать как
вероятность получить значение p = hk при измерении в момент времени t = 0 импульса
частицы, состояние которой описывается функцией \|/(jc, t). В действительности
возможные значения импульса р и координаты х образуют непрерывный ансамбль, и
величина |g(&)|2 пропорциональна плотности вероятности: вероятность d№(k)
получить значение между fik и h(k + dk) равна с точностью до постоянного множителя
| g(k) |2 dk . Более точно, если переписать формулу (С-8) в виде:
V(*,0) = -jL= \y(p)eipx,hdp , (С-20)
то, как известно, функции \j/(p) и \|/(х, 0) удовлетворяют равенству Бесселя—Парсе-
валя (дополнение I):
3*
35

Глава 1
J|\|K*,0)|&= \\x/(p)\dp. (С-21)
Если оба эти интеграла равны С, то d:lP{x)= — |V|/(jc,0)| dx есть вероятность найти
частицу в момент времени г = 0 в интервале координат между х и jc + d* ; аналогично,
величина
dnp) = ^\W(p)\2dp (C-22)
является вероятностью того, что измерение импульса даст результат, заключенный в
интервале от р до p-vdp [равенство (С-21) обеспечивает тогда, что полная вероятность
получить любое значение действительно равна 1].
Вернемся теперь к формуле (С-18). Можно записать:
&х-Ар>П (С-23)
(А/? = ЙМ — ширина кривой, описывающей |\j/(p)|). Рассмотрим частицу, состояние
которой определено волновым пакетом (С-20); мы знаем, что вероятность ее нахождения
в момент времени t - О существенно отлична от нуля лишь в области с шириной Ах
вблизи точки х0, то есть ее положение известно с неопределенностью Але. Если в тот же
момент времени измерять импульс этой частицы, то можно получить значение, лежащее
между р0+ и р0 , поскольку |\j/(/?)| практически равен нулю вне этого
интервала: тогда неопределенность измерения импульса равна Ар. Интерпретация
соотношения (С-23) может быть при этом дана следующим образом: невозможно в данный
момент времени определить положение и импульс частицы с произвольной точностью;
если достигнут нижний предел, налагаемый формулой (С-23), то увеличить точность
определения положения частицы (уменьшить Ajc ) можно лишь за счет уменьшения
точности определения ее импульса (возрастание Ар) и наоборот. Это соотношение
называется соотношением неопределенностей Гейзенберга.
В классической механике не существует ничего подобного. Ограничение,
налагаемое выражением (С-23), имеет место вследствие того, что величина h отлична от нуля.
Именно малость h в макроскопическом масштабе позволяет пренебречь этим
ограничением в классической механике (детальное изложение соответствующего примера дано в
дополнении ВО.
36

Волны и частицы. Введение основных идей квантовой механики
ЗАМЕЧАНИЕ
Исходное неравенство (С-18) само по себе не содержит ничего типично квантового.
Оно лишь отражает общее свойство преобразований Фурье, широко применяемых в
классической физике: так, например, в радиоэлектронике хорошо известно, что не существует
импульса электромагнитной волны, для которого можно было бы одновременно определить
его положение и длину волны с неограниченной точностью. Квантовым в этом рассмотрении
является лишь факт ассоциации волны материальной частице и требование, чтобы длина
волны и импульс удовлетворяли соотношению Луи де Бройля.
4. Эволюция свободного волнового пакета во времени
До сих пор мы интересовались лишь формой волнового пакета в данный момент
времени. В этом параграфе мы рассмотрим его эволюцию во времени. Вернемся к
случаю свободной частицы, состояние которой описывается одномерным волновым
пакетом вида (С-7).
Плоская волна частного вида е'{кх"ш) распространяется вдоль оси Ох со скоростью
; здесь величина
со ^
поскольку зависимость от х и t выражается лишь через член I х 1 \
\ к )
Vy(k) называется фазовой скоростью плоской волны.
Известно, что в случае электромагнитной волны, распространяющейся в вакууме,
скорость Уф не зависит от к и равна скорости света с. Напротив, известно также, что
в диспергирующей среде дело обстоит иначе, и фазовая скорость определяется
выражением:
п(к)
где п(к) — показатель преломления среды, зависящий от длины волны.
Интересующий нас случай соответствует диспергирующей среде, поскольку фазовая
скорость имеет вид [см. уравнение (С-3)]:
Пк_
2т
Уф(*) = —• (С-26)
Мы сейчас увидим, что, если различные волны имеют различные фазовые скорости,
37

Глава 1
скорость движения максимума хм волнового пакета не равна средней фазовой скорости
—^ = —-, как можно было бы ожидать.
к0 2т
Как и ранее, мы попытаемся сначала качественно понять происходящий физический
процесс и лишь потом сделаем общие выводы. В качестве примера выберем
рассмотренную выше в § С-2 суперпозицию трех волн. В произвольный момент времени
функция \\f(x, t) имеет вид:
¥(х.О- '(У
yfbi
1&к До) 1 Ак До)
л/2я
1 + COS
2
Ак До)
, —х /
^ 2 2
(С-27)
Видно, что максимум функции | \|/(jc, t) I, находившийся в момент времени / = 0 в точке
х = 0, в момент t окажется в точке
Ак
а не в точке л: = —^-г. Физическая причина такого различия ясна из рис.6. На рис. 6а
К
дано положение трех соседних максимумов A), B) и C) каждой из вещественных частей
трех волн в момент t = О. Максимумы, отмеченные индексом B), совпадают в точке
х = 0 и в результате интерференции складываются, что соответствует положению
максимума функции |\|/(jc, 0) |. Поскольку фазовая скорость увеличивается с ростом к (С-26),
максимум C) волны kQ +— постепенно приближается к максимуму волны к0, кото-
d М>1 тт
рыи, в свою очередь, «догоняет» максимум волны к0 . Через некоторое время г0
будет наблюдаться ситуация, изображенная на рис.бЬ, когда положения максимумов C)
совпадут и, следовательно, дадут максимум функции |\|/(jc, r0)| в точке хм (t0). Из ри-
сунка очевидно, что xM(tQ) отличается от —-^/0, и простейшие вычисления приводят к
К
формуле (С-28).

Волны и частицы. Введение основных идей квантовой механики
Ак
ка + —
A)
A)
*о-
Ак\
ГКО
B)
B)
1B)
1C)
1A) 1B) I
B)
!C)
l(D
1B)
1C)
1A)
1B)
1C)
1C)
C)
О
t
*лД0
Рис.6
Положения максимумов трех волн, изображенных на рис.4 в момент времени г - О (а) и
в последующий момент времени /(b). В момент f = 0 максимумы B), расположенные в
точке х = 0, интерферируют конструктивно, и положение центра волнового пакета равно
jcm@) = 0. К моменту t три волны двигались с различными фазовыми скоростями Уф,
вследствие чего теперь конструктивно интерферируют максимумы C), а центр волнового
пакета находится в точке х - xM{t). Таким образом, видно, что скорость центра
волнового пакета (групповая скорость) отличается от фазовых скоростей трех волн
Характер перемещения центра волнового пакета (С-7) можно определить также,
применив метод «стационарной фазы». Действительно, из формулы (С-7), описывающей
форму свободного волнового пакета, можно заключить, что для перехода от \|/(х, 0) к
\j/(jc, t) достаточно заменить g(k) на g(k)e~'*°{li)[. При этом все рассуждения,
приведенные в § С-2, остаются справедливыми при условии замены аргумента а(к) в формуле
для g(k) на
а(&)-со(Л:)/.
Тогда условие (С-16) дает:
хм(*)'-
did
~dk
t -
da
Ik
(C-29)
(C-30)
и мы приходим к результату, описываемому формулой (С-28): скорость максимума
волнового пакета равна:
VG(kQ) =
~dk
(С-31)
39

Глава 1
Величину VG(kQ) называют групповой скоростью волнового пакета. Используя закон
дисперсии (С-3), получим:
М
Vc(*o) = —= 2V,(*0). (C-32)
т
Этот вывод является очень важным, так как позволяет делать сравнение с
классическим описанием свободной частицы в тех случаях, когда оно справедливо.
Действительно, если рассматривается макроскопическая частица (пример пылинки в дополнении В!
показывает, насколько она может быть мала), соотношение неопределенностей не
вводит никакого заметного ограничения на точность, с которой известны ее положение и
импульс. Это означает, что для квантового описания такой частицы можно построить
волновой пакет, характерные ширины Ах и Ар которого пренебрежимо малы. Таким
образом, можно говорить о положении xM(t) и об импульсе р0 частицы в классическом
смысле этих понятий. При этом скорость частицы должна быть равна v = —. Именно
т
этот результат и следует из формулы (С-32) квантового описания, если Axw Ар
одновременно очень малы. Максимум волнового пакета перемещается как частица,
подчиняющаяся законам классической механики.
ЗАМЕЧАНИЕ
До сих пор мы обращали внимание лишь на перемещение максимума
свободного волнового пакета. Можно также рассмотреть изменение его формы во времени.
Легко показать, что если ширина Ар остается постоянной, то ширина Ах растет
со временем, и по прошествии достаточно большого интервала времени становится
равной бесконечности («расплывание» волнового пакета). Это явление
обсуждается в дополнении Gb где рассмотрен частный случай волнового пакета гауссовой
формы.
D. ЧАСТИЦА В ПОЛЕ СКАЛЯРНОГО ПОТЕНЦИАЛА,
НЕ ЗАВИСЯЩЕГО ОТ ВРЕМЕНИ
Мы видели в § С, как квантовое описание частицы сводится к классическому, если
постоянную Планка h можно считать пренебрежимо малой. В классическом приближении
волновой характер не проявляется, так как длина волны А = —, связанной с частицей,
Р
очень мала по сравнению с характерными параметрами ее движения, имеющими
размерность длины. Эта ситуация аналогична той, которая встречается в оптике: геометри-
40

Волны и частицы. Введение основных идей квантовой механики
ческая оптика, игнорирующая волновые свойства света, является хорошим
приближением, если длина соответствующей волны пренебрежимо мала по сравнению с
интересующими нас размерами. Таким образом, классическая механика играет по отношению
к квантовой механике ту же роль, какую геометрическая оптика играет по отношению к
волновой оптике.
В данном параграфе нас будет интересовать частица, находящаяся в поле
потенциала, не зависящего от времени. Сказанное выше позволяет заключить, что типично
квантовые эффекты (то есть имеющие волновую природу) должны проявиться в том случае,
когда потенциал заметно изменяется на расстояниях, меньших длины волны, ибо уже
нельзя будет ею пренебречь. Именно поэтому мы будем рассматривать поведение
квантовой частицы в различного рода потенциалах «прямоугольной» формы, то есть когда
изменение потенциала происходит скачкообразно, как показано на рис.7а. Такой
потенциал, будучи разрывной функцией, конечно, резко меняется на расстоянии порядка
длины волны, какой бы малой она ни была, и квантовые эффекты должны при этом
обязательно проявиться. Прежде чем перейти к детальному изучению, обсудим некоторые
важные свойства уравнения Шредингера, когда потенциал не зависит от времени.
1. Разделение переменных. Стационарные состояния
Волновая функция частицы, потенциальная энергия которой V(r) не зависит от
времени, должна подчиняться уравнению Шредингера:
ih— \|/(г,0 =-— А\|/(г, r) + V(r)\|/(r, t). (D-l)
dt
2m
а. ОПРЕДЕЛЕНИЕ СТАЦИОНАРНЫХ СОСТОЯНИЙ
Посмотрим, существует ли решение этого уравнения в форме:
\|/(г, г) = Ф(г)х@.
Подстановка выражения (D-2) в (D-1) дает:
dt
2т
Аф(г)
+ Х('Шг)<р(г).
(D-2)
(D-3)
Разделив обе части равенства на произведение (p(r) %(t), получим:'
ih dx.it) 1
Х@ dt ф(г)
2т
Д(р(г)
+ V(r).
(D-4)
41

Глава 1
Это уравнение устанавливает равенство функции только времени t (левая часть) и
функции только координаты г (правая часть). Это равенство возможно лишь в том
случае, если каждая из частей является константой, которую положим равной Йсо, где О)
имеет размерность циклической частоты.
Приравняем левую часть величине //со и получим для функции %(t)
дифференциальное уравнение, которое легко интегрируется и дает:
Х@ = Ае'**. (D-5)
Аналогично, функция (р(г) должна удовлетворять уравнению:
Дф(г) + У(г)ф(г) = йсоф(г). (D-6)
2т
Если мы положим в уравнении (D-5) Л = 1 [это возможно, например, потому, что
константу Л можно включить в функцию ф(г)], то придем к следующему результату.
Функция
\|/(г, 0 = ф(г)е-/0)' (D-7)
является решением уравнения Шредингера при условии, что ф(г) — решение уравнения
(D-6). Говорят, что тем самым переменные времени и пространства оказываются
разделенными.
Волновая функция вида (D-7) называется стационарным решением уравнения
Шредингера: она приводит к не зависящему от времени значению плотности вероятности
|i}/(r, 0| =|ф(г)| • В стационарной функции появляется единственная частота со;
согласно соотношениям Планка—Эйнштейна стационарное состояние является состоянием
с точно определенной энергией £ = /Ш) (собственное энергетическое состояние). В
классической механике, если потенциальная энергия не зависит от времени, полная энергия
является интегралом движения; в квантовой механике этому соответствуют состояния с
определенной энергией.
Уравнение (D-6) можно переписать в виде:
П2
— A + V(r)
2т
ф(г) = Еф(г) (D-8)
или
Яф(г) = £ф(гI (D-9)
где Я — дифференциальный оператор:
42

Волны и частицы. Введение основных идей квантовой механики
Н = A + V(r)
2т
(D-10)
Он является линейным, так как если А, и Х2 —константы, то
Я^^ + Я^Сг^^Яф.СО + ^Яф^г). (D-11)
Таким образом, уравнение (D-9) является уравнением на собственные значения
линейного оператора Я : действие оператора Я на «собственную функцию» ф(г) состоит в
умножении этой функции на «собственное значение» Е . Допустимые значения энергии
являются собственными значениями оператора Я . Ниже мы увидим, что уравнение (D-9)
допускает квадратично интегрируемое решение ф(г) только для определенных
значений Е (см. § D-2-c и § 2-е дополнения Hi): именно в этом и состоит квантование энергии.
ЗАМЕЧАНИЕ
Уравнение (D-8) [или (D-9)] иногда называют «уравнением Шредингера, не зависящим
от времени», в противоположность уравнению (D-1), называемому «уравнением Шредингера,
зависящим от времени». Обратим внимание на их существенное отличие: уравнение (D-1)
является общим уравнением, описывающим эволюцию волновой функции в любом
произвольном состоянии частицы, тогда как уравнение на собственные значения (D-9) позволяет
найти среди всех возможных состояний частицы ее стационарные состояния.
Ь. СУПЕРПОЗИЦИЯ СТАЦИОНАРНЫХ СОСТОЯНИЙ
Чтобы различать между собой различные возможные значения энергии Е и
соответствующие им собственные функции ф(г), введем индекс п ; тогда
Яф„(г)=£„ф„(г), (D-12)
и волновые функции стационарных состояний частицы запишутся в виде:
1|/я(г,0 = Ф„(г)^£",/Л, (D-13)
где функция \|/„(r, t) является решением уравнения Шредингера (D-1). Поскольку это
уравнение линейное, то оно допускает любой набор других решений вида:
¥(г,0 = Хслфя(г)е"£я'/Л, (D-14)
43

Глава I
где коэффициенты сп могут быть произвольными комплексными константами. В
частности, имеем: ? п
У(г,0) = £спф„(г). (D-15)
Справедливо и обратное утверждение. Допустим, что нам известна функция \j/(r,0),
то есть состояние частицы в начальный момент времени. Ниже мы увидим, что любая
функция \|/(г, 0) может быть разложена по собственным функциям оператора Н , как в
формуле (D-15), при этом коэффициенты сп будут определяться функцией \|/(г,0).
Тогда соответствующее решение i|/(r, r) уравнения Шредингера будет записано в виде
формулы (D-14): чтобы доказать это, достаточно умножить обе части выражения (D-15)
на множитель е , где Еп — собственное значение, соответствующее собственной
функции ф„(г). Следует подчеркнуть, что эти фазовые множители различны для разных
членов суммы, и лишь в случае стационарных состояний зависимость от t определяется
единственной экспонентой [формула (D-13)].
2. «Прямоугольные» одномерные потенциалы. Качественный анализ
В начале § D мы отметили, что для выявления квантовых эффектов следует
рассматривать потенциалы, существенно меняющиеся на малых расстояниях. Здесь мы
ограничимся качественным исследованием, сконцентрировав внимание на простых физических
идеях, а детальный анализ будет дан в дополнениях к этой главе (дополнение НО. Чтобы
упростить задачу, остановимся на одномерной модели, в которой потенциальная энергия
зависит только от х (обоснование такой модели дано в дополнении F^.
а. ФИЗИЧЕСКИЙ СМЫСЛ ПРЯМОУГОЛЬНОГО ПОТЕНЦИАЛА
Итак, в одномерном случае мы рассмотрим потенциал вида, представленного на
рис.7а : ось Ох делится на некоторое количество областей, в которых потенциал
остается постоянным, а на границе соседних областей испытывает резкий скачок. В
действительности такая функция не может отражать реальный физический потенциал, ибо он не
может иметь разрывов, и мы используем ее для приближенного описания потенциальной
энергии V(x), вид которой изображен на рис.7Ь: она не имеет разрывов, но меняется
очень быстро вблизи определенных значений х. Когда интервалы, в пределах которых
происходит это изменение, очень малы по сравнению со всеми размерами, характерными
для задачи (и в частности, с длиной волны, связанной с частицей), то можно заменить
реальный потенциал прямоугольным вида, изображенного на рис.7а. Речь идет, конечно,
44

Волны и частицы. Введение основных идей квантовой механики
о приближении, которое перестает быть справедливым, например, для частицы с очень
большой энергией, длина волны для которой очень мала.
Выводы классической механики относительно поведения частицы в потенциальном
поле, подобном рис.7, нетрудно предвидеть. Достаточно, например, представить себе,
что V(x) — потенциальная энергия поля гравитации, тогда рис.7Ь представляет собой
энергетический профиль пространства, в котором движется частица: резкие перепады
потенциала разделяют области горизонтальных «плато». Заметим, что, если полная
энергия частицы Е фиксирована, то области оси Ох , где V > Е , запрещены для движения,
так как кинетическая энергия Ес = Е - V должна быть положительной.
"Прямоугольный"
ПО10ИШК1.1
Сила
Рис.7
Прямоугольный потенциал (а), схематически изображающий реальный потенциал (Ь),
которому соответствует сила, изображенная на рис (с)
ЗАМЕЧАНИЕ
Сила, действующая на частицу, равна F(x) = ; на рис.7с представлена
dx
эта сила для потенциала, изображенного на рис.7Ь. Видно, что в областях
постоянного потенциала частица не подвержена действию никакой силы, и, следовательно,
ее скорость остается неизменной. Лишь в пограничных зонах, разделяющих эти
области, на частицу действует некоторая сила, в зависимости от знака производной
ускоряющая или тормозящая ее движение.
45

Глава 1
b. АНАЛОГИЯ С ОПТИКОЙ
Пусть нас интересуют стационарные состояния (§ D-1) частицы в поле одномерного
прямоугольного потенциала.
В области, где потенциал V остается постоянным, уравнение на собственные
значения (D-9) имеет вид:
2т dx2
■ + V
ф(*)=Еф(*)
(D-16)
или
d_2
dx
2т.
П2
2+it(e-v)
ф(*) = 0.
(D-17)
Вспомним, что в оптике существует совершенно аналогичное уравнение.
Действительно, рассмотрим прозрачную среду, показатель преломления п которой не зависит
ни от г, ни от времени. В этой среде может распространяться электромагнитная волна,
электрическое поле Е(г, t) которой не зависит ни от у , ни от z и имеет вид:
Е(г, 0 = еЕ(х)е~
(D-18)
где е — единичный вектор, перпендикулярный к оси Ох. Таким образом, функция
Е(х) должна удовлетворять уравнению:
n2Q2
dx2
Е(х) = 0.
(D-19)
Видно, что уравнения (D-17) и (D-19) становятся идентичными, если положить:
h2[t V) с2 '
(D-20)
С другой стороны, в точке х, где потенциальная энергия V [и, следовательно,
коэффициент преломления п, определяемый формулой (D-20)] испытывает разрыв, условия
сшивания функций ф(д:) и Е(х) одинаковы: эти функции и их первые производные
должны быть непрерывными (см. дополнение Нь § 1-Ь). Аналогия структуры уравнений
(D-17) и (D-19) позволяет связать задачу квантовой механики для потенциала рис.7а с
задачей оптики, в которой исследуется распространение электромагнитной волны с
частотой Q в среде, в которой коэффициент преломления п испытывает разрыв такого же
46

Волны и частицы. Введение основных идей квантовой механики
вида; согласно формуле (D-20) связь между оптическими и механическими параметрами
имеет вид:
n(Q) = —pmc2(E-V). (D-21)
Область, где Е > V , соответствует прозрачной среде, в которой коэффициент
преломления для световой волны является вещественным, и, следовательно, волна описы-
ikx
вается членом вида е .
Что происходит, если Е < V ? Формула (D-20) определяет коэффициент преломления
как чисто мнимую величину; в формуле (D-19) величина п2 является отрицательной,
и решение пропорционально экспоненте е~рх, то есть волна является «проникающей»;
эта ситуация напоминает определенным образом проникновение электромагнитной
волны в металл*.
Таким образом, мы можем перенести известные выводы волновой оптики на
рассматриваемые здесь задачи. Но нужно четко понимать, что речь идет только лишь об
аналогии: интерпретация, которую мы даем волновой функции, коренным образом
отличается от интерпретации, которую волновая оптика приписывает электромагнитной волне.
с. ПРИМЕРЫ
а. Ступенька потенциала и потенциальный барьер
Рассмотрим частицу с энергией Е, которая, двигаясь из области отрицательных
значений координаты х, падает на «ступеньку» потенциала высотой VQ, как показано на
рис.8.
| У[х)
►
Скачок потенциала
Небольшое различие связано с тем, что показатель преломления п в металле не является
чисто мнимой величиной, а имеет и вещественную часть.
47

Глава 1
Если Е > V{) (случай, когда классическая частица преодолеет скачок потенциала и
продолжит движение слева направо с меньшей скоростью), оптическая аналогия приводит
к следующему выводу: световая волна движется слева направо в среде с показателем
преломления пх:
п{ = —л12тЕ (D-22)
и в точке х = х, падает на плоскую границу, где для х > х{ показатель преломления
становится равным:
n2=^-pm(E-VQ). (D-23)
Мы знаем, что падающая слева волна порождает отраженную и прошедшую волны.
Переведем этот результат на язык квантовой механики: частица имеет определенную
вероятность ZP быть отраженной от скачка потенциала и лишь вероятность A-.^) пройти
направо и продолжить свой путь. Этот вывод полностью противоречит предсказанию
классической механики.
Если же £ < У0, то показатель преломления п2 в области х > х, становится чисто
мнимым, и падающая световая волна полностью отражается. В этом смысле
предсказания квантовой и классической механики полностью совпадают. Однако существование в
области х > jCj «проникающей» волны указывает на то, что квантовая частица имеет
отличную от нуля вероятность проникнуть в эту область.
t H.v)
к\- 1 1
•vi л: Потенциальный барьер
Роль «проникающей» волны наиболее ярко проявляется в случае потенциального
барьера (рис. 9). Если Е < V0, классическая частица всегда отражается от него. Но при
рассмотрении соответствующей задачи в оптике, барьер представлял бы собой слой
конечной толщины с мнимым показателем преломления, помещенный в прозрачную среду.
Если толщина слоя не слишком велика по сравнению с параметром глубины 1 / р про-

Волны и частицы. Введение основных идей квантовой механики
никновения «проникающей» волны, то часть падающей волны пройдет в область х> хх.
Итак, даже для энергии Е < VQ существует отличная от нуля вероятность того, что
частица пройдет через барьер: это явление называют «туннельным эффектом».
C. Потенциальная яма
В этой задаче функция V(x) имеет форму, показанную на рис. 10. Классическая
механика приводит к следующим выводам: если частица имеет отрицательную энергию (но
превышающую значение -V » °на может лишь колебаться между координатами jc, и х2
с кинетической энергией Ес = Е + VQ; если же энергия частицы положительна и частица
движется слева направо, она сначала в точке хх испытает резкое ускорение, а затем в
точке х2 — столь же резкое замедление и далее продолжит свое движение вдоль оси Ох .
А'
Рис.10
Потенциальная яма
В рамках оптической аналогии, если -V0 < Е < 0, коэффициенты преломления я, и
п2 в областях х < jc, и х> х2 являются мнимыми, тогда как в интервале [х{, х2 ]
коэффициент преломления п2 — вещественное число. Таким образом, этот интервал
эквивалентен, например, слою воздуха между двумя отражающими средами. Волны,
последовательно отражающиеся в точках х{ и х2, взаимно уничтожаются благодаря
интерференции, за исключением некоторых строго определенных частот («собственные моды»),
на которых устанавливаются стабильные стоячие волны. На квантовом языке это
означает, что отрицательные значения энергии квантуются*, тогда как при классическом
рассмотрении все значения между -V0 и 0 допустимы.
* Разрешенные значения энергии не определяются хорошо известным условием х2 - х, = kX21 2 ,
так как нужно учитывать проникающие волны, вносящие сдвиг фаз при отражениях в точках
х = хх и х = х2 (см. дополнение Hj, § 2-е).
4 Квантовая механика
49

Глава 1
При Е > О коэффициенты преломления п{, п2 и /?3 являются вещественными:
AM/
п{ = пъ = —л12тЕ v (D-24)
«2=77Тл/2т(£ + уо). Ф-25)
Поскольку л2 больше, чем л, и п3, ситуация аналогична стеклянной пластинке в
воздушной среде. Чтобы получить отраженную волну в области х <х{ или прошедшую в
области х > х2, нужно просуммировать бесконечно большое количество волн,
образующихся при последовательных отражениях в точках jc, и х2 (многолучевой интерферометр,
подобный интерферометру Фабри—Перо). При этом, например, может оказаться, что
для некоторых частот падающая волна полностью проходит через пластинку. С
квантовой точки зрения частица в общем случае имеет определенную вероятность быть
отраженной, однако имеются значения энергии, называемые резонансными, для которых
вероятность прохождения равна 1 и, следовательно, вероятность отражения равна 0.
Эти примеры показывают, насколько предсказания квантовой механики могут
отличаться от выводов классической механики, и ясно иллюстрируют первостепенную роль
точек разрыва потенциала, приближенно отображающих его быстрое изменение.
ЗАКЛЮЧЕНИЕ
В этой главе мы ввели и обсудили качественно и количественно некоторые
фундаментальные идеи квантовой механики. Мы еще вернемся к этим понятиям в гл. III, чтобы
уточнить их и систематизировать. Однако уже теперь понятно, что квантовое описание
физических систем радикально отличается от того, что дает классическая механика, хотя
последняя и составляет в многочисленных случаях отличное приближение. В этой главе
мы ограничились физическими системами, образованными только одной частицей.
Описание этих систем в заданный момент времени классической механикой базируется на
задании шести величин, представляющих собой компоненты радиуса-вектора г (г) и
вектора скорости \(t) частицы; все динамические переменные (импульс, энергия,
момент импульса) определяются через г (г) и v(r). Законы Ньютона позволяют вычислить
г (г) как решение дифференциальных уравнений второго порядка по времени и,
следовательно, найти г@ и v(r) в произвольный момент времени t, если они известны в
начальный момент времени.
В квантовой механике используется более сложное описание явлений: динамическое
состояние частицы в заданный момент времени характеризуется волновой функцией и
50

Волны и частицы. Введение основных идей квантовой механики
зависит теперь не от шести параметров, а от бесконечного их количества [значения
\|/(r, t) во всех точках г пространства]. Кроме того, все предсказания результатов
измерений имеют лишь вероятностный характер (вероятность получить некоторый результат
при измерении динамической переменной). Волновая функция является решением
уравнения Шредингера, позволяющего найти i|/(r, t) по известной функции \|/(г,0); это
уравнение допускает применение принципа суперпозиции, из которого следуют эффекты
волнового типа.
Это потрясение наших концепций механики было порождено экспериментом:
структура и поведение материи на атомном уровне оказались необъяснимыми в рамках
классической механики. Теория при этом потеряла простоту описания, но зато гораздо
больше выиграла в единстве взглядов, ибо материя и излучение стали описываться по
одной схеме (корпускулярно-волновой дуализм). Обратим внимание, что эта схема хотя
и нарушила некоторые наши идеи и привычные понятия, полученные в макроскопической
области, полностью оправдала себя: никто и никогда не смог придумать эксперимент,
который бы поставил под сомнение соотношения неопределенностей (см. дополнение Dr
к данной главе). В более общем плане до настоящего времени никакое наблюдение не
обнаружило противоречий с основными принципами квантовой механики. Однако в
наши дни еще нет общей теории релятивистских и квантовых явлений, и новые
потрясения основ, конечно, не исключены.
4*

ДОПОЛНЕНИЯ К ГЛАВЕ I
А]. Порядок величины длин волн,
ассоциированных с материальными
частицами.
В]. Ограничения, налагаемые
соотношением неопределенностей.
Ci. Соотношение неопределенностей
и атомные параметры.
Dp Соотношение неопределенностей
и дополнительность.
Ei. Простое исследование двумерного
волнового пакета.
Fi. Связь между одномерной и трехмерной
задачами.
Gi. Одномерный гауссов волновой пакет.
Расплывание волнового пакета.
Н,. Стационарные состояния частицы
в поле прямоугольного одномерного
потенциала.
Ji. Поведение волнового пакета
на скачке потенциала.
К]. Упражнения.
А|, Вь Cf. очень простые, но
фундаментальные рассуждения относительно порядка
величины квантовых параметров.
Dj: обсуждение простого эксперимента,
который можно было бы представить, чтобы
попытаться опровергнуть дополнительность
волнового и корпускулярного аспектов света
(легкий пример, который можно рассмотреть
и позже).
Еь F,, Gj: дополнения, посвященные
волновым пакетам (§ С главы I):
Ej: качественная простая демонстрация связи,
существующей между боковым расширением
двумерного волнового пакета и угловой
дисперсией волнового вектора (простой пример).
F\: обобщение результатов § С главы I на
трехмерный случай; показано, как
исследование частицы в трехмерном пространстве в
ряде случаев может быть сведено к
одномерной задаче (средняя трудность).
Gi: подробный анализ частного случая
волнового пакета, у которого можно точно
вычислить свойства и эволюцию (расчеты
несколько сложнее, но принципиальных
трудностей не представляют).
H|i количественное уточнение выводов § D-2
главы I; настоятельно рекомендуется
проработать, поскольку потенциалы
прямоугольной формы часто применяются для простых
иллюстраций выводов квантовой механики
(многочисленные упражнения и дополнения
будут в дальнейшем опираться на
полученные здесь результаты).
Ji: уточненный расчет квантового поведения
частицы в поле потенциала прямоугольной
формы (частый случай); частица считается
достаточно хорошо локализованной в
пространстве, чтобы можно было следить за ее
«движением» (задача средней трудности;
важна с точки зрения физической интерпретации
физической интерпретации результатов.
52

Волны и частицы. Введение основных идей квантовой механики
Дополнение Ai
" .-!НГ
ПОРЯДОК ВЕЛИЧИНЫ ДЛИН ВОЛН,
АССОЦИИРОВАННЫХ С МАТЕРИАЛЬНЫМИ ЧАСТИЦАМИ
Соотношение Луи де Бройля:
^ A)
указывает, что длина волны, соответствующей частице с массой т и скоростью v, тем
больше, чем меньше т и v .
Чтобы показать, что волновые свойства материи невозможно наблюдать в
макроскопической области, возьмем, например, пылинку диаметром 1 мкм с массой т~ 10~15 кг.
Даже для такой малой массы и скорости v ~ 1 мм/с формула A) дает:
f\ f\ v 1П-"^
X « —Цт метра = 6,6 х 10'16 метра = 6,6 х 10~6 ангстрем. B)
1(Г,5х1(Г3
Такая длина волны пренебрежимо мала в масштабах пылинки.
Теперь рассмотрим тепловой нейтрон, то есть нейтрон (тп = 1,67 х 10~27 кг), имеющий
скорость v, соответствующую средней энергии теплового движения при абсолютной
температуре Т. Скорость v определяется из равенства:
1 2 P2 3
— m v = ~—£7\ C)
2 " 2шн 2
где к — постоянная Больцмана (к =1,38х10~23 Дж/градус). Длина волны,
соответствующая такой скорости, равна:
ХЛ = -Ь. D)
Р ^ЪтпкТ
Для температуры Т = 300° К имеем:
X = 1,4 ангстрем, E)
т. е. длина волны имеет порядок расстояния между атомами в кристаллической решетке.
Пучок тепловых нейтронов, падающих на кристалл, породит, таким образом, явления
дифракции, аналогичные тем, которые наблюдаются в рентгеновских лучах.
53

Глава 1
Рассмотрим теперь порядок величины длин волн Луи де Бройля, связанных с
электронами (те = 0,9 х 10~30 кг). Если ускорить пучок электронов разностью потенциалов V
(выраженной в вольтах), им будет сообщена кинетическая энергия:
£ = 4К = 1,6х1(Г,9УДж F)
2
(q= 1,6х10~19 кулон — заряд электрона). Поскольку Е = -*—, длина волны будет
2/72
равна:
или численно:
Р ртеЕ
. 6,6xlQ-34 12,3 ...
А = , м = —j= ангстрем. (8)
V2 х 0,9 х Ю-30 х 1,6 х Ю-19V VV
При разности потенциалов в несколько сотен вольт можно получить длины волн,
сравнимые с длиной волн рентгеновских лучей, и, следовательно, наблюдать явления
дифракции на кристаллах или кристаллических порошках.
В настоящее время большие ускорители способны сообщить частицам значительные
энергии. При этом осуществляется выход из нерелятивистской области, которую мы до
сих пор рассматривали. Например, сегодня без особого труда получают пучки электронов,
энергия которых превышает 1 ГэВ=109 эВ A эВ=1 электрон-Вольт = 1,6хЮ",9Дж),
тогда как масса покоя электрона эквивалентна примерно тес2 =0,5х106эВ; иначе
говоря, соответствующая скорость очень близка к скорости света с. В таких случаях
нерелятивистская квантовая механика, которую мы здесь рассматриваем, неприменима, но
соотношения
Е = Av; (9-а)
Х = - (9-Ь)
Р
остаются справедливыми и в релятивистской области. Напротив, соотношение G)
следует изменить, так как в релятивистском случае энергия частицы с массой покоя Wq уже
определяется не формулой р212т^, а выражением:
E = {l
pV + WoC4. A0)
54

Волны и частицы. Введение основных идей квантовой механики
В рассмотренном выше примере электрона с энергией 1 ГэВ величина тес2
пренебрежимо мала по'сравнению с£и, следовательно:
Х =— = — г: м= 1,2x10 ,5м= 1,2 ферми (И)
Е 1,6 х100
A ферми = 105 м). С помощью таких быстрых электронов можно исследовать структуру
атомных ядер и, в частности, протона; действительно, размеры ядер имеют порядок ферми.
ЗАМЕЧАНИЯ
(i) Укажем на часто встречающуюся ошибку при вычислении длины волны
материальной частицы с массой т Ф 0, если известна ее энергия Е . Эта ошибка состоит
в том, что вычисляют частоту v, используя формулу (9-а), а затем по аналогии с
электромагнитной волной принимают значение civ за длину волны де Бройля.
Безусловно, правильным будет следующее рассуждение: найти импульс р ,
соответствующий энергии Е, например, по формуле A0) (или в нерелятивистской области
2
из соотношения Е = -—), а затем использовать формулу (9-Ь), чтобы определить X .
2т
(ii) Согласно формуле (9-а) частота v зависит от начала отсчета энергии. То же
относится и к фазовой скорости V = — = vX . Напротив, групповая скорость
t/o) ^ dv ^ _
VG = — = 2я— не зависит от выбора начала отсчета энергии. Это очень важно
dk dk
для физической интерпретации VG .
Дополнение Bi
ОГРАНИЧЕНИЯ,
НАЛАГАЕМЫЕ СООТНОШЕНИЕМ НЕОПРЕДЕЛЕННОСТЕЙ
1. Макроскопическая система.
2. Микроскопическая система.
В § С-3 главы I мы видели, что положение и импульс частицы не могут быть
одновременно определены с произвольной точностью, так как соответствующие
неопределенности Ах и Ар должны удовлетворять соотношению:
55

Глава 1
Ах-Ар>П. A)
. о\
Здесь мы предлагаем численно оценить степень; этого ограничения: мы покажем
сейчас, что оно пренебрежимо мало в макроскопической области и, напротив,
становится весьма заметным на микроскопическом уровне.
1. Макроскопическая система
Вернемся к рассмотренному ранее (дополнение АО примеру пылинки, диаметр
которой имеет порядок 1 мкм, с массой т ~ 1СГ15 кг, движущейся со скоростью v = 10~3м/с.
Ее импульс равен:
p = mv ~ КГ18 кг м/с. B)
Если ее положение измеряется, например, с точностью до 0,01 мкм, то
неопределенность Пар ее импульса должна удовлетворять приближенно равенству:
Ар « — * 1°_ = Ю6 кг м/с. C)
У Ах 10"8
Соотношение неопределенностей практически не накладывает никаких
ограничений, так как в опыте никакой измерительный прибор не способен обеспечить
относительную точность измерения импульса порядка 10"8.
С точки зрения квантовой механики пылинка представляет собой волновой пакет с
групповой скоростью v= 10м /с и средним импульсом р = 10~18 кг м/с. Но для этого
волнового пакета можно принять такое пространственное распределение Ах и такую
дисперсию импульса Ар, что их можно считать совершенно несущественными. При
этом максимум волнового пакета определяет положение пылинки, и его движение
полностью идентично движению классической частицы.
2. Микроскопическая система
Рассмотрим теперь электрон в атоме. Модель Бора описывает его как классическую
частицу. Разрешенные орбиты определены правилами квантования, заданными априори:
например, радиус г круговой орбиты с импульсом p-mv электрона на ней должен
удовлетворять соотношению:
pr = nh, D)
где п — целое число.
56

Волны и частицы. Введение основных идей квантовой механики
Чтобы можно было говорить о траектории электрона в классическом понимании,
нужно, чтобы неопределенность его положения и его импульса были бы пренебрежимо
малы в сравнении с г и р соответственно:
Ах « г ; E-а)
Ар« р, E-Ь)
откуда следует:
Ах Ар
£«1. F)
г р
Но соотношение неопределенности требует, чтобы:
Д£.Д£*Л. G)
г р гр
Если использовать формулу D) для подстановки в правую часть выражения G) гр
вместо nfi, то это неравенство преобразуется к виду:
**.*£*!. (8)
г р п
Видно, что выражения (8) и F) совместимы лишь в случае, если п »1; таким образом,
соотношение неопределенностей заставляет нас отклонить полуклассическую картину
орбит Бора.
Дополнение Q
СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ
И АТОМНЫЕ ПАРАМЕТРЫ
Соотношение неопределенностей лишает физической реальности понятие орбиты Бора
(см. дополнение Вг). Далее мы рассмотрим квантовую теорию атома водорода (гл. VII).
Тем не менее мы покажем сейчас, как соотношение неопределенностей позволяет понять
стабильность атомов и даже весьма просто определить размеры и энергию атома
водорода в его основном состоянии.
Рассмотрим электрон, находящийся в кулоновском поле протона, считая последний
зафиксированным в начале системы координат. Если две частицы отстоят друг от друга
на расстоянии г, то потенциальная энергия электрона равна:
57

Глава 1
V(r) = --^—-, A)
где q — его заряд (равный и противоположного знака заряду протона). Пусть
-£- = е\ B)
Предположим, что состояние электрона описывается волновой функцией, имеющей
сферическую симметрию, пространственное положение которой характеризуется
параметром г0 (это означает, что вероятность нахождения частицы на расстояниях более 2 г0
или 3 г0 практически равна нулю). Соответствующая потенциальная энергия в таком
состоянии примерно равна:
V=~—. C)
'о
Для того чтобы она была минимальной, следует выбрать минимально возможное
значение г0, то есть волновую функцию, максимально сконцентрированную вокруг протона.
Но нужно принять во внимание и кинетическую энергию. Именно здесь приходится
учитывать принцип неопределенности: действительно, если электрон находится в
объеме с линейным размером г0, неопределенность Ар его импульса имеет порядок h I r0.
Иначе говоря, если даже средний импульс равен нулю, кинетическая энергия Т ,
связанная с рассматриваемым состоянием, отлична от нуля:
f^fBta=-L(Ap)J5-*lr. D)
2m 2mr0
Если уменьшать г0, чтобы уменьшить потенциальную энергию, то минимальная
кинетическая энергия D) увеличивается.
Самая меньшая энергия, совместимая с соотношением неопределенностей, равна
минимуму функции:
., * тт Ь1 е2
2mr0
Этот минимум имеет место для значения:
*2 ^
те
58

Волны и частицы. Введение основных идей квантовой механики
и равен:
Е =-—
0 2П2 '
Рис.1
Зависимость потенциальной энергии V ,
кинетической энергии Т и полной энергии
Т + V атома водорода от г0
(протяженности волновой функции). Изменение энергий
Т и V происходит с разными знаками,
вследствие чего полная энергия проходит
через минимум, определяемый
компромиссом между Т и V . Значение а0 дает
порядок величины размеров атома водорода
Выражение F) совпадает с тем, которое получается в модели Бора для радиуса первой
орбиты, а выражение G) дает значение энергии основного состояния атома водорода
(см. главу VII; действительно, волновая функция основного состояния равна е~г/а°). Такое
количественное совпадение может быть только случайным, поскольку все наши
рассуждения строились лишь на основе оценки порядков величин. Однако приведенный выше
расчет позволяет сделать важный физический вывод: из соотношения неопределенностей
следует, что кинетическая энергия электрона тем больше, чем меньше пространственное
распределение его волновой функции, и основное состояние атома является компромиссом
между кинетической и потенциальной энергиями.
Обратим особое внимание на то, что этот компромисс, основанный на соотношении
неопределенностей, полностью отличен от того, что можно было ожидать в классической
механике. Действительно, если электрон движется по классической круговой орбите
с радиусом г0, его потенциальная энергия равна:
Vc/=--. (8)
Соответствующую кинетическую энергию можно получить, приравняв
электростатическую и центробежную силы*:
* На самом деле законы классического электромагнетизма указывают, что электрон,
движущийся с ускорением, излучает энергию, вследствие чего существование стабильных орбит
оказывается невозможным.
59

Глава 1
откуда следует:
2 2
V —> (9)
Td=^mv2=~. A0)
2 2 г0
Тогда полная энергия равна:
£d=rd+Vd=-~. A1)
2 г0
Наиболее выгодная энергетически ситуация реализуется при г0= 0, что соответствует
бесконечно большой энергии связи. Поэтому можно в некотором смысле говорить, что
соотношение неопределенностей позволяет понять существование атомов.
Дополнение Di
СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ
И ДОПОЛНИТЕЛЬНОСТЬ
Эксперимент Юнга, который мы анализировали в § А-2 главы I, привел нас к
следующим выводам: с одной стороны, волновой и корпускулярный аспекты света
одновременно необходимы для объяснения наблюдаемых явлений; с другой стороны, они
взаимно исключают друг друга в том смысле, что невозможно определить, через какую
конкретно щель проходит каждый фотон, не разрушив тем самым картину
интерференции. Говорят, что волновые и корпускулярные свойства являются дополнительными.
Это понятие дополнительности является следствием постулатов квантовой механики,
которые будут сформулированы в главе III; если бы его удалось поставить под сомнение,
то вся квантовая теория была бы глубоко потрясена.
Мы снова вернемся к эксперименту Юнга, чтобы показать, насколько тесно связаны
друг с другом дополнительность и соотношение неопределенностей. В попытке отвергнуть
принцип дополнительности можно представить себе более тонкий эксперимент, чем тот,
который в главе I предполагал установку за каждой из щелей по фотоумножителю.
Проанализируем здесь одну из таких установок.
60

Волны и частицы. Введение основных идей квантовой механики
Рис.1
Схема установки, в которой
установлена подвижная пластинка &,
импульс которой может измеряться
до и после прохождения фотона, что
позволяет определить, через какую
из щелей F! или F2 прошел фотон,
прежде чем попасть в точку М
экрана.
Допустим, что пластинка &, в которой прорезаны щели, смонтирована так, что может
двигаться в вертикальной плоскости, чтобы иметь возможность измерять переданный ей
вертикальный импульс. Рассмотрим фотон (рис.1), который попал на экран наблюдения
в точку М (для простоты будем считать, что источник фотонов ^находится слева в
бесконечности). Импульс этого фотона меняется всякий раз, когда он проходит через ^
закон сохранения импульса требует, чтобы разность была поглощена пластинкой &>. Но
таким образом переданный пластинке ^ импульс зависит от траектории фотона и равен
(в зависимости от того, проходит он через ¥\ или F2):
hv .
р, = sinQ{
с
О)
или
hv .
р2 = sinv2,
с
B)
где
hv
импульс фотона, а 0, и 02 — углы между направлением падения фотона и
линиями FtM и F2M соответственно.
Теперь будем посылать фотоны по одному, чтобы постепенно на экране
образовывалась интерференционная картина. Для каждого из фотонов определяется, через какую
из щелей он прошел, путем измерения импульса, переданного пластинке &. На первый
взгляд кажется, что таким образом на экране можно одновременно обнаружить и
корпускулярные и волновые свойства света.

Глава 1
На самом деле это не так: мы покажем сейчас, что с помощью такого устройства
картина интерференции наблюдаться не будет. Действительно, ошибка приведенного
рассуждения состоит в допущении, что лишь одни фотоны являются объектами
квантовой природы. Но нельзя забывать, что квантовая механика применима и к пластинке ^(к
макроскопическому объекту). Если желательно знать, через какую щель прошел фотон,
необходимо, чтобы неопределенность Ар вертикального импульса, полученного #>, была
бы достаточно мала, чтобы можно было отличить р, от р2:
Ьр«\р2-р\. C)
Но тогда соотношение неопределенностей требует, чтобы положение пластинки ^было
бы известно с точностью до Ajc , где
AxZ-^—r. D)
Если обозначить символом а расстояние между щелями, а символом d — расстояние
между пластинкой ^и экраном, то в предположении малости углов 8, и 62 (т.е. d I а»\)
найдем (рис.1):
. х-а/2
sin 6, = 0. = ;
1 ! d
sinQ2=Q2 = X*a/2, E)
d
где х — координата точки попадания М фотона на экран. При этом формулы A) и B)
дают:
|л-л|-^|е,-е2|зА£, (б)
С
где X = длина световой волны. Подставив это значение в формулу D), получим:
v
Xd
Ajc>—. G)
а
Xd
Но величина — в точности равна расстоянию между интерференционными полосами,
а
которые образуются на экране. При этом возможность наблюдения интерференционной
62

Волны и частицы. Введение основных идей квантовой механики
картины существует только в том случае, если вертикальное положение щелей F| и F2
определено с точностью более высокой, чем расстояние между полосами.
Полученные здесь выводы демонстрируют тесную связь между соотношением
неопределенностей и принципом дополнительности. Из них можно сделать также еще одно
важное заключение: невозможно построить квантовую теорию, справедливую только для
света и не работающую для материальных систем, не сталкиваясь при этом с серьезными
противоречиями. Так, если бы в приведенном выше примере пластинку ^ можно было
рассматривать как классическую материальную систему, то была бы поставлена под
сомнение дополнительность двух аспектов света и, следовательно, вся квантовая теория
излучения. Впрочем, справедливо и обратное утверждение: чисто квантовая теория
вещества встретилась бы с аналогичными трудностями. Чтобы получить непротиворечивое
описание, следует применять идеи квантовой механики ко всем физическим системам.
Дополнение Ei
ПРОСТОЕ ИССЛЕДОВАНИЕ
ДВУМЕРНОГО ВОЛНОВОГО ПАКЕТА
1. Введение.
2. Угловая дисперсия и боковые размеры.
3. Физическое обсуждение результатов.
1. Введение
В § С-2 главы I мы изучали форму одномерных волновых пакетов, образованных
путем суперпозиции плоских волн, распространяющихся в одном направлении [формула
(С-7)]. Если это направление выбрано вдоль оси Ох, то результирующая функция не
зависит от у и z . Вдоль оси Ох она ограничена, но не имеет границ в
перпендикулярных к ней направлениях: ее значение одинаково во всех точках плоскостей,
параллельных плоскости yOz.
Здесь мы предлагаем исследовать иной простейший случай волнового пакета:
плоские волны, образующие суперпозицию, имеют копланарные волновые векторы, модули
которых практически равны, но направления слегка отличны друг от друга. Цель
анализа — показать, что угловая дисперсия влечет за собой ограничение размеров волнового
пакета в направлениях, перпендикулярных среднему волновому вектору.
В §С-2 главы I мы видели, как, исследуя суперпозицию трех конкретно выбранных
волн одномерного волнового пакета, можно понять существо явления и, в частности,
63

Глава I
найти фундаментальное соотношение (С-18) этой главы. Здесь мы также ограничимся
подобной упрощенной моделью, и обобщение полученных результатов будет сделано
согласно методу, использованному в главе I (см. также дополнение Fj).
• 2. Угловая дисперсия и боковые размеры
Итак, рассмотрим три плоских волны с волновыми векторами к,, к 2 и к 3,
представленными на рис.1: все они лежат в плоскости хОу , причем вектор к, направлен вдоль
оси Ох , а векторы к2 и к3 расположены симметрично по отношению к к, и образуют
с ним равные углы А9, которые мы будем считать достаточно малыми, вследствие чего
проекции векторов к,, к2 и к3 на ось Ох практически равны:
к -к = к ~\к \ = к
A)
Модули этих трех векторов отличаются лишь членами второго порядка малости по А9,
которыми мы будем пренебрегать. Их проекции на ось Оу соответственно равны:
B)
Как и в § С-2 главы I, будем считать амплитуды g(k) вещественными и
удовлетворяющими соотношениям:
g(k2) = ^(k3) = ^(k1).
C)
ДК
Рис.1
Расположение волновых векторов к,, к2 и к3,
определяющих три плоских волны, суперпозиция
которых образует двумерный волновой пакет
Эта модель схематически отражает более сложную ситуацию настоящего волнового
пакета, чем, например, в равенстве (С-6) главы I, со следующими характеристиками: все
волновые векторы перпендикулярны оси Oz и имеют одинаковые проекции на ось Ох
(изменяется лишь проекция на ось Оу); функция |g(k)| по отношению к этой единст-
64

Волны и частицы. Введение основных идей квантовой механики
венной переменной к имеет вид пика, изображенного на рис.2, с шириной Ак ,
связанной с угловой дисперсией 2 Д6 простым соотношением:
МУ=2*Д6.
Суперпозиция определенных выше трех волн дает:
D)
ikx t}_pUкх-кДО.у) , _j_ i(кх+кДОу)
gik^e^ll + cosdcAQy)]
E)
(зависимость от г отсутствует, из-за чего такой волновой пакет получил название
двумерного).
к
1
/
/
/
/
/ ,
/ 1
/
/
/
/
/
-к
О
—
0
ле
►мм
>*.
S
\
\
\
\
\
к
\
\
\
\
\
ч.
АО
Рис.2
Три выбранных значения ку позволяют
качественно понять, как выглядит функция |g(k)|
при изменении ку
Чтобы понять физический смысл, можно опереться на рис.3, где представлены
волновые плоскости всех трех составляющих, соответствующие фазам, кратным 2я.
Функция |\j/(jc,)>)| максимальна при у = 0, где три волны интерферируют
конструктивно на оси Ох. Если же имеет место отклонение от этой оси, то функция |v|/(jc,y)\
уменьшается (сдвиг фаз между компонентами возрастает) и обращается в нуль в точках
Ау
у = ±——, где Ау определяется равенством:
cos
*де
Ау
-1
F)
или
k-AQ-Ay = 2n,
G)
5 Квантовая механика
65

Глава 1
Волны (к2) и (к3) находятся при этом в противофазе с волной (ki) (рис.3). Используя
равенство D), можно переписать соотношение G) в форме, аналогичной соотношению
(С-11) главы!:
Ay-AkY =4n ,
(8)
Рис.3
Плоскости равной фазы для трех
волн, связанных с тремя волновыми
векторами, приведенными на рис.1.
Эти волны находятся в фазе
при у = 0 ив противофазе при
y = ±2n/Mv
Итак, угловая дисперсия волновых векторов ограничивает боковые размеры
волнового пакета; количественно это ограничение принимает форму соотношения
неопределенностей [формулы G) и (8)].
3. Физическое обсуждение результатов
Рассмотрим плоскую волну с волновым вектором к, распространяющуюся вдоль
оси Ох . Всякая попытка ограничить ее размеры в направлении, перпендикулярном Ох ,
приведет к угловой дисперсии, то есть преобразует плоскую волну в волновой пакет,
аналогичный рассмотренному выше.
Действительно, предположим, например, что на пути плоской волны установлен
экран с прорезанной в нем щелью шириной А у. Она породит дифрагированную волну
(см.рис.4). Известно, что угловая ширина пятна дифракции равна:
2.Д6 = 2—,
Ау
(9)
66

Волны и частицы. Введение основных идей квантовой механики
где А, = -г-г — длина падающей волны. Мы вновь приходим к той же ситуации, что и
lkl
ранее: формулы G) и (9) оказываются идентичными.
Рис.4
При уменьшении неопределенности Ау
дифракция волны на диафрагме увеличивает
неопределенность Му.
Дополнение Fi
СВЯЗЬ МЕЖДУ ОДНОМЕРНОЙ И ТРЕХМЕРНОЙ ЗАДАЧАМИ
1. Трехмерный волновой пакет.
a. Простой случай.
b. Общий случай.
2. Обоснование использования одномерных моделей.
Пространство, в котором движется классическая или квантовая частица, является,
конечно, трехмерным. Именно поэтому в главе I мы записали уравнение Шредингера (D-1)
для волновой функции\|/(г), зависящей от трех координат jc, у, z радиуса-вектора г.
Однако в этой главе мы неоднократно пользовались одномерной моделью лишь с одной
переменной х практически без серьезных обоснований. В данном дополнении мы
преследуем две цели: во-первых, обобщить в § 1 на три измерения результаты, полученные
в § С главы I, и, во-вторых, показать в § 2, как можно в определенных случаях строго
обосновать применение такой модели.
Лу
5*
67

Глава 1
1. Трехмерный волновой пакет
а. ПРОСТОЙ СЛУЧАЙ
Рассмотрим сначала простейший случай, для которого справедливы следующие
гипотезы.
Волновой пакет является свободным [V(r) = 0] и может быть представлен так же,
как и в равенстве (С-6) главы I:
¥(r,/) = ^37Fjg(k)e"kr-m(k,"rf^. A)
Кроме того, функция g(k) имеет вид:
g(k) = gx(kx)xg2(ky)xg3(k2). B)
Вспомним выражение для зависимости (о(к):
ш(к) = ^ = А(^ + *; + *,2). C)
2т 2т v v'
Подставим B) и C) в A) и заметим, что имеется возможность разбить интеграл на три
по кх, куЧ кг, вследствие чего
\|/(г, 0 = ViU Oxv|/2()>, Ox\|/3(z, t), D)
где
л/2я -ее
М2
со(*,)А. E)
2т
Аналогичные выражения получаются для \|/2(у, О и \|/3(z, 0 .
Функция \|/,(;у, О действительно имеет форму одномерного волнового пакета.
Таким образом, в этом частном случае \|/(r, t) получается простым перемножением D)
трех одномерных волновых пакетов, которые изменяются во времени совершенно
независимым образом.
68

Волны и частицы. Введение основных идей квантовой механики
Ь. ОБЩИЙ СЛУЧАЙ
В общем случае, когда V(r) — произвольная функция, формула A) не может быть
использована. Тогда полезно ввести трехмерное преобразование Фурье g(k, t) от
функции \|/(г, /) с помощью соотношения:
i|/(r,f) =
1
BяK'
-jg(k,t)eikrd3k
F)
Априори зависимость от t функции g(k, г), которая определяется формой потенциала
V(r), может быть произвольной; кроме того, в общем случае нет никаких причин, чтобы
g(k, t) имела вид произведения типа B). Чтобы обобщить результаты, приведенные в
§С-2 главы I, воспользуемся следующим предположением относительно ее зависимости
от к : модуль | g(k, t) | в некоторый момент времени t является функцией, вид которой
имеет явно выраженный максимум для значений к , близких к к0, и быстро
уменьшается до пренебрежимо малых значений, если к оказывается вне пределов области Dk с
центром к0, имеющей размеры Мл., М , М,. Как и ранее, положим
g(kyt) = \g(k,t)\e>
/a(k,/)
G)
для того, чтобы фазу волны с волновым вектором к можно было записать в виде:
Ф(к, г, 0 = сс(к, t) + kxx + kyy + kzz . (8)
Теперь можем продолжить рассуждения так же, как и в § С-2 главы I. Сначала волновой
пакет имеет максимум, когда все волны, для которых экстремумы по к находятся в
области Dk, имеют практически одну и ту же фазу, то есть когда ф мало меняется в
области Dk. При этом всегда можно разложить ф(к, г, t) вблизи к0 и ограничиться членами
первого порядка малости по 8к = к - к0:
5ф(к, г, t) = 8kx
dk
-Ф(к,г, г)
+ 8*
Э*.
-ф(к, г, t)
+ 8k
dk
-ф(к, г, t)\
(9)
69

Глава I
или, если использовать (8), в сжатом виде*:
5ф(к,г,г) = 5к.[ Укф(к,г,г)]к=ко=5к.[г + [Ука(кл)]к=ко]. A0)
Из A0) следует, что изменения функции ф(к, г, t) в области Dk минимальны, если
г = r„@ = -[Vka(k,f )]„.„„. A1)
Мы видели, что при этих условиях модуль |\|/(г, 01 максимален, и соотношение A1)
определяет положение rM(t) центра волнового пакета и является обобщением равенства
(С-15) главы I на трехмерное пространство.
В какой области Dr с центром г^ и размерами Длс, Ду, Дг волновой пакет F)
имеет существенные размеры? Модуль |\|/(r, t) | становится малым в сравнении с модулем
| ц/(гм, 0|, если волны с различным к , интерферируя, уничтожают друг друга, то есть
если изменения фазы ф(к, г, г) в области Dk близки к значению 2п — имеют порядок
одного радиана. Пусть 5r = r-rM ; если учесть формулу A1), то равенство A0)
запишется в виде:
5ф(к, г, 0 = 5к-5г. A2)
Условие 8ф(к, г, 0>1 дает немедленно соотношения, связывающие размеры области
Dr с размерами области Dk:
[Дх-Мл>1;
JAyA*v>l; A3)
[Дг-М2>1.
Соотношения неопределенностей Гейзенберга следуют непосредственно из
соотношения р = Йк :
[ Дх • Арх > Ь\
|ДуДр,£Й; A4)
[&z-&pz>h.
* Символ V обозначает «градиент»: по определению V / (х, у, z) есть вектор с
координатами Э//Эх, df /ду , df /dz . Индекс к в Vk означает, что, как и в (9), производные берутся по
переменным кхУ ку, kz.
70

Волны и частицы. Введение основных идей квантовой механики
Эти неравенства и являются обобщением выражения (С-23) главыЛ на трехмерное
пространство.
Заметим, наконец, что групповая скорость Vc волнового пакета может быть
получена простым дифференцированием выражения A1) по V.
Vc=~[V„a(k./)]„.„.. A5)
В частном случае свободного волнового пакета, но не обязательно удовлетворяющего
услрвию B), имеем;
a(k,r) = a(k,0)-(o(k)f, A6)
где со(к) описывается формулой C). Тогда из формулы A5) следует:
йк
Vc=[Vkco(k)]klk()=—A, A7)
т
и это выражение является обобщением равенства (С-31) главы I.
2. Обоснование использования одномерных моделей
Если потенциал не зависит от времени, то, как мы видели в § D-1 главы I, имеется
возможность разделить в уравнении Шредингера временную и пространственные
переменные, что позволяет получить уравнение (D-8) на собственные значения. Мы намерены
показать здесь, как в некоторых случаях можно продвинуть далее подобную методику и
разделить также переменные х, у, z в уравнении (D-8).
Действительно, допустим, что потенциальная энергия У(г) может быть записана в
виде:
V(r) = V(x, у, z) = Vl(x) + V2(y) + V3(z), A8)
и попытаемся узнать, существуют ли решения уравнения на собственные значения вида:
Ф(дг, у, г) = Ф,(.*)хф2(;у)хфзи). A9)
Рассуждения, аналогичные тем, которые были приведены в главе I (§ D-1-а),
показывают, что это возможно при условии:
Ъ2 d2 „, ч
ф1(д:) = £1чр1и). B0)
71

Глава 1
Справедливы еще два аналогичных уравнения, в которых х следует заменить на у (или г),
V\ на V2 (или V3) и Е\ на Е2 (или Е3). Кроме того, необходимо также, чтобы выполнялось
соотношение:
Е = Е{+Е2 + Е3. B1)
Уравнение B0) того же вида, что и уравнение (D-8), но оно одномерное, и,
следовательно, переменные х, у, z оказываются разделенными*.
Что происходит, если, например, потенциальная энергия частицы У(г) зависит только
от координаты xl В этом случае У(г) можно записать в виде A8), где У, = У и У2 = У3 = 0.
Уравнения B0) по у и по z соответствуют уже рассмотренному в главе I случаю (§ С-1)
одномерной свободной частицы, и их решениями являются плоские волны е •v и e'kzZ.
Теперь остается решить лишь уравнение B0), что является одномерной задачей. Однако
полная энергия трехмерной частицы теперь равна:
£=£1+^-[*J + *?]. B2)
2т L *J
Таким образом, рассмотренные в главе I одномерные модели соответствуют на деле
трехмерной частице, двигающейся в поле потенциала У (г), который зависит лишь от х\
при этом решения <р2(у) и cp3(z) являются предельно простыми и соответствуют
частицам, «свободной по оси Оу» и «свободной по оси Oz». Именно поэтому мы
сосредоточили все наше внимание на изучении уравнения по х.
Дополнение Gi
ОДНОМЕРНЫЙ ГАУССОВ ВОЛНОВОЙ ПАКЕТ.
РАСПЛЫВАНИЕ ВОЛНОВОГО ПАКЕТА
1. Определение гауссова волнового пакета.
2. Вычисление Ал: и Ар . Соотношение неопределенностей.
3. Эволюция волнового пакета.
a. Вычисление функции \|/(д\ t).
b. Скорость распространения волнового пакета.
c. Расплывание волнового пакета.
* Можно показать (см. главу II, §F-4-a-C), что, если V(r) имеет вид A8), все решения уравнения
на собственные значения (D-8) являются линейными комбинациями найденных здесь выражений.
72

Волны и частицы. Введение основных идей квантовой механики
В этом дополнении предполагаем исследовать частный случай одномерного
свободного волнового пакета, для которого функция g(k) имеет гауссову форму. Интерес к
этому примеру обусловлен тем, что расчет может быть выполнен точно до самого конца.
Мы сможем сначала доказать для данного частного случая ряд свойств волновых пакетов,
о которых говорилось в § С главы I. Затем воспользуемся полученными результатами,
чтобы исследовать эволюцию во времени ширины волнового пакета и продемонстрировать
эффект расплывания пакета во времени.
1. Определение гауссова волнового пакета
Рассмотрим в рамках одномерной модели свободную частицу [V(jc) = 0], волновая
функция которой в момент времени t = О имеет вид:
¥UO) = -^j-0,Md%fcA. A)
B71) _то
Этот волновой пакет получен путем суперпозиции плоских волн elkx с коэффициентами:
1 4 а -—а--*,,J
8«,0) = -г^ге 4 , B)
л/2я B71)
которые соответствуют функции Гаусса с центром к = к0, умноженной на численный
коэффициент для нормировки волновой функции. Именно такой волновой пакет
называют гауссовым.
В дальнейшем вычислении мы неоднократно встретим интегралы типа:
/(а,C)= J<fe2(WJ£/$, C)
где а и C — комплексные числа [чтобы интеграл C) сходился, нужно, чтобы Re а2 > О ].
Метод вычетов позволяет показать, что этот интеграл не зависит от Р :
/(сс,Р) = /(а,0) D)
и при условии -тг / 4 < Arg а < +я / 4 , что всегда справедливо, если. Re а2 > 0, интеграл
/(а, 0) выражается следующим образом:
/(а,0) = -/A,0). E)
а
73

Глава 1
Теперь остается лишь определить /A,0), что можно сделать классическим образом
благодаря двойному интегрированию в плоскости хОу и переходу к полярным координатам:
/A,0)= JY^ = Vrc. F)
Таким образом, имеем:
7 е'*2^''(£, = —
G)
а
где -71 / 4 < Arg а < +я / 4 .
Затем вычислим \|/(х, 0). Для этого перегруппируем зависящие от к показатели
экспонент в выражении A) следующим образом:
Л2 2
(к-к.у + ikx =
4 ° 4
а
х2
+ ikQx- — . (8)
а
Теперь можно воспользоваться формулой G) и записать:
( 7 Vм
V|/(jc,0)= -—- eik"xe-xha\ (9)
Мы видим, что преобразование Фурье гауссовой функции действительно дает также
гауссову функцию (см. приложение I).
В момент времени t = 0 плотность вероятности нахождения частицы определяется
формулой:
И*,оГ=,|Х
\ е~2х2,а2 . A0)
па
График функции |\|/ (х, 0)| является классической колоколообразной кривой. Центр
волнового пакета [максимум функции |\|/(х, 0)| ] находится в точке х = 0, что и должно
было получиться в результате применения общей формулы (С-16) главы I, так как в этом
частном случае функция g(k) является вещественной.
74

Волны и частицы. Введение основных идей квантовой механики
2. Вычисление Ах и Ар. Соотношение неопределенностей
При введении гауссовой функции f(x) = е~х 1Ь удобно явно определить ее ширину
Аде с помощью соотношения:
Ах = -^. (И)
л/2
Еслих изменяется от 0 до ± Аде, то функция f(x) уменьшается в раз; это
определение, хотя и является, конечно, произвольным, имеет то преимущество, что оно совпадает
со «среднеквадратичным» значением переменной х (см. главу III, §С-5).
С учетом этого обозначения ширину Адг волнового пакета A0) можно
переопределить следующим образом:
Ajc = ~. A2)
2
Ширину Ак можно определить аналогично, поскольку |g(&,0)| также является
гауссовой функцией, и тогда
А*=- A3-а)
а
или
В результате получим:
Ар = ~. A3-Ь)
а
Ад:.Ар = |, A4)
что вполне совместимо с соотношением неопределенностей Гейзенберга.
3. Эволюция волнового пакета
а. ВЫЧИСЛЕНИЕ ФУНКЦИИ \|/(дс, t)
Чтобы найти волновую функцию \|/(дг, t) в момент времени t, достаточно
воспользоваться общей формулой (С-6) главы I, полученной для свободной частицы. То есть:
75

Глава 1
V(*, 0 =
Га
BтгK/
-t('-*»Jj
Ikx-w(k)t)
dk,
A5)
где (D(/:) = — закон дисперсии для свободной частицы. Мы увидим сейчас, что
2т
в момент времени t волновой пакет сохраняет гауссову форму. Действительно,
выражение A5) можно преобразовать, перегруппируя, как это было сделано выше, все
зависящие от к члены в показателе экспоненты. Затем можно использовать выражение G)
и записать:
VU0:
'Та""
4 AhU
т
2.2Л
V*°'vexp
Пк0
т
а" +-
liht
т
A6-а)
где ф — вещественная величина, не зависящая от х:
ф = -Э °-t и tg2Q = —г.
2т та
A6-Ь)
Найдем теперь плотность вероятности \\\f(x, t)\ для частицы в момент времени /:
|\|/(лг, г)|2 =
•м" I 4h2t2
1 + -ТТ
т а
ехр
2a2\x-^t
т
4 4/zV
а +—=-
A7)
Покажем, что норма волнового пакета, т. е. J|\|/(jc, t)\2dx, не зависит от времени
(в главе III мы увидим, что это свойство вытекает из эрмитовости гамильтониана Н
частицы). Для этого можно было бы использовать равенство G) для интегрирования
выражения A7) в пределах от -©о до +«>. Но быстрее просто заметить в выражении A5), что
преобразование Фурье от функции \\f(x, t) имеет вид:
g(*,r) = e-'wa)'g(*,0), A8)
то есть g(k, t) неизбежно имеет ту же норму, что и g(k,0). Поскольку равенство Бес-
76

Волны и частицы. Введение основных идей квантовой механики
селя—Парсеваля указывает на то, что функции \\f(x, t) и g(k, t) имеют одинаковую
норму, то и функции \|/(дг, 0) и g(k, 0) имеют одинаковую норму. Отсюда следует, что
нормы функций 1|/(jc, t) и \|/(jc, 0) равны.
b. СКОРОСТЬ РАСПРОСТРАНЕНИЯ ВОЛНОВОГО ПАКЕТА
Из формулы A7) следует, что плотность вероятности |\|/(*, t)\ является гауссовой
функцией с центром в точке х = V01, где скорость V0 определяется равенством:
V„=^- A9)
т
Именно этот результат можно было бы предвидеть из общего выражения (С-32)
главы I, которое определяет групповую скорость VG.
с. РАСПЛЫВАНИЕ ВОЛНОВОГО ПАКЕТА
Вернемся к формуле A7). Ширина Ax(t) волнового пакета в момент времени t
согласно определению A1) равна:
a I 4h2t2
A*@ = -Jl + -rr- B0)
2 V та
Мы видим (см. рис.1), что эволюция волнового пакета не сводится к простому
перемещению со скоростью V0, и он испытывает деформацию во времени. При изменении t от
-<*> до 0 ширина волнового пакета уменьшается, в момент времени t = 0 она становится
минимальной и при дальнейшем возрастании t ширина Ах (г) увеличивается до
бесконечности (расплывание волнового пакета).
Из выражения A7) видно, что меняется и высота волнового пакета, но в
направлении, обратном ширине, так что норма функции \|/(jc, t) остается неизменной.
Свойства функции g{k, t) совершенно иные. Действительно [см. формулу A8)]:
|*(*,0| = |*(*,0)|. B1)
Отсюда следует, что средний импульс волнового пакета (hk0) и его дисперсия (tiAk) не
изменяются во времени. Ниже мы увидим (см. главу III), что это обусловлено тем, что
импульс является интегралом движения для свободной частицы. Физически вполне по-
77

Глава I
нятно, что распределение по импульсам не может измениться, если на своем пути
частица не встречает никакого препятствия.
Существование дисперсии импульса Ар = fiAk = ft/a означает, что скорость
частицы может быть определена лишь с точностью до Av = Ар I m = h I та . Представим себе
множество классических частиц, исходящих в момент времени t = 0 из точки х = О
|№М2
t <0
t ^0
t > 0
Рис.1
В моменты времени t < 0 гауссов волновой пакет распространяется с уменьшением ширины.
В момент t = 0 волновой пакет имеет минимальную ширину: произведение Аде • Ар равно
ft/2 . Затем при t > 0 волновой пакет распространяется с увеличением ширины
+ Лх
Рис.2
Зависимость ширины Ах волнового пакета, изображенного на рис.1, от времени. При
больших г ширина Ах стремится к дисперсии Ьхс1 положения ансамбля классических
частиц, которые вышли в момент времени t = 0 из точки х = 0 с дисперсией скоростей Ар/т
78

Волны и частицы. Введение основных идей квантовой механики
с разбросом скоростей Av . В момент времени t дисперсия их положений будет равна
i i лИ
oxcl = AvU =—— ; эта дисперсия линейно возрастает со временем г, как показано на
та
рис.2. Нанесем на этот же график кривую, определяющую эволюцию Ах (О ; при
стремлении г к бесконечности кривые Ax(t) и 8хс1 практически совпадают [прямые линии,
соответствующие 8хс1, являются асимптотами гиперболы Ax(t)]. Таким образом, можно
утверждать, что при больших t может быть использована квазиклассическая
интерпретация ширины Ajc . Напротив, если t стремится к 0, функция Ах (г) принимает значения,
существенно отличающиеся от Ъхс1. Действительно, квантовая частица должна постоянно
удовлетворять соотношению неопределенностей Гейзенберга Ах • Ар > h 12, которое
налагает нижний предел на Ах, поскольку Ар остается постоянной. Именно этот вывод
и следует из анализа рис.2.
ЗАМЕЧАНИЯ
(i) Расплывание свободных волновых пакетов является общим явлением, не
ограниченным рассмотренным частным случаем. Можно показать, что изменение во
времени ширины волнового пакета имеет вид, представленный на рис.2,
независимо от конкретной его формы (см. упражнение 4 в дополнении Ьш).
(И) В главе I простые рассуждения привели нас согласно (С-17) к приближенному равенству
Ах- А/: = 1 без конкретизации формы функции g(k), с одним лишь предположением, что
g(k) имеет максимум с шириной Ak вида кривой на рис.3 главы I (что, конечно,
соответствует случаю, рассмотренному в данном дополнении). Как же можно тогда получить
Ах • ДА: » 1, например, для гауссового волнового пакета при очень больших значениях tl
Конечно, это противоречие является лишь кажущимся. В главе I при получении
выражения Ах-Ак = \ мы предположили в формуле (С-13), что аргумент OL(t) в функции
g(k) может быть представлен в области Ак линейной функцией. Таким образом, мы
неявно допустили, что нелинейные члены дают в области Ак пренебрежимо малый вклад в
фазу g(k). Так, например, для членов второго порядка по (к- к0) нужно, чтобы
« 271. B2)
к=к0
Если, напротив, фаза Ct(k) не может быть представлена в области Ак линейной функцией
с ошибкой, существенно меньшей 2я , то действительно путем рассуждений, аналогичных
приведенным в главе I, следует заключить, что волновой пакет шире, чем дает формула (С-17).
М'
d2a
dk2
79

Глава I
В случае рассматриваемого здесь гауссового волнового пакета имеем А к = — и
а
Пк2 ГП2ЙГ „
ОС (А:) = 1, и условие B2) запишется в виде — —« 2п . Из формулы B0) не-
2m . \ a J m
трудно видеть, что при этом произведение Ах- Ак равно приблизительно 1.
Дополнение Hi
СТАЦИОНАРНЫЕ СОСТОЯНИЯ ЧАСТИЦЫ
В ПОЛЕ ПРЯМОУГОЛЬНОГО ОДНОМЕРНОГО ПОТЕНЦИАЛА
1. Поведение стационарной волновой функции ф(х).
a. Области, где потенциальная энергия постоянна.
b. Поведение ф(х) в точке разрыва потенциальной энергии.
c. Принцип расчета.
2. Анализ некоторых простых случаев.
a. Скачок потенциала.
b. Потенциальный барьер.
c. Связанные состояния. Прямоугольная потенциальная яма.
В главе I мы отмечали (см.§ D-2), что исследование движения частицы в поле
потенциала «прямоугольной» формы представляет интерес потому, что быстрое
пространственное изменение потенциала при некоторых значениях х приводит к возникновению
чисто квантовых эффектов. О ходе волновых функций, связанных со стационарными
состояниями частицы, мы догадывались благодаря оптической аналогии, которая
позволила нам очень просто понять, как возникают эти новые физические эффекты.
В этом дополнении мы приведем принцип количественного расчета стационарных
состояний частицы, примеры такого расчета в некоторых простейших случаях и
обсудим физический смысл полученных результатов. Для простоты ограничимся
одномерными моделями (см. дополнение Fi).
1. Поведение стационарной волновой функции ф(дс)
а. ОБЛАСТИ, ГДЕ ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ПОСТОЯННА
В случае прямоугольного потенциала функция V(x) остается постоянной V(jc) = V
в некоторых областях пространства. В такой области уравнение (D-8) главы I имеет вид:
80

Волны и частицы. Введение основных идей квантовой механики
d2 , ч 2т
Ф(*) + — (£-У)ф(дс) = 0. A)
dxz Т h
Будем различать несколько частных случаев.
(i) E>V
Введем положительную константу k9 определенную выражением:
Й2*2
E-V= . B)
2m
Решение уравнения A) запишется тогда как
<p(x) = Aeikx + A'e-ikx' C)
где А и А' — комплексные постоянные.
(ii) E<V
Это условие соответствует областям пространства, в которых движение по законам
классической механики запрещено. В этом случае мы введем положительную
постоянную р, определенную равенством:
V-еЖ. D)
2т
и решение уравнения A) записывается в виде:
ф(*) = Дер' + Я/*-р\ E)
где В и В' — комплексные постоянные.
(iii) E = V
В этом частном случае ф(лг) является линейной функцией координаты х.
Ь. ПОВЕДЕНИЕ ф(дг) В ТОЧКЕ РАЗРЫВА ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ
Как ведет себя волновая функция в точке х = х], где потенциал V(x) испытывает
разрыв? Априори можно было бы предположить, что в ней ф(лс) имеет некоторую
особенность — например, также имеет разрыв. Цель данного параграфа — показать, что это
не так: функции ф(лс) и d(p I dx остаются непрерывными, и лишь вторая производная
й?2ф / dx2 имеет разрыв при х = *,.
6 Квантовая механика
81

Глава I
Не вдаваясь в строгое доказательство этого утверждения, попытаемся понять, почему оно
оказывается справедливым. Для этого вспомним, что потенциал прямоугольной формы должен
рассматриваться (см. главу I, § D-2-a) как предел при £ —» О функции Ve(x), равной V(x) вне
интервала [jc, - £, х{ + £j, и непрерывно меняющейся внутри этого интервала. Рассмотрим тогда
уравнение:
—тФеи) + -^[£-УЕи)]фЕ(х) = 0, F)
ах п
где предполагается, что функция VE(x) в интервале [х, - £, х{ + £] ограничена независимо от £ .
Выберем решение фе(х), которое при х < х1 -£ совпадает с решением A). Задача состоит в
том, чтобы показать, что при £—>0 функция фе(лО стремится к непрерывной и
дифференцируемой в точке х = х, функции ф(х). Допустим, что фе(л:) остается ограниченной при любых
значениях £ вблизи точки х = хх ; физически это означает, что плотность вероятности остается
конечной величиной. Проинтегрируем уравнение F) от хх - У] до х{ + Т) и получим:
^Ч*.+т,)-^Ч*, -ti) = ^ *f [ад-Е]<р,(*)&. (?)
аде ах п '
В пределе, когда £ —» 0, подынтегральная функция в правой части этого равенства, как мы только
что допустили, остается ограниченной, и, если теперь устремить Г] к нулю, то
(Л,+Т1)--^и1-л)-^о->0. (8)
Таким образом, в пределе при х = д, производная dty / dx является непрерывной, как и сама
функция ф(х) (первообразная от непрерывной функции). Напротив, d"ty / dx испытывает
разрыв и, как можно непосредственно заметить в уравнении A), в точке х = х{ происходит скачок,
2т
равный —г- ф(х )<3V , где Gv представляет собой скачок функции V(x) в точке х = х{.
Ь
ЗАМЕЧАНИЕ
В проведенных выше рассуждениях существенно важно, чтобы Ve(x)
оставалась ограниченной. В некоторых упражнениях дополнения Кь например, рассмат-
* Это допущение может быть математически обосновано, исходя из свойств
дифференциального уравнения A).
82

Волны и частицы. Введение основных идей квантовой механики
ривается случай, когда V(x) = cc5(jc) , то есть функция является неограниченной,
но ее интеграл остается конечным. В подобном случае cp(jc) остается
непрерывной, но с/ср / dx таковой уже не является.
с. ПРИНЦИП РАСЧЕТА
Следующим шагом для определения стационарных состояний в поле
«прямоугольного» потенциала является следующее: во всех областях, где функция V(x) постоянна,
следует записать ф(дс) в виде подходящей из двух форм C) или E) и затем сшить эти
функции, наложив условия непрерывности ф(лс)и dty/dx в точках разрыва V(x).
2. Анализ некоторых простых случаев
Выполним теперь количественный расчет стационарных состояний, следуя
описанному выше методу, для всех форм потенциала V(x), упомянутых в § D-2-c главы I; мы
сможем убедиться, что форма решений именно та, которую мы предвидели на основе
оптико-механической аналогии.
а. СКАЧОК ПОТЕНЦИАЛА
а. Случай E>V0; частичное отражение
Обозначим:
И
,РР^. СО)
Решение уравнения A) имеет форму C) в обеих областях I(jc<0)hII(jc<0):
Ф1(дг) = АУ*" + а;^дг; (И)
q>u(x) = A2eik2X + A'2e-ik2X. A2)
Поскольку уравнение A) однородное, метод расчета, предложенный в § 1-е, позволяет
6*
83

Глава I
найти лишь отношения Л[/Л,, А21 А, и А2/ А{.В действительности, два условия
согласования решений в точке х = О недостаточны для определения этих трех отношений.
Поэтому мы положим А2 - О, что соответствует случаю частицы, движущейся со
стороны х = -оо . Условия сшивания решений тогда дают:
©
i
уо
i V(x)
®
0
►А'
Рис.1
Скачок потенциала.
К *,-*■
2 .
Л,
кх +к2
2kt
кх+к2
A3)
A4)
Функция ф7(дс) является суперпозицией двух волн: первая с амплитудой Л,
соответствует падающей частице с импульсом p = hk{, движущейся слева направо; вторая с
амплитудой А[ соответствует отраженной частице с импульсом -hk{, движущейся в
противоположном направлении. Поскольку мы приняли А2 = 0, функция (ри(х)
описывает лишь одну волну, связанную с прошедшей частицей. В главе III (см. §D-l-c-C) мы
увидим, как можно, благодаря понятию тока вероятности, ввести коэффициенты
прохождения Т и отражения R на скачке потенциала (см. также §2 дополнения Вш): эти
коэффициенты определяют вероятности того, что частица, движущаяся со стороны х = -<» ,
преодолеет скачок потенциала в точке х = 0 или отразится в обратном направлении.
Мы найдем выражения для R:
R
а:
A5)
и для Т\
* Физическая причина появления множителя к21 кх в выражении для Т обсуждается в §2
дополнения Jj.
84

Волны и частицы. Введение основных идей квантовой механики
Г = -2-
А,
Л
A6)
С учетом A3) и A4) получим:
4*,*,
Д = 1 llLj-t; A7)
(*,+*2J
Г= 4^22. A8)
(*,+*2J
Легко доказать, что Я + Г = 1. Это значит, что частица может либо пройти через скачок
потенциала, либо отразиться от него. В противоположность тому, что предсказывает
классическая механика, падающая частица имеет отличную от нуля вероятность
отразиться в обратном направлении; этот вывод мы уже обсуждали в главе I на основе
оптической аналогии, рассматривая отражение световой волны на границе раздела двух сред
(rtj > п2). Кстати, из оптики известно, что такое отражение происходит без отставания
волны по фазе, и, действительно, равенства A3) и A4) указывают, что отношения А\ I А,
и А2 / А{ являются вещественными числами. Таким образом, квантовая частица не
испытывает запаздывания ни при отражении, ни при прохождении (см. дополнение Jb § 2).
И наконец, легко видеть из равенств (9), A0) и A8), что при Е » V0 практически Т= 1:
частица с энергией, существенно большей высоты скачка потенциала, проходит за него,
почти не замечая его существования.
Р. Случай Е < V0 ; полное отражение
Введем в A0) и A2) обозначения:
2т(У0-Е)
П
2 =р2; A9)
ф/Д*) = Д2еР2Л + #2>-р2Л. B0)
Чтобы решение оставалось ограниченным при х = +<» , нужно положить:
Я2=0. B1)
Граничные условия в точке х = 0 в этом случае дают:
85

Глава 1
Л1=*!-Ч'Р2
Л, *,+/р2
К 2ki
*,+/р2
B2)
B3)
Коэффициент отражения R при этом равен:
|2
\А\
Ai
*.-ф2
*1+'Р2
= 1.
B4)
Как и в классической механике, частица всегда отражается (полное отражение). Однако
существует важное различие, на которое уже указывалось в главе I: вследствие наличия
проникающей волны е'*2* частица имеет отличную от нуля вероятность проникновения
в область пространства, которая по законам классической физики недоступна. Эта
вероятность экспоненциально уменьшается с ростом х и становится пренебрежимо малой,
если х превышает «глубину проникновения» 1 / р2 проникающей волны. Заметим также,
что коэффициент А\ I А{ является комплексным числом. Это свидетельствует о
существовании при отражении некоторого сдвига фазы, который физически обусловлен
запаздыванием частицы при ее проникновении в область jc> 0 (см. дополнение Jb § 1 и Вш, § 3).
Этот сдвиг фазы аналогичен тому, что происходит при отражении света от границы
раздела с металлической средой, и, напротив, он не имеет аналогов в классической
механике.
ЗАМЕЧАНИЕ
Если V0 —> +°о, то р2 —>-к», так что из B2) и B3) следует:
B5)
В области х> 0 волна, глубина проникновения которой бесконечно уменьшается,
стремится к нулю. Поскольку (А, + Л[)-> 0, волновая функция ф(лг) обращается
в нуль в точке х = 0и остается непрерывной в этой точке. Напротив, ее производная
внезапно изменяется от значения 2/&Д,до нуля, то есть испытывает разрыв. Это
происходит потому, что потенциал в точке х = 0 бесконечно велик, и интеграл G)
более не стремится к нулю при т^ —> 0.
86

Волны и частицы. Введение основных идей квантовой механики
Ь. ПОТЕНЦИАЛЬНЫЙ БАРЬЕР
а. Случай Е > V0 ; резонансы
Рис.2
Потенциальный барьер
Используя обозначения (9) и A0), найдем решения в трех областях: I (х<0),
II @ < jc < /) и III ( jc> Z):
9/W = A/v-+A^'v;
Ф//и) = А2^ + А^-'^;
<рш(х) = А3е*>х + А',е-**х.
B6-а)
B6-b)
B6-с)
Как и ранее, допустим, что А'ъ = 0 (частица движется со стороны х = -©о).
Граничные условия в точке х = / позволяют выразить А2 и А2 через А3, а граничные условия
в точке х = 0 — выразить Ах и А\ через А2 и А2, а следовательно, и А3. Таким образом,
можно найти:
cos k2l~i
kt + Ц
2kxk2
sin k2l
e^A3 ■
k2-k2
A'i=i!^Jli.sink2i.e^Ai
2ktk2
B7)
* Значение V0 может быть положительным (как, например, на рис.2) или отрицательным
(потенциальная яма).
87

Глава I
Отношения A[/Al и Аг1 Ах позволяют найти коэффициенты отражения R и
прохождения Г, которые оказываются равными:
|2
I л;
R
(k2-k2Jsin2k2l
Т =
Аз
4k2k2+(k2-k2Jsin2k2l
4к2к2
" 4k2k2+(k2-k22Jsin2k2l '
B8-а)
B8-Ь)
Легко доказать, что R + Т = 1. С учетом (9) и A0) получим:
^_ 4Е(Е-У0)
4E(E-V0) + V2 sin2y2m(E-VQ)-l/n\
B9)
Зависимость коэффициента прохождения Т от / представлена на рис.3 (считается,
что величины Е и VQ зафиксированы): величина Т периодически изменяется от своего
-1
минимального значения
1 + -
до максимального значения, равного 1. Эта
4£(£-V0)_'
функция аналогична той, которая описывает пропускание интерферометра Фабри—Перо;
как и в оптике, резонансы (при выполнении соотношения к21 = пп, когда Т- 1)
4Е(£ - V0) + VI
Рис.3
Зависимость коэффициента
прохождения Т через барьер
от ширины барьера (высота
барьера V0 и энергия Е
частицы остаются постоянными).
Резонансы имеют место
всякий раз, когда / кратна
полуволне п/ к2 в области II.
соответствуют значениям /, являющимся кратными половине длины волны частицы в
области П. Если Е > V0, отражение частицы на каждом скачке потенциала происходит
без сдвига фазы волновой функции (см. §2-а-сс), и именно поэтому условие резонанса
к21 = пп соответствует значениям /, для которых в области II может существовать сие-

Волны и частицы. Введение основных идей квантовой механики
тема стоячих волн. Напротив, вдали от резонансов различные волны, отражающиеся в
точках х = О и х - /, уничтожают друг друга за счет интерференции, вследствие чего
значения волновой функции резко уменьшаются. Анализ распространения волнового
пакета, аналогичного тому, который рассматривался в дополнении Jb показал бы, что при
выполнении условий резонанса волновой пакет проводит относительно много времени в
области II, и это явление называется в квантовой механике резонансным рассеянием.
Р. Случай Е < V0 ; туннельный эффект
В этом случае достаточно заменить решение B6-Ь) функцией B0), где по-прежнему
величина р2 определяется формулой A9). Граничные условия в точках х = 0 и х = /
позволяют найти коэффициент пропускания барьера. На самом деле нет необходимости
вновь производить все расчеты: достаточно в равенствах, полученных в § а, заменить к2
на -/р2. В результате получим:
а,
4g(V°'£) C0)
4E(V0 -E) + V02 sh2 [V2w(V0 - E) 11 h\ '
причем, конечно, R = 1 - Т. Если р2/»1, то
TJ6E(V-E)e_2p,
v2
Мы уже видели в главе I, почему в противоположность классическим предсказаниям
частица имеет отличную от нуля вероятность пройти через потенциальный барьер:
волновая функция в области II не равна нулю, а имеет характер «проникающей» волны на
глубину проникновения 1 / р2; если / < 1 / р2, то частица имеет достаточно большую
вероятность пересечь потенциальный барьер посредством «туннельного эффекта». Этот
эффект имеет много физических приложений: инверсия молекулы аммиака (дополнение
Giv), туннельный диод, эффект Джозефсона, ос-распад некоторых ядер и т.д.
Глубина проникновения «проникающей» волны для электрона равна:
Рг)
е, VV1^
1,96
ангстрем, C2)
где Е и Vo выражены в электрон-вольтах [эта формула получается непосредственной
подстановкой в формулу (8) дополнения А[ вместо X = 2л / к величины 2я/ р2 ]. Рассмотрим теперь
89

Глава I
электрон с энергией 1 эВ, налетающий на барьер с параметрами V0 = 2 эВ, / = 1 ангстрем. Для
него глубина проникновения оказывается равной 1,96 ангстрем, то есть одного порядка с /: иными
словами, электрон должен иметь значительную вероятность преодолеть барьер. Действительно,
формула C0) в этом случае дает:
7=0,78. C3)
Таким образом, квантовый результат радикально отличается от классического: у электрона почти
8 шансов из 10 пройти через барьер.
Предположим теперь, что падающей частицей является протон, масса которого примерно в
1840 раз больше массы электрона. Глубина проникновения 1 / р2 для него равна:
1Р2
1.96 4,6 1Л_2
, ангстрем =—===10 ангстрем. C4)
Vl840(V0-E) JVb-E
Если мы сохраним те же значения Е = 1 эВ, V0 = 2 эВ, / = 1 ангстрем, то получим, что при этом
глубина проникновения 1 / р2 гораздо меньше величины /; формула C1) дает:'
Г=4х109. {35)
В этих условиях вероятность прохождения протона через потенциальный барьер пренебрежимо
мала. По той же причине, если мы применим формулу C1) к макроскопическим объектам, то
получим столь ничтожные значения вероятности, что они не могут играть никакой роли в
физических явлениях.
с. СВЯЗАННЫЕ СОСТОЯНИЯ.
ПРЯМОУГОЛЬНАЯ ПОТЕНЦИАЛЬНАЯ ЯМА
а. Яма конечной глубины
Здесь мы ограничимся случаем, когда -V0 < Е < 0 (случай, когда Е > 0,
непосредственно входит в расчеты §Ь-а, выполненные выше).
В областях I I х < —
2)
II I < х < — , III х> — \ имеем соответственно:
2 2 { 2)
(f>l(x) = Blepx+B{e-px\ C6-а)
<fH(x) = A2eikx + A'2e~na\ C6-b)
90

Волны и частицы. Введение основных идей квантовой механики
р* л. »' г>~Р-1
(f>lll(x) = Biepx + B'3e
C6-с)
где
\2тЕ
_ \2т(Е + У0)
"V л2
C7)
C8)
Рис.4
Прямоугольная потенциальная яма
Поскольку функция ф(дг) должна быть ограниченной в области I, необходимо, чтобы
в;=о.
C9)
Граничные условия в точке х = — дают:
А <-P"W2P+i*„
2 2ik '
A'=-e-(<"lk)a'2^-B,,
2 2ik '
D0)
а условия в точке х = — дают:
Въ _ е»
В2 4ikp
[(p+/it)Vte-(p-/ifc)V4;
B'3=p2+k2
В, 2kp
sin ka.
D1)

Глава I
Но функция ф(лг) должна быть ограниченной также и в области III. Отсюда следует, что
Въ - О, то есть
'p-*V
VP + *J
= е
D2)
Поскольку р и к зависят от £, уравнение D2) допускает решения лишь для
определенных значений Е. Таким образом, наложенное на функцию ф(х) условие
ограниченности влечет за собой квантование энергии. Точнее, возможны лишь два случая.
(i) Если
Р-й = _eika
p + ik
D3)
то
Р (ка
D4)
Положим:
К=^=^7?
D5)
и после подстановки получим:
1
cos
2 ка к2 +р2
D6)
Таким образом, уравнение D3) эквивалентно системе уравнений:
cos
ка
У 2
кп
D7-а)
,(||>о.
D7-Ь)
Уровни энергии определяются как точки пересечения прямой с наклоном 1 / kQ с
отрезками синусоиды (на рис.5 они представлены длинным пунктиром). Так можно найти
92

Волны и частицы. Введение основных идей квантовой механики
некоторое количество уровней энергии, волновые функции которых являются четными;
действительно, если подставить D3) в D0) и D1), нетрудно убедиться, что В'ъ = В{ и
А2 = А'2, то есть (р(-л) = ф(х).
Зк/а 4п/а k0 Sn/a
Рис.5
Графическое решение уравнения D2), определяющего энергии связанных состояний
частицы в прямоугольной потенциальной яме. В случае, представленном на рисунке, имеется
пять связанных состояний: три четных (точки Р на рисунке) и два нечетных (точки I)
(ii) Если
= е
p + ik
D8)
то аналогичные вычисления приводят к следующей системе уравнении:
sin
ka
D9-а)
(ka
2
'*[—1<0-
D9-b)
В этом случае уровни энергии определяются точками пересечения той же прямой с
другими отрезками синусоиды (на рис.5 они изображены коротким пунктиром). Эти
значения чередуются с полученными в пункте (i), и нетрудно показать, что соответствующие
волновые функции являются нечетными.

Глава 1
ЗАМЕЧАНИЕ
Если к0 < —-, то есть
а
0 , = 2^Т' E0)
то рис.5 показывает, что существует лишь одно связанное состояние частицы с четной
волновой функцией. Затем, если Vl<V0 < 4V,, появляется первый нечетный уровень и т. д.:
с ростом V0 попеременно появляются четные и нечетные уровни. Если V0 >> V{, наклон
1 / к0 прямой на рис.5 очень мал, и для низших уровней энергии практически
*-^. E0
а
где п — целое число, и, следовательно:
E.*™—V E2)
2та2 °- E)
Р. Бесконечно глубокая яма
Пусть потенциал V(x) равен нулю в области 0<х<а и бесконечно велик в
остальном пространстве. Положим:
\2тЕ
:"V h2
l2mE ,__v
k = J—y- . E3)
Согласно замечанию в конце § 2-а-C этого дополнения функция ф(дг) должна равняться
нулю вне интервала [0, а] и быть непрерывной в точках х = 0 и х = а. Итак, для
интервала 0 < х < а :
<p(jr) = A**4AV*. E4)
Поскольку ф@) = 0, получим А' = -Л , и, следовательно:
ф(*) = 2iA sin kx. E5)
Кроме того, ф(я) = 0, и, следовательно:
94

Волны и частицы. Введение основных идей квантовой механики
* = —, E6)
а
где п — целое положительное число. Если функцию E5) пронормировать с учетом E6),
то получим стационарные волновые функции:
с энергиями:
2та2
Я„=-Т-Т-- E8)
Квантование энергетических уровней в этом случае оказывается относительно простым.
ЗАМЕЧАНИЯ
(i) Соотношение E6) отражает тот факт, что стационарные состояния определены
условием равенства ширины а ямы целому числу полуволн п I k . Это не так, если
яма имеет конечную глубину (см. § а); различие этих двух случаев обусловлено
сдвигом фазы волновой функции при отражении от скачка потенциала (см. § 2-а-C).
(ii) Легко доказать, используя E1) и E2), что если устремить глубину ямы V0 к
бесконечности, то получим уровни энергии бесконечно глубокой ямы.
Дополнение Ji
ПОВЕДЕНИЕ ВОЛНОВОГО ПАКЕТА
НА СКАЧКЕ ПОТЕНЦИАЛА
1. Полное отражение: Е < V0 .
2. Частичное отражение: Е >V0 .
В дополнении Hj мы определили стационарные состояния частицы в поле
«прямоугольного» потенциала. В некоторых случаях, например, когда потенциал имеет форму
скачка, полученные стационарные состояния образованы бесконечными плоскими
волнами (падающей, отраженной и прошедшей). Конечно, поскольку их невозможно
нормировать, волновые функции не могут представлять истинное физическое состояние
95

Глава 1
частицы. Однако можно взять их линейную суперпозицию и образовать волновые
пакеты, поддающиеся нормированию. Кроме того, поскольку такой волновой пакет
непосредственно может быть разложен по стационарным волновым функциям, его эволюция
во времени поддается простому определению: достаточно умножить каждый из
коэффициентов разложения на мнимую экспоненту e~lE,lh с точно определенной частотой
El h (см. главу I, § D-1-b).
В этом дополнении мы построим такие волновые пакеты и исследуем их эволюцию
во времени в случае, когда потенциал испытывает скачок величиной V(), как на рис. 1
дополнения Н[. Мы рассчитаем квантовое поведение частицы, когда она падает на скачок
потенциала, определим движение и деформацию связанного с ней волнового пакета. Это
позволит, кроме всего прочего, подтвердить ряд результатов, полученных в дополнении Н|
путем анализа стационарных состояний (коэффициенты отражения и прохождения,
запаздывание при отражении,...).
Положим:
\2тЕ ,
и, как в дополнении Нь будем различать два случая в зависимости от того, больше или
меньше к значения К0 .
1. Полное отражение: Е < V0
В этом случае стационарные волновые функции определяются формулами A1) и
B0) дополнения Hj (просто здесь величина к\ обозначена символом к), а коэффициенты
А ,, А[, В2 и #2 в этих формулах связаны соотношениями B1), B2) и B3)
дополнения Нг.
Сейчас мы построим волновой пакет путем линейной суперпозиции стационарных
волновых функций. Выберем только те значения к, которые меньше К0, чтобы все
образующие пакет волны испытывали полное отражение. Чтобы получить это, будем считать
характеризующую волновой пакет функцию g(k) равной нулю для к> К0. Сосредоточим
внимание на отрицательной области оси Ох, слева от потенциального барьера. В
дополнении Hj равенство B2) указывает, что коэффициенты Л, и А\ в выражении A1)
для стационарной волновой функции в этой области имеют одинаковый модуль, то есть
можно положить:
96

Волны и частицы. Введение основных идей квантовой механики
К(к)
АЛк)
= е
-2Ю<*>
B)
где [см. формулу A9) в HL
tgQ(k) =
^l^
C)
Окончательно рассматриваемый здесь волновой пакет в момент времени t = 0 для
отрицательных значений координаты х можно записать в виде:
^^o^^^dk-gw^+е'тк}е'^].
D)
Как и в § С главы I, предположим, что \g(k)\ представляет собой явно выраженный
максимум с шириной А к вблизи значения k = k0<KQ.
Чтобы получить выражение для волновой функции \j/(jc, t) в произвольный момент
времени /, достаточно использовать общее соотношение (D-14) главы I:
1 К
\|/(дс, t) = -j=j °dkg(k)e
\2п
i[kx-<a(k)t] {
+
л/2я
tfdkg{k)e4
[кх+ш(кI+2в(к))
E)
где (д(к) = fik212т. Это выражение справедливо только при х < 0. Его первый член
представляет падающий волновой пакет, а второй — отраженный пакет. Для простоты
предположим, что g(k) — вещественная функция; условие стационарной фазы (см.
глава I, § С-2) позволяет найти положение х, центра падающего волнового пакета: для
этого достаточно обратить в нуль производную по к от аргумента первой экспоненты
при к = к0 и приравнять:
X: ~t
dco
dk
Mn
-t.
F)
Аналогично, положение хг центра отраженного волнового пакета получается путем
дифференцирования по к аргумента второй экспоненты. Дифференцируя равенство C),
получим:
[i+/£2e]</e =
К2-к2
dk
d^-^^f^--rr-T^
G)
7 Квантовая механика
97

Глава I
то есть
К(Л ,л Кх
- f d0 = ?■ . dk, (8)
*2 *2 ^Г1^
откуда следует:
х=-
da ^d6
J*=A0
.^r + -r-2_. (9)
m V^o-Ao2
Формулы F) и (9) позволяют определить движение частицы, локализованной в малой
области А* с центром дг. или хг.
Рассмотрим сначала, что происходит при отрицательных значениях t. Центр jc,
падающего волнового пакета распространяется слева направо с постоянной скоростью
М0/т. С другой стороны, из формулы (9) видно, что хг >0, то есть находится вне
области х < О, где справедливо выражение E) для волновой функции; это означает, что для
всех отрицательных значений х волны, описываемые вторым членом выражения E),
интерферируют деструктивно: для отрицательных значений t нет отраженного
волнового пакета, а имеется лишь падающий волновой пакет, подобный тем, которые мы
изучали в § С главы I.
Центр падающего волнового пакета приходит на барьер в момент времени г = 0.
В течение некоторого интервала времени вблизи t = 0 волновой пакет локализован в
области х = 0 скачка потенциала, и его форма имеет относительно сложный вид. Но для
больших значений г из формул F) и (9) видно, что падающий волновой пакет исчезает,
и остается лишь отраженный волновой пакет. Действительно, теперь хх > 0, тогда как
хг становится отрицательным: волны падающего пакета интерферируют деструктивно
для всех отрицательных значений х, тогда как волны отраженного пакета интерферируют
конструктивно для х = хг < 0. Отраженный волновой пакет распространяется справа
налево со скоростью -nk01 m, противоположной скорости падающего на барьер пакета;
его форма остается неизменной* (с точностью до свойств симметрии). Кроме того,
формула (9) указывает, что отражение вносит запаздывание т, определяемое формулой:
dQ/dk
dw/dk
*=*о hk^Kl-kl
2т A0)
* Мы полагаем, что Ак достаточно мала, чтобы можно было пренебречь расплыванием
волнового пакета в течение рассматриваемого интервала времени.
98

Волны и частицы. Введение основных идей квантовой механики
В противоположность тому, что предсказывает классическая механика, частица
отражается не мгновенно; отметим, что запаздывание т связано со сдвигом фазы 2Q(k) между
падающей и отраженной волнами для данного значения к\ заметим, однако, что
запаздывание волнового пакета не просто пропорционально значению 0(&о), как было бы
в случае бесконечной плоской волны, а производной dQ/ dk , взятой при к = к0.
Физически это запаздывание обусловлено тем, что для значений г, близких к нулю, вероятность
нахождения частицы в области х > О (запрещенной классической механикой) отлична
от нуля [проникающая волна, см. ниже замечание (i)]: можно сказать, пользуясь образным
языком, что частица теряет время т в этой области, прежде чем отразится в обратном
направлении. Формула A0) показывает, что запаздывание т тем больше, чем ближе
П2к2
средняя энергия — волнового пакета к высоте потенциального барьера V0.
2т
ЗАМЕЧАНИЯ
(i) Здесь мы исследовали поведение волнового пакета в области х < 0, но можно также
рассмотреть и область х > 0. Действительно, в этой области волновой пакет может быть
представлен функцией:
4(x,t) = -j^=\l°dk-g{k)-B'2(k)e-«k)
х -iio(k)t
(И)
где
p(*) = V^-*2 .
A2)
Функция В'2(к) определена равенством B3) дополнения Н|, где следует заменить Ах на 1,
/:, на к и р9 на р . Рассуждение, аналогичное проведенному в § С-2 главы I, показывает,
что модуль |\|/(/) | выражения A1) максимален, если фаза подынтегральной функции по к
остается неизменной. Но согласно B2) и B3) дополнения Н| аргумент функции В\ вдвое
меньше аргумента А[, равного согласно B) величине ~2Э(/:), вследствие чего при
разложении С0(/:) и 6(&) вблизи к = к0 получим для фазы подынтегральной функции в A1):
</9
dk
d(u
dk
т \ 2)
A3)
[здесь использовано равенство A0) и предположение о вещественности функции g(k)].
7*
99

Глава 1
Отсюда следует, что |\|/(jc, t) | максимален в области х> 0 при t = X / 2 *: момент
времени, когда волновой пакет начинает двигаться в обратном направлении, равен Т / 2, что
позволяет найти полученное выше время запаздывания т при отражении. Из выражения A3)
становится больше интервала А/, определенного равенством:
видно, что как только
Т
t
2
Pik
^АЬАг = 1, A4)
т
где А/: — ширина функции g(k), волны сдвигаются по фазе, и выражение A1) для
|\|/(л:, 0| становится пренебрежимо малым; таким образом, волновой пакет остается в
области х > 0 в течение интервала времени At порядка:
Лг = , A5)
hk01 m
который примерно соответствует времени, необходимому для его перемещения в области
х < 0 на величину, сравнимую с 1/А&.
(ii) Поскольку мы предположили, что Ак меньше, чем к0 и К0 , сравнение выражений A0) и
A5) показывает, что
АГ»Т. A6)
Запаздывание при отражении выражается тем, что смещение отраженного волнового пакета
мало по сравнению с его шириной.
2. Частичное отражение: Е > V0
Теперь рассмотрим функцию g(k) с шириной А/: в окрестности к = к0> К0 и равную
нулю для к< К0. Волновой пакет формируется в этом случае путем суперпозиции
стационарных волновых функций с коэффициентами g(k), выражения которых определены
формулами A1) и A2) дополнения Нь примем А\ =0 для изучаемой частицы, которая
падает на барьер из отрицательной области оси Ох, и выберем Ах = 1; тогда коэффици-
* Заметим, что фаза A3) не зависит от х в противоположность тому, что мы нашли в главе I
для свободного волнового пакета. Отсюда следует, что в области х > 0 модуль \x\f(x, t)\ не
образует выраженного максимума, перемещающегося в зависимости от времени.
100

Волны и частицы. Введение основных идей квантовой механики
енты А[(к) и А2(к) получаются с помощью формул A3) и A4) дополнения Нь в
которых Л, заменяется на 1, к\ на к, и к2 — на ^к2 - К2. Чтобы описать волновой пакет
единым выражением, справедливым для любых значений х, можно использовать
ступенчатую функцию Хэвисайда, определенную выражениями:
0(;с) = О, если jc<0;
0(;с) = 1, если х>0. A7)
Исследуемый волновой пакет можно при этом записать в виде:
11/и,Г) = е(-х)^Г^.^(/:).е/1^а)/] +
^{-x)^rdk^{k)^Ax{kye-i{kx^k)t^
+ еи)^Г^^(^).л2(^).И^^л-и,а)/1. A8)
V27I *°
На этот раз мы имеем три волновых пакета: падающий, отраженный и прошедший.
Как и в § 1, условие стационарной фазы определяет положение их соответствующих
центров хпхги лг,. Поскольку А[{к) и А2(к) —вещественные величины, то
*,=Af; A9-а)
т
xr=-^t; A9-b)
т
fiJkl - Kl
л =_2U! °-t. A9-c)
m
Обсуждение, аналогичное тому, что было сделано для формул F) и (9), приводит к
следующим заключениям: для отрицательных значений t существует лишь падающий
волновой пакет; для полоэюительных и достаточно больших значений t существуют лишь
отраоюенный и прошедший волновые пакеты (рис. 1). Заметим, что нет запаздывания ни
при отражении, ни при прохождении [вследствие вещественности коэффициентов
А\{к) и А2(кI
Падающий и отраженный волновые пакеты распространяются со скоростями hk01 m
и -hk{) I m соответственно. Допустим, что А к достаточно мала, чтобы в интервале
101

Глава 1
V(x)
Рис.1
Поведение волнового пакета на скачке потенциала, если E>V0. Форма потенциала
представлена на рис. а. Приближение к скачку (Ь). Форма пакета в переходный период,
когда он начинает делиться на две части: интерференция падающих и отраженных волн
приводит к появлению осцилляции в волновом пакете в области х < О (рис. с). Через
некоторое время (рис. d) образуются два волновых пакета. Первый из них (отраженный)
движется справа налево, его высота меньше высоты падающего пакета, а ширина
остается прежней. Второй пакет (прошедший) движется слева направо, его высота несколько
больше высоты падающего, но ширина оказывается меньше.
Ак , Ак
2 ° 2
можно было пренебречь изменением А[(к) в сравнении с
изменением g(k). Тогда в правой части выражения A8) можно заменить А\{к) функцией
Л[(к0) и вынести ее из-под интеграла. Отсюда сразу же следует, что отраженный вол-
102

Волны и частицы. Введение основных идей квантовой механики
новой пакет имеет ту же форму (с точностью до соображений симметрии), что и
падающий пакет; его высота, однако, будет меньше, поскольку, согласно формуле A3)
дополнения Нь величина А[(к0) меньше 1. Коэффициент отражения R по определению есть
отношение вероятности нахождения частицы в отраженном волновом пакете и в
падающем пакете; таким образом, имеем R = \А^(к0) | , что соответствует уравнению A5)
дополнения Н\ [напомним, что мы приняли А,(/:0) = 1 ].
Для прошедшего волнового пакета ситуация иная. Действительно, можно использовать
то, что Д£ мала, чтобы упростить ее выражение; для этого заменим А2(к) на А2(к0) и
tJIc2 - К% на его приближенное значение:
^k2-Kl=Jkl-Kl+(k-kQ)
dyjk2-K20
dk
s%+(*-*o)—• B0)
где
Тогда прошедший волновой пакет запишется в виде:
^t(x4 t) = A2(k0)ei(l-X^Jiyk-g(k)-el
Сравним это выражение с выражением для падающего волнового пакета:
/(*-*„ H*-jc-o>(*)/
л/2я *°
[(k-kQ)x-io(k)t\
Видно, что
|v,Uf)| = A2(*0)
V/
Uo
-х, t
B1)
B2)
B3)
B4)
Таким образом, прошедший волновой пакет слегка выше падающего пакета: согласно
формуле A4) дополнения \\х величина А2(к0) больше 1. Однако его ширина меньше, так
как если ш/. (х, t)\ имеет ширину Длс, то из формулы B4) следует, что ширина функции
\|/, (лс, t)\ равна:
103

Глава 1
(Ах\=^Ах. B5)
Коэффициент пропускания (отношение вероятностей нахождения частицы в прошедшем
и падающем волновых пакетах) можно выразить в виде произведения двух
сомножителей:
Г = ^-|Л,(*0)|2. B6)
Это вполне согласуется с формулой A6) дополнения Нь поскольку Л,(А:0) = 1. Заметим,
наконец, что с учетом сжатия прошедшего волнового пакета по оси Ох, можно найти
скорость его перемещения:
V|=Ax&«A. B7)
т к0 т
Дополнение Kj
УПРАЖНЕНИЯ
1. Пучок нейтронов с массой Мп = 1,67 х10~27 кг и энергией Е, имеющих одинаковую
скорость, падает на линейную цепочку атомных ядер, расположенных регулярно, как
показано на рисунке (например, ядра в длинной линейной молекуле). Пусть / —
расстояние между двумя соседними ядрами, ad — их диаметр (d « I). На большом
расстоянии от нее расположен нейтронный детектор D, ось которого составляет с направлением
падения нейтронов угол 0 .
а) Дать качественное описание явлений, наблюдаемых с помощью D при изменении
энергии Е падающих нейтронов.
104

Волны и частицы. Введение основных идей квантовой механики
b) Скорость счета, как функция энергии Е, имеет характер резонансного максимума
вблизи значения £ = £,. Зная, что в области Е < Ех других резонансов больше нет, показать,
что по этим данным можно определить величину /. Вычислить значение /, если 6 = 30° и
£1 = 1,Зх10-20Дж.
c) Начиная с каких значений энергии Е следует учитывать конечные размеры ядер?
2. Связанное состояние частицы в потенциальной яме вида 8-функции
Рассмотрим частицу, гамильтониан которой Н [оператор, определенный формулой
(D-10) главы I] имеет вид:
2т dx
где а — положительная константа, величину которой требуется оценить.
a) Проинтегрировать уравнение на собственные значения оператора Н между -8 и +8
в пределе е—>0 и показать, что производная собственной функции ф(.х) в точке х = 0
испытывает скачок; выразить его величину через а, т и ф@).
b) Предположим, что энергия частицы отрицательна (связанное состояние). Тогда
функция ф(лг) может быть представлена в виде:
л:<0 (р(х) = А1ерх + А[е'рх;
*>0 <p(jc) = А2ерх + А'2е~*" ,
где р — константа, которую следует выразить через Е и т. Используя результаты
предыдущего вопроса, определить матрицу М, заданную равенством:
(АА
Uj
= м
(АЛ
и; J
Показать, что функция ф(х) является квадратично интегрируемой и найти
возможные значения энергии. Вычислить соответствующие нормированные волновые функции.
c) Изобразить графически полученные волновые функции. Каков порядок величины
их ширины Ajc?
d) Какова вероятность d@* (p) того, что измерение импульса частицы в одном из
вычисленных выше нормированных стационарных состояний даст результат, заключенный между
р и р + dpi При каком значении р эта вероятность максимальна? В какой области размером
Ар ее значения достаточно велики? Дать порядок величины произведения Ajc • Ар.
105

Глава I
3. Прохождение через потенциальный барьер вида 5-функции
Рассматривается частица в поле потенциала, рассмотренного в предыдущей задаче,
но движущаяся теперь по оси Ох слева направо с положительной энергией Е.
a) Показать, что стационарное состояние частицы может быть описано равенствами:
если х < О, <р(jt) = eikx + A e~ikx ;
если х > О, ф(л:) = Ве,кх ,
где к, А и В — константы, которые следует выразить через Е, т и а (обратить внимание
на разрыв производной — в точке х = 0).
dx
b) Пусть - EL - -та212h2 (энергия связанного состояния частицы). Выразить
через безразмерный параметр ЕI EL коэффициенты отражения R и прохождения Т через
барьер. Проанализировать их зависимость от Е ; что происходит, если Е —> °° ? Дать
интерпретацию. Показать, что если распространить выражение для Т на отрицательные
значения энергии Е , то оно расходится при Е —> -EL ; дать объяснение.
4. Рассмотреть задачу 2, используя преобразование Фурье.
a) Записать уравнение на собственные значения оператора Н и Фурье-образ этого
уравнения. Получить непосредственно выражение для ф(р), Фурье-образа функции
ф(х), и выразить его через р, £, а и ф@). Показать, что при этом возможным является
лишь отрицательное значение Е. Таким образом, так можно найти только связанное
состояние частицы, а не состояния движущейся частицы. Объяснить, почему. Рассчитать
ф(л:) и показать, что этим способом можно получить все результаты задачи 2.
b) Средняя кинетическая энергия частицы может быть записана как
2т ' '
Показать, что если ф(р) — «достаточно регулярная» функция, то справедливо и
выражение:
Эти формулы позволяют найти энергию Ес частицы в связанном состоянии,
рассмотренном в пункте (а), двумя различными способами. Какой результат получится?
106

Волны и частицы. Введение основных идей квантовой механики
Нужно отметить, что в этом случае функция ф(;с) не является «регулярной» в точке
jc = 0, где ее производная терпит разрыв; следует тогда выводить ф(х) в смысле
распределения, что позволит получить вклад точки х = О в искомое среднее значение. Объяснить
этот вклад физически; для этого рассмотреть прямоугольную яму с центром в точке
jc = 0, ширина которой а стремится к нулю, а глубина V0— к бесконечности (так, чтобы
aV0 = а), и изучить поведение волновой функции в этой яме.
5. Яма, состоящая из двух 8-функций
Рассмотрим частицу с массой т, потенциальная энергия которой может быть
записана в виде:
V(jc) = -a5(jc)-a5(jt-/), a>0,
где / — постоянная, имеющая размерность длины.
а) Рассчитать связанные состояния частицы, положив Е = . Показать, что
2га
возможные значения энергии определяются соотношением:
е~91 = ±
\.ш
2m0L тт л.
где ц = —=— • Дать графическое решение этого уравнения.
Й
(i) Основное состояние. Показать, что это состояние является четным (инвариантно
относительно симметрии в точке х = 112) и что его энергия Es меньше энергии -EL9
введенной в задаче 3. Объяснить этот результат физически. Представить графически
соответствующую волновую функцию.
(ii) Возбужденное состояние. Показать, что если / превышает некоторое значение,
которое нужно уточнить, существует нечетное состояние с энергией ЕА >-EL\
представить соответствующую волновую функцию.
(Hi) Объяснить, как предшествующие вычисления позволяют построить модель
ионизированной двухатомной молекулы (например, Я2+), ядра которой находятся на
расстоянии /. Как зависит от / энергия каждого из двух уровней? Что происходит в пределе,
когда / —> 0 и / —> ©о? Какова полная энергия системы, если учесть силы отталкивания
двух ядер? Показать, что кривые зависимости от / полученных значений энергии позволяют
в некоторых случаях предсказать существование связанных состояний Я2+ и определить
значение / в равновесии (так формулируется элементарная модель химической связи).
107

Глава 1
b) Рассчитать коэффициенты отражения и прохождения для всего ансамбля из двух
барьеров вида 5-функции. Изучить их зависимость от /; существуют ли полученные ре-
зонансы, если / кратна длине волны де Бройля частицы? Почему?
6. Рассмотреть потенциальную яму прямоугольной формы с шириной а и глубиной V0
(в этой задаче систематически используются обозначения, введенные в § 2-с-ос
дополнения Н\). Исследовать свойства связанного состояния частицы в яме, когда ее ширина а
стремится к нулю.
a) Показать, что в действительности существует лишь одно связанное состояние, и
mVfa2
вычислить его энергию (Е = ~— >то есть пропорциональна квадрату площади ямы).
2Ь
b) Показать, что р —»0 и А2 = А'2 = В{ /2 ; получить, что в связанном состоянии
вероятность нахождения частицы вне ямы стремится к 1.
c) Как применить предыдущие рассуждения к частице, подверженной действию
потенциала V(x) = -cc8(jc) , как в задаче 2?
7. Рассматривается частица в поле потенциала:
V(x) = 0, если х > а;
V(x) = - V0, если 0 < х < а
и V(x) —> ©о при отрицательных значениях х. Пусть (р(х) — волновая функция, связанная
со стационарным состоянием частицы. Показать, что ф(лс) можно продлить так, чтобы
получить нечетную волновую функцию, соответствующую стационарному состоянию
для прямоугольной ямы с шириной 2а и глубиной V0 (см. дополнение Нь § 2-с-ос).
Обсудить количество связанных состояний частицы при изменении а и Vb; существует ли
по крайней мере одно такое состояние, как в случае симметричной потенциальной ямы?
8. Рассматривается в рамках двумерной задачи наклонное отражение частицы от скачка
потенциала:
V(x, у) = 0, если х < 0;
V(x, у) = Vo> если х > 0.
Изучить движение центра волнового пакета. В случае полного отражения физически
объяснить различие между траекторией этого центра и классической траекторией
(боковое отклонение при отражении). Показать, что при V0 —> +°° квантовая траектория
асимптотически стремится к классической.

Глава II
МАТЕМАТИЧЕСКИЙ АППАРАТ
КВАНТОВОЙ МЕХАНИКИ

ПЛАН ГЛАВЫ II
А. ПРОСТРАНСТВО 1. Структура пространства // волновых функций.
ВОЛНОВЫХ ФУНКЦИЙ а. Векторное пространство & .
ЧАСТИЦЫ. Ь. Скалярное произведение.
с. Линейные операторы.
2. Дискретные ортонормированные базисы в пространстве
^:{и,(г)}.
a. Определение.
b. Компоненты волновой функции в базисе { и,-(г) ).
c. Выражение скалярного произведения через
компоненты.
d. Соотношение замкнутости.
3. Введение базисов, не принадлежащих к ./ .
a. Пример плоских волн.
b. Пример «дельта-функций».
c. Обобщение: непрерывные «ортонормированные»
базисы.
1. Введение.
2. Векторы «кет» и векторы «бра».
a. Элементы в пространстве $: кет-векторы.
b. Элементы в дуальном пространстве <?*:
бра-векторы.
c. Соответствие между кет- и бра-векторами.
3. Линейные операторы.
a. Определения.
b. Примеры линейных операторов: проекционные
операторы.
4. Эрмитово сопряжение.
a. Действие линейного оператора на бра-вектор.
b. Оператор А+, эрмитово сопряженный линейному
оператору А .
c. Свойства соответствия между оператором и его
эрмитово сопряженным.
d. Эрмитово сопряжение в обозначениях Дирака.
e. Эрмитовы операторы.
В. ПРОСТРАНСТВО
СОСТОЯНИЙ.
ОБОЗНАЧЕНИЯ ДИРАКА.
С. ПРЕДСТАВЛЕНИЯ
В ПРОСТРАНСТВЕ
СОСТОЯНИЙ.
1. Введение.
a. Определение представления.
b. Цель данного параграфа.

2. Соотношения, характеризующие ортонормированный
базис.
a. Соотношение ортонормировки.
b. Соотношение замкнутости.
3. Представление векторов кет и бра.
a. Представление векторов кет.
b. Представление векторов бра.
4. Представление операторов.
a. Представление оператора А «квадратной»
матрицей.
b. Матричное представление кет-вектора |\|/') = A |V|/) .
c. Выражение числа (ф| A \\\f/ .
d. Матричное представление оператора Л+ , эрмитово
сопряженного оператору А .
5. Изменение представления.
a. Постановка задачи.
b. Преобразование компонент кет-вектора.
c. Преобразование компонент бра-вектора.
d. Преобразование матричных элементов оператора.
D. УРАВНЕНИЯ
НА СОБСТВЕННЫЕ
ЗНАЧЕНИЯ.
НАБЛЮДАЕМЫЕ.
1. Собственные значения и собственные векторы оператора.
a. Определения.
b. Нахождение собственных значений и собственных
векторов оператора.
2. Наблюдаемые.
a. Свойства собственных значений и собственных
векторов эрмитова оператора.
b. Определение наблюдаемой.
c. Пример: проекционный оператор Р^ .
3. Ансамбли коммутирующих наблюдаемых.
a. Важные теоремы.
b. Полные наборы коммутирующих наблюдаемых.
Е. ДВА ВАЖНЫХ ПРИМЕРА
ПРЕДСТАВЛЕНИЙ
И НАБЛЮДАЕМЫХ.
1. Представления {|г) } и {|р) }.
a. Определение.
b. Соотношения ортонормировки и замкнутости.
c. Компоненты кет-вектора.
d. Скалярное произведение двух векторов.
e. Переход от представления {| г) } к представлению
(|р>|.

2. Операторы R и Р.
a. Определение.
b. Эрмитовостъ операторов R и Р.
c. Собственные векторы операторов R и Р.
d. R и Р — наблюдаемые величины.
F. ТЕНЗОРНОЕ
ПРОИЗВЕДЕНИЕ
ПРОСТРАНСТВ
СОСТОЯНИЙ.
1. Введение.
2. Определение и свойства тензорного произведения.
a. Тензорное произведение пространств Ъ .
b. Тензорное произведение операторов.
c. Обозначения.
3. Уравнения на собственные значения в произведении
пространств.
a. Собственные значения и собственные векторы опе-
раторов-продолжений.
b. Полные наборы коммутирующих операторов в
пространстве $.
4. Примеры применения.
a. Состояния частицы в одномерном и трехмерном
пространствах.
b. Состояния системы, состоящей из двух частиц.

Эта глава представляет собой обзор математического аппарата, используемого в
квантовой механике. Последующее изложение адресовано читателю, мало знакомому с
этим аппаратом, и имеет целью облегчить ему изучение следующих глав путем сжатого
изложения основ математики. Мы не намереваемся представить здесь полно и строго весь
математический формализм, нам кажется более предпочтительным ограничиться лишь
практическим руководством, сгруппировав в одной главе различные понятия,
используемые в квантовой механике. Так, в частности, особое внимание уделим удобству
обозначений Дирака для выполнения разнообразных вычислений, которые нам придется делать.
В том же духе мы будем стараться максимально упрощать изложение, и читатель не
найдет здесь ни общих определений, ни строгих доказательств, которые удовлетворили
бы профессионального математика. Например, нам часто придется обсуждать
пространства с бесконечным количеством измерений как пространства с конечной размерностью;
кроме того, многие термины (квадратично интегрируемая функция, базис и т.д.) будут
применяться в смысле, характерном для их использования в физике и не всегда в
точности совпадающем с тем, что вкладывает в них «чистая» математика.
В § А приведены некоторые полезные понятия относительно пространства волновых
функций; в § В обобщена концепция состояния физической системы и введено
пространство состояний (Г системы с применением обозначений Дирака. Изучению понятия
представления посвящен § С. Чтение следующего § D особенно рекомендуется
читателю, мало знакомому с диагонализацией оператора: этой операцией мы постоянно будем
пользоваться в дальнейшем. После рассмотрения двух важных примеров представлений
в § Е мы введем в § F понятие тензорного произведения, и оно более конкретно будет
проиллюстрировано на простом примере в дополнении Dlv.
А. ПРОСТРАНСТВО ВОЛНОВЫХ ФУНКЦИЙ ЧАСТИЦЫ
Вероятностная интерпретация волновой функции \|/(г,г) частицы была дана в
предыдущей главе: величина |\|/(r,0| d*r равна вероятности нахождения частицы в момент
времени t в элементе объема d3r -dxdydz вблизи точки г. Полная вероятность найти
частицу во всем пространстве равна 1, вследствие чего
Jrf3r|v(r,0|2 = l, (A-1)
где интеграл берется по всему объему пространства.
8 Квантовая механика
ИЗ

Глава II
Таким образом, нам предстоит исследовать ансамбль квадратично интегрируемых
функций, то есть функций, для которых интеграл (А-1) сходится. Этот ансамбль
математики обозначают символом L2, и он имеет структуру гильбертова пространства.
С физической точки зрения понятно, что ансамбль L2 слишком широк: с учетом
смысла, приданного величине |\|/(г,г)| , реально используемые волновые функции имеют
ряд особенностей. Можно оставить лишь те функции \|/(г,/), которые являются повсюду
определенными, непрерывными и даже бесконечно дифференцируемыми (например,
утверждение о том, что функция в некоторой точке имеет истинный разрыв не имеет
никакого физического смысла, так как никакой эксперимент не позволит получить
сведения о реальных явлениях, происходящих в предельно малых размерах, скажем 10~30 м);
можно также рассматривать волновые функции лишь в ограниченных областях
пространства (например, с уверенностью утверждать, что частица находится в конечном
объеме лаборатории). Мы не собираемся уточнять здесь эти дополнительные условия в
общем случае и будем обозначать символом & ансамбль волновых функций,
составленный достаточно регулярными функциями из L2 (J является подпространством L2).
1. Структура пространства 'J волновых функций
а. ВЕКТОРНОЕ ПРОСТРАНСТВО 9
Если \|/1(г)е:/ и \|/2(г)е#\то
\|/(г) = Х,\|/,(г) + X2v2(r) е J, (A-2)
где А, и Х2 —произвольные комплексные числа.
Для того чтобы показать квадратичную интегрируемость функции \|/(г), раскроем |\|/(г)| :
|\l/(r)|2 =|?^I|2|\|/1(r)|2 + |Х2|2|м/2(г)|2 +X*1X2V|/;(r)\j/2(r) + XIX,*2Vi(r)M/2(r)- (А-3)
Два последних члена равенства (А-3) имеют одинаковый модуль, и их можно мажорировать
формулой:
NN[lV.(r)|2+IV2(D|2]-
Таким образом, |\|/(г)| меньше функции, интеграл от которой сходится, так как и Vj/,, и \|/2
являются квадратично-интегрируемыми функциями.
114

Математический аппарат квантовой механики
Ь. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
а. Определение
Каждой паре элементов ф(г) и \j/(r) пространства & , взятых в указанном порядке,
можно сопоставить комплексное число, обозначаемое символом (ф,\|/) и равное по
определению:
(ф,\|/) = ]>3гф*(г)у(г)
(А-4)
Это число называется скалярным произведением i|/(r) на ф(г) [этот интеграл всегда
сходится, если ф и ц/ принадлежат пространству & ].
C. Свойства
Они вытекают непосредственно из определения (А-4):
(ф,\|/) = (\1/,ф)*; (А-5)
(фД,\|/1+А.2\|/2) = А,1(ф,\|/|) + Х2(ф,\|/2); (А-6)
(Х1ф1+Л2ф2,\1/) = Х;(ф,,\|/) + Г2(ф2,1|/). (А-7)
Скалярное произведение линейно по отношению ко второй функции пары и антили-
нейно по отношению к первой функции. Если (ф,\|/) = 0, говорят, что функции ф(г) и
l|/(r) ортогональны. Величина
(\^\|/) = JdV|i|/(r)|2
(А-8)
является положительным вещественным числом, равным нулю лишь в том случае, если
\|/(г) = 0 . Величина <yj(\\f,\\f) называется нормой \|/(г) [можно без труда показать, что это
число имеет все свойства нормы]. Таким образом, определенное выше скалярное
произведение позволяет определить норму в пространстве & .
Напомним, наконец, неравенство Шварца (см. дополнение Ац):
|vp\|/2|<V(VpVi)V(V2.V2)- (A-9)
Равенство имеет место лишь в том случае, если функции \|/, и \|/2 пропорциональны.
8*
115

Глава II
с. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
а. Определение
Линейным оператором А , по определению, является математическая операция,
позволяющая сопоставить любой функции \\f(r)e^ другую функцию V|//(r)G.^ , причем
это соответствие является линейным:
\|/'(г) = АЩт); (А-10-а)
Л[Х1\|/1(г) + Х2\|/2(г)] = Х1Л\1/1(г) + Х2Л\|/2(г). (A-10-b)
Приведем несколько примеров простых линейных операторов: оператор четности П ,
по определению, удовлетворяет равенству:
Щ(х, у, z) = \|/(-дс, - у, - z), (А-11)
оператор умножения на х (обозначим его символом X) определяется равенством:
ХЩх, у, z) = jo|/(jc, yt z) (A-12)
и, наконец, оператор дифференцирования по х (обозначим его символом Dx)
определяется равенством:
0Мх.У.г)-Щ^ (А-13)
дх
[два оператора X и Dx, действуя на функцию V|/(r) G #", могут преобразовывать ее в
функцию, которая не обязательно должна быть квадратично-интегрируемой].
р. Произведение операторов
Пусть А и В — линейные операторы. Их произведение определяется равенством:
(А-14)
(А%(г) = А[Яу(г)]
Сначала на функцию \|/(г) действует оператор В, дающий ф(г) = #\|/(г), а затем
оператор А действует на полученную функцию ф(г).
В общем случае АВФ ВА . Коммутатором операторов А и В называют оператор,
который обозначается символом [А, В\ и определяется равенством:
|[А, д]=АВ-ВА| (А-15)
116

Математический аппарат квантовой механики
В качестве примера вычислим коммутатор [X, Dj. Для этого выберем произвольную
функцию \|/(г):
[Х.Од]¥(г) = (,1.~^(г)-4^)-|г^(ГI-
= jc—V|/(r)-\|/(r)-jc—V(r)=-\|/(r). (A-16)
dx djc
Поскольку последнее равенство справедливо для произвольной функции \|/(г), то
[X,Aj=-l. (A-17)
2. Дискретные ортонормированные базисы в пространстве & : {и.(г)}
а. ОПРЕДЕЛЕНИЕ
Пусть имеется счетное множество функций пространства & , пронумерованных
дискретным индексом / = 1,2,..., и,...:
м,(г)е^,и2(г)е#\..., м,.(г)е#\...
— Множество { м,(г)} является ортонормированным, если
(W/.,W.) = J^V.w;(r)^(r) = 50., (A-18)
где 8/;/ — символ Кронекера, равный 1, если / = j, и 0, если / Ф j.
— Оно образует базис*, если любая функция \j/(r) € #* может быть разложена
единственным образом по функциям и,(г):
V(r) = Zc/M/(r)
(А-19)
* Если множество { и, (г)) образует базис, иногда говорят, что оно является полной системой
функций. Следует отметить, что слово «полная» используется здесь в ином смысле, чем это
принято в математике.
117

Глава II
b. КОМПОНЕНТЫ ВОЛНОВОЙ ФУНКЦИИ В БАЗИСЕ { М,(г) }
Умножим обе части равенства (А-19) на и* (г) и проинтегрируем по всему
пространству. Согласно формулам (А-6) и (А-18) получим*:
(и., у) = и., £сд. = Ес,Ц, и,) = Хс;8/у = сj, (А-20)
v i / i i
то есть
c/=(n„v) = Jrf3r-«*(r)V(r). (A-21)
Таким образом, проекция с, функции \|/(г) на и,, (г) равна скалярному
произведению \|/(г) на м,(г). Если базис { м,(г)} выбран, то задания функции \|/(г) в явном виде
или в виде множества ее проекций (компонент) с,- на базисные функции являются
эквивалентными. Говорят, что множество чисел ci представляет функцию \j/(r) в базисе
{"/(г)}.
ЗАМЕЧАНИЯ
(i) Отметим аналогию между обычным трехмерным пространством R и ортонормированным
базисом { е,, е2, е3}. Тот факт, что векторы е,, е2, е3 являются единичными и
ортогональными, можно выразить соотношением:
е,.-е. = 8,у,где /, j = 1,2,3. (А-22)
Любой вектор V в пространстве R3 может быть разложен по векторам е,:
V = iv|.e/f (A-23)
»=1
где
v,. = е, • V . (А-24)
* Строго говоря, следует убедиться, что можно переставить ^ и ]d'r. Анализ подобных
вопросов мы систематически будем опускать.
118

Математический аппарат квантовой механики
Формулы (А-18),(А-19) и (А-21) обобщают в некотором смысле хорошо известные
выражения (А-22), (А-23) и (А-24). Однако следует заметить, что v, являются вещественными
числами, тогда как ci — комплексные числа,
(ii) Одна и та же функция \|/(г) имеет, очевидно, различные компоненты в двух различных
базисах. Далее мы изучим задачу изменения базиса,
(iii) В базисе { и, (г)} можно также представить линейный оператор А набором чисел, которые
образуют матрицу. Мы вернемся к этому вопросу в § С после введения обозначений Дирака.
с. ВЫРАЖЕНИЕ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ ЧЕРЕЗ КОМПОНЕНТЫ
Пусть ф(г) и \|/(г) — две волновые функции, которые можно записать в виде
разложений в ряды:
Ф(г) = Щ(г);
V(r) = £c,H,(r). (A-25)
J
Можно вычислить их скалярное произведение, используя формулы (А-6), (А-7) и (А-18):
(ф. V) = 2>Л Ъсм = S^c/w,., Uj) = 5>*сfiy,
то есть
(ф.у) = Х*^|.
В частности:
(v.v) = Zh|
(А-26)
(А-27)
Скалярное произведение двух волновых функций (или также квадрат нормы
волновой функции) выражается, таким образом, очень просто через компоненты этих
функций в базисе { мДг)}.
ЗАМЕЧАНИЕ
Пусть V и W — два вектора в пространстве R , имеющие компоненты v, и w-.
Аналитическое выражение их скалярного произведения хорошо известно:
119

Глава II
V-W = 5>,-wf. . (A-28)
Таким образом, формула (А-26) может рассматриваться как обобщение формулы (А-28).
d. СООТНОШЕНИЕ ЗАМКНУТОСТИ
Равенство (А-18), называемое также соотношением ортонормировки, говорит о том,
что функции множества { мДг)} нормированы на 1 и ортогональны друг к другу. Сейчас
мы установим еще одно соотношение, называемое соотношением замкнутости, из
которого следует, что это множество образует базис.
Если { и, (г)} является базисом в пространстве J , то любая функция ц/(г)б^
может быть разложена согласно формуле (А-19). Подставим в (А-19) выражение (А-21) для
компонент с( [нужно только изменить символ переменной интегрирования, поскольку
переменная г уже имеется в (А-19)]:
V(r) = ЕсЛ(г) = 2(Ч-. V) «/(г) = S[J^Vи;(г')] иДг).
Переставив местами операции £ и JdV, получим:
(А-29)
\|r(r) = JrfV\|f(rl)
5>,0г) "/Ю
(А-30)
где
]►>,.(!•)• и* (г')
- такая функция F(r, г') переменных гиг', что для любой
функции \|/(г) справедливо равенство:
\|/(r) = JdV\|/(r,)F(r,r'). (А-31)
Уравнение (А-31) является характеристическим для функции S(r-r') (см. примечание
II). Отсюда следует, что
Dn,(r)n;(r,) = 6(r-ri)
(А-32)
Справедливо и обратное: если ортонормированный ансамбль функций { и.(г)}
удовлетворяет соотношению замкнутости (А-32), то он образует базис. Действительно,
произвольную функцию \|/(г) можно записать в форме:
120

Математический аппарат квантовой механики
\|/(г) = J tf V \|/(r') 5(r - г'). (A-33)
Подставив выражение (А-32) для 6(г-г'), получим формулу (А-30), после чего
достаточно снова поменять порядок суммирования и интегрирования, чтобы вернуться к
формуле (А-29). Таким образом, это уравнение подтверждает, что функция Vj/(r) всегда
может быть разложена по w,(r), и можно определить коэффициенты этого разложения.
ЗАМЕЧАНИЕ
Мы вернемся к соотношению замкнутости с обозначениями Дирака в § С и увидим,
что ему можно дать простую геометрическую интерпретацию.
3. Введение базисов, не принадлежащих к J
Рассмотренные выше базисы { м,(г) Образованы из квадратично интегрируемых
функций. Иногда удобно ввести «базисы» из функций, не принадлежащих ни
пространству ;/, ни пространству L2, но по которым, тем не менее, можно разложить любую
волновую функцию \|/(г). Ниже мы приведем примеры таких базисов и покажем, как
можно распространить на них важнейшие формулы, установленные в предыдущем
параграфе.
а. ПРИМЕР ПЛОСКИХ ВОЛН
Для простоты рассмотрим одномерный случай квадратично интегрируемых
функций \|/(jc) , зависящих лишь от одной переменной х. В главе I мы видели, что зачастую
представляет интерес ввести преобразование Фурье \\f(p) функции x\f(x):
у(х) = -^1Ур-Щр)е*х"'; (А-34-а)
Л/27Ш
f(p) = -7i—Г dx-\\f(x)e'ipx,h. (A-34-b)
V27i/i
Рассмотрим теперь функцию v (x), определенную выражением:
v(x)=*e'i>x"'
1 J2nh
(А-35)
121

Глава II
Функция vp(x) представляет собой плоскую волну с волновым вектором р I h . Инте-
I I2 1
грал по х от 0 до ©о от функции v (х) = расходится. Таким образом, v (х) £ Jx.
1 ' 2nh
Обозначим символом {vp(x)} множество плоских волн, то есть все функции vp(x),
соответствующие различным значениям р. Величину р, которая может изменяться
непрерывно от -©о до +оо 9 будем рассматривать как непрерывный индекс, позволяющий
отличать между собой различные функции множества { vp(x)} [вспомним, что индекс /,
использованный выше для множества { мДг)}, был дискретным].
Формулы (А-34) можно переписать с учетом (А-35) в виде:
VM = H^-VO>)vpM
v(p)=(vp,v)=E.£fa,vpWvw
(А-36)
(А-37)
Эти две формулы могут быть сопоставлены с формулами (А-19) и (А-21). Равенство
(А-36) выражает, что любая функция \\f(x) e &х может быть разложена единственным
образом по функциям v (jc), то есть по плоским волнам. Индекс р изменяется
непрерывно, а не дискретно, вследствие чего суммирование в (А-19) заменяется интегралом
по р . Равенство (А-37) определяет, как и формула (А-21), компоненту \|/(р) разложения
функции i|/(x) no vp(x) в виде скалярного произведения* fv/;,\|/J; множество этих
компонент, соответствующих всем возможным значениям р, образует функцию от р,
которая является Фурье-образом \\f(p) функции \|/(х).
Итак, \|/(р) является аналогом сг Эти комплексные числа, зависящие или от р,
или от /, представляют собой компоненты одной и той же функции i|/(;c) в двух
различных базисах — { vp(x)} и { ut{x)}.
Это положение еще более подтверждается, если вычислить квадрат нормы функции
\|/(;с). Согласно равенству Парсеваля [приложение I, формула D5)] имеем:
(v,v) = C*'lv(p)l:
(А-38)
* Мы определили скалярное произведение только двух квадратично-интегрируемых функций,
но это определение без труда обобщается на случаи, подобные рассматриваемому, при условии,
что соответствующий интеграл сходится.
122

Математический аппарат квантовой механики
Эта формула напоминает выражение (А-27), если в последнем заменить сх на \|/(р) и
S на JdP-
Покажем, что функции vp(x) удовлетворяют соотношению замкнутости.
Действительно, используя формулу [см. приложение II, равенство C4)]:
_1_
271
£</*•«?*" =8(и),
найдем:
]_ф-у/,(х)у/,(х,) = —J-^^ Л =8(х-х')
(А-39)
(А-40)
Эта формула аналогична формуле (А-32), если в последней произвести замену
X на \dp.
i
Вычислим, наконец, скалярное произведение (v/;, vp.j, чтобы посмотреть,
существует ли эквивалент соотношению ортонормировки. Используя снова выражение (А-39),
получим:
(vp,vp.) = J^-v*U)vp.U)
или
k-^-i-jT'""'-"-^-^
(А-41)
Сравним (А-41) с (А-18). Вместо использования двух дискретных индексов /, j и
символа Кронекера 5ij в ней фигурируют два непрерывных индекса р и /?', а также
дельта-функция разности индексов 5(/? - р'). Заметим, что при р = р' скалярное
произведение (v^, v;j расходится, и, следовательно, действительно vp(x) £ Jx. Несмотря на то,
что приходится злоупотребить терминологией, в дальнейшем будем называть
выражение (А-41) соотношением «ортонормировки». Иногда говорят также, что функции vp(x)
«ортонормированы в смысле Дирака».
Обобщение на трехмерный случай не представляет трудностей. Рассматривается
плоская волна:
'.«-Ш '*"*■
(А-42)
123

Глава II
Базисные функции { vp(r)} зависят теперь от трех непрерывных индексов рх, ру, pz,
объединенных в обозначении р. Легко показать, что формулы:
\|/(r) = JrfVv(P)vp(r);
?(Р) = (V v) = Jd3r v*(r) v(r);
(<p,\|/)=J</V<p*(p)¥(p);
JdVvp(r)v;(r') = 8(r-r,);
(vp.Vp.J^SCp-p1)
(A-43)
(A-44)
(A-45)
(A-46)
(A-47)
являются обобщением выражений (A-36), (A-37), (А-38), (А-40) и (А-41).
Таким образом, можно считать, что функции vp(r) образуют «непрерывный базис».
Все полученные выше для дискретного базиса { мДг)} формулы могут быть
распространены на этот непрерывный базис при условии применения правил соответствия,
указанных в табл. II-1.
Таблица II-1
/ <-> р
5,;<->8(р-р')
Ь. ПРИМЕР «ДЕЛЬТА-ФУНКЦИЙ»
Введем таким же образом множество функций {£Го(г)} переменной г,
перечисленных непрерывным индексом г0 (конденсированное обозначение для jc0, yQ9 z0) и
определенных выражением:
£ro(r) = 5(r-r0). (A-48)
Множество {£Го (г) } описывает набор дельта-функций с центрами в различных точках г0
пространства. Естественно, что функции £Го (г) не являются квадратично
интегрируемыми и £г (г) £ .¥ .
Рассмотрим следующие равенства, справедливые для любой функции \|/(г) е if :
124

Математический аппарат квантовой механики
\|f(r) = Jd3r0\|/(r0)8(r-r0);
\|/(r0) = Jflf3r5(r0-r)V|/(r).
Согласно (А-48) их можно переписать в виде:
\|f(r) = Jrf3r0\|f(r0)^ (г)
V(r0) = (^re,v) = Jrf3^;e(r)v(r)
(А-49)
(А-50)
(А-51)
(А-52)
Равенство (А-51) выражает, что любая функция Щг)е& может быть разложена
единственным образом по £г (г). Равенство (А-52) указывает, что проекция функции \|/(г)
на функцию £г (г) (здесь мы имеем дело с вещественными базисными функциями) в
точности равна значению \|/(г0) функции \|/(г) в точке г0. Выражения (А-51) и (А-52)
аналогичны формулам (А-19) и (А-21), где мы просто заменили дискретный индекс / на
непрерывный индекс г0 и X на jd3r0.
Итак, \|/(г0) и с{ эквивалентны: это комплексные числа, зависящие либо от г0,
либо от i и представляющие координаты одной и той же функции \|/(г)в двух различных
базисах {£Го(г) }и { м,(г)}.
Формула (А-26) принимает тогда вид:
(ф, \|/) = /^3г0ф*(г0)\|/(г0)
(А-53)
Определение (А-4) скалярного произведения оказывается тогда простым
применением формулы (А-26) в непрерывном базисе {£г (г) }.
Отметим, наконец, что функции £Гц (г) удовлетворяют соотношениям «ортонорми-
ровки» и замкнутости того же типа, что и vp(r); действительно, имеем [формула B8)
приложения II]:
ГТ_ = ~ ' (А-54)
(А-55)
{AMr^>'HA5(r-r0)8(r'-r0) = S(r-r')
(^ ,£,.) = иъг б(г - г0) б(г - г0') = 5(г0 - г0')
125

Глава II
Все формулы, установленные для дискретного базиса { иДг)}, могут быть, таким
образом, обобщены и на непрерывный базис {t>T (r) } при условии соблюдения правил
соответствия, обобщенных в табл. И-2.
Таблица II-2
/ог„
IWA
8« <-» 5(го -
Го)
ВАЖНОЕ ЗАМЕЧАНИЕ
Полезность только что введенных непрерывных базисов станет ясна в
последующих главах. Однако, не следует упускать из виду следующее: физическому
состоянию должна всегда соответствовать квадратично-интегрируемая волновая
функция. Ни в коем случае функции vp(r) или ^Го(г) не могут представлять
состояние частицы. Они являются лишь очень удобным промежуточным средством
вычислений при выполнении операций с волновыми функциями \|/(г),
способными служить для описания физического состояния.
Аналогичная ситуация встречается в классической оптике, где плоская
монохроматическая волна является очень удобной математической абстракцией, никогда
не реализуемой физически: даже самые лучшие фильтры всегда имеют конечную
полосу пропускания Av, малую, но никогда не равную нулю.
То же самое можно сказать и относительно функций £г (г). Можно
представить себе квадратично-интегрируемую волновую функцию, строго
локализованную вблизи г(), например, Ql\r) = Ve)(r-r0) = bU)(x-x0)8(e)(y-y0)SU)(z~z0),
где 8(е)— функции, имеющие максимум с шириной е и высотой 1/ е с центром в
точках jc0, 3>0, z0, для которых £~8(E)(*-.*o)d* = 1 (в § 1-Ь приложения II
приведены примеры таких функций). Когда е->0, функция £(ге)(г)—> £Го(г), которая
уже не является квадратично-интегрируемой. Но в действительности реализовать
физическое состояние, соответствующее такому пределу, невозможно: как бы ни
была локализована частица в некотором физическом состоянии, величина е
никогда не равна в точности нулю.

Математический аппарат квантовой механики
с. ОБОБЩЕНИЕ: НЕПРЕРЫВНЫЕ «ОРТОНОРМИРОВАННЫЕ» БАЗИСЫ
а. Определение
Обобщая результаты, полученные в двух предыдущих параграфах, будем называть
непрерывным «ортонормированным» базисом ансамбль функций { wa(r) } переменной г,
выделенных непрерывным индексом а и удовлетворяющих следующим соотношениям
ортонормировки и замкнутости:
(wa, wa,) = ^3r^(r)wa,(r) = 5(a-a')
(А-56)
Idaw^wliY^^bir-Y4)
(А-57)
ЗАМЕЧАНИЯ
(i) Если a = a', то скалярное произведение (wa, wa ) расходится, и, следовательно,
wa(r)<2^.
(ii) Под а можно подразумевать несколько индексов, как это было для г() и р в приведенных
выше примерах,
(iii) Можно представить себе базисы, содержащие одновременно функции иДг),
перечисляемые дискретным индексом, и функции wa(r), перечисляемые непрерывным индексом.
В этом случае ансамбль и,(г) не образует базиса сам по себе, и к нему следует добавить
ансамбль wa(r).
Приведем пример такой ситуации. Ниже мы увидим, что множество стационарных
состояний частицы в поле потенциала, не зависящего от времени, образует базис. Вспомним
случай прямоугольной потенциальной ямы, рассмотренный в § D-2-c главы I (см. также
дополнение Hi). В области Е < О существуют дискретные уровни энергии, которым
соответствуют квадратично-интегрируемые волновые функции, пронумерованные дискретным
индексом. Но это еще не все возможные стационарные состояния. Уравнение (D-17) главы I
допускает также для любого значения Е > О ограниченные, но простирающиеся во всем
пространстве решения, квадрат которых расходится.
В случае «смешанного» базиса (дискретного и непрерывного) { м,(г), wa(r) }
соотношения ортонормировки запишутся в форме:
(и/.«у) = 5в
127

Глава II
(wa, wal) = 5(a-a');
(и,., wa) = 0.
Что касается соотношения замкнутости, то оно приобретает вид:
Xw/(r)w*(r,) + J^awu(r)w*(r,) = 8(r-r,).
(А-58)
(А-59)
Р. Компоненты волновой функции V|/(r)
Всегда можно записать:
\|/(г) = \ d\' \|/(г') 5(г - г').
(А-60)
Подставив выражение (А-57) для б(г-г') и допустив, что можно переставить
местами JdV и jcta , получим:
\|/(r) = J da [JdV w*(r') \|/(r')] wa(r)
или
где
\|/(r) = Jdac(a)wa(r)
c(a) = (wa, \|/) = JdV и/(г') \|/(r")
(A-61)
(A-62)
Выражение (A-61) показывает, что любую волновую функцию \i/(r) можно разложить
единственным образом по функциям wa(r), причем проекция с(ос) функции \|/(г) на
wa(r) равна согласно (А-62) скалярному произведению (wa, i|/).
у. Выражение скалярного произведения и нормы через компоненты
Пусть ф(г) и \|/(г) — две квадратично-интегрируемые функции с известными
компонентами в базисе wa(r):
9(r) = ^afc(a)wa(r); (A-63)
\|f(r) = Jrfa'c(a')wa(r).
(А-64)
128

Математический аппарат квантовой механики
Найдем их скалярное произведение:
(ф, у) = JVV ф*(г) i|/(r) =Jda jda1 b*(a) с(сс') Jrf3r vv* (r) wa.(r).
Последний интеграл определяется выражением (А-56):
(ф, \j/) = j da j da' b* (а) с(а') Ь(а- а*),
(А-65)
то есть
В частности:
(ф, \y) = jda-b*(a)c(a)
(\|/, i}/) = j*da-|c(a)|~
(А-66)
(А-67)
Все формулы § А-2 обобщаются с помощью правил соответствия табл. И-3:
Таблица П-3
i <->a
2<*\<t<*
■8jj <->8(a-
a')
Наиболее важные формулы, установленные в этом параграфе, сведены в табл. И-4.
В действительности, нет необходимости запоминать их в этом виде: далее мы увидим,
что введение обозначений Дирака позволяет установить их чрезвычайно просто.
Таблица П~4
Показатель
Соотношение ортонор-
мировки
Соотношение
замкнутости
Разложение волновой
функции \|/(г)
Выражение
для компонент \|/(г)
Скалярное
произведение
Квадрат нормы
Дискретным базис { мДг) }
(".'"i) = 5v
£ ((,(г) M,*(r') = 5(r-r')
1|/(г) = £с,.н,.(г)
i
с,. =(/(,, \|/) = J>Yi/*(r)y(r)
(<p.v) = Ifo
(v.v)=Skl2
Непрерывный базис { Wu(l*) }
(wa, wa.) = 5(a-a')
Jrfa wa(r) w*(r') = 5(r-r')
\|/(r) = /6/ac(a)wa(r)
c(a) = (wa, \|/) = J>Vw* (r) \|/(r)
(ф, \|/) = J^aZ?*(ot)c(a)
(\|/, \v) = jda\c(a)\2
9 Квантовая механика
129

Глава II
В. ПРОСТРАНСТВО СОСТОЯНИЙ. ОБОЗНАЧЕНИЯ ДИРАКА
1. Введение
В главе I был сформулирован следующий постулат: квантовое состояние частицы
в данный момент времени определено волновой функцией \|/(г). Вероятностная
интерпретация волновой функции требует, чтобы она была квадратично-интегрируемой, что
приводит к необходимости введения пространства & (§ А). В частности, тогда было
найдено, что одна и та же функция \|/(г) может быть представлена в зависимости от
избранного базиса различными ансамблями компонент (табл. П-5). Этот результат можно
интерпретировать следующим образом: задание величин {с,}, ij/(p) или с(сс) (если
предварительно установлен используемый базис) характеризует состояние частицы так же
точно, как и волновая функция \|/(г). Впрочем, и сама волновая функция i|/(r) в табл. И-5
фигурирует наравне с компонентами { с,}, \|/(р) и с(сс): значение \|/(г0), которое
принимает волновая функция в точке г0 пространства, может рассматриваться как ее
компонента на определенную функцию £Го(г) некоторого частного базиса.
Таблица 11-5
Базис
и, (г)
vp(r)
5,. (г)
wa(r)
Компоненты ty(r)
с,, где
J = 1,2, ...,/!,...
V(P)
V(r0)
c(a)
Таким образом, мы встречаемся с ситуацией, аналогичной той, которая хорошо
известна в обычном пространстве R3: положение точки в пространстве может быть
определено набором из трех чисел, являющихся координатами в заранее выбранной системе
отсчета; при изменении системы отсчета той же точке будет соответствовать другой
набор координат. Но введение понятия геометрического вектора и векторный анализ
позволяют устранить эту зависимость от системы осей и значительно упростить все
формулы и рассуждения.
Ниже мы проделаем совершенно аналогичную процедуру: каждое квантовое
состояние частицы будем характеризовать вектором состояния, принадлежащим абстрактному
пространству <fr, названному пространством состояний частицы. То, что пространство
J является подпространством L2, требует, чтобы пространство #г было подпростран-
130

Математический аппарат квантовой механики
ством гильбертова пространства. Далее мы определим обозначения и правила векторных
вычислений в пространстве #г.
На самом деле введение векторов состояний и пространства состояний приводит не
только к упрощению формализма. Оно позволяет также и обобщить его. Действительно,
существуют физические системы, квантовое описание которых не может быть
произведено лишь на основе понятия волновой функции: в главах IV и IX мы увидим, что так
бывает даже при рассмотрении единственной частицы, если учитывать спиновые
степени свободы. Поэтому первый постулат, который мы введем в главе III, будет
сформулирован так: квантовое состояние произвольной физической системы характеризуется
вектором состояния, принадлежащим пространству #, которое является
пространством состояний системы.
Таким образом, в оставшейся части этой главы будем развивать векторный анализ в
пространстве £. Вводимые здесь понятия и полученные результаты остаются
справедливыми для любой физической системы. Однако для их иллюстрации ограничимся
простым случаем частицы без спина, поскольку до сих пор мы им и занимались.
Этот параграф начнем с определения обозначений Дирака, очень удобных для
выполнения необходимых формальных операций.
2. Векторы «кет» и векторы «бра»
а. ЭЛЕМЕНТЫ В ПРОСТРАНСТВЕ <f КЕТ-ВЕКТОРЫ
а. Определение
Любой элемент (или вектор) пространства £ называется кет-вектором или просто
кет. Его обозначают символом | ) с указанием в скобках отличительного признака,
позволяющего выделить данный кет из всех возможных, например: |\|/).
В частности, поскольку нам уже привычно понятие волновой функции, определим
пространство £г состояний частицы, ассоциируя со всякой квадратично-интегрируемой
функцией \|/(г) кет-вектор |\|/) пространства £г:
\|/(г) е #•<=>! \|/)e£r. (B-1)
Далее перенесем в пространство tr операции, введенные для пространства & . Хотя &
и £г являются изоморфными пространствами, мы будем их тщательно различать, чтобы
избежать путаницы и сохранить возможность дальнейшего обобщения, упомянутого
выше в § В-1. Особенно подчеркнем, что в |\|/) уже нет зависимости от г, а есть лишь
буква \|/, напоминающая, с какой функцией связан вектор: \|/(г) будет интерпретиро-
9*
131

Глава II
ваться (§ Е) как множество компонент вектора |i|/) в некотором базисе, где г играет
роль индекса (см. § A-3-b и табл. И-5). Вследствие этого принятое здесь определение
позволяет сразу же характеризовать вектор его компонентами в избранной системе
отсчета, которая впоследствии будет считаться равноправной с другими системами отсчета.
Будем обозначать символом $х одномерное пространство состояний частицы без
спина, то есть абстрактное пространство, построенное так же, как и в (В-1), но на базе
волновых функций, зависящих от одной переменной х.
C. Скалярное произведение
Каждой паре двух кет-векторов |ф) и |\|/), взятых именно в таком порядке,
сопоставляется комплексное число, являющееся их скалярным произведением (|ф),|ч/)),
удовлетворяющим всем свойствам, описанным уравнениями (А-5), (А-6) и (А-7); далее
после введения понятия бра-вектора перепишем эти формулы в обозначениях Дирака.
В пространстве ^г скалярное произведение двух кет-векторов совпадает с уже
полученным ранее выражением для связанных с ними волновых функций.
Ь. ЭЛЕМЕНТЫ В ДУАЛЬНОМ ПРОСТРАНСТВЕ F : БРА-ВЕКТОРЫ
а. Определение дуального пространства $*
Вспомним сначала, что называется линейным функционалом, определенным в
системе кет-векторов пространства £. Линейный функционал % есть линейная операция,
ставящая в соответствие любому кет-вектору |\|/) комплексное число:
|v)e*—*-»х(к»;
x(X1|vi/1) + X2|ii/2)) = X1x(|\l/1)) + X2x(|i|/2)). (B-2)
Не следует смешивать линейный функционал с линейным оператором. В обоих случаях речь
идет о линейных операциях, но любому кет первая из них ассоциирует комплексное число, тогда
как вторая ассоциирует другой кет-вектор.
Можно показать, что множество линейных функционалов, определенных на кет-
векторах |i|/) e $ , образует векторное пространство, которое называют пространством,
дуальным пространству <•, и обозначают символом <f .
132

Математический аппарат квантовой механики
C. Обозначение «бра» для векторов пространства Р*
Любой элемент (или вектор) пространства #* называется бра-вектором или просто бра
и обозначается символом ( |. Например, бра (х| обозначает линейный функционал % ,
и теперь символом (%|у) будем обозначать число, полученное путем действия линейного
функционала (%| е #'* на кет |\|/) е $ :
x(|v» = (x|v>
(В-3)
На английском языке символ ( ) называется «bracket» (скобка), откуда и следует название
«бра» для левой половины символа ( и «кет» — для правой его половины ).
с. СООТВЕТСТВИЕ МЕЖДУ КЕТ- И БРА-ВЕКТОРАМИ
а. Каждому кет-вектору соответствует бра-вектор
Существование скалярного произведения в пространстве # позволит сейчас
показать, что любому кет |ф) е $ можно поставить в соответствие элемент пространства $*,
то есть бра-вектор, который будем обозначать символом (ф|.
Действительно, кет |ф) позволяет определить линейный функционал, а именно
такой, который ставит в соответствие линейным образом любому кет \\\f) e <? комплексное
число, равное скалярному произведению (|ф), |\|/)V Пусть (ф| — этот линейный
функционал, это означает, что он определяется соотношением:
(фк)=(|ф).к»
(В-4)
C. Это соответствие антилинеино
В пространстве ^ скалярное произведение антилинеино по отношению к первому
вектору. В обозначениях (В-4) это записывается следующим образом:
(Х^ф1> + Х2|ф2>,|\|/)) = Л,;(|ф1),|ч/>) + Л,;(|ф2>,|\1/)) =
= Х*1(ф1|\1/) + Х*2(ф2|\1/) = (Г1(ф1| + Г2(ф2|)|\|/). (В-5)
133

Глава II
Из (В-5) следует, что с кет-вектором А^^ф,) + Л2|ф2) ассоциируется бра-вектор
*"i (<Pi 1 + ^*2(ф2| •
Цц) + ^2\у2)^7Сх(($х\ + \\(ц2\. (В-6)
Таким образом, соответствие «кет» => «бра» является антилинейным.
ЗАМЕЧАНИЕ
Если X — комплексное число и |\|/) — кет-вектор, то Х\\у) — также кет-
вектор ($ — векторное пространство). Его часто записывают в виде |Л\|/):
|Ху) = А,|\|/).
(В-7)
При этом следует помнить, что (Ал|/| представляет бра-вектор,
соответствующий кет-вектору |Х\|/). Поскольку соответствие между кет и бра антилинейно,
имеем:
(Ал|г| = АГ(у|.
(В-8)
у. Обозначения Дирака для скалярного произведения
Теперь мы располагаем двумя различными обозначениями скалярного произведения
|\|/) на |ф): (|ф), |\|/)]или (ф|\|/), где (ф| — бра-вектор, соответствующий кет-вектору |ф).
С этого момента мы всегда будем использовать только обозначение (ф|\|/), называемое
дираковским. Ниже сведены в обозначениях Дирака все свойства скалярного
произведения, уже сформулированные ранее в § A-1-b.
(ф|\|/) = (\|/|ф)*
(ф|Х1ч/|+Х2\|/2) = Х1(ф|\|/1) + Х2(ф|\|/2)
(Хм + Х2ф21\|/> = ^(ф, |\|/> + Х2(ф2| v>
(\|/1\|/) > 0 — вещественное число, равное нулю только если | V|/) = О
(В-9)
(В-10)
(В-П)
(В-12)
134

Математический аппарат квантовой механики
8. Всякому ли бра соответствует кет ?
Если любому кет соответствует бра, то, как мы сейчас увидим на двух примерах в
пространстве & , можно найти такие бра, которым нельзя указать соответствующие кет. Затем покажем,
почему это затруднение не очень существенно в рамках квантовой механики.
(i) Примеры в пространстве &
Для простоты рассмотрим одномерный случай. Пусть Ь>1 (х)— достаточно регулярная
вещественная функция, для которой J dx ^£)(-*) = 1, имеющая форму пика с шириной £ и
высотой 1 / £ с центром в точке х = х0 [см. рис.1; например, £(v£)(*) является одной из функций,
рассмотренных в § 1-Ь приложения II]. Если £ Ф О, то Q* (x) G 3>х (квадрат ее нормы порядка 1 / £ );
обозначим
£')
соответствующий кет-вектор:
Если £ Ф О, то
имеем:
^'«Нс)- (в-,з)
£*£)) е $х • Пусть (^д£) — бра, соответствующий этому кет; для любого | \|/) G ^
:(«)
Рис.1
Функция Q*\x) описывает максимум в
точке х = х0 с шириной £ и высотой 1 / £ ,
интеграл от которой от -<*> до +оо равен 1
(&V|v)=(ttV.v)=jr*-Cwvw-
(В-14)
Устремим теперь 8 —» 0. С одной стороны:
е-»0 ° "
(В-15)
135

Глава II
[квадрат нормы функции £>^(х) имеет величину порядка 1/ 8 и расходится при 8 —> 0];
следовательно:
lim
е->0
е;)^(- (в-16)
С другой стороны, интеграл (В-14) при 8 —> 0 стремится к вполне определенному пределу \J/(jc0)
[так как для достаточно малых 8 в формуле (В-14) можно заменить \\f(x) на \|/(л:0) и вынести ее
из-под интеграла]. Вследствие этого (^е) стремится к бра, который обозначим символом (£v
(это линейный функционал, который ставит в соответствие любому кет |\|/у пространства #г
значение \\f(x0), принимаемое соответствующей волновой функцией в точке х0):
limkf\ = k< I е »;.
е-*0 \ Л" I \ ч \ "
Если | \|/) е $х , то
(%»0|V> = VUo)- (B-17)
Таким образом, видно, что бра (£
существует, но ему не соответствует никакой кет.
Рассмотрим также плоскую волну, обрезанную вне интервала шириной L :
v^(JC) = -T==^o^ сли -L/2<x<+L/2. (B-18)
"° V2nft
Вне этого интервала функция у^М быстро стремится к нулю, оставаясь непрерывной и
дифференцируемой. Обозначим кет, соответствующий функции ^\х) символом v^M:
v%\x)ev,<*\v£)e«x. (B-19)
Квадрат нормы v^ix), равный практически L12nfi, расходится, если L —> ©о . Таким образом:
Z/m|v<L)\>etf . (В-20)
Рассмотрим теперь бра (v^J , связанный с v{pLJ V Для любой функции | \|/) е (£. имеем:
136

Математический аппарат квантовой механики
(СИ=(С Ф^СА"*"^- (В-21)
Когда L —> о© , эта величина стремится к пределу, равному значению \|/(р0) Фурье-образа \|/(р)
функции \|/(*) при р = р0 . Таким образом, если L—» ©о , бра (i/^ стремится к вполне
определенному вектору (v :
Ziw(v(.L)| = (v- |е<.
Если |\|/)е^Л. ,то
(VA,k) = V(Po)- (B-22)
И снова видим, что ни odww кет «в соответствует бра (v .
(ii) Физическое разрешение указанных выше трудностей
Такая асимметрия соответствия между кет и бра связана, как показывают приведенные выше
примеры, с существованием «непрерывных базисов» в пространстве (JX: функции, образующие
эти «базисы», не принадлежат к (JX , и, следовательно, им нельзя сопоставить кет пространства <£х ;
однако их скалярное произведение с произвольной функцией пространства 91х определено, что
позволяет сопоставить им линейный функционал пространства fx, то есть бра, принадлежащий
пространству £Л. .
Причина использования таких «непрерывных базисов» состоит в их удобстве в некоторых
практических расчетах. Та же причина (в дальнейшем мы поясним это более четко) побуждает
восстановить симметрию между кет- и бра-векторами путем введения «обобщенных» кет-
векторов, определенных на основе функций, которые не являются квадратично-интегрируемыми,
но скалярное произведение которых с любой функцией пространства &х существует: таким
образом, в дальнейшем будем иметь дело с такими «кет», как £ ) или v ), которым
соответствуют функции £v (х) или v (х). Не нужно забывать, что эти обобщенные «кет» не могут, строго
говоря, представлять физические состояния и являются всего лишь удобным промежуточным
этапом некоторых операций, которые выполняются с истинными кет-векторами пространства %х ,
характеризующими действительно реализуемые квантовые состояния.
Такой способ расчета создает некоторые математические проблемы, которые могут быть
разрешены, если принять следующую физически обоснованную точку зрения: КЛ()) (или v )) на
137

Глава II
деле обозначают векторы
^Е)) (или vpL))), где £ — очень малое расстояние (или L
большое расстояние) по сравнению с другими параметрами с размерностью длины, входящими в
&е)\ (или |v("\),
^Л<) / V | ft/''
рассматриваемую задачу. Во всех промежуточных вычислениях, куда входят
никогда не следует переходить к пределу 6 = 0 (или L —» «>), чтобы все время оставаться в
пространстве Wx . Полученный в конце вычислений результат будет очень слабо зависеть от значения
£ , если только оно существенно меньше других параметров с размерностью длины: тогда можно
будет пренебречь величиной £ , то есть положить £ = 0 в конечном результате (аналогичная
процедура справедлива и для L).
Можно было бы возразить, что в противоположность [^Х{)(х)} и [vp(x)} множества
{ £>хе)(х) } и { vpL){x) } не являются в действительности базисами в пространстве 97х в той мере,
что они со всей строгостью не удовлетворяют соотношению замкнутости. Они подчиняются ему
лишь приближенно. Действительно, видно, например, что выражение J dx0 £,{xe)(x) £(хЕ)(л:')
является функцией разности (* — *') и может служить отличным приближением для 8(лг - х*):
графически она имеет практически треугольную форму с основанием 2£ , высотой 1 / £ и центром в
точке (х — х1) = 0 (приложение II, § 1-c-iv); если величина £ значительно меньше всех величин,
имеющих размерность длины в задаче, то ее отличие от Ь(х -х*) будет ничтожным с физической
точки зрения.
В общем случае пространство #*, дуальное пространству состояний £, не
изоморфно ему, за исключением, конечно, того случая, когда пространство £ является
конечномерным*: если любому кет |\|/)пространства & соответствует бра пространства #'*,
то обратное несправедливо. Однако, кроме векторов, принадлежащих £ (норма которых
конечна), будем использовать обобщенные кет с бесконечной нормой, скалярное
произведение которых с любым кет-вектором пространства V является конечным. В этом
случае каждому бра (ф| пространства <f* будет соответствовать кет-вектор. Но
обобщенные кет-векторы не представляют физические состояния системы.
* Известно, что пространство, дуальное гильбертову пространству L , ему изоморфно;
однако мы взяли в качестве пространства волновых функций .9" подпространство L , что и объясняет,
почему & «больше», чем & .
138

Математический аппарат квантовой механики
3. Линейные операторы
а. ОПРЕДЕЛЕНИЯ
Они такие же, что и в § А-1-е. Линейный оператор А ставит в соответствие любому
кет |\|/) G # другой кет |\|/') е #, причем это соответствие линейно:
|V) = %); (B-23)
A(X]\\vl) + X2\\v2)) = XlA\\v]) + X2A\\v2). (В-24)
Произведение двух линейных операторов А и В, обозначаемое ЛЯ, определяется
следующим образом:
(АД)|\|/)=А(%)). (В-25)
Сначала оператор Я действует на |\|/) и образует кет 2?|\|/), а затем Л действует на кет
#|\|/). В общем случае АВфВА . Коммутатором [А, #] операторов Л и В по
определению является оператор:
[Л, В]=АВ-ВА. (В-26)
Пусть имеются два кет-вектора |ф) и |ц/). Матричным элементом оператора А
между |ф) и |\|/) называют скалярное произведение:
(ф1Иу)). (в-27)
Это число, линейно зависящее от |\|/) и антилинейно — от |ф).
Ь. ПРИМЕРЫ ЛИНЕЙНЫХ ОПЕРАТОРОВ:
ПРОЕКЦИОННЫЕ ОПЕРАТОРЫ
а. Важное замечание относительно обозначений Дирака
Читатель уже, наверное, обратил внимание на простоту и удобство обозначений
Дирака. Действительно, символом (ф| обозначают линейный функционал (бра) и символом
(vj1!^) — скалярное произведение двух кет |\|/,) и |\|/2). Число, которое линейный
139

Глава II
функционал (ф| сопоставляет произвольному кет-вектору |\|/), записывается просто
путем объединения символов (ф| и |\|/) в символ (ф|\|/): это скалярное произведение
|\|/) на кет |ф), соответствующий бра (ф| (именно этим объясняется стремление иметь
взаимно однозначное соответствие между кет- и бра-векторами).
Допустим теперь, что мы записали (ф| и |\|/) в обратном порядке:
И(ф|. (В-28)
Если придерживаться правила объединения символов, это выражение представляет
собой оператор. Действительно, возьмем произвольный кет \х) и рассмотрим:
И(ф|%). (В-29)
Мы знаем уже, что (ф|%) — комплексное число, то есть выражение (В-29) является кет-
вектором, полученным путем умножения |\|/) на скаляр (ф|%). Но \\\i) (ф|, приложенное
к произвольному кет, дает другой кет, следовательно, это оператор.
Видно, что порядок, в котором следуют символы, имеет первостепенное значение.
Без последствий можно менять местами только комплексные числа вследствие линейности
пространства # и используемых нами операторов. Действительно, если X — число, то
|V>X = X|V>;
(v|X = X(v|;
ЛХ|\|/) = АА|\|/), где А — линейный оператор;
(ф|Х|\|Г> = А.(ф|у> = (ф|\|/)Х. (В-30)
Но для кет, бра и операторов следует всегда соблюдать их порядок следования в
формулах — это цена простоты в формализме Дирака.
Р. Проекционный оператор Р^ пакет |\|/)
Пусть |\j/) — кет, нормированный на единицу:
(V|V> = 1. (B-31)
140

Математический аппарат квантовой механики
Рассмотрим оператор Р¥ , определенный равенством:
/;=k>(v|. (в-32)
и применим его к произвольному кет-вектору |ф):
/;|фНу)(у|ф). (в-зз)
Оператор Р¥ , действуя на произвольный кет |ф), дает кет, пропорциональный |\|/), причем
коэффициент пропорциональности (ж|ф) является скалярным произведением |ф) на |\j/).
Таким образом, понятен «геометрический» смысл оператора Р : это оператор
«ортогональной проекции» на кет |\|/).
Такая интерпретация подтверждается еще и тем, что Р* = Pv (двукратная проекция
на заданный вектор дает тот же результат, что и однократная). Действительно:
pv2 = p¥/;=|vi/>(v|v>(v|. (в-34)
В этом выражении (\|/|\|/) — число, равное 1 (В-31), и, следовательно:
/>¥2 = |v)(v| = />¥. (в-35)
у. Оператор проекции на подпространство
Пусть |ф,),|ф2),.», |<lO — Ч нормированных и ортогональных друг к другу векторов:
(ф,|ф,) = 5*; /,; = 1,2, ...,<?. (В-36)
Обозначим символом ^ подпространство пространства W, «натянутое» на эти векторы.
Пусть Рц — линейный оператор, определенный равенством:
^=ik)(<p,|- (в-37)
'=1
Найдем Р^\
^2=1Е|ф,)(ф,|ф;>(ф;| (В-38)
/=1 у=1
141

Глава И
откуда получим, используя (В-36):
р:=i ±|ф,>(фу ь=±|ф,Хф> I=рч ■ (в-з9>
1=1 у=1 /=1
Таким образом, /^ является проекционным оператором. Нетрудно видеть, что Р
осуществляет операцию проекции на подпространство fq. Действительно, каким бы ни
был кет | \|/) е $ :
Ф)=ъШФ)- <в-4°)
Оператор Pq, действуя на |\|/), дает линейную суперпозицию проекций вектора |\|/) на
различные |ф;), то есть проекцию |\|/) на подпространство $q.
4. Эрмитово сопряжение
а. ДЕЙСТВИЕ ЛИНЕЙНОГО ОПЕРАТОРА НА БРА-ВЕКТОР
До сих пор мы определяли действие линейного оператора А только на кет-векторы.
Сейчас мы увидим, что можно также определить действие А на бра-векторы.
Пусть (ф|— определенный бра-вектор, и рассмотрим все возможные кет-векторы
|\|/). Каждому из этих кет можно поставить в соответствие комплексное число (ф|(Л|\|/)],
уже определенное выше как матричный элемент оператора А между |ф) и |\|/).
Поскольку А — линейный оператор и скалярное произведение линейно зависит от кет,
число (ф|(л|\|/)) также линейно зависит от |\|/).
Мы можем, таким же образом зафиксировав (ф| и А, поставить в соответствие
любому кет |\|/) число, линейно зависящее от |\j/). Задание (ф| и А определит новый
линейный функционал на кет-векторах пространства #, то есть новый бра-вектор,
принадлежащий пространству £*. Обозначим этот новый бра символом (ф|А . Итак,
определяющее его соотношение запишется в виде:
«ф|А)к)»(ф|Ицг»
(В-41)
Оператор А , действуя на любой бра (<р|, дает новый бра (ф| А . Покажем, что это
142

Математический аппарат квантовой механики
соответствие линейно. Для этого рассмотрим линейную комбинацию двух бра (ф, I
и (ф2|:
(х| = Мф,|+^(ф2| (в-42)
(это означает, что \%\\у) = X,^Ф11\|/) -4- А,2^ф21\|/^). Согласно (В-41) имеем:
«хМк>=(х1ИУ»«Х1(ф1|(А|¥» + Х2(ф2|(л|Чг» =
= X,«ф, |Л)| v> + Л.2«ф2 |Л)| V). (В-43)
Поскольку кет |\|/} произвольный, отсюда следует, что
(хИ = (Х1(ф1| + Х2(ф2|)л = Х1(ф1|Л + Х2(ф2|Л. (В-44)
Итак, уравнение (В-41) определяет линейный оператор, действующий на бра-
векторы. Бра (ф|Л является результатом действия линейного оператора А на бра (ф|.
ЗАМЕЧАНИЯ
(i) Из определения (ф|Л в (В-41) следует, что место круглых скобок в символе,
определяющем матричный элемент оператора А между |ф) и |\|/), не имеет значения.
Поэтому теперь мы можем обозначать этот матричный элемент следующим
образом:
(Ф|А|\|/> = ((ф|А)И = (ф|(%>). (В-45)
(ii) Относительный порядок (ф| и А очень важен в обозначении (ф|А (см. § 3-Ь-а).
Нужно писать (ф|А , а не А (ф|. Действительно, (ф|А , действуя на кет |\|/), дает
число ц)|а|\|/) , то есть (ф|Л является бра-вектором. Напротив, Л(ф|, действуя на
кет |\|/), дал бы А(ф|\|/), то есть оператор (оператор А умножается на число (ф| у)).
Но мы не определяли подобным образом никакой математический объект, и,
следовательно, символ А(ф| не имеет смысла.
143

Глава И
b. ОПЕРАТОР Л+ , ЭРМИТОВО СОПРЯЖЕННЫЙ ЛИНЕЙНОМУ ОПЕРАТОРУ А
Сейчас мы покажем, что соответствие между кет- и бра-векторами, изученное в
§ В-2-с, позволяет сопоставить любому линейному оператору Л другой линейный
оператор Л+ , называемый эрмитово сопряженным оператору А .
Пусть, действительно, |\|/) —произвольный кет пространства ^.Оператор А
ставит ему в соответствие другой кет |\|/') = А|\|/) из пространства $ (рис.2).
Кет-вектору |\|/) соответствует бра (\|/|; аналогично кет-вектору |\|/') соответствует
бра (\|/'|. Это соответствие между кет- и бра-векторами позволяет теперь определить
действие оператора А+ на бра. Бра-вектору (\|/|, соответствующему кет-вектору |\|/),
оператор Л+ сопоставляет бра (\|/'|, соответствующий кет-вектору |\|/') = A\\\f); принято
обозначать (у'| = (\|/| Л+.
\ф) Л v \Р>=А\ф>
Рис.2
Определение оператора А+,
эрмитово сопряженного оператору А , на
основе соответствия между кет- и
< ф | ^t —^ < Ф' | = < Ф \л* бра-векторами
Покажем, что соотношение (ц/'| =(\|/|Д+ является линейным. Действительно, бра-
вектору ^ i (ty 11 + ^ 2 (V 21 соответствует кет Х\|\у{} + Х\|\|/2} (соответствие между бра и кет
антилинейно). Оператор А преобразует вектор А.*|\|/,) + ^Уг) в ^l^Vi) + А.*2 А|\[/2) =
= Л,*J\j/1'^ -нХ*2JЧ1^2'^ - Этому кет соответствует бра ^1(v|/1'| + X2(\|/2,| = Я,(\|/1|Л+ + А.2(\|/2|Д+.
Отсюда можно заключить:
(A.,(v, | + *2(v2IK = A.,(v, |A+ + Х2(\|/2 |Л+. (В-46)
Таким образом, Л+ является линейным оператором, определяемым формулой:
(В-47)
Х|/') = Л|Ч/)^(^| = (Ч/|А+
Из формулы (В-47) нетрудно вывести еще одно важное соотношение, которому
удовлетворяет оператор Л+ . Действительно, согласно свойствам скалярного
произведения всегда можно записать:
144

Математический аппарат квантовой механики
МфНфИ*, (В-48)
где |ф)— произвольный кет пространства $. Используя выражения (В-47) для |\|/') и
(\|/'|, получим:
A|/|Л+|ф) = (ф|л|\|/)*
(В-49)
Это соотношение справедливо для любых |ф) и |ц/).
ЗАМЕЧАНИЕ ПО ОБОЗНАЧЕНИЯМ
Выше мы уже отмечали, что обозначения |А\|/) и (Х\|/|, где X — скалярная
величина [формулы (В-7) и (В-8)], могут привести к недоразумению. Та же
проблема возникает и в связи с обозначениями | А\|/) и (A\\f |, где А — линейный
оператор. |Л\|/) всего лишь иное обозначение кет-вектора Л|\|/):
|А\|/) = А|х|/), (B-50)
тогда как (А\|/| — бра-вектор, связанный с кет-вектором |А\|/). Используя
выражения (В-50) и (В-47), получим:
(А\|/| = (\|/|А\ (В-51)
При выносе линейного оператора А из-под символа бра-вектора его следует
заменять на эрмитово сопряженный оператор А+ и выносить его вправо от вектора.
с. СВОЙСТВА СООТВЕТСТВИЯ МЕЖДУ ОПЕРАТОРОМ
И ЕГО ЭРМИТОВО СОПРЯЖЕННЫМ
Используя (В-47) и (В-49), нетрудно показать, что
(а+)+ =А; (В-52)
(ХАУ =Х*А+ (где X —число); (В-53)
(А + Д)+ = А+ + Я\ (В-54)
10 Квантовая механика
145

Глава II
Вычислим, наконец, оператор (АВ)+ . Для этого рассмотрим кет |ф) = АВ\\у).
Запишем его в виде |ф) = Л|%), где |%) = #|\|/). Тогда :
(ф(у\(АВу=(Х\А+=(ч\В+А\
так как (%| = (\|/|#+. Отсюда следует:
(ДД)+ = В+А+
(В-55)
Нужно подчеркнуть, что при эрмитовом сопряжении произведения операторов их
порядок меняется.
ЗАМЕЧАНИЕ
Поскольку (Л+J = А , то согласно формуле (В-51) можно записать:
(д+ф| = (ф|(л+)+=(ф|л.
Таким образом, левую часть равенства (В-41) можно переписать в виде
(А+ф ш . Одновременно правую часть этого же равенства с учетом обозначений
(В-50) можно представить в форме (ф|А\|/) • Отсюда следует равенство, часто
применяемое для определения оператора Л+, эрмитово сопряженного оператору А :
(л+ф|\1/) = (ф|Л1|/). (В-56)
d. ЭРМИТОВО СОПРЯЖЕНИЕ В ОБОЗНАЧЕНИЯХ ДИРАКА
В предыдущем параграфе мы ввели понятие эрмитово сопряженного оператора,
используя соответствие между кет- и бра-векторами. Относительно векторов кет |\[/) и бра
(\|/| говорят, что они «эрмитово сопряжены» друг другу. Операция эрмитова
сопряжения представлена волнистыми стрелками на рис.2; видно, что она связывает Л+ и А.
По этой причине оператор А+ также называется эрмитово сопряженным оператору А .
Операция эрмитова сопряжения изменяет порядок объектов, к которым она приме-
146

Математический аппарат квантовой механики
няется. Так, на рис.2 мы видим, что Л|\|/) превращается в (\|/|Л+: кет |\|/) меняется на
бра (\|/|, оператор А на А+ , и, кроме того, порядок символов изменяется на обратный.
В формуле (В-55) мы также видели, что эрмитово сопряжение произведения двух
операторов равно произведению эрмитово сопряженных операторов, взятых в обратном
порядке. Покажем, наконец, что
(ИНГ = ИИ (в-57)
(кет \и) меняется на бра (и|, бра (v| на кет |v), и их порядок меняется на обратный).
Действительно, применим соотношение (В-49) к оператору \и) (v| и получим:
<vlO«XvO>) = M«Xv|)k>r (B-58)
Или, если использовать свойство (В-9) скалярного произведения:
[(Ф)Ш1=ШШ'=ШФНЧМ-Ы- (в-59)
Сравнив (В-58) с (В-59), сразу же получаем (В-57).
Остается найти, каков результат действия операции эрмитова сопряжения на
константу. Из (В-6) и (В-53) видно, что эта операция просто преобразует А, в X*
(комплексное сопряжение). Этот вывод вполне согласуется с равенством (ф| \}/) = (v|<p) •
Итак, эрмитово сопряженным кет-вектору является бра-вектор, и наоборот,
оператору соответствует его эрмитово сопряженный, числу соответствует его комплексно
сопряженное. В обозначениях Дирака операция эрмитова сопряжения осуществляется
очень легко, достаточно применить следующее правило:
ПРАВИЛО
Чтобы выполнить операцию комплексного сопряжения некоторого выражения,
содержащего константы, кет- и бра-векторы и операторы, нужно:
— заменить константы их комплексно сопряженными;
кет-векторы — соответствующими бра-векторами;
бра-векторы — соответствующими кет-векторами;
операторы — их эрмитово сопряженными;
— обратить порядок следования сомножителей (место констант не имеет значения).
10*
147

Глава II
ПРИМЕРЫ
Выражение X(m|a|v)|w)(\|/| является оператором (так как X и (w|a|v) — числа).
Получим эрмитово сопряженный ему оператор, применив вышеприведенное правило:
|i|/)(w|(v|A+|w)A,*. Это выражение можно переписать иначе: A,*(v|A+|w)|\|/)(w|, если
изменить позиции чисел А* и (v|A+|w).
Подобным образом выражение X|w)(v|w) является кет-вектором (А, и <v|w) суть
константы). Сопряженный ему бра-вектор равен (w|v)(m|X* или A*/w|v)(w|.
е. ЭРМИТОВЫ ОПЕРАТОРЫ
Оператор А называется эрмитовым, если он совпадает со своим эрмитово
сопряженным:
А = А+. (В-60)
Подставив (В-60) в (В-49), увидим, что эрмитов оператор удовлетворяет
соотношению:
A|/|А|Ф) = (ф|А|ч/)\ (В-61)
справедливому для любых векторов |ф) и |\|/).
Для эрмитова оператора равенство (В-56) принимает вид:
(Аф|\|/) = (ф|А11/). (В-62)
Далее вернемся к эрмитовым операторам более подробно в связи с задачей о
собственных значениях и собственных векторах. Кроме того, в главе III увидим, что
эрмитовы операторы играют в квантовой механике важнейшую роль.
Если применить формулу (В-57) к случаю, когда \и) = |v) = |\у), то можно
констатировать, что проекционный оператор Ру = |\|/)(ц/| является эрмитовым:
p;=|v)(vi/| = pv. (в-63)
ЗАМЕЧАНИЕ
Произведение двух эрмитовых операторов А и В является эрмитовым оператором
лишь тогда, если [А, в] = 0 . Действительно, если А = А+ и В - В+ , то из (В-55) следует,
что (АВ)+ = В+А+ = ВА и ВА = АВ лишь в случае, если [А, В\ = 0 .
148

Математический аппарат квантовой механики
С. ПРЕДСТАВЛЕНИЯ В ПРОСТРАНСТВЕ СОСТОЯНИЙ
1. Введение
а. ОПРЕДЕЛЕНИЕ ПРЕДСТАВЛЕНИЯ
Выбрать представление — значит выбрать ортонормированный базис, дискретный
или непрерывный, в пространстве состояний £ . Тогда в этом базисе векторы и
операторы представляются числами: компонентами векторов и матричными элементами
операторов. Векторный анализ, введенный в § В, превращается в матричный расчет для этих
чисел. Выбор представления в принципе произволен, но в реальности он, естественно,
зависит от изучаемой задачи: в каждом конкретном случае он осуществляется так, чтобы
максимально упростить вычисления.
Ь. ЦЕЛЬ ДАННОГО ПАРАГРАФА
В обозначениях Дирака для произвольных пространств <? будем пользоваться всеми
понятиями, введенными в § А-2 и § А-3 для дискретных и непрерывных базисов в
пространстве lJ.
Сначала запишем в обозначениях Дирака два соотношения, характеризующих базис:
соотношения ортонормировки и замкнутости. Затем покажем, как, исходя из этих двух
соотношений, можно решить все конкретные задачи, связанные с переходом из одного
представления в другое.
2. Соотношения, характеризующие ортонормированный базис
а. СООТНОШЕНИЕ ОРТОНОРМИРОВКИ
Дискретное {|и,)} или непрерывное {|wa)} множество кет-векторов называется
ортонормированным, если все кет-векторы этого множества удовлетворяют
соотношению ортонормировки:
{ui\uj) = *U
или
(wa\wa,) = 6(a-a')
(С-1)
(С-2)
149

Глава II
Видно, что для непрерывного множества скалярное произведение (wa|wa) не
существует: векторы | wa) имеют бесконечную норму и, следовательно, не принадлежат
пространству <f. Можно, однако, разложить векторы пространства # по | wa), и в
последующем представляется целесообразным рассматривать векторы | wa) как обобщенные
кет-векторы (см. обсуждение этих вопросов в §А-3 и в §В-2-с).
Ь. СООТНОШЕНИЕ ЗАМКНУТОСТИ
Дискретное {|и.)} или непрерывное {|wa)} множество образует базис, если любой
кет |\|/), принадлежащий пространству £, может быть разложен единственным образом
по векторам |м.) или |wa):
" (С-3)
У) = Еф,)
|v) = Jdac(a)|we)
(С-4)
Допустим еще, что базис ортонормирован. Умножим скалярно равенство (С-3) на
бра (uj\ и равенство (С-4) — на 6pa(wa|. Используя (С-1) и (С-2), получим выражения
для компонент с. или с(сс'):
(и» = с,; (С-5)
(wa,|\|/) = c(a'). (C-6)
Заменим теперь в (С-3) с;. на (u:\\\f) и в (С-4) с(а) на (wa |\|/):
|v) = Sc,.|«,.) = S(«,.|M/>|«,)=S|",X«,k)=fslM.)(M-lV) (с-7)
\\v) = jdac(a)\wa) = jda(wa\\v)\wa) = lda\wa)(wa\\v) =
= (lda\wa)(wa\)\w) (C-8)
[действительно, в формуле (С-7) число (wjij/) можно переставить после кет-вектора|и(),
а в формуле (С-8) можно поставить число (w |\|/) после кет-вектора | wa) ].
150

Математический аппарат квантовой механики
Мы видим, что появились операторы X|M,)(W,| и п da|wa)(wa|j, которые, действуя
i
на любой кет |\|/) пространства %, дают тот же кет |vj/) . Поскольку кет |\|/) произвольный,
то неизбежно:
Р(М/) =S|w/>(W/| = l
P(»a)=lda\Wa)M=l
(С-9)
(С-10)
где 1 — единичный оператор в пространстве £ . Соотношения (С-9) или (С-10)
называются соотношениями замкнутости. Покажем, что эти же соотношения (С-9) и (С-10)
отражают то, что множества {|и.)} и {|wa) } образуют базисы. Действительно, для
любого |\|/) пространства #' можно записать:
где
Аналогично:
где
/ i
|v>=l|v> = ^Jv> = Jrfa|wa>(we|v) = Jrfac(a)|we)f
c(a) = (wa|v).
(СИ)
(С-12)
(С-13)
(С-14)
Таким образом, всякий кет |\j/) может быть разложен единственным образом по
векторам |м,) или |wa). Каждое из этих двух множеств образует базис (дискретный или
непрерывный). Мы видим также, что соотношение (С-9) или (С-10) позволяет сразу же
без усилий получить выражения (С-12) и (С-14) для компонент с, и с(ос).
ЗАМЕЧАНИЯ
(i) Далее в § Е мы увидим, что в пространстве & соотношения (А-32) и (А-57) легко
выводятся из формул (С-9) и (С-10).
(и) Геометрическая интерпретация соотношения замкнутости.
151

Глава 11
Как следует из обсуждения в § B-3-b, S|wi)(M/1 является проекционным оператором:
он осуществляет проекцию на подпространство #', образованное векторами \щ ), \и2) , ...,
(и,.), ... Если кет-векторы образуют базис, то любой кет пространства $ может быть
разложен по |w,y; тогда подпространство #:| совпадает с самим пространством К . Поэтому
естественно, что Х|и.дм. | равен единичному оператору: проекция кет-вектора простран-
ства <$ на это же пространство # не меняет этот вектор. Аналогичное рассуждение
справедливо и для оператора \d(X | wa )(wa |.
Теперь можно найти эквивалент соотношению замкнутости для трехмерного
пространства с обычной геометрией R . Если ер е2, е3 — три ортонормированных вектора этого
пространства и Рх, Р2, Р3 — проекционные операторы на эти три вектора, то условие, что
{ е,, е2, е3} образуют базис в пространстве R , выражается соотношением:
/> + Р2 + Р3 = 1.
(С-15)
Напротив, ( е,, е2 } образует ортонормированный ансамбль, но не базис в пространстве
R . Это отражается в том, что проекционный оператор Р{ + Р2 (проекция на плоскость,
определяемую векторами е,, е2) не равен 1; например, (f[ + Р2 )е3 = 0.
В табл. И-6 сведены основные формулы, которые следует запомнить, чтобы
выполнять все операции в представлениях {|м,)} или {|wa) }.
Таблица 11-6
Представление { ш{) )
(и \и) = 8.
^,,=х|",Х«,|=1
Представление { Wa ) }
(wa|vv) = 5(a-a')
^)=!rf«ka)K|=l

Математический аппарат квантовой механики
3. Представление векторов кет и бра
а. ПРЕДСТАВЛЕНИЕ ВЕКТОРОВ КЕТ
В базисе {[«,)} кет-вектор |\|/) представлен множеством своих компонент, то есть
множеством чисел с, =(м,|\|/). Все эти числа можно расположить вертикально, чтобы
образовать матрицу-столбец (в общем случае со счетным множеством строк):
f(w.k>
(w2|\|/)
(иМ
(С-16)
В непрерывном базисе {|wa)} кет |\|/) представлен бесконечным непрерывным
множеством чисел c(a) = (wa|\j/), то есть функцией переменной а. Таким образом,
можно выделить вертикальную ось, на которой откладывать возможные значения а.
Каждому из этих значений соответствует число (wa |\|/):
a
т
( ■ \
Ы^)
i ■ 1
(С-17)
Ь. ПРЕДСТАВЛЕНИЕ ВЕКТОРОВ БРА
Пусть (ф| — произвольный бра-вектор. В базисе {|м,)} можно записать:
<Ф[ = <Ф| 1 = <фИ„4) = Х<ф|",)<", | -
(С-18)
153

Глава II
Бра (ф| единственным образом разлагается по бра (и.| ; а компоненты вектора (ф|,
равные (ф|м,), являются числами, комплексно сопряженными компонентам bi = (м,|ф) кет-
вектора |ф), связанного с бра (ф|.
Аналогично в базисе {|wa)}:
(Ф| = (Ф| 1 = (Ф|/>1(/) = \da (ф| wa)(wa |. (С-19)
Компоненты бра (ф|, равные (ф|и>а), являются числами, комплексно сопряженными
компонентам b(a) = (wa |ф) кет-вектора |ф), связанного с (ф|.
Мы условились располагать вертикально компоненты кет-вектора. Прежде, чем
договориться о расположении компонент бра-вектора, покажем, как соотношение
замкнутости позволяет очень просто записать выражение для скалярного произведения двух
кет-векторов через их компоненты. Действительно, всегда можно вставить единичный
оператор 1 между (ф| и |\|/) в выражении скалярного произведения:
(Ф|¥)= (ф|1И= (ф| /?.>>=Е(Ф|и,Хи/к)=2>;*, • (с-20)
Аналогично:
(Ф|\|/)= (ф|1|\|/>= (ф| PWa |v> = Jrfa(9|wa>(wa|v)= jdab\a)c(a). (C-21)
Расположим горизонтально компоненты (ф|«,) бра, чтобы образовать матрицу-строку
с одной строкой и множеством столбцов:
((фК)(фК) (ф|к.) ) (С-22)
С учетом этой договоренности (ф|\|/) с матричной точки зрения является произведением
матрицы-столбца, представляющей кет |\|/), на матрицу-строку, представляющую бра (ф|.
При этом образуется матрица с одной строкой и одним столбцом, то есть число.
В базисе {|wa) } имеется непрерывное и бесконечное множество компонент (ф|и>а),
представляющих бра (ф|. Им соответствует горизонтальная ось различных a. Каждому
из них соответствует своя компонента (ф|и>а) вектора (ф|:
( (Фк) , ) a _ (С_23)
154

Математический аппарат квантовой механики
ЗАМЕЧАНИЕ
В приведенной выше интерпретации матрицы, представляющие кет |\|/) и связанный с
ним бра (ф|, являются эрмитово сопряженными друг к другу (в матричном смысле).
Действительно, для перехода от одной матрицы к другой нужно взять комплексно сопряженное
значение каждого элемента матрицы и поменять строки и столбцы местами.
4. Представление операторов
а. ПРЕДСТАВЛЕНИЕ ОПЕРАТОРА А «КВАДРАТНОЙ» МАТРИЦЕЙ
Если А — линейный оператор, то в базисах {\и{) } и {|wa) } ему можно сопоставить
набор чисел, определяемых выражениями:
лНФк-)
(С-24)
или
A(a,a') = (wa|j4|wa.)
(С-25)
Эти числа зависят от двух индексов и будут располагаться в виде квадратной
матрицы, имеющей счетное или непрерывное множество строк и столбцов; общепринято,
что первый индекс указывает номер строки, а второй — номер столбца. Так, в базисе
{|и,)} оператор А будет представлен матрицей:
(А,, А12
А2, А22
А-1 А-2
л2]
(С-26)
Видно, что 7-тый столбец в базисе {|м.) } образован компонентами А и Л кет-век-
торабазиса иЛ.
В непрерывном базисе имеется две перпендикулярные оси, и точке с абсциссой а' и
ординатой а соответствует число А (а, а'):
155

Глава II
ОС
1
а
(
. . Л (ос, а') .
1
л
)
(С-27)
Используем соотношение замкнутости для вычисления матрицы, представляющей
оператор АВ в базисе {|н.)}:
(И/|АВ|ИЛ=(И/|л1в|н;>=(И/|А^)в|И;) = 2(и/|Л|и1)(и4|в|Иу). (С-28)
Принятая ранее договоренность о расположении элементов А~ [или Л (а, а')] вполне
совместима с условными обозначениями произведения двух матриц: действительно,
формула (С-28) выражает, что матрица, представляющая оператор АВ, является
произведением матриц, представляющих операторы А и В в отдельности.
Ь. МАТРИЧНОЕ ПРЕДСТАВЛЕНИЕ КЕТ-ВЕКТОРА |\|/') = Д|\|/)
Задача состоит в том, чтобы, зная компоненты вектора \x\f) и элементы матрицы
оператора А в заданном представлении, вычислить компоненты вектора |\|/') = Л|\|/) в
том же представлении.
В базисе {|«,)} координаты с' вектора |\|/') определяются выражением:
c,'=(M,.|V')=(M,.|A|v). (C-29)
Достаточно теперь ввести соотношение замкнутости между А и |\|/), чтобы получить:
с; = (u,\a i|v)= (м,.|л^/)|Ч/> = Е(«,И|М;.)(«» = 1Д,с>. (с-зо)
j J
Для базиса {|wa) } получим аналогично:
c\a) = (wa\\v) = (wa\A\\v) = jda'(wa\A\w^^^ (C-31)
Таким образом, матричная запись формулы |\|/') = л|\|/) оказывается очень простой. Из
156

Математический аппарат квантовой механики
(С-30) видно, например, что матрица-столбец, представляющая |\|/'), равна
произведению матрицы-столбца, представляющей |\|/}, на квадратную матрицу, представляющую
оператор А :
fs\
с->
с.
(А
А21
АХ2 .
А22 .
Ап .
■■ A,j
•• Аг,
■■ Ау
...^
...)
с1
с2
CJ
(С-32)
с. ВЫРАЖЕНИЕ ЧИСЛА (ф| А |\|/)
Введя соотношение замкнутости дважды (между (ф| и А , а также между А и |у)),
получим:
для базиса {| ui)}:
(ф|л|у) = (ф|^)Л^^) = Е(ф|и,Хи,Н";)("у|¥> = 1:^А^у; (С-33)
для базиса {|wa)}:
• \\dada:b\a)A(a, a')c(a')
(C-34)
Эти формулы интерпретируются в матричной форме следующим образом:
величина (ф|А|\{/) является числом, то есть матрицей с одной строкой и одним столбцом,
которая получается в результате перемножения матрицы-столбца, представляющей кет |\j/),
квадратной матрицы, представляющей оператор А , и матрицы-строки, представляющей
бра (ф|. Например, в базисе {|и.)}:
157

Глава II
(<p|a|v)=(a> ь; ... ь; ...)
А21 А22
Ач
( ^ \
(С-35)
ЗАМЕЧАНИЯ
(i) Подобным же образом можно было бы показать, что бра (ф| А представляет собой
матрицу-строку, являющуюся произведением квадратной матрицы, представляющей оператор А ,
на матрицу-строку, представляющую бра (ф| [две первых матрицы в правой части
равенства (С-35)]. Снова мы видим, насколько важен порядок следования символов: выражение
А (ф| привело бы к несуществующей матричной операции (произведение матрицы-строки
на квадратную матрицу),
(и) С матричной точки зрения равенство (В-41), определяющее (ф| А , всего лишь отражает
ассоциативность произведения трех матриц, фигурирующих в (С-35).
(iii) С учетом вышеуказанных соглашений |\|/) (\|/| представляется квадратной матрицей.
Действительно:
(п \
«
•)-
с, с,
с2с\
С; С,'
с{с2 .
сгс\ .
с, с\
■ с. CJ •••
. с2с] ...
■ сА -
(С-36)
Это выражение действительно представляет собой оператор, тогда как (\\f\ \\f/ ,
произведение матрицы-столбца на матрицу-строку, является числом.
d. МАТРИЧНОЕ ПРЕДСТАВЛЕНИЕ ОПЕРАТОРА А+ ,
ЭРМИТОВО СОПРЯЖЕННОГО ОПЕРАТОРУ А
Используя (В-49), нетрудно получить:
(а+) =(м,.|л+|и.> = («у|л|«,)* = л*.
(С-37)
158

Математический аппарат квантовой механики
или
A^aya1) = (wa\A+\wa) = (wa,\A\way = A\a\a). (C-38)
Таким образом, матрицы, представляющие А и Л+ в заданном представлении, являются
эрмитово сопряженными друг другу в матричном понимании: переход от одного
оператора к другому при эрмитовом сопряэюении производится путем симметричного
отображения матрицы относительно главной диагонали.
Если оператор А эрмитов, то А+ = А, и можно заменить [А*)., на Ai} в (С-37), и
A*(a, а') на Л(а, а') в (С-38):
Аи = 4 ; (С-39)
Л(а, а') = Л*(ос',а). (С-40)
Таким образом, эрмитов оператор представляется эрмитовой матрицей, то есть
матрицей, в которой произвольная пара элементов, симметричных относительно главной
диагонали, комплексно сопряжены друг другу. В частности, если / = j или а = а',
выражения (С -39) и (С-40) принимают вид:
а, = а:; (с-41)
Л(сс, а) = А\а, а). (С-42)
Диагональные элементы эрмитовой матрицы всегда являются вещественными числами.
5. Изменение представления
а. ПОСТАНОВКА ЗАДАЧИ
В заданном представлении кет-вектору, бра-вектору или оператору сопоставляется
матрица. Если представление изменяется, то есть меняется базис, те же кет, бра или
оператор будут иметь иной вид матриц. Как связаны между собой матрицы одного
математического объекта в двух разных представлениях?
Для простоты допустим, что осуществляется переход от одного дискретного орто-
нормированного базиса {|и,.)} к другому дискретному ортонормированному базису {\tk)}.
В §Е рассмотрим пример перехода от одного непрерывного базиса к другому
непрерывному базису.
159

Глава II
Изменение базиса определяется заданием компонент (**|и,-) каждого кет старого
базиса на множество кет-векторов нового базиса. Обозначим:
Su={tk\u,). (C-43)
Матрица 5 является матрицей изменения базиса. Ее эрмитово сопряженная S+
определяется элементами:
Ий= &,)'=<«, К). (с-44)
Дальнейшие вычисления выполняются предельно просто и не требуют запоминания,
так как в них используются два соотношения замкнутости:
^> = Е|и/)(и»| = 1; (С-45)
I
к
и два соотношения ортонормировки:
(",>,) = 8„; (C-47)
('*|',) = V (С-48)
ЗАМЕЧАНИЕ
Матрица S изменения базиса является унитарной (дополнение Си); действительно,
она удовлетворяет равенству:
SS+=S+S = /f (C-49)
где / — единичная матрица. Действительно:
(ss*)H = ssa5; = E(rt |«,}(«,. Ю=(r41/,)=8Ы. (c-50)
Аналогично:
(s+s)o = zs;kstj = £<M,k)('* Ь)=(ч\ъ)=8*- (C1)
160

Математический аппарат квантовой механики
Ь. ПРЕОБРАЗОВАНИЕ КОМПОНЕНТ КЕТ-ВЕКТОРА
Чтобы получить компоненты (tk \\\f) кет-вектора в новом базисе, исходя из его
компонент (м;. |\|/) в старом базисе, следует просто ввести соотношение (С-45) между (rj
и|\|/):
<^ k>=(^ |i|v»/>=</, !^)|vi/>=s<^ |ч><^ k>=s^<"/ k>. (c-52)
С помощью формулы (С-45) нетрудно доказать и обратные соотношения:
(ttJv> = <ttJl|v> = («/K,|v> = S(«/|^>^|v> = S5i(rft|V>. (C-53)
с. ПРЕОБРАЗОВАНИЕ КОМПОНЕНТ БРА-ВЕКТОРА
Принцип расчета совершенно тот же. Например:
(v|/t> = <v|l|^> = (vH.l,ki> = S(v|«/X"/l'*) = S<v|»<)Si. (C-54)
d. ПРЕОБРАЗОВАНИЕ МАТРИЧНЫХ ЭЛЕМЕНТОВ ОПЕРАТОРА
Если в выражение (tk|д|г,) ввести (С-45) между (tk\ и А , с одной стороны, и
между А и \t,) — с другой, то получим:
('* 14<>=('* КмМ=Kh \Ф< \Auj){uM) <с-55>
и
или
A, = Zs«v;,- (с-56)
Аналогично:
АЧ =DH|";> = DK,^,,)|w>)=Z("ik^('*HI'/)('/|">) = X5*A^ • (С7)
kj k,l
1 1 Квантовая механика * & 1

Глава II
D. УРАВНЕНИЯ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ.
НАБЛЮДАЕМЫЕ
1. Собственные значения и собственные векторы оператора
а. ОПРЕДЕЛЕНИЯ
Говорят, что |\|/) — собственный вектор (или собственный кет) линейного
оператора А ,если
1,4 (D-1)
Л|у) = Х|\|/)
где X — комплексное число. Сейчас мы рассмотрим некоторые свойства уравнения (D-1),
которое называется уравнением на собственные значения линейного оператора А . Это
уравнение имеет в общем случае решение лишь тогда, когда X принимает определенные
значения, которые называются собственными значениями оператора А . Множество
собственных значений называется спектром оператора А .
Отметим, что если |\j/) — собственный вектор оператора А с собственным
значением X , то oc|\j/), где а — произвольное комплексное число, также является собственным
вектором оператора А с тем же собственным значением:
л(а|\|/)) = аЛ|\|/) = aX\\\f) = X(a\x\f)). (D-2)
Чтобы преодолеть эту неопределенность, можно было бы условиться нормировать на 1
собственные векторы:
(V|V> = 1. (D-3)
Но это не снимает неопределенность полностью, поскольку е1 |\|/), где 0 — произвольный
вещественный угол, имеет ту же норму, что и |\|/) . В дальнейшем мы увидим, что в квантовой
механике физические выводы, следующие из |\|/у и е' |\|/у, одинаковы.
Собственное значение X считается невырожденным (или простым), если ему
соответствует единственный собственный вектор с точностью до постоянного множителя, то
есть если все связанные с ним собственные кет-векторы коллинеарны. Напротив, если
существует по крайней мере два линейно независимых кет-вектора, являющихся
собственными векторами оператора Л для одного собственного значения, то они называются
вырожденными', степень (или порядок) выроэюдения равна при этом количеству линейно
независимых собственных векторов, соответствующих этому значению (степень вырож-
162

Математический аппарат квантовой механики
дения собственного значения может быть конечной или бесконечной). Если степень
вырождения собственного значения X равна g, ему соответствуют g независимых кет-
векторов \|/Л (/ = 1,2,..., g ), удовлетворяющих условию:
А|\|/'') = Х|\|/''). (D-4)
Но тогда всякий кет |\|/) вида:
k> = tc|.|\|//) (D-5)
является собственным вектором оператора А с собственным значением X независимо
от значения коэффициентов с,. Действительно:
^k)=ic/.A|i|//)=xtc/|\|/')=^k). (d-6)
Таким образом, ансамбль собственных кет оператора А с собственным значением X
образует векторное пространство с размерностью g (оно может быть
бесконечномерным), называемое собственным подпространством, соответствующим
собственному значению X . В частности, сказать, что X — невырожденное собственное значение,
эквивалентно тому, что его степень вырождения равна g = 1.
Чтобы проиллюстрировать эти определения, возьмем в качестве примера проекционный
оператор (§B-3-b) Pv =|\}/д\|/| при условии, что (\|/|\|/) = 1. Уравнение на собственные значения
этого оператора имеет вид:
^|ф)=*|ф>
или
|\|/>(\|/|ф> = Х|ф). (D-7)
Кет в правой части всегда коллинеарен вектору |\|/) или равен нулю. Вследствие этого
собственными векторами оператора Р^ являются: с одной стороны, сам кет |\|/) с собственным значением
X = 1, с другой — все кет-векторы |фу , ортогональные к |\|/у с собственными значениями X = 0 .
Спектр собственных значений оператора Р^ состоит только из двух значений: 1 и 0. Первое
является простым, а второе — бесконечно вырожденным (пространство состояний считается
бесконечномерным); собственное подпространство, соответствующее X = 0, является дополнительным
к |\|/) (см. §D-2-c).
11*
163

Глава II
ЗАМЕЧАНИЯ
(i) Взяв комплексно сопряженное для обеих частей уравнения (D-1), получим:
(\|/|Л+=Х*(\|/|. (D-8)
Итак, если |\|/) — собственный кет оператора А , соответствующий собственному
значению А,, можно утверждать, что бра (\j/1 является собственным вектором
оператора Л+, соответствующим собственному значению А, . Обратим, однако,
внимание на то, что за исключением случая, когда А — эрмитов оператор (§ D-2-a),
априори нельзя ничего сказать относительно (\|/1 А .
(ii) Строго говоря, необходимо решить уравнение на собственные значения (D-1) в
пространстве <> , то есть рассматривать только собственные векторы |\|/у с конечной нормой. В
действительности нам часто придется использовать операторы, собственные векторы которых
не удовлетворяют этому условию (§ Е); таким образом, будем считать, что векторы,
являющиеся решениями (D-1), могут быть «обобщенными кет-векторами».
Ь. НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И СОБСТВЕННЫХ ВЕКТОРОВ ОПЕРАТОРА
Считая заданным линейный оператор А , как можно найти все его собственные
значения и соответствующие им собственные векторы? Здесь будем интересоваться этим
вопросом чисто с практической точки зрения. Рассмотрим случай N -мерного
пространства состояний и допустим, что результаты могут быть обобщены на бесконечномерное
пространство состояний.
Выберем некоторое представление, например, {1м,)}, и спроектируем векторное
уравнение (D-1) на векторы | и,) ортонормированного базиса:
(i<l.|A|v> = X(ii/|\|f>. (D-9)
Введя соотношение замкнутости между А и |\|/), получим:
£(ф|м,)(м,.|х|/) = Л(м,|ч/) (D-10)
J
С обычными обозначениями:
(ul\A\uJ)^Au (D-11)
164

Математический аппарат квантовой механики
уравнения (D-10) запишутся в виде:
5>,л=Хс/
(D-12)
или
Е[л,-Л5,]су = 0.
(D-13)
Можно рассматривать (D-13) как систему уравнений с неизвестными с,, компонентами
собственного вектора в выбранном представлении. Эта система является линейной и
однородной.
а. Характеристическое уравнение
Система (D-13) состоит из N уравнений (/ = 1,2,..., N) с N неизвестными с.
G = 1,2,..., N). Поскольку уравнения линейные и однородные, то нетривиальное их
решение (отличное от нулевого) возможно лишь в том случае, если детерминант,
составленный из коэффициентов уравнений, равен нулю. Это условие имеет вид:
det[.c/-AJ] = 0,
(D-14)
где ic/ — матрица, имеющая NxN элементов Aij, и / — единичная матрица.
Уравнение (D-14), называющееся характеристическим (или секулярным), позволяет
определить все собственные значения оператора А , то есть его спектр. Можно
представить (D-14) в форме:
Ап-Х
К
An\
А22-Х
^N3
ANN-\
(D-15)
Это уравнение N-ной степени по X, оно имеет N корней, вещественных или мнимых,
различных или кратных. Впрочем, легко показать, выполнив произвольное изменение
базиса, что характеристическое уравнение не зависит от выбранного представления.
Итак, собственные значения оператора являются корнями его характеристического
уравнения.
165

Глава II
Р. Определение собственных векторов
Выберем теперь собственное значение Х0, являющееся решением
характеристического уравнения (D-14), и найдем соответствующие собственные векторы. Будем
различать два случая.
(i) Сначала рассмотрим случай, когда Х0 является простым корнем
характеристического уравнения. Можно показать, что при этом система (D-13) при Х = Х0 состоит из
[N -1) независимых уравнений, причем N-ное уравнение является следствием
остальных. Итак, имеется N неизвестных и, следовательно, бесконечное множество решений,
но все значения Cj могут быть определены единственным образом через одно из них,
скажем, через сх. Действительно, если зафиксировать сх, то получим для остальных
(N -1) значений Cj систему из (N -1) линейных и однородных уравнений (правая часть
каждого из этих уравнений является членом, определенным через С\) с отличным от нуля
детерминантом [ (/V -1) независимых уравнений]. Решение этой системы имеет вид:
Ъ=а°с19 (D-16)
поскольку исходная система уравнений (D-13) линейна и однородна. Конечно, а" = 1 по
определению и (N -I) коэффициентов а у при j Ф 1 определяются через матричные
элементы Aij и Х0. Собственные векторы, связанные с Х0, отличаются друг от друга
только через выбранное значение с,, то есть выражаются соотношением:
коМ^а-с^.^фо). (D-17)
j
где
ко) = 1°ф,). (D-18)
j
Итак, если Х0 — простой корень характеристического уравнения, ему соответствует
единственный собственный вектор (с точностью до постоянного множителя), это
невырожденное собственное значение.
(и) Если Х0— корень характеристического уравнения кратности q > 1, то возможны
два варианта:
— в общем случае система (D-13) при Х-Х0 содержит еще (N-l) независимых
уравнений. Собственному значению Х0 соответствует только один собственный вектор.
166

Математический аппарат квантовой механики
В этом случае оператор А не диагонализируется: собственных векторов оператора А
недостаточно, чтобы из них можно было построить базис в пространстве состояний;
— может оказаться, что система (D-13) содержит при Х = Х0 лишь (/V - р)
независимых уравнений A < р < q). Тогда собственному значению Х0 соответствует
собственное подпространство с размерностью р, и Х0 является р -кратно вырожденным
собственным значением. Предположим, например, что при Х = Х0 система (D-13) состоит из
(/V - 2) линейно независимых уравнений. Они позволяют вычислить коэффициенты с.
через два из них, например, через с, и с2, которые можно выбрать произвольным
образом:
с.=р(;с1+у-с2 (D-19)
(очевидно, что C" = Y2 = 1 > Yi^P^O); все собственные векторы, связанные с Х0,
имеют вид:
|Vo(ci.c2)> = ^i|v!)) + c2|Vo), (D-20)
где
К)=хр;К);
j
j
Векторы |i|/0(c,, c2)) образуют двумерное векторное пространство, являющееся
характерным для дважды вырожденного собственного значения.
Если оператор эрмитов, можно показать, что кратность вырождения р собственного
значения X всегда равна кратности q корня характеристического уравнения. Поскольку
в дальнейшем в большинстве случаев будем иметь дело с эрмитовыми операторами,
достаточно знать кратность каждого из корней уравнения (D-14), чтобы сразу же получить
размерность соответствующего собственного пространства. В пространстве с конечной
размерностью N эрмитов оператор всегда имеет N линейно независимых собственных
векторов (далее мы увидим, что их можно выбрать ортонормированными): таким
образом, этот оператор является диагонализируемым (§ D-2-b).
167

Глава II
2. Наблюдаемые
а. СВОЙСТВА СОБСТВЕННЫХ ЗНАЧЕНИЙ
И СОБСТВЕННЫХ ВЕКТОРОВ ЭРМИТОВА ОПЕРАТОРА
Рассмотрим очень важный в квантовой механике случай, когда оператор А эрмитов:
А+ = А. (D-22)
(i) Собственные значения эрмитова оператора вещественны.
Умножим скалярно уравнение на собственные значения (D-1) на |\|/) и получим:
(\|/|A|v> = X(v|v>. (D-23)
Но (\|/|а|ц/) — вещественное число, если А — эрмитов оператор, так как
(i|/H\|/>*=(\|f|A+|v> = (\|f|A|v>, (D-24)
где последнее равенство вытекает из гипотезы (D-22). Поскольку величины (\|/|а|\|/) и
(\|/|\|/) — вещественные, уравнение (D-23) требует, чтобы вещественной была и
величина X. Получим тогда:
(\|г|А = Х(\|/|, (D-25)
и это равенство показывает, что (\|/| является также собственным бра-вектором
оператора А с вещественным собственным значением А,. Итак, каким бы ни был кет |ф):
(\|/|А|Ф) = Х(\|/|ф). (D-26)
Говорят, что в равенстве (D-26) эрмитов оператор А действует слева.
(ii) Два собственных вектора эрмитова оператора, соответствующие двум
различным собственным значениям, ортогональны.
Рассмотрим два собственных вектора |\|/) и |ф) эрмитова оператора А:
A|v> = X|\|f>; (D-27-a)
А|ф) = ц|<р). (D-27-b)
168

Математический аппарат квантовой механики
Поскольку А — эрмитов оператор, равенство (D-28) можно переписать в форме:
(ф|Л = ц(Ф|. (D-28)
Умножим (D-27-a) слева на (ф| и (D-28-b) справа на |\|/):
(ф|А|\|/) = А.(ф|у); (D-29-a)
(ф|А|\|/) = |г(ф|\|/>. (D-29-b)
Вычтя почленно второе равенство из первого, получим:
(X-|i)(q>|\|/) = 0. (D-30)
Таким образом, если только (X - ц) Ф О , векторы |ф) и |\|/) ортогональны.
Ь. ОПРЕДЕЛЕНИЕ НАБЛЮДАЕМОЙ
В § D-1-b мы видели, что если пространство $ имеет конечную размерность, всегда
можно образовать базис из собственных векторов эрмитова оператора. Если же
размерность пространства £ бесконечна, то это утверждение не всегда справедливо. Именно
поэтому необходимо ввести новое понятие — наблюдаемая величина или просто
наблюдаемая.
Рассмотрим эрмитов оператор А . Для простоты допустим, что ансамбль его
собственных значений образует дискретный спектр { ап, где п = 1,2,...}, и укажем затем,
какие изменения следует внести, если весь спектр (или его часть) непрерывен. Кратность
вырождения собственного значения ап будем обозначать символом gn (если gn = 1,
то ап — невырожденное собственное значение) и символом ц/М (/ = 1,2,..., gn) —
линейно независимые векторы собственного подпространства #„, соответствующего
собственному значению ап:
А\<) = ««№): i = 1.2. ...,*,. (D-31)
Мы только что показали, что любой вектор, принадлежащий подпространству <fn,
ортогонален любому вектору другого подпространства £л., соответствующего ап, Ф ап,
то есть
(v!, \vi) = 0 Для п ф п' и любых I, j. (D-32)
169

Глава II
В пределах каждого подпространства #п всегда можно выбрать векторы т'п) так,
чтобы они были ортонормированы, то есть чтобы
(ч'«М = Ьи-
(D-33)
Если сделать такой выбор, то получим ортонормированную систему собственных
векторов оператора А , ибо Ы'п) удовлетворяют соотношению:
(<|<) = 5,ш,5,,
(D-34)
полученному после группировки равенств (D-32) и (D-33).
По определению эрмитов оператор А является наблюдаемой, если ортонормиро-
ванная система векторов образует базис в пространстве состояний. Это может быть
выражено соотношением замкнутости:
8,
л=1 /=1
il|v'„)(v!,| = i
(D-35)
ЗАМЕЧАНИЯ
(i) Поскольку векторы ш'п) (i = 1,2,.... gn), образующие собственное подпространство
$„, соответствующее собственному значению ап, ортонормированы, проекционный
оператор Рп на это подпространство может быть записан в виде (см.§ B-3-b-y):
^ = t|v'.)(vi|.
Тогда наблюдаемая А определяется как
(D-36-a)
(D-36-b)
(легко доказать, что действие обеих частей этого равенства на все кет-векторы
\|/М дает один и тот же результат).
(ii) Равенство (D-35) можно обобщить на случай, когда спектр собственных значений непрерывен,
если использовать правила, приведенные в табл. Н-3. Возьмем, например, эрмитов оператор,
спектр которого имеет дискретную часть { ап с кратностью вырождения gn } и непрерывную
часть tf(v) (предположительно невырожденную), то
170

Математический аппарат квантовой механики
^К) = аяК); л = 12,... ; / = 1,2,..., £„; (D-37-a)
A|l|/V) = a(v)|\|/V); V, <V<V2. (D-37-b)
Всегда можно выбрать эти векторы так, чтобы они образовывали «ортонормированную»
систему:
(<Ю = 8„А..;
(Vv|Vv) = S(V-V);
(v!.|Vv> = 0. (D-38)
Будем говорить, что А — наблюдаемая, если эта система образует базис, то есть
X £|vi)(v!,| + j;arfv|Vv><Vv| = l- (D-39)
с. ПРИМЕР: ПРОЕКЦИОННЫЙ ОПЕРАТОР Р^
Покажем, что Pv = | V|/)(\|/|, при условии (\|/|\|/) = 1, является наблюдаемой. В § В-4-е
мы уже отметили, что этот оператор эрмитов и что его собственными значениями являются
1 и 0 (§ D-1-a); первое их них является простым (собственный вектор |у)), а второе —
бесконечно вырожденным (собственные векторы — все кет, ортогональные к | \|/)).
Рассмотрим произвольный кет |ф) пространства состояний. Его всегда можно
записать в виде:
|ф) = Р¥|ф> + A-Р¥)|ф), (D-40)
где Ру\<р) — собственный кет оператора Ру с собственным значением 1. Действительно,
поскольку Р* = Pv :
Вектор A-Р¥]|ф) также является собственным вектором оператора Pv, но с
собственным значением 0. Действительно:
171

Глава II
Р¥A-Р¥)|ф) = (Р¥-^)|ф) = 0. (D-42)
Таким образом, любой кет |ф) может быть разложен по собственным кет-векторам
оператора Pv, и оператор Р¥ является наблюдаемой.
В § Е-2 мы встретимся еще с двумя важными примерами наблюдаемых.
3. Ансамбли коммутирующих наблюдаемых
а. ВАЖНЫЕ ТЕОРЕМЫ
а. Теорема I
Если два оператора А и В коммутируют и |\|/) — собственный вектор
оператора А ,то вектор В\\у) также является собственным вектором оператора А с тем же
собственным значением.
Действительно, если |\|/}— собственный вектор оператора А , то
А|\|/) = а|ч>)- (D-43)
Применим оператор В слева к равенству (D-44):
ЯА|\|/) = яЯ|\|/). (D-44)
Поскольку согласно нашей гипотезе операторы А и В коммутируют, то
А(я|1|/)) = я(я|\|/)). (D-45)
Это равенство выражает, что вектор В\ \\f) является собственным вектором оператора А
с собственным значением а , что и требовалось доказать.
При этом возможны два случая.
(i) Если а — невырожденное собственное значение, то все связанные с ним
собственные векторы коллинеарны по определению, и кет В\\у) должен быть
пропорционален кету |\j/). Таким образом, |\|/) также является собственным вектором оператора В.
(и) Если а — вырожденное собственное значение, можно лишь сказать, что кет #|\|/)
принадлежит собственному подпространству $а оператора А, соответствующему
собственному значению а . Таким образом, каким бы ни был кет |\|/) е $а, имеем:
172

Математический аппарат квантовой механики
В\у)е$0. (D-46)
Говорят, что пространство $а является глобально инвариантным (или стабильным)
относительно действия оператора В. Теорема I может быть, таким образом, сформулирована
иначе.
Теорема /. Если два оператора А и В коммутируют, то любое собственное
подпространство оператора А глобально инвариантно относительно действия оператора В.
C. Теорема II
Если две наблюдаемые А и В коммутируют и если \\\f^ и |\j/2) — два
собственных вектора оператора А с различными собственными значениями, то матричный
элемент (\|/, | В |\|/2) равен нулю.
Действительно, если |\|/,) и |\j/2) — собственные векторы оператора А , можно
записать:
%i) = «i|Vi);
А\у2) = а2\у2). (D-47)
Согласно теореме I из коммутативности операторов А и В следует, что #|\|/2) является
собственным вектором оператора А с собственным значением а2. Таким образом, кет
#|i|/2) (см.§ D-2-a) ортогонален к \\\f{) (собственный вектор, соответствующий
собственному значению я, Ф а2), что можно выразить равенством:
{чх\в\у2) = 0, (D-48)
что и требовалось доказать. Можно, впрочем, привести и другое доказательство, не
прибегая к теореме I: поскольку коммутатор [Л, В] равен нулю, имеем:
(у1\(АВ-ВА)\ц2) = 0. (D-49)
Используя (D-47) и эрмитовость оператора А [см. уравнение (D-25)], получим:
(\|/1|ЛВ|\|/2) = д1(\|/1|5|\|/2);
(ч1\ВА\у2) = а2(у1\в\у2), (D-50)
173

Глава II
и равенство (D-49) можно переписать в виде:
(а1-а2)(у1\в\у2) = 0.
Поскольку (я, - а2) * 0 , равенство (D-48) доказано.
(D-51)
у. Фундаментальная теорема III
Если две наблюдаемые А и В коммутируют, можно образовать ортонормиро-
ванный базис пространства состояний из общих для А и В собственных векторов .
Рассмотрим две коммутирующие наблюдаемые А и В. Для упрощения
обозначений допустим, что их спектр дискретен. Поскольку А — наблюдаемая, существует по
крайней мере одна система ортонормированных собственных векторов оператора А,
образующая базис в пространстве состояний Ъп. Обозначим эти векторы символом ш'п):
А \и') = а \и' >: я = 1,2,...; / = 1,2 s t
/I / II IX I ' ' ' ' ' ' * Oil >
(D-52)
где g„ — кратность вырождения собственного значения ап, то есть размерность
соответствующего собственного подпространства <*,,. Тогда:
(":,| «:,'•> = 8„„.8,,. (D-53)
Каков же вид матрицы, представляющей оператор В в базисе {Л}? Мы знаем
(теорема II), что матричные элементы Ып \в\и'п.) при п Ф vl равны нулю (напротив, мы ничего
не можем сказать априори, если п - п' и / Ф /'). Расположим базисные векторы \и'п) в
таком порядке:
Ц1),^2),..., |wf); |i<j),..., |w,*2); |«4).-
Тогда для оператора В получим матрицу, «диагональную по блокам», то есть
имеющую вид:
(D-54)
*1
*2
h
».
###
0
0
0
if2
0
###
0
0
*3
0
0
###
0
0
0
0
###
174

Математический аппарат квантовой механики
Только те блоки матрицы, которые отмечены цепочкой символов ###, содержат
отличные от нуля элементы. Такая структура матрицы наглядно показывает, что
собственные подпространства Уп являются глобально инвариантными относительно действия
оператора В (см. § - а).
При этом возможны два случая.
(i) Если ап — невырожденное собственное значение оператора А , то существует
единственный собственный вектор \ип) с этим собственным значением (индекс / в
обозначении | ип) при этом не нужен), и размерность пространства $п равна gtl = 1. В матрице
(D-54) соответствующий «блок» сводится к простому числу (матрице 1x1). В столбце,
связанном с |м„), все остальные матричные элементы равны нулю. Это отражает тот
факт (см. § a-i), что |и„) является общим собственным вектором операторов А и В.
(ii) Если ап — вырожденное собственное значение оператора А (gn > 1), «блок»,
представляющий оператор В в подпространстве #л, в общем случае не диагоналей, и
кет-векторы ш'п) не являются собственными векторами оператора В.
Можно, однако, заметить, что поскольку действие оператора А на каждый из gn
векторов ш'п) сводится к простому умножению на ап, то матрица, представляющая
«сужение» оператора А в пространстве £я, равна ап I (где / — единичная матрица с
размерностью gn x gn). Это говорит о том, что любой кет пространства $п является
собственным вектором оператора А с собственным значением ап. Таким образом, выбор в
пространстве £;| базиса, подобного базису { и',); / = 1,2,..., gn }, произволен: каким бы
ни был этот базис, матрица, представляющая оператор А в tf„, всегда диагональна и
равна ап I. Сейчас используем это свойство, чтобы получить базис пространства <?„,
составленный из векторов, являющихся также собственными векторами оператора В.
Если выбран базис { ш'п); / = 1,2,..., gn }, то матрица, представляющая в $п
оператор В, имеет матричные элементы:
РГ=(Ф1"«>- (°-55)
Эта матрица эрмитова (C(^° = C^'° ), поскольку В— эрмитов оператор, и, следовательно,
она диагонализируется, то есть можно в пространстве $п найти новый базис {Ь^);
/ = 1,2,..., gn }, в котором оператор В будет представлен диагональной матрицей:
(v;,|B|vi> = prr (D-56)
175

Глава II
Это означает, что новые базисные векторы в пространстве #л являются собственными
векторами оператора В :
s|v;,) = P<'iv;). (D-57)
Как мы видели выше, эти векторы являются автоматически собственными векторами
оператора А , соответствующими собственному значению ап, так как они принадлежат
пространству #п. Обратим внимание на то, что собственные векторы оператора А,
связанные с вырожденными собственными значениями, не обязательно являются
собственными векторами оператора В; но, как мы только что доказали, всегда возможно
в каждом собственном подпространстве оператора А выбрать базис собственных
векторов, общих для операторов А и В.
Если мы проделаем эту операцию во всех подпространствах $п, то получим базис V,
образованный из собственных векторов, общих для А и В, что и требовалось доказать.
ЗАМЕЧАНИЯ
(i) Начиная с этого параграфа, будем обозначать символом \и'п р) собственные
векторы, общие для операторов А и В.
40=*pkp)- (D8)
Индексы пир, фигурирующие в U,'f/J, позволяют зафиксировать собственные
значения ап и Ьр операторов А и В; дополнительный индекс / служит в случае
необходимости для отличия разных базисных векторов, соответствующих
одинаковым значениям ап и Ър (см. ниже § Ь).
(И) Теорему, обратную теореме III, легко доказать: если существует базис
собственных векторов, общих для операторов А и В, то эти наблюдаемые коммутируют.
Действительно, нетрудно получить из (D-58):
ae\u*.p) = b,>A\u»<i>) = V«R/>);
ВА|||^) = £1яв|<р) = а||*р|<,) (D-59)
и, вычтя эти равенства одно из другого, найдем:
176

Математический аппарат квантовой механики
[А,В]\и'„р) = 0. (D-60)
Это равенство справедливо для любых /, п, р ; поскольку векторы \и'п р)
образуют базис, из (D-60) следует, что [Д, В] = 0 .
(Ш) В дальнейшем нам придется решать уравнение на собственные значения
наблюдаемой С, удовлетворяющей равенству:
С = А + В при условии, что [Л, в] = 0, (D-61)
где А и В — наблюдаемые.
Если известен базис {\и'п ) } общих собственных векторов операторов А и В,
задача решена. Действительно, сразу же видим, что \и'п р) является также и
собственным вектором оператора С с собственным значением ап + Ър. Естественно,
очень важно, чтобы векторы \и'пр) образовывали базис; это позволяет, например,
без труда показать, что все собственные значения оператора С имеют вид:
b. ПОЛНЫЕ* НАБОРЫ КОММУТИРУЮЩИХ НАБЛЮДАЕМЫХ**
Рассмотрим наблюдаемую А и базис £, образованный собственными векторами
\и'п) оператора А. Если ни одно из собственных значений оператора не вырождено,
различные базисные векторы базиса Ш могут различаться по собственному значению ап
(индекс / в этом случае не нужен). Тогда все собственные пространства %п имеют
размерность 1, и задание выбранного собственного значения определяет единственным
образом соответствующий собственный вектор с точностью до постоянного множителя.
Другими словами, существует единственный базис пространства И7, образованный
собственными векторами оператора А (мы не считаем различными два базиса, векторы
которых пропорциональны); говорят тогда, что наблюдаемая А сама по себе образует
полный набор коммутирующих операторов.
* Слово «полный» используется здесь в смысле, который не имеет ничего общего с тем
смыслом, который уже был отмечен в §А-2-а. Его использование общепринято в квантовой механике.
** Чтобы правильно разобраться в понятиях, вводимых в этом параграфе, читателю
рекомендуется опираться на конкретный пример, предложенный в дополнении Ни (упражнения 11 и 12).
12 Квантовая механика
177

Глава II
Если, напротив, некоторые из собственных значений А вырождены (достаточно,
чтобы было вырождено одно из них), ситуация существенно меняется: задания значения
ап более не достаточно для характеристики базисного вектора, поскольку вырожденным
собственным значениям соответствуют несколько независимых векторов. В этом случае
базис собственных векторов А уже не является единственным: действительно, можно
взять любой базис внутри каждого из собственных подпространств %п с размерностью,
большей 1.
Возьмем теперь другую наблюдаемую В, коммутирующую с А , и образуем орто-
нормированный базис из собственных векторов, общих для А и В. По определению А
и В образуют полный набор коммутирующих операторов, если этот базис единственный
(с точностью до фазового множителя для каждого из образующих его векторов), то есть
если каждой возможной паре собственных значений { ап, Ъ } соответствует единственный
базисный вектор.
ЗАМЕЧАНИЕ
В §а мы построили базис собственных векторов, общих для А и В, решая уравнение
на собственные значения оператора В внутри каждого собственного подпространства fn.
Чтобы А и В образовали полный набор коммутирующих операторов, необходимо и
достаточно, чтобы внутри каждого из этих подпространств все gn собственных значений
оператора В были бы различными: поскольку все векторы #п соответствуют одному и тому же
собственному значению ап оператора А , gn векторов v\t) могут быть различимы
связанными с ними собственными значениями оператора В. Отметим, что нет необходимости,
чтобы все собственные значения оператора В были бы не вырождены: векторы v,',),
принадлежащие двум различным подпространствам fin, могут иметь одно и то же собственное
значение оператора В. Впрочем, если все собственные значения В не вырождены,
достаточно было бы взять лишь оператор В, чтобы образовать полный набор коммутирующих
операторов.
Если же, по крайней мере, для одной из возможных пар { ап, Ър } существовало бы
несколько независимых векторов, которые были бы собственными векторами
операторов А и В с этими собственными значениями, то набор { А , В } не является полным.
Добавим тогда третью наблюдаемую С , коммутирующую одновременно и с А и с В.
Можно повторить те же рассуждения, что и в § а , обобщив их: если паре { ап, Ър )
соответствует единственный вектор, то он должен быть собственным вектором оператора С ;
если же их несколько, то они образуют собственное подпространство $ПгР, в котором
можно выбрать базис, составленный из векторов, которые были бы собственными век-
178

Математический аппарат квантовой механики
торами и оператора С. Так строится ортонормированный базис, образованный из
собственных векторов, общих для операторов А, В, и С, действующих в пространстве
состояний. Эти операторы образуют полный набор коммутирующих операторов, если
этот базис единственный (с точностью до множителей), то есть если задание возможного
набора собственных значений { ап, Ър, сг} операторов Л , В, С характеризует
единственный из векторов этого базиса. Если же это не так, можно добавить еще один оператор
наблюдаемой D , коммутирующий с каждым из трех предыдущих, и т. д. В общем случае
следует сказать:
по определению набор наблюдаемых А , В, С ... называется полным набором
коммутирующих операторов, если:
(i) все наблюдаемые попарно коммутируют;
(и) задание собственных значений всех операторов А , В, С... достаточно для
определения единственного общего собственного вектора (с точностью до постоянного
множителя).
Можно сформулировать иначе (это утверждение эквивалентно):
набор наблюдаемых А , В, С ... является полным набором коммутирующих
операторов, если существует ортонормированный базис собственных векторов и если этот
базис единственный (с точностью до фазовых множителей).
Понятие полного набора коммутирующих операторов играет важную роль в квантовой
механике. В дальнейшем мы встретимся с многочисленными примерами этого (в
частности, см. § E-2-d).
ЗАМЕЧАНИЯ
(i) Если { А, В} — полный набор коммутирующих операторов, можно получить
другой полный набор, если добавить к нему произвольную наблюдаемую С при
условии, что она коммутирует с А и В. Однако обычно удобно ограничиваться
«минимальными» наборами, то есть такими, которые перестают быть полными,
если из них исключается любая из наблюдаемых.
(ii) Пусть {Л, В, С...} — полный набор коммутирующих операторов. Поскольку
задание собственных значений ап, Ьр, сг, ... достаточно для характеристики кет-
вектора соответствующего базиса (с точностью до множителя), то иногда
обозначают этот кет символом \ап, Ьр, сг,...).
(iii) Для каждой данной физической системы существует несколько полных наборов
коммутирующих операторов. Мы увидим это уже в частном случае в § E-2-d.

Глава 11
Е. ДВА ВАЖНЫХ ПРИМЕРА ПРЕДСТАВЛЕНИЙ
И НАБЛЮДАЕМЫХ
В этом параграфе вернемся к пространству J волновых функций частицы, а
точнее, к связанному с ней пространству состояний tfr, которое определим следующим
образом. Любой волновой функции \|/(г) ставят в соответствие кет |\|/), принадлежащий
пространству Vr, причем это соответствие является линейным. Кроме того, скалярное
произведение двух кет-векторов совпадает со скалярным произведением
соответствующих функций:
(ф|11/) = {^3гф>)\|/(г), (Е-1)
где $г — пространство состояний частицы без спина.
Сейчас определим и исследуем в этом пространстве два представления и два
оператора, имеющих особенно важное значение, поскольку их будем ассоциировать в главе
III с положением и импульсом рассматриваемой частицы. Кроме того, они позволят нам
применить и использовать понятия, введенные в предыдущих параграфах.
1. Представления {|г)} и { |р)}
а. ОПРЕДЕЛЕНИЕ
В § А-З-а и § A-3-b мы ввели два частных «базиса» в пространстве & : { £Го(г)} и
{ vpo(r)}. Они составлены из функций, не принадлежащих пространству J :
£ro(r) = S(r-r0); (E-2-a)
уро(г) = BтсЛ)/2^РоГ, (E-2-b)
но любая достаточно регулярная квадратично интегрируемая функция может быть
разложена по одному из этих «базисов».
Именно поэтому уберем кавычки и каждой из функций этих базисов поставим в
соответствие кет-вектор (см. § В-2-с). Обозначим кет, связанный с £г (г), символом |г()),
а кет, связанный с vPo(r), символом |р0):
£гв<г)«|г0);
(Е-З-а)

Математический аппарат квантовой механики
^(г)«|р0>. (E-3-b)
С помощью базисов { £Г()(г)} и { vpo(r)} в пространстве Я определим в
пространстве #г два представления: представление {|г0}} и представление (|р0) }• Базисный
вектор первого представления характеризуется тремя «непрерывными индексами»
x0i y0, z0, являющимися координатами точки в трехмерном пространстве, а второго —
тремя индексами — компонентами обычного вектора.
Ь. СООТНОШЕНИЯ ОРТОНОРМИРОВКИ И ЗАМКНУТОСТИ
Вычислим (г0|г0'). По определению скалярного произведения в пространстве $г:
(г0|г0'> = \d'r %\(rM,0 (r) = 8(r0 -r0'), (E-4-a)
где использовано соотношение (А-55). Аналогично:
<Ро|Ро) = Wr v;,(r) vpo(r) = 8(p0 -p(',). (E-4-b)
Базисы, которые мы только что ввели, являются ортонормированными в широком
смысле слова.
То, что ансамбли векторов |г0) или |р0) образуют базис в пространстве £г, можно
выразить с помощью соотношения замкнутости в tfr, записанного способом, аналогичным
равенству (С-10), при условии, однако, суммирования по трем индексам вместо одного.
Таким образом, имеем фундаментальные соотношения:
(Е-5)
1*
^
(Ро
\U;
г;)=8(г0-
*о|гоХго| =
Ро) = 5(Ро
Ро|Ро)(Ро|
-о
1
-Ро)
= 1
(а)
(Ь)
(с)
(d)
с. КОМПОНЕНТЫ КЕТ-ВЕКТОРА
Рассмотрим произвольный кет |\|/), соответствующий волновой функции \|/(г).
Приведенные выше соотношения замкнутости позволяют записать его в одной из двух
форм:
181

Глава II
|v> = JAkoXrok>; (E-6-a)
|\l/) = j^3Po|Po)(Pok). (E-6-b)
Коэффициенты (г0|\|/) и (р0|\|/) могут быть найдены по формулам:
(r0|\|r> = Jrf3r§;e(r)V(r); (Е-7-а)
(Po|v> = Jrf3rv;o(r)V(r). (E-7-b)
Тогда имеем:
(r0|\|/) = \|/(r0); (Е-8-а)
<Рок> = ?(Ро). (Е"8-Ь)
где \|/(р) — Фурье-образ функции \|/(г).
Итак, значение \|/(г0) волновой функции в точке г0 имеет смысл проекции кет-
вектора \\\f)na базисный вектор\г0) представления {|г0) }; «волновая функция в
импульсном пространстве» \|/(р) интерпретируется аналогично. Возможность
охарактеризовать кет |\|/) функцией i|/(r) является просто частным случаем результатов § С-З-а.
Например, для |\|/) = |р0) формула (Е-8-а) дает:
<ro|Po) = vpo(r0H2^,2>r0. (E-9)
Для |у)= |го) результат хорошо согласуется с соотношением ортонормировки (Е-5-а):
(r0|r0/) = ^(r0) = 8(r0-r(;). (E-10)
Теперь, когда мы дали новую интерпретацию волновой функции \|/(г) и ее Фурье-
образа \|/(р), будем пользоваться обозначениями |г) и |р) вместо |г0) и |р0) для
рассматриваемых здесь базисных векторов двух представлений. Тогда формулы (Е-8)
примут вид:
(r|\|/) = v(r); (E-8-a)
(p|v) = ¥(P) (E-8-b)
182

Математический аппарат квантовой механики
и соотношения ортонормировки и замкнутости (Е-5) перепишутся в форме:
(a) (r|r') = 5(r-r'); (с) (р|р') = 8(р-р');
(b) Jrf3r|r><r| = l; (d) ^Зр|р)(р| = 1. (Е-5)
Конечно, переменные г и р по-прежнему считаются здесь двумя наборами
непрерывных индексов { л\ у, z } и { рх, ру, р.}, позволяющими идентифицировать базисные кет-
векторы представлений {|г) }и {|р)} соответственно.
Пусть в пространстве 'J имеется ортонормированный базис { и, (г)}. Каждой функции
и, (г) ставится в соответствие кет и.) пространства <?г. Множество { ш,) } образует в #г
ортонормированный базис, удовлетворяющий соотношению замкнутости:
1Ь)(к,| = 1- (Е-П)
i
Возьмем матричный элемент от обеих частей равенства (Е-11) между |г) и |г') :
S(r|«,.)(M,.|r') = (r|l|r') = (r|r'). (E-12)
Согласно (Е-8-а) и (Е-5-а) это равенство можно записать в виде:
Х«Дг)^(г') = 5(г-г'). (Е-13)
Соотношение замкнутости для ( и, (г) } [формула (А-32)! является просто переводом в
представление {|г) } векторного соотношения замкнутости (Е-11).
d. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
Мы определили скалярное произведение двух кет в пространстве £г как
произведение двух соответствующих волновых функций пространства i'J (Е-1). В свете сказанного
выше, это определение является просто частным случаем формулы (С-21).
Действительно, формулу (Е-1) можно получить, введя соотношение замкнутости (E-5-b) между (ф|
h|v):
<ф|\|/> = J^/V <M/|r><r|v|/> (E-14)
и интерпретируя, как в (Е-8-а), компоненты (г|\|/) и (г |ф).
183

Глава II
Если перейти в представление {|р) }, то нетрудно доказать хорошо известное
свойство преобразования Фурье (приложение I, § 2-е):
(ф| V> = RV (ф|р)(р| V) =Кр Ф*(р) ?(Р) • (Е-15)
е. ПЕРЕХОД ОТ ПРЕДСТАВЛЕНИЯ {|г) } К ПРЕДСТАВЛЕНИЮ {|р) )
Он осуществляется с помощью метода, описанного в § С-5, с той лишь разницей,
что здесь мы имеем дело с двумя непрерывными базисами. Переход из одного базиса в
другой потребует знания чисел:
(г|р> = (р|г>* =Brcu)VP"r. (Е-16)
Любой данный кет |\|/) в представлении {|г)} задается функцией (r|\j/) = \|/(г) и
функцией (р|\|/) = vj/(p) — в представлении {|р)}. Мы уже знаем (E-7-b), что \|/(г) и \[/(р)
связаны преобразованием Фурье. Именно на это указывают формулы изменения
представления:
(r|V) = Jrf3p(r|pXp|v)
ИЛИ
V(r) = {2пПУт\с1ър е'РГ vj7(p). (Е-17)
Обратное преобразование:
(p|v(/) = Jrf3r(p|r)(r|i|/),
то есть
\j7(p) = B7i^)-3/2J^3r^pri|/(r). (E-18)
Применив общую формулу (С-56), можно легко перейти от матричных элементов
(г'|л|г) = А(г\ г) оператора А в представлении {|г) } к матричным элементам
(р'Ир) = Мр\ Р) того же оператора в представлении {|р)}:
184

Математический аппарат квантовой механики
А(р', р) = BкПУ3 \йъг Jrf V е»(РГ~Р'Г') A(r', r).
(Е-19)
Аналогичная формула позволяет выразить А(г\ г) через А(р\ р).
2. Операторы R и Р
а. ОПРЕДЕЛЕНИЕ
Пусть |\|/) — произвольный кет пространства ffr и (г|\|/) = \|/(г) = \|/(лс, у, z) —
соответствующая волновая функция. По определению оператора X кет:
И=%) (Е-20)
определяется в базисе {|г)} функцией (г|\|/') = \|/'(г) = у'(ху у, z), причем:
\|/'(*. )\z) = x\|/(*, у, z). (E-21)
В представлении {|г)} оператор X совпадает с оператором умножения на х. Хотя
мы и характеризуем X так, что он преобразует волновую функцию, этот оператор
действует в пространстве состояний tfr. Аналогично введем и два других оператора Y и Z.
Определим все три оператора формулами:
: ГТ~~ГП (Е-22-а)
(E-22-b)
(Е-22-с)
где числа х, у, z являются тремя индексами, определяющими кет |г). Операторы
X, У, Z будут рассматриваться как «компоненты» «векторного оператора» R : пока это
следует рассматривать лишь как компактное обозначение, опирающееся на то, что
лг, у, z являются компонентами обычного вектора г.
Действия с операторами X, К, Z особенно просты в представлении {|г)}.
Например, чтобы вычислить матричный элемент (ф|х|\|/), достаточно вставить соотношение
замкнутости (Е-5-а) между (ф| и X , используя определение (Е-22):
|(r|x|V> =
\(*Ш =
|(r|z|V> =
■-х{г\ц,)\
y(r\v)\
= z(r|v)|
(Ф|%Н^(ф|г)(г|х|1|;) = |^ф>)л1|/(г).
(Е-23)
185

Глава II
Аналогично определяется векторный оператор Р через компоненты Рх, Pyi Pz,
действие которых в представлении {|р) } определяется выражениями:
(Е-24-а)
(E-24-b)
(Е-24-с)
Ф) = рЛт)
(р№) = р,(рк)
{j>\Pz№)=Pz(l>№)
где рх, р , pz —три индекса, определяющие кет |р).
Найдем, как оператор Р действует в представлении {|г) }. Для этого достаточно
(§ C-5-d) использовать соотношение замкнутости (E-5-d) и матрицу изменения базиса
(Е-16):
(г\ф) = \d3p (r|p)(p|P» = {2nhYm\d'p е~*"рхЩ\>) ■ (Е-25)
В выражении (Е-25) сразу же можно узнать Фурье-образ рх \|/(р), то есть ——\|/(г)
/ дх
[приложение I, C8-а)]. Таким образом:
<r|P|V> = 4v<r|V>.
(Е-26)
В представлении {|г)} оператор Р совпадает с дифференциальным оператором —V,
примененным к волновым функциям. Вычисление матричного элемента оператора вида
(ф|Рг|\|/) осуществляется следующим образом:
(ф|Р^) = /^3г(ф|г)(г|Рг|1|/) = /Лф*(г)
i дх
1|/(г).
(Е-27)
В представлении {|г) } можно также вычислить коммутаторы операторов X, У, Z ,
Рд, Pv, Pz. Например:
(г\[Х,Рх]\ч) = (г\ХРх-РхХ\у) = х(г\Рх\у)-
1JL
i дх
<r|x|V) =
1хтхш-7тххШ=тш-
(E-28)
186

Математический аппарат квантовой механики
Эти вычисления справедливы для произвольного |\|/) и любого кет в базисе |г), из
чего следует, что*
[X4Px] = ih. (E-29)
Аналогично можно найти и другие коммутаторы между компонентами R и Р.
Результат запишем в виде:
[*,
■IP,,
[*,
Rjh
Pj\--
.Pj]--
= 0 |
:0
= '4J
И, где/,./' = 1,2,3,
(Е-30)
где /?,, #2, /?3 и fj, Р2, Р3 обозначают соответственно операторы X, У, Z и Рх, РуУ Pz.
Формулы (Е-30) называются каноническими соотношениями коммутации.
Ь. ЭРМИТОВОСТЬ ОПЕРАТОРОВ R И Р
Чтобы доказать, например, эрмитовость оператора X, достаточно использовать
формулу (Е-23):
(ф|х|\|/) = /^3гф*(г)х\|/(г)=[/^3г\|/*(г)^ф(г)[ =(\|/|х|ф)\ (Е-31)
Согласно §В-4-е равенство (Е-31) является характеристикой эрмитова оператора.
Подобные же рассуждения доказывают, что операторы Y и Z также эрмитовы.
В том, что касается операторов Рх, РуУ Pz, можно использовать аналогичные вычисления
в представлении {| р)}.
Интересный способ доказательства эрмитовости оператора Р основан на использовании
уравнения (Е-26), описывающего его действие в представлении {|г) }. Возьмем, например,
формулу (Е-27) и проинтегрируем ее по частям:
* Коммутатор [Х, Рх\ — это оператор, и со всей строгостью следует писать [X, Рх\ = /Й1.
В дальнейшем мы часто будем использовать в одинаковой роли и оператор 1 и число 1, если только
их различие не будет иметь принципиального значения.
187

Глава II
((p\Px\\v) = -\dy'dzl+_2dxq\r) — \|/(r) =
- \dy'dz\\(p\r)^r)Y~^ -Г~ cU-y(r)— ф*(г)
(E-32)
Поскольку интеграл, определяющий скалярное произведение (ф|^)» сходится, произведение
ф (г)\|/(г) стремится к нулю, если х —> ±°° ; после интегрирования первый член обращается в
нуль и, следовательно:
— -.*
:(\1/|Р,|ф)*. (Е-33)
Э
(ц>\Ф) = -* jd3ry(r)-^<P'(r) =
-JrfVv|/*(r)|-9(r)
i дх
Видно, что наличие мнимого числа i существенно важно: дифференциальный оператор
дх'
действующий на функции пространства &• , не является эрмитовым вследствие изменения знака
. Э П д
при интегрировании по частям; напротив, оператор j— , так же как и оператор ——, является
ox i дх
эрмитовым.
с. СОБСТВЕННЫЕ ВЕКТОРЫ ОПЕРАТОРОВ R И Р
Рассмотрим действие оператора X на кет |г0). Согласно формуле (Е-22-а) имеем:
(г |х|г0) = *(г |г0) = *8(г - г0) = х0д(т - г0) = ^о(г|г0>. (Е-34)
Это равенство означает, что в представлении {|г)} координаты кет-вектора х|г0)
равны координатам кет-вектора |г0), умноженным на х0, то есть
Х|г0) = д:0|г0). (Е-35)
Аналогичные рассуждения сразу же показывают, что кет-векторы |г0) являются также и
собственными векторами операторов Y и Z. Опустив ставший ненужным нулевой
индекс, перепишем полученные равенства в следующей форме:
Х|г) =
Ио=
И;
-х\г)
-М\
= z|r)
(Е-36)
188

Математический аппарат квантовой механики
Таким образом, кет-векторы |г) являются собственными векторами, общими для
операторов X , У и Z, что еще раз свидетельствует в пользу выбранного обозначения |г):
каждый собственный вектор соответствует вектору г с координатами х, уч z,
образующими три непрерывных индекса, соответствующих собственным значениям
операторов X , У и Z.
Подобные аргументы могут быть приведены и в отношении оператора Р, если их
сформулировать в представлении {|р) }. Получим:
|^|р) = р»|
Л|р) = /Ф)
Ир) = Р;|р>|
(Е-37)
ЗАМЕЧАНИЕ
Этот же результат можно получить, исходя из уравнения (Е-26), описывающего
действие оператора Р в представлении {|г)}. Используя (Е-9), получим:
(#)-* £(г|р) Л JL^-'V'' = Р,{Щ'Ш^ = А<г|р>. (E-38)
Все компоненты кет-вектора Рх\р) в представлении {|г)} получаются путем
умножения компонент |р) на константу рх : кет |р) есть собственный вектор
оператора Рх с собственным значением рх.
d. R И Р —НАБЛЮДАЕМЫЕ ВЕЛИЧИНЫ
Соотношения (E-5-b) и (E-5-d) означают, что векторы {|г)} и {|р) } образуют базисы
в пространстве #г. Следовательно, R и Р — наблюдаемые.
Кроме того, задание трех собственных значений jc0, y0, z0 операторов X, У, Z
определяет единственным образом соответствующий собственный вектор |г0): в
представлении {|г)} его координатами являются 8(х - х0) 8( у - yQ) 5(z - z0). Отсюда следует,
что набор трех операторов X , У, Z образует полный набор коммутирующих
операторов в пространстве #г.
189

Глава II
Аналогично можно показать, что три компоненты Рх, Р, Pz также образуют
полный набор коммутирующих операторов в #г.
Отметим, что один оператор X не образует полного набора коммутирующих
операторов в пространстве £г: если индекс х0 зафиксирован, то индексы у0 и z0 могут
принимать любые вещественные значения, так что собственное значение х0 является
бесконечно вырожденным. Напротив, в пространстве состояний <fK в одномерном случае
оператор X образует полный набор коммутирующих операторов, при этом собственное
значение х0 определяет единственным образом соответствующий собственный кет |jc0),
и его координатой в представлении {\х) } является д(х - х0).
ЗАМЕЧАНИЕ
В пространстве %г мы нашли два полных набора коммутирующих операторов: {X, Y , Z }
и { Рх, Ру, Pz }. Далее мы встретим и другие. Отметим, например, набор { X, Ру, Pz }: эти
наблюдаемые коммутируют [уравнения (Е-30)]; с другой стороны, если зафиксировать три
собственных значения xQ, p0y, p0z, им соответствует единственный кет с
соответствующей волновой функцией:
F. ТЕНЗОРНОЕ ПРОИЗВЕДЕНИЕ ПРОСТРАНСТВ СОСТОЯНИЙ
1. Введение
Выше мы ввели пространство состояний физической системы, исходя из понятия
волновой функции частицы. Однако далее рассматривались волновые функции — как
одномерные, так и трехмерные. Понятно, что пространства квадратично интегрируемых
функций одной переменной \\f(x) или трех переменных \|/(г) не совпадают: ^ и tfr,
естественно, различны. Вместе с тем можно ожидать, что пространство #г является
обобщением пространства Кv. Существует ли более точное соотношение между этими
двумя пространствами?
В этом параграфе мы определим и изучим операцию тензорного произведения
векторных пространств* и применим ее к пространству состояний. Это даст нам ответ на
* Эта операция часто называется «произведением Кронекера».
190

Математический аппарат квантовой механики
только что поставленный вопрос: пространство #г можно построить, исходя из
пространства У'х и двух других изоморфных ему пространств ¥-у и %-г (см. ниже § F-4-a).
Подобным же образом в дальнейшем (главы IV и IX) будем поступать в случае
существования у некоторых частиц собственного (или спинового) момента количества
движения: кроме внешних степеней свободы (положение, импульс), которые связаны
с наблюдаемыми R и Р, определенными в tfr, нужно будет учитывать внутренние
степени свободы и вводить спиновые наблюдаемые, действующие в спиновом
пространстве <fs. Тогда полное пространство состояний £ частицы со спином образуется
как тензорное произведение tfr и fts .
Наконец, понятие тензорного произведения пространств состояний позволяет
разрешить следующую проблему. Пусть имеются две отдельные физические системы (S,)
и E2) (например, они могут быть достаточно удалены друг от друга, так, чтобы их
взаимодействием можно было пренебречь); назовем соответствующие им пространства
состояний #", и #2. Допустим теперь, что из этих двух систем образуется единая
физическая система (S ), то есть они сближаются и начинают взаимодействовать между собой.
Каким будет пространство состояний #' такой совокупной системы?
Мы видим, насколько будут полезными определения и результаты этого параграфа
для квантовой механики.
2. Определение и свойства тензорного произведения
Пусть имеются два* пространства: первое — #, с размерностью N, и второе — £2
с размерностью N2 (значения N{ и N2 могут быть конечными или бесконечными).
Векторы и операторы этих пространств будут обозначаться символами с
соответствующими индексами A) или B).
а. ТЕНЗОРНОЕ ПРОИЗВЕДЕНИЕ ПРОСТРАНСТВ <Г
а. Определение
По определению векторное пространство # называется тензорным произведением
пространств if, и $2:
<f = ^®tf2, (F-1)
* Последующие определения без труда распространяются на тензорное произведение
конечного количества пространств.
191

Глава II
если любой паре — вектору ФA)) , принадлежащему пространству #,, и вектору ХB))»
принадлежащему пространству #2,— ставится в соответствие один вектор пространства $,
обозначаемый символом*:
|ф(,))®|%B)), (F-2)
который называется тензорным произведением векторов Ф(,)) и ЗСB)). Это
соответствие должно обладать следующими свойствами:
(i) линейностью относительно умножения на комплексные числа:
[х|фA,)]®|хB,) = а[|фA))®|хB)>];
|ф<")®[ц|Х'2))] = ц[|ф"»)<8)|Х'2')]; (F-3)
(ii) дистрибутивностью относительно векторного сложения:
|ф<1,)®[|х!2)>+1^2,)]Н(р<1)>®1^,)+1ср(',>®1^));
[|фГ)>+|(Р2)>]®|х<2,> = |фГ,>®|х<2))+1(р",)®|х<2,>; (р-4)
(iii) при выборе базиса в каждом из пространств ({ и/1/ ) в ^ и ( г/ / } в ^) ан~
самбль векторов щ образует базис в пространстве # . Если Nl и N2 конечны,
то размерность пространства F равна NlxN2.
Р. Векторы пространства $
(i) Рассмотрим сначала вектор тензорного произведения ф°М®Х( /• Какими бы
ни были векторы Ф(,)) и Х<2))> их всегда можно разложить в базисах {и//} и
(|v/2))}
соответственно:
* Этот вектор можно обозначать как ф ) ® \% )> так и ПС ) ® ф ) : порядок двух
векторов не имеет значения.
192

Математический аппарат квантовой механики
\xm) = lb,\v^). (F-5)
Согласно свойствам, сформулированным в §а, разложение вектора ФA))®ЬсB)) в
базисе { U; (,,)®|v,B)) } имеет вид:
|9(I))®|x,2,)=S«a|",(,,)®|v,,2))- (f-6)
1,1
Итак, компоненты вектора тензорного произведения равны произведениям
компонент двух векторов сомножителей.
(ii) В пространстве W существуют векторы, не являющиеся тензорными
произведениями вектора из Щ на вектор из $2. Действительно, поскольку { w,A)\® v/ / }
является базисом в пространстве %, самый общий вид записи вектора в # имеет вид:
k)=Zc,,|B;,>)®|v/B>). (f-7)
При этом, если мы возьмем Nx x N2 произвольных чисел си, то их не всегда можно
представить в форме произведений а( Ъ{, являющихся результатом перемножения N,
чисел ai на N2 чисел Ъ{. Таким образом, в общем случае нельзя указать такие векторы
Ф(,)) и ХB))> тензорным произведением которых был бы произвольный вектор |\|/).
Однако любой вектор пространства # может быть всегда представлен в виде линейной
комбинации векторов тензорного произведения, как это следует из формулы (F-7).
у. Скалярное произведение в пространстве W
Существование скалярных произведений в пространствах £, и tf2 позволяет
определить также скалярное произведение в #. Сначала определим скалярное произведение
вектора |фС1)%B)) = |ф(,))®|хB)) на вектор |ф'(,) Х'B)) = |ф,A))®|х'<2)), положив:
(Ф>С1>ЗС1B)|ФA>ХС2>> = <Ф>A)|ФС1)> (Х1С2)|ХС2)>- С*"*)
Для двух произвольных векторов пространства $ достаточно тогда использовать
фундаментальные свойства скалярного произведения [уравнения (В-9), (В-10) и (В-11)], по-
13 Квантовая механика
193

Глава II
скольку каждый из этих векторов является линейной комбинацией векторов тензорного
произведения.
В частности, заметим, что базис { w,(,)v/B)) = шAМ® v,B) И ортонормирован, если
каждый из базисов { U// } и ( г/ / ) также ортонормирован:
(и^у™ |W;(,)v;2)> = D° |",{,)>(v/B) | vj2)) = 5,.5/r. (F-9)
b. ТЕНЗОРНОЕ ПРОИЗВЕДЕНИЕ ОПЕРАТОРОВ
(i) Рассмотрим сначала линейный оператор ЛA), определенный в пространстве ^,.
Ему ставят в соответствие линейный оператор ЛA), действующий в пространстве <*,
который называют продолжением оператора ЛA) в пространстве W и определяют
следующим образом.
Если применить оператор ЛA) к вектору — тензорному произведению ФA))®%B)),
то по определению получим:
Л(l)[|ф(,))®|xB))] = [A(l)|ф(l,)]®|xB,). (F-10)
Сделанного выше предположения о линейности ЛA) достаточно, чтобы полностью
определить этот оператор. Действительно, любой вектор |\|/) пространства К можно
представить в форме (F-7). Тогда определение (F-10) позволяет установить действие
АA) на |v>:
AA)|\1/) = Sc,/[aA)[W/A)I(E)|v/B)). (F-ll)
I,/ L 'J I
Аналогично можно получить продолжение ВB) оператора ВB), определенного
исходно в пространстве £2 •
(и) Пусть теперь АA) и ВB) — два линейных оператора, действующих
соответственно в ^ и $2. Их тензорное произведение ЛA) ® ВB) является линейным оператором
в #, определенным следующим соотношением, описывающим его действие на векторы —
тензорные произведения:
[ЛA)®^B)][|ф(,))(х)|хB))] = [лA)|фA))]®[Ж2)|хB)>]. (F-12)
Так же, как и ранее, этого определения достаточно, чтобы охарактеризовать АA) ® ВB).
194

Математический аппарат квантовой механики
ЗАМЕЧАНИЯ
(i) Продолжения операторов являются частными случаями тензорных произведений: если 1A)
и 1B) — единичные операторы в пространствах #, и #2 соответственно, то АA) и
ВB) могут быть записаны в виде:
ЛA) = АA)®1B);
ВB) = 1A)® ВB). (F-13)
Справедливо и обратное утверждение о том, что тензорное произведение АA) ® ВB)
совпадает с обычным произведением двух операторов ЛA) и ВB) в пространстве $ :
АA)®#B) = ДA)ЯB). (F-14)
(ii) Нетрудно показать, что два оператора, например, ЛA) и ВB), коммутируют в
пространстве # :
[ЛA),ВB)] = 0. (F-15)
Для этого достаточно доказать, что ЛA) В{2) и В{2) А{\) дают одинаковый результат,
если подействовать ими на произвольный вектор базиса {\u\l)) ® vj2))}:
^a)fiC2)|M#cl>H|V/C2>) = ДС1) [|и/С1>)в>[вB) |vf<2>)J| = [ACD l**/0)]® [вС2) I v#C2>)]; (F-16)
5c2) acd l^;0)®! v#c2>)=Sc2) [[acd l^j0)]®! v*2>)]=[^(o l^j0)]®^251 v/2>>] • (PM7)
(iii) Проекционный оператор на вектор — тензорное произведение фA))С( / =
= ф(,))® Х( /» являющийся оператором, действующим в пространстве tf, получается
путем тензорного произведения проекционных операторов на векторы ф(,)) и X* /:
|ф(,)ХB,ХфA)ХB) | = |ф("Хф(,) | ® |Х<2,)(Х<2) | • (F-18)
Это соотношение вытекает непосредственно из определения скалярного произведения в
пространстве $ .
(iv) Как и для обычных векторов, в пространстве f существуют операторы, не являющиеся
тензорными произведениями оператора в #, на оператор в #2.
13*
195

Глава II
с. ОБОЗНАЧЕНИЯ
В квантовой механике обычно используют упрощенные по сравнению с
приведенными выше обозначения. Мы также будем пользоваться ими, но в свете дальнейшего
изложения важно четко их сформулировать.
Прежде всего мы уберем символ ®, обозначающий тензорное произведение, и векторы
или операторы, перемножаемые тензорно, будем просто ставить рядом друг с другом:
|ф(,)) |хB)) означает |ф(,))® |%B)); (F-19)
АAЩ2) означает A(l)®BB). (F-20)
Кроме того, будем обозначать одинаковыми символами и продолжение в пространстве
£ оператора пространств £, и £2, и сам этот оператор:
ЛA) означает ЛA) или ЛA). (F-21)
В том, что касается формулы (F-19), то в ней нет никакой двусмысленности, так как
мы никогда не записываем два кет-вектора подряд, как это сделано здесь. Заметим, в
частности, что выражение \\\f) |ф), где |\|/} и |ф) принадлежат одному и тому же
пространству $, в этом пространстве никак не определено: оно представляет собой вектор
пространства V, умноженный тензорно сам на себя.
Напротив, обозначения (F-20) и (F -21) несколько двусмысленны, особенно
последнее, допускающее одно и то же обозначение для двух различных операторов. Однако на
практике мы сможем различать их по вектору, к которому прикладывается тот или иной
оператор: в зависимости от того, идет ли речь о пространстве $ или #,, мы будем иметь
дело с операторами ЛA) или ЛA) в строгом смысле слова. Что касается формулы
(F-20), она не вызывает проблем, если пространства Щ и ^ различны, ибо до сих пор
мы имели дело лишь с произведениями операторов, действующих в одном и том же
пространстве. Можно, однако, рассматривать ЛAMB) как обычное произведение
операторов пространства $, если интерпретировать ЛA) и В{2) как обозначения для ЛA)
и В B) [уравнение (F-14)].
3. Уравнения на собственные значения
в произведении пространств
В предыдущем параграфе важная роль отводилась векторам пространства tf,
которые были образованы путем тензорного перемножения вектора пространства #, на век-
196

Математический аппарат квантовой механики
тор пространства #2. Сейчас мы увидим, что не менее важную роль играют
продолжения операторов пространств #, и #2.
а. СОБСТВЕННЫЕ ЗНАЧЕНИЯ
И СОБСТВЕННЫЕ ВЕКТОРЫ ОПЕРАТОРОВ-ПРОДОЛЖЕНИЙ
а. Уравнение на собственные значения оператора А(\)
Рассмотрим оператор АA), действующий в пространстве £■',, с известными
собственными состояниями и собственными значениями. Допустим, например, что спектр
этого оператора дискретный:
ЛA)|ф;1A)) = а/г|Ф;1A)>; / = 1,2 gn. (F-22)
Будем искать в пространстве $ решение уравнения на собственные значения
продолжения оператора А(\):
A(l)|\|f) = X|v>; |\|/)e*. (F-23)
Из формулы (F-10) сразу же следует, что любой вектор вида (pj,(l)) |%B)) является
собственным вектором оператора АA) с собственным значением ап независимо от
выбора |хB)). Действительно:
АA) | ф!, A))| х B)> [АA) | ф'я A))] | х B)> = а„ | ф'я A))| х B)>. (F-24)
Покажем, что если АA) является наблюдаемой в пространстве #,, то можно найти
все решения уравнения (F-23). При этом ансамбль векторов ф),A)) образует базис в ^ ,
и, следовательно, система ортонормированных векторов U/J;') вида:
|v;;/) = hUD)|v1B)), (F-25)
где {| v, B)) } — базис в пространстве <Г2, образует базис в пространстве #. Таким
образом, известен один ортонормированный базис, составленный из собственных векторов
оператора АA) в %,— hC), а это значит, что решение уравнения (F-23) найдено.
Сказанное выше позволяет сделать следующие заключения:
197

Глава II
— если оператор ЛA) — наблюдаемая в пространстве ^,, то он является также
наблюдаемой в пространстве ¥ . Этот вывод непосредственно следует из того, что
продолжение оператора ЛA) является эрмитовым оператором и что ансамбль { \|/);')}
образует базис в #';
— спектр оператора ЛA) одинаков в пространствах % и <г,, в равенствах (F-22) и
(F-24) фигурируют одни и те же собственные значения ап;
— однако собственное значение ап, имеющее кратность вырождения gn в £,, в
пространстве $ имеет кратность вырождения N2 x gn. Действительно, собственное
подпространство, связанное с ап, в пространстве ^ натянуто на кет-векторы
V!,/= Ф«A))КB)) с фиксированным значением п и / = 1,1,..., #я; / = 1,2,..., N2.
Таким образом, если даже ап в пространстве ^ не вырождено, оно вырождено N2 раз
в пространстве $.
Проекционный оператор на собственное подпространство, соответствующее собственному
значению ап , в пространстве # примет вид [см. (F-18)]:
Ек;^(^:;'|=Е|ф;,A)>(ф;,A)|®|^B))(у/B)|=5:|ф,„>(Ф:1A)|®1B), <f-26)
если воспользоваться соотношением замкнутости для базиса {| vyB)y } в пространстве ^2. Таким
образом, это выражение является продолжением проекционного оператора:
^,A)=1|ф:,A)(ф:,A)|)
в пространстве £, .
Р. Уравнение на собственные значения оператора А{\) + ВB)
В дальнейшем нам часто придется сталкиваться с поиском решения уравнений на
собственные значения в пространстве — тензорном произведении операторов вида:
С= АA) + ЯB), (F-27)
где ЛA) и ВB) — наблюдаемые, для которых известны собственные значения и
собственные векторы в пространствах #*, и <*2 соответственно:
ЛA)|ф„A)) = а„|ф„A));
198

Математический аппарат квантовой механики
ВB)|х/)B)) = Ь/)|х;)B)) (F-28)
[для упрощения записи допустим, что спектры операторов ЛA)и 5B) дискретны и не
вырождены в пространствах К", и tf2].
Известно, что ЛA) и ВB) коммутируют [формулы (F-16) и (F-17)], и векторы
|ф„A)) %/;B)), образующие базис в пространстве #*, являются собственными
векторами, общими для операторов ЛA) и ВB):
АA)|ф„A))|х„B))=ал|ф„A))|х;,B)>;
ВB) |Ф„A)> |х„B)> = *>„(!)) |x,B)). (F-29)
Они являются также собственными векторами оператора С :
Ф„A)) |ХРB)) =(а.+Ь„)|фяA)> |хРB)>, (F-30)
откуда сразу же следуют решения уравнения на собственные значения оператора С .
Итак, собственные значения оператора С = А(\) + ВB) являются суммами
собственного значения оператора АA) и собственного значения оператора ВB); моэюно
всегда найти базис собственных векторов оператора С, которые являются
тензорными произведениями собственного вектора оператора АA) и собственного вектора
оператора ВB).
ЗАМЕЧАНИЕ
Уравнение (F-30) показывает, что собственные значения оператора С имеют вид
суммы с = ап + Ь . Если нельзя найти две различные пары значений пир, дающих
одно и то же значение с , то оно является невырожденным (напомним, что мы
предположили, что ап и Ъ не вырождены в пространствах #", и #'2 соответственно); собственный
вектор соответствующего оператора С неизбежно является тензорным произведением
ФнA)) РС»B)/ • Если, напротив, собственное значение с вырождено, например, дважды
(имеются такие т и q , что с — с ), можно лишь утверждать, что любой собственный
вектор оператора С , соответствующий этому собственному значению, равен:
^|ф„A))|х/,B)) + ц|ф„,A)>|х(/B)), (F-31)
199

Глава II
где X и |Ы — произвольные комплексные числа; в этом случае существуют лишь
собственные векторы оператора С , не являющиеся тензорными произведениями.
Ь. ПОЛНЫЕ НАБОРЫ КОММУТИРУЮЩИХ ОПЕРАТОРОВ В ПРОСТРАНСТВЕ £
Сейчас мы, наконец, покажем, что если выбрать полные наборы коммутирующих
операторов в пространствах <f, и <?2, то сразу же получаем полный набор
коммутирующих операторов в пространстве <f.
Для определенности предположим, что оператор ЛA) сам по себе образует полный
набор коммутирующих операторов в пространстве #',, а аналогичный набор в
пространстве £2 состоит из двух наблюдаемых ВB) и СB). Это означает (см.§ D-3-b), что все
собственные значения ап оператора ДA) в пространстве <?\ являются простыми:
АA)|фД1)) = д,,|ф,,A)), (F-32)
поскольку кет |ф„A)) с точностью до постоянного множителя является единственным;
напротив, в пространстве Щ некоторые из собственных значений Ь оператора В{2)
являются вырожденными, как и некоторые собственные значения сг оператора СB);
однако базис собственных векторов, общих для В{2) и СB) в пространстве £2, является
единственным, так как существует лишь один кет (с точностью до множителя), который
был бы собственным вектором операторов В{2) и СB) с фиксированными
собственными значениями Ьр и сг:
|5B)|х,гB)) = ф,„B));
СB) |x„B)) = ф„B)); (F-33)
Р„Д2)).
В пространстве # кратность вырождения собственных значений ап равна N2 (см.
§F-3-a); и, следовательно, оператор АA) сам по себе уже не образует полного набора
коммутирующих операторов. Кроме того, существуют Nl линейно независимых кет-
векторов, являющихся собственными векторами операторов ВB) и СB) с
собственными значениями Ъ и сг соответственно, и набор операторов (ВB), СB) } не является
полным. Однако в § F-3-a мы видели, что собственные векторы, общие для трех
коммутирующих наблюдаемых АA), В{2) и СB), имеют вид |фпA) %7,гB))= |ф„A)) |%,,Д2)) :
200

Математический аппарат квантовой механики
ЛA) |ф„A)Х/,Д2)) =а/1|Ф;1A)%/,Д2));
Ж2) |ф„A)ХрД2)) =^|ФлA)х^B));
СB) |фяA)Х„B)) = сг |ф/Д1)Х„Д2)). (F-34)
Ансамбль векторов { Ф/,A)%/,гBп } образует в пространстве V базис, поскольку то же
можно сказать относительно наборов векторов {|ф„A))} и { %;„.Bп } в пространствах
£, и £2 соответственно. Кроме того, если зафиксировать набор из трех собственных
значений { ап, Ьр9 сг}, ему соответствует единственный вектор ф„A) % Bп. Таким
образом, операторы ЛA), В{2) и СB) образуют полный набор коммутирующих операторов
в пространстве £.
Сказанное выше можно без труда обобщить: объединяя два набора коммутирующих
наблюдаемых, полных в пространствах $Л и $2 соответственно, получаем полный
набор коммутирующих наблюдаемых в пространстве $.
4. Примеры применения
а. СОСТОЯНИЯ ЧАСТИЦЫ В ОДНОМЕРНОМ И ТРЕХМЕРНОМ ПРОСТРАНСТВАХ
а. Пространства состояний
В свете изложенного выше вернемся к задаче, сформулированной в § F-1: как связаны
пространства #х и ^г ?
#х — одномерное пространство состояний частицы, то есть пространство состояний,
связанное с волновыми функциями ф(х). В $х рассмотренная в § Е-2 наблюдаемая X
сама по себе составляет полный набор коммутирующих операторов (§ E-2-d), ее
собственными векторами являются базисные кет-векторы представления {\х)}. В этом
представлении кет |ф) пространства fx характеризуется волновой функцией ф(лг) =(х|ф);
в частности, кет-вектору \х0) соответствует функция £,х0(х) = 8(х-х0).
Аналогично можно ввести пространства $у и ttz с помощью волновых функций
%(у) и co(z). Наблюдаемая Y образует полный набор коммутирующих операторов в $ ,
то же самое можно сказать относительно наблюдаемой Z в пространстве £.. Соответ-
201

Глава II
ствующие собственные векторы — это базисные кет-векторы {| у) } и {| z) } в Fv и Yz
соответственно. Вектор \%) пространства V (или вектор |со)пространства Vz) в
представлении {| у)} (или {| z)}) характеризуется функцией%(у) = (у\х) (или <o(z) = (г|х));
функция, соответствующая базисному кет | у0) (или | z0)), равна 5(у - у0) [или 8(г - г0) ].
Образуем теперь тензорное произведение:
^=^®^®tf.. (F-35)
Базис в пространстве ^, получим путем тензорного перемножения базисов [\х)}9
{| у)} и (\z) } и обозначим его символом { |jc, j, z)}, то есть
\x,y,z) = \x)\y)\z). (F-36)
Кет-векторы этого базиса являются одновременно собственными векторами
продолжений операторов X , Y и Z в пространстве <fvy,:
х|дг, у, г) = *|*, у, г);
У\х* у, z) = y\x, у, z)\
Z\x, у, z) = z\x, у, z). (F-37)
Таким образом, пространство # совпадает с £Г — трехмерным пространством частицы,
и кет | х, у, z) совпадает с |г):
\x,y,z) = \r) = \x)\y)\z). (F-38)
где ху у, z в точности равны декартовым координатам радиуса-вектора г.
В пространстве tfr имеются кет-векторы |ф%со) = |(р) |%) |со), являющиеся тензорным
произведением трех кет-векторов из пространств ^, # и ¥<z. Их компоненты в
представлении {|г) } равны [см. формулу (F-8)]:
(г|фХю)=(дг|<р)(у|хХгИ. (F-39)
Таким образом, соответствующие волновые функции являются факторизованными:
4>(х), %()>), со(г). Это касается и самих базисных векторов:
202

Математический аппарат квантовой механики
(r\rQ) = 8(r-r0) = 8(x-x0)8(y-y0M(z-z0). (F-40)
Отметим, что самый общий вид состояния в пространстве ftr не таков. Он выглядит как:
\\p) = jdx-dydz-\V(x4 у, z)\x, у, z). (F-41)
В функции \|/(дс, у, z) = (x, у, z |\|/) зависимости от переменных х, у, z в общем случае
не факторизуются: соответствующие кет-векторам пространства ftr волновые функции
являются функциями всех трех переменных.
Результаты, полученные в § F-3, позволяют понять, почему оператор X , сам по себе
образующий полный набор коммутирующих операторов в %х, не обладает этим
свойством в пространстве ftr (см. § F-2-d): собственные значения его продолжения в ftr и в ftt
одни и те же, но они становятся бесконечно вырожденными вследствие того, что
пространства ftv и ft, имеют бесконечные размерности. На основе полного набора
коммутирующих операторов в Yx, ftv и ft. можно сконструировать новые в пространстве ftr:
например, { X, У, Z } или { РЛ, У, Z}, поскольку Рх образует полный набор
коммутирующих операторов в ftv, или { Рх, Ру, Z } и т.д.
C. Важное приложение
Если в пространстве ftr требуется решить уравнение на собственные значения
оператора Я вида:
H = HX + Hy + Hz, (F-42)
где Яг, Яу и Яг — продолжения наблюдаемых, действующие в пространствах fx, fty
и ftz , можно использовать рассуждения, приведенные в § F-3-a-p (на практике бывает,
например, что оператор Нх является продолжением наблюдаемой пространства $х, так
как он построен из операторов X и Рх). Тогда сначала ищут собственные значения и
векторы операторов Нх в ftx, Яу в ftv и Hz в ft,:
я,|х,)=*;к);
Яг|<ог) = Егг|а)г). (F-43)
203

Глава II
Собственные значения оператора Н будут тогда иметь вид:
Я"'"''= £;+£; + £;, (F-44)
и соответствующий собственный вектор является тензорным произведением
|ф;1) \Хр) |wr)' a волновая функция, связанная с этим вектором, является
произведением:
Ф„(*) ХР(У) ©r(z) = {A^n){y\xP)(z\^r).
Именно такая ситуация рассмотрена в дополнении FT (§ 2) для обоснования
важности одномерных моделей. Речь там шла о дифференциальных операторах, действующих
на волновые функции:
Я = -—A + V(r). (F-45)
2т
Этот оператор можно разложить, как и в (F-42), для частного случая, когда потенциал
может быть представлен в виде суммы:
V(r) = Vx(x) + V2(y) + V3(z). (F-46)
Ь. СОСТОЯНИЯ СИСТЕМЫ, СОСТОЯЩЕЙ ИЗ ДВУХ ЧАСТИЦ
Рассмотрим физическую систему, состоящую из двух частиц без спина, которые
будем различать по нумерации A) и B). Чтобы описать ее в рамках квантовой механики,
можно обобщить понятие волновой функции, введенное для одной частицы: состояние
системы в данный момент времени характеризуется функцией шести пространственных
переменных \|/(гр r2) = V|/(*,, ух, z,; х2, у2, z2). Вероятностная интерпретация такой
волновой функции двух частиц формулируется следующим образом: вероятность
df?(rx, r2) того, что в рассматриваемый момент времени частица A) находится в объеме
d*rx=dx{dyxdzx вблизи точки с радиусом-вектором г, и частица B) — в объеме
d3r2 = dx2dy2dz2, определяется выражением:
d9(jx, г2) = С\щгх, r2 )|2 d\ d\ . (F-47)
Константа нормировки С получается из условия, что полная вероятность равна 1
(сохранение числа частиц; см. § В-2 главы I):
204

Математический аппарат квантовой механики
± = jd\.d\2\y(r{,r2)\\ (F-48)
что требует квадратичной интегрируемости функции \|/(г,,г2) в шестимерном
пространстве.
Рассмотрим теперь пространство £г состояний частицы A). В нем можно
определить представление (|г,) } и наблюдаемые X,, Yx, Z,. Аналогично, в пространстве #ri
состояний частицы B) можно ввести представление {|г2) } и наблюдаемые Х2, К>, Z2.
Найдем тензорное произведение:
я =jr ®£r . (F-49)
г,г2 г, г2 v /
Ансамбль векторов:
|r1,r2) = |rI)|r2) (F-50)
образует базис в пространстве #гг и, следовательно, произвольный кет |\|/) этого
пространства может быть представлен в виде:
| V> = J A d\ \|/(rp r2)|rp r2), (F-51)
где
V(r1,r2) = (rl,r2|\|/}. (F-52)
Кроме того, квадрат нормы вектора |\j/) равен:
(V|V> = JA ^г2|\|/(грг2)|2. (F-53)
Для того чтобы эта величина была конечной, нужно, чтобы функция \j/(r,,r2) была
квадратично интегрируемой. Итак, каждому кет-вектору пространства #
соответствует волновая функция V|/(r,,r2): пространство состояний системы двух частиц есть
тензорное произведение пространств, соответствующих каэюдой из частиц. Полный
набор коммутирующих операторов в пространстве Ш-Т Ti получается путем объединения
операторов (например, XX,YX,ZX и Х2, F2,Z2).
205

Глава 11
Предположим, что состояние системы описывается кет-вектором — тензорным произведением:
kHv,)|v|/2)- (P-54)
Соответствующая волновая функция тогда факторизуется:
\|/(r„r2)= (r,,r2|i|/}= (r,^,) (r2jl|/2) = \|/1(r,)\j/2(r2). (F-55)
В этом случае говорят, что между двумя частицами отсутствует корреляция. В дополнении Dm
мы проанализируем физические последствия такой ситуации.
Выводы этого параграфа могут быть обобщены: если физическая система
образована из двух или нескольких более простых систем, ее пространство состояний является
тензорным произведением пространств, соответствующих каждой из составляющих ее
частей.

ДОПОЛНЕНИЯ К ГЛАВЕ II
Ац. Неравенство Шварца.
Вц. Некоторые полезные свойства
линейных операторов.
Сц. Унитарные операторы.
Dn. Детальное рассмотрение
представлений ||г)| и ||р)}«
Ец* Несколько общих свойств наблюдаемых
Q и Р, коммутатор которых равен ih .
Fh. Оператор четности.
Gn. Применение свойств тензорного
произведения: двумерная
потенциальная яма бесконечной
глубины.
Нц. Упражнения.
Ац, Вц, Сц: повторение некоторых
определений и полезных математических результатов
(элементарный уровень), предназначенное
для читателей, не очень хорошо знакомых с
этими понятиями; на эти дополнения будем
ссылаться в дальнейшем (особенно на
дополнение Вц)..
Dn: можно читать сразу на уровне главы II.
Ец: вводит общий формализм и оператор
трансляции; можно изучать в другое время.
Fu: изучение оператора четности, очень
важного в квантовой механике; простая
иллюстрация понятий главы II; рекомендуется для
первого чтения.
Gn: простое применение тензорного
произведения (§ F главы II); можно рассматривать
как упражнение.
Ни: упражнения 11 и 12 приведены с
решениями; их цель — ознакомление со
свойствами коммутирующих операторов.
207

Глава II
Дополнение Ац
НЕРАВЕНСТВО ШВАРЦА
Каким бы ни был кет |\|/) пространства Р, имеем:
(\\f | \|/) — вещественное число > 0; A)
обращение в нуль возможно лишь в том случае, когда вектор \\\f) тождественно равен
нулю [см. уравнение (В-12) главы II]. Сейчас мы увидим, что из неравенства A) можно
вывести неравенство Шварца; последнее говорит о том, что если |ф,) и |ф2) —
произвольные кет-векторы пространства % , то
!(<PiM ^(ф1|Ф|)(ф2|ф2>
B)
Равенство возможно лишь в том случае, если |ф,) и |ф2) пропорциональны.
Действительно, считая известными |ф^ и |ф2), рассмотрим кет |\|/), определенный
формулой:
kH<p,)+*|<p2), C)
где X — произвольный параметр. Независимо от X имеем:
<Ч/|^> = <Ф,|ф1> + ^(ф1|ф2)-н^(ф2|ф1> + Л,Я*(ф2|ф2>>0. D)
Выберем для X значение:
х-Ж- E)
(Ф2|Ф2>
Тогда в формуле D) второй и третий члены правой части равны и противоположны по
знаку четвертому члену, вследствие чего она приводится к виду:
У (Ф2|Ф2>
Поскольку (ф21 ф2) > 0, можно умножить это неравенство на (ф21 ф2) и получить:
208

Математический аппарат квантовой механики
(Ф.|ф.)(ф2|ф2>^(ф.|ф2)(ф2|ф.)^ G)
что совпадает с неравенством B). В формуле G) равенство может быть реализовано
только в том случае, если (\|/|\|/) = 0, то есть согласно C), если |ф,) = -А. |ф2) (кет-
векторы |ф,) и |ф2) пропорциональны).
Дополнение Вц
НЕКОТОРЫЕ ПОЛЕЗНЫЕ СВОЙСТВА
ЛИНЕЙНЫХ ОПЕРАТОРОВ
1. След оператора.
a. Определение.
b. След является инвариантом.
c. Важные свойства.
2. Алгебра коммутаторов.
a. Определение.
b. Свойства.
3. Сужение оператора в подпространстве.
4. Функции операторов.
a. Определение. Простейшие свойства.
b. Важный пример: оператор потенциала.
c. Коммутаторы с функцией оператора.
5. Дифференцирование оператора.
a. Определение.
b. Правила дифференцирования.
c. Примеры.
d. Применение: полезная формула.
Цель данного дополнения — напомнить некоторые определения и полезные свойства
линейных операторов.
14 Квантовая механика
209

Глава II
1. След оператора
а. ОПРЕДЕЛЕНИЕ
Сумма диагональных элементов матрицы оператора А называется следом и
обозначается символом tr A .
Если пространство <f определяется дискретным ортонормированным базисом {|wf.) },
то по определению:
trA = £(M/|A|M/), A)
если же этот ортонормированный базис {| wa) } является непрерывным, то
tvA = \da(wa\A\wa). B)
Если & — бесконечномерное пространство, то след оператора А определен лишь при
условии сходимости выражений A) и B).
Ь. СЛЕД ЯВЛЯЕТСЯ ИНВАРИАНТОМ
Сумма диагональных элементов матрицы, представляющей оператор А в некотором
базисе, не зависит от выбора этого базиса.
Докажем это свойство на примере перехода из одного дискретного ортонормиро-
ванного базиса {|и.) } в другой ортонормированный базис [\tk) }. Имеем:
S(",HI",> = S(",|[s|'*>(^|]^|»,) О)
I I L к J
(здесь использовано соотношение замкнутости для состояний \tk}). Правая часть
выражения C) может быть преобразована следующим образом:
1Ы1к)Aк\А\и1) = ^Aк\А\и,)(и,\1к) D)
i,k i,k
(действительно, можно переставить местами два числа в произведении). Затем можем
заменить в формуле D) £|и/)(м/| на 1 (соотношение замкнутости для состояний |w,)) и
в конце концов получим:
210

Математический аппарат квантовой механики
£(«Ф|и,> = Х('*14*>. E)
i k
Это равенство в выбранном частном случае подтверждает сформулированное выше
свойство.
ЗАМЕЧАНИЕ
Если оператор А — наблюдаемая, можно вычислить tr А в базисе
собственных векторов оператора А . Диагональные матричные элементы равны при этом
собственным значениям ап оператора А (с кратностью вырождения gn), и след
окажется равным:
fr Л = ££,.*„• F)
с. ВАЖНЫЕ СВОЙСТВА
tr АВ = tr BA ; G-а)
tr ABC = tr BCA = tr CAB . G-b)
В общем случае след произведения любого количества операторов инвариантен по
отношению к циркулярной перестановке этих операторов.
Докажем, например, равенство G-а). Имеем:
tr АВ = £(«, | АВ\щ) = 2(и, | A\Uj){uj \в\и,)= 2(и, | В |и,)(и, | a\Uj) =
= £(w;J#A|w7.} = tr£A (8)
(здесь дважды использовано соотношение замкнутости в базисе {\и:) }). Таким образом,
равенство G-а) доказано, а его обобщение G-Ь) не представляет трудностей.
2. Алгебра коммутаторов
а. ОПРЕДЕЛЕНИЕ
Коммутатор [А, В] двух операторов по определению равен:
[А,В] = АВ-ВА. (9)
14*
211

Глава II
b. СВОЙСТВА
[Л, д] = -[/?, А]; A0)
[А,(Д + С)] = [А,Д] + [А,С]; A1)
[А, ВС] = [А, В]С+ В[АУ С]; A2)
[а, [Б, С]] = [5, [С, А]] + [С [А, ^]] = 0; A3)
[А,Я]+=[/Г,А+]. A4)
Доказательство этих свойств не представляет трудностей: достаточно раскрыть обе части
равенств и сравнить их между собой.
3. Сужение оператора в подпространстве
Пусть Рц — проекционный оператор в q -мерном подпространстве # ,
образованном q ортонормированными векторами |ф,):
П = £|ф,)(ф,! A5)
По определению сужение Aq оператора А в подпространстве $ равно:
\ = PqAPq. A6)
Если | \|/) — произвольный кет, это равенство требует, чтобы
Aj\|/)=^A|^), A7)
где
является ортогональной проекцией вектора | \|/) в пространстве $ . Таким образом, чтобы
подействовать оператором Ац на произвольный кет | \|/), нужно сначала спроектировать
212

Математический аппарат квантовой механики
этот кет на пространство # ; затем нужно подействовать оператором А на эту проекцию
и сохранить лишь проекцию полученного кет-вектора в пространстве tq. Оператор Ац,
преобразующий любой кет пространства # в кет, принадлежащий тому же
подпространству, является оператором, действие которого ограничено пространством #q.
Что можно сказать относительно матрицы, представляющей оператор Aq ? Выберем
базис {|^)}, в котором первые q векторов принадлежат пространству £ (например,
это векторы | ф,)), а другие принадлежат дополнительному подпространству. Тогда имеем:
(И/| Д,|иу) = (И/|Р,АР,|Иу), A9)
то есть
/ I - I \ \Ы\ a\u\ если I, j<q\
W/ AL.)= Л 'I I '/' . \ B0)
x ' q] J/ lo, если i, j>q.
Матрица, представляющая Aq, оказывается в некотором смысле «вырезана» из
матрицы Л: сохраняются лишь те матричные элементы оператора А, которые связаны с
базисными векторами \и() и шЛ, принадлежащими пространству ^ , а остальные матричные
элементы заменяются нулями.
4. Функции операторов
а. ОПРЕДЕЛЕНИЕ. ПРОСТЕЙШИЕ СВОЙСТВА
Рассмотрим произвольный линейный оператор А\ нетрудно определить оператор А":
это оператор, соответствующий л-кратному последовательному применению оператора А .
Определение оператора А, то есть оператора, обратного оператору А , хорошо известно:
А-1, если он существует, удовлетворяет равенству:
А-1А = АА_1=1. B1)
Как определить в общем случае произвольную функцию оператора? Для этого
рассмотрим функцию F переменной z ; предположим, что в некоторой области можно
разложить F в ряд по z :
F(z)=tfnzn. B2)
л=0
213

Глава U
По определению функция, соответствующая оператору А, является оператором F(A),
определенным рядом, имеющим те же самые коэффициенты fn:
^(А)=2/ЯАЯ. B3)
/1=0
Например, оператор еА определяется как
еА = % — = l+A + A2/2\ + ... + An/n\+... B4)
„=о п\
Мы не станем заниматься проблемами, связанными со сходимостью ряда B3),
зависящими от собственных значений оператора Л и от радиуса сходимости ряда B2).
Заметим, что если F(z) является вещественной функцией, то коэффициенты fn
также являются вещественными; если, кроме того, А — эрмитов оператор, то из B3)
видно, что F(z) — также эрмитов оператор.
Пусть |фя) — собственный вектор оператора А, соответствующий собственному
значению а:
А|фа) = *|фЯ)- B5)
Применив оператор А последовательно п раз, получим:
А-|фв) = а-|Фв>. B6)
Применим теперь ряд B3) к |фа) и получим:
KA)\V.)= ifna"\(pa) = F(a)\(pa). B7)
/« = 0
Отсюда следует правило: если |фа)— собственный вектор оператора А с
собственным значением а, то |фа) также является собственным вектором оператора F(A) с
собственным значением F(a).
Это свойство позволяет нам дать второе определение функции оператора:
рассмотрим диагонализируемый оператор А (это всегда справедливо, если Л — наблюдаемая)
и будем считать, что работаем в базисе, где матрица оператора А диагональна (ее
элементы являются собственными значениями а{ оператора А ); тогда F(A) по
определению является оператором, который в том же базисе представлен диагональной матрицей
с элементами F(a{).
214

Математический аппарат квантовой механики
Например, если о: — матрица вида:
(I 0]
а, =
* 10 -lj
е 0 ^
сразу же имеем:
;о \/е)
B8)
B9)
ЗАМЕЧАНИЕ
При использовании функции операторов следует проявлять осторожность в
отношении порядка следования операторов. Например, операторы елев, евеА,ел*в
в общем случае не равны, если А и В —.операторы, а не числа. Действительно,
имеем:
АР ЦЧ APRq
еАев =1^1^-1^', C0)
R4 Ap Rq Ap
еВел =1—1^=1^-', CD
ч q\ р Р}- р.ч PW-
еА+в=Ъ(А + ВУ . C2)
р Р1
Если А и В — произвольные операторы, то правые части уравнений C0),
C1) и C2) не обязательно должны быть равны (см. упражнение 7 дополнения Нц).
Лишь при условии, что А и В коммутируют, имеем:
[АчВ] = 0=>еАев=евеА=еА + в C3)
(это соотношение, впрочем, очевидно, если рассматриваются диагональные
матрицы, представляющие ел и ев в базисе собственных векторов, общих для
операторов А и В).
Ь. ВАЖНЫЙ ПРИМЕР: ОПЕРАТОР ПОТЕНЦИАЛА
В одномерных задачах мы часто будем встречаться с оператором «потенциала» (его
так называют, поскольку он соответствует классической потенциальной энергии V(x)
частицы в силовом поле), где V(X) — функция оператора положения X .
215

Глава II
Из предыдущего параграфа следует, что V(X) допускает в качестве собственных
векторы | х) оператора X , в результате чего
V(X)\x) = V(x)\x). C4)
Матричные элементы оператора V(X) в представлении {\х)) равны:
(x\V{X)\x') = V(x)8(x-x'). C5)
Применив C4) и используя эрмитовость оператора V(X) (функция V(x)
вещественная), получим:
(x\V(X)\xv) = V(x)(x\\v) = V(x)xv(x). C6)
Это равенство показывает, что в представлении {\х)} действие оператора V(X) состоит
в простом умножении на V(x).
Обобщение формул C4), C5) и C6) на трехмерные задачи производится без труда:
в этом случае получим:
V(R)|r) = V(r)|r); C7)
(r|K(R)|r') = V(rM(r-r'); C8)
(r|V(R)|\|/) = V(r)\|/(r). C9)
с. КОММУТАТОРЫ С ФУНКЦИЕЙ ОПЕРАТОРА
Определение B3) показывает, что оператор А коммутирует с любой функцией
оператора А :
[Л, F(A)] = 0. D0)
Аналогично, если операторы А и В коммутируют, то коммутируют операторы F(A) и В:
[В,А] = 0 =>[£,F(A)] = 0. D1)
Какой результат получится, если вычислить коммутатор некоторого оператора с
функцией другого оператора, не коммутирующего с ним? Ограничимся лишь случаем
операторов X и Р, коммутатор которых равен:
216

Математический аппарат квантовой механики
[X,P] = ih. D2)
Используя соотношение A2), можно найти:
[х, Р2] = [X, РР] = [X, Р]Р + Р[X,Р] = 2/ЙР . D3)
В более общем виде можно показать, что
[x9Pa] = ihnP*-1. D4)
Если допустить, что это равенство доказано, то
[х, Р"+1] = [х, РР"] = [х, р]р" + р[х, Pn] = ihP" +тпРР"'* = ih(n + l)P". D5)
Тогда соотношение D4) устанавливается путем рекурсии.
Вычислим теперь коммутатор [X, F(P)]:
[x,F(P)] = S[x,/„P"] = E//in/;jP'»-1. D6)
/> /i
Если F'(z) — производная от функции F(z), то выражение D6) является
определением оператора F(P). Итак:
[XyF(P)] = ihF(P). D7)
Аналогичные рассуждения позволяют установить симметричное соотношение:
D8)
[P,G(X)] = -//*G'(X)
ЗАМЕЧАНИЯ
(i) Приведенные выше рассуждения основаны на том, что F(P) (или G(X)) зависят
только от Р (или от X). Труднее вычислить коммутатор вида [ Х,Ф(Х,Р)], где
Ф(Х,Р) — оператор, зависящий одновременно от X и от Р: трудность состоит
в том, что операторы X и Р не коммутируют.
(ii) Уравнения D7) и D8) могут быть обобщены на случай двух операторов А и В,
коммутирующих со своим коммутатором. Действительно, совершенно
аналогичные предыдущим рассуждения показывают, что если
[А,С] = [Я,С] = 0 D9)
217

Глава II
С = [АЧВ], E0)
то
[AyF(B)] = [A,B]F(B). E1)
5. Дифференцирование оператора
а. ОПРЕДЕЛЕНИЕ
Пусть A(t) — оператор, зависящий от некоторой переменной t. По определению
dA
производной —от оператора A(t) no t является предел (если он существует):
dt
dA=l.mA(t + b)-m
dt *'-о Ar
Матричные элементы оператора A(t) в некотором базисе векторов |м,), не
зависящих от t, являются функциями переменной t:
(щ\А\и,) = Ац{г). E3)
/ I dA I \ ^ *
= ^w, I — иj) матричными элементами оператора — ; можно без труда
Назовем —
\dt)
доказать, что
'dA\ d
А \ Л V E4>
dt )ij dt J
Таким образом, получается очень простое правило: чтобы получить матричные элементы
- dA
оператора производной —, достаточно взять матрицу, представляющую оператор А
dt
и продифференцировать каждый из ее элементов (не меняя его положения).
Ь. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
Они аналогичны правилам, известным для обычных функций:
d , ^ лч dF dG ,^ч
— (F + G)=—+—-; E5)
dt dt dt
218

Математический аппарат квантовой механики
dt dt dt
E6)
Однако следует соблюдать осторожность и не менять порядка следования операторов в
формуле E6).
Докажем, например, второе из этих равенств. Матричные элементы оператора FG
равны:
(M/|FG|W>) = S(",|F|W,)(W,|G|Wy).
E7)
Мы видели, что матричные элементы оператора —(FG) являются производными по t от
dt
элементов оператора (FG); таким образом, дифференцируя правую часть формулы E7),
получим:
d ,_i \ уГ/ xdFx v/ , „\ \ . / , „, х/ xdG
к
^1^(те)К)-х|<ц,|^к><«*|сК)+(«,|гк>(«.15-к>
Х '■ At At I J/
E8)
Это равенство справедливо для любых / и j , и, следовательно, формула E6) доказана.
с. ПРИМЕРЫ
Вычислим производную оператора ем . По определению имеем:
/, = 0 П\
Дифференцируя ряд почленно, получим:
dt
е» ш % п^-?—АЪ
,.=0 И!
„-I (п-1)!
(АО"
.-I (п-1)!
А.
E9)
F0)
В квадратных скобках стоит ряд, сходящийся к е ' (в качестве индекса
суммирования следует взять р = п -1). В результате получим:
" „AI Л„Л1 „At л
— е = Ае = е А.
dt
F1)
219

Глава II
В этом простом случае, когда в функцию входит только один оператор, нет
необходимости следить за порядком множителей, ибо операторы eAt и А коммутируют.
Дело обстоит иначе, если, например, дифференцируют оператор вида eA,eBt;
применив формулы E6) и F1), получим:
— (eAteBt) = AeAteBt + eAtBeBt. F2>
Правую часть этого равенства можно преобразовать к виду eAtAeBt + eAtBeBt или
eAtAeBt + eAteBlB ; однако получить выражение типа (А + В)еAtеfl/невозможно (конечно,
за исключением случая, когда операторы А и В коммутируют). В этом случае порядок
операторов существенно важен.
ЗАМЕЧАНИЕ
Даже в том случае, когда в функцию входит один оператор,
дифференцирование не всегда может быть выполнено по правилам, определенным для обычных
функций. Например, если A(t) зависит от времени произвольным образом,
производная —емп в общем случае не равна —емп; действительно, разложив емп в
dt dt
ряд по А@ > нетрудно увидеть, что для реализации равенства необходимо, чтобы
dA
операторы A(t) и — коммутировали.
d. ПРИМЕНЕНИЕ: ПОЛЕЗНАЯ ФОРМУЛА
Рассмотрим два оператора А и В, которые коммутируют с их коммутатором.
Докажем, что в этом случае выполняется соотношение:
е е = е е1 , F3)
„А В A+B-tl*'*]
называемое иногда формулой Глаубера.
Действительно, определим оператор F(t), как функцию вещественной переменной t,
формулой:
F(t) = eAteBt. F4)
Имеем:
— = АеА,ет + eAtBeBt = (А + eAtBe~At )F{t). F5)
dt
220

Математический аппарат квантовой механики
Поскольку А и В коммутируют с коммутатором этих операторов, можно применить
формулу E1) и вычислить равенство:
[И\я] = г[А, B]eAt. F6)
Тогда:
eAtB = BeAt +t[Ay B]eAt. F7)
Умножим справа обе части равенства на e~At и, подставив соотношение, полученное
в F5), получим:
^ = (л + 5 + г[Л, B])F(t). F8)
Операторы А + В и [А, В] в соответствии со сделанным предположением
коммутируют; следовательно, можно проинтегрировать дифференциальное уравнение F8) так,
как если бы А + В и [Л, В] были числами, то есть
(A + B)t + -\A,b]t2
F(t) = F@)e 2l ] . F9)
Положив t = О, заметим, что F@) = 1 и, следовательно:
F(t) = e 2l J . G0)
Теперь положим t = 1 и получим равенство F3), что и требовалось доказать.
ЗАМЕЧАНИЕ
Если операторы А и В произвольные, то равенство F3) в общем случае не
удовлетворяется: необходимо, чтобы и оператор А , и оператор В коммутировали бы
с коммутатором [Л, В\. Это условие может казаться весьма жестким, но на самом
деле в квантовой механике часто встречаются операторы, коммутатор которых
является числом: примерами могут служить операторы X и Р или операторы а
и а* гармонического осциллятора (см. главу V).

Глава II
Дополнение Си
УНИТАРНЫЕ ОПЕРАТОРЫ
1. Общие свойства унитарных операторов.
a. Определение. Простые свойства.
b. Унитарные операторы и изменение базиса.
c. Унитарная матрица.
d. Собственные значения и собственные векторы унитарного оператора.
2. Унитарное преобразование операторов.
3. Инфинитезимальный унитарный оператор.
1. Общие свойства унитарных операторов
а. ОПРЕДЕЛЕНИЕ. ПРОСТЫЕ СВОЙСТВА
По определению оператор U называется унитарным, если обратный ему оператор
U~x и эрмитово сопряженный [/""равны:
U+U=UU+=1. A)
Рассмотрим два произвольных вектора |\|/,) и|\|/2) пространства f и два
результирующих вектора |\j/,) и |\j/2), полученных в результате действия на них оператора U :
|9i> = t/|Vi>;
|ф2) = £ф2). B)
Вычислим их скалярное произведение:
D\\4i) = {V\\V*U\\f2) = tyx\y2). C)
Таким образом, при унитарном преобразовании, связанном с оператором U, сохраняется
скалярное произведение (а следовательно, и норма) в пространстве К .
ЗАМЕЧАНИЯ
(i) Если А — эрмитов оператор, то оператор Т = е'Л является унитарным.
Действительно:
222

Математический аппарат квантовой механики
Т+ = еЧА* = e'iA D)
и, следовательно:
T+T = e~iAeiA=l;
7T+=e'VM=l, E)
так как, естественно, операторы -/А и /А коммутируют друг с другом,
(ii) Произведение двух унитарных операторов также является унитарным оператором.
Действительно, при условии, что
U+U = UU+ =1;
V+V = W+ =1, F)
без труда получим:
(UVY(UV) = V+U+UV = V*V = 1;
(t/V) (£/V)+ = £/W+£/+ = £Д/+ = 1. G)
Эти равенства доказывают, что оператор произведения унитарен. Это свойство,
впрочем, можно было предвидеть, так как если два преобразования в отдельности
сохраняют скалярное произведение, то при последовательном применении этих
двух преобразований оно также сохраняется.
(Ш) В обычном пространстве трехмерных вещественных векторов нам известны
операторы, сохраняющие норму и скалярное произведение: вращения, операции
симметрии относительно центра или плоскости симметрии и т.д. В случае
вещественного пространства говорят, что эти операторы ортогональны. Унитарные операторы
являются обобщением ортогональных операторов на комплексные пространства
(с произвольной размерностью).
Ь. УНИТАРНЫЕ ОПЕРАТОРЫ И ИЗМЕНЕНИЕ БАЗИСА
а. Пусть {|v,.) } —ортонормированный дискретный базис пространства
состояний #. Обозначим символом |у,) преобразование вектора |v,)b результате действия
оператора U :
|v,) = f/|v,.). (8)
Поскольку U — унитарный оператор, то
223

Глава U
(v,|v,) = (v,|v,) = S, (9)
и векторы | v.) ортонормированы. Покажем, что они образуют базис в пространстве £.
Для этого рассмотрим произвольный вектор |\|/) пространства £; поскольку ансамбль
{|v;) } является базисом, вектор £/ + |\|/) можно разложить по | v,):
U*\v) = lc,\Vl). A0)
l
Применим теперь к этому равенству оператор U :
UU+\\V) = ^ciU\vi) (И)
или
k> = 2c,|v,). A2)
Это уравнение говорит о том, что произвольный вектор |\|/) может быть разложен по
векторам | ?,.), и, следовательно, последние образуют базис. Таким образом, полученный
результат можно сформулировать так: для того, чтобы оператор U был унитарным,
необходимо, чтобы его применение к ортонормированному базису векторов
пространства F также давало бы ортонормированный базис.
Р. Покажем теперь, что это условие является достаточным. Согласно сделанному
предположению:
|?,) = ф,);
i
И
{vj\u*=(vj\- A4)
Произведем вычисления:
^^|v,.) = ^1v;.) = Z|vy)(v^1v-) = X|vy>(v~|v;.) = i:|v;.)§,=|^>- (И)
224

Математический аппарат квантовой механики
Соотношение A5), справедливое для любых /, доказывает, что оператор U+U является
единичным. Покажем также, что UU+ = 1. Для этого рассмотрим действие оператора U*
на вектор | v,.):
иЪ) = 1\*№Ли>д = Ъ\*М*^
Тогда имеем:
J J
откуда следует, что UU* = 1, то есть оператор U — унитарный.
A6)
A7)
Пусть
с. УНИТАРНАЯ МАТРИЦА
и<НФЬ)
A8)
элементы матрицы оператора U . Можно ли узнать по матрице, представляющей U , что
этот оператор унитарен? Соотношение A) дает:
или
{MU+U\^) = ^{vi\U%)MU\vj}
5X^=V
A9)
B0)
Если матрица унитарна, то сумма произведений элементов одного столбца на
комплексно сопряженные элементы другого столбца равна:
— нулю, если два столбца различны;
— единице в ином случае.
Приведем несколько примеров, когда это правило легко проверяется.
ПРИМЕРЫ
(i) Матрица вращения на угол 0 вокруг оси Oz в обычном трехмерном пространстве:
'оюб -sinQ 0\
Я(в) =
sin 9 cos 0 0
М 0 1.
B1)
15 Квантовая механика
225

Глава II
(ii) Матрица вращения в пространстве состояний спина 1/2 (см. главу IX):
ЯA/2)(а,р,у):
-(cx+Y)
cos-
3
r(Y-a)
^(а-Y) . C ^(а+Y)
2*
sin —
2
Р
2 .
B2)
d. СОБСТВЕННЫЕ ЗНАЧЕНИЯ
И СОБСТВЕННЫЕ ВЕКТОРЫ УНИТАРНОГО ОПЕРАТОРА
Пусть |\|/„) — нормированный собственный вектор унитарного оператора U ,
соответствующий собственному значению и:
Квадрат нормы вектора £/|i|/M) равен:
(\|/м \U+U |\J/M) = w*w (\|/„ |\|/и) = и и . B4)
Поскольку унитарный оператор сохраняет норму, то неизбежно и и = 1. Таким
образом, собственными значениями унитарного оператора могут быть лишь комплексные
числа с модулем, равным 1:
B5)
где фм — вещественное число.
Рассмотрим два собственных вектора |\|/и) и \|/м.) оператора U ; тогда:
B6)
Из формулы B6) видно, что если собственные значения и и м' различны, то скалярное
произведение (у„Ч/мЛ равно нулю, так как два собственных вектора унитарного
оператора, соответствующие различным собственным значениям, ортогональны.
2. Унитарное преобразование операторов
В § 1-Ь мы видели, что унитарный оператор U позволяет преобразовать ортонорми-
рованный базис {| v,) } пространства V в другой базис {| v;) }. В этом параграфе мы
определим, как подобное преобразование осуществляется не с векторами, а с операторами.
226

Математический аппарат квантовой механики
По определению преобразованием А оператора А будем называть оператор, который
в базисе {| v,) } имеет те же матричные элементы, что и оператор А в базисе {| v,) }:
№КИФК)- B7)
Подставим выражение (8) в это равенство:
<v/|^/ + At/|vy) = <v/|A|vy), B8)
поскольку индексы / и j — произвольные, то из формулы B8) следует, что
U+AU = A B9)
или, если умножить это равенство слева на U и справа на U+:
A = UAU+. C0)
Равенство C0) может быть взято в качестве определения формулы перехода от
оператора Л к оператору А с помощью унитарного преобразования. В квантовой механике
такие преобразования используются достаточно часто, и первый пример такой операции
приведен в дополнении F этой главы (§2-а).
Можно ли получить собственные векторы оператора А , зная собственные векторы
оператора А? Рассмотрим собственный вектор |ф„) оператора А, соответствующий
собственному значению а:
Л|фв) = а|Фв>. C1)
Пусть |фя) —Фурье-преобразование вектора |фв) оператором U 9 то есть |\j/„) = £/|фй).
Тогда:
Л|фв> = (УАУ + I/|ф^ = УА(У+У)|ф^ = Ш|фв) = АГ/|фв) = А|фв>. C2)
Таким образом, вектор |фд) является собственным вектором оператора,
соответствующим собственному значению а. В общем случае можно сформулировать следующее
правило: собственные векторы оператора Л, преобразованного из оператора А ,
являются унитарным преобразованием |фа) собственных векторов |ф„) оператора А , тогда
как собственные значения остаются неизменными.
15*
227

Глава II
ЗАМЕЧАНИЯ
(i) Эрмитово сопряжение оператора А, полученного из Л с помощью унитарного
преобразования U, достигается путем преобразования эрмитово сопряженного
оператора Л+ с помощью того же преобразования U :
(Л)+ =(UAU + y =UA+U+ = A\ C3)
Из этого равенства, в частности, вытекает, что, если А — эрмитов оператор,
той Л — также эрмитов оператор,
(ii) Аналогично:
(ЛJ = UAU+UAU+ = UAAU + = А2
и в общем случае:
(А)" =А". C4)
Используя определение B3) дополнения Вп, можно показать:
F(A) = F(A), C5)
где F(A) — функция оператора А .
3. Инфинитезимальный унитарный оператор
Пусть U(e) — унитарный оператор, зависящий от бесконечно малой вещественной
величины е ; допустим, что U(e) —> 1 при е —> 0 . Разложим U(e) в ряд по степеням 8 :
£/(e) = l + eG + ... C6)
Получим тогда:
U+(e) = l + eG+ + ... C7)
и
U(E)U+(£) = U4z)U(z) = l + e(G + G+) + ... C8)
Поскольку /7(e) — унитарный оператор, члены первого порядка по 8 в правой части
равенства C8) должны равняться нулю, то есть
228

Математический аппарат квантовой механики
(G + G+) = 0. C9)
Это соотношение свидетельствует о том, что оператор G антиэрмитов. Удобно
записать:
F = iG D0)
и получить уравнение:
F-F+=0, D1)
из которого следует, что F — эрмитов оператор. Таким образом, унитарный инфините-
зимальный оператор можно записать в виде:
£/(e) = l-/eF, D2)
где F — эрмитов оператор.
Подставив D2) в C0), получим:
A = (l-feF)A(l + /eF+) = (l-/eF)A(l + ieF) D3)
или
A-A = -/e[F,A]. D4)
Это означает, что зависимость оператора А от действия преобразования U в первом
порядке по е пропорциональна коммутатору [F, А].
Дополнение Dn
ДЕТАЛЬНОЕ РАССМОТРЕНИЕ ПРЕДСТАВЛЕНИЙ {|г)} и {|р>}
1. Представление {|г) }.
a. Оператор R и функции от R .
b. Оператор Р и функции от Р.
c. Уравнение Шредиыгера в представлении {|г) ).
2. Представление {| р) }.
a. Оператор Р и функции от Р.
b. Оператор R и функции от R .
c. Уравнение Шредингера в представлении (|р) }.
229

Глава II
1. Представление {|г)}
а. ОПЕРАТОР R И ФУНКЦИИ ОТ R
Вычислим в представлении {|г) } матричные элементы операторов X, К, Z ; используя
формулу (Е-36) главы II и соотношения ортогональности кет-векторов |г), сразу же
получим:
(r| X|r') = ;c8(r-r');
(г|У|г') = j5(r-r');
(r|z|r') = z8(r-r').
Эти три уравнения можно записать в компактной форме:
(r|R|r,) = r5(r-r').
Матричные элементы функции F(R) в представлении {|г) } определяются также
весьма просто [см. уравнение B7) дополнения Вц]:
(r|F(R)|r') = F(rM(r-r'). C)
A)
B)
b. ОПЕРАТОР Р И ФУНКЦИИ ОТ Р
Вычислим матричный элемент (r|Pv|r'):
(г|Р>') = \d>p{r\ Рх |р)(рИ = Id3p Р,ШШ = Girt)JdV» P.JPi"n -
2лй
ЦФхРх*
-рх(х-х')
2пП
Л>,
-Ру(у-у')
оо tpAz-z')
2пП
\ZdPz"h
D)
откуда, используя интегральную форму «дельта-функции» и ее производной [см. прил. II,
уравнения C4) и E3)], получим:
(v\Px\v) = -b\x-x')b{y-y)b(z-z*). E)
Матричные элементы других компонент оператора Р могут быть получены аналогично.
230

Математический аппарат квантовой механики
Докажем, что с помощью формулы E) можно установить действие оператора Рх в
представлении {|г) }. Для этого вычислим:
(r|PjV) = JdV(r|Px|r')(riv). F)
Согласно формуле E):
{г\Р>\ц) = - jVix-SW jS(y-/W jd(z-z)y(x\ y\ z')dz'. G)
Используя соотношение:
j5\-u)f(u)du = - \b\u)f(u)du = /'@) (8)
и обозначив и = х'-х , получим:
{г\Ф) = -^-Щх,у,г) (9)
I ОХ
и снова найдем равенство (Е-26) главы И.
Чему равен матричный элемент (r|G(P)|r') функции G(P) оператора Р?
Аналогичный расчет дает:
i
(r|G(P)|r') = \йър (r| G(P) |p)(p|r') = Bяй) игрС(Р)е^'("г) = BntiYm G(r-r'),
(Ю)
где G(r) — обратное преобразование Фурье функции G(p):
/■
G(r) = Bnh)~V2ld3p ^PTG(p). A1)
с. УРАВНЕНИЕ ШРЕДИНГЕРА В ПРЕДСТАВЛЕНИИ {|г) }
В главе III мы введем уравнение Шредингера, фундаментальное уравнение
квантовой механики:
/й4И0) = Я|\|/@), A2)
at
где Я — гамильтониан (оператор Гамильтона), который мы определим в свое время.
231

Глава II
Для частицы без спина в поле скалярного потенциала V(r) [см. уравнение (В-42)
главы III]:
Я = — P2+V(R).
2т
A3)
Сейчас запишем это уравнение в представлении {|г)}, введя в него волновую
функцию vj/(r, t), определенную выражением:
\|/(r,0= <r|\j/(r)>.
A4)
Спроектировав равенство A2) на |г), если гамильтониан Н определяется формулой
A3), получим:
//z^(r|\|/@)=^(r|P2|\|/(r))+(r|V(R)|\|/@).
A5)
Величины, входящие в это равенство, могут быть выражены через \|/(r, t).
Действительно, имеем:
^(r|v@) = -v(r.O;
(r|V(R)|v|/(r)) = V(r)v|/(r,r).
A6)
A7)
Матричный элемент (r| Р21\|/) можно вычислить, используя тот факт, что в
представлении {|г) } оператор Р действует как — V :
(г | Р21 V(/)> = (г| (РЛ2 + Р* + ?}) | vi/@) = - П:
( 32
32 Л
^Э*2+Эз>2 + Э^
Щх, у, z, 0 =
= -/г2А\|/(г, г).
Тогда уравнение Шредингера примет вид:
/Й — \|/(г, 0 =
2т
A + V(r)
V(r, О
A8)
A9)
Именно в этой форме мы ввели волновое уравнение в главе I (§ В-2).
232

Математический аппарат квантовой механики
2. Представление {|р)}
а. ОПЕРАТОР Р И ФУНКЦИИ ОТ Р
Формулы, аналогичные B) и C), получаются без труда:
(р|Р|р') = р8(р-р'); B0)
(p|G(P)|p') = G(pM(p-p'). B1)
b. ОПЕРАТОР R И ФУНКЦИИ ОТ R
Рассуждения, аналогичные приведенным в § 1, дают выражения, подобные
формулам E) и A0):
(р| Х|р')= №'(Рх - р'х) 5(Ру - р'у) 5(/л - р[) B2)
и
(p|F(R)|p')= Bяй)"мГ(р-р'), B3)
F(p) = BпП)~т jd'r e~T'prF(r). B4)
с. УРАВНЕНИЕ ШРЕДИНГЕРА В ПРЕДСТАВЛЕНИИ {|р) }
Введем «волновую функцию в импульсном представлении» формулой:
V(P.O=(p|v@> B5)
и найдем, опираясь на равенство A2), каким уравнением описывается эволюция во
времени функции \j/(p, t). Спроектировав формулу A2) на кет |р), получим:
^|:(p|v@)=^(p|P2|v|/@)+(p|V(R)|\i/@), B6)
откуда
где
233

Глава И
g^(p|v@)=^v(p,0;
(P|P2|V@>=p2\j7(p,f).
Остается вычислить величину:
(р| V(R) \Щ0) = JrfV (p| V(R) |p') (р'| V@) •
Используя B3), получим:
(p\V(R)\y(t))=Bnhymjd3p,V(p-p'Li(p',t),
где V (р) —преобразование Фурье от функции V(r):
B7)
B8)
B9)
C0)
V(р) = BтЛ) jd3re " V(r).
Таким образом, уравнение Шредингера в представлении {|р)) имеет вид:
Э о2
iti-^Щр, 0 = ^ ?(р, О + BnhTm Jd3/»' Г(р-р') ?(р\ О
C1)
C2)
ЗАМЕЧАНИЕ
Поскольку \j7(p, t) является Фурье-образом функции \|/(r, t) [см. формулу
(Е-18) главы И], можно было бы найти уравнение C2) путем преобразования
Фурье уравнения A9).

Математический аппарат квантовой механики
Дополнение Ец
НЕСКОЛЬКО ОБЩИХ СВОЙСТВ ДВУХ НАБЛЮДАЕМЫХ Qu P,
КОММУТАТОР КОТОРЫХ РАВЕН ih
1. Оператор S(k): определение, свойства.
2. Собственные значения и собственные векторы оператора Q.
a. Спектр оператора Q.
b. Кратность вырождения.
c. Собственные векторы.
3. Представление {| q) }.
a. Действие оператора Q в представлении {\q/ }.
b. Действие оператора S(k) в представлении [\qj }. Оператор трансляции.
c. Действие оператора Р в представлении {\q/ }.
4. Представление {| р) }. Симметрия наблюдаемых Р и Q .
В квантовой механике часто встречаются операторы, коммутатор которых равен ih.
Это, например, случай, когда два оператора соответствуют двум классическим
сопряженным величинам q. и pi (координата qt в системе ортонормированных осей и со-
пряженный ей импульс pi = ——): в квантовой механике величинам q( и р{ сопостав-
dq,
ляют операторы Qt и Pi, удовлетворяющие соотношению:
[а.^Н». со
В § Е главы II такие операторы уже встречались: X и Рх. В этом дополнении мы
покажем, придерживаясь более общей точки зрения, что можно установить целую серию
важных свойств, присущих двум наблюдаемым Р и Q, коммутатор которых равен ih .
Все они являются следствием только одного соотношения коммутации A).
1. Оператор S(X): определение, свойства .
Рассмотрим две наблюдаемые Р и Q, удовлетворяющие соотношению:
[е,/*]=/», B)
235

Глава II
и определим оператор S(X), зависящий от вещественного параметра X следующим
образом:
S(k) = ечкт C)
Этот оператор унитарен, что легко доказать с помощью соотношений:
S+(X) = S-l(X) = S(-X). D)
Вычислим коммутатор [<2, S(X)]; для этого можно применить формулу E1)
дополнения В1Ь так как коммутатор [<2, Р] = ih коммутирует с операторами Q и Р :
[G,S(X)]=i^-jj«-AW»=X5(X). E)
Это соотношение можно представить в виде:
QS(X) = S(X)[Q + X]. F)
Заметим, наконец, что
S(X)S0i) = S(X + H). G)
2. Собственные значения и собственные векторы оператора Q
а. СПЕКТР ОПЕРАТОРА Q
Допустим, что оператор Q имеет отличный от нуля собственный вектор \q) с
собственным значением q:
Q\q) = q\q)- (8)
Применим равенство F) к вектору | q):
QS(X) \q) = S(X)(Q + X) \q) = S(X)(^ + X) |^> = (q + X)S(X) \q) . (9)
236

Математический аппарат квантовой механики
Это равенство выражает, что S(X) \q) является другим отличным от нуля
собственным вектором оператора Q с собственным значением (q + X) (вектор S(X) \q) отличен
от нуля, так как S(X) — унитарный оператор). Таким образом, исходя из собственного
вектора оператора Q, путем применения к нему оператора S(X) можно построить
другой собственный вектор оператора Q с любым вещественным собственным значением
(действительно, X может принимать любое вещественное значение), и спектр оператора
Q оказывается непрерывным, образованным любыми числами, лежащими на
вещественной оси*.
Ь. КРАТНОСТЬ ВЫРОЖДЕНИЯ
Для простоты допустим пока, что собственное значение q оператора Q является
невырожденным (полученные ниже результаты легко обобщаются на случай, когда q —
вырожденное собственное значение). Покажем, что, если значение q — не вырождено,
то и все остальные собственные значения оператора Q не вырождены. Предположим,
например, что собственное значение (q + X) дважды вырождено, и покажем, что такое
предположение приводит к противоречию, заключающемуся в том, что при этом одному
собственному значению (q + X) соответствовало бы два ортогональных собственных
вектора \q + X, а) и \q + Xy C):
(q + X,$\q + X,a) = 0. A0)
Рассмотрим два вектора S(-X)\q + X, a) nS(-X)\q + X4 р). Согласно формуле (9) они
являются собственными векторами оператора Q с собственным значением q + X-X = q .
Они не коллинеарны, так как ортогональны; поскольку S(X) — унитарный оператор, их
скалярное произведение имеет вид:
* Видно, что в пространстве tf с конечной размерностью N не существует наблюдаемых Q
и Р , коммутатор которых равен ifi; действительно, количество собственных значений оператора
Q не может быть одновременно меньшим или равным N и бесконечным. Впрочем, этот
результат можно получить и непосредственно, если взять след соотношения B):- tr QP - tr PQ = tr Hi.
Если N — конечная величина, то два следа левой части равенства существуют, они являются
конечными и равными по величине [см. дополнение Вц , формула G-а)]. Тогда вышеуказанное
равенство принимает вид: 0 = tr ih = Nifi, что невозможно.
237

Глава II
(q + K $\S + (-X)S(-X) \q + X,a) = (q + X,$\q + X,a) = 0. A1)
Таким образом, приходим к выводу, что собственное значение q вырождено по
меньшей мере двукратно,.что противоречит исходному предположению, и, следовательно, все
собственные значения оператора Q должны иметь одну и ту же кратность вырождения.
с. СОБСТВЕННЫЕ ВЕКТОРЫ
Зафиксируем относительные фазы различных собственных векторов оператора Q
по отношению к собственному вектору |0) с собственным значением 0, положив:
\q) = S(q)\0). A2)
Подействуем оператором S(X) на обе части равенства A2) и, воспользовавшись
равенством G), получим:
S(X)\q) = S(X)S(q)\0) = S(X + q)\0) = \q + X). A3)
Выражение, сопряженное формуле A3), имеет вид:
(q\S + (X)=(q + X\ A4)
или с учетом формулы D) и после замены X на - X :
(q\S(X) = (q-X\. A5)
3. Представление {\q)}
Поскольку Q — наблюдаемая, ансамбль ее собственных векторов {\q) } образует
базис в пространстве К . Каждому кет-вектору можно поставить в соответствие
«волновую функцию в представлении {\q) }»:
VteH^lv). A6)
238

Математический аппарат квантовой механики
а. ДЕЙСТВИЕ ОПЕРАТОРА Q В ПРЕДСТАВЛЕНИИ {\q) }
Вычислим в представлении {\q) } волновую функцию, связанную с вектором (?|v).
Она имеет вид:
(?|Q|v) = *Mv) = *¥(?) A7)
[здесь мы использовали (8) и эрмитовость оператора Q]. Действие Q в представлении
{\q) } состоит в простом умножении на величину q .
b. ДЕЙСТВИЕ ОПЕРАТОРА S(X) В ПРЕДСТАВЛЕНИИ { \q) }.
ОПЕРАТОР ТРАНСЛЯЦИИ
Волновая функция, соответствующая кет-вектору S(X) |\|/)в представлении {\q) },
имеет вид (формула A5)):
(q\S(X)\\v) = (q-X\w) = y(q-X). A8)
Таким образом, действие оператора S(X) в представлении {\q) } состоит в
перемещении волновой функции на величину X параллельно оси q *. По этой причине
оператор S(X) называется оператором трансляции.
с. ДЕЙСТВИЕ ОПЕРАТОРА Р В ПРЕДСТАВЛЕНИИ {\q) }
Если 8 — бесконечно малая величина, то
S(-e) = e/em=l + i-P + 0(e2). A9)
h
Тогда:
^|5(-e)|\|/) = \i/(^) + /|^|p|V) + 0(e2). B0)
* Функция f(x-а) есть функция, которая в точке х = х0 + а принимает значение f(x0),
то есть это функция, полученная из f(x) путем трансляции на Л-а .
239

Глава II
С другой стороны, равенство A8) дает:
(?|S(-e)|\|/) = v(? + e). B1)
Сравнение выражений B0) и B1) показывает, что
\V(q + z) = \V(q) + iUq\P\\V) + 0(E2), B2)
п
откуда следует:
/ i г, I \ Л ,. \|/(<7 + е)-1|/(<7) Ь d , ч ^ч
(? Р ¥> = ~ й™ — yv<" = т — y(q). B3)
Действие оператора Р в представлении {\q) } состоит в дифференцировании ,
i dq
и тем самым мы обобщили равенство (Е-26) главы И.
4. Представление {|р) }• Симметрия наблюдаемых Р и Q
Соотношение B3) позволяет без труда получить волновую функцию vp(q)9
соответствующую собственному вектору \р) оператора Р с собственным значением р в
представлении {\q) }:
vp(q)={q\p)={2nh)-l/2 eT'Hl. B4)
Тогда можно записать:
\p)={2nnyn-\Zdq^"\q). B5)
Можно определить кет-вектор |\|/) через «волновую функцию в представлении {\р)}»:
Щр)=(р№). B6)
Используя соотношение, сопряженное B5), получим:
240

Математический аппарат квантовой механики
Щр) = BпП)'У2 \yq е"> Щд), B7)
то есть ij7(/?) является Фурье-образом функции \\f(q).
Действие оператора Р в представлении {| р)} соответствует умножению на р, а
действие оператора Q соответствует, как нетрудно показать, используя B7), операции
dp
Таким образом, мы получили результаты, симметричные в представлениях {\q) } и
{\р)}. Это неудивительно, так как согласно сделанным предположениям можно
переставить местами операторы Р и Q при условии изменения знака коммутатора в B). Мы
могли бы также вместо оператора S(X) рассмотреть оператор Т(\'), определенный
выражением:
T(X%)=e'VQ,\ B8)
и выполнить те же операции, заменив повсюду Р на Q и i: на -1:.
Дополнение Fh
ОПЕРАТОР ЧЕТНОСТИ
1. Изучение оператора четности.
a. Определение.
b. Простые свойства оператора П .
c. Собственные подпространства оператора П .
2. Четные и нечетные операторы.
a. Определения.
b. Правила отбора.
c. Примеры.
d. Функции операторов.
3. Собственные состояния четной наблюдаемой В+ .
4. Приложение к важному частному случаю.
16 Квантовая механика
241

Глава II
1. Изучение оператора четности
а. ОПРЕДЕЛЕНИЕ
Рассмотрим физическую систему в пространстве состояний £г. Оператор четности П
определяется по его действию на базисные векторы |г) пространства &г *:
П|г) = |-г). A)
Матричные элементы оператора П в представлении {|г) } равны:
(г|П|г,) = (г|-г,) = 8(г + г'). B)
Рассмотрим произвольный вектор |\j/) пространства $г:
|v) = JdV\|/(r)|r). C)
Если произвести замену переменной г'= -г, то вектор |\|/) можно переписать в виде:
|\|f> = JdV\|/(-rl)|-rl). D)
Вычислим теперь П| \\f):
n|v>=JdVv(-r,)|-rl>. E)
Сравнение C) и E) показывает, что действие оператора П в представлении {|г) }
состоит в замене г на - г:
(г|П|1|/) = \|/(-г). F)
Рассмотрим тогда физическую систему У*, вектор состояния которой равен |\|/); то-
* Следует четко различать |- г{)) и - |г0) ; первый является собственным вектором
оператора R с собственным значением —г0 и волновой функцией \_х (г) = 5(г + г0); второй —
собственным вектором оператора R с собственным значением г 0 и волновой функцией
Чг„(г) = -5(г-г0).
242

Математический аппарат квантовой механики
гда вектор П|\|/) будет описывать физическую систему, полученную из системы ,(/ с
помощью операции симметрии относительно начала отсчета.
Ь. ПРОСТЫЕ СВОЙСТВА ОПЕРАТОРА П
Оператор П2 является единичным оператором. Действительно, согласно формуле
A) имеем:
П2|г) = П(п|г)) = П|-г) = |г), G)
то есть, поскольку кет-векторы |г) образуют базис в пространстве £г:
П2 = 1 (8-а)
или
П = П-'. (8-Ь)
Используя рекурсию, легко показать, что оператор П" равен:
— 1, если п — четное число;
— П, если п — нечетное число.
Равенство F) можно переписать в виде:
(r|n|V) = <-r|V). (9)
Это равенство справедливо при любых |\|/), откуда следует,что
(г|П = (-г|. A0)
С другой стороны, выражение, эрмитово сопряженное формуле A), имеет вид:
(г|ГГ=(-г|. A1)
Поскольку векторы |г) образуют базис, из формул A0) и A1) следует, что оператор П
эрмитов:
П+=П. A2)
Комбинируя это равенство с (8-Ь), получим:
ГР=ГГ'. A3)
Таким образом, оператор П — унитарный.
16* 243

Глава II
с. СОБСТВЕННЫЕ ПОДПРОСТРАНСТВА ОПЕРАТОРА П
Пусть |фл) — собственный вектор оператора П с собственным значением рп.
Применив формулу (8-а), получим:
|фл) = П2|Фя) = Рл2|Фя). A4)
Таким образом, р\ = 1, то есть собственными значениями оператора П могут быть
только 1 и -1. Поскольку пространство Fr бесконечномерное, сразу же видим, что эти
собственные значения вырождены. Собственный вектор оператора П с собственным
значением +1 называется четным, а с собственным значением -1 — нечетным.
Рассмотрим два оператора Р+ и Р_, определенные равенствами:
Р+=\ A + П);
Р_=1A-П). A5)
Эти операторы эрмитовы, и, используя (8-а), легко получить равенства:
Р2 = Р •
1 + i + »
Л2 = Р_. A6)
Таким образом, операторы Р+ и Р являются проекционными операторами на два
подпространства £г, которые мы будем обозначать символами £+ и £_. Вычислим
произведения Р+Р_ и Р_Р+ :
Р+Р =-A + П-П-П2) = 0;
Р_Р+=-A-П + П-П2) = 0, A7)
и два подпространства оказываются ортогональными. Покажем, что они являются еще и
дополнительными: действительно, из определения A5) немедленно следует, что
Р++Р. =1. A8)
244

Математический аппарат квантовой механики
Каким бы ни был кет |i|/) пространства #, имеем:
|i|/) = (P+ + P)|\|/) = |x|/+) + |x|/_), A9)
где
k+) = n|v>;
|V.) = />.|V>. B0)
Вычислим произведения ПР+ и ПР_:
n/>+=in(l + n) = i(n + l)=P+;
П/>_=-ПA-П) = -(П-1) = -Р_. B1)
Эти равенства позволяют показать, что векторы |\у+) и|\|/_) , введенные в B0), являются
соответственно четным и нечетным:
n|V+> = nP+|V> = P+|V> = |V+);
П|v.) = ПР.|i|/) = -P_|v|/) = -|i|/_). B2)
Пространства £+ и £_ являются, таким образом, собственными подпространствами
оператора П с собственными значениями +1 и -1 соответственно. В представлении {|г) }
равенства B2) принимают вид:
(г|\|/+) = \|/+(г) = (г|п|\|Г+) = \|/+(-г);
(г|\|/_) = \|/_(г) = -(г |П| \|/_> = -\|/.(-г). B3)
Волновые функции \|/+(г)и \|/_(г) являются соответственно четной и нечетной.
Соотношение A9) выражает, что произвольный кет |\j/) пространства <fr может
быть разложен на сумму двух собственных векторов оператора П , а именно, |\|/+) и
|\|/_), принадлежащих соответственно четному £+ и нечетному #_ подпространствам.
Таким образом, оператор П является наблюдаемой.
245

Глава II
2. Четные и нечетные операторы
а. ОПРЕДЕЛЕНИЯ
В §2 дополнения С мы определили понятие унитарного преобразования операторов.
В случае оператора П [унитарного, как следует из A3)] преобразование произвольного
оператора В имеет вид:
В = ПЯП B4)
и подтверждается соотношением [см. уравнение B7) дополнения Сц]:
(г|в|г,) = (-г|В|-г,>. B5)
Говорят при этом, что оператор В получен из оператора В в результате преобразования
четности.
В частности: если В = +В, говорят, что оператор В четный;
если В = -В, говорят, что оператор В нечетный.
Таким образом, четный оператор В+ таков, что
В+ = ПВ+П B6)
или, если умножить это равенство слева на П и воспользоваться формулой (8-а):
ПВ+ = Д+П ; B7)
[П,Д+] = 0. B8)
Четный оператор всегда коммутирует с оператором П . Нетрудно увидеть, что нечетный
оператор В_ должен антикоммутировать с оператором П :
ПВ_ + В Л = 0. B9)
Ь. ПРАВИЛА ОТБОРА
Пусть В+ — четный оператор. Вычислим матричный элемент (ф| B+\\\f); согласно
сделанному предположению имеем:
(ф|в+|у> = (ф|ПЯ+П|у> = (ф||В+|^>, C0)
246

Математический аппарат квантовой механики
где
|ф') = П|ф);
И = П|\|/). C1)
Если один из двух кет-векторов |ф) и |\|/) четный, а другой — нечетный (|ф') = ±|ф) и
|\|/') = +|\|/)), соотношение C0) дает:
(ф|5+|\|/) = -(ф|В+|\|/> = 0. C2)
Из этого следует правило: матричные элементы четного оператора между векторами
противоположной четности равны нулю.
Если взять нечетный оператор В_ , то соотношение C0) дает:
(ф|5_|х|/) = -(Ф,|Б_|1|/') C3)
что также равно нулю, если оба вектора |ф), |\|/) либо четные, либо нечетные. Отсюда
следует правило: матричные элементы нечетного оператора равны нулю между
векторами одинаковой четности. В частности, диагональный матричный элемент (\|/| #_|ty)
(среднее значение В_ в состоянии |ij/), см. главу III, § С-4) равен нулю, если |\|/) имеет
определенную четность.
с. ПРИМЕРЫ
а. Операторы X, Y, Z
В этом случае имеем:
ПХ |г> = ПХ |jc, у, z) = xTl\x, y,z) = x\-x,-y,-z) = x |-г> C4)
и
XTl\r)=X\-r)=X\-x,-y,-z) = -x\-x,-y,-z) = -x\-r). C5)
Суммируя эти равенства, получим:
(ПХ + ХП)|г) = 0 C6)
или, поскольку векторы |г) образуют базис:
247

Глава И
ПХ + ХП = 0, C7)
то есть оператор X — нечетный.
Аналогичные доказательства легко выполнить и для операторов Y и Z, вследствие
чего можно утверждать, что оператор R — нечетный.
C. Операторы Рх, Р , Pz
Вычислим кет П |р):
П|р) = {2Tth)'m \dlr е"""'П |r) = Bя»)-и \d3r е*п |-г) =
= {2ith)'n Jrfv е-""' lr') = |-p). C8)
С помощью рассуждений, аналогичных приведенным в пункте а, нетрудно
получить:
Ш>» = р,|-р);
Р,П|р) = -Л|-р) C9)
И
ПРХ + РЛП = 0, D0)
тЪ есть оператор Р является нечетным.
у. Оператор четности
Очевидно, что оператор П коммутирует сам с собой, то есть является четным.
d. ФУНКЦИИ ОПЕРАТОРОВ
Пусть В+ — четный оператор. Используя соотношение (8-а), получим:
ГШ; П = (ПВ+П) (ПВ+П) ... (ЛВ+Л) = В?. D1)
N у /
II
Любая степень четного оператора является четным оператором. Обобщая, можно
сказать, что оператор F(B+) всегда является четным.
248

Математический аппарат квантовой механики
Пусть В_ — нечетный оператор. Вычислим оператор ПВ" П :
ПЯ_" П = (ПВ_П) (ПВ_П) ... (ПВ_П) = (- 1)я(Д.)". D2)
То есть п -ная степень нечетного оператора является четной, если п — четное
число, и нечетной, если п — нечетное число. Рассмотрим оператор F(B_). Он является
четным, если соответствующая функция F(z) — четная, и нечетным, если она нечетная.
В общем случае F(B_) не имеет определенной четности.
3. Собственные состояния четной наблюдаемой В+
Рассмотрим произвольную четную наблюдаемую В+ и собственный вектор |фЛ)
оператора В+ с собственным значением Ъ . Поскольку В+ — четный оператор, он
коммутирует с оператором П . Применив теоремы § D-3-a главы И, получим следующие
результаты:
а. Если Ъ — невырожденное собственное значение, то \tyb) обязательно является
собственным вектором оператора П , то есть это либо четный, либо нечетный вектор.
Среднее значение (ф/,|#-|ф6) любой нечетной наблюдаемой В_ (например, R, Р, ...)
равно нулю.
Р. Если Ъ — вырожденное собственное значение, соответствующее собственному
подпространству %ь, то векторы этого подпространства не обязательно имеют
определенную четность: может оказаться, что вектор П|фь)не коллинеарен вектору |ф/;), но
имеет то же самое собственное значение Ъ. Кроме того, возможно, что в каждом
подпространстве tb существует базис общих для операторов П и5+ собственных векторов.
4. Приложение к важному частному случаю
В последующем мы часто будем искать собственные состояния гамильтониана Я ,
действующего в пространстве £г и имеющего вид:
// = JL + V(R). D3)
2т
Поскольку Р — нечетный оператор, то оператор Р2 — четный; кроме того, если
функция V(r) — четная (V(r) = V(-r)), то оператор Н является четным. Как мы
только что видели, в этом случае следует искать собственные состояния оператора Н среди
четных или нечетных состояний, что часто значительно упрощает вычисления.
249

Глава II
Мы уже встречали ряд случаев, когда гамильтониан Я является четным:
прямоугольная потенциальная яма, яма бесконечной глубины (дополнение Нт); позже мы увидим
и другие примеры: гармонический осциллятор, атом водорода и т.д. На этих частных
случаях легко продемонстрировать все указанные здесь свойства.
ЗАМЕЧАНИЕ
Если Я — четный оператор и если найдено одно из его собственных
состояний |фЛ), не имеющее определенной четности (вектор П |фЛ) не коллинеарен
вектору |фл)), можно утверждать, что соответствующее собственное значение
является вырожденным: действительно, поскольку П коммутирует с Я , вектор
П |фЛ) является собственным вектором оператора Я с тем же собственным
значением, что и |фЛ).
Дополнение Gn
ПРИМЕНЕНИЕ СВОЙСТВ ТЕНЗОРНОГО ПРОИЗВЕДЕНИЯ:
ДВУМЕРНАЯ ПОТЕНЦИАЛЬНАЯ ЯМА
БЕСКОНЕЧНОЙ ГЛУБИНЫ
1. Определение. Собственные состояния.
2. Анализ энергетических уровней.
a. Основной уровень.
b. Первые возбужденные уровни.
c. Систематические и случайные вырождения.
В дополнении Н\ (§ 2-е) мы уже изучали в рамках одномерной задачи стационарные
состояния частицы в потенциальной яме бесконечной глубины. Использование понятия
тензорного произведения (см. главу II, § F) позволит нам обобщить полученные
результаты на случай двумерной потенциальной ямы (введение третьего измерения не добавит
никаких принципиальных трудностей).
1. Определение. Собственные состояния
Рассмотрим частицу с массой т в плоскости хОу внутри «прямоугольной» ямы со
стороной а : ее потенциальная энергия V(x,y) обращается в бесконечность, как только
одна из координат х или у выходит за пределы интервала [0, а] :
250

Математический аппарат квантовой механики
V(x,y) = V00(x) + VJy), A)
где
Ко(и) =0, если 0<и<а\
= -и» , если и < 0 или и > а . B)
Гамильтониан квантовой частицы запишется тогда в виде (глава III, § В-5):
H = ^(P? + P?) + VJX) + VJY) C)
или
Н = Нх + НуУ D)
где
Hy=^-Pt+Vm(Y). E)
2w
Таким образом, задача соответствует важному частному случаю, отмеченному в главе II
(§ F-4-a-P), и мы можем искать собственные состояния оператора Н в виде:
|фНф>»,. F)
Я,|ф), = Е,|Ф)х;|ф),е8,;
">>, = £,l<p),H<p),eiV G)
я|ф) = е|ф),
Е = ЕХ + Еу. (8)
где
Тогда имеем:
где
251

Глава II
Таким образом, от двумерной задачи переходим к одномерной задаче, которая уже
была решена выше (см. дополнение Нг). Применив полученные результаты и формулы
G) и (8), заметим, что:
— собственные значения оператора Н имеют вид:
Ев.,=^(п2 + />2)я2»2, (9)
где пир — положительные целые числа;
— этим энергиям соответствуют собственные состояния Ф„,/;), имеющие вид
тензорного произведения:
K„)=k),k,).v- (Ю)
которым соответствует нормированная волновая функция:
^ ч , ч , ч 2 . mix . рпу /11Ч
Фя„(*. У) = Фя(*)Фр(>0 = --ил sin^-. (И)
а а а
Нетрудно доказать, что эти волновые функции обращаются в нуль на границах
«квадратной ямы» (х или у равны 0 или а), где потенциальная энергия обращается в
бесконечность.
2. Анализ энергетических уровней
а. ОСНОВНОЙ УРОВЕНЬ
Числа пир являются целыми и положительными*. Таким образом, основной
уровень соответствует п = I и р = I. Его энергия равна:
TT2fc2
£„~ A2)
та
и достигается лишь при условии п = р = 1, то есть основной уровень не вырожден.
* Мы исключаем значения п = 0 и р = 0 , дающие нулевые волновые функции, которые
невозможно ортонормировать.
252

Математический аппарат квантовой механики
Ь. ПЕРВЫЕ ВОЗБУЖДЕННЫЕ УРОВНИ
Первый возбужденный уровень получается либо при п = 1 и р = 2 , либо при п = 2
и р = 1:
£,, = £,., Л*!*!. A3)
2 та
Этот уровень дважды вырожден, так как векторы Ф^) и Ф2.1/ независимы.
Второй возбужденный уровень соответствует п = р = 2, он не вырожден, и его
энергия равна:
£22=4 г. A4)
та
Третий уровень соответствует и = 1, р = 3 и и = 3, р = 1 и т.д.
с. СИСТЕМАТИЧЕСКИЕ И СЛУЧАЙНЫЕ ВЫРОЖДЕНИЯ
В общем случае можно констатировать, что все уровни, для которых пФ р, вырождены,
поскольку:
К, = £,.„ • A5)
Это вырождение связано с симметрией задачи. Действительно, рассмотренная квадратная яма
симметрична относительно первой биссектрисы плоскости хОу . Это отражается в том, что
гамильтониан Н инвариантен относительно подстановки:
Рх+*Ру A6)
(Можно было бы определить в пространстве состояний оператор, соответствующий операции
симметрии относительно первой биссектрисы, и этот оператор коммутировал бы с Н .) Если
известно собственное состояние оператора Н с волновой функцией Ф(х, у), то состояние,
соответствующее функции Ф'(*, у) = Ф(у, х), также является собственным состоянием Н с тем же
собственным значением. Вследствие этого, если функция Ф(*, у) не симметрична по х и у , то
соответствующее собственное значение неизбежно вырождено. Именно в этом состоит причина
вырождения A5): если пФ р, функция Ф (дг, у) не симметрична по х и у [формула A1)].
Эта интерпретация подтверждается еще и тем, что если нарушить симметрию, выбрав ширины
253

Глава II
ямы по осям Ох и Оу различными (а и Ъ соответственно), то соответствующее вырождение
исчезает. Действительно, формула (9) принимает вид:
Е -"^(«l^
"" 2m [a2 b2
A7)
и соответственно:
£„.„*£,,„• (is)
Такие вырождения, природа которых заключается в симметрии задачи, называются
систематическими вырождениями.
ЗАМЕЧАНИЕ
Другие свойства симметрии двумерной квадратной ямы не влекут за собой
систематического вырождения, так как все собственные состояния оператора Н инвариантны во
всех остальных преобразованиях симметрии. Например, для любых пир функции
Ф/|>р(дс, у) просто умножаются на фазовый множитель при замене х на {а - х) и у на
{а - у) (симметрия относительно центра ямы).
Возможно также существование вырождений, непосредственно не связанных с симметрией
задачи. Их принято называть случайными вырождениями. Например, в рассмотренном случае
оказывается, что Е55 - Е1Л или Е7 4 = £8, .
Дополнение Нц
УПРАЖНЕНИЯ
Обозначения Дирака. Коммутаторы.
Собственные векторы и собственные значения
1. Обозначим символом |ф„) собственные состояния эрмитова оператора Н (например,
гамильтониана любой физической системы). Предположим, что они образуют
дискретный ортонормированный базис. Оператор U(m, n) определен равенством:
U(my и) = |ф„,)(ф„
254

Математический аппарат квантовой механики
a. Вычислить оператор /7+(т, п), эрмитово сопряженный оператору U{m, n).
b. Вычислить коммутатор
c. Доказать соотношение:
U{m,n)U\p,q) = bnqU(m, p).
d. Вычислить след tr {U(m, n)} оператора U(m, n).
e. Пусть А — оператор с матричными элементами Атп - (фт|л|ф„). Доказать
соотношение:
т, п
/. Показать, что А = tr [AU + (p, q)}.
2. В векторном двумерном пространстве рассматривается оператор, матрица которого в
ортонормированном базисе {|l) ,|2)} имеет вид:
Ov =
у
(°
{'
-А
J
a. Является ли этот оператор эрмитовым? Вычислить его собственные значения и
собственные векторы в виде нормированного разложения в базисе {|1) ,|2)} .
b. Вычислить матрицы проекционных операторов на эти собственные векторы.
Проверить, удовлетворяют ли они соотношениям ортогональности и замкнутости.
c. Аналогичные вопросы в отношении матриц:
М =
itf
-iyfl
и в трехмерном пространстве:
L =
2/
О V2 О4
-л/2 О V2
О -V2 О
3. Пространство состояний некоторой физической системы является трехмерным; пусть
(|wi), |w2), |w3)} — ортонормированный базис этого пространства. Определим кет-
векторы |\|/0) и |\|/,) соотношениями:
255

Глава U
a. Нормированы ли эти кет-векторы?
b. Вычислить матрицы р0 и р,, представляющие в базисе {|и,), \и2), |и3))
проекционные операторы на состояния |\j/0) и |\|/|)- Проверить, являются ли эти матрицы
эрмитовыми.
4. Пусть К — оператор, определенный выражением К = |(р)(\|/|, где |ф) и |\j/) —
векторы пространства состояний.
a. При каких условиях К является эрмитовым оператором?
b. Вычислить К2. При каких условиях К является проекционным оператором?
c. Показать, что К всегда можно представить в форме К = ХРХР2, где X —
константа, подлежащая определению, а Рх и Р2 — проекционные операторы.
5. Пусть Р{ — ортогональный проекционный оператор в подпространстве #", ,а Р2 —
ортогональный проекционный оператор в подпространстве #2. Показать, что для того,
чтобы произведение РХР2 было ортогональным проекционным оператором, необходимо
и достаточно, чтобы Рх и Р2 коммутировали. Каким является подпространство, на
которое проектируется оператор Рх Р2 в этом случае?
6. Матрица ах определена выражением:
Gv =
f° Ч
[i oj
Доказать соотношение:
е,аа* = / cos a + iax sin a,
где / — единичная матрица 2x2.
7. Для матрицы оу, введенной в упражнении 2, установить соотношение, аналогичное
доказанному для ох в предыдущем упражнении. Обобщить на любую матрицу вида:
256

Математический аппарат квантовой механики
ои = Ха х + [iG v,
где
\2+\х2=1.
Вычислить матрицы, представляющие е2'а", (еЮх) и ^'(°v+°v). Определить, равны ли
е2** и(е^J1 еКа^] и *'V°'?
8. Рассмотрим в рамках одномерной задачи гамильтониан Н частицы, определенный
формулой:
Н = — P2+V(X),
2т
где X и Р — операторы, определенные в § Е главы II и удовлетворяющие
соотношению: [XyP] = ih. Собственные векторы оператора Н обозначены символом |ф„):
Н |ф„) = Еп |ф„), где п — дискретный индекс.
a. Показать, что
(ф„|/>|ф„,) = а(ф„|х|Ф„.),
где а — коэффициент, зависящий от Еп и Еп, только через их разность. Найти а (для
доказательства советуем рассмотреть коммутатор [X, Н]).
b. Вывести, используя соотношение замкнутости, равенство:
Е(£„-£,J|(ф„|х|ф,)|2 = 4(ф^2|фл>-
9. Пусть Н — гамильтониан физической системы. Обозначим символом |ф„)
собственные векторы оператора Н с собственными значениями Еп:
а. Если А — произвольный оператор, доказать соотношение:
(ф„|[Л,Я]|ф„) = 0.
17 Квантовая механика
257

Глава II
Ъ. Рассмотреть одномерную задачу [частица с массой т в поле потенциала V(X) ];
в этом случае Н имеет вид:
Я= — P2+V(X).
2т
а. Вычислить через Р, X, V(X) коммутаторы: [Я,Р], [Я,Х], [Н,ХР].
C. Показать, что матричный элемент (ф/}| Р\ц>„) (в главе III мы будем
интерпретировать его как среднее значение импульса в состоянии |ф„)) равен нулю.
Р2
у. Установить соотношение между Ес = (фи| — |ф„) (среднее значение кинетиче-
2т
ской энергии в состоянии |ф„)) и (фм| X— |ф«)- Среднее значение потенциальной
ил.
энергии в состоянии |ф;|) равно (ф;11 V(x) |ф„). Как оно связано со средним значением
кинетической энергии, если:
V(X) = V0Xk
D = 2,4,6, ...;V0>0)?
10. Используя соотношение (х\р) = BпЬ) e'px,t\ вычислить через \\f(x) выражения
(х\ ХР |\|/) и (х\ PX\\\f). Можно ли получить результат непосредственно, используя тот
факт, что в представлении л оператор Р действует как ?
/ dx
Наборы коммутирующих наблюдаемых.
Полный набор коммутирующих операторов
11. Рассмотрим физическую систему, трехмерное пространство состояний которой
связано с ортонормированным базисом, образованным тремя кет-векторами: |м,), |м2), |и3).
В базисе этих трех векторов, взятых именно в таком порядке, два оператора Н и В
определены матрицами:
(\ 0 0^1 (\ 0 (Л
Н = йсо,
0-10
^0 0 -I)
в = ь
0 0 1
10 1 0)
гдесо0 и Ъ —вещественные константы.
258

Математический аппарат квантовой механики
a. Эрмитовы ли операторы Я и В ?
b. Показать, что Я и В коммутируют. Определить базис собственных векторов,
общих для Я и В.
c. Какие из наборов операторов { Я }, {В}, { Я , В], { Я 2, #} образуют полный
набор коммутирующих операторов?
12. Оставаясь в рамках введенного в предыдущей задаче пространства, рассмотрим два
оператора L. и S , определенные соотношениями:
5|и,) = 1иэ); s|) = h); 5|из> = |и,).
я. Записать матрицы, представляющие в базисе {|м,), \и2), |w3)} операторы Lz, l}z,
S , S2. Являются ли эти операторы наблюдаемыми?
b. Указать наиболее общую форму матрицы, представляющей оператор,
коммутирующий с Lz. Аналогичный вопрос для операторов lJz и S2.
c. Образуют ли операторы ]}г и S полный набор коммутирующих операторов?
Получить базис общих собственных векторов.
Решение упражнения 11
a. Операторы Я и В эрмитовы, так как соответствующие матрицы симметричны и
вещественны.
b. \щ) — общий собственный вектор операторов Я и В, поэтому НВ \щ) =
= ВН и, ). Мы видим, что для того, чтобы Я и В коммутировали, достаточно, чтобы
блоки этих операторов в подпространстве 82, порожденном векторами |м2) и |и3)>
коммутировали. Так, в этом подпространстве матрица оператора Я равна -Й0H/ (где
/ — единичная матрица 2 х 2) и коммутирует с любыми матрицами 2x2. Таким образом,
операторы Я и В коммутируют (этот же результат можно было бы получить
непосредственным вычислением матриц Я В и В Я и проверкой их равенства). Блок оператора В
в подпространстве $2 имеет вид:
(о Г|
R BPf =b\
Нормированные собственные векторы этой матрицы 2x2 получаются легко. Они равны:
17*
259

Глава II
\р2)~ -т= [|и2)+1иъ) 1 (собственное значение +Ь);
л/2
| р3) = —;=■ [| w2) ~ | мз)] (собственное значение -Ь ),
эти векторы автоматически являются собственными векторами Я , поскольку $2 —
собственное подпространство оператора Я, соответствующее собственному значению
-/гаH . Таким образом, общими собственными векторами операторов Я и В являются:
собственные значения: Я В
|Pi) = h) йсоо Ь
|Р2) = ^[К)+|Мз)] -»©0 *
1л)=^[|>-К)] -*®о -&
Эти векторы являются единственно возможными (конечно, с точностью до фазового
множителя) нормированными собственными векторами, общими для операторов И и В.
с. Из приведенной таблицы видно, что оператор Н имеет дважды вырожденное
собственное значение, то есть он не образует полный набор коммутирующих
операторов. Аналогично, оператор В также имеет дважды вырожденное собственное значение
и сам по себе не образует полного набора коммутирующих операторов: собственный
вектор оператора В с собственным значением Ъ может быть или [/?,), или|/?2), или
даже, например, —т= |и,) + -=- |м2)+-т=г |м3). Напротив, ансамбль двух операторов Н и В
V3 V3 V3
образует полный набор коммутирующих операторов. Действительно, в приведенной
выше таблице нет двух векторов \pj), которые имели бы одинаковые собственные
значения для операторов Я и В одновременно. Именно поэтому, как ранее отмечалось,
система нормированных собственных векторов является единственной (с точностью до
фазового множителя). Заметим, что внутри собственного подпространства К2 оператора
Я , связанного с собственным значением —/гсо0, собственные значения оператора В
различны (+Ь и -Ь); аналогично, в собственном подпространстве оператора В (|р,) и
\р2)) собственные значения оператора Я также различны (йсо0 и -Йсо0).
Оператор Я2 допускает |/?,), \р2) и |р3) в качестве собственных векторов с
собственным значением Й2@^. Нетрудно видеть, что Я2 и В не образуют полного набора
260

Математический аппарат квантовой механики
коммутирующих операторов, так как паре собственных значений { Й2@„, Ь }
соответствуют два линейно независимых собственных вектора [/?,) и \р2) ■
Решение упражнения 12
а. Воспользуемся правилом, позволяющим построить матрицу оператора: «в п -ном
столбце матрицы записываются компоненты преобразования оператором п -ного
базисного вектора». Без труда получим:
f\ О (Л (О О Л
L =
L:
0 0 0
0 0-1
f\ 0 0Л
0 0 0
10 0 lj
s =
52 =
0 1 0
1 0 0,
(\ о о\
0 1 0
10 0 lj
Эти матрицы симметричны и вещественны и, следовательно, эрмитовы. Поскольку
пространство имеет конечную размерность, их можно диагонализировать, а поэтому они
являются наблюдаемыми.
Ь. Пусть М — оператор, коммутирующий с Lz; оператор М не может иметь
матричных элементов ни между \щ) и |м2), ни между \и2) и |м3), ни между \щ) и |и3)
(собственные векторы оператора Lz с различными собственными значениями). Таким
образом, матрица, представляющая М , обязательно диагональна, то есть имеет вид:
[М, Lz] = 0
<=>
М =
тИ
0
0
0
т2г
0
0
0
т.
Если оператор N коммутирует с оператором Isz, то матрица N может иметь элементы
между 1^) и |м3) (собственные векторы оператора l}z с одинаковым собственным
значением), но не может между \и2), с одной стороны, и |и,) и |и3) — с другой. Тогда
матрица N имеет вид:
(г
[n, l2z] = o
N =
0 п.
0 п
22
0 п
зз;
Итак, условие коммутации оператора N с l}z является менее строгим, чем с L,, так как
N не обязательно должен быть представлен диагональной матрицей. Можно лишь сказать,
что оператор N не смешивает векторы подпространства Э^, порожденного векторами
\щ) и |и3), с векторами подпространства, порожденного \и2); это свойство легко дока-
261

Глава II
зывается, если записать матрицу ЛГ , представляющую оператор N в базисе {1^), |и3)>
\и2) } (изменение порядка базисных векторов):
ЛГ =
1
О
3
О л,
Наконец, поскольку S2 — единичный оператор, любая матрица 3x3 коммутирует с 52
и в общем случае:
\Рп Р\г Р\ъ
[Л52] = 0 <=> Р = \р21 р22 р2Ъ
\Ръ\ РЪ2 Рп)
с. \и2) — общий собственный вектор операторов L2 и S ; в подпространстве &г>
порожденном векторами |и,) и |и3), матрицы Ц, и S примут вид:
(\ Ф
ЪАЪ =
p?sp, =
0 1
'О О
1 0
Собственные векторы последней матрицы имеют вид:
k)=^[h)+h)];
k)=^[k)-h)L
и базис собственных векторов, общих для L2 и S , запишется следующим образом:
вектор
Ы=к)
k)=^[h)+h)]
b)=^[h)-h)]
L]
0
1
1
S
1
1
-1
В таблице нет двух одинаковых строк для собственных значений Lz и S , и эти операторы
образуют полный набор коммутирующих операторов (но не каждый из них, взятый в
отдельности).

Глава III
ПОСТУЛАТЫ
КВАНТОВОЙ МЕХАНИКИ

ПЛАН ГЛАВЫ III
А. ВВЕДЕНИЕ.
В. ФОРМУЛИРОВКА
ПОСТУЛАТОВ.
1. Описание состояния системы.
2. Описание физических величин.
3. Измерение физических величин.
a. Возможные результаты.
b. Принцип спектрального разложения.
c. Редукция волнового пакета.
4. Эволюция системы во времени.
5. Правила квантования.
a. Постановка задачи.
b. Важные примеры.
С. ФИЗИЧЕСКАЯ
ИНТЕРПРЕТАЦИЯ
ПОСТУЛАТОВ
О НАБЛЮДАЕМЫХ
И ИХ ИЗМЕРЕНИИ.
1. Правила квантования согласуются с вероятностной
интерпретацией волновой функции.
2. Квантование некоторых физических величин.
3. Механизм измерения.
4. Среднее значение наблюдаемой в заданном состоянии.
5. Среднеквадратичное отклонение.
6. Совместимость наблюдаемых.
a. Совместимость и коммутативность.
b. Приготовление состояния.
D. ФИЗИЧЕСКИЙ СМЫСЛ
УРАВНЕНИЯ
ШРЕДИНГЕРА.
1. Общие свойства уравнения Шредингера.
a. Детерминизм в эволюции физических систем.
b. Принцип суперпозиции.
c. Сохранение вероятности.
d. Эволюция среднего значения наблюдаемой. Связь
с классической механикой.
2. Случай консервативных систем.
a. Решение уравнения Шредингера.
b. Стационарные состояния.
c. Константы движения.
d. Частоты Бора системы. Правила отбора.
e. Соотношение неопределенностей время — энергия.

Е. ПРИНЦИП
СУПЕРПОЗИЦИИ
И ФИЗИЧЕСКИЕ
ПРЕДСКАЗАНИЯ.
1. Амплитуда вероятности и эффекты интерференции.
a. Физический смысл линейной суперпозиции состояь
b. Суммирование по промежуточным состояниям.
c. Заключение: важность понятия амплитуды
вероятности.
2. Случай, когда несколько состояний могут быть
ассоциированы с одним и тем же результатом
измерения.
a. Вырожденные собственные значения.
b. Недостаточно селективные измерительные
приборы.
c. Резюме: следует суммировать амплитуды
или вероятности?
d. Применение к анализу непрерывных спектров.

А. ВВЕДЕНИЕ
В классической механике движение произвольной материальной системы
определено, если известна зависимость от времени положения r(jc, у, z) и скорости v(i, у, z)
каждой из ее точек. В общем случае (приложение III) для описания такой системы вводят
обобщенные координаты д;@,где / = 1,2, ...,7V и обобщенные скорости qt(t)\ задание
G,@ и q.(t) позволяет в любой момент времени определить положение и скорость любой
точки системы. Исходя из лагранжиана #(<?,-, #,-, О* для каждой из обобщенных
координат q{ определяется сопряженный ей момент pi:
й~. (А-1>
Величины д,@ и q.{t) называются основными динамическими переменными. Все
физические величины, связанные с системой (энергия, момент импульса и т.д.)
выражаются через них. Так, например, полная энергия системы определяется функцией
Гамильтона Jf{q^q.,t). Движение системы можно определить, пользуясь уравнениями
Лагранжа или каноническими уравнениями Гамильтона—Якоби, имеющими вид:
^ = |^; (А-2-а)
^ = ~. (A-2-b)
dt dqi
В частном случае системы, составленной из единственной материальной точки с
массой т, обобщенные координаты qt являются просто тремя координатами этой точки,
а обобщенные скорости qi — компонентами ее скорости v. Если силы, действующие на
частицу, определяются скалярным потенциалом V(r, t), то три момента, сопряженные
ее положению г, то есть компоненты ее импульса р, равны компонентам количества
движения т\. Тогда полная энергия равна:
2
£ = f- + V(r,r) (A-3)
2т
266

Постулаты квантовой механики
dr
It
dt
= JP .
m'
- V V.
и момент количества движения относительно начала координат равен:
# = rxp. (A-4)
2
Поскольку .Ж(г, р, t) - — + V(r, t), уравнения Гамильтона—Якоби (А-2) принимают
2т
хорошо известную форму:
(А-5-а)
(A-5-b)
Классическое описание материальной системы состоит, таким образом, в следующем,
(i) Состояние системы в данный момент времени t0 определено заданием N
обобщенных координат <7,(?0) и N сопряженных им моментов Pj(t0).
(ii) Значение любой физической величины в заданный момент времени полностью
определено, если известно состояние системы в этот момент времени: исходя из
мгновенного состояния системы, можно предсказать результат измерения любой физической
величины в момент времени t0.
(iii) Эволюция системы во времени определяется уравнениями Гамильтона—Якоби.
Поскольку эти уравнения являются дифференциальными уравнениями первого порядка,
их решение {#,@* #,@ }является единственным, если зафиксировать в этот момент
времени значения функций {дД*о)> ^/('оН1 состояние системы в некоторый момент
времени определено, если известно ее начальное состояние.
В этой главе рассмотрим постулаты, на которых базируется квантовое описание
физических систем. В главе I мы уже ввели их качественно и частично, сейчас же уточним
их в рамках формализма, развитого в главе И. Эти постулаты дадут нам ответы на
следующие вопросы (соответствующие трем пунктам классического описания):
(i) Как математически описать состояние квантовой системы в заданный момент
времени?
(ii) Как предсказать результаты измерения различных физических величин в
заданном состоянии?
(iii) Как найти состояние системы в произвольный момент времени t, если известно
ее состояние в момент времени t0 ?
Начнем с формулировки постулатов квантовой механики (§ В), обсудим затем их
физический смысл и рассмотрим их следствия (§§ С, D, Е).
267

Глава 111
В. ФОРМУЛИРОВКА ПОСТУЛАТОВ
1. Описание состояния системы
В главе I мы ввели понятие квантового состояния частицы. Сначала мы
охарактеризовали это состояние в некоторый момент времени квадратично интегрируемой
волновой функцией. Затем, в главе И, мы связали с каждой волновой функцией кет-вектор
пространства состояний #т: задание вектора |\|/), принадлежащего пространству £г,
эквивалентно заданию соответствующей функции \|/(г) = (г|\|/). Таким образом,
квантовое состояние частицы в заданный момент времени характеризуется кет-вектором в
пространстве $г. Именно в этой форме обобщается понятие состояния любой
физической системы.
I постулат. В любой фиксированный момент времени t0 состояние физической
системы определяется заданием кет-вектора |i|/(f0))> принадлежащего пространству
состояний £.
Важно отметить, что, поскольку £ — векторное пространство, этот первый
постулат требует соблюдения принципа суперпозиции: линейная комбинация векторов
состояния является вектором состояния. Это важное положение и его связь с другими
постулатами мы обсудим в § Е.
2. Описание физических величин
В § D-1 главы I мы уже использовали дифференциальный оператор Я ,
описывающий полную энергию частицы в поле скалярного потенциала. Он является всего лишь
частным случаем постулата И:
II постулат. Всякая измеряемая физическая величина .<*/ описывается
оператором А , действующим в пространстве $ ; этот оператор является наблюдаемой.
ЗАМЕЧАНИЯ
(i) Тот факт, что А — наблюдаемая (см. главу И, § D-2), окажется весьма важным
для дальнейшего изложения (§3).
(П) В противоположность классической механике (см. § А) квантовая механика
описывает состояние системы и связанные с ней физические величины совершенно иным
способом: состояние описывается вектором, а физическая величина — оператором.
268

Постулаты квантовой механики
3. Измерение физических величин
а. ВОЗМОЖНЫЕ РЕЗУЛЬТАТЫ
Связь между оператором Н и полной энергией частицы была установлена в § D-1
главы I следующим образом: единственно возможными значениями энергии являются
собственные значения оператора Н . Здесь мы обобщим этот вывод на все физические
величины.
III постулат. Результатом измерения физической величины «с/ может быть только
одно из собственных значений соответствующей наблюдаемой А .
ЗАМЕЧАНИЯ
(i) Измерение величины .?/ дает всегда вещественное число, так как по определению
А — эрмитов оператор.
(ii) Если спектр оператора А дискретный, то результаты, которые могут быть
получены при измерении ,«/, квантуются (§ С-2).
Ь. ПРИНЦИП СПЕКТРАЛЬНОГО РАЗЛОЖЕНИЯ
Сейчас уточним и обобщим выводы, сделанные в § А-3 главы I, где мы
анализировали простой эксперимент с поляризованными фотонами.
Рассмотрим систему, состояние которой в некоторый момент характеризуется кет-
вектором |vj/) , нормированным на 1:
(v|v) = i. (в-1)
Мы хотим предсказать результат измерения в этот момент времени физической величины
.«/ системы, которой соответствует наблюдаемая А . Это предсказание, как мы уже
знаем, должно носить вероятностный характер: сформулируем правила, которые позволяют
вычислить вероятность получения того или иного собственного значения оператора А .
ос. Случай дискретного спектра
Допустим сначала, что спектр оператора А дискретный. Если все собственные
значения не вырождены, то каждому из них соответствует единственный собственный
вектор |ия) (с точностью до постоянного множителя):
А\и„) = ан\ип). (В-2)
269

Глава III
Поскольку А —наблюдаемая, ансамбль нормированных векторов |и„) образует базис в
пространстве £, и произвольный вектор состояния |\|/) может быть записан в виде:
k) = Sc„|M„). (B-3)
п
Постулируем, что вероятность &(ап) получить значение ап при измерении величины .с/
равна:
*(*„)=kf =h И2- <в-4)
IV постулат (дискретный невырожденный спектр). При измерении физической
величины «с/ в нормированном состоянии системы |\|/) вероятность &{ап) получить
собственное невырожденное значение ап соответствующей наблюдаемой А равна:
*(о=|(«пН2.
где \ип) — собственный нормированный вектор оператора А , соответствующий
собственному значению ап.
Если теперь допустить, что некоторые собственные значения вырождены, то им
соответствует несколько собственных ортонормированных векторов м'Л :
А\и\) = ап\и\), где/ = 1,2, ...,*„. (В-5)
Кет |\|/) можно разложить по ортонормированному базису {\и'п)}:
|v)=x i<|«:>- (в-б)
Л 1 = 1
В этом случае вероятность &(ап) оказывается равной:
^п) = 1\4 = 1\{ф}\ ■ (В-7)
= 1 I = 1 '
Формула (В-4) является частным случаем формулы (В-7), и последнюю можно принять
в качестве общего выражения.
270

Постулаты квантовой механики
IV постулат (случай дискретного спектра). При измерении физической
величины .</ системы в нормированном состоянии |\|/) вероятность получить собственное
значение ап соответствующей наблюдаемой А равна:
;АО=|;|(ф)|2-
I = 1' '
Здесь gn — кратность вырождения собственного значения ап, и { м,',) }
(i = 1,2,..., gn) — система ортонормированных векторов, образующих базис в
собственном подпространстве #п, связанном с собственным значением оператора А .
Чтобы этот постулат имел смысл при вырожденном значении ап, необходима
независимость вероятности 1?(ап) от выбора базиса { ш'п)} в пространстве #я. Для
доказательства рассмотрим вектор:
|чО=£4К), (в-8)
где коэффициенты с'п те же, что и в разложении (В-6) вектора |\j/):
< = (М»М- (В-9)
Вектор |\|/„) является частью вектора |\|/), принадлежащей пространству ^, то есть
проекцией вектора | \|/) на пространство #;|. Впрочем, именно к этому выводу можно
прийти, если подставить (В-9) в (В-8):
I v„> = S |«-Хи-1 v) = ^.1 v), (в-ю)
где
Рп = 1\<){<\ (В-П)
проекционный оператор на пространство $п (§ B-3-b главы II). Вычислим теперь квадрат
нормы вектора |\|/„) в соответствии с формулой (В-8):
271

Глава III
(ч>„к)=£К|2. (в-12)
«= г
Таким образом, №(ап) является квадратом нормы вектора |\|//}) = f;;|\j/), то есть
проекции вектора |\|/) на пространство $п. Из этой формы записи явно следует, что
изменение базиса в пространстве $п не влияет на ^(ап). Эта вероятность имеет вид:
^„Hvl^.lv) (в-13)
или, если использовать эрмитовость оператора Рп (то есть Р* = Рп) и свойство
проекционного оператора (Р] = Ря):
>Пап) = (у\ф) (В-14)
C. Случай непрерывного спектра
Допустим теперь, что спектр оператора А непрерывен, и для простоты будем
считать его невырожденным. Ортонормированная в широком смысле система собственных
векторов |va) оператора А :
A\va) = a\va) (B-15)
образует в пространстве £ базис, по которому можно разложить вектор |\|/):
|v> = Jdac(a)|va). (B-16)
Поскольку возможные результаты измерения величины .с/ образуют непрерывный
ансамбль, следует определить плотность вероятности, как мы уже делали для
интерпретации волновой функции частицы (§ В-2 главы I): вероятность d&(a) получить значение,
лежащее между а и a + da , равна:
яЬУЧсО = p(a)Ax,
где
p(a) = |c(a)|2=|(va|\|/)|2. (B-17)
272

Постулаты квантовой механики
IV постулат (случай непрерывного и невырожденного спектра). При измерении
физической величины .<•/ в нормированном состоянии |\|/) системы вероятность
d^(a) получить значение, лежащее между а и а + da, равна:
d^a;=|(vj\|/)|2rfcc,
где |va) — собственный вектор, соответствующий собственному значению а
наблюдаемой А , связанной с величиной .?/.
ЗАМЕЧАНИЯ
(i) Во всех рассмотренных выше случаях можно в явной форме доказать, что полная
вероятность равна 1. Так, например, исходя из* формулы (В-7), получим:
S^K) = ES|c;;|2=(\|/|\|/) = i, (в-18)
п п / = 1
так как вектор |\|/) нормирован. Это последнее условие должно быть выполнено,
чтобы все приведенные выше формулировки были бы справедливыми. Однако оно
не является абсолютным: если оно не выполняется, достаточно заменить (В-7) и
(В-17) соответственно выражениями:
Wlv//Bl
p(a) = -^-|-y|c(a)|2. (B-20)
(ii) Для того чтобы IV постулат был справедливым, необходимо, чтобы оператор Л ,
связанный с произвольной физической величиной, был наблюдаемой:
действительно, нужно, чтобы любое состояние могло бы быть разложено по системе
собственных векторов оператора А.
(Hi) Мы не привели здесь IV постулат в его самой общей форме,' но, основываясь на
анализе приведенных выше случаев, можно без труда распространить принцип
спектрального разложения на любую ситуацию (непрерывный вырожденный
спектр, спектр, имеющий непрерывную и дискретную составные части и т.д.). В § Е
18 Квантовая механика
273

Глава III
и затем в главе IV мы применим IV постулат в ряде примеров, и, в частности, для
того, чтобы продемонстрировать некоторые следствия принципа суперпозиции,
рассмотренного в § В-1.
у. Важное следствие
Рассмотрим два кет-вектора |\|/) и |\|/'), связанных между собой равенством:
где Ь — вещественное число. Если вектор |\|/) нормирован, то нормирован и вектор
И:
(V,k,>=(v|^^w|v>=(vk>- (B-22)
Вероятности некоторого измерения одинаковы как для вектора |\|/), так и для вектора |\|/'),
ибо, независимо от \и\\):
|(ф)|2=|е1в(ф)|2=|(м;,|¥)|2. (в-23)
Аналогично, можем заменить |\|/) выражением:
|у") = ссе'в|ч/) (В-24)
без изменения физических результатов. Действительно, в выражениях (В-19) и (В-20) в
числителе и знаменателе появляются сокращающиеся множители |ос| . Таким образом,
два пропорциональных вектора состояния представляют одно и то же физическое
состояние.
Следует очень осторожно интерпретировать этот результат. Так, например,
предположим, что
|V> = XI|V|> + X2|V2>, (B-25)
где Я, и Х2 — комплексные числа. Действительно, вектор е,Ь[ |\|/,) представляет,
независимо от вещественного значения д,, одно и то же физическое состояние, что и | \|/,),
а е1®21\|/2) — то же состояние, что и |\|/2). Но в общем случае вектор:
274

Постулаты квантовой механики
|V) = Xie'e'|v|/,) + X2e'e=|x|/2) (B-26)
не описывает то же состояние, что и |\|/) (действительно, в § Е-1 мы увидим, что
относительные фазы коэффициентов разложения вектора состояния играют важную роль),
за исключением частного случая, когда Ь{ = Ф2 + 2пп, где
\ч>) = е*[Х1\у1) + К2\щ)] = е»'\у). (В-27)
Иначе говоря, общий фазовый множитель не влияет на физические предсказания, но
относительные фазы коэффициентов разложения имеют существенное значение.
с. РЕДУКЦИЯ ВОЛНОВОГО ПАКЕТА
Это понятие уже было введено в связи с измерением поляризации фотонов в § А-3
главы I. Здесь мы обобщим его, ограничиваясь случаем дискретного спектра
(непрерывный спектр рассмотрим в § Е).
Допустим, что в заданный момент времени нужно измерить физическую величину .с/.
Если известен кет |\|/), представляющий состояние системы до акта измерения, то
IV постулат позволяет предсказать вероятности получить различные результаты после
измерения. Однако, если производится реальное измерение, то получается, конечно,
лишь один из этих возможных результатов. Сразу же после акта измерения уже нет
вопроса о «вероятности получения» того или иного значения, поскольку уже известно
реально полученное значение. Таким образом, имеется уже дополнительная информация,
и вполне понятно, что состояние системы после измерения отлично от |\|/).
Рассмотрим сначала случай, когда измерение величины #/ дает невырожденное
собственное значение ап наблюдаемой А . Тогда можно постулировать, что состояние
системы сразу же после акта измерения описывается собственным вектором | ип) с
собственным значением ап:
|Ф> -^ Ю- (В-28)
ЗАМЕЧАНИЯ
(i) Мы рассматривали состояния «до измерения» (|ty)) и «после измерения» (|м„)).
Точный смысл этих выражений можно сформулировать так: пусть измерение
производится в момент времени t0 >0, и мы знаем состояние системы |\|/@)) в
момент времени t = 0; VI постулат (см. § 4) показывает, как система эволюционирует
18*
275

Глава 111
во времени, то есть позволяет вычислить, исходя из |\|/@)), состояние |\|/(f0))
«перед измерением». Если измерение дает в результате невырожденное собственное
значение ап, то состояние |y'(fi)) в момент времени t{>t0 нужно рассчитывать,
исходя из Iv'C'o)K1!",,)* то есть состояния «немедленно после» измерения, и
использовать VI постулат для определения эволюции вектора состояния между
моментами времени t0 и г, (рис. 1).
(и) Если вслед за первым измерением производится второе измерение величины .?/
(то есть ранее, чем система смогла испытать эволюцию), то с полной уверенностью
можно получить тот же результат ап, так как состояние системы перед вторым
измерением было \ип), а не|\|/) .
I Ф@) >
Измерение, дающее
результат ап \
\
|Wo)>
k>
И*.)>
-•►/
Рис.1
При измерении наблюдаемой А в момент времени tQ% дающем результат ant вектор
состояния системы испытывает внезапное изменение и становится вектором \ип). Затем
он испытывает эволюцию из этого нового начального состояния
Когда собственное значение ап, полученное при измерении, вырождено, то постулат
(В-28) обобщается следующим образом. Если разложение состояния |\|/) сразу же перед
измерением имеет вид:
k)=is<K),
(В-29)
то изменение вектора состояния в процессе измерения выразится формулой:
М
/ = 1
2 /=»
1 cik).
(В-30)
276

Постулаты квантовой механики
Сумма Y, с'п \и'п) представляет собой определенный выше вектор |\|/;1) [формула (В-8)],
то есть проекцию вектора |\|/) на собственное подпространство, определенное
собственным значением ап. В формуле (В-30) этот вектор был нормирован, так как всегда
удобнее использовать нормировку векторов состояния на 1 [замечание (i) в § b]. Применяя
обозначения (В-10) и (В-11), выражение (В-30) можно переписать в виде:
V => ■ "|¥ ■ (В-31)
V постулат. Если измерение физической величины .«/ системы в состоянии |\|/)
дает результат ап, то состояние системы немедленно после измерения является нор-
мированной проекцией , ' =- вектора |\|/) на собственное подпространство,
соответствующее собственному значению ап.
Таким образом, состояние системы сразу же после измерения всегда равно
собственному вектору оператора А, соответствующему собственному значению ап.
Подчеркнем особо, что это не просто какой-нибудь кет подпространства tf;l, а часть вектора
|\|/), принадлежащая #л, (нормированная соответствующим образом). В свете
изложенного выше (§ З-b-y) равенство (В-28) можно рассматривать как частный случай формулы
(В-30); действительно, если gn -1, то суммирование по / в формуле (В-30) исчезает, и,
следовательно:
-LCl,\u„) = e^^\u„). (B-32)
Этот кет описывает то же физическое состояние, что и \ип).
4. Эволюция систем во времени
В § В-2 главы I мы уже встречали уравнение Шредингера для частицы. Здесь
запишем его в общем виде:
277

Глава III
VI постулат. Эволюция
нением Шредингера:
где
вектора состояния во времени
Л±Ш-
= Я@|ч/@),
|V@)
H(t) — наблюдаемая, связанная с полной энергией системы.
описывается
урав-
Оператор Н называется гамильтонианом системы, так как он получен на основе
классической функции Гамильтона (приложение III и § 5).
5. Правила квантования
В этом параграфе мы увидим, как для физической величины .с/, определенной в
классической механике, можно построить оператор А, описывающий ее в квантовой
механике.
а. ПОСТАНОВКА ЗАДАЧИ
Рассмотрим сначала систему, состоящую из одной частицы без спина, находящуюся
в поле скалярного потенциала. Тогда:
Положению r(jc, у, z) частицы соответствует наблюдаемая R(X, У, Z).
Импульсу р(рх, pv, pz) частицы соответствует наблюдаемая P(PV, PY, Pz).
Напомним, что операторы R и Р удовлетворяют каноническим соотношениям
коммутации [глава II, равенства (Е-30)]:
[я,.,р.] = //*5,у. (в-зз)
Любая физическая величина .V, характеризующая частицу, выражается через
основные динамические переменные г и р, то есть ,<У(г, р, г). Чтобы получить
соответствующую наблюдаемую А , можно было бы просто заменить в выражении для .c/(r, p, t)
переменные г и р на наблюдаемые R и Р *:
* Определение функции от операторов дано в дополнении Вц.
278

Постулаты квантовой механики
Л(Г) = .е/(К, Р, Г). (В-34)
Однако такой подход страдает в общем случае неоднозначностью. Допустим,
например, что в .o/(R, P, t) имеется член вида:
r-p = xpx + ypy+zpz. (B-35)
В классической механике скалярное произведение г • р коммутативно, и можно в равной
мере использовать выражение:
p-r = pxx + pyy + pzz. (B-36)
Но после замены г и р на соответствующие наблюдаемые R и Р операторы,
полученные по формулам (В-35) и (В-36), не совпадают [см. формулы (В-33)]:
RP*PR. (B-37)
Кроме того, ни R • Р , ни Р • R не являются эрмитовыми операторами:
(R-P)+=(XPt + 17>v+ZPc)+=P.R. (B-38)
Поэтому к перечисленным постулатам необходимо добавить правило симметризации.
Например, наблюдаемая, соответствующая г • р, запишется в виде:
-(R P + P R) (В-39)
и является эрмитовой. Для более сложных наблюдаемых следует также выполнять
аналогичную симметризацию.
Наблюдаемая А , описывающая физическую величину ,с/, определенную
классически, получается путем замены в надлежащим образом симметризованном выражении
для ..с/ величин г и р на наблюдаемые R и Р соответственно.
Однако далее мы увидим, что существуют квантовые физические величины, не
имеющие классического эквивалента, и они определяются непосредственно
соответствующими наблюдаемыми (например, спин частиц).
ЗАМЕЧАНИЕ
Сформулированные выше правила, и, в частности, правила коммутации (В-33),
верны лишь в декартовых координатах. Однако они могут быть обобщены таким
279

Глава III
образом, чтобы их можно было использовать и в других системах координат, но
при этом они не будут иметь столь простой и наглядной формы.
Ь. ВАЖНЫЕ ПРИМЕРЫ
а. Гамильтониан частицы в поле скалярного потенциала
Рассмотрим частицу без спина, имеющую заряд q и массу т, помещенную в
электрическое поле, созданное скалярным потенциалом U(r). Потенциальная энергия
частицы равна V(r) = qU(r), а соответствующая функция Гамильтона имеет вид
[приложение III, формула B9)]:
2
.7^(r,p) = iL- + V(r), (B-40)
2т
где
р = т— = mv (B-41)
и v — скорость частицы.
Квантовый оператор Н , соответствующий функции Ж , строится без труда, так как
нет необходимости прибегать к симметризации. Действительно, ни Р2 = Р* + Р2 + Рг2,
ни V(R) не содержат произведения операторов, не коммутирующих друг с другом.
Таким образом:
Р2
Я = —+ V(R), (B-42)
2т
где V(R) — оператор, полученный путем замены в выражении V(r) переменной г на
оператор R (см. дополнение В1Ь § 4).
В этом частном случае уравнение Шредингера, вытекающее из VI постулата,
принимает вид:
|V@>. (B-43)
р. Гамильтониан частицы в поле векторного потенциала
Если теперь частица находится в произвольном электромагнитном поле, то
классическая функция Гамильтона имеет вид [приложение III, формула F6)]:
*-|¥@>-
2т
+ V(R)
280

Постулаты квантовой механики
Ж(г% р)~ [p-<?A(r, t)]2+qU(r> г), (В-44)
2т
где £/(г, О и A(r, t) — скалярный и векторный потенциалы, описывающие
электромагнитное поле, а р определяется формулой:
dv
р = т— + <?А(г, /) = т\ + <?A(r, t). (В-45)
dt
И в этом случае построение квантового оператора A(R, r) не составляет труда, ибо
А(г, t) зависит лишь от г и параметра t (но не зависит от р). Поэтому гамильтониан Н
имеет вид:
Я@ = тЦр-9А(Н, t)f+V(R9 Г), (В-46)
2т
где
V(R,f) = 9t/(R,f), (В-47)
и уравнение Шредингера записывается в форме:
|»^|V@> = {^[P-^A(R,0]2+V(R.0J|V@>. (B-48)
ЗАМЕЧАНИЕ
Следует соблюдать осторожность и не путать р (импульс частицы, или момент,
сопряженный координате г) с т\, количеством движения частицы: различие этих
двух величин отчетливо проявляется в формуле (В-45). В квантовой механике,
конечно, имеется оператор, соответствующий скорости частицы:
Г = — (Р-?А). (В-49)
т
Тогда оператор Н имеет вид:
H(t) = -mV2+V(R, t). (B-50)
281

Глава III
Это сумма двух членов, первый из которых соответствует кинетической энергии, а
второй — потенциальной энергии частицы.
Однако именно импульс р, а не количество движения т\ превращается в
квантовой механике в оператор Р, удовлетворяющий каноническим
соотношениям коммутации (В-33).
С. ФИЗИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ПОСТУЛАТОВ
О НАБЛЮДАЕМЫХ И ИХ ИЗМЕРЕНИИ
1. Правила квантования согласуются
с вероятностной интерпретацией волновой функции
Совершенно естественно связать наблюдаемые R и Р, действие которых было
определено в § Е главы II, с положением и импульсом частицы. Каждая из наблюдаемых
X, У, Z и Рх> Pv, Pz обладает непрерывным спектром, и эксперимент действительно
показывает, что шесть переменных положения и импульса могут принимать любые
вещественные значения. Применение IV постулата к этим наблюдаемым лишь подчеркивает
вероятностную интерпретацию волновой функции и ее Фурье-образа (см. § В-2 и § С-3
главы I).
Для простоты остановимся на одномерной задаче. Если частица находится в
нормированном состоянии |\|/), вероятность того, что измерение положения даст результат,
заключенный между х и х + dx , равна (В-17):
^?(д:) = |(д:|1|/)|2^, (С-1)
где \х) — собственный кет оператора X с собственным значением х. Видно, что
квадрат модуля волновой функции 1|/(jc) = (x\\\f) есть плотность вероятности найти частицу
в точке х. С другой стороны, собственный вектор | р) наблюдаемой Р соответствует
плоской волне:
{'м'шл- (С-2)
и мы уже видели в § С-3 главы I, что соотношения Луи де Бройля связывают с этой
волной определенный импульс, в точности равный р . Кроме того, вероятность получить у
частицы в состоянии |\|/) импульс в пределах от р до р Л-dp равна:
282

Постулаты квантовой механики
d;Hp)^\y)\2dp = \\v(pfdp. (С-3)
Именно это было установлено в § С-3 главы I.
2. Квантование некоторых физических величин
Выше мы уже отмечали, что III постулат позволяет установить правила квантования
некоторых величин, как, например, энергия атомов. Но его нельзя применить для
квантования всех величин, так как имеются наблюдаемые, спектр которых непрерывен.
Физические предсказания, основанные на III постулате, априори не могут считаться
очевидными. Например, далее при изучении атома водорода (глава VII) будем исходить из
полной энергии электрона в поле кулоновского потенциала протона, и из нее получим
выражение для гамильтониана. Решив уравнение на собственные значения, найдем, что
связанные состояния системы могут соответствовать лишь определенным дискретным
значениям энергии, которые затем будут найдены. Таким образом, мы не только
объясним квантование уровней атома водорода, но и предскажем возможные значения
энергии, которые можно обнаружить экспериментально. Подчеркнем, что эти результаты
будут получены на основе того же фундаментального закона взаимодействия, что и в
классической механике для макроскопических объектов.
3. Механизм измерения
Четвертый и пятый постулаты порождают определенные проблемы
фундаментального характера, которые здесь не будут рассмотрены. К ним, в частности, относится
проблема понимания природы «фундаментального» возмущения, вносимого в квантовую
систему при наблюдении (см. главу I, § А-2 и § А-3). Сущность этих проблем состоит
в том, что изучаемая система рассматривается изолированно от измерительного
прибора, тогда как их взаимодействие существенно влияет на систему в процессе измерения.
В действительности следовало бы рассматривать ансамбль, состоящий из системы и
измерительного прибора, но это связано с появлением очень деликатных вопросов,
касающихся подробностей самого механизма измерения.
Мы удовлетворимся лишь констатацией связи индетерминистской формулировки
четвертого и пятого постулатов с только что затронутыми проблемами. Например,
внезапный переход при измерении от одного вектора состояния к другому как раз и связан
с фундаментальным возмущением, о котором мы говорили выше. Но невозможно
предсказать, каким будет это возмущение, так как оно зависит от заранее неизвестного
результата измерения*.
* За исключением, конечно, случая, когда мы уверены в получении того или иного результата
(вероятность равна 1, процесс измерения не изменяет состояния системы).
283

Глава III
Уместно также заметить, что мы рассматриваем здесь лишь идеальные измерения.
Чтобы понять смысл этого понятия, вернемся к примеру эксперимента в § А-3 главы I
с поляризованными фотонами. Ясно, что когда допускаем, что все поляризованные в
определенном направлении фотоны пройдут через анализатор, мы предполагаем, что он
является совершенным. На практике, естественно, анализатор частично поглощает
фотоны, которые он должен был бы пропустить. Таким образом, в общем случае
предполагается, что используемые измерительные приборы являются идеальными, то есть
производимое ими возмущение системы связано исключительно с квантовым механизмом
измерения. Конечно, все реально существующие приборы всегда имеют отклонения от
совершенства, влияющие как на измерение, так и на саму систему. Но в принципе их
можно совершенствовать бесконечно, приближаясь тем самым к идеальному пределу,
определенному сформулированными выше постулатами.
4. Среднее значение наблюдаемой в заданном состоянии
Предсказания, которые можно сделать с помощью IV постулата, выражаются в
терминах вероятностей. Чтобы подтвердить их, нужно было бы выполнить большое
количество измерений в идентичных условиях, то есть измерять одну и ту же величину для
большого количества систем, приготовленных в одном и том же квантовом состоянии:
если эти предсказания правильны, мы должны обнаружить, что из общего количества
идентичных экспериментов N пропорция тех, которые соответствуют данному
событию, должна стремиться при N —> °о к вероятности & события, предсказанной теорией.
Такое подтверждение можно получить только при N —» ©о 9 но на практике N — всегда
конечная величина, и для интерпретации полученных результатов нужно применять
статистическую обработку.
Среднее значение наблюдаемой* А в состоянии |\|/), которое далее мы будем
обозначать символом (Л) или просто (Л), определяется как средний из результатов,
полученных при большом количестве N измерений этой наблюдаемой на системах,
находящихся в состоянии |\|/). Если вектор |\|/) известен, то известны вероятности получить
все возможные результаты, и можно предсказать среднее значение (Л) . Сейчас мы
покажем, что если кет |\|/) нормирован, величина (Л) определяется формулой:
(A) =(vHv>
(С-4)
* В дальнейшем мы будем использовать слово «наблюдаемая» для обозначения как
физической величины, так и связанного с ней оператора.
284

Постулаты квантовой механики
Рассмотрим сначала случай, когда спектр оператора А — дискретный. Если из N
измерений величины ,<*/ (каждый раз система приготовлена в состоянии |\|/))
собственное значение ап получено *Л\ап) раз, то
•*(«„)
N
■N=nr->^(«.)
(С-5)
!•*(*.) = N.
(С-6)
Среднее значение результатов N измерений равно сумме всех полученных значений,
разделенной на N (конечно, если в .Г измерениях получен один и тот же результат, в
сумму он входит ,/Г раз), то есть
— У\аМа„).
(С-7)
Используя формулу (С-5), получим, что при N —> оо среднее значение стремится к:
(А\=1а„0>(ап). (С-8)
п
Подставим в эту формулу выражение (В-7), полученное для Р7>(ап):
(-4}w=E^E(v|/|<>(«:|v|/>. (C-9)
п / = 1
Поскольку:
А\и') = а \и! ),
можно переписать формулу (С-9) в виде:
(a)v=ZS(v|a|«;,)(m:|4/> = (v|a[s£|«:>(m»I
k>.
(С-10)
(С-11)
Так как ансамбль векторов {\и'\} образует ортонормированный базис в пространстве
К, выражение в квадратных скобках равно единичному оператору (соотношение
замкнутости), и результатом является формула (С-4).
285

Глава III
В случае, если спектр оператора А непрерывный (для простоты допустим, что он не
вырожден), то все рассуждения остаются теми же. Рассмотрим N одинаковых
экспериментов и обозначим символом d I (а) число экспериментов, которые дали результат,
заключенный между а и а + da . Как и ранее:
iLM__^(a). (C-12)
Среднее значение полученных результатов равно —iadJ'(a) и стремится при N —> «>
к значению:
(A)¥=Jad?(a). (C-13)
Подставим в (С-13) выражение (В-17) для di?(a):
(>i)¥=Ja(v|vaXva|v)rfa. (C-14)
Можно воспользоваться уравнением:
A|va) = a|va) (C-15)
и преобразовать (С-14) в:
(A)v=/(V|A|va){vtt|Vya = D/|A[^a|vaXv0||¥)]. (C-16)
С учетом соотношения замкнутости для состояний | va) получаем формулу (С-4).
ЗАМЕЧАНИЯ
(i) Не следует путать (л), среднее по ансамблю идентичных измерений, со средним
по времени, что иногда бывает при изучении явлений, зависящих от времени,
(ii) Если кет |\|/), представляющий состояние системы, не нормирован, то формулу (С-4)
нужно изменить [см. замечание (i) в § B-3-b] на:
(А) _МАМ (С-17)
(}* т • (С17)
(ш) На практике для вычисления (л) часто переходят в определенное представление.
Например:
286

Постулаты квантовой механики
{Х)щ =(\|/| X |i|/) = J</3r(V|r)(r| X |i|/) = Jrf3/-y*(r)x\)/(r) (С-18)
в соответствии с определением оператора X [см. главу II, (Е-22)]. Аналогично:
(РХ =Wp,M = U3pW'(p)p.Mp) (С-19)
или в представлении {| г)}:
(P,)w=J^r(V|r)(r|Pv|v|/)=J^Vu/4r)|
ttVW
I ОХ
(С-20)
так как оператор Р определен выражением — V [формула (Е-26) главы II].
/
5. Среднеквадратичное отклонение
Значение (л) указывает на порядок величины наблюдаемой А, когда система
находится в состоянии |\|/). Однако это среднее значение не дает никакого ответа на
возможный разброс результатов измерения. Допустим, например, что спектр оператора А
непрерывен и что в определенном состоянии |\|/) кривая, описывающая зависимость
плотности вероятности p(oc) = Kva|\|/) от а, имеет форму, изображенную на рис. 2.
Для системы в состоянии |\|/) значения, которые можно получить при измерении Л,
заключены практически в интервале с шириной 8Л вблизи (л). Величина 5А является
характеристикой ширины кривой: чем она меньше, тем плотнее результаты измерения
концентрируются вокруг значения (л).
<*> «,
>сг
Рис.2
Зависимость плотности вероятности р(ос).
Среднее значение (л) равно абсциссе
центра тяжести площади под кривой (она не
обязательно совпадает с абсциссой аш
максимума функции)
287

Глава III
Как в общем случае определить число, характеризующее дисперсию результатов
вокруг (а) ? Априори можно было бы попытаться сделать это следующим образом: для
каждого измерения найти разность между полученным значением и величиной (л),
затем усреднить эти разности, разделив их сумму на количество N экспериментов.
Однако легко видеть, что при этом был бы получен результат, равный нулю. Действительно:
(а-(а)) = (а)-(а) = 0. (С-21)
По определению (а) отрицательные отклонения в среднем скомпенсировали бы
положительные отклонения.
Чтобы избежать компенсации, достаточно определить АЛ через квадрат (АЛ) , то
есть усреднять квадраты отклонений:
(ДАJ = ((а-(а))^. (С-22)
Итак, по определению введем среднеквадратичное отклонение ДА формулой:
АА
-№-wt
(С-23)
Согласно выражению (С-4) для среднего значения получим:
ДА = ij(y\(A-(A)J\y). (С-24)
Это соотношение можно переписать в несколько ином виде, поскольку,
действительно:
((Л-(А)J)=((л2-2(л)Л + (лJ)) = (л2)-2(лJ+(лJ=(л2)-(лJ.(С-25)
Таким образом, среднеквадратичное отклонение А А можно записать и так:
ДЛ = )/(Л2)-(АJ. (С-26)
Например, в случае непрерывного спектра рассмотренной выше наблюдаемой А
величина А А определяется из равенства:
(а аJ = J_^ [a-(A)]2p(a)da = О*2 p(a)da-[f_+>p(a)da]2. (С-27)
288

Постулаты квантовой механики
Если применить определение (С-23) к наблюдаемым R и Р, можно показать
(дополнение Сш), используя их соотношения коммутации, что в любом состоянии |\|/) имеем:
(ДХ-ДРг>/*/2;
|дУ-ДРу>/?/2; (С-28)
[AZ'APz>ti/2.
Иначе говоря, мы снова получили соотношения неопределенностей Гейзенберга, но с
точной нижней границей, которая получилась из точного определения отклонений.
6. Совместимость наблюдаемых
а. СОВМЕСТИМОСТЬ И КОММУТАТИВНОСТЬ
Рассмотрим две коммутирующие наблюдаемые Л и В:
[л, В] = О . (С-29)
Для простоты допустим, что их спектры дискретны. Согласно теореме, доказанной в
§ D-3-a главы И, в пространстве состояний, образованном общими собственными
векторами операторов А и /?, существует базис, который мы обозначим как \ап, Ьр, Л :
A\"n*bpj) = an\aH9bp,i)\
в\ан,Ьр,1) = Ьр\ая,Ьр,1) (С-30)
(индекс / позволит нам в случае необходимости различить разные векторы,
соответствующие одной и той же паре собственных значений). Таким образом, какими бы ни
были ап и Ь (выбранные соответственно из спектров операторов А и В), существует по
меньшей мере одно состояние \ап, bp, n , для которого измерение А даст с
достоверностью значение ап и измерение В — значение Ьр, и они могут быть одновременно и
точно определены, или, как говорят, совместимы.
Напротив, если операторы А и В не коммутируют, состояние в общем случае не
может быть" собственным вектором одновременно для этих двух наблюдаемых, и они
называются несовместимыми.
* Может оказаться, что некоторые кет-векторы будут одновременно собственными векторами
А и В. Но их при этом недостаточно, чтобы образовать базис, в противоположность тому, что
имеет место , если А и В коммутируют.
19 Квантовая механика
289

Глава III
Рассмотрим более подробно измерение двух совместимых наблюдаемых в системе, которая в
начальный момент времени находилась в произвольном нормированном состоянии |\|/) . Его
всегда можно представить в виде:
|V>= Ic„,,M.| <*„,*>„,*). (С-31)
л. p,i
Предположим сначала, что мы измеряем величину А и сразу же после нее — величину В
(прежде, чем система смогла изменить состояние). Вычислим вероятность !?(ап, Ьр) получить
ап в первом измерении и Ьр — во втором. Начинаем с измерения А в состоянии |\|/) ;
вероятность получения ап равна:
^K) = Ek.J
(С-32)
Если затем измеряем В, то система уже не находится в состоянии |\|/у , а в состоянии | \|/;'у, если
в результате первого измерения получено значение ап :
1
1*;)=
\р.1
2Х;),,. кЛ-')-
(С-ЗЗ)
Вероятность получить Ь после того, как первое измерение дало значение ап , равна:
1 ^ I
Ъ.ФрУ-
(С-34)
Искомая вероятность ^(я,,, Ъ ) соответствует «сложному событию»: сначала нужно получить
ап , а затем (после реализации первого условия) — Ъ . Тогда:
Пап,Ьр) = :Па„)х?а (Ьр). (С-35)
Подставив в эту формулу выражения (С-32) и (С-34), получим:
^(*.Л)в2К„.,|2. (С-Зб)
i
Кроме того, сразу же после второго измерения состояние системы изменится и станет равным:
(С-37)
I ¥".„) = I 2е».,./ K'V i) .
\У\с \ '
290

Постулаты квантовой механики
Таким образом, если снова пытаться измерить или А или В, то результат (ап или Ър) будет
полностью определен, так как V,",,} —общий собственный вектор операторов А и В с
собственными значениями ап и Ър соответственно.
Вернемся теперь к системе в состоянии |\|/) и измерим две наблюдаемые в обратном порядке
(сначала В, затем А ). Какой будет вероятность -J?{bp, ап) получения тех же результатов, что и
ранее? Рассуждения остаются теми же, и в конце концов получим:
Из формулы (С-31) видно, что
Р(Ьр,ая) = Р(Ьр)х&(ая).
oj>(b ) = Y \с .1 .
(С-38)
(С-39)
После измерения В, давшего Ь , состояние системы станет равным:
Тогда:
к) = i iicn.pj \an. v «■) •
/V I l/i,/
\jLj \ n,p,i\
*ъ. ("„) = ■
1
Cn.p.i
V
2 Ь
i
n,p,i
(C-40)
(C-41)
i
После измерения сначала bp, а затем ап система перейдет в состояние:
|ф/',/,) = -Г= 2 IX;,/ \*п>Ьр>1)-
(С-42)
(С-43)
Если две наблюдаемые совместимы, то физические предсказания одинаковы
независимо от порядка, в котором производятся два измерения (при условии, конечно, что ин-
19*
291

Глава 111
тервал между ними должен быть достаточно малым). Вероятности получения
результатов (ап, затем Ьр)и(Ьр, затем ап ) одинаковы:
!?(*„, Ьр) = ПЪР, а„) = S \cnJ =2 \{an,bp, i\vf . (С-44)
Кроме того, финальные состояния, в которые приходит система после двух измерений и
получения соответствующих результатов, также одинаковы:
\К„) = \<„)= , 1 2 Zc„.„,h, К, г). (С-45)
Все последующие измерения А и В с достоверностью дали бы те же значения.
Итак, проведенный выше анализ позволил нам получить следующий результат: если
две наблюдаемые А и В совместимы, то измерение В не приводит к потере
информации, полученной перед этим при измерении А (и наоборот), напротив, оно дополняет
их, при этом порядок, в котором измеряются А и В, не имеет значения. Это
утверждение, впрочем, допускает возможность и одновременного измерения А и В. Как можно
убедиться, формулы (С-44) и (С-45) позволяют обобщить IV и V постулаты на подобные
случаи одновременного измерения: результату {ап, Ър } соответствуют ортонормиро-
ванные собственные векторы \ап, bp, i), и, следовательно, формулы (С-44) и (С-45)
оказываются непосредственно вытекающими из постулатов (В-7) и (В-30).
Напротив, если А и В не коммутируют, все приведенные выше рассуждения
несправедливы. Чтобы понять это, представим себе, что пространство состояний #
заменили на пространство двумерных вещественных векторов. Векторы \щ) и \и2) на рис.3
являются собственными векторами оператора А с собственными значениями я, и а2
соответственно; |v,)h |v2) являются собственными векторами оператора В с
собственными значениями Ь{ и Ь2 соответственно. Каждый из двух ансамблей {|mi),|m2)} и
{|v,) ,|v2) } образует ортонормированный базис в пространстве ^ . На рис.3 мы
представили их двумя парами перпендикулярных единичных векторов. Тот факт, что
наблюдаемые А и В не коммутируют, требует, чтобы эти две пары не совпадали. Изучаемая
физическая система первоначально находилась в нормированном состоянии | ij/), что
представлено на рисунке некоторым произвольным единичным вектором. Измеряем А
и получаем, например, я, — при этом система переходит в состояние \щ). Затем
измеряем В и получаем, например, Ь2 — при этом система переходит в состояние | v2):
292

Постулаты квантовой механики
|1М2> __
Рис.3
Схема, иллюстрирующая последовательное
измерение двух несовместимых наблюдаемых А и В.
Вектор состояния системы |\|/); собственные векторы
оператора А обозначены символами и Л и \и2)
(собственные значения я, и я2), они отличаются от
собственных векторов оператора В — v,) и \v2)
(собственные значения Ъх и Ъ2)
|¥) _<*)_» )„,)_<&)_> |„2). (С-46)
Если же мы выполняем измерения в обратном порядке, получая при этом в каждом из
них те же результаты, то
M-^Hv2)-^h). (C-47)
Видно, что в этих двух случаях финальное состояние не одно и то же. Из рисунка также
видно, что
^>(«1,Ь2) = |ОН1|2х|ОК2|2;
^(Ь2, «1) = |ОН2|2х|ОК1|2. (С-48)
Несмотря на то, что |ОК,| = |ОК2|, в общем случае |ОН,| Ф |ОН2| и
&{Ь2,ах)Ф#(с1х,Ь2). (С-49)
Итак, две несовместимые наблюдаемые не могут быть измерены одновременно. Из
выражений (С-46) и (С-47) видно, что при втором измерении теряется информация,
полученная при первом измерении: если, например, после последовательности измерений,
схематически представленной выражением (С-46), вновь пытаться измерить
величину А , то результат оказывается не достоверным, так как |v2) не является
собственно
293

Глава III
ным вектором оператора А, и все преимущества первого измерения А оказываются
потерянными.
Ь. ПРИГОТОВЛЕНИЕ СОСТОЯНИЯ
Рассмотрим физическую систему в состоянии |\|/) и попытаемся измерить
наблюдаемую А , предполагая, что ее спектр является дискретным.
Если измерение дает невырожденное собственное значение ап, то состояние системы
сразу же после измерения является соответствующим собственным вектором \ип). В этом
случае знание результата измерения достаточно для недвусмысленного определения
состояния системы после измерения, и оно является одним и тем же, каким бы ни был
исходный кет |\|/). Как мы уже отмечали в конце § В-З-с, это связано с тем, что вектор
т-^т \ип) физически представляет то же состояние, что и сам кет \ип).
Ы
Дело обстоит иначе, если собственное значение ап, полученное в измерении,
является вырожденным. В формуле:
k:)=-r=£cJk) (c-5°)
модули коэффициентов с'п и их относительные фазы существенно важны (§В-3-Ь-у).
Поскольку с'п зафиксированы заданием начального состояния |\|/), состояние |\|/,')
после измерения оказывается зависящим от |\|/).
Однако мы видели выше, что можно одновременно измерять две совместимые
наблюдаемые А и В. Если результат (ап, Ьр) этого комбинированного измерения таков,
что ему соответствует единственный собственный вектор ап, Ър), общий для
операторов А и В, то суммирование по / в формуле (С-37) отсутствует, и, следовательно:
\с
Это состояние физически эквивалентно вектору \ап, Ьр). И снова задание результатов
измерения фиксирует единственным образом финальное состояние системы, не
зависящее от начального кет-вектора |\|/).
294

Постулаты квантовой механики
Если набору (ап, Ьр) соответствует несколько собственных векторов \ап, bp, i)
операторов А и В, можно всякий раз снова повторить сделанные рассуждения и
измерить одновременно с А и В третью наблюдаемую С, совместимую с каждой из двух
предыдущих. При этом приходим к следующему заключению: чтобы состояние
системы после измерения было определено, в любом случае при наличии полученного
результата нужно, чтобы это измерение выполнялось на полном наборе коммутирующих
наблюдаемых (§ D-3-b главы И). Именно это свойство физически оправдывает введение
понятия полного набора коммутирующих операторов.
Методы, которые можно использовать для приготовления системы в определенном
квантовом состоянии, аналогичны в принципе методам, позволяющим получить
поляризованный свет: если вставить на пути луча света поляризатор, то после него свет
выходит поляризованным в направлении оси поляризатора, независимо от состояния
начальной поляризации. Так реализуется устройство, предназначенное для приготовления
квантовой системы в некотором определенном состоянии, соответствующем
определенному собственному значению каждой из наблюдаемых избранного полного набора.
Рассмотрим конкретный пример приготовления квантовой системы в главе IV (§ В-1).
ЗАМЕЧАНИЕ
Измерение всех наблюдаемых некоторого полного набора коммутирующих
операторов позволяет приготовить систему лишь в одном из базисных состояний,
образующих этот набор. Однако достаточно изменить набор наблюдаемых, чтобы
получить другие состояния системы. На конкретном примере в § В-1 главы IV
увидим, что так можно приготовить систему в любом состоянии пространства # .
D. ФИЗИЧЕСКИЙ СМЫСЛ УРАВНЕНИЯ ШРЕДИНГЕРА
Уравнение Шредингера играет фундаментальную роль в квантовой механике, так
как согласно сформулированному выше VI постулату оно описывает эволюцию во
времени физической системы. В этом параграфе мы рассмотрим наиболее важные свойства
этого уравнения.
1. Общие свойства уравнения Шредингера
а. ДЕТЕРМИНИЗМ В ЭВОЛЮЦИИ ФИЗИЧЕСКИХ СИСТЕМ
Уравнение Шредингера:
/Й-f |V@) = #@|V@> (D-l)
at
295

Глава III
является дифференциальным уравнением первого порядка по t. Отсюда следует, что
задание начального состояния |i|/(f0)) достаточно для определения |\|/(/)) в любой
последующий момент времени. Никакой индетерминизм не вносится во временную
эволюцию квантовой системы. Он проявляется только на этапе измерения физической
величины, когда вектор состояния подвергается непредвиденным изменениям (см. V
постулат); напротив, между двумя измерениями вектор состояния эволюционирует
совершенно определенным образом в соответствии с уравнением (D-1).
Ь. ПРИНЦИП СУПЕРПОЗИЦИИ
Поскольку уравнение (D-1) линейное и однородное, его решения допускают
применение принципа суперпозиции.
Пусть |\|/,(f)) и |\|/2@) —два решения уравнения (D-1). Если начальное состояние
системы равно |\|/(r0)) = X,|\j/l(r0)) +А>2|\|/2(г0)), где А,, и Х2 —комплексные константы,
то в момент времени t система находится в состоянии \y(t)) = X1|\|/1(/)) + X2|ij/2(r)).
Таким образом, соответствие между |i|/(/0)) и |ty@) является линейным. Далее (в
дополнении Fni) более подробно рассмотрим свойства линейного оператора U(t, tQ),
преобразующего |v|/(r0)) в |\|/@)-
|v(o>=£/a^o)|va0)>- (D-2)
с. СОХРАНЕНИЕ ВЕРОЯТНОСТИ
а. Норма вектора остается постоянной
Эрмитовость гамильтониана Я(г), фигурирующего в уравнении (D-1), требует,
чтобы квадрат нормы вектора состояния (i|/@| V@) не зависел от времени t.
Действительно, можно показать, что —(i|/(f)| V@) = 0;
^(Щф(О):
>>1
|v(o)+D/(o
■ii«.»
(D-3)
Или, согласно (D-1), можно записать:
iL|V@) = ^#(r)|v@>. (D-4)
296

Постулаты квантовой механики
Возьмем эрмитово сопряжение от обеих частей равенства (D-4):
T(V(')| = ~Ы0\ Н+@ = ~(Щ0\ H(t), (D-5)
так как H{t) — эрмитов оператор (то есть наблюдаемая). Подставив (D-4) и (D-5) в (D-3),
получим:
^(V@|¥@) = ~{Ш\ ЖО | V@) + ^(V@| Я(г) | V@>. (D-6)
Свойство сохранения нормы оказывается очень полезным в квантовой механике.
Так, например, оно совершенно необходимо для интерпретации квадрата модуля
|\|/(r, t)\" волновой функции частицы без спина как плотности вероятности нахождения
ее в точке с радиусом-вектором г. Действительно, тот факт, что состояние |\|/(f0))
частицы нормировано в момент времени t0, выражается соотношением:
<Va0)|vUo)> = J^3^|v(r, r0)|2 =1, (D-7)
где \|/(r, f0)= (r|v|/(/0)) — волновая функция, соответствующая вектору |v(/0)).
Равенство (D-7) означает, что полная вероятность найти частицу во всем пространстве равна 1.
Доказанное выше свойство сохранения нормы выражается формулой:
(v@| v(o> = RV |vd\ o|2=(ч/а0)| va„)> = 1, (d-8)
где |\|/(r)) — решение уравнения (D-l), соответствующее начальному условию |\|/(r0)).
Иначе говоря, эволюция во времени не изменила полную вероятность найти частицу в
любой точке пространства, которая всегда остается равной 1, то есть |\|/(r, t)\
действительно можно интерпретировать как плотность вероятности.
Р. Локальное сохранение вероятности. Плотность и ток вероятности
В этом параграфе ограничимся случаем физической системы, образованной из
единственной частицы без спина.
Тогда, если \j/(r, t) нормирована, то функция:
p(r,0 = |v(r,0|2 (D-9)
297

Глава HI
является плотностью вероятности: вероятность d^(r, t) найти частицу в момент t в
бесконечно малом объеме d3r, окружающем точку с радиусом-вектором г, равна:
d0»(r, 0 = p(r, t)d3r. (D-10)
Мы только что показали, что интеграл от р(г, О по всему пространству остается
постоянным во времени и равным 1, если \|/(r, t) нормирована. Это, однако, не означает, что в
каждой точке пространства г функция р(г, г) не должна зависеть от времени.
Действительно, ситуация совершенно аналогична той, которая существует в электромагнетизме:
если в данной изолированной физической системе имеется заряд, распределенный в
пространстве с объемной плотностью р(г, г), то общий заряд системы (то есть интеграл
от p(r, t) по всему пространству) сохраняется во времени, но в системе могут существовать
электрические токи, связанные с пространственным перераспределением этого заряда.
Эта аналогия может быть продолжена и далее. Сохранение полного электрического
заряда основано на законе его локального сохранения: если заряд Q, содержащийся в
некотором объеме V , изменяется во времени, это значит, что через замкнутую
поверхность S , окружающую V , протекает электрический ток. Точнее, изменение dQ заряда
за время dt в объеме V равно -/ dt, где / — сила тока через поверхность S , то есть
поток вектора плотности тока J(r, t), выходящего из S . Классический векторный
анализ позволяет выразить локальное сохранение электрического заряда формулой:
J-p(r,r) + divJ(rfO = 0. @-11)
Покажем, что можно ввести вектор J(r, t) плотности тока вероятности так, что
равенство, идентичное (D-11), останется справедливым, то есть будет иметь место
локальное сохранение вероятности. Все происходит так, как будто мы имеем дело с «потоком
вероятности», плотность и движение которого описываются функциями р(г, г) и
J(r, t). Если вероятность найти частицу в фиксированном объеме d3r вблизи г
изменяется во времени, это значит, что поток тока вероятности через ограничивающую этот
объем поверхность отличен от нуля.
Допустим сначала, что рассматриваемая частица подвержена действию лишь поля
скалярного потенциала V(r, t). Тогда ее гамильтониан имеет вид:
Р2
Я =— + V(R, О (D-12)
2т
и уравнение Шредингера запишется в представлении {|г) } в виде (см. дополнение Dn):
298

Постулаты квантовой механики
Э П2
ih — \j/(r, r) = A\|/(r, t) + V(r, r)\|/(r, r). (D-13)
at 2m
Функция V(r, г) должна быть вещественной, чтобы оператор Я был эрмитов.
Уравнение, комплексно сопряженное уравнению (D-13), запишется в форме:
Э h2
-ih —\|/*(г, 0 = -—AV(r, 0 + V(r, r)\|/*(r, r). (D-14)
at 2т
Умножим обе части равенства (D-13) на \|/*(r, t) и равенства (D-14) на -\|/(г, /), затем
сложим получившиеся уравнения:
Э h2
ihj- (У (г, 0 V(r, ')] = -— [\|/*A\|/-\|/Ai|/*] (D-15)
или
—p(r, 0 + т—: [V(r, 0A\j/(r, r)-\|/(r, 0AV>, 0l = 0. (D-16)
<tt 2mi L J
Если ввести вектор:
J(r, 0 = f\|/* V V|/-\|/ V V|/*l= —Re \\f\ —V\|/
2mi L A m \ \ i j
(D-17)
то равенство (D-16) примет форму (D-l 1), так как
divj(r,0= V J =
= ;гт К v ¥*)•( V \|0 + \|f'( V 2V)-( V \|/).( V \|/*)-V( V V)l =
2mi
= —[\|/*Ai|/-i|/Ai|/*l. (D-l 8)
2m/ L J
Таким образом, доказано существование уравнения, описывающего локальное
сохранение вероятности, и найдено выражение для тока вероятности, определенного через
нормированную волновую функцию \|/(r, t).
ЗАМЕЧАНИЕ
Форма выражения (D-17) для плотности тока вероятности физически понятна.
Действительно, J(r, t) имеет вид среднего значения оператора К(г) в состоянии \|/@/ > если
он задан формулой:
299

Глава III
K(r)=^[|r)(r|P + P|.r)(r|]. (D-19)
Поскольку оператор |г)(г| имеет среднее значение |\|/(г, /)| , то есть плотность вероятно-
Р
сти, а — — оператор скорости Т, то оператор К является квантовым оператором, по-
m
строенным с учетом соответствующей симметризации как произведение плотности на
скорость частицы, что полностью совпадает с вектором плотности тока классической жидкости
(например, хорошо известно, что плотность электрического тока, ассоциирующегося с
потоком наэлектризованных частиц, записывают в виде произведения объемной плотности
заряда на скорость перемещения этих частиц).
Если частица находится в электромагнитном поле, описываемом потенциалами
Ц(т, t) и А(г, /), можно продолжить рассуждения, высказанные ранее по поводу
гамильтониана (В-46). Тогда можно записать:
J(r,r) = -Re
m
\|Л yV-gA|\|(
(D-20)
Видно, что это выражение получается из (D-17) с помощью того же правила, что и
гамильтониан: простой заменой Р на Р - qX .
Пример плоской волны. Рассмотрим волновую функцию вида:
\|/(г, 0 = Л*" \ (D-21)
п\2
где Йсо = . Соответствующая плотность вероятности равна:
2т
p(r,0=k(r,0|2=|A|2. (D-22)
Она одинакова во всем пространстве и не зависит от времени. Вычисление J(r, t) с
помощью формулы (D-17) не представляет трудностей и дает:
. .? frk
J(r,/)= Л — =p(r,Ovc, (D-23)
т
hk
где vG = — — групповая скорость, соответствующая импульсу ftk (глава I, § С-4).
т
И снова мы видим, что ток вероятности равен произведению плотности вероятности на
групповую скорость частицы. В данном случае р и J не зависят от времени: режим
300

Постулаты квантовой механики
потока вероятности соответствует стационарной плоской волне (так как эти величины
не зависят и от г, то этот режим является еще и однородным).
d. ЭВОЛЮЦИЯ СРЕДНЕГО ЗНАЧЕНИЯ НАБЛЮДАЕМОЙ.
СВЯЗЬ С КЛАССИЧЕСКОЙ МЕХАНИКОЙ
Пусть А — наблюдаемая. Если состояние системы |\|/(/)) нормировано (и мы
только что видели, что это свойство сохраняется во времени), то среднее значение
наблюдаемой А в момент времени t равно*:
(A)@ = <V(OHv@).
(D-24)
Видно, что (а)(/) зависит от t через зависимость от времени вектора |i|/(/)) (и,
конечно, (\|/@|). Кроме того, наблюдаемая А может явно зависеть от времени, что является
еще одной дополнительной причиной изменения (а)(г) во времени.
В этом параграфе мы рассмотрим эволюцию (а)(г) и покажем, как можно связать
классическую механику с квантовой.
а. Общая формула
Дифференцируя (D-24) по времени, получим:
-(V(oHv(o) =
dt
(V@|
A(o|v(o)+(v(oH(o
dt
|V@)
+ <V@|£|V(»>.
dt
(D-25)
Используя формулы (D-4) и (D-5) для
>»
>"l
, найдем:
j{y{t)| A(t) |\|/@> = ^(V(r)| [A(t) H{t) - H(t) Ait)] |\|/@) + (V@1 ^ |V@>, (D-26)
то есть
>->»M%-
(D-27)
* Обозначение (A /it) означает, что среднее значение (А) есть число, зависящее от
301

Глава III
ЗАМЕЧАНИЕ
Среднее значение (л) есть число, зависящее только от t, и важно понимать,
с чем связана эта зависимость. Для определенности рассмотрим случай частицы
без спина. Пусть .с/(г, р, г) — классическая величина; в классической механике
величины г и р зависят от времени (они изменяются в соответствии с
уравнениями Гамильтона), так что ,V(r, p, t) зависит от t одновременно и явно и неявно
через переменные г и р. Классической величине ,</(r, p, t) соответствует эрмитов
оператор Д = .</(К, Р, г), полученный путем замены в выражении для .с/
переменных г и р операторами R и Р (правила квантования, см.§ В-5).
Собственные состояния и собственные значения операторов R и Р, а следовательно, сами
эти наблюдаемые, не зависят более от t. Временная зависимость г и р,
характеризующая эволюцию классического состояния, оказывается теперь перенесенной
не в R и Р, а в вектор квантового состояния |\|/@)» которому в представлении
{|г) } соответствует волновая функция \|/(r, 0 = (r|v@)- В этом представлении
среднее значение наблюдаемой А записывается в форме:
(Л) = \d3r \|/*(г, f).«/(г, - V , 0Ч>A\ О • (D-28)
/
Ясно видно, что интегрирование по г дает в результате число, зависящее только
от времени. Чтобы установить связь с классической механикой, необходимо
сравнивать именно это число, а не оператор .«-/(г, — V , г), со значением, принимае-
/
мым классической величиной .с/(г, р, t) в момент времени t (см. ниже § у).
C. Применение к наблюдаемым R и Р (теорема Эренфеста)
Применим теперь общую формулу (D-27) к наблюдаемым R и Р. Для простоты
рассмотрим случай частицы без спина в поле стационарного скалярного потенциала
V(r). Имеем:
//~ + V(R), (D-29)
2т
так что можно записать:
302

Постулаты квантовой механики
dtx ' ihv J/ ih
2m
>4«p'"]>->• ^
(D-30)
(D-31)
Входящий в (D-30) коммутатор легко находится из канонических соотношений
коммутации. Нетрудно получить:
(D-32)
Для вычисления коммутатора в выражении (D-31) нужно использовать следующее
обобщение формулы (В-33) [см. дополнение Вц, формула D8)]:
Г« р21
R,—
2т
*«
= — Р.
т
[Р, V(R)] = -ih V V(R),
(D-33)
где V V(R) означает набор из трех операторов, полученных путем замены г на R в
трех компонентах градиента функции V(r). Таким образом:
dt
(К) = 1(Р)
т
^(P) = -(VVR)
(D-34)
(D-35)
Эти два уравнения отражают сущность теоремы Эренфеста. Они имеют форму,
которая напоминает классические уравнения Гамильтона—Якоби для частицы
(приложение III, § 3):
d 1
—r = —p;
dt m
dt
р = -V V(r),
которые приводятся в простейшем случае к известному уравнению Ньютона:
dp d v „...
-f. = m—T = - VVr.
dt dr
(D-36-a)
(D-36-b)
(D-37)
303

Глава HI
у. Обсуждение теоремы Эренфеста. Классический предел
Проанализируем физический смысл теоремы Эренфеста, то есть уравнений (D-34) и
(D-35). Предположим, что волновая функция \|/(r, t), описывающая состояние частицы,
является волновым пакетом, схожим с тем, который мы изучали в главе I. Величина
(R) представляет ансамбль трех чисел, зависящих от времени {(х), (Y), (z)}; мы
будем называть центром волнового пакета* в момент времени t точку с координатами
(R)(r). Ансамбль этих точек, соответствующих различным значениям t, образует
траекторию, по которой следует центр волнового пакета. Напомним, однако, что, строго
говоря, никогда нельзя говорить о траектории самой частицы: состояние последней
описывается всем волновым пакетом, занимающим неизбежно определенную область
пространства. Тем не менее видно, что если эта область мала по сравнению с другими
длинами рассматриваемой задачи, то можно связать волновой пакет с его центром; в
предельном случае не должно быть заметных расхождений между квантовым и
классическим описаниями частицы.
Таким образом, важно знать ответ на следующий вопрос: подчиняется ли движение
центра волнового пакета законам классической механики? Ответ на этот вопрос дает
теорема Эренфеста. Уравнение (D-34) свидетельствует о том, что скорость центра
волнового пакета равна отношению среднего импульса волнового пакета и массы т. Таким
образом, левая часть уравнения (D-35) записывается как т—t(R) » так чт° ответ на
предыдущий вопрос будет положительным, если правая часть равенства (D-35) будет
равна классической силе Fc/ в точке, где находится центр волнового пакета:
FcI=[- VV(r)]r=(R). (D-38)
Действительно, правая часть выражения (D-35) равна среднему значению силы,
приложенной к центру волнового пакета, и в общем случае:
( VV(R))*[VV(r)]r=(R) (D-39)
(иначе говоря, среднее значение функции не равно его значению для среднего значения
переменной). Ответ на заданный вопрос, таким образом, строго говоря, является
отрицательным.
* Центр и максимум волнового пакета в общем случае различны. Они совпадают, если
волновой пакет имеет симметричную форму (§С-5, рис. 2).
304

Постулаты квантовой механики
ЗАМЕЧАНИЕ
В справедливости равенства (D-39) нетрудно убедиться, если взять конкретный
пример. Для простоты выберем одномерную модель и предположим, что
V(x) = Хх", (D-40)
где X — вещественная константа им — целое положительное число. Тогда оператор,
соответствующий V(x), имеет вид:
V(X) = XX\ (D-41)
Левая часть равенства (D-39) запишется в виде Хп(Х"']) (при замене V на — ). Что ка-
х ' dx
сается правой части, то она равна:
dV] =К~'Ц)=^Х>"~'- (D-42)
dx
=<*> - Мх>
Хорошо известно, что в общем случае (Хп /^{Х/ : например, для п = 3 имеем
(Х2) ■£ (X) (так как в формулу для нахождения среднеквадратичного отклонения АХ
входит разность этих двух величин).
Заметим, однако, что при п = 1 или п = 2 имеем (Х"~ ) = {X/ ,то есть обе части
выражения (D-39) равны. Впрочем, это имеет место и при п = 0 , так как при этом обе его
части обращаются в нуль. Для свободной частицы (/2 = 0) в однородном силовом поле
(п = 1) или в параболической потенциальной яме (гармонический осциллятор, п = 2)
движение центра волнового пакета строго подчиняется законам классической механики.
Впрочем, этот результат уже был получен для свободной частицы (п = 0 ) в главе I (см. §С-4).
Несмотря на то, что в общем случае обе части выражения (D-39) не равны, имеются
ситуации (называемые квазиклассическими), когда разность между ними пренебрежимо
мала: это соответствует случаю, когда волновой пакет достаточно четко локализован.
Чтобы заметить это, запишем в явной форме в представлении {|г)} левую часть этого
уравнения:
( V V(R)> = jd\ ч/*(г, t)[ V V(r)]\|/(r, r) = Кф(г, ttf V V(r). (D-43)
Предположим, что волновой пакет достаточно хорошо локализован в пространстве:
точнее говоря, величина |\|/(г, /)| принимает существенные значения лишь в очень ма-
20 Квантовая механика
305

Глава III
лой области по сравнению с расстояниями, где V(r) изменяется достаточно заметно.
Тогда в этой области с центром вблизи (R) величина V V(r) практически не меняется,
и можно в (D-43) заменить величину V V(r) на ее значение в точке г = (R), а затем
вынести это значение из-под интеграла, который становится при этом равным 1, поскольку
функция \|/(г, г) нормирована. Таким образом, для достаточно четко локализованных
волновых пакетов можно записать:
<VV(R)>»[ VV(r)]r=(R). (D-44)
В макроскопическом пределе (длина волн де Бройля много меньше расстояний, на
которых потенциал изменяется достаточно сильно*) можно сформировать достаточно малые
волновые пакеты, чтобы удовлетворить соотношению (D-44), сохранив в то же время
достаточную определенность импульса; при этом движение волнового пакета
практически совпадает с движением классической частицы с массой т в поле потенциала V(r).
Установленный здесь результат очень важен, так как позволяет показать, что уравнения
классической механики вытекают из уравнения Шредингера при таких граничных
условиях, которые свойственны большинству макроскопических систем.
2. Случай консервативных систем
Если гамильтониан физической системы явно не зависит от времени, говорят, что
такая система является консервативной. В классической механике самым важным
следствием такой ситуации является сохранение энергии системы во времени. Говорят еще,
что полная энергия системы является константой движения. В этом параграфе мы
увидим, что и в квантовой механике консервативные системы обладают важными
особенностями, дополняющими те общие свойства, которые были отмечены в предыдущем
параграфе.
а. РЕШЕНИЕ УРАВНЕНИЯ ШРЕДИНГЕРА
Рассмотрим сначала уравнение на собственные значения оператора Н :
Я|ф„,т) = £„|ср„,х). (D-45)
Для простоты допустим, что спектр оператора Я дискретный; обозначим символом т
набор индексов, отличных от индекса п и необходимых для однозначной характеристи-
* В дополнении А| получен порядок длин волн де Бройля, связанных с макроскопической
системой.
306

Постулаты квантовой механики
ки вектора Ф„,т) (эти индексы в общем случае составляются из собственных значений
операторов, образующих вместе с Н полный набор коммутирующих операторов).
Поскольку согласно сделанному предположению Н явно не зависит от времени, время /
не входит ни в собственное значение Еп, ни в собственный кет Ф„т):
к@) = 1с,,л@|ф,,(Т), (D-46)
где
^@ = (ф,,,т|¥@). (D-47)
Поскольку векторы Ф„,т) не зависят от t, вся временная зависимость |\}/(/)) заключена
в сп т(/). Для их вычисления спроектируем уравнение Шредингера на каждое из
состояний |ф„,т). Тогда*:
1П^ипАщо) = ипАн\Щг)). (D-48)
at х ' ' N '
Так как Н — эрмитов оператор, из формулы (D-45) можно получить:
(ф„,т|я = £„(ф„,т|, (D-49)
и уравнение (D-48) примет вид:
/Й-^сял(г) = £.с..т(/). (D-50)
at
Это уравнение интегрируется без труда:
cnJt) = clux(t0)e-E"(t-1^. (D-51)
* В равенстве (D-48) бра-вектор (ф„ J можно поставить справа от —, так как (ф„ J не за-
* ' • dt \ • I
висит от t.
20* 307

Глава HI
Итак, чтобы найти |\|/@), зная |\|/(f0)), нужно сделать следующее.
©Разложить |\|/(>0)) по базису собственных состояний Н :
|v.('o)) = SZ<Vt(f0)|<P,t), (D-52)
п х
где с/1Т(/0) имеет обычную форму:
^.т(^о) = (фя.т|^о))- (D3)
(ii) Получить |\|/(г)) в любой момент времени, умножив каждый из
коэффициентов cnx(t0) разложения (D-52) на e~,En(t~h)lh, где Еп — собственное значение
оператора Н в состоянии Ф„,т/.
|V@) = Х1сЛ>т(/0)^'£"(^)/Л|фп,т) . (D-54)
Все приведенные выше рассуждения легко обобщаются на случай непрерывного
спектра оператора Н . Формула (D-54) принимает вид (все обозначения очевидны):
МО) = ЦdE cx(E, t0) е-™"*»' |ф£>т) . (D-55)
Ь. СТАЦИОНАРНЫЕ СОСТОЯНИЯ
Важным частным случаем является ситуация, когда сам кет М'о)) является
собственным состоянием оператора Н . Тогда разложение (D-52) содержит лишь члены с
одинаковым собственным значением (например, Еп):
k('o)) = 5>„,,(/0)|cp„,t). (D-56)
Т
В формуле (D-56) отсутствует суммирование по п , и переход от М*0)) к МО) вклю~
чает лишь один множитель еЧЕ»^ч»IЬ у который можно вынести из-под знака
суммирования по т :
308

Постулаты квантовой механики
(D-57)
Таким образом, кет-векторы |\|/(г))и |i|/(f0)) отличаются лишь общим фазовым
множителем е~'£'»('~'о)/Л. Такие два состояния физически неразличимы (см. §В-3-Ь-у). Отсюда
можно заключить, что все физические свойства системы, которая оказывается в
собственном состоянии оператора Н , не меняются во времени, и поэтому эти собственные
состояния называются стационарными.
Интересно также выяснить, как в квантовой механике проявляется закон сохранения
энергии консервативной системы. Допустим, что в момент времени г0 измеряется ее
энергия и получено значение Ek. Сразу же после измерения система оказывается в
собственном состоянии Н с собственным значением Ek (постулат о редукции волнового
пакета). Мы только что увидели, что собственные состояния оператора Н являются
стационарными. Таким образом, после первого измерения состояние системы не будет
более изменяться и всегда будет оставаться собственным состоянием Я с собственным
значением Ек. Все последующие измерения энергии системы в любой момент времени
всегда будут давать тот же результат, что и первое измерение.
ЗАМЕЧАНИЕ
Переход от (D-52) к (D-54) осуществляется путем умножения каждого
коэффициента c/JT(/0) выражения (D-52) на e~'E,,(t~to)/fi. Тот факт, что этот множитель
фазовый, еще не обязательно говорит о физической неразличимости состояний
|\|/@) и |\|/(/0)) • Действительно, в общем случае в разложение (D-52) входят
несколько собственных состояний Н с различными собственными значениями.
Этим различным значениям Еп соответствуют различные фазовые множители,
что изменяет относительные фазы коэффициентов разложения вектора состояния
и приводит, конечно, к состоянию |\|/(f)) > физически отличающемуся от |i|/(f0)) •
Лишь в том случае, когда в выражении (D-52) имеется только одно значение
п (если |\|/(f0)) — собственное состояние Н ), эволюция во времени выражается
единственным фазовым множителем. Он является глобальным и не имеет
физического значения. Иначе говоря, физическая эволюция во времени имеет место
только тогда, когда начальное состояние известно с некоторой неопределенностью.
Далее мы еще вернемся к вопросу связи между эволюцией во времени и
неопределенностью энергии (§ D-2-e).
309

Глава III
с. КОНСТАНТЫ ДВИЖЕНИЯ
По определению константой* движения называют наблюдаемую А, не зависящую
явно от времени и коммутирующую с Н :
^ = 0;
bt (D-58)
[А,Я] = 0.
Для консервативной системы сам гамильтониан Н является константой движения.
Константы движения обладают важными свойствами, которые будут рассмотрены
ниже.
(i) Если подставить (D-58) в общую формулу (D-27), получим:
^■(A) = -|-(\|f@|A|\|f@> = 0. (D-59)
Каким бы ни было состояние |i|/(/)) физической системы, среднее значение оператора
А в этом состоянии не изменяется со временем (именно поэтому введено название
«константа движения»).
(П) Если А и И — две коммутирующие наблюдаемые, можно всегда найти
систему общих собственных векторов { (p„t/,tT) }:
^|ф„./,х) = ^|ф„,/,х);
А\уНшРЛ) = ар\<рИщРчХ). (D-60)
Допустим для простоты, что спектры А и Н дискретны, а индексом т будем
обозначать собственные значения наблюдаемых, образующих с Я и Л полный набор
коммутирующих операторов. Поскольку состояния Ф;1/,т) являются собственными
состояниями Н , то они стационарны. Если бы система в начальный момент времени
находилась в состоянии Фл/,т), то она оставалась бы в нем неограниченно долго. Но
состояние ф„ ) является также и собственным состоянием оператора А . Когда Л —
константа движения, существуют такие стационарные состояния физической системы,
которые остаются в любой момент времени / собственными состояниями оператора А
* В отечественной литературе используется также термин «интеграл движения» (прим.
переводчика).
310

Постулаты квантовой механики
с тем же собственным значением ар. По этой причине собственные значения оператора А
называются хорошими квантовыми числами.
(ш) Покажем, наконец, что для произвольного состояния |\|/@) вероятность
получить собственное значение ар при измерении константы движения А не зависит от
времени. Действительно, кет |\|/(£0)) всегда можно разложить во введенном выше базисе
ка0)> = 22Еся,,.т(г0)|ф|1^т), (D-6D
п р т
откуда сразу же следует:
где
|М) = 22Х*я.,д@|фя.,.т), (D-62)
п р х
W(O = c„,„.t(?0)e-^'-'«"\ (D-63)
Согласно постулату о спектральном разложении вероятность &(а , t0) получить
значение ар при измерении А в состоянии |\|/(г0)) в момент времени t0 равна:
п т '
Аналогично:
Пар,0 = Ц
си.р,т@
(D-64)
(D-65)
Из этих выражений видно, что модули cnpz(t) и cnpx(t0) одинаковы, то есть
&(а , О = .Ф(а , t0), что и доказывает сформулированное выше свойство.
ЗАМЕЧАНИЕ
Если все вероятности 0>(ар, t0) равны нулю, кроме одной из них &(ak, t0) -1,
то физическая система в момент времени tQ находится в собственном состоянии А
с собственным значением ак. Поскольку вероятности ZP{ap, t) не зависят от t,
311

Глава III
состояние системы в любой момент времени г остается собственным состоянием А
с собственным значением ак .
d. ЧАСТОТЫ БОРА СИСТЕМЫ. ПРАВИЛА ОТБОРА
Пусть В — произвольная наблюдаемая изучаемой системы (не обязательно
коммутирующая с Н ). Формула (D-27) позволяет найти производную —(В) среднего значения
dt
наблюдаемой В:
jw-> "»♦(£)•
Для консервативной системы известна общая форма (D-54) кет-вектора |\|/@) • Поэтому
в этом случае можно вычислить в явном виде не только —(#), но и (\|/@| В | \|/(/)) •
Выражение, эрмитово сопряженное формуле (D-54), запишется в виде (после
изменения индексов суммирования):
(V(')| =ХЕС.х(гп)^'£"('"",/"(ф„д|- (D-67)
п' т'
Таким образом, в (\|/(r)| Z?|\|/(f)) можно заменить соответственно |i|/@) и (\|/@|
разложениями (D-54) и (D-67). В результате получим:
(¥(г)|в|у(о) = (в)@ = 1ЕЕЕ4.Л'о)с,,1^)(ф-,'.1|^|ф„.хУ(
|(£И.-£'И)(/-/0)М
S'.T'V'O^Si.TV'oy^,,',:'! ^ l^n.t/^
/J Т /»' Т'
(D-68)
Теперь допустим, что В не зависит явно от времени, то есть остаются постоянными
матричные элементы (ф/1Л- В Ф„,т)- Из формулы (D-68) следует, что эволюция (B)(t)
описывается набором осциллирующих членов, частоты которых равны:
Е ,-Е
1 К-Еп\
2я П
и являются характеристиками изучаемой системы, не зависящими от В и начального
состояния системы. Эти частоты получили название частот Бора. Так, для атома
средние значения всех атомных величин (дипольные электрический и магнитный моменты
и т.д.) осциллируют на различных частотах Бора атома, именно эти частоты могут быть
испущены или поглощены атомом. Это замечание позволяет интуитивно понять правило
312

Постулаты квантовой механики
Бора, связывающее частоты испущенных или поглощенных спектральных линий с
различными уровнями энергии атома.
Из формулы (D-68) видно также, что если частоты, с которыми изменяется (B)(t),
не зависят от В, то дело обстоит иначе в том, что касается относительных вкладов этих
частот в суммарную эволюцию (в). Действительно, каждая частота v,,.,, дает вклад,
определяемый матричным элементом (ф„>т- В Ф„,т)- В частности, если для некоторых
значений п и пу эти элементы равны нулю, то соответствующие частоты отсутствуют
в разложении (B)(t), каким бы ни было начальное состояние системы. Отсюда
вытекают правила отбора, указывающие, какие частоты могут быть испущены или поглощены
в заданных условиях. Чтобы установить эти правила, нужно проанализировать
недиагональные (пФ ri) матричные элементы различных атомных операторов (например,
дипольные электрический и магнитный моменты и т. д.).
Наконец, вклад различных частот Бора зависит и от начального состояния через
произведение c*.T.(r0) cnx(t0). В частности, если начальное состояние является
стационарным с энергией Ek, то в разложении вектора |\|/(/0)) фигурирует только одно
значение п (и = £), и произведение с*.т.(Г0) cnx(t0) отлично от нуля лишь для п = п'=к .
В этом случае (в) не зависит от времени.
ЗАМЕЧАНИЕ
Пользуясь непосредственно формулой (D-68), можно доказать, что среднее
значение константы движения всегда остается неизменным во времени.
Действительно, если В коммутирует с Я , то матричные элементы оператора В, взятые
между двумя собственными состояниями оператора Н и соответствующие
различным собственным значениям, всегда равны нулю (см. главу II, § D-3-a). Таким
образом, если п Ф пу, то соответствующие матричные элементы (ф„л- В фм) = 0,
и единственные отличные от нуля члены в (в) являются константами.
е. СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ ВРЕМЯ — ЭНЕРГИЯ
Сейчас мы увидим, что в консервативной системе эволюция во времени оказывается
тем более быстрой, чем с меньшей точностью определена энергия системы. Точнее
говоря, если А/ — интервал времени, к концу которого система изменяется заметным
образом, и, если Д£—неопределенность энергии, то At и А Я должны удовлетворять
соотношению:
313

Глава III
At-AE>h
(D-69)
Прежде всего, заметим, что если система находится в собственном состоянии
оператора Н , то ее энергия точно определена и Д£ = 0. Но мы уже видели, что такое
состояние является стационарным и не изменяется. Можно сказать, что в некотором смысле
время его эволюции А/ бесконечно велико (соотношение (D-69) действительно
указывает, что при Д£ = О величина Дг должна быть бесконечной).
Предположим теперь, что |\|/(/0)) является линейной суперпозицией двух
собственных состояний |ф,) и |ф2) оператора Я с двумя различными собственными значениями
£, и £2:
\щ*0)) = ф1)+ф2). (D-70)
Тогда:
|\|/@> = сх <Г'£'('-'»)/Л |ф1) +с2еЧЕ>{'-'°)/» |ф2). (D-71)
Если измеряется энергия, то можно получить либо £,, либо Е2. Неопределенность
энергии Е имеет порядок величины:
Д£ = |£2-£,|. (D-72)
Рассмотрим теперь некоторую наблюдаемую В, не коммутирующую с Н . Вероятность
получить при измерении В в момент времени t собственное значение Ьт (для
простоты будем считать его невырожденным), связанное с собственным вектором \ит), дается
выражением:
ПЬт, 0 =|(и„,|ч/@)|2 =|с,Г |(«т|ф,)|2 +|с2|2 |(ит|ф2)|2 +
+ 2Ке[с2*с/е-£''<'-'°"Л(Ит|ф2)*(М„,|Ф1)]. (D-73)
Это равенство показывает, что &(Ьт, t) осциллирует между двумя предельными значе-
\Е2~Е\
ниями с частотой Бора v21 = J L. Таким образом, характерное время эволюции
h
системы равно:
А*5|а? Н ., (D-74)
|£2-£,|
и, действительно, с учетом (D-72), имеем AE-At~h.
314

Постулаты квантовой механики
Допустим теперь, что спектр оператора Н непрерывен (но не вырожден).
Состояние |ty(/0)) B самом общем случае может быть записано в виде:
|v(f0)) = Jd£c(£)|<pfc.), (D-75)
где |ф£) — собственное состояние оператора Н с собственным значением Е .
Предположим, что функция \с(Е)\ имеет максимум в области шириной АЕ вблизи значения
Е0 (рис.4), то есть АЕ характеризует неопределенность энергии системы. Используя
(D-55), можно представить |\|/(/)) в виде:
\\V(t)) = ldEc(E)e-iE{t-'»),h\4>E). (D-76)
| |с(£)|2 Рис.4
В результате суперпозиции стационарных состояний
|ф£) с коэффициентами с(Е) получается
состояние системы |\|/), энергия которого определена не
точно; неопределенность АЕ равна ширине кривой,
описывающей зависимость |с(£)|~. Согласно
четвертому соотношению неопределенностей эволюция
состояния |\|/@) окажется существенной в течение интервала времени А/,
удовлетворяющего неравенству At-AE>h
Введенная выше величина #*(&,„, 0> представляющая вероятность найти
собственное значение Ът при измерении наблюдаемой В в состоянии |\|/(г)) системы, равна:
•<т„>') = |(«„,k@)f = | \dE с(£)е-'£('-'">"' (ия |ф£)|2. (D-77)
В общем случае при изменении Е вблизи Е0 величина («,„|ф£) меняется достаточно
медленно. Тогда при малом значении АЕ можно пренебречь в интеграле (D-77)
изменением (м„,|ф£) в сравнении с изменением с(Е), вследствие чего допустимо заменить
(м,„|ф£) на (мш Ф£ ) и вынести его из-под интеграла:
ПК, 0 = |(«„, |ф£о>|2 \\dEc(E)e-m-^ . (D-78)
А
315

Глава 111
Если такое приближение справедливо, то 9?(Ът, t) с точностью до множителя совпадает
с квадратом модуля Фурье-образа функции с(Е). Согласно свойствам преобразования
Фурье (см. приложение I, § 2-Ь) ширина У(Ът, t) во времени, то есть Дг, связана с
шириной АЕ функции \с(Е)\ соотношением (D-69).
ЗАМЕЧАНИЕ
Формулу (D-69) можно установить непосредственно из анализа одномерного
свободного волнового пакета. Неопределенности импульса Ар этого пакета можно поставить в
dE
соответствие неопределенность энергии АЕ = Ар . Поскольку Е - ЙО) и р -fik ,
dp
dE da ,
имеем = = vG, где vG — групповая скорость волнового пакета (глава I,§ C-4).
dp dk
Итак:
AE = vGAp. (D-79)
Вспомним, что время эволюции А/, характерное для волнового пакета, представляет собой
время его прохождения через определенную точку пространства со скоростью vG . Если
Ах — пространственная протяженность пакета, то
Ах
At « . (D-80)
Комбинируя (D-79) и (D-80), получим:
AE-At~Ax-Ap>h. (D-81)
Соотношение (D-69) часто называют четвертым соотношением
неопределенностей Гейзенберга. Оно, однако, заметно отличается от трех других соотношений
неопределенностей, относящихся к трем компонентам R и Р (формулы A4) дополнения ¥х).
Действительно, в (D-69) лишь энергия является физической величиной, как R и Р,
тогда как параметру t в квантовой механике не сопоставляется никакой оператор.
Е. ПРИНЦИП СУПЕРПОЗИЦИИ И ФИЗИЧЕСКИЕ ПРЕДСКАЗАНИЯ
Теперь нам остается рассмотреть физический смысл первого постулата, согласно
которому состояния физической системы принадлежат векторному пространству и, как
следствие, для них справедлив принцип суперпозиции.
316

Постулаты квантовой механики
Одним из важнейших следствий первого постулата в комбинации с другими
постулатами является предсказание интерференционных эффектов, подобных тем, которые
привели к формулировке понятия корпускулярно-волнового дуализма (глава I).
Понимание этих явлений базируется на понятии амплитуды вероятности, которое будет здесь
уточнено с помощью нескольких простых примеров.
1. Амплитуда вероятности и эффекты интерференции
а. ФИЗИЧЕСКИЙ СМЫСЛ ЛИНЕЙНОЙ СУПЕРПОЗИЦИИ СОСТОЯНИЙ
а. Различие между линейной суперпозицией и статистическим ансамблем
Пусть |\|/,) и |\|/2) —два нормированных ортогональных состояния:
(Vi|Vi>=(v2|V2> = 1;
(Vi|v2> = 0 (E-l)
(кет-векторы |\|/,) и |\|/2), например, могут быть собственными состояниями одной
наблюдаемой В, соответствующими различным собственным значениям Ьх и Ь2).
Если физическая система находится в состоянии |v|/,), то можно вычислить все
предсказания относительно результатов измерения данной наблюдаемой А . Например,
если \ип) — нормированный собственный вектор оператора Л, соответствующий
невырожденному собственному значению ап, то вероятность получить значение ап при
измерении наблюдаемой А в состоянии системы \\\f{) равна:
•^(я„Н(«„к,)|2. (Е-2>
Можно также определить аналогичную вероятность Щ(а1Х) для состояния |\|/2):
з(«.Н(и«М2- (Е)
Рассмотрим теперь нормированное состояние |\|/), являющееся линейной
суперпозицией |\|/,} и |\|/2):
|v> = ^,|v,) + X2|v2);
N2+N2 = i. (е-4)
317

Глава HI
Говорят, что если система находится в состоянии |\|/), то вероятность обнаружить ее в
состоянии |\|/,) равна |Х,| , а в состоянии |\|/2) — |Л2| . Более точная формулировка
этого утверждения звучит так: поскольку |\|/,) и |\|/2) являются нормированными
собственными векторами наблюдаемой В с собственными значениями Ь, и Ь2, то
вероятность получить значение Ь, при измерении В равна |Л,| , и значение Ь2 — |Л2| .
Однако не следует думать, что состояние вида (Е-4) представляет собой
статистическую смесь (ансамбль) состояний \\\f{) и |\|/2)с относительными весами |Х,| и |Х2| .
Иначе говоря, если имеется большое количество N одинаковых систем, находящихся в
состоянии |\|/), то казалось бы, что можно считать такой ансамбль эквивалентным
другому ансамблю, в котором N |Х,| систем находятся в состоянии |i|/j) и N |Л2| систем —
в состоянии |\|/2). Такая интерпретация состояния |\|/) является совершенно ошибочной
и приводит к неверным физическим выводам.
Действительно, предположим, что нужно вычислить вероятность №(ап) получить
собственное значение ап при измерении наблюдаемой А в состоянии системы |\|/),
описываемом формулой (Е-4). Если мы интерпретируем состояние |i|/) как
статистическую смесь состояний |\|/,) и |\|/2) с весовыми коэффициентами |Л,|~ и |Х2| , то
величину @*(ап) следует искать как взвешенную сумму вероятностей Щ(ап) и Щап)
(формулы [Е-2) и (Е-3)]:
0>(а„) = |Л,|2 ^(ая) +\Х2\2 Р2(аа). (Е-5)
На самом деле постулаты квантовой механики недвусмысленно указывают, как нужно
вычислять /У)(ап). Точное выражение для этой вероятности имеет вид:
то есть №(ап) равна квадрату модуля амплитуды вероятности (un\\\f). Согласно
формуле (Е-4) эта амплитуда является суммой двух членов:
(ип\уу) = Х1(ип\у1) + Х2(ии\у2). (E-7)
Тогда:
318

Постулаты квантовой механики
|2
+
+ гКе^Хг^п I V.)<w„ | V2>*} • (Е-8)
С учетом выражений (Е-2) и (Е-3) правильная формула для ^(ап) записывается в виде:
^(flJ = |Xj2^(flJ + |X2|V2(flJ + 2Re{x^(«Jv,>(«„|V2>*}- (E-9)
Этот результат, естественно, отличается от формулы (Е-5).
Таким образом, нельзя рассматривать состояние |\|/) как статистическую смесь
состояний, ибо такая интерпретация полностью игнорирует интерференционные
эффекты, содержащиеся в последнем члене формулы (Е-9). Относительная фаза* величин Л,
и Х2 также очень важна, поскольку они явно входят в физические предсказания через
произведение А.,Х*2.
C. Иллюстрация на конкретном примере
Рассмотрим поток фотонов, движущихся вдоль оси Oz , состояние поляризации
которых описывается единичным вектором (рис.5):
e = -j=(ev+ev). (E-10)
Это состояние является линейной суперпозицией двух ортогональных состояний
поляризации ед и ev. Оно описывает свет, линейно поляризованный под углом 45° к ех и
е v. Было бы абсурдным считать, что N фотонов в состоянии е эквивалентны
Nx
1
4i
N
= — фотонам в состоянии е „ и N х
2 *
1
Л
— фотонам в состоянии е v.
2 *
Действительно, если поставить на пути пучка света анализатор, ось е' которого
перпендикулярна вектору е, то ни один из N фотонов в состоянии е не пройдет через этот
анализатор. Напротив, в случае статистического ансамбля {N12 фотонов в состоянии ех
uN/2 фотонов в состоянии ev) половина фотонов должна пройти через анализатор.
* Умножение |\|/) на общий фазовый множитель ехЬ эквивалентно замене А,, и Х2 на Х{ е'д
и Х2 е'ь . Из формулы (Е-9) следует, что такая операция не изменяет физических предсказаний,
так как они зависят лишь от А,,Г , \Х2\ и ХХХ2.
319

Глава III
На этом конкретном примере ясно видно, в чем состоит физическое различие
между линейной суперпозицией (Е-10), образующей свет, поляризованный под углом 45 к
еЛ. и е v, и статистической смесью взятых в равных пропорциях состояний е v и е v,
образующих естественный (неполяризованный) свет.
-►z
Рис.5
Простой эксперимент, иллюстрирующий
различие между линейной суперпозицией и
статистической смесью состояний: если все падающие
фотоны находятся в состоянии поляризации
1 /
е = -7=-(е_г + е v), то ни один из них не пройдет
через анализатор, ось которого е'
перпендикулярна к вектору е; напротив, если имеется
статистическая смесь фотонов, поляризованных
в равных пропорциях вдоль ед и ev
(естественный свет), то половина из них пройдет через
анализатор
Важно понять также значение относительной фазы коэффициентов разложения
вектора состояния. Рассмотрим четыре случая:
«.-^(•х+е,);
е2=-^(е,-е„);
e3=-7r(e.v + ''ev);
(Е-П)
(Е-12)
(Е-13)
e4 = jr (*,-'*,).
(Е-14)
отличающихся только относительными фазами коэффициентов (в этих выражениях они,
соответственно, равны 0, я, +—, —). Эти четыре состояния совершенно различны
физически: первые два представляют свет, поляризованный линейно вдоль биссектрисы
угла между ev и еу, а два последних — свет, поляризованный по правому и левому
кругу.
320

Постулаты квантовой механики
Ь. СУММИРОВАНИЕ ПО ПРОМЕЖУТОЧНЫМ СОСТОЯНИЯМ
а. Предсказание результатов измерения в двух простых экспериментах
(i) Эксперимент 1. Предположим, что в некоторый момент времени при измерении
наблюдаемой А в системе получено невырожденное собственное значение а. Если
|wfl) — собственный вектор, соответствующий значению а, то сразу же после
измерения физическая система окажется в состоянии \иа).
Прежде чем система изменила это состояние, измеряется другая наблюдаемая С, не
коммутирующая с А . Используя обозначения, введенные в § С-6-а, назовем ^(с)
вероятность того, что при втором измерении может быть получен результат с. Перед
измерением С система была в состоянии | иа), и, следовательно, если | vc) — собственный
вектор оператора С , соответствующий невырожденному собственному значению с, то
постулаты квантовой механики позволяют утверждать, что
W = |(v>X (E-15)
(ii) Эксперимент 2. Теперь представим себе другой эксперимент, в котором
последовательно и очень быстро измеряются три наблюдаемые А, В, С, не коммутирующие
между собой (время, разделяющее два последовательных измерения, считаем столь
коротким, что система не успевает испытать эволюцию между измерениями). Назовем
Уа(Ь, с) вероятность того, что в первом измерении было получено значение а , а во
втором и в третьем — Ъ и с соответственно. 9Ра(Ъ, с)равна произведению вероятности
&а(Ь) того, что измерение наблюдаемой А дало результат а , а измерение наблюдаемой
В дало результат Ъ , на вероятность .^(с) того, что измерение наблюдаемой В дало Ь ,
а измерение наблюдаемой С дало с:
3(*,с)=3(*)^(с). (Е-16)
Если предположить, что все собственные значения оператора В не вырождены, и если
обозначить символом \wb) соответствующие собственные векторы, то
■№0=\{кЫ2\Ы»а)\2- (Е-17)
21 Квантовая механика
321

Глава III
Р. Фундаментальное различие между двумя экспериментами
В этих двух экспериментах вектор состояния системы после измерения
наблюдаемой А становится равным \иа), и роль этого измерения состоит в том, чтобы
зафиксировать начальное состояние. После последнего измерения (измерение наблюдаемой С)
вектор состояния системы становится равным | vc) (будем называть его «конечным
состоянием»). В обоих случаях состояние системы можно разложить перед измерением С
по собственным векторам \wb) оператора В и утверждать, что между состояниями \иа)
и |vc) система «может пройти» через несколько различных «промежуточных
состояний» \wh) * причем каждое из этих промежуточных состояний определяет некоторый
возможный «путь» перехода между начальным состоянием \иа) и конечным состоянием
|vt.) (рис. 6).
к>
Рис.6
Возможные «пути»
изменения вектора
состояния системы, если
его эволюция является
свободной (то есть без
промежуточного
измерения), между
начальным состоянием \иа) и
конечным состоянием
|vc). При этом нужно
суммировать не вероятности, а амплитуды вероятностей эволюции системы по всем
возможным «путям»
Различие между описанными выше двумя экспериментами состоит в следующем: в
первом путь перехода из \иа) в |vc) экспериментально не определен (измеряется только
вероятность №а(с) самого факта, что система, покидая состояние \иа), переходит в
состояние | vc.); напротив, во втором эксперименте благодаря измерению наблюдаемой В
этот путь определен, так как i?a(b, с) — вероятность того, что система перейдет из \иа)
в |vc) через конкретное промежуточное состояние | wb).
Казалось бы, чтобы установить связь между ^(с) и №а(Ь, с), достаточно прибегнуть
к следующему рассуждению: в 1-м эксперименте система может «свободно» перейти
322

Постулаты квантовой механики
через все промежуточные состояния | wb), то есть вероятность :?а(с) должна равняться
сумме всех вероятностей j£(&, с), связанных с каждым из возможных путей перехода.
Можно ли записать следующее выражение?
3(*)=ЕЗ(*.с). (Е-18)
b
Как мы сейчас увидим, эта формула неверна. Действительно, вернемся к точной
формуле (Е-15) для .fa{c). В нее входит амплитуда вероятности (vf |иЛ), которую можно
представить, используя соотношение замкнутости для состояний \wh), в виде:
(»\>e) = X(v,h)H«e). (E-19)
b
Подставим это выражение в (Е-15):
^(c) = \l{v(]wh)(wh\ua)\ =l\(vc\wh)\ \(wh\ua)[ +
\ b \ b
+ 1 ЪЫ"ь)Ы»а)Ы">ь-)'Ыи<.У ■ (Е-20)
b b'*b
Используя (Е-17), получим:
ЗД = ЪЪ(Ь, с) + 1 S Mwh}(Wb\ua)(vc\w,)'(W,\uay . (Е-21)
b b V*b
Это равенство позволяет понять, почему формула (Е-18) неверна: в ней отсутствуют
«перекрестные члены», которые неизбежно появляются в квадрате модуля суммы (Е-19).
Таким образом, в формуле (Е-18) потеряны все интерференционные эффекты между
возможными путями перехода.
Итак, если мы хотим установить связь описанных выше экспериментов, необходимо
рассуждать с использованием понятий амплитуд вероятностей: если промежуточное
состояние, через которое система совершает переход, не определено
экспериментально, суммируются не вероятности, а амплитуды вероятностей.
Ошибка в рассуждениях, которые привели к неверному соотношению (Е-18),
становится предельно ясной, если корректно применить пятый постулат (редукция волнового
пакета). Действительно, во втором эксперименте измерение наблюдаемой В можно
выполнить только при таком возмущении изучаемой системы, что в ходе измерения вектор
ее состояния испытывает резкое изменение (проекция на один из векторов \wb)); имен-
21*
323

Глава 111
но это неизбежное возмущение ответственно за исчезновение эффектов интерференции.
В первом же эксперименте, напротив, совершенно неправильно утверждать, что
физическая система совершает переход «через то или иное из состояний |и^)», ибо со всей
строгостью следует сказать, что переход осуществляется одновременно через все
состояния \wb).
ЗАМЕЧАНИЯ
(i) Приведенное выше обсуждение со всех точек зрения напоминает анализ
эксперимента Юнга, выполненный в § А-2-а главы I. Чтобы определить вероятность того,
что фотон, испущенный источником, попадет в заданную точку М экрана, нужно
сначала вычислить полное электрическое поле в точке М . Именно оно играет в
этой задаче роль амплитуды вероятности. Если же нам безразлично, через какую
щель проходит фотон, то для нахождения полного поля в точке М нужно
суммировать не интенсивности, а электрические поля, испущенные двумя щелями, и
лишь затем квадрат амплитуды полного поля даст искомую вероятность. Иначе
говоря, поле, испущенное одной из щелей в точку М, представляет амплитуду
вероятности того, что фотон, будучи испущенным источником, проходит через эту
щель и попадает в точку М .
(ii) Можно без труда избежать сделанного выше предположения о том, что измерения
наблюдаемых Л и С в первом эксперименте и измерения наблюдаемых А, В,
С — во втором должны быть очень близки друг к другу во времени. Если система
успевает каким-то образом эволюционировать между двумя измерениями,
достаточно использовать уравнение Шредингера для определения изменения состояния
системы (см. дополнение Frii, замечание (ii) в § 2).
с. ЗАКЛЮЧЕНИЕ: ВАЖНОСТЬ ПОНЯТИЯ АМПЛИТУДЫ ВЕРОЯТНОСТИ
Рассмотренные выше примеры демонстрируют важность понятия амплитуды
вероятности. Формулы (Е-5) и (Е-18), так же как и приводящие к ним рассуждения, являются
неправильными, ибо в них производится попытка вычисления вероятностей без
использования соответствующих амплитуд вероятности. В обоих случаях правильное
выражение (Е-8) или (Е-20) имеет форму квадрата суммы (точнее, квадрата модуля этой
суммы), тогда как неверная формула (Е-5) или (Е-18) содержит лишь сумму квадратов, и в
ней забыты перекрестные члены, ответственные за интерференционные эффекты.
Итак, из проведенного выше обсуждения можно вынести следующие основные
идеи.
(i) Вероятностные предсказания в квантовой теории всегда должны выполняться на
основе амплитуд вероятности с последующим вычислением квадрата модуля.
324

Постулаты квантовой механики
(И) Если в некотором эксперименте нет необходимости выполнять измерения в
промежуточном состоянии, никогда не следует рассуждать о вероятности различных
результатов, которые можно было бы получить при таких измерениях, а только об
амплитудах вероятности.
(Hi) Из того факта, что для состояний физической системы справедлив принцип
линейной суперпозиции, следует, что амплитуда вероятности часто может быть
представлена в виде суммы частных амплитуд, а соответствующая вероятность равна квадрату
модуля суммы членов, ибо разные частные амплитуды могут интерферировать,
2. Случай, когда несколько состояний могут быть ассоциированы
с одним и тем же результатом измерения
В предыдущем параграфе мы подчеркнули и продемонстрировали то
обстоятельство, что вероятность события определяется в квантовой механике квадратом суммы
членов (точнее, речь идет о квадрате модуля такой суммы). Но в формулировку четвертого
постулата (В-7) входит сумма квадратов (сумма модулей в квадрате), если результат
искомого измерения относится к вырожденному собственному значению. Важно
отчетливо понимать, что эти правила не противоречат друг другу и, напротив, дополняют
друг друга: каждый член суммы квадратов (В-7) может быть равен квадрату суммы.
Именно на этой точке зрения мы остановимся в данном параграфе. Ее обсуждение
позволит нам одновременно дополнить формулировку постулатов; затем мы изучим
свойства измерительного прибора, точность которого в реальных случаях не может быть
бесконечно большой, и увидим, как можно при этом найти теоретические предсказания
для возможных результатов измерения. И, наконец, мы обобщим пятый постулат
относительно редукции волнового пакета на случай непрерывных спектров.
а. ВЫРОЖДЕННЫЕ СОБСТВЕННЫЕ ЗНАЧЕНИЯ
В примерах, приведенных в § Е-1, мы всегда предполагали, что результатами
различных измерений были простые собственные значения соответствующих
наблюдаемых. Эта гипотеза была нужна лишь для упрощения примеров, чтобы наиболее явно
выделить природу эффектов интерференции.
Теперь рассмотрим вырожденное собственное значение ап наблюдаемой А .
Связанные с ним собственные состояния образуют векторное подпространство с
размерностью gn, в котором можно выбрать ортонормированный базис {\и'п) ; / = 1,2,..., gn }.
Обсуждение в § C-6-b показало, что для определения состояния физической
системы недостаточно знать только то, что в результате измерения наблюдаемой А получено
значение ап. Действительно, одному и тому же результату ап может
соответствовать несколько конечных состояний. Если начальное (то есть перед измерением) со-
325

Глава 111
стояние задано, то конечное состояние (после измерения) вполне определено. Однако,
если изменить начальное состояние, то в общем случае изменится и конечное состояние
(даже для одного и того же результата измерения ап). Все конечные состояния,
связанные с ап, являются линейными комбинациями gn ортонормированных векторов \и'п).
Формула (В-7) однозначно указывает, как найти вероятность f^(an) получения
результата ап при измерении А в состоянии системы |\|/). Для этого выбирается ортонорми-
рованный базис, например, {\и'п); / = 1,2,..., gn } в собственном подпространстве,
соответствующем ап, и вычисляется вероятность \(и'п \|Л найти систему в каждом из состояний
этого базиса. Вероятность &{ап) равна тогда сумме этих gn вероятностей. Однако не
следует забывать, что каждая вероятность \(и'п \|Л может быть квадратом модуля суммы
членов. Действительно, вернемся, например, к случаю, рассмотренному в § Е-1-а-сс,
и допустим, что собственное значение ап наблюдаемой А , вероятность которой &(ап)
мы ищем, имеет кратность вырождения g;j. Тогда формулу (Е-6) нужно заменить на
8,
1
где
^@ = Ц(ф)|\ (Е-22)
(<|\1/) = я1(<|\1/1) + х2(<|Ч/2). (Е-23)
Все рассуждения, приведенные в § Е-1-а-а, остаются справедливыми для каждого из
членов формулы (Е-22): величина \{и'п ш , полученная из (Е-23), остается квадратом
суммы, а 9*{с1п) — суммой этих квадратов. Совершенно так же можно обобщить на
случай вырожденных собственных значений измеряемых наблюдаемых результаты,
полученные в § E-1-b.
Прежде, чем резюмировать изложенные выше рассуждения, рассмотрим еще одну
важную ситуацию, когда несколько конечных состояний соответствуют одному и тому
же результату измерения.
Ь. НЕДОСТАТОЧНО СЕЛЕКТИВНЫЕ ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
а. Определение
Предположим, что для измерения наблюдаемой А в заданной физической системе мы
располагаем прибором, действующим следующим образом.
326

Постулаты квантовой механики
(i) Этот прибор может дать только два различных* значения, которые, ради удобства, будем
обозначать символами «да» и «нет».
(ii) Если система находится в собственном состоянии оператора А , собственное значение
которого принадлежит заранее заданному интервалу значений А вещественной оси, то ответ
прибора равен определенно «да»; аналогичный ответ прибор дает, если состояние системы является
произвольной линейной комбинацией собственных состояний оператора А , связанных с
собственными значениями, лежащими в интервале А .
(Hi) Если состояние системы является собственным состоянием оператора А с собственным
значением, лежащим вне интервала А , или любой линейной комбинацией таких собственных
состояний, то ответ будет определенно «нет».
Таким образом, значение А характеризует разрешающую способность рассматриваемого
измерительного прибора. Если имеется лишь одно собственное значение ап оператора А в
интервале А , все происходит так, как если бы разрешающая способность была бесконечной: если
система находится в любом состоянии, то вероятность № («да») получить ответ «да» равна
вероятности получить значение ап при измерении А , а вероятность У* («нет») получить ответ «нет»
очевидно равна Г-.У* («да»). Если, напротив, А содержит несколько собственных значений А,
то разрешающая сила прибора недостаточна, чтобы различить эти разные собственные значения, и
мы будем говорить, что прибор недостаточно селективен. Сейчас мы увидим, как вычислить в
этом случае У («да») или J* («нет»).
Чтобы иметь возможность оценить возмущение, вносимое таким измерением в состояние
системы, добавим следующее предположение: прибор не вносит возмущений в собственные
состояния оператора А , связанные с собственными значениями, лежащими в интервале А , равно
как и в любую линейную комбинацию таких собственных состояний, но «блокирует» все
собственные состояния оператора А , связанные с собственными значениями, лежащими вне интервала
А или со всеми их линейными комбинациями. То есть прибор ведет себя как идеальный фильтр
состояний, принадлежащих интервалу А .
Р. Пример
Большинство практически используемых измерительных приборов являются недостаточно
селективными.
Так, например, для измерения абсциссы электрона, движущегося в направлении оси Oz,
можно (рис. 7) поместить в плоскости хОу (ось Оу перпендикулярна плоскости рисунка)
пластинку, в которой просверлена щель, ось которой параллельна Оу , а края имеют абсциссы хх и
х2. Тогда видно, что весь волновой пакет, заключенный между плоскостями х = х{ и х = х2
(суперпозиция собственных состояний оператора X с собственными значениями в интервале
* Последующие выводы легко обобщаются на случай, когда прибор может давать несколько
различных результатов, имеющих свойства, подобные описанным в (ii) и (Hi).
327

Глава III
*,, х2\), пройдет в область справа от щели (ответ «да») и при этом не подвергнется никакому
изменению. Напротив, волновой пакет, расположенный вне интервала \хх, х2 ], будет блокирован
пластинкой и не пройдет в правую область пространства (ответ «нет»).
Рис.7
Схема прибора, измеряющего абсциссу х
частицы. Интервал [х]у х2] не может быть
равным нулю, вследствие чего такой
прибор оказывается всегда недостаточно
селективным
у. Квантовое описание
В случае недостаточно селективного прибора после измерения, дающего ответ «да»,
возможны несколько конечных состояний. Например, ими могут быть собственные состояния оператора
А , соответствующие собственным значениям, лежащим в интервале А .
Возникающая для таких приборов физическая задача, к анализу которой мы сейчас перейдем,
состоит в том, чтобы предвидеть ответ, который может быть получен, если измерению
подвергнется система, находящаяся в произвольном состоянии. Например, выясним для устройства,
изображенного на рис. 7, что произойдет, если волновой пакет распределен так, что он и не заключен
между плоскостями х = хх и х = х2 (ответ «да»), и не находится полностью вне этой области
(ответ «нет»)? Сейчас мы увидим, что такую задачу можно свести к измерению наблюдаемой с
вырожденным спектром.
Действительно, рассмотрим подпространство tfA , образованное всеми собственными
состояниями оператора А , собственные значения которых ап заключены в интервале Д .
Проекционный оператор Рд на это подпространство имеет вид (см. §В-3-Ь-у главы II):
Р.= 1 1\<}{<\ (Е-24)
о„бЛ /=1
(собственные значения ап в интервале А могут быть вырождены, вследствие чего введен
дополнительный индекс /; векторы \и'п) считаются ортонормированными). Подпространство £д
образовано всеми возможными состояниями системы после измерения, давшего результат «да».
Если учесть определение измерительного прибора, нетрудно видеть, что ответ «да» будет
получен для любого состояния подпространства #д, то есть для любого собственного состояния
-+г
328

Постулаты квантовой механики
оператора Рд с собственным значением +1, а ответ «нет» — для любого собственного состояния
оператора Рд с собственным значением 0. Ответы «да» и «нет», выдаваемые измерительным
прибором, соответствуют собственным значениям +1 и 0 наблюдаемой Рд , и можно сказать, что
измерительный прибор на самом деле измеряет наблюдаемую Рд , а не А .
Благодаря такой интерпретации случай недостаточно селективного измерительного прибора
может быть рассмотрен в рамках уже сформулированных постулатов. Вероятность ijP («да»)
получить ответ «да» равна вероятности получить собственное (вырожденное) значение +1 оператора
Рд. Нам известен ортонормированный базис в соответствующем собственном подпространстве:
он образован ансамблем состояний и'п), являющихся собственными состояниями оператора А с
собственными значениями, заключенными в интервале А . Применив формулу (В-7) к
собственному значению +1 наблюдаемой РА , получим:
^>(«да»)= £ ilk И • (Е-25)
а„еД i=l ' '
Поскольку имеется лишь два возможных ответа, имеем очевидно:
0> («нет») = 1 - 9Р («да»). (Е-26)
Проекционный оператор на собственное подпространство наблюдаемой Рд , связанное с
собственным значением +1, равен самому оператору Рд , вследствие чего применение формулы (В-14) дает:
<7>(«да») =(\|/|Рд|\|/) (Е-27)
[эта формула эквивалентна выражению (Е-25)].
Аналогично, поскольку прибор не возмущает состояния, принадлежащие пространству Рд , и
блокирует состояния, дополняющие его, то сразу же после измерения, дающего результат «да»,
состояние системы станет равным:
1 v, &
in I/ . I \l^ д ед ,=1 '
И = -1—— 2 1\<)(<\ч), (Е-28)
' in I/ . I \|2 а г- -•-■' /Х ' '
а,,еД i=l '
М= I/ iDi \р^- (Е_29)
Если в интервале А содержится лишь одно собственное значение ап , то оператор Рд
сводится к Рп, а формулы (В-14) и (В-31) оказываются частными случаями формул (Е-27) и (Е-29).
329

Глава III
с. РЕЗЮМЕ: СЛЕДУЕТ СУММИРОВАТЬ АМПЛИТУДЫ ИЛИ ВЕРОЯТНОСТИ?
Итак, существуют случаи (§ Е-1), когда для вычисления вероятности нужно брать
квадрат суммы, так как необходимо сложить несколько амплитуд вероятностей; в
других случаях (§ Е-2) следует брать сумму квадратов, так как нужно сложить несколько
вероятностей. Конечно, очень важно не путать такие случаи друг с другом и твердо
знать в конкретной ситуации, что следует суммировать — амплитуды вероятности или
сами вероятности.
Эксперимент Юнга снова послужит нам очень удобным физическим примером для
иллюстрации и резюмирования приведенных выше обсуждений. Допустим, что мы
хотим вычислить вероятность того, что определенный фотон попадет на пластинку между
двумя точками М, и М2 с абсциссами jc, и х2 (рис.8). Вероятность пропорциональна
полной интенсивности света, попавшего на данный участок пластинки. Таким образом,
это значение равно «сумме квадратов», точнее, это интеграл от интенсивности 1(х)
между значениями хх и х2. Но каждый член 1(х) этой суммы получен путем возведения в
квадрат электрического поля $(х), равного сумме электрических полей $А(х) и Рв(х),
испущенных в точку М щелями А и В\ таким образом, 1{х) пропорциональна
величине |#А(.х) + #д(дО| > то есть квадрату суммы. $А(х) и $в(х) являются амплитудами,
связанными с двумя возможными путями SAM и SBM , заканчивающимися в одной и
той же точке М . Чтобы получить амплитуду вероятности в точке М , нужно
суммировать амплитуды, так как не существенно, через какую щель прошел фотон. Затем, чтобы
вычислить полную интенсивность света на участке М, М2, нужно сложить
интенсивности, попадающие в разные точки этого интервала.
Рис.8
Эксперимент Юнга. Для вычисления
плотности вероятности регистрации фотона в
точке М нужно сложить электрические
поля, испущенные щелями А и В, затем
возвести суммарное поле в квадрат
(«квадрат суммы»). Вероятность
обнаружить фотон в интервале [jc, , jc2] далее
может быть получена путем суммирования
плотности вероятности между точками jc,
и х2 («сумма квадратов»)
Основная идея, следующая из обсуждения в параграфе Е, может быть выражена
схематически в следующей формулировке:
330

Постулаты квантовой механики
Сначала нужно суммировать амплитуды, соответствующие одному и тому же
конечному состоянию, а затем — вероятности, соответствующие конечным
ортогональным состояниям.
d. ПРИМЕНЕНИЕ К АНАЛИЗУ НЕПРЕРЫВНЫХ СПЕКТРОВ
Если измеряемая наблюдаемая имеет непрерывный спектр, можно использовать лишь
недостаточно селективные измерительные приборы: невозможно представить себе физический прибор,
способный выделить единственное собственное значение, если оно принадлежит непрерывному
ансамблю. Сейчас мы увидим, как анализ, предложенный в § E-2-b, позволяет уточнить и
дополнить рассуждения относительно наблюдаемых с непрерывным спектром.
а. Пример: измерение положения частицы
Пусть \|/(г) = (г|\|/) — волновая функция частицы без спина. Какова вероятность
обнаружить абсциссу этой частицы в интервале [х{, х2 ] оси Ох , если, например, используется
измерительный прибор, подобный изображенному на рис.7?
Подпространство #д , связанное с рассматриваемым результатом измерения, является
пространством, порожденным кет-векторами |r) = |*, у, z), удовлетворяющими неравенству
JCj < х < х2. Поскольку эти кет-векторы ортонормированы в широком смысле слова, применение
правила, сформулированного в вышеупомянутом параграфе, дает:
.*>(*, <х<х2) = J>r>£>K*. У. *И2 = J>L>L>|¥(r)|2 • (Е-30)
Формула (Е-27) приводит, естественно, к тому же результату. Действительно, проекционный
оператор Рд имеет вид:
^=С *£>£> I*'у- гХ*- у< г1 (Е-31)
и, следовательно:
Я>(Х1<х<х2) = (у\РА\ч} = %с1х1Уу1Уг(у\х, у, z){x, у, г|ч/), (Е-32)
Чтобы узнать состояние |\|/') частицы после измерения, дающего результат «да», достаточно
применить формулу (Е-29):
И = -Uk) = -U>' \Tjy £>у, у, z%x; у, ф>, (Е-зз)
331

Глава III
где нормирующий множитель N = j(\|/|P|\|/) известен [формула (Е-32)]. Вычислим волновую
функцию Ц/'(г) = (rill/') , связанную с кет-вектором |\|/') :
(Г1V') = -£■ С Л* Г> С*'(гИ V(r'). (Е-34)
Отметим, что (г|г') = 5(г-г') = 8(л:-;с')Ь(у- У)8(г-Z1). Интегрирование по у' и г'
производится немедленно: оно заключается в замене / и z' на у и z в подынтегральной функции.
Тогда равенство (Е-34) становится равным:
1 ех
\|/'(*, )>, г) = —ГЛ'би-*') V(*\ з>, z). (E-35)
дг «^i
Если точка л:' = х расположена внутри интервала интегрирования [jc, , Jt2 ], результат
интегрирования оказывается тем же, что и при интегрировании от -оо до + °°:
\|/'(л\ У, z) =—\|/(jc, у, z) при jc, < jc<x2 . (Е-36)
N
Напротив, если точка х'=х расположена вне интервала интегрирования, то 8(;с-;с') = 0 для
всех значений х', заключенных в этом интервале, и
\\f\x, у, z) = 0 при х>х2 и jc < jc, . (Е-37)
Часть функции \j/(r), соответствующая интервалу измерения прибора, сразу после измерения
остается без изменения [множитель 1/N обеспечивает нормировку], а остальная часть просто
подавляется процессом измерения. Таким образом, волновой пакет \|/(г), представляющий
начальное состояние частицы, в некотором смысле «обрезается» краями щели.
ЗАМЕЧАНИЯ
(i) На этом примере наглядно виден конкретный смысл «редукции волнового пакета»,
(ii) Если в измерительный прибор последовательно посылать большое количество частиц в
одном и том же состоянии | \|/}, то получаемый результат будет иногда «да» и иногда «нет»
[с вероятностями @* («да») и У («нет»)]. Если результат равен «да», то частица продолжит
свой путь из «редуцированного» состояния |\|/у ; если же результат «нет», то частица будет
поглощена экраном.
В рассматриваемом здесь примере измерительный прибор оказывается тем селективнее, чем
меньше разность х2 — х1 . Однако видно, что сделать его идеально селективным невозможно из-за
332

Постулаты квантовой механика
непрерывности спектра оператора X : какой бы узкой ни была щель, определяемый ею интервал
[jc, , х2 ] всегда будет содержать бесконечное множество собственных значений. Тем не менее, в
предельном случае, когда ширина щели Д* становится бесконечно малой, можно установить
эквивалент формулы (В-17), который уже был приведен как выражение четвертого постулата в
Ajc Ax
случае непрерывного спектра. Действительно, обозначим х1 = х0 и х2 = х0 + (щель
шириной Ах с центром в точке д:0) и допустим, что волновая функция \|/(г)мало меняется в
пределах этого интервала. Тогда в формуле (Е-30) можно заменить |\|/(г)| на |v|/(a:0, у, z)\ и
проинтегрировать по х:
01*о- — <х<х0+— J
= Axj+_yyj+_yZ\\V(x0,y,z)\ . (Е-38)
Видно, что вероятность равна произведению Ах на положительную величину, имеющую смысл
плотности вероятности в точке х0. Отличие от формулы (В-17) состоит в том, что последняя
применялась в случае непрерывного невырожденного спектра, тогда как здесь собственные
значения оператора X бесконечно вырождены в пространстве #г; именно поэтому появились
интегралы по у и по z в (Е-38) (суммирование по индексам, определяющим вырождение).
C. Постулат о редукции волнового пакета в случае непрерывного спектра
В § В-З-с при формулировке пятого постулата мы ограничивались случаем дискретного
спектра. Формула (Е-33) и сопровождающие ее рассуждения позволяют понять форму, которую
принимает этот постулат, если речь идет о непрерывном спектре: достаточно применить результаты
§ E-2-b , относящиеся к недостаточно селективному прибору.
Пусть А — наблюдаемая с непрерывным спектром (для простоты считаем его
невырожденным). Обозначения будут теми же, что и в § B-3-b-p.
Если измерение величины А в состоянии |\|/у дает результат 0С0 с точностью Да , то
состояние системы сразу же после измерения описывается волновой функцией:
И= /, ,D \ ч, .^a(«o)k). (E-39)
где
Да
^(a0)= \da\va){Va\. (E-40)
Да
ссо--7-
333

Глава HI
Рис. 9а и рис. 9Ь иллюстрируют эту формулировку: если функция (va|v) , представляющая
вектор |у) в базисе {|va) }, имеет вид, приведенный на рис.9а, то состояние системы сразу же
после измерения с точностью до нормировочного множителя совпадает с функцией,
изображенной на рис. 9Ь [вычисления совершенно аналогичны тем, которые дают формулы (Е-36) и (Е-37),
если исходить из выражения (Е-33)].
<*.!*>
<*>.\P*JM\*>
Г\
Ла
Рис.9
Иллюстрация постулата о редукции волнового пакета в случае непрерывного спектра:
измеряется наблюдаемая А , имеющая собственные векторы |va) и собственные
значения а. Измерительный прибор имеет разрешающую способность Да. Если получено
значение ос0 с точностью Да, то действие процесса измерения на волновую функцию
(vaJ\|/) состоит в ее «вырезании» вокруг значения а() (чтобы нормировать эту новую
волновую функцию, следует, конечно, умножить ее на множитель, превышающий 1)
Видно, что даже если ширина Да очень мала, никогда не удастся приготовить систему в
состоянии vaoy, которое представлено в базисе {|va) } функцией (va vao у = 5(a-a0): можно
лишь получить функцию прямоугольной формы с центром в точке а0, так как нельзя получить
в точности Да = 0.

ДОПОЛНЕНИЯ К ГЛАВЕ III
Аш. Частица в потенциальной яме
бесконечной глубины: физический анализ.
Вш. Изучение тока вероятности в
некоторых частных случаях.
Сщ. Среднеквадратичные отклонения
двух сопряженных наблюдаемых.
Dm. Измерения, выполняемые в части
физической системы.
Еш. Оператор плотности.
Fm. Оператор эволюции.
Gin* Представления Шредингера
и Гейзенберга.
Нш. Калибровочная инвариантность.
JHI. Пропагатор уравнения Шредингера.
Аш, Вш: непосредственное применение к
простейшим случаям, внимание
сосредоточено на физическом смысле результатов
(элементарный уровень).
Сш: формальные вычисления; общая
демонстрация соотношения неопределенностей
Гейзенберга; можно пропустить при первом
чтении.
Dm: обсуждение результатов измерения,
выполненного в части системы; простое, но
формальное применение результатов главы III;
можно опустить при первом чтении.
Ещ, F|jj, Gin, Нш, тш: дополнения к введению в
квантовую механику более высокого уровня;
за исключением дополнения Fm, могут быть
поняты на базе материала главы III;
рекомендуются для более глубокого изучения.
Еш: определение и свойства оператора
плотности, используемого в квантовом описании
систем, состояние которых известно не
совсем точно (статистический ансамбль
состояний); основной метод статистической
квантовой механики.
Fm: введение в оператор эволюции, дающий
возможность определения квантового
состояния системы в любой момент времени t,
если известно состояние в момент tQ.
Gin: описание эволюции квантовой системы с
помощью иного, но эквивалентного
представления, отличающегося от изложенного в
главы III; зависимость от времени заключена
в наблюдаемых, а не в состоянии системы.
Нщ: обсуждение квантового формализма в
случае, когда система подвержена действию
электромагнитного поля: хотя в описании
системы используются электромагнитные
потенциалы, физические свойства зависят
только от величин электрического и
магнитного полей; они остаются инвариантными
при изменении потенциалов, описывающих
рассматриваемое электромагнитное поле.
335

Кш. Нестабильные уровни. Время жизни.
LIH. Упражнения.
Мш. Связанные состояния частицы
в потенциальной яме произвольной
формы.
Nin. Несвязанные состояния частицы
в присутствии потенциальной ямы
или потенциального барьера
произвольной формы.
Ош. Квантовые свойства частицы
в одномерной периодической
структуре.
Jm: некоторые сведения относительно иного
подхода в квантовой механике, основанного
на принципе, аналогичном принципу
Гюйгенса в классической волновой оптике.
Кш: простой способ введения важных
физических понятий (нестабильность и время
жизни), необходимо для дальнейшего чтения.
Мш, Nin, Ош: повторение одномерных задач,
рассмотренных с более общей точки зрения,
чем в главе I.
Мш: обобщение полученных ранее
результатов на произвольную форму ямы.
Рекомендуется для физического понимания задачи.
Nin: анализ стационарных несвязанных
состояний в поле произвольного потенциала;
определения и результаты нужны для
понимания дополнения Ош.
Ош: введение понятия зон энергии, очень
важного в физике твердого тела, в поле
потенциала, имеющего периодическую
структуру (рассмотрение отличается от
предложенного в FXi); материал достаточно сложен
и рекомендуется для последующего
изучения.

Постулаты квантовой механики
Дополнение Ащ
ЧАСТИЦА В ПОТЕНЦИАЛЬНОЙ ЯМЕ
БЕСКОНЕЧНОЙ ГЛУБИНЫ: ФИЗИЧЕСКИЙ АНАЛИЗ
1. Распределение значений импульса в стационарном состоянии.
a. Вычисление функции ф„(р), \Р/ и АР.
b. Физический анализ.
2. Эволюция волновой функции частицы.
a. Волновая функция в момент времени t.
b. Эволюция формы волнового пакета.
c. Движение центра волнового пакета.
3. Возмущение, вносимое измерением положения.
В дополнении Нг (§ 2-с-р) мы уже рассматривали стационарные состояния частицы
в бесконечно глубокой одномерной потенциальной яме. Здесь мы предлагаем вернуться
к этой задаче с физической точки зрения, что позволит применить в конкретном случае
некоторые из постулатов главы III. В особенности нас будут интересовать результаты,
которые могут предсказать результат измерения положения или импульса частицы.
1. Распределение значений импульса
в стационарном состоянии
а. ВЫЧИСЛЕНИЕ ФУНКЦИИ ф^(р), (Р) и АР
Мы видели, что стационарные состояния частицы соответствуют значениям энергии*:
Е = ^!*1 A)
" 2та2 ()
и волновым функциям:
Ф»(х) = А|~5/п(~)' B)
где а — ширина ямы ил — целое положительное число.
* Использованы обозначения дополнения Hj.
22 Квантовая механика
337

Глава III
Рассмотрим частицу в состоянии |ф,;) с энергией Еп; вероятность того, что
измерение импульса Р частицы даст результат, заключенный между р и р + dp, равна:
^(/?)ф = |ф„(р)| dp
где
1
Этот интеграл легко берется и равен:
ФА?)-"*-
ф„(р)=
1
2iy/nha
Г
i[!!*-JL)x J™ + JL)
,{ a hi _e [a h)
dx =
liyfnha
^« n> -\ e -1
nn p
. nn p
a n
C)
D)
E)
то есть
F|p_^+(_ir-F^ + ^
F)
где
F(p) =
sin {pa 12b)
pa 12fi
G)
С точностью до коэффициента пропорциональности функция ф„(р) равна сумме
(или разности) двух «дифракционных» функций F
„ , nnh\ _ nnh
\ р ± с центрами р = + ;
V а ) а
«ширина» этих функций (расстояние между двумя первыми нулями, симметричными
Ann
относительно центрального значения) не зависит от п и равна , а их «высота» так-
а
же не зависит от п.
Функция, стоящая в квадратных скобках выражения F), является четной, если п —
338

Постулаты квантовой механики
нечетное число, и нечетной, если п — четное число. Плотность вероятности .'^(/?),
определенная выражением C), всегда является четной функцией переменной р, так что
(P)„=!Z%(P)pdp = 0. (8)
Таким образом, среднее значение импульса частицы в состоянии с энергией Еп равно
нулю.
Аналогично вычислим среднее значение квадрата импульса (Р2) . Поскольку в
представлении { ис) } оператор Р действует, как , то, интегрируя по частям, полу-
i dx
чим :
о
Из (8) и (9) получим:
dx
0а\ a J
2
ппх
cos
a J
nnh\
dx = \—\. (9)
Таким образом, среднеквадратичное отклонение линейно растет с увеличением п .
Ь. ФИЗИЧЕСКИЙ АНАЛИЗ
Построим графики плотности вероятности ^п(р) для различных значений п. Для
этого начнем с рассмотрения функции, стоящей в квадратных скобках выражения F).
В случае основного состояния (п = 1) она является суммой двух функций F, то есть
двух дифракционных кривых, центры которых отстоят друг от друга на половину их
ширины (рис. 1а). Для первого возбужденного уровня (п = 2 ) расстояние между
центрами вдвое больше, и следует вычислять разность функций F (рис.2а). И, наконец, для
больших значений п дифракционные кривые отстоят друг от друга на расстоянии,
значительно большем их ширины.
Возведя в квадрат изображенные здесь функции, можно получить плотность
вероятности &п(р) (см. рис. lb и рис. 2Ь). Можно, впрочем, заметить, что для больших п член,
Результат (9) можно получить, исходя из формулы F), путем вычисления интеграла
\Р ) -}_оо ФпС/7) Р dp; это вычисление, хотя и не представляет существенных трудностей,
более громоздко, чем приведенное здесь.
22*
339

Глава III
f(p - |) _F(, + |)
Рис.1
Волновая функция ф,(р), связанная в представлении {\р)} с основным уровнем частицы
в бесконечно глубокой потенциальной яме, представляет собой сумму двух дифракционных
функций F (пунктирные кривые на рис. а). Центры этих функций отстоят на половину их
ширины, и их сумма имеет вид кривой, изображенной сплошной линией. Возведение в
квадрат этой суммы дает плотность вероятности &[{р) измерения импульса частицы,
изображенную на рис. Ъ
J nnh)
описывающий перекрытие F\ р и F
тельного удаления центров двух кривых:
nnh ,
р + , пренебрежимо мал из-за значи-
а
4яя
F\p-
nnh
а )
+ (-1ГЛр +
nnh
а
4nh
„,, nnh .
F-\ p | + F^
r nnh\
p + —
a )
A1)
Функция i'Pn(p) имеет форму, изображенную на рис.3.
340

Постулаты квантовой механики
i
а
2nh Ч
-"><Ч^ 1 ^.*_ • Л
F(p-—)-F{p+—)
/у - ^Ч
/s „-— ^^^
"^ 1 -»*^' 1 ~^"*^.«
* р
Рис.2
Функция ф2(р) первого возбужденного уровня является разностью двух функций F,
имеющих ту же ширину, что и на рис. 1а, но значительно дальше раздвинутых друг от друга
(пунктирные кривые на рисунке а); результирующая кривая изображена сплошной линией.
Плотность вероятности ^2(р) характеризуется двумя максимумами, расположенными
вблизи р = ±
а
Видно, что при больших п плотность вероятности представлена двумя симметрич-
„ 4nh , nnfi
ными пиками с шириной и с центрами в точках р = ± ; можно почти точно
а а
предвидеть результат измерения импульса частицы в состоянии |ф„), так как будут по-
nnfi _ nnh „ *
лучены значения либо + , либо с относительной точностью тем более вы-
а а
сокой, чем больше значение п (оба значения с разными знаками ± равновероятны).
а
Нетрудно понять, почему дело обстоит именно так: при больших п функция (p„(jc),
изменяющаяся синусоидально, испытывает в яме большое количество осцилляции, и,
* Абсолютная точность ие зависит от п , так как ширина кривых всегда равна
Anh
341

Глава III
следовательно, может рассматриваться как сумма двух бегущих волн, соответствующих
, nnti
противоположно направленным импульсам р = ± .
\*1р)
кяЛ
-+р
Рис.3
При больших п (высокий возбужденный уровень) плотность вероятности характеризуется
, nnti
двумя острыми максимумами с центрами в точках р = ± , соответствующих импуль-
а
сам классической движущейся частицы с одинаковыми значениями энергии
Если п уменьшается, относительная точность, с которой можно предсказать
возможные значения импульса, также уменьшается. Из рис.2Ь видно, например, что при
п = 2 функция &*п(р) имеет вид двух пиков, ширина которых сравнима с расстоянием
между ними; действительно, в этом случае волновая функция испытывает в яме всего
лишь один период колебаний, и неудивительно, что для такой «усеченной» в точках
х = О и х = а синусоиды длина волны (и, следовательно, импульс частицы) плохо
определены. И, наконец, для основного состояния волновая функция представлена лишь
одним полупериодом синусоиды, то есть длина волны и импульс частицы могут быть
определены с очень плохой относительной точностью (рис.lb).
ЗАМЕЧАНИЯ
(i) Найдем импульс классической частицы с энергией Еп, определяемый формулой A):
„2 „2_2*2
2т 2та2
A2)
то есть
342

Постулаты квантовой механики
, nnh
Ры=±~- (»3)
а
При больших п два максимума функции ^(р) точно совпадают с классическими
значениями импульса,
(ii) Видно, что при больших п модуль импульса точно (в относительном смысле)
определен, но его знак неизвестен. Именно по этой причине величина АРп велика:
действительно, для распределения вероятности, имеющего вид двух максимумов,
как на рис.3, среднеквадратичное отклонение отражает расстояние между двумя
пиками, и оно не связано с их шириной.
2. Эволюция волновой функции частицы
Состояния |ф„) с волновой функцией (p„(jt) являются стационарными, ибо не
изменяются во времени. Эволюция во времени появляется только тогда, когда вектор
состояния является линейной комбинацией нескольких кет-векторов |ф„). Здесь будет
рассмотрен простейший случай, когда в момент времени t = 0 вектор состояния |\|/@))
имеет вид:
к@)> = ^[|ф,) + |ф2>]. A4)
а. ВОЛНОВАЯ ФУНКЦИЯ В МОМЕНТ ВРЕМЕНИ t
Применим формулу (D-54) главы III и сразу же получим:
|*0»-£
' 2та2 '
°2 |ф,) + е -2 |ф2)
или, если убрать в |\|/(/)) общий фазовый множитель:
A5)
где
о)«
@21
1
:7?
=Ь
h)
п
^-"*г|'|ф
_ Зл2Й
2та2
.)]•
A6)
A7)
343

Глава 111
b. ЭВОЛЮЦИЯ ФОРМЫ ВОЛНОВОГО ПАКЕТА
Форма волнового пакета определяется плотностью вероятности:
|\|/'Сх, г)|2 =-ф'(х)+-ф^и) + ф1и)ф2и)с^оJ1г.
A8)
Видно, что изменение плотности вероятности во времени описывается только
интерференционным членом, пропорциональным ф,(лс)ф2(лг). В нем фигурирует только одна
частота Бора v21 = (Е2 -Ex)l h , так как начальное состояние состояло лишь из двух
состояний |ф,) и |ф2) • Кривые, соответствующие изменению функций ф^, ф2 и ф^ ,
изображены на рис. 4а, 4Ь и 4с.
Рис.4
Графическое представление функций ф^ (плотность вероятности для основного уровня),
Ф2 (плотность вероятности для первого возбужденного уровня) и ф,ф2 (перекрестный
член, ответственный за эволюцию формы волнового пакета).
Используя эти рисунки и выражение A8), нетрудно изобразить графически
изменение формы волнового пакета во времени (рис.5): он осциллирует между двумя стенками
ямы.
с. ДВИЖЕНИЕ ЦЕНТРА ВОЛНОВОГО ПАКЕТА
Вычислим среднее значение (x)(t) положения частицы в момент времени t\ для
этого удобно ввести обозначение:
Х'=Х-а/2, A9)
так как вследствие симметрии диагональные элементы матрицы оператора X1 равны нулю:
344

Постулаты квантовой механики
t = л/ш21
г= Зя/2а>21
t = 2я/о>21
Рис.5
Периодическое движение волнового пакета, полученного в результате суперпозиции
основного и первого возбужденного состояний частицы в бесконечно глубокой
потенциальной яме. Частота движения равна частоте Бора @21 / 2я
<ф1|Х'|Ф|)«:|[*-|],й1[Н|Л = 0;
Тогда:
где
(X,)@ = Re{e-'"'"(q>1|xi<P2)},
(ф| | Х'|ф2) = (ф, | X |ф2)-^(ф, |ф2) = - \°х sin — sin —dx = ■
2 а и а а
16а
9я2
Таким образом:
/лл\/ ч а 16а
w 2 9я2 21
B0)
B1)
B2)
B3)
345

Глава III
График функции (x)(t) представлен на рис.6; пунктиром изображена зависимость
положения классической частицы от времени: она движется между стенками ямы с
частотой со21 (поскольку на частицу в интервале между соударениями со стенками не
действует никакая сила, то ее координата изменяется линейно во времени от 0 до а в течение
каждого полупериода).
Различие классического и квантового движения проявляется очень четко: центр
квантового волнового пакета, вместо того, чтобы отразиться от стенки ямы, испытывает
замедление движения и поворачивает обратно раньше, чем достигнет области с
отличным от нуля потенциалом. Здесь мы снова сталкиваемся с результатом, полученным в
§ D-2 главы I, а именно: поскольку потенциал в точках х = О и х - а меняется
бесконечно быстро, его изменение в области порядка размеров волнового пакета является
заметным, и движение центра волнового пакета не подчиняется законам классической
механики (см. также гл. Ill, § D -l-d-у). Физическое объяснение этого явления таково:
прежде чем центр пакета достигнет стенки, действие потенциала на «основание» пакета
оказывается достаточно сильным, чтобы заставить его повернуть обратно.
Ч*>
Рис.6
Зависимость от времени среднего значения (x)(t), соответствующего волновому пакету,
приведенному на рис.5. Пунктиром представлено движение классической частицы,
имеющее тот же период. Квантовая механика предсказывает, что центр волнового пакета
изменяет направление движения раньше, чем достигнет края ямы, что объясняется
взаимодействием с потенциалом «подставки» волнового пакета
ЗАМЕЧАНИЕ
Среднее значение энергии частицы в состоянии |\|/@) нетрудно вычислить с
помощью формулы A5):
346

Постулаты квантовой механики
(Я> = ^£,+|£2=|£,, B4)
а также:
откуда следует:
(H*) = U*+±I%=%E>9
B5)
Д# = --£,. B6)
Отметим, в частности, что (//), (#/ и АЯ не зависят от времени, и это вполне
нормально, так как Н — константа движения. С другой стороны, согласно
выполненному выше анализу, видно, что волновой пакет заметно изменяется за
интервал времени порядка:
Д/« —. B7)
@21
Используя B6) и B7), получим:
AH-At~-Elx = -, B8)
2 ' ЪЕХ 2
то есть мы вновь получили соотношение неопределенностей время — энергия.
3. Возмущение, вносимое измерением положения
Рассмотрим частицу в состоянии |ф,). Допустим, что в момент времени t = О
измеряется положение частицы и получено значение jc = а 12 . Какова при этом вероятность
получения различных результатов измерения энергии, которое выполняется сразу же
после первого измерения?
Следует сразу же отказаться от следующего неверного рассуждения: после
измерения частица находится в собственном состоянии оператора X, соответствующем
найденному результату, и ее волновая функция пропорциональна 8(лс-я/2); если теперь
выполнить измерение энергии, то можно найти различные значения Еп с вероятностями,
пропорциональными:
347

Глава III
£л5(*-§]ф«И
<Ы §
21а, если л = 2/:+ 1;
О, если п-2к.
B9)
Такое неправильное рассуждение приведет к равенству вероятностей для всех значений
Еп, соответствующих нечетным значениям п , что совершенно абсурдно, ибо приводит
к бесконечной сумме вероятностей.
Ошибка состоит в том, что при таком рассуждении не учитывалась норма волновой
функции. Для корректного применения четвертого постулата главы III необходимо
записать нормированную волновую функцию сразу же после первого измерения. Но
невозможность нормировки функции д(х-а/2)* требует уточнения поставленной
выше задачи.
Как мы уже видели в § E-2-b главы III, эксперимент, в котором производится
измерение наблюдаемой с непрерывным спектром, никогда не может дать результат с
бесконечно большой точностью, то есть в данном случае мы можем лишь утверждать, что
а е ^ а е
<х<—+—
2 2 2 2
C0)
где величина е зависит от измерительного прибора, но никогда не может равняться
нулю.
Если допустить, что б мала по сравнению с размерами волнового пакета перед
измерением (то есть по сравнению с а), то волновая функция после измерения будет
практически равна Ve8(E) he-- , где 8(е)(;с)— функция, равная нулю везде, кроме
интервала, определенного неравенством C0), где она равна 1/е (см. приложение II, § 1-а).
Эта функция нормирована, так как:
\dx
V^5('
а
Х~~~2
= 1.
C1)
Что же произойдет при измерении энергии? Каждое из значений Еп можно найти
с вероятностью:
,2
■ПЕ„) =
SVIWSH x-^\dx
8aQ
sm'\ еслил = 2л-1;
e \nn I \ 2a )
0 если п = 2k.
C2)
* На этом примере явно видно, что 8-функция не может представлять физически реализуемое
состояние.
348

Постулаты квантовой механики
Рис.7
Зависимость вероятности ./(Еп)
получить значение энергии Еп
после измерения положения частицы,
дающего результат all с
точностью е « а от п . Чем меньше г ,
тем больше вероятность получения
больших значений энергии
Зависимость ./(£„) от п для фиксированного значения 8 и нечетных п
представлена на рис.7. Из него видно, что вероятность ./(£„) ничтожно мала при значениях п,
больших, чем а/г. Таким образом, каким бы малым ни было значение е ,
распределение вероятности сильно зависит от 8 , и именно поэтому первое рассуждение, в котором
мы сразу же полагали, что е = 0, не могло привести нас к правильному выводу. Из
рисунка видно также, что, чем меньше е, тем сильнее кривая №(Еп) расширяется на
большие значения п. Интерпретация этого факта проста: согласно соотношению
неопределенностей Гейзенберга (глава I, § С-3), если положение частицы измеряется с
большой точностью, то значение импульса становится неопределенным, ибо частице
сообщается тем большая кинетическая энергия, чем меньше 8 .
Дополнение Вщ
ИЗУЧЕНИЕ ТОКА ВЕРОЯТНОСТИ
В НЕКОТОРЫХ ЧАСТНЫХ СЛУЧАЯХ
1. Выражение для тока в областях, где потенциал постоянен.
2. Применение к задачам с потенциальными барьерами.
a. Случай Е > V0 .
b. Случай Е <V0.
3. Ток вероятности падающей и проникающей волн в случае отражения .на двумерном скачке
потенциала.
Плотность тока вероятности, связанная с частицей с волновой функцией \|/(г,/)»
была определена в главе III формулой:
1 3 5 7 9 11 13 15 17
349

Глава 111
J(r, o=™[v*(r, t) V V|/(r, 0-c.c] (l)
2/шL
(где аббревиатура с.с. означает комплексно сопряженное выражение). В этом
дополнении мы более строго рассмотрим ток вероятности в некоторых частных случаях
(прямоугольные потенциалы в одномерном и двумерном пространствах).
1. Выражение для тока в областях,
где потенциал постоянен
Рассмотрим в рамках одномерного пространства частицу с энергией Е в поле
постоянного потенциала V(). В дополнении Н[ мы различали несколько частных случаев.
(i) Если E>V0, то волновая функция может быть записана в виде:
Щх) = АеЛх + Аечкх, B)
где
Е-Уп~. C)
2т
Подставим B) в A) и получим:
J,=^[\Af-\Af}. D)
Интерпретация этой формулы проста: волновая функция B) соответствует двум
плоским волнам с противоположно направленными импульсами р = ±hk и с плотностями
|2 I ,,|2
вероятности |л| и |Л'|
(и) Если Е < V0 , то
где
Щх) = Верх + В,е-рх, E)
Уо-еЖ. F)
2т
Подставив E) в A), получим:
350

Постулаты квантовой механики
J = — [ш*ЯЧс.с.1.
G)
В этом случае видно, что обе экспоненциальные волны должны обязательно иметь
отличные от нуля коэффициенты, иначе ток вероятности обращается в нуль.
2. Применение к задачам с потенциальными барьерами
Применим эти результаты к задачам с потенциальными барьерами, рассмотренным
в дополнениях Hi и Jb Пусть частица с массой т и энергией Е движется вдоль оси Ох
и в точке х = 0 встречает скачок потенциала высотой V0 (рис.1).
©
Цх)
®
Рис.1
Скачок потенциала высотой V0
а. СЛУЧАЙ E>V0
Применим формулу D) к волновым функциям A1) и A2) дополнения Нь положив,
как и в этом дополнении:
а;=о.
(8)
В области I ток вероятности равен:
л =
м,
т
N I2 I 121
I hi -hi J
(9)
и в области II:
т ' '
(Ю)
В формуле (9) ток J{ является разностью двух членов, первый из которых соответствует
351

Глава III
падающему току, а второй — отраженному току. Отношение этих токов определяет
коэффициент отражения барьера:
Д =
а;
(id
что совпадает с формулой A5) дополнения Hi.
Аналогично, коэффициент прохождения Т через барьер равен отношению
прошедшего тока Ju к падающему:
A2)
к, \А,
и вновь мы получаем формулу, аналогичную выражению A6) дополнения Нт.
Ь. СЛУЧАЙ E<Vn
Поскольку выражение для волновой функции фД*) то же, что и в § а, то равенство
(9) остается справедливым. Напротив, в области II волновая функция равна:
[напомним, что в уравнении B0) дополнения Hi амплитуда В2
G), получим:
J и = 0.
A3)
= 0]. Используя формулу
A4)
Прошедший поток равен нулю, что соответствует равенству B4) дополнения Uh
Как интерпретировать вывод о том, что в области II ток вероятности равен нулю,
а вероятность нахождения частицы отлична от нуля? Вернемся к результатам,
полученным в § 1 дополнения Jr. Мы видели, что часть падающего волнового пакета
проникает в область И, запрещенную классической механикой, затем производит в этой области
поворот и движется в обратном направлении в сторону отрицательных значений х
(именно это проникновение в область II является причиной запаздывания при отражении).
В стационарном режиме в области II существуют два тока вероятности: положительный
ток, соответствующий проникновению в эту область части падающего волнового пакета,
и отрицательный ток, соответствующий возвращению в область I проникающей части
волнового пакета. Эти два тока в точности компенсируют друг друга, вследствие чего
суммарный ток равен нулю.
352

Постулаты квантовой механики
Итак, в одномерной задаче структура тока вероятности проникающей волны
замаскирована компенсацией двух противоположно направленных токов вероятности.
Именно поэтому сейчас мы рассмотрим двумерную задачу о наклонном падении частицы,
которая позволит получить отличный от нуля ток и выяснить его структуру.
3. Ток вероятности падающей и проникающей волн
в случае отражения на двумерном скачке потенциала
Рассмотрим следующую двумерную задачу: частица с массой т движется в
плоскости хОу в поле потенциала V(x, у), заданного соотношениями:
V(jc, >0 = 0, если х<0;
V(x, у) = У0,если х>0. A5)
Этот случай соответствует рассмотренному в § 2 дополнения Fi, если принять, что
потенциальная энергия V(x, у) является суммой двух членов: V{(x) (одномерный скачок
потенциала) и V2(y) = 0. Тогда решение уравнения на собственные значения
гамильтониана можно искать в виде произведения:
9U у) = <р{М<р2(у). A6)
Функции ф,(х) и ф2()>) удовлетворяют одномерным уравнениям на собственные
значения, соответствующим потенциалам V,(jc) и V2(y) и таким энергиям Ех и £2, сумма
которых равна:
Е, + Е2- Е (полная энергия частицы). A7)
Допустим, что £j < V0, тогда ф,(х) соответствует полному отражению в
одномерной задаче, и можно воспользоваться формулами A1) и B0) дополнения Нь что касается
функции <р2(у), то ее можно записать сразу же, так как она соответствует случаю
свободной частицы (V2 = 0) и представляет собой плоскую волну. Таким образом, в
области I (л;<0):
,« / \ a i(kxx + kvy) , A, i(-kxx + kvv) /io\
Ф/(*> У) = &е +Ne v , A8)
где
2тЕ, , 12тЕ>>
V2
^х - \\ 4-2 ' *У ~~ V t.2 > 09)
23 Квантовая механика
353

Глава 111
и в области II (х> О):
ф„(*,;у) = Д*-р**е'\
B0)
где
Р,
2т(У0-Е1)
B1)
Уравнения B2) и B3) дополнения Ь^ дают нам отношения А/А и В1А\ введем
параметр Ь соотношением:
«f> = -
Р. _ 1Уо-Д.
L; 0<д<
B2)
и получим:
B3)
Б 2*
А кх + /рл.
1— = 2 cos 1
B4)
Применим теперь соотношение A), определяющее ток вероятности, и получим для
области I:
Ji
f nk*
(J'^="^
m
П |2 1 121
Л -Л'
[ii j
= 0
У 1 ik x -ik x\2
(Л)=—- \Aekx X + A'e '*'*
hky | |2
m ' '
2 + 2 cos B*х*+ 2Ф)
B5)
и для области II:
Jn
^v I 12 ^v I 12 ,
(^/)у= в вм=—4А cos2be~2Px\
B6)
m
В области I отлична от нуля только компонента (/,) тока вероятности. Она
является суммой двух членов:
354

Поспи ntnibi квантовой мс\ iпаки
■ член, пропорциональный 2|л| , образованный суммой током падающей и отра
женной волн (рис.2);
Рис.2
Сумма токов вероятности, связанных с падающей
и отраженной волнами, дает ток вероятности,
параллельный оси Оу
■ член, содержащий cosBkxx + 2b) и отражающий интерференцию этих волн; он
порождает осциллирующее поведение тока вероятности при изменении х (рис.3).
4 Л
К © А
Л *\
\
©
ь-_
->JC
Рис.3
Вследствие интерференции падающей и отраженной волн ток вероятности в области I
является осциллирующей функцией координаты х\ в области II он убывает
экспоненциально (проникающая волна)
В области II ток вероятности также направлен вдоль оси Оу , он испытывает
экспоненциальное затухание, отражающее уменьшение проникающей волны. Этот ток
вероятности вызван проникновением волнового пакета во вторую среду (рис.4), где он,
прежде чем вернуться обратно, продолжает свое движение в направлении оси Оу в течение
времени порядка времени запаздывания т при отражении [см. дополнение Jb уравнение
(8)]; он также связан с боковым отклонением волнового пакета при отражении (рис.4).
23*
355

Глава III
Рис.4
Возможность проникновения частицы в область II проявляется
боковым отклонением при отражении
Дополнение Сщ
СРЕДНЕКВАДРАТИЧНЫЕ ОТКЛОНЕНИЯ
ДВУХ СОПРЯЖЕННЫХ НАБЛЮДАЕМЫХ
1. Соотношение неопределенностей для Р и Q.
2. «Минимальный» волновой пакет.
Коммутатор [б, Р] двух сопряженных наблюдаемых Р и Q равен ih . В этом
дополнении мы покажем, что среднеквадратичные отклонения (см.§ С-5 главы III) АР и
Д<2 независимо от состояния изучаемой системы удовлетворяют соотношению:
др.де>|. A)
Затем покажем, что если система находится в таком состоянии, где произведение
AP-AQ в точности равно —, то волновая функция, связанная с этим состоянием в
представлении {\q) }, является гауссовым волновым пакетом (впрочем, это верно и для
волновой функции в представлении {\р)}).
356

Постулаты квантовой механики
1. Соотношение неопределенностей для Р и Q
Рассмотрим кет:
|ф)=(е+а/>)|1|/), w
где X — произвольный вещественный параметр. Каким бы ни было значение X ,
квадрат нормы (ф|ф) — положительное число:
fa|9Hv|(G-a^(Q+^
= (Q2)^iX([Q,P])^X2(p2) = (Q2)-Xh + X2(p2)>0, (З)
Дискриминант этого трехчлена второго порядка по X либо отрицателен, либо равен
нулю:
Й2-4(Р2)B2)<0, D)
откуда следует, что
(г')(е'L- »)
Считая вектор |\|/) заданным, введем теперь две наблюдаемые Q' и Р',
определенные соотношениями:
P/=P-(P)=P-(\|/|P|\|/);
Q, = G-(Q) = Q-(v|e|4/>. F)
Операторы Р' и Q' также являются сопряженными наблюдаемыми, так как:
[е/,р/]=[е,р]=1й. G)
Результат E), полученный выше для Р и Q, справедлив и для операторов Р' и Q':
(>}(<Г2>4- (8)
С другой стороны, исходя из определения [глава III, формула (С-23)]
среднеквадратичного отклонения и используя F), нетрудно получить:
357

Глава III
АР
-jp>=
AQ = ^). (9)
Соотношение (8) можно переписать в виде:
(Ю)
П
APAQ>-
Таким образом, если две наблюдаемые являются сопряженными (как, например,
операторы, соответствующие классическому положению xt и сопряженному импульсу pt),
то существует точный нижний предел произведения APAQ. Итак, тем самым мы
получили обобщение соотношения неопределенностей Гейзенберга.
ЗАМЕЧАНИЕ
Все приведенные выше рассуждения без труда обобщаются на две
произвольные наблюдаемые А и В:
ДЛ.ДЯ>^|([Д,Д])|. (И)
2. «Минимальный» волновой пакет
В том случае, если достигнуто минимальное значение произведения APAQ:
AP-AG = |, A2)
говорят, что вектор состояния |\|/) соответствует минимальному волновому пакету для
наблюдаемых Р и Q.
Согласно сказанному выше равенство A2) требует, чтобы квадрат нормы вектора:
|(p') = (Q' + *XP')k) A3)
являлся бы полиномом второй степени по X , имеющим двойной корень XQ. Если
Х = Х0, кет |ф') равен нулю:
358

Постулаты квантовой механики
(e/+ix0p/)|\i/> = [e-(e>+^o('>-<^>]|v> = o. (i4)
Напротив, если АР- AQ> — , то полином, определяющий (ф'|ф'), никогда не
обращается в нуль, так как при любых А, он больше нуля.
П
Итак, необходимым и достаточным условием равенства АРА<2 = — является
пропорциональность кет-векторов ((?-((?)) |i|/) и (Р-(Р)) |\|/). Коэффициент
пропорциональности легко вычисляется и равен -iX{). Действительно, если APAQ = —, то урав-
(ф,|ф') = л:(АР):-Х// + (АеJ =0 A5)
имеет двойной корень:
Ло=— ГГ = 7 • A6)
2(АР) Ь
Запишем равенство A4) в представлении {\q) } (для простоты допустим, что
собственные значения q оператора Q не вырождены). Зная, что в этом представлении (см.
дополнение Ец) оператор Р действует, как , получим:
/ dq
q + *k0j--(Q)-i\0{P)
¥(<?) = 0, A7)
где
V(9) = (?|V>. A8)
Чтобы проинтегрировать уравнение A7), удобно ввести функцию 0(g), определенную
равенством:
Щй) = е'^"шЩ-{а)). A9)
Подставив A9) в A7), получим более простое уравнение:
359

Глава III
л * d
dq
6(9) = 0, B0)
решение которого имеет вид:
Щ) = Се'я м, B1)
где С — произвольная комплексная постоянная. Подставив A6) и B1) в A9), получим:
НО12
V(9) = Ce'<^rt«L2a°J . B2)
Эта функция может быть нормирована, если обозначить:
C = [27i(AGJrl/4. B3)
Итак, мы приходим к следующему результату: если произведение АР • AQ принимает
свое минимальное значение /г/2 , то волновая функция в представлении {\q) } является
гауссовым волновым пакетом, полученным из функции Гаусса 9(g) путем
преобразования A9) (то есть двойного изменения начала координат — по оси q и по оси р).
ЗАМЕЧАНИЕ
Все рассуждения, приведенные выше в представлении {\q) }, могут быть
выполнены и в представлении {| р) }. При этом мы нашли бы волновую функцию
\|/(р), равную:
ЩР) = (Р\ V> = -7= j*2dqe-1"» Щд). B4)
л]2пп
Эта функция тоже гауссова и равна:
Шр) = [2п(АРJу\-^р,*е^2*р\ . B5)
360

Постулаты квантовой механики
Дополнение Dm
ИЗМЕРЕНИЯ, ВЫПОЛНЯЕМЫЕ В ЧАСТИ
ФИЗИЧЕСКОЙ СИСТЕМЫ
1. Вычисление физических предсказаний.
2. Физический смысл состояния — тензорного произведения.
3. Физический смысл состояния, не являющегося тензорным произведением.
Понятие тензорного произведения, введенное в § F главы II, позволило нам
показать, как можно построить, исходя из пространства состояний двух подсистем,
пространство полной системы, полученной путем их объединения. В данном дополнении
мы продолжим рассмотрение этого вопроса, используя введенные в главе III постулаты,
и увидим, как можно найти результаты измерений в какой-либо из подсистем, если
известно состояние системы в целом.
1. Вычисление физических предсказаний
Рассмотрим физическую систему, состоящую из двух частей A) и B) (например,
систему двух электронов). Если Щ) и £B) — пространства состояний частей A) и B),
то полное пространство системы A) + B) является тензорным произведением
пространств £A)®£B). Например, состояние системы двух электронов описывается
волновой функцией шести переменных \|/(jcp y2, z{',x2, y2> z2), связанной с кет-вектором
пространства ffr(l)®ffrB) (см. главу И, § F-2-b).
Можно представить себе, что некоторые измерения производятся только в одной из
двух частей полной системы [например, в части A)]. Наблюдаемые АA),
соответствующие этим измерениям, определены в пространстве ^A)®^B) продолжением
наблюдаемых АA), действующим только в пространстве £A) * (см. главу II, § F-2-b):
АA)=>АA)=АA)®1B), A)
где 1B) — единичный оператор в пространстве #B).
Спектр оператора АA) в пространстве #A)®£B) тот же, что и спектр оператора
* Для удобства мы сохраним в этом дополнении иные обозначения для АA) и его
продолжения АA).
361

Глава III
А{\) в пространстве ^A). Напротив, мы видели, что все собственные значения
оператора ЛA) вырождены в пространстве ?{\)®tB), если даже ни одно из них не вырождено
в пространстве #A) для оператора ЛA) [конечно, при условии, что размерность
пространства tfB) больше 1]. Если производится точное измерение в системе A), то это
значит, что полная система может находиться после измерения в различных состояниях,
независимо от результата измерения (состояние после измерения зависит не только от
результата, но и от состояния перед измерением). С физической точки зрения такая
множественность состояний вполне понятна: она соответствует степеням свободы
системы B), относительно которой мы не стремимся получить какую-либо информацию в
процессе измерения.
Пусть Рп(\) — проекционный оператор в пространстве *f(l) на собственное
подпространство, соответствующее собственному значению ап оператора ЛA):
^o)=£|<a))ka)L B)
где gn кет-векторов ^',A)) являются ортонормированными векторами, связанными со
значением ап. Пусть Рп(Х) — проекционный оператор в пространстве tf(l)®tfB) на
собственное подпространство с тем же собственным значением ап оператора ЛA); тогда
оператор Рп(\) получается как продолжение оператора Рп(\) в пространстве ^A)®^B):
/>A)=/>яA)®1B). C)
Чтобы записать единичный оператор 1B) в пространстве #B), используем
соотношение замкнутости в произвольном ортонормированном базисе {| vA:B))} этого
пространства:
K2) = S|v,B))(v,B)|. D)
к
Если подставить D) в C), используя формулу B), получим:
£ш=£s|«;a)v*B))(ni(i) v,B)|. E)
/ = 1 к
Зная нормированное на 1 состояние |\|/} полной системы, можно вычислить
вероятность 9?{Х\ап) получить значение ап при измерении наблюдаемой ЛA) в части A) этой
системы. Используя общую формулу (В-14) главы III, запишем:
362

Постулаты квантовой механики
^\ап) = (\у\Р,Д)\у) F)
и, следовательно:
^(,)K)=is|(«i(l)viB)|V>| . G)
Аналогично можно вычислить состояние |\|/') системы после измерения, и оно в
соответствии с формулой (В-31) главы III равно:
,/М ЗД I»)
или, если воспользоваться формулой E):
ES|":a)v,B))(w;;(i)v,B)|n/)
|1|(":A)^B)|ц/)|2
ЗАМЕЧАНИЯ
(i) Выбор ортонормированного базиса {| vA:B))} в пространстве $B) произволен. Из
формул C), F) и (8) видно, что предсказания относительно подсистемы A) от него
не зависят. Физически нетрудно понять, что если в системе B) не производится
никакое измерение, то ни одно из состояний или ансамбль состояний этой
системы не могут быть привилегированными,
(ii) Если состояние |\|/) перед измерением было тензорным произведением:
|V) = |<PA))®|XB)> A0)
[здесь |фA)) и |%B))— два нормированных состояния в пространствах £A) и
*?B)], то нетрудно видеть, что состояние |\|/') также является тензорным
произведением:
|уНф'A))®|хB)), (ii)
363

Глава III
где
!„■(■))■ , "■(')|Ф0)) ■ A2)
Таким образом, состояние системы A) изменилось, а состояние системы B) — нет.
(ш) Если собственное значение ап оператора ЛA) в пространстве <£A) не вырождено,
или, если говорить в более общем плане, оператор ЛA) образует в £A) полный
набор коммутирующих операторов, то индекс / в формуле B) и последующих
формулах более не нужен. Видно, что состояние системы после измерения,
дающего результат ап, можно всегда представить в виде произведения двух векторов.
Действительно, равенство (9) может быть записано в форме:
|i|/') = |Wn(l))(x)|x42)), A3)
где нормированный вектор |х'B)) пространства ifB) описывается формулой:
2KB)X4,(l)v4B)|V)
1%'B))= ' , A4)
|Е|("„AКB)|¥)|
Итак, каким бы ни было состояние |ц/) полной системы перед измерением, ее
состояние после измерения в одной лишь ее части A) всегда является тензорным
произведением, если только это измерение было полным в подсистеме A) [хотя и
частичным в полной системе A) + B)].
2. Физический смысл состояния — тензорного произведения
Чтобы выяснить физический смысл состояния, являющегося тензорным
произведением, применим результаты предыдущего параграфа в частном случае, когда начальное
состояние полной системы имеет вид A0). Используя формулы F) и C), сразу же получим:
^(,)Ю = (фA)%B)|Р„A)®1B)|фA)ХB)). A5)
Определение тензорного произведения Рп{\)®\{2) и нормировка вектора |хB))
позволяют записать:
#(,)К) = (<рA)| Pn(D |ФA))(ХB)| 1B) |хB)) = (фA)| РйA) |ФA)). A6)
364

Постулаты квантовой механики
Вероятность &{Х)(ап) не зависит от |%B)), а только от |(рA)) .Таким образом, если
состояние полной системы имеет вид A0), все физические предсказания относительно
одной из двух систем не зависят от состояния, в котором находится другая, и полностью
выражаются через состояние |фA)) [или |хB)) ] в зависимости от того, производится ли
наблюдение в одной системе A) или в одной системе B).
Это значит, что состояние, являющееся тензорным произведением |фA))®|хB)),
представляет собой простое соединение двух систем, одна из которых находится в
состоянии |фA)), а другая — в состоянии |%B)). Говорят еще, что в таком состоянии две
системы не коррелируют (точнее говоря, результаты измерения в той или другой
системе являются случайными независимыми переменными). Такая ситуация реализуется,
если обе системы были приготовлены в состояниях |фA)) и |%B)) независимо друг от
друга и лишь потом были объединены без какого-либо взаимодействия друг с другом.
3. Физический смысл состояния,
не являющегося тензорным произведением
Рассмотрим теперь случай, когда состояние полной системы не является тензорным
произведением, то есть когда |\j/) нельзя представить в форме |фA))®|хB)). Теперь
уже нельзя считать результат измерения в одной из двух систем как функцию одного
кет-вектора |фA)) или |%B)) . В этом случае нужно использовать общие формулы F) и
G) для вычисления вероятностей возможных результатов. Без доказательства отметим
только, что такая ситуация в общем случае отражает существование корреляций между
системами A) и B). Это означает, что результаты измерений в системе A) или в системе
B) не являются случайными независимыми переменными и могут коррелировать друг с
другом. Так, например, можно показать, что взаимодействие между системами
трансформирует начальное состояние, являющееся тензорным произведением, в состояние,
которое не является таковым: любое взаимодействие между двумя системами в общем
случае вносит корреляцию между ними.
Можно задаться вопросом, как охарактеризовать каждую из систем A) или B), если
состояние полной системы не равно произведению |фA))®|%B)), поскольку для этого
уже нельзя использовать |фA)) или |%B)). Этот вопрос очень важен, ибо любая
физическая система в общем случае взаимодействовала в прошлом с другими системами,
если даже в интересующий нас момент времени она изолирована. Состояние полной
системы [система A) + системы B), с которыми она взаимодействовала в прошлом] в
общем случае не является произведением состояний, и связывать систему A) только
лишь с кет-вектором |фA)) было бы неправильным. Чтобы преодолеть это затруднение,
365

/ ':шва III
нужно описывать систему A ) не иск юром состояния, а опера-юром, называющимся
оператором плотности. Некоюрые смоления относительно соответс i »> юшего формализма,
основанного на статистической кванювой механике, даны в дополнении Г.т (§ 5-b).
Однако вектор состояния все-таки можно применять для описания системы A) в тех
случаях, когда в ней'производится полный набор измерений. Действительно, каким бы
ни было состояние полной системы A) + B) перед измерением, полный набор
измерений в системе A) переводит ее в состояние, являющееся тензорным произведением |см.
формулы A3) и A4)], так как вектор состояния системы A) при этом равен
единственному собственному вектору (с точностью до множителя), связанному с полным набором
измерений в системе. Таким образом, этот набор измерений снимает все корреляции,
имевшие место вследствие предшествующих взаимодействий между системами. Если в
момент измерения система B) уже удалилась и более не взаимодействует с системой A),
то о ней можно больше не вспоминать.
ЗАМЕЧАНИЕ
С помощью формулы A4) легко доказать, что вектор состояния |х'B))
системы B) после измерения в случае, когда состояние |\j/) перед измерением не являлось
произведением состояний, зависит от результата полного набора измерений,
полученного для системы A) [напомним, что это не так, если |\|/) является
произведением состояний; см. замечание (ii) к § 1]. Этот результат априори может показаться
удивительным: действительно, состояние системы B) после набора измерений,
выполненных в системе A), зависит от результата этих измерений даже в том случае,
когда в момент измерения система B) уже настолько удалена от системы A), что
более с ней не взаимодействует. С этим «парадоксом», детально
рассматривавшимся некоторыми физиками, связаны имена Эйнштейна, Подольского и Розена.
Дополнение Ещ
ОПЕРАТОР ПЛОТНОСТИ.
1. Постановка задачи.
2. Понятие статистического ансамбля состояний.
3. Чистое состояние. Введение оператора плотности.
a. Описание вектором состояния.
b. Описание оператором плотности.
c. Свойства оператора плотности чистого состояния.
366

Постулаты квантовой механики
4. Смешанный ансамбль состояний («не чистый» ансамбль).
a. Определение оператора плотности.
b. Общие свойства оператора плотности.
c. Населенности и когерентности.
5. Примеры использования оператора плотности.
a. Система в термодинамическом равновесии.
b. Отдельное описание части физической системы. Понятие парциального следа.
1. Постановка задачи
До сих пор мы рассматривали системы, состояние которых было точно известно, и
показали, как можно исследовать их эволюцию во времени и предсказать результат
выполненных в них измерений. Чтобы определить состояние системы в заданный момент
времени, достаточно выполнить в ней совокупность измерений, соответствующую
полному набору коммутирующих операторов. Например, в описанном в § А-3 главы I
эксперименте состояние поляризации фотонов точно известно, если луч света пропускается
через поляризатор.
Однако на практике состояние системы часто оказывается известным не полностью.
Именно это имеет место, например, при определении состояния поляризации фотонов,
испущенных источником естественного света (не поляризованного), или состояния
атомов, вылетающих из печи с температурой Г, кинетическая энергия которых известна
лишь статистически. Задача, которая возникает при квантовом описании таких систем,
заключается в следующем: как включить в формализм недостаточность информации,
имеющейся относительно состояния системы, чтобы в дальнейшем иметь возможность
получить результаты, максимально использующие эту неполную информацию? Для
этого введем здесь очень удобный математический аппарат — оператор плотности,
значительно облегчающий одновременное применение постулатов квантовой механики и
формализма теории вероятности.
2. Понятие статистического ансамбля состояний
Во всех областях физики, если информация об изучаемой системе оказывается
неполной, используется понятие вероятности. Например, известно, что фотон,
испущенный естественным источником света, может иметь с равной вероятностью любое
состояние поляризации. Аналогично, система, находящаяся в термодинамическом
равновесии при температуре Т, имеет вероятность находиться в состоянии с энергией Еп,
-Е IkT
пропорциональную е " .
В общем случае неполнота информации относительно состояния системы может
быть выражена в квантовой механике следующим образом: состояние системы может
367

Глава III
быть или состоянием |\|/,) с вероятностью рх, или состоянием |\|/2) с вероятностью р2,
или и т.д. Очевидно, что
а + л + ... = £л=1. A)
Говорят при этом, что имеется смешанный (статистический) ансамбль состояний \у{),
|\|/2),... с вероятностями рх, р2,... .
Посмотрим теперь, как изменятся предсказания результатов измерений,
выполненных в системе. Если бы состояние системы было |у*)> то, используя постулаты главы
III, можно было бы найти вероятность того или иного результата измерения. Поскольку
такое событие (состояние \цк)) имеет вероятность рк, то нужно взвесить полученные
результаты по рк и затем суммировать по различным значениям к , то есть по всем
состояниям статистического ансамбля.
ЗАМЕЧАНИЯ
(i) Различные состояния |xj/J , |\|/2),... не обязательно должны быть ортогональными.
Однако можно всегда считать их нормированными, что мы и будем использовать
в дальнейшем,
(ii) Следует заметить, что в рассматриваемом случае вероятности входят на двух
разных уровнях:
— прежде всего, в начальную информацию о системе (до сих пор мы не
вводили вероятность на этой стадии и полагали, что вектор состояния был
точно известен или что все вероятности рк равны нулю, кроме одной, которая
равна 1);
— и далее в ходе применения постулатов, касающихся измерения (они имеют
вероятностный характер даже в том случае, если начальное состояние системы
точно известно).
Таким образом, две существенно различные причины требуют введения
вероятностей на этих двух уровнях: неполный характер информации относительно
начального состояния системы (такие ситуации встречаются в классической
статистической механике) и неопределенность (специфически квантовая), связанная
с процессом измерения.
(Hi) He следует отождествлять систему, информация о которой дана статистическим
ансамблем состояний (вероятность рк того, что вектор состояния равен |\|/*)),
368

Постулаты квантовой механики
с системой, состояние которой |\|/) является линейной суперпозицией состояний*:
к>=5>*к)- B)
к
Действительно, в квантовой механике часто говорят, что если кет \\\f) определен
выражением вида B), то «система имеет вероятность \ск\ находиться в состоянии
|\|/*)». Точнее говоря, под этим нужно подразумевать, что в результате
совокупности измерений, соответствующих полному набору коммутирующих операторов,
допускающих кет \\\fk) в качестве собственного вектора, вероятность получить
набор собственных значений, связанных с \\\fk), равна \ск\ . В § Е-1 главы III мы
уже обращали внимание на то, что система в состоянии |\j/), определяемом
формулой B), не обязательно эквивалентна системе, имеющей вероятность
|с,| находиться в состоянии |\|/j), вероятность \с2\ находиться в состоянии |\|/2)
и т.д. Действительно, в случае линейной комбинации векторов \\\fk) могут
существовать эффекты интерференции между этими состояниями, описываемые
перекрестными членами вида ск с*к,, возникающими при вычислении квадрата модуля
амплитуд вероятности и имеющими большое значение в квантовой механике.
Итак, понятно, что в общем случае нельзя описывать статистический ансамбль
«средним вектором состояния», который был бы суперпозицией состояний |\|/*),
ибо, как показано выше, путем вычисления взвешенной суммы вероятностей
никогда нельзя получить интерференционные члены, существующие между
различными векторами |\|/А) смешанного ансамбля.
3. Чистое состояние. Введение оператора плотности
Для изучения поведения статистической смеси состояний мы предложили
следующий метод: вычисление физически предсказуемых результатов, соответствующих
возможному состоянию |\|/А), затем взвешивание полученных результатов с вероятностями
рк, связанными с этим состоянием, и, наконец, суммирование по к . Хотя этот метод в
принципе корректен, подобные расчеты редко бывают удобными. Мы уже отмечали
[замечание (iii)], что нельзя сопоставлять системе «средний вектор состояния». И дейст-
* Здесь мы предполагаем, что состояния |\|/ kj ортонормированы. Эта гипотеза не
обязательна, но она существенно упрощает рассуждения.
24 Квантовая механика
369

Глава III
вительно, не «средний вектор», а «средний оператор» позволяет получить простой и
удобный способ описания статистической смеси состояний. Этот оператор получил
название оператора плотности.
Прежде чем перейти к общим вопросам, рассмотрим сначала простейший случай,
когда состояние системы точно известно, то есть все вероятности рк, кроме одной, равны
нулю. В этом случае будем говорить, что система находится в чистом состоянии. Сейчас
мы покажем, что можно охарактеризовать систему эквивалентным образом, используя
вектор состояния |\}/) или некоторый оператор, действующий в пространстве состояний
(оператор плотности). Его значение в полной мере будет продемонстрировано в § 4, где
мы покажем, что практически все формулы, в которые входит этот оператор (мы докажем
это в случае чистого состояния) остаются справедливыми и при описании смешанного
ансамбля состояний.
а. ОПИСАНИЕ ВЕКТОРОМ СОСТОЯНИЯ
Рассмотрим систему, вектор состояния которой в момент времени t равен:
k(o)=2X(ok), о)
п
где векторы {\ип) } образуют ортонормированный базис в пространстве состояний,
который мы будем считать дискретным (обобщение на случай непрерывного базиса
производится без труда). Коэффициенты cn{t) удовлетворяют соотношению:
Zh(of = i, D)
п
выражающему нормировку вектора |\|/@) •
Если А — наблюдаемая с матричными элементами:
(и„\А\ир)=А„р, E)
то среднее значение А в момент времени t равно:
(A)(t)= (i|/(f)| A |V@>= ^c'n(t)cp{t)Ani>. F)
И, наконец, уравнение эволюции вектора |i|/(r)) является уравнением Шредингера:
370

Постулаты квантовой механики
/ft4v(')=wawo, (?)
dt
где H(t) — гамильтониан системы.
Ь. ОПИСАНИЕ ОПЕРАТОРОМ ПЛОТНОСТИ
Формула F) показывает, что коэффициенты сп(t) входят в средние значения в виде
квадратичных форм типа с*(/)с @, которые совпадают с матричными элементами
оператора |\|/@) (v@|» являющегося проекционным оператором на кет |\|/@) (см-
§ B-3-b главы II). Действительно, согласно формуле C):
(W/;|ii/(o)(ii/(o|^) = c;(oc/;(o. (8)
Естественно ввести оператор плотности р(t) выражением:
P@=|V@>(V@|. (9)
В базисе {|w„) } оператор плотности представлен матрицей, которая получила название
матрицы плотности, элементы которой равны:
PlJt) = (ul,\p(t)\u„) = c:(t)cp(t). A0)
Покажем, что задание оператора р(г) достаточно, чтобы охарактеризовать
квантовое состояние системы, так как он позволяет получить все физические предсказания,
которые можно вычислить с помощью вектора |\|/(f)) • Для этого запишем формулы D),
F) и G) через оператор р(г). Согласно формуле A0) выражение D) указывает, что
сумма диагональных элементов матрицы плотности равна 1:
Zk(o|2 = £p«n(') = trp(o = i. (id
п п
С другой стороны, используя формулы E) и A0), можно преобразовать выражение F) к
виду:
(A>@=Z(kJp@|OW^ A2>
Наконец, эволюция во времени оператора р(г) описывается уравнением Шредингера G):
24*
371

Глава HI
d /ч
—P@ =
dt
d
{dt
—|vw> (v(o| + |v@>\-(v(t)\
d
[dt
= l#@|\|/@>(v@| + 7^|v@>(v@|«@ = ^ A3)
Таким образом, в формализме оператора плотности сохранение вероятности
выражается формулой:
trp(r) = l. A4)
Среднее значение наблюдаемой А вычисляется по формуле:
(A)(r) = tr{Ap(r)} = tr{p(r)A}, A5)
и эволюция во времени описывается уравнением:
/Й^р@ = [Я@,р@]. A6)
Для полноты следует указать, как вычисляются с помощью р(г) вероятности £Р(ап)
результатов измерения наблюдаемой Л в момент времени t. Для этого можно
использовать формулу A5). Действительно, известно [см. уравнение (В-14) главы III], что
^(ап) можно записать как среднее значение проекционного оператора Рп на
собственное подпространство, связанное с ап:
^K) = (V@|PJV@>. A7)
Используя A5), получим:
&(ая) = 1т{Рн№}- A8)
с. СВОЙСТВА ОПЕРАТОРА ПЛОТНОСТИ ЧИСТОГО СОСТОЯНИЯ
В чистом состоянии система может быть описана как оператором плотности, так и
вектором состояния. Однако описание с помощью оператора плотности представляет
определенные преимущества.
Прежде всего, из формулы (9) видно, что два вектора состояния |\|/@) и e'e|ij/@)
(где 0 — вещественное число), описывающие одно и то же физическое состояние,
соответствуют одному оператору плотности. Таким образом, использование этого опера-
372

Постулаты квантовой механики
тора устраняет неудобства, связанные с существованием произвольного фазового
множителя для вектора состояния. Кроме того, из A4), A5) и A6) видно, что формулы,
использующие оператор плотности, линейны по отношению к этому оператору, тогда как
выражения F) и A7) квадратичны по отношению к |i|/@)> и это важное свойство
окажется полезным в дальнейшем.
Отметим, наконец, несколько свойств оператора р(г), непосредственно следующих
из определения (9):
Р+@ = Р@, A9)
то есть оператор плотности эрмитов;
р2(г) = р@; B0)
trp'(f) = l. B1)
Последние два равенства следуют из того, что р(г) является проекционным
оператором, и они справедливы только для чистого состояния. Ниже мы увидим, что они не
выполняются в случае смешанных состояний.
4. Смешанный ансамбль состояний («не чистый» ансамбль)
а. ОПРЕДЕЛЕНИЕ ОПЕРАТОРА ПЛОТНОСТИ
Вернемся теперь к общему случаю, описанному в § 1, и рассмотрим систему, для
которой в заданный момент времени t вероятности р{, р2,..., рк,... имеют
произвольные значения, но удовлетворяющие соотношениям:
Как при этом вычисляется вероятность 9?{ап) получения результата ап при измерении
наблюдаемой А ?
Пусть:
^(«.HvJf.hO B3)
вероятность получить значение ап, если вектор состояния равен |\|/^). Чтобы получить
искомую вероятность 0>{ап), нужно, как уже указывалось ранее, взять &к(ап) с весом рк
и просуммировать по к :
373

Глава III
*(«.) = ХлЗЮ- B4)
*
Но согласно A8) имеем:
4(a„) = tv{pkPn}, B5)
где
Р* =|V*><V*| B6)
оператор плотности, соответствующий состоянию |yt) • Подставим B5) в B4) и получим:
Пап) = S fttr {Pi /»,} = tr {Х Л р, Р.} = tr К }, B7)
где введено обозначение:
Р = 2ЛР*- B8)
Таким образом, мы видим, что благодаря линейности формул, в которые входит
оператор плотности, все физические предсказания могут быть выражены через оператор р,
являющийся средним из операторов плотности р^. По определению р есть оператор
плотности системы.
Ь. ОБЩИЕ СВОЙСТВА ОПЕРАТОРА ПЛОТНОСТИ
Поскольку коэффициенты рк являются вещественными, оператор р эрмитов, так
же как и каждый из операторов рк.
Найдем след оператора р :
trp = EfttrP* . B9)
к
Как мы видели в § 3-Ь, след оператора р^ всегда равен 1, откуда следует, что
trp = 2ft=l. C0)
к
Таким образом, соотношение A4) доказано и в общем случае.
Приведенное выше выражение B7) позволяет выразить через р вероятность &*(ап).
Используя его, можно без труда обобщить формулу A5) на смешанный ансамбль:
374

Постулаты квантовой механики
(A) = Jlalina„) = tT^a„P„^ = tr{pA} C1)
[здесь была использована формула (D-36-b) главы II].
Найдем теперь эволюцию оператора плотности во времени. Для этого допустим, что
в противоположность состоянию системы ее гамильтониан H(t) точно известен.
Отсюда следует, что если в начальный момент времени система имела вероятность рк
находиться в состоянии \\\fk), она имеет ту же вероятность рк находиться в последующий
момент времени / в состоянии |\|/А@) > которое определяется выражениями:
i»|-|\MO) = /*@|v*@); C2)
llv*('o)) = |v*>-
Тогда в момент времени t оператор плотности будет равен:
р@ = Елр*@, C3)
к
где
P*@=|V*@)<V*@|. C4)
Согласно выражению A6) оператор р* (г) подчиняется уравнению эволюции:
ih^-pk(t) = [H{t\pk(t)}. C5)
at
Из линейности формул C3) и C5) по отношению к pk(t) следует:
ih^p(t) = [H(t),p(t)]. C6)
Таким образом, можно обобщить на смешанное состояние все равенства § 3 за
исключением формул B0) и B1), так как, поскольку р уже не является проекционным
оператором, в общем случае*:
* Допустим, например, что состояния К|0 ортогональны. В ортонормированном базисе,
содержащем \|/ к) , оператор р диагоналей, и его элементы равны рк . Чтобы получить р ,
достаточно заменить рк на рк . Тогда соотношения C7) и C8) следуют из того, что рк всегда меньше 1,
за исключением частного случая, когда отличен от нуля единственный из них (случай чистого
состояния).
375

Глава III
Р2*Р, C7)
и, следовательно:
tr р2 < 1. C8)
Впрочем, достаточно справедливости одного из уравнений B0) или B1), чтобы можно
было утверждать, что состояние является чистым.
Наконец, из равенства B8) видно, что для любого кет-вектора \и) можно записать:
Нр|") = £р*Нр*И = £р*|(кМ2- C9)
к к
и, следовательно:
(и|р|к)>0, D0)
то есть оператор р является положительным.
с. НАСЕЛЕННОСТИ И КОГЕРЕНТНОСТИ
Каков физический смысл элементов матрицы рпр оператора р в базисе {\ип) }?
Сначала рассмотрим диагональные элементы рпп. Согласно B8) имеем:
P„=ZMP*L- D1)
к
Если использовать формулу B6) и ввести компоненты:
^ =(«>*> D2)
вектора \\\fk) в базисе {\ип)}, то:
Р*=1лК°|2. D3)
к
Так как \с{пк)\ — вещественное положительное число, ему можно дать следующую
физическую интерпретацию: это вероятность того, что при измерении в системе,
находящейся в состоянии |v|/ft), будет обнаружено, что система находится в состоянии \ип).
Согласно формуле D1) элемент рпп с учетом неопределенности состояния системы пе-
376

Постулаты квантовой механики
ред измерением представляет собой среднюю вероятность найти систему в состоянии
\ип). По этой причине р;ш называют населенностью состояния \ип): если одно и то же
измерение производится при одинаковых начальных условиях N раз, то в состоянии
\ип) будет найдено iVp/m систем. Из формулы D3) следует, что р;ш всегда является ве-
щественным положительным числом, равным нулю лишь в том случае, когда все скп
равны нулю.
Аналогичные вычисления дают следующую формулу для недиагональных
элементов рпр:
P,4,=lPkc{nk)cf. D4)
Перекрестное произведение c\k) cpk) того же вида, что и в § Е-1 главы III, описывает
интерференционные эффекты между состояниями \ип) и \ир) , существующие, если
состояние \\\fk) является когерентной линейной суперпозицией этих состояний. Согласно
формуле D4) величина рпр есть среднее значение этих перекрестных членов, взятое по
всем возможным состояниям смешанного ансамбля. В отличие от населенностей
элементы рпр могут равняться нулю, если даже ни одно из произведений c{k) cpk) не равно
нулю. Действительно, тогда как рт есть сумма вещественных положительных (или
равных нулю) чисел, рпр является суммой комплексных чисел. Если рпр = 0, это значит,
что усреднение D4) приводит к исчезновению всех интерференционных эффектов
между \ип) и \ир) . Напротив, если р^ Ф О, то между этими состояниями сохраняется
некоторая когерентность. Именно поэтому недиагональные элементы матрицы оператора р
часто называют когерентностями.
ЗАМЕЧАНИЯ
(i) Различие между населенностями и когерентностями зависит, конечно, от выбора
базиса {[«„)} в пространстве состояний. Поскольку оператор р эрмитов, можно
всегда найти ортонормированный базис {\%t)}, в котором матрица р диагональна.
Тогда:
Р = 2>,|Х,)(%,|. D5)
377

Глава III
Поскольку оператор р положителен и tr р = 1, имеем:
D6)
и можно считать, что р описывает статистическую смесь состояний |х,) с
вероятностями я, (когерентности между состояниями |х/) отсутствуют),
(ii) Если |м,;) — собственные векторы гамильтониана И , не зависящего от времени:
Н\и„)=Е„\ы„). D7)
то из формулы C6) сразу же следует:
dJ <4X)
/й^-р„„(П = (£„-£„)(>„„
или
\pmU) = const;
Ue,-e.» D9)
[piip(t) = e" p„„@).
Населенности остаются постоянными, а когерентности осциллируют на частотах
Бора системы,
(iii) Используя формулу D0), можно доказать неравенство:
P„„P/VHPJ2- E°)
Из него следует, что когерентности в операторе р могут существовать только
между состояниями, населенности которых не равны нулю.
5. Примеры использования оператора плотности
а. СИСТЕМА В ТЕРМОДИНАМИЧЕСКОМ РАВНОВЕСИИ
Первый пример взят из статистической квантовой механики. Рассмотрим систему,
находящуюся в термодинамическом равновесии с термостатом при абсолютной
температуре Т . Можно показать, что ее оператор плотности имеет вид:
378

Постулаты квантовой механики
p = Z-le~H/k\ E1)
где Н — гамильтониан системы, к — постоянная Больцмана и Z — нормировочный
коэффициент, выбранный так, чтобы след матрицы р был равен 1:
Z = ir(e~H/kT). E2)
В базисе {\ип) } собственных векторов оператора Н имеем (см. дополнение Вп, § 4-а):
P,„,=Z>>-H'>„) = Z-V^ E3)
р„„ = Z>„ | e-"'tT\up) = Z-le-E'nr{u„\Up) = 0 . E4)
В термодинамическом равновесии населенности стационарных состояний описываются
экспоненциально убывающими функциями энергии (это убывание тем сильнее, чем
ниже температура Т), а когерентности между стационарными состояниями равны нулю.
Ь. ОТДЕЛЬНОЕ ОПИСАНИЕ ЧАСТИ ФИЗИЧЕСКОЙ СИСТЕМЫ.
ПОНЯТИЕ ПАРЦИАЛЬНОГО СЛЕДА
Здесь мы вернемся к задаче, рассмотренной в § 3 дополнения Dm. Пусть имеются две
различные системы A) и B), а также полная система A) + B), пространство состояний которой является
тензорным произведением:
 = РA)®К'B). E5)
Выберем {м„A)) }-базис в пространстве £A), { v Bп } — базис в пространстве #"B), тогда
кет-векторы |ww(l)) v B)) образуют базис в пространстве if .
Оператор плотности р полной системы действует в пространстве <? . В главе II (§ F-2-b) мы
уже видели, как получить продолжение оператора, действующего только в £A) [или в КB)], в
пространство £ . Здесь мы покажем, как можно выполнить обратную операцию, то есть, исходя из
оператора р, построить оператор рA) [или рB) ], действующий только в пространстве КA)
[или в пространстве ^B)] и позволяющий получить все физические предсказания измерений,
производимых только в системе A) [или в системе B)]. Эта операция получила название
парциального следа в системе A) [или в системе B)].
Введем оператор рA) с матричными элементами:
379

Глава III
(«,AI p(l) |«,,(l)> = S((«„(l)|(v„B)|)p(|M„.(l))|v,B))). E6)
P
По определению оператор рA) получается из оператора р с помощью операции парциального
следа в системе B):
p(l) = tr2p. E7)
Аналогично оператор:
PB) = tr,p E8)
имеет матричные элементы:
(v,B)| pB) |vp.B)) = i:(("„(l)|(v;)B)|)p(|«„(l))|v,).B))). E9)
Нетрудно понять, почему эти операции называются парциальным следом. Действительно, след
(полный) оператора р равен:
trp = EE((«„(l)|(v,B)|)p(|M„(l))|vpB))). F0)
п р
Различие между формулами F0) и E6) [или E9)] заключается в следующем: при вычислении
парциального следа не накладывается требование равенства индексов п и гС (или р и /?'), а
суммирование производится только по р (или п). Впрочем, справедливы соотношения:
tr p = tr, (tr2 p) = tr2 (tr, р) . F1)
Итак, операторы рA) и рB), как и оператор р , имеют след, равный 1. По определению они
эрмитовы и в общем случае имеют все свойства, присущие оператору плотности (см. § 4-Ь).
Пусть теперь ЛA) — наблюдаемая, действующая в пространстве £A), и ЛA) =
= ЛA) ® 1B) — ее продолжение в пространстве # . Используя формулу C1), определение следа
и соотношение замкнутости в базисе {|м„A)) v B)у }, получим:
(АA)) = tr{рЛA)} = I 2,(("„A)|(v,B)|)p(|м„.A)>|v,,B)})x
x((M„.(l)|(vp.B)|)A(l)®lB)(|M„(l))|v;)B))) =
= I i((«A(l)|(vpB)|)p(|M|I.(l))|vp.B)))(ii..(l)|A(l)|«A(l))(v,.B)|v,B)). F2)
380

Постулаты квантовой механики
Известно, что
(v,,B)|v;)B)) = 6;,/), F3)
и формулу F2) можно переписать в виде:
(Ml)}=2\l{u,,(\)vl,B)\p\u,,.(l)vllB))
(М„.A)|ЛA)|и„A)}- F4)
В квадратных скобках правой части F4) нетрудно узнать матричный элемент оператора рA),
определенный формулой E6). Тогда:
(аA)>=Х(«„A)|рA) k(i))(Mi)| ло) к,о))=
= Е(и„0)|рA)ДA)|"„A)) = 1г{рA)ЛA)}. F5)
п
Сравним этот результат с формулой C1). Мы видим, что парциальный след оператора рA)
позволяет вычислить все средние значения (А(Ш так, как если бы система A) была
единственной и имела в качестве оператора плотности рA) . С учетом того же замечания, что и для
формулы A7), можно сказать, что рA) позволяет также получить вероятности всех результатов
измерений, производимых в одной системе A).
ЗАМЕЧАНИЯ
(i) В дополнении Dlu мы видели, что нельзя вводить вектор состояния в системе A) [или B)],
если состояние полной системы {A) + B)} не является произведением состояний. Мы
видим теперь, что оператор плотности является значительно более простым способом
описания, чем вектор состояния. Во всех случаях, является ли состояние полной системы
произведением состояний или нет, соответствует ли оно чистому состоянию или смешанному,
благодаря операции парциального следа можно ввести оператор плотности в подсистеме A)
[или B)], позволяющий вычислить все физические предсказания в этой подсистеме.
(ii) Если даже р описывает чистое состояние и tr р2 = 1, то в общем случае это равенство не
выполняется для операторов рA) и рB), полученных с помощью операции парциального
следа. Действительно, из формулы E6) [или E9)] видно, что tr {p A)} в общем случае
отличается от 1 [это верно и для tr {р B)} ]. Тем самым мы иным способом показали, что в
общем случае нельзя вводить вектор состояния в системе A) [или B)], если состояние
полной системы не является тензорным произведением.
381

Глава III
(iii) Если полная система находится в состоянии, являющемся тензорным произведением
состояний:
|\|/) = |срA))|хB)), F6)
то сразу же можно записать соответствующий оператор плотности в виде:
р = аA)®ТB), F7)
где
аA) = |фA))(фA)|:
тB) = |хB))(хB)|. F8)
Вообще говоря, можно представить себе состояния полной системы, в которых
оператор плотности р факторизуется, как в формуле F7) ( G(l) и тB) могут соответствовать
как чистым, так и смешанным состояниям]. Тогда операция парциального следа дает:
tr2{a(l)®TB)} = a(l);
tr,{a(l)®TB)} = TB). F9)
Выражение вида F7) представляет собой простое сопоставление системы A) с оператором
плотности аA) и системы B) с оператором плотности тB) .
(iv) Вычислим для произвольного оператора плотности р [не факторизующегося по формуле
F7)] операторы плотности рA) = tr2 p и рB) = tr, p и затем образуем произведение:
р'=рA)®рB). G0)
В отличие от случая, рассмотренного в замечании (iii), p' в общем случае отличается от р :
если оператор плотности не факторизуется по формуле F7), то это значит, что между
системами A) и B) имеется определенная корреляция, которая более не содержится в
операторе р' [формула G0)].
(v) Если эволюция полной системы описывается уравнением C6), то в общем случае
невозможно найти гамильтониан отдельной системы A), который бы позволил записать
аналогичное уравнение для рA): если получить в любой момент времени рA) из р достаточно
просто, то описать эволюцию рA) во времени гораздо сложнее.

Постулаты квантовой механики
Дополнение Fni
ОПЕРАТОР ЭВОЛЮЦИИ
1. Общие свойства.
2. Случай консервативных систем.
В § D-1-b главы III мы видели, что преобразование, позволяющее перейти от
|\|/(г0)) (вектор состояния в начальный момент времени) к |\|/@) (вектор состояния в
произвольный момент времени) является линейным. Таким образом, существует
линейный оператор £/(/, г0), выполняющий операцию:
|i|/@> = f/a,r0)|i|/(rc))>. A)
В этом дополнении мы рассмотрим основные свойства оператора U(t, t()), по
определению являющегося оператором эволюции системы.
1. Общие свойства
Поскольку кет |\|/(f0)) может быть произвольным, из формулы A) сразу же следует,
что
U(t0,tQ) = l. B)
С другой стороны, подставив A) в уравнение Шредингера, получим:
/Л!"*/('. 'о) | V('o)) = #(')*/(', tQ) | v(r0)> C)
и,следовательно:
ih$-U(t,t0) = H(t)U(t,tQ). D)
at
Дифференциальное уравнение D) первого порядка полностью определяет U(t, t0), если
известны начальные условия B). Заметим, что формулы B) и D) могут быть
объединены в одно интегральное уравнение:
U(t,t0) = l-U'toH(t'mt\t0)dt'. E)
383

Глава III
Теперь параметр t0, входящий в U(t, t0), будем рассматривать как переменную ? ,
равноправную с переменной t. Тогда уравнение A) можно переписать в виде:
|у(г)) = 1/(лОк@). F)
Но сам вектор |\|/(г')) может быть получен с помощью формулы того же вида:
\\V(t')) = U(t\t")\\v(t")). G)
Подставим G) в F):
\Ш) = и«*Пи«\П\щп). (8)
Поскольку |\|/(f)) = £/(f, t") |\|/(/")), где |\|/(f")) —произвольный кет, то
U{t<t") = U(t,t')U{t\t"). (9)
Эту процедуру можно обобщить:
</(',. 'i> = */('„. '„-i) - U{t,, t2) U(t2, /,), A0)
где /,, f2,..., tn — произвольные моменты времени. Если допустить, что f,<r2<
< Г3 < ... < f„, то формула A0) интерпретируется очень просто: при переходе от г, к tn
система сначала переходит от г, к /2, затем от t2 к г3,..., и, наконец, от tn_x к tn.
Полагая в формуле (9) t"' -t, получим с учетом B):
\ = U{t%nU{t\t) A1)
или, если поменять местами переменные гиг':
l = U(t\t)U(t,f). A2)
Таким образом:
U(t\t) = U-\t4tx). A3)
Вычислим теперь оператор эволюции в интервале между двумя бесконечно
близкими моментами времени. Для этого запишем уравнение Шредингера в иной форме:
384

Постулаты квантовой механики
то есть
МО). A5)
М* + Л))
Используя определение U(t + dt, t), получим:
1--H(t)dt
fi
U(t + dt,t) = l--H(t)dt. A6)
h
Оператор U(t + dty t) получил название инфинитезимального оператора эволюции.
Поскольку H(t) — эрмитов оператор, U(t + dt,t) является унитарным оператором (см.
дополнение Сц, § 3). Отсюда следует, что и оператор U{t, ?) также является унитарным:
действительно, интервал времени [/, г'] можно разделить на множество инфинитези-
мальных интервалов, и тогда формула A0) показывает, что U{t, r') является
произведением унитарных операторов и, следовательно, дает в результате унитарный оператор.
Далее можно переписать выражение A3) в виде:
U+(t,n = U-\t,t') = U(t\t). A7)
Не стоит удивляться, что преобразование U(t, /') является унитарным, то есть оно
сохраняет норму векторов, на которые оно действует: мы уже видели в главе III (§ D-1-c),
что норма вектора состояния не изменяется со временем.
2. Случай консервативных систем
Если оператор Н не зависит от времени, уравнение D) интегрируется без труда.
С учетом начального условия B) получим:
U{t.t{)) = e-iH{t-h)lh. A8)
Можно непосредственно доказать, что это выражение обладает всеми свойствами
оператора эволюции, введенного в § 1.
Переход от формулы (D-52) к формуле (D-54) главы III осуществляется простым
применением выражения A8). Достаточно применить оператор U(t, t0) к обеим частям
выражения (D-52), заметив, что, поскольку кет Ф/1Т) является собственным вектором
оператора Н с собственным значением Еп, справедливо равенство:
U(t, Г0) |ф..т> = в-"'('-",),*|ф..х) = «"'£-("",),1ф..т>- A9)
25 Квантовая механика
385

Глава III
ЗАМЕЧАНИЯ
(i) Если оператор Н зависит от времени, то по аналогии с формулой A8) можно
было бы подумать, что оператор эволюции равен оператору V(t, t0), определенному
выражением:
-jfH{f)df
V(t,t0) = e '"> . B0)
В действительности это не так, ибо производная оператора вида eF{t) в общем
случае не равна F(t) eF(t) (см. дополнение Вп, § 5-с):
ih^-V(t,t0)*H(t)V«,tQ). B1)
ot
(ii) Вернемся к опытам, описанным в § E-1-b главы III. Как уже отмечалось
[замечание (ii) § E-l-b-C], не обязательно предполагать, что измерения различных
наблюдаемых должны быть близкими во времени. Если система успевает измениться
между двумя последовательными измерениями, то нетрудно учесть изменение
вектора состояния, используя оператор эволюции. Если обозначить моменты
времени, когда реализуются измерения наблюдаемых А, В и С, символами г0,г, и /2,
то выражение (Е-15) можно заменить на
ад=|(усИ'2>'о>к>|2 B2)
и формулу (Е-17) на
^^b,c) = |(v^(r2,rj|w,)|2|(vv^(rl,r0)|Wrt)|2. B3)
Тогда, используя (9), получим:
(vc\U(t2,t0)\ua)=(Vc\U(t2,tl)U(tl,t0)\ua) =
= Ш£/('2,',)к)Ыс/(,,л0)к). B4)
ь
После подстановки B4) в B2) видно, как и в выражении (Е-21), что ^(с) не равно
Ъ
386

Постулаты квантовой механики
Дополнение Gm
ПРЕДСТАВЛЕНИЯ ШРЕДИНГЕРА И ГЕЙЗЕНБЕРГА
В формализме, развитом в главе III, наблюдаемым системы в общем случае
соответствовали операторы, не зависящие от времени (см. главу III, § D-1-d); например,
операторы координаты, кинетической энергии частицы не зависели от времени. Эволюция
системы полностью содержалась в зависимости от времени вектора состояния |\|/@)
[здесь мы будем обозначать его символом |\|/5@) по причине, которая станет понятной
немного позже] и определялась уравнением Шредингера. Именно поэтому такой подход
к решению задачи получил название представления (или картины) Шредингера.
Можно, однако, заметить, что все предсказания квантовой механики (вероятности,
средние значения) выражаются через скалярные произведения кет- и бра-векторов или
через матричные элементы операторов. Так, мы видели в дополнении Сц, что эти
величины инвариантны, если выполняется одно и то же унитарное преобразование кет-
векторов и операторов. Это преобразование можно выбрать таким образом, что
преобразованный кет |\j/5@) не будет зависеть от времени. Конечно, преобразованные
наблюдаемые при этом окажутся функциями времени. Полученная в результате ситуация
называется представлением (или картиной) Гейзенберга.
Чтобы избежать недоразумений, в этом дополнении будем использовать
систематически индекс S для векторов и операторов в представлении Шредингера и индекс Н —
в представлении Гейзенберга (поскольку это представление используется только в данном
дополнении, во всех других главах и дополнениях индекс S может просто
подразумеваться).
Вектор состояния |\|/5@) в момент времени t выражается через |\|/5(г0))
соотношением:
|l|/5@) = ^(M0)ks('o)), A)
где U(t, t0) — оператор эволюции (см. дополнение Fm); поскольку этот оператор
унитарен, достаточно выполнить унитарное преобразование, определяемое оператором
U+(t, t0), чтобы получить преобразованный вектор \ун), остающийся неизменным:
В представлении Гейзенберга постоянный вектор состояния совпадает с вектором
|\|/5(г0)) в момент времени t0.
25*
387

Глава III
Оператор AH(t), полученный в результате преобразования оператора As(t) , равен
(дополнение Си, § 2):
AH{t) = U + 0,t0)As(t)U(t,tQ). C)
Как мы уже видели выше, в общем случае оператор Ан (t) зависит от времени, если даже
As от времени не зависит.
Существует, однако, интересный частный случай, когда и As, и Ан от времени не
зависят: случай консервативной системы, когда оператор Hs не зависит от времени и
As коммутирует с Hs (при этом As является константой движения; см. § D-2-c гл. III).
Действительно, в этом случае:
U(t,t0) = e'iH'{,-'°)">. D)
Если оператор As коммутирует с Hs , то он коммутирует также и с U(t, t0) (см.
дополнение Ви, § 4-с), так что:
AH(t) = U4t,t0)U(t,tQ)As=As. E)
Операторы As и Ан в этом случае просто равны друг другу (в частности, Hs = Нн,
и индексы S и Н просто не нужны). Поскольку они не зависят от времени, то
действительно операторы As и Ан соответствуют константе движения.
Найдем эволюцию оператора Ля(г)для произвольной функции As(t). Используя
соотношение D) дополнения Fin и сопряженное ему выражение, получим:
4ля@ = -^^Ч^r0)я5(OAs(o^(^r0)+^Ч^ro)^^^^o)+
dt ih dt
+ ^-U+(t,t0)As(t)Hs(t)U(t,t0). F)
in
Введем в первый и в последний члены этого выражения между А5 и Hs произведение
U(t, tQ) C/+(f, r0), равное единичному оператору [формула A7) дополнения Fni]:
^ГАн@ = ~ U+(t, t0)Hs(t)U(t, t0)U+(t, t0)As(t)U(t, t0) + U+(t, h)^^- £/(*, r0) +
dt ifi dt
+ ^rU+(t, tQ) As(t)Щи tQ)U4t> t0) Hs(t)U{U t0), G)
in
388

Постулаты квантовой механики
и в соответствии с определением C) окончательно получим:
ih^AH(t) = [AH(tlHH(t)] + ih^As(t)] . (8)
ЗАМЕЧАНИЯ
(i) Исторически первой была развита картина Шредингера (именно она привела к
получению уравнения, которое было названо его именем), и второй — картина
Гейзенберга (он вычислил эволюцию матриц, представляющих операторы AH{t),
откуда и пошло название «матричная механика»). И лишь впоследствии была
доказана эквивалентность обеих картин,
(ii) Используя формулу (8), можно сразу же получить уравнение (D-27) главы III.
Действительно, в рамках картины Гейзенберга можно найти эволюцию среднего
значения (Л)@ = (\|/5(/)| Л5(г)|\|/5(г)), ибо справедливо также и следующее равенство:
<а)@ = (ч/„|ан@К). (9)
В правой части формулы (9) только Ан (г) зависит от времени, и формулу (D-27)
можно сразу получить путем дифференцирования. Заметим, однако, что уравнение (8)
является более общим, чем уравнение (D-27), так как оно выражает равенство двух
операторов, а не двух средних значений (то есть двух элементов матриц операторов),
(iii) Если рассматриваемая система является частицей с массой т, находящейся в
потенциальном поле, то уравнение (8) становится очень простым. Действительно,
имеем в этом случае (для простоты — одномерном):
Р2
Hs(t) = ^- + V{Xs,t) (Ю)
2т
и, следовательно:
Р2
HH(t) = -f- + V(XH,t). A1)
2т
Подставив (И) в (8) и используя соотношения [Хн, PH] = [XS, Ps] = ih, с
помощью рассуждений, аналогичных приведенным в § D-1-d главы III, получим:
£x„(,)-iiv(,)i
389

Глава 111
Эти уравнения обобщают теорему Эренфеста [см. соотношения (D-34) и (D-35)
главы III]; они подобны уравнениям, описывающим эволюцию классических
величин х и р [формулы (D-36-a) и (D-36-b) главы III]. Таким образом,
преимуществом представления Гейзенберга является то, что оно приводит к уравнениям,
формально напоминающим уравнения классической механики.
Дополнение Нщ
КАЛИБРОВОЧНАЯ ИНВАРИАНТНОСТЬ
1. Постановка задачи. Скалярный и векторный потенциалы
электромагнитного поля. Понятие калибровки.
2. Калибровочная инвариантность в классической механике.
a. Уравнения Ньютона.
b. Гамилыпонов формализм.
3. Калибровочная инвариантность в квантовой механике.
a. Правила квантования.
b. Унитарное преобразование вектора состояния.
Инвариантность формы уравнения Шредингера.
c. Инвариантность физических предсказаний
при калибровочном преобразовании.
1. Постановка задачи. Скалярный и векторный потенциалы
электромагнитного поля. Понятие калибровки
Рассмотрим электромагнитное поле, характеризующееся векторами напряженности
электрического поля Е(г; t) и магнитной индукции B(r; t) в любой точке пространства
в произвольный момент времени. Величины Е(г; /) и B(r; t) не являются
независимыми, они связаны друг с другом уравнениями Максвелла. Вместо этих векторных полей
можно ввести скалярный (У(г;г)и векторный А(г; t) потенциалы, удовлетворяющие
соотношениям:
390

Постулаты квантовой механики
E(r;0 = -V£/(r;f)-r-A(r;0;
dt
В(г;0= V xA(r;0. (I)
С помощью уравнений Максвелла можно показать (см. приложение III, § 4-Ь-а), что
всегда можно найти функции £/(r; t) и А(г; Г), которые позволяют выразить Е(г; г) и
B(r; t) в виде A), то есть любое электромагнитное поле может быть описано скалярным
и векторным потенциалами. Однако, если Е(г; /) и В(г; г)заданы, то £/(г; /) и A(r; t)
определены неоднозначно. Действительно, можно легко доказать, что наряду с набором
возможных значений (/(г; t) и A(r; t) имеется возможность подобрать и другие
потенциалы i/'(r; r) и А'(г;г), описывающие то же самое электромагнитное поле и связанные
между собой преобразованием:
£/Чг;г) = 1/(г;/)-|-х(г;0;
ш
АЧг;г) = А(г;0+Vx(r;0, B)
где %(r, t)— произвольная функция гиг. Чтобы убедиться в этом, достаточно
заменить (/(г; t) на f/'(r; t)w A(r; t) на А'(г; г) в выражении A) и заметить, что Е(г; t) и
B(r; t) остались неизменными. Кроме того, можно показать, что соотношения B)
определяют все возможные скалярные и векторные потенциалы, определяющие заданное
электромагнитное поле.
Если производится выбор конкретной частой формы потенциалов для описания
электромагнитного поля, говорят, что осуществляется выбор калибровки. Как мы только
что отметили, для одного и того же поля, описываемого векторами E(r; t) и В(г; г),
существует бесконечное множество возможных калибровок. При переходе от одной из
них к другой говорят, что производится изменение калибровки.
В физических задачах часто бывает, что в уравнения движения системы входят не
поля Е(г; t) и B(r; t), а потенциалы (/(г; t) и A(r; t). Такой пример нам уже встречался
в § B-5-b главы III, когда записывалось уравнение Шредингера для частицы с зарядом q ,
взаимодействующей с электромагнитным полем [см. формулу (В-48) этой главы]. Тогда
возник следующий вопрос: зависят ли предсказываемые теорией физические результаты
только от значений полей Е(г; t) и В(г; г) в любой точке пространства, или имеется
зависимость также и от выбора калибровки, использованной при записи уравнений?
В последнем случае, конечно, для того, чтобы теория имела смысл, необходимо
уточнять, в какой калибровке справедливы записанные уравнения.
391

Глава III
Ответ на этот вопрос является целью данного дополнения. Мы увидим, что и в
классической (§ 2) и в квантовой (§ 3) механике физические результаты не меняются при
изменении калибровки. Скалярный и векторный потенциалы выступают в расчете лишь
в качестве посредников. В реальности имеют значения только значения электрического
и магнитного полей в любой точке пространства. Этот результат выражается в
утверждении о том, что классическая и квантовая механики обладают свойством
калибровочной инвариантности.
2. Калибровочная инвариантность в классической механике
а. УРАВНЕНИЯ НЬЮТОНА
В классической механике движение частицы* с зарядом q и массой т в
электромагнитном поле можно рассчитать с помощью силы, действующей на частицу и
описываемой законом Лоренца:
f = ?[E(r;/) + vxB(r;0], C)
где v — скорость частицы. Чтобы получить уравнения движения, позволяющие
вычислить в любой момент времени положение r(f) частицы, это равенство нужно
подставить в фундаментальное уравнение динамики (закон Ньютона):
т4т r@ = f. D)
В такой формулировке в расчет входят только значения электрического и магнитного
полей, и проблема калибровочной инвариантности не возникает.
Ь. ГАМИЛЬТОНОВ ФОРМАЛИЗМ
Кроме подхода, изложенного выше, можно использовать другие уравнения
движения, а именно, уравнения Гамильтона—Якоби. Нетрудно показать (см. приложение III),
что они полностью эквивалентны уравнениям Ньютона. Однако, поскольку для
квантования физической системы в главе III мы исходили из гамильтонова формализма, полезно
рассмотреть, как в рамках этого формализма осуществляется изменение калибровки.
Действительно, если скалярный и векторный потенциалы не входят в уравнения Ньютона,
то при записи уравнений Гамильтона они просто необходимы, но свойство калибровочной
инвариантности проявляется в этом случае гораздо менее явно.
* Для простоты в этом дополнении мы будем предполагать, что система состоит из одной
частицы. Обобщение на более сложную систему, образованную из нескольких частиц, подверженных
действию электромагнитного поля, не представляет трудностей.
392

Постулаты квантовой механики
ос. Динамические переменные системы и их эволюция
Чтобы найти движение частицы, подверженной действию силы Лоренца C), можно
использовать лагранжиан*:
ЭГ(г, v; t) = -m\2-q[U{Y\ r)-v-A(r; tj\. E)
Это выражение позволяет вычислить импульс р:
р= Vv ЗГ(г, v; t) = m\ + qA(r\ t) F)
и ввести функцию Гамильтона:
Ж(г, р; 0 = т- [р-^А(г; f)]2+?I/(r; t). G)
2т
В рамках гамильтонова формализма состояние частицы в заданный момент времени
определено ее положением г и импульсом р. Эти величины будем называть основными
динамическими переменными, а не координатой и скоростью, как это было выше в
рамках формализма Лагранжа. Не следует также отождествлять импульс р (момент,
сопряженный радиусу-вектору г) и количество движения п :
я = т\ . (8)
В действительности это разные величины, так как согласно формуле F):
71 =p-fA(r;r). (9)
Это соотношение позволяет определить в любой момент времени количество движения
(и, следовательно, скорость), если известны значения г и р. Аналогично, в рамках
гамильтонова формализма все другие характеризующие частицу величины (кинетическая
энергия, момент импульса и т. д.) выражаются также через основные динамические
переменные гири, возможно, являются функциями времени.
Эволюция рассматриваемой системы подчиняется уравнениям Гамильтона:
^-r(r)=Vp ЛГ[г@,р@;ф
* Здесь мы напомним без доказательства некоторые результаты аналитической механики,
обобщенные в приложении III.

Глава III
^p@ = -Vv./4r(r),p(/);r], A0)
где Ж — функция переменных г и р, определенная выражением G). Эти уравнения
позволяют определить в любой момент времени значения всех основных динамических
переменных, если их начальные значения известны.
Чтобы правильно записать уравнения A0), необходимо выбрать калибровку $ (то
есть пару потенциалов { £/(r; r), A(r; t)}, описывающих электромагнитное поле. Что
произойдет, если вместо этой калибровки jf мы выберем другую (f,
характеризующуюся иными потенциалами U'(r; t), А'(г; О» но описывающими те же самые поля
E(r; t) и В(г; г)? Будем обозначать символами со штрихом динамические переменные
частицы, если выбрана калибровка f . Как отмечалось выше, из уравнений Ньютона
следует, что радиус-вектор г и скорость v не зависят от выбора калибровки, и,
следовательно:
г'@ = г(г); A1-а)
71' (Г) =71 (Г) A1-Ь)
или, согласно формуле (9):
n(t) = v(t)-qA[r(t);t];
7i'@ = p'@-<7A'[r40;'], A2)
откуда следует, что значения р(г) и р'@ должны быть различными в калибровках jf и
f и связаны соотношением:
р|@-^А|[г|@;г] = р@-9А[г@;/]. A3)
Если х(г; г) — функция, позволяющая с помощью формул B) перейти от калибровки
jf к калибровке с/', то основные динамические переменные должны преобразовываться
при изменении калибровки согласно формулам:
г'@ = г@; A4-а)
р'@ = Р@ + 4 V%[r(r);r]. A4-b)
В рамках гамильтонова формализма описывающие данное движение динамические
переменные зависят от выбранного калибровочного преобразования. Этот результат не
может казаться удивительным, так как скалярный и векторный потенциалы
непосредственно входят в уравнения, описывающие эволюцию радиуса-вектора и импульса.
394

Постулаты квантовой механики
C. «Истинно физические» величины и «нефизические» величины
(i) Определения
Мы только что увидели [например, соотношения A4)], что можно различить два
типа величин, характеризующих частицу: с одной стороны, такие, которые, подобно г и
я, в любой момент времени идентичны друг другу при различных калибровках, и, с
другой стороны, такие, которые, подобно р, зависят от выбора калибровочных
соотношений. Это обстоятельство приводит к формулировке следующего общего определения:
— Истинно физической величиной рассматриваемой системы будем называть такую
величину, значение которой для данного движения системы в произвольный момент
времени не зависит от выбора калибровочных соотношений, используемых для
описания электромагнитного поля.
— Нефизической величиной будем называть такую величину, значения которой
изменяются при изменении калибровочных соотношений; такая величина (например,
скалярный и векторный потенциалы) появляется в теории скорее как промежуточный
инструмент вычислений, чем реально наблюдаемая величина.
В связи с этим возникает вопрос, как узнать, является ли некоторая величина
истинно физической или нет, если в рамках гамильтонова формализма все описывающие
систему величины имеют вид функций основных динамических переменных г и р ?
(ii) Соотношение,
характеризующее истинно физические величины
Прежде всего допустим, что описывающая частицу величина в калибровке jf
выражается функцией г и р (возможно, и времени t), которую обозначим как ^(г, р; /).
Если этой величине при другой калибровке f соответствует та же функция
#"(г\ р'; г), то немедленно можно констатировать, что эта величина не является
истинно физической (за исключением случая, когда функция :7 зависит только от г и не
зависит от р). Действительно, поскольку значения импульса различны в двух
калибровках jf и jC , то это касается, конечно, и значений функции ff .
Чтобы получить истинно физические величины, связанные с системой, мы должны
рассматривать только такие функции У;(г, р; t), форма которых не зависит от
выбранных калибровочных соотношений (именно поэтому мы ввели в обозначение этих
функций индекс jf). Впрочем, мы уже видели ранее пример такой функции: количество
движения я является функцией г и р через векторный потенциал А [см. формулу
(9)]; в этом случае функция различна для двух различных калибровок J и jC , то есть
следует записать ее в виде п f/ (r, p; t). Введенное выше определение требует, чтобы
395

Глава 111
функция .fy(r, p; t), описывающая истинно физическую величину, удовлетворяла
соотношению:
^[г@, р@; /] = ^[гЧО, рЧО; 0. A5)
где г@ и р@— значения положения и импульса в калибровке jf, а г'@ и р'@ —
эти же значения в калибровке jf'. Подставив A4) в A5), получим:
^[г@, Р@; г] = ^[г@, Р@ + «Vx(r(r); r); г], A6)
причем это равенство должно удовлетворяться в любой момент времени t для всех
возможных движений системы. Поскольку при фиксированном значении t можно
независимо выбирать значения координат и импульса, обе части равенства A6) должны быть
одинаковыми функциями г и р, то есть
^[r, p; t] = Jf[r,p + <?Vx(r; t)' t]. A7)
Это соотношение характеризует функции ^[г, р; /], описывающие истинно
физические величины. Итак, если рассматривается функция ^Дг, р; t] в рамках калибровки
jf' и в ней производится замена р на p + q V %(г; г)Р [где %(г; /) определяет согласно
формуле B) переход от калибровки jf к калибровке jf ], то новая функция от г и р
должна быть идентична функции Jf/[r, p;f]. В противном случае рассматриваемая
функция соответствует «нефизической» величине.
(Hi) Примеры
Приведем несколько примеров функций ^[г, р; /], описывающих истинно
физические величины. Две таких величины, представляющие положение и количество
движения системы, мы уже встречали: первая из них просто равна г, а вторая равна:
я,(г, p;r) = p-<yA(r;r). A8)
Поскольку равенства A1) свидетельствуют о том, что г и я являются истинно
физическими величинами, соотношение A7) удовлетворяется априори.
396

Постулаты квантовой механики
Чтобы потренироваться в применении этого соотношения, докажем его в явной форме. В том,
что касается г , ясно, что это функция, не зависящая от р, форма которой не зависит от
калибровочных соотношений*, откуда сразу же следует выражение A7). Для П формула A8) дает:
тс/(г,р;0 = р-?А,(г;0. 09)
Заменим в этой функции р на р + q V %(г; /):
p + q V х(г; 0-?А'(г; г) = р-^А(г; г), B0)
что в точности равно 71 Дг, р; t). Таким образом, соотношение A7) выполняется.
К истинно физическим величинам относится кинетическая энергия:
Y(/(r, р; 0 = — [р-«А(г; tjf, B1)
а также момент количества движения относительно начала координат:
Х,(г,р;0 = гх[р-9А(г;0]- B2)
Можно отметить, что в общем случае, когда образуется функция переменных г и р
вида:
^[r,p;r]=F[r,p-^A(r;0] B3)
(где F — функция, форма которой не зависит от выбранной калибровки), то эта
функция описывает истинно физическую величину**. Этот вывод понятен физически, так как
из формулы B3) следует, что описываемая ею величина вводится через г и тг, то есть
через величины, не зависящие от выбора калибровочных соотношений.
Приведем также несколько примеров функций, описывающих «нефизические»
величины. Кроме уже упоминавшегося импульса р, можно указать на
р2
^(Р) = Т- B4)
* Нетрудно доказать, что в общем случае любая функция .^(г, /), зависящая лишь от г (и
возможно от времени t), форма которой одинакова при любых калибровочных соотношениях,
описывает истинно физическую величину.
** В принципе можно построить функции, соответствующие истинно физическим величинам,
и более сложного вида, чем B3). Например, скалярное произведение скорости частицы на
электрическое поле в точке, где она находится, и т. д.
397

Глава III
[которую не следует отождествлять с кинетической энергией B1)] и в общем случае на
любую функцию импульса р (и, возможно, времени). Так, момент импульса:
#(г, р) = гхр B5)
должен рассматриваться как «нефизическая» величина. И, наконец, отметим функцию
Гамильтона, образующуюся согласно формуле G) в виде суммы кинетической энергии
у;(г, р; г), являющейся истинно физической величиной, и потенциальной энергии qU .
Поскольку последняя, строго говоря, является функцией Ut/(r, r), зависящей от
калибровки, то функция Гамильтона не может рассматриваться как истинно физическая
величина, ибо ее значение в произвольной точке пространства зависит от выбора
калибровочных соотношений.
3. Калибровочная инвариантность в квантовой механике
В главе III мы ввели постулаты квантовой механики, основываясь на гамильтоновой
формулировке классической механики. В связи с этим проблема калибровочной
инвариантности, легко разрешаемая в классической механике, основанной на уравнениях
Ньютона, оказывается более сложной в квантовой механике. При этом может возникнуть
вопрос: справедливы ли постулаты, сформулированные в главе III, для любой
выбранной калибровки, или только в некотором частном случае?
Чтобы ответить на этот вопрос, будем ориентироваться на полученные в
предыдущем параграфе результаты. Следуя теми же этапами рассуждений, придем к выводу, что
существует тесная аналогия между последствиями изменения калибровки в рамках
классического гамильтонова формализма и квантового формализма. В итоге установим
условия калибровочной инвариантности в квантовой механике.
Для этого в § а исследуем, к каким результатам приводит применение правил
квантования в двух различных калибровках. Затем в § b мы увидим, что, как и в классической
механике, где значения динамических переменных в общем случае изменяются при
изменении калибровочных соотношений, физическую систему следует характеризовать
математическим вектором состояния |\|/), зависящим от выбора калибровки. Переход
от вектора состояния, соответствующего одной калибровке f/ , к другой калибровке f
производится с помощью унитарного преобразования, всегда сохраняющего форму
уравнения Шредингера (как в классической механике сохранялась форма уравнений
Гамильтона). И, наконец, рассмотрим, как ведут себя при изменении калибровки наблюдаемые
рассматриваемой системы (§ с). Мы увидим, что одновременные изменения вектора состояния
и наблюдаемых таковы, что физическое содержание квантовой механики остается
неизменным при изменении калибровки. Это положение будет доказано тем, что значения
плотности и тока вероятности инвариантны относительно калибровочных преобразований.
398

Постулаты квантовой механики
а. ПРАВИЛА КВАНТОВАНИЯ
Пространство состояний частицы без спина, как и ранее, будем обозначать
символом £г. Согласно выводам, полученным в § 2, можно ожидать, что оператор,
соответствующий некоторой заданной величине, может иметь разную форму в разных калибровках.
По этой причине будем дополнять обозначения операторов индексом Jf.
Правила квантования ставят в соответствие положению г и импульсу р частицы
операторы R и Р, действующие в пространстве #г и удовлетворяющие соотношениям
коммутации:
[X,P^ = [k,Pv] = [Z,pJ = i» B6)
(все остальные коммутаторы между компонентами R и Р равны нулю). В
представлении {|г)} оператор R действует, как просто умножение на г, а Р — как дифференци-
Ь
альный оператор — V . Эти правила одинаковы в любой калибровке. Итак:
i
Rr = Ry; B7-а)
Р,. = Р,. B7-b)
Эти равенства позволяют убрать индексы у наблюдаемых R и Р, что мы и будем делать
в дальнейшем.
Правила квантования других характеризующих частицу величин вытекают из только
что сформулированных: в заданной калибровке функция величин г и р, определяющая
в классической механике рассматриваемую величину, заменяется (после соответствующей
симметризации в случае необходимости) такой же функцией операторов (г заменяется
на R и р заменяется на Р). В результате получается оператор, описывающий данную
величину в выбранной калибровке. Приведем конкретные примеры:
— оператор момента, полученный в соответствии с формулой г х р, одинаков при
любых калибровках:
Lr=L,; B8)
— оператор количества движения, напротив, зависит от выбора калибровки.
Действительно, в калибровке J он имеет вид:
П, =P-$A(R;r). B9)
Если изменить калибровку, то он должен иметь форму:
399

Глава III
nr = P-<7A'(R;0, C0)
действие которого в пространстве <f г отлично от действия П у:
П,.=П,-я Vx(R;0; CD
— аналогично, оператор*:
Л5 = R х П,( = R х [Р - <?A(R; t)], C2)
описывающий момент количества движения, содержит в себе векторный потенциал в
явном виде;
— наконец, гамильтониан записывается согласно формуле G) в виде:
Н(/ = -±- [P-?A(R; Of +*I/(R; t). C3)
Очевидно, что при другой калибровке он превращается в иной оператор, так как:
Hf =i [p-^A'(R; '>f +?£/,(R; 0* я,. C4)
b. УНИТАРНОЕ ПРЕОБРАЗОВАНИЕ ВЕКТОРА СОСТОЯНИЯ.
ИНВАРИАНТНОСТЬ ФОРМЫ УРАВНЕНИЯ ШРЕДИНГЕРА
а. Унитарный оператор Т (t)
В классической механике для обозначения основных динамических переменных в
двух разных калибровках J и f мы использовали обозначения {г(г), р(г) } и
{г'@> р'@ }• В квантовой механике векторы состояния в этих калибровках обозначим
символами |\|/@)и |\|/'@) > и тогда аналоги соотношений A4) будут представлены
равенствами для средних значений:
(i|/'(r)|Rr|ii/4r)) = (\|/@|R,;|v|/@); C5-а)
(\|/'@|Pr| V40> = (V@|P, +Я V X(R; /)|v@>. C5-b)
* Используя соотношения коммутации между R и FL , нетрудно доказать, что симметризо-
вать выражение C2) нет необходимости.
400

Постулаты квантовой механики
Используя формулу B7), можно сразу же установить, что такая запись возможна только
в том случае, если кет-векторы |\|/@) и | V'@) различны. Попытаемся найти такое
преобразование T%(t), которое позволило бы перейти от |\|/(/)) к |\|/'@):
И0) = Гх@М0>; (Зб-а)
Гх+@7-ха) = Гх@Гх+@ = 1. C6-Ь)
Если учесть формулу B7), то станет ясно, что равенства C5) будут удовлетворены для любого
вектора |V/(f)), если
r;(/)R7x@ = R,- C7-а)
Tx4t)PTx(t) = P + qVx(r,t). C7-b)
Умножим C7-а) слева на Tx(t), тогда:
R7x(r) = rx(r)R. C8)
Искомый унитарный оператор должен коммутировать с тремя компонентами оператора R , и,
следовательно, его можно записать в форме:
Tx(t) = eiF(Rl\ C9)
где F(R; t) — эрмитов оператор. Формула D8) дополнения Вц позволяет записать соотношение:
[P,7;@]=w{F(R;/)}rx@. D0)
Умножим D0) слева на T*(t) и подставим в C7-Ь), после чего получим:
ftV{F(R;f)}=*Vx(r;0. D1)
Последнее равенство будет всегда справедливо, если
F(R;r)=/ro@ + 7X(R;0. D2)
п
Первый член F0(t) можно просто убрать, так как для вектора состояния |\|/@/ он представляет
общий фазовый множитель, не имеющий физического смысла, в результате чего искомый
оператор T%(t) будет иметь вид:
26 Квантовая механика
401

Глава III
Tx(t) = e» ' . D3)
Если в формулу C6-а) входит именно этот оператор 7^@, то соотношения C5) будут
автоматически удовлетворены.
ЗАМЕЧАНИЯ
(i) В представлении {|г) } из равенств C6-а) и D3) следует, что волновые функции
\|/(r, f) = (r|\j/@) и \|/'(г, /) = (г|\|/'@) связаны соотношением:
'-Х(«\0
\|/'(г, t) = efl y(r,t). D4)
Изменение калибровки приводит к изменению фазы волновой функции,
зависящему от координаты, и, следовательно, не являющемуся общим фазовым
множителем. Таким образом, калибровочная инвариантность физических предсказаний,
полученных с помощью волновых функций, не является очевидной,
(ii) Если изучаемая система состоит из множества частиц, расположенных в точках
гр г2,... с зарядами ql9 q2J..., то нужно заменить формулу D3) на
Tx(t) = ГХ"»(Г) Г'2>(Г)... = >«"-"♦"**'•'>♦-'. D5)
Р. Эволюция вектора состояния во времени
Покажем теперь, что если в калибровке jf кет |\|/@) подчиняется уравнению
Шредингера:
/»^|v@)=^(r)|\|f(r)), D6)
то вектор состояния |\|/'@) > определяемый формулами C6), подчиняется уравнению той
же формы в калибровке f :
^Ио)=#(/(оИо), D7)
где Нr(t) выражается формулой C4).
402

Постулаты квантовой механики
Для этого вычислим левую часть равенства D7). Получим:
»^|v40> = «-»|-{rx@|v@)}=/»{^rx(/)}|V@) + /»7'x@|-|4/(r)>. D8)
то есть, согласно выражениям D3) и D6)*:
«•»^-|v,@) = -9{^x(R;o}7x(r)|v@>+7x(r)«ir(o|v@> =
= j-^x(R;0+#,(oW@). D9)
где символом Нf(t) обозначен оператор Н„ (/), преобразованный с помощью унитарного
оператора Tx(t):
н,о)=тхо)н,т;о). (so
Таким образом, уравнение D7) будет справедливым, если:
Hr(t)=Hf(t)-q^x(Kt)- E1)
Итак, оператор Н At) определяется выражением:
Hj(t)=^-[P-qA(R;t)f+qU(R;t)], E2)
в котором R и Р обозначают операторы, преобразованные из R и Р унитарным оператором
T%(t) по формуле C7):
R = Tx(/)Rrx+(r) = R; E3-а)
Р = Гх(г)РГх+@ = Р - ^V%(R; t). E3-b)
Эти соотношения, будучи подставленными в E2), указывают, что
* Функция X зависит от R, а не от Р, и поэтому %(R, t) коммутирует с — %(R, 0- Поэтому
at
можно дифференцировать Tx(t), как если бы %(R, 0 была простой функцией времени, а не
оператором (см. дополнение В1Ь замечание к §5-с).
26* 403

Глава III
HAt) = -L [P-<?A(R; 0- <?Vx(R; t)]2 + $£/(R; t). E4)
J 2m
Используя выражения B) для замены потенциалов в калибровке j[ на потенциалы в калибровке J',
получим с учетом C4) равенство E1). Таким образом, уравнение Шредингера может быть записано
в одной и той же форме, независимо от выбранной калибровки.
с. ИНВАРИАНТНОСТЬ ФИЗИЧЕСКИХ ПРЕДСКАЗАНИЙ
ПРИ КАЛИБРОВОЧНОМ ПРЕОБРАЗОВАНИИ
а. Поведение наблюдаемых
В результате действия унитарного преобразования Tx(t) любая наблюдаемая К
преобразуется в К с помощью преобразования:
К = Тх0)КТ;0). E5)
Из формулы E3) видно, что R = R и Р * Р . Аналогично, оператор П; отличен от П^
так как:
П, = Р-<zA(R; 0 = Р - <?V%(R; /)-<?A(R; 0 = П, - ^V%(R; t). E6)
С учетом B7-а) и C1) соотношения E3-а) и E6) требуют, чтобы наблюдаемые R и
П^, связанные с истинно физическими величинами положения и количества движения,
были такими, что
R^ = К у>;
П,=ПГ. E7)
Напротив, импульс Р (не являющийся истинно физической величиной) не
удовлетворяет аналогичному соотношению, так как согласно формулам B7-Ь) и E3-Ь):
Р,*Р/- E8)
Мы увидим сейчас, что полученный результат является общим: всякой истинно
физической величине в квантовой механике сопоставляется оператор Gj(t),
удовлетворяющий соотношению:
404

Постулаты квантовой механики
Gr/(t) = Gf(t). E9)
Это равенство является квантовым аналогом классического соотношения A6); оно
показывает, что, за исключением частного случая оператора R или функции от R ,
оператор, соответствующий истинно физической величине, зависит от калибровочных
преобразований; примеры тому мы уже видели в B9) и C2).
Чтобы доказать соотношение E9), достаточно применить правила квантования,
сформулированные в главе III относительно функции ^(г, р; t), и использовать выражение A7),
характеризующее истинно физические классические величины. Заменив г и р операторами R и Р,
получим (если необходимо, после симметризации, подходящей для этих операторов) оператор Gj{t).
Если форма функции $« зависит от выбранной калибровки, то оператор G^(t) также зависит от J .
Если же величина, связанная с 3„ , является истинно физической, то согласно формуле A7):
^[R, P; t] = Jr[R, Р + 4V%(R; /); t]. F0)
Применим к этому равенству унитарное преобразование T%(j):
33[R, Р; /] = Jr[R, Р + ?Vx(R; 0; t] = Jr[ft, P + <?x(R; r); t]. F1)
To есть с учетом формулы E3) имеем:
Js[R9P\t] = Js.[R9F;t]. F2)
После возможной симметризации обоих членов равенства получается формула E9).
Приведем еще несколько примеров истинно физических величин. Кроме R и П f,
можно указать на момент количества движения Л; [см. C2)] или кинетическую
энергию:
!1 2т 2т1
Г,=-^ = —[P-*A(R;/)f. F3)
Напротив, Р и L не являются истинно физическими величинами, как и гамильтониан,
ибо соотношение E1) в общем случае требует, чтобы
Hs{t)*Hr(t). F4)
405

Глава III
ЗАМЕЧАНИЕ
В классической механике хорошо известно, что полная энергия частицы,
двигающейся в электромагнитном поле, не зависит от времени и является константой
движения. Действительно, в этом случае можно ограничиться рассмотрением
потенциалов, не зависящих от времени, и согласно формуле E1), видно, что
Я, = Ну . F5)
В этом частном случае Я; является истинно физической наблюдаемой
величиной, которую можно интерпретировать как полную энергию частицы.
Р. Вероятности возможных результатов измерения
истинно физической величины
Допустим, что в момент времени t измеряется истинно физическая величина. В
калибровке $ состояние системы описывается кет-вектором* |\|/), а физическая величина —
наблюдаемой G^ . Пусть |фп) — собственный вектор оператора Gy с собственным
значением gn (предположительно не вырожденным):
С/|Ф„) = ^,|Ф„). F6)
Вычисленная в калибровке jf на основе постулатов квантовой механики вероятность
получения при измерении значения gn равна:
<Н(ф.|ч»)|2. F7)
Как изменится этот результат при изменении калибровки? Согласно формуле E9),
оператор Gr рассматриваемой величины в новой калибровке jf/ образует кет:
|Ф:) = Г,|Ф„) F8)
с тем же собственным значением gn, что и в формуле F6). Действительно:
СА<) = ТхСЛТхЮ = Тх*М=8№)- F9)
* Мы не указываем зависимость от времени, так как все величины должны быть определены в
момент t.
406

Постулаты квантовой механики
Таким образом, собственное значение gn в калибровке $' всегда выступает как
результат возможного измерения. Кроме того, вычисление соответствующей вероятности даст
то же значение, что и в калибровке у , так как согласно C6-а) и F8):
(ф:к/) = (Ф,|г;гх|¥)=(Ф».
G0)
Итак, мы доказали, что постулаты квантовой механики приводят к физическим
результатам, не зависящим от выбора калибровочных соотношений, ибо все вероятности
оказываются инвариантными относительно изменения калибровки.
у. Плотность и ток вероятности
Вычислим с помощью формул (D-9) и (D-20) главы III плотность p(r, t) и ток
вероятности J(r, t) в двух различных калибровках jf и/.В первом случае имеем:
p(r, r) = |\|/(r, г)|2
G1)
J(r, /) = — Re{\|/*(r, t)
-V -qk{r\t)
V(r, О}-
Из соотношения D4) следует, что
рЧг, /) = |\|/Чг, г)|2 = р(г, г),
а также
1 -/-У(г;/) *
J'(r,r)=-Re e »*-У(г.О
т
tV -оА'(г;0
i
4х<г:<>
У(г, 0 =
т
Re i|/ (r, г)
то есть, с учетом формулы B):
-V-qA'(r,t) + qVx(r\t)
J'(r,/) = J(r,0.
V(r.Ok
G2)
G3)
G4)
G5)
Итак, плотность и ток вероятности инвариантны относительно изменения калибровки.
Этот результат можно было бы предвидеть на основе выводов, сделанных выше в § |3.
407

Глава III
Действительно [см. формулу (D-19) главы III], р(г, г) и J(r, t) можно рассматривать как
средние значения операторов |г) (г| и
K'(r)eifrX'ln/+n>X4 G6)
Нетрудно показать, что эти два оператора удовлетворяют соотношению E9) и,
следовательно, описывают истинно физические величины, среднее значение которых
инвариантно относительно калибровочных соотношений.
Дополнение Jm
ПРОПАГАТОР УРАВНЕНИЯ ШРЕДИНГЕРА
1. Введение. Физическая идея.
2. Существование и свойства пропагатора АГB,1).
a. Существование пропагатора.
b. Физическая интерпретация К B,1) .
c. Выражение КB,1) через собственные состояния оператора Н.
d. Уравнение, которому удовлетворяет КB,1).
3. Лагранжева формулировка квантовой механики.
a. Понятие траектории в пространстве-времени.
b. Разложение КB,1) на сумму парциальных амплитуд.
c. Постулаты Фейнмана.
d. Классический предел. Связь с принципом Гамильтона.
1. Введение. Физическая идея
Рассмотрим частицу, описываемую волновой функцией \|/(г, /). Уравнение Шре-
дингера позволяет вычислить — \j/(r, t), то есть скорость изменения i|/(r, r), опреде-
ot
ляющую эволюцию волновой функции во времени. Можно спросить себя, а нельзя ли
принять более общую точку зрения (кстати, вполне эквивалентную), которая позволила
бы непосредственно определить значение \|/(r0, t), принимаемое волновой функцией в
точке г0 в заданный момент времени t, если известна функция \|/(г, t') в иной момент
времени, не обязательно бесконечно близкий к моменту t.
408

Постулаты квантовой механики
Для этого удобно вспомнить некоторые положения электромагнетизма, где
применимы две точки зрения. Уравнения Максвелла (дифференциальная точка зрения)
позволяют записать скорости изменения компонент электрического и магнитного полей.
Принцип Гюйгенса (интегральная точка зрения) позволяет, зная распределение
монохроматического поля на поверхности Z, непосредственно вычислить поле в
произвольной точке М путем суммирования полей, испущенных в точку М фиктивными
вторичными источниками Nx, N2, /V3,..., расположенными на поверхности I, волновое
состояние которых зависит от значения полей в точках N,, 7V2, N3,... (рис.1).
М
Рис.1
Принцип Гюйгенса позволяет вычислить в эксперименте
по дифракции электрическое поле в точке М в виде
суммы полей, испущенных вторичными источниками
N{, N2, N3i..., расположенными на поверхности Z
В этом дополнении мы намерены показать, что в квантовой механике имеется
аналог принципа Гюйгенса. Точнее говоря, для времени t2 > tx можно записать формулу:
\|/(r2,f2)= Jd3r,A:(r2, /2;г|э /,) V(rlf /,)f A)
физическая интерпретация которой заключается в следующем: амплитуда вероятности
найти частицу в точке г2 в момент времени t2 равна сумме всех амплитуд, «испущенных»
«вторичными источниками» (r,,^), (г,', r,)..., расположенными в «пространстве-
времени» на поверхности t = tx, причем вклад каждого их этих «источников»
пропорционален значениям \|/(гр tx), \|/(r[, t{),... (рис. 2). Докажем приведенную выше
формулу, вычислим функцию К , которая называется пропагатором уравнения Шредингера, и
изучим ее свойства. Затем укажем качественным образом, как можно было бы построить
всю квантовую механику, используя пропагатор К (лагранжева формулировка квантовой
механики; точка зрения Фейнмана).
2. Существование и свойства пропагатора К{2,1)
а. СУЩЕСТВОВАНИЕ ПРОПАГАТОРА
Задача состоит в том, чтобы связать друг с другом состояния системы в два разных
момента времени. Это можно сделать благодаря оператору эволюции, введенному в
дополнении Fffl. Действительно, можно записать:
409

Глава III
|v(f2))= U(t2,tx)\y{txj).
Зная |\|/(г2)), можно сразу же найти волновую функцию \j/(r2, t2):
\|/(r2,/2)=(r2|\|/(r2)).
B)
C)
Рис.2
Амплитуда вероятности V|/(r2, t2) может быть получена
путем суммирования амплитуд \y(rx,tx), \|/(r[, r,) и т.д.,
соответствующих одному и тому же предшествующему
моменту времени / = tx. Каждой из стрелок на рисунке
сопоставляется свой «пропагатор» К{т2, /2; г,, tx),
K(Y2,t2\r[,t{) и т.д.
Подставим B) в C) и введем соотношение замкнутости:
/А|г,)(г,| = 1 D)
между U(t2, tx) и |\|/(^,)). Получим:
\|/(г2, t2)= jd3rx (r2| £/(r2, /,) |r,) (г, | V(rl)>= J A (r2| £/(r2, r.) |r,) V(rlf tx). E)
В результате получим формулу, совпадающую с формулой A), если положить:
(r2\U(t2,tx)\rx) = K(r2j2\rx,tx).
Формулы вида A) будут, естественно, применяться только при t2 > tx, и, следовательно,
удобно принять К = О для времен t2<tx, так что корректное определение К имеет
следующий вид:
К(т2У *2;Г|, tx)= (г2| £/(Г2, Г,) |г.) 6(f2 -Г,), F)
где d(t2 - tx) — «ступенчатая функция»*:
0(г2 -/,) = !, если t2>tx\
* В литературе эта функция называется также функцией Хэвисайда (прим. переводчика).
410

Постулаты квантовой механики
6(Г2 - Г,) = 0 ,если t2 < tx . G)
Введение функции 0(/2 - /,) представляет двойной интерес — физический и
математический. С физической точки зрения она означает просто, что вторичные источники,
расположенные на поверхности t = /, (рис.2), «излучают» только «в будущее», и
функция K(r2, t2; г,, г,), определенная формулой F), по этой причине может быть названа
запаздывающим пропагатором. С математической точки зрения далее увидим, что
АГ(г2, t2\ г,, /,), благодаря множителю 6(/2 - г,), подчиняется уравнению в частных
производных, имеющих в правой части дельта-функцию, то есть уравнению, определяющему
функцию Грина.
ЗАМЕЧАНИЯ
(i) Отметим, однако, что уравнение E) остается справедливым, если даже t2 < tx.
С другой стороны, подчеркнем, что можно было бы математически ввести и
«опережающий» пропагатор, который был бы отличен от нуля только при t2 < tx и
который также подчинялся бы уравнению, определяющему функцию Грина.
Поскольку на этом этапе физический смысл такого пропагатора не просто объяснить,
мы его не будем рассматривать.
(ii) Для простоты в дальнейшем для пропагатора K(r2, f2;r,, /,) будем использовать
обозначение АГB,1), если только такое обозначение не будет приводить к
двусмысленности.
Ь. ФИЗИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ КBУ 1)
Физическая интерпретация вытекает непосредственно из определения F):
выражение КB,1) описывает амплитуду вероятности того, что частица, первоначально
находившаяся в точке г, в момент времени tx, окажется в точке г2 в последующий момент
времени t2. Действительно, выберем в качестве начального состояния в момент времени
tx состояние, локализованное в точке г,:
|va,)) = |r,>. (8)
В момент времени t2 вектор состояния станет равным:
|v(f2))=£/(f2, О |1|/(г,))= Uit^t,)^). (9)
411

Глава III
Амплитуда вероятности найти частицу в этот момент времени в точке г2 равна:
Ы\У(*2))={*2\и(*г'*х)\гх)- (Ю)
с. ВЫРАЖЕНИЕ #B,1) ЧЕРЕЗ СОБСТВЕННЫЕ СОСТОЯНИЯ ОПЕРАТОРА Я
Допустим, что гамильтониан Я не зависит явно от времени, и обозначим
символами |ф„) и Еп его собственные векторы и собственные значения:
Я|ф„)=£„|ф„). A1)
Согласно формуле A8) дополнения Fin, имеем:
U(t2itx)=e-iH{l^)fh. A2)
Соотношение замкнутости:
S|<p„)(<pJ = 1 A3)
позволяет переписать выражение A2) в виде:
c/(f2,o=«_W('2W,v'Xk.H<p.l A4)
или, с учетом A1):
£/(':,/,) =2 е-'£^-",м|ф„)(Ф„|. A5)
п
Чтобы вычислить АГB,1), достаточно взять матричный элемент от двух частей
этого равенства между (г21 и |г,), а затем умножить на 0(г2 - г,). Поскольку:
<г2|ф„)= Ф,.(г2); A6)
(ф>,)=Ф>,), A7)
получим:
К(г2, г2;г„ /,) = в(г2 -г,) 5»,) Ф„(г2) е-,Е^IП. A8)
412

Постулаты квантовой механики
d. УРАВНЕНИЕ, КОТОРОМУ УДОВЛЕТВОРЯЕТ КB,1)
-iE„t2lh
Функция ф„(г2) е  является решением уравнения Шредингера. Из этого следует,
что в представлении {|г) }:
/ft—-я
dt2
< ft
r„TV,
(p„(r2)e =0
(здесь символ V2 используется для компактного обозначения трех операторов
A9)
Э
дх2
д д д ( П Л
-т—, -г—). Применим к обеим частям равенства A8) оператор /ft-г—-Я r2,TV2 L
оу2 az2 ™г V i )
действующий только на переменные г2 и t2. Известно [см. приложение II, формула
D4)], что
^-е(г2-/,)= 50,-0, B0)
ot2
и, следовательно, с учетом A9), получим:
/ft —-я(г2,уУ2]|К(^
B1)
Вследствие наличия 5(г2 -г,)в сумме по и в правой части равенства можно положить
(t2-tl) = 0, и тогда экспонента обращается в 1. В результате остается сумма
2Ж»(Г|) Ф»(г2) > равная согласно A3), A6) и A7) 8(г2 -г,) [достаточно вычислить мат-
п
ричный элемент A3) между (r21 и |г,) ]. Окончательно получим:
' Э ( ft \]
/ft — -Я1 г2, у V2J JC(r2, r2;r,, *,) = ift8(/2 -/,) 5(r2 -г,).
B2)
Решения уравнения B2), правая часть которого пропорциональна четырехмерной
дельта-функции, называются функциями Грина. Можно показать, что для полного
определения КB,1) достаточно дополнить уравнение B2) граничным условием:
АГ(г2, г2;гр f,) = 0, если t2<tx.
B3)
413

Глава III
Заметим, что на базе уравнений B2) и B3) могут быть развиты интересные
приложения, в частности, это касается теории возмущений, которая будет изложена в главе XI.
3. Лагранжева формулировка квантовой механики
а. ПОНЯТИЕ ТРАЕКТОРИИ В ПРОСТРАНСТВЕ—ВРЕМЕНИ
Рассмотрим в пространстве-времени две точки с координатами (гр г,) и (r2, t2) (см.
рис. 3, где время t условно откладывается по оси абсцисс, а ось ординат схематически
изображает все три пространственные оси). Выберем N промежуточных моментов
времени ta (/ = 1,2,..., N), равномерно распределенных между г, и г2:
'.<'а, <'а2 <-<'«„_,<'«„<'2 >
B4)
и для каждого из них определим положение га в пространстве. Если теперь устремить N
к бесконечности, то получим, вообще говоря, непрерывную функцию г(/), для которой:
r(r1) = rI; B5-а)
г(/2) = г2. B5-Ь)
Говорят, что г (г) определяет траекторию в пространстве-времени между (г,,М и
(r2, t2\\ эта траектория может быть реальной траекторией материальной точки,
выходящей в момент времени tx из точки г, и прибывающей в момент времени t2 в точку г2.
¥
V
-+t
Рис.3
Схема эволюции системы в
«пространстве — времени»: выбираются N
промежуточных моментов времени
ta (/ = 1,2,..., N), равномерно
распределенных между г, и t2, и для каждого
из них определяется значение г
414

Постулаты квантовой механики
Ь. РАЗЛОЖЕНИЕ АГB,1) НА СУММУ ПАРЦИАЛЬНЫХ АМПЛИТУД
Вернемся сначала к случаю, когда число N промежуточных моментов времени
конечно. Формула A0) дополнения F\U позволяет записать:
U{t2, t,) = U(l2, taH) U(taii, tttNi)... U(ta2, /„,) U(tat Л,) • B6)
Вычислим матричные элементы от обеих частей равенства B6) между векторами /г2 и
г Л и вставим соотношение замкнутости для представления {|г)} в каждый
промежуточный момент времени ta . В соответствии с формулами F) и B4) получим:
К{2Л) =fd\N \d\M_r..ld\2 jd\ K(laN)K(aN,aN_l)...K(a2,al)K(al,\).
B7)
Рассмотрим произведение:
К{2, aN)K(aN, aN_,)... ЛГ«х2, а,)/Г(ар1). B8)
Обобщив рассуждения, приведенные в § 2-Ь, этот член можно интерпретировать как
амплитуду вероятности того, что частица, выйдя из точки 1 (г,, г,), попадет в точку 2
(г2, г2), пройдя последовательно через все точки а, (га , ta ), как показано на рис. 3.
Заметим, что в формуле B7) суммирование ведется по всем возможным положениям
ra в каждый момент времени ta .
Устремим теперь N к бесконечности*. Последовательность точек а,, превратится в
траекторию между точками 1 и 2 в пространстве-времени, а произведение B8) — в
амплитуду вероятности того, что частица следует данной траектории. Конечно, в формуле
B7) количество интегралов стремится к бесконечности. Вместе с тем, понятно, что
суммирование по всем возможным положениям в каждый момент времени эквивалентно
суммированию по всем возможным траекториям, а К{2,1) имеет смысл суммы (на
самом деле интеграла), соответствующей возможным траекториям от точки 1 к точке 2.
с. ПОСТУЛАТЫ ФЕЙНМАНА
Понятия пропагатора и траектории в пространстве-времени позволяют ввести
новую формулировку постулата относительно эволюции физических систем во времени.
Укажем здесь общие идеи этой формулировки в случае частицы без спина.
* В предлагаемом здесь изложении мы не стремимся к предельной математической строгости.
415

Глава III
Определим КB,1) непосредственно как амплитуду вероятности того, что частица
выходит в момент времени t{ из точки г, ив момент времени t2 приходит в точку г2.
Далее постулируем, что:
(i) КB,1) является бесконечной суммой парциальных амплитуд по одной для
каждой траектории в пространстве-времени, соединяющей (г,, г,) и (r2, t2);
(ii) парциальная амплитуда /СгB,1), соответствующая одной из таких траекторий Г,
определяется следующим образом: пусть 5Г — классическое действие, вычисленное
вдоль траектории Г, то есть
Sr= j3T(r, p, t)dt4 B9)
(Г)
где Х(гу р, /) — лагранжиан частицы (см. приложение III). Тогда АггB,1) можно
записать в виде:
KrB,l) = Netl , C0)
где N — нормировочный множитель (его можно найти в явном виде).
Можно показать, что уравнение Шредингера является следствием этих двух
постулатов. Аналогично можно вывести канонические соотношения коммутации компонент
наблюдаемых R и Р. Таким образом, приведенные выше постулаты позволяют
реализовать другую, но эквивалентную формулировку квантовой механики.
d. КЛАССИЧЕСКИЙ ПРЕДЕЛ. СВЯЗЬ С ПРИНЦИПОМ ГАМИЛЬТОНА
Формулировка, о которой шла речь, особенно интересна с точки зрения
установления связи между квантовой и классической механиками.
Действительно, представим себе ситуацию, в которой действие 5Г существенно
больше, чем ti. В этом случае разность А5Г действия между различными траекториями,
если даже она относительно мала
С-«1
5Г
, в общем случае значительно больше h .
При этом фаза КгB,1) быстро меняется, и вклады в полную амплитуду #B,1)
большинства различных траекторий Г вследствие интерференции уничтожают друг друга.
Допустим, однако, что имеется некоторая траектория Г0, для которой действие
является стационарным (то есть в первом приближении оно не меняется при переходе от Г0 к
бесконечно близкой траектории). Тогда амплитуда Кг B,1) интерферирует с амплиту-
416

Постулаты квантовой механики
дами ближайших траекторий конструктивным образом, так как на этот раз их фазы
практически одинаковы. В результате, если действие 5Г существенно больше h,
ситуация становится «квазиклассической»: чтобы получить КB,1), можно пренебречь всеми
траекториями, кроме Г0 и бесконечно близкими к ней, и можно говорить, что между
точками 1 и 2 частица движется именно по траектории Г0. Конечно, такая траектория
совпадает с классической, поскольку принцип Гамильтона определяет ее как траекторию,
вдоль которой действие минимально. Итак, постулаты Фейнмана переходят в
классическом пределе в принцип наименьшего действия Гамильтона. Кроме того, они позволяют
придать наглядность этому движению: волна, связанная с частицей, «ощупывает»
различные допустимые траектории и выбирает такую, для которой действие оказывается
минимальным.
Лагранжева формулировка квантовой механики имеет и другие преимущества, в
детали которых мы не будем здесь вдаваться. Отметим, например, что она очень удобна
для релятивистских обобщений, так как имеет дело непосредственно с понятиями
пространства и времени. Кроме того, ее можно применять к любой классической системе
(не обязательно механической), для которой справедлив вариационный принцип
(например, поле). Но в математическом плане она имеет ряд неудобств (суммирование по
бесконечному количеству траекторий, предел iV->«» и т.д.).
Дополнение Кщ
НЕСТАБИЛЬНЫЕ УРОВНИ. ВРЕМЯ ЖИЗНИ
1. Введение.
2. Определение времени жизни.
3. Феноменологическое описание нестабильности уровня.
1. Введение
Рассмотрим консервативную систему (то есть систему, гамильтониан которой Я не
зависит от времени) и допустим, что в момент t = О она находилась в одном из
собственных состояний |фл) гамильтониана с энергией Еп:
Мо)Нф„) а)
и
Ф.)=Я.|ф„>- B)
27 Квантовая механика
417

Глава III
В этом случае система остается неограниченно долго в одном и том же состоянии
(стационарное состояние; § D -2-Ь главы III).
В главе VII мы будем рассматривать атом водорода, решая уравнения на собственные
значения его гамильтониана, не зависящего от времени. Уровни энергии атома водорода
(то есть возможные значения его энергии), вычисленные с помощью гамильтониана,
очень хорошо совпадают со значениями, полученными экспериментально. Однако
известно, что большинство этих уровней в действительности нестабильны: если атом
в момент времени г - О находится в возбужденном состоянии, то есть в собственном
состоянии |ф„) с энергией Еп, превышающей энергию основного состояния (состояния
с наименьшей энергией), то в общем случае он «возвращается» в основное состояние,
испустив один или несколько фотонов. Таким образом, состояние |ф;1) не является,
вообще говоря, стационарным.
Этот «парадокс» возникает потому, что в таких вычислениях, как в главе VII,
изучаемая система (атом водорода) считается совершенно изолированной, тогда как в
реальности она постоянно взаимодействует с электромагнитным полем. Если эволюция
полной системы «атом + электромагнитное поле» может быть полностью описана
гамильтонианом, то, строго говоря, для отдельного атома водорода нельзя определить
гамильтониан [см. замечание (v) § 5-b дополнения Еш ]. Однако связь между атомом и
полем является слабой (можно показать, что ее «сила» характеризуется постоянной
тонкой структуры а « 1/137, которую мы введем в главе VII), и приближение, состоящее
в пренебрежении существованием электромагнитного поля, оказывается достаточно
хорошим, если только нас не интересует нестабильность уровней.
ЗАМЕЧАНИЯ
(i) Если изолированная и строго консервативная система находится в начальный
момент времени в состоянии, образованном линейной суперпозицией нескольких
стационарных состояний, то в процессе эволюции она не остается в одном и том
же состоянии. Однако ее гамильтониан является константой движения, и,
следовательно, вероятность найти то или иное значение энергии, как и среднее значение
энергии, не зависит от времени (см. § D-2-c главы III). Напротив, в случае
нестабильного уровня имеет место необратимый переход из одного состояния в другое,
связанный с потерей энергии: эта энергия уносится испущенными фотонами*.
(и) Нестабильность возбужденных уровней атома связана со спонтанной эмиссией
фотонов. Основное состояние является стабильным, поскольку уровней с еще меньшей
энергией просто не существует. Вспомним, однако, что атомы могут также и
поглощать световую энергию, переходя при этом на уровень с большим значением энергии.
* Испущенные атомом фотоны могут уносить также импульс и кинетическую энергию.
418

Постулаты квантовой механики
В данном дополнении мы намерены показать, как можно учесть нестабильность
уровня феноменологически. Ясно, что мы не будем стремиться к полной строгости
описания, так как система по-прежнему будет считаться изолированной, однако такой
подход является простым способом учета нестабильности в квантовом описании системы.
2. Определение времени жизни
Эксперимент показывает, что нестабильность уровня можно часто охарактеризовать
единым параметром т, имеющим размерность времени и называющимся временем
жизни уровня. Точнее говоря, если в момент времени t = 0 система приготовлена в
нестабильном состоянии |ф„), то вероятность #>(/) того, что в последующий момент
времени система останется в этом состоянии, равна:
Ш = е-1,\ C)
Этот же результат можно получить иначе. Пусть большое количество . I' идентичных
независимых систем приготовлены в момент времени г = 0 в состоянии |ф„). Тогда в
момент времени / в этом состоянии их останется N(t) = .Ye~t/X. Между моментами
времени t и t + dt некоторое количество dn(t) систем покинет нестабильное состояние:
dn(t) = N(t) - N(t + dt) = -^^-dt = N(t)—. D)
dt t
Для каждой из N(t) систем, которые находятся в момент времени / в состоянии |(рл),
можно определить вероятность:
**)-%£-*- E)
N(t) т
того, что она покинет это состояние в интервале времени dt, следующим за моментом t.
Видно, что dxn(t) не зависит от t, и при этом говорят, что система имеет вероятность
— покинуть нестабильный уровень в единицу времени.
т
ЗАМЕЧАНИЯ
(i) Вычислим среднее значение времени, в течение которого система остается в
нестабильном состоянии. Оно равно:
27*
419

Глава 111
?АГ"Т- = Т. F)
о Т
Таким образом, т представляет собой среднее время, проводимое системой в
состоянии |ф„), и поэтому называется временем жизни состояния.
Для стабильного уровня &(t) = 1, и время жизни т равно бесконечности.
(ii) Замечательная особенность времени жизни т состоит в том, что оно не зависит от
способа приготовления системы в нестабильном состоянии, то есть от его
«истории». Время жизни является характеристикой, присущей самому нестабильному
уровню.
(Ш) Согласно соотношению неопределенностей «время — энергия» (глава III, § D-2-e)
характеристическому времени эволюции нестабильного уровня соответствует
неопределенность энергии Д£, равная:
ДЕ«-. G)
т
Эта формула утверждает, что энергия нестабильного уровня не может быть
определена с произвольной точностью, и ее неопределенность в лучшем случае имеет
порядок А£ . Величина АЕ называется естественной шириной рассматриваемого
уровня. В случае атома водорода ширина уровней гораздо меньше расстояния
между ними, и в первом приближении их можно считать стабильными.
3. Феноменологическое описание нестабильности уровня
Рассмотрим сначала консервативную систему, приготовленную в начальный момент
времени в собственном состоянии |ф„) гамильтониана Н . Согласно правилу (D-54)
главы III, вектор состояния в момент времени t имеет вид:
|V@>= *-*"'>,)• (8)
Вероятность &*n(t) того, что в момент времени t система находится в состоянии |ф„),
равна:
Поскольку энергия Еп — вещественная величина (ибо Н — наблюдаемая), эта
вероятность не зависит от времени и равна 1, то есть состояние |ф„) является стационарным.
420

Постулаты квантовой механики
Рассмотрим, каковы будут последствия, если в выражении (9) энергию Еп заменим
комплексным числом:
E'„=En-ih^. A0)
Тогда вероятность й£@ окажется равной:
^,@ =
-/(£„-/Л Ь.),/;,
е 2
2
-У,,'
= *"*"'. (И)
В этом случае вероятность найти систему в состоянии |фл) уменьшается со временем
экспоненциально, как в формуле C). Таким образом, для того чтобы феноменологически
учесть нестабильность состояния |ф„) с временем жизни тп, достаточно дополнить
энергию в формуле A0) мнимой частью, положив:
Y.=7". A2)
ЗАМЕЧАНИЕ
При замене Еп на Е'п норма вектора состояния (8) становится равной е~Уп'/2 и
зависит от времени. Не следует удивляться такому результату, ведь мы уже видели
в § D-1 -с главы III, что сохранение нормы вектора состояния обусловлено эрмито-
востью гамильтониана, тогда как оператор, собственные значения которого
комплексны, как Е'п, не может быть эрмитовым. Конечно, как отмечалось в § 1, это
произошло потому, что рассматриваемая система является частью большой
системы (она взаимодействует с электромагнитным полем) и, строго говоря, ее
эволюцию нельзя описывать с помощью гамильтониана. Заметим, что сама возможность
учета этой эволюции, если ввести «гамильтониан» с комплексными собственными
значениями, кажется очень интересной.

Глава III
Дополнение Ьщ
УПРАЖНЕНИЯ
1. Рассмотрим в одномерном случае частицу с волновой функцией:
jPQxIh
\\f(x) = N
V*2+a2
где а и р0 — вещественные константы и N — нормировочный множитель.
a. Определить N так, чтобы \\f(x) была нормирована.
b. Измеряется положение частицы. Какова вероятность того, что результат измере-
а а .
ния окажется в интервале между —j= и + -т=- ?
c. Вычислить среднее значение импульса частицы с волновой функцией \\f(x).
2. В одномерном случае рассматривается частица с массой т, волновая функция
которой в момент времени / равна \\f(x, t).
a. В момент времени t измеряется расстояние d от этой частицы до начала
системы координат. Записать с помощью \|/(jc, t) вероятность ^(d0) получить в результате
измерения значение, большее заранее заданной величины d0. Каковы пределы ^(d0)
при J0->0h при d0 —> ©о ?
b. Чтобы выполнить измерения, отмеченные в вопросе (а), измеряется скорость v
частицы в момент времени t. Выразить через \j/(jc, t) вероятность найти результат,
превышающий заданную величину v0.
3. Волновая функция свободной частицы в рамках одномерной задачи в момент времени
t = 0 имеет вид:
\V(x,0) = N\^dke-W,kQeik*,
где к0 и N — константы.
a. Какова вероятность &(рх, 0) того, что при измерении импульса в момент времени
t = 0 будет получен результат, заключенный между -/?, и +/?, ? Дать краткий анализ
функции ^(/?р0).
b. Чему равна вероятность .^(рр 0 , если измерение производится в момент
времени t ? Объяснить полученный результат.
422

Постулаты квантовой механики
с. Определить форму волнового пакета в момент времени t = О. Вычислить в этот
момент времени произведение АХ • АР, проанализировать результат. Качественно
рассмотреть дальнейшую эволюцию волнового пакета.
4. Расплывание свободного волнового пакета
Рассматривается свободная частица.
a. Применив теорему Эренфеста, показать, что (х) является линейной функцией
времени, а среднее значение (Р) остается постоянным.
b. Записать уравнения эволюции средних значений \Х2) и (ХР+ РХ) и
проинтегрировать их.
c. Доказать, что при соответствующем выборе начала отсчета времени
среднеквадратичное отклонение определяется формулой:
(AXJ=-^(APHV+(AXH\
т
где (АХH и (АРH — среднеквадратичные отклонения в начальный момент времени.
Как изменяется во времени ширина волнового пакета (см. §3-с дополнения GO? Дать
физическую интерпретацию.
5. Частица под действием постоянной силы
В рамках одномерной модели рассматривается частица, потенциальная энергия
которой равна V(X) = -fX , где / —положительная постоянная [например, V(X) имеет
природу поля тяготения или однородного электрического поля].
a. Записать теорему Эренфеста для средних значений положения X и импульса Р
частицы. Проинтегрировать эти уравнения и сравнить с классическим движением частицы.
b. Показать, что среднеквадратичное отклонение АР не зависит от времени.
c. Записать уравнение Шредингера в представлении {| р)}. Получить из него соот-
ношение между 3~|(p|v@)| и "Т~ КИ1^'))! • Проинтегрировать полученное при
этом уравнение и дать физическую интерпретацию результата.
6. Рассматривается трехмерная волновая функция:
\\ЛМЛ
\V(x9y,z) = Net2« 2b 2c
где а, Ь, с — три положительных параметра с размерностью длины.
423

Глава III
a. Определить N так, чтобы функция \|/ была нормированной.
b. Определить вероятность того, что измерение X даст результат, заключенный
между 0 и а .
c. Вычислить вероятность того, что одновременные измерения Y и Z дадут
результаты, заключенные соответственно между -Ъ и +Ь , а также между -с и +с .
d. Определить вероятность того, что измерение импульса даст результат,
заключенный в элементарной области dpxdpydpz с центром в точке рх = ру = 0; рг = Й / с.
7. Пусть \|/(;с, у, г) = V|/(r)— нормированная волновая функция частицы. Выразить через
\|/(г) вероятность того, что:
а. при измерении абсциссы X будет получен результат в интервале между х{ и х2;
&. при измерении компоненты импульса Рх будет получен результат в интервале
между рх и р2\
с. при одновременном измерении X и Pz будет получен результат:
jc, < х < х2 и pz > 0 ;
<£ при одновременном измерении Pt, Ру, Pz будет получен результат:
Pi ^ р, ^ Р2;
Ръ ^ Ру ^ Ра ;
Ps^Pz^Pe*
выполнить задание пункта (Ь), если ръ, р5 —> -©о и р4, /?6 —> +<*> ;
e. при измерении компоненты [/ = —f=(X + Y + Z) будет получен результат в
интервале между и, и м2.
8. Частица с массой т описывается волновой функцией \|/(г), которой соответствует
ток вероятности J(r) [гл. III, формулы (D-17) и (D-19)].
a. Показать, что
mJtf3rJ(r) = (P),
где (Р)— среднее значение импульса.
b. Оператор орбитального момента L определен выражением L = R х Р . Являются
ли его три компоненты эрмитовыми операторами? Доказать равенство:
424

Постулаты квантовой механики
mJaf3r[rxJ(r)] = (L).
9. Показать, что физическое состояние частицы без спина полностью определено, если
известны плотность вероятности р(г)= |\|/(г)| и ток вероятности J(r).
a. Допустим, что заданы функция \j/(r) и ее аргумент 9(г):
\Кг) = 7рЙ«*(г)-
Показать, что
J(r) = -p(r) V0(r).
т
Доказать, что две волновые функции, дающие одинаковые плотность р(г) и ток J(r)
вероятности, могут отличаться друг от друга только глобальным фазовым множителем.
b. Пусть р(г) и J(r) — произвольные функции. Показать, что им можно сопоставить
квантовое состояние \|/(г) только в том случае, если V х v(r) = 0, где v(r) = J(r) / p(r) —
скорость потока вероятности.
c. Теперь предположим, что частица находится под действием магнитного поля
В(г)= V х А(г) [см., например, определение (D-20) тока вероятности в этом случае].
Показать, что
J=^p(r)[V6(r)-<7A(r)]
т
Vxv(r) = —-В(г).
т
10. Теорема вириала
а. В одномерном случае рассматривается частица, гамильтониан которой равен:
Р2
Н = — + У(Х),
2т
где V(X) = XX". Вычислить коммутатор [#, ХР\. Если в этом потенциале существует
некоторое количество стационарных состояний |ф), показать, что средние значения ки-
425

Глава III
нетической (г) и потенциальной (у) энергии в этих состояниях удовлетворяют
равенству 2(Т) = n(v).
b. В трехмерном случае оператор Я имеет вид:
Р2
Я = — + V(R).
2m
Вычислить коммутатор [Я, RP]. Допустим, что V(R) — однородная функция
степени п переменных X, У, Z . Какое соотношение должно обязательно существовать
между средними значениями кинетической и потенциальной энергий частицы в
стационарном состоянии?
Применить к частице, движущейся в поле потенциала V(r) = -е21 r (атом водорода).
Напомним, что однородная функция V степени п переменных х, уу z должна по
определению удовлетворять соотношению V(ax, ay, az) = ос" V(x, у, z) и равенству Эйлера:
dV dV д
х—+ у—+ z— = nV(x, у, z).
ox ay oz
c. Рассмотрим систему, состоящую из N частиц, определенных положениями R, и
импульсами Р,, где / = 1,2,..., N . Если их потенциальная энергия является однородной
функцией степени п ансамбля компонент X,, Y{, Z,, то можно ли обобщить полученные
выше результаты на эту систему? Возможное приложение этой задачи — произвольная
молекула, образованная ядрами с зарядами -Zxq и электронами с зарядами q . Все эти
частицы попарно взаимодействуют кулоновскими силами. Какое соотношение
существует между кинетической энергией ансамбля частиц и их энергией взаимодействия в
стационарном состоянии молекулы?
11. Волновая функция двух частиц
В рамках одномерной модели рассматривается система, состоящая из двух частиц
A) и B), которая описывается волновой функцией \у(х{, х2).
а. Вычислить вероятность получения при измерении положений X, и Х2 двух
частиц значений:
х < х1 < х + dx ;
cx<jc2<C.
426

Постулаты квантовой механики
b. Какова вероятность найти частицу A) в интервале между х и х + dx [измерение
положения частицы B) не производится]?
c. Определить вероятность найти абсциссу по крайней мере одной из частиц в
интервале между а и Р.
d. Какова вероятность получить значение импульса частицы A) в интервале между
р и /?" наряду с положением частицы B) между а и C ?
e. Измеряются импульсы Р{ и Р2 двух частиц. Какова вероятность получить
значения р'<рх< р" и р'" <р2< р"" ?
/. Единственной измеряемой величиной является импульс Р{ первой частицы.
Пользуясь результатами, полученными в пункте (d) и пункте (е), вычислить вероятность
найти значение импульса в интервале между р и р" . Сравнить полученные в двух
случаях результаты.
g. Измеряется алгебраическое расстояние Хх - Х2 между двумя частицами. Какова
вероятность получить результат, заключенный между -d и +d ? Чему равно среднее
значение этого расстояния?
12. Бесконечно глубокая потенциальная яма
Рассматривается частица с массой т в поле потенциала:
V(x) = 0, если 0 < х < а ;
V(x) = +°о , если х < 0 или х > а .
Обозначим символом |фп) собственные состояния гамильтониана Н системы с собст-
n2n2h2 , ттч ^
венными значениями Еп = т- (см. дополнение НО. Состояние частицы в момент
2та
времени t = 0 равно:
|у@)> = в1|ф|> + А2|ф2) + £1з|фз> + «4|ф4>-
a. Какова вероятность при измерении энергии частицы в состоянии |\|/@)) получить
Зя2й2 „
значение меньше, чем г~ ?
та
b. Определить среднее значение и среднеквадратичное отклонение энергии частицы
в состоянии |\|/@)).
c. Вычислить вектор состояния |\|/@) в момент времени t. Останутся ли результаты,
полученные в пунктах (а) и (Ь) для t = 0 , верными в произвольный момент времени t ?
427

Глава 111
,п 87i2fi2
а. При измерении энергии получен результат =~ • Каково состояние системы по-
та
еле измерения? Какой результат будет получен при повторном измерении энергии?
13. Двумерная потенциальная яма (см. дополнение Gn)
В рамках двумерной задачи рассматривается частица с массой т; ее гамильтониан
имеет вид:
Н = Нх + Ну,
где
Р2 Р?
-f- + V(X);Hy=-±
2т 2т
Hx=^f- + V(X)\ Hy=-^- + V(Y).
Потенциальная энергия V(x) [или V(y)] равна нулю, если х (или у ) принадлежит
интервалу [О, а], и бесконечно велика в остальных точках пространства.
a. Какие из перечисленных ниже операторов образуют полный набор
коммутирующих операторов:
[Н)лнх)лнх,ну)лн,нх}1
b. Рассматривается частица, описываемая волновой функцией:
тис пу . 2пх . 2пу
\j/(jc, у) = N cos — cos — sin sin ,
a a a a
если 0 < jc < а и 0 < ;y < д , и равной нулю в остальном пространстве (N — постоянная).
а. Найти среднее значение энергии (#) частицы. Какие результаты будут
получены при измерении энергии Я и с какими вероятностями?
Р. Какие результаты могут быть получены при измерении наблюдаемой Нх и с
какими вероятностями? Если в этом измерении получено значение ="> то каки^ ре-
2та
зультаты даст последующее измерение Ну и с какими вероятностями?
у. Производится одновременное измерение Нх и Ру. С какими вероятностями
можно получить значения:
9n2h2
2та2
и p0<Py<pQ + dp?
428

Постулаты квантовой механики
14. Рассматривается физическая система в трехмерном пространстве состояний,
определенном ортонормированным базисом {|м,), |и2), |м3)}. В этом базисе гамильтониан
системы Н и две наблюдаемые А и В имеют матрицы:
// = Йсо,
(\ о о"|
0 2 0
[О 0 2}
; А = а
(\ 0 0^
0 0 1
[о 1 oj
/
; в = ь\
\
0 1 0\
1 0 0
10 0 lj
где @0, а и Ъ — положительные вещественные константы. В начальный момент
времени t = 0 система находилась в состоянии | \|/@)) = -j= | м,) + — | и2) + — | и3).
a. В момент времени t = 0 измеряется энергия системы. Какие значения могут быть
получены и с какими вероятностями? Вычислить среднее значение (Н) и
среднеквадратичное отклонение АЯ для системы в состоянии |\|/@)).
b. В момент времени г = 0 измеряется наблюдаемая А . Какие значения могут быть
получены и с какими вероятностями? Какой вектор будет характеризовать состояние
системы сразу же после измерения?
c. Найти вектор состояния |\|/@) системы в момент времени t.
d. Определить средние значения (л)@ и (#)@ наблюдаемых А и В в момент
времени t. Дать физическую интерпретацию полученным результатам.
e. Наблюдаемая А измеряется в момент времени t. Какие будут получены
результаты? Аналогичный вопрос относительно наблюдаемой В. Дать физическую
интерпретацию.
15. Представление взаимодействия
Прежде чем выполнять это упражнение, рекомендуется прочитать дополнения Frn и Gni.
Рассматривается произвольная физическая система. Обозначим ее гамильтониан
символом #0@ и символом U0(t, t') —соответствующий оператор эволюции:
ot
^о('о>'о) = 1-
Допустим теперь, что система подвергается действию возмущения, в результате чего ее
гамильтониан принимает вид:
Я(/) = #0@ + ЩО.
429

Глава III
Вектор состояния системы в «представлении взаимодействия» |\|/,@) определяется
через вектор состояния |\|/5@) в представлении Шредингера уравнением:
|\MO) = tfo^'o)|Vs(')).
a. Показать, что эволюция вектора |\|/7@) описывается уравнением:
ihjt \yl(t)) = Wl(t)\\vl(t))i
где W,(t) — оператор, полученный из W(t) с помощью унитарного преобразования
wt(t)=u;(t,t0)wo)uQ(t9t0).
Качественно объяснить, почему в случае, когда возмущение W(t) значительно меньше,
чем Я0(г), движение вектора |\|/,@) происходит гораздо медленнее движения вектора
b. Показать, что приведенное выше дифференциальное уравнение эквивалентно
интегральному уравнению:
|v,(OHv,(f0))+ T 1Л'W)|v,@),
1П 'о
где|у;(*0))= |\|/s@).
c. Решив это интегральное уравнение методом итераций, показать, что кет |\|/,@)
можно разложить по степеням W в ряд вида:
|\|/Дг))= 1 + ^}^Х(П + ~ |4>,('o))-
[ Л h W ,0 ,0 У
16. Корреляции между двумя частицами
Чтобы ответить на вопрос (е) этого упражнения, рекомендуется прочитать
дополнение Еш.
Рассмотрим физическую систему, образованную из двух не взаимодействующих
между собой частиц A) и B), имеющих одинаковые массы т и помещенных в беско-
430

Постулаты квантовой механики
нечно глубокую потенциальную яму шириной а (см. дополнение Нь § 2-е). Обозначим
символами //A) и #B) гамильтонианы каждой из двух частиц, символами |ф„A)) и
I ,*л г- ~ n2n2h2
ф B)) — собственные состояния первой и второй частицы с энергиями т~ и
я2^2 о ~ * - I \
г-. В пространстве состоянии полной системы введем базис состоянии Ф„ф0),
2та ' '
определенный произведением фпф \ = |ф„A))® ф^B)у.
a. Каковы собственные состояния и собственные значения оператора # = //A)+#B),
то есть полного гамильтониана системы? Указать кратность вырождения двух
энергетических уровней с минимальными энергиями.
b. Допустим, что в момент времени / = 0 система находилась в состоянии:
I V@)> = -гг |<Pi<P.) + -7^ |<Pi<P2) + -nr |ф2Ф.) + -7^ |ф2Ф2) •
а. В каком состоянии находится система в момент t ?
р. Измеряется полная энергия Н . Какие результаты и с какими вероятностями
будут получены?
у. Тот же вопрос, если измеряется энергия Н(\).
c. а. Показать, что |\|/@)) является тензорным произведением. Вычислить средние
значения (ЯA)), (#B)) и (#A)#B)). Сравнить (ЯA)) (ЯB)) с (ЯA)ЯB)); как
объяснить полученный результат?
Р. Показать, что полученные выше результаты справедливы и в том случае, если
система находится в состоянии |\|/@)» полученном в пункте (Ь).
d. Допустим теперь, что в момент / = 0 система находилась в состоянии:
1 lb 1
|м/@)) = -^|ф1Ф1) + у-|ф1Ф2) + -^|ф2Ф1).
Показать, что состояние |\|/@)) не может быть представлено в виде тензорного
произведения. Как изменятся ответы на вопросы, поставленные в пункте (с)?
е. а. Записать матрицу, представляющую в базисе { Ф^Ф^) } оператор плотности
р@), соответствующий кет-вектору |\|/@)), данному в пункте (Ь). Какой вид имеет
матрица р(г)в момент времени tl Вычислить в момент времени f = 0 два парциальных
следа:
431

Глава III
p(l) = tr2p и pB) = tr,p.
Описывают ли операторы плотности р, рA)и рB) чистые состояния? Сравнить р и
рA) ® рB), дать физическую интерпретацию.
Р. Ответить на те же вопросы, что и в пункте (а), если выбрать кет |у@)) в
виде, данном в пункте (d).
Следующие упражнения следует решать, используя понятия и результаты,
приведенные в дополнении Еш.
17. Пусть р — оператор плотности произвольной системы, а %,) и п1— его
собственные векторы и собственные значения. Записать р и р2 через %,) и п1; каков вид матриц,
представляющих эти два оператора в базисе {%,}}, если р описывает чистое состояние
и смешанный ансамбль состояний? (Следует доказать, что в случае чистого состояния
единственный отличный от нуля диагональный элемент равен 1, тогда как в случае
смешанного состояния значения диагональных элементов могут лежать в диапазоне от 0 до 1.)
Показать, что р соответствует чистому состоянию только в случае, когда след р2 равен 1.
18. Рассматривается система с оператором плотности р(г), подчиняющаяся
гамильтониану H{t). Показать, что след оператора р2 не зависит от времени. Может ли система
эволюционировать так, что последовательно оказывается в чистом состоянии и в
статистическом ансамбле состояний?
19. Пусть имеется полная система A) + B), составленная из двух подсистем A) и B).
Обозначим символами А и В два оператора, действующих в пространстве состояний
£A)®#B). Показать, что два парциальных следа tr, {АВ} и tr, {ВА} равны, если А
(или В) действует только в пространстве £A), то есть когда можно записать:
Л = ЛA)®1B) [или В=В(\)® 1B)].
Вычислить —рA) редуцированного оператора плотности рA), если гамильтониан Н
dt
полной системы равен сумме двух операторов, действующих по отдельности только в
пространствах £A) и #B):
Я = ЯA)+ЯB).
Дать физическую интерпретацию полученному результату.
432

Постулаты квантовой механики
Возврат к одномерным задачам
Теперь, когда мы познакомились с математическим формализмом и физическим
содержанием квантовой механики, можно уточнить и дополнить результаты,
полученные в главе I. В последующей ниже серии, состоящей из трех дополнений, рассмотрим в
общем случае квантовые свойства частицы, подверженной действию поля скалярного
потенциала* произвольной формы, ограничившись для простоты одномерными
задачами. Нас будут интересовать связанные стационарные состояния частицы, энергии
которых образуют дискретный спектр (дополнение Мш), затем несвязанные состояния,
соответствующие энергетическому континууму (дополнение Nm), и далее исследуем очень
важный частный случай (особенно для приложений в области физики твердого тела)
периодического потенциала (дополнение Ош).
Дополнение Мщ
СВЯЗАННЫЕ СОСТОЯНИЯ ЧАСТИЦЫ
В «ПОТЕНЦИАЛЬНОЙ ЯМЕ» ПРОИЗВОЛЬНОЙ ФОРМЫ
1. Квантование энергии связанных состояний.
2. Минимальное значение энергии основного уровня.
В дополнении Hi мы уже рассматривали связанные состояния частицы в
потенциальной яме для частного случая, когда яма имела прямоугольную форму конечной или
бесконечной глубины. Там мы уже установили некоторые свойства связанных состояний:
дискретный энергетический спектр, энергия основного уровня, превышающая минимум
классической энергии. На деле эти свойства являются общими и имеют многочисленные
физические следствия. Именно это мы и хотим показать в данном дополнении.
Если потенциальная энергия частицы имеет минимум (см. рис. 1а), говорят, что
частица находится в потенциальной яме **. Прежде чем приступить к качественному
рассмотрению стационарных состояний квантовой частицы в такой яме, напомним
характер движения соответствующей классической частицы. Когда ее энергия Ес1 принимает
минимально допустимое значение Еы = -V0, где V0 — глубина ямы, частица неподвиж-
* Влияние векторного потенциала А будет рассмотрено ниже в дополнении EVi.
** Конечно, потенциальная энергия определена с точностью до постоянной величины. Как
обычно, мы примем потенциал на бесконечности равным нулю.
28 Квантовая механика
433

Глава III
на в точке М0 с абсциссой х0. В случае, если -VJ, < Ес1 < О, частица осциллирует в яме
с амплитудой, описываемой нарастающей функцией энергии Ес1. Наконец, если Ес1 > О,
частица уже не остается в яме и уходит в бесконечность. «Связанные состояния»
классической частицы соответствуют всем отрицательным значениям энергии, заключенным
в интервале между -V0 и 0.
Для квантовой частицы ситуация выглядит существенно иначе. Состояния с точно
определенной энергией Е являются стационарными состояниями, волновая функция
(р(лс) которых есть решение уравнения на собственные значения гамильтониана Я :
П2 d2
2т dx
ф(х) = £ф(х). A)
Это дифференциальное уравнение второго порядка допускает бесконечное множество
решений для любого фиксированного значения Е. Если в произвольной точке х
задаться произвольными значениями ф(*) и ее производной, то путем продолжения можно
получить ф(лс) в любой точке х. Таким образом, уравнение A) само по себе не
накладывает никаких ограничений на возможные значения энергии. Однако ниже мы
покажем, что наложение на функцию ф(х) некоторых граничных условий влечет за собой
ограничение на допустимые значения энергии (квантование уровней энергии).
1. Квантование энергии связанных состояний
Будем называть «связанными состояниями» частицы такие состояния, волновая
функция которых ф(дс) удовлетворяет уравнению на собственные значения A) и
является квадратично интегрируемой [это условие необходимо для того, чтобы ф(лг) могла
реально описывать физическое состояние частицы]. Таким образом, это стационарные
состояния, для которых плотность вероятности |ф(*)| существенно отлична от нуля только
в ограниченной области пространства [для того, чтобы интеграл j dx |ф(дс)| сходился,
нужно, чтобы квадрат модуля |ф(*)| стремился к нулю достаточно быстро при х -> ±<» ].
Связанные состояния в некотором смысле напоминают классическое движение частицы,
когда она осциллирует в яме, никогда не выходя за ее пределы, то есть случай, когда
энергия Ес1 отрицательна (но больше, чем -V0).
434

Постулаты квантовой механики
Рис.1
Потенциальная яма глубиной V0, расположенная между точками х = jc, и х = х2 (риса).
Сначала берется решение (р(;с) уравнения на собственные значения оператора Н ,
которое экспоненциально стремится к нулю в области х<х] при х —> -°° ; затем это
решение продолжается на всю ось х. Для произвольного значения энергии Е функция ф(х)
расходится, как В(Е)ерх при jc->-h»: на рис.Ь представлен случай, когда В(Е)>0, а
на pnc.d -— случай В(Е)<0. Однако, если выбрать энергию Е так, чтобы при х—> +°о
функция экспоненциально стремилась к нулю (рисе), то ф(лг) является квадратично
интегрируемой функцией
28*
435

Глава III
Сейчас мы увидим, что условие квадратичной интегрируемости функции ф(лг) в
квантовой механике означает, что возможные значения энергии образуют дискретный
ансамбль, заключенный в интервале между -V0 и 0. Для этого снова вернемся к
потенциалу, изображенному на рис. 1а. Для простоты предположим, что V(x) в точности равна
нулю вне интервала [jc,, х2]. Если х < хх (область I), то V(x) = 0, и решение уравнения A)
записывается сразу же:
— если Е > 0, то
фД*)=Ле'ь + А'<Г*\ B)
где
\lrnE
V П2
2тЕ О)
— если £<0,то
<p/0c) = Bep* + £Vpx, D)
где
>-{
*£• E)
Мы ищем квадратично интегрируемое решение и, следовательно, должны отказаться от
формулы вида B), где (р,(х) является суперпозицией плоских волн с постоянным
значением модуля, вследствие чего интеграл
]л|ф,(*)|2 F)
расходится. Итак, остается единственная возможность D), и мы можем сформулировать
первый результат: все связанные состояния частицы имеют отрицательную энергию.
В формуле D) мы не можем оставить член с экспонентой е~рх, так как он расходится,
если х —> -°о . Остается только одна возможность:
фДд:) = ер* при х<х{ G)
[мы опустили множитель В, ибо однородность уравнения A) позволяет определить ф(д)
с точностью до постоянного коэффициента].
436

Постулаты квантовой механики
Значение ф(лс) в интервале х{<х<х2 (область II) получается путем использования
непрерывности граничных условий: мы должны искать решение уравнения A), равное
е* при х = хх, производная которого в этой точке равнялась ре^1 . Полученная таким
образом функция ф7/(д:) зависит от р и, конечно, от точного выражения V(x). Однако,
поскольку уравнение A) является дифференциальным уравнением второго порядка, то
(p/7(jc)определена единственным образом указанными выше граничными условиями, и
видно, кроме того, что она должна быть вещественной (это позволяет нам изобразить ее
графики так, как это сделано на рис.lb, lc и Id).
Остается только получить решение при х > х2 (область III). Оно может быть
записано в виде:
9/l/(jc) = B^ + BVtt> (8)
где В и В' — вещественные константы, определяемые условиями непрерывности
ф(х) и dq/dx в точке х = х2. Коэффициенты В и В' зависят от р йот V(x).
Итак, мы построили решение уравнения A), имеющее, например, вид,
изображенный на рис ЛЬ. Является ли это решение квадратично интегрируемым? Из формулы (8)
видно, что в общем случае это не так, кроме случая, когда В = О (этот вариант изображен
на рис. 1с). Так, для заданной функции V(x) коэффициент В зависит от Е через р.
Единственными значениями Е, для которых существует связанное состояние, являются
решения уравнения В(Е) = 0. Эти решения £,, £2,... (см. рис.2) образуют дискретный
спектр, зависящий, конечно, от выбранного потенциала V(x) (в следующем параграфе
мы увидим, что все значения Et энергии больше -V0).
В(Е)
Рис.2
Графическое представление функции В(Е). Нули этой функции дают значения Е, для
которых функция ф(;к) является квадратично интегрируемой (ситуация соответствует рис.1с),
то есть энергии £,, £2,... связанных состояний. Все эти значения лежат между -V0 и О
437

Глава III
Таким образом, мы пришли к следующему результату: возможные значения энергии
связанных состояний частицы в потенциальной яме произвольной формы образуют
дискретный ансамбль (часто говорят, что энергия связанных состояний квантуется).
Этот результат можно сопоставить с квантованием электромагнитных мод в резонаторе.
В классической Механике аналогий нет, ибо, как мы уже видели, все значения энергии,
заключенные между -V0 и 0, допустимы. Уровень энергии с самым малым значением
энергии Е{ в квантовой механике называется основным, следующий за ним с энергией
Е2 — первым возбужденным уровнем, с энергией Е3 — вторым возбужденным
уровнем и т.д. Часто их схематически изображают следующим образом: внутри
потенциальной ямы, представляющей зависимость V(x), рисуют горизонтальные линии, ордината
которых соответствует энергии уровня, а длина напоминает пространственное
распределение волновой функции (она отмечает точки оси, которые могла бы достигнуть
классическая частица, имеющая ту же энергию). Для всей совокупности уровней энергии
схема выглядит так, как представлено схематически на рис.3.
Рис.3
Схематическое изображение связанных состояний частицы в потенциальной яме. Для
каждого из стационарных состояний проводится горизонтальная линия, ордината которой
равна энергии соответствующего уровня. Длина линии ограничивается точками ее
пересечения с кривой потенциала V(x), то есть характеризует область, в которой движется
классическая частица, имеющая ту же энергию. Эта область иллюстрирует
пространственную протяженность волновой функции
Явление квантования энергии, как мы видели в главе I, было одним из тех, которые
привели к введению квантовой механики. Оно встречается в большинстве физических
систем: дискретные энергетические уровни атомов (см. главу VII, атом водорода),
гармонический осциллятор (см. главу V), атомные ядра и т.д.

Постулаты квантовой механики
2. Минимальное значение энергии основного уровня
В этом параграфе мы покажем, что все значения энергии £,, Е2,... превышают
минимальное значение потенциальной энергии -V0, и увидим, что этот вывод легко
интерпретируется на основе соотношения неопределенностей Гейзенберга.
Если ф(лс) — решение уравнения A), то, умножив это уравнение на ф*(*) и
проинтегрировав его, получим:
-^C^Vto^W + J^ . (9)
Для связанного состояния функцию <р(лс) можно нормировать, и тогда равенство (9)
просто запишется в виде:
£ = (Г) + (У), A0)
где
d
<.).-AL,>ywiLpu,=|Lj:>'
ах
(И)
[здесь выполнено интегрирование по частям и использован тот факт, что ф(*)
стремится к нулю, если | дс | —> ©о ] и
(v) = £2dx.V(x)\(p(x)\2. A2)
Равенство A0) выражает просто, что энергия Е является суммой средних значений
кинетической:
<7>-<ф|£|Ф> (»)
и потенциальной энергии:
(у) = (ф|У(Х)|ф). A4)
Из равенств A1) и A2) сразу же следует, что
(Г)>0; A5)
439

Глава III
(v)>jZdx<-V0)\(p(x)\2=-V0. A6)
Итак:
E = (T) + (V}>(V)*-V0. A7)
Впрочем, Е < О, как было показано в § 1, и, следовательно, мы видим, что, как и в
классической механике, энергия связанных состояний всегда заключена между -V0 и 0.
Существует, однако, важное различие между классической и квантовой ситуациями:
в классической механике частица может иметь энергию, равную -V0 (неподвижная
частица в точке М0) или слегка превышающую ее (малые колебания вблизи М0), тогда
как в квантовой механике наименьшим значением энергии частицы является энергия £,
основного уровня, всегда превышающая значение -V0 (см. рис.3). Соотношения
неопределенностей Гейзенберга позволяют понять физическую природу такого результата.
Действительно, если мы хотим построить состояние частицы, в котором средняя
потенциальная энергия была бы минимальной, то, как видно из формулы A2), нужно
выбрать волновую функцию, практически локализованную в точке М0. Тогда
среднеквадратичное отклонение АХ очень мало, вследствие чего АР должно быть по
необходимости очень велико. Поскольку:
(Р2) = (ДРJ+(Р2)>(ДР)\ A8)
кинетическая энергия (т) = (Р2)/2т должна быть очень большой. Таким образом, если
потенциальная энергия стремится к минимальному значению, кинетическая энергия
бесконечно возрастает. Волновая функция основного состояния соответствует
компромиссу, при котором сумма двух энергий остается минимальной. Основное состояние
квантовой частицы характеризуется волновой функцией, имеющей некоторое
пространственное распределение (см. рис.3), и ее энергия обязательно превышает -VJ,; в
противоположность классической механике в квантовой механике не существует состояния со
строго определенной энергией, когда частица «покоится» на дне потенциальной ямы.
ЗАМЕЧАНИЕ
Поскольку энергия связанных состояний заключена между -V0 и 0, такие
состояния могут существовать лишь в том случае, если потенциал V(x) принимает
отрицательные значения в одной или нескольких областях оси Ох. Именно
поэтому в этом дополнении мы выбрали потенциал, имеющий форму,
представленную на рис. 1а (в следующем дополнении это ограничение будет снято).
440

Постулаты квантовой механики
Не исключено, однако, что для некоторых значений х потенциал V(x) может
быть положительным, например, «яма» может быть окаймлена потенциальными
«барьерами», как показано на рис.4 (по-прежнему предполагается, что на
бесконечности потенциал равен нулю). В этом случае некоторые классические движения
с положительной энергией оказываются ограниченными, тогда как в квантовой
механике вышеприведенные рассуждения показывают, что связанные состояния
всегда имеют энергию в интервале между -V0 и 0. Физически это различие
обусловлено тем, что потенциальный барьер конечной высоты никогда не может
полностью препятствовать движению квантовой частицы, и всегда имеется отличная
от нуля вероятность проникновения частицы через барьер (туннельный эффект).
-V,
**х
Рис.4
Потенциальная яма глубиной -V0, заключенная между двумя потенциальными
барьерами высотой V, и V2 (предполагается, что V, < V2). С классической точки зрения
существуют движения с энергией, заключенной между -V0 и Vx, ограниченные в пространстве
двумя барьерами. В квантовой механике частица с энергией в интервале от 0 до V,
может проникать через потенциальные барьеры путем туннельного эффекта; вследствие
этого связанные состояния всегда имеют энергию, заключенную между -V0 и 0

Глава III
Дополнение Nm
НЕСВЯЗАННЫЕ СОСТОЯНИЯ ЧАСТИЦЫ
В ПРИСУТСТВИИ ПОТЕНЦИАЛЬНОЙ ЯМЫ
ИЛИ ПОТЕНЦИАЛЬНОГО БАРЬЕРА ПРОИЗВОЛЬНОЙ ФОРМЫ
1. Матрица передачи М(к) .
a. Определение М(к).
b. Свойства М(к).
2. Коэффициенты отражения и прохождения.
3. Пример.
В дополнении Мш мы показали, что связанные состояния частицы в поле потенциала
V(x) имеют отрицательную энергию* и существуют только в том случае, если V(x) —
потенциал притяжения (потенциальная яма, допускающая классическое ограниченное
движение). Мы должны отвергнуть положительные значения энергии, так как им
соответствуют собственные функции ф* (х) гамильтониана Н , ведущие себя как суперпозиции
экспонент е±1кх , не допускающие квадратичное интегрирование. Однако в главе I мы видели, что
линейная суперпозиция таких функций может дать квадратично интегрируемую волновую
функцию \\f(x) (волновой пакет), способную представлять физическое состояние частицы.
Конечно, поскольку полученные в результате состояния состоят из членов с различными к ,
то есть с различными энергиями, они не являются стационарными состояниями, и волновая
функция изменяется во времени (распространение в пространстве, деформация и т.д.).
Однако эти изменения можно определить, так как \\f(x) может быть разложена по
собственным функциям ф^ (х) [именно это было сделано, например, в дополнении Jb где, пользуясь
свойствами ф^ (х), мы нашли коэффициенты прохождения и отражения для
потенциального барьера, определили запаздывание при отражении и т.д.]. В связи с этим, несмотря на то,
что каждая из функций (рк (х) не может представлять физическое состояние, полезно
исследовать собственные функции оператора Я с положительными значениями энергии**,
как это делалось в дополнении Нт для некоторых потенциалов прямоугольной формы.
Напоминаем, что мы выбрали начало отсчета энергии так, чтобы в бесконечности V(x)
стремилась к 0.
Можно было бы попытаться исследовать не интегрируемые квадратично собственные
функции Н с отрицательными значениями энергии, однако эти функции очень быстро
(экспоненциально) стремятся к бесконечности, и их линейная суперпозиция не может дать квадратично
интегрируемый волновой пакет.
442

Постулаты квантовой механики
В этом дополнении рассмотрим в общем виде (в рамках одномерной модели) влияние
формы потенциала V(x) на собственные функции (рк(х) с положительными значениями
энергии. Относительно формы V(x) не будет сделано никаких предположений (ямы,
барьеры и т.д.), за исключением требования обращения в нуль вне конечного интервала
[jc,, х2] оси Ох. Будет показано, что во всех случаях влияние V(x) на функцию (f>k(x)
может быть описано с помощью квадратной матрицы 2x2, обозначаемой М(к) и
обладающей рядом общих свойств. Тем самым сможем получить результаты, не зависящие
от конкретной формы V(x). Так, например, коэффициенты отражения и прохождения
для потенциального барьера (симметричного или нет) одинаковы для частицы,
двигающейся слева, и частицы той же энергии, движущейся справа. Кроме того, дополнение Nm
может служить отправной точкой для расчетов, выполненных в дополнении Ош,
касающихся свойств частицы в потенциале V(x), имеющем периодическую структуру.
1. Матрица передачи М(к)
а. ОПРЕДЕЛЕНИЕ М(к)
В рамках одномерного случая рассмотрим потенциал, равный нулю вне интервала
\хх, х2 ] длиной / и изменяющийся произвольным образом внутри этого интервала
(рис.1). Выберем начало отсчета оси Ох в середине интервала [jc,, x2] с тем, чтобы все
изменения V(x) происходили при |*|<//2. Любая волновая функция ф(х),
соответствующая стационарному состоянию с энергией Е , удовлетворяет уравнению:
\У(х)
Рис.1
Рассматриваемый потенциал V(x)
*х изменяется произвольно внутри
интервала -1/2 < х < + 1/2 и
становится равным нулю вне этого
интервала
443

Глава III
^- + ^[E-V(x)]\(p(x) = 0. A)
dx2 fi2
Для характеристики энергии частицы в дальнейшем будем использовать величину:
\2тЕ
"-{—■ т
В области х<-1/2 функция ^удовлетворяет уравнению A). Обозначим
символом vk(x) решение этого уравнения, совпадающее с е,кх при х<-1/2. Если же
х > +112, то vk (x) неизбежно является линейной комбинацией двух независимых
решений ехкх и е~,кх уравнения A), то есть
если х< —,то vk(x) = e,kx; C-а)
если х>+-, то vk(x) = F(k)eikx+G(k)e'ikxy C-b)
где F(k) и G(k) — коэффициенты, зависящие от к и от формы рассматриваемого
потенциала. Аналогично можно ввести решение, которое равно е~,кх при х < —:
если jc < —, то v* (л:) = e~lkx; D-а)
если jc>+-,to vf(jc) = F'{k)eikx +G'(k)e4kx. D-b)
2
Общее решение ф*(;с) уравнения A) для выбранного значения Е (т. е. данного к )
является линейной комбинацией v^ (x) и v'k (x):
(f>k(x) = Avk(x) + AVk(x). E)
Равенства C-а) и D-а) требуют, чтобы
при jc < --: ф, (х) = Aeikx + А V*, F-а)
тогда как равенства C-Ь) и D-Ь) дают:
444

Постулаты квантовой механики
при х> +— : ipk(л:) = Ле,Ь: + А'е /Ьг.
F-Ь)
где
A = F(k)A+F'(k)A'\
A' = G{k)A + G\k)A'.
По определению введем матрицу 2x2, обозначаемую М{к):
(С(к) G\k))
благодаря которой равенства G) можно переписать в матричной форме:
G)
(8)
(9)
Таким образом, матрица М (к) позволяет, зная поведение волновой функции F-а) слева
от потенциала, определить ее поведение F-Ь) справа от него. По этой причине будем
называть М (к) «матрицей передачи».
ЗАМЕЧАНИЕ
Ток вероятности, связанный с волновой функцией <p(jc), равен:
'<*) = —
2mi
*. .dip . .dip
Ф (*)-г-ф(*)-т-
dx dx
(Ю)
После дифференцирования получим:
d2ip
— /(*) =
dx 2mi
d2ip
Ф (*)—у-ф(*)- 2
dx dx
A1)
С учетом формулы A) можно записать:
— Л*) = 0,
A2)
445

Глава III
Таким образом, ток </(*), соответствующий стационарному состоянию, одинаков
в любой точке оси Ох. Впрочем, можно заметить, что равенство A2) является
простым аналогом в одномерном пространстве выражения:
divj(r) = 0,
A3)
справедливого, согласно (D-11) главы III, для любого стационарного состояния
частицы, двигающейся в трехмерном пространстве. В соответствии с формулой
A2) ток Jk(x), связанный с волновой функцией (рк(х), может быть вычислен в
любой точке х как для вида F-а), так и для вида F-Ь) по формуле:
Пк
Л(*) = —
т
I |2 I |2
\а\ -\а'\
т
12 I |2
-Мл
A4)
Ь. СВОЙСТВА М(к)
а. Поскольку функция V(x) является вещественной, легко показать, что если (р(х) —
решение уравнения A), то и ф*(дг) — также решение этого уравнения. Рассмотрим
теперь функцию v*k(x); она является решением уравнения A), и сравнение C-а) с D-а)
показывает, что она совпадает с v. (х), если х < —. Итак, для любых х имеем:
2
v*k(x) = v'k(k).
Подставим равенства C-Ь) и D-Ь) в это соотношение. Тогда:
F*(*) = G'(*);
G*(k) = F'(k).
Отсюда следует, что матрицу М (к) можно записать в упрощенном виде:
(F(k) G*(k))
М(к) =
G(k) F\k)
A5)
A6)
A7)
A8)
р. Выше мы видели [см.A2)], что ток вероятности J(x) в случае стационарного
состояния не зависит от х. Тогда должно выполняться равенство:
446

Постулаты квантовой механики
к>\2
|2 I ~,|2
А\-А'\= А -А' ,
A9)
какими бы ни были А и А'. Но соотношения (9) и A8) дают:
|д |2 -\Ц2 = [f(/:)A + G*(^)A/][f*U)A4G(A:)A/*]-
^(*)A + f4*)A'][g4*)A4F(A^
Таким образом, условие A9) эквивалентно равенству:
\F(k)\2-\G(k)\2 =DttM(k) = \.
B0)
B1)
ЗАМЕЧАНИЯ
(i) Мы не делали никаких предположений относительно формы потенциала. Если он
четный, то есть если V(x) = V(-x), то матрица M(k) обладает дополнительным
свойством: можно показать, что G(k) — чисто мнимая величина.
(и) Равенства F) показывают, что А и А' являются коэффициентами «падающих»
плоских волн, то есть волн, связанных с частицами, двигающимися от х = -°о и
х = +<х> в сторону зоны действия потенциала (падающие частицы); напротив, А и
А' — коэффициенты, соответствующие «выходящим» волнам, связаны с
частицами, удаляющимися от потенциала (прошедшие или отраженные частицы).
Интересно iBecTH матрицу S , позволяющую вычислить амплитуду выходящих волн
через амплитуду падающих волн:
А'
■■S(k)
( А\
А'
B2)
Функция S(k) может быть без труда выражена через элементы матрицы М(к).
Действительно, равенства:
A = F(k)A + G'(k)A';
A' = G(k)A + F'(k)A',
B3-а)
B3-b)
требуют, чтобы:
447

Глава III
A' = —}—[A'-G(k)A]. B4)
Подставив это равенство в B3-а), получим:
7 1
[(.F(k)F*(k)-G(k)G"(k))A + G*(k)A']. B5)
F\k)
С учетом равенства B1) матрица S(k) запишется в виде:
S(k) = —1
(
F (к)
1 G'(k)
B6)
-G(k) l
Нетрудно показать, используя дважды равенство B1), что:
S(k)S+(k) = S+(k)S(k) = l, B7)
то есть матрица S(k) унитарна. Она играет важную роль в теории столкновений.
Можно было бы доказать, что она унитарна, исходя из унитарности оператора
эволюции (см. дополнение F ш), выражающейся просто из сохранения во времени
полной вероятности найти частицу в любой точке на оси Ох (норма волновой
функции).
2. Коэффициенты отражения и прохождения
Чтобы вычислить коэффициенты отражения и прохождения для частицы,
налетающей на потенциал V(x), в принципе нужно, как в дополнении Jb построить волновой
пакет из только что рассмотренных собственных функций оператора Н . Пусть,
например, падающая частица имеет энергию Ei и движется слева направо. Соответствующий
волновой пакет получается путем суперпозиции функций ук (х), в которых полагаем
Л' = 0 , с коэффициентами, заданными функцией g(k), имеющей вид выраженного пика
вблизи к = к{ = ^ImEJfi2 . Мы не будем вдаваться здесь в подробности вычислений, во
всех деталях аналогичных приведенным в дополнении ]\ и показывающих, что
коэффициенты отражения и прохождения равны соответственно | A\ki) I А(к() | и
|А(*,)М(*,)|\
Поскольку Л' = 0 , равенства B2) и B6) дают:
448

Постулаты квантовой механики
А(к)--
F\k)
А(к);
B8)
А\к) = -Ш-А{к).
F (к)
Коэффициенты отражения и прохождения равны:
ВД) =
Wi)-
А\к,)
А(к,)
\Мк,)
\А(к,)
2
2
G(k,) I
F(kt) I
1
№>Г
B9-а)
B9-b)
[нетрудно показать, что условие B1) обеспечивает равенство Rl(k,) + Tl(ki) = l].
Если теперь частица падает справа налево, нужно взять А = 0, откуда следует:
Д,*,.||2дТО;
C0)
А\к):
F (к)
■А'(к).
Теперь коэффициенты прохождения и отражения равны:
ТЛк) =
А\к)
А'(к)
\F(k)f
C1-а)
*,(*)=-
А(к)
А\к)
2
G(k)
F(k)
C1-b)
Сравнение формул B9) и C1) показывает, что Тх(к) - Т2(к) и что R{(k) = R2(k): для
заданной энергии степень проникновения через барьер (симметричный или нет) всегда
одинакова для частиц, падающих слева или справа.
С другой стороны, согласно B1), имеем:
29 Квантовая механика
449

Глава HI
|F(*)|>1.
C2)
Если выполняется равенство, то коэффициент отражения равен нулю, а коэффициент
прохождения равен 1 (резонанс). Напротив, обратная ситуация невозможна: поскольку
равенство B1) требует, чтобы |F(fc)|>|G(fc)|, невозможно иметь 7 = 0 и R = 1 [за
исключением предельного случая, когда \F(k)\ и \G(k)\ одновременно стремятся к
бесконечности].
3. Пример
Вернемся к прямоугольной форме потенциала, рассмотренной в §2-Ь дополнения Нг:
в области —<х<— потенциал V(x) равен константе V0* (см. рис.2, где выбрано
значение VQ > 0).
Допустим сначала, что Е < VQ, и положим:
Элементарный расчет, подобный приведенному в дополнении Hi, дает:
C3)
Мх)
I
+ 2
Рис.2
Прямоугольный потенциальный барьер
* Здесь мы выбрали форму барьера, сдвинутую по отношению к барьеру дополнения Нь так
как предполагаем, что он расположен между х = -1/2 и х = +//2,ане между х = 0 и х = /.
450

Постулаты квантовой механики
М{к) =
, , -*2-Р2 , ,
cnpl + i shpl
2кр
к2
2кр
-iJ^-shpl
2кр
к2-р2
chpl-i — shpl
2кр
C4)
где
_ j2mV(L
C5)
(величина V0 по необходимости больше нуля, так как мы предположили, что Е < V0).
Если теперь предположить, что Е > V0, то можно обозначить:
*'-Jf?<*-v.)
C6)
*.-^
C7)
(где е = +1, если V0 > 0, и е = -1, если V0 < 0). Тогда получим:
/г
М(к) =
cos k'l + i
к2+к'2
2кк'
sin k'l
ie-^-sin k'l
2кк'
2кк
к2+к'2
cos k'l-i —- sin k'l
2kk'
C8)
Нетрудно доказать, что матрицы М(к), записанные в виде выражений C4) и C8),
полностью удовлетворяют соотношениям A6), A7) и B1).
29*

Глава III
Дополнение Ощ
КВАНТОВЫЕ СВОЙСТВА ЧАСТИЦЫ
В ОДНОМЕРНОЙ ПЕРИОДИЧЕСКОЙ СТРУКТУРЕ
1. Последовательное прохождение нескольких одинаковых потенциальных барьеров.
a. Обозначения.
b. Условия согласования.
c. Матрица итерации Q(OL).
d. Собственные значения Q((X).
2. Физический смысл: понятие энергетической зоны (разрешенной или запрещенной).
a. Поведение волновой функции фа (х).
b, Отражение Брэгга. Возможные значения энергии частицы в поле периодического потенциала.
3. Квантование уровней энергии в потенциале с периодической структурой. Влияние граничных
условий.
a. Условия, налагаемые на волновую функцию.
b. Разрешенные энергетические зоны: стационарные состояния частицы внутри цепочки.
c. Запрещенные зоны: стационарные состояния, локализованные на краях цепочки.
В этом дополнении изучим квантовые свойства частицы, находящейся в поле
потенциала V(x), имеющего периодическую структуру. Функции V(x), которые мы будем
рассматривать, не обязательно должны быть периодическими в строгом смысле этого
термина. Достаточно, чтобы они имели периодическую форму в ограниченной области
оси Ох (рис.1), то есть повторялись бы в течение N регулярных интервалов [ибо только
при N—>©о функция V(x) будет действительно периодической].
Рис.1
Периодический потенциал V(x), полученный путем повторения N раз отрезка функции
одной и той же формы (на рисунке количество повторений N = 4)
452

Постулаты квантовой механики
Такие периодические структуры встречаются, например, в линейных молекулах,
образованных из N одинаковых атомов (или групп атомов), регулярно распределенных в
пространстве. В физике твердого тела иногда используется одномерная модель для
понимания хода уровней энергии электрона в кристалле. Если N очень велико (случай
линейной макромолекулы или макроскопического кристалла), то потенциал V(x) может
быть задан в обширной области пространства периодической функцией, и с большой
точностью можно считать, что свойства частицы будут практически теми же, что и в
случае действительно периодического потенциала V(x). Однако с физической точки
зрения бесконечный предел значения N никогда не может быть реализован, и нас будет
интересовать случай произвольного значения N .
Чтобы выяснить влияние формы потенциала V(x) на собственную функцию (р(лс)
гамильтониана Н с собственным значением Е, мы введем матрицу 2x2, называемую
матрицей итерации Q , зависящую от Е . Покажем, что ф(х) ведет себя совершенно по-
разному в зависимости от того, являются ли собственные значения матрицы итерации
вещественными или мнимыми. Поскольку эти собственные значения зависят от
выбранного значения энергии, нам придется различать области энергии, соответствующие
вещественным собственным значениям, и области, соответствующие мнимым
собственным значениям. При этом будут введены понятия разрешенных и запрещенных зон
энергии.
ЗАМЕЧАНИЯ
(i) Ради удобства будем говорить о потенциальном «барьере» для обозначения
повторяющейся N раз формы функции, образующей потенциал V{x) (рис.1).
Однако эта форма может представлять собой не только «яму», но и любую
повторяющуюся форму.
(ii) В отличие от ранее принятых обозначений в физике твердого тела обычно
резервируют букву к для обозначения параметра, входящего в выражения для
стационарных волновых функций, который не связан простой пропорциональностью с
квадратным корнем из энергии. Чтобы сохранить эти условности, слегка изменим
принятые в дополнении Ыш обозначения и заменим к на а:
УЪпЕ /1Ч
а = у-£з-. A)
букву к будем использовать позже (мы увидим, что величина к непосредственно
связана с собственными значениями матрицы Q, когда они оказываются
комплексными).
453

Глава III
1. Последовательное прохождение
нескольких одинаковых потенциальных барьеров
Рассмотрим потенциал V(x), образованный путем повторения N барьеров
одинаковой формы, как показано на рис.1. Центр первого барьера находится в точке jc = 0,
центр второго — в точке х = /, центр третьего — в точке х = 2/,..., центр последнего —
в точке x = (N -1I . Требуется исследовать поведение собственной функции (ра(х)
гамильтониана Н , являющейся решением уравнения на собственные значения:
\^ + ^[E-V(x)]Ua(x) = 0, B)
[ах п J
где Е и а связаны соотношением A).
а. ОБОЗНАЧЕНИЯ
Слева от N барьеров, то есть при х< —, потенциал V(x) равен нулю, и общее
решение уравнения B) имеет вид:
Фо0с) = V/CU + К*** > если х<-~. C-а)
Рассмотрим, как и в § 1-а дополнения Nm, две функции vk(x) и v^(jc) , записав их в
принятых здесь обозначениях в виде va(jc) и v^(jc) . В области первого барьера с
центром в точке х - 0 общее решение уравнения B) имеет вид:
Фа U) = А К М + A[v'a (х), если - - < х < - . C-Ь)
Аналогично в области второго барьера с центром в точке х = /:
/3/
(pa(x) = A2va(x-l) + A'2v'a(x-l),ecjm --~<x<-- C-е)
и так далее. В области п -ного барьера с центром в точке х = (п -1)/:
фа(д:) = Д^ув[д:-(п-1)/]+А>;[ж-(/1-1)/],если (л-1)/—i^x-S(л-1)Z + |-. C-d)
454

Постулаты квантовой механики
И наконец, справа от N барьеров, то есть при x>(N-l)l + —, потенциал V(x)
снова обращается в нуль и, следовательно:
Фв(*) = С0*/о[*-(^ C-е)
Теперь следует согласовать все эти различные выражения для (ра(х) в точках:
* = -! +1 ,(tf-l)/ + JL.
2 2 2
Именно этому посвящен следующий параграф.
Ь. УСЛОВИЯ СОГЛАСОВАНИЯ
Функции va(x) и v'a(x) зависят от выбранной формы потенциала. Однако сейчас
мы покажем, что их значения, а также значения их производных, в граничных точках
каждого из барьеров легко найти, используя результаты, полученные в дополнении Ыш.
Для этого представим себе, что все барьеры, за исключением одного из них
(например, п -ного с центром в точке х = (п -1I), удалены. Внутри этого барьера по-прежнему
справедливо решение (З-d), но оно должно быть продолжено налево и направо с помощью
суперпозиции плоских волн, которые получатся, если в формулах F-а) и F-Ь)
дополнения Nm заменить х на х = (п - 1)/, k — на а и добавить индекс п к коэффициентам
Л, А\А,А'. Итак, если бы п -ный барьер был изолирован, для х<(п-\I— мы бы
имели:
д eia[x-(n-\)l] + д/^-/ак-(/1-1)/]
D)
и для х > (п -1)/ +
/
А.еК
(n-Dl] + д'e-iOi[x-(n-l)l}
E)
где
Я:
= М(а)
(К
F)
455

Глава III
В этом выражении с учетом изменения обозначений М(а) представляет матрицу М(&),
введенную в дополнении Nm. Стало быть, на левой границе п -ного барьера функция
фа(х), определенная выражением (З-d), должна иметь то же значение и ту же
производную, что и суперпозиция плоских волн D); аналогично, на правой границе этого барьера
она должна иметь то же значение и ту же производную, что и решение E). Эти выводы
позволяют очень просто записать условия согласования в периодической структуре.
Так, с левой стороны первого барьера (то есть при х = —) достаточно записать, что
C-а) имеет то же значение и ту же производную, что и Л{е,ах + А[е~,ах, откуда сразу же
следует, что
А0 - Лх
Л' = Л'
л0 - л,
G)
(впрочем, этот результат очевиден из Nln).
На правой границе первого барьера, совпадающей с левой границей второго барье-
ia(x-l) , л' -/а(лг-/)
pa, нужно записать, что Ахе1 + Ахе ' и А2е' u + А2е
ния и производные, откуда следует:
имеют одинаковые значе-
I л2 = V
(8)
Аналогично, на стыке п -ного и (п +1) -го барьеров
п
x = nl —
2
получим, приравнивая
значения и производные формулы E) и выражения, полученного путем замены в D)
индекса п на (п +1):
Ai+i
-А'е~ш.
(9)
И, наконец, на правой границе последнего барьера
х = (N -1)/ + — | нужно
записать, что формула C-е) имеет то же значение и ту же производную, что и выражение,
полученное из E) путем замены п на N :
С - V
(Ю)
456

Постулаты квантовой механики
с. МАТРИЦА ИТЕРАЦИИ Q((X)
Введем матрицу D(a), определенную выражением:
0(а) =
(еш О Л
О е~
Она позволяет записать условия согласования (9) в форме:
(И)
Га \
А„.
= D(a)
'V
Л J
A2)
или с учетом F):
fA,
А„,,
= D(a)M(a)
ГаЛ
v л)
A3)
Используя G) и применив метод итераций, получим:
<А ^
(а Л f a ^
:[D(a)Af(a)f 4 = [D(a)Af(a)J
V 1 у
д
[ Д J
A4)
И, наконец, благодаря равенствам F) и A4) можно преобразовать условие согласования
A0) в следующее:
или
(с Л
С
(г \
С
= M(a)
^4 А
д:
:M(a)[D(a)M(a)f"
= M(a)D(a)M(a)D(a)...D(a)M(a)
N-матриц М (a)
V ^7
A5)
A6)
f л Л
В этой формуле, позволяющей перейти от
А,
f С ^
С
, матрица. М(а) связана с
каждым барьером, а матрица D(a) определена каждым интервалом между двумя
последовательными барьерами.
Равенства A3) и A4) показывают, что очень важную роль играет матрица:
457

Глава III
е«х) = £>(а)М(а),
A7)
которая входит в степени п, если осуществляется переход от
(А)
W
(А Л
л'
л»+1
, то есть
когда производится трансляция с амплитудой nl вдоль периодической структуры. По
этой причине будем называть Q(a) «матрицей итерации». Используя формулу A8)
дополнения Nm и выражение A1) для £>(ос), получим:
б(сс) =
(eialF(a) eicUG*(a)^
e~iaJG(a) e~ialF\a)
A8)
Вычисление матрицы [<2((x)j станет легче, если изменить базис так, чтобы Q(a)
приобрела диагональный вид, и именно поэтому представляет интерес нахождение
собственных значений матрицы Q(a).
d. СОБСТВЕННЫЕ ЗНАЧЕНИЯ Q((X)
Пусть А, — собственное значение B(a). Характеристическое уравнение матрицы
A8) запишется в виде:
[eiaJF(a)-x][e-ialF\a)-x]-\G(a)\2 =0, A9)
то есть с учетом соотношения B1) дополнения Nin:
X2-2XX(a) + l = 0,
где Х(а) — вещественная часть комплексного числа е'а F(a):
X (a) = Re [em F(a)] = - tr Q(a)
B0)
B1)
Напомним [см. дополнение Ыш, равенство B1)], что модуль F(a) больше 1, и,
следовательно, то же можно сказать и о модуле выражения e,alF(a).
Дискриминант уравнения второй степени B0) равен:
А, = [Х(а)р-1. B2)
Возможны два случая:
458

Постулаты квантовой механики
(i) Энергия Е такова, что
|*(а)|<1 B3)
(например, если на рис.2 значение а заключено между ос0 и а{) и можно положить:
X(a) = cos[k(a)l], B4)
где
О < jfc(cc) < -. B5)
Рис.2
Зависимость от а комплексного
числа ёы F(a) = X (а) + /Г(а).
Поскольку |F(oc)| > 1, кривая в
комплексной плоскости
расположена вне круга единичного
радиуса с центром в точке О.
Последующий анализ
показывает, что при |Х(сс)|<1 для
выбранного значения а точка
находится на кривой, заключенной
между двумя вертикальными
прямыми, изображенными на
рисунке пунктиром, то есть
соответствующая энергия попадает в
«разрешенную зону». В
противном случае энергия принадлежит
«запрещенной зоне»
Нетрудно показать, что в этом случае собственные значения матрицы Q(a) равны:
Х = *±Л(в)\ B6)
то есть это два комплексно сопряженных числа с модулем 1.
(ii) Если, напротив, энергия Е соответствует такому значению а, что
|*(а)|>1 B7)
(например, если на рис.2 это значение заключено между а, и а2), то можно положить:
459

Глава III
X(a) = E-ch[p(a)l],
B8)
где
p(a)>0 B9)
и е = +1, если Х(а) > 0, и б = -1, если X(a) < О . Отсюда следует, что
А = е-е±р(а)/. C0)
В этом случае оба собственных значения Q(a) являются вещественными и обратными
друг другу.
2. Физический смысл: понятие энергетической зоны
(разрешенной или запрещенной)
а. ПОВЕДЕНИЕ ВОЛНОВОЙ ФУНКЦИИ фа(л)
Начнем с вычисления двух матриц-столбцов Л! (а) и Л 2 (а), соответствующих
собственным векторам оператора <2(°0 с собственными значениями X, и Х2; затем разло-
(АЛ
жим матрицу
по этим векторам:
ч
а:
= с{ (а)Л, (а) + с2(а) Л2 (а),
C1)
откуда сразу же можно получить:
А'
\ п j
= Х,с](а)А1(а) + кп2']с2(а)А2(а)
C2)
Ясно, что поведение волновой функции существенно зависит от области энергии, от
того, каким является модуль |ЛГ(ос)| по сравнению с 1. Действительно, в первом случае
формула B6) показывает, что последовательный переход через барьеры выражается в C2)
сдвигом фазы проекций матрицы-столбца
а:
на векторы Aj(a) и Л2(а), и при этом
поведение функции фа(л:) напоминает поведение суперпозиции мнимых экспонент.
Напротив, если энергия такова, что |Х(а)| > 1, формула C0) указывает, что только одно
460

Постулаты квантовой механики
из собственных значений (например, А.,) по модулю превышает 1; тогда для достаточно
больших п имеем:
л:
se'-V'-'^VaMite). C3)
Таким образом, Лп и А'п с ростом п увеличиваются экспоненциально [за исключением
частного случая, когда с,(а) = 0]. Итак, волновая функция фа(;с) становится все
большей и большей по модулю по мере того, как она проходит последовательно через
потенциальные барьеры, и ее поведение напоминает поведение суперпозиции
вещественных экспонент.
Ь. ОТРАЖЕНИЕ БРЭГГА. ВОЗМОЖНЫЕ ЗНАЧЕНИЯ ЭНЕРГИИ ЧАСТИЦЫ
В ПОЛЕ ПЕРИОДИЧЕСКОГО ПОТЕНЦИАЛА
В зависимости от того, ведет ли себя функция фа (х) как вещественная или как
мнимая экспонента, происходящие явления будут существенно различными.
Оценим, например, коэффициент прохождения TN(a) через совокупность N
одинаковых барьеров. Равенство A5) показывает, что для них матрица M(ol)\Q(ol)\~1
играет роль, аналогичную роли матрицы М (а) для одиночного барьера. Согласно
соотношению B9-Ь) дополнения Nm коэффициент прохождения Т(а) выражается через
элемент этой матрицы, стоящий на пересечении первой строки и первого столбца
[величина, обратная TN(a), равна квадрату модуля этого элемента].Что произойдет, если
энергия частицы Е окажется такой, что собственные значения матрицы 2(a) будут
вещественными, то есть определяться формулой C0)? Если только N достаточно
велико, собственное значение А,, =е-ер(о0/ станет доминирующим, и матрица [Q(a)]N_1
экспоненциально возрастает с увеличением N [именно это, впрочем, и выражает
равенство C3)]. В результате коэффициент прохождения экспоненциально убывает:
TN(a)oce-2Npia)l. C4)
В этом случае для больших значений N совокупность N потенциальных барьеров
практически обязательно отразит частицу. Этот вывод базируется на том обстоятельстве,
что волны, рассеянные различными потенциальными барьерами, интерферируют
полностью деструктивным образом для прошедшей волны и конструктивным образом — для
волны отраженной. Это явление можно сопоставить с отражением Брэгга. Заметим,
однако, что такая деструктивная интерференция для прошедшей волны может иметь
461

Глава III
место даже в том случае, если энергия Е больше высоты барьера (в классической
механике в этом случае частица проходит через барьер).
Можно заметить, что если коэффициент прохождения одиночного барьера мало
отличается от 1, то |F(a)| = l [например, на рис.2 |F(oc)|—И, если а, то есть энергия
стремится к бесконечности], в результате чего точка, представляющая комплексное
число eialF(a), очень близка к окружности единичного радиуса с центром О. Из рис.2
видно тогда, что области оси энергии, где |Х(а)|>1, то есть области, в которых имеет
место полное отражение, очень узкие, и практически их ширина близка к нулю.
Физически это объясняется тем, что если энергия Е падающей частицы велика по сравнению с
максимальным изменением потенциала V(x), то ее импульс точно определен, как и свя-
X
занная с ним длина волны. При этом условие Брэгга / = п— (где п — целое число) дает
вполне определенные значения энергии.
Если, напротив, энергия Е частицы попадает в область, где собственные значения
равны по модулю 1, как в B6), то элементы матрицы [Q(cl)]n~1 более не стремятся к
бесконечности с ростом N . В этих условиях коэффициент прохождения TN (а) не
стремится к нулю с увеличением количества барьеров. Речь при этом идет о чисто квантовом
явлении, связанном с колебательным характером волновой функции, позволяющим ей
распространяться в регулярной периодической потенциальной структуре без
экспоненциального затухания. Заметим, в частности, что коэффициент прохождения 7^ (а) при
этом резко отличается от произведения индивидуальных коэффициентов отражения
каждого из барьеров (это произведение стремится к нулю, если N —> <» , так как все
сомножители меньше 1).
Другая интересная задача, с которой встречаются в физике твердого тела, состоит в
квантовании уровней энергии частицы, помещенной в серию одинаковых
потенциальных ям, регулярно распределенных в пространстве, то есть в случае, когда потенциал
V{x) также обнаруживает периодическую структуру. Эта задача подробно
рассматривается в следующем параграфе, однако мы можем уже сейчас догадаться, каким будет
спектр возможных энергий. Действительно, допустим, что энергия частицы такова, что
> 1, тогда уравнение C3) показывает, что коэффициенты Ап и А'п стремятся
к бесконечности при п —> °о . Это значит, что подобную возможность нужно отклонить,
так как волновая функция оказывается неограниченной. Соответствующие значения
энергии не могут быть реализованы и образуют запрещенные зоны, в которых |Х(ос)| > 1.
Напротив, если энергия частицы такова, что |Х(а)|<1, то Ап и А'п остаются
ограниченными, если п —> ©о . Соответствующие области энергии называют разрешенными
зонами. Таким образом, спектр энергий состоит из конечных интервалов, в пределах
\Х(а)\
462

Постулаты квантовой механики
которых все энергии разрешены, разделенных интервалами, в которых все значения
энергии запрещены.
3. Квантование уровней энергии
в потенциале с периодической структурой.
Влияние граничных условий
Рассмотрим частицу с массой т, помещенную в поле потенциала V(x), представленного на
рис.3: в области < х< N1 Н— потенциал имеет периодический характер и состоит из N +1
последовательных барьеров высотой V0 с центрами в точках х = 0, /, 2/,..., N1 ; вне этой области
функция V(x) испытывает изменение на расстоянии, сравнимом с /, а затем остается равной
постоянной и положительной величине Ve. В дальнейшем область [О, MJ будем называть
«внутренней областью цепочки», а граничные области jc = и дг = М + — будем называть «краями
цепочки».
Физически такая функция V(x) может представлять потенциал, который «чувствует»
электрон в линейной молекуле, или (если ограничиться одномерной моделью) в кристалле. Потенци-
/ 3/
альные ямы, расположенные в точках х = —, —, ...соответствуют тогда притяжению электрона
различными ионами кристалла; вдали от него (или от молекулы) электрон не испытывает
никакого притяжения, вследствие чего V(x) быстро становится постоянной величиной, как только элек-
/ /
трон оказывается вне области <х< N1 + —.
2 2
С точностью до начала отсчета энергии представленный здесь потенциал V(x) остается в
рамках задачи, рассмотренной в дополнении Мш: мы уже знаем, что энергии связанных состояний
частицы образуют дискретный спектр со значениями, меньшими Ve. Однако потенциал V(x)
обладает замечательной особенностью: он имеет периодическую структуру того же типа, что и
рассмотренная ранее в § 1. Опираясь на полученные там результаты, покажем, что здесь выводы
принимают особенную форму. Например, в дополнении Мш мы утверждали, что именно граничные
условия [ ф(х) —> 0, если х —> °о ] приводят к квантованию уровней энергии. Можно было бы
подумать, что и в этой задаче граничные условия на краях цепочки играют критическую роль,
определяющую возможные значения энергии. На деле это не так: мы убедимся в том, что эти
значения практически зависят только от значений V(x) в области, где потенциал испытывает
периодичность, а не от краевых эффектов (при условии, конечно, что количество потенциальных ям
достаточно велико). Кроме того, мы докажем интуитивно полученный в § 2-Ь результат, показав,
что большинство допустимых значений энергии группируются в разрешенные зоны, и лишь некото-
463

Глава 111
рые стационарные состояния, локализованные вблизи границ цепочки, критическим образом зависят
от изменения V(x) в этих областях и могут иметь энергию, попадающую в запрещенную зону.
Рис.3
Зависимость потенциала, с которым взаимодействует электрон в «одномерном»
кристалле и на его краях, от координаты х. Внутри кристалла потенциал имеет периодическую
структуру; V{x) максимален между ионами (барьеры в точках х = 0, /, 2/,...) и минимален
в точках, соответствующих позициям ионов (ямы в точках х~—,—,...). На краях
кристалла функция V{x) изменяется более или менее сложным образом на расстояниях
порядка /, а затем быстро стремится к постоянному значению Ve
Итак, в основном мы будем следовать методике, использованной ранее в дополнении Мщ, и
исследуем сначала условия, наложенные на волновую функцию стационарного состояния.
а. УСЛОВИЯ, НАЛАГАЕМЫЕ НА ВОЛНОВУЮ ФУНКЦИЮ
В области, где потенциал V(x) периодичен, соотношение (З-d) определяет форму волновой
функции фа(х), коэффициенты которой Ап и Ап находятся из равенства C2). Чтобы записать
его в максимально явном виде, положим:
с, (ОС) Л, (ОС) =
с2(а)Л2(ОС) =
/i'«x)
/2'(а)
C5)
464

Постулаты квантовой механики
При этом получим:
A.=/i(a)^",+/2(a)XVl:
^//(аиГ'+Л'Са)^-'. Об)
Исследуем теперь граничные условия, которым должна удовлетворять волновая функция
фа(х). Прежде всего, далеко слева от цепочки потенциал V(x) равен Ve, и фа(х) записывается
в форме:
<ра(х) = Ве^>\ C7-е)
где
■-#«
И(а) = Л/—(Ve-£) C7-Ь)
(мы исключаем решение вида е~ц(а)лг, которое расходится при х —»-°°). Ток вероятности,
связанный с функцией C7), равен нулю (см. дополнение Вш , § 1); поскольку для стационарного
состояния ток не зависит от х [см. дополнение Nni, формула A2)], то он остается равным нулю в
любой точке х и, в частности, внутри цепочки. Согласно формуле A4) дополнения Nni,
коэффициенты Ап и А'п должны обязательно быть равны по модулю. Итак, если выразить граничные
условия слева через соотношение между Ап и А'п [то есть записать, что выражение функции
фа(лг) при < х < — является продолжением волновой функции C7)], то получим равенство:
А = е*(а\ C8-а)
А
где Х((Х) — вещественная функция а ( и, следовательно, энергии Е ), зависящая от конкретной
формы потенциала V(x) на левой границе цепочки [в дальнейшем нам не потребуется явная
форма выражения для %((Х), существенно лишь то, что граничные условия слева имеют вид
формулы C8-а)].
Такие же рассуждения применимы, очевидно, и на правой границе (х —> +©°), где граничные
условия запишутся в виде:
^L = e*(a\ C8-b)
А
где вещественная функция % (Об) определяется поведением V(x) на правой границе цепочки.
30 Квантовая механика
465

Глава III
Чтобы закончить, сформулируем правила квантования уровней энергии:
— исходными являются два коэффициента Д и А[, удовлетворяющие соотношению C8-а),
обеспечивающему ограниченность функции фа(*) при х —> -оо . Поскольку фа(л:) определена с
точностью до множителя, можно выбрать, например:
Ах-е
_^'Х(а)/2.
_ -0С(а)/2
д; = *-**""<; C9)
— затем, используя C6), вычисляют коэффициенты Ап и А'п с целью получить продолжение
выбранной волновой функции во всем кристалле. Заметим, что условие C9) требует, чтобы
функция Ц>а(х) была вещественной (см. дополнение Nnb §1-Ь).Тогда по необходимости:
к=<-, D0)
— наконец, записывают, что коэффициенты AN+l и Л^+1 должны удовлетворять равенству
C8-Ь), обеспечивающему ограниченность функции фа(х) при х —> -Н» . Действительно,
равенство D0) показывает, что отношение AN+] к Л^+1 автоматически является комплексным числом,
модуль которого равен 1, вследствие чего условие C8-Ь) сводится к равенству между фазами двух
комплексных чисел. В результате получается вещественное уравнение относительно переменной
ОС, допускающее определенное количество вещественных решений, дающих разрешенные
значения энергии.
Мы сейчас применим эти правила, различая два случая в зависимости от того, являются ли
собственные значения матрицы Q((X) вещественными [случай Х(ос) > 1 ] или мнимыми [случай
|Х(сс)|<1.
Ь. РАЗРЕШЕННЫЕ ЭНЕРГЕТИЧЕСКИЕ ЗОНЫ:
СТАЦИОНАРНЫЕ СОСТОЯНИЯ ЧАСТИЦЫ ВНУТРИ ЦЕПОЧКИ
Допустим сначала, что энергия Е находится в области, где Х(ос) < 1.
а. Форма уравнения квантования
С учетом B6) соотношения C6) записываются в виде:
А, = fl(a)ea"-ima)l +f2(a)e-il"-,Wa)';
К = /•1'(а)е'("-1,'(а>' +/2'(а)e-'("-1)*<а,'
D1)
466

Постулаты квантовой механики
С другой стороны, мы видели, что выбор C9) коэффициентов Ап и А'п влечет за собой равенство
А'п = Ап независимо от значения п . Тогда нетрудно убедиться в том, что соотношения D1) дают
два комплексно сопряженных числа только в том случае, если:
/,*(а) = /2'(а);
/2*(а) = /,'(а). D2)
Условие C8-Ь) тогда перепишется в форме:
/|(а)е2Ш,а„+Л(а)_^(а)
/;(а)^,а"+/,-(а)
е'Л,и\ D3)
Это уравнение относительно Ct и является тем уравнением, которое дает квантование
уровней энергии. Для его решения положим:
= [/Г(аУ^2-Л(а)е-^Ч
[функция в(а) может быть в принципе вычислена, если известны %@t), %'@С) и Q((X)]. Тогда
уравнение D3) принимает простой вид:
e2iNk(a)l = ета) D5)
Уровни энергии определяются равенством:
,, ч 0(a) п
&(ос) = —^-+р—, D6)
2NI N1
где
p = 0,l,2,...,(W-l) D7)
[другие значения р должны быть исключены, так как условие B5), наложенное здесь на А: (а),
требует, чтобы эта функция изменялась в интервале шириной Till ]. Заметим, что если N очень
велико, то уравнение D6) можно записать в упрощенном виде:
к(а) = р—. D8)
И N1
Р. Графическое решение. Определение энергетических уровней
Если подставить определение B4) функции к((Х) в D6), получим уравнение относительно a ,
определяющее разрешенные значения энергии. Чтобы решить его графически, изобразим сначала
30*
467

Глава III
кривую, представляющую функцию Х(ос) = Re[e' F(oc)]; из-за наличия экспоненты с мнимым
показателем можно ожидать, что эта кривая будет иметь осциллирующий характер, как,
например, изображено на рис.4а. Поскольку |F(a)| > 1 [см. дополнение Nni, формула C2)],
\Х(а)
Рис.4
Зависимость функции Х(а) = Re[elcdF(a)] (см.рис.2) и к(а) = -Arc cos {X(a)} от а.
Значения переменной а (то есть энергии Е) , соответствующие стационарным
состояниям, при N »1 получаются в точках пересечения графика функции к(а) горизонталь-
ными прямыми с уравнениями у = р— , где р = 0,1, 2,..., (N -1). Так образуются раз-
М
решенные зоны, включающие в себя N близко расположенных уровней а0<а<а, и
т.д., и запрещенные зоны, для которых а} <а<а2 и т.д. Изображенные пунктиром
кривые соответствуют частному случаю, когда V(x) - 0 (свободная частица)
468

Постулаты квантовой механики
то амплитуда колебаний больше 1, так что эта кривая пересекает две прямые Х((х) = ±1 при
некоторых значениях СС0, 0СР СС2,... переменной а . Таким образом, мы выделяем все области оси
а, ограниченные этими значениями, где условие Х((Х)| <1 не выполняется. С помощью
полученного набора дуг кривой X (а) мы должны теперь представить функцию:
k(a) = -arccos{X(a)}.
D9)
С учетом формы кривой arc cos z (рис.5) получим кривые, имеющие вид, представленный
на рис.4Ь. Уравнение D6) указывает, что уровни энергии определяются точками пересечения этих
I/ ч 0(а) п
кривых кривыми, изображающими функции А: (а) = V р—, то есть практически (при
71
N » 1) горизонтальными прямыми с уравнениями у = р— , где р = 0,1, 2,..., (N -1).
Таким образом, имеются группы, состоящие из N уровней, связанных с эквидистантными
значениями к((Х) и расположенных в разрешенных зонах, определяемых неравенствами:
СС0 < а < (Xj, а2 < а < а3 и т.д. Между этими разрешенными зонами находятся запрещенные
зоны (их свойства мы уточним в § с).
Рис.5
Функция arc cos z
Если нас интересует вполне определенная разрешенная зона, то каждый из соответствующих
уровней можно обозначить значением к((Х). Тогда можно принять к в качестве переменной и
рассматривать а и, следовательно, энергию Е как функции <Х(к) и Е(к). Зависимости <Х(к)
469

Глава HI
непосредственно даны кривой, изображенной на рис.4Ь, и достаточно найти функцию
чтобы получить энергию Е{к). Эта зависимость представлена кривой, изображенной на рис.6.
2т
\т
/
/
\/
У
к
N
^\
| \\
1 —
V
-*•"""""
\
N
I
1
[
1
1
1
1
1
1
1
1 /
__ж
^"
1
1
1
-1
/
/
►
*//
Рис.6
Зависимость энергии от параметра к. Сплошными
кривыми изображены энергии двух первых
разрешенных зон (значения к , определяющие эти энергии,
эквидистантны в интервале 0<к<п/1). Пунктиром
изображены кривые для частного случая V(x) = 0
(свободная частица), при этом разрешенные зоны
смыкаются, и запрещенные зоны отсутствуют
ЗАМЕЧАНИЕ
Из рис.4Ь ясно, что заданному значению к соответствуют несколько значений ОС и,
следовательно, энергии. Именно поэтому на рис.6 представлено несколько отрезков кривой.
Однако если в данной разрешенной зоне функция Х(сс) плавно увеличивается от -1 до +1
(или плавно уменьшается от +1 до -1), то каждому значению к в этой зоне соответствует
лишь один уровень энергии, и эта зона состоит из N энергетических уровней.
у. Физический анализ
Приведенные выше вычисления показывают, как можно перейти прогрессивно от ансамбля
дискретных уровней к разрешенным энергетическим зонам путем увеличения N от 1 до очень
больших значений. Строго говоря, и эти зоны образованы дискретными уровнями, но расстояние
между ними для макроскопических цепочек столь мало, что практически их можно считать
непрерывными. Если выбрать к в качестве параметра, то плотность состояний (количество
возможных значений энергии в единичном интервале к ) постоянна и равна Nlln. Это свойство
очень удобное и объясняет, почему в качестве переменной обычно выбирают к .
При переходе от D6) к D8) следует отметить важную деталь: если N велико, то влияние
470

Постулаты квантовой механики
границ цепочки, проявляющееся через функции Х(°0» Х'(°0 и в формуле D6) через <2(сс), не
играет никакой роли, и лишь периодичность потенциала внутри цепочки существенна для
определения возможных энергий.
Интересно рассмотреть два предельных случая.
(i) Если V(x) = 0 (свободная частица), то
>(а) = 1;
E0)
X(a) = cos(al)
и легко получить:
Я
к(а) = а , если 0 < а < — ;
/
2тг 71 2я
к(а) = а,если — <а<— E1)
III
и так далее. Соответствующая ломаная линия представлена на рис.4Ь пунктиром. Равенство E0)
показывает, что условие |Х(а)| < 1 реализуется всегда, и, следовательно, для свободной частицы
не существует запрещенных зон энергии.
Рис.6 позволяет продемонстрировать влияние потенциала V{x) на кривую Е(к): наряду с
тем, что появляются запрещенные зоны, описывающие энергию, кривые деформируются так, что
допускают появление горизонтально расположенных касательных для значений /; = 0 и к = п/1
(края зоны); в противоположность тому, что наблюдалось для свободной частицы, в каждой зоне
имеется точка перегиба, вблизи которой энергия изменяется с к линейно.
(И) Если коэффициент прохождения Г(а) практически равен нулю, то [см. дополнение Nm,
уравнения B9) и B1)]:
f|F(a)|»l;
E2)
1|С(а)|»1.
На рис.2 точка, изображающая комплексное число eia F(Oi), очень далека от начала координат, и
из этого же рисунка видно, что области оси а, где |Х((Х) < 1, очень узки. Таким образом,
разрешенные зоны сужаются, если уменьшается коэффициент прохождения для отдельного барьера.
В пределе, когда прохождение отсутствует вовсе, эти зоны сужаются до отдельных уровней в
изолированной потенциальной яме. И обратно, как только туннельный эффект позволяет частице
перейти из одной ямы в следующую, каждый из дискретных уровней порождает
энергетическую зону, ширина которой тем больше, чем больше коэффициент прохождения через барьер.
Мы еще вернемся к этому свойству в дополнении FXi.
471

Глава III
с. ЗАПРЕЩЕННЫЕ ЗОНЫ:
СТАЦИОНАРНЫЕ СОСТОЯНИЯ, ЛОКАЛИЗОВАННЫЕ НА КРАЯХ ЦЕПОЧКИ
а. Форма уравнений; уровни энергии
Допустим теперь, что а принадлежит области, где Х(а) >1. Согласно C0), соотношения
C6) можно переписать в виде:
А„ = е" [/, (а)е(,,-1)р(а)/ + /2 (а)^-(")р(а)/ ]
А'п =е"-,[/1,(аУМ)р(а)/ +/;(а)^(л-1)р(а)/]
Тот факт, что А'п = Ап при любых п , требует, чтобы
/,,(а) = /1*(а);
/2'(а) = /2*(а).
Условие квантования C8-Ь) принимает тогда форму:
An* = /i(a)+/2(g)e-2Wp(a); = ,У(а,
A'N+l А'(а)+/;(а)е-2^'
E3)
E4)
E5)
e-2/vp(a)/=L(a)i E6)
где вещественная функция L(cc) определена выражением:
L{a)-~f;(a)e*^-f2(a)e-*^- E7)
Пусть N » 1, тогда е~ Np{a)l = 0 , и уравнение E6) сводится к
Да) = 0. E8)
Уровни энергии, расположенные в запрещенных зонах, определяются нулями функции L@t) (см.
рис.7). Значение N не входит ни в формулу E7), ни в E8), и количество этих уровней не зависит
от N ъ противоположность количеству уровней, расположенных в разрешенной зоне. Итак, если
N » 1, то можно сказать, что практически все уровни сгруппированы в разрешенных зонах.
472

Постулаты квантовой механики
Р. Физический анализ
В рассматриваемом случае ситуация радикально отличается от той, с которой мы встречались
в § Ь. Число N , то есть длина цепочки, не играет никакой роли (хотя и должно быть достаточно
большим). Напротив, определение E7) функции L(a) показывает, что функции %@С), %'@С)
существенно важны. Поскольку известно, что эти функции зависят от поведения потенциала
V(x) на краях цепочки, следует ожидать, что они позволят определить состояния,
локализованные в этих областях.
Рис.7
Зависимость L(oc) в запрещенной зоне.
Нули функции Ца) определяют
стационарные состояния, локализованные
на краях цепочки
И это действительно так. Уравнения E7) и E8) допускают две возможности,
(i) если /, (а) Ф О, то обращение в нуль функции Цех) требует, чтобы
/i(g) ^/i(a) _ciX>(a)
/Г(а) /Да)
E9)
Вернемся к определению C5) функций /,(ос) и /,'(сс). Мы видим, что равенство E9) выражает
просто тот факт, что волновая функция, построенная для первого собственного вектора оператора
<2@С), удовлетворяет граничным условиям справа. И это понятно: если в точке х = 0 имеется
(АЛ
произвольная волновая функция, удовлетворяющая граничным условиям слева, то матрица ,
имеет проекции на два собственных вектора оператора Q((X); коэффициенты AN+l и A'N+] тогда
473

Глава III
практически (если N » 1) определяются формулой C3), которая утверждает, что матрица
пропорциональна матрице-столбцу первого собственного вектора оператора Q(OC).
А
А'
Отметим, что поскольку собственное значение Х{ (а) больше 1, волновая функция
экспоненциально растет с увеличением х . Таким образом, стационарное состояние, определяемое первым
собственным вектором оператора Q(OL), локализовано у правой границы цепочки.
(ii) Если /,((Х) = 0 , то выражение E4) дает /,'@С) = 0, и из определения C5) следует, что
с, (а) = 0 . Это означает, что соответствующее стационарное состояние связано со вторым
собственным вектором оператора Q(Ct). Все выводы, сделанные в пункте (i), остаются справедливыми,
но только это состояние оказывается локализованным у левой границы цепочки.

Глава IV
ПРИМЕНЕНИЕ ПОСТУЛАТОВ
К ПРОСТЫМ СЛУЧАЯМ:
СПИН 1/2
И ДВУХУРОВНЕВЫЕ СИСТЕМЫ

ПЛАН ГЛАВЫ IV
А. ЧАСТИЦА СО СПИНОМ 1/2:
КВАНТОВАНИЕ
МЕХАНИЧЕСКОГО
МОМЕНТА ЧАСТИЦЫ.
1. Экспериментальное обнаружение спина.
a. Опыт Штерна и Герлаха.
b. Классический расчет отклонения.
c. Результаты и выводы.
2. Теоретическое описание.
a. Наблюдаемая Sz и пространство спиновых
состояний.
b. Другие спиновые наблюдаемые.
В. ИЛЛЮСТРАЦИЯ
ПОСТУЛАТОВ В СЛУЧАЕ
СПИНА 1/2.
1. Конкретное приготовление различных спиновых
состояний.
a. Приготовление состояний +) и —).
b. Приготовление состояний ±) . i/ > ±) •
c. Приготовление состояния в общем случае.
2. Измерения спина.
a. Первый эксперимент.
b. Второй эксперимент.
c. Третий эксперимент.
d. Средние значения.
3. Эволюция спина 1/2 в однородном магнитном поле.
a. Гамильтониан взаимодействия и уравнение
Шредингера.
b. Прецессия Лармора.
С. ОБЩИЙ АНАЛИЗ
ДВУХУРОВНЕВЫХ
СИСТЕМ.
1. Постановка задачи.
a. Обозначения.
b. Последствия связи.
2. Статический аспект: влияние связи на стационарные
состояния системы.
a. Выражения для собственных значений и
собственных состояний оператора Н.
b. Физическое обсуждение.
c. Важное применение: явления квантового резонанса.
3. Динамический аспект: осцилляции системы между
двумя невозмущенными состояниями.
a. Эволюция вектора состояния.
b. Вычисление У[2(£). Формула Раби.
c. Физическое обсуждение.
d. Конкретный пример осцилляции между двумя
состояниями.

В этой главе мы предполагаем проиллюстрировать постулаты квантовой механики,
введенные и рассмотренные в главе III. Применим их к конкретным простым случаям,
когда размерность пространства состояний конечна и равна двум. Интерес к этим
примерам связан не только с их математической простотой, позволяющей лучше понять
постулаты и их следствия, но и с физическим смыслом этих задач, так как в них мы
встретимся с типично квантовыми эффектами, которые четко подтверждаются
экспериментом.
В § А и § В изучим случай спина 1/2 (его более полное рассмотрение будет
предложено в главе IX). Сначала в § А-1 опишем фундаментальный эксперимент, позволивший
доказать квантование простой физической величины — механического момента. Мы
увидим, что проекция механического (или магнитного) момента нейтрального
парамагнитного атома на ось Oz может принимать только дискретный набор значений. Так, для
атома серебра, находящегося в основном состоянии, существует лишь два возможных
значения проекции Sz его механического момента, равных +fill и -hi2. Говорят, что
атом серебра в основном состоянии является частицей со спином 1/2. Далее в § А-2
покажем, как в квантовой механике описывают «спиновые» переменные такой частицы:
в ситуациях, когда можно не применять квантовый подход к «внешним» переменным г
и р, размерность пространства состояний частицы (пространство «спиновых»
переменных) равна двум. После этого проиллюстрируем и обсудим применение постулатов
квантовой механики к особенно простому частному случаю: мы увидим, как можно в
рамках конкретного эксперимента приготовить систему атомов серебра в любом заранее
заданном спиновом состоянии. Затем покажем, каким образом можно экспериментально
доказать справедливость постулатов квантовой механики при измерении спиновых
физических величин в системе атомов серебра. Интегрируя уравнение Шредингера,
мы сможем исследовать эволюцию системы спинов 1/2 в однородном магнитном поле
(прецессия Лармора). И, наконец, в § С рассмотрим методы анализа двухуровневых
систем. Несмотря на то, что такие системы в общем случае не составлены из частиц со
спином 1/2, их анализ очень похож на вычисления, выполненные в § А и § В. Детально
исследуем влияние внешнего возмущения на стационарные состояния двухуровневой
системы и покажем, что эта простая модель позволяет объяснить важные физические
эффекты.
477

Глава IV
А. ЧАСТИЦА СО СПИНОМ 1/2:
КВАНТОВАНИЕ МЕХАНИЧЕСКОГО МОМЕНТА ЧАСТИЦЫ
1. Экспериментальное обнаружение спина
Сначала опишем и проанализируем эксперимент Штерна и Герлаха, позволивший
впервые обнаружить квантование проекций механического момента (называющееся
иногда «пространственным» квантованием).
а. ОПЫТ ШТЕРНА И ГЕРЛАХА
Сущность эксперимента состоит в изучении отклонения пучка нейтральных
парамагнитных атомов (в первом эксперименте атомов серебра) в резко неоднородном
магнитном поле. Схема эксперимента представлена на рис. Г.
Атомы серебра, содержащиеся в сосуде Е , нагретом до высокой температуры,
вылетают из него через узкое отверстие и продолжают двигаться в высоком вакууме по прямой
линии. Коллимирующая щель F выбирает из пучка такие атомы, скорость которых
параллельна заранее выбранному направлению, которое обозначим как ось Оу. Образованный
пучок атомов проходит далее через зазор электромагнита А и падает на пластинку Р.
Уточним характеристики магнитного поля В , созданного электромагнитом А. Это
магнитное поле симметрично относительно плоскости (обозначим ее yOz), в которой
лежит начальное направление Оу атомного пучка, и в зазоре магнита оно одинаково во
всех точках, расположенных на прямых, параллельных оси Оу (края электромагнита
параллельны Оу, и мы пренебрежем их влиянием), и, следовательно, поле В не имеет
компоненты, направленной вдоль Оу. Максимальная компонента поля направлена вдоль
оси Oz и сильно меняется вдоль этой оси: на рис.lb видно, что силовые линии
магнитного поля сближаются у северного полюса магнита и становятся значительно более
редкими у южного его полюса. Конечно, поскольку поток вектора индукции сохраняется
(divB = 0), должна существовать компонента поля, направленная вдоль оси Ох,
изменяющаяся с координатой х в плоскости симметрии.
Ь. КЛАССИЧЕСКИЙ РАСЧЕТ ОТКЛОНЕНИЯ**
Заметим сначала, что атомы серебра, будучи нейтральными, не испытывают
действия силы Лапласа. В то же время они обладают постоянным магнитным моментом Л
* Мы приводим только важнейшие узлы установки. Детальное описание экспериментальной
техники можно найти в любой книге по атомной физике.
** Здесь мы ограничимся только основными идеями расчета, ссылаясь на детальное
изложение в работах по атомной физике.
478

Применение постулатов к простым случаям
(так как являются парамагнитными атомами), потенциальная энергия взаимодействия
которого с магнитным полем равна:
W = -Jt В.
(А-1)
b
>
Ч\\
V>
к -
Sud
,'/V
Nord
Рис.1
Схема эксперимента Штерна и Герлаха. На рис. а изображена траектория атома серебра,
вылетевшего из сосуда Е , нагретого до высокой температуры. Атом отклоняется
градиентом магнитного поля, созданного электромагнитом А , и затем конденсируется на
пластинке Р. На рис. b изображено сечение электромагнита А плоскостью xOz; силовые
линии магнитного поля даны пунктиром. Предполагается, что Bz>0 и dBz/dz<0,
вследствие чего траектория, приведенная на рисунке, соответствует отрицательной
компоненте Лг магнитного момента, то есть положительной компоненте момента $fz (для
атома серебра величина у отрицательна)
Существование у атома электронного магнитного момента Л и механического
момента £Р обусловлено двумя причинами: движением электронов вокруг ядра (вращение
зарядов всегда связано с появлением орбитального магнитного момента) и собственным
479

Глава IV
механическим моментом (или спином) электронов, с которым также связан спиновый
магнитный момент. Можно показать (здесь мы принимаем утверждение без
доказательства), что для данного атомного уровня величины Ж и У> пропорциональны*:
Ж = у9>. (А-2)
Коэффициент пропорциональности у называется гиромагнитным отношением
рассматриваемого уровня.
Магнитные моменты атомов серебра, образующих атомный пучок, перед
попаданием в область электромагнита ориентированы случайным образом (то есть изотропно).
Рассмотрим теперь влияние магнитного поля на один из этих атомов, магнитный момент
которого Ж при вхождении в межполюсный зазор имел определенное направление. Из
выражения (А-1) для потенциальной энергии нетрудно вывести, что действующие на
атом силы имеют равнодействующую:
F= V (ж-В) (А-3)
(эта равнодействующая будет равна нулю, если поле В является однородным), и что
полный момент силы относительно положения атома:
Г = ЖхВ. (А-4)
Теорема о механическом моменте записывается в виде:
^ = Г (А-5)
Л
или
d<P
— = Y^xB. (A-6)
dt
Таким образом, атом ведет себя, как гироскоп (рис.2): производная dtP/dt
перпендикулярна к У и механический момент вращается вокруг магнитного поля, причем угол Ь
* В случае атомов серебра в основном состоянии (как это имеет место в пучке) механический
момент $Р равен просто спину внешнего электрона, ответственного за существование магнитного
момента Ж . В действительности этот внешний электрон оказывается единственно ответственным
за существование магнитного момента Ж. Его орбитальный механический момент равен нулю;
кроме того, орбитальный и спиновый моменты внутренних электронов также равны нулю. И,
наконец, практически реализованные условия эксперимента таковы, что влияние спина ядра
оказывается пренебрежимо малым. По этой причине можно считать, что атом серебра в основном
состоянии, как и электрон, имеет спин 1/2.
480

Применение постулатов к простым случаям
между векторами 9> и В остается постоянным. Угловая скорость вращения равна
произведению гиромагнитного отношения у на модуль магнитного поля. Компоненты
вектора Л, перпендикулярные магнитному полю, осциллируют относительно нуля, тогда
как компонента, параллельная В , остается постоянной.
Для вычисления силы F [формула (А-3)] в энергии W с хорошим приближением
можно пренебречь членами, пропорциональными Jtx и . Нх, и принять JL , равной
постоянной величине.
1 В
Рис.2
Атом серебра обладает магнитным моментом JL и
механическим моментом У>; однородное магнитное поле В
вызывает прецессию вектора Л вокруг В с постоянной угловой
скоростью (прецессия Лармора)
Действительно, частота осцилляции из-за вращения Ж слишком велика, чтобы Jlx
и Jty могли бы войти иначе, чем через их среднее во времени значение, равное нулю.
Таким образом, дело обстоит так, как если бы атом был подвержен действию одной
единственной силы:
F' = grad (Jlz Bz) = Jtz grad Bz. (A-7)
С другой стороны, компоненты grad Bz вдоль осей Ох и Оу равны нулю, так как
dBz /ду = 0 вследствие независимости магнитного поля от у (см. выше) и dBz /Элс = 0 в
любой точке плоскости симметрии yOz . Таким образом, сила, действующая на атом,
параллельна оси Oz и пропорциональна проекции Jtz. Поскольку именно эта сила
является причиной смещения пучка атомов HN (см. рис.1), то величина HN
пропорциональна Jlz (или ffz) и, измеряя ее, можно измерить Jtz (или У>г).
Поскольку при входе в зазор магнита моменты различных атомов в пучке
распределены изотропно (реализуются все возможные значения Лг от | JC \ до -| JC |), то можно
31 Квантовая механика 481

Глава IV
было бы ожидать, что при попадании пучка на пластинку Р образуется единственное
пятно, симметричное относительно точки Я. Верхний Я, и нижний Я2 края этого пятна в
принципе должны соответствовать максимальному | Ж | и минимальному -| Ж |
значениям Jlz. Дисперсия скрростей и конечная ширина щели F должны быть причинами того,
что атомы, имеющие данное значение Jtz, не будут конденсироваться в одной точке,
а дадут пятно с центром, соответствующим средней скорости движения.
с. РЕЗУЛЬТАТЫ И ВЫВОДЫ
Результаты эксперимента, впервые выполненного Штерном и Герлахом в 1922 г.,
оказались в полном противоречии с предложенными выше рассуждениями.
На деле наблюдалось не одно пятно с центром вблизи точки Я, а два пятна (рис.3)
с центрами Я, и Я2, симметрично расположенные относительно точки Я (их ширина
действительно соответствовала дисперсии скоростей и ширине щели F). Таким
образом, предсказания классической механики были опровергнуты экспериментом.
Посмотрим теперь, как можно интерпретировать полученные результаты. Среди
физических величин, связанных с атомом серебра, можно различить, с одной стороны, такие,
которые соответствуют его внешним степеням свободы (то есть являются функциями
положения г и импульса р атома), и, с другой стороны, соответствующие его
внутренним степеням свободы (называемым еще спиновыми степенями свободы) Ж или У>.
Рис.3
Пятна, наблюдаемые на пластинке Р в эксперименте Штерна и
Герлаха. Поскольку магнитные моменты Ж атомов, испущенных
источником Е, случайно распределены по всем направлениям,
классическая механика предсказывает, что измерение . (lz может
дать с равной вероятностью любые значения от -\Ж\ до +\Ж\,
вследствие чего должно наблюдаться одно пятно, показанное на
рисунке пунктиром. В действительности опыт дает иной результат:
наблюдаются два пятна с центрами Я, и Я2; это означает, что
измерение Жг может дать только два возможных результата
(квантование результатов измерений)
Покажем сначала, что в условиях данного эксперимента нет необходимости
рассматривать внешние степени свободы с квантовых позиций. Для этого докажем, что для
описания движения атомов серебра можно построить волновой пакет, ширина которого
482
|Я
\Н
Я,

Применение постулатов к простым случаям
Az и дисперсия импульса Ар, будут пренебрежимо малы. Эти величины должны
удовлетворять соотношению неопределенностей:
Az • &pz > Й . (А-8)
Поскольку численно масса М атома серебра равна 1,8x10~25 кг, то Аг и
неопределенность измерения скорости Avz = Apz IM должны быть такими, чтобы:
Az-Avc >ЫМ «10"9 МКСА. (А-9)
Посмотрим, какие расстояния и скорости входят в данную задачу. Ширина щели
примерно равна 0,1 мм, расстояние N{N2 между двумя пятнами составило несколько
миллиметров, расстояние, на котором магнитное поле изменяется достаточно сильно, может
быть получено из значения поля внутри зазора магнита (#~104 Гс) и его градиента
(дВ } 1дВ
— = 105 Гс/см и равно В —— = 1 мм. С другой стороны, скорость атомов серебра,
[dz ) I oz
выходящих из печи с абсолютной температурой 1000° К, близка к 500 м/с; как бы ни
был точно сформирован пучок атомов, дисперсия их скоростей вдоль оси Oz не намного
меньше нескольких метров в секунду. Теперь можно без труда оценить
неопределенности Az и Avz, которые, вполне удовлетворяя неравенству (А-9), оказываются
пренебрежимо малыми в масштабах рассматриваемого эксперимента. Таким образом, нет
необходимости рассматривать внешние переменные г и р каждого атома с квантовой
точки зрения и можно считать их квазиточечными волновыми пакетами, движущимися
по классическим траекториям. Итак, можно считать доказанным, что измерение
отклонения HN соответствует измерению Jiz или У>,.
Результаты эксперимента неизбежно заставляют сделать следующий вывод: при
измерении компоненты Уг собственного механического момента атома серебра в
основном состоянии можно получить только одно из двух возможных значений,
соответствующих отклонениям HN{ и HN2. Таким образом, мы должны отказаться от
классического представления о векторе У , угол которого Ь относительно направления
магнитного поля может принимать любые значения, и признать, что Уг является квантованной
физической величиной, дискретный спектр которой может состоять только из двух
собственных значений. Когда мы будем изучать квантовую теорию момента (глава VI), мы
увидим, что эти собственные значения равны ± — , а пока примем это без доказательства
и будем говорить, что спин атома серебра в основном состоянии равен 1/2.
31*
483

Глава IV
2. Теоретическое описание
Здесь мы расскажем, как квантовая механика описывает степени свободы атома
серебра, то есть спина 1/2.
Пока еще мы не располагаем всеми необходимыми данными, позволяющими
развить строгую дедуктивную теорию спина 1/2. Это тема главы IX, где будет изложена
общая теория момента. Поэтому несколько результатов этой теории, которые будут
доказаны в главе IX, мы приведем пока без доказательства. Такой подход оправдан и тем,
что главная цель данной главы состоит в том, чтобы проиллюстрировать применение
формализма квантовой механики в простом конкретном случае, а не рассматривать
строгую теорию спина 1/2: мы получим точные выражения для кет-векторов и
наблюдаемых и покажем, как можно рассчитать результаты физических измерений, а также
научимся различать отдельные этапы эксперимента (приготовление системы, ее
эволюция, измерение и т.д.).
В главе III мы видели, что любой измеряемой физической величине в квантовой
механике сопоставляется наблюдаемая, то есть эрмитов оператор, собственные векторы
которого могут образовать базис в пространстве состояний. Таким образом , мы должны
выбрать это пространство и указать, какие наблюдаемые соответствуют компонентам
вектора 9> (например, ^x.SPy. У>г или в общем случае У>и = У>• и , где и —
произвольный единичный вектор), поддающимся измерению, как это следует из § 1.
а. НАБЛЮДАЕМАЯ Sz И ПРОСТРАНСТВО СПИНОВЫХ СОСТОЯНИЙ
Компоненте Уг нужно сопоставить наблюдаемую Sz, принимающую в
соответствии с описанными в § 1 результатами эксперимента два собственных значения с
противоположными знаками ± — . Допустим, что эти собственные значения не вырождены, и
обозначим символами |+) и |-) соответствующие ортонормированные собственные
векторы:
s»-+fl+>;
*|-> = -f|->.
(А-10)
где
W+H-I-H:
(А-П)
484

Применение постулатов к простым случаям
Таким образом, оператор Sz сам по себе образует полный набор коммутирующих
операторов, и пространство спиновых состояний является двумерным пространством Щ,
связанным с собственными векторами | +) и | -). Тот факт, что они образуют базис,
выражается с помощью соотношения замкнутости:
1+Х+М-Х-К
(А-12)
Любой нормированный вектор пространства #s может быть представлен в виде
линейной суперпозиции | +) и | -):
где
М=«1+>+Р|->.
|а|Ч|Р|2=1.
В базисе {| +), | -) } матрица оператора Sz диагональна и имеет вид:
М-5
1 0^
0 -1
(А-13)
(А-14)
(А-15)
Ь. ДРУГИЕ СПИНОВЫЕ НАБЛЮДАЕМЫЕ
Компонентам Ух и Уу вектора У сопоставляются наблюдаемые Sx и Sy.
Операторы St и Sy должны быть представлены в базисе {|+), |-) ) эрмитовыми матрицами 2x2.
В главе VI мы увидим, что в квантовой механике три компоненты механического
момента не коммутируют между собой, а удовлетворяют определенным правилам
коммутации. Это позволит показать, что в случае интересующего нас спина 1/2 матрицы,
представляющие операторы Sx и 5V в базисе собственных векторов |+) и |-)
оператора 5г, имеют вид:
-Го О
&) =
W-
1 0
о
(А-16)
(А-17)
Временно примем эти выражения без доказательства.
485

Глава IV
Что касается проекции Уи момента У> на единичный вектор и,
характеризующийся полярными углами Ь и ф (рис.4), то она описывается формулой:
.cftJ = У> • u = .(/v sin Ь cos ф + У}у sin Ь sin ф + !f: cos в .
(А-18)
Используя формулы (А-15), (А-16) и (А-17), легко вычислить матрицу, представляющую
наблюдаемую Su = S • и в базисе {|+), |-)}:
[Slt) = [Sx)sinft cosy + \Sy)sin® sinф + [SJcosft ■
cost* sin
sin be,<p - cosft
-/фЛ
(A-19)
Рис.4
Определение полярных углов й и ф, характеризующих
единичный вектор и
В дальнейшем нам понадобятся собственные векторы и собственные значения
наблюдаемых Sx, Sy и Su. Вычисления, позволяющие получить их с помощью матриц
(А-16), (А-17) и (А-19), не представляют трудностей, и здесь мы приведем только
окончательные результаты.
Операторы Sx, Sv и Su имеют те же собственные значения +— и — , что и
оператор Sz. Этот результат понятен физически: действительно, всю установку Штерна и
Герлаха можно поворачивать так, чтобы ось, определяемая магнитным полем, была
параллельна любой из осей Ох, Оу или и. Поскольку все направления в пространстве
имеют одни и те же свойства, то и явления, регистрируемые на пластинке установки, не
должны зависеть от таких поворотов, а измерения Ух, У> или У>и могут дать только два
h Ь
результата: + — и .
Что касается собственных векторов операторов Sx, S и Su, то мы обозначим их
486

Применение постулатов к простым случаям
соответственно символами |±) , |±) и |±) (знак, фигурирующий в обозначении кет-
вектора, является знаком соответствующего собственного значения). Их разложения в
базисе собственных векторов |±) оператора Sz записываются в виде:
1±>, = ^Н±|->]; (А-20)
|±)у = ^[|+}±/|-)]; (А-21)
\+)M=cos-e*'4+) + sin-e*'2\-)-,
(А-22)
В. ИЛЛЮСТРАЦИЯ ПОСТУЛАТОВ В СЛУЧАЕ СПИНА 1/2
Используя описанный выше формализм, покажем, как применяются постулаты
квантовой механики к анализу некоторых экспериментов, реализуемых с атомами
серебра на установке Штерна и Герлаха. После этого мы сможем обсудить последствия
этих постулатов на конкретных примерах.
1. Конкретное приготовление различных спиновых состояний
Чтобы иметь возможность предсказать результат того или иного измерения,
необходимо знать состояние системы (здесь спин атома серебра) непосредственно перед
актом измерения. Сейчас мы увидим, как можно реально приготовить пучок атомов
серебра так, чтобы все они находились в заданном спиновом состоянии.
а. ПРИГОТОВЛЕНИЕ СОСТОЯНИЙ |+) И |-)
Допустим, что в пластинке Р установки, изображенной на рис. 1а, в точке с
центром в месте расположения пятна N{ просверлено отверстие (рис.3). Атомы,
отклоняющиеся вниз, продолжают конденсироваться вокруг точки N2, тогда как некоторая
часть отклоняющихся вверх пройдет через отверстие в пластинке Р (рис.5). Каждый из
атомов пучка, прошедших через отверстие, является физической системой, в которой
только что выполнили измерение наблюдаемой Sz, давшее результат + —, и согласно
487

Глава IV
пятому постулату главы III этот атом находится в собственном состоянии,
соответствующем этому результату, то есть в состоянии |+) (поскольку оператор Sz сам по себе
образует полный набор коммутирующих операторов, результат измерения достаточен,
чтобы определить состояние системы после этого измерения). Таким образом, устройство,
изображенное на рис.5, обеспечивает получение пучка, в котором все атомы находятся в
спиновом состоянии |+). Иначе говоря, оно функционирует как «атомный
поляризатор», поскольку осуществляет с атомами ту же операцию, какую обычный оптический
поляризатор делает с фотонами.
к*
-+У
Рис.5
Если в пластинке Р просверлено отверстие в точке расположения пятна Nx, то все
атомы, прошедшие через это отверстие, окажутся в спиновом состоянии |+), и установка
Штерна и Герлаха функционирует как поляризатор
Конечно, если просверлить пластинку в точке N2, а не в точке Nx, то справа от
пластинки будет получен пучок, в котором все атомы будут находиться в спиновом
состоянии |-).
Ь. ПРИГОТОВЛЕНИЕ СОСТОЯНИЙ |±) , |±) И |±)
Наблюдаемая Sx тоже образует сама по себе полный набор коммутирующих
операторов, так как ни одно из ее собственных значений не является вырожденным. Чтобы
приготовить одно из ее собственных состояний, достаточно после измерения Sx
отфильтровать все атомы, для которых это измерение дало соответствующее собственное
значение. Так, если установку, изображенную на рис.5, повернуть на угол +я/2 вокруг
оси Оу , то будет получен пучок атомов, спиновое состояние которых будет равно |+)^
(рис.6).
488

Применение постулатов к простым случаям
Рис.6
Повернув на угол +я/2 вокруг оси Оу установку, изображенную на рис.5, получим
поляризатор, приготавливающий атомы в спиновом состоянии |±)
Этот метод нетрудно обобщить: повернув установку Штерна и Герлаха так, чтобы
ось магнитного поля оказалась параллельной произвольному единичному вектору и, и
просверлив отверстия любо в точке Nx, либо в точке N2, можно приготовить систему
атомов серебра в спиновом состоянии |+) или |-) *.
с. ПРИГОТОВЛЕНИЕ СОСТОЯНИЯ В ОБЩЕМ СЛУЧАЕ
Выше мы отмечали, что нормированный кет-вектор в пространстве спиновых
состояний в самом общем случае можно представить в виде:
|v> = «|+> + P|->.
(В-1)
где
Н2+|Э|2-1.
(В-1)
Возможно ли приготовить атомы так, чтобы их спиновое состояние описывалось
соответствующим вектором | \|/) ?
Ниже мы покажем, что каким бы ни был | у), всегда существует единичный вектор и,
коллинеарный кет-вектору |+}ц. Для этого нужно найти два комплексных числа а и C,
* Направление атомного пучка не обязательно будет совпадать с осью Оу , но для
рассматриваемых здесь вопросов это не имеет значения.
489

Глава IV
которые в принципе могут быть любыми, но должны удовлетворять формуле (В-2).
Естественно, что при этом должен существовать угол Ф , связанный с а и C соотношениями:
Если еще наложить условие:
v i i
cos— = ос ;
2 ' '
sin- = \$\.
0<в<я,
(В-3)
(В-4)
то уравнение tg — =
определяет угол д единственным образом. Мы знаем уже, что
фазы чисел а и C входят в физические результаты только в виде их разности,
вследствие чего можно обозначить:
Тогда
(p = Arg(|3)-Arg(a);
% = Arg(C) + Arg(a).
Arg(C) = -(% + (p);
Arg(a) = -0c-(p).
(B-5)
(B-6)
(В-7)
В этих обозначениях кет |ц/) запишется в виде:
Iv>-
cos—e
'ТИ+
ъ
sin—е
I")
(В-8)
Если это выражение сравнить с формулой (А-22-а), то можно заметить, что |\|/)
отличается от кет-вектора |+) , соответствующего единичному вектору и и характеризующегося
углами в и ф , только фазовым множителем е'х'2, не имеющим физического смысла.
Таким образом, чтобы приготовить атомы серебра в состоянии |\|/), достаточно
расположить установку Штерна и Герлаха (с отверстием в пластинке в точке Nl) так,
490

Применение постулатов к простым случаям
чтобы ее ось была направлена вдоль вектора и, полярные углы которого определяются
формулами (В-3) и (В-5).
2. Измерения спина
В § А мы видели, что установка Штерна и Герлаха позволяет измерить проекцию
механического момента У> атомов серебра на выделенную ось. В § В-1 мы узнали, что
такая же установка может быть использована для приготовления пучка атомов в
заданном спиновом состоянии. Таким образом, располагая две аналогичные установки одну
за другой, можно было бы экспериментально проверить все предсказания, полученные
на основе постулатов. Первая из них должна функционировать в режиме
«поляризатора»: выходящий из нее пучок будет состоять из атомов серебра в одном и том же
спиновом состоянии. Затем этот пучок направляется во вторую установку, служащую для
измерения определенной компоненты механического момента У>: в некотором смысле она
выполняет роль «анализатора» (отметим аналогию с оптическим экспериментом,
описанным в § А-3 главы I). Будем предполагать, что спиновое состояние атомов пучка не
изменяется между его выходом из «поляризатора» и входом в «анализатор», то есть
между приготовлением системы и измерением ее состояния. В принципе это ограничение
можно снять, для чего достаточно использовать уравнение Шредингера и определить
эволюцию спина между моментами приготовления и измерения (см. § В-3).
а. ПЕРВЫЙ ЭКСПЕРИМЕНТ
Выберем направления осей двух установок параллельными Oz (рис.7): первая из
них готовит атомы в состоянии |+), а вторая — измеряет значение У}г. Что же мы
увидим на пластинке второй установки?
J
\*г
\*2\
|
Рис.7
Первая установка (поляризатор, образованный из источника ^.щели ^.магнита А, и
пластинки с отверстием Р]) готовит атомы в состоянии |+); вторая-(анализатор,
образованный из магнита А2 и пластинки Р2) измеряет компоненту ^,: полученный результат
П
определенно дает значение + —
491

Глава IV
Поскольку состояние, в котором находится изучаемая система, является
собственным состоянием наблюдаемой Sz, которую мы намереваемся измерить, постулаты
указывают, что результат измерения будет строго положительным, то есть совершенно
уверенно мы получим соответствующее собственное значение + —. Таким образом, все
атомы пучка должны сконденсироваться на пластинке второй установки, образовав
П
единственное пятно, расположение которого соответствует + — .
Именно это и констатируется в реальном эксперименте: все атомы попадают на
пластинку вокруг точки N{, и ни один не попадает на нее вблизи точки N2.
b. ВТОРОЙ ЭКСПЕРИМЕНТ
Расположим теперь ось первой установки вдоль единичного вектора и с полярными
углами f} , ф = 0 (вектор и лежит в плоскости xOz), оставив ось второй установки
параллельной Oz (рис.8). Согласно формуле (А-22-а) спиновое состояние атомов на
выходе такого «поляризатора» может быть описано выражением:
i \ #i \ . ei \
(В-9)
/ Ш-
Р2
Рис.8
Первая установка готовит спины в состоянии |+) (где и — единичный вектор в плоскости
xOz, образующей угол f> с осью Oz); вторая установка измеряет компоненту У>г:
возможными результатами являются + — (с вероятностью cos2 f} / 2 ) и — (с вероятностью
sin2bl2).
492

Применение постулатов к простым случаям
«Анализатор» измеряет величину У>г для этих атомов. Какой же результат будет
получен?
В этом случае мы обнаружим, что часть атомов сконденсируется вблизи точки N,, а
другая часть — вблизи точки N2, хотя все они готовились одним и тем же образом, что
свидетельствует о том, что в индивидуальном поведении атомов присутствует
некоторый индетерминизм. Постулат о спектральном разложении позволяет лишь предсказать
вероятности попадания атомов в точки Nx или N2. Поскольку формула (В-9)
определяет разложение спинового состояния атома по собственным состояниям измеряемой
наблюдаемой, то сразу же можно сказать, что эти вероятности равны соответственно
cos2bll и sin2bll. И эксперимент действительно подтверждает это: количество
атомов, сконденсировавшихся вблизи точек Nx и N2, пропорционально этим величинам.
ЗАМЕЧАНИЕ
Каким бы ни было значение угла Ь (за исключением, когда он точно равен О
или я), при измерении Sz всегда можно получить два значения: + — и —.
В некотором смысле этот вывод может вызвать удивление: например, если угол Ь
очень мал, направление спина на выходе из первой установки практически совпа-
дает с осью Oz, но вместе с тем при измерении Sz можно получить как + — , так
и — (классическая механика дает результат — cosi) = — ). Тем не менее, чем
меньше О , тем меньше вероятность получить значение — . Кроме того, ниже мы
увидим (В-11), что среднее значение результатов измерения при большом числе
одинаковых опытов равно (S.) = — cosb , что совпадает с классическим результатом.
с. ТРЕТИЙ ЭКСПЕРИМЕНТ
Допустим, что «поляризатор» расположен так, как это было в § 2-Ь, то есть готовит
атомы в состоянии (В-9), а ось «анализатора» выберем параллельной оси Ох с тем,
чтобы он измерял проекцию У>х механического момента.
Чтобы вычислить, какие предсказания дадут постулаты в этом случае, нужно
разложить состояние (В-9) по собственным состояниям наблюдаемой Sx [формула (А-20)].
Без труда найдем:
493

Глава IV
JMv)-
Гг
1 ( Ь . ЬЛ (п Ь
cos — + sin — = cos
2 2) U 2
/ i \ l f * • ^ . (n Ъ
(- Ш ) = —==■ COS 5Ш — = 5Ш
Л |У/ V?l 2 2) U 2
(B-10)
Таким образом, вероятность получить собственное значение + — наблюдаемой Sx рав-
2^7Г ЬЛ h . 2Гя Ь
на cos , а вероятность получить — равна sin
Эти равенства можно проверить количественно, измеряя интенсивность пятен на
пластинке, расположенной на выходе второй установки Штерна и Герлаха.
ЗАМЕЧАНИЕ
Не следует удивляться, что в формулы входит угол . В § 2-Ь угол
между осями двух установок был равен $ , а после поворота второй установки он
стал равным | 1
d. СРЕДНИЕ ЗНАЧЕНИЯ
В ситуации, описанной в § 2-Ь, в эксперименте обнаруживается, что из большого
количества , Г атомов в точку N{ попадает ,i'cos2b/2, а в точку N2 попадает
h h
«Г sin2b/2 . Измерение У)г дает значение + — для первой группы и для второй
группы атомов. Если вычислить среднее значение этих результатов, получим:
<°-Н
П 2 в П . 2 Ь
— .У cos Л'sin —
2 2 2 2
= — cos \
2
(В-11)
Легко доказать, исходя из формул (В-9) и (А-10), что именно этому значению равен
матричный элемент (\\f | Sz | \|/).
Аналогично средний результат измерений, полученных в эксперименте, описанном
в §2-с, равен:
м-±
П «
.i'cos'l \--Л sin*\
я Ъ
h .
= — sin}
2
(В-12)
494

Применение постулатов к простым случаям
Чтобы вычислить матричный элемент (ч/^у), можно использовать матрицу (А-16),
представляющую оператор Sx в базисе {|+), |-) }• В этом же базисе кет |\|/)
представав/2"\ . ,
и бра (\|/| — соответствующим вектором-строкой.
лен вектором-столбцом
Таким образом:
sinbll
(\|/|5A.|v) = -{cosbjl sinbll)
О 1
[I Oj
cosbll
sinbll
h .
= — sin i
1
(B-13)
Действительно, среднее значение У>х равно матричному элементу наблюдаемой Sx в
состоянии |\|/).
Интересно заметить, что если бы речь шла о классическом механическом моменте с
модулем h 11, направленном вдоль оси «поляризатора», то его проекции на оси Ох и
Ог были бы в точности равны —sinb и — cosb. В общем случае, если вычислить
средние значения Sx, Sy и Sz, применяя тот же формализм, что и в (В-13), в состоянии |+)
[формула (А-22-а)], получим:
u(+\SM)u = 2Sinbc°S(?;
H{+\Sy\+)K=lsin*sin(p;
(+k 1+) =-cos$.
(B-14)
Эти средние значения равны по величине проекциям, которые имел бы классический
механический момент с модулем h/2, направленный вдоль вектора и с полярными
углами О и ф. Таким образом, через эти средние значения можно установить связь
классической механики с квантовой. Однако не следует забывать, что измерение, напри-
мер, величины У>х у определенного атома никогда не даст значения —sinb costy,
а единственными результатами измерения могут быть только значения +Ы1 и -А / 2 .
И только после усреднения значений, полученных в результате большого количества
измерений одной и той же наблюдаемой (здесь Sx) в одном и том же состоянии системы
(здесь |+) ), можно получить приведенное выше значение — sinft cos(p .
495

Глава IV
ЗАМЕЧАНИЕ
На этом этапе небесполезно снова вернуться к рассмотрению проблемы внешних
степеней свободы (положение, импульс).
Если атом серебра попадает во вторую установку Штерна и Герлаха, находясь в
спиновом состоянии |\|/), определяемом формулой (В-9), то, как мы только что увидели,
невозможно с полной уверенностью утверждать, в какой точке ( N, или N2) пластинки он
сконденсируется. Кажется, что трудно совместить эту неопределенность с понятием
классической траектории, которая точно известна, если задано начальное состояние системы.
В действительности это лишь кажущийся парадокс: говорить, что можно классически
интерпретировать внешние степени свободы, означает считать, что можно сформировать
волновой пакет, размеры которого много меньше, чем характерные размеры задачи, и это совсем не
означает, что мы обязательно должны думать, что частица следует по классической траектории.
Рассмотрим сначала атом серебра, который попадает в установку, находясь в начальном
спиновом состоянии |+). Описывающая внешние степени свободы этой частицы волновая
функция представляет собой волновой пакет очень малых размеров, центр которого следует
по классической траектории (рис.9а). Аналогично, если атом серебра при входе в установку
Рис.9
Если спин находится в состоянии |+) (а) или в состоянии |-) (Ь), центр волнового пакета
движется по определенной траектории, которую можно вычислить классически. Если же
спиновое состояние является линейной суперпозицией состояний |+) и |-), то волновой
пакет делится на две части, и уже нельзя говорить о следовании атома по классической
траектории, несмотря на то, что пространственные размеры каждого из пакетов малы по
сравнению с характерными размерами задачи
496

Применение постулатов к простым случаям
находится в спиновом состоянии |-), то связанный с ним волновой пакет следует по
другой классической траектории (рис.9Ь).
Если теперь выбрать атом в спиновом состоянии |ц/) [формула (В-9)], то ему
соответствует вполне определенная линейная суперпозиция отмеченных выше начальных
состояний. Поскольку уравнение Шредингера является линейным, то волновая функция частицы в
последующий момент времени (рис. 9с) будет линейной суперпозицией двух волновых
пакетов, изображенных на рисунках 9а и 9Ь. Таким образом, частица имеет определенную
амплитуду вероятности существовать в одном или другом из двух волновых пакетов. Видно,
что она совсем не следует классической траектории в противоположность тому, что
происходит с центрами двух волновых пакетов. По прибытии на экран волновая функция отлична
от нуля лишь в двух областях, локализованных вокруг двух различных точек. Два волновых
пакета имеют, впрочем, определенное фазовое соотношение между собой, так как они
порождены одним и тем же начальным волновым пакетом, который затем разделился на две
части под действием градиента поля В . Его можно было бы, впрочем, восстановить, если
убрать экран (то есть не выполняя измерения), и снова подвергнуть действию другого
градиента поля со знаком, противоположным первому.
3. Эволюция спина 1/2 в однородном магнитном поле
а. ГАМИЛЬТОНИАН ВЗАИМОДЕЙСТВИЯ И УРАВНЕНИЕ ШРЕДИНГЕРА
Рассмотрим атом серебра, помещенный в однородное магнитное поле В0, и
выберем ось Oz вдоль поля В0. Классическая потенциальная энергия магнитного момента
Л = уУ> этого атома равна:
W = -Л В0 = -Jtz В0 = -уВ0У>г . (в5)
где В0 — модуль магнитного поля. Пусть:
ОH=-уЯ0. (В-16)
Легко видеть, что со0 имеет размерность обратного времени, то есть частоты.
Поскольку мы квантуем только внутренние степени свободы частицы, то следует
заменить У, на оператор Sz, и классическая энергия (В-15) становится оператором:
гамильтониан Н описывает эволюцию спина атома в поле В0:
Я = ш05г. (В-17)
32 Квантовая механика
497

Глава IV
Поскольку этот оператор не зависит от времени, решение соответствующего
уравнения Шредингера сводится к решению уравнения на собственные значения
оператора Н. Сразу же видно, что его собственные векторы являются собственными
векторами оператора Sz:
я|+) = .
ЙСОп
0:
Й0)п
"|->=-^|->
(В-18)
Таким образом, имеются два уровня энергии Е+ = +Йсо0/2 и Е_ = -Йш0/2 (рис.10).
Расстояние между ними Йсо0 пропорционально магнитному полю; они определяют
единственным образом «частоту Бора»:
V+ =-(£-£) = —2-.
Й V + ' 271
(В-19)
М
Ясоп
1 + >
!->
Рис.10
Уровни энергии спина 1/2 с гиромагнитным отношением у
в магнитном поле В0, параллельном оси Oz ; частота со0
определяется равенством ш0 = -уВ0
ЗАМЕЧАНИЯ
(i) Если поле В0 параллельно единичному вектору и с полярными углами $ и ф , то
формулу (В-17) нужно заменить на
Я = (О05и,
(В-20)
где Su = S • и — проекция вектора S на направление вектора и.
(ii) Для атома серебра у < 0, и, следовательно, 0H > 0 [формула (В-16)], что
объясняет положение уровней на рис.10.
498

Применение постулатов к простым случаям
Ь. ПРЕЦЕССИЯ ЛАРМОРА
Допустим, что в момент времени t = 0 спин находится в состоянии:
|\|/@)) = со5-^/2|+) + 5ш-£/ф/2|-) (В-21)
(в §В-1-с было показано, что произвольное состояние можно записать в этом виде). Чтобы
определить состояние |\|/@) в любой момент времени г > 0 , применим правило (D-54)
главы III. В выражении (В-21) функция |i|/@)) уже разложена по собственным
состояниям гамильтониана, и, следовательно:
|\|/@) = cos-e-i{e,E^ |+) + sin -Л"'^ |-) (В-22)
или, используя значения Е+ и Е_:
\\V(t)) = cos-e-i(^t)/2 \+) + sin-ei{^l)/21-). (В-23)
Магнитное поле В0 вносит сдвиг фазы между коэффициентами при кет-векторах |+) и
|-), пропорциональный времени.
Сравнивая выражение (В-23) для |\|/@) с выражением (А-22-а), описывающим
собственный кет |+) наблюдаемой Su, можно заметить, что направление и (г), вдоль
которого проекция спина точно равна +fi I 2 , определяется полярными углами:
*(*) = «;
(В-24)
Ф@ = Ф + со0г.
Угол между и (О и осью Oz (то есть направлением магнитного поля В0) остается
неизменным, но и@ вращается вокруг Oz с угловой скоростью со0, пропорциональной
магнитному полю. Таким образом, в квантовой механике мы снова встретились с
явлением, которое уже рассматривалось для классического магнитного момента (§ A-1-b) и
называлось прецессией Лармора.
Из выражения (В-17) гамильтониана следует, что наблюдаемая Sz является
константой движения. Формула (В-23) показывает, что вероятности получить значения
+п/2 или -Ы2 при измерении этой наблюдаемой не зависят от времени: поскольку
32*
499

Глава IV
модуль выражений е±,{ч>+@°1) равен 1, эти вероятности соответственно равны cos2 Ы2
и sin2 Ы2. Среднее значение Sz также не зависит от времени:
(\V(t)\Sz\\v(t)) = ^cosb. (B-25)
Напротив, операторы Sx и Sy не коммутируют с Я [в этом легко убедиться,
используя матрицы операторов Sx, Sy и Sz, определяемые формулами (А-15), (А-16)
и (А-17)]. Действительно, формулы (В-14) дают:
(\\i(t)\Sx\\\f(t)) = -sinbcos((p + M0t)\
(\j/@1 Sy | у @) = - sin Ь sin (ф + @0r). (B-26)
В эти выражения входит единственная частота Бора со0/271 системы. Кроме того,
средние значения Sx , Sy и Sz ведут себя так же, как и компоненты классического
механического момента с модулем h 12 , подверженного прецессии Лармора.
С. ОБЩИЙ АНАЛИЗ ДВУХУРОВНЕВЫХ СИСТЕМ
Простота представленных в § В расчетов обусловлена тем, что пространство
состояний имеет только два измерения.
В физике встречаются и другие случаи, которые в первом приближении могут
рассматриваться в таком упрощенном виде. Например, физическая система, обладающая
двумя состояниями с близкими значениями энергии, но значительно отличающимися от
энергии всех других состояний, в которой исследуется реакция на внешнее возмущение,
действующее на эти два уровня. Если интенсивность возмущения достаточно мала,
можно показать (см. гл. XI), что в первом приближении его влияние на два уровня
можно рассчитать, пренебрегая существованием других уровней системы. При этом все
вычисления можно вести в двумерном подпространстве пространства состояний.
В данном параграфе мы исследуем некоторые общие свойства двухуровневых
систем (не обязательно имеющих спин 1/2). Интерес такого исследования обусловлен тем,
что с помощью очень простой математической модели можно получить важные и
достаточно общие физические заключения (квантовый резонанс, осцилляции между двумя
уровнями и т.д.).
500

Применение постулатов к простым случаям
1. Постановка задачи
а. ОБОЗНАЧЕНИЯ
Рассмотрим физическую систему, пространство состояний которой является
двумерным (как мы только что отметили, чаще всего речь при этом идет о приближении:
иногда можно ограничиться двумерным подпространством в пространстве состояний).
В качестве базиса выберем систему двух собственных состояний |ф,) и |ф2)
гамильтониана Я0, соответствующих собственным значениям Ех и Е2:
Я0|ф1> = £1|ф|>;
//0|ф2> = ^2|ф2>. (С-1)
Этот базис ортонормирован:
(ф, |фу) = 8^, где U = l,2. (C-2)
Допустим, что нужно учесть внешнее или внутреннее возмущение системы, которое
сначала не было включено в гамильтониан Я0. Тогда полный гамильтониан можно
представить в виде суммы:
H = H0+W. (С-3)
Обозначим символами |ij/±) и Е± собственные векторы и собственные значения
оператора Я:
Н\у_)=Е_\у_). (С-4)
Гамильтониан Я0 часто называют невозмущенным гамильтонианом, а оператор W —
возмущением (или связью). Здесь допустим, что W не зависит от времени. В базисе
{[ф^, |ф2) } собственных состояний гамильтониана Я0 (называющихся
невозмущенными состояниями) оператор W может быть представлен эрмитовой матрицей:
(w) =
Kw2l w22
(C-5)
где Wu и W22 —вещественные числа, а недиагональные элементы:
Цг=К- (С-6)
501

Глава IV
В отсутствие связи Е{ и Е2 —возможные значения энергии системы, а |ф,) и |ф2) —
ее стационарные состояния (если система оказывается в одном из этих состояний, то она
остается в нем неограниченно долго). Задача состоит в определении изменений,
возникающих при введении связи W .
Ь. ПОСЛЕДСТВИЯ СВЯЗИ
а. Ех и Е2 не являются возможными энергиями системы
Измерение энергии системы может дать только одно из двух собственных значений
Е+ и Е_ гамильтониана Я, которые в общем случае отличны от £,и£2.
Прежде всего, нужно выразить Е+ и Е_ через Ех и Е2 и матричные элементы Wtj
матрицы W, то есть определить влияние связи на положение энергетических уровней.
C. |ф,) и |ф2) не являются стационарными состояниями
Поскольку |ф,) и |ф2) в общем случае не являются собственными состояниями
полного гамильтониана Я, то они не являются и стационарными состояниями. Если,
например, в момент времени г = 0 система находилась в состоянии [ф^, то в момент
времени t имеется вероятность ;j/\2(t) оказаться в состоянии |ф2), то есть оператор W
вызывает переходы между двумя невозмущенными состояниями, откуда и появился
термин «связь» (между |ф,) и |ф2)), приписываемый этому оператору.
Этот динамический аспект оператора W составляет другую сторону интересующей
нас задачи.
ЗАМЕЧАНИЕ
В дополнении Cjv отмеченные выше проблемы рассмотрены с помощью понятия
фиктивного спина. Действительно, можно показать, что гамильтониан Я может быть диагона-
лизирован к той же форме, что и спин 1/2 в статическом магнитном поле В с
компонентами Вх, Ву и В,, выражающимися через Ех и Е2, а также через матричные элементы W-..
Другими словами, любой двухуровневой системе (не обязательно со спином 1/2) можно
сопоставить спин 1/2 (называемый фиктивным спином), помещенный в статическое
магнитное поле В и описываемый гамильтонианом той же формы. Все результаты, относящиеся
в данном параграфе к двухуровневой системе, могут быть интерпретированы
геометрически в терминах магнитного момента, прецессии Лармора и других понятий, введенных в § А
и § В этой главы по поводу спина 1/2. Эта же геометрическая интерпретация развита в
дополнении Civ-
502

Применение постулатов к простым случаям
2. Статический аспект:
влияние связи на стационарные состояния системы
а. ВЫРАЖЕНИЯ ДЛЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ И СОБСТВЕННЫХ СОСТОЯНИЙ
ОПЕРАТОРА Н
В базисе {|ф,), |ф2) } матрица оператора Н имеет вид:
(н) =
El+Wlt Wl2 ^
W2l E2 + W22j
(С-7)
Диагонализация матрицы (С-7) не представляет трудностей (она подробно
выполнена в дополнении Brv). Ее собственные значения равны:
E+=UE[+Wll+E2+W22) + ^{Ei+Wll-E2-W22J+4\Wn\2 ;
Е_ Л(Е, +W„ + £2 + W22) -^(Е, +Wn-E2 -W22f + Щ2\2 (С-8)
(нетрудно доказать, что при W = О энергии Е+ и Е_ совпадают с Е{ и Е2 *). Что
касается собственных векторов с собственными значениями Е+ и Е_, то они имеют вид:
\y+) = cos^e-" |Ф|) + лп|^/2 |ф2); (С-9-а)
|V_) = -лп|е-' |Ф|) + с0Д^/2 |ф2), (C-9-b)
где углы д и ф определены равенствами:
2JW.J
4?А= ' '!.' w . приО<в<л; (С-10)
W21=|W21|e*. (C-ll)
Если Е{> Е2, то £+ —> £, и £_ —» £2, если W —> 0 ; напротив, если £, < Е2, то
£+ -> £2 и £_ —> £\ .
503

Глава IV
b. ФИЗИЧЕСКОЕ ОБСУЖДЕНИЕ
а. Графическое представление влияния связи
Все интересующие нас эффекты, обсуждаемые далее, связаны с тем, что оператор
возмущения имеет недиагональные матричные элементыWl2 = W2\ (если Wj2=0, то
собственные состояния оператора Н те же, что и оператора Я0, а новые собственные
значения равны Е{ +WJ, и Е2 + W22). Для простоты предположим, что матрица (W) не-
диагональна, то есть Wn = W22 = 0 *. Формулы (С-8) и (С-9) запишутся тогда в виде:
E+=±(Ex+E2) + ^(Ex-E2J+A\Wn\* ;
£.=|(£, + £2)-|V(£,-£2J+4|iy12|2; (C-12)
2|W12|
fgft = ' ' , приО<#<я. (С-13)
£,-£2
Посмотрим теперь, как влияет IV на значения Е+ и Е_ в зависимости от £, и Е2.
Для этого допустим, что Wl2 = con^f и введем два параметра:
Е,„=±(Е1+Е2);
Д = |(£,-£2). (С-14)
Из формулы (С-12) сразу же следует, что зависимость Е+ и Е_ от £*,„ очень проста:
изменение Ет просто смещает начало отсчета по оси энергии. Кроме того, из (С-9),
(С-10) и (С-11) следует, что векторы |ц/+) и |\|/_) не зависят от Ет. Поэтому нас будет
интересовать лишь влияние параметра Д . Изобразим на одном графике зависимость
четырех энергий Ех, Е2, Е+ и Е_ от параметра А . Для Е{ и Е2 получим две прямые
с наклонами +1 и -1 (на рис.11 они представлены пунктиром). Подставив (С-14) в (С-12),
получим:
* Если Wj j Ф 0 и W22 Ф 0 , достаточно положить Ех = Е{ + Wn и Ё2 = Е2 + W22. Тогда все
результаты этого параграфа остаются справедливыми.
504

Применение постулатов к простым случаям
£+=£,,,+^A2+|Wl2|2 ;
Е_ = £т-^Д2+|ИУ2.
(С-15)
(С-16)
Графики зависимостей Е+ и Е_ от А представляют собой две ветви гиперболы,
симметрично расположенные относительно осей координат и асимптотически стремящиеся
к двум прямым, характеризующим невозбужденные уровни. Вершины гипербол отстоят
друг от друга на расстояние 21 Wj21 (сплошные линии на рис. 11 )*.
Энергии
> Л
Рис.11
Зависимость энергий Е+ и Е_ от разности энергии А = (£, - Е2) 12 . В отсутствие связи
уровни пересекаются в начале системы отсчета (пунктирные прямые). Под действием
недиагональной связи W возмущенные уровни «отталкиваются», то есть имеет место
«антипересечение»: кривые зависимостей £+ и Е_ являются ветвями гиперболы
(сплошные кривые), асимптотами которых являются невозмущенные уровни
C. Влияние связи на положение уровней энергии
В отсутствие связи прямые, изображающие энергии Е, и Е2 двух уровней,
«пересекаются» в точке А = 0. Из рис. 11 видно, что при наличии связи уровни
«отталкиваются» друг от друга, то есть разность между их значениями возрастает. Изображенная на
Из рис. 11 видно, что при W —» 0: Е+ —> Ех, Е_ -* Е2, если £, > Е2, и £+ —> £2,
£_—>£,, если £, < Е2.
505

Глава IV
рис.11 сплошными линиями диаграмма уровней по этой причине называется
диаграммой «антипересечения».
С другой стороны, каким бы ни было значение А , всегда:
\Е.-Е_\> Е,-Е2
Тем самым мы пришли к выводу, который часто встречается в других областях физики
(например, в теории электрических цепей): связь раздвигает собственные частоты.
Вблизи асимптот, то есть при | Д|»|Wj2|, можно записать выражения (С-15) и (С-16)
в виде ограниченного разложения по степеням
W„
Е=Е+А
Е =Е - А
1 + -
1 +
W„
Wn
+ ...
2 Л
+ ..
)
(С-17)
Напротив, в центре гиперболы вблизи Е2 = Е, (Д = 0) формулы (С-15) и (С-16) дают:
Е. = Ет + \Ц2\;
E- = Em-\Wn\. (C-18)
Таким образом, влияние связи значительно сильнее, если два невозмущенных уровня
имеют одну и ту же энергию: в этом случае влияние связи является эффектом первого
порядка (С-18), тогда как при А »|Wj2| оно является эффектом второго порядка
[формула (С-17)].
у. Влияние связи на собственные состояния
Если воспользоваться выражением (С-14), то формула (С-13) примет вид:
tg* = -
\W„
(С-19)
Отсюда следует, что при А «| Wj2| (сильная связь) -& = п 12 ; напротив, при А »| \У12|
(слабая связь) 0 = 0 (предполагается, что А > 0).
506

Применение постулатов к простым случаям
В центре гиперболы, когда £, = £, (то есть Д = 0) имеем:
1
(С-20)
тогда как вблизи асимптот (то есть при Д »|WI2|) в первом порядке по | Wn\ IД имеем:
|V+) = e-'2
|ф,) + е*™|ф2> + ...
|V-H*
!ф/2
|ф2>-
2Д |V,/
(С-21)
Другими словами, при слабой связи (£, - Е2 »\Wl2\) возмущенные состояния мало
отличаются от невозмущенных: действительно, из формулы (С-21) видно, что с
точностью до глобального фазового множителя е~'ф/2 кет |\|/+) равен вектору |ф,), слегка
«загрязненному» малым вкладом состояния |ф2)- Напротив, в случае сильной связи
(Е{- Е2 «\W12\), формулы (С-20) указывают, что состояния |\|/+) и |\|/_) существенно
отличаются от состояний |ф,) и |ф2), поскольку они являются линейными
суперпозициями с коэффициентами, имеющими одинаковый модуль.
Итак, как и энергии, собственные состояния значительно изменяются вблизи точки
пересечения двух невозмущенных состояний.
с. ВАЖНОЕ ПРИМЕНЕНИЕ: ЯВЛЕНИЯ КВАНТОВОГО РЕЗОНАНСА
Если Е{ = Е2= Ет, то энергия, соответствующая Н0, дважды вырождена. Как мы
только что видели, связь Wl2 снимает это вырождение и, в частности, порождает
уровень, энергия которого уменьшена на |Wj2|. Иначе говоря, если основное состояние
физической системы дважды вырождено (и достаточно далеко отстоит от всех других
уровней), то любая связь (чисто недиагональная) между двумя соответствующими
состояниями понижает энергию основного состояния системы, в результате чего оно
становится более стабильным.
507

Глава IV
^х
Рис.12
Две возможные конфигурации двойных связей
в молекуле бензола
В качестве первого примера этого явления стоит упомянуть резонансную
стабилизацию молекулы бензола С6Н6. Эксперимент показывает, что шесть атомов углерода
расположены в вершинах правильного шестиугольника, и априори можно ожидать, что
в основном состоянии между соседними атомами углерода существуют три двойных
связи. На рис. 12а и рис.12Ь представлены два возможных варианта этих связей. Если
считать, что ядра атомов неподвижны вследствие их большой массы, то электронные
состояния |ф,) и |ф2), соответствующие рис. 12а и рис.12Ь, различны. Если бы структура,
изображенная на рис. 12а, была единственно возможной, основной уровень электронной
системы имел бы энергию Ет = (ф, |#|ф,), где Н — гамильтониан электронов в поле
потенциала, созданного ядрами. Но связи могут иметь конфигурацию, изображенную на
рис.12Ь: естественно, что благодаря симметрии (ф2|я|ф2) = (ф, |я|ф,), и можно
заключить, что основное состояние молекулы дважды вырождено. Однако
недиагональный матричный элемент (ф21 #|ф,) гамильтониана Н не равен нулю, и эта связь между
состояниями |ф,) и |ф2) порождает два различных уровня, из которых один имеет
энергию меньшую, чем Ет. Таким образом, молекула бензола оказывается более
стабильной, чем можно было бы ожидать. Кроме того, в реальном основном состоянии
конфигурация молекулы не может быть представлена ни рис. 12а, ни рис.12Ь: это
состояние является линейной суперпозицией |ф,) и |ф2) [коэффициенты этой
суперпозиции, как и в формуле (С-20), имеют одинаковые модули]. Именно это обстоятельство
выражает двойная стрелка на рис.12, как принято в химических обозначениях.
Другим примером является ион Н2 молекулы водорода, образованный из двух
протонов рх и р2 и одного электрона. Поскольку массы протонов существенно больше
массы электрона, можно считать их фиксированными. Обозначим буквой R расстояние
между ними и символами |ф,) и |ф2) состояния, образующиеся, когда электрон
локализован либо вблизи р19 либо вблизи р2 с водородоподобной волновой функцией
(рис.13). Как и в рассмотренном выше случае, вследствие симметрии диагональные
элементы гамильтониана (ф2|#|ф2) = (ф,|#|ф,), и мы обозначим их символом Em(R).
Состояния |ф,) и |ф2) не являются, однако, стационарными, так как матричный элемент
508

Применение постулатов к простым случаям
•п *п
Рг Р\
Рис.13
В ионе Н2 электрон может быть локализован или вблизи протона рх (а), или вблизи
протона р2 (Ь). В основном состоянии иона волновая функция электрона является линейной
суперпозицией волновых функций, изображенных на рисунках (а) и (Ь): вероятность
нахождения электрона симметрична относительно срединной плоскости рх р2
(ф,|я|ф2) отличен от нуля. И в этом случае образуется уровень, энергия которого
меньше Em(R), то есть в основном состоянии волновая функция электрона является
линейной комбинацией ситуаций, изображенных на рис. 13а и рисЛЗЬ: электрон
оказывается делокализованным относительно двух протонов, что понижает его
потенциальную энергию и приводит к образованию химической связи*.
3. Динамический аспект:
осцилляции системы между двумя невозмущенными состояниями
а. ЭВОЛЮЦИЯ ВЕКТОРА СОСТОЯНИЯ
Пусть
|У@) = *1@|Ф,) + *2(')|Ф2> (С-22)
вектор состояния системы в момент времени /. При наличии связи эволюция |\|/(/))
описывается уравнением Шредингера:
*^-|v@> = (#o+^)k@>. (C-23)
Спроектируем это уравнение на базисные векторы |<р,) и |ф2). Используя формулы
(С-5) (где положим Wu = W22 = 0) и (С-22), получим:
* Более глубокий анализ ионизированной молекулы Н2 будет дан в дополнении GXi.
509

Глава IV
d
in— я,(г) = Exax(t) + Wxla^t)\
at
ih— a,(t) = W2]al(t) + E2a,(t) . (C-24)
dt
Если |W12| Ф 0, эти уравнения образуют линейную систему связанных однородных
дифференциальных уравнений. Классический метод решения такой системы состоит в
применении правила (D-54) главы III: нужно найти собственные векторы |\|/ + ) и |\|/_) с
собственными значениями Е+ и Е_ оператора Н = Н{) + W, матричные элементы
которого являются коэффициентами уравнений (С-24), и разложить |\|/@)) по |\[/ + ) и |\|/_):
|\|/@)) = Х|\|/ + ) + |х|\|/_) (С-25)
(где А, и \х определяются начальными условиями). Тогда
|х|/(Г)) = к,-**1'* |\|/ + ) + |1б>-/£-'/Л |v.) (С-26)
[это позволяет получить a{{t) и я2(г), спроектировав |\|/@) на |ф,) и |ф2) ].
Можно показать, что система, вектор состояния |\|/@) которой описывается
формулой (С-26), осциллирует между двумя невозмущенными состояниями |ф,) и |ф2).
Чтобы доказать это, допустим, что в момент времени t = 0 система находилась в
состоянии |ф]):
|¥@))=|ф,), (С-27)
и вычислим вероятность .^2@ обнаружить ее в состоянии |ф2) в момент времени /.
Ь. ВЫЧИСЛЕНИЕ tfn (t) . ФОРМУЛА РАБИ
Разложим, как и в формуле (С-25), кет |\|/@)), определенный выражением (С-27), в
базисе {|ф,), |ф2) }. Обратив формулы (С-9), получим:
|V@)) = |<Pi) = **'2
Используя (С-26), получим:
*1 \ • д1 \'
(С-28)
510

Применение постулатов к простым случаям
к(о)=«
,/ф/2
ш-^'"»||+)-ш-«*>.}
(С-29)
Тогда амплитуда вероятности найти систему в момент времени t в состоянии |ф2)
запишется в виде:
(<Р2к(')):
а'»'2
cos-e-iE*t,n D>2\y + )-sin-e-iE-"h (ф2|у_)
— cos—
2 2
2.
к-£"
/ft -iE_tlh
].
и далее можно найти ^12W = | (ф21 V@) |
Я2@ =-^ш
\-cos
Е-Е_
-t
sin2b sin2
2П
(C-30)
(C-31)
или, если применить выражения (С-12) и (С-13):
|2
«|2@ = -
4W,
5Ш
>/4К2|2+(£,-£2J^
(С-32)
4|W12| +(Et-E2)
Формулу (С-32) иногда называют формулой Раби.
с. ФИЗИЧЕСКОЕ ОБСУЖДЕНИЕ
Из формулы (С-31) следует, что вероятность .г^2(г) осциллирует во времени с
частотой (Е+ - Е_) I h, которая совпадает с единственной частотой Бора системы.
Величина #|2 (г) изменяется между нулем и максимальным значением, равным согласно
формуле (С-31) sin2b всякий раз, когда t = {2k + l)nh/(E+ - Е_), где £ = 0,1,2,... (рис.14).
Частота осцилляции (£+ - Е_) I h, как и максимальное значение вероятности <ГУ|2(/) ,
являются функциями \Wl2\ и (Е, - Е2), характерные особенности которых мы сейчас
отметим.
Если £, = Е2, то (£+ -E_)lh- 2|W|2| / h, и величина sin2b принимает
максимально возможное значение, то есть 1: в моменты времени t = B& + 1) 7i/j/2|Wi2| система
оказывается в состоянии |ф2), если в начальный момент времени система находилась в
состоянии |ф,).
511

Глава IV
,^_>(')
тг*/(£+ - Я J
Рис.14
Зависимость от времени
вероятности .^2 @ найти
систему в состоянии |ф2), если
первоначально она
находилась в состоянии |ф,). Если
невозмущенные энергии этих
состояний равны, то #J2(/)
может достигать значения 1
Таким образом, всякая связь между двумя состояниями с одинаковой энергией
вынуждает систему периодически переходить из одного состояния в другое с частотой,
пропорциональной величине связи*.
С увеличением разности Е] - Е2 возрастает частота (Е+- Е_I /г, тогда как sin2b
уменьшается. В случае слабой связи ( £, -Е2 »|W12|) разность (Е+ - Е_) мало
отличается от Ех-Е2,ъ sin2b становится очень малым. Это неудивительно, так как в случае
слабой связи состояние |ф,) мало отличается от состояния |\|/+) [см. формулы (С-21)],
то есть система, выйдя из состояния |ф,), очень мало меняется со временем.
d. КОНКРЕТНЫЙ ПРИМЕР ОСЦИЛЛЯЦИИ МЕЖДУ ДВУМЯ СОСТОЯНИЯМИ
Вернемся к примеру молекулы Н2 и допустим, что в некоторый момент времени
электрон локализован вблизи протона р,, то есть, например, находится в состоянии,
изображенном на рис. 13а. В соответствии с выводами предыдущего параграфа он
должен осциллировать между двумя протонами с частотой, равной частоте Бора, связанной
с двумя стационарными состояниями |\|/+) и |\|/_) молекулы. Этим осцилляциям
электрона между двумя состояниями, изображенными на рис. 13а и рисЛЗЬ, соответствует
осцилляция среднего значения дипольного электрического момента молекулы (диполь-
ный момент отличен от нуля, когда электрон локализован у одного из двух протонов, и
* С таким явлением можно встретиться во многих областях физики. Например, два
одинаковых маятника A) и B) с одинаковой собственной частотой подвешены к одному основанию.
Допустим, что в момент времени t = О возбуждаются колебания маятника A); известно (см.
дополнение Hv), что из-за связи между маятниками за счет общего основания через некоторое время
(тем меньшее, чем сильнее связь) эти колебания окажутся переданными маятнику B), затем снова
маятнику A) и т.д.
312

Применение постулатов к простым случаям
меняет знак в зависимости от того, у какого из протонов он находится). Итак, видно, что
у молекулы может возникнуть осциллирующий дипольныи электрический момент, если
она не находится в стационарном состоянии. Известно, что такой осциллирующий
диполь способен обмениваться энергией с электромагнитной волной той же частоты, то
есть эта частота должна появиться в спектре поглощения и испускания иона Я2+.
Другие примеры осцилляции между двумя состояниями обсуждаются в
дополнениях Fiv, Gjv и Hiv.
33 Квантовая механика

ДОПОЛНЕНИЯ К ГЛАВЕ IV
AIV. Матрицы Паули.
BIV. Диагонализация эрмитовой матрицы
2x2.
Qy. Фиктивный спин 1/2 в двухуровневой
системе.
Div. Система из двух спинов 1/2.
EIV. Матрица плотности спина 1/2.
FIV. Спин 1/2 в статическом
и вращающемся магнитных полях:
магнитный резонанс.
Giy. Исследование молекулы аммиака
с помощью простой модели.
Hiv Влияние связи между стабильным
и нестабильным состояниями.
A|V, B|V: технический анализ простейших
матриц 2x2, важных для решения некоторых
задач квантовой механики.
C|V: устанавливает связь между §В и §С
главы I; дает простую геометрическую
интерпретацию свойств двухуровневых систем
(простой анализ, необходимый для
дальнейшего рассмотрения).
DjV: простая иллюстрация тензорного
произведения и постулатов (может рассматриваться
как совокупность контрольных работ).
EjV: иллюстрация понятий, введенных в
дополнении Еш, для спина 1/2.
F|V: анализ очень важного физического явления
(вследствие многочисленных применений)
магнитного резонанса. Будет рассмотрен
позже.
Giv: пример физической системы, анализ
которой можно свести в первом приближении
к анализу двухуровневой системы; задача
среднего уровня сложности.
HjV: исследование влияния связи двух уровней
с различными временами жизни; легкое, но
необходимое упражнение, требующее
понимания понятий, введенных в дополнении Кш.
Jiv Упражнения.

Применение постулатов к простым случаям
Дополнение Aiv
МАТРИЦЫ ПАУЛИ
1. Определение. Собственные значения и собственные векторы.
2. Простейшие свойства.
3. Удобный базис в пространстве матриц 2x2.
В § А-2 главы IV мы уже ввели матрицы, представляющие операторы проекций
Sx, 5 и Sz спина S в базисе {| +), | -)} собственных векторов оператора Sz. В
квантовой механике часто удобно вводить безразмерный оператор а, пропорциональный S и
определенный выражением:
S=|a. A)
Матрицы, представляющие в базисе {| +), | -)} три компоненты оператора a, получили
название «матриц Паули».
1. Определение. Собственные значения и собственные векторы
Сошлемся на уравнения (А-15), (А-16) и (А-17) главы IV. Используя A), получим,
что определение матриц Паули имеет вид:
Ог -
@ \Л
\\ oj
; tfv =
' У
f°
I'
-i\
о)
1 0^
a'=:o -i
B)
Эти матрицы эрмитовы, и все три имеют одно и то же характеристическое уравнение:
А2-1 = 0. C)
Собственные значения операторов ox,Gy,oz равны:
Х = ±1, D)
и снова видим, что собственные значения операторов Sx, Sy и Sz равны ±hl2.
Из определения B) нетрудно получить, что собственные векторы операторов ах, ау
и az равны соответственно собственным векторам операторов S x ,Sy и Sz, уже
введенным в § А-2 главы IV:
33*
515

Глава IV
где
<Ф>,=Ф>,:
<Ф),«Ф>,;
<Ф) = Ф>. E)
1±>,^[1+>±1->];
|±>,.=^[|+>±<1->]. F)
2. Простейшие свойства
Из определения B) нетрудно увидеть, что матрицы Паули удовлетворяют
соотношениям:
det (Gj) = -1, где j = x,y,z\ G)
tr (ay) = 0; (8)
с] = а* = а* = / , где / — единичная матрица 2x2; (9)
охоу =-оуох =/а,, A0)
а также все иные равенства, получающиеся из формулы A0) путем круговых
перестановок х, у, z .
Уравнения (9) и A0) иногда записывают в сжатом виде:
где символ zjkl антисимметричен относительно перестановки любых двух индексов и
равен:
£jkl ~
0, если хотя бы два индекса j,k,l равны;
1, если (у, *, /) = A,2,3), B,3,1), C,1,2); A2)
-1, если (у, jfc, /) = B,1,3), A,3,2), C,2,1).
516

Применение постулатов к простым случаям
Из формулы A0) сразу же следует, что
[ад,су] = 2/аг
A3)
(а также все остальные равенства, полученные круговой перестановкой индексов), и,
следовательно:
[Sx,Sy] = ihSz;
[Sy,Sz] = ihSx\
[S:,Sx] = ihSY.
A4)
Далее мы увидим (глава VI), что уравнения A4) характерны для любого углового
момента. Из равенства A0) следует также, что
ста +С7 а =0
A5)
(говорят, что матрицы а, антикоммутируют между собой), и с учетом формулы (9)
можно записать:
ovon, = //.
A6)
Укажем еще на одно тождество, зачастую оказывающееся полезным при квантово-
механических вычислениях. Если А и В — два вектора, компоненты которых являются
числами (или операторами, коммутирующими со всеми иными операторами,
действующими в двумерном пространстве спиновых состояний), то
(о-А)(а-В) = А-В-/ + /а-(АхВ).
(П)
Действительно, используя формулу A1) и то обстоятельство, что векторы А и В
коммутируют с а, можно записать:
(a-\Ka-B)=2loJAJotBk=2AjBk
j.k j.k
Se«0/+8*/
/
2j e jkl Aj Bk
+ 1AjBjI.
A8)
В правой части нетрудно узнать скалярное произведение А • В ; с другой стороны, в
соответствии с формулой A2) выражение в квадратных скобках правой части представляет
собой /-компоненту векторного произведения АхВ, что и доказывает формулу A7).
517

Глава IV
Отметим, что если А и В не коммутируют, то они должны появиться в одном и том же
порядке с двух сторон тождества.
3. Удобный базис в пространстве матриц 2x2
Рассмотрим произвольную матрицу 2x2:
М =
J
A9)
\т2х т22
Ее всегда можно представить в виде линейной комбинации четырех матриц:
/,а„ст,,аг. B0)
Действительно, используя формулы B), можно сразу показать, что
ЛМ тп+т„ ж тп-пг>7 т^+пи. .тп-пц, ,_1Ч
м=_и 22_/+_п 2L0^+_J2 2L0 +J_J2 ^_а B1)
2 2 ь 2 2 y
Таким образом, любая матрица 2x2 может быть представлена в форме:
М=я0/ + а-а, B2)
где коэффициенты a0,ax,ayiaz являются комплексными числами.
Сравнивая B1) и B2), легко убедиться, что М — эрмитова матрица только в том
случае, если коэффициенты а0 и а — вещественные числа. Формально их можно
определить следующим образом:
a0=-tr(M); B3-а)
а = -(Мсг). B3-Ь)
Эти формулы легко доказать, исходя из равенств (8), (9) и A0).

Применение постулатов к простым случаям
Дополнение Brv
ДИАГОНАЛИЗАЦИЯ ЭРМИТОВОЙ МАТРИЦЫ 2x2
1. Введение.
2. Изменение начала отсчета собственных значений.
3. Вычисление собственных значений и собственных векторов.
a. Углы й мф.
b. Собственные значения К .
c. Собственные значения Н .
d. Нормированные собственные векторы Н.
1. Введение
В квантовой механике часто приходится диагонализировать матрицы 2x2. Если
интерес представляют только собственные значения, решение характеристического
уравнения обычно находится без труда, ибо оно всего лишь второго порядка. В принципе,
вычисление нормированных собственных векторов также очень простое, но, если его
производить не очень умело, оно может оказаться чересчур громоздким и неудобным
для пользования.
Цель данного дополнения — предложить простой метод расчета, применимый в
любом случае. После изменения начала отсчета собственных значений вводятся углы Ь
и ф, определяемые матричными элементами, в результате чего нормированные
собственные векторы записываются в простой и удобной форме. Введение углов в и ф
представляет интерес и с физической точки зрения: в дополнении Civ мы увидим, что им
можно придать интересный физический смысл при анализе двухуровневых систем.
2. Изменение начала отсчета собственных значений
Рассмотрим эрмитову матрицу:
V И2\ Н12 )
где Ни и Н22 —вещественные числа, а
я12=//;,. B)
519

Глава IV
Таким образом, матрица (я) в ортонормированном базисе {|ф,), |ф2) } представляет
некоторый эрмитов оператор Я *.
Введя полусумму и полуразность диагональных элементов Я,, и Я22, можно
записать (я) следующим образом:
(")■
(я„ + я22)
^(Ни+Н22)
я„
я,.
■^(Ни-И22)
C)
Отсюда следует, что сам оператор Я может быть разложен на два оператора:
Я = 1(Я„+Я22I + 1(ЯП-Я22)К,
D)
где 1— единичный оператор и К — эрмитов оператор, представленный в базисе
{|ф,), |ф2) } матрицей:
(*) =
1
2Я,
2НУ
Нп -Я22
Яп -Я22
-1
E)
Из формулы D) ясно видно, что операторы Я и К имеют одинаковые собственные
векторы. Обозначим их символами |v|/±), а символами Е± и к± — соответствующие
собственные значения операторов Я и К :
Я|чг±)=£±|¥±);
*k±)=*±|v±).
F)
G)
Из формулы D) сразу же следует:
£±=^(Я1|+Я22) + ^(Я|1-Я22)/с±.
(8)
* Мы используем букву Я, так как оператор, подлежащий диагонализации, эрмитов и
обычно является гамильтонианом. Однако, естественно, представленные здесь вычисления можно
применить к любой эрмитовой матрице 2x2.
520

Применение постулатов к простым случаям
Первая матрица в правой части выражения C) играет несущественную роль, и ее
можно исключить соответствующим выбором начала отсчета собственных значений
(Яп + Я22)/2\
3. Вычисление собственных значений и собственных векторов
а. УГЛЫ в И ф
Пусть f> и ф — углы, введенные через матричные элементы #,y выражениями:
21//,. I
tg ft = ' ^ , гдеО<«<тс; (9)
Нп -Н22
н2\ =|//21к/фэ где 0<ф<2тг. A0)
Угол ф является аргументом комплексного числа Н2Х, и согласно B) имеем |Я12| = |#21| и
Н12=\Н12\еч*. A1)
Если воспользоваться формулами (9), A0) и A1), то матрица (к) примет вид:
1 tg f) е4^
w=
U*e«* -i J
A2)
b. СОБСТВЕННЫЕ ЗНАЧЕНИЯ К
Характеристическое уравнение матрицы A2) записывается как:
det [(#)-*/] = к2-1-г#2г} = 0 A3)
и сразу дает собственные значения к+ и к_ матрицы (к):
к+=+—1-г; A4-а)
COSV
Это новое начало отсчета не зависит от начального выбора базиса, так как величина
#,, + //22 = tr (Я) инвариантна относительно изменения ортонормированного базиса.
521

Глава IV
*-= -. A4-b)
cosv
Нетрудно доказать, что они являются вещественными числами (эрмитовость матрицы,
CM.§D-2-a главы II). Чтобы выразить \fcosb через Н~, достаточно использовать
формулу (9) и заметить, что cos Ь и tgb имеют одинаковые знаки, так как 0 < Ь < и :
1 _^Ни-НпJ+4\Н12
cosb Hn-H22
A5)
с. СОБСТВЕННЫЕ ЗНАЧЕНИЯ Я
Используя формулы (8), A4) и A5), сразу же получим:
£+=1(Яп+«и) + ^(Д11-ЯаJ+4|Я12|2; A6-а)
Е.
= |(ЯИ+Я22)-1А/(ЯП-Я22J+4|Я12|2. A6-Ь)
ЗАМЕЧАНИЯ
(i) Как мы уже отметили, собственные значения A6) могут быть легко получены из
характеристического уравнения матрицы (я). Если нас интересуют только они,
вводить углы Ь и ф нет необходимости. Напротив, в следующем параграфе мы
увидим, что этот метод весьма удобен, если нужно находить нормированные
собственные векторы оператора Я.
(ii) Исходя из формул A6), легко доказать, что
£++£_ = Яи + Я22=1г(Я); A7)
Е+£„ = ЯиЯ22~|Я12|2=ёе1(Я). A8)
2 I |2
(iii) Чтобы Е+ =£_, нужно выполнить равенство (Я,,-Я22) +4|Я,2| =0, то есть
Н\\ = ^22 и Hl2 = ^21 = 0- Таким образом, эрмитова матрица 2x2, имеющая
вырожденный спектр, обязательно пропорциональна единичной матрице.
522

Применение постулатов к простым случаям
d. НОРМИРОВАННЫЕ СОБСТВЕННЫЕ ВЕКТОРЫ Я
Пусть а и Ь — проекции вектора |\|/+) на |ф,) и |ф2). Согласно равенствам G),
A2) и A4-а) они должны удовлетворять уравнению:
[tgbe*
tgbe~
-1
ГгЛ
\ь)
cosb
(а\
Ы
A9)
откуда следует, что
1--
^ cos Ь )
a + tgbe~4 = 0,
B0)
то есть
sin-ei(\a +
cos — e ф
2
Ь = 0,
и, следовательно, нормированный собственный вектор |\|/+) имеет вид:
. * УФ/2 I
!*♦>=
C0S—£
2
Ф ^-др/2
ф1) + лп^е'ф'2|ф2).
Аналогично:
|¥.) = -,ш|е-^|Ф1) + с0Де^|ф2).
Без труда доказывается, что векторы |\|/+) и |\j/_) ортогональны.
B1)
B2)
B3)
ЗАМЕЧАНИЕ
Тригонометрические функции угла Ь выражаются через матричные элементы
Ну достаточно просто [см. формулы (9) и A5) ]. Иначе обстоит дело с выражениями
для угла Ы2\ формулы B2) и B3), определяющие нормированные собственные
векторы |\|/+) и |v|/_), значительно сложнее, если заменять cosbll и sinbll их
выражениями через Htj, и оказываются менее удобными. Проще использовать
непосредственно выражения B2) и B3), сохраняя функции угла й/2 в течение всех
вычислений, где требуется введение собственных векторов оператора Н. Впро-
523

Глава IV
чем, часто бывает, что явное выражение для угла Ь в конечный результат не
входит (например, § C-3-b главы IV), и последний выражается через Н^. При этом
формулы B2) и B3) позволяют выполнить все промежуточные расчеты, избегая
сложных выражений, особенно в тех случаях, когда конечный результат
достаточно прост. Именно в этом заключается достоинство рассмотренного здесь метода.
Другое его преимущество станет очевидным в следующем дополнении.
Дополнение Civ
ФИКТИВНЫЙ СПИН 1/2 В ДВУХУРОВНЕВОЙ СИСТЕМЕ
1. Введение.
2. Интерпретация гамильтониана в терминах фиктивного спина.
3. Геометрическая интерпретация эффектов, обсуждаемых в §С главы IV.
a. Фиктивные магнитные поля, ассоциирующиеся с Я0, W и Я.
b. Влияние связи на собственные значения и собственные векторы гамильтониана.
c. Геометрическая интерпретация ;^2@ •
1. Введение
Рассмотрим двухуровневую систему, гамильтониан которой Я представлен в орто-
нормированном базисе {\(р{), |ср2)} эрмитовой матрицей (Я) [формула A) дополнения
Biv]*. Если выбрать величину (Яп + Я22)/2 в качестве начала отсчета энергии, то
матрица (Я) примет вид:
(«) =
(Я,, - Я22) Я12
2
Н2\ -^H\\~H2l)
(О
Несмотря на то, что спин рассматриваемой двухуровневой системы не обязательно
равен 1/2, ей можно приписать спин 1/2, гамильтониан которого Я представлен в
базисе {|+), |-)} собственных состояний компоненты Sz этого спина такой же матрицей
(Я). Здесь мы увидим, что в этом случае можно интерпретировать (Я) как оператор,
* Здесь мы используем обозначения, принятые в дополнении B|V главы IV.
524

Применение постулатов к простым случаям
описывающий энергию взаимодействия «фиктивного» спина с постоянным магнитным
полем В , направление и модуль которого простым образом связаны с введенными
выше при диагонализации матрицы (Я) параметрами. Этим параметрам можно придать
простой физический смысл.
Кроме того, если гамильтониан Я может быть представлен в виде суммы двух
операторов Я = H0+W, то всем трем операторам Я, Я0 и W можно сопоставить три
магнитных поля В , В0 и b, причем В = В0 +Ь : введение связи W в терминах
фиктивного спина означает добавление поля b к полю В0. Мы покажем, что такой подход
позволяет очень просто интерпретировать ряд эффектов, рассмотренных в § С главы IV.
2. Интерпретация гамильтониана в терминах фиктивного спина
В главе IV мы видели, что гамильтониан связи между спином 1/2 и магнитным
полем В с компонентами Вх, Ву, Bz имеет вид:
# = -yb-s = -y(b*sx + *,s, + *zsz).
B)
Чтобы вычислить матрицу этого оператора, достаточно подставить в это равенство
матрицы операторов Sx,SyySz [главам, формулы (А-15), (А-16), (А-17)]:
(Я) = -
yh
в,
В -iB
KBx+iBy -В,
C)
Тогда для идентификации матрицы A) с (Я) достаточно определить «фиктивное» поле
В проекциями:
S,=--Re{tf12};
уп
Ву=\\т{НпУ,
уп
Bt-±(Hn-Hu).
D)
Отметим, что модуль Вх проекции В± поля В на плоскость хОу равен:
\Ну
^-\
E)
525

Глава IV
Согласно формулам (9) и A0) дополнения BiV углы Ь и ф, входящие в матрицу
(Я) = (Я), определяются выражениями:
M-rTiJ- при0<О<я; F)
\-у(Вх +iBy) = |у Bl\ е'ф при 0<ф < 2я.
Гиромагнитное отношение у здесь имеет смысл лишь промежуточного параметра
вычислений и априори может иметь любое значение. Если договориться считать величину у
отрицательной, то из равенств F) следует, что углы Ь и ф , входящие в матрицу (Я),
являются просто полярными углами, определяющими направление поля В (если бы
приняли у > 0, то это было бы противоположное направление).
Итак, мы видим, что можно даже забыть о двухуровневой системе, с которой мы
начинали, и считать, что матрица (Я) представляет в базисе собственных состояний |+)
и |-) оператора Sz гамильтониан Я спина 1/2, помещенного в поле В с компонентами,
определенными выражениями D). При этом
Я = 0MМ, G-а)
где Su — оператор S • и , описывающий проекцию спина на направление и с
полярными углами Ь и ф , а со — частота Лармора:
со = |у||в|. G-b)
В приведенной ниже таблице обобщены все соответствия, существующие между
двухуровневой системой и сопоставленным с ней фиктивным спинам 1/2.
Двухуровневая система
|ф->
|Ч>2>
М
к-)
Е.-Е.
Углы Ь и ф , введенные в BjV.
Я,, -Я22
К\
Фиктивный спин 1/2
1+)
I-)
1+>.
|->.
йсо
Полярные углы фиктивного поля В
-УЩ
-yhBji
526

Применение постулатов к простым случаям
3. Геометрическая интерпретация эффектов,
обсуждаемых в главе IV
а. ФИКТИВНЫЕ МАГНИТНЫЕ ПОЛЯ, АССОЦИИРУЮЩИЕСЯ С Я0 , W И Н
Допустим, как и в § С главы IV, что Н представлен в виде суммы двух членов:
H = H0+W.
(8)
В базисе {|ф,), |ф2)} невозмущенный гамильтониан Я0 представлен диагональной
матрицей, которая при соответствующем выборе начала отсчета энергии имеет вид:
М=
2
О
^1 ^2
(9)
Что касается оператора взаимодействия W, то, как и в § С главы IV, допустим, что его
матрица чисто недиагональная:
(И0 =
О Щ7
[W2I О
(Ю)
Сказанное в предыдущем параграфе позволяет сопоставить матрицы (Я0) и (W)
двум полям В0 и b с компонентами [формулы D) и E)]:
(И)
в -Е>
-£,
В°<- yh
B0L=0.
[Ьг=0;
м
1 Ь
ЩА
у 1
A2)
Здесь поле В0 параллельно оси Oz и пропорционально (£, -£2)/2, а поле b
перпендикулярно Oz и пропорционально \Wl2\. Поскольку (Я) = (H0)-(W), поле В,
ассоциирующееся с полным гамильтонианом, является векторной суммой полей В0 и b :
B = B0+b
A3)
527

Глава IV
Все три поля изображены на рис. 1; угол О , введенный в § С-2-а главы IV, является
углом между полями В и В0, поскольку поле В0 параллельно оси Ог .
Рис.1
Относительное расположение фиктивных полей: поле
В 0 соответствует оператору Н0, поле b — оператору
W и поле В — полному гамильтониану Н = HQ + W
Условие сильной связи (|И^2| »|£, - Е2\), введенное в §С-2 главы IV, эквивалентно
неравенству |b|»|В0| (рис.2а), а условие слабой связи (|Wj2| «\El - Е2\) эквивалентно
неравенству |ь|«|В0| (рис.2Ь).
Рис.2
Относительное расположение фиктивных полей В0, В и b в случае сильной (а) и
слабой (Ь) связи

Применение постулатов к простым случаям
Ь. ВЛИЯНИЕ СВЯЗИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
И СОБСТВЕННЫЕ ВЕКТОРЫ ГАМИЛЬТОНИАНА
Величины (Е{-Е2) и (Е+-Е_) пропорциональны соответственно частотам Лар-
мора оH=|у||В0| и (о = |у||в| в полях В0 и В.Из рис.1 видно, что В0, b и В
образуют прямоугольный треугольник, гипотенузой которого является поле В , откуда
следует, что всегда имеет место неравенство |в| > |В0| и, следовательно, (Е+- Е_) всегда
больше, чем |Е, - Е2\.
Для слабой связи (рис.2Ь) различие между |В| и |В0| очень мало и является
величиной второго порядка малости по отношению к |b|/|B0|, откуда сразу же следует, что
величины (Е+- Е_) и (£, - Е2) отличаются друг от друга во втором порядке
отношения |W,2|/|£, - Е2\. Напротив, в случае сильной связи (рис.2а) |в| »|В0| и практически
равен |b|, вследствие чего (Е+ - Е_) гораздо больше, чем \Е1 - Е2\ и почти
пропорционален модулю |Wj2|. Таким образом подтверждаются все результаты, полученные выше
в § С-2 главы IV.
Что касается влияния связи на собственные векторы, то его нетрудно обнаружить из
рис.1 и рис.2. Действительно, собственные векторы операторов Н и Я0,
соответственно, связаны с собственными векторами проекций S на оси Ои и Oz . Эти две оси в
случае слабой связи практически параллельны (рис.2Ь) и почти перпендикулярны в случае
сильной связи (рис.2а). Таким образом, собственные векторы операторов Su и S,, а
следовательно, и операторов Н и Я0, очень близки в первом случае и сильно
отличаются — во втором.
с. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ГУ|2(Г)
Используя понятие фиктивного спина, можно сформулировать задачу,
рассмотренную в § С-3 главы IV, следующим образом. В момент времени t = 0 фиктивный спин,
описывающий двухуровневую систему, находится в собственном состоянии |+)
оператора Sz; какова вероятность №+_(t) обнаружить спин в состоянии |-) в момент времени
t, если к полю В0 добавляют поле b ? Согласно приведенной выше таблице
соответствий вероятность 9J\2(t) должна совпадать с вероятностью #>+_@ •
Вычисление вероятности &+_(t) становится теперь особенно простым, так как
эволюция спина во времени приводится к прецессии Лармора вокруг поля В (рис.3). В
ходе прецессии угол Ь между спином и направлением Ои поля В остается постоянным.
34 Квантовая механика
529

Глава IV
В момент времени t спин оказывается ориентированным в направлении On,
составляющим угол а с осью Oz, и телесный угол, образованный плоскостями (Oz, Ои) и
(Ои , On ), равен cor. Простая тригонометрическая формула позволяет записать:
cos(X = cos Ь+sin f} cos COT.
A4)
Рис.3
Геометрическая интерпретация формулы Раби с
помощью понятия фиктивного спина: под действием
связи, представленной полем Ь, спин,
ориентированный первоначально вдоль оси Oz , прецессирует
вокруг поля В; вероятность получить значение
-fill при измерении его проекции Sz на ось Oz
является осциллирующей функцией времени
Итак, если направление спина составляет угол а с осью Oz, то вероятность найти
его в состоянии |-) оператора Sz равна (см. § B-2-b главы IV) sin2a/2 = (\-cosa)/2 .
Из этой формулы легко получить, используя A4):
т ОС 1 о
y+At) = sin — = — sin -&(l-cos(ut).
A5)
Если заменить со на (Е+ - E_)/h, получим формулу (С-31) главы IV. Таким образом,
эта формула получает чисто геометрическую интерпретацию.

Применение постулатов к простым случаям
Дополнение Div
СИСТЕМА ИЗ ДВУХ СПИНОВ 1/2
1. Квантовое описание.
a. Пространство состояний.
b. Полные наборы коммутирующих операторов.
c. Общий случай состояния системы.
2. Предсказание результатов измерений.
a. Измерения, выполняемые на двух спинах одновременно.
b. Измерения, выполняемые на одном спине.
В этом дополнении предлагается применить формализм, развитый в § А-2 главы IV, для
описания системы, состоящей из двух частиц со спинами 1/2. Этот случай не сложнее
рассмотренного выше случая одной частицы. В том, что касается постулатов, интерес к
нему обусловлен тем, что ни одна из спиновых наблюдаемых сама по себе не составляет
полного набора коммутирующих операторов, как это было в случае одного спина, и
поэтому мы можем считать, что измерения производятся как для одной наблюдаемой,
имеющей вырожденный спектр, так и для двух наблюдаемых одновременно. Вторая
цель этого дополнения состоит в том, чтобы на очень простом примере
проиллюстрировать понятие тензорного произведения, введенное в § F главы II. Как и в главе IV,
мы будем интересоваться только внутренними степенями свободы (спиновыми
состояниями) и допустим, кроме того, что образующие систему две частицы не являются
тождественными (системы тождественных частиц будут рассмотрены в общем виде в
главе XIV).
1. Квантовое описание
В главе IV мы увидели, как в квантовой механике следует описывать состояние
одной частицы со спином 1/2. Чтобы узнать, как нужно действовать в случае систем,
состоящих из двух спинов 1/2, достаточно использовать результаты § F главы И.
а. ПРОСТРАНСТВО СОСТОЯНИЙ
Чтобы различать частицы, пронумеруем их индексами 1 и 2. Если частица A) одна,
то ее спиновое состояние определено кет-вектором, принадлежащим двумерному
пространству состояний #:s(l). Аналогично, спиновые состояния одной частицы B)
образуют двумерное пространство ?5B). Обозначим символами S, и S2 спиновые
наблюдаемые частиц A) и B) соответственно. В пространстве tf5(l) [или tfsB)] в качестве
34*
531

Глава IV
базиса выберем собственные векторы оператора Su [или S2z ], которые обозначим как
11: +) и 11: -) [или |2 : +) и |2: -) ]. В общем случае кет пространства Fs(l) может быть
записан в виде:
|фA)> = а1|1:+> + Р1|1:-) A)
и кет пространства #5B) — в виде:
|хB)) = <х2|2:+) + Р2|2:-), B)
где а,, C,, а2, C2 — некоторые комплексные числа.
Если объединить две частицы в одну систему, то пространство состояний #s такой
системы является тензорным произведением двух определенных выше пространств:
*5=*5A)®ад. О)
Это означает, прежде всего, что базис пространства 85 образуется путем тензорного
перемножения двух введенных выше базисов в пространствах #5A) и #5B).
Используем следующие обозначения:
|++>-|1:+>|2:+);
|+->=|1:+>|2:->;
|-+)=|1:-)|2:+);
|-)=|1:->|2:-). D)
Так, например, в состоянии |+ -) проекция на ось Oz спина частицы A) с уверенностью
равна +/? / 2, а проекция спина частицы B) с уверенностью равна -й / 2. Условимся
обозначать символом (+ -1 бра-вектор, сопряженный кет-вектору | + -): порядок
символов внутри скобок одинаков для кет и бра, то есть первый символ всегда связан с
частицей A), а второй — с частицей B).
Таким образом, пространство <fs является четырехмерным. Поскольку базисы
(|l:±) } и (|2:±)} ортонормированы в пространствах tf5(l) и tf5B) соответственно,
базис D) ортонормирован в пространстве £s :
(e,e2|e;e;) = 8eie.8e2ei E)
532

Применение постулатов к простым случаям
(символы £,, Ер е2, г2 заменяют + или - в зависимости от случая; 8ее, = 1, если г = е' и
О, если е Ф е'). Таким образом, векторы D) удовлетворяют соотношению замкнутости в
пространстве #s:
1|е1б2>(е1е2| = |++>(++|+|+-)(+-| + |-+>(-+|+|~)(~| = 1. F)
Е,£2
в. ПОЛНЫЕ НАБОРЫ КОММУТИРУЮЩИХ ОПЕРАТОРОВ
Продолжим в пространство $s наблюдаемые S, и S2, определенные первоначально
в пространствах £5A) и £sB) (как и в § F главы II, будем обозначать эти продолжения
такими же символами S, и S2). Их действие на кет-векторы базиса D) понятно: так,
например, компоненты оператора S, действуют только на те части кет-вектора, которые
относятся к частице A). В частности, векторы базиса D) являются одновременно
собственными векторами операторов Slz и S2z:
| \ _ Ь | \
^1г|е1е2/- TEj|6l£2/i
^2z|ei£2)= -^e2|e1e2). G)
Для других компонент операторов S, и S2 применим формулы, приведенные в § А-2
главы IV. Например, известно [формула (А-16) главы IV], как действует оператор S]x на
кет-векторы 11: ±):
*,,|1:+> = £|1:->;
5u|l:->-f|l:+>. (8)
Из этих формул можно заключить, как действует Slx на кет-векторы D):
*.1->-£|~>:
533

Глава IV
^|-+)-fM:
^|--) = fl+-)- <9>
Нетрудно доказать, что, несмотря на то, что три компоненты S, (или S2) не
коммутируют между собой, любая компонента S, коммутирует с любой компонентой S2.
В пространстве £5A) наблюдаемая Slz сама по себе образует полный набор
коммутирующих операторов, и то же самое можно сказать о наблюдаемой S2z в пространстве
$s B). Однако в пространстве $s собственные значения операторов Slz и S2z, оставаясь
равными ±h 12, оказываются дважды вырожденными: например, собственному
значению +Н/2 оператора Siz соответствуют два ортогональных вектора |++) и |+-)
[формулы G)] и все их линейные комбинации. Таким образом, в пространстве #5 ни 5|т,
ни S2z, взятые в отдельности, не образуют полной системы коммутирующих
операторов. Напротив, ансамбль { Slz, S2z } является в этом пространстве полным набором, как
это видно из формул G).
Конечно, это не единственный полный набор коммутирующих операторов, который
можно построить. Например, им также является ансамбль { Slz, S2x}. Действительно,
эти две наблюдаемые коммутируют, как уже было отмечено выше, и каждая из них
образует полный набор коммутирующих операторов в том пространстве, в котором она
была определена первоначально. Собственные векторы, общие для операторов Slz и
S2x, образуются путем тензорного произведения собственных векторов в пространствах
#5A) и tfsB). Используя равенство (А-20) главы IV, получим:
M|2:-), = ;£D++H+->];
|1:->|2:+>,=^[|-+Н-->];
1И|2:-),=^0-+Н->]- ™
534

Применение постулатов к простым случаям
с. ОБЩИЙ СЛУЧАИ СОСТОЯНИЯ СИСТЕМЫ
Векторы D) были получены путем тензорного умножения кет-вектора пространства
(fs(l) на кет-вектор пространства #5B). В более общем случае из произвольного кет-
вектора пространства #s(l) [например, A)] и произвольного кет-вектора пространства
$s B) [например, B)] можно построить кет пространства Щ:
|фA))|хB)) = а1а2| + +> + а1Р2| + -> + а2Р1|-+> + Р1Р2|~>. A1)
Компоненты кет-вектора в базисе D) являются произведениями компонент |фA)) и
|%B)) в базисах пространств £s(l) и #5B), которые служили для построения D).
Но не все кет-векторы пространства Щ являются тензорными произведениями.
В общем случае кет этого пространства является произвольной линейной комбинацией
базисных векторов:
|v) = a|++> + p| + -) + Y|-+) + 8|—>. A2)
Если желательно нормировать | \|/), то следует принять условие:
|af+|p|2+|Y|4|5|2 = l. A3)
Если вектор \\\f)задан, то в общем случае невозможно найти два кет-вектора |фA)) и
|%B)), произведением которых он является. Действительно, чтобы формула A2) могла
быть представлена в виде A1), необходимо, в частности, чтобы
a Y
И- <14)
и это условие не всегда может быть выполнено.
2. Предсказание результатов измерений
Сейчас мы рассмотрим некоторые измерения, которые можно выполнить в системе
двух спинов 1/2, и вычислим результаты, предсказываемые постулатами для этих
измерений. Всякий раз будем считать, что состояние системы непосредственно перед
измерением описывается нормированным кет-вектором A2).
535

Глава IV
а. ИЗМЕРЕНИЯ, ВЫПОЛНЯЕМЫЕ НА ДВУХ СПИНАХ ОДНОВРЕМЕННО
Поскольку любая компонента S, коммутирует с любой компонентой S2, можно
измерить их одновременно (глава III, § С-6-а). Чтобы вычислить результат,
предсказывающий их измерения, достаточно использовать собственные векторы, общие для двух
наблюдаемых.
а. Первый пример
Допустим сначала, что измеряются одновременно проекции 5,, и S2z. Чему при
этом равны вероятности получения различных результатов?
Ансамбль { S]z, S2z } является полным набором коммутирующих операторов, и,
следовательно, с каждым результатом измерения связано только одно состояние
системы. Если перед измерением она была в состоянии A2), то можно получить:
+ — для S]z и + — для S2z с вероятностью |(+ + |v|/)| =|a| ;
+ — для 5J, и для S2z с вероятностью |(+-|ty)| =|P| ;
— для Slz и + — для S2z с вероятностью (~ + |v) =|y| »
— для »Slr и — для S2z с вероятностью K""~|v) =|8| • A5)
Р. Второй пример
Предположим теперь, что измеряются 5, и S2z. Какова вероятность получить
значение +h 12 для каждой их двух наблюдаемых?
И в этом случае ансамбль { Sly, S2z } образует полный набор коммутирующих
операторов. Собственный вектор, общий для операторов Sly и S2z и соответствующий
собственным значениям +fi 12 и +Й / 2 , является тензорным произведением вектора 11: +) и
|2:+>:
536

Применение постулатов к простым случаям
Применив четвертый постулат главы III, получим, что искомая вероятность равна:
•/ =
^[<++ИМ]к>
^|<x-;Y|2. о?)
Полученный результат имеет вид «квадрата суммы»*.
После измерения, если действительно получено значение +Й/2 для 5lv и +Ы2
для S2z, то система окажется в состоянии A6).
Ь. ИЗМЕРЕНИЯ, ВЫПОЛНЯЕМЫЕ НА ОДНОМ СПИНЕ
Можно, конечно, измерять только одну компоненту одного из двух спинов. В этом
случае, поскольку ни одна из этих компонент не образует сама по себе полный набор
коммутирующих операторов, существует несколько собственных векторов,
соответствующих одному и тому же результату измерения, и соответствующая вероятность равна
«сумме квадратов».
а. Первый пример
Измеряется только Slz. Какие результаты и с какими вероятностями могут быть
получены?
Возможными результатами являются собственные значения ±h 12 оператора SXz,
причем каждое из них дважды вырождено. В соответствующем собственном
подпространстве можно выбрать ортонормированный базис: пусть, например, им будут
векторы {|+ +), |+ -)} для значения +Й/2 и {|- +), |—)} для значения -й 12 .Тогда
&
rfj4Mv>|4<H^HY|48f. A8)
* Следует обратить внимание на смену знака перед / при переходе от A6) к сопряженному
бра-вектору; если забыть об этом, то получится неправильный результат ( Ot + m Ф ОС-т ,
так как а / у не является в общем случае вещественным числом).
537

Глава IV
ЗАМЕЧАНИЕ
Поскольку над спином B) не выполняется никакое измерение, выбор базиса в
пространстве £5B) произволен. Можно, например, выбрать в качестве базиса
собственного подпространства оператора S]z с собственным значением +Й/2
векторы:
H|2:±>,=-tM±|+->].
V2
что дает:
K+fLia+pi24ia"pi2=iai24Pi2
A9)
B0)
Общее доказательство того, что в случае вырожденного собственного
значения полученная вероятность не зависит от выбора базиса в соответствующем
собственном подпространстве, дано в § B-3-b-a главы III.
C. Второй пример
Пусть теперь измеряется S2x. Какова вероятность получить значение -Й / 2 ?
Собственное подпространство, связанное с собственным значением -й / 2 , является
двумерным. В качестве базиса в нем можно выбрать векторы:
1
|1:+>|2:->,=^[М-|+->];
1Н|2:->,=^0-+Н->]-
B1)
Тогда
? =
^[(+ЧЧ+Н]к> +^[(ЧЧ--1]к>
eI|a-pf + I|Y-5f
B2)
В этом результате каждый из членов «суммы квадратов» сам является «квадратом суммы».
Если измерение действительно дало значение -Й/2, то состояние |\|/') системы
сразу же после измерения является нормированной проекцией вектора \\\f) на
соответствующее собственное подпространство. Мы только что вычислили проекции вектора
538

Применение постулатов к простым случаям
|\|/) на базисные векторы B1) этого подпространства, и они равны соответственно
—f= (а - Р) и -pKY ~ 5) • Поэтому
V2 V2
И=
1
!|a-pf + I|Y-8fL
I(a-P)(| + +)-| + -»4(Y-8)(|-+>-|-))
B3)
ЗАМЕЧАНИЕ
В этом дополнении мы полагали, что компоненты операторов S, и S,
определялись как проекции на оси координат. Конечно, совершенно так же можно
определять компоненты S, u и S, v на любые единичные векторы и и v. При
этом все рассуждения остаются такими же, как и ранее.
Дополнение Eiv
МАТРИЦА ПЛОТНОСТИ СПИНА 1/2
1. Введение.
2. Матрица плотности идеально поляризованного спина (чистое состояние).
3. Пример статистического ансамбля: неполяризованный спин.
4. Спин 1/2 в статическом поле при термодинамическом равновесии.
5. Разложение матрицы плотности по матрицам Паули.
1. Введение
Цель данного дополнения — на примере очень простой физической системы (спин
1/2) проиллюстрировать общие положения, развитые в дополнении Еш. Мы изучим
матрицы плотности, описывающие спин 1/2 в ряде случаев: идеально поляризованный спин
(чистое состояние), неполяризованный или частично поляризованный спин
(статистический ансамбль). Тем самым мы сможем подтвердить и интерпретировать общие
свойства, сформулированные в дополнении Еш. Кроме того, увидим, что разложение матрицы
плотности по матрицам Паули очень просто выражается через средние значения
компонент спина.
539

Глава IV
2. Матрица плотности идеально поляризованного спина
(чистое состояние)
Рассмотрим спин 1/2, выходящий из «атомного поляризатора», описанного в § В
главы IV, и находящийся в собственном состоянии |+) (собственное значение +Ы2)
компоненты S • и спина (напомним, что полярные углы единичного вектора и
обозначены символами й иф). При этом состояние спина точно известно и может быть
представлено [см. формулу (А-22-а) главы IV] в виде:
\4) = cos-e-*n\+) + sin-e*n\-). A)
В дополнении Еш мы видели, что по определению такая ситуация соответствует чистому
случаю. Можно сказать, что выходящий из «поляризатора» пучок идеально
поляризован. Впрочем, напомним, что для каждого спина среднее значение (S) равно —и [глава
IV, выражения (В-14)].
В базисе {|+), |-)} матрица плотностир@, ф), соответствующая состоянию A),
находится без труда: для этого записывается матрица проекционного оператора на это
состояние:
Р(в,Ф) =
2«
COS —
2
ш — cos — е v
2 2
sin — cos — е ^
2 2
• 2*
sin —
2 J
B)
Эта матрица в общем случае не диагональна. «Населенности» р++ и р__ имеют очень
простой физический смысл: их разность равна cosb = 2(S,)/ft [см. уравнения (В-14)
главы IV], а их сумма равна 1, то есть действительно населенности связаны с
продольной поляризацией (Sz). Аналогично, модуль «когерентностей» р+_ и р_+ равен
|р+_| = |р_+| = — sinft = — (Sjl) , где (S±) — проекция (S) на плоскость хОу ; аргумент
р_+ равен ф, то есть это угол, образуемый (SL) с осью Ох , вследствие чего
когерентности связаны с поперечной поляризацией (S±).
Легко доказать также, что
[р(д,ф)]2=р(в,ф), C)
что является характеристикой чистого состояния.
540

Применение постулатов к простым случаям
3. Пример статистического ансамбля: неполяризованный спин
Пусть теперь нас интересует спин атома серебра, выходящего из нагревателя (рис. 1
главы IV) и не проходящего через «атомный поляризатор» (при этом спин не
подвергается никакой предварительной подготовке). Все, что можно сказать об этом спине,
заключается в утверждении, что априори он может оказаться направленным в любом
направлении пространства, и все эти направления равновероятны. Используя понятия
дополнения Ель можно утверждать, что такая ситуация соответствует статистической
смеси состояний |+) с равными весами. Формула B8) дополнения Еш определяет
соответствующую матрицу плотности. Однако дискретную сумму £ нужно заменить HHTerpa-
лом по всем возможным направлениям:
р = -L jdQ рF, ф) = -L J2*rf<p£«яв М р(в, Ф) D)
4я An ° °
(множитель 1 / 4я обеспечивает нормировку вероятностей по всем направлениям).
Вычисление интегралов, определяющих матричные элементы, не представляет затруднений
и приводит к следующему результату:
A/2 0 ^
р=(о I/2J- <5>
Из формулы E) следует, что р2 = р/2, и, следовательно, в случае статистического
ансамбля р2 отличается от р .
С другой стороны, если с помощью E) вычислить средние значения Sx, S , Sz,
получим:
(Si) = tr [pS, ] = 1 tr 5,- = 0, где i = x, у, z . F)
Тем самым мы доказали, что спин не поляризован: поскольку все направления
эквивалентны, средние значения проекций спина равны нулю.
ЗАМЕЧАНИЯ
(i) Из этого примера понятно, как недиагональные элементы матрицы р
(когерентности) могут обратиться в нуль при суммировании по всем возможным
состояниям статистического ансамбля: как мы уже видели в § 2, когерентности р+_ и р_+
связаны с поперечной спиновой поляризацией (S±), и суммирование векторов
541

Глава IV
(S±) по всем равновероятным направлениям плоскости хОу дает, естественно,
нулевой результат,
(ii) Случай неполяризованного спина также весьма поучителен, ибо дает возможность
понять, почему нельзя описать статистическую смесь состояний «средним
вектором состояния». Действительно, допустим, что нужно найти такие а и C, чтобы
вектор
|V) = <x|+) + P|-), G)
где
|а|2+|р|2 = 1, (8)
представлял неполяризованный спин, для которого все средние (Sv), (Sy) и (Sz)
равны нулю. Простые вычисления дают:
(S,) = ^(a*P + ap*);
(sv) = ^(a*p-ap*);
(Sz) = |(a*a-p*P). (9)
Чтобы среднее значение (Sv) обратилось в нуль, нужно выбрать аир так, чтобы
произведение а*Р было чисто мнимым; аналогично, чтобы (Sy) обратилось в
нуль, нужно, чтобы произведение а*Р было вещественным, откуда следует, что
а*Р = 0, то есть
или а = 0 , что влечет за собой |Р| = 1 и (S,) = -h 12 ;
или Р = 0, что влечет за собой | а | = 1 и (S,) = +h 12 .
Итак, (Sz) не может равняться нулю одновременно с (Sv) n(Syу, и состояние
G) не может представлять неполяризованный спин.
Впрочем, обсуждение в § В-1-е главы IV показало, что, какими бы ни были a
и Р, удовлетворяющие условию (8), им всегда можно поставить в соответствие
два угла д и ф , определяющие направление вектора и так, чтобы | \|/) был
собственным вектором оператора S • и с собственным значением +h 12 . Таким обра-
542

Применение постулатов к простым случаям
зом, видно, что состояние вида G) всегда описывает спин, идеально
поляризованный в некотором направлении пространства,
(iii) Матрица плотности E) представляет статистическую смесь состояний |+) , все
направления и которых равновероятны. Можно, однако, представить себе другие
статистические ансамбли, дающие такую же матрицу плотности. Такова,
например, статистическая смесь состояний |+) и |-), взятых в равных пропорциях; или
статистическая смесь трех состояний |+)м, определенных так, что концы трех
векторов и образуют равносторонний треугольник с центром в точке О и также взятых
в равных пропорциях, и т.д. Видно, что одна и та же матрица плотности может
быть получена различными способами. Поскольку все физические предсказания
зависят только от матрицы плотности, невозможно различить физически такие типы
статистических ансамблей, которые приводят к одной и той же матрице плотности.
Их следует рассматривать как разные формы одной и той же неполной информации
о системе.
4. Спин 1/2 в статическом поле
при термодинамическом равновесии
Рассмотрим спин 1/2 в статическом поле В0, параллельном оси Oz. Мы видели в
§В-3-а главы IV, что стационарными состояниями этого спина являются состояния |+) и
|-) с энергиями +/ШH /2 и -Ш0/2 (где со0 = -уВ0, а у — гиромагнитное отношение
спина). Если известно, что система находится в термодинамическом равновесии при
температуре Т, то можно утверждать, что она имеет вероятность находиться в
состоянии |+), равную z~xe~tmQ,2kT, и вероятность находиться в состоянии |—), равную
Z~le+fi{ao,2kT, где величина z = е~ш°,2кт + e+tm°,2kT — нормировочный множитель (часто
называют Z «функцией распределения»). Здесь мы имеем другой пример
статистического ансамбля, описываемого матрицей плотности:
9 = 1"
(e-tm0/2kT q ^
П +Л(о0ШГ
^2
(Ю)
И в этом случае можно убедиться, что р Ф р. Обращение в нуль недиагональных
элементов матрицы плотности обусловлено тем, что все направления, перпендикулярные к
полю В0, то есть к оси Oz, и определенные углом ф, эквивалентны.
Из формулы A0) нетрудно получить:
543

Глава IV
(S,) = tr(pS,) = 0;
(sv) = tr(pSv) = 0;
fc>-««*.>~M&)-
Видно, что спин приобретает поляризацию, параллельную полю, в котором он находится,
величина которой тем больше, чем больше 0H( то есть В0) и чем ниже температура Т.
Поскольку |гЛдс|<1, эта поляризация меньше значения h/2, соответствующего
идеально поляризованному вдоль Oz спину. Можно сказать, что равенство A0) описывает
«частичную» поляризацию спина вдоль оси Oz .
ЗАМЕЧАНИЕ
Намагниченность (Mz) равна у(^) • Исходя из формулы A1), можно
вычислить парамагнитную восприимчивость х спина, определяемую выражением:
(Mz) = y(Sz) = xB0. A2)
Тогда получим (формула Бриллюэна):
x=*LJ*t*Am A3)
2В0 \2кТ)
5. Разложение матрицы плотности по матрицам Паули
В дополнении AiV мы видели, что единичная матрица / и матрицы Паули
Gx,oy,Gz образуют базис, в котором удобно производить разложение матриц 2x2.
Поэтому для матрицы плотности р спина 1/2 можно записать:
p = a0I + ac>, A4)
где коэффициенты ах определяются формулами [см. дополнение AiV, формулы B3)]:
1
fl0=-trp;
544

Применение постулатов к простым случаям
2 * Й
Итак:
1
0 2
ax=\tT(pox) = ±lr(pSx);
2 п
av=-tr(pav) = -tr(pSv);
2 п
a =^tr(p<r£) = jtr(p5J. A5)
a»4(S), A6)
я
и матрица плотности может быть записана в виде:
p = I/+i(S).a. A7)
Таким образом, матрица плотности репина 1/2 очень просто выражается через
среднее значение спина (S).
ЗАМЕЧАНИЕ
Возведем в квадрат выражение A7). Используя тождество A7) дополнения
Aiv, получим:
e24/+F<sJ/4<s)-CT- A8)
Условие р2 = р, характерное для чистого случая, эквивалентно для спина 1/2
условию:
<SJ=y- A9)
Оно, конечно, не реализуется для неполяризованного спина ((S) = 0) или для спина,
находящегося в термодинамическом равновесии (мы видели, что в этом случае
35 Квантовая механика
545

Глава IV
S)| < й / 2). Напротив, из формул (В-14) главы IV следует, что для спина в состоянии
|v) [формула A)] (SJ= —.
Дополнение Fiv
СПИН 1/2 В СТАТИЧЕСКОМ
И ВРАЩАЮЩЕМСЯ МАГНИТНЫХ ПОЛЯХ:
МАГНИТНЫЙ РЕЗОНАНС
1. Классическое рассмотрение. Вращающаяся система координат.
a. Движение в статическом поле. Прецессия Лармора.
b. Влияние вращающегося поля. Резонанс.
2. Квантовое рассмотрение.
a. Уравнение Шредингера.
b. Переход во вращающуюся систему координат.
c. Вероятность перехода. Формула Раби.
d. Случай, когда два уровня нестабильны.
3. Связь классического и квантового подходов: эволюция (М).
4. Уравнения Блоха.
a. Анализ конкретного примера.
b. Решение в случае вращающегося поля.
В главе IV мы рассмотрели с позиций квантовой механики эволюцию спина 1/2,
помещенного в статическое магнитное поле. В этом дополнении нас будет интересовать
случай, когда спин 1/2 подвержен одновременному действию нескольких магнитных
полей, которые могут зависеть от времени, как это имеет место в экспериментах по
магнитному резонансу. Прежде чем перейти к квантовому анализу задачи, вспомним
некоторые результаты классической механики.
1. Классическое рассмотрение. Вращающаяся система координат
а. ДВИЖЕНИЕ В СТАТИЧЕСКОМ ПОЛЕ. ПРЕЦЕССИЯ ЛАРМОРА
Рассмотрим механический момент j , обладающий магнитным моментом m = у j,
коллинеарным с j (постоянная у называется гиромагнитным отношением системы), в
546

Применение постулатов к простым случаям
статическом магнитном поле В0. Это поле создает момент силы тхВ0, действующий
на систему, и классическое уравнение движения момента j имеет вид:
у = тхВ0 A)
dt
или
— т@ = ут(ОхВ0. B)
at
Умножив скалярно оба члена уравнения сначала на т(г) и затем на В0, получим:
4"[т(О]2=0; C)
dt L J
-f [m(r).B0] = 0. D)
dt
Таким образом, т(/) изменяется во времени так, что его модуль и угол с полем В0
остаются постоянными. Далее достаточно спроектировать уравнение B) на плоскость,
перпендикулярную В0, чтобы увидеть, что т(/) вращается вокруг В0 (прецессия Лар-
мора) с угловой скоростью со0 = -уВ0 (если у > О, вращение происходит в обратном
направлении).
Ь. ВЛИЯНИЕ ВРАЩАЮЩЕГОСЯ ПОЛЯ. РЕЗОНАНС
Допустим теперь, что, кроме статического поля В0, имеется еще поле В,(О,
перпендикулярное к В0, имеющее постоянный модуль и вращающееся вокруг В0 с
угловой скоростью со (см. рис.1). Пусть
to,=-YB,- E)
Обозначим символом Oxyz неподвижную систему координат с единичными
векторами осей ev,ev,e, ,ось Oz которой направлена вдоль поля В0, и символом OXYZ систему
координат, образованную из Oxyz путем поворота на угол cor вокруг оси Oz,
имеющую единичные векторы ех, ек, ez , ось ОХ которой направлена вдоль вращающегося
35*
547

Глава IV
поля В,(/). Уравнение эволюции m(f) в присутствии полного поля В(г) = В0+В,(г)
имеет вид:
dt
m(r) = Ym(Ox[B0 + BI@].
F)
Рис.1
Oxyz — неподвижная система
координат, ось Oz которой
направлена вдоль постоянного
магнитного поля В0. Система координат
OXYZ, ось ОХ которой
направлена вдоль поля В,(г), вращается
вокруг Oz с угловой скоростью со
Чтобы решить это уравнение, удобно перейти из неподвижной системы координат
Oxyz во вращающуюся систему координат OXYZ, в которой относительная скорость
движения вектора m(r) равна:
dm} dm
= сое х
dt ). dt
m@-
Обозначим:
и подставим F) в G):
Дсо = со - соп
dm\
= m(r)x[Acoez -co,ex].
G)
(8)
(9)
Это уравнение значительно удобнее для решения, чем уравнение F), так как в этом слу-
548

Применение постулатов к простым случаям
чае коэффициенты правой части не зависят от времени. Кроме того, оно имеет форму,
аналогичную уравнению B): относительное движение вектора ш(г) представляет собой
вращение относительно «эффективного поля» BeJf (во вращающейся системе координат
это поле неподвижно), определяемого равенством (см. рис.2):
>Г
Рис.2
Во вращающейся системе координат OXYZ
эффективное поле В^ имеет постоянное
направление, вокруг которого прецессирует магнитный
момент т(/) с постоянной угловой скоростью
(прецессия во вращающейся системе координат)
В
1
eff
[Acoez-co.eJ.
(Ю)
Чтобы получить абсолютное движение m(r), достаточно сложить прецессию вокруг
Beff с вращением вокруг оси Oz с угловой скоростью (О .
Уже эти первые результаты позволяют нам понять сущность явления магнитного
резонанса. Действительно, рассмотрим магнитный момент, который в момент времени
t = 0 был параллелен полю В0 (именно так ориентируется магнитный момент при
термодинамическом равновесии при очень низких температурах: он оказывается в самом
низшем энергетическом состоянии в присутствии поля В0). Что произойдет, если
теперь приложить слабое вращающееся поле B{(t) ? Если частота вращения (о/2я этого
поля очень далека от собственной частоты 0H /2я (точнее говоря, если Асо = 0) - со0
значительно больше со,), то направление эффективного поля практически совпадает с
осью Oz, вследствие чего прецессия m(t) вокруг Beff происходит с очень малой
амплитудой и почти не меняет направления магнитного момента. Напротив, если
выполнено условие резонанса @ = 0H (то есть До) «со,), поле Beff образует с осью Oz зна-
549

Глава IV
чительный угол. При этом прецессия магнитного момента имеет большую амплитуду, и
в условиях точного резонанса (Ао = 0) магнитный момент может оказаться полностью
перевернутым.
2. Квантовое рассмотрение
а. УРАВНЕНИЕ ШРЕДИНГЕРА
Пусть |+) и |-) — два собственных вектора оператора проекции Sz спина на ось
Oz, соответствующие собственным значениям +Й / 2 и -h 12 . Вектор состояния
системы можно представить в виде суперпозиции:
|v(f)) = MO|+) + a-@|-).
Гамильтониан системы H(t) равен*:
H(t) = -M-B(t) = -yS[B0+Bl(t)]
или после раскрытия скалярного произведения:
H(t) = u>0Sz +(D1[cas(Dr Sx + smco/ Sy].
(И)
A2)
A3)
Используя формулы (А-16) и (А-17) главы IV, получим матрицу, представляющую Н в
базисе {|+), |-)}:
V
со«
-соп
A4)
С учетом выражений A1) и A4) уравнение Шредингера может быть записано в
форме:
at 2 2
at 2 2
A5)
В выражении A2) М-В@ является скалярным произведением MX Bx(t)+ MyBy(t) +
+ MzBz(t), где Mv, M , М, — операторы (наблюдаемые исследуемой системы), a Bx(t),
Bv(t)y Bz(t) — числа, так как мы рассматриваем магнитное поле как классическую величину,
значение которой определяется внешним устройством, не зависящим от рассматриваемой системы.
550

Применение постулатов к простым случаям
Ь. ПЕРЕХОД ВО ВРАЩАЮЩУЮСЯ СИСТЕМУ КООРДИНАТ
Уравнения A5) образуют систему линейных однородных уравнений с зависящими
от времени коэффициентами. Удобно выбрать ее решения в виде:
ь+ @ = ^4@;
ЬЛ0 = е-Ш2а_@. A6)
Подставив A6) в A5), получим систему уравнений с постоянными коэффициентами:
. d До) 0),
яг 2 2
i — МО = -г1 МО + — МО-
а/ 2 2
Эту систему можно записать также в виде:
м1-\то)=й\що),
at
если ввести кет |\j?@) и оператор Н, определенные формулами:
|Ф(*)) = М0|+) + М0|->;
A7)
2
-Асо О),
со, Асо
A8)
A9)
B0)
Благодаря преобразованию A6) мы получили уравнение A8), аналогичное
уравнению Шредингера, в котором оператор Я, определенный формулой B0), играет роль
гамильтониана, не зависящего от времени. Он описывает взаимодействие спина с
постоянным полем, компоненты которого равны просто компонентам эффективного поля,
введенного выше во вращающейся системе координат OXYZ [формула A0)]. Таким
образом, можно считать, что преобразование A6) является квантовым эквивалентом
перехода из неподвижной системы координат Oxyz во вращающуюся OXYZ .
Этот результат можно доказать и вполне строго. Действительно, согласно A6) можно запи-
|ф@) = Л(г)|ч/@),
B1)
где R(t) — унитарный оператор, определяемый равенством:
551

Глава IV
R{t) = eimS-Jh . B2)
Ниже мы увидим (см. дополнение B!V), что R(t) описывает поворот системы осей на угол Ш
вокруг оси Oz ; таким образом, формула A8) действительно является записью уравнения Шре-
дингера во вращающейся системе координат OXYZ .
Решение уравнения A8) находится без труда. Чтобы определить |\j/@) , зная |\j/@)),
достаточно разложить |\j/@)) по собственным векторам оператора Я (они могут быть
вычислены совершенно точно) и затем применить правило (D-54) главы III (это
возможно, поскольку Я не зависит явно от времени). Дальнейший переход от |ф@) к |\|/@)
производится с помощью формул A6).
с. ВЕРОЯТНОСТЬ ПЕРЕХОДА. ФОРМУЛА РАБИ
Рассмотрим спин, который в момент времени t = 0 находился в состоянии |+):
|v@))=|+>. B3)
Согласно формуле A6) это соответствует:
|Ф@> = |+>. B4)
Какова вероятность №+_(t) найти спин в момент времени t в состоянии |-)? Поскольку
a_(t) и b_(t) имеют одинаковые модули, можно записать:
^+-@ = |(-|V@)|2 =K@|2 =М0|2 =|(~|Ф@)|2. B5)
Поскольку |ф@) является решением уравнения A8) с начальным условием B4), то
нужно вычислить (-|чКО)Г •
Эта задача фактически уже была решена в § C-3-b главы IV. Чтобы использовать
полученные там результаты, достаточно применить следующие соответствия:
|ф.)->1+>:
|ф2И->;
* л
Е, -> —Дсо ;
1 2
552

Применение постулатов к простым случаям
Е2 -> —До) ;
WI2->-©,.
Тогда формула Раби [уравнение (С-32) главы IV] примет вид:
ч2
со:
со2 + (ЛеоJ
sin2
д/со'+САо)J^
B6)
B7)
Таким образом, вероятность ^._@, равная нулю в момент времени t = О ,
изменяется со временем синусоидально между значениями 0 и
cof
GJ+(ACDJ
. Здесь мы также
видим, что имеет место явление резонанса. Действительно, если |Дсо|» |со,|,
вероятность 0*+_(t) остается близкой к нулю (см. рис.З-а), и, напротив, вблизи резонанса
амплитуда осцилляции Pf+_(t) становится большой и, если условие Дсо = 0 реализовано
Bи +1O1
точно, имеем .^_@ = 1 в моменты времени t - -
со,
(см. рис.ЗЬ).
1 +
^+-(/)
со - со, = Зсо.
ЮУ\/\У\,
->/
Рис.3
Зависимость вероятности перехода между состояниями |+) и |-) от.времени под
действием вращающегося магнитного поля В,(г). Вне резонанса (а) вероятность мала, а в
точном резонансе (Ь), каким бы малым ни было поле B{(t), существуют моменты
времени, когда вероятность перехода равна 1
553

Глава IV
Итак, мы получили результат, уже знакомый из классического рассмотрения: при
резонансе даже очень слабое вращающееся поле способно изменить направление спина
на обратное. Заметим, впрочем, что частота осцилляции вероятности ;?+_(t) равна
д/cof +(ДшJ = YBrJ ; эти осцилляции, соответствующие во вращающейся системе
координат проекции на ось OZ прецессии магнитного момента вокруг эффективного
поля, иногда называют «прецессией Раби» [см. также вычисления .^_@ в дополнении Civ,
§ 3-е].
d. СЛУЧАЙ, КОГДА ДВА УРОВНЯ НЕСТАБИЛЬНЫ
Здесь мы предположим, что два уровня |±) соответствуют двум подуровням одного
возбужденного атомного уровня, механический момент которого равен 1/2. В единицу времени
возбуждается п атомов, и все они попадают в состояние |+) *. Атом теряет возбуждение через
спонтанную эмиссию с вероятностью в единицу времени, равной 1 / Т и одинаковой для обоих
подуровней I ±) . Известно, что в этих условиях атом, возбужденный в момент времени -t, имеет
вероятность e~tlx еще находиться в возбужденном состоянии к моменту времени t = 0 (см. дополнение
К,„).
Предполагаем также, что эксперимент проводится в непрерывном режиме, то есть что в
присутствии полей В0 и В,(t) в единицу времени постоянно возбуждается п атомов в состояние
|+). Следует определить, какое количество N атомов будет переходить на основной уровень из
состояния |-у в моменты времени, существенно большие, чем время жизни X . Если атом был
возбужден в момент времени —t, то вероятность найти его в момент времени / = 0 в состоянии
|-) равна ^+_(t)e~t/x, где ^+_@ описывается формулой B7). Полное число атомов в состоянии
|—) может быть получено путем суммирования атомов, возбужденных во все моменты времени
—X, то есть путем интегрирования по времени:
\~dte-tlxn^_{t). B8)
Этот расчет не представляет трудностей; умножив полученное количество атомов на вероятность
спонтанного перехода 1 / X в основное состояние, получим:
* Практически такое возбуждение может быть реализовано с помощью облучения атомов
лучом света: если падающие фотоны поляризованы, то из закона сохранения момента следует, что
поглощающие их атомы должны попадать только в состояние |+), а не в состояние |—) . Измеряя
поляризацию переизлученных атомами фотонов, можно узнать, из какого именно состояния
совершаются обратные переходы на основной уровень.
554

Применение постулатов к простым случаям
*-£.. ., "I ,...,■ B9)
2 (ЛеоJ+со,+A/т)
Зависимость /V от А@ представляет собой лоренцеву кривую с полушириной
1 = д/ш;ЧA/тJ. (зо)
-а>/у
Рис.4
Кривая резонанса. Чтобы обнаружить
явление резонанса, ставится эксперимент, когда
в единицу времени п атомов возбуждаются
в состояние |+); под действием поля В,(г),
^ *#о вращающегося с частотой со/2я, атомы
испытывают переходы в состояние |-);
в стационарном режиме регистрируется количество атомов, переходящих в единицу
времени из состояния |-), и при этом наблюдается резонансное увеличение этого
количества, если поле В0 изменяется вблизи значения -о/у
В описанном выше эксперименте измеряется число атомов, переизлучающих фотоны из
состояния |-) при различных значениях магнитного поля В0 и при постоянной частоте СО (то есть
для разных значений АО)). В результате в соответствии с формулой B9) должна быть получена
кривая резонанса, имеющая форму, представленную на рис.4.
Подобные явления представляют значительный интерес. Действительно, можно использовать
несколько параметров кривой резонанса:
— если частота СО известна, то измерение значения магнитного поля В'0п , соответствующего
вершине резонансной кривой, позволяет найти гиромагнитное отношение у = -0) / Bq ;
— может оказаться также, что величина у известна заранее: тогда измерение частоты
(О / 2я, соответствующей резонансу, позволяет измерить постоянное магнитное поле В0. На
этом принципе основаны многочисленные схемы магнитометров, обладающих очень высокой
чувствительностью. В ряде случаев такое измерение поля дает возможность получить интересную
физическую информацию: так, например, если спин принадлежит ядру в некоторой молекуле или
в кристаллической решетке, то можно узнать значение локального поля в месте расположения
этого ядра, зависимость его от положения в кристаллической решетке и т. д.;
— если построить график зависимости квадрата полуширины линии резонанса L2 от
квадрата @, , то получится прямая, экстраполяция которой к О), = 0 даст значение времени жизни X
возбужденного уровня (см. рис.5).
555

Глава IV
т
L2
Л'
^А' Рис.5
Экстраполяция квадрата ширины L2 кривой
, резонанса (рис.4) к со, =0 позволяет опреде-
-> со,
лить время жизни т исследуемого уровня
3. Связь классического и квантового подходов:
эволюция (М)
Результаты, полученные в § 1 и § 2, очень схожи, хотя в первом случае
использовался классический подход, а во втором — квантовый. Сейчас мы покажем, что такое
совпадение не является случайным, а имеет вполне определенную причину: квантовые
уравнения, описывающие эволюцию среднего значения магнитного момента в
произвольном магнитном поле, идентичны соответствующим классическим уравнениям.
Среднее значение магнитного момента спина 1/2 равно:
(M)(f) = Y(S)@. CD
Чтобы найти (М)(г), используем теорему (D-27) главы III:
1Й^-(М>@ = ([М,Я@]), C2)
где H(t) —оператор:
Я@ = -М-В(/). C3)
Вычислим, например, коммутатор [Mx,H(t)]. Поскольку компоненты поля By(t) и
Bz(t) являются числами (см. замечание к § 2-а), получим:
[Mx,H(t)] = -y2[sx,SxBx(t) + SyBy(t) + SzBz(t)] =
= ^%(t)[sx9S,]-y%(t)[sx9Sl]. C4)
Используя соотношения A4) дополнения AIV, запишем:
556

Применение постулатов к простым случаям
[Mx,H(t)] = ihy2[Bz(t)Sy-By(t)S:]. C5)
Подставим C5) в C2):
j (Mx)(t) = y[Bz(t) (Му) (/)- By(t) (М:) (t)]. C6)
С помощью круговой перестановки можно найти аналогичные выражения для
компонент вдоль осей Оу и Oz, а затем записать все три уравнения в сжатом виде:
^(M)@ = Y(M)(r)xB(r). C7)
Сравним теперь формулы C7) и F): видно, что среднее значение (М)(г) подчиняется в
точности классическим уравнениям, какой бы ни была зависимость от времени
магнитного поля В (г).
4. Уравнения Блоха
На практике в экспериментах по магнитному резонансу наблюдается магнитный момент не
одного изолированного спина, а большого числа одинаковых спинов, как и в описанном в § 2-d
эксперименте, где регистрировалось количество атомов, возвращающихся на основной уровень из
возбужденного состояния |-у . Кроме того, интересуются не только вычисленной ранее
вероятностью .^_@ » можно измерять также полную намагниченность Л исследуемого образца,
являющуюся суммой средних значений наблюдаемой М всех спинов, входящих в образец*. Таким
образом, представляет интерес получить уравнения эволюции величины Ж , названные
уравнениями Блоха.
Чтобы понять физический смысл входящих в эти уравнения членов, мы рассмотрим простой
конкретный случай. Его выводы легко обобщаются на иные более сложные ситуации.
а. АНАЛИЗ КОНКРЕТНОГО ПРИМЕРА
Рассмотрим пучок атомов, вылетающих из атомного поляризатора типа тех, которые
описывались в §В-1-а главы IV. Все атомы пучка** находятся в спиновом состоянии +) и имеют маг-
Можно регистрировать, например, электродвижущую силу, индуцированную в
окружающей образец катушке при изменении Л во времени.
** Например, атомы серебра или водорода в основном состоянии. Для простоты пренебрежем
всеми эффектами, связанными с существованием спина атомного ядра.
557

Глава IV
нитный момент, направленный вдоль оси Oz . Через малое отверстие они проникают в ячейку С
(рис.6), многократно сталкиваются с внутренними стенками ячейки и через некоторое время
вылетают из нее через то же отверстие.
Обозначим буквой п число поляризованных атомов, проникающих в ячейку в единицу
времени. Обычно п — малая величина, так как плотность атомов в ячейке достаточно мала, чтобы
можно было пренебречь взаимодействием между ними.
Если внутренние поверхности стенок ячейки покрыты соответствующим покрытием, можно
считать, что столкновения атомов со стенками ячейки очень мало влияют на спиновое состояние
атомов*. Допустим, что 1 / TR — вероятность того, что в единицу времени элементарная
намагниченность, внесенная в ячейку поляризованными атомами, исчезла либо вследствие
деполяризующих столкновений со стенками, либо просто потому, что атом покинул ячейку. Время TR
называют «временем релаксации». Ячейка помещается в магнитное поле В(Г) , имеющее постоянную
составляющую и вращающуюся компоненту. Нужно найти уравнение эволюции полной
намагниченности Jt(t) атомов, находящихся в ячейке в момент времени t.
Рис.6
Схема экспериментальной установки, позволяющей наполнить ячейку атомами,
находящимися в состоянии |+)
Запишем сначала точное выражение для Jt{t) :
N
ли) = Z(v(,,)(o|M|\|f(/)(o) = I>(/)@.
C8)
В формуле C8) суммирование ведется по ,/Г спинам, которые уже вошли в ячейку, но к моменту
времени t еще не вышли из нее-и не испытали деполяризующих столкновений. \|/(,)@/
—вектор состояния такого спина (i) в момент времени t [мы не учитываем в формуле C8) спины,
которые испытали деполяризующее столкновение и еще не вышли из ячейки, так как их полный
вклад равен нулю: их спины случайно ориентированы во всех направлениях].
* Например, для атомов водорода требуются десятки тысяч столкновений со стенками,
покрытыми фторопластом, чтобы магнитный момент атома водорода оказался дезориентированным.
558

Применение постулатов к простым случаям
Между моментами времени t и t + dt намагниченность Jt{t) изменяется под действием
трех различных факторов.
(i) Некоторая часть dt I ТИ из . Г спинов испытывает деполяризующие столкновения или
выходит из ячейки; эти спины вычитаются из суммирования C8), то есть
dJt(t) = Jt(t). C9)
(ii) Другие спины испытывают эволюцию в поле B(f) . Мы видели в §3, что для каждого из
них эволюция среднего значения М , равного:
^@@ = (v(/,@|m| \|/(,'Ч0).
подчиняется классическому закону:
dJtU)(t) = YJlU)(t)xB(t)dt . D0)
Правая часть равенства D0) линейна по отношению к М{' (t), вследствие чего вклад этих спинов
в общее изменение Jt(t) определяется формулой:
dJt(t) = yJl(t)xB(t)dt . D1)
(iii) Наконец, некоторое количество новых атомов п dt пополняет ячейку и дает вклад JA0 в
полную намагниченность, равный среднему значению М в состоянии |+) (момент Ц0
параллелен оси Oz и равен по модулю |jl10| = Y Й/2 ), вследствие чего Л увеличивается на
dJC(t) = n \i0dt. D2)
Полное изменение Ж является суммой C9), D1) и D2). Разделив обе части суммы на dt,
получим уравнение, описывающее эволюцию Jt{t) (уравнение Блоха):
—Ji(t) = п ц0 JL(t) + yJC(t) х В(Г). D3)
dt TR
Уравнение D3) установлено для конкретного случая с учетом некоторых предположений.
Однако характерные свойства этого уравнения остаются справедливыми для большого количества
других экспериментов, когда скорость изменения JC(t) образуется как сумма трех членов:
— член, описывающий приготовление системы (здесь п\1{)); действительно, магнитный
резонанс невозможно наблюдать без предварительной поляризации спинов, которая может быть
реализована с помощью градиента магнитного поля (как в приведенном выше примере),
поляризованного оптического возбуждения (пример, рассмотренный в §2-d), охлаждения образца в
сильном постоянном магнитном поле и т.д.;
559

Глава IV
— член, описывающий затухание (здесь -Jt{t) ITR), то есть исчезновение (релаксацию)
полной намагниченности под действием различных факторов: столкновения, уход атомов,
изменение атомного уровня за счет спонтанной эмиссии и т. д.;
— член, описывающий прецессию Ji(i) в магнитном поле В(/) [последний член в D3)].
Ь. РЕШЕНИЕ В СЛУЧАЕ ВРАЩАЮЩЕГОСЯ ПОЛЯ
Если поле В(£) является суммой статического поля В0 и вращающегося поля В,@, как
рассматривалось выше, то уравнения D3) можно решить точно. Как и ранее, используется переход
во вращающуюся систему координат OXYZ , в которой относительное изменение Jl(t) можно
записать в виде:
—Л I = п [10 -^-Л{1) + yM(t) xBeJf D4)
*" ' rel *R
[где Bejj- определяется равенством A0)].
Проектируя это уравнение на оси ОХ, О К, OZ , получим три линейных дифференциальных
уравнения с постоянными коэффициентами, стационарными решениями которых (справедливых
для времен, существенно больших времени релаксации TR ) являются функции:
(jlx)s=-n\L0TR 1—
(А@J+@^+A/Г/?J
Ws- nJX«(AcaJ+CD2l+A/7iJ
{j(z)s=nii0TR
■ -L
(Ао)J+со2+A/Г/?J
D5)
Три компоненты стационарной намагниченности \Л) при изменении поля В0 изменяются
резонансным образом вблизи значения В0 = -0) / у (см. рис.7). При этом функции \ЛУ) и \Л2)
Z / 2 2
имеют вид кривых поглощения (лоренцевы кривые с шириной — у СО, +(\/TR) ), а функция
\.llx J — кривой дисперсии с той же шириной.
560

Применение постулатов к простым случаям
*(//v).
► ,!<•>
:л),
Лш
Лм
Рис.7
Зависимость стационарных
значений компонент вектора JC во
вращающейся системе координат от
Асо = со - со0. Зависимости (JtY)s и
{•H'z)s имеют форму кривых
поглощения, а зависимость (Jtx)s —
кривой дисперсии. Ширины всех
трех кривых одинаковы и равны
2д/@^ +(\/TRJ ; они
увеличиваются с ростом о,. На данном рисунке
предполагается, что со, = \ITR
Относительно практического интереса этих кривых можно повторить те же замечания, что и
в §2-d.
Дополнение Giv
ИССЛЕДОВАНИЕ МОЛЕКУЛЫ АММИАКА
С ПОМОЩЬЮ ПРОСТОЙ МОДЕЛИ
1. Описание модели.
2. Собственные функции и собственные значения гамильтониана.
a. Бесконечно высокий потенциальный барьер.
b. Потенциальный барьер конечной высоты.
c. Эволюция молекулы. Частота инверсии.
3. Молекула аммиака как двухуровневая система.
a. Пространство состояний.
b. Уровни энергии. Снятие вырождения вследствие прозрачности потенциального барьера.
c. Влияние статического электрического поля.
36 Квантовая механика
561

Глава IV
1. Описание модели
В молекуле аммиака NH3 три атома водорода образуют основание пирамиды, в
вершине которой находится атом азота (см. рис.1). Рассмотрим эту молекулу на базе
упрощенной модели, характеризующейся следующими свойствами: атом азота, будучи
более тяжелым, чем атомы водорода, считается неподвижным; атомы водорода
образуют равносторонний треугольник, длина сторон которого считается постоянной, а его ось
симметрии всегда проходит через атом азота; потенциальная энергия системы является
функцией единственного параметра, которым является алгебраическое расстояние х
между атомом азота и плоскостью, определяемой тремя атомами водорода*. Ход
функции, описывающей потенциальную энергию V(x), представлен сплошной кривой на
рис.2. Симметрия задачи относительно плоскости х = 0 требует, чтобы V(x) была
четной функцией координаты х. Два минимума V(x) соответствуют двум симметричным
конфигурациям молекулы, в которых она находится в стабильном состоянии с точки
зрения классической механики, и энергию этого состояния примем за нулевую.
Потенциальный барьер в точке х = 0 с высотой V, отражает то обстоятельство, что, когда
атом азота находится в плоскости атомов водорода, он их отталкивает. И наконец,
нарастание V(x) при |jc|>Z? соответствует силам химической связи, которые сохраняют
молекулу как стабильное образование.
АХ
о! mN
Н *(-- 1-—-± Н Рис.1
^"ч\^ I / Схема молекулы аммиака; х — алгебраическое зна-
\^ чение расстояния между плоскостью атомов водорода
" и атомом азота, который считается неподвижным
В рамках этой модели задача становится одномерной: фиктивная частица с массой
т (можно показать, что «приведенная масса» т этой системы равна ) дви-
Ътн + mN
жется в поле потенциала V(x). Какие уровни энергии предсказывает в этом случае
* В этой одномерной модели, естественно, не учитываются эффекты, связанные с вращением
молекулы.
562

Применение постулатов к простым случаям
квантовая механика? В сравнении с классической механикой могут появиться два
принципиальных отличия.
(i) Соотношение неопределенностей Гейзенберга запрещает молекуле иметь
энергию, равную минимальному значению функции V(x), то есть Vmin = 0; мы уже видели в
дополнениях Q и Мш, почему ее энергия должна быть обязательно больше, чем Vmhl.
Рис.2
Зависимость потенциальной энергии V(x) молекулы от координаты х. Имеются два
минимума, соответствующие положениям классического равновесия, разделенные
потенциальным барьером, связанным с наличием сил отталкивания между атомом азота и тремя
атомами водорода. Пунктиром изображен «прямоугольный» потенциал, используемый
для аппроксимации функции V(x)
(ii) С классической точки зрения потенциальный барьер в точке х = 0 непроницаем
для частицы, если ее энергия меньше V,, то есть атом азота остается всегда с какой-то
одной стороны относительно плоскости атомов водорода, и молекула не может испытать
инверсионную трансформацию. С квантовой точки зрения молекула может пройти через
барьер за счет туннельного эффекта независимо от значения энергии, то есть инверсия
молекулы всегда возможна. Следствия этого эффекта будут обсуждаться в дальнейшем.
Здесь нас будет интересовать лишь качественная сторона явлений, а не их точный
количественный расчет, который в рамках данной упрощенной модели не имеет
большого смысла. Так, мы покажем сам факт существования определенной частоты
инверсии молекулы аммиака, не пытаясь определить ни точное, ни даже приблизительное
значение этой частоты. Более того, для еще большего упрощения задачи заменим
функцию V(x) прямоугольным потенциалом, изображенным на рис.2 пунктиром и
состоящим из двух бесконечных скачков потенциала в точках х = ±(b + a 12) и
потенциального барьера с высотой V{) и центром в точке х = 0 [его ширина равна (lb - а) ].
36*
563

Глава IV
2. Собственные функции
и собственные значения гамильтониана
а. БЕСКОНЕЧНО ВЫСОКИЙ ПОТЕНЦИАЛЬНЫЙ БАРЬЕР
Прежде чем вычислить собственные функции и собственные значения
гамильтониана, соответствующего «прямоугольному» потенциалу, изображенному на рис.2,
допустим на первом этапе, что потенциальный барьер в центре ямы V0 бесконечно высок (при
этом туннельный эффект невозможен). Это позволит нам затем лучше понять
последствия туннельного эффекта через барьер конечной высоты (рис.2). Поэтому будем сначала
считать, что частица находится в поле потенциала V(x), состоящего из двух бесконечно
глубоких ям с шириной а и центрами в точках х = ±Ь (рис.3). Если частица находится
в одной из этих ям, она, конечно, не может перейти в другую.
аУМ
-Ь
—f—
+ *
■>х
Рис.3
Если высота
У0 потенциального барьера
(рис.2) очень велика, то можно считать, что
имеются две бесконечно глубокие
потенциальные ямы с шириной а , центры которых
отстоят друг от друга на расстоянии 2Ь
Каждая из ям, изображенных на рис.3, подобна той, которую мы уже рассматривали
в §2-с-р дополнения Hi, и можно использовать полученные там результаты. Возможные
энергии частицы при этом равны:
h2kl
Е„ =-
2т
A)
где
_ пп
B)
(здесь п — целое положительное число). Каждое из этих значений энергии дважды
вырождено, так как им соответствуют две волновые функции:
564

Применение постулатов к простым случаям
<р?<*) =
Ф2« =
2
— sin
а
/2"-
J— 5/W
k,\ b + --x
b + — + jc
2
если & — < jc < Z? + —
2 2
вне этого интервала
если Z? — <-х<Ь + —
2 2
C)
О вне этого интервала
В состоянии ср'Л частица находится в правой бесконечной яме, а в состоянии ф^) — в
левой.
На рис.4 представлены два первых дважды вырожденных уровня энергии молекулы.
Частота Бора (Е2 -£,)//i, связанная с этими двумя уровнями, соответствует, как мы
уже видели в § 2-Ь дополнения Ащ, колебательному движению частицы между двумя
стенками правой (или левой) ямы, когда ее состояние является линейной суперпозицией
векторов ф[\ и ж) (или ш2) и ф^)). Физически такое движение представляет собой
колебания плоскости, в которой находятся три атома водорода, около положения
устойчивого равновесия, соответствующего х = +Ь (или х = -Ь). Частота таких колебаний
лежит в инфракрасном диапазоне.
т£
Е2 =
4л2Ь2
2та2
Л1*2
£,-£,
г — п п
0 +
Рис.4
Первые уровни энергии в потенциальных ямах, изображенных на рис.3. Колебания
системы в одной из двух ям с частотой Бора v = (Е2 - £,) I h отражают осцилляции
молекулы вокруг одного из двух классических положений равновесия
Для последующих вычислений удобно выполнить замену базиса в каждом из
собственных подпространств гамильтониана частицы. Поскольку функция V(x) четная, этот
565

Глава IV
гамильтониан коммутирует с оператором четности П (см. § 4 дополнения Fn). В этом
случае можно найти базис собственных векторов оператора #, которые могут быть
четными или нечетными. Их волновые функции являются симметричными и
антисимметричными линейными комбинациями:
1
Ф;(дс) = -7=г[ф:(д:) + ф;(дс)];
Ф:и) = -^[ф';и)-ф^и)].
D)
В состояниях ф'Л и ф") частицу можно найти в одной или в другой потенциальной яме.
В дальнейшем ограничимся рассмотрением только основного уровня, для которого
волновые функции (р\(х), (р[(х), (р\(х) и (р[(х) имеют вид, изображенный на рис.5.
ь. потенциальный барьер конечной высоты
Попытаемся найти вид собственных функций первых уровней энергии в случае,
когда потенциальный барьер имеет конечную высоту VQ, которую все же будем считать
существенно большей энергии этих уровней.
В пределах двух прямоугольных потенциальных ям, изображенных пунктиром на
рис.2, потенциал V(x) = О. Таким образом, волновая функция там имеет вид:
Х(х) = A sin
%(х) = A'sin
k\b + х
2 .
к\ b + — + x
если о — <х<Ь + —;
2 2
если о — <-х<Ь + —
2 2
где величина к связана с энергией Е уровня равенством:
h2k2
2т
E)
F)
В предыдущем параграфе функция %(х) обращается в нуль в точках х - ±{Ь + а 12), так
как в этих точках потенциал V(x) становится равным бесконечности. Напротив, если
V() является конечной величиной, %(х) уже не обращается в нуль в точках
х = ±(Ь - а 12), и к более не удовлетворяет соотношению B).
Так как V(x) — четная функция, можно найти собственные функции гамильтониана
%s(x) и %а(х), являющиеся соответственно четной и нечетной. Обозначим символами
566

Применение постулатов к простым случаям
As и А', а также Аа и Д' значения коэффициентов А и Л', введенных в формуле E) и
соответствующих функциям %s(x) и %w (*). Очевидно, что
,**(*)
А<р{(*)
о
9lW
-►*
~+х
Рис.5
Представленные на риса состояния ф](дс) и фзОО являются стационарными состояниями
системы с одинаковой энергией, локализованными соответственно в правой и левой
потенциальной яме рис. 3. Чтобы воспользоваться симметрией задачи, удобно выбрать в качестве
стационарных состояний симметричную (f>[(x) и антисимметричную ф],(л*) линейные
комбинации состояний ф|(л) и (р[(х) (рис.Ь)
567

Глава IV
Собственные значения, связанные с Х.Д*) и Ха (*)> обозначим символами Es и £Л,
и с помощью формулы F) определим соответствующие значения ks и £fl параметра к .
В интервале -(& -а12)<х<(Ь-а!2) волновая функция уже не обращается в нуль,
как это было раньше, так как значение У0 конечно: она должна быть четной или
нечетной линейной комбинацией (в зависимости от того, идет ли речь о функции %s(x) или
%а (х)) экспонент еч',вХ и e~q'"x ,где qs и qa определяются через Es, Ea и V0
соотношением:
«••-"$г(Уо~Е1'')~№~к'--'
где
Vn =
ti2a2
2т
(8)
(9)
Таким образом, при -{Ь-а12)<х<(Ь-а12) функции %s(x) и ХаМ имеют вид:
Xs(x) = B5ch(qsx);
Xa(x) = Bash(qax). A0)
Теперь остается только обеспечить непрерывность собственных функций и их
производных в точках х = ±(Ь-а/2). Четное решение %я(х) должно удовлетворять
граничным условиям:
A5sin(ksa) = Bsch
*i»-t.
• As kscos(ks a) = Bs qssh
ф-\,
(И)
Поскольку As и Bs не могут одновременно равняться нулю, можно взять отношение
формул A1):
tg(ksa) = —Lcth
..!»-§,
Для нечетного решения %а (х) можно получить аналогично:
tg(k„a) = —±th
«J*-i
A2)
A3)
568

Применение постулатов к простым случаям
, ' cth
- ■ *" th\
№-к]\ь-Щ
Если заменить qs и qa их значениями, то соотношения A2) и A3) примут вид:
tg{ksa) = —^=±=:cth\^az-k; |*~E-||; A4)
tg(kaa) = - t ?' thUa£-k;\b~\\. A5)
V« -К L v i)\
Таким образом, в принципе задача решена, так как соотношения A4) и A5)
определяют квантование энергии, ибо дают возможные значения ks и ка, а следовательно, и
допустимые значения энергий Es и Еа (при условии, что они меньше VJ,). Решение
трансцендентных уравнений A4) и A5) можно найти, например, графически. При этом
будут определены корни kls, к], ..., кха, к] , ...и т.д. Корень к" отличается от корня к",
так как уравнения A4) и A5) различны, а следовательно, различны и значения энергий
Е" и Епа. Конечно, когда величина V0 становится очень большой, то и к", и k"t
стремятся к значению пп/ а , найденному в предыдущем параграфе. Это можно показать,
устремив угол а к бесконечности в уравнениях A4) и A5), откуда следует, что
tg(ks аа) = 0 — уравнение, эквивалентное уравнению B). Значения энергии Е" и Е"
стремятся при этом к Еп = h2n2n212ma2, что было вычислено в предыдущем параграфе
в предположении, что V0 —> °°. Наконец, нетрудно заметить, что, чем больше V() по
сравнению с Еп, тем ближе друг к другу значения Е" и Е".
Точные значения Е" и Е" здесь не имеют большого интереса, поэтому
удовлетворимся лишь анализом общих свойств спектра, изображенного на рис.6, где сделана
попытка представить, что происходит с уровнями энергии £, и Е2 (рис.4), если учесть,
что высота потенциального барьера V{) конечна. Видно, что туннельный эффект через
барьер снимает вырождение уровней £, и Е2 и порождает два дублетных уровня
(£', Б},) и (е2, Е2)(конечно, предположение о малости этих энергий по сравнению с
V{) остается без изменения). Поскольку дублет (£', £4 расположен ниже по оси
энергий, то \е1 - Е1 < \Е2 - Е2 . И, наконец, расстояние между дублетами существенно
больше расщепления внутри каждого из них (экспериментально было найдено, что это
отношение составляет по величине примерно три порядка). Сказанное выше позволяет
определить новые частоты Бора соотношениями:
569

Глава IV
и т. д., физический смысл которых рассмотрим в следующем параграфе
(соответствующие переходы изображены стрелками на рис.6).
El
El
Ell
О +
! W2,
Шх
Рис.6
Если учесть, что высота VQ потенциального барьера конечна,
получим, что энергетический спектр изменяется по сравнению
с рис.4: каждый уровень расщепляется на два. Частоты Бора
£2, /2я и £12/2п, соответствующие туннельному переходу из
одной ямы в другую, равны частотам инверсии молекулы
аммиака для двух первых колебательных уровней. Туннельный
эффект оказывает большее влияние на верхнем
колебательном уровне, вследствие чего Q2 > Q,
Наконец, на рис.7 изображен ход собственных функций %](х) и xlM > определенных
уравнениями E), G) и A0) для значений к] и кха, найденных по формулам A4) и A5).
Видно, что они очень похожи на функции <$\(х) и ф^(д:), представленные на рис.5, но
отличаются тем, что в интервале -{b-а/2)<х<(Ь-а/2) они не равны нулю. Теперь
понятно, почему мы ввели в предьщущем параграфе базис ty[s и ф',: собственные функции %\ и
х\ при наличии туннельного эффекта значительно более схожи с ф*. и ф^, чем с ф[ и (р12.
-6
I хЦх)
Ь 01 + b
Xl(x)
+ 6
-+х
-► х
Рис.7
Волновые функции уровней Е\ и Е1а,
изображенных на рис.6. Отмечается аналогия с
функциями, представленными на рис.бЬ, но эти
функции не обращаются в нуль в интервале
~(Ь-а/2)<х<(Ь-а/2)

Применение постулатов к простым случаям
с. ЭВОЛЮЦИЯ МОЛЕКУЛЫ. ЧАСТОТА ИНВЕРСИИ
Допустим, что в момент времени t = 0 молекула находится в состоянии:
1
ka = o)) = -^[|xl)+|x:>]. A6)
Вектор состояния |\|/@) в момент времени t можно получить, используя общую
формулу (D-54) главы III:
\W)) = ^iib^'[e^'2\xl) + e-ia'''2\X:,)l A7)
и сразу же вычислить плотность вероятности:
\Щх,1)\2 =|[xiU)]2+^[xiW]2 + ^(Q,OxiWxiW. A8)
Ее зависимость от времени нетрудно получить графически, исходя из кривых рис.7. Она
представлена на рис.8. В момент времени t = О (рис.8а) начальное состояние A6)
соответствует ситуации, когда плотность вероятности сконцентрирована в правой
потенциальной яме (в левой яме функции %\ и х], имеют разные знаки и близкие по величине
абсолютные значения, в результате чего их сумма практически равна нулю). Таким
образом, можно сказать, что в исходном состоянии частица находится в правой яме. В
момент времени t = 71/2Q, (рис.8b) она за счет туннельного эффекта заметно переходит в
левую яму, где практически полностью концентрируется к моменту t = я/Q, (рис.8с), и
далее осуществляет обратное движение (рис.8A и рис.8е).
Итак, фиктивная частица переходит с частотой Q.J2n то в одну, то в другую
сторону от потенциального барьера, и это соответствует тому, что плоскость атомов
водорода попеременно переходит в разные стороны относительно атома азота. Именно
поэтому частота Q, /2п получила название частоты инверсии молекулы. Отметим, что
эта частота не имеет классического аналога, так как ее существование связано с
туннельным переходом фиктивной частицы через потенциальный барьер.
Поскольку атом азота стремится притянуть к себе электроны трех атомов водорода,
молекула аммиака обладает дипольным электрическим моментом, пропорциональным
среднему значению (х) координаты введенной фиктивной частицы; из рис.8 видно, что
этот момент является осциллирующей функцией времени. Таким образом, молекула
аммиака способна испускать или поглощать электромагнитное излучение с частотой
£2,/2я.
571

Глава IV
И*.'I2
iZ^l
У~^ •
Рис.8
Эволюция волнового пакета, полученная в результате суперпозиции двух стационарных
волновых функций, изображенных на рис.7. Сначала частица находится в правой яме (а),
затем за счет туннельного эффекта переходит в левую яму (Ь), далее снова движется в
сторону правой ямы (d) и, наконец, возвращается в исходное состояние. Далее процесс
повторяется периодически
Этот факт был подтвержден экспериментально, причем частота Q, / 2я попадает в
область сантиметровых волн. В радиоастрономии удалось обнаружить поглощение и
излучение радиоволн этой частоты молекулами аммиака, находящимися в межзвездном
пространстве. Отметим также, что принцип действия мазера на молекулах аммиака
основан на стимулированном испускании этих волн молекулой NH3.
3. Молекула аммиака как двухуровневая система
Из рис.6 видно, что в рассматриваемом случае мы встречаемся с ситуацией,
аналогичной той, которая была рассмотрена в §С главы IV: изучаемая система имеет два
уровня с близкими значениями энергии (е] , Е Ч, но достаточно далеко удаленных от
других уровней \Е25, Е]\ и т.д. Если интерес представляют лишь два уровня (El5, E]aY
572

Применение постулатов к простым случаям
то можно «забыть» о существовании остальных уровней (точное доказательство
законности подобной аппроксимации будет дано в рамках теории возмущений в главе XI).
Сейчас же снова вернемся к рассмотренной выше задаче, но с несколько иной точки
зрения, и покажем, что общие рассуждения главы IV, касающиеся двухуровневых
систем, могут быть использованы для анализа молекулы аммиака. Эта точка зрения
позволит нам с помощью очень простого формализма исследовать воздействие на молекулу
внешнего постоянного электрического поля.
а. ПРОСТРАНСТВО СОСТОЯНИЙ
Рассматриваемое ниже пространство состояний образовано двумя ортогональными
векторами ф|у и ф,), волновые функции которых определены формулой C). Как уже
говорилось, будем игнорировать другие состояния ф'Л и Ф?), для которых п > 1.
В состояниях ф|у и фо) атом азота находится либо выше, либо ниже плоскости
атомов водорода. Формулой D) мы ввели другой ортонормированный базис пространства
состояний, образованный четным и нечетным векторами:
K)=^[W-K)]- <19>
В этих двух состояниях вероятность найти азот выше или ниже плоскости атомов
водорода одинакова.
Ь. УРОВНИ ЭНЕРГИИ. СНЯТИЕ ВЫРОЖДЕНИЯ
ВСЛЕДСТВИЕ ПРОЗРАЧНОСТИ ПОТЕНЦИАЛЬНОГО БАРЬЕРА
Когда высота потенциального барьера V0 бесконечна, состояния ф|у и W2) имеют
одну и ту же энергию (как, впрочем, и состояния ф') и ф',у ), в результате чего
гамильтониан Н{) системы может быть записан в виде:
Я0 = £,х1, B0)
где 1 — единичный оператор в двумерном пространстве состояний.
Чтобы феноменологически учесть конечность высоты потенциального барьера,
добавим к Н0 возмущение W, имеющее недиагональную форму в базисе { ф[), фО } и
представленное матрицей:
573

Глава IV
W = -A\
B1)
где А — вещественный положительный коэффициент*.
Если нас интересуют стационарные состояния молекулы, нужно диагонализировать
полный гамильтониан Н = #0 + W , матрица которого равна:
Н =
£, -А
EJ
B2)
Элементарный расчет дает собственные значения и собственные векторы оператора Н :
Е1 + А соответствует собственному вектору |ф^ \ ;
Е] - А соответствует собственному вектору ф j. B3)
Мы видим, что под действием возмущения W два уровня, вырожденные при А = 0,
расщепляются: между ними появляется разность энергий, равная 2 А, а новые состояния
представлены векторами W) и фМ . Тем самым приходим к результату, полученному
в §2.
Если в момент времени t = 0 молекула находилась в состоянии ф|у :
1чг(/=о»-|ф!>-^[|ф:)+|ф:)].
то в момент времени / вектор состояния будет равен:
B4)
| VW) = ^ *-'£"/Л [eiAtlh k) + е— |ф1)] = е-"*1" [««[^] |Ф') + ismffi |ф')
B5)
В результате измерения, выполненного в момент времени t, с вероятностью
cos2 {At I К) молекула будет обнаружена в состоянии ф|) (атом азота находится выше
плоскости атомов водорода) и с вероятностью sin2(At/h) — в состоянии W2) (атом
азота находится ниже плоскости атомов водорода). Таким образом, под действием связи
W молекула аммиака периодически «выворачивается наизнанку» (инверсия молекулы).
* Действительно, чтобы относительное расположение уровней Es и Еа было таким, как
изображено на рис.6 [см. собственные значения B3)], необходимо, чтобы А > 0.
574

Применение постулатов к простым случаям
ЗАМЕЧАНИЕ
Феноменологическая оценка влияния конечности потенциального барьера с
помощью возмущения W, определенного формулой B1), менее точно описывает
ситуацию, чем развитый выше формализм, так как здесь вывод основан на
собственных функциях ф' (х) и ф^ (х), равных нулю в интервале (-b + a/2)<x<(b-a/2)
в отличие от функций %1 и %\ • Этот подход, будучи значительно более простым,
позволяет, тем не менее, учесть два важнейших физических эффекта: снятие
вырождения в мультиплете £, и периодические колебания молекулы между
состояниями ф|) и фт) (инверсия).
с. ВЛИЯНИЕ СТАТИЧЕСКОГО ЭЛЕКТРИЧЕСКОГО ПОЛЯ
Выше мы увидели, что в состояниях ф[) и W2) дипольный электрический момент
молекулы принимает два противоположных по знаку значения, которые обозначим +т)
и -Г). Пусть D — наблюдаемая, связанная с этой физической величиной. Можно
предположить, что в базисе { ф]), ф!) } оператор D представлен диагональной матрицей с
собственными значениями +г) и -Г):
,о -л]'
D =
B6)
Если молекула помещена в статическое электрическое поле f *, то энергия
взаимодействия с этим полем имеет вид:
W(V) = -W. B7)
Этот член гамильтониана** в базисе { ф[) , w\) } представлен матрицей:
^) = -л*10 _{)
B8)
Запишем теперь матрицу, представляющую в базисе { ф[), W2) } полный гамильтониан
молекулы Н0 + W + W'(Y<) :
* Для простоты предположим, что это поле направлено вдоль оси Ох на рис. 1 (одномерная
модель).
** В выражении для энергии D — наблюдаемая, тогда как $ — классическая величина,
определяемая внешними условиями (см. замечание к формуле A2) дополнения FiV).
575

Глава IV
#0 + w + w'09 =
{ -А ех+т\$)
B9)
Эту матрицу легко диагонализировать, а ее собственные значения Е+ и Е_ и
собственные векторы |\|/+) и |\|/_) равны соответственно:
где принято обозначение:
я+ = i?! + V-a2 + л2*2;
£_=£,- д/А2 + Л2^'2
I \ • #1 i\ *l i\
tg$ = — приО<в<я
C0)
C1)
C2)
[см. формулы (9), A0), B2) и B3) дополнения BiV; поскольку А — вещественное
отрицательное число, то угол ф, введенный в дополнении, здесь равен я ].
Если if = 0, то в = я / 2, и мы снова получаем результат § 3-Ь, так как
Е+(Р = 0) = Е, + А;
£_ (£ = ()) = £,-А
C3)
|v+<8 = 0)) = |q>i);
|V-(8 = 0)) = |<pl).
C4)
Если А = 0 (что соответствует абсолютно непрозрачному потенциальному барьеру),
то при любых значениях #■ получим:
Е_(А = 0) = Е1-Г]Щ,
C5)
576

Применение постулатов к простым случаям
где при У- >СГ:
|i|/_U = 0)) = |(p!);
|v + (A = 0)) = -|q>i). C6)
В этом случае энергия линейно связана с t (см. пунктирные прямые на рис.9). Физически
результаты, полученные в формулах C5) и C6), нетрудно понять: если на молекулу
действует только электрическое поле, то оно «оттягивает» заряженные положительно водороды
выше и ниже атома азота, вследствие чего стационарными являются состояния ф[) и W2\ .
Если же и электрическое поле % и константа связи А могут принимать любые
значения, то состояния |\|/+) и |\|/_) являются линейными суперпозициями состояний ф|\ и
Фз) (впрочем, как и состояния W) и W) ) и образуются вследствие совместного
действия электрического поля, стремящегося оттянуть атомы водорода от атома азота, и связи W,
которая способствует прохождению атома азота через потенциальный барьер. Зависимость
энергий Е+ и Е_ от tf представлена графически на рис.9, из которого видно, что имеет
место явление антипересечения уровней (см. § C-2-b главы IV) за счет связи W. При этом Е+
и Е_ образуют две ветви гиперболы, асимптотами которых являются пунктирные прямые,
соответствующие энергиям в отсутствие связи.
Рис.9
Влияние электрического поля 6 на два
первых уровня молекулы аммиака (их
расщепление 2 Л в нулевом поле
обусловлено туннельным эффектом). При
малых # молекула приобретает дипольный
><? момент, пропорциональный t , а энергия
молекулы пропорциональна Y<2. При
больших У дипольный момент стремится к
пределу, соответствующему положению
атома азота выше или ниже плоскости
атомов водорода, при этом энергия
становится линейной функцией Y>
Наконец, можно вычислить средние значения дипольного электрического момента
D в каждом из стационарных состояний |\|/+) и |\|/_). Используя формулы B6) и C1),
получим:
* Если ?< < О, то в выражении C6) роли функций ф[\ и ф!) меняются местами.
37 Квантовая механика
577

Глава IV
(\|/+|D|\|/ + ) = -(\|/_|D|\|/_) = TK<«fl C7)
или согласно формуле C2):
• (Vt|Phy,)HV-|PK_) = - ,f\ • C8)
у] А + трг
При £ = О эти значения равны нулю, что согласуется с отмеченным выше фактом
равенства вероятностей нахождения частицы в той или другой потенциальной яме в состояниях
ф]. а) . Напротив, если r\V » А, то дипольный момент равен +Г) (или -Г)) в состоянии
|ф|) (или |ф')).
В слабом электрическом поле (r|tf « А) формулы C8) можно переписать в виде:
(V+|D|i|/+) = -(v|/_|D|V.) = -^l. C9)
Видно, что в стационарном состоянии |\}/+) (или |\|/_)) молекула приобретает
дипольный электрический момент, пропорциональный поляризующему полю V . Если
определить диэлектрическую восприимчивость молекулы в состоянии |\|/_) соотношением:
(\|/_|£>|\|/_) = е_£, D0)
то согласно формуле C9) получим:
л2
8 = -±- D1)
" А
(аналогичный расчет дает для |\|/+) значение е+ = -е_).
ЗАМЕЧАНИЕ
В слабом поле формулы C0) можно разложить в ряд по степеням г|£ / А:
Е =£ -A-I.DJL+...; D2-а)
1 2 А
1 Л2#2
Е = £, + А + - -! + .... D2-Ь)
1 2 А
Рассмотрим теперь ситуацию, когда молекулы аммиака перемещаются в область
пространства, где К невелико, но f2 имеет значительный градиент в направлении
оси Ох , которое является направлением оси молекул:
578

Применение постулатов к простым случаям
В соответствии с формулой D2-а) молекулы, которые находятся в состоянии
|\|/_), подвержены действию силы, параллельной Ох и равной:
F=-^=lk£. D4)
dx 2 Л
Равенство D2-Ь) указывает, что молекулы в состоянии |\|/+) будут подвержены
действию силы противоположного направления:
dE
F+=-^ = -F_. D5)
ах
Этот результат является основой метода, который служит для сортировки молекул
аммиака по состояниям в аммиачном мазере, где отбираются молекулы в
состоянии с большим значением энергии. Используется устройство, во многом
напоминающее установку Штерна и Герлаха: пучок молекул аммиака пересекает область
с большим градиентом электрического поля; молекулы движутся по разным
траекториям в зависимости от состояния, в котором они находятся, и с помощью
соответствующей диафрагмы можно изолировать молекулы, находящиеся в любом из
двух состояний.
Дополнение Нгу
ВЛИЯНИЕ СВЯЗИ
МЕЖДУ СТАБИЛЬНЫМ И НЕСТАБИЛЬНЫМ СОСТОЯНИЯМИ
1. Введение. Обозначения.
2. Влияние слабой связи на уровни с различной энергией.
3. Влияние произвольной связи на уровни с одинаковой энергией.
1. Введение. Обозначения
Влияние связи W между состояниями |ф,) и |ф2) с энергиями £, и Е2 детально
обсуждалось в § С главы IV. Что нужно изменить в этом анализе, если одно из двух
состояний (например, |ф,)) является нестабильным?
37*
579

Глава IV
Понятия нестабильного состояния и времени жизни были введены в дополнении Кш.
Допустим, например, что |ф,) — возбужденное состояние атома. Если атом находится в
этом состоянии, то при спонтанном испускании одного или нескольких фотонов он
может вернуться в состояние с меньшим значением энергии с вероятностью 1/т, в
единицу времени. Здесь т, — время жизни нестабильного состояния |ф,). Напротив, будем
считать, что в отсутствие связи W состояние |ф2) является стабильным, то есть т2
бесконечно велико.
В дополнении Кш мы видели, что учесть нестабильность состояния можно простым
введением мнимой части в значение соответствующей энергии. Итак, заменим энергию
Е{ состояния |ф,) величиной:
£.' = £,-<'tY,,
A)
где
Y,=-
B)
(поскольку т2 бесконечно велико, то у2 =0 и Е'2 = Е2). В отсутствие связи матрица
«гамильтониана» Н0 в базисе {|ф,), |ф2) 1 имеет вид*:
"о =
Е[ 0 ")
О Е'г)
10 Е,
C)
2. Влияние слабой связи на уровни с различной энергией
Допустим теперь, как и в § С главы IV, что к оператору Я0 добавляется возмущение
W, матрица которого в базисе {|(р,), |ф2) } имеет вид:
W =
0 WtA
W2l 0
D)
Что произойдет при этом с энергиями и временами жизни уровней?
Вычислим собственные значения е{ и г'2 матрицы:
* Оператор Н0 не является эрмитовым, и, следовательно, не может быть «истинным»
гамильтонианом (см. замечание в конце дополнения Кш).
580

Применение постулатов к простым случаям
H = H()+W
( П ^
\w2i
Ег)
Тогда г\ и г'2 являются решениями уравнения:
е2-е[ £, +Е2-/-у, +£,£2 -'-Yi£2 Ч^Г =0-
1 IVU UI Т 11UVTV1I1 1 U U Ш 1 X.
( \ fh
\\Wl2\«1l(El-E2J+—y2l
e;sE,-i-Y,+
е; = £,+-
£|_£2_/_Yi
i2-£i+«2 Yi
E)
F)
Чтобы упростить вычисления, ограничимся случаем слабой связи
и получим:
К. Г
G)
Энергии собственных состояний в присутствии связи являются вещественными
частями г\ и е2, а времена жизни обратно пропорциональны их мнимым частям. Из формул
G) видно, что связь изменяет и значения энергии, и значения времен жизни во втором
порядке по |Wj2|. В частности, можно констатировать, что если |WI2| * 0, то и е\ , и е2
являются комплексными, то есть при наличии связи не существует более стабильного
состояния. Величину е2 можно представить в виде:
2 "
где
Д, = Е, + -
(£,-Е,)|УУ|2|2
T2=Y,
\w„
(8)
(9-a)
(9-b)
(E2-ElJ + — y2
Итак, время жизни (9-b) состояния |ф2) под действием связи становится конечным
581

Глава IV
(формула Бете). Физически этот результат вполне понятен: если в момент времени t = О
система находилась в стабильном состоянии |ф2), то в последующий момент времени t
имеется отличная от нуля вероятность обнаружить систему в состоянии |ф,), где ее
время жизни является конечным. Иногда образно говорят, что «связь передает
стабильному уровню часть нестабильности другого уровня». Кроме того, из выражений G) видно,
что, как и в случае, рассмотренном в § С главы IV, возмущение действует на значения
энергии и времен жизни тем эффективнее, чем меньше разность невозмущенных энергий
£, и Е2. В следующем параграфе рассмотрим случай, когда эта разность равна нулю.
3. Влияние произвольной связи
на уровни с одинаковой энергией
Если энергии Ех и Е2 равны, то оператор Н можно представить в таком виде,
чтобы выделить его след, как это было сделано в § 2 дополнения BIV:
tf^E.-i^Yijl+K. (Ю)
где 1 — единичный оператор, а оператор К имеет в базисе {|(р,), |ф2)} матрицу:
f ь Л
Wl2 i-Yi
(И)
Собственные значения кх и к2 оператора К являются решениями характеристического
уравнения:
*2=K-£y?- A2)
Они противоположны по знаку:
*i=-*2, A3)
вследствие чего собственные значения оператора Н равны:
e; = E,-i-Y,+*,;
е2 = Е,-/^у,-*,. A4)
582

Применение постулатов к простым случаям
Собственные векторы |\|/{) и \^'2)операторов И и К одинаковы, и простой расчет
позволяет получить их в виде:
к0 = ^12|ф^ + и+/^у,)|ф2);
к/2) = ^2|ф.) + (-^+^У,)|ф2>. A5)
Допустим, что в момент времени г = О система находилась в состоянии |ф2),
которое было бы стабильным в отсутствие связи:
|у(' = о)Нф2) = ^[|\|/0-№)]. Об)
Используя формулу A4), легко показать, что в момент времени / вектор состояния
будет иметь вид:
I /.Л А '7 ~IY,/ Г -ikitJtii Л ik,t/h\ ,\1 /ЛП.
IХ|/(Г)> = —— е " е 4 \е \у\)-ех |\|/'2)j. A7)
Вероятность -A\U) найти систему в состоянии |ф,) в момент времени t равна:
•4,@ = |(ф.к@>|2 = -^ е^ \е-'к"п> (Ф, | V;> - /"'" (Ф, |ч/;>|2 =
= —:—-п е \Wn\ \е -е A8)
4 UM
Мы будем различать несколько частных случаев.
(О |W12|>|y,. A9)
Используя формулу A2), получим:
к.=-к2 = лШ'~
U-Y,| B0)
и собственные значения е[ и е'2 определяются выражениями:
583

Глава IV
*>El + l\Waf-(±b
*г = Е>-Мг\2
UY'
B1)
Величины г\ и е2 имеют одинаковые мнимые и различные вещественные части. То
есть состояния |\|/{) и |\|/2) характеризуются одним и тем же временем жизни 2т,, но
имеют различные энергии.
Подставив B0) в A8), получим:
^2,@="
\W
W,
h ^
4Y|
-Yi//2 . 2
- е sin
B2)
Этот результат напоминает по форме формулу Раби [см. уравнение (С-32) главы IV].
Функция .^,@ описывает синусоиду, затухающую с постоянной времени 2т, (рис.1).
Условие A9) выражает, что связь достаточно сильна, чтобы вызвать колебания системы
между двумя состояниями |ф,) и |ф2) прежде, чем нестабильность состояния |ф,)
успеет проявиться заметным образом.
А*1|(')
* /
Рис.1
Влияние сильной связи между стабильным
состоянием |ф2) и нестабильным состоянием
|ф,): если система первоначально находилась
в состоянии |ф2), то вероятность .^,@ найти
ее в момент времени t в состоянии |ф,)
имеет характер затухающих колебаний
(и) Fi2 <TY,.
Тогда
к, - к2 -1.
^у.\-Ы
B3)
B4)
584

Применение постулатов к простым случаям
г\ = £",-/
82=£,-/
г
w\\
4 у
/ \ ^
»-W']
Т Yi
2
-\wJ2
U "j ■ -
B5)
Состояния |\|/{) и \у'2) имеют при этом одинаковую энергию, но различные
времена жизни. Формула A8) принимает вид:
г г. — л
4,@ =
Wn
h v
— у, !
4YlJ
-Y.'/2 /2
■e sh
W,
Ь -Wi
B6)
то есть .^,@ имеет вид суммы затухающих экспонент (рис.2).
Результат нетрудно понять физически: условие B3) говорит о том, что время жизни
т, слишком мало, чтобы связь W успела вызвать заметные колебания системы между
состояниями |ф,) и |ф2).
(iii)|Wl2| = ^Yl.
B7)
Из формулы A4) видно, что состояния |\|/{) и |\|/2) имеют при этом одинаковую
энергию £, и время жизни 2т,.
f^iiO
Рис.2
Если связь слабая, колебания системы между
состояниями |ф,) и |ф2) просто не успевают произойти
Уравнения B2) и B6) после раскрытия получающейся неопределенности приводятся
к одному и тому же виду:
\W
-Л , ч rV12 -> -Yi//2
B8)
585

Глава IV
ЗАМЕЧАНИЕ
Приведенный выше анализ очень напоминает классическое движение
затухающего гармонического осциллятора: условия A9), B3) и B7) совпадают
соответственно со случаями слабого, сильного и критического затухания.
Дополнение Jrv
УПРАЖНЕНИЯ
1. Рассматривается частица со спином 1/2 и магнитным моментом М = yS.
Пространство спиновых состояний определяется базисными векторами |+) и |-), являющимися
собственными векторами оператора Sz с собственными значениями +# / 2 и -h 12.
В момент времени t - О состояние системы равно:
|v(f = o))=|+).
a. Если в момент времени t = О измеряется наблюдаемая Sx, то какие результаты
можно получить и с какими вероятностями?
b. Не производя описанного выше измерения, предоставляют системе свободно
эволюционировать в присутствии магнитного поля В{), параллельного оси Оу . Определить
состояние системы в момент времени t в базисе {|+), |-)}.
c. В момент времени t измеряются наблюдаемые Sx, Sv, Sz. Какие значения и с
какими вероятностями могут быть получены? Какое соотношение нужно выполнить
между значениями В0 и t, чтобы одно из этих измерений дало бы априори точный
результат? Дать физическую интерпретацию.
2. Рассматривается спин 1/2, как и в предыдущей задаче; используются те же
обозначения.
a. В момент времени t = 0 измеряется Sy и получено значение +Л / 2 . Каков вектор
состояния |\|/@)) немедленно после этого измерения?
b. Немедленно после измерения прикладывается зависящее от времени однородное
поле, направленное вдоль оси Oz. Гамильтониан H(t) спина можно представить в виде:
Я@ = о0@^.
Предполагая, что со0(/) = 0 при t < 0 и t >Т и линейно нарастает от 0 до со0 в ин-
586

Применение постулатов к простым случаям
тервале 0<t<T (где Т — заданный параметр, имеющий размерность времени),
показать, что в момент времени t вектор состояния можно представить в виде:
|v@) = JL[e»<''|+) + fc^''|-)],
где д(/)— вещественная функция времени, которую нужно определить.
с. В момент времени t = х > Т измеряется 5V. Какие результаты могут быть
получены и с какими вероятностями? Определить соотношение, которое должно выполняться
между о)() и Т, чтобы результат был точно известен. Дать физическую интерпретацию.
3. Рассматривается спин 1/2, помещенный в магнитное поле В0 с компонентами:
Вх = 0;
Использованы обозначения задачи A).
a. Вычислить матрицу, представляющую гамильтониан Н системы в базисе
П+>.|->}-
b. Найти собственные значения и собственные векторы оператора Н .
c. В момент времени t = 0 система находилась в состоянии |-). Какие значения
энергии можно было бы получить при измерении и с какими вероятностями?
d. Вычислить вектор состояния |\|/@) в момент времени t. В этот момент времени
производится измерение Sx; найти среднее значение результатов, которые могут быть
получены. Дать геометрическую интерпретацию.
4. Рассматривается экспериментальная установка, описанная в § B-2-b главы IV (см.
рис.8): пучок атомов, имеющих спин 1/2, проходит через первое устройство,
работающее как «поляризатор» в направлении, образующем в плоскости xOz угол Ь с осью
Oz, затем через второе устройство («анализатор»), измеряющее компоненту спина S,.
Между поляризатором и анализатором на длине пучка L приложено однородное
магнитное поле В0, параллельное оси Ох . Пусть v — скорость атомов, Т' = L / v — время,
в течение которого атомы подвергаются воздействию поля В(), и со0 = -уВ().
а. В каком спиновом состоянии \\\f^ находятся атомы в момент времени, когда они
попадают в анализатор?
587

Глава IV
b. Показать, что при измерении в анализаторе вероятность получить значение +fi 12
равна — (l + cosb cos(d0T), а значение -hi2 {\-cosb cos(u0T). Дать физическую
интерпретацию.
c. (Этот и последующий вопросы потребуют знания понятия оператора плотности,
определенного в дополнении Еш; советуем также вспомнить дополнение EiV.) Показать,
что матрица плотности р{ проникающего в анализатор спина в базисе {|+), |-)} имеет вид:
1
р'=1
^ l + cosb cos(ti0T sinft+ icosft sin(d0T^
\sin-d-icos-d sin(O0T i-cosft cos(d0T
Вычислить tr{p,5v}, trlp,^} и tr{p,Sz}. Дать интерпретацию. Описывает ли оператор
плотности Pj чистое состояние?
d. Теперь допустим, что скорость атома является случайной величиной, и
вследствие этого время Т известно с неопределенностью АГ. Кроме того, будем считать, что
поле В0 достаточно велико, чтобы выполнялось условие (О0АГ » 1; тогда возможными
значениями произведения ш0Г являются значения в интервале от 0 до 2тг, и они
равновероятны.
Каков в этих условиях оператор плотности р2 атома в момент времени, когда он
проникает в анализатор? Соответствует ли р2 чистому состоянию? Вычислить величины
tr{p25v}, tr{p25y} и tr{p25J . Дать интерпретацию. В каких случаях оператор
плотности описывает полностью поляризованный или полностью деполяризованный спин?
Качественно описать явления, наблюдаемые на выходе анализатора, если со0
изменять от нуля до значения, когда выполняется условие ш0АГ » 1.
5. Оператор эволюции спина 1/2 (см. дополнение Fm).
Рассматривается спин 1/2 с магнитным моментом М = yS , помещенный в
магнитное поле В0 с компонентами Вх = -сол / у , Вх - -cov /у , Bz - -со, /у .
Положим: со0 = -у|В0| •
а. Показать, что оператор эволюции этого спина имеет вид:
U(t,0) = e-m9
где М —оператор, определенный выражением:
М = 1 К5* + со А +с°А1 = ^ К°л +<оуа, + согаг]
и at, Gy, а, — матрицы Паули (см. дополнение AJV).
588

Применение постулатов к простым случаям
Вычислить матрицу оператора М в базисе {|+), |-)} собственных векторов
оператора S.. Показать, что
4[w;.+cd;+g):i = i (Dn
b. Представить оператор эволюции в форме:
U(t,0) = cos\
'со0Л
М sin\ —iL-
(On V 2
с. Пусть спин в момент времени t = О находится в состоянии |\|/@)) = |+). Показать,
что вероятность ./++@ найти его в момент времени t в состоянии |+) равна:
<+(/) = |(+|£/(/,0)|+)|2
и установить соотношение:
Дать геометрическую интерпретацию.
6. Рассматривается система, состоящая из двух спинов 1/2 S, и S2, и базис, состоящий
из четырех векторов | ±, ±), определенных в дополнении DiV. В момент времени / = О
система находится в состоянии:
1 . v 1 , v 1
1^@)> = ^ 1++>+^ К-)+т?'—^
a. В момент времени t = О производится измерение S,,. Какова вероятность
получить значение -til21 Каков вектор состояния после этого измерения? Если затем
измеряется Slx, какие результаты и с какой вероятностью можно получить? Ответить на эти
же вопросы, если измерение Su дало значение +Й/2 .
b. Считая, что начальным является состояние |\|/@)), записанное выше, какова
вероятность получить равные по величине, но обратные по знаку результаты при
одновременном измерении Sl: и S2: ?
c. Вместо того, чтобы проводить отмеченные выше измерения, дают возможность
системе свободно эволюционировать под действием гамильтониана:
Я = @,5,. +со252,.
589

Глава IV
Каким будет вектор состояния |\|/(г)) в момент времени / ? Найти средние значения
(S,) и (S2) в момент времени t. Дать физическую интерпретацию.
d. Показать, что длины векторов (S,)h (S2) меньше fill. Какова должна быть
форма |\|/@)), чтобы эти длины были равны til21
7. Рассматривается та же система из двух спинов 1/2, как и в предыдущей задаче, в
пространстве состояний, определенном базисными векторами |±, ±).
a. Записать матрицу 4x4, представляющую в этом базисе оператор Su,. Найти
собственные значения и собственные векторы этой матрицы.
b. Нормированное состояние системы имеет вид:
|¥) = а| + +) + р| + -) + у|-+) + 8|-->,
где а, C, у,5 — заданные комплексные коэффициенты. Какие результаты и с какими
вероятностями могут быть получены при одновременном измерении Slx и S2y ? Как
изменятся эти вероятности, если |ij/) будет тензорным произведением вектора из
пространства состояний первого спина на вектор из пространства состояний второго спина?
c. Такие же вопросы, если измеряются наблюдаемые Sly и S2y.
d. Измеряется только 52у. Пользуясь результатами, полученными в пункте (Ь) и в
пункте (с), найти вероятность получения значения -Ь12 .
8. Рассматривается электрон в линейной трехатомной молекуле, образованной из трех
эквидистантных атомов. Обозначим |фд), |фя), |фс) три нормированных
ортогональных состояния этого электрона, соответствующие трем волновым функциям,
локализованным вблизи ядер атомов Л, В, С. Ограничимся только подпространством состояний,
образованным |фА), |фя)> |фс)-
0—®—©
Если пренебречь вероятностью «перескока» электрона от одного ядра к другому, то
его энергия описывается гамильтонианом Я0, допускающим в качестве собственных
состояний три состояния |фА), |фя)> |фс) с одинаковым собственным значением Е0.
Связь между состояниями |фл), |фд), |фс) описывается дополнительным
гамильтонианом W, определенным формулами:
590

Применение постулатов к простым случаям
*"|ф>1) = -«|фв>;
^|фя) = -«|Фл>-а|фс);
W|<pc.) = -«|(pB),
где а — положительная вещественная постоянная.
1. Вычислить энергии и стационарные состояния гамильтониана Н = Н{) + W .
2. В момент г = 0 электрон находится в состоянии |фА). Рассмотреть качественно
его локализацию в последующие моменты времени t. Имеются ли такие моменты
времени, когда электрон точно локализован вблизи ядер атомов А,В,С1
3. Пусть D — наблюдаемая, которой соответствуют собственные состояния |фЛ),
|ф/*)' |фс) с собственными значениями -d,Q4d . В момент времени t измеряется D.
Какие значения и с какими вероятностями можно получить?
4. Если начальное состояние электрона произвольно, какие частоты Бора могут
проявиться в эволюции среднего значения (D) ? Дать физическую интерпретацию величине D .
Электромагнитные волны каких частот могут поглощаться или испускаться молекулой?
9. Молекула образована из 6 одинаковых атомов А1% Л2,..., Л6, образующих правильный
шестиугольник. Рассматривается электрон, который может
быть локализован на каждом из атомов. Назовем |фм)
состояние, в котором он локализован на п -ном атоме (п = 1, 2,..., 6).
Ограничимся рассмотрением пространства состояний
электрона, образованного векторами |ф„), считая их ортонорми-
рованными.
a. Определим оператор R следующими соотношениями:
/?|ф1) = |ф2);/?|ф2) = |Фз);...;/?|ф6) = |ф.)-
Найти собственные значения и собственные состояния оператора R . Показать, что
собственные векторы оператора R образуют базис в пространстве состояний.
b. Если пренебречь возможностью перехода электрона от одного узла ячейки к
другому, то его энергия описывается гамильтонианом Н0, допускающим в качестве
собственных состояний шесть состояний |ф„) с одинаковыми собственными значениями Е{).
Как и в предыдущей задаче, возможность перехода электрона от одного атома к другому
опишем дополнительным возмущением W, складывающимся с гамильтонианом Я0 и
определенным соотношениями:
591

Глава IV
W|9,) = -fl|<p6)-fl|<p2); ^|ф2> = -а|ф|)-а|ф3>;..-
^|фб> = -о|ф5>-в|ф|>-
Показать, что R коммутирует с полным гамильтонианом Н = Н0 + W. Найти
собственные значения и собственные векторы оператора Н. Локализован ли электрон в этих
собственных состояниях? Применить полученные результаты к молекуле бензола.

Глава V
ОДНОМЕРНЫЙ ГАРМОНИЧЕСКИЙ
ОСЦИЛЛЯТОР
38 Квантовая механика

ПЛАН ГЛАВЫ V
А. ВВЕДЕНИЕ.
1. Важность гармонического осциллятора в физике.
2. Гармонический осциллятор в классической механике.
3. Общие свойства квантового гамильтониана.
В. СОБСТВЕННЫЕ ЗНАЧЕНИЯ
ГАМИЛЬТОНИАНА.
1. Обозначения.
a. Операторы X и Р.
b. Операторы а , а+ и N .
2. Определение спектра.
a. Леммы
b. Спектр оператора N состоит из
неотрицательных целых чисел.
c. Интерпретация операторов а , а+.
3. Вырождение собственных значений.
a. Основной уровень не вырожден.
b. Все уровни не вырождены.
С. СОБСТВЕННЫЕ
СОСТОЯНИЯ
ГАМИЛЬТОНИАНА.
1. Представление {|ф„) }•
a. Выражение базисных векторов через |ф()).
b. Соотношения ортонормировки и замкнутости.
c. Действие различных операторов.
2. Волновые функции стационарных состояний.
D. ФИЗИЧЕСКОЕ
ОБСУЖДЕНИЕ.
1. Средние значения и среднеквадратичные отклонения
операторов X и Р в состоянии |ф„).
2. Свойства основного состояния.
3. Эволюция средних значений во времени.

А. ВВЕДЕНИЕ
1. Важность гармонического осциллятора в физике
Эта глава посвящена изучению особенно важной физической системы —
одномерного гармонического осциллятора.
Самым простым примером такой системы является частица с массой т,
движущаяся в поле потенциала, зависящего только от координаты х:
V(x) = -kx\ (A-1)
где к — положительная вещественная постоянная. Частица притягивается к плоскости
jc = 0 [минимум функции V(jc), соответствующий устойчивому равновесию]
возвращающей силой:
Fx = — = -**, (А-2)
dx
пропорциональной расстоянию х, отделяющему ее от плоскости х = 0. Из
классической механики известно, что проекция движения частицы на ось Ох представляет собой
синусоидальное колебание около положения равновесия х = 0 с циклической частотой:
, = t
со= -. (А-3)
V т
В реальности огромное количество систем ведут себя (по крайней мере
приближенно) как гармонические осцилляторы. Практически каждый раз, когда исследуется
поведение физической системы вблизи положения устойчивого равновесия, уравнения
движения в пределе малых колебаний сводятся к уравнениям гармонического осциллятора
(см. § А-2). Поэтому результаты, которые будут получены в этой главе, применимы к
широкому классу важных физических явлений, как, например, колебания атомов в
молекуле вблизи их положения равновесия или колебания атомов или ионов
кристаллической решетки (фононы)*.
* Дополнение Av посвящено качественному исследованию некоторых физических примеров
гармонических осцилляторов.
38*
595

Глава V
Гармонический осциллятор необходим также и при изучении электромагнитного
поля. Известно, что в резонаторе существует бесконечное количество возможных
стоячих волн (собственные моды резонатора). Электромагнитное поле можно разложить по
этим модам, и с помощью уравнений Максвелла можно доказать, что коэффициенты
такого разложения, описывающего состояние поля в каждый данный момент времени,
подчиняются дифференциальным уравнениям, полностью совпадающим с уравнением
гармонического осциллятора, частота со которого равна собственной частоте
соответствующей моды. Другими словами, формально электромагнитное поле эквивалентно
ансамблю независимых гармонических осцилляторов (см. дополнение Kv). Квантование
поля получается путем простого квантования этих осцилляторов, связанных с
различными собственными модами резонатора. Напомним, впрочем, что именно анализ
поведения этих осцилляторов при тепловом равновесии (излучение абсолютно черного тела)
исторически побудил Планка впервые в физике ввести постоянную h , которая с тех пор
носит его имя. Действительно, мы увидим (дополнение Ly), что средняя энергия
гармонического осциллятора, находящегося в термодинамическом равновесии при
температуре Т, различна для классического и квантового осцилляторов.
Гармонический осциллятор играет также важную роль в описании ансамбля
одинаковых частиц, находящихся в одном и том же квантовом состоянии (речь, конечно, идет
только о бозонах, см. главу XIV). Это связано с тем, что, как мы увидим далее,
энергетические уровни гармонического осциллятора эквидистантны, и разделяющий два
соседних уровня интервал энергии равен Йсо . При этом любому уровню энергии,
определенному целым числом п (то есть отстоящему на расстоянии пйсо от основного
уровня), можно сопоставить ансамбль, состоящий из п одинаковых частиц (или квантов),
каждая из которых имеет энергию /го. Переход осциллятора с уровня п на уровень
п + 1 или п - 1 соответствует рождению или уничтожению кванта энергии Ш . Мы
введем в этой главе операторы а+ и а , позволяющие описать этот переход с уровня п на
уровень п +1 или п - 1. Эти операторы, названные операторами рождения и
уничтожения, часто используются в квантовой статистической механике и в квантовой теории
поля*.
Таким образом, подробное изучение гармонического осциллятора очень важно с
физической точки зрения. Кроме того, речь здесь идет о такой квантовой системе, для
которой можно получить строгое решение уравнения Шредингера. После спина 1/2 и
двухуровневых систем, рассмотренных в предыдущей главе, эта тема будет еще одним
простым примером, позволяющим иллюстрировать общий формализм квантовой
теории. В частности, мы покажем, как можно получить решение уравнения на собственные
* Цель квантовой теории поля — описать взаимодействие между частицами в релятивистской
области, а именно, взаимодействие между электронами, позитронами и фотонами. Понятно, что
операторы рождения и уничтожения частиц играют очень важную роль, тем более, что такие
процессы действительно наблюдаются экспериментально (поглощение или испускание фотонов,
образование пар и т. д.).
596

Одномерный гармонический осциллятор
значения в чисто операторной форме, базируясь исключительно на соотношениях
коммутации (этот метод будет использован в главе VI в отношении момента). Мы также
детально рассмотрим движение волнового пакета, в том числе и в классическом пределе
(см. дополнение Gv, где рассматриваются квазиклассические состояния).
В § А-2 мы напомним некоторые результаты для классического осциллятора, после
чего сформулируем в § А-3 общие свойства собственных значений гамильтониана Н.
Далее, в § В и в § С определим эти значения, а также собственные векторы, введя
операторы рождения и уничтожения и используя только следствия канонического
соотношения коммутации [Ху Р] = ifi и определенным образом выбранную форму оператора Н .
Следующий § D посвящен физическому анализу стационарных состояний осциллятора и
волновых пакетов, образованных путем линейной суперпозиции этих стационарных
состояний.
2. Гармонический осциллятор в классической механике
Потенциальная энергия V(x) [формула (А-1)] представлена на рис.1
тицы определяется уравнением динамики:
d2x dV
т—г- = = -кх.
dt2 dx
\V(x)
Рис.1
Потенциальная энергия V(x)
одномерного гармонического
осциллятора. Амплитуда классического
движения с энергией Е равна хм
Общее решение этого уравнения имеет вид:
х = хм cos(m - ф), (А-5)
где частота со определена формулой (А-3), а постоянные интегрирования хм и ф
находятся из начальных условий. Таким образом, частица испытывает синусоидальные
колебания вблизи точки О с амплитудой хм и частотой @ .
Движение час-
(А-4)
597

Глава V
Кинетическая энергия частицы равна:
Г-IwteV-^., (А-6)
2 U 2и
dx
где р = т импульс частицы. Таким образом полная энергия:
dt
2 |
Е = Г +V = -£- + -/hg)V . (А-7)
2т 2
Подставив в это выражение решение (А-5), получим:
Е = -ты2х2м . (А-8)
Энергия частицы не зависит от времени (это общее свойство консервативных систем) и
может принимать любые положительные значения или равняться нулю, так как хм
может априори принимать любые значения.
Если полная энергия Е зафиксирована, то пределы х = ±хм классического
движения могут быть определены графически (рис.1) как абсциссы точек пересечения
параболы с прямой, параллельной оси Ох , ордината которой равна Е. В этих точках
потенциальная энергия максимальна и равна Е, а кинетическая энергия равна нулю. Напротив,
в точке х = 0 потенциальная энергия равна нулю, а кинетическая энергия максимальна.
ЗАМЕЧАНИЕ
Рассмотрим произвольный потенциал V(x), обладающий минимумом в точке
х-х0 (рис.2). Разложим функцию V{x) в ряд Тейлора в окрестности точки
х = х0:
V(x) = a + b(x-x0J+c(x-x0K + ... (A-9)
Коэффициенты разложения равны:
a = V(x0);
b = -
lf d2V
2[ dx2
(A-10)
lfrfV"!
3\[dx3)
598

Одномерный гармонический осциллятор
и линейный по (х-х0) член равен нулю, так как х = х0 соответствует минимуму
V{x). Сила со стороны потенциала V{x) вблизи точки х0 может быть
представлена в виде ряда:
F = --
dV
dx
-2b(x-x0)-3c(x-x0J + ...
(A-ll)
Поскольку точка х = х0 соответствует минимуму V(x), коэффициент Ъ
положителен.
Точка х = х() соответствует положению устойчивого равновесия частицы:
действительно, Fx(x0) = 0, и для малых отклонений (х-х0) сила FX и разность
(х - х0) имеют разные знаки, так как Ь > О .
Если амплитуда смещения частицы относительно точки х - х0 достаточно
мала, чтобы можно было пренебречь в выражении (А-9) членом (х-х0K [и,
следовательно, членом (х - х0J в формуле (А-11)], то система может
рассматриваться как гармонический осциллятор, поскольку описывающее ее динамику
уравнение приближенно может быть представлено в виде:
т-
л2
= -2b(x-x0).
(А-12)
Соответствующая частота @ связана со второй производной от потенциала V(x)
в точке х = х0 формулой:
@ =
dx2
(А-13)
Рис.2
Вблизи точки л: = х0, где имеет место
минимум, потенциал любой формы
может быть аппроксимирован
параболическим (пунктир). В поле потенциала
V(x) классическая частица с энергией
Е осциллирует между точками jc, и х2
599

Глава V
Поскольку амплитуда движения должна оставаться малой, энергия
гармонического осциллятора невелика.
В случае больших значений Е частица будет двигаться между предельными
точками хх и х2 (рис.2). Это движение будет периодическим, но не
синусоидальным. Если разложить в ряд Фурье функцию x(t), определяющую положение
частицы, то в нем будет присутствовать несколько синусоидальных членов с
кратными частотами. Говорят, что в подобных случаях имеют дело с ангармоническим
осциллятором. Заметим также, что в этом случае период движения, вообще
говоря, отличается от 2я/со, где ш определяется формулой (А-13).
3. Общие свойства квантового гамильтониана
В квантовой механике классические величины х и р должны быть заменены
соответственно наблюдаемыми X и Р, удовлетворяющими соотношению:
[Х,Р] = /й. (А-14)
Тогда из равенства (А-7) легко получить гамильтониан системы:
Р2 1
Я = — +-mco2X2. (A-15)
2т 2
Поскольку Н не зависит от времени (консервативная система), то квантовый анализ
гармонического осциллятора сводится к решению уравнения на собственные значения:
Я|ф) = £|ф), (А-16)
которое в представлении { |jc) } имеет вид:
Ь2 d2 1 2 2
г- + - тсо х
2т dx 2
<p(jc) = £<p(jc). (A-17)
Прежде чем перейти к решению уравнения (А-16), отметим некоторые важные
свойства, вытекающие из формы (А-1) потенциала.
(i) Собственные значения гамильтониана являются положительными числами.
Действительно, в общем случае можно показать (дополнение Мш), что если
потенциальная энергия V(x) ограничена снизу, то собственные значения Е гамильтониана
Р2
Н = — + V(X) превышают минимальное значение функции V(x):
2т
£>У/;/,если V(x)>Vm. (A-18)
600

Одномерный гармонический осциллятор
В случае интересующего нас гармонического осциллятора начало отсчета энергии
выбрано так, что Vm = 0 .
(ii) Собственные функции оператора Н имеют определенную четность. Это
свойство следует из четности функции V(x):
V(-x) = V(x). (A-19)
В этом случае (см. дополнения Fn и Cv) собственные функции оператора Н в
представлении {|jc) } можно искать среди функций с определенной четностью (действительно,
ниже мы увидим, что собственные значения Н не вырождены, и, следовательно,
волновые функции, описывающие стационарные состояния, должны быть либо четными, либо
нечетными).
(Hi) Спектр энергий является дискретным. Классическое движение частицы имеет
место в ограниченной области оси Ох независимо от значения полной энергии (рис.1),
и можно показать (дополнение Мш), что в этом случае собственные значения
гамильтониана образуют дискретный ансамбль.
Конечно, мы снова встретимся с перечисленными свойствами в уточненной форме в
последующем изложении. Но интересно отметить, что их можно получить путем
простого применения к гармоническому осциллятору общих теорем, сформулированных
для одномерного случая.
В. СОБСТВЕННЫЕ ЗНАЧЕНИЯ ГАМИЛЬТОНИАНА
Вернемся к уравнению на собственные значения (А-16) и, используя только
каноническое соотношение коммутации (А-14), найдем спектр гамильтониана Я, имеющего
вид, приведенный в формуле (А-15).
1. Обозначения
Введем несколько обозначений, которые окажутся очень удобными в дальнейшем.
а. ОПЕРАТОРЫ X И Р
Наблюдаемые X и Р имеют размерность координаты и импульса соответственно.
Зная, что размерность величины со — обратное время, а размерность fi — действие
(произведение энергии на время), нетрудно заметить, что наблюдаемые X и Р,
определенные формулами:
601

Глава V
являются безразмерными.
Используя эти новые операторы, можно переписать каноническое соотношение
коммутации в форме:
[x,P] = i (B-2)
и представить гамильтониан в виде:
Н = ЙсоЯ, (В-3)
где
Я = -(*2 + Р2). (В-4)
Теперь можно искать решения уравнения на собственные значения:
tf|(p'v) = ev|cp'v), (B-5)
где оператор Н и собственные значения ev являются безразмерными величинами.
Индекс v априори может принадлежать непрерывному или дискретному ансамблю, а
дополнительный индекс / позволит различать возможные различные собственные
ортогональные векторы, соответствующие одному собственному значению ev.
b. ОПЕРАТОРЫ Я, Я+и N
Если бы X и Р были числами, а не операторами, то сумму квадратов (X2 + Р2),
входящую в выражение (В-4) оператора Н, можно было бы представить в виде
произведения двух линейных комбинаций: ( X -iP) (x +/P]. На самом деле, поскольку X и
Р— операторы, не коммутирующие друг с другом, (х2 + Р2)ф (х -iP) (x +iPJ.
Сейчас мы покажем, однако, что введение операторов, пропорциональных (X-iPj и
(x+iP) , позволяет значительно упростить поиск собственных значений и собственных
векторов оператора Н.
Итак, положим*:
* До настоящего времени для обозначения операторов использовались заглавные буквы.
Чтобы не противоречить общепринятым обозначениям, мы будем использовать строчные буквы а и
а+ для обозначения операторов (В-6).
602

Одномерный гармонический осциллятор
Эти
формулы
можно
без
труда
а =
а+ ■
■£(*♦*):
'Я'
обратить, чтобы
Х-
Р--
■тг(«-
-*)•
получить:
(В-6-а)
(B-6-b)
(В-7-а)
(B-7-b)
Хотя операторы X и Р — эрмитовы, операторы а и а* таковыми не являются из-за
множителя I*, но они сопряжены друг с другом.
Коммутатор операторов а и а* вычисляется без труда с помощью формул (В-6) и
(В-2):
.♦1 !
то есть
[в.в+] = -[х+|Ах-1Р] = 1[Ах]-1[х,р], (в-8)
[*,*+] = 1. (B-9)
Это равенство полностью эквивалентно каноническому соотношению коммутации (А-14).
Установим, наконец, несколько простых формул, полезных для дальнейших
расчетов данной главы. Найдем сначала произведение а*а :
а+а = - (X-iP) (X+iP) = - (X2 + Р2 +iXP-iPX) = - (X2 + Р2 -1). (В-10)
Сравнивая этот результат с выражением (В-4), заметим, что:
Н = а+а + - =-(X-iP)(X+/P) + -. (В-11)
2 2 2
Таким образом, в отличие от классического случая, оператор Н нельзя представить в
форме произведения двух линейных комбинаций. Некоммутативность операторов X и
Р является причиной появления дополнительного члена 1/2 в правой части (В-11).
Аналогично можно получить:
Я = ая+--. (В-12)
Введем теперь оператор N , определенный формулой:
603

Глава V
N = a+a. (В-13)
Этот оператор эрмитов, так как:
N+ =а+(а+У =a+a = N . (В-14)
Кроме того, согласно формуле (В-11) имеем:
H = N+-, (B-15)
так что собственные векторы оператора Н являются собственными векторами
оператора N и наоборот.
Вычислим, наконец, коммутаторы оператора N с а и а+:
[N, а] = \а*а, я] = д+[я, а\ + [я+, а]а = -а ;
[yV,a + ] = [a+a,a+] = fl^[a,a+] + [fl+,a+]fl = a+, (B-16)
то есть
[N,a] = -a; (В-17-а)
[N,a+] = a\ (B-17-b)
Дальнейший анализ гармонического осциллятора основан на использовании
операторов а, а+ и N . Мы должны теперь заменить уравнение на собственные значения
оператора Н, записанное ранее в форме (В-5), на уравнение для оператора N:
7У|Ф;) = у|ф^). (В-18)
Когда это уравнение будет решено, мы узнаем, что собственный вектор фу у оператора
N является также собственным вектором оператора Н с собственным значением
£v =(v +1/2)/ко [формулы (В-3) и (В-15)]:
я|ф'у) = (У + 1/2)йсо|ф'у). (В-19)
Решение уравнения (В-18) будет основано на коммутационном соотношении (В-9),
эквивалентном исходному соотношению (А-14), и на вытекающих из него формулах
(В-17).
604

Одномерный гармонический осциллятор
2. Определение спектра
а. ЛЕММЫ
а. Лемма I {свойство собственных значений оператора N )
Собственные значения v оператора N либо положительны, либо равны нулю.
Действительно, рассмотрим произвольный собственный вектор ф'уу и запишем, что
квадрат нормы вектора а фу) положителен или равен нулю:
|я|фу)| = (ф'у|я+а|фу)>0. (В-20)
Используем теперь определение (В-13) оператора N :
(ф'у|а^|Ф'у> = (ф'у|^|ф'у> = у(ф'у|ф'у). (В-21)
Поскольку (ф'у фу) — положительная величина, то сравнение формул (В-20) и (В-21)
показывает, что
v>0. (B-22)
C. Лемма II (свойства вектора а фу))
Пусть ф'уу — отличный от нуля собственный вектор оператора N с собственным
значением v.
(i) Если v = 0, то кет а ф'у=о) = 0 •
Согласно формуле (В-21) квадрат нормы вектора а фу) равен нулю, если v = 0, но
норма вектора равна нулю тогда и только тогда, если сам вектор равен нулю. Поэтому,
если v = 0 — собственное значение оператора N , то все собственные векторы Фо),
связанные с этим собственным значением, удовлетворяют равенству:
«|фо> = °- (В3)
Впрочем, можно показать, что равенство (В-23) справедливо для всех этих
собственных векторов. Действительно, рассмотрим вектор |ф), удовлетворяющий равенству:
д|ф) = 0. (В-24)
605

Глава V
Умножим обе части этого равенства слева на а+:
я+я|ф) = Лг|(р) = 0. (В-25)
Любой вектор, удовлетворяющий равенству (В-24), является собственным вектором
оператора N с собственным значением v = 0.
(ii) Если v>0, то кет a фу) является отличным от нуля собственным вектором
оператора N с собственным значением v - 1.
Допустим, что значение v строго положительно. Согласно формуле (В-21) вектор
а ф'уу не равен нулю, так как квадрат его нормы отличен от нуля.
Покажем, что кет а ф'у) является собственным вектором оператора N . Для этого
применим операторное равенство (В-17-а) к вектору ф'у):
[^ф'у) = -я|Ф'у);
Na |<p'v) = aN |ф'у)-я |ф'у) = av |фу)-в |ф'у) . (В-26)
Таким образом:
^[а|ф'у)] = (У-1)[«|ф'у)], (В-27)
откуда следует, что кет а ф у) является собственным вектором оператора N с
собственным значением (v -1).
у. Лемма III (свойства вектора а+ фу))
Пусть ф'у)— собственный отличный от нуля вектор оператора N с собственным
значением v.
(i) Вектор а+ ф'у) всегда отличен от нуля.
Используя формулы (В-9) и (В-13), вычислим норму вектора а* ф'у):
\\а+н)\2={< iаа+\<)=(<pv и+1} ко=(v+чф'» \<) ■ (в-28)
Поскольку согласно лемме I величина v является положительной или нулем, то кет
а+ фу) всегда имеет норму, отличную от нуля и никогда не может равняться нулю.
606

Одномерный гармонический осциллятор
(ii) Кет а+ kp'v) является собственным вектором оператора N с собственным
значением (v + 1).
Доказательство того, что а+ ф'у) является собственным вектором оператора N ,
аналогично приведенному в лемме I. Достаточно взять в качестве исходного равенство
(B-17-b) между операторами, откуда последует:
[^а+]|Ф'у) = ^|ф'у);
^+|ф'у) = а + ^|ф'у) + а+|ф',) = (У + 1)а+|ф;). (В-29)
Ь. СПЕКТР ОПЕРАТОРА N СОСТОИТ ИЗ НЕОТРИЦАТЕЛЬНЫХ ЦЕЛЫХ ЧИСЕЛ
Рассмотрим произвольное собственное значение v оператора N и собственный
отличный от нуля вектор ф'у) , связанный с этим значением.
Согласно лемме I значение v по необходимости или положительно или равно нулю.
Допустим сначала, что v — не целое число. Сейчас мы покажем, что это
предположение противоречит лемме I и должно быть исключено. Действительно, если v — не
целое, то всегда можно найти такое целое число п > 0, что
п < v < п + 1. (В-30)
Затем рассмотрим последовательность векторов:
|ф;),«|ф;),...^"|ф'у). (в-зо
Согласно лемме II каждый из векторов ар ф'у) (где 0< р<п) этой последовательности
отличен от нуля и является собственным вектором оператора N с собственным
значением v-p (см. рис.3). Доказательство далее осуществляется по шагам: ф'у) отличен от
нуля по предположению; а ф'уу отличен от нуля, так как v > 0 и соответствует
собственному значению v-1 оператора N ...; вектор ар ф'у) получается в результате
действия оператора а на ар~1 Фу), собственный вектор оператора N с положительным
собственным значением v - р +1, так как р < п и v > п [см. формулу (В-30)].
Подействуем теперь оператором а на кет а" ф'у). Поскольку из формулы (В-30)
следует, что v - п > 0, то действие а на а" ф'у) (собственный вектор оператора N с
собственным значением v - п > 0) дает отличный от нуля (лемма II) вектор. Кроме того,
607

Глава V
вследствие леммы II вектор «" |ф'у) также является собственным вектором оператора
N с собственным значением v - п - 1, то есть числом, строго отрицательным согласно
формуле (В-30). Таким образом, если v — не целое число, мы можем сконструировать
отличный от нуля собственный вектор оператора N со строго отрицательным
собственным значением. Поскольку это невозможно (лемма I), то гипотеза о том, что v — не
целое число, должна быть отброшена.
v — л v — л + 1 V—1 v
I !
■н 1 1 н 1 1 ►
О 1 2 п - 1 п п + I
a"|pi> a* -1 |«р{> а|ф1> |<*>1>
Рис.3
Собственные векторы оператора N с собственными значениями v-l,v-2,...
образуются в результате многократного действия оператора а на кет ф'у\
Что же произойдет, если
v = п , (В-32)
где п — целое положительное число или О? В последовательности векторов (В-31)
вектор а" ф|Л отличен от нуля и является собственным вектором оператора N с
собственным значением 0. Тогда согласно лемме II (i) имеем:
a"+'|cp;,) = 0. (В-33)
Таким образом, последовательность векторов, полученная в результате многократного
действия оператора а на вектор ф!,)> оказывается ограниченной, если п — целое
число, и получить отличный от нуля собственный вектор оператора N с отрицательным
собственным значением невозможно.
Итак, собственное значение v может быть только целым неотрицательным числом.
Теперь можно воспользоваться леммой III и показать, что спектр оператора N
состоит только из положительных целых чисел и нулей. Действительно, выше был построен
собственный вектор а" \(р'п) оператора N с нулевым собственным значением; достаточно
подействовать на него оператором (а+)к, чтобы получить собственный вектор
оператора N с собственным значением к , где к — произвольное положительное целое число.
i
608

Одномерный гармонический осциллятор
Если обратиться к формуле (В-19), то можно заключить, что собственные значения
оператора Н имеют вид:
£„=(" + {)*•>, (В-34)
где п = 1,2 Итак, в квантовой механике энергия гармонического осциллятора
квантуется и не может принимать произвольные значения. Заметим также, что самое малое
возможное значение энергии (основной уровень) равно не нулю, а величине /ко / 2 (см.
ниже § D-2).
с. ИНТЕРПРЕТАЦИЯ ОПЕРАТОРОВ а и а +
Если исходным является собственное состояние фМ оператора Я,
соответствующее собственному значению Еп - (п +1 / 2) Лео, то действие на него оператора а даст
собственный вектор с собственным значением Еп_х = (п +1 / 2) Лео - Лео , тогда как
действие оператора а+ даст вектор с собственным значением Еп+[ = (п +1 / 2) /ко + /ко .
По этой причине говорят, что я — оператор уничтожения и я+ — оператор
рождения: их действие на собственный вектор оператора УУ приводит к исчезновению
или появлению кванта с энергией /"ко .
3. Вырождение собственных значений
Сейчас покажем, что уровни энергии одномерного гармонического осциллятора,
определенные формулой (В-34), не вырождены.
а. ОСНОВНОЙ УРОВЕНЬ НЕ ВЫРОЖДЕН
Собственные состояния оператора Н с собственным значением Е0 = Лео / 2 , то есть
связанные с собственным значением п = 0 оператора N , согласно лемме II (§ 2-а-C)
должны удовлетворять уравнению:
я|фо) = 0- (В-35)
Чтобы определить кратность вырождения уровня Е0, достаточно определить, сколько
линейно независимых кет-векторов могут удовлетворять уравнению (В-35).
Используя определение (В-6-а) оператора а и соотношения (В-1), можно
переписать (В-35) в форме:
39 Квантовая механика
609

Глава V
1
-X + -
В представлении { |jc) } это равенство имеет вид:
|<Ро) = 0. (В-36)
—-* + — ф^(дс) = 0 (В-37)
п ах)
где
Ф;)и) = (х|ф'0). (В-38)
Таким образом, нужно решить дифференциальное уравнение первого порядка, и его
общее решение равно:
<р10(х) = се~Т*~х , (В-39)
где с — постоянная интегрирования. Таким образом, все различные решения уравнения
(В-37) пропорциональны друг другу, и с точностью до постоянного множителя имеется
всего лишь один кет-вектор |ф0), удовлетворяющий уравнению (В-35), то есть основной
уровень Е0 = йсо / 2 является невырожденным.
Ь. ВСЕ УРОВНИ НЕ ВЫРОЖДЕНЫ
Только что мы увидели, что основной уровень не вырожден. Покажем с помощью
рекуррентного метода, что это же утверждение справедливо для всех других уровней.
Для этого достаточно доказать, что если уровень Еп = (и + 1/2)Йсо не вырожден, то
и уровень Еп+1 = (п +1 +1 / 2) /Ш) оказывается невырожденным. Допустим, что существует
единственный (с точностью до постоянного множителя) вектор |ф„), удовлетворяющий
равенству:
л|ф„>=«|ф„>- (в-4°)
Рассмотрим собственный вектор ф',+1), соответствующий собственному значению
и + 1:
^|ф^> = (" + 1)|ф:'!+1). (В-41)
Известно, что кет a Wn+i) отличен от нуля и является собственным вектором оператора
N с собственным значением п (лемма II). Поскольку в соответствии с нашим
предположением он не вырожден, то существует такое число с', что
610

Одномерный гармонический осциллятор
я|<р:,+,) = Ф„)- (В-42)
Это уравнение легко обратить, подействовав оператором а* на обе его части:
«+а|Ф;,+,) = с'«+|ф„), (в-43)
то есть если учесть (В-13) и (В-41):
|ф:,+1> = ^Т«+|ф„)- (В-44)
1 ' /г + 1
Мы знаем уже, что я+|ф„) является собственным вектором оператора N с
собственным значением (л + 1), и видим, что все кет-векторы Ф',|+1) , связанные с собственным
значением (п + 1), пропорциональны вектору а+ |ф„), и следовательно, пропорциональны
друг другу, что и свидетельствует о том, что собственное значение (п + 1) не вырождено.
И, наконец, поскольку собственное значение п = 0 не вырождено (см. § а), то не
вырождено собственное значение п = 1, затем я = 2 и т.д.: то есть все собственные
значения оператора N , а следовательно, и оператора Н являются невырожденными. Это
позволяет в дальнейшем опустить индекс / и просто записывать собственный вектор
оператора Н с собственным значением Еп = (п +1 / 2) hco в виде |ф„).
С. СОБСТВЕННЫЕ СОСТОЯНИЯ ГАМИЛЬТОНИАНА
В этом параграфе рассмотрим главные свойства собственных состояний оператора
N и гамильтониана Я .
1. Представление {|ф„)}
Допустим, что операторы N и Н являются наблюдаемыми, то есть система их
собственных векторов образует базис в пространстве состояний <fr частицы в одномерной
задаче (это можно было бы доказать, рассмотрев волновые функции, связанные с
собственными состояниями оператора N , которые будут найдены ниже в § 2). Поскольку
ни одно из собственных значений оператора N (или Н) не является вырожденным (см.
§ В-3), то оператор N (или Н) сам по себе образует в пространстве Ъх полный набор
коммутирующих операторов.
39*
611

Глава V
а. ВЫРАЖЕНИЕ БАЗИСНЫХ ВЕКТОРОВ ЧЕРЕЗ |ф0)
Вектор |ф0), связанный с собственным значением я = 0, является вектором
пространства £v, удовлетворяющим условию:
я|Фо} = 0. (С-1)
Он определен с точностью до постоянного множителя. Допустим, что |ф0) нормирован,
в связи с чем остающаяся неопределенность связана с общим фазовым множителем вида
е'ь, где в — вещественное число.
Согласно лемме III (§ В-2-а) вектор |ф,), соответствующий п = 1, пропорционален
я+|фо)-
|<Pi) = ^+|<Po)- (C-2)
Определим с\9 наложив на вектор |ф,) условие нормировки и выбрав фазу вектора |ф,)
относительно фазы вектора |ф0) так, чтобы с, было вещественным положительным
числом. Согласно (С-2) квадрат нормы вектора |ф^ равен:
(<Pi |Ф1> = Ы^Фо| аа* |ф0) = |с,|2(ф01 (а+а + 1) |ф0), (С-3)
где было использовано равенство (В-9). Поскольку |ф0) — нормированное собственное
состояние оператора N = а+а с нулевым собственным значением, то
(ф||ф|) = к,Г=1. (С-4)
С учетом сделанного выбора фазы имеем сх = 1 и, следовательно:
|ф,) = *+|фо>- (С)
Аналогично можно построить вектор |ф2) из вектора |ф,):
|ф2) = с2а+|Ф1). (С-6)
Потребуем, чтобы вектор |ф2) был нормирован, и выберем его фазу так, чтобы с2 было
вещественным положительным числом:
(ф2|ф2) = к2Г(ф1|««+|ф1)к2Г(ф,|(а+« + 1)|ф1) = 2|с2|2=1. (С-7)
612

Одномерный гармонический осциллятор
Таким образом:
|ф2) = -^а+|ф1) = -^(«+J|Фо) (С-8)
с учетом формулы (С-5).
Описанная процедура без труда обобщается. Если известен нормированный вектор
|ф„ч), то нормированный вектор |ф„) имеет вид:
|ФП) = ^+|Ф„-,)- (С-9)
Поскольку:
(фя|Фл)=КГ<Ф..1|вв+|ф(..1>=иКГ = 1- (с-10>
то с учетом тех же условий для фазы, что и ранее, получим:
с„=А=. (С-П)
При последовательных выборах фазы можно выразить все векторы |ф„) через
вектор |<р0):
|фЛ = ^а1ф^) = ^т^(а+J1ф"-2) = -" = "ГТ=Г'--~^(а+)''1(р0)
л/я \n yjn-l л/л л/л-1 л/2
(С-12)
ИЛИ
|ф„> = -тЦ («+)"|ф0>. (С-13)
л/я!
Ь. СООТНОШЕНИЯ ОРТОНОРМИРОВКИ И ЗАМКНУТОСТИ
Поскольку оператор Н эрмитов, кет-векторы |ф„), соответствующие различным
значениям п, ортогональны. Так как, кроме того, каждый из них нормирован, то они
удовлетворяют соотношению ортонормировки:
(Ф„-|Ф„> = 5»„<- (С-14)
С другой стороны, Я — наблюдаемая (пока примем это утверждение без
доказательства), и поэтому ансамбль |ф„) образует базис в пространстве $х, что выражается с
помощью соотношения замкнутости:
х|ф,ЖИ- (с-15)
613

Глава V
ЗАМЕЧАНИЕ
С помощью формулы (С-13) можно непосредственно доказать, что векторы \tyn) ор-
тонормированы:
fa»' К<)= Trr; (ф<> Iа"а+П |фо> • (С-16)
Ып\п !
Но
я"'а+" |ф0) = а"'~{(аа + )а+"~1 |ф()) = я"'_,(я+я + 1)я+"-1 |ф0) = пап'~1а+п~1 |ф0) (С-17)
(здесь использовано то обстоятельство, что я+ ф0у является собственным состоянием
оператора N = а*а с собственным значением п — 1). Таким образом, можно шаг за шагом
повторять подобную операцию и в конце концов получить:
(ф01 а"'а+" |ф()) = п х (п -1) х ... 2 х 1 (ф01 ап'~п |ф0), если и < и'; (С-18-а)
(ф01 а"'а+п |ф0) = л х (л - 1)... (л - и' + 1)(ф() | (я+ )"~"' |ф0) , если п > п'; (C-18-b)
(ф0|а"'я+" |ф0) = их(л-1) х...2х1(ф0|ф0), если и = п'. (С-18-с)
Выражение (С-18-а) равно нулю, так как а ф()) = 0 . Аналогично, (C-18-b) равно нулю, так
как матричный элемент (ф()| {а + )п~п |ф0у можно рассматривать как скалярное
произведение |ф0) на бра-вектор, сопряженный вектору (а)"~" |ф0), который равен нулю, если
п > п'. И, наконец, если подставить (С-18-с) в (С-16), нетрудно видеть, что (ф;, флу = 1.
с. ДЕЙСТВИЕ РАЗЛИЧНЫХ ОПЕРАТОРОВ
Наблюдаемые X и Р являются линейными комбинациями операторов а и а+
[формулы (В-1) и (В-7)], и поэтому все физические величины могут быть выражены в
виде функций операторов а и а*. Но мы знаем (и ниже покажем это более строго), что
действие операторов а и а+ на векторы |ф„) является особенно простым. Таким
образом, представляет интерес использовать представление {|ф„)} для вычисления
матричных элементов и средних значений различных наблюдаемых.
С учетом введенных выше соглашений относительно фазы действие операторов а и
а+ на базисные векторы {|ф;1)} описывается выражениями:
Ифп) = ^^|ф||+1)|; (С-19-а)
614

Одномерный гармонический осциллятор
Ыф„) = >/п |ф„_,)
(C-19-b)
Мыуже доказали равенство (С-19-а): достаточно заменить п на п + 1 в уравнениях (С-9)
и (С-11). Чтобы получить (C-19-b), умножим слева обе части равенства (С-9) на
оператор а и используем формулу (С-11):
а|ф^ = -^^+|ф/1.1) = -^(а+а + 1)|ф/,_1) = л/^|ф//.1). (С-20)
л/я л/и
ЗАМЕЧАНИЕ
Уравнения, сопряженные (С-19-а) и (C-19-b), имеют вид:
(ф„|я = 7лТГ(ф„+1|;
(ф;1|«+ = л/я'(ф;1_1|.
(С-21-а)
(C-21-b)
Нужно только помнить, что оператор а уменьшает или увеличивает п в
зависимости от того, действует ли он на кет |ф„) или на бра (ф„ |. Аналогично, оператор
а+ увеличивает или уменьшает п в зависимости от того, действует ли он на кет
|ф„) или на бра (ф„|.
С помощью формулы (С-19) и используя (В-1) и (В-7), сразу же найдем выражения
для кет-векторов X |ф/;) и Р |ф«):
х,ф^=Ж^(а++а)|ф^=^[л/^1<р"^+л/"|(р"-|^; (С2"а)
Р|ф,^ = л/^^^(а+-а)|Ф„) = /)|^[л^ТТ|ф,,+1)-л^|ф„_|)]. (C-22-b)
Матричные элементы операторов а , а*, X и Р в представлении {|ф„)} равны:
(ф,,|а|ф„) = ^8„,„.1; (С-23-а)
(C-23-b)
(С-23-с)
(C-23-d)
615

Глава V
Матрицы, представляющие а и а*, эрмитово сопряжены друг другу, так как имеют вид:
'о VI о о 1
О О V2 0 ••• •
0 0 0 л/3 ••• •
(а) =
0 0 0
4~п
(С-24-а)
И-
'00 О
VI о о
О V2 О
о о &
0 0 0
л/я + 1
(C-24-b)
Что касается матриц, представляющих операторы X и Р, то они эрмитовы: матрица
оператора X с точностью до постоянного множителя совпадает с суммой двух
предыдущих, а матрица оператора Р пропорциональна их разности, но наличие множителя /
в равенстве (C-22-b) восстанавливает ее эрмитовость.
2. Волновые функции стационарных состояний
Перейдем в представление {\х) } и запишем функции (рп(х) = (*|ф„),
представляющие собственные состояния гамильтониана.
В § В-З-а мы уже определили функцию (p0(jc), представляющую основное
состояние |ф0):
Фо(*) = (*|ф0) =
т@
nh )
I /НО) 2
(С-25)
Фигурирующая перед экспонентой константа обеспечивает нормировку функции |ф0).
Чтобы получить функции ф„(.х), связанные с другими стационарными состояниями
гармонического осциллятора, достаточно использовать выражение (С-13) для кет-
вектора |ф/2) и тот факт, что в представлении {\х) } оператор а* представлен выраже-
616

Одномерный гармонический осциллятор
нием
V?
П d
moo dx
h d
, поскольку X представлен умножением на х, а Р
дифференцированием [формула (B-6-b)]. Тогда:
/ dx
ф"и)=(л|ф")=^И(а+)"|фо)=^Т^г]¥
b_d_
I отсо dx
Фо(х) (С-26)
или
ф.(*) =
1 ( Ь У
1/2
wcoV
nh J
m(Q d
~TX~~dx~
" 1 ш
(C-27)
2ял!Ысо,
Нетрудно видеть из этого выражения, что ф„(д:) является произведением экспоненты
I ШО) з
е 2 Л на полином степени п и четности (-1)", который называется полиномом
Эрмита (см. дополнения By и Су).
Несложные вычисления дают первые функции ф„(л:):
Ф,0*) =
4f/лсоУ
хе
1 //1@
2~Л
ф2(*) =
W0)
4тсй
I W0) 2
"IT'1
(С-28)
Рис.4
Волновые функции трех первых уровней гармонического осциллятора
Эти функции представлены на рис.4, а соответствующие им плотности вероятности
приведены на рис.5. Рис.6 иллюстрирует ход волновой функции ф„(;с)и плотности ве-
|2
роятности |ф„(.х)| для случая п = 10 .
617

Глава V
w:,
t*:
А,лКлк[\
Рис.5
Плотность вероятности трех первых уровней гармонического осциллятора
Рис.6
Ход волновой функции (а) и плотности
вероятности (Ь) возбужденного уровня
п = 10 гармонического осциллятора
Из этих рисунков видно, что с увеличением п область оси Ох , в которой функция
Ф„(х) заметно отличается от нуля, становится все шире. Это соответствует известному
из классической механики факту, что амплитуда колебаний частицы увеличивается с
ростом ее энергии [см. рис.1 и соотношение (А-8)]. Отсюда следует, что среднее
значение потенциальной энергии также увеличивается с ростом п [см. замечание (ii) к § D-1],
так как при больших значениях п функция ф„ (х) заметно отлична от нуля в тех
областях оси Ох, где потенциал V(x) увеличивается. Кроме того, из этих рисунков можно
заключить, что число нулей функции ф„(*) равно п (см. дополнение Bv, где это свойство
строго доказано), и средняя кинетическая энергия частицы увеличивается с ростом п
[см. замечание (ii) в § D-1]. Действительно, она определяется формулой:
618

Одномерный гармонический осциллятор
т- (рг) = ~т~ 1->»(х) ттф-w^ • (с-29)
2га х ' 2га ах"
С увеличением количества нулей функции ф/? (х) кривизна волновой функции возраста-
ет, и в формуле (С-29) вторая производная —- ф„(х) принимает все большие и боль-
dx
шие значения.
Наконец, при больших п (см., например, рис.6) плотность вероятности |ф„0)|
принимает наибольшие значения при х~±хм [где хм — амплитуда классического
колебания с энергией Еп; см.(А-8)]. Этот результат напоминает характеристику
движения, которую предсказывает классическая механика: классическая частица имеет
нулевую скорость в точках х = ±хм ; то есть она в среднем проводит больше времени вблизи
этих точек, чем в центре интервала -хм < х < хм .
D. ФИЗИЧЕСКОЕ ОБСУЖДЕНИЕ
1. Средние значения и среднеквадратичные отклонения операторов X и Р
в состоянии |ф„)
Ни X , ни Р не коммутируют с Я, и собственные состояния |ф„) оператора Н не
являются собственными состояниями операторов X и Р. В связи с этим, если
гармонический осциллятор находится в стационарном состоянии |ф„), то измерение
наблюдаемой X или наблюдаемой Р априори может дать любой результат, так как спектры
операторов X и Р содержат все вещественные числа. Здесь мы вычислим средние
значения X и Р в таком стационарном состоянии, а затем их среднеквадратичные
отклонения АХ и ДР, что позволит еще раз проверить соотношение неопределенностей.
Как указывалось в § С-1-е, вычисления удобно проводить с помощью операторов а
и а+. Что касается средних значений X и Р, результат сразу же вытекает из формул
(С-22), которые показывают, что ни X ни Р не имеют диагональных матричных
элементов:
(ф„|х|ф„) = 0;
(ф„Мфя) = 0. (D-1)
Чтобы получить среднеквадратичные отклонения АХ и АР, нужно вычислить
средние значения X2 и Р2:
619

Глава V
(АХJ=(ф„|Х2|ф„)-((ф„|х|ф„)J=(ф„|Х2|ф„);
М2-(Ф.|'>1|Ф.)-«Ф.|'»|Ф.»2=(Ф.|^|Ф.>- (D-2)
Но согласно формулам (В-1) и (В-7):
X2 = —— (а+ +а)(а+ +а) = —— (д+2 +аа+ +а+а + а2);
2/7203 2/WG)
Р = (а -а)(а -а) = (а -аа -а а + а ). (D-3)
Члены а2 и а+ не дают вкладов в диагональные матричные элементы, так как а2 |ф„)
пропорционален |ф„_2) и а* |ф„) пропорционален |ф/|+2), то есть векторам, которые
ортогональны к вектору |ф„). Напротив:
(уп\(а+а + аа + )\ч>п) = (ч)„\Bа+а + \)\ч>п) = 2п + \ (D-4)
и, следовательно:
(АХJ=(ф„|Х2|ф„) = (п+1)-^; (D-5-a)
(ДРJ=(ф„|Р2|ф„)=^ + ^тй@. (D-5-b)
Произведение АX • А Р оказывается равным:
АХАР = | л + -
П. (D-6)
И снова (см. дополнение Сш) мы видим, что оно больше или равно Ь12.
Действительно, эта нижняя граница достигается, если п - О, то есть в основном состоянии (см.
ниже § 2).
ЗАМЕЧАНИЯ
(i) Если обозначить символом хм амплитуду классических колебаний с энергией
Еп = (п +1 / 2) /Ш), то нетрудно видеть из формул (А-8) и (D-5-a), что
AX=-^jcm. (D-7)
V2
620

Одномерный гармонический осциллятор
Аналогично, если рм — амплитуда колебаний соответствующего классического
импульса:
рм = тшм , (D-8)
получим:
AF = ipM. (D-9)
Неудивительно, что величина А X оказывается того же порядка, что и
интервал [-л^.+дгуи], в котором происходит классическое движение (см. рис.1),
поскольку, как мы уже видели в конце предыдущего параграфа, примерно в этом
интервале функция ф„(лО принимает существенно отличные от нуля значения.
С другой стороны, нетрудно понять, почему с увеличением п величина А X также
растет. Действительно, плотность вероятности |ф„(*)| в случае больших
значений п имеет форму двух пиков, симметрично расположенных вблизи значений
х = ±хм, и среднеквадратичное отклонение не может быть слишком малым по
сравнению с расстоянием между пиками, даже если каждый из них окажется очень
узким (см. § С-5 главы III и рассуждения в § 1-Ь дополнения Аш). Аналогичные
рассуждения могут быть сделаны и для величины АР (см. дополнение Dv).
(ii) Средняя потенциальная энергия частицы в состоянии |фн) равна:
(V(X)) = |m@2(x2), (D-10)
то есть, поскольку (х) = О [см формулу (D-1)]:
(У(Х)) = -ты2(АХJ. (D-11)
Можно также показать, что средняя кинетическая энергия частицы равна:
-(АРJ. (D-12)
Р2\ 1
2т 2т
Подставим равенства (D-5) в (D-11) и (D-12) и получим:
Е„
<^»4Н)
2
Р2\ \( П. Е
,=- и + - йа> = -*-. (D-13)
2m/ 2 1 2 2

Глава V
Итак, средние значения кинетической и потенциальной энергии равны, и мы снова
встречаемся с частным случаем теоремы вириала (см. упражнение 10 дополнения
Lm).
(iii) Стационарное состояние |ф„) не имеет никакого эквивалента в классической
механике. Действительно, его энергия отлична от нуля, тогда как средние значения
(х) и (р) равны нулю. Однако между состоянием |ф;/) и состоянием
классической частицы имеется некоторая аналогия. Положение последней определяется
формулой (А-5), где хм связана с энергией Еп соотношением (А-8), но при этом
начальная фаза ф колебания может быть случайной величиной (то есть она
принимает с равной вероятностью все значения между 0 и 2п). Тогда средние
значения переменных х и р оказываются равными нулю, так как
*d =^Г Jo*cos(M-<р)Лр = 0;
27l1 (D-14)
Кроме того, можно было бы вычислить среднеквадратичные отклонения
положения и импульса, и они оказываются такими же, что и в состоянии |фм) [формулы
(D-7)h(D-9)]:
ti = 4 — J02W(cd/-^) £/ф = 4f;
Й=Pi^Jo2,l«л2((or-ф)rfф==^■, (D-15)
то есть
5-^/ = V ■**
.(г У =ZM--
ЬРы = yjPd
■(PclJ=^- (D-16)
2. Свойства основного состояния
В классической механике наименьшая энергия гармонического осциллятора имеет
место тогда, когда частица неподвижна (импульс и кинетическая энергия равны нулю)
и находится в начале координат (точка х = 0, где потенциальная энергия равна нулю).
622

Одномерный гармонический осциллятор
В квантовой механике все обстоит иначе: состояние с минимальной энергией |ф0) имеет
отличную от нуля энергию, и связанная с ним волновая функция имеет некоторую
пространственную протяженность, характеризующуюся среднеквадратичным отклонением
ДХ=лМ/2т@ .
Это наиболее существенное различие квантового и классического результатов
можно рассматривать как следствие соотношения неопределенностей, запрещающего
одновременно минимизировать кинетическую и потенциальную энергию. Как мы уже
отмечали в дополнениях Q и Мщ, основное состояние является компромиссом, в котором
сумма этих энергий имеет минимально возможное значение.
В частном случае гармонического осциллятора эти качественные рассуждения можно
уточнить полуколичественно и определить порядок величины энергии и пространственной
протяженности основного состояния. Если длина £ характеризует пространственную
протяженность, то средняя потенциальная энергия по порядку величины равна:
V=-mOJ£2. (D-17)
Но тогда АР равна примерно ЬI £, и средняя кинетическая энергия приближенно равна:
2т 2т£
Г=-£- = т-тг. (D-18)
Таким образом, полная энергия по порядку величины равна:
_ _ _ п2 1
E = T+V =—-r- + -mco2£2. (D-19)
Зависимость величин Т , V и Е от переменной £ представлена на рис.7. Для малых
значений £ кинетическая энергия Т превышает потенциальную V , тогда как при
больших значениях £ имеет место обратное соотношение между ними. Таким образом,
основное состояние соответствует приближенно минимуму функции (D-19), и значение
переменной £, соответствующее минимуму, равно:
Vmco
а энергия равна:
£,„=/*). (D-21)
Тем самым мы снова находим по порядку величины уже известные значения Е0 и АХ в
состоянии |ф0) •
623

Глава V
Рис.7
Зависимость потенциальной V и кинетической Т
энергии от параметра % , характеризующего пространственную
протяженность волновой функции вблизи х = О.
Поскольку гармонический потенциал минимален при х = О,
функция V растет с увеличением \ (то есть V ©с £2).
Напротив, согласно соотношению неопределенностей Гейзен-
берга, кинетическая энергия убывает с ростом £.
Минимально возможное значение полной энергии имеет место
при \ - \т в результате компромисса между Т и V
Гармонический осциллятор обладает той особенностью, что из-за формы
потенциала V(x) произведение АХ АР действительно достигает в основном состоянии |(р())
своего нижнего порога ft/2 [формула (D-6)], и это связано с гауссовой формой волновой
функции основного состояния (см. дополнение Сщ).
3. Эволюция средних значений во времени
Рассмотрим гармонический осциллятор, состояние которого в момент времени
/ = О записывается в виде:
к@))=|с„@)|Ф„) (D-22)
(предполагается, что функция |\|/@)) нормирована). Его состояние |\|/(/)) в момент
времени t можно получить благодаря правилу (D-54) главы III:
к(о)=Ес„@)е-'£"'/"|ф„) = х^@)^ [ 2> |ф„)- (°-23)
Среднее значение любой физической величины А определяется функцией времени:
(\|/@| А\Щ») = £ £с;,@)с„@)А„шен"-"ш , (D-24)
где
Л,,,,=ЫЛН> (D-25)
a /и и и — целые числа. Таким образом, эволюция со времени средних значений
происходит с частотой со / 2л и кратными ей, причем все они образуют набор частот Бора
гармонического осциллятора.
624

Одномерный гармонический осциллятор
Обратим внимание на средние значения наблюдаемых X и Р . Согласно формулам
(С-22) единственными отличными от нуля матричными элементами Хтп и Рпт
являются такие, для которых т = п ± 1, вследствие чего средние значения операторов X и Р
изменяются пропорционально е±т! и, следовательно, являются гармоническими
функциями времени с частотой со . Это, очевидно, напоминает классическое решение задачи
о гармоническом осцилляторе. Впрочем, как мы уже отмечали при обсуждении теоремы
Эренфеста (глава III, § D-1-d-y), форма потенциала гармонического осциллятора говорит
о том, что средние значения X и Р должны строго соответствовать классическим
уравнениям движения в любом состоянии |\|/). Действительно, согласно общим
формулам (D-34) и (D-35) главы III:
±(X) = U[X,H]) = &; (D-26-a)
dt x ifi x J/ m
Если эти уравнения проинтегрировать, получим:
(X)(t) = (X)@)cosm + —(P)(Q)sin cor ;
(Р)@ = (P)@)cosat - m(»(x)@)sinm (D-27)
и снова находим синусоидальную функцию вида (D-24).
ЗАМЕЧАНИЕ
Важно заметить, что аналогия с классической ситуацией имеет место только
тогда, когда |\|/@)) является суперпозицией состояний |ф„)вида (D-22), где по
крайней мере несколько коэффициентов сп @) отличны от нуля. Если все
коэффициенты, кроме одного, равны нулю, это значит, что осциллятор находится в
стационарном состоянии, и все средние значения всех наблюдаемых остаются
постоянными во времени.
Отсюда следует, что в стационарном состоянии |ф„) поведение
гармонического осциллятора существенно отличается от того, что предсказывает
классическая механика, если даже п очень велико (предел больших квантовых чисел).
Если требуется построить волновой пакет, среднее положение которого осциллирует
во времени, необходимо воспользоваться суперпозицией различных состояний
|ф;/) (см. дополнение Gy).
40 Квантовая механика
625

ДОПОЛНЕНИЯ К ГЛАВЕ V
Av. Анализ некоторых физических
примеров гармонического
осциллятора.
By. Стационарные состояния
в представлении {\х) }. Полиномы
Эрмита.
Су. Решение уравнения на собственные
значения гармонического осциллятора
методом полиномов.
Dv. Анализ стационарных состояний
в представлении {|р) }.
Еу. Трехмерный изотропный
гармонический осциллятор.
Fv. Гармонический осциллятор с зарядом
в однородном электрическом поле.
Gv. «Квазиклассические» когерентные
состояния гармонического
осциллятора.
Ну. Собственные моды колебаний двух
связанных гармонических
осцилляторов.
Av: на нескольких примерах из различных
областей физики показана важность задачи о
гармоническом квантовом осцилляторе в
физике; решение полуколичественное и
достаточно простое; рекомендуется для первого
чтения.
Bv: формальный анализ стационарных
волновых функций гармонического осциллятора;
предназначается в качестве справочного
пособия.
Cv: иной метод получения результатов
главы V; показана связь между квантованием
энергии и поведением волновой функции на
бесконечности; задача средней трудности.
Dv: показано, что в стационарном состоянии
гармонического осциллятора распределение
вероятности импульса имеет ту же форму,
что и распределение вероятности положения
частицы; простое решение.
Ev: обобщение результатов главы V на
трехмерный случай; рекомендуется для первого
чтения, поскольку задача достаточно проста
и важна в физическом плане.
Fv: простое и непосредственное приложение
результатов главы V (кроме §3, в котором
используется оператор трансляции,
введенный в дополнении Еп); рекомендуется для
первого чтения.
Gv: детальный анализ «квазиклассических»
состояний гармонического осциллятора,
позволяющий установить связь между квантовой
и классической механиками; важен своими
многочисленными применениями в
квантовой теории излучения; задача средней
трудности, может быть пропущена при первом
чтении.
Hv: анализ простого случая двух связанных
гармонических осцилляторов; нормальные
моды колебаний системы; рекомендуется при
первом чтении из-за простоты и важности
физических результатов.
626

Jv. Моды колебаний бесконечной
линейной цепочки связанных
гармонических осцилляторов.
Фононы.
Kv: Моды колебаний непрерывной
физической системы. Применение
к излучению. Фотоны.
Jv, Kv: введение в рамках упрощенных
моделей особенно важных в физике понятий;
достаточно трудный материал, может быть
отложен для последующего изучения.
Jv: нахождение собственных мод колебаний
линейной цепочки связанных осцилляторов,
приводящее к введению понятия фонона,
фундаментального понятия в физике
твердого тела.
Kv: собственные моды колебаний
непрерывной системы; позволяют легко понять введение
понятия фотона в квантовой теории
электромагнитного поля.
Одномерный гармонический
осциллятор в термодинамическом
равновесии при температуре Г.
Lv: применение оператора плотности,
введенного в дополнении Еш, к задаче о
гармоническом осцилляторе в условиях теплового
равновесия; задача важна с физической точки
зрения, но требует знания дополнения Еш.
Mv. Упражнения.
40*

Глава V
Дополнение Ay
АНАЛИЗ НЕКОТОРЫХ ФИЗИЧЕСКИХ ПРИМЕРОВ
ГАРМОНИЧЕСКОГО ОСЦИЛЛЯТОРА
1. Колебания ядер двухатомной молекулы.
a. Энергия взаимодействия между двумя атомами.
b. Движение ядер.
c. Экспериментальное проявление колебаний ядер.
2. Колебания ядер в кристаллах.
a. Модель Эйнштейна.
b. Квантовый характер колебаний кристалла.
3. Торсионные колебания молекулы: пример молекулы этилена.
a. Структура молекулы этилена С2Н4 .
b. Классические уравнения движения.
c. Квантовый анализ.
4. Тяжелые мюонные атомы.
a. Сравнение с атомом водорода.
b. Тяжелый мюонный атом как гармонический осциллятор.
c. Порядок величины энергий и протяженности волновых функций.
Во введении к главе V мы уже отмечали, что результаты изучения гармонического
осциллятора применимы к множеству физических задач и, в частности, ко всем задачам,
связанным с малыми колебаниями системы вблизи положения устойчивого равновесия,
где ее потенциальная энергия минимальна. Цель этого дополнения — описать несколько
примеров подобных колебаний и показать их физическую важность: колебания ядер
двухатомной молекулы или кристаллической решетки, торсионные колебания молекулы,
движение мюона \х~ внутри тяжелого ядра. Естественно, мы не станем вдаваться в детали
рассматриваемых явлений и ограничимся лишь простым и качественным обсуждением.
1. Колебания ядер двухатомной молекулы
а. ЭНЕРГИЯ ВЗАИМОДЕЙСТВИЯ МЕЖДУ ДВУМЯ АТОМАМИ
Образование молекулы из двух нейтральных атомов происходит вследствие того,
что потенциальная энергия взаимодействия V(r) этих атомов (г — разделяющее их
расстояние) имеет минимум. На рис.1 представлен ход функции V(r): если г очень ве-
628

Одномерный гармонический осциллятор
лико, два атома практически не взаимодействуют, и функция V(r) стремится к
некоторой постоянной величине, которую можно выбрать в качестве начала отсчета энергии.
Затем, когда г уменьшается, функция V(r) изменяется приблизительно как -1/г6:
силами притяжения являются силы Ван-дер-Ваальса (они рассматриваются в
дополнении Cxi). Если г достаточно мало, чтобы электронные волновые функции двух атомов
перекрылись, потенциал V(r) уменьшается быстрее, затем проходит через минимум при
г = геи начинает возрастать, стремясь к бесконечности при г —» 0.
Рис.1
Форма потенциала взаимодействия между двумя
атомами, способными образовать стабильную
молекулу: с классической точки зрения V0 —
энергия диссоциации молекулы, ге —
расстояние между двумя ядрами в положении
равновесия. В рамках квантовой механики образуются
колебательные уровни (горизонтальные линии
внутри ямы), энергия которых всегда
превышает -V0
Минимум потенциала V(r) ответственен за химическую связь между атомами: мы
уже указывали в § С-2-с главы IV (на примере молекулы Я2+ ), что понижение энергии в
минимуме связано с явлением делокализации электронных состояний (квантовый
резонанс), которое позволяет электронам воспользоваться притяжением со стороны двух
ядер. Быстрое увеличение У (г) на малых расстояниях связано с отталкиванием ядер.
Если бы ядра были классическими частицами, их положение устойчивого
равновесия соответствовало бы расстоянию г = ге. Глубина V0 потенциальной ямы в точке
г = ге в классической модели называется энергией диссоциации молекулы: это такая
энергия, которую нужно сообщить двум атомам, чтобы удалить их друг от друга. Чем
больше V0, тем стабильнее молекула.
Теоретическое и экспериментальное исследование кривой, изображенной на рис.1,
является в атомной и молекулярной физике очень важной задачей. Мы увидим сейчас, что
анализ колебаний ядер позволяет получить важные сведения относительно этой кривой.
ЗАМЕЧАНИЕ (приближение Борна—Оппенгеймера)
Поставленная задача квантового описания двухатомной молекулы в реальности очень
сложна, так как требует нахождения стационарных состояний многих частиц, ядер и элек-
0
,
- к
\
\
V
V^J
гс
/^
/
/
I/
629

Глава V
тронов, взаимодействующих друг с другом. Точное решение уравнения Шредингера такой
системы в общем случае невозможно. Задачу можно существенно упростить, если учесть,
что масса электронов мала по сравнению с массой ядер, вследствие чего движение
электронов является гораздо более быстрым, чем движение ядер. Отсюда следует, что в первом
приближении эти два вида движения можно изучать отдельно. Можно начать с анализа
движения электронов при фиксированном расстоянии г между ядрами, получить набор
стационарных состояний для электронной системы с энергиями Е{(г), Е2(г).... Затем
выбрать основное состояние электронной системы с энергией Ех(г). Если г изменяется
вследствие движения ядер, электронная система остается всегда для каждого значения г в
основном состоянии, ибо ее волновая функция очень быстро адаптируется к любому
изменению координаты г : говорят, что электроны, будучи очень мобильными, «адиабатически»
отслеживают движение ядер. Если теперь нужно исследовать это движение, то электронная
энергия Е{(г) играет роль потенциальной энергии взаимодействия между ядрами,
зависящей от расстояния г, которая должна быть добавлена к их электростатическому
отталкиванию Z{Z2e I г, где Z, и Z2 — атомные номера двух ядер, а е = q /4я£0, где q —
заряд электрона. Полная потенциальная энергия V{r) системы двух ядер, позволяющая
определить их движение, практически равна:
V(r)=£1(r) + ^^-. A)
Г
Именно эта функция представлена на рис.1.
Ь. ДВИЖЕНИЕ ЯДЕР
а. Разделение движений вращения и колебания
Таким образом, задача сводится к анализу движения двух частиц с массами т, и пц ,
взаимодействующими друг с другом, причем потенциал взаимодействия V(r) имеет
вид, изображенный на рис.1, и зависит только от расстояния между частицами. Задача
все еще остается достаточно сложной из-за наличия нескольких степеней свободы:
колебания (изменение г) и вращения (изменение полярных углов 6 и ф, определяющих
направление оси молекулы в пространстве). Эти степени свободы связаны друг с
другом: если молекула колеблется, изменяется ее момент инерции вследствие изменения г,
и, конечно, энергия вращения.
Если ограничиться колебаниями малой амплитуды, то можно показать, что связь
между колебательными и вращательными степенями свободы пренебрежимо мала, так
как момент инерции относительно мало меняется при колебательном движении. Таким
образом, как мы увидим более строго в дополнении FVn, задача сводится к двум незави-
630

Одномерный гармонический осциллятор
симым задачам: вращение системы, напоминающей «гантель», образованной из двух
масс т{ и щ, разделенных фиксированным расстоянием ге *, и одномерное колебание
фиктивной частицы с массой т, равной приведенной массе тх и т^ (см. §В главы VII):
т. т,
т = ——?— B)
в поле потенциала V(r), изображенного на рис.1. При этом потребуется решить уравнение
на собственные значения:
r- + V(r)
2т dr2
ф(г) = £ф(г). C)
Остановимся именно на этой последней задаче.
Р. Колебательные уровни
Если ограничиться колебаниями малой амплитуды, то можно взять лишь первые
члены разложения функции V(г) вблизи точки минимума г = ге:
V(r) = -V0+V/(r€)(r-reJ+^Vw(rJ(r-rJ3 + ... D)
2 о
Обсуждение, проведенное в §А-2 главы V, показывает, что если в выражении D)
пренебречь членами порядка выше второго, то уравнение сводится к уравнению одномерного
гармонического осциллятора с центром в точке г = ге и частотой:
-,Р2. E)
V т
Колебательные уровни |ч\.), изображенные на рис.1 горизонтальными линиями,
имеют энергию:
£v=^v + |j/ia)-V0, F)
где v = 0,1,2,... (здесь используется символ v вместо п , как это принято в
молекулярной спектроскопии).
* Квантовый анализ такой системы, называющейся «жестким ротатором», будет выполнен в
дополнении CVi после введения механического момента.
631

Глава V
Согласно обсуждению в § D-3 главы V среднее значение (/?) расстояния между
двумя ядрами осциллирует вблизи значения ге с частотой со / 2тс, которая имеет смысл
частоты колебания молекулы.
ЗАМЕЧАНИЯ
(i) Даже в основном состоянии волновая функция гармонического осциллятора имеет
конечную протяженность порядка yjh 12тС0 (см. §D-2 главы V). Это значит, что расстояние
между двумя ядрами молекулы в основном колебательном состоянии определено с
точностью до yjh 12/ЖО . Таким образом, важным условием возможности отдельного рассмотрения
колебательных и вращательных степеней свободы является неравенство:
2/ЖО
« ге. G)
(ii) Если приведенная масса т известна, то измерение частоты со позволяет найти вторую
производную V"(re) по формуле E). С увеличением квантового числа v уже нельзя будет
пренебрегать членами вида (г-ге)ъ в выражении D), характеризующими отклонение
формы потенциальной ямы от параболической. При этом осциллятор становится
ангармоническим. Анализ влияния члена (г — ге) в выражении D) с помощью теории возмущений
(это будет сделано в дополнении AXi), показывает, что разность энергий двух соседних
уровней Ev+] - Ev для больших и малых квантовых чисел v различна. Зависимость
разности Ev+l — Ev от v позволяет определить коэффициент V'"{re) члена (г-ге)ъ. Теперь
понятно, как путем изучения колебаний молекулы можно определить форму потенциала
взаимодействия V(r) вблизи точки минимума.
у. Порядок величины частот колебаний
Принято выражать частоты колебаний молекул в см"', то есть вычислять величину, обратную
длине волны X , выраженной в см, для электромагнитного излучения с частотой v . Напомним,
что 1 см соответствует частоте 3-1010 герц или энергии 1,24 • 10~4 эВ.
Значения частот колебаний двухатомных молекул лежат в диапазоне между десятками и
тысячами см. Соответствующие значения длин волн находятся в интервале от нескольких микрон
до нескольких сотен микрон и лежат в инфракрасной области.
Из формулы E) видно, что частота СО тем больше, чем меньше масса т и чем больше
величина V'\re), то есть чем больше крутизна потенциальной ямы вблизи г = ге. Поскольку
величина ге почти всегда имеет порядок нескольких ангстрем, значение V (ге) увеличивается с глуби-
632

Одномерный гармонический осциллятор
ной V0 ямы, то есть частота СО может служить мерой химической стабильности.
Проиллюстрируем сказанное несколькими конкретными примерами.
Частоты колебаний молекул водорода и дейтерия (Н2 и D2) равны соответственно (без
учета поправок на ангармоничность):
VH =4401смч ;
VD, =3112 см. (8)
Кривые V(r) в обоих случаях одинаковы: действительно, химическая связь между двумя
атомами определяется только электронной оболочкой. Напротив, приведенная масса Н2 в два раза
меньше приведенной массы D2. Поэтому согласно формуле E) V^ = V2vD^ . Именно такое
отношение имеют экспериментально полученные значения (8).
Рассмотрим теперь пример двух молекул, имеющих примерно одинаковые приведенные
массы, но существенно различную химическую стабильность. Молекула Br Rb химически
стабильна (связь между галогеном и щелочным металлом); частота ее колебаний равна 181 см-1.
Молекулы 84Kr85Rb были недавно обнаружены в экспериментах по оптической накачке.
Их стабильность гораздо меньше, так как криптон, будучи инертным газом, с химической точки
зрения практически инертен (связь в молекуле практически обусловлена только силами Ван-дер-
Ваальса). Для этих молекул частота колебаний составляет 13 см ~1. Значительное различие с
предыдущим значением отражает исключительно различие химической стабильности этих двух
молекул, так как их приведенные массы совпадают с точностью до нескольких процентов.
с. ЭКСПЕРИМЕНТАЛЬНОЕ ПРОЯВЛЕНИЕ КОЛЕБАНИЙ ЯДЕР
Остается объяснить, как колебания ядер проявляются экспериментально, в
частности, при взаимодействии молекулы с электромагнитной волной.
а. Поглощение и испускание инфракрасного излучения
Допустим сначала, что молекула гетерополярная, то есть образована из двух
различных атомов. Поскольку электроны притягиваются более электроотрицательным атомом,
в общем случае молекула должна обладать постоянным дипольным моментом D(r),
зависящим от расстояния г между двумя ядрами. Разложим D(r) вблизи положения
равновесия г = ге\
О(г) = йГ0+^(г-ге) + ..., (9)
где dQ и dx — вещественные постоянные.
633

Глава V
Когда молекула находится в линейной суперпозиции |\|/@) нескольких
стационарных колебательных состояний |ф,,), то среднее значение (\|/@| D(R)\\\f(t)) ее диполь-
ного электрического момента осциллирует вблизи значения d0 с частотой о / 2тс. Этот
осциллирующий член появляется за счет среднего значения члена dx{R-re) в
выражении (9) (в нем R-re играет ту же роль в нашей задаче, что и наблюдаемая X
гармонического осциллятора в §D-3 главы V). Поэтому оператор (R-re) имеет отличные от
нуля матричные элементы только между такими состояниями |(pv) и |(pv.), для которых
v-v' = ±1. Это правило отбора позволяет понять, почему в изменении величины
(D(/?))(r) появляется только одна частота Бора со /2тс [естественно, если учесть
ангармоничность потенциала и члены высших порядков в разложении (9), то появятся и более
высокие гармоники, но их интенсивность значительно слабее].
Колебания дипольного момента являются физической причиной связи молекулы с
электромагнитным полем, благодаря чему она может поглощать или испускать
излучение с частотой v. Применяя понятие фотона, можно сказать, что молекула может
поглотить фотон с энергией hv и перейти из состояния |cpv) в состояние |cpv+1) (рис.2а)
или испустить фотон hv , перейдя при этом в состояние |фг_!) (рис.2Ь).
Р. Эффект Рамана
Рассмотрим теперь гомеополярную молекулу, образованную из двух одинаковых
атомов. Вследствие симметрии постоянный электрический дипольный момент у такой
молекулы равен нулю при любых значениях г, вследствие чего молекула оказывается
«неактивной» в инфракрасном диапазоне длин волн.
a b
к> •—^— к> +
Рис.2
Поглощение (а) и испускание (Ь) фотона с энергией hv гетерополярной молекулой,
переходящей из колебательного состояния |cpv) в состояние |фу+1) или |cpv_i)
634

Одномерный гармонический осциллятор
Представим себе, что на такую молекулу падает оптическая волна с частотой Q / 2л .
Ее частота значительно выше характерных колебательных частот, и волна может
возбудить электронную оболочку молекулы. Под действием оптической волны электроны будут
совершать вынужденное движение и переизлучать в пространство фотоны той же частоты.
Это явление хорошо известно под названием молекулярного рассеяния света (рассеяние
Рэлея)*. Какие же новые эффекты могут появиться при наличии колебаний молекулы?
Рис.3
Колебания молекулы модулируют
амплитуду осциллирующего
электрического диполя,
индуцированного падающей световой волной
Можно предложить следующее качественное объяснение. Электронная
поляризуемость** молекулы в общем случае является функцией расстояния г между ядрами. При
изменении г (напомним, что это изменение по сравнению с движением электронов
происходит гораздо медленнее) амплитуда индуцированного дипольного электрического
момента, осциллирующего с частотой Q/2n , будет изменяться. Зависимость
дипольного момента от времени может быть представлена в виде синусоиды с частотой Q / 2я ,
амплитуда которой промодулирована значительно меньшей частотой молекулярных
колебаний со / 2тг (рис.3). Распределение частот света, испущенного молекулой,
описывается преобразованием Фурье движения электрического диполя, представленного на
рис.3. Как видно из рис.4, существует центральная линия с частотой £>/2л (рассеяние
Рэлея) и две боковых линии с частотами (П-со)/2я (рассеяние Рамана, стоксова
линия) и (Q + со) / 2я (рассеяние Рамана, антистоксова линия).
Интерпретация этих линий очень проста, если использовать понятие фотонов.
Рассмотрим оптический фотон с энергией Ш , падающий на молекулу, находящуюся в состоянии
* В дополнении АХш с помощью формализма квантовой механики мы рассмотрим
вынужденное движение электронов в атоме под действием светового излучения.
Под действием поля Е0е' ' падающей световой волны электронная оболочка молекулы
приобретает индуцированный дипольный момент D , определяемый формулой D = %(Q) E0e'Qt ,
где %(&) по определению называется электронной поляризуемостью молекулы. Важно отметить,
что %(£2) зависит от расстояния г .
635

Глава V
Q — (о
In
In
Q + со
In
Рис.4
Спектр колебаний, представленных на рис.3. Кроме
центральной линии с частотой, равной частоте
падающей волны (линия Рэлея), появляются две
смещенные линии (стоксова и антистоксова линии
эффекта Рамана); расстояния между ними и
центральной линией равны частоте колебаний молекулы
|(pv) (рис.5а). Если в процессе рассеяния фотона молекула не изменяет свое
колебательное состояние, то рассеяние является упругим: согласно закону сохранения энергии
рассеянный фотон имеет ту же энергию, что и падающий (рис.5Ь, рэлеевская линия). Но
в процессе рассеяния молекула может перейти с колебательного уровня |фг) на
колебательный уровень |фг+1). Увеличение энергии молекулы может произойти только за счет
уменьшения энергии рассеянного фотона, которая станет равной Й(й-О)) (рис.5с):
рассеяние при этом оказывается неупругим (стоксова рамановская линия). И, наконец,
молекула может перейти из состояния |ф^) в состояние |фу_,), тогда рассеянный фотон
будет иметь энергию Й(й + со) (рис.5с1; антистоксова рамановская линия).
b
gk>
м>\
\ч\)
па
с
@k+l>
h(Q - w)V
d
0 k-
ЦП + wK
i>
a
Рис.5.
Схематическое представление рассеяния фотона с энергией йй молекулой,
первоначально находящейся в колебательном состоянии |фг); (а) — релеевское рассеяние без
изменения колебательного состояния; (Ь) —- рамановское стоксово или антистоксово
рассеяние с переходом молекулы из состояния |фг) в состояние <Pv+i) (с) или в
состояние |фг.,) (d)
636

Одномерный гармонический осциллятор
ЗАМЕЧАНИЯ
(i) Эффект Рамана можно наблюдать и на гетерополярных молекулах.
(ii) С появлением лазеров интерес к эффекту Рамана резко возрос. Помещая в лазерный
резонатор, настроенный на частоту Q / 2тг, кювету, заполненную веществом, активным с точки
зрения рамановского рассеяния, можно получить в ряде случаев усиление
(стимулированный эффект Рамана) и даже генерацию лазерных колебаний на частоте (£2-О))/271, где
0) — частота колебаний молекул, находящихся в кювете (рамановский лазер). Изменяя
вещество, можно в значительной степени изменять частоту лазерного излучения.
(iii) Изучение инфракрасных и рамановских спектров молекул имеет большое значение для
химии, так как позволяет определить существующие в сложных молекулах связи. Так,
например, частота колебаний образования, состоящего из двух атомов углерода, в значительной
мере зависит от того, является ли химическая связь простой, двойной или тройной.
2. Колебания ядер в кристаллах
а. МОДЕЛЬ ЭЙНШТЕЙНА
Кристалл состоит из совокупности атомов (или ионов), регулярно распределенных в
пространстве в узлах периодической решетки. Для простоты остановимся на
одномерной модели, то есть рассмотрим линейную цепочку атомов. Среднее положение ядра
g-того атома обозначим:
x°q=qd, A0)
где d — параметр решетки, имеющий величину порядка нескольких ангстрем.
Пусть £/(jcp дг2,..., xqy...) — потенциальная энергия ансамбля образующих кристалл
ядер, зависящая от их положения jc,, jc2, ..., xq,.... Если разность xq - xq не слишком
велика, то есть если отклонение каждого из ядер от своего положения равновесия мало, то
во многих случаях функция U(xx, х2,..., х ,...) может быть записана в упрощенном виде:
U(xl,x2,...,xq,...)~U0 + %Uxq-x°qJUZ+...9 A1)
q 2
где U0 и Uq — вещественные постоянные, причем Uq> 0. Линейные по xq - xq члены
отсутствуют, так как предполагается, что xq является положением устойчивого
равновесия ядра q (минимум потенциальной энергии). Если прибавить к A1) полную
кинетическую энергию:
7 = 2^-, A2)
ц 2т
631

Глава V
где р — импульс ядра q с массой т , то гамильтониан Н полной системы с точностью
до постоянного слагаемого U0 равен сумме гамильтонианов одномерных гармонических
осцилляторов, связанных с каждым ядром q :
я-и„ + £
&^-°^'
A3)
Таким образом, в этой упрощенной модели каждое ядро колеблется независимо от
соседних ядер около своего положения равновесия с частотой:
co = J—. A4)
V т
Как и в случае двухатомной молекулы, частота со тем больше, чем меньше масса т и
чем больше крутизна потенциала, притягивающего ядро к положению равновесия.
ЗАМЕЧАНИЕ
В изложенной выше простейшей модели каждое ядро колеблется независимо от других
ядер системы. Это происходит потому, что выбранная форма потенциала U не содержит
членов, зависящих одновременно от нескольких переменных х , которые могли бы
описывать взаимодействие между различными ядрами. Данная модель далека от реальности, так
как такие взаимодействия непременно существуют. В дополнении Jv будет рассмотрена
более точная модель, в рамках которой будет учтена связь каждого ядра с двумя ближайшими
соседями. Мы увидим, что даже в этой модели гамильтониан полной системы может быть
представлен в виде суммы гамильтонианов независимых гармонических осцилляторов.
Ь. КВАНТОВЫЙ ХАРАКТЕР КОЛЕБАНИЙ КРИСТАЛЛА
Модель Эйнштейна, хотя и достаточно схематично, все же позволяет понять ряд
явлений, связанных с квантовым характером колебаний в кристаллах. Поведение
теплоемкости при постоянном объеме в области низких температур, которое не объясняется
классической механикой, будет описано в дополнении Lv в связи с изучением свойств
гармонического осциллятора в условиях термодинамического равновесия. Здесь мы
попытаемся обсудить замечательный эффект, связанный с конечной протяженностью
волновых функций основного состояния в месте расположения каждого атома.
При атмосферном давлении и температуре абсолютного нуля все вещества, за
исключением гелия, являются твердыми телами. Чтобы получить твердый гелий, нужно
приложить дополнительное давление не менее 25 атмосфер. Можно ли качественно
объяснить такое особое поведение?
638

Одномерный гармонический осциллятор
Попытаемся сначала понять явление плавления обычных веществ. При температуре
абсолютного нуля атомы практически локализованы в своих положениях равновесия;
протяженность их волновых функций вблизи х^ определяется выражением [см.
формулу (D-5-a) главы V]:
in I Г
АХ =
2тсо
4т£/0"
A5)
[здесь использовано выражение A4) для частоты ш ]. В общем случае величина АХ
очень мала. При нагревании кристалла ядра переходят на все более высокие колебательные
уровни: на классическом языке это означает, что амплитуда их колебаний возрастает,
тогда как с квантовой точки зрения увеличивается протяженность их волновой функции
[пропорционально квадратному корню из колебательного квантового числа; см.
формулу (D-5-a) главы V]. Когда эта протяженность становится сравнимой с межатомным
расстоянием d , кристалл плавится (см. § 4-с дополнения Lv, где это явление рассмотрено
полуколичественно).
Невозможность затвердевания гелия при обычном давлении соответствует тому, что
даже при температуре абсолютного нуля протяженность волновой функции A5) нельзя
считать малой по сравнению с d . Происходит это из-за очень малой массы гелия и
очень слабого химического сродства (крутизна Uq потенциала вблизи каждого
минимума очень мала, так как мала глубина потенциальных ям). Эти два фактора действуют
в формуле A5) в одном направлении и дают большое значение АХ . Увеличение
давления приводит к росту Uq , и, следовательно, частоты со , в результате чего уменьшается
значение АХ . Можно сказать, что при повышенном давлении каждый атом гелия как
бы «зажат» между своими соседями, вследствие чего минимум потенциала становится
тем острее (увеличение Uq ), чем меньше среднее расстояние между соседними
атомами, то есть, чем больше давление. Таким образом, сказанное выше объясняет, почему
увеличение давления дает возможность достигнуть затвердевания гелия.
3. Торсионные колебания молекулы: пример молекулы этилена
а. СТРУКТУРА МОЛЕКУЛЫ ЭТИЛЕНА С2Н4
Структура молекулы С2Н4 хорошо известна: шесть атомов молекулы лежат в одной
и той же плоскости (рис.6), а углы между связями С - Н и С - С близки к 120°.
Представим теперь, что не изменяя относительного положения связей, исходящих
из каждого атома углерода, одна из групп СН2 поворачивается вокруг оси С - С
относительно другой группы на угол а. На рис.7 молекула показана в проекции вдоль оси
639

Глава V
С - С: связь С - Н одной группы СН2 изображена сплошной линией, а второй —
пунктирной. Как же зависит от угла а потенциальная энергия молекулы?
Рис.6
Плоская структура молекулы этилена
И
МН
сш4 *
н«
Рис.7
Торсионные колебания молекулы этилена (вид вдоль оси,
соединяющей атомы углерода): одна из групп СН2
поворачивается относительно другой на угол а вокруг оси С - С
Поскольку стабильной конфигурацией является плоская, угол а = 0 должен
соответствовать минимуму функции V(oc). С другой стороны, ясно, что а = я
соответствует другому минимуму V(a), так как структуры а = 0 и а = я неразличимы. Таким
образом, ход зависимости V(a) выглядит так, как изображено на рис.8 [угол а на нем
изменяется от -я/2 до Зя / 2, а значение V@) принято за начало отсчета энергии].
аИ(<х)
>а
Рис.8
Потенциальная энергия молекулы
зависит от угла а поворота:
функция V(a) минимальна при
а = 0 и при а = я (плоские
структуры)
Два стабильных состояния а = 0 и а = я разделены потенциальным барьером
высотой V0. Форму потенциала, изображенную на рис.8, часто аппроксимируют простой
формулой:
У(а) = -2-A-сю2а).
A6)
640

Одномерный гармонический осциллятор
ЗАМЕЧАНИЕ
Квантовая механика позволяет интерпретировать все характеристики молекулы
С2Н4. В этой молекуле каждый атом углерода имеет четыре валентных электрона. Три из
них (а-электроны) имеют волновые функции с симметрией вращения относительно трех
копланарных прямых, образующих друг с другом углы 120° и определяющих направления
химических связей (рис.6). Перекрытие этих волновых функций с функциями электронов
ближайших атомов весьма велико и обеспечивает стабильность связей С - Н и частично
связи С - С (это явление называют «sp -гибридизацией», оно будет детально рассмотрено
в дополнении Еуц- Последний валентный электрон каждого атома углерода (Я-электрон)
имеет волновую функцию с симметрией вращения вокруг прямой, проходящей через С и
перпендикулярной к плоскости, определенной углеродом С и его тремя соседями.
Перекрытие волновых функций двух 71-электронов максимально, и, следовательно, химическая
стабильность двойной связи оказывается максимально возможной, если две прямые,
связанные с Я-электронами, будут параллельны, то есть если шесть атомов молекулы будут
находиться в одной плоскости. Так полностью объясняется структура, изображенная на
рис.6.
Потенциал У(а) может быть аппроксимирован вблизи двух минимумов параболой,
и молекула может испытывать торсионные колебания относительно двух положений
равновесия, которые и будут рассмотрены ниже. Но прежде всего мы кратко напомним
соответствующие классические уравнения движения.
Ь. КЛАССИЧЕСКИЕ УРАВНЕНИЯ ДВИЖЕНИЯ
Обозначим символами а, и а2углы, образованные двумя группами СН2 с
фиксированной плоскостью, проходящей через ось С - С (рис.9). Угол а, изображенный на
рис.7, очевидно, равен:
а = а,-а2. A7)
Пусть / — момент инерции одной из групп СН2 относительно оси С - С. Поскольку
потенциальная энергия зависит только от а = а, -а2, уравнения динамики,
описывающие вращение каждой из групп, имеют вид:
d2a, Э .., ч d
d2a, Э „, % d
dt2 Эа, ' 2 da
Aо)
dr Эа9 da
41 Квантовая механика
641

Глава V
Складывая и вычитая эти уравнения, получим:
4т(а1+а2) = 0; A9-а)
at
I^=-2±v{a). A9-b)
df da
jsrb
/
/
/
Рис.9
Чтобы записать уравнения движения, положение плоскостей
двух групп СН2 определяют углами а, и а2, которые они
образуют с фиксированной плоскостью
Уравнение A9-а) показывает, что, независимо от торсионного движения, вся
молекула может свободно вращаться вокруг оси С-С: угол (ос,+а2)/2, определяющий
биссектральную плоскость двух групп СН2, является линейной функцией времени.
Уравнение A9-Ь) описывает движение торсионного типа (вращение одной из групп
относительно другой). Рассмотрим эти движения вблизи положения устойчивого
равновесия а = 0 , для чего разложим выражение A6) в окрестности точки а = 0 :
V(a) = V0a\ B0)
Подставив B0) в A9-Ь), получим:
d2a 4V,
dtl I
+ _Aa = 0. B1)
В выражении B1) нетрудно узнать уравнение гармонического одномерного осциллятора
с частотой:
(О, =2^L. B2)
Для молекулы С2Н4 частота со, равна примерно 825 см.
с. КВАНТОВЫЙ АНАЛИЗ
В окрестности двух положений равновесия a = 0 и a = я молекула находится в
«торсионных» состояниях с квантованной энергией Еп = (п +1 /2)/ко,, где п - 0,1,2,....
В первом приближении каждый из уровней Еп = (л + 1/2)Й@г является дважды вырож-
642

Одномерный гармонический осциллятор
денным, так как соответствует двум состояниям |ф„) и |ф;'), волновые функции
которых ф„(а) и ф'Дос) отличаются только тем, что одна из них относится к среднему
положению а = 0, а другая — к положению ос = п (рис. 10а и рис. 10Ь).
Рис.10
Если пренебречь туннельным
эффектом через потенциальные
барьеры в точках а = 71/2 и
а = Зтг / 2, торсионные
состояния молекулы оказываются
локализованными в потенциальных
ямах с центрами а = 0 и а = я
В действительности мы должны еще учитывать типично квантовый эффект,
заключающийся в туннельном переходе через потенциальный барьер, разделяющий два
минимума (рис.8). Ранее мы уже встречали подобную ситуацию в связи с инверсией
молекулы NH3 (дополнение Giv). Вычисления, аналогичные приведенным в этом
дополнении, показали бы, что вырождение состояний |ф„) и |ф^) снимается при учете
туннельного эффекта. В результате для каждого значения п два стационарных состояния
Ufl) и \|/'Л, которые в первом приближении являются симметричной и
антисимметричной линейными комбинациями векторов |ф/?) и |ф^), разделяются интервалом энергии
Й8П, который тем больше, чем больше квантовое число п , то есть чем ближе энергия Еп
к значению У0 (вклад туннельного эффекта увеличивается). Однако Шп всегда значи-
41*
643

Глава V
тельно меньше энергетического интервала ftw,, разделяющего два соседних мультипле-
тас квантовыми числами п и п±\ (рис.11).
Рис.11
Туннельный эффект снимает вырождение
уровней энергии, изображенных на рис.10, тем
сильнее, чем ближе уровень к вершине
потенциального барьера Et >50); новыми
стационарными состояниями становятся состояния
|v0+).|v0-). К), И
Таким образом, предсказываемый квантовой механикой характер движения для
некоторого среднего значения угла а можно представить в виде быстрых осцилляции с
частотой со, относительно двух значений углов а = 0 и а = я на фоне значительно
более медленных колебаний между а = 0 и а = я с частотами Бора 50/2я, 8,/271,
62/2я....
ЗАМЕЧАНИЕ
Конечно, существуют и уровни, энергия которых больше высоты V0 потенциального
барьера, изображенного на рис.8. Эти уровни соответствуют кинетической энергии
вращения, достаточной для того, чтобы можно было считать, что одна из групп СН2 вращается
практически свободно относительно другой [но периодически затормаживаясь или
ускоряясь потенциалом (рис.8)].
Именно так ведет себя молекула этана С2Н6. Отсутствие Я-электронов в этой
молекуле допускает значительно более легкое вращение групп СН3 относительно друг друга
(потенциальный барьер V0 имеет значительно меньшую высоту). В этом случае потенциал
V(a), стремящийся противостоять свободному вращению групп СН3, вследствие
симметрии молекулы имеет период 2я / 3.
4. Тяжелые мюонные атомы
Мюон \х~ (иногда называемый по историческим причинам «ji-мезоном») — это
частица, имеющая свойства, аналогичные свойствам электрона, за исключением массы,
*Е
Mi {|*J>,|*!M
*<5n
i {|*;x I *->>
644

Одномерный гармонический осциллятор
которая в 207 раз больше массы электрона*. В частности, он не чувствителен к сильному
взаимодействию, а его связь с ядрами имеет существенно электромагнитный характер.
Мюон \хГ , замедленный в веществе, может быть притянут кулоновским полем атомного
ядра и образовать с последним связанное состояние. Образующийся при этом атом
называется мюонным атомом.
а. СРАВНЕНИЕ С АТОМОМ ВОДОРОДА
В главе VII (§ С) будут рассмотрены связанные состояния двух частиц с
противоположными зарядами и, в частности, состояния атома водорода. Мы увидим, что результаты
квантовой механики, касающиеся энергии связанных состояний, совпадают с выводами,
следующими из модели Бора (§ С-2, глава VII). В частности, протяженность
описывающих эти состояния волновых функций имеет порядок радиуса боровских орбит. Для
начала с помощью упрощенной модели рассчитаем энергии и протяженности первых
связанных состояний мюона \х~ в кулоновском поле тяжелого ядра (например, ядра
свинца Z = 82, А = 207).
Если считать ядро бесконечно тяжелым, то энергия л-ной орбиты Бора равна:
Z2me4 1
2П2
Еп= Г7^— • B3)
где Z — атомный номер ядра, е2 = q2 /47ie0 (здесь q — заряд электрона), aw — масса
электрона или мюона в зависимости от рассматриваемого случая. Если перейти от
водорода к рассматриваемому здесь мюонному атому, то энергию Еп следует умножить на
коэффициент Z2m)i I те = (82J • 207 = 1,4 • 106. Отсюда следует, что для мюонного атома:
£, =-19МэВ;
B4)
Е2 = -4,7 МэВ.
Что касается радиуса л-ной орбиты Бора, то он дается формулой:
B5)
п2П2
Zme~
Для водорода г, = 0,5 ангстрем. Здесь это значение нужно разделить на Zm^ I me,
вследствие чего:
* Мюон — нестабильная частица, он распадается с образованием электрона и двух нейтрино.
645

Глава V
"=3-'0Г: B6)
г2 = 12-1(Г,3см.
В приведенных вычислениях мы неявно предположили, что ядро является точечным
(в модели Бора и в рамках теории, представленной в главе VII (§ С), потенциальная
энергия принята равной - Ze2 /r). Малость значений г, и г2 [формулы B6)]
свидетельствует о том, что такое предположение нельзя считать обоснованным для тяжелого мюон-
ного атома. Действительно, ядро свинца имеет радиус порядка 8,5-10~13 см (напомним, что
радиус ядра изменяется пропорционально Ат), что нельзя считать пренебрежимо малой
величиной. Изложенный выше качественный расчет позволяет полагать, что протяженность
волновых функций мюона может оказаться меньше размеров ядра*. По этой причине
задача должна быть полностью пересмотрена, и сначала должен быть найден потенциал,
который «видит» мюон как вне, так и внутри распределения заряда ядра.
Ь. ТЯЖЕЛЫЙ МЮОННЫЙ АТОМ КАК ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
Примем достаточно грубую модель ядра свинца, предполагая, что его заряд
равномерно распределен по объему сферы с радиусом р0= 8,5-10~13 см.
Если расстояние г от мюона до центра этой сферы больше р0, то потенциальная
энергия определяется формулой:
V(r) = -— дляг>р0. B7)
г
Для расстояний г < р0 можно найти электростатическую силу, действующую на мюон,
по теореме Гаусса: она направлена к центру сферы и по модулю равна нулю:
( \ъ
Ze2
г
IP(J
1 Ze1
-=—r- B8)
г Ро
Эта сила соответствует потенциальной энергии:
2
1 Ze 2
2 Р^ '
V(r) = Гг2+С приг<р0. B9)
* Для водорода протяженность волновых функций имеет порядок нескольких ангстрем, то
есть в 105 раз больше размеров протона, что позволяет считать протон точечным. Новая ситуация,
с которой мы здесь сталкиваемся, является следствием нескольких факторов, действующих в
одинаковом направлении: увеличение массы т и увеличение Z приводит к росту
электростатической силы и большему радиусу ядра.
646

Одномерный гармонический осциллятор
Постоянная С определяется из приравнивания друг другу выражений B7) и B9) в точке
г = Ро:
с = -- —
2 Ро
C0)
На рис.12 представлена результирующая зависимость потенциальной энергии мюона от
координаты г.
Рис.12
Ход потенциала V(r), действующего
на мюон ц", при его притяжении
ядром, расположенным в точке г = 0 и
имеющим радиус р0. Если г<р0>
форма потенциала близка к
параболической (плотность заряда ядра считаем
одинаковой в объеме ядра); при г > р0
потенциал пропорционален \/г (закон
Кулона)
Внутри ядра потенциал имеет параболическую форму. Порядки величины,
вычисленные в предыдущем параграфе, указывают, что было бы нереалистично принимать
чисто кулоновский потенциал для основного состояния мюонного атома свинца, так как
его волновая функция сосредоточена в область, где потенциал имеет параболическую
форму. Поэтому предпочтительнее в этом случае рассматривать мюон связанным с
ядром «упругой» связью. Тогда задача сводится к трехмерному гармоническому
осциллятору (дополнение Ev), имеющему частоту:
@ =
Zez
"VPo
C1)
На деле мы увидим, что волновая функция основного состояния такого гармонического
осциллятора не равна нулю вне ядра, вследствие чего гармоническое приближение
также нельзя считать удовлетворительным.
ЗАМЕЧАНИЕ
Интересно отметить, что рассматриваемая здесь физическая система во многом похожа
на первую модель атома, предложенную Дж. Дж. Томсоном. Этот физик предположил, что
положительный заряд атома распределен по сфере, радиус которой имеет порядок нескольких
647

Глава V
ангстрем, и он представил себе, что электроны движутся в поле потенциала параболической
формы, существующем внутри такого распределения заряда (модель упруго связанного
электрона). Но эксперименты Резерфорда вскоре доказали, что ядро имеет существенно
меньшие размеры и что такая модель не соответствует реальности атомного мира.
с. ПОРЯДОК ВЕЛИЧИНЫ ЭНЕРГИЙ И ПРОТЯЖЕННОСТИ ВОЛНОВЫХ ФУНКЦИЙ
Если подставить в выражение C1) численные значения:
2 1
Z = 82; с = 3-108м/с; — = —;
Пс 137
т^ = 201те = 1,86-108 кГ ; П = 1,05-КГ34 Джс ; р0 = 8,5-КГ15 м,
то нетрудно получить:
(О = 1,3-1022 рад/с, C2)
что соответствует энергии Йсо порядка:
йш = 8,4 МэВ . C3)
Можно сравнить //со с полной глубиной потенциальной ямы, которая равна:
3 Ze2
- — = 21 МэВ. C4)
2 Ро
Видно, что ЙО) меньше этой глубины, но недостаточно, чтобы можно было бы
полностью пренебречь частью потенциала V(r), отличной от параболической формы.
Аналогично, протяженность волновой функции основного состояния, если бы яма
имела чисто параболическую форму, равнялась бы:
П =4,7-КГ13 см. C5)
2тцсо
Таким образом, качественные оценки, сделанные в предыдущем параграфе,
подтверждаются: значительная часть волновой функции мюона оказывается внутри ядра, но
тем не менее полностью пренебречь частью, остающейся вне ядра, нельзя.
Точный расчет энергий и волновых функций становится более сложным, чем в
случае простого гармонического осциллятора. Нужно решить уравнение Шредингера,
соответствующее потенциалу, изображенному на рис.12 (кроме того, следует учесть наличие
спина, сделать релятивистские поправки и т. д.). Эта задача достаточно важна, ибо
изучение энергии фотонов, испущенных тяжелым мюонным атомом, дает возможность
648

Одномерный гармонический осциллятор
получить информацию о структуре ядра и, в частности, о характере распределения заряда
по объему ядра.
ЗАМЕЧАНИЕ
В случае обычных атомов (электрон вместо мюона) с достаточной степенью точности
можно пренебречь влиянием отклонения потенциала от закона - Ze2 I r . Но и это
отклонение можно учесть с помощью теории возмущений (глава XI). В дополнении DXi мы
рассмотрим влияние объема ядра на уровни энергии атома.
Дополнение By
СТАЦИОНАРНЫЕ СОСТОЯНИЯ В ПРЕДСТАВЛЕНИИ {|*)}.
ПОЛИНОМЫ ЭРМИТА
1. Полиномы Эрмита.
a. Определение и важнейшие свойства.
b. Производящая функция.
c. Рекуррентные соотношения. Дифференциальное уравнение.
d. Примеры.
2. Собственные функции гамильтониана гармонического осциллятора.
a. Производящая функция.
b. Выражение функции ф„ (х) через полиномы Эрмита.
c. Рекуррентные соотношения.
В этом дополнении мы рассмотрим подробнее, чем это было сделано в § С-2 главы V,
волновые функции ф;,(;с) = (-*|ф„) стационарных состояний |фп) гармонического
осциллятора. Прежде чем перейти к основной теме, определим полиномы Эрмита и рассмотрим
их важнейшие свойства.
1. Полиномы Эрмита
а. ОПРЕДЕЛЕНИЕ И ВАЖНЕЙШИЕ СВОЙСТВА
Рассмотрим гауссову функцию:
F(z) = -2z*-*\ A)
649

Глава V
представленную колоколообразной кривой на рис.1. Последовательные производные
функции F(z) даются формулами:
F'{z) = -2ze~v ;
F"(z) = Dz2-2)e-:\
B)
C)
Рис.1
Ход гауссовой функции F{z) и ее
первых производных F\z) и F"{z)
Покажем, что в общем случае производная л-ного порядка F{n)(z) может быть
записана в виде:
F(")(z) = (-l)"Hn(z)e-z\ D)
где Hn(z) — полином переменной z степени п . Доказательство формулы D)
производится методом рекурсии. Указанное равенство справедливо для п = 1,2 [см. формулы
B) и C)]. Допустим, что оно справедливо для п - 1:
_,2
F{"-l)(z) = (-l)"-{Hn_i(z)e-~
E)
где #„_, (г) — полином степени п -1. Тогда путем непосредственного
дифференцирования можно получить равенство D), если положить, что
я"(г)=|2г"£К|(г)'
F)
Поскольку Hn_{(z) является полиномом переменной z степени п- 1, из последнего
соотношения видно, что Hn(z) является действительно полиномом степени п. Полином
Hn(z) называется полиномом Эрмита степени п . Его определением является равенство:
//„(z) = (-l)"*r—-e-
dz
G)
650

Одномерный гармонический осциллятор
Из формул B) и C) следует, что #,(z) и H2(z) являются соответственно нечетной и
четной функциями переменной z. С другой стороны, соотношение F) показывает, что
если #„_,(z) имеет определенную четность, то Hn(z) имеет противоположную
четность, то есть четность полинома #„(z) равна (-1)".
Нули полинома Hn(z) соответствуют нулям я-ной производной функции F(z).
Можно показать, что #„(z) имеет л вещественных нулей, между которыми чередуются
нули полинома Hn_x(z). Действительно, это непосредственно видно из рис.1 и равенств
A), B) и C) для п = 1,2 . С помощью рекурсии этот результат можно обобщить: пусть
#;l_,(z) имеет (и-1) вещественных нулей; если z, и z2 —два последовательных нуля
полинома Hn_x{z), а следовательно, и F("-1)(z), то из теоремы Ролля следует, что
производная F(n)(z) от функции F(n~l)(z) обращается в нуль в точке z3, лежащей между z,
и г2, и, следовательно, #;l(z3) = 0. Кроме того, поскольку F("_,)(z) обращается в нуль
при z—»-°° и при z—■»+°° , то Fin)(z) и #„(z) имеют по меньшей мере я
вещественных нулей [но не более, так как порядок полинома Hn(z) равен п ], между которыми
стоят нули полинома Hn_x(z).
b. ПРОИЗВОДЯЩАЯ ФУНКЦИЯ
Рассмотрим функцию переменных z к X :
F(Z + X) = е~и+ХJ. (8)
Формула Тейлора позволяет записать:
F(z + X)= £ —F{"\z)=l —(-\)nHn(z)e-z2. (9)
Умножим это равенство на ez и заменим X на -X . Получим:
00 Я,"
ez2F(z-X)=l— H„(z), (Ю)
то есть, если заменить F(z - X) его значением:
00 X"
e-*2+2Xz = £— яя(г). A1)
л=0 П\
Таким образом, полиномы Эрмита могут быть получены путем разложения в ряд по
651

Глава V
степеням X функции е~х *2Xz, которая по этой причине получила название
производящей функции.
Соотношение A1) позволяет дать другое определение полиномов Hn(z):
с. РЕКУРРЕНТНЫЕ СООТНОШЕНИЯ. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ
В формуле F) мы уже получили первое рекуррентное соотношение. Другие
соотношения нетрудно получить, дифференцируя равенство A1). Действительно, производная
по z дает:
2Xe-x2+2Xz = l—^-Hn(z), A3)
„=о п\ dz
то есть, заменив е~х +2Xz разложением A1) и сравнив члены одинаковой степени X ,
получим:
l-Hn(z) = 2nHn_{{z). A4)
dz
Аналогично, взяв производную от выражения A1) по X , получим:
Hn(z) = 2zHfl_](z)-2(n-l)Hn_2(z). A5)
И, наконец, можно без труда получить дифференциальное уравнение, которому
удовлетворяют полиномы Hn(z). Дифференцируя A4) и используя F), получим:
d2
2 Hn(z) = 2n — Hn_l(z) = 2n[2zHn_l(z)-HnU)], A6)
dz1 n dz
то есть, если заменить Hn_x(z) его значением A4):
—- -2z— +2л
dz" dz
#„(£) = 0. A7)
d. ПРИМЕРЫ
Определение G) или рекуррентное соотношение F) позволяют без труда вычислить
первые полиномы Эрмита:
652

Одномерный гармонический осциллятор
В общем случае:
ВД = 1;
H2(z)=4z2-2;
Я3(г) = 8г3-12г.
ВД>-|*-- -1.
A8)
A9)
2. Собственные функции гамильтониана
гармонического осциллятора
а. ПРОИЗВОДЯЩАЯ ФУНКЦИЯ
Рассмотрим функцию:
АГ(Х,л)=1ттХ-(ф1|).
л=о vw!
Используя соотношение [см. формулу (С-13) главы V]:
1
|ф>^(*+)''|фо>'
получим:
B0)
B1)
B2)
Как и в главе V, введем безразмерные операторы X и Р выражениями:
где параметр C, имеющий размерность обратной длины, определен равенством:
-I
т(Л
B3)
B4)
653

Глава V
Оператор
е"=е*
IX-iP)
B5)
может быть вычислен, если использовать формулу F3) дополнения Ви, где введено
обозначение:
Тогда:
у/2
Подставив этот результат в формулу B2), получим:
К(Х, х) = е-х1'А{х\ еа'Г2)* е^1^ |<р0) =
Х2/4 3lxl4llv\ _(-Л/72)Р/Рй
!(*l
Поскольку [см. дополнение Еп, формула A5)]
. \р
формулу B8) можно переписать в виде:
K(\,x) = e-x2,Ae^ir2(x-\l$S\<Vb) = e-x21* epWI (p0(x--X/pV2).
Используя формулу (С-25) главы V, получим:
( СО-
К(ХУ х) =
Р2
ехр<-
2 2
B6)
B7)
|ф0>- B8)
B9)
C0)
C1)
Согласно определению B0) достаточно разложить это выражение по степеням X,
чтобы найти волновые функции ф„(дс) = (*|ф„):
~ А,"
К(Х, х) = £-=ф „(•*),
где функция К(К, х) называется производящей функцией для ф„ (х).
654
C2)

Одномерный гармонический осциллятор
Ь.ВЫРАЖЕНИЕ ФУНКЦИИ (p„(jc) ЧЕРЕЗ ПОЛИНОМЫ ЭРМИТА
Заменим в формуле A1) X на X / V2 и z на Pjc; получим при этом:
ехр
+ PAjcV2 = S
f 1 v
I л/2 J
1
И!
Я„(Р*).
Подставим это выражение в C1):
К(Х, х) =
71
/
1
Ш ^"'"".^
Сопоставляя коэффициенты при одинаковых степенях X , получим:
Гч2ЛУ4
ф„и) =
я
^ «-Р2*2'2Яя(Рх).
V2"n!
C3)
C4)
C5)
Ход функции фя (дс) подобен производной n-ного порядка от гауссовой функции F(x),
рассмотренной в § 1. Функция фя (х) четности (-1)" имеет п нулей, расположенных
между нулями функции ф;|+,(лг). В § С-2 главы V мы уже указывали, что это свойство
определяется возрастанием средней кинетической энергией состояний |ф/}) при
увеличении квантового числа п .
с. РЕКУРРЕНТНЫЕ СООТНОШЕНИЯ
Запишем в представлении {\х) } уравнения:
«|ф«) = ^|фя_,>;
Д+|фл) = л/^й|ф„+1).
C6)
Используя определения операторов а и а* [см. выражения (В-6) главы V], нетрудно
установить, что в представлении {|лг) } действие этих операторов описывается формулами:
р
4i
х +
'
X ""
1
V
1
з2
d]
—
dxj
d~
dx_
C7)
655

Глава V
Тогда уравнения C6) примут вид:
р
р
Л
х + -
\_d_
р2 Л
(З2 <£с
Суммируя и вычитая эти уравнения, получим:
*р./2~Ф„ (•*) = л/й"ф„-, (*) + л/й+Тфя+, (л;);
42 d г- /
Т л ф"(х) = ^"ф""'(дс)" "vn+! Фп+| (х) ■
C8)
C9)
D0)
ЗАМЕЧАНИЕ
В формулах C9) и D0) заменим функции ф„(л:)их выражениями C5) и после
упрощения получим (введено обозначение х = $х):
2хН„(х) = 2nHa_t(x) + Ня+1(х); D1)
-хН„{х) + — Нп{х)
ах
= 2пН„_1(х)-Нп+1(х),
D2)
Суммируя и вычитая эти равенства, получим соотношения F) и A4).
Дополнение Су
РЕШЕНИЕ УРАВНЕНИЯ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
ГАРМОНИЧЕСКОГО ОСЦИЛЛЯТОРА
МЕТОДОМ ПОЛИНОМОВ
1. Изменение функции и переменной.
2. Метод полинома.
a. Асимптотическая форма функции ф(х).
b. Вычисление h(x) в виде разложения в ряд.
c. Квантование энергии.
d. Стационарные волновые функции.
656

Одномерный гармонический осциллятор
Метод, позволивший найти энергии стационарных состояний |ф„) гармонического
осциллятора в § В главы V, основан на использовании операторов а , а+, N и их
соотношений коммутации. Те же результаты можно получить совершенно иным способом,
решая уравнение на собственные значения гамильтониана Н в представлении {\х) },
что и будет целью данного дополнения.
1. Изменение функции и переменной
В представлении {\х) } уравнение на собственные значения гамильтониана Н
имеет вид:
ft2 d2 1
2т dx2
+ —т(й2х2
Ф(дс) = Еф(лг).
A)
Как и в главе V, введем безразмерные операторы X и Р выражениями:
B)
где параметр Р, имеющий размерность обратной длины, определяется формулой:
Обозначим символом |£.) собственный вектор оператора X , соответствующий
собственному значению х:
Х%) = х%). D)
Соотношения ортонормировки и замкнутости кет-векторов |£.) имеют вид:
(Щ,) = Щ-х')- E)
Кет |^.), очевидно, является собственным вектором оператора X с собственным
значением х IP, и, следовательно, при
* = |3д: G)
42 Квантовая механика
657

Глава V
два кет-вектора \х) и |£«) пропорциональны. Тем не менее они не равны:
действительно, запишем соотношение замкнутости для векторов \х):
П&|*><*| = 1. (8)
Если в этом интеграле произвести замену переменной G), то
£f 1*=*'РХ*=*'РН- (9)
Сравнение с выражением F) показывает, что можно, например, положить:
\х = х/&) = $\Ъ), A0)
чтобы кет-векторы |£е) были ортонормированы по отношению к переменной х, если
кет-векторы \х) ортонормированы по отношению к переменной х.
Пусть |ф) — произвольный кет, a ф(*) = (*|ф) — его волновая функция в
представлении {\х) } и (p(Jc) = (jc|(p) — его волновая функция в представлении {|£f)}.
Согласно равенству A0):
ф(х) = (^.|ф) = -^(х = л/р|ф), A1)
то есть
p(i) = -jLcp(jr = Jr/P). A2)
Если кет |ф) нормирован, то из равенства (8) следует:
<ф|ф> = (ф| (П> |*)(*|) |ф) = \ZvWvWdx = 1, A3)
а из равенства F):
(ф|ф) = (ф| (D** |$,)fe |)|<р) = Сф*(*>Ф(*)<** = 1 • A4)
Таким образом, волновая функция ф(лс) нормирована по отношению к переменной х, и
<p(jc) — по отношению к переменной Jc [впрочем, это можно увидеть непосредственно,
если в интеграле A3) произвести замену переменных G) и использовать равенство A2)].
Подставив G) и A2) в A), получим:
d2
dx2
+ jc"
ф(*) = ефсг), A5)
658

Одномерный гармонический осциллятор
если приравнять:
е = -
Ш
A6)
Уравнение A5) удобнее, чем уравнение A), так как все входящие в него величины не
имеют размерности.
2. Метод полинома
а. АСИМПТОТИЧЕСКАЯ ФОРМА ФУНКЦИИ ф(х)
Уравнение A5) можно переписать в виде:
ах
ф(*) = 0.
(П)
Попытаемся интуитивно определить поведение ф(х) при больших значениях х. Для
этого рассмотрим функции:
G±(jc) = e±i2/2, A8)
являющиеся решениями дифференциальных уравнений:
3F-(*±1)
G±(jc) = 0.
Если х стремится к бесконечности, то
х2 ± 1« х2 ~ х2 - 2е
A9)
B0)
и уравнения A7) и A9) асимптотически принимают одинаковую форму. Таким образом,
можно ожидать, что решения уравнения A7) при больших х будут вести себя, как
е+х п или как е~х /2 *. С физической точки зрения нас будут интересовать лишь такие
функции ф(х), которые ограничены с двух сторон, то есть решения уравнения A7) вида
(если оно существует). Поэтому положим:
(p(x) = e-*2,2h(x)
B1)
±.v2/2
* Решения уравнения A7) не обязательно эквивалентны е Л при Jc—>«»: приведенное
выше интуитивное обоснование не исключает, например, варианта, когда ф(х) эквивалентна
произведению е
на некоторую степень переменной х.
42*
659

Глава V
и, подставив B1) в A7), получим уравнение:
-^-rh(x) - 2x—h(x) + Be - l)A(Jc) = 0 . B2)
dx dx
Сейчас покажем, как можно найти решение этого уравнения, разложив h(x) в ряд, а
затем потребуем, чтобы эти решения были приемлемыми физически.
Ь. ВЫЧИСЛЕНИЕ h(x) В ВИДЕ РАЗЛОЖЕНИЯ В РЯД
Как было отмечено в § А-3 главы V, решения уравнения A) [или, что в принципе то
же самое, уравнения A7)] можно искать среди четных или нечетных функций.
Поскольку функция е~х'12 четная, можно записать:
h (jc) = хр (а0 + а2х2 + а4х4 + ... + а2тх2т + ...), B3)
где а0 Ф 0 (так как а^хр по определению является первым отличным от нуля членом
разложения). Запишем B3) в виде:
h(x)=ta2mx2m+p. B4)
м=0
Нетрудно получить:
^h(x)=l{2m + p)a2mxBm*p-l) B5)
CIX ш=0
и
7TW) = 1Bт+ р)Bт+ p-\)a2mxi2l"+p-2) . B6)
ах ш=о
Подставим B4), B5) и B6) в B2). Чтобы равенство имело место, нужно, чтобы
разложение в ряд правой части B2) равнялось нулю почленно. Для общего члена,
пропорционального х2т+р, это условие запишется в виде:
Bw+p + 2)Bw+p + l)fl2lfl+2=Dm + 2p-2e + l)a2lll. B7)
Член самой низшей степени Jc p~2 имеет равный нулю коэффициент, если
р(р-\)а()=0. B8)
Поскольку а0 ^0, то есть только две возможности: или р = 0 [функция ф(х) четная],
или р = 1 [функция cp(jc) нечетная].
Теперь равенство B7) можно переписать в виде:
660

Одномерный гармонический осциллятор
_ 4т + 2р + \-2г
а2т+2 ~ ,~ , ,лил , , 1Ч а2т> B")
Bт + р + 2) Bт + р + 1)
и оно является рекуррентным соотношением для коэффициентов а2т . Поскольку а0 Ф 0,
соотношение B9) позволяет выразить а2 через я0, затем аА через а2 и т.д.
Таким образом, разложение в ряд двух линейно независимых решений уравнения
B2), соответствующих р - 0 и р = 1, можно считать известным.
с. КВАНТОВАНИЕ ЭНЕРГИИ
Теперь остается выбрать среди всех найденных выше решений такие, которые
соответствуют физическому условию, требующему, чтобы функция (p(Jc) была ограниченной
во всей области определения.
Для большинства значений е числитель выражения B9) не обращается в нуль ни
при каких положительных или равных нулю значений т. Это значит, что ни один из
коэффициентов а2т не равен нулю, и ряд содержит бесконечное количество членов.
Можно показать, что асимптотическое поведение решения таково, что делает его
неприемлемым с физической точки зрения. Действительно, из B9) следует, что
^^ - - C0)
т—*°°
т
Рассмотрим теперь разложение в ряд функции екх , где X — вещественный параметр:
e^'=lb2mx2\ C1)
где
У"
Ь2т= — . C2)
т\
Таким образом, для этого второго ряда имеем:
Кп (л* +1)! А,'" т +1 ш-^оо т '
Если параметр X выбрать так, что
0<Х<1, C4)
то из C0) и C3) следует, что существует такое значение М , что при т> М :
661

Глава V
а2т+2 > Ь2т+2 >q
а2т Ь2т
и можно сделать вывод, что при выполнении условия C4):
\x'ph(x)-P(x)\>
12М
J2M
Vй -Q(x)\,
C5)
C6)
где Р(х) и Q(x) —полиномы степени 2 М , определяемые первыми М + 1 членами
рядов B3) и C1). Если х —> °°, то из C6) следует:
№)\ ^
J2M
хреи2
и,следовательно:
х—>«
Можно было бы выбрать X так, что
*2М
£/yX-l/2).v2
1/2<Х<1,
C7)
C8)
C9)
но при х->°о величина |ф(х)| не ограничена, то есть это решение следует отбросить,
как не имеющее физического смысла.
Остается только одна возможность, если числитель выражения B9) обращается в
нуль при конкретном значении щ целой переменной т. Тогда имеем:
а2т *0, если т<т();
<22w=0, если т>т0,
D0)
и разложение в ряд функции h{x) сводится к полиному степени 2т^ + р. Поведение
функции (р(х) на бесконечности определяется экспонентой е~х'12, и ф(х) приемлема с
физической точки зрения, так как она квадратично интегрируема.
Обращение в нуль числителя формулы B9) при т = щ требует выполнения
условия:
2е = 2B/^ +/0 + 1. D1)
Если положить:
то уравнение D1) примет вид:
2гщ + р = п ,
D2)
662

Одномерный гармонический осциллятор
6 = ея = л + 1 / 2 ,
D3)
где п — произвольное целое положительное число или нуль, так как т должно быть
целым положительным числом или нулем, а р равняется 0 или 1. Условие D3) требует
квантования энергии гармонического осциллятора, так как дает:
я + -
2)
лес.
D4)
Таким образом, мы снова приходим к выражению (В-34) главы V.
d. СТАЦИОНАРНЫЕ ВОЛНОВЫЕ ФУНКЦИИ
Метод полинома позволяет также вычислить собственные функции, связанные с
уровнями энергии Еп, в виде:
<pn(x) = e-x'nh„(x),
D5)
где hn(x) — полином степени п . Согласно формулам B3) и D2) функция hn(x)
является четной, если п — четное число, и нечетной, если п — нечетное число.
Основное состояние соответствует п = 0, то есть т^ = р = 0 . Функция 1\{х)
является поэтому константой и
%(х) = а0е-*2'2. D6)
Легко получить, что для нормировки функции ф0(х) достаточно положить:
Итак, с учетом A2) получим:
Фо(*) =
{ и)
-PV/2
D7)
D8)
что совпадает с выражением (С-25), приведенным в главе V.
Энергия первого возбужденного уровня £, = 3/гсо / 2 соответствует п = 1, то есть
т0 = 0 и /7 = 1. Функция hx{x) состоит из единственного члена, и ее можно вычислить
аналогично:
Ф,С*) =
Ф,С*):
171
Г4Р6У
D9)
хе
663

Глава V
При п = 2 имеем т0 = 1 и /; = 0. Тогда из выражения B9) следует:
а2 =-2а0,
и окончательно:
2 У'4
Ф2С*) =
An)
E0)
E1)
BPV-1KP
В случае произвольного значения п функция hn(x)является полиномиальным
решением уравнения B2), которое может быть записано с учетом условия квантования
D3) в виде:
dx2
- 2х— + 2п
dx
h(x) = 0.
E2)
В формуле E2) нетрудно узнать дифференциальное уравнение, которому удовлетворяет
полином Эрмита Нп{х) [см. уравнение A7) дополнения Bv]. Таким образом, полином
hn(x) пропорционален Нп(х), причем коэффициент пропорциональности определяется
нормировкой функции ф(х). В результате мы вновь приходим к формуле C5)
дополнения Bv.
Дополнение Dy
АНАЛИЗ СТАЦИОНАРНЫХ СОСТОЯНИЙ
В ПРЕДСТАВЛЕНИИ {|р)}
1. Волновые функции в импульсном пространстве.
a. Изменение переменной и функции.
b. Определение ф;| (р).
c. Вычисление фазового множителя.
2. Физическое обсуждение.
Возможное распределение импульса частицы в состоянии |ф„) определяется волновой
функцией ф„(/?) в представлении {\р)}, которая является преобразованием Фурье вол-
664

Одномерный гармонический осциллятор
новой функции ф„(*) в представлении {\х) }. В этом дополнении мы покажем, что
в случае гармонического осциллятора функции ф„ и ф„ одинаковы с точностью до
постоянных множителей, так что в стационарном состоянии распределение вероятности
по импульсу аналогично распределению по координате.
1. Волновые функции в импульсном пространстве
а. ИЗМЕНЕНИЕ ПЕРЕМЕННОЙ И ФУНКЦИИ
В дополнении Cv для простоты был введен оператор:
* = РХ, A)
где
Там же мы ввели собственные кет-векторы [£.) оператора X и волновую функцию
ф(х) в представлении {|^)}. Здесь мы сделаем то же самое для оператора:
Р
? = ТГ- C)
Назовем я Л собственные векторы оператора Р:
P\nj) = p\n,} D)
и обозначим символом Щр) волновую функцию в представлении { я Л }:
Ф(р) = (я*|ф). E)
Аналогично тому, как кет |£-) пропорционален вектору |jc = Jc/p), кет я Л
пропорционален вектору \р = рйр). Если заменить Р на 1/рЛ [см. формулы A) и C)],
соотношение A0) дополнения Су указывает, что
\п.) = ^\Р = Щ. F)
Волновая функция ф(р) в представлении {я/})} связана с волновой функцией ф(р) в
представлении {| р)} выражением:
665

Глава V
Жр) = №Шр = №р).
G)
С другой стороны, можно воспользоваться формулой F) и выражением A0) дополнения
Cv, чтобы получить:
Таким образом, используя E) и соотношение замкнутости в базисе {|£{)}, получим:
to=ЕЫъ%\<№ = ^= £>"** vmdx. (9)
Итак, функция Щ является преобразованием Фурье функции ф .
Ь. ОПРЕДЕЛЕНИЕ $„ (р)
Мы видели [см. уравнение A5) дополнения Су], что стационарные волновые
функции ф(£) гармонического осциллятора удовлетворяют уравнению:
dx2
+ Г
ф(*) = еф(х).
(Ю)
т2
Поскольку преобразованием Фурье от —- ф(х) является функция - р2 ф(р), а
преобрази
зованием от х^ф(х) — функция г- ф(р), то уравнение A0) может быть
представая
лено в виде:
<#2
Ф(р) = еф(р).
(И)
Сравним A0) и A1) между собой. Видно, что обе функции фп и ф„ удовлетворяют
одному и тому же дифференциальному уравнению, и, как мы знаем, это уравнение при
8 = п +1 / 2 (где п — положительное целое число или нуль) допускает единственное
квадратично интегрируемое решение (собственные значения е„ не вырождены; см. §В-3
главы V), вследствие чего функции ф„ и ф„ должны быть пропорциональны. А так как
они нормированы, то коэффициент пропорциональности должен быть комплексным
числом с модулем, равным 1, то есть
666

Одномерный гармонический осциллятор
Ъ«(р) = е"-$я(х = р), A2)
где е'*" — фазовый множитель, который будет сейчас определен.
с. ВЫЧИСЛЕНИЕ ФАЗОВОГО МНОЖИТЕЛЯ
Волновая функция основного уровня [см. формулы D6) и D7) дополнения Cv]
записывается в виде:
Ф0а)=7г1/4^2/2. (И)
Это функция Гаусса, и ее преобразование Фурье равно[см. приложение I, равенство E0)]:
Ф0(р) = я",/4^2/2, A4)
откуда следует, что фаза Ь0 = 0.
Чтобы найти Ьп, запишем в представлениях {|^)} и { тс Л } равенство:
В представлении {|£Л } операторы X и Р действуют, как Jc и , то есть опе-
' i dx
ратор а* действует, как -= Jc—- . В представлении {\р)} операторы X и Р дей-
. d Л + . i ( d
ствуют, как / — и р, то есть оператор а действует, как -т=н р
dp V2 V dp
В представлении {|£f) } равенство A5) принимает вид:
♦-'w-:j55To (*-*)♦■">■ A6)
тогда как в представлении {\пЛ } оно дает:
(и
-РШр)- A7)
A8)
Таким образом:
то есть, зная, что О0 = 0:
ф Л о) =
V2(n + 1)
e'e-=-,*"■,
667

Глава V
<Л =(-/)" A9)
и окончательно:
Ъя(р) = Н)"ФЛх = р) B0)
или, если вернуться к функциям ф„ и ф„:
I ( п\
B1)
Ф„(Р) = НГ^Ф„
х=п)
2. Физическое обсуждение
Рассмотрим частицу в состоянии |ф„). При измерении абсциссы частицы
вероятность p;j (x)dx получить результат, лежащий между х и x + dx , равна:
pn(x)dx = \q>n(x)\2dx. B2)
Аналогично, при измерении импульса частицы вероятность pn(p)dp получить
результат, лежащий между р и p + dp , равна:
РЯ(Р)Ф = |Ф„(Р)|2Ф. B3)
Тогда соотношение B1) дает:
1 ( п Л
B4)
Р„(Р) = Р„
mix)
m(Oj
и это соотношение показывает, что распределение импульса в стационарном состоянии
имеет ту же форму, что и распределение координаты.
Так, например, видно (см. рис.6 главы V), что при больших п функция рп(р) имеет
вид двух максимумов, соответствующих значениям:
р = ±тахм =±рм, B5)
где рм — максимальный импульс классической частицы, испытывающей движение с
энергией Еп в потенциальной яме. Рассуждения, аналогичные тем, которые были
сделаны в конце § С-2 главы, позволяют понять этот результат. Если импульс классической
частицы равен ±рм , то ее ускорение равно нулю (постоянная скорость), и значения
импульса ±рм в среднем во времени являются наиболее вероятными. Замечание (i) § D-1
главы V, касающееся плотности вероятности р„ (х), может быть без труда перенесено
668

Одномерный гармонический осциллятор
на рассматриваемый здесь случай. Например, для больших п среднеквадратичное
отклонение АР можно интерпретировать как порядок величины расстояния между
максимумами функции рп(р), расположенными при р = ±рм .
Можно также непосредственно понять из рис.6а главы V, почему именно эти
значения импульса являются наиболее вероятными при больших п . Действительно, при этом
волновая функция испытывает большое количество осцилляции, подобных синусоиде,
между двумя крайними пиками, так как дифференциальное уравнение, которому
подчиняется волновая функция [см. формулу (А-17) главы V], при Е » raw2*2 /2 принимает
вид:
4тф(д0 + ^ф(*) = 0, B6)
и тогда в соответствии с определением величины рм :
VWzAeW + A'e-*»*. B7)
Таким образом, волновая функция подобна синусоиде с длиной волны h I pM в довольно
широкой области оси Ох (при больших п ), и эта синусоида может рассматриваться как
сумма двух бегущих волн [см. B7)], связанных с противоположно направленными
импульсами ±рм , соответствующими прямому и обратному движениям частицы в
потенциальной яме. Поэтому нет ничего удивительного в том, что плотность вероятности
р„(р) возрастает вблизи значений р = ±рм .
Аналогичное рассуждение позволяет также понять порядок величины произведения
АХ -АР . Это произведение равно [см. соотношения (D-6), (D-7) и (D-9) главы V]:
ДХ-ДР = Г/1 + -1й = ^1^.. B8)
Если п растет, амплитуды хм и рм колебаний нарастают, и произведение АХ • АР
принимает значения, значительно превышающие минимальное значение h 12. Можно
спросить, почему это так, ведь неоднократно мы видели, что при увеличении ширины
АХ некоторой функции ширина АР ее преобразования Фурье уменьшается.
Действительно, именно так обстоит дело для функций ф„(х), если в интервале -хм <х< +хм ,
где они существенно отличны от нуля, их изменение является медленным и, например,
характеризуется лишь одним экстремумом. Впрочем, эта ситуация справедлива для
малых значений п , когда произведение АХ -АР близко по величине к своему
минимальному значению. Напротив, если п велико, функции фп(дг) характеризуются
многочисленными колебаниями в интервале -хм <х< +хм, где они имеют п нулей. Тогда им
669

Глава V
можно поставить в соответствие длины волн порядка Х = хм /п = АХ In,
соответствующие импульсам частицы, лежащим в области с размерами АР :
Дрф — • B9)
X АХ
Тогда нетрудно получить:
AXAP = nh. C0)
В некотором смысле положение очень похоже на рассматривавшуюся в § 1 дополнения
Аш задачу о бесконечно глубокой одномерной потенциальной яме.
Дополнение Еу
ТРЕХМЕРНЫЙ ИЗОТРОПНЫЙ
ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
1. Гамильтониан.
2. Разделение переменных в декартовых координатах.
3. Вырождение уровней энергии.
В главе V мы рассматривали одномерный осциллятор. Здесь же мы покажем, как
можно обобщить результаты этого рассмотрения на трехмерный гармонический
осциллятор.
1. Гамильтониан
Рассмотрим частицу без спина с массой т, движущуюся в трехмерном пространстве
под действием центральной силы, то есть силы, всегда направленной к началу отсчета О
системы координат, модуль которой пропорционален расстоянию от частицы до точки О:
F = -Jfcr, A)
где к — положительная постоянная.
Потенциальная энергия такого силового поля имеет вид:
V(r) = -*r2=~mco2r2, B)
2 2
где частота со определяется так же, как для одномерного гармонического осциллятора:
670

Одномерный гармонический осциллятор
o) = J-. C)
V т
Классическая функция Гамильтона равна:
2 |
Ж(г, р) = ■£- + -/ио) V. D)
2т 2
Согласно правилам квантования (§ В-5 главы III) из нее сразу же следует гамильтониан:
р2 1
Н = — +-mw2R2. E)
2т 2
Поскольку гамильтониан Н не зависит от времени, можно решить соответствующее
ему уравнение на собственные значения:
/ф)=Е|\|/), F)
где кет |\|/) принадлежит пространству состояний $г частицы, движущейся в
трехмерном пространстве.
ЗАМЕЧАНИЕ
Поскольку V(r) зависит только от расстояния г = |г| частицы от начала
координат [вследствие этого потенциал V(r) инвариантен относительно
произвольного вращения], то говорят, что гармонический осциллятор является изотропным.
Однако приведенные ниже расчеты легко обобщаются на анизотропный
гармонический осциллятор, для которого:
V(r) = ^((Oxx2+(uyy2+uzz2), G)
где все три постоянные со г, со у, сог различны.
2. Разделение переменных в декартовых координатах
Вспомним, что пространство состояний £Г можно рассматривать (см. § F главы II)
как тензорное произведение:
?г=^®?у®^, (8)
где ^Л — пространство состояний частицы, движущейся вдоль оси Ох, то есть про-
671

Глава V
странство, связанное с волновыми функциями (р(;с), и пространства йу и %z определены
аналогично.
Тогда выражение E) для гамильтониана Я можно переписать в виде:
Я = -^-(Рх2 + Р2 + Р2) + -mco2(X2 + Y2 +Z2) = Нх + Я + Я , (9)
2т ■ " 2
где
D2 1
Р2 1
#х=Т^+Т^ lX \ A0)
2т 2
и аналогично определены операторы Нг и Ну. Итак, Яд. зависит только от X и Рх, то
есть он является продолжением в пространстве £г оператора, действующего на самом
деле только в пространстве #х. Аналогично, операторы Н и Я, действуют только в
пространствах V и frz соответственно. Оператор Нх является гамильтонианом
одномерного гармонического осциллятора в пространстве £х. То же самое можно сказать и
относительно операторов Н и Яг в пространствах tfv и $z.
Операторы Нх, Яу и Я, коммутируют между собой, и каждый из них
коммутирует с их суммой Я. Таким образом, уравнение на собственные значения F) можно
решить путем отыскания собственных векторов оператора Я, которые будут также
собственными векторами операторов Нх, Н и Яг. Итак, мы знаем собственные векторы
оператора Нх в пространстве %х, а также собственные векторы операторов Ну в $у и
Hz в JT:
я*|фО = (л*+^)Нф"*); |ф„г)е^; A1-а)
я.|^) = (,г^^)^|ф,,); |ф„,)е*,; (п-Ь)
(в этих выражениях квантовые числа /2Х, nv, nz — целые положительные числа или
нули). Отсюда следует (см. § F главы II), что собственные векторы операторов Я, ЯЛ, Ну
и Hz могут быть представлены в форме:
| ¥„,.„,..,, ) = К)|ф.г)К>- <12>
672

Одномерный гармонический осциллятор
Согласно уравнениям (9) и A1):
я|уя,.«,,Яг) = [п* +пу +nz + ^JH^.»,.*) • A3)
то есть собственные векторы оператора Я являются тензорными произведениями
собственных векторов операторов Нх, Ну и ЯГ соответственно, а собственные значения
оператора Я являются суммами собственных значений этих операторов.
Согласно уравнению A3) уровни энергии Еп изотропного трехмерного
гармонического осциллятора имеют вид:
'/ко, A4)
Е„ =\ п +
где п — положительное целое число или нуль. A5)
Действительно, п является суммой п х +ny+nz трех чисел, каждое из которых является
произвольным целым неотрицательным числом.
С другой стороны, формула A2) позволяет вывести свойства векторов \\\fn п п у,
общих для собственных векторов операторов Я, Нх, Ну и Я,, из свойств векторов
фн ) (одинаково справедливых для (р„ ) и фм )), которые были получены в § С-1
главы V.
Введем три пары операторов рождения и уничтожения:
JWCO
a =J — X +
2h V2m^co
av=l—y+ i - f>; ^ =
|m@
2Й ' ' V2m^C0 'v
Imco ^ / . / wo)
: J Z+ , P,; < = J
V 2/i у[2тШ ' z \ 2h
X--T=Px>
2ft V2/wftco
Г^.у-—^—Р ■
2ft V2/nft@ v'
ffl@ z ' л
2Й V2mftco l"
A6-a)
A6-b)
A6-c)
Эти операторы являются продолжениями в пространстве £г операторов, действующих в
пространствах %х, tf v или <?,. Канонические соотношения коммутации компонент R и
Р требуют, чтобы единственными отличными от нуля коммутаторами шести
операторов A6) были бы:
[*,,<] = [*,, <] = [«г, <] = !• (П)
43 Квантовая механика
673

Глава V
(Стоит отметить, что операторы с различными индексами коммутируют всегда, и это
вполне нормально, так как на деле они действуют в различных пространствах.) Действие
же операторов ах и а+х на состояния \у„хч пп) определяется формулами:
**1 уя,.я,.Яг) = (*, |ф„, » |фя, ) |ф,, > = V"T |ф,,-.) |фя,) |фЯ: > = лЯ~ 14V».„V,,);
A8-а)
< |4>„r.,Jv,„:) = (< |фя,)) |фя,) |ф„:) = 7лх + 1|фЯх+1)|фЯу) К ) = V^V^| V,,f+uv,,, ) •
A8-b)
Формулы для операторов ау, а *, яг, я г+ совершенно аналогичны.
Кроме того, известно [см. уравнение (С-13) главы V], что
1
1п'\
ф'0 = "ГТ(а;Гл1ф«)' A9)
где |ф0) — вектор пространства #Л, удовлетворяющий условию:
^|фо> = 0. B0)
Векторы ф \ и ф;1 ) в пространствах $у и £. соответственно описываются
аналогичными выражениями. Таким образом, из выражения A2) следует, что
К.-,.,.) = / / , , Ю"' «>"' «)"г |Vo.o.o). BD
1 Ч Jnx\ny\nz\
где Vo.o.o) — тензорное произведение основных состояний трех одномерных
осцилляторов, удовлетворяющее равенству:
flx|Vo,o.o) = fl.v|Vo.o.o):=:fl2|Vo.o.o)=sO. B2)
Напомним, наконец, что, поскольку \|/„ п п ) является тензорным произведением,
соответствующая ему волновая функция имеет вид:
(г|Уя„я,.Яг) = Ф«, М Ф*, (У) ФЯг (г). B3)
где ф„ , ф/? , фЛ являются стационарными волновыми функциями одномерного
гармонического осциллятора (см. § С-2 главы V). Например:
/ | v ГтшУ'4 _^u2 + y2+:2)
674

Одномерный гармонический осциллятор
3. Вырождение уровней энергии
В § В-3 главы V мы показали, что в пространстве #Л. оператор Нх образует полный
набор коммутирующих операторов. То же самое можно сказать относительно оператора
Яу в пространстве tfv и относительно оператора Я, в пространстве #,. Тогда в
соответствии с § F главы II ансамбль операторов { Нх, Яу, Я, } образует полный набор
коммутирующих операторов в пространстве #г. Таким образом, существует единственный
кет-вектор (с точностью до множителя) \|/л „ „.} пространства £г, соответствующий
заданному набору собственных значений операторов Нх, Яу, Hz, то есть набору целых
неотрицательных чисел пх, п , nz.
Напротив, оператор Я сам по себе не образует полного набора коммутирующих
операторов, так как уровни энергии Еп вырождены. Действительно, выберем собственное
значение оператора Я, равное Еп = (п + 3 / 2) /гсо, где п должно быть целым
положительным числом.
Все кет-векторы базиса { шп п \ }, удовлетворяющие условию:
пх+пу+пг=п, B5)
являются собственными векторами оператора Я с собственным значением Еп.
Кратность вырождения gn энергии Еп равна числу различных наборов чисел
{пх,п ,nz}, удовлетворяющих условию B5). Чтобы найти gn, можно рассуждать
следующим образом. Считая п фиксированным числом, выберем сначала пх из
следующего ряда значений:
л, =0,1,2,...,л. B6)
Тогда должно выполняться равенство:
п +nz =n- пх B7)
и имеется (п - пх +1) возможностей составить пары:
{пу%пг} = {0,/1-л,}, {1,/1-пх-1},...,{п-пх,0}. B8)
Итак, кратность вырождения gn энергии Еп равна:
gn= S(n-/iv+l). B9)
43*
675

Глава V
Эта сумма вычисляется без труда:
» " (л + 1)(л + 2)
gn=(n-i)ll-lnx= * '-. C0)
;,t=() пх=0 £
з
Таким образом, только уровень £0 = — Йа) оказывается невырожденным.
ЗАМЕЧАНИЕ
Кет-векторы И|/ ) образуют ортонормированную систему собственных
векторов оператора Я, являющуюся базисом в пространстве <*г. Поскольку
собственные значения Еп вырождены, эта система не является единственной. В
частности, в дополнении Вуц мы увидим, что для решения уравнения F) можно
использовать ансамбль постоянных движения, отличный от { Нх, Яу, Я, }: при этом будет
получен базис пространства #г, отличающийся от приведенного выше, хотя и
образованный из собственных векторов оператора Я. Кет-векторы этого нового базиса
будут линейными ортонормированными комбинациями векторов Ж,ч,я.,„, )> ПРИ~
надлежащими каждому из собственных подпространств оператора Я, то есть
соответствующими одному и тому же фиксированному значению суммы пх +ny+nz.
Дополнение Fy
ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР С ЗАРЯДОМ
В ОДНОРОДНОМ ЭЛЕКТРИЧЕСКОМ ПОЛЕ
1. Уравнение на собственные значения оператора Я'($) в представлении {\х/ }.
2. Физическое обсуждение.
a. Электрическая поляризуемость упруго связанного электрона.
b. Интерпретация сдвига энергии.
3. Использование оператора трансляции.
Рассмотренный в главе V одномерный гармонический осциллятор был образован
частицей с массой т, находящейся в поле потенциала:
676

Одномерный гармонический осциллятор
V(X) = -m(u2X2. A)
2
Предположим также, что эта частица имеет электрический заряд q и находится в
однородном электрическом поле £ , параллельном оси Ох . Каковы в этом случае ее
стационарные состояния и соответствующие им значения энергии?
Классическая потенциальная энергия частицы в однородном поле $ равна*:
w($) = -q$x. B)
Чтобы получить квантовомеханический оператор Гамильтона #'(<?) в присутствии поля
$ , нужно к потенциальной энергии гармонического осциллятора A) добавить член:
ЩЩ = -qt X , C)
в результате чего получим:
Р2 1
//'(£) = + -m(u2X2-q%X . D)
2т 2
Таким образом, задача состоит в нахождении собственных значений и собственных
векторов этого оператора. С этой целью мы воспользуемся двумя различными
методами: сначала мы будем непосредственно решать уравнение на собственные значения
гамильтониана #'(£) в представлении {\х) }, так как полученные результаты имеют очень
простую физическую интерпретацию, а затем мы покажем, как эта задача может быть
решена чисто операторным методом.
1. Уравнение на собственные значения оператора //'(#)
в представлении { |jc) }
Пусть |ф') — собственный вектор оператора #'(#'):
ЯЧ8)|Ф') = Я'|Ф'>- E)
Используя D), это уравнение можно переписать в представлении {\х) }:
2т dx2 2
2 +— шсо х -q$x
ф'(*) = EVU). F)
* Мы сохраним условие о том, что в точке х = 0 потенциальная энергия частицы равна нулю.

Глава V
В правой части равенства F) можно сгруппировать члены с х и с х2:
I vnfrt'l у 1
п
d2 1 2,
- +-AWCO X .
2т dx2 2 { mco2
2шоJ
ф'(*) = £'(p'(jc).
Далее заменим х на новую переменную w согласно равенству:
и = х-
тсо
G)
(8)
Поскольку функция ф' становится функцией переменной и , уравнение G) можно
представить в форме:
Ь2 d2
1
r- + — mcoV
2m dw 2
ф'(к) = £"ф'(и),
где
*" = £' + -**
2mo2
(9)
(Ю)
Видно, что уравнение (9) имеет тот же вид, что и уравнение, определяющее в
представлении {|*) } стационарные состояния гармонического осциллятора в отсутствие
электрического поля [см. выражение (А-17) главы V]. Таким образом, решение уже имеется,
и возможные значения энергии Е" можно вычислить по формуле:
Ея"=|/1 + ||Ла>,
(И)
где п — целое положительное число или нуль.
Равенства A0) и A1) показывают, что в присутствии электрического поля энергии
Е' стационарных состояний гармонического осциллятора изменяются согласно
выражению:
Е:{Щ=\п + -\Ш-^-^. A2)
2mor
Таким образом, спектр гармонического осциллятора «целиком» сдвигается на величину
q4212mco2.
Что касается собственных функций Ц)'п(х), соответствующих энергиям A2), то все
они могут быть получены из функций ф„(л:) с помощью такой же трансляции.
Действительно, решение уравнения (9), соответствующее данному значению п, есть функция
Ф„(м) [где функция ф„, например, дана формулой C5) дополнения Bv], и согласно
формуле (8) получим:
678

Одномерный гармонический осциллятор
ф;(*) = фя| *--^2"
тсс
A3)
Эта трансляция физически связана с тем, что со стороны электрического поля на
частицу действует сила*.
V + W
Рис.1
Наличие однородного электрического
поля # приводит к добавлению
линейного члена W к потенциальной
энергии гармонического осциллятора.
Полный потенциал V + W изображен
«смещенной» параболой
ЗАМЕЧАНИЕ
Замена переменной по формуле (8) позволила свести задачу с произвольным
электрическим полем к уже известному случаю, когда поле равнялось нулю,
то есть действие электрического поля приводит лишь к изменению начала отсчета
по оси абсцисс [см. A3)] и энергии A2). Этот вывод нетрудно интерпретировать
графически (рис.1): если поле равно нулю, потенциальная энергия изображается
параболой, вершина которой находится в точке О ; если же поле отлично от нуля,
к этой потенциальной энергии нужно добавить величину -q$ х,
соответствующую пунктирной прямой на рис.1. Кривая, изображающая V + W, опять-таки
является параболой, то есть и в присутствии электрического поля система остается
гармоническим осциллятором. Поскольку эти две параболы могут быть
совмещены простым перемещением, они соответствуют одному и тому же значению (О и,
следовательно, одинаковым энергетическим интервалам между уровнями. Однако
положения их вершин различны, о чем как раз и свидетельствуют формулы A2)
и A3).
* Из формулы A3) видно, что функция ф^(дг) получена из функции ф„(х) путем
трансляции на величину q% I miu2; если произведение q$ положительно, то трансляция происходит в
положительном направлении оси Ох , совпадающем с силой, действующей со стороны поля # .
679

Глава V
2. Физическое обсуждение
а. ЭЛЕКТРИЧЕСКАЯ ПОЛЯРИЗУЕМОСТЬ УПРУГО СВЯЗАННОГО ЭЛЕКТРОНА
В ряде случаев электроны в атоме или в молекуле с хорошим приближением могут
рассматриваться как имеющие «упругую связь», то есть так, как если бы каждый из них
представлял собой гармонический осциллятор. В случае атомов докажем это в
дополнении АХш с помощью теории возмущений, зависящих от времени.
Вклад каждого электрона в электрический дипольный момент атома описывается
оператором:
D = qX, A4)
где q — заряд электрона (g < 0) и X — соответствующий оператор координаты. Здесь
мы вычислим среднее значение D в рамках модели электрона с упругой связью.
В отсутствие электрического поля среднее значение дипольного электрического
момента осциллятора в стационарном состоянии равно нулю:
(D) = <7(<P„|X|CP„) = 0 A5)
[см. формулы (D-1) главы V].
Допустим теперь, что поле # устанавливается достаточно медленно, чтобы
электрон последовательно переходил из состояния |ф„) в состояние |ф,') без изменения
квантового числа п. В этом случае среднее значение дипольного момента отлично от
нуля, так как
(D) = <?<ф;, | X |Ф;) = q\Zdx х\<р'п(х)(. A6)
Используя формулы (8) и A3), получим:
(о)'=^;>|ф„(")|2^+-^||Г|ф„(")|2^ = -^|, A7)
moo таг
так как первый интеграл обращается в нуль из-за симметрии. Итак, среднее значение
(р) пропорционально #, и в этой модели электрическая поляризуемость электрона в
рассматриваемом атоме равна:
% тог
Она положительна независимо от знака заряда q .
Физическая интерпретация полученного результата достаточно проста:
электрическое поле смещает электрон из его классического положения равновесия, то есть от
680

Одномерный гармонический осциллятор
среднего значения его положения в квантовой механике [см. формулу A3)], что
проявляется в возникновении индуцированного дипольного момента. Уменьшение % с
ростом со согласуется с тем, что с увеличением упругой силы, пропорциональной со2,
деформировать осциллятор становится все труднее.
Ь. ИНТЕРПРЕТАЦИЯ СДВИГА ЭНЕРГИИ
В рамках только что изложенной модели формулу A2) можно интерпретировать,
вычислив изменение средних значений кинетической и потенциальной энергии
электрона при его переходе из состояния |ф„) в состояние |ф,').
На самом деле изменение кинетической энергии равно нулю (это нетрудно понять
интуитивно, анализируя, например, рис.1), так как
2т \2т 2т
d2 d2
= 0 A9)
в соответствии с формулой A3).
С другой стороны, изменение потенциальной энергии можно представить в виде
суммы двух членов:
— первый их них (W(%)) соответствует потенциальной энергии электрического
диполя в поле % ; поскольку диполь и поле параллельны, согласно A7) имеем:
(WW) =-%(D) =-££?; B0)
х ' N ' ты
— второй, равный (V(X)) -(V(X))9 обусловлен изменением волновой функции,
определенной квантовым числом п, за счет действия электрического поля: «упругая»
потенциальная энергия частицы изменяется как
(V(X))-(V(X)) = ±mu2[lZx2\v:(x)\2dx-lZx2\<VnW\2cbc]. B1)
Первый интеграл можно вычислить, используя A3) и замену переменной (8):
£У|ф:м|2&«
2?» r~..U,.,\2,..J Я9
-£У|Ф.00| А + ^ОФР.И <*+ 5J Пф.<«>1 *• B2)
\
681

Глава V
Поскольку функция фм(м) нормирована, а интеграл от м|фя(и)| равен нулю
вследствие симметрии, окончательно получим:
(V(X))'-(V(X)) = -2-*L. B3)
2 war
Понятно, что этот результат всегда положителен, так как электрическое поле
удаляет частицу от точки О и притягивает ее в ту область, где «упругая» потенциальная
энергия V(x) имеет большее значение. Суммируя B0) и B3), получим, что энергия
состояния |ф„) всегда меньше энергии состояния |ф„), равной q2%2 /2mco2.
3. Использование оператора трансляции
В этом параграфе мы увидим, что вместо использования представления {\х) }, как
было сделано выше, можно непосредственно оперировать с оператором Н'($),
определенным формулой D). Точнее говоря, мы сейчас покажем, что унитарное
преобразование, соответствующее трансляции волновой функции вдоль оси Ох , позволяет перейти
от оператора # = #'(£ = 0), собственные значения и собственные векторы которого
были определены в главе V, к оператору //'(#) с точностью до аддитивной постоянной,
которая не изменяет собственные векторы.
Итак, рассмотрим оператор:
U(X) = e~Ma-a*\ B4)
где X —вещественное число. Сопряженный ему оператор U + (X) равен:
U + (\) = eMa-a+). B5)
Нетрудно видеть, что
U(X)U + (X) = U + (X)U(X) = 1. B6)
Таким образом, U(X) является унитарным оператором. Соответствующее ему
унитарное преобразование оператора Н запишется в виде:
H = U(X)HU + (X) = h(d
и теперь нужно определить оператор:
- + U(X)a+aU + (X)
B7)
682

Одномерный гармонический осциллятор
U(X)a+aU + (X) = a+a,
B8)
где
a=U(X)aU + (X)\
а+ =U(X)a+U + (X).
B9)
Чтобы получить а и а*, используем формулу F3) дополнения Вп (ее можно
применить, так как коммутатор операторов а и а+ равен 1), что дает:
= е ее ;
-Ха^ + Ха -Лл+ Ум -К 12
= е ее
U(k) = e'
U + (X) = e~
С другой стороны, формула E1) дополнения Вп позволяет записать:
[*"**, fl+] = -X*-**;
[е^\а] = -Хе^\
то есть
и, следовательно:
Аналогично:
я=е е яе е = е (а-А)е =а-А.
а+ =а+-Х.
Оператор Н тогда определяется выражением:
Я = Йсо
- + (а+-Х)(а-Х)
= Ш
+ а+а-Х(а + а+) + Х2
C0)
C1)
C2)
C3)
C4)
= Н - Айсо (а + а+) + X2h(d .
C5)
Поскольку (д + а+) пропорционален оператору X [формулы (В-1) и (В-7) главы V],
достаточно обозначить:
683

Глава V
чтобы получить:
X=S5»J-J_. C6)
(О V 2тШ
2иг>2 2ir2
H = H-q%X+-t^ = HW) + -?—T. C7)
2ma) 2 war
Таким образом, операторы Я и Я'(#) имеют одинаковые собственные векторы, а их
собственные значения отличаются на q2%212т(д2. Но уже известно (см. дополнение Сц,
§ 2), что если собственными векторами оператора Я являются кет-векторы |ф„), то
собственными векторами оператора Я являются кет-векторы:
|ф,,) = [/(Л)|ф,,), C8)
и что соответствующие собственные значения операторов Я и Я одинаковы.
Стационарными состояниями |ф,') гармонического осциллятора в присутствии поля #
оказываются состояния |ф„), определенные выражением C8), с собственным значением
оператора Н'(Щ, равным:
£.'« = („ + 1)»Ш-£?- C9)
И снова получим формулу A2) предыдущего параграфа. Что касается выражения C8)
для собственных векторов, то его можно представить в виде:
-1-4L-P
Ю = Ю = * '"Л(°2 |ф„). D°)
если использовать формулы B4) и C6), а также формулы (В-1) и (В-7) главы V. В
дополнении Ей мы интерпретировали оператор е~шРПх как оператор трансляции на
расстояние (алгебраическое) а вдоль оси Ох . Тогда |ф,') является состоянием, полученным из
|ф;|) путем трансляции на qtt I шсо2. Именно это и выражает формула A3).

Одномерный гармонический осциллятор
Дополнение Gv
«КВАЗИКЛАССИЧЕСКИЕ» КОГЕРЕНТНЫЕ СОСТОЯНИЯ
ГАРМОНИЧЕСКОГО ОСЦИЛЛЯТОРА
1. Определение квазиклассических состояний.
a. Введение параметра 0С0 для характеристики классического движения.
b. Условия, определяющие квазиклассические состояния.
c. Квазиклассические состояния являются собственными векторами оператора а .
2. Свойства состояний |ос) .
a. Разложение вектора |ос) в базисе стационарных состояний ф„).
b. Возможные значения энергии в состоянии |ос) .
c. Вычисление значений \Х/, (Р), АХ и АР в состоянии \(Х/.
d. Оператор D((X). Волновые функции \|/а(.х) .
e. Скалярное произведение двух состояний | Ос). Соотношение замкнутости.
3. Эволюция квазиклассического состояния во времени.
a. Квазиклассическое состояние неизменно совпадает с собственным вектором оператора а.
b. Эволюция физических свойств.
c. Движение волнового пакета.
4. Пример применения: квантовый анализ макроскопического осциллятора.
Свойства стационарных состояний |ф/2) гармонического осциллятора были
рассмотрены в главе V. Например, в § D мы видели, что средние значения (х) и (р)
положения и импульса осциллятора в таком состоянии равны нулю. Так, в рамках
классической механики хорошо известно, что положение д: и импульс р частицы являются
осциллирующими функциями времени, которые могут оставаться равными нулю только
в том случае, если энергия движения равна нулю [см. соотношения (А-5) и (А-8) главы V].
С другой стороны, известно также, что квантовая механика должна давать те же
результаты, что и классическая, в пределе, когда гармонический осциллятор имеет энергию,
существенно превышающую энергию одного кванта Йсо (предел больших значений
квантовых чисел).
Итак, можно поставить следующий вопрос: существует ли возможность построить
такие квантовые состояния, которые бы обеспечили практически полную идентичность
предсказаний квантовой и классической теорий по крайней мере для макроскопического
685

Глава V
осциллятора? В этом дополнении мы увидим, что такие квантовые состояния
действительно существуют. Они являются когерентными линейными суперпозициями всех
состояний |фл), и мы в дальнейшем будем называть их «квазиклассическими состояниями»
или «когерентными состояниями гармонического осциллятора». Сформулированная
здесь задача представляется очень важной для квантовой механики. Действительно, как
мы отмечали во введении к главе V и в дополнении Av, многочисленные физические
системы могут рассматриваться как гармонические осцилляторы, по крайней мере в
первом приближении. Во всех таких случаях любопытно понять с помощью формализма
квантовой механики, как происходит прогрессивный переход от случая, когда
классическое приближение дает достаточно верные результаты, к ситуации, где преобладают
квантовые эффекты. Одним из наиболее важных примеров такой системы является
электромагнитное излучение, которое в некоторых экспериментах проявляет существенно
квантовый характер (см. эксперимент, обсуждавшийся в § А-2-а главы I, при очень малой
интенсивности светового потока), а в других — может рассматриваться с классических
позиций. «Когерентные состояния» электромагнитного излучения были введены совсем
недавно Глаубером и широко применяются в наши дни в области квантовой оптики.
Положение, импульс и энергия гармонического осциллятора описываются в рамках
квантовой механики операторами, не коммутирующими друг с другом, то есть
соответствующие им физические величины являются несовместимыми. Это значит, что
невозможно построить такое состояние, в котором все три величины были бы полностью
определены. Поэтому наша задача будет состоять в том, чтобы найти такой вектор
состояния, для которого в любой момент времени средние значения (х), (Р) и (#) были бы
максимально близки к соответствующим классическим величинам. Такая постановка
задачи неизбежно приведет к компромиссу, когда ни одна из перечисленных
наблюдаемых не будет точно определена, но в макроскопическом пределе среднеквадратичные
отклонения АХ , АР, АЯ будут ничтожно малыми.
1. Определение квазиклассических состояний
а. ВВЕДЕНИЕ ПАРАМЕТРА СС0
ДЛЯ ХАРАКТЕРИСТИКИ КЛАССИЧЕСКОГО ДВИЖЕНИЯ
Классические уравнения движения одномерного гармонического осциллятора,
имеющего массу т и частоту со , записываются в виде:
f d г ч 1 ,ч
— X(t)=— P{t)\
\d m A)
— p(t) = -mu2x(t).
[at
686

Одномерный гармонический осциллятор
Квантовый формализм, который будет развит ниже, окажется более простым, если уже
сейчас ввести безразмерные величины:
jc@ = MO;
ftp
или
l mil)
B)
C)
В этих переменных уравнения A) имеют вид:
d
jc(r) = сор(г);
p(t) = -coJc(r).
D)
Классическое состояние гармонического осциллятора определено в момент времени t,
если известно его положение x(t) и импульс p(t), то есть величины x(t) и p(t). Эти
два вещественных числа можно объединить в одно комплексное безразмерное число
ос(г), определенное выражением:
a(t) = -=[x(t) + ipO)].
E)
Теперь система D), состоящая из двух уравнений, может быть заменена одним
уравнением:
—a(/) = -/(oa@,
dt
решением которого является функция:
где
<х@ = а0*-|Ш,>
a0=a@) = -j=[i@) + ip@)].
F)
G)
(8)
Построим в комплексной плоскости точки Л/() и М, изображающие комплексные
числа а0 и а(г) [рис.1]. Точка М совпадет с точкой М0 в момент времени г = 0 и далее
будет двигаться по окружности с центром О и радиусом ОМ0 с угловой скоростью -со .
687

Глава V
Поскольку согласно формуле E) координаты точки М равны x(t) и p(t), в результате
получается очень простое геометрическое представление эволюции состояния системы
во времени. Любое возможное движение, соответствующее заданным начальным
условиям, полностью характеризуется точкой М0 (модуль а0 определяет амплитуду
колебания, а аргумент сс0 дает его фазу), то есть комплексным числом ос0. Согласно
равенствам E) и G) имеем:
Alma(r)
Рис.1
Точка M(t), изображающая комплексное
число ос(г) и характеризующая состояние
гармонического осциллятора в каждый момент
времени, перемещается по кругу с угловой
скоростью -со. Абсцисса и ордината точки
М определяют положение и импульс
осциллятора
т = -^[а0е-ш+а^еш]; (9-а)
p{t) = -J^{a0e-^-a^}. (9-b)
Что касается классической энергии Ж системы, то она остается постоянной и равной:
Ж = — [р@)]2 +-тш2 [x@)f = -у {[*@)]2 + [ЖО)Г}, (Ю)
и с учетом формулы (8):
Ж = Ны\а0\2. (И)
Для макроскопического осциллятора энергия Ж значительно больше энергии одного
кванта Йш , то есть
|ос0|»1. A2)
688
Rea(r)

Одномерный гармонический осциллятор
Ь. УСЛОВИЯ, ОПРЕДЕЛЯЮЩИЕ КВАЗИКЛАССИЧЕСКИЕ СОСТОЯНИЯ
Будем искать такое квантовое состояние, в котором средние значения (х), (Р) и
(я) были бы практически равны в каждый момент времени значениям дс, р и Ж ,
соответствующим заданному классическому движению.
Чтобы найти (X), (/>) и (я), используем выражения:
1
Х=$Х=-;=г(а + а+);
V2
ftp V2
tf = ftco
2J
A3)
A4)
Для произвольного состояния |\|/@) эволюция во времени матричного элемента
(a)(t) = (i|/(f)| a |v|/@) определяется уравнением (см. § D-1-d главы III):
Но
откуда следует:
то есть
m-(a)(t) = ([a,H])(t).
[а, Н] = /ко [а, а*а\ = Йсоа,
i—(а)@ = ш(а)(?),
A5)
A6)
A7)
(a)(t) = (a)@) е-'ш. A8)
Эволюция среднего значения (a+Vf) = (v@|a+|v(*)) описывается комплексно
сопряженным выражением:
(a+yt) = (a+)@)eiw ={а)'@)еш. A9)
Формулы A8) и A9) аналогичны классическому равенству G).
Подставив A8) и A9) в A3), получим:
(*)(г) = -j= [(а>@)е-'ш' + (а)*@)е'ш' ];
(Р)@ = "^ [(а)@)е-'ш' -(a)'@)eiw\
B0)
44 Квантовая механика
689

Глава V
Сравним полученные результаты с формулами (9). Видно, что для того, чтобы в
произвольный момент времени г:
f(*)(r) = jc@;
[(р)(г) = р@,
необходимо и достаточно, чтобы в начальный момент времени t = О было выполнено
условие:
(a)@) = <х0, B2)
где ос0 — комплексный параметр, характеризующий классическое движение, который
нужно выбрать так, чтобы получить наилучшее совпадение с квантовым результатом.
Таким образом, нормированный вектор состояния |\|/@) осциллятора должен
удовлетворять первому условию:
(i|/@)H\|/@)) = a0. B3)
Остается теперь потребовать, чтобы среднее значение:
(я) = /Цд+я)@) + — B4)
равнялось классической энергии Ж, определяемой выражением A1). Поскольку для
классического осциллятора |сс0|»1 [см. формулу A2)], то можно пренебречь членом
I |2
/КО/2, имеющим чисто квантовую природу, по сравнению с Йсо|а()| , вследствие чего
второе условие, которому должен удовлетворять вектор состояния, можно представить
равенством:
(fl+£i)@) = |a0|2 B5)
или
(\|/@)|a+«|V@)) = |a0|2. B6)
Ниже мы покажем, что условия B3) и B6) достаточны для определения нормированного
вектора состояния |\|/@)) с точностью до фазового множителя.
с. КВИЗИКЛАССИЧЕСКИЕ СОСТОЯНИЯ
ЯВЛЯЮТСЯ СОБСТВЕННЫМИ ВЕКТОРАМИ ОПЕРАТОРА а
Введем оператор Ь(а0), определяемый выражением:
Ь(а0) = а-а0. B7)
690

Одномерный гармонический осциллятор
Тогда
b+ (a0)b(a0) = а*а-а0а+ -а*0а + а*а0, B8)
и квадрат нормы кет-вектора Ь(а0) |\|/@) равен:
(\|/@)|^+(а0Жа0)|1|/@)) =
= <\|/@) | «+^г | V@)> - сх0<\|/@) |«+1 м/@)> - oc;<v|/@) |«| v@)> + oc;oc0. B9)
Подставим в это равенство условия B3) и B6):
(\|/@)|Ь+(а0)Ь(а0)|\|/@))= а;а0 -а0а; -<xja0 + а;а0 = 0. C0)
Кет Ь(ос0) |\|/@)) имеет нулевую норму и, следовательно, равен нулю:
Ка0)|\|/@)) = 0, C1)
то есть
я|\|/@)) = а0|\|/@)). C2)
И напротив, если нормированный вектор удовлетворяет этому равенству, очевидно,
что условия B3) и B6) выполнены.
Таким образом, мы пришли к следующему результату: квазиклассическое
состояние, соответствующее классическому движению, характеризующемуся параметром ос0,
таково, что кет |\|/@)) является собственным вектором оператора а с собственным
значением сс0.
В последующем мы будем обозначать символом |а) собственный вектор оператора
а с собственным значением а:
а|а) = а|а) C3)
[далее покажем, что решение C3) является единственным с точностью до постоянного
множителя].
2. Свойства состояний |а)
а. РАЗЛОЖЕНИЕ ВЕКТОРА |(х) В БАЗИСЕ СТАЦИОНАРНЫХ СОСТОЯНИЙ |ф„)
Определим кет |ос) как решение уравнения C3) с использованием разложения по
состояниям \<рп)'.
44*
691

Глава V
|а) = Хс„«х)|фл}. C4)
/1
Тогда
«|а> = 1^(а)^|фя.,>, C5)
п
и, подставив это равенство в C3), получим:
Сп+1(а) = -Д=сп(а). C6)
Это соотношение позволяет определить рекуррентным методом все коэффициенты
с„(сс) через с0(а):
а"
ся(а) = -=с0(а). C7)
Из него следует, что при фиксированном значении с0(ос) все значения сл(сс) также
остаются фиксированными. Это значит, что вектор |а) определен единственным образом
с точностью до постоянного множителя. Выберем значение с0(а) вещественным и
положительным, будем считать кет |а) нормированным. Тогда коэффициенты с„(ос)
должны удовлетворять равенству:
ХК«х)|2=1, C8)
то есть
I 12 ^ ОС | |2 I |2
|с0(сс)| Sj-Jr = |c0(a)| ен =1.
С учетом принятого соглашения:
C9)
c0(a) = e-|tt|/2 D0)
получим окончательно:
-\а\-12 v^ ОС
п л/л'
D1)
Ь. ВОЗМОЖНЫЕ ЗНАЧЕНИЯ ЭНЕРГИИ В СОСТОЯНИИ |сс)
Рассмотрим осциллятор в состоянии |ос). Из формулы D1) видно, что измерение
энергии может дать результат Еп = (п +1 / 2) Йсо с вероятностью:
692

Одномерный гармонический осциллятор
12 ОС
^(<х)= ся(сс) =■
D2)
Полученное распределение вероятности &*п (а) является распределением Пуассона.
Поскольку
а
jj(a) = ^^,(a),
п
можно без труда доказать, что вероятность &п (а) максимальна, если
i i2
п = целая часть a .
D3)
D4)
Чтобы вычислить среднее значение энергии (#) , можно использовать формулу
D2) и выражение:
<")a=5>.(a)
п + —
2
Йсо.
D5)
Однако значительно проще заметить, что соотношение, сопряженное формуле C3),
имеет вид:
(а|я+=ос*(а|, D6)
и
(а|я+д|а) = а*сс, D7)
то есть
(//>„=М«1
а а + -
1
|а) = йсо
н'4
D8)
Сравнив этот результат с формулой D4), можно констатировать, что при |<х| » 1
величина (Я) относительно мало отличается от значения энергии Еп, соответствующего
максимуму функции й?,(а).
Вычислим среднее значение (Я2) :
( \\г
D9)
(n')e=»W<a|(e*e + I)|a>.
Используя формулу C3) и тот факт, что [а, а* 1 = 1, получим:
kV
|a|4+2|af+I
E0)
693

Глава V
откуда следует:
ДЯа=йш|а|. E1)
Сравним формулы D8) и E1). Эти равенства показывают, что при больших значениях
|сс| имеем:
^-*А«1. E2)
то есть энергия состояния |сс) в относительных значениях очень хорошо определена.
ЗАМЕЧАНИЕ
Поскольку:
Н =
N + - ,
2)
Й@, E3)
то из выражений D8) и E1) сразу же следует:
}iw„=|a|.
Таким образом, видно, что для получения квазиклассического состояния, нужно
линейно суммировать очень большое количество состояний |фл), так как ANa » 1.
Однако относительное значение дисперсии по N остается достаточно малым:
А^,_!_«!. E5)
И. И
с. ВЫЧИСЛЕНИЕ (X), (Р), АХ И АР В СОСТОЯНИИ |(х)
Средние значения (х) и (/>) могут быть получены, если выразить операторы X и Р
через а и а* [формула A3)] и затем использовать выражения C3) и D6). В результате
получим:
(x)o=(a|x|a) = ^Re(a);
(Р)а = (<х| Р\а) = л/2/ийю Im(a). E6)
694

Одномерный гармонический осциллятор
Аналогичные вычисления дают без труда:
Й
и, следовательно:
/ХЛ =JL- (a+ccT + l
2mco L
чШ Г
~2~L
*\2
/ 2\ И*Й@ Г, / *\:
E7)
АХ,
-1^
V 2тсо
АР =
w/jG)
E8)
Ни АХа, ни АРа не зависят от а, и можно заметить, что произведение АХ • АР
принимает свое минимально возможное значение:
ДХа-Д/>а=Й/2-
E9)
d. ОПЕРАТОР D(a). ВОЛНОВЫЕ ФУНКЦИИ \|/а(*)
Рассмотрим оператор D(a), определенный выражением:
D(a) = eaa'-a'".
Этот оператор является унитарным, так как
D+(a) = ea'a-aa*
и
D(a) D* (a) = D+ (a) D(a) = 1.
F0)
F1)
F2)
Поскольку коммутатор операторов ota+ и -а*а равен числу a*a, можно
воспользоваться равенством F3) дополнения Вц и записать:
D(a) = <r|a|!/VaVa*a
Вычислим кет-вектор D(a) |ф0) . Легко видеть, что
-"">«) =
a
1-сс а + а + ...
2!
|Фо) = |Фо>.
F3)
F4)
695

Глава V
и можно записать:
D(a)\%) = e-^e^M = e-^l^\%)=e'a X ^|cp„). F5)
Сравним теперь выражения D1) и F5). Видно, что
|a) = D«x)|q>0), F6)
и, следовательно, оператор D(a) описывает унитарное преобразование, преобразующее
основное состояние |ф0) в квазиклассическое состояние |сс).
Формула F6) теперь даст возможность получить волновую функцию:
Va(*) = (x|a), F7)
характеризующую квазиклассическое состояние |сс) в представлении {\х)}. Чтобы
вычислить функцию:
Va(x) = (*|D(a)|<p0),
выразим оператор аа+ -а*а через операторы X и Р:
аа -aa =
mco
a-a ,x__ ,
^а + а*Л
\ yjl } Jmhto \ V2 J
P.
Снова используя формулу F3) дополнения В1Ь получим:
D(a) = e°
\тш a-a*
«*« _ J л VI х
= е
JmtHo v2
F8)
F9)
G0)
Подставим этот результат в формулу F8) и получим:
V|/a(jc) = e 4 (x\eU Гг e4S*,R |ф0) =
a _a- //иш a-a
= е
Л VI
<4
Jmhta V2
|фо>-
G1)
Но оператор вида е lXPIh является оператором трансляции на величину X вдоль оси Ох
(см. дополнение Ец):
(x\e~f*Z V2 ' = (*_
2wca
(a + a*)
G2)
696

Одномерный гармонический осциллятор
Таким образом, из равенства G1) следует, что
а -а} |/жо а-а
Г ГЦ
[Х v2wco
(а + а*)
G3)
Если выразить а и а* через (х) и (р) [формулы E6)], то функция \\fa(x)
принимает форму:
Wa(x) = e^ei{p)"M%(x-(x)a), G4)
где общий фазовый множитель elba определяется формулой:
eiK = е 4
G5)
Равенство G4) указывает, что функцию \|/а(х) можно получить сразу же, если известна
волновая функция ф0(*) основного состояния осциллятора: для этого достаточно
переместить ее вдоль оси Ох на расстояние (х) и умножить на осциллирующую
экспоненту e^P'uXlh (множитель elba не играет никакой физической роли и его можно
опустить)*.
Если подставить в G4) явное выражение функции ф0, в результате получим:
И/4
н*>.
2ДХ„
+ 1
Up) -
G6)
Таким образом, форма волнового пакета, связанного с состоянием |а), описывается
выражением:
I , ч,2 /то)
ехр
ЛХ„
G7)
Каким бы ни было состояние |а), волновой пакет имеет гауссову форму. Этот результат
нужно сопоставить с тем, что произведение АХа • АРа всегда минимально (см.
дополнение Сш).
„ i(P) xlh
Экспонента е " не является, конечно, общим фазовым множителем, так как ее значение
зависит от х. Наличие этой экспоненты в формуле G4) обеспечивает равенство среднего
значения наблюдаемой Р в состоянии, описываемом волновой функцией \|/а(*) , величине (Р) .
697

Глава V
е. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ СОСТОЯНИЙ |ос) . СООТНОШЕНИЕ ЗАМКНУТОСТИ
Состояния |сс) являются собственными векторами оператора а , который не является
эрмитовым. Таким образом, нет никаких оснований для того, чтобы эти состояния удовлетворяли
соотношениям ортогональности и замкнутости. В этом параграфе мы посмотрим, что же имеет
место на самом деле.
Рассмотрим сначала два собственных кет-вектора |сс) и \(Х/ оператора а . Равенство D1)
позволяет сразу же записать их скалярное произведение, так как
(а|а') = 2>;(а)с„(а'). G8)
Таким образом:
<<х|<х'> = е-М2'2 е-^'п Ъ^т~ = е'^12 e^n eaV, G9)
п П\
откуда следует:
|(ос|а')|2=е-|а-а1\ (80)
Это скалярное произведение никогда не может быть равным нулю.
Однако сейчас мы убедимся, что состояния |ос) удовлетворяют соотношению замкнутости,
имеющему вид:
- JJ |a)(a|d{Rea}d{lma}=l. (81)
Для этого в левой части равенства (81) заменим ос) его выражением D1) и получим:
1 _^ п ^у /и
-Я«На| 2-Г7к)Ет=т(<^№еаМ1та}' »2)
то есть, если перейти в полярные координаты на комплексной плоскости а (положим a = ре'ф):
Ij;Prfpf dveS S^-" P |ф11)(ф.|. (83)
я пт yjnlmi
Интеграл по ф вычисляется без труда:
£"е«—"<йр = 2718(И1, (84)
в результате чего выражение (83) примет вид:
1',А|фЖ|. <85>
п т
698

Одномерный гармонический осциллятор
где
/„ =2/;Рф^р2р2" =£due-u" . (86)
Интегрируя по частям, найдем рекуррентную формулу для 1п :
/„=<-.. (87)
которой удовлетворяет решение:
/я=л!/0=л! (88)
Подставив полученный результат в формулу (85), заметим, что правая часть равенства (81)
принимает вид:
п
что и доказывает тождество.
3. Эволюция квазиклассического состояния во времени
Рассмотрим гармонический осциллятор, который в момент времени t - О находился
в некотором частном состоянии |ос):
|V@)) = |(X0). (90)
Какова эволюция физических свойств осциллятора во времени? Мы уже знаем (см. § 1-Ь),
что средние значения (х)(/)и (P)(t) все время остаются равными соответствующим
классическим величинам. Ниже будут рассмотрены другие интересные свойства вектора
состояния |\|/@).
а. КВАЗИКЛАССИЧЕСКОЕ СОСТОЯНИЕ НЕИЗМЕННО СОВПАДАЕТ
С СОБСТВЕННЫМ ВЕКТОРОМ ОПЕРАТОРА а
Опираясь на формулу D1), можно использовать общее правило, позволяющее
получить |\|/@) > когда гамильтониан не зависит от времени (см. § D-2-а главы III):
\у¥фе^а2^е-т-,п\9т)^е^пе^п11ЦТ-\9а). (91)
Сравним этот результат с формулой D1). Нетрудно видеть, что для того, чтобы перейти
из состояния |\|/@)) = |а0) в состояние |\|/(/))> достаточно заменить а0 на а0 е~ш и
умножить полученный кет на множитель е~шП , являющийся общим фазовым
множителем, не имеющим физического смысла:

Глава V
\yV(t)) = e-Hot,2\a = a0e-k").
(92)
Иначе говоря, видно, что квазиклассическое состояние всегда остается собственным
вектором оператора а с собственным значением ос0 е~ш , являющимся параметром
а@ на рис.1, определенным точкой М и характеризующим в каждый момент времени
классический осциллятор, состояние которого |\[/@) воспроизводит движение.
Ь. ЭВОЛЮЦИЯ ФИЗИЧЕСКИХ СВОЙСТВ
Используя формулу (92) и заменив в E6) а на ос0 е~ш , сразу же получим:
<Х>@ =
2Й
Re[a0^];
(P)(t) = V2m/20) Im[a0 е~ш ].
(93)
Как и можно было предвидеть, эти уравнения совпадают с классическими уравнениями (9).
Средняя энергия осциллятора не зависит от времени:
(Я) = /ко
I I2 !
Ы +2
(94)
Что касается среднеквадратичных отклонений АЯ, АХ и АР, то согласно формулам
E1) и E8) они равны:
АЯ = /ко|а0|; (95)
АХ =
АР =
2ш@
т/г со
(96)
При этом АХ и АР не зависят от времени, то есть в каждый момент времени волновой
пакет остается минимальным.
с. ДВИЖЕНИЕ ВОЛНОВОГО ПАКЕТА
Вычислим волновую функцию в момент времени t:
\{/(х,г) = (х|\|/@),
где кет |\|/(г)) определен выражением (92). Тогда из G6) получим:
(97)
700

Одномерный гармонический осциллятор
\|/(jt, t) = е'»<>
mix)
nfi
-/им/2 л
е е
x(P)(t) I v-(X)(/)
е
Й
2ДХ
(98)
В момент времени / волновой пакет остается гауссовым. Его форма не меняется во
времени, так как
|v|/(jc, 0|2 =|ф0[д:-<Х>@]|2. (99)
То есть мы снова видим, что он остается «минимальным» в любой момент времени [см.
формулу (96)].
На рис.2 изображено движение волнового пакета, осуществляющего осцилляции без
изменения формы с периодом Т = 2я / со вдоль оси Ох . В дополнении Gi мы видели,
что свободный гауссов волновой пакет деформируется при распространении, ибо его
ширина изменяется («расплывание» волнового пакета). Здесь же мы видим, что если на
волновой пакет действует параболический потенциал, ничего подобного не происходит.
A J
А
0
1
|*М2
> X
* X
А,
► X
* X
Рис.2
Движение гауссова волнового пакета,
связанного с состоянием |а): под действием
параболического потенциала V(x)
волновой пакет осциллирует, не деформируясь
Физически такой результат можно объяснить тем, что тенденция к расплыванию
волнового пакета компенсируется действием потенциала, стремящегося оттолкнуть волновой
пакет в сторону начала отсчета в областях, где У(х) возрастает.

Глава V
Что же происходит, если модуль |ос| очень велик? Как показывают формулы (96),
отклонения АХ и АР не изменяются. Напротив, амплитуды колебаний (x)(t) и (P)(t)
становятся значительно больше, чем АХ и АР. Выбрав достаточно большое значение
|ос|, можно получить такое квантовое движение, для которого положение и импульс
осциллятора по относительной величине будут как угодно точно определены. Если
| ос | » 1, состояние |ос) хорошо описывает движение макроскопического
гармонического осциллятора, для которого положение, импульс и энергия могут рассматриваться как
классические величины.
4. Пример применения:
квантовый анализ макроскопического осциллятора
Для определенности рассмотрим макроскопическое тело с массой т = 1 кг,
подвешенное к концу нити длиной / = ОД м и находящееся в поле силы тяжести
(g = 10м/с2). Известно, что в случае малых колебаний период Т колебательного
движения равен:
-WF-
A00)
V 8
В нашем случае получим:
Т = 0,63 с;
A01)
(О = 10 рад/с.
Допустим теперь, что этот осциллятор испытывает периодическое движение с
амплитудой хм = 1 см. Какое квантовое состояние наилучшим образом описывает такие
колебания?
Выше мы видели, что таким состоянием является состояние |ос), в котором
согласно формуле (93) величина а должна удовлетворять соотношению:
, . /та)
A02)
V in
то есть в нашем случае:
|сс| = 4b х 1015 = 2,2х 1015 » 1 A03)
(аргумент величины а определяется начальной фазой движения).
702

Одномерный гармонический осциллятор
При этом отклонения АХ и АР равны:
AX="\fc н2,2хЮ-,8м«хм;
AP = J-y- = 2,2х1(Г,7кгм/с.
A04)
Что касается среднеквадратичного отклонения AV скорости, то оно равно:
АУ = 2,2х1(Г,7м/с. A05)
Максимальная скорость осциллятора равна 0,1 м/с, вследствие чего
неопределенность его положения и скорости пренебрежимо мала по сравнению с порядком величин
всех физических наблюдаемых, входящих в задачу. Например, АХ меньше одного
ферми A0~15 м), то есть имеет размеры порядка атомного ядра. Вполне понятно, что
невозможно измерить макроскопическую длину с такой точностью.
Наконец, энергия осциллятора известна с великолепной относительной точностью,
так как согласно формуле E2):
ДО 1
-г-г = т-т = 0,4х10"'5«1. A06)
(Я) |<х|
Таким образом, законы классической механики более чем достаточны, чтобы описать
эволюцию рассматриваемого макроскопического осциллятора.
Дополнение Ну
СОБСТВЕННЫЕ МОДЫ КОЛЕБАНИЙ
ДВУХ СВЯЗАННЫХ ГАРМОНИЧЕСКИХ ОСЦИЛЛЯТОРОВ
1. Колебания двух частиц в классической механике.
a. Решение уравнений движения.
b. Физический смысл каждой из мод.
c. Движение системы в общем случае.
2. Колебательные состояния системы в квантовой механике.
a. Соотношения коммутации.
b. Преобразование гамильтониана.
c. Стационарные состояния системы.
d. Эволюция средних значений.

Глава V
Это дополнение посвящено изучению движения двух одномерных связанных
гармонических осцилляторов. Главная цель его состоит в том, чтобы на простом примере
ввести одно из важнейших физических понятий — понятие собственных мод колебаний.
Как в классической, так и в квантовой механике с этим понятием связано множество
задач. Примерами могут служить колебания атомов в кристалле (дополнение Jv),
электромагнитное излучение (дополнение Ку).
Рассмотрим две частицы A) и B), имеющие одинаковую массу т и движущиеся
вдоль оси Ох . Их положение будем определять координатами хх и х2. Допустим
сначала, что потенциальная энергия системы частиц равна:
£/0(jc,,Jt2) = — m(D2(jc, -яJ +—m@2(jc2 +aJ.
A)
При jc, = а и х2 = -а потенциальная энергия ио(х{, х2) минимальна, и эти точки
соответствуют положениям устойчивого равновесия частиц. Если частицы отклонены от
положений равновесия, то на них действуют силы F, и F2, равные:
F] = -—U0(xx,x2) = -т(д2(х1 -я);
OJC,
Э 2
F2 =--—и0(х],х2) = -т(й {х2+а\
ох-.
B)
и движение частиц описывается уравнениями:
т-
d2 ,..
dt
jc1(/) = -mw (x, -я);
2 •*!
nidi4
x2(t) = -w@2(jc2 + я).
C)
Таким образом, движения обеих частиц являются гармоническими колебаниями
относительно соответствующих положений равновесия, не зависящими друг от друга.
Амплитуды колебаний могут быть произвольными* и определены однозначно путем выбора
подходящих начальных условий.
Предположим теперь, что потенциальная энергия £/(*,,*2)частиц определяется
суммой:
U(xl,x2) = U0(xl,x2) + V(xl,x2), D)
где
* Естественно, выбор формы потенциала A) требует, чтобы амплитуды колебаний были
такими, чтобы не было столкновений частиц между собой.
704

Одномерный гармонический осциллятор
У(х{, *2) = Хт(й2(*, -х2J
E)
(здесь X — положительный безразмерный коэффициент, который мы будем называть
коэффициентом связи). Теперь к силам F, и F2 следует добавить соответственно силы
F,' и F2, определенные выражениями:
F,' = --— V(jc,,x,) = 2Xmco2(x, -jc,);
Эх,
F2' = --— V(x,, д:2) = 2Am(D2(x, -x2).
ox.
F)
Видно, что введение потенциала V(x{,x2) означает учет силы притяжения между
частицами, пропорциональной разделяющему их расстоянию. Таким образом, в этих
условиях частицы уже не являются независимыми. Каким же будет их движение?
Прежде чем исследовать задачу с квантовой точки зрения, напомним результаты, известные в
классической механике.
1. Колебания двух частиц в классической механике
а. РЕШЕНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ
При наличии связи V(jc,,jc2) нужно заменить уравнения C) системой связанных
дифференциальных уравнений:
Л2
т-
dt
2 Л\
xl(t) = -m(u (jcj -а) + 2\т(й (х2-х.);
G)
т-
dt
*2 @ = ~т®2 (*2 + я) + 2\т(д2 (х, - х2).
2 Л2
Метод решения такой системы известен (см., например, § С-З-а главы IV). Диагона-
лизируется матрица К, составленная из коэффициентов, входящих в правую часть
уравнений G):
/1 + 2Х -2\Л
•2\ 1 + 2AJ'
K = -m@"
(8)
и затем вместо переменных х,@ и x2(t) вводятся линейные комбинации этих функций,
определяющие собственные векторы матрицы К . Временная зависимость новых
переменных подчиняется линейным дифференциальным уравнениям, которые уже не связаны друг
с другом, а входящие в них коэффициенты определяют собственные значения матрицы К .
45 Квантовая механика
705

Глава V
В интересующем нас случае такими линейными комбинациями являются:
*g@ = -[*i@ + *2@], (9)
определяющая положение центра тяжести двух частиц, и
xR(t) = [xl(t)-x2(t)] A0)
абсцисса, определяющая относительное положение двух частиц. Действительно, если
подставить (9) и A0) в G), нетрудно получить путем суммирования и вычитания:
dt
Yxc(t) = -(ii2xG(ty,
—j xK(t) = -u>2[xR(t)-2a]-4X(iJxR(t).
at
(ID
Эти уравнения интегрируются сразу же:
где
xG(t) = x°G cos((x)Gt + eG);
**(') = —^ + x°Rcos(<uRt + QR\
0)с =w;
@Л =0)^1 + 4^,
A2)
A3)
а величины xG , xlR, 9С и QR являются постоянными интегрирования, определяемые
начальными условиями. Чтобы найти движение частиц A) и B), достаточно обратить
формулы (9) и A0):
*|@ = *с@+ -**(*);
x2(t) = xG(t)--xR(t)
(И)
и подставить в эти равенства выражения A2).
Ь. ФИЗИЧЕСКИЙ СМЫСЛ КАЖДОЙ ИЗ МОД
Благодаря замене переменных (9) и A0) оказалось возможным такое описание
движения взаимодействующих частиц, когда его можно представить в виде независимых
колебаний двух фиктивных частиц (G) и (R) с абсциссами xG(t) и xR(t), в результате
706

Одномерный гармонический осциллятор
чего путем выбора начальных условий можно зафиксировать любые значения амплитуд
и фаз этих колебаний. Так, например, можно потребовать, чтобы одна из этих
фиктивных частиц все время оставалась неподвижной, тогда как другая испытывала колебания:
в этом случае говорят, что в системе возбуждается одна собственная мода колебания.
Нужно отчетливо понимать, что в собственной моде колебания обе реальные частицы
A) и B) испытывают колебательное движение с одной и той же частотой ((йк или 0)с в
зависимости от возбуждаемой моды). Не существует решений уравнений движения, для
которых одна из реальных частиц A) или B) оставалась бы неподвижной, а другая
находилась в состоянии колебательного движения, ибо, если в момент времени / = 0
придать начальную скорость только одной из них, сила связи неизбежно приведет вторую
частицу в движение (см. последующий параграф).
Конечно, наиболее простым частным случаем является такой, когда ни одна из двух
мод не возбуждается. Эта ситуация соответствует в формулах A2) равенству
xG = x°R =0 и означает, что функции xG(t) и xK(t) постоянно остаются равными нулю
и значению 2а I A + АХ) соответственно, что дает согласно A4) равенство:
Xi=-x2=^. A5)
Система не осциллирует, и две частицы A) и B) остаются неподвижными в своих новых
положениях равновесия, определенных равенствами A5) (действительно, можно
показать, что для этих значений jc, и х2 силы, действующие на частицы, равны нулю; тот
факт, что эти положения равновесия являются ближайшими друг к другу при наличии
связи, если X = О, физически обусловлен их взаимным притяжением).
Чтобы возбудить лишь одну моду xG(t), достаточно в начальный момент времени
поместить обе частицы A) и B) на то же самое расстояние , как и в предыдущем
1 + 4 А
случае, и придать им равные скорости. При этом видно, 4TOxR(t) остается всегда
равной — (начальные условия требуют, чтобы х^ = О), то есть обе частицы движутся
вместе как одно недеформируемое тело с массой 2т, на которое действует сила
F, + F2 = -2mu>2xG(t); теперь нетрудно понять, почему частота этой моды равна
@С = со [см. формулу (А-3) главы V].
Чтобы возбудить только одну моду, соответствующую xR(t), достаточно выбрать
начальное состояние так, чтобы начальные положения и начальные скорости двух частиц
были бы противоположными по знакам. Тогда в любой последующий момент времени
xG(t) = 0 , и движение двух частиц будет симметричным относительно начала отсчета О .
Для такой моды расстояние (х2 - х{) изменяется, и сила притяжения двух частиц входит
45*
707

Глава V
в уравнения движения. Именно по этой причине частота данной моды увеличивается до
Динамические переменные xG(t) и xR(t), связанные с собственными независимыми
модами, то есть с фиктивными частицами (G) и (/?), называются нормальными переменными.
с. ДВИЖЕНИЕ СИСТЕМЫ В ОБЩЕМ СЛУЧАЕ
В общем случае возбуждаются две моды, то есть две координаты x{(t) и x2(t)
задаются двумя суперпозициями двух колебаний с разными частотами со^ и coG [см.
формулы A4)]; движение системы будет периодическим лишь в том случае, если
отношение частот coG /сод является рациональной величиной*.
Исследуем, например, что происходит, если в начальный момент времени t0 части-
ца A) остается неподвижной в своем положении равновесия хх = —, тогда как час-
1 + 4 А
тица B) имеет отличную от нуля скорость (в классической механике имеется аналогия с
задачей в §С-3-Ь главы IV). В отсутствие связи будет колебаться только частица B), а
частица A) останется неподвижной. Сейчас мы покажем, что связь вызывает движение
частицы A). Действительно, эволюция во времени jc,(f) и x2(t) происходит с двумя
разными частотами 0)Л и сос , что дает в результате биения (рис.1) с частотой:
v = -
сой
со,
271
i[vra-.].
A6)
>*
Рис.1
Колебания частицы A) в
предположении, что в момент времени t = О
она была неподвижной в положении
равновесия, а частица B) получила
начальную скорость. Движение
имеет характер биений двух
собственных мод, в результате чего
амплитуда колебаний частицы A) зависит
от времени
* Если С0С /С0д = 1/V1 + 4A, равно неприводимой рациональной дроби /?, / р2, то период
движения равен Т = 2пр1 I @С = 2пр2 / (Ок.
708

Одномерный гармонический осциллятор
Если связь слабая (X « 1), то эта частота v = Ло) / я пренебрежимо мала по
сравнению с частотами со^ и шс . В этом случае, пока (t -10) « 1 / v , частица B) осциллирует
практически в одиночестве; затем энергия колебаний медленно передается частице A),
то есть амплитуда ее колебаний нарастает, а амплитуда колебаний частицы B)
уменьшается. В дальнейшем ситуация становится обратной: частица A) осциллирует с
максимальной амплитудой, тогда как частица B) остается практически неподвижной. Далее
амплитуда колебаний частицы A) начинает уменьшаться, а амплитуда колебаний
частицы B) увеличивается до тех пор, пока вся энергия не окажется сосредоточенной в
осцилляторе B). Затем те же процессы будут повторяться бесконечно долго. Таким
образом, слабая связь между осцилляторами приводит к постоянному обмену энергией
между ними с частотой, пропорциональной степени связи.
ЗАМЕЧАНИЯ
(i) Если р] и р2 — импульсы частиц A) и B) соответственно, то функция
Гамильтона рассматриваемой системы равна:
2 2
W(xi,x,,pl,p2) = ^+j2-+UQ(xl,x,) + V(xl,x2). A7)
2т 2т
Положив:
[рс(') = р,@ + />2@;
|мо = ^[л(о+р2(о] A8)
и
{\ic =2т;
т A9)
ГЛ=Т'
можно представить функцию Гамильтона в виде:
ж = !Ь_+1 ю2 2 jPL+i iir(o2r(xr ^-1 +w(oV-^-. B0)
2\iG 2^° G G 2\iR 2^R 4 1 + 4AJ 1 + 4X
Путем соответствующего выбора начала отсчета энергии можно исключить из
этого выражения постоянный последний член. Тогда функция Ж оказывается
равной сумме двух энергий, соответствующих двум модам колебаний. В отличие
от формулы A7), где члены потенциала V(x{, х2) , пропорциональные х{х2,
ответственны за связь между частицами, в формуле B0) член связи между модами
отсутствует: это свидетельствует о том, что они независимы.
709

Глава V
(ii) Для простоты мы предполагали ранее, что массы т, и щ частиц A) и B)
одинаковы. Это ограничение нетрудно преодолеть, если заменить формулы (9), A0),
A8) и A9) выражениями:
*g@:
mlxl(t) + m2x2(t)
pG(t) = p{{t) + p2{t)\
[iG =ml+m2,
B1)
описывающими положение, импульс и массу «центра тяжести» системы, и
xR(t)
Pr@
= *,@
т2р
т1т2
~Х7
@
т,
@;
-ш,
+ т2
Л@
B2)
w, + т2
описывающими положение, импульс и массу «сопряженной» частицы. В
результате получим выражения, аналогичные B0).
(iii) В отсутствие связи обе моды имеют одинаковые частоты о), тогда как при
наличии связи частоты со^ и coG различны. Здесь обнаруживается явление, часто
встречающееся в физике: в большинстве случаев связь между двумя
осцилляторами раздвигает их собственные частоты (аналогичное явление имеет место и в том
случае, если в отсутствие связи осцилляторы имели разные частоты). Если, вместо
двух осцилляторов, их число стремится к бесконечности (но, будучи
изолированными, они имеют одинаковые частоты), то влияние связи, как мы увидим в
дополнении Jv, состоит в возникновении бесконечного количества различных частот
собственных мод колебаний.
2. Колебательные состояния системы в квантовой механике
Рассмотрим теперь эту же задачу с квантовой точки зрения. Как известно, следует
заменить переменные положения jc,(/), x2(t) и импульсы p,(r), p2(t) частиц
операторами X,, Х2, Рр Р2. По аналогии с формулами (9), A0) и A8) введем наблюдаемые:
710

Одномерный гармонический осциллятор
\Xg --^{Xi + X2h B3)
k = ^i + ^2;
\'.-\i*-n)- <24)
Чтобы определить, можно ли представить гамильтониан системы в форме, аналогичной
выражению B0), исследуем соотношения коммутации операторов XG , PG , XR и PR .
а. СООТНОШЕНИЯ КОММУТАЦИИ
Поскольку все наблюдаемые, относящиеся к изолированной частице A),
коммутируют с наблюдаемыми, относящимися к изолированной частице B), единственными
отличными от нуля коммутаторами, в которые входят операторы Х{, Р,, Х2 и Р2,
будут:
[Х2,Р2] = /Й. B5)
Поскольку X, и Х2 коммутируют, то
[XG,XR} = 0 B6)
и аналогично:
[Рс,Р«] = 0- B7)
Вычислим коммутатор [Хс, Рс]:
[^.^1= ^{[^1>Р,] + [х„Р2] + [х2,Р|] + [х2,Р2]} = -{/Й + гй} = /Й. B8)
Аналогично:
[Х«,Р«Нй. B9)
Остается исследовать коммутаторы [XR, PG] и [Хс, PR]. Они равны:
[*с Р«}= \ {[Х„ Р,]-[Х„ Р2] + [*2, Р,]-[х2, Р2]}=Д {/»-,%} = 0. C0)
Аналогично:
711

Глава V
[XR,Pc] = 0. C1)
Таким образом, можно рассматривать XG , PG, а также Хл и PR как операторы
положения и импульса двух различных частиц. Действительно, формулы B8) и B9)
являются каноническими соотношениями коммутации для каждой из этих частиц; кроме
того, соотношения B6), B7), C0) и C1) выражают, что все наблюдаемые, относящиеся к
одной из них, коммутируют со всеми наблюдаемыми, относящимися к другой.
Ь. ПРЕОБРАЗОВАНИЕ ГАМИЛЬТОНИАНА
При наличии связи V(X{, X2) имеем:
H = T + U, C2)
где
Т = ±(Р? + Р?) C3)
(оператор кинетической энергии) и
\
2
U =- тсо2 \(Х1 -аJ +(Х2 +яJ +2Х(Х, - Х2J] C4)
(оператор потенциальной энергии). Поскольку Р] и Р2 коммутируют друг с другом, то
формулу C3) можно раскрывать так, как если бы эти операторы были числами, то есть
Г = — Рс2+ — PR, C5)
2цс G 2\iR R
где (lic и \iR определены формулой A9). Аналогично, поскольку коммутируют X, и
Х2, получим:
/
^/ =— |^СС0^ Х^ +— JLl^CO^
хв-
2а
1 2 v2 - * 2 I v _ *« 1 +таJд2_^? C6)
I R 1 + 4A.J
4Х
1 + 4Х'
где сос и со^ определены формулой A3).
Таким образом, мы видим, что гамильтониан Н записывается в форме, аналогичной
выражению B0), в котором отсутствует член, ответственный за связь:
H = HG + HR+ m(xJa2 -^-, C7)
G R 1 + 4X
где
712

Одномерный гармонический осциллятор
на =
2ЦС
Р2
+ -liGa2GX2G;
Нр = -^- +—ц„о)р
R 1 + 4А
C8)
с. СТАЦИОНАРНЫЕ СОСТОЯНИЯ СИСТЕМЫ
Пространство состояний системы является тензорным произведением £A)®^B)
пространств состояний частиц A) и B). Одновременно оно является тензорным
произведением £(G)®£(#) пространств состояний фиктивных частиц «центра тяжести» и
«сопряженной», связанных с каждой из двух собственных мод. Поскольку Я — сумма
двух операторов Яс и HR, действующих соответственно только в пространствах <<(G)
и £(/?) (постоянная величина тсо а — вносит лишь добавку к началу отсчета
энергии), можно утверждать (§ Е главы II), что базис собственных векторов оператора
Я может быть выбран в форме:
|Ф) = |фс)|ф/?), C9)
где фс) и фЛ) являются соответственно собственными векторами операторов Яс и
HR в пространствах if(G) и £(/?). Поскольку эти операторы являются
гамильтонианами одномерных гармонических осцилляторов, то их собственные значения и
собственные векторы нам уже известны. Если определить операторы aG и а\ выражениями:
1
■у/^С Й»С
a* = V2
V^w7
D0-а)
где
2а
D0-Ь)
Фо ) и Фо ) —соответственно основные состояния операторов Яс и Hr,to
собственными векторами Яс будут векторы:
713

Глава V
с собственными значениями
|ф,?)=-тЦю"|фо) DD
Е?=\п + Цп<ос. D2)
Аналогично для оператора HR собственные векторы равны:
1
и собственные значения:
<> = T(fl«)'K> D3)
Е*р=\р + ^Ы„. D4)
Таким образом, ситуация оказывается совершенно аналогичной случаю двумерного
анизотропного @)с ^оо^) гармонического осциллятора. Стационарные состояния
системы описываются выражениями:
|Ф...> = |Ф?> |ф;> --^Ш^|ФМ> . D5)
и их энергии равны:
"'" " " 1+4X I 2 J
йсог + /? + — ЙсОо+шсоя -. D6)
G {И 2 R 1 + 4Х
Операторы aG и а£ (или а^ и а^) имеют смысл операторов уничтожения и
рождения квантов энергии соответствующих мод (G) или (R). Путем последовательного
действия операторов a*G и <я*, как видно из формулы D5), можно получить стационарные
состояния системы для случая, когда число квантов в каждой моде является произвольным.
Действие этих операторов на стационарные состояния W„tP) описывается формулами:
*£|фп,,) = ^^|фя+11|,);
всК^^Ф,.,.,);
я*|ф,м>) = л/^|ф,,,/,+1);
714

Одномерный гармонический осциллятор
В общем случае в системе нет вырожденных уровней, так как не существует двух таких
пар целых чисел {л, /?} и [п\ //}, чтобы выполнялось равенство:
яо)с + p(dR = /i'o)G + p'odR . D8)
(за исключением случая, когда отношение (uR/(dG =Л/1 + 4Я является рациональным
числом).
d. ЭВОЛЮЦИЯ СРЕДНИХ ЗНАЧЕНИЙ
Произвольное состояние системы можно представить в виде линейной
суперпозиции стационарных состояний (p,lt/,):
|ф('))=Ес„.р(о|ф„,,), D9)
где
ся.РЮ = сНщР@)е-1Б--'''\ E0)
Согласно соотношениям D0) и сопряженным им оператор XG (или XR) является
линейной комбинацией операторов ас и aG (или aR и a+R). Используя формулу D7),
можно установить, что оператор XG имеет отличные от нуля матричные элементы
только между двумя такими состояниями Ф/;/,) и kvw/), что п-п' = ±1, р = р' (для
оператора XR имели бы п = п\ р- р' = ±1). Отсюда следует, что в функциях,
описывающих эволюцию во времени средних величин (Хс)(г) и (Х/?)(г), могут появиться
только те частоты Бора, которые определяются равенствами*:
Е - Е
_JllL£ ^L = ±COc;
Kp±\Kp=±<*R. E1)
п
Таким образом, мы снова видим, что средние значения (хс)(г) и (XR)(t) осциллируют
с частотами ос, со^ , что напоминает классические результаты, полученные в § 1-а.
* Чтобы эти частоты появились на самом деле, необходимо, чтобы по крайней мере было
отличным от нуля одно из произведений с/1±, с или сп ±] с .

Глава V
Дополнение Jv
МОДЫ КОЛЕБАНИЙ БЕСКОНЕЧНОЙ ЛИНЕЙНОЙ ЦЕПОЧКИ
СВЯЗАННЫХ ГАРМОНИЧЕСКИХ ОСЦИЛЛЯТОРОВ. ФОНОНЫ
1. Классический анализ.
a. Уравнения движения.
b. Простейшие решения уравнений движения.
c. Нормальные переменные.
d. Полная энергия системы и энергия каждой из мод.
2. Квантовый анализ.
a. Стационарные состояния в отсутствие связи.
b. Влияние связи.
c. Нормальные операторы. Соотношения коммутации.
d. Стационарные состояния при наличии связи.
3. Применение к изучению колебаний в кристалле. Фононы.
a. Постановка задачи.
b. Собственные моды колебаний. Скорость звука в кристалле.
В дополнении Hv мы изучали движение системы двух связанных гармонических
осцилляторов. Из выполненного анализа следует важный вывод: несмотря на то, что
индивидуальные динамические переменные каждого осциллятора взаимосвязаны, можно
ввести новые динамические переменные (нормальные координаты), являющиеся их
линейными комбинациями и обладающие очень важной особенностью — отсутствием
связи между собой. Такие переменные описывают собственные моды колебаний на вполне
определенных частотах. Если полный гамильтониан системы выразить через эти новые
переменные, он оказывается равным сумме гамильтонианов независимых
гармонических осцилляторов, что существенно облегчает дальнейшее квантование.
В этом дополнении мы покажем, что все сказанное выше применимо также и к
системе, образованной бесконечной последовательностью одинаковых гармонических
осцилляторов, регулярно расположенных вдоль оси и связанных между собой.
Для этого определим различные собственные моды колебаний системы и покажем,
что каждая из них соответствует некоторому коллективному движению частиц,
характеризуемому частотой Q и волновым вектором к . В результате в значительной степени
упрощается поиск собственных состояний и векторов квантового гамильтониана, так
как полная энергия системы оказывается равной сумме энергий всех собственных мод
колебаний.
Выполненный анализ позволит нам узнать, как распространяются колебания в кри-
716

Одномерный гармонический осциллятор
сталле, и ввести понятие фонона, являющееся фундаментальным в физике твердого тела.
Конечно, в рамках данного дополнения особое внимание будет уделено введению и
квантованию собственных мод, а не свойствам фононов, что является предметом
изучения физики твердого тела.
1. Классический анализ
а. УРАВНЕНИЯ ДВИЖЕНИЯ
Рассмотрим бесконечную цепочку одинаковых одномерных гармонических
осцилляторов, каждый из которых определен целым индексом q (положительным,
отрицательным или нулевым). Частица Mq с массой т, образующая осциллятор (q) имеет
положение равновесия в точке с абсциссой ql (рис.1) где / — расстояние между
соседними осцилляторами в состоянии равновесия. Обозначим символом хц алгебраическое
значение отклонения осциллятора (q) от своего положения равновесия. Тогда состояние
системы в момент времени t будет определено, если известны все динамические
переменные xq(t) и их производные по времени xq(t).
(<7-l)/u ., Я1 ., (* + 1)/
Рис.1
Бесконечная цепочка осцилляторов; смещение g-той частицы относительно положения
равновесия ql обозначается символом хц
В отсутствие взаимодействия между частицами потенциальная энергия системы
запишется в виде:
+~ 1
£/(...,*_,,.*o»*+i»---)= X:w(o\2, A)
где со — частота каждого осциллятора. Тогда эволюция системы будет определяться
уравнениями:
d2
т—хч0) = -ты2хдA), B)
решения которых имеют вид:
717

Глава V
x4{t) = x™cos{m-<p(l), C)
М
где постоянные интегрирования xq и ф^ определяются начальными условиями
движения. Таким образом, все осцилляторы колеблются независимо друг от друга.
Представим теперь, что частицы взаимодействуют между собой. Для простоты
допустим, что достаточно учесть только те силы, с которыми на каждую частицу
действуют ее ближайшие соседи и что это силы притяжения, пропорциональные расстоянию
между взаимодействующими частицами. Иначе говоря, на частицу (q) действуют
дополнительно две силы притяжения со стороны частиц (д + 1)и(д-1),
пропорциональные соответственно смещениям \Mq Mq+A и \Mq Мц\ (будем считать коэффициент
пропорциональности одинаковым в обоих случаях). Тогда полная сила Fq, действующая
на частицу (q ), равна:
Fq = -mU2xq-m(u2[ql + xq-(q + \)l-xq+l]-
-mu>][ql + xq-(q-l)l-xq_l] = -m(u2xq-m(d*(xq-xq+l)-m D)
где О),— постоянная, имеющая размерность обратного времени, характеризующая
интенсивность связи. Тогда уравнения B) следует заменить уравнениями:
j2
т— xq(t) = -ma2xq(t)-m(u2[2xq(t)-xq+l(t)-xq_l(t)]. E)
Нетрудно доказать, что силы взаимодействия [члены выражения D), пропорциональные
со J ], соответствуют потенциальной энергии связи V , имеющей вид:
1 +°°
V(...,*_l,*o.*+P-») = -mco? E(*,-*,+i>2- F)
Согласно уравнению E) эволюция х (t) зависит от х +l(t) и х _,(t). Таким
образом, необходимо решить бесконечную систему связанных дифференциальных
уравнений. Прежде чем ввести новые переменные, позволяющие сделать эти уравнения
независимыми, интересно найти простейшие решения уравнений E) и рассмотреть их
физический смысл.
Ь. ПРОСТЕЙШИЕ РЕШЕНИЯ УРАВНЕНИЙ ДВИЖЕНИЯ
а. Существование простейших решений
Бесконечная цепочка связанных осцилляторов подобна бесконечной
макроскопической пружине. Мы знаем, что в такой пружине способны распространяться продольные
718

Одномерный гармонический осциллятор
бегущие волны, сопровождающиеся чередующимися растяжениями и сжатиями витков
пружины. Под действием такой волны гармонической формы с волновым вектором к и
частотой Q точка пружины с абсциссой х в условиях равновесия в момент времени t
окажется смещенной в точку х + и(х, /), где
M(jc,r) = M^,"(Ar"fi')+JiV/(fa-Q'). G)
Действительно, уравнения движения E) допускают решения такого вида. Однако,
поскольку цепочка осцилляторов является дискретной системой, волновое движение
затрагивает только наборы точек, соответствующих абсциссам х = ql, причем функция
u(qU t) будет представлять смещение осциллятора (q) в момент времени t:
xq(t) = u{ql t) = \лепкя1-т +nVW~ft/) • (8)
Легко доказать, что это выражение является решением уравнений E), если Q. и к
удовлетворяют уравнению:
- mQr = -woJ - /и©? [2 - е'А/ - <ГШ ]. (9)
Таким образом, частота О, связана с к «законом дисперсии»:
который мы детально обсудим в § 1-Ь-8.
C. Физический смысл
В решении (8) уравнений движения все осцилляторы колеблются с одной и той же
частотой Q/2n и одной и той же амплитудой |2ц|, но с разными фазами, которые
периодически зависят от начального положения частиц. Все происходит так, как если бы
смещения отдельных осцилляторов определялись бегущей синусоидальной волной с
волновым вектором к и фазовой скоростью:
v,<*) = -^. (И)
к
Действительно, из (8) следует, что
A2)
ф J
то есть осциллятор {q{ +q2)осуществляет то же самое движение, что и осциллятор
(д,), но с запаздыванием на время, которое тратит волна на прохождение со скоростью

Глава V
уф расстояния q21, разделяющего два осциллятора. Поскольку при этом все
осцилляторы находятся в состоянии движения, решения (8) получили название «коллективных
мод» колебаний системы.
у. Возможные значения волнового вектора к
Рассмотрим два значения волнового вектора к и к', отличающиеся на целое число
значений 2тг / /:
к' = к+ , где п — целое число, большее или меньшее 0. A3)
Очевидно, что
eik'ql =eikql;
Q(k') = Q.(k\
A4)
причем второе равенство непосредственно следует из формулы A0).
Тогда из формулы (8) следует, что две бегущие волны с волновыми векторами к и
к' соответствуют одинаковым движениям осцилляторов и, следовательно, неразличимы
физически. Поэтому в рамках рассматриваемой здесь задачи достаточно изменять к в
интервале с шириной 2я / /. Вследствие симметрии выберем:
-*<*<*. A5)
II
Соответствующий интервал часто называют «первой зоной Бриллюэна».
8. Закон дисперсии
Закон дисперсии A0), определяющий зависимость частоты Q(k) от волнового
числа к, позволяет исследовать распространение колебаний в системе. Если, например,
образовать «волновой пакет» путем суперпозиции волн с различными волновыми
векторами, то, как известно, он будет распространяться с групповой скоростью, определяемой
выражением:
(Щк)
dk
A6)
и эта скорость отличается от фазовой скорости уф .
На рис.2 изображен ход зависимости Q(k) при изменении к в первой зоне
Бриллюэна.
720

Одномерный гармонический осциллятор
- п/1 0 + п/1
Рис.2
Закон дисперсии, определяющий зависимость частоты собственных мод колебаний от
волнового числа к в первой зоне Бриллюэна [-я//, + я//]; пунктирная кривая
соответствует случаю со = О
Из этого рисунка сразу же видно, что функция Q(k) не может принимать
произвольные значения, то есть колебание с частотой v может свободно распространяться в
среде только в том случае, если частота лежит в пределах «разрешенной полосы»:
со
~2п
<v<^
со2 +4@?
2я
A7)
Другие значения частот относятся к «запрещенным». Две граничные частоты интервала
A7) часто называются «частотами среза».
Мода с самой малой частотой £2@) = со имеет волновой вектор к , равный нулю: он
соответствует колебаниям всех осцилляторов с одной и той же фазой, то есть частицы
колеблются все вместе как единое целое, и расстояния между ними не изменяются
(рис.3), в результате чего частота этой моды колебания равна частоте колебаний одного
осциллятора в отсутствие связи с другими (см. § 1-Ь дополнения Hv).
(q-2)l ((/-I)/ ql
-—I • 1 • h-
(q + I)/ (q + 2I
1 • h ►
xa-
q-2
Рис.3
xa-
4-i
Мода с наименьшей частотой [к = 0; О, = со) соответствует синфазному смещению всех
осцилляторов, вследствие чего ее частота не зависит от связи V
46 Квантовая механика
721

Глава V
Что касается наивысшей частоты моды Q(±ti//) = ^/со2 +4(о2 , то ей соответствует
такое колебание системы, когда два соседних осциллятора находятся в противофазе
(рис. 4), при таком колебании силы связи V максимально влияют на движение системы.
(q-2)l (q-\)I ql (q + \)l (q + 2I
1—» »—i 1—• *_, 1—*_►
Xq-2 Xq-1 Xq Xq + 1 Xq + 2
Рис.4
Моды к - ±7i / / соответствуют случаю, когда соседние осцилляторы смещаются в
противофазе, вследствие чего связь V значительно изменяет их частоту
с. НОРМАЛЬНЫЕ ПЕРЕМЕННЫЕ
а. Получение несвязанных уравнений
Вернемся к уравнениям движения E) и попытаемся найти новые динамические
переменные, являющиеся линейными комбинациями переменных xq, но эволюция
которых во времени не зависит от других переменных.
Для этого умножим обе части уравнения E) на экспоненту e~'kql и просуммируем по
q . Если заметить, что
X V. г"*" = е±М X *,±i е"'(,±,)И = е±ш 1 хч е-*" , A8)
и если обозначить:
X *,(*)*-*" =£(*,*), A9)
то нетрудно увидеть, что уравнение примет вид:
^Ык,»*-^2 +<о21B-еш -е-ш)]&к,», B0)
то есть с учетом (9):
^(*,0 = -Q2(*)S(*,0. B1)
Это равенство показывает, что эьилюция £,(к, t) во времени не зависит от £(&', /), если
722

Одномерный гармонический осциллятор
к' Фк . Таким образом, введенные выражением A9) величины полностью независимы
друг от друга и имеют замечательно простую зависимость от времени.
ЗАМЕЧАНИЯ
(i) Возможность устранить члены связи в уравнениях E) вытекает из инвариантности
задачи относительно трансляции ансамбля осцилляторов на величину ±1 (замена
q на q ± 1). Причина же этой инвариантности заключается в том, что цепочка
осцилляторов имеет бесконечную длину и регулярное строение,
(ii) В реальности, конечно, любая цепочка имеет конечную длину, если даже она содержит
очень большое количество .Г осцилляторов. Чтобы найти ее собственные моды
колебаний, нужно учесть граничные условия на двух концах цепочки, и задача становится гораздо
сложнее (краевой эффект). При этом вместо непрерывного и бесконечного множества
собственных мод колебаний, соответствующих различным значениям к первой зоны Бриллю-
эна, образуется конечное количество собственных мод, равное числу . Г осцилляторов.
Если интерес представляет поведение системы вдали от границ цепочки, то часто вводят
искусственные граничные условия, отличающиеся от реальных, но значительно упрощающие
вычисления при сохранении всех существенных физических выводов. Они состоят в том,
что два находящихся на концах цепочки осциллятора считаются движущимися одинаково
(«периодические» граничные условия, называемые еще «условиями Борна — фон
Кармана»). Поскольку мы еще вернемся к этому вопросу в связи с изучением других
периодических структур (дополнение FXi и § 1-е дополнения CXiv), то здесь ограничимся только
простейшим примером бесконечной цепочки.
Введенная формулой A9) функция £>(k,t) по определению является суммой ряда
Фурье, коэффициентами которого являются смещения х (t). Эта периодическая
функция с периодом 2п/1 вполне определена, если заданы ее значения в интервале
-nll<k<nll [то есть в зоне Бриллюэна A5)], и £,(k,t) зависит от положений всех
осцилляторов в момент времени t. Справедливо и обратное утверждение: положения
осцилляторов однозначно определены, если известны значения £ в интервале A5) в
момент времени /. Действительно, равенство A9) можно обратить, так как с учетом
интеграла:
Г"<1кеПч-ч')к1=—8 . B2)
можно записать:
^L&5(U)^. B3)
46*
723

Глава V
Заметим, впрочем, что поскольку смещения x(j(t) являются вещественными
величинами, то функция £(£, t) должна удовлетворять условию:
£(-*,*) = £*(*, О- B4)
Аналогично можно определить с помощью импульсов pq{t) = mxq(t) функцию:
я(М) = 5>,(')*_Л*, B5)
-ikql
q
через которую можно также выразить:
Pq{t) = ±\:y(Kt)eik«dk. B6)
Вещественность pq(t) требует, чтобы
n(-kj) = n{kj). B7)
Почленно дифференцируя обе части равенства A9) и используя сначала B5), а затем
B1), окончательно получим:
/я—5(*,0 = я(*,г);
/' B8)
—n(*,0 = -wQ2(JfcM(*,0.
В любой момент времени t динамическое состояние системы может быть задано
как переменными xq{t) npq(t) для всех значений q, так и «нормальными
переменными» £(&, t) и п(к, t), где к принимает все возможные значения в первой зоне Бриллю-
эна. Уравнения эволюции B8) нормальных переменных, соответствующих каждому
значению к, представляют собой уравнения, описывающие положение и импульс
гармонического осциллятора с массой т и частотой £1(к), однако функции £ и п
являются комплексными. Таким образом, задача о бесконечной (но дискретной) цепочке
связанных гармонических осцилляторов сводится к задаче о непрерывной цепочке
независимых фиктивных осцилляторов, обозначенных индексом к.
ЗАМЕЧАНИЕ
Строго говоря, эти фиктивные осцилляторы не являются совершенно
независимыми, так как условия вещественности B4) и B7) требуют, чтобы начальные
значения £(&,()) и п(к,0) удовлетворяли условиям:
724

Одномерный гармонический осциллятор
$(*,0) = £•(-*,());
я(Л,0) = 71*(-*,0).
B9)
р. Нормальные переменные a(fc, t), связанные с бегущими волнами
Удобно объединить (см. также § 1-а дополнения Gv) две нормальные переменные
£(&,f) и n(k,t) в одну ос(£, О, определенную формулой:
а(*,г) = 4=[|(А:,0 + йс(*,0], C0)
где t{kj) и ii(k,t) — безразмерные величины, пропорциональные £(&,*) и n{k,t)\
£(*,/) = Р(*)$(*,0;
й(*,0 =
1
»Р(*)
я(*,г).
C1)
Для упрощения последующих квантовых вычислений обозначим:
Р(*)
^
т£1(к)
C2)
Легко показать с помощью равенства C0), что два уравнения B8) эквивалентны одному
уравнению:
'Л
i—a(k,t) = Q(k)a(k,t) C3)
dt
первого порядка по t [функция сс(&, t) полностью определена, если задана функция
а{к, 0), тогда как £(&, t) определяется двумя функциями £(&, 0) и я(£, 0) ]. Общее
решение уравнения C3) записывается в виде:
a(k9t) = a(k,0)e"iaik)'. C4)
Используя формулы A9) и B5), нетрудно выразить сс(&, /) через х (t) и р (t):
V2 ,
x(t) + i—
q mQ(k)
C5)
Покажем теперь, что функции х (t) и pq(t) также могут быть выражены через a(£, t).
Согласно формулам B4) и B7) имеем:

Глава V
C7)
a4-/:^) = i[|4-A:,0-m4-^^)] = i[^^)-m(^,o], C6)
откуда следует:
|(*,r) = ^[a(M) + aVM)];
п(к, t) = —j= [a(£, t)-a*(-k, г)],
[ л/2
что позволяет переписать формулу B3) в виде:
х (,) = -J— ( Г' ^А e^dk + Г" a'{~kj) e^'dkl. C8)
" 2nV2l Р(*) Р(*) J
Заменив во втором интеграле & на —к , окончательно получим [функция ${к) — четная]:
, (,) = _J_ (г-' ^МЛ + Г» «Ii*i£> в^л 1. C9)
2лл/2 V""" Р(*) J-"" P(Jfc) J
Если использовать формулу B6), то аналогичные вычисления дают:
Pq(t) = ^ij у {С P(*)a(Jfc,/)Л* -С p(*)a'(*, t)e-^dk). D0)
Таким образом, состояние системы может быть описано как функцией a(&, t), так и
совокупностью функций х (t) и р (t).
Если в выражении C9) заменить функцию a(£,r) ее общим выражением C4), то
формула для xq(t) примет вид:
*'@ = ^/Г {С ^l^T^'-^" +»мпл. сопр]. D1)
Таким образом, самое общее решение задачи о цепочке связанных осцилляторов
является линейной суперпозицией бегущих волн, форма которых была введена ранее в § 1-Ь
(коэффициенты этой суперпозиции равны j= —-1—). Эти бегущие волны образуют
271V2 р(*)
набор собственных мод колебаний системы*.
* Можно было бы ввести также и набор стоячих волн в системе, образованный двумя
бегущими волнами одной частоты и противоположно направленными скоростями. Полученные при
этом результаты были бы совершенно эквивалентными, только лишь движение системы было бы
разложено в ином «базисе». Разложение такого вида используется в дополнении Kv.
726

Одномерный гармонический осциллятор
ЗАМЕЧАНИЕ
Для фиксированного значения к оба члена в правой части выражений C9) и
D0) являются комплексно сопряженными друг другу, и это обеспечивает
вещественность функций х (t) и р (t) без наложения дополнительных условий на
а(к, t). Поэтому именно переменные ос(£, t) являются истинно независимыми.
d. ПОЛНАЯ ЭНЕРГИЯ СИСТЕМЫ И ЭНЕРГИЯ КАЖДОЙ ИЗ МОД
Полная энергия рассматриваемой системы равна сумме кинетической энергии всех
частиц (q) и потенциальных энергий A) и F):
— Р\ +-ma2x2q + -m(»2(xC]-xq + lJ
^'С..,л_1,дс0,дс+|,...,/7ч,р0,р+1,...)= £
D2)
В этом параграфе мы увидим, что энергия системы может быть просто выражена через
энергии каждой из мод колебаний.
Для этого вычислим суммы, входящие в D2). Поскольку смещения х являются
коэффициентами ряда Фурье, определяющего функцию £(/:, t), то из равенства Парсеваля
[приложение I, формула A8)] сразу же следует:
^,J-~С1«*.0|2Л; D3)
&^)!4С1*')|2Л. D4)
д = -оо Z71
Остается вычислить сумму в D2), ответственную за связь. Для этого заметим, что,
поскольку в формуле A8) смещения xq являются коэффициентами ряда Фурье,
описывающего t[kj), то xq + [ являются коэффициентами ряда, описывающего e'kl%(к, г), а
величины (xq-xq + l) являются коэффициентами ряда Фурье, описывающего (l-e,kl)<^(k,t).
Равенство Парсеваля дает при этом:
Подставив D3), D4) и D5) в D2), получим:
727

Глава V
2л ]-п" 2
<й2+<
■4cof jw2(— j |^(*,r)|2 + —|я(*,0|2|л • D6)
Запишем полученный результат в виде:
где
й(*) = ^mQ2(*) |£(*. 0|2 + ^- |я(Л, г)|2. D8)
2 2т
Таким образом, ./<? оказывается равной сумме (точнее говоря, интегралу) энергий
фиктивных невзаимодействующих гармонических осцилляторов, для которых функция
£(£,0 определяет положение, а функция n(k,t) —импульс.
Можно выразить h(k) также и через переменные OL(k,t) каждой из собственных
мод. Действительно, с помощью формулы C7) можно преобразовать выражение D8) в
ft(Jt) = -Ш(к) [сс(*.t)a(k,t) + а (-к,t)a(-k% t)\ D9)
или с учетом C4):
Л(*) = -Ш(*)[а(*>0)а*(*,0) + а*(-*,0)а(-*,0)]. E0)
Таким образом, h(k) не зависит от времени, и это понятно, так как h(k) является
энергией гармонического осциллятора. С другой стороны, из D7) следует, что фиктивные
осцилляторы независимы, так как полная энергия Ж является простой суммой энергий
всех осцилляторов.
Подставив выражение D9) в D7), получим:
•^ = ^С^^Ш(^)[а(/:,0аЧ^,0 + аМ,г)аЧ^,0]. E1)
Можно заменить во втором слагаемом под интегралом к на -к и рассматривать Ж
как сумму энергий h'(k) собственных мод, характеризуемых переменными a(kyt):
■* = ^П>Л'(*). E2)
где
h'(k) = HQ.(k)a(k, t)a(k, t) = hQ(k)a(k, 0)a(Jfc, 0). E3)
728

Одномерный гармонический осциллятор
2. Квантовый анализ
Квантовый подход к решению задачи о бесконечной цепочке связанных
осцилляторов в соответствии с общими правилами квантования основан на замене классических
величин x(j{t) и р (г) наблюдаемыми Хц и Pq, удовлетворяющими каноническим
соотношениям коммутации:
К-^Н5^- E4)
а. СТАЦИОНАРНЫЕ СОСТОЯНИЯ В ОТСУТСТВИЕ СВЯЗИ
В отсутствие связи (со, =0) гамильтониан Н системы имеет вид:
Я(ш1=0) = £
{***>&
-2Л.
E5)
где Hq — гамильтониан одномерного гармонического осциллятора, действующий в
пространстве состояний частицы (q).
Введем оператор aq, определенный выражением:
1
•-Ц
W'-
у/тШ q
E6)
Тогда оператор Н можно представить в виде:
Ня = j (fl А+ + аяая)П@ = ( аяая + 2)'
E7)
где а и а* — операторы уничтожения и рождения фотона с энергией, присущей
осциллятору (q). Мы знаем (§ С-1-а главы V), что собственные состояния гамильтониана
Hq определяются как
E8)
где kpjj) — вектор основного состояния осциллятора (q), а квантовое число nq
является нулем или целым положительным числом. Если обозначить символом Eqn энергию
729

Глава V
состояния Ф* ), приняв за начало отсчета энергию основного состояния [при этом в
выражении E7) можно опустить член 1/2], то получим:
E4n,=nqha>. E9)
В отсутствие связи стационарные состояния полной системы являются тензорными
произведениями вида:
с энергией*:
£ = ££,? =[...+л_1+л0+л1 + ...]йсо. F1)
ч "
Основной уровень, энергия которого выбрана в качестве начала отсчета, не
вырожден. Действительно, Е = 0 в формуле F1) возможно лишь в том случае, если
nq - О при любых q . F2)
Таким образом, состояние F0) является единственным. Напротив, все остальные уровни
оказываются бесконечно вырожденными. Так, например, первый уровень с энергией
Ш соответствует случаю, когда все числа nq равны нулю, кроме одного, равного 1.
При этом все осцилляторы находятся в основном состоянии, кроме единственного, ибо
возбуждение может быть локализовано на одном из осцилляторов, уровень которого
Е = /KD бесконечно вырожден.
Ь. ВЛИЯНИЕ СВЯЗИ
При наличии связи гамильтониан становится равным:
Я = Я(со|=0) + У, F3)
где
V=\ma2lZ(Xq-Xq + lJ. F4)
При этом состояния F0) уже не являются стационарными состояниями системы. Дейст-
* Если бы мы не изменили начало отсчета энергии каждого осциллятора, убрав в формуле
E7) член 1/2, то мы получили бы бесконечно большую энергию, независимо от квантового числа
nq. Это затруднение не возникло бы, если бы рассматривалась не бесконечно длинная цепочка
осцилляторов, а состоящая из большого, но конечного числа осцилляторов. Но в таком случае
возникла бы проблема «краевых» эффектов.
730

Одномерный гармонический осциллятор
вительно, они будут собственными состояниями оператора Я(ш, = 0), но не оператора V .
Чтобы показать это, запишем V через операторы ац и aq:
V =■%■ ^ 2(ач +а; -а1п1 -<+|J. F5)
Ц- СО q
Тогда становится понятным, что действие оператора V на состояние вида F0) не может
дать то же самое состояние: числа nq не являются более «хорошими квантовыми
числами», так как оператор V может передать возбуждение, например, от ячейки (q ) ячейке
(q +1) благодаря наличию члена aq+] aq.
Чтобы найти стационарные состояния системы при наличии связи, удобно, как и в
классической механике, ввести «нормальные переменные», то есть операторы,
соответствующие собственным модам системы.
с. НОРМАЛЬНЫЕ ОПЕРАТОРЫ. СООТНОШЕНИЯ КОММУТАЦИИ
Нормальным переменным t>{k,t) и n(k, t) соответствуют операторы Е(к) и Щк),
определенные выражениями:
hw = ev~'V/"; F6-a)
ч
П(к) = ^Ряе-!"к1 . F6-Ь)
ч
Область изменения непрерывного параметра к по-прежнему ограничена первой зоной
Бриллюэна A5). Заметим, что, поскольку переменные \(k,t) и n(k,t) являются
комплексными, операторы Е(к) и Щк) не могут быть эрмитовыми в противоположность
операторам Xq и Р. Соотношениям B4) и B7) здесь соответствуют:
Е(-к) = Е+(к)\ F7-а)
Щ-к) = П+(к). F7-Ь)
Канонические соотношения коммутации E4) позволяют вычислить коммутаторы
операторов Е(к) и Щк). Сразу же видно, что Е(к) и Е(к') коммутируют, как и
операторы Щк) и Щк') . Однако коммутатор [Н(/:), П+ (к')]имеет вид:
[е(*),ГГ(*')] = Е1 \xq, Pq]e~iqkl e+iq'k'1 =i»S^(ft"r)/ . F8)
ч ч ч
731

Глава V
Согласно формуле C1) приложения II получим (так как волновые числа к и к'
принадлежат одному и тому же интервалу):
[Е(*),ГГ(*')]='Л — 5(*-*').
F9)
В § 1-с-Р мы видели, что удобно объединить две нормальные переменные £(&,/) и
n(k,t) в одну a.(k,t) [формула C0)]. Соответствующий оператор имеет вид:
а(к) =
Р(*)Н(*) +
ЛР(*)
П(*)
G0)
где функция $(к) определена формулой C2). Заметим, что оператор, сопряженный
а(к), имеет вид:
1
G1)
Используя выражения F9) и F7), без труда получим, что
[а(к),а(к')] = [а+(к\а+(к')] = 0\ G2-а)
[а{к\а+{к')]~Ь(к-к'). G2-Ь)
Классической величине h(k), определенной формулой D8), соответствует оператор:
G3)
Н(к) = — Щк)П+(к) + -т0.2(к)Е(к)Е+(к),
2т 2
так как операторы Е(к) и Е+(к), а также Щк) и П+(£) коммутируют. Чтобы
получить эквивалент классической формулы D9), необходимо учесть, что операторы а(к) и
а+(к) не коммутируют, и нужно сохранять порядок их следования в ходе выполнения
вычислений. Если обратиться к формулам F7), то соотношения C7) примут здесь
следующую форму:
P(t)S(*) = -ir[fl(t)+fl + (-*)];
Подставив эти выражения в G3), найдем:
G4-а)
G4-Ь)
Н{к) = -ККк)[а(к)а*(к) + а+(-к)а(-к)].
G5)
732

Одномерный гармонический осциллятор
Как и в формуле E2), полный гамильтониан системы И можно привести к виду:
2я J-n/l
где
H'(k) = -hQ(k)[a(k)a+(k) + a + (k)a(k)]. G7)
Тогда операторы а(к) и а+(к) приобретают здесь смысл операторов уничтожения и
рождения, как и в случае гармонического осциллятора, однако поскольку индекс к
непрерывный, то в соотношения коммутации G2) будет входить не символ Кронекера,
а функция 8(к-к'), и это вынуждает сохранять Н\к) в симметричной форме G7).
Нетрудно показать, что операторы Н'(к) коммутируют друг с другом:
[Н\к),Н'{к')] = 0. G8)
d. СТАЦИОНАРНЫЕ СОСТОЯНИЯ ПРИ НАЛИЧИИ СВЯЗИ
Согласно формулам G6) и G7) основное состояние |0) системы связанных
осцилляторов определяется условием:
*(*)|0) = 0 G9)
для всех значений к . Другие стационарные состояния получаются из состояния |0)
путем действия на него операторов а+(к). Их энергия равна интегралу от энергий каждой
из мод. Вследствие непрерывной бесконечности собственных мод появляются
некоторые затруднения; так, в частности, энергия основного состояния, которую можно найти
из G6) и G7), оказывается бесконечно большой. Здесь мы не станем обсуждать эти
трудности, которые, впрочем, никогда не проявляют себя в случае реальных цепочек,
имеющих конечную длину (см. замечание к § 2-а).
Формула A0) определяет значение энергии кванта, с которым ассоциируется каждая
из мод. Таким образом, она указывает, какие кванты энергии может поглощать или
излучать рассматриваемая система: они обязательно соответствуют частотам, лежащим в
разрешенной полосе A7).
3. Применение к изучению колебаний в кристалле. Фононы
а. ПОСТАНОВКА ЗАДАЧИ
Рассмотрим твердое тело, образованное из большого количества атомов (или
ионов), равновесные положения которых регулярно расположены в пространстве в узлах
733

Глава V
кристаллической решетки. Для простоты допустим, что решетка одномерная, и ее можно
представить в виде линейной бесконечной цепочки атомов. Здесь используем
полученные в предыдущих параграфах результаты, чтобы изучить движение ядер этих атомов
вблизи положений равновесия.
С этой целью воспользуемся тем же приближением, что и в анализе молекулярных
колебаний (приближение Борна—Оппенгеймера; см. дополнение Av, замечание к § 1-а).
Предположим, что сначала можно рассчитать движение электронов, считая положения
ядер фиксированными параметрами xq, то есть решить соответствующее уравнение
Шредингера (в действительности это уравнение само по себе слишком сложное, чтобы
его можно было решить точно, и на практике для его решения приходится
довольствоваться приближением). Затем мы обозначим символом Eel(...y jc_,, х0, *,,...) энергию
электронной системы в основном состоянии, где xq будет определять отклонение
ядра с номером (q) от его равновесного положения. Можно показать, что в этом случае
возможно рассчитать движение ядер с достаточно хорошей точностью, считая, что они
обладают полной потенциальной энергией UN (..., х_х, х0, х{,...), равной сумме энергий
их электростатического взаимодействия и Ее1 (..., х_х, х0, *,,...).
На деле мы еще больше упростим задачу, сделав несколько разумных предположений
относительно UN (это необходимо, поскольку мы не знаем Ее1). Во-первых, допустим,
что UN описывает в основном взаимодействия каждого из ядер с ближайшими соседями
(в линейной бесконечной цепочке каждое ядро имеет два таких соседа), то есть считаем,
что можно пренебречь силами между ядрами, не находящимися в непосредственной
близости. Кроме того, предположим, что в области возможных значений смещения xq
энергию UN можно представить выражением вида:
UN=\m^^(xq-x^J , (80)
где т — масса ядра и величина со, характеризует интенсивность его взаимодействия с
соседними ядрами. Мы не будем принимать во внимание члены высших порядков по
(xq -х х), то есть ангармоничностью потенциала.
Поскольку выражение (80) идентично выражению F), можно использовать
результаты предыдущих параграфов в рамках простейшей модели твердого тела, которую мы
только что определили. Заметим, однако, что поскольку UN является полной
потенциальной энергией системы ядер, нужно положить со = 0 : ядра взаимодействуют со
своими соседями, но не связаны упругими связями со своими равновесными положениями*.
* Модель Эйнштейна, которую мы описали в дополнении Av, основана на иной гипотезе: она
предполагает, что каждое ядро «видит» средний потенциал, обусловленный взаимодействиями с
ансамблем других ядер, но практически не зависящий от точного положения других ядер. В пер-
734

Одномерный гармонический осциллятор
Ь. СОБСТВЕННЫЕ МОДЫ КОЛЕБАНИИ. СКОРОСТЬ ЗВУКА В КРИСТАЛЛЕ
Каждая из собственных мод колебаний кристалла характеризуется волновым
вектором к и частотой Q,(k). В физике твердого тела «фононом» называют квант энергии,
связанный с этой модой. Фононы можно рассматривать как частицы с энергией Ш(/с) и
импульсом fik . На самом деле фонон не является истинной частицей, так как его
существование отражает коллективное колебание реальных частиц, образующих кристалл.
Говорят иногда, что фононы являются «квазичастицами»: они полностью аналогичны
фиктивным частицам с положением xG(t) и xR(t), которые были введены в дополнении Hv.
Кроме того, можно создать или уничтожить фонон, передав кристаллу или отняв у
кристалла энергию соответствующего колебания, тогда как (по крайней мере в
рассматриваемой здесь нерелятивистской области) невозможно создать или уничтожить такую
частицу, как, например, электрон. По этому поводу заметим, что число фононов в заданной
моде может быть любым, и, следовательно, фононы являются бозонами (глава XIV).
Закон дисперсии, определяющийся функцией £1(к), для фононов отличается от уже
рассматривавшегося в §1-Ь-5, так как со = 0. Подставив это значение в A0), получим:
Q(*) = 2(D,
kl
sm-
(81)
AQ
Рис.5
Закон дисперсии для фононов (кривая рис.2 для со = 0); наклон кривой в начале отсчета
определяет скорость звука в кристалле
вом приближении этот средний потенциал рассматривается как параболический, и в этом случае
ансамбль ядер может считаться набором независимых гармонических осцилляторов. Здесь же мы
будем иметь дело с менее грубой моделью, в рамках которой явно (хотя и приближенно)
учитывается взаимодействие ядер друг с другом.
735

Глава V
Описываемая этой формулой кривая приведена на рис.5. Она состоит из двух
четвертей синусоиды. В отличие от того, что имеет место при со Ф О, при к = 0 функция Q(k)
обращается в нуль и близка к линейной зависимости при малых к . Действительно, пока
И «у, (82)
имеем:
Q(/:) = col|)t/| = vJ^, (83)
где
v, = со^ . (84)
Условие (82) выражает, что длина волны 27t/|fc|, связанной с рассматриваемой
модой, очень велика по сравнению с параметром решетки /. Для таких длин волн
дискретность структуры цепочки не влияет на их распространение, и среда оказывается не
диспергирующей, то есть фазовая скорость Q(fc)/|&| = vv не зависит от к . Поэтому
волновой пакет, составленный из волн с малыми значениями к одного знака,
распространяется в ней без деформации со скоростью vy. Поскольку длина акустических волн
удовлетворяет неравенству (82), v5 является скоростью звука в кристалле.
Если же \к\ того же порядка, что и 1 / /, дискретность структуры среды становится
заметной, в результате чего частота Q(k) увеличивается с ростом к медленнее, чем это
предусматривает формула (83) (на рис.5 кривая дисперсии отклоняется от прямых,
изображенных пунктиром, являющихся касательными в начале координат). В этом случае среда
является диспергирующей, и волновой пакет распространяется с групповой скоростью:
rfQ(fc) ^ Q(*)
vG=—— *—— • (85)
ак к
И, наконец, в том случае, когда значение к приближается к границам первой зоны
Бриллюэна (к —>±я//), из рис.5 видно, что групповая скорость стремится к нулю. Как
и в электромагнитных волноводах, скорость распространения обращается в нуль на
частоте среза системы (здесь она равна со, / 2я).
Рис.5 можно рассматривать и как спектральное распределение возможных значений
энергии frQ(k) фононов в зависимости от импульса hk. Для реальных кристаллов
очень важно знать форму такого распределения, так как она позволяет установить
значения энергии и импульса, которые кристалл способен излучать или поглощать при
взаимодействии с другими системами. Так, например, можно интерпретировать
неупругое рассеяние света в кристалле (эффект Бриллюэна) как результат процессов
уничтожения и рождения фонона, сопровождающихся изменением энергии и импульса
падающего фотона (полные энергия и импульс совокупной системы при этом сохраняются).
736

Одномерный гармонический осциллятор
ЗАМЕЧАНИЕ
Рассмотренная здесь простая одномерная модель позволила получить важные
физические результаты, остающиеся справедливыми и для реальных кристаллов:
квантование энергии собственных мод колебаний, дисперсия среды, разрешенные
и запрещенные полосы частот. Реальные кристаллы имеют трехмерную решетку, и
собственная мода должна характеризоваться в действительности волновым
вектором к. Тогда в общем случае частота Q будет зависеть не только от модуля
вектора к, но и от его направления. Кроме того, может случиться (обычно в ионных
кристаллах), что не все узлы решетки будут заняты одинаковыми частицами
(например, в кристаллах, образованных двумя различными типами частиц с регулярной
структурой)*. В подобных случаях каждому волновому вектору может
соответствовать несколько значений частот £2(к). Некоторые из них, обращающиеся в нуль
при |к|—>0, образуют так называемые «акустические ветви», с которыми мы
встретились только что. Другие частоты могут принадлежать к так называемым
«оптическим ветвям»**, в которых фонон с нулевым импульсом имеет отличную
от нуля энергию. Несмотря на всю важность этих вопросов в физике твердого тела,
мы не имеем возможности рассматривать их в данном дополнении.
Дополнение К у
МОДЫ КОЛЕБАНИЙ НЕПРЕРЫВНОЙ ФИЗИЧЕСКОЙ СИСТЕМЫ.
ПРИМЕНЕНИЕ К ИЗЛУЧЕНИЮ. ФОТОНЫ
1. Постановка задачи.
2. Моды колебаний непрерывной механической системы. Пример колеблющейся струны.
a. Обозначения. Динамические переменные системы.
b. Классические уравнения движения.
c. Введение нормальных переменных.
d. Классический гамильтониан.
e. Квантование.
* В реальном кристалле имеются также примеси и дефекты кристаллической решетки,
распределенные по кристаллу случайным образом. Здесь же речь идет только об идеальных кристаллах.
** Причина такого названия состоит в том, что в ионном кристалле «оптические» фононы
связаны с электромагнитными волнами, длина волны которых существенно превышает параметр
решетки, как в видимой области.
47 Квантовая механика
737

Глава V
3. Моды колебаний излучения. Фотоны.
a. Обозначения. Уравнения движения.
b. Введение нормальных переменных.
c. Классический гамильтониан.
d. Квантование.
1. Постановка задачи
В дополнениях Ну и Jv мы ввели идею нормальных переменных для системы двух
или бесконечного множества связанных гармонических осцилляторов. Цель данного
дополнения состоит в том, чтобы показать, что те же самые идеи могут быть применены
для описания электромагнитного поля, которое является непрерывной физической
системой (нет никакого естественного нижнего предела для длины волны излучения).
Прежде чем начать дальнейший анализ, в котором встретится немало проблем, и
реализовать плавный переход от изложенных ранее дополнений Ну и Jv, § 2 мы начнем с изучения
мод колебаний непрерывной механической системы: колеблющейся струны. Конечно, в
атомных масштабах такая система не является непрерывной, так как струна состоит из очень
большого количества атомов. Тем не менее мы будем игнорировать атомное строение струны и
будем считать ее непрерывной системой, поскольку главная цель вычислений состоит в том,
чтобы показать, как можно ввести нормальные переменные для изучения непрерывных
систем. Кроме того, поскольку речь идет о механической системе, можно без труда ввести
моменты, сопряженные нормальным переменным, вычислить гамильтониан системы и показать,
что он действительно является суммой гамильтонианов одномерных независимых
гармонических осцилляторов. Далее детально обсудим, как нужно квантовать такую систему.
Полученные в § 2 результаты позволят нам в § 3 ввести понятие колебательных мод
излучения. Мы покажем, что исследование излучения в прямоугольной полости
приводит к уравнениям, аналогичным уравнениям колеблющейся струны. Аналогичные
преобразования позволяют ввести нормальные переменные для излучения, связанные со
стоячими волнами, существующими в полости и совершенно не зависящими друг от
друга. Удовлетворимся обобщением результатов, полученных в § 2, чтобы ввести
понятие фотона (в рамках простейшего обсуждения весьма сложно строго ввести такие
понятия, как сопряженные моменты, лагранжиан и гамильтониан, для такой «не
механической» системы, как электромагнитное поле).
2. Моды колебаний непрерывной механической системы.
Пример колеблющейся струны
а. ОБОЗНАЧЕНИЯ. ДИНАМИЧЕСКИЕ ПЕРЕМЕННЫЕ СИСТЕМЫ
Пусть струна зафиксирована в точке О (рис.1). Далее она проходит через отверстие
в пластине и растягивается (через блок) силой натяжения F с помощью прикрепленной
738

Одномерный гармонический осциллятор
ф. t)
Рис.1
Колеблющаяся струна, проходящая через
две фиксированные точки О и Р,
подверженная силе натяжения F. Величина
u(x,t) характеризует отклонение от
положения равновесия точки струны,
расположенной на расстоянии х от начала О
к ее концу массы. Для простоты допустим, что струна все время остается в одной и той
же плоскости, проходящей через точки О и Р. Ее состояние определено в момент
времени /, если в этот момент времени известно смещение и(х, t) различных точек в
плоскости ОР и их скорости du(xj)ldt. Ограничения, наложенные в точках О и F,
выражаются граничными условиями:
n@,f) = K(L,f) = 0, A)
где 0 и L — абсциссы точек О и Р.
Следует отдавать себе отчет, что в рамках этой задачи динамическими переменными
являются смещения и(х, t) каждой точки с абсциссой х : при этом имеется непрерывное
бесконечное множество динамических переменных. И, как следствие, величина х не
является динамической переменной, а всего лишь непрерывным индексом, позволяющим
определить интересующую нас динамическую переменную (х играет ту же роль, что и
индексы 1 и 2 в дополнении Hv или индекс q в дополнении Jv).
b. КЛАССИЧЕСКИЕ УРАВНЕНИЯ ДВИЖЕНИЯ
Пусть \1 — линейная масса струны. Если допустить, что струна идеально упругая и
ограничиться случаем малых смещений ее элементов, то классическая теория позволяет
получить уравнение в частных производных для переменной и :
v2dt2
12 Л
дх2
u(x,t) = 0,
где
•=7^7ц
B)
C)
скорость распространения волны вдоль струны.
Это уравнение свидетельствует о том, что эволюция переменной и в точке х
зависит от значений переменной и в бесконечно близких точках, что и описывается членом
47*
739

Глава V
д2и/дх2. Отсюда следует, что переменные и(х, t) связаны друг с другом, и резонно
поставить следующий вопрос: можно ли, как в дополнениях Hv и Jv, ввести новые
переменные, являющиеся линейными комбинациями переменных и(х, t) для разных точек
х, которые были бы не связаны друг с другом?
с. ВВЕДЕНИЕ НОРМАЛЬНЫХ ПЕРЕМЕННЫХ
Рассмотрим ансамбль функций переменной х:
=/z™
/*W = Jt sin
{ пх
kT\. D)
где к — целое положительное число: к = 1,2, 3,.... Все функции fk(x)удовлетворяют
тем же граничным условиям, что и функции и{хУ t):
Л@) = Л(Ю = 0. E)
Кроме того, нетрудно доказать, что
£/»«/*.(*)& = 8«. F)
(это равенство является соотношением ортонормировки), а также
( d2 *V^
-+-
[dx2 L2 )
/»W = 0. G)
Можно показать, что любая функция, обращающаяся в нуль в точках х - 0 и х = L
[в том числе и функция и(х, t) ], может быть разложена единственным образом по
функциям ft (x). Таким образом, можно записать:
u(x,t) = tqk(t)ft(x), (8)
где функции qk(t), благодаря равенству F), определяются соотношением:
qk(t) = \L0u{x,t)fk(x)dx. (9)
Состояние струны в момент времени t в равной мере можно определить как ансамблем
значений \и(х, t),—u(x, t)>, соответствующих различным точкам х, так и ансамблем
чисел {qk(t),qk(t)}. Новые переменные qk(t), как следует из формулы (9), являются
740

Одномерный гармонический осциллятор
линейными комбинациями старых переменных и(х, t). Между ними имеется и обратное
соотношение (8).
Чтобы получить уравнение, которому удовлетворяют функции qk(t), достаточно
подставить разложение (8) в уравнение движения B). Простые вычисления с
использованием выражения G) дают:
2Л(*>
k = l
Id2 , г k2n2 . .
v at L
= 0,
(Ю)
то есть если учесть линейную независимость функций fk (x):
dr
где
9,@ = 0,
knv
(И)
A2)
Таким образом, видно, что новые переменные, называющиеся нормальными
переменными, изменяются во времени независимо друг от друга. Кроме того, уравнение A1)
идентично уравнению одномерного гармонического осциллятора с частотой соЛ, откуда
следует:
qk(t) = Akcos((ukt-<f>k). A3)
Каждый из членов qk(t)fk(x), фигурирующих в правой части равенства (8),
представляет собой стоячую волну с частотой соА /2тс и длиной волны 2LI к . Таким образом,
каждая нормальная переменная qk{t) связана с собственной модой колебаний струны, а
движение струны в самом общем случае представляет собой линейную суперпозицию
собственных мод.
ЗАМЕЧАНИЕ
В дополнении Jv мы исходили из того, что имеется бесконечный дискретный
набор гармонических осцилляторов, и ввели непрерывную и бесконечную
совокупность нормальных переменных. Здесь же имеет место противоположная
ситуация: функции w(jc, f) образуют по отношению к индексу х непрерывный ансамбль,
тогда как из-за наложенных граничных условий нормальные переменные qk(t)
образуют дискретный ансамбль, определяемый дискретным индексом к .
741

Глава V
d. КЛАССИЧЕСКИЙ ГАМИЛЬТОНИАН
а. Кинетическая энергия
Кинетическая энергия бесконечно малого отрезка струны, заключенного между х и
х + *. равна 1м*
ны равна:
3w(jt, t)
dt
Таким образом, полная кинетическая энергия J стру-
2 ^
Д&.
Используя формулу (8), можно выразить ее через qk :
A4)
М- rv^*W dM0 r^
*■ = *!!
z k k'
dt
dt
\ofkMfk'Mdx9
и с учетом F) получим:
ir_V^(dqk
2f(dt
A5)
A6)
P. Потенциальная энергия
Рассмотрим бесконечно малый отрезок струны, заключенный между х и х + dx
В общем случае он составляет угол Э с осью Ох , определяемый выражением:
tgQ =
du(x,t)
дх
Его длина равна:
dx
cosQ
= dx[l + tg2Q\*.
A7)
A8)
Поскольку смещения считаются малыми, то мал и угол 0 , вследствие чего можно записать:
dx
cos В
= dx
1 + -
'du(x,t)^2
дх
A9)
Отсюда следует, что полное удлинение струны по сравнению с ее длиной в состоянии
равновесия, соответствующем и = 0 при произвольном значении х, равно:
( ди(х, r)N
9 Jo
dx
dx.
B0)
742

Одномерный гармонический осциллятор
Величина AL представляет собой высоту подъема участка струны. Потенциальная
энергия 7 струны по отношению к значению, соответствующему положению равновесия,
равна:
Энергию Г можно выразить через нормальные переменные qk . Простой расчет
позволяет получить с помощью формул (8) и D):
F ^ k2n2 2
у. Моменты, сопряженные qk. Гамильтониан
Лагранжиан У, системы (см. приложение III) имеет вид:
* = J-r=^l[fi-<u\q\]. B3)
2
к
Из этого выражения можно сразу же получить формулу для момента рк, сопряженного qk:
Рк=^7-:=Мк> B4)
одк
так, чтобы в конце концов получить гамильтониан Jf(qk, рк) системы:
Ж = J + 7 • = £
Pk I 2 2
B5)
или
•*" = ХА*, B6)
где
hk=^+±liu2kql B7)
Поскольку переменные рА и ^ являются сопряженными, то в функции hk нетрудно
узнать гамильтониан одномерного гармонического осциллятора с частотой (йк. Таким
образом, Ж является суммой гамильтонианов независимых одномерных гармонических
осцилляторов (они независимы, так как это нормальные переменные, не связанные друг
с другом).
743

Глава V
Как и в дополнениях Bv и Cv, удобно ввести безразмерные переменные
Як = $кЯк;
1
М
где
является безразмерной константой. Тогда гамильтониан Ж принимает вид:
к I
е. КВАНТОВАНИЕ
а. Предварительное замечание
Выполненные в данном параграфе вычисления, конечно, не предназначены для
демонстрации квантовых эффектов в движении макроскопической колеблющейся струны.
Частоты колебаний 0)Л /2я, возбуждаемые в такой струне, столь малы по частоте
(порядка килогерц) и соответственно по энергии /КО* по сравнению с макроскопической
энергией струны, что классический анализ оказывается вполне достаточным и
справедливым. Можно было бы подумать, что (х)к может оказаться столь угодно большой,
поскольку величина к в формуле A2) ничем не ограничена сверху. В реальности для
достаточно малых длин волн 2L/ к уже нельзя пренебрегать жесткостью струны, и
уравнение B) уже не является справедливым. Кроме того, как мы указывали во введении,
струна не является в действительности непрерывной системой, и нет никакого смысла
рассматривать длины волн меньше межатомного расстояния.
Вычисления, которые мы здесь представим, следует рассматривать как первое
приближение для задач, связанных с квантовым описанием излучения, которое на самом
деле является непрерывной системой, поскольку нет никакого естественного нижнего
предела для длины волны излучения, и которое описывается уравнением, аналогичным
уравнению B), независимо от значений частот и длин волн, описывающих систему*.
* Если бы нас интересовала настоящая микроскопическая «колеблющаяся струна» (например,
линейная макромолекула), то было бы более реалистичным взять в качестве модели, как это было
сделано в дополнении Jv, цепочку атомов и исследовать не только продольные, но и поперечные
колебания (поперечные фононы).
744
B8-а)
B8-Ь)
B9)
C0)

Одномерный гармонический осциллятор
Р. Собственные состояния и собственные значения квантового гамильтониана Н
Квантование любого осциллятора можно осуществить, сопоставляя переменным qk
и рк наблюдаемые Qk и Рк, удовлетворяющие соотношению:
[&,/>] = ;. on
Поскольку нормальные переменные не связаны друг с другом, можно предположить,
что операторы, относящиеся к двум различным осцилляторам, коммутируют. В общем
случае имеем:
[&Л] = '8м-- C2)
Пусть
Я4=1»а>4(# + £2) C3)
квантовый гамильтониан осциллятора к. Согласно результатам главы V, собственные
состояния и собственные значения известны:
nM = [nk+fy«>k\nk), C4)
где пк — неотрицательное целое число (для упрощения обозначений вместо ф^)
будем писать \пк).
Поскольку операторы Нк коммутируют между собой, можно выбрать собственные
состояния оператора Я в виде тензорных произведений состояний \пк):
|л,>|п2)...|ла)... = |л1>п2,...,яа,...). C5)
Основное состояние, которое называют «вакуумом», соответствует нулевым значениям
квантовых чисел пк:
|0,0,...,0,...) = |0). C6)
Энергия состояния C5), если ее отсчитывать от энергии состояния |0), равна:
£„„„2 *.... = 2М<*>*- . C7)
Можно считать, что состояние C5) содержит л, квантов с энергией /гсо,,..., пк квантов
с энергией Йсо*,... и т. д. Эти кванты колебаний аналогичны фононам, рассмотренным в
дополнении Jv.
745

Глава V
И, наконец, можно ввести операторы рождения и уничтожения кванта с энергией Шк
через операторы Рк и Qk, как это было сделано в § В главы V:
at=-^(Qk+iPk). C8)
Оператор ак является сопряженным оператору ак. Тогда
[at, <*;.] = 8 и. C9)
И
ak\nl,n2,...,nk,..) = <fc\nl,n2,...,nk-l..)\
ак+\п1,п2,...упк,..) = У1пк+\\п1,п2,...,пк +1,...). D0)
Все состояния C5) могут быть выражены через состояние вакуума |0):
I \ '< Г W W ш)
D1)
у. Квантовое состояние системы
В самом общем случае состояние системы является линейной суперпозицией
состояний |n,,n2,...,nt.,...):
\що) = 2 c„it4 И1..„@|я,.«2 n4,...). D2)
Уравнение эволюции вектора |\|/(/)) является уравнением Шредингера:
т^\щп) = н\що). D3)
Используя выражения C7) и D3), нетрудно получить:
<V„: ....(') = с, 2 (,...@)е ' . D4)
746

Одномерный гармонический осциллятор
8. Наблюдаемые, связанные с динамическими переменными и(х, t)
При квантовании переменная u(xj) становится наблюдаемой U(x), не зависящей
от t *, которую можно получить, заменив в формуле (8) qk{t)наблюдаемой Qk:
i/w=z/«wa =Sp-^/*c*>h+e*]- D5)
Таким образом, видно, что можно определить наблюдаемую U(x) для каждого значения х,
линейно зависящую от операторов рождения и уничтожения ак и а[.
Интересно сравнить среднее значение наблюдаемой £/(*), то есть
(\|/(r)|£/(jt)|\|/(f)) с классической величиной и(х, t). Поскольку согласно формуле D0)
операторы ак и а\ могут связывать лишь такие состояния, разность энергий между
которыми равна ТЙсо^, то из выражения D5) следует, что в эволюции (U(x))(t) могут
появиться частоты iujln, со2/2я,..., соА/2я,..., связанные соответственно с
пространственными функциями /,(*), f2(x),..., fk(x),.... И вновь мы приходим к выводу,
что среднее значение (U(x))(t) является линейной суперпозицией стоячих волн,
способных существовать на струне. Эту аналогию можно продолжить и далее. Действи-
Э2
тельно, вычислим вторую производную т-у(£/(*))@; используя равенство [см.
дополов
нение Gv, уравнение A7)]:
— (ak) = -i<ok(ak) D6)
и соотношения G) и A2), без труда найдем, что среднее значение наблюдаемой U(x),
определяемое формулой D5), удовлетворяет дифференциальному уравнению:
v2 Эг2 дх2
(£/(*))@ = 0, D7)
идентичному уравнению B).
Заметим, наконец, что поскольку Qk не коммутирует с Нк, то U(x) не
коммутирует с Н. Таким образом, в квантовой механике полная энергия и смещение являются
несовместимыми физическими величинами.
* Напомним, что в квантовой механике временная зависимость в общем случае содержится в
векторе состояния, а не в наблюдаемых (см. §D-l-d главы III).
747

Глава V
3. Моды колебаний излучения. Фотоны
а. ОБОЗНАЧЕНИЯ. УРАВНЕНИЯ ДВИЖЕНИЯ
Классическое состояние электромагнитного поля в данный момент времени /
определено, если известны компоненты электрического Е и магнитного В полей в каждой
точке г пространства. Таким образом, как и в § 2, имеется бесконечное количество
непрерывных динамических переменных — шесть компонент полей Ех, Еу, £,,
ВхУ #v, Bz в каждой точке пространства г .
Чтобы сосредоточить внимание на важнейшей идее нормальных переменных (или
собственных мод) поля, воспользуемся упрощенным вариантом задачи, в рамках
которого мы временно забудем о векторном характере полей Е и Н, а введем некоторое
скалярное поле У (г, t), подчиняющееся, как и каждая из компонент полей Е и Н,
уравнению:
1 Э2 д
с дг
У(г,/) = 0,
D8)
где с — скорость света.
Допустим, что поле заключено в прямоугольную полость, стенки которой с
внутренней стороны являются идеально проводящими, а ребра полости, параллельные осям
Ox, Oy, Oz, имеют соответственно длину L,, L,, Lj. В качестве граничных условий
наложим равенство функции if (r, t) нулю на всех стенках полости (в реальной задаче на
стенках должны равняться нулю, например, тангенциальные компоненты
электрического поля Е). Таким образом:
ff(x = 0, у, z, г) = У(х = L,, у, z, t) = <f(x9 у = 0, z, t) ■■
<f(x,y,z=Lt,t) = 0.
D9)
b. ВВЕДЕНИЕ НОРМАЛЬНЫХ ПЕРЕМЕННЫХ
Рассмотрим ансамбль функций переменных x,y,z:
/«*(*• У» *) =
ккх
LXL2L,
sin
V U ,
sin
(toy)
\ ^2 )
sin
mnz
V ^з )
E0)
где k,l,m — целые положительные числа (к,I,m= 1,2,...). Функции fkim{x,y,z)
обращаются в нуль на стенках полости и удовлетворяют, следовательно, тем же
граничным условиям, что и функции !f(x4 у, z, /):
/««. (* = 0, у, z) = /,,„, (х = L,, у, z) ■
■fkif„(^y^=L3) = 0.
E1)
748

Одномерный гармонический осциллятор
Кроме того, нетрудно доказать, что
£"Л 1о ЛУ Jo* dz /«»,U У. z) /Иу (л, У, z) = bu. 8„. 6И,„.
E2)
Д +
2^
/2 т
/««(*. У. z) = 0.
E3)
Любая функция, обращающаяся в нуль на стенках полости, и, в частности, функция
^(г, /), может быть разложена единственным образом по функциям fklm(x, у, z). Итак:
#>(*, у, z, 0 = £ <W0 /***(*» У. ^) •
E4)
Формула E4) легко обращается при использовании E2):
Яш (О = \о d* № йУ № dz /*/*<*' У, z)y?(xi у, z, t).
E5)
Видно, что состояние поля в момент времени t полностью определяется либо
ансамблем переменных qklm(t), либо ансамблем переменных У>(х, у, z, t). Формулы E4) и E5)
позволяют перейти от одного представления к другому.
Подставив E4) в D8) и используя E3), после простых вычислений получим:
Г + со*/«
4ш,@ = 0,
где
2 2 2
1 *1
ТГ"^
E6)
E7)
Таким образом, нормальные переменные qklm(t) независимы друг от друга. Согласно
формуле E6) функция qklm(t) изменяется как A cos (со шг - ф), и каждый из членов
qkim(t)fUm(x,y,z) разложения описывается стоячей волной (или собственной модой
колебания поля в полости), характеризующейся своей частотой (йЫт/2п и
пространственным распределением в трех направлениях Ox, Оу, Oz с длинами полуволн, равными
соответственно Ljk, Ц/1, Ц/т .
Итак, мы смогли без труда обобщить результаты, полученные в § 2-е. Отметим,
однако, что если бы мы учли векторный характер электромагнитного поля, то структура
мод была бы еще сложнее, но общая идея осталась бы той же, а полученные результаты
были бы очень похожи на приведенные здесь.
749

Глава V
с. КЛАССИЧЕСКИЙ ГАМИЛЬТОНИАН
Основываясь на очень тесной аналогии между результатами § 2-е и § 3-Ь, примем
без доказательства, что полю ^(r, t) можно поставить в соответствие лагранжиан 5Г , из
которого можно вывести уравнение движения D8), сопряженные моменты pUm(t)
нормальных переменных и, наконец, гамильтониан системы. Нас будет интересовать в этом
лишь то обстоятельство, что гамильтониан будет аналогичен выражению C0):
Ж = X -Шк1т\(дк1тJ^(рк1тJ],
к.1,т £ L J
где qklm и pklm — безразмерные переменные, пропорциональные qklm и рк1т :
1
Qklm ~ Р*/ж Qklm ' Pklm ~"
»Р*
'Pklm
Здесь Рш — размерная постоянная, аналогичная уже введенной в B9).
E8)
E9)
ЗАМЕЧАНИЯ
0)
Уравнения эволюции каждой из нормальных переменных qklm E6) аналогичны уравнению
гармонического одномерного осциллятора с частотой (йк1т. Таким образом, понятно, что
для Ж мы получим сумму гамильтонианов независимых одномерных гармонических
осцилляторов. Формулу E6), впрочем, можно было бы получить непосредственно из
формулы E8). Уравнения Гамильтона—Якоби (приложение III) с учетом E9) запишутся в виде:
1 дЖ
dqkl
dt
dPklm
1 дЖ
F0)
то есть
Л
d4h
dt
Фит
dt
h дЯщ, '
: ®klm Pklm
— ® Urn Qklm
F1)
Исключив в этих уравнениях рк1т , получим формулу E6).
(ii) В случае реального электромагнитного поля, состоящего из двух полей Е и В , можно
также непосредственно установить выражение E8) без перехода к лагранжиану. Можно
750

Одномерный гармонический осциллятор
просто записать, что полная энергия поля есть сумма энергии электрического и магнитного
полей в полости:
.Г = -|1>{>П>г[Е2+с2В2], F2)
и использовать для Е и В разложения, аналогичные формуле E4). При этом получим, что
члены, пропорциональные pklm и qklm , соответствуют электрической и магнитной энергиям.
d. КВАНТОВАНИЕ
Теперь, исходя из уравнения E8), можно осуществить такие же разложения, как и в
§2-е.
а. Собственные состояния и собственные значения оператора Н
Величинам qklm и pklm сопоставляем две наблюдаемые Qklm и Pklm, коммутатор
которых равен /. Поскольку наблюдаемые разных мод коммутируют, то в общем случае:
[&/„,» Kiw] = *'8**' 8//'5w • F3)
Пусть Hklm — гамильтониан моды (klm):
*~* trln, —
2
Его собственные состояния и собственные значения известны:
F4)
( П
Нит\ПЫт)=\ nkl,n+-\h®klm\nkln)> F5)
где пк1т — целое неотрицательное число.
Поскольку все операторы Нк1т коммутируют между собой, то собственные состояния
оператора Н = ]£ Нк1т можно выбрать в виде тензорного произведения векторов \пк1т):
Urn
>• F6)
Основное состояние, называемое «вакуумом», соответствует всем квантовым числам,
равным нулю:
|0,а0,0,...,0,...) = |0). F7)
Тогда энергия состояния F6), отсчитанная от энергии вакуума, равна:
751

Глава V
Е„ nUm =5>tfa. *<">№.• F8>
"ill nklm
kin,
Можно считать, что состояния вида F6) соответствуют пп] квантам с энергией
Йсот, ..., пк1т квантам с энергией Йсош и т.д. Эти кванты есть не что иное, как фотоны.
Мы видим, что каждой собственной моде в полости соответствует определенный тип
фотона.
Как и в формуле C8), можно ввести операторы уничтожения и рождения фотона
типа [klm):
а klm = ~ПГ \У>к1т + l"klm J >
allm=-^(Qklm-iPklm) F9)
и установить формулы, совпадающие с C9), D0) и D1):
[аЫт > акГт' ] = 5М' 5Н' 8 W > G0)
G2)
I \ (°ГпГ" (<■)"" ,nv
Р. Квантовое состояние поля
В самом общем случае состояние поля описывается линейной суперпозицией
состояний F6):
|v@)= S c„m 1и @|/!ш,...,лш,...). G3)
яш л */»»'•••
Уравнение Шредингера:
/Й^|\|/(г)) = Я|\|/@) G4)
позволяет получить коэффициенты ся w (r) в виде:
с„ „ @ = с„ я @) <? *"" . G5)
752

Одномерный гармонический осциллятор
у. Оператор поля
В результате квантования поле ^(r, t) становится наблюдаемой 5(г), не зависящей
более от /, которую можно получить путем замены в формуле E4) qklm(t) на Qklm:
S(r) = 2^-fklm(r)Qklm. G6)
С помощью формулы F9) можно выразить 5(г) через операторы рождения и
уничтожения:
S(r) = -т= 2 — fklm(r)[aklm +a+klm]. G7)
V2 Urn Pk{m
Рассуждения, аналогичные сделанным в § 2-е-8, помогают показать с помощью
формул G1) и G5), что единственными частотами Бора, способными проявиться в ходе
эволюции во времени среднего значения поля E(г))(г) = (\|/(г)| 5(г) |\|/(/)), являются
частоты а)ш/2я, co211/27i,..., a>klm/2n,..., связанные с пространственными
распределениями /ш(г),/2П(г),...,/ш(г),... Таким образом, (S(r))(f) является линейной
суперпозицией классических стоячих волн, способных существовать в полости. Вычисления,
аналогичные выполненным в §2-е-8, позволили бы показать, что (S(r)) удовлетворяет
уравнению D8).
И, наконец, можно констатировать, что 5(г) и Я не коммутируют. Поэтому в
квантовой теории невозможно с уверенностью и одновременно знать количество
фотонов и значение электромагнитного поля в произвольной точке пространства.
ЗАМЕЧАНИЕ
Для электромагнитного поля можно сконструировать когерентные состояния,
аналогичные тем, которые были введены в дополнении Gy, реализующие наилучшее совпадение
между несовместимыми величинами: полем и энергии.
8. Флюктуации вакуума
В § D-1 главы V мы видели, что в основном состоянии гармонического осциллятора (Ху = 0 ,
тогда как (X ) Ф 0, и мы обсуждали физический смысл этого типично квантового эффекта.
В рассматриваемой здесь задаче оператор 5(г) имеет много общего с оператором X главы V:
действительно, из формулы G7) видно, что S(г) является линейной комбинацией операторов
рождения и уничтожения. Рассмотрим среднее значение 5(г) в основном состоянии |0) поля,
48 Квантовая механика
753

Глава V
то есть в «фотонном вакууме». Поскольку диагональные элементы матриц операторов рождения и
уничтожения равны нулю, то
@|5(г)|0) = 0. G8)
Напротив, элемент матрицы, соответствующей оператору р(г)] , отличен от нуля.
Действительно, согласно G1):
к,„|0) = 0;
@kr„,,=0; G9)
[ (°| fl*vw aL I °) = 5«- S,r 5m„,.,
и простой расчет позволяет установить на основании формулы G7), что
@|[5(r)]2|0) = iS-i-[/w„,(r)]2. (80)
1 *''" 9 Urn
Отсюда следует, что в вакууме, то есть в отсутствие фотонов, электромагнитное поле S(г) в
любой точке пространства в среднем равно нулю, но его среднеквадратичное отклонение не равно
нулю. Это, например, означает, что при измерении S(r) можно получить результат, не равный
нулю, если даже в пространстве нет ни одного фотона. Этот вывод не имеет эквивалента в
классической теории, где в отсутствие поля энергия в точности равна нулю. Такой результат часто
интерпретируют как существование «флюктуации фотонного вакуума», характеризуемых
выражениями G8) и (80).
Введение понятия флюктуации вакуума имело интересные физические последствия для
теории взаимодействия атомных систем с электромагнитным полем. Рассмотрим, например, атом в
состоянии I Е/ с энергией Е , облучаемый электромагнитной волной в ее классическом
понимании. В дополнении АХш с помощью теории возмущений покажем, что такое облучение может
перевести атом в состояние с большей энергией (поглощение фотона) или в состояние с меньшей
энергией (индуцированное испускание фотона). Напротив, в рамках полуклассической теории
атом остается в состоянии | Е) неограниченно долго, если поле в пространстве отсутствует. Мы
только что установили, что даже в отсутствие падающих фотонов атом «чувствует» флюктуации
вакуума, связанные с квантовым характером электромагнитного поля. Под действием этих
флюктуации он может испустить фотон и перейти в состояние с меньшей энергией (полная энергия
системы при этом сохраняется): такое явление получило название спонтанной эмиссии, которую
можно рассматривать как испускание фотона, «индуцированное флюктуациями вакуума»
(«спонтанное поглощение», сопровождающееся переходом атома в состояние с большей энергией
существовать не может, так как поле в основном состоянии не может отдать энергию).
Можно показать также, что существует еще один эффект, связанный с флюктуациями
вакуума. Они вынуждают атом испытывать хаотическое движение, которое слегка изменяет энергию
уровней. Открытие этого эффекта в спектре атома водорода (сдвиг Лэмба) стало отправной точкой
для развития современной квантовой электродинамики.
754

Одномерный гармонический осциллятор
ЗАМЕЧАНИЕ
Ранее мы всегда выбирали за начало отсчета энергии состояний поля энергию вакуума.
На самом деле теория гармонического осциллятора дает нам абсолютное значение энергии
вакуума:
E0 = l\b«>klm- (81)
klm I
Естественно, имеется тесная связь между Е0 и магнитной и электрической энергиями
«флюктуации вакуума». Одна из трудностей квантовой электродинамики состоит в том, что
сумма (81) стремится к бесконечности, как и сумма (80)! Однако это затруднение можно
преодолеть: путем «перенормировки» удается избежать бесконечных значений и вычислить
действительно наблюдаемые эффекты, как, например, сдвиг Лэмба, с замечательной
точностью. Эти важные проблемы, естественно, требуют отдельного рассмотрения.
Дополнение Ly
ОДНОМЕРНЫЙ ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
В ТЕРМОДИНАМИЧЕСКОМ РАВНОВЕСИИ
ПРИ ТЕМПЕРАТУРЕ Т
1. Средняя энергия.
a. Нормировочный множитель.
b. Вычисление \Н/.
2. Физическое обсуждение.
a. Сравнение с классическим осциллятором.
b. Сравнение с двухуровневой системой.
3. Приложения.
a. Излучение абсолютно черного тела.
b. Закон распределения Бозе-Эйнштейна.
c. Удельная теплоемкость твердых тел при постоянном объеме.
4. Распределение вероятности наблюдаемой X .
a. Определение плотности вероятности р(х).
b. Вычисление р(х) .
c. Физическое обсуждение.
d. Теорема Блоха.
48*
755

Глава V
Это дополнение посвящено изучению физических свойств одномерного
гармонического осциллятора, находящегося в равновесии с термостатом при температуре Т.
Известно (см. дополнение Еш), что такой осциллятор не может находиться в чистом
состоянии (его нельзя описать кет-вектором |v)). Неполнота информации и
статистическая механика позволяют охарактеризовать его состояние как статистическую смесь
стационарных состояний |ф;1) с весовыми коэффициентами, пропорциональными
е-Е„/кт ^ ^ — постоянная Больцмана, Еп — энергия состояния [ф,,)). В § 5-а дополнения
Еш мы видели, что соответствующий оператор плотности записывается в виде:
где Н — гамильтониан системы и
p = Z-le-H,kT, A)
Z = tr e~Hlkr B)
нормировочный множитель, обеспечивающий равенство:
trp = l. C)
Сейчас мы найдем среднее значение (#) энергии осциллятора, дадим физическую
интерпретацию полученному результату и покажем, что он используется во многих
физических задачах (излучение черного тела, удельная теплоемкость и т.д.). И, наконец,
установим выражение для плотности вероятности наблюдаемой X (положение
частицы) и обсудим вытекающие из него следствия.
1. Средняя энергия
а. НОРМИРОВОЧНЫЙ МНОЖИТЕЛЬ
Значения энергии Еп состояний |ф,}) в соответствии с результатами § В главы V
равны (п +1 / 2) /Ш). Поскольку уровни энергии не вырождены, согласно формуле B)
имеем:
Z= Ё(ф L-"/A7U)= £*-<»+i'2)i»»/«- = е-Ш2кт\\ + е-Шкт + е'2Шкт -^ ..]. D)
В квадратных скобках выражения D) нетрудно узнать геометрическую прогрессию со
знаменателем e~tmlkT. Тогда
-Ш2кТ
^ = 1 -ШкТ ' E)
756

Одномерный гармонический осциллятор
Ь. ВЫЧИСЛЕНИЕ (Я)
Согласно формуле C1) дополнения Е1П и выражению A) для р :
(Н) = tr (Яр) = Z"'tr (He'H,kT). F)
Используя явное выражение для следа в базисе {|ф„) }, получим:
<#> = Z"' £ (п +1 / 2) йсог4'"^7 . G)
Чтобы вычислить эту величину, продифференцируем обе части равенства D) по Т:
^ = Т^Ё(п + 1/2)йше-("+""»«г. (8)
а! к! п=о
Видно, что
(Я) = *Г21 —, (9)
и простой расчет дает с учетом E):
(//) = — + -
2 е"ш/" -1
2 S 2(«i+i/2)»(oe-[("'+)+("'t)+("'+,/2,)to,*r
„v=0 /;v=0 н_=0
Y V V -1К + 1/2) + (лу + !/2) + (я.+1/2)]Аш/АГ
n =() л =0 /;.=0
757
A0)
ЗАМЕЧАНИЯ
(i) Изотропный трехмерный осциллятор
Используя результаты и обозначения дополнения Ev, можно записать:
где \НХ/ определяется выражением:
(Hx) = Z-,tv(Hxe-H'kT) =
A2)

Глава V
Суммирования по пу и по nz факторизуются и идентичны в числителе и знаменателе,
вследствие чего:
ЁК + 1/2)йсое-<"'+,Лш"г
• М = ^—. . A3)
V p-(nx + \/2)hia/kT
пх=0
Это выражение идентично вычисленному в предыдущем параграфе (отличается лишь заменой
п на пх ), и, следовательно, \НХ) равно значению, приведенному в A0). Нетрудно показать,
что для Шу) и \HZ) получаются аналогичные выражения. Таким образом, мы установили
следующее: при термодинамическом равновесии средняя энергия трехмерного изотропного
осциллятора равна утроенной энергии одномерного осциллятора, имеющего ту же частоту.
(ii) Классический осциллятор
Энергия Ж(х, р) классического одномерного осциллятора равна:
2 1
Ж(Х, р) = ^-+ -тсо V . A4)
2т 2
В выражении A4) величины х и р могут принимать любые значения между -°° и
+оо. В соответствии с положениями классической статистической механики
средняя энергия такого осциллятора определяется выражением:
, % rr.r(x,p)e-^p),kTdxdp
J1L« ; ,kTdxdp
Подставим A4) в A5) и после несложных вычислений получим:
(ж) = 1сТ. A6)
Рассуждения, аналогичные приведенным в замечании (i), показывают, что результат,
полученный в формуле A6), нужно умножить на 3 при переходе к трехмерному случаю.
2. Физическое обсуждение
а. СРАВНЕНИЕ С КЛАССИЧЕСКИМ ОСЦИЛЛЯТОРОМ
На рис. 1 сплошной кривой изображена зависимость средней энергии (я)
одномерного квантового осциллятора от температуры Т и пунктиром — аналогичная
зависимость средней энергии (.ж) классического осциллятора.
758

Одномерный гармонический осциллятор
ж Средняя шергпя
Рис.1
Зависимость средней энергии квантового
осциллятора от температуры (сплошная кривая) в сравнении
со средней энергией классического осциллятора
(пунктирная кривая)
При Г = 0 имеем (#) = Йоо/2 . Этот результат соответствует тому факту, что при
абсолютном нуле достоверно известно, что осциллятор находится в основном состоянии
|ф0) с энергией /ко/2 (по этой причине величину /Ш)/2 иногда называют «нулевой
энергией»). Что касается классического осциллятора, то он при этом остается
неподвижным (р = 0) в положении устойчивого равновесия (х = 0), и его энергия равна
нулю, то есть (ж) = 0.
При малых значениях Т, а точнее, пока кТ « Ш , преобладает лишь населенность
основного уровня, и (я) остается практически равной /Ко / 2: сплошная кривая на рис. 1
близка к горизонтали. Это же можно получить, исходя из выражения A0), так как при
малых Т оно приближенно равно:
(Н) = — + Ьш-Шкт. A7)
Напротив, при больших Т, то есть, когда кТ »/гсо , это же выражение дает:
то есть
(H)~kT A9)
с точностью до бесконечно малых величин порядка kT(hu> I кТJ, таким образом,
прямая (я) = кТ является асимптотой функции (н)(Т).
В заключение отметим, что при больших температурах (кТ»Ш) и квантовый и
классический осцилляторы имеют одну и ту же энергию, равную кТ . Заметное различие
между ними может проявляться только при низких температурах, так как игнорировать
квантование энергии осциллятора в случае, когда характеризующая термостат энергия кТ
становится того же порядка, что и интервал /гсо, разделяющий два соседних уровня
осциллятора, уже невозможно.
759

Глава V
b. СРАВНЕНИЕ С ДВУХУРОВНЕВОЙ СИСТЕМОЙ
Интересно сравнить полученные выше результаты с выводами, известными для
двухуровневой системы. Пусть |\|/,) и |\|/2) — состояния системы с энергиями Ех и
Е2, причем Ех< Е2. Для такой системы общее решение F) дает:
, ч Е{е-Е>/кТ + Е2е-Е>,кт
(")= e-^rJE2«r ■ B0)
Рис.2
Зависимость средней энергии квантовой
системы двух уровней с энергиями Е{ и Е2 от
температуры Т при термодинамическом
равновесии
Средняя энергия двухуровневой системы, определяемая формулой B0),
представлена на рис.2. Для малых температур (кТ« Е2-Ех) члены с е~Е{,кт являются
преобладающими как в числителе, так и в знаменателе выражения B0), ибо Е2 > Ех, и тогда:
<Я)-ТЗГ»Я.- B1)
Можно доказать, что вблизи Т = 0 касательная к кривой практически горизонтальна.
Для больших значений Т (то есть при кТ » Е2- Ех) кривая асимптотически стремится
к значению (£, + Е2) 12. Эти результаты легко объяснить: при 7 = 0 система находится
в основном состоянии | \|/ х) с энергией Ех, а при высоких температурах населенности
уровней практически выравниваются, и энергия стремится к значению, равному
полусумме энергий Ех и Е2.
Если кривые, изображенные на рис. 1 и рис.2, имеют похожее поведение при низких
температурах, то при высоких температурах их ход существенно отличается. Средняя
энергия гармонического осциллятора ничем не ограничена и линейно возрастает с
увеличением температуры, тогда как для двухуровневой системы средняя энергия не может
быть больше некоторого значения. Это различие объясняется тем, что спектр энергии
гармонического осциллятора не имеет предела со стороны высоких частот: при
увеличении температуры занимаются уровни со все большими значениями квантового числа п ,
что и приводит к увеличению средней энергии. Напротив, в двухуровневой системе, как
только населенности двух уровней стали равными, дальнейшее повышение температуры
не изменяет ее средней энергии.
760

Одномерный гармонический осциллятор
3. Приложения
а. ИЗЛУЧЕНИЕ АБСОЛЮТНО ЧЕРНОГО ТЕЛА
Во введении к главе V мы уже отмечали (а в дополнении Kv приводили более точное
доказательство), что электромагнитное поле в полости эквивалентно ансамблю независимых одномерных
гармонических осцилляторов, причем каждый из этих осцилляторов связан с одной из стоячих
волн, способных существовать в полости (собственные моды), и имеет ту же частоту, что и такая
волна. Покажем, что этот вывод в комбинации с полученными выше результатами для средних
энергий (ж) и (я) сразу же позволяет получить законы Рэлея—Джинса и Планка для излучения
абсолютно черного тела.
Пусть 7 — объем полости, стенки которой будем считать идеально отражающими. Первые
моды полости (то есть моды с минимальными частотами) критическим образом зависят от формы
полости. Напротив, для мод с большими частотами, длины волн которых X = с IV малы по
сравнению с размерами полости, путем классического электродинамического расчета можно без труда
доказать следующий результат: если обозначить число мод, частота которых заключена между V
и V + dv, символом N(v)dv ,то N(v) практически не зависит от формы полости и равняется:
N(v) = ^-r. B2)
С
Пусть u(v)dv — объемная плотность электромагнитной энергии в полосе частот от V до
V + dv , заключенной в полости в условиях термодинамического равновесия при температуре Т.
Чтобы получить энергию Tu(y)dv), нужно умножить число мод с частотами между V и V + dv
на среднюю энергию соответствующих гармонических осцилляторов. Ранее мы находили эту
энергию, которая была равна (Ж/ или (#)-#0)/2 * в зависимости от того, рассматривалась
задача классически или квантово. В итоге, используя формулы A0), A6) и B2), получим:
иа{у) = Щ-кТ B3)
С
при классическом рассмотрении и
* Мы используем (//) - /КО / 2 , а не (#) по следующей причине: и(у) обозначает
электромагнитную энергию, которую можно извлечь из полости. При абсолютном нуле все осцилляторы
находятся в своем основном состоянии и никакая энергия не может быть испущена полостью во
внешнее пространство, так как система находится в состоянии с минимально возможной энергией.
Поэтому функция w(v) должна равняться нулю при абсолютном нуле, что, впрочем,
подтверждается экспериментально. Приведенные рассуждения показывают, почему среднюю энергию поля в
полости следует отсчитывать от ее значения при Т = 0.
761

Глава V
«fl(v) = —5--TwiT7 B4)
С £ - 1
при квантовом рассмотрении.
Нетрудно заметить, что формула B3) представляет собой закон Рэлея—Джинса, а формула
B4) совпадает с законом Планка, который переходит в пределе малых частот или высоких
температур (hvI кТ« 1) в закон Рэлея—Джинса. Различие этих двух законов отражает различия,
существующие между двумя кривыми, изображенными на рис. 1. Именно для преодоления
трудности применения закона Рэлея—Джинса в области больших частот (ис1 (V) —> <*> , если V —» <*> , что
абсурдно с физической точки зрения) Планк был вынужден постулировать, что энергия каждого
осциллятора должна изменяться дискретным образом, то есть скачками, пропорциональными
частоте (квантование энергии). И он получил формулу B4), прекрасно описывающую
экспериментальные результаты.
Ь. ЗАКОН РАСПРЕДЕЛЕНИЯ БОЗЕ—ЭЙНШТЕЙНА
В предыдущем параграфе вычислялось среднее значение энергии (#), теперь же мы
вычислим среднее значение оператора N . Поскольку согласно формуле (В-15) главы V:
# = [ЛГ + -]йоо, B5)
из выражения A0) следует, что
Н=7^гг B6)
Эквидистантность уровней одномерного гармонического осциллятора позволяет
ассоциировать осциллятор в состоянии ф,Л с ансамблем, состоящим из п одинаковых частиц (квантов) с
одинаковой энергией hv . В такой интерпретации операторы а+ и а , описывающие переходы из
состояния |ф„) в состояние \Ц)п+\) или в состояние [ф,,^), создают или уничтожают одну
частицу. В этом смысле N является оператором числа частиц ( ф„) является собственным
состоянием оператора N с собственным значением п ).
В частном случае электромагнитного поля кванты, ассоциированные с каждым
гармоническим осциллятором, являются фотонами. Каждой моде полости, рассмотренной в предыдущем
параграфе, соответствуют фотоны определенного типа, характеризуемые частотой, поляризацией,
пространственным распределением моды. Выражение B6) определяет среднее количество
фотонов, ассоциированных с модой, имеющей частоту V, при термодинамическом равновесии. В нем
нетрудно узнать закон распределения Бозе—Эйнштейна, который может быть доказан и в более
общей формулировке. Здесь же мы получили его просто из анализа гармонического осциллятора
с учетом интерпретации состояний |ф;|у .
762

Одномерный гармонический осциллятор
ЗАМЕЧАНИЕ
Строго говоря, распределение Бозе—Эйнштейна для бозонов, имеющих энергию £ ,
имеет вид:
(А,)%.е-Л_Г B7)
где \1 — химический потенциал. В случае фотонов \1 = 0. Это связано с тем, что полное
число фотонов в полной системе «излучение + термостат» не является постоянным из-за
возможности поглощения и испускания фотонов стенками.
с. УДЕЛЬНАЯ ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛ ПРИ ПОСТОЯННОМ ОБЪЕМЕ
Здесь мы ограничимся моделью Эйнштейна (см. дополнение Av), в рамках которой твердое
тело рассматривается как ./Г атомов, независимо колеблющихся относительно своих положений
равновесия с одной и той же частотой а)£ . Таким образом, внутренняя энергия U твердого тела
при температуре Т равна сумме средних энергий Л изотропных трехмерных осцилляторов,
находящихся в термодинамическом равновесии при этой температуре. Используя замечание (i)
предыдущего параграфа, запишем:
и = Щн), B8)
где (//) — средняя энергия одномерного гармонического осциллятора с частотой @Е . С другой
стороны, известно, что удельная теплоемкость при постоянном объеме cv является производной
от внутренней энергии U по температуре:
Cv = *L = 3..r—(H), B9)
что дает с учетом формулы A0):
\ кТ
[еы*
] еЬ»Е1кТ
1кт-\]2
С"=3"Г* [g^^-!f • C0)
Зависимость cv от Т представлена на рис.3. Согласно формуле B9) cv пропорциональна
производной от сплошной кривой, изображенной на рис. 1, по температуре, что дает возможность
простым способом определить поведение зависимости cv от Т.
Из рис.1 видно, что (Я) вблизи нулевой температуры нарастает очень медленно и угол наклона
касательной в точке Т = 0 также равен нулю, то есть при Т = 0 величина cv равна нулю и
медленно увеличивается. Напротив, в области больших температур (кТ » Й00£ ) среднее значение (//)
763

Глава V
Рис.3
Зависимость удельной теплоемкости
твердого тела при постоянном давлении
cv от температуры в рамках модели
Эйнштейна. Предел, к которому стремится cv
при высоких температурах, соответствует
классическому закону Дюлонга и Пти
стремится к кТ , то есть cv стремится к постоянной величине 3. I к , не зависящей от @t .
Переход между этими двумя областями происходит, когда ЙСО£ / кТ = 1.
Асимптота на рис.3 соответствует закону Дюлонга и Пти: если взять грамм-атом любого
твердого вещества, .Г равно числу Авогадро, и предельное значение cv оказывается равным 3/?,
где R — универсальная газовая постоянная, то есть примерно 6 кал/(град моль).
Как отмечалось выше, квантовый характер колебаний кристалла проявляется при низких
температурах, когда кТ по порядку величины меньше или равно ЙО) Е . Что касается cv , то при
стремлении температуры к абсолютному нулю удельная теплоемкость также стремится к нулю.
Все происходит так, как если бы степени свободы, соответствующие колебаниям кристалла,
оказались «замороженными» ниже некоторой температуры и более не влияли на теплоемкость.
Физически такое поведение нетрудно понять: при абсолютном нуле каждый осциллятор находится в
своем основном состоянии |ф0) , и, пока тепловая энергия кТ меньше /Ш)£ , он не может
поглотить ее, так как первый возбужденный уровень оказывается значительно выше.
ЗАМЕЧАНИЯ
(i) Сравнение с удельной теплоемкостью двухуровневой системы
Аналогичные рассуждения можно применить и в отношении образца, содержащего
двухуровневые системы (например, парамагнитный образец, состоящий из .Г спинов 1/2).
С точностью до постоянного множителя его удельная теплоемкость cv равна производной
от кривой, изображенной на рис.2. Для такой системы зависимость cv от Т представлена
на рис.4.
Поведение cv вблизи Т ~ О подобно изображенному на рис.3. Напротив, видно, что
при кТ» (Е2 - Ех) величина cv стремится к нулю, так как средняя энергия становится
не зависящей от Г и равной (Ех + Е2}/2 (см. рис.2). Для двухуровневой системы
функция cv(T) имеет максимум (аномалия Шоттки), интерпретация которого такова: как и
гармонический осциллятор, двухуровневая система не может поглощать тепловую энергию
при столь низких температурах, что кТ <<{Е2- Ех), то есть начальным является нулевое
глк
764

Одномерный гармонический осциллятор
значение; затем уровень Е2 заселяется, и по мере увеличения Т теплоемкость возрастает.
При достаточно высокой температуре населенности уровней выравниваются, система более
не может поглощать тепловую энергию, так как населенности не могут больше изменяться,
в результате чего теплоемкость снова стремится к нулю, если Т —> °° .
Рис.4
Зависимость удельной теплоемкости cv от Т
для ансамбля двухуровневых систем. При
высоких температурах теплоемкость стремится к
нулю, что объясняется тем, что спектр энергий
ограничен сверху
(ii) Модель Эйнштейна позволяет объяснить, почему удельная теплоемкость cv стремится к
нулю, когда Т —> 0 (этот результат невозможно объяснить классически). Но такое
объяснение страдает схематичностью и не позволяет найти точную зависимость от Т при низких
температурах.
В реальном кристалле все осцилляторы связаны друг с другом, и это взаимодействие
порождает ансамбль собственных мод колебаний (фононы), частоты которых могут
принимать значения от нуля до некоторой частоты среза (см. дополнение Jv). Поэтому выражение
C0) следует просуммировать по всем возможным частотам V с учетом зависимости от
частоты количества мод, заключенных между V и V + dv . В результате получится выражение
для удельной теплоемкости, которое при низких температурах пропорционально Т , что
хорошо подтверждается экспериментом.
4. Распределение вероятности наблюдаемой X
а. ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ ВЕРОЯТНОСТИ р(х)
Вернемся к задаче об одномерном гармоническом осцилляторе, находящемся в
условиях термодинамического равновесия, и определим вероятность p(jt) найти в
результате измерения положения X частицы значение, заключенное между х и х + dx .
Функция р(х) играет важную роль во многих физических задачах: например, в модели
Эйнштейна твердого тела ширина функции р(дс) определяет амплитуду колебаний
атомов; зависимость этой ширины от Т позволяет понять явление плавления [оно
происходит в том случае, если ширина функции р(;с) не может считаться малой по сравнению
с межатомным расстоянием].
Если осциллятор находится в стационарном состоянии | Ф„), соответствующая
плотность вероятности р(д:) равна:
765

Глава V
р„(*Нф„(л:)|2=(*|ф„)(ф„|х). C1)
В условиях термодинамического равновесия осциллятор описывается статистической
смесью состояний |ф,;) с весовыми коэффициентами Z~le~E",kT. Тогда плотность
вероятности приобретает вид:
pW = Z-,2pll(j:)^/*r> C2)
п
то есть р{х) является взвешенной суммой плотностей вероятности р„(х), связанных с
различными состояниями |ф„), некоторые из которых представлены на рис.5 и рис.6
главы V. Ниже мы увидим, что осцилляции функций рп(х), изображенные на этих
рисунках, постепенно исчезают по мере увеличения индекса суммирования п;
действительно, покажем, что р(х) имеет простую гауссову форму.
Плотность вероятности р(х), определенная формулой C2), связана с оператором
плотности р гармонического осциллятора при термодинамическом равновесии.
Используя формулы C1) и C2), получим:
р(х) = г-*Ъе-Е°,кт(х\<р„)(ч>,1\х). C3)
В правой части можно выделить оператор е~Н1кт, записываемый с учетом соотношения
замкнутости по состояниям |ф„) в виде:
е-н„т = е-„пт J. |фп)(фл | = 1е-с„«т |фя)(фл | C4)
п п
Видно, что
p(x) = Z-](x\e-H,kT\x) = (x\p\x), C5)
где оператор плотности р определяется формулой A). Таким образом, р(х) равняется
диагональному элементу матрицы р, соответствующему кет-вектору | х).
Ь. ВЫЧИСЛЕНИЕ р(х)
Известно, что
Н = Ш\ а+а + —
2
C6)
так что р(х) можно представить в форме:
p(x) = Z-'e-mFx{x), C7)
766

Одномерный гармонический осциллятор
где
Х =
Й@
Иг
C8)
Fx(x) = (x\e-^a\x). C9)
Чтобы найти р(х), достаточно вычислить этот диагональный матричный элемент.
Для этого определим зависимость Fx (х), заменив х на х + dx . Поскольку кет | х + dx)
известен [см. дополнение Еи, соотношение B0)]:
\x + dx) =
\-i — P]
ft
\x).
D0)
то, подставляя это равенство и равенство, сопряженное ему, в C9), пренебрегая, как и ранее, бес
конечно малыми второго порядка малости по dx , получим:
dx
"ft
Fx(x + dx) = Fk(x) + i— (х\[р,е-*"*°\\х).
D1)
Матричный элемент, стоящий в правой части равенства D1), включает в себя оператор Р,
пропорциональный (а-а+). Известно также действие оператора X, пропорционального
la + а+) на кет \х/. Поэтому следует преобразовать оператор Р, е
-Ха+а
так, чтобы явно
выделить X. С этой целью найдем соотношение, существующее между ае ° " и е аа . В
представлении ( ф„) } оно выглядит наиболее просто:
то есть
е а = е ае
D2-а)
D2-Ь)
D3)
\-th-
e-hr"a ■■
\ + th-\ae-Ua.
Аналогично можно показать, что
е'^'а* = еЛг Vх"*"
l + th-
2)
а =\ \-tn—\a e
D4)
D5)
D6)
767

Глава V
Теперь вычтем почленно равенства D4) и D6):
X
{a-a\e-^aY-th-\a + a\e-^a)i ,
D7)
где символ [А, В\ обозначает антикоммутатор:
[Л, В]+ = АВ + ВА. D8)
Если учесть численные множители, следующие из формул (В-1) и (В-7) главы V, то равенство D7)
примет вид:
Гр>в"Ал+<,] = 1та)Л-[х,в"Ал+в] . D9)
Подставим этот результат в соотношение D1):
тсо X , ,г , + 1 . v mco X
Fx(x + dx)-Fx(x) = -—dxth-(x\\X,e-}Ma\ \x) = -2x—th-~FAx)dx. E0)
n 2 L J+ n 2
Таким образом, функция Fk (x) удовлетворяет дифференциальному уравнению:
2х
dx'^'l2
— ^W + tt^W^O. E1>
где величина £ , имеющая размерность длины, определена равенством:
5 .iJLcb* =Jj_crAf^-V E2)
ъ Vwco 2 \та> \2кТ)
Уравнение E1) интегрируется сразу же:
Fk(x) = Fk@)e-x2li\ E3)
Итак, нам известна функция р(лг) с точностью до постоянного множителя, так как согласно C7)
имеем:
р(*) = Z-le-x,2Fx@)e-x2,e . E4)
Поскольку интеграл от р(лг) по всей оси Ох должен равняться 1, то окончательно:
у ч 1 -Г2/?2
р(х) = —ге х1% . E5)
£л/Я
Таким образом, функция p(jc) является гауссовой, ширина которой характеризуется параметром % ,
определенным в формуле E2).
768

Одномерный гармонический осциллятор
с. ФИЗИЧЕСКОЕ ОБСУЖДЕНИЕ
С помощью выражения E5) для плотности вероятности нетрудно найти:
<Х> = 0;
(хг) = (АХJ=|-. E6)
На рис.5 представлена зависимость (АХJ от температуры Т. Из формулы E2) следует,
что при Т = О величина (АХJ равна h / 2mco . Этот результат можно было ожидать, так
как при абсолютном нуле осциллятор находится в основном состоянии, и р(;с) совпадает
с |ф(,(л:)| ; затем (АХJ начинает расти и при кТ» /ко :
(А*J - -^7- E7)
В этом случае р(лс) совпадает с плотностью вероятности классического осциллятора,
находящегося в термодинамическом равновесии при температуре Т:
-V(x)lkT
e-vwm j
р (jc) = — = . е 2kT , E8)
Vmco2
которая приводит к выражению (Ajcc/) = кТ/т(хJ (пунктирная прямая на рис.5). И в
этом случае предсказания классической и квантовой теорий совпадают при кТ » #@ .
Рис.5
Зависимость среднеквадратичного отклонения
(АХ)*" от температуры для гармонического
осциллятора в условиях термодинамического
равновесия. При Г -» «> оно стремится к
классическому значению, изображенному
пунктиром; при низких температурах квантовые
эффекты (соотношение неопределенностей
* ^ Гейзенберга) мешают ему обратиться в нуль.
Применим теперь полученные результаты к задаче о плавлении твердого тела (для
простоты примем одномерную модель Эйнштейна; см. дополнение Av)» Эксперимент
показывает, что твердое тело плавится, когда АХ имеет порядок доли ч) от межатомного
49 Квантовая механика
769

Глава V
расстояния d . Приближенное значение температуры плавления Tf определяется
выражением:
|г-л'. E9,
где для £ взято значение E2) при Т-Tf. Допустим, что температура Tf достаточно
велика, чтобы выполнялось неравенство kTf »ШЕ; тогда в формулу E9) можно
подставить асимптотическое значение E7)*, в результате чего получим:
—f— = r]2d2. F0)
т(д2Е
Если положить:
Йй)£=ШЕ F1)
(величину 0£ называют «температурой Эйнштейна») и заметить, что d мало меняется
от одного вещества к другому (во всяком случае гораздо меньше, чем со£, то есть ©Е),
то можно записать приближенное выражение:
7}
— = const. F2)
mQE
Итак, температура плавления кристалла приблизительно пропорциональна квадрату
частоты колебаний, характерных для кристалла.
d. ТЕОРЕМА БЛОХА
Рассмотрим оператор е~щХ , где q — вещественная переменная. Его среднее значение:
(e-**) = tr[pe-"<x] F3)
[где р определяется формулой A)] является функцией q . Обозначим ее символом f(q):
f{q) = (e-iqX). F4)
В теории вероятностей f(q) называют характеристической функцией случайной переменной х.
* Это возможно не всегда. Вспомним, что гелий остается жидким при атмосферном давлении
даже при Т = 0, то есть нельзя пренебречь значением £ по сравнению с d при любых
температурах (см. дополнение Av).
770

Одномерный гармонический осциллятор
В представлении {\х/ } эта функция легко вычисляется:
f(q) = j*dx(x\ pe~ikx \x) = n^(jc| p |x)e'ikx = fcdx p(x)e'ikx . F5)
С точностью до множителя \2п функция f{q) совпадает с преобразованием Фурье от функции
р(х) , вычисленной выше (§ 4-Ь). Обе функции имеют гауссову форму, и интеграл F5) равен:
/(9)=eV/4 F6)
или в соответствии с формулой E6):
(e-,qX) = e 2К '. F7)
Вычисления, аналогичные тем, которые были выполнены в § 4-а и § 4-Ь, можно сделать и для
наблюдаемой Р , в результате чего будет получена плотность вероятности р(/?) :
p(p) = Z-lZe-E°lkT\4>„(P)\2- F8)
/I
Формула B4) дополнения Dv указывает, что
Р0>) = — р|* = —|. F9)
тсо V т(й ,
Таким образом:
Р(Р) = —г=е mW? . G0)
Соответственно, вычисление \£~' / привело бы к результату, подобному формуле F7):
_±_/р2
(е-*р) = е~*К К G1)
Обобщение формул F7) и G1) известно под названием теоремы Блоха: если G(X, Р) —
произвольная линейная комбинация операторов положения X и импульса Р одномерного
гармонического осциллятора, находящегося в термодинамическом равновесии при температуре Т, то
(е-"с) = е~^ >. G2)
Эта теорема используется в физике твердого тела, например, в теории испускания фотонов без
отдачи ядрами кристаллической решетки (эффект Мессбауэра).
49*
771

Глава V
Дополнение My
УПРАЖНЕНИЯ
1. Рассматривается гармонический осциллятор с массой т и частотой со. В момент
времени г = О состояние осциллятора задано выражением:
к@)) = Есл|Ф„),
п
где |ф;1) —стационарные состояния с энергиями (л + 1/2)/гсо .
a. Какова вероятность 0 того, что измерение энергии осциллятора в произвольный
момент времени t > О даст результат, превышающий 2/KD ?
b. Далее предполагается, что отличны от нуля только два коэффициента с() и с,.
Записать через с0 и сх условие нормировки вектора |\|/@)) и среднее значение (#)
энергии. Положить (я) = /zco ; вычислить \с0\ и |с,| .
c. Поскольку нормированный вектор состояния |\|/@)) определен с точностью до
общего фазового множителя, выбрать его так, чтобы коэффициент с0 был
вещественным и положительным. Обозначить с, = |с,|е'в|. Положить (#} = Ш и допустить, что
Х ' 2Vw©
Вычислить О,.
d. Определив, таким образом, вектор |\|/@)), записать |\|/(/)) для / >0 и найти
значение Ьj в момент времени г. Найти среднее значение (x)(t) положения в момент
времени г.
2. Трехмерный анизотропный гармонический осциллятор
В трехмерной задаче рассматривается частица с массой т и потенциальной энергией:
тоJ
i3l(x4r2) + fi-^]z2
где со и X — постоянные, удовлетворяющие неравенствам:
@>0, 0<Х<3/4.
а. Каковы собственные состояния гамильтониана и соответствующие им энергии?
772

Одномерный гармонический осциллятор
Ъ. Вычислить энергию и обсудить ее зависимость от X , найти четность и кратность
вырождения основного уровня и двух первых возбужденных уровней.
3. Гармонический осциллятор, состоящий из двух частиц
Две частицы, имеющие одинаковую массу т и определенные положениями Х[9
Х2 и импульсами Р{, Р2, находятся в поле действия потенциала:
У(Х) = -ты2Х2.
2
Частицы не взаимодействуют друг с другом.
a. Записать оператор Я, то есть гамильтониан системы, состоящей из двух частиц.
Показать, что Я можно записать в виде:
Н = Н]+Н2У
где Я, и Я2 действуют соответственно только в пространстве состояний частицы A) и
частицы B). Вычислить энергии системы двух частиц, кратность их вырождения и
соответствующие волновые функции.
b. Образует ли оператор Я полный ансамбль коммутирующих операторов? Такой
же вопрос для ансамбля { Я,, Я2 }. Обозначим символом Ф;| п ) собственные векторы,
общие для операторов Я, и Я2. Записать соотношения ортонормировки и замкнутости
для состояний Ф„ п ).
c. Рассматривается система, находящаяся в момент времени г = О в состоянии:
|¥@))Л(|ф0,0) + |Ф,,0) + |Ф0.1) + |Фи».
Какие результаты и с какими вероятностями можно ожидать, если в этот момент
времени измеряется:
— полная энергия системы?
— энергия частицы A)?
— положение или скорость этой частицы?
4. (Это упражнение следует из предыдущего и использует те же обозначения).
Система из двух частиц в момент времени г = 0 находится в состоянии |\|/@)),
определенном в упражнении 3.
а. В момент времени t = 0 измеряется полная энергия Я и получен результат 2Ш .
773

Глава V
а. Вычислить средние значения в произвольный положительный момент времени
t для положения, импульса и энергии частицы A). Аналогичный вопрос для частицы B).
р. В этот момент времени t >0 измеряется энергия частицы A). Какие
результаты и с какими вероятностями можно получить? Аналогичный вопрос, если измеряется
положение частицы A); изобразить кривую, определяющую соответствующую
плотность вероятности.
Ъ. Вместо измерения в момент времени г - О полной энергии Я измеряется энергия
Я2 частицы B), и получен результат Ш/2. Как изменится ответ на вопросы а и Р
пункта а?
5. (Это упражнение является продолжением упражнения 3 с сохранением обозначений.)
Обозначим символами
Фя,,л ) собственные состояния, общие для операторов Я,
и Я2 с собственными значениями (л,+1/2)/Ш) и (п2 +1/2)/ко. Оператор Ре «обмена»
двумя частицами определяется выражением:
PeWn n ) = Wn n )•
е\ п I • " 2 / | " 2 • " I /
a. Доказать, что Р~х = Ре и что оператор Ре унитарный. Найти собственные
значения оператора Ре. Пусть В' = РеВРе+ — преобразованная с помощью оператора Ре
произвольная наблюдаемая В . Показать, что условие В' -В (В — инвариант
относительно обмена двух частиц) эквивалентно равенству [В, Ре] = 0.
b. Показать, что
рен2р; = нх.
Коммутирует ли Я с Pf? Вычислить преобразование наблюдаемых Х{, Р,, Х2, Р2 с
помощью оператора Ре.
c. Построить базис собственных векторов, общих для операторов Я и Ре.
Образуют ли эти два оператора полный набор коммутирующих операторов? Что произойдет со
спектром оператора Я и вырождением его собственных значений, если из собственных
векторов |ф) оператора Я сохранить только такие векторы, что Ре |ф) = -|Ф) ?
6. Гармонический осциллятор с зарядом в переменном электрическом поле
Одномерный гармонический осциллятор состоит из частицы с массой т и зарядом
q в поле потенциала V(X) = — wco2X2; в этом упражнении предполагается, что частица
774

Одномерный гармонический осциллятор
находится в электрическом поле $(t), параллельном оси Ох и зависящим от времени,
так что к V(x) нужно добавить потенциальную энергию:
W(t) = -qHt)X .
a. Записать гамильтониан H(t) частицы через операторы а и а+. Вычислить
коммутаторы этих операторов с H(t).
b. Пусть а@ — число, определяемое выражением:
a(r) = (v@|e|v@>,
где |\|/@) — нормированный вектор состояния рассматриваемой частицы. Ответить на
предыдущий вопрос, если a(f) удовлетворяет дифференциальному уравнению:
—a(f) = -i'coa(f) + /X(f).
dt
где X(t) определяется равенством:
у12тШ
Проинтегрировать это дифференциальное уравнение. Чему равны средние значения
положения и импульса частицы в момент времени t ?
c. Кет |ф@) определен выражением:
|Ф@) = [а-а(/)]|х|/@),
где а(г) имеет значение, вычисленное в (Ь). Используя результаты вопросов (а) и (Ь),
показать, что эволюция вектора |(p(f)) определяется выражением:
1Й^|Ф@> = [Я@ + Йю]|ф@>-
Как изменяется норма вектора |ф@) в зависимости от времени?
d. Предположим, что |\|/@)) является собственным вектором оператора а с
собственным значением ос@); показать, что |v|/(r)) также является собственным вектором
оператора а, собственное значение которого следует определить.
Вычислить через сс@) среднее значение невозмущенного гамильтониана
775

Глава V
Н0 = H(t)-W(t) в момент времени t. Определить среднеквадратичные отклонения
АХ , АР и АЯ0; как изменяются эти величины во времени?
е. Предположим, что в момент времени t = О осциллятор находится в основном
состоянии |ф@)). Электрическое поле действует между моментами времени 0 и Г, а
затем обращается в нуль. Какова эволюция при t>T средних значений (х)(/)и (P)(t) ?
Приложение: предполагая, что между моментами времени 0 и Г поле #'(/) имеет вид
${t) = tf()aw(a)'0, обсудить зависимость наблюдаемых явлений от разности частот
Асо = со7 — со (резонанс). Если в момент t > Т измеряется энергия, то какие результаты и
с какими вероятностями будут получены?
7. Рассматривается одномерный гармонический осциллятор, у которого гамильтониан Н
и стационарные состояния |ф„) удовлетворяют соотношению:
Я|ф„) = (п + 1/2)й(о|ф„).
Оператор U(k) определен выражением:
U(k) = eikx ,
где к — вещественная величина.
a. Является ли оператор U(k) унитарным? Показать, что его матричные элементы
удовлетворяют приведенному ниже соотношению независимо от п :
£|(<p„|t/(*)|<p„,)|2 = l.
п'
b. Выразить U(к) через операторы а и а+. Чтобы представить U(k) в виде
произведения экспоненциальных операторов, использовать формулу Глаубера (формула F3)
дополнения Вп).
c. Установить соотношения:
«ЧфоНфо);
<ф»К1фо) = -п>
VA2!
где X — произвольный комплексный параметр.
d. Выразить через Ек =ft2k212m и E^-fiix) матричный элемент (ф0| U(k)\q>n).
Что происходит, если к —> 0 ? Можно ли было заранее предвидеть этот результат?
776

Одномерный гармонический осциллятор
8. Оператор эволюции U(t, 0) одномерного гармонического осциллятора имеет вид:
£/(/,0) = *-'""*,
где
H = hJa+a + -).
a. Рассмотреть операторы:
a(t) = U + (t,0)aU(t,0)\
a + (t) = U*(ty0)a+U(t,0).
Вычислив их действие на собственные векторы |ф„) оператора Я, выразить a(t) и
a + (t) через а и а*.
b. Вычислить операторы X(t) и P(t), полученные из X и Р с помощью
унитарного преобразования:
X(t) = U + (t,0)XU(t,0);
P(t) = U + (t,0)PU(t,0).
Как интерпретировать полученные соотношения?
с. Показать, что кет U+\ —,0
'2@
11 х) является собственным вектором оператора Р с
собственным значением, которое следует определить, а также, что U+\ —, 0 | р)
явля-
V 2@ ; '" '
ется собственным вектором оператора X .
d. В момент времени t = 0 волновая функция осциллятора равна \|/(х, 0). Как
можно получить, исходя из \|/(;с, 0), волновую функцию в последующие моменты времени
tq = qn 12@, где q — целое положительное число?
e. В качестве функции \|/(jc, 0) взять волновую функцию ф„(х) стационарного
состояния. Вывести из предыдущего вопроса соотношение, которое должно существовать
между функцией ф„(;с) и ее преобразованием Фурье ф„(р).
/. Качественно описать эволюцию волновой функции в следующих случаях:
(i) \|/(jc, 0) = elkx, где k — заданное вещественное число;
(ii) \|/(jc, 0) = е~рх, где р — вещественное положительное число;
777

ва V
(iii) l|/(x,0)
1 a a
= —=•, если — <x<—\
V^ 2 2
= 0 при других x
(iv) \|/(jc, 0)-epx , где p — вещественное

Глава VI
ОБЩИЕ СВОЙСТВА УГЛОВЫХ МОМЕНТОВ
В КВАНТОВОЙ МЕХАНИКЕ

А. ВВЕДЕНИЕ: ВАЖНОСТЬ
ПОНЯТИЯ УГЛОВОГО
МОМЕНТА.
ПЛАН ГЛАВЫ VI
В. СООТНОШЕНИЯ
КОММУТАЦИИ
ОПЕРАТОРОВ УГЛОВЫХ
МОМЕНТОВ.
1. Орбитальные угловые моменты.
2. Обобщение: определение углового момента.
3. Постановка задачи.
С. ОБЩАЯ ТЕОРИЯ
УГЛОВОГО МОМЕНТА.
1. Определения и обозначения.
a. Операторы J + и J_.
b. Обозначения собственных значений операторов J"
uJz.
c. Уравнения на собственные значения операторов J~
и Л .
2. Собственные значения операторов J" и У, .
a. Леммы.
b. Определение спектра операторов J~ и J. .
3. «Стандартные» представления I\k, у, т) }.
a. Базисные состояния.
b. Подпространства Y<{k, j) .
c. Матрицы операторов углового момента.
D. ПРИМЕНЕНИЕ
К ОРБИТАЛЬНОМУ
УГЛОВОМУ МОМЕНТУ.
1. Собственные значения и собственные функции
операторов L и L,.
a. Уравнения на собственные значения в
представлении {|гу }.
b. Значения I и т.
c. Основные свойства сферических гармоник.
d. «Стандартные» базисы пространства волновых
функций частицы без спина.
2. Физические соображения.
a. Анализ состояния | к, /, пг) .
b. Вычисление физических предсказаний при измерении
L2 и L. .

А. ВВЕДЕНИЕ:
ВАЖНОСТЬ ПОНЯТИЯ УГЛОВОГО МОМЕНТА
Данная глава является первой из серии четырех глав (VI, VII, IX и X), посвященных
изучению угловых моментов в квантовой механике. Речь идет о чрезвычайно важной
проблеме, и установленные здесь результаты будут использованы во многих областях
физики: классификация атомных, молекулярных и ядерных спектров, спин
элементарных частиц, магнетизм и т.д.
Угловой момент играет важную роль и в классической механике. Известно, что
полный угловой момент изолированной физической системы является константой
движения. Это, впрочем, имеет место и в ряде случаев, когда система не является
изолированной: так, например, если материальная точка Р с массой т движется в поле
центрального потенциала (то есть потенциала, зависящего только от расстояния точки
Р от фиксированной точки О пространства), то сила, действующая на Р, постоянно
направлена в сторону точки О, и, следовательно, ее момент относительно точки О
равен нулю, и теорема об угловом моменте требует, чтобы
^# = 0, (А-1)
dt
где <£ — угловой момент точки Р относительно точки О. Отсюда следуют важные
выводы: движение частицы Р происходит в фиксированной плоскости, проходящей
через точку О и перпендикулярной к угловому моменту 5?; кроме того, это движение
подчиняется закону Кеплера.
Все эти свойства имеют свой эквивалент в квантовой механике. Угловому моменту (£
классической системы соответствует наблюдаемая L , то есть набор, состоящий из трех
наблюдаемых Lv, Lv и L,, соответствующих трем компонентам момента У> в декартовой
системе координат. Если изучаемая физическая система является материальной точкой,
движущейся в поле центрального потенциала, то, как мы увидим в главе VII,
операторы Lx, Lv и Lz являются константами движения в квантовом понимании этого понятия,
то есть они коммутируют с гамильтонианом, описывающим частицу в поле центрального
потенциала V(r). Это важное свойство позволяет значительно упростить поиск и
классификацию собственных состояний оператора Н .
781

Глава VI
С другой стороны, в главе IV мы описали опыт Штерна и Герлаха, который
позволил открыть квантование углового момента: компонента собственного момента атома
вдоль фиксированной оси может принимать только некоторые дискретные значения.
Мы увидим, что все угловые моменты квантуются подобным образом, и это, в
частности, позволяет понять природу атомного магнетизма, эффекта Зеемана и т.д. Кроме того,
анализ этих явлений требует введения типично квантовых угловых моментов, то есть
не имеющих никакого кчассического эквивалента (собственные моменты элементарных
частиц; глава IX).
С этих пор мы будем называть орбитальным угловым моментом любой момент,
имеющий классический эквивалент, и обозначать символом L соответствующие
наблюдаемые, и спиновым угловым моментом — любой собственный угловой момент
элементарной частицы, для обозначения которого будет использоваться буква S. В
таких сложных системах, как атом, ядро или молекула, орбитальные моменты L,
различных частиц, составляющих систему (электроны, протоны, нейтроны и т.д.)
комбинируются друг с другом и со спиновыми моментами S, этих же частиц и образуют полный
угловой момент J системы. Способ, с помощью которого комбинируются моменты
(сложение угловых моментов), будет изучен в главе X. Отметим, наконец, что буквой J
мы будем также обозначать любой момент, если не будет необходимости уточнять,
является ли он орбитальным или комбинацией нескольких угловых моментов.
Прежде чем перейти к рассмотрению упомянутых выше физических задач (уровни
энергии частицы в поле центрального потенциала, спин, эффект Зеемана, сложение
моментов и т.д.), мы установим в данной главе общие квантовые свойства, которыми
обладают все угловые моменты, независимо от их природы.
Эти свойства вытекают из соотношений коммутации, которым удовлетворяют три
наблюдаемые 7Д, Jv и Jz, соответствующие компонентам произвольного момента J.
Природа этих соотношений обсуждается в § В: для орбитального углового момента они
являются просто следствиями правил квантования (§ В-5 главы III) и канонических
соотношений коммутации [формулы (Е-30) главы И]; для спиновых моментов, не
имеющих классического эквивалента, они на самом деле служат определением
соответствующих наблюдаемых*. В § С проанализированы следствия соотношений коммутации
для угловых моментов. В частности, будет доказано пространственное квантование
момента, то есть дискретность спектра значений любых компонент момента. И, наконец, в
§ D полученные общие результаты будут применены к исследованию орбитального
момента частицы.
* Глубинная природа этих соотношений коммутации в самом деле является чисто
геометрическим эффектом. Эту точку зрения мы подробно обсудим в дополнении BVi, где будет
установлена тесная связь углового момента системы относительно точки О с геометрическими
вращениями этой системы вокруг точки О .
782

Общие свойства угловых моментов в квантовой механике
В. СООТНОШЕНИЯ КОММУТАЦИИ ОПЕРАТОРОВ
УГЛОВЫХ МОМЕНТОВ
1. Орбитальные угловые моменты
Чтобы получить наблюдаемые Lx,Ly,Lz, соответствующие в квантовой механике
трем компонентам углового момента $ частицы без спина, достаточно применить
правила квантования, сформулированные в § В-5 главы III, особенно простые в этом случае.
Действительно, рассмотрим компоненту ?£х классического углового момента:
Хх=УРг~Фу. (В-1)
Переменным положения у и Z сопоставим наблюдаемые Y и Z, а переменным
импульса р и pz —наблюдаемые Ру и Pz. Хотя в формулу (В-1) входят произведения
двух классических переменных, нет необходимости соблюдать предосторожности при
их замене соответствующими наблюдаемыми, так как Y и Pz коммутируют, как и
переменные Z и Ру [см. канонические соотношения коммутации (Е-30) главы II]. Таким
образом, не требуется симметризовать выражение (В-1), чтобы получить оператор Lx:
Lx = YPz-ZPy. (B-2)
По этой же причине полученный оператор является эрмитовым.
Совершенно так же можно найти операторы Ly и Lz, соответствующие
компонентам Aу и (£z классического углового момента, что позволяет записать:
L = RxP. (B-3)
Зная канонические соотношения коммутации наблюдаемых положения R и
импульса Р, можно легко вычислить коммутаторы операторов Lx, Ly и Lz друг с другом.
Найдем, например, коммутатор \bx9 Lv]:
[Lx^y] = [YPz-ZPy,ZPx- XPz] = [YPz,ZPxMZPy, XPZ], (B-4)
так как YPZ коммутирует с XPZ и ZPV с ZPX. Тогда имеем:
[Lxf Ly] = Y[Pl9 Z]PX + X[Z, Pz]Py = -ihYPx +ihXPy = ifiLz. (B-5)
Аналогичные вычисления дают два других коммутатора, и окончательно получим:
783

Глава VI
[Ly,Lz] = ibLx;
[Lz,Lx] = ihLy. (B-6)
Итак, мы установили соотношения коммутации для операторов компонент углового
момента частицы без спина.
Этот результат немедленно обобщается для системы, состоящей из N частиц без
спина. Полный угловой момент такой системы в рамках квантовой механики равен:
L = £l,, (B-7)
1=1
где
L,=R,xP,. (B-8)
Поскольку каждый из индивидуальных моментов L, удовлетворяет соотношениям
коммутации (В-6) и коммутирует с L., если j Ф i (операторы, действующие в
пространствах состояний различных частиц); тогда без труда видно, что соотношения (В-6)
остаются справедливыми и для полного углового момента L .
2. Обобщение: определение углового момента
Три оператора, соответствующие компонентам произвольного классического
углового момента, удовлетворяют правилам коммутации (В-6). Впрочем, можно показать
(см. дополнение BVi), что глубинный смысл этих соотношений заключаются в
геометрических свойствах вращений в трехмерном пространстве. Именно поэтому, принимая
самую общую точку зрения, мы будем называть угловым моментом J (или просто
моментом) ансамбль из трех наблюдаемых Jx,Jy и Jz, удовлетворяющий равенствам:
[jx4Jv] = ihJz;
[jy,Jz] = ihJx;
[Л,УЛ.] = /&/у. (В-9)
Введем оператор:
j2 = y2 + y2+y2, (В-10)
являющийся скалярным квадратом углового момента J. Этот оператор является
эрмитовым, так как операторы Jx, J и J, эрмитовы. Допустим, что он является
наблюдаемой. Тогда оператор J2 коммутирует с тремя компонентами момента J :
784

Общие свойства угловых моментов в квантовой механике
|[J2,J] = 0| (В-11)
Действительно, выполним, например, вычисление для Jx:
[j2,Jx] = [j2,+J2y+J2z,Jx} = [j;,Jx} + [jlJx], (B-12)
так как Jx коммутирует как сам с собой, так и со своим квадратом. Два остающихся
коммутатора нетрудно найти из (В-9):
[уу2, УЛ] = Jy [yv, Jx]+[jy, j]jy = 4hJyJt -ihJzJy; (B-13-a)
[Л2, Ул.]= Л [л, У,] + [л, Jx]jz =ibJJv + /Й/УЛ- (B-13-b)
Сумма двух коммутаторов, входящих в (В-12), конечно, равна нулю.
Теория углового момента в квантовой механике полностью основана на
соотношениях коммутации (В-9). Заметим, что эти соотношения утверждают невозможность
одновременного измерения всех трех компонент углового момента. Напротив, операторы
J2 и любой из компонент J являются совместимыми.
3. Постановка задачи
Вернемся к примеру частицы без спина в поле центрального потенциала,
приведенному во введении. В главе VII мы увидим, что в этом случае три компоненты углового
момента L частицы коммутируют с гамильтонианом Н, как и оператор L2. Таким
образом, мы располагаем четырьмя константами движения: L2, Lr, Ly и Lz. Но эти
операторы не коммутируют друг с другом; чтобы образовать вместе с гамильтонианом Я
набор коммутирующих операторов, можно только взять L2 и один из трех остальных
операторов (например, Lz). Для частицы в поле центрального потенциала можно,
например, найти собственные состояния гамильтониана Н, являющиеся также
собственными векторами операторов L2 и L, без ограничения общности задачи. Но эти четыре
оператора не коммутируют между собой, и, следовательно, невозможно получить базис
пространства состояний, образованный из собственных векторов, общих для трех
компонент оператора L , поскольку эти три наблюдаемые не коммутируют.
В общем случае имеем ту же ситуацию: компоненты произвольного углового
момента J не коммутируют между собой, и их нельзя диагонализировать одновременно.
Таким образом, будем искать систему собственных векторов, общих для операторов J2
и Jz, то есть наблюдаемых, соответствующих квадрату модуля углового момента и его
компоненте вдоль оси Oz .
50 Квантовая механика
785

Глава VI
С. ОБЩАЯ ТЕОРИЯ УГЛОВОГО МОМЕНТА
В этом параграфе мы определим в общем случае спектр операторов L2 и Jz, а
затем изучим их общие собственные векторы. Рассуждения будут очень похожи на те,
которые были изложены в главе V для гармонического осциллятора.
1. Определения и обозначения
а. ОПЕРАТОРЫ /+ И У_
Вместо того, чтобы использовать компоненты Jx, J углового момента J, удобнее
ввести следующие линейные комбинации:
J+ = Jx+uy\
J- = JX-Uy. (C-1)
Как и операторы а и а+ гармонического осциллятора, операторы У+ и У_ не
являются эрмитовыми, но сопряжены друг с другом.
В последующем будем использовать только операторы У+, У_, Jz и J2. С
помощью выражений (В-9) и (В-И) легко показать, что эти операторы удовлетворяют
следующим соотношениям коммутации:
[jt,J.] = hJ.; (С-2)
[Jt,J_] = -fiJ_; (С-3)
[j.,J_] = 2hJz; (C-4)
[j2,/+] = [j2.-/-] = [j2-^] = 0. (C-5)
Вычислим произведения У+У_ и J_J+:
JJ_ = (jx + Uy)(jx -Uy)=J2x+J2y -i[jx, Jy]=J2x+J2y+bJz; (C-6-a)
У_У+ = (jx~Uy) (jx +Uy) = J] + J] + i[jx. Jy]=J2x + J) -hft. (C-6-b)
Согласно определению (В-10) оператора J2 эти выражения можно переписать в виде:
J+J.=32-J2+Mz; (C-7-a)
J.J+=J2-J2-hJz. (C-7-b)
786

Общие свойства угловых моментов в квантовой механике
Сложив почленно равенства (С-7), получим:
J2=\(j+J- + J.J+)+J2z. (C-8)
Ь. ОБОЗНАЧЕНИЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ ОПЕРАТОРОВ J2 И У,
Согласно формуле (В-10) оператор J2 является суммой квадратов трех эрмитовых
операторов, вследствие чего для любого вектора |\|/) матричный элемент (\|/| J2|\|/)
положителен или равен нулю:
= (v | j] | v)+(v | J; I v)+(v I Jl | v) = IЛ | v)f +1 J, k)f +1 л | v)|f z о. (c-9)
Заметим, что физически это свойство вполне понятно, так как J2 соответствует
квадрату модуля углового момента J . В частности, из этого следует, что все собственные
значения оператора J2 положительны или равны нулю; действительно, если |\|/) —
собственный вектор оператора J2, то (\j/| J2|\|/) является произведением соответствующего
собственного значения на квадрат нормы вектора | \|/) и всегда положительно.
Собственные значения оператора J2 будем записывать в форме j(j + l)h2 при
условии, что
7>0. (С-10)
Введение такого обозначения приводит к упрощению последующих рассуждений, но
никак не влияет на их результат. Действительно, поскольку J имеет ту же размерность,
что и h , то любое собственное значение оператора J2 можно представить в форме Xh2,
где X — вещественное безразмерное число. Мы только что видели, что X по
необходимости положительно или равно нулю, и тогда можно без труда показать, что
уравнение второй степени по j :
Л7 + 1) = Х (С-11)
всегда имеет единственный положительный или равный нулю корень. Итак, если
потребовать выполнения условия (С-10), то задание X определяет j единственным образом,
и собственное значение оператора J2, априори произвольное, можно записать как
j(j +1) h2 с положительным или равным нулю значением числа j .
Что касается собственных значений оператора У., имеющих размерность h , то их
традиционно обозначают символом mh , где т — безразмерное число.
50*
787

Глава VI
с. УРАВНЕНИЯ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ ОПЕРАТОРОВ J2 И У.
Общие собственные векторы операторов J2 и Jz будем обозначать индексами j и т,
характеризующими соответствующие собственные значения. Однако в общем случае
эти операторы не образуют полного набора коммутирующих операторов (см., например,
§ А главы VII), и необходимо ввести третий индекс, который позволил бы отличить
разные собственные векторы, соответствующие одинаковым собственным значениям
УО' + ОЙ2 и mh операторов J2 и Л (эту точку зрения мы еще уточним ниже в § 3), и
обозначим его буквой к (однако следует иметь в виду, что это не обязательно
дискретный индекс).
Таким образом, будем искать решения системы уравнений на собственные значения
вида:
J2\k,j,m)= j(j + W2\kJ,m);
jz \kj,m) =mh\kj,m). (С-12)
2. Собственные значения операторов J2 и Jz
Как и в § В-2 главы V, начнем с доказательства трех лемм, которые позволят нам
затем определить спектр операторов J2 и Jz.
а. ЛЕММЫ
а. Лемма I (свойства собственных значений операторов J2 и У.)
Если j{j + \)h2 и mh — собственные значения операторов J2 и Л,
соответствующие одному собственному вектору \к, j, m), то числа jam удовлетворяют
неравенству:
~j<m<j. (C-13)
Действительно, рассмотрим векторы J+\k,j,m) и J_\k,j,m) и запишем, что
квадрат их нормы положителен или равен нулю:
||у+|/:,7,/г2)||2=(/:,;,т|У_У+|^,7,т)>0; (С-14-а)
||у_|^,у,т)||2=(/:,7\т|У+У_|^,у,т)>0. (C-14-b)
Чтобы вычислить левые части этих неравенств, можно использовать формулы (С-7).
Тогда, предполагая нормированным вектор \к, у, т), получим:
788

Общие свойства угловых моментов в квантовой механике
(k,j\m\jJ+\kJfm) = (kJ,m\(j2-J2-hJz)\kJ,m) =
= Д./ + 1)Й2 -rrfti1 -rnfi2; (С-15-а)
(jfc, 7, т\ J+J_\k, j\ m) = (k, j, m\ (j2 - J2 +ЙУг)| Jt, 7, m) =
= j(j +1)^2 -ю2й2 + w/z2. (C-15-b)
Подставив эти выражения в неравенства (С-14), получим:
j(j + l)-m(m + \) = (j-m)(j + m+\)>0\ (С-16-а)
7О, + 1)-/я(п1 + 1) = О,-/я + 1)ОЧ|11)>0 (C-16-b)
или
-ОЧ1)<т<У; (С-17-а)
-j<m<j + l. (C-17-b)
Эти два условия могут быть выполнены только в том случае, если т удовлетворяет
неравенствам (С-13).
Р. Лемма II (свойства вектора J_\k, у, ш) )
Пусть кет \k,j,m) является собственным вектором операторов J2 и У, с
собственными значениями j(j + l)h2 и mfi.
(i) Если т = -у, то J_\k, j, - у) = 0.
(И) Если т> -j , то кет У_ |&, 7, m) является отличным от нуля собственным
вектором операторов J 2 и 7, с собственными значениями j{j + \)b2 и (m-l)ft.
(i) Согласно выражению (C-15-b) квадрат нормы вектора J_\k,jtm) равен
h2[j(j + l)-m(m-l)] и обращается в нуль, если m = -j. Поскольку норма вектора
обращается в нуль тогда и только тогда, если вектор равен нулю, то все векторы
J.\k, j,- j) равны нулю:
m = -j=>J_\k,j9-j) = 0. (С-18)
Впрочем, легко доказать и утверждение, обратное (С-18):
j \kj,m) = 0=*m = -j. (С-19)
Подействовав оператором 7+ на обе части уравнения (С-19) и используя (С-7-а), получим:
789

Глава VI
h2[j(j + l)-m2+m]\kJ,m) = h2U + m)(j-m + l)\kJ,m) = 0. (C-20)
Если учесть (С-13), нетрудно видеть, что уравнение (С-20) имеет только одно решение:
т = -у.
(и) Предположим теперь, что т строго больше (-у ). Согласно (C-15-b) кет J_\k, у, mj
является отличным от нуля вектором, так как квадрат его нормы отличен от нуля.
Покажем, что он является собственным вектором операторов J 2 и У,. Операторы
J_ и J 2 коммутируют, вследствие чего
[j\j_]\kj,m) = 0 (C-21)
или
J2J_\kJ,m) = JJ2\kJym) = j(j + l)b2J-\k,j\m). (C-22)
Это равенство выражает, что кет J_ \k, у, m) является собственным вектором оператора
J 2 с собственным значением у (у + \)h2.
С другой стороны, применим операторное равенство (С-3) к вектору \к, у, т):
[Jz,J_]\kJ,m) = -hJ_\kJ,m) (C-23)
или
JzJ_\k, у,m) = J_Jz\k, j,rn}-hJ_\k, у, m) =
= mhJ_\kJ,m)-hJ_\kJ,m) = (m-l)hJ_\kJ,m). (C-24)
Итак, кет J_\k, у, т) является собственным вектором оператора Jz с собственным
значением {m-\)fi.
у. Лемма III (свойства вектора У+ | к, у, w))
Пусть кет \к, у, т) является собственным вектором операторов J2 и Jz с
собственными значениями y(y + l)ft2 и mfi.
(i) Если m = у\ то У+1£, у, у) = 0.
(и) Если т < у , то кет У+ \к, у, т) является отличным от нуля собственным
вектором операторов J2 и Jz с собственными значениями у'(./ + 1)Й2 и (т + 1)Й.
(i) Доказательство аналогично приведенному выше в § С-2-а-C. Согласно (С-14-а)
квадрат нормы вектора J+ | к, у, т) равен нулю, если т = j. Тогда:
790

Общие свойства угловых моментов в квантовой механике
m = j=>J+\kJj) = 0. (C-25)
Можно доказать и обратное утверждение:
J+\kJ,m) = 0<am = j. (C-26)
(ii) Если т < j , то рассуждения, аналогичные приведенным в § C-(ii), дают с учетом
формул (С-5) и (С-2):
JV+ \k, j9m) = j(j + \)h2J+\k9 j,m); (C-27)
JtJ+\k, Лm) = (m + 1)ЙУ+1*, ;,m). (C-28)
b. ОПРЕДЕЛЕНИЕ СПЕКТРА ОПЕРАТОРОВ J2 И Jz
Теперь мы покажем, что три сформулированные выше леммы позволяют
определить возможные значения j и т.
Пусть кет \k,j,m) является отличным от нуля собственным вектором операторов
J2h Jz с собственными значениями j(j + l)ti2 и mfi. Согласно лемме I имеем
-j<m< j. Таким образом, обязательно существует такое целое положительное или
равное нулю число р, что
-;<m-p<-7 + l. (C-29)
Рассмотрим последовательность векторов:
\kj,m)9j_\kj,m),...9(j_)p\kj9m). (С-30)
Согласно лемме II каждый из векторов (/_)"[/:, j, m) этой последовательности
(п - 1,2,..., р ) является отличным от нуля собственным вектором операторов J2 и У, и
соответствует собственным значениям j(j + l)ft2 и {m-ri)ti.
Доказательство осуществляется шаг за шагом: согласно предположению кет
|&, у, т) отличен от нуля и соответствует собственным значениям j{j + \)h2 и тй ; кет
(«/_)" |&, 7»т) получается путем действия оператора J_ на кет (•/_)" |^, 7,т) > который
является собственным вектором операторов J2 и Уг с собственными значениями
j(j + l)h2 и (m-n + l)h. Последнее собственное значение строго превышает -у, так
как согласно формуле (С-29):
m-/i + l>m-/? + l>-y + l. (C-31)
791

Глава VI
Из пункта (ii) леммы II следует, что (•/_)" \к, Л т) является отличным от нуля
собственным вектором операторов J2 и Jz с собственными значениями j(j + l)h2 и (m-n)h.
Подействуем теперь оператором J_ на кет (У_)''|/;, у, т). Допустим сначала, что
собственное значение (m-ri)ti оператора Л, связанное с вектором (/_)''\к, j, m),
строго превышает -jh , то есть
m-p>-j. (C-32)
Согласно пункту (ii) леммы II кет J_{j_Y\ky у, m) тогда отличен от нуля и
соответствует собственным значениям j(j + l)h2 и (т- р- 1)й, что противоречит лемме I, так как
согласно (С-29):
m-p-\<-j. (С-33)
Таким образом, необходимо, чтобы т-p = -j. Действительно, в этом случае
вектор (j_)P\k, у, ш) соответствует собственному значению -j оператора У, и согласно
пункту (i) леммы II кет J_(J_)P\k, j, m) равен нулю. Таким образом,
последовательность векторов (С-30), полученная путем повторяющегося действия оператора J_ на кет
|&, у, т), ограничена, и противоречие с леммой I устраняется.
Итак, мы только что доказали, что существует такое целое положительное или
равное нулю число р, что
m-p = -j. (C-34)
Совершенно аналогичные рассуждения позволяют показать с помощью леммы III,
что существует такое целое положительное или равное нулю число q , что
/я + 9 = у, (С-35)
так как последовательность векторов:
\kj,m)j+\kj,m),...,{j,)q\kj,m) (С-Зб)
должна быть ограничена, чтобы не было противоречия с леммой I.
Комбинируя (С-34) и (С-35), получим:
P + q = 2j< (C-37)
то есть j равняется целому положительному или равному нулю числу, разделенному на 2.
Следовательно, число j должно быть обязательно целым или полуцелым*. С другой
* «Полуцелым» традиционно называют число, равное частному от деления нечетного целого
числа на 2.
792

Общие свойства угловых моментов в квантовой механике
стороны, если существует отличный от нуля вектор \k, j, m), то все другие векторы
последовательностей (С-30) и (С-36) также отличны от нуля и являются собственными
векторами оператора J2 с собственным значением j(j + l)h2, а также собственными
векторами оператора Jz с собственными значениями:
-уйэ (-7 + D». ("У+ 2)Л 0"-2)Й, (У- 1)Й, 7Й . (С-38)
Таким образом, можно резюмировать полученные результаты следующим образом:
Пусть J — произвольный угловой момент, подчиняющийся соотношениям
коммутации (В-9). Если j(j + \)Ti2 и mfi —собственные значения операторов J2 и Jz ,то
— единственно возможными значениями j являются целые, полуцелые
положительные числа или нули, то есть: 0, 1/2, 1, 3/2, 2,...(эти значения единственно
возможны, но это не означает, что все они реализуются для всех угловых моментов);
— для фиксированного значения j единственно возможными значениями т
являются B./ + 1) чисел: -у, -7 + 1,..., у-1, j'; итак, т является целым, если j —
целое число, и полуцелым, если j — полуцелое число; все значения т
действительно реализуются, если реализуется одно из них.
3. «Стандартные» представления {\к, j, m)}
Изучим теперь общие собственные векторы операторов J2 и Jz, образующих базис
в пространстве состояний, так как мы предполагали, что эти операторы являются
наблюдаемыми.
а. БАЗИСНЫЕ СОСТОЯНИЯ
Рассмотрим оператор углового момента J, действующий в пространстве состояний £ .
Сейчас мы покажем, как можно построить в пространстве # ортонормированный базис
из собственных векторов, общих для операторов J2 и Jz.
Возьмем пару собственных значений j(j + i)h2 и mh, действительно
реализующихся в рассматриваемом частном случае. Ансамбль собственных векторов, связанных
с этой парой собственных значений, образует векторное подпространство, которое мы
обозначим #"(у, т). Размерность g(j,m) этого подпространства априори больше 1, так
как в общем случае операторы J2 и Jz не образуют полного набора коммутирующих
операторов. Выберем в подпространстве <f(y, m) произвольный ортонормированный
базис [\kj,m) },где к = 1,2,..., g(j,m).
793

Глава VI
Если т Ф j, то неизбежно существует другое подпространство £(у, w +1)
пространства £, образованное собственными векторами операторов J2 и Л , связанными с
собственными значениями У(У + 1)Й2 и (w+l)ft. Аналогично, если тФ-j, то неизбежно
существует подпространство £(У, w-1). Сейчас мы построим в случае, когда т
отличается и от j, и от -j, ортонормированный базис в подпространствах F(y\ m+1) и
£(У, т-1), исходя из базиса, выбранного в подпространстве ${j, m).
Покажем сначала, что если кх и к2 различны, то векторы J+\klJj\m) и
J+1 к2, 7, w) ортогональны, как и векторы J_ | кх, 7, w) и У_ | &2, у, m). Для этого можно
вычислить скалярное произведение векторов J+\klt j\m) и J±|к2, 7, w), используя
формулы (С-7):
\к2, у, т\ J^J± j кх, у, т) = \к2, у, т| (j2 - У2 + ЙУг) | кх, у, т) =
= [У(У +1) -т(т± D]й2(*2, У, т | *,, у, /я). (С-39)
Эти скалярные произведения равны нулю, если к{Фк2, так как базис F(y\ m) ортонор-
мирован; если же кх = к2, то квадрат нормы 7± | кх, у, m) равен [j(j +1) - m(w ± 1)]/г2.
Рассмотрим для этого ансамбль, состоящий из g(jy m) векторов, определенных
выражением:
\к, j,m + \) = —, 1 = jAk, у, т). (С-40)
Эти векторы, как мы только что показали, ортонормированы. Кроме того, они образуют
базис в подпространстве £(у, m + 1). Действительно, предположим, что в этом
подпространстве существует вектор |сс, у, m+l), ортогональный всем векторам \k,j, m+l),
полученным с помощью формулы (С-40). Вектор /_|сс, у, m + l) не равнялся бы при
этом нулю, так как (т +1) не может равняться -j ; он принадлежал бы
подпространству if (у, т) и был бы ортогонален всем векторам J_\k, у, m+1); но согласно (С-40) кет
J_\k, у, w+l) пропорционален вектору J_J+\k, у,т), то есть вектору \k,j,m)
[формула (C-7-b)], тогда У_|а, у, m + l) был бы отличным от нуля вектором подпространства
#ХУ, т), ортогональным ко всем базисным векторам {|&, у, w) }, что невозможно. Итак,
ансамбль векторов (С-40) образует базис в подпространстве £(у\ w +1).
С помощью совершенно таких же рассуждений можно было бы показать, что
векторы | к, у, т -1), определенные выражением:
794

Общие свойства угловых моментов в квантовой механике
l^'^K/v' + n ( ny-Mm>' (C1)
образуют ортонормированный базис в подпространстве $(j, m-1).
В частности, видно, что размерность подпространств $(j, m+1) и $(j,m-\) равна
размерности подпространства £G, т). Иначе говоря, размерность подпространств не
зависит от т *:
S0\m + 1) = *0\m-l) = #0\m) = g(y). (C-42)
Далее поступим следующим образом. Для каждого значения j , действительно
реализуемого в рассматриваемой задаче, выделим подпространства, соответствующие этим
значениям j , например, #(./, Л соответствует т = j . В этом подпространстве выберем
произвольный ортонормированный базис {\k, j, j)\ к = 1,2,..., g(Л }• Затем удобно
воспользоваться пошаговым применением формулы (С-41) и построить базис, с которым будут
связаны каждое из 2j других подпространств $(j, m): стрелки в таблице (VI-1)
схематически иллюстрируют используемый метод. Применив его ко всем значениям j ,
реализуемых в задаче, получим так называемый стандартный базис пространства состояний $ .
Для такого базиса соотношения ортонормировки и замкнутости запишутся в виде:
(*, j, т |*', Г, т') = bkk,bjybnm, ; (С-43-а)
2 2 l\k,j,m)(k,j,m\ = l. (C-43-b)
j m=-j k = \
ЗАМЕЧАНИЯ
(i) Применение формулы (С-41) требует, в частности, выбора фаз: условно
принимают, что базисные векторы в подпространстве <f(j, m - 1) пропорциональны
векторам, полученным путем действия оператора J_ в базисе подпространства #'(у\ т),
с вещественным положительным коэффициентом пропорциональности,
(ii) Формулы (С-40) и (С-41) совместимы. Действительно, если подействовать
оператором У+ на обе части равенства (С-41) и учесть формулу (С-7-а), то вновь получим
выражение (С-40), где вместо т будет стоять (т-1). Это, в частности, означает,
что не обязательно исходить, как мы это сделали, из максимального значения т - j
и из одной формулы (С-41), чтобы построить базисы в подпространствах <г(у, т) ,
соответствующих данному значению j .
* Если эта размерность бесконечна, то полученный результат следует интерпретировать
следующим образом: имеется взаимно однозначное соответствие между базисными векторами двух
подпространств, соответствующих одному значению./.
795

Глава VI
Таблица VI. 1
Схематическое представление построения Bj + Y) g(j) векторов «стандартного базиса» для
фиксированного значения j ; для каждого из g(j) векторов \к, j, j/ первой строки с помощью
оператора J_ строятся Bj + 1) векторов одного столбца. Каждое подпространство <f{j, m)
образуется из g(j) векторов, стоящих в одной строке. Напротив, чтобы образовать подпространство
£(/:, j) , нужно сгруппировать Bу + 1) векторов одного столбца.
g(j) различных значений к
B; + 1)
остранств
Hj.m)
к =
Ч], т =
НУ.
Hj,m =
Ну.
Hj.m)
НУ.
Hj,m =
Л
7-D
-Л
I. 2,
\UJ) \2JJ) -
Ну. Ну.
\UJ.j-l) \2JJ-l) ■■
Ну. Ну.
\l,j,m) \2J,m)
Ну. Ну.
\U.-j) |2.7.-7) -
Hk = l,j) Hk = 2,j) ■
•• g(f)
• \g(J)Jj)
Ну.
• \g(j)>jJ-i)
Ну.
• \g(J)J<m)
Ну.
• |*(y).y'.-y)
- Hk = g(j)J)
g(j) пространств f (k, j)
В большинстве случаев для определения стандартного базиса используют наблюдаемые
А у /?,..., коммутирующие с тремя компонентами J и образующие полный набор
коммутирующих операторов в совокупности с операторами J и Jz (мы увидим конкретный пример этого в
§А главы VII):
[A,J] = [*,J] = ... = 0. (C-44)
Для простоты предположим, что достаточно лишь одной наблюдаемой А , чтобы образовать
полный набор коммутирующих операторов в совокупности с операторами J и /,.В этих
условиях каждое из подпространств F(j, m), определенных выше, глобально инвариантно
относительно действия оператора А : если V;,,») — произвольный вектор подпространства <s(j,m),
* Оператор, коммутирующий с тремя компонентами полного углового момента физической
системы, называется «скалярным» (см. дополнение BVi).
796

Общие свойства угловых моментов в квантовой механике
то вектор A \\\f ■: т) также является согласно выражению (С-44) собственным вектором
операторов J~ и Jz:
J2A |v,.m) = AJ2 |x|/y,m) = У0 + 1)Й2Л |чгу,,„);
J*A\Vj.m) = Mz\Vj,m) = mhA |l|/,,,„) (C-45)
с теми же собственными значениями, что и \|/.. ;||). Таким образом, вектор А \J/ , т) также
принадлежит подпространству <£(у, т). Если мы выберем теперь значение j , то внутри
подпространства W{j, j) можно диагонализировать матрицу оператора А . Обозначим символами
дополученные собственные значения: индекс j напоминает, в каком подпространстве <f(y, j) они
были получены, а индекс к (для простоты будем считать его дискретным) позволяет различать
их. Каждому собственному значению ак . соответствует единственный вектор \k,j9jj в
подпространстве #(у, j), так как в соответствии с нашим предположением операторы А , J и У,
образуют полный набор коммутирующих операторов:
A\k,j,j) = akj\kJ,j). (C-46)
Ансамбль {\к, у, jj ; у, к = 1,2,..., g(j) ) образует в подпространстве tf(y, у) ортонормированный
базис, исходя из которого описанным выше методом можно построить базис в других
подпространствах ^(у, т), связанных с рассматриваемым значением у . Применив этот метод
последовательно ко всем значениям у , в результате получим «стандартный» базис {\к, j> j) } пространства
состояний, все векторы которого являются собственными состояниями не только операторов J
и У,, но также и оператора А :
Л |*, у, т) = akj \к% у\ т) . (С-47)
Действительно, если справедливы соотношения (С-44), то оператор А коммутирует с оператором
J_, в результате чего кет J_ \к, у, у) , то есть |к, у, у -1/ , является собственным вектором
оператора Л с тем же самым собственным значением, что и кет \к, j, j/ :
AJ_\kJj) = J_A\kJj) = akjJ.\kJj). (C-48)
Повторяя эту операцию, можно без труда доказать равенство (С-47).
ЗАМЕЧАНИЯ
(i) Наблюдаемая, коммутирующая с операторами J и Jz, не обязательно коммутирует с
операторами J x и Jy (примером является сам оператор У,). Поэтому для того, чтобы об-
797

Глава VI
разовать полный набор коммутирующих операторов в совокупности с операторами J и
Jz, нет необходимости выбирать наблюдаемые, коммутирующие с тремя компонентами
оператора J , как это сделано в (С-44). Однако если А не коммутирует с операторами У+
и J_ (то есть с J x и Jv), то кет J± \kt у, т/ не обязательно будет собственным вектором
оператора А с тем же собственным значением, что и кет \к, у, т) .
(и) Спектр оператора А одинаков во всех подпространствах <£(у, m), связанных с данным
значением у . Однако собственные значения ак . в общем случае зависят от у (это
утверждение встретится в конкретных примерах, рассмотренных в § А и § С главы VII).
Ь. ПОДПРОСТРАНСТВА £(у, т)
В предыдущем параграфе мы ввели «стандартный» базис пространства состояний,
построив, исходя из выбранного базиса в подпространстве И~(у, т = у), базис в
подпространстве ?(у,ш=у-1), затем в подпространствах £'(у,т= у-2),..., #'(у\т) и т.д.
Пространство состояний может рассматриваться как прямая сумма всех ортогональных
подпространств F(y, га), где га изменяется скачками на целое число от - у до + у и где у
принимает значения, действительно реализуемые в рассматриваемой задаче. Тем самым
подразумевается, что любой вектор пространства f может быть представлен
единственным образом в виде суммы векторов, каждый из которых принадлежит
определенному подпространству (^(у, га).
Тем не менее, использование подпространств £(у, га) представляет некоторые
неудобства. Прежде всего, их размерность g(j) априори неизвестна и зависит от
рассматриваемой физической системы. Кроме того, подпространства #(у\ га) не инвариантны
относительно действия оператора J, так как из самого принципа построения векторов
|&, у, га) видно, что операторы У+ и J_ имеют отличные от нуля элементы между
векторами подпространств #(у, га) и (^(у, mil).
Именно поэтому введем сейчас другие подпространства $(к, у). Для этого
сгруппируем те кет-векторы \к, у, га), для которых индексы к и j имеют заданные значения, и
обозначим образованные ими подпространства символами <f(k,j). Эта операция
соответствует объединению в таблице (VI-1) Bу + 1) векторов одного столбца
(подпространство tf(y, га) объединяло g(j) векторов одной строки).
Теперь пространство $ оказывается прямой суммой ортогональных подпространств
$(к, у), обладающих более простыми свойствами:
— размерность подпространства #(&,у) равна Bу + 1) независимо от к и от
рассматриваемой системы;
798

Общие свойства угловых моментов в квантовой механике
— подпространство #(kyj) глобально инвариантно относительно действия
оператора J : любая компонента Ju оператора J [или функция F( J) ], действуя на кет
подпространства <£(&, j), дает другой кет, также принадлежащий этому же
подпространству*. Этот результат нетрудно установить, так как Ju [или F( J) ] всегда можно выразить
через Л, У+и J_. Так, оператор Jz, действуя на кет |&,у,т), даст кет,
пропорциональный \ку у, т), оператор У+ даст кет, пропорциональный \ку j, m+1), и оператор J_
даст кет, пропорциональный \k,j,m-l). Это свойство непосредственно вытекает из
самих правил построения «стандартного» базиса {\к, j, m) }.
с. МАТРИЦЫ ОПЕРАТОРОВ УГЛОВОГО МОМЕНТА
Использование подпространств £(к, j) позволяет значительно упростить поиск
матрицы, представляющей в «стандартном» базисе любую компоненту Ju оператора J
[или любую функцию F(J) ]. Действительно, элементы этой матрицы между двумя
базисными векторами, принадлежащими различным подпространствам <?(k,j), равны
нулю. Поэтому матрица имеет следующую форму:
HkJ)
Hk'J)
WJ')
HkJ)
матрица
0
0
0
Hk'J)
0
матрица
<2y+l)xB;+l)
0
0
Hk'J')
0
0
матрица
B/+l)xBy' + l)
0
0
о
0
0
и достаточно вычислить матрицы конечных размеров, представляющих рассматриваемый
оператор внутри каждого из подпространств $(к9 j).
Второе очень важное упрощение состоит в том, что каждая из этих конечных
подматриц не зависит от к и изучаемой физической системы. Она зависит только от j и,
конечно, от оператора, который требуется представить. Действительно, определение
вектора \к, j, т) [см. формулы (С-12), (С-40) и (С-41)] требует, чтобы
* Кроме того, нетрудно доказать, что подпространство #'(£, j) является «неприводимым» по
отношению к J : не существует другого подпространства <?(к, j), кроме самого (£(/:, j) ,
которое было бы глобально инвариантно относительно действия всех компонент оператора J .
799

Глава VI
то есть
Jz | к, j, m) = mfi | k, 7, m);
J+\k4 7,m) = hyljU + l)-m(m+l) \k, j,m +1);
J-\kJ,m) = h ylj(j + l)-m(m-l) \ к, ;, m -1),
(*, 7, m| Уг j*', 7", m) = m/iSM, 8^ 8„„„,;
(C-50)
(*. 7, H Л I*', /. m'> = hJjU + D-m'(m'±l) 8tt. 8^ 8„,ж±1. (C-51)
Эти равенства показывают, что матричные элементы компонент оператора J
действительно зависят только от ; и m, но не зависят от к .
Таким образом, чтобы знать во всех случаях матрицу любой компоненты Ju в
стандартном базисе, достаточно вычислить один раз и навсегда все «универсальные»
матрицы (JU)J , представляющие Ju внутри подпространств ${к, j) для всех возможных
значений j , то есть j = 0, 1/2, 1, 3/2, ... При изучении конкретной физической системы и
ее углового момента J выбираются те значения j , которые действительно реализуются
в поставленной задаче, а также количество подпространств Р(к> j), связанных с каждым
из них [то есть кратность их вырождения g(j) ]. Известно, что матрица,
представляющая Ju в таком частном случае, имеет форму, «диагональную по блокам» (С-49), и
можно построить ее из только что рассмотренных «универсальных» матриц: для
каждого значения j будем иметь g(j) «блоков», идентичных (JU)J .
Дадим несколько примеров матриц (J„)J :
0O=0.
Подпространства #(£,7 = 0) имеют размерность 1, так как существует
единственное возможное значение т = 0 ; матрицы (Уи)J вырождаются в числа, которые к тому
же равны нулю согласно формуле (С-51).
00 7 = 1/2.
Подпространства <^{к, j -112) имеют размерность 2 (т=\/2 или w = -l/2). Если
базисные векторы расположить именно в этом порядке (т= 1/2, т = - 1/2), то из
формулы (С-51) следует:
(лГ *Г1 °^
('♦)
A/2)
= Й
0 1
[о о)
[0 -I)
A/2)
(С-52)
(/_)=*
(l oj
(С-53)
800

Общие свойства угловых моментов в квантовой механике
то есть, если использовать формулу (С-1):
СУ
A/2)
) П@ П
■■ (лГ-
211 0)
Таким образом, матрица, представляющая оператор J2, имеет вид:
A/2) Ь
2
2
О -i
I' «J
iJV,n)_2*J
4
И "I*
lo i)
(С-54)
(С-55)
Мы теперь явно видим матрицы, введенные без доказательства в § А-2 главы IV.
(Hi) 7 = 1-
В этом случае в порядке базисных векторов от = 1, от = 0, от = -1 имеем:
(\ О 0Л
('♦)=»
fo V2 О'
О 0 42
0 0 0
0 0 0
0 0-1
; СГ = »
^о о 6\
L/2 0 0
[ 0 V2 oj
и, следовательно:
Шт-
Л
Го
1
U
1 ti\
0 1
1 oj
= w-£
( -i 0")
i 0 -i
lo «• oj
а также
(J2)(,,=2*2
(I 0 0")
0 1 0
lo о lj
(C-56)
(C-57)
(C-58)
(C-59)
ЗАМЕЧАНИЕ
Можно доказать, что матрицы (С-56) и (С-58) действительно удовлетворяют
соотношениям коммутации (В-9).
(iv) j — произвольное число
Воспользуемся соотношениями (С-51), которые можно [см. формулу (С-1)]
переписать в виде:
51 Квантовая механика
801

Глава VI
<А, У, т| У, |Л', у',т') = -|б„. 5^ х
х [yljU + D-m'im' + l) 5т,тЧ| + Jj{j+\)-m'{m'-\) 5„,„,,.,] (С-60)
И
(kJ,m\jy\k'J',m') = ji5kk.SjJ.x
xyjU + V-m'irn' + DS^-ylKJ + D-m'im'-l)^^]. (C-61)
Таким образом, матрица (JZ)J диагональна, и ее элементами являются B/ + 1)
значения mh . Матрицы (Jx)J и (j) имеют отличные от нуля элементы только непосред-
ственно выше или ниже главной диагонали, причем матрица [Jx) — симметричная и
вещественная, а матрица (У J — антисимметричная и чисто мнимая.
С другой стороны, поскольку векторы \k,j,m) являются собственными векторами
оператора J2, имеем:
(*. j,m\ i2\k', j',т') = Л] + т2Ькк.8,.8тт.. (С-62)
Итак, матрица (J2) пропорциональна единичной матрице Bу + 1) х Bу +1): все ее
диагональные элементы равны j(j +1) ft1.
ЗАМЕЧАНИЕ
Ось Oz, выбранная нами в качестве «оси квантования», совершенно
произвольна: все направления пространства физически эквивалентны, и можно ожидать,
что собственные значения операторов J\ и J должны быть такими же, как и
собственные значения оператора J, (их собственные векторы будут, однако,
различными, так как J x и /v не коммутируют с Jz). Действительно, можно доказать,
что собственные значения матриц (Jx) * и и\ [формулы (С-54)] равны ± —,
а собственные значения матриц (У,)A) и (Уу) [формулы (С-58)] равны +h , 0 и
-h. Это свойство является общим: внутри определенного подпространства
<f(k, j) собственные значения операторов J x и Jv (впрочем, как и любой проек-
802

Общие свойства угловых моментов в квантовой механике
ции Ju = J • и оператора J на произвольный единичный вектор и) равны
jhy (j -1) /*,..., (-j -1)Л, - jfi, а соответствующие собственные векторы (общие
для операторов J2 и Jx, J2 и Jy или J2 и Ум) являются линейными
комбинациями векторов \k, j, m) с фиксированными значениями к и j .
В заключение этого параграфа, посвященного «стандартному» представлению,
сформулируем важный вывод.
Ортонормированный базис [\k,j,m) } пространства состояний, образованный
из общих собственных векторов операторов J2 и Jz:
j21*. л m) = уО" + 1)й21*. Л ^>;
Jz | к, у, ш) = тй | к, j, /w)
называется «стандартным», если действие операторов У+ и J_ на базисные векторы
описывается выражениями:
J+\k, j,m) = hyjj(j +1)-т(т+1) |*,у, w+1);
D. ПРИМЕНЕНИЕ
К ОРБИТАЛЬНОМУ УГЛОВОМУ МОМЕНТУ
В предыдущем параграфе мы рассмотрели общие свойства угловых моментов,
основываясь исключительно на соотношениях коммутации (В-9). Сейчас мы вернемся к
рассмотрению орбитального углового момента L частицы без спина [формула (В-3)] и
посмотрим, как применяется развитый выше общий формализм в этом частном случае.
Будем использовать представление {|г)} и покажем, что собственные значения
оператора L2 равны /(/ + 1)й2, где / — любое целое положительное число или нуль. Таким
образом, среди всех возможных значений j , которые мы нашли в § C-2-b, реализуются
в этом случае только все целые значения. Затем укажем, какими должны быть собственные
функции, общие для операторов L2 и Lz, и найдем их основные свойства. И, наконец,
обсудим собственные состояния с физической точки зрения.
51*
803

Глава VI
1. Собственные значения
и собственные функции операторов L2 и L,
а. УРАВНЕНИЯ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ В ПРЕДСТАВЛЕНИИ {|г) }
В представлении {|г}} наблюдаемые R и Р соответствуют умножению на г и
дифференциальному оператору —V. Три компоненты углового момента L записыва-
ются в виде:
L=-
{ dz ду)
т Ч э э I
о
г
\
i х~^—Уч~~ i
I oy dx)
(D-1-a)
(D-l-b)
(D-l-c)
Удобнее работать в сферической (или полярной) системе координат. Действительно,
мы увидим сейчас, что различные операторы углового момента действуют только на
угловые переменные в и ф , а не на переменную г. Вместо того, чтобы характеризовать
вектор г декартовыми координатами х, у, z, мы зафиксируем положение точки М в
пространстве (ОМ = г ) ее сферическими координатами г, Ь и ф (рис.1):
Рис.1
Определение положения произвольной точки
в сферической системе координат г, в и ф
804

Общие свойства угловых моментов в квантовой механике
где
х = г sin $ cos ф;
у = г sin Ь sin ф;
z = rcosb,
r>0;
0<в<я;
0<ф<2я.
(D-2)
Элемент объема d3r = dxdydz записывается в сферических координатах
следующим образом:
d3r = r2 sinЬ dr db dip = r2dr dQ,, (D-3)
где
dQ = sinbdbd(p
(D-4)
является элементом телесного угла вблизи направления, выделенного полярными
углами О и ф.
Применив классическую технику замены переменных, получим из формул (D-1) и
(D-2) следующие выражения (их вычисление не представляет большой сложности, но
достаточно громоздко):
.*■ . Э cos(D Э 1
1 db tgb Эф J
L=ih
Э sinip Э
-cos(f>— +
дЪ tgb Эф J'
z /Эф
откуда следует:
V=-h2
( 32
1 Э 19
2 Л
\ЬЬ2 tgbdb sin2bd<p2)
/ Э . „ Э
L = he
' э . . э
^ ЬЬ Эф
(D-5-a)
(D-5-b)
(D-5-c)
(D-6-a)
(D-6-b)
(D-6-c)
L. = Ье'щ
В представлении {|r)) собственные функции, соответствующие собственным зна
805

Глава VI
чениям /(/ + 1)Й2 оператора L2 и mh оператора Lz, являются решениями уравнений в
частных производных:
Н Sj-+-т-й:+—ттттК(г' в' ф> = /(/+1} v(^ *. ф);
I [дЬ2 tg& 9f> sin2 Ь Эф2 J Ф_7ч
-/ —\|/(г, в, ф) = m\|/(r, в, ф).
I Эф
Мы уже знаем из общих выводов § С, применимых к орбитальному угловому моменту,
что / является целым или полуцелым числом и что при фиксированном / число т может
принимать только такие значения: -/,-/ +1,...,/-1, /.
В уравнениях (D-7) переменная г не входит ни в один из дифференциальных
операторов, то есть можно рассматривать г как параметр и учитывать зависимость функции
\|/ только от углов Ь и ф. Обозначим символом 17"(т}*Ф) собственную функцию,
общую для операторов L2 и Lz, соответствующую собственным значениям l(l + l)h2
и mh:
L217"(в,ф)= /(/ + 1)й2 1Г(«,ф); (°-8"а)
L, }f (в, ф) = тй I?"(в, ф). (D-8-b)
Строго говоря, следовало бы ввести еще один дополнительный индекс, чтобы различать
между собой другие решения уравнений (D-8), соответствующие той же паре значений
/ и т . На деле, как мы увидим ниже, эти уравнения допускают только одно решение
(с точностью до множителя) для каждой пары разрешенных значений / и т, вследствие
чего этих введение дополнительного индекса не потребуется.
ЗАМЕЧАНИЯ
(i) Уравнения (D-8) определяют зависимость собственных функций операторов L2 и
Lz от углов f) и ф. Если найдено решение У/"(т}, ф) этих уравнений, то
собственные функции записываются в виде:
1|/,ш(г,д,ф) = /(г)^'(^Ф), (D-9)
где f(r) — функция расстояния г *, возникающая как постоянная интегрирования
* Функция f(r) должна быть всегда такой, чтобы У/,,, (г, в, ф) была квадратично
интегрируемой.
806

Общие свойства угловых моментов в квантовой механике
уравнений в частных производных (D-7). Тот факт, что f(r) может быть любой
функцией, показывает, что операторы L2 и Lz не образуют полного набора
коммутирующих операторов в пространстве #г функций от г (или от г, f) и ф).
(ii) Чтобы нормировать функции у,„,(г, f}, ф), удобно (и мы именно так и поступим)
нормировать отдельно У/'ЧЬ, ф) и /(г). Тогда с учетом (D-4) получим:
/02яф10Л5шд|Г(в,ф)|2^ = 1 (D-10)
и
J0V|/(r)|2</r = l. (D-11)
b. ЗНАЧЕНИЯ / И Ш
ос. Числа I и т могут быть только целыми
Используя выражение (D-5-c) для Lz, можно записать (D-8-b) в форме:
-—УГФ, ф) = тПУГ(Ъ, ф), (D-12)
i аф
откуда следует, что У/"(д,ф) равна:
1Г(в.ф)= F^me""*. (D-13)
Изменяя угол ф от 0 до 2я, можно определить любую точку пространства. Поскольку
волновая функция должна быть непрерывной во всех точках пространства*, то, в
частности, должно выполняться равенство:
Г/&,Ф = 0)= }f0M = 27i) (D-14)
и, следовательно:
е2Ш=1. (D-15)
В соответствии с результатами § С число т может быть только целым или полуцелым.
* Если при ф = 0 функция ^'"(в,ф) не была бы непрерывной, то. ее было бы нельзя
продифференцировать и она не была бы собственной функцией дифференциальных операторов (D-5-c)
и (D-6-a). Так, например, производная -— Y"'(b, ф) дала бы 8(ф), что несовместимо с выраже-
Эф
нием@-12).
807

Глава VI
Равенство (D-15) показывает, что в случае орбитального углового момента число т
может быть только целым (экспонента е2тп равнялась бы -1, если бы т было
полуцелым числом). Но мы знаем, что т и / могут быть либо оба целыми, либо оба
полуцелыми, и это означает, что / может также быть только целым числом.
Р. Реализуются все целые (положительные или нули) значения числа I
Зафиксируем целое значение / (положительное или нулевое). Мы знаем, что в
соответствии с общей теорией (§С) функция К/(д, ф) должна удовлетворять равенству:
L+y/0M) = 0, (D-16)
что дает с учетом формул (D-6-b) и (D-13):
j~/c^F/(fl) = 0. (D-17)
Это уравнение первого порядка интегрируется без труда, если заметить, что
ctgdM = ^!HEl. (D-18)
sin-Q
Его общее решение равно:
F/(d) = c/Emd)/, (D-19)
где с{ — постоянная нормировки.
Таким образом, для каждого целого положительного или нулевого значения числа /
существует единственная функция Y/ (д, ф), с точностью до постоянного множителя равная:
^Чв,Ф)=^шв)'е,/ф. (D-20)
Путем повторного действия оператора L_ можно построить ряд функций
Yt" ,..., Y"\...4 Y{ . Итак, мы доказали, что паре собственных значений l(l + \)h2 и тП
(где / — произвольное целое положительное число или нуль, aw — другое целое
число, принимающее значения -1<т<1) соответствует одна и только одна собственная
функция Y'(Ф,ф), однозначно определяемая формулой (D-20). Эти собственные
функции ^т(в,ф) называются сферическими гармониками.
с. ОСНОВНЫЕ СВОЙСТВА СФЕРИЧЕСКИХ ГАРМОНИК
Сферические гармоники ^'м(д,ф) подробно рассмотрены в дополнении Ащ. Здесь
же мы ограничимся только перечислением их основных свойств без доказательства.
808

Общие свойства угловых моментов в квантовой механике
а. Рекуррентные соотношения
В соответствии с изложенным в § С имеем:
L±}f (О, ф) = /Ц//(/ + 1)-/и(/п±1) У;п±1(Ъ, ф). (D-21)
Теперь достаточно использовать выражения (D-6-b) и (D-6-c) для операторов L+ и L_ и
тот факт, что У/'ЧЬ, ф) является произведением функции угла Ь на е"щ, чтобы получить:
( г) А
е\ 3 mctg$\Ylm($,(()) = yll(l + l)-m(m+\)Ylm+l(Vyq))\ (D-22-a)
Ue
*"* ( -gT—mc/g* J^w(«, ф) = Jl(l + \)-m(m-l) С'^ Ф) • (D-22-1
b)
Р. Соотношения ортонормировки и замкнутости
Уравнения (D-7) определяют сферические гармоники с точностью до постоянного
множителя. Этот множитель в дальнейшем будем выбирать из условия, что }^т(в,ф)
ортонормированы как функции углов Ь и ф :
£" Лр£ял6 Y«\b, ф) Г F, ф) <tf> = 8n8,„,„,. (D-23)
С другой стороны, произвольная функция /(в,ф) может быть разложена по
сферическим гармоникам:
/(«,<р) = Х 2 с(,Х(«-Ф). (D-24)
/=0 т=-1
где
с,„, = iTd^sinb db YtmЪ, ф) /(в, ф). (D-25)
Таким образом, сферические гармоники образуют ортонормированный базис в
пространстве #а функций углов в и ф , что и отражает соотношение замкнутости:
/=0 ;»=-/
= -1-8(в-в'M(ф-ф') (D-26)
sinv
[в правую часть соотношения замкнутости вошла функция 8(casfl-casO')> a не
809

Глава VI
8(f}-d')» так как интегрирование по переменной Ь ведется с дифференциалом
sin$db = -d(cos$)].
у. Четность и комплексное сопряжение
Вспомним сначала, что изменение г на -г (преобразование симметрии
относительно начала системы координат) в сферических координатах выражается
соотношениями (рис.2):
г => г;
fl=>7t-d; (D-27)
ф=>71 + ф.
Легко показать (см. дополнение AVi), что
У/п,(я-д,я + ф) = (-1)/^(д,ф).
(D-28)
Таким образом, сферические функции являются функциями определенной четности, не
зависящей от т: они четные, если / — четное число и нечетные, если / — нечетное
число.
Рис.2
Преобразование сферических координат
произвольной точки в результате операции
симметрии относительно начала координат;
г не изменяется, Ь преобразуется в п-Ь
и ф преобразуется в я + ф
С другой стороны, легко видеть, что
[г(*.ф)Г=(-irirm(*.<p).
(D-29)
810

Общие свойства угловых моментов в квантовой механике
d. «СТАНДАРТНЫЕ» БАЗИСЫ
ПРОСТРАНСТВА ВОЛНОВЫХ ФУНКЦИЙ ЧАСТИЦЫ БЕЗ СПИНА
Как мы уже отмечали [замечание (i) в § D-1-a], операторы L2 и Lz не образуют
полного набора коммутирующих операторов в пространстве волновых функций
частицы без спина. Сейчас мы покажем, опираясь на результаты, полученные в § С-3, какова
форма «стандартных» базисов этого пространства.
Пусть # (/, т = /) — подпространство собственных функций, общих для операторов
L2 и Lz, с собственными значениями /(/ + 1)#2 и lh, где / — фиксированное целое
положительное число или нуль. Первый этап построения «стандартного» базиса (см. § С-3)
состоит в выборе произвольного ортонормированного базиса в каждом из
подпространств (f(/,w = /). Обозначим символом \|/ы/(г) функции, составляющие выбранный
в £(/, т = /) базис, где индекс к (для простоты считаем его дискретным) служит для
различения функций этого базиса. В результате последовательного повторения действия
оператора L_ на \|/^м(г) построим функции \\fkJm(г), дополняющие «стандартный»
базис для т* I. Они удовлетворяют уравнениям (С-12) и (С-50), которые примут здесь
форму:
^ц^^Иц^г) (D-30)
и
kVu.mW = hjl(l + l)-m(m±\) \|/,,,,„,(r). (D-31)
Но мы уже видели в § D-1-a, что все собственные функции, общие для операторов
L2 и Lz, соответствующие заданным собственным значениям /(/ + 1)Й2 и rrih, имеют
одинаковую угловую зависимость вида Y"l(b,(p) и отличаются только радиальной
зависимостью. Из уравнений (D-30) можно получить, что функция \ук1 т(г) имеет вид:
v*./.«(r) = «*.,.«(»•) 1Г(*.ф)- (°-32)
Покажем теперь, что если функции V|/Af/tW(r) образуют «стандартный» базис, то
радиальные функции RkJm(r) не зависят от индекса т . Действительно, поскольку
дифференциальные операторы L± не влияют на зависимость от г, то согласно формуле (D-21) имеем:
L±Wu,m(r) = Rk.,,m(r)L±Yr(b^) =
= hjl(l +1) -т{т± \)RkXm(r)Y;"±l{b, <p). (D-33)
811

Глава VI
Сравнение с формулой (D-31) показывает, что радиальные функции для всех значений г
должны удовлетворять соотношению:
Кы±М) = К.,М) (D-34)
и, следовательно, не зависят от т. Функции \\fk, ,M(r) «стандартного» базиса
пространства волновых функций частицы без спина должны обязательно иметь форму:
1|/и^г) = Я^)У/м(в,Ф). (D-35)
Соотношение ортонормировки такого базиса имеет вид:
\dWu.m(T)Vv.r.Ar) = £r2dr K,(r) Rk,,.(r) x
x j^d^sinb db Yfib, Ф) Y?\b, ф) = 8w.8r8mm- ■ (D-36)
Поскольку сферические гармоники уже ортонормированы, как функции углов Ф и ф
[формула (D-23)], окончательно получим:
J0Vdr<,(r)/?,.,(/•) = 5Ы.. (D-37)
Таким образом, радиальные функции Ru(r) нормированы по отношению к переменной г.
Кроме того, две радиальные функции, соответствующие одному и тому же значению /,
но разным значениям к, ортогональны.
ЗАМЕЧАНИЯ
(i) Формула (D-37) является следствием того, что выбранные в качестве базиса в
подпространстве £(/,т = /) функции i|/u„,(r) = /?u(r)}f(д,ф) ортонормированы.
Существенно важно, чтобы индекс / в функциях Rkl левой части равенства был
бы одинаковым. Если /*/', то функции \|/м>т(г) и \|/ГГш.(г)все равно остаются
ортогональными из-за их угловой зависимости (они являются собственными
функциями эрмитова оператора L2 с разными собственными значениями), но
интеграл:
i~r2drR'u(r)Rt,r (D-38)
априори может иметь любое значение,
(ii) Радиальные функции Rkl(r) в общем случае зависят от /. Это можно доказать
следующим образом. Функция формы /(г) #(д,ф) может быть непрерывной в
812

Общие свойства угловых моментов в квантовой механике
начале координат (г = 0, углы й иф — произвольны) только в том случае, если
g@, ф) равна постоянной или если /(г) = 0 в точке г = О [действительно, в
противном случае предел, к которому стремится /(г) gF,(p) при г—>0, зависит от
направления, с которого мы приближаемся к началу координат]. Отсюда следует,
что если мы хотим, чтобы базисные функции У *,,,„, (г) были непрерывными,
только радиальные функции, соответствующие / = 0, могут быть отличными
от нуля при г = 0 [так как ^0(d,(p) — постоянная величина]. Аналогично, если
потребовать, чтобы функции Ч/м>Я|(г) были дифференцируемыми (один или
несколько раз) в начале координат, то можно получить для функций Rkl(r)
условия, зависящие от значения /.
2. Физические соображения
а. АНАЛИЗ СОСТОЯНИЯ | к, I, т)
Рассмотрим частицу без спина в собственном состоянии \к,1,т) операторов L2 и
Lz, волновая функция которого \|/Uw(r). В этом состоянии квадрат углового момента
частицы и его проекция на ось Ог имеют вполне определенные значения, равные
/(/ + 1)Й2 и тЬ соответственно.
Допустим, что мы интересуемся измерением проекции момента этой частицы на ось
Ох или Оу . Поскольку операторы Lx и Lv не коммутируют с Lz, то кет \к, /, т) не
является собственным вектором ни Lx, ни Ly, и предсказать с определенностью
результат такого измерения невозможно. Вычислим средние значения и среднеквадратичные
отклонения этих наблюдаемых в состоянии | к, I, т) .
Эти вычисления значительно упрощаются, если Lx и Ly выразить через операторы
L+ и L_, обратив формулы (С-1):
Ly=j:{L+-L_). (D-39)
Видно, что Lx | к, /, т) и Ly | к, I, m) являются линейными комбинациями векторов
| к, I, т +1) и | к, /, т -1), и, следовательно:
(*,/,т\ Lx\k,/,т) = (fc/,m\ Ly\k,l,m) = 0. (D-40)
813

Глава VI
С другой стороны:
(^/,m|L^,/,m) = -(^/,m|(L^ + L^ + L+L. + L.L+)|fc/,m);
(fc/,m|*L2^^,m) = ~(fc/,m|(L^ + L!-L+L.--L_L+)|A:,/,m). (D-41)
Члены, содержащие L2 и L2 , дают нулевой вклад, так как кет L2± \k, 1,т)
пропорционален \k,l,m±l). Кроме того, формула (С-8) дает:
L+ L_ + L_L+= 2(L2 - L]). (D-42)
В результате получим:
(к, /, т\ L] \ку /, т) = (к, /, т\ (L2V) \k, /, т) =
1 h2
= -(kJ,m\(L2-L2z)\kJ,m) = — [/(/ + l)-m2]. (D-43)
Окончательно, в состоянии \kj,m):
(Lr) = (Lv) = 0; (D-44-a)
К. i2l
ALX = ALV = h J- [/(/ +1) - ml ] . (D-44-b)
Эти результаты могут быть интерпретированы следующим образом. Пусть имеется
классический угловой момент, модуль которого равен h<y] 1A + 1) , а проекция на ось Oz
равна mh (рис.3):
|ОЬ| = й^(/ + 1);
Ш = тП. (D-45)
Обозначим символами 0 и Ф полярные углы, характеризующие его направление.
Поскольку треугольник OLI имеет в вершине J прямой угол и ОН = JL, то
О J = VOL2 - ОН2 = /ц//(/ + 1)-т2 . (D-46)
Таким образом, компоненты такого классического момента были бы равными:
01 = hyll(l + i)-m2 cos<& ;
~ОК = ti^l(l + \)-m2 шФ;
Ш = *Ц//(/ + 1) cos в = тП. (D-41)
814

Общие свойства угловых моментов в квантовой механике
Рис.3
Классическая модель орбитального углового
момента частицы без спина в состоянии
|/, т). Предполагается, что длина |OL| и
угол 0 известны, а угол Ф является
случайной переменной, плотность вероятности
которой остается постоянной в интервале
углов [0,2тс]; классические средние
значения компонент вектора OL и их квадратов
при этом равны средним значениям
соответствующих квантовых величин
Допустим теперь, что |OL| и 0 известны, а Ф — случайная величина,
принимающая любые значения в интервале [0,2я] с одинаковой вероятностью (равновероятная
случайная переменная). Тогда, усреднив по Ф , получим:
(pi) ос |о2я cosФ d<S> = 0 ; (D-48-a)
(pR) ос |2я Sin ф с1Ф = 0, (D-48-b)
что полностью соответствует формуле (D-44-a). Кроме того:
(pl2]^ — п2[l(l + l)-m2]\2Qncos2 ФAФ = — [/(/ + l)-m2] (D-49)
и также
@K2)^[KUl)-m2}.
(D-50)
Эти средние значения совпадают с теми, которые были найдены в (D-44). Итак, угловой
момент частицы в состоянии | k, /, т) ведет себя (в том, что касается средних значений
его компонент и их квадратов) как классический угловой момент длиной Лд//(/ +1) ,
имеющий проекцию mh на ось Oz, угол Ф которого является равновероятной
случайной функцией со значениями между 0 и 2я .
Конечно, этот образ нужно использовать с осторожностью, и на протяжении всей
главы мы многократно подчеркивали, насколько квантовые свойства угловых моментов
отличаются от их классических свойств. В частности, обратим внимание на то, что ин-
815

Глава VI
дивидуальное измерение Lx или Lv для частицы в состоянии \k,l,mj не может дать
любое значение, заключенное между - fi^l{l +1) - т2 и + h^Jl(l +1) - т2 , как можно
было бы предполагать на основании изложенной выше модели, и единственно
возможными результатами измерения могут быть только собственные значения Lx или Ly
(в конце §С мы видели, что они совпадают с собственными значениями оператора L.),
то есть в данном случае фиксированного числа / могут принимать одно из 2/ +1
значений /Й,(/-1)Й,...,(-/ + 1)Й,-/Й.
Ь. ВЫЧИСЛЕНИЕ ФИЗИЧЕСКИХ ПРЕДСКАЗАНИЙ ПРИ ИЗМЕРЕНИИ V И L,
Рассмотрим частицу, состояние которой описывается нормированной волновой
функцией:
(r|\|/) = \|/(r) = \|/(r,fl,(p). (D-51)
Мы знаем, что измерение L2 может дать только дискретный ряд значений
0,2/i2,6/j2,...,/(/ + l)/i2,..., а измерение Lz —только значения 0,±й,±2Й,...,тй,... Как
найти вероятности получения этих различных результатов, если известна волновая
функция \|/(г, 0,ф)?
а. Общие формулы
Обозначим символом ;^2 (Lm) вероятность получить при одновременном
измерении L2 и Lz результаты /(/ + \)fi2 и mh .Ее можно вычислить, разложив \|/(г) в
базисе собственных функций операторов L2 и L,. На самом деле мы возьмем
«стандартный» базис типа тех, которые были введены в § D-1-d:
М/,,/,,Дг) = ^/(г)Г/"@,ф). (D-52)
Тогда функция \|/(г) запишется в виде:
V(r)= 111^Л„Л,>)Г(^Ф)> (D-53)
к I m
где коэффициенты ск1т вычисляются по обычной формуле:
= J0V</r Kj{r) j20nd(f> fisinbd* У/"*(в, ф) V(r, 6, Ф). (D-54)
816

Общие свойства угловых моментов в квантовой механике
Согласно постулатам главы III вероятность .^2 L{Um) в этих условиях
определяется как:
^l2,z..(/'w)= 2 к,/,-
Если измеряется только L2, то вероятность получить результат /(/ + \)Ь равна:
+/
1
^,@= S^L(/,«)=II
+/
(D-55)
(D-56)
Аналогично, если измеряется только L , то вероятность получить результат nth равна:
Л (m)=S^a ,(/,и) = 12
L'.L. '
(D-57)
(ограничение />|m| удовлетворяется автоматически, так как коэффициентов ск , ш с
индексами |т| > / просто не существует).
В действительности, поскольку операторы L2 и Lz действуют только на углы Ь и
ф, ясно, что именно угловая зависимость волновой функции является наиболее
существенной при вычислении вероятностей. Чтобы убедиться в этом, представим функцию
\|/(г,О,ф) как функцию углов й и ф, зависящую от параметра г. Как и любая
функция углов, она может быть разложена по сферическим гармоникам:
У(г,в,Ф) = :ЕЕ«|,ж№(«.Ф).
(D-58)
Коэффициенты а1%т этого разложения зависят от «параметра» г и определяются
выражением:
*/.*@ = Г</Ф \lsinb db У/"*(д, ф) V(r, в, Ф). (D-59)
Если сравнить выражения (D-58) и (D-53), видно, что Ск, т являются коэффициентами в
разложении а1т{г) по функциям Rkl(r):
4mir)^cklmRkl{r),
к
где с учетом (D-54) и (D-59):
c*./.«=sJrr2rfr**./(r)fl/.-.(r)'
Используя (D-37) и (D-60), получим также:
(D-60)
(D-61)
52 Квантовая механика
817

Глава VI
£r2dr\aLm(r)\ =Хк,.-Г- (°-62)
Вероятность ^2 (/, m) [формула (D-55)] может быть теперь записана в форме:
^ L(l,m)=j;r2dr\altm(r)\\ (D-63)
и, как в формулах (D-56) и (D-57), можно получить:
^@= S fcr2drUm(r)\2 (D-64)
^( = S J^rL (r)| (D-65)
[в этой формуле коэффициенты а1 т(г) также не существуют, если / > \т\ ]. Итак, чтобы
предсказать результаты измерения L2 и Lz, достаточно рассмотреть волновую
функцию, как зависящую только от углов Ф и ф , и разложить ее по сферическим
гармоникам, как это сделано в (D-58), а затем применить формулы (D-63), (D-64) и (D-65).
Совершенно аналогично можно показать, что поскольку оператор Lz действует
только на ф , именно зависимость от угла ф волновой функции \|/(г) существенна для
вычисления вероятности 9>и (т). Для этого используем тот факт, что сферические
функции являются произведением функции от угла Ь на функцию от угла ф . Запишем их
в таком виде:
/икр
Г(^,Ф) = ^ (*)-=, (D-66)
чтобы каждая из функций произведения была нормированной. Действительно:
fK=s- (D'67)
Подставив эту формулу в соотношение ортонормировки (D-23) для сферических
гармоник, получим:
j*sinb d$ zfF)ZP(b) = 8„, (D-68)
[по причинам, аналогичным уже указанным в замечании (i) § D-1-d, в обе функции Z™
левой части равенства входит одно и то же значение т ].
818

Общие свойства угловых моментов в квантовой механике
Если рассматривать \|/(г, О, ф) как функцию угла ф, определенную в интервале
[0,2я] и зависящую от «параметров» г и д , то ее можно разложить в ряд Фурье:
1/Иф
v(r, в, ф)=5Л0-. *) т= • (D-69)
m -\/2Я
где коэффициенты bm(r, Ь) могут быть вычислены по формуле:
6w(r,«) = 7= £* J(P *"""* V(r,«, ф). (D-70)
Если сравнить формулы (D-69), (D-70) с формулами (D-58), (D-59), то коэффициенты
а{ т(г) для фиксированного значения т могут быть представлены как коэффициенты
разложения Ьт(г,Ь) по функциям Z"', соответствующим одному значению т:
*-,('".*) = Е«/.«М2Г(в), (D-71)
/
где
«/.»(') = Jo«*e M Zf{b)bm{r% Ь). (D-72)
Учитывая формулу (D-68), из разложения (D-71) следует:
ЦзтЬ db\bm{ry Ц2 = £ \altm(r)\2. (D-73)
Подставив эту формулу в выражение (D-65), получим 9>L (m) в форме:
•^ (т) = \~r2dr ЦзтЬ db\bm(r, Ъ)(. (D-74)
Итак, если измеряется только Lz, достаточно считать волновую функцию зависящей
только от переменной ф и разложить ее в ряд Фурье подобно (D-69), чтобы иметь
возможность вычислить вероятности возможных результатов.
Можно было бы подумать, что аналогичные рассуждения должны дать значение
^2 @ с помощью разложения \|/(г, д,ф) по переменной Ь . Однако это не так: все
предсказания относительно измерения L2 включают в себя зависимость волновой
функции от углов Ь и ф, что связано с тем обстоятельством, что оператор L2
действует одновременно и на Ь, и на ф, вследствие чего следует использовать формулу
(D-64).
52*
819

Глава VI
Р. Частные случаи и примеры
Допустим, что волновая функция \|/(г), описывающая состояние частицы, имеет
вид произведения функции переменной г на функцию переменных Ь и ф :
V(r,«,q>) = /(r)gF,<p). (D-75)
Можно всегда предположить, что функции /(г) и g($, ф) нормированы в отдельности:
JoVrfr|/(r)|2=l; (D-76-a)
j20ndq> $inbdB\g&,v)\2 =1. (D-76-b)
Чтобы разложить в соответствии с выражением (D-58) волновую функцию, достаточно
разложить g(d, ф) по сферическим гармоникам:
*(*,Ф) = ЕХ4.«>Г(в.Ф). (D-77)
/ т
где
<*/.« = fd(P Jo^« rf6 Г*№» Ф) *(*. Ф) • (D~78)
В этом случае все коэффициенты а1 „,(г) формулы (D-58) пропорциональны /(г):
a,.M = duJ{r). (D-79)
С учетом формулы (D-76-a) выражение (D-63) для вероятности .<?f2 (/, т) приобретает
L ,LZ
вид:
^L(/,m)=|^m|2. (D-80)
Эта вероятность совершенно не зависит от радиальной части волновой функции /(г).
Аналогично рассмотрим случай, когда функция \|/(г, О, ф) является произведением
трех функций одной переменной:
У(г,в,Ф) = /(г)А(в)*(ф), (D-81)
которые мы будем считать нормированными в отдельности:
\~r2dr\f{r)\2 = J*«ne £»|Л@)|2 = J02*rfcp |*:(Ф)|2 = 1. (D-82)
Конечно, формула (D-81) является частным случаем формулы (D-75), и полученные
только что результаты применимы и здесь. Но, кроме того, если мы интересуемся лишь
измерением Lz, достаточно разложить &(ф) в ряд:
820

Общие свойства угловых моментов в квантовой механике
*(ф)=1>„,
ЙЯф
л/2л"
где
и получить эквивалент формулы (D-69) с подстановкой:
bm(r9b) = emf(r)h(b).
Согласно формуле (D-82) вероятность &и (т) определяется выражением:
(D-83)
(D-84)
(D-85)
(D-86)
Изложенные выше рассуждения можно проиллюстрировать простыми примерами.
Допустим сначала, что волновая функция ц/(г) не зависит от углов 6 иф, так что
*(Ф) =
72я'
Тогда:
Я(в,<р)=-= = #(в,ф).
(D-87)
(D-88)
Измерение L2 или измерение Lz может дать только нулевой результат.
Введем теперь только зависимость от Ь , выбрав:
А(в)
= ^-cos&\
*(Ф) = -
В этом случае:
(D-89)
(D-90)
Результаты измерения L2 или Lz точно определены: для L2 можно получить только
значение 2Й2, а для Ьг — нуль. Нетрудно видеть, что это введение зависимости от Ь
никак не влияет на физические предсказания, касающиеся измерения Lz.
821

Глава VI
Напротив, если имеется зависимость от ф, например, вида:
£(ф);
(D-91)
л/2я '
то функция g(-&, ф) уже не является сферической гармоникой. Согласно формуле (D-86)
все вероятности &>L (m) равны нулю, кроме:
^(m = l) = l. (D-92)
Но предсказания результатов измерения L2 также изменяются по сравнению с (D-87).
Чтобы убедиться в этом, достаточно разложить функцию:
*(*,Ф) =
л/4тт
Л'ф
(D-93)
по сферическим гармоникам. Можно доказать, что все функции 17"(Ф, ф) с нечетными
значениями / и т = 1 действительно входят в разложение функции (D-93), вследствие
чего невозможно точно предсказать результат измерения L2 (вероятности различных
возможных результатов могут быть вычислены с помощью выражений для сферических
гармоник). Таким образом, на этом частном примере можно заметить, что, как указано в
конце § а, зависимость волновой функции от ф входит также и в результаты
вычисления предсказаний измерения L2.

ДОПОЛНЕНИЯ К ГЛАВЕ VI
Avi- Сферические гармоники.
BVI. Угловой момент и вращения.
Cyi. Вращение двухатомных молекул.
DVI. Угловой момент стационарных
состояний двумерного
гармонического осциллятора.
Evi- Заряженная частица в магнитном
поле. Уровни Ландау.
FVi. Упражнения.
AVj: формальный анализ сферических
гармоник ^w(f), ф) ; устанавливаются некоторые
свойства, использованные в главе VI и в
некоторых других дополнениях.
Вуь устанавливается тесная связь между
угловым моментом J произвольной квантовой
системы и пространственными вращениями,
которые она может испытывать. Показано,
что соотношения коммутации между
компонентами J отражают чисто геометрические
свойства этих вращений. Вводятся понятия
скалярной и векторной наблюдаемых,
используемые в других дополнениях, в частности,
в дополнении Dx. Материал существенно
важен в теоретическом плане, но иногда
труден для понимания, вследствие чего
рекомендован для более позднего изучения.
Сщ. простое и непосредственное применение
квантовых свойств углового момента:
спектры чистого вращения гетерополярных
двухатомных молекул и рамановские
вращательные спектры. Уровень элементарно простой.
Из-за важности рассмотренных явлений в
физике и химии рекомендуется для изучения
при первом чтении.
Dvi: может рассматриваться как упражнение
с решением. Изучаются стационарные
состояния двумерного осциллятора. Для
классификации этих состояний в зависимости от
углового момента вводится понятие
«циркулярных квантов». В принципе материал легок
для понимания. Некоторые результаты будут
использованы в дополнении Ещ.
Ещ. общий анализ квантовых свойств
заряженной частицы в магнитном поле, после
чего рассмотрен частный случай
однородного магнитного поля (уровни Ландау).
Трудности не представляет: рекомендуется при
первом чтении, но можно ограничиться § 1 -а,
§ 1-Ь, § 2-а, § 2-Ь, § 3-а.
823

Глава VI
Дополнение Avi
СФЕРИЧЕСКИЕ ГАРМОНИКИ
1. Вычисление сферических гармоник.
a. Определение функций Yt (Ф, ф).
b. Общее выражение для Y}n(b, ф).
c. Явные выражения для сферических гармоник при I = 0,1, 2.
2. Свойства сферических гармоник.
a. Рекуррентные соотношения.
b. Соотношения ортонормировки и замкнутости.
c. Четность.
d. Комплексное сопряжение.
e. Связь сферических гармоник с полиномами Лежандра и другими функциями.
Это дополнение предназначено для уточнения основных свойств сферических
гармоник. Здесь будут доказаны некоторые результаты, сформулированные в § D- 1-е главы VI.
1. Вычисление сферических гармоник
Чтобы вычислить различные сферические гармоники У(Ь^), используем метод,
предложенный в § D-1-c главы VI. Возьмем в качестве исходного выражение для
У1(Ъ, ф) и применим к нему оператор L_ , чтобы затем шаг за шагом получить
сферические гармоники, соответствующие одному значению / и связанным с ним B1 +1)
значениям т. Вспомним, что операторы L+ и L_ действуют только на угловую
зависимость волновой функции и имеют вид:
L±=/te±/<p
±-гт + '<*$д —
Эв Эф
A)
а. ОПРЕДЕЛЕНИЕ ФУНКЦИЙ У{ (в, ф)
В § D-1-c главы VI мы видели, что функцию 5^(в,ф) можно вычислить, исходя из
уравнения:
L+r/(e,q» = 0 B)
824

Общие свойства угловых моментов в квантовой механике
благодаря существованию соотношения:
1?(«,Ф)= Ffme"*. C)
Ранее было получено:
Yll(bi(p)=cl(sin^)leil\ D)
где с, — произвольная постоянная.
Определим сначала модуль с,, считая У/@, ф) нормированной относительно
переменных Ь и ф:
/(^ф/0Л5ш«^|у/@,ф)|2 =|с,|2 j2Qnd(p j*sin$db(sin$J1 = 1, E)
откуда получим:
|с;|2 = 1/271/,, F)
где /, определяется равенством:
/, = j*sin$d$(sin$J1 = \l\du{\-u2I G)
(здесь и = cosb ); интеграл /, вычисляется рекуррентным методом:
//=J!Il^(l-ii2)(l-ii2)M=//.I-J*lrfiiii2(l-ii2)M. (8)
Интегрирование последнего интеграла по частям дает:
/, = /,_,-!/,. (9)
Итак:
/, =-^-/, ,, A0)
' 2/+1 "
где
/„ = £'<& = 2. A1)
Таким образом, получим:
B/)!! 22/+|(/!J
/ = 1 ч'- i =±—!±±-. A2)
' B/+1)!! ° B/ + 1)!
Итак, функция Y,'(b,<p) нормирована, если
,, 1 /B/ + 1)!
\С, =—:—J . A3)
1 'I 2'/! V 4я
825

Глава VI
Чтобы полностью определить коэффициент с,, нужно выбрать его фазу. Обычно
принимают:
tlL ШМ A4)
' 2'/! Ч 471
Далее мы увидим, что с этим условием фазы функция У1°(Ф), которая не зависит от ф,
имеет вещественное и положительное значение при f> = 0.
Ь. ОБЩЕЕ ВЫРАЖЕНИЕ ДЛЯ YJ" (в, ф)
Путем последовательного действия оператора L_ на функции ^'(ф.ф) можно
получить и все другие сферические гармоники У,т@, ф). Для упрощения вычислений
докажем справедливость более удобной формулы.
а. Действие операторов (L±)P на функцию вида em(pF(f>)
Действие операторов L+ и L_ на функцию вида emF{b), где п — произвольное
целое число, определяется выражением:
L\e^FW]^nei{n±XLsinb)x±" * Vsinbf"F{b)\. A5)
В общем случае:
АР г 1
(L±r[e^F(b)] = (+nrei<n±pLsinbr±n-——[(sinbf*F&)\. A6)
Докажем сначала формулу A5). Известно, что
d db d
1 d
откуда следует:
d(cosb) d(cosb) db sinb db
d
(sinft)
= (sin$y
{ 1 Л
sin г
,±n—^—UsinVf" F($)] =
d(cosv)L J
?n(sind)*n-lcosf> F($) + (sinb)
„dF&j
Tnctgd F(d) +
dF(b)
db
A7)
A8)
826

Общие свойства угловых моментов в квантовой механике
Итак:
+ £?'
/(«±1)Ф
^*)lt"^^[<jfa*)*"',w] =
d{cosb)
= е
±/ф
Эв Эф
-ис/^±э?
e**F(d),
?.(«±d<pF(^) =
A9)
и в последнем выражении нетрудно узнать формулу A) для операторов L+ и L_ : тем самым
равенства A9) и A5) идентичны.
Чтобы доказать теперь формулу A6), можно применить рекуррентный способ, так как при
/7 = 1 формула A6) сводится к формуле A5), которую мы только что доказали. Поэтому
допустим, что соотношение A6) справедливо при ( р - 1):
(l±)P~1 [ein«F($)] = (mp-lei("±pTlLsinb)p-l±n- T7^[(smtf)*''F(f3)] B0)
и докажем, что оно справедливо также и при индексе, равном р . С этой целью подействуем
операторами L± на обе части равенства B0). Что касается правой части, то там можно использовать
формулу A5), где следует произвести замену:
л => л±р +1;
F(b) => (япв)'*" —?-—г Usin$)*n F(d)l.
d(cost))p l J
B1)
В результате получим:
d(cosb)
(L±)P [e,mpF(f})] = (+h)p ei(n±p)*(sin$)±n + " x
(sinbf"-p+l (sin$y-{±" d". [(sin*)** F(f3)][ =
d{cosbY
= (+/*)" *'<»*"• (jihO)^' ., **' [(sinb)Tn F(f3)]. B2)
Таким образом, путем рекуррентных преобразований формула A6) доказана.
&. Вычисление ^'"(т>,ф) через ^'(т},ф)
Как было указано в § D-1-c-cc, требуется, чтобы сферические гармоники У;"Ч#»Ф)
удовлетворяли соотношению:
ад-ф.ф) = /Ц//(/ + 1)-т(т±1) У,т±|(^Ф) = »>/(Z=Fm)(Z±m+l) ^w±,(^,Ф). B3)
827

Глава VI
Эти соотношения автоматически обеспечивают нормировку функции Y",±l, если
нормирована функция Y, и фиксируют относительные фазы сферических гармоник,
соответствующих одному и тому же значению / и разным значениям т .
В частности, можно вычислить }у"(т},ф), основываясь на 1^($,ф) и используя
оператор L_ [формулы A) и B3)]. В результате непосредственно получим
нормированную функцию Yjm(b, ф), фаза которой будет определена на базе условия, наложенного
на Y,l(ft, ф) [формула A4)]. Чтобы перейти от 1^0&,ф) к ^т(Ф, ф)» нужно оператор L_
применить A-т) раз, и, согласно формуле B3), получим:
(l.)'-tf«>,q>) =
= (И)'"'B0A) xB/-l)B)x...x(/ + m + l)(/-/n) Ч"(в,ср), B4)
то есть
/1 N § / Т \1-1П
A + т)\ (L
B/)!(/-/и)!
I Й
Г(*• Ф) = JJ.T, ' "тН Y!(*.Ф) • B5)
И окончательно, используя выражение D) для У/ (в, ф) [коэффициент С,
определяется формулой A4)] и формулу A6), в которой п-1 и р = 1-т, можно преобразовать
B5) к виду:
(-1У |2мао+^^ _^--
2'/! V 4я (/-/я)! </(аюв)'
Г@,Ф) = Vrr J^ т^т: ^(«я*)-1" „ Ач|.„, (^J/. B6)
у. Вычисление Y (Ъ,($) через Y{ Ч#*Ф)
Чтобы получить выражение B6), мы исходили из результатов § 1-а. Конечно, можно
было бы также сначала вычислить yj_/(t}, ф) и использовать оператор L+ . Полученное
при этом выражение для Y™ отличается от B6), но оказывается полностью ему
эквивалентным.
Вычислим Yf~l(b, ф), исходя из B6)*. Поскольку:
* Можно было бы, конечно, найти Yt l из уравнения L_Yt l(t), ф) = 0, но при этом фаза
осталась бы произвольной. Используя B6), мы полностью определим Yt~l (Ф, ф), и ее фаза
останется выбранной в соответствии с условием, наложенным в § 1 -а.
828

Общие свойства угловых моментов в квантовой механике
(sinftJ1 = (l-aw26)'
B7)
является полиномом степени 2/ по cosb, то вклад в ^~'(Ф> ф) дает только его член
наивысшей степени:
d21
d(cosb)
-(s*W=(-l)'B/)!
При этом:
' 2'/!\ 4я
<Г"ф(*шд)'
B8)
B9)
Тогда функцию ^ш(д,ф) можно получить, подействовав A + т) раз оператором L+
на функцию Y/''i-д, ф). Используя B3) и A6), получим окончательно:
(-1)'- [2/ + 1 (/-,)! ^(Лд)._^1_(й|в)«в C0)
у«(«, ф) = ^— рш ^-^: *"*(,
d(awfl)'
с. ЯВНЫЕ ВЫРАЖЕНИЯ ДЛЯ СФЕРИЧЕСКИХ ГАРМОНИК ПРИ / = 0, 1 И 2
Из общих формул B6) и C0) нетрудно получить сферические гармоники для первых
значений /:
1 C1)
У° =
°~^'
Ylt'(b,(p) = T^—sin^etl,f-
C2)
15
32п
К2"(#, ф) = лЬг- im2* е±2лр-
КЛ^-Ф) = *л|— «ид cosfl е*'ф;
C3)
К2°(в,ф) = д|—(Зсо/д-1).
829

Глава VI
2. Свойства сферических гармоник
а. РЕКУРРЕНТНЫЕ СООТНОШЕНИЯ
В соответствии с принципом построения сферические гармоники должны
удовлетворять соотношениям B3), то есть с учетом формулы A):
0±'"ф
±- mctgb
Г(^Ф) = л//(/ + 1)-т(/п±1)Г±,(^Ф). C4)
С другой стороны, отметим следующую формулу, оказывающуюся часто полезной:
' Л' B/ + 1)B/ + 3) '
B/ + 1)B/-1) "
C5)
Эту формулу можно очень просто доказать, и ниже мы вкратце приведем это доказательство.
Согласно B5):
cosbY;" =
(/ + /и)!
cosb
'B/)!(/-m)!
и легко доказать, используя выражение A) для L_ , что
[L_,cos&] = tte~i,fsin$
и
[L.,e-'<p5md] = 0.
у| У/(д.ф).
C6)
C7)
C8)
Тогда рекуррентный метод позволяет вычислить коммутатор оператора | — | с cosft ;
действительно, если предположить, что
то получим:
I Л
,COS$
ft '
,cos$
f , N*-.
= (Jfc-l)e"*smd
*-2
C9)
l Л
-,C051
I ft
+
го" J
— , cayfi
U J J
L
h
('- ^"'
-»<p
sin®
h
•
D0)
830

Общие свойства угловых моментов в квантовой механике
L.
, COSX
ke4* sinb
П)
= к
D1)
Это соотношение установлено с помощью рекуррентного метода, и теперь его можно
использовать, чтобы записать формулу C6) в виде:
costi Y™ =
(Z + m)!
B/)!(/-m)!
( т Л
I П )
cosbY/-(l-m) — J e'* sintiYf
Используя D) и A4), без труда покажем, что
е~* sin® Y/ = -Л^- (l-cos2 «) Y;
i-i
1 •
D2)
D3)
Если теперь с помощью общей формулы B6) вычислить явные выражения для Yl+l и Yl+ll, получим:
costi Y! =
' V2/ + 3
Yl •
cos2 Ь Y}:{ =
I yl-\ i 1 y/-l
2/ + 1 V2/ + 3 /+1 2/ + 1 '-1 '
D4-a)
D4-b)
Чтобы доказать выражение C5), достаточно подставить равенства D3) и D4) в D2) и
воспользоваться формулой C5).
Ь. СООТНОШЕНИЯ ОРТОНОРМИРОВКИ И ЗАМКНУТОСТИ
Из самого метода, использованного для построения сферических гармоник, следует,
что они образуют ансамбль нормированных функций, которые к тому же оказываются
ортогональными друг другу, так как являются собственными функциями эрмитовых
операторов L2 и Lz, соответствующими различным собственным значениям. Тогда
соотношение ортонормировки можно записать в форме:
J02> Hsinb db У/"*(*. Ф) 1ГЧ*. Ф) = 5/r8,„„,,.
D5)
Можно показать (и мы будем здесь так считать), что любая квадратично
интегрируемая функция углов f) и ф может быть разложена единственным образом по
сферическим гармоникам:
/(«,ф) = 21с,.жГ(«,ф), D6)
831

Глава VI
где
cl». = f<*P ]>'"* <ю уГ*&< ф) Я*, ф) • D?)
Таким образом, ансамбль сферических гармоник образует ортонормированный базис в
пространстве квадратично интегрируемых функций й и ф, что можно выразить с
помощью соотношения замкнутости:
ЕЕ^ГФ. Ф) ^/"'(в'.ф') = &(cosb-cosu') 8(ф-ф'). D8)
с. ЧЕТНОСТЬ
Операция четности над некоторой функцией обычного пространства состоит в
замене (см. дополнение Fn) в этой функции координат текущей точки пространства на
координаты точки, симметричной к данной относительно начала системы координат:
г => -г. D9)
В системе сферических координат эта операция сводится к замене (рис.2 главы VI):
д=>я-д; E0)
ф => п + ф.
Вследствие этого, если связать пространство волновых функций частицы без спина со
стандартным базисом (§ D-1-d главы VI), то радиальная часть базисных функций
хук {,„(г) останется неизменной при операции четности, и их преобразование коснется
только сферических гармоник, что мы сейчас и продемонстрируем.
Прежде всего, заметим, что в преобразовании:
sin$=> sinb\
casO=>-casf); E1)
eim*=*(-l)meim*.
В этих условиях функция У/(О, ф), вычисленная в § 1-а, преобразуется как
#(я-6,я + ф) = (-1)' #(в,Ф). E2)
С другой стороны:
А А
Эф Эф*
E3)
832

Общие свойства угловых моментов в квантовой механике
Формулы E1) и E3) показывают, что операторы L+ и L_ [формулы A)] остаются
неизменными, и это значит, что эти операторы являются четными в том смысле, который мы
определили в дополнении Fn (§ 2-а). Вследствие этого и в соответствии с формулами
E2) и B5) получим:
К/"(я-«,я + ф) = (-1)/ ТО.ф). E4)
Таким образом, сферические гармоники являются функциями определенной
четности, не зависящей от числа т : они являются четными, если / — четное число, и
нечетными, если / — нечетное число.
d. КОМПЛЕКСНОЕ СОПРЯЖЕНИЕ
Благодаря зависимости от ф сферические гармоники являются комплексными
функциями. Из сравнения выражений B6) и C0) сразу же видно, что
[Г(^,ф)[ =(-1ПГ"(#,ф). E5)
е. СВЯЗЬ СФЕРИЧЕСКИХ ГАРМОНИК
С ПОЛИНОМАМИ ЛЕЖАНДРА И ДРУГИМИ ФУНКЦИЯМИ
Зависимость сферических гармоник от угла Ь аналогична зависимости функций,
известных под названием полиномов Лежандра и связанных с ними функций Лежандра.
Здесь мы не намерены ни доказывать, ни даже перечислять все свойства этих функций,
но все-таки отметим их связь со сферическими гармониками.
а. Функция У?(Ъ) пропорциональна полиному Лежандра
Если т - 0 , то формулы B6) и C0) дают:
У,° (*) = ^r W^TT^r (**•*>" • E6)
2 /! V 4я d(cosb)
и это выражение можно переписать в форме:
У/0(д^^Р/(С™0)' E?)
если положить:
P((m)=w^A-m2)'- E8)
53 Квантовая механика
833

Глава VI
Из определения E8) видно, что Р{{и) является полиномом степени / от и с
четностью* (-1) :
/>(-и) = (-1)'/>(н). E9)
Здесь РДи) — полином Лежандра степени /. Легко показать, что у него может быть /
нулей в интервале [-1, +1], и численный коэффициент в E8) обеспечивает равенство:
*50) = 1- F0)
Можно показать также, что полиномы Лежандра образуют ансамбль ортогональных
функций:
\l\du Р» Pr(u) = fisinb d$ P^cosb) Pr(cos$) = ^Л* , F1)
по которым могут быть разложены любые функции угла Ь :
/W = Sc/P/(c^f)), F2)
где
с, = 2И1 fisJnQ db Px (cosb) /(f>). F3)
ЗАМЕЧАНИЕ
Согласно формулам E7) и F0) имеем:
*?@) = Д^. F4)
»>=]¥•
Как отмечалось в § 1-а, выбранное для }^(#,ф) соглашение о фазе означает, что
У;°@) является положительным вещественным числом.
C. Функция ^w(f>, ф) пропорциональна присоединенной функции Лежандра
Для положительных значений т функцию У^Чб, ф) можно получить путем
действия оператора L+ на Yt°(f>); с учетом формулы B3):
* Речь идет о четности относительно переменной и . Заметим, однако, что операция четности в
пространстве [формулы E0)] заключается в изменении cos$ на -cosb ; при этом свойство E9)
выражается соотношением Yt (п - д) = (-1) Y{ (f)) , являющимся частным случаем выражения E4).
834

Общие свойства угловых моментов в квантовой механике
(l-m)\(L+\
таФ) = ^^!111 Y'm' (w-0b F5)
Используя формулы A) и A6), получим:
К;Чв,ф) = (-1)\|^^-^ РГ(созЬ)е1п1\ (m>0), F6)
11 4я (/ + m)!
где Р"' — присоединенная функция Лежандра, определяемая выражением:
Plm(u) = yl(l-u2)m—Pl(u), (-1<м<1). F7)
аи
Функция Р"\и) является произведением д/A-м2) на полином степени (/-т) с
четностью (-1) ; функция />°(и) совпадает с полиномом Лежандра Р{ (и). Ансамбль
функций Р/" при фиксированном значении т образует систему ортогональных функций:
Vхdu Р;\и) Р;!\и) = Fsinbdb P^cosb) P,m(cosb) = —^— A + тIЬи,, F8)
по которой можно разложить любую функцию угла 6 .
Формула F6) справедлива для положительного или равного нулю значения т. Для
отрицательных значений т достаточно использовать соотношение E5), чтобы
получить:
у;"(Ъ, ф) = J^li У-^ p-'"(cosb) eim\ (m < 0). F9)
1 V 1' An (/-m)! '
у. Теорема о сложении сферических гармоник
Рассмотрим два произвольных направления в пространстве Ои' и Ои",
выделенных полярными углами ($', ф') и F", ф") соответственно, и обозначим символом а
угол между этими двумя направлениями. Можно доказать следующее соотношение:
^Pt(cosa)= Х(-1ГГ(^фОГЧв",Ф">, G0)
где Р1 — полином Лежандра степени /. Это соотношение известно под названием
«теоремы сложения сферических гармоник».
53*
835

Глава VI
Укажем основные этапы элементарного доказательства соотношения G0). Заметим сначала,
что если cosOL выразить через полярные углы (f}', ф') и (f}", ф"), левая часть равенства G0)
может рассматриваться как функция углов (тУ, ф') и может быть разложена по сферическим
гармоникам Y™ (тУ, ф') . Коэффициенты этого разложения, являющиеся, естественно,
функциями двух других углов (в", ф"), также могут быть разложены по сферическим гармоникам
Y/" (f}", ф") . Тогда должно выполняться равенство:
2L±±Pl(cosa) = £ 1 cr,m,r,m~ Yr"(*W)Yf (*",*"). G1)
и задача сводится к вычислению коэффициентов сг т,.г т„ . Их можно получить в результате
следующих рассуждений:
(i) Прежде всего, эти коэффициенты отличны от нуля только при условии, что
/' = /" = /. G2)
Чтобы показать это, зафиксируем сначала направление Ои"; тогда Р{ (cosOL) будет зависеть
только от углов (f}', ф') • Если ось Oz выбрана вдоль Ои", то cosOL = cos$', и полином
f) (cosOL) пропорционален У5°(тУ) [см. соотношение E7)]. Далее нужно перейти к общему
случаю, где направление Ои" произвольное, путем поворота, приводящего ось Oz к этому
направлению: cosOL при этом остается неизменным, как и Pt (cosа). Поскольку операторы вращения
(§ 3-с-у дополнения BVi) коммутируют с оператором L2, то результат преобразования 5^0(т}')
остается собственной функцией оператора L с собственным значением l(l + \)h , то есть
линейной комбинацией сферических гармоник Y™ (тУ, ф'), и, следовательно, V -I. Аналогично
устанавливается, что /" = /.
(и) При повороте совокупности двух направлений Ои' и Ои" на угол Р вокруг оси Oz
угол а не изменяется, как не меняются и углы f}' и f}" , тогда как углы ф' и ф" становятся
равными ф'+Р и ф"+р. Таким образом, левая часть равенства G1) сохраняется, а каждый
член правой части умножается на е1(т +т , и единственными отличными от нуля
коэффициентами в сумме правой части остаются те, которые удовлетворяют равенству:
m' + m" = 0. G3)
(Hi) Комбинируя результаты G2) и G3), заметим, что формулу G1) можно переписать в виде:
^ pt(cosa)= £(-1)ч,Г(^фосч^ф"). G4)
Если подставить гУ = f}" и ф' = ф" , то согласно F0) получим:
836

Общие свойства угловых моментов в квантовой механике
Цг-= 1(-1ГстГЛ«',ф')Г"(в',Ф'). G5)
Поскольку (-l)wK/~m совпадаете Y™ , интегрирование равенства G5) по dQ/ = sinb'db'dty' с
учетом соотношения ортонормировки дает:
2/ + 1= %ст. G6)
m=-l
С другой стороны, можно взять квадрат модуля обеих частей равенства G4) и
проинтегрировать по dQf и dSl" . Если воспользоваться выражением D5), легко заметить, что правая часть
+/
получившегося равенства равна £ \ст\2 . В левой же части можно воспользоваться инвариант-
т = -I
ностью угла а при вращении, чтобы показать независимость интеграла J <Й2'| Р, (cos Ct)|2 от
(f)", ф"). Если еще при вычислении этого интеграла выбрать направление Ои" вдоль оси Oz ,
то в соответствии с соотношением F1) получим:
\d&'\Pl(cosa)f = JdQ|P,(co5«)|2 = 2ic-^—. G7)
Интегрирование по d£l" теперь производится без труда, и мы приходим ко второму
соотношению между коэффициентами ст:
2/ + l= Z kf. G8)
« = -/
(iv) Уравнений G6) и G8) достаточно, чтобы определить B1 +1) коэффициентов ст, и все
они равны 1. Чтобы доказать это, рассмотрим в B1 +1) -мерном нормированном пространстве
с 1
вектор X с компонентами х = , т и вектор Y с компонентами у = , . Неравенст-
V2/ + 1 V2/ +1
во Шварца указывает, что
(X*-X)(Y*-Y)>|Y*.X|\ G9)
причем равенство в этом выражении реализуется тогда и только тогда, если векторы X и Y
пропорциональны. Но выражения G6) и G8) показывают, что оно действительно реализуется, и,
следовательно, хт, ст и ут не зависят от т, в результате чего ст = 1. Итак, формула G0)
доказана.

Глава VI
Дополнение Byi
УГЛОВОЙ МОМЕНТ И ВРАЩЕНИЯ
1. Введение.
2. Краткий анализ геометрических вращений 31.
a. Определение. Параметризация.
b. Инфинитезимальные вращения.
3. Операторы вращения в пространстве состояний. Пример частицы без спина.
a. Существование и определение операторов вращения.
b. Свойства операторов вращения R .
c. Выражение операторов вращения через наблюдаемые углового момента.
4. Операторы вращения в пространстве состояний произвольной системы.
a. Система, состоящая из нескольких частиц без спина.
b. Произвольная система.
5. Вращение наблюдаемых.
a. Общий закон преобразования.
b. Скалярные наблюдаемые.
c. Векторные наблюдаемые.
6. Инвариантность относительно вращения.
a. Инвариантность физических законов.
b. Следствие: сохранение углового момента.
c. Приложения.
1. Введение
В § В-2 главы VI мы указывали, что соотношения коммутации между компонентами
углового момента отражают геометрические свойства вращения в обычном трехмерном
пространстве. Именно это мы и намерены показать в данном дополнении, уточнив связь,
существующую между вращениями и операторами углового момента.
Рассмотрим физическую систему (S), квантовое состояние которой в некоторый
момент времени характеризуется кет-вектором |\|/) пространства состояний #.
Выполним над этой системой операцию поворота 31. В ее новом положении состояние
системы будет описываться вектором |\|/'), отличным от |\|/). Требуется выразить |\|/') через
| \|/), если известно геометрическое преобразование 31. Мы увидим, что решение этой
838

Общие свойства угловых моментов в квантовой механике
задачи таково: всякому геометрическому вращению 01 можно поставить в соответствие
такой линейный оператор R , действующий в пространстве состояний #, что
|у')=Д|у). A)
Сразу же обратим внимание на необходимость четко отличать геометрическое вращение 01,
действующее в обычном пространстве, от его «отражения» R, действующего в
пространстве состояний:
<й=>Д. B)
В § 2 мы начнем с напоминания основных свойств геометрических вращений 01.
Естественно, нет необходимости приводить здесь их детальный анализ, достаточно
лишь отметить некоторые его результаты, которые окажутся полезными в дальнейшем.
Затем в § 3 мы на простом примере частицы без спина уточним форму операторов
вращения R, изучим их важнейшие свойства и покажем их связь с операторами углового
момента L . Это даст возможность интерпретировать соотношения коммутации между
компонентами углового момента как отражение в пространстве #г чисто
геометрических характеристик вращений 01. Далее в § 4 мы обобщим эти понятия на произвольные
квантовые системы. В § 5 исследуем поведение наблюдаемых, описывающих
измеряемые физические величины системы при ее вращении, что приведет нас к возможности
классификации наблюдаемых в зависимости от способа их преобразования при
вращении (скалярные, векторные и тензорные наблюдаемые). И, наконец, в § 6 кратко
затронем проблему инвариантности относительно вращения и укажем на несколько важных
следствий такой инвариантности.
2. Краткий анализ геометрических вращений 01
а. ОПРЕДЕЛЕНИЕ. ПАРАМЕТРИЗАЦИЯ
Вращение 01 является взаимно однозначным преобразованием в трехмерном
пространстве, в котором сохраняются точка пространства, углы, расстояния и
относительная ориентация* трех базисных векторов. Здесь нас будет интересовать ансамбль таких
вращений, при которых сохраняется заданная точка О в пространстве, которую мы
примем за начало отсчета координат. Тогда вращение можно охарактеризовать осью
вращения (задаваемой единичным вектором и или его полярными углами) и углом
вращения ос @ < а < 2тг). Чтобы полностью определить вращение, нужно задать три
параметра, которые иногда рассматривают как компоненты вектора:
* Последнее условие налагается для того, чтобы исключить операцию симметрии
относительно точки или плоскости.
839

Глава VI
а = au , C)
модуль которого равен углу поворота, а направление определяет ось вращения
(отметим, что можно охарактеризовать вращение также и заданием трех углов, которые
называются обычно углами Эйлера). Мы будем обозначать символом .#u(a) геометрическое
вращение на угол а вокруг оси, определенной единичным вектором и.
Ансамбль вращений Л образует группу: произведение двух вращений (то есть
преобразование, образуемое последовательным применением этих двух вращений) также
является вращением. Существует тождественное вращение (то есть вращение на угол,
равный нулю, относительно любой оси); всякому вращению .#u(a) можно поставить в
соответствие обратное вращение Я1_и (ос). Группа вращений не коммутативна: в общем
случае произведение двух вращений зависит от порядка, в котором они применяются*:
<йи (ос) .яи, (а') * tfu, (а') <яи (а). D)
Напомним, однако, что два вращения, выполненные вокруг одной и той же оси, всегда
коммутируют:
яи(а)Яи(а') = Яи(а')Ми(а) = гт + а'). E)
b. ИНФИНИТЕЗИМАЛЬНЫЕ ВРАЩЕНИЯ
Инфинитезимальным вращением называют вращение, бесконечно близкое к
тождественному, то есть вращение 01^ (da) на бесконечно малый угол da вокруг
произвольной оси и. Нетрудно видеть, что вектор, преобразованный с помощью инфинитези-
мального вращения #?u (da) из заданного вектора ОМ, в первом приближении по da
может быть записан в виде:
tfu (da) ОМ = ОМ + dau x ОМ. F)
Всякое конечное вращение можно разложить на бесконечное количество инфините-
зимальных вращений, так как угол поворота может изменяться непрерывно и согласно
формуле E):
tfu (a + da) = #u (a).% (da) = Ж, (da) .% (a), G)
* Если запись имеет вид 012 У1Л, это означает, что первым выполняется вращение У1Х, а затем
к полученному результату применяется вращение Щ .
840

Общие свойства угловых моментов в квантовой механике
где &u(da) — инфинитезимальное вращение. Таким образом, можно свести изучение
группы вращений к изучению инфинитезимальных вращений*.
Прежде чем закончить этот короткий обзор свойств геометрических вращений,
отметим следующее равенство, полезное для последующего изложения:
;йг (-da') ^ (da) Me (da') Ме% (-da) = .%г (da da'), (8)
где ед.,е ,ег — единичные векторы трех осей координат OxyOy,Oz соответственно.
Если da w da' — бесконечно малые углы первого порядка, то это равенство
справедливо с точностью до второго порядка малости включительно. В частном случае оно
уточняет некоммутативную структуру группы вращений.
Чтобы доказать соотношение (8), применим левую часть равенства к произвольному вектору
ОМ и используем формулу F), чтобы найти вектор ОМ', образованный из ОМ с помощью
последовательного действия четырех инфинитезимальных вращений. Можно сразу же заметить,
что если da = 0, то левая часть выражения (8) сводится к произведению Же (-da')ffle (da'),
то есть к тождественному преобразованию [см. E)]; вектор ОМ'-ОМ должен быть
пропорционален da. По тем же причинам он должен быть пропорционален da\ и, следовательно, разность
ОМ'-ОМ пропорциональна da da' .
Итак, чтобы вычислить ОМ', достаточно ограничиться первым порядком относительно двух
бесконечно малых углов da и da' в отдельности. Сначала в соответствии с формулой F):
tfe% (-da) ОМ = ОМ - da ех х ОМ. (9)
Затем нужно применить к этому вектору #?е (da') , снова используя формулу F):
те (da')tfe (-da)OM =
= (OM-daexxOM) + da'eyx(OM-daexxOM) =
= ОМ - da ед. х ОМ + da' еу х ОМ - da da' e v x (ех x ОМ). A0)
Действие 31г (da) на вектор, фигурирующий в правой части выражения A0), состоит в
добавлении к этому вектору следующих инфинитезимальных членов:
daexxOM + dada'exx(eyxOM), A1)
* Отметим, что поступая таким образом, мы не можем быть уверены, что вращение на угол
2тс, построенное с помощью последовательности инфинитезимальных вращений, совпадает с
тождественным вращением.
841

Глава VI
полученных в результате векторного умножения правой части равенства A0) на ел и сохранения
лишь членов первого порядка по da. Итак:
31^ (da) ,%y (da') ^ (-da) ОМ =
= ОМ + Лх'еу xOM + rfa da' [exx(ey xOM)-ey х(еЛ хОМ)]. A2)
Окончательно, ОМ' равен сумме только что полученного вектора и его векторного произведения
на (-da' ev) ; в первом порядке по da' это векторное произведение равно:
-da'evxOM, A3)
откуда сразу же следует:
теу (-da') 31^ (da) 3lty (da') Щ,х (-da) ОМ =
= ОМ + da da' [ex x (ey x OM) - ey x (ex x OM)], A4)
и после преобразования двойных векторных произведений получим:
4?ev (-da') MCx (da) ,%v (da') Ж^х (-da) ОМ = ОМ + da da' ег х ОМ = .%x (da da') OM .
A5)
Это равенство справедливо для любого вектора ОМ , то есть формула (8) доказана.
3. Операторы вращения в пространстве состояний.
Пример частицы без спина
В этом параграфе мы рассмотрим физическую систему, образованную единственной
частицей без спина, движущейся в трехмерном пространстве.
а. СУЩЕСТВОВАНИЕ И ОПРЕДЕЛЕНИЕ ОПЕРАТОРОВ ВРАЩЕНИЯ
В любой данный момент времени квантовое состояние частицы в пространстве
состояний $т характеризуется вектором |\|/), которому соответствует волновая функция
\j/(r) = (r|\|/). Выполним над системой операцию вращения 01, которая ставит в
соответствие точке г0(*0, у0, z0) пространства другую точку т^(х'0, у'0, z'0), такую, что
r0' = ^r0. A6)
Пусть |\|/') — вектор состояния системы после вращения, и \\f'(r) = (г|\|/') —
соответствующая волновая функция. Естественно предположить, что значение исходной
волновой функции \|/(г) в точке г0 преобразуется вращением в значение конечной волновой
функции \|/'(г) в точке г0' так, как определяется формулой A6):
842

Общие свойства угловых моментов в квантовой механике
\|/'(г0') = \|/(г0), A7)
то есть
V/(r0/) = V(«"lr0/). A8)
Поскольку это уравнение справедливо для любой точки г0' пространства, то можно
переписать его в виде:
\|/'(г) = Щ0Г1 г). A9)
По определению оператор R, действующий в пространстве состояний £г и
соответствующий рассматриваемому геометрическому вращению .9?, является оператором,
который, действуя на состояние |\|/) перед вращением, дает состояние |\|/') после
вращения ,<#:
И = *к). B0)
Оператор R называется «оператором вращения». Равенство A9) характеризует его
действие в представлении {|г)}:
(r|/?|\|/) = (^-,r|i|/), B1)
где ш~х г) — базисный кет-вектор этого представления, определяемый компонентами
вектора У1~х г.
ЗАМЕЧАНИЕ
Состояние частицы после поворота могло бы быть е'в|\|/'), а не |\|/') (здесь Ь —
произвольное вещественное число), при этом его физические свойства остаются
неизменными. Иначе говоря, равенство A7) можно было бы заменить равенством:
\|/'(r0') = e'Vr0), B2)
где Ь , конечно, не зависит от г0 , но может зависеть от рассматриваемого вращения #?.
Эту особенность здесь мы рассматривать не будем.
Ь. СВОЙСТВА ОПЕРАТОРОВ ВРАЩЕНИЯ R
ос. Оператор R линейный
Это весьма важное свойство операторов вращения вытекает непосредственно из их
определения. Действительно, если кет |\|/) перед вращением являлся линейной
суперпозицией состояний, например:
843

Глава VI
|v|/) = Xl|Vl) + X2|¥2), B3)
то формула B1) дает:
<г| /?|\|/> = ^.(^г-1 г|m/i>h-A.2(^_1 r|\|/2) = X1<r|/?|M/1>H-X2<r|/?|\|/2>. B4)
Это равенство справедливо для любого базисного вектора пространства {|г)}, и из него
следует, что оператор R линеен:
R|v) = i?[Xj\|fl) + X2|v2>] = M|Vi> + M|V2>- B5)
C. Оператор R унитарен
В формуле B1) кет \\\f) может быть произвольным, поэтому действие оператора R
на бра (г| дает:
(г|/? = (^-,г|, B6)
и, применив эрмитово сопряжение к обеим частям уравнения B6), получим:
Д+|г)=|я_|г). B7)
С другой стороны, если вспомнить, что кет |г) представляет состояние, в котором
частица точно локализована в точке г , то
Д|г) = |&г). B8)
Это уравнение выражает, что если перед вращением частица была локализована в точке г ,
то после вращения она будет локализована в точке г' = У1 г . Чтобы получить формулу
B8) из формулы B1), выберем в качестве вектора |v|/) базисное состояние |г0):
(r|/?|r0> = (^-,r|r0) = 5[(^-lr)-r0], B9)
где использовано соотношение ортонормировки базиса {|г)}. Но, с другой стороны:
8[(^-1г)-г0]=8[г-(Яг0)]. C0)
Подставив C0) в B9), получим:
(r|/?|r0) = 5[r-(^r0)] = (r|^r0) C1)
или, поскольку {|г)} является базисом в пространстве £г:
844

Общие свойства угловых моментов в квантовой механике
Л|г0) = |Яг0). C2)
Исходя из формул B7) и B8), легко показать, что
RR+=R+R = l. C3)
Действительно, действие операторов RR* и R+R на любой вектор базиса {|г)} дает тот
же самый вектор. Например:
RR+ |r) = R \&Г1 г) = |я ЯГХ г) = |г), C4)
то есть оператор R — унитарный.
ЗАМЕЧАНИЕ
Оператор R сохраняет скалярное произведение и норму векторов, которые он
преобразует:
Это очень важное с точки зрения физики свойство, так как амплитуды
вероятности, определяющие физические предсказания, всегда имеют форму скалярного
произведения двух кет-векторов.
у. Ансамбль операторов R образует представление группы вращений
В § 2 мы указывали, что геометрические вращения образуют группу. В частности,
произведение двух вращений У1Х и &2 также является вращением:
У12(ЖХ = 31Ъ. C6)
В пространстве состояний tfr трем геометрическим вращениям 211У (М2 и 01 ъ
сопоставляются три оператора вращения Rl9R2 и R3 соответственно. Если три
геометрических вращения удовлетворяют соотношению C6), можно показать, что
соответствующие операторы вращения таковы, что справедливо равенство:
ВД = Я з C7)
(здесь R2RX — произведение операторов пространства £г, как мы определили его в § В-З-а
главы II).
Действительно, рассмотрим частицу, состояние которой описывается произвольным
845

Глава VI
вектором IГ) базиса, характеризующего представление {| Г)}. Если выполнить
операцию вращения 31х, то состояние частицы по определению оператора Rl станет равным:
Я, |г) = !#,!•). C8)
Выполним затем вращение 312, исходя из только что полученного нового состояния.
После второго вращения в соответствии с C8) и с определением R2:
Л2/?1|г) = Л2|.да1г) = |^2^| г). C9)
Если учесть равенство C6), нетрудно видеть, что формула C9) эквивалентна выражению:
ВД|г) = |#3г). D0)
Итак, оператор R3, связанный с вращением 31 ъ, таков, что
Лзк> = |*,г). D1)
Соотношение C7) доказано, так как рассматриваемый кет |г) может быть выбран в
базисе {|г)} произвольно.
Чтобы отразить полученный только что важный результат, говорят, что
соответствие 31=$ R между геометрическими вращениями и операторами вращения сохраняет
закон группы или что ансамбль операторов R образует «представление» группы
вращений. Конечно, тождественному вращению соответствует в пространстве £г единичный
оператор, а вращению ЗСХ, обратному по отношению к вращению 31, соответствует
оператор R'1, обратный оператору R (впрочем, мы уже показали, что /Г1 = R+ ).
с. ВЫРАЖЕНИЕ ОПЕРАТОРОВ ВРАЩЕНИЯ
ЧЕРЕЗ НАБЛЮДАЕМЫЕ УГЛОВОГО МОМЕНТА
а. Операторы инфинитезимального вращения
Рассмотрим сначала инфинитезимальное вращение вокруг оси Oz, то есть 31 г (da).
Если мы применим его к частице, состояние которой описывается волновой функцией
\|/(г), то в соответствии с A9) волновая функция \\f'(r), описывающая состояние
частицы после вращения, удовлетворяет соотношению:
V'(r)= v[<(da)r]. D2)
846

Общие свойства угловых моментов в квантовой механике
Но если ( jc, у, z ) — компоненты вектора г , то компоненты #?е' (da) г без труда
вычисляются с помощью формулы F):
\х + у da;
М~*(da) = .#_e (da)г = (г - da ег х г) \
y-xda\
z.
D3)
Таким образом, уравнение D2) можно переписать в виде:
\|/'(*, у, z) = \\f(x + yda,y-xda, z),
что в первом порядке малости по da дает:
\\f'(xyy,z) = \\i(x,y,z) + da
D4)
Э\|/ _ Э^
Э* ду
= \y(xiyfz)-da
ду дх
У(х, у, Z).
D5)
Нетрудно заметить, что в квадратных скобках с точностью до множителя — стоит выра-
V'(r) = (r|V') = (r| (l™<fazJ|V).
жение для оператора Lz = ХРу - YPX в представлении {|г) }. Итак, в результате получим:
D6)
Но по определению оператора Re (da), соответствующего вращению 3£е (da):
|v') = J?es(da)|\|f), D7)
и, следовательно, если учесть, что начальное состояние |\|/) было произвольным, то
окончательно получим:
Re (Ax) = l—daLz
D8)
Изложенные рассуждения легко обобщаются на инфинитезимальное вращение
вокруг произвольной оси. В общем случае имеем:
Ru(da) = l—daL-u
D9)
847

Глава VI
ЗАМЕЧАНИЕ
Равенство D6) можно также получить, используя сферические координаты
(г, О, ф), так как Lz соответствует дифференциальному оператору —— .
i Эф
C. Интерпретация соотношений коммутации между компонентами
углового момента L
Посмотрим, как будет выглядеть в пространстве состояний #г соотношение (8).
В соответствии с результатами, полученными в §3 -b-у, и доказанными выше
выражениями, его можно представить в первом порядке по углам da и da' в виде:
l + -da'L
ft
1—daL
ft
1—da'L
ft
l + -daZ,
ft
= 1—da da'L. E0)
ft
Раскрыв левую часть равенства и приравняв коэффициенты при членах, содержащих
da da', без труда увидим, что равенство E0) приводится к
[K^y] = ihLz
E1)
Конечно, два других соотношения коммутации между компонентами L могли бы быть
получены совершенно аналогично из формул той же формы, что и (8) при циклической
перестановке единичных векторов еЛ, е , е..
Итак, соотношения коммутации орбитального углового момента частицы
являются следствием некоммутативной структуры группы геометрических вращений.
у. Операторы конечного вращения
Рассмотрим теперь вращение .^е (а) на произвольный угол а вокруг оси Oz .
Согласно формуле G) оператор Re (a), связанный с таким вращением, должен
удовлетворять равенству:
Re (a + da) = Rtz (a) Re (da), E2)
где два оператора в правой части коммутируют. Но выражение для Re (da) нам
известно, в результате чего имеем:
Re (a + da)= Re (a)
1—da U
ft
E3)
или
848

Общие свойства угловых моментов в квантовой механике
Де.(ос + Жх)- Яе.(а)= —7daRt{a)Lz
E4)
Здесь также операторы в правой части коммутируют. Хотя в этом равенстве
фигурируют операторы, формальное решение уравнения E4) имеет тот же вид, что и для
обычных функций переменной а:
Re (а)^""^
E5)
Действительно, если вспомнить (§ 3 дополнения Ви), что операторная экспонента определяется
разложением в ряд, легко доказать, что E5) является решением уравнения E4). Кроме того,
«постоянная интегрирования» равна 1, так как известно, что
Л..@) = 1.
E6)
Как и в § 3-с-а, полученный результат легко обобщается на конечное вращение
вокруг произвольной оси:
*u(a) = ^aLu
E7)
ЗАМЕЧАНИЯ
(i) Формула E7) может быть представлена в форме:
—a(L, и. + Lvuv + L,u.)
Л.(а)=е »
E8)
где ux,uy,ut — компоненты единичного вектора и. Вспомним, однако, что
поскольку операторы Lx,Ly, Lz не коммутируют, то:
Ru(a)*e » e
—aL.u. —aLvuv —aL, и.
E9)
(и) С помощью выражения E7) легко доказать, что оператор /?u(a) унитарный.
Действительно, поскольку компоненты оператора L эрмитовы:
[Ku(a)]+=^aL\ F0)
откуда следует (оператор Lu очевидно коммутирует сам с собой):
[tfu(a)]+tfu(a) = tfu(a)[/?u(oo]+ = i. F1)
54 Квантовая механика
849

Глава VI
(iii) В рассматриваемом здесь частном случае (§ 3) имеем:
Д„Bя) = 1. F2)
Ограничимся доказательством этого результата только для вращения на 2я вокруг
оси Oz (обобщение не представляет трудностей). Для этого рассмотрим
произвольный кет |\|/) и разложим его в базисе, образованном собственными векторами
наблюдаемой Lz:
к)=2>и,,|т,т), F3)
/л,т
где
Lz\m4x)-mh\m,x) F4)
(число т заменяет отличные от т индексы, необходимые для характеристики
используемых базисных векторов; так, например, ими могут быть векторы
«стандартного» базиса, введенного в § С-3 главы VI). Действие Re (а) на кет |\|/) описывается
выражением:
*,.(a)|v) = E^T^^|m,x)=Ecm,T^^|m,T). F5)
т, х m, x
Но мы уже знаем, что для орбитального углового момента частицы число т всегда
целое. Поэтому, если а достигает значения 2я , все экспоненциальные множители
станут равными 1, и
^Bя)|\1/)=1стт|т,т) = |\1/). F6)
т,х
Это равенство доказано для произвольного вектора | \|/), то есть Re Bя) —
единичный оператор.
Приведенные выше рассуждения свидетельствуют о том, что формула F2)
была бы неверна, если бы полуцелые значения т не были бы исключены.
Действительно, в дополнении А1Х мы увидим, что для спина 1/2 оператор вращения на 2я
равен не 1, а -1. Этот вывод связан с тем, что конечное вращение строилось как
последовательное применение бесконечно малых вращений [см. примечание к
формуле G)].
4. Операторы вращения
в пространстве состояний произвольной системы
Ниже мы обобщим на произвольные системы понятия и результаты предыдущего
параграфа.
850

Общие свойства угловых моментов в квантовой механике
а. СИСТЕМА, СОСТОЯЩАЯ ИЗ НЕСКОЛЬКИХ ЧАСТИЦ БЕЗ СПИНА
Прежде всего, покажем, что сказанное выше без труда можно распространить на
системы, состоящие из нескольких частиц без спина. Для упрощения выберем в качестве
примера систему двух частиц A) и B) без спина.
Пространство состояний # такой системы является тензорным произведением
пространств состояний $г и £г двух частиц:
£ = $Г)®£Г2. F7)
Далее будем использовать те же обозначения, что и в § F-4-b главы И. Для каждой из
частиц можно определить орбитальный угловой момент:
Ld I = .К. i х ",:
_ F8)
Компоненты L, и L2 удовлетворяют соотношениям коммутации, свойственным для
углового момента.
Рассмотрим вектор, являющийся тензорным произведением вектора пространства
£г на вектор пространства #г :
Н = |ФA))®|ХB)>. F9)
Здесь |\|/) — кет, представляющий состояние системы, образованной объединением
частицы A) в состоянии |фA)) и частицы B) в состоянии |%B)). Если осуществить
вращение системы двух частиц на угол а вокруг и, то состояние системы после
вращения соответствует объединению двух частиц в «повернутых» состояниях |ф'0)) и
\у/B)) соответственно:
| V') = |ф'Ц))® |хЧ2)> = [К(а) |ФA))]® [R2u(a) |XB)>], G0)
где R1 и R2 — операторы вращения в пространствах #г и #г :
/?» = e~*aL,u; G1-а)
R2u(a) = e~~»aL2\ G1-b)
Равенство G0) можно переписать в соответствии с определением тензорного
произведения двух операторов (§ F-2-b главы II):
54*
851

Глава VI
| V') = [R[ (a) ® R2U (a)] |ФA)> ® | xB)>. G2)
Поскольку любой вектор пространства # является линейной комбинацией векторов-
произведений, аналогичных F9), вектор |\|/'), преобразованный путем вращения
произвольного вектора |\|/) пространства #, имеет вид:
|\|0 = [*i(a)®^(cO]|v). G3)
Используя формулу (F-14) главы II и тот факт, что L, и L2 коммутируют, получим
операторы вращения в пространстве £ :
Я»® Rl(a) = <f >,u .->2U = <Г> , G4)
где
L = L,+L2 G5)
полный угловой момент системы из двух частиц. Все формулы предыдущего параграфа
остаются справедливыми при условии, что L — полный угловой момент.
ЗАМЕЧАНИЯ
(i) L — оператор, действующий в пространстве #. В формуле G5) оператор Lp
строго говоря, является продолжением в пространстве^ оператора L,,
действующего в пространстве #г (аналогичное замечание можно сделать относительно
L2). Для упрощения обозначений будем использовать одинаковые символы для L,
и для его продолжения в пространстве # (см. § F-2-c главы II).
(ii) Можно было бы осуществить вращение только одной из двух частиц, например,
частицы A). В ходе такого «парциального» вращения вектор вида F9)
преобразуется следующим образом:
[д>)|ФA))]®|%B)), G6)
где изменяется состояние только одной частицы, например, A). Как и ранее,
можно показать, что действие вращения одной частицы A) на произвольное состояние
| \|/) пространства £ описывается оператором:
/?i(a)®lB) = /»aL,u, G7)
где 1 — единичный оператор в пространстве #г [в формуле G7) оператор Li
действует в пространстве W ].
852

Общие свойства угловых моментов в квантовой механике
Ь. ПРОИЗВОЛЬНАЯ СИСТЕМА
Отправной точкой вышеприведенных рассуждений была формула A9),
определяющая закон преобразования вектора состояния системы на базе преобразования его
волновой функции. В случае произвольной квантовой системы (не обязательно имеющей
классический аналог) этот метод применять нельзя. Так, например, для частицы со
спином операторы Х,У и Z уже не образуют полного набора коммутирующих
операторов, и состояние частицы не может быть определено волновой функцией \|/(дс, у, z) (см.
главу IX), и нужно действовать непосредственно в пространстве состояний $ системы.
Не вдаваясь в детали, допустим здесь, что любому геометрическому вращению f/i
можно поставить в соответствие оператор R , действующий в пространстве # : если система
сначала находилась в состоянии | ц/), то вращение У1 переводит ее в состояние:
|х|/') = Як)> G8)
где оператор R является линейным и унитарным (см. замечание к § 3-Ь-Р).
В том, что касается закона группы вращений 31, то он сохраняется и для операторов R ,
но только локально: произведение двух геометрических вращений, из которых по крайней
мере одно является инфинитезимальным, представлено в пространстве #
произведением соответствующих операторов R (в частности, из этого следует, что «изображением»
вращения на нулевой угол является единичный оператор). Однако оператор, связанный
с геометрическим вращением на угол 2п , не обязательно совпадает с единичным
оператором [см. замечание (Ш) в § 3-с-у и дополнение А1Х].
Рассмотрим теперь инфинитезимальное вращение Re (da) вокруг оси Oz.
Поскольку закон группы справедлив для инфинитезимальных вращений, оператор Re (da)
должен обязательно иметь вид:
Re (da) = l~daJz9 G9)
п
где Jz — эрмитов оператор, так как оператор Re (da) унитарный (см. § 3 дополнения
Сц). Это равенство является по существу определением оператора Jz. Совершенно так
же можно ввести эрмитовы операторы Jx и Jy с помощью инфинитезимальных
вращений вокруг осей Ох и Оу , и тогда полный угловой момент J системы можно
определить, исходя из его трех компонент Jx, Jy и Jz.
Далее нужно вернуться к рассуждениям, приведенным в § 3-C-J3: из геометрического
соотношения (8) следует, что компоненты J удовлетворяют тем же соотношениям
коммутации, что и компоненты орбитального момента. Итак, полный угловой момент
произвольной квантовой системы связан с соответствующими операторами вращения,
откуда непосредственно следуют соотношения коммутации между его компонен-
853

Глава VI
тами; их можно использовать, как это уже было сделано в § В-2 главы VI, для
характеристики любого углового момента.
И, наконец, покажем, что в соответствии с определенными выше операторами
компонент Jх, J и Jz оператор Ru (da) произвольного инфинитезимального вращения
(где их, и , uz — компоненты единичного вектора и) можно записать в виде:
Ru(da) = l-jda(jxux + Jyiiy + Jzuz) (80)
или в сжатой форме:
Ru(da) = l--daj-u. (81)
fi
Формула (80) является простым следствием геометрического соотношения:
Лм (da) = Яе (их da) Же (иу da) .% (uz da), (82)
справедливого в первом порядке по da, которое немедленно следует из формулы F).
Итак, мы обобщили выражения D8) и D9) для операторов инфинитезимального
вращения. Поскольку закон группы локально сохраняется, равенство E2) и вытекающие
из него выводы остаются справедливыми, то есть операторы конечного вращения имеют
вид, аналогичный выражениям E5) и E7):
-i- i
Ru(a) = e~~*a \ (83)
5. Вращение наблюдаемых
Теперь мы знаем, как преобразуется вектор, описывающий состояние квантовой
системы при вращении. Но в квантовой механике состояние системы и физические
величины описываются независимым образом. Поэтому следует рассмотреть, как при
вращении преобразуются наблюдаемые.
а. ОБЩИЙ ЗАКОН ПРЕОБРАЗОВАНИЯ
Рассмотрим наблюдаемую А некоторой физической системы. Для упрощения
обозначений предположим, что спектр А дискретный и невырожденный:
А\и„) = ап\и„). (84)
Чтобы лучше понять, как влияет вращение на эту наблюдаемую, представим себе, что
имеется прибор, позволяющий измерить А в рассматриваемой физической системе.
Тогда наблюдаемая А', преобразованная из Л с помощью геометрического вращения &,
854

Общие свойства угловых моментов в квантовой механике
по определению является значением, которое измеряет прибор, также подвергнутый
вращению &.
Допустим, что система находится в собственном состоянии \ип) наблюдаемой А.
Прибор, предназначенный для измерения А, даст в этом случае точно значение ап.
Если же непосредственно перед измерением мы приложим одновременно к физической
системе и к измерительному прибору вращение 31, то их относительное расположение
не изменится, и, следовательно, если наблюдаемая А, описывающая физическую
величину, связана исключительно с повернутой системой (то есть не зависит от других
систем или приборов, не испытавших вращения), то и в новом положении измерительный
прибор с уверенностью даст тот же результат ап. Но по определению прибор измеряет
наблюдаемую Л', и система находится в состоянии:
К) = *!"„>• (85)
Таким образом, мы должны получить:
А\ип) = ап\ип)=*А'\и'п) = ап\и'п). (86)
Комбинируя (85) и (86), получим:
A'R\un) = anR\un) (87)
или
ЛМ'Л|И|1) = в.|и.), (88)
так как оператор, обратный оператору R, равен R*. Ансамбль векторов \ип) в
пространстве состояний образует базис (так как А — наблюдаемая), и, конечно:
Й+А'Я = Л, (89)
то есть
Л' = RAR+
(90)
В частном случае инфинитезимального вращения &lu(da) общее выражение (81)
после его подстановки в (90) в первом порядке по da дает:
А' =
ЗАМЕЧАНИЯ
l--AxJ-ii| A\ l + -£/aJ-u| = A--dafj-u,Al. (91)
h ) \ h ) h
(i) В случае частицы без спина из равенства (90) следует:
(г|А'|г') = (г|ЯАД+|г'). (92)
855

Глава VI
Используя B6) и B7), получим:
(г|Л/|г/> = Й",г|л|^-,г/). (93)
Таким образом, преобразование, позволяющее получить Л'из Л, совершенно
аналогично преобразованию, дающему |\|/') из |\|/) [формула A9)].
(и) Рассмотрим случай, когда наблюдаемая А соответствует классической величине .с/
являющейся функцией положений г,, и импульсов р, частиц, образующих систему.
Оператор А получается из этой функции с помощью правил квантования,
изложенных в главе III. В классической механике имеются правила отыскания
величины .<•/', полученной из величины .с/ при операции вращения: так, например, если
.</ — скалярная величина, то .V' = .«/ ; если ,*/ — проекция векторной величины
на ось Ои , то .</' является проекцией этой же величины на новую ось Ои,
полученную при вращении &. Квантовый оператор, соответствующий .с/', можно
построить, применяя те же правила квантования. Можно показать, что этот оператор
совпадает с оператором А', определенным формулой (90), что и отражено на
рис. 1.
£
I . I
Рис.1
Поведение классической физической величины .<>/ и
связанной с нею наблюдаемой А при вращении Ж
Ь. СКАЛЯРНЫЕ НАБЛЮДАЕМЫЕ
Наблюдаемая А называется скалярной, если
А' = А (94)
независимо от R . Из выражения (91) следует, что
[A,J] = 0. (95)
Скалярная наблюдаемая коммутирует с тремя компонентами полного углового
момента.
Можно привести многочисленные примеры скалярных наблюдаемых: так, J2 всегда
является скалярной наблюдаемой, что следует из соотношений коммутации для
углового момента (§ В-2 главы VI); для частицы без спина наблюдаемые R2,P2,RP,
соответствующие классическим скалярным величинам, также являются скалярными, и
нетрудно показать (см. далее § 5-с), что они удовлетворяют соотношению (95). В § 6
856

Общие свойства угловых моментов в квантовой механике
мы увидим, что гамильтониан изолированной физической системы также является
скалярным.
с. ВЕКТОРНЫЕ НАБЛЮДАЕМЫЕ
Векторная наблюдаемая — это ансамбль, состоящий из трех наблюдаемых Vx, Vy и
Vz, являющихся ее декартовыми компонентами, преобразующимися при вращении по
правилам преобразования векторных величин. При вращении 31 компонента Vu = V • и
вектора V вдоль выделенной оси с единичным вектором и преобразуется в компоненту
Vu. - V -и' вектора V вдоль новой оси Ои , полученной из Ои с помощью вращения Ж.
Рассмотрим, например, компоненту Vx такой наблюдаемой и исследуем ее
поведение при инфинитезимальных вращениях вокруг каждой из трех осей координат. Если
вращение происходит вокруг оси Ох , то, очевидно, Vx не изменяется, и это можно
выразить соотношением:
[/,,V,] = 0. (96)
Если выполнить вращение .# (da) вокруг оси Оу , то компонента Vx преобразуется в
наблюдаемую (Vx)', определенную в соответствии с (91) формулой:
<y,Y=Vx-±da[j,,Vx]. (97)
Но Vx является проекцией вектора V на ось Ох с единичным вектором е х. Вращение
Ле (da) переводит ех в ех, где
ех =ех +daey xex =ex-daez. (98)
Если V —векторная наблюдаемая, то проекция (V,)' должна совпасть с V-e^:
(Ух)'= V-e, -da\-ez=Vx-daVz. (99)
Сравнив (97) с (99), получим:
[vx,Jy] = ihVt. A00)
Аналогичные рассуждения для инфинитезимального вращения &е (da) вокруг оси Oz
приводят к соотношению:
[Jz,Vx] = ihVy. A01)
Конечно, при исследовании поведения компонент Vy и Vz в инфинитезимальных
вращениях будут получены формулы, связанные с (96), A00) и A01) циклической переста-
857

Глава VI
новкой индексов x,y,z. Совокупность полученных соотношений характерна для
векторной наблюдаемой. Эти соотношения предполагают, что в результате произвольного
инфинитезимального вращения скалярное произведение V • и преобразуется в
произведение У-и',где и' получен при рассматриваемом вращении единичного вектора и.
Из сказанного видно, что угловой момент является векторной переменной, а
равенства (96), A00) и A01) вытекают из соотношений коммутации для угловых моментов.
Если система состоит из одной частицы без спина, то R и Р являются векторными
наблюдаемыми, что без труда доказывается с помощью канонических соотношений
коммутации. В результате введенные векторные обозначения для R , Р, L и J
оказываются оправданными.
ЗАМЕЧАНИЯ
(i) Скалярное произведение V • W двух векторных наблюдаемых, определенное по
известной схеме:
\.\V = VxWx+VvWy+VzWz4 A02)
является скалярным оператором. Чтобы доказать это, вычислим, например,
коммутатор произведения V • W с оператором Jх:
[v.W,yJ = [vy\yy,7jr] + [vz^,yjt] =
= -ihVy Wz - ihVz Wy + ihVz Wy + ifiVy Wz = 0. A03)
Выше мы вполне справедливо утверждали, что R2, Р2 и RP являются
скалярными операторами,
(ii) В соотношения (96), A00) и A01) входит полный угловой момент системы. В
следующем примере мы продемонстрируем всю важность этого положения. Если для
системы, состоящей из двух частиц, использовать не L = Lt + L2, a Lt, то величина
R2 оказалась бы ансамблем трех скалярных наблюдаемых, а не векторной
наблюдаемой.
6. Инвариантность относительно вращения
Проведенный в предшествующих параграфах анализ имел целью не только оправдать
определение угловых моментов через их соотношения коммутации. Важность вращений
в физике весьма тесно связана с тем, что физические законы инвариантны относительно
вращения. В данном параграфе мы уточним, что же понимается под таким утверждением,
и изучим ряд следствий этого фундаментального обстоятельства.
858

Общие свойства угловых моментов в квантовой механике
а. ИНВАРИАНТНОСТЬ ФИЗИЧЕСКИХ ЗАКОНОВ
Пусть (S) — классическая или квантовая физическая система, которая в заданный
момент времени испытывает вращение (Л. Если вместе с этой системой мы повернем
все другие системы или приборы, которые могут с ней взаимодействовать, то ни
физические свойства, ни поведение системы (S) не изменятся. Это значит, что физические
законы, определяющие эволюцию системы, остаются неизменными: при этом говорят,
что физические законы инвариантны относительно вращения. Заметим, что это свойство
не является априори очевидным. Существуют преобразования (например, подобие*),
относительно которых физические законы не являются инвариантными**. Таким
образом, можно принять инвариантность относительно вращения как постулат, следствия
которого подтверждаются экспериментом.
В том случае, когда говорят, что физические свойства и поведение системы не
изменяются при вращении, выполненном в момент времени г0, констатируются два
обстоятельства.
(i) Свойства системы в этот момент времени не изменяются, несмотря на то, что
способ описания состояния системы и физические величины изменяются (см.
предыдущий параграф). В квантовой механике это означает, что наблюдаемая А', полученная в
результате преобразования наблюдаемой А, имеет тот же спектр и что вероятность
получения любого из собственных значений этого спектра при измерении А' в системе
после вращения остается той же, что и при измерении А в системе до вращения. Из
этого можно сделать вывод, что операторы R , описывающие вращения в пространстве
состояний, являются линейными и унитарными или антилинейными и унитарными (то
есть антиунитарными***).
(и) Эволюция системы во времени не изменяется. Чтобы уточнить это утверждение,
обозначим символом |\|/(f0)) состояние системы. Если в момент времени t0
осуществляется вращение системы, то это состояние преобразуется в
|v/a0)>=^|v(r0)). A04)
* Возьмем, например, атом водорода. Если умножить расстояние между протоном и
электроном на постоянную величину X Ф 1 (не меняя заряда и массы частиц), то получим систему,
эволюция которой более не будет подчиняться физическим законам (классическим или квантовым).
** Отметим также, что эксперимент показал, что законы, управляющие C -распадом ядер, не
инвариантны относительно операции отражения в плоскости (несохранение четности).
*** Все преобразования, оставляющие инвариантными физические законы, описываются
унитарными операторами, кроме оператора обращения времени, который является антиунитарным.
859

Глава VI
Оставим систему свободной и сравним ее состояние |\}/'@) в последующий момент
времени t с состоянием, в которое оно пришло бы, если бы эволюционировало
свободно из состояния |\|/(^0)) • Если поведение системы не изменилось, то
|х|/'@) = /ф@), A05)
то есть, каким бы ни был момент времени t, состояние |\|/'@) получается из состояния
|\|/(г)) с помощью того же вращения, что и в A04). Таким образом, если |\|/@) является
решением уравнения Шредингера, то /?|\|/(/)) также является его другим решением:
преобразование от возможного движения системы является другим возможным
движением системы. В § b мы увидим, что это предполагает, что гамильтониан Я системы
является скалярной наблюдаемой.
Инвариантность физических законов относительно вращения выражается
свойствами симметрии уравнений, математически описывающих эти законы. Чтобы понять
природу таких свойств симметрии, рассмотрим, например, систему, состоящую из одной
частицы без спина. В выражения для физических законов, управляющих такой
системой, в явном виде входят параметры г(;с, у, z) и р(рх, ру, pz), характеризующие
положение частицы и ее импульс: в классической механике г и р в каждый момент времени
определяют состояние системы; в квантовой механике, несмотря на то, что значение
этих параметров не столь простое, они появляются в волновой функции \|/(г) и в ее
преобразовании Фурье \j7(r). Если подвергнуть систему мгновенному вращению {Л, то оно
так преобразует г ирвг' ир', что
г' = Ж г ;
р' = #р. A06)
Если в уравнениях, описывающих физические законы, заменить г на 31л г' и р на
УСХ р', то получим соотношения, в которые входят г' и р'. Инвариантность
физических законов относительно вращения требует, чтобы форма уравнений по г' и р' была
бы той же, что и форма уравнений по г up. Иначе говоря, если убрать штрихи,
которые мы использовали для обозначения новых параметров, то мы вновь должны
получить исходные уравнения. Понятно, что при этом возможные формы уравнений
оказываются ограниченными.
ЗАМЕЧАНИЯ
(i) Что произойдет при вращении системы, которая не является изолированной? Рассмотрим,
например, частицу, которая находится во внешнем поле некоторого потенциала. Если осу-
860

Общие свойства угловых моментов в квантовой механике
ществить вращение системы, не поворачивая в то лее время источник потенциала, то
последующая эволюция системы в общем случае изменится*: в классической механике
действующие на частицу силы не остаются теми же в новом положении; в квантовой механике
\|/'(r, t) = \\f(&l~l г, t) является решением уравнения Шредингера, в котором потенциал
V(r) должен быть заменен на V(ffl.~l г) , который в общем случае отличен от V(r). Таким
образом, преобразование возможного движения не является более возможным движением.
В некотором смысле наличие внешнего потенциала разрушает однородность пространства,
в котором движется изучаемая система.
Однако может оказаться, что внешний потенциал обладает определенной симметрией,
позволяющей физической системе реализовать некоторые вращения, не изменяя ее
поведения. Если существуют такие частные вращения .<%0, что V(.^0~ г) совпадает с V(r), то
свойства системы оказываются неизменными при таких вращениях. Именно это имеет
место в поле центрального потенциала, зависящего только от расстояния до фиксированной
точки О, при этом вращениями 01^ являются любые вращения, сохраняющие точку О
неизменной (см. главу VII).
(ii) Вернемся к случаю изолированных систем. До сих пор мы занимали «активную» точку
зрения: наблюдатель оставался неподвижным, а физическая система поворачивалась. Но
можно также представить себе и «пассивную» точку зрения, когда поворачивается
наблюдатель: не затрагивая систему, он разворачивает связанную с собой систему координат,
получая при этом новую систему координат, связанную с прежней операцией заданного
вращения. Инвариантность относительно вращения интерпретируется тогда следующим
образом: в новом положении (то есть при использовании новых осей координат) наблюдатель
описывает физические явления законами, которые имеют ту же форму, что и в старой
системе координат. Нет никаких причин утверждать, что одна из этих систем координат более
предпочтительна, чем другая, и нельзя определить абсолютную ориентацию в
пространстве, изучая какое-то физическое явление. Впрочем, нетрудно видеть, что для изолированной
системы «пассивное» вращение эквивалентно «активному» вращению на такой же угол
вокруг противоположно направленной оси.
* Если частица находится в поле векторного потенциала, ее свойства сразу же после вращения
подвергнутся глубоким изменениям. Рассмотрим, например, частицу без спина во внешнем
магнитном поле. В соответствии с законом преобразования A9) ток вероятности, определяемый
формулой (D-20) главы III, в общем случае невозможно получить путем вращения исходного тока, так
как он зависит от векторного потенциала, описывающего магнитное поле.
Физическая интерпретация этого явления следующая. Пусть вращается не частица, а быстрый
поворот на обратное направление испытывает магнитное поле. Волновая функция не успевает
измениться, о чем свидетельствует формула A9). Если же физические свойства системы
меняются, то это может произойти только за счет взаимодействия с частицей поля электромагнитной
индукции. Это взаимодействие не зависит от конкретной формы поворота магнитного поля, если
только он выполняется достаточно быстро.
861

Глава VI
b. СЛЕДСТВИЕ: СОХРАНЕНИЕ УГЛОВОГО МОМЕНТА
В § 6-а мы указывали, что инвариантность относительно вращения выражается
через свойства симметрии уравнений, описывающих физические законы. Здесь мы
рассмотрим случай уравнения Шредингера и покажем, что гамильтониан изолированной
физической системы является скалярной наблюдаемой.
Пусть изолированная система находится в состоянии |\|/(/0)). Выполним в момент
времени t0 некоторое вращение 31. Тогда состояние системы станет:
|v'(f0)) = *|v(f0)), <107)
где R — оператор, соответствующий вращению 31. Если затем мы предоставим
системе возможность свободно изменяться из состояния |\|/'('0))> то ее состояние в момент
времени r0 + dt будет описываться согласно уравнению Шредингера выражением:
|v/a0+A)>=|v/ao)>+^#|v/(/0)>- (Ю8)
Если бы мы не производили вращения, то состояние системы в тот же момент времени
t0 + dt описывалось бы выражением:
|va0+A)> = |vao)> + ^|va0)>. A09)
Инвариантность относительно вращения требует, чтобы
|\|//а0+л)) = л|\|г(/0+л)>. (но)
где оператор R тот же, что и в формуле A07). Из приведенных выше двух уравнений
следует, что
ЯЯ|\|/(г0)) = Я|\|/'(г0)) AН)
или
/?Я|х1/(г0)) = Я/?|\|/(г0)). A12)
Поскольку кет |\|/(f0)) произволен, то гамильтониан Я коммутирует со всеми
операторами вращения. Чтобы это утверждение было справедливым, необходимо и достаточно,
чтобы Я коммутировал с операторами инфинитезимальных вращений, то есть с тремя
компонентами полного углового момента J системы:
[#,j] = 0f (ИЗ)
и, следовательно, оператор Я является скалярной наблюдаемой.
862

Общие свойства угловых моментов в квантовой механике
Инвариантность относительно вращения выражается, таким образом, в том, что
полный угловой момент изолированной системы является константой движения:
сохранение углового момента проявляется как следствие инвариантности относительно
вращения.
ЗАМЕЧАНИЯ
(i) Гамильтониан неизолированной системы в общем случае не является скалярным. Однако,
если существуют некоторые частные вращения, оставляющие систему инвариантной
[примечание (i) в §6-а], то гамильтониан коммутирует с соответствующими операторами. Так,
гамильтониан частицы в поле центрального потенциала коммутирует с оператором L
углового момента частицы относительно центра силы.
(и) Гамильтониан изолированной системы, состоящей из нескольких взаимодействующих
частиц, коммутирует с полным угловым моментом системы. Напротив, в общем случае он не
коммутирует с индивидуальным моментом каждой из частиц. Действительно, чтобы
преобразование возможного движения оставалось возможным движением, нужно осуществить
вращение всего ансамбля частиц, а не только некоторых из них.
с. ПРИЛОЖЕНИЯ
Только что было показано, что инвариантность относительно вращения приводит к
тому, что полный угловой момент J изолированной системы является константой
движения в квантово-механическом смысле. Поэтому удобно выбирать стационарные
состояния таких систем (собственные состояния гамильтониана), которые были бы также
собственными состояниями операторов J2 и Jz; тогда в качестве базиса пространства
состояний можно выбрать стандартный базис [\k,jtm)}9 образованный собственными
векторами, общими для операторов Н, J2 и Jz:
H\kJ%m) = E\kJ%m)\
J2\kJ,m) = j(j + \)h2\kJ,m);
Jz\kJ,m) = mh\kJ,m). A14)
а. «Существенное» вырождение при вращении
Поскольку гамильтониан является скалярной наблюдаемой, он коммутирует с
операторами У+ и J_. Отсюда следует, что векторы \k,j, m+l) и \k, j,m-l),
соответственно пропорциональные векторам J+\k,j9m) и J_\k9 j,m), являются собственными
863

Глава VI
векторами гамильтониана Я с тем же собственным значением, что и вектор |&,у, т)
[ход доказательства тот же, что для формулы (С-48) главы VI]. Шаг за шагом можно
доказать, что Bj + l) векторы стандартного базиса, характеризуемого заданными
значениями квантовых, чисел к и j, имеют одну и ту же энергию. Соответствующее
вырождение собственных значений гамильтониана Н называется «существенным», так
как оно обусловлено инвариантностью относительно вращения и не зависит от
конкретной формы гамильтониана. Конечно, в ряде случаев уровни энергии могут
характеризоваться дополнительным вырождением, которое называется «случайным». Пример его
мы увидим в § С главы VII.
C. Матричные элементы наблюдаемых в стандартном базисе
При изучении конкретной физической величины изолированной системы знание
даже одного лишь поведения наблюдаемой при вращении часто позволяет установить
ряд ее важных свойств без проведения детальных вычислений. Так, можно предсказать,
что только некоторые из ее матричных элементов отличны от нуля в стандартном базисе
{\к, у, т) }, и записать связь между ними. Скалярная наблюдаемая имеет отличные от
нуля матричные элементы только между базисными векторами с равными значениями
j и т [ причиной этого является коммутативность скалярной наблюдаемой с
операторами J2 и Jz ]; кроме того, эти элементы не зависят от квантового числа т, так как
скалярная наблюдаемая коммутирует и с операторами У+ и J., Для векторных или
тензорных наблюдаемых подобные свойства сформулированы в теореме Вигнера-Эккарта,
которую мы докажем ниже в частном случае (дополнение Ех) и которая постоянно
применяется во всех областях физики, исследуемых с помощью квантовой механики
(атомная и молекулярная физика, ядерная физика, физика элементарных частиц и т. д.).
Дополнение Cvi
ВРАЩЕНИЕ ДВУХАТОМНЫХ МОЛЕКУЛ
1. Введение.
2. Жесткий ротатор. Классический анализ.
a. Обозначения.
b. Движение ротатора. Угловой момент и энергия.
c. Фиктивная частица, сопоставляемая ротатору.
864

Общие свойства угловых моментов в квантовой механике
3. Квантование жесткого ротатора.
a. Квантовое состояние и наблюдаемые ротатора.
b. Собственные состояния и собственные значения гамильтониана.
c. Изучение наблюдаемой Z.
4. Экспериментальное проявление вращения молекул.
a. Гетерополярные молекулы. Спектр чистого вращения.
b. Гомеополярные молекулы. Рамановские спектры вращения.
1. Введение
В § 1 дополнения Av мы рассмотрели колебания ядер в двухатомной молекуле
относительно их равновесного положения, не обращая внимания на возможность вращения
двух ядер относительно их центра массы. Были получены стационарные колебательные
состояния с энергиями Ev, волновые функции которых (pv (r) зависели только от
расстояния между ядрами.
Здесь же мы рассмотрим в некотором смысле дополняющую задачу и исследуем
вращение двух ядер относительно их центра масс, не интересуясь колебаниями, то есть
предполагая, что разделяющее их расстояние г остается неизменным и равным ге —
расстоянию, соответствующему положению устойчивого равновесия молекулы (см.
рис.1 дополнения Av). Волновые функции стационарных состояний при этом могут
зависеть только от полярных углов f> и ф, определяющих направление оси молекулы.
Мы увидим, что эти функции являются сферическими гармониками Y"\b, ф),
изученными в § D-1 главы VI и в дополнении AVi, соответствующими энергии вращения Ех,
которая зависит только от квантового числа /.
В действительности в системе центра масс молекула вращается и колеблется
одновременно, и волновые функции ее стационарных состояний должны быть функциями
трех переменных г, Ь и ф . Мы покажем в дополнении Fvn, что в первом приближении
волновые функции имеют форму — фДг)?)ш(в,ф) и соответствуют энергии Ev + Et.
г
Этот результат апостериори оправдает принятый до сих пор упрощенный подход,
который состоит в отдельном рассмотрении одномерного вращения или одномерного
колебания*. В § 2 мы вновь вернемся к классической модели системы, состоящей из двух
масс, разделенных постоянным расстоянием (жесткий ротатор). Квантовый анализ этой
задачи в § 3 будет основан на результатах главы VI, полученных для орбитального
углового момента. И, наконец, в § 4 мы опишем некоторые экспериментальные проявления
В дополнении FVn мы рассмотрим также поправки, возникающие при учете связи между
вращательными и колебательными степенями свободы.
55 Квантовая механика
865

Глава VI
вращения двухатомных молекул (спектры чистого вращения и рамановские
вращательные спектры).
2. Жесткий ротатор. Классический анализ
а. ОБОЗНАЧЕНИЯ
Две частицы с массами тх и щ разделены постоянным расстоянием ге. Центр их
масс О примем за начало отсчета в системе координат Oxyz, и в ней углами Ь и ф
определим направление связывающей их оси (рис.1). Расстояния ОМх и ОМ2
обозначим символами гх и г2 соответственно. По определению центра масс:
тхгх=т2г2, A)
откуда следует:
г.
щ тх тх+т2
B)
Рис.1
Параметры, определяющие положение жесткого
ротатора М, М2 относительно начала координат О,
совпадающего с его центром масс; расстояния гх и
г2 остаются постоянными, изменяться могут только
полярные углы в иф
Момент инерции / системы относительно точки О равен:
/ = тх гх + п^ г2
или, если ввести приведенную массу:
ц = -
1т2
тх+т2
866
C)
D)

Общие свойства угловых моментов в квантовой механике
и использовать соотношение B), то
1 = \хге2. E)
Ь. ДВИЖЕНИЕ РОТАТОРА. УГЛОВОЙ МОМЕНТ И ЭНЕРГИЯ
Если на ротатор не действуют внешние силы, то полный угловой момент £
системы относительно точки О является константой движения. Ротатор вращается вокруг
точки О в плоскости, перпендикулярной к фиксированному вектору 9В, с постоянной
угловой скоростью Од . Модуль вектора SB связан с со^ формулой:
\SB\ = mlrlr](uR+m2r2r2(uR = I(uR, F)
то есть с учетом E):
|#| = »аг>л. G)
Частота вращения системы v^ = u>R /2n пропорциональна модулю |#| и обратно
пропорциональна моменту инерции / .
В системе центра масс полная энергия Ж системы сводится к кинетической
энергии вращения:
Ж=^\, (8)
и ее можно переписать в виде:
SB2 SB2
Ж= = г-. (9)
2/ 2(ir/
с. ФИКТИВНАЯ ЧАСТИЦА, СОПОСТАВЛЯЕМАЯ РОТАТОРУ
Формулы E), G) и (9) показывают, что рассматриваемая здесь задача формально
эквивалентна задаче о фиктивной частице с массой |ы, остающейся на фиксированном
расстоянии ге от точки О, вокруг которой она вращается с угловой скоростью @R , при этом
SB оказывается угловым моментом этой фиктивной частицы относительно точки О.
3. Квантование жесткого ротатора
а. КВАНТОВОЕ СОСТОЯНИЕ И НАБЛЮДАЕМЫЕ РОТАТОРА
Поскольку расстояние ге остается неизменным, то параметрами, определяющими
положение ротатора (то есть связанной с ним фиктивной частицы), являются полярные
55*
867

Глава VI
углы ft и ф (рис.1). Таким образом, квантовое состояние ротатора описывается
волновой функцией \}/(Ф, ф), зависящей только от этих двух параметров. Допустим, что эта
функция квадратично интегрируема и нормирована:
j2ondq> j*sin bdft |V(«, ф)|2 = 1. A0)
Ее физическая интерпретация такова: величина |\|/(д,ф)| sinft db dtp представляет
собой вероятность обнаружить ось ротатора направленной в элементе телесного угла
dQ. = sin Ь d$ dcp вблизи направления, определяемого полярными углами Ь и ф .
Чтобы иметь возможность применить обозначения Дирака, удобно связать с каждой
квадратично интегрируемой функцией \|/(#, ф) кет | ц/) пространства состояний VQ:
\|/(«,ф)^|Ч/>€^. (И)
Скалярное произведение двух кет-векторов |ij/) и |%) по определению равно:
(х|у) = ^охЧ*,фЖ«.ф). A2)
где х@, ф) и \|/(Ф, ф) — волновые функции, связанные с |%) и с |\|/).
Квантовый гамильтониан Я ротатора (или связанной с ним фиктивной частицы)
получается путем замены в выражении (9) для классической энергии $2 на оператор
L2, изученный в §D главы VI:
Я = -Ц-. A3)
Оператор Я действует в пространстве &п. Согласно формуле (D-6-a) главы VI, если кет
|\|/) представлен волновой функцией \|/(Ф, ф), то кет Я|\|/) будет представлен функцией:
tf|v)<->-
ft2
2цг/
Э2 1 Э 1 Э2
т- + + ; г
дЪ2 tgb db sin2b Эф2
У(«,Ф). A4)
Другими представляющими интерес наблюдаемыми являются операторы трех
алгебраических проекций х, у, z отрезка М,М2 (координаты фиктивной частицы):
х = re sinb costy ;
у = re sin Ь sin ф ;
z = recos-&. A5)
868

Общие свойства угловых моментов в квантовой механике
Причина интереса, проявляемого к этим наблюдаемым, станет ясна в § 4-а.
Операторы X, У, Z , соответствующие величинам x,y,z, действуют в пространстве $а. Кет-
векторам X |\|/), Y\\\f), Z|\|/) сопоставляются функции:
X |\|/)<-> /; $шдсоуф\|/(д,ф);
y|i|/)<-> resin$ ^шф\|/(в,ф);
Z |\|/) <-> re cos® \|/@, ф). A6)
ЗАМЕЧАНИЕ
Как мы уже отмечали во введении, истинные волновые функции молекулы зависят от
г, О и ф . Аналогично, наблюдаемые, полученные для молекулы из соответствующих
классических величин с помощью правил квантования (глава III), действуют на эти функции
трех переменных, а не только на функции полярных углов. В дополнении FVn мы докажем
допустимость использования принятой здесь упрощенной точки зрения, в рамках которой
радиальная зависимость волновых функций игнорируется, а величина г принимается в
качестве постоянного параметра, равного ге [см. формулы A4) и A6)].
Ь. СОБСТВЕННЫЕ СОСТОЯНИЯ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ ГАМИЛЬТОНИАНА
В § D главы VI мы определили собственные значения оператора L2, имеющие вид
/(/ + 1)Й2, где / — произвольное целое неотрицательное число. Кроме того, нам
известна система ортонормированных собственных функций оператора L2 [сферические
гармоники ¥"'($, ф) ], образующих базис в пространстве квадратично интегрируемых
функций $ и ф (см. § D-1-c-P главы VI). Обозначим символом \1,т) кет пространства
isn, связанный с функцией 1У"(Ф, ф):
^т(*,Ф) <->|/,т>. A7)
Из формулы A3) следует, что
, \ /(/ + 1)Й2|У v ,1Й,
Н\1,т) = — /,т). A8)
1 ' 2цг/ ' '
Удобно обозначить:
* = —= -^-. 09)
4я/ 4я|1г;
869

Глава VI
Величину В называют «вращательной постоянной»*, имеющей размерность частоты.
Тогда собственные значения оператора Я имеют вид:
Е, = Bhl(l +1). B0)
Поскольку для каждого квантового числа / существует B/ +1) сферических гармоник
У/"(в,ф), где т = -/,-/ +1,...,/, то каждое собственное значение £, вырождено
B/ +1) раз. На рис.2 представлены первые уровни энергии ротатора. Расстояние между
двумя последовательными уровнями энергии I к 1-1 равно:
Е, - £,_, = Bh [/(/ +1) - /(/ -1)] = 2Bhl, B1)
и оно линейно возрастает с увеличением /.
Собственные состояния оператора Н удовлетворяют следующим соотношениям
ортогональности и замкнутости, полученным из соотношений для сферических
гармоник (см. § D -1-с-Р главы VI):
£ £|/,m)(/,m| = l.
/=0/и = -/
B2)
/ = 5
/ =4
/ = 3
/ =2
/ = 1
/ =0
10 Bh
8 5/;
6Bh
4Bh
2Bh
Рис.2
Первые уровни жесткого ротатора с энергиями
£, = ВЫ(/ +1), где / = 0,1,2,.... Каждый
уровень Е{, для которого / > 1, отделен от
ближайшего, лежащего ниже, отделен
интервалом энергии 2ВЫ
В общем случае квантовое состояние ротатора можно разложить по состояниям |/,т):
|v@)=i tclm{t)\Um). B3)
Его компонента:
'/.«(О = ('- Н v@)= IdQ Y>m'^ Ф) v(«, ф; О
B4)
* Иногда в знаменатель правой части формулы A9) вводят скорость света с. Тогда В имеет
размерность обратной длины и в системе СГС измеряется в см-1.
870

Общие свойства угловых моментов в квантовой механике
изменяется во времени в соответствии с уравнением:
cl,Jt) = cLm@)e-iE,t,\ B5)
с. ИЗУЧЕНИЕ НАБЛЮДАЕМОЙ Z
Выше мы ввели наблюдаемые X,Y, Z, соответствующие проекциям сегмента
М, М2 на оси системы координат. В данном параграфе рассмотрим эволюцию средних
значений этих наблюдаемых и сравним с результатами, полученными в рамках
классической механики. Вычисления будут выполнены только для (z)(t), так как величины
(x)(t) и (Y)(t) имеют аналогичные свойства.
Частота Бора (Et - Er)Ihможет появиться в функции (z)(f) только в том случае,
если отличны от нуля матричные элементы оператора Z между состоянием |/, т) муль-
типлета Е1 и состоянием |/', т') мультиплета Ег . Таким образом, прежде всего
следует найти отличные от нуля матричные элементы Z. Для этого воспользуемся
следующим соотношением, которое можно установить, исходя из математических свойств
сферических гармоник [формула C5) дополнения AvJ:
^^Г(^Ф) = ^^У.(^Ф) + ^(^OГ12 С(О.Ф)- B6)
С помощью формул A6), A7) и B2) получим:
(l\m'\z\l,m) = reSi
ЗАМЕЧАНИЕ
Согласно формуле B7) правила отбора, которым удовлетворяет оператор Z, таковы:
А/ = ±1, Дт = 0. Можно показать, что для операторов X и У они имеют вид: А/ = ±1,
Ат = ±\. Поскольку энергии уровней зависят только от /, частоты Бора для
(Х), (К), (Z) одинаковы.
Итак, оператор Z может связывать только два соседних мультиплета рис.2
(соответствующие переходы представлены на рисунке вертикальными стрелками). Поэтому
единственные частоты Бора, появляющиеся в эволюции (z)(r), имеют вид:
VmV«
-т- 1A + 1)
+ 5г.;+!
■т
4(/ + 1J-1
B7)
871

Глава VI
v/M=^-£=L = 2B/. B8)
h
Они образуют последовательность эквидистантных частот, разделенных интервалами
2В (рис.3).
1«—*0 2—-М 3<-*2 4—►З 5*-* 4
J I I I L
-**v
О 2В АВ 6В W 10 Д
Рис.3
Частоты, возникающие в эволюции среднего значения наблюдаемой Z. Правило отбора
А/ = ±1 требует, чтобы существовали лишь частоты Бора 25/, где />1, связанные с
переходами между уровнями Е{ и Ем рис. 1
Таким образом, среднее значение (z)(t) может изменяться во времени лишь на
вполне определенной серии частот в отличие от классического случая, где частота
вращения vR ротатора может принимать любые значения.
Если система находится в стационарном состоянии |/,ш), то (z)(t) всегда равно
нулю [формула B7)], даже при больших числах /. Чтобы получить квантовое
состояние, в котором (z) вело бы себя аналогично соответствующей классической
переменной Z, нужно суммировать большое количество состояний |/,т). Допустим, что со-
I I2
стояние системы описывается формулой B3) и что числа сЛ/и@) имеют значения,
зависящие от / так, как представлено на рис.4: наиболее вероятное значение /, равное
1М , очень велико, дисперсия А/ значений / также велика по абсолютной величине, но
ее относительная величина очень мала:
^,A/»1; B9-а)
— «1. B9-Ь)
Тогда можно показать, что в этом состоянии:
(LJ=(L2) = lM(lM+l)ti2=l2Mh2. C0)
Однако частоты Бора, характерные для эволюции (z)(r), расположены очень близко
друг к другу (по относительной величине) и примерно равны:
872

Общие свойства угловых моментов в квантовой механике
М°)|2
Л1
I
Рис.4
Квадраты модулей коэффициентов в
разложении «квазиклассического»
состояния по стационарным состояниям
|/,т) жесткого ротатора. Дисперсия
А/ достаточно велика, но, поскольку
наиболее вероятное значение 1М
очень велико, относительная ошибка
А/
L
■« 1 достаточно мала
vM=2BlM.
Исключив 1М с помощью равенств C0) и C1), получим с учетом A9):
п 2тг/
что совпадает с классическим соотношением F).
C1)
C2)
ЗАМЕЧАНИЕ
Представляет интерес более подробный анализ движения волнового пакета,
соответствующего состоянию, изображенному на рис.4. Он описывается функцией углов тЭ и ф , и
можно полагать, что его эволюция происходит по сфере единичного радиуса. Выполненный
выше анализ показывает, что волновой пакет движется по сфере со средней частотой V м .
Из-за дисперсии А/ квантовых чисел / и соответствующей дисперсии частот Бора 2 В А/
волновой пакет деформируется с течением времени. Деформация становится значительной
в течение интервала времени порядка:
1
2ВМ
Поскольку относительное значение дисперсии по / невелико:
А/
C3)
C4)
Таким образом, деформация волнового пакета происходит существенно медленнее его
вращения.
На деле частоты Бора системы образуют дискретную последовательность эквиди-
873

Глава VI
стантных частот, разделенных интервалом 2 В . Результирующая суперпозиция движений
с этими частотами является периодическим движением с периодом:
Т = , C5)
2В
и согласно формуле B9-а):
Т » X » . C6)
Таким образом, деформация волнового пакета не является необратимой, а периодически
повторяется. Это связано с ограниченностью поверхности сферы единичного радиуса, по
которой движется волновой пакет. Подобное поведение можно сравнить с движением
свободного волнового пакета (с его необратимым расплыванием, как показано в дополнении
Gj) и с поведением квазиклассических состояний гармонического осциллятора (колебания
без деформации, дополнение Gv).
4. Экспериментальное проявление вращения молекул
а. ГЕТЕРОПОЛЯРНЫЕ МОЛЕКУЛЫ. СПЕКТР ЧИСТОГО ВРАЩЕНИЯ
а. Описание спектра
Если молекула состоит из двух различных атомов, электроны притягиваются в
сторону более электроотрицательного атома, и молекула обычно имеет постоянный ди-
польный электрический момент d0, направленный вдоль оси молекулы. Проекция этого
момента на ось Oz в квантовой механике превращается в наблюдаемую,
пропорциональную оператору Z. Выше мы видели, что в эволюции среднего значения (z)(t)
присутствуют все частоты Бора 2В1 (здесь / = 1,2,3,...), представленные на рис.3. Поэтому
понятно, как молекула оказывается связанной с электромагнитным полем и почему она
может поглощать или испускать излучение, поляризованное параллельно оси Oz *, при
условии, что частота этого излучения совпадает с одной из частот Бора 2 В1.
Соответствующий спектр поглощения или испускания молекулы называется
«спектром чистого вращения». Он состоит из серии эквидистантных линий, частотный
интервал между которыми равен 2В, как изображено на рис.3. Линия поглощения (или
испускания) с частотой 2В1 соответствует переходу молекулы с уровня /-1 на уровень /
(или с уровня / на уровень / -1) при одновременном поглощении (или испускании)
фотона с частотой 2В1, как это схематически показано на рис.5.
* Изучая движение средних значений (х)@ и (у)@ , нетрудно заметить, что молекула
может также поглощать и испускать излучение, поляризованное параллельно осям Ох и Оу .
874

Общие свойства угловых моментов в квантовой механике
Рис.5
Схематическое представление
перехода молекулы между двумя
вращательными уровнями: а) при
поглощении фотона и Ь) при
испускании фотона
Таким образом, вращательные спектры двухатомных молекул позволяют
экспериментально проверить выводы, полученные при изучении квантования наблюдаемой L2.
Р. Сравнение со спектром «чистого колебания»
В § 1-с-а дополнения Av мы рассматривали «чисто колебательный» спектр гетеро-
полярной двухатомной молекулы. Представляет интерес сравнить этот спектр с
рассматриваемым здесь «чисто вращательным» спектром.
(i) Частоты вращения двухатомной молекулы в общем случае значительно меньше
частот колебаний. Интервал 2ВI с между двумя линиями вращения изменяется от
нескольких десятых до нескольких десятков см. При этом частоты 2В1 для малых
значений квантового числа / соответствуют длинам волн порядка сантиметров или
миллиметров. Так, например, для молекулы НС1 интервал 2ВI с равен 20,8 см, тогда как
частота колебаний, соответствующая волновому числу 2886 см, в сотни раз больше.
Таким образом, спектры чистого вращения лежат в области далекого инфракрасного
излучения или в диапазоне сверхвысоких частот.
ЗАМЕЧАНИЕ
В дополнении FVn мы покажем, что вращение молекул может проявиться
также в тонкой структуре колебательного спектра (колебательно-вращательные
спектры). При этом можно измерить константу 2В в области длин волн, лежащих
совсем в другом диапазоне. Аналогичное замечание касается и рамановского
вращательного спектра (см. ниже § 4-Ь), который проявляется в виде вращательных
линий в структуре оптического спектра.
(ii) В «чисто колебательном» спектре, описанном в дополнении Av, имелась только
одна линия колебания. Это было связано с тем, что все колебательные уровни
эквидистантны (если пренебречь ангармоничностью потенциала) и в движении диполя имелась
лишь одна частота Бора (правило отбора Av = ±1). Напротив, «чисто вращательный»
спектр представляет собой серию эквидистантных линий.
(Hi) В дополнении Av мы указали, что дипольный электрический момент гетеропо-
лярной молекулы может быть разложен в ряд по степеням (г-ге) вблизи положения
устойчивого равновесия молекулы:
Ж
875

Глава VI
D(r) = d0+dl(r-re) + ... C7)
Спектр чистого колебания может появиться только в том случае, если D(r) явно зависит
от г, и, следовательно, коэффициент dx должен быть отличен от нуля. Напротив, если
даже расстояние г остается неизменным и равным ге, вращение молекулы модулирует
проекцию электрического диполя на одну из осей, при условии, что d0 отличен от нуля.
Можно понять теперь, что изучение интенсивности колебательных и вращательных
линий позволяет определить коэффициенты d, и d0 разложения C7) в отдельности.
у. Приложения
Изучение спектров чистого вращения имеет интересные приложения, из которых
мы приведем только три примера.
(i) Измерение интервала 2 В между двумя соседними линиями согласно формуле
A9) определяет момент инерции / молекулы. Если известны массы т, и т2, то можно
вычислить расстояние ге между двумя ядрами в положении устойчивого равновесия
молекулы [ге — абсцисса минимума кривой V(r) на рис.1 дополнения Av]. Напомним,
что измерение частоты колебания дает крутизну этой кривой в точке г = ге.
(ii) Рассмотрим две двухатомные молекулы N - М и N - М', где два изотопа М и
М' одного элемента связаны с одним и тем же атомом N . Поскольку расстояния ге
между ядрами в этих двух молекулах равны, то измерение отношения коэффициентов
В, которое может быть выполнено с большой точностью, дает возможность получить
отношение масс двух изотопов М и М'.
Можно также сравнить частоты колебаний двух молекул, но предпочтительнее
использовать вращательный спектр, так как частоты вращения изменяются
пропорционально 1/jli [формула A9)], а частоты колебаний — пропорционально 1/уц [формула
E) дополнения Av].
(Hi) При изучении образца, содержащего большое количество одинаковых молекул,
относительные интенсивности линий поглощения или испускания в спектре чистого
вращения дают информацию о распределении молекул между различными мультипле-
тами Е,. Действительно, в противоположность тому, что имеет место в колебательном
спектре, переходу между двумя заданными соседними мультиплетами (стрелки на рис.2)
соответствует своя собственная частота, являющаяся характерной для этих двух муль-
типлетов, откуда следует, что интенсивность соответствующей линии зависит от
количества молекул, находящихся в состояниях, образующих эти мультиплеты.
Все эти сведения можно использовать для определения температуры среды*. Дей-
* Для этого чаще используется колебательно-вращательный спектр или вращательный рама-
новский спектр, попадающие в более удобный диапазон частот, чем спектр чистого вращения.
876

Общие свойства угловых моментов в квантовой механике
ствительно, если достигнуто термодинамическое равновесие, то вероятность
нахождения молекулы в состоянии с определенной энергией Е( пропорциональна e~E,lkT . Кроме
того, поскольку кратность вырождения вращательного уровня Е1 равна B/ +1), то
полная вероятность Щ того, что рассматриваемая молекула находится в каком-то из
состояний уровня Et («населенность» уровня Е{), запишется как:
9>=±B1 + 1)е-Е',кТ =~B/ + 1)^-/(/+,),,5МГ,
где
Z = 2B/ + l)e
-Щ+WB/kT
C8)
C9)
нормировочный множитель. Если исследуется система, содержащая большое
количество молекул, взаимодействием которых можно пренебречь, то (J\ определяет пропорцию
тех из них, которые имеют энергию Е{.
При обычной температуре hB «кТ, и заполнены многие вращательные уровни.
Заметим, впрочем, что наличие множителя B/ +1) говорит о том, что наиболее
населенными являются не самые нижние уровни. На рис.6 показан ход зависимости .^ от /
для такой температуры Г, что отношение hB/kT по порядку величины равно 1/10.
Вспомним, что колебательные уровни не вырождены, и их расщепление велико по
сравнению с hB, вследствие чего в том случае, когда распределение молекул между
вращательными уровнями соответствует рис.6, практически все молекулы находятся в
основном колебательном состоянии (v = 0).
(
0,3 .
0,2.
0,1 .
fl
hB _ 1
кТ ~10
1 . . .
0 12 3
6 7
Рис.6
Населенности Щ различных вращательных уровней с энергиями Е, при термодинамическом
равновесии. При малых / населенности увеличиваются вследствие B/+1)-кратного
вырождения уровней; при достаточно больших / показатель Болыдмана преобладает, что
приводит к уменьшению населенностей
877

Глава VI
b. ГОМЕОПОЛЯРНЫЕ МОЛЕКУЛЫ.
РАМАНОВСКИЕ СПЕКТРЫ ВРАЩЕНИЯ
Как уже указывалось в § 1-с-р дополнения Av, гомеополярная молекула (то есть
молекула, образованная из двух одинаковых атомов) не имеет постоянного дипольного
электрического момента, и в формуле C7) все коэффициенты dt = 0. При этом ни
колебания, ни вращение молекулы не могут привести к взаимодействию с электромагнитным
полем, вследствие чего она не может поглощать или испускать излучение в ближней
инфракрасной области (колебания) или в диапазоне СВЧ-радиоволн (вращение). Вместе
с тем, как и в случае колебаний (см. § 1-с-C дополнения Av), можно наблюдать
вращение молекул благодаря неупругому рассеянию световой волны (эффект Рамана).
а. Вращательный эффект Рамана. Классический анализ
В дополнении Av мы ввели восприимчивость % молекулы в оптическом диапазоне:
падающая световая волна, электрическое поле которой равно Е e,Qt, вызывает
вынужденное движение электронов в молекуле и индуцирует электрический дипольный
момент D elQ*, осциллирующий с частотой падающей волны, причем % является
коэффициентом пропорциональности между D и Е . Если вектор Е параллелен оси
молекулы, то х зависит от расстояния между ее ядрами: когда молекула колеблется, величина
X колеблется с той же частотой, что и является причиной колебательного эффекта
Рамана, описанного в § 1 -с-C дополнения Av.
Фактически двухатомная молекула является анизотропной системой. Если
ориентация оси молекулы произвольна по отношению к Е, то в общем случае вектор D не
параллелен вектору Е, и соотношение между D и Е является тензорным (х — тензор
восприимчивости). Вектор D параллелен Е в двух простейших случаях: если Е
параллелен молекулярной оси (при этом % = Хц) и если Е перпендикулярен к этой оси (при
этом х = Х± )• Выберем ось Oz параллельной электрическому полю Е поляризованной
световой волны и рассмотрим молекулу, ось которой имеет направление, определяемое
полярными углами й иф. Вычислим проекцию на ось Oz диполя, индуцированного в
молекуле полем Е. Вектор Е можно разложить на компоненту Е|, параллельную оси
молекулы, и компоненту Е±, перпендикулярную к линии М{М2 и находящуюся в
плоскости, образованной Oz и М,М2 (рис.7). Диполь, индуцированный полем EcosQ.t,
равен:
D = (x,E,+x1E±)cojQr. D0)
878

Общие свойства угловых моментов в квантовой механике
Рис.7
Разложение электрического поля Е на компоненту
Ец, параллельную оси молекулы, и компоненту Е±,
перпендикулярную к этой оси. Эти поля индуцируют
в молекуле электрические диполи Х\Щ и ЗС±ЕХ;
однако, поскольку Х\ и х± различны (анизотропия
молекулы), индуцированный диполь D = %цЕц + %1Е1
не коллинеарен полю Е
Его проекция на ось Oz вычисляется без труда:
Dz = (cos® Х\\|Ец| + sinb Xi |Ei|)cos &t = (cos2$ %i + sin2 ®X±)E cosQ.t =
= [%i +(X| -X±)cos2 b]EcosOa . D1)
Видно, что Д зависит от ft потому, что Х\ и ЗС± не равны (анизотропия молекулы).
Чтобы установить, что происходит при вращении молекулы, начнем с классических
рассуждений. Вращение молекулы с частотой оз^ /2я приводит к тому, что cosb
осциллирует с той же частотой:
cos Ь = a cos (со Rt - C), D2)
где а и Р зависят от начальных условий и от ориентации углового момента & (он
зафиксирован). Тогда видно, что член формулы D1), пропорциональный cos2 Ь, порождает
компоненты дипольного момента, осциллирующие с частотами (£2±2со/г)/2я и
добавляющиеся к компоненте, изменяющейся с частотой £2/2я (возникновение модуляции
поляризуемости на удвоенной частоте вращения 0)л / 2я молекулы нетрудно понять: после
поворота на угол я за половину периода молекула снова оказывается в таком же
геометрическом положении по отношению к вектору падающей световой волны). Свет,
переизлученный молекулой с поляризацией, параллельной оси Oz, испущен диполем Д и содержит
линию с несмещенной частотой Q / 2я (линия Рэлея) и две линии Рамана со смещенными
частотами, расположенными симметрично относительно линии Рэлея: «стоксову» линию с
частотой (Q - 2ш R) / 2я и «антистоксову» линию с частотой (Q + 2@ R) / 2я .
Р. Квантовые правила отбора. Характер романовского спектра
С квантовой точки зрения рассеяние Рамана соответствует процессу неупругого
рассеяния, в ходе которого молекула переходит с уровня Et на уровень Ег при одно-
879

Глава VI
временном изменении энергии фотона с Ш на Ш + Е, - Е,, (при этом полная энергия
системы в процессе рассеяния сохраняется).
Квантовая теория эффекта Рамана (здесь она излагаться не будет) приводит к тому,
что вероятность такого процесса включает в себя матричные элементы оператора
(%H-%1)cos2'& + x1 между начальным состоянием У/"(в, ф) и конечным состоянием
К//''(#,Ф) молекулы:
JrfQ^^^jJtxi-XiJc^O + XxJr^^)-
D3)
Можно показать, исходя из свойств сферических гармоник, что такой матричный
элемент отличен от нуля лишь в том случае, если*
/'-/ = 0, + 2, -2.
D4)
Линия рассеяния Рэлея, соответствующая / = /', одиночная. Поскольку уровни
вращения не эквидистантны, имеется множество антистоксовых линий Рамана,
соответствующих Г = / - 2 , с частотами:
£2 Er+2 Er ^
271 h
где Г = 0,1,2,...
Q 3)
2^ + 4Т+2>
D5)
и множество стоксовых линий Рамана, соответствующих Г = / + 2, с частотами:
Q Е,- £,.
2я h
где I = 0,1,2,
Q ( 3
■ = —-4В / + -„
2я V 2J
D6)
Вид рамановского вращательного спектра представлен на рис.8. Стоксовы и
антистоксовы линии расположены симметрично по обе стороны линии Рэлея. Интервал
между двумя соседними стоксовыми (или антистоксовыми) линиями равен 45, то есть
удвоенному значению расщепления между двумя соседними линиями чистого
вращения, если бы они существовали. Поскольку В значительно меньше частоты колебаний,
стоксовы и антистоксовы рамановские линии колебательного спектра располагаются
очень далеко с правой и с левой сторон от линии Рэлея (впрочем, и они также обладают
аналогичной вращательной структурой).
* Интеграл D3) также равен нулю, если тФт'. Если же интересуются светом, испущенным
с иным состоянием поляризации, чем поляризация падающего света, то будут получены
следующие правила отбора для квантового числа т : Am = 0, ± 1, ± 2 .
880

Общие свойства угловых моментов в квантовой механике
Линия Рэлея
Стоксовы линии
Рамана
4В | 6В
it
-ы
Антистоксовы линии
Рамана
6В | 4В
111
i!i
3-5 2-4 1-3 0-2 / = /' 2-0 3-1 4-2 3-5
Рис.8
Рамановский спектр вращения молекулы. Молекула, первоначально находившаяся на
вращательном уровне Et, рассеивает неупругим образом падающий фотон с энергией
Ш и переходит на вращательный уровень Ег, а энергия фотона становится равной
Ш+ Е, - Ег (сохранение энергии). Если / = /' , рассеянный фотон имеет ту же частоту
v = Q / 271, что и падающий фотон (линия Рэлея); если Г - / = ±2 , то при Г = 1 + 2
частота рассеянного фотона меньше (стоксова линия), и, если Г = 1-2 % частота рассеянного
фотона больше (антистоксова линия). Поскольку вращательные уровни не эквидистантны
(рис.2), количество стоксовых или антистоксовых линий равно количеству значений числа /;
эти линии обозначены на рисунке символом / —» Г , где Г = I ± 2
ЗАМЕЧАНИЯ
(i) Вернемся к волновому пакету типа тех, которые были рассмотрены выше в § 3-е,
для которого значения / были сгруппированы вблизи очень большого значения 1М
(см. рис.4). Согласно выражениям D5) и D6) частоты различных стоксовых и
антистоксовых линий будут очень близки (по относительному значению) к частоте:
£±4*/„ D7)
или в соответствии с C1):
£±2v„. D8)
где v м — средняя частота вращения молекулы. Так квантовая теория позволяет
перейти к классическому пределу от полученных в §4-Ь-а результатов,
(ii) Во вращательных спектрах Рамана стоксовы и антистоксовы линии имеют
сравнимые интенсивности, так как величина hB мала по сравнению с кТ, и уровни с
большими квантовыми числами / имеют значительные населенности, что
необходимо для наблюдения антистоксовых линий, для которых начальным состоянием
56 Квантовая механика
881

Глава VI
молекулы должно быть по меньшей мере состояние 1 = 2. Напротив, антистоксо-
вы колебательные линии имеют интенсивность существенно меньшую, чем сто-
ксовы. Действительно, энергия колебаний мала по сравнению с кТ, и
населенность основного колебательного уровня v = 0 значительно больше, чем других, в
результате чего стоксовы переходы v = 0 —> v = 1 оказываются значительно более
вероятными, чем антистоксовы v = 1 —> v = 0.
(iii) Вращательный эффект Рамана существует также и в случае гетерополярных молекул.
Дополнение Dvi
УГЛОВОЙ МОМЕНТ СТАЦИОНАРНЫХ СОСТОЯНИЙ
ДВУМЕРНОГО ГАРМОНИЧЕСКОГО ОСЦИЛЛЯТОРА
1. Введение.
a. Напоминание классических результатов.
b. Постановка задачи в квантовой механике.
2. Классификация стационарных состояний с помощью квантовых чисел пх и п .
a. Энергии. Стационарные состояния.
b. Нху не образует полного набора коммутирующих операторов в пространстве #vv.
3. Классификация стационарных состояний в зависимости от их углового момента.
a. Значение и свойства оператора L,.
b. Кванты, поляризованные по правому и левому кругу.
c. Стационарные состояния с хорошо известным угловым моментом.
d. Волновые функции собственных состояний, общих для операторов Н^ и Lz.
4. Квазиклассические состояния.
a. Определение состояний СС^, ОС ) и OC^,OCg).
b. Средние значения и среднеквадратичные отклонения некоторых наблюдаемых.
В этом дополнении нас будут интересовать квантовые свойства двумерного
гармонического осциллятора. Значение этой задачи состоит не только в том, что она решается
точно без особо сложных вычислений. Кроме того, она является простым примером
применения свойств орбитального углового момента L, так как стационарные
состояния такого осциллятора могут быть классифицированы в зависимости от возможных
значений наблюдаемой Lz. Полученные здесь результаты будут полезны для задачи,
приведенной в дополнении EVi.
882

Общие свойства угловых моментов в квантовой механике
1. Введение
а. НАПОМИНАНИЕ КЛАССИЧЕСКИХ РЕЗУЛЬТАТОВ
Физическая частица всегда движется в трехмерном пространстве. Однако, если ее
потенциальная энергия зависит только от координат х и у, то задача оказывается
двумерной. Здесь мы допустим, что потенциальная энергия имеет вид:
У(*,у) = уС02(х2+у2), A)
где [I — масса частицы и со — постоянная величина. Функция Гамильтона такой
системы запишется в форме:
Ж = Жх+Жг, B)
где
**=ч^(р1 + р1)+\^2(х2 + у2)'
2|ы
JC=^-p2z. C)
Здесь рх, ру, pz — три компоненты импульса р частицы, a Ж^ — гамильтониан
двумерного гармонического осциллятора.
Уравнения движения интегрируются без труда и дают:
z(t) = ^t + Zo; D)
x(t) = xMcos(M-<f>x)\
рх (t) = -\шсм sin (cor - фх);
y(t) = yMcos(m-yy);
py(t) = -\LV>yMsin(m-(py),
E)
F)
где р0, Zq, хм , (рх, ум , фу — постоянные, определяемые начальными условиями
(далее мы будем считать хм и у^ положительными).
Видно, что проекция траектории частицы на ось Oz является равномерным
движением со скоростью р011!, а проекция на плоскость хОу представляет собой эллипс,
вписанный в прямоугольник ABCD, изображенный на рис. 1. Направление движения по
эллипсу зависит от разности фаз фу -фх. Если фу - фл = ±п, то эллипс вырождается в
56*
883

Глава VI
прямую АС; если разность углов фу - ф^ заключена между -тс и 0, движение по
эллипсу осуществляется в направлении часовой стрелки («левое» движение), причем при
ф v - фЛ = -я / 2 оси эллипса параллельны осям Ох и Оу . Если (ру - фЛ. = 0, то эллипс
вырождается в отрезок прямой BD , и, наконец, если разность углов (ру - (рх заключена
между 0 и тг, то движение по эллипсу происходит против часовой стрелки («правое»
движение), причем оси эллипса параллельны осям Ох и Оу , если фу -фх = +п/2.
Заметим, что эллипс превратится в круг, если фу - фЛ = ±п 12 и хм = ум .
А
~ \м
1
э
к
о
^У
Ум
-Ум
Б
Л
с
+ *.!/
Рис.1
Проекция на плоскость хОу
классической траектории частицы, движущейся
в поле двумерного гармонического
потенциала; траектория представляет
собой эллипс, вписанный в
прямоугольник ABCD
В том, что касается проекции движения на плоскость хОу, можно определить ряд
величин, остающихся неизменными:
— полная энергия Ж^, равная:
JL
2
- энергии:
JC = ^co2D + y«);
G)
проекций движения на оси Ох и Оу ;
— проекция орбитального углового момента Я! частицы на ось Ог:
равная согласно формулам E) и F):
(8-а)
(8-Ь)
(9)
884

Общие свойства угловых моментов в квантовой механике
<P.Z = ц@*м yM sin(q>y -фг). A0)
Видно, что У*г больше или меньше нуля в зависимости от того, является ли движение
правым или левым. Проекция У.г = 0, если эллипс вырождается в одну из прямых.
И, наконец, для движения с заранее заданной энергией, то есть для фиксированного
значения суммы х2м + у2м , модуль \(fz\ максимален, если фу -фг = ±я/2 , и произведение
хм ум оказывается максимально возможным, то есть при хм = ум . Из всех движений с
фиксированной энергией правоциркулярное (или левоциркулярное) движение
соответствует максимальному (или минимальному) алгебраическому значению (fz.
b. ПОСТАНОВКА ЗАДАЧИ В КВАНТОВОЙ МЕХАНИКЕ
Правила квантования, введенные в главе III, позволяют получить операторы Я,
Я , Я,, исходя из классических величин Ж, Ж , Жг. Стационарные состояния |ф)
частицы определяются выражением:
Я|ф) = (ЯЛ7 + Яс)|ф) = £|Ф), (И)
где
:>2 , п2
#.„=—^ + ^ЦС02(Х2+У2); A2-а)
Р2
Hz=-^-. A2-b)
Из результатов дополнения Fj известно, что можно выбрать базис собственных
состояний оператора Н из векторов вида:
|ф> = |ф„)®|Фг), A3)
где фЛ — собственный вектор оператора Нхув пространстве состояний %ху,
связанном с переменными х и у:
^Ю = £,>,,)> A4)
и |фт) — собственный вектор оператора Hz в пространстве состояний #г, связанном с
переменной z:
Hz\<f>z)=E:\<pz). A5)
Полная энергия состояния A3) равна:
885

Глава VI
E = Exy, + Ez. A6)
Уравнение A5), определяющее стационарные состояния свободной частицы в
одномерной задаче, можно решить сразу же:
<*>=жг*""- <17)
где pz — произвольная вещественная константа и
Е---Ь ,18)
Таким образом, задача сводится к нахождению решений уравнения A4), то есть к
нахождению энергий и собственных состояний двумерного гармонического осциллятора.
Именно эту задачу мы и попытаемся решить в дальнейшем изложении.
Мы увидим, что собственные значения Еху операторов Н^ вырождены, и Н^ сам
по себе не образует в пространстве $ху полного набора коммутирующих операторов.
Таким образом, чтобы получить полный набор, нужно добавить к Н^ одну или
несколько других наблюдаемых. В квантовой механике мы встречаем те же константы
движения, что и в классической механике: энергии проекций движения Нх и Яу на оси
Ох и Оу , проекция L, орбитального углового момента L на ось Oz. Поскольку L, не
коммутирует ни с Нх ни с Н , можно построить полный набор коммутирующих
операторов или из Нху, Нх и Н (§ 2), или из Н и L. (§ 3).
ЗАМЕЧАНИЯ
(i) Формула A8) указывает, что собственные значения Ег оператора Hz дважды вырождены
в пространстве <-z. Кроме того, вырождение в пространстве #'" = #ДЛ, ® #, собственных
значений A6) полного гамильтониана имеет место не только за счет вырождения Еху в
пространстве $ху и Ez в пространстве %z: действительно, два собственных вектора оператора
Н вида A3) могут иметь одинаковую полную энергию Е, если даже соответствующие
значения Еху (и Ez) различны.
(и) Оператор Н коммутирует с компонентой L, оператора L , но не коммутирует с
операторами Lx и L . Это происходит из-за того, что потенциальная энергия A) не инвариантна
относительно вращения вокруг оси Oz . Впрочем, их трех операторов Lx , Lv, Lz лишь
один оператор Lz действует только в пространстве tfvy . Поэтому для анализа двумерного
886

Общие свойства угловых моментов в квантовой механике
гармонического осциллятора мы будем использовать только наблюдаемую L,. В
дополнении Вуц будем рассматривать трехмерный изотропный гармонический осциллятор,
потенциальная энергия которого инвариантна относительно любой оси, проходящей через начало
координат. Мы увидим, что в этом случае все три компоненты оператора L коммутируют
с гамильтонианом.
2. Классификация стационарных состояний
с помощью квантовых чисел пг и и
а. ЭНЕРГИИ. СТАЦИОНАРНЫЕ СОСТОЯНИЯ
Чтобы решить уравнение A4) на собственные значения, заметим, что
Нху=Нх + Ну, A9)
где операторы Нх и Н — гамильтонианы одномерных гармонических осцилляторов:
Р2 1
х 2[i 2^
Р2 1
Я=-^- + -цаJУ2. B0)
Собственные состояния \(рп ) оператора Нх в пространстве Шх и собственные
состояния ф„ ) оператора Ну в пространстве $у имеют соответственно значения энергий
Ех = (пх +1 / 2) /Ш) и Еу = (пу +1 / 2) /гсо , где пх и пу — целые положительные числа
или нули. Тогда собственные состояния оператора Н^ можно записать в виде:
причем соответствующая энергия равна:
Е,у = [пх + -1йа> + 1 пу +-) йш = (л, + лу +1)й@ . B2)
В соответствии со свойствами одномерного гармонического осциллятора значение Ех
не вырождено в пространстве ^, как и значение Еу в пространстве $у, вследствие чего
паре чисел |л,,иЛ соответствует в пространстве #rv единственный вектор ф„ „ \,
887

Глава VI
то есть в этом пространстве операторы Нх и Ну образуют полный набор
коммутирующих операторов.
В дальнейшем удобно использовать операторы ах и ау (операторы уничтожения
квантов, относящихся к осям Ох и Оу соответственно), определенные формулами:
ъ-И*™*}- B3)
где
*■■¥?■ B4>
Поскольку операторы ах и а действуют в различных пространствах %х и £у1
единственными отличными от нуля коммутаторами операторов ах, а*, а^,, я* являются:
[йд.,а;] = [^,а;] = 1. B5)
С другой стороны, операторы Nx (число квантов, относящихся к оси Ох) и N (число
квантов, относящихся к оси Оу ) равны:
Nx=a*ax;
Ny=a*yay, B6)
что позволяет записать оператор Нху в форме:
HX7 = Hx + Hy=(Nx + Ny + l)M. B7)
Очевидно,что
^л|фл,.л,.)=^|ф„д,и>);
^,|ф„г.п,.) = «у|фп,.„¥)- B8)
Основное состояние Ф0,о) определяется формул ой :
|фо,о> = |ф„,=о)®|ф„у=о)- B9)
Состояние ф„ ), определенное формулой B1), можно получить из Ф0,о) путем
многократного последовательного применения операторов а* и а* :
888

Общие свойства угловых моментов в квантовой механике
К»>)=1^&Т(<Т'М- C0)
Соответствующая волновая функция является произведением ф„ (х) на ф„ (у) [см.
формулу C5) дополнения Bv]:
ЧЧ.", (*' У) = / „J е-*^I2НПх фх) Н фу). C1)
^яB)я'+я'(ях)!(пу)!
Ь. Я^ НЕ ОБРАЗУЕТ ПОЛНОГО НАБОРА
КОММУТИРУЮЩИХ ОПРЕРАТОРОВ В ПРОСТРАНСТВЕ ^
Из формулы B2) видно, что собственные значения оператора Нху имеют вид:
£<, = £„= (л+ 1)»а>, C2)
где
п = пх+ пу C3)
равно произвольному положительному целому числу или нулю. Этому значению
энергии соответствуют различные ортогональные собственные векторы:
|фяж.я.Яг.о).|фЯ,.Я-1.Яг.1). —|фЯ^О.п,вЯ)- C4)
Поскольку общее число таких векторов равно (п +1), то собственное значение Еп
оказывается (л+1)-кратно вырожденным в пространстве $ 9 и, следовательно, оператор
Н сам по себе не образует полного набора коммутирующих операторов. Напротив,
как мы видели выше, совокупность операторов 1нх, НА является таким набором. То же
самое можно, очевидно, сказать и о совокупностях операторов 1нху, Нх} и 1нху, Ну}.
3. Классификация стационарных состояний
в зависимости от их углового момента
а. ЗНАЧЕНИЕ И СВОЙСТВА ОПЕРАТОРА Lz
В предыдущем параграфе стационарные состояния классифицировались с помощью
квантовых чисел \пх ,пу\. Если оси Ох и Оу не играют существенной роли в задаче,
889

Глава VI
так как потенциальная энергия инвариантна относительно вращения вокруг оси Oz, то
почему бы не выбрать другую систему ортогональных осей Ох' и Оу' в плоскости хОу ,
в которой стационарные состояния выглядели бы иначе, чем приведенные выше.
Поэтому, чтобы наилучшим образом использовать свойства симметрии данной
задачи, рассмотрим компоненту Lz углового момента:
LZ = XPY-YPX. C5)
Выразив X и Рх через ах и ах, a Y и Р через ау и а*, без труда получим:
Lz =i^(axay~a+xay)' C6)
Если через эти же операторы выразить Нху , то мы получили бы:
Я*=(вХ+в,Ч+1)А@- C7)
Поскольку:
то сразу же получим:
[ахау, ахах + д*а_у ] = аха+ - аха* = 0;
[а+хау,а+ах +а+уау\ = -a>v +<av = 0, C8)
Кл] = о. C9)
и нужно искать базис собственных векторов, общих для операторов Н и L,.
Ь. КВАНТЫ, ПОЛЯРИЗОВАННЫЕ ПО ПРАВОМУ И ЛЕВОМУ КРУГУ
Введем операторы ad и а , определенные формулами:
ag =-j=(ax+iay). D0)
Из этого определения видно, что действие оператора ad (или ag) на вектор ф;| „ )
дает состояние, являющееся линейной комбинацией векторов ф;| _, п ) и фл /} _Л,
то есть стационарное состояние, имеющее энергию на 1 квант Йсо меньше. Аналогично,
действие оператора ad (или a J) на ф„ fI ) дает состояние с энергией, на 1 квант большей.
Действительно, сейчас мы увидим, что действие оператора ad (или а ) очень похоже
890

Общие свойства угловых моментов в квантовой механике
на действие оператора ах (или а ), то есть операторы ad и ag могут
интерпретироваться как операторы уничтожения «правого» и «левого» циркулярно-поляризованного
фотона соответственно.
Сначала докажем, используя выражения D0) и B5), что единственными отличными
от нуля коммутаторами четырех операторов ad , ag, ad и ag являются:
K-«;]=k-<]=i- D1)
имеющие явное сходство с выражениями B5). Кроме того, оператор Нху можно
представить через эти операторы в виде, сходном с выражением C7); действительно, поскольку
adad = т(*Х + а+уау - Кау + "*Х) ;
fl* fl* = - («t ^Л + ^ X' + *fl* fly " ^Х ) > D2)
имеем:
^,у=(^Ч+^Ч+1)ЙС0- D3)
Если учесть выражение C6), получим:
Lz=h(a+dad-a;ag). D4)
Если ввести операторы Nd и Ng (число квантов с правой и левой круговой
поляризацией):
Nd = a*ad ;
N, =«;*,> D5)
то формулы D3) и D4) перепишутся в форме:
Я<у = К + Л, + 1)йа>;
£г=й(лг,-Л^). D6)
Сохраняя для оператора Я простейшее выражение вида B7), мы смогли упростить
выражение для Lz.
с. СТАЦИОНАРНЫЕ СОСТОЯНИЯ С ХОРОШО ИЗВЕСТНЫМ УГЛОВЫМ МОМЕНТОМ
Теперь мы можем выполнить с операторами ad и ag те же действия, что и с
операторами ах и ау. Тогда окажется, что спектры операторов Nd и Ng образованы целыми
891

Глава VI
положительными числами или нулями; кроме того, задание пары чисел \nd, ng}
единственным образом (с точностью до постоянного множителя) определяет общий
собственный вектор операторов Nd и Ng с этими же квантовыми числами:
Итак, Nd и Ng образуют полный набор коммутирующих операторов в пространстве $„. .
Используя D6), нетрудно заметить, что Ьс,,^,, ) также является собственным вектором
операторов Н^ и Lz с собственными значениями (п +1) Йсо и rrih, где пит —
квантовые числа, равные:
n = nd+ng;
m = nd- ng. D8)
Равенства D8) позволяют понять природу названия «циркулярно-поляризованных»
правых или левых квантов. Действительно, действие оператора ad на кет \ХпA,п ) Дает со"
стояние, имеющее на 1 квант больше, которому, поскольку число т увеличилось на 1,
следует приписать угловой момент +h (вращение вокруг оси Oz в прямом
направлении), и, аналогично, действие оператора а* дает состояние, имеющее на 1 квант
больше, но с моментом -h (вращение в противоположном направлении).
Поскольку nd и ng — целые положительные (или равные нулю) числа, то мы снова
приходим к уже встречавшимся ранее выводам: собственные значения оператора Н
имеют форму (л + 1)/гш, где п — целое положительное (или равное нулю) число, и
кратность их вырождения равна (п +1), так как при фиксированном п можно иметь:
D9)
С другой стороны, мы видели, что собственные значения оператора Lz равны mti,
где т — любое целое число или нуль, что совпадает с общими выводами главы VI.
Кроме того, таблица D9) позволяет определить, какие значения т связаны с заранее
заданным значением п. Например, для основного уровня имеем nd =ng = 0, то есть
т = 0; для первого возбужденного уровня могут быть комбинации nd = 1 и ng = 0 или
п{1 = п\
nd=n-\\
п,=0;
ns=0;
/.,=1;
ng=n.
892

Общие свойства угловых моментов в квантовой механике
nd ~ О и ng - 1, что дает т = +1 или т = -1. В общем случае формулы D8) и D9)
показывают, что для заданного уровня энергии (п +1) Йсо возможными значениями т могут быть:
т = л,я-2, л-4, ...,-л + 2, -п
E0)
Отсюда следует, что паре значений пит соответствует единственный вектор (с
точностью до постоянного множителя):
п+т п-т
Таким образом, операторы Н и Lz образуют полный набор коммутирующих
операторов в пространстве £ .
ЗАМЕЧАНИЕ
Для заданного значения полной энергии, определенного числом п , состояния
Хн</=и,/| =о/ и X/irf=o,/i =л) соответствуют максимальному значению пЬ и
минимальному значению -пЬ проекции Lz. Эти состояния напоминают классические
круговые движения (правое и левое), связанные с данным значением полной
энергии, для которых 2?z достигает своего максимального (или минимального)
значения (см. § 1-а).
d. ВОЛНОВЫЕ ФУНКЦИИ СОБСТВЕННЫХ СОСТОЯНИЙ,
ОБЩИХ ДЛЯ ОПЕРАТОРОВ Н^ И L,
Чтобы сохранить симметрию задачи при вращении вокруг оси Oz , используем полярные
координаты, полагая:
jt = pcas(p, p>0;
у = р5шф, 0<ф<2я.
E1)
Посмотрим, как действуют операторы ad и а на функцию переменных риф. Сначала
определим их действие на функцию переменных х и у. Зная действие операторов X и Рх и,
следовательно, ах, можно воспользоваться формулой D0) и записать:
1
flrf=>2
Р(*-о0+^
_Э__._Э_
[дх ду)
E2)
893

Глава VI
С помощью правил дифференцирования функции нескольких переменных получим:
Аналогично:
а.
а 1 д ' Э
6р +
р Эр (ЗрЭф
3p_1A__lA
Р Эр рр Эф
E3)
E4)
о 1 Э / Э
р Эр рр Эф]
о 1 Э id
Рр + .
Р Эр рр Эф]
E5)
Чтобы вычислить волновую функцию %п (р, ф), достаточно применить
дифференциальные операторы, представляющие a*d ии*,к функции Хо,о(Р' Ф)> имеющей вид C1):
Хо.о(Р,Ф)=-М!рг'2
V71
E6)
Теперь несложно установить, что действие операторов a J и а* на функцию вида e'mF(p)
описывается выражениями:
.|(/И+1)ф
a;[^F(p)] =
a;[^F(p)] =
2
,/(/М-1)ф
PpJ
Рр-—■
РР PpJ
™ ч 1 dF
^(Р)-х—
РФ
„, ч 1 dF
РФ
E7)
Путем повторяющегося действия этих равенств к функции E6) получим, что зависимость функ
ции %п п (р, Ф) от угла ф определяется простой экспонентой е  "' ф. Тем самым мы
убедились в справедливости общего правила, установленного в главе VI: зависимость от угла ф
собственной функции оператора Ьг, соответствующей собственному значению mh , имеет вид е""ф.
Допустим, что в формуле E7) F(p) = рт е~* р /2. Тогда:
a+d[eim*pn
^-Л2/2 | _ О^Ои+ПФ т+\ e-?>Vl2
E8)
894

Общие свойства угловых моментов в квантовой механике
Подействовав пA раз на функцию %0,о(Р) оператором я,), получим:
х (р,ф) =-P.^VPp^^v^
и аналогично:
Хо.„ (Р>Ф):
V^K)!
*-,я'ф(Рр)я'*-р2р2/2.
E9)
F0)
Нетрудно доказать, что эти волновые функции нормированы, что видно хотя бы из самого
принципа их построения. Для заданного уровня энергии (п + 1) Л@ волновые функции E9) и F0)
соответствуют предельным значениям +п и —п квантового числа т . Их зависимость от р
предельно проста: имеется максимум (по модулю) при р = ^п 113 , вследствие чего, как и в случае
одномерного гармонического осциллятора, пространственное распределение волновых функций
становится шире с увеличением энергии (п + 1) /ztt) .
Применение операторов я J (или а* ) к функциям E9) и F0) позволило бы построить таким
же способом функции %п п (р, ф) для произвольных nd и ng . Результаты, полученные для
первых возбужденных уровней, приведены в табл. I.
Таблица I
Общие собственные функции гамильтониана Нху и наблюдаемой L, для первых уровней
двумерного гармонического осциллятора
я = 0,
п = \
п = 2
т = 0,
/и=1,
т- -1,
/и = 2,
т = 0,
т- -2,
л/я
х,0(р,ф)=-^(Зр^2р:'2А
х0,1(р,ф)=-^Рре"рУ/2^'ф;
л/я
X2.0(P)9) = -|=(PpJ,-pV'2^;
Xu(p,p) = -^[(PpJ-l]^v'2;
Х0,2(р,ф) = -^(РрJ^гр2/2е-2Лр
895

Глава VI
ЗАМЕЧАНИЕ
Функции Хп ,о(Р» Ф)» приведенные в E9), пропорциональны е~^ р ' (рре'ф)"'/ . В
более общей форме все их линейные комбинации имеют вид:
F(p,(p) = e-p2p2/2/(PP^) F1)
(где / — произвольная функция одной переменной) и являются собственными функциями
оператора N с нулевым собственным значением. С помощью выражения E5) нетрудно
доказать, что
aeF(p,q>) = 0. F2)
Аналогично подпространство собственных функций оператора Nd с нулевым
собственным значением состоит из функций вида:
С(р,<р) = е-^2п8фре-*). F3)
4. Квазиклассические состояния
Свойства одномерного гармонического осциллятора позволяют достаточно просто
определить эволюцию вектора состояний и средних значений различных наблюдаемых
двумерного осциллятора во времени. Можно показать, что средние значения (x)(t) и
(У)@, а также (Px)(t) и (^v)@ должны содержать единственную частоту Бора со.
Кроме того, можно доказать, что эти средние значения в точности подчиняются
классическим законам эволюции. В этом параграфе нас будут интересовать свойства и
эволюция квазиклассических состояний двумерного гармонического осциллятора.
а. ОПРЕДЕЛЕНИЕ СОСТОЯНИЙ | ОС,, ОС Л И |ctrf,(X Л
Чтобы построить квазиклассическое состояние двумерного гармонического
осциллятора, можно опереться на выполненный ранее расчет в случае одномерного
осциллятора (см. дополнение Gv). Напомним, что в квазиклассическом состоянии, связанном с
заданным классическим движением, средние значения (x)(t) и (P)(t) в каждый
момент времени совпадают с x(t) и p(t), а также среднее значение гамильтониана Я
равно (с точностью до половины кванта /КО / 2) классической энергии. В дополнении Gv
было показано, что в любой момент времени квазиклассические состояния являются
собственными состояниями оператора уничтожения а и имеют вид:
896

Общие свойства угловых моментов в квантовой механике
|а) = 1с„(а)|Ф„)( F4)
/J
где а — собственное значение оператора а и
с„(а) = -^е-|а|2/2. F5)
л/и!
В интересующем нас случае можно использовать правила тензорного произведения
и записать квазиклассические состояния в виде:
av>av) = K)®К)= 2 2^(«х)с (ау) ф ), F6)
пх=0 nv=0 I /
где
ау\ах,ау) = ау\ах,ау). F7)
При этом можно с уверенностью считать, что (х), (Рх), (#v), (Y), (^v)> (#v)
совпадают с соответствующими классическими величинами. Если вернуться к определению
D0) и использовать выражение F7), то нетрудно видеть, что
*d\*x*<*y) = ad\ax,ay)\
в,|а*.а,) = а,|а,,а,), F8)
где
"V2
а,=-^(а,-/осу);
а, =-7= (а, + /ау). F9)
Таким образом, состояние cct,av) является также собственным вектором операторов
ad и ag с собственными значениями, определенными выражением F9). Обозначим
символом а^аЛ собственный вектор, общий для операторов ad и ag и связанный с
собственными значениями ос^ иаг Можно показать, что разложение вектора \ad, a \
в базисе {%„,,„ )} имеет ту же форму, что и разложение вектора ос^осЛ в базисе
(|ф-ж.-,) ):
57 Квантовая механика 897

Глава VI
„.=0 и =0 I */
G0)
где коэффициенты с„ определены выражением F5). Из формул F8) и F9) следует, что
К'а>)=
ос -юс
а, =■
4г ' ,а,= Л
G1)
С учетом свойств состояний |а) (см. дополнение Gv, § 3-a) можно заметить, что если
|\|/@)> = |aJC,ay) = |a</,ag), G2)
то вектор состояния в момент t будет равен:
|\|/@) = е~ш \е-шах,е~ш<1у) = е~'т \е'шо.^ешо.^. G3)
Ь. СРЕДНИЕ ЗНАЧЕНИЯ И СРЕДНЕКВАДРАТИЧНЫЕ ОТКЛОНЕНИЯ
НЕКОТОРЫХ НАБЛЮДАЕМЫХ
Пусть:
a, =Kk
ay = aje
'Фу
Используя формулы (93) дополнения Gv, получим:
л/2
(X)(t) = — \ax\cos(M-<px)\
/ч л/2 i i
(К)@ = — |av|c<9s(wf-(pv);
л/2
(рс)@ = ~№-рг |ал.|^ш(шг-фл);
/ \ л/2 | |
(Py}(t) = -\uu — |av|sm(co/-(pv).
Сравнив G5) и G6) с E) и F), установим, что
_ Р*м /фл .
a =^l^
' л/2 '
G4)
G5)
G6)
G7)
898

Общие свойства угловых моментов в квантовой механике
где хм , ф^, ум , ф v — параметры, определяющие такое классическое движение, которое
наилучшим образом совпадает с состоянием ссх, ccv).
С другой стороны:
Ю = |ах|2;
(^,) = |а,|2 G8)
и
К)=1а<'Г=^[1алГ+|ау|2+''(аХ -«>,)];
W=Kf =|[КНа/~КаХ-<«,)] • G9>
то есть в соответствии с формулой D6):
(Я^> = Ц|а,|2 +|avf +1) = /Kojja/ +\agf +1) (80)
И
(Lz} = 2h\ax\\ay\sin(<py-q>,) = h(\ad\2 -\ag\2). (81)
Согласно формуле G7) величина (L2) также совпадает с классическим значением (£z
[см. формулу A0)].
Рассмотрим теперь среднеквадратичные отклонения положения, импульса, энергии
и углового момента в состоянии ах,ау). Применив непосредственно результаты
дополнения Gy, получим:
1
АХ=АУ =
fr/T
Среднеквадратичные отклонения положения и импульса не зависят от ах и осу. Если
\ах\ и a J велики по сравнению с 1, то дисперсия положения и импульса осциллятора
очень мала вблизи (X), (У) и(Рх),(Ру).
Вычислим, наконец, среднеквадратичные отклонения А//^ энергии и ALZ углового
момента. Как и в дополнении Gv, имеем:
899

Глава VI
ДЛГ,=|ах|;
ANy =|а_»|;
AJV„=K|;
ANg=\ag\. (83)
Но в гамильтониан Нху входит сумма N = Nx + Nv, a L, пропорционален разности
Ncl - Ns, и нужно вычислить, например:
(ANJ = Ik(nx + Nyj)-{(NX + A/,.))' = (ANxf +(ANyJ +2[(^Nv)-(^)(iVv)].
(84)
В соответствии с выражением F6) состояние системы является тензорным
произведением, откуда следует, что наблюдаемые Nx и Ny не коррелируют:
(NxNy) = (Nx)(Ny), (85)
и, следовательно:
(ANJ = (&NX f + (ДЛГУ J, (86)
то есть
Аналогично:
Wxy=hwij\ax\2+\ay\2 =йш^|а,|2+|а8|2 . (87)
|2
(88)
Дополнение Evi
ЗАРЯЖЕННАЯ ЧАСТИЦА В МАГНИТНОМ ПОЛЕ.
УРОВНИ ЛАНДАУ
1. Классические результаты.
a. Движение частицы.
b. Векторный потенциал. Лагранжиан и гамильтониан.
c. Константы движения в однородном поле.
900

Общие свойства угловых моментов в квантовой механике
2. Общие квантовые свойства частицы в магнитном поле.
a. Квантование. Гамильтониан.
b. Соотношения коммутации.
c. Физические следствия.
3. Случай однородного магнитного поля.
a. Собственные значения гамильтониана.
b. Анализ наблюдаемых для частного случая калибровки.
c. Анализ стационарных состояний.
d. Эволюция во времени.
Свойства частицы, находящейся в поле скалярного потенциала V(r), который
может описывать, например, действие электрического поля на заряженную частицу, были
проанализированы в некоторых частных случаях в главе I; в главе V (гармонический
осциллятор) и в главе VII (частица в поле центрального потенциала) рассматривались
другие примеры скалярных потенциалов. Здесь мы обратимся к дополняющей задаче и
рассмотрим свойства частицы в поле векторного потенциала А(г), то есть заряженной
частицы в магнитном поле. Будет обнаружен ряд чисто квантовых эффектов, как,
например, существование в однородном магнитном поле эквидистантных уровней энергии
(уровни Ландау)*. Прежде чем перейти к квантовому анализу задачи, вспомним вкратце
некоторые классические результаты.
1. Классические результаты
а. ДВИЖЕНИЕ ЧАСТИЦЫ
Если частица с зарядом q находится в точке с радиусом-вектором г под действием
магнитного поля В (г), то на нее действует сила, определяемая законом Лапласа:
f=<yvxB(r), A)
где
v = — B)
dt
скорость частицы. Ее движение подчиняется фундаментальному закону динамики:
* Эквидистантность проявляется, впрочем, как следствие свойств гармонического осциллятора,
и могла быть уже рассмотрена в рамках главы V. Однако мы увидим, что для изучения и
классификации стационарных состояний частицы окажутся очень полезными свойства углового момента,
и именно поэтому мы внесли эту тему в главу VI.
901

Глава VI
ц— = f,
C)
где \i — масса частицы.
В дальнейшем мы часто будем обращаться к случаю, когда магнитное поле будет
однородным, и в таком случае будем считать, что его направление будет совпадать с
осью Oz. Решив уравнение C), можно доказать, что в этом случае зависимость трех
координат частицы от времени лс(г), y(t), z{t) определяется выражениями:
x(t) = *0+Gcas(oocf-(p0);
у@ = Уо+сг5ш(сосг-ф0);
D)
где х0, у0, z0, а, ф0 и v0z — шесть постоянных параметров, зависящих от начальных
условий, а «циклотронная частота» сос определяется равенством:
сос=-<7-
В
E)
Рис.1
Классическая траектория заряженной частицы
в однородном магнитном поле, параллельном
оси Oz . Частица движется с постоянной
скоростью по круговой спирали, ось которой
параллельна Oz и проходит через точку С0.
На рисунке изображен случай q < 0 (электрон),
то есть 0)„ > О
Уравнения D) показывают, что проекция положения М частицы на плоскость хОу
осуществляет равномерное движение с угловой скоростью сос и начальной фазой ф0 по
окружности с радиусом а и с центром в точке С0, имеющей координаты х0 и у0. Что
902

Общие свойства угловых моментов в квантовой механике
касается проекции точки М на ось Oz, то ее движение является равномерным и
прямолинейным. Таким образом, частица движется в пространстве по круговой спирали
(рис.1), ось которой параллельна Oz и проходит через точку С0.
Если интерес представляет лишь движение точки Q (проекция точки М на
плоскость хОу ), то можно исследовать эволюцию вектора:
р = хех + уеу, F)
где ev и ev —единичные векторы осей Ох и Оу . Скорость точки Q равна:
d
v,=-p. G)
Удобно ввести компоненты х' и у' вектора C()Q:
х - х - х{);
у' = У~Уо- (8)
Поскольку точка Q осуществляет равномерное движение по окружности вокруг точки
С0, то скорость этого движения можно описать формулой:
v±=coc.ezxC0Q, (9)
где е, — единичный вектор оси Oz . Отсюда следует, что координаты точки С0 связаны
с координатами точки Q и компонентами вектора скорости v± выражениями:
(Ю)
Ь. ВЕКТОРНЫЙ ПОТЕНЦИАЛ. ЛАГРАНЖИАН И ГАМИЛЬТОНИАН
Чтобы описать магнитное поле В(г), можно использовать векторный потенциал
А(г), связанный с В(г) выражением:
A(r)=VxA(r). A1)
Например, если поле В однородное, можно записать:
А(г)= --гхВ. A2)
*0
Уо
= х-
= у-
1
«с
1
со.
Л
■*х
903

Глава VI
Впрочем, известно, что при заданной функции В(г) условие A1) определяет А(г)
неоднозначно: к А(г) можно добавить градиент произвольной функции от г , и при этом
В(г) не изменится*.
Можно показать (см. приложение III, § 4-Ь), что функция Лагранжа ЗГ(г, v) частицы
определяется выражением:
X(r,v) = -Vv2+<?v-A(r). A3)
Тогда импульс р, то есть момент, сопряженный положению г , связан с v и А(г)
формулой:
р= Vv5T(r,v) = |nv + ^A(r) A4)
и функция Гамильтона Ж(г, р) равна:
ЛГ(г,р)=^[р-4А(г)]2. A5)
2|i
Для последующего изложения удобно ввести:
ЛГ(г,р)= ЛГ±(г,р) + ЛГ^(г,р), A6)
где
•#± (г> Р) = ^ {[р* - чК (г)]2 + [рУ - чАу (г)]2};
Ж„(г,р)=±-[Р1-дАг(г)}2. A7)
ЗАМЕЧАНИЕ
Соотношение A4) показывает, что в противоположность тому, что имело
место для частицы в поле скалярного потенциала, импульс р здесь не равен
количеству движения jiv . Сравнивая A4) и A5), можно увидеть, что функция
Гамильтона Ж равна кинетической энергии jliv2 /2 частицы, так как сила Лапласа A)
всегда перпендикулярна к скорости v и не дает вклада в работу в ходе движения.
Аналогично, следует иметь в виду, что угловой момент:
* Например, для однородного поля, параллельного оси Oz, можно было бы вместо вектора
А (г), определенного формулой A2), выбрать вектор с компонентами АХ=0У Ау = хВ,
А=0.
904

Общие свойства угловых моментов в квантовой механике
# = гхр A8)
отличается от момента количества движения:
Х = гху,\. A9)
с. КОНСТАНТЫ ДВИЖЕНИЯ В ОДНОРОДНОМ ПОЛЕ
Рассмотрим частный случай, когда поле В однородно. Характеристики движения частицы
(§ 1-а) требуют, чтобы Ж± и Ж„ , определенные формулами A7), были бы константами движения*.
Если подставить A4) в A0), получим:
Уо = У + -^-[р,-ЯАЛг)]- B0)
Отсюда следует, что радиус цилиндра, по которому проходит траектория частицы, удовлетворяет
равенству:
G2 =(х-х0J+(У~УоJ =
V И™ с ) ^ - j р,шс
B1)
И {U-^H2+U-^^r)]2}=^.
Таким образом, О2 пропорционален гамильтониану Ж± .
Аналогично, если обозначить символом 6 момент количества движения JIV относительно
центра окружности С0:
0 = CoMx|!v, B2)
то компонента 0г этого момента с учетом равенства B0) имеет вид:
B3)
Таким образом, 8. является константой движения, как и можно было ожидать. Напротив,
компонента Xz момента |XV относительно точки О в общем случае не остается постоянной, так как
Xz=Qz+\i[xQvy(t)-yoVx(t)]. B4)
Итак, согласно D) величина Xz изменяется синусоидально во времени.
* Такой вывод следует из того, что согласно формулам A4) и A7) Ж1 и Ж'и соответственно
равны кинетической и потенциальной энергии движения, перпендикулярного и параллельного оси Oz .
905

Глава VI
Рассмотрим, наконец, проекцию (£z углового момента £ на ось Oz :
К = ХРу - УРх • ' B5)
Согласно формуле A4) она имеет вид:
<P.Z = x[[ivy+qAy(r)]-y[[ivx+qAx(r)]. B6)
Таким образом, это выражение явно зависит от выбранной калибровки, то есть от векторного
потенциала А , принятого для описания магнитного поля. В большинстве случаев (£г не остается
константой движения. Однако, если выбрать калибровку вида A2), то с помощью выражения D)
можно получить:
Vz=^(xl+yl-02). B7)
Таким образом, У\ является константой движения.
У равенства B7) нет простой физической интерпретации, так как оно справедливо только при
определенной калибровке. Тем не менее, оно будет полезно в последующих параграфах при
рассмотрении квантового решения задачи.
2. Общие квантовые свойства частицы в магнитном поле
а. КВАНТОВАНИЕ. ГАМИЛЬТОНИАН
Рассмотрим частицу в произвольном магнитном поле, описываемом векторным
потенциалом A(jc,)\z). В квантовой механике векторный потенциал становится
оператором, зависящим от трех наблюдаемых X, К, Z . Гамильтониан частицы Н можно
получить с помощью равенства A5):
tf = -i-[P-<7A(X,r,Z)f. B8)
2jli
Согласно формуле A4) оператор V скорости частицы имеет вид:
V=-[P-<?A(X,r,Z)], B9)
что позволяет записать Н в виде:
Н = ^\2. C0)
906

Общие свойства угловых моментов в квантовой механике
Ь. СООТНОШЕНИЯ КОММУТАЦИИ
Наблюдаемые R и Р удовлетворяют каноническим соотношениям коммутации:
[X,Px] = [y,Pv] = [Z,Pj = i», C1)
все остальные коммутаторы между компонентами R и Р равны нулю. Две компоненты
оператора Р коммутируют между собой, и, напротив, из формулы B9) видно, что для
вектора V подобное утверждение не справедливо. Например:
[v*-V,]= -jj \PX, A,(R)] + [a,(R), Py]}. C2)
Это выражение вычисляется без труда в соответствии с правилами, изложенными в
дополнении Вп [см. формулу D8)]:
г I iqfi ГЭЛ дАх} iqb
1у-Мв^{аГ-э^|-^A1)- C3"а)
Аналогично можно показать, что
K.vJ = ^r*,(R); (зз-b)
k^,] = TTBy(R). C3-c)
М-
В соотношения коммутации оператора скорости явно входит магнитное поле.
Однако, поскольку A(R) коммутирует с операторами X, У, Z , равенство B9)
приводит к
[Х,УХ]Л[Х,Р,] = ± C4-а)
и также к
[Y,V,] = [Z.Vt] = £ C4-b)
(другие коммутаторы между компонентами оператора R и любой компонентой V
равны нулю). Из этих соотношений можно вывести (см. дополнение Сш), что
АХ-АУ>— C5)
х 2ц
(аналогичные неравенства справедливы для компонент вдоль осей Оу и Oz). Таким
образом, физические следствия соотношений неопределенностей Гейзенберга не
изменяются в присутствии магнитного поля.
907

Глава VI
Вычислим в заключение соотношения коммутации между компонентами оператора:
Л= \iR х V , C6)
связанного с моментом количества движения относительно точки О *. Получим:
[Ax,Ay] = li2[YVz-ZVy,ZVx-XVz} =
= H2K{[y:,z]VA.+z[K,Vv]}-n2Z2[vv)yv]+n2x{z[Kv,yJ + [z,Vz]l/v}, C7
то есть с учетом формул C3) и C4):
[лх> Л J = /ft{-|il% +qYZBy +qZ2Bz +qXZBx+\LXVy). C8)
Тогда:
[Лх, Лу] = /ft{Л. + qZR -B(R)} C9)
(другие коммутаторы могут быть получены путем круговой перестановки индексов х,
у, z). Если поле В отлично от нуля, соотношения коммутации для компонент
оператора Л совершенно отличаются от соотношений для оператора L . Таким образом,
оператор Л априори не обладает теми свойствами, которые мы получили в главе VI.
с. ФИЗИЧЕСКИЕ СЛЕДСТВИЯ
а. Эволюция (R)
Изменение среднего положения частицы во времени определяется теоремой Эрен-
феста [см. формулу C0)]:
*£<*> = ([*. 4'
R,iiv2
D0)
Теперь нетрудно интерпретировать выражения C4): если подставить их в формулу D0),
получим:
|(R) = (V). D1)
Как и в случае отсутствия магнитного поля, средняя скорость равна производной от
среднего значения положения по времени, то есть соотношение D1) является квантовым
аналогом формулы B).
* Конечно, компоненты углового момента L = R X Р всегда удовлетворяют обычным
соотношениям коммутации.
908

Общие свойства угловых моментов в квантовой механике
C. Эволюция (V) . Закон Лапласа
Вычислим производную от среднего значения (V) скорости по времени:
**H
v, -!V-
2
D2)
Поскольку согласно равенствам C3) коммутатор определяется как:
= уу К- VJ + h'v*\v> +v< fc'VJ + \УгУ,]чг =
= ^ {-Vy Bz(R) - Bz (R) V, + Vz By (R) + Д, (R)Vz}, D3)
нетрудно видеть, что
^(V) = (F(R,V)), D4)
где оператор F(R,V) равен:
F(R,V) = ^-{VxB(R)-B(R)xV}. D5)
Два последних равенства являются простыми аналогами классических выражений A) и C);
для оператора F(R,V) получено симметризованное выражение (см. § В-5 главы III),
так как R и V не коммутируют. Таким образом, соотношения коммутации C3)
соответствуют закону Лапласа.
^.Эволюция (Л)
Вычислим теперь:
/й|-(Л) = ([Л,Я]). D6)
Для этого найдем, например, коммутатор:
[XV, -VJ, Н] = X[vy, Н] + [X, H]Vy - Y[VX, H] - [Y, H]VX =
= £ (XFy -YFx) + ih(v,V, -VyVx). D7)
Поскольку операторы X и Vv, а также Y и Vx коммутируют, то в результате:
909

Глава VI
vy x -vxy, н] = уу[х, н] + [уу, н]х -vx[y, h]-[vx, h]y =
= ^(FyX-F>Y)+in(VyV>-V*Vy)- («)
Вычислив полусумму этих двух выражений, найдем:
±(AZ) = 1(XF,-YFX-FXY+F,X). D9)
Аналогичные вычисления дадут производные по времени от (ЛЛ) и (Л \ , и в
результате получим:
—(A)=-(RxF(R,V)-F(R,V)xR). E0)
Классический аналог этого соотношения имеет вид:
-^X = rxf(r,v) E1)
dt
и выражает хорошо известную теорему: производная по времени от момента количества
движения относительно фиксированной точки О равна моменту силы, действующей на
частицу, относительно той же точки.
3. Случай однородного магнитного поля
Если магнитное поле однородное, то приведенные выше вычисления можно
продолжить. Выберем направление оси Oz вдоль направления вектора В . Тогда
соотношения коммутации C3) с учетом определения E) принимают вид:
\Vx,Vy] = -i^-- E2-а)
К^] = КЛ] = 0. E2-Ь)
ЗАМЕЧАНИЕ
Применив результаты дополнения Сщ к операторам Vx и Vy, можно
заключить из формулы E2-а), что их среднеквадратичные отклонения удовлетворяют
неравенству:
910

Общие свойства угловых моментов в квантовой механике
где
Й CD J
Д^-ДУу>-^1. E3)
Таким образом, компоненты скорости V± являются несовместимыми физическими
величинами.
а. СОБСТВЕННЫЕ ЗНАЧЕНИЯ ГАМИЛЬТОНИАНА
По аналогии с формулой A6) гамильтониан Я можно записать в виде:
H = HL+HV E4)
«i=f (V?+V,2); E5-a)
Я„ = - К2. E5-Ь)
II 2 г
Согласно формуле E2-Ь):
[Я±>Я,] = 0. E6)
Теперь мы можем попытаться найти базис собственных векторов, общий для операторов
Н± (с собственными значениями EL) и Щ (с собственными значениями Е\). Они
будут автоматически собственными значениями оператора Я с собственными значениями:
E = EL+Ey E7)
а. Собственные значения оператора Я.
Собственные векторы оператора V. являются также собственными векторами
оператора Я|. Поскольку Z и Vz являются эрмитовыми операторами, удовлетворяющими
соотношению:
[Z,VZ] = -, E8)
ц
то к ним можно применить результаты дополнения Ец. В частности, спектр оператора Vz
содержит все вещественные числа.
Тогда собственные значения гамильтониана #( имеют вид:
£, =-v.2, E9)
1 2 *
911

Глава VI
где v, — произвольная вещественная постоянная, и спектр гамильтониана #j является
непрерывным: энергия £, может принимать любое положительное или нулевое значение.
Физическая интерпретация этого результата очевидна: оператор Щ описывает
кинетическую энергию свободной частицы, движущейся вдоль оси Oz (как и в
классической механике, § 1-а).
^.Собственные значения Н±
Допустим, например, что рассматриваемая частица несет отрицательный заряд q, и
ее циклотронная частота сос положительна [формула E)].
Обозначим:
F0)
Тогда выражение E2-а) можно
и оператор
и,
примет вид:
переписать в форме:
[&s] = /,
F1)
Я±=-^(B2+52), F2)
то есть тот же вид, что и гамильтониан одномерного гармонического осциллятора [см.
формулу (В-4) главы V]. Таким образом, операторы Q и S , удовлетворяющие
соотношению коммутации F1), играют роль операторов положения X и импульса Р такого
осциллятора.
Все рассуждения, выполненные в § В-2 главы V для операторов X и Р, можно
повторить здесь для операторов Q и S . Например, легко показать, что если кет |ф±)
является собственным вектором Н±, то
я±|ф±) = я±|ф±) F3)
и кет-векторы:
\<?'1) = j^(Q + iS)\<pL); F4-а)
\<Pl) = -^(Q-iS)\<p±) F4-b)
912

Общие свойства угловых моментов в квантовой механике
также являются собственными векторами оператора Я± :
Я±|ф1> = (Я±-Ла>с)|ф'±); F5-а)
Я1|ф1/) = (Я1+Ло)г)|Ф:). F5-Ь)
Таким образом, возможные значения энергии Е± определяются формулой:
Е±= /1 + - йсос, F6)
где п — целое положительное число или нуль.
у. Собственные значения Н
В соответствии с полученными ранее результатами собственные значения полного
гамильтониана Н имеют вид:
П 1 2
Й(Ос+-~цуг2. F7)
«л,
^Несоответствующие уровни энергии называются уровнями Ландау.
Для заданного значения v, эффективно реализуются все возможные значения п
(положительные целые или нуль). Действительно, путем многократного последовательного
действия операторов —j=(Q±iS) на собственный вектор гамильтониана Н с собственным
л/2
значением Е(п, vz) можно получить [см. формулу F5)] состояние с энергией Е(п\ v,), где
п может быть любым целым числом, но при этом скорость vz не изменяется, так как
операторы Q и S коммутируют с #|. Итак, видно, что энергия движения вдоль оси Oz
не квантуется в отличие от энергии проекции движения на плоскость хОу .
ЗАМЕЧАНИЕ
В § В-3 главы V мы показали, что уровни энергии одномерного
гармонического осциллятора в пространстве $х Ех не вырождены. Здесь же ситуация иная, так
как изучаемая частица движется в трехмерном пространстве. Поскольку
оператор уничтожения кванта Шс, собственные векторы гамильтониана Н19
соответствующие п = 0, являются решениями уравнения:

Глава VI
(Vv+/Vv)|cp) = 0. F8)
С одной стороны, эти векторы могут быть собственными векторами
гамильтониана #| с произвольными (положительными) собственными значениями, а с другой
стороны, даже для фиксированного значения vz уравнение F8) является
уравнением в частных производных по х и по у, допускающим бесконечное множество
решений. Таким образом, энергии Е(п = 0, vz) бесконечно вырождены. Используя
оператор рождения кванта, нетрудно показать, что это замечание справедливо для
всех уровней E(n,vz) с произвольным неотрицательным целым значением п.
Ь. АНАЛИЗ НАБЛЮДАЕМЫХ ДЛЯ ЧАСТНОГО СЛУЧАЯ КАЛИБРОВКИ
Чтобы конкретизировать полученные выше результаты, найдем стационарные
состояния изучаемой системы, так как это позволит проанализировать их физические
свойства. Для этого нужно выбрать калибровочное соотношение. Мы возьмем
соотношение, приведенное в формуле A2). Тогда компоненты скорости примут вид:
V,
v,
Уг =
2
со
2
Р.
Y;
X;
F9)
аТамильтонианы HL и Щ. Связь с двумерным гармоническим осциллятором
Подставим F9) в E5) и получим:
Рх + Pv (О ЦОJ •> -у
Я, = — ^ + ^L,+-^-(X2 + r2); G0-а)
1 2ц 2 * 8
#, = -£-, G0-Ь)
где L, — проекция углового момента L = R х Р на ось Oz .
В представлении {|г)} оператор Ну действует только на переменную г, тогда как
Н± действует только на переменные х и у. Таким образом, можно определить базис
собственных векторов гамильтониана Я, решив сначала в пространстве % уравнение
914

Общие свойства угловых моментов в квантовой механике
на собственные значения #|, а затем в пространстве ^ — уравнение на собственные
значения HL, после чего найти тензорное произведение полученных векторов.
Действительно, уравнение на собственные значения Щ дает волновые функции:
ф(г)= * ^'» G1)
и
е'=! <72)
[снова получаем выражение E9)]. Поэтому сосредоточим внимание на решении уравнения
на собственные значения оператора Н± в пространстве ^ . Соответствующие волновые
функции будут зависеть не от z, а от х и у.
Сравнив G0-а) с выражением A2-а) дополнения DVi, нетрудно заметить, что
оператор Н± выражается через гамильтониан Нху двумерного гармонического осциллятора:
HL=Hxy+^Lz, G3)
если в качестве константы со , входящей в Нху, подставить значение:
@ = ^-. G4)
2
В дополнении DVi мы видели, что Н^ и Lz образуют полный набор коммутирующих
операторов в пространстве txy, и построили базис собственных векторов Ьс„^„ ),
общих для этих двух наблюдаемых [формула D7) дополнения DVi]. Эти векторы являются
также собственными векторами оператора HL, вследствие чего изложенные там
результаты дают немедленно решения уравнения на собственные значения оператора Н± .
ЗАМЕЧАНИЯ
(i) В § 3-а мы видели, что оператор Я± может быть представлен в такой же форме,
что и гамильтониан одномерного гармонического осциллятора. Здесь же мы
убедились, что путем подходящего выбора калибровочного соотношения этот же
оператор оказывается связанным простым выражением с гамильтонианом Н^
двумерного гармонического осциллятора. Оба вывода не противоречат друг другу:
просто речь идет о двух различных разложениях одного и того же гамильтониана,
приводящих, конечно, к одинаковым физическим результатам.
58*
915

Глава VI
(ii) He следует упускать из виду, что гамильтониан Ях связан с физической задачей,
совершенно иной, чем задача о двумерном осцилляторе. Заряженная частица
взаимодействует с однородным магнитным полем, определяемым векторным
потенциалом, а не скалярным гармоническим потенциалом (который в частном
случае может описывать неоднородное электрическое поле). Оказывается, что при
выбранном соотношении калибровки действие магнитного поля напоминает
действие фиктивного гармонического скалярного потенциала.
Р. Выражение наблюдаемых через операторы рождения и уничтожения
циркулярно поляризованных квантов
Выразим сначала наблюдаемые, описывающие величины, связанные с частицей,
через операторы ad и ag, определенные формулами D0), и сопряженные им операторы
ad и а* (в дальнейшем мы будем использовать также операторы Nd = adad и
Вставим выражения D6) дополнения DVi в формулу G3):
и,
и энергия состояния Ьс^,, ) равна:
V+i|/KQ, G5)
£i=K + 2j
Й©с. G6)
Этот результат совпадает с выражением F6). Кроме того, поскольку Е± не зависит от
ng, ясно, что все собственные значения оператора Н± бесконечно вырождены.
Опираясь на выражения B3) и D0) дополнения DVi, можно доказать, что
Y = ^(ad-a;-ag+a+g), G7)
где с учетом формулы G4) величина C определена следующим образом:
2й
Аналогично
0 = ^. G8)
916

Общие свойства угловых моментов в квантовой механике
p>=Y («„+«; -«,-«;>• G9)
Эти равенства можно подставить в F9) и получить:
Поскольку операторы <яг/ и я J" не коммутируют с оператором Nd, используя
выражение G5), можно заметить, что, как и в классической механике, компоненты Vx и Vy не
являются константами движения. Кроме того, из соотношений коммутации операторов
ad и ad можно сразу же получить формулу E2-а).
Представляет интерес рассмотреть также операторы, соответствующие в квантовой
механике переменным, введенным в классической механике: координатам (*0, у0)
центра С0 классической траектории, компонентам (х\ у') вектора C0Q и т.д. Как и ранее,
мы будем обозначать каждый из операторов заглавной буквой того обозначения,
которое используется для соответствующей классической величины. По аналогии с
формулой A0) положим:
(81-а)
(81-Ь)
Операторы ag и а* коммутируют с оператором Nd, откуда следует, что Х0 и У0
являются константами движения. Кроме того, из формул (81) следует, что
и, следовательно, Х0 и YQ являются несовместимыми физическими величинами, а их
среднеквадратичные отклонения связаны неравенством:
ЛХ0-ДК0>-£-. (83)
*0
Уо
= х-
= У +
1
1
■v,
V,"
=^(fl<
■i(e--
+<);
-"„>•
Определим также:
917

Глава VI
2C
Х' = Х-Х0=— (ad+a;,);
Y' = Y-Y0=j^(ad-a+d). (84)
Сразу же видно, что X' и К' , как и в классической механике, не являются константами
движения. Впрочем, эти операторы просто пропорциональны операторам компонент
скоростей:
v,=-fl)fi";
Vy=(dcX', (85)
как и соответствующие классические переменные (9). Согласно выражению E3) из
равенств (85) сразу же следует:
ДЛ"-ЛГ>——. (86)
2\иае
С другой стороны, пусть £ обозначает оператор, соответствующий а (квадрат радиуса
классической траектории):
Z2=(X-X0J+(Y-Y0J. (87)
Согласно формуле (81) имеем:
i2 =
м^2
(V'+V2)=^yHl. (88)
Таким образом, Е2 является константой движения, как и а2 в классической механике.
Наконец, оператор, соответствующий моменту количества движения |iv относительно точки О,
равен:
et=\i[(X-X0)V,-(Y-Y0)Vx\, (89)
и формулы (81) указывают, что
ez=—HL. (90)
«с
как и в формуле B3), то есть 0, — константа движения. Напротив, оператор Л,, то есть
проекция вектора JLlR X V на ось Oz , выражается формулой:
Az=—H±+h(adag+a*a;) (91)
и не коммутирует с оператором Н± .
918

Общие свойства угловых моментов в квантовой механике
с. АНАЛИЗ СТАЦИОНАРНЫХ СОСТОЯНИЙ
Выше мы отмечали, что все собственные значения гамильтониана Н± бесконечно
вырождены в пространстве $ . Таким образом, для каждого неотрицательного целого числа п
существует подпространство (^° пространства ^ с бесконечной кратностью вырождения, все кет-
векторы которого являются собственными векторами оператора Н± с одним и тем же
собственным значением (п +1/ 2)ЙС0С. В этом параграфе мы исследуем различные базисы, которые
можно выбрать в каждом из этих подпространств. Для начала укажем на общие свойства
стационарных состояний, справедливые для любого базиса собственных состояний оператора Н± .
ОС. Общие свойства
Равенства (88) и (90) показывают, что любое стационарное состояние обязательно должно
быть собственным вектором операторов Е2 и 0г . В таком состоянии соответствующие им
физические величины всегда полностью определены и равны:
для I2 => Bл +1) ;
для ez=>Bn + l)h. (92)
Значения I2 и 0г пропорциональны энергии, что хорошо согласуется с классическим
описанием движения (см. §1).
Из формул (80) и (84) вытекает, что операторы X', У , Vx и Vv не имеют матричных
элементов внутри заданного подпространства ^), и в стационарном состоянии:
(Х') = (Г) = 0. (93)
Однако, поскольку Vx и Vy (а следовательно, и X', У) не являются константами движения,
соответствующие физические величины не могут иметь точно определенных значений в
стационарном состоянии. Действительно, используя формулы (80), (84) и свойства одномерного
гармонического осциллятора [выражение (D-5) главы V], можно показать, что
йУг = СО АГ :
г
п + ~
П Йод
V-
AK,=a),AX' = JU + ^
ЙС0„
И
(94)
919

Глава VI
что полностью соответствует неравенству E3). Кроме того, мы видим, что единственными
стационарными состояниями, в которых произведение AV^ • AVV (или АХ'АУ) принимает
минимальное значение, являются основные состояния, в которых /2 = 0.
ЗАМЕЧАНИЕ
Основные состояния можно найти как решения уравнения:
а,|ф) = 0, (95-е)
то есть с учетом формулы (80):
(v,+iV,)|q>) = 0. (95-b)
и мы снова получаем выражение F8).
C. Состояния \Хп„.пя)
Как мы видели в дополнении DVi, для построения базиса собственных векторов, общих для
операторов Н± и L,, можно использовать то обстоятельство, что они образуют полный набор
коммутирующих операторов. Этот базис состоит из векторов \%п п ), так как согласно
выражению G5) и формуле D6) дополнения DVi:
»± |x„.„f) = (л, +!]«Юс |%„„.П1); (96-а)
^|х,,,.„,) = (",/-«*)л|х„,.„в)- (96-Ь)
Подпространство #^и), определяемое при выборе конкретного неотрицательного целого
числа п , порождается ансамблем векторов \%п п ), в которых nd =n\ собственные значения
оператора Lz, соответствующие этим векторам, имеют форму тЬ , и для фиксированного значения п
число т может изменяться от ~©о до п (например, все основные состояния соответствуют
отрицательным значениям т, и это связано со сделанным ранее предположением о том, что
@С>0.
Волновые функции, соответствующие состояниям \%п п ), были вычислены в дополнении
Dvi (§3-d).
Отметим, что состояния \%п п ) являются собственными состояниями оператора Lz, но не
920

Общие свойства угловых моментов в квантовой механике
оператора Лг, соответствующего моменту количества движения. Это немедленно следует из
формулы (91).
В состоянии %„ „ ) средние значения \Х0/ и {Y0/ согласно формуле (81) равны нулю.
Однако ни Х0, ни Y0 не соответствуют строго определенным физическим величинам.
Действительно, если воспользоваться свойствами одномерного гармонического осциллятора, нетрудно
показать, что в состоянии \Хп ,п )'•
AXn= In +
V0 1П "g
П п
2)№с
^=^4]^' (97)
Минимальное значение произведения AX0-AY0 достигается в состояниях \%п п =0), то есть в
таких состояниях каждого энергетического уровня EL = (п +1 / 2) Н(Ос, в которых L. принимает
свое максимальное значение rih [см. формулу (96)].
Определим оператор Г2 выражением:
Г? = Х02+К02. (98)
Он соответствует квадрату расстояния от центра траектории движения до начала координат. Из
выражения (81) находим:
Г2 = — (аX +яV) = —BNg + 1). (99)
Ц@С * * * * |и1@с *
Итак, состояние \%п ,„ ) является собственным состоянием оператора Г2 с собственным значе-
h
нием Bи +1) . Тот факт, что это значение никогда не может обратиться в нуль, связан с
некоммутативностью операторов Х0 и Y0.
ЗАМЕЧАНИЕ
Согласно формулам G5) и (99) оператор L. равен:
Lz=h(Nd-Ng) = h
то есть с учетом (88):
/id). 2 2п 2
A00)
921

Глава VI
Lz=^(I.2-r2) = ^-(r2-Z2). A01)
Тем самым мы снова получаем эквивалент классического соотношения B7).
у. Другие типы стационарных состояний
Любая линейная комбинация векторов \Хп ,п )» соответствующих одному и тому же значению
nd , является собственным состоянием оператора Н± и, следовательно, обладает свойствами,
сформулированными в § 3-с-а. Выбрав соответствующим образом коэффициенты линейной
комбинации, можно получить стационарные состояния, обладающие и другими интересными свойствами.
Так, например, мы знаем (§ 3-с-C), что Х0 и Y0 являются константами движения. Однако,
поскольку эти операторы не коммутируют друг с другом, у них нет общих собственных
состояний. В квантовой механике это означает, что невозможно измерить одновременно две координаты
точки С().
Чтобы построить собственные состояния, общие для операторов Н± и Х0, можно использовать
свойства одномерного гармонического осциллятора. Действительно, формула (81-а) показывает,
что выражение для оператора Х0 с точностью до постоянного множителя совпадает с выражением
для оператора Xg одномерного осциллятора, оператор уничтожения которого был бы равен ag :
X0=-^Xg. A02)
Поскольку волновые функции tyk(x), соответствующие стационарным состояниям |ф^
одномерного гармонического осциллятора (см. § 2-Ь дополнения Bv), известны, то собственные векторы | х)
оператора положения частицы записываются в форме линейных комбинаций состояний |ф*) :
|*)=2|Ф*)(Ф*|*)=£ф**(*)|Ф*>- <103>
Чтобы получить собственные состояния, общие для операторов HL и Х0, достаточно применить
этот результат к состояниям \%п п =к). Кет:
кп.дь)= ЁФ1 (PV2^o)|x^.„. „,.*) A04)
является собственным вектором операторов HL и Х0 с собственными значениями
(п + \/2)Шс и jc0.
922

Общие свойства угловых моментов в квантовой механике
Аналогично можно найти собственные состояния \Т\п ), общие для операторов Н± и Y0.
Равенство (81-Ь) утверждает, что оператор Y0 пропорционален оператору импульса Р только
что использованного фиктивного одномерного осциллятора:
У»=ЩГ, О05)
Таким образом [см. формулу B0) дополнения Dv]:
k,v„)= Ё'*Ф1(Ра/2 Уо)|х „ Л. A06)
Мы только что построили состояния, в которых или Х0, или Y0 точно определены. Можно
также найти стационарные состояния, в которых произведение АХ0 • AY0 достигает минимально
возможного значения, определенного формулой (83). В дополнении Gv мы рассматривали
состояния одномерного гармонического осциллятора, в которых произведение АХ • АР минимально.
Ими являются квазиклассические состояния, определяемые выражением:
|а)=Ё^(а)|фА), A07)
где
с4(а) = -^е>14 A08)
В этих состояниях:
АХ=АР = -рг. A09)
Отсюда следует, что в интересующем нас случае состояние:
|в..ав)=Ё^(ао)|х^...,...*) (И°)
AX0 = AY0 = —. (Ill)
дает для величин Х0 и Ya среднеквадратичные отклонения
_1
2Р
При этом произведение АХ0 • AY0 минимально.
ЗАМЕЧАНИЕ
Поскольку магнитное поле однородно, рассматриваемая физическая задача
инвариантна относительно трансляции. Во всем предшествовавшем изложении эта симметрия
маскировалась частной формой A2) соотношения калибровки, выделяющей начало координат О
923

ва VI
из других точек пространства. Поэтому ни гамильтониан Н , ни его собственные состояния
не инвариантны относительно трансляции. Однако мы знаем (см. дополнение Нш), что
физические предсказания квантовой механики инвариантны относительно калибровочных
соотношений. Они должны оставаться теми же, как бы мы ни выделяли с помощью
калибровки ту или иную точку пространства. Таким образом, симметрия относительно трансляции
должна снова появиться при изучении физических свойств заданного состояния.
Чтобы продемонстрировать это более строго, допустим, что в заданный момент
времени состояние частицы характеризовалось в калибровке A2) кет-вектором |\}/), которому
соответствовала волновая функция (г|\|/) = \|/(г). Произведем теперь заранее известную
операцию трансляции J , определенную вектором а , и рассмотрим кет 1|/г) , связанный
с исходным соотношением:
|l|/r) = e~*Pa|l|/), A12)
с которым связана волновая функция:
\|/7.(г) = (г|\|/7-) = \|/(г-а). (ИЗ)
Аналогичную операцию трансляции можно применить к векторному потенциалу, который
примет вид:
Аг(г) = А(г-а) = —(г-а)хВ. A14)
Потенциал А7(г), конечно, описывает то же самое магнитное поле, что и А(г) .
Поскольку физические свойства заданного вектора состояния зависят только от самого вектора и
выбранного потенциала А , они также подвержены трансляции J при замене \|/(г) и
А (г) выражениями A13) и A14). Эти равенства можно использовать также для
нахождения плотности вероятности, связанной с вектором \|/г) :
pr(r) = |\Mr)f=|\|/(r-a)|2=p(r-a) A15)
и тока вероятности Jr(r), найденного с векторным потенциалом Аг(г):
-Мг)~К(г)
-V + ^(r-a)xB
/ 2
4/r(r) + компл. conp.V =
= J-Wr-a)
-v4(r-a)xB
/ 2
\|/r(r-a) + компл. conp.l = J(r-a) A16)
[где J(r) — ток вероятности, связанный с волновой функцией \|/(г) в калибровке А(г) ].
Таким образом, кет V|/r> описывает в повой калибровке Аг(г) состояние, физические
924

Общие свойства угловых моментов в квантовой механике
свойства которого могут быть получены путем трансляции J свойств, соответствующих
кет-вектору |\|/} в калибровке А(г) .
Покажем еще, что возможное движение, полученное путем трансляции, также является
возможным движением, чем и закончим доказательство инвариантности задачи
относительно вращения. Для этого рассмотрим уравнение Шредингера в представлении {|г) } в
калибровке А (г):
•* Э / ч J
ifi — V(r,f) = —
dt 2\X
-V-gA(r)
\|/(r,r).
A17)
Заменим в этом уравнении г на г-а . Используя выражения A13) и A14), нетрудно
получить:
ч- д / ч 1
Л — \|/г(г,г) =
dt
2\i\_i
-V-qAT(r)
\|/г(г,0-
A18)
Оператор, фигурирующий в правой части равенства A18), является гамильтонианом в
калибровке АТ(г). Итак, если lj/(r, /) описывает возможное движение системы в
калибровке А(г), то \\fT(r,t) описывает в эквивалентной калибровке Аг(г) другое возможное
движение, которое, как показано выше, получено в результате преобразования трансляции,
выполненного над первым движением. В частности, если
\|/(г,г)=Ф(г)е-'й"'
является стационарным состоянием в калибровке А (г), то
Ч/г(г,0=Фг(г)<Г,£'м
является другим стационарным состоянием, имеющим ту же энергию, в калибровке А7(г).
Если желательно использовать калибровку A2) после того, как выполнена трансляция J
физического состояния системы, нужно описывать транслированное состояние
математическим кет-вектором |V|/7), отличающимся от \\\fT/ . Согласно § З-Ь-а дополнения Нш
кет \у'Т) получается из вектора |\|/г) с помощью унитарного преобразования:
Ю = Тг\Чт)-
где оператор Т определяется формулой:
Т =eh
ю(Ю
A19)
A20)
a %(R) — функция, характеризующая выполняемое изменение калибровки. В данном
случае потенциал после изменения калибровки запишется в виде:
925

Глава VI
A(r) = —rxB = Ar(r)--axB, A21)
так что
Х(г) = -—г-(ахВ). A22)
Подставив A12), A20) и A22) в A19), получим окончательно:
|\|/'г) = £/(а)|\|/), A23)
где
,,, ч -/^7R(axB) -7Р а
U(a) = e 2Л е л . A24)
Таким образом, если оставаться в калибровке А (г), то оператор трансляции £/(а) должен
быть определен формулой A24).
В формулу A24) входят компоненты операторов R и Р вдоль двух
перпендикулярных осей, коммутирующие друг с другом, в результате чего можно записать:
1/(а) = «-'*"-,",,,-*"\ A25)
Если вектор а лежит в плоскости хОу , то несложные вычисления с помощью формул A0)
и F9) дают:
WT, ч 17(вхК0)-В
У(а) = еА , A26)
где
R0 = X0et+roey, A27)
то есть операторы Х0 и Y0 (координаты центра круга) связаны с инфинитезимальными
трансляциями вдоль осей Оу и Ох соответственно.
d. ЭВОЛЮЦИЯ ВО ВРЕМЕНИ
а. Средние значения наблюдаемых
Мы уже встречали ряд физических величин, остающихся константами движения:
Х0, Y0, ©z, Z2. Каким бы ни было состояние системы, их средние значения не зависят
от времени.
Исследуем эволюцию во времени средних значений (х), (y) , (Vx), (Vy) и (X'), (Y').
Из выражений, приведенных в § 3-Ь-р, сразу же следует, что соответствующие операторы
926

Общие свойства угловых моментов в квантовой механике
ДЛЯ
имеют отличные от нуля матричные элементы только между состояниями \%п п ),
которых значения квантовых чисел nd отличаются на ±1 или 0. Таким образом,
эволюция этих средних значений во времени происходит так, что в ней участвует только одна
частота Бора, равная здесь циклотронной частоте шс / 2я, определенной формулой E).
Этот результат полностью аналогичен выводам классической теории.
р. Квазиклассические состояния
Допустим, что в момент времени t = 0 состояние частицы описывается вектором:
к±@))=К'а*)' A28)
где кет 06^,0^ ) определен выражением G0) дополнения DVj. Поскольку в выражение G5) для
HL входит Nd , а не Ng ,в момент времени t получим вектор состояния |\|/1@/ > если просто
I /.\\ -йо,//2 I -fto-f \
|\М0)= е \ade ,ag}
[см. выражение (92) дополнения Gv].
Положим:
ссНа.к"";
A29)
««= а««
Тогда равенства (80), (81) и (84) дают:
(хо) = ^(а,+а;) = о1с^ф8
ос.
W^K"»^ [~у *йф,;
A30)
A31)
1лг/\, ч * • -1A),./ * /0)-/х V^d\ , , ч
' ' 26 "е  ^=QC0S^ct-4>j)\
фр) = —(аЛе -ade ) = !—ISOT(a>f f-<p,)
A32)
927

Глава VI
(^) = -^а>,«'пам-Ф,/);
W(') = ^coc«"(G>cf-<l\,).
A33)
Кроме того, из свойств состояний |а) следует, что
(tfx)=fco,(kf+^
<*2>=fH4
A34)
Все эти результаты исключительно близки к результатам классической механики [см. формулу
D)]; видно, что ОС J связан с радиусом G классической траектории, а ф^ — с начальной фазой
ф0, тогда как ОС связан с расстоянием ОС0,ифаза ф соответствует полярному углу вектора
ос0
С другой стороны, свойства состояний |ос) могут быть использованы, чтобы показать, что
_1_
2Р;
0),
АХ0 = АУ0=АХ' = АГ = -
AV =AV =■
2C
A35-а)
A35-Ь)
(при этом произведения АХ0 • А^}, АХ' • АУ и AVx • AVv принимают минимальные значения) и
АН± =Шс\а(,\;
А0, = 2/i|ocJ;
AS -т#Ы
A36)
Что касается отклонений АХ и А У, то их можно найти, используя выражение:
|vM0) =
-но ,л
а.е +ос
а. =■
V?
-/0), t
« а =La"e ~1<хх
V2
A37)
928

Общие свойства угловых моментов в квантовой механике
где кет Otv, 0CV) определен соотношением F6) приложения DV|. Тогда:
Г" 1
ЛХ=АК =
№с (Зл/2
A38)
Величины APV и АРу могут быть получены аналогично.
Если выполнены условия:
Kl»i, K|»i,
A39)
то различные физические величины (положение, скорость, энергия и т.д.) точно определены, и
состояния A29) являются «квазиклассическими» состояниями заряженной частицы в однородном
магнитном поле.
ЗАМЕЧАНИЕ
Если а^ = 0, то
(Я1) = -Л©с;
АЯ± =0.
Таким образом, состояния:
|а,,ау=-/аЛ.)
соответствуют основному уровню энергии.
A40)
A41)
Дополнение Fvi
УПРАЖНЕНИЯ
1. Рассматривается система с угловым моментом j = 1, пространство состояний
которого допускает в качестве базиса ансамбль || +1), | б), | -1)|, состоящий из трех
собственных векторов, общих для операторов J2 (собственное значение 2ft2) и Jz (собственные
значения +/*, 0, - Ь ). Состояние системы описывается вектором:
|v) = <x|+i)+P|o)+y|-i),
где а, Р, у — три заданных комплексных параметра.
59 Квантовая механика
929

Глава VI
a. Вычислить среднее значение (j) углового момента в зависимости от а, C, у .
b. Записать через эти же параметры выражения для трех средних значений (./*),
2. Пусть некоторая физическая система, пространство состояний которой образовано
базисом из четырех собственных векторов \j,mz), общих для операторов J2 и У,
(j = 0 или 1; -j<mz< +j), с собственными значениями j(j + \)fi2 и mz fi, для которых
справедливы равенства:
J±\j,mz) = hJj(j + \)-mz(mz±\)\j,mz±l);
J+\jj) = J-\j*-j) = o.
a. Выразить через векторы |у,mz) собственные состояния, общие для операторов
J2 и Jxi которые мы обозначим символом | j, mx).
b. Рассмотрим систему в нормированном состоянии:
|\1/) = а|у = 1,тг = 1) + Р|; = 1,тг=0) + у|; = 1^г=-1) + 8|7 = 0,тг=0).
(i) Какова вероятность получить значения 2/г2 и Ь при одновременном
измерении J2 и Jх ?
(ii) Вычислить среднее значение Jz, когда система находится в состоянии |\j/),
а также вероятности возможных различных результатов при измерении только этой
наблюдаемой.
(Hi) Аналогичный вопрос относительно наблюдаемой J2 и затем Jx.
(iv) Теперь измеряется У2; какие возможны результаты, каковы их вероятности
и средние значения?
3. Пусть L = R х Р — угловой момент системы в пространстве состояний #г. Доказать
соотношения коммутации:
[L,.,P,.] = //*e,^;
[l/.,p2] = [l/,r2] = [l/,r-p] = o,
где L^Rj, Pj — компоненты операторов L, R,P на оси ортонормированной системы
координат, a Eijk определяется выражениями:
930

Общие свойства угловых моментов в квантовой механике
eijt
= 0, если два (или три) индекса ij, k равны;
= 1, если индексы образуют четную перестановку ху у, z\
= -1» если перестановка нечетная.
4. Вращение многоатомной молекулы
Рассматривается система, состоящая из N различных частиц, векторы положения
которых равны Rj,...,Rw,...,RN, а импульсы— Р,,...,Р/Н,...,Р^ . Положим:
т
где
I = R х Р
т т
я. Показать, что оператор J удовлетворяет соотношениям коммутации, которые
определяют угловой момент. Из них вывести, что если V и V обозначают два
обычных вектора в трехмерном пространстве, то
[j-V,J-V'] = ift(VxV').J.
b. Вычислить коммутаторы оператора J с тремя компонентами оператора Rm,
а также с компонентами оператора Рт . Показать, что
[J,R„,-R„] = 0.
c. Установить, что
[j,JRm] = 0
и вывести соотношение:
[j-rw,j-rh,] = ^(r^xrw).j = ^j.(rw,xrw).
Положим, что
w = 2>MRm;
т
W' = Ia:RM,
т
где коэффициенты ат и а'т известны. Показать, что
[j-W,J-W'] = -/ft(WxW')-J.
59*
931

Глава VI
Заключение: определить разницу, существующую между соотношениями коммутации
компонент оператора J на фиксированную систему координат и на движущуюся
систему координат, связанную с изучаемой системой.
d. Рассматривается молекула, образованная из N неупорядоченных атомов,
относительные расстояния между которыми остаются постоянными (жесткий ротатор).
Назовем символом J сумму угловых моментов атомов относительно центра тяжести
молекулы, расположенного в фиксированной точке О; оси Oxyz образуют
фиксированную ортонормированную систему координат. Три главных оси инерции
рассматриваемой системы обозначим Оа , #Р и Оу и предположим, что эллипсоид инерции
аксиально симметричен при вращении вокруг оси Оу (симметричный ротатор). Энергия
вращения молекулы запишется в виде:
1 Гу2 /2 + /21
2[h 7i J
где Уа,Ур,Уу —проекции оператора J на единичные векторы wa,wp,wy подвижных
осей Оа, ОР и Оу , связанных с молекулой, /( и /х — соответствующие моменты
инерции. Допустим, что
Jl+jl+j* = j]+j2y+jl=i\
(i) Вывести из результатов, полученных в пункте (с), соотношения коммутации
для компонент Уа, Ур, Уу.
(ii) Введем операторы N± = Уа ± Ур. Повторив общие рассуждения главы VI,
показать, что можно найти собственные векторы, общие для операторов J2 и Уу с
собственными значениями У(У + 1)Й2 и #Й,где К- -У,-У + 1,..., У-1, У.
(Hi) Выразить гамильтониан Н ротатора через J2 и У2, вычислить его
собственные значения.
(iv) Показать, что можно найти собственные состояния, общие для операторов
J2, У,, Уу, и обозначить их символом |у, М, К) [соответствующие собственные
значения равны У(У + \)fi2, Mfi, Kfi ]. Показать, что эти состояния являются также
собственными состояниями гамильтониана Н.
(v) Вычислить коммутаторы операторов У± и N± с операторами J2, Уг, Уу. С их
помощью определить действие У± и N± на вектор |У, М, К). Показать, что
собственные значения оператора Н по меньшей мере 2BУ + 1) -кратно вырождены, если КФО,
или B У +1) -кратно вырождены, если К = 0 .
932

Общие свойства угловых моментов в квантовой механике
(vi) Нарисовать энергетическую диаграмму жесткого ротатора (J — целое
число, так как J — сумма орбитальных угловых моментов, см. главу X). Как изменится эта
диаграмма, если /( = 1± (сферический ротатор)?
5. Система, пространство состояний которой #г, описывается волновой функцией:
\|/(х, у, z) = N(x + у + z)e~r2,a2,
где а — заданное вещественное число и N — нормировочный множитель.
a. Измеряются наблюдаемые Lz и L2; найти вероятность получения результатов О
и 2h2. Напомним, что
У°($,ф)=— cos$e
V 4я
b. Можно ли, используя выражение:
^(в.Ф)^/— sinbe**
V 8тс
непосредственно получить вероятности всех возможных результатов измерения L2 и Lz в
системе с волновой функцией \|/(jc, у, z) ?
6. Рассматривается система с угловым моментом / = 1. Базис ее собственных состояний
образован тремя собственными векторами оператора L,: |+1), |o), |-1), имеющими
собственные значения +й, О, -Ь. соответственно:
L±|m) = W2|m±l),
L+|1)=L_|-1) = 0.
Эта система, обладающая квадрупольным электрическим моментом, помещена в
электрическое неоднородное поле, в результате чего ее гамильтониан имеет вид:
0)
"■^(Ч-Ч).
где Lu и Lv — компоненты L на направления Ои и Ov плоскости хОу,
расположенные под углом 45 градусов к осям Ох и Oz ; со0 — вещественная константа.
933

Глава VI
a. Записать матрицу, представляющую гамильтониан Н в базисе {| + l),|o),|-l)}.
Каковы стационарные состояния системы и их энергии? (Обозначить эти состояния
символами |£,), |£2), |£3) в порядке убывания энергии).
b. В момент времени t = О система находилась в состоянии: | \|/@)) = —==■ [ | +1) -1 -1I.
л/2
Каким будет вектор состояния |\|/@) в момент времени t ? В этот момент измеряется L.;
каковы вероятности получения различных результатов измерения?
c. Вычислить средние значения (L^)@,(£y)@>(£,)(') в момент времени t. Как
движется вектор (L) ?
d. В момент времени t измеряется величина l3z.
(i) Существуют ли такие моменты времени, когда возможен лишь один
результат измерения?
(и) Допустим, что это измерение дало результат h2. Каково состояние системы
сразу же после измерения? Указать без вычислений ее последующую эволюцию.
7. Рассматриваются вращения в обычном трехмерном пространстве #?и(а), где и —
единичный вектор, определяющий ось вращения, и а — угол вращения.
a. Показать, что если М' есть преобразование точки М в результате инфинитези-
мального поворота на угол е , то ОМ' = ОМ + eu x ОМ.
(х~)
b. Представим вектор ОМ матрицей-столбцом
Какой вид имеет матрица,
представляющая вращение #u (e) ? Получить матрицы, описывающие компоненты
оператора Л , определенного выражением .<#и (е) = 1 + гМ • и.
c. Вычислить коммутаторы Ly^,.//^];L/^,.,/M;[./C,^]. Каковы квантовые аналоги
полученных чисто геометрических соотношений?
d. Исходя из матрицы, описывающей Jtz, вычислить матрицу, представляющую £а/':,
и показать, что .^ (а) = е " . Каков аналог этого соотношения в квантовой механике?
8. Рассмотреть в трехмерном пространстве частицу, вектор состояния которой равен
|\|/), а волновая функция — \|/(г) = (г |\|/). Пусть А — наблюдаемая, коммутирующая с
L = R х Р, угловым орбитальным моментом частицы. Допустим, что А , L2 и Lz
образуют полный набор коммутирующих операторов в пространстве #г, а их собственные
934

Общие свойства угловых моментов в квантовой механике
общие векторы обозначены символом \п, /,т) с собственными значениями ап, где
индекс п предполагается дискретным, равными /(/ + 1)Й2 и тЬ .
Пусть £/(ф) —унитарный оператор, определенный формулой £/(ф) = е~щ1г,ь, где ф —
вещественный безразмерный параметр. Считая, что К — произвольный оператор,
обозначим символом К его преобразование с помощью унитарного оператора £/(ф):
£ = *У(Ф)К£/ + (Ф).
а. Пусть L± = Lx ± iLy. Вычислить L+|n, /, m) и показать, что L+ и L+
пропорциональны; найти коэффициент пропорциональности. Аналогичный вопрос для операторов
L_ и L_.
&. Выразить операторы Lx,LyJ Lz через Lx,Ly,Lz. Какое геометрическое
преобразование можно сопоставить переходу от L к L ?
c. Вычислить коммутаторы [X±iY,Lz] и [ZyLz]. Доказать, что кет-векторы
и Z|m, /,m) являются собственными векторами оператора Lz с
собственными значениями, которые требуется вычислить. Какое соотношение должно
обязательно существовать между т и т', чтобы матричный элемент (п\ /', m'| X ±iY \n, /, т)
был бы отличен от нуля? Аналогичный вопрос относительно матричного элемента
(rt',/',m'|z|rt,/,m).
d. Сравнив матричные элементы X ±iY и Z с матричными элементами X±iY и Z,
вычислить X, ?, Z через X, К, Z . Дать геометрическую интерпретацию.
9. Пусть имеется физическая система с фиксированным угловым моментом / и вектором
состояния |\|/) в пространстве состояний Щ . Обозначим оператор орбитального момента
символом L , и допустим, что базис пространства Щ образован из 2/ +1 собственных
векторов |/,т) оператора Lz (где -/<т<+/), которым соответствуют волновые функции
/(г) ^'"(в, ф). Обозначим среднее значение оператора L символом (L) = (\|/1 L | \|/).
а. Предположим сначала, что (Lx) = (Lyy = 0. Какие из всех возможных состояний
системы имеют минимальное значение суммы (AL,) + (&Ly) +('ALZ) ? Показать, что
для этих состояний среднеквадратичное отклонение ALa компоненты L , составляющей
угол а с осью Oz, равно AL(
,„ = Й-/— sina.
a V2
935

Глава VI
b. Предположим теперь, что вектор (L) имеет произвольное направление в системе
координат Oxyz. Обозначим OXYZ правую систему координат, ось OZ которой
направлена так же, как и вектор (L), а ось OY лежит в плоскости хОу .
(i) Показать, что состояние |\|/0) системы, для которого сумма
(ALt) + (ALV J + (AL.) минимальна, определено равенствами:
(Lx+iL,)|Vo) = 0;
L2|\|/0) = /%0).
(ii) Пусть Ь0 — угол между осями Oz и OZ, а ф0 — угол между осями Оу и
OY. Установить соотношения:
Lx + iLY = cos2 ^-е'*0 L+ - sin2 -V*0 L_ - ял fl0 Lz;
L = ял ^ cos^-e-** L+ + ял ^ соДе L + ow60L..
2 2 + 2 2" ° *
При условии, что |i|/0) = ]£din |/, m), доказать равенство:
Ьа |@ IT+m+T f
dm=tg^e^J- dm+l.
2 V /-m
Выразить dm через dM d0, ф0, /.
(iii) Чтобы найти <iz, показать, что волновая функция, связанная с вектором
|vj/0), равна \|/0(Х, У, Z) = с; -. /(г) [коэффициенты с, определяются уравнени-
г
ем (D-20) главы VI], так как функция, связанная с вектором I/, /), равна с, , f{r).
г
Заменив затем в выражении для \|/0(Х, К, Z) операторы Х,У, Z их значениями x,y,z,
получить значение dx и равенство:
С s\ \l-'nf s\ \l+m
отМ^Г._.*рГ".-*-. I_M_
2;
«wrf I e ",,<p"
(l + m)\(l-m)\ '
(iv) Измеряется компонента Lz системы, находящейся в состоянии |\|/0).
Каковы вероятности получения различных возможных результатов? Чему равен наиболее
936

Общие свойства угловых моментов в квантовой механике
вероятный результат измерения? Показать, что если / существенно больше 1, то результат
измерения хорошо совпадает с классическим пределом.
10. Пусть J — оператор углового момента некоторой физической системы, находящейся
в состоянии |\|/).
a. Можно ли найти такие состояния системы, в которых среднеквадратичные
отклонения Ых, ДУУ и AJZ были бы равны нулю одновременно?
b. Доказать соотношение AJX AJy > — \(JZ)\, а также соотношения, полученные из
приведенного путем циркулярной перестановки индексов. Пусть (j) — среднее
значение углового момента системы. Предполагаем, что координаты Oxyz выбраны так,
чтобы (jx) = (yv) = 0. Показать, что (AJxf +(л/,J > n\(Jz)\.
c. Показать, что два неравенства, полученные в пункте (Ь), переходят одновременно
в равенства тогда и только тогда, если J+1 \|/) = 0 или J_ \ \\f) = 0.
d. Рассматривается система, представляющая собой частицу без спина, для которой
J = L = R х Р. Показать, что одновременно выполнить равенства ALX • ALy = — \(Lz)\ и
(ДУ,) +(Д»0 =^(Лл можно только в том случае, если волновая функция системы
имеет вид \|/(r, d, (p) = F(ry sinft e±,<p).
11. Рассматривается трехмерный гармонический осциллятор, вектор состояния которого
равен |\|/) = |а^)® аЛ®|ос,), где |осг), \ау) и |аг) —квазиклассические состояния
(см. дополнение Gy) для одномерных гармонических осцилляторов, движущихся
соответственно вдоль осей Ох , Оу , Oz . Пусть L = R х Р — орбитальный угловой момент
трехмерного осциллятора.
a. Доказать равенства (Lz) = ifi(axay -ос* ocv) и ALZ = hд/|осЛ| + ос J , а также
аналогичные соотношения для компонент L вдоль осей Ох и Оу .
b. Допустим теперь, что (Lv) = ih\ - 0, (Lz) = Xh > 0. Доказать, что при этом
обязательно осг = 0. Зафиксируем значение X и минимизируем сумму ALt + ALy; показать,
что для этого нужно, чтобы
«, =-''«,= j! ^
937

Глава VI
где ф0 — произвольное вещественное число. Имеют ли выражения ALV • ALy и
(ALV) +(aLvJ в этом случае минимальные значения, совпадающие с неравенствами,
полученными в пункте (Ь) предыдущего упражнения?
с. Показать, что состояние системы, для которой выполнены указанные выше
условия, обязательно имеет вид:
к ' * " '
где
I \ _(<+*'<) I \
\Xnd = k,nx = 0,nz=0/ ~~ Г~к Ф/1Л = 0,лу=0,/!г=0/ »
c,(a) = -^l^al2/2; ad=e»*JX.
При доказательстве можно опираться на результаты дополнения Gv и § 4 дополнения DVi.
Показать, что угловая зависимость X«rf=*,« =o,/i,=o) пропорциональна функции (sin® е,(*) .
Измеряется L2 системы в состоянии | \|/). Показать, что вероятности получения
различных возможных результатов распределены по закону Пуассона. Какие значения
может дать измерение Lz после измерения L2, которое дало значение /(/ +1) h2 ?

ОГЛАВЛЕНИЕ
ТОМ I
Предисловие переводчика 5
Предисловие к русскому изданию 6
Важное предупреждение: как работать с книгой 7
Введение 8
Глава I. Волны и частицы. Введение основных идей квантовой механики 11
A. Электромагнитные волны и фотоны 14
B. Материальные частицы и волны материи 23
C. Квантовое описание частицы. Волновой пакет 28
D. Частица в поле скалярного потенциала, не зависящего от времени 40
Дополнения к главе I 52
А\. Порядок величины длин волн, ассоциированных с материальными частицами 53
Bj. Ограничения, налагаемые соотношением неопределенностей 55
С\. Соотношение неопределенностей и атомные параметры 57
D|. Соотношение неопределенностей и дополнительность 60
Е|. Простое исследование двумерного волнового пакета 63
Fj. Связь между одномерной и трехмерной задачами 67
G|. Одномерный гауссов волновой пакет. Расплывание волнового пакета 72
Н|. Стационарные состояния частицы в поле прямоугольного одномерного
потенциала 80
J|. Поведение волнового пакета на скачке потенциала 95
Kj. Упражнения 104
Глава И. Математический аппарат квантовой механики 109
A. Пространство волновых функций частицы 113
B. Пространство состояний. Обозначения Дирака 130
C. Представления в пространстве состояний 149
939

D. Уравнения на собственные значения. Наблюдаемые 162
E. Два важных примера представлений и наблюдаемых 180
F. Тензорное произведение пространств состояний 190
Дополнения к главе II 207
Ап. Неравенство Шварца 208
Вп. Некоторые полезные свойства линейных операторов 209
Си. Унитарные операторы 222
Dn. Детальное рассмотрение представлений {|г)| и {|Р/} 229
Еп. Несколько общих свойств двух наблюдаемых Q и Р, коммутатор которых
равен ifi . 235
F|i. Оператор четности 247
G[i. Применение свойств тензорного произведения: двумерная потенциальная яма
бесконечной глубины 250
Нп. Упражнения 254
Глава III. Постулаты квантовой механики 263
A. Введение 266
B. Формулировка постулатов 268
C. Физическая интерпретация постулатов о наблюдаемых и их измерении 282
D. Физический смысл уравнения Шредингера 295
E. Принцип суперпозиции и физические предсказания 316
Дополнения к главе III 335
Ащ. Частица в потенциальной яме бесконечной глубины: физический анализ 337
ВП|. Изучение тока вероятности в некоторых частных случаях 349
С\\]. Среднеквадратичные отклонения двух сопряженных наблюдаемых 356
Dm. Измерения, выполняемые в части физической системы 361
Ец». Оператор плотности 366
Fin- Оператор эволюции 383
Gjn. Представления Шредингера и Гейзенберга 387
Нш. Калибровочная инвариантность 390
Jm. Пропагатор уравнения Шредингера 408
Кш. Нестабильные уровни. Время жизни 417
L||j. Упражнения 422
Мш. Связанные состояния частицы в потенциальной яме произвольной формы 433
Njh. Несвязанные состояния частицы в присутствии потенциальной ямы или
потенциального барьера произвольной формы 442
Оц|. Квантовые свойства частицы в одномерной периодической структуре 452
Глава IV. Применение постулатов к простым случаям: спин 1/2 и двухуровневые
системы 475
А. Частица со спином 1/2: квантование механического момента частицы 478
940

B. Иллюстрация постулатов в случае спина 1/2 487
C. Общий анализ двухуровневых систем 500
Дополнения к главе IV 514
Aiy. Матрицы Паули 515
BjV. Диагонализация эрмитовой матрицы 2x2 519
Ciy. Фиктивный спин 1/2 в двухуровневой системе 524
DJV. Система из двух спинов 1/2 531
EJV. Матрица плотности спина 1/2 539
F|V. Спин 1/2 в статическом и вращающемся магнитных полях: магнитный
резонанс 546
Giy. Исследование молекулы аммиака с помощью простой модели 561
H|V. Влияние связи между стабильным и нестабильным состояниями 579
Jiv. Упражнения 586
Глава V. Одномерный гармонический осциллятор 593
A. Введение 595
B. Собственные значения гамильтониана 601
C. Собственные состояния гамильтониана 611
D. Физическое обсуждение 619
Дополнения к главе V 626
Ау. Анализ некоторых физических примеров гармонического осциллятора 628
By. Стационарные состояния в представлении \\х/\. Полиномы Эрмита 694
Су. Решение уравнения на собственные значения гармонического осциллятора
методом полиномов 656
Dv. Анализ стационарных состояний в представлении Цр)} 664
Еу. Трехмерный изотропный гармонический осциллятор 670
Fv. Гармонический осциллятор с зарядом в однородном электрическом поле 676
Gv. «Квазиклассические» когерентные состояния гармонического осциллятора 685
Ну. Собственные моды колебаний двух связанных гармонических осцилляторов 703
Jv. Моды колебаний бесконечной линейной цепочки связанных гармонических
осцилляторов. Фононы 716
Ку. Моды колебаний непрерывной физической системы. Применение к излучению.
Фотоны 737
Lv. Одномерный гармонический осциллятор в термодинамическом равновесии
при температуре Т 755
Му. Упражнения 772
Глава VI. Общие свойства угловых моментов в квантовой механике 779
A. Введение: важность понятия углового момента 781
B. Соотношения коммутации операторов угловых моментов 783
C. Общая теория углового момента 786
941

D. Применение к орбитальному угловому моменту 803
Дополнения к главе VI 823
AVj. Сферические гармоники 824
BV|. Угловой момент и вращения 838
Сщ. Вращение двухатомных молекул 864
DV|. Угловой момент стационарных состояний двумерного гармонического
осциллятора 882
EV|. Заряженная частица в магнитном поле. Уровни Ландау 900
Fvi- Упражнения 929

Коэн-Таннуджи К., Диу Б., Лалоэ Ф.
К767 Квантовая механика/Пер. с фр. Л. Н. Новикова: В 2-х т. Т. 1. Екатеринбург: Изд-
во Урал, ун-та, 2000.— 944 с.
ISBN 5-7525-1085-6
ISBN5-7525-1131-3 (T.I)
Книга представляет собой изложение важнейших положений нерелятивистской
квантовой механики, содержит большое количества задач и упражнений, основанных на
практически интересных примерах из различных областей атомной физики и спектроскопии.
Предназначена для студентов, аспирантов и молодых научных сотрудников, а также
преподавателей высших учебных заведений физико-математического профиля.
„ 1604030000
К ББК 22.314я73-1
182@2) - 2000

Клод Коэн-Таннуджи
Бернар Диу
Франк Лалоэ
КВАНТОВАЯ МЕХАНИКА
Том 1
КВАНТОВАЯ МЕХАНИКА
Том 1
Ответственный за выпуск Н. А. Тишенкова
Редактор С. Г. Галинова
Технический редактор Т. М. Канула
Оригинал-макет подготовлен М С. Будимировой, Н. П. Сорокиной
Изд. лиц. ЛР № 020257 от 22.11.96.
Подписано в печать 29.08.00. Формат 70x90/16. Усл. печ. л. 69,03.
Бумага офсетная. Печать офсетная.
Тираж 1025 экз. Заказ № 76.
Издательство Уральского университета.
620083, г. Екатеринбург, ул. Тургенева, 4.
Отпечатано с готовых диапозитивов на ГИПП «Уральский рабочий»
620219, г. Екатеринбург, ул. Тургенева, 13.