МТФ НГТУ и
ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО НАРОДНОМУ ОБРАЗОВАНИЮ
представляют бестселлер:
Утверждено Главным учебно-методическим управлением высшего образования
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ
для студентов-заочников машиностроительных, строительных, транспортных, приборостроительных специальностей высших учебных заведений
Издание четвертое
Под редакцией проф. С. М. ТАР Г А
SCAN
KNEKER
МОСКВА «ВЫСШАЯ ШКОЛА» 1989
ББК 22.21
Т 33
УДК 531.8
Л. И. Котова, Р. И. Надеева, С. М. Тарг, В. Л. Цывильский, И. М. Шмарова
Теоретическая механика: Методические указания Т 33 и контрольные задания для студентов-заочников машиностроительных, строительных, транспортных, приборостроительных специальностей высших учебных заведений/Л. И. Котова, Р. И. Надеева, С. М. Тарг и др.; Под ред. С. М. Тарга — 4-е изд. — М..: Высш, шк., 1989. — 111 с.: ил.
ББК 22.21 1603020000(4309000000)—384	531
Т ---------2----—г——------- 105—89
001(01)—89
© Издательство «Высшая школа», 1989
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
В курсе теоретической механики студенты изучают три ее раздела: статику, кинематику и динамику.
1.	Для изучения курса необходимо иметь соответствующую математическую подготовку. Во всех разделах курса, начиная со статики, широко используется векторная алгебра. Необходимо уметь вычислять проекции векторов на координатные оси, находить геометрически (построением векторного треугольника или многоугольника) и аналитически (по проекциям на координатные оси) сумму векторов, вычислять скалярное и векторное произведения двух векторов и знать свойства этих произведений, а в кинематике и динамике — дифференцировать векторы.. Надо также уметь свободно пользоваться системой прямоугольных декартовых координат на плоскости и в пространстве, знать, что такое единичные векторы (орты) этих осей и как выражаются составляющие вектора по координатным осям с помощью ортов.
Для изучения кинематики надо совершенно свободно уметь дифференцировать функции одного переменного, строить графики этих функций, быть знакомым с понятиями о естественном трехграннике, кривизне кривой и радиусе кривизны, знать основы теории кривых 2-го порядка, изучаемой в аналитической геометрии.
Для изучения динамики надо уметь находить интегралы (неопределенные и определенные) от простейших функций, вычислять частные производные и полный дифференциал функций некольких переменных, а также уметь интегрировать дифференциальные уравнения 1-го порядка с разделяющимися переменными и линейные дифференциальные уравнения 2-го порядка (однородные и неоднородные) с постоянными коэффициентами.
2.	При изучении материала курса по учебнику нужно прежде всего уяснить существо каждого излагаемого там вопроса. Главное — это понять изложенное в учебнике, а не «заучить».
Изучать материал рекомендуется по темам (пунктам приводимой ниже программы) или по главам (параграфам) учебника. Сначала следует прочитать весь материал темы (параграфа), особенно не задерживаясь на.том, что показалось не совсем понятным; часто это становится понятным из последующего. Затем надо вернуться к местам, вызвавшим затруднения, и внимательно разобраться в том, что было неясно. Особое внимание при повторном чтении обратите на формулировки
соответствующих определений, теорем и т. п. (они обычно бывают набраны в учебнике курсивом или разрядкой); в точных формулировках, как правило, бывает существенно каждое слово и очень полезно понять, почему данное положение сформулировано именно так. Однако не следует стараться заучивать формулировки; важно понять их смысл и уметь изложить результат своими словами.
Необходимо также понять ход всех доказательств (в механике они обычно не сложны) и разобраться в их деталях. Доказательства надо уметь воспроизводить самостоятельно, что нетрудно сделать, поняв идею доказательства; пытаться просто их «заучивать» не следует, никакой пользы это не принесет.
Закончив изучение темы, полезно составить краткий конспект, по возможности не заглядывая в учебник.
При изучении курса особое внимание следует уделить приобретению навыков решения задач. Для этого, изучив материал данной темы, надо сначала обязательно разобраться в решениях соответствующих задач, которые приводятся в учебнике, обратив особое внимание на методические указания по их решению. Затем постарайтесь решить самостоятельно несколько аналогичных задач из сборника задач И. В. Мещерского и после этого решите соответствующую задачу из контрольного задания.
3.	Закончив изучение темы, нужно проверить, можете ли вы дать ответ на все вопросы программы курса по этой теме (осуществить самопроверку).
Поскольку все вопросы, которые должны быть изучены и усвоены, в программе перечислены достаточно подробно, дополнительные вопросы для самопроверки здесь не приводятся. Однако очень полезно составить перечень таких вопросов самостоятельно (в отдельной тетради) следующим образом.
Начав изучение очередной темы программы, выписать сначала в тетради последовательно все перечисленные в программе вопросы этой темы, оставив справа широкую колонку (поле). При этом если, например, в программе сказано «Условия равновесия пространственной и плоской систем сходящихся сил», то следует записать отдельно вопросы «Условия равновесия пространственной системы сходящихся сил» и «Условия равновесия плоской системы сходящихся сил» и т. п.
Затем по мере изучения материала темы (чтения учебника) следует в правой колонке указать страницу учебника, на которой излагается соответствующий вопрос, а также номер формулы или уравнения (уравнений), которые выражают ответ на вопрос математически. В результате в данной тетради будет полный перечень вопросов для самопроверки, который можно использовать и при подготовке к экзамену. Кроме того, ответив на вопрос или написав соответствующую формулу (уравнение), вы можете по учебнику быстро проверить, правильно ли это сделано, если в правильности своего ответа сомневаетесь. Наконец,
по тетради с такими вопросами вы можете установить, весь ли материал, предусмотренный программой, вами изучен (если изучен весь материал, то против каждого вопроса в правой колонке будет указана соответствующая страница учебника).
Следует иметь в виду, что в различных учебниках материал может излагаться в разной последовательности. Поэтому ответ на какой-нибудь вопрос данной темы может оказаться в другой главе учебника, но на изучении курса в целом это, конечно, никак не скажется.
Указания по выполнению контрольных заданий приводятся ниже после рабочей программы. Их надо прочитать обязательно и ими руководствоваться. Кроме того, к каждой задаче даются конкретные методические указания по ее решению и приводится пример решения.
РАБОЧАЯ ПРОГРАММА*
Введение. Механическое движение как одна из форм движения материи. Предмет механики. Теоретическая механика и ее место среди естественных и технических наук. Механика как теоретическая база ряда областей современной техники. Объективный характер законов механики. Основные исторические этапы развития механики. Связь механики с общественным производством и ее роль в решении народнохозяйственных задач, поставленных партией и правительством.
СТАТИКА ТВЕРДОГО ТЕЛА
I Предмет статики. Основные понятия статики: абсолютно твердое тело, сила, эквивалентные системы сил, равнодействующая, уравновешенная система сил, силы внешние и внутренние. Исходные положения (аксиомы) статики. Связи и реакции связей. Основные виды связей: гладкая плоскость, поверхность и опора, гибкая нить, цилиндрический шарнир (подшипник), сферический шарнир (подпятник), невесомый стержень; реакции этих связей.
Система сходящихся сил. Геометрический и аналитический способы сложения сил. Сходящиеся силы. Равнодействующая сходящихся сил. Геометрическое условие равновесия системы сходящихся сил.
* Составлена на основе Программы по теоретической механике инд. ГУМУ—4/1, утвержденной Главным учебно-методическим управлением высшего образования 2 июня 1988 г. По решению кафедры для отдельных специальностей в рабочую программу могут включаться дополнительные вопросы, перечень которых должен быть сообщен студентам. Вопросы, поставленные в данной программе в скобках, в зависимости от их актуальности для данной специальности и от числа часов, отведенных на курс учебным планом, могут включаться в программу не полностью или не включаться совсем, о чем тоже должно быть сообщено студентам.
Аналитические условия равновесия пространственной и плоской систем сходящихся сил. Теорема о равновесии трех непараллельных сил.
пДеория пар сил. Момент силы относительно точки (центра) как вектор. Пара сил. Момент пары сил как вектор. Теоремы об эквивалентности пар. Сложение пар, произвольно расположенных в пространстве. Условия равновесия системы пар.
Приведение произвольной системы сил к данному центру. Теорема о параллельном переносе силы. Основная теорема статики о приведении системы сил к данному центру. Главный вектор и главный момент системы сил.
Система сил, произвольно расположенных на плоскости (плоская система сил). Алгебраическая величина момента силы. Вычисление главного вектора и главного момента плоской системы сил. Частные случаи приведения: приведение к паре сил, к равнодействующей и случай равновесия. Аналитические условия равновесия плоской системы сил. Три вида условий равновесия: а) равенство нулю сумм проекций сил на две координатные оси и суммы их моментов относительно любого центра; б) равенство нулю сумм моментов сил относительно двух центров и суммы их проекций на одну ось; в) равенство нулю сумм моментов сил относительно трех центров. Условия равновесия плоской системы; параллельных сил. Теорема Вариньона о моменте равнодействующей.
(Сосредоточенные и распределенные силы. Силы, равномерно распределенные по отрезку прямой, и их равнодействующая.) Реакция жесткой заделки. Равновесие системы тел. Статически определимые и статически неопределимые системы. Равновесие при наличии сил трения. Коэффициент трения. Предельная сила трения. Угол и конус трения. (Трение качения; коэффициент трения качения.)
. Система сил, произвольно расположенных в пространстве (пространственная система сил). Момент силы относительно оси и его вычисление. Зависимость между моментами силы относительно центра и относительно оси, проходящей через этот центр. Аналитические формулы для вычисления моментов силы относительно трех координатных осей. Вычисление главного вектора и главного момента пространственной системы сил. (Частные случаи приведения пространственной системы сил: приведение к паре сил, к равнодействующей, к динамическому винту и случай равновесия.) Аналитические условия равновесия произвольной пространственной системы сил. Условия равновесия пространственной системы параллельных сил. Теорема Вариньона о моменте равнодействующей относительно оси.
Центр параллельных сил и центр тяжести. Центр параллельных сил. Формулы для определения координат центра параллельных сил. Центр тяжести твердого тела; формулы для определения его координат. Центры тяжести, объема, площади и линии. Способы определения
положения центров тяжести тел. Центры тяжести дуги окружности, треугольника и кругового сектора.
КИНЕМАТИКА
Введение в кинематику. Предмет кинематики. Пространство и вре-мй в классической механике. Относительность механического движейия. Система отсчета. Задачи кинематики.
Кинематика точки. Векторный способ задания движения точки. Траектория точки. Скорость точки как производная ее радиуса-вектора по времени. Ускорение точки как производная от ее скорости по времени.
Координатный способ задания движения точки (в прямоугольных декартовых координатах). Определение траектории точки. Определение скорости и ускорения точки по их проекциям на координатные оси.
Естественный способ задания движения точки. Естественный трехгранник. Алгебраическая величина скорости точки. Определение ускорения точки по его проекциям на оси естественного трехгранника; касательное и нормальное ускорения точки. (Скорость и ускорение точки в полярных координатах.)
Кинематика твердого тела
г
) Поступательное движение. Поступательное движение твердого тела. Теорема о траекториях, скоростях и ускорениях точек твердого тела при поступательном движении.
^Вращение твердого тела вокруг неподвижной оси (вращательное движение). Уравнение (или закон) вращательного движения твердого тела. Угловая скорость и угловое ускорение твердого тела. Законы равномерного и равнопеременного вращения. Скорость и ускорение точки твердого тела, вращающегося вокруг неподвижной оси. Векторы угловой скорости и углового ускорения тела. Выражение скорости точки вращающегося тела и ее касательного и нормального ускорений в виде векторных произведений.
(П Плоскопараллельное (плоское) движение твердого тела. Плоское движение твердого.тела и движение плоской фигуры в ее плоскости. Уравнения движения плоской фигуры. Разложение движения плоской фигуры на поступательное вместе с полюсом и вращательное вокруг полюса. Независимость угловой скорости и углового ускорения фигуры от выбора полюса. Определение скорости любой точки плоской фигуры как геометрической суммы скорости полюса и скорости этой точки при вращении фигуры вокруг полюса. Теорема о проекциях скоростей двух точек фигуры (тела). Мгновенный центр скоростей. Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей.

Определение ускорения любой точки плоской фигуры как геометрической суммы ускорения полюса и ускорения этой точки при вращении фигуры вокруг полюса. (Понятие о мгновенном центре ускорений.)
{^(Движение твердого тела вокруг неподвижной точки или сферическое движение. Углы Эйлера. Уравнения движения твердого тела вокруг неподвижной точки. Мгновенная ось вращения тела. Векторы угловой скорости и углового ускорения тела. Определение скоростей и ускорений точек твердого тела, имеющего одну неподвижную точку.)
|/ (Общий случай движения свободного твердого тела. Уравнения движения свободного твердого тела. Разложение этого движения на поступательное движение вместе с полюсом и движение вокруг полюса. Определение скоростей и ускорений точек свободного твердого тела.)
ЕСложное движение точки и твердого тела или составное движение, элютное и относительное движения точки; переносное движение. Относительная, переносная и абсолютная скорости и относительное, переносное и абсолютное ускорения точки. Теорема о сложении скоростей. Теорема Кориолиса о сложении ускорений. Модуль и направление кориолисова ускорения. Случай поступательного переносного движения.
Ш (Сложное движение твердого тела. Сложение поступательных движений. Сложение мгновенных вращений твердого тела вокруг пересекающихся и параллельных осей. Пара мгновенных вращений. Кинематический винт. Мгновенная винтовая ось.)
ДИНАМИКА
| Введение в динамику. Предмет динамики. Основные понятия и определения: масса, материальная точка, сила. Силы, зависящие от времени, от положения точки и от ее скорости. Законы классической механики или законы Галилея — Ньютона. Инерциальная система отсчета. Задачи динамики.
Динамика точки
^(Решение первой и второй задач динамики. Дифференциальные уравнения движения свободной и несвободной материальной точки в декартовых координатах.
Уравнения в проекциях на оси естественного трехгранника.
Две основные задачи динамики для материальной точки. Решение первой задачи динамики.
Решение второй задачи динамики. Начальные условия. Постоянные интегрирования и их определение по начальным условиям. Примеры интегрирования дифференциальных уравнений движения точки.
h- Несвободное и относительное движения точки. (Несвободное движение материальной точки. Дифференциальные уравнения движения точки по заданной гладкой неподвижной кривой. Определение закона движения и реакции связи.)
Относительное движение материальной точки. Дифференциальные уравнения относительного движения материальной точки; переносная и кориолисова силы инерции. Принцип относительности классической механики. Случай относительного покоя.
j,/Прямолинейные колебания точки. Свободные колебания материальной точки под действием восстанавливающей силы, пропорциональной расстоянию от центра колебаний. Амплитуда, начальная фаза, частота и период колебаний. Затухающие колебания материальной точки при сопротивлении, пропорциональном скорости; период этих колебаний, декремент колебаний. Апериодическое движение.
Вынужденные колебания материальной точки при действии гармонической возмущающей силы и сопротивлении, пропорциональном скорости; случай отсутствия сопротивления. Амплитуда вынужденных колебаний и сдвиг фаз, их зависимость от отношения частот; коэффициент динамичности. Явление резонанса.
у Введение в динамику механической системы. Механическая система. Классификация сил, действующих на механическую систему: силы активные (задаваемые) и реакции связей; силы внешние и внутренние. Свойства внутренних сил. Масса системы. Центр масс; радиус-вектор и координаты центра масс.
Моменты инерции. Момент инерции твердого тела относительно оси; радиус инерции. Моменты инерции тела относительно плоскости и полюса. Теорема о моментах инерции относительно параллельных осей или теорема Гюйгенса. Примеры вычисления моментов инерции: моменты инерции однородного тонкого стержня, тонкого круглого кольца или полого цилиндра и круглого диска или сплошного круглого цилиндра. (Формула для вычисления момента инерции относительно оси любого направления. Центробежные моменты инерции. Главные и главные центральные оси инерции и их свойства.)
Общие теоремы динамики
£ ф Теорема о движении центра масс. Дифференциальные уравнения движения механической системы. Теорема о движении центра масс механической системы. Закон сохранения движения центра масс.
Теорема об изменении количества движения. Количество движения материальной точки. Элементарный импульс силы. Импульс силы за конечный промежуток времени и его проекции на координатные оси. Теорема об изменении количества движения материальной точки в дифференциальной и конечной формах.
Количество движения механической системы; его выражение через
массу системы и скорость ее центра масс. Теорема об изменении количества движения механической системы в дифференциальной и конечной формах. Закон сохранения количества движения механической системы.
(Понятие о теле и точке переменной массы. Уравнение Мещерского. Формула Циолковского.)
лдГеорема об изменении момента количества движения. Момент колййества движения материальной точки относительно центра и относительно оси. Теорема об изменении момента количества движения материальной точки. Центральная сила. Сохранение момента количества движения материальной точки в случае центральной силы. (Понятие о секторной скорости. Закон площадей.)
Главный момент количеств движения или кинетический момент механической системы относительно центра и относительно оси. Кинетический момент вращающегося твердого тела относительно оси вращения. Теорема об изменении кинетического момента механической системы. Закон сохранения кинетического момента механической системы. (Теорема об изменении кинетического момента механической системы в относительном движении по отношению к центру масс.)
у'/ Теорема об изменении кинетической энергии. Кинетическая энергия материальной точки. Элементарная работа силы; аналитическое выражение элементарной работы. Работа силы на конечном перемещении точки ее приложения. Работа силы тяжести, силы упругости и силы тяготения. Теорема об изменении кинетической энергии материальной точки в дифференциальной и конечной формах.
Кинетическая энергия механической системы. Формулы для вычисления кинетической энергии твердого тела при поступательном движении, при вращении вокруг неподвижной оси и в общем случае движения (в частности, при плоскопараллельном движении). Теорема об изменении кинетической энергии механической системы в дифференциальной и конечной формах. Равенство нулю суммы работ внутренних сил в твердом теле. Работа и мощность сил, приложенных к твердому телу, вращающемуся вокруг неподвижной оси.
Понятие о силовом поле. Потенциальное силовое поле и силовая функция. Выражение проекций силы через силовую функцию. Поверхности равного потенциала. Работа силы на конечном перемещении точки в потенциальном силовом поле. Потенциальная энергия. Примеры потенциальных силовых полей: однородное поле тяжести и поле тяготения. Закон сохранения механической энергии.
(/'Динамика твердого тела. Дифференциальные уравнения поступательного движения твердого тела. Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси. Физический маятник. Дифференциальные уравнения плоского движения твердого тела.
Принцип Даламбера. Принцип Даламбера для материальной точки; сила инерции. Принцип Даламбера для механической системы.
Приведение сил инерции точек твердого тела к центру; главный вектор и главный момент сил инерции.
(Определение динамических реакций подшипников при вращении твердого тела вокруг неподвижной оси. Случай, когда ось вращения является главной центральной осью инерции тела.)
’^/.Принцип возможных перемещений и общее уравнение динамики. Связи, налагаемые на механическую систему. Возможные (или виртуальные) перемещения материальной точки и механической системы. Число степеней свободы системы. Идеальные связи. Принцип возможных перемещений. Общее уравнение динамики.
Уравнения движения системы в обобщенных координатах (уравнения Лагранжа). Обобщенные координаты системы; обобщенные скорости. Выражение элементарной работы в обобщенных координатах. Обобщенные силы и их вычисление; случай сил, имеющих потенциал. Условия равновесия системы в обобщенных координатах. Дифференциальные уравнения движения системы в обобщенных координатах или уравнения Лагранжа 2-го рода. Уравнения Лагранжа в случае потенциальных сил; функция Лагранжа (кинетический потенциал).
Понятие об устойчивости равновесия. Малые свободные колебания механической системы с одной степенью свободы около положения устойчивого равновесия системы и их свойства.
И7" Элементы теории удара. Явление удара. Ударная сила и ударный импульс. Действие ударной силы на материальную точку. Теорема об изменении количества движения механической системы при ударе. Прямой центральный удар тела о неподвижную поверхность; упругий и неупругий удары. Коэффициент восстановления при ударе и его опытное определение. Прямой центральный удар двух тел. Теорема Карно.
СПИСОК ЛИТЕРАТУРЫ
Основной
Бутенин Н. В., Лунц Я. Л., Меркин Д. Р. Курс теоретической механики. Т. 1, 2. М., 1985 и предыдущие издания.
Добронравов В. В., Никитин Н. Н. Курс теоретической механики. М., 1983.
Старжинский В. М. Теоретическая механика. М., 1980.
Тарг С. М. Краткий курс теоретической механики. М., 1986 и предыдущие издания.
Яблонский A. А., Никифорова В. М. Курс теоретической механики. Ч. 1. М., 1984 и предыдущие издания.
Яблонский А. А. Курс теоретической механики. Ч. 2. М., 1984 и предыдущие издания.
Мещерский И. В. Сборник задач по теоретической механике. М., 1986 и предыдущие издания.
Сборник задач по теоретической механике/Под ред. К. С. Колесникова. М., 1983.
Дополнительной
Бать М. И., Джанелидзе Г. Ю., Келъзон А. С. Теоретическая механика в примерах и задачах. Ч. 1, 2. М., 1984 и предыдущие издания.
Сборник задач по теоретической механике/ Б ражниченко Н А., Кан В. Л., Минцберг Б. Л. и др. М.» 1987.
Новожилов И. В., Зацепин М. Ф. Типовые расчеты по теоретической механике на базе ЭВМ. М., 1986,
Сборник заданий для курсовых работ по теоретической механике /Под ред. А. А. Яблонского. М., 1985 и предыдущие издания (содержит примеры решения задач).
КОНТРОЛЬНЫЕ ЗАДАНИЯ
СОДЕРЖАНИЕ ЗАДАНИЙ, ВЫБОР ВАРИАНТОВ, ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТ, ПОЯСНЕНИЯ К ТЕКСТУ ЗАДАЧ
(статика) — задачи С1 — С4У (кинематика) — задачи К1 — К4У (динамика) — задачи Д1 — Д4> (динамика) задачи Д5 — Д8. (динамика) — задачи Д9 — Д12.
Студенты выполняют 5 контрольных заданий (работ}к
Задание 1
Задание 2
Задание 3
Задание 4
Задание 5
К каждой задаче дается 10 рисунков и таблица (с тем же номером, что и задача), содержащая дополнительные к тексту задачи условия. Нумерация рисунков двойная, при этом номером рисунка является цифра, стоящая после точки. Например, рис. С 1.4 — это рис. 4 к задаче С1 и т. д. (в тексте задачи при повторных ссылках на рисунок пишется просто рис. 4 и т. д.). Номера условий от 0 до 9 проставлены в 1-м столбце (или в 1-й строке) таблицы.
Студент во всех задачах выбирает номер рисунка по предпоследней цифре шифра, а номер условия в таблице — по последней; например, если шифр оканчивается числом 46, то берутся рис. 4 и условия № 6 из таблицы.
Каждое задание выполняется в отдельной тетради (ученической), страницы которой нумеруются. На обложке указываются: название дисциплины, номер работы, фамилия и инициалы студента, учебный шифр, факультет, специальность и адрес. На первой странице тетради записываются: номер работы, номера решаемых задач и год издания контрольных заданий.
12 а	s
~	- l/V
Решение каждой задачи обязательно начинать на развороте тетради (на четной странице, начиная со второй, иначе работу трудно проверять). Сверху указывается номер задачи, далее делается чертеж (можно карандашом) и записывается, что в задаче дано и что требуется определить (текст задачи не переписывается). Чертеж выполняется с учетом условий решаемого варианта задачи; на нем все углы, действующие силы, число тел и их расположение на чертеже должны соответствовать этим условиям. В результате в целом ряде задач чертеж получается более простой, чем общий.
Чертеж должен быть аккуратным и наглядным, а его размеры должны позволять ясно показать все силы или векторы скорости и ускорения и др.; показывать все эти векторы и координатные оси на чертеже, а также указывать единицы получаемых величин нужно обязательно. Решение задач необходимо сопровождать краткими пояснениями (какие формулы или теоремы применяются, откуда получаются те или иные результаты и т. п.) и подробно излагать весь ход расчетов. На каждой странице следует оставлять поля для замечаний рецензента.
Работы, не отвечающие всем перечисленным требованиям, проверяться не будут, а будут возвращаться для переделки.
К работе, высылаемой на повторную проверку (если она выполнена в другой тетради), должна обязательно прилагаться незачтенная работа.
На экзамене необходимо представить зачтенные по данному разделу курса работы, в которых все отмеченные рецензентом погрешности должны быть исправлены.
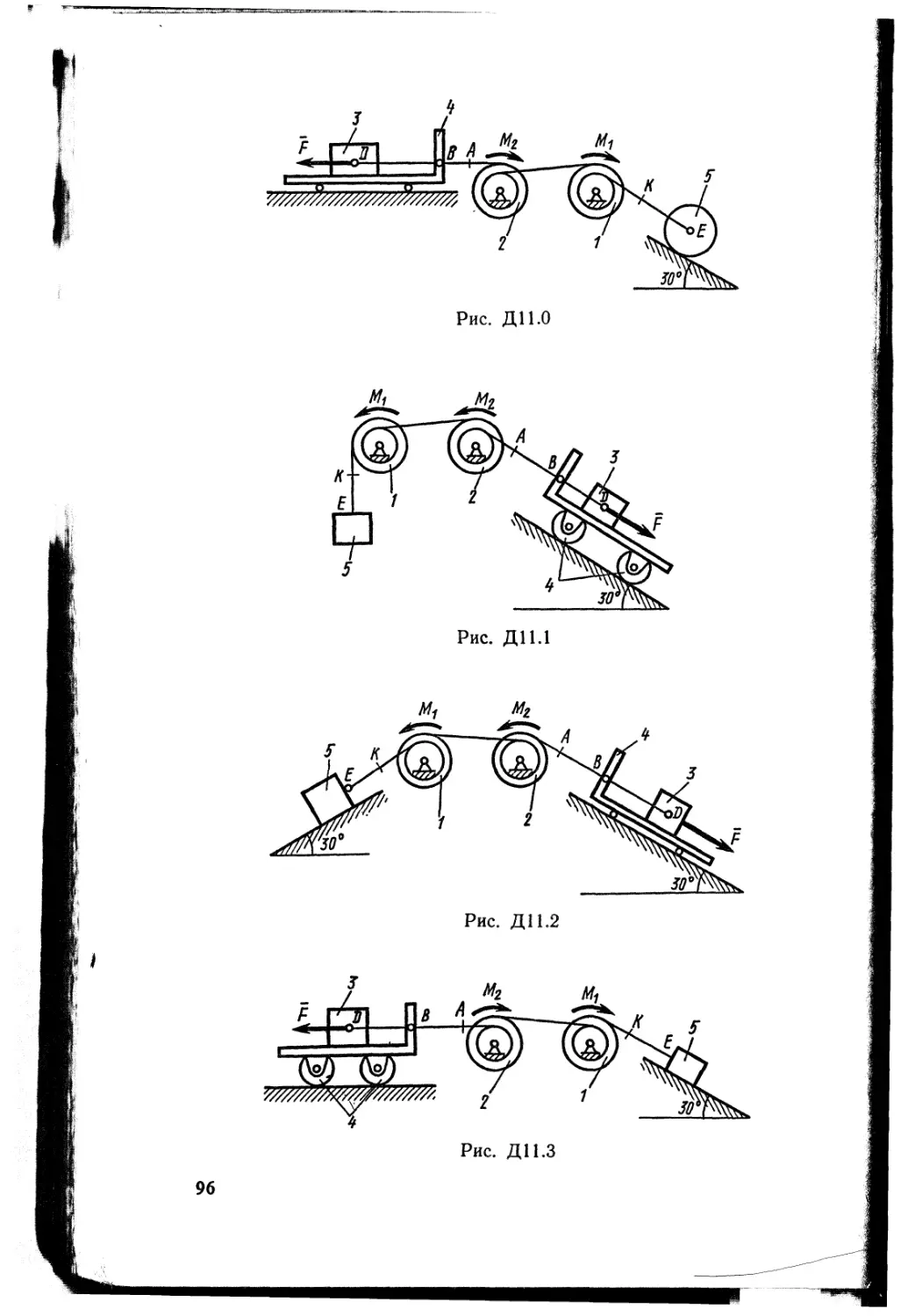
При чтении текста каждой задачи учесть следующее. Большинство рисунков дано без соблюдения масштабов. На рисунках к задачам С1 —С4 и Д1 — Д12 все линии, параллельные строкам, считаются горизонтальными, а перпендикулярные строкам — вертикальными и это в тексте задач специально не оговаривается. Также без оговорок считается, что все нити (веревки, тросы) являются нерастяжимыми и невесомыми, нити, перекинутые через блок, по блоку не скользят, катки и колеса (в кинематике и динамике) катятся по плоскостям без скольжения. Все связи, если не сделано других оговорок, считаются идеальными.
Когда тела на рисунке пронумерованы, то в тексте задач и в таблице Pi, h, гх и т. п. означают вес или размеры тела /; Р2, /2, г2 — тела 2 и т. д. Аналогично, в кинематике и динамике ав означают скорость и ускорение точки В; vc, ас— точки С; сси, ei — угловую скорость и угловое ускорение тела /; g)2, е2 — тела 2 и т. д. В каждой задаче подобные обозначения могут тоже специально не оговариваться.
Следует также иметь в виду, что некоторые из заданных в условиях задачи величин (размеров) при решении каких-нибудь вариантов могут не понадобиться, они нужны для решения других вариантов задачи.
Из всех пояснений в тексте задачи обращайте внимание только на относящиеся к вашему варианту, т. е. номеру вашего рисунка или вашего условия в таблице.
Методические указания по решению задач, входящих в контрольные задания, даются для каждой задачи после ее текста под рубрикой «Указания», затем дается пример решения аналогичной задачи. Цель примера — разъяснить ход решения, но не воспроизвести его полностью. Поэтому в ряде случаев промежуточные расчеты опускаются. Но при выполнении задания все преобразования и числовые расчеты должны быть обязательно последовательно проделаны с необходимыми пояснениями; в конце должны быть даны ответы.
ЗАДАЧИ К КОНТРОЛЬНЫМ ЗАДАНИЯМ
СТАТИКА
Задача С1
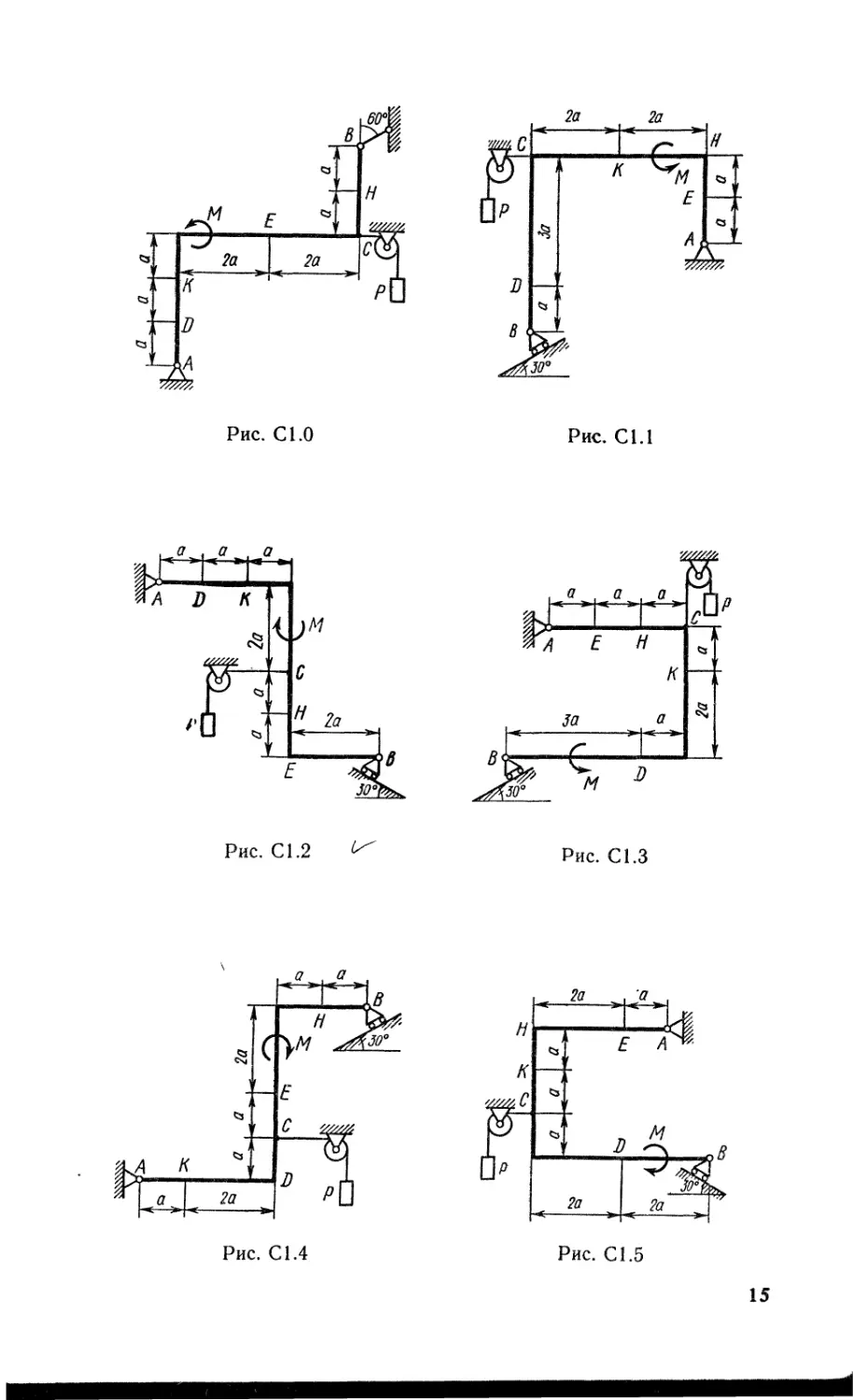
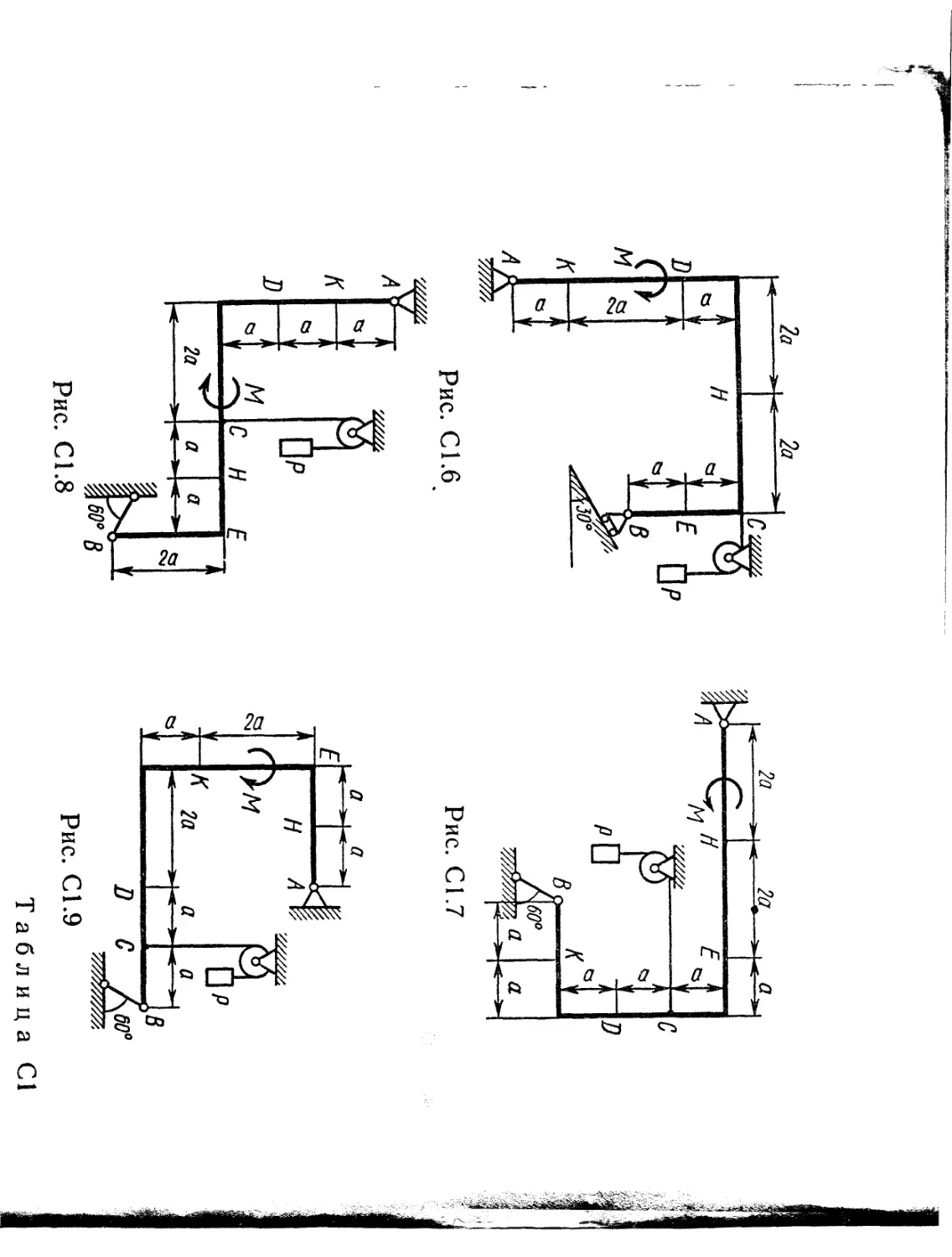
Жесткая рама, расположенная в вертикальной плоскости (рис. С1.0 — С1.9, табл. С1), закреплена в точке А шарнирно, а в точке В прикреплена или к невесомому стержню с шарнирами на концах, или к шарнирной опоре на катках.
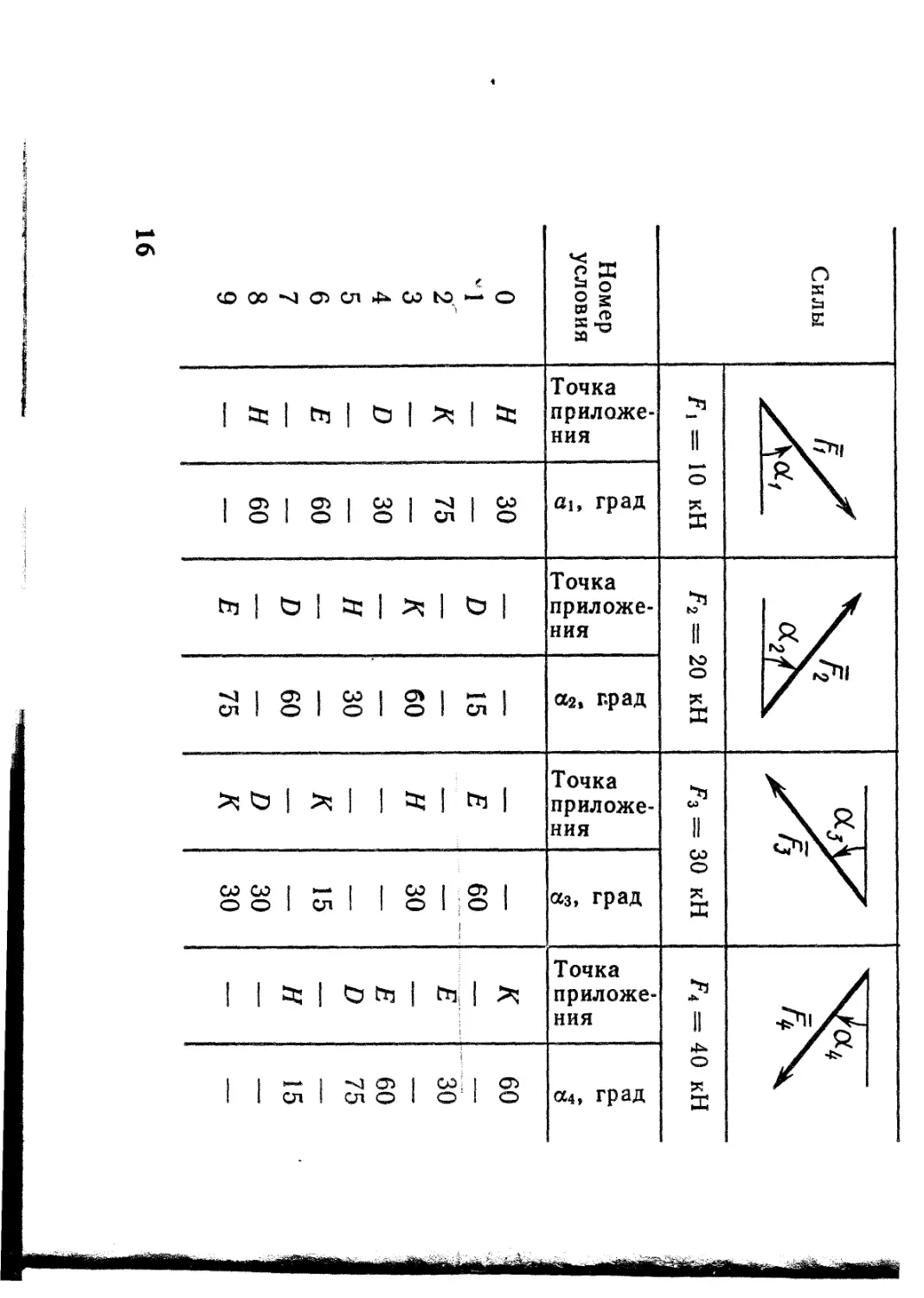
В точке С к раме привязан трос, перекинутый через блок и несущий на конце груз весом Р = 25 кН. На раму действуют пара сил с моментом М = 100 кН’М и две силы, значения, направления и точки приложения которых указаны в таблице (например, в условиях № 1 на раму действует сила А под углом 15° к горизонтальной оси, приложенная в точке D, и сила Рз под углом 60° к горизонтальной оси, приложенная в точке Е, и т. д.).
Определить реакции связей в точках Л, В, вызываемые действующими нагрузками. При окончательных расчетах принять а = 0,5 м.
Указания. Задача С1 — на равновесие тела под действием произвольной плоской системы сил. При ее решении учесть, что натяжения обеих ветвей нити, перекинутой через блок, когда трением пренебрегают, будут одинаковыми. Уравнение моментов будет более простым (содержать меньше неизвестных), если брать моменты относительно точки, где пересекаются линии действия двух реакций связей. При вычислении момента силы F часто удобно разложить ее на составляющие F' и F", для которых плечи легко определяются, и воспользоваться теоремой Вариньона; тогда mo(F) = m0(F') -f- mo(F"}.
Рис. Cl. 1
CO 00 -J Oi СП 4^ 00 to. '-* О	Номер условия	Силы			
I | tn | Сз |	|	Точка приложения	II о ж Д			
					
J	CT>	I	O') I	00	I	I	00 1	O	1	O 1	O	1	СЛ 1	о	ан град				
					
Гп | ts |	| >: | b |	Точка приложения	II ко о я Д			
сл 1 о 1 о 1 о 1 сл 1	а2» г.р ад				
>:	| >: | | I tn |	Точка приложения	F3 = 30 кН	\ * СпгЛ-		
00 00 1 — I I 00 I О | о о 1 ел 1 1 о lol	а3, град				
| |	| tn | tni; | >:	Точка приложения	II о ж К			
I I a I as 1ёIs	а4, град				
Рис. Cl.6
Рис. С 1.8
2а
2а
а
Таблица С1
Пример Cl. Жесткая пластина ABCD (рис. С1) имеет в точке А неподвижную шарнирную опору, а в точке В — подвижную шарнирную опору на катках. Все действующие нагрузки и размеры показаны на рисунке.
Дано: F — 25 кН, а = 60°, Р = 18 кН, у = 75°, М = 50 кН«м, р = 30°, а = 0,5 м. Определить: реакции в точках А и В, вызываемые действующими нагрузками.
Решение. 1. Рассмотрим равновесие пластины. Проведем координатные оси ху и изобразим действующие на пластину силы: силу Г, пару сил с моментом М, натяжение троса Т (по модулю Т = Р) и реакции связей ХА, YA, RB (реакцию неподвижной шарнирной опоры А изображаем двумя ее составляющими, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости).
2. Для полученной плоской системы сил составим три уравнения равновесия. При вычислении момента силы F относительно точки А воспользуемся теоремой Вариньона, т. е. разложим силу F на составляющие F', F" (F'=i Fcosa, jF" = Fsina) и учтем, что mA(F) = = mA{F') + mA(F"). Получим:
2F*x=0, ХА 4-7?j3sinp — Fcosa+ Tsiny = 0 ;	(1)
2/^ = 0, Ya + /?flcosP4-Fsina— Tcosy — 0 ;	(2)
2тл(А) = 0, M — 7?BCosp«4a +Fcosa*2a—Fsina’3a— Tsiny*2a = 0.
(3)
Рис. Cl
Подставив в составленные уравнения числовые значения заданных величин и решив эти уравнения, определим искомые реакции.
Ответ: Хл=-8,5 кН; Ул = -23,3 кН; RB = 7,3 кН. Знаки указывают, что силы ХА и Ул направлены противоположно показанным на рис. С1.
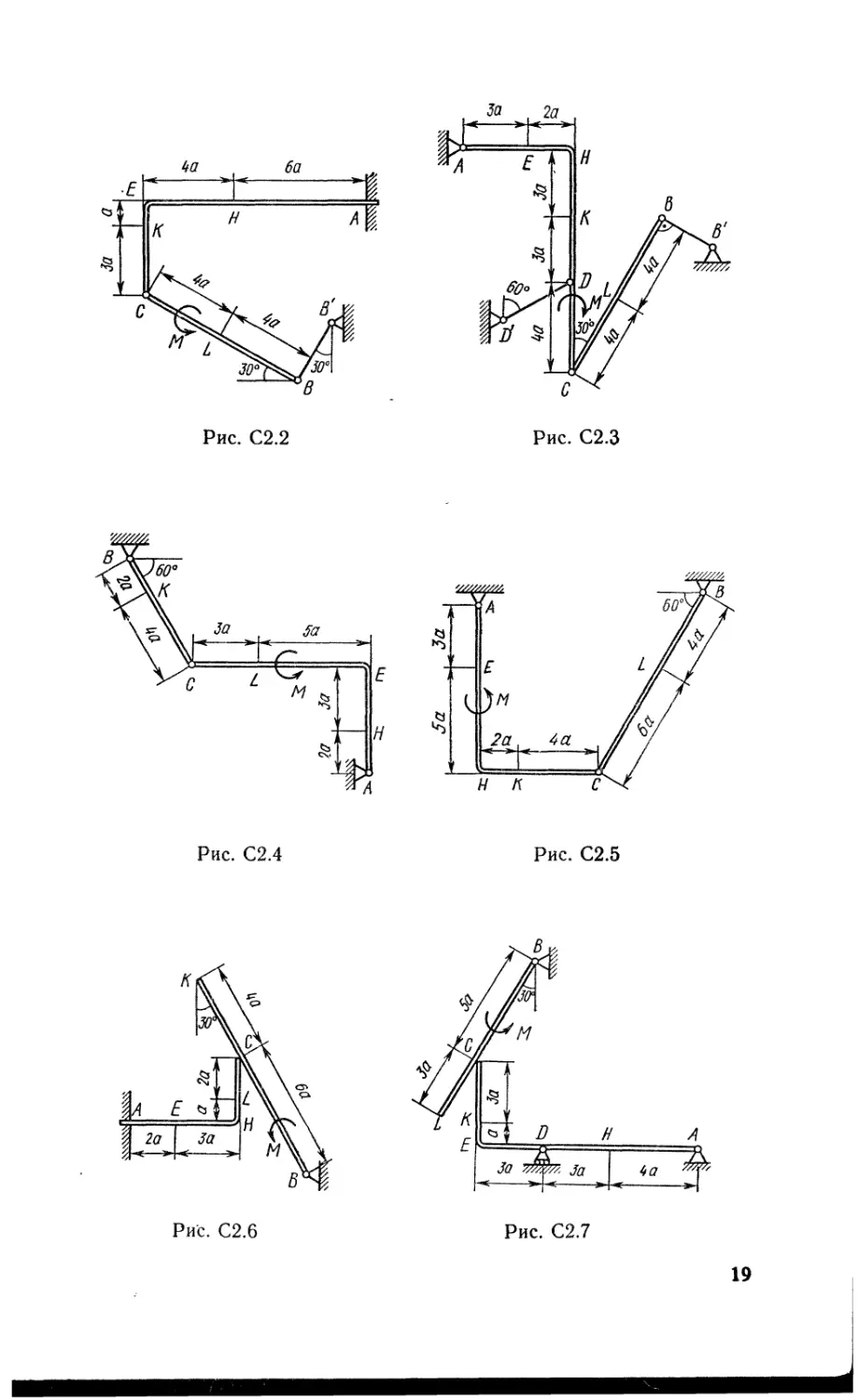
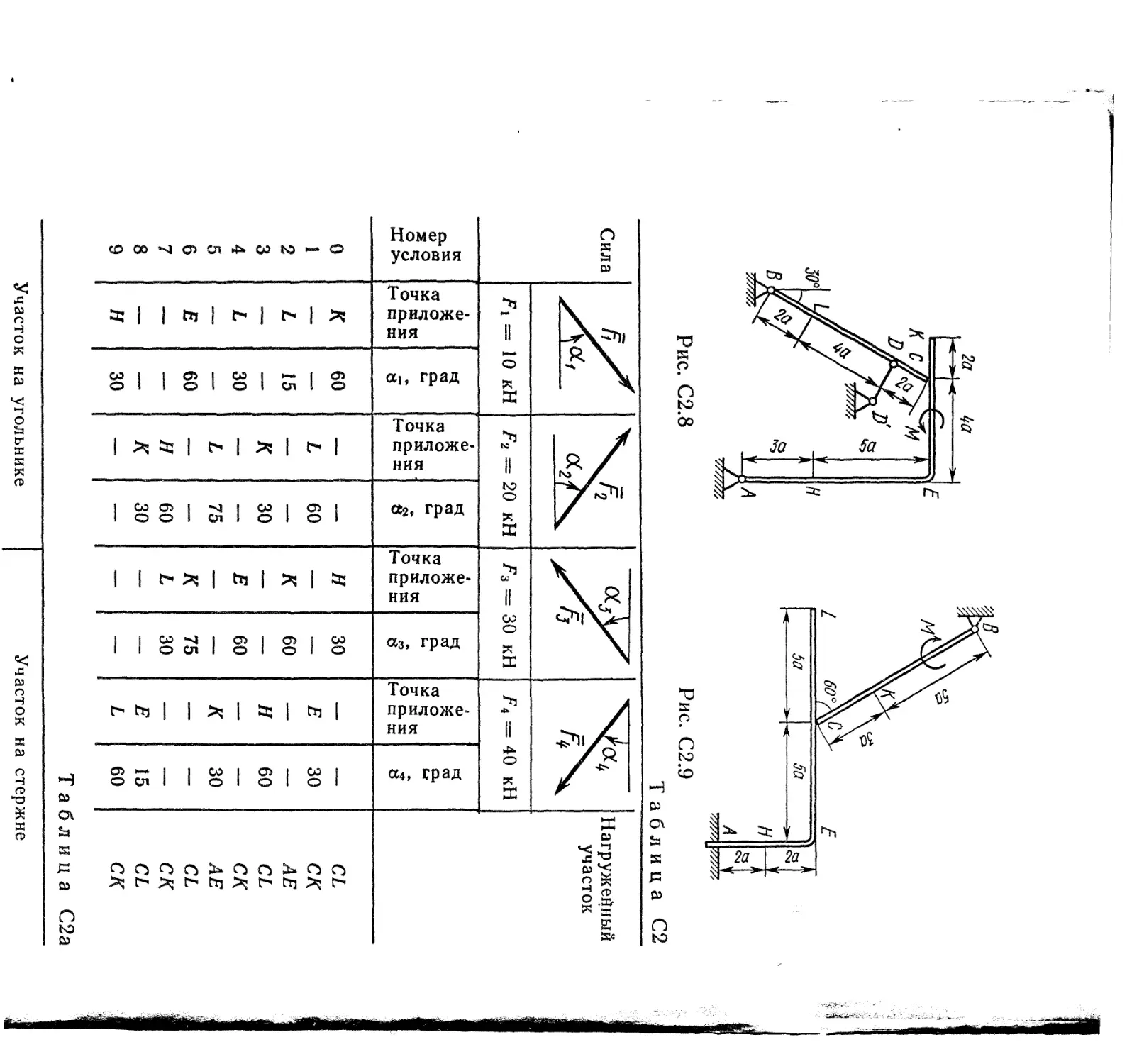
Конструкция состоит из жесткого угольника и стержня, которые в точке С или соединены друг с другом шарнирно (рис. С2.0 — С2.5), или свободно опираются друг о друга (рис. С2.6— С2.9). Внешними связями, наложенными на конструкцию, являются в точке А или шарнир, или жесткая заделка; в точке В или гладкая плоскость (рис. О и 1), или невесомый стержень ВВ' (рис. 2 и 3), или шарнир (рис. 4—9); в точке D или невесомый стержень DD' (рис. О, 3, 8), или шарнирная опора на катках (рис., 7).
На каждую конструкцию действуют: пара сил с моментом М = ==60 кН«м, равномерно распределенная нагрузка интенсивности # = = 20 кН/м и еще две силы. Эти силы, их направления и точки приложения указаны в табл. С2; там же в столбце «Нагруженный участок» указано, на каком участке действует распределенная нагрузка (например, в условиях № 1 на конструкцию действуют сила А под углом 60° к горизонтальной оси, приложенная в точке L, сила А под углом 30° к горизонтальной оси, приложенная в точке Е , и нагрузка, распределенная на участке СК).
Определить реакции связей в точках А, В, С (для рис. 0, 3, 7, 8 еще и в точке £>), вызванные заданными нагрузками. При окончательных расчетах принять а — 0,2 м. Направление распределенной нагрузки на различных по расположению участках указано в табл. С2а.
Указания. Задача С2 — на равновесие системы тел, находящихся под действием плоской системы сил. При ее решении можно или рассмотреть сначала равновесие всей системы в целом, а затем равновесие одного из тел системы, изобразив его отдельно, или же сразу расчленить систему и рассмотреть равновесие каждого из тел в отдельности, учтя при этом закон о равенстве действия и противодействия. В задачах, где имеется жесткая заделка, учесть, что ее реакция представляется силой, модуль и направление которой неизвестны, и парой сил, момент которой тоже неизвестен.
Рис. С2.0	Рис. С2.1
Рис. С2.6
Рис. С2.7
20
2а
Рис. С2.8
Таблица С2
Сила	^Х Xt*,				°^Х X*		/я.		Нагружейный участок
	Fi = 10 кН		F2 = 20 кН		Г3 = 30 кН		F4 = 40 кН		
, Номер условия !		6 * СП о М Ч S" X к Ofts Нею	j аь град	Точка приложения	«2, град	Точка приложения	а3, град	6 * сП О Ю Ч 5" К К о as Нею	а4, град	
0 1 2 3 4 5 6 7 8 9	1 1 t4 1 Г" 1	1	60 15 30 60 30	L К L Н К	60 30 75 60 30	Н К Е К L	30 60 60 75 30	Е И К Е L	30 60 30 15 60	CL СК АЕ CL СК АЕ CL СК CL СК
Т а б л и ц а С2а
Участок на угольнике
Участок на стержне
Пример С2. На угольник ABC (Z-ABC = 90°), конец А которого жестко заделан, в точке С опирается стержень DE (рис. С2, а). Стержень имеет в точке D неподвижную шарнирную опору и к нему приложена сила Дак угольнику — равномерно распределенная на участке КВ нагрузка интенсивности q и пара с моментом М.
Дано: F-Ю кН, М = 5 кН«м, ^ = 20 кН/м, а =0,2 м. Определить: реакции в точках Л, С, D, вызванные заданными нагрузками.
Решение. 1. Для определения реакций расчленим систему и рассмотрим сначала равновесие стержня DE (рис. С2,б). Проведем координатные оси ху и изобразим действующие на стержень силы: силу F, реакцию N, направленную перпендикулярно стержню, и составляющие XD и Yd реакции шарнира D. Для полученной плоской системы сил составляем три уравнения равновесия:
SFu = О, Xd + F — zVsin60° = 0;	(1)
2/^=0, Уа-f-Afcos 60° = 0 ;	(2)
S то(Г*) = 0, AF2а —F-5asin 60° = 0.	(3)
2. Теперь рассмотрим равновесие угольника (рис. С£, в). На него действуют сила давления стержня N', направленная противоположно реакции N, равномерно распределенная нагрузка, которую заменяем силой Q, приложенной в середине участка КВ (численно Q = q*4a = = 16 кН), пара сил с моментом М и реакция жесткой заделки, слагающаяся из силы, которую представим составляющими Ха, Уа, и пары
с моментом Ма. Для этой плоской системы сил тоже составляем три уравнения равновесия:
£Fkx = 0, ^ + Qcos60° + #'sin60° = 0;	(4)
£Г^ = 0, Ya-Qsin60° — N'cos60° = 0 ;	(5)
£tnA(Fk) = 0, MA + M + Q-2a + .V'cos60o.4a + ^'sin60°-6a = 0.(6) При вычислении момента силы N' разлагаем ее на составляющие N'i и М и применяем теорему Вариньона. Подставив в составленные уравнения числовые значения заданных величин и решив систему уравнений (1) — (6), найдем искомые реакции. При решении учитываем, что численно N' — N в силу равенства действия и противодействия.
Ответ: #=21,7 кН, Уо=-10,8 кН; XD = 8,8 кН, ХА = = -26,8 кН, Ya = 24,7 кН, МА = -42,6 кН • м.
Знаки указывают, что силы YD, ХА и момент МА направлены противоположно показанным на рисунках.
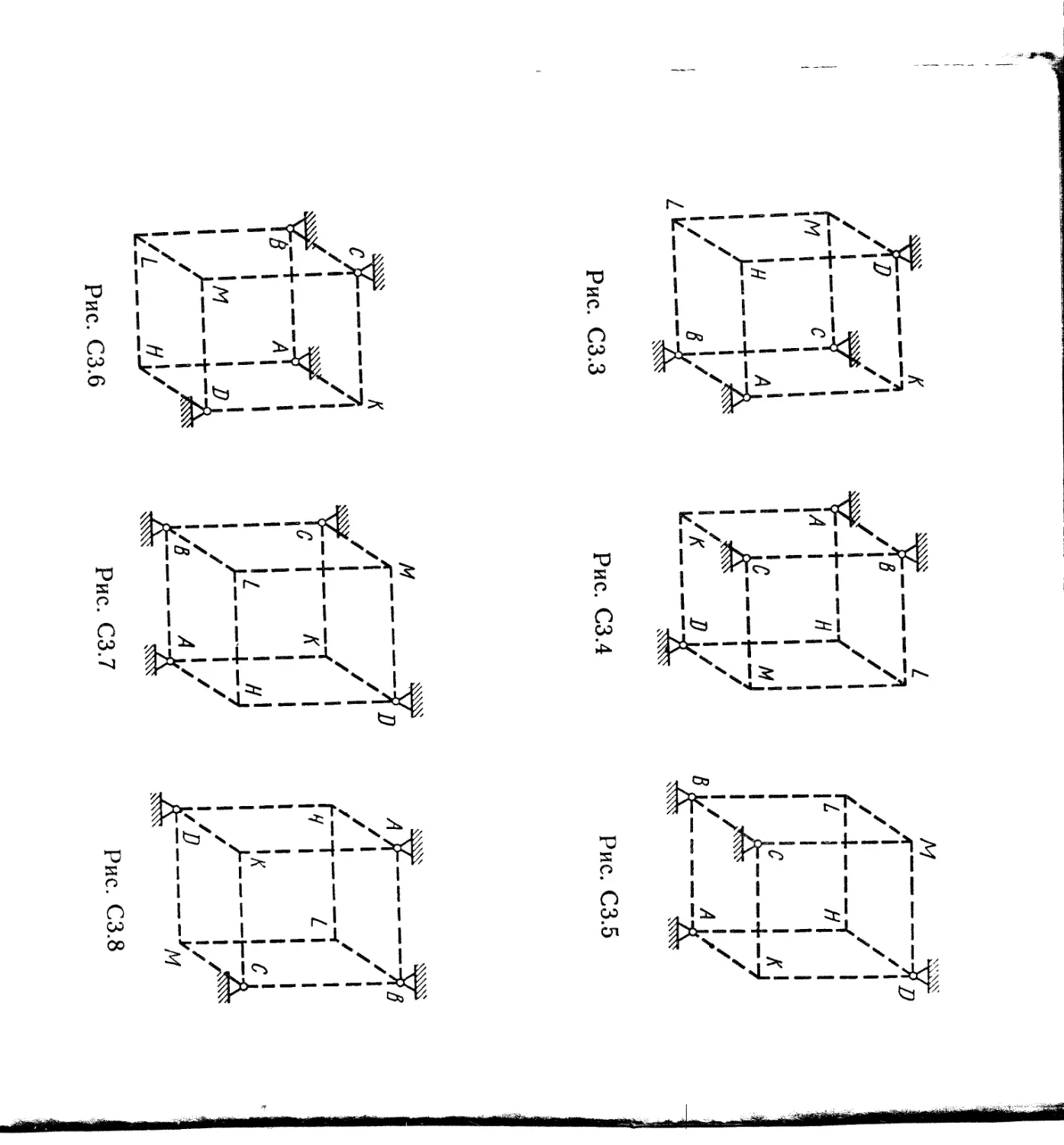
Задача СЗ
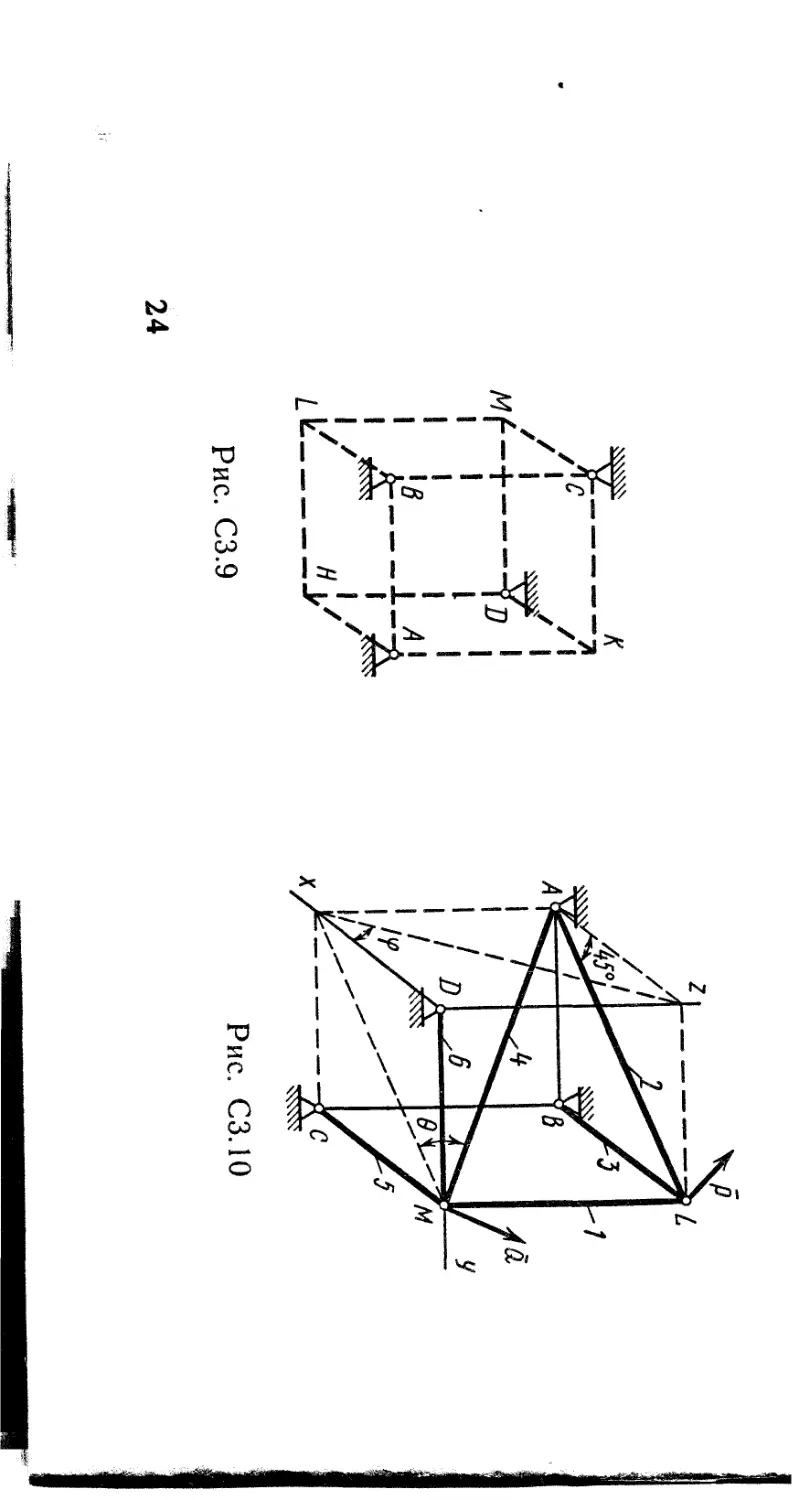
Шесть невесомых стержней соединены своими концами шарнирно друг с другом в двух узлах и прикреплены другими концами (тоже шарнирно) к неподвижным опорам Л, В, С, D (рис. СЗ.О — С3.9, табл. СЗ). Стержни и узлы (узлы расположены в вершинах Н, К, L или М прямоугольного параллелепипеда) на рисунках не показаны и должны быть изображены решающим задачу по данным таблицы. В узле, который в каждом столбце таблицы указан первым, приложена сила Р = 200 Н; во втором узле приложена сила Q = 100 Н. Сила Р образует с положительными направлениями координатных осей х, у, z углы, равные соответственно ai = 45°, 0i = 60°, yi = 60°, а сила Q — углы (Х2 = 60°, 02 = 45°, у2 — 60°; направления осей х, у, z для всех рисунков показаны на рис. СЗ.О.
Грани параллелепипеда, параллельные плоскости ху, — квадраты. Диагонали других боковых граней образуют с плоскостью ху угол ф = 60°, а диагональ параллелепипеда образует с этой плоскостью угол 0= 51°. Определить усилия в стержнях.
На рис. С3.10 в качестве примера показано, как должен выглядеть чертеж С3.1, если по условиям задачи узлы находятся в точках L и М, а стержнями являются LM, LA, LB; МА, МС, MD. Там же показаны углы ф и 0.
Указания. Задача СЗ — на равновесие пространственной системы сходящихся сил. При ее решении следует рассмотреть отдельно равновесие каждого из двух узлов, где сходятся стержни и приложены заданные силы, и учесть закон о равенстве действия и противодействия; начинать с узла, где сходятся три стержня.
Изображать чертеж можно без соблюдения масштаба так, чтобы лучше были видны все шесть стержней. Стержни следует пронумеровать в том порядке, в каком они указаны в таблице; реакции стержней обозначать буквой с индексом, соответствующим номеру стержня (например, М, и т. д.).
Таблица СЗ
Номер условия	0	1	2	3	4
Узлы	Я, М	L, М	К, М	L, Н	X, н
Стержни	ЯЛ1, НА, НВ, МА, МС, MD,	LM, LA, LD, МА, МВ, МС,	КМ, КА, КВ, МА, МС, MD,	LH, LC, LD, НА, НВ, НС	кн, кв, КС, НА, НС, HD
Номер условия	5	6	7	8	9
Узлы	М, Н	L, Н	К, н	L, М	X, м
Стержни	МН, МВ, МС, НА, НС, HD	LH, LB, LD, НА, НВ, НС	КН, КС, KD, НА, НВ, НС	LM, LB, LD, МА, МВ, МС	КМ, КА, KD, МА, МВ, МС
Рис. СЗ.О	Рис. С3.1	Рис. С3.2
24
Рис. С3.9
Рис. С3.10
Рис. СЗ.З
Рис. С3.6
Рис. С3.4
м
Рис. С3.5
Рис. С3.7
Рис. С3.8
Пример СЗ. Конструкция состоит из невесомых стержней 1, 2, .... 6, соединенных друг с другом (в узлах X и М) и с неподвижными опорами А, В, С, D шарнирами (рис. СЗ). В узлах К и М приложены силы Р и Q, образующие с координатными осями углы щ, pi, yi и а2, р2, ?2 соответственно (на рисунке показаны только углы pi, yi).
Дано: Р=100 Н, = 60°, Pi = 60°, у} - 45°; Q = 50 Н, а2 = 45°, р2 = 60°, у2 = 60°, ф = 30°, ф = 60°, 6 — 74°. Определить: усилия в стержнях 1—6.
Решение. 1. Рассмотрим равновесие узла К, в котором сходятся стержни 1, 2, 3. На узел действуют сила Р и реакции Ni, N2, N3 стержней, которые направим по стержням от узла, считая стержни растянутыми. Составим уравнения равновесия этой пространственной системы сходящихся сил:
2X^ = 0, Pcosai + Л^зтф-ф- Л7зsin ф = 0 ;	(1)
TtFky—0, Pcospi-—Afi — Л^созф = 0 ;
(2)
S Fkz = 0, Pcosyi — /Уз cos ф = 0 .
(3)
Решив уравнения (1), (2), (3) при заданных числовых значениях силы Р и углов, получим Ni = 349 Н, N2 — = -345 Н, N3 = 141 Н.
2. Рассмотрим равновесие узла М. На узел действуют сила Q и реакции Nf2, N4, Л^5, N& стержней. При этом по
Рис. СЗ
закону о равенстве действия и противодействия реакция N2 направлена
противоположно ТУ2, численно же N2 = Составим уравнения равно-
весия:
^Fkx — 0, Qcosa2 —Л^зтф —7/4 —Л^зтбзшф = 0 ;	(4)
— Qcosp2 + М>со8ф +Af5sinбсозф = 0;	(5)
2/^г = 0, Qcosy2 — N5cos6 — N6 = 0 .	(6)
При определении проекций силы Ns на оси х и у в уравнениях (4) и (5) удобнее сначала найти проекцию N's этой силы на плоскость хОу (по числовой величине М — Ns sin 6), а затем найденную проекцию на плоскость спроектировать на оси х, у.
Решив систему уравнений (4), (5), (6) и учитывая, что N2 = — N2 = —345 Н, найдем, чему равны N4, N5, N6.
Ответ: Ni = 349 Н; N2=-345 Н; N3 = 141 Н; N4 = 50 Н; Ns — 329 Н; N6 — —66 Н. Знаки показывают, что стержни 2 и 6 сжаты, остальные — растянуты.
Задача С4
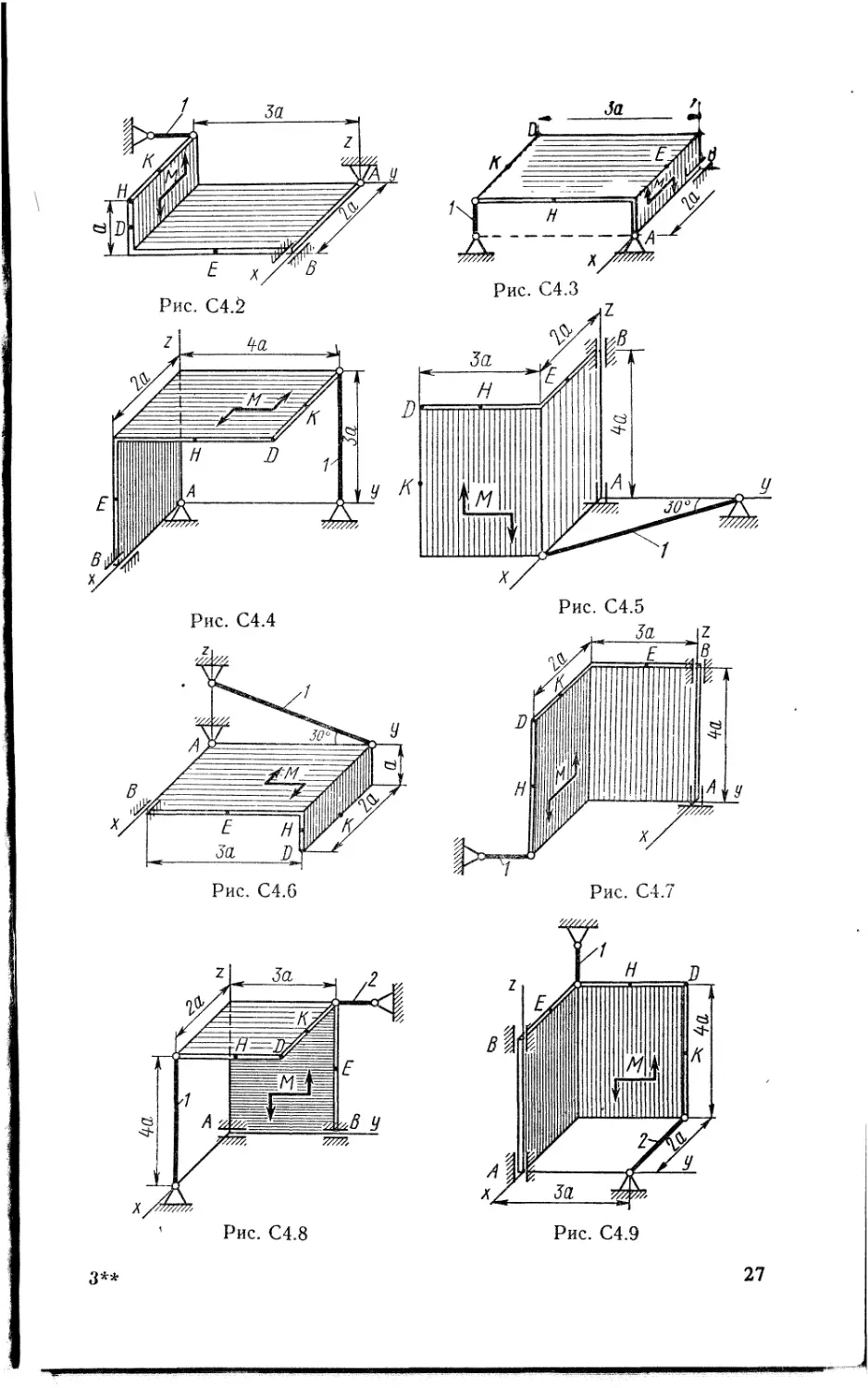
Две однородные прямоугольные тонкие плиты жестко соединены (сварены) под прямым углом друг к другу и закреплены сферическим шарниром (или подпятником) в точке А, цилиндрическим шарниром (подшипником) в точке В и невесомым стержнем 1 (рис. С4.0 — С4.7) или же двумя подшипниками в точках Л и В и двумя невесомыми стержнями 1 и 2 (рис. С4.8, С4.9); все стержни прикреплены к плитам и к неподвижным опорам шарнирами.
Размеры плит указаны на рисунках; вес большей плиты Pi — 5 кН, вес меньшей плиты Р2 = 3 кН. Каждая из плит расположена параллельно одной из координатных плоскостей (плоскость ху — горизонтальная).
На плиты действуют пара сил с моментом М = 4 кН-м, лежащая в плоскости одной из плит, и две силы. Значения этих сил, их направления и точки приложения указаны в табл. С4; при этом силы Fi и F4 лежат в плоскостях, параллельных плоскости ху, сила А — в плоскости, параллельной xz, и сила F3 — в плоскости, параллельной yz. Точки приложения сил (/), Е, И, К) находятся в углах или в серединах сторон плит.
Определить реакции связей в точках А и В и реакцию стержня (стержней). При подсчетах принять а — 0,6 м.
Указания. Задача С4 — на равновесие тела под действием произвольной пространственной системы сил. При се решении учесть, что реакция сферического шарнира (подпятника) имеет три составляющие (по всем трем координатным осям), а реакция цилиндрического шарнира (подшипника) — две составляющие, лежащие в плоскости, перпендикулярной оси шарнира (подшипника). При вычислении момента силы F часто удобно разложить ее на две составляющие Р и F", параллельные координатным осям (или на три); тогда, по теореме Вариньона, mx(F) — mx(Fr') + mx(F") и т. д.
Рис. С4.0
Рис. С4.1
Рис. С4.6
Рис. С4.7
Таблица С4
Пример С4. Горизонтальная прямоугольная плита весом Р (рис. С4) закреплена сферическим шарниром в точке А, цилиндрическим (подшипником) в точке В и невесомым стержнем DD'. На плиту в плоскости, параллельной xz, действует сила Дав плоскости, параллельной yz, — пара сил с моментом М.
Дано: Р = 3 кН, F = 8 кН, М = 4 кН • м, а = 60°, А С ~ 0,8 м, АВ = 1,2 м, BE ~ 0,4 м, ЕН = 0,4 м. Определить: реакции опор Л, В и стержня DD'.
Решение. 1. Рассмотрим равновесие плиты. На плиту действуют заданные силы Р, F и пара с моментом М, а также реакции связей. Реакцию сферического шарнира разложим на три составляющие Ад, Уд, 2д, цилиндрического (подшипника) — на две составляющие Хв, (в плоскости, перпендикулярной оси подшипника); реакцию N стержня направляем вдоль стержня от D к D', предполагая, что он растянут.
2. Для определения шести неизвестных реакций составляем шесть уравнений равновесия действующей на плиту пространственной системы сил:
2Лх=0, ХА +
+Л'в + Fcos60° = 0 ;
(1)
2Ftl/ = 0, Ya — Wcos30° = 0 ;
(2)
2Лг=0, Za + Zb— P + Wsin30° — Fsin60° = 0;	(3)
S/пХЛ) = 0, M - P • AB/2 + ZS-AB — Fsin 60° • AB + N sin 30° • AB = 0;
(4)
Zm^Ft) = 0, Р-ДС72-^8Й130°-ЛС + .р8Й160о-ЛС72-
— Fcos60°-B£ = 0;	(5)
2тг(А) = 0, -Fcos60°-AB—N_cos30°-AC — Xb-AB = 0.	(6)
Для определения моментов силы F относительно осей разлагаем ее на составляющие F' и F", параллельные осям х и z (F' = Fcosa, F" = Fsina), и применяем теорему Вариньона (см. «Указания»). Аналогично можно поступить при определении моментов реакции N.
Подставив в составленные уравнения числовые значения всех заданных величин и решив эти уравнения, найдем искомые реакции.
Ответ: Хл = 3,4 кН; Ул = 5,1 кН; ZA = 4,8 кН; Хв — — 7,4 кН; ZB = 2,1 кН; 7V = 5,9 кН. Знак минус указывает, что реакция Хв направлена противоположно показанной на рис. С4.
КИНЕМАТИКА
Задача(кл)'/’
Под номером К1 помещены две задачи К1а и К16, которые надо решить.
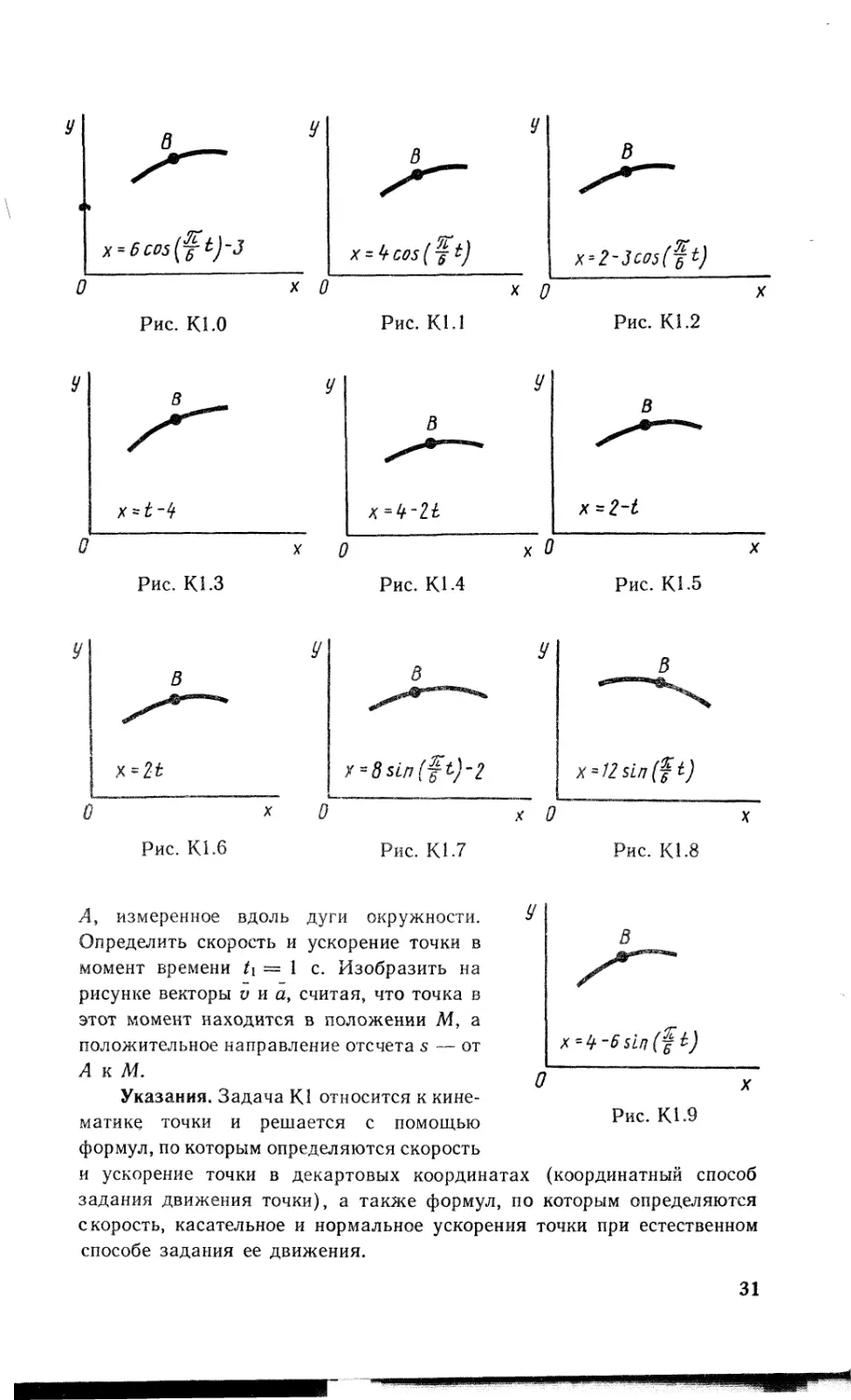
Задача К1а. Точка В движется в плоскости ху (рис. К1.0 — К 1.9, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями: х = у = f2(Z), где х и у выражены в сантиметрах, t — в секундах.
Найти уравнение траектории точки; для момента времени t\ = 1 с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Зависимость x—f\(f) указана непосредственно на рисунках, а за-
Таблица KI
Номер уело-ВИЯ	У = Ы/)			s = Kt)
	рис. 0—2	рис. 3—6	рис. 7—9	
1	2	3	4	5
0	2 sinGz)	2/2 + 2	4cos(iz)	4cos(i0
1	-6cos(fz)	8 sin (-J/)	6c°S2(^)	2sin(fz)
2	-3sin2(fz)	(2 + /)2	4cos(t0	6/ - 2t2
3	9sin(iz)	2/3	IOcos^-^-/)	~2sin(-JZ)
4	3cos(fz)	2cos(t0	-4c°s’(y/)	л ( л A 4 cos/ — / J
5	!Osin(iz)	2 —3/2	i2cos(10	-3sin(yz)
6	6Sm2(y/)	2 sin (-J/)	-3c°S(^)	3/2 - 10/
7	“2sin(^)	(/+1)3	“8coS(tZ)	-2cos(-^/)
8	9cos(|r)	2 — t3	9cos(tz)	3sm(-Jz)
9	-8sin(^)	4cos(-^/)	-6cos(tz)	-2c°s(-J/)
висимость у = f2(t) дана в табл. К1 (для рис. О—2 в столбце 2, для рис. 3—6 в .столбце 3, для рис. 7—9 в столбце 4). Как и в задачах С1 — С4, номер рисунка выбирается по предпоследней цифре шифра; а номер условия в табл. К1 — по последней.
Задача К16. Точка движется по дуге окружности радиуса R = 2 м по закону s = f(/), заданному в табл. К1 в столбце 5 (s — в метрах, t — в секундах), где s — AM — расстояние точки от некоторого начала
Рис. К1.3
Л, измеренное вдоль дуги окружности. Определить скорость и ускорение точки в момент времени /1=1 с. Изобразить на рисунке векторы v и а, считая, что точка в этот момент находится в положении М, а положительное направление отсчета 5 — от А к М.
Указания. Задача К1 относится к кинематике точки и решается с помощью формул, по которым определяются скорость
и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются
скорость, касательное и нормальное ускорения точки при естественном способе задания ее движения.
В задаче все искомые величины нужно определить только для момента времени 6 = 1 с. В некоторых вариантах задачи К1а при определении траектории или при последующих расчетах (для их упрощения) следует учесть известные из тригонометрии формулы: cos 2а = 1—2 sin2 а = 2 cos2 а — 1; sin 2а — 2 sin acos а.
Пример Kia. Даны уравнения движения точки в плоскости ху:
х = — 2cos4-3, у = 2sin^-g-z) — 1
(%, у — в сантиметрах, t —в секундах).
Определить уравнение траектории точки; для момента времени 6 = 1 с найти скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Решение. 1. Для определения уравнения траектории точки исключим из заданных уравнений движения время t. Поскольку t входит в аргументы тригонометрических функций, где один аргумент вдвое больше другого, используем формулу
cos2a= 1— 2sin2a или cos^-^~/) = 1— 2sin2^-^-^ .	(1)
Из уравнений движения находим выражения соответствующих функций и подставляем в равенство (1). Получим
следовательно,
- 1	2 (j/+1)2
2	4
Отсюда окончательно находим следующее уравнение траектории точки (параболы, рис. К1а):
х=(г/4-1)24-1.	(2)
2. Скорость точки найдем по ее проекциям на координатные оси:
dx	л . / л X
^ = -dF = — s4—7 
d#	я / л Л
^ = -аГ==-1-С04-8-9 ;
V = V 0? + ^
и при 71 = 1 с
= 1,11 см/с, V\y = 0,73 см/с, щ = 1,33 см/с .	(3)
3. Аналогично найдем ускорение точки:
и при t\ = 1 с
«и = 0,87 см/с2, а\у = —0,12 см/с2, а\ — 0,88 см/с2. (4)
4.	Касательное ускорение найдем, дифференцируя по времени равенство V2 = и2 4- Uy. Получим
du dux du„
2a-dF=^Tr+2^-df’
откуда
du	Uxdx + Vydy
a' = ~ =------v----•	(5)
Числовые значения всех величин, входящих в правую часть выражения (5), определены и даются равенствами (3)- и (4). Подставив в (5) эти числа, найдем сразу, что при 6 = 1 с air— 0,66 см/с2.
5.	Нормальное ускорение точки ап = ~^а2 — а2. Подставляя сюда найденные числовые значения ai и ан, получим, что при t\ — 1 с ain = 0,58 см/с2.
6.	Радиус кривизны траектории р = и2/ал. Подставляя сюда числовые значения ui и а\п, найдем, что при t\ — 1 с pi = 3,05 см.
Ответ: ui = 1,33 см/с, ai = 0,88 см/с2, aiT = 0,66 см/с2, а\п — — 0,58 см/с2, pi — 3,05 см.
Пример К1б. Точка движется по дуге окружности радиуса jR — = 2 м по закону s — 2sin^-^-^ (s — в метрах, t — в секундах), где s = AM (рис. К1б). Определить скорость и ускорение точки в момент времени 6 = 1к с.
Решение. Определяем скорость точки:
ds л
у	cos |
При t\ — 1 с получим ui — лу/2 /4 — — 1,11 м/с.
Ускорение находим по его касательной и нормальной составляющим:
При ti = 1 с получим, учтя, что R = 2 м,
ан = — л2У2”/16 — 0,87 м/с2, ain — ui/2 = зт2/16 — 0,62 м/с2 .
Тогда ускорение точки при Л = 1 с будет
ai = -\/а\х + а\п~ л2д/3 /16 = 1,07 м/с2.
Изобразим на рис. К1б векторы oi и щ, учитывая знаки щ и а1х и считая положительным направление от А к М.
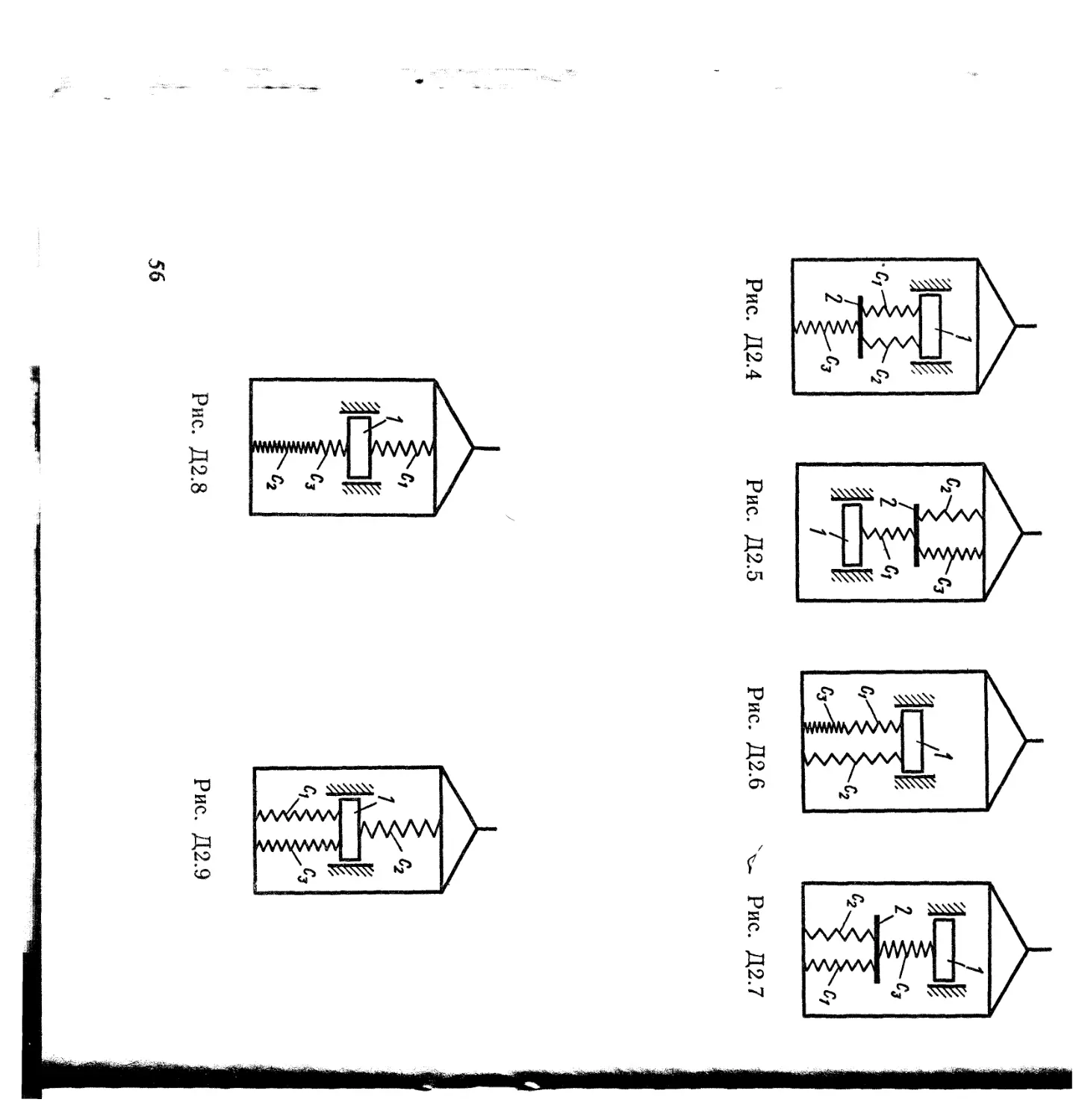
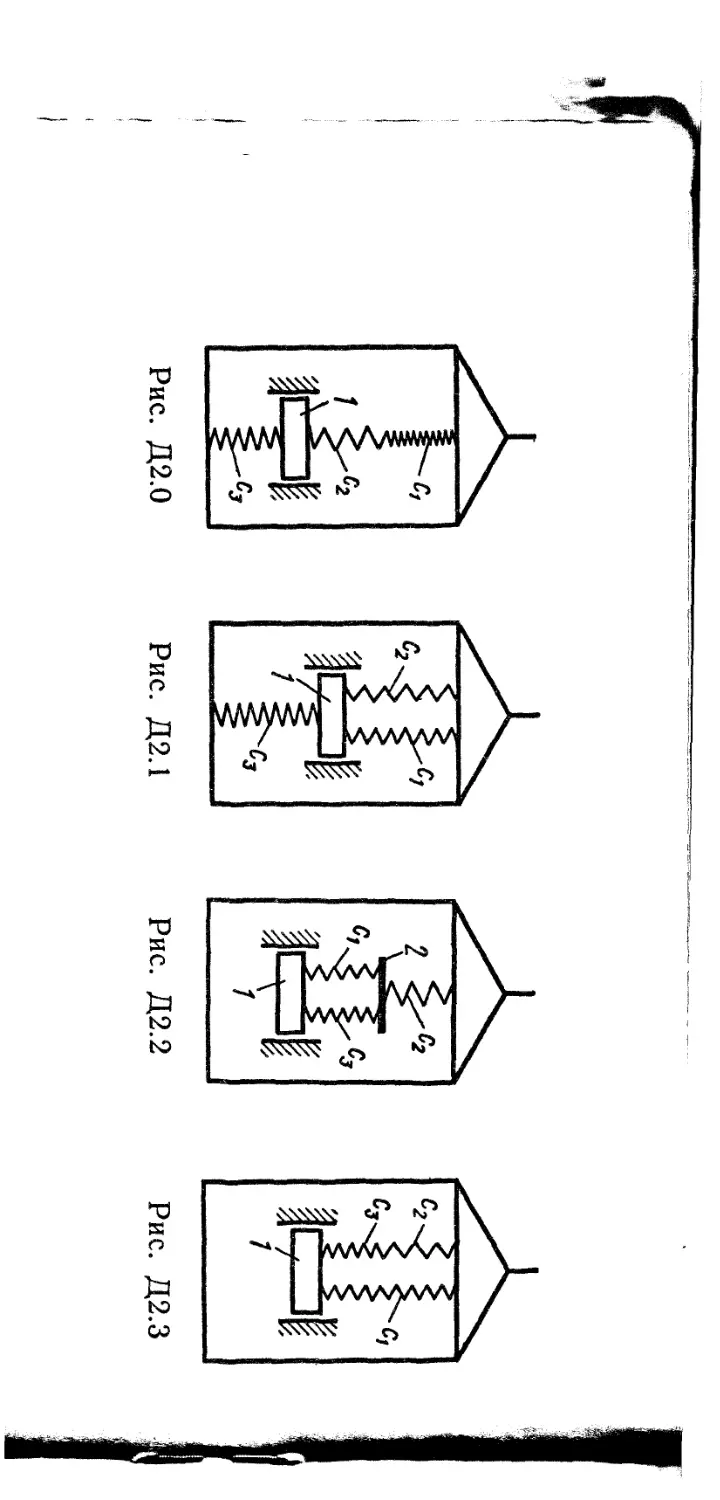
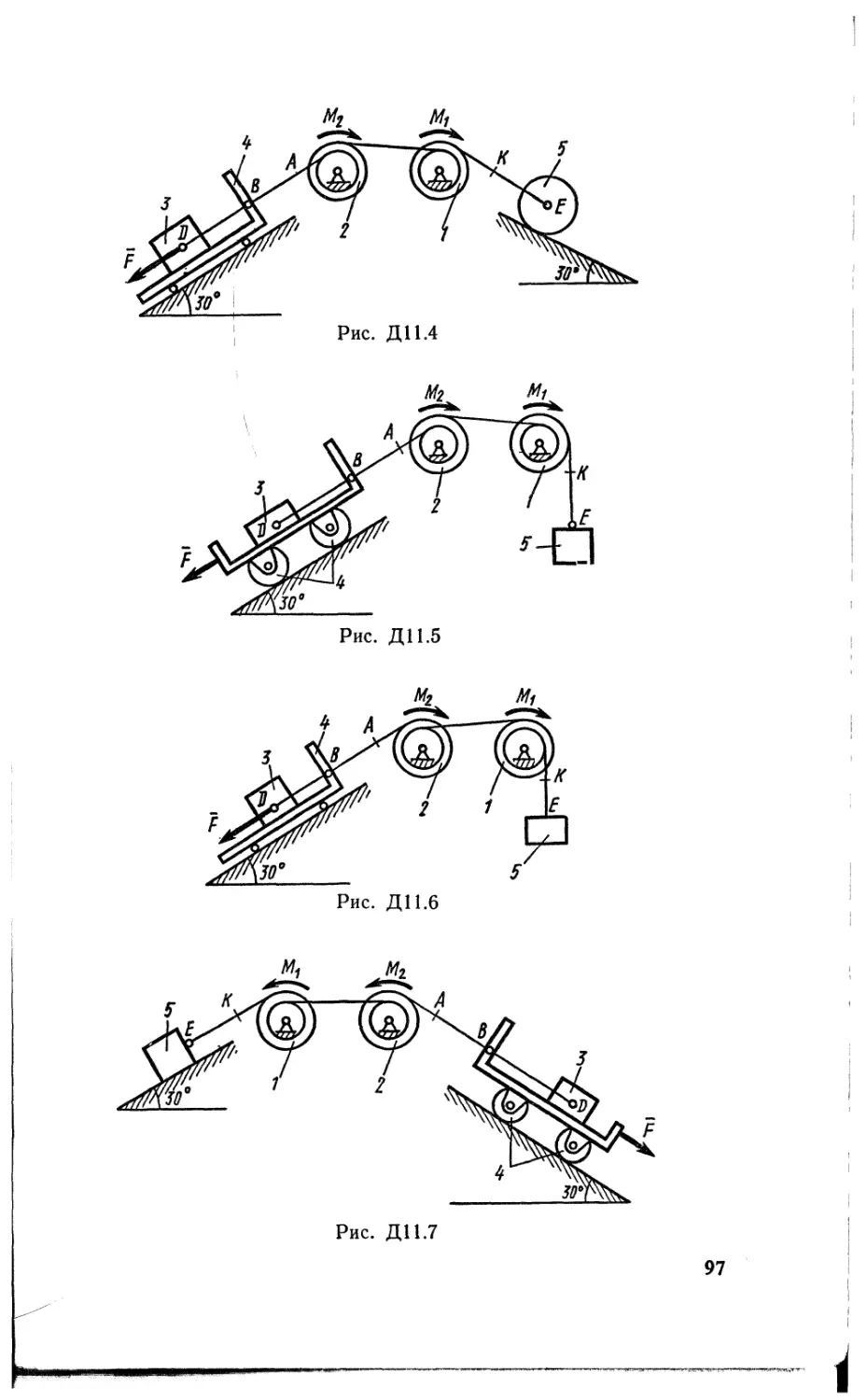
Задача^К2у
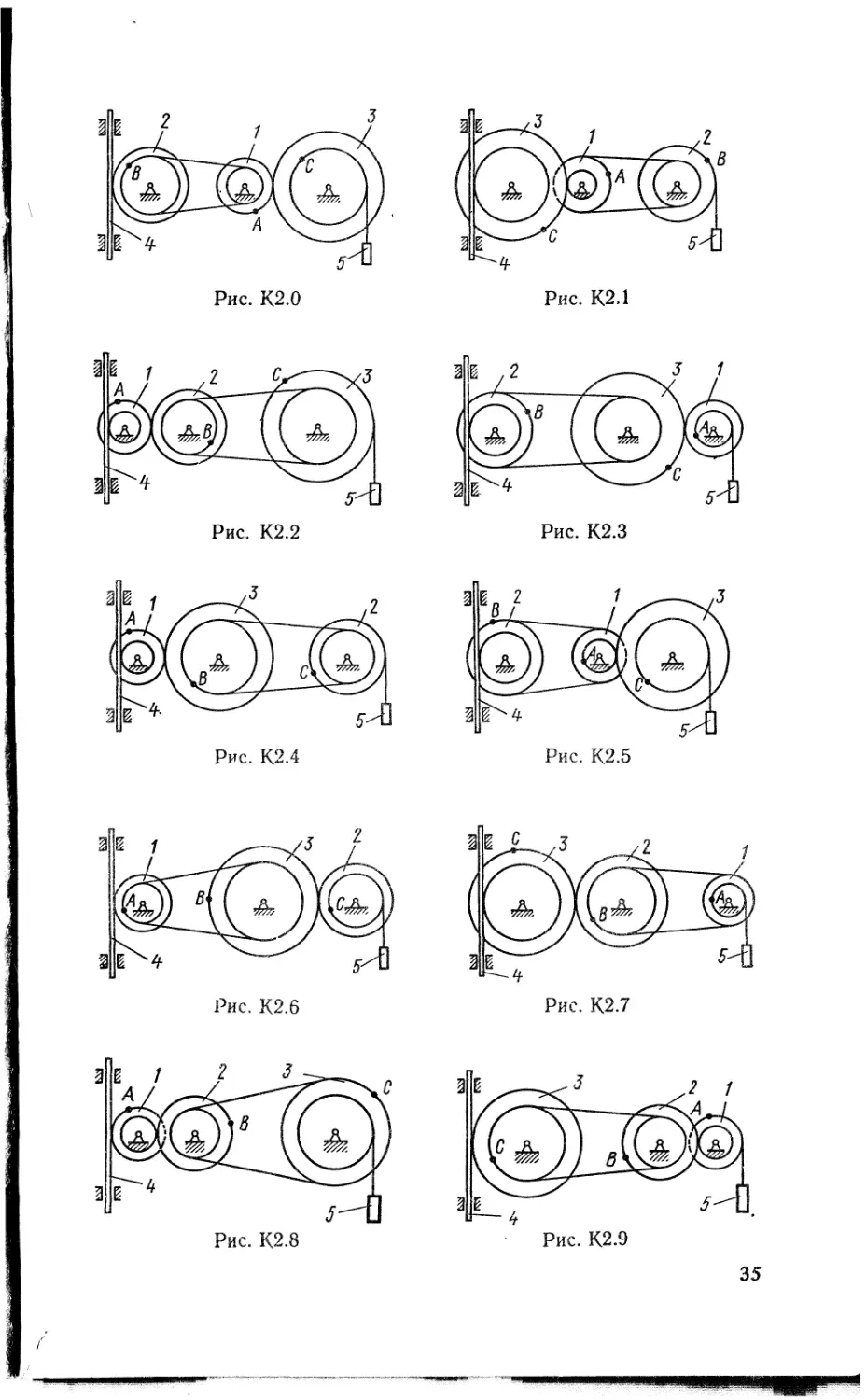
Механизм состоит из ступенчатых колес 1—3, находящихся в зацеплении или связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес (рис. К2.0 — К2.9, табл. К2). Радиусы ступеней колес равны соответственно: у колеса 1 — г\ — 2 см, Ri = 4 см, у колеса 2 г- г2 = 6 см, Т?2 = 8 см, у колеса 3 — гз — 12 см, R3 = 16 см. На ободьях колес расположены точки А, В и С.
В столбце «Дано» таблицы указан закон движения или закон изменения скорости ведущего звена механизма, где <pi(£) — закон вращения колеса /, s<(0 — закон движения рейки 4, (о2(/) — закон изменения угловой скорости колеса 2, v$(t) — закон изменения скорости груза 5 и т. д. (везде <р выражено в радианах, s — в сантиметрах, t — в секундах). Положительное направление для ф и (о против хода часовой стрелки, для s4, $5 и vs ~~ вниз.
Определить в момент времени h — 2 с указанные в таблице в столбцах «Найти» скорости (и — линейные, со — угловые) и ускорения (а—линейные, е — угловые) соответствующих точек или тел (и& — скорость груза 5 и т. д.).
Указания. Задача К2 — на исследование вращательного движения
Таблица К2
Номер условия	Дано	Найти	
		скорости	ускорения
0		V В, Vc	E2,
1	WS 	 о 2 ~	vA, Vc	e3, ав, щ
2	<pi = 2г— 9	V4, (02	e2, etc,
3	<о2= 7/-3/2	Vs, (03	e2, aA} U4
4	фз = 3/ — t2	V4, (01	Ei, aB, as
5	mi = 5t — 2t2	V5, VB	E2, He, Cl4
6	ф2 = 2(/2-3/)	V4, (01	Ei, a,ct as
7	Vf == Зг — 8	vA, (o3	e3, as
8	Ss = 2/2 —5/	V4, (02	ei, ac, a4
9	<03 = 8/- 3t2	V5, VB	e2, aAt П4
Рис. К2.1
Рис. К2.4
Рис. К2.5
Рис. К2.7
Рис. К2.8
Рис. К2.9
Рис. К2
тое колесо 2 с радиусами /?2 и
твердого тела вокруг неподвижной оси. При решении задачи учесть, что, когда два колеса находятся в зацеплении, скорость точки зацепления каждого колеса одна и та же, а когда два колеса связаны ременной передачей, то скорости всех точек ремня и, следовательно, точек, лежащих на ободе каждого из этих колес, в данный момент времени численно одинаковы; при этом считается, что ремень по ободу колеса не скользит.
Пример К2. Рейка /, ступенча-г2 и колесо 3 радиуса /?з, скрепленное
с валом радиуса гз, находятся в зацеплении; на вал намотана нить с грузом 4 на конце (рис. К2). Рейка движется по закону si — f(t).
Дано: Т?2 = 6 см, г2 — 4 см, /?з = 8 см, гз = 3 см, $i = 3t3 (s — в сантиметрах, t — в секундах), А — точка обода колеса 3, t\ = = 3 с. Определить: соз, и4, ез, ал в момент времени t — h.
Решение. Условимся обозначать скорости точек, лежащих на внешних ободах колес (радиуса /?<•), через а точек, лежащих на внутренних ободах (радиуса п), — через щ.
1.	Определяем сначала угловые скорости всех колес как функции времени t. Зная закон движения рейки /, находим ее скорость:
v\ = s’j = 9/2.
(1)
Так как рейка и колесо 2 находятся в зацеплении, то и2 = или со27?2 = Но колеса 2 и 3 тоже находятся в зацеплении, следовательно, и2 = или со2г2 = (£)3/?з. Из этих равенств находим
Vi 3 /2 г2 з _2
<Й2 = “«Г = ^' ’ 6,3 - "/Г*02 ~ ~ •
(2)
Тогда для момента времени 6 = 3 с получим ©з = 6,75 с-1.
2.	Определяем и4. Так как v4 = vB — (о3гз, то при Л = 3 с v4 ~ = 20,25 см/с.
3.	Определяем 83. Учитывая второе из равенств (2), получим ез = = со3 = 1,5/. Тогда при 6 — 3 с е3 = 4,5 с-2.
4.	Определяем аА. Для точки А ал — аАх4гаАп, где численно аЛх = R3&3, аАп — /?зсо2. Тогда для момента времени t\ = 3 с имеем
аАх — 36 см/с2, аАп = 364,5 см/с2;
аА — (Ах 4~ о?Ап — 366,3 см/с2.
Все скорости и ускорения точек, а также направления угловых скоростей показаны на рис. К2.
Ответ: со3 — 6,75 с-1; и4 = 20,25 см/с; е3 = 4,5 с-2; «д = — 366,3 см/с2.
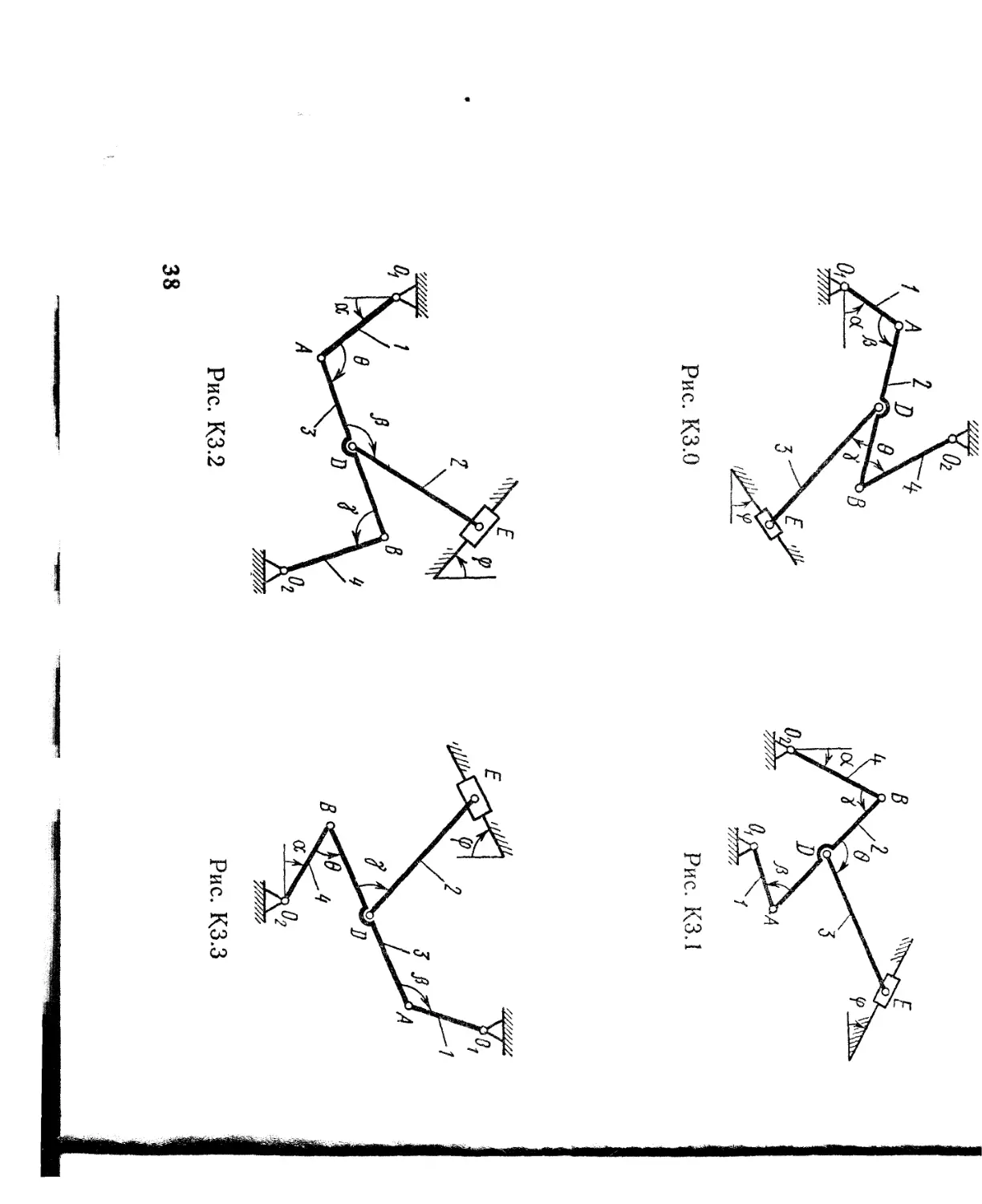
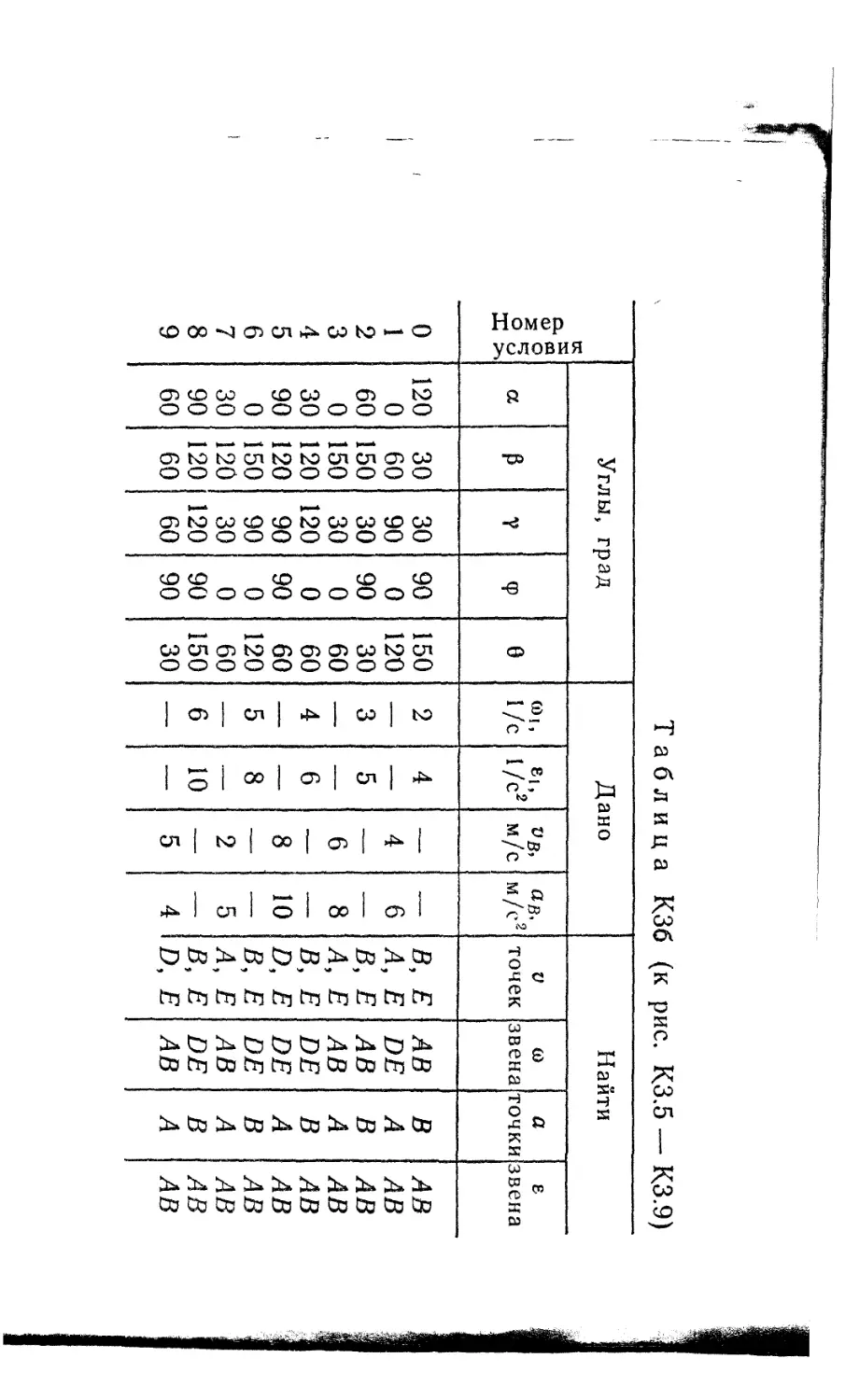
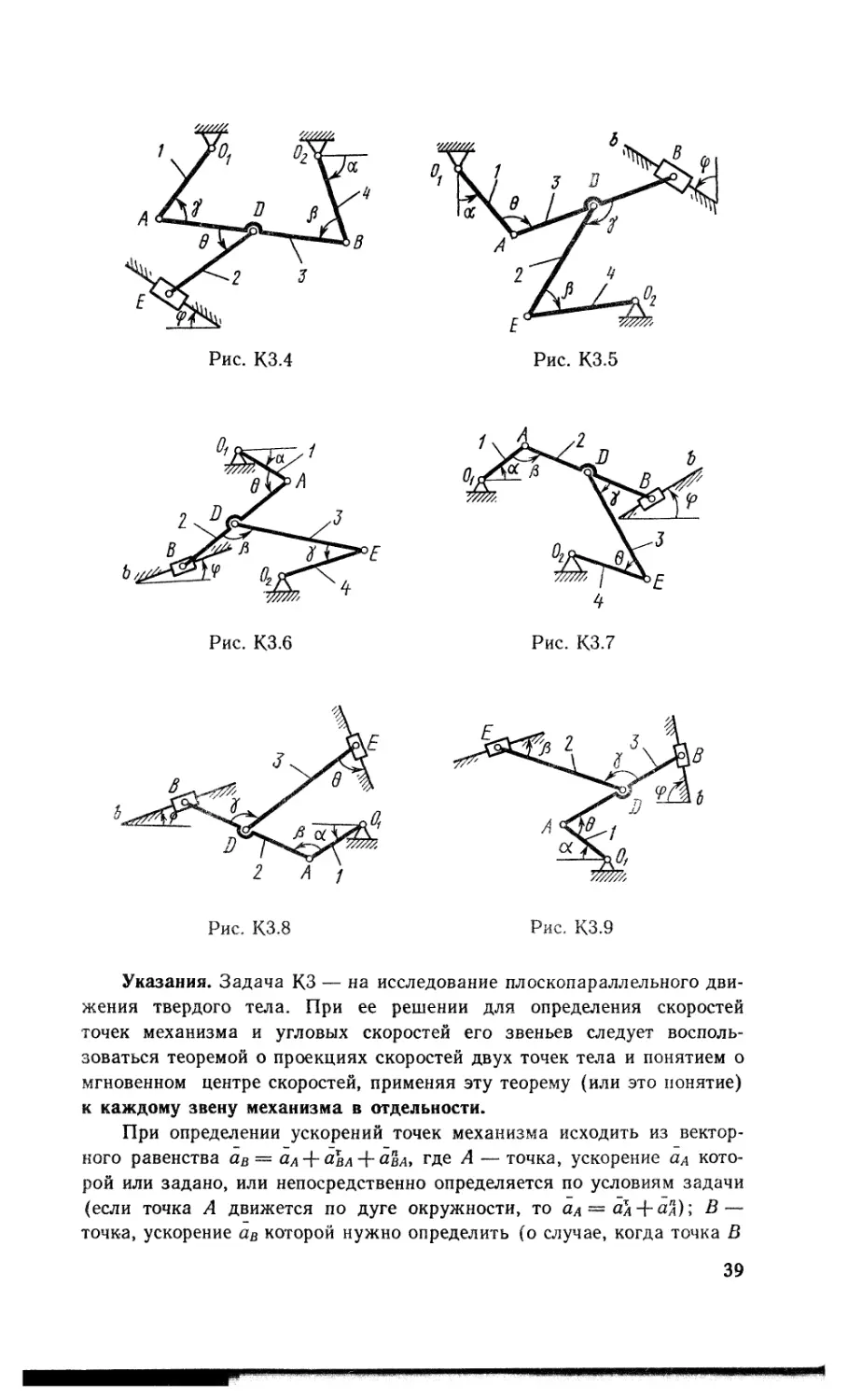
Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна В или Е (рис. КЗ.О — К3.7) или из стержней 1, 2, 3 и ползунов В и Е (рис. К3.8, К3.9), соединенных друг с другом и с неподвижными опорами Oi, О2 шарнирами; точка D находится в середине стержня АВ. Длины стержней равны соответственно 1\ = 0,4 м, I2 ~ 1,2 м, Z3 = 1,4 м, Ц ~ 0,6 м. Положение механизма определяется углами а, р, у, <р, 0. Значения этих углов и других заданных величин указаны в табл. КЗа (для рис. 0—4) или в табл. КЗб (для рис. 5—9); при этом в табл. КЗа (Di и (о4 — величины постоянные.
Определить величины, указанные в таблицах в столбцах «Найти».
Дуговые стрелки на рисунках показывают, как при построении чертежа механизма должны откладываться соответствующие углы: по ходу или против хода часовой стрелки (например, угол у на рис. 8 следует отложить от DB по ходу часовой стрелки, а на рис. 9 — против хода часовой стрелки и т. д.).
Построение чертежа начинать со стержня, направление которого определяется углом а; ползун с направляющими для большей наглядности изобразить так, как в примере КЗ (см. рис. КЗб).
Заданные угловую скорость и угловое ускорение считать направленными против часовой стрелки, а заданные скорость vB и ускорение ав — от точки В к b (на рис. 5—9).
Т а блица КЗа (к рис. КЗ.О — К3.4)
Номер условия	Углы, град					Дано		Найти			
	а	V	Y	Ф	0	(01, 1/с	(О4, 1/с	V точек	£0 звена	а точки	е звена
0	0	60	30	0	120	6		В, Е	DE	В	АВ
1	90	120	150	0	30				4	Л, Е	АВ	А	АВ
2	30	60	30	0	120	5		В, Е	АВ	В	АВ
3	60	150	150	90	30	—	5	А, Е	DE	А	АВ
4	30	30	60	0	150	4		D, Е	АВ	В	АВ
5	90	120	120	90	60	—	6	Л, Е	АВ	А	АВ
6	90	150	120	90	30	3	—_	В, Е	DE	В	АВ
7	0	60	60	0	120	—	2	Л, Е	DE	А	АВ
8	60	150	120	90	30	2		.	D, Е	АВ	В	АВ
9 ।	30	120	150	0	60	—	8	А, Е	DE	А	АВ
Рис. КЗ.О
38
Рис. КЗ.З
Таблица КЗб (к рис. К3.5 — К3.9)
Номер условия	Углы, град					Дано				Найти			
	а	Р	7	Ф	0	(Й1, 1/с	8|, 1/С2	VB, м/с	ав, м/с2	V точек	(0 звена	а точки	в звена
0	120	30	30	90	150	2	4			—	В, £	АВ	В	АВ
1	0	60	90	0	120	—	—	4	6	Д, Е	DE	А	АВ
2	60	150	30	90	30	3	5	—	—	В, Е	АВ	В	АВ
3	0	150	30	0	60	—	—	6	8	Д, Е	АВ	А	АВ
4	30	120	120	0	60	4	6	—	—	В, Е	DE	В	АВ
5	90	120	90	90	60	—	—.	8	10	D, £	DE	А	АВ
6	0	150	90	0	120	5	8	—_	—	В, Е	DE	В	АВ
7	30	120	30	0	60	—	—	2	5	Д, Е	АВ	А	АВ
8	90	120	120	90	150	6	10	—	—	Bt Е	DE	В	АВ
9	60	60	60	90	30	—	.—	5	4	D, Е	АВ	А	АВ
Указания. Задача КЗ — на исследование плоскопараллельного движения твердого тела. При ее решении для определения скоростей точек механизма и угловых скоростей его звеньев следует воспользоваться теоремой о проекциях скоростей двух точек тела и понятием о мгновенном центре скоростей, применяя эту теорему (или это понятие) к каждому звену механизма в отдельности.
При определении ускорений точек механизма исходить из векторного равенства ав — ад + «вл + яВа> где А — точка, ускорение ад которой или задано, или непосредственно определяется по условиям задачи (если точка А движется по дуге окружности, то ал — ал + «д); В— точка, ускорение ав которой нужно определить (о случае, когда точка В
Ог
тоже движется по дуге окружности, см. примечание в конце рассмотренного ниже примера КЗ).
Пример КЗ. Механизм (рис. КЗа) состоит из стержней 1, 2, 3, 4 и ползуна В, соединенных друг с другом и с неподвижными опорами Oi и О2 шарнирами.
Дано: .«=60°, ₽ = 150°, у = 90°, <р = 30°, 0= 30°, AD = DB, li = 0,4 м, /2 — 1,2 м, /3 = 1,4 м, (01 = 2 с-1, ei = 7 с~2 (направления он и 81 — против хода часовой стрелки). Определить: vB, ve , (02,	S3-
Решение. 1. Строим положение механизма в соответствии с заданными углами (рис. КЗб; на этом рисунке изображаем все векторы скоростей).
2. Определяем vB. Точка В принадлежит стержню АВ. Чтобы найти надо знать скорость какой-нибудь другой точки этого стержня и направление vB. По данным задачи, учитывая направление (Di, можем определить va, численно
vA = (O1/1 = 0,8 м/с; vA -L OiA .	(1)
Направление vB найдем, учтя, что точка В принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь, зная иА и направление vB, воспользуемся теоремой о проекциях скоростей двух точек тела (стержня АВ) на прямую, соединяющую эти точки (прямая АВ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор ив (проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
yBcos30°= vacos60° и vB — 0,46 м/с.	(2)
3. Определяем ив. Точка Е принадлежит стержню DE. Следовательно, по аналогии с предыдущим, чтобы определить надо сначала
найти скорость точки D, принадлежащей одновременно стержню АВ. Для этого, зная va и vb, строим мгновенный центр скоростей (МЦС) стержня АВ; это точка Сз, лежащая на пересечении перпендикуляров к va и vb, восставленных «из точек А и В (к va перпендикулярен стержень /). По направлению вектора va определяем направление поворота стержня АВ вокруг МЦС Сз. Вектор vd перпендикулярен отрезку C3D, соединяющему точки D и С3, и направлен в сторону поворота. Величину Vd найдем из пропорции
vD _ Vb
~cjT -~~с7в~ ‘
(3)
Чтобы вычислить C3D и СзВ, заметим, что ААСзВ — прямоуголь- . ный, так как острые углы в нем равны 30° и 60°, и что С3В = = ДВэшЗО0 = 0,5ДВ = BD. Тогда ABC3Z) является равносторонним и СзВ — C3D. В результате равенство (3) дает
vd — vB = 0,46 м/с; vD _L С3£> .
(4)
Так как точка Е принадлежит одновременно стержню О2Е, вращающемуся вокруг О2, то Ve-LOzE. Тогда, восставляя из точек Е и D перпендикуляры к скоростям ve и vd, построим МЦС 6*2 стержня DE. По направлению вектора vD определяем направление поворота стержня DE вокруг центра 6*2. Вектор ve направлен в сторону поворота этого стержня. Из рис. КЗб видно, что /_C$ED = /_C$DE — 30°, откуда С2Е = C2D. Составив теперь пропорцию, найдем, что
vE	vd
С2Е	C2D
vE — Vd ~ 0,46 м/с .
(5)
4. Определяем (02. Так как МЦС. стержня 2 известен
(точка 6*2) и
C2D = /2/(2cos30°) = 0,69 м, то
vD
0,2 С^Г
5. Определяем ав (рис. КЗв, на котором изображаем все векторы ускорений). Точка В принадлежит стержню АВ. Чтобы найти ав, надо знать ускорение какой-нибудь другой точки стержня АВ и траекторию точки В. По данным задачи можем определить аА — ад-\~ал, где численно
аА — sUi = 2,8 м/с2;
ад = «1/1 = 1,6 м/с2.	(7)
4 — 1722
Вектор ~апА направлен вдоль АО\, а ахА— перпендикулярно ДОг, изображаем эти векторы на чертеже (см. рис. КЗв). Так как точка В одновременно принадлежит ползуну, то вектор ав параллелен направляющим ползуна. Изображаем вектор ав на чертеже, полагая, что он направлен в ту же сторону, что и vB.
Для определения ав воспользуемся равенством
ав~ аА Д- аА 4- ахВА 4~ аВА .	(8)
Изображаем на чертеже векторы о^д (вдоль В А от В к А) и аВА (в любую сторону перпендикулярно ВА); численно аВА — соз/з- Найдя (Оз с помощью построенного МЦС С3 стержня 3, получим
vAvA
=	^30- = °’66 с й = °’61 м/с •
Таким образом, у величин, входящих в равенство (8), неизвестны только числовые значения ав и ахВА; их можно найти, спроектировав обе части равенства (8) на какие-нибудь две оси.
Чтобы определить аВу спроектируем обе части равенства (8) на направление ВА (ось х), перпендикулярное неизвестному вектору аВА. Тогда получим
aBcos30° = аА cos60° — cfAcos30° 4~ cfBA .	(10)
Подставив в равенство (10) числовые значения всех величин из (7) и (9), найдем, что
ав = 0,72 м/с2.	(11)
Так как получилось ав>0, то, следовательно, вектор ав направлен как показано на рис. КЗв.
6.	Определяем Ез. Чтобы найти ез, сначала определим ахВА. Для этого обе части равенства (8) спроектируем на направление, перпендикулярное АВ (ось у). Тогда получим
— ав sin 30° = аА sin 60° + <Л sin 30° 4- аВА .	(12)
Подставив в равенство (12) числовые значения всех величин -из (11) и (7), найдем, что аВА = —3,58 м/с2. Знак указывает, что направление ахВА противоположно показанному на рис. КЗв.
Теперь из равенства аВА = E3Z3 получим
|аЬл1 _2 е3 = __	2,56 с .
/з
Ответ: vB = 0,46 м/с; vE — 0,46 м/с; сог = 0,67 с~’; ав = = 0,72 м/с2; Е3= 2,56 с““2.
Примечание. Если точка В, ускорение которой определяется, движется не прямолинейно (например, как на рис. КЗ.О — КЗ.4, где В движется по окружности радиуса О2В), то направление ав заранее неизвестно.
В этом случае ав также следует представить двумя составляющими (ав = ав + апв) и исходное уравнение (8) примет вид
ab + <?ff= ахА + й + ®ва + йл •	(13)
При этом вектор апв (см., например, рис. КЗ.О) будет направлен вдоль ВО2, а вектор ав — перпендикулярно ВО2 в любую сторону. Числовые значения 34, й и апвА определяются так же, как в рассмотренном примере (в частности, по условиям задачи может быть ахд — 0 или бД = О, если точка А движется прямолинейно).
Значение бД также вычисляется по формуле сРв — и2в/р — Й/4 где I — радиус окружности О2В, a vB определяется так же, как скорость любой другой точки механизма.
После этого в равенстве (13) остаются неизвестными только значения ахв и ахВА и они, как и в рассмотренном примере, находятся проектированием обеих частей равенства (13) на две оси.
Найдя axBi можем вычислить искомое ускорение «в = л/(й)2+(й)2« Величина ахВА служит для нахождения 8дв (как в рассмотренном примере).
Задача К4
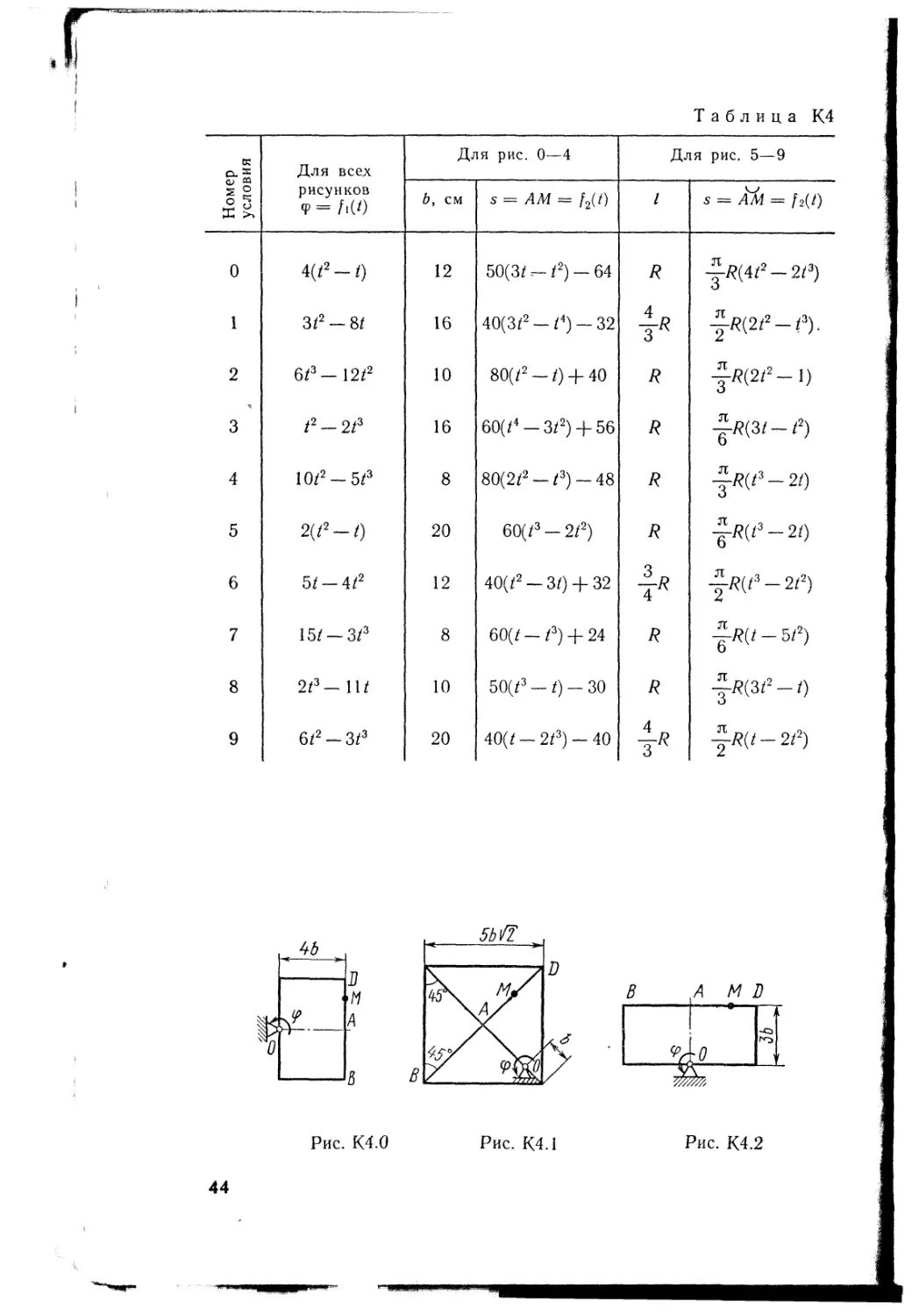
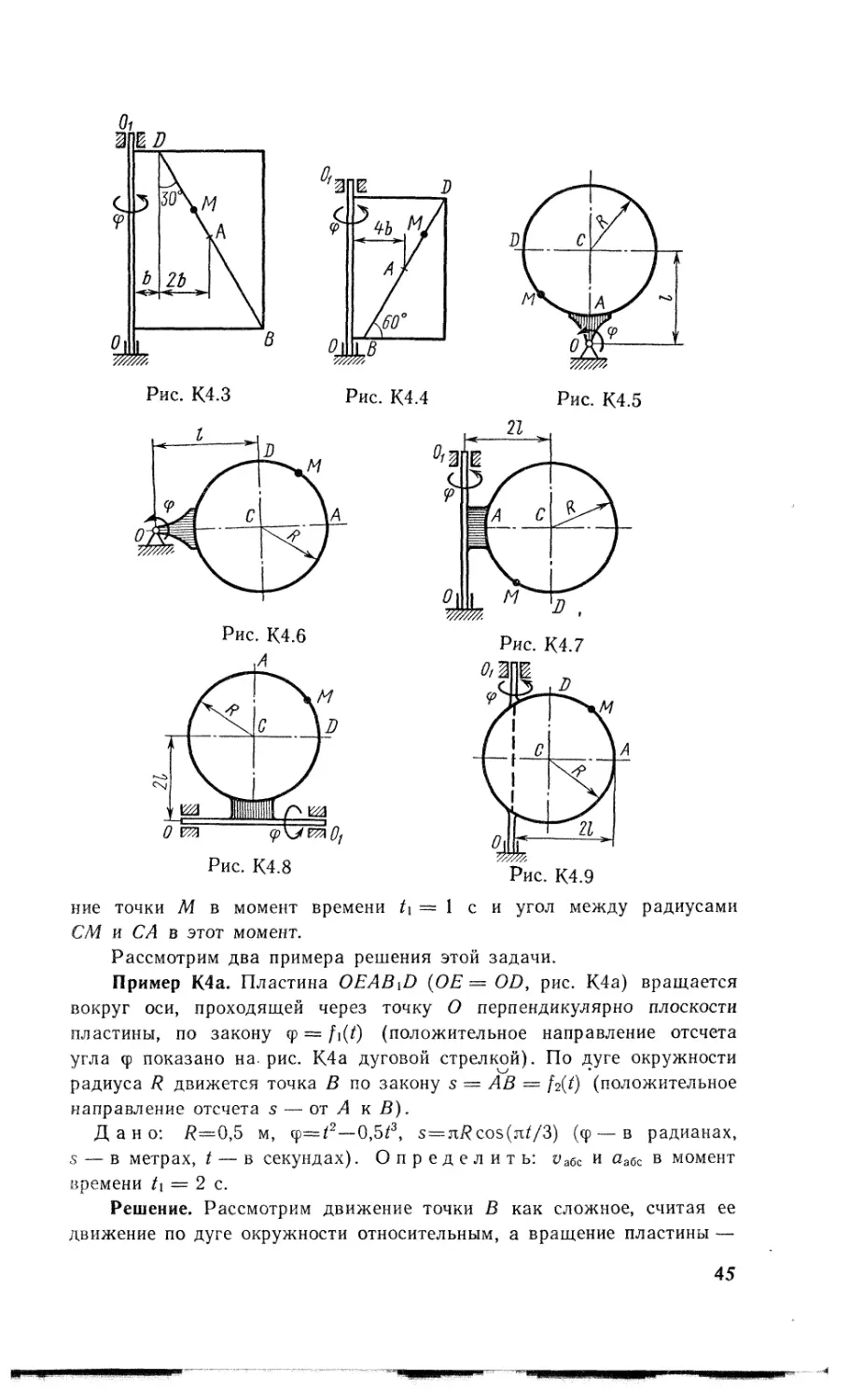
Прямоугольная пластина (рис. К4.0 — К4.4) или круглая пластина радиуса /? = 60 см (рис. К4.5 — К4.9) вращается вокруг неподвижной оси по закону ф = заданному в табл. К4. Положительное направление отсчета угла ф показано на рисунках дуговой- стрелкой. На рис. 0, 1, 2, 5, 6 ось вращения перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. 3, 4, 7, 8, 9 ось вращения OOi лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой BD (рис. 0—4) или по окружности радиуса R (рис. 5—9) движется точка М; закон ее относительного движения, т. е. зависимость s = AM — fdj) (s выражено в сантиметрах, Z — в секундах), задан в таблице отдельно для рис. 0—4 и для рис. 5—9; там же даны размеры b и I. На рисунках точка М показана в положении, при котором s = 4M>0 (при s<0 точка М находится по другую сторону от точки Л).
Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t\ = 1 с.
Указания. Задача К4 — на сложное движение точки. Для ее решения воспользоваться теоремами о сложении скоростей и о сложении ускорений. Прежде чем производить все расчеты, следует пб условиям задачи определить, где находится точка М на пластине в момент времени t\ = 1 с, и изобразить точку именно в этом положении (а не в произвольном, показанном на рисунках к задаче).
В случаях, относящихся к рис. 5—9, при решении задачи не подставлять числового значения /?, пока не будут определены положе-
Рис. К4.0	Рис. К4.1	Рис. К4.2
10/2 — 5/3	8	80(2/2/3) — 48 R
Таблица К4
O1
g О
Рис. K4.3	Рис. K4.4	Рис. K4.5
ние точки М в момент времени h = I с и угол между радиусами СМ и СА в этот момент.
Рассмотрим два примера решения этой задачи.
Пример К4а. Пластина OEAB\D (ОЕ = OD, рис. К4а) вращается вокруг оси, проходящей через точку О перпендикулярно плоскости пластины, по закону <р = fi(f) (положительное направление отсчета угла ф показано на. рис. К4а дуговой стрелкой). По дуге окружности радиуса R движется точка В по закону s — АВ = /г(0 (положительное направление отсчета s — от Л кВ).
Дано: В—0,5 м, ф==/2—0,5/3, s=nBcos(n^/3) (ф — в радианах, s — в метрах, t — в секундах). Определить: иабс и пабс в момент времени t\ — 2 с.
Решение. Рассмотрим движение точки В как сложное, считая ее движение по дуге окружности относительным, а вращение пластины —
переносным движением. Тогда абсолютная скорость уабс и абсолютное ускорение аабс точки найдутся по формулам:
^абс —’ ^отн ~h ^пер »
«абс === «отн 4“ «пер "Т" « кор »	( 1)
где, в свою очередь,
П^отн == «отн 4“ «отн, «пер=±: «пер~|“ «пер •
Определим все, входящие в равенства (1) величины.
1.	Относительное движение. Это движение происходит по закону
s = АВ = nR соз(л//3) .	(2)
Сначала установим, где будет находиться точка В на дуге окружности в момент времени h. Полагая в уравнении (2) h = 2 с, получим
si = ji/?cos(ji2/3) = — 0,5л/? .
Тогда
Z4CB = -^- = -0,5л. А
Знак минус свидетельствует о том, что точка В в момент ti = 2 с находится справа от точки А, Изображаем ее на рис. К4а в этом положении (точка £h).
Теперь находим числовые значения иотн, Яотн, «”тн-‘
n2R . , ./ох
UOTH = S = — —— sin (jtZ/3) ,
О
_•	Л3/? /о\ л	У°тн
«отн — ^отн —‘	”q COS(n7/3) , «отн — ~~~	— ~ п ' >
У	Роти А
где ратн — радиус кривизны относительной траектории, равный радиусу окружности R. Для момента ti = 2 с, учитывая, что R ~ 0,5 м, получим
%тн = — - -—sm(2jt/3) = —-Ь— = — 1,42 м/с , м	1Z
«отн = ~--^“СО8(2л/3) =	= 0,86 м/с2, 6ЙТН =	= 4,06 м/с2е
9	оо	24
Знаки показывают, что вектор floTH направлен в сторону положительного отсчета расстояния s, а вектор уотн — в противоположную сторону; вектор а"отн направлен к центру С окружности. Изображаем все эти векторы на рис. К4а.
2.	Переносное движение. Это движение (вращение) происходит по закону ф = t2 — 0,5/3. Найдем сначала угловую скорость со и угловое ускорение е переносного вращения?
со = ф = 2t — 1,5/2, е — со = 2 — 31
и при ti = 2 с
со = —2 с-1, е= — 4 с~2.	(4)
Знаки указывают, что в момент t\ = 2 с направления со и е противоположны направлению положительного отсчета угла ф; отметим это на рис. К4а.
Для определения упер и апер находим сначала расстояние hi = OBi точки Bi от оси вращения О. Из рисунка видно, что hi —	=
= 1,41 м. Тогда в момент времени t\ = 2 с, учитывая равенства (4), получим
Упер = |со| •/?! = 2,82 м/с ,
«пер — 1е| • hi = 5,64 м/с2, с^ер = co2/ij = 5,64 м/с2.	(5)
Изображаем на рис. К4а векторы упер и Ядер с учетом направлений со и е и вектор йер (направлен к оси вращения).
3.	Кориолисово ускорение. Модуль кориолисова ускорения определяем по формуле акор = 2|уотн| • 1«| • sin а, где а — угол между вектором иотн и осью вращения (вектором со). В нашем случае этот угол равен 90°, так как ось вращения перпендикулярна плоскости пластины, в которой расположен вектор уотн. Численно в момент времени /1 = 2 с, так как в этот момент |у0Тн1 = 1,42 м/с и Iсо| — 2 с-1, получим
«кор = 5,68 м/с2.	(6)
Направление акор найдем по правилу Н. Е. Жуковского: так как вектор Уотн лежит в плоскости, перпендикулярной оси вращения, то повернем его на 90° в направлении со, т. е. по ходу часовой стрелки. Изображаем акор на рис. К4а. [Иначе направление акор можно найти, учтя, что «кор = 2(соХ «отн)-]
Таким образом, значения всех входящих в правые части равенств (1) векторов найдены и для определения уабс и аабС остается только сложить эти векторы. Произведем это сложение аналитически.
4.	Определение уабс. Проведем координатные оси В\ху (см. рис. К4а) и спроектируем почленно обе части равенства
Уабс = Уотн + Упер НЗ ЭТИ ОСИ. ПолуЧИМ ДЛЯ МОМСНТЭ Времени /1 = 2 с:
Уабсх = Уотнх+ Уперх = 0 — |vпер| cos45° = — 1,99 м/с ;
Уабсу === У отну *4“ У перу === I Уотн1 "4” I Упер! COS 45 = 3,41 м/С .
После этого находим
Уабс == ~\/ Уабсх*4” У абсу == 3,95 м/с .
Учитывая, что в данном случае угол между иотн и ипер равен 45°, значение иабс можно еще определить по формуле
Уабс === Уотн "4" Упер ~4~ 2|уотн| • |Упер1 ’ COS 45 = 3,95 м/с .
5.	Определение аабс. По теореме о сложении ускорений
#абс #отн + #от + #пер + #пер 4~ #кор •	(7)
Для определения аабс спроектируем обе части равенства (7) на проведенные оси В\ху. Получим
У^абсх == У'отн Ч- У^кор "4” У^пер COS 45  l^nepl COS 45 ,
У^абсу == ^nepCOS45 -J-l^nepl COS 45	’ I^oth! •
Подставив сюда значения, которые все величины имеют в момент времени /1 = 2 с, найдем, что в этот момент
«абсх= 9,74 м/с2 ; Лабсу= 7,15 м/с2.
Тогда
Дабе = -у а2бсх 4- al6cy = 12,08 м/с2.
Ответ: иабс = 3,95 м/с, аабс= = 12,08 м/с2.
Пример К4б. Треугольная пластина ADE вращается вокруг оси z по закону ср = fi(/) (положительное направление отсчета угла ф показано на рис. К4б дуговой стрелкой). По гипотенузе AD движется точка В по закону s = АВ = f2(/); положительное направление отсчета s от А к D.
Дано: ф = 0,1 /3 — 2,2/, s = = А В = 2 + 15/ —• З/2; (ф — в радианах, s — в сантиметрах, / — в секундах) . Определить: уабс и аабс в момент времени /1 = 2 с.
Решение. Рассмотрим движение точки В как сложное, считая ее
движение по прямой AD относительным, а вращение пластины — переносным. Тогда абсолютная скорость vaQC и абсолютное ускорение аабс найдутся по формулам:
Уабс == Уотн + Упер, «абс == «отн 4“ «пер "4" «кор »	( 1 )
где, в свою очередь, апер = ЯпеР + ^ер •
Определим все входящие в равенство (1) величины.
1.	Относительное движение. Это движение прямолинейное- и происходит по закону
s = ЛВ = 2-ф-15/—- З/2.	(2)
Поэтому
Уогн — *5 — 15 6/ , «отн — Уотн —	6 .
В момент времени ti = 2 с имеем
si — ABi = 20 см, иотн — 3 см/с, аотн = — 6 см/с2.	(3)
Знаки показывают, что вектор аотн направлен в сторону положительного отсчета расстояния s, а вектор аотн — в противоположную сторону. Изображаем эти векторы на рис. К4б.
2.	Переносное движение. Это движение (вращение) происходит по закону ср = 0, И3 —2,2/.
Найдем угловую скорость со и угловое ускорение с переносного вращения: -со — ф = 0,3/2 — 2,2; е — со = 0,6/ и при Л = 2 с,
со — — 1 с-1 , 8 = 1,2 с~2.	(4)
Знаки указывают, что в момент ti — 2 с направление е совпадает с направлением положительного отсчета угла ф, а направление со ему противоположно; отметим это на рис. К4, б соответствующими дуговыми стрелками.
Из рисунка находим расстояние hi точки Bi от оси вращения z: hi = ЛВ^ш 30° = 10 см. Тогда в момент t\ = 2 с, учитывая равенства (4), получим
Упер = 1<Ю|-hi = 10 СМ/С,
«пер = |е|-hl = 12 см/с2 , CZnep = O)2/li = 10 см/с2 .	(5)
Изобразим на рис. К4б векторы ипер и cznep (с учетом знаков со и е) и аппер; направлены векторы апер и Япер перпендикулярно плоскости ADE, а вектор йеР — по линии В\С к оси вращения.
3.	Кориолисово ускорение. Так как угол между вектором уотн и осью вращения (вектором со) равен 30°, то численно в момент времени h = 2 с
«кор = 2- |уотн| • |со| • sin 30° = 3 см/с2.
(6)
49
Направление акор найдем по правилу Н. Е. Жуковского. Для этого вектор Уотн спроектируем на плоскость, перпендикулярную оси вращения (проекция направлена противоположно вектору а"ер) и затем эту проекцию повернем на 90° в сторону со, т. е. по ходу часовой стрелки; получим направление вектора акор. Он направлен перпендикулярно плоскости пластины так же, как вектор ипер (см. рис. К4б).
4.	Определение уабс. Так как пабс — иОТн + ПпеР, а векторы потн и упер взаимно перпендикулярны, то иабс = д/^отя + Ар5 в момент времени 6 = 2 с уабс = 10,44 см/с.
5.	Определение аабс. По теореме о сложении ускорений
&абс == &отн	^пер “F ^пер “F ^кор •	(7)
Для определения аабс проведем координатные оси B{xyz\ и вычислим проекции аабс на эти оси. Учтем при этом, что векторы Япер и акор лежат на оси х, а векторы а"еР-и аотн расположены в плоскости Bxyzt, т. е. в плоскости пластины. Тогда, проектируя обе части равенства (7) на оси Bixyzi и учтя одновременно равенства (3), (5), (6), получим для момента времени 6 = 2 с:
^абсх == i^nepl &кор === 9 См/с , Яабсу = Ар + I^othI Sin 30° = 13 СМ/С2 , «абс^ = |aOTHlcos30° = 5,20 см/с2.
Отсюда находим значение аабС
«абс =	+	Acs.= 16,64 СМ/с2 .
Ответ: уабс = 10,44 см/с, аабс = 16,64 см/с2.
ДИНАМИКА
Задача Д1\/
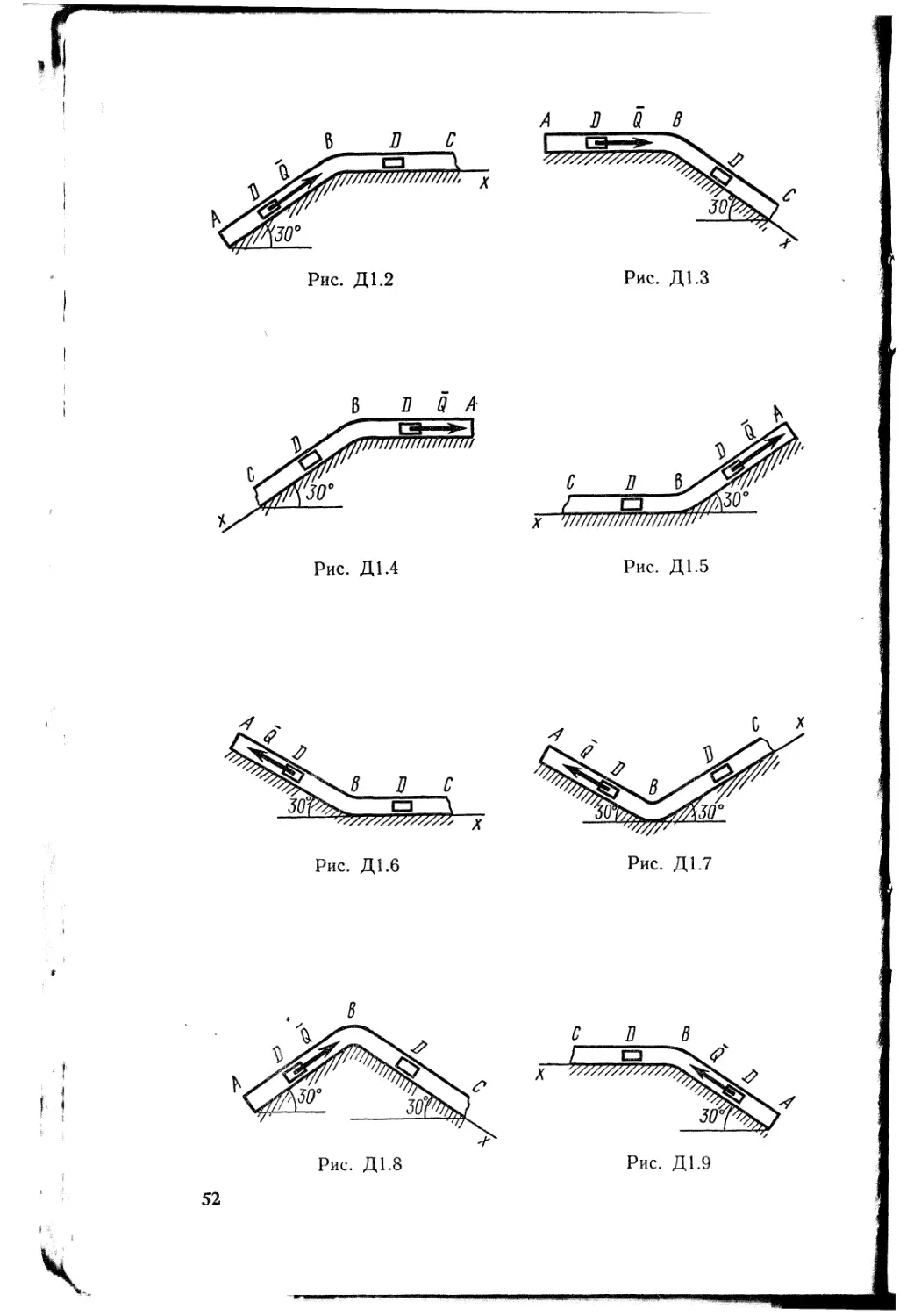
Груз D массой т, получив в точке А начальную скорость ио, движется в изогнутой трубе АВС, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д1.0 —Д1.9, табл. Д1).
На участке АВ на груз кроме силы тяжести действуют постоянная сила Q (ее направление показано на рисунках) и сила сопротивления среды R, зависящая от скорости v груза (направлена против движения); трением груза о трубу на участке АВ пренебречь.
В точке В груз, не изменяя своей скорости, переходит на участок ВС трубы, где на него кроме силы тяжести действуют сила трения (коэффициент трения груза о трубу f = 0,2) и переменная сила F, проекция которой Fx на ось х задана в таблице.
Считая груз материальной точкой и зная расстояние АВ = I или
время ti движения груза от точки А до точки В, найти закон движения груза на участке ВС, т. е. х — f(t), где х = BD.
Указания. Задача Д1 — на интегрирование дифференциальных уравнений движения точки (решение основной задачи динамики). Решение задачи разбивается на две части. Сначала нужно составить и проинтегрировать методом разделения переменных дифференциальное уравнение движения точки (груза) на участке АВ, учтя начальные условия. Затем, зная время движения груза на участке АВ или длину этого участка, определить скорость груза в точке В. Эта скорость будет начальной для движения груза на участке ВС. После этого нужно составить и проинтегрировать дифференциальное уравнение движения груза на участке ВС тоже с учетом начальных условий, ведя отсчет времени от момента, когда груз находится в точке В, и полагая в этот момент t — 0. При интегрировании уравнения движения на участке АВ в случае, когда задана длина I участка, целесообразно перейти к переменному х, учтя, что
chx d/ Vx dx
Таблица Д1
Номер условия	т, кг	Vo, м/с	Q, Н	R, Н	/, м	/ь с	Fx, Н
0	2	20	6	0,4и					2,5	2 sin (4/)
1	2,4	12	6	0,8о2	1,5		6/
2	4,5	24	9	0,5и	-—	3	3sin(2/)
3	6	14	22	0,6и2	5		— 3cos(2/)
4	1,6	18	4	0,4и	—	2	4 cos (4/)
5	8	10	16	0,5и2	4	—	— 6 sin (2/)
6	1,8	24	5	0,Зи	___	2	9/2
7	4	12	12	0,8и2	2,5	—	— 8 cos (4/)
8	3	22	9	0,5и	—	3	2cos(2/)
9	4,8	10	12	0,2и2	4	—	— 6 sin (4/)
Рис. Д1.0
Рис. Д 1.1
Рис. Д1.3
Рис. Д1.4
Рис. Д1.9
X
Рис. Д1
Пример Д1. На вертикальном участке АВ трубы (рис. Д1) на груз D массой т действуют сила тяжести и сила сопротивления R; расстояние от точки 4, где v = о0, до точки В равно I. На наклонном участке ВС на груз действуют сила тяжести и переменная сила F = F(/), заданная в ньютонах.
Дано: m — 2 кг, R = ци2,где р = 0,4 кг/м, о0 = 5 м/с, I = 2,5 м, Fx = 16sin(4/). Определить: х — f(t) — закон движения груза на участке ВС.
Решение. 1. Рассмотрим движение груза на участке АВ, считая груз материальной точкой. Изображаем груз (в произвольном положении) и действующие на него силы Р — mg и R. Проводим ось Az и составляем дифференциальное уравнение движения груза в проекции на эту ось:
dvz	dvz
т—гг-= ^Fkz или mvz—z—= Pz + Rz •	0)
сп	dz
Далее находим Р2 — Р = mg, Rz = — R = — ро2; подчеркиваем, что в уравнении все переменные силы надо обязательно выразить через величины, от которых они зависят. Учтя еще, что vz = и, получим
do	2 do р / mg 2\ zov
—= mg— poz или о—г— = -£—(—2—— о ).	(2)
dz	dz tn \ p /
Введем для сокращения записей обозначения
k = -И- = 0,2 м~' , п =	= 50 м2/с2,	(3)
т	р
где при подсчете принято	м/с2. Тогда уравнение (2) можно
представить в виде
2о .	~ 2k(v2 — ri} .	(4)
az
Разделяя в уравнении (4) переменные, а затем беря от обеих частей интегралы, получим
-Д-Р-Р- — — 2&dz и ln(v2 — п) =—2kzA~ Ci.	(5)
о —и
По начальным условиям при z — 0 о = оо, что дает Ci — 1п(о2 —м) и из равенства (5) находим In (v2 — n) = — 2kz~F ln(oo — n) или ln(o2 — — n) — ln(oo —n) = — 2kz. Отсюда
, v2 — n	v2-—n _2kz
In—y-----= — 2kz и ——— = e 2kz.
Vo — n	VQ — n
।	В результате находим
v2 = п + (vl — n)e~2kz .	(6)
।	Полагая в равенстве (6) z = / = 2,5 м и заменяя k* и п их значе-
i	ниями (3), определим скорость vB груза в точке В (t»o = 5 м/с, число
е = 2,7):
vB = 50 — 25/е = 40,7 и vB — 6,4 м/с.	(7)
|	2. Рассмотрим теперь движение груза на участке В.С\ найденная
!	скорость vB будет для движения на этом участке начальной скоростью
।	(уо = Ув). Изображаем груз (в произвольном положении) .и действую-
щие на него силы Р = mg,N,Frp и F. Проведем из точки В оси Вх и
;	By и составим дифференциальное уравнение движения груза в проекции
-	на ось Вх:
dvx
= Рх+ N *+ FTpx + Fx
или
dvx
т—^— = mgsina—FTp-j-Fx ,	(8)
где FTp = fN. Для определения N составим уравнение в проекции на ось By. Так как ау = 0, получим 0 == N — mg cos а, откуда N = mg cos а. Следовательно, Гтр = fmgcosa; кроме того, Fx— 16sin(4Z) и уравнение (8) примет вид
dux
W~37 — m^(sina —fcosa) + 16sin(4/) .	(9)
Разделив обе части равенства на т, вычислим g(sina —/cosa) = = g( sin 30° — 0,2 cos 30°) = 3,2; 16/m==8 и подставим эти значения в (9). Тогда получим
dyx
—^-== 3,2 + 8 sin (4/) .	(10)
Умножая обе части уравнения (10) на d/ и интегрируя, найдем
ух == 3,2/ —2cos(4/)+С2 .	(11)
Будем теперь отсчитывать время от момента, когда груз находится в точке В, считая в этот момент t = 0. Тогда при t = 0 v = Vo = vB, где vB дается равенством (7). Подставляя эти величины в (11), получим
|	С2 = Ув + 2cos0 = 6,4 + 2 = 8,4 .
|	При найденном значении С2 уравнение (11) дает
*	dx
Гх==—= 3,2/ — 2 cos (4/) + 8,4.	(12)
К
Умножая здесь обе части на d/ и снова интегрируя, найдем
х = 1,6/2 - 0,5 sin (40 + 8,4/ + С3 •	(13)
Так как при / = 0 х=-0, то С3 — 0 и окончательно искомый закон движения груза будет
х = 1,6/2 +8,4/—0,5sin(4/),	(14)
где х — в метрах, / — в секундах.
Задача Д2
Груз / массой т укреплен на пружинной подвеске в лифте (рис. Д2.0 —- Д2.9, табл. Д2). Лифт движется вертикально по закону z = 0,5ai/2 + a2 sin (со/) + a3cos(co/) (ось z направлена по вертикали вверх; z выражено в метрах, / — в секундах). На груз действует сила сопротивления среды R = ру, где v — скорость груза по отношению к лифту.
Найти закон движения груза по отношению к лифту, т. е. х = /(/); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х>0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с2. Массой пружин и соединительной планки 2 пренебречь.
В таблице обозначено: С[, С2, Сз — коэффициенты жесткости пружин, — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, vq — начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах сь Сз означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить
Таблица Д2
Номер условия	т, кг	Ci, Н/м	С2, Н/м	X	s' 8	a2, м	s §	3	-5. X	Ло, M	Vo, м/с
0	1	300	150	____	0	0,1	0	15	0	0	0
1	0,8	—	240	120	-1,5g	0	0	—	8	0,1	0
2	0,5	—	100	150	0	0,8	0	5	0	0	4
3	1	240	—	160	0	0	0,5	6	0	0	0
4	0,5	80	120	___	— g	0	0	—	6	0,15	0
5	2	—	400	400	0	0	0,1	16	0	0	0
6	0,4	60	.—	120	g	0	0	—_	4	0	2
7	0,5	120	—	180	0	0,1	0	20	0	0	0
8	0,4	50	200	—-	0	0	0,2	20	0	0,15	0
9	1	200	—	300	h5g	0	0	—	20	0	3
Рис. Д2.4
Рис. Д2.5
Рис. Д2.8
56
₽
Рис. Д2.6
Рис. Д2.7
Рис. Д2.9
Рис. Д2.0	Рис. Д2.1	Рис. Д2.2	Рис. Д2.3
в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
Условие ц = 0 означает, что сила сопротивления R отсутствует.
Указания. Задача Д2 охватывает одновременно относительное движение и колебания материальной точки.
Сначала нужно составить дифференциальное уравнение относительного движения (по отношению к лифту) рассматриваемого в задаче груза, для чего присоединить к действующим силам переносную силу инерции. Затем прикрепленные к грузу пружины (по условиям задачи их будет две) заменить эквивалентной пружиной с коэффициентом жесткости сэкв = с, произведя соответствующий расчет.
а)	Если пружины соединены друг с другом последовательно (как пружины с жесткостями Ci и С2 на рис. Д2.0), то при равновесии под действием некоторой силы Q, приложенной к свободному концу пружины, усилия в любом поперечном сечении пружин одинаковы и равны Q. Удлинения пружин М = Q/c\, X2=Q/c2, удлинение эквивалентной пружины Л = Q/c и Л= Xi+^2. Отсюда-
0^2 с — ——. 4-6’2
б)	Если груз прикреплен к двум параллельным пружинам (как к пружинам с жесткостями Ci и £2 на рис. Д2.1) или находится между двумя пружинами, то при равновесии под действием некоторой силы Q каждая из пружин и эквивалентная пружина имели бы одно и то же удлинение Л. Тогда для двух пружин сД-|-с2А,= Q, а для эквивалентной пружины сК = Q, отсюда с = Ci + С2.
После того как уравнение будет составлено (это будет линейное дифференциальное уравнение 2-го порядка), его следует проинтегрировать, учтя начальные условия.
Пример Д2. В приборе для измерения вертикальных колебаний (рис. Д2) груз массой т прикреплен к пружине с коэффициентом жесткости с. Другой конец пружины прикреплен к корпусу прибора, который движется по закону z — A sin (о>/) (неподвижная ось z направлена по вертикали вниз). Начальное удлинение пружины равно Хо, а начальная скорость груза по отношению к корпусу прибора Vo (направлена вертикально вниз).
Дано: т — 0,4 кг, с — 40 Н/м, = = 0,05 м, Vo ~ 0,5 м/с, А — 0,03 м, со = 20 1/с. Определить: х = f(t) — закон движения груза по отношению к корпусу прибора.
пер
Рис.. Д2
Решение. 1. Свяжем с корпусом прибора подвижную систему отсчета, начало О которой поместим в конце недеформированной пружины (ее длина обозначена /0), а ось х направим в сторону удлинения пружины (см. рис. Д2). Рассмотрим груз в положении, при котором пружина растянута. На груз действует сила тяжести Р и сила упругости F. Для составления уравнения относительного движения груза присоединим к этим силам переносную <щл.у инерции F„eP = — шапер, кориолисова сила инерции равна нулю, так как переносное движение (движение корпуса прибора) является поступательным. Тогда уравнение относительного движения в векторной форме будет иметь вид
maOTli = P + F + Fnep •
Проектируя обе его части на ось х, получим
mx = Px + Fx + F»epx.	(i)
Здесь Рх = Р, Fx = ~ сК = — сх, где К—х — удлинение пружины, Fnepx = — тапгрх. Учитывая, что оси х иг направлены одинаково, получим Яперх = Яперг = Z = — 4й)2 5Ш (<й/) И Fnepx = ГП,А (л)2 SH1 ((л)/).
Подставляя все найденные выражения проекций сил в уравнение (1), получим
тх = Р — сх + mA со2 sin (со/).	(2)
Дифференциальное уравнение (2) может быть записано в виде х’ + k2x = bi + &2sin((o/) ,	(3)
где обозначено
k2 = с/т = 100 с-2, bi = g = 10 м/с2; b2 = Аса2 = 12 м/с2. (4)
2. Для определения закона движения груза надо проинтегрировать уравнение (3). Его общее решение, как известно из теории дифференциальных уравнений:
Х = Х1+^2,	(5)
где Xi — общее решение однородного уравнения х’ + /?2х ~ 0, т. е.
Xi = Ci sin (kt) + C2cQs(kf) ,	(6)
a x2— частное решение уравнения (3). Учитывая, каковы правая и левая части этого уравнения, ищем х2 в виде
х2 — В +Z) sin (со/) .	(7)
Для определения постоянных В и D находим х2 — —D со2 sin (со/), подставляем значения х2 и х2 в уравнение (3) и приравниваем в его
обеих частях свободные члены и коэффициенты при sin (со/). В результате, принимая во внимание обозначения (4), получим
Ь\	Ь2
В = —— 0,1 м, D = —---------~~ — — 0,04 м.
k2	k — со
Тогда из равенств (5) — (7), учитывая, что k — 10 с"1, а со — 20 с-1, получим следующее общее решение уравнения (3):
х = Ci sin (10Z) + С2 cos (10/) — 0,04 sin (20/) + 0,1.	(8)
Для определения постоянных интегрирования С\ и С2 найдем еще vx = х;
Ух = 1 ОС! cos (10/) - 10С2 sin (10/) — 0,8 cos (20/).	(9)
По условиям задачи при t = 0 vx = vq — 0,5 м/с, Xq = Хо — 0,05 м. Подставив эти начальные данные в уравнения (8) и (9), найдем из них, что Ci = 0,13, С2=—0,05. В результате уравнение (8) примет окончательно вид
х = 0,13 sin (10/) — 0,05 cos (10/)-0,04 sin (20/) + 0,1 .	(10)
Это уравнение и определяет искомый закон относительного движения груза, т. е. закон совершаемых им колебаний.
Задача^)7
Механическая система состоит из грузов Di массой т\ = 2 кг и В2 массой т2 — 6 кг и из прямоугольной вертикальной плиты массой тз — 12 кг, движущейся вдоль горизонтальных направляющих (рис. ДЗ.О — Д3.9, табл. ДЗ). В момент времени /о=вО, когда система находилась в покое, под действием внутренних сил грузы начинают двигаться по желобам, представляющим собой окружности радиусов г = 0,4 м и Я = 0,8 м.
При движении грузов угол <pi == 2.Л1Сз/>1 изменяется по закону Ф1 = Л(/), а угол <р2 = Z.A2C3D2 — по закону <р2 == f2(/). В табл. ДЗ эти зависимости даны отдельно для рис. 0—4 и 5—9, тде <р выражено в радианах, / — в секундах.
Считая грузы материальными точками и пренебрегая всеми сопротивлениями, определить закон изменения со временем величины, указанной в таблице в столбце «Найти», т. е. хз = /з(/) и N = f(/), где х3 — координата центра Сз плиты (зависимость хз = f3(/) определяет закон движения плиты), N — полная нормальная реакция направляющих.
Указания. Задача ДЗ — на применение теоремы о движении центра масс. При этом для определения хз = /з(/) составить уравнение в проекции на горизонтальную ось х, а для определения N — на вертикальную ось у.
59
i

Рис. ДЗ.О
60

Рис. О—4
Номер условия		
	= fi(0	<₽2 = f2(0
0	4о2+>) О	fO2-2)
1	3i(2 - 0	^ + 3)
2	^42)	-^5-Z2)
3	л/ "з	
4		^2- 4) О
5	^ + 2)	-Т<1-0
6	л/2	-J(l-2/2)
7	-£<5-0	fV + 4)
8	>2+з)	-^2-Z2)
9	-£<4-0	X< + 5)
Таблица 1ДЗ
Рис. 5—9		Найти
Ф1 = Л(0	ф2 = /г(^)	
^з-/2)	y^ + 2)	Хз
т<2/-1)	nt T	N
	n/2	Хз
-^-2)		N
л/2 Т	-J<2-/2)	Хз
л(3 — t)		N
-J<2/2 —3)	^(2-/2)	Хз
nt Т	-^4-/)	N
^4-Z2)	л(/2 + 2)	Хз
>-D	-J<2-/)	
19


6 £tr эиа
s err ’эиа

wewew

z eir эм
WWWzWW
э еи ’эи^
'//М7/////////////////////////////,

S'Ctt '^d	rstf -эиа
2 £tr 'эиа

£•£17 ’эиа
Рис. ДЗ
Пример ДЗ. Механическая система состоит из грузов Di массой mi и D2 массой т2 и из прямоугольной вертикальной плиты массой т3, движущейся вдоль горизонтальных направляющих (рис. ДЗ). В момент времени tQ = 0, когда система находилась в покое, под действием внутренних сил грузы начинают двигаться по желобам, представляющим собой окружности радиусов г и R, по законам дл = f\(t) И ф2 = Ь(/).
Дано: mi — 6 кг, т2 = 8 кг, т3 = 12 кг, г = 0,6 м, R = 1,2 м,
Ф1 = л/ рад, <р2 ==-—-( 1/) рад (/— в секундах). Определить: х3 == f3(t) — закон движения плиты, N = f(t) — закон изменения со временем полной нормальной реакции направляющих.
Решение. Рассмотрим механическую систему, состоящую из плиты и грузов D\ и Z)2, в произвольном положении (рис. ДЗ). Изобразим действующие на систему внешние силы: силы тяжести Pi, Р2, Р3 и реакцию направляющих N. Проведем координатные оси Оху так, чтобы ось у проходила через точку С3о, где находился центр масс плиты в момент времени /о = 0.
а)	Определение перемещения х3. Для определения х3 = /3(/) воспользуемся теоремой о движении центра масс системы. Составим дифференциальное уравнение его движения в проекции на ось х Получим
Мхс = SFfx или Мхс = 0 ,	(1)
так как SFL — 0, поскольку все действующие на систему внешние силы вертикальны.
Проинтегрировав уравнение (1), найдем, что Мхс — Ci, т. е. проекция скорости центра масс системы на эту ось есть величина постоянная. Так как в начальный момент времени vc% = 0, то Ci = 0.
Интегрируя уравнение Мхс = 0, получим
Мхс= const,	(2)
т. е. центр масс системы вдоль оси Ох перемещаться не будет.
Определим значение Мхс. Из рис. ДЗ видно, что в произвольный момент времени абсциссы грузов равны соответственно х\ — х3 — Rtoscpi, х2 = х3-|-г sincp2. Так как по формуле, определяющей координату хс центра масс системы, Мхс — miXi т2х2т'3х3, то
Мхс = (mi 4- m2 + т3)%з — miRtos(ji/)4- m2rsin(jt/2 — л//2).	(3)
В соответствии с равенством (2) координаты центра масс хс всей системы в начальном и произвольном положениях будут равны. Следовательно, учитывая, что при /о = 0 хз = 0, получим
— miR^m2r — (mi + т24-т3)х3 — mi/?tos(n/)+m2rcos(n//2). (4)
Отсюда получаем зависимость от времени координаты
Ответ: х3 — O,O9[3cos(ji0 — 2cos(n//2)— 1]м, где t — в секундах.
б)	Определение реакции N. Для определения N = f(f) составим дифференциальное уравнение движения центра масс системы в проекции на вертикальную ось у (см. рис. ДЗ):
Мус — Tfky ИЛИ Мус — N — Pi~~P2 — P3 .	(1)
Отсюда получим, учтя, что Pi — m\g, и т. д.:
N == Myc-p(mi-p т2-Р m3)g .	(2)
По формуле, определяющей ординату ус центра масс системы,
Мус= miyi т2у2 т3у3, где yi = Я + /^sincpi,
у2 — Н — гсоэфг, уз — Н — ОСзо — const, получим
Мус — (mi + т2 + т3)Н + т i R^in (nt)— m2r cos (п/2 — л//2) или
Мус — (mi + т2-ф т3)Н + miR^m(nt) — m2r sin (nt/2).
Продифференцировав обе части этого равенства два раза по времени, найдем
Мус — т i Rn cos (nt)—т2г(п/2) cos (nt/2) ;
Мус — — miRft2sin(n0+ m2r(n2/4)sin(3xf/2) .
Подставив это значение Мус в уравнение (2), определим искомую зависимость N от t.
Ответ: N = 254,8—1,2л2 [6 sin (nt) — sin (nt/2) ], где t — в секундах, N — в ньютонах.
Задача
Механическая система состоит из прямоугольной вертикальной плиты / массой mi = 18 кг, движущейся вдоль горизонтальных направляющих, и груза D массой т2 — 6 кг (рис. Д4.0 — Д4.9, табл. Д4). В момент времени to — 0, когда скорость плиты и0 — 2 м/с, груз под действием внутренних сил начинает двигаться по желобу плиты.
На рис. О—3 желоб RE прямолинейный и при движении груза расстояние s = AD изменяется по закону s == fi(t), а на рис. 4—9 желоб — окружность радиуса R — 0,8 м и при движении груза угол y—^ACiD изменяется по закону ср = f2(t). В табл. Д4 эти зависи-
Рис. Д4.0
Рис. Д4.1
Рис. Д4.2
Рис. Д4.3
Рис. Д4.4
Рис. Д4.5	Рис. Д4.6	Рис. Д4.7
Рис. Д4.8
Рис. Д4.9
Таблица Д4
I1омер уело-ВИЯ	s = Л(/)		ф = h(0	
	рис. 0,1	рис. 2,3	рис. 4,5,6	рис. 7,8,9
0	0,8 sin (л/2)	0,4(3/2- 2)	л(3-2/2)/3	л(2/2— 1)
1	1,2.соз(л//2)	0,6зт(л/2/2)	л(1-зг2)/4	л(1—4/2)/3
2	0,6(2/2 - 1)	0,8 cos (лЛ	л(/2-3)/6	л(3 + 4/2)/6
3	0,4зш(л/2/3)	0,5зт(лг/6)	л(2-/2)	л(/2+1)/2
4	0,5соз(л//6)	1,2соз(л//3)	л(1+2/2)/6	л( 1-50/4
5	0,6 sin (лг/4)	0,5(3-—4г)	л(5/+1)/4	л(/2 —4)/3
6	0,8(2 - З/2)	0,8sin(n/2/3)	л(/2 - 2)/2	л/2/4
7	0,6соз(л//3)	0,4соз(л/74)	л(3 + /2)/3	л(3/2— 1)/6
8	1,2 sin (лг/6)	1,2 sin (лг)	л/2/2	л(/2 + 3)/2
9	0,8соз(л//4)	0,6соз(л//6)	л(г + 2)/6	л(2—/2)/4
мости даны отдельно для рис. О и 1, для рис. 2 и 3 и т.д., где $ выражено в метрах, ф — в радианах, t — в секундах.
Считая груз материальной точкой и пренебрегая всеми сопротивлениями, определить зависимость и — f(t), т. е. скорость плиты как
функцию времени.
Указания. Задача Д4 на применение теоремы об изменении количества движения системы. При решении составить уравнение, выражающее теорему, в проекции на горизонтальную ось.
Пример Д4. В центре тяжести А тележки массой mi, движущейся по гладкой горизонтальной плоскости, укреплен невесомый стержень AD длиной I с грузом D массой т2 на конце (рис. Д4). В момент времени /о = 0, когда скорость тележки и = стержень AD начинает вращаться вокруг оси А по закону ф — ф(/).
Дано: mi = 24 кг, т2 — 12 кг, uq = 0,5 м/с, I = 0,6 м, ф = (л/ЗХ1 4-2/3) рад (/ — в секундах). Определить: и — f(f) —
закон изменения скорости тележки.
Решение. Рассмотрим механическую систему, состоящую из тележки и груза Dy в произвольном положении. Изобразим действующие
на систему внешние силы: силы тяжести Pi, Р2 и реакции плоскости N', N". Проведем координатные оси Оху так, чтобы ось х была горизонтальна.
Чтобы определить w, воспользуемся юоремой об изменении количества движения системы Q в проекции на ось х. Так как все действующие на систему внешние силы вертикальны (рис. Д4), то = 0 и теорема дает
dQ. dt
= 0 , откуда Qx = C\ .
(1)
Для рассматриваемой механической системы Q = QT4-QD, где QT= = пци и Qd = m2vD — количества движения тележки и груза D соответственно (и — скорость тележки, vD — скорость груза по отношению к осям Оху). Тогда из равенства (1) следует, что
или miux-}- m2vDx= Ci.
(2)
Для определения vdx рассмотрим движение груза D как сложное, считая его движение по отношению к тележке относительным (это движение, совершаемое при вращении стержня AD вокруг оси Л), а движение самой тележки — переносным. Тогда vD'~ иор4- vdh и
vDx=v^+v^x.	(3)
Но vnDp = и и, следовательно, vnD$—ux. Вектор направлен перпендикулярно стержню и численно Vo — l‘(nAD — /ф = 2/л/2.
Изобразив этот вектор на рис. Д4 с учетом знака (р, найдем, что v°dx== — уЬтcos ф. Окончательно из равенства (3) получим
(т+т‘‘).
vDx =
Ux~— ЬрСОБф = их — 2/л/2 cos
(4)
(В данной задаче величину vDx можно еще найти другим путем, определив абсциссу xD груза D, для которой, как видно из рис. Д4, получим xD = хА — /эшф; тогда vDx = xD — хА — /фсоэф, где хА — их, а Ф = 2л/2,)
При найденном значении vqx равенство (2), если учесть, что их — и, примет вид
пци + т2и — т22/л/2со8-4^ 4"	(5)
Постоянную интегрирования Ci определим по начальным условиям: при t = 0 и — uq. Подстановка этих величин в уравнение (5) дает Ci = (mi 4- т2)ио и тогда из (5) получим
(mi + т2)и — 2m2W2cos^-^-4—=	’
Отсюда находим следующую зависимость скорости и тележки от времени:
2/лт2	/ л , 2л А
и = Wo4-_------—— fcos (-т~4—/3) .	(6)
mi 4~	\ 3	3	/	'
Подставив сюда значения соответствующих величин, находим искомую зависимость и от t.
Ответ: и — 0,5 4-0,4л/2 • соз(л/3 4~2л/3/3) м/с.
Однородная горизонтальная платформа (круглая радиуса R или прямоугольная со сторонами £ и 2R, где R'— 1,2 м) массой mi — 24 кг вращается с угловой скоростью <оо = Ю с-1 вокруг вертикальной оси z, отстоящей от центра масс С платформы на расстоянии ОС = b (рис. Д5.0 — Д5.9, табл. Д5); размеры для всех прямоугольных платформ показаны на рис. Д5.0а (вид сверху).
В момент времени to — 0 по желобу платформы начинает двигаться (под действием внутренних сил) груз D массой т2 = 8 кг по закону s — AD — F(f), где s выражено в метрах, t — в секундах. Одновременно на платформы начинает действовать пара сил с моментом М (задан в ньютонометрах; при М<0 его направление противоположно показанному на рисунках).
Определить, пренебрегая массой вала, зависимость со — f(f), т. е. угловую скорость платформы, как функцию времени.
На всех рисунках груз D показан в положении, при котором s>0 (когда $<0, груз находится по другую сторону от точки Л). Изображая чертеж решаемой задачи, провести ось z на заданном расстоянии ОС — b от центра С.
Указания. Задача Д5 — на применение теоремы об изменении кинетического момента системы. При применении теоремы к системе, состоящей из платформы и груза, кинетический момент Кг системы относительно оси z определяется как сумма моментов платформы и груза. При этом следует учесть, что абсолютная скорость груза складывается из относительной уотн и переносной vпер скоростей, т. е. v — уОтн+ ^пеР. Поэтому и количество движения этого груза mv = т^отн+^пер- Тогда можно воспользоваться теоремой Вариньона (статика), согласно которой tnz(mv) = mz(mv0TH) + т2(т упер); эти моменты вычисляются так же, как моменты сил. Подробнее ход решения разъяснен в примере Д5.
При решении задачи полезно изобразить на вспомогательном чертеже вид на платформу сверху (с конца оси г), как это сделано на рис. Д5.0, а — Д5.9, а.
Момент инерции пластины с массой т относительно оси Cz, перпендикулярной пластине и проходящей через ее центр масс С, равен: для прямоугольной пластины со сторонами а\ и а2
Icz^ m(a2i + аг)/12 ;
для круглой пластины радиуса R
ICz^mR2/2,
z
Рис. Д5.0
68
R
Номер условия	b
0	R
1	R/2
2	R
3	R/2
4	R
5	R/2
6	R
7	R/2
8	R
9	R/2
	Таблица Д5
s = F(t)	M
— 0,4/2 0,6/2 — 0,8/2 10/ 0,4/3 — 0,5/ — 0,6/ 0,8/ 0,4/3 0,5/2	6 4/ — 6 - 8/ 10 - 9/2 8 6/2 — 10/ 12/2
Рис. Д5.2
70
z
Рис. Д5.8
Рис. Д5.9
Рис. Д5.6
Е
Рис. Д5
Пример Д5. Однородная горизонтальная платформа (прямоугольная со сторонами 21 и /), имеющая массу ть жестко скреплена с вертикальным валом и вращается вместе с ним вокруг оси z с угловой скоростью соо (рис. Д5, а). В момент времени to — 0 на вал начинает действовать вращающий момент М, направленный противоположно со©; одновременно груз D массой т2, находящийся в желобе АВ в точке С, начинает двигаться по желобу (под действием внутренних сил) по закону s — CD = F(t).
Дано: mi = 16 кг, m2 = 10 кг, I = 0,5 м, ®о = 2 с"1, s = 0,4/2 (s — в метрах, / — в секундах), М — kt, где k = 6 Н-м/с. Определить: со = f(Z) ~ закон изменения угловой скорости платформы.
Решение. Рассмотрим механическую систему, состоящую из платформы и груза D. Для определения со применим теорему об изменении кинетического момента системы относительно оси z:
-^- = 2тг(Й).	(1)
Изобразим действующие на систему внешние силы: силы тяжести Pi, Рг реакции Ле, Rh и вращающий момент М. Так как силы Pi и Л2 параллельны оси z, а реакции Ле и Ля эту ось пересекают, то их моменты относительно оси z равны нулю. Тогда, считая для момента положительным направление со0 (т. е. против хода часовой стрелки), получим Sm2(Pl) = — М = — kt и уравнение (1) примет такой вид:
Умножая обе части этого уравнения на d/ и интегрируя, получим Кг=-'|/2 + С1.	(3)
Для рассматриваемой механической системы
Kz=	(4)
1 де КТ и К? — кинетические моменты платформы и груза D соответственно.
Так как платформа вращается вокруг оси z, то /С"л = /?(о. Значение 4 найдем по теореме Гюйгенса: /2 ==/СУ4-mj .(ОС)2 == =	Цсгг— момент инерции относительно оси г', параллельной
оси z и проходящей через центр С платформы).
Но, как известно,
Icz= m1[(2/)2 + /2]/12 = 5mi/2/12.
Тогда
= 5miZ2/12 + mi/2 = 1701^/12.
Следовательно,
Kr=(i7mil2/12)^.	(5)
Для определения обратимся к рис. Д5, б и рассмотрим движение груза D как сложное, считая его движение по платформе относительным, а вращение самой платформы вокруг оси z переносным движением. Тогда абсолютная скорость груза и — уотн+ ^пер. Так как груз D движется по закону s = CD — 0,4/2, то уОтн = s = 0,8/; изображаем вектор уотн на рис. Д5, б с учетом знака 5 (при s<0 направление уотн было бы противоположным). Затем, учитывая направление со, изображаем вектор ипер(ипер ± О£>); численно ипер = со-OD. Тогда, по теореме Вариньона,
К? = mz(tn2v) = тг(т2йОтн) + игг(т2^пеР) = — т2и0ТП'0С + tn2uneP-OD =
—’ — m2-0,8/Z+ tn2(d[OD)2 .	(6)
Но на рис. Д5, б видно, что OD2 — I2 -\-s2 — I2 4- 0,16/4. Подставляя эту величину в равенство (6), а затем значения К? и К?л из (6) и (5) в равенство (4), получим с учетом данных задачи
17
/(г —	+ m2co(Z2 -J- 0,16/4) — m2(0,8/)/ =
= (8,17 -Ь 1,6/4)ш — 4/.	(7)
Тогда уравнение (3), где k = 6, примет вид
(8,17 4- 1,6/4)со - 4/ = - З/2 4- Ci .	(8)
Постоянную интегрирования определяем по начальным условиям: при /==0, со = соо- Получим Ci = 8,17соо = 16,34. При этом значении С\ из уравнения (8) находим искомую зависимость со от /. Ответ: (0= (16,34 4- 4/ —- З/2) / (8,17 4* 1,6/4), где / -—-в секундах, со — в с"1.
Задача Д6
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней 7?3 = 0,3 м, г3= 0,1 м и радиусом инерции относительно оси вращения р3 — 0,2 м, блока 4 радиуса
Рис. Д6.2
Рис. Д6.1
Рис. Д6.3
11омер условия
ms, кг
W2, кг
Шз, кг
о 1 2 3 4 5 6 7 8 9
О 8 О
О 5 О
8 О
4 О
6 О
4 6 О
5 О 4 О
5
4 О
6 О
4 О 5 О О
6
Таблица Д6
п4, кг	™5, кг	с,Н/м	М.Н-м	W(+ Н	Найти
0	5	200	1,2	80(4 + 5s)	0)3
4	6	320	0,8	50(8 + 3s)	
0	5	240	1,4	60(6 + 5s)	v2
5	4	300	1,8	80(5 + 6s)	(i)4
0	6	240	1,2	40(9 + 4s)	Vi
6	4	200	1,6	50(7 + 8s)	&C5
0	6	280	0,8	40(8 + 9s)	(1)3
6	5	300	1,5	60(8 +5s)	
5	6	320	1,4	50(9 + 2s)	(1)4
0	4	280	1,6	80(6 + 7s)	VC5
il
I
— 0,2 м и катка (или подвижного блока) 5 (рис. Д6.0 — Д6.9, табл. Д6); тело 5 считать сплошным однородным цилиндром, а массу блока 4 — равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При дви-
жснии на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным si — 0,2 м. Искомая величина указана в столбце «Найти» таблицы, где обозначено: Vi, V2, vcs— скорости грузов 1, 2 и центра масс тела 5 соответственно, соз и о)4 — угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 2), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если m2 — 0; остальные тела должны изображаться и тогда, когда их масса равна нулю.
Указания. Задача Д6 — на применение теоремы об изменении кинетической энергии системы. При решении задачи учесть, что кинетическая энергия Т системы равна сумме кинетических энергий всех входящих в систему тел; эту энергию нужно выразить через ту скоррсть (линейную или угловую), которую в задаче надо определить. При вычислении Т для установления зависимости между скоростями точек тела, движущегося плоскопараллельно, или между его угловой скоростью и скоростью центра масс воспользоваться мгновенным центром скоростей (кинематика). При вычислении работы надо все перемещения выразить через заданное перемещение si, учтя, что зависимость между перемещениями здесь будет такой же, как между соответствующими скоростями.
Пример Д6. Механическая система (рис. Д6, а) состоит из сплошного однородного цилиндрического катка /, подвижного блока 2, ступенчатого шкива 3 с радиусами ступеней 7?3 и г3 и радиусом инерции относительно оси вращения рз, блока 4 и груза 5 (коэффициент трения груза о плоскость равен f). Тела системы соединены нитями,
намотанными на шкив 3. К центру Е блока 2 прикреплена пружина с коэффициентом жесткости с; ее начальная деформация равна нулю.
Система приходит в движение из состояния покоя под действием силы F = f(s), зависящей от перемещения s точки ее приложения. На шкив 3 при движении действует постоянный момент М сил сопротивления.
Дано: mi — 8 кг, т2 = 0, /Из = 4 кг, т4 == 0,	= 10 кг, /?з =
= 0,3 м, гз = 0,1 м, рз = 0,2 м, f = 0,1, с = 240 Н/м, М = 0,6 Н-м, F = = 20(3 + 2s) Н, si = 0,2 м. Определить: со3 в тот момент времени, когда s = si.
Решение. 1. Рассмотрим движение неизменяемой механической системы, состоящей из весомых тел 1, 3, 5 и невесомых тел 2, 4, ьъекъ-ненных нитями. Изобразим действующие на систему внешние силы: активные F, Fynp, А, Рз, Ps, реакции jV3, W4, AZ5, натяжение нити S2, силы трения Pip, FF и момент М.
Для определения ©з воспользуемся теоремой об изменении кинетической энергии:
Г~Г0 = 2Л1.	(1)
2. Определяем Го и Г. Так как в начальный момент система находилась в покое, то Го — 0. Величина Г равна сумме энергий всех тел системы:
Г=Г1 + Г3 + Г5.	(2)
Учитывая, что тело 1 движется плоскопараллельно, тело 5 — поступательно, а тело 3 вращается вокруг неподвижной оси, получим
Т1 =	Н—^-/ciwi;
Тз = ~1з<>>1; 7'5 = -^-m5vl.	(3)
Все входящие сюда скорости надо выразить через искомую со3. Для этого предварительно заметим, что Vci = V5 — va, где А — любая точка обода радиуса г3 шкива 3 и что точка Ki — мгновенный центр скоростей катка /, радиус которого обозначим л. Тогда
Vci	Vci	Гз	, *
Vci = ^5 == (О3Г3 ; (01 = -гт-тт— = --= (Оз--.	(4)
Л1С1	Г1	Г1	__у
Кроме того, входящие в (3) моменты инерции имеют значения
/С1 = 0,5/И1Г1 ; 1з = тзрз •	(5)
Подставив все величины (4) и (5) в равенства (3), а затем, используя равенство (2), получим окончательно
Г =	----1_тзр2 _|-.	(6)
3. Теперь найдем сумму работ всех действующих внешних сил при перемещении, которое будет иметь система, когда центр катка 1 пройдет путь si. Введя обозначения: «5 -— перемещение груза 5 («5 — ™ 51), фз — угол поворота шкива 5, Хо и М — начальное и конечное удлинения пружины, получим
A(F) = 20(3 + 2s)ds = 20(3si + s?); о
?l(Pj) = Pis, sin 60° ;
Л(ЯР)== -F5Tps5= -fP5si ;
Л(М) = -Мфз;
Л(^упр) = -y(^0 ~ ^1) •
Работы остальных сил равны нулю, так как точки Ki и /G, где приложены силы Ni, FIP и §2 — мгновенные центры скоростей; точки, где приложены силы Р3, N3 и — неподвижны; а реакция TV5 перпендикулярна перемещению груза.
По условиям задачи, Хо = 0- Тогда М = sE, где sE — перемещение точки Е (конца пружины). Величины s£ и ф3 надо выразить через заданное перемещение «г, для этого учтем, что зависимость между перемещениями здесь такая же, как и между соответствующими скоростями. Тогда так как соз = va/гз = vci/гз (равенство vci = va уже отмечалось), то И фз = 51/Гз.
Далее, из рис. Д6, б видно, что vd = vb = (O3F3, а так как -точка К2 является мгновенным центром скоростей для блока 2 (он как бы «катится» по участку нити K2L), то vE — 0,5vd — 0,5со3/?з; следовательно, и Xi = sE = 0,5ф3/?3 = 0,б517?3/гз. При найденных значениях фз и Л1 для суммы вычисленных работ получим
s	/?2
= 20(3s1+s?) + P1s,sin60°-/P6si-M—!-----------. (7)
Гз 8 Гз
Подставляя выражения (6) и (7) в уравнение (1) и учитывая, что То = 0, придем к равенству
+“4~тзрз Ч—"-т5гз^ со2 = 20(351 + $i) + PiSi sin 60° —
fD M c Rl 2
— fPbSi——-51 ---------—St.	(8)
r3 8 Гз
Из равенства (8), подставив в него числовые значения заданных величин, найдем искомую угловую скорость со3.
Ответ: со3 = 8,1 с"1.
Задача Д7
Барабан радиуса 7? весом Р имеет выточку (как у катушки) радиуса г = 0,67? (рис. Д7.0 — Д7.9, табл. Д7). К концам намотанных на барабан нитей приложены постоянные силы F\ и Ё2, направления которых определяются углом 0; кроме сил на барабан действует пара с моментом Л4; когда в таблице М<0, направление момента противоположно показанному на рисунке. При движении, начинающемся из состояния покоя, барабан катится без скольжения по шероховатой наклонной плоскости с углом наклона а так, как показано на рисунках.
Пренебрегая сопротивлением качению, определить закон движения центра масс С барабана, т. е. Хс = /(/), и наименьшее значение коэффициента трения f о плоскость, при котором возможно качение без скольжения. Барабан рассматривать как сплошной однородный цилиндр радиуса 7?.
Указания. Задача Д7 — на применение дифференциальных уравнений плоскопараллельного движения твердого тела. При составлении уравнений следует во избежание ошибок в знаках направить координатную ось х в ту сторону, куда предполагается направленным движение центра С барабана, и считать тогда все моменты положительными, когда они направлены в сторону вращения барабана. Если фактически направление движения центра С другое, то в ответе получится &с<0, но найденное значение \ас\ будет верным. Силу трения, когда неясно, куда она направлена, можно направлять в любую сторону (результат от этого не зависит).
Определяя наименьшее значение коэффициента трения, при котором возможно качение без скольжения, учесть, что сила трения не может быть больше предельной, т. е. что |Ртр| fN, откуда f > |Ртр1/^. Следовательно, fmin = SFtp|/jV. Очень существенно, что во все эти выражения входят модули сил (мы не пишем |Л^|, так как в данной задаче
Таблица Д7
Номер условия	а	0	Fi	F2	м
	гр	ад			
0	30	60	0	ОДР	0
1	30	30	0,2Р	0	0
2	0	30	0	ОДР	ОД PR
3	30	—	0	0	0,4PR
4	30	90	ОДР	0	- 0 ДР7?
5	0	60	0,ЗР	ОДР	0
6	30	0	0	0,ЗР	0ДР7?
7	0	60	ОДР	0	0,ЗР7?
8	30	90	0	ОДР	— 0,4Р7?
9	30	60	ОДР	0	- 0,ЗР7?
Рис. Д7.3
Рис. Д7.4
Рис. Д7.5
не может быть Л^сО). Если при расчетах получится Гтр<;0, то это означает лишь, что фактически сила FTp направлена в другую сторону; в остальном весь расчет будет верен.
Пример Д7. Барабан (сплошной однородный цилиндр) радиуса Р и весом Р начинает катиться без скольжения из состояния покоя по наклонной плоскости с углом наклона а; на барабан действуют сила F и пара сил с моментом М (рис. Д7).
Дано: Р, F= 0,8Р, М = 1,1PR, а = 30°, р == 30°. Определить: 1) хс = /(/) — закон движения центра масс барабана; 2) fmin — наименьший коэффициент трения, при котором возможно качение без скольжения.
Решение. Барабан совершает плоскопараллельное движение под действием сил Р, F, N, Frp и момента М. Так как направление силы трения Ётр заранее неизвестно, выбираем его произвольно. Проводим оси Оху и составляем дифференциальные уравнения плоскопараллельного движения:
тхс = S Fkx ; тхс = F cos р + Р sin а + Ртр ;	(1)
myc = ^Fky} = ^V — Pcosa — Fsinp ;	(2)
- тР2
ICz^ = S mcz{Fk); —= FR — FTpP - M .	(3)
За положительное направление для моментов принято направление по ходу часовой стрелки, т. е. в ту сторону, куда будет вращаться барабан при движении центра С от оси Оу.
1) Определение хс— f(t). Так как ясно, что в нашей задаче ус = R = const и ус = 0, то уравнения (1) — (3) содержат четыре неизвестные величины (хс, е, N и FTp).
Поэтому необходимо найти еще одно соотношение, связывающее эти величины, Для этого учтем, что хс—ас (так как центр С движется прямолинейно) и что при качении без скольжения в точке В находится мгновенный центр скоростей. Тогда
vc —	, ас == ic = ®R = нА или
Хс = zR .	(4)
Теперь из уравнения (3) можно исключить в, подставив в (3) найденное значение zR; деля одновременно обе части уравнения (3) на R, получим
-^-тхс = F — Гтр--(5)
Z	/у
Далее, сложив почленно равенства (1) и (5), исключим из них / 1р и получим
ч	М
-^-тхс = F( 1 + cos р) + Р sin а -	= 0,8Р( 1 + cos 30°) + Р sin 30° —
2	R
- 1,1Р= 0,89Р.
Отсюда, так как Р = mg, найдем для определения хс = f(t) следующее дифференциальное уравнение:
хс = 0,6g.	(6)
Интегрируя уравнение (6), получим
£с = Ofigt + Ct ; хс= О.З^+С^ + Сг.	(7)
По начальным условиям при / = 0 ис= хс — 0 и хс= 0 (ось у проводим через начальное положение точки С). Подстановка этих величин в равенства (7) дает Ci = 0, С2 = 0. Окончательно находим следующий закон движения центра С:
xc=0,3gt2.	(8)
2) Определение fm-m. Для определения f исходим из того, что при качении без скольжения сила трения должна удовлетворять неравенству
|FTp|<fAf,	(9)
куда, подчеркиваем, входят модули сил. Величину N находим из уравнения (2), учитывая, что ус = 0. Получим
7V = Pcosa+Fsinp = Pcos30°+0,8Psin30° — 1,27P.	(10)
Значение FTp проще всего найти из уравнения (5), заменив в нем хс его значением (6). Получим
Q,3mg^ F — F^ — M/R.
Отсюда, так как mg — Р, то
FTP = F - M/R — О.ЗР = 0,8Р - 1,1Р - 0,ЗР = - ОДР .	(11)
Знак указывает, что сила Ртр направлена противоположно показанному на рисунке.
Подставляя значения FTp и N из равенств (11) и (10) в неравенство. (9), получим 0,6Р^1,27РД откуда f^0,47. Следовательно, наименьший коэффициент трения, при котором возможно качение барабана без скольжения fmin — 0,47.
Задача Д8
Вертикальный вал AR (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью «о — 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DE =	= а). К валу жестко прикреплены
тонкий однородный ломаный стержень массой т = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где 6 = 0,1 м, а их массы mi и m2 пропорциональны длинам), и невесомый стержень длиной I = 4Ь с точечной массой т3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы а, 0, у, ф даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.
Указания. Задача Д8 — на применение к изучению движения системы принципа Даламбера. При решении задачи учесть, что когда
Таблица Д8
Номер условия	Подшипник в точке	Крепление в точке		а, град	0, град	Т» град	Ф, град
		ломаного стержня	невесомого стержня				
					рис. 0—4	рис. 5—9	
1	2	3	4	5	6	7	8
0	В	D	К	45	135	225	60
1	К	В	D	60	240	150	45
2	К	Е	В	30	210	120	60
3	D	К	В	60	150	240	30
4	К	D	Е	30	120	210	60
5	Е	В	К	45	225	135	60
6	Е	D	К	60	60	150	30
7	К	В	Е	30	30	120	60
8	D	Е	К	60	150	60	30
9	Е	К	D	30	120	210	60
Рис. Д8.0
Хт
Рис. Д8.2
Рис. Д8.3
Рис. Д8.4
Рис. Д8.8
*т
D
‘В
Рис. Д8.9
силы инерции частиц тела (в данной задаче стержня) имеют равнодействующую R", то численно 7?и = тас, где ас — ускорение центра масс С тела, но линия-действия силы R* в общем случае не проходит через точку С (см. пример Д8).
Пример Д8. Вертикальный вал длиной За(ЛВ = = BD — DE = а), закрепленный подпятником А и подшипником D (рис. Д8, а), вращается с постоянной угловой скоростью со. К валу жестко прикреплен в точке Е ломаный однородный стержень массой tn и длиной 106, состоящий из двух частей / и 2, а в точке В прикреплен невесомый стержень длиной I = 5Ь с точечной массой т3 на конце; оба стержня лежат в одной плоскости.
Дано: со = 8 с-1, m = mi + /zz2 =10 кг, m3 = 2 кг, а = 30°, р = 150°, ср = 60°, а = 0,3 м, 6 = 0,1 м. Определить: реакции подпятника А и подшипника D, пренебрегая весом вала.
Решение. 1. Изображаем (с учетом заданных углов) вал и прикрепленные к нему в точках В и Е стержни (рис. Д8, б). Массы и веса частей 1 и 2 ломаного стержня пропорциональны длинам этих частей и соответственно равны гп\ = 0,6m; m2 = 0,4m;
Pi = 0,6mg ; Р2 = 0,4 mg ; Р3 = m3g .
(1)
2. Для определения искомых реакций рассмотрим движение заданной механической системы и применим принцип Даламбера. Проведем
вращающиеся вместе с валом координатные оси Аху так, чтобы стержни лежали в плоскости ху, и изобразим действующие на систему силы: активные силы — силы тяжести Pi, А>, Рз и реакции связей — составляющие реакции подпятника Ха, Ya и реакцию цилиндрического подшипника Rd-
Согласно принципу Даламбера, присоединим к этим силам силы инерции элементов однородного ломаного стержня и груза, считая его материальной точкой.
Так как вал вращается равномерно, то элементы стержня имеют только нормальные ускорения ank, направленные к оси вращения, а численно ank = a>2hk, где hk — расстояния элементов от оси вращения. Тогда силы инерции Fk будут направлены от оси вращения, а численно Fk = \mka,kn = A.mk(o2hk, где Д/щ — масса элемента. Так как все Fk пропорциональны hk, то эпюры этих параллельных сил инерции стержня образуют для части 1 треугольник, а для части 2 — прямоугольник (рис. Д8, б).
Каждую из полученных систем параллельных сил инерции заменим ее равнодействующей, равной главному вектору этих сил. Так как модуль главного вектора сил инерции любого тела имеет значение Ри = тас, где т — масса тела, ас—ускорение его центра масс, то для частей стержня соответственно получим
PF = т\аС\, RS = т2аС2 •	(2)
Сила инерции точечной массы 3 должна быть направлена в сторону, противоположную ее ускорению и численно будет равна
F§ = т3а3 .	(3)
Ускорения центров масс частей 1 и 2 стержня и груза 3 равны: асл = &2hci , Q-C2 — ^2hc2, аз = со26з,	(4)
где hci, hC2 — расстояния центров масс частей стержня от оси вращения, а 63 — соответствующее расстояние груза:
hC\ = 3b sin 30° = 0,15 м ,
hC2~ 66 sin 30° =^0,3 м ,	(5)
Из = /sin60° = 56 sin60° = 0,43 м .
Подставив в (2) и (3) значения (4) и учтя (5), получим числовые значения Rf, R2 и F%:
Rf = 0,6mco26a = 57,6 Н ,
R2 = O,4mco26c2 = 76,8 H ,	(6)
FS = m3co263 = 55,0 H .
При этом линии действия равнодействующих R" и RS пройдут через центры тяжестей соответствующих эпюр сил инерции. Так, линия
действия У?” проходит на расстоянии —^~Н от вершины треугольника Е, где Н = 6b cos 30°.
3. Согласно принципу Даламбера, приложенные внешние силы (активные и реакции связей) и силы инерции образуют уравновешенную систему сил. Составим для этой плоской системы сил три уравнения равновесия. Получим
2Лх = 0;	+
= Гл-Л-Р2-Рз = 0;
2тл(^) = 0; -RD^a-Plhci~P2hC2+P^-~	1 ’
- RiHi - R$H2 + W3 - 0 ,
где Hi, Н2, Н3 — плечи сил R", R2, F3 относительно точки Л, равные (при подсчетах учтено, что И = 6b cos30° = 0,52 м)
Hi = За—(2/3)Zf = 0,55 м, Н2 = За-(Я + 2&) = 0,18 м , Н3 = а + /cos 60° = 0,55 м .
Подставив в уравнения (7) соответствующие величины из равенств (1), (5), (6), (8) и решив эту систему уравнений (7), найдем искомые реакции.
Ответ: ХА = -33,7 Н; УА = 117,7 Н; RD = -45,7 Н.
Задача Д9
Механизм, расположенный в горизонтальной плоскости, находится под действием приложенных сил в равновесии; положение равновесия определяется углами а, р, у, ср, 0 (рис. Д9.0 — Д9.9, табл. Д9а и Д9б). Длины стержней механизма (кривошипов) равны: Zi — 0,4 м, Z4 = 0,6 м (размеры 12 и /3 произвольны); точка Е находится в середине соответствующего стержня.
На ползун В механизма действует сила упругости пружины Ё; численно F = ск, где с — коэффициент жесткости пружины, X — ее деформация. Кроме того, на рис. 0 и 1 на ползун D действует сила Q, а на кривошип OiA — пара сил с моментом М; на рис. 2—9 на кривошипы OiA и O2D действуют пары сил с моментами Mi и М2.
Определить, чему равна при равновесии деформация 1 пружины, и указать, растянута пружина или сжата. Значения всех заданных величин приведены в табл. Д9а для рис. 0—4 и в табл. Д9б для рис. 5—9, где Q выражено в ньютонах, а М, Mit М2 — в ньютонометрах.
Построение чертежа начинать со стержня, направление которого определяется углом а; для большей наглядности ползун с направляющими и пружину изобразить так, как в примере Д9 (см. рис. Д9, а также рис. Д9.10, б). Если на чертеже решаемого варианта задачи прикрепленный к ползуну В стержень окажется совмещенным с пружи-

ной (как на рис. Д9.10, а), то пружину следует считать прикрепленной к ползуну с другой стороны (как на рис. Д9.10, б, где одновременно иначе изображены направляющие).
Указания. Задача Д9 — на определение условий равновесия механической системы с помощью принципа возможных перемещений. Механизм в рассматриваемой задаче имеет одну степень свободы, т. е. одно независимое возможное перемещение. Для решения задачи нужно сообщить механизму возможное перемещение, вычислить сумму элементарных работ всех действующих активных сил и пар на этом перемещении и приравнять ее нулю. Все вошедшие в составленное уравнение возможные перемещения следует выразить через какое-нибудь одно.
Чтобы найти X, надо из полученного условия равновесия определить силу упругости F. На чертеже эту силу можно направить в любую сторону (т. е. считать пружину или растянутой, или сжатой); верно ли выбрано направление силы, укажет знак.
Таблица Д9а (к рис. Д9.0 — ДЭЛ)
Номер уело-ВИЯ	Углы, град					с, Н/см	Для рис. 0— 1		Для рис. 2—4	
	а	Р	У	Ф	0		М	Q	Mi	Мг
Рис. Д9.2
Рис. Д9.3
Пример Д9. Механизм (рис. Д9, а), расположенный в горизон-I альной плоскости, состоит из стержней 1, 2, 3 и ползунов В, В, соеди-пенных друг с другом и с неподвижной опорой О шарнирами. К ползуну В прикреплена пружина с коэффициентом жесткости с, к ползуну D приложена сила Q, а к стержню / (кривошипу) — пара сил с моментом М.
Дано: а =60°, ₽ = 0°, у = 60°, <р=0°, 9=120°, Z = 0,4 м, Л Е — ED, с = 125 Н/см, М = 150 Н • м, Q = 350 Н. Определить: деформацию X пружины при равновесии механизма.
Решение. 1. Строим положение механизма в соответствии с заданными углами (рис. Д9, б); при этом согласно последнему из указаний к задаче Д9 прикрепляем пружину к ползуну с другой стороны (iaK, как если бы было р= 180°).
Для решения задачи воспользуемся принципом возможных перемещений, согласно которому
»Л=0,	(1)
1 де bAk — элементарные работы активных сил на соответствующих возможных перемещениях.
Изображаем действующие на механизм активные силы: силу Q, силу упругости F пружины (предполагая, что пружина растянута) и пару с моментом М.
Неизвестную силу F найдем с помощью уравнения (1), а зная F и учитывая, что F == сХ, определим X.
2. Чтобы составить уравнение (1), сообщим механизму возможное перемещение и введем следующие обозначения для перемещений звеньев, к которым приложены активные силы: 6ф1 — поворот стержня / вокруг оси О, 8sd и 8sв—перемещения ползунов (точек) D и В.
Из перемещений 6<pi, 8sDt 8sв независимое от других — одно (у механизма одна степень свободы). Примем за независимое возможное перемещение 6ф1 и установим, какими тогда будут 6sd и 8s в, выразив их через бфь при этом важно верно определить и направления 8sо, 8sв, так как иначе в уравнении (1) будут ошибки в знаках.
При расчетах учтем, что зависимость между возможными перемещениями здесь такая же, как между соответствующими скоростями звеньев механизма при его движении и воспользуемся известными из- кинематики соотношениями (ход расчетов такой же, как в примере КЗ).
Сначала найдем и изобразим (направление 65л определяется направлением 6ф1); получим
6s л — /16ф1 ; б5л-ЬОЛ .	(2)
Теперь определим и изобразим 6s D, учитывая, что проекции 6sд и 6sл на прямую AD должны быть равны друг другу (иметь одинаковые модули и знаки). Тогда
6s£)cos30° — б5лсоз30° и 6s£>= 6sл = Л6ф1 .	(3)
Чтобы определить 8s в> найдем сначала 6se. Для этого построим мгновенный центр вращения (скоростей) С2 стержня 2 (на пересечении перпендикуляров к 6sл и 8sd> восставленных из точек А и D) и покажем направление поворота стержня 2 вокруг С2, учтя направление 6sл или 8sD. Так как Z.C2AD ~ AC2DA — 60°, то ДДС21)— равносторонний и С2Е в нем высота, поскольку АЕ — ED. Тогда перемещение 8s е, перпендикулярное С2Е, будет направлено по прямой ЕА (при изображении 6sе учитываем направление поворота вокруг центра С2).
Воспользовавшись опять тем, что проекции 6sе и 6sл на прямую ЕА должны быть равны друг другу, получим (значение 8sE можно найти и составив соответствующую пропорцию)
6se= 65лсоз30° = /16ф1соз30° .	(4)
Наконец, из условия равенства проекций 8s в и 8s Е на прямую BE находим и изображаем 8s в- Численно
6sв — 6secos60° — /16ф1 cos30° • cos60° = 0,43/|6ф1 .	(5)
3. Теперь составляем для механизма уравнение (1); получим
Af6<pi 4- Q8sd— F8sb = 0,	(6)
пли, заменяя здесь 6$д и 6sв их значениями (3) и (5) и вынося одновременно 6ф| за скобки,
(М + ZiQ-0,43/^)6ф1 = 0.	(7)
Так как 6ф1^0, то отсюда следует, что
M + /iQ-0,43/iF= 0.	(8)
Из уравнения (8) находим значение F и определяем А = F/c.
Ответ: А = 13,5 см. Знак указывает, что пружина, как и предполагалось, растянута.
Задача ДЮ
Механическая система состоит из однородных ступенчатых шкивов 1 и 2, обмотанных нитями, грузов 3—6, прикрепленных к этим нитям, и невесомого блока (рис. Д10.0 —- Д10.9, табл. ДЮ). Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом М, приложенной к одному из шкивов. Радиусы ступеней шкива 1 равны: Ri = 0,2 м, и = 0,1 м, а шкива 2 — /?2 = 0,3 м, f2 — 0,15 м; их радиусы инерции относительно осей вращения равны соответственно pi = 0,1 м и р2 — 0,2 м.
Пренебрегая трением, определить ускорение груза, имеющего больший вес; веса Pi, ..., Ре шкивов и грузов заданы в таблице в ньютонах. Грузы, веса которых равны нулю, на чертеже не изображать (шкивы 1, 2 изображать всегда как части системы).
Указания. Задача ДЮ —- на применение к изучению движения < истемы общего уравнения динамики (принципа Даламбера — Лагранжа). Ход решения задачи такой же, как в задаче Д9, только предварительно надо присоединить к действующим на систему силам соответствующие силы инерции. Учесть при этом, что для однородного юла, вращающегося вокруг своей оси симметрии (шкива), система < ил инерции приводится к паре с моментом Мн = /2е, где 1г — момент инерции тела относительно оси вращения, е — угловое ускорение тела; направление Ми противоположно направлению е.
Рис. Д10.4
92
Рис. Д10.5
Таблица ДЮ
Номер условия	Pi	Р2	Рз	Р*	Рб		М, Н-м
0	10	0	20	30	40	0	10
1	0	40	0	10	20	30	12
2	20	30	40	0	10	0	16
3	0	20	10	30	0	40	18
4	30	0	20	0	40	10	12
5	0	10	30	40	20	0	16
6	40	0	0	20	30	10	10
,7	10	20	0	40	0	30	18
8	0	40	10	0	30	20	12
9	30	0	40	20	10	0	16
Рис. ДЮ.8
Пример ДЮ. Механическая система (рис. ДЮ) состоит из обмотанных нитями блока / радиуса Ri и ступенчатого шкива 2 (радиусы ступеней R2 и г2, радиус инерции относительно оси вращения р2), а также из грузов 3 и 4, прикрепленных к этим нитям. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом М, приложенной к блоку 1.
Дано: А == О, Р2 = 30 Н, Р3 = 40 Н, Р4 = 20 Н, М = 16 Н«м, Rt = 0,2 м, R2 = 0,3 м, г2 = 0,15 м, р2 — 0,2 м. Определит ь: ускорение груза 3, пренебрегая трением.
Рис. ДЮ
Решение. 1. Рассмотрим движение механической системы, состоящей из тел 1, 2, 3, 4, соединенных нитями. Система имеет одну степень свободы. Связи, наложенные на эту систему, — идеальные.
Для определения о3 применим общее уравнение динамики:

(1)
где 56Л| — сумма элементарных работ активных сил; 26Л& — сумма элементарных работ сил инерции.
2. Изображаем на чертеже активные силы Р2, Рз, А и пару сил с моментом М. Задавшись направлением ускорения о3, изображаем на чертеже силы инерции Гз, FI и пару сил инерции с моментом Л12, величины которых равны:
Гзи
Рз g
Р4 g а* ’
МЦ = -у-р282 
(2)
3. Сообщая системе возможное перемещение и составляя уравнение (1), получим
(P3sin60° - ГзйЖз ™ Wq)2 - F4h6s4 -	= 0 .	(3)
Выразим все перемещения через 6ф2:
6s3 — Р26ф2 j 6S4 = Г2бф2 J
6<Pi = -^-5<Р2 •	(4)
Подставив величины (2) и (4) в уравнение (3), приведем его к виду
[ P3(sin60°----------------------7-Л4'’2~~Л41^_] 6(Р2 = °- (5)
Входящие сюда величины е2 и си выразим через искомую величину а3: Оз	г2
е2 — —— j д4 = &2Г2 =	—аз.
Д2	Л2
Затем, учтя, что 6ф2#=0, приравняем нулю выражение, стоящее в (5) в квадратных скобках.
Из полученного в результате уравнения найдем Р3Р2 sin 60° ~ Л1(г2/Р1) P3R2 + P2pi/P2"+ P4(d/P2) g ’
Вычисления дают следующий ответ: ц3 = — 0,9 м/с2. Знак указывает, что ускорение груза 3 и ускорения других тел направлены противоположно показанным на рис. ДЮ. >	94
Задача ДИ
Механическая система состоит из тел 1, 2,	5 весом Pi, Рг, ...» Рб
соответственно, связанных друг с другом нитями, намотанными на оупенчатые блоки 1 и 2 (рис. Д11.0— Д11.9, табл. Д11). Радиусы ступенчатых блоков 1 и 2 равны соответственно Pi = Р, и = 0,4Р, /\2 = Р, Г2 = 0,8Р. При вычислении моментов инерции все блоки, катки и колеса считать однородными сплошными цилиндрами радиуса Р.
На систему кроме сил тяжести действует сила F, приложенная к телу 3 или 4 (если тело 3 в систему не входит, сила приложена в точке В к тележке), и пары сил с моментами Mi, М2, приложенные к блокам 1 и 2; когда М<0, направление момента противоположно показанному на рисунке.
На участке нити, указанном в таблице в столбце «Пружина», включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если AD, то AD — пружина и т. д.); в начальный момент времени пружина не деформирована.
Составить для системы уравнения Лагранжа и найти закон изменения обобщенной координаты х, т. е. х ~ f(t), считая, что движение начинается из состояния покоя; определить также частоту и период колебаний, совершаемых телами системы при ее движении (о выборе координаты х см. «Указания»).
Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит; для колес, обозначенных номером 4, Р4 — их общий вес (вес платформы такой Iслежки не учитывается).
Указания. Задача Д11 —на применение к изучению движения системы уравнений Лагранжа. В задаче система имеет две степени свободы; следовательно, ее положение определяется двумя обобщенны-
Таблица Д11
Помер условия		Р2	Рз	Ра	Рь	F	Mi	М2	Пружина
0	4Р	0				ЗР			4Р	0	0	АВ
1	0	2Р	—	—	ЗР	0	0	— 2PR	КЕ
2	0	2Р	—	Р	—	0	2PR	0	АВ
3	—	0	2Р	ЗР	—.	0	0	2PR	BD
4	р	—	—	.—	4Р	0	— PR	0	КЕ
5	—	—	4Р	ЗР	—_	Р	0	0	BD
6	2Р	0	—	—	Р	0	0	-PR	КЕ
7	—	4Р	.—	2Р	—	ЗР	0	2PR	АВ
8\	—	4Р	2Р	0	.—	0	0	3PR	BD
9\	2Р	0	—.	Р	—	0	2PR	0	АВ
Рис. Д11.3
Рис. Д11.6
Рис. Д11.7
ми координатами qi и q2 и для нее должны быть составлены два уравнения.
Решение начать с выбора обобщенных координат, обозначив их qi = х и q2 = ф или q\ = х и q2 — у. За координату х принять удлинение пружины, отсчитываемое в сторону того из тел 3, 4 или 5 системы, к которому пружина прикреплена; например, если пружина прикреплена к этому телу в точке В и ее длина в произвольный момент времени равна АВ, то х = ДВ —/0, где Zo— длина недеформи-рованной пружины. За координату ф принять угол поворота крайнего блока (этот блок может быть и невесомым), отсчитывая ф от начального положения. Если в систему ни один блок не входит, а входят лишь тела 3 и 4, за координату у принять расстояние тела 4 от 98
Рис. Д11
начального положения. Соот-|и*1ствующие примеры даны на рис. Д 11.10. Дальнейший ход решения разъяснен в примере Д11.
Пример Д11. Механическая система (рис. Д11) со-< юит из барабана / радиуса /?, к которому приложена пара сил с моментом М, тележки ? и катка 3 (барабан и каюк — однородные цилиндры) ; веса всех тел равны соот-шчственно Р], Рг, Рз; весом колес тележки пренебречь. Тележка соединена с барабаном намотанной на него нитью, а с катком — пружиной BDt коэффициент жесткости которой равен с. Система начинает движение из состояния покоя; пружина в этот момент не деформирована.
Дано: Р, с, Pi == 2Р; Р2 = 4Р; Р3 = 2Р; М = 4РР, а = 30°. Определить: 1) х = /(/), где х — удлинение пружины (или перемещение центра D катка по отношению к тележке 2); 2) частоту k и период т колебаний.
Решение. 1. Для решения задачи воспользуемся уравнениями Лагранжа. Рассматриваемая система имеет две степени свободы. Выберем в качестве обобщенных координат угол поворота барабана <р и удлинение пружины x(qi = tp, q2 ~ х). Тогда уравнения Лагранжа будут иметь вид
d f дТ\ дТ п _ d ( дТ\ дТ dt \ дф / dtp	1 ’	дх ) дх 2 ’
2. Определим кинетическую энергию Т системы, равную сумме энергий всех тел:
Т=Т1 + Т2 + Тз.	(2)
Так как барабан вращается вокруг оси О, тележка движется поступательно, а каток — плоскопараллельно, то
т 1 Т 2 Т 1^2
Ti =	; Т2 ==	--j^—v2,
1 Ря 1
(3)
1Де /0 =(Pi/2g)R2, ID = (P3/2g)Rl (/?з — радиус катка 3).
Все входящие сюда скорости надо выразить через обобщенные < корости <р и х. Очевидно, что сщ == ср, v2 — R®i = Ry. Для определения у,, рассмотрим движение катка как сложное. Учитывая, что х определи-
ет положение точки D по отношению к тележке, получим = =	где численно v°d = х, иЬер= у2 — Ry- Тогда, принимая во
внимание, что при возрастании <р и х скорости v°o и Урпер направлены в разные стороны и что точка Е для катка — мгновенный центр скоростей, получим
n- Vd x~Rq
vD = x-R<t, о>з = -^- =.....£— •
Подставляя все найденные значения скоростей и 'значения Ю и ID в равенства (3) и учитывая, что Pi = Р3 = 2Р, а Р2 = 4Р, получим окончательно из (2) следующее выражение для Т:
т = -^- (4/?V - 3/?ф*+-|-X2).	(4)
Отсюда находим
¥-= — (8/?2ф-3/?х),	=0;
дф g	Оф
3-- 7 l-3ST+3i).	<s>
3. Теперь определим обобщенные силы Qi и Q2. Изображаем действующие на систему активные силы: силы тяжести Pi, Р2, Р3, силы упругости F и F', где численно F' = F = сх, и пару с моментом М.
а)	Для определения Qi сообщим системе возможное перемещение, при котором координата ф получает приращение б<р>0, а х не изменяется, т. е. бх = 0 (пружина при таком перемещении системы не изменяет свою длину). Тогда тележка и центр D катка получают одинаковые перемещения 6s2 = 6sD = Рбф и элементарная работа действующих сил будет равна
б Д i = Мбф — Р2 sin30° • 6s2 — Рз sin 30° • 6s D — F'6s2 + F6sD.
Заменив здесь все величины их значениями, найдем в результате, что
6Д1 = (М - 0,5Р2Р - 0,5Р3Р)бф = РРбф .	(6)
б)	Для определения Q2 сообщим системе возможное перемещение, при котором координата х получает приращение 6х>0, а ф не изменяется, т. е. бф = 0 (барабан не поворачивается и тележка не перемещается). Тогда элементарную работу совершат только силы Р3 и F, учтя, что Рз = 2Р, получим
6Д2 = P3sin30° • 6х — F6x = (Р — сх)дх .	(7)
Коэффициенты при бф и бх в равенствах (6) и (7) и будут искомыми обобщенными силами; следовательно,
Qi = PR ; Q2 = Р— сх .	(8)
Подставляя величины (5) и (8) в уравнения (1), получим следующие дифференциальные уравнения движения системы:
- 3Rx) = PR , -у-(— ЗЯ? + 3х) = Р — сх .	(9)
4. Для определения х = /(/) исключим из уравнений (9) ф. Получим дифференциальное уравнение вида
х + k2x = а ,
где
Общее решение уравнения (10), как известно из высшей математики, имеет вид х = Xi -J- х2, где х\ — общее решение однородного уравнения x-\~k2x — 0, т. е. Xi = Cisin (&/) + С2 cos (&/), а х2— частное решение уравнения (10). Будем искать решение х2 в виде х2 = Л— == const. Подставляя значение х2 в уравнение (10), получим А = a/k2. Таким образом, общее решение уравнения (10) имеет вид
х = Ci sin (6/) + C2cos(&/) + a/k? ,	(11)
где Ci и С2 — постоянные интегрирования. Для их определения найдем еще производную х от х по времени:
х = Ci&cos (kt) — C2k sin (kt).	(12)
По начальным условиям при t = 0 х = 0, х = 0 (движение начинается из состояния покоя и пружина в этот момент не деформирована). Подставляя эти величины в уравнения (11) и (12), найдем из них, что Ci = 0, С2 = — a/k2.
Окончательно получим искомую зависимость х — f(t) в виде
x = -^-(l-cos«).	(13)
где значения а и k2 даются последними двумя из равенств (10). Таким образом, центр D катка совершает по отношению к тележке колебания, закон которых дает равенство (13). Круговая частота k и период т этих колебаний:
<»>
Задача Д12
Механизм, расположенный в вертикальной плоскости (рис. Д12.0 — Д12.9), состоит из ступенчатых колес 1 и 2 с радиусами Ri = 0,4 м, Г1 — 0,2 м, /?2 = 0,5 м, г2 = 0,3 м, имеющих неподвижные оси враще-
Таблица Д1^
Номер условия	Шх	ГПч	т3	т4	т5	Cl	Сч	Сз
0	12	16			8			1200				
1	10	8	4	_—	—	—	—	1000
2	16	12	—	—	6	_—	800	—.
3	20	—_	.—	6	—	1500	—	—
4	—	18	—	—	4	—	1000	—
5	18	14	6	—	—	1000	—	—_
6	12	—	8	4	-—	—	—	1200
7	16	10	—	—	4	800	—	—
8	20	16	—	8	—	—	1200	—
9	10	—	6	4	—	1000	—	—
Рис. Д12.2
Рис. Д12.5
Рис. Д12.6
Рис. Д12.7
Рис. Д12.8
Рис. Д12.9
ния; однородного стержня 3 длиной I = 1,2 м, закрепленного шарниром на одном из концов; грузов 4 и 5, подвешенных к нитям, намотанным на колеса. На стержне расстояние АВ = 2//3.
Стержень 3 соединен с колесом 2 невесомым стержнем 6. Колеса / и 2 или находятся в зацеплении (рис. О—4), или соединены невесомым стержнем 7 (рис. 5—9). К колесам и стержню 3 прикреплены пружины.
В табл. Д12 заданы массы пи тел (кг) и коэффициенты жесткости Ci пружин (Н/м). Прочерки в столбцах таблицы означают, что соответствующие тела или пружины в систему не входят (на чертеже эти тела и пружины не изображать); в результате в каждом конкрет
ном варианте получается довольно простои механизм, содержащий три или даже два тела. Стержень 6 или 7 входит в состав механизма, когда в него входят оба тела, соединенные этим стержнем.
В положениях, изображенных на рисунках, механизм находится в равновесии. Определить частоту и период малых колебаний системы около положения равновесия. Найти также, чему равно статическое удлинение (сжатие) пружины Хст в положении равновесия.
При подсчетах считать колеса 1 и 2 сплошными однородными цилиндрами радиусов Ri и R2 соответственно.
Рассмотрим два примера решения этой задачи.
Пример Д12а. Находящаяся в равновесии механическая система состоит из колеса 1 радиуса Ri, ступенчатого колеса 2 с радиусами R2 и г2 и груза 3, подвешенного на нити, намотанной на колесо 2; колеса соединены невесомым стержнем АВ (рис. Д12а). К колесу 1 прикреплена вертикальная пружина с коэффициентом жесткости с.
Дано: mi — 12 кг, т2 = 6 кг, тз = 3 кг, Ri — R2 — R, r2 = 0,5/?, с — 900 Н/м. Колеса считать сплошными однородными цилиндрами. Определить: частоту k и период т малых колебаний системы около положения равновесия и значение Хст.
Решение. 1. Система имеет одну степень свободы. Выберем в качестве обобщенной координаты угол ср поворота колеса / от равновесного положения (при равновесии ф = 0 и sD — 0, s3 = 0); при движении системы, рассматривая малые колебания, считаем угол ф малым.
Поскольку все действующие на систему активные силы потенциальные (сила тяжести и сила упругости), выразим обобщенную силу Q через потенциальную энергию П системы. Тогда исходным уравнением будет
d / дТ \ дТ _	_ ОТ	...
- т;~(	)---3“— — Q » гДе Q — ~~~з— •	(О
d/ \ оф / дф	дф
Рис. Д12а
2.	Определим кинетическую энергию системы, равную сумме энергий всех тел:
+	(2)
Так как колеса 1 и 2 вращаются вокруг осей О\ и О2, а груз 3 движется поступательно, то
Л = /01(о?/2, T2 = ZO2(d!/2,
Гз = m3v3/2 ,	(3)
где
Z01 == miZ??/2 , IO2=tn2R22/2.	(4)
Все скорости, входящие в равенства (3), надо выразить через обобщенную скорость <р. Тогда = <р. Далее, ввиду малости угла ф можно считать в каждый момент времени vB = Уд, т. е. (о2Г2 = (oiRi, откуда ©г = ®iRi/r2 и v3 = (O2R2 == (O1R1R2A2. Отсюда, учтя, что Ri = = R2 — R, r2~ 0,5/?, получим
(0i = Ф, (02 = /?1ф/г2 = 2ф , Уз = 2/?ф .	(5)
Подставляя величины (4), где Ri — R2 = R, и (5) в равенства (3), получим из равенства (2)
Т — 0,5а0ф2, где а0 — (0,5/ni + 2m2 + 4m3)R2.	(6)
Отсюда находим
дТ • дТ a d / дТ \
__==аоч),__=о,-^^5-)=ао<р.	(7)
3.	Определим потенциальную энергию П системы, учитывая, что для пружины П = 0,5сХ2, где X — удлинение (сжатие) пружины, а для поля сил тяжести П = mgzc, где zc — координата центра тяжести (ось z направлена по вертикали вверх).
Тогда для всей системы
П — 0,5сX2 + m3gz Сз •	(8)
Определяя X, учтем, что в положении равновесия пружина может иметь некоторое статическое (начальное) удлинение или сжатие Хст, необходимое для сохранения равновесия (в нашем случае для уравновешивания силы тяжести, действующей на груз 3). При повороте колеса / на угол ф пружина получит дополнительное к Хст удлинение sD = /?кр. Следовательно, 1 = XCt4“$d = XCT+R<p-
Для zc3, направляя ось г из точки О3 вверх, получим zC3 = — s3. Чтобы выразить $3 через ф, заметим, что зависимость между малыми перемещениями здесь будет такой же, как между соответствующими скоростями. Тогда по аналогии с последним из равенств (5) s3 .= 2/?ф и Zc3 = —2/?ф.
Подставляя все найденные величины в равенство (8), получим
П = О,5с(Хст + Яф)2 - 2т3£/?Ф •	(9)
4.	Определим обобщенную силу Q и ZCT. Сначала находим
Q=-----^-=-c/?(X„+/?ip) + 2mjg/?.	(10)
Входящую сюда неизвестную величину Хст найдем из условия, что при равновесии, т. е. когда ф = 0, должно быть и Q — 0. Полагая в (10) ф = 0 и Q = 0, получим c/?XCT — 2m3gR, откуда
XCT=2m3g/c.	(11)
Заменяя в (10) Хст этим значением, найдем, что
Q=-cR2<p.	(12)
5.	Составляем уравнение Лагранжа. Подставляя значения производных из равенств (7) и значение Q из (12) в уравнение (1), получим аоф = — с/?2ср или, с учетом обозначения в (6),
ftp
ф 4- /г2ф = 0 , где k2 =-= ———-----------.	(13)
ао mi + 4т2 + 8тз
Из теории колебаний известно, что когда уравнение приведено к виду (13), то в нем k является искомой круговой частотой, а период колебаний т = 2n/k. При заданных числовых значениях mi, m2, m3 и с, произведя соответствующие подсчеты, получим из (13) и (11) ответы: k — 5,48 с"1, т ~ 1,11 с, %ст — 0;065 м — 6,5 см.
Пример Д126. Находящаяся в равновесии механическая система состоит из однородного стержня /, ступенчатого колеса 2 с радиусами ступеней Т?2 и г2, груза 3, подвешенного на нити, перекинутой через блок 4 и намотанной на колесо 2, и невесомого стержня 5, соединяющего тела / и 2 (рис. Д12, б). В точке (?i шарнир; в точке А прикреплена горизонтальная пружина с коэффициентом жесткости с.
Рис Д12
Дано: mi = 10 кг, m2 = 12 кг, m3 — 4 кг, m4 — 0, R2 — R, 1	0,5/?, с = 750 Н/м, О\А = 1=1 м, О\В = 1/3. Колесо 2 считать
< плотным однородным цилиндром. Определить: частоту k и период т малых колебаний системы около положения равновесия и значение Хет-
Решение. 1. Рассмотрим произвольное положение системы, когда • •на выведена из состояния равновесия и совершает малые колебания (рис. Д12, в). Система имеет одну степень свободы. Выберем в качестве обобщенной координаты угол ф отклонения стержня от вертикали, считая ср малым, и составим для системы уравнение Лагранжа. Поскольку все действующие активные силы (сила упругости и силы 1яжести) потенциальные, выразим обобщенную силу Q через потенциальную энергию II системы. Тогда исходным уравнением будет
d / дТ \ дТ _ п <Ш
—т; (---•»- -1 -—-— = Q , где Q =-ч— .	(1)
dt \ дф / дф	ду>
При исследовании малых колебаний в уравнении сохраняют малые величины ф, ф в первой степени, отбрасывая малые более высокого порядка. Для этого надо найти выражения Т и П с точностью до ф2 и Ф2, так как в (1) входят первые производные от Т и П по ф и ф, а при дифференцировании многочлена его степень понижается на единицу
2.	Определим кинетическую энергию Т системы, равную сумме энергий всех тел:
Т=Т1 + Т2 + Т3.	(2)
Так как стержень 1 и колесо 2 вращаются вокруг осей О\ и С2 соответственно, а груз 3 движется поступательно, то
Л - /01со?/2 ; Т2 = 1с^1/2 ;	(3)
Гз = т3у3/2, • де
/01== W1/73; IC2=m2R2/2.	(4)
Все скорости, входящие в равенства (3), надо выразить через обобщенную скорость ф. Тогда coi — ф. Затем ввиду малости ф можно считать vd = vB — wi//3. Учтя это, найдем со2 = vD/r2 = vd/^,3R и
= ve— (o2R. Таким образом, он = ф; со2 = 2/ф/З/?;
V3 = 2/ф/З .	(5)
Подставляя величины (4) и (5) в равенства (3), получим из (2)
Г	/ mi	2m2	4m3 \ „
т = —ао<р2, где а0 =	—|—5---1--5—У-	(6)
Z	\ О	<7	<7 /
Отсюда находим
дТ . дТ d / дТ \ . = 0, ^-_-J = ao(p	(7)
3.	Определим потенциальную энергию П системы, учитывая, что для пружины П = 0,5сХ2, где X — удлинение (сжатие) пружины, а для поля сил тяжести П = mgzc, где zc — координата центра тяжести (ось z направлена по вертикали вверх). Тогда для всей системы
П = 0,5сХ2 + /И1^гС1 + m2^zc2+ m3gzC3,	(8)
где величины X, zCp zC2, £с3 должны быть выражены через ср.
Определяя X, учтем, что в положении равновесия пружина может иметь некоторое статическое (начальное) удлинение или сжатие Хст, необходимое для сохранения равновесия (в нашем случае для уравновешивания силы тяжести Р3). В произвольном положении (см. рис. Д12, в) пружина получит дополнительное удлинение, равное причем ввиду малости <р можно считать =/ф. Тогда Х=Хст + $л = = Хст~Т /ф.
Для гСр направляя ось z\ из точки Oi вверх, получим zCi = = 0,5/cos ф. Разлагая здесь coscp в ряд и сохраняя член с ф2, получим*
1 У?	1 (1 Ф2 \
cosq>= 1---2“ и Zc>=f"V-------2~) 
Для zc2, взяв начало координат в точке С2, получим zC2 = 0.
Для 2Сз, совмещая начало координат Оз с положением центра тяжести груза 3 при равновесии, получим zC3 — — $з» где «з — перемещение груза. Чтобы выразить $3 через ф, заметим, что зависимость между малыми перемещениями здесь будет такой же, как между соответствующими скоростями. Тогда по аналогии с последним из равенств (5) s3 = 2/ф/З и гСз — — 2/ф/З.
Подставляя все найденные величины в равенство (8), получим
П —-^%ст + /ф)2+-^т1^ 1 —------------у~т3^/ф.	(9)
4.	Определим обобщенную силу Q и Хст. Сначала находим
Q = = — [ cZ(x« + ZlF)------5-тI&l'f--•	(10)
Входящую сюда неизвестную величину Хст найдем из условия, что при равновесии, т. е. когда ф = 0, должно быть и Q = 0. Полагая в равенстве (10) ф=0и Q ~ 0, получим c/XCT —2m3g//3 = 0, откуда
2 m3g ““”“F с
(П)
* В случае когда стержень OiA горизонтален (поверните рис. Д12,в на 90°), будет zc—0»5/зтф, и нужное приближение получится, если считать sin ф = ф.
Заменяя в (10) Хет этим значением, найдем окончательно
Q = — &ф, где b = (cl-— 0,5mig)l.	(12)
5.	Составляем уравнение Лагранжа. Подставив значения произ-ш»дных из равенств (7) и значение Q из (12) в уравнение (1), получим
- —- &ф или
«о	„ b	9(2cl — mig)
Ф-f-&2ф = 0, где k? =---=  -------————гт».	(13)
«о 2(3/П1 4- 2т2 4- 4/Пз)/
Из теории колебаний известно, что когда уравнение приведено к виду (13), то в нем величина k является искомой круговой частотой, в период т-= 2n/k. При заданных числовых значениях, произведя соответствующие расчеты, получим из (13) и (11) следующие отве-। ы: k — 9,49 с-1; т = 0,66 с; Хст = 0,035 м = 3,5 см.
Д ругое решение. Рассмотрим другой путь решения задачи, пригодный и когда действующие силы не потенциальны.
Выберем опять в качестве обобщенной координаты угол ф, считая по малым, и составим для системы уравнение Лагранжа
4(^)	(14)
dt х (?ф ' ^ф
Для кинетической энергии Т системы и для соответствующих производных получим, как и раньше, значения (6) и (7).
Чтобы найти обобщенную силу Q, надо изобразить на чертеже (рис. Д12,б) действующие активные силы, совершающие работу при перемещении системы, т. е. силу упругости пружины F, приложенную к стержню 1 в точке А и направленную вправо (пружину считаем растянутой), силу тяжести приложенную к стержню 1 в точке Ci, и силу тяжести Рз, приложенную к грузу _5; обе эти силы направлены по вертикали вниз (на рис. Д12,б силы Г, Pi, Рз не показаны, но при решении задачи таким путем их надо изображать).
Теперь сообщаем системе возможное перемещение, при котором угол ф получает положительное приращение бф, и вычисляем работу 6Д всех названных сил на этом перемещении. Получим
6Д = (—р/созф4-7>1-~“8тф)дф4-/>зб5з .	(15)
В равенстве (15) надо выразить б$з через бф. По аналогии с последним из равенств (5) найдем, что
6s3 = 2/бф/З .	(16)
Определим еще значение силы упругости F. По модулю F — ск, где К — удлинение пружины, слагающееся из начального удлинения £ст и дополнительного удлинения $л, которое ввиду малости угла ф можно считать равным /ф. Тогда Х = Хст4~/ф и
F = с(%ст4-/ф) •	(17)
Подставив величины (16) и (17) в равенство (15) и учтя, что Pi = m\g, а Р3 = rri3g и что ввиду малости ф можно считать зшф = ф, cos ф = 1, приведем окончательно равенство (15) к виду
6А = [—с(Хст4-/ф)/4-Щ1Я/ф/24-2т3^А]бф.
Коэффициент при бф в правой части полученного равенства и является искомой обобщенной силой. Следовательно,
Q = [ — cXCT+(mig/2 — cl)q>+2m3g'/3]l.	(18)
Величину Хет опять находим учитывая, что при равновесии, т. е. при ф = 0, будет и Q = 0. В результате получим для Хст значение, даваемое формулой (11). При таком Хст найдем из (18) окончательно, что
Q = (mig/2 —c[)lq>.	(19)
Подставляя значения соответствующих производных из равенств (7) и значение Q, даваемое формулой (19), в уравнение (14), приведем его окончательно к виду
^ + (с/-ОТ|§/2)Ар=0.	(20)
ао
Решение уравнения (20) существенно зависит от знака коэффициента при ф. Если этот коэффициент положителен, т. е.
c>m,g/2l,	(21)
то, введя обозначение
(22) получим, как известно, решение уравнения (20) в виде
Ф == Ci sin (kt) + Czcos(kt).
Если при / = 0 ф = фо и ф = фо, то С2 == фо, С\ — ф0//г. Но фо и фо всегда можно выбрать столь малыми, что угол ф во все время движения тоже будет оставаться малым и, следовательно, система будет совершать малые колебания около положения ее равновесия, определяемого углом ф — 0. Равновесие системы в таком случае называют устойчивым; условие устойчивости равновесия определяется в данной задаче неравенством (21).
Если же коэффициент при ф в уравнении (20) будет отрицательным, т. е. будет c<m\g/2l, то введя обозначение tv = (m\g/2 — cl)l/aa, приведем уравнение (20) к виду ф — п2ф = 0. Решением этого уравнения, как тоже известно, будет
Ф= Cieni^C2e~nt
и, каковы бы ни были начальные условия, множитель ent, а с ним и угол ф, будут со временем возрастать, т. е. система, выведенная из равновесного положения сколь угодно малым смещением (толчком), будет от этого положения все больше и больше отклоняться. Равновесие системы в таком случае называется неустойчивым.
В решаемой задаче с = 750 Н/м, a tn\g/2l ж 49 Н/м и неравенство (21) выполняется. Следовательно, равновесие системы является устойчивым и она может совершать около положения равновесия малые колебания. Круговая частота k этих колебаний определяется из равенства (22), а период т = 2л/&. Числовые значения искомых величин получаются, конечно, те же, что и в п. 5.
содержание
Методические указания....................................... 3
Рабочая программа .......................................... 5
Список литературы.......................................... II
Контрольные задания ....................................... 12
(.одержание заданий, выбор вариантов, порядок выполнения ра-
бот, пояснения к тексту задач.............................. 12
Задачи к контрольным заданиям.............................. 14
(батика..................................................   14
Кинематика ....... ........................................ 29
Динамика.................................................   50

Учебное издание
Котова Людмила Ивановна, Надеева Раиса Ивановна, Тарг Семен Михайлович, Цывильский Василий Львович.
Шмарова Инна Мироновна
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Методические указания и контрольные задания
Зав. редакцией А. В. Дубровский Редактор О. Г. Подобедова Мл. редактор Н. М. Иванова Художественный редактор Л. К. Громова Технический редактор А. К. Нестерова Корректор Г. Н. Буханова
Н/К
Изд. № ОТ-727. Сдано в набор 06.12.88. Подп. в печать 02.06.89. Формат 84ХЮ8’/з2. Бум. кн.-журн. Гарнитура литературная. Печать высокая. Объем 5,88 усл. печ. л. 5,98 усл. кр.-отт. 5,35 уч.-изд. л. Тираж 160 000 экз. Зак. № 1722. Цена 15 коп.
Издательство «Высшая школа», 101430, Москва, ГСП-4, Неглинная ул., д. 29/14.
Ярославский полиграфкомбинат Госкомиздата СССР. 150014, Ярославль, ул. Свободы, 97.