Сборник,
заданий
ДЛЯ КУРСОВЫХ РАБОТ
ПО ТЕОРЕТИЧЕСКОЙ
МЕХАНИКЕ
ПОД ОБЩЕЙ РЕДАКЦИЕЙ
ПРОФ. А. А. ЯБЛОНСКОГО
ИЗДАНИЕ ПЯТНАДЦАТОЕ, СТЕРЕОТИПНОЕ
Допущено Министерством
высшего и среднего специального образования СССР
в качестве учебного пособия для студентов
высших технических учебных заведений.
МОСКВА
«ИНТЕГРАЛ-ПРЕСС»
2006
ББК 22.21
С23
УДК 531.8
А. А. Яблонский, С. С. Норейко, С. А. Вольфсон, Н. В. Карпова,
Б. Н. Квасников, Ю. Г. Минкин, Н. И. Никитина, В. Б. Павлов,
Ю. М. Тепанков, Д. Д. Акимов-Перетц, В. С. Доев, Ф. А. Доронин,
К. Ю. Красносельский
Рецензент: д-р техн, наук, проф. М. М. Гернет (Московский
технологический институт пищевой промышленности)
Сборник заданий для курсовых работ по теоретической
механике: Учебное пособие для технических вузов. —
15-е изд., стереотипное — М.: Интеграл-Пресс, 2006. — 384 с.
ISBN 5-89602-016-3
Сборник содержит 45 заданий в 30-ти вариантах по статике, кинематике, ди-
намике, аналитической механике и колебаниям механической системы для курсо-
вых работ по теоретической механике.
Ряд заданий требует проведения исследований. Приведены примеры выполнения
заданий. Предназначен в качестве учебного пособия для студентов втузов очной, ве-
черней и заочной систем обучения.
Учебное издание
Формат 60 X ЭОУхб- Объем 24 п. л. Доп. тираж 3000 экз. Издательство «Интеграл-
Пресс». 125130. г. Москва, а/я 240. ЛР №065120 от 18.04.97. Отпечатано с готовых
диапозитивов в ГУП ППП «Типография «Наука» Академиздатцентра «Наука» РАН.
121099, Москва, Шубинский пер., 6. Заказ № 4268.
ISBN 5-89602-016-3
© Коллектив авторов, 2006
© Издательство «Интеграл-Пресс», 2006
9 785896 020165
ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
В настоящем издании сборника исправлены замеченные опечатки и
ошибки предыдущего издания. Большую работу по подготовке нового
издания сборника провели авторы Доев В. С. и Доронин Ф. А.
Коллектив авторов
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
Теоретическая механика как одна из важнейших физико-матема-
тических дисциплин играет существенную роль в подготовке инже-
неров любых специальностей.
На основных законах и принципах теоретической механики базиру-
ются многие общеинженерные дисциплины, такие, как сопротивление
материалов, строительная механика, гидравлика, теория механизмов
и машин, детали машин и др.
В различных курсах по машиностроительным, механическим, стро-
ительным, приборостроительным и многим другим специальностям
также широко используются положения теоретической механики. На
основе теорем и принципов теоретической механики решаются многие
инженерные задачи и осуществляется проектирование новых машин,
конструкций и сооружений.
Хорошее усвоение курса теоретической механики требует не только
глубокого изучения теории, но и приобретения твердых навыков в ре-
шении задач. Для этого необходимо самостоятельно решить большое
количество задач по всем разделам.
Четвертое издание настоящего сборника содержит 45 заданий, ка-
ждое в 30 вариантах, по всем основным темам программ, утвер-
жденных Минвузом СССР: 9 — по статике, 9 — кинематике, 13 —
динамике, 9 — аналитической механике и 5 — колебаниям механи-
ческой системы.
В некоторые задания, входившие в третье издание, внесены изме-
нения и дополнения, некоторые из них существенно переработаны,
отдельные задания, сходные по тематике, объединены, добавлены
новые задания.
5
В сборнике помещены три задания (по статике, кинематике и
динамике), при выполнении которых целесообразно использование
ЭВМ. По каждому из этих заданий дан пример с алгоритмом решения
и результатами расчета на ЭВМ.
Примеры выполнения заданий не содержат программ и рекоменда-
ций по их составлению, так как в вузах страны могут применяться
различные языки программирования и операционные системы и ис-
пользоваться разные ЭВМ.
Для выполнения заданий по статике и кинематике необходимо ре-
шать системы линейных алгебраических уравнений, а при выполнении
задания по динамике — численно интегрировать дифференциальное
уравнение. В библиотеке стандартных программ любой ЭВМ такие
программы имеются.
Большое число заданий по каждому из разделов курса обеспе-
чивает возможность устанавливать тематику и количество курсовых
работ в зависимости от профиля подготовки специалистов, т. е. от
объема и содержания изучаемого курса теоретической механики.
Набор вариантов индивидуальных заданий, входящих в курсовую
работу, студент может определить по своему шифру, пользуясь спе-
циальной таблицей, приведенной в конце книги. Шифр каждому сту-
денту устанавливает преподаватель.
В сборнике приведены примеры выполнения заданий. Основываясь
на этих примерах, студенты (особенно заочных и вечерних факуль-
тетов) смогут самостоятельно выполнять задания из этого сборника.
При выполнении ряда заданий требуется проведение некоторых
исследований. Они могут служить основой для организации учебно-
исследовательской работы студентов по теоретической механике.
Сборник могут использовать также инженеры и техники для углу-
бления знаний по теоретической механике.
В подготовке настоящего издания сборника наряду с автора-
ми предыдущих изданий приняли участие Д. Д. Акимов-Перетц,
В. С. Доев, Ф. А. Доронин и К. Ю. Красносельский.
Авторы выражают искреннюю благодарность профессору М. М. Бер-
нету за обстоятельный разбор рукописи сборника и ряд ценных пред-
ложений, а также коллективам кафедр и отдельным преподавателям
за полезные советы, учтенные при подготовке настоящего издания.
Авторы
6
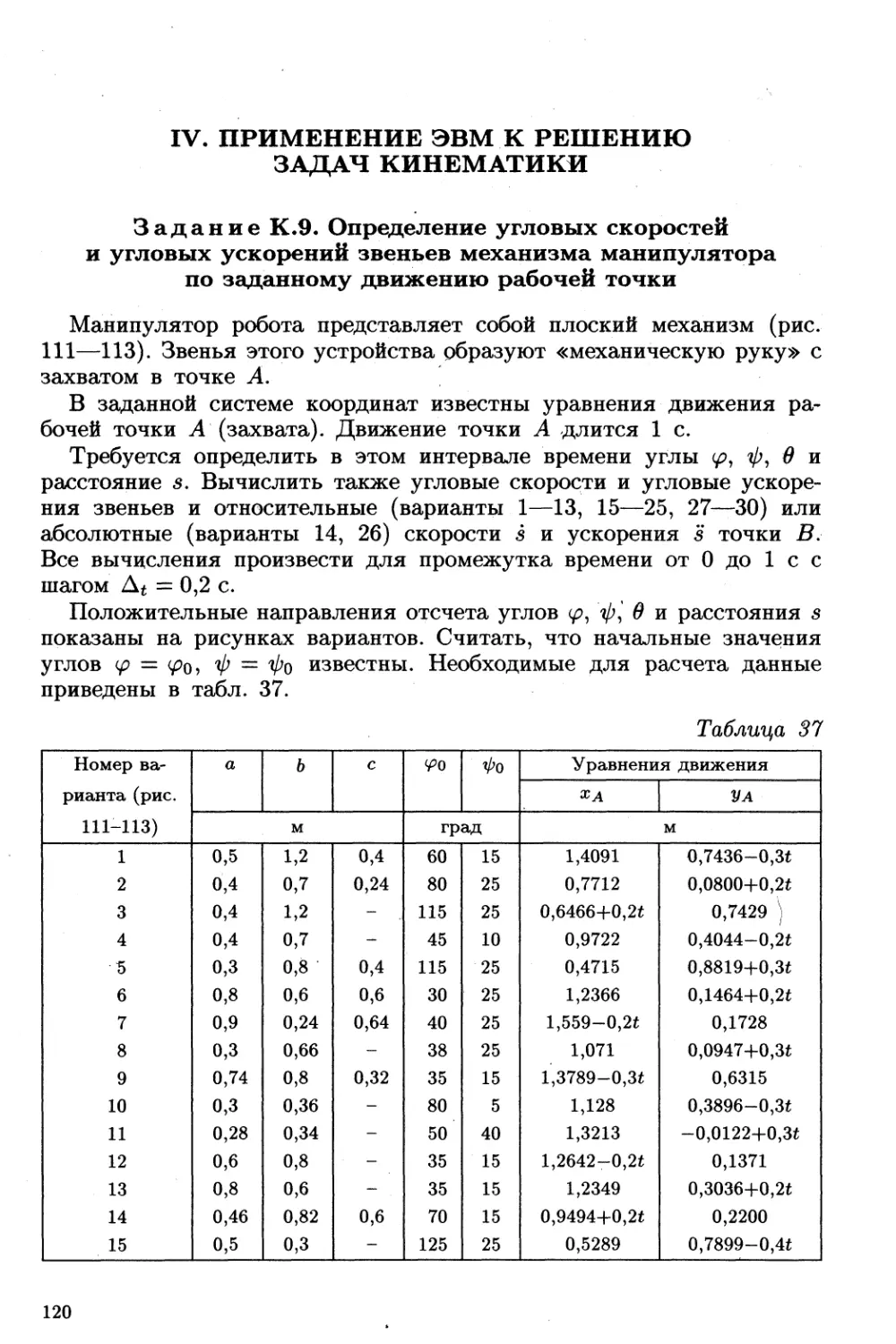
Используемые обозначения.
о	шарнир
	основание неподвижной опоры
^7	основание подвижной опоры
Г	жесткая заделка
w" ¥	скользящая заделка
Bill	бискользящая заделка
s	шарнирно-подвижная опора
й	демпфер
7
РАЗДЕЛ ПЕРВЫЙ
СТАТИКА ТВЕРДОГО ТЕЛА
I.	ПЛОСКАЯ СИСТЕМА СИЛ
СИСТЕМА ПРОИЗВОЛЬНО РАСПОЛОЖЕННЫХ СИЛ
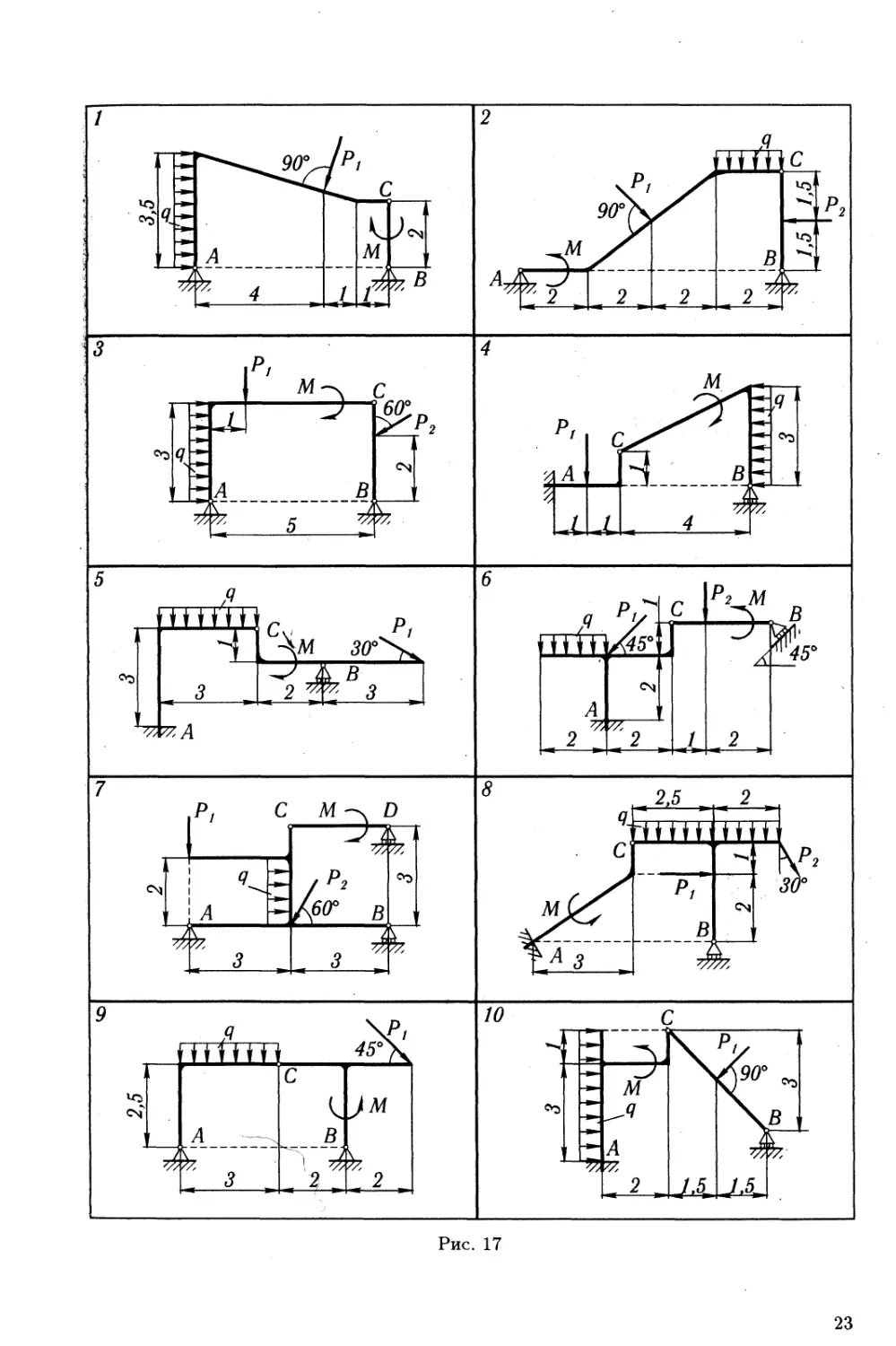
Задание С.1. Определение реакций опор твердого тела
На схемах (рис. 1—4) показаны для каждого варианта три спо-
соба закрепления бруса, ось которого — ломаная линия. Задаваемая
нагрузка (см. табл. 1) и размеры (м) во всех трех случаях одинаковы.
Определить реакции опор для того способа закрепления бруса, при
котором реакция, указанная в табл. 1, имеет наименьший модуль.
Таблица 1
Номер варианта (рис. 1-4)	Р, кН	М, кН-м	кН/м	Иссле- дуемая реакция	Номер варианта (рис. 1-4)	P, кН	кН-м	Я, кН/м	Иссле- дуемая реакция
1	10	6	2	Ya	16	12	6	2	МА
2	20	5	4	МА	17	20	4	3	Уа
3	15	8	1	Yb	18	14	4	2	ХА
4	5	2	1	Yb	19	16	6	1	Rb
5	10	4	—	ХВ	20	10	—	4	Уа
6	6	2	1	МА	21	20	10	2	МА
7	2	4	2	Ха	22	6	6	1	Уа
8	20	10	4	Rb	23	10	4	2	Ма
9	10	6	—	Ya	24	4	3	1	Уа
10	2	4	2	Ra	25	10	10	2	Ха
11	4	10	1	Rb	26	20	5	2	мА
12	10	5	2	Ya	27	10	6	1	ХА
13	20	12	2	Ya	28	20	10	2	Уа
14	15	4	3	Ya	29	25	—	1	МА
15	10	5	2	XA	30	20	10	2	Rb
Пример выполнения задания. Дано: схемы закрепления бруса
(рис. 5, а, б, в); Р = 5 кН; М = 8 кН-м; q — 1,2 кН/м.
Определить реакции опор для того способа закрепления, при ко-
тором момент Ма в заделке имеет наименьшее числовое значение.
Решение. Рассмотрим систему уравновешивающихся сил, прило-
женных к конструкции. Действие связей на конструкцию заменяем
их реакциями (рис. 6): в схеме а — Ха, Уа, Ма, в схеме б — Уд,
8
Рис. 1
9
от
г эиа
Рис. 3
11
Рис. 4
12
Мд и Rb, в схеме в — Мд, Хв и Ув- Равномерно распределенную
нагрузку интенсивностью q заменяем равнодействующей
Q = q • 2 = 2,4 кН.
Чтобы выяснить, в каком случае момент в заделке является наи-
меньшим, найдем его для всех трех схем, не определяя пока осталь-
ных реакций.
Для схемы а
^2 MiA =0; МА - Р • 2sin45° + М - Q • 5 = 0.
Вычисления дают
Мд = 11,07 кН-м.
Для схемы б
^МгС =0; М'а + М-Q-5 = 0 и М'А = 4,00 кН-м.
Для схемы в
= M'i + P BD + M + Q «1 = 0 и M'i = -31,61 кН-м.
Здесь
BD = BE + ED = V2 + 2д/2 = 4,24 м.
Таким образом, наименьший момент в заделке получается при
закреплении бруса по схеме б. Определим остальные опорные реакции
для этой схемы:
^Хг = 0; Р cos 45° — Rb = 0, откуда Rb = 3,54 кН;
52 Уг = 0; Уд — Р • sin 45° — Q = 0, откуда Уд = 5,94 кН.
Результаты расчета приведены в табл. 2.
13
Таблица 2
Схема по рис. 6	Момент Ма(М'а, М"),кНм	Силы, кН	
			Rb
а	11,07	-	—
б	4,00	5,94	3,54
в	-31,61	-	-
Задание С.2. Определение реакций опор и сил
в стержнях плоской фермы
Определить реакции опор фермы на заданную нагрузку, а также
силы во всех ее стержнях способом вырезания узлов. Схемы ферм
показаны на рис. 7—9. Необходимые для расчета данные приведены
в табл. 3.
Таблица 3
Номер варианта	Р1	Р2	Рз	а	h	а, град	Номера
(рис. 7-9)	кН			м			стержней
1	4	9	2	2,0	—	30	3, 8, 9
2	10	3	4	2,5	—	60	2, 5, 7
3	2	12	6	3,0	—	60	4, 5, 10
4	10	10	5	4,0	—	60	5, 6, 11
5	2	4	2	—	2,0	60	4, 5, 10
6	3	7	5	4,0	3,0	—	8, 9, 11
7	4	6	3	4,0 '	—	60	4, 6, 12
8	5	7	7	3,2	—	45	3, 4, 5
9	10	8	2	5,0	—	60	6, 7, 12
10	3	4	5	4,4	3,3	—	3, 5, 7
11	2	6	8	2,5	3,0	—	2, 7, 8
12	5	7	2	4,0	—	60	4, 5, 10
13	4	6	2	4,8	3,6	—	4, 5, 10
14	3	5	5	3,0	—	60	5, 6, 8
15	2	2	10	4,0	6,0	—	2, 6, 9
16	5	6	2	5,0	—	60	3, 5, 6
17	4	4	10	4,0	6,0	—	4, 7, 8
18	5	2	8	—	5,0	60	1, 4, 8
19	8	4	10	5,0	10,0	60	4, 5, 7
20	2	3	5	4,0	6,0	—	5, 6, 8
21	’ 3	2	7	6,0	—	45	5, 8, 9
22	4	2	9	4,0	—	45	2, 6, 8
23	5	8	8	4,0	9,0	30	4, 7, 9
24	6	10	2	3,6	—	45	4, 5, 10
25	7	10	5	• 4,4	3,3	—	8, 10, 11
26	8	12	2	4,0	—	30	4, 5, 9
27	9	4	4	4,0	3,0	—	5, 9, 11
28	10	5	3	5,0	—	30	3, 5, 6
29	12	8	2	6,0	—	45	5, 6, 11
30	5	10	4	4,0	2,0	-	6, 7, 12
Дополнительно определить силы в трех стержнях фермы от той
же нагрузки способом Риттера (номера стержней указаны в табл. 3).
14
Рис. 7
15
Рис. 8
16
Рис. 9
17
Пример выполнения задания. Дано: схема фермы (рис. 10);
Pi = 2 кН, Р2 = 4 кН, Р3 = 6 кН, а = 4,0 м; h = 3,0 м.
Решение. 1. Определение реакций опор. Покажем внешние силы,
приложенные к ферме: активные (задаваемые) силы Р1? Р2, Рз и
реакции опор А и В (рис. 11).
Так как линия действия реакции опоры А неизвестна, определим
ее составляющие по координатным осям ХА и Уд.
Опора В — стержневая; линия действия ее реакции известна —
она направлена вдоль опорного стержня.
Составим уравнения равновесия сил, приложенных к ферме:
V MiA = 0; Pi • ЗЛ + Р2 • 2Л + RBa = 0; '
£Xi = 0;	Хд-Р1-Р2=0;	►
£ у. = 0; Ya + Rb - Рз = 0.
(1)
Из этих уравнений
RB = -10,5 кН; Уд = 6,0 кН; ХА = 16,5 кН.
2.	Определение сил в стержнях фермы способом вырезания узлов.
Стержни, сходящиеся в узле фермы, являются для узлового соеди-
нения связями. Отбросим мысленно связи и заменим их действие на
узлы реакциями. На рис. 12 показаны узлы фермы с приложенными
к ним активными и реактивными силами.
Силу в стержне с номером г обозначим Si. Реакцию стержня с
номером г, приложенную к узлу М, обозначим SiM- Для стержня,
соединяющего узлы М и N
SiM = ^iN •) ИО SiM = Sift = Sz.
Направления реакций всех стержней показаны от узлов внутрь
стержней в предположении, что стержни растянуты. Если в резуль-
тате решения реакция стержня получится отрицательной, это будет
означать, что соответствующий стержень сжат.
18
Для каждого узла составим два уравнения равновесия:
(2)
^Х = 0и ^У = 0.
Рис. 13
Нетрудно убедиться, что из этих уравнений можно определить не
только все силы, но и реакции опор, так что предварительное опреде-
ление реакций опор не является необходимым. Действительно, узлов
7 (А, В, С, D, Е, F, Н), уравнений, следовательно, 14, а неизвестных
тоже 14, т. е. 11 усилий в стержнях и 3 составляющих опорных ре-
акций. Ранее найденные реакции опор могут служить для проверки
решения.
Если уравнения предполагается решать без применения ЭВМ, ре-
комендуется рассматривать узлы в такой последовательности, чтобы
каждый раз в уравнения (2) входило не более двух неизвестных.
Начнем с узла Н:
Xi = 0; -Pi - Sih cos а = 0;
ЕУ = 0; -SiHsina -	= 0,
откуда определяем
Sin = Si = —2,5 кН (стержень сжат) и Szh ~ Sz = 1,5 кН.
Для узла Е
52 Xi = 0; SiE cos а 4- S^e = 0;
IS Yi - °; S1E sin a - P3 - $4E = o,
откуда находим
Sse = S3 = 2,0 кН, $4e = S4 = —7,5 кН (стержень сжат).
19
гоугольник сил (рис.
.. Сжатый стержень
..—- Растянутый стержень
..Стержень, сила в
котором равна нулю
Рис. 14
Затем составляем уравнения равновесия сил, приложенных к узлам
F, С, D, В, А.
Для проверки расчета полезно для каждого узла построить мно-
13).
Для узла Н откладываем в масштабе силу
Pi и проводим через конец и начало этого
вектора направления реакций Sih и S^h Д°
их взаимного пересечения. Стрелки векторов
Siн и Szh ставим так, чтобы силовой тре-
угольник был замкнут. Для этого на рис. 13
стрелку Sih пришлось направить в сторону,
противоположную показанной на рис. 12,—
это соответствует знаку минус в аналитиче-
ском решении. При построении многоуголь-
ника сил для узла Е откладываем силы Рз
и Sie (направляется противоположно Sih) и
проводим до взаимного пересечения направле-
ния реакций Ззя и S±e и т. д. Измеренные в
масштабе построения реакции стержней должны мало отличаться от
найденных аналитически.
Приводим таблицу сил в стержнях (табл. 4) и схему фермы с
фактической картиной сил (рис. 14).
Таблица 4
Номер стержня	1	2	3	4	5	6	7	8	9	10	11
Знак силы	—	+	+	—	—	+	+	—	-	+	
Сила, кН	2,5	1,5	2,0	7,5	7,5	6,0	6,0	12,0	7,5	10,5	0
3.	Определение сил в стержнях способом се-
чений (способом Риттера). Требуется опреде-
лить силы в стержнях 4, 5 и 8.
По способу Риттера каждая сила должна
быть определена из отдельного уравнения и
не должна выражаться через силы в других
стержнях.
Для определения сил S4 и мысленно раз-
режем ферму сечением I—I (рис. 15).
Рассматриваем равновесие сил, приложенных
к верхней части фермы*. Действие отброшенной нижней части на
верхнюю представлено силами S4, S$ и Sq.
По-прежнему условно предполагаем все стержни растянутыми.
Знак минус в ответе укажет на то, что стержень сжат.
* Выбор части фермы обычно определяется объемом вычйслительной работы.
В данном случае следует отметить, что выбор верхней части позволяет получить
искомые силы, выраженные только через заданные силы, независимо от ранее най-
денных опорных реакций.
20
Для определения составим уравнение моментов сил относитель-
но точки F, где пересекаются линии действия сил S& и Sq (точки
Риттера для стержня 4):
MiF = О» S^a 4- P^d 4“ P±h = 0.
Отсюда получим
S4 = -7,5 кН. ‘
Для определения S5, чтобы исключить из уравнения усилия S4 и
5б, проецируем силы на ось х:
Xi = 0; —Pi — Р2 - S5 cos о = 0.
Отсюда получим S$ = —7,5 кН.
Для определения силы S$ проводим сечение
II—II (можно было бы провести его и через
стержни 8, 7 и 6). Рассмотрим равновесие сил,
приложенных к нижней части фермы (рис. 16).
Точкой Риттера для стержня 8 является узел Р, где пересекаются
линии действия сил Sg и Sio, исключаемых из уравнения:
Мц) — 0; —Sgd — ^Ad 4- ХдЛ — 0.
Отсюда получим
Ss = -12,0 кН.
Задание С.З. Определение реакций опор
составной конструкции
(система двух тел)
Конструкция состоит из двух частей. Установить, при каком спо-
собе соединения частей конструкции модуль реакции, указанной в
табл. 5, наименьший, и для этого варианта соединения определить
реакции опор, а также соединения С.
На рис. 17—19 показан первый способ соединения — с помощью
шарнира С. Второй способ соединения — с помощью скользящей
заделки, схемы которой показаны в табл. 6.
Пример выполнения задания. Дано: схема конструкции
(рис. 20); Р1 = 5 кН, Р2 = 7 кН; М = 22 кН • м; q = 2 кН/м; а = 60°.
Определить реакции опор, а также соединения С для того способа
сочленения (шарнир или скользящая заделка), при котором модуль
опоры А наименьший.
Решение. 1. Определение реакций опоры А при шарнирном со-
единении в точке С.
21
Таблица 5
Номер вари- анта	Р1	Р2	М,		Иссле- дуемая	Номер вари- анта	Pl	P2	M,		Иссле- дуемая
(рис. 17-19)	кН		кН • м	кН/м	реакция	(рис. 17-19)	кН		кН • м	кН/м	реакция
1	5,0	-	24,0	0,8	хА	16	7,0	10,0	14,0	3,8	Rb
2	6,0	10,0	22,0	1,0	Ра	17	9,0	12,0	26,0	4,0	Ra
3	7,0	9,0	20,0	1,2	Rb	18	11,0	10,0	18,0	3,5	MB
4	8,0	-	18,0	1,4	мА	19	13,0	9,0	30,0	3,0	MB
5	9,0	-	16,0	1,6	Ra	20	15,0	8,0	25,0	2,5	Rb
6	10,0	8,0	25,0	1,8	мА	21	10,0	7,0	20,0	2,0	Ra
7	11,0	7,0	20,0	2,0	Rb	22	5,0	6,0	15,0	1,5	Ra
8	12,0	6,0	15,0	2,2	мА	23	8,0	5,0	10,0	1,4	Ra
9	13,0	-	10,0	2,4	хА	24	11,0	4,0	5,0	1,3	MA
10	14,0	-	12,0	2,6	Ra	25	14,q	6,0	7,0	1,2	Rb
11	15,0	5,0	14,0	2,8	Rd	26	12,0	8,0	9,0	1,1	Rb
12	12,0	4,0	16,0	3,0	Rb	27	10,0	7,0	11,0	1,0	xA
13	9,0	6,0	18,0	3,2	Ra	28	8,0	9,0	13,0	1,2	Ra
14	6,0	-	20,0	3,4	мА	29	6,0	10,0	15,0	1,4	ma
15	5,0	8,0	22,0	3,6	Mb	30	10,0	12,0	17,0	1,6	MB
Рассмотрим систему уравновешивающихся сил, приложенных ко
всей конструкции (рис. 21). Составим уравнение моментов сил отно-
сительно точки В. упрощения вычисления момента силы
разложим ее на вертикальную и горизонтальную составляющие:
Р[ = Pi cos 60° = 2,5 кН; Р/ = Pi sin 60° = 4,33 кН,
^MiB =0; Р[ • 3 +Р" • 8 — Q • 1— YA • 5 +ХА -1 — М+
+Р2т/1,02 + 1,52 = 0,	(1)
где Q = q- 4 = 2- 4 = 8 кН.
После подстановки данных и вычислений уравнение (1) получает
вид
ХА - 5YA = -24,74 кН.	(1')
Второе уравнение с неизвестными ХА и YA получим, рассмотрев
систему уравновешивающихся сил, приложенных к части конструк-
ции, расположенной левее шарнира С (рис. 22):
Y^MiC =0; Pf • 6 + Q • 2 + ХА  4 - YA • 3 = 0,
или после вычислений
4Ха - ЗУд = -41,98 кН.	(2)
Решая систему уравнений (1') и (2), находим:
ХА = -7,97 кН, Уд = 3,36 кН.
22
Рис. 17
23
vz
81 Э1Ч
Рис. 19
25
Таблица 6
Номер варианта	Вид скользящей заделки	Номер варианта	Вид скользящей заделки	Номер варианта	Вид скользящей заделки
1, 2, 3	-1	|	14	Ф'	23	yl—1-
4	Ф'	15		24	ф-
5	4р	16	-ф	25	ч-t-
6, 7, 8	Ф-	17	ф	26	Л
9	н—1—	18	—1—1-	. 27	
10	йк	19	-ф	28	Ч—|-
11	-1—1—	20	иг	29	r^j
12	Йк	21	—1—1-	30	-й
13		-1	22			
Модуль реакции опоры А при шарнирном соединении в точке С
равен
R'a =	+ У2 = у/7$72 + 3,362 = х/74,81 = 8,65 кН.
2. Расчетная схема при соединении частей конструкции в точке
С скользящей заделкой показана на рис. 23. Системы сил, показанных
Рис. 20
на рис. 21 и 23, ничем друг от друга не отличаются. Поэтому
уравнение (!') остается в силе. Для получения второго уравнения
26
рассмотрим систему уравновешивающихся сил, приложенных к части
конструкции, расположенной левее скользящей заделки С (рис. 24, а).
Составим уравнение равновесия:
22^ = 0; Xa + Q-P[ = 0,	(3)
откуда
ХА = -5,50 кН,
и из уравнения (1') находим
УА = 3,85 кН.
Следовательно, модуль реакции опоры А при скользящей заделке
в С равен
ra = \]xa+Ya = а/5,502 + 3,852 = ^/45,07 = 6,71 кН.
Итак, при соединении в точке С скользящей заделкой модуль
реакции опоры А меньше, чем при шарнирном соединении (~ на 22%).
Найдем составляющие реакции опоры В и скользящей заделки.
Для левой от С части (рис. 24, а)
52 К = 0; -Pf + Уд + Гс =0, (4)
откуда
Yc = Р" - Ya = 0,48 кН.
Составляющие реакции опоры
В и момент в скользящей задел-
ке найдем из уравнений равнове-
сия, составленных для правой от
С части конструкции (рис. 24, б):
52 MiB = 0; Мс + Ус • 2 - М + Р2 • 1,80 = 0,	(5)
52 xi = °;	~р2	+ Хв = 0,	(6)
52^ = 0; -Ус+ Yb-P2 sin/3 = 0.	(7)
Рис. 24
27
Из прямоугольного треугольника BCD
sin/? = BD/BC = 2,0/5/22+12 = 2,0/3,61 = 0,555;
cos /3 = CD/ВС = 3,0/3,61 = 0,832.
Решая уравнения (5)—(7) относительно Мс, Хв, Yb, получим:
Мс = 8,44 кН • м; Хв = 5,82 кН; YB = 4,37 кН.
Для проверки правильности определения реакций убедимся, что
соблюдается не использованное ранее уравнение равновесия для сил,
приложенных ко всей конструкции (см. рис. 21), например
MiA =	• 4 + Р[' • 3 - Q • 2 - М - Р2 sin/3 • 4 + F2 cos/? • 2,5 - Хв  1+
+YB -5 = 2,5-4 + 4,33 -3-8-2-22-7- 0,555 -4 + 7- 0,832 • 2,5-
-5,82 • 1 + 4,37 • 5 = 59,40 - 59,36 « 0.
Результаты расчетов приведены в табл. 7.
Таблица 7
	Силы, кН						Момент, кН • м
	ХА	УА		Ус	ХВ	Ув	Мс
Для схемы на рис. 20	-7,97	3,36	8,65	-	-	-	-
Для схемы на рис. 23	-5,50	3,85	6,71	±0,48	5,82	4,37	±8,44
Задание С.4. Определение реакций опор
составной конструкции
(система трех тел)
Найти реакции опор конструкции, состоящей из трех тел, соеди-
ненных либо в одной точке (варианты 1-20), либо в двух точках
(варианты 21—30). Схемы конструкций представлены на рис. 25—27
(размеры — в м), нагрузка указана в табл. 8. В вариантах 1—15, 21—
30 составные части соединены с помощью шарниров, а в вариантах
16—20 — с помощью гладкой втулки малой длины.
Пример выполнения задания. Дано: схема конструкции (рис.
28); нагрузка: Р± = 10 кН, Р% = 204 кН, М = 40 кН • м, q = 2 кН/м.
Определить реакции опор в точках 4, В, С и Е.
Решение. На рис. 29 изображены отдельно все три тела, образу-
ющие систему. К каждому из тел приложены задаваемые (активные)
силы и реакции связей.
Так как направления составляющих реакций и реактивных момен-
тов в соединении D заранее не известны, покажем их направленными
28
Рис. 25
29
Рис. 26
30
Рис. 27
31
Таблица 8
Номер	Р1	Р2	Mi	М2	Qy	Номер	Р1	Р2	Mi	М2	Ч,
варианта						варианта					
(рис. 31-33)	кН		кН • м		кН/м	(рис. 31-33)	кН		кЬ	I • м	кН/м
1	6,0	— '	25,0	—	0,8	16	13,0	—	26,0	—	0,9
2	11,0	8,0	34,0	-	1,0	17	7,0	7,0	23,0	34,0	-
3	9,0	12,0	20,0	—	1,0	18	9,0	9,0	29,0	—	1,3
4	10,0	14,0	30,0	20,0	-	19	12,0	7,0	33,0	-	1,2
5	8,0	15,0	22,0	-	1,1	20	11,0	—	38,0	—	1,5
6	10,0	17,0	28,0	—	1,0	21	6,0	-	25,0	-	0,8
7	16,0	10,0	-	30,0	-	22	11,0	8,0	34,0	-	—
8	13,0	12,0	25,0	34,0	—	23	9,0	12,0	20,0	—	1,0
9	11,0	-	29,0	37,0	—	24	10,0	14,0	30,0	—	—
10	12,0	-	34,0	35,0	1,4	25	8,0	15,0	22,0	. - .	1,1
11	8,0	—	28,0	-	1,0	26	10,0	17,0	28,0	-	-
12	12,0	14,0	36,0	28,0	-	27	16,0	—	36,0	3,0	-
13	15,0	—	30,0	21,0	-	28	13,0	—	25,0	34,0	-
14	10,0	16,0	35,0	-	-	29	11,0	—	29,0	37,0	-
15	12,0	8,0	32,0	-	1,2	30	12,0	-	34,0	-	1,4
одинаково для каждой части конструкции. Истинные направления
реакций и моментов определяются по знаку ответа: знак плюс укажет
на то, что истинные их направления соответствуют показанным на
рисунке.
Рис. 29
Общее количество неизвестных реакций в задаче — 11 (Хд, Уд,
Mb, YD1, Yd2, YD3, MD1, MD2, MD3, Rc, Re)-
Для каждого из трех тел может быть составлено три независимых
уравнения равновесия, что даст в совокупности девять уравнений.
Для того чтобы получить недостающие два уравнения, рассмо-
трим силы и моменты, приложенные в Z?i, D% и 7?з. Из закона о
32
равенстве действия и противодействия вытекает, что геометрическая
сумма этих сил и сумма реактивных моментов должны быть рав-
ны нулю. Следовательно, сумма проекций на любую ось всех сил,
приложенных в точках Pi, Р2 и Рз, должна быть равна нулю. Ал-
гебраическая сумма моментов всех пар в Pi, Р2, Р3 также равна
нулю. Эти уравнения дополняют уравнения равновесия до системы
11 уравнений.
В рассматриваемом примере сначала рассмотрим систему уравно-
вешивающихся сил, приложенных к телу ABDi (рис. 29):
£Х,=О; ХА + Р2 =0;	(1)
£К = 0; Ya + YD1=0-,	(2)
Y,MiA = 0;	-P2-1 + MB + M + MD1 +YD1 -2 = 0.	(3)
Уравнения равновесия сил, приложенных к телу CD^:
52^ = 0; Pi cos 60°-Яс = 0;	(4)
^2 У; = 0; -Р, cos 30° + Yd2 = 0;	(5)
^2М;К=0; MD2 +Picos30° -2-Picos60° • 1 = 0.	(6)
Уравнения равновесия сил, приложенных к телу ED%'.
£^ = 0; Pe-Q = 0;	(7)
£У=О; Ур3 = 0;	(8)
MD3 +Ql = 0.	(9)
Уравнения, вытекающие из аксиомы о равен-
стве действия и противодействия:
52 YDi = 0;	yD1 + YD2 + Yd3 = 0;	(10)
52 MDi = 0;	MD1 + Md2 + MD3 = 0. (11)
Решая последовательно уравнения (1), (4), (5) — (10), (2), (11)
и (3), получим числовые значения искомых величин. Результаты
вычислений приведены в табл. 9.
Для проверки правильности
расчетов требуется убедиться
в том, что соблюдаются урав-
нения равновесия сил, прило-
женных ко всей конструкции
(рис. 30).
Рис. 31
33
Например:
= ХА + Р2 + Рх sin30° - Rc - Q + Re =
= -20 + 20 + 10 • 0,5 - 5 - 4 + 4 ±= 0;
^Yi = Ya -Pi cos 30° = 8,66 - 10 • 0,866 = 0;
^2 MiA = -P2 • 1 + MB + M + Pi sin 30° • 3 - Rc • 4 + RE • 4 - Q • 3 =
= -20 + (-19) + 40 + 10 • 0,5 • 3 - 5 • 4 + 4 • 4 - 4 • 3 = -71 + 71 = 0.
Таблица 9
Силы, кН							Моменты, кН • м			
А'а	Уа	Яс	Ре		Уп2	УОз	Мв	MD1	Мр2	Md3
-20	8,66	5	4	-8,66	8,66	0	-19	16,32	-12,32	—4
Примечание. Если тела соединены в точке D шарниром и к нему приложена
сосредоточенная сила, то ее можно отнести к любой составной части. На рис. 31 в
качестве примера показан случай, когда сила Р отнесена к части I конструкции.
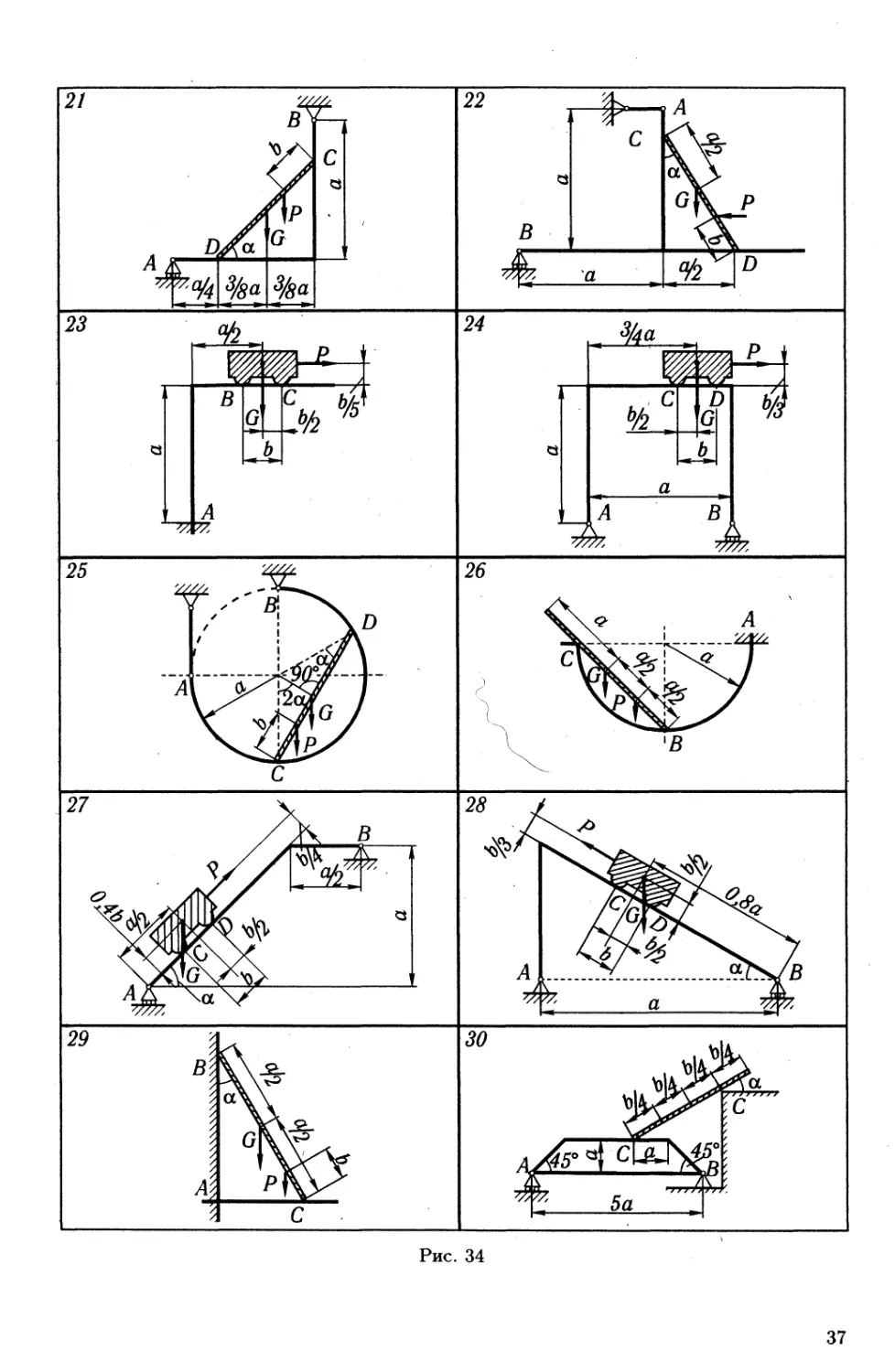
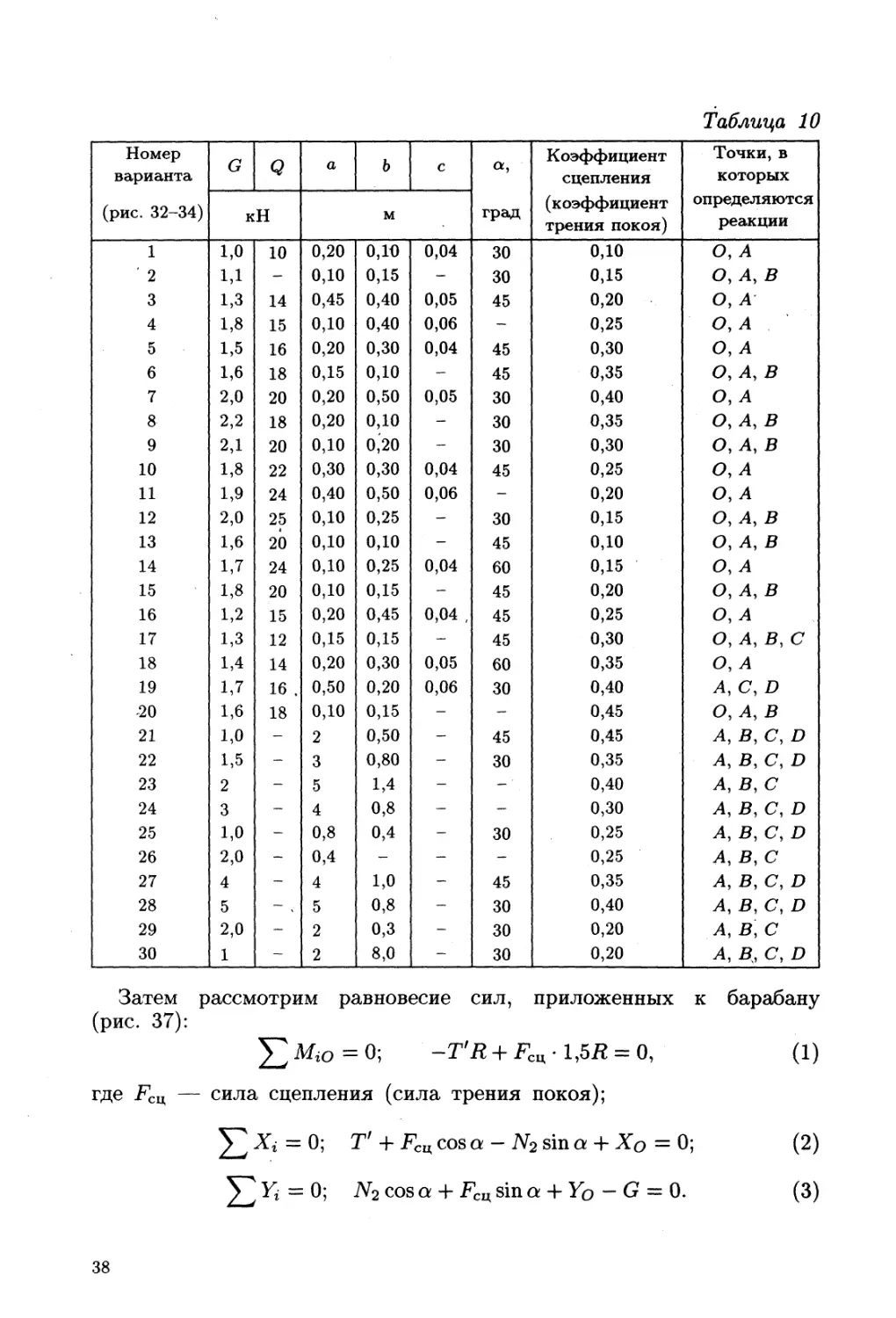
Задание С.5. Равновесие сил с учетом сцепления
(трения покоя)
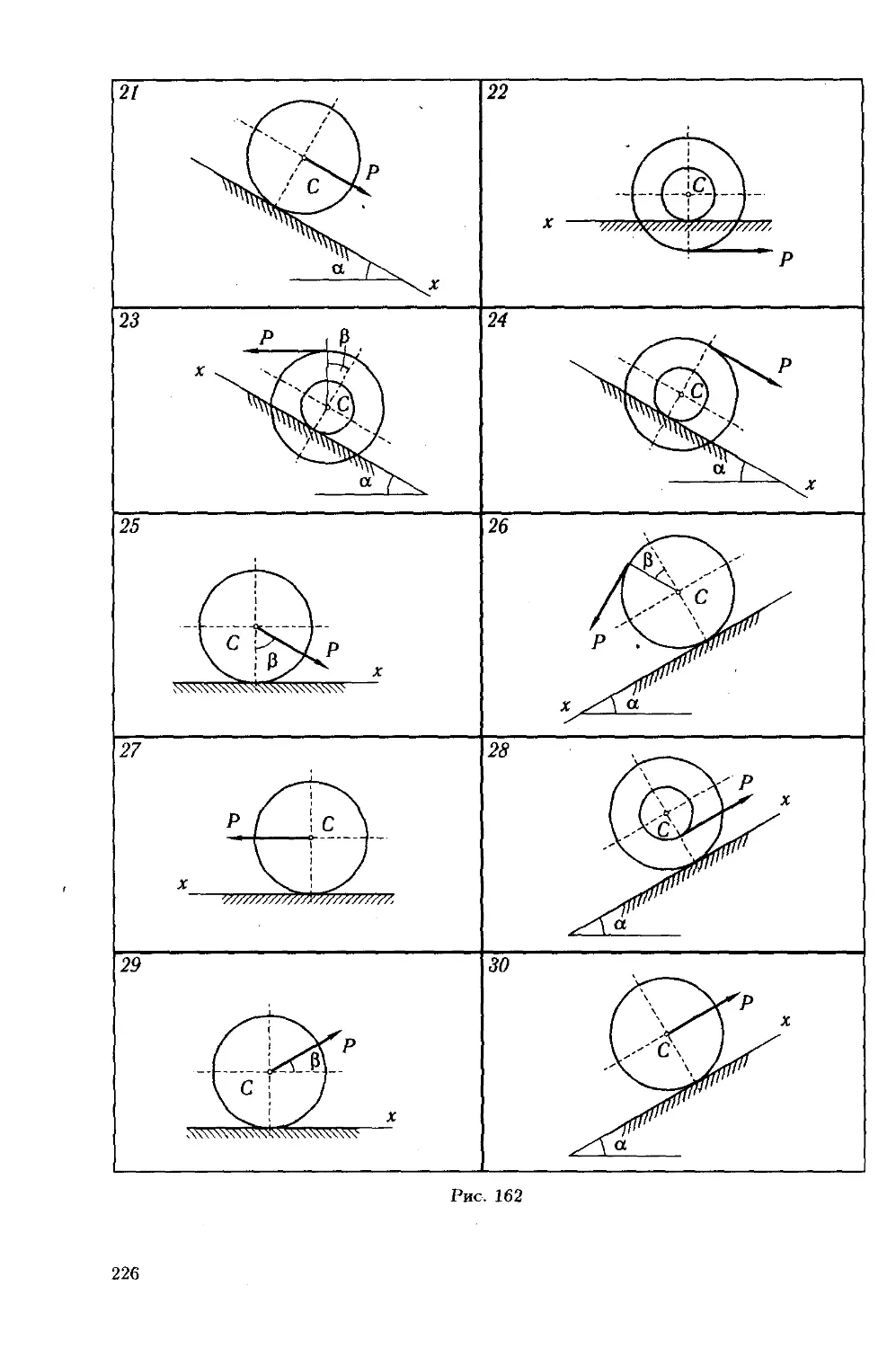
Определить минимальное (в вариантах 1—20, 25, 26, 29, 30) или
максимальное (в вариантах 21—24, 27, 28) значение силы Р и реакции
опор системы, находящиеся в покое. Схемы вариантов представлены
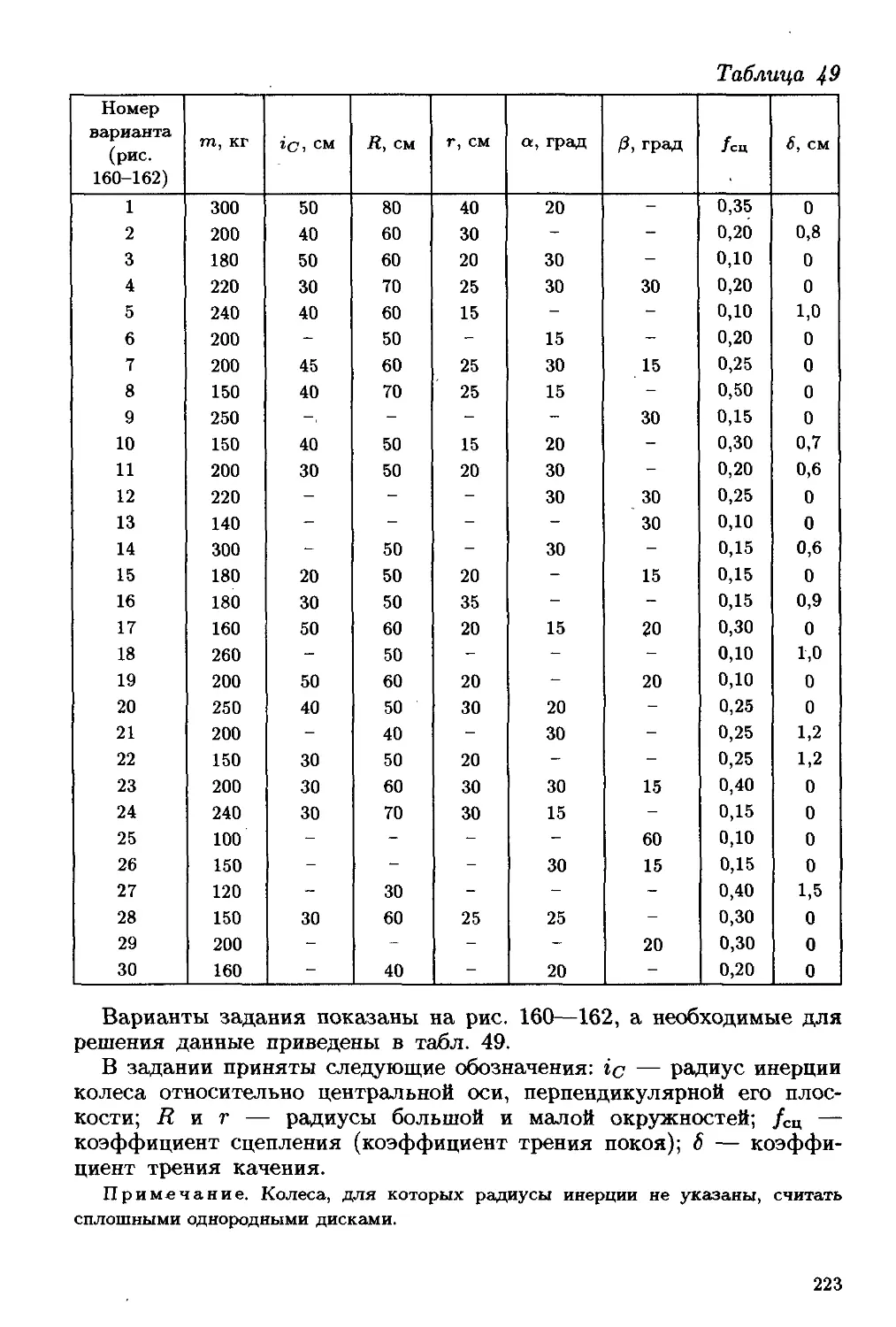
на рис. 32—34, а необходимые для расчета данные — в табл. 10.
В вариантах 1—20 сцепление (трение покоя) учесть только между
колодкой и барабаном. В вариантах 21—30 учесть сцепление в двух
опорных точках тела весом G.
Пример выполнения задания (варианты 1—20). Дано: G =
= 2 кН; Q = 20 кН; коэффициент сцепления (трения покоя) /сц = 0,1;
а = 20°; а — 10 см; b = 20 см (рис. 35).
Определить минимальное значение силы Р и реакции опор О, А
и В.
Решение. Рассмотрим сначала систему уравновешивающихся сил,
приложенных к телу Q (рис. 36). На тело действуют сила тяжести
Q, реакция нити Т и нормальная реакция N±.
Рассматривая тело Q как материальную точку, составим уравнения
равновесия указанных сил:
52*г=О; Q cos 45° — Т = 0;
52*i = O; Ni - <2sin45° = 0.
Отсюда
T = Qcos45°; M=Qsin45°.
34
Рис. 32
35
Рис. 33
36
Рис. 34
37
Таблица 10
Номер варианта	G	Q	а	b	с	а,	Коэффициент сцепления	Точки, в которых
(рис. 32-34)	кН			м		град	(коэффициент трения покоя)	определяются реакции
1	1,0	10	0,20	0,10	0,04	30	0,10	О, А
2	1Д	-	0,10	0,15	-	30	0,15	Оу А, В
3	1,3	14	0,45	0,40	0,05	45	0,20	О, А
4	1,8	15	0,10	0,40	0,06	-	0,25	Оу А
5	1,5	16	0,20	0,30	0,04	45	0,30	О, А
6	1,6	18	0,15	0,10	-	45	0,35	Оу Ау В
7	2,0	20	0,20	0,50	0,05	30	0,40	Оу А
8	2,2	18	0,20	0,10	-	30	0,35	Оу Ау В
9	2,1	20	0,10	0,20	-	30	0,30	Оу Ау В
10	1,8	22	0,30	0,30	0,04	45	0,25	Оу А
11	1,9	24	0,40	0,50	0,06	-	0,20	Оу А
12	2,0	25	0,10	0,25	-	30	0,15	Оу Ау В
13	1,6	20	0,10	0,10	-	45	0,10	Оу А, В
14	1,7	24	0,10	0,25	0,04	60	0,15	Оу А
15	1,8	20	0,10	0,15	-	45	0,20	Оу А, В
16	1,2	15	0,20	0,45	0,04 ,	45	0,25	Оу А
17	1,3	12	0,15	0,15	-	45	0,30	Оу А, В, С
18	1,4	14	0,20	0,30	0,05	60	0,35	Оу А
19	1,7	16 .	0,50	0,20	0,06	30	0,40	Ау Су D
20	1,6	18	0,10	0,15	-	-	0,45	Оу Ау В
21	1,0	-	2	0,50	-	45	0,45	А, В, С, D
22	1,5	-	3	0,80	-	30	0,35	Ay By Су D
23	2	-	5	1,4	-	-'	0,40	Ay By С
24	3	-	4	0,8	-	-	0,30	Ay By Су D
25	1,0	-	0,8	0,4	-	30	0,25	Ay By Су D
26	2,0	-	0,4	-	-	-	0,25	Ay By С
27	4	-	4	1,0		45	0,35	Ay By Су D
28	5		5	0,8	-	30	0,40	Ау В, С, D
29	2,0	-	2	0,3	-	30	0,20	Ay By С
30	1	-	2	8,0	-	30	0,20	А, В. С, D
Затем рассмотрим равновесие сил, приложенных к барабану
(рис. 37):
52 MiO = 0; -T'R + Fcu • 1,57? = 0,	(1)
где FC4 — сила сцепления (сила трения покоя);
Tf + Fcu^cos а - Ж sin о 4- Хо = 0;	(2)
Yi = 0; 7V2 cos а + Гсц sin а + Yq - G = 0.	(3)
38
В состоянии предельного равновесия
сила Р минимальна, а сила сцепления
(трения покоя) между тормозной ко-
лодкой и барабаном определяется ра-
венством
Рсц = /сц^.	(4)
Из уравнений (1) — (4) получим:
FC4=T'/1,5; № = Рсц//сЦ;
Хо = -Т' — FCU; cos a -F Nz sin а;
Yq = —Nz cos a — FC4 sin a + G.
Рис. 35
Для определения минимального значения силы Р и реакций опор
А и В (эти реакции перпендикулярны направляющим А и В, так
как трением здесь пренебрегаем) рассмотрим равновесие сил, прило-
женных к штоку тормозного устройства (рис. 38):
2 MiA — 0$ -^сца 4" Rbb — 0;
№-Pmin=0;
(5)
(6)
(7) Рис. 36
/ . = 0; Ра 4- Rb - РСц/= 0-
Решая эти уравнения, получаем:	I
Рв = —F^a/fy Pmin = 7^2; Ra = —Rb + РсЦ-
Учитывая заданные в
условии числовые значения,
М = 14,1 кН;
Nz = 94 кН;
Yo = -89,6 кН;
ЯА = 14,1 кН;
FC4 = 9,4 кН;
Хо = 9,2 кН;
RB = -4,7 кН;
Pmin — 94 кН.
Для определения реакций опоры С достаточно
составить уравнения равновесия сил, приложенных
к блоку.
Пример выполнения задания (варианты
получим:
Рис. 37
21—30). Дано: G = 1 кН; /сц = 0,4; а = 6 м; b = 2 м (рис. 39).
Определить максимальное значение силы Р и реакции в точках
Л, В, D и Е.
Решение. Рассмотрим сначала систему уравновешивающихся сил,
приложенных к телу весом G (рис. 40). К телу приложена сила
тяжести G, сила Р, нормальные составляющие реакции Nd и Ne,
а также касательные составляющие силы сцепления Fc^d) и -^сц(е)
(силы трения покоя).
39
Рис. 38
Составим три уравнения равновесия указанных сил:
Xi = 0;	“^сц(Р) ~ ^сц(Я) + Р = 0;	(1)
22^ = 0; Nd + Ne-G = 0-,	(2)
52 MiD = 0;	—Gb/2 + NEb - Pb/4 = 0.	(3)
В случае предельного равновесия Р = Fmax. В этом случае силы
сцепления (силы трения покоя) принимают экстремальные значения,
а система уравнений (1) — (3) дополняется равенствами
^сц(Г>) = /сцАЪ,	(4)
^сц(Е) = /сц№-	(5)
Решая систему уравнений (1) — (5), получаем:
Ртах = /сцС; Ne = (G/2)(l + 0,5/сц); Nd = (G/2)(l - 0,5/сц).
Отсюда
Fmax = 0,4 кН;
Nd = 0,4 кН;
Рсц(Е) — 0,24 кН.
Ne = 0,6 кН;
^сц(Р) = 0,16 кН:
Совокупности сил Nd
ственно опорные реакции
и Fcu(d), Ne и Рсц(е) образуют соответ-
в точках D и Е.
Рис. 40
Рис. 39
Рассмотрим теперь равновесие системы сил Хв, Yb, G и
P = Fmax, приложенных ко всей системе (см. рис. 39):
52^г = О; Хв + Ртах=0;	(6)
52Уг = О; Ra-G + Yb=&,	(7)
52л/гВ=О; -Ртах • Ь/4 + G • а/2 - Ra • а = 0.	(8)
40
Решая эти уравнения, получаем:
Хв = Рmax', Ra = (G ' в/2 Ртах ' &/4)/л‘, Ув — G Ra-
Отсюда Хв = -0,4 кН; RA = 0,467 кН; YB = 0,533 кН.
II. СИСТЕМА СИЛ,
НЕ ЛЕЖАЩИХ В ОДНОЙ ПЛОСКОСТИ
Задание С.6. Приведение системы сил к простейшему виду
Определить главный вектор R* и главный момент Мо заданной
системы сил относительно центра О и установить, к какому про-
стейшему виду приводится эта система. Размеры параллелепипеда
(рис. 41), а также модули и направления сил указаны в табл. 11.
Таблица И
Номер варианта	Размеры прямоугольного параллелепипеда (рис. 41), см 1			Силы системы											
				А			Pi			Рз			Pl		
	с		и	модуль, Н	точка при- ложения	направление	модуль, Н	точка при- ложения	направление	модуль, Н	точка при- ложения	направление	модуль, Н	точка при- ложения	направление
1	60	30	20	4	F	FK	6	А	АЕ	8	В	ВА	10	D	DK
2	30	40	40	20	А	АС	24	О	OD	10	К	КВ	—	—	—
3	20	10	10	4	В	ВА	2	С	СК	8	Е	ED	—	—	 —
4	30	40	20	15	А	АВ	20	К	КС	— .	—	—	—	—	—
5	20	20	20	8	О	OD	10	D	DF	8	К	КС	10	В	во
6	30	40	20	8	А	АО	4	Е	EF	6	F	FB	20	D	DF
7	30	40	40	10	В	ВК	16	С	СО	20	D	DF	—	 —	—
8	20	30	10	10	О	ОА	10	В	BF	10	D	DK	—	—	—
9	30	40	30	10	А	АС	20	К	КВ	—	—	—	—	—	—
10	10	10	20	20	А	АС	30	О	OD	20	К	КЕ	30	Е	ЕА
11	10	40	30	8	А	АЕ	12	С	СВ	20	О	ОК	16	К	KD
12	4	8	6	6	А	АЕ	20	F	FA	10	с	СК	8	D	DK
13	20	20	20	8	О	ОВ	8	С	CD	8	Е	ЕК	—	—	—
14	20	5	8	40	В	ВА	30	О	OD	—	' —	—	—	—	—
15	40	20	40	15	Е	АЕ	10	F	FE	15	В	BF	10	D	DK
16	30	30	30	6	О	ОС	10	В	ВК	20	к	КО	—	—	—
17	15	15	20	30	Е	ЕВ	40	В	ВК	10	о	ОС	32	D	DO
18	10	15	20	40	А	АВ	20	К	КС	16	D	DE	—	—	—
19	20	15	15	40	С	СА	20	D	DF	—	—	—	—	—	
20	20	20	10	10	А	AD	20	В	ВО	10	К	КВ	20	D	DF
21	20	20	20	10	О	OD	8	В	ВА	6	к	KF	8	D	DK
22	40	20	30	30	О	ОА	50	Е	ЕВ	50	с	CD	25	D	DK
23	50	20	40	10	О	ОА	5	F	FB	8	к	KD	—	—	—
24	30	40	30	40	А	AD	2(К	К	КЕ	-	-	-	-	-	-
41
Продолжение табл. 11
	Размеры прямоугольного параллелепипеда			v	Силы системы											
				.А			Pi			Рз			Pi		
и д	(рис. 41),		см												
св S а «3 д а ф О К	с		•О	модуль, Н	точка при- ложения	направление	модуль., Н	точка при- ложения	направление	модуль, Н	точка при- ложения	направление	модуль, Н	точка при- ложения	направление
25	30	20	40	25	А	АС	20	В	ВА	25	К	КЕ	20	D	DK
26	30	40	20	10	Е	ЕА	12	О	ОС	10	С	СК	8	К	KF
27	30	20	40	8	О	OD	6	С	СВ	4	D	DK	—	—	—
28	10	14	40	4	О	ОА	10	F	FE	16	С	СК	—	—	—
29	30	30	40	80	В	ВК	100	D	DC	—	—	—	—	—	—
30	40	20	30	,10	А	AD	5	В	ВО	10	К	КВ	5	D	DF
Рис. 41
на чертеже.
При выполнении задания необходимо сделать
следующее.
1. Изобразить заданную систему сил, выполнив
построение параллелепипеда в масштабе, показав
АхОу на чертеже равным 135°; сокращение раз-
меров по оси Ох принять равным 1:2.
2. Выбрав систему координатных осей, опре-
делить модуль и направление главного вектора
заданной системы сил по его проекциям на коор-
динатные оси и изобразить Я* на чертеже.
3. Вычислить главный момент заданной системы сил относительно
центра О по его проекциям на координатные оси и изобразить Мо
4. Вычислить наименьший главный момент
заданной системы сил.
5. На основании результатов вычислений глав-
ного вектора и наименьшего главного момен-
та М* установить, к какому простейшему виду
приводится заданная система сил. При этом не-
обходимо сделать следующее:
а) если заданная система сил приводится к
паре сил, то показать момент этой пары, при-
ложив его к точке О;
б) если заданная система сил приводится к равнодействующей, то
найти уравнение линии действия равнодействующей, определить точ-
ки пересечения этой линией координатных плоскостей и изобразить
R на чертеже;
в) если заданная система сил приводится к динаме (силовому
винту), то найти уравнения центральной оси, определить точки пере-
сечения этой осью координатных плоскостей и изобразить R* и М*
на чертеже.
42
Пример выполнения задания. Дана система сил Pi, Р2, Рз,
Д; модули, точки приложения и направления этих сил указаны в
табл. 12.
Таблица 12
Размеры прямоугольного параллелепипеда, см			Силы системы											
			Р1			Р2			Рз			Pi		
а	Ь	с	модуль, Н	точка при- ложения	направление	модуль, Н	точка при- ложения	направление	модуль, Н	точка при- ложения	направление	модуль, Н	точка при- ложения	направление
30	50	40		О	ОС	4	F	FB	4	С	СВ	11	D	DA
Решение. 1. Определение главного вектора заданной системы
сил. Заданная система сил показана на рис. 42.
Предварительно определяем
cos а = а/\/а2 + с2; / v _ sin а = cf\Jo? + с2.
В данном случае cos а = 0,6; sin а = 0,8.
Проекции главного вектора на оси координат:
X = Рз 4- Р4 cos о; У = Pi; Z = -Р2 - Р4 sin а.
Модуль главного вектора
д* = у/х2 + У2 + Z2.
Направляющие косинусы:
cos(P*, Г) = Х/Р*;
cos(P*,/) = У/Р*;
cos(P*, fc) = Z/R\
В соответствии с исходными данны-
ми получаем: X = 10,6 Н; У = 10,0 Н;
Z = -12,8 Н; Р* = 19,4 Н;
cos(P*, Г) = 0,547; cos(P*, j ) = 0,515; cos(P*, fc) = -0,660.
Главный вектор показан на рис. 43.
2.	Определение главного момента заданной системы сил относи-
тельно центра О.
Главные моменты заданной системы сил относительно координат-
ных осей:
Мх = —РъЪ-, Му = Pza -I- Р4 cos а с; Mz = —РзЬ.
43
Модуль главного момента
Мо = у/м^ + M^ + Ml
Направляющие косинусы:
cos(Mq, Г) = Мх/Мо\ cos(Mq, j) = Му/Мо, cos(Mq, к) = Mz/Mo-
В результате вычислений имеем:
Мх = —200 Н ♦ см;	Му = 384 Н • см;
Mz = -200 Н • см;	Мо = 477 Н ♦ см;
cos(Mo, Г) = -0,419;
Таблица 13
Точки	Координаты, см		
	X	У	Z
Л1	0	5,1	25,5
^2	—5,4	0	32,0
Аз	21,1	25,0	0
cos(Mo, J) = 0,805; cos(Mq, к) = —0,419.
Главный момент Мо показан на рис. 43.
3.	Вычисление наименьшего главного мо-
мента заданной системы сил:
М* = (ХМх + YMy + ZMz)/R\
По этой формуле получаем
М* = 221 Н ♦ см.
4.	Так как R* 0, М* ф 0, то заданная система сил приводится
к динаме (силовому винту).
Уравнение центральной оси таково:
[Mx — (yZ—zY)]/X = [My — (zX—xZ)]/Y = [Mz-(xY-yX)]/Z = M*/R*.
Из этих трех уравнений независимыми являются только два. Под-
ставляя в два из этих уравнений найденные числовые значения ве-
личин, находим:
[Мх - (yZ - zY)]/X = M*/R\	6,4г/ + bz = 160;
[Му - (zX - xZ)]/Y = M*/R*',	5,3z + 6,4т = 135.
Значения координат точек пересечения центральной осью коорди-
натных плоскостей, определенные с помощью этих уравнений, поме-
щены в табл. 13.
Центральная ось системы сил показана на рис. 43.
Примечание. Если силы приводятся к равнодействующей, т. е.
М* — 0, a R = R* / 0, то уравнения линии действия равнодействую-
щей:
Mx=yZ- zY; My = zX- xZ; Mz=xY - yX,
где X, У, Z — проекции равнодействующей силы на координат-
ные оси; Мж, Му, Mz — главные моменты заданной системы сил
относительно координатных осей.	ч
Из этих трех уравнений независимыми также являются только
два.
44
Задание С.7. Определение реакций опор твердого тела
Найти реакции опор конструкции. Схемы конструкций показаны на
рис. 44—46. Необходимые для расчета данные приведены в табл. 14.
Таблица 14
Номер варианта (рис. 44—46)	Силы, кН			Размеры, см					Номер варианта (рис. 44—46)	Силы, кН			Размеры, см				
	Q	т	G	а	Ъ	с	R	г		Q	Т	G	а	Ъ	с	R	г
1	2	-	20	20	30	10	15	5	16	4	-	2	50	30	-	-	-
2	4	—	2	20	10	30	10	10	17	2	-	1	15	10	20	20	5
3	20	—	18	400	400	450	-	-	18	6	-	2	60	40	60	-	-
4	3	-	2	30	20	40	15	10	19	-	8	2	20	30	40	20	15
5	5	-	3	30	40	20	20	15	20	4	-	-	60	40	20	-	-
6	1	4	2	40	30	20	20	10	21	2	-	-	40	60	30	-	-
7	-	3	1	30	10	5	18	6	22	-	-	5	20	50	30	-	
8	4	6	3	20	40	15	20	10	23	-	-	4	40	30	50	-	-
9	5	-	3	20	15	10	30	40	24	5	-	2	-	-	-	-	-
10	1	4	2	30	40.	20	20	10	25	-	-	3	50	50	60	-	-
11	-	2	1	20	30	15	15	10	26	-	-	1	20	60	40	-	-
12	4	-	1	25	20	8	15	10	27	10	-	-	50	30	50	-	-
13	10	-	5	40	30	20	25	15	28	35	-	32	400	200	200	-	-
14	-	2	1	30	90	20	30	10	29	-	4	3	15	20	15	15	10
15	3	-	2	60	20	40	20	5	30	5	-	-	40	40	10	-	-
Примечания. 1. Считать, что в вариантах 16, 18, 22—26 петли не препятствуют
перемещению рамы вдоль АВ. ,
2. В вариантах 20 и 21 соприкасающиеся поверхности считать
абсолютно гладкими.	)
Пример выполнения задания. Дано: рама ABCD весом G =
= 1 кН, Р = 2 кН, Р || Ay. AD — ВС = 60 см;АВ = CD = 100 см,
а = 30°, /3 = 60° (рис. 47). Найти реакции опор А, В и С (А —
шаровой шарнир, В — петля, С — стержневая опора).
Решение. К раме ABCD приложены сила тяжести G, сила Р,
реакция S стержня СЕ и реакции опор А и В. Реакция шарово-
го шарнира А определяется тремя составляющими: Хау Ya, % a, а
реакция петли В — двумя: Хв и Yb (рис. 48).
Из этих сил — шесть неизвестных. Для их определения можно
составить шесть уравнений равновесия.
Уравнения моментов сил относительно координатных осей:
Y,Mix=0-, -PADcos30o-GAB/2+Scos30°AB+ZbAB = 0, (1)
^Miy = 0-, G(BC/2)sin30° — S'• BCsin60° = 0,	(2)
45
Рис. 44
46
It
I
в
3(Г
SSIO^R
T-2t
TlAy
P и t\\ Ax
N\\Az;N-2G
Рис. 45
47
Рис. 46
48
XMlz = O; P- AD sin 30° + 5cos60° AB- XB- AB = 0.	(3)
Из уравнения (2) определяем S, затем из уравнений (1) и (3)
находим Zb и Хв- Уравнения проекций сил на оси координат:
= ХА + Хв - 5cos60° = 0,	(4)
£> = 0; Ya + Р = 0,	(5)
^2^ = 0; ZA - G + ZB + 5cos30° = 0.	(6)
Из этих уравнений находим Ха, У а и Za-
Результаты вычислений приведены в табл. 15. J
Таблица 15
Силы, кН					
S	ХА	Уа	ZA	ХВ	Zb
0,289	-0,600	-2,00	-0,54	0,744	1,29
ЦЕНТР ТЯЖЕСТИ
Задание С.8. Определение положения центра тяжести тела
Найти координаты центра тяжести плоской фермы, составленной
из тонких однородных стержней одинакового погонного веса (вари-
анты 1—6), плоской фигуры (варианты 7—18 и 24—30) или объема
(варианты 19—23), показанных на рис. 49—51. В вариантах 1—6
размеры указаны в метрах, а в вариантах 7—30 — в сантиметрах.
Пример выполнения задания. Определить координаты центра
тяжести плоской фигуры, показанной на рис. 52.
49
Рис.49
50
Рис.50
51
Рис.51
52
Решение. Координаты центра тяжести плоской фигуры опреде-
ляем по формулам
%с = Sy/F, ус = Sx/F.	(1)
Здесь Sy — ^FiXi, Sx = J^Fit/i — статические моменты фигуры
относительно осей у и ж, F — площадь фигуры.
Чтобы воспользоваться формулами (1), делим плоскую фигуру на
части, для которых известны или легко определяются площади Fi и
координаты центров тяжести Xi и t/i-
В данном случае в качестве таких частей принимаем прямоуголь-
ник, треугольник и половину круга (рис. 53). Площадь половины
круга, вырезанной из прямоугольника, считаем отрицательной.
Все расчетные данные заносим в таблицу (табл. 16).
Таблица 16
Номер элемента	Fi, см2	Xi, см	У г, СМ	Siy — FiXi, см3	Six = Fiyi, см3
1	1200	15,0	20,0	18000	24000
2	1000	46,7	13,3	46700	13300
3	-628	8,5	20,0	-5338	-12560
Е	1572	—	—	59362	ххЖоо	
По формулам (1) вычисляем фигуры:			координаты центра тяжести плоской		
хс = 59362/1572 = 37,8 см; ус = 24700/1572 = 15,7 см.
Центр тяжести площади указан на рис. 53.
Таблица 17
53
Продолжение табл. 17
Плоская фигура				Площадь	Координаты центра тяжести
	а = тг/2 (полукруг)			Г = 1гК2/2	хс = AR/(Зтг)
	а = 7г/6			F = к/?2/6	хс = 2Я/тг
Круговой сегмент			X	F = ^R2x х(2а — sin 2а)	— 4Я sin3 а _ хс ~ 3(2а — sin 2а) ~ ь3 ~ V1F
Примечание. Площади и координаты центров тяжести некоторых плоских фи-
гур, встречающихся при выполнении заданий, приведены в табл. 17.
III. ПРИМЕНЕНИЕ ЭВМ
К РЕШЕНИЮ ЗАДАЧ СТАТИКИ
Задание С.9. Определение реакций опор составных
конструкций с внутренними односторонними связями
Найти реакции опор и силы во внутренних двусторонних и одно-
сторонних связях составной конструкции.
Схемы конструкций представлены на рис. 54—56 (размеры — в м),
нагрузка указана в табл. 18. Учесть, что при заданной схеме нагру-
жения конструкции реакция возникает только в одной из односто-
ронних связей Е или F. Зазоры отсутствуют. При снятии внешних
сил реакции внешних и внутренних связей обращаются в ноль.
Таблица 18
Номер варианта	Р1, кН	Р2, кН	М, кН м	q, кН/м	Примечания
1	8	9	10	1,5	ЕК и NF — нити
2	9	10	12	1	ЕК и NF — нити
3	12	15	20	2	
4	7	5	13	1,2	
5	8	12	16	1	ЕК и NF — нити
6	9	14	8	3	
7	9	6	10	1,5	
8	8	10	12	2	ЕК и NF — нити
9	6	7	8	1	
10	7	5	14	1,8	NF — нить
11	12	14	6	1,4	
12	20	15	23	3	
13	11	12	16	2,2	
14	8	10	12	1,5	
15	22	18	20	1,8	
54
Продолжение табл. 18
Номер варианта	Р1, кН	Р2, кН	М, кН-м	q, кН/м	Примечания
16	8	7	10	1,2	
17	20	18	24	2	
18	16	15	20	2,8	
19	18	14	12	3	ЕК и NF — нити
20	19	14	18	2,5	ЕК — нить
21	6	11	15	1,8	
22	10	10	11	2	
23	16	15	9	3	ЕК и NF — нити
24	14	11	20	2	NF — нить
25	8	9	18	1,6	
26	6	5	7	1,6	
27	16	16	20	2,5	
28	14	11	15	1,9	
29	16	12	14	2 "	ЕК и NF — нити
30 *	17	23	18	1,7	ЕК и NF — нити
Пример выполнения задания. Дано: схема конструкции (рис. 57);
Pi = 10 кН, Рэ = 3 кН, М = 20 кН - м, q = 1 кН/м.
Определить реакции опор А и В, а также усилия во внутренних
двусторонних связях (шарнирах С и D) и в односторонних связях
(В и F).
Решение. Так как в условии задачи отсутствует информация о
том, в какой из односторонних связей Е или F возникает реакция,
необходимо рассмотреть два случая.	----
1-й случай: Rf = 0. В этом случае (рис. 58) элементы ED и АС
конструкции прижаты один к другому и, следовательно, направле-
ние реакции Re будет таким, как показано на рис. 59. Связь F
«не работает».
Сначала рассмотрим силы, приложенные к части АС конструкции
(рис. 59). Уравнения равновесия этой системы имеют следующий вид:
^M-iC=Q- Re • 2 + М — ХА  3+ Ya  7 = 0-,	(1)
^Xt=0; Хс + ХА = 0-,	(2)
52^ = 0; Ya + Re+Yc = 0.	.	(3)
Затем запишем систему уравнений равновесия для сил, приложен-
ных к элементу CD (рис. 60):
^2 MiD = 0; -Х'с  1 -	• 10 - Р2 • 10 = 0;	(4)
52^ = 0;	X'c+XD=0-,	(5)
52^ = 0; Y^ + P2+Yd=0.	(6)
55
9S
frS *эиа
ZS
ее эиа
и
91
гп			
11Н			
	//		
ь'			
	Т777. 9 Х9		J
8S
9S ohj
LI
Далее переходим к рассмотрению системы уравновешивающихся
сил, приложенных к элементу ED (рис. 61).
Уравнения равновесия сил, приложенных к этой части конструк-
ции, имеют следующий вид:
= R'e -6 + Pi sin 60° р-фЦ-У/, -2 = 0;	(7)
^2	= 0; X'D+XB- Pi cos60° = 0;	(8)
22^ = 0;	—— Pi sin60° + YB-Q + Y^ = 0.	(9)
Рис. 59
Рис. 60
Помимо уравнений равновесия (1) — (9) запишем уравнения, выра-
жающие равенство действия и про-
тиводействия в шарнирах С и D.
Дл£ шарнира С
^У=0;	Ус+У^=0; (10)
Хс + Х'с=0. (11)
Для шарнира D
Y,Yi = 0-, Yd + Y^=0- (12)
59
£>i = 0; Xd + X'd = O.	(13)
Из уравнений (10) — (13) следует:
YC = -Y^ Хс = -Х'с, Yd = -Y^ Xd = -X'd.
Учитывая это, а также R'E = Re, представим систему уравнений
(1) — (9) в следующем виде:
2Re + М - ЗХЛ + TYa = 0;'
Хс + Ха = 0;
Ya + Re + Yc = 0;
Хс + 10Yc - WP2 = 0;
-Xc + XD=0-, ►
-Yc + P2 + Yd = 0;
&Re + 6Pi sin 60° - Q • 1 - 2YD = 0;
~Xd + Xb — Pi cos 60° = 0;
-Re - Pi sin 60° + YB - Q - YD = 0.,
(14)
Система линейных алгебраических уравнений (14) определяет ис-
тинные значения всех искомых сил
Re > 0-
Рис. 62
лишь при условии, что ее корень
2-й случай: Re = 0. В этом
случае (рис. 62) элементы FD и
CD прижаты один к другому и,
следовательно, направление реак-
ции Rf будет таким, как показа-
но на рис. 63 и 64 (R'f = Rf)-
Связь Е ”не работает”.
Рассмотрим систему сил, при-
ложенных к части АС конструк-
ции (рис. 65). Уравнения равно-
весия этой системы сил имеют
следующий вид:
^MiC = 0-, М+ YA • 7 — ХА-3 = 0;	(15)
£xi = 0; XA + Xc=0;	(16)
60
£K = 0; YA + YC = O.	(17)
Запишем уравнения равновесия сил, приложенных к элементу CD
конструкции (см. рис. 63):
—Y^  10 — Х'с • 1 — Р2 -10 + RF  6 = 0;	(18)
^Хг = 0; X'C + XD=O-,	(19)
^У = 0; Y^+P2-Rf + Yd = 0.	(20)
Уравнения равновесия сил, приложенных к элементу FD (см.
рис. 64):
£MlB=0;	6Р1 sin 60° - Rf • 4 - Q • 1 + YB • 2 = 0;	(21)
^Xi = 0; XB+X'D -Pi cos 60° =0;	(22)
2^ = 0; YB+ Y/j-Q + RF - P1Sin60° = 0.	(23)
Учитывая и здесь результаты, вытекающие из уравнений (10) —
(13), перепишем систему уравнений (15) — (23) в следующем виде:
М + 7Ya - ЗХА = 0п
ХА + Хс = 0;
Ya + Yc = 0;
10Ус + Хс - ЮР2 + 6Rf = 0;
-XC+XD =0; >
—Yc + Р2 — RF + YB = 0;
6Pi sin 60° - 4RF - Q - 2Yd = 0;
XB - XD - Л cos 60° = 0;
Yb-Yd-Q + Rf-P! sin 60° = 0. ,
(24)
Система линейных уравнений (24) определяет истинные значения
всех неизвестных лишь в случае, когда ее корень Rp > 0.
61
Системы уравнений (14) и (24) с учетом значений Р,
перепишем в матричной форме:
М и Q
ЛЛ = В;
а2х2 = в.
(25)
(26)
Здесь
	(	2	-3	7	0	0	0	0	0	°\
		0	1	0	0	0	0	0	1	0
		1	0	1	0	0	0	0	0	1
		0	0	0	0	0	0	0	1	10
Л =		0	0	0	0	0	1	0	-1	0
		0	0	0	0	0	0	1	0	-1
		6	0	0	0	0	0-	-2	0	0
		0	0	0	1	0	-1	0	0	0
		-1	0	0	0	1	0-	-1	0	0/
	/	0	-3	7	0	0	0	0	0	°\
		0	1	0	0	0	0	0	1	0
		0	0	1	0	0	0	0	0	1
		6	0	0	0	0	0	0	1	10
А2 —		0	0	0	0	0	1	0	-1	0
		-1	0	0	0	0	0	1	0	-1
		—4	0	0	0	0	0-	-2	0	0
		0	0	0	1	0	-1	0	0	0
	1	1	0	0	0	1	0-	-1	0	0/
Х1 =	(re\ Ха Ya хв YB	; х2 —	( Rf\ Xa Ya xB YB	; b =	(~20 \ 0 0 30 0
	xD		xD		-3
	Yd		yd		-49,96
	Хс		Xc		5
	\ Yc /	\YCJ			\ 10,66 /
Системы (25) и (26) должны решаться совместно с неравенства-
ми «ключами», выбирающими систему уравнений равновесия. Если
в процессе решения системы (25) выясняется, что Re > 0, то уравне-
ниями равновесия рассматриваемой составной конструкции являются
уравнения (25). Если же оказывается, что Re < 0, то, следовательно,
Rf > 0, а поэтому уравнениями равновесия являются уравнения (26).
62
Рис. 64
Рис. 63
Для решения полученных систем ал-
гебраических уравнений можно исполь-
зовать метод Гаусса (метод последова-
тельного исключения неизвестных).
Блок-схема программы решений си-
стем (25) и (26) совместно с «ключа-
ми» представлена на рис. 66, где Фг —
ввод исходных данных; $2 — решение
системы (25) методом Гаусса; Фз —
если Re > 0, то переход к Ф4, если
Же Re С 0, то переход к Фе; Ф4 —
печать результатов; Ф5 — конец рабо-
ты программы, Фе — решение системы
(26) методом Гаусса.
Результаты расчета приведены в табл. 19.
С А
Рис. 65
ф(
Ф,-—Ф,——Ф.,
№/
Рис. 66
Ф5
Силы, кН								
Rf	xA	XB	xD	XC	yA	Ув	Yd	Yc
9,949	11,023	-6,023	-11,023	-11,023	1,867	5,793	5,082	-1,B67
Из таблицы видно, что реакция Rf оказалась положительной. Это
означает, что при заданной схеме нагружения составной конструкции
«работает» связь Г, а в связи Е усллие не возникает.
Для проверки правильности произведенных расчетов следует убе-
диться в том, что соблюдаются уравнения равновесия для сил, при-
ложенных ко всей конструкции:
52 MiA = M + Fisin60o-5-F1cos60o-4-F2'7 + yBl + XB-4-Q-2 =
= 20 + 10 • 0,866 • 5 - 10 • 0,5 • 4 - 3  7 + 5,703 - 6,023 • 4 - 2 • 2 =
= 49,093 - 49,092 « 0;
52 Yi = Ya + Yb + Л - Pi sin 60° - Q = 1,867 + 5,793 + 3 - 8,66 - 2 =
= 10,66 - 10,66 = 0;
52	= XA + XB - Pi cos 60° = 11,023 - 6,023 - 10 • 0,5 = 0.
63
РАЗДЕЛ ВТОРОЙ
КИНЕМАТИКА
I. КИНЕМАТИКА ТОЧКИ
Задание К.1. Определение скорости и ускорения точки
по заданным уравнениям ее движения
По заданным уравнениям движения точки М установить вид ее
траектории и для момента времени t = ti (с) найти положение точ-
ки на траектории, ее скорость, полное, касательное и нормальное
ускорения, а также радиус кривизны траектории.
Необходимые для решения данные приведены в табл. 20.
Таблица 20
Номер варианта	Уравнения движения		h, c
	х = х(*), см	у = y(t), CM	
1	—2*2 + 3	-5*	1/2
2	4cos2(tt*/3) 4- 2	4sin2(7rt/3)	1
3	— cos(7r*2/3) 4- 3	sin(7rt2/3) — 1	1
4	4*4-4	-4/(t4-l)	2
5	2sin(7rt/3)	—3cos(ir*/3) 4- 4	1
6	3*2 4-2	— 14*	1/2
7	3*2 - t 4- 1	5*2 - 5t/3 - 2	1
8	7 sin(Trt2/6) 4- 3	2 — 7 cos(tt*2/6)	1
9	—3/(* 4-2)	3*4-6 (	2
10	—4 cos(tf*/3)	—2sin(Trt/3) — 3	1
11	—4*2 4-1	8-3*	1/2
12	5sin2(7r*/6)	—5 cos2(7t*;/6) — 3	1
13	5cos(tt*2/3)	—5sin(?rt2/3)	1
14	-2*-2	-2/(*4-l)	2
15	4cos(tt*/3)	—3sin(7r*/3)	1
16	3*	4t2 4-1	1/2
17	7sin2(7rt/6) — 5	—7 cos2(tt*/6)	1
18	1 4- 3cos(tt*2/3)	3sin(7r*2/3) 4- 3	1
19	—5*2 - 4	3*	1
20	2 — 3* — 6*2	3 - 3*/2 - 3*2	0
21	6sin(?r*2/6) — 2	6cos(tt*2/6) 4- 3	1
22	7*2 -3	5*	1/4
23	3 - 3*2 4- t	4 — 5*2 4~ 5*/3	1
64
Продолжение табл. 20
Номер варианта	Уравнения движения		ti, c
	х = x(t), см	у = y(t), cm	
24	—4cos(7rf/3) — 1	—4sin(7rt/3)	1
25	-6t	-2t2 — 4	1
26	8cos2(tt£/6) 4- 2	—8sin2(4r£/6) — 7	1
27	—3 — 9sin(7rt2/6)	—9cos(?rt2/6) 4- 5	1
28	—4t2 4-1	-3t	1
29	5t2 4- 5t/3 - 3	3t2 4-1 4- 3	1
30	2cos(tt£2/3) — 2	—2 sin(7rt2/3) 4- 3	1
Пример выполнения задания. Исходные данные:
x = 4t; у = 1Ы2 - 1;	(1)
= 0,5 (х и у — в см, t и t\ — вс).
Решение. Уравнения движения (1) можно рассматривать как па-
раметрические уравнения траектории точки. Чтобы получить урав-
нения траектории в координатной форме, исключим время t из урав-
нений (1).
Получаем у = х2 — 1, т. е. траекторией точки является парабола,
показанная на рис. 67.
Вектор скорости точки
V = ихг 4- Vyj.	(2)
Вектор ускорения
а = axi 4~ ^yj •
Здесь г, j — орты осей х и у; vx, vy, ах, ау — проекции скорости и
ускорения точки на оси координат.
Найдем их, дифференцируя по времени уравнения движения (1):
vx = х = 4 см/с;	ах = х = 0;
vy — У = 32£;	ау = у = 32 см/с2.
По найденным проекциям определяются мо-
дуль скорости:
v =	+	(4)
и модуль ускорения точки:
а = \Jal+ay-	(5)
Модуль касательного ускорения точки
аг = | ch/cU |,	(6)
или
аг = | v • a/v	(6')
аг = | (vxax 4- vya,y)lv |;	(6")
llUiUlIll I .. I
2J 2 4 6 8 10см/с
5 0 5 15 25см/c
। । । । ।
Рис. 67
65
dv/dt выражает проекцию ускорения точки на направление ее скоро-
сти. Знак «4-» при ch/d£ означает, что движение точки ускоренное,
направления ат и v совпадают; знак «—», — что движение замедлен-
ное.
Модуль нормального ускорения точки
ап = v2/p.	(7)
Ёсли радиус кривизны траектории р в рассматриваемой точке неиз-
вестей, то ап можно определить по формуле
ап = |v х a\/v.	(8)
При движений точки в плоскости формула (8) принимает вид
— | Ux&y Vy(J>x |/^*	(3 )
Модуль нормального ускорения эдожно определить и следующим
образом:
ап = \/а2 ~ ат-	(9)
После того, как найдено нормальное ускорение по формулам (8)
или (9), радиус кривизны траектории в рассматриваемой точке опре-
деляется из выражения
p=iv2/an.	(10)
Результаты вычислений по формулам (3)—(6), (8) и (10) для
заданного момента времени t± =0,5 с приведены в табл. 21.
Таблица 21
Координаты, см		Скорость, см/с			Ускорение, см/с2					Радиус кривизны, см
X	У	V®	Vy	У	а®		а	О>Т		р
2,0	3,0	4,0	16,0	16,5	0	32,0	32,0	31,0	7,8	35,0
На рис. 67 показано положение точки М в заданный момент вре-
мени. Вектор v строим по составляющим vx и vy, причем этот вектор
должен по направлению совпадать с касательной к траектории. Век-
тор а строим по составляющим ах и ау и затем раскладываем на
составляющие ат и ап. Совпадение величин ат и ап, найденных
из чертежа, с их значениями, полученными аналитически, служит
контролем правильности решения.
Дополнение к заданию К.1. Данное задание может быть ис-
пользовано для определения скорости и ускорения точки при ее дви-
жении по пространственной траектории. Для этого к двум уравнениям
движения (см. табл. 20) добавляется третье уравнение (табл. 22).
Общий порядок выполнения задания в этом случае такой же, как
и в приведенном выше примере.
66
Таблица 22
Номер вари- анта	z — z(t), см	Номер вари- анта	z = z(t), CM	Номер вари- анта	z = z(t), CM	Номер вари- анта	z = z(t), CM	Номер вари- анта	z = z(t), CM
1	3t	7	2,5t	13	l,5t	19	6t	25	5t
2	2t	8	5t	14	2t+2	20	2t	26	6t
3	l,5t	9	4t + 8	15	3t	21	4t	27	3,5t
4	4t + 4	10	t	16	l,5t	22	t	28	4t
5	t	11	2t	17	5t	23	l,5t	29	5t
6	3t	12	3t	18	3,5t	24	2t	30	l,5t
II. КИНЕМАТИКА ТВЕРДОГО ТЕЛА
ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ
ТВЕРДОГО ТЕЛА
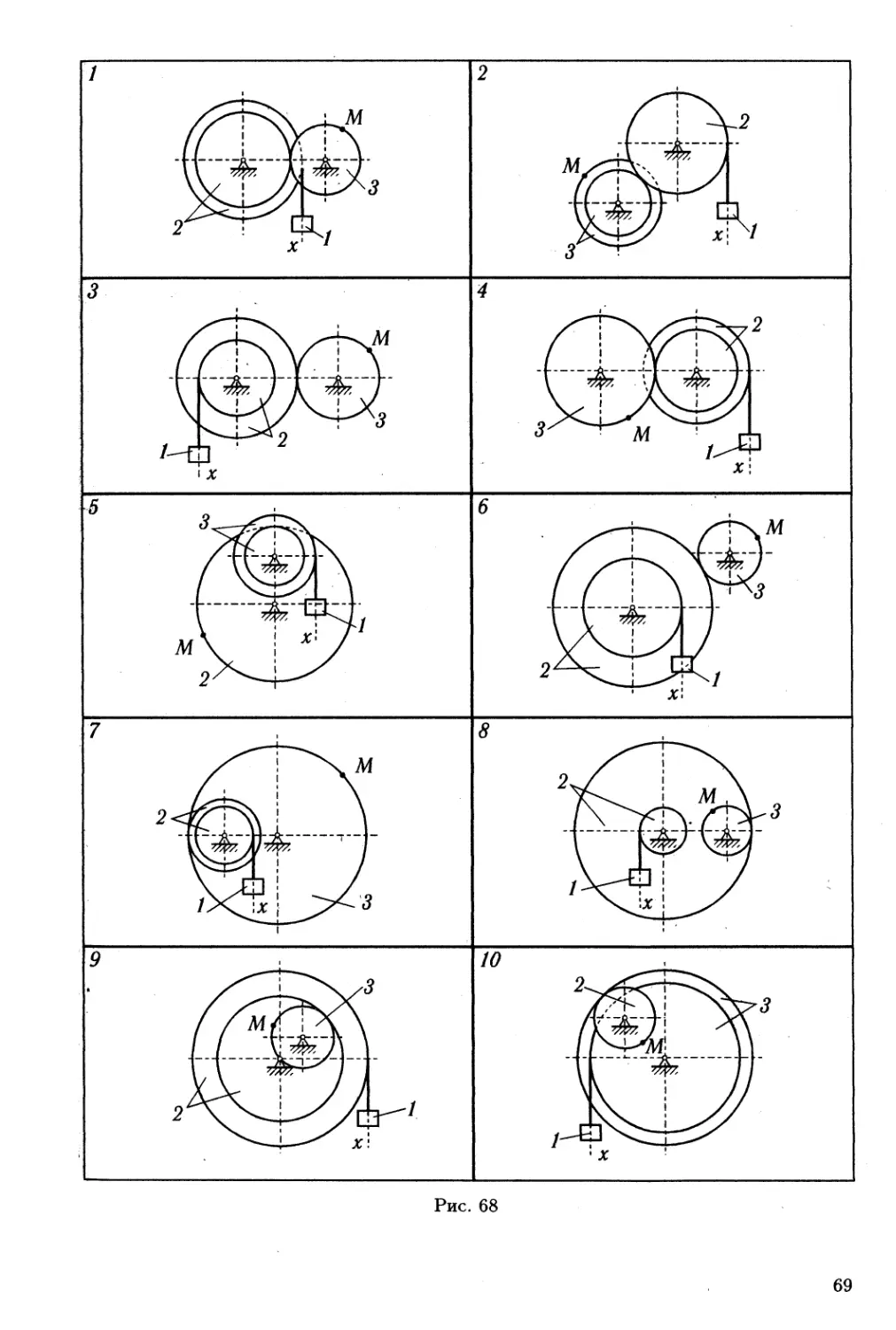
Задание К.2. Определение скоростей и ускорений
точек твердого тела при поступательном и
вращательном движениях
Движение груза 1 должно описываться уравнением
х = c2t2 + c^t + со,	(1)
где t — время, с; со, ci, с2 — некоторые постоянные.
В начальный момент времени (t — 0) положение груза определяется
Координатой хо, и он имеет скорость Учесть, что в момент времени
t = t2 координата груза равна х2.
Определить коэффициенты Со, ci и с2, при которых осуществляется
требуемое движение груза 1. Определить также в момент времени
t = ti скорость и ускорение груза и точки М одного из колес
механизма.
Схемы механизмов показаны на рис. 68—70, а необходимые данные
приведены в табл. 23.
Пример выполнения задания. Дано: схема механизма (рис. 71);
j?2 = 50 см, г2 = 25 см, R% = 65 см, гз = 40 см, xq = 14 см, vq = 5 см/с,
х2 = 168 см, ti = 1 с, t2 = 2 с.
Найти уравнение движения груза, а также скорости и ускорения
груза и точки М в момент времени t — ti.
Решение. Уравнение движения груза 1 имеет вид
х = c2t2 + dt + с0.	(1)
67
Таблица 23
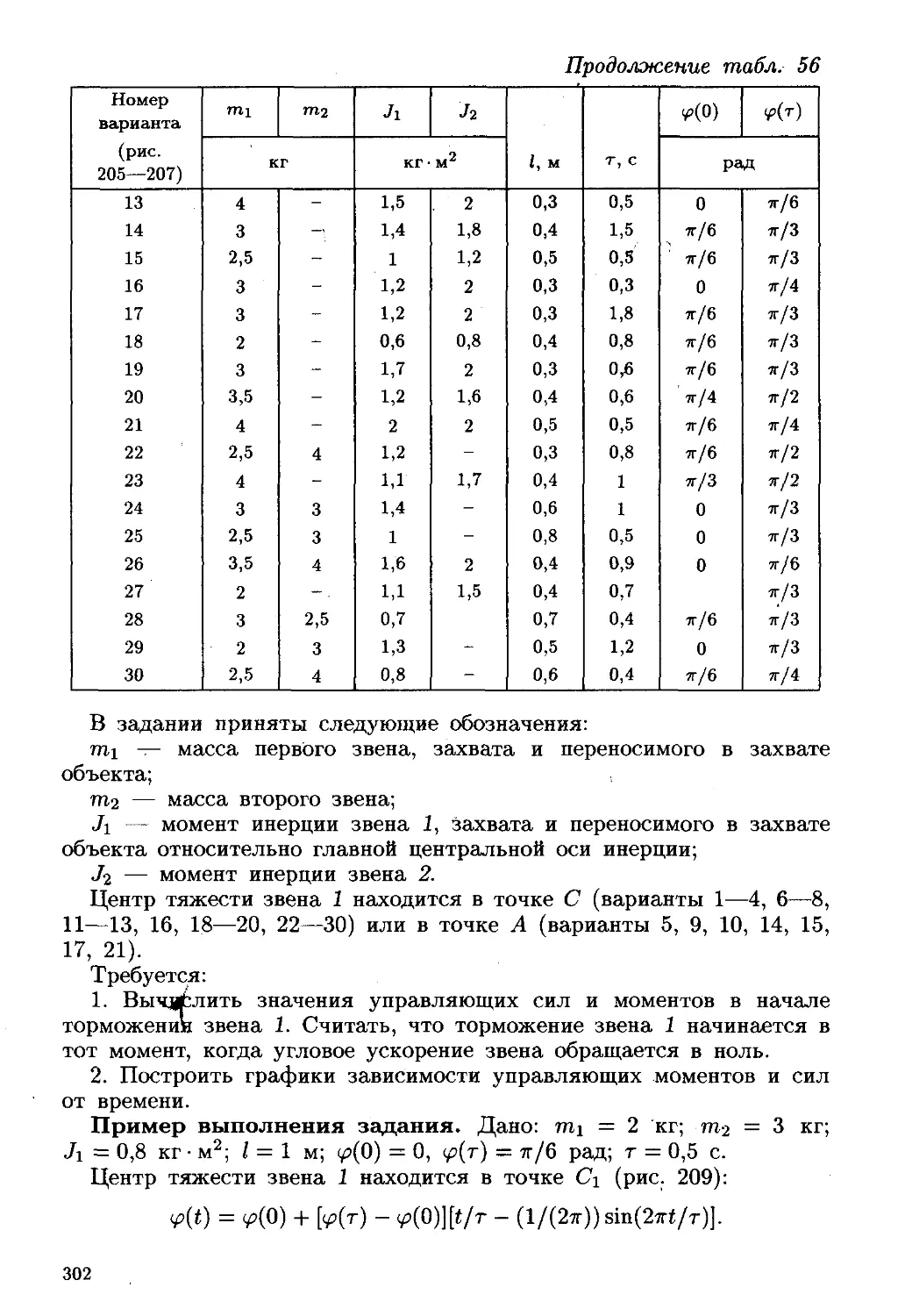
Номер варианта (рис. 68-70)	Радиусы, см				Координаты и скорости груза 1			Расчетные моменты времени, с	
	R2	Г2	Яз	гз	XQ, см	г>0, см/с	Ж2, СМ	*2	ti
1	60	45	36	—	2	12	173	3	2
2	80	—	60	45	5	10	41	2	1
3	100	60	75	—	8	6	40	4	2
4	58	45	60	—	4	4	172	4	3
4 5	80	—	45	30	3	15	102	3	2
6	100	60	30	—	7	16	215	4	2
7	45	35	105	—	' 8	5	124	4	3
8	35	10	10		6	2	111	3	2
9	40	30	15	—	10	7	48	2	1
10	15	—	40	35	5	3	129	4	3
11	40	25	20	—	9	8	65	2	1
12	20	15	10	—	5	10	179	3	2
13	30	20	40	—	7	0	557	5	2
14	15	10	15	—	6	3	80	2	1
15	15	10	15	—	5	2	189	4	2
16	20	15	15	—	4	6	220	4	3
17	15	10	20		8	4	44	2	1
18	20	15	10	—	3	12	211	4	1
19	15	10	20	—	5	10	505	5	3
20	25	15	10	—	10	8	277	3	1
21	20	10	30	10	6	5	356	5	2
22	40	20	35	<—	7	6	103	2	1
23	40	30	30	15 -	5	9	194	3	2
24	30	15	40	20	9	8	105	4	2
25	50	20	60	—	8	4	119	3	2
26	32	16	32	16	6	14	862	4	2
27	40	18	40	18	5	10	193	2	1
28	40	20	40	15	8	5	347	3	2
29	25	20	50	25	4	6	32	2	1
30	30	15	20	—	10	7	128	2	1
Коэффициенты со, с± и могут быть определены из следующих
условий:
при t = 0 то —14 см,	±о = 5 см/с,	(2)
при t2 = 2 с Х2 = 168 см.	(3)
Скорость груза 1
v = х = 2c2t 4- ci.	(4)
Подставляя (2) и (3) в формулы (1) и (4), находим коэффициенты
со = 14 см, ci = 5 см/с, с2 = 36 см/с2.
Таким образом, уравнение движения груза 1
х = 36f2 + 5t +14.	(5)
Скорость груза 1
v — х — 72t 4- 5.	(6)
68
Рис. 68
69
Рис. 69
70
Рис. 70
71
Ускорение груза 1
а = х = 72 см/с2.
Для определения скорости
и ускорения точки М запишем
уравнения, связывающие ско-
рость груза v и угловые ско-
рости колес о>2 и <^з-
В соответствии со схемой ме-
ханизма
v = r2v2A
R2w2 — B3CU3, J
откуда
с^з = vR2/(r2R3),
или с учетом (6) после подста-
новки данных
а?з = 2,215* + 0,154.
Таблица 24
V,	а,		S3,		аМ’		«м,
см/с	см/с2	рад/с	рад/с2	см/с	см/с2	см/с2	см/с2
77	72	2,37	2,22	94,8	224	88,6	241
Угловое ускорение колеса 3
£з = Дз = 2,215 рад/с2.
Скорость точки М, ее вращательное, центростремительное и полное
ускорения определяются по формулам
vm = эд;
авм = г3£з;	а^=г3^з;
ам = У(ам)2 + («м)2-
Результаты вычислений для заданного момента времени *1 = 1 с
приведены в табл. 24.
Скорости и ускорения тела 1 и точки М показаны на рис. 72.
ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
Задание К.З. Кинематический анализ плоского механизма
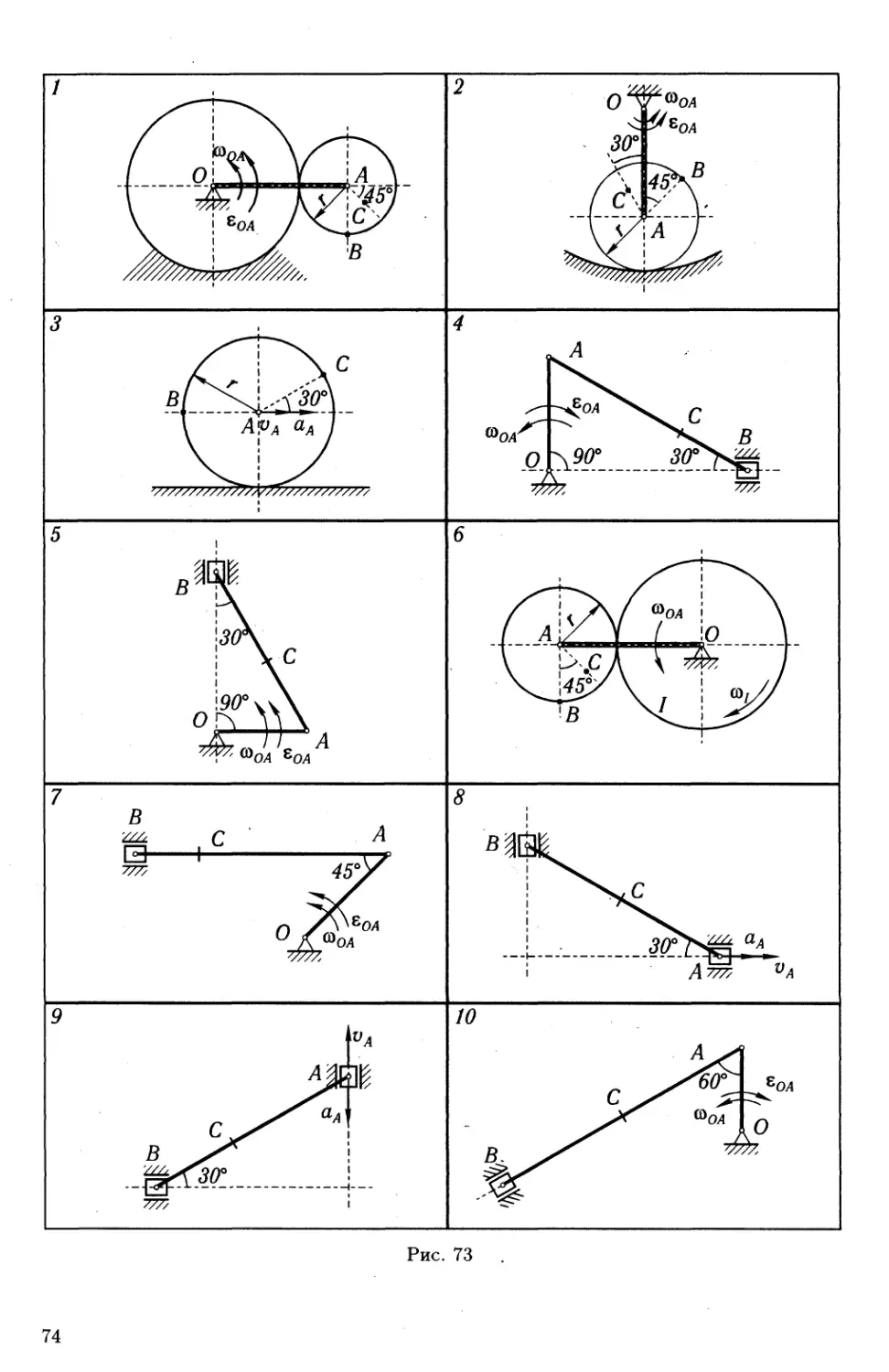
Найти для заданного положения механизма скорости и ускорения
точек В и С, а также угловую скорость и угловое ускорение звена,
которому эти точки принадлежат.
72
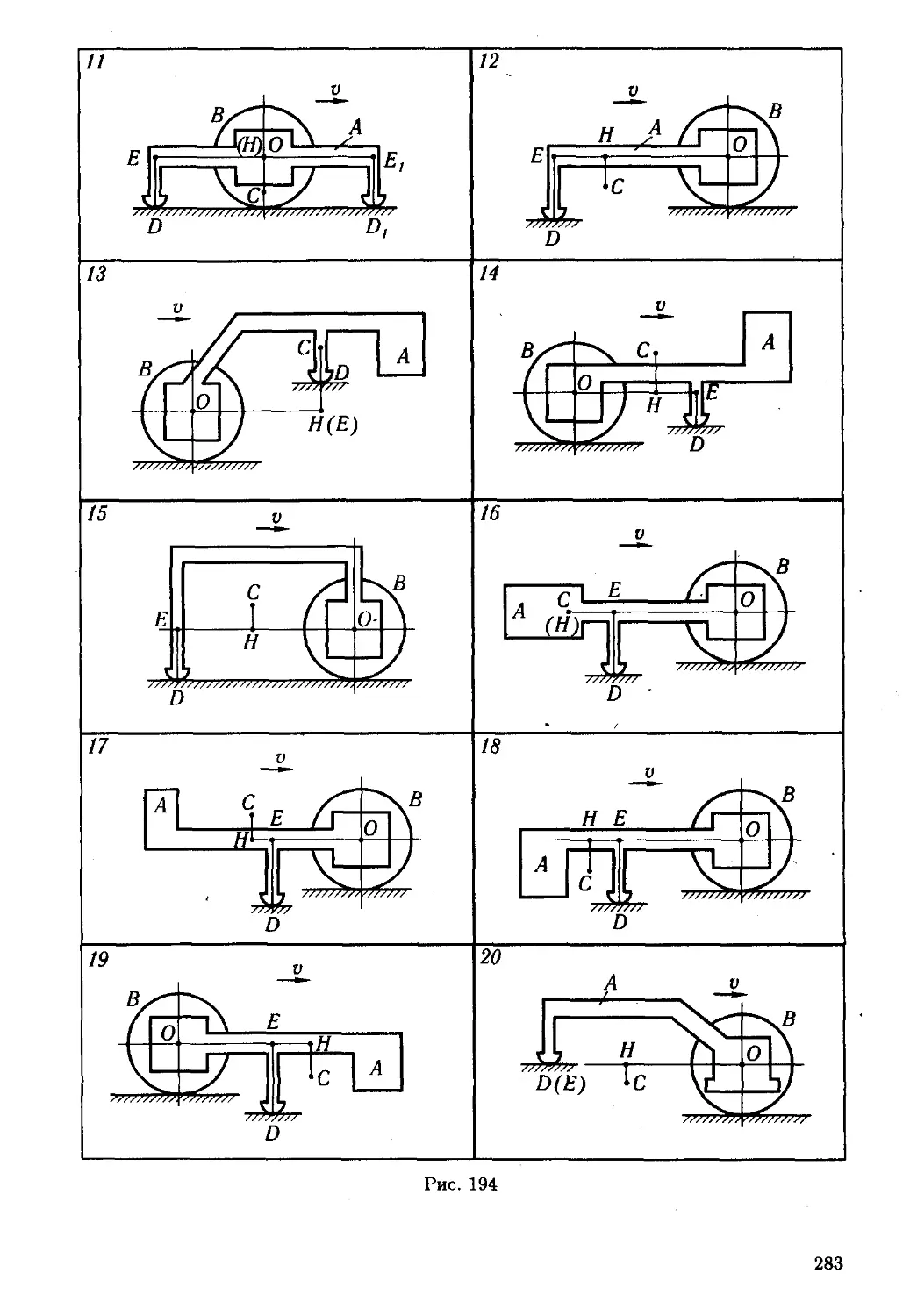
Схемы механизмов помещены на рис. 73—75, а необходимые для
расчета данные приведены в табл. 25.
Таблица 25
Номер варианта (рис. 73-75)	Размеры, см				ЫОА, рад/с	^1, рад/с	£(ЭА, рад/с2	У А, см/с	аА-> см/с2
	ОА	г	АВ	АС					
1	40	15	-	8	2	—	2	—	—
2	30	15	—	8	3	—	2	—	—
3 .	—	50	—	—	—	—	—	50	100
4	35	—	—	45	4	—	8	—	—
5	25	—	—	20	1	—	1	—	—
6	40	15	—	6	1	1	0	—	—
7	35	—	75	60	5	—	10	—	—
8	—	—	20	10	—	—	—	40	20
9	—	—	45	30	•—	—	—	20	10
10	25	—	80	20	1	—	2	—	—
11	—	—	30	15	—	—	—	10	0
12	—	—	30	20	—	—	—	20	20
13	25	—	55	40	2	—	4	—	—
14	45	15	—	8	3	12	0	—	—
15	40	15	—	8	1	—	1	—	—
16	55	20	—		2	—	5	—	—
17	—	30	—	10	—	—	—	80	50
18	10	—	10	5	2	—	6	—	—
19	20	15	—	10	1	2,5	0	—	—
20	—	—	20	6	—	—	—	10	15
21	30	—	60	15	3	—	8		—
22	35	—	60	40	4	—	10	—	—
23	—	—	60	20	—	—	—	5	10
24	25	—	35	15	2	—	3	—	—
25	20	—	70	20	1	—	2	—	—
26	20	15	—	10	2	1,2	0	—	—
27	—	15	—	5	—	—	—	60	30
28	20	—	50	25	1	—	1	—	—
29	12	—	35	15	4	—	6	—	—
30	40	—	—	20	5	-	10	-	-
Примечание, со о А и со А — угловая скорость и угловое ускорение кривошипа
О А при заданном положении механизма; од — угловая скорость колеса I (посто-
янная); и а а — скорость и ускорение точки А. Качение колес происходит без
скольжения.
Пример выполнения задания. Дано: схема механизма в задан-
ном положении (рис. 76); исходные данные (табл. 26).
Таблица 26
Размеры, см			&ОА, рад/с	so А, рад/с2
ОА	АВ	АС		
10	60	20	1,5	2
Решение. 1. Определение скоростей точек и угловой скорости
звена (рис. 77). Вычисляем модуль скорости пальца А кривошипа
О А при заданном положении механизма:
VA = Мо А • О А.
73
Рис. 73
74
Рис. 74
75
Рис. 75
76
Скорость точки А перпендикулярна кривошипу
ОА, Скорость ползуна В направлена по вертикали.
Мгновенный центр скоростей Рав шатуна АВ нахо-
дится в точке пересечения перпендикуляров, прове-
денных из точек А и В к их скоростям.
Угловая скорость звена АВ
ШАВ = V А/АРАВ-
Модули скоростей точек В и С
VB = ШАВ ’ ВРаВ', Vc = ЫАВ • СРаВ-
Расстояния АРав-> В Рав и С Рав определяются из рассмотрения
треугольников АВ Рав и АС Рав-
АРав = 52,0 см; ВРав = 30,0 см; СРав = 36,1 см.
В соответствии с этим va = 15,0 см/с; шав = 0,29 рад/с;
vB = 8,7 см/с; vc = 10,5 см/с.
Вектор vc направлен перпендикулярно отрез-
ку СРав в сторону, соответствующую направле-
нию вращения звена АВ,
Для проверки определим скорость точки В
другим способом. Воспользуемся теоремой о ра-
венстве проекции скоростей точек на ось, прове-
денную через эти точки.
Направим ось х вдоль шатуна АВ в напра-
влении от В к Л.
Имеем va соз(дд, х) = vb cos(vb, х), или, как
видно из рис. 77,
va cos 60° = vb cos 30°.
Рис. 77
Отсюда
vB = 3,7 см.
Полезно убедиться, что и найденная ранее скорость точки С удо-
влетворяет этой теореме.
2. Определение ускорений точек и углового ускорения звена
(рис. 78). Ускорение точки А складывается из вращательного и цен-
тростремительного ускорений:
оа = авА + а*А ~ еОА ’ ОА; = coqA ’ О А.
Согласно теореме об ускорениях точек плоской фигуры,
а в — а а 4- а ав + ^дю
или
ав — Од + Од Л- ОаВ + ОдВ.
(1)
77
Центростремительное ускорение точки В во вращательном движе-
нии шатуна АВ вокруг полюса А
а\в = и2дв ‘ &В.
По приведенным формулам вычисляем:
(^4=20,0 см/с2; а^=22,5 см/с2; а^в=5,0 см/с2.
Вектор Од направлен от А к О. Вектор Йд перпендикулярен
вектору и направлен противоположно va (вращение кривошипа
О А — замедленное).
Вектор а\в направлен от В к А Что касается
ускорения а в точки В и вращательного ускоре-
ния ОдВ, то известны только линии действия этих
векторов: а в — по вертикали вдоль направляю-
щих ползуна, ОдВ — перпендикулярно АВ.
Зададимся произвольно их направлениями по
указанным линиям (рис. 78, а). Эти ускорения
определим из уравнений проекций векторного ра-
венства (1) на оси координат. Знак в ответе по-
казывает, соответствует ли истинное направление
вектора принятому при расчете.
Выбрав направление осей х и ?/, как показано
на рис. 78, г, получаем:	#
а в cos 30° = —авА cos 60° + а^в cos 30° + а^в; (2)
а в cos 60° = авА cos 30° + cos 60° + а\в. (3)
Из уравнения (2) находим
ав = 16,7 см/с2.
Ускорение а в направлено, как показано на
рис. 78, а.
Из уравнения (3) получаем
а\в — —20,2 см/с2.
Рис 78	Направление а^в противоположно показанному
на рис. 78, а.
Ускорение а в и все его составляющие с учетом их истинных
направлений и масштаба показаны на рис. 78, б.
Угловое ускорение шатуна АВ с учетом того, что здесь а^в —
алгебраическая величина, определяется по формуле
£ав — \аАв\/АВ.
Вычисляя, находим
£ав = 0,34 рад/с2.
78
Направление ускорения аАВ относительно полюса А определяет
направление углового ускорения sab- Здесь под направлением угло-
вого ускорения понимается направление дуговой стрелки, которое
при ускоренном вращении звена совпадает с направлением его вра-
щения, а при замедленном — противоположно ему. В данном случае
угловое ускорение противоположно направлению вращения шатуна.
Определить а в и ОдВ можно и графически — построением мно-
гоугольника ускорений.
Отложим из точки В согласно (1) в выбранном масштабе после-
довательно векторы ад, и а*дВ (рис. 78, в). Через конец вектора
а?дВ проведем прямую, параллельную вращательному ускорению ОдВ,
т. е. перпендикулярно а#, до пересечения ее с прямой, по которой
направлено ускорение ав>
Последнее определяется как замыкающая сторона многоугольника
ускорений.
Модули а в и авАВ могут быть найдены измерением на чертеже.
Определяем ускорение точки С:
Вращательное и центростремительное ускорения точки С во вра-
щательном движении АВ вокруг полюса А
о^ас = £ав ‘ АС] а^Ас = ^‘ав ‘
или
а\с = 6,8 см/с2; а^с = 1,7 см/с2.
Вектор ОдС перпендикулярен вектору а\с и направлен соответ-
ственно угловому ускорению £ав-
Ускорение точки С находим способом проекций (рис. 78, а):
&Сх = ObAC + аА COS 30° “ аA COS 60° >
/р!
ас у = «д cos 60° + авА cos 30° - авАС,	/I
аС =	+ facy)2'	'уа J
W 'У
В результате вычислений получаем: асх — И,2 см/с2;
асу — 21,8 см/с2; ас — 24,5 см/с2 (рис. 78, г).	Рис. 79
Приведем решение этой же задачи другим, более общим методом.
На рис. 79 показана схема механизма в некотором произвольном
положении.
Проведем оси координат. Уравнениями связи для данного меха-
низма являются условия
г в = ОА 4- АВ	(4)
79
(fB — радиус-вектор точки В, проведенный из центра О),
хв = а = const.	(5)
Проецируя (4) на ось ж, с учетом (5) имеем
—О А • sin а 4-АВ • sin/3 = а,	(6)
Для определения угловой скорости шав = (3 звена АВ и углового
ускорения sab — & нет необходимости выражать (3 из (6). Проще
непосредственно дважды продифференцировать (6).
Имея в виду, что а = шоа, получаем в результате первого диф-
ференцирования
—О А • cos а • (jJqa 4- АВ • cos /3 • u>ab = 0-	(7)
Отсюда
шав = ^оа ' о A cos а/{АВ • cos /3).	(8)
Дифференцируя (7) и учитывая, что шоа — £оа> имеем
О А • sin а ♦ WqA — О А • cos а • sqa ~ АВ • sin (3 • J^b + АВ ‘ cos Р ’ еАВ — 0;
£ав = tg/3 4-ОА(бол coso - sino)/(AB -cos/3).	(9)
Выражения (8) и (9) позволяют вычислять шав и £ав для любого
положения механизма, в частности для заданного (о = 0°, (3 — 30°).
Заметим, что с^оа и sqa входят в эти выражения со знаком «4-»
или «—» в соответствии с принятым направлением отсчета угла а.
В данном случае (Xqa = 1,5 рад/с, еоА = — 2,0 рад/с2. Смысл знако₽
о>ав и &ав определяется направлением отсчета угла {3.
Модуль скорости точки В vb = \ ув |- Модуль ускорения а в = \ ув |-
Проецируя (4) на ось ?/, получаем
у в = О А • cos а 4- АВ • cos /3.
Отсюда после дифференцирования получаем
у в = —ОА • sin а • о^оа ~ АВ • sin /3 • ш'дв:
у в = —ОА ♦ cos а • ojqa ~ О А • sin а • sqa — АВ ♦ cos (3- ш2Ав ~ АВ * sin /3 ♦ sab •
Для определения скорости и ускорения точки С следует составить
уравнения ее движения в координатной форме, проецируя радиус-
вектор г с = О А 4- АС на оси х и у.
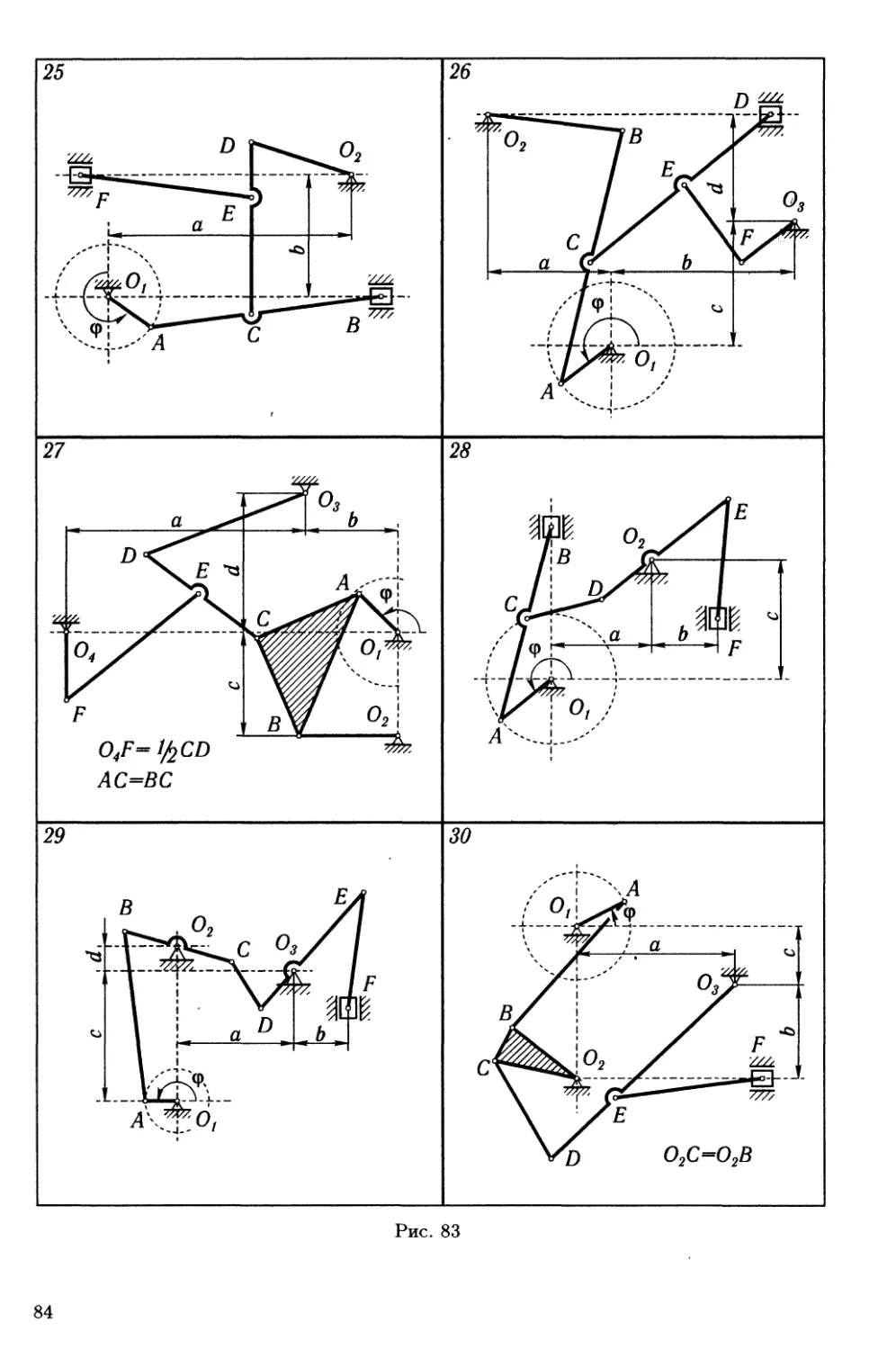
Задание К.4. Кинематический анализ
многозвенного механизма
Кривошип 01А вращается с постоянной угловой скоростью шогА =
= 2 рад/с. Определить для заданного положения механизма:
1)	скорости точек А, В, С, ... механизма и угловые скорости всех
его звеньев с помощью плана скоростей;
80
Рис. 80
81
9
Рис. 81
82
Рис. 82
83
Рис. 83
84
2)	скорости этих же точек механизма и угловые скорости звеньев
с помощью мгновенных центров скоростей;
3)	ускорения точек А и В и угловое ускорение звена АВ;
4)	положение мгновенного центра ускорений звена АВ;
5)	ускорение точки М, делящей звено АВ пополам.
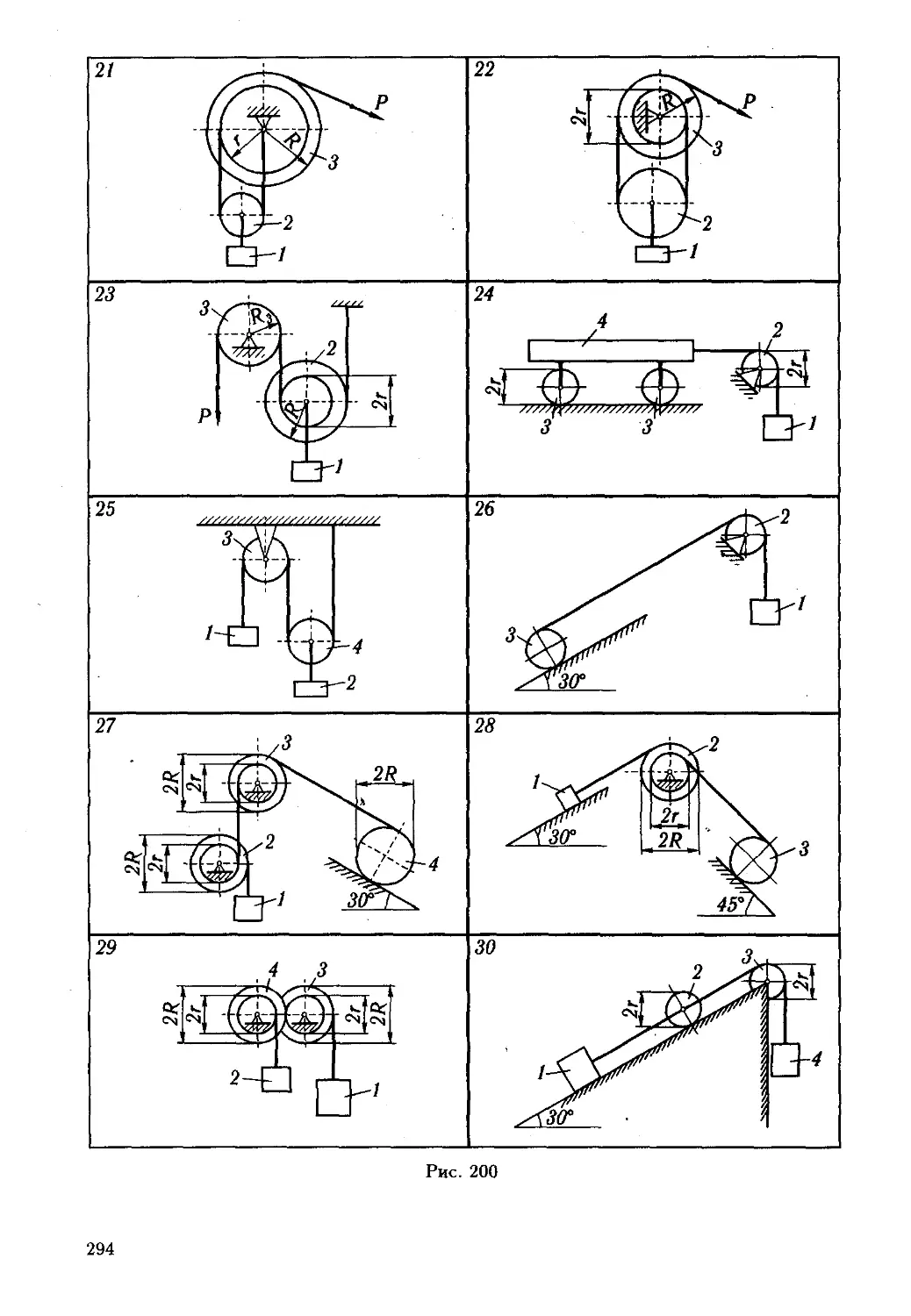
Схемы механизмов показаны на рис. 80—83, а необходимые для
расчета данные приведены в табл. 27.
Таблица 21
Номер вари- анта (рис. 80-83)	град.	Расстояния, см					Длина звеньев, см										
		а	b	с	d	е	ОгА	О2В	o2d	O3D	O3F	АВ	ВС	CD	СЕ	DE	EF
1	200	18	23	18	22	23	14	28	—	28	—	21	21	48	38	—	42
2	60	56	10	26	16	25	21	25	—	—	20	54	52	69	35	—	32
3	90	15	25	54	35	—	15	28	—	58	—	42	21	47	26	—	31
4	155	26	15	23	—	—	15	65	—	—	—	51	22	38	—	—	—
5	125	19	19	10	22	—	12	—	19	—	—	55	19	23	—	38	22
6	60	65	49	—	—	—	15	29	—	24	—	50	25	32	23	—	39
7	250	11	42	11	7	24	16	34	—	—	41	25	25	42	21	—	49
8	90	27	18	14	15	30	14	29	—	23	—	55	32	15	—	45	—
9	200	23	19	20	28	21	21	31		25	—	65	62	31	—	11	29
10	20	55	21	25	—	—	15	—	24	—	—	70	35	33	—	17	12
11	50	50	30	—	—	—	14	29	—	—	—	45	54	34	—	37	—
12	55	10	86	32	28	—	21	—	—	55	—	60	30	19	60	—	49
13	315	17	54	—	—	—	15	—	40	—	—	50	35	40	22	22	50
14	0	28	40	6	18	15	15	31	—	15	—	50	25	70	35	—	50
15	220	46	31	—	—	—	15	20	—	20	—	45	15	31	17	17	37
16	40	36	22	15	—	—	15	20	40	—	—	45	20	24	—	40	—
17	145	96	—	—	—	—	15	28	—	—	—	84	20	51	—	—	—
18	45	70	9	37	—	—	16	—	39	—	25	78	38	41	19	—	57
19	40	42	39'	—	—	—	20	—	20	—	—	71	30	—	—	57	—
20	145	27	24	30	—	—	20	50	—	—	30	80	32	58	29	—	35
21	115	46	—	—	—	 —	15	—	45	—	—	78	39	26	52	—	38
22	305	46	23	11	—	—	15	15	—	38	—	44	25	30	22	15	40
23	130	31	30	50	—	—	15	30	—	50	—	40	16	60	30	—	30
24	115	36	39	13	31	—	17	23	—	17	—	35	11	45	25	25	44
25	325	72	36	—	—	—	15	—	30	—	—	76	46	50	35	—	51
26	215	36	53	36	32	—	19'	40	—	—	19	76	38	68	35	—	29
27	140	71	27	32	40	—	16	30	—	50	—	46	33	40	20	—	50
28	215	30	20	35	—	—	19	—	19	—	—	59	29	24	—	48	36
29	180	35	15	38	7	—	10	16	—	15	—	50	33	16	—	45	33
30	25	46	28	17	-	-	16	25	—	75	—	50	11	33	—	26	44
Пример выполнения задания. Дано: 1) схема механизма в за-
данном положении (рис. 84); 2) исходные данные (табл. 28).
Решение. 1. Определение скоростей точек и угловых ускорений
звеньев механизма с помощью плана скоростей.
а)	Определяем скорости точек. Строим схему механизма в вы-
85
бранном масштабе (рис. 85). Вычисляем модуль скорости точки А
кривошипа OiA:
va = ^огА • OiA = 2 ♦ 12 = 24 см/с.
Рис. 84
Вектор va перпендикулярен OiA
и направлен в сторону вращения
кривошипа.
Строим план скоростей. Из про-
извольно выбранного полюса О про-
водим отрезок Оа, изображающий в
выбранном масштабе скорость точ-
ки А. Для определения скорости
точки В через полюс О прово-
дим прямую, параллельную скоро-
сти vb, через точку а — прямую,
перпендикулярную АВ. Получаем
точку 6; отрезок ОЬ определяет ско-
рость точки В. Измеряем длину от-
резка ОЬ и, пользуясь масштабом
скоростей, находим vb = 17,5 см/с.
Таблица 28
град.	Расстояние, см					Длина звеньев, см									
	а	Ь	с	d	е	О1А	АВ	AD	o2d	DE	О3Е	FG	GH	FH	O±G
52	32	4	39	19	32	12	46	29	32	53	18	25	14	14	20
Для определения скорости точки С делим отрезок ab плана ско-
ростей в отношении ас/cb = АС /СВ.
Рис. 85
Отрезок Ос изобра-
жает скорость точки С.
Пользуясь масштабом
скоростей, получаем
vc = 17,5 см/с.
Продолжая построе-
ние плана скоростей,
находим ид, vb, v<j,
vd, ve, vf, vg, vh
(табл. 29).
На чертеже меха-
низма концы вёкторов
скоростей точек пря-
молинейного звена (на-
пример А, В, С или В,
В) находятся на одной
прямой.
86
Таблица 29
Способ определения	Скорости точек, см/с							
По плану скоростей С помощью мгновенных центров скоростей	24 24	17,5 17,3	17,5 17,5	17,5 17,4	17,5 17,4	17,5 17,4	14,8 14,6	14,4 14,1
б)	Определяем угловые скорости звеньев механизма. Отрезок аЬ
плана скоростей выражает вращательную скорость точки В вокруг
точки А:
аЬ = vab = шав * АВ;
отсюда угловая скорость звена АВ
шав = аЬ/AB = 19,5/46 = 0,424 рад/с.
Аналогично определяются угло-
вые скорости звеньев AJD, DE,
FGH:
wad = ad/AD;
wde — de/DE;
^FGH = fg/FG.
Угловую скорость lofgh можно
определить также из соотношений
UFGH = gh/GH = fh/FH.
Угловая скорость звена O?D
определяется по вращательной
скорости точки D вокруг непо-
движного центра О2’
wo2d = vd/O^D.
Аналогично определяются угло-
вые скорости звеньев О$Е, О 4G:
wq3e = ое/О^Е; wo4g = vq/O^G.
Вычисленные по этим форму-
лам угловые скорости приведены
в табл. 30.
Таблица 30
Способ определения	Угловые скорости звеньев, рад/с						
	АВ	AD	DE	o2d	О3Е	FGH	O4G
По плану скоростей	0,424	0,500	0	0,547	0,972	0,272	0,740
С помощью мгновенных центров скоростей	0,421	0,505	0	0,544	0,967	0,278	0,730
2.	Определение скоростей точек и угловых скоростей звеньев ме-
ханизма с помощью мгновенных центров скоростей.
87
а)	Определяем положения мгновенных центров скоростей звеньев
механизма. Строим схему механизма в выбранном масштабе (рис. 86).
Звенья 01 A, O2D, О3Е, O4G вращаются вокруг неподвижных центров
Oi, О2, О3, О4.
Мгновенный центр скоростей Рав звена АВ находится как точ-
ка пересечения перпендикуляров, проведенных из точек А и В к
их скоростям. Аналогично определяется положение мгновенных цен-
тров скоростей Pad и Pfgh- Мгновенный центр скоростей звена DE
находится в бесконечности.
б)	Определяем скорости точек. Скорости точек звеньев механизма
пропорциональны расстояниям от этих точек до мгновенных центров
скоростей соответствующих звеньев.
Эти расстояния измеряются на чертеже.
Для определения скоростей точек В и С звена АВ имеем пропор-
ции
va/vb — АРав/ВРав',
va/vc = АРав/СРав-
Следовательно,	‘
vb = va ’ ВРав/АРав\
vc = va • СРав/АРав-
Аналогично, для точки D звена AD
va/vd = APad/DPad,
откуда
vd = va • DPad/APad-
Так как мгновенный центр скоростей звена DE находится в бес-
конечности, то ve = vf = vd.
Для определения скоростей точек G и Н имеем пропорции
vf/vg — FPfgh/GPfgh, vf/vh = FPfgh/HPfgh<
С л едовате л ьно,
vG = vf • GPfgh/FPfgh',
vh = vf • HPfgh/FPfgh-
Пользуясь масштабом длин, определяем расстояния от точек до
мгновенных центров скоростей.
Эти расстояния (в см) приведены в табл. 31.
Таблица 31
АРав	ВРав	СРав	APad	DPad	FPfgh	GPfgh	HPfgh
57	41	41,5	47,5	34,5	62,7	52,8	50,8
Скорости точек, вычисленные по указанным формулам, приведены
в табл. 29.
Одновременно с определением модулей скоростей точек находим
их направления, а также направления вращений звеньев механизма.
88
Например, по направлению скорости точки А и положению мгно-
венного центра скоростей Рав устанавливаем, что вращение звена
АВ происходит по часовой стрелке. Поэтому скорость точки В при
данном положении механизма направлена вверх.
Аналогично определяем направления вращений остальных звеньев
и направления скоростей точек механизма (рис. 86).
в)	Определяем угловые скорости звеньев механизма. Скорость лю-
бой точки звена равна произведению угловой скорости этого звена
на расстояние от точки до мгновенного центра скоростей:
VA = UАВ ’ АРва = ^AD ’ APaD-
Отсюда определяем угловые скорости звеньев АВ и AD\
wab = va/APab', mad = va/APad-
Угловая скорость звена O2D определяется по скорости точки D:
Wq2D — VD/O2D.
Угловая скорость звена DE при данном
положении механизма равна нулю, так как
мгновенный центр скоростей звена в этом
случае находится в бесконечности: wde = 0.
Аналогично определяем угловые скорости
остальных звеньев механизма:
ШО3Е = Ve/O^E',
WFGH = Vf/FPfGH',
&o4g = vg/O±G.
Угловые скорости звеньев, вычисленные по
указанным соотношениям, приведены в табл.
30.
3.	Определение ускорений точек А, В, D
и угловых ускорений  звеньев АВ и BD*.	ис'
а)	Определяем Sa, а в и sab (рис. 87). С помощью теоремы об
ускорениях точек плоской фигуры определяем ускорение точки В:
а в — А “Ь О АВ О АВ'
Так как кривошип О\А вращается равномерно, то ускорение точки
А направлено к центру и равно
ад — (^а ~ О±А •	= 12 • 22 = 48 см/с2.
* Условие задания предусматривает определение ускорений точек А, В и углово-
го ускорения звена АВ. Однако в примере определяются также ускорение точки D
и угловое ускорение звена AD в соответствии с двумя случаями, встречающимися
в задачах такого типа.
89
Центростремительное ускорение точки В во вращательном движе-
нии шатуна АВ вокруг полюса А направлено от точки В к точке А
и равно
'	авд = А& * шав = 46 • 0,42 = 7,36 см/с2.
Откладываем от точки В в соответствующем масштабе ускорение
полюса ад. Из конца вектора ад строим вектор ОдВ, проводя его
параллельно ВА. Через конец вектора а1АВ проводим прямую, пер-
пендикулярную В А, т. е. параллельную вращательному ускорению
Точка пересечения этой прямой с прямой, по которой направлен
вектор ускорения ползуна В, определяет концы векторов а в и o^B.
Измерением на чертеже получаем а в = 39 см/с2; а?АВ = 30 см/с2.
Так как а\в = АВ • елв, то угловое ускорение звена АВ
е ав = аъАв1АВ ~ 30/46 = 0,652 рад/с2.
б)	Определяем ав и sad (рис. 88). Точка D принадлежит двум
звеньям: AD и O2D. Взяв за полюс точку А, получаем
Sd — <7д А a^D +
Ускорение точки А найдено выше: ад =48 см/с2.
Центростремительное ускорение точки D во вращательном движе-
нии звена AD вокруг полюса А направлено от точки D к точке А
и равно
a\D = AD • u2ad = 28,5 • 0,52 = 7,1 см/с2.
Откладываем из точки D в соответствующем масштабе ускорение
полюса ад. Из конца вектора ад строим вектор а^, проводя его
параллельно DA. Через конец вектора a^D проводим прямую JK
перпендикулярно ВА, т. е. параллельно вращательному ускорению
(Рав' Однако определить ускорение а в этим построением невозможно,
так как его направление неизвестно.
90
Чтобы найти ускорение точки D, необходимо выполнить второе
построение, рассматривая D как точку звена O2D. В этом случае
UD = а%) + SPD.
Центростремительное ускорение точки D
do = O2D  Wq2D = 8 см/с2.
Откладываем от точки D вектор , направив его к центру О2.
Через конец вектора проводим прямую LN перпендикулярно/O2-D,
т. е. параллельно вращательному ускорению	*
Точка пересечения этой прямой с JК определяет концы векторов
dD, o?ad и Со-
измерением на чертеже получаем а© = 42 см/с2; a\D — 30 см/с2.
Так как a?AD = AD • cad, то угловое ускорение звена AD
cad — <?ad/AD = 30/29 = 1,03 рад/с2.
4.	Определение положения мгновенного центра ускорений эвена
АВ (рис. 89). Примем точку А за полюс. Тогда ускорение точки В
ав = а>А + аАВ-
Строим параллелограмм ускорений при точке В по диагонали ад и
стороне а а- Сторона параллелограмма Sab выражает ускорение точки
В во вращении АВ вокруг полюса А. Ускорение Sab составляет с
отрезком АВ угол а, который можно измерить на чертеже.
Направление вектора S?AB относительно полюса А позволяет опре-
делить направление сав, в данном случае соответствующее напра-
влению вращения часовой стрелки. Отложив угол а от векторов Sa
и Sb в этом направлении и проводя два луча," найдем точку их
пересечения Qab — мгновенный центр ускорений звена АВ.
5.	Определение ускорения точки М. Найдем ускорение точки М с
помощью мгновенного центра ускорений.
Ускорения точек плоской фигуры пропорциональны их расстояни-
ям до мгновенного центра ускорений:
ам/ал — MQab/MQab-
Подставив расстояния, определенные по чертежу, MQab = 67,5 см,
AQab = 77 см, получим ускорение точки М:
ам = Q'A • MQab/AQab = 48 • 67,5/77 = 42,1 см/с2.
Ускорение ам составляет с прямой MQab угол а; направление
этого вектора соответствует угловому ускорению сав-
91
СФЕРИЧЕСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
Задание К.5. Определение кинематических характеристик
движения твердого тела и его точек по уравнениям Эйлера
Заданы уравнения сферического движения твердого тела -0 = -0(£),
в = f)(t) и р = p(t), где ф, 0 и р — углы Эйлера (рис. 90).
Определить для момента времени t = угловую скорость и угловое
ускорение тела, а также скорость и ускорение точки М, координаты
которой в подвижной системе, жестко связанной с телом, £, ту, (ф
Необходимые данные приведены в табл. 32.
Пример выполнения задания. Исходные данные: ф = 2£2+3t рад,
0 = 7г/6 рад, р = 24£ рад, £ = 3 см, у = 2 см, £ = 5 см, ф = 1 с.
Решение. 1. Определение угловой скорости тела. Проекции угло-
вой скорости тела на подвижные оси координат определяются по
следующим формулам:
Рис. 90
щ = ф sin в sin р + в cos р\
^Г] — ф sin 0 cos р — 0 sin р;
щ = ф cos# + р.
Используя исходные данные, находим:
= (4t + 3)0,5 sin 24t;
= (4t -h 3)0,5 cos 24t; >
= (4Z + 3)0,866 + 24. >
(1)
Таблица 32
Номер варианта	Уравнения движения тела			Координаты точки M, см			ti, с
	Ф = ^(t), рад	0 = 0(t), рад	= <^(t), рад	е	V	С	
1	3t2 + 6t	ТГ / 3	4t	2	5	4	1
2	2t	(тг/6) sin 2t	25t	3	1	2	2
3	-4t	(тГ/4) cos 3t	15t	4	-3	5	1
4	2t2 + 3t	ТГ / 6	-2t	—2	4	4	3
5	4t2	—тг/4	20t	3	2	-3	2
6	3t	—(тг/З) cos 4t	6t	2	3	2	1
7	4t2 - 2t	Тг/4	—20t	6	2	3	0,5
8	t2 + 4t	тг/З	(	18t	7	4	1	1
9	- 3t2 + 2t	ТГ / 6	30t	-4	5	3	2
10	5t	(тг/З) cos 2t	lOt	5	3	3	0,5
92
Продолжение табл. 32
Номер варианта	Уравнения движения тела			Координаты точки M, см			ti, с
	= -0(f), рад	0 = 0(t), рад	P = ^(t), рад	е	*7	с	
11	—2t	(тг/4) sin 3t	— 12t	4	—2	4	2
12	2i2 - 4t	—тг/4	15t	-6	4	2	1
13	3t2 + 2t	—Тг/З	24t	3	10	5	0,5
14	-3t	(тг/6) sin 8t	-30*	10	—4	3	1
15	—4t2 + 3t	тг/4	16t	9	5	5	2
16	2t	(тг/З) cos 6t	3t	6	8	10	1
17	—2t2 + 5t	Тг/5	5t	1	3	-2	1
18	4t2 + 3t	Тг/9	25t	7	5	4	0,5
19	t2 - 2t	— Тг/6	—4t	5	4	3	2
20	4t	(тг/5) cos 3t	18t	-3	2	1	2
21	—5t	(тг/4) sin 6t	12t	8	6	10	1
22	—2t2 - 2t	—тг/5	2t	4	-1	3	4
23	3t2 - 2t	тг/4	-5t	-5	7	4	3
24	2t	—(тг/5) sin 3t	-30t	10	8	-6	1
25	-t	(тг/9) cos 8t	18*	7	4	5	2
26	3t	(тг/З) sin 2t	lot	—2	1	3	1
27	- 3t2 + 4t	. —тг/9	5t	8	9	6	2
28	-5t	—(тг/З) sin 3t	8t	4	—2	—2	2
29	t	(тг/4) cos 6t	9t	7	6	10	3
30	-3t	(тг/6) cos 4t	— 15t	6	8	5	1
Проекции угловой скорости на неподвижные оси координат:
шх = ф sin ф sin 0 4- в cos ф\
шу = —фсоъфътО + 0Б1пф;
шг = </>cos0 4- ф,
или в данном случае
шх = 24 • 0,5 sin (2t2 4- 3t);
шу = -24 • 0,5 cos (2t2 4- 3t); ►
шг = 24 0,866 + 4f+ 3.
(2)
Для определения угловой скорости тела при tj = 1 с предвари-
тельно вычисляем:
sin 242 = sin 24 = sin(8?r - 1,133) = sin(-l,133) = -0,906;
cos 24* = 0,424;
sin(2£2 + 3f) = sin 5 = зт(2тг - 1,283) = sin(-l,283) = -0,959;
cos(2£2 + 3f) = 0,284.
93
Тогда согласно (1) и (2) в результате вычислений получаем (рад/с):
= -3,17;	= 1,48;	щ = 30,1;
= —11,5;	wy = —3,41;	wz = 27,8.
Модуль угловой скорости
СО = yjcoj +	+ О>2,
или	____________
W	+0)2 4- ц?2
Можно определить модуль угловой скорости, минуя вычисление ее
проекций на оси координат, по формуле
(jj =	+ V’2 + 2фф cos#.
По любой из этих формул находим
со = 30,3 рад/с.
Направление угловой скорости, а следовательно, и мгновенной оси
вращения тела можно определить направляющими косинусами, на-
пример	х
cos(cj, £) = cu^/cj.
Совершенно аналогичны формулы для других направляющих ко-
синусов.
В результате вычислений получаем:
в подвижной системе координат
cos(o>, £) = —0,105; cos(o>, ц) = 0,049; cos(o>, С) = 0,993;
в неподвижной системе
cos(a), х) = —0,380; cos(c5, у) = —0,113; cos(o>, z) = 0,917.
2.	Определение углового ускорения тела. Проекции углового уско-
рения тела на подвижные оси координат определяются следующим
образом:
— со^] — со^.
В соответствии с (1)
= 2sin24£ 4- (2t + 1,5)24 cos 24^;
£^ = 2 cos 24t - (2t 4-1,5)24 sin 24£;
= 3,46.
Проекции углового ускорения на неподвижные оси координат:
&Х ~~ ^х\ £у —	£ Z — &Z'
В соответствии с (2)
ех = 12(4£ 4- 3) cos(2£2 4- 3£); еу = 12(4/: 4- 3) sin(2£2 4- 3£); ez = 4.
94
При ti = 1 с находим (рад/с2):
= 33,8;	= 76,9;	= 3,46;
гх = 23,9;	£у = -80,5;	ez = 4.
Модуль углового ускорения
£ = vM+£*+£c>
или	___________
£ = +
По любой из этих формул
£ = 84,1 рад/с2.
Направление углового ускорения определяется направляющими ко-
синусами.
В подвижной системе координат
cos(e*, £) = 0,402; cos(e*, ту) = 0,914; cos(e, С) = 0,041.
В неподвижной системе координат
cds(s, х) = 0,284; cos(e, у) = -0,957; cos(e, z) = 0,048.
3.	Определение скорости точки Af(£, р, £). Проекции скорости
точки на подвижные оси координат определяются по формулам
“ Щр; Vrj =	vc = щр -
Для момента времени t± = 1 с и заданных значений £, т/, £ имеем
(см/с):
= —52,8;	= 106,2;	= —10,7.
Модуль скорости точки
v =	+ vc
Вычисляя, находим v = 119 см/с. Направляющие косинусы: cos(tf, £)=
= —0,444; cos(i7, 77) = 0,892; cos(#, £) = —0,090.
4.	Определение ускорения точки М(& р, С). Проекции ускорения
точки на подвижные оси координат определяются по формулам
ае =	+ ЦуП +	- ^2£;
av =	- ^2j?;
аС = £iV -	+ МуЧ + WC<) - ^2С-
В момент времени ti = 1 с имеем (см/с2):
а( = -2829; av = -1780;	= -414.
Модуль ускорения точки
а ” \/а1 + ал +
95
или
а = 3367 см/с2.
Направляющие косинусы:
cos(a, £) = —0,841; cos(a, т?) = —0,529; cos(a, Q = -0,123.
Задание К.6. Кинематический анализ движения
твердого тела, катящегося без скольжения
по неподвижной поверхности
и имеющего неподвижную точку
Тело А катится без скольжения по поверхности неподвижного
тела В, имея неподвижную точку О. Ось ОС> тела А вращается
вокруг неподвижной оси Oz и имеет при заданном положении тела
А угловую скорость и угловое ускорение ед.
Определить угловую скорость и угловое ускорение тела А, а также
скорость и ускорение точки М в указанном положении тела А.
Схемы показаны на рис. 91 — 93, а необходимые для расчета
данные приведены в табл. 33.
Таблица 33
Номер варианта (рис. 91-93)	ОМ0, см	<^1, рад/с	£1, рад/с2	М0М, см	Номер варианта (рис. 91-93)	ОМ0, см	о>1, рад/с	£1, рад/с2	М0М, см
1	30	2,3	4,0	16	16	45	2,4	5,4	20
2	45	3,0	3,0	5	17	50	3,5	-3,0	10
3	50	1,2	-3,6	-	18	30	1,0	2,2	10
4	40	2,0	4,2	10	19	50	2,7	4,4	20
5	40	0,8	2,0	10	20	30	3,3	-4,6	10
6	70	4,0	5,6	30	21	40	4,0	-5,0	25
7	60	1,5	—2,5	-	22	30	1,6	2,8	5
8	40	2,1	3,2	20	23	40	2,0	3,7	5
9	50	з;2	—4,7	10	24	60	3,5	4,1	10
10	20	1,3	1,8	10	25	40	1,6	-3,0	15
11	30	0,9	2,6	20	26	40	2,2	3,3	'15
12	40	2,2	3,0	. -	27	30	4,1	-5,5	10
13	20	3,8	4,3	10	28	45	3,0	4,2	5
14	30	1,4	-2,8	10	29	40	1,4	3,6	15
15	40	0,7	2,2	15	30	50	2,9	-5,2	/15
Примечание. Положительный и отрицательный знаки у si означают соответ-
ственно, что вращение оси вокруг оси Oz происходит в направлении, показанном
на схеме, ускоренно или замедленно.
96
Рис. 91
97
Рис. 92
98
Рис. 93
99
Пример выполнения задания. Тела А и В представляют собой
прямые круговые конусы (рис. 94).
Рис. 94	Рис. 95	Рис. 96
Дано: а — 60°, /3 = 90°, OMQ = I = 30 см, о>1 — 1,2 рад/с,
£1 = 27 рад/с2, MqM = 10 см.
Решение. 1. Определение угловой скорости тела. Конус А совер-
шает сферическое движение. Мгновенная ось вращения OQ совпадает
с общей образующей конусов (рис. 95).
Выберем направления координатных осей Ох и Оу так, чтобы ось
ОС, а следовательно, и OQ находились в плоскости xOz.
Скорость vc точки С является вращательной скоростью вокруг
мгновенной оси.
Следовательно,
vc = <3 х ОС,	(1)
где <3 — угловая скорость тела А.
С другой стороны, vc — вращательная скорость вокруг оси Oz,
поэтому
vc = <3i х ОС.	(2)
Из (1) и (2) следует
cusin(a/2) = о>1 sin[(a + /3)/2].	(3)
С учетом исходных данных находим си = 2,32 рад/с.
Направление (3 определяется направлением vc в соответствии с
(1).
Угловую скорость тела А можно найти также путем сложения вра-
щений вокруг пересекающихся осей — построением параллелограмма
угловых скоростей (рис. 96):
CU — CU1 4" Сс>2.
Здесь (32 — угловая скорость конуса А во вращении вокруг соб-
ственной оси О£>
По теореме синусов,
си/ sin[(a + /3)/2] = cui / sin(a/2),
что совпадает с выражением (3).
100
2. Определение углового ускорения тела. Угловое ускорение
£ = dcu/dt	(4)
Вектор угловой скорости запишем в виде
Со = cuzq,
(5)
где со — модуль вектора Со; zq — орт его направления.
Следовательно,
£ = (dcj/dt)^ -I- codan/dt.	(6)
Заметим, что
din/dt = Coi х in ,
а с учетом направлений coi и zq (рис. 97)
dan/dt = coi sin(/3/2)J.
Теперь вместо (6) имеем
или
где
ё*= (du>/d^)zn 4- cocoi sin(/3/2)j
£ = €|| + €_l.
ё|| = (dw/dt)in,
ej. = wwi sin(/3/2)J.
(7)
(8)
(9)
(10)
Эти же выражения составляющих £ непосредственно следуют из
условия, что угловое ускорение геометрически равно скорости и конца
вектора йо. Ее составляющие пц = sj| и и± = бд. — соответственно
радиальная и трансверсальная (поперечная) скорости этой точки.
Вектор £|| направлен по мгновенной оси вращения OQ. Его модуль
бц = |du;/d£|.
Согласно (3) и учитывая, что dcui/dt = £i,
duj/dt = si sin[(a 4- /?)/2] / sin(o/2),
или с учетом исходных данных
dco/dt = 5,22 рад/с2.
Следовательно,
бц = 5,22 рад/с2.
Знак «4-» при dcu/dt (при si) показывает, что направления sj| и Со
совпадают.
Вектор €j_, как следует из (10), имеет направление орта j. Его
модуль
£j_ = <0(01 sin(/3/2),
или
= 1,97 рад/с2.
101
Так как бд. и еу взаимно перпендикулярны, то
£ = ^+s2j_,
или
£ = 5,58 рад/с2.
Векторы еу, ед. и е пока-
заны на рис. 97.
‘ 3. Определение скорости
точки тела. Скорость точ-
ки М определяем как враща-
тельную вокруг мгновенной
оси:
Рис. 97	>
= СЗ х ОМ. (11)
Векторы сЗ и ОМ расположены в плоскости xOz; следовательно,
вектор им параллелен оси Оу. Он имеет одинаковое направление с
вектором vC-
Модуль скорости
vm = • OMsin(cj, ОМ}.	(12)
Как видно из рис. 95,
ОМ • sin(w, ОЛ?) = MN = DM  cos(a/2);
DM = 2/sin(a/2) - MM0.
С учетом этих соотношений по формуле (12) находим
им = 40,2 см/с.
4. Определение ускорения точки тела. Ускорение точки М нахо-
дим как геометрическую сумму осестремительного и вращательного
ускорений:
а>м — Щ •
Осестремительное ускорение
= C3xvM,'
оно направлено по перпендикуляру к мгновенной оси вращения
(рис. 97). Его модуль
а°м = wvm sin 90° = cu-им-
Вращательное ускорение
а?м = ех ОМ,
или, учитывая (9),
102
где
z
п

£
о__
м0
Рис. 98
перпендикулярен ОМ.
У
1^-
' А Ч
ф
и
Sm|| = x ом,	(13)
4f± = Ё1 х ОМ.	(14)
Сравнивая (13) с (11) и принимая во вни-
мание, что направления ej| и о? совпадают,
заключаем, что и направления и vm
тоже совпадают.
Модуль составляющей ускорения точ-
ки М
амц = ец-OAf-sin(ej|, ОМ) =‘£ц-£>М-cos(a/2).
Вектор расположен в плоскости xOz
Его модуль
ам± =	* ОМ * sin 90° =	♦ ОМ]
ОМ = у/12 + (М0М)2 - 21  М0М  sin(a/2).
В результате вычислении находим:
ам|| = 90,4 см/с2;	= 52,2 см/с2.
Ускорение точки М найдем как геометрическую сумму трех со-
ставляющих:
= 3°м + Ом\\ + ^мг-
Векторы и расположены в плоскости xOz, а вектор
ей перпендикулярен.
Поэтому модуль ускорения точки М (рис. 97)
ам = ^/(ам)2 + (ам±)2 - 2амам± cos7 + (амц)2-
Здесь
со§7 = cos 4.MOD = (I — DM • sin(a/2))/OM.
Окончательно после вычислений получаем
ам — 110,9 см/с2.
Если бы в этой задаче требовалось определить кинематические
характеристики движения тела и его точки не в некоторый заданный,
а в любой момент времени, условие задачи удобно было бы записать
в форме уравнений Эйлера.
Полагая, например, что = const, cui — начальное значение
угловой скорости вращения оси ОС> вокруг Oz (рис. 98), имеем
ф =	+ ^it2/2
(принято, что начальное значение угла V’o = 0),
0 = (а + /?)/2.
103
Для определения = <^(£) заметим, что угловые скорости ф и
обратно пропорциональны длинам окружностей или радиусам осно-
ваний конусов, т. е.
ф = [sin(/?/2)/sin(o!/2)]^ (то же следует из рис. 96),
или
Ч> = [sin(z3/2)/ зш(а/2)]^	(<Л) = 0).
Следовательно,
ip = [sin(/8/2)/sin(a/2)](a;i^ + £it2/2).
В условиях данной задачи
ф = 1,35г2 + 1,20г; 0 = 5тг/12; 9? = ^2-ф.
Координаты точки М в подвижной системе координат:
С = I sin(a/2) - М0М = 30 • 0,5 - 10 = 5,0 см,
т] = 0,
С = I cos(a/2) = 30 • 0,866 = 26,0 см.
Порядок решения такой задачи показан в примере выполнения
задания К.5.
III. СЛОЖНОЕ ДВИЖЕНИЕ
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
Задание К.7. Определение абсолютной скорости
и абсолютного ускорения точки
Точка М движется относительно тела D. По заданным уравнениям
относительного движения точки М и движения тела D определить
для момента времени t = t\ абсолютную скорость и абсолютное
ускорение точки М.
Схемы механизмов показаны на рис. 99 — 101, а необходимые для
расчета данные приведены в табл. 34.
Пример выполнения задания. Дано: схема механизма (рис. 102),
sr — ОМ = 16 — 8cos3tt£ см; <ре = 0,9£2 — 9t3 рад; t± = 2/9 с.
Решение. Будем считать, что в заданный момент времени плос-
кость чертежа (рис. 102) совпадает с плоскостью треугольника D.
Положение точки М на теле D определяется расстоянием sr = ОМ.
При t = 2/9 с
sr = 16 — 8cos(3?r • 2/9) = 20,0 CM.
Абсолютную скорость точки М найдем как геометрическую сумму
относительной и переносной скоростей:
v = vr + уе.
104
Таблица 34
Номер варианта (рис. 99-101)	Уравнение относительно- го движения точки М ОМ = зг = = sr(t), см	Уравнение движения тела		tl, c	K, CM	a, CM	a, град	Дополни- тельные данные
		¥>e = <^e(t), рад	Xg — CM					
1	18sin(Trt/4)	2t3 -12	-	2/3	-	25	-	
2	20 sin Trt	0,4t2 + t	' —	5/3	20	—	—	
3	6t3	2t + 0,5t2	—	2	—	30	—	
4	10sin(7rt/6)	0,6t2	I —	1	—		60	
5	407Г cos(?rt/6)	3t - 0,5t3	—	2	30	—	—	
6	—	—	3t + 0,27t3	10/3	15	—	—	<pr = 0,157rt3
7	20 cos 2?rt	0,5t2	-	3/8	-	40	60	
8	6(t+0,5t2)	t3- 5t	-	2	-	-	30	
9	10(1 4- sin 2%^)	4t + l,6t2	—	1/8	—		—	
10	207Г cos(tf£/4)	l,2t - t2	—	4/3	20	20	—	
11	25sin(7rt/3)	2t2 - 0,5t	—	4	—	25	—	
12	15irt3/8	5t — 4t2	-	2	30	30	-	
13	120irt2	8t2 -3t	—	1/3	40	• —	—	
14	3 + 14 sin 7rt	4t- 2t2	—	2/3	—	—	30	
15	5\/2(t2 +t)	0,2t3 + t	-	2	-	60	45	
16	20 sin Tvt	t - 0,5t2	—	1/3	—	20	—	
17	St3 + 2t	0,5t2	-	1	-	4>/5		
18	lOt +t3	8t -t2	—	2	—	—	60	
19	6t + 4t3	t + 3t2	—	2	40	—	—	
20	307Г COs(7Tt/6)	6t + t2	—	3	60	—	—	
21	257r(t +12)	2t - 4t2	-	1/2	25	-	-	
22	10тг sin(Trt/4)	4t - 0,2t2	—	2/3	30	-	-	
23	67Tt2	— .	—	1	18	—	—	p — ?rt3/6; O\O = O^A — = 20 cm
24	75Tr(0,lt+ +0,3t3)	2t - 0,3t2	—	1	30	—	—	
25	15sin(7rt/3)	lOt - 0,lt2	—	5	—	—	—	
26	8cos(?rt/2)	—2jrt2	—	3/2	—	—	45	
27	-	-	50t2	2	75	-	-	<pr = 5?rt3 /48
28	2,5?rt2	2t3 - 5t	—	2	40	—	—	
29	57rt3 /4	—	—	2	30	—	—	<p = ?rt3/8; OiO = О2Л = = 40 cm
30	4?rt2	—	t3 + 4t	2	48	—	—	
Примечания. Для каждого варианта положение точки М на схеме соответ-
ствует положительному значению sr; в вариантах 5, 10, 12, 13, 20—24, 28—30
ОМ = 8Г — дуга окружности; на схемах 5, 10, 12, 21, 24 ОМ — дуга, соответствую-
щая меньшему центральному углу. Относительное движение точки М в вариантах
6 и 27 и движение тела D в вариантах 23 и 29 определяются уравнениями, приве-
денными в последнем столбце табл. 34.
105
Рис. 99
106
Рис. 100
107
Рис. 101
108
Рис. 102
Модуль относительной скорости
Vr = Ы,
где
vr = dsr/dt = 247rsin37rt
При t = 2/9 с
vr = 65,2 см/с; vr = 65,2 см/с.
Положительный знак у vr показывает, что вектор
vr направлен в сторону возрастания sr.
Модуль переносной скорости
ve = Rwe,	(1)
где R — радиус окружности L, описываемой той точкой тела, с
которой в данный момент совпадает точка М, г = srsin30° = 10,0 см;
— модуль угловой скорости тела:
= |£>е|;	= type/dt = 1 fit — 27t2.
При t = 2/9 с
cue = —0,93 рад/с; ие = 0,93 рад/с.
Отрицательный знак у величины с5е показывает, что вращение
треугольника происходит вокруг оси Oz в сторону, обратную напра-
влению отсчета угла ц>. Поэтому вектор сие направлен по оси Oz
вниз (рис. 103, а).
Модуль переносной скорости, по формуле (1),
ve = 9,3 см/с.
Вектор ve направлен по касательной к окружности L в сторону
вращения тела. Так как ve и vr взаимно перпендикулярны, модуль
абсолютной скорости точки М
v =
или
v = 65,9 см/с.
109
Абсолютное ускорение точки равно геометрической сумме относи-
тельного, переносного и кориолисова ускорений:
CL —— CLf 4” ttg I ,
или в развернутом виде
а = агт + агп +	+ flg+flc.
Модуль относительного касательного ускорения
(Ltt —
где
агт = d2sr/dt2 = 727r2cos37rt
При t = 2/9 g>	/
arT = —355 см/с2; агт = 355 см/с2.
Отрицательный знак агт показывает, что вектор агт направлен
в сторону отрицательных значений sr. Знаки vr и агт различны;
следовательно, относительное движение точки М замедленное.
Относительное нормальное ускорение
arn = v2r/p = 0,
так как траектория относительного движения — прямая (р = оо).
Модуль переносного вращательного ускорения
a* = Rce,	(2)
где ее = |бе| — модуль углового ускорения тела D:
ёе = d2(pe/dt2 = 1,8 — 54Л
При t = 2/9 с
ёе = —10,2 рад/с2; е = 10,2 рад/с2.
Знаки ёе и одинаковы; следовательно, вращение треугольника D
ускоренное, направления векторов а?е и ее совпадают (рис. 103, а, б).
Согласно (2),
а® = 102 см/с2.
Вектор of направлен в ту же сторону, что и ve.
Модуль переносного центростремительного ускорения
= Ru% или а? = 9 см/с2.
Вектор а* направлен к центру окружности L.
Кориолисово ускорение
(Хе —	.
110
Модуль кориолисова ускорения
ас = 2wevr sm(a>€, vr),
где
sin(a/e, vr) = sin 150° = 0,5.
С учетом найденных выше значений ше и vr получаем
ас = 61 см/с2.
Вектор ас направлен согласно правилу векторного произведения
(рис. 103, б).
Модуль абсолютного ускорения точки М находим способом про-
екций:
ах ~~~~	ас,	~~~ ^тт COS 60 ,
az = —arT cos30°; a \Ja2 + a2 + a2z.
Результаты расчета сведены в табл. 35.
Таблица 35
а>е, рад/с	Скорость, см/с			ее, рад/с2	Ускорение, см/с2								
	Ve	Vr	V		а?	а;	<1гп	dp	ас	(X®	(Ху	а2	а
-0,93	9,3	65,2	65,9	-10,2	9	102	0	-355	61	163	-186	308	395
СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА,
СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПАРАЛЛЕЛЬНЫХ
И ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
Задание К.8. Определение угловых скоростей звеньев
планетарного редуктора
Найти угловые скорости ведомого вала II и сателлитов редукто-
ра. Схемы редукторов показаны на рис. 104—106, необходимые для
расчета данные приведены в табл. 36.
Пример выполнения задания (варианты 1—20). Редуктор с
цилиндрическими колесами. Исходные данные: схема редуктора
(рис. 107); радиусы колес (см): ri = 30, г2 = 15, гз = 30,	= 75;
угловые скорости (рад/с): cjj = 80,	= 20.
Решение. Применим способ мгновенных центров скоростей. По
угловым скоростям ведущих звеньев найдем скорость точки А
оси блока сателлитов и скорость точки В касания колес 1 и 2
(рис. 108, а).
va = ^i(ri 4- r2); vb = ^1Г1,
или
va =^ 3600 см/с; vb = 600 см/с.
111
Таблица 36
Номер ва- рианта (рис. 104-106)	Радиус, см				Угловая скорость, рад/с				
	Г1	Г2	гз	Г4			CV3	О>4	U5
1	15	20	15	20	200	—	—	-40	—
2	30	30	15	45	350	50	—	—	—
3	15	30	15	60	240	—	—	—	40
4	20	30	20	120	10	-30	—	—	—
5	40	10	20	10	60	—	—	—	-20
6	80	15	35	30	120	—	—	50	—
7	50	10	15	55	80	-20	—	—	—
8	20	15	25	60	300	—	—	—	30
9	15	7	5	17	70	—	—	20	—
10	10	10	12	54	200	—	—	-10	—
11	50	10	15	55	30'	—	—	-30	—
12	30	15	30	75	330	—	—	70	—
13	20	30	15	35	30	100	—		—
14	100	30	20	50	40	-50	—	—	—
15	15	5	9	11	270	—	—	—	20
16	40	10	20	50	40	—	—	—	-30
17	50	15	10	25	50	-30	—	—	—
18	50	10	10	50	40	40	—	—	—
19	20	15	10	25	200	50	—	—	—
20	50	10	15	25	90	-40	—	—	—
21	100	92	52	60	20	-10	—	—	—
22	50	28	16	30	70	—	—	-150	—
23	40	42	22	22	90	—	—	200	—
24	20	44	20	— 	250	—	40	—	—
25	20	10	20	30	40	150	—	—	—
26	45	60	45	—	50	-120	—	—	—
27	30	30	30	—	100		—	40	—
28	40	42	20	20	130	-250	—	—	—
29	20	20	40	40	320	—	—	50	—
30	15	15	20	20	30	-350	-	-	-
Примечание. Положительный и отрицательный знаки угловых скоростей
означают соответственно направление вращения против и по часовой стрелке, 'если
смотреть со стороны ведущего вала I (для редуктора с цилиндрическими колесами)
или со стороны положительного направления соответствующей оси (для редуктора
с коническими колесами).
Отложив векторы бд и зд, найдем мгновенный центр скоростей
Р2-3 сателлитов 2 — 3. Покажем также скорость vc точки С и
направления вращений сателлитов 2—3 и колеса 4 (ведомого вала II).
Согласно чертежу, угловая скорость сателлитов
W2-3 = (VA ~ VB)/AB.
Скорость точки С
Vc — УД 4- О>2—з * АС.
112
Рис. 104
113
Рис. 105
114
115
Угловая скорость ведомого вала
Рис. 107
=074= vc/ri.
Вычисляя, находим:
о?2-з = 200 рад/с; vc = 9600 см/с;
= 128 рад/с.
Для проверки решения используем способ,
основанный на применении теории сложения
вращений твердого тела вокруг параллельных
осей (способ Виллиса).
Колеса редуктора участвуют: 1) в относи-
тельном вращении (по отношению к водилу) вокруг собственных осей
и 2) в переносном вращении вместе с водилом вокруг его оси.
Переносной угловой скоростью для каждого колеса является угло-
вая скорость водила cjq.
Относительные угловые скорости колес определяются как разности
абсолютных и переносных угловых скоростей:
— cuo;

^kr —	•
Эти относительные скорости являются угловыми скоростями колес
при мысленно оставленном водиле.
В этом случае между относительными угловыми скоростями име-
ются такие же соотношения, как в зубчатых передачах с неподвиж-
ными осями вращений. Следовательно,
(wi - wo)/(cjfc - а>о) -	(1)
где т — число внешних зацеплений между колесами 1 и к; i —
передаточное число от колеса 1 к колесу к в относительном движении
(при остановленном водиле).
116
Отметим, что в это соотношение (формулу Виллиса) входят алге-
браические значения угловых скоростей; знак «+» примем соответ-
ствующим вращению против часовой стрелки, а «—» — вращению
по часовой стрелке.
Применим формулу (1) к решению рассматриваемой задачи (рис.
108, 0. Так как колеса 1 и 2 находятся во внешнем зацеплении, а
колеса 3 и 4 — во внутреннем и угловая скорость водила равна u?i
(рис. 108, а, б), то
(а>1 -wi)/(w4-wi) = (-l)1r2r4/(rir3),
откуда
WK = w4 = wi - (wi - ад)г1Тз/(г2г4).
, Угловую скорость t^2-3 сателлитов 2—3 определяем из следующего
отношения:
(и>1 - сл)/(а;2-з ~ &i) = -г2/п,
откуда
^2-3 = <0 - (cui - CUi)ri/r2.
Используя исходные данные, находим:
= 128 рад/с; ^2-3 = 200 рад/с.
Знаки «+» в ответах указывают на то, что ** у 1
вал II и сателлиты 2—3 вращаются в направле-
нии, противоположном вращению часовой стрелки. Рис- 109
Пример выполнения задания (варианты 21—30). Редуктор с
коническими колесами. Исходные данные: схема редуктора (рис. 109),
радиусы колес (см): п = 24, Г2 = 30, тз = 40, г 4 = 44 см, угловые
скорости (рад/с): — 60, o>i = —40.
Решение. Движение блока сателлитов 2—3 может рассматри-
ваться как совокупность двух вращательных движений. При этом в
качестве переносного движения можно принять не только вращение
водила вокруг оси Oz (в рассматриваемой задаче угловая скорость
водила равна угловой скорости ведущего вала o>i), но и вращение
колеса 1 или колеса 4. Следовательно,
CJc — CJi 4- CUc — О>1 + (31с,	~ ^4 + (J4C.	(2)
Здесь — угловая скорость сателлитов; a>ic, u5ic, ^4с — угло-
вые скорости сателлитов относительно водила, колеса 1 и колеса 4
соответственно.
Заметим, что линии действия любых двух составляющих вектора
CSс известны. Угловые скорости (Ji, и направлены по оси Oz
(рис. 110, а), а?1С — по оси OQ-, и &4С — соответственно по линиям
О а и ОЬ (по мгновенным осям вращения в относительном движении).
Из произвольного полюса Oi (рис. 110, б) отложим векторы за-
данных угловых скоростей cuj и cui параллельно оси Oz, а векторы
o?ic, (31с и й?4С — параллельно О£, Оа и ОЬ соответственно.
117
б) а
/®1к
ь/
Рис. 110
Спроецировав векторные выражения (2) на оси (иг получим:
(vc^ ~~ ^IC;	^cz ~ tvj;
^сС = ^ic sin a;	ucz = — cvi 4- (Vic cos а;	(3)
^c< = tU4C cos /3;	, a>cz = ^4 ~ ^4c sin (3.
Решая систему уравнений (3), находим:
wcf = (wi + wi)tga;
^cC, = cui;
CV4 = <^I + (<^I + cvi) tgotg/3.
При вычислениях заметим, что tgo = п/гг; tg/3 = Г3/Г4; сиц = CV4.
Учитывая исходные данные и имея в виду, что здесь cvi = 40 рад/с
(знак «—» учтен в направлении <vi на рис. 110, б), получаем (рад/с):
(vc£ — 80; (vC2 — 60; и>ц = 132,7.
Угловая скорость сателлитов 2—3
+wj?2,
или
шс = 100 рад/с.
Отметим, что векторные уравнения (2) могут быть решены и гра-
фически. Для этого из произвольного центра О2 (рис. 110, в) отложим
в выбранном масштабе параллельно оси Oz векторы заданных угло-
вых скоростей (Vi и d>i. Через конец вектора cvi проводим прямую
KL, параллельную ОС> (линии действия tvic), из конца вектора (Vi —
прямую MN, параллельную О а (линии действия tvic). Точка пересе-
чения этих прямых определяет конец вектора cvc, а также (Vic и cvic.
Измерением на чертеже находим
= 100 рад/с.
Направление определяет положение мгновенной оси вращения
сателлита OQ (рис. 110, а).
Для определения а?ц разложим tvc на две составляющие, напра-
вленные параллельно Oz и ОЬ. Полученные векторы представляют
собой (VII (си4) И CVnc((V4c).
118
Измерением на чертеже находим сиц = 135 рад/с.
Приведем также решение этой задачи способом Виллиса. Формулу
(1) можно применять и для механизма с коническими колесами, т. е.
когда оси вращения колес пересекаются. В этом случае надо иметь
в виду следующее:
1. Сателлиты 2—3 участвуют во вращениях вокруг пересекаю-
щихся осей. Поэтому их угловая скорость относительно водила не
может быть выражена алгебраической разностью между абсолютной
и переносной угловыми скоростями.
2. Знаки передаточного числа от одного колеса к другому в фор-
муле Виллиса определяются из следующего условия: ,«+», если глядя
со стороны положительных направлений осей, видеть вращения со-
ответствующих колес происходящими (при остановленном водиле) в
одном направлении; «—», если вращения колес видеть происходящими
в разных направлениях.
В рассматриваемой задаче угловая скорость водила равна угловой
скорости ведущего вала ojj. Угловая скорость сателлитов относитель-
но водила обозначена ицс- Тогда для колес 1 и 2 имеем
(wi-wi)/wic =-г2/п.	(4)
Для колес 3 и 4
^1с/(оЛ1-O>i) = г4/г3.	(5)
Перемножая (4) и (5), получаем	)
(О>1 - м)/(^4 ~ <Vl) = -Г2Г4/(Г1Гз),
откуда
0,11 =OJ4=UI- (wi - О?1)Г1Гз/(Г2Г4).	(6)
Подставляя в (6) числовые значения, находим а>ц = 132,7 рад/с.
Положительный знак у показывает, что ведомый вал вращается
в направлении против вращения часовой стрелки (если смотреть со
стороны положительного направления оси Oz).
Для определения угловой скорости сателлита из (4) определяем
сначала его угловую скорость относительно водила:
^1с = “(^1 -O?l)ri/r2,
или
= 80 рад/с.
Абсолютная угловая скорость сателлита
причем вектор cfo направлен по оси Oz, a d?ic — по оси О(.
Так как cjic и aJj взаимно перпендикулярны, то
wc = ^Ic + ^I2,
или
о>с = 100 рад/с.
119
IV. ПРИМЕНЕНИЕ ЭВМ К РЕШЕНИЮ
ЗАДАЧ КИНЕМАТИКИ
Задание К.9. Определение угловых скоростей
и угловых ускорений звеньев механизма манипулятора
по заданному движению рабочей точки
Манипулятор робота представляет собой плоский механизм (рис.
111—113). Звенья этого устройства образуют «механическую руку» с
захватом в точке А.
В заданной системе координат известны уравнения движения ра-
бочей точки А (захвата). Движение точки А длится 1 с.
Требуется определить в этом интервале времени углы в и
расстояние s. Вычислить также угловые скорости и угловые ускоре-
ния звеньев и относительные (варианты 1—13, 15—25, 27—30) или
абсолютные (варианты 14, 26) скорости з и ускорения s точки В.
Все вычисления произвести для промежутка времени от 0 до 1 с с
шагом At = 0,2 с.
Положительные направления отсчета углов <р,	0 и расстояния s
показаны на рисунках вариантов. Считать, что начальные значения
углов — <ро, Ф = Фо известны. Необходимые для расчета данные
приведены в табл. 37.
Таблица 37
Номер ва- рианта (рис. 111-113)	а	b	с		Фо	Уравнения движения	
						ХА	УА
		м		град		м	
1	0,5	1,2	0,4	60	15	1,4091	0,7436-0,3*
2	0,4	0,7	0,24	80	25	0,7712	0,0800+0,2*
3	0,4	1,2	-	115	25	0,6466+0,2*	0,7429 )
4	0,4	0,7	-	45	10	0,9722	0,4044-0,2*
5	0,3	0,8	0,4	115	25	0,4715	0,8819+0,3*
6	0,8	0,6	0,6	30	25	1,2366	0,1464+0,2*
7	0,9	0,24	0,64	40	25	1,559—0,2*	0,1728
8	0,3	0,66	-	38	25	1,071	0,0947+0,3*
9	0,74	0,8	0,32	35	15	1,3789—0,3*	0,6315
10	0,3	0,36	-	80	5	1,128	0,3896-0,3*
11	0,28	0,34	-	50	40	1,3213	-0,0122+0,3*
12	0,6	0,8	-	35	15	1,2642-0,2*	0,1371
13	0,8	0,6	-	35	15	1,2349	0,3036+0,2*
14	0,46	0,82	0,6	70	15	0,9494+0,2*	0,2200
15	0,5	0,3	-	125	25	0,5289	0,7899-0,4*
120
Продолжение табл. 37
Номер ва- рианта (рис. Ш-113)	а	b	с	<ро	V’o	Уравнения движения	
						ха	УА
		м		град		м	
16	0,6	1,2	0,54	35	25	0,59614-0,2*	0,8513
17	0,42	1,0	0,56	50	15	1,236	0,5806-0,2*
18	0,4	0,46	-	40	20	1,6032-0,3*	0,7291
19	0,34	0,9	-	65	12	1,024	0,1214-0,3*
20	0,4	0,5	-	60	17	1,6345—0,3*	0,785
21	0,3	0,9	-	50	30	0,5866	0,6798-0,2*
22	0,3	1,3	0,34	60	20	1,3716-0,3*	0,7044
23	0,24	0,82	0,4	135	35	0,502	0,64-0,2*
24	0,3	0,5	-	32	17	1,2264-0,2*	0,0987
25	0,4	0,9	0,6	40	15	1,4056-0,2*	0,6839
26	0,4	0,8	0,34	50	20	1,1374	0,7332—0,2*
27	0,2	0,3	-	65	20	1,339—0,3*	0,0427
28	0,3	0,3	0,4	130	35	0,54444-0,3*	0,746
29	0,34	0,24	-	55	30	1,0264	-0,20154-0,2*
30	0,28	0,86	0,4	135	41	0,45114-0,2*	0,7622
В конструкции манипуляторов использовано соединение,схема ко-
торого и условное обозначение приведены на рис. 114, а, б; взаимное
относительное движение звеньев 1—3 — поступательное, 2 и 3 —
вращательное, 1 и 2 — плоское.
Пример выполнения задания. На рис. 115, а изображен в на-
чальном положении механизм манипулятора и показаны положи-
тельные направления отсчета углов </>,	0 и расстояния <9. Размеры
звеньев (м): а = 1,30, b = 1,10, с = 0,55.
Захват (точка А) движется согласно уравнениям
xA(t) = 1,5329-0,2* 1
yA(t) = 0,5487 — 0,089*/
(1)
в течение 1 с.
В начальный момент времени (* = 0)
^ = <^0=62°;	^ = ^0 = 33°.
Определить значения углов <р,	0 и расстояние s для указанного
промежутка времени.
Вычислить также угловые скорости ср, ф, 0, угловые ускорения ф,
0, относительную скорость з и относительное ускорение 5 точки В.
Вычисления произвести для моментов времени 0; 0,2; 0,4; 0,6; 0,8; 1 с.
121
Рис. Ill
122
11	'	12
Рис. 112
123
Рис. 113
124
Рис. 114
Решение. Для любого положения механиз-
ма справедливы векторные соотношения (рис.
115, б)
ol = od + cl,	(2)
DB = D(5 + cfi,	(3)
Рис. 115
где	___>	___>
|ОС| = а = const;	(С'уЦ = b = const; 1
|5С| ~ 0,31а = const;	\DB\ = с = const. J	)
Равенства (2) — (4) являются уравнениями связей, наложенных
на систему.
Спроецируем (2) и (3) на оси координат:
ха = a cos р 4- b cos ф,
у a = asintp — bsin^;
(5)
c cos 9 = 0,31a cost/? 4- s cos ф\ 1
c sin 9 = 0,31a sin p — з sin ф. /	'
Продифференцируем (5) и (6) дважды по времени, учитывая (4).
В результате первого дифференцирования получим уравнения, содер-
жащие неизвестные угловые скорости 0, ф, 9 и скорость $:
—аф sin (/? — Ьф sin ф =	1	;
аф cos р — Ьф cos ф = у a, /
—0,31at^ sin р — зф sin ф 4- з cos ф 4- с9 sin 9 = 0; 1
0,31a(£ cos р — зф cos ф — s sin ф — с9 cos 0 = 0./
После второго дифференцирования получим две системы урав-
нений, связывающих угловые ускорения </?, ф, 9 и относительное
ускорение 5:
—аф sin р — Ьф sin ф = ха + аф2 cos р 4- Ьф2 cos ф,}	,qx
ар cos р — Ьф cos ф = у а 4- аф2 sin р — Ьф2 sin ф, J	'
125
,	—O,31a0 sin — зф cos ф 4- s cos ф 4- св sin 0 =	1
= О,31а02 cos 4- 2зф sin 0 4- зф2 cos ф — св2 cos 0; I
О,31а0 cos — зф cos ф — s sin 0 — св cos в =	|	'
= 0,31аф2 sin <р 4- 2зф cos ф — з'ф2 sin ф — св2 sin в. J
Величины ггд, уАч %Ач УАч входящие в выражения (7) и (9), опреде-
ляются дифференцированием уравнений движения захвата (1):
%а = ~ 0,2;	ха — 0; 1
уА = -0,089; #A = OJ	lii;
Для начального момента времени t = to = 0 системы уравнений
(7) и (8) имеют следующий вид:
-афо sin (ро - Ьфо sin фо = -0,2; 1
афосоз(ро - Ьфо cos фо = —0,089; J	.	'
-О,31а0о sin ipo — зофо sin фо 4- «о cos фо 4- сво sin 0О = 0; 1
О,31а0о costpo —-$о0о cos0o — so sin0o — c0q cos0q = 0. f ' '
Для определения «о и 0о воспользуемся системой (6) для началь-
ного положения (t = 0):
с cos 0о = 0,31а cos (^о 4- $о cos0o;
с sin 0о = 0,31а sin <ро — «so sin фо.
Разрешив данную систему относительно $о и tg0o, получим:
so — \/(0,31а)2 4- с2 — 0,62а • с • cos((^o — 0о); so = 0,4102 м;
е = 0,31a sin у>0 — $0 sin V’O t Q 0 2483
°	0,31а cos (/?о 4- so cos V’o
откуда
0о = 13,946°.
Подставляя значения а, 6, с, </?о, Фоч Овч <$о в (7'), (8'), имеем
следующую систему уравнений:
—1,14780о - О,59910о = -0,2;
О,61О30о - О,92250о = 0,089;
—О,35580о - О,22340о 4- O,8387so 4- О,13260о = 0;
О,18920о - О,3440о - O,5446so - О,53380о = 0.
Решая эту систему уравнений, получим:
0о = 0,0921 рад/с;	0о = 0,1574 рад/с;
во = —0,1806 рад/с;	so = 0,1095 м/с.
Заметим, что первые два уравнения решаются совместно, незави-
симо от двух последних.
126
Используя найденные результаты, составим систему уравнений (9)
и (10) для начального положения манипулятора:
—1,147800 - О,59910о = 0,028;
0,61O3(£o - О,92250о = -0,0051;
-О,35580о - 0,223400 + О,8387зо + О,13260о = 0,0115;
О,18920о ~ О,3440о - О,5446зо - О,53380о = 0,0221.
Решая эту систему уравнений, получим:
0О = -0,0203 рад/с2;	0о = -0,0079 рад/с2;
0q = -0,0555 рад/с2;	з’о = 0,0118 м/с2.	'
Отметим, что и в этом случае первые два уравнения решаются
независимо от двух последних.
Следующим моментом времени, при котором необходимо опреде-
лить искомые величины, является t = t± = At = 0,2 с. Считая А
малой величиной, можно записать*:	х х
Vi = <Ро + <Pokt + 0>oAt2/2;	/
01 = 0о + 0оД< + 0оД«2/2;	/12ч
@1 = 4~	4~ 0оД^/2;
$1 = Зо 4“ soAt 4" s’oAt2/2.
Выражения (12) непосредственно вытекают из разложения функций
y?(t), 0(t), 0(t), s(ty в ряд Маклорена.
Вычислим согласно (12) <^i, 0i,0i и 3i:
<pi = 1,1001 рад;	0i = 0,6073 рад;
01 = 0,2062 рад;	31 = 0,4323 м.
В общем случае переход от <а, 0», 0i, $i к <a+i, 0;+i, #i+i, s^+i
будет осуществляться по формулам
<A+i =	4- 0;At 4- 0\At2/2;
0i+i = 0i + A* + 0tAi2/2;	, >
ff-+1 =0i + eiAt + 6i^t2/2;	k ’
s»+i — Si + SiAt + s'iAt2/2,
где i — порядковый номер рассчитываемого положения механизма.
Отметим, что уравнения (13) соответствуют закону изменения па-
раметров (/?, 0, з в интервале времени [ti, £*-+-1] с постоянным
ускорением (равнопеременное движение).
* Следует учесть, что для решения системы дифференциальных уравнений не-
обходимо правильно выбрать численный метод, иначе полученное решение может
оказаться неверным.
127
По найденным согласно (12) ^>1,	01, $1 записываем системы
уравнений (7) и (8) для положения 1 (г = 1) манипулятора:
-1,1586^1 - 0,6277^1 = —0,2;
0,5896(^1 - 0,9033^1 = —0,089;
-0,3592(^1 - 0,2467^1 + 0,8212$i + 0,112601 = 0;
0,1828^i - 0,3550^i - 0,5707$i - 0,538301 = 0.
Решая эту систему уравнений, получим:
<pi = 0,0881 рад/с; Ф1.= 0,1560 рад/с;
01 = —0,1913 рад/с; $i = 0,1116 м/с.
Используя полученные результаты, записываем системы уравнений
(9) и (10) для положения 1 (г = 1) манипулятора:
-1,1586^1 - 0,6277^1 = 0,0265;
0,5896^1 - 0,9033^1 = -0,0063;
-0,3592^1 - 0,2467^1 + 0,8212$! + 0,112601 = 0,0102;
0,1828<^i - 0,3550^i - 0,5707$i 4- 0,538301 = 0,0212.
Решая эти системы уравнений, получаем:
Ф1 = —0,0197 рад/с2;	ф1 = —0,0059 рад/с2;
01 = -0,0520 рад/с2;	$\ = 0,0092 м/с2.
Очередным моментом времени, при котором необходимо определить
искомые величины, является t =	— 2Д£ = 0,4 с.
Воспользовавшись (13), при г = 1 найдем ^2? 02, <§2-
Описанная выше вычислительная процедура выполняется к раз,
где
i = zi + 1 = ^ + 1 = 6-
Здесь т — длительность процесса движения (т = 1 с).
Блок-схема описанного алгоритма показана на рис. 116.
4/ *" А2 А4 *г А5 ** А6 * Af-^-Ag-^Ag
Рис. 116
Здесь Ai — ввод исходных данных;
Л2 — решение	системы	(7),	определение	ф,	ф\
Аз — решение	системы	(8),	определение	0,	$;
А4 — решение	системы	(9),	определение	ф,	ф;
А5 — решение	системы	(10),	определение	0,	$;
Aq — печать результатов;
128
A? — вычисление р, фу 0, s для следующего
момента времени согласно (13);
— если i < 6, вычисления повторить;
А$ — конец работы.
После проведения всех вычислений составляется таблица значений
фу Оу Sy фу фу 0у S, фу фу 0у s для различных моментов времени.
Для приведенного примера результаты вычислений с точностью
до третьего десятичного знака приведены в табл. 38.
Таблица 38
t, с	рад	Фу рад	в, рад	S, м
0,000	1,082	0,576	0,243	0,410
0,200	1,100	0,607	0,206	0,432
0,400	1,117	0,638	0,167	0,455
0,600	1,134	0,669	0,126	0,478
0,800	1,150	0,700	0,083	0,501
1,000	1,164	0,731	0,038	0,524
t, с	фу рад/с	Фу рад/с	0, рад/с	3, м/с
0,000	0,092	0,157	-0,181	0,110
0,200	0,088	0,156	-0,191	0,112
0,400	0,084	0,155	-0,201	0,113
0,600	0,080	0,154	-0,211	0,114
0,800	0,077	0,154	-0,220	0,115
1,000	0,073	0,154	-0,228	0,115
t, с	Фу рад/с2	ф, рад/с2	0, рад/с2	3, м/с2
'	0,000	-0,020	-0,008	-0,056	0,012
0,200	-0,020	-0,006	-0,052	0,009
0,400	-0,019	-0,004	-0,049	0,007
0,600	-0,019	-0,002	-0,046	0,004
0,800	-0,019	0,000	-0,043	0,002
1,000	-0,020	0,001	-0,040	-0,001
129
РАЗДЕЛ ТРЕТИЙ
ДИНАМИКА
I. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
МАТЕРИАЛЬНОЙ ТОЧКИ
Задание Д.1. Интегрирование дифференциальных
уравнений движения материальной точки,
находящейся под действием постоянных сил
Варианты 1—5 (рис. 117, схема 1). Тело движется из точки
А по участку АВ (длиной I) наклонной плоскости, составляющей
угол а с горизонтом, в течение т с. Его начальная скорость гд.
Коэффициент трения скольжения тела по плоскости равен /.
В точке В тело покидает плоскость со скоростью 1'в и попадает
со скоростью vc в точку С плоскости BD, наклоненной под углом
/3 к горизонту, находясь в воздухе Т с.
При решении задачи тело принять за материальную точку; сопро-
тивление воздуха не учитывать.
Вариант 1. Дано: а = 30°; г>д = 0; f = 0,2; I = 10 м; /3 = 60°.
Определить т и h.
Вариант 2. Дано: а = 15°; цд = 2 м/с; / = 0,2; h = 4 м; /3 = 45°.
Определить I и уравнение траектории точки на участке ВС.
Вариант 3. Дано: а = 30°; тд = 3,5 м/с; f 0; I = 8 м; d = 10 м;
/3 = 60°. Определить vg и т.
Вариант 4. Дано: тд = 0; т — 2 с; I = 9,8 м; /3 = 60°; f = 0.
Определить а и Т.
Вариант 5. Дано: а = 30°; сд = 0; I = 9,8 м; т = 3 с; /3 = 45°.
Определить f и vc.
Варианты 6—10 (рис. 117, схема 2). Лыжник подходит к точке
А участка трамплина АВ, наклоненного под углом а к горизонту и
имеющего длину I, со скоростью тд. Коэффициент трения скольжения
лыж на участке АВ равен f. Лыжник от А до В движется г с; в
точке В со скоростью vg он покидает трамплин. Через Т с лыжник
приземляется со скоростью v<j в ±очке С горы, составляющей угол
/3 с горизонтом.
130
При решении задачи принять лыжника за материальную точку и
не учитывать сопротивление воздуха.
Вариант 6. Дано: а = 20°; f = 0,1; т = 0,2 с; h = 40 м; /3 = 30°.
Определить I и vc-
Вариант 7. Дано: а = 15°; f = 0,1; va = 16 м/с; 1 = 5 м; (3 = 45°.
Определить vb и Т.
Вариант 8. Дано: va = 21 м/с; / = 0; т = 0,3 с; vb = 20 м/с;
(3 = 60°. Определить а и d.
Вариант 9. Дано: а = 15°; т = 0,3 с; f = 0,1; h = ЗОд/2 м; /3 = 45°.
Определить vb и va-
Вариант 10. Дано: а = 15°; f = 0; va = 12 м/с; d = 50 м; /3 = 60°.
Определить т и уравнение траектории лыжника на участке ВС.
Варианты 11—15 (рис. 117, схема 3). Имея в точке А скорость
va, мотоцикл поднимается т с по участку АВ длиной /, составля-
ющему с горизонтом угол а. При постоянной на всем участке АВ
движущей силе Р мотоцикл в точке В приобретает скорость Vb и
перелетает через ров шириной d, находясь в воздухе Теи приземля-
ясь в точке С со скоростью vc- Масса мотоцикла с мотоциклистом
равна т.
При решении задачи считать мотоцикл с мотоциклистом матери-
альной точкой и не учитывать силы сопротивления движению.
Вариант 11. Дано: а = 30°; Р / 0; I = 40 м; va = 0; vb = 4,5 м/с;
d = 3 м. Определить т и h.
Вариант 12. Дано: а = 30°; Р = 0; I = 40 м; vb = 4,5 м/с;
h = 1,5 м. Определить va и d.
Вариант 13. Дано: а = 30°; m = 400 кг, va = 0; т = 20 с; d = 3 м;
h = 1,5 м. Определить Р и I.
Вариант 14. Дано: а = 30°; тп = 400 кг; Р = 2,2 кН; va — 0;
I = 40 м; d = 5 м. Определить vb в vc-
Вариант 15. Дано: а = 30°; va = 0; Р = 2 кН; I = 50 м; h = 2 м;
d = 4 м. Определить Тит.
Варианты 16—20 (рис. 117, схема 4). Камень скользит в течение
т с по участку АВ откоса, составляющему угол а с горизонтом и
имеющему длину I. Его начальная скорость va- Коэффициент трения
скольжения камня по откосу равен /. Имея в точке В скорость vb,
камень через Т с ударяется в точке С о вертикальную защитную
стену. При решении задачи принять камень за материальную точку;
сопротивление воздуха не учитывать.
Вариант 16. Дано: а = 30°; va = 1 м/с; I = 3 м; f = 0,2; d = 2,5 м.
Определить h и Т.
Вариант 17. Дано: а = 45°; I = 6 м; vb = 2г>л; т = 1 с; h = 6 м.
Определить d и /.
Вариант 18. Дано: а = 30°; I = 2 м; va = 0; f = 0,1; d = 3 м.
Определить h и т.
т Вариант 19. Дано: а = 15°; I = 3 м; vb = 3 м/с; / 0; т = 1,5 с;
d = 2 м. Определить va и h.
131
ш
ли =>иа
Вариант 20. Дано: а = 45°; va = 0; f = 0,3; d = 2 м; h = 4 м.
Определить I и т.
Варианты 21—25 (рис. 117, схема 5). Тело движется из точки А
по участку АВ (длиной /) наклонной плоскости, составляющей угол
а с горизонтом. Его начальная скорость сд. Коэффициент трения
скольжения равен /. Через т с тело в точке В со скоростью vb по-
кидает наклонную плоскость и падает на горизонтальную плоскость
в точку С со скоростью vc', при этом оно находится в воздухе Т с.
При решении задачи принять тело за материальную точку и не
учитывать сопротивление воздуха.
Вариант 21. Дано: а = 30°; f = 0,1; va = 1 м/с; т = 1,5 с;
h — 10 м. Определить vb и d.
Вариант 22. Дано: va = 0; а = 45°; I = 10 м; т = 2 с. Определить
/ и уравнение траектории на участке ВС.
Вариант 23. Дано: / — 0; va = 0; I = 9,81 м; т — 2 с; h = 20 м.
Определить а и Т.
Вариант 24. Дано: va = 0; а = 30°; f = 0,2; I = 10 м; d = 12 м.
Определить т и h.
Вариант 25. Дано: va =0; а = 30°; / = 0,2; 1=6 м; h = 4,5 м.
Определить т и vr.
Варианты 26—30 (рис. 117, схема 6). Имея в точке А скорость
va , тело движется по горизонтальному участку АВ длиной I в течение
т с. Коэффициент трения скольжения тела по плоскости равен f.
Со скоростью vb тело в точке В покидает плоскость и попадает в
точку С со скоростью vc, находясь в воздухе Т с. При решении
задачи принять тело за материальную точку; сопротивление воздуха
не учитывать.
Вариант 26. Дано: va = 7 м/с; / = 0,2; 1 = 8 м; h = 20 м.
Определить d и vc-
Вариант 27. Дано: va — 4 м/с; / = 0,1; г = 2 с; d = 2 м.
Определить vb и h.
Вариант 28. Дано: vb = 3 м/с; f = 0,3; 1 = 3 м; h = 5 м.
Определить va и Т.
Вариант 29. Дано: va = 3 м/с; vb = 1 м/с; Z = 2,5 м; h = 20 м.
Определить f и d.
Вариант 30. Дано: f = 0,25; I = 4 м; d = 3 м; h = 5 м..Определить
va и т.
Пример выполнения задания (рис. 118). В железнодорожных
скальных выемках для защиты кюветов от попадания в них с откосов
каменных осыпей устраивается «полка» DC. Учитывая возможность
движения камня из наивысшей точки А откоса и полагая при этом
его начальную скорость «о = 0, определить наименьшую ширину
полки b и скорость vc, с которой камень падает на нее. По участку
АВ откоса, составляющему угол а с горизонтом и имеющему длину
I, камень движется тс.
При решении задачи считать коэффициент трения скольжения f
камня на участке АВ постоянным, а сопротивлением воздуха прене-
бречь.
133
Дано: va = 0; а = 60°; 1 = 4 м; т = 1 с; / ^ 0; h = 5 м; (3 = 75°.
Определить b и vc-
Решение. Рассмотрим движение камня на участке АВ. Принимая
камень за материальную точку, покажем (рис. 118) действующие на
него силы: вес G, нормальную реакцию N и силу трения скольже-
ния F. Составим дифференциальное уравнение движения камня на
участке АВ-.
mxi = У Хц; mx1 = G sin а - F.
Сила трения
F = fN,
где
N = Geos а.
Таким образом,
тпх1 = G sin а — fG cos а
или
= д sin а — fg cos а.
Интегрируя дифференциальное уравнение дважды, получаем
xt = g(sin а — f cos a) t + Ci;
Xi = [</(sina - /cosa)/2] t2 + C\t + C2.
Для определения постоянных интегрирования воспользуемся на-
чальными условиями задачи: при t = 0 а?ю = 0 и £ю = 0*.
Составим уравнения, полученные при интегрировании, для t = 0:
iio = Ci;	а?ю = С2.
Найдем постоянные:
С1 =0,	С2 = 0.
Тогда
= g(sin a — f cos a) t;
Ti = [<?(sina — /cosa)/2] t2.
Для момента т, когда камень покидает участок,
ii = vb', Xi = I,
т. е.	• •
vb = <?(sina — /cos а)т;
I = [g(sina - /cosa)/2] г2,
* Постоянные интегрирования Сд — Cq во всех 30 вариантах задания можно най-
ти, вводя начальные условия на первбм и втором участках движения точки. Тем не
менее в ряде вариантов более естественно воспользоваться граничными условиями,
когда значения координат и скоростей заданы не для одного, а для разных моментов
времени.
134
откуда
vb = 21/т,
т. е.
vb = 2 • 4/1 = 8 м/с.
Рассмотрим движение камня от точки В до точки С.
Показав силу тяжести G, действующую на камень, составим диф-
ференциальные уравнения его движения:
тх - 0;	ту = G.
Начальные условия задачи: при t = 0
ТО =0;	Уо = 0;
To=VBCosa;	yo = vesina.
Интегрируем дифференциальные	уравнения	дважды;
т = С3;	y = gt + C4;
х = Сз1 + Сз;	у = gt2/2 + C^t + Cq.
Напишем полученные уравнения для t = 0:
хо = Сз; уо = С4;
хо = С5; уо = Со-
Отсюда найдем, что
Сз = vb cos а; С4 = Vb sin а;
С5 = 0;	Св = 0.
Получим следующие уравнения проекций скорости камня:
x = vecosa, y = gt + vBsina
и уравнения его движения:
т = тдсо8а-^,	у = gt2/2 + vb sin а  t.
Уравнение траектории камня найдем, исключив параметр t из
уравнений движения. Определив t из первого уравнения и подставив
его значение во второе, получаем уравнение параболы:
у = gx2/(2v2B cos2 а) + ztga.
В момент падения у = h, х = d.
Определяя d из уравнения траектории, найдем
di = 2,11 м, ^2 = —7,75 м.
Так как траекторией движения камня является ветвь параболы с
положительными абсциссами ее точек, то d = 2,11 м.
Минимальная ширина полки
b — d — ED = d — h/tg75°, или Ь = 0,77 м.
135
Используя уравнение движения камня х = vb cos a t, найдем время
Т движения камня от точки В до точки С:
Т = 0,53 с.
Скорость камня при падении найдем через проекции скорости на
оси координат
x = vecosa, у = gt + vesina
по формуле
V = \/ х2 + у2.
Для момента падения t = Т = 0,53 с
vc = y/(vB cos а)2 + (дТ + vb sin а)2,
или
vc = 12,8 м/с.
Задание Д.2. Интегрирование дифференциальных
уравнений движения материальной точки,
находящейся под действием переменных сил
Найти уравнения движения тела М массой m (рис. 119—121),
принимаемого за материальную точку и находящегося под действием
переменной силы Р = Xi+Yj + Zk при заданных начальных условиях.
Во всех вариантах ось z (где показана) вертикальна, за исключением
вариантов 8 и 30.
Необходимые для решения данные приведены в табл. 39, в которой
приняты следующие обозначения: г, j, к — орты координатных осей
(соответственно х, у, z); д — ускорение свободного падения (9,81
м/с2); f — коэффициент трения скольжения; t — время, с; х, у, z,
х, у, z — координаты точки и проекции ее скорости на оси координат
соответственно, м и м/с.
Во всех случаях, где сила Р зависит от х, х, z, z, рассмотреть
движение точки, при котором эти величины только положительны.
Пример выполнения задания. Дано: m = 1 кг, xq = 0, z<j = 10 м,
хо — 20 м/с, zq = 0, Р — —cr(i cos + к sin <р); R = ~аг, с = 4 Н/м,
а = 2 Н • с/м.
Найти уравнения движения точки без учета и с учетом силы R.
Решение. На материальную точку действуют силы тяжести G и
сила Р, линия действия которой проходит через неподвижный центр
О (рис. 122). Силой R пренебрегаем. Сила Р притягивает точку М
к центру О. Модуль этой силы прямо пропорционаден расстоянию г
от точки до полюса.
В начальный момент времени (t = 0) точка М находится на оси
z на расстоянии 10 м от начала отсчета и ей сообщается начальная
скорость 20 м/с, направленная параллельно оси х.
136
ЛЕТ
6П Э1Ч
Рис.120
138
Рис.121
139
Таблица 39
Номер				Начальные условия						
варианта	т,	Р, н-	f	XQ	Уо	ZO	io	У0	zo	Примечание
(рис. 119121)	кг			M				M	/<=	
1	2	—0,5(ii + zfc)	-	0	-	0	20	-	20	
2	0,25	— 100(ж — lo)i	0,3	0,03	-	-	0,5	-	-	Iq = 0,02 м
3	2	—(20® — 4i)i	0	0,15	-	-	1	-	-	
4	т	—p,z~2k	-	-	-	a	-	-	у/2цЦта)	Учесть только силу P;
										a — положительные
										постоянные
5	50	—(5® — 25®)г	0	0	-	-	1	-	-	
6	т	_ O'? —ггщх °г	0	a	-	--	VO	—	-	г>о > 0, р > 0 (const)
7	2	4icos(irt/6) + yj	0	0	0	-	0	3	-	
8	150	120t(i cos 30° + j sin 30°)	0	0	0	0	0,5	2	0	
9	1	4r(i cos <p + fcsintp)	-	0	-	2	5	-	0	
10	1	—3>/ii	0	0	-	-	16	-	-	
И	20	—3v	-	-	0	0	—	15	0	Рассмотреть движение при у > 0, z > 0
12	т	—mgR2 z~2k	-	-	-	R	-	-	vwt	Учесть только силу Р,
										(R > 0) (const)
13	т	-9mr(i coso! + j cos /3 + kcosy)	-	2	2	2	1	0	i	
14	1,5	(4,5 + 3x)i	0,1	1	-	-	0,3	-	-	
Продолжение табл. 39
Номер варианта	т,	Р, Н	f	Начальные условия						Примечание
				XQ	3/0	ZO	io	yo	io	
. (рис. 119—121)	кг				M			м/с		
15	1,5	(6 — l,5z + i)k	0	-		0,5	-	-	1	
16	100	~20xi	0	0	-	-	2,5	-	-	
17	1	5(1 — e-2t)i	0	0	-	-	0	-	-	
18	2	—6x2i	0	0	-	-	10	-	-	
19	6	(30e-3t - 18i - 12®)7	0	0	-	-	10	-	-	
20	0,1	—0,2z4fc	-	-	-	200	-	-	0,1	Учесть только силу Р
21	0,1	0,lz3fc	-	-	-	300	-	-	2,5	То же
22	т	-4mr(i cos ip + j cos <p)	0	20	0	0	0	8	0	
23	100	50(3 + x)i	0,2	0	-	-	1	-	-	
24	3	—3(3i + 2x)i	0	0		-	2	-	-	
25	1,5	—7,5(x3i — 2gk)	-	0	-	100	4	-	0	
26	0,1	—(2z3 - 0,981)fc	-	-	-	20	-	-	0,7	
27	2	3ti	0	0	0	-	3	4	0	
28	4	-2(xt + у] + zfc)	-	0	0	0	1	1	2	
29	0,01	—3\/ik		—	—	0	-	—	125	Влиянием силы тяже- сти пренебречь
30	100	120(7,5 + t)(i cos 30° + к sin 30°)	0,25	0	-	0	0,5	-	0	
Заданные силы Р, G и вектор vq начальной скорости расположены
в плоскости xOz, и поэтому дальнейшее движение точки происходит
в этой плоскости. Дифференциальные уравнения движения матери-
альной точки имеют вид
тх  —er cos <р;
где
mz = —cr sin <р — G. 
Так как
cosy> = ;r/r; sintp = z/r,
то
тх = —ex;	mz — —cz — G
или
х + к2х = 0; z + k2z = —д, (1)
к = у/с)т, к = 2 рад/с.
Уравнения (1) — линейные дифференциальные уравнения второго
порядка с постоянными коэффициентами. Первое из них однородное,
а второе — неоднородное.
Решения уравнений (1) имеют вид
х = Ci cos kt + С2 sin kt; 1	, .
z = C3 cos kt + C4 sin kt — g/k2 J	'
и, следовательно,
x = — Cifcsin kt + C3k cos kt; 1	, .
z = — C3k sin kt + C^k cos kt. )	'
Постоянные интегрирования Ci, C3, C3, C4 найдем из начальных
условий
при t — 0	Xq = 0; Zq = 10; 1	, .
х0 = 20; z0 = 0. J	W
Подставляя (4) в (2) и (3), получим:
ar0 = Ci; z0 = C3-g/k2;
xq = С3к; zq = С^к.
Отсюда
Ci = 0;	С3=х0/к; C3 = z0+g/k2; C4 = 0.	(5)
Подставляя (5) в (2), будем иметь окончательно
х = (х0/к) sin kt = 10sin2i;	1	. .
z — (z0 + g/k2) cos kt - g/k2 = 12,45 cos 2t - 2,45. J
142
Следовательно,
(7)
х = io cos,kt = 20 cos 2t;
z = —k(zo + g/k2) sin kt = —24,9 sin 2t.
В рассматриваемом примере может быть получено уравнение тра-
ектории точки. Для этого запишем уравнения движения (6) в виде
х . , . z-f-g/R-	. .
= sin kt; --------= cos kt.
ха/к	го + д/к*
Возведя эти выражения в квадрат и сло-
жив результаты, получим
х2 , (z + g/fe2)2 _ ,
(io/fc)2 (zo+g/fc2)2
ИЛИ
х2 (z + 2,45)2 _
Ю2 +	2,452	“ Ъ
Это уравнение эллипса, центр которого
А смещен по оси z относительно начала	Рис
координат на 2,45 м вниз. Полуоси элли-	ис'
пса: горизонтальная а = 10 м, а вертикальная Ь = 12,45 м (рис. 123).
В процессе движения точки М по эллипсу сумма моментов сил Р
и G относительно центра А остается все время равной нулю. Ины-
ми словами, равнодействующая сил Р и G во все время движения
проходит через точку А.
Период обращения точки по эллипсу
Т = 2-к/к = тг = 3,14 с.
Площадь, заметаемая радиус-вектором точки за период, равна:
F = тгаЬ = 7r(zo + д/к2)хо/к.
Обратимся теперь к изучению движения точки с сопротивлением.
Сила сопротивления движению
R=—ar = —av = —a(ix+jy).	(8)
Дифференциальные уравнения движения материальной точки при-
мут вид	mx = —сх — ах; mz = —cz — az — G,	
или	x + 2nx + k2x = 0; z + 2nz + k2z = —g,	(9)
где	2n = a/m; n = 1 c-1.	
Так как	n < к, то решения уравнений (9) имеют вид	
	х = e~nt(Ci cos k*t + C2 sin k*t);	1 z = e~nt(C3 cos ktt + C4 sinfc*£) - g/k2, J	(10)
143
где
А:* = \/к2 — п2 — \/4 — 1 » 1,73 рад/с,
и, следовательно,
х = е nt(—Ci_k* sin k*t + С2к* cosfc*Z) — '
—е ntn(Ci cos k*t + C2 sin
z = е~п*(—С3к* sin + C4k* cos fc*t)—
-e ntn(C3 cos ktt + C4 sin k*t").
Подставив начальные условия (4) в (10) и (11), получим:
откуда
т0 = Ci;	то = С2к* — nCi;
zo = <53-g/k2;	z0 = C4k* - пС3,
Ci=0;	С2 = ^;
Сз = zo + ff/k2; С4 = ^-(г0 + д/к2).
(И)
(12)
Подставляя (12) в (10), окончательно имеем
Рис. 124
х = еое-"‘ sin k^t = 11,56е~‘ sin 1,73t;
/с»
z = (z0 + g/k2)e~nt(cos k*t + sin fc*£) - g/fc2,
 или
z = 12,45e“‘(cos l,73i + 0,577sin l,73i) - 2,45.
Нетрудно понять, что траектория точки представ-
ляет собой, спираль, навивающуюся на точку А
(рис. 124), в которой силы Р и G взаимно уравновешиваются. Отме-
тим, что материальная точка будет асимптотически приближаться к
точке А. Радиус-вектор точки будет делать один полный оборот за
Т* = 2тг/Ад; Т* = 3,63 с.
При этом расстояние от центра А до движущейся точки будет каждые
Т* с убывать в епТ* раз, т. е. примерно в 37,7 раза.
Задание Д.З. Исследование колебательного движения
материальной точки
В задании рассматриваются колебания груза D или системы грузов
D и Е. Во всех вариантах, представленных ниже, считать, что сила
сопротивления движению R измеряется в Н, скорость движения v —
в м/с, а величина / — в см.
144
Рис. 125
Варианты 1—5 (рис. 125). Найти уравнение движения груза D
массой то (варианты 2 и 4) или системы грузов D и Е массами тпр
и то (варианты 1, 3, 5), отнеся их движение к оси ж; начало отсчета
совместить с положением покоя груза D или соответственно системы
грузов D и Е (при статической деформации пружин). Стержень,
соединяющий грузы, считать невесомым и недеформируемым.
Вариант 1. Груз D (то = 2 кг) прикреплен к бруску АВ, подве-
шенному к двум одинаковым параллельным пружинам, коэффициент
жесткости каждой из которых с = 3 Н/см. Точка прикрепления груза
,D находится на равных расстояниях от осей пружин.
В некоторый момент времени к грузу D подвешивают груз Е
(т,Е = 1 кг). Сопротивление движению системы двух грузов пропор-
ционально скорости: R =Ь 12 г’ (Н), где v — скорость (м/с).
Массой абсолютно жесткого бруска АВ и массой части демпфера,
прикрепленной к бруску, пренебречь.
Вариант 2. В момент, когда стержень, соединяющий грузы D
(mp = 1 кг) и Е (ше = 2 кг),*перерезают, точка В (верхний конец
последовательно соединенных пружин) начинает совершать движение
по закону £ = l,5sinl8t (см) (ось £ направлена вертикально вниз).
Коэффициенты жесткости пружин Q = 12 Н/см, сг = 36 Н/см.
Вариант 3. Груз D (то = 0,8 кг) висит на пружине, прикре-
пленной к точке F бруска АВ и имеющей коэффициент жесткости
Ci = 10 Н/см. Брусок подвешен к двум параллельным пружинам,
коэффициенты жесткости которых = 4 Н/см, сз = 6 Н/см; точка
F находится на расстояниях а и Ь от осей этих пружин: а/b = сз/сг-
В некоторый момент времени к грузу D подвешивают груз Е
(т,Е = 1,2 кг). В этот же момент системе грузов сообщают скорость
по = 0,2 м/с, направленную вниз. Массой абсолютно жесткого бруска
АВ пренебречь.
Вариант 4. Статическая деформация двух одинаковых парал-
лельных пружин под действием грузов D (то = 0,5 кг) и Е
(то = 1,5 кг) /ст = 4 см. Грузы подвешены к пружинам с помо-
щью абсолютно жесткого бруска АВ. В некоторый момент времени
стержень, соединяющий грузы, перерезают. Сопротивление движению
груза D пропорционально скорости: R = 6п, где v — скорость. Массой
бруска и массой прикрепленной к бруску части демпфера пренебречь.
Вариант 5. Одновременно с подвешиванием к грузу D (то =
= 1,6 кг), висящему на пружине, коэффициент жесткости которой
с = 4 Н/см, груза Е (то = 2,4 кг) точка В (верхний конец пружины)
начинает совершать движение по закону £ = 2 sin 5t (ось £ направлена
вертикально вниз).
Примечание. Положение начала отсчета на оси х соответствует среднему по-
ложению точки В (£ = 0).
Варианты 6—10 (рис. 125). Найти уравнение движения груза
D массой т по гладкой наклонной плоскости, составляющей с го-
ризонтом угол а, с момента соприкасания груза с пружиной или с
системой пружин, предполагая, что при дальнейшем движении груз
146
от пружин не отделяется. Движение груза отнести к оси х, приняв за
начало отсчета положение покоя груза (при статической деформации
пружин).
Вариант 6. Пройдя без начальной скорости по наклонной плос-
кости (а = 30°) расстояние з = 0,1 м, груз D (т = 4 кг) ударяется
о недеформированные, последовательно соединенные пружины, име-
ющие коэффициенты жесткости Ci = 48 Н/см и сг = 24 Н/см.
Вариант 7. В некоторый момент времени груз D (т = 2 кг)
присоединяют без начальной скорости к концу А недеформирован-
ных последовательно соединенных пружин, имеющих коэффициенты
жесткости ci = 12 Н/см, = 6 Н/см. В тот же момент времени
(t — 0) другой конец пружин В начинает совершать движение вдоль
наклонной плоскости (о = 45°) по закону / = 0,02 sin 20t (м) (ось £
направлена вдоль наклонной плоскости вниз).
Примечание. Положение начала отсчета на оси х соответствует среднему по-
ложению точки В (£ = 0).
Вариант 8. Две параллельные пружины 1 и 2, имеющие коэффи-
циенты жесткости ci = 4 Н/см и С2 = 6 Н/см, соединены абсолютно
жестким бруском АВ, к точке К которого прикреплена пружина 3
с коэффициентом жесткости сз = 15 Н/см. Точка К находится на
расстояниях а и b от осей пружин 1 и 2: a/b = C2/C1. Пружины
1, 2 и 3 не деформированы. Груз D массой 1,5 кг присоединяют к
концу N пружины 3; в тот же момент грузу D сообщают скорость
по =0,5 м/с, направленную вниз параллельно наклонной плоскости
(о = 45°). Массой бруска АВ пренебречь.
Вариант 9. Груз D (т = 1,2 кг), пройдя без начальной скорости
по наклонной плоскости (а = 30°) расстояние з = 0,2 м, ударяет-
ся о недеформированную пружину, коэффициент жесткости которой
с = 4,8 Н/см. В этот же момент (t = 0) точка В (нижний конец
пружины) начинает совершать вдоль наклонной плоскости движение
по закону £ = 0,03 sin 12t (м) (ось £ направлена вдоль наклонной
плоскости вниз) (см. примечание к варианту 7).
Вариант 10. Груз D (m = 1 кг) прикрепляют в середине абсо-
лютно жесткого бруска АВ, соединяющего концы двух одинаковых
параллельных пружин, не сообщая начальной скорости; пружины не
деформированы. Коэффициенты жесткости пружин с = 1,5 Н/см. Со-
противление движению груза пропорционально скорости: R = 8г, где
v — скорость, а = 60°. Массой бруска АВ и массой прикрепленной
к бруску части демпфера пренебречь.
Варианты 11—15 (рис. 126). Груз D массой т укреплен на
конце невесомого стержня, который может вращаться в горизон-
тальной плоскости вокруг оси Е. Груз соединен с пружиной или с
системой пружин; положение покоя стержня, показанное на чертеже,
соответствует недеформированным пружинам. Считая, что груз D,
принимаемый за материальную точку, движется по прямой, опреде-
лить уравнение движения этого груза (трением скольжения груза по
плоскости пренебречь).
147
Движение отнести к оси х, за начало отсчета принять точку,
соответствующую положению покоя груза.
Вариант 11. Груз D (т = 2,4 кг) соединен с точкой F бруска
АВ, связывающего концы двух параллельных пружин, коэффициенты
жесткости которых ci = 1 Н/см и сг = 1,4 Н/см. Точка F находится
на расстояниях а и b от осей пружин: а/Ь = съ/с-о
Груз D отклоняет на величину А = 2 см влево от положения,
показанного на чертеже, и отпускают без начальной скорости. Со-
противление движению груза пропорционально скорости: R = 6v, где
v — скорость. Массой абсолютно жесткого бруска АВ и массой
демпфера пренебречь.
Вариант 12. В некоторый момент времени груз D (т = 3 кг),
удерживаемый в положении, при котором пружина сжата на величину
А = 2 см, отпускают без начальной скорости. Коэффициент жесткости
пружины с = 9 Н/см. Одновременно (t = 0) точка В (правый конец
пружины) начинает совершать движение по закону £ = 1,2 sin 8t (см)
(ось £ направлена влево).
Примечание. Положение начала отсчета на оси х соответствует среднему по-
ложению точки В (£ = 0).
Вариант 13. Груз D (т = 1 кг) прикреплен к концу пружины,
имеющей коэффициент жесткости ci = 12 Н/см и соединенной другим
концом с точкой F бруска АВ. Брусок АВ связывает концы двух
параллельных пружин, коэффициент жесткости каждой из которых
с = 3 Н/см. Точка F находится на равных расстояниях от осей
параллельных пружин. Грузу в положении стержня, показанном на
чертеже, сообщают скорость vq = 0,5 м/с, направленную вправо.
Сопротивление движению груза пропорционально скорости: R =
= 12v, где v — скорость.
Шток демпфера пропущен через отверстие в невесомом бруске АВ
и соединен с грузом D.
Вариант 14. Груз D (т = 1,5 кг) прикреплен одной стороной
к концу пружины, имеющей коэффициент жесткости с\ = 4,4 Н/см,
а другой стороной — к концу двух последовательно соединенных
пружин, коэффициенты жесткости которых = 2 Н/см, сз = 8 Н/см.
Груз отклоняют на величину А = 2,5 см влево от его положения,
показанного на чертеже, и отпускают, одновременно сообщая грузу
начальную скорость vq — 0,4 м/с, направленную вправо.
Вариант 15. Груз D (т = 1 кг) прикреплен к концу А после-
довательно соединенных пружин. Другой конец пружин В движется
по закону £ = 1,8 sin 12t (см) (ось £ направлена влево). Коэффици-
енты жесткости пружин ci = 4 Н/см, сг = 12 Н/см. При t = 0 груз
находится в положении покоя, соответствующем недеформированным
пружинам (см. примечание к варианту 12).
Варианты 16—20 (рис. 126). Найти уравнение движения груза D
массой то (варианты 17 и 19) или системы грузов D и Е массами то
и то (варианты 16, 18, 20), отнеся движение к оси х: начало отсчета
совместить с положением покоя груза D или соответственно системы
148
Рис. 126
149
грузов D и Е (при статической деформации пружин). Предполагается,
что грузы D и Е при совместном движении не отделяются.
Вариант 16. Пружина 1, на которой покоится груз D (то =
= 10 кг), опирается в точке F на брусок АВ, соединяющий концы
двух параллельных пружин 2 и 3. Коэффициенты жесткости (Н/см)
пружин 1, 2 и 3: с\ = 200, c-i = 160, сз = 140,-
Точка F находится на расстояниях а и b от осей пружин 2 и 3:
а^Ъ = с^с?..
В некоторый момент времени на груз D устанавливают груз
Е (т,Е — 20 кг); одновременно системе грузов сообщают скорость
ц0 = 0,4 м/с, направленную вниз. Массой абсолютно жесткого бруска
АВ пренебречь.
Вариант 17. В некоторый момент времени груз Е снимают с
груза D (оба груза находятся в состоянии покоя, соответствующем
статической деформации пружины). Циклическая частота собствен-
ных колебаний системы грузов D и Е на пружине к = 20 рад/с,
отноЩение масс тв/тЕ = 2/3.
Вариант 18. Статическая деформация каждой из двух одина-
ковых параллельных пружин под действием груза Р (то — 20 кг)
равна fcrD = 2 см. В некоторый момент времени на груз Р уста-
навливают груз Е (тпе = Ю кг). Сопротивление движению грузов
пропорционально скорости: R = 60\/Зи. где v — скорость. Массой
абсолютно жесткого бруска АВ и массой части демпфера, связанной
с ним, пренебречь.
Вариант 19. Два груза Р и Е (то — 15 кг, тле = 25 кг) покоятся
на последовательно соединенных пружинах, имеющих коэффициенты
жесткости Ci = 250 Н/см и & = 375 Н/см. В момент, когда снимают
груз Е, точка В опирания пружин начинает совершать движение по
закону £ = 0,5sin301 (ось £ направлена вертикально вниз).
Примечание. Положение начала отсчета на оси х соответствует среднему по-
ложению точки В ~ 0).
Вариант 20. На груз Р, находящийся в состоянии покоя, соот-
ветствующем статической деформации пружины, в некоторый момент
времени устанавливают груз Е. В этот же момент времени системе
двух грузов сообщают скорость Со — 0,3 м/с, направленную вниз.
Циклическая частота собственных колебаний груза D на пружине
кв = 24 рад/с, отношение масс чпе/шв = 3.
Варианты 21—25 (рис. 127). Найти уравнение движения груза
Р массой т по гладкой наклонной плоскости, составляющей с гори-
зонтом угол а, отнеся движение к оси ж; за начало отсчета принять
положение покоя груза (при статической деформации пружин).
Вариант 21. В некоторый момент времени груз D (т = 2 кг)
прикрепляют к концам недеформированных пружин, имеющих коэф-
фициенты жесткости ci = 7 Н/см и сг — 3 Н/см; одновременно грузу
сообщают скорость п0 = 0,4 м/с, направленную вдоль наклонной
плоскости (а = 45°) вниз.
150
Рис. 127
151
Вариант 22. Груз D находится на наклонной плоскости (а = 30°)
в состоянии покоя, соответствующем статической деформации пру-
жины /ст = 2 см. В некоторый момент времени (1 = 0) точка В
(верхний конец пружины) начинает совершать движение по закону
£ = 0,01 sin ЮЛ (м) (ось £ направлена вдоль наклонной плоскости
вниз).
Примечание. Положение начала отсчета на оси х соответствует среднему по-
ложению точки В (£ = 0).
Вариант 23. Груз D (т = 3 кг) прикрепляют к точке F бруска
АВ, соединяющего концы двух недеформированных параллельных
пружин, и отпускают без начальной скорости. Коэффициенты жест-
кости пружин ci = 2 Н/см и Сг = 4 Н/см*. Точка F находится на
расстояниях а и b от осей пружины: а/b = сг/си а = 60°.
Сопротивление движению груза пропорционально скорости: R =
— 12г>, где v — скорость. Массой бруска АВ и массой демпфера
пренебречь.
Вариант 24. В некоторый момент времени груз D (т = 1 кг)
прикрепляют к концу А недеформированных последовательно соеди-
ненных пружин, имеющих коэффициенты жесткости ci = 12 Н/см и
сг = 4 Н/см, и отпускают без начальной скорости.
Одновременно (1 = 0) другой конец пружин В начинает совершать
движение по закону £ = 1,5 sin 101 (см). Ось £ направлена вдоль
наклонной плоскости вниз (о = 30°) (см. примечание к варианту 22).
Вариант 25. Концы двух одинаковых параллельных пружин со-
единены бруском АВ. Статическая деформация каждой из пружин
под действием груза D (т = 1,5 кг), находящегося на наклонной
плоскости (а = 30°), /ст — 4,9 см. В некоторый момент грузу D со-
общают скорость vq = 0,3 м/с, направленную вверх вдоль наклонной
плоскости. Сопротивление движению груза пропорционально скорости
груза: R = 6v, где v — скорость.
Массой абсолютно жесткого бруска АВ и массой части демпфера,
связанной с бруском, пренебречь.
Варианты 26—30 (рис. 127). Пренебрегая массой плиты и считая
ее абсолютно жесткой, найти уравнение движения груза D массой т
с момента соприкасания его с плитой, предполагая, что при даль-
нейшем движении груз от плиты не отделяется.
Движение груза отнести к оси х, приняв за начало отсчета поло-
жение покоя этого груза (при статической деформации пружин).
Вариант 26. Плита лежит на двух параллельных пружинах,
имеющих коэффициенты жесткости ci = 600 Н/см и = 400 Н/см.
Груз D (т = 50 кг) падает без начальной скорости с высоты h = 0,1 м
в точку F плиты, находящуюся на расстояниях а и b от осей пружин:
а/Ь-с^/с^.
Вариант 27. Коэффициент жесткости каждой из двух парал-
лельных пружин, на которых лежит плита, с = 130 Н/см. Груз D
(т = 40 кг) устанавливают на середину плиты и отпускают без
152
начальной скорости при недеформированных пружинах. Сопротивле-
ние движению груза пропорционально скорости: R = 400г, где v —
скорость. Массой плиты и демпфера пренебречь.
Вариант 28. Груз D падает на плиту с высоты h = 5 см.
Статический прогиб пружины под действием этого груза /ст = 1 см.
Вариант 29. Плита лежит на двух одинаковых параллельных
пружинах 1 и 2, коэффициенты жесткости которых ci = c-i = с =
= 400 Н/см. В некоторый момент времени груз D (т = 200 кг)
устанавливают на середину плиты и одновременно прикрепляют к
недеформированной пружине 3, имеющей коэффициент жесткости
с3 = 200 Н/см. В тот же момент времени (при недеформирован-
ных пружинах) грузу сообщают скорость vq = 0,6 м/с, направленную
вниз.
Вариант 30. В некоторый момент времени груз D (т = 100 кг)
устанавливают на плиту и отпускают (при недеформированной пру-
жине) без начальной скорости. В этот же момент времени точка В
(нижний конец пружины) начинает совершать движение по верти-
кали согласно закону £ = 0,5 sin 204 (см) (ось £ направлена вниз).
Коэффициент жесткости пружины с = 2000 Н/см.
Примечание. Начало отсчета на оси х соответствует среднему положению точ-
ки В (£ = 0).
Пример выполнения задания (рис. 128). Два груза D и Е
массами mjj = 2 кг и ше = 3 кг лежат на гладкой плоскости,
наклоненной под углом а = 30° к горизонту, опираясь на пружину,
коэффициент жесткости которой с = 6 Н/см = 600 Н/м.
В некоторый момент времени груз Е
убирают; одновременно (4 = 0) нижний
конец пружины В начинает совершать
вдоль наклонной плоскости движение по
закону £ = 0,02sin 104 (м). Найти урав-
нение движения груза D.
Решение. Применим к решению за-
дачи дифференциальные уравнения дви-
жения точки. Совместим начало коор-
динатной системы с положением покоя
груза D, соответствующим статической
деформации пружины, при условии, что
точка В занимает свое среднее положе-
ние (£ = 0).
Направим ось х вверх вдоль наклон-
ной плоскости (в сторону движения груза
D после снятия груза Е).
Движение груза D определяется по следующему дифференциальному
уравнению:
moi = 5? Xj,
где 52 Xi — сумма проекций на ось х сил, действующих на груз
D (рис. 128, a): Gr> — веса, N — нормальной реакции наклонной
плоскости, Р — силы упругости пружины.
153
Таким образом,
твх = -Gd sin а — Р.
Здесь
Р = с(х - /стр - С),
где /стр — статическая деформация пружины под действием груза
D; £ — перемещение точки прикрепления нижнего конца пружины,
происходящее по закону £ = sin pt (d = 0,02 м, р = 10 рад/с).
Статическую деформацию пружины /СТ£> найдем из уравнения,
соответствующего состоянию покоя груза D на наклонной плоскости
(рис. 128, б):
2>< = 0;
—Gd sin а + Ро = 0,
т. е.
—Gd sin а + c/сто = 0,
откуда
/ctD = Gd sin а/с.
Дифференциальное уравнение движения груза D примет вид
moi = —Gd sin а — с(х — fCTD — £),
или после преобразования
твх + сх = cd sin pt.
Разделив все члены уравнения на тр и введя обозначения
с/то = к2, cd/m-D = h,
приведем дифференциальное уравнение к следующему виду:
х + к2х = hsinpt.
Решение этого неоднородного уравнения складывается из обще-
го решения х* соответствующего однородного уравнения и частного
решения х** данного неоднородного уравнения:
х = х*+х**.
Общее решение однородного уравнения имеет вид
х* = Ci cos kt + С2 sin kt.
Частное решение неоднородного уравнения:
х** = [h/(k2 — р2)] sin pt.
Общий интеграл
х = Ci cos kt + G2 sin kt + \h/(k2 — p2)] sin pi.
154
Для определения постоянных интегрирования Ci и С2 найдем,
кроме того, уравнение для х
х — —С\к sin kt + С2к cos kt + [hp/(k2 — p2)] cos pt
и используем начальные условия Задачи.
Рассматриваемое движение начинается в момент (t = 0), когда
деформация пружины является статической деформацией под дей-
ствием грузов D и Е. При принятом положении начала отсче-
та О начальная координата груза D равна х0 = —/сте, причем
/ст£ = Ge sin а/с — статическая деформация пружины под действи-
ем груза Е.
Таким образом, при t = 0
Ж0 — /стЕ, #0 — 0.
Составим уравнения х = x(t) и х = x(t) для t = 0:
To=Ci; х0 = С2к + hp/(k2 - р2),
откуда
Ci = -Ате, С2 = —hp/[k(k2 - р2)].
Уравнение движения груза D имеет следующий вид:
х = -ferE cos kt - к{к2 2р2) sin kt + sin^-
Найдем числовые значения входящих в уравнение величин:
к =	= 17,3 с"1;
V тг> и 2
Gf е sir Ct 3'9,81’0,5 _ r\ a pt
/стЯ =	= -6	= 0,0245 m;
h _ cd _ 600  0,02 _ „ „„
fc2 — p2 mp(fc2 — p2)	2(300 — 100)	’	’
ftp 0,03 10	„ nl
fc(fc^7) = -17^=0’0173M-
Следовательно, уравнение движения груза D
х = —2,45cos 17,3/ — 1,73sin 17,3/ + 3sin 10/ (cm).
Задание Д.4. Исследование относительного движения
материальной точки
Шарик М, рассматриваемый как материальная точка, перемещает-
ся по цилиндрическому каналу движущегося тела А (рис. 129—131).
Найти уравнение относительного движения этого шарика х = f(t),
приняв за начало отсчета точку О.
155
Рис. 129
Рис. 130
157
SSI
тет эиа
Таблица 40
Номер варианта (рис. 129-131)	Q, град	т, кг	w, рад С	Начальные данные		h, с	С, Н см	^0) м	Уравнение движения тела А	г, h м	/
				®(Ъ м	ХО, м/с						
1	—	0,02	-7Г	0	0,4	0,5	-	-	-	-	0
2	-	0,02	7Г	0	0,2	0,4	-	-	-	0,15	0
3	45	0,03	2%	0,5	0	0,2	—	-	-	-	0
4	-	0,09	4%	0,2	-0,8	0,1	0,36	0,15	-	-	0
5	60	0,02	-	0,6	0	0,2	-	-	щ=0,6 — 2t3 (м)	-	0
6	-	0,01	10%	0,5	0	0,2	-	-	-	0,10	0
7	-	0,03	2%	0,3	0	0,2	-	-	-	0,20	0
8	30	0,03	-	0,8	0	0,1	-	-	zi=0,lcos2%t (м)	-	0
9	30	0,02	-	0,4	0	0,1	0,20	0,20	S/l=4t3 (м)		0
10	60	0,05	бтг	0,4	0	0,1	-	-	-	0,20	0
11	30	0,05	7Г	0	0	0,4	-	-	-	-	0
12	-	0,08	бтг	0,05	0	0,1	0,20	0,10	-	-	0
13	-	0,01	-	0	0,5	0,2	-	-	zi=5 — 10t2 (м)	-	0,1
14	-	0,05	4%	0,5	0	0,1	-	-	-	0,20	0,2
15	-	0,01	7Г	0,5	0	1,0	-	-	-	-	0
16	45	0,02	-	1,0	2,0	0,1	-	-	j/i=0,06t3 (м)	-	0
17	-	0,02	бтг	0	4,0	0,2	-	-	-	0,20	0
18	40	0,02	-	0,6	0	0,1	-	-	щ=0,1 sin%t (м)	-	0
19	-	0,08	-	0,4	-0,8	0,1	0,40	0,20	yi=8t - t3 (м)	-	0
20	-	0,01	10%	0,1	0	0,2	0,20	0,10	-	-	0
21	30	0,05	-	0,5	0,1	0,1	-	-	yi=2 + t2 (м)	-	0,2
22	-	0,03	4тг	0,1	3,0	0,1	-	-	-	0,10	0
23	-	0,01	2%	-0,5	-0,1	0,2	-	-	-	-	0
24	60	0,01	-	0	0,2	0,2	-	-	щ=0,1 cos l,5%t (м)	-	0
25	-	0,05	2%	0,1	-0,4	0,1	0,20	0,20	-	-	0
26	-	0,09	ТГ	0,2	0,3	0,1	0,20	0,1	-	-	0
27	75	0,02	-	1,0	0,6	0,3	-	-	zi=0,lsin0,5%t (м)	-	0
28	-	0,93	-	0,8	0	0,3	-	-	Щ=8 - 5t3 (м)	-	0,1
29	60	0,10	-	0,4	1,0	0,1	0,20	0,20	г/1=8 +13 (м)	-	0
30	50	0,02	%/2	0	0,5	0,2	-		-	0,50	0
Тело А равномерно вращается вокруг неподвижной оси (в вариан-
тах 2, 3, 4, 7, 10, 11, 14, 20, 23, 26 и 30 ось вращения zi вертикальна,
в вариантах 1, 12, 15 и 25 ось вращения Xi горизонтальна). В вариан-
тах 5, 6, 8, 9, 13, 16, 17, 18, 19, 21, 22, 24, 27, 28 и 29 тело А движется
поступательно, параллельно вертикальной плоскости yiOiZi-
Найти также координату х и давление шарика на стенку канала
при заданном значении t = ti. Данные, необходимые для выполнения
задания, приведены в табл. 40.
159
*М Ф’
В задании приняты следующие обозначения:
т — масса шарика М; и — постоянная угло-
вая скорость тела А (в вариантах 1—4, 7,
10—12, 14, 15, 20, 23, 25, 26, 30) или криво-
шипов PiB и О2С (в вариантах 6, 17, 22);
с — коэффициент жесткости пружины, к ко-
торой прикреплен шарик М; 1о — длина неде-
формированной пружины; f коэффициент
трения скольжения шарика по стенке канала;
х0, io — начальная координата и проекция
.начальной скорости на ось х.
Пример выполнения задания (рис. 132).
Дано: а = 30°, ш = тг рад/с; т = 0,01 кг;
т = 0,2 с; хо = 0,3 м; ±о = 2 м/с; с = 1 Н/м;
1о = 0,2 м; г = 0,2 м.
1
Рис. 132
Найти уравнение х = x(t) относительного движения шарика М,
а также координату х± и давление шарика на стенку канала при
заданном t = ti.	/
Решение. Свяжем подвижную систему отсчета Oxyz с вращаю-
щимся каналом (трубкой), совместив ось х с траекторией относи-
тельного движения шарика М.
Вращение этой системы вокруг оси zi является переносным движе-
нием для шарика М. Относительным движением шарика М является
его движение вдоль трубки. В том случае, когда переносное дви-
жение является равномерным вращением, относительное движение
точки определяется уравнением
mar = Pi + Ф“ + Фс.
К шарику М приложены силы: вес G. реакция пружины Р и
нормальная реакция стенки трубки; эту реакцию можно разложить
на две взаимно перпендикулярные составляющие и N^-
Присоединяем к силам, действующим на шарик М, переносную
центробежную силу инерции Ф/ и кориолисову силу инерции Фс,
направленные противоположно ускорениям и ас. Направление
ускорения ас найдем по известному правилу. Предположим, что
направление относительной скорости vr точки М совпадает с по-
ложительным направлением оси х. В этом случае кориолисова сила
инерции Фс перпендикулярна плоскости xOz и направлена, как по-
казано на рис. 132.
Модули сил инерции определяются по формулам
Ф/ = та" = mw^(r + a; sin a);
Фс = тас = 2mwevr sin a,
где
а)е = w, vr = |i|.
160
Основное уравнение относительного движения точки М в данном
Случае имеет вид
mar = G + Р + N1 + TV2 + Фе + Фс-	(1)
Составим дифференциальное уравнение относительного движения
шарика М вдоль оси х:
тх =	Xi = Ф“ sin а — G cos а — Р;
тх = mw2(r + х sin a) sin а — mg cos а — с(х — 10)
(реакция пружины Р равна произведению коэффициента жесткости
на деформацию пружины).
Последнее уравнение представим в виде
х + {с/т — u/2 sin2 а)х = w2r sin а — д cos а + clo/m. (2)
Общее решение полученного дифференциального уравнения (2)
имеет вид
х = х* + х**,
где х* — общее решение соответствующего однородного уравнения;
х** — частное решение уравнения (2).
Составим характеристическое уравнение и найдем его корни:
Л2 + с/т — и2 sin2 о = 0;
Ai — ^/a>2sin2a — с/т = л/тг2 • 0,52 — 1/0,01 = 9,876г;
А2 = —9,876г.
Таким образом, общее решение однородного уравнения имеет вид
х* = Ci cos 9,8761 + С2 sin 9,8761.
Частное решение уравнения (2) находим,в форме
х** = В.
Из дифференциального уравнения (2) находим
** _ д _ ш2г sin а — geos а + do/m
X — .О —	.	л . п ' •
с/т — (лг sin* а.
В результате вычислений получаем
В = 0,128 м.
Решение дифференциального уравнения (2) относительного движе-
ния шарика М получает вид
х = Ci cos9,876t + С2 sin 9,8761 + 0,128.	(3)
161
Скорость этого движения
х = -9,8766*! sin 9,876* 4- 9,876С2 cos 9,876*.	(4)
Постоянные Ci и Сг определяем, используя начальные условия:
при t = 0 хо = 0,3 м, io = 2,0 м/с.
Составим уравнения (3) и (4) для t = 0:
xq — Ci + 0,128; io = 9,876C2,
откуда
Pi = 0,172; C2 = 0,202.
Уравнение относительного движения шарика М принимает вид
х = 0,172 cos9,876* 4- 0,202 sin 9,876* + 0,128.
Скорость относительного движения шарика i = -l,69sin9,876*4-
4-1,99 cos 9,876*.
Для определения составляющих реакции стенки трубки Ni и N2
при t = ti = 0,2 с выразим векторное уравнение (1) в проекциях на
оси у и z. Учитывая, что вектор аг перпендикулярен этим осям,
получаем
0 = ТУ2 — Фс, 0 = N1 - Gcos60° - Ф“cos30°.
Из этих уравнений находим
JV2 = Фс = 2mwvr sin о;
М = G cos 60° 4- Ф^ cos 30° = mg cos 60° 4- тш2 (г 4- х sin a) cos 30°.
Для получения числовых значений Ni и N2 необходимо опреде-
лить координату Xi и проекцию относительной скорости точки ii,
соответствующие значению *1 = 0,2 с:
ц = 0,172cos(9,876  0,2) 4- 0,202sin(9,876 • 0,2) 4- 0,128 =
= 0,172 cos 113° 4-0,202 sin 113° 4-0,128 = 0,246 м;
ii = -1,69 sin 113° 4-1,99 cos 113° = -2,33 м/с.
Следовательно, составляющие реакции Л/i = 0,077 Н; N2 = 0,080 Н.
Реакция стенки трубки
W = \/n? + N? = у/0,0772 4- 0,0802 = 0,111 Н.
Искомое давление шарика М на стенки трубки по числовому зна-
чению равно найденной реакции N и направлено в противоположную
сторону.
162
ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ
МАТЕРИАЛЬНОЙ ТОЧКИ
Задание Д.5. Применение теоремы
об изменении количества движения к определению скорости
материальной точки
Телу массой т сообщена начальная скорость vq, направленная
вверх по наклонной плоскости, составляющей угол а с горизонтом.
На тело действует сила Р, направленная в ту же сторону (рис. 133).
Зная закон изменения силы Р = P(t) и ко-
эффициент трения скольжения /, определить
скорость тела в моменты времени ti, to, <з и
Проверить полученный результат для момен-	(б
та времени ti с помощью дифференциального
уравнения движения.	Рис. 133
Необходимые для решения данные приведены в табл. 41.
При построении графика изменения силы Р по заданным ее зна-
чениям Ро, Pi, Pi, Рз для моментов времени to, ti, to, to считать
зависимость Р = P(t) между указанными моментами времени линей-
ной. Значение силы Р, задаваемое в табл. 41 в виде дроби, указывает
на то, что модуль силы в заданный момент времени претерпевает
«скачок»: в числителе указан модуль силы в конце промежутка вре-
мени, а в знаменателе — в начале следующего промежутка времени.
Таблица Ц
Номер	т,	г>0,	tl	«2	1з	Ро	Р1	Рз	Рз	а,	f
варианта	кг	м/с		С			Н			град.	
1	35	5,4	4	10	18	100	200	150	250	25	0,10
2	20	0	6	io	15	200	160	160	180	37	0,25
3	25	0	4	10	16	200	200/120	120	0	21	0,10
4	10	4,5	5	10	16	0	180	40	100	32	0,12
5	16	9,0	4	8	16	120	120/0	0	160	24	0,08
6	40	4,0	4	8	12	400	300	300	0	40	0,06
7	20	8,0	5	8	11	0	300	0	0	25	0,20
8	16	7,6	6	11	13	75	200	0	0	23	0,12
9	12	0	6	10	14	100	140	0	0	20	0,20
10	50	12,0	2	6	12	0	300	200	200	27	0,08
11	10	5,0	6	10	16	50	100	100	200	35	0,24
12	12	3,0	3	8	14	60	180	120	120	42	0,15
13	10	8,0	4	12	16	0	150	150	100	30	0,18
14	20	8,5	5	8	15	40	100	150	0	23	0,07
15	14	9,0	7	12	18	0	140	0	100	18	0,15
163
Продолжение табл. 41
Номер	ш,	«р,	*1	*2	G	Ро	Р1	Pi	Рз	а,	f
варианта	кг	м/с		С				Н		град.	
16	20	3,0	5	9	17	300	150	100	100	39	0,12
17	24	10,0	6	10	15	0	180	60	140	15	0,20
18	15	13,0	8	16	20	110	150	0	90	26	0,22
19	15	7,2	3	10	16	150	110	90	120	30	0,30
20	22	8,2	2	9	11	70	110	110	50	15	0,15
21	13	10,0	8	12	16	0	200/0	0/200	100	28	0,14
22	11	6,0	7	9	14	160	0	0/100	120	31	0,11
23	12	4,5	5	10	16	50	120	40	80	21	0,22
24	10	7,0	4	14	29	100	50	50	0	18	0,09
25	18	0	8	10	16	180	160/0	0/140	180	33	0,17
26	8	9,0	4	8	12	0	150	0	120	45	0,10
27	17	5,0	7	10	18	190	170/0	100	280	38	0,21
28	9	7,5	4	12	17	0	140/70	100/70	70	26	0,20
29	20	9,5	5	6	11	0	400	400/100	200	15	0,25
30	10	10,2	6	7	10	120	70	0	120	33	0,15
Пример выполнения задания. Дано: т = 40 кг, «о = 10 м/с;
ti = з с, t2 = 8 с, t3 = 12 с; Ро = 0; Pi = 250 Н; Р2 = 300/200 Н;
Р3 = 150 Н; а = 30°; / = 0,1.
Определить vi, v2 и v3 для ii, t2, t3.
Решение. Покажем силы, действующие на тело: вес G, нор-
мальную реакцию плоскости N, силу Р и силу трения скольжения
F, направив ее противоположно начальной скорости, т. е. вниз по
наклонной плоскости.
Построим график Р = P(t) по заданным значениям Ро, Pi, Р2 и
Р3 (рис. 134).
1.	Для тела, принимаемого за материальную точку, составим урав-
нение, выражающее теорему об изменении количества движения в
проекциях на ось х для промежутка времени от 0 до ф
mvix - mvOx — Six, (1)
где
У2 = -Gti sin о - Fti + Spx.
Проекция импульса переменной
силы Р за время ti
ti
Spx = У Pdf.
о
164
Этот интеграл определим как площадь треугольника ОВМ на
графике Р = P(t):
Spx=3- 250/2 = 375 Н  с.
Учитывая, что сила трения скольжения F = fN = fG cos а, полу-
чаем уравнение (1) в следующем виде:
mv\x — mvox = —mgti sin a — fmgti cos a + 375,
откуда
«is = vox — gti sin a — fgti cos a + 375/m.
С учетом исходных данных находим
«1 = \vix I = 2,10 м/с.
Примечание. Сила трения скольжения F направлена противоположно скоро-
сти, и поэтому, прежде чем производить приведенный расчет, нужно выяснить, не
изменит ли скорость тела за время t первоначального направления вверх по наклон-
ной плоскости (увх > 0), а следовательно, сила трения — направления вниз.
Для этого надо установить, возможен ли такой момент времени
t* < fi, при котором скорость тела станет равной нулю под действием
постоянных сил G, N, F и силы Р, изменяющейся по закону прямой
OB : Р = (250/3)1.
Составим уравнение, выражающее теорему об изменении количе-
ства движения, для предполагаемого промежутка времени от 0 до t*:
mvx — mvox = —mgt* sin a — fmgt* cos a + Spx,
где в данном случае
t*	t*
vx = 0, Spx = J Pxdt = У (250/3)1 dl = (125/3)!*2.
о	о
В результате получим следующее уравнение для определения 1*:
(125/3)!*2 — mg(sina + / cosa)t* + mvox = 0,
т. е.
I*2 - (196,2 + 34,1)31*/125 + 400 • 3/125 = 0,
или
I*2 - 5,521* 4- 9,6 = 0.
Решая это уравнение, делаем вывод, что не существует такого
момента времени, для которого скорость тела, находящегося под
действием указанных сил, будет равна нулю.
2.	Для определения скорости тела в момент времени 1г составим
уравнение, выражающее теорему об изменении количества движения,
для промежутка времени 1г — ti:
mv2x - mvlx = ^2	(2)
165
где
57	- -G(t2 - fi)sin a - F(f2 - ti) + Spx.
Проекция импульса переменной силы Р за t2 —, ti выражается
площадью трапеции MBCI на графике Р = P(t):
Spx = 5(250 + 300)/2 = 1375 Н с.
Поэтому уравнение (2) имеет вид
mv^x — mvix — —mg(t2 — Н) sin a — /mgcosa(i2 — H) + 1375,
откуда
V2x = vlx - gfa-ti) sin a- fg cos a(t2 - H) + 1375/m,
или
V2 = |п2ж| = 7,68 м/с.
Примечание. Прежде чем составить уравнение (2), нужно убедиться, что за
время t2 — ti первоначальная скорость гц (уix > 0) не изменит своего направления.
Действительно, в начале движения на этом участке сила Р > (Gsina + /Geosа) и
продолжает расти, значит, скорость тела не может изменить своего первоначального
направления.
3.	Уравнение, выражающее теорему об изменении количества дви-
жения и составленное для промежутка времени t3 —12, дает возмож-
ность определить скорость тела v3 в момент i3:
mv3x - mv2x = ^Six,	(3)
где
57 Six = -G(t3 - f2) sin a - fG cos a(t3 -t2) + Spx.
Проекция импульса переменной силы Р за (t3 — t2) выражается
площадью трапеции IDEK-.
Spx = 4(200 + 150)/2 = 700 Н  с.
Тогда
v3x = v2x - g(t3 - t2)sina - fg cosa(t3 - t2) + 700/40,
откуда
V3 = |«3x| = 2,15 м/с.
Примечание. Уравнение (3) можно составить после того, как установлено, что
и на третьем участке тело не изменяет направления своей первоначальной скорости
(у2х > 0) и сила трения скольжения направлена в течение всего промежутка времени
t3 — t2 вниз по наклонной плоскости. Для этого следует выяснить, возможен ли такой
момент времени т* < <з, когда скорость тела станет равной нулю под действием
постоянных сил G, N, F и силы Р, закон изменения которой представлен на третьем
участке графика (см. рис. 133) прямой DE. Уравнение DE имеет вид
Р = 200 - [(200 - 150)/4]т = 200 - 12,5т,
где т — время, отсчитываемое от момента t2 = 8 с.
166
Составим уравнение, выражающее теорему об изменении количе-
ства движения, для промежутка времени от то = О до т = т*:
mvx — mv2x = —тдт* sin а — fmgr* cos а + Spx,
где для данного случая vx = 0, а
Spx = у Рх dr = У (200 - 12,5т) dr = 200т* - 6,25т*2.
о	о
В результате получим следующее уравнение, позволяющее опреде-
лить т*:
6,25т*2 - 200т* + mg(sina 4- f cos а)т* — mv2x = 0,
т. е.
*2 . 230,3-200 *	40-7,68	п
т 6,25	6,25	’
ИЛИ
т*2 + 4,85т* - 49,1 = 0,
откуда
т* = -2,42 ± -/5,86 + 49,1 = -2,42 ± 7,41 с.
Таким образом,
т* = 4,99 с.
Скорость станет равной нулю при т = 4,99 с, но (/3 — t2) < т*,
поэтому изменения скорости в рассматриваемый промежуток времени
ts — t2 не произойдет.
4.	Найдем в момент /1 значение скорости щ с помощью диффе-
ренциального уравнения
тх = У/ Xi.
Раскроем правую часть уравнения:
тх = — G sin а — F + Р,
или
тх = —mg sin а — fmg cos а + Р,
т. е.
х = — sin о — fgcos а + Р/т,
где Р = (250/3)/ — уравнение прямой ОБ, а поэтому
х = —gsino - fgcos а + (25/12)/.
Интегрируя полученное дифференциальное уравнение, получаем
х = -«/(since + /cos а)/ + (25/24)/2 + С.
Для определения С используем начальное условие задачи: при
/ = 0 vqx = io — 10 м/с.
167
Составим уравнение, полученное интегрированием, для t = 0; най-
дем, что С = 10 м/с. Таким образом, уравнение, определяющее из-
менение скорости за промежуток времени от 0 до Д, имеет вид
х = — gfsina + f cosa)t + (25/24)i2 + 10.
При t = tj
гд = |;rt=tl | = 2,10 м/с.
Задание Д.6. Применение основных теорем динамики
к исследованию движения материальной точки
Шарик, принимаемый за материальную точку, движется из поло-
жения А внутри трубки, ось которой расположена в вертикальной
плоскости (рис. 135—137). Найти скорость шарика в положениях В
и С и давление шарика на стенку трубки в положении С. Трением
на криволинейных участках траектории пренебречь. В вариантах 3,
6, 7, 10, 13, 15, 17, 19, 25, 28, 29 шарик, пройдя путь ho, отделяется
от пружины.
Необходимые для решения данные приведены в табл. 42.
В задании приняты следующие обозначения: m — масса шарика;
va — начальная скорость шарика; т — время движения шарика
на участке АВ (в вариантах 1, 2, 5, 8, 14, 18, 20, 21, 23, 24, 27,
30) или на участке BD (в вариантах 3, 4, 6, 7, 9—13, 15—17,
19, 22, 25, 26, 28, 29); / — коэффициент трения скольжения шари-
ка по стенке трубки; ho — начальная деформация пружины; h —
наибольшее сжатие пружины; с — коэффициент жесткости пружины;
Н — наибольшая высота подъема шарика; s — путь, пройденный
шариком до остановки.
Пример выполнения задания (рис. 138). Дано: m = 0,5 кг,
Va = 0,8 м/с; г = 0,1 с (время движения на участке BD); R = 0,2 м;
f = 0,1; а = 60°; /3 = 30°; h0 = 0; с = 10 Н/см=1000 Н/м.
Определить vb, vc, Nc, vd, h.
Решение. Для определения vb и vc применим теорему об изме-
нении кинетической энергии материальной точки. Движение шарика
на участках АС и АВ траектории происходит под действием силы
тяжести G (силы трения на криволинейных участках не учитываем):
mvg/2 — mv\/2 = А, = GH\ = mg АВ sin а = mg&R sin а;
vb~va = 2g67?sina;
vb — 4,59 м/с;
mn^./2 — mv2A(2 = Ai = GH% = mg(47?sina + 27?cos a);
168
Рис. 135
169
ОЛТ
9£1 эиа
Рис. 137
171
Таблица 42
Номер варианта (рис. 135—137)	т, кг	va, м/с	С	Ч 2	f	а, град	б, град	Ло, см	с, Н/см	Величины, которые требуется определить дополнительно
1	0,5	20	2,0	2,0	0,20	30	45	-	-	-
2	0,6	16	0,2	4,0	0,10	45	20	-	-	н
3	0,4	0	2,0	0,2	0,15	30	-	10	1	VD
4	0,2	5	0,5	1,0	0,10	45	-	-	-	VD
5	0,1	8	1,5	2,0	0,20	30	-	-	-	-
6	0,3	2	2,0	4,0	0,10	30	20	30	2	VD
7	0,4	5	1,0	1,0	0,10	30	-	50	5	VD
8	0,2	1	0,5	1,5	0,15	30	60	0	4	h
9	0,5	2	1,5	4,0	0,25	20	60	-	-	VD
10	0,4	4	0,1	0,5	0,10	30	60	0,2	0,2	VD
11	0,2	6	1,0	1,0	0,30	45	-	-	3	VD, h
12	0,4	5	0,4	2,0	0,20	30	60	-	-	vd
13	0,3	0	0,1	1,0	0,10	30	60	50	10	VD
14	0,6	0	2,0	3,0	0,20	60	30	-	-	s
15	0,1	1	0,1	1,0	0,15	60	20	50	0,2	VD
16	0,4	2	0,2	2,0	0,40	30	-	-	-	 VD
17	0,2	0	0,1	1,0	0,20	30	-	40	1,0	VD
18	0,3	3	0,4	1,5	0,10	45	-	-	-	-
19	0,1	4	0,1	0,4	0,30	30	60	10	0,5	VD
20	0,2	10	1,0	0,5	0,10	60	-	0	1,2	h
21	0,7	3	0,3	0,3	0,20	45	-	-	-	-
22	0,4	1	0,2	0,2	0,40	45	-	0	1,1	vd, h
23	0,6	2	0,4	0,2	0,20	45	-	-	-	-
24	0,5	0	0,5	0,6	0,30	60	30	-	-	H
25	0,1	. 0	0,2	0,5	0,25	-	30	30	0,4	vd
26	0,2	2	0,1	0,2	0,20	30		-	-	VD
27	0,8	3	0,2	0,4	0,15	45	-	-	-	VD
28	0,3	4	0,1	0,6	0,35	30	15	60	0,1	VD
29	0,5	0	0,2	0,5	0,20	45	30	50	0,8	VD
30	0,8	5	0,3	0,6	0,15	30	-	-		tDE
172
vc ~va= 4gJ?(2sin a + cos a);
vc = \/va + 4g/?(2 sin a + cos «),
или
vc = 4,26 м/с.
Определяем давление шарика на стенку канала в положении С.
В соответствии с принципом Даламбера для материальной точки
геометрическая сумма сил, приложенных к точке, и силы инерции
этой точки равна нулю:
G + N'c + $ = 0.
Силу инерции материальной точки
можно разложить на нормальную и ка-
сательную составляющие:
Ф = Фп 4- Фг-
Сумма проекций сил G, N'c и Ф на
ось х должна быть равна нулю:
N'c -Geos60° — Фп = 0.
Отсюда
2
N'c = Geos 60° + Ф„ = mg cos 60° +
или
N'c = 25,2 Н.
Реакцию N'c можно также определить с помощью естественного
уравнения движения:
pi cos(A, n). = N'c - G cos60°.
Отсюда
2
N'c = Geos 60° + ^.
Искомое давление Nc с шарика на стенку трубки по числовому
значению равно найденной реакции N^, и направлено в противопо-
ложную сторону.
Скорость шарика в положении D найдем, применив на участке
BD теорему об изменении количества движения материальной точки
(рис. 139):
mvpx - mvBx = Six.
173
К точке приложены сила тяжести G, реакция стенки трубки N
и сила трения F:
F = fN' = fQ cos/3.
Так как
vDa. = vd, vbx — vb, SiX = — G sin/З-t—Ft = —mg sin /З-t—f mg cos /3-t,
TO
mvD — mve = —mg sin /3 • t — f mg cos /3  t,
откуда
vd = 4,01 м/с.
Для определения максимального сжатия h пружины воспользу-
емся на участке DE теоремой об изменении кинетической энергии
материальной точки:
mv^/2 — mvjy/2 =	Ai = —ch2/2 — GH3 — Fh.
Учитывая, что Ve = 0 и Н3 = hsin/З, получаем
ch2/2 + G(sin /3 + f cos (3)h — mv2D/2 = 0,
или
h,2 + 2G/i(sin (3 + f cos (3)/c — mv2D /с = 0.
Решая полученное квадратное уравнение относительно h, получим
h = (-0,003 ± 0,090) м.
Принимаем в качестве искомой величины положительный корень
квадратного уравнения:
h = -0,003 + 0,090 = 0,087 м.
II. ДИНАМИКА МЕХАНИЧЕСКОЙ СИСТЕМЫ
ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ
МЕХАНИЧЕСКОЙ СИСТЕМЫ
Задание Д.7. Применение теоремы о движении центра масс
к исследованию движения механической системы
Тела 1 и 2 (рис. 140—142) движутся по отношению к телу 3 с по-
мощью механизмов, установленных на этом теле (силы, приводящие
в движение механизмы, являются внутренними силами данной меха-
нической системы). Тело 3 находится на горизонтальной плоскости.
1. Предполагая горизонтальную плоскость гладкой, определить за-
висимость между перемещением .S3 = зз(1) тела 3 и относительным
174
szt
он эиа
ЭЛТ
ти ;|ч
ш
ей Э1м
Таблица 43
Номер варианта	mi	m2	тз					а		
(рис. 140—142)	кг			Да ГА	RB гв	Ri П	Д2 Г2	град '		Примечание
1	800	200	800	2	2	3	—	30	—	ГА = Г в
2	200	600	1000	3/2	-	-	-	30	45	Ла = Лв
3	300	800	500	3	2	-	-	60	30	Ла = Лв
4	200	800	1000	2	2	-	-	15	-	га = гв', Лв1 = Лв
5	100	700	600	3/2	-	—	—	45	-	
6	600	300	600	3	2	—		30	45	г А = гв
7	300	500	1000	—	2	—	4	45	—	г А = гв
8	500	200	400	2	2	-	-	60	-	г а = гВ', ЛА, = Ra',
9	400	200	500	2	—	—	2	30	—	Rb' = Лв Массой подвижного блока пренебречь
10	500	300	600	2	—	—	—	45	—	г А = гв
11	600	200	800	2	2	—	3	30	60	ГА = Гв
12	300	600	500	2	3	—	—	30	60	Ла = Rb; га> = га Г В' = ГВ
13	700	300	600	3	—	—	—	30	30	
14	400	500	1000	2	2	—	3	45	—	ГА=ТВ '
' 15	400	900	500	2	2	—	—	60	30	га = гв
16	600	200	700	2	3	-	-	30	45	Ra — Лв
17	500	400	800	2	—	—	—	30	—	Массой подвижного блока пренебречь
18	700	400	800	2	—	—	—	30	15	
19	300	600	700	3/2	2		—	45	—	г а — г в; Ла1 = Ла; Лв> = Лв
20	800	200	1000	2	2	—	3	—	—	га = гв
21	500	180	300	3	2	—	—	45	60	га = г в; Л а' = ra ; ЛВ' = Лв
22	300	700	500	2	—	—	3	30	—	
23	600	300	500	2	—	2	—	30	60	
24	400	300	600	2	—	—	—	30	—	Массой подвижного блока пренебречь
25	200	700	600	2	2	—	—	15	45	г а = гв
26	600	300	800	2	2	—	—	30	60	г а = Лв
27	200	600	800	2	2	—	—	30	60	г а = г в; Ra1 = Ra
28	500	200	600	2	—	2	—	30	60	
29	600	300	800	2	—	—	4	45	—	Ra = Rb
30	300	800	600	2	2	—	4	30	15	г A = гв
перемещением sir = siT(f) тела 1 (по отношению к телу 3), если
механическая система в начале рассматриваемого движения (t = 0)
находилась в состоянии покоя, причем siro = s2ro = «зо = 0; опреде-
лить также зависимость горизонтальной составляющей реакции Rx
одного из упоров, которые удерживали бы тело 3 от перемещения,
от относительного перемещения sir = sir(t) тела 1.
178
2. Предполагая горизонтальную плос-
кость шероховатой, написать диффе-
ренциальное уравнение движения те-
ла 3; определить условие, при кото-
ром тело 3 (при заданных параметрах
системы) придет в движение, и най-
ти зависимость между Зз(<) и sir(i),
считая, что дальнейшее движение про-
исходит при соблюдении этого усло-
вия (при t = 0 SirO = «2г0 = «30 = 0,
SlrO = ^2г0 — s30 = 0).
Известны: mi, m2 — массы тел 1
и 2; m3 — масса тела 3 с находя-
щимися на нем механизмами привода
(центр масс Сз по отношению к телу
3 не перемещается); R, г — радиусы
больших и малых окружностей тел 1
и 2 или звеньев А и В механизмов
привода; а, /3 — углы наклона граней
призм (тел 3) и лент транспортеров
к горизонтальной плоскости; /сц, / —
коэффициенты трения покоя (сцепле-
ния) и трения скольжения соответ-
ственно, принимаемые одинаковыми во
всех вариантах: /сц = 0,11, f = 0,10;
slr = = sir(t) — непрерывная и возра-
стающая функция времени (ее произ-
водная тоже непрерывна и возрастает).
Качение тел происходит без проскальзывания; нити невесомы и
нерастяжимы.
На схемах тела 1, 2, 3 — в отклоненных от начального (t = 0)
положениях; показаны относительные перемещения sir, 82г тел 1 и
2 и предполагаемое абсолютное перемещение «з тела 3 в сторону
возрастания этих перемещений. Необходимые для решения данные
приведены в табл. 43. Массой зубчатой рейки (варианты 1, 6, 7, 14,
15, 20, 22, 29) пренебречь.
Пример выполнения задания (рис. 143). Дано: mi = 600 кг;
m2 = = 240 кг; m3 = 400 кг; Нд/гд = 3; а = 30°; /3 — 60°; /сц = 0,11;
/ = 0,10.
Решение. 1. Горизонтальная плоскость — гладкая. Напишем
дифференциальное уравнение, выражающее теорему о движении цен-
тра масс механической системы (рис. 143, а), в проекциях на ось х:
"W = ^ХгЕ.
В данном случае
тхс = 0,	(1)
где m = mi + m2 + m3 — масса всей системы.
179
Проинтегрируем уравнение (1) дважды при следующих начальных
условиях: при t = 0 хсо / 0, хсо = 0.
Получаем
xc—Ci, xc = C1t + C2. 
Эти уравнения для t = 0 имеют вид
ico=Ci; хсо = С2,
откуда Ci — 0, С2 = хсо- Таким образом, для любого момента вре-
мени
хс = 0, хс = хсо-	(2)
Из уравнений (2) видно, что вдоль оси х центр масс механической
системы не перемещается и что движение тел 1 и 2 возможно только
с одновременным движением тела 3.
Приравняем на основании (2) абсциссу центра масс системы в
любой момент времени t
_ mixci + Ш2ХС2 + "‘ЗгСЗ
ХС ~	т
его абсциссе в начальный момент рассматриваемого движения:
_	_ raiXQio 4- ГП2ХС20 + ТП-З^СЗО	/д\
.	m	’	' '
Покажем перемещение зз тела 3, предполагая его направленным
в сторону возрастания координаты S3.
В выражении (3)
тел = хсю + S3 + Sir cos а;
ХС2 = ХС20 + S3 - S2rCOS/3 = ХС20 + «з - з1ггА cos/3/RA;	(5)
ХСЗ = Хсзо + 83.
В (5) следует выразить з2г через sir- Для этого устанавливаем
связь между относительными скоростями v2r = s2r и vir = sir.
Из чертежа (рис. 143, а) находим
virlv2r = Ra/ta, откуда v2r = virrA/RA,
т. е.
ds2r/di = (dsir/dt)rx//?A, или ds2r = dsirrA/RA-
Интегрируя это выражение при нулевых начальных условиях, име-
ем
$2r = Sit-Ta/Ra-
Из полученного видно, что линейные перемещения находятся в
такой же зависимости, что и соответствующие линейные скорости.
Приравняв (3) [с учетом (5)] и (4), имеем
mi (хсю + «з + sir cos о) +т2 (хС20 + s3 - slrr a cos f3!RA) + m3 (хсзо + s3) =
= mi^cio + wi2^C20 + тзхсзо,
180
откуда найдем искомую зависимость
—mi cos а + тагА cos/3/Яд	, .
«3 = ---------~----------«1г,	(6)
или, используя числовые данные, получим
S3 = —0,39sir (м).
Знак «—» означает, что при заданных параметрах системы поло-
жительной координате sir тела 1 соответствует координата зз < О,
т. е. тело 3 перемещается из первоначального положения влево (а не
в положительном направлении отсчета зз, как первоначально пред-
полагалось).
Очевидно, что зависимость между абсолютной скоростью г>з = зз
тела 3 и относительной скоростью vir = sir тела 1 определяется на
основании (6) выражением
—mi cosa 4-Ш2Гд cos/3/Яд	Z(_x
V3 = -----------------------------------  (7)
m	4
ИЛИ
Уз = — 0,39i>ir (м/с).	(7')
Пусть тело 3 на гладкой горизонтальной плоскости удерживается
упорами (на рис. 143,6 они показаны пунктиром).
Учитывая по (7') направление скорости тела 3, покажем горизон-
тальную составляющую Rx реакции левого упора.
Для определения ее величины составим дифференциальное урав-
нение движения центра масс системы:
mxc=^Xf.
В данном случае ^Xf = Rx.
Выразим проекцию ускорения центра масс системы на ось через
соответствующие проекции ускорений центров масс тел системы, взяв
производные по времени от выражения (3):
_ mixgi + т2хС2 + тзхсз	(g)
Тогда
miici + т2хС2 + тзхСз = Rx.	(9)
Вторые производные от координат (5) центров масс тел системы:
£<71 = S3 + Sir COS а, £<72 = «3 - 51гГдСО8^/7?А,	£<73 = «з-	(10)
При наличии упоров тело 3 перемещаться не будет (зз = 0 = const),
т. е.
зз = 0.	(11)
Из уравнения (9) с учетом (10) и (11) находим
Rx = (mi coso - m2ra cos 0/Ra)Sit,	(12)
или
Rx = 479,6 s\r Н.
181
Выражение (12) позволяет заключить, что упор будет испытывать
горизонтальное давление тела 3 (а тело 3 — реакцию Rx) только
тогда, когда тела 1 и 2 движутся с ускорением (s’ir / 0).
Заметим, что Rx может оказаться равной нулю, когда s'ir / 0,
при некоторых сочетаниях параметров системы. Например, в данной
задаче, как это видно из (12), при mi cos а = тпгГд cos/З/Ra-
2. Горизонтальная плоскость шероховата. Составим дифференци-
альное уравнение движения центра масс системы:
mic =^ХгЕ-
В данном случае (рис. 143, в) на ось х проецируется сила трения
скольжения F между телом 3 и горизонтальной плоскостью, напра-
вленная противоположно скорости тела 3, а направление скорости
тела 3 определяется выражением (7'), поэтому ^2	= F.
Используя (8), напишем
mixci + т2тС2 + т3хСз = F
или, учитывая (10), имеем
тДз’з + sir cosa) + т2(5з - siri'A cos/3/Ra) + m3s3 = F. (13)
Найдем силу трения скольжения:
F = fN',	(14)
где N' — нормальное давление системы на горизонтальную плос-
кость.
Для определения величины N' составим уравнение, выражающее
теорему о движении центра масс системы, в проекциях на ось у:
тус =
Выразим проекцию ускорения центра масс системы на ось у через
соответствующие проекции ускорений центров масс отдельных тел
системы [по аналогии с (8)]:
.. miyci + т2ус2 + пгзз/сз
УС = --------т---------•
Тогда дифференциальное уравнение примет вид
miyci + т3ус3 + т3усз = -Gi -G2-G3+N.-	(15)
Здесь N — нормальная реакция горизонтальной плоскости: N = —N';
Gi, G3, G3 — силы тяжести тел 1, 2, 3.
Составим выражения ординат центров масс тел системы:
УС1 = УСЫ + Sir Sin а, УС2 = УС20 + S2rSin/3 = УС20 + SirTASin/3/RA,
УСЗ = Усзо-
182
Взяв производные по времени от этих выражений, получим:
УС1 = Sir sin О, УС2 = SlrTA sin 0/RA, УСЗ = o. (16)
Из (15) с учетом (16) найдем величину реакции:
N = G + mi'sir sin a + т231гГд sin [3/Ra	(17)
(G = Gi + G2 + G3 — сила тяжести всей системы).
Используя (14) и (17), напишем дифференциальное уравнение (13)
в следующем виде:
mi(s3 + sir coset) + m2(s3 - 81гГа cos Р/Ra) + т3з3 =
= /(G + mi'sir sin a + т231Ггд sin 0/Ra)-
Ускорение тела 3 определяется выражением
fG - [mi cosa — (т2гд cosj3/RA) - /(mi sina -f- т2гд sin ^/Лд)]51г Q4
S3 - -4----------------------------------------------------. (18)
Отсюда заключаем, что движение тела 3 на шероховатой плоскости
возможно только тогда, когда тела 1 и 2 движутся с ускорениями,
причем ускорение s’ir превосходит некоторую величину Sjr.
В самом деле, |.$з| > 0, когда
|/G - [mi cosa - (т2гЛ cos/3/йд) - /(mi sina + т2гд зт/3//?д)]51Г| > 0,
т. e.
|mi cosa —(т2гд cos/3//?д) — /(т! sina + m2TA sin/3//?A)|s’ir > /G. (19)
Движение тела 3 начинается из состояния покоя, когда на него
действует максимальная сила трения покоя (сцепления) Fc4 тах =
= fcu.N = fcuG; поэтому, определяя Sjr из выражения (19), следует
ввести коэффициент сцепления /сц:
lr0 |mi cosa — (т2гд cos—/Cu(mi sina + т2гд sin/3/7?д)|'	'
Произведя вычисления, получим
з;г0 > 3,05 м/с2.
Пусть относительное ускорение изменяется по некоторому непре-
рывному закону s’ir = sir(Z) так, что в любой момент времени
Sir > s’ir-
Тогда движение тела 3 описывается дифференциальным уравне-
нием (18). Разделив каждое из слагаемых числителя правой части
(18) на знаменатель и обозначив
[mi cos a — (т2гд cos /3/RA) — f(mi sin a + т2гд sin 0/RA)\	D
m
получим это уравнение в следующем виде:
з'з = fg- B'sir-	(20)
183
Заметим, что условие (19') при принятом обозначении имеет вид
"*	/сц<7
*1г ' в 
Интегрируем (20) (начальные условия: при t = 0 siro = •<,'2r0 = «Зго = 0,
SlrO = S2r0 = $3r0 = 0):
з3 = fgt - Bsir +C, s3 = (fgt2/2) - Bslr + Ct + D.
Напишем эти уравнения для t = 0:
S30 = — Bs^rO + С,	5зо = — BsirO + О,
откуда найдем (имея в виду начальные условия) постоянные инте-
грирования:
С = 0,	0 = 0.
Таким образом, з3 = fgt — Bslr, 83 = (fgt2/2) - Bslr.
Сделав числовые расчеты, имеем
з3 = 0,98t - 0,36slr,	83 = 0,49t2-0,36slr.	(21)
Задание Д-8. Применение теоремы об изменении количества
движения к исследованию движения механической системы
Механическая система (рис. 144—146) состоит из тел 1, 2, 3 с
массами соответственно mi, m2 и m3. Массами остальных тел, со-
ставляющих систему, пренебречь.
На тело 1 наложены две связи. Опора А препятствует переме-
щению по нормали к опорным поверхностям (по вертикали). Опора
В не препятствует перемещениям по вертикали и горизонтали, но
исключает возможность поворота.
В некоторый момент времени (принятый за начальный), когда ско-
рость тела 1 равна «о, а угловая скорость тела 2 — й?2о, движение тел
2 и 3 относительно тела 1 начинает замедляться (направление вра-
щения тела 2 и направление скорости vq показаны на рис. 144—146).
Торможение осуществляется внутренними для всей системы силами.
Устройство, осуществляющее торможение, на схемах не показано.
В процессе торможения угловое ускорение е2 (замедление) тела 2
остается постоянным.
Определить скорость vT тела 1 в тот момент времени Т, когда й?2
становится равным нулю, т. е. когда движение тел 2 и 3 относитель-
но тела 1 прекращается. Вычисление vT произвести для одного из
следующих условий*:
* Выбор условий — по усмотрению преподавателя. Условие б) рекомендуется
для самостоятельного исследования.
184
Рис. 144
185
Рис. 145
186
Рис. 146
187
Таблица 44
Номер варианта	7П1	7712	m3	я2	Яз	а,	Номер варианта	7П1	ТП2	7713	R2	«3	а,
(рис. 144-146)		КГ		м		град	(рис. 144-146)		КГ		В	4 •	град
1	10	5	2	0,5	-	40	16	10	5	2	0,9	0,4	30
2	12	4	3	0,5	-	30	17	15	4	1	0,8	0,2	30
3	10	4	5	0,35	0,5	20	18	12	2	4	0,8	-	40
4	12	4	2	0,7	-	40	19	12	2	6	0,6	0,8	30
5	10	1	6	0,5	0,4	30	20	14	2	4	0,8	0,5	20
6	15	1	6	0,5	- 	40	21	13	1	6	0,8	0,4	25
7	16	' 4	4	0,7	-	40	22	12	4	2	0,6	0,4	20
8	19	2	6	0,7	0,7	40	23	20	1	8	0,8	-	35
9	10	5	5	0,7	0,5	30	24	13	1	6	0,6	-	30
10	12	4	6	0,8	0,6	30	25	10	2	4	0,6	-	25
11	18	6	4	0,8	0,4	25	26	11	2	4	0,7	-	25
12	13	1	6	0,8	0,6	35	27	20	1	6	0,7	-	30
13	12	2	6	0,4	-	40	28	14	1	6	0,8	0,6	20
14	12	6	2	0,8	0,4	40	29	10	4	3	0,8	0,6	20
15	10	5	3	0,8	0,4	30	30	12	4	4	0,8	0,6	25
а)	на тело 1 со стороны направляющих А действует сила куло-
новского (сухого) трения F = —/|Л'г|г/|,г| (/ — коэффициент трения
скольжения, |Л7| — модуль реакции в точке Л);
б)	на тело 1 кроме силы трения скольжения F в опоре А действует
сила «вязкого» трения R со стороны опоры В: R = — bv (b —
коэффициент «вязкого» сопротивления, v — вектор скорости тела 1).
Вычисление vT произвести точно и приближенно. В приближенном
расчете пренебречь величинами первого и более высоких порядков
малости относительно промежутка времени Т = шгоАг-
Для всех вариантов принять г>о = 2 м/с; = 10 рад/с;
|е2| — 250 рад/с2; f = 0,25; b = 10 Н • с/м.
Считать, что проскальзывание колес по соответствующим поверх-
ностям отсутствует.
Необходимые для расчета данные приведены в табл. 44.
Пример выполнения задания. Дано (рис. 147): mi = 12 кг,
m2 = 4 кг, тз = 3 кг; R2 = 0,5 м; г2 = 0,25 м; а = 30°; vg — 2 м/с;
<д2о — Ю рад/с; |е2| = 250 рад/с2; / = 0,25; Ь = 10 Н • с/м;
W2 — а>2о ~	(0 t sj шгоДг)-	(1)
Определить ит — скорость тела 1 в момент времени Т = cj2o/e2-
Решение, а). На механическую систему действуют внешние си-
лы: F — сила сухого трения в опоре A; Gi, G2, G3 — силы тяжести
188
тел 1, 2 и 3; N — сила нормальной реакции в точке А; Мв —
реактивный момент в опоре В.
Применим теорему об изменении количества движения механи-
ческой системы в дифференциальной форме. В проекциях на оси
координат
dKx/dt = ^Х^, dKy/dt = ^Yf,	(2)
где Кх. Ку — проекции вектора количества движения системы на
оси координат; ^Xf,	— суммы проекций внешних сил на
соответствующие оси.
Рис. 147
Количество движения системы тел 1, 2 и 3
К = К3+К2+К3,	(3)
где
Ki =m1ni; К2 = m2vc2 = m2(vc2e + vcir)',
K3 = m3vc3 = m3(vc3e + vc3r)-	(4)
Здесь ft, vc2, vc3 — скорости центров масс тел 1, 2, 3; Vc2e, Усзе,
vc2r, vcsr — соответственно переносные и относительные скорости
центров масс (рис. 147).
Очевидно, что
VC2e = VC3e = V;	1	/gx
vc2r = w2R2; vl = 2R2uj2- vk = w2(R2 + r2); J	'
VK =	+ г>к)/2 = w2(3R2 + r2)/2;	1
Ш3 = (vL - vK)/(2r3) = w2(T?2 - re)/(2r3). J	11 J
189
Проецируя обе части векторного равенства (3) на координатные
оси, получаем с учетом (4), (5) и (6)
Кх = тх — цшг cosa, Ку = /za>2 sin a,	(7)
где x — проекция вектора v на ось х;
m = mi + т2 + пг3; М = ТП2Я2 + 0,5m3(3J?2 + Лг)-
Проекции главного вектора внешних сил на координатные оси
= =р/|ЛГ|;	52^в = -G1-G2-G3 + N. (8)
Здесь знак «—» соответствует случаю, когда х > 0, а знак «+» —
случаю, когда х < 0.
Подставляя (7) и (8) в (2), получим
тх + cosa = т/|ЛГ|;	— Ц£2 sin a = — Gi — G2 — G3 + N. (9)
Выразим из второго уравнения системы (9) алгебраическую ве-
личину нормальной реакции и подставим ее в первое уравнение. В
результате получим
х = — а	при х > 0;	(10)
х = —а	при х < 0,	(11)
где
а - — е2 cosa + f\g — — е2 sinal; а = —£2 cosa - f\q - sin al.
m	' m	1	m	J m	1
Рассмотрим промежуток времени 0 C t T,, в течение которого
тело 1 движется в направлении vq. Из (10) следует, что
х = —at + С = —at + и0,	(12)
где С — постоянная интегрирования, определяемая из начального
условия: при t = 0
x0=v0.	(13)
При t = Т* скорость тела 1 обращается в ноль, поэтому
Т* = v0/a.	(14)
Для дальнейшего решения необходимо сравнить найденную вели-
чину Т* с величиной Т =
Если окажется, что Т* > Т, то искомая скорость vT может быть
найдена по формуле (12) при t = Т.
Если Т* = Т, то очевидно, что vx = 0, т. е. движение всех тел в
системе прекращается одновременно при t = Т.
Если Т* < Т, то тело 1 либо останавливается при t = Т, (гд = 0 при
любом t > Т*), либо начинает двигаться в обратном направлении.
Первая из этих возможностей реализуется при а = 0, а вторая —
при а > 0. Справедливость этих утверждений вытекает из дифферен-
циального уравнения (11).
190
В рассматриваемом примере
а = 57,92 м/с2; а = 47,60 м/с2;
= 0,0346 с; Т = 0,04 с,
т. е. Т* < Т и а > 0. Следовательно, тело 1 начинает при t = Т*
двигаться в обратную сторону. Это движение описывается дифферен-
циальным уравнением (11) при начальном условии: при t = Т*
х = 0.	(15)
Интегрируя (11) с учетом (15), получим при Т* t Т
x = —a(t — T*}.	(16)
При t = Т получим из (16) искомое значение скорости тела 1 в
момент, когда о>2 — 0:
vTX = х(Т) = —а(Т — 71*); vTa; = —0,26 м/с.
Интересно сопоставить этот результат со скоростью vT, вычислен-
ной при отсутствии силы трения. В этом случае надо положить
во всех выкладках / — 0. В результате вычислений будем иметь
dT2. = —0,11 м/с, что в два раза меньше, чем в системе с трением.
б) На механическую систему помимо перечисленных в предыдущем
пункте внешних сил действует сила «вязкого» трения R.
Точное решение задачи. Воспользовавшись методикой, изложен-
ной в п. а), получим дифференциальное уравнение движения тела 1:
х + (Зх = —а	при х > 0;	(17)
х + (Зх = — а	при х < 0,	(18)
где /3 = b/m (/3 = 0,526 рад/с).
Из (17) и начальных условий (13) следует, что при 0 t Т*
х = (^о + a//3)e-/?t - а//3,
откуда
Т* = |ln(vo/?/a +1),
или
Г* = 0,0343 с.
Из (18) и начальных условий (15) получаем при Т, t Т:
. х = (а//3)[е-^‘-т‘) - 1].	(19)
При t = Т из (19) находим
vxx = —0,27 м/с.
191
Приближенное решение задачи*. Воспользуемся теоремой об
изменении количества движения механической системы в конечной
форме для промежутков времени 0 t Т* и Т* t < Т:
Kx*-Kx0 = YSfx;
кхт - Кх* = Ysl\
-Ky0 = Ys&]
(20)
где Y^fy-> Y$iy — сумма проекций импульсов внеш-
них сил на координатные оси соответственно за первый и второй
промежутки времени.
Очевидно, что проекции количества движения системы равны
Kxq = hwqx - sin а;'
Куо = Д^20 sin а;
Кх* = — да>2* cos а;
Ку* = ДШ2* sin а;
Кхт — Tfivxx,
Кут = 0,
(21)
где а>2* — угловая скорость тела 2 при t = Т*.
Если предположить, что N = const, то проекции импульсов внеш-
них сил примут вид
Е = - J bidt - ?/|N|dt = -Ъх* - f\N\T*-
о	о
Y S^y = -(Gt + G2 + G3)T* + NT*-,
Ysfx = ~fbxdt + ff |7V|dt = —b(xT - x* + /|jV|T - TJ;
T.	T.
YК = -(Gi + G2 + G3)(T - T*) + N(T - T*),
(22)
где x*; xT — смещения тела 1 соответственно за Т* и Т с.
Подставим (21) и (22) в (20):
—до>2* cosof — mvox + ЦШ20 cos а = —bx* — /|-ZV|T*;	(23) ,
(^2* — W2o)m sin a = — (Gi + G2 + G3yr* + NT*-,	(24)
mvTX + /zu>2* coso = -b(xT - x*) + /|7V|(T - T*);	(25)
—ци?2* sin a = —(Gj + G2 + Сз)(Т — T*) 4- N(T — T*).	(26)
Порядок приближенного решения задачи для условия а) такой же.
192
Выразим из уравнений (24) и (26) соответственно NT* и N(T — Т*)
и подставим эти результаты в (23) и (25):
cosa - mvOx + //w20cosa = -bxt - /|(Gi + G2 + Сз)Т* +
+(w2* - w20)/zsina|;	(27)
mvxx + ЦШ2* cosa = -b(xT - xt) + /](Gi + G2 + Gs)(T - T*)-
—//w2sina|.	(28)
Текущая координата x, описывающая поступательное движение
тела 1, является некоторой функцией времени t. Разложим х = x(t)
в ряд Маклорена по степеням t:
x(t) = Xq + XOt + . . .
Так как х0 = 0, a t Т, где Т — малая величина, то, пренебрегая
величинами первого и более высоких порядков малости относительно
Т, мы тем самым пренебрегаем смещением тела 1 за любой проме-
жуток времени, меньший Т, т. е.
х* » 0 и хт ю 0.
Из тех же соображений следует в (27) и (28) пренебречь слагае-
мыми (Gi + G2 + G3)T* и (Gj + G2 + Gs)(T — Т*).
С учетом сказанного строгие равенства (27) и (28) переходят в
более простые приближенные:
—ЦШ2* cos а — mvox + /iw2o cos а » —/(w2o — w2> )д sin <*;	(29)
тптж + cos а » /w2*/r sin а	(30)
Из (29) определяем ш2*, а из (30) — vTX:
w2* « w20 - mvQX/[д(cosa + /sina)];	(31)
vTX « w2*(^/m)(/sina — cosa).	(32)
Произведя вычисления по формулам (31) и (32), будем иметь
vTX и —0,31 м/с. Этот результат приемлемо согласуется с полученным
выше точным.
Задание Д.9. Применение теоремы об изменении
кинетического момента к определению
угловой скорости твердого тела
Тело Н массой mi вращается вокруг вертикальной оси z с по-
стоянной угловой скоростью wo; при этом в точке О желоба АВ
тела Н на расстоянии АО от точки А, отсчитываемом вдоль же-
лоба, закреплена материальная точка К массой т2. В некоторый
момент времени (£ = 0) на систему начинает действовать пара сил с
моментом Mz = Mz(t). При t = т действие пары сил прекращается.
Определить угловую скорость wT тела Н в момент t = т.
193
Рис. 148
194
Рис. 149
195
Рис. 150
196
Таблица 45
рианта -150)	mi	m2	^0,	а,	ь,	Я,	а,	АО,	Mz =		OK =	T,
Номер ва (рис. 148-	к		рад/с	м	м	м	град	м	= Нм	c	= s = s(tj)	c
1	32	10	-1	1	1,5	1,2	-	тг/?/6	-29,6t2	3	(5тгЯ/12)П	1
2	200	60	—2	-	-	2	120	у/3/2	101	5	V3tj	1
3	120	40	0	2	-	-	-	0	—120t	4	(V2/4)tj	2
4	16	5	-3	-	-	1	30	0,4	21t	2	0,6ti	2
5	66	10	1,5	2	1’,5		-	0	15\/t	4	0,5ti	2,5
6	160	80	-1,25	1,5	-	2,5	-	тга/6	—700t	V3	(5ira/18)t2	V3
7	300	50	—2	1,6	1	0,8	-	0	968	1	(%fl/2)t2	1
8	80	20	0	1,2	-	2	-	тга/2	240\/t	4	(Tra/4)ti	2
9	20	5	5	1,2	-	0,4	45	TtR/4	-29,2t '	3	(3irR/4)t^	1
10	100	40	2	2	л/2	-	-	у/2/2	-ЭОл/t	4	(V2/4)t2	1
11	60	20	-1	2	-	-	15	0	40t	2	0,4tf	2
12	40	10	-3	1	-	2	-	0	50t2	3	(ira/3)ti	2
13	24	4	4	1	-	-	-	0,5	-27Vt	1	0,3ti	2
14	40	10	2	-	-	1	-	0	120t	1	0,5ti	3
15	120	50	-4	1	-	2	-	0	330t2	2	(та/2)42	1
16	60	10	-5	1	1,2	-	30	0,4	74	2	0,3t2	л/2
17	50	10	—2	-	-	1,6	30	0,6	69t	4	0,6ti	2
18	120	50	3	2	3	0,8	-	тгЯ/2	324	3	(irK/8)t2	2
19	90	30	1	1,5	-	-	-	0	— 135t	2	(%a/4)t2	1
20	50	12	3	1	-	1,2	-	тга/6	— 14t2	3	(Tra/12)tJ	2
21	40	10	-6	-	-	1	-	V2/2	75y/t	1	(T2/16)t2	2
22	150	50	-1	1,6	1,2	0,6	-	тгЛ/2	163	4	(%K/2)t2	1
23	90	20	2	л/2	1	-	-	л/3/2	-210	2	(>/3/2)ti	1
24	50	12	-3	0,6	-	-	60	0,2	27t2	2	0,4ti	2
25	36	8	-5	-	-	0,5	-	0	20t	2	(тгЯ/6)12	2
26	150	40	—4	1,5		2	-	тга/6	1170Vt	1	(?ra/2)t2	1
27	120	30	0	1	-	-	60	0	—25t	2		1
28	15	4	—2	0,6		-	-	0,1	5,6t	3	0,4ti	1
29	20	5	5	0,6	-	0,6	-	0	-6,ЗлЛ	4	(5irR/6)ti	1
30	150	50	0	1,6	1,2	-	-	1,6	652t	2	0,2t2	2
Примечание. Знак минус перед Mz и ш соответствует направлению вращения
часовой стрелки, если смотреть со стороны положительного направления оси z.
197
Таблица 46
Осевые моменты инерции однородных пластинок
Тело Н вращается по инерции с угловой скоростью шг.
В некоторый момент времени Н = 0 (ii — новое начало отсчета
времени) точка К (самоходный механизм) начинает относительное
движение из точки О вдоль желоба АВ (в направлении к В) по
закону ОК = s = s(ij).
Определить угловую скорость шт тела Н при ti = Т.
Тело Н рассматривать как однородную пластинку, имеющую фор-
му, показанную на рис. 148—150. Необходимые для решения данные
приведены в табл. 45—46.
198
= 0,5q м; ti = Т = 2 с.
Рис. 151
Пример выполнения задания (рис. 151). Дано: mi = 200 кг;
m2 = 80 кг; Mz — 592t Н • м; шц = — 2 рад/с; АО = 0,8 м; R = 2,4 м;
а = 1,2 м; t = т = 4 с; ОК = з
Определить и шт, счи-
тая тело Н однородной круг-
лой пластинкой.
Решение. К решению
задачи применим теорему об
изменении кинетического мо-
мента механической системы,
выраженную уравнением
где Lz — кинетический мо-
мент системы, состоящей в
данном случае из тела Н и
точки К, относительно оси г;
^МЕ — МЕ — главный момент внешних сил, приложенных к си-
стеме, относительно оси z.
На систему за время от t = 0 до t = т действуют силы: вес Gi тела
Н, вес G2 точки К, пара сил с моментом M.z и реакции подпятника
и подшипника (рис. 151, а).
Предположим, что вращение тела Н происходит против вращения
часовой стрелки, если смотреть со стороны положительного напра-
вления оси г; будем считать это направление положительным при
определении знаков кинетических моментов.
Найдем выражение кинетического момента Lz системы, который
складывается из кинетического момента тела Jziv и момента количе-
ства движения точки К, находящейся в точке О тела Н и имеющей
скорость v = со • OiO:
m2v • OiO = m2w • OiO2.
Таким образом,
Lz = Jzlj 4* m2cj • OiO2 — (.72 + m2 • GiG2)u?.
Главный момент внешних сил равен вращающему моменту Мг, так
как другие силы момента относительно оси z не создают.
Уравнение, выражающее теорему об изменении кинетического мо-
мента, примет вид
d[(Jz +m2 О1О2М _ м
(1)
d t
где Mz = ct (с = 592 Н • м/с).
199
Разделим в уравнении (1) переменные и проинтегрируем левую и
правую части уравнения:
(Jz + га2 • О1
ctdt.
Тогда
(Л + т2 • OiO2)(wT - (Д0) = ст2/2.	(2)
Найдем числовые значения входящих в уравнение (2) величин.
Момент инерции тела Н относительно оси z найдем, используя
теорему о зависимости между моментами инерции относительно па-
раллельных осей:
Jz = Jzc+mia2,
где JzC — момент инерции тела Н — однородной круглой пластинки
относительно вертикальной оси, проходящей через центр масс тела
параллельно оси z:
Jzc = m1R2/2.
Тогда
Jz = m\R?/2 — пца2,
т. e.
Jz = 864 кг • M2.
Из чертежа (рис. 151, б) находим
(О±О2) = (ОС)2 + (О-^С)2, или (<9i<9)2 = 4 м2,
поэтому
Jz + т2 • О1О2 = 864 + 80 • 4 = 1184 кг • м2.
Таким образом, из уравнения (2)
1184[сдт - (-2)] = 592 • 42/2
имеем
шТ = 2 рад/с.
После прекращения действия момента Mz тело Н вращается по
инерции с угловой скоростью сдг; при этом к системе приложены
силы Gi, G2, реакции подпятника и подшипника (рис. 151, б).
Те же внешние силы действуют на систему и в течение промежутка
времени от ti = 0 до ti = Т при движении самоходной тележки.
Уравнение, выражающее теорему об изменении кинетического мо-
мента системы, имеет для этого периода времени вид
dLz/dt = 0,
т. е.
Lz — const.
200
Определим значения кинетических моментов Lzq при ti = 0 и Lzt
при Zi = Т и приравняем эти значения.
Для £1=0
Lzo = ( Jz + гп'2  OiO2)u>T = 2368 кг • м2/с.
При Н > 0 скорость точки К складывается из относительной
скорости vr по отношению к телу Н и переносной скорости ve в
движении вместе с телом Н. Поэтому для Н = Т покажем два
вектора количества движения точки: m2vr и m2ve (рис. 151).
Для ti = Т
LZT = Jz^T + т2шт(О1Кт)2 + m2vr  OlC.
Найдем
(О1КГ)2 = (О1С)2 + (СКГ)2,
где
СКТ = ОКТ - ОС, ОКТ = stl=T = 0,5Т2 = 0,5 • 22 = 2 м,
т. е.
СКт = 2-1,6 = 0,4 м, (OiКт)2 = 1,22 + 0,42 = 1,6 м2.
Относительная скорость
vr = ds/dt = ti,
при ti = Т = 2 с
vr = 2 м/с.
Поэтому
Lzt = 864шу + SOcuy • 1,6 — 80 • 2 • 1,2 = 992шг — 192.
Приравнивая Lzq и Lzt-
2368 = 992о>г - 192,
находим
ivt = 2,58 рад/с.
Задание Д.10. Применение теоремы об изменении
кинетической энергии
к изучению движения механической системы
Механическая система под действием сил тяжести приходит в дви-
жение из состояния покоя; начальное положение системы показано
на рис. 152—154. Учитывая трение скольжения тела 1 (варианты
1—3, 5, 6, 8—12, 17—23, 28—30) и сопротивление качению тела
3, катящегося без скольжения (варианты 2, 4, 6—9, 11, 13—15, 20,
21, 24, 27, 29), пренебрегая другими силами сопротивления и массами
201
Рис. 152
202
Рис. 153
203
Рис. 154
204
нитей, предполагаемых нерастяжимыми, определить скорость тела 1
в тот момент, когда пройденный им путь станет равным з.
В задании приняты следующие обозначения: mi, т2, т3, т4 —
массы тел 1, 2, 3, '4; R3, Г2, Из, гз — радиусы больших и малых
окружностей; г2х, г3{ — радиусы инерции тел 2 и 3 относительно
горизонтальных осей, проходящих через их центры тяжести; а, 0 —
углы наклона плоскостей к горизонту; t — коэффициент трения
скольжения; б — коэффициент трения качения.
Необходимые для решения данные приведены в табл. 47. Блоки в
катки, для которых радиусы инерции в таблице не указаны, считать
сплошными однородными цилиндрами.
Наклонные участки нитей параллельны соответствующим наклон-
ным плоскостям.
Пример выполнения задания. Дано: mi — масса груза 1,
m2 = 2mi, m3 = mi, т^ = 0,5mi, ms = 20mi, Я2 = J?3 = 12 см,
r2 = 0,5Л2, гз = 0,757?з, R& = 20 см, АВ = I — 4R3, г2^ = 8 см,
i3x = Ю см, о: = 30°, f = 0,1, б = 0,2 см, з = 0,06тг м. Сопротивление
качению тела 2 не учитывать. Шатун 4 считать тонким однородным
стержнем; каток 5 — однородный сплошной цилиндр. Массами звена
ВСз и ползуна В пренебречь. На рис. 155, а показана механическая
система в начальном положении.
Найти щ — скорость груза 1 в конечном положении.
Решение. Применим теорему об изменении кинетической энергии
системы:	1
T-T0 = ^Af + ^^,	(1)
где То и Т — кинетическая энергия системы в начальном и конеч-
ном положениях; £Af — сумма работ внешних сил, приложенных
к системе, на перемещении системы из начального положения в ко-
нечное; 52 -А/ — сумма работ внутренних сил системы на том же
перемещении.
Для рассматриваемых систем, состоящих из абсолютно твердых
тел, соединенных нерастяжимыми нитями и стержнями,
ЕЛ/=0-
Так как в начальном положении система находится в покое, то
То = 0.
Следовательно, уравнение (1) принимает вид
т = £ав.	(2)
Для определения кинетической энергии Т и суммы работ внешних
сил надо изобразить систему в конечном положении (рис. ,155, б, в).
Напишем кинематические соотношения между скоростями и пере-
мещениями точек системы, т. е. уравнения связей, при этом скорости
и перемещения выразим соответственно через скорости и перемеще-
ния груза 1.
205
206
Таблица
Номер варианта	mi	ГП2	тз	Ш4	R2	Лз	iix		а	б	f	<5, см	S, м	
(рис. 152-154)	кг				см		СМ		град					Примечание
1	т	4т	1/5т	4/Зт	-	-	-	-	-	60	0,10	-	2	
2	т	1/2т	1/Зт	-	-	30	-	20	30	45	0,22	0,20	2	
3	т	т	1/10т	т	-	-	-	-	45	-	0,10	-	2	
4	т	2т	40т	т	20	40	18	-	-	-	-	0,30	0,17Г	Массами звеньев АВ, ВС и пол- зуна В пренебречь
5	т	2т	т	-	20	15	18	-	60	-	0,12	-	0,28%	Массой водила пренебречь
6	т	Зт	т	-	-	28	-	-	30	45	0,10	0,28	1,5	
7	т	2т	2т	-	16	25	14	-	30	-	-	0,20	2	
8	т	1/2т	1/Зт	-	-	30	-	-	30	45	0,15	0,20	1,75	
9	т	2т	9т	-	-	30	-	20	30	-	0,12	0,25	1,5	
10	т	1/4т	1/4т	1/5т	-	-	-	-	60	-	0,10	-	3	
11	т	1/2т	1/4т	-	-	30	-	25	30	45	0,17	0,20	2,5	
12	т	1/2т	1/5т	т	30	-	20	-	30	-	0,20	-	2,5	
13	т	2т	5т	2т	30	20	26	-	30	-	-	0,24	2	
14	т	1/2т	5т	4т	-	25	-	-	-	-	-	0,20	2	Массы каждого из четырех колес
														одинаковы
15	т	1/2т	4т	1/2т	20	15	18	-	60	-	-	0,25	1,5	
16	т	1/10т	1/20т	1/10т	10	12	-	-	-	-	-	-	0,05%	Массой водила пренебречь
17	т	1/4т	1/5т	1/10т	20	-	15	-	60	-	0,10	-	0,16тг	Шатун 3 рассматривать как тонкий однородный стержень
Продолжение табл.
207
Номер варианта	7П1	Ш2	m3	m4	R2	Яз	»2x		a	<3	f	6, CM	s, M	
(рис. 152-154)	КГ				CM		CM		град					Примечание
18	m	3m	m	-	35	15	32	-	60	-	0,15	-	0,2%	Массой водила пренебречь
19	m	l/3m	l/10m	m	24	-	20	-	60	-	0,15	-	1,5	
20	m	2m	20m	-	20	15	16	-	30	-	0,10	0,20	0,2%	Массами звеньев АВ, ВС и ползу- на В пренебречь
21	m	m	2m	-	20	20	16	-	30	45	0,20	0,32	1,2	
22	m	l/2m	l/4m	-	20	10	-	-	60	-	0,17	-	0,1%	Массой водила пренебречь
23	m	m	l/10m	4/5m	20	-	18	-	30	-	0,10	-	1	
24	m	3m	20m	-	20	30	18	-	-	-	—	0,60	0,08%	Массами звеньев АВ, ВС и ползу- на В пренебречь
25	m	l/3m	l/4m	-	16	20	-	-	-	-	-	-	0,04%	Массой водила пренебречь
26	m	l/2m	m	l/3m	30		20						0,6%	Массы и моменты инерции блоков 2 и 5 одинаковы Шатун 3 рассматривать как тонкий однородный стержень
27	m	m	6m	l/2m	20	20	16	-	30	-	-	0,20	2	
28	m	2m	3m	-	20	-	14	-	60	-	0,10	-	0,1%	Шатун 3 рассматривать как тонкий однородный стержень
. 29	m	l/4m	l/8m	-	-	35	-	-	15	30	‘ 0,20	0,20	2,4	
30	m	l/2m	3/10m	3/2m	26	20	20	18	30	-	0,12	-	2	
Рис. 155
Скорость центра масс С катка 2 равна скорости груза 1:
VC2 = VX.	(3)
Угловая скорость катка 2, мгновенный центр скоростей которого
находится в точке Р2,
<^2 = УсгЛС'г.Рг)-
Учитывая (3), получим
^2 = V\/R2.	(4)
Скорость точки D катка 2
Vd = w2 • DP2,
т. е.
vd = ^(-^2 + v2).
Скорость точки Е блока 3 равна скорости точки D катка 2:
VE=VD-	(5)
208
Но
VE — <^>3^3 
Следовательно, по (5),	Ш3Т3 =	+ Г2). Л2	
Так как	R2 — 2г 2,	
то	^згз=3/2д1,	
откуда	3 щ шз - 2~3-	 (6)
Заменяя в формуле (6)		
d tf>3	d s
= -dT’ V1 = Tt'
получим
d <рз ____________________________ 3 d s
d t 2гз d t ’
ИЛИ
d¥,3 = JLds.
После интегрирования (при нулевых начальных
условиях)
Когда груз 1 пройдет путь s = 0,06тг м, блок 3 повернется на угол
При этом повороте блока 3 на 180° его точка Ло перейдет в
конечное положение А и шатун 4 из начального положения Л о Во
перейдет в конечное положение АВ.
Каток 5 переместится влево при повороте блока 3 на угол тг/2 и
вправо при довороте блока еще на тг/2; значит, конечное положение
катка 5 совпадает с его начальным положением.
Таким образом, конечное положение всей системы вполне опреде-
лено (рис. 155, б).
Вычислим кинетическую энергию системы в конечном положении
как сумму кинетических энергий тел 1, 2, 3, 4, 5:
Т = Т1+Т2+Тз+Т4 + Т5.	(8)
Кинетическая энергия груза 1, движущегося поступательно,
Тх = пц^/2.	(9)
209
Кинетическая энергия катка 2, совершающего плоское движение,
n I n
(10)
где — момент инерции катка 2 относительно его продольной
центральной оси С24:
= Wl2»2f-	(11)
Подставляя (3), (4), (11) в формулу (10), получаем
Кинетическая энергия тела 3, вращающегося вокруг оси Ох,
Тз =	(13)
где J3x — момент инерции блока 3 относительно оси Ох:
J3X = m3ilx.	(14)
Подставляя (6), (14) в формулу (13), получаем
т _ m^3x (3vi\2 _ 9	«Зх„2	/1е-ч
Тз-^-{2Г3) ~8m3TlV^	(15)
Кинетическая энергия шатуна 4, совершающего плоское движение,
m4t£4	J4{^4
-*3 =  о----1-Й—,
где уса — скорость центра масс C4 шатуна 4; щ4 — угловая скорость
шатуна 4;	— момент инерции шатуна относительно центральной
оси .
Для определения 17(74 и w4 найдем положение мгновенного центра
скоростей шатуна 4. Так как скорости точек Л и В в этот момент
параллельны, то мгновенный центр скоростей шатуна 4 находится
в бесконечности; следовательно, угловая скорость шатуна в данный
момент <*>4 = 0, а скорости всех его точек параллельны и равны
между собой. Таким образом, кинетическая энергия шатуна 4
Ti = miVci/2,	(16)
где
va = vA.	(17)
Вращательная скорость точки А тела 3
va=^sR3,	(18)
или с учетом (14)
vA = 3/2R3vi/r3-
210
Поскольку гз — 3/4/?з, получим
vA = 2П1-
По (17)
VC4=VA, VC4=2V1.	(19)
После подстановки (19) в (16) выражение кинетической энергии
шатуна 4 принимает вид
Т4 = 1/2тп4(2п1)2 = 27714^1.	(20)
Кинетическая энергия катка 5, совершающего плоское движение,
Ть = m5v|;5/2 + Л{^2/2,
где т?с5 — скорость центра масс С5 катка 5;	— момент инерции
катка 5 (однородного сплошного цилиндра) относительно его цен-
тральной продольной оси Csj, Jsj = 7715Я5/2; W5 — угловая скорость
катка 5.
Так как каток катится без скольжения, то мгновенный центр
скоростей находится в точке Р&. Поэтому
^5 = vcs/Rs-
Следовательно,
Т5 ~ ~Г" + 2 • 2Л| - 4m5V^'
Так как звено ВС& совершает поступательное движение, то
vc5 = vв, но vb = Vc4 — 2тд. Значит, т?с'5 = 2т?1.
Поэтому выражение кинетической энергии катка 5 принимает вид
Т5 — 3/47715 (2т?1)2 = 37775 7? 2.	(21)
Кинетическая энергия всей механической системы определяется по
формуле (8) с учетом (9), (12), (15), (20), (21): \
Т = 77727?2/2 + 7772(1 + i^lB^)v1l2 + Э/вТТ^Т?2^/?-2 + 277747?f + 377157?2.
Подставляя сюда заданные значения масс, получаем
Т = 77717?!2 [1 + 2(1 + iljRl} + 9/47^/^ + 2 + 120]/2,
ИЛИ
Т = 129777177^/2.	(22)
Найдем сумму работ всех внешних сил, приложенных к системе,
на заданном ее перемещении. Покажем внешние силы, приложенные
к системе (рис. 155, в).
Работа силы тяжести Gi
Aq1 = Gihi = 777igssina.
(23)
211
Работа силы трения скольжения FTp
^FTp = —FTps.
Так как
FTp = fNi = fGi cos а,
то
AFtp =-fnngscosa.	(24)
Работа силы тяжести G?
Ag2 = Gzhcz = mzgssina.	(25)
Работа сил сцепления Fcu?, Fca5 катков 2 и 5 равна нулю, так как
эти силы приложены в мгновенных центрах скоростей этих катков.
Работа силы тяжести G4
Ag4 = Giha,
где ha — вертикальное перемещение центра тяжести С4 шатуна 4
из начального положения в его конечное положение (рис. 155, г):
hc4 = R3,
Ag4 = т4дВ3.	(26)
Работа пары сил сопротивления качению катка 5
Амс = —Мс<Рь,	(27)
где Me = 6N5 = 6G3 — момент пары сил сопротивления качению
катка 5; <р3 — угол поворота катка 5.
Так как каток 5 катится без скольжения, то угол его поворота
= scs/Rs,	(28)
где 5с5 — перемещение центра тяжести С3 катка 5.
В данном примере работу пары сил сопротивления вычислим как
сумму работ этой пары при качении катка 5 влево при повороте
тела 3 на угол тг/2 и качении вправо, когда тело 3 повернется еще
на угол тг/2.
Перемещение центра тяжести С3 катка 5 равно перемещению пол-
зуна В влево и вправо:
5С5 = 2(В0В').	(29)
Определим перемещение Bq В' при повороте тела 3 на угол тг/2.
За начало отсчета координаты точки В выберем неподвижную точку
К плоскости (рис. 155, г). При этом повороте тела 3 шатун из
положения AqBo перейдет в положение КВ'. Тогда
В0В' = КВо- КВ',
212
где
К Во = КО + О Во = R3 + у/(АоВо)2 - (AqO)2 = R3 + y/l2 - R23,
KB' = l = 4R3.
Следовательно,
B0B' = R3 + yjp - R2 — l = R3 + ^(4Я3)2-Л| - 4Я3 = 0,88Я3. (30)
Подставляя (30) в (29), а затем в (28), находим полный угол
поворота катка 5:
<р5 = 1,76Я3/Я5.	(31)
Работа пары сил сопротивления качению по (27)
АМс = ~ёт5д • 1,76R3/R5.	(32)
Сумма работ внешних сил определится сложением работ, вычисля-
емых по формулам (23)—(26) и (32):
У2 Af = migssina — fmigscosa+m2gssina+m4ffR3:-Sm5ff-l,76R3/R5.
Подставляя заданные значения масс, получаем
лЕ	( •	/	, о •	. Яз	<5 • 20 • 1,76Я3 \
2 ^4, = migs I sina — j cosa -I- 2sina +	----------),
или
У2 Af = l,51migs.	(33)
Согласно теореме (2), приравняем значения Т и ^2Af, определя-
емые по формулам (22) и (33):
129 • miv2/2 = l,51migs,
откуда
vi = 0,21 м/с.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
ТВЕРДОГО ТЕЛА
Задание Д. 11. Исследование поступательного
и вращательного движений твердого тела
Механическая система состоит из механизма (колес 1 и 2) и гру-
за 3.
К колесу 1 приложена пара сил с моментом М = M(t) (движущий
момент) или движущая сила Р = P(t).
213
Время t отсчитывается от некоторого момента (t = 0), когда <ро = 0,
а угловая скорость колеса 1 равна шщ- Момент сил сопротивления
ведомого колеса 2 равен Мс. Другие силы сопротивления движению
системы не учитывать.
Массы колес 1 и 2 равны mi и m2, а масса груза 3 — m3.
Радиусы больших и малых окружностей колес 7?i, п, R?, г?.
Схемы механических систем показаны на рис. 156—158, а необхо-
димые для решения данные приведены в табл. 48.
Найти уравнение движения тела системы, указанного в последней
графе табл. 48.
Определить также натяжение нитей в заданный момент времени,
а в вариантах, где имеется соприкасание колес 1 и 2, найти, кроме
того, окружное усилие в точке их касания. Колеса 1 и 2, для которых
радиусы инерции гХ1 и iX2 в табл. 48 не заданы, считать сплошными
однородными дисками.
Пример выполнения задания. Дано: тг = 100 кг; т2 = 150 кг;
m3 = 400 кг; М = 4200+200t Нм; Мс = 2000 Н м = const; Ri = 60 см;
R2 = 40 см; г2 = 20 см; iX1 = 20>/2 см; iX2 = 30 см; o?io = 2 рад/с.
Найти уравнение <р2 = / (t) вращательного движения колеса 2 ме-
ханизма, а также окружное усилие S в точке касания колес 1 и 2
и натяжение нити Т в момент времени G = 1 (рис. 159, а).
Решение. В данной механической системе колеса 1 и 2 меха-
низма вращаются вокруг неподвижных осей, а поднимаемый груз 3
совершает поступательное движение.
Напишем дифференциальные уравнения движения каждого из этих
трех тел, для чего отделим одно от другого, разрезав нить, удержи-
вающую груз 3, и разъединив колеса 1 и 2 в точках соприкасания
зубцов (рис. 159, 6).
К колесу 1 механизма приложены сила тяжести Gi, движущий
момент М, составляющие реакции подшипника Уд, 2д, окружное
усилие Si и нормальная реакция Ni' колеса 2.
К колесу 2 механизма приложены сила тяжести G2, момент сил
сопротивления Мс, составляющие реакции подшипника Уд, Zb, на-
тяжения Т нити, к которой подвешен груз 3, окружное усилие .S2 и
нормальная реакция колеса 1.
К грузу 3 приложены сила тяжести G3 и натяжение нити Т'.
Очевидно,
S2 = -Si, 2У1 = -ЛГ2 и =
Составим дифференциальное уравнение вращательного движения
колеса 1 вокруг оси x±:
JX1$i=ME,
здесь MXJ = 52	— главный момент внешних сил, приложенных
к колесу 1, относительно оси вращения Xi:
^мгЕХ1=м-з^.
214
Рис. 156
215
Рис. 157
216
Рис. 158
217
218
Таблица 48
Номер варианта (рис.	mi	Ш2	тз	R1	Г1	R?	Г2	^xl	ix2	М,	P,	Me,	With	h,	Тело, для ко- торого нужно определить
156-158)		КГ					СМ			Нм	H	Нм	рад/с	c	уравнение движения
1	100	300	500	20	-	60	40	-	50	2100+20t	-	1000	2	2	1
2	300	80	500	70	50	20	-	60	-	-	10200+100t	600	1	0,5	2
3	200	100	400	60	-	30	20	60	20>/2	6100+20t	-	800	0,5	2,5	1
4	100	250	300	20	-	50	30	-	40	1000+40t	-	1400	1,5	2	1
5	150	300	600	30	-	50	20	-	30	-	5500+200t	1500	2	1	3
6	400	250	600	70	-	30	20	70	20-/2	4800+10t	-	800	3	4	1
7	300	200	400	60	40	30	20	50	20	-	3000+loot	500	0	3	3
8	300	250	700	50	30	40	20	40	30	-	9700+50t	500	1	2	1
9	200	100	500	80	60	20	-	50\/2.	-	5900+30t	-	600	2	3	2
10	250	100	400	40	20	30	-	30	-	250Q+504	-	1200	0	1,5	. 2
11	150	300	700	40	30	60	30	30	40	-	3900+50t	1000	1	2	1
12	100	200	600	30	20	60	-	20+2	60	-	5700+50t	1500	2	2	1
13	180	100	300	50	40	80	20	30\/2	20	-	2700+200t	400	0,5	1	2
14	150	80	400	40	20	30	-	30	-	1800+20t	-	700	1,5	2,5	3
15	300	180	500	20'	10	50	-	10>/2	50	700+40t	-	300	0	1,5	1
Продолжение табл. 4$
Номер варианта (рис.	mi	m2	тз	Ri	Г1	К2	Г2	^х1	Ъх2	м,	р,	МС,	и>10,	*1,	Тело, для ко- торого нужно определить
156-158)		кг					СМ			Нм	н	Нм	рад/с	С	уравнение движения
16	300	250	400	60	40	50	30	50	40	-	7300+100*	1200	1	2	1
17	250	100	800	50	30	20	-	40	-	5400+501	-	900	2	2	1
18	200	100	600	20	-	50	-	-	50	1900+20*	-	1500	0,5	1	2
19	250	150	400	50	30	30	20	40	20д/2	-	14200+200*	500	0,5	2	1
20	400	100	800	50	20	30	-	40	-	3700+50*	-	1200	2	1	2
21	200	150	300	50	40	30	20	30\/2	20	-	3800+100*	800	1	1,5	2
22	250	100	800	60	20	10	-	50	-	-	9700+200*	700	2	0,5	1
23	200	80	400	40	20	30	-	30	-	2300+20*	-	900	0,5	1	2
24	100	200	500	30	-	40	20	-	30	-	12600+100*	500	1,5	1	1
25	150	80	400	60	-	20	-	60	-	4900+40*	-	800	0	1,5	2
26	250	200	500	50	20	40	30	40	30	-	3500+150*	600	2	2	1
27	250	150	500	50	30	40	30	30д/2	30	-	15200+100*	700	1,5	1	1
28	60	200	900	20	-	60	10	-	50	900+10*	-	1500	0	2	2
29	50	200	500	20	-	40	30	-	25\/2	2100+20*	-	1000	2	0,5	1
30	300	60	600	50	30	20	-	40	• -	-	7200+50*	700	1,5	1	2
Примечание. Радиусы инерции звеньев 1 и 2 ixi и ix2 заданы относительно неподвижных осей этих звеньев.
219
(Момент М приводит в движение колесо 1 и поэтому принят положи-
тельным, а момент, создаваемый окружным усилием Si, препятствует
вращению колеса 1 и, следовательно, отрицателен.)
Рис. 159
Дифференциальное уравнение вращательного движения колеса 1
примет вид
Jxi(pi = М - SRi-	(1)
Составим дифференциальное уравнение вращательного движения
колеса 2 вокруг оси Х2'-
JX2$2 = МЕ.
Здесь МЕ2 = МЕ2 — главный момент внешних сил, приложенных
к колесу 2, относительно оси вращения Х2‘-
^MtEX2 = S2R2-Tr2-Mc.
(Момент, создаваемый окружным усилием S2, приводит в движение
колесо 2 и поэтому принят положительным, а момент силы натяже-
ния нити Т и момент сил сопротивления Мс препятствуют движению
колеса и, следовательно, отрицательны.)
Дифференциальное уравнение вращательного движения колеса 2
имеет вид
Jx2$2 — S2R2 — Тг2 — Мс.	(2)
Составим дифференциальное уравнение поступательного движения
груза 3:
тпз'г = ZE.
Здесь ZE = ZE — проекция главного вектора внешних сил, при-
ложенных к грузу 3, на ось z, направленную в сторону движения
груза, т. е. вверх:
Y,ZE = T’-G3.
220
Дифференциальное уравнение поступательного движения груза 3
tn-i'z = Т' — G3.	(3)
В уравнениях (1), (2), (3) неизвестными являются силы Т' = Т
и Si = S2 = S', а также функции <£г(*) и 23(f) — угловые
ускорения колес 1, 2 и ускорение груза 3 соответственно.
Но указанные функции связаны между собой соотношениями
Ф1/Фч = Я2/Л1,	(4)
z = Ф2Г2	(5)
так, что в трех уравнениях — три неизвестные: Т, S и ф?.
Выразим ф1 из (4):
Ф1 = ф2^/^
и подставим в (1):
Jx^R^IRi = М — SRi. ,	(6)
Исключим из дифференциального уравнения (2) силу Т, для чего
выразим Т(Т = Т") из (3):
Т = ти-зз + G3.
Учитывая (5), напишем
Т = ТП2Ф2Т2 + G3.
Тогда (2) приобретает вид
Л2Й = S2R2 — ('ГП3Ф2Г2 + Сз)г2 — Мс,
или
{JX2 + тзг^фч = S2R2 — СзГ2 — Мс.	(7)
Исключим S(S = Si = S2) из (6) и (7), для чего умножим (6) на R2,
а (7) — на Ri:
•^Х1Ф2^^1 R\ — MR2 — S\R\R2,
(JX2 + тзг^фзЯх = S2R2R1 ~ G3r2Ri - McRi.
Сложив соответствующие части полученных уравнений, имеем
(R2/R1) 4"	+ msr^Ri] = MR2 — СзГзЛх — McRi,
откуда
.. _ MR2R1 - {тздт^ + MC}R\	, .
“ JXIR22 + {JX2 +m3r|)K2 •	W
Выражение (8) определяет в общем виде угловое ускорение коле-
са 2 механизма.
Моменты инерции колес 1 и 2 относительно осей Xi и хз-
JX1=m1i2X1-, Jx2=m2il2.
221
Учитывая исходные данные, находим
JX1 = 8 кг • м2; JX2 = 13,5 кг - м2.
Теперь по формуле (8) получаем
<£2 = 4,034t + 0,4597.	(9)
Интегрируем это уравнение дважды, используя следующие началь-
ные условия задачи: при t = 0
<£20 = 0;	020 = wio7?i/7?2, или <£2о = з рад/с.
Первый интеграл <£2 — 2,017t2 + 0,4597^ 4- Ci.
Второй интеграл <£2 = 0,672t3 4- 0,230t2 4- Cit + Сг-
Напишем полученные уравнения <£2 = <£2 (0 и <£2 = £г(0 для t = 0:
<£20 = Ci; <£20 = С2,
откуда
Ci = 3 рад/с, С2 = 0.
Уравнение угловой скорости звена 2 имеет вид
<£2 = 2,017£2 + 0,4597^ 4- 3 (рад/с).
Искомое уравнение вращательного движения колеса 2 имеет вид:
<£2 — 0,672£3 4- 0,23СИ2 4- 3£ (рад).
Натяжение нити Т найдем, как было показано, из уравнения (3):
Т - m3z 4- G3,
или
Т — т3<£г2 4- т3д.
При t = 1 с, учитывая (9) и исходные данные, имеем
Т = 4285 Н. .
Окружное усилие определяем из уравнения (2):
S = S2 = (*7Ж2<£2 4- Тг2 4- Mc)/T?2i
при t = 1 с S = 7295 Н.
Задание Д. 12. Исследование плоского движения
твердого тела
Определить значение постоянной силы Р, под действием которой
качение без скольжения колеса массой m носит граничный характер,
т. е. сцепление колеса с основанием находится на грани срыва.
Найти также для этого случая уравнение движения центра масс
колеса С, если в начальный момент времени его координата хсо = 0
и скорость vco = 0.
222
Таблица 49
Номер варианта (рис. 160-162)	т, кг	ic, см	R, см	Г, см	а, град	б, град	/сц	6, см
1	300	50	80	40	20	-	0,35	0
2	200	40	60	30	-	-	0,20	0,8
3	180	50	60	20	30	-	0,10	0
4	220	30	70	25	30	30	0,20	0
5	240	40	60	15	-	-	0,10	1,0
6	200	-	50	-	15	-	0,20	0
7	200	45	60	25	30	15	0,25	0
8	150	40	70	25	15	-	0,50	0
9	250		-	-	-	30	0,15	0
10	150	40	50	15	20	-	0,30	0,7
11	200	30	50	20	30	-	0,20	0,6
12	220	-	-	-	30	30	0,25	0
13	140	-	-	-	-	30	0,10	0
14	300	-	50	-	30	-	0,15	0,6
15	180	20	50	20	-	15	0,15	0
16	180	30	50	35	-	-	0,15	0,9
17	160	50	60	20	15	20	0,30	0
18	260	-	50	-	-	-	0,10	1,0
19	200	50	60	20	-	20	0,10	0
20	250	40	50	30	20	-	0,25	0
21	200	-	40	-	30	-	0,25	1,2
22	150	30	50	20	-	-	0,25	1,2
23	200	30	60	30	30	15	0,40	0
24	240	30	70	30	15	-	0,15	0
25	100	-	-	-	-	60	0,10	0
26	150	-	-	-	30	15	0,15	0
27	120	-	30	-	-	-	0,40	1,5
28	150	30	60	25	25	-	0,30	0
29	200	-	-	-	-	20	0,30	0
30	160	-	40	-	20	-	0,20	0
Варианты задания показаны на рис. 160—162, а необходимые для
решения данные приведены в табл. 49.
В задании приняты следующие обозначения: г’с — радиус инерции
колеса относительно центральной оси, перпендикулярной его плос-
кости; R и г — радиусы большой и малой окружностей; /Сц —
коэффициент сцепления (коэффициент трения покоя); 6 — коэффи-
циент трения качения.
Примечание. Колеса, для которых радиусы инерции не указаны, считать
сплошными однородными дисками.
223
Рис. 160
224
Рис. 161
225
Рис. 162
226
Пример выполнения задания. Дано: т = 200 кг; R = 60 см;
г = 10 см; ic = 50 см; а = 15°; в = 30°; /сц = 0,10; 6 = 0 (рис. 163, а).
Решение. На колесо дей-
ствуют силы: сила тяжести ко-
леса G, нормальная реакция N,
сила Р и сила сцепления Рсц
(рис. 163, б) (в случае, если
6/0, необходимо показать мо-
мент пары сил сопротивления
качению).
Силу FCIX направляем условно
вления оси х.
Дифференциальные уравнения
’тгжс=^2Хгв; тус =
или в данном случае
тхс = Р cos /3
тус = N — G
1сФ = f
Положительным направлением отсчета угла поворота колеса при-
нято направление по часовой стрелке, что соответствует движению
центра колеса в положительном направлении оси х.
В соответствии с этим направление по часовой стрелке принято
положительным и при определении знаков моментов внешних сил в
уравнении (3).
К дифференциальным уравнениям (1)—(3) добавим уравнения свя-
зей
ус = R = const;	(4)
ш = ф = vc/R — ic/R-	(5)
Рис. 163
в сторону положительного напра-
плоского движения колеса:
— G sin а + Есц;	(1)
' cos а — Р sin /3;	(2)
V - FcaR.	(3)
Последнее уравнение, связывающее угловую скорость колеса ш со
скоростью центра vc, выражает условие качения колеса без сколь-
жения.
Из (4) следует
Ус = 0.	(6)
Дифференцируя (5) по времени, получаем
Ф = xc/R-
(7)
* Дифференциальное уравнение вращения колеса может быть записано в такой
же форме и относительно оси, перпендикулярной плоскости движения и проходящей
Be через его центр масс, а через мгновенный центр скоростей (точку контакта колеса
с основанием). Такая возможность обусловлена тем, что расстояние между центром
масс и мгновенным центром скоростей остается при движении колеса постоянным.
227
Подставляя (6) и (7) в (2) и (3) и учитывая, что G = mg, Jc = mic,
получим
N = Psin/3 + mg cosa-, 	(2')
mi^‘ic/R = Pr - FCUR.	(3')
Исключая хс из уравнений (1) и (3'), находим
Рсц = [P(Rr — ip cos/3) + icing sin a]/(R2 + ip),
или с учетом исходных данных
Рсц = - 0,257 Р + 208.	(8)
График зависимости (8) показан на рие. 164. График пересекает
ось Р в точке Ро = 809 Н.
При 0 Р < Ро Гсц >0 — сила сцепления направлена, как
показано на рисунке, в положительном направлении оси х.
При Р > Ро Feu, <0 — сила сцепления направлена в противопо-
ложную сторону.
Модуль силы сцепления, обеспечивающей качение колеса без
скольжения, подчинен следующему ограничению:
|Рсц| < NfCu
(имеется в виду, что всегда N > 0).
Предельное значение модуля силы сцепления согласно (2')
|РСЦ|* = Nfeu = (Psin/З + тдсоза)/Сц,
или с учетом исходных данных
|ГСЦ|* = 0,05Р+190.	(9)
На рис. 164 показан график зависимости |РСЦ| от Р, представля-
ющий собой ломаную линию. Там же проведена прямая (9). Она
пересекает график |РСЦ| в точках А и В с абсциссами Pi и Р2.
Область значений силы Р, при которых колесо катится без сколь-
жения (|Рсц| < Nfeu),
Pl Р Р2-
228
Граничные значения силы Р находим, пользуясь (8) и (9), из
условий
FC4 = |FCU|* и -ГСЦ = |ГСЦ|*.
В результате вычислений получаем Pi = 58,6 Н, Р% = 1923 Н.
Дифференциальное уравнение движения центра колеса после ис-
ключения Fcu из (1) и (3') принимает вид
Хс = -R[F(/?cos/3 + г) — mgsina  R]/[m(R2 + г^)],
или с учетом исходных данных
хс = 0,003047Р - 1,498.	(10)
График зависимости (10) показан на рис. 165: хс = 0 при
Р = 492 Н.
При Р - Pi имеем хс = —1,32 м/с2.
Дважды интегрируя это дифференциальное уравнение и имея в
виду нулевые начальные условия, находим
Хс = — 0,66t2;
колесо катится вниз по наклонной плоскости.
При Р — Р^
хс = 4,36 м/с2, хс = 2,18/2.
Колесо катится в сторону положительного направления оси х вверх
по наклонной плоскости.
Примечание. Равнодействующая всех сил, приложенных к колесу, катящемуся
без скольжения, проходит через точку К, расположенную на диаметре, перпенди-
кулярном скорости центра масс, на расстоянии СК = i^/R от него.
При этом точка К и мгновенный центр скоростей колеса находятся по разные
стороны от центра масс.
В данном примере
СК = 502/60 = 41,7 см.
Точка К показана на рис. 163, б.
Сумма моментов всех сил, приложенных к колесу, относитель-
но оси, проходящей через точку К и перпендикулярной плоскости
движения, равна нулю:
'£iMiK = 0.	(11)
Условие (11) позволяет без составления дифференциальных урав-
нений найти зависимость силы сцепления от других сил, действующих
на колесо.
Это условие можно также использовать для проверки результатов
вычислений, произведенных при решении задачи на основе диффе-
ренциальных уравнений плоского движения твердого тела.
229
УДАР
Задание Д.13. Исследование соударений твердых тел
Варианты 1—10 (рис. 166). Вариант 1. Тележка 1 общей мас-
сой mi = 6000 кг, движущаяся со скоростью Vi =2,5 м/с по гори-
зонтальному прямолинейному пути, наталкивается на неподвижную
тележку 2, имеющую вместе с контейнером массу т? = 4000 кг. В
конце соударения тележка 2 приобретает скорость 1/2 = 2 м/с, а кон-
тейнер — угловую скорость вращения вокруг ребра А, закрепленного
упорной планкой. Считать контейнер массой то = 500 кг однородным
прямоугольным параллелепипедом (а = 0,8 м, h = 1,5 м). Вертикаль-
ные плоскости соударения тележек полагать гладкими. Поверхность
рельсов абсолютно шероховата, т. е. препятствует проскальзыванию
колес при соударении тележек. Моменты инерции колес относительно
их осей пренебрежимо малы.
Определить скорость тележки 1 в конце соударения с тележкой 2,
а также ударный импульс, воспринимаемый упорной планкой.
Вариант 2. Груз массой то = 500 кг падает с высоты h = 1 м в
точку D абсолютно жесткой балки, имеющей шарнирно-неподвижную
опору А и упругую опору В, коэффициент жесткости которой
с = 20000 Н/см; удар груза о балку — неупругий. Масса балки
m = 6000 кг, ее длина I = 4 м. Горизонтальное положение балки,
показанное на чертеже, соответствует статической деформации упру-
гой опоры под воздействием веса балки. Принять балку за тонкий
однородный стержень, а груз — за материальную точку.
Определить ударный импульс, воспринимаемый балкой в точке
D, а также наибольшую деформацию упругой опоры, считая, что
движение точки В происходит по прямой.
Вариант 3. Вследствие разрыва удерживающего троса груз мас-
сой то = 500 кг падает с высоты h = 1 м на платформу, покоящуюся
на одинаковых и симметрично расположенных рессорах. Точка А, в
которую падает груз, находится в вертикальной поперечной плоско-
сти симметрии платформы и отстоит от центра тяжести С платформы
на расстоянии d = 0,6 м.
Удар груза о платформу — неупругий. Масса платформы m =
= 5000 кг, ее радиус инерции относительно горизонтальной продоль-
ной оси симметрии ic = 0,5 м.
Принимая платформу за абсолютно твердое тело и считая груз
материальной точкой, определить скорость центра тяжести и угло-
вую скорость платформы в конце удара. Определить также ударный
импульс в точке А.
Вариант 4. Груз — однородный сплошной цилиндр массой
т = 200 кг и радиусом г = 0,2 м — перемещается транспор-
тером. Лента транспортера горизонтальна, ее постоянная скорость
v — 0,6 м/с; скольжение ленты по шкивам 1 и 2 отсутствует. В некото-
рый момент времени движение транспортера внезапно прекращается.
230

99Т эил
Поскольку поверхность ленты транспортера абсолютно шероховата,
т. е. не допускает скольжения тела при ударном воздействии, цилиндр
вследствие внезапной остановки транспортера-покатится по ленте.
Сопротивление качению пренебрежимо мало.
Определить ударный импульс, воспринимаемый абсолютно шеро-
ховатой поверхностью ленты при внезапной остановке транспортера.
Проверить найденную для этого скорость центра тяжести (или
угловую скорость) цилиндра по теореме Карно.
Определить ударный импульс, воспринимаемый упорной ступень-
кой высотой h = 0,03 м, о которую ударяется цилиндр, пройдя не-
которое расстояние, если не происходят отрыв цилиндра при ударе
о ступеньку и его проскальзывание.
Вариант 5. Транспортируемые грузы катятся из положения А
без начальной скорости по наклонной плоскости, составляющей угол
а = 15° с горизонтом, проходя вдоль нее расстояние si = 3 м,
и продолжают катиться по горизонтальной плоскости. Скольжение
отсутствует; коэффициент трения качения 6 = 0,8 см.
Определить, на каком расстоянии $2 должна быть поставлена упор-
ная ступенька высотой h. = 0,2 м, чтобы грузы, ударившись о ребро
F ступеньки, лишь поднимались на нее, не перемещаясь дальше
ребра F.
Расчет произвести для груза — однородного сплошного цилиндра
массой т = 500 кг и радиусом г = 0,5 м.
Считать, что отрыва цилиндра от ступеньки не происходит, а по-
верхность ступеньки абсолютно шероховата, т. е. препятствует сколь-
жению цилиндра при ударном воздействии.
Определить также горизонтальную и вертикальную составляющие
ударного импульса, воспринимаемого цилиндром со стороны ступень-
ки, при указанных условиях.
Вариант 6. Маятник состоит из стержня длиной I = 1,2 м и
однородного круглого диска радиусом г = 0,1 м. Масса стержня
пренебрежимо мала; масса диска то — 5 кг.
Маятник, отклоненный от положения устойчивого равновесия, па-
дает под действием собственного веса, вращаясь вокруг неподвиж-
ной octi О; в вертикальном положении, имея угловую скорость
ш = 3 рад/с, маятник ударяется о точку В боковой грани тела
D — однородного прямоугольного параллелепипеда массой т = бто
(а = 0,8 м, b = 0,4 м, h = 0,2 м).
Коэффициент восстановления при ударе к = 0,5. Поверхности ма-
ятника и тела D в точке соударения гладкие. Плоскость, на которой
покоится тело D, абсолютно шероховата, т. е. не допускает сколь-
жения тела при ударном воздействии.
Определить угловую скорость вращения тела D вокруг ребра А в
конце удара, а также ударный импульс, воспринимаемый шероховатой
поверхностью в точке А.
Вариант 7'. Рычаг состоит из двух абсолютно жестких стержней
АВ и AD, соединенных под прямым углом. Рычаг имеет неподвижную
232
горизонтальную ось вращения А и удерживается в точке В пружиной;
АВ - а = 1,5 м.
В точку D горизонтального стержня рычага, находящегося в по-
кое, с высоты h = 0,5 м падает груз массой то = 100 кг. Масса
рычага т = 1000 кг, радиус его инерции относительно оси враще-
ния гл = 0,5 м. Положение центра тяжести С рычага определяется
координатами хс = 0,4 м и ус = 0,3 м. Считать груз материальной
точкой, а удар груза о рычаг принять неупругим.
Определить ударный импульс, испытываемый грузом, а также го-
ризонтальную и вертикальную составляющие ударного импульса, вос-
принимаемого опорой А.
Вариант 8. На тележке 1 лежит груз — однородный полый тон-
костенный цилиндр массой то = 500 кг и радиусом г = 0,4 м, который
удерживается от возможного перемещения по тележке ступенькой и
наклонной плоскостью, составляющей угол а = 60° с горизонтом.
Тележка 1, имеющая вместе с грузом массу mi = 3000 кг, дви-
гаясь по горизонтальному прямолинейному пути, наталкивается со
скоростью vi = 3 м/с на неподвижную вагонетку 2 общей массой
m2 = 6000 кг. В конце соударения тележка 1 останавливается, а
цилиндр, ударясь о наклонную плоскость, начинает катиться по ней.
Отрыва цилиндра при ударе о наклонную плоскость не происходит;
абсолютная шероховатость наклонной плоскости исключает сколь-
жение цилиндра при ударном воздействии. Считать вертикальные
плоскости соударения тележки и вагонетки гладкими. Поверхность
рельсов абсолютно шероховата, т. е. препятствует проскальзыванию
колес при соударении тележек. Моменты инерции колес относительно
их осей пренебрежимо малы.
Определить угловую скорость цилиндра в конце удара о наклон-
ную плоскость; проверить найденное выражение угловой скорости
цилиндра по теореме Карно.
Определить скорость вагонетки 2 в конце соударения с тележкой 1.
Вариант 9. Тело D массой то, поступательно движущееся по
горизонтальной плоскости, ударяется со скоростью vq = 3 м/с об узел
С покоящейся фермы. Поверхности тела D и узла С в точке соуда-
рения — гладкие; коэффициент восстановления при ударе к — 0,5.
Абсолютно жесткая ферма имеет шарнирно-неподвижную опору О и
упругую опору А; ВС = а = 2 м. Масса фермы т = 2Ото, радиус ее
инерции относительно горизонтальной оси вращения О io — 1 м.
Определить угловую скорость фермы в конце удара и проверить
ее по теореме Карно.
Определить, какую скорость поступательного движения по гладкой
горизонтальной плоскости получит тело D после удара.
Вариант 10. Отклоненный на угол а = 60° от положения устой-
чивого равновесия маятник падает без начальной скорости под дей-
ствием собственного веса, вращаясь вокруг неподвижной оси О. В
вертикальном положении маятник ударяется точкой F о покоящееся
тело, находящееся в положении А.
233
Расстояния от точки О пересечения оси вращения вертикальной
плоскостью симметрии маятника до его центра тяжести С и до точки
F, находящейся в той же плоскости, ОС — d = 0,9 м и OF = / =? 1,1 м.
Масса маятника т = 18 кг, радиус его инерции относительно оси
вращения го = 1 м. Тело имеет массу то = 6 кг и может быть
принято за материальную точку. Коэффициент восстановления при
ударе маятника о тело к = 0,2.
Вследствие удара тело падает из точки А плоскости АВ в точку D
сладкой горизонтальной плоскости DE. Плоскость DE расположена
ниже плоскости АВ на Л = 1 м. Удар тела в точке D можно считать
неупругим (fci = 0).
Определить ударный импульс в точке D и уравнение движения те-
ла после этого удара, отнеся движение к координатной системе xDy.
Определить также угол /3 отклонения маятника после удара о
тело в точке А.
Варианты 11—20 (рис. 167). Вариант 11. При испытании на
ударную нагрузку маятник копра массой то = 500 кг, отклоненный
из положения устойчивого равновесия на угол а = 60°, падает без на-
чальной скорости под действием собственного веса, вращаясь вокруг
неподвижной оси О.
В вертикальном положении маятник ударяется точкой А о сере-
дину D покоящейся вертикальной балки BF массой то — 2000 кг,
имеющей шарнирно-неподвижную опору В и упругую опору F
(BF = 2а = 3,2 м); балку можно считать однородным тонким стерж-
нем; коэффициент Восстановления при ударе к = 0,4.
Расстояние от точки О пересечения оси вращения маятника вер-
тикальной плоскостью его симметрии до центра тяжести С маятника
ОС = d = 1,5 м, а расстояние от точки О до точки А, лежащей в той
же плоскости симметрии, О А = 1 = 2 м; радиус инерции маятника
относительно оси вращения io = 1,8 м. Отклонившийся после удара
на угол /3 маятник задерживается в этом положении специальным
захватом.
Определить ударный импульс в точке D и расстояние от точки
В до точки, в которую следует наносить удар, чтобы опора В не
испытывала ударного импульса.
Вариант 12. Тележка 1, имеющая вместе с контейнером массу
mi = 2000 кг и движущаяся по горизонтальному прямолинейному
пути со скоростью г>1 = 2,5 м/с, наталкивается на тележку 2 общей
массой т2 = 8000 кг, движущуюся со скоростью и2 = 0,5 м/с по тому
же пути и в том же направлении.
В конце соударения тележка 1 останавливается, а контейнер при-
обретает угловую скорость вращения вокруг ребра А, закрепленного
упорной планкой. Считать контейнер массой то = 500 кг однородным
прямоугольным параллелепипедом (а = 0,9 м, h = 1,2 м), а верти-
кальные плоскости соударения тележек — гладкими. Поверхность
рельсов абсолютно шероховата, т. е. препятствует проскальзыванию
234
S£Z
291 Э1Ч
колес при соударении тележек. Моменты инерции колес относительно
их осей пренебрежимо малы.
Определить угловую скорость контейнера в конце соударения теле-
жек и проверить найденное выражение по теореме Карно. Определить
скорость тележки 2 в конце соударения с тележкой 1.
Вариант 13. Ось О подвеса маятника движется поступательно в
горизонтальной плоскости с постоянной скоростью, при этом маят-
ник занимает вертикальное положение относительного покоя. Радиус
инерции маятника относительно оси О io = 0,8 м.
При внезапной остановке оси подвеса маятник, находясь в том
же положении и приобретя угловую скорость, ударяется точкой А
о покоящееся тело D, имеющее массу то = 2,5т, где т — масса
маятника. Поверхности маятника и тела D в точке соударения —
гладкие. Коэффициент восстановления при соударении маятника и
тела к = 0,6.
Расстояния от точки О до точки Л и до центра тяжести С маят-
ника, отсчитываемые вдоль его вертикальной оси симметрии, I = 1 м
и d = 0,7 м соответственно.
В конце соударения с маятником тело D приобрело скорость
и = 0,5 м/с поступательного движения по гладкой горизонтальной
плоскости.
Определить скорость оси О подвеса маятника перед внезапной
остановкой, а также угол /3 отклонения маятника после удара о
тело D.
Вариант 14. Абсолютно жесткая конструкция, имеющая фор-
му прямоугольного треугольника со сторонами АВ = а = 1 м и
BD = Ь = 2 м, опирается на шарнирно-неподвижную опору А и
удерживается в точке В пружиной.
В точку О конструкции, находящейся в состоянии покоя, при
котором сторона BD горизонтальна, с высоты h = 0,5 м падает груз
массой то = 200 кг; удар груза — неупругий. Считать конструкцию,
масса которой т = 20000 кг, однородным треугольником, а груз —
материальной точкой.
Определить угловую скорость системы в конце удара и проверить
найденное выражение угловой скорости по теореме Карно. Опреде-
лить также ударный импульс, испытываемый опорой А.
Вариант 15. При транспортировке грузы из положения А сколь-
зят без начальной скорости по наклонной плоскости, составляющей
угол а — 30° с горизонтом, проходя вдоль нее расстояние .Si = 3 м,
и продолжают движение по горизонтальной плоскости.
Определить, на каком наименьшем расстоянии BD должен быть
поставлен упор D для остановки грузов, чтобы они при этом не
опрокидывались. Расчет произвести для груза — однородного пря-
моугольного параллелепипеда массой т = 500 кг (6 = 2а = 1 м).
Принять коэффициент трения скольжения f = 0,2.
Определить также ударный импульс, воспринимаемый упором при
указанных условиях.
236
Вариант 16. Вагонетка 1 общей массой mi = 6500 кг, движущаяся
по горизонтальному прямолинейному пути, наталкивается на непо-
движную тележку 2, имеющую вместе с грузом массу = 4000 кг.
Груз — однородный полый тонкостенный цилиндр массой то = 500 кг
и радиусом г = 0,5 м — удерживается от возможного перемещения
по тележке двумя упорами — ступеньками.
В конце соударения вагонетка 1 и тележка 2 приобретают одина-
ковую скорость движения по горизонтальному прямолинейному пути,
а цилиндр — угловую скорость вращения вокруг ребра Е ступеньки
DE. Поверхность ступеньки абсолютно шероховата, т. е. препятствует
проскальзыванию цилиндра при ударном воздействии; отрыва цилин-
дра при ударе о ребро Е не происходит. После удара цилиндр подни-
мается на ступеньку DE высотой h = 0,1 м. Считать, что .за время
подъема цилиндра на ступеньку скорость тележки 2, приобретенная
ею в конце удара, остается постоянной, а вертикальные плоскости
соударения вагонетки и тележки — гладкие. Поверхность рельсов аб-
солютно шероховата, т. е. препятствует проскальзыванию колес при
соударении тележек. Моменты инерции колес относительно их осей
пренебрежимо малы.
Определить ударный импульс, испытываемый цилиндром со сто-
роны ступеньки DE, а также скорость вагонетки 1 до столкновения
ее с тележкой 2.
Вариант 17. Ось О подвеса маятника движется поступательно
в горизонтальной плоскости с постоянной скоростью v — 2 м/с, при
этом маятник занимает вертикальное положение относительного по-
коя. Маятник — однородный тонкий стержень длиной I = 1 м и
массой то = 20 кг.
При внезапной остановке оси подвеса маятник, находясь в том
же положении и приобретя угловую скорость, ударяется точкой Е
о неподвижный однородный полый тонкостенный цилиндр радиусом
г = 0,2 м и массой т = 2то- Коэффициент восстановления при со-
ударении тел к = 1/3. Поверхности маятника и цилиндра в точке
соударения — гладкие. Плоскость, на которой покоится цилиндр, аб-
солютно шероховата, т. е. не допускает скольжения тела при ударном
воздействии.
Определить ударный импульс, испытываемый осью О подвеса ма-
ятника при ее внезапной остановке, а также угловую скорость ци-
линдра в конце соударения с маятником.
Вариант 18. Абсолютно жесткая балка массой т = 8000 кг и
длиной I = 4 м имеет упругую опору А и шарнирно-неподвижную
опору В. Балка занимает в состоянии покоя, соответствующем ста-
тической деформации пружины А, горизонтальное положение; коэф-
фициент жесткости пружины с = 10000 Н/см. Радиус инерции балки
относительно горизонтальной оси вращения В ig = 2,2 м.
Балка испытывается на воздействие ударной нагрузки с помо-
щью парового молота, в котором масса молота, штока и поршня
то — 800 кг. Молот и связанные с ним части падают под давлением
237
пара на середину балки с высоты h = 0,8 м, имея в момент соприкос-
новения с балкой скорость, в два раза превышающую скорость при
свободном падении. Коэффициент восстановленйя при ударе молота
о балку к = 0,2.
Принять молот и связанные с ним элементы за материальную
точку; считать, что движение точек балки происходит по прямым.
Определить наибольшую деформацию упругой опоры А, считая,
что молот, отскочив от балки, не падает снова, а удерживается
обратным давлением пара; определить также ударный импульс, вос-
принимаемый опорой В.
Вариант 19. При испытании упорных (буферных) брусьев на
удар маятник копра массой т = 500 кг, радиус инерции которого от-
носительно неподвижной горизонтальной оси вращения О io = 1,2 м,
отклоняют от положения устойчивого равновесия на угол а = 90° и
отпускают без начальной угловой скорости. Падая, маятник точкой
А ударяется о буферный брус массой то = 1000 кг, коэффициент
жесткости комплекта пружин которого с = 10000 Н/см. Коэффици-
ент восстановления при ударе к = 0,5. Отклонившийся после удара
на угол /3 маятник задерживается в этом положении специальным
захватом.
Расстояние от точки О пересечения оси вращения вертикаль-
ной плоскостью симметрии маятника до его центра тяжести С
ОС = d = 0,9 м; расстояние от точки О до точки А, находящей-
ся в той же плоскости симметрии, О А = I = 1,5 м.
Пренебрегая трением скольжения бруса о горизонтальную плос-
кость, определить величину наибольшего сжатия буферных пружин,
ударный импульс в точке А, а также расстояние от точки О до
центра удара.
Вариант 20. В гипоциклическом механизме кривошип ОС массой
т = 2 кг и зубчатое колесо 1 радиусом г = 30 см вращаются с
угловыми скоростями wo = 1,5 рад/с и wj = 1 рад/с соответственно.
Зубчатое колесо 2 имеет массу = 8 кг и радиус г<2 = 10 см. В
некоторый момент времени колесо 1 внезапно останавливают.
Считая кривошип однородным тонким стержнем, а колесо 2 —
однородным сплошным диском, определить угловую скорость криво-
шипа в конце удара, а также ударные импульсы в точках А и С.
Варианты 21—30 (рис. 168). Вариант 21. Лента транспортера
составляет угол а = 15° с горизонтом. Радиусы шкивов г = 0,2 м.
На ленте транспортера, скольжение которой по шкивам 1 и 2 от-
сутствует, находится груз — однородный куб массой то = 200 кг
с ребрами длиной а = 0,5 м. В некоторый момент времени движе-
ние транспортера внезапно прекращается, при этом груз приобретает
угловую скорость вращения вокруг ребра А, закрепленного упорной
планкой.
238
6£Z
89T MJ
Определить наименьшую угловую скорость шкивов в момент оста-
новки, если груз опрокидывается; определить также ударный им-
пульс, воспринимаемый упорной планкой, при внезапной остановке
шкивов, вращающихся с этой угловой скоростью.
Вариант 22. Груз — однородный полый тонкостенный цилиндр
массой т = 800 кг и радиусом г = 0,4 м — покоится на движущейся
платформе между упорами — ступеньками. При внезапной остановке
платформы ступенька АВ не удерживает груз: цилиндр, поднимаясь
на ступеньку, прокатывается по участку BD = s = 1 м горизон-
тальной площадки BE и, ударившись о ребро F другого упора —
ступеньки EF высотой h = 0,1 м, поворачивается вокруг ребра F,
вследствие чего центр тяжести цилиндра поднимается по вертикали
на высоту hi = 0,07 м. Качение цилиндра от В до F происхо-
дит без скольжения; коэффициент сопротивления качению цилиндра
<5 = 0,1 см. Отрыва цилиндра при ударе о ступеньку не происходит,
абсолютно шероховатая поверхность ступеньки не допускает сколь-
жения цилиндра при ударном воздействии.
Определить, какую скорость имеет центр тяжести цилиндра в
начале движения на участке BD, а также ударный импульс, испы-
тываемый ребром F ступеньки EF.
Вариант 23. Маятник состоит из тонкого однородного стержня
АВ массой т = 4 кг, длиной I = 0,7 м и однородного сплошного шара
массой то = 2 кг и радиусом г = 0,1 м. Ось А маятника движется
поступательно в горизонтальной плоскости с постоянной скоростью
v = 1,4 м/с, при этом маятник занимает вертикальное положение
устойчивого равновесия.
Вследствие внезапной остановки оси подвеса маятник получает
угловую скорость вращения вокруг этой оси и, находясь в том же
вертикальном положении, ударяется точкой D о неподвижную вер-
тикальную плоскость. Поверхности маятника и вертикальной плос-
кости в точке соударения — гладкие. Коэффициент восстановления
при ударе к = 0,4.
Определить угловую скорость маятника при внезапной остановке
оси его подвеса и проверить найденное выражение по теореме Кар-
но. Определить также угол отклонения /3 маятника после удара о
вертикальную плоскость и ударные импульсы, испытываемые осью
А маятника.
Вариант 24. При испытании фундамента на ударную нагруз-
ку маятник копра, вращаясь вокруг неподвижной оси, падает из
вертикального положения, показанного на чертеже, под действием
собственного веса без начальной угловой скорости. В горизонтальном
положении маятник точкой А ударяется о середину верхней грани
покоящегося фундамента.
Масса маятника то = 500 кг, радиус его инерции относительно оси
вращения io = 1,8 м, масса однородного фундамента т = 10000 кг.
Коэффициент восстановления при ударе к = 0,2. Отклоняющийся
240
после удара маятник задерживается в этом положении специаль-
ным захватом. Расстояния от точки О пересечения оси вращения
вертикальной плоскостью симметрии маятника до его центра тяже-
сти С и до точки А, находящейся в той же плоскости симметрии,
ОС = d = 1,5 м и О А = 1 = 2 м.
Определить наибольшую упругую осадку основания, имеющего ко-
эффициент жесткости с= 16-105 Н/см, ударный импульс в точке А
и расстояние от точки О до центра удара.
Вариант 25. Тележка 1 общей массой тгц = 3000 кг, двигаясь по
горизонтальному прямолинейному пути со скоростью щ = 5 м/с,
наталкивается на тележку 2, имеющую вместе с грузом массу
m2 = 2000 кг и движущуюся по тому же пути и ‘в том же на-
правлении СО скоростью 1)2 = 1 м/с.
Груз — однородный полый тонкостенный цилиндр массой то =
= 500 кг и радиусом г = 0,5 м — удерживается от возможного
перемещения по тележке двумя упорами — наклонными плоскостями.
В конце соударения скорости движения тележек по тому же гори-
зонтальному прямолинейному пути изменяются, а цилиндр, ударяясь
о наклонную плоскость АВ, составляющую угол а = 60°, начинает
качение по ней.
Цилиндр по наклонной плоскости проходит без скольжения рассто-
яние 5 = 0,1 м; сопротивление качению пренебрежимо мало. Отрыва
цилиндра при ударе о наклонную плоскость не происходит, абсо-
лютная шероховатость наклонной плоскости исключает скольжение
цилиндра при ударном воздействии.
Считать, что за время подъема цилиндра на наклонную плос-
кость скорость тележки 2, полученная ею в конце удара, остается
постоянной, а вертикальные плоскости соударения тележек — глад-
кие. Поверхность рельсов абсолютно шероховата, т. е. препятствует
проскальзыванию колес при соударении тележек. Моменты инерции
колес относительно их осей пренебрежимо малы.
Определить скорость тележки 1 в конце соударения с тележкой 2,
а также ударный импульс, воспринимаемый наклонной плоскостью
со стороны цилиндра.
Вариант 26. В эпициклическом механизме кривошип ОС мас-
сой т = 3 кг и длиной I = 30 см вращается с угловой скоро-
стью wo = 2 рад/с, а зубчатое колесо 1 — с угловой скоростью
= 3 рад/с. Масса зубчатого колеса 2 m2 = 10 кг, а радиус
Г2 = 10 см.
В некоторый момент времени колесо 1 внезапно останавливают.
Считая колесо 2 однородным сплошным диском, а кривошип — од-
нородным тонким стержнем, определить угловую скорость колеса 2
в конце удара, а также ударные импульсы, в точках А и С.
Вариант 27. В точку D абсолютно жесткой балки массой
т = 5000 кг и длиной I = 3 м с высоты h = 1,2 м падает груз
массой т = 400 кг. Балка имеет шарнирно-неподвижную опору А и
241
упругую опору В; в состоянии покоя балка занимает горизонтальное
положение, показанное на чертеже. Удар груза о балку — неупругий.
Считать балку однородным тонким стержнем; а груз — матери-
альной точкой.
Определить угловую скорость балки в конце удара и проверить
найденное выражение угловой скорости по теореме Карно. Опреде-
лить также ударный импульс, воспринимаемый опорой А.
Вариант 28. Механизм состоит из шестерни с кулачками, кото-
рая приводится во вращение вокруг неподвижной горизонтальной оси
О. Масса механизма т = 50 кг, радиус инерции относительно оси
вращения io = 0,2 м. Механизм сбрасывает металлические болван-
ки массой то = 2 кг из точки А горизонтальной плоскости АВ на
горизонтальную плоскость ED на расстояние d = 1,5 м, отсчитыва-
емое по горизонтали от точки А. Цлоскость ED расположена ниже
плоскости АВ на высоту h = 1 м.
Неупругий удар между кулачком и болванкой (ki — 0) происходит
на расстоянии I = 0,4 м от оси вращения механизма. Коэффици-
ент восстановления при ударе болванки о гладкую горизонтальную
плоскость в точке Е к% = 0,2.
Принимая болванку за материальную точку, определить угловую
скорость шестерни в начале удара, а также ударные импульсы, ис-
пытываемые болванкой в точках А и Е.
Вариант 29. Маятник, отклоненный от положения устойчивого
равновесия на некоторый угол а, падает без начальной скорости
под действием собственного веса, вращаясь вокруг неподвижной оси
О, и в вертикальном положении точкой А ударяется о покоящийся
однородный полый тонкостенный цилиндр массой то = 200 кг и ра-
диусом г = 0,2 м. Масса маятника т — 100 кг, радиус его инерции
относительно оси вращения io = 1 м. Расстояния от точки О пересе-
чения оси вращения вертикальной плоскостью симметрии до центра
тяжести С маятника и до точки А, находящейся в той же плос-
кости симметрии, ОС = d = 0,8 м и О А = Z = 1,2 м. Коэффициент
восстановления при соударении маятника и цилиндра к = 0,6.
После удара цилиндр скользит, не вращаясь, по гладкой гори-
зонтальной плоскости и, натолкнувшись на ступеньку DE высотой
h = 0,05 м, поднимается на нее, не перемещаясь дальше ребра Е.
Отрыва цилиндра от ребра Е при ударе о ступеньку не происходит, а
абсолютно шероховатая поверхность ступеньки исключает проскаль-
зывание цилиндра при ударном воздействии.
Определить угол а первоначального отклонения маятника, а также
ударный импульс, испытываемый цилиндром со стороны маятника.
Вариант 30. Рычаг состоит из двух абсолютно жестких стерж-
ней OD и OF, соединенных под прямым углом; OD = а = 1 м,
OF = Ь = 1,5 м. Рычаг имеет шарнирно-неподвижную опору О и
удерживается в точке Е пружиной. Масса рычага т = 400 кг, ради-
ус его инерции относительно оси вращения О io = 0,4 м.
242
Рычаг находится в покое, соответствующем статической деформа-
ции пружины, при этом его стержень OD горизонтален. В точку
D рычага падает груз А массой гпа = 20 кг с высоты h = 0,5 м.
Удар груза о стержень OD рычага — неупругий (fci = 0). Приобретя
угловую скорость, рычаг точкой F ударяется о неподвижное тело В
массой тв = 120 кг; коэффициент восстановления при этом ударе
fc2 = 0,2. Считать груз А и тело В материальными точками.
Определить, какую скорость получает тело В в конце его соуда-
рения со стержнем OF, а также ударный импульс, воспринимаемый
телом В.
Пример выполнения задания (]
сплошной цилиндр массой т = 500
лежит на движущейся платформе :
перемещения по платформе упорами
При внезапной остановке плат-
формы цилиндр ударяется о ребро
D ступеньки BD высотой h =
= 0,1 м и поднимается вверх на
эту ступеньку. Далее цилиндр ка-
тится по участку DE горизонталь-
ной площадки DK и, ударившись
о другой упор — наклонную плос-
кость KN, составляющую угол
а = 60° с горизонтом, проходит по ней расстояние FN = s = 0,1 м.
Качение цилиндра не сопровождается скольжением, сопротивление
качению пренебрежимо мало.
Отрыва цилиндра при ударах о ступеньку и о наклонную плоскость
не происходит, абсолютная шероховатость ступеньки и наклонной
плоскости исключает скольжение цилиндра при ударном воздействии.
Определить скорость платформы до ее остановки, а также удар-
ные импульсы, испытываемые цилиндром со стороны ступеньки и
наклонной
»ис. 169). Груз — однородный
кг и радиусом г = 0,5 м —
I удерживается от возможного
— ступеньками.
Рис. 169
Поверить найденные выражения угловых скоростей цилиндра после
ударов о ступеньку и наклонную плоскость с помощью теоремы
Карно.
Решение. При внезапной остановке платформы поступательное
движение цилиндра мгновенно изменяется на вращательное движение
вокруг ребра D ступеньки BD, т. е. цилиндр испытывает удар.
Составим уравнение, выражающее теорему об изменении кинетиче-
ского момента механической системы при ударе, взяв за ось моментов
горизонтальную ось, проходящую вдоль ребра D (положения I и II,
соответствующие началу и концу удара о ребро D ступеньки BD,
совпадают; рис. 170, а):
Гцо - Lid =
243
Рис. 170
Сумма моментов внешних ударных импульсов, приложенных к ци-
линдру, относительно оси D равна ^2	= 0 (ударный импульс
Sd пересекает ось D) и потому
Lhd = Lid-
Кинетический момент цилиндра относительно оси D в начале уда-
ра
Ью = mvci(r - К),
где vci — v — скорость центра тяжести цилиндра в начале удара,
равная; скорости платформы до внезапной остановки.
Кинетический момент цилиндра относительно оси D в конце удара
Liid —
где Jd — момент инерции цилиндра относительно оси D; шц —
угловая скорость цилиндра в конце удара
Liid = (Jc + тг2)шц = (mr2/2 + тг2)о>ц = 3/2тг2шц.
244
Но
Lud = Lid,
т. e.
3/2mr2ti>n = mv{r — h),
откуда
wii = 2(r - h)v/(3r2).	(1)
Проверим полученное выражение (1) угловой скорости цилиндра
по теореме Карно:
- Гц = Т*,
где Т[ — кинетическая энергия системы материальных точек в начале
удара; Гц — кинетическая энергия системы в конце удара; Т* —
кинетическая энергия, соответствующая потерянным скоростям точек
системы.
Кинетическая энергия цилиндра в начале удара о ступеньку
Ti = l/2mv2.
Кинетическая энергия цилиндра в конце удара о ступеньку
Тп = l/2(znt£ + Jc^n)-
Теперь выведем выражение кинетической энергии, соответствую-
щей потерянным скоростям Ап, точек Mi твердого тела при плоском
движении:
Ari = vn - vai,
где
ГЦ = VCI + VcMi ’ Гщ = Ген + VcMi>
причем вращательные скорости вокруг оси С имеют выражения
^СМ, = WI X rt, v£M. = X п-
Кинетическая энергия тела, соответствующая потерянным скоро-
стям его точек,
Г* = 1/2	[(гС1 - ген) + tfCM, - $м.)]2 ,
т. е.
Т* = 1/2 mi(rci - ген)2 + 2 У2	- гсп)(гсм< ~ ^см,)+
+	-17см,)2] 
Здесь
У2 пч(гст - ген)2 = m(rci - ген)2;
У2 "ii(rci - vcn^cMt ~	) = (vci - ген) У2 m№i ^п х п) =
245
= (vci - ven) [(<^i - <3ц) x mifi] = 0;
так как
57 тЛ = т?с = 0;
52т№см< ~ ^cMt) = 52m^Win ~ wnn)2 = Jc(wi - ип)2.
Таким образом,
Т* = l/2m(vci — ven)2 + l/2<7c(<^i — шп )2,
или
Т* = l/2m [(«cix ~ ^сщ)2 + (vciy ~ vcnv)2] + l/2Jc(wi - о>п)2. (2)
Выражение (2) является общей формулой кинетической энергии,
соответствующей потерянным скоростям точек твердого тела при
плоском движении.
Для цилиндра (рис. 170, б) в рассматриваемой задаче '
Т* = l/2m[(t>ci - vCn cos/?)2 + г2.п sin/3] + l/2Jcu>n,
т. e.
T* = l/2m(^! - 2vCiVen cos/3 + i£n) + 1/2 Jc^'h-
Так как
t’ci = v, vCn = Wir, Jo = mr2/2,
то, приравнивая 7j — Tn и T*, получаем
l/2mv2 — l/2mu2lr2 — l/47nr2Wn = l/2mv2 + mvcjnr cos /3+
+l/2mw2Ir2 + 1/4т7гг2алр1,
или
3/2mw2Ir2 = пгаддцг cos/3,
где
cos /3 = (r — h)/r.
Отсюда,.
o?ii = 2(r — /i)r/(3r2).
Составим уравнение, выражающее теорему об изменении кине-
тической энергии механической системы и соответствующее подъ-
ему цилиндра на ступеньку BD из положения II в положение III
(рис. 170, в):
Tm-Tn^Af.
Так как перемещение осуществляется поворотом вокруг оси D, то
1/27дси2ц — 1/2Jdu?2j = —Gh,
или
3/4mr2w2II — 3/4mr2cj[2[ = —mgh,
246
откуда
шш = ^/ч21 -4<z/i/(3r2).	(3)
Составим уравнение, выражающее теорему об изменении кинетиче-
ской энергии механической системы и соответствующее качению ци-
линдра на участке DE из положения III в положение IV (рис. 170, г):
Tiv - Тш = 52 •
Так как на рассматриваемом перемещении ^2 Af = 0, то
Ты = Tin,
т. е.
v-сы = fcin и wvi = tuin-	(4)
При соприкосновении цилиндра с наклонной плоскостью мгновен-
ная ось вращения цилиндра (мгновенный центр скоростей) мгновенно
перемещается из Е в F, т. е. цилиндр испытывает удар.
Составим уравнение, выражающее теорему изменения кинетическо-
го момента механической системы при ударе, взяв за ось моментов
горизонтальную ось, совпадающую с образующей F цилиндра (по-
ложения цилиндра IV и V, соответствующие началу и концу удара,
совпадают; рис. 170, д):
Lvf — Livf = 52	).
Но	=0, так как ударный импульс Sp, приложенный к
цилиндру, пересекает ось F. Поэтому
Lvf = Tivf-
При вычислении кинетических моментов цилиндра Livf и Lvf
используем теорему о кинетическом моменте системы в общем случае
ее движения.
Кинетический момент относительно оси F в начале удара
Livf = mvcwrcosa + Jc^iv,
где vciv — i^ivEC, поскольку мгновенный центр скоростей — в точке
Е\
' Livf = тмы?2 cosa + {тг2/2)шы = mwivr2(cosa + 1/2).
Кинетический момент относительно оси F в конце удара
Lvf = mvcyr + .7с wy,
где vcv = ^\'CF\ так как мгновенный центр скоростей — и точке F;
Lve = mwyr2 + (mr2/2)wv = 3/2mwyr2 •
Но Lvf = Livf, т. е.
3/2mwyr2 = mwvir2(coso + 1/2),
247
поэтому
щу = wiv(2cosa + l)/3.	.	(5)
Проверим найденное выражение угловой скорости цилиндра по
теореме Карно:
Tiv - 7v = Т*.
Кинетическая энергия цилиндра в начале удара о наклонную плос-
кость
Tiv = 1/2(z7W£IV + Jc^jv)-
Кинетическая энергия цилиндра в конце удара о наклонную плос-
кость
Tv = l/2(nw^v + Теле-
кинетическую энергию, соответствующую потерянным скоростям
точек цилиндра, найдем, используя формулу (2) (рис. 170, д'):
Т* = l/2m[(vcTV„ - vcvx)2 + («civ,, - «cv„)2] + l/2Jc,(wiv - ^v)2,
т. e.
T* = 1/2т[(цсту -vevcosa)2 + r/;vsin2a] 4-1/2Jc(i^iv — wv)2,
или
T* = l/2m(v0lv — 2vcivvcv cosa +	+ l/2Jc(^iv — w)2-
Так как
Very =	Vcv = WC
то, приравнивая Zjy — Ту и T*, получаем
l/2mcv2vr2 + l/4mr2u>2v — 1/2тшуГ2 — 1/4иЛ( = l/2mw2yr2 +
+тш\ушуг2 cosa + 1/2та)уГ2 + l/4mr2wfv —
— l/2mr2 адуШу + l/4mr2Wy,
или
3/2<z>y = wiya>v(cosa + 1/2),
откуда -
cjy = wiv(2cosa + l)/3.
Составим уравнение, выражающее теорему об изменении кинети-
ческой энергии механической системы и соответствующее качению
цилиндра по наклонной плоскости из положения V в положение VI
на расстояние s (рис. 170, е):
Tvi - Ту = 5? Д£ •
Так как Tyi = 0, то
(mt£v Jc^y\	
2CV -I-2^" I = ~Gsslna'
248
или
mw?,r2 (mr2/2)ul
----£----------—- = -mgs sin а,
т. е.
3/4а?уГ2 = gssina,
откуда 
2 /gssina
Используя выражения (3)—(5), находим
_	/	. 4gh
И у (2 cos а 4- I)2	Зг2
Учитывая выражение (6), имеем
__ 2 / 3gssina gh
*^11 г у (2cosa + l)2	3
Таким образом, скорость платформы, по (1),
_ Зг2 2 / 3g s sina	, gh
V 2(r-h)ry (2cosa + l)2	3 ’
t. e.
v = 3,68 м/с.
Найдем ударный импульс, воспринимаемый цилиндром со стороны
ступеньки, для чего составим уравнения, выражающие теорему об
изменении количества движения механической системы при ударе, в
проекциях на оси х и у (рис. 170, а):
mvcnx - mvCi, =	mvCuy - mvciy = Y,Sitn
или
-maciicos(3 - (-nwci) = Sdx', macii sin/3 = Sdv,
откуда
Sdx — mvci — mvcu cos /3 = mv — mw(r — h)/r = mv[l — 2/3(r — 7i)2/r2],
t. e.
SDx = 1055 H • c,
Soy = mvcn sin (3 = тх'цг\/1 — cos2 (3 =
= 2/3(r — /i)(ma/r)y/l — (r — h)2/r2,
t. e.
Soy = 589 H • c.
Ударный импульс, воспринимаемый цилиндром со стороны сту-
пеньки,
SD = y/s2Dx + S2Dy,
или Sq = 1208 Н • с.
249
Найдем ударный импульс, воспринимаемый цилиндром со стороны
наклонной плоскости, для чего составим уравнения, выражающие
теорему об изменении количества движения системы при ударе, в
проекциях на оси £ и т] (рис. 170, д):
mvcvt - mvcive =	mvcvr, - mvcwrj =
или
—(—mvciv sin о) — Sfs.', mvcv — rnvcty cos a = Sfu,
откуда
Sf£ = mvcrv sin a = muryr sin a = тЗиуг sin o/[(2 cos a 4- 1)];
Sf$ = mvcy — mvcw cos a = mwyr — тодут cos <a = mwyr—
—m3LJyrcosa/[(2cosa -4-1)].
Используя выражение (б), найдем
Sf(, = 6mi/gssina/3sina/[(2 cosa 4-1)],
т. e.
SF( = 691 H • c;
Sfti = 2m\/gS sina/3[l - 3 cos «/(2 cos a 4-1)],
t. e.
Sftj = 133 H • c.
Ударный импульс, воспринимаемый цилиндром со стороны наклон-
ной плоскости,
или '
SF = 704 Н • с.
III. АНАЛИТИЧЕСКАЯ МЕХАНИКА
ПРИНЦИП ВОЗМОЖНЫХ ПЕ РЕМЕЩЕНИЙ
Задание Д.14. Применение принципа возможных
перемещений к решению задач о равновесии сил,
приложенных к механической системе
с одной степенью свободы
Схемы механизмов, находящихся под действием взаимно уравнове-
шивающихся сил, показаны на рис. 171—173, а необходимые данные
приведены в табл. 50.
Применяя принцип возможных перемещений и пренебрегая сила-
ми сопротивления, определить величину, указанную в предпоследней
графе табл. 50.
Примечание. Механизмы в вариантах 3, 6, 10, 1—4, 16, 18, 19, 25 и 30 располо-
жены в вертикальный плоскости, а остальные — в го]ризонтальной-
250
Хаблица 50
Номер варианта (рис. 171-173)	Линейные размеры	Силы, Н		Момент пары сил М, Н м	1 Коэффициент жесткости с, Н/см	Деформация пружины h, см	Величины подлежа- щие определению	Примечания
		Q	р					
1	ОА=Ю см	—	—	20	—	—	р	
2	О1Л=20 см	—	100	—	—	—	м	
3	ri=20 см, Г2=30 см, г$=40 см	—	—	100	—	—	Q	
4	ОС:ОА=4 : 5	—	200	—	—	4	С	
5	ОА=ЮО см	—	—	10	—	—	р	
6	П=15 см Г2=50 см, гз=20 см, О1Л=80 см	200					р	Вес рукоятки О1А не учи- вать
7	ОС=ОА		—	—	10	3	р	Пружина сжа- та
8	ОС=АС	—	200	—	10	2	Q	То же
9	ОА=20 см	200	—	—	—	—	м	
10	7*1=15 см, 7*2=40 см, гз=30 см, ОЛ=ЮО см	2 • 103		—	—	4	С	Вес рукоятки О А не учиты- вать
11	ОА=20 см	—	—	300	—	—	р	
12	01.0=60 см, ОА= =20 см	—	—	100	—	—	р	
13	ОА=40 см	—	—	200	—	—	р	
14	ОВ=2  ОА	20			25	3	р	Вес стержней ОА и ОВ не учи- тывать; пружи- на растянута
15	AC=OC=OD	3 • 103	—	—	250	3	р	Пружина сжа- та
16	di=SO см, d.2=25 см £1 = 100 см, I2 = 50 см	5 • 103			100	4	р	Вес стержней О, А и О^В не учитывать. Пружина сжа- та
17	ОА=20 см	—	—	200	—	—	р	
18		200	200	—	100	—	h	Р — вес блока радиусом Г2
19	7*1=20 см, Т2=30 см, ОЛ=25 см	—	—	100	—	—	Р	Вес звена АВ не учитывать
20	ОА=АВ=АС=50 см	50	100	—	—	—	М	
21	OA=AB=AC=DC= =25 см	—	200	—	—	—	М	
22	ОА=40 см	—	—	400	—	—	Р	
23	00=204=100 см	—	200	50	50	—	h	
24	AD=OD=OB см	—	250	—	150	2,5	Q	Пружина сжа- та 
25	OD=DB=Ofi АО	400			120	3	р	Вес стержней АО и ВО не учи- тывать. Пружи- на растянута
26	ОЛ=25 см	—	500	120	—	2	С	Пружина рас- тянута
27	ОВ=АВ	—	—	—	180	2	р	
28	ОВ=Ь/4ОА	—	450	—			Q	
29	AO=3Q см, BD=OiO	—	—	120	100	—	h	
30	П = 15 см, Г2=36 см, гз=10 см, Г4=20 см	—	600	—	—	—	Q	
251

ш эиа
ESS


£2.1 эиа
Пример выполнения
задания. Дано: Q = 100 Н;
с = 5 Н/см; ri = 20 см;
Г2 = 40 см; гз = 10 см;
О А = I = 50 см; а = 30°;
/3 = 90° (рис. 174).
Определить деформацию
h пружины, пренебрегая ве-
сом звеньев ОА и АВ.
Решение. Рассматрива-
емый механизм (рис. 174)
находится под действием
следующей системы урав-
новешивающихся сил: силы
упругости F, сил тяжести
Gi вала 1 с шестерней 2,
Оз шестерни 3, G4 ползуна
В, Q груза и реакций опор.
Составим уравнение работ,
выражающее принцип возможных пе-
ремещений:
57 Pi$Si СО8(Л 6Si) - 0.
Связи, наложенные на механизм, допускают следующие возможные
перемещения его звеньев: поворот вала 1 с шестерней 2 на угол
Stpi, поворот шестерни 3 на угол <5<^з и поступательное перемещение
груза по вертикали на 6sq. Ползун В может иметь перемещение
6s в (перемещение по горизонтали), а точка А.— перемещение 6sа
(отрезок 6sa перпендикулярен ОА). Уравнение работ, выражающее
принцип' возможных перемещений, получает вид
Q6sq — F6sb — 0.
(1)
Найдем зависимость между возможными перемещениями точек си-
стемы. Поскольку нить, к которой привязан груз Q, нерастяжима и
скольжение между нитью и валом 1 отсутствует, перемещение груза
Q равно перемещению точки обода колеса 1. Поэтому угол поворота
вала 1 и шестерни 2
6^1 = 6sq/ti.
Перемещение точки К обода колеса 2
6si = r2&Pi = (r2/n)6sQ.
Так как скольжение между шестернями 2 и 3 отсутствует, то
возможные перемещения точек касания этих шестерен равны и угол
поворота шестерни 3
бсрз - бзх/тз = [г2/(пгз)]<5«<э•
255
Перемещение точки А кривошипа, жестко соединенного с колесом,
dsA - ОА&Рз = [ril/tnr^SQ.
Для определения зависимости между возможными перемещениями
ds а и ds в найдем положение мгновенного центра вращения звена
АВ — точки Р.
Тогда
dsB/dsA = РВ/РА\ dsB = (PB/PA)dsA.
можных перемещении точек системы, пол;
QdsQ — сК[г21/(гзГз cos 30°
откуда
Из ДАРВ
РВ/РА = 1/cos 30°.
Теперь
dSB = [Г21/(Г1Гз cos30o)]^5<2-
Сила упругости пружины пропорциональна ее деформации: F = ch.
Подставив в уравнение работ (1) выражения силы упругости и воз-
учим
)]6sq = 0,
1,74 см.
Следовательно, пружи-
на сжата на 1,74 см.
Решим ту же задачу
составлением уравнения
мощностей, выражающего
принцип возможных ско-
ростей:
57 =
или
57 PiVi СО8(Л, Vi) = 0.
Сообщим валу 1 с ше-
стерней 2 возможную уг-
ловую скорость W1-2 вр-
круг ОСИ О1, допустив,
по часовой стрелке
(рис. 175). Груз Q по-
лучит вертикальную ско-
рость vq. Шестерня 3 вместе с жестко соединенным с нею кривоши-
пом О А приобретает угловую скорость вокруг оси О. Звено АВ
будет иметь угловую скорость шдв, которую покажем вокруг мгно-
венного центра скоростей Рав-, находящегося на пересечении перпен-
дикуляров к скоростям va и vb точек А и В звена АВ (скорость va
256
точки А, принадлежащей кривошипу ОА, направлена перпендикуляр-
но ОА, а скорость vb точки В, принадлежащей ползуну, направлена
параллельно его направляющим).
Составим уравнение мощностей:
-Qvq + FvB = О,
или
-Qvq + chve = 0.
Здесь неизвестными являются деформация пружины h, а также
скорости Vq и Vb-
Скорость груза равна скорости точек обода колеса, так как нить,
к которой подвешен груз, нерастяжима, й поэтому
z>Q=wi-2n-
Скорости точек касания К шестерен 2 и 3 выражаются соответ-
ственно следующим образом:
vK = й>1_2г2; vK = ш3г3;
они равны между собой, так как проскальзывание шестерен отсут-
ствует.
Скорость точки А можно выразить двояко, поскольку она принад-
лежит кривошипу О А и звену АВ одновременно:
VA = и?з • О A; VA = Ш АВ  АР.
Скорость точки В звена АВ
vb = oJab  BP.
Таким образом,
u>i_2г2 = ш3г3;	и3 • ОА = шав • АР,
откуда
Ш1-2Г2	ш3  ОА Ш1-2Г2 • ОА
=	; ШАВ =	= гзАр 
Скорость точки В
г> г> Ш1-2Г2  ОА • ВР
vb=^ab-BP=------------------.
Из ДАРВ
АР = ВР • cos 30°.
Следовательно,
_____________________________ Ш1—2Г2• О А
Vb Г3 cos 30°
Итак, уравнение мощностей приобретает вид
_QU1_2r1+ch^^=0.
Г3 cos 30
257
Разделив все члены этого уравнения на од_2, найдем искомую
деформацию пружины:
__ Qrir3cos30°
CT2I
Задание Д.15. Применение принципа возможных
перемещений к определению реакций опор
составной конструкции
Применяя принцип возможных перемещений, определить реакции
опор составной конструкции.
Схемы конструкций показаны на рис. 176—178, а необходимые для
решения данные приведены в табл. 51. На рисунках все размеры
указаны в метрах.
Таблица 51
Номер варианта (рис. 176—178)	Нагрузка				Номер варианта (рис. 176—178)	Нагрузка			
	Л, кН	Pi, кН	Я, кН/м	М, кН • м		Л, кН	Pi, кН	Я, кН/м	ЛГ, кН  м
1	15	14	3	10	16	3	10	2	10
2	13	12	2	6	17	1	8	1	8
3	11	10	1	5	18	3	6	3	6
4	9	8	3	14	19	5	4	2	7
5	7	6	2	12	20	7	2	1	5
6	8	5	1	4	21	10	9	2	4
7	7	4	2	10	22	8	7	1	7
8	6	6	1	7	23	6	. 5	2	8
9	5	8	3	8	24	4	3	1	3
10	4	10	2	6	25	2	1	2	2
11	12	11	1	12	26	7	1	2	7
12	10	6	2	10	27	6	2	1	5
13	9	5	1	6	28	5	3	2	10
14	7	10	2	13	29	4	4	1	5
15	6	8	1	5	30	3	5	2	10
Пример выполнения задания. Дано: составная рама (рис. 179)
Pi = 2 кН; = 4 кН; М = 5 кН • м; q = 1,5 кН/м.
Определить реакции опор рамы.
258
Рис. 176
096
Z21 эи<1
Рис. 178
261
Решение. Заменим равномерно распределенную нагрузку сосре-
доточенной силой Q — q  4 = 1,5 • 4 = 6 кН, приложенной в середине
загруженного участка.
Найдем реакцию подвижной опоры А, для чего мысленно отбросим
эту связь, заменив ее действие реакцией (рис. 180).
Составим уравнение работ, выражающее принцип возможных пере-
мещений, при этом учтем, что работа силы при повороте тела равна
произведению момента силы относительно центра вращения на угол
поворота тела:
Q  26ip + М&р — Ra  4<5<р = 0,
откуда
Ra = (Q  2 + М)/4;	RA = 4,25 кН.
Для определения реакций заделки воспользуемся уравнением воз-
можных мощностей
57 = °’
где v — возможные скорости.
Сначала найдем реактивный момент Мв- Для этого отбросим
связь, препятствующую повороту правой части рамы, заменив за-
делку шарнирной неподвижной опорой и приложив искомый момент
Мв (рис. 181).
Сообщим правой части рамы возможную угловую скорость wj во-
круг оси В по направлению вращения часовой стрелки. Левая часть
рамы получит угловую скорость а>2 вокруг мгновенного центра скоро-
стей О1, находящегося на пересечении перпендикуляров к скоростям
262
vc и va точек С и А (скорость точки С направлена перпендикуляр-
но СВ, а скорость точки подвижной опоры направлена параллельно
опорной плоскости).
, Скорость точки С можно выразить двояко, поскольку эта точка
принадлежит левой и правой части: vc = wi - СВ; vc = u>2 COi, т. е.
LVl • СВ = U?2 ’ СО1,
откуда
= W2 = поскольку СВ = СО1-
Составим уравнение возможных мощностей:
Мш — Q • 2и — Pi  2ш — Р% • 5о> — Mgcv = О,
где
Р2 = Л sin 30°.
Из уравнения следует
Мв = М - Q • 2 - Pi • 2 - F2 • 0,5 • 5.
Отсюда
Мв — —21 кН • м.
Для определения вертикальной составляющей Уь реакции заделки
отбросим связь, препятствующую вертикальному перемещению точки
В, заменив жесткую заделку скользящей (вертикальными направля-
ющими) и приложив реакцию YB (рис. 182).
Сообщим правой части рамы возможную скорость v поступательно-
го движения вверх (направляющие исключают возможность поворота
правой части).
Левая часть рамы получит угловую скорость ш вокруг мгновенного
центра скоростей О2, находящегося на пересечении перпендикуляров
к скоростям vc и va точек С и A (vc = v)- Составим уравнение
возможных мощностей:
Мы — Q • 2о> — Pi • v — Р." • v + Yb • v = 0,
263
где
Р% = Р2 cos 30°, v = vc = ш • CO2 = a>  4.
Следовательно,
Mcv — Q  2a> — Pi  4cv + Рг  0,866 • 4u> + Yb • 4w = 0,
откуда
YB = (-M + Q • 2 + Pi • 4 - P2 • 0,866 • 4)/4 = 0,29 кН.
Для определения горизонтальной составляющей Хв реакции задел-
ки отбросим связь, препятствующую горизонтальному перемещению
точки В, заменив жесткую заделку скользящей (горизонтальными
направляющими) и приложив реакцию Хв (рис. 183).
Сообщим правой части рамы возможную скорость v поступатель-
ного движения вправо (направляющие исключают возможность по-
ворота правой части). Скорости точек С и А левой части будут
параллельны. Следовательно, левая часть рамы, как и правая, по-
лучит скорость v поступательного движения.
Составим уравнения возможных мощностей:
—Р2 cos 60° • v + Хв • v = 0,
откуда
Хв = 4 • 0,5 = 2 кН.
Проверим правильность решения задачи.
Убедимся, что найденные числовые значения величин удовлетво-
ряют уравнениям равновесия сил для всей рамы (рис. 184):
=° и 52MiB =0.
Имеем
^Yt = Ra-Q- Р1+Р2 cos 30° 4- YB = 4,25 -6-24-4- 0,87 4- 0,29 =
= 8,02 - 8,00 с; 0;
5 Mib — —Ra  8 4- M 4- Q • 6 4“ Pi • 2 + P2 cos 60° • 5 4-	—
= -4,25 • 8 4- 5 4- 6 • 6 4- 2 • 2 4- 4 • 0,5 • 5 — 21 = 55 — 55 = 0.
ПРИНЦИП ДАЛАМБЕРА
Задание Д.16. Применение принципа Даламбера
к определению реакций связей
Определить реакции внешних связей механической системы:
а)	в произвольный момент времени — для вариантов 4, 5, 10,
12—14, 16—18, 21—30 (рис. 185—187);
б)	в момент времени t = ti — для вариантов 1, 8, 9, 11, 20;
в)	в тот момент времени, когда угол поворота = y>i, — для
вариантов 2, 3, 6, 7;
264
г)	в положении, показанном на чертеже для вариантов 15 и 19.
На схемах (рис. 185—187) плоскость хОу (хАу) горизонтальна,
плоскость yOz (у Az) вертикальна. Необходимые для решения данные
приведены в табл. 52, в которой и — угловая скорость, и uJq —
значения угла поворота и угловой скорости в начальный момент
времени.
Таблица 52
ь «О я <»	Ш1	Ш2	1	R	м,	о — I	tl	¥>1			
Номер вар1 (рис. 185-1	кг		м		Нм	"и Й О з	С	град		5- а о 3	Примечания
1	20	-	0,60	-	1,0		10	-	0	0	
2	25	-	0,50	-	-	-	-	60	0	0	
3	40	-	0,80	-	-	-	-	60	0	6,3	
4	20	-	0,80	-	-	-	-	-	-	-	
5	30	1,5	0,60	-	-	-	-	-	-	-	
6	40	-	-	0,30	-	-	-	30	0	0	
7	20	-	-	0,25	-	-	-	60	0	5,5	
8	50	-	-	0,30	4,0	-	5	-	0	0	
9	20	30	0,50	0,10	20-0,11		200			0	При t=ti коорди- наты центров тяже- сти шкивов Ci иСг; ®С1 =0; ус! = = — 0,1 см; = =а + 5; зсс2=0,1 см; ус2=°; zC2=a
10	20	5	0,25	-	-	-	-	-	-	-	
11	25	40 .	0,30		5-0,11		50			0	При t = ti ось стержня 1 парал- лельна оси у, а ось стержня 2 парал- лельна оси X, 11 — =25, 1% — 40 см
12	30	-	0,40	-	-	10	-	-	-	-	
13	25	25	0,40	-	-	15	-	-	-	-	
14	20	20	0,40	-	-	-	-	-	-	-	
15	20	45	0,20	-	-	8	-	-	-	-	
16	80	20		0,10	65	-		-	-	-	
17	100	10	1,50		160		—	—		—	Радиус инерции ротора 2 двигате- ля 3 ix=0,10 м
18	30	-	0,40	-	-	12	-	-	-	-	
265
Продолжение табл. 52
Номер варианта (рис. 185-187)	mi	ГП2	1	R	М, Нм	(const) рад/с	ti	VI	V0	шо, рад/с	Примечания
	кг		м				С	град			
19 20 21 22 23 24 25 26 27 28 29 30	40 40 80 100 30 60 50 80 100 80 20 50	10 40 20 70 200 150 40 20	0,60 1,20 0,60 0,50 1,50 1,20 0,42 0,60	0,30 0,15 0,20 0,20 0,25 0,20	3,0 124 216	9 9 12	Illi!	1	1	1	1	1	1	-	0	2,0	Радиус инерции ротора 2 двигате- ля 3 гх=0,12 м Радиус инерции шкива 3 ta,=0,18 м То же, гш=0,22 м » io: =0,15 м Р=1300 Н
Примечания: 1. Вращающиеся тела, для которых не указан радиус инерции,
рассматривать как тонкие однородные стержни (варианты 1—5,
11—15, 18, 19, 23, 24, 29, 30) или сплошные однородные диски
(варианты 6—9, 16, 20, 22, 28); в варианте 10 тело 2 рассматри-
вать как материальную точку.
2. На схемах 1, 8, 9, 11, 16, 17, 20—22 указаны внешние момен-
ты М.
Пример выполнения задания. Дано: mi = 3 кг, т2 = 2 кг,
тз = 5 кг; li = 0,30 м, 12 = 0,20 м; а = 30°; си = 120 рад/с = const.
Схема системы и необходимые размеры приведены на рис. 188, а.
Найти реакции подпятника А, подшипника В, а также пружины
DN. Поперечными размерами стержней 1, 2, 3 и массой пружины
пренебречь.
Решение. Для определения реакций связей воспользуемся прин-
ципом Даламбера. Так как со — const, рассмотрим только центробеж-
ные силы инерции частиц каждого стержня. Известно, что главный
вектор сил инерции точек вращающегося тела определяется по фор-
муле
Ф* = —тас,
где т — масса тела, а ас — ускорение центра масс тела.
Равнодействующая сил инерции точек тела равна их главному
вектору. Поэтому для стержней 1 и 2
Ф1 = miaci = miw2(0,5Zi sina + Z2);
Ф2 = m2aC2 = т2а>2  0,Ы2.
266
Рис. 185
267
Рис. 186
268
Рис. 187
269
Для определения реакций опор необходимо знать точку приложе-
ния силы Фх (линия действия силы Фг совпадает с осью стержня
2 и поэтому определена). Так как сумма моментов параллельных
сил инерции точек стержня относительно точки О равна моменту
равнодействующей этих сил, то
Ф1Л
h
о
созобФ,
где h — плечо силы Фх относительно точки О; 6Ф — сила инерции
элемента стержня длиной d£; £ — координата элемента стержня
(рис. 188, б).
Используя значение силы Фх и учитывая, что
d Ф = (/г + С sin a)u>27 d £,
где 7 — масса участка стержня единичной длины, получаем
Рис. 188
270
h
micu2(0,5/i sina + Z2)h = j\h + £ sina)w27£cosad£,
о
откуда после интегрирования
, Z1G2 + 2/3h sina)cosa: - - .
h =	^-7 .-r-=r---= 16,4 cos a.
41 Sina + 242
Показываем составляющие реакции подпятника Ха, Ya, %а и под-
шипника Хв, Yb, силы тяжести стержней Gy., G3, G3 и силы инерции
Ф1 и Ф2 (рис. 188, в). Эти силы должны удовлетворять уравнениям,
вытекающим из принципа Даламбера:
52 Mix = 0; -YB • 50 - Ф2 • 40 - G2 • 10 - Gi • 27,5-
—Ф1(40 — 16,4 cos a) = 0 => Yb = -8,47 кН;
52^ = 0; Ya + YB + Ф1 + Ф2 = 0 => YA = -6,28 кН;
52 Zi = 0; ZD - Gi - G2 - G3 = 0;
ZD = 0,098 кН.
Так как рассматриваемые силы расположены в плоскости у Az, то
Хв = ХА = 0.
Для определения реакции пружины DN составим уравнение
= 0, рассматривая силы, приложенные к стержню 1 (рис.
188, г):
-Gi(Zi/2)sina + Ф1/1 - Ply cosa = 0,
откуда Р = 6,47 кН.
Задание Д.17. Определение реакций опор
при вращении твердого тела вокруг неподвижной оси
Однородное тело Q массой т вращается вокруг неподвижной вер-
тикальной оси z под действием пары сил с моментом М, расположен-
ной в горизонтальной плоскости. Определить реакции подпятника А
и подшипника В в момент времени t = ty, считая, что в этот момент
плоскость материальной симметрии тела совпадает с плоскостью yAz.
Начальная угловая скорость и>о = 0. Массой стержней, связанных с
телом Q, пренебречь.
Варианты задания показаны на рис. 189—191, необходимые
данные — в табл. 53.
Пример выполнения задания. Тело Q (однородный цилиндр,
из которого вырезан конус) вращается вокруг неподвижной оси z
(рис. 192, а).
271
Рис. 189
272
Рис. 190
Рис. 191
274
Таблица 53
Номер варианта	т,	R	Н	УС	гС	7,	АВ,	М,	*1,	Дополнительные
(рис. 189-191)	кг	СМ				град	СМ	Нм	С	размеры, см
1	40	25	-	0	60	20	120	10,0	10,0	
2	42	10	50	0	32	16	70	2,8	8,0	
3	20	8	30	3	30	20	55	2,0	3,5	
4	38	10	45	-20	38	25	80	18,0	7,0	
5	120	-	60	0	50	18	110	22,0	10,0	а = 40, Ь = 40
6	45	10	50	0	33	20	75	3,6	7,0	
7	40	-	30	-20	55	30	100	12,0	12,0	а = 24, 6 = 20
8	40	10	40	5	28	10	60	2,2	6,0	
9	26	12	48	33	50	20	100	16,0	15,0	
10	12	15	-	3	32	15	70	1,2	5,0	
11	50	10	40	-	28	12	48	4,0	6,0	
12	28	-	50	0	36	30	80	1,8	11,0	а = 18, Ь - 30 <ц = 14, bi = 24
13	90	12	50	14	35	10	75	13,0	7,0	а = 15
14	36	6	42	1	25	-	52	0,8	5,0	
15	8	12	50	15	36	8	70	2,4	4,5	
16	48	20	10	-22	32	30	65	15,0	18,0	
17	55'	8	70	5	55	12	120	4,0	14,0	а — 30
18	60	16	50	0	28	10	60	5,0	16,0	
19	32	15	6	0	15	15	35	4,5	5,5	
20	65	6	30	0	36	15	75	6,2	9,0	
21	80	15	40	-	35	30	78	16,0	10,0	
22	24	10	40	0	28	10	60	0,6	6,5	
23	55	16	50	0	42	5	80	3,8	8,5	
24	85	14	60		30	10	90	4,4	9,5	
25	22	-	48	-	42	15	75	5,0	4,0	
26	64	18	8	3	36	12	70	7,0	9,0	
27	80	14	55	-6	50	15	80	9,0	6,0	
28	85	15	45	-	48	25	76	8,5	7,0	
29	80	12	56	—2	42	20	80	9,5	8,0	
30	110	16	52	-	50	8	85	10,5	9,0	
Дано: т — 32 кг; М = 60 Н • м; г = 0,25 м; OCR =0,5 м; h = 1 м;
7 = 30°; а = 1 м; 6 = 2 м; г = 2‘с. Стержень OOi совпадает с осью
симметрии тела Q. Массой стержней пренебречь. Найти Ra и Rb-
Решение. Показываем главные центральные оси инерции тела
Q: £, г) и а также силу G, момент М и составляющие реакции
опор Ха, Ya, Za, Хв, Yb (рис. 192, б).
275
Рис. 192
Для решения задачи используем систему уравнений, вытекающую
из принципа Даламбера:
Ха + Хв + тхс^2 + тусе = 0;
Ya + Yb + тусш2 - тхсе = 0; ZA - G = 0;	, .,
-YB(a + b) - G ОС sin7 - Jyzu2 + Jzx£ = О',
%в(а + b) + Jzx'-^2 + Jyz& = 0; M — Jzc = 0. .
Для определения углового ускорения е из последнего уравнения
системы (1) найдем момент инерции тела Q относительно оси вра-
щения z по формуле
Jz — J21 Y md2,	(2)
где Jzi — момент инерции тела Q относительно центральной оси
Сzi, параллельной оси z; d — расстояние между осями z и Zj.
Воспользуемся формулой
Jzi = cos2 а + Jn cos2 /3 + cos2 7,	(3)
где a, /3 и 7 — углы, составленные осью Z\ с осями £, 1/, С, соответ-
ственно.
Так как а = 90°, то
Jzi = Л cos2 /3 + Jr cos2 7.	(4)
Определим моменты инерции и как разности моментов инер-
ции тела I (сплошного цилиндра) и тела II (конуса) (рис. 192):
Л = A - Jc - Jc - Jc -	(5)
Зная массу тела Q, равную т, определим массу тела I и тела II:
mi = pirr2h, mu = l/3pirr2h,
где p — плотность тела; г — радиус основания цилиндра и конуса.
Следовательно,
тц = l/3mi,
276
т = mi — тн = 2/3mj = 32 кг.
Отсюда
mi = 3/2 • 32 = 48 кг; mj = 48/3 = 16 кг.
Для вычисления моментов инерции тела Q необходимо знать по-
ложение его центра тяжести — расстояние от точки Oi. (Во всех
вариантах координаты центра тяжести заданы, а определению под-
лежат другие величины, необходимые при решении задачи.)
Это расстояние
OiC = (miO^i - mn<?iC'n)/(m/ - тц),
где
OiQ = 1/2Л = 1/2 м; OiCn = 3/4Л = 3/4 м.
Следовательно,
п 48  1/2 - 16 • 3/4 _ 3	•
48-16	8
Момент инерции цилиндра относительно оси Ст)
J^J^+m^C)2,	(6)
где = mi(r2/4 + h2/12)* — момент инерции цилиндра относи-
тельно оси тух, проходящей через центр тяжести Cj этого тела;
CiC = OiCi — О\С = 1/2 — 3/8 =1/8 — расстояние между осями
7? и /?1.
Подставляя в (6) значение этих величин, получим
J* = 48(0,252/4 + I2/12) + 48(1/8)2 = 5,5 кг • м2.
Момент инерции конуса относительно оси Ст)
J" = /У2 + тп(СцС)2,	(7)
где — момент инерции конуса относительно оси т?2, проходящей
через центр тяжести Сц этого тела.
В свою очередь, для конуса имеем
^^^з-тпСОгСп)2.	(8)
Здесь — момент инерции конуса относительно оси т)з, прохо-
дящей через центр основания конуса Оз и параллельной оси %•
Подставляя (8) в формулу (7), получим
J” =	- тп(О2Сп)2 + mn(CnC)2 = J” + mn[(CnC)2 - (O2Cn)2],
* См., например, Лойцянский А. Г. иЛурьеА. И. Теоретическая механика.
Физматгиз, 1954; Фаворин М. В. Моменты инерции тел. М., 1977.
277
причем момент инерции конуса относительно оси % определяется по
формуле
J"3 = 0,15тпг2 + 0,1тцЛ2 = (0,15 • 0,252 + 0,1 • 12)16 = 1,75 кг • м2;
СПС = О1СИ - OiC = 3/4 - 3/8 = 3/8 м;
О2С11 = Л./4 =1/4 м.
Таким образом,
J*1 = 1,75 + 16[(3/8)2 - (1/4)2] = 3 кг • м2.
Теперь и можно вычислить по формулам (5):
Jr, = Jy — j” = 5,5 — 3 = 2,5 кг • м2;	= J* — J*1,
где
= mir2/2 = 48 • 0,252/2 = 1,5 кг • м2;
J™ = 0,Зтцг2 = 0,3 • 16 • 0,252 = 0,3 кг • м2.
Тогда
= 1,5 — 0,3 = 1,2 кг • м2.
По формуле (4) вычисляем J21, учитывая, что /3 = 120°, 7 = 30°:
JZ1 = cos2 120° + cos2 30° = 2,5(l/2)2 + 1,2(у/З/2)2 = 1,525 кг • м2.
Момент инерции тела Q относительно оси вращения z вычисляем
по формуле (2):
Л = Л1 + md2,
где
d = ОС sin 7 = (OOj +O1C)sin7 = (1/2 + 3/8) sin30° = 0,437 м;
Jz = 1,525 + 32(0,437)2 = 7,65 кг • м2.
Из последнего уравнения системы (1)
е = M/Jz = 60/7,65 = 7,85 рад/с2 = const.
Угловая скорость при равноускоренном вращении тела
W =	+ £t,
поэтому при wq = 0 и t = т = 2 с
ш = 7,85  2 = 15,7 рад/с.
Для определения реакций опор следует определить центробежные
моменты инерции Jyz и Jzx тела Jzx = 0, так как ось х, перпендику-
лярная плоскости материальной симметрии тела Q, является главной
осью инерции в точке А.
278
Центробежный момент инерции тела Jyz определим по формуле
Jyz — JyXzx +myczc, где JyXzX — (.d?) <7^)(sin 27)/2,
т. е.
Jyizx = (2,5 - l,2)(sin60°)/2 = 562 кг • м2.
Координаты центра тяжести тела D следующие:
хс = 0; ус = d = 0,437 м;
zc = а + ОС cos 7 = а + (OOi + OiC) cos 7 = 1,76 м.
Таким образом,
Jyz = 0,562 + 32 • 0,437 -1,76 = 25,16 кг  м2.
Подставляя известные величины в систему уравнений (1) и учи-
тывая, что d = 0,437 м, получаем следующие равенства:
ХА + Хв + 32 • 0,437 • 7,85 = 0;
Ya + YB + 32 • 0,437 • (15,7)2 = 0;
ZA - 32 • 9,81 = 0;
-ЗУВ - 32 • 9,81 • 0,437 - 25,16 • (15,7)2 = 0;
-ЗХВ + 25,16 • 7,85 = 0.
Отсюда
ХА = -43,6 Н; УА = -1340 Н; ZA = 314 Н;
Хв = -65,8 Н; YB = -2120 Н.
Задание Д.18. Применение теорем и принципов динамики
к исследованию движения механической системы
Механическая система состоит из тела А массой тА, колеса В
массой тв и электродвигателя, приводящего систему в движение.
Тело А опирается на ось колеса В и на горизонтальную шероховатую
плоскость. Вращающиеся части двигателя жестко связаны с колесом
В, и их массы и моменты инерции учтены соответственно в массе и
моменте инерции колеса В.
Вращающий момент M(t), развиваемый электродвигателем, опре-
деляется дифференциальным уравнением
b^+b2M = Ьз~аш,	(1)
где bi, Ьз, Ьз и а — постоянные коэффициенты, аш — угловая
скорость вращения вала двигателя. Проскальзывание колеса В по
опорной плоскости отсутствует.
279
Корпус двигателя в вариантах 1—7, 9, 11—20, 30 жестко связан
с телом А и его масса учтена в тд.
В вариантах 8, 10, 21—29 корпус двигателя не связан с телами
А и В и, следовательно, вращающий момент является внешним по
отношению к системе этих тел.
Двигатель включается в начальный момент времени (t = 0), когда
система находится в покое. Наличие силы трения покоя (сцепления),
приложенной к телу А со стороны опорной плоскости, приводит к
тому, что движение механической системы начинается только че-
рез т с после включения двигателя. Затем скорость поступательного
движения системы возрастает до некоторого значения г*. В дальней-
шем производится торможение и скорость поступательного движения
системы на пути s снижается до значения 0,9 щ.
Требуется:
1.	Определить зависимость М — M(t) при 0 t т, значение
Мя = М(т) в начальный момент движения и время т.
2.	Определить зависимость v = v(t) при t т, найти значение
установившейся скорости г>* и значение установившегося момента
М*.
3.	На этапе торможения определить пути, проходимые системой
при снижении v до значения 0,9 г* для двух режимов торможения.
1-й режим — торможение двигателем — двигатель работает
как тормоз. При этом момент на валу двигателя определяется урав-
нением
, dM
Ь1ЧГ = -а“-
2-	й режим — механическое торможение. При этом М = const = 0.
Сравнить пути торможения s и I при первом и втором режимах
торможения.
Схемы механизмов приведены на рис. 193—195, а необходимые
данные для расчета — в табл. 54.
На рис. 193—195 С — центр тяжести тела А, О — центр тяжести
однородного колеса В, стрелкой указано направление движения; D —
точка опирания тела А на шероховатую поверхность.
В вариантах 9, 11, 30 при разгоне тело А контактирует с опорной
поверхностью в точке D, а при торможении — в точке Di.
В табл. 54 приведены значения следующих параметров: пгд, mg —
массы тел А и В; г — радиус колеса В; г — радиус инерции колеса В
относительно оси вращения; / — коэффициент трения, ОН, НС, ОЕ,
ED — см. рис. 193 —195, a, bi, b%, b3 — постоянные коэффициенты.
Пример выполнения задания. Дано: тд = 20 кг, тв = 100 кг;
г = 0,5 м; i = 0,4 м; / =‘0,35; ОН = а = 1,4 м; ОЕ = b = 2,0 м;
CH = h = 0,4 м; ED = с = 0,7 м; а = 2; bi = 2,5 • 10“2, Ь2 = 0,25,
Ь3 = 50.
Найти: М = M(t) при 0 i Sj т; Мп, т, v = v(t) при t > т, щ; М*,
з и I.
280
Таблица 54
Номер варианта	тд,		Г,	г,	/	ОН	НС	ОЕ	ED	а	Ь1	ь2	5з	Примечание
(рис. 193-195)	КГ	кг	м	м		м					10“2			
1	30	80	0,6	0,3	0,2	1,2	0,25	0,8	0,8	3	1,00	0,33	40	
2	10	50	0,3	0,2	0,35	0,5	0,3	1,0	0,7	3	1,33	0,27	30	
3	50	120	0,5	0,35	0,25	1,1	0,2	1,5	0,5	4	1,25	0,32	70	
4	40	90	0,45	0,4	0,4	1,6	0,1	1,7'	0,6	3,5	2,28	0,20	60	
5	25	70	0,4	0,3	0,3	2,0	0	1,5	0,5	3	2,33	0,28	50	
6	is	60	0,35	0,25	0,35	1,2	0,2	1,8	0	4,5	1,33	0,27	40	
7	35	105	0,5	0,3	0,4	1,6	0	1,0	0,5	5	1,0	0,19	50	
8	7	18	0,4	0,3	0,3	1,0	0	0,3	0,5	4	0,75	0,22	40	
9	25	80	0,6	0,4	0,4	0	0,3	0,8	0,8	4	1,75	0,17	60	ОЕ, = ОЕ-, E,D, = ED
10	5	15	0,3	0,2	0,3	0,7	0,1	0,5	0,4	4,5	1,33	0,44	40	
11	30	110	0,7	0,5	0,3	0	0,4	1,2	0,7	3	2,67	0,30	55	OEi — ОЕ', E^Di == ED
12	20	85	0,3	0,25	0,4	1,3	0,3	1,3	0,15	4	2,25	0,42	60	
13	20	70	0,4	0,3	0,4	0,9	0,3	1,8	0,4	2	1,50	0,50	50	
14	30	95	0,5	0,4	0,3	1,7	0,3	1,3	0,8	3	2,67	0,46	70	
15	25	80	0,55	0,4	0,2	1,8	0,3	1,5	0,7	3,5	2,00	0,17	50	
16	40	100	0,6	0,5	0,25	0,5	0,6	1,9	0,9	4	1,50	0,17	60	
17	35	ПО	0,65	0,5	0,45	0,8	0,25	1,4	0,25	5	1,60	0,16	40	Размерности коэффици-
18	35	120	0,6	0,5	0,4	2,0	0	1,0	0,8	5	1,60	0,14	80	ентов a, b,, 62 и 5з,
19	10	40	0,4	0,3	0,4	1,9	0,2	1,2	0,7	3	3,00	0,26	50	имеющих электромеха-
20	25	85	0,55	0,4	о,з	1,1	0,1	2,3	0	4	1,0	0,22	45	ническую природу, не
21	2	10	0,1	0,06	0,3	0,7	0,05	1,0	0,2	1,5	3,33	1,33	30	приводятся. Их числен-
22	4	30	0,2	0,15	0,4	0,5	0,1	0,9	0,3	2	3,50	0,75	40	ные значения даны в СИ.
23	3	20	0,2	0,1	0,3	0,8	0,2	0,6	0,4	3	2,67	0,66	35	
24	5	15	0,3	0,2	0,3	0,9	0,1	0,7	0,4	2	3,00	0,45	40	
25	2,5	15	0,25	0,2	0,3	0,5	0,2	1,2	0,2	3	2,33	0,56	35	
26	4,5	18	0,35	0,25	0,4	1,9	0,2	1,2	0,5	4	1,50	0,35	40	
27	3,2	16	0,3	0,2	0,2	1,4	0	1,0	0,9	3	2,00	0,43	35	
28	2,8	15	0,25	0,2	0,3	1,1	0,3	1,3	0,2	4	1,25	0,45	45	
29	4,7	21	0,3	0,25	0,4	1,8	0,2	0,8	0,1	3,5	2,57	0,43	40	
30	10	60	0,6	0,5	0,4	0	0,3	0,8	0,7	4	1,75	0,15	70	ОЕ, = 0,9; E,D, = 0,6
Рис. 193
282
Рис. 194
283
Рис. 195
284
Решение. 1. Определение параметров движения системы на эта-
пе разгона до установившейся скорости.
Механическая система представлена на рис. 196. Расчетная схема
этой системы — на рис. 197.
Составим дифференциальные
уравнения, описывающие движе-
ние механической системы (рис.
197,а). К колесу В приложены
вращающий момент М, сила тя-
жести G — твд, нормальная ре-
акция Yk в опорной точке К и
сила сцепления Fc^, предположи-
тельно направленная вправо. На
Рис. 196
тело А действуют сила тяжести Q = тдд, приложенная в центре
тяжести С, реакция Yd, сила трения Xd = /Хо и реактивный мо-
мент корпуса двигателя М'. Силы взаимодействия в точке О между
телом А и колесом В являются реакциями внутренних идеальных
связей и не показаны на рисунке. При расчленении системы на части
(рис. 197, б, в) в точках О прикладываются силы взаимодействия
Хо = Х'о и Yq = Yq между телами Ап В.
Q
D
и
Для получения дифференциальных уравнений движения восполь-
зуемся теоремой об изменении кинетической энергии в дифференци-
альной форме
T = ^Ni,	(2)
где мощность определяется для всех сил и моментов, как внешних,
так и внутренних.
Составим выражение для кинетической энергии системы:
_ mAv2A mBv2 Joiw2
1 ~	2	+	2	+	2
Уравнения связей:
х = v = vA = vc = по; ш = х/т.	(4)
Подставив (4) в (3), будем иметь
Т = 1/2тпр±2,	(5)
285
где приведенная масса
тпр = тА + тв ^1 + ^2
Составим выражение для мощности сил и моментов в системе:
N = Mu-XDi= (y-XD^x.	(6)
Подставляя выражения (5) и (6). в (2), получаем
тарх = М/г- fYD.	(7)
Это уравнение содержит неизвестную силу Yd- Чтобы ее исключить,
составим для тела А (рис. 197, в) в соответствии с принципом
Даламбера сумму моментов всех сил и силы инерции Ф относительно
точки О и приравняем ее нулю:
М' - Qa - fYDc 4- YDb + Ф • h = 0.
Учитывая, что Ф = тАх, получим уравнение
mAxh = —М' + тАда — Yd<1,	(8)
где
d = b — fc.
Исключая из уравнений (7) и (8) силу Yd, получаем
а%х = а^М - аг,	(9)
где
ai — f + d/r; аг = famAg; аз = mnpd — fhmA. (9')
Дифференциальное уравнение (9) описывает движение системы
вдоль оси х.
Определим зависимость М = M(t) в интервале изменения t от 0
до г. Для этого проинтегрируем уравнение (1), положив в нем ш = 0.
Учитывая начальное условие M(t=Oj = 0, будем иметь
M(t) = g(l-e-^).	(10)
Условие трогания с места имеет вид х > 0.
Используя уравнение (9), получаем условие трогания с места для
вращающего момента:
М > аг/ai •
Начальное значение момента М„, при котором система приходит
в движение,
М„=а2/а1.	'	(11)
286
Определим интервал времени т от момента включения двигате-
ля до начала движения системы. Учитывая, что Мя = М(т), из
уравнения (10) получаем
.М„ =	; т = ^1п(.	(12)
Найдем зависимость v = v(t) при t т.
Учитывая, что х = v, уравнения (1) и (9) запишем в виде
Ь1> + б2м=ЬЗ’^;)	(13)
a3~fr = Л1М — 0,2-
Из второго уравнения этой системы находим
M=02+O3dy	(И)
ai ai dt	'	'
Продифференцируем это уравнение по t:
dM _ аз d2t>	/1
dt ~ ai dt2 ‘
Подставим (14) и (15) в первое уравнение системы (13).
После преобразований получаем
^+2n%+k2v = D,	(16)
dt dt	'
где
П=^-;	к=.Г^- D = Qlfe3-a2fe2	(17)
2bi	V ra3t>i	0361	v '
Начальные условия для уравнения (16):
при t = т v = 0 и du/dt = 0.	(18)
Значение dv/dt = 0 следует из второго уравнения системы (13) при
М(т) = М„.
Как известно, решение уравнения (16) при п > к имеет вид (в том,
что п > к, легко убедиться подстановкой числовых значений)
v = Ae~nt • sh(k*t + /3) + D/к2,	(19)
где
fc* = \/п2 — к2.
Постоянные интегрирования А и 0 определим по начальным усло-
виям (18):
4=ge-; th(fc,T + /3) = ^;
/3 = 0,51п(^±£Л -к„т.
\п — К* /
287
Установившееся значение скорости г* определяется вторым членом
правой части выражения (19), так как первый стремится к нулю:
v* = D/k2.	(20)
Отметим, что при движении с установившейся скоростью момент
на валу электродвигателя достигает установившегося значения М*,
определяемого из второго уравнения системы (13) при dr/dt = 0:
Mt = Мн = a2/ai-	(21)
Подставим исходные данные и определим значения параметров
движения на этапе разгона.
Значения коэффициентов, входящих в уравнение (9): тпр = 184 кг,
d = 1,735 м; ах = 3,82; а2 = 96,04 Н • м; а3 = 316,44 Н • с2.
Момент электродвигателя М = M(t) на этапе разгона [см. (10)]
M(t) ~ 200(1 — e-10t).
Начальное значение момента Мн при трогании с места, определя-
емое (11)
Мп = 25,14 Н • м.
Интервал времени т от момента включения двигателя до начала
движения, вычисленный в соответствии с (12), равен
т = 0,0134 с.
Определим зависимость v(t). Для этого вычисляем значения пара-
метров, входящих в уравнения (16) и (19): п = 5 с-1; к = 1,39 с-1;
D = 21,11 м/с3; к* = 4,80 с"1; А = -3,38 м/с; /3 = 1,89.
Значения установившейся скорости [см. (20)]
v* = 10,93 м/с.
Подставляя значения величин А, /3 и г* в равенство (19), получаем
зависимость r(Z) при t т: v{t) = —3,38e-5i sh(4,80t + 1,89) -I-10,93.
Значение установившегося момента на этапе разгона, как показы-
вает (21), совпадает с начальным значением Ми:
М» = 25,14 Н • м.
2. Определение пути при торможении. Торможение начинается
при скорости поступательного движения v = v* и моменте М = М„,
а заканчивается при и = 0,9г».
Исследуем два режима торможения.
1-й режим торможения. Для определения тормозного пути s
составим теорему об изменении кинетической энергии механической
системы в конечной форме:
Т2-Т1=^Д,	(22)
288
где 52 Ai — сумма работ внешних и внутренних сил:
Ч>2	Х2	Х2	Х2
^Ai = у Mdp- jXDdx = ± У Mdx — f jYDdx.
ifil	Xi	Xi	Xl
Используя выражение (5), представим (22) в виде
Х2	Х2
^х2-х2) = ± J Mdx-f j^dx.	(23)
Х\	Х\
Здесь индексом 1 обозначены значения неизвестных в момент t\
начала торможения, а индексом 2 4- в момент t>2 конца торможения.
Второе слагаемое правой части уравнения (23) содержит неизвестную
Yd- Поэтому необходимо составить еще уравнение, содержащее ту же
неизвестную. Проинтегрируем выражение (8) по х.
/j.2\
Учитывая, что х da: = d I 1, получаем
JC2	Х2
—^—(х^ — ж?) = — У М dx + тлда(х2 - xi) — jУо d.r • d. (24)
XI	Хд
Исключим из уравнений (23) и (24) интеграл от Yd и, используя
обозначения (9'), будем иметь
*1 ~
2

а3(
М dx — <12(22 — 2i).
(25)
Заметим, что это уравнение можно также получить, проинтегри-
ровав (9) по 2. Дифференциальное уравнение для момента на валу
двигателя при торможении имеет вид
, АМ
Проинтегрируем это уравнение в пределах от до t:
М — М2 = —-^-(2 — 21).
ГОД 4	'
Проинтегрируем (26) по 2 в пределах от 21 до 22:
(26)
(27)

Подставим (27) в (25):
=Д1 (М1 + ^) (22-21)-^ (^Va2(22-21). (28)
\	"	/	\	' 1'1 /	' “1 \	"	/
289
В этом выражении следует принять:
Xi = 0,	ii=vt, Mi = M*=a2/ai,
%2 = 3,	±2=0,917».
Подставляя эти значения в (28), получим
у-(0,92 -
Путь s торможения, на котором скорость снижается до значения
0,9 и*,
з = г»»/22^-049.	-	(29)
у aai	'	7
2-й режим торможения. Уравнение, характеризующее движение
системы при втором режиме торможения, получается из (28) при
— 0:
У (±2 - ±?) = -«2(12 - Х1).	(30)
Принимая а?! =0; ±1 = п»; £2 = /; ±2 = 0,9га, получаем
Подставляя значения параметров в формулы (29) и (31), получаем
s = 3,43 м; I = 37,39 м.
Сравнивая пути s и I при первом и втором режимах торможения,
заключаем, что приложение тормозного момента двигателя значи-
тельно сокращает тормозной путь.
ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
Задание Д. 19. Применение общего уравнения динамики
к исследованию движения механической системы
с одной степенью свободы
Для заданной механической системы определить ускорения гру-
зов и натяжения в ветвях нитей, к которым прикреплены грузы.
Массами нитей пренебречь. Трение качения и силы сопротивления в
подшипниках не учитывать. Система движется из состояния покоя.
Варианты механических систем показаны на рис. 198—200, а не-
обходимые для решения данные приведены в табл. 55.
Блоки и катки, для которых радиусы инерции в таблице не ука-
заны, считать сплошными однородными цилиндрами.
Пример выполнения задания. Дано: Gi = G2 = 2G; G3 = G4 =
= G; R = 2г; i2x = ry/2; f = 0,2.
Блок 3 — сплошной однородный цилиндр (рис. 201). Определить
ускорения грузов I и 4 и натяжения ветвей нити 1—2 и 3—4.
290
Таблица 55
Номер ва- рианта(рис. 198—200)	Сила тяжести				R/r	Радиусы инерции		р	Коэффициент трения скольжения /	Дополнительные данные
	G1	g2	G3	g4		t2x	«Зх			
1	G	G	3G	-	2	ту/2	-	-	-	
2	G	G	G	-	2	ту/2	-	-	-	
3	3G	G	G	-	2	ту/2	-	-	0,1	
4	G	G	2G	-	-	-	-	-	0,2	7*2 =гз
5	2G	G	G	G	3	2т	-	-	-	
6	2G	G	2G	-	3	2т	-	-	0,2	
7	2G	G	2G	-	3	2т	-	-	0,2	
8	2G	G	2G	-	3	2т	-	-	0,2	
9	2G	G	2G	-	3	2т	-	0,2G	0,2	
10	2G	2G	G	-	4	-	2г	G/3	0,4	
11	2G	G	2G	0,2G	3	2т	-	-	0,2	
12	2G	G	2G	0,2G	3	2т	-	-	0,2	
13	4G	2G	G	4G	-	Г2л/2	2гз	-	-	Г2=2гз; /?2—-^3
14	-	G	G	4G	-	Г2л/2	2г3	8G	-	Т2— 2гз; Яз—1,5Яг
15	4G	2G	2G	4G		Г2л/2	2гз	-	-	Г2 — 2гз; Яз=1,5Й2
16	-	G	2G	4G	-	Г2л/2	2г3	4G	-	Г2— 2гз; Яз=1,5Яг
17	2G	G	G	-	2	гл/2	-	-	0,1	
18	3G	0,2G	0,lG	0,5G	2	-	-	-	0,4	
19	4G	0,3G	0,2G	3G	3	2г	1,2г	-	0,1	гз=1,2г; Яз=1,2гз
20	4G	0,2G	0,lG	3G	2	1,6г	гл/2	-	0,2	Г2=1,5г; 7?2=1)2г2
21	5G	0,lG	0,2G	-	3	-	гл/2	G	-	
22	G	0,2G	0,3G	-	2	-	гл/2	G	-	
23	G	0,2G	0,lG	-	1,5	1,2г	-	2G	-	Яз=1,2г
24	2G	G	G	8G	-	-	-	-	-	Массы четырех колес одинаковы
25	6G	2G	2G	G	—	—	—	—	—	Гз=Гф
26	6G	G	2G	-	-	-	-	-	-	Гз=Г2
27	G	G	G	4G	2	гл/2	г-\/2	-	-	
28	3G	G	G	-	2	га/2	-	-	0,1	
29	6G	3G	G	G	2	-	гл/2	-	-	*4®
30	8G	G	G	2G	-	-	-	-	0,1	
Примечания: 1. Радиусы инерции даны относительно центральных осей, пер-
пендикулярных плоскости чертежа (рис. 198—200).
2. Коэффициент трения принимать одинаковым как при сколь-
жении тела по плоскости, так и при торможении колодкой (ва-
рианты 9—12).
291
Рис. 198
292
Рис. 199
293
Рис. 200
294
Решение. Применим к решению задания общее уравнение дина-
мики. Так как система приходит в движение из состояния покоя,
направления ускорений тел соответствуют направлениям их движе-
ния.
Ввиду того, что среди сил, действующих на тела системы, есть
сила трения, целесообразно по исходным данным найти истинное на-
правление движения системы, чтобы правильно показать направление
силы трения.
Рис. 202
Если направление движения системы выбрано ошибочно, то иско-
мое ускорение получается со знаком «—». В этом случае необходимо
изменить направления силы трения и сил инерции и внести соответ-
ствующие поправки в общее уравнение динамики.
В данном примере движение системы таково, что груз 1 опускается.
Покажем задаваемые силы: силы тяжести Gi — груза 1, G3 —
блока 2, вз — блока 3 и 64 — груза 4, а также F — силу трения
скольжения груза 1 по наклонной плоскости (рис. 202).
Приложим силы инерции. Сила инерции груза 1, движущегося
поступательно с ускорением Si, выражается вектором
Ф1 = — miai.
Силы инерции блока 2, вращающегося вокруг неподвижной оси с
угловым ускорением е2, приводятся к паре, момент которой
Л/2Ф =
Силы инерции блока 3, совершающего плоское движение, приво-
дятся к вектору
Ф3 = —т3а3,
295
где а3 — ускорение центра масс блока 3, и к паре сил, момент
которой
М3ф = 73^з, '
где Ез — угловое ускорение блока.
Сила инерции груза 4, движущегося поступательно с ускорени-
ем <?4,
Ф = — пцсц.
Сообщим системе возможное перемещение в направлении ее дей-
ствительного движения (рис. 202) (можно сообщить возможное пере-
мещение и в обратном направлении).
Составим общее уравнение динамики:
Gitisi sin60° - F6s! -	- G36s3 - Ф3<5з3 - Mffy>3-
— G46S4 — Ф4^54 = 0,	(1)
где 6ip2 и 6ip3 — углы поворотов блоков 2 и 3.
Зависимости между возможными перемещениями такие же, как и
между соответствующими скоростями.
Выразим скорости центров масс и угловые скорости тел системы
через скорость тела 1 (составим уравнения связей).
Как показано на рис. 202, мгновенный центр скоростей блока 3
находится на одной вертикали с центром блока 2. Расстояние между
мгновенным центром скоростей и центром блока 3
b — Зг/2 — г = г/2.
Теперь находим
W2 = W3 = vi/R = «1/2г; 1
v3 = «4 = ш3Ь — щ/4. J	' '
Такие же зависимости и между возможными перемещениями:
^2 =	= £si/(2r); 1
6s3 = 6S4 = 6sj/4. J	'
Уравнение (1) с учетом (3) принимает вид
Gi sin60° - F - Ф1 - Mf/(2r) - G3/4 - Ф3/4 - М3ф/(2г)-
—G4/4 — Ф4/4 = 0*.	(4)
Учитывая, что
Gi = G2 ~ 2G — 2mg\ G3 = G4 ~ G = mg,
* Это же уравнение можно получить, если вместо (1) составить уравнение мощ-
ностей, сообщив системе возможные скорости. Соотношения (2), приведенные для
действительных скоростей тел системы, те же, что и для любых возможных скоро-
стей.
296
имеем
F = /Gi cos 60° = fmg;
$i = midi = 2mai;
= Ш2^х£2 = 4mr2e2;
Ф3 = m3a3 = ma3;
M3 = J3xe3 = [m3(l,5r)2/2]e3 = 9mr2£3/8;
Ф4 = //140.4 = 7/10,4.
Зависимости между ускорениями в соответ-
ствии с (2)
е2 = ез = ai/(2r); 1
а3 = а,4 = ai/4. J
Подставляя (5) и (6) в (4), получим
ду/з — fg — 2aj — aj — <?/4 — «j/16 — 9aj/32 — g/4 — «1/16 = 0,
откуда
а(\/з - / - 0,5)	„ _o , 2
ai = —----jj-ji--«1 = 2,69 м/с ,
a4 = a3/^\ a4 = 0,74 м/с2.
Для определения натяжения в ветви нити 1—2
мысленно разрежем нить и заменим ее действие на
груз 2 реакцией Д-г (рис. 203).
Общее уравнение динамики
Рис. 204
Gi^si sin60° — Fdsi — Ф1<5«1 — 7i-26si = 0,
откуда
Д-2 = Gi sin 60° - F - Ф1 = 2Gsin60° - 2G/cos60° - 2(G/g)ai;
Ti—2 = 0,93G.
Для определения натяжения в нити 3—4 мысленно разрежем эту
нить и заменим ее действие на груз 4 реакцией 7з_4 (рис. 204).
Не составляя общего уравнения динамики, на основании принципа
Даламбера имеем
Т3_4 = G4 + Ф4 = G + (G/g)a4;	Т3_4 = 10,8G.
УРАВНЕНИЯ ЛАГРАНЖА II РОДА
Задание Д.20. Применение уравнений Лагранжа II рода
к определению сил и моментов, обеспечивающих
программное движение манипулятора
Манипулятор (рис. 205—207), состоящий из звеньев 1, 2 и захвата
Z), приводится в движение приводами А и В. Захват D перемещается
вдоль прямой ON. Со стороны привода А к звену 1 прикладывается
297
Рис. 205
298
Рис. 206
299
Рис. 207
300
либо управляющий момент Ма (варианты 2, 4, 7, 8, 12, 22, 24—26,
29), либо управляющее усилие Ра (варианты 1, 3, 5, 6, 9—11, 13—21,
23, 27, 28, 30). Привод В воздействует на звено 2 либо моментом
Мв (варианты 1—3, 5, 6, 8—11, 13—21, 23, 27), либо управляющим
усилием Рв (варианты 4, 7, 12, 22, 24—26, 28—30).
Перемещение звена 1 (варианты 3, 4, 7, 12, 22, 24—26, 28—30) или
звена 2 (варианты 1, 2, 5, 6, 8—11, 13—21, 23, 27) манипулятора
ограничено препятствиями К и L, поэтому изменение угла поворота
р = p(t) этого звена возможно лишь в интервале [<р(0), <р(т)], где т —
время движения звена.
Технические условия работы манипулятора требуют, чтобы ука-
занное звено сошло со связи К при t = 0 и «мягко» коснулось
препятствия L при t = т, т. е. так, чтобы были удовлетворены усло-
вия
3>>L,.„=Oi
Программные движения звена 1, удовлетворяющие требованиям «мяг-
кого» касания, приняты в таком виде:
1) y?(t) = <р(0) + [<р(т) — <р(0)](10 — 15</т + 6t2/r2)t3/r3 (варианты 2,
4, 6, 7, И, 12, 16, 19, 22, 24—26, 28—30);
2) <^(f) = <Д0) + [<Дт) — </>(0)][£/т — (1/(2тг)) sin(27rt/r)] (варианты 1,
3, 5, 8—10, 13—15, 17, 18, 20, 21, 23, 27).
Значения <Д0) и р(т) заданы в табл. 56, а график р = p(t) показан
на рис. 208. Силами сопротивления движению пренебречь. Механизм
расположен в горизонтальной плоскости. Движением захвата относи-
тельно звена 1 пренебречь.
Таблица 56
Номер варианта (рис. 205—207)	mi	тг	J1	J2	1, м	т, с	¥>(0)	^(т)
	к	г	кг	м2			ра	
1	3	-	0,5	0,6	0,5	1	тг/3	2тг/3
2	4	-	1	2	0,3	0,25	0	%/3
3	2	-	1	2	0,2	1	0	тг/3
4	2,5	2,5	0,8		0,8	0,5	тг/6 .	тг/3
5	4	-	2	2	0,5	2	тг/б'-	тг/3
6	2,5	-	1,2	1,5	0,3	0,9	0	тг/3
7	2	3	0,6	-	0,7	0,5	7г/6	7Г/3
8	3	-	0,9	2	0,4	0,3	Тг/6	тг/3
9	2	-	0,8	1,4	0,3	1	0	тг/3
10	3,5	-	1,4	1,6	0,4	2	0,1%	тг/6
11	2,5	-	1	1,4	0,5	0,5	0	тг/4
12	3	3	0,7	-	0,7	0,4	тг/6	тг/3
301
Продолжение табл. 56
Номер варианта (рис. 205—207)	mi	m2	J1	Ji	1, м	т, с	¥>(0)	
	к	г	КГ	м2			ра	Д
13	4	-	1,5	2	0,3	0,5	0	-тг/6
14	3		1,4	1,8	0,4	1,5	тг/6	7Г/3
15	2,5	-	1	1,2	0,5	0,5	тг/6	тг/З
16	3	-	1,2	2	0,3	0,3	0	тг/4
17	3		1,2	2	0,3	1,8	ТГ/6	тг/З
18	2	-	0,6	0,8	0,4	0,8	ТГ/6	тг/З
19	3	-	1,7	2	0,3	0,6	-тг/6	тг/З
20	3,5	-	1,2	1,6	0,4	0,6	тг/4	тг/2
21	4		2	2	0,5	0,5	тг/6	тг/4
22	2,5	4	1,2	-	0,3	0,8	ТГ/6	тг/2
23	4	-	1,1	1,7	0,4	1	тг/З	тг/2
24	3	3	1,4	-	0,6	1	0	тг/З
25	2,5	3	1	-	0,8	0,5	0	тг/З
26	3,5	4	1,6	2	0,4	0,9	0	тг/6
27	2	- .	1,1	1,5	0,4	0,7		тг/З
28	3	2,5	0,7		0,7	0,4	тг/6	тг/З
29	2	3	1,3	-	0,5	1,2	0	тг/З
30	2,5	4	0,8	-	0,6	0,4	тг/6	тг/4
В задании приняты следующие обозначения:
mi — масса первого звена, захвата и переносимого в захвате
объекта;
m2 — масса второго звена;
Ji — момент инерции звена 1, захвата и переносимого в захвате
объекта относительно главной центральной оси инерции;
J2 — момент инерции звена 2.
Центр тяжести звена 1 находится в точке С (варианты 1—4, 6—8,
11—13, 16, 18—20, 22—30) или в точке А (варианты 5, 9, 10, 14, 15,
17, 21).
Требуется:
1. Вычислить значения управляющих сил и моментов в начале
торможения звена 1. Считать, что торможение звена 1 начинается в
тот момент, когда угловое ускорение звена обращается в ноль.
2. Построить графики зависимости управляющих моментов и сил
от времени.
Пример выполнения задания. Дано: mi = 2 кг; m2 = 3 кг;
Ji = 0,8 кг • м2; I = 1 м; <р(0) = 0, <р(т) = тг/6 рад; т = 0,5 с.
Центр тяжести звена 1 находится в точке Ci (рис. 209):
<p(t) = <р(0) + [<^(т) - <р(0)][£/т - (1/(2тг)) sin(27rt/r)].
302
Найти управляющий момент М и управляющую силу Р.
Решение. Для решения задачи применим уравнения Лагранжа
II рода. Будем рассматривать механическую систему как систему с
двумя степенями свободы, приняв за обобщенные координаты угол
поворота звена 1 и смещение х звена 2.
Для рассматриваемой механической системы можно записать:
уС2 = const; xci = х + I cosip;	yci = Z sin </?.	(1)
Эти равенства играют роль уравнений связей.
В соответствии с выбранными обобщенными координатами имеем
A (&L\ _дт _п .'
dt \дф J др
d (дТ\ _ дТ _ п	’
dt \ дх ) дх	,
Совокупность уравнений (1) и (2) позволяет составить дифферен-
циальные уравнения движения механической системы.
Составим выражение для кинетической энергии системы Т как
функцию обобщенных скоростей ф я х и обобщенных координат <р и х.
Кинетическая энергия системы равна сумме кинетической энергии
Т\ звена 1 и кинетической энергии Тг звена 2.
Кинетическая энергия звена 1, совершающего плоское движение,
T1 = ~2~~ + — •
Кинетическая энергия звена 2, совершающего поступательное дви-
жение,
_ m2vl
Т2 2 ,
где
wi = <р; V2 — х.
Продифференцировав (1) по времени, будем иметь
xci = х — 1ф sin <р; yci = 1ф cos <р.
откуда
uci = %ci + Ус1 = х2 + 12ф2 — 21фх sin ip.
303
Таким образом,
Т =	+ тп^ф2/2 — 2mi/i<£(sin<p)/2 + З^ф2/2 4- m%x2/2 =
= (mi + т2)х2/2 + (т\12 + Зф)ф2/2 — ттцИфзнкр.
Найдем значения слагаемых уравнений Лагранжа:
= (mj+m-jji — mi/^sin<y5;
1Д = (mi 777-2 — тП11ф sin <p — т\1ф2 cos p;
&L =0-
dx U’
(3)
— = (mJ2 + 31)ф — mi/isin^?;
= (mi/2 + 3^)ф — myl'ismip — т\1хф cos
= —ГП11хф cos <p.
Определим обобщенные силы Qx и Q^.
Для определения Qx мысленно наложим на систему связь <р = const
и, сообщив системе возможную скорость х, вычислим возможную
мощность сил, действующих на нее:
Nx = Qxx = Рх,
отсюда
Qx = Р.	(4)
Аналогично, мысленно наложив на механическую систему связь
х = const и сообщив ей возможную скорость ф, получим выражение
возможной мощности Nv:
Np —	= Мф,
отсюда
Q„ = M.	(5)
Обобщенные силы Qx и Qv можно определить и из выражения ра-
боты сил на элементарных перемещениях системы, соответствующих
вариации каждой обобщенной координаты:
f>Ax = Qx6x = Р6х\ ЬАу, =	= Мбр.
Подставляя (3), (4) и (5) в (2), получим
(mi + тг)т — milpsinp — т\1ф2 cosy> = F; 1
(тД2 + 3\)ф — milxsinp = М. J	' ’
304
Так как захват D манипулятора по условию задачи должен дви-
гаться вдоль прямой, перпендикулярной оси х, на механизм допол-
нительно оказывается наложенной связь а: + 2/соз</> = Хо, или
х = хо — 21 cos (хо = const),
следовательно,
х = 21ф sin ip.
Отсюда
х = 21ф sin <р + 21ф2 cos <р.
(П
Подставляя (7) в (6), приходим к соотношениям
М = (m^l2 + Л)<р — 2Z2mi<psin2 <р — 12т.1ф2 sin 2ср;
Р = (mi + 2тп2)(<Э sin 4- ф2 cos <p)l.
(8)
Равенства (8) представляют собой зависимость управляющего мо-
мента М и управляющего усилия Р от известных функций <р, ф и
ф. Так как является заданной функцией времени, то вычисление
производных ф и ф, а следовательно, и управляющего момента М и
усилия Р не представляет труда.
Вычислим М и Р в момент начала торможения звена 1.
В этот момент угловое ускорение ф обращается в нуль. Производ-
ные ф и ф соответственно равны:
ф = [<^(т) - <^(0)](1 - со8 27г(/т)/т; ф = 2тг[<р(т) - <^(0)](sin27rt/T)/r2.
Отсюда
или
2тг[у(т) - у(0)] 2тг . _ 0
2	ОХАЛ V 1 v
2% ,	. т
—t — 7Г И t =
305
Таким образом, торможение звена 1 начинается в момент времени
t = т/2. В этот момент времени
¥>(т/2) = [99(0) + <р(т)]/2,	1	, .
<Д(т/2) = 2[<р(т) - ^(0)]/т,	ф(т/2) = 0. /
Подставляя (9) в (8), получаем
М(т/2) = -4mJ2[^(r) - </>(0)]2(l/r2)sin[y>(0) 4- </>(т)];
Р(т/2) = 4Z(mi + 2тп2)[у(т) - <р(0)]2(1/т2) cos[(</?(0) + <£>(т))/2].
Учитывая условие задачи, имеем
М (т/2) = -4,39 Н • м;	Р(т/2) = 33,90 Н.
Обратимся, наконец, к построению графиков зависимостей упра-
вляющих моментов и сил от времени.
Вычисления будем производить в интервале [0;т] с шагом 0,1т.
Графики зависимостей М и Р от времени показаны на рис. 210, 211.
Так как вычисления заключены в простом обсчете формул (8) при
разных значениях аргумента, то они могут быть легко организованы
на любых клавишных вычислительных машинах.
Задание Д.21. Применение уравнений Лагранжа II рода
к исследованию движения механической системы
с двумя степенями свободы
Механическая система тел 1—6 (рис. 212—214) движется под воз-
действием постоянных сил Р и пар сил с моментами М или только
сил тяжести.
Найти уравнения движения системы в обобщенных координатах
Qi и q% при заданных начальных условиях. Необходимые данные
приведены в табл. 57; там же указаны рекомендуемые обобщенные
координаты (т и <р — обобщенные координаты для абсолютного
движения, а £ — для относительного движения).
При решении задачи массами нитей пренебречь. Считать, что каче-
ние колес происходит без проскальзывания. Трение качения и силы
сопротивления в подшипниках не учитывать. Колеса, для которых
в таблице радиусы инерции не указаны, считать сплошными одно-
родными дисками. Водила (кривошипы) рассматривать как тонкие
однородные стержни. Принять, что в вариантах 6, 9, 11, 20, 22 и 30
механизм расположен в горизонтальной плоскости.
306
Рис. 212
307
Рис. 213
60£
viz эиа
310
Таблица 57
Номер варианта (рис. 212-214)	Массы тел					Радиус инерции		Силы P	Момен- ты M	Коэффи- циенты		Обобщен- ные коор- динаты		Начальные условия				Дополнительные данные
	1	2	3	4	5	’2»	’3»			трения скольже- ния	вязкого сопро- тивления	«1	92	910	920	910	920	
1	2т	6m	m	m	-	-	-	-	-	-	-	X	c	0	0	0	0	
2	т	3m	-	-	-	-	-		M	-	-	f	X	0	xo	0	0	Массу ленты не учитывать
3	т	3m	2m	-	-	r\/2	-	-	M	-	-	' f	X	0	0	0	0	Момент М приложен
																		к водилу
4	т	4m	-	-	-	-	-	-	-	0	b	X		0	0	Xo	0	1 — материальная точка
5	m	2m	4m	2m	2m		—	—	—	f	—	Xl	x2	0	0	0	0	Блоки 5 и 6 насажены на общую ось свобод- но, их массы одинаковы
6	m	2m	3m	-	-	2r	-	-	; Л/2	-	-	fl	f2	0	0	0	0	Момент Mi приложен
																		к водилу
7	3m	3m	m	m	-	-	-	Pv, Pi	-	-	-	Xl	Xi	0	0	0	0	
8	m	2m	2m	2m	2m	-	-	-	-	f	-	X	i	0	0	0	Co	
9	m	2m	3m	-	-	-	-	-	Afi; Л^2	-	-	fl	f2	0	0	0	0	Момент Mi приложен
																		к водилу
10	2m	2m	m	2m	m	-	-	-	-	f	-	X	c	0	0	io	0	
11	m	3m	2m	m	-	4r	r\/2	-	Mi; М2	-	-	fl	f2	0	0	0	0	
12	2m	5m	m	-	-	-	-	p	-	f	-	X	t	0	Co	0	0	
13	m	3m	2m	-	-	-	-	-	-	-	b	X	c	0	0	0	Co	1 — материальная точка
14	2m	m	m	2m	-	-	-	-	M	-	-	f	c	0	0	0	Co	
15	3m	m	2m	-	-	-	-	p	M	-	-	f	X	0	0	0	0	Массу ленты не учитывать
16	2m	3m	2m	m	-	2r	-		M	-	—	f	X	0	0	0	Xo	Момент М приложен к водилу
Продолжение табл. 57
>ианта 214)		Массы		тел		Радиус инерции				Коэффи- циенты		Обобщен- ные коор- динаты		Начальные условия				
Номер вар (рис. 212-	1	2	3	4	5	«2у	iay	Силы P	Момен- ты M	трения скольже- ния	вязкого сопро- тивления	91	92	910	920	910	920	Дополнительные данные
17	т	3m		-	-	-	-	P	-	0	b	X	c	0	Co	0	0	1 — материальная точка
18	2т	2m	m	m	3m	-	-	-	M	f	-	X	c	0	0	0	0	
19	2т	2m	3m	m	-	-	ry/2	-	-	f	-	X	c	0	0	io	0	
20	2т	3m	m	3m	-	-	-	-	Mi; М2	-	-	Vl	<?2	0	0	0	0	Момент Mi приложен к водилу
21	2m	2m	3m	2m	m	-	ту/2	-	-	-	-	X	c	0	0	io	0	
22	т	3m	2m	m	-	-	-	-	Mi; М2	-	-	¥>1	<P2	0	0	0	0	То же
23	2т	m	m	m	3m	-	-	-	-	/	-	X	c	0	0	0	Co	
24	т	3m	m	-	-	-	-	p	-	-	b	X	t	0	Co	0	0	1 — материальная точка
25	2т	2m	m	-	-	-	-	Pi; Рз	-	f	-	XI	X2	0	0	0	0	
26	т	3m	2m	3m	-	-	T	-	M	-	-	¥>	t	0	0	0	Co	
27	2т	2m	3m	m	2m	r\/2	ry/3	-	M	-	-	V	c	0	0	0	0	
28	т	3m	m	-	-	-	-	p	-	-	-	X	€	0	0	0	Co	
29	2т	4m	m	m	-	-	-	p	-	f	-	X		0	0	XQ	0	
30	3m	2m	2m	-	-	-	-	-	Mi; М2	-	-	Vl	9>2	0	0	Ф10	0	Момент Mi приложен к
								-										водилу
Примечаия: 1. Радиус инерции тела 2 или 3 определены относительно центральной оси, перпендикулярной плоскости
чертежа.
2. Коэффициентом вязкого сопротивления назван коэффициент пропорциональности в выражении силы
сопротивления относительному движению тел 1 и 2 R = — bv, где v - относительная скорость тела.
Пример выполнения задания. Дано: массы тел механической си-
стемы (рис. 215) mi = 3m; m2 = 8m; тз*= т< — т@ = 2т;	= 4т;
тг = т; Р — постоянная сила, приложенная к телу 2; М\— по-
стоянный момент, приложенный к колесу 6; b — коэффициент про-
порциональности в выражении силы сопротивления движению тела
5 R = —bvs (Ц5 — скорость тела 5), L — длина нити 3; г — радиус
колес 4 и 6.
Все колеса считать сплошными однородными дисками. Трение
скольжения тела 2 не учитывать.
Найти уравнения движения системы в обобщенных координатах
91 = xj; §2 =
Начальные условия: дю = 0 (при этом начальное расстояние по
вертикали от нижнего конца нити 3 до ее горизонтального участка
равно /0), д2о = 0, фо = 0, фо = Фо-
На рис. 215 система изображена в начальном положении.
Решение. Для решения задачи применим уравнения Лагранжа
II рода:
d ат _ дт_ _ _ ап
dtaix	дХ1	дХ1 +	V1'
jd ат_ _ вт_ _ _ ап о
dt di2	дх2	дх2 +
Здесь Т — кинематическая энергия системы; П — потенциальная
энергия; Qi и Q2 — обобщенные силы, соответствующие неконсерва-
тивным силам.
Для данной системы
7
Г =	.	(3)
г=1
Выразим скорости центров масс твердых тел системы через обоб-
щенные скорости:
fi = V5 = Ф;
1>2 = V6 = i2;	>
f? = (Ф + Ф)2/4 + х2 - (Ф + Ф)Ф coso, _
(4)
* Здесь нить 3 принята весомой — это усложнение в сравнении с общим условием
задания. Провисание нити не учитывается.
312
или, имея в виду, что а = 30°,
v27 = 0,25[i2! + (5 - 2\/3)±| - 2(\/3 - 1 )±i±2].
Здесь учитывалось, что (х7+х2)/2 — скорость центра масс тела 7
относительно тела 2, а х2 — его переносная скорость (рис. 216).
Угловые скорости тел (см. рис. 215—217)
w4=ii/r;	1
О)в = О>7 = (±1 + x2)/r. J	* '
Моменты инерции колес относительно центральных осей
J4 = J6 = 2тт2/2 = тг2;
Jr = (т/2)(г/2)2 = тг2/8.
Кинетическая энергия тел 1, 2, 4—7:
Ti = m7v2/2 = Зт±1/2;
Т2 = т2хЦ2 = 4m±2;
Т4 = J4a>l/2 = mil /2,'
T5 = 77151)3/2 = 2mxl;
Tq = m^vl/2 + Je^e/2 = O,577i(ii 4- 3±2 + 2±i±2);
T7 = mrvl/2 + J7rf/2 = (тп/16)[3±? + (11 - 4v/3)±i - 2(2ч/3 - 3)±i±2]-
Кинетическую энергию нити 3 T3 = 0,5	, находим, учиты-
вая, что скорости всех ее точек одинаковы, т. е. 1)31 = ц3 = х7 и
£ 77l3i = 771:
Т3 = m3vl/2 = mil-	'VTXi
Подставляя все эти величины в (3), получим	“
Т=(77г/16)[754 + (99-4У^)^ + 2(11-2х/3)±1±2]. (6)	6
Потенциальную энергию системы находим как рабо-
ту сил тяжести твердых тел 1 и 7 и нити 3 при их Рис- 217
перемещении из данного положения, характеризуемого координатами
и х2, в некоторое исходное нулевое, например то, от которого
ведется отсчет обобщенных координат:
П = П1+Пт+Пз; П1 = —7711 дх\; П? = т7д • у2,	(7)
где у7 — высота центра колеса 7 над уровнем, где он находится при
xi = 0 и х2 = 0. Так как проекция скорости центра колеса на ось у
(см. рис. 216)
v7y —У7 = (xi + ±2)0,5 sin а,
313
Следовательно,
а а
"3
b
-л-Ь' Рис. 218
то, интегрируя это выражение при нулевых начальных условиях,
получим
2/7 = (£1 + £2)0,5 sin а.
П7 = т7д(х1 +£2)0,5 sin а.
Для определения П3 заметим, что работа силы
тяжести нити 3 при ее перемещении из положения
а'Ь' в положение ab, при котором £1 = 0, равна
работе силы тяжести участка нити bb' при его
перемещении в положение аа' (рис. 218).
Таким образом,
П3 = -m3£i#(£i/2 + l0)/L.
Подставляя эти значения в (7), находим
П = g[—mixi + m7(£i + £2)0,5sina - m3£!(£i/2 + Z0)/i],
или
П = mg[-xj/L - (2,75 + 2l0/L)xi + £2/4].	(8)
Обобщенные силы Qi и Q2 можно определить из выражений рабо-
ты неконсервативных сил на элементарных перемещениях системы,
соответствующих вариации каждой обобщенной координаты, или, что
то же самое, из выражений мощности Ni и У2 неконсервативных
сил на возможных скоростях системы, соответствующих возрастанию
каждой обобщенной координаты
Qi = Ni/ii; Q2 = АГг/£2-
В данном случае
^1	^^5(х2=0)	^^6(х2=0),
или с учетом (4) и (5)
Ni = — Rxi — Mil/г.
Отсюда
Qi = -R- М/г,
или
Qi = — tel — М/г.	(9)
Аналогично,
N% = 75£2(±2=о) — Afw6(i1=o)-
Учитывая (4) и (5), имеем
-У2 = Рх2 - Af£2/r;
(?2 = Р - М/г.	(10)
314
Подставляя (6), (8), (9) и (10) в (1) и (2), получаем дифференци-
альные уравнения движения системы:
ymii + -11	= 2тд^~ + mg ^2,75 +	— bxi —	(11)
99 -	। 11 ~	= -l р _ М	(12)
-г g /«а-1 —	। л г .	V1Zi/
Выражая х2 из (12) и подставляя в (11), получаем
Si + 2nxi — cxi — а.	(13)
Здесь п = 0,0538b/m; с = 0,215g/L; а = д(0,298 + 0,215/о/Ь)—
—0,099Л7/(гт) — 0,0088Р/т. Найдем решение линейного неоднород-
ного дифференциального уравнения (13).
Характеристическое уравнение
г2 + 2nz — с = 0.
Его корни 
21,2 = — П ± V П2 + С.
Общее решение дифференциального уравнения (13) имеет вид
хг = e-nt(C1e'/”*+'t + C2e-y/^ct) -	(14)
Для определения постоянных Ci и С2 дифференцируем (14):
X! = e-nt[(-n + \/п2 + с)С1е7^‘ - (п + х/п2 + с)^"7^1]. (15)
Пользуясь начальными условиями: при t = 0 Xi = 0; Xi = 0,—
находим из (14) и (15)
0*1 + С2 — а/с = 0;
(—п + \/п2 + c)Ci — (п + у/п2 + с)С2 = 0.
Отсюда
Ci = А (п + х/n2 + с); )
2cVn2 + c	I
с2 = —	(-п + хЛ^ТЕ). /
2суп2 + с	)
Уравнение (14) с учетом (16) является уравнением движения си-
стемы, описывающим изменение первой обобщенной координаты.
Чтобы получить второе уравнение движения, находим из (12)
= _______________§___ (_9 + Р _ _М_\ _ ll-.2_yg-
2	99-4^ V 4^m тг) 99-4^3 Ъ
ИЛИ
х2 = к- 0,0818^1,	(17)
где к = 0,0869 [- (р - —") -	.
’ [m \ г ) 4J
315
Интегрируя (17), получаем
±2 — kt - 0,0818^! + Сз;	(18)
%2 — kt?/2 — 0,0818xi 4~ C$t 4- Сд.	(19)
Для определения постоянных Сз и С4 используем все четыре
начальных условия: при t = 0	= 0; z2 = 0; ii = 0; i2 = i'20-
Из (18) и (19) следует
Сз = Х20;	С4 = 0.
Теперь вместо (19) с учетом (14) имеем
х2 =	- 0,0818 ^“"‘(Cie77^* + C2e~'^T+it) -	+ x20t
Это второе уравнение движения системы.
УСТОЙЧИВОСТЬ СОСТОЯНИЯ РАВНОВЕСИЯ (ПОКОЯ)
КОНСЕРВАТИВНОЙ МЕХАНИЧЕСКОЙ СИСТЕМЫ
Задание Д.22. Определение положений равновесия (покоя)
консервативной механической системы с одной степенью
свободы и исследование их устойчивости
Для консервативной механической системы с одной степенью сво-
боды требуется:
1. Определить положения равновесия, пренебрегая массами упругих
элементов.
2. Провести исследование устойчивости найденных положений рав-
новесия.
Варианты механических систем показаны на рис. 219—221, а не-
обходимые соотношения приведены в табл. 58.
В качестве обобщенной координаты выбрать угол <р. На рис. 219—
221 показаны механические системы при некотором положительном
угле <р. Во всех вариантах качение колес происходит без проскаль-
зывания и трение в сочленениях отсутствует. При решении задачи
считать все стержни и диски однородными.
Пример выполнения задания. Консервативная механическая си-
стема (рис. 222) состоит из однородного стержня АВ длиной 2/, тел
1 и 2, пружины с коэффициентом жесткости с и тяжелой нити BE
длины L. Вес единицы длины нити р. В качестве обобщенной коорди-
наты примем угол р. При р = 0 пружина сжата на величину /. Вес
тел 1 и 2 соответственно Gi и G2. Провисанием нити пренебречь.
316
Рис. 219
317
Рис. 220
318
Рис. 221
319
Таблица 58
Номер ва- рианта (рис. 219—221)	Соотношения между параметрами	Примечания
1	ZGi = 8RG2	Весом нити пренебречь
2	G2 = l,5Gi; l0 = 2Z; 5cZ = 12Gj	
3	G2 = l,5Gi; cZ = 4Gi; Zo = 21	
4	16cZ = 5Gi; l0 = 2R	
5	G% 3Gi; Zq = 2Z'f cl — 8G1	
6	G2 = 2,5Gi; Zo = 1,5Z; cl = 12Gi	
7	G2 — Gi; 4cZ = 5Gi; Iq = b	
8	Gi + 2G2 = 2cR; f = 0	
9	Gi = G2 = ct; Zo = I	Трением пренебречь
10	Gi = 2G2; cR = 6G2; / = 27?	
11	R = 2ч/2/; Gi = cf	
12	Gi = cZ; to = 0,5J	
13	Gi — G2; Gi = cZ; Zq = 0,5Z	
14	G2 = 3Gi; G2 = ct; l0 = 0,51	
15	l0 = l-,G2 = 0,1cZ; Gi = 4ct(l - V2/2')	
16	G2 = l,5Gi = 0,15сз/; ci = C2 = 2сз; /1 = 0,2Z; f2 = 0; /3 = I	
17	0,5Gi + G2 = cf - f = I	
18	Gil = 2pR2	К цилиндру приклеивается лента 2
19	Gil = 4G2R	Весом нити пренебречь
20	G1 = 2G2; Zo = R;cR = 0,5G2; I = 2R	
21	Gi = 2G2; I = 0,52a	Весом нити пренебречь
22	Gi = 6cZ; a — 21] Ь = l,5Zo; Zo — \/3Z	То же
23	Gi = 3G2 = 3cZ; b = 2l + l0	Весом стержней пренебречь
24	Gi = G2 = cl- b = 3Z; l0 = 41	То же
25	G2 = 1,5^1; 4cZo — I87Z — 5cl = 0	Учесть вес стержней
26	Gi = cZ; 4(5 - Zo - L) = 31	Весом нити пренебречь
27	Gi = 0,57Z	Учесть вес стержней
28	4G2 = 15Gi	Весом стержней пренебречь
29	Gi = cZ; G2 = c(/ + 0,5Z)	Весом нити пренебречь
30	Gi = 0,5pl; L = 2l	Провисанием нити прене- бречь
В таблице обозначено: Gi, G2 — веса тел; р — вес единицы длины тяжелой нити,
ленты; L — длина нити; с — коэффициент жесткости пружины; f — деформация
пружины при <р — 0; 7 — вес единицы длины стержня; Iq — длина недеформирован-
ной пружины; R — радиус диска; Ь, I — конструктивные размеры.
320
Параметры системы удовлетворяют условиям
L = 3Z; G2=c/-7pJ/4; Gi=(p + c)l.
Найти положения равновесия системы и иссле-
довать их на устойчивость.
1. Определение положений равновесия систе-
мы. Для исследования равновесных состояний си-
стемы составим выражение потенциальной энер-
гии. Потенциальная энергия системы складывает-
ся из потенциальной энергии элементов системы в
поле силы тяжести Пс.т и потенциальной энергии
сил упругости деформированных пружин Псу
П — Пс.т + Пс.у.
Рис. 222
В качестве нулевого уровня потенциальной энер-
гии элементов в поле сил тяжести выберем горизонтальную прямую,
проходящую через точку О. Тогда для каждого г-го элемента при
выбранном направлении оси Оу получим
Пс.т(^|) — ОгУгу
где Gi — вес г-го элемента, a yi — вертикальная координата центра
тяжести г-го элемента.
Для рассматриваемой системы Пс.т имеет
вид
Пс.т = Gi?/i + G27/2 + СвкУз + ОкеУа-
Здесь Gbk и Gke — вес участков В К и КЕ
тяжелой нити BE, а уз и у4 — вертикальные
координаты их центров тяжести (рис. 223):
Gbk = P-BK-, Gke = P-KE = p(L-BK).
Длину ВК определим из равнобедренного тре-
угольника ОВК, в котором OB = ОК = I:
ВК = 21 |sin .
Модуль при sin введен для того, чтобы фор-
мула была верна как для ср > 0, так и для
ср < 0. Тогда имеем
Gbk = 2pl sin | ; GKE = р (b - 21 sin f
321
Координаты yi равны:
yt = I cos р = I — 2 sin2 i0 ;
y3 = — OIcos £ = — I cos2 = —I (1 — sin2 0 ;
y4 = - {/ + \KE\ = - {/ + | (l - 21 |sin f J) } ;
У2 — —{/ + KE + e} = — ^i+e + jL — 21 |sin 10
Подставив найденные соотношения в выражения для Пс.т, имеем
Пс.т = вг1 (1 - 2sin2 0 - G2 {/ + е + L - 21 |sin ^|} -
- 2pl2 |sin	(l-sin20 - р (l - 21 |sin | |)	+ | (l - 21 |sin |.
Потенциальная энергия силы упругости пружины определяется
равенством
Пс.у = 1/2сА2,
где А — деформация пружины, равная
А = / + ВК = / + 2/|sin ;
f > 0, если при р = 0 пружина растянута,
f < 0, если при = 0 пружина сжата,
Пс.у = § (/ + 21 |sin £|)2 .
Складывая выражения для Пс.т и Пс.у, получаем выражения для
потенциальной энергии системы в виде
П = П(9?) = <?i/(l-2sin20 -G2 (z + e + L-2/|sin^|)
-2pl2 |sin^| (1 - sin2 0 - p (l - 21 |sin 0) p + 0,5 (b - 21 |sin +
(/ + 2;|sin^|)2.
Функция П(</?) зависит от sin2 и |sin | и потому является четной,
т. е. П(у>) = П(—<р).
Так как функции sin2 и |sin^j удовлетворяют равенствам
sin2 = sin2	; |sin | = |sin (а?тг + 101 для любого целого
к, то график функции П(<р) симметричен относительно вертикалей
р = ктг.
322
Это позволяет провести анализ функции П(<р) только на участке
О <р тг и, пользуясь соображениями симметрии, распространить
результаты на любой другой интервал изменения <р.
Удобно ввести обозначение
•
х = sin у.
Тогда
П = П(т (<р)) = GJ(1 - 2х2) — G2(l + е + L — 2/|т |) — 2р Z2| х |(1 — х2) —
-p(L - 2/| х |)[Z + 0,5(L - 2/| х |)] + |(/ + 2/| х |)2.	(2)
Положения равновесия определим из условия равенства нулю об-
общенной силы Q:
ЙП п дП ЙП дх n
^ = -й7 = 0 или й? = й^ = 0-	<3)
Выражение (2) содержит функцию | х |, график которой при х = О
(<р = 0) имеет излом, т. е. производная при х = 0 не определена.
Поэтому сначала определим корни уравнения (3) при х > 0 (<р > 0),
а затем проведем исследование положения х = 0 (р = 0).
Для интервала 0 < <р тг потенциальная энергия может быть
представлена выражением
П(т (<р)) = 21	- Ъх2 + d - х^ + const,	(4)
где а = 3pl; b = Gi + (р — c)l; d = G2+pL + cf. Учитывая соотношения,
заданные в условии, получаем:
a = 3pl; b = (р + с)1 + (р — с)1 — 2р1;
d = c\f\ + yi + pl-c\f\ = lpl-
П(т (<р)) = 2р12(х3 — 2х2 + 1,25т) + const.	(5)
Слагаемые в правой части (4) и (5), не зависящие от х, выписывать
подробно нет надобности.
Получим и
= 2р/2(3т2 — 4т + 1,25);	= 0,5cos (£) .
Условие (3) дает два уравнения:
= 0, или cos = 0;	(6)
др ’	2	’	' ’
дТ\./дх = 0, или Зт2 — 4х + 1,25 = 0.	(7)
В интервале 0 < <р тг уравнение (6) имеет единственный корень
<Р1 = тг (<Р1 = 180°).
323
Рассмотрим квадратное уравнение (7). Его корни:
4 + 716 - 4 • 3  1,25	5	4-716-4-3-1,25	_
= --------6------------ = б; *2 = -----6-------- = °’'
Так как Xi и x-i по модулю меньше единицы, то им соответствуют
положения покоя системы, определяемые равенствами
siny-=Ti; smy-=T2-
П В интервале 0 < 7 С я получаем два положения равновесия:
q	<Р2 = 2 arcsine = 2arcsin(5/6) = 112,89°,
7з = 2arcsinx2 = 2arcsin0,5 = 60°.
Исследуем теперь положение системы при 7 = 0. Легко
В К видеть, что при 7 = 0 (х — 0) механическая система на-
ходится в равновесии, так как все активные силы направ-
лены вдоль вертикали OD и уравновешиваются реакцией
pL Ro опоры О (рис. 224).
£	Отметим, что при 7 = 0 нить растянута вдоль всей дли-
।	। ны L, так как, по условию задачи, с| f\ < G2.
< ,q Итак, в интервале 0 < 7 тг система имеет четыре поло-
> 2 жения равновесия: 71 = 180°; 72 = 112,89°; 73 = 60°; 74 = 0.
Л< >С“	ГТ	ГТ
Примечание. При других значениях параметров механическая си-
Р 224 стема может иметь в интервале 0	тг три или два положения рав-
новесия.
Положения равновесия рассматриваемой системы в интервале
тг 7 2тг (или —7Г ^7^0) определяются из условия четности
функции П(7) и равны
75 = -7з = -60° = 300°;
76 = -72 = -112,89° = 247,11°.
2. Исследование положений равновесий на устойчивость. Иссле-
дуем на устойчивость положения равновесия в интервале 0	7 тг.
Для этого определим вид экстремума функции П(7) (максимум или
минимум) в положениях равновесия. Составим вторую производную
от П по 7:
Э2П _ Э2П (дх\2 , ЭП Э2х
.	dp2 дх2 \dp) dx д<р2'	'
При 7 = 71 = я производная дх/др = 0 [см. (6)], поэтому из (8)
имеем
Учитывая, что при 71 = тг х = 1, получаем
= 2p/2(3-4+l,25)(-0,25sinf) =-^
dp )	\	°
324
Следовательно, при = </д = тг функция П(<^) имеет максимум. При
ЛГТ
р = </>2 и р = Рз производная = 0 [см. (7)], поэтому
Э2П
дх2
(9)
<Р2,<РЗ
Из (9) следует, что знак второй производной при р = рз и р = рз
<Э2П
определяется знаком gjr-
Так как д2Х\./дх2 = 2р/2(6ж — 4), то при р = рз х = Xi = 5/6 и
д2П/дх2 = 2р12(6 • 5/6 - 4) = 2р12 > 0, при р = рз х = хз = 0,5 и
0 = 2дР(6 • 0,5 - 4) = —2pl2 < 0.
Таким образом, при р = рз функция П(</>) имеет минимум, а при
р = рз — максимум.
В положении равновесия при р = р± — 0 не определены ни первая,
ни вторая производные от потенциальной энергии по углу р. Поэтому
проведем исследование функции П(</?) при р = 0 по знаку в
окрестности положения р = 0.
Производная в нуле справа
dip ) v>=+o
<^>0
х>0
9»>0
= lim 2pl2(5x2 — 4х + 1,25) lim 0,5 cos = l,25pZ2 > 0.
х —»4-0	<р —»+0	Z
® >0	»р>0
Так как производная в нуле справа положительна, то функция П(^)
возрастает при увеличении р (р > 0), т. е.
П(Д|/?) > П(</? = 0)
при малом Д<£ > 0.
Вследствие четности функции П(<р)
она удовлетворяет также неравен-
ству П(—Д<р) > П(<£ = 0). Следова-
тельно, при р = 0 функция П(</>)
имеет минимум. Таким образом,
при р = (pi = 180° и р = рз = 60°
функция П(у>) имеет максимум, а
при р = рз = 112,89° и р = р4 =
= 0 — минимум. На основании те-
оремы Лагранжа—Дирихле при р =
жения устойчивого равновесия, а на
при р = p-з и р = рз — положения
рз и р = pi система имеет поло-
основании теоремы Н. Г. Четаева
неустойчивого равновесия.
325
Теорема Н. Г. Четаева. Если в изолированном положении равно-
весия потенциальная энергия, предполагаемая аналитической функ-
цией обобщенных координат, не имеет минимума, то равновесие не-
устойчиво.
Положение равновесия = <ps является, как и = <рз, неустойчи-
вым, а положение равновесия	соответствующее положению
(р = </>2, - УСТОЙЧИВЫМ.
Сведем результаты исследования в табл. 59 и отметим положения
равновесия на графике функции П(<р) (рис. 225).
Таблица 59
Положение равновесия	Устойчивость положения равновесия	Положение равновесия	Устойчивость положения равновесия
<Р1 = 180°	Неустойчиво	Ч>4 = 0	Устойчиво
<р2 = 112,89°	Устойчиво	— —60°	Неустойчиво
<рз = 60°	Неустойчиво	<рв = -112,89°	Устойчиво
IV. КОЛЕБАНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ
Задание Д.23. Исследование свободных колебаний
механической системы с одной степенью свободы
Определить частоту и период малых свободных колебаний меха-
нической системы с одной степенью свободы, пренебрегая силами
сопротивления и массами нитей.
Найти уравнение движения груза 1 у = 3/(0, приняв за нача-
ло отсчета положение покоя груза 1 (при статической деформации
пружин). Найти также амплитуду колебаний груза 1.
Схемы систем показаны на рис. 226—228, а необходимые данные
приведены в табл. 60.
В задании приняты следующие обозначения: 1 — груз массой
mu 2 — блок массой тг и радиусом г 2 (сплошной однородный
диск); 3 — блок массой тз и радиусом инерции гх; 4 — сплошной
однородный диск массой т4 и радиусом г4; 5 — диск массой ms
и радиусом инерции г'х\ 6 — тонкий однородный стержень массой
mg и длиной Z; 7 — стержень, масса которого не учитывается; с —
коэффициент жесткости пружины; уо — начальное отклонение груза
1 по вертикали от положения покоя, соответствующего статической
деформации пружины; уо — проекция начальной скорости vq груза
1 на вертикальную ось.
На рис. 226—228 системы тел 1—7 показаны в положении покоя
(при статической деформации пружин).
В вариантах 5, 6, 14 и 23 стержень 6 жестко соединен с диском 4.
326
Рис. 226
327
Рис. 227
328
Рис. 228
329
Таблица 60
Номер варианта	1	ix		Г4	ТГЦ	Ш2	m3, 7П4, W5	"16,	с	Начальные условия (t = 0)	
(рис. 226-228)	м				кг				Н/см	УО, см	УО, м/с
1	0,5	-	-	-	1	2	-	3	40	0,1	5,0
2	0,5	-	-	0,2	1	2	2	3	40	0	6,0
3	0,5	3/2г	-	-	1	-	4.	3	20	0,2	7,0
4	0,6	-	-	-	1	2	3	2	36	0,2	0
5	0,6	-	-	0,15	1	-	3	3	16	0	8,0
6	0,6	-	-	0,15	1	-	1	1	40	0,3	7,0
7	-	-	-	-	1	-	2	2	40	0,4	0
8	-	-	-	-	1	3	2	-	40	0	6,0
9	0,6	-	-	-	1	2	-	3	38	0,5	5,0
10	0,6		-	-	1	2	-	3	32	0	6,0
11	-				1	2	-	3	30	0,4	7,0
12	0,5	-	-	-	1	2	-	3	20	0,2	0
13	0,3	-	-	-	1	1	1	2	32	0	8,0
14	0,4	-	-	0,1	1	-	2	3	20	0	7,0
15	0,4	г\/3	-		1	-	2	2	20	0,1	0
16	-	-	-	-	1	2	3	-	32	0,3	6,0
17	-	-	-	-	1	2	-	2	20	0	5,0
18	-	-	-	-	1	2	1	-	40	0	6,0
19	0,2	-	-	-	1	1	-	1	32	0,1	0
20	0,5	-	-	-	1	2	-	3	20	0,4	7,0
21	-	2г	-	-	1		2	3	32	0	8,0
22	-	-	гл/2	-	1	2	4	-	40	0,1	7,0
23	0,4	-	-	0,2	1	2	2	3	40	0,3	0
24	-	-	г\/3	-	1	-	3	2	40	0	6,0
25	0,3	-	-	0,1	1	2	2	1	40	0,2	5,0
26	-	гу/2	-	-	1	-	2	-	40	0,3	0
27	-	-	Зг/2	-	1	2	3	-	40	0	6,0
28	-	-	г\/3	—	1	2	3		40	0,2	0
29	-	-	4г/3	-	1	2	3	-	40	0	7,0
30	-	-		-	1	2	3	-	40	0,3	7,0
Пример выполнения задания. Дано: ту = 1 кг, т? = 2 кг,
mt = 1 кг, те =3 кг, I = 0,6 м; с = 20 Н/см; уо = 0,2 см; уо = 8 см/с
(рис. 229).
Определить циклическую частоту к и период Т малых свободных
колебаний системы, а также получить уравнение у = y(t) колебаний
груза 1 и найти амплитуду а его колебаний.
330
Решение. Воспользуемся уравнением Лагранжа II рода для кон-
сервативной системы. Приняв за обобщенную координату системы
вертикальное отклонение у груза 1 от положения покоя, соответ-
ствующего статической деформации пружины, имеем
А (дТ\ _ (9Т\ - _9П	/П
dt \ ду J	\ ду J ду'	' '
где Т — кинетическая энергия системы; П — потенциальная энергия
системы.
Рис. 229	Рис. 230	Рис. 231
Кинетическую энергию Т вычислим с точностью до величин вто-
рого порядка малости относительно у и у, а потенциальную энергию
П — с точностью до величин второго порядка малости относительно
обобщенной координаты у.
Найдем кинетическую энергию системы, равную сумме кинетиче-
ских энергий тел 1, 2, 6 и 4:
Выразим скорость центра масс тела 4 и угловые скорости тел 2,
4 и 6 через обобщенную скорость у:
vi = у; о>2 = у/т2', мв=ш2 = у/г2.
Так как рассматриваются малые колебания, то vg = гд, а ввиду
того, что диск 4 катится без скольжения, vc = vg/2\ следовательно,
vc = va/2 = LOel/2 = u2l/2 = y//(2r2) = 2j/;
w4 = vc/ri  2jr/r4.
Момент инерции тела 4 относительно центральной оси
Jc = m4r4/2.
Моменты инерции тел 2 и б относительно оси вращения
J2 = mai’i/2; Je = mel2/3.
Кинетическая энергия тел 1, 2, 4 и 6 имеет следующий вид:
_ rn-iv2 _ miy2 rp _ J2U>2 _ m2y2
41-^---у-, т2 _ —,
331
т4 = =£ +	= з™4!л	=	=
Таким образом, кинетическая энергия рассматриваемой механиче-
ской системы
Т = Ti + Т2 + Те + Tt = m1y2/2 + m2y2/4 + 8/3mey2 + Зтп^у2 = •
= l/2[mx + m2/2 + 16/3mg + 6m<]^2.
Найдем потенциальную энергию системы, которая определится ра-
ботой сил тяжести системы и силы упругости пружины на переме-
щении системы из отклоненного положения, когда груз имеет коор-
динату у, в нулевое положение, которым считаем положение покоя
системы:
П = П1 + Пп.
Потенциальная энергия, соответствующая силам тяжести при ука-
занном перемещении,
П[ = ~Giy — GqH,
где h — вертикальное смещение центра тяжести стержня 6, кото-
рое вычисляем с точностью до величины второго порядка малости
относительно обобщенной координаты у.
По рис. 230
h — l/2 — (1/2) cost/? = (7/2)(1 — cost/?).
Ограничиваясь в формуле разложения
cost/? = 1 — </?2/2! + </?4/4! — ...
двумя первыми членами и учитывая, что
V = у/т2 = 4у/1,
имеем
h = (1]2)<р2/2 = (1/4) (^) = 4у2/1.
Таким образом,
Hi = -Gry-Ge -4у2/1.
Потенциальная энергия деформированной пружины при указанном
перемещении системы равна
Пц = c(fCT + Ак)2/2 — с/2т/2,
где /ст — статическая деформация пружины; Хк — перемещение
точки прикрепления пружины К, соответствующее координате у.
Так как (см. рис. 229)
X к _ 3/41
~V ~ G41'
т. е. = Зз/, то
Птт — С^ст +	— С^т — 3 f у 5С?У2
11П —	2	2	— д/сту и 2^5/ •
332
Потенциальная энергия системы
П = П] + Пи = —Giy - (4G6/l)y2 + 3c/CT?/ + 9/2q/2.
Так как в положении покоя, соответствующем статической дефор-
мации пружины,
(дП/ду)у=о = 0, то - Gi + 3cfCT = 0.	(а)
Уравнение (а) можно получить также, составив уравнение момен-
тов сил ^Mio2 =0 для положения покоя системы (рис. 231):
MiO2 = Ро • 3/4/ - Gxr2 = 0,
или
с/ст • 3/4/ — Gil/4 = 0, т. е. 3cfCT - Gi = 0.
Таким образом, потенциальная энергия рассматриваемой механи-
ческой системы
П = 9/2су2 - ^у2 = 1/2 (9с -	у2.
Найдем значения членов уравнения (1):
S ( ад ) = (”*' + Т + Т““+ в“‘) й
g=0; ш =
Уравнение (1) приобретает вид
(mi + ^ + yW + 6т4) у + (9с - у = 0,
или
9c-8G6/J	_
1/ -J-----------—-------у = (J
y mi + m2/2 + 16me/3 + 6m4
Обозначив к2 коэффициент при у, имеем
у + к2у = 0.	(2)
Циклическая частота свободных колебаний
к = «/ 9c-'SGe/l	л _ 27 1 л /„
У mi+m2/2 + 16me/3 + 6m4’	’	'
Период свободных колебаний
Т = 2я/к = 2 • 3,14/27,1 = 0,23 с.
Интегрируя уравнение (2), получаем уравнение движения груза 1:
у = Ci cos kt + С2 sin kt.
Для определения постоянных Сг и С2 найдем уравнение скорости
груза
у = —kCi sin kt + kC-i cos kt
333
и воспользуемся начальными условиями .задачи. Из уравнений у =
= y(t) и у = y(f) при t = 0 имеем:
Уо = Cii	Уо = кС2.
Следовательно,
С1=2/о;	С2=Уо1к.
Подставляем эти значения Ci и С2 в уравнение у = y(t):
у = уо cos kt + (у/к) sin kt-,
у = 0,2 cos 27, It + 0,3 sin 27,It.
Уравнение у — y(t) можно получить в другом виде, если перейти
к другим постоянным интегрирования а и (3, приняв
Ci=asin/3; C2 = acos/3.
Тогда у = asin(fct + /3), где а = у/С% + Cf, /3 = arctg(Ci/C2) или
а = у/Уо + (Уо/kJ2; в = arctg(fcj/o/yo)-
Найдем числовые значения а и /3: а — 3,6 • 10-2 м, 0 = arctg0,68.
Так как sin /3 > 0 (С/ > 0), то /3 = 34° 12' = 0,597 рад.
Окончательно
у = 3,6 • 10~2 sin(27,lt + 0,597) м.
Задание Д.24. Исследование свободных колебаний
механической системы с двумя степенями свободы
Определить частоты малых свободных колебаний и формы главных
колебаний системы с двумя степенями свободы, пренебрегая силами
сопротивления, массами пружин и моментами инерции скручиваемых
валов.
Схемы механических систем тел 1—3 в положении покоя показаны
на рис. 232—234, а необходимые для решения данные приведены в
табл. 61.	•
Примечание. Во всех вариантах колеса считать сплошными однородными дис-
ками, стержни — тонкими однородными. Во всех случаях качение колес происходит
без скольжения.
Пример выполнения задания. Определить частоты свободных
колебаний и найти формы главных колебаний системы с двумя сте-
пенями свободы, указанной на рис. 235.
Дано: li = 0,2 м; 12 = 0,6 м; 12 — 0,3 м; масса груза mi = 0,5 кг,
масса однородного стержня ED т2 = 3 кг; коэффициенты жесткости
пружин: ci = 60 Н/см; с2 — 40 Н/см; с2 = 40 Н/см.
Решение. Система состоит из груза В, подвешенного к рычагу
ED на пружине с коэффициентом жесткости с2. В точках Е и D
рычаг опирается на пружины с коэффициентами жесткости ci и с2.
334
SEE
ZES эиа
Рис. 233
Рис. 234
337
338
Таблица 61
Номер варианта (Рис. 232-234)	Масса тел, кг			Ради- ус R, м	Радиус инерции тела 1 от- носитель- но оси вра- щения гх, м	Коэффициенты жесткости упругих элементов						Расстояние 1, м	Примечания
	mi	Ш2	тз			С1		С2		сз			
						Н см	Нм рад	н см	Нм рад	н см	Нм рад		
1	1	2	—	—	—	40	—	30	—	20	—	0,5	
2	10	2	4	0,2	0,6	400			2 • 103			1	Корпус редуктора имеет возможность поворачиваться вокруг оси колеса 3. Ось колеса 2 неизменно связана с корпусом. Центр тяжести корпуса совпадает с цент- ром колеса 2
3	4					30		20		10			Система расположена в горизонталь- ной плоскости, в которой происходит движение. В положении покоя пружины не деформированы. Тело 1 принять за материальную точку
4	2	5	—	—	—	6	—	8	—	7	—	0,5	
5	5	2	—	—	—	8	—	6	—	7	—	0,5	
6	8	2	—	—	—	20	—	15	—	—	—	—	
7	3	1	—	—	—	6	—	4	—	8	—	0,5	
8	4	1	—	0,2	—	40	—	30	—	—	—	0,3	
9	1	0,5	—	—	—	80	—	10	-	60	—	0,4	
10	6	4		0,2	0,3	4		3				0,1	Центр тяжести тела 1 находится на оси пружины с коэффициентом жесткости cj. В положении покоя пружины не дефор- мированы
11	10	3	—			10		10	—	5		0,4	В положении покоя пружина с коэф- фициентом жесткости ci не деформиро- вана
12	6	—	—	—	—	20	—	30	—	40	—	0,5	-
13	30	30	10	0,4	—	—	2 • 104	—	1 • ю4	200	—	—	
14	40	20	'10	-	-	-	3 • 104	100	-	150	-	. —	
Продолжение табл. 61
339
Номер варианта (Рис. 232-234)	Масса тел, кг			Ради- ус R, м	Радиус инерции тела 1 от- носитель- но оси вра- щения i®, м	Коэффициенты жесткости упругих элементов						Расстояние !, м	Примечания
	ГП1	Ш2	тз			С1		С2		СЗ			
						Н см	Нм рад	н см	Нм рад	Н см	Нм рад		
15	6	—	—	—	0,6	40	—	30		50		1	ix — радиус инерции относительно оси, проходящей через центр тяжести и пер- пендикулярной плоскости рисунка
16	4	6	—	—	—	60	—	100	—	80	—	0,4	
17	50	60	40	0,2	—	—	2 • 104	—	3 • 104	— .	1 • 104	—	7П4 — ТГЦ
18	2	3	8	0,4	—	20	—	40	—	30	—	—	
19	40	60	30	0,35	—	—	1  ю4	—	ЗЮ4	—	—	—	7П4 — Ш1
20	8	10	—	—	—	40	—	60	—	—	—	0,5	
21	4	2			0,6	20		30		30		0,5	Система расположена в горизонталь- ной плоскости, в которой происходит движение. В положении покоя пружины не деформированы
22	30	40	20	0,4	0,5	—	1 • ю4	—	5  103	—	2 • 104	—	
23	3					10		20		30			Система расположена в горизонталь- ной плоскости, в которой происходит движение. В положении покоя пружины не деформированы. Тело 1 принять за материальную точку
24	40	2				2		1				0,4	В положении покоя пружины не де- формированы. Тело 1 состоит из трех одинаковых стержней
25	2	1	0,5	—	—	20	—	40	—	30	—	0,3	
26	6	2	3	—	—	40	—	30	—	10	—	0,2	ТП4 = 7П1
27	8	2	—	—	—	30	—	60	—	—	—	—	
28	6	4	—	—	—	20	—	10	—	30	—	—	
29	4	3	—	—	—	30	—	20	—	40	—	—	
30	30	30	-	-	0,4	-	2 • 104	80	-	100	—	0,5	— ^Х2
Рис. 235
В .состоянии покоя рычаг за-
нимает горизонтальное положе-
ние. Пружины с коэффициентами
жесткости ci и сг деформированы
(сжаты или растянуты) соответ-
ственно на величины /CTi; /СТ2.
Пружина с коэффициентом жест-
кости сз растянута на величину
/стЗ-
За обобщенные координаты
примем: z — вертикальное смещение груза от положения покоя; р —
угол поворота рычага ED от положения покоя. На рис. 236 показано
положение системы при положительных обобщенных координатах.
Найдем кинетическую и по-
Рис. 236
Момент инерции
тенциальную энергии системы.
Кинетическая энергия.системы
состоит из кинетической энер-
гии груза и кинетической энер-
гии рычага:
Т = m\z2/2 + J0<p2/2,
где z, ф — обобщенные ско-
рости; Jq — момент инерции
стержня ED относительно оси
вращения О.
Jo = 7П2/2/12 4-
где I — длина стержня ED, d = ОС — расстояние от центра тяжести
С стержня до оси вращения О (см. рис. 235):
d — (Zi + ^)/2 — li — (^2 — ^1)/2.
Момент инерции стержня будет Jq =0,28 кг-м2.
Потенциальная энергия системы равна работе сил при переме-
щении системы из отклоненного положения в нулевое (положение
статического равновесия).
Потенциальную энергию системы вычислим как сумму:
П = П] + Пц,
где П[ — потенциальная энергия груза и рычага в поле сил тяжести;
Пц — потенциальная энергия деформированных пружин;
П1 — —Giz + С?2^-
Так как
h = ОСр =
340
то
nt = -G1Z + G2l-^±<p.
Потенциальную энергию пружин найдем, рассматривая сначала
перемещение системы из отклоненного положения в положение, со-
ответствующее недеформированным пружинам, а затем из этого по-
ложения — в положение покоя.
Деформации пружин следующие: Л1 = h ± /Ст1 — для пружины
с коэффициентом жесткости ci; Х2 = 12<р ± fCT2 — для пружины с
коэффициентом жесткости с2; Лз = /стз + l3tp + z — для пружины с
коэффициентом жесткости с3.
Следовательно,
Пп = 1/2C1(Z1V ± /ст1)2 - 1/2С1/2т1 + 1/2c2(Z2^ ± /ст2)2-
-1/2с2/2т2 + 1 /2Сз(/стз + 1зЧ> + z)2 - 1/2с/2т3,
или после упрощений
Пп = l/2cj^2 + l/2c2Z2<£2 + 1/2с3(/з<р + z)2 ± ciZifCTi<p±
+ C3.At3(W + z).
Потенциальная энергия всей системы
П = — G\Z + [G2(Z2 — Zi)/2]</> + 1 /2c3l2<p2 + 1/2c2/2¥’2 + 1/2сз/3<р2+
+c3l3pz + l/2c3z2 ± cJi/CTi</? ± c2l2fCT2p + c3/ct3/3<p + c3fCT3z.
Из условий покоя рассматриваемой системы, находящейся под дей-
ствием сил, имеющих потенциал, имеем
(<ЭП/Дг) г—о = -Gi + сз/стз = 0;
ip=0
(дП/др) г=о = G21— 11 ± C1/1/CT1 ± c2Z2/ct2 + Сз/з/стз = о.
95=0
Потенциальная энергия системы с учетом условий покоя имеет
вид
П = 1/2ciZ2(/?2 + 1/2с2/2(^2 + 1/2сз/з<£2 + c3l3zip + l/2c3z2.
Таким образом,
Т = l/2miz2 + 1/2Jq02;
П = l/2c3z2 + c3l3ztp + l/2(ciZ2 + c2Z2 + c3l3)ip2
или
T = 1/2(ац22 + 2а±2гф + a22<p2);
П — l/2(ciiz2 -I- 2c\2zip + c22y>2).
Здесь aij — коэффициенты инерции:
an = тц ai2 = 0;	a22 = Jo',
341
Cij — коэффициенты жесткости:
Cll = С3,	С12 = С3/3,	С22 = Cilf + С2/2 + с3^з-
Для рассматриваемой консервативной системы уравнения Лагран-
жа имеют вид
d (ЭТ\ _ дТ _ ЭП.	А (&L\ - ОТ. = эп
dt \di ) dz dz ’	dt / dip dip'
Вычислив производные
dT _ n	dT	_ n .
dz -0’	di	~ ailZ'
dT n	dT
dij = Q'	дф	=a^'
d (dT\
dt {di) =a^
d (dT \
й[дф) =a^
— C11 z 4- Ci2^;
an
= С12г + C22<p
а) Первое главное колебание системы
k,=-66,4c';	,49рад/м
и подставив их в уравнения Ла-
гранжа, получим
anz = -сиг - ci2ip;
а22<Р = — C21Z - С22<Р,
где c2i = с12.
Таким образом, для данной си-
стемы дифференциальные урав-
нения свободных колебаний име-
ют вид
йц2 4- Сц2 4- си1/? = 0;
0.2242 + C21Z + C22V = 0.
Частное решение этих уравне-
ний:
z = Az sin(kt + /?);
ip = Ay, sin(kt 4- /3),
где Az n Ay, — амплитуды главных колебаний; k — частоты сво-
бодных колебаний; (3 — начальная фаза колебаний.
Уравнение частот, вытекающее из данной системы дифференци-
альных уравнений, имеет вид
(di - aiifc2)(c22 - 0.22k2) - с22 = 0.
Корни этого биквадратного уравнения, соответствующие квадратам
частот, определим по формулам
2	«11С22 + «22С11 Т Ц (“11С22 + Я22С11)2 - 4аца22(сцС22 - С?2)
2аца22
В рассматриваемой задаче: ац = ту — 0,5 кг; сц = сз = 4000 Н/м;
Ci2 = C3Z3 = 1200 Н, а2 = Jo = 0,28 кг  м2; с22 = CxZ2 + C2I2 + с3/2 =
= 2040 Н • м.
342
Следовательно, частоты свободных колебаний
fci = 66,4 с-1; к? = 104 с-1.
Коэффициенты распределения, соответствующие частотам fci и к?,
в общем случае имеют вид
_ А?! _ СИ ~ “U^l _	с12 —	«12^1
A*t	CJ2 — «32^1	С22 — «22^1	’
__ AV2 	 СЦ—dllfcj 		С12	—	<112^2
Az2___________________________С12 — «12^2_с22 —	«22^2
В данном случае Д1 = —1,49 рад/м; д2 = 1,2 рад/м.
Уравнения, определяющие первое главное колебание, примут сле-
дующий вид:
zi = Л21 sin(66,4t + ,31);	— — 1,49А21 sin(66,4t + /31).
Уравнения, определяющие второе главное колебание,
z2 — AZ2 sin(104t + /32);	= 1,2А22 sin(104t + /32).
Формы колебаний показаны на рис. 237, а, б.
Общее решение дифференциальных уравнений представляет собой
сумму частных решений:
z = zi + z2 = AZ1 sin(66,4i + /31) + Л22 sin(104i -I- /32);
V = 4->i + Ч>2 = —0,0149Л21 sin(66,4< + /31) + 0,012Л22 sin(104Z + /32).
Значения Azi и Д определяются по начальным условиям задачи.
Задание Д.25. Исследование вынужденных колебаний
механической системы с одной степенью свободы
Исследовать вынужденные колебания механической системы с од-
ной степенью свободы при силовом (варианты 2—5, 7—9, 12—15, 17,
18, 20, 22—25, 27, 28, 30) или кинематическом (варианты 1, 6, 10,
11, 16, 19, 21, 26, 29) возмущении.
Схемы механических систем показаны на рис. 238—240.
Силовое возмущение. Необходимые сведения о параметрах си-
стемы и силового возмущения приведены в табл; 62. Диссипативные
свойства системы заданы логарифмическим декрементом затухания
системы ц.
В вариантах 9, 23, 30 механические системы расположены в гори-
зонтальной плоскости.
В вариантах 2, 7, 9, 18 пружины с коэффициентом жесткости ci
в положении покоя не деформированы.
Определить: коэффициент а, характеризующий вязкое сопротивле-
ние, осуществляемое в демпфере, уравнение вынужденных колебаний
343
Рис. 238
344
Рис. 239
345
9К
от-г эис1
Таблица 62
Номер варианта (рис. 238-240)	Масса тел, кг			Радиус Я, м	Расстояние 1, м	Радиус инерции тела 1 относительно оси м	Коэффициенты жесткости пружин				р, н	А, м	Р		Логарифмический декремент
	ТП1	m2	тз				С1		с2				с 1		
							Н см	Нм рад	н см	Нм рад					
2 3 4 5 7 8 9 12 13 14 15 17 18 20 22 23 24 25 27 28 30	8 2 20 40 5 40 40 40 30 20 45 40 50 80 40 30 70 10 40 25 40	2 4 5 10 5 30 15 30 15 30 30 10 20 15 50	10	0,3 0,2 0,4 0,3 0,2 0,3 0,2 0,3 0,4 0,4 0,2 0,3 0,2 0,3	0,9 0,1 0,6 0,5 0,4 0,6 0,4	0,4 0,5	50 10 20 15 20 10 18 12 14 10 22 16 12 14 25 14 15 12	2104 1104 2 104	30	ЗЮ4 ЗЮ4	50 40 30 10 15 35 8 12 25 20 16 24 26 18 14 18 24 40 12 18 20	0,2 0,1 0,4 0,1 0,15 0,1 0,05	2я 4я 4я 3,5я 2я 1,5я 2,5я 4,5я 2,2я Зя 2я Зя 1,4я 3,2я 2,2я Зя 2,5я 1,5я 3,2я 2,5я		0,48 1,75 0,50 0,40 0,35 0,62 1,70 0,66 1,32 0,50 1,10 1,08 0,56 1,60 1,04 0,95 1,62 0,98 1,14 0,86 1,35
системы при заданной частоте возмущения; максимальные и резо-
нансные значения амплитуд изменения обобщенных координат, ско-
рости и ускорения в предположении, что частота возмущения может
изменяться.
Примечание. Во всех вариантах колеса считать сплошными однородными дис-
ками, стержни — тонкими однородными, качение колес происходит без скольжения.
Кинематическое возмущение. Условия к вариантам с кинема-
тическим возмущением 1, 6, 10, 11, 16, 19, 21, 26, 29 см. в табл. 63.
Система состоит из подвижного якоря массы т, который с помо-
щью пружины удерживается в положении покоя, изображенном на
чертеже (см. рис. 238—240).
347
Таблица 63
Номер варианта	т,	D IO"5	б	6	1	f	d	6
(рис. 238240)	кг	Нм2	Нм/с	м				
1	0,08	1	0,009	0,005	0,12	0,02	0,01	0,07
6	0,09	2	0,009	0,006	0,12	0,04	0,06	0,05
10	0,1	2,5	0,008	0,008	0,09	—	—	0,07
11 .	0,08	1	0,008	0,005	0,008	0,02	0,06	0,04
16	0,15	1,5	0,01	0,006	0,1	—	0,06	0,08
19	0,05	1	0,007	0,007	0,08	0,03	0,06	0,05
21	0,07	1,1	0,08	0,014	0,12	0,03	0,09	0,04
26	0,1Й	3,6	0,08	0,011	0,08	—	—	0,07
29	0,1	1,5	0,007	0,006	0,12	-	—	0,06
Якорь считать тонким однородным стержнем. Центр тяжести яко-
ря находится в точке С. При движении якоря на него действует со
стороны шарнира момент сил вязкого сопротивления, пропорциональ-
ный угловой скорости якоря (коэффициент пропорциональности В).
На якорь со стороны постоянного магнита действует сила притяже-
ния, направленная вдоль оси воздушного зазора. Эта сила F = D/62,
где D — некоторая постоянная; 6 — величина воздушного зазора.
Плоскость чертежа совпадает с вертикальной плоскостью. Вели-
чина воздушного зазора в положении покоя равна <5о-
Корпус устройства вибрирует, перемещаясь поступательно вдоль
указанного на чертеже направления, по закону £ = £о sin pt, где —
малая величина; р — циклическая частота вибрации.
Для нормального функционирования устройства должны быть удо-
влетворены следующие условия:
1. Амплитуда относительного перемещения конца якоря при резо-
нансе Арез (р = к, где к — циклическая частота свободных колебаний)
должна составлять 2/3 величины 6q.
2. Амплитуда относительного перемещения конца якоря Аж при
высоких частотах возмущения (р » к) должна быть равна 1/3 от
величины 6о.
Исходя из этих требований, определить:
1.	Циклическую частоту малых свободных колебаний якоря.
2.	Статическую деформацию Ао и коэффициент жесткости cj пру-
жины.
3.	Максимально допустимую величину £о амплитуды вибрации
корпуса устройства.
4.	Максимальную амплитуду вынужденных колебаний якоря.
Необходимые для решения данные приведены в табл. 63.
Пример выполнения задания к вариантам 2—5, 7—9, 12—15,
17, 18, 20, 22—25, 27, 28, 30.
Дано: mi = 20 кг, т2 = 5 кг, тз = 2 кг, ггц = 18 кг; 7? = 0,3 м;
I = 0,9 м; ci = 40, С2 = 70 Н/см; Р = 20 Н; х = A sin pt; А = 0,1 м;
р = 4тг с-1; ц = 0,812. Обе пружины в положении покоя не деформи-
рованы.
348
Вычислить коэффициент а,
характеризующий вязкое сопро-
тивление, осуществляемое в
демпфере, включенном в сис-
тему 1—3 в соответствии с
рис. 241.
Определить уравнение выну-
жденных колебаний системы
при заданной частоте возму-
щения р. Найти также макси-
мальные и резонансные значе-
ния амплитуд изменения обоб-
щенных: координаты, скорости
и ускорения.
Решение. За обобщенную координату примем — угол поворота
колеса 1 (рис. 242).
Уравнение Лагранжа в рассматриваемом случае имеет вид
А (дТ _ дП ЭФ . о
dt \дф4 ) dtp\	дф±
(1)
где Т — кинетическая энергия системы; Ф — функция рассеяния си-
стемы (диссипативная функция Релея); П — потенциальная энергия
системы; Qp — обобщенная
Функции Т, Ф и П вычи-
сляются с точностью, при
которой справедливы фор-
мулы
Т = 1/2аф%;
Ф = 1/26^2;
П = 1/2ар4,
где а и с — коэффици-
енты инерции и жесткости
системы, а b — коэффици-
ент, характеризующий со-
противление в системе.
Найти кинетическую энер-
возмущающая сила.
гию системы как сумму кинетических энергий тел 1, 2, 3 и 4:
Т = Т1+Т2+Т3+ Т4.
Выразим скорости центров масс vci и тез тел 1 и 3, скорость
тела 2 и угловые скорости оц, ш3 и ш4 тел 1, 3 и 4 через обобщенную
скорость ф4:
= Ф1;	^<71 =	= Wi ;	^2 = 2vm = 2Лф4.
Стержень 3 совершает плоское движение. Мгновенный центр ско-
ростей этого звена при его положении, совпадающем с положением
349
покоя, находится в бесконечности. Следовательно, для обеспечения
указанной выше точности выражения кинетической энергии систе-
мы можно считать, что о?з = 0 и ъсз — Vd = Vb = V2 = 27?ipi,
cj4 = vd/1 = 2R<pi/l.
Момент инерции тела 1 относительно центральной оси Jfi =
= miR2/2. Момент инерции тела 4 относительно оси вращения
Ji = mil2/3. Кинетическая энергия тел 1, 2, 3 и 4 имеет вид
Ti = 1/277111,^ 4-1/2701^1 = 3/4mi.R2<Pi;
Тъ = \/2т^2 = 2ni2-R2<Pi;
7з = 1/2тзД^3 = 2тз/?2<р2;
Ti = I/2J4W2 = 2/Зт^2ф2.
Кинетическая энергия всей системы
Т = 3/4mi/?2<pf + 2т2Я2<^1 + 2m3jR2y>2 + 2/3m4J?2y>2 = 1/2аф2,
где коэффициент инерции системы
а = [3/2/771 + 4/772 + 4/773 + 4/3/774]/?2.
Найдем функцию рассеяния системы:
Ф = l/2av| = 1/2о(2й^1)2 = 1/26^,
где
b = 4R2a.
Переходим к определению потенциальной энергии системы.
В положении покоя
= О,
поэтому в выражении для П сумма всех членов первого порядка
малости равна нулю. Это позволяет непосредственно производить
определение потенциальной энергии системы, вычисляя только члены
второго порядка малости.
Найдем потенциальную энергию системы как сумму работ сил
тяжести и сил упругости пружин на перемещении системы из откло-
ненного положения, определяемого углом <pi, в нулевое положение,
каковым считаем положение покоя системы. При этом в выражени-
ях для деформации пружин, не загруженных в положении покоя,
учитываются только те слагаемые, которые имеют первый порядок
малости относительно <pi, а в. выражениях для вертикальных сме-
щений центров тяжести элементов системы — слагаемые, имеющие
350
второй порядок малости. Деформации пружин, загруженных в поло-
жении покоя, вычисляются с точностью до величин второго порядка
малости включительно.
Потенциальная энергия П1, соответствующая силам тяжести, равна
П1 = — G3hcs ~ Giha,
где hcs и het — вертикальные смещения центров тяжести элементов
3 и 4, вычисленные с точностью до величин второго порядка малости.
Из рис. 242 видно, что
^•<74 = Z/2 “ (//2)cos<p4 = (7/2)(1 - cos<р4).
Ограничиваясь в формуле разложения
cos <р4 = 1 - 924/2! + у>1/4! - ...
двумя первыми членами и учитывая, что
924 = Ад// = Ад/Z = Ад/Z = 2Rtp4/l,
имеем
ha = (V2)^/2 = (Z/4)47?292?/Z2 = (Я2//)^-
Учитывая, что hcs = ho/2 = ha, получаем
Hi = -G3hC3-G4ha = -Gs-R^/l-Gi-R2?2/! = -(fl2/Z)(G3+G4)^.
Потенциальная энергия Пц деформированных пружин при указан-
ном перемещении системы равна
Пц = 1/2С1АД + 1/2сг(Ак cos45° — Ад-)2,
где Хе, Xf, Ад- — перемещения точек прикрепления пружин, вы-
званные поворотом диска 1 на угол
Вычисляя эти величины с точностью до слагаемых первого поряд-
ка малости относительно 921, имеем
Хе = LE  <pi =	; Ад = LF  924 = Ry/2ip3-,
Хк = ОК • <р4 = 4/3R(p\.
Таким образом,
Пц = (ci + с2/18)Я2<9>2.
Потенциальная энергия системы
П = П[ + Пц = — (Я2//)(С3 + С4)<р2 + (ci + с2/18)Я29?2 = I/2C922,
где коэффициент жесткости системы
с = [2ci + с2/9 - 2(G3 + G4)//]7?2-
Определим обобщенную силу Qp, соответствующую возмущающей
силе Р:
Qp = Px6tpl/{6(pi') = Рх = Р • Asmpt.
351
Здесь 6<pi — приращение обобщенной координаты; РхЬ^у — работа
силы Р на элементарном перемещении системы, соответствующем
приращению <5<Pi обобщенной координаты.
Используя полученные для Т, Ф, П и Qp выражения, получаем
уравнение (1) в следующем виде:
афу 4- Ьфу + c<pi — Р  A sin pt,
или
фу + 2пфу + k2<pi = hsinpt,	(2)
где b/а = 2п; с/а = к2; РА/а = h.
Уравнение вынужденных колебаний системы является частным
решением неоднородного дифференциального уравнения (2) и имеет
вид
<pi = AV1 sin(pt - е),	(3)
где Ар} — амплитуда вынужденных колебаний; е — сдвиг фазы
вынужденных колебаний;
,	_	h	,	__ 1пр
*’1 - 7(к2_р2)2 + 4п2р2;	£ - к2 - р2 •	W
Определим h, к, п:
h -- Р  А/а\ к = у/с/а-,
откуда h = 0,271 с~2; к — 10,2 с-1.
Величину п определим по заданному логарифмическому декремен-
ту затухания системы:
__	7Г71	__ Т	/т»*	2?Г
71 ~ Vfc2 - П2 ~ П”2-’ ГД “ Vk2 - п2 '
Отсюда
п = к - =, т. е. п = 2,55 с-1.
Vl+TT2/»)2’
Коэффициент а, характеризующий сопротивление, осуществляемое
в демпфере, вычисляем по формуле
__ Ь ___ ап
” 4Л2 “ 2R2
Таким образом, а = 104,5 Н-с/м.
Амплитуду изменения угла (pi и сдвиг фазы вынужденных колеба-
ний системы при р = 4тг с-1 = 12,57 с-1 определяем по формулам (4):
Alfil = 0,00325 рад; tge = —1,19; е = 130°04' = 2,27 рад.
Окончательно по формуле (3) имеем
<pi = 0,00325 sin(4?rt — 2,27) рад.
Определяем максимальные значения амплитуд изменения фу
и фу при условии, что частота возбуждения р может изменяться.
352
Амплитуда колебаний AV1 имеет максимум при
p = pi = у/к2 - 2п2 = 00,22 - 2 • 2,552 = 9,53 с"1,
откуда
А - h
юах ~ 2nVk^^
_________0,271__________
2 • 2,55-^/10,22 - 2,552
= 0,00537 рад.
Обобщенная скорость
01 =  ; -----к ~ cos(pZ — е) = . „	J1..........—_ cos(pt — е).
^/(fc2 — р2)2 + 4п2р2	-/(А:2 — р2)2 /р2 + 4п2
Следовательно, амплитуда обобщенной скорости имеет максимум
при р = р2 = к:.
Афг max =	Аф! max — 0,0531 рад/с.
Обобщенное ускорение
0! —-----.	—....... sin(pt — е) =----, h — sin (pt - е).
у/(к2 - р2)2 + 4п2р2	fk2 _р2\2	(п\2
+4Ь)
Найдем то значение р = рз, при котором амплитуда обобщенного
ускорения имеет максимум, а следовательно, подкоренное выраже-
ние [(к2 — р2)/р2]2 + 4(п/р)2 имеет минимум. Для этого вычислим
производную этого выражения по р и приравняем ее нулю:
—2рр2 — 2p(fc2 — р2)
После упрощений получаем
А:4 — р2к2 + 2п2р2 = 0,
откуда
р = к2/\/к2 — 2п2.
В рассматриваемой задаче
р = рз = 10,9 с-1.
Максимальное значение амплитуды обобщенного ускорения
А 	=	h	
таХ 1/[(^/Рз)2 - I]2 + 4(п/р3)2 ’
после вычислений получим А^1тах= 0,559 рад/с2.
353
Определим теперь амплитуды изменения обобщенных координат,
скорости и ускорения при резонансе:
AV1 {р=к) = h/(2nk) = 0,271/(2 • 2,55 • 10,2) = 0,00520 рад;
(p=fc) — АР1 max — 0,0531 рад/с,
АР1 (Р=к) = hk/2n = 0,271 • 10,2/(2 • 2,55) = 0,54 рад/с2.
Из вычислений следует, что амплитуды изменения обобщенной
координаты и ускорения при резонансе (р — к) весьма близки к
максимальным значениям.
Пример выполнения задания к вариантам 1, 6, 10, 11, 16, 19,
21, 26, 29.
Схема устройства показана на рис. 243.
Дано: т = 0,1 кг, /3 = 0,01 Н-м-с; Йо = 0,006 м; I = 0,1 м; f = 0,04 м;
d = 0,05 м; b = 0,08 м; D = 3 • 10“5 Н • м2.
Решение. За обобщенную ко-
ординату примем угол <р поворо-
та якоря (рис. 244), который бу-
дем отсчитывать от положения
покоя в сторону уменьшения воз-
душного зазора 6.
Уравнение Лагранжа II рода,
описывающее относительное дви-
жение якоря, имеет вид
а. (дт\_аг = 0
где Qv = Qn + Qm + Qr + <?ф-
Здесь Т — кинетическая энергия якоря; Qn = —	— обобщенная
сила от механических сил, имеющих потенциал (П — потенциаль-
ная энергия); Qm — обобщенная сила от сил притяжения якоря;
=	— обобщенная сила от сил вязкого сопротивления; Q$ —
обобщенная сила от переносной силы инерции Фе.
При изучении колебательного движения систе-
мы функции Г, П и Ф будем вычислять с точно-
стью до величин второго, а обобщенные силы —
до величин первого порядка малости относительно
<Е, Ф, С и
Вычисление обобщенных сил. Обобщен-
ную силу Qm найдем по формуле
z~i _ Nr _ F • vM
У'
В
Е
х
G
Рис. 244

Ф
где Nf — мощность силы притяжения якоря F; vm — скорость
точки приложения силы F.
354
Так как vm = 1ф, а векторы vm и F направлены по одной прямой
в одну сторону, то, учитывая, что 6 = б0 - 1<р, будем иметь
вм = S = Fl =	= DKSo - lv}-\
Разложим Qm в РЯД Маклорена с точностью до величин, первого
порядка малости относительно у:
Qm = Qm(0) + Q'm(0W1! + ..., (Q' = d(?/d^).	(2)
Так как
Q'm = D/(-2)№ - /<Р)-3(-/),
ТО
Ы = 2D12/Sq.
Учитывая, что Qjw(O) = DI/<5q, получим
Qm = Wo +	(3)
Обобщенная сила Qr равна
Qr = Nr/Ф = -MRф|ф = —Mr,
где Nr — мощность момента сил вязкого сопротивления; Mr = &ф —
момент сил вязкого сопротивления.
Таким образом,
Qr = -0Ф-	(4)
Обобщенную силу <5ф, соответствующую переносной силе инерции
Фе, определим по формуле
Qi = Nz/ф = Фе • vc !Ф,	(5)
где А7ф — мощность переносной силы инерции Фе; vc — скорость
точки приложения силы Фе; vc = (1/2)ф.
Переносная сила инерции
Фе = —тае,
где ае = б — переносное ускорение.
Подставляя значения Фе и vc в (5), получаем
Q$ = —т£(1/2)фсо5<р/ф= — m£(//2) cos</>.
Разложив Qф в ряд Маклорена и удержав в этом разложении сла-
гаемые не выше первого порядка малости относительно <р, получим
(?ф = —тГб/2.	(6)
Для вычисления Qn найдем потенциальную энергию П, склады-
вающуюся из потенциальной энергии якоря П1 в поле сил тяжести
и потенциальной энергии Пц деформированной пружины:
П = П1 + Пц.	(7)
355
Потенциальная энергия Пт с принятой выше точностью
ni = -G(//2)sin^^-G(//2)^.	(8)
Потенциальная энергия Пц определяется выражением
Пц = Ci(Ao + А<р)2/2 - ciAq/2,	(9)
где Aq — деформация пружины в положении покоя; Xv — дополни-
тельная деформация пружины, вызванная поворотом якоря на угол р.
Из (9) следует, что для обеспечения принятой погрешности в вычи-
слении потенциальной энергии достаточно Ау подсчитать с точностью
до величин второго порядка малости относительно <р.
Вычисление А^ удобно произвести следующим образом. Придадим
отрезкам ОА, АВ и BE ориентацию, показанную на рис. 244. Тогда
О А + АВ + BE = const.	(10)
Спроецируем (10) на оси хну, выбранные так, чтобы одна из
осей была параллельна оси пружины в положении покоя:
b + d = dcos р + f sin p + (b — Av) cos
f — — damp + f cos<p + (b — Av)sinip, f	( '
где ip — угол поворота оси пружины (рис. 244).
Разложим (11) в ряд по степеням малых величин р, Xv и ip и
удержим слагаемые до второго порядка малости включительно:
b + d = d(l — р2/2) + fip + b — Xv — bip2/2,	(12)
f——dp + /(l-^2/2) + (b-Av)V>.	(13)
Перепишем эти уравнения так, чтобы слагаемые, содержащие пер-
вые порядки малости относительно искомых величин Xv и ip, нахо-
дились в левых частях равенств:
Xv = ftp - dp2/2 - bip2/2,	(14)
bip = dp + fp2/2 + Xvip.	(15)
Выражение (14) содержит квадрат угла ip, поэтому для сохранения
принятой точности вычисления А^ нужно угол подсчитывать с точ-
ностью до величин первого порядка малости относительно р. Для
этого отбросим в (15) величины второго порядка малости:
bip = dp или ip = (d/b)p.
Следовательно,
= Л? - d(p2/2)(l + d/b) = fp- ср212,	(16)
где е = d(l + d/b).
356
Подставим (16) в (9). С точностью до величин второго порядка
малости относительно у функция (9) принимает вид
Пп = (1/2)сх(/2 - Л0е)<£2 + сМо/у.	(17)
Складывая (8) и (17) в соответствии с (7), получим
П = -G(Z/2)V + 1/2С1(/2 - А0е)</?2 + cXofp.	(18)
Отсюда обобщенная сила
Qn = -g = G//2-ci(/2-Aoe)^-ciAo/.	(19)
Подставив выражения Qm, Qr, <Эф и Qn из (3), (4), (6) и (19) в (2),
получаем
Qv = Dlffi + 2DZ2<p/^ -13ф- ml£/2 + Gl/2 - C1(f2 - Xoe)p - aXof,
или
Qv = -ар -РФ- ml£/2 - C1Xof + Gl/2 + Dl/8%,	(20)
где
с = С1(/2-А0е)-2Г>/2/^.
Условие относительного покоя (равновесия) механической системы
при р = 0, ф = Q и £ = 0 имеет вид
„о = 0-
4=о
Отсюда
Gl/2-aXof + DI/81 = 0.	(21)
Таким образом,
Qv = —ср - РФ - (т//2)£.	(22)
Вычисление кинетической энергии. Так как в относи-
тельном движении якорь совершает вращение вокруг оси, проходящей
через точку О, то его кинетическую энергию вычисляют по формуле
Т = Jop2 /2,
где Jo — ml2/3 — момент инерции якоря относительно оси вращения,
т. е.
Т = (ml2/3)(ф2/2) = аф2/2,	(23)
где а = ml2/3 — коэффициент инерции системы.
Дифференциальное уравнение вынужденных колебаний якоря по-
лучим, подставив (22) и (23) в (1):
ар + рф + ср = —(ml/2)£,
или
ф + 2пф + к2р — hp2 sin pt,	(24)
где 2п = PI a, h — m.l£o/(2a)', к = \Jcfa — циклическая частота
свободных колебаний.
357
Рис. 245
Вынужденные колебания сис-
темы описываются частным ре-
шением неоднородного диффе-
ренциального уравнения (24)
sin(pt — е),
где А,? — амплитуда выну-
жденных колебаний; е — сдвиг
фазы вынужденных колебаний
по отношению к фазе возмуща-
ющей силы:
__ ________hp2___________
у/(к2 — р2)2 + 4п2р2 ’
(25)
,	2пр
Функция Av = Л^(р) имеет максимум (см. аналогичную функцию
в предыдущем примере) при
р* = к2/у/к2 - 2п2	(к2 > 2п2).
Этот максимум будет равен
Av max — , —	'~Ti2'~~5-л/- / Д'	(^®)
V {(к/Р*Г - Ч + 4(п/р*)2
При неограниченном увеличении р амплитуда вынужденных коле-
баний Av асимптотически стремится к h.
При резонансе, когда к = р, имеем
Аррез = hk/(2n).	(27)
На рис. 245 показан вид графика функции Av = Av(p) при раз-
личных п. Сплошной линией выделен график Av = ЛДр) для рас-
сматриваемой задачи.
Вычисляем искомые параметры. Из условия известна амплитуда
относительного перемещения конца якоря при резонансе; следователь-
но, из (27) можно определить циклическую частоту его свободных
колебаний. Учитывая, что .4рез = /.4^рез и А^. = lh, получим
к = 2Alfipe3n/h = ЗАреэ/З/^РАоо).	(28)
Для определения статической деформация пружины Ло и ее коэф-
фициента жесткости cj выразим Aq из уравнения (21):
A0 = [l/(C1/)](G//2 + r>Z/^02).	(29)
Тогда из (20) находим
с = ci/2 - С1Аое - 2D126q = C1f2 - (e//)(G//2 + Dl/62) - 2Dl2/S3.
358
Так как с = ак2, то
ci = [ml2k2/3 + (e//)(G?/2 4- Dl/620) + 2D12/bf]/ f.	(30)
Для вычисления £o воспользуемся тем, что задается амплитуда
относительного перемещения конца якоря Аж при высоких частотах
возмущения. При р 3> к имеем Av ~ h = £omZ/(2a). Отсюда макси-
мально допустимая амплитуда вибрации корпуса устройства может
быть найдена по формуле
£о = 2аК/(т1) = 2aAoo/(ml2) = 2/ЗАоо-	(31)
Подставляя в формулы (28)—(31) числовые значения входящих в
них величин, получаем: к = 60 с-1; Ci = 2654 Н/м; Ао = 0,00125 м =
= 1,25 мм; £о = 0,00133 м = 1,33 мм.
Подсчитаем с помощью формулы (26) максимальную амплитуду
вынужденных колебаний конца якоря и частоту возмущающей силы,
при которой этот максимум наступает:
р„. = к2/у/к2 — 2п2 = № jyjk2 — 9/32/(2т2/Р) = 64,14 с-1,
Лпах = IAV max ~	.2 °?2	, . .3 = 0,0041 М.
VKfc/P*)2 - I]2 + 4(п/р.)2
Видно, что Лтах практически не отличается от 4рез.
Задание Д.26. Исследование вынужденных колебаний
механической системы с двумя степенями свободы
Механическая система с двумя степенями свободы находится
под действием силового гармонического возмущения в виде силы
Р = Ро cos pt или момента М = Mq cos pt. Пренебрегая сопротивлени-
ем, исследовать вынужденные колебания системы.
Схемы механических систем в положении покоя показаны на
рис. 232—234. Необходимые сведения об инерционных и упругих свой-
ствах системы, а также ее размеры приведены в табл. 61. Массами
пружин и скручиваемых валов пренебречь.
В табл. 64 указано, к какому из тел системы приложена возму-
щающая сила Р или пара сил с моментом М. Линия действия силы
Р во всех случаях проходит через центр тяжести тела, к которому
она приложена. В процессе колебаний линия действия силы остается
либо вертикальной, либо горизонтальной.
Пара сил с моментом М расположена в плоскости колебаний
тела, к которому она приложена. Во всех вариантах положительное
направление силы Р и момента М, изменяющихся по гармоническому
закону, можно выбирать произвольно.
В табл. 64 задано линейное или угловое смещение от положения
покоя для тела, к которому приложено силовое возмущение при
условии воздействия постоянной силы Р = Ро или момента М = Мо
359
Таблица 64
Номер варианта (рис. 232—234)	Вид возму- щения	Номер тела, к которому приложено возмущение	Линия дей- ствия силы Р	Линейное смещение при Р ~ Ро, м	Угловое смещение при М — Мо, рад
1	м	1		-	0,01
2	м	3	-	-	0,01
3	р	1	Вертикальна	0,002	-
4	м	2	-	-	0,005
5	м	1	-	-	0,02
6	р	1	Горизонтальна	0,001	-
7	р	1	»	0,002	-
8	р	1		0,001	-
9	м	1	-	-	0,005
10	м	1	-	-	0,01
11	р	1	Вертикальна	0,001	-
12	р	1	»	0,002	-
13	р	3	Горизонтальна	0,003	-
14	р	2	Вертикальна	0,001	-
15	м	1	-	-	0,01
16	м	1	-	-	0,02
17	м	2	-	-	0,005
18	р	2	Горизонтальна	0,002	-
19	м	1	-	-	0,005
20	р	2	Вертикальна	0,001	-
21	м	1	-	-	0,01
22	м	2	-	-	0,005
23	р	1	Горизонтальна	0,003	-
24	м	1	-	-	0,01
25	р	2	Вертикальна	0,005	-
26	м	1	-	-	0,02
27	р	1	Горизонтальна	0,004	-
28	р	1	»	0,003	-
29	р	2	»	0,002	-
30	м	1	-	-	0,005
(случай нулевой частоты изменения возмущения силы или момента).
Для систем, находящихся под действием силы, смещение задается
вдоль линии ее действия, а для систем, находящихся под действием
пары сил, задается угловое смещение в плоскости действия этой
пары сил.
360
Пример выполнения зада-
ния. Пренебрегая сопротивле-
нием, исследовать вынужденные
колебания системы с двумя сте-
пенями свободы, изображенной
в положении покоя (рис. 246).
Колебания происходят под дей-
ствием пары сил, приложенной
к стержню DE и расположен-
ной в плоскости чертежа. Мо-
мент возмущающей пары изме-
няется по закону
, г	Рис. 246
М = Мо cos pt.
Дано: массы элементов системы mi = 0,5 кг, ms = 3 кг, коэффи-
циенты жесткости пружин (Н/см): cj = 60, с2 — 40, сз = 40; линейные
размеры (см): li = 20, Is = 60, /3 = 30. Угол поворота стержня DE
под действием пары сил с постоянным моментом М = Мо равен
= 0,01 рад.
Решение. За обобщенные координаты примем: z — вертикальное
смещение груза от положения покоя и ip — угол поворота рычага
DE от положения покоя.
На рис. 246 пунктиром показано положение системы при положи-
тельных обобщенных координатах.
Уравнения Лагранжа для рассматриваемой системы имеют вид
d (8Т\	_ ОТ	_ _дП	о . d	дТ	_ дП
dt \ dz) dz dz	dt	\d<pj dip dip
где Qz и Qv — обобщенные возмущающие силы.
Выражения для кинетической и потенциальной энергии получены
в примере к заданию Д.24, где исследовались свободные колебания
рассматриваемой системы:
Т = l/2«ui2 -I- ai2i¥> + l/2a22p2; 1
П = l/2cnz2 + ciszip + 1/2с22<д2, J	'
где aij и Cij — коэффициенты инерции и жесткости системы, равные:
ац = пи = 0,5 кг, ai2 = 0, а22 = Jo = 0,28 кг-м2; сц = сз = 4000 Н/м,
Cis = c2i = C3I3 = 1200 Н; с22 = с\12 + с212 + C3I3 = 2040 Н • м.
Частоты свободных колебаний и соответствующие коэффициенты
распределения получены в примере к заданию Д.24:
ki = 66,4 с-1; Д! = —1,49 рад/м; fc2 = 104 с-1; д2 — 1,2 рад/м.
Определим обобщенные силы Qz и Qv. увязанные с действием
возмущающего момента:
Qz = 6AMz/(f>z)-, Qv = бА'м^К&р),	(4)
361
где 8Amz — элементарная работа возмущающего момента на переме-
щении системы, вызванном элементарным приращением обобщенной
координаты z при р = const; 8Ам<р — элементарная работа возмуща-
ющего момента на перемещении системы, вызванном элементарным
приращением обобщенной координаты при z = const; 8z, 8р —
элементарные приращения обобщенных координат.
Если принять направление возмущающего момента при t = 0 по-
ложительным и считать, что оно совпадает с направлением отсчета
положительных значений угла р, то из соотношений (4) получаем
Q? =0;
Qv = Mo cos pt.
Следовательно, дифференциальные уравнения (1), описывающие
вынужденные колебания системы в обобщенных координатах z и р,
имеют вид
O-11Z + Сц2 + С12Р — 0; й22Р + С21Z+ С22р = Мо cos pt. (5)
Частное решение системы дифференциальных уравнений (5), опре-
деляющее вынужденные колебания, находим в виде
z = Az cos pt, р = Av cos pt.
Подставляя эти выражения в дифференциальные уравнения (5), по-
лучаем
(сц — а12р2)Аг + €12-4^, = 0; C2iAz + (с22 — а-22Р2)Ач, = Мо-
Из этой системы двух алгебраических уравнений относительно Az
и Аф находим:
Az = М0С12/[(сц - ацр2)(с22 - О22Р2) - С22],	(6)
Аф = Мо(сц - ацр2)/[(сц - ацр2)(с22 - «22Р2) ~ <д2]-	(7)
Амплитуды вынужденных колебаний равны абсолютным значениям
Az и Аф. Воспользуемся формулой (7) для определения амплитуды
Мд возмущающего момента. По условию задачи при р = 0 угол
поворота стержня DE равен ро', следовательно, при р = 0
Аф0 = Ро - МоС\\/{с^с22 - cl2),
откуда Мо = у>о(с22 - с^2/сц) = 16,8 Н • м.
Перемещение груза под действием постоянного момента М = Мо,
приложенного к стержню DE, можно найти из соотношения (6) при
р — 0:
Az0 = zo = -Moc12/(ci1c22 - c22); Az0 = -0,003 м.
Так как знаменатель в формулах (6) и (7) является квадратным
многочленом относительно р2, а корнями этого многочлена являются
362
квадраты частот свободных колебаний системы kl и к%, то формулы
(6) и (7) можно представить в виде
л _____________Mpci2________ ________у 144000_______.	/о\
Z »11«2г(р2 — k2)(p2 — fc2) (р2 — 4414)(р2 — 10870) ’	' '
_ Мо(сц - ацр2)	120(4000 - 0,5р2)	, .
V аца22(р2 — fc2)(p2 — fc2)	(Р2 ~ 4414)(р2 — 10870)	'
Формулы (6), (7) или (8), (9) позволяют проследить за зависимо-
стью Az и Av от частоты р и построить соответствующие графики
(рис. 247, а, б).
Рассмотрим поведение Az и Av для трех интервалов изменения
циклической частоты возмущающего момента:
0 < р < fci, fci < р < fc2 и fc2 < р < оо.
1.	0 < р < ki. Так как ki < къ, то р2 — fc2 < 0 и р2 — к2. < 0;
следовательно, знаменатель формул (8) и (9) положителен. Из этого
вытекает, что в первом интервале Az < 0 и Av > 0. С ростом вели-
чины р амплитуды колебаний стержня и груза возрастают, при этом
колебания стержня происходят в одной фазе с изменением возмуща-
ющего момента, а колебания груза — в противофазе (рис. 248,а).
363
При р = 0 имеем Ау, = <ро = 0,01 рад и Az = zq — —0,03 м.
При р =	= 66,4 с-1 в системе наступает первый резонанс и
функции Az и Ау, претерпевают бесконечный разрыв (см. рис. 247).
2.	ki < р < к2. Так как ki < к2, то рР—к^ > 0, а р2 — к% < 0. Следова-
тельно, знаменатель формул (8) и (9) отрицателен. Из этого следует,
что во втором интервале Az > 0, т. е. колебания груза происходят
синфазно с изменением возмущающего момента (рис. 248, б, в).
При определении знака функции Av необходимо рассмотреть чи-
слитель формулы (9). Если ki < р < у/сц/ац, то Av < 0 и коле-
бания стержня происходят в противофазе с возмущающим моментом
(рис. 248, б). Если у/сц/ац < р < к-2, то Av > 0 и колебания стержня,
так же как и груза, синфазны с изменением М (рис. 248, в).
При р = у/сц/ац = ^/4000/0,5 = 89,4 с-1 первая парциальная
частота (частота собственных колебаний системы, изображенной на
рис. 249, а) амплитуды вынужденных колебаний стержня равна нулю
(Ау, = 0 — случай антирезонанса). В этом случае груз массой mi
может рассматриваться как гаситель колебаний стержня. Величину
Az в этом режиме проще определить по формуле (6): Az — Mq/ci2‘,
Az = 0,014 м.
Амплитуда колебаний стержня | Az | убывает до нуля при возра-
стании р от ki до у/сц/ац, а затем с увеличением р от у/сц/ац до
&2 возрастает. При р = ^22/^22 = 2040/0,28 = 85,4 с-1, т. ё. при вто-
рой парциальной частоте (частоте собственных колебаний системы,
изображенной на рис. 249, б), амплитуды вынужденных колебаний
Az и Ау,, определяемые по формулам (6) и (7) равны:
.42 — M0/ci2; А2 = 0,014 м;
Ау, = -М0(сц - ацс22/а22)/с12; Av = -0,00414 м.
364
При изменении р в интервале от fci до fca функция Аг для амплиту-
ды вынужденных колебаний груза имеет минимум, соответствующий
максимуму знаменателя формул (6) и (7). Взяв от этого выражения
производную по р и приравняв ее нулю, получим
2ацй22Р2 — («11С22 + Я22С11) = О,
откуда найдем значение р, при котором Az достигает минимума:
Р = л/0,5(с22/а22 + сц/ац) = 87,4 с \	(10)
При р =	= 104 с-1 в системе наступает второй резонанс.
3.	к-2 < р < оо. Так как fci < к%, то
р2 —	> 0 и р2 — к2 > 0; следователь-
но, знаменатель формул (8) и (9) поло-
жителен. Учитывая, что к2 > y/сц/ац,
можно заключить, что в этом интервале
и Az < 0, и Av < 0, т. е. колебания про-
исходят в противофазе с возмущающим
моментом (см. рис. 248, г). С возрастани-
ем р амплитуды вынужденных колеба-
ний | Az | и | Av | уменьшаются, стремясь
к нулю.
Отношение функций Av и Az, опре^
жденных колебаний, получим, разделив
Av/Az = -(сп - ап^)/с12 = -(4000 - 0,5р2)/1200.	(11)
При р = 0 А<р1Аг = —cn/ai2; Av/Az = —3,33 рад/м. При р = fci =
— 66,4 с-1 A^,/Az =	= —1,49 рад/м. При р = ^/сц/ац = 89,4 с-1
А^/А2 = 0. При р = fc2 = Ю4 с'1; AVIAZ = р2 = 1,2 рад/м.
График зависимости Av/Az от частоты возмущения р показан на
рис. 250. При резонансах формы вынужденных и свободных колеба-
ний совпадают (см. рис. 247).
Для исследования резонансных колебаний (р = кг и р = fo) осуще-
ствим переход к главным координатам системы: pi и рг- Они связаны
с координатами z и <р соотношениями
z = pi + р2; v = gipi + М2Р2-
(12)
365
Дифференциальные уравнения колебаний механической системы
с двумя степенями свободы в главных координатах щ и 7?2 при
обобщенных возмущающих силах Qi — Н\ sin(p/+6); Q2 = Н2 sin(pt+<5),
соответствующих обобщенным координатам qi и q2, имеют вид
iji + kfm =	sin(pt + <5),	(13)
' «1
% + к%т)2 =	Sin(pf + (j),	(14)
где ai = яц + 2ai2/ii + аггМ?; а>2 = ац + 2й12Д2 + а>22^ Mi и М2 —
коэффициенты распределения обобщенных координат q\ и <72 при
свободных колебаниях.
В данном случае Hi =0; Н2 = Мо; 6 = тг/2.
Поэтому дифференциальные уравнения (13) принимают вид
7)1 + kfyi =	sin (pt + 70 ;
7)2 + ^772 =	sin (pt +	.
(15)
При p = fci (первый резонанс) частный интеграл первого диффе-
ренциального уравнения системы (15) имеет вид
т?1 = sin к^.
di
Частный интеграл второго дифферен-
циального уравнения:
Л2 =
«2(^2 — ^1)
sin
(kit + 70
Переходя к обобщенным координатам
z и р, по формулам (12) получаем
z ~ 2^*sin klt+ a2(fc| -°fc?) cos klt’
* = ^ftsinfc^+^l^^cosfcH.
При p = fc2 (второй резонанс) частные интегралы дифференциаль-
ных уравнений (15) имеют вид
т =
ai(fcj — ^2
_ Р.2М0
12	2к2а2
t sin k2t,
366
откуда обобщенные координаты z и <р:
Sin Ы ~ ajk^-k*) COS fc2f-
(17)
Параметры, входящие в уравнения (16) и (17), имеют следующие
числовые значения: Мо = 16,8 Нм; pi = —1,49 рад/м; ц2 = 1,2 рад/м.
Согласно (14) ai = 1,13 кг; а2 = 0,9 кг.
Подставляя эти значения в формулы (16) и (17), получаем урав-
нения вынужденных колебаний при первом и втором резонансах.
Первый резонанс: р=к\ = 66,4 с-1;
z = —0,168/sin 66,4/ + 0,0035 cos 66,4/;
ip = 0,252/ sin 66,4/ 4- 0,0042 sin 66,4/.
Второй резонанс: р = fc2 — 104 с-1;
z — 0,108£ sin 104t + 0,0035 cos 104/;
<p = 1,30/ sin 104/ — 0,0052 cos 104/.
Полученные результаты позволяют оценить колебания, происходя-
щие в системе при резонансе в том случае, когда силы сопротивления
незначительны, а резонансные режимы кратковременны.
V. ПРИМЕНЕНИЕ ЭВМ
К РЕШЕНИЮ ЗАДАЧ
ДИНАМИКИ
Задание Д.27. Интегрирование дифференциального
уравнения свободных колебаний механической системы
с помощью ЭВМ
Механическая система с одной степенью свободы (рис. 251—253)
может совершать колебания относительно положения равновесия. В
начальный момент (/ = 0) система выведена из положения равнове-
сия и скорости всех ее точек равны нулю. Предоставленная далее
самой себе система колеблется, находясь под действием только кон-
сервативных сил.
В схемах вариантов 8 и 20 применены пружины, сила упругости
которых связана с деформацией А соотношением Р(А) = сА + аА3. В
остальных схемах использованы пружины, для которых зависимость
силы упругости Р от деформации А — линейная, т. е. Р = сА.
В вариантах 3, 4, 7, 9—11, 21, 22 пружины имеют деформацию f
в положении покоя (предварительный натяг). В схемах вариантов
12—17, 23—28 пружины установлены с зазором s.
367
00
Рис. 251
Рис. 252
369
0Л£
ess эм
371
Таблица 65
Номер	mi,	7П2,	г,	С1>	С2,	а,	/,	/3,	1	d	Ь	R	9о,	S,	
варианта (рис. 251-253)	кг	КГ	м	н см	н см		м	град			м		град	м	Примечание
1	15	-	0,25	-	-	-	-	-	0,2	-	0,4	-	0,122	-	sin q « q
2	25	-	0,22	-	-	-	-	-	0,1	-	0,39	-	0,07	-	sin q^i q
3	10	15	-	5	-	-	0,05	60	-	-	-		0,1	-	Массой диска пренебречь При q = 0 пружина сжата
4	15	10	-	7	-	-	0,08	-	-	-	-	0,2	0,12	-	Пружины сжаты при q = 0
5	30	-	-	-	-	-	-	30	-	-	-	0,25	1,2	-	
6	20	15	-	-	-	-	-	45	-	-	-	-	0,2	-	Массой роликов пренебречь
7	30	20	-	8	-	-	0,05	-	-	-	0,2	0,2	0,35	-	Пружина растянута при q = 0
8	7	12	0,2	3	-	0,02	0	-	-	-	-	-	0,8	—	Параметры пружин одина- ковы
9	14	5	-	14	-	-	0,15	-	-	-	-	0,3	0,2	-	Пружины сжаты при q = 0
10	10	16	-	20	-		0,1	30	-	-	-		0,1	-	Массой ролика пренебречь Пружина сжата при q = 0
11	12	8	-	15	-	-	0,08	30	-	—	-	-	0,14	—	Массой ролика пренебречь Пружина сжата при q = 0
12	25	5	-	5	10	-	0	-	-	-	-	-	0,2	0,1	
13	20	10	-	12	8	-	-	-	-	-	-	0,15	1,0	0,06	
14	12	-	-	15	10	-	-	-	0,8	-	0,5	-	0,122	0,03	sin q « q
15	15	-	-	23	-	-	-	-	0,7	-	-	-	0,1	0,02	sin q q
16	10	10	0,25	5	2	-	-	-	0,6	-	0,4	-	0,11	0,02	il = «2
17	16	0,24	0,35	21	-	-	-	-	-	0,35	-	0,3	0,04	0,01	sin(g/fl) и
372
Продолжение табл. 65
Номер варианта	mi,	m2,	г,	С1,	С2,	а,	f,	/?,	1	d	ь	R	9о,	S,	
(рис. 251-253)	кг	кг	м	н см	н см	Н см'З	м	град			и		град	м	Примечание
18	12	20	-	-	-	-	-	-	0,6	-	-	0,25	0,5	-	sing as q -
19	20	30	-	3	-	-	-	-	0,8	-	-	0,3	0,35	-	sing и g -
20	30	-	-	10	-	0,1	0	-	-	-	-	0,35	0,5	-	Пружины одинаковы. АВ и ВС — нити
21	12	10	-	15	-	-	0,2	-	-	-	0,6	0,2	0,3	-	Пружина растянута при g = 0
22	10	14	0,43	25		-	0,1	-	—	0,48	0,3	0,4	0,14	—	Пружина растянута при g = 0, sin g ~ g
23	25	-	0,3	20	-	-	-	-	-	-	-	0,35	0,6	0,08	
24	30	10	0,3	22	-	-	-	-	-	-	-	0,4	0,75	0,06	r/R = 0,5
25	12	20	-	20	-	-	-	-	-	-	-	0,3	0,5	0,07	
26	16	-	-	5	-	-	-	-	0,4	-	-	-	0,13	0,016	
27	18	18	0,04	26	-	-	-	-	0,5	0,35	-	-	0,15	0,03	Й = «2
28	8	18	-	6	-	-	-	-	0,5	0,1	0,3	0,3	0,10	0,015	
29	20	10	—	7	—		0		0,4		—		0,4		Механнизм расположен в го- ризонтальной плоскости, sing ps g — g3/6
30	25	10	-	23	-	-	-	30	-	-	-	0,15	0,15	-	
Примечание. В вариантах 7, 21 и 22 выражение для обобщенной силы разложить в ряд Маклорена и удержать члены не
выше третьего порядка малости относительно обобщенной координаты. В вариантах 1 и 2 принять, что колебания «перевалки»
вокруг опорных ребер происходят без потери энергии.
В задании требуется:
1.	Составить дифференциальное уравнение, описывающее движение
системы (свободные колебания системы).
2.	Численным интегрированием на ЭВМ найти решение дифферен-
циального уравнения при заданных начальных условиях.
3.	По результатам численного интегрирования определить цикли-
ческую частоту к и период Т колебаний.
Схемы механических систем приведены на рис. 251—253 в поло-
жении покоя. На каждой схеме указана координата, которую нужно
принять в качестве обобщенной. Необходимые для расчета данные
приведены в табл. 65. Здесь mi, m2 — массы тел системы; г —
радиус инерции тела, участвующего во вращательном движении от-
носительно центральной оси; ci, C2 — коэффициенты жесткости для
линейных пружин; Ci и а — коэффициенты для определения зависи-
мости силы упругости от деформации для нелинейных пружин, f —
деформация пружины в положении покоя (в примечании указано,
сжата пружина или растянута); qo — начальное значение обобщенной
координаты, s — величина зазора, d — расстояние от оси вращения
до центра тяжести тела. Качение тел во всех случаях происходит
без проскальзывания. Тела, для которых радиус инерции не указан,
считать сплошными цилиндрами.
Рис. 254
Пример выполнения задания. Механическая система предста-
влена на рис. 254, а. При поступательном движении тела 1 в на-
правляющих диск 2 катится без проскальзывания по горизонтальной
поверхности. Система удерживается в положении равновесия двумя
пружинами, которые сжаты в положении покоя на величину /. Силы
упругости пружин передаются на тело 1 через шайбы 3. Перемещение
правой шайбы ограничено левым упором, а левой — правым. Рассто-
яние между упорами равно длине тела 1. Поэтому при перемещении
тела 1 от положения равновесия влево на него действует сила упру-
гости только от левой пружины (рис. 254, б), а при перемещении
вправо от положения равновесия — только правой. Сила упруго-
сти Р каждой пружины связана с ее деформацией А зависимостью
Р(А) = сА + аА3 (рис. 255, а). Зависимость силы Р(х), действующей
на тело 1 со стороны пружин, представлена на рис. 255, б, где Ро —
значение силы упругости в положении покоя, ах — смещение тела
1 по горизонтали. При решении задачи не учитывать массы шайб 3
и силы сопротивления движению.
373
Рис. 255
Решить задачу при следующих данных: mi = 20 кг, m2 — 40 кг,
с = 10 Н/см, а = 0,03 Н/см3, R — 0,3 м, to = 0, qo = 0,5 рад; qo = 0;
f = 0,1 м.
Решение. Для получения дифференциального уравнения дви-
жения системы воспользуемся уравнением Лагранжа II рода для
консервативных систем:
d (дт\ _ дТ _ ап
dt \dq ) dq dq '
(1)
где T и П — кинетическая и потенциальная энергии системы. В
качестве обобщенной координаты q примем угол поворота диска 2
= <р).
Кинетическая энергия системы
т _ mix2 т2Уд , JC2^2
1	2 "г 2 + 2 '
Учитывая уравнения связей
vc = РФ = Rq; х = 2Rq
(2)
и выражение для момента инерции Jc2 = Ш22Д однородного диска 2
относительно центральной оси, получаем выражение для кинетиче-
ской энергии:
.<>
(3)
где
а = (4mi + l,5m2)R2; а = 12,6 кг • м2.
Потенциальная энергия системы определяется как работа сил
упругости на перемещении из отклоненного положения в нулевое
(положение покоя):
0	х
П(ж) = j P(x)dx = j\—P(x))dx.
х	О
(4)
Зависимость Р(х) (рис. 255, б) определяется выражением
Р(х) = <
—Ро — b\x — b?x2 — ах3,
0,
Ро — Ь\х + b%x2 — ах3,
х > 0;
х = 0;
х < 0,
(5)
374
где Ро = /(с + а/2); i>i = с + За/2; Ь2 = За/. Это выражение можно
представить более компактной записью, если использовать функцию
j-щ, которая принимает значение +1 при х > 0 и —1 при х < 0.
Условимся, что значение при х = 0 равно нулю.
Зависимость Р(х) принимает вид
Р(х) = -(Ро + b2x2) А? - brx - ах3.		(6)
Iх I
Подставляя (6) в (4), получаеу выражение для П(ж):
П(х) = (Р0 + ^2)!т| + ^2 + ^.	(7)
Выразим потенциальную энергию, как функцию от д, учитывая, что
х = 2Rq
П(д) = (2РР0 + ^-q2)\q | + 2R2biq2 + 4aP4g4.	(8)
В уравнение Лагранжа II рода следует подставить производную
от П по q.
Функция (8) имеет производную = F(q) всюду, кроме точки
9 = 0,
F(g) = (2Р0Я + 8Ь2Я3?2)р^ + 4R2biq + 16aP4g3.	(9)
При q = 0 функция F(g) должна быть принята равной нулю, ибо в
этом положении силы, действующие на тела системы, взаимно урав-
новешены. Подставляя (3) и (9) в уравнение (1), получим нелинейное
дифференциальное уравнение движения системы:
aq + F(q) = 0. '	(10)
Вычислим коэффициенты выражения (9):
Ро = cf + a/3 = 103  0,1 + 0,3 • 105 • 0,13 = 130 H;
2RPq = 2 0,3 130 = 78 Н м; 6i = 1900 Н/м; 4Я261 = 684 H • м;
16a Л4 = 16 • 0,3 • 105 • 0,34 = 3888 Н  м; 8Л3Ь2 = 1944 Н • м.
Функция F(g) имеет вид:
F(g) = (78 + 1944g2)	+ 684g + 3888g3.	(11)
Дифференциальное уравнение движения рассматриваемой системы
12,6g + (78 + 1944g2)	+ 684g + 3888g3 = 0.	(12)
375
Для определения движения системы следует численно проинтегри-
ровать на ЭВМ уравнение (12) при начальных условиях:
Рис. 256
при t= О
<fo = 0,5 рад,	, .
9 = 0.
Результаты вычислений сведены в
табл. 66. На рис. 256 по результатам вы-
числений представлена зависимость р =
= p(t). Достаточно построить лишь ту
часть графика, где р изменяется от мак-
симального значения <ро ДО нуля. Продол-
жение графика можно построить из со-
ображений симметрии.
По графику легко определить четверть периода колебаний 0,25 Т: в
момент t* = 0,25Т значение р обращается в ноль. Так как Z* = 0,114 с,
то период колебаний составляет Т = 0,456 с, а циклическая частота
к = 13,77 с"1.
Таблица 66
£, с	¥?(*), рад	t, с	¥>(t), рад	t, с	¥>(<), рад	£, с	рад
0,000	0,5000	0,088	0,1618	0,176	-0,3687	0,264	-0,4268
0,011	0,4933	0,099	0,0927	0,187	-0,4164	0,275	-0,3814
0,022	0,4737	0,110	0,0220	0,198	-0,4546	0,286	-0,3279
0,033	0,4420	0,121	-0,0488	0,209	-0,4818	0,297	-0,2682
0,044	0,3999	0,132	-0,1189	0,220	-0,4966	0,308	-0,2038
0,055	0,3491	0,143	-0,1871	0,231	-0,4982	0,319	-0,1363
0,066	0,2913	0,154	-0,2524	0,242	-0,4867	0,330	-0,0667
0,077	0,2284	0,165	-0,3134	0,253	-0,4625	0,341	+0,042
376
ТАБЛИЦА ВАРИАНТОВ ЗАДАНИЙ,
ВХОДЯЩИХ В КУРСОВЫЕ РАБОТЫ
ш	Номера заданий						ш	Номера заданий						Ш	Номера заданий					
	1 7	2 8	3 9	4 10	5 11	6 12		1 7	2 8	3 9	4 10	5 11	6 12		1 7	2 8	3 9	4 10	5 11	6 12
и	13	14	15	16	17	18	и	13	14	15	16	17	18	И	13	14	15	16	17	18
ф	19	20	21	22	23	24	ф	19	20	21	22	23	24	ф	19	20	21	22	23	24
р	25	26	27				р	25	26	27				р	25	26	27			
	Вари		1НТЬ	заданий				Варианты заданий							Варианты заданий					
1	23	25	19	3	5	1	35	19	4	8	18	17	13	69	21	9	29	7	1	24
2	20	22	2	6	8	3	36	16	30	11	21	24	16	70	18	6	1	10	29	27
3	17	19	20	9	11	6	37	13	27	14	24	21	19	71	15	3	7	13	18	2
4	14	10	28	12	17	9х	38	10	24	17	27	28	22	72	12	1	6	16	6	5
5	11	13	22	15	14	12	39	7	21	20	30	1	25	73	9	29	9	19	8	18
6	8	10	5	18	20	15	40	4	18	23	4	29	28	74	6	26	12	22	15	11
7	5	7	8	21	23	18	41	30	15	20	7	3	30	75	3	23	15	25	12	14
8	2	4	11	24	26	21	42	27	12	29	10	6	4	76	1	20	18	28	11	17
9	19	30	14	27	29	24	43	24	9	1	13	9	7	77	29	17	21	2	19	20
10	16	27	17	30	1	27	44	21	6	3	16	12	10	78	26	14	24	5	20	23
11	13	24	20	4	3	2	45	18	3	6	19	15	12	79	9	11	27	8	23	26
12	10	21	23	7	6	5	46	15	1	9	22	18	16	80	20	8	30	11	3	29
13	7	18	26	10	9	8	47	12	29	12	25	21	19	81	17	5	4	14	18	2
14	15	29	13	12	30	11	48	9	26	15	28	24	22	82	14	2	7	17	8	5
15	30	12	1	16	15	14	49	6	23	18	2	27	25	83	11	19	10	20	16	8
16	27	9	3	19	18	17	50	3	20	21	5	30	28	84	8	16	13	23	7	11
17	24	6	9	11	21	20	51	1	17	24	8	4	1	85	5	13	16	26	6	14
18	21	3	6	25	24	23	52	29	14	27	11	7	30	86	2	10	19	29	9	17
19	18	1	12	28	27	26	53	26	11	30	14	10	6	87	25	7	2	1	22	20
20	15	29	18	5	4	29	54	23	8	4	17	13	9	88	21	4	5	9	25	23
21	12	26	15	2	30	2	55	20	5	7	20	16	12	89	7	27	8	12	28	26
22	9	23	21	8	7	5	56	17	2	10	23	19	15	90	19	24	11	15	2	29
23	6	20	24	11	10	8	57	28	19	13	26	22	18	91	30	21	19	18	5	30
24	3	17	27	14	13	11	58	25	16	19	29	25	21	92	27	18	17	21	8	4
25	1	14	30	17	16	14	59	22	13	16	6	28	24	93	24	15	20	24	11	7
26	29	11	4	20	19	17	60	18	10	15	9	2	27	94	21	12	23	27	14	10
27	28	8	7	23	22	20	61	16	4	5	12	5	17	95	18	9	26	30	17	13
28	23	5	10	26	25	23	62	13	30	8	15	11	3	96	15	6	29	4	9	16
29	20	2	13	29	28	26	63	10	27	11	18	8	16	97	12	3	1	7	23	22
30	14	19	22	3	2	29	64	7	24	14	21	14	9	98	9	1	3	10	26	25
31	11	16	25	6	5	30	65	4	21	17	24	17	12	99	6	29	6	13	19	28
32	8	13	28	9	8	4	66	30	18	20	27	20	15	100	.26	28	16	1	2	16
33	5	10	2	12	11	7	67	27	15	23	30	23	18							
34	2	7	5	15	14	10	68	24	12	26	4	26	21							
377
ЛИТЕРАТУРА
Бабаков И. М. Теория колебаний, М., 1965.
Бутенин Н. В. Введение в аналитическую механику. М., 1971
Бутенин Н. В. Теория колебаний. М., 1963.
Бутенин Н. В., Лунц Я. Л., Меркни Д. Р. Курс теоретической
механики, ч. I и II. М., 1971 и последующие издания.
Воронков И. М. Курс теоретической механики. М., 1954 и после-
дующие издания.
Гернет М. М. Курс теоретической механики. М., 1965 и последу-
ющие издания.
Добронравов В. В., Никитин Н. Н. Курс теоретической механики.
М., 1983.
Космодемьянский А. А. Курс теоретической механики. М., 1954.
Лойцянский Л. Г., Лурье А. И. Курс теоретической механики, ч.
I и II. М., 1954 и последующие издания.
Николаи Е. Л. Теоретическая механика. М., 1952.
Пановко Я. Г., Губанова И. И. Устойчивость и колебания упругих
систем. М., 1964
Пановко Я. Г. Введение в теорию механических колебаний. М.,
1971.
Пановко Я. Г. Введение в теорию механического удара. М., 1977.
Савин Г. П., Кильчевский Н. А., Путята Т. В. Курс теоретиче-
ской механики. Киев, 1963.
Старминский В. М. Теоретическая механика. М., 1980.
Таре С. М. Курс теоретической механики. М., 1963 и последующие
издания.
Яблонский А. А., Никифорова В. М. Курс теоретической механики,
ч. I, М., 1971 и последующие издания.
Яблонский А. А. Курс теоретической механики, ч. II. М., 1971 и
последующие издания.
Яблонский А. А., Норейко С. С. Курс теории колебаний. М., 1966
и последующие издания.
378
Сборники задач и руководства к решению задач
Айзенберг Т. Б., Воронков И. М., Осецкий В. М. Руководство к
решению задач по теоретической механике. М., 1968.
Бать М. И., Джанелидзе Г. Ю., Келъзон А. С. Теоретическая
механика в примерах и задачах, ч. I и II. М., 1961 и последующие
издания.
Бражниченко Н. А. и др. Сборник задач по теоретической меха-
нике. М., 1967 и последующие издания.
Мещерский И. В. Сборник задач по теоретической механике. М.,
1971 и последующие издания.
Пятницкий Е. С., Турхан Н. М., Ханукаев Ю. И., Яковенко Г. Н.
Сборник задач по аналитической механике. М., 1980.
Светлицкий В. А., Стасенко И. В. Сборник задач по теории
колебаний. М., 1973 и последующие издания.
Сборник задач по теоретической механике/Под ред. проф. К. С. Ко-
лесникова М., 1984.
379
СОДЕРЖАНИЕ
Предисловие....................................................... 5
Используемые обозначения.......................................... 7
РАЗДЕЛ ПЕРВЫЙ
СТАТИКА ТВЕРДОГО ТЕЛА
I.	Плоская система сил............................................ 8
Система произвольно расположенных сил.......................... 8
Задание С.1. Определение реакций опор твердого тела............ 8
Задание С.2. Определение реакций опор и сил в стержнях плоской фермы	14
Задание С.З. Определение реакций опор составной конструкции (система
двух тел)..................................................... 21
Задание С.4. Определение реакций опор составной конструкции (система
трех тел)..................................................... 28
Задание С.5. Равновесие тел с учетом сцепления (трения покоя). 34
II.	Система сил, не лежащих в одной плоскости.................... 41
Задание С.6. Приведение системы сил к простейшему виду........ 41
Задание С.7. Определение реакций опор твердого тела........... 45
Центр тяжести................................................. 49
Задание С.8. Определение положения центра тяжести тела........ 49
III.	Применение ЭВМ к решению задач статики...................... 54
Задание С.9. Определение реакций опор составных конструкций с внутрен-
ними односторонними связями..................................  54
РАЗДЕЛ ВТОРОЙ
КИНЕМАТИКА
I.	Кинематика точки.............................................. 64
Задание К.1. Определение скорости и ускорения точки по заданным урав-
нениям ее движения............................................ 64
II.	Кинематика твердого тела...................................   67
Поступательное и вращательное движения твердого тела.......... 67
Задание К.2. Определение скоростей и ускорений точек твердого тела при
поступательном и вращательном движениях....................... 67
Плоское движение твердого тела................................ 72
Задание К.З. Кинематический анализ плоского механизма......... 72
380
Задание К.4. Кинематический анализ многозвенного механизма .... 80
Сферическое движение твердого тела............................. 92
Задание К.5. Определение кинематических характеристик движения твер-
дого тела и его точек по уравнениям Эйлера..................... 92
Задание К.6. Кинематический анализ движения твердого тела, катящегося
без скольжения по неподвижной поверхности и имеющего неподвижную
точку.......................................................... 96
III.	Сложное движение............................................ 104
Сложное движение	точки........................................ 104
Задание К.7. Определение абсолютной скорости и абсолютного ускорения
точки ........................................................ 104
Сложное движение твердого тела, сложение вращений вокруг параллель-
ных и пересекающихся осей..................................... 111
Задание К.8. Определение угловых скоростей звеньев планетарного редук-
тора.......................................................... 111
IV.	Применение ЭВМ к решению задач	кинематики................ 120
Задание К.9. Определение угловых скоростей и угловых ускорений звеньев
механизма манипулятора по заданному движению рабочей точки...	120
РАЗДЕЛ ТРЕТИЙ
ДИНАМИКА
I. Динамика материальной точки..................................... 130
Дифференциальные уравнения движения материальной точки.......... 130
Задание Д.1. Интегрирование дифференциальных уравнений движения
материальной точки, находящейся под действием постоянных сил...	130
Задание Д.2. Интегрирование дифференциальных уравнений движения
материальной точки, находящейся под действием переменных сил...	136
Задание Д.З. Исследование колебательного движения материальной точки 144
Задание Д.4. Исследование относительного движения материальной точки 155
Основные теоремы динамики материальной точки.................... 163
Задание Д.5. Применение теоремы об изменении количества движения к
определению скорости материальной точки......................... 163
Задание Д.6. Применение основных теорем динамики к исследованию дви-
жения материальной точки.....................................    168
II. Динамика механической системы.................................. 174
Основные теоремы динамики механической системы.................. 174
Задание Д.7. Применение теоремы о движении центра масс к исследова-
нию движения механической системы............................... 174
Задание Д.8. Применение теоремы об изменении количества движения к
исследованию движения механической системы.....................  184
Задание Д.9. Применение теоремы об изменении кинетического момента к
определению угловой скорости твердого тела.....................  193
Задание Д.10. Применение теоремы об изменении кинетической энергии к
изучению движения механической системы.......................... 201
Дифференциальные уравнения движения твердого тела............... 213
Задание Д.11. Исследование поступательного и вращательного движений
твердого тела................................................... 213
Задание Д.12. Исследование плоского движения твердого тела...... 222
Удар........................................................     230
Задание Д.13. Исследование соударений твердых тел............... 230
381
III.	Аналитическая механика.......................................... 250
Принцип возможных перемещений..................................... 250
Задание Д.14. Применение принципа возможных перемещений к решению
задач о равновесии сил, приложенных к механической системе с одной
степенью свободы.................................................. 250
Задание Д.15. Применение принципа возможных перемещений к опреде-
лению реакций опор составной конструкции.......................... 258
Принцип Даламбера................................................  264
Задание Д.16. Применение принципа Даламбера к определению реакций
связей............................................................ 264
Задание Д.17. Определение реакций опор при вращении твердого тела во-
круг неподвижной оси.............................................. 271
Задание Д.18. Применение теорем и принципов динамики к исследованию
движения механической системы....................................  279
Общее уравнение динамики.......................................... 290
Задание Д.19. Применение общего уравнения динамики к исследованию
движения механической системы с одной степенью свободы...........  290
Уравнение Лагранжа II рода........................................ 297
Задание Д.20. Применение уравнения Лагранжа II рода к определению
сил и моментов, обеспечивающих программное движение манипулятора .	297
Задание Д.21. Применение уравнения Лагранжа II рода к исследованию
движения механической системы с двумя степенями свободы........... 306
Устойчивость состояния равновесия (покоя) консервативной механической
системы........................................................... 316
Задание Д.22. Определение положений равновесия (покоя) консерватив-
ной механической системы с одной степенью свободы и исследование их
устойчивости...................................................... 316
IV.	Колебания механической системы................................... 326
Задание Д.23. Исследование свободных колебаний механической системы
с одной степенью свободы.......................................... 326
Задание Д-24. Исследование свободных колебаний механической системы
с двумя степенями свободы......................................... 334
Задание Д.25. Исследование вынужденных колебаний механической си-
стемы с одной степенью свободы.................................... 343
Задание Д.26. Исследование вынужденных колебаний механической си-
стемы с двумя степенями свободы..................................  359
V.	Применение ЭВМ к решению задач динамики........................... 367
Задание Д.27. Интегрирование дифференциального уравнения свободных
колебаний механической системы с помощью ЭВМ...................... 367
Таблица вариантов заданий, входящих в курсовые работы................ 377
Литература........................................................... 378
382