СБОРНИК
ЗАДАНИЙ
для
курсовых
работ
по
теоретической
механике
Под общей редакцией
проф. А. А. Яблонского
Издание 3-е, исправленное
Допущено
Министерством высшего и среднего
специального образования Г.СГД'
в качестве учебного пособия
для студентов иыешнх
технических учебных заведения
МОСКВА «ВЫСШАЯ ШКОЛА» 19

531
C23
УДК 531.8@75)
Рецензенту:
Кафедры теоретической механики Московского авиационного и Харь-
Харьковского политехнического институтов;
профессор М. М. Гернет
Л.Л.Яблонский, С. С. Н о р е й к о, С. А. В о л ь ф с о н,
Н. В. Карпова, Б. Н. Квасников, Ю. Г. Мппкин,
II. И. Никитина, В. Е. Павлов, Ю. М. Те пан ко в
20302-063
© ИЗДАТЕЛЬСТВО «ВЫСШАЯ ШКОЛА», 1978 г.

ПРЕДИСЛОВИЕ
Теоретическая механика как одна из важнейших физико-
математических дисциплин играет существенную роль
в подготовке инженеров любых специальностей.
На основных законах и принципах теоретической меха-
механики базируются многие общеинженерные дисциплины,
такие, как сопротивление материалов, строительная меха-
механика, гидравлика, теория механизмов и машин, детали
машин и др.
В различных курсах по машиностроительным, механи-
механическим, строительным, приборостроительным и по другим
специальностям также широко используются важнейшие
положения теоретической механики.
На основе теорем и принципов теоретической механики
решаются многие инженерные задачи и осуществляется
проектирование новых машин, конструкций и сооружений.
Хорошее усвоение курса теоретической механики требует
не только глубокого изучения теории, но и приобретения
твердых навыков в решении задач. Для этого необходимо
самостоятельно решить большое количество задач по всем
разделам курса из соответствующих сборников и выпол-
выполнить ряд специальных заданий.
Третье издание настоящего сборника содержит 50 зада-
заданий по всем разделам курса: 12 — по статике, 12 — но кинема-
кинематике и 26 — по динамике, из которых 14 — по аналитической
механике. Каждое задание содержит тридцать вариантов.
Большое число заданий по каждому из разделов курса
обеспечивает возможность устанавливать тематику и коли-
количество курсовых работ в зависимости от профиля подго-
подготовки специалистов, т. е. от объема и содержания изучае-
изучаемого курса теоретической механики.
Набор вариантов индивидуальных заданий, входящих
в курсовую работу, студент может определить по своему
шифру, пользуясь специальной таблицей, приведенной
в конце книги. Шифр каждому студенту устанавливает
преподаватель.
В сборнике приведены примеры выполнения заданий.
Основываясь па этих примерах, студенты (особенно заоч-

ных и вечерних факультетов), а также специалисты, желаю-
желающие углубить своп знания по теоретической механике,
смогут самостоятельно выполнять задания из этого сбор-
сборника.
В сборник включен ряд заданий, выполнение которых
требует проведения некоторых исследований. Эти задания
могут служить основой для организации учебно-исследо-
учебно-исследовательском работы студентов по теоретической механике.
При подготовке к печати рукописи третьего издания
учтены замечания кафедры Московского авиационного инсти-
института, давшей развернутую рецензию сборника, замечания
коллективов ряда кафедр и отдельных преподавателей,
а также профессоров В. Г. Веретенникова, М. М. Гернета
и А. Г. Ишковой, которым авторы выражают глубокую
благодарность.
Отзывы и пожелания, направленные па улучшение
этого издания, просим посылать в адрес издательства
^ Высшая школа».
Авторы

РАЗДЕЛ ПЕРВЫЙ.
СТАТИКА ТВЕРДОГО ТЕЛА
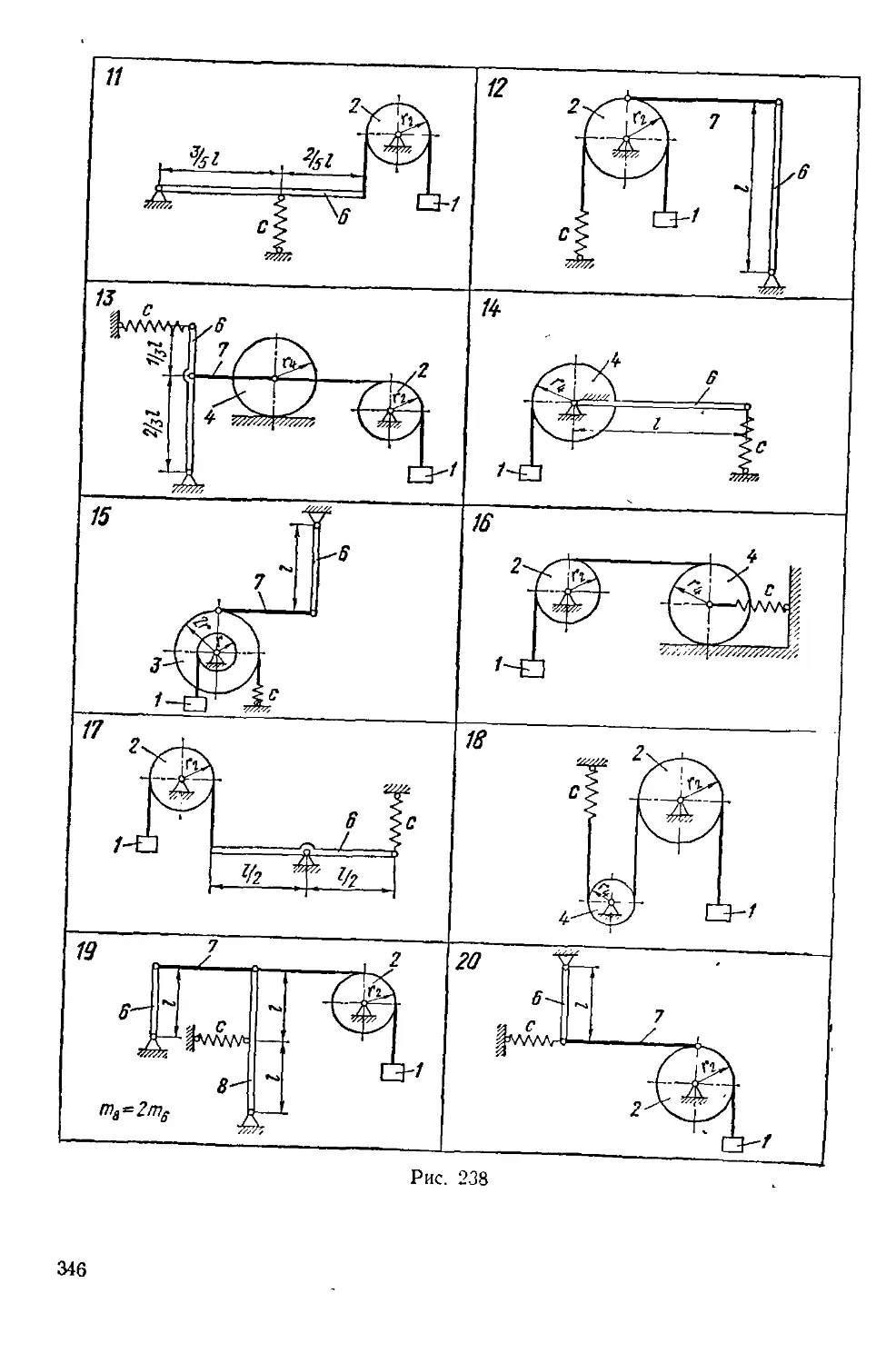
В этом разделе содержатся 12 заданий. По некоторым темам
предлагаются задания различной сложности. Так, на плоскую систему
сил наряду с простейшими схемами (задание С-2), требующими приме-
применения только трех уравнений равновесия, включены задания
на составные конструкции из двух (С-5) и трех (С-4 и C-G) тел.
На равновесие пространственной системы сил имеются два задания
(С-10 и С-11). Выбор каждого из них может определяться профилем
подготовки студентов.
I. Плоская система сил
СИСТЕМА СХОДЯЩИХСЯ СИЛ \
Задание С-1. Определение реакций опор '
и усилий в стержнях плоской фермы
К одному из узлов плоской фермы приложена сила Р. Опреде-
Определить реакции опор фермы (при помощи теоремы о равновесии трех
непараллельных сил), а также усилия во всех ее стержнях спосо-
способом вырезания узлов. Вес стержней не учитывать. Результаты ана-
аналитического расчета проверить для каждого узла путем построения
силового многоугольника.
Основываясь на полученных значениях усилий в стержнях,
определить реакции опор фермы также и аналитическим способом.
Схемы ферм и необходимые для расчета данные приведены
на рис. 1-3.
Пример выполнения задания. Дано: схема фермы (рис. 4, а);
Р = 11 кН, а = 30°. Найти реакции RA, RB и усилия в стержнях.
Решение. 1. Определение реакций опор. Рассмотрим внешние
силы, приложенные к ферме: задаваемую силу Р и реакции опор
R~a и Rb- Так как опора А стержневая, то линия действия реакции RA
известна: она направлена по оси стержня AD. Линию действия
реакции /?л определяем, применяя теорему о равновесии трех
непараллельных сил (рис. 4, а).
Три силы Р, Ra и Rfi взаимно уравновешиваются, следовательно,
линии их действия пересекаются в одной точке.

P=8kH
P=7hH
a .
p
4
a
и
5П
|йг|
\
\
i
7
(
Л
a t
V
\
7 /
a a*p
8
/11 \
I
T
6
ft
Р=5кй
/
nso°
a
\
a
J
У
/
a
P
\
P=10?.H
Pi-с 1

12
A
J?
ff
15
17
,, о
\
7 '
{ *
^?\
5
A^&° з
p rl
1
4
A
?
и
X
/.
V
i ^
sll
A
—^¦
•?/
A6
a
¦
a
i
^\
4
С"
4
/*
г
/7
G
A
'
\
V
Y
f}
3
2.
/
a
n
в
8\
7
—7
/
a ,
И
A
N
* /
/a
\
?l
(
1,'/
//
a
12
w7
/V
d
¦xr
?• 1
A
p
Ю
\
№
' rA's
"^ Р-ЮнН
J
/I
1/
P = 10kH
1L
F-SHH
16
P
и
/
p
Д
A
/г
1 "
\P 1
P-12M
РЧ2,
t
В
- t
и ькн
2y/
a "
4
V
/
'-
~?
/
\
a
/
q_
i
\
\
6,
i
\
\
ft/
Г
/
\
J
/
a
?
/
77
7
3
\
t
4
7
V
\
"Z
p_
7 У
/
6
f
в
s\
S
a
a.
y7
v
N
7
/
ВЛ
10
a V
9
'у
11
P
^\
P
iz
ff /Lr
a ¦]'
Рис. 2

21
Р-ЮкН
25
€
Р8кН\
28
P'ShH
Р=Ш
г
г
л
Л1
а
3
а
11
Р
\29
о , a j
30
Рис 3

Находим точку пересечения липни действия сил Р и RA. Линия
действия реакции Rn проходит через эту точку (точку С) и центр
шарнира В. Строим замкнутый силовой треугольник (рис. 4, б). Его
построение начинаем с силы Р. Через начало вектора Р проводим
прямую, параллельную линии действия одном реакции, например ИА,
а через конец —прямую, параллельную линии действия Rn до их
взаимного пересечения.
Стороны полученного замкнутого
силового треугольника определяют
модули и направления опорных реак-
реакций RA и RB. Из подобия силового
треугольника и треугольника ABC
находим RA и Rti
Приняв АВ-а, получим:
Л С = ЗС? = За tg а = За J/3/3 = а
Следовательно,
откуда
RA г-. Р |/3 = 11 УЗ = 19,05 кН;
RB--2P = 2 11=22 кН.
Рис 4
2. Определение усилий в стержнях фермы. Кроме внешних сил,
которые могут быть приложены к узлу фермы, па каждый ее узел
действуют реакции сходящихся в нем стержней Эти реакции равны
усилиям в стержнях.
Рассматриваем равновесие сил, приложенных к каждому узлу
фермы, выбирая узлы в такой последовательности, чтобы число
неизвестных сил в узле не превышало двух
Условно предполагаем, что все стержни растянуты, т. е. реакции
стержней направлены от узлов (рис. 5). Отрицательные знаки найден-
найденных реакций показывают, что соответствующие стержни не растянуты,
а сжаты, т. е. реакции этих стержней направлены к узлам
Реакции каждого стержня обозначим 5 и 5', причем 5 = — S'.
Расчет начинаем с узла С.
Составим два уравнения равновесия сил, приложенных к этому
узлу:
-S1-S2cob60° = 0,

откуда
11 -2
= —12,7 кН;
cos 30' Y 3
Sl = — Si cos 60° = — (— 12,7) 0,5 = 6,35 кН.
Значение S., получается отрицательным, S, — положительным.
Следовательно, стержень / растянут, а стержень 2 сжат.
Для проверки расчета строим в масштабе треугольник сил Р,
St и S2, учитывая, что направление S2 в этом треугольнике должно
быть противоположно направ-
направлению Si на рис. 5, так как
стержень 2 сжат (рис. 6). 5,
Треугольник сил получа-
получается замкнутым, т. е. реакции
SL и S2 определены правиль-
правильно. Реакции других стержней
Рис. 5
Рис. 6
фермы определяем аналогично. Замкнутые многоугольники сил, при-
приложенных к каждому из узлов фермы, показаны на рис. 6.
Узел К:
Подставляя в эти уравнения 5^ = 52 = — 12,7 кН, получаем:
S'i = — S:, cos 30° = — (— 12,7) У3/2 = 11 кН;
56 = S't cos 60° = — 12,7 • 0,5 = — 6,35 кН.
10

Узел Е:
SXf = O; 53 + 55cos30° = 0;
ЕУг = О; Si-St- Sb cos 60° = 0,
откуда
Sb = — 53/cos 30° = — 11,0/0,866 = — 12,7 кН,
S, = Si - 55 cos 60° = 6,35 - (— 12,7) 0,5 = 12,7 кН.
Узел L:
S X, = 0; - S; - Si cos 30° = 0;
2У,- = 0; Sl + Sicos60°-S10 = 0,
откуда
S; = — S~ cos 30° = — (— 12,7) 0,866 = 11,0 кН;
S10 = SI + SJcos60o = -6,35-12,7-0,5 = -12,7 кН.
Узел D:
2X; = 0; S,+ S9 cos 30° = 0;
откуда
S9 = — S7/cos 30° = — 11,0/0,866 = — 12,7 кН;
S8 - 51 -S, cos 60° -12,7 -(-12,7) -0,5 =19,05 кН.
Таким образом, реакции всех стержней фермы определены.
Заметим, что реакции опор рассматриваемой фермы можно опре-
определить, составив уравнения равновесия сил, приложенных к узлам
А и В (рис. 7).
Р с
Рис. 7
Узел А:
Узел 5:
Рис. 8
= S',= 19,05 кН.
И

Решая совместно эти уравнения, получаем:
#„-22 кН, P = arctg 1,73 = 60°.
Числовые^'значепия реакций RA и /?л, полученные двумя спосо-
способами, совпадают.
Замкнутые многоугольники сил, приложенных к опорным узлам
фермы, показаны на рис. 6.
3. Составление таблицы усилий в стержнях фермы и построе-
построение схемы фермы с действительными направлениями этих усилий.
По результатам расчета составляем таблицу усилий в стержнях
фермы (табл. 1).
Таблица 1
Номер стержня
Знак усилия
Усилие (кН)
1
+
6,35
2
—
12,7
3
+
11,0
4
+
12,7
5
—
12,7
G
—
6,35
7
+
11,0
8
4-
19,05
9
12,7
10
—
12,7
Схема фермы с действительными направлениями усилий в стерж-
стержнях показана на рис. 8.
СИСТЕМА ПРОИЗВОЛЬНО
РАСПОЛОЖЕННЫХ СИЛ ^ '
Задание С-2. Определение реакций опор
твердого тела '
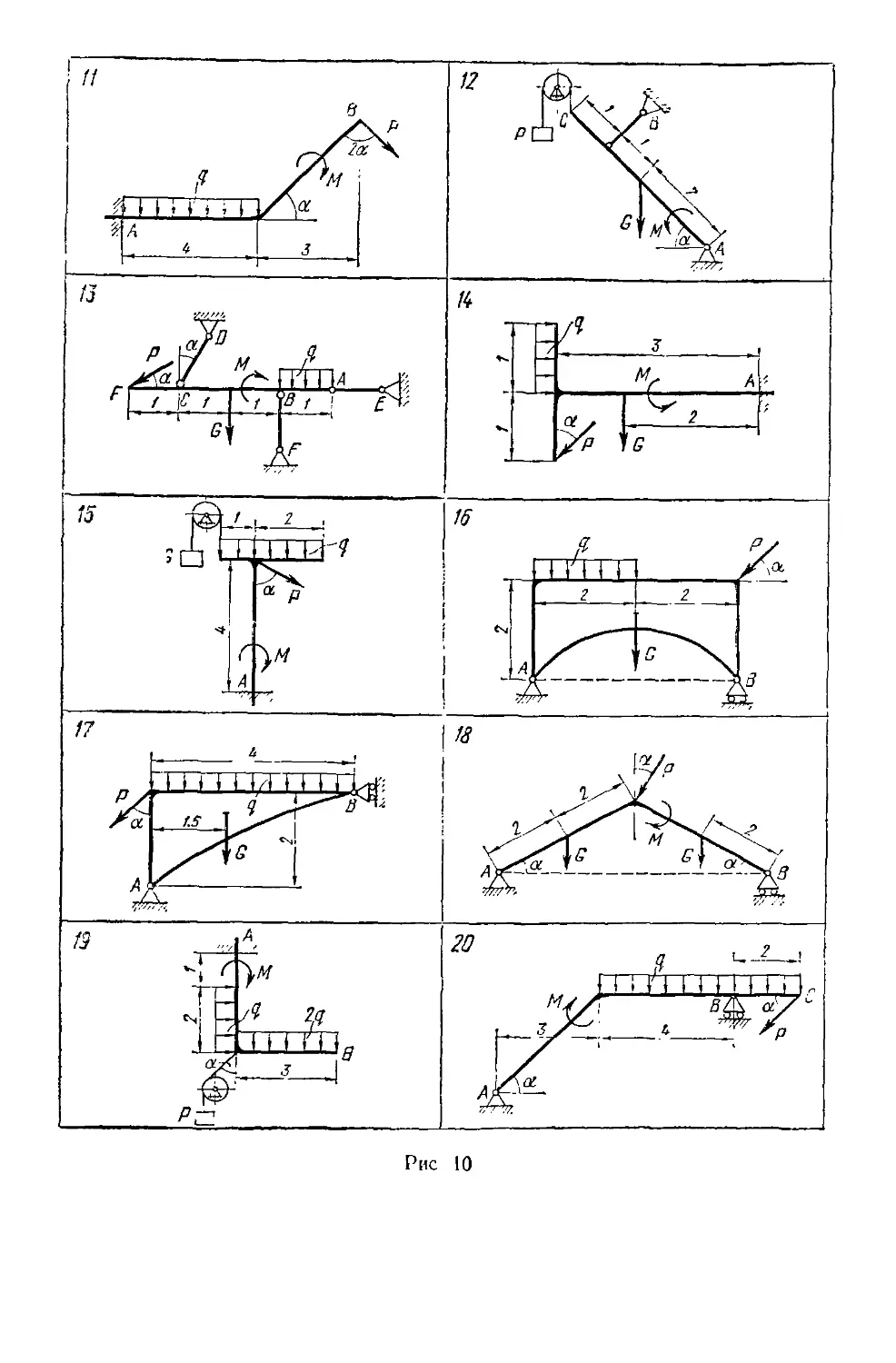
Найти реакции опор конструкции. Схемы конструкций представ-
представлены на рис. 9—11 (размеры —в м), нагрузка указана в табл. 2.
Номер п три-
антя задания
(pi.c. 9-II)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
G
р
кН
10
12
8
14
__
, _
1G
б
10
10
12
10
4
5
8
4
. _
G
10
0
7
6
8
4
Г)
10
Ь
4
Л1
Л1 ,
кНм
20
10
5
8
7
4
S
G
4
9
7
8
6
10
4
кН' м
1
4
2
3
1
Ч
1
2
2
1
0,5
—
2
I
2
а, град
30
G0
(>0
30
45
60
45
00
30
30
45
45
30
45
60
Номер пари-
¦л нта здании
(рис 9 — 11)
IG
17
18
19
20
21
22
23
24..
25
2G
27
28
29
30
а
к
20
25
20
—
—
—
—
—
—
5
—
—
15
Р
f
10
5
10
4
10
8
10
7
6
14
IG
4
10
G
10
Т а б л
м
кНм
_
10
8
G
7
8
10
7
20
14
8
7
8
14
кН м
2
0,5
—
1
0,5
0,5
1
2
1,5
0,5
I
2,5
3
1
—
и ц а 2
а. град
45
45
30
45
45
30
30
30
30
45
30
45
30
15
30
12

A '-n
2
1 KM t
о
M
?
Гд
2Щ
¦9:
t i ,,, ¦
/
10
\9> i
V//MA
1,5
Рис. 9

П 1 1 1 »' t i 1
12
13
(Y
Mr
2
A
ttu-1
16
17
fa
M I I/I
f.s
/3
M
/f
2 ,
Я/[\ Ol/
г П
Рис 10

Рис. II

Пример выполнения задания. Дано: схема конструкции (рис. 12);
G=10 кН; Р г=5 кН, М = 8 кНм- 4 = 0,5 кН/м; а = 30°, размеры —
Рис. 12
в м.
Определить реакцию опоры А и реакцию стержня CD.
Решение. Рассмотрим
систему уравновешивающихся
сил, приложенных к балке
АВ. Отбрасываем связи: шар-
нирно-неподвижную опору А,
стержень CD и нить. Дей-
Действие связей на балку заме-
заменяем их реакциями (рис. 13).
Так как направление реак-
реакции шарнирно-неподвижной
опоры А неизвестно, то
определяем ее составляющие
Ха и Yа. Покажем также
реакцию SCr> стержня CD
и реакцию S нити, модуль
которой равен Р.' Равномер-
Равномерно-распределенную нагрузку
интенсивностью q заменяем
сосредоточенной силой Q, рав-
равной Q = 2-<7 = 2-0,5 = l кН
и приложенной в центре тя-
тяжести эпюры этой нагрузки.
Для плоской системы сил, приложенных к балке, составляем три
уравнения равновесия:
5 = 0; A)
B)
C)
; X
Рис. 13
,- = 0; Хл - SCD cos 30° = 0;
Из уравнения (I)
5=
.I + I0-3 + 8-5.G . ,. „
ж = ТТо^ 4<5 кН>
Из уравнения B)
Хл = Sen cos 30° = 4,5 • 0,866 = 3,90 кН.
Из уравнения C)
-SCDcos60°-S = 1 + 10 -4,5- 0,5-5 = 3,75 кН.
Значения Ха, У a, Sen получаются положительными. Это указы-
указывает на то, что принятые направления этих сил совпадают с их дейст-
действительными направлениями.
16

Задание С-3. Определение усилий п стержнях
плоской фермы способом Риттера
Найти способом Риттера усилия п стержнях /, 2, 3, 4, 5 фермы.
Схемы ферм представлены на рис 14 —16, а нагрузка указана
в табл. 3.
Таблиц л 3
Номер гяри-
анта (put.
14 - 16)
I
2
3
4
5
6
7
8
9
10
11
12
13
14
13
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Pi
о
0
10
10
5
10
о
10
10
20
10
10
10
10
10
10
10
10
10
10
К)
10
3
10
10
10
10
20
10
10
5
10
5
30
5
20
10
20
20
10
20
20
10
10
20
20
20
40
10
40
20
10
10
20
'0
20
20
20
20
10
Pi
hll
5
20
20
50
20
10
20
30
30
10
40
30
10
10
10
20
20
20
40
20
10
20
10
20
20
20
10
10
20
20
Pt
20
30
20
20
10
20
30
20
10
30
20
20
40
30
40
20
40
30
Р5
30
—
—
20
20
20
—
—
—
—.
—
—
L0
—
—
.
—
—
30
2
—
—
—
—
2
—
2
—
3
3
3
—.
3
—
—
2
2
2
2
—
2
—
Л, м
—
6,0
—
5,0
—
t;,o
—
—
1.5
—
5,0
3,5
3,5
—
4,0
—
—
2,4
2,4
2,3
3,0
—
2,2
—
о, град
__
30
—
30
30
30
.
45
45
4j
—
—
—
—.
—
—
—
—
—
—
—.
—
.
—
—
—
Пример выполнения задания. Дано: схема фермы (рис. 17); Pt ~
= 58 кН; Р.2 -50 кН; Рч -=85 кН. Найти усилил S,, S2, S.,, S4, S5.
Решение. 1. Аналитическое определение реакций опор. Рас-
Рассмотрим систему уравновешивающихся сил, приложенных к ферме.
Отбросим связи (опоры А В), заменяя их действие на ферму
реакциями. Реакцию опоры А разложим на составляющие ХА и Y,\,
направленные вдоль осей координат. Реакцию шарнира В направ-
направляем вверх по оси опорного стержня BN.
Силу ~Р3 разложим на две составляющие Р'Л и Р, имеющие
модули P'3 = Pscosa и />3 = P3sina (рис. 18).
17

— a j^a __ о a ¦. a , ' . g .
Рис. 14

12
13
ft
1S
'y //,'/
V//W1 ? /'-УЛ
18
Рис. 13

23
Рг
—i
Pi
6a
*
J*/ //)/
Pi. . з
,JFV
6a
25
26
Pf
\
5 '
N
p*
/
a.
/
i
B
1
T
30
¦/
5
\
\
Ps
\
p*
3a
\
\
P3
tP<
tp*
f
Pnc. 16

Вычисляем sin а и cos а:
sin а = ?{; = - = 0,447;
CD 2 ^ аЧ-(в/2J
СГ:
а*
= 0,894.
Рис. 17
Рис. 18
Определяем модули сил Р\ и Р\:
Р\ = 85 ¦ 0,894 --= 76,0 кИ; Р\ =-85 -0,447 = 38,0 кН.
Для плоской системы сил, приложенных к ферме, составляем три
уравнения равновесия:
1-a-P2-2a-P.;-5a + P;-a + /?/J-5a = 0; A)
ХХ, = 0; -Ра'-Х.4 = 0; B)
0; КА-Р1-Р2-Р5 + «п = О. C)
Из уравнения A)
;-РУ,-5-РГ_ 58 + 50-2 + 76-5-38
21

Из уравнения B)
Из уравнения C)
= Р; = 38 кН.
0-\-76- 100-84 кН.
2. Определение усилий в стержнях ферм. Найдем усилия в пяти
стержнях фермы способом Риттера. Для определения усилий в стерж-
у
у
H S,
1
1
/
\
^4
\
6 2a
г)
В
/p
/
Ж
а.'
Рис. 19
нях 1, 2, 3 (рис. 19, а) делаем разрез / — /и рассматриваем равно-
равновесие сил, приложенных к одной части фермы (рис. 19, б).
Целесообразно рассматривать равновесие той части фермы, для
которой объем вычислительной работы меньше. Следует составлять
такие уравнения равновесия, каждое из которых содержало бы лишь
22

одно неизвестное — искомое усилие. Это позволит определить каждое
устие независима ог усилии в других стержня^.
По-прежнему условно предполагаем все стержни растянутыми.
Знак минус в ответе укажет на то, что стержень сжат.
Для определения Sx составляем уравнение моментов относительно
точки пересечения линий действия S, и 53:
Ш,г = 0; — S1 ¦ 1,5а - Р'л ¦ 2а - PJ • 0,5а -f Ra ¦ 2а = 0,
откуда
Rn-2-P'-2 - Р[ -0,5 100-2 —76-2 —38 0,5
Si = - П5 = П5 =19'3 КН«
Для определения S, проектируем силы на ось Ау:
, = 0; — 5, cos $ - Р'л + Rn = 0,
где
cos p = F<j- = 77==== = 0,832,
откуда
^х'~ cosp ~~ 0,832 -zo'° к"'
Для определения S3 составляем уравнение моментов относительно
точки пересечения линий действия SL и S\:
2 М,я = 0; Sj ¦ 1,5а - Я^ • За + PJ • а + Лд • За = 0,
откуда
^З-Р' —/?й-3 76 3—38—100-3
= ЦТ
S3= v ;, п = Т-. =-73,3 кН.
Для определения усгг.чия в стержне Сделаем paipe3 ll —ff и
рассматриваем равновесие сил, приложенных к левой части фермы
(рис. 19, в). Составляем уравнение
lV = 0; —YA-a-St-VK = Q,
где
VK=VL coscc = a-0,894.
Отсюда
S4 =-- — К л ¦ й/0,894а = — 84/0,894 = — 94 кН.
Для определения усилия S,-, делаем разрез III — III и рассматри-
рассматриваем равновесие сил, приложенных к правой части фермы (рис. 19 г).
Составляем уравнение
Отсюда
23

Задание С-4. Опредслепис реакций опор
составной балки
Найти реакции опор и давления в промежуточных шарнирах
составной балки. Схемы балок представлены на рис. 20 — 22 (раз-
(размеры-в м), нагрузка указана в табл. 4.
Таблица 4
Номер
варианта
(рис 20 — 22)
1
2
Я
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
6.0
7,0
12,0
8,0
0,0
10,0
4,0
5,0
10,0
8,0
10,0
7,0
8,0
10,0
14,0
11.0
8,0
10,0
9,0
12,0
6,0
12,0
8,0
9,0
9,0
6,0
10,0
7,0
5,0
18,0
кН
10,0
4,0
18,0
10,0
15,0
7,0
6,0
4,0
7,0
14,0
5,0
12,0
12,0,
7,0
9,0
15,0
12,0
15,0
13,0
6,0
10,0
20,0
14,0
15,0
15,0
12,0
16,0
10,0
13Л
7,0
р,
—
—
5,0
—
9,0
—
14,0
—
13,0
—
6,0
5,0
—
8,0
—
—
—
—
_
—
12,0
16,0
—
14,0
.—
12,0
25,0
20,0
36,0
30,0
32,0
18,0
20,0
16,0
24,0
2fi,0
12,0
15,0
24,0
30,0
26,0
40,0
20,0
35,0
25,0
32,0
30,0
30,0
25,0
28,0
24,0
26,0
32,0
20,0
30,0
16,0
1 М г
I
—
•—
25,0
.—
—
28,0
—
—
—
20,0
—
—
—
18,0
—
28,0
—
—
—
—
24,0
—
—
3">,0
—
—
—
—
<7, KlliM
0,8
1,0
1,4
1,8
0,9
—
1,5
1,2
1,0
.—
1,5
1,6
1,2
—
1,0
—
—
1,4
0,8
1,5
2,0
1,0
1,2
—
1,5
1,4
1,3
2,0
~
Пример выполнения задания. Дано: схема составной балки
(рис. 23); Z3!^ 12,0 кН; Р.2 = 20,0 кН; М =- 50,0 кНм; ?-2,0 кН/м.
Решение. Составная балка представляет собой систему простых
балок, соединенных шарнирами. Поэтому рассматриваем системы
уравновешивающихся сил, приложенных к каждой простой балке
в отдельности, учитывая давления в шарнирах, соединяющих эти
балки.
Начинаем с балки DE (рис. 24), так как число неизвестных сил
(RF_, Xd, Yd) приложенных к этой балке, равно числу уравнений
равновесия:
2М,п=-0; RE-i-P,¦2cosW-Ql-l=0, A)
24

OS
ПП/1П
У >d
1ШШШ
»«t
CTZ
'И
S'l
oz .„\
J
•e-
Иж,
*</
oz .„
« »
Si
~w
HHIHI/IIH tTft \ >
™ ot
S'Z I G'<? ^
¦e-
ж si
т
& -
'd
j?,
г Л
W- п
o'z »L/, fg
¦^
*v
i?^
!!f
ог
7,, X"# ^
J
oz
srz
Л al
Ъ тмнитьптттгпн
'd bJ
S? I SZ
J -"и
Ш1
~O'Z .„I,/, ОТ
W
~oT
^1? ff
ПТТ1
f-
OZ

13
'a4!
птптт!
~W
hi
'IT
I f It t t f Ы ГТТПТтТТГГ ff
st
S'i
'HI
o'z
14
> В
о?
oz
st
g
¦711111 м rm m
bJ
~~or
\\\\\\\XV
sz
02 и.
/ей?
¦JE-
S'Z
С
о? .,
O'l
у— t
9'Z
Vfe
о'г
0$
~W
{es tt\ t ГП11 M t f 111 И f f f f
'Л

LZ
S't I O'Z S?
1\ °°%
ti^9
.ЙГ
0?
'rfN
3^%
Jill f f ГГШ )/))))))) t t
V
6Z
'o'i л*, "o'i _a. o'z "
/7I4
М
9Z
'in
Tz"
a
st ~t
X
.7) I ) ! H/t ) ) )
a
O'Z 01
7
"s'z
_?,
л )) t j/t m 11
zd\
St
\\\\v
'd
9Z
's'j T
S't
V
SZ
jrrrm шлицI
»
O'? ~ -A* S'Z "~ ' S'Z
t H 11 f П 1,1 N ll I И f t
CtE' I OT
Yd
?Z
3} -s
о'г "ТГ-ЯГ
fflL
•€-
ZZ
o'z
~W
4
v Oo9\
IZ

где
= q. 2 = 2 2 = 4 кН;
Из уравнения A)
B)
C)
Из уравнения B)
''4 А
„ - Я, cos 60° = 20 • 0,5 = 10,0 кН.
[ттпУгг
4/7
Рис 23
W
\S0°
1,0 2,0
x^
ШШТ
л го
rmrm
"
Рис 24
Рис. 25
Из уравнения C)
Уп = <?i + Pi cos 30э -RE = 4+ 20 (КЗ/2) - 9,66 = 11,6 кН.
Для балки BD (рис. 25):
где
кН;
D)
E)
F)
Из сравнения D)
50-I-8-6+11.6-8
= 47,7 кН.
Из уравнения E)
Из уравнения F)
V 1 Л Л tj-T f
В — Л о — 1U,VJ КП|
Ь = —47,7 + 8+11,6== —28,1 кН.
28

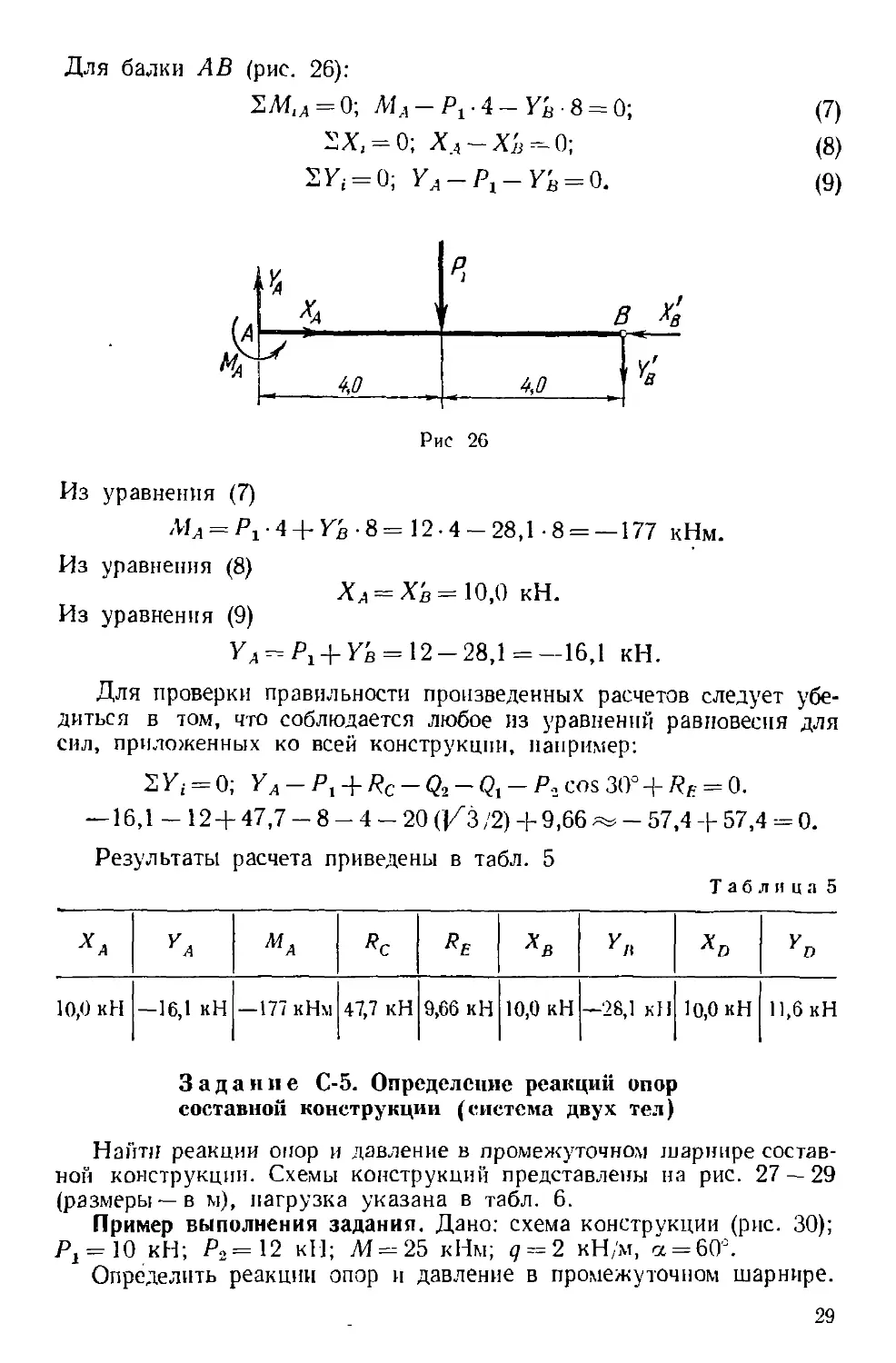
Для балки АВ (рис. 26):
G)
(8)
(9)
Из
Из
Из
(л
ft
уравнения G)
уравнения (8)
уравнения (9)
Ул
Уа
¦4 + Y
— Я, 4
4/7
Рн
в-8=12
- Ув = 12
с 26
4-
= 10
-28
28
,0
ь
•«,/7
,1-8 =
кН.
= —16
о V1
О лв
* 1
— 177 кНм.
,1 кН.
Для проверки правильности произведенных расчетов следует убе-
убедиться в том, что соблюдается любое из уравнений равновесия для
сил, приложенных ко всей конструкции, например:
; = 0; YA-Pl + Rc-Qi-Ql- P, cos 30° + RE = 0.
— 16,1 - 12+47,7 - 8 - 4 - 20 (|/3/2) + 9,66 ъ* - 57,4 + 57,4 --= 0.
Результаты расчета приведены в табл. 5
X
10,0
кН
УА
-16,1
кН
—17'
А
кНм
47,7
С
кН
/?
9,66
кН
л
10,0
в
кН
у*
—28,1
кН
10,0
аб
3
кН
п и
11
ц а 5
YD
,6кН
Задание С-5. Определение реакции опор
составной конструкции (система двух тел)
Найти реакции опор и давление в промежуточном шарнире состав-
нон конструкции. Схемы конструкций представлены на рис. 27 — 29
(размеры —в м), нагрузка указана в табл. 6.
Пример выполнения задания. Дано: схема конструкции (рис. 30);
^ = 10 кН; Я2=12 кМ; М=25 кНм; q = 2 кН/м, а = 60°.
Определить реакции опор и давление в промежуточном шарнире.
29

м
J
L
M
M
АЪ
М
T* г I. _^__
<к8
Н
ТТТТУП
А
w/'
7?. 7Г
Рис. 27

Pi
2 _^J_
15
16
/7
2 .,
HEl.
z' -Ч
Л/
/V
В
м .
,60°
А
Рис. 28

21 P,
2k
V- J—i
22
M
( t
2 л
г Л. «
L
P.
2.5
25
j4
p,

TTT'tTTlj
h q-
27
Zd
м
рг.
B\
Рис 29
32

Номер
варнянтя
(рис. 27 — 29)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Р,
к
fi,0
5,0
8,0
10,0
! 2,0
14,0
16,0
l'.\0
14,0
8,0
1 ~\0
1 л,0
7,0
5,0
6,0
II
8,0
10,0
—
1 2,0
8,0
6.0
—
.._
10,0
8 0
0.0
—
10,0
Л(
и 11м
2"),0
2()()
,п'.о
2ri,0
'27,0
—
18,0
'20 0
28,0
2fi,0
20 0
28,0
15,0
¦:о,О
24,0
q
к! 1 м
0,8
—
1,1
\',о
0,9
1 4
1,0
1,4
О/'
1,0
1 г)
1,1
0,9
1,5
Номер
(рис 27 — 20)
16
17
18
19
20
21
22
23
24
2т
20
O
2S
29
ЯО
р,
к
8,0
9,0
7,0
(i.O
7,0
8,0
5,0
14,0
10,0
11,0
Г\0
11,0
12,0
10,0
9,0
/'2
1
11 0
п,о
10,0
18,0
1П.0
17,0
6,0
10,0
13,0
10,0
Г>,0
1 1,0
12,0
9,0
10,0
Табл
М,
к 11 м
31,0
26,0
27,0
ЗтО
,!2,0
30,0
34,0
36,0
;g()
¦i.-iO
1 8,0
36,0
30,0
Зг),0
29,0
ii ц а б
и,
0,8
1,1
0,8
1,4
0 S
1,2
1 ri
й
1,4
i (;
1 4
1 т
и
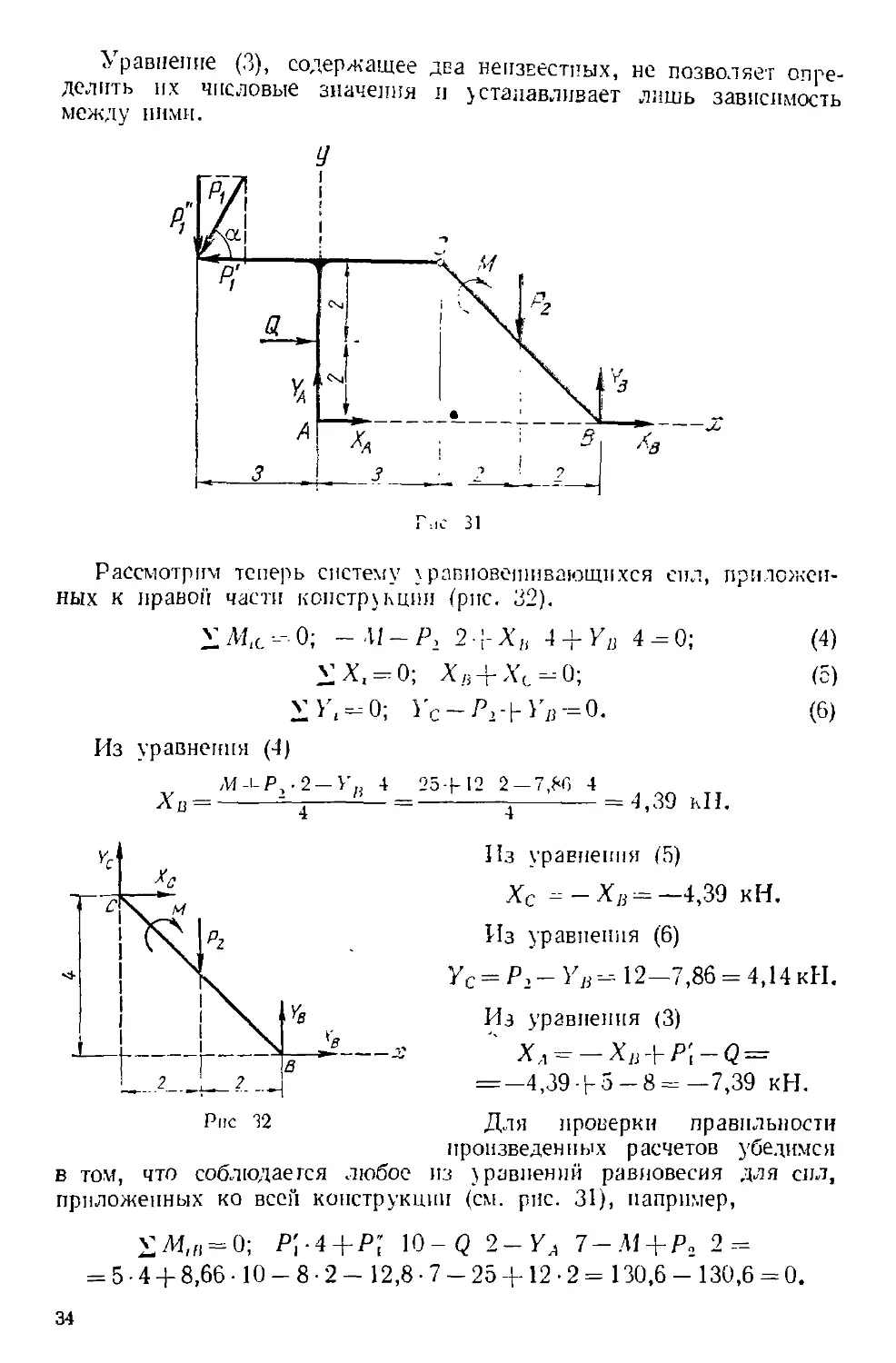
Ре шеи lie. Сначала рассмотрим систему уравновешивающихся
сил, приложенных ко всей конструкции (рис. 31J, что позволит опре-
определить вертикальные составляющие реакции опор А и В.
Для упрощения вычисления момента силы Pt раскладываем ее
на составляющие Р\ н Р{:
P[^Plnos'x =10 0,5 =5 кИ;
Я; =PlSrnrx= 10 0,866---8,66 кН.
Уравнения разиовесич имеют вид
2Л1.4-0, Р\ 4 + Л' 3-Q 2 —
_уц_Я, 5 + ^„ 7-0, A)
где<? = 4 д = 4 2-8 кН,
2У, = 0; - Р; -|- Уд - Р, + Ки = 0;
B)
Из уравнения A)
_р; 4- P,
-: Р2 5
— 5 4-8.66-3 + 8 2-;-2Г)-;-12 5
7
-7.86 кН.
Из уравнения B)
уд ^ р; + Р2 - У'й = 8,66 + 12 - 7,86 = 12,8 кН.
2 н/р Ябюпсиого А А
33

Уравнение C), содержащее два неизвестных, не позволяет опре-
определить их числовые значения и устанавливает лишь зависимость
между ними.
,.с 31
Рассмотрим теперь систему уравновешивающихся сил, приложен-
приложенных к правой части конструкции (рис. 32).
Из
Ус1
с
уравнения
/VI-
у
лц
\ м
1 1
с-
0;
V
D)
_р
.
\
• 2 —
Ув
1 ^
- .11-
х, = о
-0;
v'/i 4
_^
J
Ус
25
9 ' У
2-г Л;
-1-12 2-
Пз
X
Из
Ус = Р
Из
¦
¦i + Ya 4
, ^0;
1'я-=0.
-7,80 4
1
— т
ураЕнення
с — ~~ Хн —
уравнения
-0;
39 tiH
= —4,39
F)
2-Уд-12-7,86 =
уравнения
4,39-ho-
C)
8 = -7,5
кН.
4,14
D)
E)
F)
кЫ.
19 кН.
Рис 12 Для проверки правильности
произведенных расчетов убедимся
в TOVf, что соблюдается любое из jравнений равновесия для сил,
приложенных ко всей конструкции (см. рис. 31), например,
; 10- С? 2-YA 7-M + P» 2 =
= 5 • 4 + 8,66 ¦ 10 - 8 • 2 - 12,8 • 7 - 25 + 12 • 2 = 130,6 - 130,6 = 0.
34

Результаты расчета приведены в табл. 7.
Таблица 7
Ctf/TU, кН
—7,39
Уа
12,8
хв
4,39
Ув
7,86
*с
-4,39
YC
4,14
Задание С-6. Определение реакций опор
составной конструкции (система трех тел)
Найти реакции опор п давтения в промежуточных шарнирах со-
составной конструкции. Схемы конструкций представлены на рис. 33—35
(размеры —в м), пагр\зка указана в табл. 8.
Табтица 8
Номер
варилита
(pi'c
33-35)
1
2
3
4
.5
6
7
8
9
10
11
12
13
14
15
Pi
к
6,0
11,0
9,0
10,0
8,0
10,0
16,0
13,0
по
12,0
8,0
12,0
15,0
10,0
12,0
р,
?
.
8,0
12,0
14,0
15,0
17,0
—
—
—
—
14,0
16.0
8,0
Л',
кПм
2=>,0
34,0
20,0
30,0
22,0
28,0
36,0
25,0
29,0
31,0
28,0
Jti,0
30,0
35,0
32,0
_
—
—
—
—
30,0
34,0
37,0
—
—
—
21,0
—
Q
lift м
0,8
1,0
1,1
—
-_
1,4
1,0
—
—
—
1,2
\ 11 iep
варнам га
(,Ч1С
33-35)
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
р,
К
13,0
7,0
9,0
12,0
11,0
8,0
14,0
13,0
10,0
15,0
12,0
0,0
6,0
8,0
15,0
Рг
—
—
7,0
9,0
—
—
.—
—
—
14,0
—
л<,
мг
К|1м
26,0
23,0
29,0
33,0
38,0
30,0
28,0
32,0
35,0
40,0
37,0
29,0
25,0
30,0
34,0
34,0
.—
—
.
—
.—
—
—
—
—
—
—
—
—
к
0,9
1
—
,3
—
,5
,0
,4
,2
,5
,1
0,8
,0
1,2
Пример выполнения задания. Дано: схема конструкции (рис. 36);
Р1=--10,0 кН; Я, = 15,0 кН; М = 40,0 кИм; q = 1,6 кН/м.
Определить реакции опор и дазления в промежуточных шар-
шарнирах.
Решение. Сначала рассмотрим систему \равковешивающихсл
сил, приложенных к балке ВС, и определим вертикальные состав-
составляющие реакций шарнироз В и С (рис. 37).
Уравнения равновесия имеют вид.
-P., 2sin604-Vc 4 = 0;
-YB 4 + P2 2sui60n =0;
XB-Pj.cos603-Xc = 0.
A)
B)
C)
35

ш.
ч
А
2.5
1_Ж._| 7,0
яг^НАда» п
~ J,0
4Л± ci
N5
\П
| 2,0
Вя
f*
3.1
_ ?^_ ^^<?..^. ¦?"
10
2,о
v, ;!
."О
J,
-»E
Рис 33

12
\°г
/
\60"
1.0
1,0
к JM,
1_
F \F
-Ш 20У7*77' 3,n vty- 2.0 Л%
15
15
\\'\\\
\Е
2,5
17
13
13
20 , м_
D
1Г| У у ь \ ^г
fffT?
3,0
Рнс. 34
37

\21
Чф
vh
20,
п
so"
22
2,0
I п. А<
5,0
\23
2.0 \2,0
°к\ <7,g \t,p\ i,q\&
Ch '-
,25 ,_ 25
В "
1
1
26
М
hi rrr^g
Of
'-
<^
Ш
(S
p,
'—»-
\ 1
o
A
iJL/P,
С Е
30
w
JJL
3,0
Рис 35
38

?
щ
р,
1—н
—т*
li
2,0
*
2,0
7 .
lf\/!i)
/r\w i
^0_
2,0
Рис. 3G
6
/\60° С Xc
f - 2.0 1 . 2.0
4
P»c. 37
Pkc. 33
Рис. 39

Из уравнения A)
у __ /V 2 sin 60- _ '5 ¦ 2 ¦ \' 3/2 _ g г
4 4 '
Из уравнения B)
„ _ Л ¦ 2Ч1П 60е _ у __ „ ,. „
Составляющие Хп и Хс определятся из уравнений равновесия
сил, приложенных к элементу CD.
Рассмотрим систему уравновешивающихся сил, приложенных
к элементу CD (рис. 38):
fA'D-4=0; E)
:«-о. F)
Из уравнения D)
if) — J с — 0,0 К П.
Из уравнения E)
Из уравнения F)
Х'с = — Хй--13,3 кН.
Из уравнения C)
0э + Хс= 15 0,5+13,3-20,8 кН.
Переходим к рассмотрению системы уравновешивающихся сил,
приложенных к элементу АВ (рис. 39):
1Х, = 0; XA+Q-X'B = 0, G)
»де Q=-q-2=lfi 2--,3,2 кН;
vy.-O; У^-^-УЬ-О; (8)
v Л1 |В - 0, Af д -h X, 2 - }',, ¦ -И I\ 2 + Q 1=0. (9)
Из уравнения G)
*.,=-- —Q + Xa-=—32-I-20,8 =17,6 кН.
Из \равнения (8)
YA =-. Р1 + Y'B -- Ю,0 + 6,5 = 16,5 кН.
Из уравнения (9)
MA--- — X.i-2 + Y/ 4 — Pj 2 — Q- 1 ==
-----17,0-2+16,5 4-10 2-3,2 1-7,6 кНм.
Для проверки правильности произведенных расчетов следует убе-
убедиться в том, что соблюдается любое из уравнении равновесия для
40.

сил, приложенных ко всей конструкции. Например,
V X, = 0; ХА + Q - Р2 cos 60° -{- Хп =-- 0;
17,6 + 3,2 - 15 ¦ 0,5 - 13,3 - 20,8 - 20,8 - 0;
16,5-10-15 (|/3/2) -\- 6,5 - 23,0 - 23,0 = 0.
Результаты расчета приведены в табл. 9.
Момент Л/ ^,
кНм
7,6
*А
17,6
YA
16,5
ХВ
20,8
Силы
Ув
С,5
хс
13,3
Ус
6,5
Таб.?
XD
-13,3
i и ц а 9
6,5
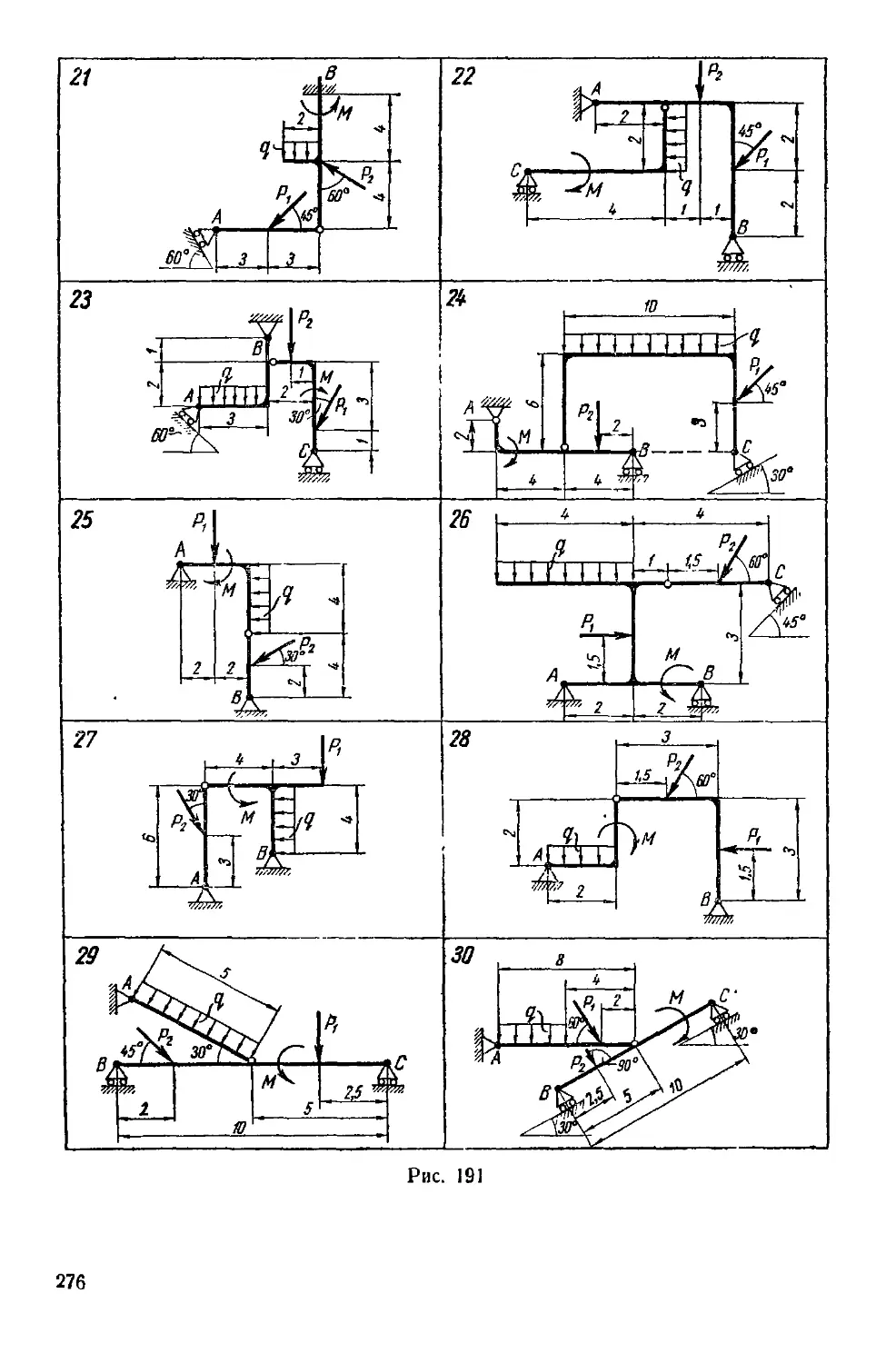
Задание С-7. Равновесие сил с учетом
сцепления (трения покоя)
Определить минимальное (в вариантах 1 —20, 25, 26, 29, 30) или
максимальное (в вариантах 21—24, 27, 28) значение силы Р и реак-
реакции опор системы, находящейся в покое. Схемы вариантов представ-
представлены на рис. 40—42, а необходимые для расчета данные —в табл. 10.
Трением в опорных устройствах пренебречь. Веса стержней, колодок
и нитей не учитывать.
Пример выполнения задания (к вариантам 1—20). Дано: G —
-•¦• 2 кН; Q = 20 кН; коэффициент сцепления (трепня покоя) /са— 0,1;
а-. 20-, а -10 см; 6=20 см (рис. 43).
Определить минимальное значение силы Р и реакции опор О,
А н В.
Решение. Рассмотрим сначала систему уравновешивающихся
сил, приложенных к телу Q (рис. 44). На тело действуют: сила тя-
уьесми Qt реакция нити Т и нормальная реакция .Vj.
Рассматривая тело Q как материальнаю точку, составим уравне-
уравнения равновесия указанных сил:
V X, = 0; Q соъ 4Г)° -7 = 0,
откуда Т = Q cos 45° -20 -0,707-14,1 кН.
Затем рассмофнм равновесие сил, приложенных к барабану
(рис. 45):
v,Mw-0; -T'-R-\-Far],nR--Q, D)
где ^ц — сила сиепления (сила трепня покоя);
v X, ¦= 0; Т -f Fcn cos a - Д/2 sin ъ -}- Х„ =¦ 0;
E)
F)
41'

Таблица 10
Помер
R.ipiMHT-1
(рис.
40-42)
1
О
3
4
5
E
7
8
lJ
10
11
12
13
14
П
10
17
13
И)
20
21
22
23
24
¦>-¦>
2E
27
24
20
30
а
к
1,0
1,1
1,3
1,8
1,5
1,6
2,0
2,2
2,1
1,8
1,9
2,0
1,6
1,7
1.S
1,2
1,3
1,4
1,7
1,6
1,0
1,5
2
3
1,0
2,0
4
5
2,0
1
Q
11
10
—
14
15
16
18
20
18
20
22
24
25
20
24
20
15
12
14
16
18
—
—
—
—
—
—
—
—
—
а
0,20
0,10
0,45
0,10
0,20
0,15
0,20
0,20
0,10
0,30
0,40
0,10
0,10
0,10
0,10
0,20
0,15
0,20
0,50
0,10
2
3
5
4
0,8
0,4
4
5
2
2
ь
м
0,10
0,15
0,40
0,40
0,30
0,10
0,50
0,10
0,20
0,30
0,50
0,25
0,10
0,2о
0,15
0,45
0,15
0,30
0,20
0,15
0,50
0,80
1,4
0,3
0,4
1,0
0,8
0,3
8,0
с
0,04
—
0,05
0,06
0,04
—
0,05
—
—
0,04
0,06
—
0,04
—
0,04
—
0,05
0,06
—
—
—
—
—
—
—
—
а.
град-
30
30
45
—
45
45
30
30
30
45
—
30
45
60
45
45
45
GO
30
—
45
30
—
—
30
—
45
30
30
30
Kos |)фи циет
сцсплешт
(ктффициеш
трепия п<жоя)
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,35
0,30
0,25
0,20
0,15
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,45
0,35
0,40
0,30
0,25
0,25
0,35
0,40
0,20
0,20
Точки, в котормас
определяются
реакции
0, А
0, А, В
0, А
0, А
0, Л
0, А, В
0, А
0, А, В
0, А, В
0, А
0, А
0, А, В
0, А, В
0, А
0, А, В
О, Л
0, Л, В, О
О, А
А, С, D
0, А, В
А, В, С, D
А, В, С, D
А, В, С
А, В, С, D
А, В, С, D
А, В, С
А, В, С, D
А, В, С, D
А, В, С
А, В, С, D
Для случая прсделыюго равновесия система уравнений D)—F)
дополняется уравнением
Из уравнения D)
F^ = T'R/l,5R = 14,1/1,5 = 9,4 кН.
Из уравнения G)
tfa = /W/ci, = 9,4/0,1=94 кИ. !
Из уравнения E)
XT1/ Г1 1 А Г •
— ^^_ ? г- COS fJ ~л /V S IП С? —
= —14,1-9,4-0,940 + 94-0,342 = 9,2 кН.
Из уравнения F)
= —94 • 0,940 - 9,4 • 0,342^ + 2 = —89,6 кН.
42

у *
Ю
Рис. 40

Рис. 41

21
23
25
26
28
29
30
—i
Рис. 42
45

Рис. 43
Рис. 44
Рис. 47
Рис. 46
Рис. 43
4R

Для определения минимального значения силы Р и реакции
опор А и В (эти реакции перпендикулярны к направляющим А и В)
рассмотрим равновесие сил, приложенных к тормозному устройству
(рис. 46):
2М,л = 0\ Fcra + Rn-b^O; (8)
VX, = O; N',-Pmin = Q; (9)
vyi = 0; RA + Rn-F'ca--=0. A0)
Решая эти уравнения, получаем;
Rb - - (Яц • а)/Ь = - (9,4 • 0,1)/0,22 = -4,7 кН;
Яш1п==Л^ = 94 кН;
Да = -Ди + Яц = -(-4,7) + 9,4=14,1 кП.
Пример выполнения задания (к вариантам 21—30). Дано: G =
— 1 кН; /сЦ = 0,4; а = 6 м; Ь = 2 м (рис. 47). Определить максималь-
максимальное значение силы р и реакции в точках Л, В, D и /Г.
Решение. Рассмотрим сначала систему уравновешивающихся
сил, приложенных к телу весом G (рис. 48). К телу приложены:
сила тяжести G, сила Р, нормальные реакции Nn и NE, а также
силы сцепления 1\1иП) и ^Сц<^) (.силы трения покоя).
Составим три уравнения равновесия указанных сил:
VX; = O; -FtniD)-FCHlE) + P = 0; A)
vy; = 0; Nn + NE-G = 0; B)
VAflD = 0; -G-b/2 + A/?-b-P-b/4 = 0. C>
В случае предельного равновесия P = Pmav. В этом случае си-
система уравнении @—C) дополняется уравнениями
fcuD = /c.AT»; D)
F^v^UNr:. E)
Подставив D) и E) в уравнение A), получаем
-/Л-/с^-!-/)п,« = 0. (Г)
Из уравнения B)
Nn + NE~G. B')
Из уравнений (Г) и B')
Ртах = /Сц (#0 + N я) = /cllG = 0,4 -1-0,4 кН.
Из уравнения C)
0,4 ¦ 1 -0,5+1 -2/2 л - „
= ft = ъ 2
Из уравнения B)
ND=G-NE= 1-0,6 = 0,4 кН.
Из уравнений D) и E)
= 0,4 • 0,6 = 0,24 кН.
47

Совокупности сил Nn и РацП), N,; и F~cll{E) образуют соответст-
соответственно опорные реакции в точках D и Е.
Рассмотрим теперь равновесие системы сил RA, Хп, Ytu GnP =
= Ртах, приложенных ко всей системе (см. рис. 47):
VX,=-0; Xn + Pma< = 0; F)
(8)
1 MiB = 0; — Pmax ¦ b/4 + G ¦ a/2 - RA ¦ a = 0.
Решая эти уравнения, получаем:
Xn — Рт . = 0 4 кН-
G.a/2 — Pma«-A'4 I -3-0,4-0,5 А ,С7 „
Я л = = б = 0,467 кН;
YB = G- Ял = 1 - 0,467 = 0,533 кН.
II. Система сил, не лежащих в одной плоскости
СИСТЕМА СХОДЯЩИХСЯ СИЛ
Задание С-8. Определение усилии в стержнях
пространственной конструкции
Найти методом вырезания узлов усилия в шести стержнях шар-
ннрно-стержневой конструкции. Сила Р действует в направлении АВ,
сила Q (в вариантах 2,4—6,8, 10—14, 16—25, 27, 29, 30) - в нап-
направлении DE. Схемы конструкций показаны на рис. 49—51, а необ-
необходимые для расчета данные приведены в табл. 11.
Таблица 11
11омер
варианта
(рис
4D—51)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Нагрузка,
Р
9
6
3
5
7
8
2
4
5
6
8
7
4
5
9
Q
8
5
3
5
6
6
6
4
4
9
6
7
Размеры, м
прямоугольного
II
.1 пллле-
лепипеда
а
4,0
4,5
2,0
3,5
4,0
4,5
4$
4,5
3,5
4,0
4,5
2,0
3 5
4,5
Ь
5,0
5,0
3,0
5,5
5,0
5,5
5,0
5,0
5,0
5,0
5,0
5,0
3,5
5.5
5,5
С
4,0
4,0
2,5
4,0
4,5
4,0
4,0
3,5
3,5
4,5
3,5
4,0
2,5
4,0
•1,0
d
1,0
—
—
—
—
—
—
—
—
—
1,5
"
Номер
варианта
(рис
49—5!)
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Нагрузка,
кП
Р
2
3
4
6
8
3
5
6
2
4
8
9
3
7
6
Q
4
5
6
4
6
5
3
Л
3
6
—
7
—-
6
5
Размеры, м
прямоугольно! о
паратк
лепипеда
а
4,0
3,5
4,0
4,5
2,5
4,5
4,0
3,5
4,0
3,5
4,0
2,0
4,5
3 5
4,0
Ь
5,0
4,5
5,0
5,0
3,0
5,0
5,5
5,0
5,5
5,0
0,0
3,0
5,5
5,0
5,5
с
4,5
4,0
4,5
4,0
3,0
4,0
4,5
3,5
4,0
4,0
4,5
2,5
3.5
1.0
3,5
d
—
—
—.
-*-
—
1,0
—
—
—
—
1,5
1.0

Pnc 49
40

/У
12
А\Р
13
15
fff
17
18
го
Рис 50
50

21
Q в
23
25
28
27
23
Рис. 51

Пример выполнения задания. Дано: стержневая конструкция
(рнс. 52); Я = 4кН; а = 4 м; Ь = 5м; с — 4 м; с/=1л).
Определить усилия 5,, 5а, 5Я, S(, .Ss, 50.
Решение. Рассмотрим сначала \зел А (рис 53), так как в нем
сходятся три стержня. На этот узел действует сила Я. Предполагаем,
что все стержни растянуты и поэто-
поэтому направляем реакции Slt S2, S3
от узла А. Сила Я и реакции Sx,
S^ S:i взаимно уравновешиваются.
Составим три уравнения равно-
равновесия сил, сходящихся в узле А:
VX, = 0; — Я cos iE sin ф—
— S, sin р - S^-Sj sin ф = 0; A)
V У, -^ 0; — Р cos if cos ф —
B)
VZ, = 0; —
Р„о 52 SlCosp^O. C)
По заданным размерам вычисляем синусы и косинусы углов ф, if>, p:
Sill ф=" —,-
cos ф = -р
h
sin ф =
c
cos ty =- —
1 1у
Va\_
?57 '
У57 '
a a 4
SID p = -7— -—- = —-. = ;
JIj уравнения C)
P sin vj
cosp
4 • А У'Л
hV'2
= —2,99 kH.
Из уравнения B)
S3 = -7>cosi|; = -4i^- = -3>39 kH.
|/o7
52

Из уравнения A)
<S2 = — Р cos г|; sin cp — St sin P — S3 sin tp =
~ У57' 'Т4Г
41
1 57 12
| 57 \ 41
¦- 2,12 кН.
Переходим к рассмотрению системы уравновешивающихся сил,
приложенных к узлу D:
"i ("I ~~~ — i-li)> ^4, S5, о8.
Введем угол Q. Направления осей координат сохраняем без изменения.
Ь.
Рис.
Составим три уравнения равновесия сил, сходящихся в узле D:
v X; = 0; S', sin р -Ь So sin 0 sin ip -- - 0;
vy,-.- = 0; — Ss-Se sin 6 cos ф = 0;
v Z; == 0; S\ cos p -|- S4 - Se cos 0 --= 0.
Вычисляем синус п косинус угла 0:
D)
E)
F)
с,
sin G —
Из уравнения D)
sin ft
sill 8 sin
¦=16--
V \- + 5^-|- I- \ 42
7^~ = Ttr*
" Vf
_Л_. 144--J-P- = 3,44 кН.
I'2 j 41 4
53

Из уравнения E)
S5---~-SAsin0cos(p = — 4
Из уравнения F)
^-. I-----4=- = —2,65 кН.
57 М2 I"И
i = So cos 0 - SI cos p -= -4 -Ь^- • -U- -
¦--2,65 kII.
I I 57 ¦ I 2
Результаты расчета приведены в табл. 12, в которой знак плюс
соответствует растяжению, минус —сжатию.
Таблица 12
Номер стержня
Знак усилия
Усилие, кН
1
—
2,99
2
+
2,12
3
—
3,39
4
+
2,65
5
2,65
6
+
3,4 4
Из табл. 12 видно, что стержни 2, 4, 6 растянуты, а стержни /,
3, 5, сжаты.
СИСТЕМА ПРОИЗВОЛЬНО
РАСПОЛОЖЕННЫХ СИЛ
Задание С-9. Приведение системы сил
к простейшему виду
Определить главный вектор ~%* л главный момент Мо заданной
системы сил относительно центра О и установить, к какому простей-
простейшему виду приводится эта система. Размеры параллелепипеда (рис. 54),
а также модули и направления сил указаны в табл. 13.
При выполнении задания необходимо сделать следующее:
1. Изобразить заданную систему сил, выполнив построение парал-
параллелепипеда в масштабе, показав /_ xQy на чертеже равным 135е;
сокращение размеров по оси Ох принять равным 1 : 2.
2. Выбрав систему координатных осей, определить модуль и
направление главного вектора заданной системы сил по его проек-
проекциям на координатные оси и изобразить R* па чертеже.
3. вычислить главный момент заданной системы сил относительно
центра О по его проекциям на координатные оси и изобразить Mq
на чертеже.
4. Вычислить наименьший главный момент заданной системы сил.
5. На основании результатов вычислений главного вектора и
наименьшего главного момента ~М* установить, к какому простейшему
54

виду приводится заданная система сил. При этом необходимо сделать
следующее:
а) если заданная система сил приводится к паре сил, то показать
момент этой пары, приложив его к точке О;
б) если заданная система сил приводится к равнодействующей
силе, то найти уравнение линии действия равнодействующей, опре-
определить точки пересечения этой линией координатных плоскостей
и изобразить R на чертеже;
в) если заданная система спл приводится к дипаме (силовому
винту), то найти уравнения центральной оси, определить точки пере-
L
A
n
/
0
/
в
к
/
с
//
.b J/
Рис. 54
сечения этой осью координатных плоскостей и изобразить R* и М*
на чертеже.
Пример выполнения задания. Дана система сил Я,, Я2, Рд, Я4;
модули, точки приложения и направления этих сил указаны в табл. 14.
Решение. 1. Определение модуля и направления главного вектора
заданной системы сил по его проекциям на координатные оси. Задан-
Заданная система сил показана па рис. 55. Так как
то
AD = УЛО~ + OD- = ]/30а -f 402 = 50 см,
cos а = АО/AD = 30/50 = 0,6; cos E = AE/AD = 40/50 = 0,8.
Проекции главного вектора на оси координат:
X = P3-f-P*cosa^4+ll-0,6 = 10,6 Н;
Y = Р1 = 10 Н;
Z = —P.-P4cosp = — 4-11-0,8 = —12,8 Н.
Л\одуль главного вектора
R* =УХ> + Y* + Z1 = ]Л0,62 + Ю- + (-12.8J = 1/"зЖГ= 19,4 Н.
55

3 u ^^
s 5 S =
^ ^ ^ *-
p
« s
i!
S I I
" ¦ lQ 13 ¦ I QGQ I I QiC I I i Q
I ! !чо ! I I
:q ! ! qcici I I ciitr
О i I 1 O©
— I I I —cm
0200 I . © i <N | I ©ao io
n-~ I i — I eo ' I CM c>
S00
qo о qo ioo'0©o ioocoo !ю©©'о I ccooe i
— I CN — I CN CN — I — CM. I— Ю !
U: =э о tj '<. Q эз
|©©*d-'i^O©©'MOOCOOOC©©©QOOLCOOntC©OLO
м- _._счгс — oi re — t«n:i "O ci см— —о
3 — CCi-^ — Q^-^C*^^:Q
n -^ — ¦— — см
*'— СОТТГ •— <T~. TrCl CO
<M 4- — CJ '.
©o ©o
CO ¦* — тг
; © с о ооо Ci
г со -л- — -ir сч
СЧ CN "М СЧ чг СЧ Ч-
СМ — П Г1
IcecOCNCO ^JCl-гсе СЧ04СЧ-*2->ОСОСОС:с-1 — с
n<Jea
— СЧ СО ~1г 1О '.
¦ Г}\ с ( СЧ СМ СМ СЧ CN СЧ СЧ СМ
56

Таблица 14
Размеры прямо-
лелепппеда, см
а
30
ь
50
с
40
X
Я
S
10
г.
ч
npi
1 =
si
0
он
X
с
гё
3
ОС
х
5.
Щ
4
Силы системь
г;
с"
«5
" Z
о
с.
с
г
с;
§
4
npi
к
те -:
5 с
г- *
с
пен
X
CS
Е
уль
и
5
npi
к
X
X
о>
D.
П
X
Направляющие косинусы
cos(^*, 7) = X/R* = 10,6/19,4 =0,547;
cos(R*, 7) = V//?* = 10/19,4 = 0,515;
cos (R*, k) = ZlR* = —12,8/19,4 = —0,660.
Главный вектор показан на рис. 56.
Рис 56

2. Определение главного момента заданной системы сил относи-
относительно центра О.
Главные моменты заданной системы сил относительно коорди-
координатных осей:
Мх = — Рф = — 4 • 50 = —200 Нем;
My = P2a-b^4Cospa = 4 304-11-0,8-30 = 384 Нем:
М. = — РйЬ = — 4 50 = —200 11см.
Мо = УШТЩ+Ш = V(—200J + 3842 + (—200)» = 476,9 Нем.
Направляющие косинусы:
cos (М'о, Т) = MJMO = — 200/47G.9 = —0,419;
cos (Мо, 7) = MUIMO =- 384/476,9 = 0,805;
cos (Mo, k) = Мг1 Mo = —200/476,9 = —0,419.
Главный момент показан на рис. 56.
3. Вычисление наименьшего главного момента заданной системы сил.
R* ~
= «0-6-(-200)+ 10 381 + (-12,8) (-200) =
4. Так как R* Ф0, М* =/=0, то заданная система сил приво-
приводится к динаме (силовому винту).
Уравнение центральной оси:
Mx-lyZ-zY) My-{iX-xZ) M,-(xY-yX) M*
X = V = 1 ==ТГ#
Подставляя в это уравнение найденные числовые значения вели-
величин, находим:
Мк— (yZ-zY) __ jM^ _ —200-\у (—12.3)-;-г 10] _ 220.G .
X ~ R* '• 10,0 ~~ 19,4 »
6,4у + 5г=160. A)
Mv—(iX — xZ) М* 384 —[2-10,0-*(—12,8I 220,0
F =R*~> 10 = 19,4 •
5,3z-1-6,4* =135. B)
Координаты точек пересечения центральной осью координатных
плоскостей определяем при помощи уравнений центральной оси A)
и B). Полученные значения координат помещены в табл. 15.
Центральная ось системы сил показана па рис. 56.
Примечание. Если силы приводятся к равнодействующей, т. е. М* = 04
a R = R* ф 0, то j равнения линии действия равнодействующей:
МЛ= yZ-zY; Mu--=zX-xZ, AU^-xY-yX,
где A', Y, Z — проекции равнодействующей силы на координатные оси; А1К, My,
ЛЬ — главные моменты заданной системы сил относигелоио координатных о-ей.
Из этих трех уравнений независимыми являются только два.
5S

А3
X
0
-5,4
21,1
Та б;
и ц а 15
Координаты, с\т
у
5,1
0
25,0
2
25,5
32,0
0
Задание С-10. Определение реакций опор
твердого тела
Найти реакции опор конструкции. Схемы конструкций показаны на
рис. 57 — 59. Необходимые для расчета данные приведены в табл. 16.
Таблица 16
Номер
Е.фн. чтя
(рис
57-3")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Силы, KlI
G
2
4
6
3
5
1
4
5
1
4
10
3
4
2
6
4
2
5
—
2
—
Г
4
3
6
4
2
__
2
__
8
4
—¦
G
20
2
4
2
3
2
1
3
3
2
1
1
5
1
2
2
1
2
2
5
4
2
3
1
1
6
3
4
а
20
20
15
30
30
40
30
20
20
30
20
25
40
30
60
50
15
60
20
60
40
20
40
_
50
20
50
30
15
40
ь
30
10
15
20
40
30
10
40
15
40
30
20
30
90
20
30
10
40
30
40
60
50
30
50
60
30
10
20
30
'алмеры, с\
с
10
30
20
40
20
20
5
15
10
20
15
8
20
20
40
—
20
60
40
20
30
30
50
—
60
40
—
50
15
10
R
15
10
—
15
20
20
18
20
30
20
15
15
25
30
20
—
20
—
'20
—
—
—
—
—
—
—
—
10
15
Г
5
10
15
10
15
10
6
10
40
10
10
10
15
10
5
—
5
—
15
—
—
—
—
—
—
—
—
15
10
1. Считать1, ачто'в вариантах 16, 18. 22 — 27, 30 петли не препятствуют перемещению рзмы
вдоль А в
2. В вариантах 20, 21 и 28 соприкасающиеся поверхности считать абсолютно гладкими.
59

Рис 57

I'nc. 58

22
i
1
i/
ъ
у
С
r~
в
r^ - i'
С01А4
CBLAij
cm Ax
CDWAy
27
60
СППТНЕПАХ j.
Рис 59
62

Пример выполнения задания. Дано: рама ABCD весом G=l кН;
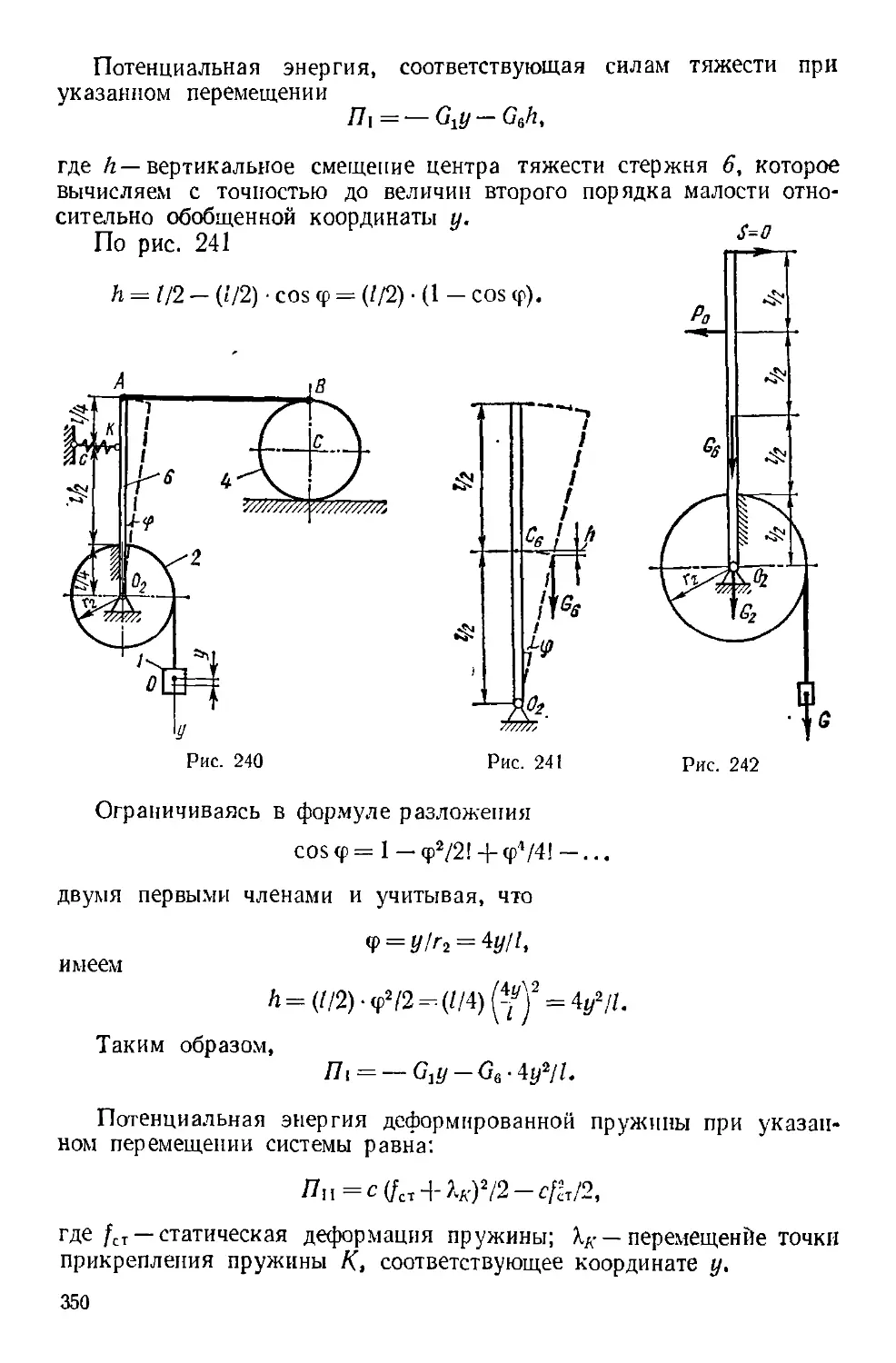
Р = 2 кН; ~Р\\Ау; AD = ВС = 60 см; АВ = CD =100 см; а = 30°;
р = 60° (рис. 60).
Найти /?., и Лл (Л — шаровой шарнир, В — петля).
Решение. Рассмотрим равновесие сил, приложенных к раме:
силы тяжести G, силы Р, реакции S стержня СЕ и составляющих
реакции опор Л и В: ХА, Yл, ZA, X1]t Za (рис. 61). Прежде всего
Рис. 60
Рис G1
составим уравнение моментов сил относительно оси, проходящей
через точки А и В:
откуда
М1у = 0; G (ВС/2) sin 30° - 5 • ВС • sin 60° = 0,
= (O- sin 30°)/B • sin 60°) = A • 0,5)/B • 0,866) = 0,289 кН.
Затем составим уравнения моментов сил относительно координат-
координатных осей Ах и Аг\
2Af,.v = 0; -P-AD cos 30° - G • ЛВ/2 + 5 cos 30° • Л В +• ZB ¦ АВ = 0;
7 _ Р./1Рсо5 30° + О/15/2-5со5 30о.,4Д _
в " АВ ~
__ 2 • GO ¦ 0,866+ 1 • 50 — 0,289 • 0,866 - 100 _ „
. = 0; P-AD sin 30° + S cos 60° • AB—XD AB = 0;
В 2-60 0,5+ 0,289-0,5-100
AB
100
= U,/44 KH.
63

Наконец, составим уравнения проекций cm на осп координат:
0; XA + X,(-S cos 60^0;
S cos 60* ¦--= -- 0,741 -'-0,289 ¦ 0,5 == — 0,6 кН;
YA = — P = — 2 кН.
IZ, = 0; 7Л - G + Z/t -!- S cos 30r' - 0.
2.4 = G ~ Zu - S cos 30° = 1 - 1,29 - 0,289 • 0,866 -.^ — 0,54 кП.
Итак, реакции всех связей рассматриваемой конструкции опре-
определены.
Задание С-11. Определение реакций стержней,
поддерягииающнх прямоугольную плиту
Найти реакции стержней, потдержипагощпх тонкчю горизонталь-
горизонтальную однородную плиту весом G, прч деист сип па нее вдоль сто-
стороны АВ силы Р. Схемы консгр\чцпй показаны на рис. 62 — 64;
необходимые для расчета данные приведены в табл. 17.
Таблиц,! 17
Помер
в ^piMiiTa
(рис
С2 — 64)
1
2
3
4
5
6
7
8
9
10
II
12
13
И
15
[larpyixa,
к!1
пес
а
20
28
18
28
32
22
20
30
36
20
8
.43
24
зз
35
сила
25
30
20
30
35
25
25
35
10
25
10
35
25
35
40
а
8,0
5,7'
4,0
7.0
К,0
0,0
1,0
5,5
6,0
8 5
3,0
6,0
'.1,5
0,0
7.0
Размеры, м
Ь
2.5
5 0
1,5
1,0
¦1,0
2,5
5,0
5,5
6,0
2,5
2,5
5,5
2,5
5 5
5,0
с
Я,5
\'i
3,5
4,0
4,0
¦1,'Т
3,0
1,0
¦1,0
'Л,'>
1,5
3,0
3,5
4,0
1,0
d
1,"
1,°
—
—
—
—
2,0
—
1,5
—
—
I ipi:<,ll I."
(i)llc
i ¦) - Ы)
16
17
IS
19
20
21
22
1Л
1\
>5
2E
27
28
i'l
30
1 |<|ГП\';|Ка,
кП
Г..Ч
6
14
20
33
20
!Ч
24
1E
20
28
30
20
3,!
30
30
20
сила
/•
25
35
25
35
30
20
25
30
35
25
35
•>5
35
25
а
4,0
8,0
0,0
•1,0
A,0
7,0
5,5
1.0
7,0
0,0
8,0
1>.О
6,0
,),5
4,0
Ратшры, и
Ь
3,5
2.5
5,5
5,0
5,5
4,0
3,0
5,0
4,0
5,0
2,5
5,5
5,0
5,0
5,0
С
3,0
3,5
4,0
1,0
4,0
4,0
3,0
3,0
4,0
4,0
О ~(
•V»
3,0
4,<)
4,0
d
1,0
—.
—
1,0
—
1,5
—
1,0
1.5
—
¦
Пример выполнения задания. Дано: схема конструкции (рис. 65);
G=--6 кН; Р-^9 кН; а = 5 м; b -5 м; с = 4 м; d -2 м.
Определить реакции 5,, S.,, S^, 54, S:>, Slr
Решение. Рассмотрим систему уравновешивающихся сил, дей-
действующих па плиту (рис. 66). Заааваемыми силами являются вес
плиты G, приложенный в ее центре тяжести, и сила Р. Предпола-
64

8
Pnc 62
О п/р, Яблоыскош A. A.

/v/r/s.
12
13
15
16
17
18
7Г
W&7
19
20
Ш
Рис. 63
6С

21
.ww?
23
25
26
W/fff
27
28
29
30
Рис. 64
67

гая, что все стержни растянуты, направляем их реакции 5„ 52,
S3, S4, 56, Se от узлов.
Выбираем оси координат Охуг так, 'чтобы эти оси пересекали
наибольшее количество стержней. В этом случае уравнения равно-
равновесия получают наиболее простой вид. Дополним построение до пря-
прямоугольного параллелепипеда и введем углы q>, ty, ц, 6. Усилие 5в
p/
Рис. 65
Рис. 66
целесообразно разложить на три составляющих по координатным
осям (см. рис. 66); их модули:
, = О; G-a/2-S'6"a = 0;
Составляем шесть уравнений равновесия:
A)
B)
C)
D)
E)
5Г = 0. F)
По заданным размерам вычисляем синусы и косинусы углоь.
с 4 -!
, = 0; -53cost|)-5o-=0;
sin ф =
cos ф =
sin if = -
соь U = -
У сР + с~
а
4
у 52 + 42
5
4
К 41
i 41

n
9 (п т> =» —- — =
b I
COiv II = , = ;
Уа* + Ь* У 2
_ s /2
Из
откуда
cos б d
уравнения B)
SS" = 1/2-G =
-d*
¦d»
1/2
V r-2 + 5*
>
/54 '
•6 = 3 кН,
+ 2*
HO
К 54
Из уравнения C)
<, Pb + S^a _ P
5 ~~ 6 cos ф cos ф '
Saa sin 9 cos т|
b cos ф cos ф ' b cos ф
= 3,3/41 = 21,1 к!
~ 5 ~ 5-5
Из уравнения A)
4
S4 = — - G - S5 sm ф - -'б- 3,3 ]/4 T
Из уравнения E)
2
= — 3-13,2 = —16,2 кН.
^ S' _ 5e sin 0 cost]
J" cos г() cos iji
1,5./Й Mli—L./4I
qiJ^^ =-9.62 кн.
Из уравнения D)
1 COS ф 5 "• COS ф COS (|i 5 "^ COS Ip
1.5^1
_ з 3 1/41 |
j
= A.8-3.3-1-1,5; K4l=0.

уравнения F)
S.t = — G — 5j sin ф - 53 sin г|з - S4 - 55 sin ф + S«" =
= — G - ^ + Sb) sin ф - 53 sin -ф - S4 + Se cos 6 --=
- (-16,2) + 1,51^54 j= = 6 kH.
Результаты расчета даны в табл. 18.
Таблица 18
Номер стержня
Знак усилия
Усилие, кН
1
0
2
+
6
3
—
9,62
4
—
16,2
5
+
21,1
6
+
11,03
Из данных табл. 18 видно, что стержни 2, 5 и 6 растянуты,
стержни 3 и 4 сжаты, а стержень — / «нулевой».
Для проверки правильности проведенных расчетов составим урав-
уравнение моментов, например, относительно оси гх.
,г, = — Sj cos ф • Ь + Sa cos ф • а + S'6b = — Sj cos ф • b + 53 cos ф • a -f-
= — 37,5 + 37,5 = 0.
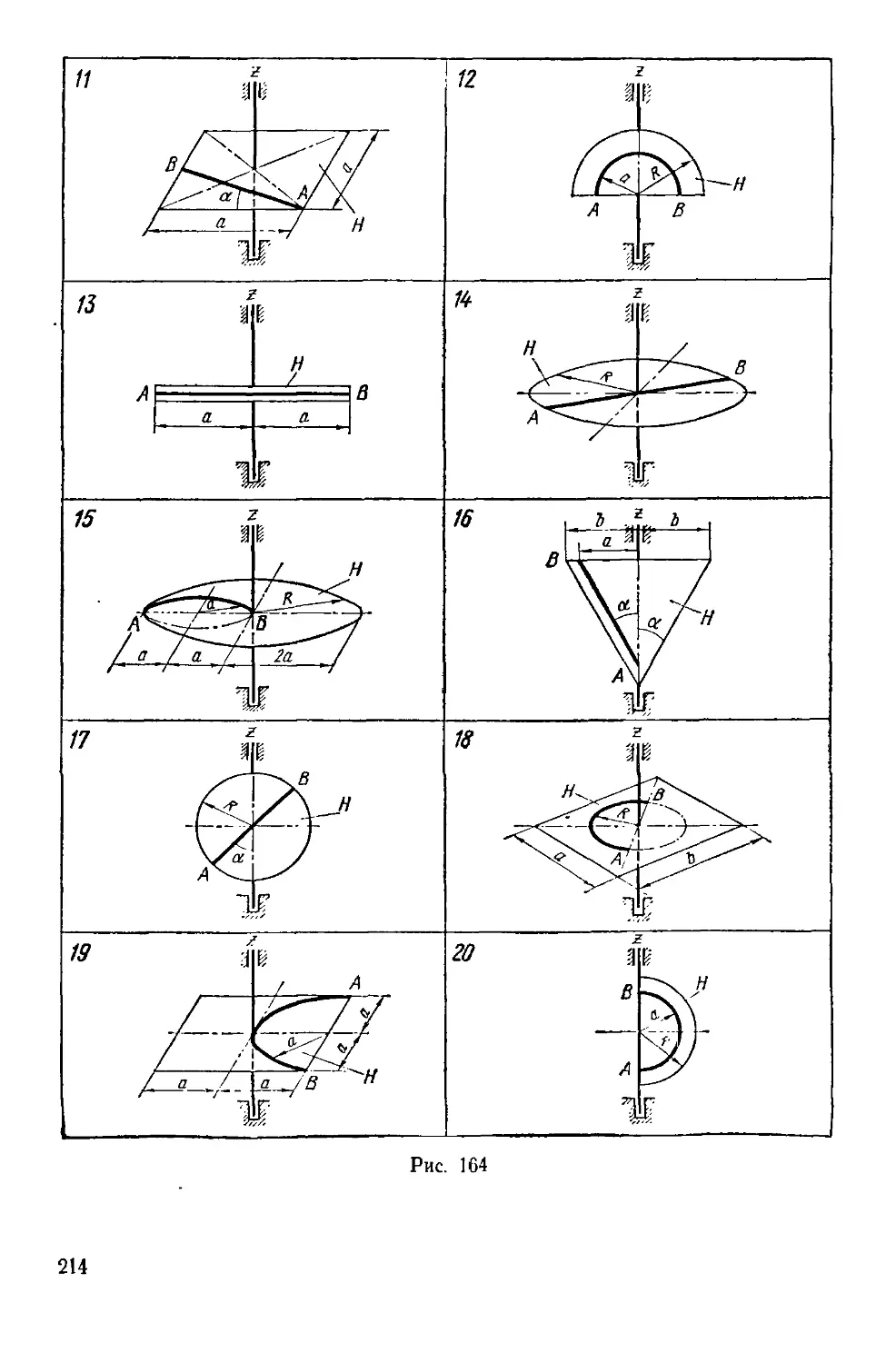
ЦЕНТР ТЯЖЕСТИ
Задание С-12. Определение положения
центра тяжести тела
Найти координаты центра тяжести плоской фермы, составленной
из тонких однородных стержней одинакового погонного веса (вари-
(варианты 1 —6), плоской фигуры (варианты 7— 18 и 24 — 30) или объема
(варианты 19 — 23), показанных на рис. 67 — 69. В вариантах 1—6
размеры указаны в метрах, а в вариантах 7 —30 —в сантиметрах.
Пример выполнения задания. Определить координаты центра
тяжести плоской фигуры, показанной на рис. 70.
Решение. Координаты центра тяжести площади определяем по
формулам:
*с = —j-^\ Ус= " р -• A)
Чтобы воспользоваться этими формулами, площадь делим на
отдельные части, положения центров тяжести которых известны.

У\
-x
У\
8
о
х
'УУУУУУУУУУУ,
30
9 n\
i
10
У\
0\
X
ш.
Рис 67
п

УI
F0
12
У\
R2
J -х
х
—х
15
16
1-^ X
17
х i
VJ
—у
х
Рис. 08
Т2

21
3D
22
25
26
u:
—i x
27 У\
28 у\
29
JO 4'I
с
ЖШй
Рис ЬЭ
73

В данном случае такими частями являются: прямоугольник тре-
треугольник и половина круга (рис. 71). Площадь половины круга,
вырезанную из площади пря-
прямоугольника, считаем отрица-
отрицательной.
Цмеем:
площадь прямоугольника
/^ = 40-30= 1200 см2;
площадь треугольника
ft=D0 -50) /2 =1000 см2;
площадь половины круга
f а =* (я ¦ 202)/2 = 200я = 628 сма.
Рис. 70
Центры тяжести рассматриваемых частей фигуры имеют следую-
следующие координаты:
для прямоугольника:
^ = 15 см; г/! = 20 см;
для треугольника
х2 = 30 + 50/3 = 46,7 см; уя = 40/3 = 13,3 см;
для половины круга
= 8,5 см; */3 =
см.
Для вычисления координат центра тяжести плоской фигуры
составляем таблицу (табл. 19).
—х
Рис. 71
По формулам A) вычисляем координаты центра тяжести плоской
фигуры:
59362 24700 . с _
^ТбТг"37'8 см; ^С==Т572~ 5<7 Ш'
П

Таблица
Номер
элемента
1
2
3
Е
Fj. см1
1200
1000
—628
1572
X,, СМ
15,0
46,7
8,5
—
У{, см
20,0
13,3
20,0
—
S -F х см»
h i 1
18000
46700
—5338
59362
S( =^(//j. см3
24000
13300
—12560
24700
Центр тяжести площади указан на рис. 71.
Примечание. Площади и координаты центров тяжести некоторых плоских
фигур, встречающихся при выполнении заданий, приведены в табл. 20.
Таблица 20
Плоская фигура
Площадь
Координаты центра тяжести
Треугольник
F=\/2-aha
где *!, х2, ха—координаты
вершин О, А, В
Круговой
сектор
/
(полукруг)
a = л/6
2fl sina
Xc- За
2/?/я
Круговой
сегмент
XBa— sin 2a)
Ba —sin 2a)

РАЗДЕЛ ВТОРОЙ.
КИНЕМАТИКА
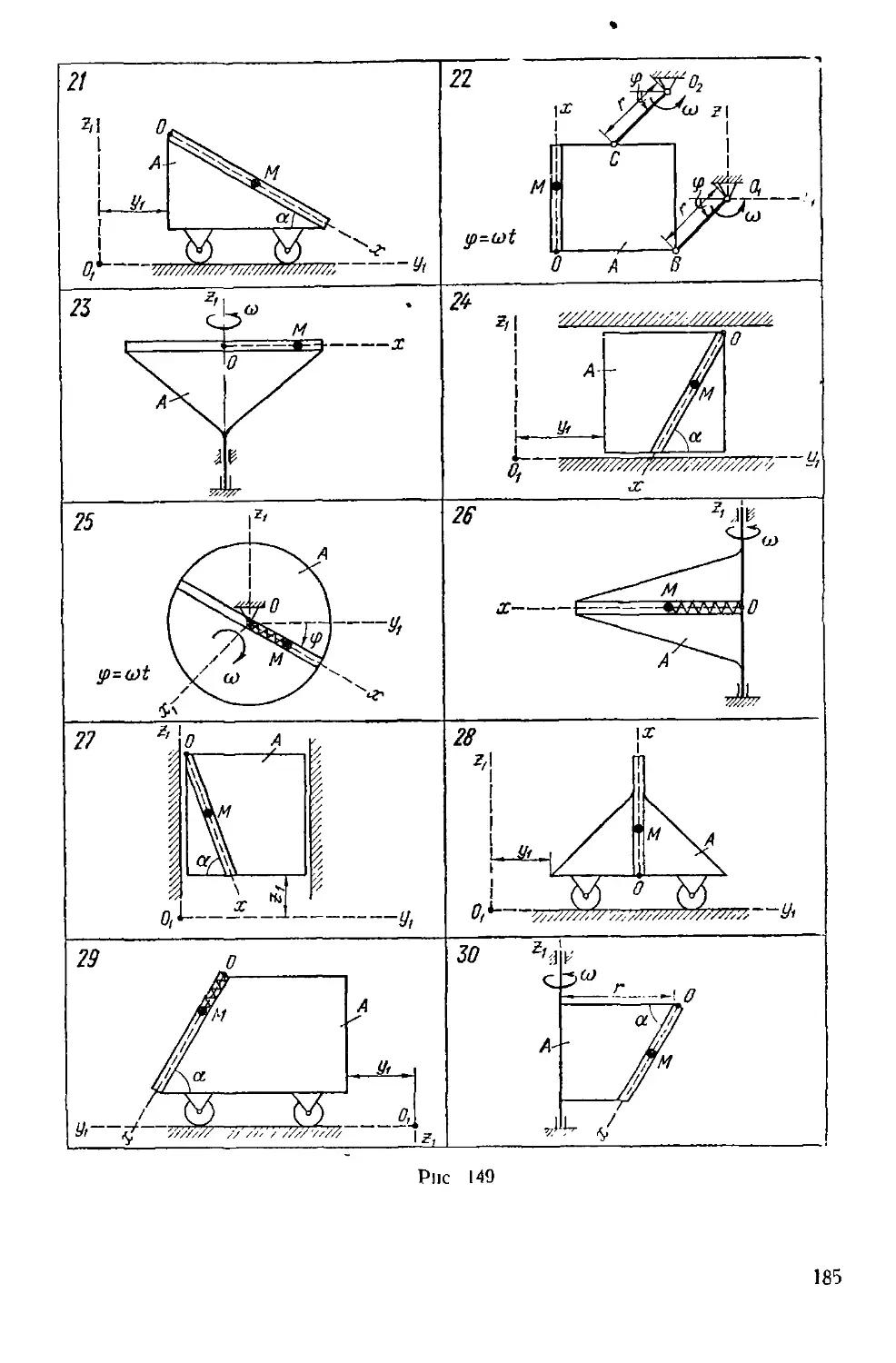
В этом разделе содержатся 12 заданий по кинематике точки,
кинематике твердого тела и сложному движению. По каждой теме
предлагаются задания различной трудности. Так, задание К-2 слож-
сложнее, чем К-1. Наиболее полно охватывающим тему плоского движе-
движения является задание К-6.
Каждое из заданий К-5, К-6, К-7, К-8, К-Н и К-12, как показано
в примерах, можно полностью или частично выполнить различными
способами. Однако обязательное использование двух способов преду-
предусмотрено только в условии задания К-6.
Предполагается, что выбор способа выполнения других заданий
произволен или определяется преподавателем.
I. Кинематика точки
ПРЯМОЛИНЕЙНОЕ И КРИВОЛИНЕЙНОЕ
ДВИЖЕНИЯ ТОЧКИ
Задание К-1. Определение скорости и ускорения
точки по заданным уравнениям ее движения
По заданным уравнениям движения точки М установить вид ее
траектории и для момента времени / = ^(с) найти положение точки
на траектории, ее скорость, полное, касательное и нормальнее уско-
ускорения, а также радиус кривизны траектории в соответствующей
точке.
Необходимые для решения данные приведены в табл. 21.
Пример выполнения задания. Исходные данные в см и с:
х = 4/; </=16*2-1; A)
/, = 1/2.
Решение. Уравнения движения A) являются параметрическими
уравнениями траектории точки М. Чтобы получить уравнение тра-
траектории в обычной координатной форме, исключим время / из урав-
уравнений движения.
Тогда
у = #-\. ¦ B)
7G

Номер
варианта
1
2
3
4
5
6
7
8
9
10
II
12
13
14
15
16
17
18
:о
20
21
22
23
24
Уравнриня
х — х «), см
-2Г- + 3
4 COS2 (л//3) + 2
— cos(.t^/3) + 3
4/ +4
2 sin (л//3)
ЗГ2 + 2
3/2-/+I
7 sin (л/2/6) + 3
-ЗД/+2)
— 4 cos (л//3)
— 4/2+1
5 sin2 (л//6)
5 cos (л/2/3)
-2/ —2
4 cos(n//3)
3/
7 sm2 (n.f/6) — 5
1 + 3сс*(д/-/3)
— 5P-4
2-3/-0/2
(ism (л/*,Г>) —2
7/' —3
3-3r- + t
— 4 «os (л//3)—1
T
движения
y = y{t), см
-5/
4 sin2 (я//3)
Sin (л/2/3) — 1
-4/(/+l)
— 3cos(-i//3) + 4
-4/
Ы2-Ы/3~2
2 — 7 cos (л/2/6)
3/ + 6
— 2 sin (л//3)—3
~3t
—5cos2(n//6) —3
—5 sin (л/2/3)
-2/U+D
— 3 sin [:it/i)
4P+1
—7 cos2 (Я//6)
3 sin {лР/3) + 3
г/
3 —"//2-3/2
(>СО8(Л/*/б)-ЬЗ
5.'
4 —5/^ + 5//3
—4 sin i.n//3)
а б л и ц а 21
'l. 0
1/2
1
1
2
1
1/2
1
1
2
1
1/2
1
1
2
1
1/2
1
1
I
0
1
1/4
1
1
77

Номер
варианта
25
26
27
28
29
30
Уравнения
х = х A) см
—&
8 C0S2 (л//6) + 2
—3 — 9 sin (л*а/6)
—4/2-1-1
5Р + 5//3-3
2 cos (л/2/3) — 2
Продолжение
движения
;/"=</ @, см
—2/2-4
—8sin2(n//6) — 7
—9 cos (л/з/6)+ 5
—3/
3/2 + / + 3
—2sm (л/3/3) + 3
табл. 21
t,. a
1
1
1
1
1
1
Это выражение есть уравнение параболы.
Для определения скорости точки находим проекции скорости
на оси координат:
vx = х = 4 см/с; vy = i) = 32/ см/с.
Модуль скорости точки
v = Уи*х + Щ. C)
Аналогично проекции ускорения точки
wx = x = 0; wu = y = 32 см/са.
Модуль ускорения точки
l = 32 см/са.
Координаты точки, а также ее скорость, ускорение и их проек-
проекции на координатные оси для заданного момента времени t=\/2 с
приведены в табл. 22.
Таблица 22
Координаты,
см
X
2
У
3
Скорость,
4
16
см/с
V
16,5
wx
0
Ускорение
32
w
32
cm/cj
31
7,94
Раднус
кривизны
см
р
34,3
Касательное ускорение находим путем дифференцирования модуля
скорости C):
dv
w<= It
dv *>x<
78

При 7=1/2 с
dv ==4IO+j6132_ j 2
dt 16,5 ~ ' *
Следовательно, модуль касательного ускорения
шх = 31 см/са.
Знак «+» при dv/dt показывает, что движение точки ускоренное
и, следовательно, направления wx и v совпадают.
Нормальное ускорение точки в данный момент времени
wn = Уш2 - wi = V 32* - 312 = 7,94 см/с2.
Радиус кривизны траектории в той точке, где при t=l/2c нахо-
находится точка М,
4 = 34,3 см.
Полученные значения wx, wn и р также приведены в табл. 22.
Пользуясь уравнением B), строим траекторию (рис. 72) и пока-
показываем на ней положение точки М в заданный момент времени.
Вектор v строим по составляющим vx и vy,
причем этот вектор должен быть направлен
по касательной к траектории точки. Вектор w
находим как по составляющим wx и wy, так \ ^ I] f vn
и по id, и эд„, чем контролируется правиль-
правильность вычислений.
Дополнение к заданию /(-/. Уравнения
движения точки на плоскости (табл. 21)
можно использовать и для задания движения
точки в пространстве, если дополнительно
к табл. 21 задать третье уравнение z = z(t),
которое приведено в табл. 23.
Пример выполнения задания. Исходные
данные (в см и с):
4 AJ , ^ , „ f1==o.
D)
У
6
[ 5
\ *
\ J
\ 2
\ 1
" V
V I
1 \1г
1
. I
I ,
1
t+\<
I....!
1 0 2 * S 8
I...1...I i iit i
50 5 10 15 ?0 2
Рис. 72
2см
Решение. Уравнения D) являются параметрическими уравне-
уравнениями траектории точки в пространстве. Исключая параметр / из
первого и второго уравнений этой системы, а также из второго и
третьего, находим:
ху = -16; E)
У = —2г. F)
Уравнение E) выражает в плоскости хОу равностороннюю гипер-
гиперболу, для которой оси координат служат асимптотами. В простран-
пространстве этому уравнению соответствует гиперболический цилиндр с обра-
образующими, параллельными оси Ог.
79

Таблица 1\
Номер
варианта
3
4
5
6
7
8
9
10
- г (/) см
3*
It
1,5*
4f-|-4
I
3/
2,5'
5'
t
Номер
нерпам га
и
12
14
14
15
16
17
18
19
20
г — г [t)m см
2^
3^
1,5^
2/ + 2
.«
1,5'
Ы
3,5<
е<
2^
Номер
смриа па
21
22
23
24
25
2G
27
28
29
30
4<
/
1,5^
Ъ
Ы
Ы
3,5<
4/
5^
1,5^
Уравнеяие F) выражает в плоскости уОг прямую, проходящую
через начало координат, а в пространстве — плоскость, содержащую
ось Ох.
Траектория точки представляет собой линию пересечения этих
двух поверхностей: гиперболического цилиндра и плоскости (рис. 73).
Проекции скорости точки на оси координат:
_ .
vx — х —
7г2- см/с;
>•„ = (/ = — 4 см/с;
с, = 2 = 2 см/с.
Модуль скорое™
o=F^ + o;-гV, = -у-^ F 4 + 5(Н-1L см/с.
80

Проекции ускорения точки
Q
wx = х = 3; wv = у = 0: гг>г = г = 0.
Модуль ускорения
w — V~w"K -\-wi-\- w\ = . , см/с2.
Координаты точки, ее скорость, ускорение и их проекции на оси
координат для заданного момента времени t = Q приведены в табл. 24.
Коорди наи.1, см
X
4
У
—4
2
2
Скорость, см/с
—4
—4
2
г)
6
8
Ускорение, см/сг
0
0
w
8
«Г
,,,3
¦[ а б
5,90
лица 24
Радиус
крипннны.
см
р
0,01
Модуль касательного ускорения
dv
di
do
где -df =
-4-8
= — 5,33 СМ/С2.
У 6
Знак «—» при dv/dt показывает, что движенне точки замедленное.
Касательное ускорение шх направлено в сторону, противоположную
скорости.
Нормальное ускорение
юп = Vw2-wi = |/~82 - 5.332 = &,96 см/с2.
Радиус кривизны
2б2/596 = 6,04 см.
Полученные значения wx, wn и р также приведены в табл. 24.
На рис. 73 показаны положение точки М в заданный момент
времени, а также ее скорость и ускорение, построенные по состав-
составляющим vx, vy, иг к шх, wu, хюг.
Вектор шт откладываем по касательной к траектории в сторону,
противоположную направлению скорости. Вектор wn определяется
как разность wn — w — wx.
Задание К-2. Составление уравнений диижспия
точки и определение ее скорости и ускорения
Для точки М заданного механизма составить уравнения движе-
движения, вычертить участок ее траектории и для момента времени / = /,
найти скорость точки, полное, касательное и нормальное ускорения,
а также радиус кривизны траектории в соответствующей точке.
81

Таблица 25
Номер
ваонанта
¦ ¦ирпиП Яи
(рис. 74—76)
1
2
3
4
5
6
7
8
Ж
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Размеры
1
15
—
54
40
60
—
10
60
~Ш
60
45
—
20
60
40
42
40
60
—
45
42
45
60
30
50
60
звеньев механизма, см
R
50
—
250
_
_
50
50
28
. .
23
45
—
г
—
30
30
15
__
50
—
35.
24
—
40
30
22
12
—
21
10
30
24
рад
2я/
Зя^
Я/
6я/
я/
„
5л/
Зя/
01
2л/
—
5nt
2я/
Зя/
Зл/
Ant
2я/
л/
—
—
л/
2л/
Зя/
—
Зя/
S ^= S (/) СМ
_
—
—
—
—
60 У 2 sin 2я/
—
—
40 sin nt
—
30 У 3 cos nt
—
—
40 sin Зя/
804in 2л/
.—.
45 sin я/
42 cos 2л/
45 ^2 sin я/
—
20 УЗ sin Зл/
—
100 cos 2n/
—
/« с
*i» ^
1/6
1/9
1/2
1/12
1/6
1/12
1/15
1/12
X&-
1/4
1/6
1/3
1/15
1/12
1/12
1/9
1/12
1/6
1/16
1/6
1/6
1/3
1/6
1/6
1/3
1/18
1/8
1/4
1/8
1/12
Схемы механизмов помещены на рис, 74—76, а необходимые для
расчета данные приведены в табл. 25.
Пример выполнения задания. Исходные данные: схема механизма
(рис. 77); ф = я/ рад; г = 20 см; #=100 см; /L=l/3 С
Решение. Из условия 0Р = МР имеем:
R<x = Лф; ос = лф/д = 0,2л/.
При /=1/3 с ф = 60°, а =12°.
Уравнения движения точки М (рис. 78):
х = (# + '¦) sin ее — т sin (ф + а);
у = (/? + /¦) cos а —/? — г cos (ф -J- а)
или окончательно
у = 20 F cos 0,2л/ - cos 1,2л/ - 5) см.
82

ор=мр
ОА=Г
ПР=МР
АВ=1
МВ=Уз1
— X
ОР=МР
10
—у
Рис 74

IX
—у
13
OP=AP
AM = 0/4
У ' ,}/ У /VjvV J^
15
--y
17 y\
AB
AM = til
AM='/!R
20
y\
<4iH м
Pm. 75

ц car- ¦•-
Рис 76

Эти уравнения являются параметрическими уравнениями траекто-
траектории точки—эпициклоиды*.
Проекции скорости точки на оси координат:
vx = х = 24л (cos 0,2я/ — cos 1,2nt) см/с;
0<, = </ = 24л(—sin 0,2л/+ sin 1,2л/) см/с.
Рис. 77
0,
Рис. 78
Модуль скорости
5 0 5 10 15 20 СИ
10 0 10 20 ЗС «0 см/с
50 0 50 100 150 200 СЛг/с2
Рис. 79
v = У vl + ь\ = 24л У 2 - 2 (cos O,2nt ¦ cos 1,2л/ -f sin 0,2я* • sin 1,2л/)
= 24л 1/2A-cos я/)
* В некоторых вариантах задания можно исключить параметр / из уравнений
движения и получить уравнение траектории в обычной координатной форме.
86

или окончательно
sin
см/с.
B)
или
Проекции ускорения точки на оси координат
(— sin 0,2л/+ 6 sin 1,2л/) см/с2;
(— cos 0,2л/+6 cos 1,2л/) см/с2.
Модуль ускорения
W = j^Wi + ш? =
= 4,8л2 /37-12 (sin 0,2л/-sin 1,2л/+ cos 0,2л/. cos 1,2я/)
да = 4,8л2 У 37 -12 cos я/ см/с2.
Так как в данном примере для модуля скорости точки получено
простое выражение, то модуль касательного ускорения находим не
по формуле
а непосредственным дифференцированием выражения B):
dt
или
wt = 24я2
см/с2.
Модули скорости и ускорения точки, их проекции на оси коор-
координат, а также касательное и нормальное ускорения, вычисленные
для заданного момента времени / = 1/3 с, приведены в табл. 26.
Таблица 26
Скорость, см/с
ох
50,4
Vy
56,0
V
75,4
Ускорение, см/с3
wx
260
Wy
41
w
263
wt
204
wn
166
Радиус
кривизны,
см
Р
34,3
Нормальное ускорение точки
ш„ - Vw2 - w\ = Vr263a - 2042 = 166 см/с2.
Радиус кривизны
2/ 7542/166 34,3 см.
Значения wn и р также приведены в табл. 26.
На чертеже (рис. 79) показан участок траектории точки М,
построенный по уравнениям A), а также ее скорость, ускорение
и все их составляющие. Таким образом, как и при выполнении зада-
задания К-1, осуществляется графическая проверка правильности вычис-
вычислений.
87

II. Кинематика твердого тела
ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ
ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Задание К-3. Определение скоростей
и ускорений точек твердого тела
при поступательном и вращательном движениях
По заданному уравнению прямолинейного поступательного дви-
движения груза 1 определить скорость, а также вращательное, центро-
центростремительное и полное ускорения точки М механизма в момент
времени, когда путь, пройденный грузом, равен s. Схемы механизмов
показаны на рис. 80—S2, а необходимые для расчета данные поме-
помешены в табл. 27.
Таблица 27
Номер
(рнс 80—82)
1
2
3
4
5
6
7
8 ¦
9
10
11
12
13
14
15
16
17
18
1!)
20
21
22
23
24
25
26
27
У8
2'.1
;;о
Радиусы, см
60
80
100
5Н
80
100
45
Й.~>
40
15
40
20
30
15
15
20
15
20
15
25
20
40
40
30
50
32
40
40
25
30
г,
45
60
45
—
60
35
10
оО
25
15
20
10
10
15
К)
15
10
15
10
20
30
15
20
16
18
20
20
15
я,
36
60
75
60
45
30
105
10
15
40
20
10
40
15
15
15
20
10
20
10
30
35
30
40
60
32
40
40
50
20
_
45
—
—
30
—
—
—
—
35
—
—
—
¦—
—
—
.—
—
10
15
20
10
18
15
25
—
Уравнение
движения
груза /
х = х (П
(X — В СМ,
t—B С)
10+100 /2
80 /2
18 + 70 /2
50 t2
8 + 40 t2
5 + 60 t2
7 + 90 /2
4 + 30 /2
3 4 80 P
70 t2
5 + 40 t-
2 + 50 /"
60 P
fi + 20 /
8 + 40 t1
3 + 40 t-
80 t2
4 + 20 /
5+80 t*
50 fi
4 + 90 t'1
10+40 t2
7-|-40 ^
SO P
2-| 50 t
5 + 60 P
6 + 30 t*
50 P
3 + 30 С
5+60 t2
S, M
0,5"
0,1
0,2
0,5
0,1
0,5
0,2
0,5
0,2
0,4
0,3
0,1
0,4
0,1
0,3
0,4
0,6
0,3
0,2
0,3
0,5
0,5
0,6
0,2
0,5
0,1
0,3
0,4
0,6
0,2
Пример выполнения задания. Исходные данные: схема механизма
(рис. 83); х = 2 + 70 I2 см; (/-вс); Я2 = 50 см; г.г = 30 см; Ra = 60 см;
г-л — 40 см; s = 40 см.

Рис. fiU

11
13
15
м
i
12
17
Рис 81
ад

2J
25
29
Рис. 82

Решение. Найдем момент времени т, когда путь s, пройденный
грузом, равен 40 см:
S = АГ(/_Х) — X(t-O) = 70 Т ,
откуда
|/770 У^0770 0,76 с.
Дифференцированием по времени уравнения движения найдем
скорость груза:
vt = | х | = 140 t см/с.
Угловая скорость звена 2
= 140 //30 = A4/3) t с1.
Р»с. 83
Рис 84
Угловые скорости колес 2 и 3, связанных гибкой передачей,
обратно пропорциональны радиусам этих колес, т. е.
ш2/со,., = R:i/R2,
отк уда
о»з - (Я2//?„) • со, = E0/G0) • A4/3) • t = C5/9) • f с 1.
Угловое ускорение
Скорость точки М
= const.
о = гя(л3 = 40 (оя
и направтепа перпендикулярно к радиусу в сторону вращения колеса.?.
92

Вращательное ускорение точки М
= 40 я3
и имеет одинаковое со скоростью направление, так как в рассматри-
рассматриваемом примере вращение колес ускоренное.
Центростремительное ускорение точки М v
ш" =/yojj = 40 <л1
и направлено по радиусу к центру колеса.
Полное ускорение
w = V(wbf-\-(waJ.
Значения этих величин для момента времени / = т сведены в табл. 28.
Таблица 28
2,94
-3,89
и, см/с
118
156
Ускорение, см/с'
346
W
379
Скорость и ускорение точки М показаны на рис. 84.
ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
Задание К-4. Определение скоростей точек
твердого тела при плоском движении
Найти для заданного положения механизма скорости точек А,
В, С и угловые скорости всех его звеньев, если известна угловая
скорость кривошипа ыОа-
Схемы механизмов показаны на рис. 85—87, а необходимые дан-
данные приведены в табл. 29.
Пример выполнения задания. Дано: 1) схема механизма в задан-
заданном положении (рис. 88); 2) исходные данные (табл. 30).
Решение. Скорость точки Л направлена перпендикулярно к криво-
кривошипу О А (рис. 89). Ее модуль
vA = w0A • ОА = 2 • 40 = 80 см/с.
Скорость центра В колеса направлена по горизонтали. Находим
для звена АВ мгновенный центр скорости Рлв, восставив перпенди-
перпендикуляры к скоростям точек Л и В.
Угловую скорость зиена АВ определяем по формуле
Как видно из рис. 89,
= А К /cos 30°; Л К = у'АВ*-АП*;
= OA- sin 30е = 40 • 0,5 = 20 см.
93

Таблица 29
Номер
варианта
(рис.
85—87)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
ОА
35
40
22
20
35
20
30
12
14
15
27
20
22
60
25
27
16
22
23
23
24
25
26
J7
28
12
55
25
16
16
i-
АВ
65
40
50
—
60
60
—
—
50
—
25
44
25
60
—
36
57
56
24
12
75
54
25
60
'азмеры. с
AD
„ . .
40
—
40
—
—
50
—
72
24
32
25
50
—
ВС
60
24
24
—
30
30
45
25
34
35
35
—
-
25
35
40
36
15
15
42
30
35
14
Г
15
11
15
_
¦
12
15
15
12
8
14
10
12
—
10
10
10
10
2
1,5
3
1
4
1,2
2
1,5
1
—
2,5
2
_
1,4
1,6
1,2
0,6
2,4
1,5
4
3
2
1
2,1
2,5
2,2
1,8
2,3
2
1,5
Дополните ль*
ные данные
()? = 30 см
ш7=1,5 с"»
OjS = 50 см
BD = BOt
оо = 80 см/с
оо= 100 см/с
со, = 3 с
О,С = 36 см
Примечание. Качение колес происходит без скольжения.
• В вариантах 5 и 16 задана также угловая скорость ац шестерни /;
задана скорость Vq центра О.
рариантвх 10 и 13
Таблица 30
Размеры, см
ОА
40
АВ
80
ВС
25
т
15
"од- с '
2
Следовательно,
См;
АРАВ = A K/cos 30° = 77,5/0,866 = 89,6 см;
= va/A Рав = 80/89,6 = 0,893 с \

S8
Of
.09

12
15
15
17
ы,
20
w?° Ф°~
%%
Рис 8G

22
23
28
—He
Рис. 87
4 а/р. Яблонского Л. А«
97

Скорость центра В колеса определяем как вращательную вокруг
мгновенного центра скоростей РАВ:
Так как
или
ВРАВ={ОА+АРАВ) sin 30°
ВРАВ= D0 + 89,6).0,5 = 64,8 см,
то скорость центра колеса
»в = <»ав ¦ ВРАВ = 0,893 • 64,8 = 57,9 см/с.
Мгновенный центр скоростей Р колеса находится в точке каса-
касания этого колеса с неподвижной плоскостью.
Рис. 88
Рис. 89
Угловая скорость колеса
о) =;
Так как
ВР = г=1Ь см, то со = 57,9/15 = 3,86 с.
Скорость точки С определим как вращательную скорость вокруг
мгновенного центра скоростей Р'.
vc = a-CP.
По теореме косинусов
СР = УВР2 + ВО - 2 • ВР ¦ ВС ¦ cos 120^
98

или
Следовательно, скорость точки С:
vc = со ¦ СР = 3,86 • 35,0 = 135 см/с.
Вектор vc направлен перпендикулярно к PC в сторону вращения
колеса.
Задание К-5. Определение скоростей
и ускорений точек твердого тела
при плоском движении
Найти для заданного положения механизма скорости и ускоре-
ускорения точек В и С. Схемы механизмов помещены на рис. 90 — 92,
а необходимые для расчета данные приведены в табл. 31.
Таблица 31
Номер
варианта
(рис
90—92)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
ОА
40
30
35
25
40
35
—
25
—
—
25
45
40
55
10
20
_
30
35
_
25
20
20
20
12
40
Размеры
г
15
15
50
15
15
15
20
30
15
.
15
15
—
, см
АВ
75
20
45
80
НО
30
55
—
—
—
—
10
20
60
60
60
35
70
—
—
50
35
—
АС
8
8
45
20
6
60
10
30
20
15
20
40
8
8
—
10
5
10
6
15
40
20
15
20
10
5
25
15
20
®ОА- с
2
3
4
1
1
5
—
1
—
—
2
3
1
2
—
2
1
,
3
4
2
1
2
,—,
1
4
5
toft с
1
—
.—
12
.—
_
2,5
.
1,2
—
—
2
2
_
8
1
0
10
—
—
2
—
—
4
0
1
5
—
6
0
8
10
3
2
0
—
i
б
10
VA.
Н •
СМ/С
50
.
—
40
20
10
20
—
—
80
10
5
—
60
_
,
—
W л ,
/1'
СМ/Са
_
100
,
,
—
20
10
0
20
—
50
,
15
10
—
.
—
30
—
Примечания, шрд а ?оА— угловая скорость и угловое ускорение кривошипа О А
при заданном положении механизма; а)] угловая скорость колеса / (постоянная)! Vj\ и шд —•
скорость н ускорение точки А. Качение колео происходит йез скольжения.
4*
99

Рис. 90
1СО

101
IG

21
А С
-e-
22
a),
'Of
23
/120'
25
26
27
28
29
A
¦¦C
18
3D
'2?
да?,
Рис. 92
102

Пример выполнения задания. Дано: 1) схема механизма в задан-
заданном положении (рис. 93); 2) исходные данные (табл. 32).
Таблица 32
Размеры, см
ОА
10
АВ
60
АС
20
ШОЛ> с 1
1,5
гОА< с 2
2
Решение. 1. Определение скоростей точек (рис. 94). Вычисляем
скорость пальца А кривошипа ОА при заданном положении меха-
механизма:
vA = олОА -ОА = 1,5-10= 15 см/с.
Скорость точки А перпендикулярна к кривошипу ОА. Скорость
ползуна В направлена по вертикали. Мгновенный центр скоростей
Рис, 93
Рис. 94
Яла шатуна АВ находится в точке пересечения перпендикуляров,
проведенных из точек А и В к их скоростям.
Угловая скорость звена А В
«да = vA/APAB = 15/F0 cos 30°) = 1/2 /3"= 0,29 сг1.
Скорости точек В и С:
• ВРАВ:, vc = шАВ • СРАВ,
10J

где
см;
= ]/02 + 302 — 2 • 40 ¦ 30-0,5 = 36,1 см.
Следовательно,
vB = 0,29 -30,0 --8,7 см/с; i?c = 0,29-36,1 =10,5 см/с.
Вектор vc направлен перпендикулярно к отрезку СРАВ в сто-
сторону, соответствующую направлению вращения звена ЛВ.
Для проверки определим скорость точки В другим способом.
Воспользуемся теоремой о равенстве проекции скоростей точек на
ось, проведенную через эти
точки.
Направим ось х из точ-
точки В вдоль шатуна ВА.
Имеем:
VA COS FА, X) =
— VLCOS(ViU X).
Или, как видно из рис. 94:
vA cos 60° = vR cos Ж.
Отсюда
Полезно убедиться, что
и найденная ранее ско-
Pllc- 95 рость точки С удовле-
удовлетворяет ьтой теореме.
2. Определение ускорений точек (рис. 95,. Ускорение точки А
складывается из вращательного и центростремительного ускорений:
wA = eQ 4 • ОА ^ 2 • 10 = 20 см/с2;
wa = ь*ол
= 22,5 см/с2.
Вектор t?'!i направлен от А к О. Вектор w\ перпендикулярен
к вектору wA и направлен в соответсгвян с направлением углового
ускорения t(jA.
Согласно теореме об ускорениях точек плосксл фигуры имеем:
или
Hi в — Wa + Wa + Шь
A)
104

Центростремительное ускорение точки В во вращательном движе-
движении шатуна А В вокруг полюса А:
wl\B = ш\в ¦ АВ = A/12) • 60 = 5,00 см/с2.
Вектор w'ab направлен от В к Л, а вращательное ускорение шЛв
перпендикулярно к нему.
Строим многоугольник ускорений. При этом воспользуемся тем,
что прямая, по которой направлено ускорение wB известна. Пол-
Ползун В движется по вертикальной прямой, вдоль которой направлено
и ускорение точки В. Отложим из точки В последовательно век-
векторы швл и w'\ составляющих ускорений полюса А и центростреми-
центростремительное ускорение wAb (параллельно звену ВА). Через конец век-
вектора w'ab проводим прямую, параллельную вращательному ускоре-
ускорению w'ab, т. е. перпендикулярно к АВ до пересечения ее прямой,
по которой направлено ускорение wB. Ускорение wn определяется
как замыкающий вектор многоугольника ускорений (рис. 95, а).
Проектируя векторное равенство A) на оси х и у, получаем:
wB cos 30°-== — тъАсъ'ъЬЪа + 1Ш\ cos30° + [?%. B)
wB cos 60° = wBA cos 30° -|- wA cos 60° — wAB. C)
Из уравнения B)
>'j| cos 30с' + ю^в — 20 • 0,5 + 22,5 . 0,866 + 5
= « 6,7cm/cj.
Для определения ускорения точки С найдем угловое ускорение
шатуна АВ.
Из уравнения C)
wAB = wA cos 30° + w* cos 60° - wB cos ?0° ^
= 20 • 0,866 + 22,5 -0,5-16,7 ¦ 0,5 = 20,2 см/с2.
Ho
wAB = eAB-AB, отсюда гАВ = wAB/AВ = 20,2/60 = 0,34 с 2.
Направление ускорения доля относительно полюса А определяет
направление углового ускорения еАВ. В данном случае оно противо-
противоположно (Dab-
Определяем ускорение4 точки С:
Вращательное и центростремительное ускорения точки С во вра-
вращательном движении шатуна А В вокруг полюса А:
w*AC = eAB- AC = 0,34 20 = 6,8 см/с2;
ш^с = ы*лв-ЛС = A/12)-20=1,7 см/с2.
Вектор ы>ас перпендикулярен к вектору Wac и направлен соот-
соответственно угловому ускорению е^д.
105

Ускорение точки С находим способом проекций:
wCx = w«AC + wlA cos 30° - ш» cos 60° =
= 1,7+ 22,5-0,866-20-0,5 =11,2 см/с2; |
WC.y = WA C0S 60° + WA C0S 30° -WAC =
= 22,5.0,5 + 20-0,866-6,8 = 21,8 см/с2;
wc = Vw'cx + why = Kl 1.22 + 21,82 = 24,5 см/са
(рис. 95, б).
\
Задание К-6. Определение скоростей
и ускорений точек многозвенного механизма
Приняв угловую скорость оH кривошипа ОгА постоянной и рав-
равной 2 с1 определить для заданного положения механизма:
1) скорости точек А, В, С, ... механизма и угловые скорости
всех его звеньев при помощи плана скоростей;
2) скорости этих же точек механизма и угловые скорости звеньев
при помощи мгновенных центров скоростей;
3) ускорения точек Л и В и угловое ускорение звена АВ;
4) положение мгновенного центра ускорений звена А В;
5) ускорение точки М, делящей звено АВ пополам.
Схемы механизмов показаны на рис. 96 — 99, а необходимые для
расчета данные приведены в табл. 33.
Пример выполнения задания. Дано: 1) схема механизма в задан-
заданном положении (рис. 100), 2) исходные данные (табл. 34).
Решение 1. Определение скоростей точек и угловых скоростей
звеньев механизма при помощи плана скоростей.
а) Определение скоростей точек. Строим схему меха-
механизма в выбранном масштабе (рис. 101). Вычисляем модуль скоро-
скорости пальца А кривошипа ОУА:
vA = (ц0А. OLA = 2 • 12 = 24 см/с.
Вектор vA перпендикулярен к 0гА и направлен в сторону вра-
вращения кривошипа.
Строим план скоростей. Из произвольно выбранного полюса про-
проводим луч Оа, изображающий в выбранном масштабе скорость точки А.
Для определения скорости точки В через полюс О проводим пря-
прямую, параллельную скорости ид, через точку а —прямую, перпенди-
перпендикулярную к АВ. Получаем точку Ь; отрезок Ob определяет ско-
скорость точки В. Измеряем длину луча Ob и, пользуясь масштабом
скоростей, находим ув=17,5 см/с.
Для определения скорости точки С делим отрезок ab плана ско-
скоростей в отношении
ac/cb = AC/CB.
Луч Ос изображает скорость точки С. Пользуясь масштабом ско-
скоростей, получаем
ус=17,5 см/с.
106

m
звень
a
Длн
О
К
ГГОЯН!
О
га
0,
е
о
с
***
к.
1ц
3
Q
и
it.
С?
о
с
о
ч
о
о
град
1анта
96—99)
вар
(рнс.
ОС
2
2!
о
ОС
-
СМ СМ —
-Ч1 СО С1-
1
1
1
1
ос ю со
се се см
СМ СП СП
ем се "Ч*
ос | 1 и-
С. см
см —
ГО 1 1 -»-
го —
см см
ос ел р- ос э; см см ю -
СМИ
] —
- <М СЕ 1С Ю С
¦з см см-
— ^f СМ -
1 см
ОС
см
1
00
\Г
-см см с
- Ю О 1С Ч
j Ю Ю CM tf
15
¦*¦ 11"
- р- р-
го
-ГО т
с t-
1СС1-
р-
с
С СМ 1С Р-
со см со —
" О С О —
J С?
-ч1 1 те 1/
¦J 1С
зс
5 •«¦ С и"
3 1Г
- р- У
^ L
3 С
3
Н ,—
ю
се со т
1 р- 1
1 1Г
о
1
1Г
1
1
СЛ СМ (М С
емюем го
00 СО О С
[Г
с
— оз о со се ^-
ю см ic се се -ч1
1 ОС \Г> СО
1 ^3
¦С 1С 1С О
см о го см
'ОС:
00 О -ч
¦ч
г см
1
г со го
ЮСМГОСО-Ч'ЮСО-Ч'СМ-
; о ос с cj се ю ее
-смсмссгогосссм —
1 О Ю О С С Ю Ю 'S
см 1 см см
СП | |
оеюоею
см см см со
- 1 ]
СМ
см с; см го
-ююсмюсо-*-
М с
гою
см см
см с
О"
— О
2
1
1
ю
СЕ
СМ
-Ю ч
i см се см
| СМ 1 Р- Ю 00
1 СМ 1 —' СМ
ос со ¦* те с
— см ю см -
м с
!•-
ю с
о
_
- см
с
t ас —
:р-р-
см
1
1
- с ос ч
- OOP- "Я
о
1
1
" С
!¦ -Ч
1
оос
го \г
ОО 1 1П
сеем 1 т
- С С ОС 1
с. смем см I
-1ОЮ Ю 1
1
1
СО
см
см
о?
ю
00
со
•3 1/
1
1
1
ю
тооююстэоэсмоооэ — осо-ч-о — ем
см — см — — -ч1 -ч1 ем се оо ю -ч- го см
ОС CD 1С СО СЕ 1С — р- ГО Ю О О Г~- С
с с с
осо <
см
см го
ИС1
N -
s с
т с
OCI
^со с
1
1
1
ОС
о
1
1
1
1 те
есм
М р- С
г
1
—
- го
- СО ОС ГО СЕ ГО —
¦ го ге см го —
1С СО СО СО С. С О
р-
С
юс се
ти-
1
I:
1?
DCj
-сеем
3 t-
-¦'
-ото
-lo-
o-
os' 0
э с
о г
а
: 1
о
ю
If
1 с:
1 -
о о
^¦се
5 С
п со с
1
1
ем с
ТО Tf
1
- р-
1
1
со ю
ПС
г
-см
DCO
1 1
1 1
- 1
СО СМ 1С 00 1^
го ее се ее —
о с
е р- с:
м -
— Г|
;СОСМСО — ОЮ(С
.ОЮООООООЮЮОООЮЮОЮЮЮОЮЮЮОЮО'Л
лемсоюооемюю —¦ ем -»з- ^r -<t -ч* -ч* — осе — см — -ч- — оосм
_^ — см см се см -— — — се — —¦ го см — см-—
X
—
~ч се
о t
7ЭО — СМСО"Ч"ЮСОР-ООСЛО
107

п
АЕ=АВ
T~-a- -I
Рис 96
103

FI
11
15
Рис. 97
109

17
02С=02д
П 02С-0гВ
Рис. 98

25
28
U,F = '/2 CD
AC = ВС
29
Рис. 99
111

грда
52
а
32
Расстояние
ft
4
С
39
, СМ
d
19
в
32
12
46
1
10 j
2Э
' ,"t; [' i зги."
1
0,0 | JC
32 Г),-!
1
!S
Ч
а б /
ОН
И
И Ц
FH
И
0,f.
20
По плану
'. коростей
При помсщм мгновенных
центров
скоростей
А
24
24
1
1
17,5 j
1 7,3 :
!
Си
г
17,5
17,5
->Р'1С ГЦ
0
17,5
17,4
точек, си
?
17,5
17,4
Т
h
1 7,0
17,4
а
б л и
G
14,8
14,6
ц а да
II
И,4
.и
Продолжая построение плана скоростей, находим скорости точек
D, E, F, G u H (табл. 35).
На чертеже механизма концы векторов скоростей точек прямо-
прямолинейного звена (например, А, В, С или D, E, F) находятся на
одной прямой.
б) Определение угловых скоростей звеньев меха-
механизма. Отрезок ab плана скоростей выражает вращательную ско-
скорость точки В вокруг точки Л:
ab = vAn = (лла- АВ,
отсюда угловая скорость звена АВ
хлАВ = аЬ/А5=19,5/46 = 0,424 с '.
Аналогично определяем угловые скорости звеньев .40, DE, FGH:
u)AD = ad/AD= 14,5/29 = 0,5 с;
мпр = de/DE = 0/DE = 0;
«»ган = fg/FG ¦= 6,8/25 = 0,272 с-1.
Угловую скорость ыгаи можно определить и следующим образом:
Угловая скорость звена 02D определяется по вращательной ско-
скорости точки D вокруг неподвижного центра 02
= 17,5/32 = 0,547 с.
Аналогично определяем угловые скорости звеньев ОЯБ, OtGi
(оОз? = у?/08? = 17,5/18 = 0,972 с1;
113

По плану скоростей
При помощи мгновенных цент-
центров скоростей
лв
0,424
0,421
Углопые скорости э
AD
0,500
0,505
DF.
0
0
O,D
0,547
0,544
Таб л и
веньев.
o,rs
0,972
0,967
FGfl
0,272
0,278
ца 36
O,G
0,740
0,730
Полученные угловые скорости звеньев механизма сведены втабл. 36.
2. Определение скоростей точек и угловых скоростей звеньев меха-
механизма при помощи мгновенных центров скоростей.
Рис. 102
а) Определен lie положения мгновенных центров
скоростей звеньев механизма. Строим механизм в выбран-
выбранном масштабе (рис. 102). Звенья ОХА, O2D, O3E, O4G вращаются
вокруг неподвижных центров О,, О2, О3, О4.
Мгновенный центр скоростей PAli звена АВ находится как точка
пересечения перпендикуляров, проведенных из точек А я В к их
П4

скоростям. Аналогично определяется положение мгновенных центров
скоростей РАп и PhQH- Мгновенный центр скоростей звена DE нахо-
находится в бесконечности.
б) Определение скоростей точек. Скорость точки А
vA = (o0-01A = 2\2 = 2i см/с.
Скорости точек звена А В пропорциональны расстояниям от точек
до мгновенного центра скоростей Р аи'-
vAlvB = РлвЛ/РАВВ; va/vc = РАВА/РАВС.
Расстояния от точек до мгновенного центра скоростей измеря-
измеряются на чертеже. Пользуясь масштабом длин, получаем:
РАВА = 57 см; Р„ДВ = 41 см; РАВС = 4\,5 см.
Определяем скорости точек В и С:
vB = vA- РАВВ/РАВА =24-41/57= 17,3 см/с;
vc = vA ¦ PabQPabA =24 • 41,5/57= 17,5 см/с.
Для определения скорости точки D воспользуемся пропорцией
A = 24 • 34,5/47,5- 17,4 см/с.
Так как мгновенный центр скоростей звена DE находится в беско-
бесконечности, то 1»я = iv= Уд = 17,4 см/с.
Для определения скоростей точек G и Н имеем следующие
пропорции:
vrjvQ =
vt./vH =
отсюда
Vq = vp-PfoHGIPfohH= 17,4-52,8/62,7= 14,6 см/с;
Vn = vF-PFQHHlPFaHF= 17,4-50,8/62,7= 14,1 см/с.
Полученные скорости приведены в табл. 35.
Одновременно с определением модулей скоростей точек находим
их направления, а также направления вращений звеньев механизма.
Например, по направлению скорости точки А и положению мгно-
мгновенного центра скоростей РАВ устанавливаем, что вращение звена
А В происходит по часовой стрелке. Поэтому скорость точки В при
данном положении механизма направлена вверх.
Аналогично определяем направления вращений остальных звеньев
и направления скоростей точек механизма (см. рис. 102).
в) Определение угловых скоростей звеньев меха-
механизма. Скорость любой точки звена равна произведению угловой
скорости этого звена на расстояние от точки до мгновенного центра
скоростей:
VA = ®АВ ¦ РавА = Шдп • PADA,
115

отсюда определяем угловые скорости звеньев АВ и AD
<OAi, = vA/PAnA = 24/57 = 0,421 с;
«М« = vA/PAr.A = 24/47,5 = 0,505 С.
Угловая скорость звена O2D определяется по скорости точки D
= 17,4/32 = 0,544 с.
Угловая скорость звена DE при данном положении механизма
.равна нулю, так как мгновенный центр скоростей звена в этом слу-
случае находится в бесконечности:
О1/-,Я =" 0.
Аналогично определяем угловые скорости сстальных звеньев
механизма:
шозя = vE/0,i: = 17,4/18 = 0,967 С,
ч>гсн = Vr/Phoif = 17,4/62,7 -., 0,278 с ];
соо4« = vo/OiG= 14,6/20 = 0,730 с К
Полученные угловые скорости приведены в табл. 36.
3. Определение ускорений точек А, В, D* и угловых ускорений
звеньев АВ и BD.
а) Определение wA, wn и eAR (рис. 103). Определяем ускорение
точки В при помощи теоремы об ускорениях точек плоской фигуры:
Так как кривошип ОХА вращается равномерно, то ускорение
течки А направлено к центру Ол и равно:
wA -= w\ = О,Л сой -^12 22 = 48 см, с2.
Центростремительное ускорение точьи В во вращательном дви-
движении шатуна АВ вокруг полю:а А направлено от точки В к точие
А и равно:
= 46• 0,42 = 7,36 см/с2.
Откладываем от точки В в соответствующем масштабе ускорение
полюса w,\. Из конца вектора wA строим вектор w'\b, проводя его
параллельно В А. Через конец вектора w'ah проводим прямую,
перпепдикупярную ВА, т. е. параллельную вращательному ускоре-
ускорению Wah- Точка пересечения этой прямой с прямой, по которой
направлен вектор ускорения ползуна В, определяет концы векторов
1Юц И т\в-
* \Члоьне чядания предусматривает определение ускорений точек А, В и
углового ускорения шека АВ Однако а примере определяются также ускорение
точки /; и у г повое ускорение ieona A.D в соответствии с двумя случаями, встре-
чаюилмммся в задичал laxoro типа.
116

Измерением t;a чертеже получаем
Wh -- 39 см/с2; w"no — 30 см/с2.
Так как ©лв = А В ¦ еАП, то углоьое ускорение звена А В
= 30/46 = 0,652 с.
б) Определение ого и г4в (рис. 104). Точка О принадлежит
двум звеньям —ЛО и O2D. Взяв на полюс точку А, имеем
Ускорение точки А найдено выше:
wA = 48 см/с2.
Центростремительное ускорение точки D во вращательном дви-
движении звена AD вокруг полюса А направлено от точки D к точке
А и равно:
wAD = AD ¦ шЛо = 28,5 • 0,52 = 7,1 см/с*.
Откладываем из точки D в соответствующем масштабе ускоре-
ускорение полюса зуд. Из конца вектора шл строим векюр ш%, проведя
В
L 7^=
гд.,'-* 20 ° г.°
Рис. 10!
Рис 104
его параллельно DA. Через конец вектора wAd проводим прямую
JK перпендикулярно к DA, т, е. параллельно вращательному уско-
ускорению wad. Однако определить ускорение wD этим построением
невозможно, так как его направление неизвестно.
Чтобы найти ускорение точки D, необходимо выполнить второе
построение, рассматривая эту точку как принадлежащую звену O2D.
117

В этом случае
Центростремительное ускорение точки D
wl = O2D ¦ (йЬ,о = 32 • 0,52 = 8 см/с2.
Откладываем от точки D вектор w'b, направив его к центру 02.
Через конец вектора а»о проводим пря.чую LN перпендикулярно
к O2D, т. е. параллельно вращательному ускорению w'd- Точка
пересечения этой прямой с
JK определяет
ров Wr>, ^>лп и
Измерением
получаем
шо = 42
шлд = 3(
Так как
концы векто-
wBD.
на чертеже
см/с2,
) см/с2.
то угловое ускорение звена AD
Рис. 105
= 30/29=1,03 с-2.
4. Определение положения
мгновенного центра ускоре-
ускорений эвена АВ (рис. 105). Примем точку А за полюс. Тогда
ускорение точки В
wB = wA-{-wAB.
Строим параллелограмм ускорений при точке В по диагонали
Эд/i и стороне wA. Сторона параллелограмма wAD выражает ускоре-
ускорение точки В во вращении АВ вокруг полюса А. Ускорение wAB
составляет с отрезком А В угол а, который можно измерить на чертеже.
Направление вектора w\b относительно полюса А позволяет
определить направление елв, в данном случае соответствующее направ-
направлению вращения часовой стрелки. Отложив угол а от векторов wA
и w1} в этом направлении и проводя две полупрямые, найдем точку
их пересечения фд/{ —мгновенный центр ускорений звена АВ.
5. Определение ускорения точки М. Найдем ускорение точки М
при помощи мгновенного центра ускорений.
Ускорения точек плоской фигуры пропорциональны их рассто-
расстояниям до мгновенного центра ускорений. Следовательно,
wM = wA ¦ MQAIi/AQAB = 48 • 67,5/77 = 42,1 см/с2.
Расстояния MQAb и AQAB определены путем измерения на чертеже.
Ускорение ши (рис. 105) составляет с прямой MQAB угол а; направ-
направление этого вектора соответствует угловому ускорению tAB.
118

СФЕРИЧЕСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
Задание К-7. Определение кинематических
характеристик движения твердого тела
и его точек по уравнениям Эйлера
Заданы уравнения сферического движения твердого тела: ij) = i{
6 = б(/) и Ф = Ф(/), где ф, б и ф —углы Эйлера (рис. 106).
Определить для момента времени t = tt угловую скорость и угло-
угловое ускорение тела, а также скорость и ускорение точки М, коорди-
координаты которой в подвижной си-
системе, жестко связанной с те-
телом I, г], ?.
Необходимые данные приве-
приведены в табл. 37.
Пример выполнения задания
Исходные данные: г|з = 2t2 -\~
+ 3/ рад, 0 = л/6 рад, гр = 24/
рад, | = 3 см, т] = 2 см, t, = 5 см,
*, = 1 с.
Решение. 1. Определение
угловой скорости тела. Проек-
Проекции угловой скорости тела на
подвижные оси координат опреде-
определяются по следующим формулам:
• «
с>1 = i|3sin 8 sin ф + 6 cosф;
(on= ij) sin б cos ф — б sin ф;
cot=ibcosl
Рис 106
Имея в виду, что в рассматриваемом случае
9 = 0; ф = 24; sin 6 = sin (л/6) =0,5;
cos б = cos (я/6) = 0,866,
находим
0,5 sin 24/;
шл = D1 + 3H,5 cos 24/;
шс = D/ + 3H,866 + 24.
Проекции угловой скорости на неподвижные оси координат:
«b. = q>sini|7Sin в + 9 cosi|>;
ыу = — ф cos iJj sin б + б sin i|)j
шг = ф cos б + tJj;
(I)
119

Таблица 37
Номер
вариинга
1
2
3
4
5
Ь
7
8
9
10
11
12
13
14
15
К)
17
18
19
20
21
22
23
24
25
2<>
27
28
29
30
Уравнения движения тела
ф = ф С), Рад
3/2+ G/
2/
- 4/
2/2 f 3/
4/2
3/
4/а - 2/
/2-И/
-3/2 + 2/
Ь/
- 2/
2/? —4/
3/-Н 2/
— 3/
— 4/2 + 3/
2/
-2/2 + 5/
4/2 + 3/
/^-2/
4/
-5/
— ?/¦> — 2/
3/-> — 2/
2/
— /
3/
-3/2 + 4/
— 5/
/
- 3/
0 — 0 ((), рад
л/3
(л/6) ып 2/
(л/4) cos 3/
л/6
-л/4
(л/3) cos4/
л/4
я/а
л/6
(л/3) cos 2/
(л/4) sin 3/
- л/4
-л/3
(л/6) sin 8/
л/4
UL/3) COS 6/
л/5
л/9
— л/6
(л/5) cos 3/
(л/4) sin 6/
— л/Ь
л/4
— (я/5) sin 3/
(я/9) cos 8/
(л/3) sm It
— л/9
- (л/3) sin 3/
(л/4) cos 6/
(л/6) cos 4/
ф = ФС), рад
4/
25/
15/
-2/
20/
6/
-20/
18/
30/
10/
- 12/
15/
24/
- 30/
1W
3/
5/
25.'
--At
18/
Ylt
•It
— r>t
- 30/
18/
10/
5/
8/
9/
-- 15/
Коорднна
точки М
2
3
4
—2
3
2
Ь
7
. 4
5
4
—Ь
3
10
9
С
1
7
В
—3
8
4
— 5
10
7
9
8
4
7
1)
it
5
1
з
4
2
3
2
4
5
3
—2
4
10
4
5
8
3
5
4
2
6
— 1
7
8
4
1
9
—2
6
8
гы
см
к
4
2
5
4
—3
2
3
1
3
3
4
2
5
3
5
10
-2
4
3
1
to
3
4
—b
5
3
6
— 2
10
5
1
2
1
3
2
1
0,5
1
2
0,5
2
1
0,5
I
2
1
1
0,5
2
2
1
4
3
1
2
1
2
2
3
1
или в данном случае
(-24-0,5 sin B/2-ЬЗ/)
rtv = —24 0,5 cos
i, = 24
Для определения угловой скорости тела при
тельно вычисляем
B)
----1 с предвари-
sin 24/ -sin 24 = sin (8л- 1,133) = sin (— 1,133) = — 0,906;
cos 24/ = cos 24 = cos (—1,133) = 0,424,
sm Bt2 + 3t) = sm 5 = sin Bл - 1,283) = sin (—1,283) = — 0,959;
cos B/3 + 30 = cos 5 = соь (—1,283) = 0,284.
120

Тогда согласно A) и B)
<^ = 7-0,5(— 0,906) = — 3,17 с-1;
wn = 7-0,5-0,424 =1,48 с1;
cot = 7-0,866 + 24 = 30,1 с J;
<¦>, = —24-0,5-0,9&9-—11,5 с1;
со,, = —24-0,5-0,284=- —3,41 с1;
ш, = 24-0,866 + 7-27,8 с >.
Модуль угловой скорости
(о = У^+Щ+Й = Y(- 3,17J + М85 +Ж11 = /918" = 30,3 с
или
со = |Ло1 + а>; + <й; = /Pi 1,5J + (- ЗТ4УJ"+Т7^ = /ЭТУ = 30,3 с1.
Модуль угловой скорости тела можно определить и, минуя вычис-
вычисление ее проекций на оси координат, по формуле
(о = V^ + G2 + ф2 + 2-фф cos 8.
В данном случае
о) = |/72 + 242 + 2 • 7 • 24 • 0,866 = /916 = 30,3 с1.
Направление угловой скорости, а следовательно, и мгновенной
оси вращения тела можно определить направляющими косинусами.
В подвижной системе координат
cos (со, I) = б^/со = — 3,17/30,3 = — 0,105;
cos (со, т)) = cot1/o) = 1,48/30,3 = 0,049;
cos (w, I) = со&/со = 30,1 /30,3 = 0,993.
В неподвижной системе
cos (со, х) = о>,До = —11 ,с/30,3 = — 0,380;
cos (со, у) = со1;/со = — 3,41 /30,3 = —0,113;
cos (со, 2) = co^/w = 27,8/30,3 = 0,917.
2. Определение углового ускорения тела. Проекции углевого уско-
ускорения тела на подвижные оси координат определяются следующим
обрачом:
^ = cot; et) = ton; ft = d)t.
Ь соответствии с A)
г,. = 2 sin 24/ + B( + 1,5) 24 cos 24/;
ел = 2 cos 24/ - Bt + 1,5) 24 sin 24/;
ч = 4-0,866 = 3,4<j.
121

Проекции углового ускорения на неподвижные оси координат:
В соответствии с B):
; е„ = 12 D* + 3) sin Bf« + 30; гг = 4.
При /-1с
г% = 2 (— 0,906) = 3,5 • 24 • 0,424 = 33,8 с;
еп = 2 • 0,424 - 3,5 • 24 ¦ (— 0,906) = 76,9 с;
еЕ = 3,46 с-2;
ех= 12-7-0,284 = 23,9 с;
е„ = 12 • 7 (— 0,959) = — 80,5 с;
ег = 4 с-2.
Модуль углового ускорения
е = У е| + Ц + е\ = /33,82 + 76,92 + 3,462 = 1/7068 = 84,1 с
или
е = /ei + ej + ej = К23,92 + (— 80,5J + 42 = j/7067 = 84,1 с~а.
Направление углового ускорения определяется направляющими
косинусами.
В подвижной системе координат
COS (в, I) = е^/е = 33,8/84,1 = 0,402;
cos (Г, T)) = etl/e = 76,9/84,1 =0,914;
cos(e, Q=es/e = 3,46/84,1=0,041.
В неподвижной системе
cos («Г, *) = ех/к = 23,9/84,1 = 0,284;
Cos (е, у) = е^/е = — 80,5/84,1 = — 0,957;
cos(e, z) = ег/е = 4/84,1 =0,048.
3. Определение скорости точки М (|, r|, Q. Проекции скорости
точки на подвижные оси координат определяются по формулам:
Для момента времени /==1 с имеем:
^=1,48.5 — 30,1-2 = — 52,8 см/с;
i»n=.30,1.3 —(— 3,17).5=106,2 см/с;
t>; = (— 3,17J-1,48.3 = —10,7 см/с.
122

Модуль скорости точки
v = Vui + uii+vi = У (- 52,87+ Ю6,22 + (- 10,7J -
= КНГ8О=119 см/с.
Направляющие косинусы:
cos (v, с) = v^v = — 52,8/119 = — 0,444;
cos (у, I-)) = ип/и = 106,2/119 = 0,892;
cos (v, 0 = v-Jv = — 10,7/119 = — 0,090.
4. Определение ускорения точки М (?, ц, ?). Проекции ускорения
точки на подвижные оси координат определяются формулами:
В момент времени t — 1 с
Ш| = 76,9-5-3,4б-2+(—3,17) (—3,17-3+1,48 .2 + 30,1-5)—
-917-3 = —2829 см/с2;
а»л = 3,46-3-33,8-5+1,48-144-917-2 = — 1780 см/с2;
шг = 33,8-2-76,9-3 + 30,Ы44-917-5 = —414 см/с2.
Модуль ускорения точки
i = V (— 2829J + (— 1780J + (— 414J--=
= 100 КП34 = 3367 см/с2.
Направляющие косинусы
cos (ш, |) = ш^ш = — 2829/3367 = — 0,841;
cos (w, Ti) = a»n/tti = — 1780/3367 = — 0,529;
cos (ш, 9 = а»с/ш = —414/3367 = —0,123.
Задание К-8. Определение скоростей
и ускорении точек твердого тела, катящегося
без скольжения по подвижной поверхности
и имеющего неподвижную точку
Тело А катится без скольжения по поверхности неподвижного
тела В, имея неподвижную точку О. Определить угловую скорость
и угловое ускорение тела А, а также скорость и ускорение точки М
при заданном положении тела А, если его ось О? вращается с посто-
постоянной угловой скоростью о)х вокруг неподвижной оси Ог.
Схемы показаны на рис. 107—109, а необходимые для расчета
данные приведены в табл. 38.
123

#//jjws...
y////////W////////'W/y//''//'v'/'/,Y/
Рис 107
124

12
1ч-
¦<¦
15
17
t-
f7777777777777.
в
20
Рис 108
125

21
22
25
29
Рис. 109
12в

Номер
варианта
(рис. 107—109)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
ом0.
см
30
4О
50
40
40
70
60
40
50
20
30
40
20
30
40
а>1,
С
2.3
3,0
1,2
2.0
0,8
4,0
1,5
2,1
3,2
1,3
0,9
2,2
3,8
1,4
0,7
мом,
см
16
5
10
10
30
—
20
10
10
20
10
10
15
Номер
варианта
(рис. 107—109)
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
см
45
50
30
50
30
40
30
40
60
40
40
30
45
40
50
Таб.
с~'
2,4
3,5
1,0
2,7
3,3
4,0
1.6
2,0
3,5
1,6
2,2
4,1
3,0
1,4
2,9
и и ц а 38
мом.
см
20
10
10
20
10
25
5
5
10
15
15
10
5
15
15
Пример выполнения задания. Тела Л и В представляют собой
прямые круглые конусы (рис. 110).
Дано: а = 60°; 0 = 90°; ОМ0 = / = 30 см; а>г = 1,2 с~\ MQM = 10 см.
Решение. 1. Определение угловой скорости тела. Конус А
совершает сферическое движение. Мгновенная ось вращения OQ соб-
Рис. ПО
Рис. 111
падает с общей образующей конусов (рис. 111). Скорость уточки С
является вращательной скоростью вокруг мгновенной оси. Следова-
Следовательно, угловая скорость конуса
(о =
127

С другой стороны, скорость точки С, описывающей окружность
радиусом CKL, можно определить но формуле
vc — С/С,. о>!.
По ряс. 111
CKt = / • cos 30° • sin 75° = 30 • 0,866 • 0.9G6 = 25,1 см.
Поэтому
«с = 25,1- 1,2 = 30,1 см/с.
Так как
CK = l- sin 30° • sin 60° = 30 • 0,5 • 0,866 = 13,0 см,
то
@ = 30,1/13 = 2,32 с-1.
Направление <м определяется направлением vc (рис. 111).
Угловую скорость конуса А можно найти также путем сложения
вращений вокруг пересекающихся осей — построением параллелограмма
угловых скоростей Срис. 112).
Здесь о>2 —угловая скорость конуса А во вращении относительно
собственной оси О?.
По теореме синусов
to/sin 75° = о»!/sin 30°,
отк уда
<и = о»! • sin 75°/sin 30° = 1,2 • 0,966/0,5 = 2,32 с1.
2. Определение углового ускорения тела. Угловое ускорение
конуса А геометрически равно скорости и конца вектора ш, кото-
который описывает окружность радиусом (о-sin 45° вокруг оси Ог
(рис. 113).
и ¦= ш • sin 45 • <ot = 2,32 • 0,707. 1,2 = 1,97 с;
в = и=1.97 сЛ
128

Вектор е приложен в точке О и направлен перпендикулярно
к плоскости zO'Q. Следовательно, ось углового ускорения ОЕ совпа-
совпадает с осью Оу.
3. Определение скорости точки тега. Скорость точки М опреде-
определяем как вращательную скорость вокруг мгновенно.! оси:
v „ --= МКг ¦ со = MD cos 30° ¦ со;
MD = 2/ ¦ sin 30° - М0М =-2-30-0,5— 10 = 20 см;
им = 20 • 0,866 ¦ 2,32 - 40,2 см/с.
Вектор vM параллелен вектору vc и имеет одинаковое с ш;м
направление (см. рис. 111).
4. Определение ускорения
точки тела. Ускорение точки
М находим как геометрическую
сумму осестремителыюго и вра-
щательного ускорений:
Осестремителыюе ускорение
направлено по перпендикуляру
к мгновенной оси вращения
(рис. И4)
= 20-0,866-2,322 = 93,3 см/с2.
Р,;с Ц4
Вращательное ускорение направлено перпендикулярно к О1Л
в плоскости zO'C,, как показано на рнс. 114,
w\, = ОМ ¦ е;
ОМ = VI- + (М0МJ ~ 2/ ¦ М0М ¦ cos 603 =
= 1^900 + 100 - 2 • 30 ¦ 10 • 0,5'= 26,5 см;
w*M = 26,5 • 1,97 = 52,2 см/с2.
Обе составляющие расположены в плоскости zO^,(zOx). Величину
ву.ц найдем как диагональ параллелограмма, построенного на этих
составляющих:
wM - у (w°jJ + (ш»,)- - 2к/« ¦ u»f cos у;
cos v = cos $: A'.,0M =
/—AID- sir, 301
од-;
30 -20 0,5
26.5
-0,75;
wM = V 93.33 + 52,22 - 2 • 93,3 ¦ 52,2 ¦ 0,75 = \ 4125 = 64,2 c\s/c2.
5 r [) яз-^т'Слого л л. jog

III. Сложное движение
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
Задание К-9. Определение абсолютной скорости
и абсолютного ускорения точки
в случае поступательного переносного движения
По заданным уравнениям относительного движения точки М и
переносного движения тела D для момента времени t = tx определить
абсолютную скорость и абсолютное ускорение точки М.
Схемы механизмов показаны на рис. 115—117, а необходимые
для расчета данные приведены в табл. 39.
Пример выполнения задания. Дано: схема механизма (рис. 118):
О,/= 02В = 20 см; Я = 16см; ф = E/48) nl* рад; sr-= AM = лР см;
tx = 2 с.
Решение. Найдем положение тела D и точки М в заданный
момент времени. Положение тела D определяется углом ф. При t = 2 с
Ф = E/48)л 2а = E/6)лрад.
Положение точки М на теле D можно определить углом
a = sr/R.
При t = 2 с
а = л • 22/16 = л/4 рад.
Тело D и точка М в заданный момент времени показаны на рис. 119.
Абсолютную скорость точки М определяем как геометрическую сумму
относительной и переносной скоростей:
Модуль относительной скорости точки М
vr = \vr\.
Здесь vr — проекция относительной скорости на касательную
к траектории относительного движения
vr = dsrldt = 2л/.
При / = 2с
vr = 2л • 2 = 4л = 12,6 см/с.
Следовательно,
vr= 12,6 см/с.
Положительный знак vr показывает, что относительное движение
точки происходит в направлении положительного отсчета sr.
Вектор относительной скорости показан на рис. 119.
Переносную скорость определяем, учитывая, что
где со —модуль угловой скорости звена OLA.
130

у//// у//////////'///////////;
-X
Y///////////////////////////7////////
0,^77777,
у///////////////////////////
Рис. 115
131

11
X
12
13
'///¦¦"/У,. У' ///У// /'//¦>//'''•//,
"i у//,//,.
18
Рис 116
132

21
22
'/г V ^
/Л '/.¦¦//уЯ1//// \
y//////V///yyyyyy7y//y///y7//y///y///
X
25
м
26
V/////.
27
Ml
28
л ,.
0,\
х
29
л
/
1 (—
\
%
/
в
i -
I
30
hi-
Рис 117
133

Таблица 39
Номер
варианта
(рис.
115—117)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
xe = fi @. см
/3 + 4/
60/2
—
2/+0,2/з
7*+4*з
20[l + sin(n//3)]
20*2+ Ш
—
250/2
— 8/+3/2
—
4(/ + 4/2)
20 [cos (я^/8)+1]
10/2-0,6/з
—
—
—
20/2+15/
25 П + sin (я//3)]
—
10 + 3 sin (л//2)
—
20[1+ап(л//2)]
24/S+7/
—
3/ + 0,27/з
18/2+2/
50/2
50[l-cos(n</2)]
ф = U @. Рад
—
—
—
1,5л/2
8.1/3/3
—
4п<*/27
—
—
л/г/8
л/2/24
2л/2/3
—
2л<2/з
—
5л*з/б
—
л/2/12
—
—
Уравнение относительного движения
точки М
OM = sr==f, A), см
4л/а
—
2^ + 3/
—
20лР
л B/»+3/)
—
9^+5/
16^2-2/+2
—
4 sin (л//3)
2^з
Юл sin (л//6)
5л^
2л<2
5яР/4
3/^+5/
4/з + Э/
—
—
1.5/ + 10*3
—
6.1/S
—
Бл/з/З
/з+2/
—
—
12л<2
тела К
<Pr = f* If), рад
0,036л/з
—
л/з/12
—
—
л/з/3
—
Зл/2
—
—
—
—
—
—
—
—
(л/3) cos Bл/)
2л/2/3
—
0,24л/2
—
0,36л/2
—
—
0,15л/2
Eл/6) sin (л//12)
5л/3/48
—
iu с
2
5/3
2
2
1/2
1
1
1/3
1/2
5/3
2
3/2
1
2
3
2
9
1/2
1/6
1
1/2
5/3
1
5/6
2
2
10/3
2
2
5/6
Л, см
48
80
15
20
30
30
20
25
30
60
—
25
30
24
54
30
20
20
15
40
20
30
18
50
40
35
15
20
75
25
Примечание
010 = 02Л = 40 СМ
О1О = О2А = 20см
Примечание. В вариантах
ствует положительному значению s ,
I, 5, fi, 13—16, 23, 25, 30
на схемах 14 и 30 ОМ
ОМ — щга окружности, для каждого варианта положение точки М на схеме соответ-
д>га, соответствующая меньшему центральному

Обозначая и> алгебраическую величину угловой скорости, имеем:
ш = с(ф/Л = E/16)-г2 с1.
При t = 2 с
w = E/4)-я с-1.
Так как а» = | а» [, то
о) = E/4)-я с-1.
Положительный знак у величины со показывает, что вращение
звена QXA происходит в направлении возрастания угла ф.
Модуль переносной скорости
ve = vA = 20- E/4) ¦ л = 25л = 78,5 см/с.
Вектор ve направлен перпендикулярно к звену OLA в сторону
его вращения.
Рис. 119
Рис. 120
Модуль абсолютной скорости точки М найдем способом проек-
проекций. Как следует из рис. 119,
vx = vr cos 45° - ve cos 30°; vy = vr cos 45° + ve cos 60°.
Следовательно,
vx = — 59,1 см/с; vy = 48,2 см/с; v = Vvx + v-y = 76,3 см/с.
Абсолютное ускорение точки при поступательном переносном
движении равно геометрической сумме относительного и переносного
ускорений:
или в развернутом виде
W = Wrx + Wrn -\- W"
135

/•Модуль относительного касательного ускорения
ы'гх —- ¦ wrz!; ш'Лт = d5r/d/ ¦= dh,/dt2.
В рассматриваемом случае
ю,т ¦= 2л --= 6,23 см/с-; wrz =¦ 6,28 см/с2.
Положительный знак у величины wrx покалывает, что вектор wrx
направлен в сторону гголожнгелыюго отсчета s., т. е. так' же, как у,-
(относительное движение--ускоренное) (рис. 120).
Относительное нормальное ускорение
wrn=.--v-r/R = 1Бл2/1Г) .-.- л2 =9,87 cv/c2.
Вектор wrn направлен по радиусу к центру кр:и'нзпы траектории
относительного движения точки М.
Переносное вращательное ускорение
шк-=юпл; w\=OxA-z,
где е —модуль углового ускорения зпена ОХА
Здесь ё = —^ — алгебраическая величина углового ускорения.
В рассматриваемом случае
к - E/8) • nt = E/4) • я = 3,93 с-2.
Совпадения знаков у величин к и oi показывает, что вращение
тела D ускоренное
е ¦= 3,93 с 2; ш" -= 20 • 3,93 ¦--. 79 см/с2.
Направление ^"соответствует направлению jjy"i (см. рис. 120). Пере-
Переносное центростремительное ускорение
w" =-- z:'\ = ОИ • od2 --- 20 • B3/16) • л2 --= 31,2Гш2 ----- 308 см/с2.
Вектор w'a направлен от Л к О1? а ш* имеет одинаковое с ним
направление.
Модуль абсолютного ускорения находим способом проекций:
ws - (ю„ - w,a) cos 45е - w* cos 30е - aCl cos 60°;
ш„ - tort -\- wrn) cos 45° -1- w" cos 60" - ^ц соь 30°
или после вычислений
шл------225 см/с2, аи!; = —21Г. см/с2,
ш = ]/ш.Н-ш^= 312 см/с2.
136

Результаты расчета сведены в табл. 40.
Таблица 40
<Р, Рад
5л/0
а, рад
л/4
ш, с •
5я/4
78,5
Скорость, tn,
"V
12,6
-50,1
с
48,2
в
70,3
Е, С"!
5л/4
е
308
к."
с
79
Ускорение, см
гп
10
ш
6
с2
ш.
-225
ы
-216
312
Задание К-10. Определение абсолютной скорости
и абсолютного ускорения точки в случае
вращательного переносного движения
По заданным уравнениям относительного движения точки М и
переносною движения тела D определить для момента времени t — tx
абсолютную скорость и абсолютное ускорение точки М.
Схемы механизмов показаны на рис. 121 —123, а необходимые
для расчета данные приведены в табл. 41.
Пример выполнения задания. Дано схема механизма (рис. 124)
Фс = 0,9/2-9^ рад; sr = ОМ = 16 - 8 cos 3rit см; /1 = 2/9 с.
Решение. Будем считать, что в расчетный момент времени
плоскость чертежа (рис. 125) совпадает с плоскостью треугольника D.
Положение точки М на теле D определяется расстоянием sr=0M.
При /=-2/9 с
sr--- 16 - 8 cos (Зл • 2/9) = 16 + 4 •=. 20,0 см.
Абсолютную скорость точки М найдем как геометрическую сумму
относительной и переносной скоростей
Модуль относительной скорости
где
vr — dsjdt — 24л sin Зл/.
При /-2/9 с
iv =- 24л ¦ |/з"/2 = 65,2 см/с; tv "= 65,2 см/с.
Положительный знак у величины vr иоказывгег, что вектор vr
направлен в сторону возрастания sr.
Мсд>ль переносной скорости
137

м
—
п
1
W
О М
8
Уе
'М
10
Рис 121
138

В
*G
12
м
13
-е
У>е
15
16
17 т
19
20
Рис. 122
139

21
22
м
23
25
0
D
M
м
3Q
Рис. 123

T .! С - i ц а 41
Ho^ep
варилигл
(р:-с
121-12"))
1
2
3
4
5
6
7
8
9
Го
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
2!)
30
Ур г псптс1 л11ижст:пя
- ( ли D
Ф /1 (»'/,* ряд
10 - V-
0,4/--W
It ¦ 0,5/-
0,с'-
3/ 0,5/3
0,75' ' 1,5/-
0,5/-
(•¦- Ы
4/-i l,t^
\,1t-~- /2
11- 0,5/
5/ At-
8/2 -3/
At -IP
0,2/:i + /
/ -0,5/2
0,5/J
6/- /2
/ + 3/2
G/ + /2
2/ -4/2
4/— 0,2/2
2/ —0,25/2
2/ -0,3/2
10/- 0,1/1!
—2л/-
/-0,5/3
2/1 5/
0.6/-1
2Z-- 3/
Ур^иненч.1 относительного
ти'жр.пя точим At
18 sin (л/; 4)
20 sin л/
G/J
lOSii! (Л/'li)
40л соа Ы G)
150л/2
20 ens-2.7/
6(/ + 0,5/a)
10+10 Sirica/
20л cos (л//4)
25 sin (л/, 3)
15 л/1/8
120л/2
3 + 14 sin л/
5 V^ (/- + /)
20 sin л/
8/3 + 2/
10/+/J
6/ + 4/J
30л cos (л//0)
25л (/ + /-)
Юл sin (л/ 4)
3/--| At
75л @,!/ +0,3/3)
15 s и (л//3)
8(<Мл//2)
10 \ 2 л ros 2л/
2,5 л/2
6 [/'(is::i (л/'lG)
5 i 3/;/3
',}..
2
1
1/6
9
1/S
4/3"
•1
2
I /3
2/.!
';
1/3
I
2
2
3
I/2
2/3
I
Г)
3/2
1/8
2
4
2
/¦>
20
-
зо
25
—
_
20
•J0
•К)
—
—
40
ею
2ri
зс
-
30
_.
--
30
40
36
20
<i.
2л
30
40
20
2."
30
т
20
1 Уз
—
-
—
-_
—
—
—
—
гряд
ео
60
30
—
30
45
—
60
—
—
—
—
30
—
—
45
—
—
30
30
Примечание И мрналтах 5, С, 10, 12, 13, 20—22, 24. :>7, 'J8 Г,М~ дугл о к
поетн; для к;)Ждо!0 нлриант.п положение точки М па схеме соотистчт i,y( i пало/кител!.
значению s , hj exeM.ix 5, 10. 12, 21, 24, 27 ОМ—дуга, cotn котч in v югцля м<*ч<..пи му !'4eurj
нему углу
где R — радиус окружности /., описываемой той точкой тела, с
торой в данный момент совпадает точка М,
R- sr- sin 30е - 20 ¦ 0,5 -- 10,0 см;
ые — модуль углевой скорости тела
и>с - ; ас I; we -- d<fe/dt --¦- 1,8/ - 27t'2 (с ').
При /=-2/9 с
ьуе = 1,8 ¦ 2/9 - 27 ¦ 4/81 ---- —0,93 с '; т, - 0,93 с К
исму
ко-
коОтрицательный знак у величины шг показывает, что р
треугольника происходит вокруг оси Oz в сторону, обратную
правлению отсчета угла ср. Поэтому вектор we направлен по оси
вниз (рис. 125, а).
на-
наOz
Н!

Переносная скорость
ve= 10-0,93 = 9,3 см/с.
Вектор ve направлен по касательной к окружности L в сторону
вращения тела. Так как ve и vr взаимно перпендикулярны, модуль
абсолютной скорости точки М
22 = 65,9 см/с.
Абсолютное ускорение точки равно геометри-
геометрической сумме относительного, переносного и ко-
риолисова ускорений:
или в развернутом виде
W = Wrx -f- Wrn + We + W'e + Wc.
Модуль относительного касательного ускорения
где
wn = d2sr/dt2 = 72л2 cos Зл/.
При / = 2/9 с
wrz — —36л2 = —355 см/с; шгт = 355 см/с2.
Рис. 124
Отрицательный знак wrt показывает, что вектор wrx направлен
в сторону отрицательных значений sr.
-у с
Рис 125
Относительное нормальное ускорение
wrn = v-/p = 0,
так как траектория относительного движения — прямая (р = оо).
142

Модуль переносного вращательного ускорения
We =
где ее = | ье | — модуль углового ускорения тела D;
При ^ = 2/9 с
?„-= 1,8-54-2/9 = —10,2 с-2, ев = 10,2 с2.
Одинаковые знаки у величин ёе и ше указывают на то, что вра-
вращение треугольника D ускоренное, направления векторов <ле и ге
совпадают (см. рис. 125, а, 6).
ауев=10-10,2 = 102 см/с2.
Вектор ш" направлен в ту же сторону, что и ve.
Модуль переносного центростремительного ускорения
а? = # со| = 10 0,932 = 8,7«^9 см/с2.
Вектор а? направлен к центру окружности L.
Кориолисово ускорение
X vr.
Модуль кориолисова ускорения
ou<: = 2o)ewl.s
Так как
то
ou<: = 2o)ewl.sin({Se, vr).
sin (со,,, vr) = sm 150° = 0,5,
, = 2-0,93 65,2 0,5 = 61 см/с2.
В соответствии с правилом векторного произведения вектор wc
направлен перпендикулярно к плоскости треугольника в ту же сто-
сторону, что и векторы ve и ш« (см рис. 125, б).
Модуль абсолютного ускорения точки М находим способом про-
проекций
Wx = We + Wc = 102 -f 61 = 163 СМ/С2,
wy = — w? — wrx cos 60° = —9 - 355 • 0,5 = -186 см/с2,
w, = — svt cos 30° = —355 j//2 = —308 см/с2,
к» = \rw"x -\-Wy-\-wz —- 395 см/с2.
Результаты расчета сведены в табл 42.
с ^
-0,93
Скорость
"е
9,3
«V
65,2
см/с
V
65,9
С 2
-10,2
9
В
102
0
Ускорение
">гх
—355
61
см'с2
wx
163
Та
wy
— 186
5 л и ц
-308
а 42
395
143

сложной дшг/кшш: твердого тгла. сложение
ВРАЩЕНИИ ВОКРУГ ИАРЛЛЛЕЧЬПЫХ
If ПЕРЕСЕКАЮЩИХСЯ ОС lift
Задание К-11. Определение угловых скоростей
звеньев планетарного редуктора
с цилиндрическими колесами
Нантн угловые скорости ведомого вааа // и сателлитов редис-
тора. Схемы редукторов показаны на рис. 125—128, а необходи-
необходимые для расчета данные приведены в табл. 43.
Пркад^р выполнения задания. Исходные данные: схема редуктора
(рис. 129); радиксы колес: г, -=39, г., = 15, л, = 30, г4 = 75 см; ча-
частоты вращения /г/— 800 об/мин, ih =200 об/мин.
H-.--P
пар' iti г '
i
2
3
4
5
6
^
¦,
1)
10
И
12
1.4
14
15
1';
17
IS
10
'hi
21
21
2!
24
25
2'i
77
2S
;)
IV)
15
30
50
20
20
ьо
•50
'0
6)
25
30
20
100
15
75
75
20
15
10
15
50
i 5
24
40
V)
30
40
15
50
20
30
15
30
2~)
1 5
10
15
10
15
20
!5
• л)
.JO
5
30
20
12
7
10
10
10
30
lo
15
10
10
!5
10
Радиус, см
15
!5
20
20
1 5
A~)
15
25
20
lo
65
30
15
20
0
20
15
16
5
12
10
15
15
48
20
10
i ~)
20
10
10
20
45
10
120
30
,40
55.
uO
70
30
15
75
35
50
11
25
70
48
17
54
5 )
55
60
12
10
25
5.")
50
¦10
.50
10
_
10
20
oO
15
15
15
IS
20
_ .
._
3
(j
10
—
10
—
—
15
10
_
_
!5
20
4
10
_..
4
—
6

2000
3500
1000
100
1600
1200
800
3000
600
200
2500
3300
,'0)
400
2700
1200
500
1 100
700
2000
3500
300
2400
500
600
500
200
400
1300
400
Частота
500
—300
—
-200
—
—
. _
1000
— 500
—
—
—
_
—300
—
—
—
400
и
-400
—
- —
--
. -
500
—
—
—
- -
700
_..
—
—
—
___
200
— 100
—
-300
.—
. —
—
—
- —
—
T а б л
и ц а 43
Я, об'МИН
п

_-
-200
—
—
—
—
300
—
—
-300
—
—
200
—
—
_-
—
400
2300
-200
—
_-
—300
п
'а
500
—
—
—
-600
400
—
—
—
—
-3000
1600
-2000
500
1000
1300
-
III
По
чают ю ^i-1-n.-ao.i
сто;ю .л . ду.црго
\ i P Ч ч E[ rr n.
л['те."ь; ыЛ ir
цатолг.^Ь'!' Miat.n v упонык ckopocic.t (частот кругценпя) оша-
ил ;ра,ленче врац.чшя против п по ча< оаоч стрсли.-. е^ли смотреть со

I—=-
1
Ш
-=—ж
Г}
— 77"
I—=-
3 —
V2
fe
n
-s—2Г
¦J" ¦¦«.
_zr
r
U-
t
К
'6
T* —
I =-
-=—ж
2-
1-
I—=-
Tft
-s- Ж
I s-
—
6
J.
4
:
1 J
T
_Г|
_ T
г
a 2Г
i
Рис 126
145

11
I 55-
-=—Л
кг-
12
.3
л
-s Ж
Тр ^_^_^^_
-=—Ж
I—3—4
-2
-3
-=—ж
2-
1-
Гт!
I в-
^— Ж
I-^=-
lil
-в JT
/7
I Вт
4
5-
-вв—Ж
Рис 127
146

-4
I2J
h
-4
127
28
-5
-5
2-
1-
и
-s—Ж
\2S
-JT
Рис. 128
147

Решение. 1. Способом Виллиса. Способ Виллиса позволяет
определять угловые скорости звеньев механизма, участвующих в двух
вращениях: переносном и относительном.
Колеса редуктора участвуют: 1) в относительном вращении (по
отношению к водилу) вокруг собственной оси и 2) в переносном
вращении вместе с воднлем вокруг
его оси.
Переносной угловой скоростью для
каждого колеса является угловая ско-
рость водила ып.
Относительные угловые скорости
колес определяются как разности
абсолютных и переносных угловых
скоростей:
со2/. = @2 — соо;
'///>
Рис. 129
«кг = WK — Щ.
Эти относительные скорости явля-
являются угловыми скоростями всех колес
при мысленно остановленном водиле.
В этом случае между относительными угловыми скоростями
имеются такие же соотношения, как в зубчатых передачах с непо-
неподвижными осями вращений. Следовательно,
(и>1 — со0)/(с>к — со0) -=(—1)тг,
где т — число внешних зацеплений между колесами 1 и k; г —пере-
—передаточное число от колеса / к колесу k в относительном движении
(при остановленном водиле).
Это соотношение носит название формулы Виллиса.
Отметим, что в эту формулу входят алгебраические значения
угловых скоростей; знак «-•-» примем соответствующим вращению
против часовой стрелки, а «—» — вращению по часовой стрелке.
В формулу Виллиса вместо угловой скорости о> можно, разумеется,
подставить частоту врашепня а (об/мин).
Применим формулу Виллиса к решению рассматриваемой задачи
(рис. 130, а). Так как колеса / и 2 находятся во внешнем зацеп-
зацеплении, а колеса 3 и 4 — во внутреннем и частота вращения водила
равна /I,, то
(Их - П\)!(п.% -Hi)--- (—II • /-^/(/Уа),
откуда
' «4 =¦• «и = «I - l/i's/fori)] («i — Я1).
Подставляя сюда числовые значения, находил»
пи = 800 - [C0 • 30)/A5 ¦ 75)] B00 - 800) ^ 1280 об/мин.
Знак «-(-» в ответе указывает, что вал // вращается в направ-
направлении, противоположном вращению часовой стрелки.
148

Частоту вращения /z2 3 шестерен 2—3 (сателлитоз) определяем
из следующего отношения:
откуда
Подставляя сюда числовые значения, находим:
AV3 - 800 - C0/15) B00 - 800) = 2000 об/мин.
Вращение шестерен 2—3 также происходит в направлении, про-
противоположном вращению часовой стрелки.
Рис. 130
2. Способом мгновенных центров скоростей. По угловым скоро-
скоростям ведущих звеньев найдем скорость точки А оси спаренных ше-
шестерен и скорость точки В касания «олес / и 2:
o)i = пп [/30 = (л • 800)/30 = (80/3) -л с1;
(Од ^ л/2„'30 = (л • 200)/30 = B0/3) л с;
vA r- mi (/-j + г2) = (80/3) л • 45 = 1200л см/с;
0Д = о)^! --= B0/3) л ¦ 30 = 200л см/с.
Отложив векторы vA и ая (рис. 130, б), найдем мгновенный центр
скоростей шестерен 2—3:
, ЯВ) = vA/vB = 1200л/200л =•¦= 6; Р., 3А = 6 • Р2-3В.
Так как
Р2 ЯА — P., .3B = r2 = 15 см,
то
Р2 3В = 15/5 = 3 см; Р.г-3А =--18 см;
= 48 см.
149

Затем определим скорость точки С:
! 2ООЛ = 32ООЛ
vr Р„ „С 48 48 48
= ° = : ° = °
va ръ -А 18> Г8 л" 18
По скорости точки А (или В) находим угловую скорость шесте-
шестерен 2—3 и частоту их вращения*
ул 1200л 200
032 з=т~^а = ~w = х л с 1;
яи2 i 30-м, •, 30 B00/3)-л оллл , ,
и2-з = —5п '' йп= — = ' ' = 2000 Об/МИН.
По скорости точки С находим угловую скорость колеса 4:
уг 3200л 128л
Частота вращения колеса 4
30 -«4 30 -A28/3) -л ,ООГ1 ,,
и4 = —— = —Ц^—-— = 1280 об/мнп.
/2//==п4=1280 об/мин.
Задание К-12. Определение угловых скоростей
звеньев планетарного редуктора
с коническими колесами
Найти угловые скорости ведомого вала // и шестерни 2—3 ре-
редуктора с коническими колесами. Схемы редукторов показаны на
рис. 131 —133, а необходимые для расчета данные приведены
в табл. 44.
Пример выполнения задания. Исходные данные: схема редуктора
(рис. 134); радиусы колес: ^ = 24, r2 = 30, r3 = 4Q, г4 = 44 см,
u)i = 60 с-1, @1 = — 40 с *.
Решение. 1. Способом Виллиса. Способ Виллиса, который
изложен в примере выполнения задания К-П, можно применять и
для механизма с коническими колесами, т. е. когда оси враще-
вращения колес пересекаются. В этом случае надо лишь иметь в виду
следующее:
1. зубчатые колеса 2 — 3 (сателлит) участвуют во вращениях
вокруг пересекающихся осей. Поэтому их угловая скорость относи-
относительно водила не может быть выражена алгебраической разностью
между абсолютной и переносной угловыми скоростями.
2. Знаки передаточного числа от одного колеса к другому
в формуле Виллиса определяются из следующего условия: -" —
если, глядя со стороны положительных направлений осей, видеть
вращения соответствующих колес происходящими (при остановлен-
остановленном водиле) в одном направлении; «—»— если вращения колес
видеть происходящими* в разных направлениях.
В рассматриваемой задаче угловая скорость водила равна угло-
угловой скорости ведущего вала сот. Угловую скорость сателлита относи-
150

7
!
J
г-
4—-
5
7
у —
Г
f
ч.
2-
' /
*
-=-
I'
1
j
—
—
А
I
7
Г—1
1
л 1
JTI
1
\
Ч.-Л
\
3
1
1
Е
У
_]¦¦
1
Z
1 /
1 /.
1
I
г
\
п
\
i ^
0
-.
-3
^ 
2
4-
6
ю
j
г
't
J
Г
и
г
1-Г
/^
\\\ж
I
i
—
\~т
-
\; ..
Z
III—-X
1
1
1
J
.1
i-zr
7
4 \
Iff
г
jl—X
I
i
Iff
/
-4
2
I»
J/
Piic. 131
151

11
13
1
15
3—-
<- —
" 1
17
T
1 1
\
1
?
1
\ ,
и
1
2
1
2
i
1
J
Jo
Vt
19
2-
y-
4
Li
0
\ t
r-zr
II
1
¦
11
II
V
d
I
Iff
7
-
'UT'
\\\Ж
i
Mi
1
г
Л
U--2-
>¦
4
-2
f
12
c-
/4
/6
20
2--
(
\
J
' ,
7
-V
7
i
!
f ,
1
I
i
Г1
i
t
i
¦
i
/
i
i
/
/
¦
II
p
Iff
11
1—^
iff
¦
II
Iff
llff
7
Г
/
1
Г
r
J
J
T
J
4
>
4
Рис. 132
152

21
>-
4 -
23
2
У
4
25
27
У _
29
¦jr- '
5"'
-
!
I
- ¦ 71
- r
i
!
f
/ ,
i
i
1/j
\
IJT
1-1
/
Ш
11 T
,
i
V2
V
I
1
IJT
II
/
1
г
17
|1
\
4
/,
y
4
-5
22
2k
2
>¦
4
26
28
У
2
30
It
I
и
ijii
0
к
1
1
i—,
1
I
4 /
f)
¦?
, \
.
-J
1
1
1
1
\H
Li
l
IE
:
2
\ '
n
m
z
Li
\
4
\E
/
\
\ '
/
^2
;
_ >-
— 4
- >
4
Pnc 133
153

Номер
варианта
(рис.
131—133)
1
2
3
4
5
G
7
8
9
10
11
12
13
14
15
1G
17
18
19
20
21
22
23
24
25
2G
27
28
29
30
'i
20
15
30
30
45
50
25
75
10
60
15
@0
50
40
60
35
16
15
20
40
60
30
15
25
20
45
30
25
10
15
Радиус, см
г,
20
9
30
30
45
40
19
57
13
18
17
92
28
42
60
15
16
12
44
42
60
13
11
21
10
60
14
20
20
15
г>
40
24
30
60
15
20
9
75
17
60
15
52
16
22
80
35
9
21
20
20
36
30
15
13
20
45
32
10
Ю
20
г.
40
24
60
35
30
15
90
20
60
30
22
80
9
25
20
30
—
15
30
—
50
15
15
20
г.
15
—
5
—
320
50
100
350
30
GO
40
330
80
310
20
70
90
340
40
150
200
250
130
180
80
110
70
40
50
220
60
310
30
Т аб л и
Угловая скорость, с 1
ш,
— 200
—
—
—
—
по
-90
—
—
—
— 10
70
—
-250
,
150
-120
80
—
-350
—
—.
—
—
,
,
-50
.
—
40
—
.
-300
—
—
,
—
—
СО»
50
40
—
—
— 300
—
30
-150
200
-80
—,
—
—
—
40
-50
—
—
—
—¦
ц а 44
а.
—
80
40
—
—,
340
30
,
—,
.
.
,
50
70
.
—.
30
.
,
—
—
40
—
200
—
Положительный и отрицательный энакн угловых скоростей означают соответственно
направление вращения против хода и по ходу часовой стрелки, если смотреть со стороны
положительного направления соответствующей оси,
тельно водила обозначим @|С. Тогда для колес 1 и 2 имеем:
(<ttx — <0[)/й>1С = — Г-i/rj.. A)
oW(co4 — (oi) = rjr3. B)
Перемножая A) и B), получаем:
(coj — <oj)/(od4 — coi) = — r2ri/rlr3,
= (o,, = (oi-((o1 — ©О •/y3//y4. C)
Подставляя в C) числовые значения, находим:
«ой = 60 - (— 40 - 60) ¦ B4 • 40)/C0 • 44) = 60 + 72,7 «* 133 с1.
154
Для колес 3 и 4
откуда

Положительный знак у величины «и показывает, что ведомый
вал вращается в направлении против вращения часовой стрелки
(если смотреть со стороны положитель-
положительного направления оси Oz).
Для определения угловой скорости ca- z
теллита из A) определяем сначала его {
угловую скорость относительно водила: HI I
или
оIс = — 24/30- (—40-60) = 80 с '.
Абсолютная угловая скорость сател-
сателлита
С0с = (!)[ + OJ,c,
причем вектор щ направлен по оси Oz,
a @ic по 01.
Так как (o[c и щ взаимно перпенди-
перпендикулярны, то
?
-*
г-
*
. II
1
1
—1
; !
I
1 <*
•
0
^
О)с = У Ш\ + «1с
\\Е
или
Рис. 134
2. Графическим способом. Графическое решение задачи основано
на том, что движение сателлита может рассматриваться как сово-
совокупность двух вращательных движений. При этом в качестве пере-
\
н
III
\
—30
20 0 20 40 СМ:
Рис. 135
Рис. 136
поеного движения можно принять не только вращение водила вокруг
оси Oz (как в способе Виллиса), но и вращение колеса 1 или
155

колеса 4. Следовательно,
сос = со i -|- со lc; сос = «! -}- ы Lc; сос -— щ + иLс.
Заметим, что линии действия любых двух составляющих вектора
(о^ известны. Угловые скорости coi, wl и о>4 направлены по оси Oz
(рис. 135); со1с —по оси 0?; ы1с. и wlc — соответственно по линиям Оа
н Ой (по мгновенным осям вращения в относительном движении).
Из произвольного полюса Ох (рис. 136) отложим в выбранном
масштабе параллельно оси Oz векторы заданных угловых скоростей и>[
и (и1. Через конец вектора coi проводим прямую KL, параллельную 0?
(линии действия ацс); из конца вектора со1 — прямую ММ, парал-
параллельную Оа (линии действия а>1с). Точка пересечения этих прямых
определяет конец вектора шс, а также щс и оIс.
Измерением на чертеже находим
сос = 100 с !.
Направление и\. определяет положение мгновенной оси вращения
сателлита OQ (см. рис. 135).
Для определения озц разложим со,, на две составляющие, направ-
направленные параллельно Oz и 0Ь. Полученные векторы представляют
СОбоЙ <Л[[(щ) И (Вис (tt>4c).
Измерением на чертеже находим:
со,, = 135 с1.
Направление а>ц соответствует положительному знаку угловой
скорости сиц, найденной способом Виллиса.

РАЗДЕЛ ТРЕТИЙ
ДИНАМИКА
Задания по динамике тематически разделены на три группы:
1) динамика материальной точки (G заданий),
2) динамика механической системы F заданий),
3) аналитическая механика A4 заданий).
Из четырех заданий первой группы, посвященных дифференци-
дифференциальным уравнениям движения материальной точки, наиболее простым
является задание Д-1, в котором рассматривается движение точки
под действием постоянных сил. Остальные три задания требуют
более глубокого знания теории дифференциальных уравнении.
Во второй группе повышенную трудность представляют задания
Д-7 и Д-12. Они могут быть отнесены к работам с элементами
самостоятельного исследования.
В третьей группе на каждую из тем даны задания различной
сложности и трудоемкости. К числу сравнительно сложных следует
отнести задания: Д-14, Д-16, Д-18, Д-20, Д-21, вторую часть зада-
задания Д-22, Д-24, Д-25, Д-26. Эти задания требуют более глубокого
знания теоретического материала и также содержат элементы само-
самостоятельного исследования.
I. Динамика материальной точки
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
МАТЕРИАЛЬНОЙ ТОЧКИ
Задание Д-1. Интегрирование дифференциальных
уравнении движения материальной точки,
находящейся под действием постоянных сил
Варианты 1—5 (рис. 137, схема 1). Тело движется нз точки Л
по участку АВ (длиной /) наклонной плоскости, составляющей
угол а с горизонтом, в течение т с. Его начальная скорость vA.
Коэффициент трения скольжения тела по плоскости равен /.
В точке В тело покидает плоскость со скоростью vH и попадает
со скоростью v(- в точку С плоскости BD, наклоненной под углом р
к горизонту, находясь в воздухе Т с.
J57

¦X,
а
в
7у
I
У
\г—" ~/уу
^>777777^'
d
|
V///////////////////, V,
У/УУХ/УуууУ/ууууУу
d
XXi-
УУУУУУ/УУУУУУУУУУУ,
d
УуУУх
L
УУУУУУ.
У,
Рис. 137
158

При решении задачи тело принять за материальную точку;
сопротивление воздуха не учитывать.
Вариант 1. Дано: а = 30°; vA=0; / = 0,2; / = 10 м; 0 = 60°.
Определить т и И.
Вариант 2. Дано: ее--15°; у4 = 2м/с; / = 0,2; Л = 4м; 0 = 45°.
Определить / и уравнение траектории точки на участке ВС.
Вариант 3. Дано: а. — 30°; vA = 2,5 м/с; / Ф 0; / = 8 м; d = 10 м;
Р = 60°. Определить vn и т.
Вариант 4. Дано: vA = Q; т = 2 с; / = 9,8 м; 0 = 60°; / = 0.
Определить а и Г.
Вариант 5. Дано: а = 30°; 1>л = 0; /--=9,8 м; т = 3 с, р = 45°.
Определить / и ис.
Варианты 6—10 (рис. 137, схема 2). Лыжник подходит к точке А
участка трамплина АВ, наклоненного под углом а к горизонту и
имеющего длину /, со скоростью vA. Коэффициент трения скольже-
скольжения лыж на участке АВ равен /. Лыжник от Л до В движется -и с;
в точке В со скоростью vB он покидает трамплин. 'Через Т (с) лыж-
лыжник приземляется со скоростью vc в точке С горы, составляющей
угол р с горизонтом.
При решении задачи принять лыжника за материальную точку
и не учитывать сопротивление воздуха.
Вариант 6. Дано: а = 20°; / = 0,1; т = 0,2 с; А = 40 м; р =
= 30°. Определить / и vc.
Вариант 7. Дано: а=15°; / = 0,1; ил = 16 м/с; / = 5 м; 0 =
= 45°. Определить vR и Т.
Вариант 8. Дано: vA — 21 м/с; / = 0; т —0,3 с; ий = 20м/с;
Р = 60°. Определить а и d.
Вариант 9. Дано: а --=15°; т = 0,3 с; / = 0,1; /г = 30 ]/2 м;
Р = 45°. Определить vK и vA.
Вариант 10. Дано: а=15°;/ = 0; ил = 12 м/с; J = 50m;P =
= 6O'J. Определить т и уравнение траектории лыжника на участке ВС.
Варианты 11—15 (рис. 137, схема 3). Имея в точке А скорость vA
мотоцикл поднимается т с по участку А В длиной /, составляющему с
горизонтом угол а. При постоянной на всем участке А В движущей
силе Р мотоцикл в точке В приобретает скорость vn и перелетает
через ров шириной d, находясь в воздухе Т (с) и приземляясь в точке
С со скоростью vc. Масса мотоцикла с мотоциклистом равна т.
При решении задачи считать мотоцикл с мотоциклистом матери-
материальной точкой и не учитывать сил сопротивления движению.
Вариант 11. Дано: ее = 30°; Р ф 0; / = 40м; vA = 0: ив = 4,5м/с;
d = 3 м. Определить т и h.
Вариант 12. Дано: а = 30°; Я^0; / = 40 м; ой = 4,5 м/с;
h =1,5 м. Определить vA и d.
Вариант 13. Дано: а = 30°; т = 400 кг, vA=0; т = 20 с; d =-=
= 3 м; /г = 1,5 м. Определить Р и /.
Вариант 14. Дано: а = 30°; т = 400 кг; Я = 2,2 кН; vA = 0;
/ = 40 м; rf = 5 м. Определить va и ас-
Вариант 15. Дано: а = 30°; vA = 0; Я = 2 кН, / = 50 м; h = 2 м;
J = 4 м. Определить 71 и //i.
159

е-
е16—.20 (рис, 137, сшйа 4). Камень скользит в тече
ние т с по участку АВ откоса, составляющему угол а с горизон-
горизонтом и имеющему длину /. Его начальная скорость vA. Коэффициент
трепня скольжения камня по откосу равен /. Имея в точке В ско-
скорость vtt, камень через Т (с) ударяется в точке С о вертикальную
защитную стену. При решении задачи принять камень за материальную
точку; сопротивленце воздуха не учитывать.
Вариант 16. Дано: а = 30°; vA = 1 м/с; / = 3 м; / = 0,2; d—
— 2,5 м. Определить /г и Т.
Вариант 17. Дано: а = 45°; / =6 м; vu~2vA\ т= 1 c;/i-6m.
Определить d и /.
Вариант 18. Дано: а = 30°; / = 2 м; ил = 0; / = 0,1; d = 3 м.
Определить ft и т.
Вариант 19, Дано: а =15°; / = 3 м; v,s^3 м/с, /=И=0; т =
= 1,5 с; d — 2 м. Определить ул и h.
Вариант 20. Дано: a = 45'J, г>д = 0; / = 0,3; d = 2 м; h = \ м.
Определить / и т.
Варианты 21—25 (рис. 137, схема 5). Тело движется из точки А
по участку АВ (длиной /) наклонной плоскости, составляющей
угол а с горизонтом. Его начальная скорость vA. Коэффициент тре-
трения скольжения равен /. Через т с тело в точке В со скоростью vB
покидает наклонную плоскость и падает на горизонтальную плоскость
в точку С со скоростью vc\ при этом оно находится в воздухе Т с.
При решении задачи принять тело за материальную точку и не учиты-
учитывать сопротивление воздуха.
Вариант 21. Дано: а -= ЗУ; /--=0,1; vA = 1 м/с; т = 1,5 с;
/г= 10 м. Определить иц и d.
Вариант 22. Дано: vA = 0; а = 45°; /=10 м; т = 2 с. Опреде-
Определить / и уравнение траектории на участке ВС.
Варп'ант 23. Дано: / = 0; ил^0; / = 9,81 м, т = 2 с; Л--20м;
Определить а и Т.
J}jy3ji^_H_T_,24. Дано: ад = 0; а-=30°; / = 0,2; / = 10 м, rf = 12 лг.
Определить т и к.
Вариант 23. Дано: vA=0; а =30"; / — 0,2; / = G м, Л = 4,5м.
Определить т н у,-.
Варианты 26—30 (рис. 137, схема 6). Имея в точке А скорость vA,
тело движется по горизонтальному участку А В длиной / в течение т с.
Коэффициент трения скольжения тела по плоскости равен /. Со ско-
скоростью и» тело в точке В покидает плоскость и попадает в точку С
со скооостыо Vq, находясь в воздухе Т с. При решении задачи при-
принять тело за материальную точк\; сопротивление возду?;а не учитывать.
Вариант 26. Дано: vA = 7 м/с; / = 0,2; /=8 м; h = 20 м.
Определить d и vc.
Вариант 27. Дано: vA = 4 м/с, /=-0,1; т=2с; ^ = 2м. Опре-
Определить v,i и к.
Вариант 28. Дано: г>„ = 3 м'с; /=0,3; /=--3 м; Л = 5 м. Опре-
Определить иА и Т.
Вариант 29. Дано: vA = 3 м/с; ив=1 м'с; / = 2,5 м; /г=--20м.
Определить / и d.
160

Вариант 30. Дано: / = 0,25; / = 4 м; d ~ 3 м; Л = 5 м. Опре-
Определить vд и т.
Пример выполнения задания (рис. 13S). В железнодорожных
скальных выемках для защиты кюветов от попадания в них с отко-
откосов каменных осыпей устраивается «полка» DC. Учитывая возмож-
возможность движения камня из наивысшей точки А откоса и полагая при
этом его начальную скорость v0 равной нулю, определить минималь-
минимальную ширину полки b п скорость vc, с которой камень падает на нее.
По участку АВ откоса, составляющему угол а с горизонтом и
имеющему длину /, камень движется т с.
Рис. 138
При решении задачи считать коэффициент трения скольжения /
камня на участке АВ постоянным, а сопротивлением воздуха пре-
пренебречь.
Дано: vA = Q; а = 60°; I = 4 м; т= 1 с; }ф 0; Л = 5 м; 0 = 75°.
Определить b и vc
Решение. Рассмотрим движение камня на участке АВ. Прини-
Принимая камень за материальную точку, покажем (см. рис. 138) дейст-
действующие на пего силы: вес б, нормальную реакцию N и силу трения
скольжения F. Составим дифференциальное уравнение движения
камня на участке А В:
тх1 = ? X,!; тх1 =¦- G s in a — F.
Сила трепня
F-fN,
где у
N — Gcosa.
Таким образом,
тл\ = G sines —{Gcosa
6 п/р. Яблонского Л А.
161

пли
xL — о ^iii х — /g coses.
Интегрируя дифференциальное уравнение дважды, получаем:
x1^g(s\na -/cosa)
*i = [g (Sin « - / c
Для определения постоянных интегрирования воспользуемся
начальными условиями задачи: при ^ = 0 xlo = 0 и ilo = O. Составив
уравнения, полученные при интегрировании, для / = 0
найдем постоянные:
° — п Г — о
Тогда
ii^g (sine: — /cosее) Г;
¦*i = [g (sm a — /cos я)/2] P.
Для момента т, когда камень покидает участок,
-*1 = г;|л; хх = /,
т. е.
wfl = ?(siiia-/cosa)T;
/ = [g (sin a — / cos a)/2] • т2,
откуда
т. е.
wn = B-4)/l=8 м/с.
Рассмотрим движение камня эт точки В до точки С.
Показав силу тяжести G, действующую на камень, составим диф-
дифференциальные уравнения его движения:
Интегрируем первое из этих уравнений:
X = С3; х — L3Z -p L4.
Постоянные интегрирования С, и С4 определим, используя началь-
начальные условия задачи: при t = 0 xo-—Q, xa = vncosa.
С помощью уравнений, полученных при интегрировании и состав-
составленных для ^ = 0,
х0 = Сз! -^o==^-"Ji
найдем, что
С3 = Уд cos а; С4 = 0.
Тогда
х- y ^
Интегрируя уравнение my = G, имеем:
162

Начальные условия: при ? —О у0 —О у0—- wnsina. Из уравне-
уравнений, полученных интегрированием и составленных для < = 0,
Уо — ^&'i Уо= ^ei
найдем, что
C=, = vi)S\na и С8 = 0.
Окончательно
y = gt + vn sin a; // = g^/2 + vB sin а • t.
Таким образом, уравнения движения камня имеют вид
x=vBcosa-t; y = gt2i2-\- vB sin a-1.
Уравнение траектории камня найдем, исключив параметр t из
уравнений движения. Определив t из первого уравнения и подста-
подставив его значение во второе, получаем уравнение параболы:
В момент падения
// = Л = 5 м, a x = d,
т. е.
5= 2-№-0,5» +dV 3>
откуда
^,2 = — 2,82 :L 4,93,
так что
rfx =- 2,11 м, ds = — 7,75 м.
Поскольку траекторией движения камня является ветвь пара-
параболы с положительными абсциссами ее точек, то d = 2,ll м.
i^\инимaльнaя ширина полки
b = d-ED = d- /i/tg 75° = 2,11 - 5/3,73 = 0,77 м.
Используя уравнение движения камня х — vB cos а-/, найдем
время Т движения камня от точки В до точки С:
2,11 =8-0,57\
откуда
Т = 0,53 с.
Скорость камня при падении найдем через проекции скорости на
оси координат:
X-= Vи COS OL, y = \
по формуле
Для момента падения ^=7" = 0,53 с
vc = У (vn cos aJ + (g7' + va sin аJ =
= V(8 • 0,5J + (9,81 • 0,53 + 8 ¦ 0,87J = 12,8 м/с
163

Задание Д-2. Интегрирование дифференциальных
уравнений движения материальной точки,
находящееся под действием переменных сил
Найти уравнения движения тела М массой т (рис. 139 — 141),
принимаемого за материальную точку и находящегося под действием
переменной силы Р — XI + Yj -f- Zk, при заданных начальных усло-
условиях. Во всех вариантах, где показана ось z, эта ось вертикальна,
за исключением вариантов 8 и 30.
Необходимые для решения данные приведены в табл. 45, в кото-
которой приняты следующие обозначения: i, j, k — орты координатных
осей (соответственно х, у, z); g —ускорение свободного падения
(9,81 м/с2); / — коэффициент трения скольжения; / — время в с; л,
у, г, х, у, г —координаты точки и проекции ее скорости па оси
координат соответственно в м и м/с.
Во всех случая:;, где сила Р зависит от л-, х, z, z, рассмотреть
движение точки, при котором эти величины только положительны.
Пример выполнения задания. Дано: т=[ кг, Р — —4r(t cosq) 4-
+ %su-\(i>) Н; хо=1О м; го = О, л = 0, го = 4О м/с (рис. 142, а).
Найти уравнения движения.
Решение. Материальная точка М находится под действием
силы тяжести G и силы Р, линия действия которой проходит через
неподвижный центр О (рис. 142, б). Сила Р притягивает точку М
к центру О. Модуль силы прямо пропорционален расстоянию г от
точки до полюса О.
В начальный момент времени (^ — 0) точка М находится на оси х
на расстоянии 10 м от начала отсчета и ей сообщается начальная
скорость 40 м/с, направленная вверх по вертикали.
Заданные силы /•*', G и вектор начальной скорости расположены
в плоскости xOz и поэтому дальнейшее движение точки происходит
в этой плоскости.
Дифференциальные уравнения движения материальной точки имеют
вид:
тх = X Хп тг — ^ Z,-.
Сумма проекций сил па оси координат равна:
XX, =/\ = — 4rcos(p, vz, = P,-G=-- 4rsin<p-G.
Так как cos<p = .v/r, sin ф —г/г, то
vXi--4.v, VZ, -.^ — 4г-С
С учетом исходных данных
х-— —Ах, z — — '\z — g
или .
A)
IC4

•>М(х,г)
О
г
X
'/as, У//7/////У7, /77////.
n 9 . г
х У -
о'Mix, у)
' /%(¦////, У,////'/' '/7/Y/7//////
/// У. У////А//////////А/////,'///////,
MfX.2)
?h
т
х м
////////'/////У///'','/;/////'
Рис. 139
165

OH
99J
)N
OZ
X
^ О
ei
X
X-
91
LI
Bl
'//////SS////A'////////. '.'/.У •////
f/
w
21

2/
II
23
1 I
M
о
26
23
У//////////, '////,¦///
23
30
>\
Nj4
\
/
/7
г
P«c. 141
167

00
Таблица 45
Номер
варианта
(рнс. 139—14 1)
1
о
3
4
5
6
7
8
9
10
11
12
т. кг
2
0,25
2
т
50
т
2
150
1
1
20
т
i
Р. Н
— 0,5 (xl + ?k)
100x7
— B0х-4дгO
— \iz~4
— Eх —25х)Г
— m\ix'H
47cos(nt/6) + yJ
120^ G со* 30s + 'k sin 30е)
4r (( cos ф + k sin ф)
-з/*Г
— 3v
~- mgR?z-4
i
i
0,3
0
—
0
0
0
0
—
0
—
—
*0
Начальные
г0
M
0
0,03
0,15
—
0
a
0
0
0
0
—
—
—
—
—
—
—
0
0
—
—
0
—
0
—
—
a
—
—
—
0
2
—
0
R
УСЛОВИ!
х„
!
г0
М/с
20
0,5
1
—
1
Vf>
0
0,5
5
16
—
—
20
—
—
—
—
—
3
2
—
15
—
—
—
V ma
—
—
0
0
—
0
Примечание
Учесть только силу
Р; jii, о—поло-
о—положительные по-
постоянные
t>o>O, ц>0 (const)
Рассмотреть движе-
движение при у >0,
?> 0
Учесть только силу
Р; R > 0 (const)

13
14
15
16
17
18
19
20
21
22
25
21
25
26
27
2S
29
30
S
m
1,5
1,5
100
1
2
6
0,1
0,1
m
100
3
1,5
0,1
9
4
0,0'
100
9mr (i cos a +./' cos В + & cos y)
D,5-f :-г)Г
F - 1,5г + 3i) I
— 20x1
5(l—e-2') Г
з'— 18х— 12дг)Т
— imr (i cos <f¦+/ sin ф)
50 C + x)T
— 3 Cx + 2x) 7
— 7,5 (д~( — 2g~k)
— Bc^_ 0,98 \)~k
— 2 {x~i + y~-i-zl)
— 3y'z k
120 G,5 + 0 Gcos 3(F + I"sm 30-)
0,1
0
0
0
0
0
—
—
0
0,2
0
—
—
0
—
—
0,25
2
1
—
0
0
0
0
—
—
20
0
0
0
—
0
0
—
0
о
—
—
—
—
—
—
—
—
0
—
—
—
—
0
0
—
—
о
—
0,5
—
—
—
—
200
300
0
—
—
100
0
—
0
0
0
1
0,3
—
2,5
0
10
10
—
—
0
1
2
4
—
H
1
—
0,5
0
—
—
—
—
—
—
—
—
8
—
—
—
—
4
1
—
—
0,1
2,5
0
0
7
0
2
125
0
Учесть только силу
P
Учесть только cnju
Р
Влиянием силы тя-
тяжести пренебречь

Уравнения A) п B)—линейные дифференциальные уравнения
второго порядка с постоянными коэффициентами; первое из нич
однородное, а второе неоднородное.
z _. Характеристическое уравнение для
^ уравнения A):
Корни этого уравнения:
tM(r,z)
Общее решение уравнения A) имеет
вид:
x = C1cos2( + Css\n2L E)
Дифференцируя но времени E), по-
получаем:
Постоянные интегрирования Си С,
находим из начальных условии
М(х,7) 0 = 2 (— С1 ¦ s i n 0 + С, cos 0),
откуда
С1 = 10, С,=0. G)
2 Искомое уравнение движения х — х (():
x=\0cos2t. (8)
Рис. 142
Общий интеграл неоднородного уравнения B) имеет вид:
z = z* + z*\ (9)
где 2*—общее решение соответствующего однородного уравнения
z" + 4z--=0, A0)
2** —частное решение неоднородного уравнения B).
Уравнения A) и A0) аналогичны и поэтому общий интеграл
уравнения A0) имеет вид:
2* -~СЛ cos 2t -|- C4 sin 21. (II)
Частное решение г** следует искать в виде
г**,-_-Л = const. A2)
Подставляя A2) в B), получаем:
0 + 4/4^-g-, A =—#/4=-- — 2,45. A3)
Таким образом,
z = C3 cos 2М-С4 sin 2^-2,43. A4)
170

Дифференцируя A4) по времени, получаем:
2 = 2(— C,sin2/ + C4cos2Q. A5)
С учетом начальных условий уравнения A4) и A5) при t^O
получают вид
0-С,.1+С4.0-2,45;
40--=2(-Са-0 + С4.1),
откуда
С, = 2,45; С4 = 20.
Окончательно
z = 2,45 cos 21 + 20 sin 2/ -2,45 (м). A6)
Уравнения (8) и A6) являются решением задачи.
Задание Д-3. Исследование колебательного
движения материальной точки
Варианты 1-5 (рис. 143). Найти уравнение движения груза D
массой тп (варианты 2 и 4) или системы грузов D и Е массами tnD
и тЕ (варианты I, 3, 5), отнеся их движение к оси х; начало отсчета
совместить с положением покоя груза D или соответственно системы
грузов D и ? (при статической деформации пружин). Стержень,
соединяющий грузы, считать невесомым и недеформируемым.
Вариант 1. Груз D (тр = 2 кг) прикреплен к бруску АВ,
подвешенному к двум одинаковым параллельным пружинам, коэф-
коэффициент жесткости каждой из которых с = ЗН/см. Точка прикрепле-
прикрепления груза D находится на равных расстояниях от осей пружин.
В некоторый момент времени к грузу D подвешивают груз Е
(тЁ—\ кг). Сопротивление движению системы двух грузов пропор-
пропорционально скорости: R—\2 v (Н), где v — скорость (м/с).
Массой абсолютно жесткого бруска АВ ц массой части демпфера,
прикрепленной к бруску, пренебречь.
Вариант 2. В момент, когда стержень, соединяющий грузы D
(mD=\ кг) и Е (т? = 2 кг), перерезают, точка В (верхний конец
последовательно соединенных пружин) начинает совершать движение
по закону |=1,5 sin 18/ (см) (ось Н направлена вертикально вниз).
Коэффициенты жесткости пружин cl==12 Н/см, с2 = 36 Н/см.
Вариант 3. Груз D (mD = Q,8 кг) висит на пружине, прикреп-
прикрепленной к точке F бруска А В и имеющей коэффициент жесткости
q=10 Н/см. Брусок подвешен к двум параллельным пружинам,
коэффициенты жесткости которых с2 = 4 Н/см, с, = 6 Н/см; точка F
находится на расстояниях а и Ь от осей этих пружин: а/Ь = ся/с2.
В некоторый момент времени к грузу D подвешивают груз Е
(тЕ—1,2 кг). В этот же момент системе грузов сообщают скорость
v0 = 0,2 м/с направленную вния. Массой абсолютно жесткого бруска А В
пренебречь.
Вариант 4. Статическая деформация двух одинаковых парал-
параллельных пружин под действием грузов D (mD = E,5 кг) и Е (rnF. --¦ 1,5 кг)
/ст = 4 см. Грузы подвешены к пружинам с помощью абсолютно
171

A ~J
г *=s
D
z с
В
Л,
¦С,
ID 3
у/Л/л
\D
to
Рис 143
172

жесткого бруска АВ. В некоторый момент времени стержень, соеди-
соединяющий грузы, перерезают. Сопротивление движению груза D про-
пропорционально скорости- R = 6v (Н), где у —скорость (м/с). Массой
бруска и массой, прикрепленной к бруску части демпфера, пренебречь.
Вариант 5. Одновременно с подвешиванием к грузу D{mn—-
— 1,6 кг), вчеящему на пружине, коэффициент жесткости которон
с = 4 Н/см, груза ?(mF = 2,4 кг) точка В (верхний конец пружьиы)
начинает совершат, движение по закону с —2 sin о/ (см) (ось |
направлена вертикально вниз).
Примечание Положение начала отсчетч на мн х соответствует среднему
лсложению точки fi(*=-0)
Варианты 6—10 (рис. 143). Найти уравнение дв [же шя груза D
ма'сой т по гладкой наклонной плоскости, составляющей с горизон-
горизонтом угол ос, с момента соприкасания груза с пружиной или с систе-
системой пружин, предполагая, что при дальнейшем движении груз от
пружин не отделяется. Движение гр\ла отнести к оси а, приняв за
начало отсчета положение покоя трупа (при статической деформации
пружин).
.,. Вариант 6 Пройдя без начальной скорости по наклонной
плоскости (а — 30') расстояние s = 0,1 м, груз Z)(m —4 кг) ударяется
о недеформи^ованпые, последовательно соединенные пружины, имею-
имеющие коэффициенты жесткости сх = 48 и с,—24 Н/см.
Вариант 7. В некоторый момент времени гр>з D(m-2 кг)
присоединяют без начальной скорости к концу А иедеформированных
последовательно соединенных пружин, имеющих коэффициенты жест-
жесткости с, = 12, с2 = 6 11/см. В тот же момент времени (/=0) другой
конец пружин В начинает совершать движение вдоль наклонной
плоскости (а —45е) по закону ? — 0,02 sin 201 (м) (ось Е, направлена
вдоль наклонной плоскости вниз)
Примечание Положение чачала отсчета на оси х соответствует среднему
положению точки fi(* = 0)
Вариант 8 Две параллельные пружины/ и 2, имеющие коэф-
коэффициенты жесткости с1 = 4 Н/см и с,--6 Н/см, соединены абсолютно
жестким броском АВ, к точке К которого прикреплена пружина 3
с коэффициентом жес1кости с., = 15 Н/см Точка К находится на
расстояниях а и ft от осей пр\жин / и 2 а/Ь ¦-с.1/с\. Пружины /,
2 и .3 не деформированы. Груз D массой 1,5 кг присоединяют к копну /V
пружины 3, в тот же момент грузу D сообщают скорость vn ==0,5 м/с,
направленную вниз параллельно наклонной плоскости (а. = 45<:) Массой
бруска АВ пренебречь.
В а р и а и t 9. Груз D (т ~ 1,2 кг), пройдя без начальной скорости
по наклонной плоскости (а -=30') расстояние s = 0,2 м, ударяется
о недеформировэиную пружину, коэффициент жесткости которон
с —4,8 Н'см В этот же момент (i-- 0) точка В (нижний конец пру-
пружины) начинает совершать вдоль наклонной плоскости движение но
закону |=-= 0,03-sin 12/ (м) (ось ? направлена вдоль наклонной плос-
плоскости вниз) (см. примечание к варианту 7).
173

Вариант 10. Груз D(m—\ кг) прикрепляют к середине абсо-
абсолютно жесткого бруска АВ, соединяющего концы двух одинаковых
параллельных пружин, не сообщая начальной скорости; пружины
не деформированы. Коэффициенты жесткости пружин с =1,5 Н/см.
Сопротивление движению груза пропорционально скорости: R = 8v (Н),
где V — скорость (м/с); а = 60°. Массой бруска А В и массой прикреп-
прикрепленной к бруску части демпфера пренебречь.
Варианты 11—15 (рис. 144). Груз D массой т укреплен на конце
невесомого стержня, который может вращаться в горизонтальной
плоскости вокруг оси Е. Груз соединен с пружиной или с системой
пружин; вертикальное положение стержня соответствует недеформи-
ровапным пружинам. Считая, что груз D, принимаемый за мате-
материальную точку, движется по прямой, определить уравнение движе-
движения этого груза.
Движение отнести к оси х, за начало отсчета принять точку,
соответствующую положению покоя 1~руза (при педеформированпых
пружинах).
Вариант 11. Груз D (т = 2,4 кг) соединен с точкой F бруска А В,
связывающего концы двух параллельных пружин, коэффициенты жест-
жесткости которых сх — 1 Н/см и б'2^=1,4 Н/см. Точка F находится на
расстояниях а и b от осей пружин: а/b =с,/с\.
Груз D отклоняют на величину а = 2 см влево от положения,
соответствующего вертикальному положению стержня, и отпускают
без начальной скорости. Сопротивление движению груза пропорцио-
пропорционально скорости: R = 6v (Н), где v — скорость (м/с). Массой абсолютно
жесткого бруска АВ и массой демпфера пренебречь.
Вариант 12. В некоторый момент времени груз D(m = 3 кг),
удерживаемый в положении, при котором пружина сжата на величину
1 = 2 см, отпускают без начальной скорости. Коэффициент жесткости
пружины с = 9 Н/см. Одновременно (/ = 0) точка В (правый конец
пружины) начинает совершать движение по закону |= 1,2 sin 8/ (см)
(ось | направлена горизонтально влево).
Примечание. Положение начала отсчета на оси х соответствует среднему
положению точки В (| = 0).
Вариант 13. Груз D(m=l кг) прикреплен к концу пружины,
имеющей коэффициент жесткости сх=12 Н/см и соединенной другим
концом с точкой F бруска АВ. Брусок АВ связывает концы двух
параллельных пружин, коэффициент жесткости каждой из которых
с = 3 Н/см. Точка F находится па равных расстояниях от осей парал-
параллельных пружин. Грузу при вертикальном положении стержня сооб-
сообщают скорость l'0 = 0,5 м/с, направленную вправо.
Сопротивление движению груза пропорционально скорости: R —
— 12 v (Н), где и — скорость (м/с).
Шток демпфера пропущен через отверстие в невесомом бруске А В
и соединен с грузом D.
Вариант 14. Груз D(m— 1,5 кг) прикреплен одной стороной
к концу пружины, имеющей коэффициент жесткости с,--=4,4 П/см,
а другой стороной —к концу двух последовательно соединенных пру-
пружин, коэффициенты жесткости которых с2 = 2, с3--8 Н/см.
174

л
F C
P
12
x
y
¦w
^3 JUAAAAlJ I  Л Л Л Л
x
U w ... f
f
Y////Y//, '/У//////////////X/////.
LJLJlJ'-J
17
18
19
E
В
20
\D
//////.У7лг77//.
P»c 144
175

Груз отклоняют на величину ^^2,5 см влево от его положения,
соответствующего вертикальному положению стержня, и отпускают,
одновременно сообщая грузу начальную скорость уо^-О,4 м/с, направ-
направленную вправо.
Вариант 15. Груз D (//; — 1 кг) прикреплен к концу А после-
последовательно соединенных пр\жнн. Другом конец пружин В движется
по закону: |-= 1,8 sin 12 t (см) (ось | направлена горизонтально влево).
Коэффициенты жесткости пружин: q = 4, с,—12 И few. При / = 0
груз находился в положении покоя, соответствующем недеЛормиро-
ванным пружинам (см. примечание к варианту 12).
Варианты 16—20 (рис. 144). Найти уравнение движения груза D
массой тп (варианты 17 и 19) или системы грузов D и ? массами тп
и nifi (варианты 16, 18, 20), отнеся движение к оси л; начало отсчета
совместить с положением покоя груза D или соответственно системы
грузов D и Е (при статической деформации пружин). Предполагается,
что грузы D и Е при совместном движении не отделяются.
Вариант 16. Пружина /, на которой покоится груз D (тп= 10 кг),
опирается в точке F па брусок АВ, соединяющий концы двух парал-
параллельных пружин 2 и 3. Коэффициенты жесткости пружин /, 2 и 3:
Гц = 200, с, = 160, с3 = 140 Н/см.
Точка F находится на расстояниях а и b от осей пружин 2 и 3:
a/b = cs/c.,.
В некоторый момент времени на груз D устанавливают груз ?
(тЕ — 20 кг); одновременно системе грузов сообщают скорость v0 ~
= 0,4 м/с, направленную вниз.
Массой абсолютно жесткого бруска А В пренебречь.
Вариант 17. В некоторый момент времени груз ? снимают
с груза D (оба груза находится в состоянии покоя, соответствующем
статической деформации пружины). Циклическая частота собственных
колебаний системы грузов D и Е на пружине & = 20 с \ отношение
масс тп/тр = 2/3.
Вариант 18. Статическая деформация каждой из двух одина-
одинаковых параллельных пружин под действием груза D (тп — 20 кг)
равна /Г1Л = 2 см. В некоторый момент времени на груз D устана-
устанавливают груз ?(т/.^10 кг). Сопротивление движению грузов про-
пропорционально скорости: ^?:=60J/3l> (Н), где v — скорость (м/с). Мас-
Массой абсолютно жесткого бруска АВ v. массой части демпфера, связан-
связанной с ним, пренебречь.
Вариант 19. Два груза D и ? (шп= 15 кг, inf.-= 25 кг) покоятся
на последовательно соединенных пружинах, имеющих коэффициенты
жесткости сх = 250 Н/см и с, = 375 Н/см. В момент, когда снимают
груз ?, точка В опирания пружин начинает совершать движение по
закону | = 0,5 sin 30/ (см) (ось ? направлена вертикально вниз).
Примечание. Положение начала отсчета на оси а-соответствует среднему
положению точки В (д,-=0).
Вариант 20. Па груз D, находящийся в состоянии покоя, соот-
соответствующем статической деформации пружины, в некоторый момент
времени устанавливают груз Е. В этот же момент времени системе
176

двух грузов сообщают скорость v0 — 0,3 м/с, направленную вниз.
Пиклическая частота собственных колебаний груза D на пружине
ко -¦= 2 I с х, отношение масс nif />пп --¦= 3.
Варианты 21—25 (рис. 145). Найти уравнение движения груза D
массой т по гладкой наклонной плоскости, составляющей с горн-
зонтом угол ос, отнеся движение к оси х; за начало отсчета принять
положение покоя груза (при статической деформации пружин).
Вариант 21. В некоторый момент времени груз D(m = 2 кг)
прикрепляют к концам недеформированных пружин, имеющих коэф- "
фицненты жесткости су — 7 и с2 — 3 Н/см; одновременно грузу сооб-
сообщают скорость v0 = 0,4 м/с, направленную вдоль наклонной плоскости
(ос = 45°) вниз.
Вариант 22. Груз D находится на наклонной плоскости (а = 30°)
в состоянии покоя, соответствующем статической деформации пру-
пружины /ст = 2 см. В некоторый момент времени (^ = 0) точка В (верх-
(верхний конец пружины) начинает совершать движение по закону | =
= 0,01 sin 10/ (м) (ось ? направлена вдоль наклонной плоскости
вниз).
Примечание. Положение начала отсчета на оси х соответствует среднему
положению точки В (? = 0).
Вариант 23. Груз D (т = 3 кг) прикрепляют к точке F бруска АВ,
соединяющего концы двух недеформированных параллельных пружин,
и отпускают без начальной скорости. Коэффициенты жесткости пру-
пружин ct = 2 и с2 = 4 Н/см. Точка F находится на расстояниях а и Ь
от осей пружины: a/b = ci/cl; a =60°.
Сопротивление движению груза пропорционально скорости: R =
----- \1о (Н), где V — скорость (м/с). Массой бруска ЛВ и массой демп-
демпфера пренебречь.
Вариант 24. В некоторый момент времени груз D(tn=l кг)
прикрепляют к концу А недеформированных последовательно соеди-
соединенных гтружии, имеющих коэффициенты жесткости сх = 12 и с, =
= 4 Н/см, и отпускают без начальной скорости.
Одновременно (/ = 0) другой конец пружин В начинает совершать
движение но закону ?= 1,5 sin 10/ (см). Ось § направлена вдоль
наклонной плоскости вниз (а = 30с) (см. примечание к варианту 22).
Вариант 25. Концы двух одинаковых параллельных пружин
соединены бруском АВ. Статическая деформация каждой из пружин
под действием груза D(m = 1,5 кг), находящегося на наклонной плос-
плоскости (ее = 30е), /ст = 4,9 см. В некоторый момент грузу D сообщают
сьорость г'0 = 0,3 м/с, направленную вверх вдоль наклонной плоскости.
Сопротивление движению груза пропорционально скорости груза:
# = 6и (Н), где у —скорость (м/с).
Массой абсолютно жесткого бруска АВ и массой части демпфера,
связанной с бруском, пренебречь.
Варианты 26—30 (рис. 145). Пренебрегая массой плиты и считая ее
абсолютно жесткой, найти уравнение движения груза D массой т
с момента соприкасания его с плитой, предполагая, что при даль-
дальнейшем движении груз от плиты не отделяется.
177

21
22
П
23
25
26
ТЛП
'Л Н
¦с,\
_ЛГFt "•
27
28
¦ П
-\т\-
а \ а ¦
—"IT"
,Х
29
30
,п
¦1Е1
Р«с. Hi
178

Движение груза отнести к осп х, приняв за начало отсчета поло-
положение покоя этого груза (при статической деформации пружин).
Вариант 26. Плита лежит на двух параллельных пружинах,
имеющих коэффициенты жесткости 6^ = 600 и с2 = 400 Н/см. Груз D
(т -= 50 кг) падает без начальной скорости с высоты /(=0,1 мв точку F
плиты, находящуюся на расстояниях а и ft от осей пружшг а/b =
Вариант 27. Коэффициент жесткости каждой из двух парал-
параллельных пружин, на которых лежит плита, с— 130 М/см. Груз D (т —
-=40 кг) устанавливают на середину плиты и отпускают без началь-
начальной скорости при недеформированпых пружинах. Сопротивление дви-
движению груза пропорционально скорости: Л! = 400у (Н), где и —ско-
—скорость (м/с). Массой плиты и демпфера пренебречь.
Вариант 28. Груз D надает на плиту с высоты ft = 5 см. Ста-
Статический прогиб пружины под действием этого груза /гт=1 см.
Вариант 29. Плита лежит на двух одинаковых параллельных
пружинах / и 2, коэффициенты жесткости которых сх = с1 = с = 400 Н/см.
В некоторый момент времени груз D(m = 200 кг) устанавливают на
середину плиты и одновременно прикрепляют к недеформироваппой
пружине 3, имеющей коэффициент жесткости ся = 200 Н/см. В тот же
момент времени (при педеформированных пружинах) грузу сообщают
скорость vQ — Q,6 м/с, направленную вниз.
Вариант 30. В некоторый момент времени груз D(m = 100 кг)
устанавливают на плиту и отпускают (при недеформированной пру-
жпье) без начальной скорости. В этот же момент времени точка В
(нижний конец пружины) начинает совершать движение по вертикали
согласно закону Н — 0,5 sin 20/ (см) (ось ? направлена вниз). Коэф-
Коэффициент жесткости пружины с —2000 Н/см.
Примечание. 1 [ачало отсчета на оси х соответствует среднему положению
точки В (|^=0).
Пример выполнения задания (рис. 146). Два груза D и Е мас-
массам 1 гпп =~= 2 и m.f = 3 кг лежат на гладкой плоскости, наклоненной
под углом а ^30° к горизонту, опираясь на пружину, коэффициент
жесткости которой 6 = 6 Н/см = 600 Н/м.
В некоторый момент времени груз Е убирают; одновременно (^ = 0)
нижний конец пружины В начинает совершать вдоль наклонной плос-
плоскости движение по закону ? = 0,02 sin 10/ (м). Найти уравнение дви-
движения груза D.
Решение. Применим к решению задачи дифференциальные урав-
уравнения движения точки. Совместим начало координатной системы
с положением покоя груза D, соответствующим статической дефор-
машш пружины, при условии,'что точка В занимает свое среднее
положение (? = 0).
Направим ось х вверх вдоль наклонной плоскости (в сторону
движения груза D после снятия груза Е). Движение груза D опре-
определяется по следующему дифференциальному уравнению:
тпа = ^ Xlt
179

где ^Xt — сумма проекций на ось х сил, действующих на груз D
(рис. 146, a): GD — веса, N — нормальной реакции наклонной плос-
плоскости, Я —силы упругости пружины.
Таким образом,
Здесь
mDx = — GD sin a — Р.
где /сгд — статическая деформация пружины под действием груза D,
Е —перемещение точки прикрепления нижнего конца пружины, про-
происходящее по закону | = d s'ui pt (d = 0,02 м, р—Ю с1).
a)
Рис. 146
Статическую деформацию пружины /clD найдем из уравнения,
соответствующего состоянию покоя груза D на наклонной плоскости
(рис. 146,6):
т. е.
откуда
VX,-0; — Go sin о+ Я0 --О,
— Gu sin a4-cfctn = О,
Дифференциальное уравнение движения груза D примет вид
mDx = — Сд sin а — с (х — /стд — Н)
180

или после преобразования:
тп lr Jr ex = cdb,[ n pt.
Разделив все члены уравнения иа тп и введя обозначения
c<mn = !i2, cd,mn — h,
приведем дифференциальное уравнение к следующему виду:
I-f/22A' = /? SIM pt.
Решение этого неоднородного уравнения складывается из общего
решения х* соответствующего однородного уравнения и частного
решения х** данного неоднородного уравнения:
х = х* +х**.
Общее решение однородного уравнения имеет вид
Частное решение неоднородного уравнения
Общин интеграл
х = С, cos kt + C2 sin kt + [h/(k2 - p2)] sm pt.
Для определения постоянных интегрирования С\ и С2 найдем,
кроме того, уравнение для х:
Ji = — Clk5wkt + C2k cos kt + [hp/ik*—p2)] cos pt
и используем начальные условия задачи.
Рассматриваемое движение начинается в момент (^ —0), когда
деформация пружины является статической деформацией под дей-
действием грузов D и Е. При принятом положении начала отсчета О
начальная координата груза D равна ха -— — /ст?-, причем Дтр—
GF sin a
~ статическая деформация пружины под действием груза Е.
Таким образом, при t = 0
А'о = — /ст?. Х0 = 0.
Составим уравнения х — x(t) и х=л(() для t~0:
х9 = С» хи = Сгк -f hp!{til -p2),
отк уда
Уравнение движения груза D имеет следующий вид:
kt-[hp/k(k2 - p2)]sin kt + [Л/(А;2- p2)]sin pt,
181

Найдем числовые значения входящих в уравнение величин:
G.. sin a 3-9,81.0,5
f^—Чг- = -1ГТ0О— = °'0245 К
h cd __ __60(Ь 0,02_ „ ^
k--p- ~ тоA^-р') ~ 'C00—100) ~" >U" М>
к(к*-р*) 17,3 -
Следовательно, уравнение движения груза D:
х--^ — 2,45cos 17 3/- i,73sm 17,3/ + 3sin 10/ (см).
Задание Д-4. Исследование относительного
движении материальной точки
Шарик М, рассматриваемый как материальная точка, перемещается
по цилиндрическому каналу движущегося тела Л (рис. 147—149).
Найти уравнение относительного движения этого шарика x==f(t),
приняв за начало отсчета точку О.
Тело А равномерно вращается вокруг неподвижной оси (в вариан-
вариантах 2, 3, 4, 7, 10, 11, 14, 20, 23, 26 и 30 ось вращения zx верти-
вертикальна, в вариантах 1, 12, 15 и 25 ось вращения х, горизонтальна).
В вариантах 5, 6, 8, 9, 13, 16, 17, 18, 19, 21, 22, 24, 27, 28 и 29
тело А движется поступательно, параллельно вертикальной плос-
плоскости l)fix2x.
Найти также координату х и давление шарика на стенку канала
при заданном значении t = x. Данные, необходимые для выполнения
задания, приведены в табл. 46.
В задании приняты следующие обозначения: т — масса шарика М;
со — постоянная угловая скорость тела А (в вариантах 1—4, 7, 10—
12, 14, 15, 20, 23, 25, 26, 30) или кривошипов OYB и 02С (в вариан-
вариантах 6, 17, 22); с — коэффициент жесткости пружины, к которой при-
прикреплен шарик М; /0 —длина недеформировапной пружины;/ — коэф-
коэффициент трения скольжения шарика по стенке капала; Хо, А'о —
начальная координата и проекция начальной скорости на ось х.
Пример выполнения задания (рис. 150). Дано: ос — 30°, (о = яс *;
/72 = 0,01 кг; т=-0,2с; хи-- 0,3 м; .v0 = 2 м/с, с-=0,01 Н/см=1 Н/м;
/0 = 0,2 м; /- = 0,2 м
Найти уравнение x = x(t) относительного движения шарика М,
а также координату х и давление шарика на стенку канала при
заданном t = т.
Решение. Свяжем подвижную систему отсчета Oxyz с вращаю-
вращающимся каналом (трубкой), совместив ось х с траекторией относитель-
относительного движения шарика М.
Вращение этой системы вокруг оси zl является переносным дви-
движением для шарика М. Относительным движением шарика М яв-
182

М
Ю
А-
а
х
Рис 147
183

12
Ifi^tOt
13 г> i
M
14
'Л»
(_3w
; x
15
~-^-\ У,
tp=oit
17
гЛ
ш x \ч
x
м
w
lfi = Ojt
I
I
'*//V/ ////////////
20
iAAA/V7^ —
X
Рис 148
184

o2
21
24-
2,\ У//////////////У///////////A
.— u.
25
26
X ?— ¦
27 *.Ю
28
\х
м
-У,
29
30
'- 1 О
у--?-
//У//// // //у / /У/УУ/УУ/
Рис 149
185

-
•с
Уравнение движения тела А
Е
<э
?
О
и
О
а ш
35
U
S
.1?
?
с
град
йЛ
оооооооооос
ю
1©
I
I
I
о с
о'с
о с
К (
0,02
1
3 С
¦J
эс
5 С
з с
DC
о о о
1 1 оо ' 1 о*
—. 'я"
й •—'
«- |?
м 11 issi
? 5i
1 IIй1
0,15
0,20
0,36
0,20
:оооо ооо;
зоооооо ос
^lo^llcS
5С
I
[
с
с
с
•;
с
If
1
0,20
г -
э с
1С
с
3 С
'с
CffiTJ -'CCCCCMiOlOO
Sooooooooc
э о' о" о" о о" о" о о' с
Ю I О I 1 О О О О
¦ч" 1 со 1 1 те то со
м с
- ^\
io'o с
°, |
о1'
>о о о с
о
г ¦%„
3 с- ^ м
" [ 18 I'iji
[ I tl
[ 1 1
[ I I
г-ч: —
5 О" О О О О О О С
о
'о-
0,20
0,10
0,40
0,20
-СМ — О—'СМ — — С
зо о"— ооо о" с
3 С
3
1 с
DO OO
у] Т О О С
1СЮО СО "*f -
з о о'—о о-о"с
0,01
0,05
0,01
III1.
IcSl |с
г> о о о с
эооос
О | О |
;ос
з о о
ЭОС
3N
1 1
и
ел
О-
U
О
II
1
" 1
О :
II
0,20
0,10
0,20
0,20
н СМ СМ —< -
зо о ос
> -
- иг
DC
0.05
0,03
IS
3 О О С
1
э —г
эоос
3 15
3 5SS
зо ос
О I
со 1
DOC
осо
DOC
"о о
о
I'o-
)°°
II
S*
0,20
0,20
3OO
э —"o"
з — o"o-o
ТЭ CM f
DOC
DOC
1 r-
м?5?
?О ^1
3"o"o"~
о о
CO 1Л
sag
18G

ляется его движение вдоль трубки. Б случае, когда переносное дви-
движение является равномерным вращением, относительное движение
точки определяется уравнением
К шарику М приложены силы: вес G, реакция пружины Р и
нормальная реакция стенки трубки; эту реакцию можно разложить
па две взаимно перпендикулярные
составляющие Nt и У2.
Присоединяем к силам, действу-
действующим на шарик М, переносную
центробежную силу инерции Ф?
и кориолисову силу инерции Фс,
направленные противоположно ус-
ускорениям w^ и wc. Направление
ускорения wc найдем по известно-
известному правилу, предположив, что про-
проекция относительной скорости vr
на ось х положительна. В рассмат-
рассматриваемом примере кориолисова си-
сила инерции Фс параллельна оси у 4
и перпендикулярна к птоскости
хОг (рис. 150).
Модули сил инерции опреде-
определяются по формулам:
Ф'г = ma'" = niti>e (r±x&\na)i
Фс = mwc — 2nvaevr sin a,
где
Рис. 150
ы,, = со, vr — \x\
Основное уравнение относительного движения в данном случае
имеет вид:
^ (О
Составим дифференциальное уравнение относительного движения
шарика М вдоль осп х:
тх = vx, = Ф'е sin а — G cos а — Р;
тх = /пса2 (r-\-x sin а) sin а — mg cos а — с (х —10)
(реакция пружины Р равна произведению коэффициента жесткости
на величину деформации пружины).
Последнее уравнение представим в виде
jc + (с/т — со2 sin2 a) x = со2/" sin a — g cos а -f clo/m. B)
Общее решение полученного дифференциального уравнения B)
имеет вид
Л — л ~~у~ Л j
187

где лf—общее решение соответствующего однородного уравнения;
хм —частное решение уравнения B).
Составим характеристическое уравнение и найдем его корни:
Ji! = |/w2sin2 а- с/т = Vn'-0,J- 1/0,01 = 9,876г.
?.., = — 9,876г.
Таким образом, общее решение однородного уравнения
л* = Сл cos 9,876/ + С2 sin 9,876/.
Частное решение уравнения B) находим в форме
*** = ?
Из дифференциального уравнения B)
х** = В — ы"'sin а~
с/т —
я2-0,2-0,5 — 9,81 -0,866 +A,0-0,2)/0,01
= ^
1,0/0,01 -п». 0,5^ U.l^« M.
Решение дифференциального уравнения B) относительного дви-
движения шарика М получает вид
х = С± cos 9,876/ + С2 sin 9,876/ + 0,128 (м). C)
Скорость этого движения
х = —9,87бСгsin 9,876/ + 9,876С2 cos 9,876/ (м/с). D)
Постоянные Сх и С2 определяем, используя начальные условия:
при t = 0
х0 = 0,3 м, х0 = 2,0 м/с.
Составим уравнения C) и D) для / = 0:
*„ = <?!+ 0,128; хо = 9,876С2,
откуда
Сх = 0,3 -0,128 = 0,172; С2 = 2/9,876 =0,202.
Уравнение относительного движения шарика М принимает вид
х = 0,172 cos 9,876/ + 0,202 sin 9,876/ + 0,128 (м).
Скорость относительного движения шарика
х = —1,69 sin 9,876/ +1,99 cos 9,876/ (м/с).
Для определения составляющих реакции стенки трубки Mt и N2
при / = т = 0,2с выразим векторное уравнение A) в проекциях на
оси у и z. Учитывая, что вектор wr перпендикулярен к этим осям,
получаем:
0 = Л/, - Фс, 0 = N1-G cos 60° - Ф? cos 30°.
188

Из этих уравнений
N2 = <Pt = 2tmavr sin a,
Л/, =-- G cos 60° + Ф? cos 30° = trig cos 6O': + шщ- (r + x sin a) cos 30°.
Для получения числовых значений Л/j и N2 необходимо опреде-
определить координату х и проекцию относительной скорости точки х,
соответствующие значению / = 0,2 с.
х = 0,172 cos (9,876 ¦ 0,2) + 0,202 sin (9,876 • 0,2) + 0,128 =
=-0,172cos 113° + 0,202s!ii ll3° + 0,128=-
= —0,172-0,391+0,202-0,92 + 0,128---0,246 м;
i=—1,69 sin 113°+1,99 cos 113° = —1,69-0,92-
- 1,99 • 0,391 = —1,55 - 0,78 = —2,33 м/с.
Следовательно, составляющие реакции jVj и jV2
Л^! = 0,01-9,81- g + 0,01л2 @,2+ 0',246-0,5)-0,866 = 0,077 Н;
N., = 2- 0,01я • 2,33 • 0,5 = 0,080 Н.
Реакция стенки трубки
= 0,111 Н.
Искомое давление шарика М на стенки трубки по величине равно
найденной реакции N и направлено в противоположную сторону.
ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ
МЛТКРИЛЛЫЮЙ ТОЧКИ
Задание Д-5. Применение теоремы об изменении
количества движения к определению скорости
материальной точки
Телу массой т. сообщена начальная скорость vn, направленная
вверх по наклонной плоскости, составляющей угол а с горизонтом.
На тело действует сила Р, направленная в ту же сторону (рис. 151).
Знай закон изменения силы
Р = Р (() и коэффициент трения
скольжения /, определить ско-
скорость тела в моменты времени
t\, 4. h и проверить получен-
полученный результат для момента
времени I. с помощью диф-
1 Риг I т1
ференциального уравнения дви- г ¦
жения.
Необходимые для решения данные приведены в табл. 47.
При построении графика из.меись'ия силы Р по заданным ее зна-
значениям Ро, Ри Р-,, Рл для моментов времени ta, 1Ъ 1.2, t3 считать
зависимость Р — Р (t) между указанными моментами Бремени лпией-
189

ной. Значение силы Р, задаваемое в табл. 47 в виде дроби, указы-
указывает на то, что модуль силы в заданный момент времени претерпе-
претерпевает «скачок»: в числителе указан модуль силы в конце промежутка
времени, а в знаменателе —в начале следующего промежутка вре-
времени.
Таблица 47
Номер
ва-
варианта
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
го
т.
КГ
35
20
25
10
16
40
20
16
12
50
К)
12
10
20
14
20
24
15
15
22
13
И
12
10
18
8
17
9
20
10
м/с
5,4
0
0
4,5
9,0
4,0
8,0
7,6
0
12.0
5,0
3,0
8,0
8,5
9,0
3,0
10,0
13,0
7,2
8,2
10,0
0,0
4,5
7,0
0
9.0
5,0
7,5
9,5
10,2
Л
4
6
4
5
4
4
5
6
6
2
6
3
4
5
7
5
6
8
3
2
8
7
5
4
8
4
7
4
5
6
и
с
10
10
10
10
8
8
8
11
10
6
10
8
12
8
12
9
10
16
10
9
12
9
10
14
10
8
10
12
6
7
и
18
15
16
16
16
12
И
13
14
12
16
14
16
15
18
17
15
20
16
11
16
14
16
29
16
12
18
17
11
10
Ра
100
200
200
0
120
400
0
75
100
0
50
60
0
40
0
300
0
ПО
150
70
0
160
50
100
180
0
190
0
0
120
Pi
I
200
160
200/120
180
120/0
300
300
200
140
300
100
180
150
100
140
150
180
150
110
НО
200/0
0
120
50
160/0
150
170/0
140/70
400
70
Р2
1
150
1G0
120
40
0
300
0
0
0
200
100
120
150
150
0
100
60
0
90
ПО
0/200
0/100
40
50
0/140
0
100
100/70
400/100
0
Р,
250
180
0
100
160
0
0
0
0
200
200
120
100
0
100
100
140
90
120
50
100
120
80
0
180
120
280
70
200
120
а
град
25
37
21
32
24
40
25
23
20
27
35
42
30
23
18
39
15
26
30
15
28
31
21
18
33
45
38
26
15
33
t
i
0,10
0,25
0,10
0,12
0,08
0,06
0,20
0,12
0,о0
0,08
0,24
0,15
0,18
0,07
0,15
0,12
0,20
0,22
0,30
0,15
0,14
0,11
0,22
0,09
0,17
0,10
0,21
0,20
0,25
0,15
Пример выполнения задания. Дано: т = 40 кг; vo~-\O м/с; tt =
= 3 с; /, = 8с; /,= 12 с; Р„ = 0; Я1 = 250Н; А, = 300/200 Н; Р3 -=
- 150 Н; а = 30=; / = 0,1.
Определить vx, v*, и v3 для tv t2, t3
Решение. Покажем силы, действующие на тело (рис. 151): вес
G, нормальную реакцию плоскости N, силу Р и силу трения сколь-
скольжения F, направив ее противоположно начальной скорости, т. е. вниз
по наклонной плоскости.
Построим график P — P(t) по заданным значениям Ро, Р,, Р2 и
Р3 (рис. 152).
1. Для тела, принимаемого за материальную точку, составим
уравнение, выражающее теорему об изменении количества движения
190

в проекциях па ось х для промежутка времени от 0 до
где
?SIV~ — Gtx sin a— FtL-\-Si>.x.
Проекция импульса переменной силы Р за tx с
A)
Этот интеграл определяется как площадь треугольника ОВМ на
графике Р = Р (t):
SPv = C ¦ 250)/2 = 375 Н • с.
Учитывая, что сила трения скольжения F = /iV=/Gcosa, полу-
получаем уравнение A) в следующем виде:
ти1Х — mvox = — tngt± sin a — fmgt{ cos a-f 375,
vlx = vox — eh sin a — jgtY cosa-f375/m,
vlx = 10 - 9,81 ¦ 3 • 0,5 - 0,1 • 9,81 ¦ 3 • 0,87 + 375/40 =
= 10-14,72-2,56 + 9,38 = 2,10 м/с.
Таким образом,
f1 = alv = 2,10 м/с.
Примечание. Cnia трения скольжения F направлена противоположно
скорости и поэтому, прежде чем производить приведенным расчет, нужно выяс-
выяснить, не изменит ли скорость тела за пречя t± первоначального направления
откуда
т. е.
вверх по наклонной плсckol'tii (у0г>0), а, следовательно, сила трения — направ-
направления вниз.
Для этого надо установить, возможен ли такой момент времени t* <С 11г пра
котором скорость тела ciaiiet равной нулю под действием постоянных сил G,
N, F и силы Р, изменяющейся по закону прямой ОВ: Р = B50/3) ¦ t.
191

Составим уравнение, выражающег теорему об изменении количества движе-
движения, дтя предполагаемого промежутка времени ог 0 до t":
cos a -\-Spxt
где в данном случае
vx = О, Spx = /* • B50/3) t* ¦ 1 /2 = A25/3) • t*>.
В резутьгате получим следующее уравнение для определения (*;
125/3 -t""- — mg (sin a + / cos a) /* + wy0A. = 0,
т. е. •
<*2- A96,2 + 34,1) 3/*/125 + D00 - 3)/125 = 0
или
г*2 —5,52е*+ 9,6 = 0.
Решал это уравнение, делаем вывод, что не существует такого момента вре-
времени, для которого скорость тела, находящегося под действием указанных сил,
будет равна нулю.
2. Для определения скорости тела в момент времени L составим
уравнение, выражающее теорему об изменении количества движения,
для промежутка времени ?, —1{.
mvlx - mvlx = v Six> B)
где
2 Su = - G (tz-tj since- FVt-tJ+Sp,.
Проекция импульса переменной силы Р за (t2 — tt) выражается
площадью трапеции MBCI на графике P = P(t):
SPx = [5 B50 + 300)]/2 = 1375 Н • с.
Поэтому уравнение B) имеет вид
mviK — mvXK = — tng (t2 — it) sin a — fmg cos a ¦ (t2 — t1)-\-1375,
откуда
t'ax^ vtx — gitz — tjsma — fgeosa- (tz — tj + 1375/m =
= 2,10-9,81-5-0,5-0,1 -9,81 -0,87-5 + 1375/40 =
= 2,10 - 24,52 - 4,27 + 34,38 = 7,68 м/с.
Таким образом,
v.1 = v.lx = 7,68 м/с.
Примечание. Прежде чем составить уравнение B), нужно убедиться,
что за время t.2 —1{ перионачальная скорость vt(vlx>-0) не изменит своего
направления. Действительно, в начало движения на этом участке сила Р>
> (G sin a +/G cos а) и продолжает расти, значит, скорость тела не может изме-
изменить своего первоначального направления.
3. Уравнение, выражающее теорему об изменении количества
движения и составленное для промежутка времени !.. — (,, дает воз-
возможность определить скорость тела va в момент /3;
tnv3x-mviA = VS.-*, C)
где
2 5;., = — G (t3 -12) sin а - /G cos a (t, - /а) + 50V.
192

Проекция импульса переменной силы Р за (/3 — 4) с выражается
площадью трапеции IDEK'.
SPl = [4 B00 + 150)]/2 - 700 Н ¦ с.
Тогда
v3< = t'2i-g(U - М sin a -fg cos a (A, -12) -]- 700/40 - 7,68 - 9,81 X
X 4 • 0,5 - 0,1 • 9,81 ¦ 0.87 • 4 + 17,5 - 7,68 - 19,62 — 3,414-
+ 17,5 = 2,15 м/с.
Таким образом,
va = v:ix = 2,lo м/с.
Примечание. Уравнение C) можно составить после того, как установ-
установлено, чго и на третьем участке тело не изменяет направления своей первона-
первоначальной скорости (v2v > 0) и сила трения скольжения направлена в течение всею
промежутка времени t3 —12 вниз по наклонной плоскости. Для этого следует
выяснить, возможен ли такой момент времени т* </3, когда скорость тела станет
равной нулю пол действием постоянных сил G, N, F и силы Р, закон изменения
которой представлен па третьем участке графика (см. рнс. 73) прямой DH. Урав-
Уравнение DE имеет вид:
Р = 200 — [B00— 150)/4] -т = 200- 12,5т,
где т — время, отсчитываемое от момента /а = 8 с.
Составим \равнение, выражающее теорему об изменении количества движе-
движения, для промежутка времени от то = О до т = т*:
то t — mvOx = — mgi* sin a — jivg т*cos a -|- SPxt
где для дансого случая vx = 0, а
В результате получим следующее уравнение, позволяющее определить т*:
G,25t*2 — 200T* + mg(sina+/'cosa)T* — /w2v = 0,
Т*М 230,3-200 40-7,68
Т ¦* 6^5 Т ~ 6,25 ~°
или
т*2 + л, 85т* — 49,1=о.
откуда
т*=— 2,42 i V 5,8li-j-49,U--— 2,41 ±7,41 (с).
Таким образом
т* = 4,99с.
Скорость станет равной нулю при т = 4,99с, по (/3 — /2)<т*, поэтому изме-
изменения скорости в рассматриваемый промежуток времени t3—t2 не произойдет.
4. Проверим полученное в момент /L значение скорости i\ с по-
помощью дифференциального уравнения
тх = v х,.
Раскроем правую часть уравнения:
тх = — Gsina — F + P
или
тх = — mg sin a — /mg cos a + Я,
7 п/р. Яблонского Л Л 193

т. е.
х = — g sin a — fg cos a + P/m,
где Р = B50/3) •/— уравнение прямой OB, а поэтому
i' = —g sin a — g/ cos a + B5/12)- /.
Интегрируя полученное дифференциальное уравнение, получаем
х = — g (sin a + / cos a) t + B5/24) • <2 + С
Для определения С используем начальное условие задачи: при
t=0 vax = x0= 10 м/с.
Составим уравнение, полученное интегрированием, для / = 0,
найдем, что С"=10м/с. Таким образом, уравнение, определяющее
изменение скорости за промежуток времени от 0 до tlt имеет вид:
х = — g (s in a + / cos a) t + B5/24) • t2 + 10.
При * = 3с
»! = ix = — 9,81 @,5 + 0,1 • 0,87) • 3 + B5/24) • 9 + 10 = 2,10 м/с.
Задание Д-6. Применение основных теорем динамики
к исследованию движения материальной точки
Шарик, принимаемый за материальную точку, движется из поло-
положения А внутри трубки, ось которой расположена в вертикальной
плоскости (рис. 153—155). Найти скорость шарика в положениях В
и С и давление шарика на стенку трубки в положении С. Трением
на криволинейных участках траектории пренебречь. В вариантах 3,
6, 7, 10, 13, 15, 17, 19, 25, 28, 29 шарик, пройдя путь 1ц, отде-
отделяется от пружины.
Необходимые для решения данные приведены в табл. 48.
В задании приняты следующие обозначения: т — масса шарика;
ид —начальная скорость шарика; т —время движения шарика на
участке АВ (в вариантах 1, 2, 5, 8, 14, 18, -20, 21, 23, 24, 27, 30)
или на участке BD (в вариантах 3, 4, 6, 7, 9—13, 15—17, 19, 22,
25, 26, 28, 29); / — коэффициент трения скольжения шарика по
стенке трубки; Ло —начальная деформация пружины; Л— величина
наибольшего сжатия пружины; с — коэффициент жесткости пружины;
Я—наибольшая высота подъема шарика; s —путь, пройденный шари-
шариком до остановки.
Пример выполнения задания (рис. 156). Дано: т = 0,5 кг; vA =
= 0,8 м/с; т = 0,1 с (время движения на участке BD)\ /? = 0,2м;
/ = 0,1; a = 60°; р = 30°; А0 = 0; с= 10 Н/см = 1000 Н/м.
Определить vK, v(:, Nc, vD, h.
Решение. Для определения vB и vc применим теорему об изме-
изменении кинетической энергии материальной точки. Движение шарика
на участках АС и А В траектории происходит под действием силы
194

2a,
Рис. 153
195

15
16
о '/////v//// '/'/A;
is
19
20
A l\
\B
Рис 154
196

22
Zj
Z5
¦ О
//////////////////////у///////,
26
/RJft
С W"""?77™r'
¦1
29
30
Рис. 155
197

Таблица 48
Помер
варианта
(рис. 153—
155)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
т,
кг
0,5
0,6
0,4
0,2
0,1
0,3
0,4
0,2
0,5
0,4
0,2
0,4
0,3
0,6
0,1
0,4
0,2
0,3
0,1
0,2
0,7
0,4
0,6
0,5
0,1
0,2
0,8
0,3
0,5
0,8
"А,
м/с
20
16
0
5
8
2
5
1
2
4
6
5
0
0
1
2
0
3
2
10
3
1
2
0
0
2
3
4
0
5
т, с
2,0
0,2
2,0
0,5
1,5
2,0
1,0
0,5
1,5
0,1
1,0
0,4
0,1
2,0
0,1
0,2
0,1 .
0,4
0,1
1,0
0,3
0,2
0,4
0,5
0,2
0,1
0,2
0,1
0,2
0,3
Н, м
2,0
4,0
0,2
1,0
2,0
4,0
1,0
1,5
4,0
0,5
1,0
2,0
1,0
3,0
1,0
2,0
1,0
1,5
0,4
0,5
0,3
0,2
0,2
0,6
0,5
0,2
0,4
0,6
0,5
0,6
F
0,20
0,10
0,15
0,10
0,20
0,10
0,10
0,15
0,25
0,10
0,30
0,20
0,10
0,20
0,15
0,40
0,20
0,10
0,30
0,10
0,20
0,40
0,20
0,30
0,25
0,20
0,15
0,35
0,20
0,15
а.
град
30
45
30
45
30
30
30
30
20
30
45
30
30
60
60
30
30
45
30
60
45
45
45
60
—
30
45
30
45
30
Р.
град
45
20
—
—
20
—
60
60
60
—
60
60
30
20
—
—
60
—
—
—
30
30
—
—
15
30
*—
Л»,
см
_
—
10
—
30
50
0
—
0,2
—
—
50
50
—
40
10
0
—
0
—
—
30
—
—
60
50
1—
с.
Н/см
—
1
.—
„
2
5
4
—
0,2
3
—
10
0,2
—
1,0
—
0,5
1,2
—
1,1
—
—
0,4
—
—
0,1
0,8
—
Величины,
которые
требуется
определить
дополни-
дополнительно
Я
VD
vn
VD
VD
h
VD
VD
vD, h
VD
VD
s
VD
VD
vn
VD
h
—
vn, h
II
VD
VD
vn
vn
vn
тяжести G (силы трения на криволинейных участках не учитываем
mv%/2 — ти'А/2 = ? Л,- —- GZ/j = mgAВ sin a = mg6R sin a;
vB = VvA + \2gRs\noi. = /0.82 + 12 ¦ 9,81 • 0,2 • 0,866=4,59 м/с;
mvh/2 - mv\l2 = ? A{ = GH2 = mg DR sin a + 2R cos a);
Vc — vA — igR B sin a + cos a);
vc = Vv'a
B sin a 4- cos a) =
= j/0,82 4-4 ¦ 9,81 •0,2B-0,866 4-0,5) = 4,26 м/с.
Определяем давление шарика на стенку канала в положении С.
198

В соответствии с принципом Даламбера для материальной точки
геометрическая сумма сил, приложенных к точке, и силы инерции
этой точки равна нулю (рис. 156):
Силу инерции материальной точки можно разложить па нормаль-
нормальную и касательную составляющие
Сумма проекций сил 5, N'c и Ф на ось х должна равняться нулю:
Отсюда
N'c = G cos 60° + Фп = mg cos 60° + ^~ =
= m'
60°
/ 4.2G2 \
,5 (9,81 • 0,5 +2^г) = 25,2 Н.
Искомое давление Nc шарика на стенку трубки по величине
равно найденной реакции N'c и направлено в противоположную сто-
сторону.
Рис. 156
Скорость шарика в положении D найдем, применив на участке BD
теорему об изменении количества движения материальной точки
(рис. 157):
К точке приложены: сила тяжести G, реакция стенки трубки
и сила трения F
FfN'fGp
199

Так как
то
откуда
, Vbx = vb, SSu = — Gsin $¦ t —Ft =
= — mg sin $t — fmg cos $t,
— mvB = — mg sin $-t —
= 4,59-9,81-0,1 @,5 + 0,1 -0,866) = 4,01 м/с.
Phc. 157
Для определения величины максимального сжатия- h пружины
воспользуемся на участке DE теоремой об изменении кинетической
энергии материальной точки (рис. 157):
mvb/2 - mvh/2 = v A, = — ch2/2 - GHa - Fh.
Учитывая, что vE = 0 и H3 — hsin$, получаем
или
с с
Решаем полученное квадратное уравнение относительно h:
G (sin
h = —
-j/"I G (si
(sin p+/cosP) |2 mvj
с r l с
_ 0,5-9,81 @,5 + 0,1-0,866)
~~ 1000
0.5-9,81 @,5 + 0,1. 0,866) J +
Принимаем в качестве искомой величины положительный корень
квадратного уравнения:
h = —0,003 + 0,090 = 0,087 м.
200

II. Динамика механической системы
ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ
МЕХАНИЧЕСКОЙ СИСТЕМЫ
Задание Д-7. Применение теорем об изменении
количества движения и о движении центра масс
к исследованию движения механической системы
Тело 2 (рис. 158—160) приводится в движение приводом, уста-
установленным на теле / (варианты 2, 3, 8, 11, 16, 17, 19, 21, 22, 23,
25, 27), или является составной частью самоходной установки
(варианты 1, 4, 5, 6, 7, 9, 10, 12, 13, 14, 15, 18, 2), 24, 26, 28,
29, 30); угловая скорость тела 2 изменяется по закону:
со2 = со0A -е ").
В начальный момент тело / неподвижно.
Найти уравнение движения и скорость v тела 1, если сила
сопротивления, действующая на это тело, R = bv-\-Ftp.
Заданы следующие величины: т, — масса i-ro тела; r;, R, — радиусы
малых и больших окружностей; Ь — постоянный коэффициент; / —
коэффициент трения скольжения тела / по неподвижной плоскости,
FTp — fN; а, р — углы, показанные на рис. 158—160.
Во всех вариантах нити считать невесомыми и нерастяжимыми;
проскальзыванием нитей и катящихся колес пренебречь.
Пример выполнения задания (рис. 161). 1. Применим теорему об
изменении количества движения системы к телам /—6:
K-7co=vsf, A)
где Ко, K — количество движения системы в начальный момент времени
t — 0 и в некоторый момент времени /; У Sf —геометрическая сумма
импульсов всех внешних сил, действующих на систему за промежуток
времени /.
Так как при ^ = 0 система находилась в состоянии покоя, то
/Со = 0, а следовательно:
tf-vSf. B)
Проектируя равенство B) на оси координат, получаем:
K, = vsFv; (За)
Kj = v Si,,. C6)
Так как количество движения рассматриваемой системы равно
геометрической сумме количеств движения всех тел, входящих в эту
систему, то
К = ~Ki + 2КЯ +'К3 + X + Кь + К».
201

/, /////////////////77///// // ////// '//77////;//////7/7.
'/УУ/У/У/УУ/У/У/УУУУУУ/У.'//'//'//'/'/'/
/7//f/7/77/7//У/У777/77/7////7///////У7,
10
///,'/ /s У/''// '/////у////////,'/ ////////'/
Рис. 158
202

eos
6SI
г
W//M///////////////////////////////////////////////
x>~\
81
91
'//////////////////////////////////////////////у///.

У//У//У/У////Я?7//7//У//,7У////.-7У////////.Г,
22
29
Pkc. 160
204

Количество движения каждого тела равно произведению массы
этого тела на абсолютную скорость движения его центра тяжести
(рис. 162).
Найдем количества движения тел 1—6.
Количество движения тела /:
Тело 2 (колеса) и тело 3 (гусеница) имеют общий центр тяжести
в точке С.,_Я) скорость которого равна скорости точки С2, т. е.
Ус2_з = °с2. Количество движения этих тел обозначим 7B-3, тогда
К2 з = 2/С2 + К3 = Bт2 + тл) ЪСг.
Количества движения тел 4, 5 и 6 равны:
где vc2, vCi, vCi, vca — абсолютные скорости центров тяжести соот-
соответствующих тел.
Неподвижную систему отсчета хОу свяжем с плоскостью (непо-
(неподвижной), по которой движется тело /, а подвижную систему отсчета
Рис. 161
-yjA#i~'c телом /. Абсолютная скорость центра тяжести каждого
тела равна геометрической сумме переносной и относительной скоро-
Iстей, причем скорость тела / явится переносной скоростью для
остальных тел, т. е.
щ --• ve.
Абсолютная скорость центра тяжести С2 3-
VC, = Ve Л' VCar = Vx -J- V c,r,
205

где vctr — относительная скорость центров колес Сг при качении этих
колес без скольжения; модуль этой скорости
Vc,r = СО2/?2.
Абсолютная скорость центра тяжести С4:
Абсолютная скорость центра тяжести Q:
Рис 162
где t><v — относительная скорость центра тяжести С5, модуль которой
где wz;^, VMr — относительные скорости точек L и М тела 5, равные
вращательным скоростям соответствующих точек тела 4, т. е.
Так как
4, ТО Uir =
С04 = VClr/Ri =
и следовательно, Ууиг = со.2/?2
oCsr = A/2) ¦ (cojRa - r^R-i/Rt) = A/2) • <B2#i A -
Абсолютная скорость центра тяжести Со:
206

Найдем проекции абсолютных скоростей центров тяжести тел на
ось х:
(где х — координата центра тяжести Cj)
,.t = ve ~ vc2r cos a — x — oj2/?2 cos a;
D)
vcbx = ve — vcbr cosp = i— A/2)-oj2/?2-A — rjRi) cos P; x '
vc,x = vClX.
Следовательно, проекция количества движения всей системы на
ось х:
Кх = tn-i.x + Bm2 + m3) (i - (a2R2 cos a) + m4x -f-
4- (т5 + тй) [x — A/2) • (a2R2 A — rt/Rt) cos p]
или
/(Л. = mx- tt>2/?2 [B/n2 + /n3) cos a + A/2) ¦ (m& + me) ¦ A - л4/Я4) cos P],
E)
где
m = tnx 4- 2m2 ¦
Сумма проекций импульсов всех внешних сил на ось х:
i t
о о
где G — вес всей системы.
Учитывая, что
J frjc dt = b \ dx = bx и FTp = /Л/,
о о
где Л/ — нормальное давление, имеем
?x = Gtsina-bx-f\Ndt. F)
о
Приравнивая E) и F), получаем
mx-u>2R2 [Bm2+m3) cos а + A/2) • (т5 + т,) ¦ A - rjR4) cos p] =
= Gts\na-bx-f\Ndt. G)
о
Проекции абсолютных скоростей центров тяжести тел на ось у.
vVJ = 0; vc3y = — t'c^r sin a = — co2#2 s'n ai
ocj, = 0; vCilJ = vCir sin p = A/2) ¦ w2tf2 A - rjRt) sin P; (8)
Следовательно, проекция количества движения всей системы
'на ось у.
A/2) (тъ + тй) со2/?гA — г4//?4) • sin P
207

или
Ки = со2/?2 [A /2) • (ms + /ne) A - rjRi) s i n ft - Bш2 + m,) si n a]. (9)
Сумма проекций импульсов всех внешних сил на ось у:
t
2Sfi = — Gt cos a + \N dt. A0)
о
Приравнивая (9) и A0), получаем
G>tRi [0,5 (m-0 + ma)(l — rjRt) sin p — Bm2 + m3) sin a] =
= — G/cosa + ^Л, (II)
о
откуда
\ N dt = Gt cos а + сог/?2[0,5 (m5 + me) A — r4//?4)sinp — Bm2 + m3) sina].
A2)
После подстановки выражения A2) в уравнение G) имеем:
тх + Ьх = (о2#2 [Bт., + т3) (cos a + / s in a) +
+ 0,5 (та + т6) A - rjRi) (cos p - / sin p)] + Gt (sin a -/ cos a), A3)
где
(о„ = (оо A —esf).
Разделив обе части равенства A3) на т, получаем
л- + г)лг = /гA-<г-")-<7Л A4)
где г| = Ыт,
- _ (dO/?8 [B/п2 + т3) (соз ее + / sin а) + 0,5 (т, + те) A — rAiRx) (соз Р — ^ sin P)|
п _ ^- . ^
<7 ~g(f cosa —sina).
Решение уравнения A4) состоит из общего решения соответствую-
соответствующего однородного уравнения х-{-цх = 0 и частного решения уравне-
уравнения A4):
л: = *, + *,. A5)
Общее решение однородного уравнения имеет вид:
х1 = Се-ч'.
Частное решение уравнения A4) найдем в виде:
Подставив частное решение х2 в уравнение A4), получим:
- QlSe «' + Qn + ц (Qie-' + QJ + Q3) = h A - e~^) - qt.
208

Приравнивая коэффициенты при переменных величинах e~st и /,
а также свободные члены, получим следующие равенства:
l = — /г;
откуда
Следовательно,
* = дсх + *., = Се-1* + [A/(s - т)I е-J' + Л/11 + <//п2 - fa/iW • A6)
Постоянную С найдем из условия: при / = О
*о==0.
Это условие приводит к следующему значению С:
Таким образом, уравнение движения тела / можно представить
в следующем виде:
х = [h/(s - Л)] (е-*' - е-*) + A/л) [(q/ц) +Л] 0 - е-") - (?/n) f. A7)
Скорость тела /:
v = i = [/2/(s - n)] (i]e -i' - se-50 + [(<7/rj) + A] e -"' -
1 -e^). A8)
Из выражения A8) следует, что скорость тела / через некоторый
промежуток времени может оказаться равной нулю и тело остано-
остановится. В таком случае уравнение движения A7) справедливо лишь
для этого промежутка времени.
2. К исследованию движения рассматриваемой механической
системы применим теорему о движении центра масс:
vPf, B0)
где v Pf — главный вектор всех внешних сил системы.
Дифференциальные уравнения движения центра масс:
= VKf = yL. B1)
Координаты центра масс данной системы:
"¦2 + тз) *<:,, +т4
т
'12 + т:,)Ус^:
Дифференцируя выражение B2) дважды по времени и учитывая, что
209

получаем:
ХС
Ус
Bm2 + та) yCi + m4ifCt + (тъ + т„) ус<
-
Найдем проекции ускорений центров тяжести тел рассматривае-
рассматриваемой системы на неподвижные оси координат х, у. Проекции скоро-
скоростей центров тяжести приведены в D) и (8).
dvr
4
Подставляем B4) в B3):
mix + Bm2 + /n3) f A' — -^- /?2 sin a j + m4* + (m3 + /я„) X
X
+ m3) -^ /?2 sin a + (m
- ^4 ) sin
ИЛИ
mx - R2 ~ [Bm2 + ms) cos a + 0,5 («5 + me) f 1 - -'4-) cos p]
й
B4)
B5)
2 ^? [o, 5
- ?-) sin p -
sin a
Найдем проекции главного вектора всех внешних сил системы
на оси хну.
XE = %xf^Gs\na-bx-Fip;}
У? = 2 Y? = — G cos a + W. j
Подставляем B5) и B6) в дифференциальные уравнения B1) дви-
движения центра масс системы:
тх - R2 *~ [Bт2 + т3) cos a -f- 0,5 (т8 + тв) х
X (l - J-
210

или
тх + bx = R2 ~ \Bт2 -f tn3) cos а + 0,5 х
X К + т6) A - g-j cos pj + G sin a - fN B7a)
= — Gcosa + N. B76)
Из уравнения B7б) найдем нормальную реакцию Ы, учитывая,
что угловое ускорение колес 2 равно: e2 = -^~ = uj0ses/;
N = w0se«R2 [о,5 (ш5 + me) (l - g-) sin p -
3) sin a]+ G cos a. B8)
Подставляя выражение B8) в B7а), получаем'дифференциальное
уравнение движения тела 1 следующего вида:
x + r\x = Iise-"-q, B9)
где r\ = b/m,
t,_(o0/?2|Bm.2 + ^3) (С08 0С+/sine)+0,5 (ms + Me) A-г4/^4) (соз р — / sin P)l
я _ , ,
<7 = g(/cosa — sina).
Общее решение дифференциального уравнения B9) имеет вид:
х = хх-{- х2,
где дг1 = С1 + Сае'—общее решение однородного уравнения;
Частное решение л:а находим в виде:
Для определения Qi и Q2 подставим частное решение в уравне-
уравнение B9):
Qts2e st — \\sQ^'st + r\Q2 = hs&-st — q.
Приравняв коэффициенты при e~s/ и свободные члены
Qi(s-r\)=-h, 4Q2 = — q,
получим:
Тогда общее решение дифференциального уравнения B9) имеет
вид:
С1 + Се-* + [ft/(s - т))] е-" - (д/ц) t. C0)
Проекция скорости тела 1:
зс = dx/dt = — т)С2е-^ - [hsfts - tj)] e's' T q/Ц. C1)
211

Постоянные интегрирования Сх и С2 определяются из начальных
условий:
при ^ = 0
При 7 = 0 уравнения C0) и C1) принимают следующий вид:
откуда
^ С — ^ _ fa I ^ * ^ 4- '
1 — 2 s — Г] т) (s — л) Л2 s — "Л " Г] ~*~ т|а *
Следовательно, уравнение движения тела / имеет вид:
х = —(e-J'-e-t>0+-—- + /i]- (l-e-1")- q t. C2)
s — 1)v Ч \ Ч / Ч
Это же уравнение получено при исследовании движения механи-
механической системы с помощью теоремы об изменении количества движе-
движения системы [см. A7)].
Задание Д-8. Применение теоремы об изменении
кинетического момента к определению угловой
скорости твердого тела
Тело Н массой тх вращается вокруг вертикальной оси z с посто-
постоянной угловой скоростью 6)О; при этом в точке 0 желоба А В тела Н
на расстоянии АО от точки А, отсчитываемом вдоль желоба, нахо-
находится материальная точка К массой т2- В некоторый момент вре-
времени G = 0) на систему начинает действовать пара сил с моментом
Л1г = /1(^). При t = x действие пары сил прекращается; одновременно
точка К начинает относительное движение из точки О вдоль желоба
АВ (в направлении к В) по закону O,K=s = f2(t — т) для t>%.
Определить угловую скорость тела Н при t = x и при t—T, пре-
пренебрегая сопротивлением вращению тела Н. Тело Н рассматривать
как пластинку, имеющую форму, показанную на рис. 163 — 165.
Необходимые для решения данные приведены в табл. 49 — 50.
В тех вариантах, в которых пластинка Н расположена в верти-
вертикальной плоскости, относительное движение точки К вызывается
силой действующей в той же плоскости; в остальных вариантах под
точкой К подразумевается самоходная тележка.
Пример выполнения задания (рис. 166). Дано: ^ = 200 кг;
т.г--- 80 кг; Мг -ЪШг Мм; шо= = —2 с1; ЛО = 0,8 м; Я = 2,4 м;
а-1,2 м; т-4 с, Т = 6 с; ОК - 0,5 (t - тJ м.
Определить ыг и а)/-, считая тело Н однородной круглой пла-
пластинкой.
212

z
/a /a
H
p
s
^~7уУ
/
I
8
i
H
///
/ a'
\
л /
Рис. 1G3
213

ж
12
в
13
II
и
н
16
17
18
19
го
Рис. 164
214

21
н
/а / а К/
23
а ,., а
/ i
н~
Z5
А
i
>-
1
1
¦
Г
26
в
Z7
28
,н
30
/ a . / a
Рис. 165
215

Таблица 49
Номер варианта
(рис. 163—165)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
* Знак минус
ьг
32
200
120
16
66
160
300
80
20
100
60
40
24
40
120
E0
50
120
00
50
¦10
150
90
50
36
150
120
15
20
150
1еред М
И! г,
КГ,
10
60
40
5
10
80
50
20
5
40
20
10
4
10
50
10
10
¦ 50
30
12
10
50
20
12
8
40
30
4
5
50
— 1
— 2
0
— 3
1,5
— 1,25
— 2
0
5
2
— 1
— 3
4
2
— 4
— 5
_2
3
1
3
— 6
— 1
2
— 3
— 5
— 4
0
— 2
5
0
н (о соответствует
а, м
1
—
2
—
2
1,5
1,6
1,2
1,2
2
2
1
1
—
1
1
—
9
U5
1
—
1,6
\ 2
0,6
—
1,5
1
0,6
0,6
1,6
Ь, м
1,5
—
—
—
1,5
1
V2
—
—
—
—
1,2
—
3
—
—
1,2
1
—
—
—
—
—
1,2
направлению i
Л, м
"to
2
—
1
—
2,5
0,8
2
0,4
—
2
!
2
1,6
0,8
1,2
1
0,6
—
0,3
2
—
—
0,6
—
а,
град
—
120
—
30
—
—
—
—
45
—
15
—
—
—
—
30
30
—
—
—
—
—
—
60
—
—
50
—
—
АО, м
я#/6
1^3/2
0
0,4
0
ла/6
0
яа/2
яЯ/4
1/2/2
0
0
0,5
0
0
0,4
0,6
лК/2
0
ля/б
У 2/2'
яЯ/2
V 3/2
0,2
0
ла/6
0
0,1
0
1,6
ращения часовой стрелки, f
М г = М0*, Нм
— 29,60
101
-120*
21*
15 (/*"
-700*
968
240 Vt
- 29,2*
- 90 Vt
40*
50*2
-27 VT
120*
330*J
74
69*
324
— 135*
— 14*-
75 V t
163
— 210
27*J
20*
1170 Vt
— 25*
5,6*
- 6,3 VT
652*
х, с
3
5
4
2
4
1/3"
1
4
3
4
2
3
1
1
2
о
4
3
2
3
1
4
2
о
2
1
2
3
4
2
Г, с
4
6
6
6
6,5
гКз
2
8
4
5
4
5
3
4
3
6
6
5
3
5
3
5
3
6
4
2
3
4
5
4
EлЯ/12)(*-т)
К3"(*-ТJ
(V2M) (*-т)з
0,6 Vt — т
0,5 (*-т)
Eяа/18)(*-тJ
(я/?/2)(*-тJ
(ла/4)^*-т
(Зя#/4)(*-тJ
(/2"/4) (*-т)
0,4(*-тJ
(ла/3)(*-т)
0,3(*-^т)
0,5 (*-т)
(ла/2) (*-тр
0,3 И —т
0,6 (* —т.)
(л/?/8)(*-тJ
(яа/4)(*-т)
(ла/12)(*-тр
0/2/16) (*-т)*
(я/?/2) К*-т
A/3/2)(*-т)
0,4 J/'*—т
(я/?/6)(*-ТJ
(яа/2)(*-т)*
(*-тР
0,1 1/*-т
Eл#/6)(/ —т)
0,2(*-тJ
.слн смотреть со стороны положнтельного направления оси г.

Таблица 50
Осевые моменты инерции однородных пластинок
mR1-
m (q2 + fc2)
3
ma2
13
"Ж
ma2
IT
Решение. К решению задачи применим теорему об изменении
кинетического момента механической системы, выраженную уравне-
уравнением:
где Lr —кинетически» момент системы, состоящей в данном случае
из тела // и точки К, относительно оси z\ У] А1% —- Alf — главный
момент внешних сил, приложенных к системе, относительно оси г.
217

На систему за время от ? = 0 до t = x действуют силы: вес Gt
тела Н, вес б2 точки К, пара сил с моментом Мг и реакции под-
подпятника и подшипника (рис. 166, а).
Предполагая вращение тела Н происходящим против вращения
часовой стрелки, найдем текущее значение кинетического момента
системы, который складывается из кинетического момента тела
/.о» и момента количества движения точки К, находящейся в точке О
тела Н и имеющей скорость и = о>010:
Таким образом,
m2v ¦ Ofi = т2ы ¦ OLO2
со.
Главный момент внешних сил равен вращающему моменту Мг,
так как другие силы момента относительно оси z не создают.
Уравнение, выражающее теорему об изменении кинетического
момента, примет вид
: = Ми A)
dt г' W
где М, = ct (с = 592 Нм/с).
Разделим в уравнении A) переменные и проинтегрируем левую
и правую части уравнения:
Alt
218

Тогда
(Jt + m2-0l0*)(<ox-<a0)=cr2/2. B)
Найдем числовые значения входящих в уравнение B) величин.
Момент инерции тела Н относительно оси г найдем, используя
теорему о зависимости между моментами инерции относительно
параллельных осей:
J2
где JiC — момент инерции тела Я —однородной круглой пластинки
относительно вертикальной оси, проходящей через центр тяжести С
тела параллельно оси г:
Лс = т1#2/2.
Тогда
Л = т1/?2/2 + т1а2,
т. е.
]г = 200 • 2,42/2 + 200-1,22 - 864 кгм2.
Из чертежа (рис. 166, а)
0х0* = 00 + OjC2 = 1,62 + 1,22 = 4 м2,
поэтому
J -i ¦ Ой02 = 864 + 80 • 4 = 1184 кгм3.
Таким образом, из уравнения B)
1184 К - (—2)] = E92 • 42)/2
имеем
сот = 2 с1.
В течение промежутка времени от t = x до t = T на систему
действуют силы Glt G2, реакции подпятника и подшипника (рис. 166,6).
Поскольку вращающий момент М. снимается, т. е. ^,М?2 = 0, то
dLjdt = 0, Lz = const.
Определим значения кинетических моментов L,x при / = т и LzT
при t — T и приравняем эти значения.
Для t = x
- Ofi*) cox = 1184 • 2 = 2368 кгмг/с.
При t>x скорость точки К складывается из относительной ско-
скорости vr по отношению к телу Н и переносной скорости ve в дви-
движении вместе с телом Н. Поэтому для t = T покажем (рис. 166, б)
два вектора количества движения точки: т<рг и m2ve.
Для t = T
LzT= J/siT-\-tn2<i}T- OtK2T — m2vr- ОгС,
Найдем

где
ОКт = st. т = 0,5 (Т - тJ = 0,5 F - 4J = 2 м,
т. е.
СКт = 2 - 1,6 = 0,4 м, OLKr = 1,22 + 0,42 = 1,6 м2.
Относительная скорость
и, --= dsidt = 2 ¦ 0,5 (t — т)
при / = Г
vr = 2- 0,5 F -4) = 2 м/с.
Поэтому
-1,6-80-2-1,2 = 992(ог-(92.
Приравнивая L.T и LzT
2368 = 992cor- 192,
находим
Задание Д-9. Применение теоремы об изменении
кинетической энергии к изучению
движения механической системы
Механическая система под действием сил тяжести приходит в дви-
движение из состояния покоя; начальное положение системы показано
на рис. 167—169. Учитывая трение скольжения тела / (варианты
1 —3, 5, б, 8— 12, 17 — 23, 28 — 30) и сопротивление качению тела 3,
катящегося без скольжения (варианты 2, 4, 6 — 9, 11, 13 — 15, 20,
21, 24, 27, 29), пренебрегая другими силами сопротивления и мас-
массами нитей, предполагаемых нерастяжимыми, определить скорость
тела / в тот момент, когда пройденный им путь станет равным s.
В задании приняты следующие обозначения: mL, m2, m3, tnl —
массы тел /, 2, 3, 4; /?2, г., R3, гя — радиусы больших и малых
окружностей; Lx, i3j —радиусы инерции тел 2 и 3 относительно
горизонтальных осей, проходящих через их центры тяжести; а, р —
углы наклона плоскостей к горизонту; / — коэффициент трения сколь-
скольжения; б — коэффициент трения качения.
Необходимые для решения данные приведены в табл. 51. Блоки
и катки, для которых радиусы инерции в таблице не указаны, счи-
считать сплошными однородными цилиндрами.
Наклонные участки нитей параллельны соответствующим наклон-
наклонным плоскостям.
Пример выполнения задания. Дано: т, — масса груза /,
т2 = 2т1, т3 = т,, тх — 0,5mj, m:, = 20/^, R2 = Ra = 12 см, f2 =
= 0,5Я2, /-3 = 0,75/?з, #5—-20 см, ЛВ = / = 4/^, U = 8 см; i,.u--=10 см,
а —30°, / = 0,1, 6 = 0,2 см, s= 0,06л м. Сопротивление качению
тела 2 не учитывать. Шатун 4 считать тонким однородным стерж-
стержнем; каток 5 —однородный сплошной цилиндр. Массами звена ВСЪ
220

AB-SR,,
г, = 0,8 R2
Puc 167
221

'У/// '-7. '/////// '. V, У/А, УУ/У/
I i
I —
/7
16 \^/
r2=O,5R2
Рис. 168
222

<a
22
23
25
26
ОС = 2,5 R2
-\
27
23
Рис. 169
223

Таблица Ы
2s-
It
о
¦ Номер
1
2
3
4
5
6
7
8
9
10
11
12
13
14
m,
m
т
in
т
т
т
т
т
т
т
т
т
т
т
кг
4т
1/2pz
т
2т
2т
Зт
2т
1/2т
2т
1/4т
1/2т
1/2т
2т
1/2т
1/5т
1/Зт
1/10т
40т
т
т
Ъп
1 /Зт
Эрг
1/4т
1/4,71
1/5т
5т
5т
4/Зт
—
т
т
—
—
—
—
—
1/ат
—
т
2т
4т
л,
R,
см
—
—
20
20
—
16
—
—
—
—
30
30
_
30
—
40
15
28
25
30
30
—
30
—
20
25
'2V
см
_
—
—
18
18
—
14
—
—
—
—
20
2G
_
20
—
—
—
—
—
20
—
25
—
—
а
р
град
СО
30
45
GO
30
30
30
30
60
30
30
30
_
45
—
—
—
45
—
45
—
—
45
—
—
*
0,10
0,22
0,10
—
0,12
0,10
—
0,15
0,12
0,10
0,17
0,20
—
б см
_
0,20
—
0,30
—
0,28
0,20
0,20
0,25
—
0,20
—
0,24
0,20
2
2
2
0,1л
0,28л
1,5
2
1,75
1,5
3
2,5
2,5
2
2
Примечания
Массами зпеньев АВ, ВС и
ползуна В пренебречь
Массой водила пренебречь
Массы каждого из четырех
колес одинаковы

15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
m
m
in
m
m
m
m
m
m
in
m
m
m
m
m
in
l/2m
1/1 0/n
1/4/n
3m
l/3m
1m
m
I/2m
m
Ы
l/3m
l/2m
m
2m
l/4m
l/2m
4m
l/20m
1/5пг
m
1/10/n
20m
2m
l/4m
1/10ш
20m
l/4m
m
Qm
3m
l/8m
3/10m
l/2m
l/10m
l/10m
m
—
—
4/5m
—
—
l/3/л
l/2m
—
З/2/л
20
10
20
35
24
20
20
20
20
20
16
30
20
20
26
15
12
—
15
—
15
20
10
—
30
20
—
20
—
35
20
18
—
15
32
20
16
16
—
18
18
—
20
16
14
_
20
—
—
—
—
—
—
—
—
—
—
—
18
GO
—
60
60
60
30
30
60
30
—
—
—
30
60
15
30
—
—
—
—
45
—
—
—
—
—
—
30
—
—
0,10
0,15
0,15
0,10
0,20
0,17
0,10
—
—
—
0,10
0,20
0,12
0,25
—
—
—
0,20
C.32
—
—
0,60
—
—
0,20
—
0,20
—
1,5
0,05л
0,16л
0,2л
1,5
0,2л
1,2
0,1л
1
0,08л
0,04л
0,6л
2
0,1л
2,4
2
Массой водила пренебречь
Шатун 3 рассматривать kjk
тонкий однородный стер-
стержень
Массой водила пренебречь
Массами звеньев АВ, ВС и
ползуна В пренебречь
Массой водила пренебречь
Массами звеньев АВ, ВС и
ползуна В пренебречь
Массой водила пренебречь
Массы и моменты инерции
блоков 2 и 5 одинаковы
Шатун 3 рассматривать как
тонкий однородный стер-
стержень
Шатун 3 рассматривать как
тонкий однородный стер-
стержень

и ползуна В пренебречь. На рис. 170, а показана механическая
система в начальном положении.
Найти Dj —скорость груза / в конечном положении.
Рис 170
Решение. Применим теорему об изменении кинетической энер-
энергии системы:
где То и Т— кинетическая энергия системы в начальном и конеч-
конечном положениях; Y.Af —сумма работ внешних сил, приложенных
к системе; У,А? — сумма работ внутренних сил системы.
Для рассматриваемых систем, состоящих из абсолютно твердых
тел, соединенных нерастяжимыми нитями и стержнями,
Так как в начальном положении система находится в покое, то
226

Следовательно, уравнение A) принимает вид:
Т=УА?. B)
Кинетическая энергия рассматриваемой системы Т в конечном ее
положении (рнс. 170, б) равна сумме кинетических энергий тел /,
2, 3, 4, 5:
+ 7'з + 7'4Н-71в. C)
Кинетическая энергия груза /, движущегося поступательно,
Тх = т#\\Ъ. D)
Кинетическая энергия катка 2, совершающего плоское движение,
T2 = m2vh /2 + J2^V2, E)
где Vc2 — скорость центра тяжести С2 катка 2
VC2 = VU ^ (б)
Ji% — момент инерции катка 2 относительно его продольной цент-
центральной ОСИ С25
h\ = mSb G)
щ — угловая скорость катка 2.
Так как каток катится без скольжения, то мгновенный центр
скоростей катка находится в точке Рг. Поэтому
a2 = vc2/C2P2 = v1/R2. (8)
Подставляя F) —(8) в формулу E), получаем
Т2 = ~+ -щ- = -2-Щ{1+ fij w,. (9)
Кинетическая энергия барабанов 3, вращающихся вокруг непод-
неподвижной оси Ох,
T<, = J3xioi>2, A0)
где J3x- — момент инерции барабанов 3 относительно их общей
оси Ох:
ojj — угловая скорость барабанов 3:
<ad = ui-/r3. A2)
Скорость точки Е барабана равна скорости точки D катка,
которую можно найти из соотношения:
а так как
t'c-2 = fI, ^2 = 2r2, то
Следовательно, ve = vd = C/2) vL. A3)
8* 227

Подставляя A3) в A2), получаем
оK=C/2)-»|//>я. A4)
После подстановки A1) и A4) в A0) выражение кинетической
энерпш барабанов 3 принимает вид:
ИЛИ
т.-\*,*?. OS)
Кинетическая энергия шатуна 4, совершающего плоское движение
где t'c4 — скорость центра тяжести С4 шатуна 4, J,^ —момент инер-
инерции шатуна относительно центральной оси C4g, оГ, — угловая ско-
скорость шатуна 4.
Для определения скорости vCi и угловой скорости со, найдем
конечное положение шатуна 4.
Когда груз / пройдет путь s = 0,06л м, барабан 3 повернется на
угол ф3. Этот угол фз можно определить на основании формулы A4);
заменяя в ней щ = кц>3/са, v1 = ds/dt, получаем
da>3 3 ds , 3 ds
-dt^^-rdt "ли d^=2 •/„¦;
после интегрирования (при нулевых начальных условиях)
cF3=C/2)-s/ra.
Из полученного видно, что линейные и угловые перемещения
находятся в такой же зависимости, как соответствующие линейные
н угловые скорости.
Вычислим угол
Ф3 = 3-0,0бя/B-0,09) = л (радиан).
Это значит, что барабан 3 повернется на 180°, при этом шатун 4
из начального положения А0В0 перейдет в конечное положение АВ
(рис. 170, 6).
Так как скорости точек А и В шатуна в этот момент парал-
параллельны, то мгновенный центр скоростей шатуна находится в беско-
бесконечности.
Следовательно, угловая скорость шатуна в этот момент м4 = 0,
а скорости всех его точек равны между собой.
Таким образом, кинетическая энергия шатуна
Tt = m4vhA/2, A6)
где
vCi = vA. A7)
228

Вращательная скорость точки А тела 3
Ид =
или с учетом A4)
Поскольку г3 = C/4) R3, получим
По A7)
va = vA.
Значит,
уС4 = 2wx.
После подстановки A9) в A6) выражение кинетическо.
шатуна 4 принимает вид:
Кинетическая энергия катка 5, совершающего плоское движение
где vCb — скорость центра тяжести Сь катка 5; J5z — момент инерции
катка 5 (однородного сплошного цилиндра) относительно его цент-
центральной продольной оси С-О1, У5| = т5/?5/2; со5 — угловая скорость
катка 5.
Так как каток катится без скольжения, то мгновенный центр
скоростей находится в точке Рь. Поэтому
Следовательно,
Так как звено БС5 совершает поступательное движение, то
Vcb = VR- н0 Vb = vci — 2vv Значит, va> = 2v1.
Поэтому выражение кинетической энергии катка 5 принимает
вид:
B1)
Кинетическая энергия всей механической системы определяется
по формуле C) с учетом D), (9), A5)^B0), B1):
Т = ? + -2"т*-11 + да)vl+i m> Щ vl + 2lUiVl +
да)Щ
Подставляя сюда заданные значения масс, получаем
или
71=129-miuI/2. B2)
229

'мму работ всех внешних сил, приложенных к системе,
' перемещении. Покажем внешние силы, приложенные
170, в).
i тяжести Gyi
AOl — G^ = /Hjgs s i n a. B3)
ibi трения скольжения Fip:
Лрт = — fmtgs cos a. B4)
абота силы тяжести G2:
4 с, = GJic, = m^s s i n a. B5)
Работа сил сцепления F^, ^cus катков 2 и 5 равна нулю, так
как эти силы приложены в мгновенных центрах скоростей этих катков.
Работа силы тяжести G4:
Aat = GAhCi,
где hс4 — вертикальное перемещение центра тяжести С4 шатуна 4 из
начального положения в его конечное положение (рис. 170, г):
Ao^migRs. B6)
Работа пары сил сопротивления качению катка 5
B7)
где Me = 6Л/5 = 6G5 — момент пары сил сопротивления качению катка 5;
<г5— угол поворота катка 5.
Так как каток 5 катится без скольжения, то угол его поворота:
где sa — перемещение центра тяжести С5 катка 5.
В данном примере работу пары сил сопротивления вычислим как
сумму работ этой пары при качении катка 5 влево при повороте
тела 3 на угол я/2 и качении вправо, когда тело 3 повернется еще
на угол л/2.
Перемещение центра тяжести С5 катка 5 равно перемещению пол-
ползуна В влево и вправо:
sC5 = 2(B0B')- B9)
Определим перемещение В0В' при повороте тела 3 на угол я/2.
За начало отсчета координаты точки В выберем неподвижную точку
К плоскости (рис. 170, г). При этом повороте тела 3 шатун из поло-
230

жения AQB0 перейдет в положение KB'. Тогда
где
КВ0 = КО + ОВ0 = R3 + 1/(Л0В0J - (А йО)* =
Следовательно,
В0В' = Я 3 + VlT^Ri -1 = R3 + l/"D/?3J-/?i - 4tfз = 0.88Я 3. C0)
Подставляя C0) в B9), а затем в B8), находим полный угол
поворота катка 5:
Ф5=1,76/?3//?5. C1)
Работа пары сил сопротивления качению по B7):
AMc = -6mbg-l,76R3/R6. C2)
Сумма работ внешних сил определится сложением работ, вычис-
вычисляемых по формулам B3)—B6) и C2):
^]Ai= niigs ¦ sin a — fmLgs cos a -\- tn^gs sin a
Xl,76i?3/i?6.
Подставляя заданные значения масс, получаем
или
^Af^lMm^s. C3)
Согласно теореме B) приравняем значения Т и ^А?, определя-
определяемые по формулам B2) и C3):
129 -т^[/2 = 1,51^^,
откуда
-•/~2 • l,51es -ш АЗ,02 n «I плл1 г,п
г<1 = У 129 = У 129" ' 9'81 ' °'06л = °-2 м/с-
ДИФФЕРЕНГЦ1АЛЬНЫБ УРАВНЕНИЯ ДВИЖЕНИЯ
ТВЕРДОГО ТЕЛА.
Задание Д-10. Исследование вращательного
движения твердого тела
На звено 1 механизма, угловая скорость которого равна coi(/, с неко-
некоторого момента времени (^ = 0) начинает действовать«пара сил с момен-
моментом М (движущий момент) или движущая сила Р.
Массы звеньев / и 2 механизма равны соответственно тг и т2,
а масса поднимаемого груза 3 — т3. Момент сил сопротивления вра-
вращению ведомого звена 2 равен Мс- Радиусы больших н малых окруж-
окружностей звеньев 1 и 2: Rlt rx, R2, r2.
Схемы механизмов показаны на рис. 171—173, а необходимые
для решения данные приведены в табл. 52.
231

2 P
м,
Y/
t
ю
Рис. 171
232

P;:c 172
233

я
22
23
м
м
25
27
28
29
з-\-
Рпс. 173
234

Найти уравнение вращательного движения звена механизма, ука-
указанного в последней графе табл. 52. Определить также натяжение
нитей в заданный момент времени, а в вариантах, где имеется сопри-
соприкасание звеньев / и 2, найти, кроме того, окружное усилие в точке
их касания. Звенья 1 и 2, для которых радиусы инерции iXl и ix>
в табл. 52 не заданы, считать сплошными однородными дисками. •
1 Пример выполнения задания. Дано: т1 — 100; т., — 150; т3 — 400 кг;
Л1 = 4200+ 200/ Нм; /Ис = 2000 Им-const; /?;¦-= 60; /?а = 40 см;
г.2 = 20 см; i.tl = 2
x, = 30 см; <oi,, = 2 С"
М
Рис. 174
Найти уравнение ф.2 = /(/) вращательного движения звена 2 меха-
механизма, а также окружное усилие 5 в точке касания звеньев 1 и 2
и натяжение нити Т в момент времени t1 = 1 с (рис. 174, а).
Решение. К звену / механизма приложены (рис. 174, б) сила
тяжести Gj, движущий момент М, составляющие реакции подшип-
подшипника Ya, ZA, окружное усилие Sln нормальная реакция Nt звена 2.
К звену 2 механизма приложены сила тяжести G2, момент сил
сопротивления Мс, составляющие реакции подшипника YB, 2B, натя-
натяжения f нити, к которой подвешен груз 3, окружное усилие 52 и
нормальная реакция Л/2 звена /.
К грузу 3 приложены сила тяжести G3 и натяжение нити Т'.
Очевидно:
Ss = —Slf Nx=—V, и f' = — f.
235

Номер
варианта
(рис. 171—
— 173)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
mi
100
300
200
100
150
400
300
300
200
250
150
100
180
150
та
кг
300
80
100
250
300
250
200
250
100
100
300
200
100
80
тз
500
500
400
300
600
600
400
700
500
400
700
600
300
400

20
70
60
20
30
70
60
50
80
40
40
30
50
40
р
R2
см
50
—
—
—
—
40
30
60
20
30
20
40
20
60
20
30
50
50
30
30
40
20
30
60
60
30
30
Г2
40
—
20
30
20
20
20
20
—
—
30
—
20
—
'х,
''х,
см
60
60
—
—
70
50
40
50 У 2
30
30
20 V 2
30У
30
50
—
20 У 2
40
30
20 У 2
20
30
—
—
40
60
20
—
М, Им
2100 + 20/
—
6100 + 20/
1000 + 40/
—
4800+10/
—
—
5900 + 30/
2500 + 50/
—
—
—
1800+20/
Р. Н
г
10200+100/
—
—
5500 + 200/
—
3000+ 100/
9700 + 50/
—
—
3900 + 50/
5700 + 50/
2700 + 200/
—
Им
1000
600
800
1400
1500
800
500
500
600
1200
1000
1500
400
700
С '
2
1
0,5
1,5
2
3
0
1
2
0
1
2
0,5
1,5
Т
11
2
0,5
2,5
2
1
4
3
2
3
1,5
2
о
1
2,5
а б л и ц а 52
Звено, для
которого
нужно опре-
делить урав-
уравнение враща-
вращательного дви-
движения
1
2
1
1
2
1
2
1
2
2
1
1
2
1

15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
300
300
250
200
250
400
200
250
200
100
1'"Ч)
250
250
60
50
300
180
250
100*
100
!50
100
J50
100
80
200
80
200
150
200
200
60
500
400
800
600
400
800
300
800
400
500
400
500
500
900
500
600
20
60
50
20
50
50
50
60
40
30
60
50
50
20
20
50
10
40
30
—
30
20
40
20
20
—
—
20
30
—
—
30
50
50
20
50
30
;ю
30
10
30
40
20
40
40
60
40
20
—
30
—
—
20
—
20
—
—
20
—
30
30
10
30
—
10^2
50
40
—
40
40
30^2
50
30
—
60
40
30 1/2
—
—
40
50
40
—
50
20^2
—
20
—
—
30
—
30
30
50
251/2
—
700+40/
5400 + 51Ч
1900 + 20/
3700 + 50/
2300 + 20/
4900+ 40*
900+10/
2100-'-20/
—
7300+ 100/
—
—
4200 + 200/
—
3800+100/
9700 + 200/
—
12600+100/
—
3500+ 1.50/
15200 -г 100/
—
—
7200+50/
300
1200
900
1500
500
1200
800
700
900
500
800
600
700
1500
1000
700
0
1
2
0,5
0,5
2
1
2
0,5
1,5
0
о
1,5
0
2
1,5
1,5
2
2
1
2
1
1,5
0,5
1
1
1,5
2
1
0,5
1
• Радиусы инерции звеньев 1 и 2, iXl и lXi заданы относительно неподвижных осей вращения этнх звеньев.

Составим дифференциальное уравнение вращения звена / вокруг
неподвижной оси xt:
Главный момент Л4п внешних сил, приложенных к звену
(рис. 174, б), относительно оси х1
Момент М приводит в движение систему и поэтому принят поло-
положительным, а момент, создаваемый усилием Su препятствует враще-
вращению звена / и, следовательно, отрицателен.
Дифференциальное уравнение вращательного движения звена /
примет вид
JA1^1 = M-SlRl. A)
Выразим угловое ускорение срх звена / через угловое ускорение
ср2 звена 2.
Так как
ipl/(f2 = R2/Ri, то <f>i = (p2-(R'>/Ri).
Тогда уравнение A) принимает следующий вид:
JJClff2-(^2/Ri) = M-S1R1. B)
Для составления дифференциального уравнения вращения вокруг
сси х2 звена 2, к которому подвешен груз 3, применим теорему
об изменении кинетического момента:
dUJdt = MEXi. C)
Кинетический момент системы 2 — 3 относительно оси х2
здесь JX:a2 — кинетический момент звена 2, вращающегося с угловой
скоростью ел, вокруг неподвижной оси хг; mAvr2 — момент количества
движения груза 3, движущегося поступательно со скоростью и.
Так как v = сй2г2,
LXt = (Jx2 + tnA) Щ = -^прх2ф2,
где Jnpx2 = JXi + m3rl — приведенный к оси х> момент инерции сис-
системы 2 — 3.
Главный момент М*г внешних сил, приложенных к системе 2 — 3
(рис. 174, б), относительно оси х2
Момент, создаваемый усилием 52, приводит в движение систему
2^—3 и поэтому принят положительным, а момент силы тяжести груза
G3 и момент сил сопротивления Мс препятствуют движению системы
и, следовательно, отрицательны.
238

Таким образом, из уравнения C)
(^Ф) SR
- G3r2 - Мс
получаем следующее дифференциальное уравнение вращения звена 2:
JnpxJh = S2Ro. — йлгг — Мс. D)
В полученной системе уравнений B) и D)
= М — Sftu Jvpxtfz = S2^2 ~ G3r2 — Mc
неизвестны усилия Sx = S2 = S и угловое ускорение ф2. Исключим
5, для чего первое из уравнений этой системы умножим на R2, вто-
второе—на /?! и сложим соответствующие части уравнений:
[/v! (ВДО + -/прхЛ] Ф2 = MR2 - (G3r2 + Мс) Rlt
отсюда
Выражение E) определяет в общем виде угловое ускорение звена
2 механизма.
Учитывая исходные данные, найдем:
JXi--:-miH-t - 100@,2\Г2J--^8 кгм2;
JnpX2 = JX2 -f m3rl ¦--= nioji, + m3r'2 ¦-= 150¦ 0,32 + 400 • 0,22 = 29,5 кгм2.
Из выражения E)
D200 + 200/) 0,^^^.0,2 + 2000) 0,6» = 4034,+ 0L597 (c-,)§
Интегрируем это уравнение дважды:
фа = 2,017^ +0,4597/+ С„
Для определения постоянных интегрирования используем началь-
начальные условия задачи: при t = 0, <jp2<, = 0,
ф2о = со2о = a>]llR1/R2 = 2¦ 60/40 = 3 С.
Следовательно,
С
т. е.
= 3 с-1,
Уравнение угловой скорости звена 2 имеет вид
ф, = 2,017*а +0,4597/+ 3 (с »).
Искомое уравнение вращательного движения звена 2 имеет вид
(рад).
230

Окружное усилие S можно определить из уравнения D):
S = S2 = (Упрх2Ф2 + G3r2 + MC)IR2;
при ^=1 с
с 29,5 D,034- 1 +0,4597) + 400 -9,81 0,2 + 2000
6= д-? =
Для определения натяжения нити Т составим дифференциальное
уравнение вращения звена 2 (рис. 175)
— 7Y2 — Мс,
в следующем виде:
из которого
при tl = 1 с
7295-0.4 — 2000-13,5 D,0334 - I +0,4597)
~ 0,2 -
= 4285 Н.
Задание Д-Н. Исследование плоского движения
твердого тела
Определить максимальную величину постоянной силы Р, под дей-
действием которой колесо массой m катится без скольжения.
Найти также Для этого случая уравнение движения-центра тяжести
колеса С, если в начальный момент времени его координата лс„ = 0
и скорость vca -— 0.
Варианты задания показаны на рис. 176—178, а необходимые
для решения данные приведены в табл. 53.
В задании приняты следующие обозначения: t'c — радиус инерции
колеса относительно центральной оси, перпендикулярной к его плос-
плоскости; R и г —радиусы большой и малой окружностей; /сЦ —коэф-
—коэффициент сцепления (коэффициент трения покоя); б — коэффициент
трения качения.
Примечание. Колеса, для которых радиусы инерции не указаны, считать
сплошными однородными дисками.
Пример выполнения задания. Дано: m =200 кг; #=60 см; г ~
— 10 см; (С = 50 см; а =15°; 0 = 30°; /сЦ = 0,Ю; 6 = 0 (рис. 179, а).
Решение. На колесо действуют силы: вес колеса G, нормаль-
нормальная реакция N, сила Р и сила сцепления Fca (рис. 179, б) (в слу-
случае, если б Ф 0, необходимо показать момент пары сил сопротивле-
сопротивления качению).
240 /

77//////// Y/, '¦//////.
¦//////////////у//, .//.:
10
Рис. [76
241

12
13
!д
V7/77777//'/77////.
... r-Г. У
~/ У//////// *"•
15
19
17
18
Y7/7/77//A
19
20
7777777777,'/77//////Л
Рис. 177
242

21
22
'/УУУЖУУУУУУгУУУУ.уУ////.
р
25
26
'/У/У/УУУУ///УУУ/у7уУУ,
27
28
'//уу/у//?уу\
29
30
V77/.',. /¦![' /,.-/////.'.
Рис 178
243

Номер
P2p*l 3 IIT3
(рис 176—
— 178)
1
о
3
4
5
6
7
8
О
10
11
12
13
14
15
10
17
18
10
20
21
22
23
24
25
26
27
28
29
30
m кг
300,
200
180
11)
240
200
200
150
24)
150
200
220
1-Ю
300
180
180
100
260
200
2W
200
150
200
240
100
150
120
150
200
160
50
40
50
30
40
—
45
40
—
40
30
—
—
—
20
30
50
50
40
30
30
30
—
30
—
—
Л, см
80
60
(Ю
70
60
50
60
70
50
50
50
50
60
50
60
50
40
50
60
70
30
60
40
г, см
40
30
20
2')
.—
2")
25
—
15
20
—
—
—
20
35
20
20
30
20
30
30
—
—
2)
—
—
а град
20
—
30
30
15
30
15
20
30
30
30
—
.
15
—
20
30
30
15
3,)
15
—
1)
Р. град
—
30
-_
15
—
30
—
—
30
30
—
15
20
20
.—
15
—
60
15
—
2)
—
Табл
'с
0,35
0,20
0,10
0,20
0,10
0,20
0,25
0,50
0/5
0,30
0,20
0,25
0,10
0,15
0,15
0,15
0,30
0,10
0,!0
0,25
0,25
0,25
0,40
0,15 -
0,10
0,15
0,40
0,30
0,30
0,20
и ц а 52
й, см
1,0
0,8
0
0
1,0
0,5
0
0
0
0,7
O,ii
0
0
0
0
0,9
0
1,0
0
0
1,2
1,2
0
0
0
0
1,5
0,8
0
0,7
В соответствии с направлением силы Р вращение колеса проис-
происходит по движению часовой стрелки, т. е колесо катится вверх
по наклонной плоскости. Силу /\.ц направляем предположительно,
как показано на рисунке. Действительное направление этой силы
устанавливается в процессе решения задачи. Оси координат выби-
выбираем так, чтобы ось х была направлена в сторону движения колеса
(рис. 179).
Дифференциальные уравнения плоского движения колеса:
тхс -= У] Xl: ¦
-^У, Y?; Jc<f =
Mct
или в данном случае
т~с = Р cos р* — Gsina — FC
nu)r = N- Gcosa- P sin p
A)
B)
C)
Знак у момента силы в уравнении C) принимаем положительным,
если момент способствует вращению колеса, и отрицательным — в обрат-
обратном случае.
244

Из уравнения B) следует, что, поскольку y = /? = const, yc = 0,
N = G cosa + Psinfl.
При качении колеса без скольжения угловая скорость
(o = vcfR или ф = л'с//?, откуда ip — Xc/R.
Таким образом, уравнение C) принимает следующий вид:
alR. C')
Для исключения Хс разделим уравнение A) на C'):
R __ PcosP — Gsin a — Fcu
откуда
р _FCn(R
h since
lc cos P — Rr
D)
Заметим, что выражение D) дает возможность судить о правиль-
правильности выбранного направления силы сцепления. Приближение силы
Р к своему предельному значению (искомой величине) сопровожда-
сопровождается, естественно, возрастанием силы сцепления. Поэтому в выра-
выражении D), приведенном к виду
коэффициент а должен быть положительным. В противном случае
следует изменить направление Рса на обратное и внести соответствую-
соответствующие изменения в дифференциальные уравнения A) —C).
Максимальное значение силы сцепления:
^сТ = UN = /сц (G cos а + Р sin p).
Подставляя максимальное значение /^ц в уравнение D) и решая
его относительно Р, найдем максимальное значение этой силы, при.
245

действии которой колесо катится без скольжения:
р _G [(У?2 + 1&)/сцСояое-'Г1& sina|
iccosp — Rr— (Яа+ Гс)/С„ sin 0
ИЛИ
р _200 |@,ба-Ю,5Ч-0,1 -0,966 + 0,5*-0,2591 -9,81 _ . . qS]_1qOn И
Г~ 0,5=-0,866-0,6-0,1-@,62+ 0,5-!) 0,1-0,5 - 1УО • у,О1 - lyzu л.
Сила сцепления
К" = /cu (G cos a + Р sin Р) = 0,1 B00 ¦ 0,966 + 196 ¦ 0,5) 9,81 =
= 29-9,81 =284 Н.
Дифференциальное уравнение движения центра колеса
™*
тхс = Р cos р - G sin а - F™
или
200*'с = 1920 • 0,866 - 200 • 9,81 ¦ 0,259 - 284,
откуда
= 4,4 м/с2.
Дважды интегрируя это дифференциальное уравнение, находим:
Имея в виду, что при ^ = 0 хс„ — 0 и хс<1 = 0, определяем:
С1 = 0 и С,-0.
Следовательно, уравнение движения центра колеса
xc--=2,2t- (ы).
УДАР
Задание Д-12. Исследование соударений
твердых тел
Варианты 1—10 (рис. 180). Вариант 1. Тележка / общей
массой тх = б000 кг, движущаяся со скоростью v1 = 2,5 м/с по гори-
горизонтальному прямолинейному пути, наталкивается на неподвижную
тележку 2, имеющую вместе с контейнером массу т2 = 4000 кг.
В конце соударения тележка 2 приобретает скорость и2 = 2 м/с,
а контейнер — угловую скорость вращения вокруг ребра А, зак-
закрепленного упорной планкой. Считать контейнер массой шо = 500 кг
однородным прямоугольным параллелепипедом (а = 0,8м, h — 1,5 м).
Вертикальные плоскости соударения тележек полагать гладкими.
Определить скорость тележки / в конце соударения с тележкой
2, а также ударный импульс, воспринимаемый упорной планкой.
Вариант 2. Груз массой mfl = 500 кг падает с высоты /i=l м
в точку D абсолютно жесткой балки, имеющей шарнирно-неподвиж-
ную опору А и упругую опору В, коэффициент жесткости которой
246

Г
и
зщ
1/7
'Ж2
/I1
e
J
Рис. 180
247

с —20000 Н/см; удар груза о балку неупругий. Масса балки т =
— 6000 кг, ее длина / = 4 м. Горизонтальное положение балки,
показанное на чертеже, соответствует статической деформации упру-
упругой опоры под воздействием веса балки. Принять балку за тонкий
однородный стержень, а груз —за материальную точку.
Определить ударный импульс, воспринимаемый балкой в точке D,
а также наибольшую деформацию упругой опоры, считая, что дви-
движение точки В происходит по прямой.
Вариант 3. Вследствие разрыва удерживающего троса груз
массой то = 500 кг падает с высоты Л=1 м на платформу, покоя-
покоящуюся на одинаковых и симметрично расположенных рессорах.
Точка А, в которую падает груз, находится в вертикальной попереч-
поперечной плоскости симметрии платформы и отстоит от центра тяжести С
платформы на расстоянии d = 0,6 м.
Удар груза о платформу неупругий. .Масса платформы т = 5000 кг,
радиус ее инерции относительно горизонтальной продольной оси
симметрии ic — 0,5 м.
Принимая платформу за абсолютно твердое тело и считая груз
материальной точкой, определить скорость центра тяжести и угло-
угловую скорость платформы в конце удара. Определить также ударный
импульс в точке А.
Вариант 4. Груз— однородный сплошной цилиндр массой т =
— 200 кг и радиусом г — 0,2 м перемещается транспортером. Лента
транспортера горизонтальна, ее постоянная скорость v = 0,6 м/с;
скольжение лепты по шкивам 1 и 2 отсутствует. В некоторый момент
времени движение транспортера внезапно прекращается.
Поскольку поверхность ленты транспортера абсолютно шерохо-
шероховата, т. е. не доп>скает скольжение тела при ударном воздействии,
цилиндр вследствие внезапной остановки транспортера покатится
по ленте. Сопротивление качению пренебрежимо мало.
Определить ударный импульс, воспринимаемый абсолютно шерохо-
шероховатой поверхностью ленты при внезапной остановке транспортера.
Проверить найденную для этого скорость центра тяжести (пли
угловую скорость) цилиндра по теореме Карно.
Определить ударный импульс, воспринимаемый упорный ступень-
ступенькой высотой Л = 0,03 м, о которую ударяется колесо, пройдя неко-
некоторое расстояние, если не происходят отрыв цилиндра при ударе
о ступеньку и его проскальзывание.
Вариант 5. Транспортируемые грузы катятся из положения Л
без начальной скорости по наклонной плоскости, составляющей угол
а=15° с горизонтом, проходя вдоль нее расстояние s, = 3 м, и
продолжают катиться по горизонтальной плоскости. Скольжение
отсутствует; коэффициент трения качения 6 = 0,8 см.
Определить, на каком расстоянии s. должна быть поставлена
упорная ступенька высотой h = 0,2 м, чтобы грузы, ударившись о ребро
F ступеньки, лишь поднимались на нее, не перемещаясь дальше
ребра F.
Расчет произвести для груза — однородного сплошного цилиндра
массой т = 500 кг и радиусом /- = 0,5 м.
248 ^

Считать, что отрыва цилиндра от ступеньки не происходит, а поверх-
поверхность ступеньки абсолютно шероховата, т. е. препятствует скольже-
скольжению цилиндра при ударном воздействии.
Определить также горизонтальную и вертикальную составляющие
ударного импульса, воспринимаемого цилиндром со стороны ступеньки,
при указанных условиях.
Вариант 6. /Маятник состоит из стержня длиной /=1,2 м и
однородного круглого диска радиусом г = 0,1 м. Масса стержня
пренебрежимо мала; масса диска тй----Ъ кг.
Маятник, отклоненный от положения устойчивого равновесия,
падает под действием собственного веса, вращаясь вокруг неподвиж-
неподвижной оси О; в вертикальном положении, имея угловую скорость
ю = 3 с х, маятник ударяется о точку В боковой грани тела D —
однородного прямоугольного параллелепипеда массой т —6т0 (а =
— 0,8 м, 6 = 0,4 л</ /г = 0,2 м).
Коэффициент восстановления при ударе /г = 0.5. Поверхности
маятника и тела D в точке соударения гладкие. Плоскость, па кото-
которой покоится тело D, абсолютно шероховата, т. е. не допускает
скольжения тела при ударном воздействии.
Определить угловую скорость вращения тела D вокруг ребра А
в конце удара, а также ударный импульс, воспринимаемый шерохо-
шероховатой поверхностью в точке А.
Вариант 7. Рычаг состоит из двух абсолютно жестких стерж-
стержней АВ и AD, соединенных под прямым углом. Рычаг имеет непод-
неподвижную горизонтальную ось вращения А и удерживается в точке В
пружиной; AD == а = 1,5 м.
В точку D горизонтального стержня рычага, находящегося в покое,
с высоты Л = 0,5 м падает груз массой то—\(Ю кг. Масса рычага
т=10(H кг, радиус его инерции относительно оси вращения iA =--
— 0,5 м. Положение центра тяжести С рычага определяется коор-
координатами лс = 0,4 м и i/c = 0,3 м. Считать груз материальной
точкой, а удар груза о рычаг принять неупругим.
Определить ударный импульс, испытываемы» грузом, а также
горизонтальную и вертикальную составляющие ударного импульса,
воспринимаемого опорой А.
Вариант 8. На тележке / лежит груз —однородный полый
тонкостенный цилиндр массой шо = 5О() кг и радиусом г = 0,4 м,
который удерживается от возможного перемещения по тележке сту-
ступенькой и наклонной плоскостью, составляющей угол а = 60° с гори-
горизонтом.
Тележка /, имеющая вместе с грузом массу ша = 3000 кг, дви-
двигаясь по горизонтальному прямолинейному пути, наталкивается
со скоростью и1 = 3 м/с на неподвижную вагонетку 2 общей массой
т.2 = 6000 кг. В конце соударения тележка / останавливается,
а цилиндр, ударясь о наклонную плоскость, начинает катиться по ней.
Отрыва цилиндра при ударе о наклонную плоскость не происходит,
абсолютная шероховатость наклонной плоскости исключает сколь-
скольжение цилиндра при ударном воздействии. Считать вертикальные
плоскости соударения тележки и вагонетки гладкими.
249

Определить угловую скорость цилиндра в конце удара о наклон-
наклонную плоскость; проверить найденное выражение угловой скорости
цилиндра по теореме Карно.
Определить скорость вагонетки 2 в конце соударения с тележ-
тележкой /.
Вариант 9. Тело D массой т0, поступательно движущееся по
горизонтальной плоскости, ударяется со скоростью vQ = 3 м/с об
узел С вертикального пояса покоящейся фермы. Поверхности тела D
и узла С в точке соударения гладкие; коэффициент восстановления
при ударе & = 0,5. Абсолютно жесткая ферма имеет шарнирно-непо-
двнжную опору 0 и упругую опору А; ВС=--а = 2 м. Масса фермы
m = 20m0, радиус ее инерции относительно горизонтальной оси вра-
вращения 0 io= 1 м.
Определить угловую скорость фермы в конце удара и проверить
ее по теореме Карно.
Определить, на какое расстояние s переместится, двигаясь посту-
поступательно, тело D после удара, если коэффициент трения скольже-
скольжения / = 0,1.
Вариант 10. Отклоненный на угол а = 60° от положения
устойчивого равновесия маятник падает без начальной скорости под
действием собственного веса, вращаясь вокруг неподвижной оси О.
В вертикальном положении маятник ударяется точкой F о покоя-
покоящееся тело, находящееся в положении А.
Расстояния от точки 0 пересечения оси вращения вертикальной
плоскостью симметрии маятника до его центра тяжести С и до
точки F, находящейся в той же плоскости: ОС = d = 0,9 м и OF—
= /=1,1 м.
Масса маятника т=\8 кг, радиус его инерции относительно оси
вращения to=l м. Тело имеет массу то = 6 кг и может быть при-
принято за материальную точку. Коэффициент восстановления при ударе
маятника о тело & = 0,2.
Вследствие удара тело падает из точки Л плоскости А В в точку D
гладкой горизонтальной плоскости DE. Плоскость DE расположена
ниже плоскости АВ на /i=l м. Удар тела в точке D можно счи-
считать неупругим (kl = 0).
Определить ударный импульс в точке D и уравнение движения
тела после этого удара, отнеся движение к координатной системе xDy.
Определить также угол р* отклонения маятника после удара
о тело в точке А.
Вариант 11—20 (рис. 181). Вариант 11. При испытании на
ударную нагрузку маятник копра массой т0 = 500 кг, отклоненный
из положения устойчивого равновесия на угол ос — 60°, падает без
начальной скорости под действием собственного веса, вращаясь во-
вокруг неподвижной оси О.
В вертикальном положении маятник ударяется точкой А о сере-
середину D покоящейся вертикальной балки BF массой т ^2000 кг,
имеющей шарнирно-неподвижную опору В и упругую опору F (BF =
— 2а =3,2 м); балку можно считать однородным тонким стержнем;
коэффициент восстановления при ударе ^ = 0,4.
250

12
rd
'//////У/////////////////////////////////////
15
16
\ 2
а/ /ууу//ууУ///у//уУ///
Г'-ф: ;(t>
17
20
'S7777777SS7//
Рис. 181
251

Расстояние от точки О пересечения оси вращения маятника вер-
вертикальной плоскостью его симметрии до центра тяжести С маятника
OC — d-^ 1,5 м, а расстояние от точки О до точки А, лежащей в той
же плоскости симметрии, 0Л=/ — 2 м; радиус инерции маятника
относительно оси вращения jo=l,8 м. Отклонившийся после удара
на угол р маятник задерживается в этом положении специальным
захватом.
Определить ударный импульс в точке D и расстояние от точки В
до точки, в которую следует наносить удар, чтобы опора В не испы-
испытывала ударного импульса.
Вариант 12. Тележка /, имеющая вместе с контейнером массу
т, = 2000кг и движущаяся по горизонтальному прямолинейному
пути со скоростью ^ = 2,5 м/с, наталкивается на тележку 2 общей
массой /п2 = 8000 кг, движущуюся со скоростью и* = 0,5 м/с по тому
же пути и в том же направлении.
В конце соударения тележка 1 останавливается, а контейнер
приобретает угловую скорость вращения вокруг ребра А, закреп-
закрепленного упорной планкой. Считать контейнер массой /по = 5ОО кг
однородным прямоугольным параллелепипедом (а = 0,9м, h =1,2 м),
а вертикальные плоскости соударения тележек гладкими.
Определить угловую скорость контейнера в конце соударения
тележек и проверить найденное выражение по теореме Карно. Опре-
Определить также коэффициент восстановления при соударении тележек.
Вариант 13. Ось О подвеса маятника движется поступательно
в горизонтальной плоскости с постоянной скоростью, при этом маят-
маятник занимает вертикальное положение устойчивого равновесия. Радиус
инерции маятника относительно оси О го = 0,8 м.
При внезапной остановке оси подвеса маятник, находясь в том
же положении и приобретя угловую скорость, ударяется точкой А
о покоящееся тело D, имеющее массу mo = 2,5m, где т — масса маят-
маятника. Поверхности маятника и тела D в точке соударения гладкие.
Коэффициент восстановления при соударении маятника и тела & = 0,6.
Расстояния от точки О до точки Л и до центра тяжести С маят-
маятника, отсчитываемые вдоль его вертикальной оси симметрии, 1 = 1 м
и d = QJ м соответственно. После удара тело D, двигаясь поступа-
поступательно, перемещается по горизонтальной плоскости на расстояние
s = 0,l м; коэффициент трення скольжения тела по плоскости / = 0,1.
Определить скорость оси О подвеса маятника перед внезапной
остановкой, а также угол р* отклонения маятника после удара
о тело D.
Вариант 14. Абсолютно жесткая конструкция, имеющая форму
прямоугольного треугольника со сторонами АВ = а=\ м и BD —
-Ь = 2 м, опирается на шарнирно-неподвижную - опору А и удер-
удерживается в точке В пружиной.
В точку D конструкции, находящейся в состоянии покоя, при
котором сторона BD горизонтальна, с высоты h = 0,5 м падает груз
массой /гсо = 2ОО кг; удар груза неупругий. Считать конструкцию,
масса которой т = 2000 кг, однородным треугольником, а груз —
материальной точкой.
252

Определить углов} ю скорость системы в конце удара и проверить
найденное выражение угловой скорости по теореме Карно. Опреде-
Определить также ударным импульс, испытываемый onopoii А.
Вариант 15. При транспортировке [рузы из положения А
скользят без начальной скорости по наклонной плоскости, состав-
составляющей у юл а -30 с горизонтом, проходя вдоль нее расстояние
s1 — 3 м, и продолжают движение по горизонтальной плоскости.
Определить, па каком наименьшем расстоянии BD должен быть
поставлен }пор D для остановки грузов, чтобы они при этом не
опрокидывались. Расчет произвести для груза —однородного пря-
прямоугольного п?раллслепь!!еда Maccoii т —500 кг (Ь = 2а=1 м).
Принять коэффициент трения скольжения /-0,2.
Определить также ударный импульс, воспринимаемый упором
при указанных условиях.
Вариант 16. Вагонетка / общей массой /«j--6500 кг, дви-
движущаяся по горизонтальному прямолинейному пути, наталкивается
на неподвижною тележку 2, имеющую смеете с грузом массу т2 -
=--4000 кг. Груз — однородным полый тонкостенный цилиндр массой
/«„=-500 кг и радиусом г =--0,5 м удерживается от возможного пере-
перемещения но тележке двумя упорами— ступеньками.
В конце соударения вагонетка / и тележка 2 приобретают оди-
одинаковую скорость движения но горизонтальному прямолинейному
пути, а цилиндр — угловую скорость вращения вокруг ребра ? сту-
ступеньки DE. Поверхность ступеньки абсолютно шероховата, т. е.
препятствует проскальзыванию цилиндра при ударном воздействии;
отрыва цилиндра при ударе о ребро Е не происходит. После удара
цилиндр поднимается на ступеньку DE высотой //--0,1 м. Считать,
что за время подъема цилиндра на ст\ пеньку скорость тележки 2,
приобретенная ею в конце }Дара, остается постоянной, а вертикаль-
вертикальные плоскости соударения вагонетки и тележки гладкие.
Определить ударный импульс, испытываемый цилиндром со сто-
стороны ступеньки DE, а также скорость вагонетки / до столкновения
ее с тележкой 2.
Вариант 17. Ось О подвеса маятника движется поступательно
в горизонтальном плоскости с постоянной скоростью v=--2 м/с, при
этом маятник занимает вертикальное положение устойчивого равно-
равновесия. Маятник — однородный тонкий стержень длиной 1-Х м и
массой та — 20 кг.
При внезапной остановке оси подвеса маятник, находясь в том
же положении и приобретя угловую скорость, ударяется точкой Е
о неподвижный однородный полый тонкостенный цилиндр радиусом
г —0,2 м п массой т-—2т0. Коэффициент восстановления при соуда-
соударении тел k--- 1/3. Поверхности маятника и цилиндра в точке соуда-
соударения гладкие. Плоскость, на которой покоится цилиндр, абсолютно
шероховата, т. е. не допускает скольжения тела при } дар ном воз-
воздействии.
Определить ударный импульс, испытываемый осью 0 подвеса
маятника при ее внезапной остановке, а также угловую скорость
цилиндра в конце соударения с маятником.
253

Вариант 18. Абсолютно жесткая балка массой т = 8000 кг и
длиной / = 4 м имеет упругую опору А и шарнирно-неподвижную
опору В. Балка занимает в состоянии покоя, соответствующем ста-
статической деформации пружины А, горизонтальное положение; коэф-
коэффициент жесткости пружины с= 10000 Н/см. Радиус инерции балки
относительно горизонтальной оси вращения В гл = 2,2 м.
Балка испытывается на воздействие ударной нагрузки с помощью
парового молота, в котором масса молота, штока и поршня rnQ =
= 800 кг. Молот и связанные с ним части падают под давлением
пара на середину балки с высоты h = 0,8 м, имея в момент сопри-
соприкосновения с балкой скорость, в два раза превышающую скорость
при свободном падении. Коэффициент восстановления при ударе
молота о балку ^ = 0,2.
Принять молот и связанные с ним элементы за материальную
точку; считать, что движение точек балки происходит по прямым.
Определить наибольшую деформацию упругой опоры А, считая,
что молот, отскочив от балки, не падает снова, а удерживается
обратным давлением пара; определить также ударный импульс, вос-
воспринимаемый опорой В.
Вариант 19. При испытании упорных (буферных) брусьев на
удар маятник копра массой /п = 500 кг, радиус инерции которого
относительно неподвижной горизонтальной оси вращения О го= 1,2 м,
отклоняют от положения устойчивого равновесия на угол а = 90°
и отпускают без начальной угловой скорости. Падая, маятник точ-
точкой А ударяется о буферный брус массой то= 1000 кг, коэффициент
жесткости комплекта пружин которого с= 10000 Н/см. Коэффициент
восстановления при ударе & = 0,5. Отклонившийся после удара на
угол р маятник задерживается в этом положении специальным
захватом.
Расстояние от точки О пересечения оси вращения вертикальной
плоскостью симметрии маятника до его центра тяжести С ОС =
= d = 0,9 м; расстояние от точки О до точки А, находящейся в той
же плоскости симметрии, ОЛ = /=1,5 м.
Пренебрегая трением скольжения бруса о горизонтальную пло-
плоскость, определить величину наибольшего сжатия буферных пружин,
ударный импульс в точке А, а также расстояние от точки О до
центра удара.
Вариант 20. В гипоциклическом механизме кривошип ОС
массой т = 2 кг и зубчатое колесо / радиусом г = 30 см вращаются
с угловыми скоростями оH=1,5 с 1 и сох = 1 с соответственно.
Зубчатое колесо 2 имеет массу т.2 = 8 кг и радиус г2 — 10 см. В неко-
некоторый момент времени колесо / внезапно останавливают.
Считая кривошип однородным тонким стержнем, а колесо 2 —
однородным сплошным диском, определить угловую скорость криво-
кривошипа в конце удара, а также ударные импульсы в точках Л и С.
Варианты 21—30 (рис. 182). Вариант 21. Лепта транспор-
транспортера составляет угол а =15° с горизонтом. Радиусы шкивов г —
^0,2 м. На ленте траспортера, ско'льжение которой по шкивам /
и 2 отсутствует, находится груз —однородный куб массой /гсо = 200 кг
254

22
25
26
¦'У/УУУУУУУУУУУУ,УУ7УУУУУУУ'77////У,УЯ7,У///у^7//У/.уУ7,
28
30
'УУУУУУ7/УУУ//УУУУ//УУУЛ7/УУУ7УУ?.
Рис.-182
255

с ребрами длиной я ^0,5 м В нехэгоры"! момент времени движение
транспортера внезапно прекращается, при этом груз приобретает
угловую скорость вращения вокруг ребра Л, закрепленного упор-
упорной планкой.
Определить наименьшую угловую скорость шкивов в момент оста-
остановки, если груз опрокидывается; определить также ударный им-
импульс, воспринимаемый упорной планкой при внезапной остановке
шкивов, вращающихся с этой угловой скоростью.
Вариант 22. Груз — однородный полый тонкостенный цилиндр
массой m — 800 кг и радиусом г = 0,4 м —покоится па движущейся
платформе между упорами—ступеньками. При внезапной остановке
платформы ступенька АВ не удерживает груз: цилиндр, поднимаясь
на ступеньку, прокатывается по участку BD = s=l м горизонталь-
горизонтальной площадки BE и, ударившись о ребро F другого упора — сту-
ступеньки EF высотой h = 0,\ м, поворачивается вокруг ребра F, вслед-
вследствие чего центр тяжести цилиндра поднимается по вертикали на
высоту /гх = 0,07 м. Качение цилиндра от В до F происходит без
скольжения; коэффициент сопротивления качению цилиндра 6^0,1 см.
Отрыва цилиндра при ударе о ступеньку ле происходит, абсолютно
шероховатая поверхность ступеньки не допускает скольжения ци-
цилиндра при ударном воздействии.
Определить, какую скорость имеет центр тяжести цилиндра в на-
начале движения на участке BD, а также ударный импульс, испыты-
испытываемый ребром F ступеньки EF.
Вариант 2,'5. Маятник состоит из тонкого однородного стержня
АВ массой т = 4 кг, длиной / = 0,7 м и однородного сплошного
шара массой то — 2 кг и радиусом /'=-0,1 м Ось А маятника дви-
движется поступательно в горизонтальной плоскости с постоянной ско-
скоростью у—-1,4 м/с, при этом маятник занимает вертикальное поло-
положение устойчивого равновесия.
Вследствие внезапной остановки оси подвеса маятник получает
угловую скорость вращения вокруг этой оси и, находясь в том же
вертикальном положении, ударяется точкой D о неподвижную верти-
вертикальную плоскость. Поверхности маятника и вертикальной плоско-
плоскости в точке соударения гладкие. Коэффициент восстановления при
ударе й = 0,4.
Определить угловую скорость маятника при внезапной остановке
оси его подвеса и проверить найденное выражение по теореме Карно.
Определить также угол отклонения р1 маятника после удара о вер-
вертикальную ллоскость и ударные импульсы, испытываемые осью А
маятника.
Вариант 24. При испытании фундамента на ударную нагрузку
маятник копра, вращаясь вокруг неподвижной оси, надает из верти-
вертикального положения, показанного на чертеже, под действием собст-
собственного веса без начальной угловой скорости. В горизонтальном по-
положении маятник точкой А ударяется о середину верхней грани
покоящегося фундамента.
Масса маятника то = 500 кг, радиус его инерции относительно
оси вращеигя /о = 1,8 м, масса однородного фундамента т = 10 000 кг.
256

Коэффициент восстановления при ударе /е = 0,2. Отклоняющийся
после удара маятник задерживается в этом положении специальным
захватом. Расстояния от точки О пересечения оси вращения верти-
вертикальной плоскостью симметрии маятника до его центра тяжести С
и до точки А, находящейся в той же плоскости симметрии: ОС =
= d= 1,5 м и О А = / = 2 м.
Определить: наибольшую упругую осадку основания, имеющего
коэффициент жесткости с=1б-105 Н/см, ударный импульс в точке Л
и расстояние от точки 0 до центра, удара.
Вариант 25. Тележка / общей массой т1 = 3000 кг, двигаясь
по горизонтальному прямолинейному пути со скоростью v1 = 5 м/с,
наталкивается на тележку 2, имеющую вместе с грузом массу т2 =
= 2000 кг и движущуюся по тому же пути и в том же направле-
направлении со скоростью v2 = 1 м/с.
Груз —однородный полый тонкостенппый цилиндр массой т0 =
= 500 кг и радиусом а = 0,5 м удерживается от возможного пере-
перемещения по тележке двумя упорами —наклонными плоскостями.
В конце соударения скорости движения тележек по тому же го-
горизонтальному прямолинейному пути изменяются, а цилиндр, уда-
ударяясь о наклонную плоскость АВ, составляющую угол а = 60°, начи-
начинает качение по ней.
Цилиндр по наклонной плоскости проходит без скольжения рас-
расстояние s = 0,1 м; сопротивление качению пренебрежимо мало. Отрыва
цилиндра при ударе о наклонную плоскость не происходит, абсо-
абсолютная шероховатость наклонной плоскости исключает скольжение
цилиндра при ударном воздействии.
Считать, что за время подъема цилиндра на наклонную плоскость
скорость тележки 2, полученная ею в конце удара, остается посто-
постоянной, а вертикальные плоскости соударения тележек гладкие.
Определить скорость тележки / в конце соударения с тележ-
тележкой 2, а также ударный импульс, воспринимаемый наклонной пло-
плоскостью со стороны цилиндра.
Вариант 26. В эпициклическом механизме кривошип ОС мас-
массой т = 3 кг и длиной / = 30 см вращается с угловой скоростью
ыо = 2 С, а зубчатое колесо / — с угловой скоростью Wj = 3 с~".
Масса зубчатого колеса 2 т2 = 10 кг, а радиус г2=10 см.
8 некоторый момент времени колесо / внезапно останавливают.
Считая колесо 2 однородным сплошным диском, а кривошип— одно-
однородным тонким стержнем, определить угловую скорость колеса 2
в конце удара, а также ударные импульсы в точках А и С.
Вариант 27. В точку D абсолютно жесткой балки массой т =
= 5000 кг и длиной / = 3 м с высоты А =1,2 м падает груз массой
т — 400 кг. Балка имеет шарнирно-неподвижную опору А и упру-
упругую опору В; в состоянии покоя балка занимает горизонтальное
положение, показанное на чертеже. Удар груза о балку пеупругий.
Считать балку однородным тонким стержнем, а груз —матери-
—материальной точкой.
Определить угловую скорость балки в конце удара и про-
проверить найденное выражение угловой скорости по теореме
9 п/р. Яблонского А. А. 257

Карно. Определить также ударный импульс, воспринимаемый опо-
опорой А.
Вариант 28. Механизм состоит из шестерни с кулачками, ко-
которая приводится во вращение вокруг неподвижной горизонтальной
оси О. Масса механизма т = 50 кг, радиус инерции относительно
оси вращения i0 = 0,2 м. Механизм сбрасывает металлические бол-
болванки массой та = 2 кг из точки А горизонтальной плоскости АВ
на горизонтальную плоскость ED на расстояние d=l,5 м, отсчи-
отсчитываемое по горизонтали от точки А. Плоскость ED расположена
ниже плоскости А В на высоту А=1 м.
Неупругий удар между кулачком и болванкой (^ = 0) происхо-
происходит на расстоянии / = 0,4 м от оси вращения механизма. Коэффи-
Коэффициент восстановления при ударе болванки о гладкую горизонталь-
горизонтальную плоскость в точке Е &2 = 0,2.
Принимая болванку за материальную точку, определить угловую
скорость шестерни в начале удара, а также ударные импульсы, испы-
испытываемые болванкой в точках А и Е.
Вариант 29. Маятник, отклоненный от положения устойчивого
равновесия на некоторый угол а, падает без начальной скорости
под действием собственного веса, вращаясь вокруг неподвижной
оси О, и в вертикальном положении точкой А ударяется о покоя-
покоящийся однородный полый тонкостенный цилиндр массой то = 2ООкг
и радиусом г = 0,2 м. Масса маятника т=100 кг, радиус его инер-
инерции относительно оси вращения io=\ м. Расстояния от точки О
пересечения оси вращения вертикальной плоскостью симметрии до
центра тяжести С маятника и до точки А, находящейся в той же
плоскости симметрии: ОС = d — 0,8 м и ОА =1=1,2 м. Коэффициент
восстановления при соударении маятника и цилиндра & = 0,6.
После удара дилиндр скользит, не вращаясь, по гладкой гори-
горизонтальной плоскости и, натолкнувшись на ступеньку DE высотой
/i = 0,05 м, поднимается на нее, не перемещаясь дальше ребра Е.
Отрыва цилиндра от ребра Е при ударе о ступеньку не происходит,
а абсолютно шероховатая поверхность ступеньки исключает про-
проскальзывание цилиндра при ударном воздействии.
Определить угол а первоначального отклонения маятника, а также
ударный импульс, испытываемый цилиндром со стороны маят-
маятника.
Вариант 30. Рычаг состоит из двух абсолютно жестких стерж-
стержней OD и OF, соединенных под прямым углом; OD — a=\ м, OF =
= ft=l,5 м. Рычаг имеет шарнирно-неподвнжпую опору О и удер-
удерживается в точке Е пружиной. Масса рычага т^400 кг, радиус
его инерции относительно оси вращения О in = 0,4 м.
Рычаг находится в покое, соответствующем статической деформа-
деформации пружины, при этом его стержень OD горизонтален. В точку D
рычага надает груз А массой тА = 20 кг с высоты /i = 0,5 м. Удар
груза о стержень OD рычага неупругий (k1 = 0). Приобретя угло-
угловую скорость, рычаг точкой F ударяется о неподвижное тело В
массой шв=120 кг; коэффициент восстановления при этом ударе
&2 = 0,2. Считать груз Л и тело В материальными точками.
258

Определить, какую скорость получает тело В в конце его соуда-
соударения со стержнем OF, а также ударный импульс, воспринимаемый
телом В.
Пример выполнения задания (рис. 183). Груз-однородный сплош-
сплошной цилиндр массой т = 500 кг и радиусом г = 0,5 м лежит на
движущейся платформе и удерживается от возможного перемещения
по платформе упорами —ступеньками.
При внезапной остановке платформы цилиндр ударяется о ребро О
ступеньки BD высотой h = 0,1 м и поднимается вверх на эту сту-
ступеньку. Далее цилиндр катится по участку DE горизонтальной пло-
площадки DK и, ударившись о другой упор — наклонную плоскость KN,
составляющую угол а = 60° с горизонтом, проходит по ней расстоя-
расстояние FN~ s~Q,\ m. Качение цилиндра не сопровождается скольже-
скольжением, сопротивление качению пренебрежимо мало.
Рис. 183
Отрыва цилиндра при ударах о ступеньку и о наклонную пло-
плоскость не происходит; абсолютная шероховатость ступеньки и на-
наклонной плоскости исключает скольжение цилиндра при ударном
воздействии.
Определить скорость платформы до ее остановки, а также удар-
ударные импульсы, испытываемые цилиндром со стороны ступеньки и
наклонной плоскости.
Проверить найденные выражения угловых скоростей цилиндра
после ударов о ступеньку и наклонную плоскость с помощью тео-
теоремы Кар но.
Решение. При внезапной остановке платформы поступательное
движение цилиндра мгновенно изменяется на вращательное движе-
движение вокруг ребра D ступеньки BD, т. е. цилиндр испытывает удар.
Составим уравнение, выражающее теорему об изменении кине-
кинетического момента механической системы при ударе, взяв за ось
моментов неподвижную горизонтальную ось, проходящую вдоль
ребра D (положения / и //, соответствующие началу и концу удара
о ребро D ступеньки BD, совпадают —рис. 184, а):
Сумма моментов внешних ударных импульсов, приложенных
к цилиндру, относительно оси D ? MD(Sf) = 0 (ударный импульс.5П
9*
259

пересекает ось D) и потому
Кинетический момент цилиндра отпосителыю оси D в начале
удара
где vc\ = v — скорость центра тяжести цилиндра в начале удара,
равная скорости платформы до внезапной остановки.
о)
Рис. 184
Кинетический момент цилиндра относительно оси D в конце удара
L\\D —
где Jr> — момент инерции цилиндра относительно оси ?>; Щ\ — угло-
угловая скорость цилиндра в конце удара.
(on
= C/2) • тгЛоп.
260

Но
Liw
т. е.
C/2) ¦mr2w[[ = mv (r -h),
откуда
соп = 2(г-/г)у/3/-2. A)
Проверим полученное выражение A) угловой скорости цилиндра
по теореме Карно (для случая наложения на механическую систему
идеальной неупругой связи):
Ji-7n = T*,
где Т\ — кинетическая энергия системы материальных точек в начале
удара; Т]г — кинетическая энергия системы в конце удара; Т* — ки-
кинетическая энергия, соответствующая потерянным скоростям точек
системы.
Кинетическая энергия цилиндра в начале удара о ступеньку
Кинетическая энергия цилиндра в конце удара о ступеньку
Теперь выведем выражение кинетической энергии, соответствую-
соответствующей потерянным скоростям Avt точек /И, твердого тела при пло-
плоском движении
Аи, = i»,-i —а.п,
где _ .
Vil = VC\ +VCMit fill = VCII +VclMt)
причем вращательные скорости вокруг оси С имеют выражения!
Кинетическая энергия тела, соответствующая потерянным ско-
скоростям его точек,
Т* = A/2) Sm, [(vCi - »сп) + (»слA-»"м,)]а,
т. е.
Т* = A/2) [2/я, (vc, -ад[)а + 2 ?/и, (ус, - vCn) X
Здесь
2 пц (va — vci iJ = m (vC\ — vcuJ;
2 mt (vci — vcu) • (vcm, — vcm{) = (vci — vCu) • У, mt (щ xn — "©ir x7,)
так как
yimiri = nirc = 0;
У J = 2 m (co^ согJ Jc (m -
261

Таким образом,
Т* = A/2) m (9ci - vCuJ + A/2) Jc (coi -со,,J
или
7* = A/2) m [(vax - vcuf + (vcly - »сп/] + A/2) Ус (со, -
Выражение (+¦) является общей формулой кинетической энергии,
соответствующей потерянным скоростям точек твердого тела при
плоском движении.
Для цилиндра (рис. 184, б) в рассматриваемой задаче
Т* = A/2) m [{vC\ - vcu cos pJ + vh\ sin2 p] + A/2) Jcco?b
т. e.
T* = A/2) m {vh - ivcWcw cos p + vhi) + A/2) Jccu|i.
Поскольку va = v, fcn = cui,/-, Jc = mr2/2, то, приравнивая
T1 — T2 и Т*, получаем
A/2) mu2 - A/2) mco1,A2 - A/4) тг2ы3п =
= l/2mv2 + mvunr cos p + A/2) mahr2 + A/4) mr2cufi
или
C/2) mcoii/ = mv(O\ir cos p,
где
cos p = (r — h)/r.
Отсюда
an = 2{r-h)v/3r2.
Составим уравнение, выражающее теорему об изменении кинети-
кинетической энергии механической системы и соответствующее подъему
цилиндра на ступеньку BD из положения // в положение ///
(рис. 184, в):
Так как перемещение осуществляется поворотом вокруг оси D, то
A/2) ¦ JDalu - A /2) • У0со?. = - Gh
или
C/4) • m/-2coin — C/4) • mrho]\ = — mgh,
откуда
со, м = Vuh-4gh/3r2. B)
Составим уравнение, выражающее теорему об изменении кинети-
кинетической энергии механической системы и соответствующее качению
цилиндра на участке DE из положения /// в положение IV
(рис. 184, г)
f
Так как па рассматриваемом перемещении 2М,Е = 0, то
т. е.
VCI\ = VCIU И CU[V = CO[ii. C)
262

При соприкасании цилиндра с наклонной плоскостью мгновенная
ось вращения цилиндра (мгновенный центр скоростей) мгновенно пе-
перемещается из Е в F, т. е. цилиндр испытывает удар.
Составим уравнение, выражающее теорему об изменении кинети-
кинетического момента механической системы при ударе, взяв за ось мо-
моментов неподвижную горизонтальную ось, совпадающую с образую-
образующей F цилиндра (положения цилиндра IV и V, соответствующие
началу и концу удара, совпадают —рис. 184,5):
Но ?MF(sf) = 0, так как ударный импульс S/.-, приложенный
к цилиндру, пересекает ось F. Поэтому
При вычислении кинетических моментов цилиндра L\yF и LyF
используем теорему о кинетическом моменте системы в общем слу-
случае ег движения.
Кинетический момент цилиндра относительно оси F в начале
удара
L\yF ¦= mvcxvr cos a -f-
где vciv = ЩуЕС, поскольку мгновенный центр скоростей — в точке Е;
L[vF = ma}ivr2 cos a + (тг*/2) -coiv = mu)ivr2 (cosa-|- 1/2).
Кинетический момент цилиндра относительно оси F в конце
удара
L\!F = mvcvr + ^wv,
где vcv = (?>vCF, так как мгновенный центр скоростей —в точке F
Lme = mcovr2 + (mr2/2) • cov = C/2)
Ho L\iF = L\vF, т. е.
C/2) • тсоу/ = mcoivr2 (cos a + 1/2),
поэтому fflv = aMvBcos«+l)/3. D)
Проверим найденное выражение угловой скорости цилиндра по
теореме Карно (для случая наложения на систему материальных точек
идеальной неуиругой связи):
Кинетическая энергия цилиндра в начале удара о наклонную
плоскость
Кинетическая энергия цилиндра в конце удара о наклонную плос-
плоскость
7\ =A/2) (mv'cv + Jc«v).
263

Кинетическую энергию, соответствующую потерянным скоростям
точек цилиндра, найдем, используя формулу (*) (рис. 184, д):
Т* = A/2) m [(vc\vK - vCVxy + (vaVl) - vcvvJ + A/2) Jc (<»iv - covJ,
т. e.
T* = A12) m [(Vciv - vc\ COS aJ -f- vh sin2 a] + A /2) Jc (со, v - wvJ
или
T* = A/2) m (ubv - 2vavvcv coS7. + ^v) + A/2) Jc (coiv -wvJ.
Поскольку nCiv = o)Iv/1,fcv = cov/'I то, приравнивая Tiv — Tv и f*,
получаем
A/2) mmvr2 + A/4) mrtofv - A/2) mcot^2 - A/4) ffzrWv =
= A/2) mcofvA2 + m(olvcuvr2cosa+A/2) mcovr2 +
+ A/4) mAofv - A/2) /n/-2(o,vwv + A/4) шгга\
или
C/2) cov^co^cov (COSa + 1/2),
откуда
(ov = coIV B cos a + l)/3.
Составим уравнение, выражающее теорему об изменении кинети-
кинетической энергии механической системы и соответствующее качению
цилиндра по наклонной плоскости из положения V в положение VI
на расстояние s (рис. 184, г):
7Vi-7V
Поскольку 7Vi=0,
j + ^
или
mo)^,/-2 (тла/2) • ч>Ь
2 g = ~ m8s sm a>
т. е.
откуда
Используя выражения B) —D), находим:
ш" ~ Г Bcosa+ l;2 "г" Зга •
Учитывая выражение E), имеем
Щ1= г V Bc<xa+\f + Г"
Таким образом, скорость платформы по A)
.. _ W 2 ./ 3gssina gA
2 (г— А) ' г К Bcosa+lJ "г 3 '
8С4

т. е.
3-0,5 -,/" 3-9,81-0,1-0,866 . 4-9,81.0,1 о со .
Р== 0,5 — 0,1 V B-0.5+1)» + 3 = 3'68 М/С-
Найдем ударный импульс, воспринимаемый цилиндром со стороны
ступеньки, для чего составим уравнения, выражающие теорему об
изменении количества движения механической системы при ударе,
в проекциях на оси хну (см. рис. 184, а):
mvcux - mvC\x = S Sfx; mvCuu - mvCiy = ZSfu
или
— то en cos P — (— mvci) = SDx; mvCu sin p = SDy,
откуда
r~
SDx — mvci — mvcii cos p = mo — тщ\г
- m, [l - ^9^] = 500- 3,68[l-^Wj= 1055 He;
sin p =mco1i/']/l — cos2p =
2{r-h)mv ЛГ\ ('-У2 2@,5-0,1M00-3,68 na -RQ „
- з^ |/ 1 ^ - gTj^g U,b-J>«y MC.
Ударный импульс, воспринимаемый цилиндром со стороны сту-
ступеньки
= ]/10552 + 5892 = 1208 Не/
Найдем ударный импульс, воспринимаемый цилиндром со стороны
наклонной плоскости, для чего составим уравнения, выражающие
теорему об изменении количества движения системы при ударе,
в проекциях на оси § и г\ (см. рис. 184, д):
mvcvt — invavi = ? S,1; moCvt\ — mvCivt\ = ? Sfn
или
— (— nwciv sin a) = Sf^; mvCv — tnvC\v cos a = SFri,
откуда
- v
sin a = mco,vr sin a = m 2cq } /¦ sin a;
SFr\ = mocv — mvcw cos a = mwy/" — mcoivr cos a =
Используя выражение E), найдем:
-^ТГ 0,866 = 691 Не;
2COS.+ !
3созa \
y — r-
cnAl /" 9,81 -0,1-0,866 /, 3-0,5 \ „„ „
2.500]/ з A~ 2-0,5 + 1 J^133 НС«
266

Ударный импульс, воспринимаемый цилиндром со стороны наклон-
наклонной плоскости,
/ /" He.
III. Аналитическая механика
ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
Задание Д-13. Применение принципа возможных
перемещений к решению задач о равновесии сил,
приложенных к механической системе
с одной степенью свободы
Схемы механизмов, находящихся под действием взаимно уравно-
уравновешивающихся сил, показаны на рис. 185—187, а необходимые для
решения данные приведены в табл. 54.
Применяя принцип возможных перемещений и пренебрегая силами
сопротивления, определить величину, указанную в предпоследней
графе табл. 54.
Примечание. Механизмы в вариантах 3, 6, 10, 14, 16, 18, 19, 25 и 30
расположены в вертикальной плоскости, а остальные — в горизонтальной.
Пример выполнения задания. Дано: Q = 100 Н; с = 5 Н/см; г1 = 20;
га = 40; а., = 10 см; ОА = / = 50 см; а = 30°; р = 90° (рис. 188).
Определить деформацию h пружины, пренебрегая весом звеньев О А
и АВ.
Решение. Рассматриваемый механизм (рис. 188) находится под
действием следующей системы взаимно уравновешивающихся сил: силы
упругости F, сил тяжести G\ —вала / с шестерней 2, G3 — шестерни 3,
G4 — ползуна В, Q —груза и реакций опор.
Связи, наложенные на механизм, допускают следующие возможные
перемещения его звеньев: поворот вала / с шестерней 2 на угол йф^
поворот шестерни 3 на угол йф3 и поступательное перемещение груза
но вертикали на dsQ. Ползун В может иметь перемещение 8sB (пере-
(перемещение по горизонтали), а точка А — перемещение &sA (отрезок dsA
перпендикулярен к ОА). Уравнение работ, выражающее принцип
возможных перемещений, получает вид
Q8sQ -FdsB = O. A)
Найдем зависимость между возможными перемещениями точек
системы. Поскольку нить, к которой привязан груз Q, нерастяжима
и скольжение между нитью и валом 1 отсутствует, перемещение
груза Q равно перемещению точки обода колеса /. Поэтому угол
поворота вала 1 и шестерни 2
Перемещение точки К обода колеса 2
2G6

-X
В P
8 y\
—У
Рис 185
267

11
18
z\
t У
ffl -4^-
'19
в
¦ у
i -¦ ... ,7"
Рис. 186
268

21
22 y[
—X
i
D о
8
25
27
y\
28
29
30
Рис. 187
269

Таблица 54
Номер
рис 1Вэ —1Ь7)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
JdnncHnuc размеры
0Л = 1О см
0^ = 20 см
/¦1 = 20 см, /=30 см,
— —— 40 см
ОС:ОЛ = 4:5
СМ = 100 см
^i == *О СМ, ^2== "-* ^ •
/¦3 = 20см, Су1 = 80 см
ОС=ОА
ОС=АС
ОЛ = 20 см
/¦х=15 см, /-2 = 40 см,
/¦3 = 20 см, СМ =100 см
СМ = 20 см
ОхО = 60см, ЛО = 20см
О/! = 40 см
ОВ = 2 ОА
Силы Н.
—
—
—
—
200
—
—
200
2- 103
—
—
—
20
Р
100
—
200
—
—
200
—
—
—
—
Момент
пары
сил М, Нм
20
—
100
—
10
—
—
—
„
300
100
200
Коэффи-
Коэффициент
жест-
жесткости с,
Н/см
—
—
—
—
—
10
10
—
—
—
—
25
Деформа-
Деформация пру-
пружины h,
см
—
—
4
—
—
3
2
—
4
—
—
—
3
Величины,
подлежа-
подлежащие опре-
определению
Р
м
Q
с
Р
Р
Р
Q
М
с
Р
Р
Р
Р
Примечания
Вес рукоятки ОгА не учи-
учитывать
Пружина сжата
Пружина сжата
Вес рукоятки ОА не учиты-
учитывать
Вес стержней ОА и ОВ не
учитывать; пружина растя-
растянута

15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
см, rf2=25 см,
О см, /2=75 см
= 20 см
/¦, = 20 см
лг=30 см, ОЛ = 25 см
ОА = АВ = АС =50 см
= DC= 25 см
ОЛ = 40 см
OD=DS = 0,8 АО
О А = 25 см
ОВ = АВ
0В = E/4) О А
ЛО=30см, BD = O1D
/¦i=15 см; г2 = 36 см;
т-3=10 см; 7-4 = 20 см
3- 103
5-103
200
—
50
—
—
—
—
400
—
—
—
—
—
—
,
200
—
100
200
—
200
250
—
500
—
450
—
600
—
—
200
—
100
—
—
400
50
—
—
120
—
—
120
—
250
100
100
—
—
—
—
50
150
120
180
—
100
—
3
4
.
—
—
—
—
—
—
2,5
3
2
2
—
—
—
P
P
P
h
P
M
M
P
h
Q
P
с
P
Q
h
Q
Пружина сжата
Вес стержней OLA и OZB не
учитывать
Пружина растянута
Р — вес блока радиусом г2
Вес звена АВ не учитывать
Пружина сжата
Вес стержней АО и ВО не
учитывать. Пружина рас-
растянута
Пружина растянута

Так как скольжение между шестернями 2 и 3 отсутствует, то
возможные перемещения точек касания этих шестерен равны и угол
поворота шестерни 3
Рис. 188
Перемещение точки А кривошипа, жестко соединенного с колесом 3
= (гл1/гхг3) ¦ bsQ.
Для определения зависимости между возможными перемещениями
bsA и &sn найдем положение мгновенного центра вращения звена
Л В —точки Р.
Тогда
откуда
б
Из треугольника АРВ
Теперь
РВ/РА = 1/cos 30°.
= (r2///Va cos 30°) • 6sQ.
272

Сила упругости пружины пропорциональна ее деформации F = ch.
Подставив в уравнение работ A) выражения силы упругости и воз-
возможных перемещений точек системы, получим
QbsQ - ch • {r2l/rir3 cos 30°) • bsQ = 0;
откуда
_ 100-20-10-0,87
с ~
h_ Q riracos 30"
= 1,74 см.
r4 5-40-50
Следовательно, пружина сжата на 1,74 см.
Задание Д-14. Применение принципа возможных
перемещений к определению реакций опор
составной конструкции
Применяя принцип возможных перемещений, определить реакции
опор составной конструкции.
Схемы конструкций показаны на рис. 189—191, а необходимые
для решения данные приведены в табл. 55. На рисунках все раз-
размеры указаны в метрах.
Таблица 55
Номер
варианта
(рис.
189—191)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Нагрузка
Pi, кП
15
13
II
9
7
8
7
6
5
4
12
10
9
7
6
Р2, к И
14
12
10
8
6
5
4
п
8
10
11
fi
5
10
8
кН/м
3
2
I
3
2
1
2
1
3
2
1
2
1
2
1
м,
кНм
10
6
5
14
12
4
К)
7
8
6
12
10
6
13
5
Номер
иарианта
(рис
189—191)
16
17
18
19
20
21
22
23
21
25
26
27
28
29
30
Нагрузка
Р„ Kll
3
1
3
5
7
10
8
П
4
2
7
О
5
4
3
Pt, кН
10
8
6
4
2
9
7
5
3
1
1
2
3
4
5
<7
кН/М
2
1
3
2
1
2
1
2
1
2
2
1
2
1
2
м
i Пм
10
8
(i
7
5
4
7
8
3
2
7
5
10
5
10
Пример выполнения задания. Дано: составная рама (рис. 192);
Я1 = 2; Р2 = 4кН; М=5кНм; </=1,5кН/м.
Определить реакции опор рамы.
Решение. Заменим равномерно распределенную нагрузку сосре-
сосредоточенной силой Q = q- 4= 1,5- 4 = 6 кН, приложенной в середине
загруженного участка.
Найдем реакцию подвижной опоры А, для чего мысленно отбро-
отбросим эту связь, заменив ее действие реакцией (рис. 193).
Возможным перемещением левой части рамы является ее поворот
вокруг шарнира С на угол бф, например, против вращения часовой
стрелки; правая часть рамы останется неподвижной.
273

n
CO
f
1
t
|
3
Co
|
11
у
л
3
-*
-j-
to
it
i
1
r
s
<
\
J
)
rt?1 Til
r—
l
I
I
4
м-
|
1
1
1
у
Ю
;
4
j
/
4
—
—
г
ri
/-J
?
7
/
J
to
1 5
1
1
I
r
\
л
1,5
\
I
Co
1
i1
"I
1 J
fsl
1
Г с
J-^r
\
, v
Щ
i
\
5
i
to
/
-Г-- i^
T-> or
1
*
1
^_
j i i Si
1,5 Г U
\

1Z
1
тУпт
м
Ш: Ш-
13
Р,
\М
Р?
ЭДИП
П,
—
яг ?
if
V,'//./,
17
«
к в
Т////Г7,
М
".ю°
Рис. 190
275

21
в
6O'r\\. 3
22
¦Be-
23
hi*-
А
_L
3
в
Л
i
Рг
/'
Ж-
i
м
m
\\w\\\\\-
? J_
5G°
А '
~'W -
2
2
/?
л»'
- s*
г
JLL
л/
^7! 7Я5 ^
я
wTTwK
А
\\ \
>,? 2
3
Ля
W77W
Рис. 191
276

Составим уравнение работ, выражающих принцип возможных
перемещений, при этом учтем, что работа силы при повороте тела
равна произведению момента силы относительно центра вращения
на угол поворота тела:
откуда
Ra = (Q •
- RA ¦ 4бф = О,
= F • 2 + 5)/4 = 4,25 кН.
Переходим к определению реакции заделки В. Сначала найдем
реактивный момент Мв. Для этого отбросим связь, препятствующую
гптйтп
c\j Hz.
' i
с
м
Рис. 192
ил
~с
i/i
V
\
Рис. 193
V
j
\
о
Рис. 194
повороту балки, заменив заделку шарнирной неподвижной опорой
и приложив искомый момент Мк (рис. 194).
Воспользуемся принципом возможных скоростей, согласно которому
где vt — возможные скорости.
Сообщим системе возможные скорости: правая часть рамы может
поворачиваться вокруг шарнира В с некоторой угловой скоростью <ли
а левая будет совершать плоское движение. Найдем мгновенный
центр скоростей левой части рамы как пересечение перпендикуля-
перпендикуляров к возможным скоростям точек А и С.
Угловые скорости обеих частей рамы связаны соотношением:
Так как О^^
то
со2 = (о1 = со.
Составим уравнение возможных мощностей:
Мы - Q2ca - Pfim - Pfiu) —
= О,
277

где
и определим
¦ Мв = М - Q ¦ 2 - Ру ¦ 2 - Р2 • 0,5 • 5 =
= 5 — 6-2 — 2-2 — 4-0,5-5 = —21 кНм.
Для определения вертикальной составляющей YB реакции заделки
отбросим связь, препятствующую вертикальному перемещению точки В,
заменив заделку ползуном В в вертикальных направляющих, жестко
скрепленным с рамой ВС, и приложив реакцию Ув (рис. 195).
Сообщим системе возможные скорости: правая часть рамы пере-
переместится поступательно с некоторой скоростью v, направленной,
р,
Рис. 195
Рис. 196
Рис. 197
например, вверх. Поступательное движение правой части является
единственно возможным, ибо поворот ползуна В в направляющих
невозможен.
Левая часть рамы будет совершать плоское движение. Мгновен-
Мгновенный центр скоростей О2 этой части лежит на пересечении перпенди-
перпендикуляров к возможным скоростям точек С и Л.
Составим уравнение мощностей:
М<& - Q2« -
= 0,
где Р{ = Р cos 30°:
Зависимость между со и v устанавливается из соотношения
4ш = vc = и.
Следовательно,
Мы - Q2oj — Pj4(o + Я2 • 0,87 • 4со + Уд4со = О,
откуда
YB = (— М + Q ¦ 2 + Рг ¦ 4 - Р2 ¦ 0,87.4)/4 = 0,29 кН.
. Для определения горизонтальной составляющей Хв реакции
заделки представим опору в виде ползуна В в горизонтальных направ-
278 *

ляющих, жестко скрепленного с рамой ВС, и приложим реак-
реакцию Хв (рис. 196).
Возможное перемещение в этом случае —поступательное перемеще-
перемещение всей рамы, например, вправо на величину 6s (поворот ползуна
в направлающих невозможен).
Составим уравнение работ:
откуда
Хв = 4-0,5 = 2 кН.
Произведем теперь проверку правильности решения задачи.
Убедимся, что найденные числовые значения величин удовлетво-
удовлетворяют уравнениям равновесия сил для всей рамы (рис. 197)
?, = 0 и Я
Имеем:
?V, = «A-Q-P1+
= 4,25 - 6 - 2 + 4 • 0,87 + 0,29 = 8,02 - 8,00 «=. 0;
X Мш = — Rл • 8 + М + Q ¦ 6 + Pt ¦ 2 + Pz cos 60° • 5 -|- MR =
- — 4,25 • 8 + 5 + 6 • 6 + 2 • 2 + 4 • 0,5 • 5 - 21 = 55 - 55 - 0.
ПРИНЦИП ДЛЛЛМБКРА
Задание Д-15. Применение принципа Даламбера
к определению реакций связей
Определить реакции внешних связей механической системы:
а) в произвольный момент времени —для вариантов 4, 5, 10,
12-18, 21-30 (рис. 198-200);
б) в момент времени t = t1— для вариантов 1, 8, 9, 11, 20;
в) в тот момент времени, когда угол поворота ф = фх —для вариан-
вариантов 2, 3, 6, 7;
г) в положении, показанном на чертеже для вариантов 15 и 19.
На схемах (рис. 198 — 200) плоскость хОу (хАу) горизонтальна,
плоскость уОг (уАг) вертикальна. Необходимые для решения данные
приведены в табл. 56, в которой о — угловая скорость, <р0 и м0 —
значения угла поворота и угловой скорости в начальный момент
времени.
Пример выполнения задания. Дано: т1 = 3; т2 = 2; /гся = 5кг;
lx — 30; 12 = 20 см; а — 30°; со = 120 с = const. Схема системы и необ-
необходимые размеры приведены на рис. 201, а.
Найти реакции подпятника Л, подшипника В, а также пружины DN.
Поперечными размерами стержней 1, 2 и 3 и массой пружины пре-
пренебречь.
Решение. Для определения реакции связей воспользуемся
принципом Да1амбера. Так как od = const, рассмотрим только центро-
центробежные силы инерции частиц каждого стержня. Известно, что глав-
главный вектор сил инерции точек вращающегося тела определяется
279

у
M-l
OA=l
10
у
Рис. 198
280

12
а=0,11
AB=2l
15 F
IS
EN=l
17
i
*f
Ш
AB=l
'2 ty ~ Ют2.
18
\г
Я1
0>
an
3
к-у
0,51
OB'=0,21
<Фи>
19
20
Рис. 199
281

21
'-0
т3 -
23
03=03=1
25
rh} = 0,2 т,
?/7/t'.vPf
r=D,8R
^ D-' й-Г
27
30"
~У
29
30
/АО=OB =0,51
Рпс 200
282

по формуле
Ф* = —
где т — масса тела, a wc — ускорение центра тяжести тела.
ф,
Р П
Рис. 201
Равнодействующая сил инерции точек тела равна их главному
вектору. Поэтому для стержней / и 2
с1 = ш1а>2 @,5/j sin a-j-A,);
Ф2 = ttiiWCt = tn-M2 • 0,5/2.
Для определения реакции опор необходимо знать точку прило-
приложения силы Ф^ (линия действия силы Ф2 совпадает с осью стержня 2
и поэтому определена). Так как с^мма моментов параллельных сил
283

Таблица 56
Номер
(рис
198— <00)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
т,
т2
кг
20
25
40
20
30
40
20
50
20
20
25
30
25
20
—
—
—
14,4
—
—
—
30
5
40
—
25
20
i
R
см
60
50
80
80
60
—
—
—
50
25
30
40
40
40
—
—
—
—
30
25
30
10
—
—
-
—
Л1, Им
1 0
4,0
20- 0,1/
— 5-0,1/
10
15
U, с
10
5
200
50
•Pi фо
град
60
60
.30
60
о
о
6,3
о
5,5
О
о
Примечания
При t = t] координаты центров тяжести
шкивов С1 и С2, хс =-0, ус =
= —0,1 см; zCi = a-\-b, *Сг = 0,1 см;
При / = ^ ось стержня 1 параллельна
оси у, а ось стержня 2 параллельна
оси х, 11 = 25 см, /2 = 40 см

15
16
17
18
19
20
21
22
23
24
2c
26
27
28
29
30
20
80
100
30
40
40
80
100
30
60
50
80
100
80
20
50
45
20
10
—
—
—
10
40
—
20
70
200
150
40
20
—
20
—
150
40
60
—
120
—
60
50
—
i50
120
—
42
60
—
Ю
—
—
—
30
15
20
—
—
20
25
20
—
—
—
—
65
160
—
—
3,0
124
216
—
—
—
—
—
—
—
—
8
—
—
12
9
—
—
—
9
—
—
—
—
—
—
12
—
—
—
—
—
4
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
0
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
2,0
—
—
—
—
—
—
—
—
—
—
Радиус инерции ротора 2 двигателя 3
tj-= 10 см
инерции ротора 2 двигателя 3
2 см
Радиус
ix — 12 см
Радиус инерции шкива 3 гж = 18 см
Радиус инерции шкива 3 ix = 22 см
Радиус инерции шкива 3 1^=15 см
Р=1300К
Примечания.
1 Тела, вводящие в состав механической системы, для которых ие указан радиус инерции, рассматривать как тонкие однородные стержня (вари-
аяты 1—5, 10, II—J5, )8, 19, 23, 24, 29, 30) или сплошные одгюреднь-е диски (варианты 6—9, 16, 20, 22, 28); в варианте 10 тело 2 рассматривать как
материальную точку.
2- На схемах I, 8, 9, II, 16, \Т, 20—22 указаны внешние моменты М

инерции точек стержня относительно точки О равна моменту равно-
равнодействующей этих сил, то
ФгН = <\?, cos а йФ,
о
где /г — плечо силы Ф1 относительно точки О; йФ — сила инерции
элемента стержня длиной d?; ?— координата элемента стержня
(рис. 201 б).
Используя значение силы Фх и учитывая, что
&ф = (/2 + gsina) co2v dg,
где у — масса участка стержня единичной длины, получаем
откуда после интегрирования
J, (/, + B/3) ¦/, sine) cos « „_ 30 B0 +B/3). 30. 0,5) .fi
"~" /lSina+2/2 ~ 30-0,5 + 2-20 СОЬ a — 10,4 COSa.
Показываем составляющие реакций подпятника ХА, YA, ZA
и подшипника Ув, YB силы тяжести стержней G1( G2, G3 и силы
(инерции Фу и Ф2 (рис. 201, б). Эти силы должны удовлетворять
уравнениям, вытекающим из принципа Даламбера
v м1х = 0; — YB ¦ 50 - Ф2 • 40 - G3 • 10 - Gt • 27,5 -
- Фх D0 - 16,4 cos a) = 0 => Уд = — 8,47 кН;
ZD = 0,098 кН.
Так как рассматриваемые силы расположены в плоскости yAz,
то Хн = Хл = 0.
Для определения реакции пружины DN составим уравнение
V Мю = 0, рассматривая силы, приложенные к стержню / (рис. 201, г)
— <?! • Aг/2) ¦ sin а + Ф{к— Plx cos a = 0,
откуда Р = 6,47 кН.
Задание Д-16. Определение реакций опор
при вращении твердого тела вокруг неподвижной оси
Однородное тело D вращается вокруг неподвижной вертикальной
осп 2 под действием пары сил, расположенной в горизонтальной
плоскости. Масса тела — т, момент пары сил — М. Определить реак-
реакции подпятника А и подшипника В в момент времени t = x, считая,
что в этот момент центр тяжести тела находится в плоскости уг,
с которой совпадает плоскость материальной симметрии тела; поло-
283

жение центра тяжести тела задано координатами ус и Zc- Началь-
Начальная угловая скорость тела соо = 0. Массой стержней, связанных
с телом D, пренебречь.
Варианты задания представлены на рис. 202 — 204, а необходи-
необходимые данные приведены в табл. 57.
Пример выполнения задания. Тело D (однородный цилиндр,
из которого вырезан конус) вращается вокруг неподвижной оси z
(рис. 205).
Дано: т = 32 кг; Л? = 60 Нм; /- = 0,25 м; 00, = 0,5 м; h=\ м;
Y = 30°; а=1 м; b = 2 м; т = 2с. Стержень ООг совпадает с ссью
симметрии тела D. Массой стержней пренебречь. Найти RA и RR.
Решение. Показываем главные центральные оси инерции тела
D: |, т) и ?, а также силу G, момент М и составляющие реакции
опор ХА, fA, ZA, Хй, Yn (рис. 205).
Для решения задачи используем систему уравнений, вытекающую
из принципа Даламбера.
Ха + Хв + тхси>2 + тусе = 0;
- У в (а + Ь) - G ¦ ОС sin у - J^2 + h^ = 0;
Хй (а + Ъ) + J2xa2 + Jyle = 0; М - Jгг = 0.
Для определения углового ускорения е из последнего уравнения
системы A) найдем момент инерции тела D относительно оси враще-
вращения 2- по формуле:
J J d> B)
где Jn — момент инерции тела D относительно центральной оси Сг1,
параллельной оси г; d — расстояние между осями z и zY.
Воспользуемся формулой:
JZ1 = J^ cos2 a -\- J^ cos2 p + Js cos2 у, C)
где а, р и у — углы, составленные осью z1 с осями |, т), %> соответ-
соответственно. ,
Так как а = 90°, то
J21 = Ул cos2 р + J; cos2 у. D)
Определим моменты инерции J^ и J^ как разности моментов
инерции тела / (сплошного цилиндра) и тела // (конуса) (рис. 205):
Jx\ = Jn — J"; Ji = Ji—J{- E)
Зная массу тела D, равную т, определим массу тела / и тела Л:
/ri[ = pnr2h, гпц = A/3) -рлг2/1,
где р —плотность тела; а —радиус основания цилиндра и конуса.
Следовательно,
т = /щ — тп = B/3) • гп\ = 32 кг.
287

•ч: и
288

s
О.
'/,10 n/p Яблонского A A.
289

290

Таблица 57
Помер
варианта
]
2
3
4
5
Ь
7
8
9
10
31
12
13
14
15
16
т. кг
40
120
60
80
60
100
80
50
85
60
100
80
75
50
60
100
м,
Нм
30
50
40
50
45
60 -
40
25
40
20
50
30
25
15
10
20
V-
град
20
30
40
25
20
25
20
15
20
30
15
30
30
30
20
15
-"С,
см
0
0
20
— 40
0
0
-30
— 40
30
15
2
0
50
30
— 25
— 20
гС,
см
60
70
50
60
50
65
60
50
55
40
25
60
75
40
40
50
лв.
см
120
140
120
125
НО
140
125
115
100
90
125
120
125
110
100
ПО
R. см
25
20
20
25
—
20
—
20
15
30
24
—
20
30
20
25
II. см
60
—
60
—
100
—
50
00
—
—
90
100
70
70
20
I. с
2,0
2,5
1,5
3,1
2,0
2,5
2,0
3,0
2,5
3,5
3,0
2,0
1,5
2,0
2,0
2,0
Дополнительные данные
Толщиной диска пренебречь
а=30; 6 = 40; с = 60 см;
tfi = 25 см-
а = 25; 6 = 30; с = 50 см
Я=1,2 г
а = 30; а, =24; Ь-=20; fcj = 16 сч
а = 6 = 5 см
R=2r
Пластинку между дисками считать тонкой однородно,"
? = 2/-; Л= 10 см

8
ко
Продолжение табл. 57
Номер
варианта
17
18
19
20
21
22
23
24
25
26
27
28
29
30
72, КГ
70
50
50
70
40
50
70
40
100
120
80
75
70
50
м.
Нм
30
10
20
15
20
15
15
5
15
20
15
12
10
7
\.
град
10
15
30
20
30
20
15
30
15
30
45
20
30
30
"С.
см
15
— 25
-20
0
-10
— 30
30
25
—
—
— 40
— 40
-20
—
гС'
см
55
70
60
40
70
55
50
70
45
40
50
60
50
60
АВ
гу
120
115
100
100
100
100
- 90
100
90
90
85
140
100
80
R. см
10
25
30
7,5
25
—
25
20
25
20
30
30
20
10
Н. см
70
25
40
25
—
—
25
25
—
40
—
20
40
т. с
1,7
1,8
2,5
1,8
2,0
2,2
2,0
3,5
3,2
3,0
2,0
2,5
2,0
2,5
Дополнительные данные
0 = 6 = 35 см; Л = 5 см
л = 0,5^
Я=о = 6 = 25 см
R = 2r
г = 0,2/?
г = 0,2/?, Й = ЗЯ
г=0,6/?, принять Л = 0
/¦ = 0,5/?, /г = 0,4Я
Н=2Ну
Пренебречь массой шарового сегмента, являющегося
основанием конуса
/¦ = 0,2/?. Пренебречь массой шаровых сегментов, являю-
являющихся основаниями цилиндра
а = 20; Ь = 50 см
о = 30 см; передняя грань параллелепипеда лежит
в плоскости уг

Отсюда
пц = C/2) • 32 = 48 кг; mn = 48/3 = 16 кг.
Для вычисления моментов инерции тела D необходимо знать
положение его центра тяжести —расстояние от точки Ot. (Во всех
вариантах координаты центра тяжести заданы, а определению под-
подлежат другие величины, необходимые при решении задачи.)
Это расстояние
где
— tnu),
OXC, = A/2) -Л= 1/2 м; О1Сц = C/4)-ft = 3/4 м.
Следовательно,
~п 48-1/2-16-3/4 3 ,.
Момент инерции цилиндра относительно оси Сп:
Ул = yT)i -\-m1 (L\LI, (о)
где У' =/пг (а2/4 +/г2/12) * — момент инерции цилиндра относительно
оси %, проходящей через центр тяжести С{ этого тела: С\С = OjCi —
— 0tC= 1/2 — 3/8= 1/8 — расстояние между осями rj и %.
Подставляя в F) значение этих величин, получим
: = 5,5 кгм2.
* См., например, А. Г. Л о й ц я н с к и й и А. И. Л у р ь е. Теоретическая
механика. Физматгиз, 1954. М. В. Ф а в о р и н. Моменты инерции тел. М., 1970.
10 п/р. Яблонского А. А.
293

Момент инерции конуса относительно оси Сл:
\l ? (СИС)\ G)
где J^ — момент инерции конуса относительно оси тJ, проходящей
через центр тяжести Сц этого тела.
В свою очередь для конуса имеем:
у;' = у;'_т„(О2С„J. (8)
Здесь J\l — момент инерции конуса относительно оси г|3, прохо-
проходящей через центр основания конуса О2 и параллельной оси i]2.
Подставляя (8) в формулу G), получим:
причем момент инерции конуса относительно оси тK определяется
по формуле*:
где
^9 1] ,1 -12) 16=1,75 кгм2;
С1]С = О1Си-О1С = 3/4 -3/8 = 3/8 м;
О2СП = Л/4 =1/4 м.
Таким образом,
JH = l,75+16[C/8J-(l/4J] = 3 кгм2.
Теперь Jj, и J^ можно вычислить по формулам E):
=Jv—j\! = 5,5-3 = 2,5 кгм2; Jt = Jl-j[1,
JJ = m1r2/2 = D8-01252)/2 = l,5 кгм2;
У» = 0,3/ипг2 = 0,3 • 16 • 0,252 = 0,3 кгм2.
Тогда
УЕ= 1,5-0,3= 1,2 кгм2.
По формуле D) вычисляем Jn, учитывая, что р = 120°, у = 30°.
jn = Уч cos2120° + J% cos2 30° = 2,5 A /2J + 1,2 A/3/2J = 1,525 кгм2.
Момент инерции тела D относительно оси вращения г вычисляем
по формуле B):
J J
где
d = ОС sin у = (ООг + О& sin у = A /2 + 3/8) sin 30° = 0,437 м;
Л= 1,525 +32 @,437J = 7,65 кгм2.
Из последнего уравнения системы A)
. e = M/JJ! = 60/7,65 = 7,85 с2 = const,
294

Угловая скорость при равноускоренном вращении тела
со == со„ + е/,
поэтому при шо = 0 и ^ = т = 2 с
@ = 7,85-2=15,7 с-1.
Для определения реакций опор следует определить центробеж-
центробежные моменты инерции Jyz и Sгх тела. Jlx = 0, так как ось х,
перпендикулярная к плоскости материальной симметрии тела D,
является главной осью инерции в точке А.
Центробежный момент инерции тела Jyz определим по формуле*:
Jyz = JyA + mycZc, где JyiIl = (Jn- J$ (sin 2v)/2,
т. e.
Jyi2i = B,5 - 1,2) (sin 60°)/2 =» 562 кгм».
Координаты центра тяжести тела D следующие;
хс = 0; yc = d = 0,437 м;
zc = а + ОС cos y = a + (OO1 + OlC) cosy =1,76 м.
Таким образом,
Jyt = 0,562 + 32 • 0,437 -1,76 = 25,16 кгм2.
Подставляя известные величины в систему уравнений A) и
учитывая, что ОСs\ny = d = 0,437 м, получаем следующие равен-
равенства:
ХА + Хв + 32 • 0,437 • 7,85 = 0;
У А + У в + 32 • 0,437 • A5,7J = о;
ZA- 32-9,81=0;
- ЗУв - 32 • 9,81 ¦ 0,437 - 25,16 ¦ A5.7J = 0j
ЗХВ + 25,16 -7,85 = 0.
Откуда
ХА = ~ 43,6 Я; УА = — 1340 Я; гл = 314Я; Хп = — 65,8 Я;
7В = — 2120 Я.
ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
Задание Д-17. Применение общего уравпения
динамики к исследованию движения механической
системы с одной степенью свободы
Для заданной механической системы определить ускорения гру-
грузов и натяжения в ветвях нитей, к которым прикреплены грузы.
Массами нитей пренебречь. Трение качения и силы сопротивления
в подшипниках не учитывать. Система движется из состояния покоя.
* См., например, А. Л. Яблонский. Курс теоретической механики.
Ч. II. Изд-во «Высшая школа», 1977, пример Ms 20.
10* 295

Варианты механических систем показаны на рис. 206 — 208,
а необходимые для решения данные приведены в табл. 58.
Блоки и катки, для которых радиусы инерции в таблице
не указаны, считать сплошными однородными цилиндрами.
Пример выполнения задания. Дано: Gt = G2 — 2G; G3 = Gi = G\
R = 2r, itx = rV% / = 0,2.
Блок 3 — сплошной однородный цилиндр (рис. 209). Определить
ускорения грузов 1 и 4 и натяжения ветвей нити 1 — 2 и 3 — 4.
Решение, Применим к решению задания общее уравнение
динамики. Так как система приходит в движение из состояния
покоя, направления ускорений тел соответствуют направлениям
нх движения.
Ввиду того, что среци сил, действующих на тела системы, есть
сила трения, целесообразно установить по исходным данным истин-
истинное направление движения системы, чтобы правильно показать
направление силы трения.
Если направление движения системы выбрано ошибочно, то иско-
искомое ускорение получается со знаком «—». В этом случае необхо-
необходимо изменить направления силы трения и сил инерции и внести
соответствующие поправки в общее уравнение динамики.
В данном примере движение системы таково, что груз /
опускается.
Покажем задаваемые силы: силы тяжести Gx —груза /, G2 —
блока 2, 0'3 — блока 3 и G4— груза 4, а также F — силу трения
скольжения груза / по наклонной плоскости (рис, 210).
Приложим силы инерции. Сила инерции груза 1, движущегося
поступательно с ускорением ш,, выражается вектором
Силы инерции блока 2, вращающегося вокруг неподвижной оси
с угловым ускорением е2, приводятся к паре, момент которой
Силы инерции блока 3, совершающего плоское движение, при-
приводятся к вектору
Фа = — ЩЩ,
где ш3 —ускорение центра масс блока 3, и к паре сил, момент
которой
Mf = J3xe3,
где е, — угловое ускорение блока.
Сила инерции груза 4, движущегося поступательно с ускоре-
ускорением ~wt
Ф4 = — miwi.
Сообщим системе возможное перемещение в направлении ее дей-
действительного движения (рис. 210) (можно сообщить возможное
перемещение и в обратном направлении).
296

?////////7////////////////// '/////////№
'//////////'Xr//////////,
~7~
V/////////7PZV/777777/////
Рис 206
2Q7

12
I 21
D-'
13
15
16
Рис 207
298

21
22
23
p
1
I
1 V
3 m
' 2
-A—i_
25
'//////////////////////////A
3~
27
2R
-I
30
Рис. 208
2Э9

Таблица 58
Номер
варианта
(рис 206—
—°08)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Веса
С
G
G
3G .
G
2G
2G
2G
2G
2G
2G
2G
2G
4G
—
G
G
G
G
G
G
G
G
G
2G
G
G
2G
2G
3G
G
G
2G
G
2G
2G
2G
2G
G
2G
2G
G
G
_
—
—
—
G
—
—
—
—
—
0.2G
0,2 G
4G
4G
Я
г
2
2
2
—
3
3
3
3
3
4
3
3
—
—
Радиусы
lix
r\f2
г\Г2
rV2
—
2т
1г
2г
2г
2,-
—
2г
2г
r,V~2
H\f2
инерции
—
—
—
—
—
—
—
—
—
—
2г3
2л,
р
_
— _
—
—
—
—
—
—
0.2G
G
3
—
—
—
8G
Коэффи-
циент
трения /
—
0,1
0,2
—
0,2
0,2
0,2
0,2
0,4
0,2
0,2
—
—
Дополнительные Данные
гг = 2гг\ R2 = R3
/¦2 = 2г3; /?з = 1,5/?а

15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
AG
2G
3G
4G
4G
5G
G
G
2G
6G
6G
G
3G
CG
8G
G
G
G
0,2G
0,3G
0,2G
O,1G
0,2G
0,2G
G
2G
G
G
G
3G
G
2G
2G
G
0,IG
0,2G
0,1 G
0,2G
0.3G
0.1G
G
2G
2G
G
G
G
G
4G
4G
0.5G
3G
3G
8G
G
4G
G
2G
2
2
3
2
3
2
1,5
2r
1,2/-
2r3
1,2/-
V'2
4G
—
—
—
—
G
G
2G
0,1
0,4
0,1
0,2
—
—
0,1
0,1
ra=l,2r; /?B=l,2r,
Массы четырех колес одина-
одинаковы
со
П риуечання'
I Радиусь' инерции даны относительно центральных ocefl. перпендикулярных к плоскости чертежа (рис 206—208)
2. Коэффициент трення принимать одинаковым как при скольжении тела по плоскости, так и при торможении колодкой (варианты Ч—12).

Составим общее уравнение динамики:
Gx8sx sin 60° -FSs^ - Ф^ - Mf бф2 -
- G?s3 - Ф3б«з - Mf бф3 - G46s4 - *46s4 = О,
где 6ф.2 и бфз — углы поворотов блоков 2 и 3.
Учитывая, что
имеем:
F = /Gx cos 60° = 2/ mg cos 60°;
Фх = т1ш1 = 2mwl;
Mf = J2Ji:e2 = т^?2хе2 = 4mr2e2;
Фа = maw3 = mw3;
Mf = J3,e3 = Kra/2) e3 = (mr2/2) e3;
ф = /niti4.
0)
B)
Устанавливаем зависимости между возможными перемещениями,
входящими в A), и между ускорениями в B), пользуясь тем, что эти
зависимости такие же, как между соответствующими скоростями.
Рис. 209
Рис. 210
Как показано на рис. 210, мгновенный центр скоростей блока 3
находится на одной вертикали с центром блока 2. Расстояние между
мгновенным центром скоростей и центром блока 3
а = (Зг/2) — г = г72.
302

Теперь находим:
6s3 = 6s4 = бф3а = dsji; \ C)
e2 = e3 = Wylir; w3 = ш4 = u»x/4.
С учетом B) и C) уравнение A), после деления всех его членов
на т и 6slt принимает вид
2gsin60°-2/gcos60°-
w,
откуда
_ g B sm 60° — 2/ cos 60°—0,5) _
_ 9,81 (l,73-2-0,2-0,5-0,5)_
— 3,25
= 3,11 м/с2,
ш4 = oUj/4 = 3,11/4 = 0,78 м/с2.
p-
Рис. 211
k
Рис. 212
Для определения натяжения в ветви нити /—2 мысленно разре-
разрежем нить и заменим ее действие на груз реакцией 7\_з (Рис- 211).
Общее уравнение динамики
G^ sin 60° - F6sx - Ф^ - Ti-^Si = 0,
откуда _
Т^2 = Gt sin 60° - F - Фх = 2G /3/2 - 2Gf cos 60° -
-2- (G/?)bf, = GA,73-2-0,2- 0,5-2 -3,11/9,81) = 0,90G.
Для определения натяжения в нити 3—4 мысленно разрежем эту
нить и заменим ее действие на груз 4 реакцией Г3_4 (рис. 212).
Не составляя общего уравнения динамики, на основании прин-
принципа Даламбера имеем:
Т3_4 = <j4 + Ф* = G + (Gig) ¦ Wt = G4 A + 0,78/9,81) = 1,08 G.
Задание Д-18. Применение общего уравнения
динамики к исследованию движения механической
системы с двумя степенями свободы
Механическая система тел 1—6 (рис. 213—215) движется под
воздействием постоянных сил Р и пар сил с моментами М или
только сил тяжести.
Найти уравнения движения системы в обобщенных координатах
qx и q2 при заданных начальных условиях. Необходимые данные
приведены в табл. 59; там же указаны рекомендуемые обобщенные
координаты (х и <р — обобщенные координаты для абсолютного дви-
движения, а I — для относительного движения).
При решении задачи массами нитей пренебречь. Считать, что
качение колес происходит без проскальзывания. Трение качения
зоз

Таблица 59
Номер
парнаита
(рис.
2K — 215)
1
2
3
4
5
6
7
8
9
10
11
12
13
1
27!
т
т
т
т
т
Зт
т
т
2т
т
2т
т
Массы 1
2
6т
Зт
Зт
4т
2т
2т
Зт
2т
2т
2т
Ът
Ът
Зт
з
т
—
2т
—
4т
Зт
т
2т
"т
т
2т
т
2т
гел
4
т
—
—
—
2т
—
т
2т
—
2т
т
—
—
—
—
—
—
2т
—
—
2т
—
т
—
—
—
Радиус
ниерции •
—
—
г\/~2
—
2г
—
—
—
—
4.
—
—
—
—
—
—
—
—
—
—
—
—
/•1/2
—
—
Силы
Р
—
—
—
Р
—
—
Pi, P*
—
—
—
—
Р
—
Момен-
Моменты AI
—
Л?
УМ
—
—
Л1, Л12
—
—
—
Mi, Л12
—
—
Коэффициент
тре-
трения
сколь-
скольжения
—
—
—
0
/
—
—
1
—
—
—
вязко-
вязкого со-
про
тивле-
ния **
—
—
—
b
—
—
—
—
—
—
—
—
ь
ОбоСщен
HbL 1чООр
дкнаты
ф
ф
«1
ф!
*1
X
?!
ф1
Qz
с
X
X
%
х*
Ф2
^2
1
Ч-;
t
Ф2
ъ
t
0
0
0
0
0
0
0
0
0
0
0
0
0
н;^о
0
с
0
0
(|
0
с
0
0
0
So
0
0
0
0
'о
0
0
0
0
0
*0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
\о
Дополнительные
данные
Массу ленты не учиты-
учитывать
Момент М приложен
к водилу
1 — материальная точка
Блоки 5 и б насажены
па общую ось свободно,
их массы одинаковы
Момент Мг приложен
к водилу
Момент Мх приложен
к водилу
/ — материальная точка

2m
Зт
2m
т.
2m
2m
2m
2m
m
2m
m
2m
m
2m
m
2m
Ът
m
m
3m
3m
2m
2m
3m
2m
3m
m
3m
2m
3m
2m
3m
4m
2m
m
2m
2m
—
m
Ът
m
3m
2m
m
m
m
2m
3m
m
m
2m
2m
—
m
—
m
m
3m
2m
m
m
—
—
3m
m
—
m
—
—
—
—
—
3m
—
—
m
—
Ът
—
—
—
2m
—
—
—
—
2r
—
—
—
—
—
—
—
—
—
г
r\r2
—
—
—
—
—
—
—
rV2
—
rV2
—
—
—
—
—
—
—
—
p
—
p
—
—
—
—
—
—
p
Pl.pt
—
—
p
p
—
M
M
M
—
—
—
MltMt
—
мимг
—
—
—
M
M
—
—
М1г Mt
—
—
0
/
/
—
—
—
/
—
f
—
—
—
—
—
—
—
—
—
—
—
—
6
—
—
—
—
—
—
Ф
Ф
Ф
X
X
X
Ф1
X
«Pi
X
X
Xl
Ф
<p
X
X
q>i
E
X
X
I
I
I
Ф2
I
Ф2
i
i
Б
1
¦ i
Ф2
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
fcO
0
0
0
0
0
0
b>
0
0
0
0
0
0
0
0
0
0
0
4
0
4
0
0
0
0
0
0
0
*0
Фю
So
0
0
0
0
0
0
0
to
0
0
io
0
4o
0
0
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
• Радиус инерции тела 2 или 3 относительно центральной осн. перпендикулярной к плоскости чертежа
м ** Коэффициентом вязкого сопротивления назван коэффициент пропорциональности в выражении силы сонротивлення отвоснтельному движе-
сл нию тел / н 2 R = —b i>T гДе ? ~ относительная скорость тела,
Массу ленты не учиты-
учитывать
Момент М приложен
к водилу
/—материальная точка
Момент /И] приложен
к водилу
Момент Мл приложен
к водилу
—материальная точка

X
\.
<зо°
4>г
г
j_
10
ч>.
%
Рис. 213
306

11
13
15
M
Yfi
' . 1
17
19
Рис. 214
3G7

21
Z5
X
V/УУУУУУУУУУУУУУУУУУУУУУУУУУУУУУУУУУ/УУУУУУУУУ/,
29
Рис 215
308

и силы сопротивления в подсгипниках не учитывать. Колеса, для
которых в таблице радиусы инерции не указаны, считать сплошными
однородными дисками. Водила (кривошипы) рассматривать как топкие
однородные стержни. Принять, что в вариантах 6, 9, 11, 20, 22 и 30
механизм расположен в горизонтальной плоскости.
Пример выполнения задания. Дано: массы тел / и 2 механической
системы (рис. 216): гпу^ — т, т2 = 5т (тело / считать материальной
точкой); Р — постоянная сила, приложенная к телу 2 (тело 2 может
двигаться только поступательно вдоль линии действия силы Р);
Ь — коэффициент пропорциональности в выражении силы сопротив-
сопротивления относительному движению тел / и 2; R = — bv, где и —отно-
—относительная скорость тел. Коэффициент трения скольжения (тела 2) / = 0.
Рис 216
?П!|||;Г |1!Пл1!1"|||1м|;.
Рис. 217
Найти уравнения движения системы в обобщенных координатах
= x, q-i = ?, (рис. 216) при начальных условиях:
Решение. Воспользуемся общим уравнением динамики. Покажем
задаваемые (активные) силы: силы тяжести тел / (шарика) и 2 — Gl
и G2, силу Р, а также силу R сопротивления движению шарика
по желобу (рис.-*217). Со стороны шарика на тело 2 действует сила
R' = — R, которая на рисунке не показана.
Приложим силы инерции. Сила инерции тела 2, движущегося
поступательно с ускорением ш2, выражается вектором
Ускорение шарика / складывается из относительного wr и пере-
переносного WP = W2.
Соответственно покажем две составляющие силы инерции шарика
Фг = — ттг ц фе— — /7гхш2.
Для того чтобы получить уравнение движения системы, применим
принцип^наложени*-дополнительных связей (принцип затвердения).
309

Мысленно закрепив тело 2, сообщчм шарику / возможное пере-
перемещение 6? и составим общее уравнение динамики:
GM cos (Glt 8t) - (R + Фг) 81 + ФМ cos (Ф„ 81) = 0.
Имея в виду, что
cos(Glt 6E) = sin30°sin45°; cos (Фе, 81) = cos 30° sin 45°,
получим
n^g sin 30° sin 45° - b| - mj -f rnxx cos 30° sin 45° = 0
или
I + (*/«) • I - (/6/4) • JB = ^ /2/4. A)
Теперь мысленно закрепив шарик / в желобе, сообщим телу 2
возможное перемещение &х.
Общее уравнение динамики в этом случае имеет вид:
(Р - ф2 _ фе) Ьх + Фг6х cos (Ф„ &с) = 0.
Учитывая, что
cos (Фг, 6x) = cos30°sin45°,
находим
Р = щ2х - тух + mj cos 30°sin 45° = °
или
6mJt - m (/6 /4) • | = Р. B)
Для решения системы дифференциальных уравнений A) и B)
из A) определяем
х = D//б) • 1 + DЬ//б т) • | -
Подставляя это значение х в B), получаем
3,75/6mf + 4Vr6bi = ,p + 2/nyr3g. C)
Введем обозначения:
3,75 Кб/и = a; 4j/^ = fi; Я + 2m/З g = A.
Тогда уравнение C) примет вид:
al + \il = h или 1 + (|х/а) • | == Л/а. D)
Общее решение этого дифференциального уравнения имеет вид:
1 = С1+С*Г{>1'аI + Ш-и E)
Постоянные Ct и С2 определяем из начальных условий. При f = 0
6 = So. lo = 0.
Следовательно, согласно E)
310

откуда
Окончательно
S = So
Для того чтобы получить второе уравнение движения x = x(t),
найдем из B)
i
- e-w«)-0 + (A/i*) • *. F)
Дважды дифференцируя F), определяем, что
Тогда
Jc = Qi/aA 1/6) • е- d»/")-' -f- P/6m
или, учитывая, что а = 3,75"|/бт,
JP = (A/90m) • е-о*/«>-< + Р/бт. G)
Интегрируя G), находим:
i = _ (faz/90mu) • е-<¦*/<»>•< + (P/Qm) -t + C3;
х = (/га2/90тц2) е- (^а>¦' + (P/l 2m) • /а + С,/ + СА. (8)
Согласно условию задачи при t = О
* = 0, Л = 0.
Следовательно,
0 = —/ia/90m(i. + C3; 0 = ha2/90m\i2 + СА.
Отсюда
С3 = /ю/90тц; С4 = — ha2/90m\is.
Подставляя эти значения постоянных в (8), получаем:
Уравнения F) и (9) являются решением задачи.
УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
Задание Д-19. Применение уравненвй Лагранжа
второго рода к исследованию движения
механической системы с одной степенью свободы
К ведущему валу / механизма приложена пара сил, момент
которой (вращающий момент) постоянен и равен Mi. К ведомому валу //
приложены силы сопротивления, создающие относительно оси //
постоянный момент Мц (момент сопротивления).
Определить угловые ускорения ведущего и ведомого валов.
В задании приняты следующие обозначения: т2_3 — масса каж-
каждого сателлита 2—3, состоящего из колес 2 и 3; У2_3 —момент инерции
сателлита 2—3 относительно собственной оси; Jj —момент инерции
311

частей, жестко связанных с ведущим валом /, относительно его оси;
Уп — момент инерции частей, жестко связанных с ведомым валом II,
относительно его оси; rlt r2, г3, г4 — радиусы колес /—4.
Схемы показаны на рис. 218—220, а необходимые для решения
данные приведены в табл. 60.
Таблица 60
Номер
(рис 2IS—220)
1
2
О*
v>
4*
5
6
7*
8
0
10
11*
J
13
1 Л*
] '1
15
16*
17
IS
19
20
21
22
2Л
24
25
ок*
27
28
29
30*
см
20
20
.г
25
15
40
15
15
20
50
30
35
15
in
i \j
15
10
10
10
10
10
20
20
15
10
30
in
1 'J
10
15
27
15
25
5
in
1U
15
10
10
12
10
15
10
8
10
10
in
i w
20
15
15
12
10
15
15
10
10
15
10
in
1 V
10
10
12
10
11/
15
10
in
10
—
18
18
15
10
15
14
15
12
in
10
12
—
—
12
—.
5
in
l и
12
5
10
1 \J
30
15
30
—
12
9
10
25
25
40
37
15
37
—
10
—
16
10
14
—
15
12
.
.
.
.
.
m
кг '
50
45
5/5
58
10
80
55
70
82
72
4,5
95
60
4/4
7
65
55
70
80
55
72
75
62
50
70
8
95
82
4/4
КГМ2
0,92
0,8
0,0015
0,0015
1,0
0,003
1,2
0,9
1,0
1,1
1,02
0,001
1,2
0,9
0,001
0,001
0,002
0,96
0,92
1,0
1,1
0,91
1,2
1,05
0,95
0,9
1,0
0,0014
0,0014
0,002
1,2
1,1
0,001
0,001
2,7
12
on
2.0
2,5
3,0
3.5
4,2
2,5
1,5
2
12
4
2,5
6
5.5
4,8
4
4,5
18
0,2
20
5,5
12
9
6,2
6,5
4
5
19
2,0
Л f\
4,0
3,0
12
15
4,5
21
20
12
18
6
16
10
12
6,0
22
16
18
5,7
5
7
18
6
22
17
1 /
20
6
12
ЧП
Ни
ПО
170
45
75
95
100
70
80
75
120
72
75
90
100
85
70
200
100
ПО
120
240
175
170
220
190
1 Ч~,
1 Oi)
130
120
60
54
90
55
18
100
91
450
35
150
30
6
160
220
Iе;
и
350
8
225
726
400
450
280
55
105
80
100
380
74
102
460
* Дополнительные данные в вариантах 4, 7, М, 14 .и 16 — раднус шестеренки, сопри-
соприкасающейся с колесом—5 — 2 см, момент инерции рамки относительно оси вращения —0,5 кгм2;
в вариантах 3, 14, 26, 30 — в числитече данные для колеса 2, в знаменателе — для колеса 3.
Пример выполнения задания. Дано:
= 4 кгм2; т2_о==100
= 2 кгм
2;
, = 100,
/и = 12
Ми = 320 Нм;
кгм2; г1 = 60;
кг; У2_3 =
г2 = 25; г3 = 5; г4 = 30см (рис. 221).
Определить угловые ускорения ei и ец.
Решение. Воспользуемся уравнением Лагранжа второго рода.
Приняв за обобщенную координату системы, имеющей одну степень
312

Ты
ы К
т2
j,
1 т
1
J
:
J
"т
L
*¦
:
L
Li «i
I V
f4 ^zr
\
J. ?////
Ж
f'
i
LLP
У777/
Г2 .
/
1
1
J ^ 1
7" -jj
1
т -
J
L2
J
77Л7
Рис. 218
313

XL у////, 4
zm x
'////( i
? '77Л/ 1
13
о
1
15
2
17
J
J- J?i/A
19
1 ША
WV/
5
"
—=-
I
/ .
г 1
И
1
I
V
[
h
1 1
i
I
1
i
l
I
J
j-
-L >/
il
-4
ri
f\
i
j
_
-
*
Ж
V777/
777-
12
J '///7a
77777,
ti-
j
Г—1
:
-s
:
Л ИИ4
У/У/.
13
4
7777?
20
W//
f
t
f
I
\
P
h
II
< . .
i
1 r
^ T
J7-1
ri
X
X
]5
T
1?
T/
r~
2
|—
г
E
I
xJ
-•///*•
1
J
J
Ij
'//7///
«ж
777
I
'//л* 77"
Рис 219
314

L_
21
г?
№
23
i «i
tat Ж
777?
ft-il
26
~i
12
I
.'I
J
4
'/
'*,
-t iiCii
H
*' 2Г
|
-71
tr
J
:
2
r
f ~
ж
Рис. 220
315

свободы, угол поворота ф| ведущего вала, имеем:
dt
dp,
0)
Найдем кинетическую энергию системы Т как функцию обобщен-
обобщенной скорости фь равной угловой скорости ведущего вала coi. Для
м,
Л/д-
Рис. 221
вычисления кинетической энергии рассматриваемой системы необхо-
необходимо знать угловые скорости всех звеньев: ведущего вала (колеса /)
coi, ведомого вала (водила) соц, сателлитов ш2-я-
Определим эти угловые скорости способом Виллиса (см. пример
выполнения^задания К-11):
(COj - COI l)/((iL - COI l) = — Г4/Г, = — 13_4- C)
Перемножая левые и правые части равенств B) и C), а также
учитывая, что cu2 = cu3, получаем:
((Ol — С0ц)/(Ш4 — СО[[) = — I) I = i\_2 ' tj- 4-
Так как колесо 4 неподвижно, т. е. со4 = 0, то
(coi —coii)/con = t.
Из этого равенства
Из B) и D)
D)
E)
Полученные значения соц и со2 показывают, что вал // и сател-
сателлиты вращаются в одном направлении с валом /.
316

Составим выражение кинетической энергии всех движущихся
частей:
где
vCi = Ясоц = (r3 + л4) con = -^
Выразив все линейные и угловые скорости через угловую ско-
скорость ведущего вала coi = (pi, получим:
Из выражения кинетической энергии находим приведенный к оси
ведущего вала момент инерции:
7TT7F F)
Таким образом,
Г = A/2)Упрф|.
Определим потенциальную энергию П. Силами, имеющими потен-
потенциал, являются силы тяжести. Но центр тяжести всех движущихся
частей неизменно находится на оси его материальной симметрии —
прямой, Совпадающей с осями валов / и //, так что потенциальная
энергия постоянна:
П = const.
Найдем обобщенную силу <2Фг, соответствующую задаваемым силам,
не имеющим потенциала. Такими силами являются: силы, приложен-
приложенные к валу / и образующие пару, момент которой (вращающий
момент) равен М\, и силы сопротивления, приложенные к валу //
и создающие относительно оси // момент сопротивления /Иц.
Сообщим углу (pi приращение d(pi и составим сумму элементар-
элементарных работ задаваемых сил на этом возможном перемещении. В эту
сумму войдет работа вращающего момента Mi и работа момента сил
сопротивления М\\, которая отрицательна,
8Аф1 = Mi бф| — Мм осрц.
Зависимость между угловыми перемещениями ведущего и ведо-
ведомого валов такая же, как и зависимость между абсолютными значе-
значениями угловых скоростей:
Тогда
6ЛФ1 =[Afi — Л1ц -1/A +
Обобщенная сила
Q<p, = 6Л„г/вф1 = Mi -Ми ¦ 1/A+0-
317

Найдем значения членов левой части уравнения (I):
дТ Л дП
-^Г = о и ^Г
Уравнение A) примет вид
Из уравнения G), учитывая выражение F), получаем:
G)
Зависимость между угловыми ускорениями ведущего и ведомого
валов такая же, как и зависимость D) между их угловыми скоростями:
en = ei/(l+t).
Подставляя в эти формулы заданные числовые значения всех
величин, находим:
е, = 0,37 с и ем =0,106 с2.
Задание Д-20. Применение уравнений Лагранжа
второго рода к исследованию движения механической
системы с двумя степенями свободы
Решить задачу из задания Д-18, пользуясь уравнениями Лаграпжа
второго рода. Условие задачи и все исходные данные, указанные в
задании Д-18 (см. рис. 213 — 215, табл. 59), остаются без изменений.
Пример выполнения
задания. Рассмотрим при-
пример, решенный в задании
Д-18.
Дано: массы тел / и
2 механической системы
(рис. 222) tnl = m,tni = 5m
(тело / считать материаль-
материальной точкой); Я —постоян-
—постоянная сила, приложенная к
телу 2 (тело 2 может дви-
двигаться только поступатель-
поступательно вдоль линии действия
силы Р); Ъ — коэффициент
пропорциональности в вы-
Рпс. 222 ражении силы сопротивле-
сопротивления относительному движению тел R = — bv, где v — относительная
скорость тел. Коэффициент трения скольжения (тела 2) / = 0.
Найти уравнения движения системы в обобщенных координатах
ql = x; q-i = \ (рис. 222) при начальных условиях:
?ю = 0, 02о = ?о. <7го = О, «L =0.
318

Решение. Для решения задачи применим уравнения Лагранжа
второго рода:
A)
&г
т'
а/
B)
Здесь Г —кинетическая энергия системы; П — потенциальная
энергия; Qx и Q| — обобщенные силы, соответствующие неконсерва-
неконсервативным силам.
Кинетическая энергия
системы (рис. 223)
где v — абсолютная ско-
скорость тела / (шарика):
',f, cos (г»„ у,).
Здесь относительная ско-
скорость vr = i, переносная
скорость ие = х
cos (vr, ve) =
= —cos 30° cos 45° =
= -J/6/4.
Учитывая, что тг = т,
/722 = 5ffz, получим
illllllllllllllllllllllllllllllllllllllllllllllllllllHMI
Рис 223
. C)
Потенциальная энергия системы зависит только от высоты, на
которой находится шарик. Принимая, что Я = 0 при | = 0, находим:
или
П = — mg\ sin 30° sin 45°
П = - (/2/4) -/ng|.
D)
Обобщенные силы Qx и Q| определяются из выражений работы
неконсервативных сил тта-элетиштар"ных перемещениях системы, соот-
соответствующих вариации каждой обобщенной координаты:
где R — b% — сила сопротивления движению шарика по желобу.
Отсюда
Определяем величины, входящие в уравнения Лагранжа A) и B).
319

Учитывая C) и D), имеем
-д— = 6mx — nt^-r-c: -г—=0; -^г—— 0j
ox 4 -' d* ' дх
дТ i Ув . дТ п дП V~2
—r- = mc, — m -— л:; — т= О, _ -.= r-— ma.
Теперь уравнения A) и B) принимают вид:
m^-i = P, E)
Дифференциальные уравнения движения системы E) и F) сов-
совпадают с уравнениями A) и B) в примере выполнения задания Д-18,
где дано их решение.
УСТОЙЧИВОСТЬ СОСТОЯНиЯ ПОКОЯ (РАВНОВЕСИЯ)
КОНСЕРВАТИВНОЙ МЕХЛНИЧКСКОЙ СИСТЕМЫ
Задание Д-21. Определение положений покоя
(равновесия) консервативной механической системы
с одной степенью свободы и исследование
их устойчивости (по теореме Лагранжа—Дирихле)
Определить положения покоя консервативной механической
системы с одной степенью свободы, пренебрегая массами упругих
элементов. Провести исследование устойчивости найденных положе-
положений покоя по теореме Лагранжа —Дирихле.
Варианты механических систем показаны на рис. 224 — 228,
а необходимые для расчета данные приведены в табл. 61.
В качестве обобщенной координаты выбрать угол (р, образован-
образованный стержнем / и вертикалью (ось Оу), считая, что при ф = 0 угол
между стержнем 2 и положительным направлением оси Оу равен
нулю. На рис. 224 — 228 показаны механические системы тел 1 — 6
при некотором положительном угле ц>. Во всех вариантах качение
колес происходит без проскальзывания и трение в сочленениях
отсутствует. При решении задачи считать все стержни и диски
однородными.
Пример выполнения задания. Дано: веса элементов системы тел
1-6 (рис. 229): G\=10; G2 = 5, G3 =-- 20; G4¦--= 5; G5=10, Ge=-15 II;
линейные размеры: ^ = 0,8, /2 = 0,2, /4 = =0,2, /в = 0,5, /6 = 0,7 м;
R = 0,1 м; коэффициенты жесткости пружин: q = 40 Н/см, с2 = 50 Н/см,
длины недеформированных пружин 1 и 2: а1 = 0,1 м, сц — 0,3 м.
Определить положения покоя рассматриваемой системы и иссле-
исследовать их устойчивость по теореме Лагранжа —Дирихле.
Решение 1. Определение положений покоя рассматриваемой
системы. Значения угла <р, соответствующие положениям покоя
исследуемой консервативной системы с одной степенью свободы,
320

Рис. 224
321

^—I
Рис. 225
322

13
h-h
17
Рис. 226
323

Рис 227
324

x
Рис 228
325

8
Таблица 61
Номер
варианта
(РНС 2.2^—2?<->)
1
2
;s
4
ft
6
<
,S
;i
10
1 1
12
13
1 !
35
16
17
IS
1!)
20
21
') >
23
21
о,"
¦>(>
27
28
29
го
С,
4
6
10
2
4
6
2
2
3
4
1
9
50
70
К)
3
100
10
40
15
')
80
100
20
4
20
4
20
20
20
Сн
2
10
4
3
<S
6-
4
5
• у
Г)
О
3
40
15
80
2
30
40
30
20
4
100
20
40
|)
20
10
20
30
60
Веса тел.
С,
6
20
15
а
20
30
6
20
10
15
20
за
00
60
120
6
150
80
70
GO
10
200
60
100
10
60
20
50
га
80
с, 1
3
15
4
4
20
12
8
12
20
¦_)
М
8
80
100
100
/
30
90
70
30
20
120
80
80
6
50
15
40
50
130
Н
G5 !
1
15
8
6
10
15
<)
10
5
4
i)
130
40
100
1
40
150
50
40
л
70
10
8.)
)
80
15
30
70
120
с.
10
—
—
—
—
5
10
—
40
50
;)
80
20
7
250
20
100
4
_..
5
. _
25
—
—
—
—
—
—
—
—
6
—
—
80
—
—
—
—
—
._
—
—
Л
0,2
0,2
0,7
0,2
0,4
0.4
0,3
(>,?
(', 1
0,1
0,1
0,'
0,5
0,7
0,1
0,3
1
0,1
0,4
0,1
0,1
о,х
03
0,08
0,1
0.2
0,0 1
0,2
0,2
0,2
Длины стержней, м
h I
0,15
0,1
0,15
0,3
0,'t
0,4
0,5
0,5
0,1
0,")
0,5
0,1
0,4
0,15
0,3
0,2
0,'i
о, t
0, i
0,1
0,1
l
0,1
0,15
0,6
0,2
0,1
0,2
0,2
0,6
h
0,4
—
—
0,7
—
—
1
—
_
1,5
—
—
0,')
—
—
--
0,7
—
2
—
—
1
—
—
0,5
—
—
0,9
0,9
0,15
0,'i
¦)
0,9
0,-i
1,1
1
0,2
1. 1
0,8
0,9
1
1,2
0,7
0,i
0,')
0,7
U,i
1
1
0/1
0,3
0,6
0,5
o,>
(),!
0,5
1,3
'5 ,
0.2
0,9
0,6
1,8
1,2
0,4
i
0,2
0,4
0,7
0,5
U
0,4
0,4
1
0,5
1,5
0,<l
0,1
0,7
ои
0,3
0,5
0,8
0,2
0,2
0,7
V-
'. •
0,6
—
—
—
—
0,8
—
0,4
—
o,a
0,2
—
o,5
0,9
—
0,8
0,4
0,7
>
0,1
1
0,1
—
0,05
—
0,2
—
—
0,0
—
—
—
0,8
—
—
—
—
_-
—
—
—
—
—
—
—
—
—
Радиус
/v'.M
0,1
0,1
—
—
0,15
—
0,1
0,05
—
0,05
0,1
—
0,05
0,05
—
0,1
0,05
0,05
0,0.5
—
0,05
0,04
—
0,1
0,02
— -
—
0,1
Длинь
i иедг-
формирован-
формированных пружин, м
at
0,05
0,8
0,1
0,03
0,6
0,2
0,05
0,5
0,1
0,2
0.;
0,1
0,4
0,2
0,1
0,6
0,6
0,1
0,8
0,2
од
0,6
0,19
0,!
0,7
0,1
0,6
0,05
1,2
0,02
0,6
0,2
0,04
0,8
0,1
0,1
0,6
0,2
0,2
0,1
(),-!
0,2
0,6
0,6
0,3
0,8
0,2
0,05
о,1;
0,2
0,3
0,7
0,05
0,2
0,6
0,1
0,3
0,05
0,2
Коэффициенты
жесткости
пружин. Н/см
с,
40
60
30
80
60
10
30
60
20
40
80
50
100
20
40
20
100
40
20
100
70
150
40
140'
20
40
20
40
100
40
60
80
20
100
40
20
60
90
40
70
120
70
ПО
80
100
10
120
60
100
40
50
200
120
60
160
80
30
40
150
120

A)
определяются корнями уравнения:
дП/dip = О,
где Я—потенциальная энергия системы.
Потенциальная энергия системы складывается из потенциальной
энергии элементов системы в поле сил тяжести и потенциальной
энергии деформированных пружин.
в
качестве нулевого уровня потенциальной энергии элементов
в поле сил тяжести выберем ось Ох. Тогда для каждого i-го эле-
элемента при выбранном направлении оси у получим:
11 Gl — ^ ilj i* \^-f
где «/( — вертикальная координата центра тяжести i-го элемента.
Так как при ф = 0 угол между стержне:и 2 и осью Оу равен
нулю, а качение подвижного колеса по неподвижному происходит
без проскальзывания, то
Z. ОС3Л = ф • ОС-,/С3Р = 2Rtf/R = 2ф,
поэтому /. ВС3А =(|1.
327

Из равенств /2 =
и h =
С3ВА =
следует, что:
С3?Л = / С3Л? =
Полученные соотношения между углами позволяют для каждого t'-ro
элемента представить соотношение B) в виде:
Пв1 = GiUi = Gi ¦ ОС1 cos ф = Gj • (/,у2) • cos ф;
По2 = G2y2 — G2 (OC3 cos ф -f- C3C2 cos 2ф) =
= G2 BR cos ф + (l2/2) • cos 2ф);
Яоз = G3y3 = Gj ¦ OCj cos ф = G32R cos cp;
nOi = G4y4 = G4 (OC3 cos ф + C3A cos 2ф + ЛС4) = C)
= G4 BR cos ф +12 cos 2ф + /4/2);
Паь = Gs//5 = G5 (OC3 cos ф + C3A cos 2ф — A C5 cos ф) =
= G5 [B/? - /5/2) cos ф + U cos 2ф)];
Лав = Gcye = Ge (ОСЯ cos ф — C3Ce) = Ge BЛ cos ф - /e/2).
Потенциальная энергия /-й деформированной пружины опреде-
определяется равенством
где ^ — деформация /-й пружины.
Для пружин с коэффициентами жесткости сг и с2 равенство D)
примет вид:
с1 () ^iiW^tf
= A /2) • сх [1а - BR + /-2 + 0С3 cos ф) - о,]2 =
= A /2) ¦ Cj [(/,-2R-l2- a,) - 2R cos ф]2 =
= A/2) с1[(/6-2Я-/2-а1J-Н/?2со52Ф-
- 4/? (/, - Л - /s - Qi) cos ф]; E)
Я„ = A/2) • с2Ц = A /2) • с2 (BF - а2у = A /2) • с2 (I, -0В- а,J =
= A/2) • с2 (^-2R- 2/2 cosф-а2J =
= A/2) cj^- 2R -at) - 2/2 cos Ф]2 =
= A12) ¦ с2 [(/, - 2R - а2J + 4/| cos2 Ф - 4/2 (/, - 2R - а2) cos rp].
Суммируем соотношения C) и E) и приводим подобные Ч1ены
cos2 со5ф и соз2ф:
s2(f —В cos <(>-]-Ccos2y + D, Fa)
при cos
где
ф и
П =
А = 2/?2С! + 2/|са = 2 (q^2 + с2г^);
В = _ [0,/,/г + G22R + G32^ + G6 BЛ - /e/2) +
4 + ,R - 2Rc, (lt-2R-l2-ax) -2/2c2 (I, -2R
= G5 • /6/2 + 2 [Rct (/, - 2f? - /a - aj + /2c3 (/L - 2R - a2)] -
- d • /i/2 - 2R (G2 + Gs + G4 + G5 + Ge);
С = G, • /2/2 + G4/a + G6/2 = /2 (G2/2 + G4 + G&), F6)
328

D —свободный член, значение которого ввиду последующей опера-
операции дифференцирования можно не вычислять.
Производную от потенциальной энергии Fа) по обобщенной коор-
координате ф представим в виде:
—— = — 2Л cos ф sin ф + В sin ф —2Csin 2ц> =
= — sinq> BЛ cos ф - В + 4С cos ф) = —sin ф[2(Л + 2Qcos ф - В]. G)
На основании равенства A) получаем, что в состоянии покоя
2C)cos<p-fi]==0, (8)
откуда следует, что значения угла ф, соответствующие состояниям
покоя, определяются двумя уравнениями:
sin ф = 0; (9)
5 Si. A0)
Для исследуемой системы значения коэффициентов А, В и С,
вычисленные по формулам F6), равны:
А = 2 (с^2 +Ы\) = 2 D000 • 0,12 + 5000 • 0,22) = 480 Нм;
В = G5• /5/2 + 2[Rcx (I,-2R-k-at) + l2c2 (lx-2R-a2)]-
- G1-/1/2-2/?(Gi+ Ga + 04 + Gs + G.) = 10-0,5/2 +
+2 [0,1 - 4000 @,7 - 2 • 0,1 - 0,2 - 0,1) +0,2 • 5000 @,8 - 2 • 0,1 - 0,3) —
-10-0,8/2-2 0,1 E + 20 + 5+10+15) = 747,5 Нм;
С = /2 (G2/2 + G4 + G5) = 0,2 E/2 + 5 + 10) = 3,5 Нм,
откуда
2 (A + 2C) = 2 D80 + 7) = 974 Нм.
Проведенные вычисления показывают, что В<2(Л + 2С). Сле-
Следовательно, система имеет четыре состояния покоя, соответствующие
корням уравнений (9) и A0):
из (9)
Фх = 0 и ф2 = я;
из A0)
Ф,(/1 = arccos [В/2 (А + 2С)] = arccos G47,5/974) = arccos 0,767,
что соответствует углам ф3 = 39с54' и ф, = — 39°54'.
В общем случае из соотношения (9) следует, чго пне зависимости от пара-
параметров системы существуют но крайнем мере два значения обобщенной коорди-
координаты ф, при которых система находится в состоянии покоя,
ф1==0 и ф,, = я. (И)
Так как при любых исходных данных А > 0 и С > 0, то уравнение A0)
имеет решение лишь при | В \ «5 2 (Л + 2С).
В зависимости от числовых значении коэффициентов А, В и С при решении
задачи возможны три следующих случая.
Первый случай:
|В;>2(Л-[-2С). A2)
Ц п'р Яб-.ouckoro А А. 329

В этом случае положения покоя, определяемые углами фг и ф2, единственные.
Втором случай:
|В| = 2(Л + 2С), т.е. В = 2(Л-Ь2С) A3а)
или
В = — 2(Л + 2С). A36)
В этом случае выражение A0) примет вид
cos ф = -1 1.
Корни этого уравнения совпадают со значениями срг и ф2 из формулы A1).
Следовательно, и в этом случае система имеет только два положения покоя,
определяемые углами <р, и ср2.
Третий случай:
] Д j <: 2 (Л-Ь 2С). A4)
В этом случае, помимо cpj и <р2, появляются еще два угла фз и ф41 соответ-.
ствующие положениям покоя.
A5)'
При ?>0
0<ф3<л/2 и — л/2<ф4<0.
При В<0
я/2 < ф3 < я и — л < ф4 < — л/2.
Случай /5 = 0 не рассматриваем, так как ввиду равенства 12 = G3E положение
системы при <р= ;i- я/2 определяется неоднозначно.
2. Исследование устойчивости положений покоя рассматриваемой системы.
Если в положении покоя (ф —фк) потенциальная энергия игслед\емой системы
имеет минимум, то по теореме Лаграпжа— Дирихле это положение покоя устой-
устойчиво *.
Известно, что условие минимума функции /7 можно представить в виде:
(<№,%% = фк>0, A6)
где фк —значение обобщенной координаты, соответствующее положению покоя.
Если представить равенство G) в виде
дП/д<р = В sin ф— (А + Щ sin 2ф,
то
д2П,Щ- =г- В cos ф - 2 (Л -;- 2С) cos 2ф. [17)
При ф = ф1=О из A7) следует:
(д*П 1дц,\ =ф] ^ 0 = В — 2 (Л -f 2C) = 747,5 - 974 = — 22E,5 Нм < 0,
т. е. условие устойчивости A6) при ф = фг не выполняется.
При ф = ф2 = л выражение A7) примет вид:
(<5'=/7/Eф2)ф==гр]^л = —В-2(/Ц-2С) = —747,5 —974 = — 1721,5 Нм < 0.
Следовательно, при ф = ф2 условие устойчивости A0) также не выполняется.
Таким образом, теорема Лагранжа —Дирихле не позволяет судить о харак-
характере состояний покоя при ф, = 0 и фа = я.
Прн ф = фл 4 = arccos 0,7G7
cos ф3 4=-0,767, cos 2Фзл = 2 cos* фзд- 1=2- 0,767-— 1 = 0,176.
* Если потенциальная энергия системы при ф =фк не имеет минимума, то
для исследования характера устойчивости состояния покоя необходимо использо-
использовать теоремы Ляпунова.
330

Тогда вторая производная от потенциальной энергии по обобщенной коорди-
координате
(?J/7/г?ф2)ф г. ^ = В cos ФаЛ- 2 (Л + 2С) cos 2<р3>4 =
= 747,5-0,767 —974-0,170 = 403 Нм>0.
Таким образом, условие A6) оказывается при <p = q>3i выполненным, откуда
следует, что положения покоя, соответствующие обоим углам, устойчивы.
Ниже приведено исследование устойчивости положений покоя в общем виде
для каждого из трех перечисленных случаен, определяемых формулам» A2) — A4).
Первый случаи. Исследованию подлежат значения ф, определяемые
формулами A1).
При ф = ф1 = О из A7) следует:
i&n/dtp% ^ = 0 = В - 2 (Л + 2С).
Отсюда условие устойчивости A6) примет вид
?>2(Л + 2С). A8)
При ф = ф1-—л
(д-П,Щ,\ = фг = я = - В - 2 (Л + 1С)
и условно устойчивости этого положения покоя определится неравенством:
В <-2(А + 2С). A9)
Неравенства A8) и A9) совместны с неравенством A2). Следовательно, в пер-
первом случае устойчивым может оказаться как первое (ф! = 0), так и второе (ф2 = л)
иоложения покоя.
Второй случай. Исследованию по-прежнему подлежат значения ф, зада-
задаваемые формулами (II); при этом величина В определяется по одному из
равенств A3).
При ф = ф1 = 0 и В=2(Л+2С)
В = 2 (Л + 2С)
Следовательно, значение второй производной не может служить критерием
минимума потенциальной энергии. В этом случае необходимо вычислить старшие
(п>2) производные уЛ/дфп)ф==ф . Если первая не равная нулю производная
имеет четный порядок и при этом положительна, то при ф = фк имеется минимум.
Если первая не равная нулю производная имеет нечетный порядок, то тео-
теорема Лагранжа —Дирихле не позволяет судить о характере состояния покоя
dsn,'d(f3 = — В sin ф + 4 (А -4- 1С) sin 2<p; B0)
д4Я/дф" = — В cos ф + 8 (Л + 1С) cos 2ф; B1)
(д3/7/дф3)ф1 = 0 =0;
BL.-= 2 (А + 2С)
{д*П>д<р% г 0 = - В + 8 (Л + 2С) = 6 (Л + 2С).
Л-=2(Л+2С)
2 (Л + 2С)
Так как А > 0 и С> 0, то
=0
В 2<1 +
Следовательно, при Ф( = 0 к В = 2(Л + 2С) состояпне покоя рассматриваемой
системы устойчиво.
При ф = ф2=л и В =
т. е. оказывается невыполненным условие устойчивости A6).
ц. 331

При ф=ф,=^О и Ь-^ — 2{Л-\-2С)
FW ,д{\ _= ф, _ ч = - В - 2 (Л + 2С) - О
й - --.(Л ;- -С)
Из B0) и B1) с,"ед\ет.
^///Ji) л =,0,
) л
А( - J (Л 1- 2G)
Равенство и\лю третье i iipoii.-iiio.i/in i or ногенцнлл.нсм энер'гш и г'отожи-
'1елыю 1Ь чсп;ерто1 позволяют з.ж почпгь, что при ф -<.2~.л и В- -2(/1-]-2С)
состояние покоя cn<ievi,r ^кичипо
Пропедсппос ни чодоняпии нспочлот сбъститт, условия хсгончинопп лля
первосо и вюрого (л\чпси. Г\. и В 2 (А . 2С), то" при ф.~((,—0 «.о гояиис
Покоя устопчяво, когдл й .. 2(Л + 2С), а при (|—фг- т коти й - 1(А-\2С).
Т р с т и и случаи I [сследоплпмо П'длс ч^т чсгмрс 11 ¦ а ч с 111 i я fp, опрсдол'с-
ш,е формулами A1) и A">).
При ф-— (г, - 0 \с--.оы,е \втопчивисти соппад ют с псряиспством (\Ь), а при
(/¦=ф., — л с неравен;. iDom A9)
HcpaB^iKTna A8) и A9) vn овм(\тпы г \ч лописм (\\\ Следов, елшо, при
] В \ < 2 (Л -\-'2С) ното/кеппя покоя, соогноапоющие j r;ia>i fp, и ф2, нц о'кмаюг
УСЛОВИЮ VCTOIIMIIMOLTH.
При ф =- (f, j
В
\ .^ ,v-4ai 2 (A -h2С) .~"Л + - >\ 2 {Л-| 2С)- " J
--И I 'L) 2(/I-|-2C) *
Условие устомчиноети A0) вырпзпая в виде
2 (Л -I 2C) > -^^гр или S^ < 4 (Л + 2С)К B2)
J-IepaiseiiiTito B2) равно нчыю условию A4), откуда следует, что углы ф:) и
ф4 tooiLcicTiiyioT положению \(.тоичивою состояния покои рассматриваемой
системы.
Задание Д-22. Определение условии устойчивости
заданного состояния покоя (равновесия)
консервативной механической системы с одной и двумя
степенями свободы (по теореме Лаграпжа — Дирихле)
А. Опрсдеченче i/слоаия устойчивости заданного состояния покоя
(равновесия) метрической системы с одной степенью свободы. Опре-
Определить условие устойчивости заданного состояния покоя механиче-
механической системы с одной степенью свободы, пренебрегая массами упру-
упругих элементов
Схемы механических систем тел 1 — 4 в состоянии покоя пока-
показаны на рис 230 — 232. Кажаяя механическая система состоит из
нескольких однородны ч тел весами G,, где i — номер соответствую-
соответствующего тела па схеме. Во всех варпачтгх пружины, коэффициенты
жесткости которых cL и с2, в положении покоя не деформированы.
332

R=0,25l
с,
/У
К
/ч
My
\
c2
Ы
^2
Ы
s//////?/////////////////////
V//////////
R=D,25l
R=0,25l
R-Q,12Sl
Рис 230
333

11
R = 0,151
15
777W*
ts
R=0,5l
17
Lz 4—•
WWWWWMM
к/ ^
7///)fr,
R~0,5l
20
Рис. 231
aii

Рис, 232
335

Трепне в шарнирах отсутствует и качение колес происходит без
скольжения. При решении задачи считать все стержни тонкими
однородными и диски однородными сплошными.
Пример решения задания. Определить условие устойчивости
состояния покоя для механической системы тел 1 — 3 с одной сте-
степенью свободы, изображенной в положении покоя на рис. 2X1.
Цапо: веса элементов G,, G>, G,; коэффициенты жесткости пружин
с,, с2 и с,; длина стержня ОЛ — 1 и радиус диска R — 0,3/. Известно,
что пружины, коэффициенты жесткости которых q и с2, в положе-
положении покоя не деформированы.
R--CH
Рис 233
Решение. Выберем в качестве обобщенной координаты угол ф,,
на который отклоняется стержень / от положения покоя (рис. 234).
Исследуемая система является консервативной, следовательно,
при фА = 0 должно выполняться равенство:
(дП/дч^.-о-^О. A)
По теореме Лагранжа— Дирихле состояние покоя рассматривае-
рассматриваемой системы являются устойчивым, если наряду с равенством A)
выполняется условие:
(Pn/dylU,. „>0. B)
При этом обобщенная координата ф1 считается малой, поскольку
проводится исследование устойчивости около положения фх--0.
Потенциальную энергию системы определим как сумму работ
сил тяжести и сил упругости при перемещении системы от откло-
отклоненного положения в нулевое, каковым считаем положение покоя
системы.
Неравенство B) позволяет при вычислении потенциальной энер-
энергии ограничиться слагаемыми второго порядка малости относительно
обобщенной координаты фг Для этого деформации пружин, не
нагруженных в положении покоя, достаточно вычислить с точно-
точностью до величин первого порядка малости, а вертикальные смеще-
смещения центров тяжести и деформации пружин, загруженных в поло-
положении покоя,—с точностью до величин второго порядка малости
включительно,
336

В рассматриваемой задаче такая точность будет достшнуга,
если при определении углов поворота элементов системы ограни-
ограничиться величинами первого порядка малости относительно ср,.
При повороте стержня / (ОА) на угол фх, все точки системы
занимают новое положение. На рис. 234 точки, обозначенные бук-
буквами с верхним индексом
в виде одного штриха, со-
соответствуют положениям,
показанным с точностью до
величин первого порядка
малости относительно ф,, а
точки, обозначенные бук-
вамп с верхним индексом
в виде двух штрихов, соот-
соответствуют положениям, в
которых учтены перемеще-
перемещения второго порядка мало-
малости.
Опишем перемещения
элементов системы, огра-
ограничиваясь величинами пер-
рого порядка малости.
Точка А перемещается
перпендикулярно к отрезку
ОА в точку А', при этом:
АЛ' -ОА -ф: ---=/</\.
Перемещение стержня 2
(отрезка А В) можно пред-
представить как поворот на не-
некоторый угол ф, вокруг
точки Р,, являющейся
мгновенным центром вращения звена
стнтся по горизонтали в точку В'
ВВ'^ЛЛ'-Р2В/Р,А;
Рис 234
А В, при этом точка И персме-
где
откуда
Р2А =
РоО - О А --= 2 • ОВ
2В = Р,0 ¦ cos 30° =-¦ U ¦
ф2 -_-- АЛ'/РгА,
О А = 4 ¦ О А - О А = 3/;
КЗ /2 = 2/ X 3,
ВВ' ---/ф, B/1/3/3/)= 1,1."/ф,; ф, = /cf4/3/ -
Перемещение стержня 3 (DF), жестко скрепленного с диском,
можно представить как поворот па угол q.,, вокруг точки Ря, являю-
являющейся мгновенным центром вращения диска, при этом перемещение
точки Е в точку Е' будет перпендикулярным к отрезку РЛЕ.
ВВ' _ _2_^3/<р, _ 2 ГЗ/у, _ .
фз "" 1Щ ~ 3R~~ ' ' ~3 ¦ 0,3/ " " Л'°';"Г1'
ЕЕ' = Фз ¦ РаЕ =
2" --- 2 |/2/3 ¦ /<рх = 1,63/Ф1.
337

Перемещение точки F перпендикулярно к P3F и равно:
FF' = ф3 • FP3 = фз (/ cos 30° + /?) = З.вбср^ @,866 + 0,3) = 4
Потенциальная энергия деформированной пружины, коэффициент
жесткости которой с,, определяется формулой
Пе, = A/2) • с, (X, rt /„)? - A/2) ¦ с/сг/ = A/2) • eft ± с,усф C)
где Яу —деформация /-и пружины, вызванная отклонением стержня /
на угол <pL от положения покоя; /„/ — деформация /-й пружины
в положении покоя (статическая деформация).
Для пружины, коэффициент жесткости которой сь имеем:
где Х1А и %iF — проекции перемещений точек А и F на ось первой
пружины.
Зная перемещения АА' и Т7/7', можно получить:
Ян = F/7' - ЛЛ' cos 30° = 4,5/фх - 0,866/ф! = 3,63%.
Для пружины, коэффицие1{т жесткости которой с2, деформация Я2
равна проекции перемещения точки Е на ось пружины:
Я2 = ЕЕ' cos 45° = 21/2/3 • % 1/2/2 = B//з) /Фх = 1,15/ф1.
Следует иметь в виду также, что /ст1 = 0 и /„г^О.
Деформация пружины с коэффициентом жесткости с3, нагружен-
нагруженной в положении покоя, должна вычисляться с точностью до вели-
величин второго порядка малости относительно ф^ Так как ось этой
пружины перпендикулярна к ОА, то легко показать, что в выра-
выражении для Я3 слагаемые второго порядка малости отсутствуют:
Подставляя найденные значения деформаций %lt Ji2 и ?.3 в выра-
выражение C), получаем значения потенциальной энергии для каждой
деформированной пружины:
П?1 = A/2) • сх C,63J /Vi = A/2) • с, ¦ 13,18Др|; D)
Пл = (\ 12) ¦ с2 D/3) • /2ф1 - A /2) • с2,j ,32/2Ф1; E)
ф.1Гст3. F)
Потенциальная энергия j-ro элемента системы в поле сил тяжести
определяется формулой:
nai = G,hlt G)
где hi — вертикальное перемещение центров тяжести элементов си-
системы, вычисленное с точностью до величин второго порядка мало-
малости относительно обобщенной координаты фх. Если при повороте
звена О А на угол фл центр тяжести j'-ro тела поднимается, то Л,>0;
в противном случае hi << 0. В рассматриваемой задаче hi для всех
элементов отрицательно.
338

Для звена О А:
ht = — (С,/С - СЩ = — [0Сг cos 30а - ОС^ cos C0° + Ф1)] =
= — 0С1 [cos 30° - (cos 30° cos <p, - sm 30° sin ф^] =
= — (//2) • [cos 30° A - cos фО +sm 30° sin ф^.
Учитывая малость ц>и получаем:
ф1 (ф1/) ф1/
Тогда
К = — И\ [(/3/2) • ф? + <р,1 = — //4
Для звена АВ:
2
так как hA = 2h1, то
Л2 = А1 = —(//4)
Для звена FD:
Лз = — (ВСЯ - В'С; cos ф3) = — ВС3 A - cos ф3) = — ВС3 ф"/2.
Так как FD — однородный стержень, то
ЯСа = A/2) (/cos 30° + /?) = 1/2 /@,866+ 0,3) = 0,583/.
Используя значение угла ф3, найденное выше, получаем
/га = — 0,583/
Подставляя выражения для вертикальных перемещений центров
тяжести в формулу G), получаем значения потенциальной энергии
элементов в поле сил тяжести
-0,25^/ @,866ф1 + ф1); (8)
, (9)
A0)
Потенциальная энергия системы равна сумме выражений D), E),
F), (8), (9) и A0). После приведения подобных членов по степеням
обобщенной координаты ф! имеем.
П = A/2) ф',7 [13,18с,+ 1,32с2 + с3)/-0,433 (G1 + G2)-8,65G3]-H
+ ф1/ [-0,25 (G^G^ + c^,].
Из условия равновесия A) следует, что
поэтому
Л = A/2) /[13,18q+l,32c2 + c3)/-0,433 (С!-1-О2)-8,65С,]ф?. A1)
После двукратного дифференцирования выражения потенциальной
энергии A0) по обобщенной координате фх получаем:
Ф? = /[A3,18с1+1,32с2 + с3)/- 0,433 (GL + G2)-8,65G3].
339

В соответствии с неравенством B) условие устойчивости рассмат-
рассматриваемого состояния покоя механической системы, изображенной на
рис. 229, примет вид:
' ?ki. . Г. I /in I О„ i I O(J \г\
П All in I
R-0,U
- 0,433 (
— 8,65G3 >
что равносильно:
Рис. 235
0,
13,18с,) >
> 0,433 (G1 + G24-20Ga).
При выполнении этого
неравенства заданное по-
положение покоя является
устойчивым.
Б. Определение условий
устойчивости состояния по-
покоя механической системы
с двумя степенями свободы.
Определить условия устой-
устойчивости заданного состояния
покоя консервативной ме-
механической системы с двумя
степенями свободы. Принять,
что варианты механических
систем в состоянии покоя
получаются из схем, изоб-
изображенных на рис. 226—228,
следующим образом: а) в
вариантах 1 —15 стержень
А В заменяется невесомой
пружиной с коэффициен-
коэффициентом жесткости с, при этом
в вариантах 4, 9, 14 диск
с центром В получает воз-
возможность вращаться, сколь-
скользя без трения но опоре;
б) в вариантах 16—30 счи-
считать, что в точке D нахо-
находится шарнир и спиральная
пружина с коэффициентом крутильной жесткости с. Во всех вариан-
вариантах пружины с коэффициентами жесткости clt c2 и с в положении
покоя не деформированы.
Пример выполнения задания. Определить условия устойчивости
для механической системы с двумя степенями свободы, изображен-
изображенной в положении покоя на рис. 235. Эта схема получена из меха-
механической системы, рассмотренной в предыдущем примере. Дано: веса
элементов Glt G2, G3; коэффициенты жесткости упругих элементов
340
Pifc. 236

C\, Co, c~ и с; длина стержня О А — / и радиус диск;] R --- 0,3/. Известно,
что спиральная пружина и пружины с коэффициентами жесткости
Cj и сг в положении покоя не деформированы.
Решение. Выберем в качестве обобщенных координат углы (р1
и 6Я, на которые стержни / и 3 отклоняются из положения покоя.
Оба утла отсчитываем в одном направлении (см. рис. 236).
Исследуемая система является консервативной, поэтому при (pj=O
и 63 = 0 должны выполняться равенства:
(дП.'дч^, -о = О; (<Э/7/дВя),Г1,_о--=О. A)
fij — 0 6, . 0
По теореме Лагранжа—Дирихле состояние покоя рассматриваемой
системы начнется устойчивым, если наряду с равенствами A) вы-
выполняются два условия Сильвестра:
1. fu>0 или с,.2>0; 2.
C2lC22
B)
где си, с22 и f12 — коэффициенты жесткости системы, вычисляемые
по формулам:
т,- о; с1г --- (дЧ1/дЬ^,и- о;
6., -0 0,-0
03)^ - о- C)
С о
При этом обобщенные координаты цх и 03 считаются малыми. Соот-
Соотношения C) при вычислении потенциальной энергии позволяют огра-
ограничиться слагаемыми второго порядка .малости относительно обоб-
обобщенных координат.
Так как потенциальная энергия системы определяется суммой
работ сил тяжести и сил упругости при перемещении системы из
отклоненного положения в нулевое (положение покоя), то деформа-
деформации пружин, не нагруженных в положении покоя, вычисляются
с точностью до величии первого порядка малости, а вертикальные
смещения центров тяжести тел и деформации пружин, нагруженных
в положении покоя, —с точностью до величин второго порядка ма-
малости включительно.
Для достижения указанной точности в выражениях углов пово-
поворота элементов рассматриваемой системы достаточно ограничиться
величинами первого порядка малости относительно ц\ и 63.
При повороте стержня / (ОА) на угол (р1, а стержня 3 (DF) на
угол б3, все точки системы занимают новое положение. На рис. 236
точки, обозначенные буквами с верхним индексом в виде одного
штриха, соответствуют положениям, показанным с точностью до ве-
величин первого порядка малости относительно <р, и 8), а точки, обо-
обозначенные буквами с верхним индексом в виде двух штрихов, соот-
соответствуют положениям, в которых учтены перемещения второго
порядка малости.
Опишем перемещения элементов системы, ограничиваясь величи-
величинами первого порядка малости. Перемещения звеньев ОА, АВ н
диска с центром в точке В полностью определяются обобщенной
341

координатой срг Перемещения точек А, В, Е, а также углы ф2 и
Ф3 получены в предыдущем примере, в котором:
Перемещеиие точки D происходит по перпендикуляру к P3D и
равно DD' = Р-Р • ф3 = 2Кф3 = 2 • 0,3/ • 3,85ф! =-- 2,31 /ф,"
Перемещение стержня FD можно представить как сумму двух
перемещений: поступательного вместе с полюсом D и вращательного
вокруг этого полюса, при этом поворот FD вокруг точки D проис-
происходит на угол 03. В соответствии с этим
FF' = DD' + F',F' =DD' + D'F'a • fl3 = 2,31 /Ф1 +
+ (/ cos 30° - R) 63 = 2,31 /ф! + @,866/ - 0,3/) % =,
Потенциальная энергия деформированной пружины с коэффи-
коэффициентом жесткости С) определяется формулой:
Пс, = A/2) • с} (к, ± faj)a - A/2) • afiij - A/2) • с,Ц ± ct\}faj, D)
где ^—деформация ;-й пружины, вызванная отклонением стерж-
стержней / и 3 на углы ф! и % соответственно; /ст/ —деформация пру-
пружины в положении покоя (статическая деформация).
Примечание. Для пружин /, 2 и 3 kj и fcl;- измеряются в единицах
длины, а для спиральной пружины —в угловых единицах.
Для пружины с коэффициентом жесткости сх имеем:
^ = llF-XlA = FF'-AA' cos 30° = I B,31 <pt + 0,56693) -
- 0,866/ф! = A,44ф! + 0,56663) /.
Для спиральной пружины:
К = В3- ф3.
Деформации Ji2 и Х3 зависят только от угла щ и вычислены
в предыдущем примере:
. Подставляя значения Хи Я, I, и А3 в D), получаем:
Па - A/2) сх/2 A,44ф1 + 0,566в3)* - A/2) -ClP B,07Ф; +
+ 2-0,814ф1Оз + 0,32е~); E)
Пп = A/2) -с2/2 A ,15Jф; = A/2) • с2/2 • l,32*pi; F)
1 ст3ф1; G)
так как 93 = 3,859!, то
Пе= A/2) -с @5 -7,76зф1 + 14,8Ф=). (8)
Потенциальная энергия г-го элемента системы в поле сил тяже-
тяжести определяется формулой
nat = Gfa, (9)
342

где h, — вертикальное перемещение центров тяжести элементов си-
системы, вычисленное с точностью до величин второго порядка малости
относительно обобщенных координат ф, и 0Я. Если центр тяжести
t'-ro тела опускается, то h, <0; в противном случае /г, >0. В рас-
рассматриваемой задаче для всех элементов ht отрицательно.
Потенциальная энергия элементов / и 2 зависит только от коор-
координаты фх и вычислена в предыдущем примере;
ЯЯ1 =-0,250^ @,866vf + Vl); A0)
tfOa = —0,25G2/@,86691 + 91)- A1)
Вертикальное перемещение центра тяжести С3 звена 3 склады-
складывается из вертикального смещения точки D при повороте диска
на угол ф3 и смещения точки С, при повороте стержня DF вокруг
точки D на угол 63:
где
hD = — (BD - B'D" cos <рл) = — (R - R cos фл) = — R A - cos rp3) =>
= — R ¦ cpi/2 = — 0,15/cp.j = —0,15 C,85)'-/<p; = —2,22/rpf;
AJ = — (DCa - D"C; cos Qj) = — DC3 6{/2 =¦ — 1 /4 (/ cos 30° - R) Oj =
= —0,25/@,866 -0,3)Oj =—0,142^;
следовательно,
Лл = - Z B,22Ф; + 0,1420,),
откуда •
/7 С/B22Н0142е;). A2)
Потенциальная энергия системы равна сумме выражений E)—(8),
A0)—A2). После приведения подобных членов по степеням обоб-
обобщенных координат ц\ и 83 получаем.
П = A /2) • Сц<р; + Сцф^а + A /2) ¦ си63 + ^4ф1,
где
сц = /2 B,07q + 1,32с2 + с3) -|- 14,8с — / [0,433 (G, + Са) + 4,44О3];
с2, =- 0,32^/2 + с - 0,284G3/:
с12 =0,814q/2-3,85с;
^4 =с3/ст3/-0,25/@,
Из условий равновесия A) следует, что
0,-0
поэтому
Л = A/2) • сиф? +с12тЛ + A/2) -с,20^. A3)
В соответствии с выражениями B) и C) условия устойчивости
рассматриваемого состояния покоя примут вид:
с,2>0 или
343

{/2 B,07Cl + 1,32c2 + c3) + 14,8c - I [0,433 (G1 + G2) + 4,44G3]} X
X[l @,32сх/ - 0,284G:)) + c] - @,814c,/2 - 3,85cJ > 0.
После перемножения, приведения подобных членов и деления
на / во втором неравенстве окончательно получаем:
и
I B,07с, + 1,32с2 + с3) (с - 0,284G3/) + 14,8с @,32^/ - 0,284G3) -
- [0,433 (G, + G,) + 4,44С3] [/ @,32q/ - 0,284G3) + с] +
+ 6,26с1/с>0.
При одновременном выполнении этих неравенств рассматриваемое
состояние покоя является устойчивым.
КОЛЕБАНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ
Задание Д-23. Исследование свободных колебаний
механической системы с одной степенью свободы
Определить частоту и период малых свободных колебаний меха-
механической системы с одной степенью свободы, пренебрегая силами
сопротивления и массами нитей.
Найти уравнение движения груза / y = y{t), приняв за начало
отсчета положение покоя груза / (при статической деформации пру-
пружин). Найти также амплитуду колебаний груза /.
Схемы систем показаны на рис. 237—239, а необходимые данные
приведены в табл. 62.
В задании приняты следующие обозначения: / — груз массой т^,
2 —блок массой т2 и радиусом г2 (сплошной однородный диск^;
3 — блок массой т3 и радиусом инерции ix; 4 — сплошной однород-
однородный диск массой т4 и радиусом г4; 5 —диск массой ть и радиусом
инерции ix; б —тонкий однородный стержень массой me и длиной /;
7 —стержень, масса которого не учитывается; с — коэффициент жест-
жесткости пружины; у0 — начальное отклонение груза / по вертикали
от положения покоя, соответствующего статической деформации пру-
пружины; г/0 — проекция начальной скорости v0 груза / на вертикаль-
вертикальную ось.
На рис. 237—239 системы тел /—7 показаны в положении покоя
(при статической деформации пружин).
В вариантах 5, 6, 14 и 23 стержень 6 жестко соединен с диском 4.
Пример выполнения задания. Дано: /^ = 1, т, — 2, т4 = 1,
/н6 = 3 кг; / = 0,6 м; с = 20 Н/см; уо = 0,2 см; уо = 8 см/с (рис. 240).
Определить циклическую частоту k и период Т малых свободных
колебаний системы, а также получить уравнение y = y(t) колебаний
груза / и найти амплитуду а его колебаний.
Решение. Воспользуемся уравнением Лагранжа второго рода
для консервативной системы. Приняв за обобщенную координату
344

ff-
is?
/-a
7 , Щъ
Рис. 237
345

12
*WZ J
15
18
v/ss/л
Рис. 238
346

21
24-
25
a c
6--
Г / 7
Ь<-2
б"/
27
28
29
30
Рис 239
347

Таблиц,) 62
Помер
варианта
(рнс 237—
239)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
1
0,5
0,г)
0,5
0,6
0 (>
0,6
—
—
0,6
0,6
—
0 т
0,3
0,4
0,4
—
—
0,'2
0,5
—
.
0,4
0,3
—
—
—
—
—
1Х
-
C/2) г
—
—
—
—
—
—
—
—
г 1/3
2т
—
—
г VI
—
—
—
1'х
—
—
—
—
—
—
—
—
—
—
—
—
.—
г V'2
г V з
—
Зг/2
т\'г
4г/3
г \ '2
0,2
—
—
0,15
0,15
—
—
—
—
—
—
0,1
0,2
0,1
—
—
-
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
2
2
—
2
—
—
Л
2
о
2
2
1
—
2
о
1
2
—
2
2
2
2
2
2
2
'"а- ш.|
"\
кг
2
4
3
3
1
2
о
—
1
2
2
3
1
—
—
2
4
2
3
2
2
3
3
3
3
3
3
3
2
3
1
о
—
,-(
3
3
2
3
1
2
—
1
3
3
3
2
1
—
—
—
—
с
Н см
40
40
?0
,1b
Hi
40
40
40
38
30
20
32
20
20
Л>
20
40
32
20
32
40
40
40
40
40
40
40
40
40
Нач.чль
ЛОГ.И>[
см
0,1
0
0,2
0/2
0
0,3
0,4
0
0 т
о'
0,4
0,2
0
0
0,1
0,3
0
0
0,1
0,1
0
0,1
0,3
0
0,2
0,3
0
0,2
0
0,3
>ше ye-
yell -0)
•
I/O.
СМ'С
5,0
6,0
7,0
0
8,0
7,0
0
6,0
5.0
E,0
7,0
0
8,0
7,0
0
6,0
5,0
(,,0
0
7,0
8,0
7,0
0
6,0
5,0
0
6,0
0
7,0
7,0
системы вертикальное отклонение (/ груза / от положения покоя,
соответствующего статической деформации пружины, имеем:
d (дТ\
dt ' ~ду )
дТ
ду
('/7
где Т — кинетическая энергия системы; Я —потенциальная энергия
системы.
Кинетическую энергию Т вычислим с точностью до величин вто-
второго порядка малости относительно обобщенной скорости у, а потен-
потенциальную энергию // — с точностью до величин второго порядка
малости относительно обобщенной координаты у.
Найдем кинетическую энергию системы, равную сумме кинети-
кинетических энергий тел /, 2, 6 и 4:
348

выразив линейные и угловые скорости, которыми определяется кине-
кинетическая энергия тел этой системы, через обобщенную скорость у.
Кинетическая энергия груза /, движущегося поступательно со
скоростью v—y:
2
Кинетическая энергия блока 2 (сплошного однородного диска),
вращающегося вокруг неподвижной оси О.гх:
Г2 = J2Acol/2, где Лх = т,г1/2, «>., = у/г2,
т. е.
Т2 = (m2r",/2 ¦ 2) • уг1г\ = т2у2/4.
Кинетическая энергия тонкого однородного стержня 6, жестко
связанного с блоком 2 и вращающегося вокруг неподвижной оси 0ix:
, где J6x = tneP/3; ю6 = со2 = у/г2,
т. е.
Te = (mJ2/3-2)(y/r2J,
так как r2 = //4, то
Тв = 8/иву2/3.
Кинетическая энергия сплошного однородного диска 4, соверша-
совершающего плоское движение,
Ti = mivy2 + Jcxal/2, где Jcx^=m4n/2.
Скорость центра тяжести диска vc и угловую скорость оL можно
определить следующим образом. Так как рассматриваются малые
колебания, то
vB = va,
а ввиду того, что диск катится без скольжения
vc = vn/2,
следовательно,
vc = vj2 = сой//2 = a.J/2 = yl/2r-z ¦=¦¦ 2y, co4 = vc/n -= 2y/rt.
Подставляем значения JCx, vc и а>4 в выражение для Т4:
Т4 = m44y2/2 +
Таким образом, кинетическая энергия рассматриваемой механи-
механической системы
Т = Тх + Г2 + Тв + Г4 = ш^-72 + т#/4 + (8/3)
Найдем потенциальную энергию системы, которая определится рабо-
работой сил тяжести системы и силы упругости пружины на перемещении
системы из отклоненного положении, когда груз имеет координату у,
в нулевое положение, которым считаем положение покоя системы:
349

Потенциальная энергия, соответствующая силам тяжести при
указанном перемещении
S=o
где Л—вертикальное смещение центра тяжести стержня 6, которое
вычисляем с точностью до величин второго порядка малости отно-
относительно обобщенной координаты у.
По рис. 241
= t/2- A/2) ¦ cos ф = A/2) • A - cos ф).
i
Рис. 240
и6*
////)/s
Рис. 241
Ограничиваясь в формуле разложения
cos ф = 1 - ф72! + ф"/4! -...
двумя первыми членами и учитывая, что
имеем
Я. = — Gj//-
Рис. 242
Таким образом,
Потенциальная энергия деформированной пружины при указан-
указанном перемещении системы равна:
где /сТ — статическая деформация пружины; кк — перемещение точки
прикрепления пружины К, соответствующее координате у.
350

Поскольку
*• *^к "^ *-*?/,
(см.
то
рис.
1
240)
2
V
г/
C/4)
A/4)
2
-/
•Г
f
*J/cij
. 9
Потенциальная энергия системы
77 = 77[ + Л,i = — G^ - DGe/7) • //2 + Зс/ст# + (9/2) • а/.
Так как в положении покоя, соответствующем статической дефор-
деформации пружины
(дЯ/ду)а_о = 0,
то
-Gi + Зс^О. (а)
Уравнение (а) можно получить также, составив уравнение момен-
моментов сил ^У] Мю2 для положения покоя системы (рис. 242)
o1 = P0-C/4)-/-G1ri = 0
или
т. е. 3c/CT-G1 = 0.
Таким образом, потенциальная энергия рассматриваемой меха-
механической системы
п- 9 ru»_40«u»_ ] for _8GM u«
2 су — — ^
Найдем значения членов уравнения A):
Уравнение A) приобретает вид
или
Обозначив fe2 коэффициент при г/, имеем:
У + « у = \J. \Z)
Циклическая частота свободных колебаний
и -г/ 9с —8Gc/< . _ 1 /"9-2000 —(8-3-9,81)/0.В_97 . _х
F m1+m2/2+A6/3) -тв+6т4 ~ F 1+2/2+ A6/3) -3 + 6- 1 — ' С '
351

Период свободных колебании
7=--2л//г-2 3,14/27,1-0,23 с.
Интегрируя уравнение B), получаем уравнение движения груза /
у- Сусы, Ut -\- C2 sin kt.
Для определения постоянных С, и С, найасм уравнение скорости
груза:
у — — kCx sin kt -\-kC2coskt
п воспользуемся начальными условиями задачи. Из уравнений
y = y(t) п у--(/(/) при Г-0 имеем
Следовательно,
Сх -г/,„ С, ---//,../*.
Подставляем эти значения Сх и С, в урасиепие y--y(t)
у -^ync.(s,kt + (y0/h) -sinki,
у ¦- 0,2 cos 27,1/ -f 0,3 sin 27,1/.
Уравнение y — y{t) можно получить в другом виде, если перейти
к другим постоянным интегрирования а и р1, приняв
Ci = asinp, C2—: a cos р.
Тогда // = a sin (?/ -f P),
где
а = |/' С\ + С-2 и р = arctfi(C1,/C2)
или
P - arctg (Ьуо/Уо)-
Найдем числовые значения а и р:
а --= >70,22 + (8,0/27,1J = 0,36 см;
Р = arctg B7,1 • 0,2/8) = arctg 0,6775.
Так как sinP>0 (C1>0), то
Р = 34с07' = 0,595 рад.
Окончательно
у - 0,36 sin B7,U + 0,595) см.
Задание Д-24. Исследование вынужденных колебаний
механической системы с одной степенью свободы
В механической системе тел 1—2 с одной степенью свободы
возникают вынужденные колебания под действием силового во.,. iy-
щения. Схемы механических систем в положении покоя показаны
на рис. 243 — 245. Необходимые сведения о параметрах системы п
силового возмущения приведены в табл. 63. Дпссипативиые свой-
свойства системы заданы логарифмическим декрементом колебаний системы.
352

= ASLtipt
4 .,
x-Asinpt
P С
31
Ш
г
|эЛМЛЛ/<|
10
^
2
tp=(t)t
P AB
Рис 243
353

tp=(Jt
РЦАВ
12
x^Asinpt
p\\ab
18
x^Asinpt
Puc 214
354

21
x=Asinpt
x=Asinpt
x= Aslnpt
1 x=ASinpt
30
\\/
Ж
Ь-1
Pile. 245
355

Таблица 63
Номер вариаи-
- 245)
1
2
3
4
5
6
7
8
9
10
И
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Масса тел
т.
2
8
40
20
40
30
5
40
40
10
15
40
80
20
60
30
40
12
50
80
24
40
30
70
10
15
40
30
25
40
4
2
—
5
10
30
5
30
15
10
30
—
—
15
—
20
30
10
10
20
20
—
15
—
50
—
—
'20
—
—
кг
».
_
—
—
4
20
—
—
—
10
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
Радиус
R. и
0,2
0,3
—
—
0,4
0,3
—
—
0,3
0,2
0,3
0,2
0,4
0,2
0,2
—
0,2
0,4
—
0,2
0,4
—
0,2
0,3
0,1
0,2
0,2
0,3
—
Расстоя-
Расстояние /, м
_
0,9
—
0,1
0,6
—
—
—
—
0,5
—
—
—
—
0,4
—
—
0,7
0,6
0,4
—
—
—
—
—
—
—
Раднус пиер
ции i* тела
относительно
оси |—|, м
_
—
0,4
—
—
—
0,6
—
0,4
—
—
0,5
—
—
—
0,6
0,5
—
—
—
0,15
—
—
—
—
Коэффициенты
Н/см
50
10
20
15
20
10
20
—
18
8
12
—
—
14
18
10
22
15
16
12
14
25
12
14
20
15
12
Нм/рад
2- 104
—
3- 104
—
1 -104
—
—
—
—
2- 104
—
—
4- 10*
1 • 104
—
—
—
—
—
—
—
—
—
—
—
—^
жесткости пружин
Н/см
40
—
20
10
—
10
25
—
—
—
—
16
20
—
—
18
20
20
—
30
—
18
24
20
10
Нм/рад
3-Ю4
—
—
—
2- 104
—
—
1 ¦ 10*
1 • 104
3- 10*
—
—
2- 104
8- 102
6-Ю3
2- 10=
1 ¦ 103
5- 102
/ , п
40
50
20
30
10
25
15
35
8
10
16
V2
18
20
25-
8
24
30
26
18
15
14
18
24
40
8
12
15
18
20
А \м
s\, М
—
0,1
0,2
0,1
0,1
—
—
—
—
0,2
0,1
.
0,15
0,1
0,05
0,05
—
р
л
2л
Зя
4 л
4л
V
1
л
о,5л
2л
1,5л
2л
Зл
2,5л
1,5я
2,2л
4л
3,5л
2л
4л
Зл
1.4л
1,8л
3,2л
2,2л
Зл
2,5
л
2,2л
1,5
2л
3,2
л
л
2,5л
i']OI dpll-
декремеит
1.75
0,48
1,15
0,j0
0,40
1,32
0,35
0,62
1.70
0,48
1,10
0,66
1.40
0,50
0,70
0,92
1,08
1,52
0,50
1,60
0,82
1,04
0,95
1.62
0,98
1,58
1,14
1,54
0,80
1,35

В вариантах 2, 5, 7, 9, 10, 12, 17, 18, 23, 25 п 2G пружины
с коэффициентом жесткости г, в положений покоя не деформиро-
деформированы, в вариантах 13, 14, 19, 22, 21 п 27-30 в положении покоя
не деформированы пружины с коэффициентамп жесткости с\ и с2.
Опре.пелпть: коэффициент а, характеризующим вязкое сопротивле-
сопротивление, осуществляемое в яемпфере, уравнение вынужденных колебании
системы при заданной частоте но:.м\ i; синя; максимальные и резо-
резонансные значения амплитуд изменения обобщенных координаты,
скорости и ускорения с предположении, что частота возмущения
ьожет измени]ься.
ripni'd ,'i!i!o По 13ч\\ вярнчиых ко ice счшат!, (П.юшпыми однородными
дис'.л.ми, аержпн топкими однородными; ки'.счяс коле ¦ происходи i без скольжения.
Пример иыполксния задания. Вычислить ко_-н1>фип.пспт а, харак-
Tcpr!.?yioi:ui''i г*я !кое сопротi.rneiiiie, осуществляемое в демпфере, ьклю-
ченпом в спс ему 1^-3 в соответствии с рис. 246.
Рис. 24G
Определить уравнение вынужденных колебаний системы при
заданной частоте возмещения р. Найти также максимальные и рсзо-
ианспые значения амплитуд изменении обобщенных: координаты, ско-
скорости и ускорения.
Дано: ш, = 20, тг--5, /«.,--= 2, т4--=9 кг; #=0,3 м; / = 0,9 м;
с, =40 Н/см; с, = 70 П/см, Р = 20 Н; х = /Ынр/, Л =0,1 м, р =
--4л с ', ц - 0,812. Обе пружины в положении покоя не деформи-
деформированы.
Р е ш с и и е. За обобщенною координату примем фх — угол поворота
колеса / (рис. 247).
Уравнение Лагранжа в рассматриваемом случае имеет вид:
где Г —кинетическая -энергия с;к:те>п/; Ф —функция рассеивания
систем:-.] (днссппатнвпая функции Рел;:>), // — потенциальная зпергия
системы; Q,, — обобщенная возмущак !чая сила.
357

Функции Т, Ф и Я вычисляются с точностью до величины второго
порядка малости: Т и Ф — относительно обобщенной скорости ф1(
/7 — относительно обобщенной координаты (pL.
Общий вид этих функций следующий:
Г=A/2)-аф1; Ф= A/2) ¦ Аф?; Я = A/2)-сФь
где а и с — коэффициенты инерции и жесткости системы, а ft —коэф-
—коэффициент, характеризующий сопротивление в системе.
Рис 247
Найдем кинетическую энергию системы как сумму кинетических
энергий тел 1, 2, 3 и 4.
Кинетическая энергия колеса / (сплошного однородного диска):
где
т. е.
\ = A/2)
! + A/2) • A/2)
oi - C/4)
Кинетическая энергия однородного стержня 2, движущегося
поступательно:
Т2 = A /2) • m2vl = (ш,/2) • К • 2ЯJ = 2ш2/?2ф|.
Стержень 3 совершает плоское движение. Мгновенный центр
скоростей этого звена при его положении, совпадающем с положе-
положением покоя, находится в бесконечности. Следовательно, для обеспе-
обеспечения указанной выше точности выражения кинетической энергии
системы можно считать, что соа = 0 и vc3 = vD = vB = и2.
Таким образом,
Т3 = A /2) • m3vl = A/2) • щр\ = 2т3/?2ф?.
358

Кинетическая энергия тонкого однородного стержня 4, вращающе-
вращающегося вокруг неподвижной оси Ох
Jixal, где Jix = A/3) • m4/2;
co4 = vnft = v,/t = щ ¦ IR/l = BR/L) ¦ ф„
т. е.
Г4 = A/2) • A /3) • т4/2 • D/?Ч1) /Р = B/3) • т4/?2ф?.
Кинетическая энергия всей системы:
Т = C/4) ¦ тх#2фт + 2m2R4? + 2т3/?2ф. +
+ B/3) ¦ т4/?2ф! == A /2) [C/2) • т, + 4/п, + 4т3 + D/3) • т4]
где коэффициент инерции системы
а = [C/2) тх + 4ш., + 4ш3 + D/3) • mj ^2.
Найдем функцию рассеивания системы:
Ф = A/2) - аи| = A/2) - а B/?фх)а = A/2L/?2афт = A/2) • 6ф?,
где
Ь = 4/?2а.
Переходим к определению потенциальной энергии системы.
В положении покоя
поэтому в выражении для П сумма всех членов первого порядка
малости равна нулю. Это позволяет непосредственно производить
определение потенциальной энергии системы, вычисляя только члены
второго порядка малости.
Найдем потенциальную энергию системы как сумму работ сил
тяжести и сил упругости пружин на перемещении системы из откло-
отклоненного положения, определяемого углом (р,, в нулевое положение,
каковым считаем положение покоя системы. При этом в выражениях
для деформации пружин, не загруженных в положении покоя, учи-
учитываются только те слагаемые, которые имеют первый порядок мало-
малости относительно ц>1г а в выражениях для вертикальных смещений
центров тяжести элементов системы —слагаемые, имеющие второй
порядок малости. Деформации пружин, загруженных в положении
покоя, вычисляются с точностью до величин второго порядка мало-
малости включительно.
Потенциальная энергия Я!, соответствующая силам тяжести, равна:
П\ = — G3hC3 — GJiCi,
где !гСз и hCi — вертикальные смещения центров тяжести элементов 3
и 4, вычисленные с точностью до величин второго порядка малости.
Из рис. 247 видно, что
hCi = 111 ~ A/2) ¦ cos ф4 = A/2) • A - cos (ft).
Ограничиваясь в формуле разложения
cos ф4 = 1 - ф?/2! + ф!/4! -...
359

двумя первыми членами и учитывая, что
=¦. г.п11 ----- XA/l = 2RipJl,
имеем
Учитывая, что hCu = hDi2 = hci, получаем*
Я, = — Gg/гсз - Giha = — G3 R2<t,/l - G4 • R^Jl = — (Ryt) (Gj + G,) ф?.
Потенциальная энергия Пи деформированных пружин при ука-
указанном перемещении системы равна
77ц = A/2) ^? + A/2) c2(bcos45°-^J,
где \Е, \f, V —перемещения точек прикрепления пружин, вызван-
вызванные поворотом диска 1 на угол <pL
Вычисляя эти величины с точностью до слагаемых первого
порядка малости относительно фи имеем.
Ф4 = B/3) / 2R4JI = D/3) Яф
Таким образом,
77ц = 2 q(/?K2 Ф1)9 + у сг (/? /2 cos 45° ф1 -
Потенциальная энергия системы
П = П1+Пи = - -f- (G3 + G4) Ф; + f ^i
— 2 1^1 +9 1 J ^'
2
где коэффициент жесткости системы
^(<33 I-G4) D2
с =
9 /
Определим обобщенную силу Qp, соответствующую возмущающей
силе Р:
р1 = Рх = Р A s]n pt.
Здесь 6ф1 — приращение обобщенной координаты, Px6(pL — работа
силы Р на элементарном перемещении системы, соответствующем
приращению бф! обобщенной координаты.
Используя полученные для Т, Ф, П и QP выражения, получаем
уравнение (I) в следующем виде:
или
ц\ + (й/а) ¦?! + (с /fl) Ф! =¦¦= (Я .4 /a) s iп
Обозначив
b/a = 2n, da = k-; Р Л/a-^/i,
360

представим дифференциальное уравнение колебаний системы в сле-
следующем виде:
+ 2ф! + k2(fy = h s in pt. B)
Уравнение вынужденных колебаний системы является частным
решением неоднородного дифференциального уравнения B) и имеет
вид:
(fl = АЧ1 sin (pt —г), C)
где ЛФ1 —амплитуда вынужденных колебаний; е —сдвиг фазы вынуж-
вынужденных колебаний.
Л h ; tge ^
Определим Л, &, /г
[C/2) ¦ /я, + inh + 4m3 + D/3) • mt| Я*
= l^i
|C/2) -20-1-4 -5 + 4 -2 + D/3)- 18) 0,32
3 + D/3)-
_ ¦!/-4000+ 7000/9—12 B + 9) -G,81|)/0,9 _ -, f 8538 _ )n p _i
~ Г C/2)-20-r4-5 + 4-2 + D 3)-18 ~ \ 82 -IU'^C •
C/2)
Величину п определим по заданному логарифмическому декре-
декременту колебаний системы:
ля Т* ~ъ 2 л
т] =, ___^^ = /г—, где Т* =— т
Отсюда
п __; * =, 1Q.2 _ = о 55 с-1
(/ 1+л2/тJ 1Л+C,142)/0,8122
Коэффициент а, характеризующий сопротивление, осуществляе-
осуществляемое в демпфере, вычисляем по формуле
_ап__ __ [C/2) ¦ m1 + 4m2 + 4rn3+D/3) - от4!
^ 1C/2)-20 + 4-5 + 4-2 + D/3)-18] 2,55 _ Ш1>
Определяем амплитуду изменения угла ц>г и сдвиг фазы вынуж-
вынужденных колебаний системы при р = 4п с1 = 12,57 с1:
Аф1 = ^- = . °'271 =г = 0,00324 рад,
1 > (А2 — р«)» + 4n'Jpa /[(Ю,22 — DлJ12 + 4-2,552 DлJ f"'
tg е = 2np/(fe2 - р2) = B ¦ 2,55 • 4л) /[A0.22 - DпJ)] = - 1,189;
е=130°04' = 2,2701 рад.
Окончательно по формуле C)
Ф! -0,00324- sin (Ы- 2,27) рад.
12 п-'р. Яблонского А. А. 361

Определяем максимальные значения амплитуд изменения <plt ф
и ip1 при условии, что частота возбуждения р может изменяться.
Амплитуда колебаний Лф1 имеет максимум при
p=pl = VP-2n2 = V 10,22- 2 • 2,552 = 9,54 c,
откуда:
л ft 0.2^1
Обобщенная скорость
ф = р cos (pt — е) = . cos (pt — г).
Следовательно, амплитуда обобщенной скорости имеет максимум
при р = р2 = &:
. 2,55) = 0,0531 с Л
Обобщенное ускорение
[k2 — р2J+4я2р2 e' ^
sin (pt — e).
Найдем то значение р = р3, при котором амплитуда обобщенного
ускорения имеет максимум, а следовательно, подкоренное выражение
имеет минимум. Для этого вычислим производную этого выражения
по р и приравняем ее нулю:
После упрощений получаем:
?4-р2А:2
откуда
р = &lVk- - 2п\
В рассматриваемой задаче
—2п* ~ 10,22-2-2,552 "~ ' ° '
Максимальное значение амплитуды обобщенного ускорения
Л
А ¦¦ =
(pimax
362
Ol271 =0,559 с2.
/ 2,55 .2

Определим теперь амплитуды изменения обобщенных координат,
скорости и ускорения при резонансе
= 0,271/B-2,55- 10,2) =0,00521 рад;
Л -, (р = А) = ftfc/2n = @,271 • 10,2)/B • 2,55) - 0,542 сЛ
Из вычислений следует, что амплитуды изменения обобщенной
координаты и ускорения при резонансе (p = k) весьма близки к мак-
максимальным значениям.
Задание Д-25. Исследование свободных колебаний
механической системы с двумя степенями свободы
Определить частоты малых свободных колебаний и формы глав-
главных колебаний системы с двумя степенями свободы, пренебрегая
силами сопротивления, массами пружин и моментами инерции скру-
скручиваемых валов.
Схемы механических систем тел 1 — 3 в положении покоя показаны
на рис. 248 — 250, а необходимые для решения данные приведены
в табл. 64.
Примечание. Во всех вариантах колеса считать сплошными однородными
дисками, стержни — тонкими однородными. Во всех случаях качение колес про-
происходит без скольжения.
Пример выполнения задания. Определить частоты свободных
колебаний и найти формы главных колебаний системы с двумя сте-
степенями свободы, указанной па рис. 251.
Дано: /1 = 20см; /2 = 60см; /а = 30см; масса груза ^ = 0,5 кг;
масса однородного стержня ED т2 — 3 кг; коэффициенты жест-
жесткости пружин: q = 60 Н/см; с.2 = 40 Н/см; са — 40 Н/см.
Решение. Система состоит из груза В, подвешенного к рычагу
ED на пружине с коэффициентом жесткости с3. В точках Е и D
рычаг опирается на пружины с коэффициентами жесткости сх и с2.
В состоянии покоя рычаг занимает горизонтальное положение.
Пружины с коэффициентами жесткости q и с2 деформированы (сжаты
или растянуты) соответственно на величины /ст1, /ст2. Пружина
с коэффициентом жесткости с3 растянута на величину /ст3.
За обобщенные координаты примем: г —вертикальное смещение
груза от положения покоя; ф —угол поворота рычага ED от поло-
положения покоя. На рис. 252 показано положение системы при поло-
положительных обобщенных координатах.
Найдем кинетическую и потенциальную энергии системы. Кине-
Кинетическая энергия системы состоит из кинетической энергии груза и
кинетической энергии рычага
где г, ф —обобщенные скорости; Jo — момент инерции стержня ED
относительно оси вращения О.
12* 363

f 1
Сг
лАЛАЛЛJ
С3 Jg **
1
s
Y///f,
УУ///уУ/УУУ1У/.//У.'/УУУУУУУУуУУУУУУУ/УУУУ.
c,
го
*vvv
-2
f
8
=лллллл|--
10
Рис. 248
364

13
15
15
\сз
цт.
17
f8
19
20
2.5i ... г
f УУ//У/
Рис 249
3f>5

"si
|vvwv<
|vww
|\ЛЛЛЛААЛЛЛ<
\T
л.
N1

Момент инерции
где / — длина стержня ED, равная 80 см; d = ОС -расстояние от
центра тяжести С стержня до оси вращения О (рис. 252)
d = (t, + h)/2- /, = (l2-IJ/2 = F0-20)/2 = 20 см.
Момент инерции стержня
Jo = C • 802)/12 + 3 • 202 = 2800 кгсм2 = 0,28 кгм2.
Потенциальная энергия системы равна работе сил при переме-
перемещении системы из отклоненного положения в нулевое (положение
статического равновесия).
г,
mmfc
Рис. 251
Рис. Г,2
Потенциальную энергию системы вычислим как сумму:
где П\ — потенциальная энергия груза и рычага в поле сил тяже-
тяжести; Ли — потенциальная энергия деформированных пружин.
Так как
/7i = ~
то Л,=-
367

Таблица 64
HoveD
(рис
24S '50)
1
2
3
4
5
6
7
8
9
10
11
12
Масса теt
m, .
1
10
4
2
5
8
3
4
]
G
10
6
m,
2
2
5
2
2
1
1
0,5
4
3
'
КГ
4
—
Ра-
Радиус
R, м
0,2
—
—
—
0,2
0,2
Радиус инер
ции тела /
л-р ипЛита Ti l_ \Mf\
Ol НОСИТсЛЬИО
оси враще-
_
0,6
—
—
—
_
.
0,3
Коэффициенты жесткости упругих элементов
с
Н/см
40
400
30
6
8
20
6
40
80
4
10
20
Нм/рад
_
—
—
—
—
—
.
—
—
с.
Н/см
30
—
20
8
6
15
4
30
10
3
10
30
Нм/рад
_
2- 10з
—
—
—
—
—
—
—
—
—
Н/см
20
—
*
10
7
7
—
—
60
—
5
40
Нм/рад
_
—
—
—
—
—
—.
—.
Рас-
стоя-
стояние
(. м
0,5
1
—
0,5
0,5
—
0,э
0,.*
0,1
0,1
0,4
0,5
Примечания
Корпус редуктора имеет воз-
возможность поворачиваться
вокруг оси колеса 3. Ось
колеса 2 неизменно свя-
связана с корпусом. Центр
тяжести корпуса совпадает
с центром колеса 2
Система расположена в гори-
горизонтальной плоскости, в
которой происходит движе-
движение. В положении покоя
пружины не деформиро-
деформированы. Тело / принять за
материальную точку
Центр тяжести тела / нахо-
находится на оси пружин с ко-
коэффициентом жесткости сг.
В положении покоя пру-
пружины не деформированы
В положении покоя пружи-
пружина с коэффициентом жест-
жесткости Ci не деформирована

13
14
15
16
17
18
10
20
21
22
23
24
25
26
27
28
29
30
30
40
6
4
50
40
8
4
30
3
40
2
6
8
6
4
30
SO
20
"
6
60
3
60
10
2
40
2
1
2
2
4
3
30
10
10
"
40
8
30
20
—
0,5
3
0.4
0,5
0,2
0,4
0,35
—
0,4
—
—
0,6
0,6
0,4
40
60
20
40
20
10
2
20
40
30
20
30
2-10*
3 10*
2 10*
1 10*
—
1 !04
—
2- lW
100
30
100
40
60
30
20
]
40
30
60
10
20
80
1 10*
—
3 I04
3 104
5- 103
—
—
200
150
50
80
30
—
30
30
—
30
10
30
40
100
—
1 • 104
—
—
—
2- Ю4
—
—
—
—
—
—
1
0,4
—
—
_—
0,5
0,5
0,4
0,3
0,2
—
0,5
тельнооси, проходящей че-
через центр ТЯЖ&.ТИ и пер-
перпендикулярной к плоскости
рисунка
Система расположена в гори-
горизонтальной плоскости, в
которой происходит движе-
движение. В положении покоя
пружины не деформиро-
деформированы
Система расположена в гори-
горизонтальной плоскости, вко-
торой происходит движе-
движение. В положении покоя
пружины не деформирова-
деформированы. Тело 1 принять за ма-
материальную точку
В положении покоя пружи-
пружины не деформированы. Те-
Тело / состоит из трех оди-
одинаковых стержней

Потенциальную энергию пружин найдем, рассматривая сначала
перемещение системы из отклоненного положения в положение,
соответствующее недеформированным пружинам, а затем из этого
положения —в положение покоя.
Деформации пружин следующие: Х1 = [1(\>±:fZT1 — для пружины
с коэффициентом жесткости сх; 12 = /2<р± /ст2 — для пружины с коэф-
коэффициентом жесткости с2; А3 =/ст3-f-/Зф-f-г — для пружины с коэффи-
коэффициентом жесткости с3.
Следовательно,
Пи = A/2) -с, (/1ф±/ст1J- A/2) -сДп + A/2) -^ (/2ф±/С12J-
— A /2) ¦ с2/ет2 + A /2) - с3 (/ст3 + /яФ + 2J — (I /2) • с/|т3
или после упрощений
Пи = A/2) -с^фЧ-A/2) ¦ с/аф» +A/2) -с3 (/3Ф + гJ±
± <VlfcU<P ± С2/2/ст2ф + С3/Ст3 (/Зф + Z) .
Потенциальная энергия всей системы
Л = — Chz + [G2 (lz-l1)/2].q> + (\/2)-c1l№+(\/2)-c2ll4,* +
+ A/2) • Сз/^ф2 + С3/зФ2 + A /2) • C3Z2 ± q/^иф ± С2/2/ст2
Из условий покоя рассматриваемой системы, находящейся под
действием сил, имеющих потенциал, имеем:
{дЩдг)г = о = — Gx + с3/ст3 = 0;
ф-=0
г = „ = G2 -^=^- rfc q/i/e,! ± с,/2/ст2 + с3/3/ст3 = 0.
Потенциальная энергия системы с учетом условий покоя имеет
вид
Л = A /2) • с,/1ф2 + A /2) • с2/1ф2 + A/2)'С3/5ф2 + с3/32Ф + A/2) • слг\
Таким образом,
или
Т = A/2) (апгМ-2а12г
Л = A /2) (си22 + 2с122ф + с22ф2).
Здесь at/ — коэффициенты инерции:
с,у — коэффициенты жесткости:
С21 = С3, С12 = С3C, С22 — Cx
Для рассматриваемой консервативной системы уравнения Лаг-
рапжа имеют вид:
JL (HL\ _ HL — _ iZL. _^_ ^^L\ _ ill — _ -^L
d/ \ di /' dz ~ dz ' dt \дц> J d(f ~ d(f '
370

Вычислив производные
дТ Л дТ d (дТ\ .. дП
дТ п дТ d I дТ\ .. дП
0 аф [} aV
и подставив их в уравнения Лагранжа, получим:
a1Lz = — cnz — с12ср; а22ф = — c21z — с22ф,
где с21 = с12.
Таким образом, для данной системы дифференциальные уравне-
уравнения свободных колебаний имеют вид:
«и2 + cuz + С12ф = 0; й22ф + cnz + с22ф = 0.
Частное решение этих уравнений:
Обозначим ц отношение обобщенных координат, равное отноше-
отношению амплитудных значений фиг:
ф/г = Л2/Л1 = (х.
Тогда
2 = ^1sin F/-J-P); ф = |яг = |ыЛ1 sin (kt-\-P).
Величина ц характеризует формы главных колебаний и назы-
называется коэффициентом распределения.
Подставив значения z и ф в систему дифференциальных уравне-
уравнений, получим:
— ank2 + cn -f cl2\i = 0; — a,2\x.k2 + сп -[- c22fi - 0,
откуда, после исключения \i, получим уравнение частот:
(сп - ank2) (С22 - aZ2k*) - си = 0.
Так как
ап = ml = 0,5 кг, сп = с3 = 40 Н/см — 4000 Н/м;
с1Я = са/3 = 4000-0,3 =1200 Н, й22 = Уо = 0,28 кгма:
с22 = Cl/| + са/1 + с-Д = 6000 • 0,22 + 4000 • 0,6а + 4000 • 0,32 = 2040 Нм,
то уравнение частот
D000'- 0,5/г2) B040 - 0.28&2) - 12002 = 0
или
0,07й4 - 1070/г2 + 3 360 000 = 0.
Квадраты корней этого уравнения
3 _ 1070:4 ^Ю70а — 4 0,07-3 3G0 000
«l.a— 0I4 i
^ = 4414, Aj= 10 870.
Следовательно, частоты свободных колебаний
А1 = 66,4с-1; *в = 104с1.
371

Коэффициенты распределения, соответствующие частотам kk и
в общем случае имеют вид
C21 — а.Ф
В данном елуча е
II, =.-_ D000 -0,5- 4414)/1200 = —1,49 рад/м = — 0,0149 рад/см;
х2 = — D000-0,5¦ 10870)/1200 = 1,2 рад/м = 0,0120 рад/см.
Первое главное колебание системы
к,= 66.4с'1; ji,= -0,0149рад/см
Второе главное колебание системы
К2= 104 С ; Ji2= 0,012рад/см
Рис 253
Уравнения, определяющие первое главное колебание, прим1
следующий вид:
z1 = /llsinF6,4/ + pi); ф,-- — 0,0149Л, sin F6,4/ -|-р\).
Уравнения, определяющие второе главное колебание:
z2 = A,sinA04/ + p\2); ф., -=0,012Л2 sin A04/ -\- р2).
372

Общее решение дифференциальных уравнений представляет собой
сумму частных решений:
г =
<р = ф1
га = Л, sin F6,4/ + Pi) + ^2 sin A04/ + Pa);
— 0,0149^i sin F6,4/ + Pj) + 0,012Л2 sin A04/-f ft,).
/c2 = Wt с
,-f
Значения А{ и р, определяются по начальным условиям задачи.
Коэффициенты распределения цх и fi2 показывают, что в первом
главном колебании с частотой ^ = 66,4 с х перемещению груза вниз,
равному 1 см, соответст-
соответствует поворот рычага по
вращению часовой стрелки
на угол, равный 0,0149 рад
(рис. 253, а); во втором
главном колебании с час-
частотой &2= 104 с1 тому же
перемещению груза вниз
на 1 см соответствует по-
поворот рычага против вра-
вращения часовой стрелки на
0,0120 рад (рис. 253,6).
Формы колебаний мож- рис 254
но представить в виде гра-
графиков. Для рассматриваемой задачи построим график сравнения пере-
перемещения груза В и точки А (точки прикрепления пружины к рычагу).
В первом главном колебании при перемещении груза В вниз на
1 см точка А перемещается также вниз на величину цхЛг ^ 0,0149 х
хЗО = О,447 см (точки В и А находятся в одной фазе) (рис. 254, а).
Во втором главном колебании при перемещении груза В вниз
на 1 см точка А перемещается вверх на величину ц2/3 = 0,012 х
X30 = 0,36 см (точки В и А находятся в противоположных фазах)
(рис. 254, б).
Задание Д-26. Исследование вынужденных колебаний
механической системы с двумя степенями свободы
Механическая система с двумя степенями свободы находится под
действием силового гармонического возмущения в виде силы Р —
^P0cospt или момента М — М0сояр(. Пренебрегая сопротивлением,
исследовать вынужденные колебания системы.
Схемы механических систем в положении покоя показаны на
рис. 248 — 250. Необходимые сведения об инерционных и упругих
свойствах системы, а также ее размеры приведены в табл. 64. Мас-
Массами пружин и скручиваемых валов пренебречь.
В табл. 65 указано, к какому из тел системы приложена возму-
возмущающая сила Р или пара сил с моментом М. Линия действия
силы Р во всех случаях проходит через центр тяжести тела, к кото-
которому она приложена. В процессе колебаний линия действия силы
остается либо вертикальной, либо горизонтальной (см. табл. 65).
373

Номер вари-
варианта (рис
243 — !>50)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
14
20
21
22
23
24
25
26
27
28
29
30
Вид воз-
мущенля
м
м
р
м
м
р
р
р
м
м
р
р
р
р
м
м
м
р
м
1*1
р
м
м
р
м
р
м
р
р
р
м
Номер тела,
к которому
приложено
возмущенно
<
[
f
1
1
С
С
1
г
'
г
1
<
1
3
2
)
>
>
г
Ллнля действия
силы Р
,
—
Вертикальна
—
—
Горизонтальна
»
»
с 1
—
Вертикальна
»
Горизонтальна
Вертикальна
—
—
—
Горизонтальна
Вертикальна
—
—
Горизонтальна
—
Вертикальна
—
Горизонтальна
»
»
Т
Линейное сме-
смещение прн
Р = Ра, м
—
0,002
—
—
0,001
0,002
0,001
—
—
0,001
0,002
0,003
0,001
—
—
0,002
0,001
—
0,003
ч
0,005
_
0,004
0,003
0,002
—
а б л и ц а 65
Угловое сме-
смещение при
М = Мп, рая
0,01
0,01
—
0,005
0,02
—
—
—
0,005
0,01
—
—
—
—
0,01
0,02
0,005
¦ п (VIе;
0,01
0,005
—
0,01
—
0,02
0,005
Пара сил с моментом М. расположена в плоскости колебаний
тела, к которому она приложена, Во всех вариантах положитель-
положительное направление силы Р и момента М, изменяющихся по гармони-
гармоническому закону, можно выбирать произвольно.
В табл, 65 задано линейное или угловое смещение от положения
покоя для тела, к которому приложено силовое возмущение при
условии воздействия постоянной силы P — PQ или момента М =
- Мп (случай пулевой частоты изменения возмущения силы или
момента), Для систем, находящихся под действием силы, смещение
задается вдоль линии ее действия, а для систем, находящихся под
действием пары сил, задается угловое смещение в плоскости дейст-
действия этой пары сил.
Пример выполнения задания. Пренебрегая сопротивлением, иссле-
исследовать вынужденные колебания системы с двумя степенями свободы,
изображенной в положении покоя (рис. 255). Колебания происходят
под действием пары сил, приложенной к стержню DE и располо-
расположенной в плоскости чертежа, Момент возмущающей пары изменяется
374

по закону:
М = Мо cos pt.
Дано: массы элементов системы т1 = 0,5, т2 = 3 кг, коэффициенты
жесткости пружин сх = 60, с2 = 40, с3 = 40 Н/см; линейные размеры:
^ = 20, /2 = 60, 1а = 30 см. Угол поворота стержня DE под действием
пары сил" с постоянным моментом М = М0 равен: ф0 = 0,01 рад.
Решение. За обобщенные координаты примем: г —вертикаль-
—вертикальное смещение груза от положения покоя и ф —угол поворота
рычага DE от положения покоя.
M=l%ctxpt А ,- Р
Рис. 255
На рис. 255 пунктиром показано положение системы при поло-
положительных обобщенных координатах.
Уравнения Лагранжа для рассматриваемой системы имеют вид:
J- (~\ — 0L. EJL\n- J-l^L\ — HL — _ ^Е-4-0 (\)
dt \di J dz дг ' dt \ д$ ) д(р дц> ' ч"
где Qz и Qtp — обобщенные возмущающие силы.
Выражения для кинетической и потенциальной энергии получены
в примере к заданию Д-25, где исследовались свободные колебания
рассматриваемой системы.
Г = A /2) • auz2 + «12гф + A /2) • а22ф2; 1
где ац и ^/ — коэффициенты инерции и жесткости системы, равные
Н/м, cia = Cji = c3/a=1200 H;
Нм.
кгм2;
Частоты свободных колебаний и соответствующие коэффициенты
распределения получены в примере к заданию Д-25
^ = 66,4 с-1; |ах = — 1,49 рад/м;
&2=104 с; (Аа = 1,2 рад/м
д/м; \
. J
C)
375

Определим обобщенные силы Qz и Qv, связанные с действием
возмущающего момента:
D)
где &AMz — элементарная работа возмущающего момента на переме-
перемещении системы, вызванном элементарным приращением обобщенной
координаты z при ф = const; бАМч — элементарная работа возмущаю-
возмущающего момента на перемещении системы, вызванном элементарным
приращением обобщенной координаты ф при z = const; 62, бф — эле-
элементарные приращения обобщенных координат.
Если принять направление возмущающего момента при / = 0
положительным и считать, что оно совпадает с направлением отсчета
положительных значений угла ф, то из соотношений D) получаем:
Qz = 0; Qy — Мо cos pt.
Следовательно, дифференциальные уравнения A), описывающие
вынужденные колебания системы в обобщенных координатах z и ф,
имеют вид:
au'i + спг Н-С|,ф = 0; а22ср + c2lz + г 2,ф = /W0cos pt. E)
Частное решение системы дифференциальных уравнений E), опре-
определяющее вынужденные колебания, находим в виде:
z = Аг cos pt, (f> = Avcos pt.
Подставляя эти выражения в дифференциальные уравнения E), полу-
получаем:
Из этой системы двух алгебраических уравнений относительно
Az и Лф находим:
Д, = —
А — —
Амплитуды вынужденных колебаний равны абсолютным значениям
А, и Лф.
Воспользуемся формулой G) для определения амплитуды Мо воз-
возмущающего момента. По условию задачи при р =0 угол поворота
стержня DE равен ф0, следовательно, при /> = 0
откуда
Мо = ф0 !с.,г - -^ \ = 0,01 B040 - -4^-) = 16,8 Нм.
Перемещение груза под действием постоянного момента М = М0,
приложенного к стержню DE, можно найти из соотношения F) при
Д - у - — М°Сп = — '6,8- '200 = _ О ПГП м
Л г0 — Ч — С] lCi2 _ саз 4000 ¦ 2040 — 12002 ' '
37G

Так как знаменатель в формулах F) и G) является квадратным
многочленом относительно р2, а корнями этого многочлена являются
квадраты частот свободных колебаний системы k\ и &;, то формулы F)
и G) можно представить в виде
л =^Vi2[44000
z W
л =
ф
[
(р2-4414)(р2-10870) '
120D000 0,5р*)
'~кГ)(рг--^) Хр1- 4414) (р*-10870) ' Р>
Формулы F), G) или (8), (9) позволяют проследить за зависи-
зависимостью А- и Лф от частоты р и построить соответствующие графики
(рис. 256).
_1_
30 +0
^ v> (радиан)
Ж»,
«3J
0,0?
0.01
о
-0,01
-0,02
-№
9
0,03
0,02
0,01
о
-0.01
-0,02
-0,03
Рис. 256
Рассмотрим поведение Л- и Лф для трех интервалоз изменения
циклической частоты возмущающего момента:
0--ss/?<*!, k1<:p<.k.i и k2<p<oo.
1. 0<гр<*!. Так как ^1<А2, то р2 — А; < 0 и р2 — &.;<0, сле-
следовательно, знаменатель формул (8) и (9) положителен. Из этого
Ю 20 20 ?3 50 60 \io во '/90 100 \
на по но
377

вытекает, что в первом интервале Лг<0 и Лф>0. С ростом вели-
величины р амплитуды колебаний стержня и груза возрастают, при этом
колебания стержня происходят в одной фазе с изменением возму-
возмущающего момента, а колебания груза —в противофазе (рис. 257, а).
При р = 0 имеем: Лф = ф0 = 0,01 рад и Аг = г0 = — 0,003 м.
При p = ky = 66,4 с в системе наступает первый резонанс и функ-
функции Аг и Лф претерпевают бесконечный разрыв (рис. 256).
2. ky<p<.k2. Так как kx<k2, то p2-k'\>0, а р2 — &!<0.
Следовательно, знаменатель формул (8) и (9) отрицателен. Из этого
А -~\В
—-9—
Рис. 257
следует, что во втором интервале Лг>0, т. е. колебания груза про-
происходят синфазно с изменением возмущающего момента (рис. 257, б, в).
При определении знака функции Лф необходимо рассмотреть
числитель формулы (9). Если kx<p <.Vcnjau, то Лф<0, и коле-
колебания стержня происходят в противофазе с возмущающим моментом
(рис. 257,6). Если Vclllall<p <k2, то /1ф>0, и колебания стержня
так же, как и груза, синфазны с изменением М (рис. 257, в).
При p=]Aw°n — У 4000/0,5 = 89,4 с1 —первая парциальная
частота (частота собственных колебании системы, изображенной на
рис. 258, а) амплитуда вынужденных колебаний стержня равняется
нулю (Аф = 0 — случай антирезонанса). В этом случае груз массой tnt
может рассматриваться как гаситель колебании стержня. Величину Аг
в этом режиме проще определить по формуле F):
Лг = Мос12/с\.2 = М0/с12= 16,6/1200 = 0,014 м.
378

Амплитуда колебаний стержня \Аг\ убывает до нуля при воз-
возрастании р от kx до У'сц/пц, а затем с увеличением р от \/Гсп/а11
до &2 возрастает. При р = /с.22/а22 = /2040/0,28 = /7290 = 85,4 с —
вторая парциальная частота (частота собственных колебаний системы,
изображенной на рис. 258, б) по формулам F) и G) находим:
А; = Ма/с12 = 16,8/1200 = 0,014 м;
_ 16,8D000-0,5-7290) _ nnn4i4 пял
i^ooti -U.UU414 рад.
и
При изменении р в интервале от kv до fe2 функция Аг для ампли-
амплитуды вынужденных колебаний груза имеет минимум, соответствую-
w77Wt
Piic. 258
щий максимуму знаменателя формул F) и G). Взяв от этого выра-
выражения производную по р и приравняв се нулю, получим:
2аиа,2р2 - (йис22 + я22си) = 0;
откуда найдем значение р, при котором Az достигает минимума:
= 87,4 с \ A0)
При р = &2 = 104 с в системе наступает второй резонанс.
3 & Т *й 2 ftJ0 2
р
3. &2<р<оо. Так как *!<й2, то р2 — ftJ>0 и р2 —
следовательно, знаменатель формул (8) и (9) положителен. Учитывая,
что ks>Vcll/all, можно заключить, что в этом интервале и Лг<0,
и Лф<0, т. е. колебания происходят в противофазе с возмущающим
моментом (см. рис. 257, г). С возрастанием р амплитуды вынужден-
вынужденных колебаний \AZ\ и \AV\ уменьшаются, стремясь к нулю.
Отношение функций Лф и Л2, определяющих амплитуды вынуж-
вынужденных колебаний стержня и груза (коэффициент формы вынужден-
вынужденных колебаний), получим, разделив (9) на (8):
Ач/Аг = - (сц - flllPs)/c18 = - D000 - 0,5р2)/1200. A1)
При р = 0
AJAг = — сп/с12 = — 4000/1200 = — 3,33 р ад/м.
379

При р = А1 =
При р = 1/"^
При p = fej =
с 1
A(flAz =
-89,4 с
= — 1,49 рад/м.
Ач1Аг = fi2 = 1,2 рад/м.
График зависимости А9\Аг от частоты возмущения р показан на
рис. 259. При резонансах формы вынужденных и свободных коле-
колебаний совпадают (см. рис. 253).
3
2
1
-1
-2
-3
Az (
10
'. '
poo
7Г
20
»—-
)
30
10 50 60
I
1
SIL,
s
/30
/
/l
_I_J 1
too no
p=kz
/
/
/
p
ktitc
Рис. 259
Для исследования резонансных колебании (p = kx и p = k.2) осу-
осуществим переход к главным координатам системы: % и тJ. Они
связаны с координатами z и <р соотношениями:
Дифференциальные уравнения колебаний механической системы
с двумя степенями свободы в главных координатах цх и тJ при
обобщенных возмущающих силах:
Q, = Ях sin (р/ + в); Q.2 = Я2 sin (р^ + б),
соответствующих обобщенным координатам </х и q.2, имеют вид:
4- А-,% =•¦
-L-'7 s i п
sin (p* -j-б),
где
aM
A3)
A4)
(j,j и |А2 —ьозффкцленты распределения обобщенных координат qx и
при свободных колебаниях.
380

В данном случае
Я1 = 0; Н2 = М0; 6 = я/2.
Поэтому дифференциальные уравнения A3) принимают вид:
42
sin
A5)
При р = ^ (первый резонанс) частный интеграл первого диффе-
дифференциального уравнения системы A5) имеет вид:
Частный интеграл второго дифференциального уравнения
Переходя к обобщенным координатам z и <р по формулам A2),
получаем:
При p = 62 (второй резонанс) частные интегралы дифференциаль-
дифференциальных уравнений A5) имеют вид:
откуда обобщенные координаты г и ср:
— пи „ * Sin «2'»
COS kj.
т^Г COS,
A7)
Параметры, входящие в уравнения A6) и A7), имеют следующие
числовые значения:
Мо=16,8 Нм; fAt = — 1,49 рад/м; щ^=1,2 рад/м.
Согласно A4):
ах = 0,5 + 0,28 (— 1,49J = 1,13 кг;
а, -= 0,5 + 0,28 ¦ 1,22 = 0,90 кг.
Подставляя эти значения в формулы A6) и A7), получаем урав-
уравнения вынужденных колебаний при первом и втором резонансах.
381

Первый резонанс: p = kx = 66,4 с1;
— 1,49 16,8, . аа .. . 1,2-16,8 сс .,
Z= 2-06,4-1,13 *sin6M*+ 0,90A0870-4414) COS 66,4/=
= — 0,168/ sin 66,4/ + 0,0035 cos 66,4/;
(— 1,49J -16,8 , . сс ,, . A.2J ¦ 16,8 rc .,
V = 2.66,4-1,13 t Sltl 66At + 0,90A0870-4414) c0S 66-« =
= 0,252/ sin 66,4/ + 0,0042 cos 66,4/.
Второй резонанс: p = k2=l04 с 1;
1,2-16,8 , . ,„., (—1,49)-16,8
2= 2-104-0,90 *s'0^- ,,13A0870-44.4-)
= 0,108/sin 104/+ 0,0035 cos 104/;
1,25-16,8 , . ,„., (—l,49J-l6,8
* 2-104-0,90 ^Sml04^- 1,13A0870-4414) COS 104/ =
= 1,30/sin 104/-0,0052 cos 104/.
Полученные результаты позволяют оценить колебания, происхо
дящие в системе при резонансе в том случае, когда силы сопротив
ления незначительны, а резонансные режимы кратковременны.

Таблица вариантов заданий, входящих в курсовые работы
Шифр
1
2
3
4
5
6
7
8
9
10
11
12
13
1
7
13
19
25
23
20
17
14
11
8
5
2
19
16
13
10
7
Номера
2
8
11
20
26
3
9
15
21
Варианты
25
22
19
10
13
10
7
4
30
27
24
21
18
19
2
20
28
22
5
8
11
14
17
20
23
26
заданий
4
10
1ь
22
5
11
17
23
заданий
3
6
9
12
15
18
21
24
27
30
4
7
10
5
8
11
17
14
20
23
26
29
1
3
6
9
6
12
18
24
1
3
6
9
12
15
18
21
21
27
2
5
8
Шифр
35
36
37
38
39
40
41
42
43
44
45
46
47
1
7
13
19
25
19
16
13
10
7
4
30
27
24
21
18
15
12
Номера
2
8
14
20
26
3
9
15
21
Варианты
4
30
27
24
21
18
15
12
9
6
3
1
29
8
11
14
17
20
23
20
29
1
3
6
9
12
заданий
4
10
16
22
5
п
17
23
заданий
18
21
24
27
30
4
7
10
13
16
19
22
25
17
24
21
28
1
29
3
6
9
12
15
18
21
6
12
18
24
13
16
J9
22
25
28
30
4
7
10
12
16
19
Шнфр
69
70
71
72
73
74
75
76
77
78
79
80
81
I
7
13
19
25
Номера
2
8
14
20
26
3
9
15
21
заданий
4
10
16
22
5
11
17
23
6
12
18
24
Варианты заданий
21
18
15
12
9
6
3
1
29
26
9
20
17
9
6
3
1
29
26
23
20
17
14
11
8
5
29
1
7
6
9
12
15
18
21
24
27
30
4
7
10
13
16
19
22
25
28
2
5
8
11
14
1
29
18
6
8
15
12
11
19
20
23
3
18
24
27
2
5
18
11
14
17
20
23
26
29
2

Ю 00 — •*
omcocNi
_ „ — CM <
ooocs
<M CM —
00
см
¦Ч"
см
ОС
й
см
00
12
8
со
СО
см
о
с»
S3
Я
см
см
00
ГС
сч
СО
то
го
со
ОО
0О
ОО
см
-
ее
со
со
см
СО
то
ю
ОО
~
00
сч
со
о>
см
о
о
см
S
8
см
со
см
см
см
г-
\п
см
00
со
о
о
го
-
СО
см
ю
см
О)
ю
ТР
0О
ОС
СП
то
¦ч-
ОО
я
00
гм
00
со
0О
см
СО
о
см
iO
S
гм
1П
-
¦Ч"
СП
8
'О
СП
то
о
сч
1Л
00
см
о
то
ОО
сч
сч
CD
то
со
ОО
см
on
сч
-
00
сч
Й
с»
о
со
см
"
см
о
см
ю
¦*
см
пэ
СП
см
00
сч
со
CD
т
сч
"
см
сч
_
см
о>
г--
см
см
с»
ю
о
ОО
,_,
то
СО
см
ел
00
S
.о
см
СО
с»
о
|П
то
¦о
00
о
га
гс
го
см
-
то
см
-
се
00
00
-
см
-
со
см
о
то
о
ОО
сч
см
г—
о
т
СО
<ъ
см
СП
8
см
см
см
со
00
со
см
100
ю
8
г*
8
ОО
то
со
то
см
о
то
см
см
со
см
¦*
со
см
см
см
iO iO iQ
LO 'О Ю О CD CD CD
S
см
ю
со
оо
CD
8
см
-
см
см
СО
см
см
0О
см
8
ю
см
8
см
ю
ОО
00
о
-
го
¦а"
со
г^
8
8
см
С4)
ГС
О]
я
1С
см
со
см
СО
см
ас
см
С5
см
СП
см
см
то
ю
со
00
ет
—
см
о
ю
— та сп со см оо
о см сэ со го — o>comot^-Tj<—.
см — см см см см — —. ™
О Г— "Г — ОС lOCl
ТО СЧ СМ СЧ —¦ — —•
C^Oi
СМ СМ <М OI — —¦
iO CD t~~ 0O ОЗ О •-¦ C^l ГС "^ 'O ^D P^ ОС CT <O <—' C^\ CO ^*
^m ^m ^ ^ ^ CM CM СЛ C^l (M (M CM CM C-l C-l CO O0 CC CO CO
384

ЛИТЕРАТУРА
Бабаков И. М. Теория колебаний. «Наука», 1965.
Б уте и и к Н. В. Введение в аналитическую механику, «Наука», 197].
Б у тении Н. В. Теория колебании. М., «Высшая школа», 1963.
Бутенин Н. В., Лунц Я. Л., Меркин Д. Р. Курс теоретической ме-
каники, ч. I и II. «Наука», 1971 и последующие издания.
Воронков И. М. Курс теоретическом механики. Физматгнэ, 1954.
Гер нет М. М. Курс теоретической механики. М., «Высшая шкома», 1965.
Добронравов В. В., Н и к и г и н Н. Н., Дворников А. А. Курс
теоретической механики. М , «Высшая школа», 1968 и последующие издания.
Космодемьянский А. А. Курс теоретической механики. Изд. 2 е, Уч-
Учпедгиз, 1954. «
Лойцянекий Л. Г., Лурье А. II. Курс теоретической механики, ч. I и
II. Физматгиз, 1954.
Николаи Е. Л. Теоретическая механика. Физмаггиз, 1952.
Па нов ко Я. Г., Губанова И. И. Устойчивость и колебания упругих
систем. «Наука», 1964.
Па нов к о Я. Г. Введение в теорию механических колебаний. «Наука»,
1971.
Пановко Я. Г. Введение в теорию механического удара. «Наука», 1977.
Савин Г. П., К и л ь ч е в с к и ii H. А., П у т я т а Т. В. Курс теоретиче-
теоретической механики. Гостсхиздат УССР, 1963.
Т а р г С. М. Курс теоретической механики. Изд. 3-е. Физматгиз, 1963 и по-
последующие издания.
Яблонский А. Д., Никифорова В. М. Курс теоретической меха-
механики, ч. 1, М., «Высшая школа», 1971 и [тслед>/юш.не издания.
Яблонский А. Л. Курс теоретической механики, ч. II, М., «Высшая
школа», 1971 и последующие издания.
Я б л о н с к и й А А., Н о р е й к о С. С. Курс теории колебаний. М. «Выс-
«Высшая школа», 1966 и последующие издания.
Сборники задач и руководства к решению задач
Айзенберг Т. Б., Воронков И. М., Осецьии В. М. Руководство
к решению задач по теоретической механике. М., «Высшая школа», 1968.
Бать М. И., Джанелидзе Г. Ю., Ксльзон А С, Теоретическая
механика в примерах и задачах, ч. I и П. Физматгиз, 1961 и последующие из-
издания.
Б р а ж и и ч е и к о Н. А. [и др.]. Сборник задич по теоретической механике.
М., «Высшая школа», 19G7 и последующие издании.
Мещерский И. В. Сборник задач по теоретической мехгчшке. Физмат-
гиз, 1971.
Светлиц к п ii В. А., С т a l с и к о И. В. Сборник задач по теории коле-
колебаний. М., «Высшая школа% 1973.
385

ОГЛАВЛЕНИЕ
Стр.
Предисловие 3
Раздел первый Статика твердого тела
I Плоская система сил ... ... . 5
Система сходящихся сил . . . .... .... 5
Задание С I Определение реакций опор и усилии в стержнях пло-
плоской фермы . ... ... . . . . 5
Система произвольно расположенных сил . . . 12
Задание С2 Определение реакции опор твердого тела . ... 12
Задание СЗ Определение усилим в стержнях плоской фермы спо-
способом Риттера . . .17
Задание С4 Определение реакций опор составном балки . . . 24
Задание С 5 Определение реакций опор составной конструкции (си-
(система двух тел) . . 29
Задание С 6 Опредеюиие реакций опор составной конструкции
(система трех тел) . . . . . 35
Задание С7 Равновесие сил с }четом сцепления (трения покоя) 41
II Система сил, не лежащих в одной тоскости 48
Система сходящихся сил . ... 48
Задание С8 Определение усилий в стержнях пространственной
конструкции . . 48
Система произвольно расположенных сил . 54
Задание С9 Приведение системы сил к простейшему виду ... 54
Задание С 10 Определение реакции опор твердого тела ... . 59
Задание СП Определение реакций стержней, поддерживающих
прямоугольною плиту . . . . 64
Центр тяжести . 70
Задание С 12 Определение положения центра тяжести тела .... 70
Раздел второп Кинематика
I. Кинематика точки 76
Прямолинейное и криволинейное движения точки 7G
Задание К 1 Опредечение скорости и ускорения точки по заданным
уравнениям ее движения . . . . 76
Задание К. 2 Составление уравнений движения точки и определе-
определение ее скорости и ускорения . 81
II. Кинематика твердого тела . . 88
Поступательное и вращательное движения твердого тела 88
Задание КЗ Определение скоростей и ускорении точек твердого
тела при поступательном и вращательном движениях ... ... 88
Плоское движение твердого тела ... . . ... 93
Задание К 4 Определение скоростей точек тпердого чела при пло-
плоском движении . ... .... 93
Задание К5 Определение скоростей и ускорении точек твердого
тела при тоском движении . . . 99
386

Стр.
Задание К-6. Определение скоростей и усмирений точек многозвен-
многозвенного механизма 106
Сферическое движение твердого тела 119
Задание К-7. Определение кинематических характеристик движения
твердого тела и его точек по уравнениям Эйлера 119
Задание К-8. Определение скоростей и ускорении точек твердого
тела, катящегося без скольжения по неподвижной поверхности и
имеющего неподвижную точку 123
III. Сложное движение 130
Сложное движение точки 130
Задание К-9. Определение абсолютной скорости и абсолютного уско-
ускорения точки в случае поступательного переносного движения 130
Задание К-10. Определение абсолютной скорости и абсолютного
ускорения точкл в случае вращательного переносного движения ... 137
Сложное движение твердого тела. Сложение вращений вокруг парал-
параллельных и пересекающихся осей 144
Задание К-П. Определение угловых скоростей звеньев планетарного
редуктора с цилиндрическими колесами 144
Задание К-12. Определение угловых скоростей звеньев планетарного
редуктора с коническими колесами 150
Раздел третий. Динамика
I. Динамика материальной точки 157
Дифференциальные уравнения движения материальной точки 157
Задание Д-1 Интегрирование дифференциальных уравнений движе-
движения материальной точки, находящейся под действием постоянных сил 157
Задание Д-2. Интегрирование дифференциальных уравнений движе-
движения материальной точки, находящейся под действием переменных сил 164
Задание Д-3. Исследование колебательного движения материальной
точки 171
Задание Д-4. Исследование относительного движения материальной
точки 182
Основные теоремы динамики материальной точки 189
Задание Д-5. Применение теоремы об изменении количества движе-
движения к определению скорости материальной точки 189
Задание Д-6. Применение основных теорем динамики к исследова-
исследованию движения материальной точки 104
II. Динамика механической системы 201
Основные теоремы динамики механической системы 201
Задание Д-7. Применение теорем об изменении количества движения
и о движении центра масс к исследованию движения механической
системы 201
Задание Д-8. Применение теоремы об изменении кинетического мо-
момента к определению угловой скорости твердого тела . 212
Задание Д-9. Применение теоремы об изменении кинетической
энергии к изучению движения механической системы 220
Дифференциальные уравнения движения твердого тела 231
Задание Д-10. Исследование вращательного движения твердого тела 231
3 а д а н и е.Д-11. Исследование плоского движения твердого тела . . . 240
Удар 246
Задание Д-12 Исследование соударений твердых теп 246
III. Аналитическая механика 266
Принцип возможных перемещении 266
Задание Д-13. Применение принципа возможных перемещений к ре-
решению задач о равновесии сил, приложенных к механической системе
с одной степенью свободы 266
387

Стр.
Задание Д-14. Применение принципа возможных перемещений
к определению реакций опор составной конструкции 273
Принцип Даламбера 279
Задание Д-15. Применение принципа Даламбера к определению ре-
реакций связей 279
Задание Д-16. Определение реакций опор при вращении твердого
тела вокруг неподвижной оси 28E
Общее уравнение динамики 295
Задание Д-17. Применение общего уравнения динамики к исследо-
исследованию движения механической системы с одной степенью свободы . . 295
Задание Д-18. Применение общего уравнения динамики к исследо-
исследованию движения механической системы с двумя степенями свободы 303
Уравнения Лагрчнжа второго рода 311
Задание Д-19. Применение уравнений Лагранжа второго рода к ис-
исследованию движения механической системы с одной степенью сво-
свободы 311
Задание Д-20. Применение уравнений Лагранжа второго рода к ис-
исследованию движения механической системы с двумя степенями сво-
свободы 318
Устойчивость состояния покоя (равноиесия) консервативной механиче-
механической системы 320
Задание Д-21. Определение положений покоя (равновесия) консерва-
консервативной механической системы с одной степенью свободы и исследо-
исследование их устойчивости (по теореме Лагранжа—Дирихле) 320
3 а д а и и е Д-22. Определение условий устойчивости заданного состоя-
мпя покоя (равновесия) консервативной механической системы с од-
одной и двумя степенями свободы (по теореме Лагранжа—Дирихле) . . 332
Колебания механической системы 344
Задание Д-23. Исследование свободных колебаний механической
системы с одной степенью свободы 344
Задание Д-24. Исследование вынужденных колебаний механической
системы с одной степенью свободы 352
Задание Д-25. Исследование свободных колебаний механической си-
системы с двумя степенями свободы 363
Задание Д-26. Исследование вынужденных колебаний механической
системы с двумя степенями свободы . 373
Таблица вариантов заданий, входящих в курсовые работы 383
Литература 385

Сборник заданий для курсовых работ по теоретической
С23 механике Под ред. проф. А. А. Яблонского. Учеб. пособие для
втузов. Изд. 3-е, испр. М., «Высш. школа», 1978.
388 стр , с ил
На обороте тит л авт А А Яблонским, С С 11оройко, С А Вольф-
сон [и др ].
Книга представляет собой сборник заданий для курсовых раГют по теоретической
механике
В сборнике имеется 50 заданий по статике, кинематике и динамике для курсовых
работ, предусмотренных программен курса г^орегичсокоп механики Каждое задание
Содержит тридцать вариантов Приведены примеры выполнения этих заданий
Предназначается п качестве учебного пособия для студентов высших техниче-
технических учебных заведений очном, вечерней и заочном систем обучения Г.е могут также
использовать инженеры и техники для углубления знаний по теоретической меха
пике
с «»И=«» 80_78 53,
С01@1)-78

Александр Александрович Яблонский.
Сиги:шунд Сильвестрович Норсйко
Саул Аронович Вольфсон
Наталия Васильевна Карпова
Борис Николаевич Квасников
Юрии Григорьевич Минфин
Нина Ивановна Никитина
Владимир Егорович Пав ion
Юрии Михайлович Тепанков
СБОРНИК ЗАДАНИЙ
для курсовых работ
по теоретической
механике
Редактор 3 Т Овсянникова
Художеством ими редактор Т А Дурасова
Художник график Н М Керезовскл i
Перегнет художника В Н Панферова
Технический редактор 3 Л М\гслимова
Корректор М А Минкова
ИБ № 1057
Сдано в набор 29/V1 1977 г Подп к печати 16/Х1 1977 г Формат 60x907i6 Бум тип
№ ! Объем 24 5 печ .ч Уел печ л 24 3 Уч 1ьд л 23 61 Изд № ОТ—283/7G Тираж
130 000 экз Заказ № 1359 Цена 80 ком
План выпуска литературы издательства
«Высшая школа» (вузы и техникумы) па 1978 г Позиция № 80
Издательство (.Высшая школа», Москва, К 51, Нсглнипая ул , Д 29/14
Ордена Октябрьской Резолюции, ордена Трудового Красного Знамени Ленинградское
производственно техническое объединение «Печатный Двор» имени А М Горького
Союзпотиграфпрома при Государственном комитете Совета Министров СССР по делам
издательств, полиграфии н книжной торговли 197I3G, Ленинград, П 136, Гатчин-
Гатчинская ул , 2G

ИЗДАТЕЛЬСТВО «ВЫСШАЯ ШКОЛА»
ВЫПУСТИТ В СВЕТ 1$ 1978 ГОДУ
для студептов машиностроительных и немашпностроитель-
пых специальностей вузов, а также для учащихся, меха-
механических, машиностроительных ц строительных технику-
техникумов следующие учебные пособия:
Левитская О IГ, Л свитский П И Курс теории меха-
механизмов и машин. Учебник 20 л l ил 82 к
Учебник написан по нстой A974 г) программе для студентов
механических специальностей вузов При изложении всех разделов
курса выделен материал, предназначенный для студентов немашиио-
строительных специальностей, н поэтому он может быть использован
при изучении курсов «Теория механизмов п машин и детали машин»
и «Прикладная механика»
В разделах кинематики и динамики механизмов рассматри-
рассматриваются пространственные механизмы промышленных роботов и ма-
манипуляторов В разделе «Основы теории машин-автоматов» изла-
излагаются методы лостроения систем управления машин-автоматов
с механическими, пневматическими и гидравлическими элементами.
Предназначается для студентов машиностроительных и немашп-
иостроительных специальностей вузов
УлитинН С , Л а у е и б у р г Л В, Перший А П Сборник
задач по технической механике. Учебное пособие 25 л с ил 87 к.
В сборник включены задачи по теоретической механике, сопро-
сопротивлению материалов и статике сооружений, составленные в соот-
соответствии с программами для специальностей промышлеиио-граж-
данские сооружения, мосты, тоннели и метрополитены, гидротехни-
гидротехнические и другие искусственные сооружения
Наряду с задачами для аудиторных и текущих домашних работ
в сборнике имеются многовариантные задачи для контрольных работ
и индивидуальных домашних заданий Типовые задачи снабжены
решениями, остальные имеют ответы
Предназначается для учащихся строительных специальностей
техникумов
Ф а м и А М Сборник задач по теоретической механике. Учебное
пособие 15 л с ил 60 к
В задачнике представлено около тысячи задач по теоретической
механике Подавляющая часть задач оригинальна Тематика их
отражает достижения современной техники В условиях задач вни-
внимание уделено выбору рациональных способов решения, проверки

результатов исходя из принципов правдоподобия и правил размер-
размерности Приведены контрольные вопросы, развивающие у учащихся
навыки применения аксиом и методов теоретической механики
в практической деятельности Для контрольных работ даны десяти-
варнантные задачи различной степени трудности
Предназначается для учащихся механических и машинострои-
машиностроительных техникумов. Может быть использовано в техникумах других
специальностей и в кружковой работе.
Уважаемые читатели!
Издательство «Высшая школа» выпускает учебники, учебные и
методические'пособия, плакаты Подробнее познакомиться с \чебнон
литературой Вам поможет аннотированный плаЕ! выпуска литера-
литературы на 1978 год (вузы и техникумы), который имеется в книжных
магазинах
Предварительные заявки на книги Вы можете сделать в мага-
магазинах Книготорга или потребительской кооперации.