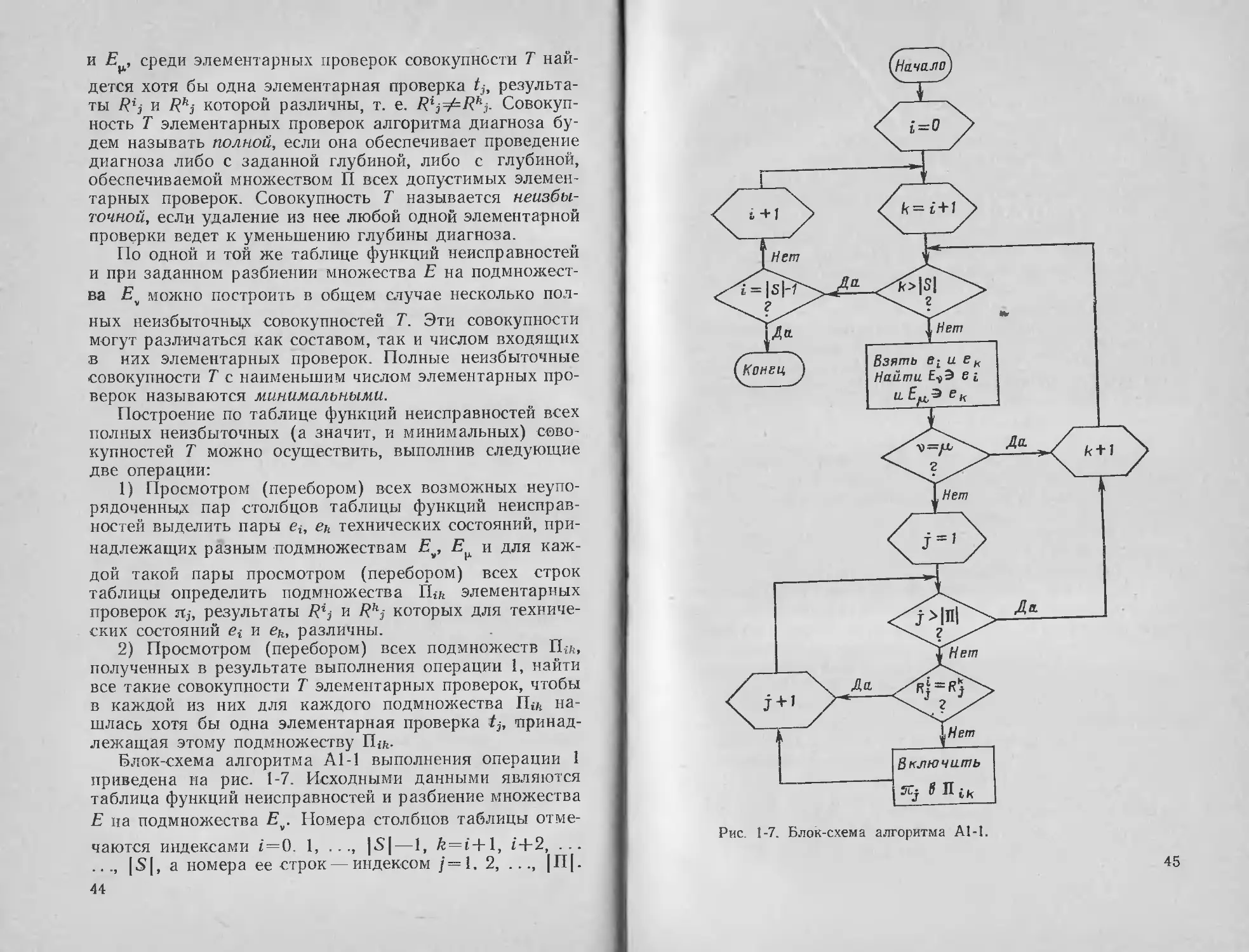
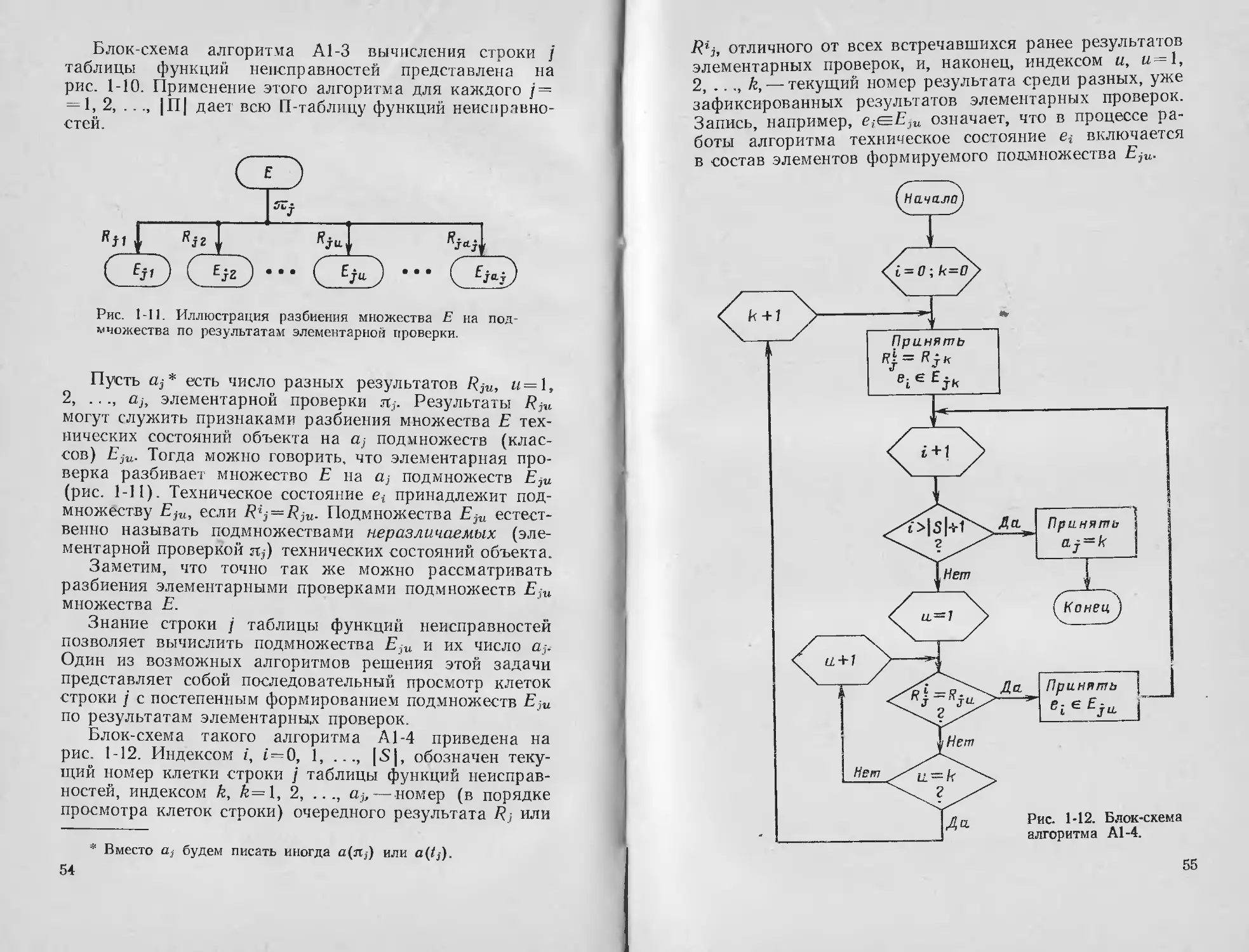
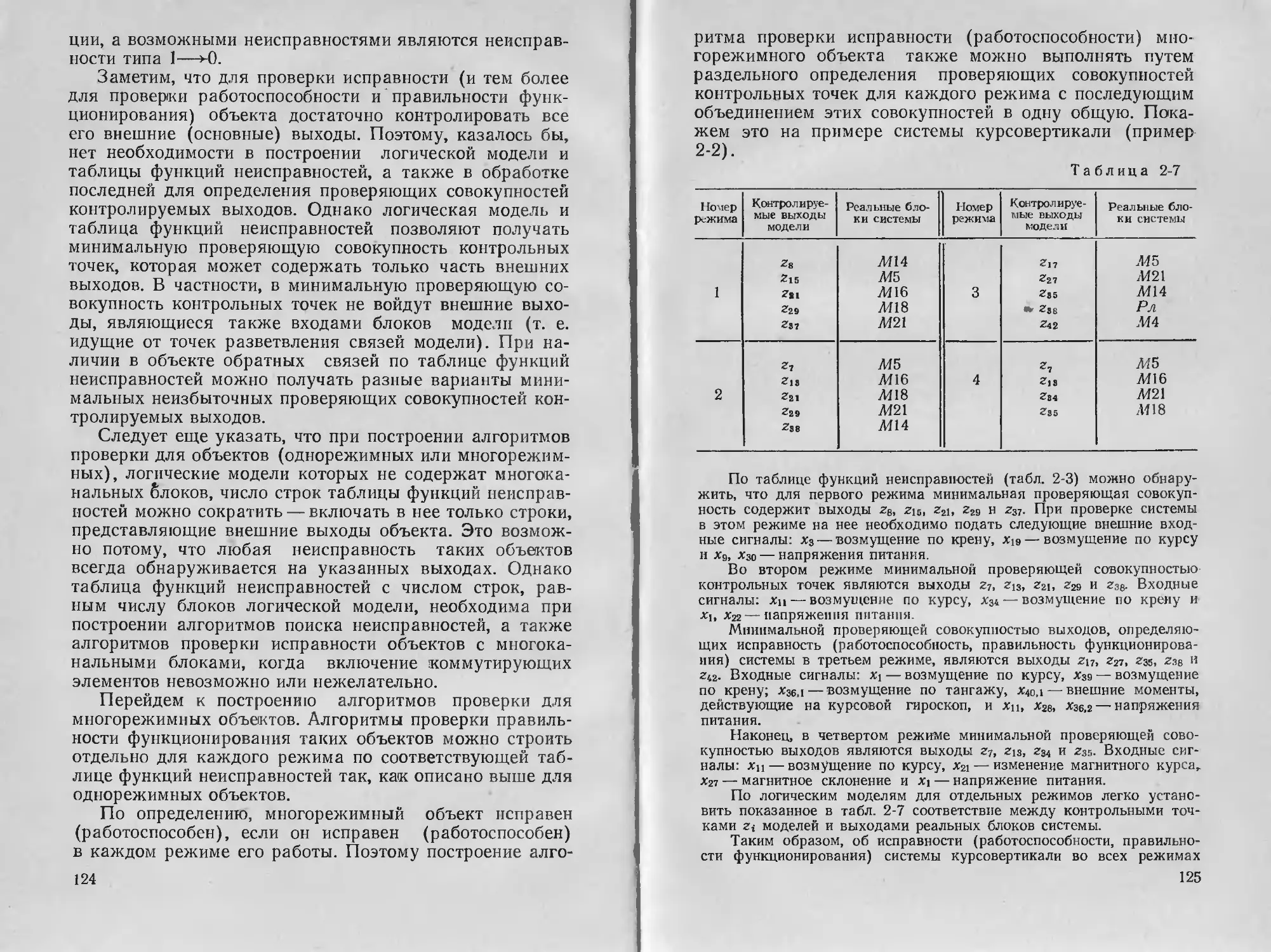
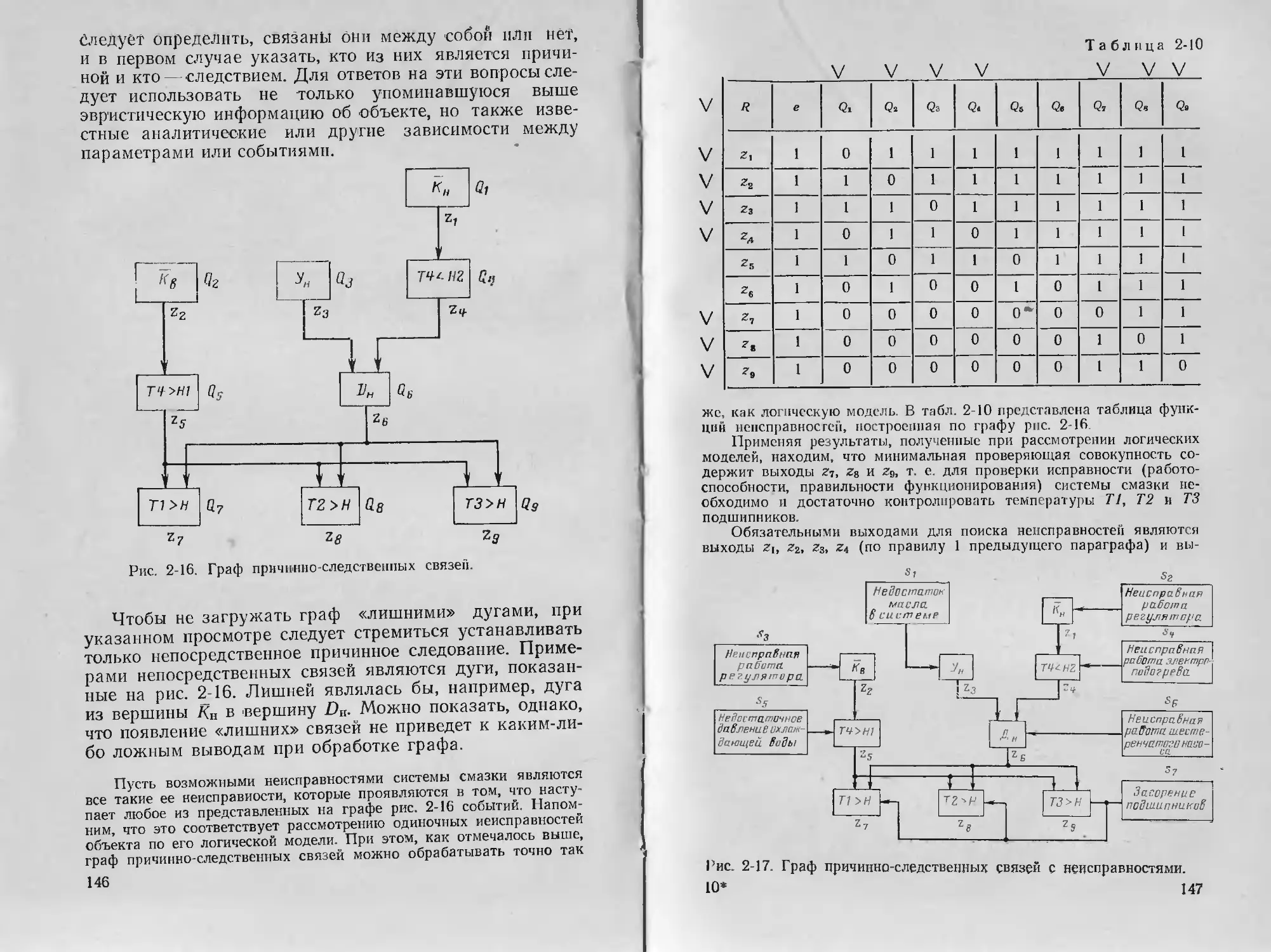
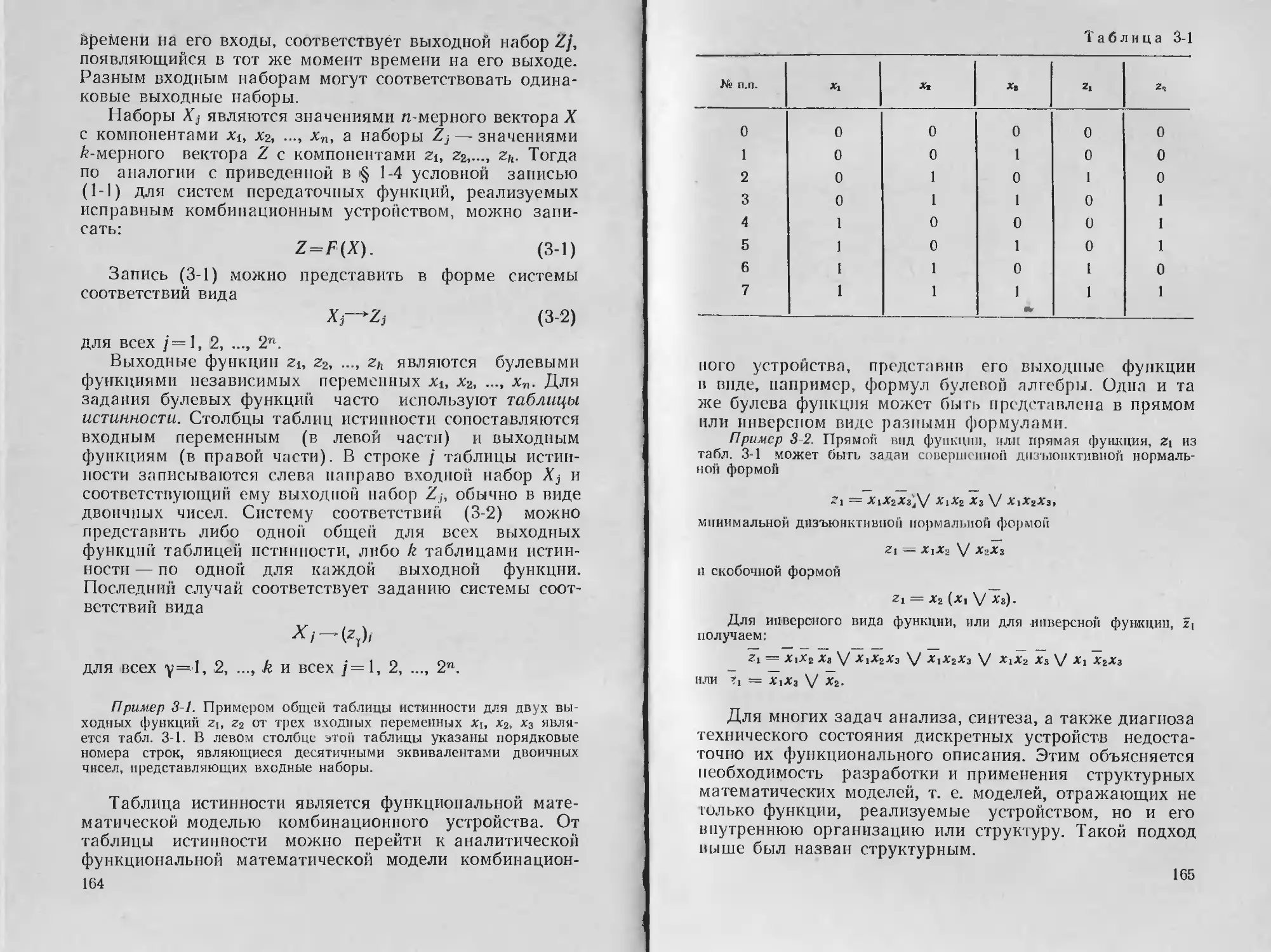
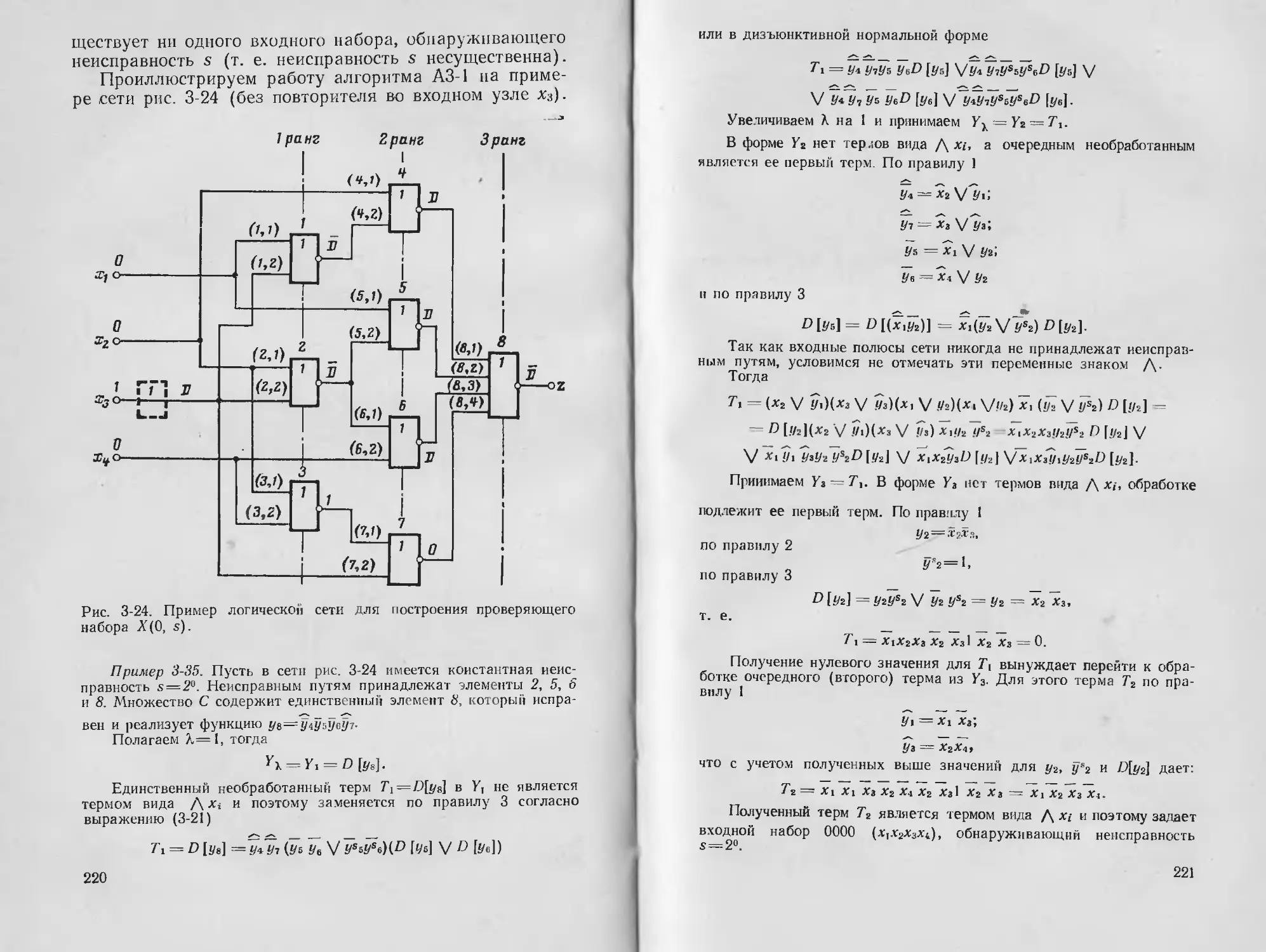
Text
основы
ТЕХНИЧЕСКОЙ
ДИАГНОСТИКИ
Применение
вычислительных
машин
в исследованиях
и управлении
производством
ИЗДАТЕЛЬСТВО
«Э Н Е Р Г И Я»
1976
Редакционная
коллегия:
академик В. А. Трапезников
академик А. А. Воронов
доктор техн, наук А. Г. Мамиконов
доктор техн, наук О. И. Авен
кандидат техн, наук Д. М. Беркович
основы
ТЕХНИЧЕСКОЙ
Под редакцией ДИАГНОСТИКИ
П. П. ПАРХОМЕНКО
В ДВУХ КНИГАХ
Книга первая
МОДЕЛИ ОБЪЕКТОВ,
МЕТОДЫ И АЛГОРИТМЫ
ДИАГНОЗА
6Ф7
0-75
УДК 658.5:681.3
Авторы: В. В. Карибский, П. П. Пархоменко, Е. С. Согомонян,
В. Ф. Халчев.
Основы технической диагностики. В 2-х книгах.
0-75 Кн. I. Модели объектов, методы и алгоритмы диаг-
ноза. Под ред. П. П. Пархоменко. М., «Энергия», 1976.
464 с. с ил. (Применение вычислительных машин в иссле-
дованиях и управлении производством).
На обороте тнт. л. авт. Кн. I: В. В. Карибский, П. П. Пар-
хоменко, Е. С. Согомонян, В. Ф. Халчев.
В книге дана классификация задач технической диагностики, рас-
смотрены принципы организации систем тестового и функционального
диагноза, изложены методы и процедуры построения алгоритмов
диагноза для проверки исправности, работоспособности и правильности
функционирования, а также для поиска неисправностей различных
объектов. Основное внимание уделено логическим аспектам техниче-
ской диагностики при детерминированных математических моделях
объектов диагноза.
Книга предназначена для научных работников и инженеров, заня-
тых проектированием, созданием и исследованием систем диагноза
технического состояния сложных объектов. Книга полезна также сту-
дентам и аспирантам ряда технических специальностей.
~ 30405-330
° 051(01)-76 220-75 6Ф7
© Издательство «Энергия», 1976 г.
ПРЕДИСЛОВИЕ
Проверка исправности, работоспособности, правиль-
ности функционирования, а также поиск неисправностей
сложных технических объектов необходимы при из-
готовлении, эксплуатации, ремонте ji хранении послед-
них. Эффективная организация процессов диагноза тех-
нического состояния объектов является основной целью
технической диагностики.
В книге излагаются основы теории технической диаг-
ностики, методы построения и анализа математических
моделей объектов диагноза, методы построения алгорит-
мов диагноза.
Объекты диагноза разделены на два класса: объек-
ты с непрерывно изменяющимися параметрами (для
краткости изложения будем их называть «непрерывные
объекты») и объекты с дискретно изменяющимися пара-
метрами (для краткости изложения будем их называть
«дискретные объекты»), «Гибридные объекты» (так
будем называть объекты, имеющие непрерывную и ди-
скретную части) не выделяются в специальный класс,
так как при их исследовании можно воспользоваться
рассмотрением моделей дискретных и непрерывных
объектов. Класс дискретных объектов разбит на два
подкласса: дискретные комбинационные объекты и
дискретные объекты с памятью. Такая классификация
позволяет выделить общие, существенные с точки зре-
ния задач технической диагностики свойства объектов
и в значительной степени абстрагироваться от специ-
фических свойств, определяемых, например, физиче-
скими или энергетическими характеристиками объектов,
их назначением, условиями применения и т. п. Специ-
фические свойства конкретных объектов учитываются
на этапах, предшествующих построению описывающих
эти объекты математических моделей, а также на за-
ключительном этапе разработки и физической реализа-
ции технических средств диагноза. Представленное
в книге общее рассмотрение не следует рассматривать
как отрицание целесообразности индивидуальных под-
ходов, продиктованных спецификой отдельных классов
объектов диагноза, в частности, таких, как универсаль-
ные вычислительные машины или сложные механиче-
ские системы типа двигателей внутреннего сгорания.
Преобладающее внимание в книге уделяется логи-
ческим аспектам технической диагностики. На выбор
такой направленности содержания книги повлияли сле-
дующие обстоятельства. Во-первых, большинство задач
построения алгоритмов диагноза, равно как и методов
их решения, носит комбинаторный (т. е. по существу
логический) характер. Во-вторых, допусковые (логиче-
ские) способы диагноза технического состояния непре-
рывных объектов благодаря присущей этим способам
простоте реализации получили самое широкое распро-
странение в практике. В-третьих, дискретные объекты
представляют большой класс устройств и систем, за-
служивающий самостоятельного рассмотрения, в осно-
ву которого, естественно, должен быть положен логиче-
ский подход. Наконец, следует указать, что большую
часть технических средств диагноза, особенно внешних,
представляют собой устройства дискретного действия.
Ряд вопросов, косвенно или даже прямо связанных
с технической диагностикой, не нашел отражения в кни-
ге. Это—вопросы оптимизации алгоритмов диагноза;
принципы построения встроенных и внешних средств
диагноза; вопросы построения сложных диагностических
систем управления, содержащих системы диагноза
в качестве составных частей; методы расчета и оценки
эффективности или достоверности систем диагноза;
вопросы применения недетерминированных математи-
ческих моделей объектов диагноза и методы их обработ-
ки, специальные физические методы диагноза техниче-
ского состояния объектов, например методы неразру-
шающего контроля; вопросы теории и практики
измерений различных физических величин; роль чело-
века-оператора в автоматизированных системах диаг-
ноза и т. п. Одна часть этих вопросов заслуживает
самостоятельного рассмотрения (над ними авторы про-
должают работать), другая часть освещена в соответ-
ствующей специальной научно-технической литературе.
6
В гл. 1 книги даны основные понятия и определения,
а также изложена обобщенная постановка задач техни-
ческой диагностики. В следующих трех главах рассмат-
риваются математические модели соответственно не-
прерывных, дискретных комбинационных и дискретных
с памятью объектов диагноза. Там же изложены мето-
цы анализа этих моделей, а также методы построения
алгоритмов диагноза технического состояния объектов
указанных классов.
Изложение материала сопровождается примерами.
В конце каждой главы дается краткая библиографи-
ческая справка по основным работам, относящимся
к тематике данной главы.
В. В. Карибским написана гл. 4, П. П. Пархоменко —
введение и гл. 1, Е. С. Согомоняном*— гл. 2, В. Ф. Хал-
чевым — гл. 3, за исключением § 3-7, который по прось-
бе авторов написан М. Ф. Караваем.
Авторы
ВВЕДЕНИЕ
Диагноз в переводе с греческого «диагнозис» озна-
чает распознавание, определение. В медицине, напри-
мер, это — определение состояния человека, а в техни-
ке— определение состояния объекта технической
природы. Объект, состояние которого определяется, бу-
дем называть объектом диагноза. Диагноз представ-
ляет собой процесс исследования объекта диагноза. За-
вершением этого исследования является получение ре-
зультата диагноза, т. е. заключения о состоянии объекта
диагноза. Характерными примерами результатов диаг-
ноза состояния технического объекта являются заклю-
чения вида: объект исправен, объект неисправен, в объ-
екте имеется такая-то неисправность.
Диагностика есть отрасль знаний, включающая в се-
бя теорию и методы организации процессов диагноза,
а также принципы построения средств диагноза. Когда
объектами диагноза являются объекты технической при-
роды, говорят о технической диагностике.
Чтобы более четко увидеть область, охватываемую
технической диагностикой, рассмотрим три типа задач
по определению состояния технических объектов.
К первому типу относятся задачи по определению со-
стояния, в котором находится объект в настоящий мо-
мент времени. Это — задачи диагноза. Задачами второ-
го типа являются задачи по предсказанию состояния,
в котором окажется объект в некоторый будущий
момент времени. Это — задачи прогноза (от греческого
«прогнозис» — предвидение, предсказание). Наконец,
к третьему типу относятся задачи определения состоя-
ния, в котором находился объект в некоторый момент
времени в прошлом. По аналогии можно говорить, что
это задачи генеза (от греческого «генезис» — происхож-
дение, возникновение, процесс образования).
8
Задачи первого типа формально следует отнести
к технической диагностике, а второго типа — к техниче-
ской прогностике (или, как чаще говорят, к техническо-
му прогнозированию). Тогда отрасль знания, которая
должна заниматься решением задач третьего типа, есте-
ственно назвать технической генетикой (по гречески
термин «генетикос» означает «относящийся к рождению,
происхождению»).
Задачи технической генетики возникают, например,
в связи с расследованием аварий и их причин, когда
настоящее состояние объекта отличается от состояния,
в котором он оказался в прошлом в результате появле-
ния первопричины, вызвавшей аварию. Решаются эти
задачи путем определения возможных или вероятных
предысторий, ведущих в настоящее "Состояние объекта.
К задачам технической прогностики относятся, напри-
мер, задачи, связанные с определением срока службы
объекта или с назначением периодичности его профи-
лактических проверок и ремонтов. Решаются эти задачи
путем определения возможных или вероятных эволюций
состояния объекта, начинающихся в настоящий момент
времени.
Таким образом, знание состояния в настоящий мо-
мент времени является обязательным как для генеза,
так и для прогноза. Поэтому техническая диагностика
представляет собой основу технической генетики и тех-
нической прогностики, и естественно, что последние раз-
виваются в тесной связи с первой.
Усиление интереса к технической диагностике в по-
следние годы объясняется созданием и применением
в народном хозяйстве все более сложных изделий,
устройств и систем (объектов) при непрерывном увели-
чении темпов их производства, росте интенсивности их
использования и повышении требований к их надежно-
сти. В этих условиях интуитивные методы и ручные
способы определения состояния сложных объектов ока-
зываются малоэффективными или даже непригодными.
В «жизни» любого объекта всегда можно выделить
два этапа: этап производства, когда объект создается,
и этап эксплуатации, когда объект применяется по на-
значению (выполняет предписанный ему рабочий алго-
ритм функционирования), подвергается профилактиче-
ским проверкам, проверкам перед применением или по-
сле применения, ремонту и т. п. Иногда целесообразно
9
выделять в качестве самостоятельного также этап хра-
нения объекта или пребывания его в резерве.
Для любого объекта на каждом этапе его жизни за-
даются определенные технические требования. Жела-
тельно, чтобы объект всегда соответствовал этим требо-
ваниям. Однако в объекте могут возникать неисправно-
сти, нарушающие указанное соответствие. Тогда задача
состоит в том, чтобы создать первоначально (на этапе
производства) или восстановить нарушенное неисправ-
ностью (на этапах эксплуатации или хранения) соответ-
ствие объекта техническим требованиям. Решение этой
задачи невозможно без эпизодического или непрерыв-
ного диагноза состояния объекта.
Во многих случаях необходимо убеждаться в том,
что объект исправен, т. е. в нем нет ни одной неисправ-
ности. Это — проверка исправности объекта. На этапе
производства, например, проверка исправности позволя-
ет узнать, содержит ли созданный объект дефектные
компоненты (детали, элементы, блоки, узлы и т. п.),
а их монтаж — ошибки. Заметим, что проверка исправ-
ности лежит в основе деятельности производственных
отделов технического контроля. В условиях ремонта про-
верка исправности позволяет убедиться, действительно
ли устранены при ремонте все имевшиеся в объекте
неисправности, а в условиях хранения — не возникли ли
какие-либо неисправности за время хранения объекта.
На этапе эксплуатации при профилактике объекта,
перед применением его по назначению или после такого
применения в ряде случаев необходимо убеждаться
в том, что объект в состоянии выполнять все функции,
предусмотренные его рабочим алгоритмом функциони-
рования. Это — проверка работоспособности объекта.
Проверка работоспособности может быть менее полной,
чем проверка исправности, т. е. может оставлять необ-
наруженными неисправности, не препятствующие при-
менению объекта по назначению. Например, резервиро-
ванный объект может быть работоспособным несмотря
на наличие неисправностей в резервных компонентах или
связях.
На этапе эксплуатации в процессе выполнения объ-
ектом его рабочего алгоритма функционирования часто
необходимо осуществлять проверку правильности функ-
ционирования объекта, т. е. следить за тем, не появи-
лись ли в объекте неисправности, нарушающие его нор-
10
мальную работу в настоящий момент времени. Провер-
ка правильности функционирования дает возможность
исключить недопустимое для нормальной работы объек-
та влияние неисправностей, возникающих в процессе
применения объекта по назначению. Проверка правиль-
ности функционирования, вообще говоря, менее полна,
чем проверка работоспособности, так как позволяет
убеждаться только в том, что объект правильно функ-
ционирует в данном режиме работы в данный момент
времени. Иными словами, в правильно функционирую-
щем объекте могут быть неисправности, которые не по-
зволят ему правильно работать в других режимах. Ра-
ботоспособный объект будет правильно функциониро-
вать во всех режимах и в течение всего времени его
работы. Таким образом, исправный объект всегда рабо-
тоспособен и функционирует правильно, а неправильно
функционирующий объект всегда неработоспособен и
неисправен. Правильно функционирующий объект может
быть неработоспособным, и значит, неисправным. Рабо-
тоспособный объект также может быть неисправным.
Одной из важнейших задач диагноза состояния объ-
екта является поиск неисправностей, т. е. указание мест
и, возможно, причин возникновения имеющихся в объ-
екте неисправностей. Поиск неисправностей необходим
для выявления и замены дефектных компонент или свя-
зей объекта, для устранения ошибок монтажа и т. п.
После устранения неисправности объект становится
исправным, работоспособным или правильно функцио-
нирующим. Поиск неисправностей является существен-
ной составляющей деятельности служб наладки на этапе
производства и ремонтных служб на этапах эксплуата-
ции или хранения объектов.
Исправное и все неисправные состояния объекта об-
разуют множество Е его технических состояний. Задачи
проверки исправности, проверки работоспособности, про-
верки правильности функционирования и поиска не-
исправностей представляют собой частные случаи об-
щей задачи диагноза технического состояния объекта.
На рис. В-1 множество технических состояний объ-
екта диагноза условно ограничено замкнутой кривой,
причем исправное состояние обозначено малым круж-
ком, а неисправные состояния — крестиками. Результа-
тами проверки исправности (рис. В-1,а), проверки рабо-
тоспособности (рис. В-1,б) и проверки правильности
11
функционирования (рис. В-1,в) является получение двух
подмножеств технических состояний. Одно из них (ле-
вое на рис. В-1) содержит либо только исправное со-
стояние (при проверке исправности), либо кроме
исправного состояния также те неисправные состояния,
находясь в которых объект остается работоспособным
или правильно функционирующим. Второе подмножест-
Рис. В-1. Представление задач диагноза через разбиения множества
технических состояний объекта.
во содержит либо все неисправные состояния (при про-
верке исправности), либо такие, пребывание в которых
делает объект неработоспособным или неправильно
функционирующим. Результатами поиска неисправно-
стей (рис. В-1,г, д, е) являются разбиения на классы
не различаемых между собой неисправных состояний
вторых подмножеств. Число классов и, следовательно,
числа входящих в них неисправных состояний (мощно-
сти классов) определяют достигаемую при поиске сте-
пень детализации мест и состава имеющихся (или по-
дозреваемых на наличие) в объекте неисправностей. Эту
степень детализации принято называть глубиной поиска
или глубиной диагноза.
Заметим, что при проверке правильности функцио-
нирования и при поиске неисправностей, нарушающих
правильное функционирование объекта, разбиения от-
носятся к определенному (настоящему) моменту време-
12
ни и поэтому могут быть разными для разных моментов
времени и разных режимов работы объекта.
Диагноз технического состояния объекта осуществ-
ляется при помощи тех или иных средств диагноза. Вза-
имодействующие между собой объект и средства диаг-
ноза образуют систему диагноза. Протекающий в систе-
ме диагноза процесс в общем случае представляет собой
многократную подачу на объект определенных воздей-
ствий (входных сигналов) и многократное измерение и
анализ ответов (выходных сигналов) объекта на эти
воздействия. Воздействия на объект либо поступают от
средств диагноза, либо являются внешними (по отно-
шению к системе диагноза) сигналами, определяемыми
рабочим алгоритмом функционирования объекта. Изме-
рение и анализ ответов объекта всеща осуществляются
средствами диагноза.
Будем различать системы тестового диагноза, отли-
чительная особенность которых состоит в возможности
подачи на объект диагноза специально организуемых
(тестовых) воздействий от средств диагноза, и системы
функционального диагноза, в которых подача воздейст-
вий на объект от средств диагноза не производится (по-
ступают только рабочие воздействия, предусмотренные
рабочим алгоритмом функционирования объекта). Си-
стемы тестового диагноза обычно решают задачи про-
верки исправности, проверки работоспособности и по-
иска неисправностей (всех или только нарушающих
работоспособность) и работают тогда, когда объект не
применяется по прямому назначению. Использование
систем тестового диагноза при работающем объекте
также возможно, но при этом тестовые воздействия мо-
гут быть только такими, которые не мешают нормаль-
ному функционированию объекта. Системы функцио-
нального диагноза используются, как правило, для
решения задач проверки правильности функционирова-
ния и поиска неисправностей, нарушающих нормальное
функционирование. Эти системы работают обычно тог-
да, когда объект применяется по назначению. В про-
тивном случае требуется имитация условий функциони-
рования объекта (в частности, имитация рабочих воз-
действий).
Процесс диагноза может состоять из отдельных ча-
стей, каждая из которых характеризуется подаваемым
па объект тестовым или рабочим воздействием и сни-
13
маемым с объекта ответом. Будем называть такие части
элементарными проверками объекта. Результатом эле-
ментарной проверки является полученное при ее реали-
зации значение ответа объекта. Тогда формальное опи-
сание процесса диагноза, т. е. алгоритм диагноза тех-
нического состояния объекта, представляет собой
безусловную или условную последовательность элемен-
тарных проверок и правил анализа результатов по-
следних.
Процесс диагноза можно рассматривать как специ-
фический процесс управления, целью которого является
определение технического состояния объекта. Это хо-
рошо согласуется с современным пониманием управле-
ния как процесса осуществления целенаправленных
управляющих воздействий на управляемый объект,
а кроме того, четко определяет предмет исследований и
задачи технической диагностики с позиций общей тео-
рии управления и контроля.
Основная цель технической диагностики состоит
в организации эффективных процессов диагноза техни-
ческого состояния сложных объектов.
Одним из факторов, существенно влияющих на эф-
фективность процесса диагноза, является качество алго-
ритмов диагноза.
Возможность оптимизации алгоритмов диагноза
определяется следующими обстоятельствами. Число
элементарных проверок, Достаточных для решения кон-
кретной задачи диагноза, как правило, меньше числа
всех допустимых (т. е. физически возможных и реали-
зуемых) элементарных проверок данного объекта. Раз-
ные элементарные проверки могут требовать разных
затрат на их реализацию и давать разную информацию
о техническом состоянии объекта. Кроме того, одни и
те же элементарные проверки могут быть реализованы
в различных последовательностях.
Поэтому для решения одной и той же задачи диагно-
за (например, для проверки исправности) можно по-
строить несколько алгоритмов диагноза, различающихся
между собой либо составом элементарных проверок,
либо последовательностью их реализации, либо, нако-
нец, тем и другим вместе, и поэтому, возможно, требую-
щих разных затрат на их реализацию.
Необходимость увеличения производительности тру-
да на операциях диагноза, сокращения времени обна-*
14
ружения, поиска и устранения неисправностей, умень-
шения объемов и сложности средств диагноза вызывает
интерес к разработке методов построения опти-
мальных алгоритмов диагноза, требующих минималь-
ных затрат на их реализацию. Построение оптимальных
алгоритмов во многих случаях сопряжено с большими
вычислительными трудностями, и поэтому зачастую
удовлетворяются оптимизированными алгоритмами ди-
агноза, затраты на реализацию которых как-то умень-
шены, но не обязательно минимальны.
Интуитивные методы построения алгоритмов диагно-
за не могут гарантировать получения объективного за-
ключения о действительном техническом состоянии
объекта. Кроме того, при интуитивном подходе алгорит-
мы диагноза могут содержать избыточные элементар-
ные проверки, последовательность реализации которых
может быть далекой от оптимальной, что в конечном
итоге приводит к непроизводительным затратам на реа-
лизацию алгоритмов в целом.
Отсюда следует необходимость разработки формаль-
ных методов построения алгоритмов диагноза техниче-
ского состояния объектов. Это особенно важно для
сложных объектов, насчитывающих десятки, сотни и
тысячи функционально и конструктивно взаимосвязан-
ных компонент и зачастую требующих многих часов
для обнаружения и поиска неисправностей интуитивны-
ми способами. Применение формальных методов, кроме
того, позволяет автоматизировать процессы построения
алгоритмов диагноза при помощи вычислительных
средств.
Эффективность процессов диагноза определяется не
только качеством алгоритмов диагноза, но и в не мень-
шей степени качеством средств диагноза. Последние
могут быть аппаратурными или программными, внеш-
ними или встроенными, ручными, автоматизированными
или автоматическими, специализированными или уни-
версальными.
Наличие объективных статистических данных о ве-
роятностях возникновения неисправностей, а также
о средних затратах на обнаружение, поиск и устранение
неисправностей, расширяет возможности эффективной
организации процессов диагноза. Сбор таких данных
требует применения надежно работающих внешних и
встроенных аппаратурных средств диагноза, обеспечи-
15
вающих высокую точность измерений и автоматическое
документирование данных. При этом будет гарантиро-
вана достоверность результатов диагноза, сведено
к минимуму влияние субъективных факторов и упроще-
на статистическая обработка результатов.
Эффективная организация процессов диагноза техни-
ческого состояния сложных объектов на всех этапах их
жизни требует совместного применения систем функ-
ционального и тестового диагноза.
Без систем тестового диагноза невозможно обойтись
на этапе изготовления и при ремонте объектов диагно-
за. На этапе эксплуатации положительный результат
тестовой проверки исправности или работоспособности
объекта, полученный непосредственно перед примене-
нием объекта по назначению, повышает вероятность
успешного выполнения объектом возложенных на него
функций. Во всяком случае, в указанных условиях эта
вероятность выше, чем тогда, когда тестовая проверка
исправности или работоспособности объекта не прово-
дится.
Системы функционального диагноза дают возмож-
ность немедленно реагировать на нарушение правильно-
сти функционирования объекта и тем самым путем за-
мены отказавших узлов, включения резерва, повторного
выполнения операций, перехода на другой режим функ-
ционирования и т. п. во многих случаях позволяют обес-
печить нормальное или хотя бы частичное (т. е. с по-
терей качества) выполнение объектом возложенных
на него функций даже при наличии неисправностей
в нем.
В настоящее время в большинстве случаев проекти-
рование сложных объектов ведется без должного учета
того, как они будут проверяться и налаживаться в усло-
виях производства или ремонта, как будут организова-
ны проверка работоспособности, правильности функцио-
нирования и поиск неисправностей в условиях их
эксплуатации или хранения. Недооценка важности свое-
временной (на этапе проектирования объектов) и глу-
бокой проработки вопросов организации эффективных
процедур диагноза, в том числе автоматизации поиска
неисправностей сложных объектов, ведет к непроизводи-
тельным материальным затратам, затратам времени и
квалифицированной рабочей силы при наладке, профи-
лактике и ремонте.
16
Среди объективных причин такого положения следу-
ет назвать недостаточное развитие теории и методов-
технической диагностики, слабую проработку принципов
построения технических средств диагноза, а также от-
сутствие налаженного производства таких средств. Су-
щественным является также психологический фактор,
состоящий в том, что почти все разработчики считают
творческим, созидательным делом непосредственно раз-
работку объектов (изделий, устройств, агрегатов, си-
стем), выполняющих заданные им функции, и не при-
дают должного значения вопросам организации налад-
ки, профилактики и ремонта проектируемых объектов.
Усугубляется это обстоятельство тем, что обязательная
проработка этих вопросов пока не всегда регламенти-
руется официальными требованиям# к проектам новых
объектов. Все это приводит к тому, что часто сложные
объекты оказываются без хорошо организованных си-
стем проверки правильности их функционирования, не
говоря уже о системах поиска неисправностей в усло-
виях применения по назначению. Задачи проверки
исправности, проверки работоспособности и поиска не-
исправностей в условиях изготовления, профилактики,
ремонта и хранения во многих случаях вынужденно
решаются после того, как объект уже спроектирован или
даже выполнен «в металле». Такой подход не позволяет
своевременно учесть те изменения и дополнения, кото-
рые целесообразно внести в объект для того, чтобы
обеспечить простоту и удобство диагноза его техниче-
ского состояния на всех этапах жизни. При существую-
щем положении заботы по созданию средств диагноза
в значительной степени ложатся на изготовителей, экс-
плуатационников и ремонтников. Создаваемые ими
средства, как правило, являются специализированными
со всеми присущими «приставной автоматике» не-
достатками. Затраты на разработку и создание та-
ких средств велики, а эффективность применения
низкая.
Многие из указанных недостатков будут исключе-
ны, если задачи диагноза решать на этапе проектиро-
вания объектов. Иначе говоря, разработку систем и
средств диагноза следует считать такой же обязатель-
ной и важной частью проекта нового объекта, как и
разработку самого объекта или других его систем и
средств управления.
2—358
17
Глава первая
ОСНОВНЫЕ ЗАДАЧИ ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ
Как отмечалось во введении, основная цель техниче-
ской диагностики состоит в организации эффективных
процессов определения технического состояния различ-
ных, особенно сложных, многокомпонентных объектов.
Диагноз осуществляется аппаратурными или программ-
ными, встроенными или внешними техническими сред-
ствами, реализующими тот или иной алгоритм диаг-
ноза.
При исследовании, разработке и реализации процес-
сов диагноза технического состояния объектов необхо-
димо решать те же задачи, которые возникают при ис-
следовании, разработке и реализации процессов управ-
ления вообще. Это, в первую очередь, задачи изучения
Рис. 1-1. Дерево классификации основных задач технической диагно-
стики.
18
физических свойств объектов и неисправностей послед-
них, задачи построения математических моделей объек-
тов и моделей неисправностей. Затем следуют задачи
анализа моделей объектов с целью получения данных,
необходимых для построения алгоритмов диагноза. Сле-
дующую группу образуют задачи, связанные с разра-
боткой принципов построения, экспериментальным
опробованием и промышленным внедрением технических
средств диагноза. Наконец, следует указать на задачи
проектирования систем диагноза в целом и исследова-
ния их характеристик и свойств.
Дерево классификации основных предметов исследо-
ваний технической диагностики представлено на рис. 1-1.
В этой главе дается общая характеристика перечис-
ленных задач. По ходу изложение материала главы
вводятся понятия и определения, необходимые для опи-
сания методов решения указанных задач.
1-1. СИСТЕМЫ ДИАГНОЗА ТЕХНИЧЕСКОГО СОСТОЯНИЯ
Па рис. 1-2 представлены обобщенные функциональ-
ные схемы системы тестового диагноза и системы функ-
ционального диагноза технического состояния. Системы
содержат объект диагноза ОД и средства диагноза СД.
Схемы даны в «однолинейном» изображении. Физически
Рабочие
Рис. 1-2. Обобщенные функциональные схемы систем диагноза техни-
ческого состояния.
а — система тестового диагноза; б — система функционального диагноза.
каждая линия схемы, снабженная стрелкой на конце,
может представлять несколько каналов передачи ин-
формации. Условимся, что при рассмотрении задач про-
верки исправности, проверки работоспособности или
проверки правильности функционирования объекта
можно говорить не о системе, объекте и средствах диаг-
2* 1&
ноза, а о системе, объекте и средствах проверки, и при
рассмотрении задач поиска неисправностей-—о системе,
объекте и средствах поиска.
Как видно из рис. 1-2,а, в системах тестового диаг-
ноза воздействия на объект поступают от средств диаг-
ноза. Поэтому как состав, так и последовательности
подачи этих воздействий можно выбирать исходя из
условий эффективной организации процесса диагноза.
Более того, каждое очередное воздействие в процессе
диагноза может назначаться в зависимости от ответов
объекта на предыдущие воздействия. Воздействия в си-
стемах тестового диагноза будем называть тестовыми.
Тестовые воздействия могут подаваться как в перио-
ды времени, когда объект не используется по прямому
назначению, так и в процессе выполнения им его рабо-
чего алгоритма функционирования. Во втором случае,
однако, тестовыми воздействиями могут быть только
такие сигналы, которые не мешают нормальной работе
объекта. Например, при инерционных исполнительных
механизмах некоторого функционирующего объекта
возможна подача кратковременных импульсных тесто-
вых воздействий на схемы управления этими механиз-
мами.
Тестовые воздействия могут подаваться как па основ-
ные входы объекта, т. е. на его входы, необходимые для
применения объекта по назначению, так и на дополни-
тельные входы, организованные специально для целей
диагноза.
В системах функционального диагноза (рис. 1-2,6)
воздействия, поступающие на основные входы объекта,
заданы его рабочим алгоритмом функционирования и
поэтому, как правило, не могут выбираться исходя из
условий эффективной организации процесса диагноза.
Эти воздействия будем называть рабочими.
Указанная на рис. 1-2,6 подача рабочих воздействий
и на средства диагноза часто имеет место в системах
функционального диагноза, хотя и не является обяза-
тельной.
Отметим, что системы функционального диагноза
могут использоваться также в режимах имитации функ-
ционирования объекта. При этом, естественно, должна
быть обеспечена имитация рабочих воздействий. Такое
использование систем функционального диагноза целе-
сообразно при наладке или ремонте объекта.
20
Ответы объекта (на тестовые или на рабочие воз-
действия) в обоих видах систем диагноза поступают
(рис. 1-2) на средства диагноза. Ответы могут снимать-
ся как с основных выходов объекта, т. е. с выходов, не-
обходимых для применения объекта по назначению,
так и с дополнительных выходов, организованных спе-
циально для целей диагноза. Эти основные и допол-
нительные выходы часто называют контрольными точ-
ками.
Как отмечалось, элементарные проверки объекта ха-
рактеризуются воздействиями, подаваемыми или посту-
пающими на объект, и его ответами на соответствую-
щие воздействия; результатами элементарных проверок
являются значения ответов.
Обратимся теперь к средствам диагноза систем, при-
веденных на рис. 1-2. Средства диагноза реализуют
некоторый алгоритм диагноза, задающий состав и оче-
редность реализации, а также способ анализа резуль-
татов элементарных проверок объекта.
Реализация элементарных проверок заключается
в выработке и подаче па обьект входных сигналов (воз-
действий) и в приеме и измерении соответствующих
выходных сигналов (ответов). Указанные операции об-
щеприняты и не нуждаются в каких-либо специальных
пояснениях. Естественно, что для реализации этих опе-
раций средства диагноза должны содержать, вообще
говоря, источники воздействий (в системах тестового
диагноза), измерительные устройства и устройства свя-
зи источников воздействий и измерительных устройств
с объектом.
Целью анализа результатов элементарных проверок
является получение результатов диагноза, т. е. опреде-
ление технических состояний, в одном из которых фа-
ктически находится объект.
Как было сказано выше, результаты элементарных
проверок представлены в виде значений сигналов в кон-
трольных точках. Результаты же диагноза должны быть
представлены в иной форме, более удобной для практи-
ческого их использования. Например, при проверке
исправности результатом диагноза должен быть один
из ответов: «обьект исправен» или «объект неисправен»,
а при поиске неисправностей — «в объекте неисправна
такая-то конкретная компонента (узел, блок, деталь)».
Другими словами, требуется расшифровка (анализ, пре-
21
образование) результатов элементарных проверок, полу-
ченных в процессе реализации алгоритма диагноза.
В простейшем случае такая расшифровка может
представлять собой обычное сравнение физических зна-
чений сигналов в контрольных точках с заданными эта-
лонными значениями этих сигналов. В других случаях
операции расшифровки являются более сложными. За-
метим, что при недостаточном уровне автоматизации
процесса диагноза, в частности при использовании руч-
ных средств диагноза, функции расшифровки результатов
элементарных проверок возлагаются на человека.
Так или иначе, для выполнения операций анализа
результатов элементарных проверок средства диагноза
должны располагать определенной информацией о по-
ведении исправного (работоспособного, правильно
функционирующего) объекта, а также, возможно, о его
поведении в неисправных состояниях. Аппаратуру
средств диагноза, хранящую информацию о поведении
объекта, или другой носитель этой информации будем
называть физической моделью объекта. Наглядным при-
мером физической модели объекта является эталонный,,
заведомо исправный его экземпляр. Однако во многих
случаях такая физическая модель информационно из-
быточна и зачастую трудно реализуема. В широко рас-
пространенных системах централизованного контроля,
являющихся системами проверки правильности функ-
ционирования, физическая модель объекта представляет
собой аппаратуру для задания допустимых значений
(уставок) контролируемых параметров, а также сред-
ства коммутации и подключения этой аппаратуры
к устройствам сравнения допустимых значений парамет-
ров с фактическими.
Средства, осуществляющие сопоставление информа-
ции об объекте, хранящейся в физической модели по-
следнего, с фактическими результатами элементарных
проверок и вырабатывающие сигнал «результаты диаг-
ноза», назовем блоком расшифровки результатов. Как
и физическая модель объекта, блок расшифровки ре-
зультатов может быть реализован различными спосо-
бами и средствами в зависимости от задач и характе-
ристик конкретных систем диагноза.
Наконец, средства диагноза должны иметь тот или
иной носитель алгоритма диагноза. Носителем жестких
или редко изменяемых алгоритмов диагноза обычно
22
является аппаратура, конструктивно объединенная
с остальной аппаратурой средств диагноза. Для задания
сменных алгоритмов диагноза часто применяются стан-
дартные программоносители — перфоленты, перфокарты,
магнитные барабаны, магнитные ленты и т. п. В послед-
нем случае, естественно, средства диагноза должны
содержать соответствующие устройства считывания ин-
формации с программоносителей.
Итак, по завершении процесса определения техниче-
ского состояния объекта средства диагноза вырабаты-
вают сигнал «результаты диагноза». Знание техническо-
го состояния объекта может быть использовано для раз-
личных целей, в том числе, например, для выбора и
применения другого алгоритма диагноза, позволяющего
более точно определить техническое состояние объекта,
или же для организации других специальных воздейст-
вий на объект. Вопросы целенаправленного использова-
ния результатов диагноза сложных объектов относятся
к области организации так называемых диагностических
систем управления, о которых кратко будет сказано в
следующем параграфе.
В качестве иллюстрации системы тестового диагноза рассмотрим
следующий пример.
Пример 1-1. Объектом диагноза является электрический кабель-
ный жгут, определение технического состояния которого осуществ-
ляется в условиях производства при помощи внешних аппаратурных
средств диагноза. Точками подключения жгута к средствам диагно-
за являются все контакты его штекерных разъемов, а также корпуса
последних. Известна схема правильной распайки проводов жгута.
Электрические соединения групп контактов между собой в соответ-
ствии со схемой назовем цепями.
Основными операциями проверки исправности жгута в условиях
производства являются: проверка правильности распайки (монтажа)
проводов, проверка сопротивления изоляции между разными цепями
(включая корпуса штекерных разъемов) и, наконец, высоковольтные
испытания изоляции. Проверка правильности монтажа состоит в про-
верке наличия всех необходимых электрических соединений (в про-
верке целости цепей) и в проверке отсутствия любых ложных соеди-
нений, т. е. коротких замыканий между разными цепями или пере-
путываний проводов. Указанным операциям соответствуют элемен-
тарные проверки, совокупность и последовательность реализации
которых образуют алгоритм проверки исправности жгута.
При проверке целости цепей элементарная проверка состоит
в подаче напряжения на один из контактов той или иной цепи (воз-
действие) и в проверке наличия этого напряжения иа некотором дру-
гом контакте этой цепи (ответ). Наличие напряжения (положитель-
ный результат элементарной проверки) говорит о том, что два вы-
бранных контакта цепи соединены между собой, а отсутствие
{отрицательный результат элементарной проверки) — о том, что тре-
23
буемого соединения нет. Если цепь содержит I контактов, то для
проверки ее целости необходимо реализовать I—1 таких элементар-
ных проверок.
Наличие ложных соединений дайной цепи с другими (в том чис-
ле с корпусами штекерных разъемов) можно обнаружить при помо-
щи элементарной проверки, состоящей в подаче потенциала па любой
контакт данной цепи и в контроле отсутствия этого потенциала на
всех других цепях. Эти другие цепи могут быть предварительно
электрически соединены между собой через общую шину. Наличию
короткого замыкания между проверяемой цепью и остальными соот-
ветствует наличие напряжения на общей шине. Если короткого за-
мыкания нет, то можно выполнять проверку сопротивления изоляции
между проверяемой цепью и остальными цепями.
Заметим, что при использовании в средствах диагноза общей
шины проверка целости цепей требует предварительного (до прове-
дения соответствующих элементарных проверок) отключения всех
контактов проверяемой цепи от общей шины. В противном случае
возможно получение ложных положительных результатов элементар-
ных проверок целости цепи при наличии перепутываний проводов.
Контроль сопротивления изоляции между некоторой цепью и
остальными цепями можно проводить при помощи элементарной
проверки, воздействием которой является создание разности потен-
циалов между любым контактом проверяемой цепи и общей шиной,
объединяющей остальные цепи, а ответом — ток утечки. Ток утечки
является результатом элементарной проверки и определяет сопро-
тивление изоляции.
Если сопротивление изоляции находится в норме, то можно пе-
реходить к высоковольтным испытаниям изоляции. Элементарная
проверка при этом состоит в приложении высокого напряжения меж-
ду проверяемой цепью и общей шиной в течение определенного про-
межутка времени и в контроле тока утечки.
Рассмотрим теперь процесс поиска неисправностей жгута. Нали-
чие обрыва в проверяемой цепи определяется с точностью до номе-
ров контактов штекерных разъемов уже при проверке исправности,
поэтому дополнительных операций по поиску мест обрыва цепей не
требуется. Однако обрыв цепи может быть вызван перепутыванием
проводов и целесообразно до устранения обрыва выяснить, не зако-
рочен ли соответствующий («оборванный») контакт проверяемой
цепи с другими цепями, — если это так, то определить, с какой
цепью или с каким контактом он закорочен.
Места коротких замыканий при проверке исправности указы-
ваются довольно грубо. Для более точного поиска места короткого
замыкания можно приложить напряжение между проверяемой цепью-
и изолированной от жгута общей шиной, а затем поочередно по
одной подключать к последней другие электрические цепи, контро-
лируя моменты появления тока короткого замыкания. Цепи, при
подключении которых появляется ток, закорочены с проверяемой
цепью. Аналогично можно выявить места пониженного сопротивле-
ния изоляции. Заметим, что в ряде случаев для нахождения дефек-
тов изоляции могут понадобиться более радикальные элементарные
проверки, например выжигание слабого места высоким напряжением
(воздействие) и визуальное наблюдение свечения и дыма (ответ).
Из приведенного описания следует, что средства диагноза тех-
нического состояния жгута должны содержать несколько источников
напряжений, устройства для измерения напряжений (потенциалов}
24
и токов, а также устройство коммутации. Физической моделью
жгута является аппаратура для задания правильных (допустимых)
значений ответов элементарных проверок, а также цепи и средства
переключения этой аппаратуры в зависимости от вида реализуемых
элементарных проверок. Блок расшифровки результатов представляет
собой устройство сравнения фактических значений ответов с пра-
вильными (допустимыми).
Процесс проверки исправности и поиска неисправностей кабель-
ного жгута можно организовать двумя способами. Например, можно
после каждого обнаружения места неисправности прекращать про-
цесс диагноза, производить ремонт жгута и затем повторять описан-
ный процесс. При другом варианте организации процесса диагноза
поступают иначе: процесс проводят до конца, фиксируя всю инфор-
мацию о местах и характере неисправностей, затем производят ре-
монт жгута, после чего повторяют процесс. Последний вариант по
затрата?.! времени на диагноз и ремонт более экономичен, чем пер-
вый, однако для сложных жгутов при это.м могут потребоваться
значительные усилия на дополнительную обработку полученной
информации с целью определения конкретных мест обрывов, корот-
ких замыканий и перепутываний.
1-2. ДИАГНОСТИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
Результаты диагноза технического состояния необ-
ходимы для активных воздействий на объекты диагно-
за и на условия их производства, эксплуатации или хра-
нения. Это могут быть такие «простые» воздействия, как
ручное или автоматическое отключение, замена или ре-
монт неисправной компоненты объекта или объекта
в целом, ввод резерва, перестройка структуры объекта
и т. п. Примерами более сложных воздействий для опре-
деленного класса объектов могут служить меры по изме-
нению технологии монтажа или качества комплектую-
щих изделий в условиях производства, влияния внеш-
ней среды или периодичности профилактических работ
в условиях эксплуатации или хранения и т. п. Так или
иначе, во всех случаях по результатам диагноза прини-
маются и осуществляются определенные решения по
дальнейшему использованию объектов. Это соответст-
вует организации процесса управления, содержащего
в себе процесс диагноза технического состояния как со-
ставную часть. Системы, в которых реализуется такой
процесс управления и которые имеют в своей основе
систему диагноза технического состояния, можно назы-
вать диагностическими системами управления. Вопросы
исследования таких систем представляют самостоятель-
ный интерес, выходящий за рамки настоящей книги,
поэтому ограничимся тем, что приведем функциональ-
25
ную схему диагностической системы управления и опи-
шем один пример.
Функциональную схему диагностической системы
управления применительно к рассматриваемому ниже
примеру можно представить так, как показано на
Рис. 1-3. Функциональная схе-
ма диагностической системы
управления.
Термины «внешняя среда»
рис. 1-3. На этом рисунке
приняты следующие обозна-
чения: ОД — объект диагно-
за, СД — средства диагноза,
ТС — технические службы,
ОУ—-объект управления,
У У — управляющее устрой-
ство, ВС — внешняя среда.
Сигналами, учитываемыми
при выработке управляюще-
го воздействия е=ф(хо, х,
yi, У2), являются: Хо-—за-
данная цель управления,
х—результат диагноза тех-
нического состояния объек-
та диагноза, у\ —состояние
технических служб и у%—
состояние внешней среды,
и «состояние внешней сре-
ды» здесь совершенно условны и означают только то,
что в процессе работы системы учитывается определен-
ная информация, поступающая на систему извне.
Пример 1-2. Рассмотрим работу диагностической системы управ-
ления на примере деятельности некоторого аэропорта. Объектами
диагноза ОД являются самолеты, техническое состояние которых
определяется перед вылето.м средствами диагноза СД, реализующими
определенные алгоритмы диагноза с учетом некоторых параметров
внешней среды (например, температуры окружающего воздуха и
атмосферного давления). В процессе диагноза осуществляется пода-
ча на бортовые системы самолета определенных тестовых воздей-
ствий и получение от него соответствующих ответов, обрабатывае-
мых аппаратурой средств диагноза. По окончании процесса диагноза
полученный результат х, характеризующий техническое состояние
самолета (например, исправен, неисправен, неисправна такая-то бор-
товая система и т. п.), поступает в управляющее устройство УУ,
которое в соответствии с заданной целью управления Хо и знанием
состояния yt технических служб и состояния у2 внешней среды вы-
рабатывает управляющее воздействие е.
Целью управления, например, может быть требование мини-
мальных отклонений от заданного расписания вылетов самолетов
при заданном уровне безопасности полетов. К числу параметров тех-
нических служб, учитываемых при выработке управляющего воз-
действия, могут относиться такие, как наличие резервных, готовых
26
к вылету самолетов, время вылета диагностируемого самолета по
расписанию, данные о дате проведения и глубине предыдущего диаг-
ноза и т. п. Учитываемыми параметрами внешней среды могут быть
данные о метеорологических и иных условиях на трассе и др.
Управляющими воздействиями могут быть следующие: разрешить
вылет самолета, произвести более детальный диагноз технического
состояния некоторой бортовой системы, отправить самолет в ремонт,
заменить самолет резервным, готовым к вылету самолетом, подать
из ангара свободный самолет подходящего типа и выполнить диаг-
ноз его технического состояния для возможной замены неисправного,
перейти к диагнозу технического состояния очередного самолета.
Для исследования и проектирования диагностических систе.м
управления рассмотренного в примере типа привлекаются соответ-
ствующие методы, описанные в специальных разделах общей теории
управления.
1-3. ОБЪЕКТЫ ДИАГНОЗА
№
Для построения математических моделей объектов
диагноза в процессе проектирования и создания систем
диагноза необходимо знать физические свойства и ха-
рактеристики этих объектов.
В получении таких знаний важное место занимает
изучение возможных физических неисправностей объек-
та, а также параметров, характеризующих исправное и
неисправные состояния объекта. При этом полезна клас-
сификация объектов по принципу их действия, по на-
значению, по сложности, по энергетическим и другим
признакам. Необходимо также классифицировать неис-
правности по их видам (например, на производствен-
ные и эксплуатационные, на катастрофические и посте-
пенные), определять вероятности или частости, анализи-
ровать причины их возникновения, разрабатывать
методы определения признаков неисправностей и т. п.
Работы по исследованию параметров объектов включа-
ют в себя разработку методов задания допусков и опре-
деления контрольных соотношений между отдельными
параметрами, изучение вопросов точности измерения
параметров при диагнозе, определение законов измене-
ния параметров во времени и т. п.
Для построения оптимальных алгоритмов диагноза
большое значение имеет организация сбора и обработ-
ки статистических данных, особенно по вероятностям
возникновения неисправностей и по затратам (времени,
энергии, материальных или денежных средств и т. д.) на
отыскание неисправностей и их устранение. Отметим, что
статистические данные важны не только для оптимиза-
27
ции алгоритмов диагноза, но также для эффективного
решения задач технической прогностики и технической
генетики.
Некоторые из перечисленных задач стали, а другие
могут стать самостоятельными предметами исследова-
ний и публикаций как общих, посвященных, например,
вопросам измерений или надежности, так и специаль-
ных, рассматривающих отдельные классы объектов, на-
пример универсальные вычислительные машины, паро
энергетические установки, двигатели внутреннего сгора-
ния и т. п. Здесь мы ограничимся самыми общими
свойствами объектов диагноза и их неисправностей.
Объектами диагноза могут быть любые технические
изделия, устройства или системы, относительно которых
имеет смысл ставить и решать задачи проверки их
исправности, работоспособности, правильности функцио-
нирования или задачи поиска неисправностей.
Объект находится в исправном состоянии или назы-
вается исправным, если он удовлетворяет всем техни-
ческим требованиям, предъявляемым к нему в данный
конкретный период его жизни (изготовления, примене-
ния по назначению, ремонта, хранения). В противном
случае объект находится в неисправном состоянии или
называется неисправным. Исправное и все неисправные
состояния объединяются термином техническое состоя-
ние объекта.
Последствия любых явлений или действий, которые
переводят объект в некоторое неисправное состояние,
называются физическими неисправностями объекта.
Объект может состоять из компонент — функциональ-
но или конструктивно выделенных частей. Тогда совокуп-
ность компонент объекта, связей между компонентами
(внутренних связей) и связей объекта с внешней средой
(внешних связей) называют структурой объекта. Понятие
исправного и неисправного состояний, а также физиче-
ской неисправности приложимы к компонентам объекта,
его внутренним и внешним связям.
Взаимодействие объекта с внешней средой осущест-
вляется через его основные и дополнительные входы и
выходы. Сигналы на входах и выходах объекта харак-
теризуются параметрами тех физических величин, с по-
мощью которых передаются указанные сигналы. Это —
входные и выходные параметры объекта. Часто возни-
кает необходимость рассматривать внутренние парамет-
28
ры объекта, т. е. такие параметры, которые не являют-
ся его входными или выходными, В частности, когда
объект представлен совокупностью взаимосвязанных
компонент, внутренними являются параметры на тех
входах и выходах компонент, которые не являются вхо-
дами или выходами объекта. Чаще всего входные и
выходные параметры объекта доступны для измерения,
чего нельзя сказать о внутренних параметрах.
Последовательности (или, в частном случае, сово-
купности) возможных значений входных параметров
образуют множество возможных воздействий на объект.
Аналогично, множество ответов объекта определяется
последовательностью (или, в частном случае, совокуп-
ностью) значений его выходных параметров. Для наших
целей удобно принять, что воздействия (ответы) могут
определяться значениями либо всех, либо только части
входных (выходных) параметров объекта. Последнее
имеет место тогда, когда значения некоторых входных
(выходных) параметров по тем или иным причинам нас
не интересуют и могут быть любыми. Аналогично может
не представлять интереса часть значений в последова-
тельности значений некоторого входного или выходного
параметра.
Таким образом, воздействие на объект (ответ объек
та) характеризуется составом входов (выходов) и теми
моментами времени, в которые поступают заданные (из-
меряются получаемые) значения параметров на этих
входах (выходах). Последовательность (совокупность)
значений указанных параметров можно называть значе-
нием воздействия (ответа).
Как уже говорилось, элементарная проверка пред-
ставляет собой некоторый физический эксперимент над
объектом и определяется значением воздействия, пода-
ваемого или поступающего на объект, а также ответом
объекта на это воздействие. Значение ответа объекта
является результатом элементарной проверки. Ясно, что
объект, находящийся в разных технических состояниях,
может выдать разные результаты одной и той же эле-
ментарной проверки. Понятие элементарной проверки
применимо также к отдельным компонентам объекта.
В этом случае, естественно, предполагается доступность
входов и выходов компонент, что может потребовать
организации дополнительных входов и выходов объ-
екта.
29
Следовательно, в каждый момент времени при за-
фиксированном составе выводов (контрольных точек)
объекта элементарные проверки могут различаться
между собой только значениями воздействий. И наобо-
рот, элементарные проверки различаются между собой
только составом выходов, если зафиксировано значение
воздействия на объект. Забегая вперед, отметим, что
в первом случае задача построения алгоритма диагноза
сводится к задаче выбора последовательности (совокуп-
ности) значений воздействий, а во втором — к задаче
выбора состава контрольных точек объекта. Первая из
этих задач характерна при разработке систем тестового
диагноза, а вторая — систем функционального диагноза.
В общем случае имеется возможность проводить выбор
как значений воздействий, так и контрольных точек.
1-4. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ ДИАГНОЗА
Формализация методов построения алгоритмов ди-
агноза технического состояния некоторого объекта пред-
полагает наличие формального описания объекта и его
поведения в исправном и неисправных состояниях. Та-
кое формальное описание (в аналитической, табличной,
векторной, графической или другой форме) будем назы-
вать математической моделью объекта диагноза. Мате-
матическая модель объекта диагноза может быть задана
в явном или неявном виде.
Явная модель объекта диагноза представляет собой
совокупность формальных описаний исправного объекта
и всех (точнее, каждой из рассматриваемых) его неис-
правных модификаций. Для удобства обработки все
указанные описания желательно иметь в одной и той же
форме. Неявная модель объекта диагноза содержит ка-
кое-либо одно формальное описание объекта, математи-
ческие модели его физических неисправностей и правила
получения по этим данным всех других интересующих
нас описаний. Чаще всего заданной является математи-
ческая модель исправного объекта, по которой можно
построить модели его неисправных модификаций.
Общие требования к моделям исправного объекта и
его неисправных модификаций, а также к моделям не-
исправностей состоят в том, что они должны с требуе-
мой точностью описывать представляемые ими объекты
и их неисправности. В неявных моделях объектов диа-
30
гноза модели неисправностей, кроме того, должны удо-
влетворять требованию удобства их «сопряжения»
с имеющимся описанием объекта и тем самым обеспе-
чить достаточно простые правила получения других опи-
саний объекта.
Оговорим возможность в выражении «математиче-
ская модель» опускать иногда первое слово. Кроме то-
го, там, где это не приведет к неправильному понима-
нию, будем наряду с выражениями «модель объекта»
или «модель неисправности» употреблять более короткие
термины «объект» или «неисправность» соответственно.
Исправный или неисправный объект может быть
представлен как динамическая система, состояние кото-
рой в каждый момент времени t определяется значения-
ми входные, внутренних и выходных координат (пара-
метров). Частным является случай^ когда состояние
объекта не зависит от времени.
Обратим внимание на то, что термин «состояние
объекта» (как динамической системы), обозначающий
совокупность значений параметров объекта в опреде-
ленный момент времени, не следует смешивать с терми-
ном «техническое состояние объекта», обозначающим
наличие или отсутствие неисправности в объекте.
Объекты диагноза разделим па классы. Объекты, все
координаты которых могут принимать значения из кон-
тинуальных множеств значений, отнесем к классу не-
прерывных объектов. К классу дискретных объектов
причислим объекты диагноза, значения всех координат
которых задаются на конечных множествах, а время
отсчитывается дискретно. Если значения части коорди-
нат объекта заданы на континуальных, а значения дру-
гих — на конечны^ множествах, то объект является гиб-
ридным.
Объекты будем называть комбинационными или
объектами без памяти, если значения их выходных ко-
ординат однозначно определяются только значениями их
входных координат. Последовательностными, или объ-
ектами с памятью, являются объекты, у которых наблю-
дается зависимость значений их выходных координат не
только от значений входных координат, но и от времени.
Приведем примеры простых объектов разных клас-
сов: резисторная электрическая сеть — непрерывный
объект без памяти, аналоговая система регулирования
с обратными связями — непрерывный объект с памятью,
31
диодный дешифратор двоичных сигналов — дискретный
комбинационный объект, двоичный счетчик—дискрет-
ный объект с памятью, аналого-цифровой преобразо-
ватель — гибридный объект.
Часто входные и внутренние координаты объекта на-
зывают входными и соответственно внутренними пере-
менными, а выходные координаты — выходными функ-
циями. Мы также будем пользоваться этими названия-
ми. Заметим, что входные переменные и выходные функ-
ции могут быть сопоставлены как основным, так и до-
полнительным входам и соответственно выходам объ-
екта.
Обозначим символом X «-мерный вектор, компонен-
тами которого являются значения п входных перемен-
ных Xi, Xz, ..., хп. Аналогично У является т-мерным
вектором значений m внутренних переменных щ, у2, ...
..., ym, a Z— ^-мерным вектором значений k выходных
ФУНКЦИЙ Zi, Zz, . . ., Zk.
Запись
Z = Y(Z, Унач, t)
(Ы)
будем рассматривать как некоторую аналитическую,
векторную, графическую, табличную или другую форму
представления системы передаточных функций исправ-
ного объекта диагноза, отражающих зависимость реа-
лизуемых объектом выходных функций Z от его входных
переменных X, начального значения У1ЮЧ внутренних
переменных и от времени t. Система (1-1) является ма-
тематической моделью исправного объекта.
Выделим для рассмотрения конечное множество воз-
можных неисправностей объекта. Принято различать
одиночные и кратные неисправности. Под одиночной
понимается неисправность, принимаемая в качестве эле-
ментарной, т. е. такой, которая не может быть представ-
лена (или не подлежит представлению) совокупностью
нескольких других, более «мелких» неисправностей.
Кратная неисправность является совокупностью одно-
временно существующих двух или большего числа оди-
ночных неисправностей. Символом S будем обозначать
множество всех рассматриваемых (не обязательно всех
возможных) одиночных и кратных неисправностей объ-
екта, а символом О — множество его одиночных неис-
правностей. Очевидно, O^S. Будем говорить, что при
наличии в объекте неисправности s^S, i=l, 2, ...
32
..|S| (или о^О, i=l, 2, |0|) он находится
в (-неисправном состоянии или является (-неисправ-
ным.
Объект диагноза, находящийся в (-неисправном со-
стоянии, реализует систему передаточных функций
Z* = 4»(X, У’нач. t), (1-2)
представленных в той же форме, что и передаточные
функции (1-1). Заметим, что начальное значение У’Нач
внутренние переменных (-неисправного объекта может
не совпадать с их начальным значением Унач в исправ-
ном объекте. Система (1-2) для фиксированного ('
является математической моделью i-неисправного объ-
екта.
Условимся запись фактически ревизуемых объектом
диагноза передаточных функций снабжать знаком *:
Z*=4'*(X, У*нач, t). (1-3)
Система (1-1) и совокупность систем (1-2) для всех
steS образуют явную модель объекта диагноза. Будем
такую модель обозначать записью (Ч1Г, {Чг}).
Часто, как отмечалось выше, в явном виде задается
только модель исправного объекта, т. е. зависимость
(1-1), а поведение объекта в (-неисправных состояниях
представляется косвенно через множество S возможных
неисправностей. В этом случае неявную модель объекта
диагноза образуют: зависимость (1-1), множество S воз-
можных неисправностей объекта (представленных их
математическими моделями) и, наконец, способ вычи-
сления зависимостей (1-2) по зависимости (1-1) для
любой неисправности s, Такую неявную модель объекта
диагноза будем обозначать записью (ЧГ, S, Ф—►ЧГ1)-
Если математические модели неисправностей известны
sz
для всех s; 5, то преобразованием ’-F — ЧГг можно полу-
чить все зависимости (1-2) и тем самым от модели (Чг, S,
sz
V —Ф') перейти к явной модели (’Г, {’У"'}). Если же
математические модели некоторых или даже всех неис-
правностей из множества 5 неизвестны, то зависимости
(1-2) могут быть получены в результате физического
эксперимента непосредственно над объектом диагноза
л 358 33
при наличии в нем соответствующие неисправностей
Модификацией этого подхода является использование
при эксперименте не самого объекта, а некоторой его
физической модели.
При построении неявной модели объекта диагноза
математическими моделями физических неисправностей
чаще всего являются определенные «искажения» зави-
симости (1-1), например изменение в последней значе-
ний коэффициентов, фиксация константами некоторых
входных переменных, исключение имеющихся или до-
бавление новых членов и т. п. При этом получение за-
висимостей (1-2) заключается в осуществлении соответ-
ствующих «искажений» зависимости (1-1). Естественно
требовать, чтобы эти искажения правильно отображали
физические неисправности объекта, т. е. чтобы получае-
мые зависимости (1-2) действительно представляли со-
ответствующие i-неисправные объекты, причем для всех
рассматриваемых неисправностей из множества S.
Указанное требование, однако, не всегда выполнимо,
если зависимость (1-1) является системой передаточные
функций исправного объекта, составленных относитель-
но его основных входов и основных выходов. Поэтому
во многих случаях зависимость (1-1) задается в виде,
учитывающем внутреннее строение объекта, и тем самым
позволяет более точно представлять его физические не-
исправности. Например, при рассмотрении дискретных
объектов диагноза используется прием «расщепления»
тех входных переменных, для которые представляемые
ими сигналы распространяются в объекте по нескольким
физическим каналам. В других случаях применяется
неявная модель объекта диагноза, в которой заданное
описание (обозначим его символом ’F) объекта содер-
жит дополнительные фиктивные аргументы. Заданием
значений этих аргументов можно получить модели как
исправного, так и всех i-неисправных объектов. Такие
~ ~ si
модели (Ф, S, 4е—►V, Ч*7) будут рассмотрены в после-
дующих главах.
Основным понятием, используемым при решении за-
дач построения и реализации алгоритмов диагноза,
является элементарная проверка объекта. Рассмотрим
вопросы задания моделей объектов диагноза в терминах
элементарных проверок объекта и их результатов.
34
Обозначим символом П множество всех допустимых
элементарных проверок л3, /=1, 2,.., |П| объекта,
т. е. таких его проверок, которые физически осуществи-
мы в конкретных условиях проведения процесса диагно-
за. Каждая элементарная проверка, по определению,
характеризуется значением воздействия, подаваемого
поступающего) на объект при реализации элементарной
проверки, и ответом объекта на это воздействие. Значе-
ние а, воздействия в элементарной проверке я,еП
определяется составом входных переменных и последова-
тельностью во времени t их значений X,, а также на-
чальным значением У3цач внутренних переменных. Ответ
объекта в элементарной проверке л3 характеризуется
составом {у}; контрольных точек и значением (резуль-
татом элементарной проверки) /?*3, зависящим от техни-
ческого состояния объекта (отсутствие индекса i соот-
ветствует исправному объекту).
Таким образом, результат элементарной провер-
ки представляется в общем случае последовательностью
|{у}3|-мерных векторов и является функцией значения
aj воздействия:
R^=W^aj, {у},).
Вместо этой записи условимся применять более ко-
роткую
^^'(л.О (1-4)
для исправного объекта и
^=^(л,) (1-5)
для i-неисправных объектов.
Описанию фактического поведения объекта соответ-
ствует запись
Я*3=Чл(л3). (1-6)
Связь между моделями типа (1-1), (1-2) и типа
(1-4), (1-5) заключается в том, что последние могут
быть получены путем подстановки в правые части (1-1)
и (1-2) значений X,, Упач, t (для каждой элементарной
проверки л,еП) и последующего вычисления значений
гех компонент векторов Z и Z’, которые сопоставлены
контрольным точкам из множеств {у}3-.
Явную модель объекта диагноза, когда зависимости
(1-5) заданы для всех будем обозначать, как и
прежде, записью (Ч7, {Чг;}) • Неявная модель объекта
диагноза в данном случае предполагает заданными мо-
:»♦ 35
дель Ч7 исправного объекта,
стей, а также множество
тарных проверок и поэтому
(ЦТ, S, П,
множество S неисправно-
П допустимых элемен-
представляется записью
1-5. ФУНКЦИОНАЛЬНЫЕ СХЕМЫ СИСТЕМ ТЕСТОВОГО
И ФУНКЦИОНАЛЬНОГО ДИАГНОЗА
Рассмотрим теперь более детально, чем это сделано
в § 1-1, функциональные схемы систем тестового и
функционального диагноза.
Рис. 1-4. Функциональная схема системы тестово-
го диагноза.
Будем считать, что алгоритм диагноза, реализуемый
в той или иной системе диагноза, задан и содержит
множество элементарных проверок.
Функциональная схема системы тестового диагноза
показана на рис. 1-4. По командам блока управления
БУ, хранящего алгоритм диагноза, источник воздейст-
вий ИВ вырабатывает воздействия а, элементарных
проверок tj^T и в соответствии с алгоритмом диагноза
в определенной последовательности подает их через
устройство связи УС на объект диагноза ОД, а также,
36
возможно, на физическую модель ФМ объекта. В общем
случае устройство связи УС может коммутировать ка-
налы связи по сигналам блока управления.
Если, например, система рис. 1-4 решает задачу про-
верки исправности объекта, то реализация физической
модели сводится к представлению функции
(1-7)
для всех tj^T. Для этого случая на рис. 1-4 рядом
с выходом физической модели указано множество сиг-
налов
При поиске неисправностей объекта возможны раз-
ные варианты организации процесса тестового диагноза.
Если до реализации процесса неизвестно, исправен
объект или неисправен, то в физической модели долж-
ны быть представлены как зависимость (1-7), так и за-
висимости
(1-8)
для всех и всех tj^T, т. е. множество выходных
сигналов физической модели образуют множества {/?,}
и {R^}.
Часто процесс тестового диагноза организуют в два
этапа: сначала реализуют алгоритм проверки исправно-
сти объекта и только в случае получения результата
проверки «объект неисправен» переходят к реализации
алгоритма поиска неисправностей. При наличии предва-
рительной информации о том, что объект неисправен,
для решения задачи поиска неисправностей достаточно,
чтобы физическая модель реализовала только зависимо-
сти (1-8), т. е. выдавала множество сигналов {/?*,}.
Таким образом, физическая модель объекта выдает
информацию о возможных технических состояниях объ-
екта в виде возможных результатов R'j элементар-
ных проверок из множества Т. Эта информация поступа-
ет в блок расшифровки результатов БРР.
Ответами объекта диагноза на воздействия а, явля-
ются фактические результаты R*j элементарных прове-
рок t^T. Эти результаты через устройство связи УС по-
ступают на измерительное устройство ИУ и затем с вы-
хода последнего (в некоторой, возможно, преобразован-
ной форме) — на вход блока расшифровки результатов.
Показанная на рис. 1-4 пунктиром обратная связь между
блоком расшифровки результатов и блоком управления
37
выполняется тогда, когда реализуемый в системе алго-
ритм диагноза представляет собой условную последова-
тельность элементарны?; проверок. В этом случае оче-
редная элементарная проверка из множества Т назнача-
ется в зависимости от фактических результатов R*j
предшествующих ей элементарных проверок.
Рис. 1-5. Функциональная схема системы функциональ-
ного диагноза.
В блоке расшифровки результатов производится со-
поставление возможных {7?3}, и фактических R*j ре-
зультатов элементарных проверок, назначаются очеред-
ные элементарные проверки и формируются результаты
диагноза.
Функциональная схема системы функционального
диагноза показана на рис. 1-5. Характерной особенно-
стью таких систем, как уже отмечалось, является от-
сутствие в средствах диагноза источника (тестовых) воз-
действий. Напомним, что теперь объект в процессе ди-
агноза применяется по своему назначению или находится
в режиме имитации такого применения: воздействия а,-
являются рабочими и поступают на основные входы
объекта.
С объекта снимаются, во-первых, сигналы управле-
ния (на рис. 1-5 они обозначены символом г/,) средства-
ми диагноза и, во-вторых, сигналы R*j ответов объек-
38
га на воздействия а,. Сигналы у, нужны тогда, когда
имеется необходимость управления физической моделью
ФМ и блоком управления БУ в зависимости от режима
работы объекта. Блок управления по сигналам yj, а так-
же, возможно, по сигналам обратной связи от блока рас-
шифровки результатов БРР осуществляет коммутацию
каналов в устройстве связи УС. Если на систему функ-
ционального диагноза возложены также функции защи-
ты объекта, то БРР выдает команды на управление
объектом.
Как и в системах тестового диагноза, блок расшиф-
ровки результатов БРР производит сопоставление фак-
тических результатов /?*,- элементарных проверок с воз-
можными результатами {7?J, выдаваемыми физи-
ческой моделью. Когда система решает задачу проверки
правильности функционирования объекта, достаточно,
чтобы физическая модель хранила и выдавала только
множество {/?;} результатов. При поиске неисправностей
необходимо знание также результатов
Примером систем функционального диагноза являют-
ся широко распространенные системы централизованно-
го контроля, в которых о техническом состоянии объек-
та судят по результатам сравнения фактических значе-
ний параметров объекта с их верхними и нижними
допустимыми значениями. В этом случае физической
моделью объекта диагноза является аппаратура хране-
ния и выдачи указанных допустимых значений контро-
лируемых параметров.
В заключение настоящего параграфа отметим, что
здесь были рассмотрены в определенном смысле общие
условия проведения процессов диагноза. Не всегда
в практике требуется или возможно проведение диагноза
с глубиной до каждой одной неисправности объ-
екта (например, часто нет необходимости различать не-
исправности одной и той же сменной компоненты объек-
та). Иногда полезно обеспечить возможность формиро-
вать результаты тестового диагноза по рсоду процесса и
тем самым прекращать jho, не дожидаясь реализации
всех элементарных проверок из множества Т.
В системах функционального диагноза не всегда мож-
но конструктивно четко отделить аппаратуру, принадле-
жащую объекту диагноза, от аппаратуры средств диаг-
ноза. Более того, встроенные средства функционального
диагноза могут использоваться для целей тестового ди-
39
агноза, а структура функционирующего объекта диагно-
за может отличаться от его структуры при тестовом
диагнозе и т. и.
Представленные на рис. 1-4 и 1-5 функциональные
схемы систем диагноза могут претерпеть те или иные
изменения в зависимости от того, какими являются
эти системы — автоматическими, автоматизированными
или ручными, какие применяются в них средства диаг-
ноза— универсальные (управляемые по сменной про-
грамме) или специализированные, программные или ап-
паратурные и т. и.
1-6. ТАБЛИЦА ФУНКЦИЙ НЕИСПРАВНОСТЕЙ
Явную математическую модель объекта диагноза ти-
па (Y, {ЧА}), т. е. совокупность функций (1-4) и (1-5),
можно представить в табличной форме.
Обозначим множество технических состояний объекта
символом Е. Пусть ееЕ обозначает исправное состояние
объекта, а е^Е — его i-неисправное состояние. Каждо-
му i-неиспр явному состоянию соответствует неисправ-
ность Si из множества S и наоборот.
Построим прямоугольную таблицу, строкам которой
поставим в соответствие допустимые элементарные про-
верки зт3- из множества П, а столбцам — технические
состояния объекта из множества Е или, что то же, функ-
ции V и V{, i=l, 2, ..., |S|, реализуемые объектом, на-
ходящимся в исправном е или i-неиспрявном ег состоя-
нии. Будем в дальнейшем значение индекса 1=0 отно-
сить к столбцу исправного состояния е. В клетке (/, i)
таблицы, находящейся на пересечении строки я,- и столб-
ца вг, проставим результат элементарной проверки
я,- объекта, находящегося в техническом состоянии е,.
Множество всех результатов /=1, 2, .. ., |П|; i=
=0, 1, ..., |S| обозначим символом R. Очевидно, |/?| =
= |П|(|5| + 1). Построенную таблицу (рис. 1-6) будем
называть таблицей функций неисправностей объекта
диагноза.
Заметим сразу, что непосредственное использование
таблицы функций неисправностей как формы представ-
ления информации при построении и реализации алго-
ритмов диагноза и физических моделей объектов диагно-
за часто невозможно по причине высокой размерности
таблицы. Однако как универсальная математическая мо-
40
дель объекта диагноза таблица функций неисправностей
очень наглядна и удобна при обсуждении и классифика-
ции принципов, а также основных процедур построения
и реализации алгоритмов диагноза, даже если эти прин-
ципы и процедуры первоначально формулируются на
языках, отличных от языка
таблиц функций неисправ-
ностей.
Задание таблицы функ-
ций неисправностей эквива-
лентно заданию системы
функций (1-4) и (1-5). Дей-
ствительно, столбец е0табли-
цы задает поведение ис-
правного объекта, т. е. функ-
цию (1-4), а остальные ее
столбцы — поведения объек-
та, находящегося в соответст-
вующих неисправных состоя-
ниях, т. е. функции (1-5). Рис. 1-6. Таблица функций не-
Для определенности при- исправностей,
мем здесь, что множество П
обладает свойством обнаружения любой неисправности
из множества S, т. е. для любой неисправности
найдется хотя бы одна элементарная проверка —
такая, что R^R*;, а также свойством различения всех
неисправностей из множества S, т е. для каждой пары
неисправностей s,, Sk^S, i^=k, найдется хотя бы одна
элементарная проверка такая, что
Наличие у множества П свойства обнаружения не-
исправностей эквивалентно тому, что столбец е таблицы
функций неисправностей отличается от каждого из
остальных ее столбцов et, i=l, 2, . . |S|, а свойства
различения — тому, что все столбцы таблицы, представ-
ляющие неисправные состояния, попарно различны.
Как всякая математическая модель объекта диагно-
за, таблица функций неисправностей нужна для двух
применений: для построения алгоритмов диагноза при
проектировании систем диагноза и для построения фи-
зической модели объекта при реализации этих систем.
Изложим основные операции процесса построения
алгоритма диагноза по таблице функций неисправностей.
Будем предполагать, что множество S неисправно-
стей объекта содержит либо все неисправности (при рас-
41
смотрении задач проверки исправности и поиска всех
неисправностей), либо только те из них, которые нару-
шают работоспособность объекта (в задачах проверки
работоспособности и поиска неисправностей, делающих
объект неработоспособным), либо, наконец, только не-
исправности, нарушающие правильное функционирова-
ние объекта (при проверке правильности функциониро-
вания и при поиске неисправностей, нарушающих функ-
ционирование объекта). Это же условие распространя-
ется на множество Е технических состояний объекта.
Задание на построение алгоритма диагноза наряду
с указанием множества Е возможных технических со-
стояний объекта (или множества S его неисправностей)
должно содержать сведения о требуемой глубине диагно-
за. Независимо от назначения алгоритма диагноза (для
проверки исправности, работоспособности, правильности
функционирования или для поиска неисправностей) тре-
буемую глубину диагноза можно задать через фиксиро-
ванное разбиение множества Е на X непересекающихся
подмножеств Еи, v= 1, 2, ..., Л,
(J Ev —Е, Ev А 0 ПРИ
Тогда проверке исправности, работоспособности или
правильности функционирования соответствует мини-
мальная глубина диагноза, при которой Z=2, причем
Ei = {e} и E2={ci/i=l, 2, .. ., |S|}. При поиске неисправ-
ностей с максимальной глубиной диагноза (т. е. с точ-
ностью до каждого одного технического состояния) Л=
= |S| + 1, E1={e}, Е ={е<}, 1=1, 2, ..., |S|, v = i+l. Про-
межуточные значения глубины диагноза характеризуют-
ся условием 2<Z< |S| + 1.
Способ задания глубины диагноза разбиением мно-
жества Е технических состояний объекта на подмноже-
ства Ev является достаточно универсальным, но он не-
удобен практически тогда, когда отсутствует соответст-
вие такого разбиения разбиению объекта на конструк-
тивные составные части. Значительно удобнее требуемую
глубину диагноза задавать через разбиение множества
конструктивных компонент объекта на непересекающие-
ся подмножества. Например, широко известно требова-
ние проведения диагноза с глубиной до сменного блока
(узла, компоненты) объекта. Рассмотрим особенности
такого способа задания глубины диагноза.
zt-
Пусть объект разбит на N сменных блоков. Сопоста-
вим /-му (/=1, 2, .. N) сменному блоку подмножество
Е) технических состояний, каждое из которых определя-
ется неисправностями только этого блока. Если предпо
лагается, что в объекте может быть неисправным толь-
ко один (любой) блок, то объединение N подмножеств
Ei вместе с исправным состоянием е объекта образует
множество Е всех возможных технических состояний.
Поэтому получаем: A,=.7V+1, Ет = {е}, Ev=Et. Этот случай
соответствует рассмотрению одиночных неисправностей
объекта, если в качестве последних принять неисправ-
ности каждого сменного блока.
Иначе дело обстоит тогда, когда нельзя исключить
возможность одновременного существавания неисправно-
стей в двух или большем числе сменных блоков (крат-
ных неисправностей). При этом, кроме указанного выше
формирования подмножеств Ei для каждого одного
сменного блока необходимо каждой группе из двух, трех
и т. д. сменных блоков сопоставить подмножества тех-
нических состояний, определяемых одновременным суще-
ствованием неисправностей во всех блоках (и только
в них) рассматриваемой группы. При этом будет полу-
чено 2N—1 непересекающихся подмножеств технических
состояний объекта, т. е. (с учетом исправного состоя-
ния е) Z=2JV.
Итак, пусть имеется таблица функций неисправностей
и задана тем или иным способом требуемая глубина
диагноза. Условимся, что в таблице нет незаполненных
клеток.
Основу любого алгоритма диагноза составляет сово-
купность (множество) Т входящих в него элементарных
проверок. Для того чтобы обеспечить требуемую глуби-
ну диагноза, эта совокупность должна различать каж-
дую пару технических состояний, принадлежащих раз-
ным подмножествам Ev и Е^ v=#p, хотя может не раз-
личать любую пару технических состояний, принадлежа-
щих одному и тому же подмножеству Е^. Первое усло-
вие означает, что для каждой пары технических состоя-
ний 6i и в/. *, принадлежащих разным подмножествам Е,
Одно из них может быть исправным состоянием е.
43
и Е , среди элементарных проверок совокупности Т най-
дется хотя бы одна элементарная проверка tj, результа-
ты и Ehj которой различны, т. е. Совокуп-
ность Т элементарных проверок алгоритма диагноза бу-
дем называть полной, если она обеспечивает проведение
диагноза либо с заданной глубиной, либо с глубиной,
обеспечиваемой множеством П всех допустимых элемен-
тарных проверок. Совокупность Т называется неизбы-
точной, если удаление из нее любой одной элементарной
проверки ведет к уменьшению глубины диагноза.
По одной и той же таблице функций неисправностей
и при заданном разбиении множества Е на подмножест-
ва £v можно построить в общем случае несколько пол-
ных неизбыточных совокупностей Т. Эти совокупности
могут различаться как составом, так и числом входящих
в них элементарных проверок. Полные неизбыточные
совокупности Т с наименьшим числом элементарных про-
верок называются минимальными.
Построение по таблице функций неисправностей всех
полных неизбыточных (а значит, и минимальных) сово-
купностей Т можно осуществить, выполнив следующие
две операции:
1) Просмотром (перебором) всех возможных неупо-
рядоченных пар столбцов таблицы функций неисправ-
ностей выделить пары ег, ек технических состояний, при-
надлежащих разным подмножествам Е^ и для каж-
дой такой пары просмотром (перебором) всех строк
таблицы определить подмножества Пгь элементарных
проверок sij, результаты и Rhj которых для техниче-
ских состояний вг и eh, различны.
2) Просмотром (перебором) всех подмножеств Ппг,
полученных в результате выполнения операции 1, найти
все такие совокупности Т элементарных проверок, чтобы
в каждой из них для каждого подмножества П,/; на-
шлась хотя бы одна элементарная проверка tj, принад-
лежащая этому подмножеству П,ь.
Блок-схема алгоритма А1-1 выполнения операции 1
приведена на рис. 1-7. Исходными данными являются
таблица функций неисправностей и разбиение множества
Е на подмножества Ev. Номера столбцов таблицы отме-
чаются индексами i=0. 1, . . ., | S |—1, A = t+1, i+2, ...
..., |S|, а номера ее строк — индексом /=1. 2, ..., |П|.
44
Включить
STf 0
J Ъп
Рис. 1-7. Блок-схема алгоритма А1-1.
45
Формальный способ выполнения операции 2 состоит
в следующем. Обозначим символом U множество всех
подмножеств nift, полученных в результате выполнения
операции 1. Пусть I — порядковый номер некоторого
подмножества как элемента (ПпЭг множества U,
1=1, 2, . . |Z7|. Возьмем два первых подмножества
(Ilift)i и (Пп<)2 и образуем все возможные пары входя-
щих в них элементарных проверок. Среди этих пар про-
изведем следующие упрощения: каждую пару вида (гт3-;
jtj) заменим одной элементарной проверкой (л3); при
наличии одной элементарной проверки (я,) и пар вида
(я.,; лд) удалим последние. Полученное после таких
упрощений множество пар и, возможно, одиночных эле-
ментарны^ проверок обозначим символом Пь Затем
возьмем множество (П<ь)з и построенное множество П1
и образуем все возможные пары их элементов. После вы-
полнения среди этих пар упрощений, аналогичных ука-
занным выше, получаем множество П2 и т. д. Подмноже-
ство (Пгь)/ и множество П;-1 дают множество П/. Каж-
дый элемент множества П. является полной неиз-
быточной совокупностью Т элементарных проверок.
Блок-схема алгоритма А1-2 выполнения операции 2
изображена на рис. 1-8. Исходными данными является
множество U подмножеств 11,-л Индексом 1=1, 2, . | С7|
отмечен порядковый номер подмножества nift. Знак 0
означает пустое множество.
Остановимся теперь на применении таблицы функций
неисправностей при построении физической модели объ-
екта в средствах диагноза.
Определение совокупности TsII элементарных про- .
верок, входящих в алгоритм диагноза, соответствует вы-
делению определенной совокупности строк таблицы
функции неисправностей. Для алгоритмов проверки ис-
правности, работоспособности или правильности функ-
ционирования объекта эта совокупность строк такова,
что столбец е образуемой ими подтаблицы функций не-
исправностей отличается от любого другого ее столбца.
Аналогично при поиске неисправностей с максимальной
глубиной все столбцы такой подтаблицы функций неис-
правностей попарно различны.
Подтаблицу, образованную совокупностью Т строк,
будем называть Т-таблицей функций неисправностей,
чтобы отличать ее от исходной таблицы функций неис-
правностей, которую можно называть П-таблицей.
46
Нетрудно видеть, что 7-таблица функций неисправно-
стей является заданием функций (1-7) и (1-8), опреде-
ляющих физическую модель объекта в средствах диаг-
ноза. При представлении
физической модели объ-
екта 7-таблицей функций
неисправностей процесс
расшифровки фактиче-
ских результатов эле-
ментарных проверок мож-
но представить следую-
щим образом. Каждая
реализованная элементар-
ная проверка tj^T выде-
ляет соответствующую
строку 7-таблицы, а ее
фактический результат
R*i делит множество
столбцов таблицы на два
подмножества. Те столб-
цы eit i=0, 1, ..., | S j,
для которых
«вычеркиваются» из таб-
лицы Оставшиеся столб-
цы, для которых Rij=R*j, представляют подмноже-
ство возможных технических состояний объекта. Завер-
шению процесса диагноза соответствует момент, когда
в таблице останется единственный «невычеркнутый»
столбец. Заметим, что «вычеркивание» столбца е озна-
чает, что объект диагноза неисправен.
Следовательно, чем меньше число строк 7-таблицы
функций неисправностей, тем (при прочих равных
условиях) проще реализация соответствующего ей алго-
ритма диагноза (во всяком случае, в системах тестового
диагноза) и представляемой ею физической модели объ-
екта. Поэтому при проектировании систем диагноза ча-
сто стремятся строить алгоритмы диагноза с как можно
меньшим числом входящих в них элементарных прове-
рок.
Чем больше разнообразие (а значит, число) элемен-
тарных проверок в множестве П, тем шире возможности
получения алгоритмов диагноза с малым числом эле-
ментарных проверок. Однако, вообще говоря, чем боль-
ше строк (а также столбцов) содержит П-таблица функ-
47
ций неисправностей, тем больше требуется операций по
ее обработке для построения экономных алгоритмов
диагноза. Отсюда можно сделать неформальный вывод
о том, что чем больше усилий будет затрачено при
построении алгоритма диагноза, тем будет проще по-
следующая техническая реализация системы ди-
агноза.
В частности, никаких усилий не требуется на по-
строение так называемого тривиального алгоритма диаг-
ноза, содержащего все элементарные проверки множе-
ства П, но при этом физическая модель должна быть
представлена П-таблицей функций неисправностей и по-
этому будет максимально сложной, а время и другие
затраты на реализацию алгоритма диагноза будут наи-
большими.
Другая крайняя, всегда желательная, но часто не-
достижимая ситуация заключается в получении всех
неизбыточных алгоритмов диагноза с целью последую-
щего выбора из них в каком-то смысле наилучшего
(например, минимального) алгоритма *. Этого можно до-
стичь, в частности, применением алгоритмов А1-1 и А1-2,
представляющих собой, по существу, полный перебор
всех возможных решений и поэтому требующих макси-
мального объема операций по обработке П-таблицы
функций неисправностей. Между этими двумя крайними
ситуациями лежит ряд промежуточны^, различающихся
объемами вычислений и соответственно размерами за-
трат на реализацию систем диагноза.
Чаще всего причиной вынужденного отказа от полу-
чения минимальных алгоритмов диагноза являются
большие размеры П-таблицы функций неисправностей.
Размеры таблицы определяются как числом ее строк
и столбцов, так и размерностью результатов Д3, R‘3^R
элементарных проверок. Рассмотрим пути уменьшения
размеров П-таблицы функций неисправностей, т. е. объе-
мов той информации, которая задается в качестве ис-
ходной для построения алгоритмов диагноза, не имея
в виду такие тривиальные возможности, как удаление
повторяющихся строк и столбцов таблицы.
1 В общем случае следует говорить о получении алгоритмов
диагноза, оптимальных в смысле экстремума некоторой заданной це-
левой функции. Здесь мы этого не делаем с целью упрощения изло-
жения.
48
Начнем с уменьшения числа строк путем укрупнения
элементарных проверок. Элементарная проверка выше
была определена как некоторый, в значительной степе-
ни произвольный, эксперимент над объектом диагноза.
Если в качестве элементарной проверки принять такой
эксперимент, реализация которого дает достаточное для
целей диагноза описание поведения объекта (в исправ-
ном и всех его неисправных состояниях), то множество
П становится одноэлементным (таблица функций неис-
правностей содержит одну строку). Такое предельно воз-
можное сокращение числа строк П-таблицы будет со-
провождаться увеличением размерности результатов
элементарной проверки, так как описание поведения
объекта будет максимально сложным. При этом теряет
смысл задача минимизации алгоритмов диагноза, ибо
существует единственный тривиальный алгоритм диагно-
за В этих условиях физическая модель и алгоритм ди-
агноза будут достаточно сложными. Тем не менее в ряде
случаев представление математической модели объекта
диагноза в виде однострочной таблицы функций неис-
правностей может иметь практическое значение. Это
имеет место, например, в том случае когда нецелесооб-
разно или невозможно расчленить эксперимент над объ-
ектом на ряд элементарных проверок.
Другой путь сокращения числа строк П-таблицы
функций неисправностей состоит в исключении части
элементарных проверок из числа всех допустимых. При-
мером может служить .задание только тех элементарных
проверок, воздействия которых могут встретиться в про-
цессе выполнения объектом его рабочего алгоритма
функционирования. Это множество элементарных прове-
рок может оказаться достаточным для решения задач
проверки исправности, работоспособности или правиль-
ности функционирования, чего нельзя сказать относи-
тельно задач поиска неисправностей объекта.
Идеальным было бы исключение из множества П всех
тех элементарных проверок, которые заведомо не вой-
дут в минимальные алгоритмы диагноза. Однако про-
стые способы нахождения всех таких «ненужных» строк
П-таблицы функций неисправностей, т. е. способы, не
требующие сложных процедур анализа состава и свойств
всех элементарных проверок множества П, неизвестны.
Общим требованием при сокращении числа строк
таблицы функций неисправностей является контроль за
4358 49
тем, чтобы у выбранного множества П элементарных
проверок сохранялось свойство полноты. Следует также
помнить, что сокращение числа строк П-таблицы, вообще
говоря, может привести к увеличению числа элементар-
ных проверок, входящих в алгоритм диагноза.
Сокращение числа столбцов таблицы функций неис-
правностей соответствует уменьшению числа рассматри-
ваемых технических состояний объекта диагноза. В ря-
де случаев такое уменьшение может быть определено
условиями решаемой задачи. Например, задача диагно-
за технического состояния объекта в условиях его экс-
плуатации в ряде случаев может решаться при рассмо-
трении только множества О одиночных неисправностей,
когда вероятности появления кратных неисправностей
принимаются равными нулю.
Принципиально возможно и всегда желательно
исключение «ненужных» столбцов таблицы, отсутствие
которых не снижает точности результатов (глубины)
диагноза. Нахождение всех таких столбцов, к сожале-
нию, является сложной задачей, решение которой тре-
бует специальных исследований и известно только для
ряда частных случаев, при которых учитываются как
свойства структуры объекта диагноза, так и классы воз-
можных неисправностей.
В общем случае при уменьшении числа столбцов
таблицы функций неисправностей следует иметь в виду,
что алгоритмы диагноза, построенные относительно не-
которого подмножества возможных технических состоя-
ний объекта, не всегда позволяют определить исключен-
ные из рассмотрения технические состояния. Более того,
необоснованное исключение столбцов таблицы может
привести к получению ложных результатов диагноза.
Например, при реализации алгоритма проверки исправ-
ности, построенного в предположении наличия только
одной неисправной компоненты, можно получить лож-
ный сигнал исправности объекта при фактическом нали-
чии в нем нескольких неисправных компонент.
Теперь остановимся на вопросе сокращения размер-
ности результатов /?;, R{^R элементарных проверок.
Результат элементарной проверки л3-, как отмечалось
выше, представляет собой последовательность |{у}3|-
мерных векторов значений сигналов в контрольных точ-
ках объекта. Значит, сокращение размерности результа-
тов элементарной проверки возможно путем уменьшения
50
размерности вектора значений указанных сигналов,
а также путем уменьшения числа векторов в их после-
довательности.
Максимальное сокращение размерности результатов
элементарных проверок П-таблицы функций неисправно-
стей дает следующий прием. В каждой строке / табли-
цы все результаты элементарной проверки л,-, удовлет-
воряющие условию Rij = Rj, i=l, 2, . . ., |S|, принимают-
ся равными 1. Остальные результаты этой элементарной
проверки, для которые имеет место неравенство Rtj^Rj,
принимаются равными 0, независимо от того, различны
они между собой или одинаковы. При этом результат
любой элементарной проверки (безотносительно к физи-
ческой природе воздействий и ответов, а также к составу
и значениям входных сигналов и сигналов в контроль-
ных точках) может трактоваться только как положи-
тельный (7?‘j=l) или как отрицательный (7?%=0).
Упрощенную таким образом таблицу функций неис-
правностей будем называть двоичной математической
моделью объекта диагноза. Заметим, что в этой модели
столбец е, соответствующий исправному состоянию объ-
екта, содержит только положительные результаты
элементарных проверок.
В общем случае сокращение размерности результа-
тов элементарных проверок сопровождается уменьшени-
ем числа различных результатов последних. Это снижа-
ет возможности различения технических состояний объ-
екта и, как следствие, может 'потребовать увеличения
числа элементарных проверок, входящие в алгоритм
диагноза. С другой стороны, сокращение размерности
результатов элементарных проверок ведет к упрощению
реализации операций передачи, измерения, сравнения и
анализа этих результатов в системах диагноза.
Конечно, всегда желательно сокращение размерности
результатов элементарных проверок за счет исключения
несущественных компонент векторов значений сигналов
в контрольных точках и несущественных векторов этих
значений, т. е. таких компонент и векторов, исключение
которые не изменяет состава и числа различных резуль-
татов элементарных проверок в П-таблице.
Заметим, что «укрупнение» элементарных проверок
увеличивает размерность их результатов. Максимума эта
размерность, как указывалось, достигает в однострочной
таблице функций неисправностей.
4*
51
Итак, эффективных путей сокращения размеров таб-
лицы функций неисправностей практически нет. Таблица
остается громоздкой и поэтому требует больших объе-
мов вычислений в процессе ее обработки. В этом состоит
основная причина поиска и разработки различных более
экономных способов представления и обработки инфор-
мации, необходимой для построения и реализации алго-
ритмов диагноза и физических моделей объектов диагно-
за. Естественно, что во многих случаях «платой» за эту
экономию является отказ от получения точных (опти-
мальных или минимальных) решений.
Как указывалось, П-таблица функций неисправностей
является табличной формой задания явной математиче-
ской модели объекта диагноза (Ч7, {Ч*'})- Информацию,
содержащуюся в П-таблице, можно получать по частям,
что соответствует работе с неявной математической мо-
si, п
делью объекта диагноза (Ч7, S, П, Ч7—-Ч71')-
Следующие два параграфа посвящены характерным
постановкам и алгоритмам решения задач в рамках не-
явной модели. Алгоритмы рассматриваются в порядке
убывания вычислительных трудностей, вызываемых боль-
шими размерами П-таблиц функций неисправностей.
1-7. ПРЯМЫЕ ЗАДАЧИ ДИАГНОЗА
Назовем прямыми задачами диагноза задачи опреде-
ления по заданной элементарной проверке л.,- той или
иной информации о технических состояниях объекта
диагноза. При построении алгоритмов диагноза (т. е.
в процессе проектирования систем диагноза) такой
информацией может быть, например, определение подмно-
жеств технических состояний объекта, дающих одинако-
вые результаты элементарной проверки л.;. А при реа-
лизации алгоритма диагноза интересующей нас инфор-
мацией может быть, например, определение по известному
результату R*j элементарной проверки л; подмноже-
ства тех технических состояний, в одном из которых
фактически находится объект. Указанная информация
может представляться не в терминах технических состоя-
ний объекта, а в терминах его неисправностей.
Пусть заданы: математическая модель Ч7 исправного
объекта диагноза, множество S возможных неисправно-
стей и множество П допустимых элементарных проверок.
52
Модель W исправного объекта такова, что она позволя-
ет, во-первых, «ввести» в нее любую неисправность
и, во-вторых, вычислить как результат так и резуль-
таты Rij любой элементар-
ной проверки луеП по изве-
стному значению ctj ее воз-
действия.
Начнем рассмотрение
прямых задач диагноза с за-
дачи вычисления одной стро-
ки таблицы функций неис-
правностей. При построении
алгоритмов диагноза это
может существенно сокра-
тить объемы памяти для хра-
Рис. 1-10. Блок-схема алгорит-
ма А1-3.
Рис. 1 -9. Иллюстрация
прямой задачи анализа
модели
нения информации, содержащейся в таблице функций
неисправностей.
Вычисление строки таблицы функций неисправностей
производится путем многократного решения прямой за-
дачи анализа модели Чг, состоящего в том, что на мо-
дель W подается (рис. 1-9) входное воздействие а3 эле-
ментарной проверки я,- и производится вычисление либо
результата Rj, либо результата Rij. В последнем случае
в модель Чг предварительно вводится неисправность
s.eS. В результате будут получены | S | +1 результатов
Rlj элементарной проверки я,- для всех t=0, 1, ..|S|.
53
Блок-схема алгоритма А1-3 вычисления строки /
таблицы функций неисправностей представлена на
рис. 1-10. Применение этого алгоритма для каждого / =
= 1,2, . . |П| дает всю П-таблицу функций неисправно-
стей.
Рис. 1-11. Иллюстрация разбиения множества Е на под-
множества по результатам элементарной проверки.
Пусть а3 * есть число разных результатов R]U, и=1,
2, .. ., а;, элементарной проверки л3. Результаты Rju
могут служить признаками разбиения множества Е тех-
нических состояний объекта на а-, подмножеств (клас-
сов) Eju. Тогда можно говорить, что элементарная про-
верка разбивает множество Е на aj подмножеств Ези
(рис. 1-11). Техническое состояние е, принадлежит под-
множеству EjU, если R^ — Rju- Подмножества Eju естест-
венно называть подмножествами неразличаемых (эле-
ментарной проверкой л,) технических состояний объекта.
Заметим, что точно так же можно рассматривать
разбиения элементарными проверками подмножеств Е,и
множества Е.
Знание строки / таблицы функций неисправностей
позволяет вычислить подмножества Е,и и их число
Один из возможных алгоритмов решения этой задачи
представляет собой последовательный просмотр клеток
строки / с постепенным формированием подмножеств Ези
по результатам элементарных проверок.
Блок-схема такого алгоритма А1-4 приведена на
рис. 1-12. Индексом г, i=0, 1, ..., |S|, обозначен теку-
щий номер клетки строки / таблицы функций неисправ-
ностей, индексом k, k=\, 2, ..., а3,— номер (в порядке
просмотра клеток строки) очередного результата R, или
Вместо aj будем писать иногда а(л3) или a(/j).
54
отличного от всех встречавшихся ранее результатов
элементарных проверок, и, наконец, индексом и, и=1,
2, .. ., А,— текущий номер результата среди разных, уже
зафиксированных результатов элементарных проверок.
Запись, например, е^Е}и означает, что в процессе ра-
боты алгоритма техническое состояние е, включается
в состав элементов формируемого подмножества EjU-
55
Отметим, что задание подмножеств EjU, и=1, 2, ...
.. а,, неразличаемых технических состояний эквива-
лентно неявному заданию всех пар технических состоя-
ний, дающих разные результаты элементарной проверки
л,, т. е. различаемых этой элементарной проверкой.
Решение прямой задачи диагноза последовательным
применением алгоритмов А1-3 и А1-4 требует для фикси-
рованной элементарной проверки л, (|S | + 1)-кратного
прямого анализа модели 'I1' исправного объекта и в худ-
шем случае около a,|S| сравнений результатов этой
элементарной проверки с результатами RjU. Это, по су-
ществу, полный перебор всех возможностей, и в этом
недостаток рассмотренного способа решения прямой за-
дачи диагноза.
Вычисление всех подмножеств Е,и и их числа aj для
элементарных проверок я,еП необходимо, как правило,
на этапе построения алгоритмов поиска неисправностей.
При построении алгоритмов проверки исправности (ра-
ботоспособности, правильности функционирования) воз-
никает более узкая задача вычисления одного подмно-
жества Ej технических состояний Cj, i=0, 1, .. ., |S|,
не обнаруживаемых элементарной проверкой nj, т. е.
таких, для которых =/?,-. Эта задача равноценна за-
даче вычисления одного подмножества Ej обнаруживае-
мых элементарной проверкой состояний, которые да-
ют R1j^=Rj, так как Ej (J Ej=E.
При реализации алгоритмов диагноза (в процессе
расшифровки фактических результатов элементарных
проверок) необходимо по известному результату R*j
элементарной проверки t^T определять также одно'
подмножество Е*, технических состояний е,-, для кото-
рых Rij=R*j. Если имеется строка / Т-таблицы функций
неисправностей (т. е. физическая модель объекта пред-
ставлена Т-таблицей), то решение этой задачи может
быть получено по алгоритму, аналогичному алгоритму
А1-4. Разница состоит лишь в том, что теперь в процессе
просмотра клеток строки / производится сравнение за-
писанных в этих клетках результатов с единственным
фактическим результатом R*j элементарной проверки
tj. Блок-схема алгоритма А1-5 вычисления подмножест-
ва Е*} приведена на рис. 1-13. Индексом i, i=0, 1, ...
..., |S|, обозначен текущий номер клетки строки табли-
цы функций неисправностей.
56
Назовем подозреваемыми
Пусть в процессе диагноза технического состояния
объекта реализовано некоторое число элементарных про-
верок и зафиксированы их результаты, т. е., другими
словами, известны результаты некоторого физического
эксперимента над объектом,
такие технические состоя-
ния, в которых поведение
объекта совпадает с из-
вестными результатами фи-
зического эксперимента над
ним.
Знание результатов лю-
бого физического экспери-
мента над объектом позво-
ляет выделить из множества
Е возможных технических
состояний объекта соответ-
ствующее подмножество его
подозреваемых технических
состояний. Примером явля-
ется рассмотренное выше
выделение тюдмножества
E*j подозреваемых техниче-
ских состояний объекта по
известному результату R*j
элементарной проверки tj.
Ясно, что фактическое техни-
ческое состояние объекта
всегда принадлежит подмно-
жеству его подозреваемых
технических состояний.
Процесс выделения под-
множества Е*3 подозревае-
мых технических состояний по алгоритму А1-5 является
формализацией рассмотренной в предыдущем параграфе
процедуры «вычеркивания» столбцов Т-таблицы функ-
ций неисправностей, представляющей физическую модель
объекта диагноза. «Вычеркиваются» столбцы, которые
соответствуют техническим состояниям, не принадлежа-
щим подмножествам E*j. По мере увеличения числа
реализованных элементарных проверок tj<=T и обработ-
ки ид результатов R*j уменьшается мощность подмноже-
ства подозреваемых технических состояний объекта. По-
сле реализации всех элементарных проверок из множе-
57
ства Т выделяется некоторое подмножество Е*т подо-
зреваемых технических состояний, мощность которого
определяется глубиной диагноза, обеспечиваемой реали-
зуемым алгоритмом диагноза.
Подчеркнем, что подозреваемые технические состоя-
ния объекта можно выделить по известным результатам
любого физического эксперимента над объектом (а не
только по результатам элементарных проверок множе-
ства Т, входящего в алгоритм диагноза). Это обстоятель-
ство используется на практике тогда, когда не представ-
ляется возможным предварительно (до реализации про-
цесса диагноза) построить алгоритм диагноза. При этом
последовательно реализуют некоторые (в общем случае
назначаемые произвольно) элементарные проверки из
множества II и по получаемым их фактическим резуль-
татам вычисляют подмножества подозреваемых техни-
ческих состояний.
Такой подход обладает рядом недостатков и должен
рассматриваться как вынужденный. К числу этих недо-
статков относится невозможность оценить заранее длину
эксперимента, т. е. число элементарных проверок, реали-
зация которых потребуется для достижения глубины
диагноза, удовлетворительной в данных конкретных
условиях. Как следствие, вообще неизвестно, достижима
ли такая глубина диагноза. Кроме того, имеется «опас-
ность» реализации большого числа безрезультатных эле-
ментарных проверок, т. е. таких проверок, результаты
которых не позволяют уменьшить мощность множества
подозреваемых технических состояний, выделенного по
результатам ранее реализованных элементарных прове-
рок.
Алгоритм А1-5 решения прямой задачи диагноза по-
добно алгоритму А1-4 также требует наличия (или вы-
числения по алгоритму А1-3) строк таблицы функций
неисправностей и последующего однократного перебора
всех их клеток, что ограничивает область применения
этого алгоритма небольшими числами | S | возможных
неисправностей объекта диагноза. Дальнейшим шагом
на пути снижения вычислительных трудностей решения
прямых задач диагноза является отказ от использования
таблицы функций неисправностей и замена перебора
возможных технических состояний вычислением только
подозреваемых технических состояний непосредственно
по математической модели V исправного объекта при
58
по-прежнему известных результатах физического экспе-
римента над объектом. Методы, использующие такой
подход, будем называть методами вычисления подозре-
ваемых технических состояний объекта.
Применительно к процедурам обработки модели
исправного объекта диагноза часто более удобно гово-
рить не о технических состояниях
исправностях. Чтобы обеспечить
взаимно-однозначное соответст-
вие между элементами множества
Е возможных технических со-
стояний объекта и элементами
множества S его возможных не-
исправностей, будем отсутствие
неисправностей в объекте считать
«нулевой неисправностью» и обо-
значать ее символом s0. Для обо-
значения множества, содержа-
щего все действительные неис-
правности S,- объекта и его «нуле-
вую неисправность» s0, сохраним
символ S. Тогда вместо вычисле-
ния подмножеств Е\ и Е*т по-
дозреваемых технических состоя-
ний (среди которых может нахо-
диться исправное состояние) объ-
объекта, а о его не-
Рис. 1-14. Иллюстрация
задачи вычисления под-
множества подозревае-
мых неисправностей.
екта можно говорить о вычислении подмножеств S*j и
соответственно S*T его подозреваемых неисправностей.
Иллюстрацией такой постановки прямой задачи
диагноза является рис. 1-14. На этом рисунке показана
модель W, подаваемое па нее вводное воздействие а;
элементарной проверки л„ а также получаемый резуль-
тат ее обработки — подмножество S*, подозреваемых
неисправностей. Стрелка, изображенная справа, и сим-
волы над ней условно показывают, что обработка моде-
ли ведется с учетом известного фактического результата
R*i элементарной проверки л, при заданном множестве
5 (или О) неисправностей.
Когда множеством возможных неисправностей объек-
та диагноза является множество S его одиночных и
кратных неисправностей, вычислительные трудности,
а также трудности хранения информации остаются боль-
шими даже для методов вычисления подозреваемых
неисправностей, если эти методы требуют прямого пере-
59
числения (составления перечня) кратных неисправно-
стей. Причина заключается в том, что число подозревае-
мых кратных неисправностей для сложных многокомпо-
нентных объектов, как правило, очень велико. Когда
множеством возможных неисправностей объекта являет-
ся множество О его одиночных неисправностей, указан-
ные трудности проявляются в значительно меньшей сте-
пени, так как обычно | О | <С | S |. В этом случае говорят
о множествах О*, и О*г подозреваемых одиночных не-
исправностей.
Уменьшить объемы вычислений и объемы памяти,
требуемые при применении методов вычисления подозре-
ваемых неисправностей, когда кратные неисправности
являются возможными, можно на основе следующих со-
ображений.
Кратная неисправность, по определению, является
совокупностью одновременно существующих в объекте
нескольких одиночных его неисправностей. Результаты
диагноза технического состояния объекта (во всяком
случае, результаты поиска неисправностей) необходимы
в большинстве случаев для устранения обнаруженных
неисправностей. Процесс устранения кратной неисправ-
ности физически представляет собой совокупность опе-
раций по независимому устранению одиночных неисправ-
ностей, образующие эту кратную неисправность, поэтому
практической необходимости в представлении кратных
неисправностей как таковых нет. Действительно, любую
кратную неисправность всегда можно представить пе-
речнем образующих ее одиночных неисправностей, а лю-
бое подмножество кратных неисправностей—перечнем
всех входящих хотя бы в одну из них одиночных неис-
правностей. Перечень одиночных неисправностей, пред-
ставляющих подмножество или S*T подозреваемых
неисправностей объекта, будем обозначать O(S*,) или
соответственно O(S*T).
Таким образом, прямая задача диагноза может быть
решена также при задании исходных данных в виде ма-
тематической модели V исправного объекта диагноза и
множества О одиночных неисправностей ‘. При этом,
естественнно, необходимо наличие способа вычисления
1 Здесь также считаем, что множество О содержит «нулевую
одиночную неисправность» о0, соответствующую исправному состоя-
нию объекта диагноза.
60
подмножеств O(S*j) подозреваемых одиночных неис-
правностей по указанным исходным данным и по из-
вестным результатам /?*,• физического эксперимента над
объектом.
Выше рассматривались методы вычисления подозре-
ваемых неисправностей по известным результатам экспе-
римента над объектом, т. е. имелось в виду применение
этих методов при реализации процесса диагноза. Эти
методы, однако, можно применять также на этапе по-
строения алгоритмов диагноза для вычисления под-
множеств EjU неразличаемыд технических состояний, т. е.
получая решение той же прямой задачи диагноза, что
и по алгоритмам А1-3 и А1-4, но без построения строк
таблицы функций неисправностей. При этом вместо из-
вестных из физического эксперимента результатов /?*,
элементарных проверок следует рассматривать заданные
результаты RjU последних.
Покажем, как это сделать для всех а, возможных
результатов Rju, и=1, 2, .. ., a:i, элементарной проверки
л> Если возможные результаты RlU известны заранее,
то получение всех подмножеств EjU неразличаемых тех-
нических состояний сводится к а;-кратному применению
того или иного метода вычисления подозреваемых неис-
правностей. При каждом таком применении роль резуль-
тата R*, играет один из результатов RjU. Примером та-
кой ситуации является случай, когда результат R*j эле-
ментарной проверки я,- является малоразрядным двоич-
ным вектором и поэтому нетрудно перечислить все его
возможные значения. Если возможные' результаты Rju
элементарной проверки л3 заранее неизвестны, то можно
поступить следующим образом. Для определенности при-
мем, что возможные неисправности объекта заданы мно-
жеством S его одиночных и кратных неисправностей.
Прямым анализом (см. рис. 1-9) модели 'Р исправного
объекта определим результат Rj элементарной проверки
я,- и для этого результата вычислим подмножество S,
неразличаемых неисправностей (см. рис. 1-14). Затем
возьмем любую одну неисправность s,, не принадлежа-
щую вычисленному подмножеству Sj, «введем» ее в мо-
дель W и прямым анализом последней определим резуль-
тат R'j той же элементарной проверки я3-. После этого
вычислим подмножество S*j для результата Rij. Очеред-
ной цикл вычислений начинается с выбора некоторой
неисправности sb, не принадлежащей ни одному из под-
61
множеств S, или S’,-, и так далее до тех пор, пока не ока-
жется, что вычисленные подмножества неразличаемых
неисправностей содержат все возможные неисправности
множества S.
Подобную рекуррентную процедуру можно использо-
вать также в случае задания возможных неисправностей
объекта множеством О его одиночных неисправностей.
При этом, однако, необходимо учитывать, что одни и те
же одиночные неисправности могут входить в разные
подмножества OjU.
1-8. ОБРАТНЫЕ ЗАДАЧИ ДИАГНОЗА
Назовем обратными задачами диагноза задачи опре-
деления некоторого подмножества элементарных
проверок, различающих заданную пару (ei; е^) техниче-
ских состояний или пару (s,, S/,) неисправностей объекта,
т. е. таких элементарных проверок jtj, которые имеют
разные результаты и Rhj. Если речь идет о парах
(е, ец) или (s0, s^), где s0 — «нулевая неисправность»
объекта, то можно говорить о подмножестве Пой элемен-
тарных проверок, обнаруживающих техническое состоя-
ние бй или неисправность s^. Двумя крайними случаями
обратных задач диагноза являются задача определения
хотя бы одной различающей или обнаруживающей эле-
ментарной проверки и, с другой стороны, задача опре-
деления всех таких элементарных проверок. Необходи-
мость решения обратных задач диагноза возникает, как
правило, при построении алгоритмов диагноза.
Как и при рассмотрении в предыдущем параграфе
прямых задач диагноза, заданными являются математи-
ческая модель W исправного объекта, множество S воз-
можных неисправностей и множество П допустимых эле-
ментарных проверок. Примем, что модель Д’ позволяет
не только вычислять результат любой элементарной
проверки л, из П для любой неисправности из S, 1=
=0, 1, ..., |S|—1, т. е. решать прямую задачу анализа,
но также для любой неисправности s; вычислять значе-
ние а, воздействия некоторой элементарной проверки л;
по известному ее результату т. е. решать обратную
задачу анализа.
Начнем рассмотрение обратных задач диагноза с за-
дачи вычисления одного столбца таблицы функций не-
исправностей. Успешное решение этой задачи позволит
62
сократить объемы памяти для хранения информации
содержащейся в таблице функций неисправностей.
Построение столбца таблицы функций неисправно-
стей состоит в последовательном вычислении по модели
Чг с введенной в нее неисправностью результатов R‘:i
каждой элементарной проверки В результате бу-
дут получены |П| результатов элементарных прове-
рке. 1-15. Блок-схема алгоритма А1-6.
рок для всех /=1, 2, ..|П|. Это та же задача прямого
анализа модели Ч’, которая упоминалась в связи с по-
строением строки таблицы функций неисправностей
в предыдущем параграфе (см. рис. 1-9). Блок-схема
алгоритма А1-6 вычисления столбца i таблицы функций
неисправностей дана на рис. 1-15. Применение этого
алгоритма для каждого i=0, 1, .. ., |S|—1 позволяет
заполнить всю П-таблицу функций неисправностей.
63
Знание пары столбцов i и k таблицы функций неис-
правностей позволяет вычислить подмножество П,-. все?:
элементарных проверок, различающих технические со-
стояния е, и ek. Для этого достаточно выполнить после-
довательный просмотр и сравнение между собой пар ре-
зультатов и Rhj с постепенным формированием под-
множества Пгя из элементарных проверок яд для кото-
рые Блок-схема алгоритма А1-7, выполняюще-
Рис. 1-16. Блок-схема алгоритма А1-7.
го эти операции, приведена на рис. 1-16. Индексом /,
/=1, 2, ..., |П|, обозначен текущий номер пары клеток
столбцов i и k таблицы функций неисправностей, а за-
пись Tj-elltt означает, что в процессе работы алгоритма
элементарная проверка л> включается в состав элемен-
тов формируемого подмножества П^.
Решение обратной задачи диагноза последователь-
ным применением алгоритмов А1-6 и А1-7 требует для
фиксированной пары (е», ek) технических состояний
64
Рис. 1-17. Блок-схема алгорит-
ма А1-8.
2|П |-кратной обработки модели 'И исправного объекта
и |П| сравнений результатов элементарных проверок.
Это, по существу, полный перебор всех возможностей,
следствием которого является практическая непримени-
мость этого метода решения обратной задачи диагноза
для сколько-нибудь больших чисел |П| допустимых эле-
ментарных проверок.
Как указывалось ранее, алгоритм диагноза должен
различать только те технические состояния, которые
принадлежат разным подмножествам Ev заданного раз-
биения множества Е возможных технических состояний
объекта. Вычисление под-
множеств Пгй, содержа-
щих все различающие
элементарные проверки,
для всех пар (щ, eh) тех-
нических состояний из
разных подмножеств Еу
необходимо при построе-
нии оптимальных алго-
ритмов диагноза. Если от-
казаться от оптимизации
алгоритмов диагноза, то
достаточно для каждой
пары (вг, вй) требующих
различения технических
состояний определить хо-
тя бы одну различающую
их элементарную про-
верку.
Эту упрощенную об-
ратную задачу диагноза
можно решить при помо-
щи алгоритма, отличаю-
щегося от алгоритма А1-7
тем, что его работа пре-
кращается, как только бу-
дет получено первое нера-
венство Rij^=Ehj. При
этом также предполагает-
ся наличие (или вычисление по алгоритму А1-6) столб-
цов i и k таблицы функций неисправностей.
Решить обратную задачу диагноза можно без пред-
варительного построения и запоминания столбцов i и k
5—358 65
дель неисправности Sj и
Рис. 1-18. Иллюстрация пря-
мой задачи анализа с ис-
пользованием двух экземп-
ляров 4r(i) и 'Г/а) модели.
таблицы функций неисправностей, если воспользоваться
алгоритмом А1-8, блок-схема которого приведена на
рис. 1-17. В основе этого алгоритма лежит операция
двукратного прямого анализа модели Чг для каждой
элементарной проверки л,: один раз при введенной в мо-
второй раз — неисправности sh.
Применение алгоритма А1-8
сокращает объемы памяти, но
не уменьшает объемов вычи-
слений, которые по-прежнему
имеют характер перебора всех
возможностей (при получении
подмножеств П,/£ всех разли-
чающих элементарных прове-
рок) или их части (при полу-
чении одной первой в порядке
перебора элементарной про-
верки, различающей техниче-
ские состояния Cj И 6k). Эконо-
мия времени, затрачиваемого на вычисления, может
быть получена при использовании нескольких, например
двух, экземпляров 4f(ij и W(2j модели исправного объекта
(рис. 1-18). Это позволяет вычислять результаты У?1, и
Rki не последовательно во времени, как в алгоритме
А1-8, а параллельно.
Характерной особенностью рассмотренного выше под-
хода к решению обратных задач диагноза и реализую-
щих этот подход алгоритмов является перебор допусти-
мых элементарных проверок из множества П с целью
выделения различающих элементарных проверок. Сни-
жения вычислительных трудностей при решении обрат-
ных задач диагноза можно достичь путем замены пере-
бора допустимых элементарных проверок вычислением
только различающих (или обнаруживающих) элементар-
ных проверок непосредственно по математической моде-
ли 'Р' исправного объекта. Методы, использующие такой
подход, будем называть методами вычисления разли-
чающих элементарных проверок объекта.
Многие методы вычисления различающих элементар-
ных проверок базируются на понятии так называемых
существенных путей в структуре объекта диагноза. При-
ведем физическую трактовку этого понятия.
Пусть в физическом объекте диагноза имеется неко-
торая одиночная неисправность гд е О, i=l, 2, . .., |О|.
66
Из очевидных соображений следует, что одиночная фи-
зическая неисправность может быть обнаружена элемен-
тарной проверкой л3еП при выполнении двух следую-
щих условий.
Первое условие состоит в том, что возникшая неис-
правность должна проявиться, т. е. вызвать появление
некоторого значения хотя бы одного входного, внутрен-
него или выходного сигнала объекта, отличного от зна-
чения, которое этот сигнал имел бы в исправном объек-
те. Назовем это условие условием проявления неисправ-
ности.
Как возникновение, так и проявление неисправности
происходят в пространстве и во времени. Место и мо-
мент времени проявления неисправности не всегда сов-
падают соответственно с местом и моментом времени ее
возникновения, хотя, как правило, и являются близкими.
Простым с точки зрения диагноза технического состоя-
ния объекта является случай, когда места, а также мо-
менты проявления и возникновения неисправностей сов-
падают. В противном случае задача диагноза становится
более трудной.
Второе условие обнаружения одиночной неисправно-
сти состоит в том, что вызванные ее проявлением значе-
ния сигналов должны быть переданы на одну или не-
сколько контрольных точек объекта, т. е. должны вы-
звать появление значений ответов объекта, отличных от
их значений в исправном состоянии объекта. Это значит,
что при подаче на объект воздействия а, элементарной
проверки л,, обнаруживающей неисправность о,-, в объек-
те должны создаться такие условия (т. е. входные, вну-
тренние и выходные переменные объекта должны при-
нять такие последовательности значений), при которых
от места проявления неисправности до какого-либо вы-
хода у объекта образуется один или несколько каналов
передачи указанных значений сигналов. Такие каналы
будем называть существенными (относительно неисправ-
ности ог и относительно элементарной проверки л,) пу-
тями. Если существенный путь один, то он называется
простым-, в противном случае — сложным. Условие обра-
зования существенного пути назовем условием транс-
портировки неисправности в контрольные точки.
С точки зрения структуры объекта существенный
путь представляет собой совокупность компонент и свя-
зей. Не следует считать, что передача значений сигналов
5'
67
по тому или иному существенному пути должна проис-
ходить сразу (без перерывов во времени) через весь
существенный путь. Последний может состоять из по-
следовательных участков, по каждому из которых пере-
даются изменения значений сигналов в свой момент
времени, отличный от таких моментов времени для дру-
гих участков.
Аналогично сказанному о соотношении мест и момен-
тов возникновения и проявления неисправности можно
говорить о соотношении мест и моментов проявления и
обнаружения неисправности. Если рассматриваемая не-
исправность проявляется на выходе объекта, то места
и моменты ее проявления и ее обнаружения совпадают.
В других случаях они всегда разнесены в пространстве
и могут оказаться разнесенными во времени.
Таким образом, необходимым и достаточным усло-
вием обнаружения одиночной неисправности является
удовлетворение как условия ее проявления, так и усло-
вия ее транспортировки, или, другими словами, данная
неисправность не обнаруживается, если не соблюдено
либо условие ее проявления, либо условие ее транспор-
тировки, либо, наконец, оба эти условия вместе.
Рисунок 1-19 является иллюстрацией условий обна-
ружения одиночной неисправности о;. Прямоугольники
представляют объект диагноза, кружки — место возмож-
ного проявления неисправности о,-, волнистые линии —
существенные пути. Точка в кружке означает, что неис-
правность проявляется. Только в первом случае (7?%#=
У=7?,) неисправность обнаруживается, так как она
проявляется, и имеется существенный путь.
Остановимся на использовании понятия существен-
ных путей для определения условий различения одиноч-
ных неисправностей. По определению необходимым и
достаточным условием различения элементарной провер-
кой л,- двух неисправностей о,- и oh является наличие
(при подаче на объект воздействия а,- этой элементарной
проверки) хотя бы одного выхода, значение выходной
функции которого при наличии в объекте неисправности
Of отличается от значения этой функции при наличии
неисправности В терминах существенных путей это
значит, что либо одна из неисправностей пары (о,, о,()
обнаруживается, а другая не обнаруживается, либо обе
неисправности обнаруживаются, но в разных контроль-
ных точках, например yi и у2, либо, наконец, обе они
68
обнаруживаются в одних и тех же контрольных точках у,
но дают разные значения результатов R\i и Rkj.
Первый случай соответствует тому, что для одной не-
исправности имеет место ситуация, отображенная на
первой слева схеме рис. 1-19, а для другой неисправно-
сти— одна из ситуаций, показанных на остальных трех
схемах этого рисунка. Два же других случая иллюстри-
Рис. 1-19. Иллюстрация условий обнаружения одиночной неисправ-
ности.
руются первыми слева двумя схемами рис. 1-20 соответ-
ственно. Третья схема на рис. 1-20 представляет случай,
когда обе неисправности о, и од обнаруживаются в одних
и тех же контрольных точках и дают одинаковые зна-
чения результатов и Rhj. Обозначения на рис. 1-20
аналогичны обозначениям, принятым для рис. 1-19.
Изложим последовательность операций при вычисле-
нии элементарной проверки, обнаруживающей некото-
рую одиночную неисправность о». Прежде всего в модели
Д исправного объекта задаются условия проявления не-
исправности о,. Затем осуществляются попытки органи-
зовать простой или сложный существенный путь от ме-
ста проявления неисправности О; до, по крайней мере,
одной контрольной точки, т. е. задать условия транспор-
тировки этой неисправности. Задание условий прояв-
ления и условий транспортировки неисправности сводит-
69
ся к заданию определенных, не противоречащих друг
другу значений (совокупностей значений, последователь-
ностей значений) некоторых внутренних переменных и
выходных функций, а также, возможно, входных пере-
менных модели V. При этом используются прямые зави-
симости между указанными переменными и функциями,
т. е решается частичная прямая задача анализа моде-
Рис. 1 20. Иллюстрация условий различения
одиночных неисправностей ot и o,t.
ли V. Эта задача отличается от упоминавшейся выше
прямой задачи анализа тем, что заданными могут быть
значения некоторых входных и некоторых внутренних
переменных, а вычислению подлежат в общем случае
значения не всех, а только некоторых выходных функций
модели. Эти выходные функции определяют состав кон-
трольных точек {у}, искомой различающей элементарной
проверки я,-, а их значения — результат /?% последней.
Следующий этап решения задачи заключается в вы-
числении воздействия а,- искомой элементарной проверки
по заданным или вычисленным на предыдущем этапе
значениям внутренних переменных и выходных функций.
При этом используются обратные зависимости между
выходными функциями, внутренними и входными пере-
менными модели, т. е. решается частичная обратная за-
70
дача анализа последней. Эта задача отличается от об-
ратной задачи анализа (см. начало этого параграфа) тем,
что заданными могут быть значения не только выходных
функций, но также некоторые внутренних переменных,
а вычислению подлежат в общем случае значения не
всех, а только некоторых входных переменных модели.
Обычно имеющая место неоднозначность обратных зави-
симостей порождает ряд допустимых вариантов задания
непротиворечащих друг другу значений переменных и
функций. Воздействие а,- искомой элементарной провер-
ки формируется как последовательность во времени t
значений входных (ЛД, и, возможно, внутренних (У,)
переменных, полученных в том или ином допустимом
варианте.
Изложенные операции позволяют*вычислить элемен-
тарную проверку, обнаруживающую одиночную неис-
правность. Аналогично поступают при вычислении эле-
ментарной проверки, различающей пару (о<, Ой) одиноч-
ных неисправностей. Отличие имеется только на первом
этапе вычислений при задании условий различения не-
исправностей. Теперь значения внутренних переменных
и выходных функций, а также, возможно, входных пере-
менных должны задаваться так, чтобы условия обнару-
жения (проявления и транспортировки) неисправностей
Oi и Ой были разными (см. рис. 1-19 и 1-20).
В общем случае в объекте диагноза для некоторых
неисправностей может не найтись ни одного входного
воздействия, обеспечивающего условия образования су-
щественных путей. Отсюда следует необходимость орга-
низации упорядоченного перебора всех возможных вари-
антов образования существенных путей на первом этапе
рассмотренных выше процедур, а также всех возможных
входных воздействий на втором их этапе.
При построении любой обнаруживающей или разли-
чающей элементарной проверки указанный перебор об-
рывается, как только будет получена такая проверка.
При построении же подмножеств Г1,й всех таких элемен-
тарных проверок перебор должен доводиться до конца.
Даже в первом случае объемы вычислений могут ока-
заться значительными. В этом заключается недостаток
рассматриваемого метода вычисления различающих эле-
ментарных проверок. Особенно заметен этот недостаток
при применении метода к дискретным объектам с па-
мя гью.
71
В ряде случаев сокращения объема вычислений мож-
но достичь, если чередовать решения обратной задачи
с решениями прямой задачи диагноза. При этом снача-
ла, используя описанные выше
® °i 4е
В)
5)
Рис. 1-21. Иллюстрация задач построе-
ния существенных путей для обнаруже-
ния одиночной неисправности и вычисле-
ния подмножества обнаруживаемых оди-
ночных неисправностей.
пути решения частичной
прямой и частичной
обратной задач ана-
лиза модели V объ-
екта, следует вычи-
слить элементарную
проверку Лу, обнару-
живающую некото-
рую неисправность
или различающую
некоторую пару не-
исправностей. После
этого следует поэле-
ментарней проверке
лу сформировать
«расширенную» эле-
ментарную проверку
л', путем некоторого
(например, произ-
вольного) доопреде-
ления значений тех
входных и, возможно
внутренних перемен-
ных, которые не
вошли в вычислен-
ное воздействие ау
проверки лу, а также
путем включения в
состав контрольных
точек проверки л'у
всех выходов объек-
та. Наконец, следует
решить прямую за-
дачу диагноза, т. е.
все пары неисправно-
определить все неисправности или
стей, обнаруживаемые или, соответственно, различаемые
элементарной проверкой л',. После этого надлежит по-
вторить цикл вычислений, выбрав новую неисправность
или новую пару неисправностей из числа не обнаружи-
ваемых или не различаемых элементарной проверкой л',
и т. д.
72
Последовательность операций одного такого цикла
при обнаружении одиночной неисправности о4 иллюстри-
руется рис. 1-21. На этом рисунке последовательно пред-
ставлены: 1) «ввод» неисправности о< в модель Т ис-
правного объекта диагноза; 2) задание условий
проявления этой неисправности; 3) образование сущест-
венного пути (т. е. задание условий транспортировки
неисправности) и определение состава контрольных то
чек {у}3; 4) вычисление вводного воздействия ад 5) об-
разование «расширенной» элементарной проверки л/,
(а'д {у}',) и вычисление ее результата 6) наконец,
определение подмножества O'j обнаруживаемых (эле-
ментарной проверкой л'.,) одиночных неисправностей.
Обозначения на рис. 1-21 аналогичны обозначениям, ис-
пользованным на предыдущих рисунках.
Методы вычисления обнаруживающих элементарных
проверок через организацию существенных путей нашли
применение для дискретных (комбинационных и после-
довательностных) объектов. В ряде методов использу-
ется аналитическая модель F исправного объекта 1 в виде
той или иной формы представления булевых (для дво-
ичных дискретных объектов) функций. Для вычисления
воздействий а,- искомых элементарных проверок при этом
применяются различные методы обработки модели F,
в том числе методы вычисления булевых производных.
Характерная особенность методов, работающих с ана-
литической моделью F, состоит в том, что условия обра-
зования и реализации существенных путей формулиру-
ются непосредственно в терминах воздействий искомых
обнаруживающих (или различающих) элементарных
проверок. Операции по обработке прямых и обратных
зависимостей между входными и внутренними перемен-
ными и выходными функциями модели объекта заменя-
ются некоторыми другими операциями по выбору или
вычислению указанных воздействий. Такая замена будет
эффективной, если сложность и число этих других опе-
раций будут ниже сложности и числа операций над пря-
мыми и обратными зависимостями между переменными
и функциями модели объекта. При этом, естественно,
возникает ряд специфических задач. К их числу отно-
сится задача установления соответствия между неис-
правностями компонент объекта и значениями аргумен-
1 Для обозначения аналитических моделей будем пользоваться
символом F вместо общего символа Ч*-.
73
тов функций, представляющих модель F. К этой задаче
тесно примыкает задача расшифровки результатов диаг-
ноза.
Применение понятия существенных путей для вычис-
ления элементарных проверок, обнаруживающих или
различающих кратные неисправности, также возможно,
но при этом возникают значительные вычислительные
трудности.
1-9. АЛГОРИТМЫ ДИАГНОЗА
Алгоритм диагноза задает совокупность элементар-
ных проверок, последовательность (или последователь-
ности) их реализации и правила обработки результатов
реализуемых элементарных проверок с целью получения
результатов диагноза.
Совокупность входящих в алгоритм диагноза элемен-
тарных проверок мы ранее обозначили символом Т. Для
обозначения любой (некоторой) элементарной проверки
из совокупности Т сохраним символ
Чтобы более наглядно представить классификацию
алгоритмов диагноза и характерные целевые функции их
оптимизации, рассмотрим некоторые вопросы представ-
ления алгоритмов диагноза в виде графов.
Результаты любой элементарной проверки могут быть
использованы как признаки разбиения множества Е тех-
нических состояний объекта или подмножеств этого мно-
жества на классы. Об этом шла речь в § 1-7 (рис. 1-11)
при рассмотрении прямых задач диагноза. Используя
такую трактовку элементарных проверок и их результа-
тов, любой алгоритм диагноза можно представить неко-
торым ориентированным графом. Здесь мы ограничимся
случаем, когда граф, представляющий алгоритм диагно-
за, является деревом.
Дерево имеет вершины двух типов: вершины, из ко-
торых исходит хотя бы одна дуга, и вершины, из кото-
рых не исходит ни одной дуги. Пример дерева дан на
рис. 1-22, где вершины первого типа представлены за-
черненными кружками, а вершины второго типа — свет-
лыми кружками. В дереве имеется единственная верши-
на первого типа, в которую не заходит ни одна дуга.
Эта вершина называется начальной или корнем дерева
(на рис. 1-22 начальная вершина отмечена символами
/о, Е). Вершины, из которых не исходит ни одной дуги,
называются конечными или висячими вершинами.
74
Остальные вершины дерева называются внутренними.
В каждую вершину дерева, кроме его корня, заходит
только одна дуга. В дереве нет контуров. Ради простоты
стрелки на дугах дерева указывать не будем.
Рангом вершины дерева называется число дуг пути,
начинающегося в начальной вершине t0 и заканчиваю-
щегося в рассматриваемой вершине. Минимальным ран-
гом р0 дерева является ранг, для которого существует
хотя бы одна висячая вершина и не существует ни одной
Рис. 1-22. Пример дерева, представляющего алгоритм диагноза,
висячей вершины ранга меньше р0. Максимальным ран-
гом рм дерева является ранг, для которого существует
хотя бы одна вершина ранга рм не существует ни одной
вершины ранга больше рм.
Будем внутренние и висячие вершины дерева нуме-
ровать (рис. 1-22) парой чисел в скобках (р, и), где р
есть ранг вершины, а о — ее порядковый (например, сле-
ва направо в заданном графическом представлении де-
рева) номер среди всех вершин одного и того же ранга.
Начальную вершину будем обозначать парой (0, 0).
75
Начальной и внутренним вершинам дерева сопоста-
вим элементарные проверки множества Т. Дугам дерева,
исходящим из некоторой (начальной или внутренней)
его вершины, сопоставим возможные результаты провер-
ки, представляемой этой вершиной. Кроме того, началь-
ной вершине дерева поставим в соответствие множество
Е возможных технических состояний объекта, а внутрен-
ним и висячим вершинам — подмножества технических
состояний, получаемые как классы разбиений по резуль-
татам соответствующих элементарных проверок. Элемен-
тарную проверку и подмножество технических состоя-
ний, сопоставленные вершине (р, о) дерева, будем обо-
значать символами / , и Е соответственно. Множе-
ство элементарных проверок t? в, сопоставленных на-
чальной и всем внутренним вершинам дерева, обозначим
символом Тя. Из правил построения дерева следует, что
объединение всех подмножеств технических состояний,
сопоставленных висячим вершинам дерева, есть множе-
ство Е возможных технических состояний объекта. Каж-
дому пути в дереве соответствует последовательность
элементарных проверок, сопоставленных вершинам пути.
Обратимся к рис. 1-22 и рассмотрим, как дерево
представляет алгоритм диагноза. Начальной вершине
дерева сопоставлены элементарная проверка t0 и мно-
жество Е всех возможных технических состояний объек-
та диагноза. Элементарная проверка t0 имеет три воз-
можных результата, т. е. о(/0)=3, и тем самым разбива-
ет множество Е на три подмножества £1, i, £1,2 и £1, 3 не
различаемых этой проверкой технических состояний.
Первые два из этих подмножеств соответствуют внутрен-
ним вершинам (1,1) и (1,2) и поэтому подлежат даль-
нейшему разбиению элементарными проверками tt t и
tit 2 соответственно. Третье подмножество Ei 3 соответ-
ствует висячей вершине (1, 3), и поэтому разбиение его
на подмножества алгоритмом диагноза не предусмотре-
но. Далее, элементарная проверка Л, 1, у которой a(tt, 1) =
=2, разбивает подмножество £i,i на два подмножества
£2,1 и £2,2 не различаемых этой проверкой технических
состояний. Одно из них, а именно £2, ь представлено
внутренней вершиной (2,1), а второе £2,2 — висячей вер-
шиной (2,2). Аналогично можно рассмотреть любую
другую внутреннюю вершину (р, о) дерева, соответст-
вующие этой вершине элементарную проверку и под-
76
множество Ера, а также разбиение последнего на
a(tp д) подмножеств.
Будем пока считать, что работа алгоритма диагноза
прекращается (т. е. выдаются результаты диагноза), как
только в процессе реализации входящих в алгоритм эле-
ментарных проверок будет достигнута висячая вершина
дерева. Фактическое техническое состояние е* объекта
диагноза принадлежит подмножеству, сопоставленному
достигнутой висячей вершине.
В дереве представлены все возможные реализации
алгоритма диагноза и соответствующие им результаты
диагноза. Каждой конкретной реализации алгоритма
диагноза соответствует единственный путь в дереве, т. е.
единственная последовательность реализации элементар-
ных проверок алгоритма. Например, если фактическое
техническое состояние е* принадлежит подмножеству
£4,2 на рис. 1-22, то последовательность реализации эле-
ментарных проверок будет t0, Л, 2, /2,3, (з, з-
Рассмотрим некоторый ненулевой ранг р дерева.
В общем случае дерево может иметь несколько внутрен-
них вершин ранга р, например две вершины (р, Oi) и
(р, 02) • Это значит, что возможны, по крайней мере, две
разные последовательности реализации элементарных
проверок, различающиеся тем, что у одной из них на
(р+1)-м месте находится элементарная проверка tp ,
а у другой —элементарная проверка tp о/ Обе эти
проверки могут являться как одной и той же элементар-
ной проверкой tj множества Т, так и разными элемен-
тарными проверками последнего
Если для каждого ранга дерева выполняется усло-
вие, состоящее в том, что всем внутренним вершинам
этого ранга сопоставлена одна и та же элементарная
проверка из множества Т, то алгоритм диагноза, пред-
ставляемый таким деревом, называется безусловным.
Это соответствует заданию одной фиксированной (жест-
кой) последовательности реализации элементарных про-
верок из множества Т, не зависящей от фактического
технического состояния объекта. Другими словами,
в безусловных алгоритмах диагноза выбор или назначе-
ние очередной элементарной проверки в последователь-
ности их реализации не зависит от результатов преды-
дущих уже реализованных элементарных проверок.
77
Если же в дереве найдется хотя бы один ранг с не-
сколькими внутренними вершинами, которым сопостав-
лены разные элементарные проверки из множества Т, то
алгоритм диагноза, представляемый этим деревом, назы-
вается условным. Это соответствует тому, что имеется
несколько разных реализаций алгоритма диагноза, зави-
сящих от фактического технического состояния объекта
и различающихся составами реализуемых элементарных
проверок или последовательностями их реализации. Дру-
гими словами, в условных алгоритмах диагноза выбор
или назначение некоторых или всех (кроме /0) эле-
ментарных проверок производится с учетом резуль-
татов предыдущей уже реализованной элементарной
проверки.
Достоинством безусловных алгоритмов является от
носительная простота их представления в средствах ди-
агноза: требуется .хранить лишь состав элементарных про-
верок множества Тп и единственную последовательность
их реализации. Для условных же алгоритмов диагноза
необходимо хранить кроме состава элементарных прове-
рок множества Тд все признаки безусловны^ и условных
переходов от данной элементарной проверки к следую
щей, т. е. хранить не одну, а несколько последовательно-
стей реализации элементарных проверок из множества
Тп. Такое усложнение представления условных алгорит-
мов диагноза по сравнению с безусловными позволяет,
однако, получать более экономичные процедуры диагно-
за благодаря выбору реализуемых элементарных прове-
рок с учетом фактического технического состояния объ-
екта.
Безусловные алгоритмы диагноза можно классифици-
ровать также по характеру их остановки, что, по сущест-
ву, определяет способ реализации алгоритма. Если вы-
дача результатов диагноза предусмотрена только после
реализации всех элементарных проверок алгоритма, то
последний является алгоритмом с безусловной останов-
кой. Таким алгоритмам соответствуют деревья, у кото-
рых все висячие вершины имеют один и тот же ранг.
Во многих случаях фактическое техническое состоя-
ние объекта может быть определено с требуемой глуби-
ной диагноза прежде, чем будут реализованы все эле-
ментарные проверки алгоритма диагноза. Безусловные
алгоритмы, у которых предусмотрена возможность выда-
чи результатов диагноза после реализации каждой эле-
78
ментарной проверки, называются алгоритмами с услов-
ной остановкой. Характерным для деревьев, представ-
ляющих алгоритмы с условной остановкой, является
наличие не менее двух висячих вершин, ранги которых
различны. Заметим, что все условные алгоритмы диагно-
за по определению являются алгоритмами с условной
остановкой. В литературе в ряде случаев алгоритмы
с безусловной остановкой называют комбинационными
(комбинаторными), а- с ус-
ловнои остановкой — после-
довательными.
Рассмотренная класси-
фикация алгоритмов диагно-
за представлена на рис. 1-23.
Все указанные виды ал-
горитмов диагноза находят
применение в системах тес-
тового диагноза. В системах
функционального диагноза
Алгоритмы
диагноза.
Рис. 1-23. Классификация алго
ритмов диагноза.
последовательность реализа-
ции элементарных проверок
алгоритма диагноза опреде-
ляется рабочим алгоритмом функционирования объекта.
В большинстве случаев в таких системах используются
алгоритмы диагноза с условной остановкой в связи с не-
обходимостью «немедленного» определения неисправного
состояния объекта. Условные алгоритмы диагноза можно
использовать тогда, когда имеется возможность органи-
зовать выборочную реализацию элементарных проверок
с учетом их результатов. В системах функционального
диагноза это, в частности, можно сделать тогда, когда
элементарные проверки множества Т различаются толь-
ко составами контрольных точек. Заметим, что в суще-
ствующих системах централизованного контроля в такой
ситуации обычно реализуются безусловные алгоритмы
проверки правильности функционирования объекта.
В предыдущем тексте книги результаты элементар-
ных проверок л;еП трактовались как признаки разбие-
ний на классы множеств (подмножеств) либо техниче-
ских состояний, либо неисправностей объекта Для алго-
ритмов поиска неисправностей с практической точки
зрения было бы удобно при диагнозе получать не классы
технических состояний или неисправностей, а классы
компонент (в том числе связей) объекта. Об этом шла
79
речь в § 1-6 этой главы при обсуждении способов зада-
ния глубины диагноза. Такой подход в принципе всегда
возможен, хотя и не всегда целесообразен.
Рассмотрим простейший случай, когда неисправной
может быть только одна компонента объекта, а резуль-
таты элементарных проверок могут принимать
только два значения. Последнее условие соответствует
рассмотрению двоичной математической модели объекта
диагноза (см. § 1-6).
Пусть 91 — множество компонент объекта. Каждой
элементарной проверке чт/ можно сопоставить совокуп-
ность 91/ проверяемых и совокупность 91/ непроверяемых,
или, как иногда говорят, охватываемых и неохватываемых
ею компонент. Очевидно, 91/ (J 91/=91. Компонента?), про-
веряется элементарной проверкой чу/, т. е. ?]/£91/, если
результат проверки зависит от технического состояния
этой компоненты. Иными словами, проверяемыми явля-
ются, очевидно, те компоненты, неисправности которых
обнаруживаются соответствующей элементарной провер-
кой. В противном случае компоненты не проверяются
данной элементарной проверкой. Таким образом, поло-
жительный результат R, элементарной проверки л,- вы-
деляет класс непроверяемых, а отрицательный ее резуль-
тат R'j — класс проверяемых компонент. Действительно,
в первом случае все проверяемые компоненты исправны
и поэтому могут быть исключены из дальнейшего рас-
смотрения, а во втором — неисправна одна из проверяе-
мых компонент.
Распространение рассмотренного подхода на случай
кратных неисправностей не вызывает никаких трудно-
стей тогда, когда возможна покомпонентная или, как
иногда говорят, поэлементная проверка объекта. При
этом каждая допустимая элементарная проверка из мно-
жества II проверяет техническое состояние только одной
«своей» компоненты объекта В общем же случае при
кратных неисправностях необходимо рассматривать раз-
биения не множества одиночных компонент, а разбие-
ния множества их подмножеств, содержащих по одной,
две, три и т. д. компоненты. Самым общим является слу-
чай, когда компоненты объекта для проверки их техни-
ческого состояния требуют нескольких элементарных
проверок. Формально в этом случае следует рассматри-
вать разбиения множества, элементами которого явля-
80
ются пары «компонента — ее неисправность» (при оди-
ночных неисправностях) или даже подмножества из
одной, двух, трех и т. д. таких пар (при кратных неис-
правностях). Указанные множества являются множест-
вами технических состояний объекта (точнее, возможных
его неисправностей).
Остановимся теперь на целевые функциях оптимиза-
ции алгоритмов диагноза.
Реализация любой элементарной проверки
требует определенных затрат времени, материальных и
энергетических ресурсов, человеческих усилий и т. п. Эти
затраты необходимы для выработки и подачи воздейст-
вия а, и для приема, измерения и анализа ответа
на это воздействие. Будем называть те или иные учи-
тываемые при конкретном рассмотрении затраты ценой
элементарной проверки и обозначать их с, или с (л.,),
c(tj). В постановках задач построения оптимальных
алгоритмов диагноза цены элементарных проверок могут
приниматься как одинаковыми для всех элементарных
проверок множества П, так и разными. В первом случае
для простоты обычно принимают с3 = 1, а во втором
(предполагая, что реализация любой элементарной про-
верки требует затрат) G>0 для всех /=1, 2, ..., |П|.
Пусть каждому техническому состоянию е^Е, i=l,
2, . . ., |Б|, объекта диагноза приписано некоторое поло-
жительное число pt или, в ином обозначении, p(e-i), на-
зываемое весом технического состояния е* и определяю-
щее «значимость» состояния ei среди остальных состояний
множества Е. Подобно ценам элементарных прове-
рок, веса состояний могут приниматься как одинаковы-
ми для всех состояний множества Е, так и разными. Ха-
рактерным является случай, когда весом технического
состояния является вероятность, с которой объект диаг-
ноза может находиться в этом техническом состоянии.
При этом 0<р(е1)<1 и %р(е1)=1.
eiGE
В любом алгоритме диагноза выделение подмножест-
ва технических состояний, содержащего фактическое со-
стояние и сопоставленного висячей вершине дерева, осу-
ществляется путем реализации одной или нескольких
элементарных проверок Е<=Т. Обозначим символом с (t0,
е{) сумму цен элементарных проверок, реализация кото-
рых в предусмотренной алгоритмом диагноза последова-
6—358
81
тельности позволяет выделить подмножество техниче-
ских состояний, содержащее состояние е,. В приведенном
обозначении символом t0 названа элементарная провер-
ка, первая в последовательности их реализации.
Тогда в качестве характеристики качества алгоритма
естественно принять средневзвешенные (средние) затра-
ты на выделение одного состояния объекта, т. е. функ-
цию
С(/о, £)= е*)р(ф)- (1-9)
Будем говорить, что функция (1-9) задает цену алго-
ритма диагноза.
Функция (1-9) часто используется как целевая функ-
ция оптимизации алгоритмов диагноза. Она позволяет
оценивать качество алгоритмов диагноза любого вида
(безусловных, условных, с безусловной и условной оста-
новкой) при неодинаковых и одинаковых ценах элемен-
тарных проверок, неодинаковых и одинаковых весах тех-
нических состояний объекта диагноза.
При одинаковых весах технических состояний, когда
р(вг) = 1/|£| для всех е^Е, вместо (1-9) получаем бо-
лее простое выражение:
С (/„, £) = -|4|- У] с(/„, ег). (1-10)
При одинаковых ценах элементарных проверок вме-
сто цены алгоритма диагноза говорят о длине алгоритма,
понимая под этим термином среднее число L(tQ, Е) эле-
ментарных проверок, реализация которых необходима
для выделения одного технического состояния.
В безусловных алгоритмах диагноза с безусловной
остановкой последовательность реализации элементар-
ных проверок единственна, причем число элементарных
проверок в этой последовательности равно |Т|. Поэтому
при одинаковых ценах элементарных проверок С(/о, щ) =
= |Т| для каждого е4, т. е.
2 с {t0, е<) = |£| |7'|- Тогда из (1-10) следует:
L(t0,E) = \T\, (1-11)
т. е. длина алгоритма диагноза с безусловной останов-
кой при одинаковых ценах элементарных проверок и
82
одинаковы^ весах технических состояний объекта равна
числу |7| элементарных проверок этого алгоритма.
Таким образом, задача построения оптимального
алгоритма диагноза состоит в выборе такого множест-
ва элементарных проверок и таких последователь-
ностей их реализации, которые обеспечивают получение
минимума целевой функции (1-9).
В основе методов оптимизации алгоритмов диагноза
лежат либо процедуры полного перебора всех возмож-
ных вариантов решений, либо процедуры отсеивания ва-
риантов, заведомо не дающих оптимального решения,
либо, наконец, процедуры улучшения исходного вариан-
та, представляющего в общем случае неоптимальное
решение. В процедурах построения оптимальных алго-
ритмов диагноза нашли применение методы обработки
таблиц покрытий, динамическое прЯ-раммирование, ме-
тод ветвей и границ, различные градиентные методы
и др. Все эти методы требуют просмотра большего или
меньшего числа вариантов решений.
Просмотр и обработка большого числа вариантов
решений при построении оптимальные алгоритмов диаг-
ноза часто сопряжены с недопустимо большими затра-
тами времени или памяти вычислительных средств. Вы-
ходом из этого положения является применение много-
шаговых процедур получения приближенных решений
(процедур построения оптимизированных алгоритмов
диагноза), в которых из числа возможных на каждом
шаге частичных решений выбирается одно, лучшее
в смысле экстремума некоторой выбранной или назна-
ченной функции предпочтения.
1-10. СПОСОБЫ И СРЕДСТВА РЕАЛИЗАЦИИ АЛГОРИТМОВ
ДИАГНОЗА
Различают аппаратурный, программный и программ-
но-аппаратурный способы реализации алгоритмов тесто-
вого и функционального диагноза.
Как показывает название аппаратурного способа ди-
агноза, средствами его реализации является аппаратура
(аппаратурные средства диагноза). Аппаратурные сред-
ства диагноза, выполненные конструктивно независимо
от объекта диагноза и подключаемые к нему только при
осуществлении процесса диагноза, называют внешними
аппаратурными средствами диагноза. Если же аппара-
6* 83
турные средства составляют с объектом диагноза конст-
руктивно и, возможно, функционально единое целое, то
говорят о встроенных аппаратурных средствах диагноза.
При реализации алгоритмов тестового диагноза аппа-
ратурным способом чаще всего используются внешние
аппаратурные средства. Внешние аппаратурные средст-
ва диагноза всегда необходимы на этапе производства
объектов, а также при ремонте, когда ни встроенные ап-
паратурные, ни программные средства (если даже они
предусмотрены) еще не работают и сами требуют диаг-
ноза цх технического состояния. Во многих случаях при-
менение внешних аппаратурных средств необходимо так-
же на этапе хранения сложных объектов. Встроенные
аппаратурные средства диагноза нашли наиболее широ-
кое применение при реализации аппаратурным способом
алгоритмов функционального диагноза. Примером
встроенных аппаратурных средств могут служить схемы
контроля по модулю, широко используемые при орга-
низации процессов функционального диагноза в вычис-
лительных машинах.
Внешние аппаратурные средства диагноза могут быть
ручными, автоматизированными и автоматическими.
Ручные средства, как правило, выполняются специали-
зированными, т. е. пригодными для диагноза техниче-
ского состояния одного конкретного объекта. Главный
недостаток ручных средств состоит в отсутствии гаран-
тии получения объективны^ результатов диагноза, осо-
бенно при большом числе повторяющихся однообразных
элементарных проверок. Кроме того, производительность
труда на операциях диагноза при этом очень низка. От
этих недостатков свободны автоматические и автомати-
зированные средства. Автоматизированные и автомати-
ческие внешние аппаратурные средства могут быть как
специализированными, так и универсальными, т. е. ра-
ботающими по сменной программе и поэтому пригодны-
ми для диагноза технического состояния многих или не-
скольких разных объектов. Специализированные автома-
тические или автоматизированные средства обладают,
как правило, высоким быстродействием и надежны в ра-
боте. Однако, когда объекты диагноза меняются более
или менее часто, целесообразно использовать универ-
сальные средства. При этом исключается необходимость
разработки, создания и постоянной наладки новых спе-
циализированных средств, что требует затрат матери-
84
альны-х средств, времени и квалифицированного труда.
Кроме того, в универсальных средствах легче реализу-
ется идея унификации их основных узлов и блоков.
Встроенные аппаратурные средства диагноза почти
всегда являются специализированными и автоматиче-
скими или автоматизированными, что определяется усло-
виями их применения. Эти средства пока трудно под-
даются унификации. Определенное исключение из этого
правила составляют применяемые в вычислительных
устройствах встроенные средства контроля по модулю,
а также простейшие устройства сравнения или голосо-
вания в объектах с резервированием каналов передачи
информации. Высокий уровень универсализации и уни-
фикации средств достигнут также в системах оператив-
ного (централизованного) контроля различных техноло-
гических процессов. Эти и другие, подобные им примеры
почти без исключения являются примерами унификации
встроенные средств систем проверки правильности функ-
ционирования объектов. Автоматизация процессов проек-
тирования систем функционального диагноза (в том чис-
ле систем поиска неисправностей при функционирова-
нии), повышение эффективности производства аппара-
турных средств диагноза и другие соображения вызыва-
ют необходимость разработки общих принципов построе-
ния и унификации встроенных аппаратурных средств
диагноза.
Программный способ диагноза в отличие от аппара-
турного способа, пригодного для любых объектов диаг-
ноза, применим только для объектов, работающих по
сменной программе. Примерами таких объектов явля-
ются универсальные или специализированные вычисли-
тельные, управляющие и логические машины. Средства-
ми реализации программного способа диагноза, т. е.
программными средствами диагноза, являются програм-
мы, записанные на носителе, с которым работает объект
диагноза.
Программы, составленные специально для целей ди-
агноза технического состояния объекта, называют испы-
тательными программами. Испытательные программы
могут не представлять, вообще говоря, никакой осмыс-
ленной задачи из класса задач, решаемых данным объек-
том диагноза. Реализация испытательных программ тре-
бует перерыва в функционировании объекта. Для целей
диагноза могут использоваться также программы реше-
85
ния рабочих задач (рабочие программы). Рабочие про-
граммы могут использоваться без каки^-либо изменений,
когда для некоторой рабочей задачи известны правиль-
ные окончательные и, возможно, промежуточные резуль-
таты решения. По фактическим результатам решения та-
кой задачи можно вынести определенные суждения
о техническом состоянии объекта диагноза.
В ряде случаев в рабочие программы вносятся спе-
циальные команды или группы команд, предназначен-
ные для улучшения условий проведения диагноза техни-
ческого состояния объекта. В качестве примера можно
указать на рабочие программы, предусматривающие
двукратное решение задачи в целом или отдельных ее
частей и сравнение результатов.
Эффективность программных средств диагноза су-
щественно повышается при сочетании их с аппаратурны
ми средствами, т. е. при реализации программно-аппара-
турного способа диагноза. В таких случаях используют-
ся главным образом встроенные аппаратурные средства.
Примером реализации программно-аппаратурного спосо-
ба диагноза может служить аппаратурное и программное
86
воплощение принципа избыточного кодирования инфор-
мации с использованием рабочих программ, а также
принципа самодиагноза технического состояния объек-
тов, работающих по сменной программе, когда испыта-
тельные программы сочетаются с встроенными аппара-
турными средствами.
На рис. 1-24 представлена рассмотренная здесь клас-
сификация средств диагноза.
1-11. ОБ ОРГАНИЗАЦИИ ПРОЦЕССОВ ДИАГНОЗА
Рассмотрим вопросы организации процессов диагноза
ради определенности в предположении, что осуществля-
ется тестовый диагноз, а заданные алгоритмы обеспечи-
вают максимальную глубину диагноза, т. е. позволяют
определить исправное состояние е ц^любое неисправное
состояние вг, 1=1, 2, .. ., |S|. Тр и типичных способа та-
Рис. 1 25 Иллюстрация способов организации
процессов диагноза.
кок организации проиллюстрированы рис. 1-25. На этом
рисунке треугольниками изображены деревья, представ-
ляющие алгоритмы диагноза. Рядом с верхними вершл-
нами треугольников указаны множества технических со-
стояний, сопоставленных корням деревьев (начальным
вершинам). Под основаниями треугольников показаны
висячие вершины деревьев и сопоставленные им техни-
ческие состояния или подмножества последних.
Рисунок 1-25,а демонстрирует тот случай, когда при-
меняется общий алгоритм тестового диагноза, решаю-
87
щий как задачу проверки исправности объекта, так и
задачу поиска его неисправностей. Применение общих
алгоритмов диагноза целесообразно, например, тогда,
когда вероятности исправного технического состояния
объекта и его неисправных технических состояний мало
различаются между собой.
Если вероятности исправного состояния объекта диаг-
ноза существенно выше вероятностей его неисправных
состояний, то может оказаться выгодным отделить про-
цесс проверки исправности объекта от процесса поиска
его неисправностей. Независимо от соотношения указан-
ны^ вероятностей такая организация процесса диагноза
типична для служб технического контроля в условиях
производства. Этот способ организации процесса диагно-
за иллюстрируется рис. 1-25,6. Верхний треугольник на
этом рисунке представляет алгоритм проверки исправно-
сти объекта, а нижний-—алгоритм поиска неисправно-
стей. Алгоритм проверки исправности объекта дает дву-
значный результат диагноза — «объект исправен» (е)
или «объект неисправен» (Е\ е). Соответственно этому
алгоритм поиска неисправностей должен обеспечить
определение фактического неисправного состояния объ-
екта среди множества Е\ е всех его неисправных со-
стояний.
Наконец, на рис. 1-25,в представлен способ органи-
зации процесса диагноза, занимающий некоторое проме-
жуточное положение между рассмотренными «крайни-
ми» случаями, соответствующими рис. 1-25,а и б. При
этом сначала применяется общий алгоритм диагноза
(этому алгоритму соответствует верхний треугольник
на рис. 1-25,в), который обеспечивает определение ис-
правного состояния е объекта, но, вообще говоря, не
обеспечивает требуемой глубины поиска неисправностей.
Когда объект неисправен, результатом диагноза являет-
ся выделение некоторого подмножества Ег перазличае-
мых неисправных состояний объекта. Соответственно
этому реализуемый затем алгоритм поиска неисправно-
стей должен определить фактическое неисправное состоя-
ние объекта среди состояний подмножества Ei.
При втором способе организации процесса диагноза
(рис. 1-25,6) проста реализация алгоритма проверки ис-
правности объекта, но алгоритм поиска неисправностей
по сложности близок к общему алгоритму диагноза тех-
нического состояния по первому способу (рис. 1-25,а).
88
По третьему способу (рис. 1-25,в) реализация процесса
проверки исправности объекта более сложна, чем по вто-
рому способу, однако процесс поиска неисправностей при
этом проще. При выборе того или иного способа органи-
зации процесса диагноза следует учитывать как количе-
ственные оценки сложности алгоритмов диагноза, т. е.
их цены, так и качественные характеристики условий
применения систем диагноза.
Все сказанное выше относительно способов организа-
ции процессов диагноза нетрудно обобщить на случай,
когда заданная глубина диагноза отличается от макси-
мальной. Аналогично могут быть организованы процес-
сы функционального диагноза.
Второй и третий способы организации процессов ди-
агноза часто применяются при сочетании функциональ-
ного и тестового диагноза. Сначала алгоритм проверки
правильности функционирования (верхний треугольник
на рис. 1-25,6 и в) определяет наличие в объекте неис-
правностей, препятствующих его нормальной работе. По-
сле этого вступает в работу соответствующий алгоритм
тестового поиска неисправностей (нижние треугольники
на рис. 1-25,6 и в).
Отметим, что в процессе восстановления неисправно-
го объекта диагноза (например, в условиях его изготов-
ления или ремонта) обычно требуется неоднократная
реализация алгоритмов диагноза. При кратных неисправ-
ностях принципиальная необходимость повторной реали-
зации алгоритмов следует из того, что одни неисправно-
сти могут препятствовать проявлению i(a значит, и обна-
ружению) других неисправностей. Поэтому процесс вос-
становления можно считать законченным только тогда,
когда очередная реализация алгоритма диагноза даст
результат «объект исправен».
ЗАМЕЧАНИЯ ПО БИБЛИОГРАФИИ
Впервые многие понятия, связанные с диагнозом тех-
нического состояния дискретных объектов, в том числе
таблица функций неисправностей, были введены в осно-
вополагающей работе [Л. 11]. Некоторые обобщения ря-
да таких понятий, а также понятие элементарной про-
верки как некоторого эксперимента, характеризуемого
воздействием, подаваемым или поступающим на объект
диагноза, и составом контрольных точек, с которых сни-
мается ответ объекта, были даны в [Л. 4].
89
Основы изложенной в гл. 1 точки зрения на задачи
технической диагностики и краткое перечисление этих
задач содержатся в {Л. 8]. Об общих задачах техниче-
ской диагностики сказано также в работе [Л. 2]. Объек-
ты диагноза, их математические модели, классификация
алгоритмов диагноза и некоторые вопросы оптимизации
последних обсуждались в [Л. 9]. Некоторые принятые
в книге изменения терминологии по сравнению с указан-
ными источниками кажутся авторам оправданными.
В основе этих изменений лежит рассмотрение систем
диагноза как специфических систем управления.
Соотношение между специализированными и универ-
сальными внешними аппаратурными средствами диагно-
за обсуждается кратко в [Л. 9]. Программные и про-
граммно-аппаратурные средства диагноза технического
состояния универсальных вычислительных машин осве-
щены, например, в [Л. 7 и 10]
Заметим, что беспрепятственное чтение книги предпо-
лагает наличие у читателя элементарных знаний по мате-
матической логике, булевой алгебре, теории релейных
устройств и конечных автоматов, а также по теории гра-
фов. Для знакомства с основами теории конечных авто-
матов и экспериментов над абстрактными автоматами
можно рекомендовать работу [Л. 3]. Для изучения тео-
рии релейных устройств рекомендуется работа [Л. 6]
в двух томах, в которой достаточно сведений также по
математической логике и булевым алгебрам. Релейно-
контактный аспект теории релейных устройств имеется
в работе [Л. 5]. С основами теории графов можно озна-
комиться, например, по [Л. 1].
ГЛАВА ВТОРАЯ
НЕПРЕРЫВНЫЕ ОБЪЕКТЫ ДИАГНОЗА
При диагнозе технического состояния непрерывных
объектов широкое распространение получили допуско-
вые (как наиболее простые и легко поддающиеся авто-
матизации) способы, характеризующиеся тем, что за-
ключение о техническом состоянии объекта делается по
результатам оценки значений сигналов в контрольных
точках или, как часто говорят, — значений контролируе-
мых параметров объекта. Результаты контроля параме-
тров во многих случаях при этом приводятся к оценкам
90
вида «в норме — не в норме», «в допуске — не в до-
пуске». Поэтому для описания поведения непрерывных
объектов, диагноз технического состояния которых про-
водится допусковыми способами, естественно применять
математические модели логического типа, а для анализа
последних — различные логические методы.
Исходные формы представления объекта диагноза, по
которым строятся математические модели логического
типа, могут быть разными. Характерными формами явля-
ются структурные, функциональные или принципиальные
схемы исправного объекта, а также системы алгебраиче-
ских, дифференциальных или других уравнений, задаю-
щих зависимости между входными, внутренними и вы-
ходными координатами объекта. Однако для построения
моделей логического типа зачастую*-достаточно знания
причинно-следственных связей между координатами или
параметрами объекта диагноза.
В этой главе основное рассмотрение ведется относи-
тельно так называемой логической модели непрерывного
объекта диагноза, получаемой по его заданной структур-
ной пли функциональной схеме. Рассматривается также
форма представления объекта диагноза в виде графа
причинно-следственных связей. Между логической мо-
делью и графом причинно-следственных связей имеется
однозначное соответствие. Это позволяет методы обра-
ботки логических моделей распространить на графы при-
чинно-следственных связей.
Простота математических моделей логического типа
является их преимущетвом. Однако вследствие этой про-
стоты на языке таких моделей некоторые задачи диаг-
ноза технического состояния непрерывных объектов не
имеют решения. Например, при помощи логической мо-
дели место неисправности может быть указано лишь
с глубиной, не превышающей части объекта, объединяю-
щей в себе все элементы замкнутого контура обратной
связи. Решение такого рода задач требует привлечения
математических моделей, являющихся более сложными
и благодаря этому описывающих поведение объекта бо-
лее точно, чем модели логического типа. Примером мо-
жет служить динамическая модель в виде совокупности
дифференциальных и других уравнений, детально описы-
вающих динамику работы непрерывного объекта диаг-
ноза. При решении задач диагноза технического состоя-
ния сложных непрерывных объектов следует в первую
91
очередь использовать модели логического типа и только
при необходимости привлекать более сложные матема-
тические модели, стремясь использовать их не для
объекта в целом, а только для некоторых его составных
частей.
Применение математических моделей, учитывающих
динамику работы непрерывны^ объектов, кратко рассмо-
трено в § 2-7. В заключительной части главы речь идет
о некоторых физических способах диагноза технического
состояния непрерывных объектов.
2-1. ПОСТРОЕНИЕ ЛОГИЧЕСКИХ МОДЕЛЕЙ
НЕПРЕРЫВНЫХ ОБЪЕКТОВ ДИАГНОЗА
Опишем сначала формальную процедуру построения
логической модели, а затем приведем примеры ее по-
строения для некоторых реальных устройств1.
Пусть непрерывный объект диагноза состоит из Af
связанных между собой компонент (блоков, узлов, агре-
гатов, составных частей и т. п.). Состав компонент, свя-
зи между ними и внешние связи представляют структуру
объекта.
Один и тот же объект может быть представлен раз-
ными его структурами, различающимися между собой
в первую очередь составом и числом компонент. Задача
в том или ином смысле оптимального разбиения объек-
та на компоненты представляет самостоятельный инте-
рес и здесь не рассматривается. Заметим только, что
с точки зрения диагноза технического состояния объек-
та при его разбиении следует учитывать такие показате-
ли, как сменность компонент, удобство измерения вы-
ходных параметров компонент, конструктивные сообра-
жения и т. п.
Будем считать, что структура объекта задана и пред-
ставлена структурной схемой. Компоненты структуры
будем называть блоками.
Каждый входной и выходной сигнал характеризуется
одним пли несколькими физическими параметрами. Если
какой-либо входной (выходной) сигнал характеризуется
несколькими параметрами, то каждый из этих параме-
тров представим отдельным входом (выходом) блока
1 Эти примеры были любезно предоставлены В. Т. Князевым, за
что авторы выражают ему глубокую благодарность.
92
Обозначим входы блока Pi, являющиеся внешними вхо-
дами объекта, символами хц, ..ХтР его входы, являю-
щиеся выходами других блоков, символами уи, ...
... , yimi, а выходы этого блока символами гц, ..., Zikr
Построим функциональную схему объекта, в которой
каждый блок Pi, i=l, . .., N, имеет число входов (выхо-
дов), равное числу его входных (выходных) параметров.
Например, если блок Pi (рис. 2-1,а) имеет два входных
сигнала Xi и уг и один выходной сигнал Zi, каждый из
хи
хи
Уи
Ун
Чг
Рис. 2-1. Иллюстрация «расщепления» входов и выхо-
дов блока.
которых характеризуется двумя физическими параметра-
ми (к примеру, амплитудой и частотой электрического
напряжения или тока), то в функциональной схеме блок
Рг будет иметь 4 входа Хц, Хц, Ун, Уг2 И 2 выхода Zil и
Zi2 (рис. 2-1,6). Таким образом, некоторые связи струк-
турной схемы окажутся на функциональной схеме «рас-
щепленными». Если некоторый выход Zi блока Рц
являющийся входом z/д блока Рк, «расщепляется» на
несколько выходов гц, то вход yh также «расщепляется»
на такое же число входов ук). Выполнив «расщепления»
входов и выходов всех блоков Pt, i= 1, 2, ..., 2V, и соеди-
нив между собой соответствующие друг другу «расщеп-
ленные» входы и выходы блоков, получим функциональ-
ную схему объекта. Довольно часто функциональная схе-
ма объекта бывает заданной наряду с его структурной
схемой.
Будем считать, что для всех входных и выходных па-
раметров блоков всегда можно выделить области их до-
пустимых значений. В установившемся режиме работы
объекта области допустимых значений параметров обыч-
но определяются постоянными верхними и нижними пре-
делами (уставками) этих значений. Если же диагноз
технического состояния объекта проводится в неустано-
вившемся режиме работы объекта, то для некоторых
93
(или даже для всех) параметров области допустимых
значений должны задаваться с учетом изменения этих
значений во времени.
Заметим, что при построении функциональной схемы
объекта указанное выше «расщепление» входов и выхо-
дов блоков структуры не является обязательным, т. е.
может не выполняться совсем или выполняться частично.
Иными словами, в функциональной схеме также могут
быть входы или выходы, сигналы которых .характеризу-
ются несколькими физическими параметрами.
Будем говорить, что значение входа или выхода (или,
короче, вход или выход) блока функциональной схемы
является допустимым, если значения всех характеризую-
щих его сигналы параметров принадлежат областям их
допустимых значений. Значение входа или выхода не-
допустимо, если значение хотя бы одного из указанных
параметров не принадлежит области его допустимых
значений.
Обозначим логическое высказывание «значение входа
допустимо» символом входа х (или у), а высказывание
«значение входа недопустимо» — символом х (или у).
Тогда символы входов можно считать двоичными логи-
ческими входными переменными, принимающими значе-
ние «истинно» (1), если значения соответствующих им
входов допустимы, п значение «ложно» (0) —в против-
ном случае. Аналогично символы выходов можно считать
двоичными логическими выходными функциями, прини-
мающими значение 1, если значения соответствующих
им выходов допустимы, и 0 — в противном случае.
Переберем все возможные сочетания значений (на-
боры) входных переменных исправного блока Pi и опре-
делим для каждого такого набора значение выхода гц,
/=1, 2, .. ., ki. Если каждому набору входных перемен-
ных соответствует одно из двух значений выхода— 1 или
0, то полученная функция является булевой. Назовем
последнюю функцией условий работы блока Pt по выхо-
ду Zij и обозначим символом Fij. Булеву функцию мож-
но записать в виде совершенной дизъюнктивной нор-
мальной формы и затем известными методами получить
ее минимальную форму. Все буквы, входящие в мини-
мальную форму, существенны. Таким образом, в резуль-
тате минимизации для каждого из выходов z,i, . .zikt
блока Pi будет получена совокупность существенных
(для данного выхода) входов.
94
Для получения логической модели объекта каждый
блок Рг функциональной схемы заменяется ki блоками,
каждый из которых имеет один выход и существен-
ные для данного выхода входы. Обозначим блоки логи-
ческой модели объекта символами Q,, Q2, ..., Q/i, где
/V
h= В общем случае каждому исходному блоку
<=1
в функциональной схеме
соответствует подмножество
Рис. 2-2. Иллюстрация к опреде-
лению понятия правильной логи-
ческой модели.
блоков логической модели из множества {Qi, . . Q/J.
В частном случае, когда все блоки имеют по одному вы-
ходу, каждый из которых характеризуется одним физи-
ческим параметром, логическая модель может совпадать
с функциональной схемой объекта.
Будем называть логическую модель правильной, если
во-первых, для любой пары ее блоков Qi и Q,— такой,
что выход Zi одного из блоков является входом у, дру-
гого (рис. 2-2,а), выполняется условие: области допусти-
мых значений входа у-, и выхода z-L и области их недопу-
стимых значении соответственно совпадают и, во-вторых,
для любой пары ее блоков Qi и Q,-, имеющих входы yi
и Уз, которые характеризуются одним и тем же параме-
тром (рис. 2-2,6), выполняется условие: области допу-
стимых значений и соответственно области недопустимых
значений этих входов совпадают. Для правильной логи-
ческой модели символы внутренних входов можно заме-
нить на символы связанных с ними выходов. На этом
завершается построение логической модели.
Логическую модель можно рассматривать как ориен-
тированный граф. Вершинами графа являются блоки ло-
гической модели, а также ее внешние входные и выход-
ные полюсы, а дугами —связи между блоками и внеш-
95
ними входными и выходными полюсами. На рис. 2-2,в
изображен граф, построенный по логической модели
рис. 2-2,а. На этом рисунке входные полюсы Xt, yt и
выходной полюс Zj представлены отдельными верши-
нами.
Большинство исправных непрерывных объектов об-
ладает тем свойством, что функция условий работы не-
которого блока Fij принимает значение, равное единице,
лишь в том случае, когда значения существенных вход-
ные переменных на данном наборе — допустимы (т. е.
равны единице). Такие функции называются монотон-
ными; для монотонных функций минимальная форма
единственна и, кроме того, не содержит переменных с от-
рицанием. В дальнейшем будем считать, что все функ-
ции Fij представлены такими минимальными формами.
В самом простом случае функция Fij является конъюнк-
цией (функцией И) входных переменных без отрицаний.
Отметим, что для обработки логических моделей,
у которых функции условий работы блоков немонотонны
(или даже являются не булевыми, а последовательност-
ными функциями), можно применить методы, описанные
в гл. 3 и 4, где рассматриваются дискретные объекты
диагноза.
Непрерывные объекты диагноза условно можно раз-
делить на однорежимиые и многорежимные. Однорежим-
ным является объект, предназначенный для выполнения
одного рабочего алгоритма функционирования, в реали-
зации которого участвуют все блоки и все связи функ-
циональной схемы объекта. Многорежимным называется
объект, рабочий алгоритм функционирования которого
состоит из нескольких подалгоритмов, каждый из кото-
рых может быть задействован или свободен от реализа-
ции, в зависимости от режима работы объекта. Сущест-
венно то, что в реализации каждого подалгоритма функ-
ционирования (в каждом режиме работы объекта)
участвуют разные совокупности блоков п связей функ-
циональной схемы объекта. Поэтому каждый режим дол-
жен рассматриваться отдельно, в том числе с точки зре-
ния выделения допустимых значений параметров.
Пример 2-1. В качестве примера рассмотрим процедуру построе-
ния логической модели для самолетной системы кондиционирования
воздуха, приведенной на рис. 2-3.
Система кондиционирования воздуха предназначена для обеспе-
чения жизнедеятельности пассажиров и экипажа и условий нор-
мального функционирования части аппаратуры самолета. Система
96
автоматически поддерживает давление и температуру воздуха в гер
метизированном отсеке (гермоотсеке), например в кабине пилота.
Для наддува, охлаждения и обогрева гермоотсека используется
сжатый теплый воздух, отбираемый от компрессоров двигателя. Этот
воздух через обратный клапан OKi поступает в воздуховоздушный
радиатор ВВР, где может охлаждаться воздухом, забираемым из
атмосферы. На липни продувки ВВР установлены обратный клапан
ОК/„ а также пневмоэлектроклапан ПЭК, управляемый извне и
включающий продувку ВВР атмосферным воздухом при необходи-
мости понижения температуры в гермоотсеке; ПЭК управляет пнев-
моклапаном ПК. Из ВВР воздух поступает в магистральный возду-
хопровод, в конце которого расходится но «холодной» и «горячей»
линиям.
Рис. 2-3. Система кондиционирования воздуха.
В «холодной» линии охлаждение воздуха осуществляется водо-
воздушным радиатором ВВПР и турбохолодпльнпком ТХ. Работа
водовоздушного радиатора состоит в охлаждении горячего воздуха,
проходящего по трубам, путем отдачи тепла испаряющейся воде,
залитой в межтрубное пространство. Охлажденный воздух посту-
пает в сопловой аппарат турбохолодильпика, где происходит падение
давления воздуха и увеличение скорости его движения. Из
соплового аппарата воздух с большой скоростью поступает на лопат-
ки турбины, которая вращает вентилятор, загруженный атмосферным
воздухом. Таким образом, воздух, совершив работу на лопатках
рабочего колеса турбины, с меньшим давлением, скоростью и темпе-
ратурой идет на охлаждение оборудования (через обратный кла-
пан ОКз), а также в гермоотсек (через смеситель СМ и обратный
клапан ОК2).
В «горячей» линии установлен регулятор давления АРД, авто-
матически поддерживающий давление воздуха в гермоотсеке.
Воздух, проходя по «холодной» и «горячей» линиям, поступает
к смесителю холодного и горячего воздуха СМ, который является
исполнительным органом автомата АТ регулирования температуры
в гермоотсеке. По сигналу автомата смеситель открывает заслонку
«холодной» или «горячей» линии в зависимости от температуры
в охлаждаемом (обогреваемом) гермоотсеке. Из смесителя воздух
7—358 97
через обратный клапан ОК2 поступает к заслонке 3 выключения
наддува, а затем в коллекторы гермоотсека.
На рис. 2-4 представлена функциональная схема системы конди-
ционирования На функциональной схеме, содержащей блоки Pi—
внешние входы обозначены символами Xi, xs и х10, внешние выхо-
ды — z5 и z8; двойные индексы введены только для входных сигна-
лов блоков, которые имеют по нескольку входов. При построении
этой схемы «расщепление» входов и выходов блоков системы не
производилось. Это значит, что внешние входные сигналы х9,
а также сигналы выходов всех блоков, кроме блоков Рп и Р13, и
соответствующих этим выходам входов, характеризуются двумя па-
раметрами каждый: давлением р и температурой t воздуха. Сигналы
внешнего входа х10 и выходов блоков Рп и Pis характеризуются
Рис. 2-4. Функциональная схема системы кондиционирования воз-
духа.
одним параметром каждый. Для всех параметров назначены области
допустимых значений.
Логическая модель системы (рис. 2-5,а), построенная по функ-
циональной схеме (рис. 2-4), содержит 13 блоков Qi—Qis.
На рис. 2-5,6 представлена логическая модель, построенная по
функциональной схеме с «расщепленными» входами и выходами.
Функциональная схема с «расщепленными» входами и выходами не
приводится. Логическая модель системы, построенная по функцио-
нальной схеме с «расщепленными» входами и выходами, содержит
24 блока.
Предполагается, что модель является правильной и поэтому
символы внутренних входов блоков заменены символами выходов Z;.
Функции условий работы блоков модели будут приведены в следую-
щем параграфе.
Рассмотренная система как объект диагноза является одноре-
жимной, потому что во всех условиях полета самолета в работе си-
стемы участвуют все блоки.
Пример 2-2. В качестве примера многорежимного объекта рас-
смотрим систему курсовертикали. Эта система предназначена для
определения курса, а также углов крена и тангажа самолета. Систе-
98
ма курсовертикали работает в режимах гирополукомпаса (ГПК) и
магнитной коррекции (ГМК). Основным функциональным узлом
•системы является курсовертикаль с блоком усилителей и регулятором
рамы, в которой вырабатываются сигналы курса, крена и тангажа.
Чувствительным элементом курсовертикали является гироскоп с тре-
мя степенями свободы, состоящий из гироузла в карданной раме
тангажа, установленной на подшипниках в следящей раме крена.
Сигналы курса передаются с курсового гироскопа курсовертикали
через дифференциальный сельсин механизма согласования блока
усилителей всем потребителям при помощи сельсинных дистанцион-
ных передач, работающих в трансформаторном режиме.
7* 99
Мы не будем подробно описывать принцип работы системы кур-
совертикали и приводить ее структуру. С этими материалами чита-
тель может ознакомиться в соответствующей литературе по навига-
ционным гироскопическим приборам, указанной в библиографической
справке к данной главе. Не будем также приводить функциональные
схемы системы, предполагая, что методика их построения ясна из
предыдущего примера. Дадим только логические модели системы,
которые будут использованы в дальнейшем как материал для демон-
страции методов построения алгоритмов диагноза для сложных мно-
горежимных объектов.
Пусть диагноз технического состояния системы курсовертикали
ведется в следующих режимах:
первый режим (ГПК, угол тангажа <><70", угол крена у>]2°);
второй режим (ГПК, угол тангажа 0<70°, угол крена у<10°);
третий режим (ГПК, угол тангажа •&>70°);
четвертый режим (ГМК, угол тангажа &<70°, угол крена
у<10°).
В логических моделях, представленных на рис. 2-6—2-9, наряду
с обозначениями блоков символами Qi использованы также следую-
щие обозначения, отражающие физическое содержание блоков:
ГУ — гироузел;
М4, MIO, М13— датчики моментов;
Ml, М5, М15, М16—сельсины-приемники курса, крена, тангажа;
МН, М14, М18 — сельсины-датчики курса, крена, тангажа;
ИД1, ИД2, ИД5 — индукционные датчики;
М2 — сельсин-датчик магнитного курса;
М3, Мб, М7, М19, М20— двигатели-генераторы;
У1, У2, УЗ, У4, УМ, УР, У ПТ, У ПС, УПК, W7M — усилители;
КП1 — ламельное устройство;
М21 — дифференциальный сельсин;
СП — стабилизатор напряжения;
М22 — интегрирующий двигатель;
Э1, Э2 — жидкостные переключатели;
Рл — реле;
/КОК — жидкостный отключатель;
Дв и Тг — двигатель и тахогенератор;
Ст, Р — статор, ротор;
R1 и R2 — сопротивления.
На рис. 2-6 приведена логическая модель системы курсоверти-
кали в первом режиме. Логическая модель построена в соответствии
с правилами, используемыми для построения логической модели
однорежимного объекта. В этом режиме задействованы 37 блоков
логической модели. Логические модели для других режимов отли-
чаются от модели (рис. 2-6) и между собой числом и составом бло-
ков, и естественно, связями. Так, модель (рис. 2-7) содержит 38 бло-
ков, рис. 2-8 — 43 блока и рис. 2-9 — 35 блоков. В третьем режиме
в работе курсовертикали принимает участие сельсинная передача,
соответствующая блокам Q21—-Q25 (рис. 2-8), в то время, как
в первом режиме (рис. 2-6) она не работает. Из этого следует, что
в каждом из режимов характер взаимодействия функциональных
блоков системы различен, поэтому одна и та же неисправность
системы курсовертикали может проявляться и обнаруживаться на
разных режимах по-разному.
100
Рис. 2-6. Логическая модель системы курсовертикали для первого режима.
101
ьо
Рис. 2-7. Логическая модель системы курссвертикали для второго режима.
Рис. 2-8. Логическая модель системы курссвертикали для третьего режима.
00
Рис. 2-9. Логическая модель системы курсовертикали для четвертого режима.
104
2-2. АНАЛИЗ ЛОГИЧЕСКОЙ МОДЕЛИ, ПОСТРОЕНИЕ ТАБЛИЦ
ФУНКЦИЙ НЕИСПРАВНОСТЕЙ
В этом параграфе излагаются методы анализа логи-
ческой модели для построения таблицы функций неис-
правностей.
Как будет показано ниже, мощность множества П
возможных элементарных проверок (число строк табли-
цы функций неисправностей) при задании непрерывного
объекта его логической моделью невелико. Это объяс-
няется тем фактом, что для непрерывных объектов
мощность множества возможных проверок зависит от
числа блоков логической модели. Для дискретных объек-
тов мощность множества возможных проверок зависит
как от числа блоков (элементов) структурной схемы
объекта, так и от числа возможных входных наборов
(последовательностей). Кроме того, при использовании
логической модели имеется возможность рассматривать
только одиночные неисправности объекта (при сохране-
нии во многих случаях требования обнаруживать и раз-
личать как одиночные, так и кратные неисправности),
благодаря чему число столбцов таблицы функций неис-
правностей также оказывается относительно небольшим.
При этих обстоятельствах применение таблицы функций
неисправностей для построения алгоритмов диагноза эф-
фективно даже для достаточно сложных непрерывных
объектов диагноза.
Рассмотрим множество П возможных элементарных
проверок объекта. Естественно предполагать, что все
параметры входных сигналов, подаваемых на объект,
имеют допустимые значения. Это значит, что па логиче-
скую модель может поступать единственное воздействие,
при котором значения всех внешних входов модели рав-
ны 1. Следовательно, все возможные элементарные про-
верки объекта имеют одинаковое воздействие и могут
различаться только составами контрольных точек.
Предположим, что контрольной точкой может быть
выход любого блока логической модели, а при всех эле-
ментарных проверках используется по одной контроль-
ной точке. При этом множество П может содержать не
более h (h— число блоков логической модели) возмож-
ных элементарных проверок. Число последних будет
меньше h, например, в тех случаях, когда выходы неко-
торых блоков модели не могут быть контрольными точ-
ками Это имеет место тогда, когда эти выходы недо-
105
сгупны, либо когда соответствующие параметры не мо-
гут быть измерены из-за отсутствия датчиков или
измерительных устройств.
Рассмотрим теперь характер возможных неисправно-
стей объекта.
Предположим сначала, что объект диагноза—одно-
режимный, а минимальные формы функций условий ра-
боты Fi, i=d, 2, ..., h всех блоков модели состоят из
одного члена, являющегося конъюнкцией, внешних и
внутренних переменных, т. е. имеют вид:
Fl — Xh ... Xin-yti ... yimi- (2'1)
Каждый блок логической модели Q, (i=l, ..., h)
имеет по одному выходу zit поэтому функции условий
работы F{ отмечены одним индексом i номера блока Qi-
Все возможные неисправности блока Qi, i=l, ..., /г,
модели можно разбить на два класса. К первому классу
относятся все ге неисправности, которые приводят к по-
явлению неправильного значения выхода хг=0 вместо
ожидаемого правильного значения выхода (соответст-
вующего исправному блоку) z*=l. Обозначим такие не-
исправности записью 1^-0. Второй класс содержит неис-
правности, переводящие правильное значение z, = 0
в неправильное значение z, = l. Эти неисправности обо-
значим записью 0—>1.
Для большинства реальных непрерывных объектов
физически могут иметь место неисправности только типа
Исключение из рассмотрения неисправностей типа
0->1 соответствует предположению, что никакая неис-
правность блока при недопустимом значении ,хотя бы
одного входного параметра, когда согласно (2-1) Fi = 0,
не приводит к появлению допустимого значения выход-
ного параметра. Укажем, что если в непрерывном объ-
екте диагноза возможны неисправности как типа 1->0,
так и типа 0->1, то для обработки его логической моде-
ли следует пользоваться методами обработки математи-
ческих моделей дискретных объектов диагноза.
Условия проявления любых неисправностей одного и
того же блока Qt модели одинаковы, что позволяет все
такие неисправности считать одной одиночной неисправ-
ностью объекта. Тем самым мощность множества (чис-
ло) возможных одиночных неисправностей непрерывного
объекта О не превышает числа h блоков его модели.
Принятая здесь математическая модель охватывает все
106
неисправности и не требует перечисления возможных
или наиболее вероятных физических неисправностей объ-
екта. Это, однако, не мешает рассматривать неисправ-
ности не всех h возможных блоков, а только некоторую
их часть. Последний случай равносилен предположений,
что некоторые блоки модели являются абсолютно на-
дежными (всегда исправны).
Фактическое значение выхода Zi блока зависит от
того, исправен этот блок или нет, а также от значения
функции Fi. Составим логическое высказывание: «блок
Qi исправен» и обозначим его символом Q, (Qt= 1, когда
высказывание истинно, т. е. блок исправен, и Qi=Q
в противном случае). В табл. 2-1 перечислены четыре
возможных набора значений двоичных переменных Fi и
Qi и указаны соответствующие им значения выхода z,.
Когда блок Qi исправен (первые две строки таблицы),
выход Zi повторяет значения функции Л- Если же блок
Qi неисправен (две последние строки таблицы), то в со-
ответствии с тем, что возможными являются только не-
исправности типа 1—>0, выход Zj недопустим независимо
от значения F-;.
Формально из табл. 2-1 следует, что Zi является
конъюнкцией переменных Е, и Qj:
(2-2)
Физически это соответствует тому, что выход Zi бло-
ка Qi будет допустим только в том случае, если все его
входы допустимы (при этом функция условий работы
Ег = 1) и блок исправный (Qi = l). Очевидно, справедлив
следующий вывод: блок Qi исправен, если при проверке
выход Zi допустим (обратное утверждение неверно)
Нетрудно показать, что при принятых условиях (объ-
ект однорежимный, условия работы всех блоков
Таблица 2-1
Fl Qi zi
1 1 1
0 1 0
1 0 0
0 0 0
107
логической модели определяются зависимостью (2-1), воз-
можны неисправности только типа 1->-0) задачи про-
верки правильности функционирования, работоспособно-
сти и исправности объекта не различаются между собой.
Не различаются между собой также и задачи поиска не-
исправностей (всех или только тех, которые иа-рушают
работоспособность или правильность функционирования
объекта). Это следует из того, что любая неисправность
делает объект неправильно функционирующим и, следо-
вательно, неработоспособным.
Информация о техническом состоянии объекта сни-
мается с выходов блоков его логической модели. Макси-
мум этой информации будет получен при условии, что
контролю подвергаются выходы всех блоков.
В частности, объект функционирует правильно (ра-
ботоспособен, исправен), если все блоки его логической
модели исправны, т. е. если конъюнкция
Zi-z2... Zh (2-3)
истинна. Чтобы установить значение конъюнкции (2-3)
(истинна она или ложна), можно проконтролировать
выходы всех h блоков модели. Однако в общем случае
в этом нет необходимости, т. е. можно проверить пра-
вильность функционирования (работоспособность, ис-
правность) объекта, контролируя выводы только части
блоков логической модели.
Аналогично обстоит дело при решении задач поиска
неисправностей объекта. Например, поиск одиночных
неисправностей объекта также, вообще говоря, не тре-
бует контроля выходов всех блоков модели. Более того,
можно говорить об определении минимального числа
выходов блоков модели (контролируемых выходов), не-
обходимых и достаточных для решения той или иной
задачи диагноза технического состояния объекта. Учи-
тывая однозначное соответствие между контрольными
точками и элементарными проверками множества П,
определение минимальной совокупности контролируемых
выходов эквивалентно определению минимального числа
элементарны^ проверок, входящих в минимальный алго-
ритм проверки правильности функционирования (рабо-
тоспособности, исправности) или поиска неисправностей
объекта.
Как отмечалось в гл. 1, существуют методы построе-
ния минимальных алгоритмов диагноза по таблицам
108
функций неисправностей. Изложим процедуру построе-
ния таблицы функций неисправностей по логической мо-
дели объекта на примере модели (рис. 2-5,а) системы
кондиционирования воздуха (пример 2-1).
Таблица функций неисправностей для этой модели представлена
в табл. 2-2. Так как рассматриваются только одиночные неисправ-
Таблица 2-2
столбцов таблицы) на 1 больше числа h—13 блоков модели, т. е.
равна 14. Неисправные состояния объекта удобно обозначить сим-
волами Qi, а за исправным состоянием сохраним символ е.
Мощность множества П возможных элементарных проверок
(число строк таблицы) примем равной числу /г== 13 блоков модели.
Ради удобства элементарные -проверки (строки таблицы, контроль-
ные точки) будем обозначать символами z, выходов блоков логиче-
ской модели (i=l, ..., h).
Для заполнения таблицы функций неисправностей необходимо
выполнить анализ логической модели. Обратимся к рис. 2-5,а и вы-
пишем функции условий работы блоков модели:
Fi — Xi, Fi = ZiZn; Fs = z2; Fa = z3; Fs = z4; F6 = z4z12z13; F, = ze;
Fa — Fq = Xu', Fio = XioZgJ F11 = ZioJ Fia - Z2> Fia = Ze, (2-4)
Составим равенства типа z, = Q,F,:
Zt — Qixr, zt = QtZiZil; z3~Qaze, zi = Qiz3- z5 = Q$z4;
Ze — QaZtZisZisl Zy—QjZe^ Za — QgZ?; Z3 = QgXgJ Zio = Qio-XioZgl
Zll=QllZloj Z12 = Q12--21 213=^1328. (2-5)
109
Содержимым клетки ij табл. 2-2 (элементом RJi множества ре-
зультатов R) является допустимое (1) или недопустимое (0) зна-
чение выхода Zi для /го, /=0, 1, ..й, технического состояния
объекта. Напомним, что единственным воздействием возможных
элементарных проверок являются допустимые значения всех внешних
входов модели, т. е. в данном случае %i=x9 = l и Хю=1. Заполнение
клеток таблицы можно вести либо по столбцам, либо по строкам.
В обоих случаях используется система равенств (2-5).
При построении по столбцам задаются техническим состоянием
объекта, подставляют в уравнения (2-5) соответствующие значения
переменных Q, и вычисляют значения z,. Первый столбец таблицы,
соответствующий исправному состоянию е объекта, вычисляется при
условии, что Qj = l для всех /=1, 2, ..., й, и поэтому все z, = l.
Второй столбец вычисляется при условии, что <21=0 и остальные
Qj=l, j=2, ..., h. При этом получаем:
zi = 0, так
z2 = 0, так
z3 = 0, так
z4 = 0, так
z5 — 0, так
z6 - 0, так
z7 = 0, так
как Qi = 0;
как zt = 0;
как z2 = 0;
как zs = 0;
как z4 — 0;
как z6 = 0;
как ze = 0;
z8 = 0, так как z7 = 0;
z9 = 1, так как Qa = 1 и х9 = 1;
zio = 1, так как Qic = 1, z9 = 1 и xi9=l;
zn = 1, так как Qu = 1 и zio = 1:
Zia = 0, так как z2 = 0;
Zib = 0, так как zs = 0.
Аналогично заполняются остальные столбцы таблицы.
Заполнение таблицы по строкам сводится к определению зависи-
мости выходов блоков модели от всех переменных Qj. Так, для пер-
вой строки имеем Zi=iQiXi, поэтому единственный нуль в этой стро-
ке содержится только в столбце Qi, когда Qi=0. Для второй строки
из системы (2-5) получаем z2= QiQaQsQioQn^i^io, откуда следуют
нули в столбцах Qi, Q2, Qt>, Qw и Qu.
Аналогично заполняются остальные строки таблицы.
При рассмотрении многорежимных объектов посту-
пают таким же образом, строя по логической модели
для каждого режима свою таблицу функций неисправ-
ностей. Индивидуальная обработка каждой такой таб-
лицы (получение совокупностей контрольных точек) по-
зволяет решать задачу проверки правильности функцио-
нирования и поиска неисправностей, нарушающих пра-
вильное функционирование, в данном режиме работы.
Решением задач проверки работоспособности и провер-
ки исправности многорежимпого объекта, а также задач
поиска всех неисправностей или неисправностей, нару-
шающих работоспособность объекта, является объедине-
ние совокупностей контрольных точек, полученных по
таблицам функций неисправностей для всех режимов
работы.
В качестве примера ниже дана система (2-6) уравнений вида
Zi = QiFi и приведена таблица функций неисправностей (табл. 2-3)
для логической модели (рис. 2-6) первого режима (ГПК О <70°,
у>12°) системы курсовертикали (пример 2-2):
ПО
Zi = QiZiC; z2 = Q2z,; z3 = QsX.iZsZV, zi=Qiz3zi; z3 = Q3zr,
ze = Q6z3; z7=Q7a5; z8 = Qsz7; z9 = Q9x9; zic = Qi9z9zr>;
= QnZio; zi2 = Qi2zn; zi3=Qi32i2; zh = Q14Z13; zi$ = QisZuii?;
«£16 = QigZisZis', £17 = Q1t£16» Z18 — QlsZ*!?» Z | g = Q) qX 19 J Z2O^QaoZifll
Z21 = Q2lZ2oZ23j Z22 = Q22Z21Z24:‘t Z23 — QisZzzj Z9t = Q24Z23j
z2s = Q2sZi3z27; z2e = z97'= QziZzg', z2s — Q28Z27J
£2э = QasZ^?; £30 = Q30X30; £31 “ Q31Z30; Z32 = Q32Z31Z3S;
Z33 = Фзз2з2> £34 = QmZwI Z35 — Q3SZ34; £36 — QsgZsoJ Z37 = Фз7£зв£з4.
(2-6)
Особенность табл. 2-3 состоит в том, что в ее клетках ради на-
глядности проставлены только значения 0, пустые клетки соответст-
вуют значениям 1.
Таблицы функций неисправностей для других трех режимов ра-
боты системы курсовертикали строятся по моделям рис. 2-7, 2-8 и
2-9 аналогично и здесь не приводятся.
Заметим, что таблица функций»неисправностей, по-
строенная по логической модели, представляет собой по
существу двоичную математическую модель объекта
диагноза, о которой шла речь в § 1-6. Полное совпаде-
ние будет иметь место, если в таблице функций неис-
правностей заменить везде значения 0 значениями 1 и
наоборот.
Обработке таблиц посвящен следующий параграф.
Ниже рассматриваются особенности анализа логических
моделей объектов с резервированием.
Пусть функции Fi условий работы всех блоков логи-
ческой модели по-прежнему являются монотонными,
однако некоторые из ни,х не удовлетворяют условию
(2-1), а имеют вид:
Fi — Да V Д/2 V ••• V ДД> (2-7)
где A,j— конъюнкция логических переменных. В дан-
ном случае функция Д блока Q, представляет собой
сумму li конъюнкций существенных входных перемен-
ных блока Qi, причем все переменные входят в конъ-
юнкции без отрицаний. Функции такого вида имеются
в логических моделях объектов с резервированием,
в частности, у блоков, соответствующих восстанавли-
вающим органам. Действительно, если восстанавливаю-
щий орган реализует функцию «2 из 3», то функция Fi,
соответствующая блоку Qi (восстанавливающему орга-
ну), будет иметь вид: Fi—XuXi2, V xi2XiS V хцх{3, где
ха, xiZ, Xi,s — логические переменные входных сигналов
блока Qi.
ill
/? e q.|q3 Q3 Q. Q» Qe Q, Q» Qio Qll | Ql2 Q13 Qu I Q16 [ Qie Qv
Zi 0 0 0 0 0
z2 0 0 0 0 0 0
Z3 0 0 0 0 0 0 0 0 0 0
Z< 0 0 0 0 0 0 0 0 0 0
26 0 0 0 0 0 0 0 0 0 0
Ze 0 0 0 0 0 0 0 0 0 0
Z7 0 0 0 0 0 0 0 0 0 0 0
Ze 0 0 0 0 0 0 0 0 0 0 0 0
Zs 0
21o 0 0 0 0
Zu 0 0 0 0
Z12 0 0 0 0
Zis 0 0 0 0 0
214 0 0 0 0 0 0
2]5 0 0 0 0 0 0 0 0 0 0
216 0 0 0 0 0 0 0 0 0 0
217 0 0 0 0 0 0 0 0 0 0
218 0 0 0 0 0 0 0 0 0 0
2ig
112
Т а б лиц а 2-3
Е
Qio Q20 j Q21 Q22 Q23 Q24 Q2B 1 Q27 [ Qae | Q29 | Qao | Q31 |<3>2 Qs | Qsi QS3 |Qsb Qs,
0
8—358
ИЗ
Г<
₽|q. |<?а 1 Оз |<2« 1 Оз | Ов |Qz | Ов 1 0» Qio Qi. | Q12] Q13 Qu Qi61 Qio| Q17 Iqi8
Z20
Z21
?22
^2з
2г t
225 0 0 0 0 0
226 0 0 0 0 0
Z27 0 0 0 0 0
228 0 0 0 0 0
31 22 s 0 0 0 0 0
2зо
^31
232
2зз
2з4
2з5 1
^36 1
237 I 1 1
fl 14
Продолжение пы(!л. 2-3
Е
Q19 [ Qao | <2.11 Qaaj Q23 1 Q241 Sac | Qae | Q» | Q2B 1 Q29 I Qae [ <2s. | Q32 1 <2гз ! Qj4 1 Qss 1 2зв | Qa
0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0 0
0
0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0
0 0 0 0 0 0 0 0 0 0
8*
115
В этом случае не все неисправности блока Qi дают
значение т. е. даже при Е,= 1 и z<=l в общем слу-
чае нельзя утверждать, что блок Qi — исправный. На-
пример, если yi2, то для г/й=1 при вы-
ходе из строя в блоке элемента, воспринимающего вход
Ун, значение х, = 1 сохраняется.
Если в (2-7) количество логических слагаемых боль-
ше, чем один, /,>1, то это означает, что в блоке Q,
имеется несколько каналов передачи информации на вы-
ход блока. Естественно считать исправным блок, у ко-
торого каждый канал исправен. Чтобы убедиться в ис-
правности некоторого канала, необходимо на время его
проверки создать условия, исключающие влияние
остальных каналов. Формально эти условия представ-
лены в табл. 2-4, где Е,,-— функция, получаемая из Fi
удалением конъюнкции A,,-, a Qu— символ логического
высказывания: «/-й канал исправен» Е,,—О (или 1),
если Рц=Лц V • • • V Ай-i V Л«я-1 V • V A«i=O (или
1), т. е. при Fij = O значение сигнала на выходе блока
Qi зависит только от значения конъюнкции А^ и от
исправности /-го канала блока. При Qi3-=1 в блоке нет
неисправностей вида 1—>4), нарушающих работу /-го
канала.
Таким образом, значения Е<;=0, представленные
в первом столбце табл. 2-4, отражают условия исклю-
чения влияния на /-Й канал остальных каналов. В ос-
тальном табл. 2-4 аналогична рассмотренной выше
табл. 2-1.
Таблица 2-4
Fu Q// г1
0 1 1 1
0 0 1 0
0 1 0 0
0 0 0 0
Многоканальный блок Qi логической модели испра-
вен, если истинны конъюнкции вида
Zi = Qi}\ij (2-8)
при E,j = O для всех / = 1, 2, ..., Л.
116
Нетрудно видеть, что при /,= 1 функция (2-7) ста*
новится функцией вида (2-1), табл. 2-4 — табл. 2-1,
а формула (2-8) — формулой (2-2). Действительно, если
блок Qi — одноканальный, то F{=Ai3-, FjjsO и, следо-
вательно, столбец Fij из табл. (2-4) можно удалить.
Итак, для проверки исправности блока Qit функция
Ft условий работы которого имеет вид (2-7), необхо-
димо для каждого / = 1, 2../,• удовлетворить одновре-
менно два равенства: А<3 = 1 и F,j=0. Теоретически это
всегда возможно, так как функция Fi представлена сво-
ей минимальной формой. Иными словами, всегда най-
дутся /;• разных наборов значений входных переменных
блока (назовем эти наборы разделяющими) — таки,х,
что на /-м наборе Д^-=1 и Ftj=O.
Любой разделяющий набор содержит значения неко-
торых переменных, равные 0. Поэтому при практической
реализации разделяющих
наборов возникает необходи-
мость в принудительном за-
дании недопустимых значе-
ний соответствующих вхо-
дов многоканального блока
Qi. Такое задание может
быть осуществлено двумя
способами: 1) путем подачи
Рис. 2-10. Блок логической мо-
дели с коммутирующим эле-
ментом.
недопустимых значений внешних входных сигналов мо-
дели; 2) путем образования управляемых разрывов свя-
зей модели при помощи коммутирующих элементов (КЭ).
Для резервированных объектов это соответствует
разделению (на время диагноза) резервных каналов
между собой. Это необходимо осуществлять для опре-
деления «исправности резерва». Кроме того, управляе-
мые разрывы требуются для поиска неисправностей
мажоритарного восстанавливающего органа. Разрывы
связей легче реализуются в системах тестового диагно-
за. Пример включения КЭ показан на рис. 2-10. В ка-
честве коммутирующего элемента в этом случае может
быть использован элемент, реализующий функцию fi,
заданную табл. 2-5.
Здесь Pj — дополнительный внешний вход для управ-
ления КЭ; fi — выход КЭ, являющийся входом блока Qi
вместо i/i.
Из табл. 2-5 видно, что при нулевом сигнале на
управляющем входе (Р, = 0) выход fi КЭ повторяет зна-
117
чения yi, а при единичном сигнале сохраняет недопусти-
мое значение цхода Д блока Qi независимо от значе-
ния yt.
Таблица 2-5
У1 fi
0 1 0 1 0 0 1 1 0 1 0 0
Установка на объекте коммутирующих элементов
является вынужденной мерой, требующей дополнитель-
ных аппаратурных затрат и усложняющей объект. По-
этому следует минимизировать число управляемых раз-
рывов, а также рассмотреть возможности организации
разрывов такими способами, как, например, временное
отключение питания некоторых блоков или удаление
сменных узлов. Задача определения строго минимально-
го числа управляемых разрывов по логической модели
в целом разрешима, но достаточно сложна. Здесь мы
ограничимся рассмотрением задачи определения мини-
мального числа управляемых разрывов на входах одного
отдельно взятого блока логической модели. При наличии
нескольких таких блоков общее число управляемы^ раз-
рывов связей логической модели в целом будет в худ-
шем случае равно сумме чисел разрывов, полученных
для блоков.
Пример 2-3. Минимизацию числа управляемых разрывов прове-
дем на примере некоторого трехканального блока Qi, функция усло-
вий работы которого
Fi = Уп V X/1W2 V Xi2yi2. (2-9)
Составим таблицу разделяющих наборов в виде табл. 2-6. В этой
таблице каждой конъюнкции Функции Ft выделено по одной
строке и по группе столбцов. Число столбцов в /-й группе равно
числу символов переменных в конъюнкции Лц. Таблица заполняется
следующим образом. В /-й строке проставляются единицы в клетках,
соответствующих символам переменных конъюнкции Л,-3-, в осталь-
ных клетках строки проставляются нули.
Обратимся к первой строке табл. 2-6. Эта строка представляет
условия независимой проверки первого канала блока Qi. Исключение
118
Таблица 2-6
W1 Х11&12 х1гУг
1 0 0 0 0
0 1 1 0 I
Xi2yi2 0 0 1 1 1
влияния второго канала (Xi1j/i2=0) может быть достигнуто прида-
нием недопустимого значения либо внешнему входу хц модели, либо
входу уц блока, либо обоим этим входам вместе, о чем гово-
рят нули, стоящие во втором и третьем столбцах первой строки
табл. 2-6. Запишем это условие в виде дизъюнкции (хц\/ х,2). Ана-
логично условия исключения влияния третьего канала (x421/i2=0)
представляются дизъюнкцией вида (xi2 \/ у 12). Тогда условия исклю-
чения влияния второго и третьего каналов одновременно представ-
ляются конъюнкцией полученных дизъюнкций: (Хц V/A?) V Угг).
После раскрытия скобок и проведения обычных для булевой
алгебры упрощений вместо последнего выражения получаем более
простое: (х,1Х42 \/Ун)- Это значит, что исключить влияние второго
и третьего каналов можно приданием недопустимых значений либо
двум внешним входам хц и х,2 модели, либо одному входу ун бло-
ка (либо всем им вместе).
Из второй строки следует, что влияние первого (третьего) кана-
ла может быть исключено единственным образом — приданием недо-
пустимого значения входу уц блока (А (внешнему входу х42 моде-
ли). Поэтому исключению влияния обоих этих каналов отвечает
конъюнкция Уг\Хг2.
Наконец, из третьей строки табл. 2-6 получаем конъюнкцию
j/iiXii, представляющую условия исключения влияния первого и вто-
рого каналов при проверке исправности третьего канала.
Совместное выполнение полученных для отдельных строк
табл. 2-6 условий отражает запись
(xiiXft V У1г)(УцХ12)(уьхц), (2-10)
после преобразования которой получаем конъюнкцию ХцХг2Ун, пред-
ставляющую единственную неизбыточную и потому минимальную
совокупность управляемых разрывов на внешних входах хц и х,2
модели и на внутреннем входе уц блока Qi. На рис. 2-11 показан
блок Qi и КЭ на его входах.
В приведенном примере получена только одна неиз-
быточная совокупность управляемых разрывов. В общем
случае может оказаться несколько вариантов таких .со-
вокупностей, различающихся составом входов, которые
требуют придания им недопустимых значений. При вы-
боре лучшего варианта можно учесть разную сложность
реализации КЭ для разных параметров, возможность
119
придания недопустимых значений внешним входам моде-
ли без установки на них КЭ и другие условия.
Пусть для каждого многоканального блока логиче-
ской модели найдены минимальные совокупности КЭ.
В результате логическая модель будет иметь внешние
основные Xi, ..., хп и дополнительные ifh, ..., pg входы.
Всегда можно построить v наборов значений входов
Xi, ..хп, Pi, ..., 'Рд (разделяющих наборов модели) та-
ких, что на всех v наборах каждая из конъюнкций A<j
Рис. 2-11. Иллюстрация к примеру выбора минималь-
ной совокупности коммутирующих элементов.
каждого блока по меньшей мере один раз примет значе-
ние, равное 1 при одновременном равенстве нулю соот-
ветствующих функций Fij.
Значение v определяется максимальным числом ка-
налов среди всех многоканальных блоков, поэтому
o>max li, где — число каналов блока Qi.
i
Подачу на модель каждого из v разделяющих набо-
ров модели можно рассматривать как задание объекту
одного из v возможных режимов его работы. Для каж-
дого такого режима может быть построена таблица
функций неисправностей так, как было описано выше.
Особенность построения таблиц функций неисправностей
при этом состоит в том, что в равенства системы вида
(2-5) или (2-6) каждый раз предварительно подставля-
ются значения входов и выходов, определяемые тем раз-
120
деляющим набором модели, который задает рассматри-
ваемый режим.
Построение v таблиц функций неисправностей (по
одной для каждого разделяющего набора модели) рав-
носильно построению одной общей таблицы функций не-
исправностей, возможные элементарные проверки кото-
рой различаются не только составами контрольных то-
чек, но также воздействиями, а мощность множества П
равна vh. Воздействиями элементарных проверок явля-
ются разделяющие наборы модели. Такой подход соот-
ветствует рассмотрению логической модели непрерывно-
го объекта как математической модели дискретного
объекта диагноза и детально рассматривается в гл. 3
и 4.
2-3. ПОСТРОЕНИЕ ПРОВЕРЯЮЩИХ СОВОКУПНОСТЕЙ
КОНТРОЛЬНЫХ ТОЧЕК
Будем предполагать здесь, что цены (затраты) на
реализацию всех возможных элементарных проверок
множества П одинаковы. Вероятности технических со-
стояний объекта учитывать не будем. При этих условиях
целесообразно строить безусловные алгоритмы диагноза,
содержащие как можно меньше элементарных проверок.
Кроме того, будем предполагать, что алгоритмы реали-
зуются как алгоритмы с безусловной остановкой.
Пусть для однорежимного непрерывного объекта
диагноза по его логической модели, содержащей только
одноканальные блоки, построена таблица функций не-
исправностей, например табл. 2-2 для системы конди-
ционирования воздуха. Рассматриваются одиночные не-
исправности объекта.
Напомним (см. § 2-2), что для таких однорежимных
объектов любая неисправность делает объект не только
неисправным, но также неработоспособным и неправиль-
но функционирующим. Поэтому для проверки правиль-
ности функционирования, работоспособности и исправ-
ности объекта пригоден один и тот же алгоритм диагно-
за. Результаты входящих в такой алгоритм элементар-
ных проверок в исправном состоянии объекта должны
отличаться от результатов в каждом неисправном его
состоянии. Таблица функций неисправностей, построен-
ная по логической модели, содержит в данном случае
121
единственный столбец е, состоящий только из единиц.
Поэтому построение алгоритма проверки правильности
функционирования, работоспособности или исправности
объекта состоит в выборе совокупности строк таблицы
таких, чтобы они содержали хотя бы по одному нулю
в каждом столбце Qi( i=il, 2, ..., h. Будем называть
такую совокупность' проверяющей совокупностью кон-
трольных точек (строк).
Минимальная проверяющая совокупность содержит
наименьшее число строк таблицы функций неисправно-
стей, т. е. требует контроля наименьшего числа выходов
блоков модели.
В простейших случаях определение минимальной про-
веряющей совокупности строк легко осуществить путем
простого просмотра таблицы. В более сложных случаях
следует применять специальные методы построения
алгоритмов диагноза.
В рассматриваемом примере 2-1 для логической мо-
дели (см. рис. 2-5,а; табл. 2-2) имеется четыре мини-
мальные проверяющие совокупности из двух строк:
{z5, Ze}, {z5, z7}, {z5, zs}, {z5, zi3}. Из этих совокупностей
можно выбрать любую одну. Из условий более удобного
измерения сигнала z8 по сравнению с сигналами Ze, Zy, z13
выберем совокупность T={z5, z&}.
Следовательно, алгоритм проверки правильности
функционирования, работоспособности и исправности
системы кондиционирования воздуха содержит две эле-
ментарные проверки. Контрольной точкой одной из них
является выход z5 (давление и температура воздуха
охлаждения оборудования системы), а для другой —
выход z8 (давление и температура воздуха в гермоотсе-
ке). Воздействием обеих элементарных проверок явля-
ется допустимое давление (х4=1) и допустимая темпе-
ратура (х9=1) воздуха на входе системы, а также сиг-
нал включения (х10=1) пневмоэлектроклапана [см. си-
стему равенств (2-5)].
Анализ логической модели (см. рис. 2-5,6) показы-
вает, что для проверки правильности функционирования,
работоспособности и исправности достаточно проверить
значения выходов и zi2 (давление и температуру воз-
духа охлаждения оборудования системы) и одного из
выходов (например, температуру воздуха в гер-
моотсеке). Таким образом, «расщепление» входов и вы-
ходов функциональной схемы позволяет в общем случае
122
сократить число контролируемых параметров. Однако
анализ непрерывного объекта при этом усложняется.
Нетрудно показать, что истинность полученной мини-
мальной проверяющей совокупности выходов (z5z8=l)
является необходимым и достаточным условием истин-
ности конъюнкции вида (2-3), т. е. условием исправности
объекта.
По физическим соображениям ясно, что полученный
алгоритм проверки может быть реализован как в систе-
ме тестового диагноза, так и в системе функционального
диагноза. В первом случае тестовое воздействие (*1=1,
х9= 1 и Xio=l) на вход объекта подается от средств
диагноза, а во втором это воздействие является рабочим
и поступает на объект в течение всего времени работы
последнего. *
В системе функционального диагноза построенный
алгоритм выступает в роли алгоритма проверки правиль-
ности функционирования объекта. Присущее алгоритмам
проверки правильности функционирования требование
«немедленного» обнаружения неисправностей, препятст-
вующих нормальной работе объекта, будет выполнено,
если осуществить параллельную во времени и непрерыв-
ную реализацию всех элементарных проверок алгоритма
(одновременный контроль и анализ их результатов).
Принципиально это всегда возможно благодаря тому,
что все элементарные проверки алгоритма имеют одно и
то же воздействие. Практически, однако, при большом
числе контролируемых выходов параллельная во време-
ни реализация всех элементарных проверок может по-
требовать значительных аппаратурных затрат. В таких
случаях обычно организуют циклическую поочередную
реализацию элементарных проверок, входящих в алго-
ритм. Так работают системы централизованного контро-
ля (системы проверки правильности функционирования
объекта), в которых контрольные точки при помощи ком-
мутатора по очереди подключаются к измерительным
устройствам.
Укажем, что алгоритмы проверки, построенные отно-
сительно одиночных неисправностей логической модели,
обнаруживают также любые кратные неисправности
(одновременно существующие неисправности нескольких
блоков модели). Этот вывод следует из того, что блоки
логической модели реализуют монотонные булевы функ-
123
ции, а возможными неисправностями являются неисправ-
ности типа 1—>“0.
Заметим, что для проверки исправности (и тем более
для проверки работоспособности и правильности функ-
ционирования) объекта достаточно контролировать все
его внешние (основные) выходы. Поэтому, казалось бы,
нет необходимости в построении логической модели и
таблицы функций неисправностей, а также в обработке
последней для определения проверяющих совокупностей
контролируемых выходов. Однако логическая модель и
таблица функций неисправностей позволяют получать
минимальную проверяющую совокупность контрольных
точек, которая может содержать только часть внешних
выходов. В частности, в минимальную проверяющую со-
вокупность контрольных точек не войдут внешние выхо-
ды, являющиеся также входами блоков модели (т. е.
идущие от точек разветвления связей модели). При на-
личии в объекте обратных связей по таблице функций
неисправностей можно получать разные варианты мини-
мальных неизбыточных проверяющих совокупностей кон-
тролируемых выходов.
Следует еще указать, что при построении алгоритмов
проверки для объектов (однорежимных или многорежим-
ных), логические модели которых не содержат многока-
нальных блоков, число строк таблицы функций неисправ-
ностей можно сократить — включать в нее только строки,
представляющие внешние выходы объекта. Это возмож-
но потому, что любая неисправность таких объектов
всегда обнаруживается на указанных выходах. Однако
таблица функций неисправностей с числом строк, рав-
ным числу блоков логической модели, необходима при
построении алгоритмов поиска неисправностей, а также
алгоритмов проверки исправности объектов с многока-
нальными блоками, когда включение коммутирующих
элементов невозможно или нежелательно.
Перейдем к построению алгоритмов проверки для
многорежимных объектов. Алгоритмы проверки правиль-
ности функционирования таких объектов можно строить
отдельно для каждого режима по соответствующей таб-
лице функций неисправностей так, как описано выше для
однорежимных объектов.
По определению, многорежимный объект исправен
(работоспособен), если он исправен (работоспособен)
в каждом режиме его работы. Поэтому построение алго-
124
ритма проверки исправности (работоспособности) мно-
горежимного объекта также можно выполнять путем
раздельного определения проверяющих совокупностей
контрольных точек для каждого режима с последующим
объединением этих совокупностей в одну общую. Пока-
жем это на примере системы курссвертикали (пример
2-2).
Таблица 2-7
Номер режима Контролируе- мые выходы модели Реальные бло- ки системы Номер режима Контролируе- мые выходы модели Реальные бло- ки системы
г8 Л414 217 .145
215 Л45 7 Л421
1 71416 3 ?35 Л414
229 Л418 w Z’sg Рл
ZS1 71421 Z42 .144
Z-1 Л45 г, Л45
213 Л416 4 Zis 71416
2 ?21 71418 234 71421
2а 9 Л421 235 АП 8
2з8 Л414
По таблице функций неисправностей (табл. 2-3) можно обнару-
жить, что для первого режима минимальная проверяющая совокуп-
ность содержит выходы ze, zi5, z2i, Zzs н z37. При проверке системы
в этом режиме на нее необходимо подать следующие внешние вход-
ные сигналы: х3 — возмущение по крену, Xi9 — возмущение по курсу
и xs, х30— напряжения питания.
Во втором режиме минимальной проверяющей совокупностью
контрольных точек являются выходы z7, zb, Z2i, г29 и г33. Входные
сигналы: хи — возмущение по курсу, х34 — возмущение по крену и
хь %22 — напряжения питания.
Минимальной проверяющей совокупностью выходов, определяю-
щих исправность (работоспособность, правильность функционирова-
ния) системы в третьем режиме, являются выходы zn, г2т, г33, z33 11
г42. Входные сигналы: Xi — возмущение по курсу, х3э — возмущение
по крену; x36,i—возмущение по тангажу, Х40.1— внешние моменты,
действующие на курсовой гироскоп, и хц, х23, х36>2 — напряжения
питания.
Наконец, в четвертом режиме минимальной проверяющей сово-
купностью выходов являются выходы z-i, zn, г34 и z35. Входные сиг-
налы: Хи — возмущение по курсу, х27 — изменение магнитного курса,
х27 — магнитное склонение и Xi — напряжение питания.
По логическим моделям для отдельных режимов легко устано-
вить показанное в табл. 2-7 соответствие между контрольными точ-
ками г, моделей и выходами реальных блоков системы.
Таким образом, об исправности (работоспособности, правильно-
сти функционирования) системы курссвертикали во всех режимах
125
ее работы можно судить по характеристикам каналов крена, курса,
тангажа и по работе регулятора рамы путем контроля н анализа
сигналов с выходов блоков М4, М5, М14, М16, М18, М21, М25, Рл.
Как и для однорежимных объектов диагноза, полу-
ченный алгоритм проверки технического состояния мно-
горежимного объекта может быть реализован в системах
тестового и функционального диагноза. В последнем слу-
чае сигналы настройки объекта на разные режимы его
работы рассматриваются как рабочие входные воздей-
ствия и должны подаваться на средства диагноза
(рис. 1-5) для перестройки физической модели объекта.
Основное назначение этой перестройки состоит в выделе-
нии из общей проверяющей совокупности контрольных
точек тех, параметры сигналов в которых подлежат кон-
тролю и анализу в соответствующем режиме.
Теперь рассмотрим проверку исправности объектов,
логические модели которых содержат многоканальные
блоки. В предыдущем параграфе было показано, что для
обеспечения раздельной проверки исправности каналов
всех многоканальных блоков на объект необходимо по-
дать v разделяющих наборов модели. Для того чтобы
установить, что такой объект исправен, достаточно за-
фиксировать, что он исправен на каждом из разделяю-
щих наборов модели. Действительно, если объект испра-
вен па каждом из v наборов, то это значит, что в каж-
дом блоке Qj, i=l, 2, ..., h, модели исправен каждый
его /-Й, / = 1, 2, ..., li, капал. Тогда по определению каж-
дый блок является исправным. А это в свою очередь
определяет исправность объекта.
Построение алгоритма проверки исправности объек-
та, содержащего многоканальные блоки, осуществляется
так, как описано здесь для многорежимных объектов.
По имеющимся для каждого из v разделяющих наборов
модели таблицам функций неисправностей находятся
проверяющие совокупности контролируемых выходов
блоков. Затем эти совокупности объединяются в одну
общую.
При реализации полученного алгоритма проверки
исправности (в системе тестового диагноза) в качестве
тестовых воздействий на объект по очереди подаются
разделяющие наборы модели, т. е. единичные и нулевые
значения сигналов на внешние входы объекта и на
управляющие входы коммутирующих элементов. На
каждом таком наборе контролируются и анализируются
126
значения сигналов, снимаемых с контрольных точек про-
веряющей совокупности для данного набора. Если пода-
ча на объект разделяющих наборов возможна в процессе
применения его по назначению, то проверку правильно-
сти функционирования объекта можно осуществить пу-
тем организации системы тестового диагноза, реализую-
щей алгоритм проверки исправности. Примерами таких
объектов являются быстродействующие устройства
управления инерционными исполнительными механизма-
ми. Для этих устройств имеется возможность проводить
тестовую проверку исправности во время их функциони-
рования, если организовать подачу разделяющих набо-
ров модели (при помощи КЭ) в виде кратковременных
(импульсных) сигналов. При этом недопустимые значе-
ния сигналов на основных выходах^ будут появляться
кратковременно и поэтому не нарушат нормальной ра-
боты исполнительных механизмов.
Когда применение коммутирующих элементов невоз-
можно или нежелательно, алгоритмы проверки исправ-
ности строятся так, как было изложено для объектов, ие
содержащих многоканальных блоков. При этом одиноч-
ные неисправности каналов многоканальных блоков не
будут обнаруживаться, несмотря на то, что получаемые
совокупности контрольных точек будут содержать кроме
внешних выходов объекта некоторые его внутренние
узлы. Такие алгоритмы проверки исправности можно
использовать в качестве алгоритмов проверки работоспо-
собности или правильности функционирования, так как
в число получаемых контрольных точек входят все не-
обходимые внешние выходы объекта. Использование при
этом также внутренних узлов объекта позволит обнару-
живать некоторые неисправности, ие нарушающие рабо-
тоспособности или правильности функционирования
объекта.
2-4. ПОСТРОЕНИЕ РАЗЛИЧАЮЩИХ СОВОКУПНОСТЕЙ
КОНТРОЛЬНЫХ ТОЧЕК
В этом параграфе также предполагается, что цены
всех элементарных проверок одинаковы, вероятности
технических состояний объекта не учитываются, а алго-
ритмы поиска неисправностей являются алгоритмами
с безусловной остановкой.
В предыдущем параграфе было показано, что для
каждого режима работы многорежимного объекта и для
127
каждого разделяющего набора модели объекта с резер-
вированием (с многоканальными блоками) строится своя
таблица функций неисправностей, соответствующая ло-
гической модели, все блоки которой являются или могут
рассматриваться как одноканальные. Здесь будут иметь-
ся в виду только такие логические модели с однаканаль-
пыми блоками.
Пусть задана таблица функций неисправностей, по-
строенная по логической модели с одноканальными бло-
ками и по-прежнему для одиночных неисправностей.
В качестве примера будем использовать табл. 2-3, по-
строенную по логической модели (см. рис. 2-6) первого
режима системы курсовертикали (пример 2-2).
Таблица функций неисправностей может содержать
одинаковые столбцы, которые представляют неразличи-
мые (по результатам элементарных проверок множества
П) технические состояния объекта. Столбец, содержащий
только единицы, в таблице функций неисправностей
единственный и представляет исправное состояние
объекта. Поэтому вместо неразличимых технических со-
стояний можно говорить о неразличимых неисправно-
стях объекта.
Нетрудно показать, что неисправности блоков моде-
ли, охваченных обратной связью, неразличимы. Дейст-
вительно, появление значения 0 па выходе любого одного
такого блока влечет за собою появление нулевых значе-
ний на всех остальных блоках, входящих в контур обрат-
ной связи. Причем это происходит независимо от того,
что явилось причиной появления недопустимого значения
на выходе блока — его неисправность или подача на его
вход недопустимого значения с выхода некоторого блока,
не входящего в рассматриваемый контур обратной свя-
зи. Как следствие получаем, что значение 1 на выходе
любого одного блока, входящего в контур обратной свя-
зи, может иметь место только тогда, когда допустимы
выходы всех других блоков этого контура.
Приведенные рассуждения показывают, что всегда
выходы всех блоков, охваченных обратной связью, имеют
одно и то же (недопустимое или допустимое) значение.
Следовательно, в таблице функций неисправностей будут
одинаковыми не только столбцы, соответствующие не-
исправностям блоков, охваченных обратной связью, но
также строки, соответствующие выходам этих блоков.
128
Указанное свойство столбцов и строк таблицы функ-
ций неисправностей можно использовать для определе-
ния групп блоков, охваченных обратными связями. Так,
обращаясь к табл. 2-3, находим следующие шесть таких
групп: {Q.i, Qit Q5, Qb}, {Qio, Qu, Q12}, {Qis, Qie, Q17, Qis},
{Q21, Q22, Q23, Q24}, {Q25, Q26, Q27, Q'/s}, {Q32, Q33, Q34, Q35}-
Найденные здесь группы понадобятся нам в дальнейшем
при выборе минимального числа управляемых разрывов
контуров обратных связей.
Рис. 2-12. Обобщенная логическая мотель системы курсовертикали
для первого режима.
Оставим в таблице функций неисправностей по одно-
му представителю от (каждой группы одинаковых столб-
цов и от каждой группы одинаковых строк. Это умень-
шает размеры таблицы и поэтому, как отмечалось в
§ 1-6, сокращает затраты на ее обработку при построе-
нии алгоритмов диагноза, особенно алгоритмов поиска
неисправностей. Заметим, что удаление повторяющихся
столбцов и строк таблицы функций неисправностей мож-
но было производить также в предыдущем параграфе
при построении проверяющих совокупностей контроль-
ных точек.
Если в алгоритм диагноза войдет элементарная про-
верка, которую представляет строка, являющаяся пред-
9—358 129
>- Таблица 2-8
vvvvvvvvvvv V V V V V V V V vvv
R e Qi <2« <234-5 <27 q8 Q» 2104-12 Q13 Q14 <2154-18 Q19 Qao <2214-24 <2’54-28 Q29 Q30 Q31 <2.324-35 Q26 Q37
V 0 0 0
V ?2 0 0 0 0
V z34-5 0 0 0 0 0
V S’? 0 0 0 0 0 0 —
V Zs 0 0 0 0 0 0 0
V Zs 0
z104-12 0 0
Z13 0 0 0
V 214 0 0 0 0
% V V V V V V V V V 1—* w - V z154-18 0 0 0 0 0
Z19 0
Z20 0 0
z214-24 0 0 0
z254-28 0 0 0 0
Z29 0 0 0 0 0
?зо » 0
Z31 0 0
z32-j-35 0 0 0
^36 0 0 0 0
Z37 0 0 0 0 0 0
ставителем некоторой группы одинаковых строк (выхо
дов блоков), то в качестве контролируемого может быть
взят любой выход из этой группы. Тем самым будут сох-
ранены все возможные варианты алгоритмов диагноза.
Таблица функций неисправностей, полученная по
табл. 2-3 путем замены в последней всех групп одина-
ковых столбцов и групп одинаковых строк их соответ-
ствующими представителями, представлена под номе-
ром 2-8.
Объединение одинаковых столбцов и строк таблицы
функций неисправностей соответствует замене в логиче-
ской модели каждой группы блоков, охваченных обрат-
ной связью, одним обобщенным блоком. Вход (выход)
обобщенного блока назовем наружным, если он является
внешним входом (выходом) модели или выходом (вхо-
дом) блока, не входящего в данный обобщенный блок.
Тогда входами обобщенного блока являются все наруж-
ные входы образующих его блоков. Все наружные выхо-
ды этих блоков заменяются единственным выходом обоб-
щенного блока.
Логическую модель, полученную по некоторой логи-
ческой модели путем замены в последней групп блоков,
охваченных обратными связями, обобщенными блоками,
будем называть обобщенной. Обобщенная логическая
модель первого режима системы курссвертикали само-
лета (рис. 2-6) показана па рис. 2-12.
Пусть в объекте возможны только одиночные не-
исправности и требуется построить алгоритм поиска не-
исправностей с глубиной до одного блока обобщенной
логической модели.
Алгоритм поиска неисправностей должен при этом
различать каждую пару (одиночных в нашем случае)
неисправностей. Это значит, что результаты входящих
в алгоритм элементарных проверок должны быть разны-
ми в каждом неисправном состоянии объекта. Поэтому
построение алгоритма поиска неисправностей состоит в
выборе совокупности строк таблицы функции неисправ-
ностей таких, чтобы все образуемые этими строками
столбцы Qe, i=l, 2, . .., й, были различны. Такая сово-
купность всегда существует, так как все столбцы таб-
лицы функций неисправностей (типа табл. 2-8) различ-
ны (множество П возможных элементарных проверок
является достаточным). Совокупность контролируемых
выходов или строк таблицы функций неисправностей,
132
различающую все различимые технические состояния
объекта, будем называть различающей.
В общем случае для определения минимальных раз-
личающих совокупностей строк необходимо применять
специальные методы минимизации, требующие обычно
значительных объемов вычислений по перебору вариан-
тов. Однако во многих случаях, когда объект диагноза
представлен своей обобщенной логической моделью, име-
ется возможность определить минимальную различаю-
щую совокупность контролируемых выходов для поиска
неисправностей объекта более простыми приемами. Эта
возможность основана на ряде свойств обобщенной логи-
ческой модели и реализуется применением следующих
двух правил.
Правило 1. Если в обобщенной логической модели
существует два блока Q, и Qj — такТ5е, что выход одного
из них, например Qj, соединен только со входом другого
Qi, то выход блока Q, является обязательным (т. е. он
необходимо входит в любую минимальную различаю-
щую совокупность). Действительно, рассмотрим столбцы
Qi и Qj обобщенной таблицы функций неисправностей;
опп отличаются только в строке z4. Поэтому для разли-
чения неисправностей блоков Q, и Qj необходимо кон-
тролировать ВЫХОД Zj.
Правило 2. Обязательным для поиска неисправностей
являются внешние выходы обобщенной логической моде-
ли, образующие минимальную проверяющую совокуп-
ность контролируемых выходов. Справедливость этого
правила следует из того, что изъятие любого одного
такого выхода из различающей совокупности контроли-
руемых выходов приведет к невозможности обнаружения
неисправности соответствующего выходного блока мо-
дели.
Исключение из правила 2 составляет случай, когда
исправность объекта проверяется на единственном внеш-
нем выходе и перед применением алгоритма поиска не-
исправностей известно, что объект неисправен. В этом
случае внешний выход модели можно не включать в раз-
личающую совокупность контролируемых выходов, а о
неисправности единственного выходного блока модели
заключать по получению допустимых значений сигналов
па всех контролируемых выходах из этой совокупности.
Правила 1 и 2 позволяют выделить в таблице функ-
ций неисправностей обязательные выходы, т. е. выходы,
133
которые войдут в любую (а значит, и в минимальную)
различающую совокупность контролируемых выходов
для поиска неисправностей с глубиной до одного блока
логической модели. Доказательства необходимости этих
выходов содержатся в обоснованиях правил 1 и 2.
В табл. 2-8 правило 1 выделяет выходы z,, z2, z34_c>
z„ zs, z14, Zi9, z25^28, z,0, z3i, 2^,_._g5, г3б, а правило 2 —
выходы z8, zir . 18, z21^_24, z29 и zS7. Эти выходы отмечены
знаком V слева от таблицы.
Теперь необходимо проверить, является ли совокуп-
ность обязательных выходов достаточной. Это можно
сделать попарным сравнением столбцов, образуемых от-
меченными (обязательными) строками. В процессе тако-
го сравнения будем отмечать тем же знаком V те
столбцы, которые отличаются от всех других. Если все
столбцы оказались отмеченными (все они различны), то
обязательные выходы образуют минимальную различаю-
щую совокупность.
В противном случае следует выбрать такую мини-
мальную совокупность неотмеченных строк, которая де-
лает различимыми все неотмеченные столбцы. Для этого
построим таблицу, строками и столбцами которой явля-
ются соответственно неотмеченные строки и неотмечен-
ные столбцы исходной таблицы функций неисправностей.
Тогда указанный выбор минимальной совокупности не-
отмеченных строк ничем не отличается от построения
минимальной различающей совокупности строк по полу-
ченной таким образом таблице. Однако размеры послед-
ней в большинстве случаев существенно меньше разме-
ров исходной таблицы функций неисправностей.
Проверка показывает, что для табл. 2-8 совокупность
обязательных выходов различает все столбцы таблицы
и поэтому образует минимальную различающую совокуп-
ность Т = {z„ z2, z^, z7, Zs, Zs, Z14, zI5<I8, z19, z ,. 24>
Z25-2B> Z2S’ Z3<>, Zsl’ Z32-35’ Z’” Z”} 113 17 ВЫХОДОВ. В T CO-
держатся выходы z:i., z^.j., г.ц..ч, ,28 и z3, .3 обоб-
щенных блоков модели. Эти выходы представляют соот-
ветствующие группы выходов блоков исходной логиче-
ской модели. Из каждой такой группы следует выбрать
по одному выходу исходя из соображений, например,
удобства его контроля.
Число контролируемых выходов в минимальной раз-
личающей совокупности может быть уменьшено, если
134
задавать меньшую глубину диагноза. Уменьшение глу-
бины диагноза имеет смысл, в частности, тогда, когда
конструктивно сменные узлы объекта включают в себя
несколько блоков обобщенной логической модели. Пусть,
например, такой узел системы курсовертикали содержит
блоки Q2, С?3. , и Qi модели рис. 2-12 (на этом рисунке
указанные блоки заключены в пунктирный прямоуголь-
ник). Тогда в минимальную различающую совокупность
пе войдут выходы z2 п г3^Г), представляющие внутрен-
ние связи сменного узла. Приведенные здесь соображе-
ния целесообразно учитывать при проектировании объек-
тов, когда имеются разные варианты конструктивного
размещения его функциональных блоков.
Как отмечалось выше, представление объекта диагно-
за его логической моделью не позволяет различать меж-
ду собой неисправности блоков, охваченных обратной
связью. Это является следствием простоты и «грубости»
логической модели. Указанные неисправности, очевидно,
станут различимыми, если па время поиска неисправно-
стей разрывать контуры обратных связей. Такие управ-
ляемые разрывы контуров обратных связей можно реа-
лизовать при помощи коммутирующих элементов, подоб-
ных тем, которые обсуждались в § 2-2, по реализующих
функцию, заданную табл. 2 9. Как и прежде, при пуле-
вом значении управляющего входа [3; выход fi КЭ по-
вторяет значения его входа //,. Однако при единичном
значении входа |3,- па выходе КЭ сохраняется допустимое
значение сигнала независимо от значения входа yi.
Таблица 2-9
т ₽,• fl
1 0 1 0 0 0 1 1 1 0 1 1
О некоторых других, более точных, чем логическая
модель, математических моделях объекта, позволяющих
различать неисправности в контурах обратных связей
без их разрывов, будет сказано в одном из следующих
135
параграфов этой главы. Здесь же рассмотрим задачу
выбора минимального числа КЭ для разрыва всех конту-
ров обратных связей логической модели объекта.
Выше по табл. 2-3 для построения обобщенной логи-
ческой модели (рис. 2-12) были определены группы бло-
ков, охваченных обратной связью. Выбор управляемых
разрывов контуров обратных связей можно осуществлять
для каждой такой группы блоков независимо.
Рис. 2 13. Фрагмент логической мотели системы курсовертикали
для первого режима, содержащий блоки, охваченные обратной
связью.
Если блоки некоторой группы охвачены единствен-
ным контуром обратной связи, то достаточно одного
управляемого разрыва любой связи между блоками это-
го контура. Выбор разрываемой связи осуществляется
с учетом простоты и удобства реализации коммутирую-
щего элемента. Если же блоки группы охвачены несколь-
кими контурами обратной связи, то, во-первых, может
потребоваться несколько управляемых разрывов и, во-
вторых, выбор минимального числа разрываемых связей
становится менее очевидным, чем в одноконтурных груп-
пах блоков.
Пример 2-4. Па рис. 2-13 представлена группа охваченных обрат-
ной связью блоков {Q3, (Д, Qr„ Q(i) логической модели, показанной
на рис. 2-6. Имеется дна контура обратной связи: Q3——Q5 и
Q., Qs Qis- Нетрудно видеть, что разрыв одной связи между бло-
ками Q4 и Qs или на выходе последнего обеспечивает разрыв обоих
контуров. Все другие варианты требуют двух управляемых разрывов.
В результате получаем логическую модель, показанную на рис. 2-14.
Для определения неисправного блока необходимо задать Ps=l и
контролировать выходы г3, г4 и Ze.
В простых случаях (как в рассмотренном примере)
определение минимальной совокупности управляемых
136
разрывов может быть определено вручную без привлече-
ния каких-либо формализованных процедур. В других
случаях формализованные методы необходимы как для
выделения отдельных конту-
ров обратной связи, так и
для определения минималь-
ных совокупностей разрывов.
Что касается задачи вы-
деления контуров обратной
связи, то для ее формально-
го решения можно привлечь
аппарат теории графов. Ло-
гическую модель объекта при
этом следует рассматривать
как ориентированный граф,
вершинам которого соответ-
ствуют блоки модели, а так-
же ее внешние входные и вы-
ходные полюсы, а дугам —
Рис. 2-Т4. Иллюстрация к при-
меру выбора минимальной со-
вокупности управляемых раз-
рывов контуров обратной
связи.
связи между блоками и внешними входными и выход-
ными полюсами. Отметим, что многие другие задачи по
обработке логических моделей также могут быть сфор-
мулированы на языке теории графов.
Получение различающих совокупностей контролируе-
мых выходов для многорежимных объектов и для объек-
тов с резервированием производится путем объединения
различающих совокупностей, полученных для каждого
режима работы и для каждого разделяющего набора
модели (так же как при получении проверяющих сово-
купностей).
Построенные описанным способом различающие сово-
купности контрольных точек представляют, по сущест-
ву, алгоритмы поиска всех неисправностей объекта и
могут быть всегда реализованы в системах тестового
диагноза. При этом, естественно, должно быть обеспече-
но управление коммутирующими элементами, установ-
ленными для отключения резервных каналов и для раз-
рыва контуров обратных связей. Реализация этих алго-
ритмов в системах функционального диагноза (т. е. ис-
пользование их в качестве алгоритмов поиска неисправ-
ностей при функционировании объекта диагноза) имеет
некоторые особенности, обсуждавшиеся в предыдущем
параграфе применительно к задачам проверки техниче-
ского состояния объектов. Эти особенности определяются
137
наличием неисправностей, Не мешакмцнх нормальной
работе объекта, а также тем, что в процессе функцио-
нирования объекта нельзя коммутировать рабочие эле-
менты.
Как и при реализации алгоритмов проверки исправ-
ности (работоспособности, правильности функциониро-
вания) объекта контроль и анализ сигналов контроли-
руемых выходов, образующих различающую совокуп-
ность, может производиться либо параллельно (одновре-
менно), либо путем последовательного их опроса при
помощи коммутатора. В качестве физической модели
объекта может выступать Е-таблица функций неисправ-
ностей, строки которой соответствуют контролируемым
выходам. Области допустимых значений контролируемых
параметров могут быть представлены в виде, например,
их пнжпих и верхних пределов (уставок), значения ко-
торых храня гея аппаратурой средств диагноза. Тогда
результатом сравнения фактических параметров с их
уставками будет некоторое | Т|-разрядное двоичное чис-
ло, где | Т|—число контролируемых выходов. Расшиф-
ровка результатов элементарных проверок (получение
результатов диагноза) состоит в сравнении этого двоич-
ного числа со столбцами 7-таблицы функций неисправ-
ностей. Совпадение со столбцом Qi, te{l, 2,..., h], ука-
зывает на то, что неисправен блок Qi, а со столбцом е —
па исправность (работоспособность, правильность функ-
ционирования) объекта.
Представление физической модели объекта Г-табли-
цей следует рассматривать как некоторое «канониче-
ское» решение этой задачи, которое может оказаться
аппаратуры© достаточно сложным.
Перейдем теперь к рассмотрению случая кратных
неисправностей, когда в объекте возможно существова-
ние произвольного числа неисправных блоков.
Различающая совокупность, обеспечивающая поиск
одиночных и кратных неисправностей с максимально
возможной глубиной, содержит выходы всех блоков логи-
ческой модели. Справедливость этого утверждения дока-
зывают следующие соображения. Различающая совокуп-
ность для поиска одиночных неисправностей не содержит
только некоторых разветвляющихся выходов блоков мо-
дели. Рассмотрим один из таких выходов (например,
выход £13 на рис. 2-12). Если этот выход не включен в
различающую совокупность, то неисправность блока, не-
138
посредственно предшествующего разветвлению (блока
Q13), будет неотличимой от кратной неисправности
всех блоков, непосредственно следующих за разветвле-
нием (блоков Qu и Q25^_28)-
Следовательно, при предположении существования
в объекте кратных неисправностей минимальная разли-
чающая совокупность контролируемых выходов единст-
венна и содержит выходы всех блоков модели.
Таблица функций неисправностей нами использова-
лась для двух применений: для построения минимальных
алгоритмов диагноза и в качестве физической модели
объекта в средствах диагноза. Число всех (включая
кратные) возможных неисправностей объекта равно
2h—1, где h — количество блоков логической модели
объекта. Работать с таблицей функций неисправностей,
содержащей 2'1 столбцов, при больших значениях h прак-
тически невозможно. В данном случае минимальная раз-
личающая совокупность содержит выходы всех блоков
модели, поэтому ее получение не требует построения и
обработки таблицы функций неисправностей. Остаются
только трудности, связанные с реализацией физической
модели объекта
По существу, необходим экономный способ расшиф-
ровки результатов элементарных проверок объекта при
наличии в нем кратных неисправностей. Покажем, что
имеется возможность поиска кратных неисправностей
объекта при условии, что физическая модель последнего
представлена таблицей функций неисправностей, пост-
роенной только для одиночных неисправностей, т. е. со-
держащей h+ 1 столбцов
Пусть в объекте неисправны два блока Q,- и Q,.
Отдельно взятая (одиночная) неисправность каждого из
этих блоков вызывает появление недопустимых значений
определенных выходов блоков модели, отмеченных нуля-
ми в столбцах Qi п Q, таблицы функций неисправностей.
Ни одно из недопустимых значений выходов блоков мо-
дели, вызванных неисправностью блока Q,, не может
быть скомпенсировано (сделано допустимым) появле-
нием неисправности блока Qj, и наоборот. Это следует
из того, что функции условий работы блоков логической
модели монотонны, а все неисправности — типа 1—>0.
Поэтому значения выходов блоков модели, когда не-
исправны оба блока Q,- и Qj, можно вычислить по столб-
цам Qj и Qj таблицы функций неисправностей, выпол-
139
нив построчное (поразрядное) логическое умножение
значений выходов в этих столбцах.
Например, для блоков Q, и Q9 логической модели
(рис. 2-12) по табл. 2-8 получаем:
Q, <2» Q1Q9 <2. <?» <2.<2»
0 0 0 1 1 1
0 0 0 1 1 1
0 0 0 1 I 1
0 0 0 1 0 0
0 0 0 1 0 0
1 0 0 1 I 1
1 0 0 1 1 1
1 0 0 1 I 1
1 0 0 1 1 1
1 0 0 1 1 1
Все здесь сказанное остается справедливым для лю-
бого числа одновременно неисправных блоков модели и
позволяет выделять подмножества блоков модели, подо-
зреваемых на наличие в них неисправностей. Это дела-
ется следующим образом.
Пусть известны фактические значения выходов всех
блоков модели. Если выход z< блока Q, допустим, z,= l,
то блок Qi заведомо исправен. Исключив из множества
всех блоков модели заведомо исправные, получаем под-
множество блоков, в которых возможны неисправности.
Теперь задача состоит в том, чтобы среди блоков,
подозреваемых на наличие в них неисправностей, найти
все действительно неисправные блоки. Решим эту задачу
методом последовательного восстановления или замены
неисправных блоков. Сущность этого метода состоит в
следующем. Алгоритм поиска неисправностей реализу-
ется многократно. После каждой такой реализации на-
ходится хотя бы один заведомо неисправный блок, кото-
рый восстанавливается или заменяется исправным. Этот
процесс повторяется до тех пор, пока не будет зафикси-
рована исправность (работоспособность, правильность
функционирования) объекта.
Итак, пусть имеется непустое подмножество подозре-
ваемых на наличие неисправностей блоков модели. Ему
соответствует подмножество столбцов таблицы функций
неисправностей. Среди этих столбцов всегда найдется хо-
тя бы один столбец Qi такой, что в строке Zj, представ-
140
ляющей выход блока Qi, содержится единственный нуль
в этом столбце. Назовем такие столбцы определяющими.
Справедливость утверждения о существовании определя-
ющих столбцов следует из того, что рассматриваемые
здесь логические модели не содержат контуров обратных
связей, поэтому все столбцы соответствующих этим мо-
делям таблиц функций неисправностей различны. Физи-
чески наличие определяющих столбцов соответствует
тому, что среди одиночных неисправностей, образующих
некоторую кратную неисправность, имеются такие (до-
минирующие) одиночные неисправности, устранение лю-
бой из которых изменяет значение хотя бы одного конт-
ролируемого выхода.
Теперь можно сформулировать процедуру поиска не-
исправных блоков методом последовательного восста-
новления:
1. Зафиксировать фактические значение всех выходов
блоков модели. Если все фактические значения допусти-
мы, то выдать результат диагноза «объект исправен» п
на этом закончить процедуру. В противном случае, вы-
полнить указанные ниже операции.
2. Исключить из дальнейшего рассмотрения столбцы
таблицы функций неисправностей, представляющие за-
ведомо исправные блоки, т. е. блоки, фактические зна-
чения выходов которых допустимы.
3. Просмотром строк, образуемых оставшимися
столбцами таблицы функций неисправностей, найти
строки, содержащие по одному нулю, и тем самым вы-
делить определяющие столбцы, которые представляют
заведомо неисправные блоки. Выдать результат диагно-
за в виде перечня заведомо неисправных блоков.
4. Восстановить найденные неисправные блоки (или
заменить их исправными) и перейти к повторному вы-
полнению операции п. 1 процедуры.
Обратимся к примеру 2-2. Пусть при поиске неисправностей
системы курсовертикали в первом режиме ее работы (рис. 2-12) полу-
чены значения 1 на выходах Zi9, z29, Z21—24 ’ ги> гз2ч-35 • 236 и
г87. На остальных выходах получены значения 0.
Заведомо исправны блоки Qi9, Q20. Q2i—24 ’ <3ЗЪ ^324-35’ @36
и Q37. После «вычеркивания» в табл. 2-8 столбцов, представляющих
неисправности этих блоков, находим единственную строку zg, со-
держащую один нуль. Следовательно, блок Qs заведомо неисправен.
Пусть после замены неисправного блока Qg исправным получе-
ны значения 0 на выходах г,, z2, z3.6, z? и z6. Остальные выходы
141
допустимы. Теперь в табл. 2-8 остаются «невычеркнутыми» столбцы
Qi. Qz, Q3-6 Qy п Qs- Строкой с одним нулем является строка Zi,
указывающая на неисправность блока Q(.
Пусть после замены блока Q, исправным все выходы оказались
допустимыми. Значит, в объекте были два неисправных блока Q9 и Qt.
2-5. ГРАФЫ ПРИЧИННО-СЛЕДСТВЕННЫХ СВЯЗЕЙ
В тех случаях, когда объект диагноза не имеет явно
выраженных функциональных блоков, построение его
логической модели может вызвать ряд практических
неудобств. Кроме того, бывают ситуации, когда точные
(аналитические, табличные и др.) зависимости между
параметрами объекта неизвестны, а известно лишь о том,
что один параметр как-то влияет на другой или как-то
зависит от другого. Такого рода влияния и зависимости
хорошо согласуются с понятием причинно-следственных
связей, которое кстати, охватывает также и строгие,
формальные зависимости между параметрами, события-
ми или явлениями.
Графом причинно-следственных связей называется
ориентированный граф, вершины которого представляют
параметры, события или явления, а дуги отражают
причинно-следственные связи между соответствующими
вершинами. Направление дуги соответствует перемеще-
нию от причины к следствию.
Графы причинно-следственных связей нашли приме-
нение при решении задач анализа работы различных
электрических, гидравлических, механических и смешан-
ных (например, электромеханических) устройств, меха-
низмов и машин, а также различных технологических
процессов. Ряд таких применений графов причинно-
следственных связей связан с решением задач диагноза
технического состояния сложных объектов.
Покажем, что логическая модель объекта, не содер-
жащего многоканальных блоков, может трактоваться
как граф причинно-следственных связей между входны-
ми, внутренними и выходными параметрами объекта.
Построим граф, вершины которого соответствуют
выходным параметрам блоков модели, а также входным
параметрам последней. Дуги графа пусть соответствуют
связям между блоками модели, а также между внешни-
ми входами и блоками модели. Наличие дуги, идущей из
вершины Qi и вершину Qj, пусть означает, что пара-
метр Zj зависит (причинно следует) от параметра 2,.
142
Следовательно, так построенный граф удовлетворяет
определению графа причинно-следственных связей.
В данном случае указанная причинно-следственная
связь между параметрами Zj и Zj задана более конкрет-
но, а именно: если параметр z,- принимает недопустимое
значение, то такое же значение принимает параметр Zj.
Отметим следующее обстоятельство: для того чтобы
по графу причинно-следственных связей можно было де-
лать строго формальные заключения относительно тех-
нического состояния представляемого им объекта диаг-
ноза, должны быть справедливыми все те предпосылки,
которые были приняты при построении логической моде-
ли (см. § 2-1). При этих условиях от графа причинно-
следственных связей можно однозначно перейти к логи-
ческой модели и наоборот. Поэтому все рассмотренные
выше методы обработки логической модели можно без
каких-либо изменений изложить в терминах графов
причинно-следственных связей.
При построении графа причинно-следственных связен
его вершинам можно сопоставлять не параметры объек-
та диагноза, а события, определяемые логическими
высказываниями типа «значение параметра z-t вышло из
заданной для него области допустимых значений». Учи-
тывая «негативный» характер такого события, условим-
ся истинность определяющего его высказывания пред-
ставлять значением 0. Тогда 1 обозначает, что событие
не наступило (параметр Zj имеет допустимое значение).
Указанная символика в то же время совпадает с той,
которая была принята ранее, при представлении объек-
тов их логическими моделями.
Заметим еще, что при построении графа причинно-
следственных связей можно, вообще говоря, представлять
не все входные, внутренние и выходные параметры (или
события, отражающие предельные допустимые значения
этих параметров) объекта, а только некоторые из них,
например те, которые доступны для измерения.
Остановимся теперь на некоторых вопросах задания
возможных неисправностей объекта диагноза. Для логи-
ческой модели объекта было принято, что возможной
неисправностью объекта является любая его физическая
неисправность, такая, которая приводит к появлению
недопустимого выхода хотя бы одного блока. Это усло-
вие может быть принято также для графа причинно-
следственных связей. При этом обработка графа для
143
построения таблицы функций неисправностей и обработ-
ка последней для построения проверяющих и различаю-
щих совокупностей контролируемых параметров должны
осуществляться так, как это изложено в предыдущих
параграфах этой главы. Однако в ряде случаев может
оказаться целесообразным ограничиться заданием под-
лежащих обнаружению или различению неисправностей
объекта путем прямого перечисления некоторых возмож
ных неисправностей. Такое задание равносильно предпо-
ложению, что неисправности, нс включенные в перечень,
невозможны или, в крайнем случае, маловероятны.
Естественно, сокращение числа рассматриваемых неис-
правностей может сопровождаться уменьшением числа
контролируемых параметров в проверяющей и особенно
в различающей их совокупности.
Рассмотрим построение графа причинно-следственных
связей па следующем примере.
Рис. 2-15. Система смазки подшип-
ников мощного редуктора.
Пример 2-5. На рис. 2-15 представлена система смазки подшип-
ников мощного редуктора. Выходными параметрами системы являют-
ся температуры Tl, Т2 и ТЗ
вкладышей подшипников вход-
ного промежуточного и выход-
ного валов редуктора соответ-
ственно. Смазка осуществляет-
ся маслом, циркуляцию которо-
го обеспечивает шестеренчатый
маслопасос.
При снижении давления
масла в напорной магистрали
ниже допустимого значения
срабатывает сигнализатор дав-
ления О„. Обогрев маслосбор
ника системы осуществляется
электроподогревателем; при не-
обходимости маслосборник ох-
лаждается проточной водой.
Подачей проточной воды в ру-
башку маслосборника управ-
ляет регулятор, стабилизирую-
щий температуру Т4 в масло-
сборнике. 1 [сполнительным ор-
ганом регулятора является кла-
пан, снабженный концевыми
выключателями Кн и Кв. Пер-
вый из них указывает на до-
стижение нижнего уровня ре-
гулирования (клапан закрыт), а второй — верхнего уровня регули-
рования (клапан полностью открыт) В маслосборнике установлен
сигнализатор нижнего уровня масла Ун. Для повышения уровня
масла в маслосборнике производится включение на определенное
время пускового маслонасоса.
144
Выберем для представления в графе причинно-следственных свя-
зей следующие события:
температура Т1 выше допустимой, Т1>Н‘,
температура Т2 выше допустимой, Т2>Н-,
температура ТЗ выше допустимой, ТЗ>Н,
температура Т4 выше допустимой, Т4>Н 1,
температура Т4 ниже допустимой, Т4<Н2,
давление масла ниже нормы. DH;
уровень масла ниже нормы, Уи;
клапан охлаждающей воды закрыт, А'н;
клапан охлаждающей воды полностью открыт, Л'в.
Эти события определяют вершины графа. Теперь необходимо
установить пли задать причинно-следственные связи между выбран-
ными событиями. Во многих практических случаях это можно сде-
лать в значительной мере интуитивно, привлекая любую имеющуюся
в распоряжении информацию об объекте. Особенно ценным при этом
является знание функциональной схемы объекта, физики его работы
и технологических особенностей.
Так, для рассматриваемого примера 2-£ системы смазки под-
шипников редуктора причинно-следственные связи между выбранны-
ми событиями определяются следующими соображениями. Превыше-
ние допустимого значения температуры Tl, Т2 и ТЗ может быть вы-
звано одной из двух причин температура Т4 масла превысила до-
пустимое значение Н1 или давление масла стало ниже допустимого
(Du). В свою очередь событие Т4>Н1 может произойти вследствие
неисправности регулятора, когда окажется разомкнутым концевой
выключатель Ки. Причинами понижения давления масла DH могут
быть понижение уровня масла Уи пли достижение температурой Т4
иижнего допустимого значения Н2. Наконец, событие Т4<Н2 может
быть вызвано неисправной работой регулятора, на что указывает
размыкание концевого выключателя /<н.
Полученный граф причинно-следственных связей
показан на рис. 2-16. Вершины графа представлены пря-
моугольниками, в которых записаны условные обозначе-
ния соответствующих событий. Прямоугольники, кроме
того, обозначены рядом стоящими символами Q{, i=l,
2, .... 9, а исходящие из них дуги — символами г,-, приня-
тыми для логических моделей. Для графа причинно-
следственных связей показывать дуги, исходящие из
концевых вершин, не требуется, поэтому символы г7, Ze
и z9 обозначают такие дуги условно.
Прежде чем перейти к заданию неисправностей и
к обработке полученного графа причинно-следственных
связей, заметим, что в сложных случаях (при большом
числе рассматриваемых параметров или событий, при
функционально сложном и малоизученном объекте
и т. п.) для определения причинно-следственных связей
следует применять те или иные процедуры упорядоченно-
го просмотра пар представляемых параметров или
событий. Для каждой пары параметров или событий
10—358 145
Следует определить, связаны они между собой пли нет,
и в первом случае указать, кто из них является причи-
ной и кто—следствием. Для ответов на эти вопросы сле-
дует использовать не только упоминавшуюся выше
эвристическую информацию об объекте, но также изве-
стные аналитические или другие зависимости между
параметрами или событиями.
z7 гв га
Рис. 2-16. Граф причинно-следственных связен.
Чтобы не загружать граф «лишними» дугами, при
указанном просмотре следует стремиться устанавливать
только непосредственное причинное следование. Приме-
рами непосредственных связей являются дуги, показан-
ные на рис. 2-16. Лишней являлась бы, например, дуга
из вершины Ян в вершину Da. Можно показать, однако,
что появление «лишних» связей не приведет к каким-ли-
бо ложным выводам при обработке графа.
Пусть возможными неисправностями системы смазки являются
все такие ее неисправности, которые проявляются в том, что насту-
пает любое из представленных на графе рис. 2-16 событий. Напом-
ним, что это соответствует рассмотрению одиночных неисправностей
объекта по его логической модели. При этом, как отмечалось выше,
граф причинно-следственных связей можно обрабатывать точно так
146
Таблица 2-10
V V V V________________V V V
V e Qi Qi <2s <21 Qs <2e <2, <2, Qo
V 1 0 1 1 1 1 1 1 1 1
V «2 1 1 0 1 1 I I 1 1 I
V z3 1 I 1 0 1 1 1 1 1 1
V гЛ 1 0 1 I 0 1 1 1 1 1
z5 1 1 0 1 1 0 1 1 1 I
z6 1 0 1 0 0 I 0 1 1 1
V ^7 1 0 0 0 0 0* 0 0 1 1
V Z8 1 0 0 0 0 0 0 1 0 1
V Z9 I 0 0 0 0 0 0 1 1 0
же, как логическую модель. В табл. 2-10 представлена таблица функ-
ций неисправностей, построенная по графу рис. 2-16
Применяя результаты, полученные при рассмотрении логических
моделей, находим, что минимальная проверяющая совокупность со-
держит выходы г7, г8 и г9, т. е для проверки исправности (работо-
способности, правильности функционирования) системы смазки не-
обходимо и достаточно контролировать температуры Tl, Т2 и ТЗ
подшипников.
Обязательными выходами для поиска неисправностей являются
выходы Zi, z2, z3, z4 (по правилу 1 предыдущего параграфа) и вы-
1’ис. 2 17. Граф причинно-следственных связей с неисправностями.
10* 147
ходы z7, z8 и zB (по правилу 2). Эти выходы и различаемые ими
неисправности отмечены знаками V слева от табл. 2-10 и над ней
соответственно. Неразличимыми остались неисправности блоков Qs
и Qs- Легко видеть, что они различаются на любом из неотмеченных
выходов z5 или z6. Учитывая, что контроль понижения температуры
Т4 масла является обязательным (выход z4), выберем вы-
ход z5, представляющий сигнал повышения температуры Т4.
Таким образом, для поиска одиночных неисправностей необходи-
мо контролировать положение концевых выключателей Кп и Кв,
уровень Ун и температуру Т4 масла в маслосборнике, а также тем-
пературы Tl, Т2 и ТЗ подшипников
Пусть теперь возможными неисправностями системы смазки счи-
таются следующие конкретные неисправности: недостаточное давле-
ние охлаждающей воды; неисправная работа регулятора; недостаток
масла в системе; неисправная работа шестеренчатого насоса; не-
исправная работа электроподогрева; засорение подшипников.
Такого рода перечни неисправностей являются в большей или
меньшей степени произвольными (и в этом состоит недостаток
рассматриваемого способа задания неисправностей), хотя они и со-
ставляются с учетом вероятностей возникновения и важности обна-
ружения конкретных неисправностей.
Сформированный перечень неисправностей теперь необходимо
«наложить» на граф причинно-следственных связей. Это делается
путем рассмотрения каждой неисправности из перечня (как причи-
ны) и определения вызываемых из-за ее возникновения отклонений
за норму параметров пли событий (как следствий) из числа вклю-
ченных в граф причинно-следственных связей.
Например, недостаточное давление охлаждающей воды может
привести к повышению температуры масла Т4 за допустимый предел
Ht, а неисправная работа регулятора-—к срабатыванию одного из
концевых выключателей Кп или /\п и т. д. На рис. 2-17 показан
граф причинно-следственных. связей с неисправностями из приведен-
ного выше перечня. Неисправности указаны в прямоугольниках и
обозначены символами Sj, j=\ 2, . .., 7. Дуги, исходящие из пря-
моугольников, представляющих неисправности, заходят в вершины,
являющиеся непосредственными следствиями возникновения соот-
ветствующих неисправностей. Заметим, что можно задавать как
одиночные, так и кратные неисправности объекта. Примером кратной
неисправности является засорение подшипников (х?).
По графу причинно-следственных связей с неисправностями мож-
но построить таблицу функций неисправностей (табл. 2-11), которая
отличается от построенной выше табл. 2-10 тем, что ее столбцы
представляют неисправности sj, наложенные на граф, а не неисправ-
ности блоков Qi.
Построение таблицы функций неисправности ведется аналогично
ее построению по логической модели. Различие состоит лишь в том,
что теперь принимаются равными пулю не каждый из выходов Z,
по очереди, а только те из них, недопустимые значения которых не-
посредственно вызываются заданными неисправностями. Например,
чтобы заполнить столбец S| табл. 2-11, необходимо задать z3=0
(см. рис. 2-17) и вычислить при этих условиях значения остальных
выходов. Заметим, что некоторые неисправности могут требовать
задания недопустимых значений нескольким выходам. Например,
неисправность s? на рис. 2-17 требует принять z7=z8=z9 = 0. По-
следнее характерно для кратных неисправностей объекта, а также
148
Таблица 2-11
_______V V V V_________у
я e Si Si S3 Si Se S7
V Z1 1 1 0 1 1 1 1 1
V Zs 1 1 1 0 1 1 1 1
V Z3 1 0 1 1 1 1 1 1
V Z4 1 1 0 1 0 1 1 1
Z5 1 1 1 0 1 0 1 1
Z6 1 0 0 1 0 1 0 1
V z, 1 0 0 0 *0 0 0 0
V Z8 1 0 0 0 0 0 0 0
V 2s 1 0 0 0 0 0 0 0
для таких неисправностей, непосредственным следствием возникнове-
ния которых являются одновременно несколько событий графа.
Обработка табл. 2-11 показывает, что имеется три минималь-
ные проверяющие совокупности контролируемых выходов. Каждая
из них состоит из одного выхода — z7, zB или z9, т. е. для проверки
исправности (работоспособности, правильности функционирования)
системы смазки при заданных неисправностях необходимо и доста-
точно контролировать температуру или Т1, или Т2, или ТЗ подшип-
ников. Напомним, что по табл. 2-10 минимальная проверяющая со-
вокупность требовала контроля каждой из этих температур. Такое
различие объясняется тем, что (см. граф. рис. 2-17) следствием не-
исправности «засорение подшипников» принято одновременное повы-
шение всех трех температур Tl, Т2 и ТЗ.
Остановимся на применении правил 1 и 2 для выделения обяза-
тельных строк таблиц функции неисправностей, построенных по гра-
фам причинно-следственных связей с неисправностями (типа
табл. 2-11). Правило 2 можно применять без каких-либо его изме-
нений, т. е. в различающую совокупность всегда входят
контролируемые выходы, образующие минимальную проверяющую
совокупность. В нашем примере обязательным по правилу 2 являет-
ся один из выходов z7, гв или z9. Все эти выходы отмечены слева
от табл. 2 11 знаком V•
Однако применение правила 1 требует некоторых оговорок.
Пусть из вершины i графа причинно-следственных связей исходит
единственная дуга в вершину /. Тогда выход г, является обязатель-
ным, если обе вершины i и / являются непосредственными следствия-
ми разных неисправностей. Согласно этому уточненному правилу
(назовем его правилом Г) по графу рис. 2-16 выделяются обязатель-
ные выходы Zi, zs, z3 и zt. Соответствующие этим выходам строки
табл. 2 11 также отмечены.
149
Проверкой табл 2 11 находим, что на обязательных выходах не
различаются неисправности Sj, Se и Для их различения необходи-
мы обе неотмеченные строки z5 и z8. Таким образом, для поиска неис-
правностей системы смазки из заданного их перечня необходимо и
достаточно контролировать положение концевых выключателей /(„.
и (выходы Z| и z2), уровень Ун и давление DH масла (выходы 2з
и zc), температуру Т4 масла (выходы z4 н z5) и одну из темпера-
тур Tl, Т2 и ТЗ подшипников (выход z7, z8 или z9).
2-6. ДИАГНОЗ ТЕХНИЧЕСКОГО СОСТОЯНИЯ ОБЪЕКТА
С УЧЕТОМ ВОЗМОЖНЫХ НЕИСПРАВНОСТЕЙ ДАТЧИКОВ
Рассмотрим вопрос о поиске неисправностей датчи-
ков и сигнализаторов (будем последние в дальнейшем
также называть датчиками). Неисправности датчиков
можно разделить на 2 класса: 1) неисправности, приво-
дящие к установлению па выходе датчика сигнала, сви-
детельствующего о недопустимом значении контроль
руемого параметра, в то время как параметр находится
в области допустимых значений; 2) неисправности, при
водящие к установлению на выходе датчика сигнала,
свидетельствующего о допустимом значении контроли-
руемого параметра, в то время как параметр вышел из
области допустимых значений.
Дальнейшее рассмотрение проведем на примере
системы смазки (пример 2-5), представленной графом
причинно-следственных связен, хотя все сказанное ниже
справедливо для логических моделей. При анализе гра-
фа причинно следственных связей системы смазки было
установлено, что для проверки исправности (работоспо-
собности, правильности функционирования) и поиска
одиночных неисправностей достаточно контролировать
параметры Кп, 7<л, У„, T4<JH, Т4~>Н1, Т1>11, Т2>Н,
ТЗ>Н (рис. 2-16). Па рис. 218 приведен граф причин-
но-следственных связен системы смазки, а также обоз-
начены датчики, контролирующие указанные параметры
(датчики Д\—Д1 обозначены па рисунке ромбами).
Предположим, что в датчике Д3, контролирующем
нижний уровень масла Уп в маслосборнике, произошла
неисправность, относящаяся к первому классу. Это зна
чит, что на выходе датчика Дз появится сигнал, свиде-
тельствующий о том, что произошло событие «уровень
масла ниже нормы». В действительности уровень масла
Ун находится в области допустимых значений. В силу
существующих между событиями (параметрами) при-
чинно-следственных связей, определяемых графом при-
150
чнпно-сЛедственпых связей, значения параметров, на
которые воздействует параметр Ун, будут допустимыми.
Поэтому на выходах датчиков Д6, Д7, Д&, контролирую-
щих параметры, которые представляются на графе при-
чинно-следственных связей концевыми вершинами, уста-
новятся сигналы, свидетельствующие о допустимых
значениях параметров Tl, Т2, ТЗ. Это позволяет сделать
вывод о неисправности датчика Дз-
Рис. 2-18. Граф прнчпппо-следствсппых связей объекта, содержащего
датчики.
Предположим далее, что неисправность, относящаяся
к первому классу, произошла в датчике, контролирую-
щем параметр, который представляется па графе при-
чинно-следственных связей концевой вершиной (напри-
мер датчик ДТ). В ээтом случае по показаниям осталь-
ных датчиков нельзя установить, неисправен ли датчик
Д7 или в действительности температура Т2 выше допу-
стимой.
Можно показать, что всегда неисправности, относя-
щиеся к первому классу, всех датчиков, контролирующих
параметры, которые представляются на графе причинно-
следственных связей внутренними (неконцевыми) верши-
нами, могут быть найдены.
Для решения задачи поиска неисправного блока
в объекте с учетом возможных неисправностей в контро-
лирующих датчиках будем пользоваться таблицей функ-
151
ций неисправностей объекта, вычеркнув из нее строки,
которые соответствуют выходам блоков, не вошедшим
в подмножество контрольных точек для проверки исправ-
ности и поиска одиночных неисправностей1. Так, из
таблицы функций неисправностей, построенной для
системы смазки подшипников редуктора (табл. 2-10),
нужно вычеркнуть строку г6. После вычеркивания полу-
чена преобразованная таблица (табл. 2-12).
Таблица 2-12
R е о. Q* <5з Q. <?. О? Qa Qa
Z, 1 0 1 1 1 1 1 1 1 1
«2 1 1 0 1 1 1 1 1 1 1
23 1 1 1 0 1 1 1 1 1 I
г* 1 0 1 1 0 1 1 1 1 1
z5 1 1 0 1 1 0 1 1 1 1
Z, 1 0 0 0 0 0 0 0 1 1
Z, 1 0 0 0 0 0 0 1 0 1
Z, 1 0 0 0 0 0 0 1 1 0
Предполагаем наличие в объекте одной из пере-
численных ниже неисправностей:
1) одиночная неисправность блока Q,;
2) одиночная неисправность датчика, относящаяся
к первому классу (неисправность Д1,);
3) одиночная неисправность датчика, относящаяся
ко второму классу (неисправность Д\).
Пусть при диагнозе технического состояния объекта
на выходах датчиков установился некоторый набор зна-
чений контролируемых параметров. В зависимости от
принадлежности (непринадлежности) этих значений
областям допустимых значений соответствующих пара-
метров полученный набор значений можно представить
в виде двоичного набора из нулей и единиц, которые
будем называть контролирующим набором.
Рассмотрим три возможных случая.
1 Другими словами, из таблицы функций неисправностей исклю-
чаются строки, которым соответствуют параметры, ие контролируе-
мые с помощью датчиков.
152
1. Контролирующий набор состоит из всех единиц.
Все функциональные блоки объекта исправны. В объек-
те может существовать одиночная неисправность датчи-
ка типа Д2{.
Для обнаружения неисправностей датчиков типа
Д2г- можно воспользоваться способом, состоящим в пода-
че на блоки объекта входных сигналов, находящихся вне
областей допустимых значений. При этом значения пара-
метров па выходах всех блоков будут недопустимыми, что
должно привести к установлению на выходах датчиков
контролирующего набора, состоящего из всех нулей.
Наличие в контролирующем наборе хотя бы одной еди-
ницы свидетельствует о неисправности соответствующе-
го датчика типа Д2,. Такой способ проверки датчиков
возможен только при тестовом диагнозе технического
состояния объекта.
При функциональном диагнозе технического состоя-
ния объекта неисправность датчика типа Д2$ будет обна-
ружена в том случае, если выйдет из области допусти-
мых значений некоторый контролируемый параметр,
который причинно воздействует на параметр, контроли-
руемый неисправным датчиком. Предположим, что
в датчике Д5 системы смазки (рис. 2-18) произошла не-
исправность типа Д25. Рассмотрим пути на графе при-
чинно-следственных связей, проходящие через вершину,
соответствующую параметру, контролируемому неисправ-
ным датчиком. В нашем примере через вершину Т4>Н1
проходят пути, содержащие дуги z2, z5, z7, z8, zg. Пусть
вышел из области допустимых значений некоторый конт-
ролируемый параметр, причем этот параметр причинно
воздействует на параметр, контролируемый неисправным
датчиком (например, параметр /<в)- Согласно графу при-
чинно-следственных связен датчики Д2, Дз, Дв, Дт, Дь
контролирующие параметры /<в, 74, 71, 72, 73, должны
выдавать сигналы о недопустимых значениях соответст-
вующих параметров. Однако датчик Д5 будет выдавать
сигнал о допустимом значении параметра 74. Тем самым
неисправность датчика Дз будет обнаружена.
2. Контролирующий набор состоит из нулей и единиц,
причем в таблице функций неисправностей нашелся
l-й столбец, совпадающий с полученным контролирую-
щим набором.
Если i-й столбец содержит всего один нуль, то не-
исправным является либо блок (параметр) Qi, соот-
153
ветствующий i-му столбцу, либо датчик (неисправ-
ность типа Д1,). Единственный нуль, содержащийся
в i-м столбце, свидетельствует о том, что блок Qi явля-
ется концевым, и поэтому неисправность блока Q, неот-
личима от неисправности датчика типа Д1;. Например,
контролирующий набор системы смазки содержит один
нуль и имеет следующий вид:
Zi z2 z3 z4 zs z7 z8 z9
11111011.
В таблице функций неисправностей (габл. 2-12)
с этим набором совпадает столбец Q7, причем блок Qi
является концевым, следовательно в объекте существу-
ет либо неисправность блока Q7 (вышел из области
допустимых значений параметр El), либо неисправность
датчика типа Д’е-
Если i-й столбец содержит более одного пуля, то
неисправным является блок, соответствующий Ему
столбцу. Пусть, например, контролирующий набор
системы смазки имеет вид:
Z1 Z2 Za Z4
1111
Zs Z, Zs Z9
10 0 0.
Этот контролирующий набор совпадает со столбцом
Qe (табл. 2-12). Неисправным является блок Q6 (пара-
метр Dn вышел из области допустимых значений).
3. Контролирующий набор состоит из нулей и единиц,
причем в таблице функций неисправностей нет столбца,
совпадающего с контролирующим набором. Если счи-
тать, что в объекте могут существовать только одиноч-
ные неисправности блоков и дачиков, то в этом случае
контролирующий набор, по совпадающий ни с одним
столбцом таблицы функций неисправностей, может
содержать только один нуль. В самом деле, при одиноч-
ной неисправности блока контролирующий набор совпа-
дает с одним из столбцов таблицы функций неисправ-
ностей, при одиночной неисправности датчика типа Д\
контролирующий набор содержит один нуль, и при этом
в таблице функций неисправностей может не оказаться
столбца, совпадающего с контролирующим набором.
В рассматриваемом случае в датчике, соответствующем
единственному нулю контролирующего набора, существу-
ет неисправность типа Д\.
154
Пусть, например, контролирующий набор системы
смазки имеет вид;
Zi z2 z3 zt z5 z7 z8 z9
1110 1111.
В табл. 2-12 нет столбца, совпадающего с контроли-
рующим набором, следовательно в датчике Д4 существу-
ет неисправность типа ДД
2-7. ДИАГНОЗ ТЕХНИЧЕСКОГО СОСТОЯНИЯ
НЕПРЕРЫВНЫХ ОБЪЕКТОВ, СОДЕРЖАЩИХ ОБРАТНЫЕ СВЯЗИ
Простота математических моделей логического типа
является их преимуществом. Однако вследствие этой
простоты некоторые задачи диагноза технического
состояния непрерывных объектов на» языке таких моде-
лей не имеют решения. Например, при помощи логи-
ческой модели места неисправностей могут быть указа-
ны с глубиной, не превышающей частей объекта, обра-
зующих замкнутые контуры обратной связи. Решение
такого рода задач требует привлечения математических
моделей, являющихся более сложными и благодаря это-
му описывающими поведение объекта более точно, чем
модели логического типа.
Поэтому при решении задач диагноза технического
состояния сложных непрерывных объектов следует
в первую очередь использовать модели логического типа
и только при необходимости затем привлекать более
сложные математические модели, стремясь использовать
их не для объекта в целом, а только для некоторых его
составных частей.
Обычно реальные объекты допускают некоторые от-
клонения (в пределах допусков) для значений основных
параметров. Поэтому оказывается целесообразным
ввести понятие степени работоспособности, которое опре-
деляется по степени отклонения контролируемых пара-
метров в пределах установленных допусков. Неисправ-
ность рассматривается как такое изменение структуры
контролируемого объекта или параметров элементов,
которое приводит к недопустимому снижению степени
работоспособности или полной потере работоспособности
объекта.
Реальные сложные системы могут иметь как большое
число параметров, так и параметры, контроль которых
оказывается довольно сложным. Все это, естественно,
155
затрудняет анализ работоспособности системы. При
рассмотрении таких систем приходится ограничиваться,
как правило, небольшим числом контролируемых пара-
метров. Для выбора ограниченного числа контролируе-
мых параметров всю совокупность параметров целесооб-
разно упорядочить по степени их влияния на
работоспособность системы.
Решение задачи определения работоспособности
системы кроме выбора параметров для контроля тре-
бует установления границ допустимых изменений конт-
ролируемых параметров. Определить границы допусти-
мых изменений контролируемых параметров можно,
анализируя временные или частотные характеристики
системы и пользуясь методами, изложенными в теории
автоматического управления и регулирования. Однако
этот путь требует предварительного получения этих
характеристик, что связано в ряде случаев с большой
вычислительной работой. Альтернативой этого пути
является метод малого параметра, использующий то
обстоятельство, что условия работоспособности опреде-
ляются ограничением областей допустимых перемещений
корней характеристического уравнения системы. Возмож-
ности метода малого параметра позволяют установить
непосредственно область допустимых изменений контро-
лируемого параметра, соответствующих перемещениям
корней характеристического уравнения системы внутри
заданной области, определяемой условиями работоспо-
собности системы.
При диагнозе технического состояния функционирую-
щей системы ее работоспособность можно определить по
результатам сравнения реакции системы с реакцией
эквивалентной модели, .включаемой параллельно контро-
лируемой системе. При построении таких моделей ис-
пользуются аналитические методы, а также аналоговая
техника,— в последнем случае необходима эксперимен-
тальная «подстройка» характеристик модели к соответст-
вующим характеристикам исследуемой системы.
Для определения динамических характеристик систем
как с постоянными, так и с переменными параметрами
применяются также специализированные модели-фильт-
ры. Они могут быть эффективно использованы для опре-
деления характеристик системы неизвестной структуры
непосредственно в процессе ее функционирования. Их-
удобно применять при наличии в системе обратных свя-
156
зей, когда аналитические методы являются слишком
сложными и не приводят к достаточно точным резуль-
татам.
Задачу диагностики непрерывных объектов можно
свести к построению дифференциального уравнения,
соответствующего полученной динамической характери-
стике. В том случае, когда структура диагностируемой
системы известна, определение дифференциального
уравнения сводится к отысканию его коэффициентов.
Если данных о структуре нет и не представляется целе-
сообразным делать какие-либо априорные предположе-
ния, наиболее удобным для нестационарных систем ока-
зывается отыскание системы дифференциальных
уравнений первого порядка, позволяющей представить
диагностическую систему в виде совокупности элемен-
тарных звеньев и, следовательно, определить структуру
модели, изоморфной по поведению исследуемому ориги-
налу. Имеется значительное количество систем, в кото-
рых выход обладает малой «чувствительностью» к опре-
деленным (малым) изменениям внутренних параметров
системы. В таких системах внутренние параметры, плав-
но достигнув некоторых «критических» значений, могут
резко изменить выходные характеристики системы.
Локализация подобных изменений параметров в систе-
ме производится с помощью специальных функций пере-
дач между определенными узлами системы на диаграм-
ме прохождения сигналов. Для некоторых классов
систем можно построить специальную «компенсирую-
щую» схему, с разным выходом при правильном и
неправильном функционировании контролируемой систе-
мы. Известны примеры построения таких «компенси-
рующих» схем для линейных систем автоматического
регулирования
Следует сказать также о выборе режимов контроля
для оценки параметров систем. Существуют два подхода
к выбору режима контроля Один из них предполагает
введение наиболее тяжелого режима, другой — наиболее
вероятного. В практике создания систем диагноза обще-
принят выбор наиболее вероятного режима работы
системы. В случае динамических систем методика изме-
рения параметров базируется на применении статисти-
ческой теории оптимальных систем.
157
2-8. О ФИЗИЧЕСКИХ МЕТОДАХ ДИАГНОЗА ТЕХНИЧЕСКОГО
СОСТОЯНИЯ ОБЪЕКТОВ
В этом параграфе дается общее краткое описание ряда спе-
циальных методов определения технического состояния объектов
диагноза по различным физическим показателям их работы Это
в первую очередь акустические, тепловые и рентгенотелевизионные
методы. Такие методы в литературе называются методами неразру-
шающего контроля.
Более подробно с этими методами читатель может ознакомиться
по литературе, указанной в библиографии.
Начнем рассмотрение с акустических методов. Техническое со
стояние различных механизмов и машин может быть оценено по
таким параметрам, как шум и вибрация в процессе их работы. Вы-
бор этих параметров обусловлен прежде всего тем, что шумовые
характеристики работы машин существенно зависят от многих
свойств участвующих в работе их узлов и деталей, в том числе
таких свойств работающих частей машин (например, состояние тру-
щихся поверхностей деталей), определение которых по иным харак-
теристикам затруднительно.
Одной из основных задач, решаемых в рамках акустических ме-
тодов диагноза, является выделение полезного акустического сигнала
на фоне маскирующих его помех. Следует заметить, что один и тот
же акустический сигнал при диагнозе может оказаться в одном
случае полезным сигналом, а в другом — помехой. Полезным являет-
ся сигнал, который связан с шумом, издаваемым исследуемой де-
талью. Все другие сигналы являются помехой. В связи с этим шум
механизма или машины можно рассматривать как сложный сигнал. Вы-
деление полезной составляющей такого сигнала может быть осу-
ществлено способами временной селекции и фильтрации. Оба эти
способа используются в акустических методах диагноза.
Один из акустических методов диагноза основан на измерении
средней мощности шума Этот метод применяется в основном для
проверки технического состояния объекта В основе метода лежит
предположение о том, что средняя мощность шума исправного ме-
ханизма ниже средней мощности шума изношенного или неисправно-
го механизма. Однако в большинстве реальных случаев уровни
шумов при исправном и неисправном состоянии объекта близки по
значению. В этом случае существует определенная вероятность
принятия исправного объекта за неисправный или неисправного за
исправный, т. е. данный метод диагноза может оказаться малоэффек-
тивным.
К распространенным акустическим методам диагноза принадле-
жит метод, основанный па выявлении скрытых периодичностей в сиг-
нале шума. При исследовании шумовых характеристик различных
механизмов (в частности, коробок передач тракторов и редукторов
станков) установлено, что при возникновении в механизме неисправ-
ности в акустическом сигнале появляется периодическая составляю-
щая. Задача состоит в том, чтобы выявить эту периодическую
составляющую, которая скрыта помехами. Следует отметить, что
если бы полезный периодический сигнал был достаточно мощным
(например, слышимый стук в работающем двигателе), то его выяв-
ление не представляло бы технических трудностей. Однако, когда
стук не прослушивается, т. е. возникшая неисправность еще не
168
привела к заметному нарушению работы механизма, необходимо
применять специальные методы анализа шумовых сигналов.
Для решения этой задачи используются корреляционные методы
анализа сложных сигналов. Эти методы принципиально позволяют
выявлять даже очень слабые периодические составляющие сигнала
на фоне заглушающих их помех. Период специально построенной
корреляционной функции позволяет определить неисправную деталь
механизма а амплитуда этой функции - степень разрушения детали.
В последнее время большое развитие получили методы теплового
(инфракрасного) контроля качества и надежности радиоэлектронно-
го оборудования. Эти методы основаны на анализе теплового излу-
чения деталей, элементов пли устройств при их функционировании.
Интенсивность теплового излучения зависит от электрических харак-
теристик отдельных элементов устройства и его структуры. Измене-
ние характеристик теплового излучения свидетельствует об изменении
режима работы устройства. Для отдельных деталей и элементов
увеличение интенсивности их теплового излучения характеризует ло-
кальные тепловые перегревы, связанные с наличием дефектов или
неоднородностей. Своевремениое обнаружен fe этих дефектов позво-
ляет принять меры по предупреждению выхода из строя деталей
элементов и устройств в целом. Так, исключение из радиоэлектрон-
ных устройств их элементов и деталей, интегральный уровень тепло-
вого излучения которых отличается от среднего (номинального)
уровня, позволяет заметно снизить число отказов
Тепловые методы по способу получения характеристик излучения
делятся на контактные и неконтактные.
К контактным методам относятся:
методы измерения температуры в различных точках объекта при
помощи термопар;
методы, основанные на использовании температурно-чувствитель-
ных красок и составов, изменяющих свой цвет или плавящихся при
определенной температуре детали, на которую они нанесены;
методы, связанные с применением жидкокристаллических соеди
нений, окраска которых обратимо меняется в зависимости от темпе-
ратуры;
методы, основанные на использовании свойства фотографических
эмульсий изменять скорость проявления в зависимости от темпера-
туры.
Наиболее перспективными методами из перечисленных выше счи-
таются методы, использующие жидкокристаллические соединения.
В настоящее время они позволяют измерять разности температур
порядка О 1°С. При помощи ряда холестерических жидкокристалли-
ческих соединений проводится измерение температур от 10 до 100GC.
Большое распространение получили также следующие неконтакт-
ные методы:
методы эвапорографии, основанные на преобразовании теплово-
го излучения объекта в видимое изображение путем испарения или
конденсации жидкости на тонкой мембране;
методы краевого поглощения, связанные с использованием за-
висимости положения границы поглощения некоторых полупровод-
ников от температуры;
методы, использующие явления фотоэмиссии и вторичной эмис-
сии электронов;
методы, основанные на свойстве люминофоров изменять интен-
сивность свечения под действием температуры;
159
методы, использующие сканирование электронным или оптиче-
ским лучом.
В настоящее время разработан ряд приборов, предназначенных
для определения теплового излучения объектов неконтактными ме-
тодами. Эвапорографы, применяемые для визуализации теплового
поля объектов, обладают высокой разрешающей способностью и по-
зволяют получать изображения объектов, температура которых отли-
чается от температуры среды на 0,5°С. Приборы, работающие на
принципе поглощения, имеют при минимальной разности температур
12°С разрешающую способность порядка 2 штрихов на миллиметр
и постоянную времени около 0,5 с. Разработаны также люминесцент-
ные термографы, изменяющие яркость свечения на 20% при измене-
нии температуры на 1°С. Широкое распространение получили различ-
ные сканирующие системы. В этих системах последовательно про-
сматриваются отдельные части схемы, тепловое излучение которых
преобразуется в электрические сигналы и затем в двумерную ви-
зуально наблюдаемую картину объекта.
Рентгенотелевизионные методы диагноза позволяют обнаружи-
вать скрытые дефекты изделий и деталей в процессе их изготовле-
ния. Дефекты радиоэлектронных изделий (полупроводниковых дио-
дов, транзисторов, резисторов, микромодулей и т. д.) могут быть
разделены на два основных класса:
дефекты формы, выражающиеся в изменении конфигурации и
нарушении геометрических размеров;
дефекты сплошности, образующиеся за счет различных неодно-
родностей, примесей, трещин.
Наличие этих дефектов существенно влияет на работоспособ-
ность изделий. Выявление скрытых дефектов осуществляется при
помощи реитгенотелевизпонпых микроскопов и стробоскопов. Назна-
чение реитгеиотелевпзиоииого микроскопа состоит в получении рент-
геновского изображения контролируемого изделия. Рептгепотелеви-
зионные стробоскопы дают неподвижные изображения вибрирующих
изделий.
Существующая рентгенотелевизионная аппаратура позволяет
контролировать почти всю номенклатуру радиоэлектронных изделий.
Исключение составляют слишком массивные изделия, а также изде-
лия, содержащие некоторые мелкие детали (например, элементы
отдельных микромодулеп), которые на экране вндеоконтрольного
устройства оказываются недостаточно различимыми. Для определе-
ния дефектов в изделиях производят сравнение получаемых рентге-
нограмм с эталонными рентгенограммами или с конструктивными
чертежами.
Результаты контроля регистрируются следующими способами:
описанием наблюдаемых на экране дефектов;
фотографированием изображения изделия с экрана видеокоп-
трольного устройства;
рентгенографированием изделия;
электрографированием в рентгеновских лучах.
Рентгенотелевизионные микроскопы позволяют получить па
экране изображение с увеличением до 30 раз при высокой разре-
шающей способности (до 20 пар линий на 1 мм).
1G0
ЗАМЕЧАНИЯ ПО БИБЛИОГРАФИИ
В [Л. 14] для описания функционирования непрерыв-
ных объектов (в частности, радиоэлектронных устройств)
в исправном и неисправном состояниях была введена
двухзначная модель. В этой работе решалась задача
построения комбинационных и последовательных алго-
ритмов диагноза. В [Л. 28] предложена логическая
модель и описаны формальные правила ее построения.
Развитие и обобщение двузначной модели состоят в рас-
смотрении объектов, состоящих из функционально свя-
занных блоков со многими выходами (выходными пара-
метрами). В [Л. 28] и впоследствии в [Л. 4, 18] была по-
ставлена и решена задача определения минимального
числа контрольных точек в объекте для проверки его
исправности и поиска неисправностей.
В [Л. 27] излагаются методы анализа и процедуры
диагностики объектов (в основном радиоэлектронных
устройств), заданных функциональными схемами и мо-
делями.
В [Л. 23] для анализа электронных схем в исправном
состоянии были введены графы причинно-следственных
связей между параметрами схемы. В [Л. 17, 20] графы
причинно-следственных связей были использованы для
диагностического анализа различных электрических,
механических устройств, механизмов и машин, а также
сложных объектов (в частности, двигателей внутреннего
сгорания). Исследованию возможности использования
теории графов при решении задач технической диаг-
ностики посвящена [Л. 25].
В [Л. 19] рассмотрены формальные процедуры поиска
неисправностей на основе дихотомического дерева реше-
ний (схемы функциональных проб) п вопросы оптимиза-
ции этих процедур. Исследованию методов поиска не-
исправностей в системах управления, содержащих об-
ратные связи, посвящены (Л. 12, 22]. В этих работах на
основе диаграммы прохождения сигналов предложена
процедура анализа характера деформации тест-сигнала
(единичного или гармонического) для целей проверки
работоспособности и поиска неисправностей.
В [Л. 15, 16[ рассматриваются методы диагностики
непрерывных объектов, основанные на анализе их дина-
мических характеристик. В [Л. 13] предложен метод
диагностики с использованием избыточных переменных.
11—358 161
Методы акустической диагностики достаточно по-
дробно рассмотрены в [Л. 24]. Сборники [Л. 21, 29] содер-
жат работы по методам перазрушающего контроля. Они
состоят из ряда обзорных и специальных статей, а так-
же содержат обширную библиографию отечественных и
зарубежных работ по методам теплового, рентгено-
телевизионного и других видов неразрушающего кон-
троля.
Описание принципов работы устройств и систем, рас-
сматриваемых в качестве примеров в гл. 2, можно най-
ти в [Л. 17, 26].
ГЛАВА ТРЕТЬЯ
ДИСКРЕТНЫЕ КОМБИНАЦИОННЫЕ ОБЪЕКТЫ
ДИАГНОЗА
В этой главе рассматриваются дискретные комбина
циоппые объекты, т. с. объекты, входные, внутренние и
выходные координаты которых заданы па конечных мно-
жествах и значения выходных координат определяются
однозначно только значениями входных координат. Об-
щепринятой идеализацией при рассмотрении дискретных
комбинационных объектов является предположение
о том, что изменения значений выходных координат
(функций) происходя г мгновенно вслед за вызвавшими
их изменениями значений входных координат (перемен-
ных). Последнее условие равносильно отсутствию в объ
екте контуров обратных связей пли элементов памяти,
в том числе задержек.
Заметим, однако, что ряд результатов рассмотрения
дискретных комбинационных объектов может быть не-
посредственно распространен на дискретные объекты
с временными задержками, но без контуров обратных
связей, а также на дискретные объекты с несуществен-
ными обратными связями Исследование дискретных
комбинационных объектов представляет интерес также
применительно к дискретным объектам с памятью,
содержащим, как правило, комбинационные части.
Физические дискретные объекты обычно называют
дискретными устройствами. В этой, а также в следую-
щей главе, посвященной рассмотрению дискретных
объектов диагноза с памятью, мы часто будем пользо-
ваться этим термином,
162
В книге рассматриваются только двоичные дискрет-
ные устройства, нашедшие наиболее широкое распрост-
ранение.
3-1. ИСПРАВНЫЕ КОМБИНАЦИОННЫЕ УСТРОЙСТВА
И ИХ МАТЕМАТИЧЕСКИЕ МОДЕЛИ
При изучении физических объектов, в том числе
объектов, предназначенных для переработки дискретной
информации, принято два подхода: функциональный и
структурный.
Функциональный подход заключается в рассмотрении
алгоритмов функционирования объекта, т. е. реализуе-
мых объектом функций, а структурный подход предусма-
тривает исследование внутренней организации или струк-
туры объекта.
функциональный подход
При функциональном подходе исследуемое устройство
рассматривается как «черный ящик», т. е как объект,
внутренняя организация или структура которого неиз-
вестна или не имеет значения. Исследователя в этом
случае интересует лишь характер переработки информа-
ции. осуществляемой устройством, и выяснение функцио-
нальных зависимостей между информацией, поступаю-
щей на входы устройства и вырабатываемой на его
выходах.
Пусть дискретное комбинационное устройство имеет
п входов и k выходов Каждая из п входных переменных
л',, х2, • • •> хю может принимать значения из двоичного
алфавита {0,1}. Комбинацию значений входных перемен-
ных будем называть входным набором или входным
словом и обозначать символом Xj, j=\, 2, ..., 2", где
2п — число всех возможных (разных) входных наборов.
Если упорядочить входные переменные, то каждый
входной набор может быть представлен /г-разрядным
двоичным числом.
Каждая из k выходных функций Zi, z2, ..., zh также
может принимать значения 0 или 1. Комбинация
значений выходных функций образует выходной
набор или выходное слово Z,. Выходные наборы Z, явля-
ются ^-разрядными двоичными числами.
По определению комбинационного устройства каждо-
му входному набору Xj, поданному в некоторый момент
11* 163
Времени на его входы, соответствует выходной набор Zj,
появляющийся в тот же момент времени на его выходе.
Разным входным наборам могут соответствовать одина-
ковые выходные наборы.
Наборы Xj являются значениями n-мерного вектора X
с компонентами х1( х2, .... хп, а наборы Zj — значениями
й-мерного вектора Z с компонентами Zi, z2,..., zh. Тогда
по аналогии с приведенной в § 1-4 условной записью
(1-1) для систем передаточных функций, реализуемых
исправным комбинационным устройством, можно запи-
сать:
Z=F{X). (3-1)
Запись (3-1) можно представить в форме системы
соответствий вида
Zj—Zj (3-2)
для всех j = l, 2, .... 2й.
Выходные функции zt, z2, zft являются булевыми
функциями независимых переменных Xt, х2, хп. Для
задания булевых функций часто используют таблицы
истинности. Столбцы таблиц истинности сопоставляются
входным переменным (в левой части) и выходным
функциям (в правой части). В строке j таблицы истин-
ности записываются слева направо входной набор Х3 и
соответствующий ему выходной набор Zj, обычно в виде
двоичных чисел. Систему соответствий (3-2) можно
представить либо одной общей для всех выходных
функций таблицей истинности, либо /г таблицами истин-
ности — по одной для каждой выходной функции.
Последний случай соответствует заданию системы соот-
ветствий вида
X i —*(2Т)/
для всех у=1, 2, ..., k и всех /=1, 2, ..., 2п.
Пример 3 1. Примером общей таблицы истинности для двух вы-
ходных функций г2 от трех входных переменных Xi, х2, х3 явля-
ется табл. 3-1. В левом столбце этой таблицы указаны порядковые
номера строк, являющиеся десятичными эквивалентами двоичных
чисел, представляющих входные наборы.
Таблица истинности является функциональной мате-
матической моделью комбинационного устройства. От
таблицы истинности можно перейти к аналитической
функциональной математической модели комбинацион-
164
Таблица 3-1
№ п.п. *1 *1 Хй Zi 2ц
0 0 0 0 0 0
1 0 0 1 0 0
2 0 1 0 1 0
3 0 1 1 0 1
4 1 0 0 0 1
5 1 0 1 0 1
6 I 1 0 I 0
7 1 1 1 1 1
кого устройства, представив его выходные функции
в виде, например, формул булевой алгебры. Одна и та
же булева функция может быть представлена в прямом
или инверсном виде разными формулами.
Пример 3 2. Прямой вид функции, или прямая функция, Zi из
табл 3-1 может быть задан совершенной дизъюнктивной нормаль-
ной формой
Z1 — JC1X2X3‘V X]X2 Х3 V Х1Х2Хз.
минимальной дизъюнктивной нормальной формой
Zt = Х1Х2 V Х2Х3
и скобочной формой
Z1 — хг (Xi V Хз).
Для инверсного вида функции, или для инверсной функции, Z|
получаем:
Z, = Х1Х2 Хз V Х1ХгХ3 V Х1Х2Х3 V Х1Х2 Хз V Xi х2х3
ИЛИ ’! = Х1Х3 V хг-
Для многих задач анализа, синтеза, а также диагноза
технического состояния дискретных устройств недоста-
точно их функционального описания. Этим объясняется
необходимость разработки и применения структурных
математических моделей, т. е. моделей, отражающих не
только функции, реализуемые устройством, но и его
внутреннюю организацию или структуру. Такой подход
выше был назван структурным.
165
Структурный подход
Дискретные устройства состоят, как правило, из ря-
да однотипных пли даже одинаковых компонент, соеди-
ненных между собой с целью получения определенных
функциональных зависимостей. Часто компонента уст-
ройства — это конструктивно и функционально закончен-
ная элементарная часть, не подлежащая дальнейшему
расщеплению. Поэтому для описания компоненты доста-
точно той или иной ее функциональной математической
модели. В частности, компонента ц,- комбинационного
устройства может рассматриваться как комбинационное
подустройство с tii входами и ki выходами, реализующее
определенную систему передаточных функций, заданных
в одном из рассмотренных выше видов. Такие компонен-
ты будем называть логическими элементами.
Ограничимся рассмотрением одновыходных логичес-
ких элементов. Многовыходные логические элементы
будем представлять совокупностями одновыходных эле-
ментов с объединением их одноименных входов (подобно
тому, как это делалось при построении логической моде-
ли в гл. 2). Основное рассмотрение будем вести относи-
тельно логических элементов обладающих свойством
односторонней проводимости (от входов к выходу),
свойством разделительное™ (независимости) входов и
свойством существенности всех /г,- входов. Примерами
таких элементов являются бесконтактные полупроводни-
ковые логические элементы.
В качестве структурной математической модели ком-
бинационного устройства обычно принимается правиль-
ная логическая сеть |(схема). Дадим неформальное опре-
деление логической сети, близкое к известному инженер-
ному понятию функциональной схемы устройства и по-
лучившее удобную интерпретацию на языке графов.
Назовем множество функционально разных логических
элементов устройства базисом логической сети и обозна-
чим его символом Н. Логическая сеть определяется мно-
жеством {'/;/} логических элементов из базиса II, множест-
вом {xj входных полюсов и множеством {z I выходных
полюсов. Каждому входному (выходному) полюсу взаимно-
однозначно соответствует входная переменная ха, а.—
= 1,2, ..., /г (выходная функция z, у=1,2, ..., k).
Кроме того, для логической сети задаются соединения
входных полюсов с входами элементов, соединения вы-
166
ходов элементов с выходными полюсами и, наконец,
соединения выходов одних элементов с входами других
элементов. В частном случае входной полюс может быть
соединен с выходным полюсом. Для представления вход-
ного полюса или выхода элемента, соединенного с нес-
колькими входами элементов или выходными полюсами,
в логической сети предусматривается узел разветвления.
Условимся под соединением или узлом сети подразуме-
вать связь входного полюса, выхода элемента или узла
разветвления с входом элемента, с выходным полюсом
или с узлом разветвления. Связь узла разветвления
с входом элемента или выходным полюсом будем назы-
вать ветвью разветвления.
Логическую сеть, представляющую комбинационное
бесконтактное устройство, называют правильной, если
никакие два выхода элементов не соединены вместе и
если каждую из k функций, реализуемых на выходных
полюсах сети, можно представить как булеву функцию
входных переменных, сопоставленных п входным полю-
сам сети.
Логической сети сопоставляется ориентированный
граф, вершинам которого соответствуют логические эле-
менты, входные и выходные полюсы сети и узлы разветв-
лений, а направленным дугам — соединения сети, при-
чем дуги, инцидентные вершинам, которым соответству-
ют логические элементы, упорядочены. Это вызвано
тем, что в общем случае функция yi, реализуемая эле-
ментом г);, несимметрична относительно перестановок
входных переменных элемента. Для одновыходных эле-
ментов достаточно упорядочить дуги, заходящие в ука-
занные вершины. Таким образом, при задании дуги
в графе логической сети, кроме указания вер-
шин, которые она соединяет, в общем случае
указывается номер входа элемента, соответствую-
щего вершине, в которую заходит рассматриваемая дуга.
Будем считать этот номер весом рассматриваемой дуги.
Дуги, заходящие в вершины, которые соответствуют
элементам, симметричным относительно перестановок их
входов, можно не взвешивать, как и дуги, заходящие
в вершины, которым соответствуют выходные полюсы
сети. Граф логической сети может быть задан графичес-
ки или посредством матрицы смежностей.
Две логические сети А и А' будем называть одинако-
выми (тождественными), если, во-первых, их графы GA и Од,
167
изоморфны1, во-вторых, совпадают их базисы, НЛ = НЛ,
и множества их полюсов входных {ла}л = {ла}л, и выход-
ных {?т}л — {гг}л, и, в-третьих, вершинам каждой пары
взаимно-однозначных вершин соответствует или один и
тот же логический элемент, или входная переменная,
или выходная функция. В противном случае логические
сети А и А' различны (нетождественны).
В дальнейшем при начертании логических схем бу-
дем использовать названия и условные обозначения
некоторых часто употребляемых логических элементов
из табл. 3-2. Пример логической сети изображен на
рис. 3-1. Входные переменные обозначены символами
а, Ь, с и cl, а выходная функция — символом г.
Элементы логической сети без обратных связей могут
быть упорядочены следующим образом. Перенумеруем
сначала в произвольном порядке входные полюсы сети и
отнесем их к пулевому рангу. Затем перенумеруем также
в произвольном порядке элементы сети, все входы кото-
рых соединены лишь с входными полюсами (указанные
элементы будем называть элементами первого ранга).
Подобным образом выполним произвольную нумерацию
элементов, входы которых обязательно соединены с вы-
ходами элементов первого ранга и, возможно, с входны-
ми полюсами (элементы второго ранга). Входами
элементов /-го ранга обязательно являются выходы эле-
ментов (/—1)-го ранга и, возможно, входные полюсы и
выходы элементов ранга, меньшего /—1. Указанная
процедура упорядочения элементов (или ранжирования
сети) заканчивается, когда все элементы сети будут про-
нумерованы и им будет присвоен некоторый ранг. Для
логической сети рис. 3-1 ранги ее элементов указаны
над сетью.
Как известно, от правильной логической сети легко
перейти к функциональному описанию представляемого
ею комбинационного устройства. Так, например, при ана-
литическом представлении функционального описания
логических элементов ранжированной сети аналитичес-
кая запись системы передаточных функций комбинаци-
онного устройства может быть получена путем последо-
1 Два взвешенных графа GA и GA называются изоморфными,
если существует такое взаимно-однозначное соответствие их вершин,
что дуга одного графа соединяет пару вершин тогда и только тогда,
когда соответствующая пара вершин другого графа соединена дугой
и вес обеих дуг одинаков (или, в частности, обе дуги не взвешены).
165
Таблица 3-2
Название реа- лизуемой функции Реализуемая функция Условное обозначе- ние Начертание в схемах
Повторение Отрицание (инверсия) Конъюнкция Отрицание конъюнкции (штрих Шеф- фера) Дизъюнкция Отрицание дизъюнкции (стрелка Пирса) Конъюнкция с запретом Дизъюнкция с запретом !/ = х у ~ . Хп y-XiX2. . ,хЛ у = Xi V Х2 V . . . V Хп у = *1 V х, V . . . V хп у = хгх,. . х[. . .хп y = j^Vx,V ... V V xt V ... V хп И НЕ И И ИЛИ > или
X 1 —у
3? 1 ~У
X,— хп т1.— & —У
& •—У
— I —У
Н Н я Й ’ГП Г"| 7 " у
" & —У
а, _ хп 1 — У
169
Продолжение табл. 3-2
Название реа-
лизуемой
функции
Неравно-
значность
(сумма по
модулю 2)
Равнознач-
ность
Реализуемая функция
Начертание в схемах
У = *1*2 V XiXa
Мажоритар-
ная
у = xtx* v Jtprs v *2*з
М
вательной подстановки выходных функций элементов
(начиная с элементов первого ранга). При этом в фор-
мулу, представляющую реализуемую некоторым элемен-
том функцию, вместо входных переменных элемента
подставляются переменные входных полюсов сети или
формулы выходных функций элементов, выходы которых
соединены с входами рассматриваемого элемента.
Пример 3-3. Обозначим выходы элементов, ие являющиеся внеш-
ним выходом сети рис. 3-1, символами у с нижним индексом, ука-
зывающим номер элемента. Тогда описанная процедура прямой под-
становки при получении прямой функции г выглядит так:
ранг 1 — yi = cd, уг = Ь, уз = d;
ранг 2 — yt = у, V а = cd \/ а, Уз = уе \/ у3 = b \/ d
ранг 3 — уй = byi = b(cd \/и), !h = tji = (г: V d) it;
ранг 4 — уга у-,уь (с \/ d) a (b V d) = it (с Ь V ^)’>
ранг 5 — г = уй\/ ys = b (cd \/ a)\Ja(c b \/ d) =
= ab V a d\/ bed V ас b
Аналитическая запись системы передаточных функ-
ций, реализуемых комбинационным устройством, может
быть получена также при помощи процедуры обратной
подстановки (от выходов к входам устройства). Сущ-
ность процедуры состоит в последовательной подстанов-
170
ке выходных функции элементов сети (начиная с эле-
ментов последнего ранга).
Пример 8-4 Проиллюстрируем процедуру обратной подстановки
на том же примере логической сети рис. 3-1 для получения реализуе-
мой ею прямой функции г:
ранг 5 — г = у6\/уе-,
ранг 4 — z = yt,\/У1У&;
ранг^ 3 — z = by<i\J ytyf,
ранг 2 — z = b (t/i V ") V V а)(Уг V Из);
ранг 1 — z = b (cd V с) V (с V Ф а (Р V d) =
= ab V а d V bed V ас b-
Обратная (или инверсная) функция z может быть
получена как путем ипвертирования»прямой функции г,
РангО РЫг1 Ранг г РалгЗ Ранг 4 Ранг 5
Рис. 3-1 Пример логической сети без обратных связей.
так и по заданной логической сети при помощи процедур
прямой или обратной подстановки. В последнем случае
выполняется подстановка инверсных входных перемен-
ных или выходных функций элементов сети.
Пример 3-5. Применим процедуру обратной подстановки к сети
(рис. 3-1) в целях получения обратной функции z:
г = J/е V Лз — Уб
Уб (у-, V?s);
171
z = (bv г/s);
Z = (ft V t/1 V a- V i/2 г/з);
z = [ft V (c V Ф al (cd bd) = «ft V bed V ab cd.
В дальнейшем под передаточной функцией комби-
национного устройства или функцией, реализуемой
устройством, будем понимать, как правило, прямую
функцию.
Заметим, что требование правильности лошческой
сети не исключает наличия в ней петель обратной связи
или циклов в соответствующем ей графе. Логическая
сеть, построенная из логических элементов без соедине-
РангО Ранг! Ранг 2
Рис. 3-2. Пример логической
сети комбинационного устрой-
ства с обратной связью.
обратной связи. Вычислив
функцию z, покажем, что
бинацнонное устройство.
ния между собой выходов
нескольких элементов и без
обратных связей, всегда яв-
ляется правильной и пред-
ставляет комбинационное
устройство. Однако наличие
в логической сети петель об-
ратной связи не является
достаточным признаком то-
го, что устройство не комби-
национное. Для примера на
рис. 3-2 изображена логи-
ческая сеть из двух мажори-
тарных элементов с петлей
реализуемую сетью выходную
последняя представляет ком-
Для вычисления передаточных функций логической
сети с обратными связями при помощи процедур под-
становки оборвем условно все обратные связи. При
этом образуются новые входные и выходные полюсы
сети. Новым входным полюсам сопоставим условные не-
зависимые переменные и произведем ранжирование сети.
После этого вычислим выражения передаточных
функций сети для всех (основных и новых) выходных
полюсов. Затем в выражения функций, реализуемых
устройством на его рабочих выходах, вместо услов-
ных независимых переменных подставим функции,
реализуемые на соответствующих новых выходных
полюсах. Если полученные после этого выходные функ-
ции, реализуемые на основных выходах устройства, не
172
зависят от условных независимых переменных, то
устройство является комбинационным. В противном
случае оно является устройством с памятью. (Об осо-
бенностях представления устройств с памятью логи-
ческой сетью будет сказано в следующей главе).
Пример 3-6. Для логической сети рис. 3-2, обозначив символом «
условную независимую переменную и символом д? — новый выход,
имеем:
ранг 1 — = z = аЬ\/ ас V Ьс;
ранг 2 — ys = а \/ аул = а.
После подстановки У2=а вместо а получаем:
z = ab V ас V Ьс.
Следовательно, логическая сеть (рис. 3-2) представляет комби-
национное устройство с несущественной обратной связью.
Две логические сети А и А', у которых системы пе-
редаточных функций одинаковы, называются эквива-
лентными. Одинаковые сети всегда эквивалентны. Но
обратное, как известно, неверно.
В полученном выше виде аналитическая запись си-
стемы передаточных функций комбинационного устрой-
ства, заданного своей логической сетью, в общем слу-
чае не отражает структуры сети. Рассмотрим другие
виды аналитической записи передаточных функций ком-
бинационных устройств, содержащие информацию о
структуре устройства и позволяющие восстанавливать
граф его логической сети.
СКОБОЧНАЯ ФОРМА
Одним из видов структурно-аналитических выраже-
ний является скобочная форма (СФ) представления
прямых (инверсных) передаточных функций комбина-
ционного устройства. Скобочная форма может быть
получена процедурой прямой или обратной подстанов-
ки в ранжированной сети с пронумерованными элемен-
тами, если выражение для прямой (инверсной) функции,
реализуемой элементом ц,, во всех его вхождениях
заключать в скобки с нижним индексом, равным i, и при
подстановках не производить никаких раскрытий скобок
и замен отрицания над скобкой преобразованием вну-
I рнскобочного выражения.
173
Пример 3-7. Применим для построения скобочной формы прямой
функции процедуру обратной подстановки на примере логической
сети рис. 3-1:
z — (у. V
г = [1/в V ('/7Лз)в]9;
[(by,). v |(/лШЬ}9;
= {[6 (ю V V {[('/> V ф,b (у*' / (/з)5}в}8;
Z = {{&[(«*). V Л] 1}6 V{{[(crf)iV"h}7 [(6)2V(dh]s}s}s.
I
(3-4)
Взяв инверсию левой и правой частей уравнения (3-4), получим
скобочную форму инверсной функции.
ЭКВИВАЛЕНТНАЯ ФОРМА ФУНКЦИИ ЛОГИЧЕСКОЙ СЕТИ
Широкое распространение получила другая структур-
но-аналитическая запись в виде эквивалентной формы
(ЭФ) или, что то же, эквивалентной нормальной формы
(ЭПФ) булевой функции, реализуемой комбинационным
устройством. Предварительно введем некоторые понятия.
Будем называть базис булевым, если он содержит
лишь логические элементы И, ИЛИ и НЕ. Любой логи-
ческий элемент может быть представлен логической
сетью в булевом базисе. I (азовем логический элемент
простым, если существует представляющая его логи-
ческая сеть в булевом базисе такая, что все ее вершины
содержат по одной исходящей дуге, т. е. в этой сети нет
узлов разветвлении. В противном случае элемент назы-
вается сложным.
Для функции, реализуемой простым элементом,
всегда существует ее дизъюнктивная нормальная форма,
каждая входная переменная которой во всех своих
вхождениях либо имеет знак отрицания, либо его не
имеет; в первом случае соответствующий вход называ-
ется инвертируемым входом простого элемента. Прос-
тыми элементами являются, например, элементы, реали-
зующие функции у = Х1Х2Х3, y = Xi\/x2—XlX2, У = Х[Х2\/Х3.
У второго элемента оба входа являются инвертируемы-
ми, у третьего—вход х2. Сложным элементом является,
например, элемент, реализующий «сумму по модулю
два» y=XiX2\/Х1Х2, мажоритарный элемент с функцией
y=xlx2\/xtX3\fX2X3 также является сложным, гак как
не может быть представлен логической сетью без раз-
174
ветвлений в булевом базисе. Базис, содержании! только
простые элементы, назовем простым, а содержащий
хотя бы один сложный элемент, — сложным. Если
характер логических элементов базиса не играет роли,
то будем называть последний произвольным.
Одновыходная логическая сеть является деревом, если
она не содержит ни одной вершины, из которой исходит
более одной дуги. Это соответствует отсутствию разветв-
лений входных полюсов п выходов логических элементов
устройства. Граф логической сети дерева, если его рас-
сматривать как неориентированный граф, не содержит
циклов. Рассмотрим одни из способов преобразования
одновыходной логической сети без обратных связей
к логической сети, имеющей вид дерева, п эквивалент-
ной исходной сети при отождествлении одноименных
входных полюсов дерева.
В исходной логической сети проверим, имеет ли она
вершины с несколькими исходящими дугами. Если та-
ких вершин пет, то заданная логическая сеть является
деревом. В противном случае отметим все вершины,
инцидентные нескольким исходящим дугам, и поместим
их в список в порядке неубывания рангов этих вершин
(входных полюсов, элементов). Возьмем первую верши
пу 1), из списка, имеющую vf^2 исходящих дуг. «Рас-
щепим» ее на вершин, имеющих по одной исходящей
дуге, с одновременным повторением v, раз подсети, для
которой вершина ф является выходным полюсом. Ука-
занную подсеть будем называть г),-подсетью. Присвоим
номерам элементов и символам входных переменных
разных ф-подсетей индексы 1, 2,..., v,-. Возьмем вторую
вершину из исходного списка к повтворим для нее ука-
занную процедуру «расщепления» в полученной па пер-
вом шаге логической сети. При этом у номеров элемен-
тов и символов входных переменных, участвующих
в «расщеплении», появляются или добавляются новые
индексы. Выполнив последовательно описанные опера
цин для каждой вершины из списка, получим искомое
дерево, эквивалентное исходной сети, если в нем отож-
дествить входные переменные, символы которых отли-
чаются только индексами. Для краткости полученную
сеть будем называть эквивалентным деревом (ЭД).
Условимся входной полюс, «не расщепившийся» в ЭД,
снабжать индексом 1. Выражение функции, реализуемой
ЭД и записанной в дизъюнктивной нормальной форме,
175
будем называть эквивалентной формой функции ЭД
или просто эквивалентной формой (ЭФ). Вначале вве-
дем ЭФ для функций логических сетей без обратных
связей, реализованных в простом базисе.
Пример 3-8. Для логической сети рис. 3-1 эквивалентное дерево
показано на рис. 3-3. Как видно из рис. 3-1, входные полюсы Ь и d,
а также выход элемента 4 разветвляются. Вначале «расщепляются»
входные полюсы b и d па Ь\, Ь2 и d,, d2, затем -/-подсеть представ
ляется дважды: 4t подсетью (элементы /ь 4, и входные полюсы Ci,
du, я,) и ^-подсетью (элементы 12, 1г и входные полюсы с2, di2, а2).
Рис. 3-3. Эквивалентное дерево логической сети рис. 3-1.
По процедурам прямой или обратной подстановки можно по-
строить эквивалентную форму функции, реализуемой деревом. Для
рис. 3-3 имеем:
£ = bid, \/ biCidn\/ а2 е2 b2 \J и2 di2 b2 \/ и2^е2 d2 \J (t2 di2d2- (3-5)
Применив одну из процедур подстановки к инверсным функциям
логических элементов дерева, получим обратную эквивалентную фор-
му (ОЭФ):
z = bifiaV biC2 diS V bib2d2 'у/ ей Ci«2 V <7i t’ic2di2 V Щ ctb2d2 V
V ЩСг dn V dnC2di2 V Щ d,,b2d2. (3-R)
При преобразованиях выражений для функций z или
z не допускаются никакие упрощения. Отметим следую-
щие особенности ЭФ (ОЭФ)
1. ЭФ (ОЭФ) имеет вид логической суммы произве-
дений, а потому является дизъюнктивной нормальной
формой.
176
2. Каждая буква ЭФ (ОЭФ) представляет входную
переменную исходной сети (возможно с отрицанием)
с приписанными ей индексами. Например, буква г/щ
в выражении (3-5) является отрицанием входной пере-
менной dK ЭД и представляет входную переменную d
исходной сети (рис. 3-1) с двумя индексами 1 и 2
(следствие двух последовательных «расщеплений»),
В ЭД от каждого входного полюса существует только
один путь до выходного полюса. Этому пути в исходной
сети однозначно соответствует вполне определенный
путь от входного полюса до выходного. Будем говорить,
что с буквой в ЭФ (ОЭФ) ассоциирован путь в исходной
сети. Например, с буквой й|2, которой в ЭД соответ-
ствует единственный путь от полюса d\2, ассоциирован
путь от полюса d через элементы 1, 4, %, 8 и 9 к полюсу z
(рис. 3-1).
3. Каждому возможному пути от входа исходной се-
ти к ее выходу в ЭФ (ОЭФ) соответствует по крайней
мере одна буква (одно вхождение буквы).
4. Каждый дизъюнктивный член (будем называть его
термом) ЭФ (ОЭФ) представляет условия равенства
1 (0) выходной функции z, т. е. г=1(0), когда все буквы
хотя бы одного терма ЭФ (ОЭФ) принимают значе-
ния 1.
Подчеркнем, что в процессе построения ЭФ (ОЭФ)
нельзя удалять никакие буквы или термы. Например,
последний терм в (3-5) логически избыточен. В ЭФ
(ОЭФ) остаются также термы, логически тождественно
равные 0, т. е. термы, содержащие, например букву
us и букву dt, где s и t разные индексы при перемен-
ных а и а, например, термы К b2 d2 (3-6). Заметим, что
гермы ЭФ (ОЭФ) логических сетей, реализованных в
простом базисе, не содержат одновременно буквы as
п а„.
Отметим еще одну особенность ЭФ (ОЭФ) для сетей,
представленных в простом базисе. Если путь S ассо-
циирован с некоторой буквой as ЭФ (ОЭФ), то он со-
держит четное (нечетное) число инверсий'. Наоборот,
в пути Т, ассоциированном с буквой at ЭФ (ОЭФ),
обязательно содержится нечетное (четное) число инвер-
сии Например, в пути, ассоциированном с буквой di2
1 Инверсия имеет место всякий раз, когда путь проходит через
инвертируемый вход логического элемента, принадлежащего данно-
му их III.
12 -358 177
ЭФ (3-5) (d, 1, 4, 7, 8, 9, г), содержится одна инверсия,
в то время как в пути, ассоциированном с буквой du
ЭФ (3-5) (d, 1, 4, 6, 9, г),— ни одной.
Для упрощения записи ЭФ (ОЭФ) различные по-
следовательности индексов при буквах, представляющих
одну и ту же входную переменную, перенумеруем
числами натурального ряда и тем самым уменьшим
«размерность» этих индексов.
Пример 3-9. В примере 3-8 примем следующую нумерацию по-
следовательностей индексов при буквах, соответствующих входной
переменной d: 1 —11, 2 12, 3—2. Тогда построенные ЭФ (3-5) и
ОЭФ (3-6) принимают соответственно вид:
z = V 6iCidi V я2 с2 62 V «г d2 Ьг V с2 V аг d2 d3; (3-7)
z = Ьмг V bic2d2 V bib-ds V «1 сша V «1 ctCsdi V
V /h Cib2d3 V aur2di V «i Фг242 V Ш dtbzds. (3-8)
се логических элементов.
Рис. 3-4. Логическая сеть
в сложном базисе к приме
ру 3-10
Эквивалентная форма может быть построена также
для функции комбинационной логической сети без
обратных связей, представленной в произвольном бази-
удем считать, что функция,
реализуемая каждым эле-
ментом сети, задана анали-
тически в некоторой мини-
мальной дизъюнктивной нор-
мальной форме (МДНФ) и,
следовательно, можно вы-
числить инверсию этой
функции. При построении
ЭФ (ОЭФ) функции сетей в
произвольном базисе, содер-
жащем сложные элементы,
возможны два подхода.
Первый подход состоит
в том, что каждый логи-
ческий элемент ц, заданной (исходной) сети, не являю-
щийся простым, заменяется эквивалентной ему одновы-
ходной подсетью, имеющей те же входы, что и эле-
мент гр, представленной в простом (например, в булевом)
базисе и реализующей функцию, реализуемую элемен-
том гр. Пусть структура рассматриваемой подсети пред-
ставляет МДНФ функции элемента гр. В результате по-
лучается сеть в простом базисе, эквивалентная исходной
сети. Все элементы полученной сети обозначаются раз-
178
ними номерами, после чего изложенным выше способом
строится ЭФ и ОЭФ.
Пример 3-10. В логической сети, изображенной на рис. 3-4,
сложным является элемент 3, реализующий функцию «сумма по мо-
дулю два» Уъ=у1Уг\/ У\уг (элемент 1 реализует функцию yi = db)
I______________________________________I
Рис. 3 5. Сеть в простом базисе, эквивалентная сети рис. 3-4.
Рис. 3-6. Эквивалентное дерево сети рис. 3-5.
12’
179
На рис. 3-5 представлена сеть, эквивалентная сети рис. 3-4, но реа-
лизованная в простом базисе. Элементы И, ИЛИ, НЕ подсети, пред-
ставляющей элемент 3 исходной сети, обозначены цифрой 3 с ниж-
ними индексами 1—5. На рис. 3-6 изображено эквивалентное дерево
для сети рис. 3-5. Переобозначим индексы входных полюсов ЭД, со-
ответствующих входной переменной b: 1—11, 2—12, 3—21, 4—22.
ЭФ и ОЭФ функции сети рис. 3-6 имеют вид:
Z = (flibi)(bi v Са) V (Ь3Х/ Ci)(a2b2) =
= Л164 VrtiO> V bibl V Z?1C2 V Gzthbs C1J (3-9)
z = V dibibi \/ aibibs V n‘bi Ci V
V a^bt сг \/ b2 bt c2 V bibi сг V btCi Ci. (3-Ю)
Получаемая при рассматриваемом подходе ЭФ
(ОЭФ) представляет все пути, имеющиеся в эквива-
лентной сети (рис. 3-5), в том числе те, которые разли-
чаются только своими частями, принадлежащими слож-
ным элементам.
Пример 3-11. Пути (а, 1, Зц З3, З3, z) и (а, /, 34, З3, z), acco
циированные с буквами ЭФ щ и а2 соответственно, различаются
только частями 31, З3, 35 и 34, 36, принадлежащими элементу 3 исход-
ной сети. Такие пути прослеживаются по исходной сети как один и
тот же путь (а, 1, 3, г).
В дальнейшем будет показано, что информация, со-
держащаяся в такого рода
Рис. 3-7. Эквивалентное дере-
во сети рис. 3-4.
путях, позволяет относитель-
но просто получить выраже-
ние функции, реализуемой
устройством при появлении
в нем неисправностей опре-
деленного класса. Если же
такая задача не ставится,
то целесообразно исключить
ненужную информацию опи-
сываемым ниже способом,
принадлежащим другому
подходу к построению ЭФ
и ОЭФ функций сетей, реа-
лизованных в сложном ба-
зисе. При этом ЭФ (ОЭФ) строится по эквивалентному
дереву исходной сети в сложном базисе без преобразо-
вания ее в эквивалентную сеть в простом базисе.
180
Пример 3-12. На рис. 3-7 изображено ЭД исходной сети
(рис. 3-4). Применяя к сети рис. 3-7 процедуру прямой подстанов-
ки, имеем:
У\ =
_ _ _ (31()
Z = УгУг V У11Л = (libib2Cx\J (lh\J 61)(Ь2 V с') =
= С1Ь2 v Citi V bib2 V biCi V Oibi b2 ci.
Обратная эквивалентная форма выглядит следующим образом:
z = aibibi \/ aibiCi V Л162С1 V bi b2 а. (3-12)
Нетрудно видеть, что формы (3-11) и (3-12) содержат в два
раза меньше разных букв, чем формы (3-9) и (3-10), а форма (3-12),
кроме того, имеет 4 терма вместо 8 в форме (3-10).
Условимся называть ЭФ и ОЭФ, построенные по сети
в сложном базисе, как, например, (3-11) и (3-12),
сжатыми. Сжатые ЭФ и ОЭФ в отличие от построенных
по сети в простом базисе могут содержать буквы as
и as, с которыми ассоциирован один и тот же путь.
В (3-11) такими буквами являются, например, а, и di,
Ь2 п Ь2. Причиной этому служит наличие разветвляю-
щихся участков путей с четным и нечетным числом ин-
верторов в подсетях, представляющих сложные элемен-
ты в простом базисе. В рассмотренном примере
(рис. 3-5) такими участками являются, например, 31,
З3, <?5 И <?4, <3g.
Завершая обсуждение математических моделей
исправных комбинационных устройств, приведем не-
сколько дополнительных замечаний.
В реальных дискретных устройствах возможны та-
кие «некорректные» соединения логических элементов,
которые не удовлетворяют формальному определению
правильной логической сети.
Пример 3-13. На рис. 3-8 изображена принципиальная схема со-
единения двух диодных логических элементов И, на которой выход
логического элемента И\ соединен с выходом элемента И2. Функция,
реализуемая на выходном полюсе z (в узле соединения выходов
элементов), представляет конъюнкцию выходных функций элемен-
тов И[ и И2: z= (ab) (cd) =abcd. На рис. 3-9 изображены две схемы
импульсно-потенциальных электрических вентилей, выходы которых
также объединены. Вентиль реализует функцию д= (dxa)xB, где
dxB обозначает изменение 1—>0 (1 здесь соответствует отрицатель-
ному потенциалу) значения переменной хи на импульсном входе,
а хв — переменная потенциального входа. Функция, реализуемая
на выходном полюсе схемы рис. 3-9, есть z= (dxj) х2 V (dx3) Xi.
181
Для описания устройств, содержащих такие соеди-
нения элементов, моделями правильных логических се-
тей каждая совокупность элементов, выходы которых
соединены, заменяется одним логическим элементом, ко-
торый па своем выходе реализует функцию, совпадаю-
щую с функцией, реализуемой в узле соединения.
Иногда с целью более точного описания процессов,
происходящих в реальных устройствах, в математичес-
ких моделях комбинационных устройств учитывается
Рис. 3-8. Первый пример «некорректного- со-
единения выходов логических элементов.
Рис. 3-9. Второй пример «некорректного^ соедине-
ния выходов логических элементов.
качество (например, форма) сигналов и вводится вре-
менная координата. В таких моделях логическим зна-
чениям (0,1) сигналов сопоставляются строго фиксиро-
ванные области значений физических параметров этих
сигналов. Значения сигналов на выходах логических
элементов определяются при помощи функциональных
зависимостей относительно предельных (напхудших)
182
значении входных сигналов и с учетом влияния пара-
метров нагрузки. При описании функционирования ло-
гических элементов могут учитываться характеристики
фронтов сигналов при изменении значений последних,
что дает возможность анализировать работу комбина-
ционных устройств на предмет выявления в них логи-
ческих состязаний.
В библиографической справке к этой главе указаны
литературные источники, в которых читатель может
найти более или мепее детальное описание такого рода
математических моделей. В данной же книге почти
исключительно будет использоваться невременное, ло-
гическое описание дискретных комбинационных
устройств в виде формул булевой алгебры, таблиц
истинности, логических сетей, прямых и обратных экви-
валентных форм. Многие задачи диагноза технического
состояния дискретных устройств могут быть решены
в рамках этих моделей.
3-2. НЕИСПРАВНОСТИ КОМБИНАЦИОННЫХ УСТРОЙСТВ
Для обозначения комбинационных устройств там,
где это будет правильно понятно, используем тот же
символ А, что в для обозначения модели устройства
в виде логической сети.
Не претендуя на точное формальное определение по-
нятия неисправности физических объектов, предназна-
ченных для переработки дискретной информации, будем
понимать под физической неисправностью s,- послед-
ствия некоторого события (явления), которое преобра-
зует исправное устройство А в некоторое другое, не-
исправное (в том пли ином смысле отличное от Д)
устройство Д’ и поддерживает его в этом неисправном
состоянии в течение интервала времени А/. Подразуме-
вается, что входы (выходы) устройства А взаимно-одно-
значно сопоставлены входам (выходам) устройства Д’.
Одни и те же последствия некоторого события,
происшедшего с устройством, в одних случаях могут
классифицироваться как неисправность последнего, а в
других случаях—нет. Это зависит в первую очередь от
условий, определяющих конкретную постановку задачи
диагноза, и находит формальное отражение в выборе
математических моделей объекта диагноза и его не-
исправностей. Например, возможны последствия, кото-
рые являются неисправностями при структурном описа-
183
ниц комбинационного устройства и не являются
таковыми при его функциональном описании.
Вне зависимости от того, какой моделью пользуются
при описании исправного устройства А, множество всех
неисправностей, которые в нем могут возникнуть, делят
на два класса. Неисправность s, называют правильной,
если i-неисправное устройство Л2 описывается моделью,
принятой для описания исправного устройства А. В про-
тивном случае неисправность называют неправильной.
При функциональном подходе, как всегда, отвле-
каются от анализа и сравнения процессов, происходя-
щих внутри устройств А и Л2, и сопоставляют лишь их
внешнее поведение. Если устройство Л является комби-
национным, то неисправность, преобразующая его в
другое, также комбинационное устройство Л2, как уже
было сказано, является правильной неисправностью.
При функциональном описании комбинационного
устройства Л в предположении, что возможные не-
исправности в нем являются правильными, сопоставле
ние устройств Л и Л2 заключается в сравнении значений
соответствующих выходных функций (Z.()j и
у=>1, 2, ..., k, на входных наборах {XJ, /е{1, 2, ..., 2п},
из множества {X} всех возможных наборов. Заметим,
что как при описании исправного устройства Л, так и
при сопоставлении устройств Л и Л2 могут интересовать-
ся их поведением лишь на заданном подмножестве
{Х}3 множества {X} входных наборов. Подмножество
{Х}3 может содержать, например, только те входные на-
боры, которые возможны в процессе рабочего функцио-
нирования устройства Л.
Исследуемое устройство А* считается содержащим
неисправность s; (или неисправным при функциональ-
ном подходе) по отношению к своему исправному эта-
лону Л, т. е. А:,:—А', если найдется по крайней мере
один входной набор Х3е{Х}3, на котором выходное слово Z,-
исправного устройства отлично от выходного слова Z%-
исследуемого устройства. В противном случае исследуе-
мое устройство считается исправным Л*=Л, так как его
внешнее поведение на множестве {Х}3 совпадает с пове-
дением исправного устройства Л. При этом не исклю-
чено, что имеется такой входной набор Х3е{Х}3, на ко-
тором Z,^Z*j, но при функциональном подходе к оцен-
ке технического состояния исследуемого устройства на
множестве наборов {Х}3с:{Х} это не имеет значения.
184
Рассмотренная постановка характерна для задач
проверки работоспособности и проверки правильности
функционирования комбинационных устройств. При ре-
шении задач проверки исправности и поиска неисправ-
ностей устройства ограничиться его функциональным
описанием, а тем более на ограниченном числе входных
наборов в большинстве случаев нельзя.
В реальных устройствах, описываемых моделью ком-
бинационных схем, возможны такие физические явле-
ния, при которых i-неисправное устройство А1 выходит
из класса комбинационных устройств. Например,
устройство Ai может потребовать описания его моделью
конечного автомата с памятью. В этом случае мы
имеем дело с классом неправильных неисправностей и
сопоставление поведения устройств А и А‘ оказывается
более сложным, требующим привлечения методов иссле-
дования дискретных устройств с памятью. Далее, в при-
мере 3-16 будет проиллюстрировав рассмотренный
случаи.
При задании комбинационного устройства А пра-
вильной логической сетью некоторое физическое явле-
ние, происшедшее в нем, классифицируется как не-
исправность Si, а устройство А‘—как неисправное, если
логическая сеть, представляющая устройство А', ие
тождественна логической сети устройства А. Как следу-
ет из определения различения двух логических сетей,
рассматриваемое явление (неисправность) приводит
либо к нарушению функционирования хотя бы одного
логического элемента сети, представляющей устройство
А, либо к искажению ее связей. Если устройство А;
описывается при этом правильной логической сетью, то
рассматриваемая неисправность s, принадлежит классу
правильных неисправностей.
Уточним это определение. Понятие неисправности
логического элемента сети подразумевает функциональ-
ный подход к оценке технического состояния элемента,
рассматриваемого как функционально заданное комби-
национное подустройство. Каждый такой элемент т]г
с rii входами описывается реализуемой им функцией,
заданной на множестве всех 2ni входных наборов.
Функционирование логического элемента нарушено
(элемент неисправен), если он реализует функцию, зна-
чение которой не совпадает с соответствующим значе-
нием функции, реализуемой исправным элементом, хотя
185
бы на одном входном наборе элемента. Неправильная
неисправность логического элемента сети рассматрива-
ется как неправильная неисправность устройства, задан-
ного логической сетью. Под искажением связей логи-
ческой сети понимается отсутствие изоморфности взве-
шенных графов логической сети исправного устройства
А и логической сети, представляющей ьнепсправное
устройство А‘.
Рис. 3-10. Иллюстрация к анализу поведения
логических элементов при задании их физиче-
ских неисправностей.
Приведем несколько примеров физических неисправ-
ностей в комбинационных устройствах.
Пример 3-14. На рис. 3-10 изображена принципиальная схема
двухвходового логического элемента И. Функция, реализуемая этим
элементом в исправном состоянии, есть у=Х{Х2. Зададимся следую-
щим перечнем физических явлении, возможных в рассматриваемом
элементе:
1) обрыв цепи коллектора триода Г;
2) короткое замыкание цепи коллектор — эмиттер;
3) короткое замыкание диода Д3;
4) короткое замыкание резистора
5) обрыв в диоде Дг,
6) обрыв в диоде Дз;
7) короткое замыкание диода Д,.
Обозначим функции, реализуемые элементом в каждом из указан-
ных случаев, соответственно через if' , ..., if7 . Эти функции могут
быть определены путем анализа поведения элемента при наличии
в нем соответствующих неисправностей. Не исключено, что для этого
в общем случае может понадобиться физическое моделирование
элемента и его неисправностей. Пусть указанные функции являются
IS6
Такими, какие показаны в табл. 3-3, представляющей собой совокуп-
ность таблиц истинности функции у и функций t/si yS1
Сравнив столбцы ys' , ..., tf1 со столбцом у табл. 3-3, отмечаем,
что с функциональной точки зрения только явления 1—5 могут быть
классифицированы как правильные неисправности элемента. Обрыв
в диоде Дз не меняет функционирование элемента (ySe — у) и по-
этому не может расцениваться как неисправность. Диод Д3 в схеме
Таблица 3-3
Х1 Х2 У if' fl ft f' f" f« fl
0 0 1 1 0 1 0 1 1 1
0 1 1 1 0 1 0 0 1 1
1 0 1 1 0 1 • 0 1 1 1
1 1 0 1 0 1 0 0 0 0
элемента не выполняет логических функций и необходим для уве-
личения надежности работы элемента, предохраняя базу триода от
положительных импульсов помех. Короткое замыкание диода Д\
также не меняет функцию, реализуемую па выходе элемента
(*/’ = //)» ио при этом нарушается условие разделителытости (не-
зависимости) входов элемента. Действительно, при подаче на входхг
сигнала 0 на входе xt будет на-
блюдаться сигнал 0 независимо от
того, какой сигнал подается па
него извне (подразумевается, чтт
входные сигналы поступают с вы-
ходов аналогичных элементов).
Таким образом, короткое замыка-
ние диода Д\ следует расценивать
как неправильную .неисправность
элемента.
Подчеркнем, что особенность
рассмотренной ,неисправности дио-
да состоит в том, что опа не
Рис. 3-11. Пример несовпаде-
ния места возникновения и ме-
ста проявления неисправности.
нарушает функциональных свойств
того элемента, в котором она воз-
никает, но может нарушить функ-
циональное поведение другого.
связанного с ним исправного элемента устройства. Иными словами,
в данном случае место возникновения неисправности не совпадает
с местом его проявления.
Пример 3-15. В схеме, изображенной на рис. 3-11, замыкание
диода Д в элементе не меняет функцию, реализуемую на его
выходе (yi = ab), но функция, реализуемая на выходе исправного
элемента И2, при этом изменяется: вместо у2 = ас будет 1/!'2 = а6с.
Нарушение условия разделительное™ входов элемента может
в некоторых случаях вывести рассматриваемое устройство из класса
комбинационных.
187
Пример 3-16. На рис. 3-12 изображена комбинационная правиль-
ная логическая сеть, в которой при замыкании диода Д в элемен-
те И образуется существенная обратная связь. Действительно, при
входном сигнале а=1 элементы Иг и И образуют потенциаль-
ный триггер с раздельными входами b и с.
В качестве неисправности может рассматриваться
ошибочная установка в процессе монтажа устройства
вместо одного логического элемента некоторого другого
элемента, реализующего функцию, отличную от функции
правильного элемента.
Рис. 3-12. Пример неисправности, вызывающей образо-
вание существенной обратной связи в логической сети.
Среди наиболее часто встречающихся физических не-
исправностей связен (соединений) элементов устройства
можно выделить следующие: 1) обрыв соединения;
2) замыкание соединения с некоторой шиной питания;
3) перепутывание связей; 4) появление лишних связей;
5) замыкание нескольких связей между собой; 6) сово-
купность перечисленных выше неисправностей. Для
большинства логических элементов обрыв входа с функ-
циональной точки зрения эквивалентен подаче на обор-
ванный вход некоторого постоянного сигнала, соответ-
ствующего одному пз логических значений 0 или 1, т. е.
константе 0 или 1.
Пример 3-17. Так, для элемента И, изображенного на рис. 3-10,
обрыв соединения, идущего на один из его входов, например Xi,
соответствует подаче на этот вход постоянного сигнала 1; при этом
функция, реализуемая элементом с оборванным входом хц соответ-
ствует столбцу ys° в табл. 3-3.
188
Пример 3-18. На рпс. 3 13,а изображена Схема с разветвляю-
щимся выходом z/i триода Т, связанным с элементами И и ИЛИ.
При обрыве соединения входа Хц функционирование элемента И
соответствует подаче на этот его вход сигнала 1; при обрыве соеди-
нения Хц функционирование элемента ИЛИ соответствует подаче
на этот его вход сигнала 0; при обрыве соединения выхода У\ логи-
Рис 3-13. Пример неисправности, преобразующей правиль-
ную логическую есть в неправильную.
ческая сеть, соответствующая рассматриваемому неисправному
устройству (рис. 3-13,6), является неправильной, так как сигнал на
входе Хц, а значит, и на входе xi2 зависит от сигнала на входе х2|.
Как правило, замыкание какого-либо соединения
с шиной питания также соответствует подаче на рас-
сматриваемое соединение постоянного сигнала 0 или 1,
т. е. соответствует изменению функции, реализуемой
элементом, на входе или выходе которого произошло
замыкание.
Пример 3-19. На рис. 3-14 изображен более сложный случай
изменения функциональных свойств элемента ИЛИ при замыкании
189
его входа d на шину питания +1/2{7Пит. При этом функция, реали-
зуемая на выходе у, становится инверсией мажоритарной функции:
у = (а V b V с V d); у‘ = (ab\/ ас\/ be).
Перепутывание связей, появление лишних связей или
лишних логических элементов в основном случаются
в процессе производства. Перепутывание входов эле-
мента, симметричного относительно перестановки его
входов (например, элемента ИЛИ), преобразует граф
Рис. 3-14. Пример сложного проявления замыкания соединения иа
шипу питания.
исходной логической сети в изоморфный граф, а пото-
му такое перепутывание не расценивается как неисправ-
ность.
Перепутывание входов элемента, несимметрично-
го относительно некоторой перестановки его входов,
эквивалентно изменению функции, реализуемой эле-
ментом.
Пример 3-20. На рис. 3-15,а изображен случай перепутывания
входов элемента 2. На рис. 3-15,6 изображена логическая сеть, пред-
ставляющая устройство с рассматриваемой неисправностью. Пере-
путывание входов различных элементов может привести к тому, что
неисправное устройство выходит из класса устройств, описываемых
правильными логическими сетями.
190
Пример 3-21. В схеме, изображенной на рис. 3-16, перепутывание
указанных входов элементов 3 и 4 приводит к образованию элемен-
та памяти — триггера (1,4).
Лишние связи, лишние элементы и замыкание сое-
динений между собой также могут вывести устройство
из класса устройств, описываемых правильными логи-
ческими сетями, и даже из класса комбинационных
устройств.
Рис. 3-15. Пример правильной неисправности вида
перепутывания соединений входов логического
элемента.
До сих пор рассматривались физические явления,
в результате которых неисправное устройство по-преж-
нему оставалось дискретным устройством для перера-
ботки двоичной информации. Количественные изменения
параметров элементов, например прямых и обратных
сопротивлений диодов, коэффициентов усиления трио-
дов и другие явления могут привести к тому, что устрой-
ство перестанет удовлетво-
рять принятому представле-
нию информации и спосо-
бам описания ее переработ-
ки. Иногда для исследова-
ния подобных явлений при-
меняется изменение условий
работы устройства, напри-
мер изменение питающих
напряжений, частоты вход-
ных сигналов, температуры,
нагрузки и др., что в неко-
торых случаях позволяет
использовать известный ап-
Рис. 3-16. Пример неправиль-
ной неисправности вида пере-
путывания соединений входов
разных логических элементов.
191
парат и модели для описания работы устройств с такого
рода неисправностями. Однако эти вопросы в книге не
рассматриваются.
Заметим, что приведенное 'выше определение не-
исправности устройства, заданного своей структурой
(логической сетью), не связано с сопоставлением вы-
ходных функций, реализуемых устройствами А и А‘
(в отличие от обсужденного в начале параграфа функ-
ционального подхода к определению технического со-
стояния устройства). Явление, в результате которого
логические сети устройств А и А* становятся различны-
ми, как это уже указывалось, расценивается как не-
исправность, хотя с функциональной точки зрения эти
сети могут быть эквивалентными (реализовать одина-
ковые выходные функции). Когда это имеет место, не-
исправности будем называть несущественными, в отли-
чие от существенных неисправностей, в результате появ-
ления которых системы передаточных функций
устройств А и А‘ становятся различными на заданном
множестве {Х}3 входных наборов. Исследование несу-
щественных неисправностей оказывается пебходпмым
потому, что они, не меняя функциональных свойств
устройства, могут менять некоторые другие важные его
показатели, например надежностные свойства, нагрузоч-
ные характеристики, могут вызвать появление в устрой-
стве логических состязании плп изменить функциональ-
ное поведение устройства при появлении в нем новых
неисправностей и т. и.
Пример 3-22. На рис. 3-17 изображена логическая сеть комбина-
ционного устройства, свободного от логических состязаний при изме-
нении значения любой одной входной переменной (это достигнуто
введением избыточного элемента 3). При наличии константы 0 на
выходе элемента 3 устройство, продолжая реализовать ту же функ-
цию, что и исправное устройство, несвободно от состязаний при пе-
реходе от входного набора 100 (Xi = l, х2=х3=0) к набору 101 или
обратно, т. е. из-за наличия разных временных задержек в элемен-
тах I и 2 во время указанного перехода па выходе у может по-
явиться импульсный сигнал 0 (1—>-0—>1).
При построении неявных математических моделей
объектов диагноза требуется задание математических
моделей их неисправностей. Это равносильно выбору из
всех возможных неисправностей объекта некоторого клас-
са неисправностей, поддающихся формальному описанию.
Так, для устройств, описываемых логической сетью, как
правило, задаются классом правильных неисправностей.
192
Среди них часто выделяют класс логических неисправ-
ностей, под которыми понимают неисправности логичес-
ких элементов, а также неисправности связей, сводя-
щиеся к изменению логических функций, реализуемых
элементами. В классе логических неисправностей очень
распространенными являются так называемые констант-
ные неисправности. Это—неисправности элементов и
связей, которые эквивалентны такому изменению функ-
ций, реализуемых логическими элементами, которое
соответствует подаче па один или несколько входов
Рис. 3-17. Пример неисправности, приводящей к по-
явлению логических состязаний в устройстве.
хотя бы одного элемента или на его выход постоянного
сигнала (константы) 0 и 1. Так, к классу константных
неисправностей относятся неисправности рассмотрен-
ного выше логического элемента И, соответствующие
столбцам ys*—ys' табл. 3-3, или обрыв, например, связи
входа Х12 элемента ИЛИ па схеме рис. 3-13, а.
Если полагают, что в устройстве возможна только
одна логическая неисправность, т. е. неисправность
одного логического элемента, то в таких случаях гово-
рят о классе одиночных логических неисправностей.
Если в устройстве допускается константная неисправ-
ность только одного входного полюса или только одного
входа (выхода) одного элемента, то тем самым выделя-
ют класс одиночных константных неисправностей. Под
классом кратных неисправностей подразумевают про-
извольные (однако имеющие физический смысл) соче-
тания одиночных неисправностей, которые в этом случае
11—358 193
называют составляющими данной кратной неисправно-
сти. Как видно из рассмотренных выше примеров, боль-
шое число реальных физических неисправностей оста-
лось за пределами только что введенных классов оди-
ночных пли кратных правильных логических или
константных неисправностей, хотя даже класс констант-
ных неисправностей является достаточно широким.
Одним из преимуществ рассмотрения правильных логи-
ческих или константных неисправностей является воз-
можность использования при этом неявных математи-
ческих моделей объектов диагноза (4f, S, /7, Ф—< Ф‘)
(см. § 1-4), что обеспечивает в ряде случаев заметное
снижение вычислительных трудностей при построении
алгоритмов диагноза. Для класса неправильных не-
исправностей, а также неисправностей, нарушающих
условия двоичного представления информации в устрой-
стве, необходимо строит!, явные математические модели
(Ф, {'И'}), что ограничивает область применения соот
ветствующих методов задачами небольших размер-
ностей.
Как уже указывалось, неисправность преобразует
устройство А в устройство А’ и поддерживает его
в этом состоянии в течение интервала времени Ай Если
этот интервал ие меньше длительности процесса диагно-
за технического состояния устройства и, кроме того,
начинается не позже, чем процесс диагноза, то не-
исправность считается устойчивой. Это значит, что
в течение времени диагноза техническое состояние
устройства ие изменяется, т. е в частности в нем ие
возникают новые и не исчезают имеющиеся неисправ-
ности. Если же за время диагноза техническое состоя-
ние устройства изменяется за счет появления в нем
новых или исчезновения имевшихся неисправностей, то
последние будем называть неустойчивыми, независимо
от абсолютных значений их интервалов \t. Неустойчивую
неисправность будем называть сбоем, если для нее \t
значительно меньше длительности процесса диагноза.
3-3. ВИДЫ И МЕТОДЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
НЕИСПРАВНЫХ КОМБИНАЦИОННЫХ УСТРОЙСТВ
О моделях исправных комбинационных устройств и
их неисправностей речь шла в двух предыдущих па-
раграфах этой главы. Здесь рассмотрим характерные
194
способы представления /-неисправных комбинационных
устройств и, в частности, способы получения их функ-
ционального описания. Предполагается, что все возмож-
ные неисправности являются правильными. Кроме того,
условимся, что все допустимые элементарные проверки
из множества П имеют одинаковые фиксированные со-
ставы контрольных точек, которыми являются все выхо-
ды Zi, ..., Zk устройства, т. е. что элементарные проверки
различаются только воздействиями (входными набора-
ми). Тогда множество П можно заменить множеством
{Х}3 заданных входных наборов Xj. Функционирование
/-неисправного комбинационного устройства Ai, как и
исправного комбинационного устройства А, может быть
описано посредством задания реализуемой им системы
функций выходов {zj, ..., Zk} на заданном множестве
входных наборов {Л'}3.
ЯВНЫЕ МОДЕЛИ
Классической явной моделью объекта диагноза
('К {Ч^}), как уже упоминалось в гл. 1, является табли-
ца функций неисправностей (ТФН), в которой для каж-
дого /неисправного Л’ и для исправного А объекта
соответствующие им системы функций выходов заданы
таблично. В данном случае строки ТФН соответствуют
входным наборам А^е{А.}3, а столбцы — исправному е
и всем неисправным е, техническим состояниям устрой-
ства. В клетках ji, i^O ТФН проставлены значения
функций выходов zi,..., г/, /-неисправного устройства Л’
па входном наборе Xj. В столбце е проставлены значе-
ния функций этих выходов исправного устройства А.
Таким образом, ТФН комбинационного устройства при
заданном списке его технических состояний представ-
ляет совокупность таблиц истинности исправного и всех
/-неисправных комбинационных устройств, определенных
на множестве входных наборов {А"}3. Примером ТФН
может служить табл. 3-3.
Чаще всего дискретное устройство задается своей
структурой (функциональной схемой, логической сетью)
и реже—аналитическим описанием. Таблицы истинности
задаются очень редко и, как правило, только для
исправных устройств. Покажем, как построить таблицу
истинности комбинационного устройства, заданного ана-
литически или структурой.
13* 195
Когда задана аналитическая запись функций выхо-
дов устройства, значения последних могут быть получе-
ны путем подстановки значений входных переменных
для каждого набора Х3е{Х}э.
Пример 3-23. Найти значение выходной функции г по формуле
(3-3), описывающей функционирование устройства (рис. 3-1), иа
входном наборе 1001 («, Ь, с, d) :
z = ab\/ad\/ bed. \/~а~с b = 1 0 V 0 0 \/ 0-0-1 V 0-11=0.
Когда устройство задано своей структурой, можно
поступить двояко. Можно сначала получить аналитиче-
скую запись реализуемых устройством выходных функ-
ций методом прямой или обратной подстановки (так,
как это было изложено в § 3-1 для исправных
устройств), а затем использовать эту запись для вычис-
ления значений выходных функций, как в примере 3-23.
Другой способ состоит в вычислении значений выход-
ных функций непосредственно по структуре. При этом
используется метод прямой подстановки, согласно ко-
торому ранг за рангом вычисляются значения выходных
функций логических элементов структуры на заданном
входном наборе до тех пор, пока не будут получены
значения выходных функций устройства.
Пример 3-24. Вычислить значение функции г по структуре
рис. 3-1 на том же, что и в предыдущем примере, входном набо-
ре 1001:
ранг 1 — yt = cd = 0-1 = 0, уг — b — I, p3 = d = 0;
ранг 2 — t/4 =^i V « = 0 V 1 = 1. {/s = ^2 V = 1 V ° = И
ранг 3 — у6 = bz/4 = 0 • 1 = 0, ут = у4 = 0;
ранг 4 — ys = уту5 = 0-1 =0;
ранг 5 — г = й V = 0 V 0 - 0.
Вычисление значений выходных функций /-неисправ-
ных устройств производится таким же образом, если
известны их структуры пли аналитические описания.
Логическая сеть неисправного устройства А' может
быть получена из логической сети исправного устройст-
ва А преобразованием функциональных свойств логиче-
ских элементов и их связей, определяемым наличием
в устройстве неисправности s<. Так, например, на
рис. 3-15,6 изображена логическая сеть комбинационно-
го устройства (рис. 3-15,а) при наличии в нем неисправ-
ности вида перепутывания входов элемента 2. Совокуп-
ность сетей исправного А и всех /-неисправных
196
устройств Л' можно рассматривать как явную структур-
ную модель (А, (А<}). Ясно, что построение такой моде-
ли для сложных устройств громоздко, а непосредствен-
ное использование ее, например при графическом пред-
ставлении сетей, неудобно.
Получив аналитические описания F и F' соответст-
венно исправного и i-неисправных устройств, можно от
модели (А, {А'}) перейти к модели (F, {£'}). С послед-
ней работать более удобно, чем с первой, но ее по-
строение требует многократного применения процедур
прямой пли обратной подстановки.
Наконец, путем вычислений значений выходных
функций исправного и всех i-неисправных устройств на
каждом входном наборе А можно перейти от моде-
лей (А, {А'}) пли (F, {F1}) к таблице функций неисправ-
ностей. При работе с ТФН многие Тадачп диагноза ре-
шаются сравнительно просто (см. гл. 1), однако платой
за эту простоту являются большие объемы вычислений
для получения ТФН и большие объемы памяти для ее
хранения. Эти недостатки модели объекта диагноза
в виде ТФН сохраняются при всех других, отличных от
описанных в данном параграфе способах ее построения.
В этом состоит причина отказа от явных моделей и
широкое распространение структурных и аналитических
неявных моделей объектов диагноза. Следует заметить,
что при работе с неявными моделями классы рассма-
триваемых неисправностей, как правило, более узкие,
чем те, с которыми можно иметь дело при работе с ТФН.
НЕЯВНЫЕ МОДЕЛИ
В гл. 1 были введены характерные виды неявных мо-
делей. В настоящем параграфе рассматриваются аналити-
~ {*}з
ческие неявные модели вида (F, S, {Х}3, F------> F, F1)
si.{ Х)з
и (F, S, {Х}з, F--->F‘) комбинационных объектов диаг-
ноза, где под F подразумевается некоторая обобщенная
функция устройства с фиктивными переменными (см.
гл. 1), позволяющая получить функции F и F1.
МЕТОД ОБОБЩЕННОЙ ФУНКЦИИ ВЫХОДА
Для описания комбинационного устройства, задан-
ного логической сетью без петель в произвольном бази-
се логических элементов, в предположении устойчивых
197
кратных константных неисправностей ""может быть ис-
пользован метод обобщенной функции выхода. Рас-
смотрим его. Узлы сети, связанные непосредственно
с входными полюсами или с выходами элементов, будем
обозначать буквами соответствующих входных перемен-
ных или номерами соответствующих элементов. Ветви
разветвления будем обозначать либо специальными
буквенными символами, либо парой цифр в скобках,
например (5, 1), где первая цифра соответствует номеру
элемента, а вторая -- номеру его входа (условимся вхо-
ды каждого элемента нумеровать начиная с единицы
сверху вниз па заданно^ графическом изображении
сети).
Относительно каждого соединения или узла сети,
например соединения а, может иметь место три логиче-
ских высказывания вида аи (а=Н, 1, 0):
ан — соединение а функционирует исправно (нахо-
дится в состоянии Н);
а1 — па соединении постоянно присутствует сигнал 1
(находится в состоянии 1);
а® — на соединении а постоянно присутствует сигнал
0 (находится в состоянии 0).
Инверсию «-состояния соединения а обозначим а"
или аа, что будет означать, что соединение а не нахо
дится в а-состояпип. При рассмотрении устойчивых не-
исправностей эти высказывания для одного и того же
соединения не являются независимыми, а именно, всегда
истинно только одно из них, т. е. верны следующие ра-
венства:
ан V а1 V а = 1; а1 = а1 V an; а — а'\/ а\
Кроме того, используя приведенные выше соотноше-
ния, нетрудно убедиться, что для устойчивых неисправ-
ностей
а —0; яа й₽ = й“; cl\J с? = cP
для всех а, 0е{Н, 1, 0} при «#=Р-
Получим для каждого выхода у сети аналитическое
выражение функции, зависящей не только от значений
входных переменных сети, но и от состояний всех ее
соединений. Эту функцию в отличие от функции
198
только входных переменных сети будем называть обоб-
щенной функцией выхода и обозначать zr Обобщен-
ные функции являются функциями, а а-состояния
переменными булевой алгебры, которую мы будем на-
зывать алгеброй ct-состояний. Проиллюстрируем полу-
чение выражения обобщенной функции па примере ло-
гической сети, изображенной на рис. 3-18.
Рис. 3-18. Пример логической сети для получения
обобщенной функции выхода.
Пример 3-25. В сети рис. 3-18 все соединения обо-
значены буквами или цифрами, проставленными около
них в соответствии с принятыми выше правилами. Через
уа, у/,, Уз обозначим обобщенные функции, реализуе-
мые па соответствующих соединениях. Тогда для соеди-
нений входных полюсов имеем:
уа = а ан у a'; yk = kk" \jk'> y<i = d d" \/ dl;
yh = hhH V h',
где a, k, d и h — булевы входные переменные сети.
Каждая из этих функций представляет логическое
условие появления па соответствующем соединении сиг-
нала 1. Условие появления на некотором соединении,
например а, сигнала 0 имеет вид:
уа — (ааИ V «') = (а V й' =
= (a а V а°) (а” V а ) а" \/ а•°-
J99
Обобщая, можно показать, что если е—некоторое
соединение, связывающее входной полюс или выход
элемента с узлом разветвления, а / — ветвь разветвле-
ния последнего, то Уз=Уе1н\/]1. Если соединение i
является выходом элемента гц сети, то обобщенная
функция, реализуемая на соединении I, yi=x\iiH\J i\ где
T]j — выражение обобщенной функции, реализуемой эле-
ментом т];. Переменными функции т), являются обоб-
щенные функции, реализуемые на соединениях, являю-
щихся входами элемента тц. Для инверсии обобщен-
ной функции справедливо выражение yi=('HiiH\/ i°).
Выражение для обобщенной функции выхода 1 в при-
мере 3-25 получим методом прямой подстановки:
yb = ykbH\/ bl = (kkH\/ k')b" V Ь1;
ус =ykcH\/ С1 = {kkH V *') с" V с';
у, = (yayb I" V 1 ') = (аа" V а) [(Л k" V *') b" V &'] 1"V
Vl’=(yol"V 1*)(уД" V‘') = [(№" V«')1"V l']X
x {[(^"V £') b" V ft'] l" V l1};
y*= [Су. V УД2" v 21 ] = [(kkH V kn )c"\jC]X
x (dd" X/ d1) 2H V 21 = {l(bk" V *°) cH V C°] V
v d°)2"v 21];
z=(ys = у. V У2 v y„) зн v 3' = (y^1 V з1) v
v (y^ V 3l) V (yh3H V 3*) = {[(go" V Й ) 1" V
J1} 3" V з1} V
V {{[(kkH V k°) cH V c°] 2W V 2’} 3" v 31} X
x {[(ddH V d?) 2H\j 21] Зн V З1} V [QdiH \J hl) Зн V 31].
(3-13)
Как видно, выражение (3-13) имеет гнездовую структуру.
Каждую из скобок, например| ^(kk" \J k") сн \J л] 2Н\/ 2'}Х
X Зн\/ 3’|, имеющую единственное вхождение одной вход-
ной переменной (в нашем примере буквы k), будем называть
200
буквенным предложением и записывать в виде /с(/г°, с°,
21, З1). Значения узлов в скобках буквенного предложе-
ния назовем его параметрами. Тогда выражение (3-13)
можно записать более сжато в терминах буквенных
предложений:
z = y3 = а(а, I1, З1) k (k\ b\ I1, З1) V
V k(k°, c°, 21, 31) d (d°, 21, З1) V h (h', 31). (3-13a)
Нетрудно показать, что для произвольной логической
сети выражение функции, реализуемой в любом соеди-
нении, может быть записано сжато в терминах буквен-
ных предложений. Аналогичным образом можно полу-
чить выражение для инверсии обобщенной функции 2.
Для нашего примера имеем:
уа—ааи V a0; yb—(kkH \/ k°) Ьн \/ b°; yh=hhH \J h°;
= (Уа V yb) 1"V 1° = V а°) Iй V1 °] V №" V
V*°)feH V^l^V i0};
У* = {ус 7Jd} 2" V 2° = {[(kk” V kl) сн V с1] 2Н V 2П} V
V [(dd" V dl) 2Н V 2°};
z - у3 == (у3 у3 у и) 3" \/ 3° = {[(аа" V а) 1" V
V 1°] 3" V 3°} {{[(kkH V fe1) сн V f'l 2" V 2°} 3" V
V з0} [(fi hH V Л°) 3" V 3°] v {[(«а" V a°) 1" V
V 1 °] 3" V 3°} {[(ddH V d‘) 2H V 2°13" V
V3°}[(ftft"v л0)3" V 3°] V
V {{[(* V ft0) bH v b°] Iй V i0} 3" v 3°} {{[(^" v
v *') cH V c1] 2" v 2°} 3" v 3°)[(Wi" V л°) з" V
V 3°] V {{[(^й V kG) ьи v b°] i" V i0} 3й V 3°} X
X {[(<w" V d') 2H V 2°] 3" V 3°}[(hhH V h") Зн V 3°]. (3-14)
201
В терминах буквенных предложений (3-15) выглядит
в виде
г = а(аа, /°, 3°)Л(&1, Ci, 2°, 3“)/г(/г°, 3°)\/
\/а(а°, 1°, 3°)d(d1, 2°, 3a)h(h°, 3®)\/
\/k(ka, ba, 1% 3a)k(k', с', 2», 3«)Й(Л», 3»)V
\/k(ka, ba, /«, 3»)d(d’, 2% 3«)Л(А°, 3°). (3-14a)
В исправном устройстве все соединения находятся
в //-состояниях. Поэтому, положив в (3-13) все буквы
соединений с индексом И равными 1, а с индексами О
или 1 равными 0, получим z = z=ak\Jkd \/h, т. е. вы-
ражение для функции, реализуемой исправным устрой-
ством. Таким же образом из (3-14) получаем инверсию
функции z: z=z=akk \J adh \J zdh для исправного
устройства.
Математической моделью рассматриваемых неис-
правностей являются константы 1 пли 0 в узлах сети.
Одиночную константную (сг=) неисправность (<j= 1
или о=0) соединений, например а, 5 или (5, 1) будем
обозначать соответственно записью Оа = а, Ой = 5’ или
Os.i =(5,lf. Для задания одиночной неисправности^
например. а1 (а0), необходимо в выражениях для z и z
принять равной 1 букву пЦй0), а также буквы, пред-
ставляющие //-состояния всех других соединений, и рав-
ными 0 остальные буквы соединений. Любая кратная
неисправность рассматривается как совокупность оди-
ночных. Так, для кратной неисправности s двух соеди-
нений s = {d°, i0} в выражениях (3-13) и (3-14) полагаем
равными 1 буквы d°, 1° и буквы ан, kH, bH, сн, 2П, hH,
Зн, а остальные буквы соединений равными 0. Тогда
z=zs = k\J h и z=zs=kh являются прямой и инверсной
функциями, реализуемыми устройством при наличии
в нем кратной неисправности s.
Рассмотренные операции получения описаний ис-
правного и неисправных устройств нетрудно перефор-
мулировать для выражения 1 и z в терминах буквенных
предложений вида (3-13а) и (3-14а).
Несмотря на простую и непосредственную процедуру
получения функции выхода неисправного устройства zs
из обобщенной функции z при заданной неисправности
s, представляющей совокупность одиночных констант-
ных неисправностей, размерность самой обобщенной
202
функции z, как это видно из правил ее построения, су-
щественно больше размерности функции z (по крайней
мере на 2L переменных, где L — число соединений се-
ти). Поэтому даже для относительно небольших
устройств формула обобщенной функции оказывается
исключительно громоздкой.
МЕТОД ЭКВИВАЛЕНТНОЙ ФОРМЫ
В § 3-1 отмечалось, что удобной формой представ-
ления исправных комбинационных устройств без петель
обратной связи является описание логической сети экви-
валентной формой (ЭФ) функции выхода. Использова-
ние ЭФ оказалось удобным и для описания неисправных
комбинационных устройств при наличии в них одиноч-
ных и кратных константных неисправностей.
Пусть одновыходное комбинационное устройство А
реализует функцию z (х1г ..., хп) и задано своей логи-
ческой сетью.
Рассмотрим некоторую кратную неисправность у,
представляющую сочетание одиночных неисправностей
т узлов сети, т. е. s = {Oi, ..., От}. Устройство при не-
исправности у реализует функцию zs. Выделим из мно-
жества у подмножество sA£s одиночных неисправно-
стей, удовлетворяющих следующему условию. Одиноч-
ная неисправность Oa^s некоторого соединения а (вход-
ного полюса, входа или выхода элемента) принадлежит
подмножеству уд тогда и только тогда, когда существу-
ет по крайней мере один путь в сети от соединения а
до выходного полюса z такой, что все соединения этого
пути (за исключением соединения а) исправны. Не-
исправность ул и входящие в нее одиночные неисправ-
ности называются доминирующими относительно задан-
ной неисправности у. Доминирующая неисправность ул
обладает тем свойством, что z Д(Х1, ..., xn)^^(xt,.. .,хп).
Пример 3-26. Для иллюстрации рассмотрим схему, изображен-
ную на рис. 3-1. Пусть в схеме имеется кратная неисправность s=
= {а°, (6, 2)1, 6°). Очевидно, что неисправность (6, 2)1 не является
доминирующей и не оказывает влияния на функцию, реализуемую
сетью при кратной неисправности s, так как в единственном пути,
соединяющем вход 2 элемента 6 с выходом сети, неисправным
является выход элемента 6. Следовательно, sH={a°, 6°).
Перейдем к построению выражения функции zs, реа-
лизуемой устройством при наличии в нем кратной не-
исправности у. Исправное устройство задано своей ЭФ.
203
Эквивалентная форма описывает функционирование
(см. § 3-1) эквивалентного исходной сети дерева (ЭД).
Любой одиночной неисправности в исходной сети соот-
ветствует либо одиночная, либо кратная неисправность
в логической сети ЭД или просто в ЭД. Первый случай
имеет место тогда, когда неисправным в исходной сети
является соединение, которое в процессе построения ЭД
не подвергалось «расщеплению». Во втором случае крат-
ность неисправности в ЭД определяется числом «рас-
щеплений» неисправного соединения исходной сети На-
пример, одиночной неисправности 6° в сети рис. 3-1
соответствует такая же одиночная неисправность в ЭД
этой сети, представленном на рис. 3-3. Однако неисправ-
ности а° в этой сети соответствует кратная неисправ-
ность {«% в ее ЭД.
Таким образом от кратной неисправности s в исход-
ной сети можно перейти к кратной неисправности s'
в ЭД, представляющей собой совокупность одиночных
неисправностей в ЭД. Выделим из s' доминирующую не-
исправность у'д
В ЭД любой узел I является выходом единственного
поддерева, которое мы будем называть /-поддеревом.
Каждому /-поддереву соответствует свое подмножество
входных переменных ЭД. Из определения доминирую-
щих неисправностей следует, что никакие две одипоч
ные доминирующие неисправности, входящие в я'д, не
лежат на одном и том же пути в ЭД Поэтому подмно-
жества входных переменных любой пары /- и /-подде-
ревьев таких, что i=/=j и о,, o^s'R, не пересекаются (не
имеют ни одной общей входной переменной ЭД).
Любая одиночная неисправность Г „принудительно" за-
дает значение а выходной функции у: /-поддерева и зна-
чение а ее инверсии у,-. Обозначим множество рабочих
наборов (наборов, па которых //,= 1) значений входных
переменных /-поддерева символом М1,-, а множество не-
рабочих наборов (наборов, па которых (л = 0 или yt=
= 1)—символом /И0,. Тогда задание любой доминирую-
щей неисправности С при <г= 1 (<т=0) состоит в том,
чтобы в ЭФ буквы, представляющие входные перемен-
ные /-поддерева, заменить значениями 1 или 0, равными
значениям этих переменных в любом рабочем (нерабо-
чем) наборе из Л!1,- (из Л!0,). Выполнив в ЭФ такую
замену (фиксацию) букв для всех одиночных домини-
204
рующих неисправностей из подмножества s л, получим
искомое представление функции zs, реализуемой устрой-
ством при наличии в нем кратной неисправности s.
Продолжая пример 3-26, получим функцию zs для устройства
рис. 3-1 при s={o°, (6, 2)1, 6°}. Эквивалентная форма выходной
функции этого устройства представлена выражением (3-5), а ЭД
изображено на рис. 3 3.
Соответствие между одиночными неисправностями из s и неис-
правностями из s' в ЭД следующее:
а»---------* {я°1, «о2};
(6, 2)1---------> (6. 2)1;
6°---------* 6».
Таким образом, заданной неисправности s соответствует крат-
ная неисправность s'={a°i, а°2, (6,2)1, 6е) в ЭД. Доминирующая
неисправность s'n (относительно s') содержит одиночные неисправ-
ности а°2 и 6°. Единственной входной переменной а2-поддерева
является переменная а2, а входными переменными 6 поддерева —
переменные 6ь сь du и щ. Из ЭФ а2-поддерева уПг=а2 находим:
п2
< = {0};
из ув =aibi V biCidu находим:
(11 bl Cl dll
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 I
0 1 0 0
Л1о6 = 0 1 0 1
0 1 1 0
* 1 0 0 0
1 0 0 1
1 0 1 0
1 0 I 1
Для фиксации букв в ЭФ (3-5) берем единственный набор 0 из
Л1°о и, например, набор 0000 из Л4"6. При этом
а, = «2 = = Ci = dn = О и 2* = cs Ьг V dizbz V ci d2\/ di2d2
или (опустив индексы и проведя упрощения)
zs = с b \/J.
(3-15)
Описанный способ получения функции zs применим
для устройств в произвольном базисе и необходим, во-
. 205
обще говоря, при задании устройств сжатой ЭФ. Заме-
тим, что вместо построения множеств АР, или 7И°,- всех
рабочих или нерабочих наборов можно воспользоваться
любым способом получения только одного рабочего или
нерабочего набора.
Если устройство с элементами произвольного базиса
описывается несжатой ЭФ, то можно воспользоваться
более простой процедурой получения функции z8, осно-
ванной на следующих соображениях. Пусть в ЭД про-
стого базиса одиночной составляющей Of неисправности
8ГЛ является неисправность t. Предположим, что име-
ется ЭФ;. Тогда для задания в узле i значения Уг=а
можно положить все буквы ЭФ; равными ст. Подчерк-
нем, что фиксации значением о подвергаются бук-
вы ЭФ,-, а не переменные, представляемые этими бук-
вами.
Обычно ЭФ; бывает неизвестна, а задана лишь не-
сжатая ЭФ всей сети. Каждой букве, например х, (xj =
=Xj или xj) из ЭФ; соответствуют все ее вхождения
в несжатой ЭФ в прямом (xj) или инверсном (xj) ви-
дах. Как это следует из рассмотренных в § 3-1 особен-
ностей ЭФ, прямой или инверсный вид этих вхождений
определяется соответственно четным или нечетным
числом инверсий в пути ЭД от узла i до выхода сети.
Тогда процедура получения zs для устройств, описан-
ных несжатой ЭФ, состоит в следующем:
1. По заданной в исходной сети кратной неисправ-
ности s определить соответствующую ей кратную не-
исправность s' в ЭД, после чего найти кратную доми-
нирующую неисправность s'n.
2. Для каждой одиночной доминирующей неисправ-
ности Г (Е s'д выделить подмножества букв несжатой ЭФ
функции сети, представляющих входные переменные
/-поддерева ЭД.
3. Для каждой неисправности /3 подсчитать число инвер-
сий на пути от узла i до выхода z сети. При четном
числе инверсий все буквы, представляющие входные пе-
ременные /-поддерева, зафиксировать значениями о,
а при нечетном — значениями о. В полученном выраже-
нии при желании или необходимости можно убрать все
индексы при буквах и произвести необходимые упро-
щения.
206
Платой за простоту процедуры получения функции
zs является необходимость работы с несжатой ЭФ, кото-
рая в общем случае может быть сложнее, чем сжатая
ЭФ той же сети.
Пример 3-27. Построить функцию zs для сети рис. 3-4 при s =
= {/*}. ЭД в простом базисе изображено на рис. 3-6, а несжатая ЭФ
представлена выражением (3-9) Кратной доминирующей неисправ-
ностью в ЭД является неисправность 5/д={Р1, Р2} (Л)-поддерево
имеет входные переменные at и йь представленные в (3-9) всеми
вхождениями букв at и Ь>. Для (Д) -поддерева такими буквами
являются буквы а2 и Ь2. От узла (/,) до выхода сети г имеется
(рис. 3-6) одна инверсия (нечетное число), а от узла (12)—ни
одной инверсии (четное число). Поэтому в несжатой ЭФ (3-9) бук-
вы а, и 5] должны быть зафиксированы значением 0, а буквы а2
н Ь2 — значением I В результате получаем:
г’ = 5зс1 = 6с. w (316)
Получение инверсной функции, реализуемой устрой-
ством, содержащим неисправность s, осуществляется пу-
тем использования ОЭФ (сжатой пли несжатой) с при
менением аналогичных правил фиксации ее букв. Един-
ственное отличие состоит в том, что при обращении к ЭД
следует предполагать, что иа его выходе включен ин-
вертор.
Распространение описанных приемов построения
функции zs на многовыходиые устройства состоит в мно-
гократном применении этих приемов для каждого выхо-
да отдельно.
Эквивалентная форма функции выхода устройства z
существенно проще обобщенной функции выхода z, так
как ее переменными являются только входные перемен-
ные сети с индексами, число которых определяется сте-
пенью разветвленности сети, тогда как обобщенная
функция выхода зависит от переменных, соответствую-
щих состояниям всех узлов сети. I (о правило фиксации
букв ЭФ для построения функции zs оказывается слож-
нее, чем подстановка в обобщенную функцию z состоя-
ний узлов сети, соответствующих рассматриваемой не-
исправности s. Это правило еще сложнее, когда сеть
описывается сжатой ЭФ.
В § 3-1 была описана скобочная форма (СФ) пред-
ставления передаточных функций комбинационного
устройства, использование которой является одним из
наиболее наглядных и экономных способов задания ком-
бинационных устройств. Действительно, заметим, что
каждому выходу элемента гр; сети в СФ соответствует
207
по крайней мере одна пара скобок, т. е. одно вхождение
выражения, заключенного между открывающей и за-
крывающей скобками с индексом i; точно так же каж-
дому входу элемента тр сети в СФ внутри пары скобок
с индексом i соответствует либо входная переменная
сети, либо другая пара скобок с индексом элемента,
выход которого соединен с рассматриваемым входом
элемента тц. Таким образом, выражение функции выхо-
да устройства при наличии в нем одиночной константной
неисправности а” может быть получено из СФ для ис-
правного устройства, если каждую пару скобок или
каждую входную переменную, соответствующую неис-
правному узлу а сети, заменить на константу о. При
наличии кратной неисправности указанная замена вы-
полняется для каждой составляющей одиночной неис-
правности.
Пример 3-28. Для сети рис. 3-1 и неисправности s= {1°, (2, /)*}
в СФ (3-4) положим равными нулю обе пары скобок с индексом I,
а входную переменную Ь в паре скобок с индексом 2— равной 1.
Тогда после указанных подстановок, опуская индексы, получим:
zs = ba \J a d •
Важно отметить, что отнюдь не любое аналитическое
выражение функции выхода z устройства можно исполь-
зовать с целью получения выражения для функции zs
путем фиксации константами 0 и 1 определенных букв
в исходном выражении для z.
Пример 3-29. Пусть устройс тво реализует функцию, аналити
ческое выражение которой в некоторой минимальной дизъюнктивной
форме имеет вид: za = XiX2 \/ XiX3 \/ хг х3, а сеть, реализующая
эту функцию (рис. 3-19,ah пусть соответствует другой минимальной
дизъюнктивной форме функции: гс = xt х3 V х' x‘ V хгх3, Выраже
ние zc может быть получено по рис. 3-19,а процедурой прямой или
обратной подстановки. На рис. 3-19,6 изображена карта Карно
функции г, где сплошными линиями обведены простые нмпликанты
выражения za, а пунктирными — простые нмпликанты выражения zc.
При неисправности s=6° функция zsc имеет вид: 2яс=х1®3\/ х^.
Выражение zsc не может быть получено из выражения zo путем
фиксации его букв значениями 0 или 1.
Введем одну существенную характеристику логиче-
ских сетей. Логическая сеть называется избыточной,
если существует хотя бы одна непустая совокупность /
соединений сети такая, что система передаточных функ-
ций сети не изменяется при замене функций, реализуе-
208
мых исправной сетью во всех узлах (соединениях) из
совокупности 1 константой 0 или 1; совокупность 1 со-
единений в этом случае называют избыточной Ч Содер-
жательный смысл избыточности сети состоит в том, что
из исходной сети могут быть удалены соединения, при-
надлежащие совокупности I при условии подачи в по-
лученной сети на образовавшиеся новые входы i (i^I)
определенной или произвольной константы; получившая-
ся в результате этого новая сеть эквивалентна исходной
(относительно одноименных выходов).
Рис. 3-19. Пример логической сети, неисправность которой не отобра-
жается посредством фиксации букв МДФ функции г.
Избыточность в логических сетях в одних случаях
ввсдят преднамеренно с целью получения определенных
качественных свойств структур, например повышения
надежности функционирования или исключения логиче-
ских состязаний; в других случаях избыточные соедине-
ния появляются бесконтрольно вследствие того, что при
проектировании устройств не применяются формальные
1 Данное определение является лишь частным случаем более
общего понятия избыточных сетей, выходящего за пределы интере-
сов настоящей книги. Тем не менее введенный тип избыточности
широко распространен и будет иас интересовать в связи с анализом
комбинационных устройств, содержащих константные неисправ-
ности.
209
Методы синтеза Минимальных структур, а анализ схемы
на неизбыточность не проводится.
Рассмотрим несколько примеров избыточных логиче-
ских сетей.
Пример 3-30. Реализуемая сетью рис. 3-20,а функция
Z = Х2Х3 Х4 V Х1Х3 Xt \/ Xi Хг Xi V X) Х2Х3
представлена картой Карно на рис. 3-20,6. В рассматриваемой сети
реализованы все простые импликанты функции. Известно, что в та
ких сетях отсутствуют логические состязания. Это свойство дости-
гается реализацией в сети избыточных импликантов. В данном слу-
чае избыточным является один из импликантов Х1Х3Х4 или Х1Х2Х4.
С точки зрения введенного определения избыточности сети это азна
чает, что одно из ее соединений 5 или 6 избыточно, т е соответст-
7
Рис. 3-20. Первый пример избыточной логической сети. Наличие со-
единений, избыточных в отдельности и неизбыточных в совокуп-
ности.
вующее соединение может быть удалено. Например, может быть уда-
лено соединение 5, а вместе с пим элемент 5 и его соединения
с входным полюсом Х|, а также с элементами 1 и 2; при подаче
константы 0 на освободившийся вход 3 элемента 8 функция г' преобра-
зованной сети которая может быть получена известными методами,
равна функции z исходной сети
z' = z = х2х8 х, V Xi Х2Х3.
Точно так же удаление избыточного соединения 6 не меняет
функцию, реализуемую преобразованной сетью. При этом
z" = Z = ХгХз Xi V Xi Хз Xi V *1 *2X3.
210
Из определения избыточности сети, а также данно-
го в § 3-2 понятия несущественной неисправности сле-
дует, что в избыточной сети одна или каждая из двух
одиночных константных неисправностей 0 или 1 избы-
точного соединения или некоторая кратная
ность совокупности избыточных соединений
несущественными. И на-
оборот, в неизбыточной
сети нет несущественных
одиночных или кратных
константных неисправно-
стей.
неисправ-
являются
Рис. 3-22. Третий пример избыточ-
ной логической сети с избыточной
совокупностью соединений, не-
избыточных по отдельности
Рис. 3-21. Второй пример избы-
точной логической сети, в ко-
торой несущественны обе кон-
стантные неисправности вход-
ного полюса.
Очевидно, что в рассмотренном примере (рис. 3-20,а) одиночные
неисправности os = 5° и ов = 6° несущественны, так как г*1 = г' —
= z, z°* = г" = z. Однако при кратной неисправности s = {5°. 6°}
zS = Хг Хз Xi \/ Х1 ХгХз ф г'
т. е кратная неисправность s является существенной; также являют-
ся существенными кратные неисправности {5°, б1}, {51, 6°} и
{51, б1), что означает псизбыточиость совокупности соединений 5
и 6 (1={5, 6}—неизбыточпа)
Для иллюстрации возможной избыточности в логиче
ских сетях рассмотрим два примера.
Пример 3-31. В схеме рис. 3-21 избыточным соединением являет-
ся вход 1 элемента 1 (входной полюс а):
z = ab\J b = b.
Обе неисправности оа = {а0} и оа = {а1} оказываются несущест-
венными (/= {о} — избыточна).
Пример 3-32. В схеме рис. 3-22 выходная функция z — C. Каждая
из неисправностей Si={/*}, s2= {7°}, s3={2‘). st={2»} существен-
на, так как
zSl =zs> = а с у Ь с V аЬс Ф г;
zSa =г®* = ab с V ас V Ьс ф z.
14’
211
т. е. каждое из соединений 1 и 2 в отдельности не является избы-
точным (Д={/}, /г={2}—неизбыточны). Однако кратные неис-
правности s5={/1 *, 2'}, se—{l°, 2°} не меняют функционирования
сети, так как zs‘ =zs‘ =г=с, т. е. совокупность 13={1, 2} соеди-
нений I и 2 избыточна.
В заключение отметим одну важную особенность
структур без разветвлений, т. е. деревьев. Логическая
сеть вида дерева неизбыточна и, следовательно, в ней
нет несущественных константных неисправностей. Фор-
мально это утверждение будет доказано позже.
3-4. ПОСТРОЕНИЕ ПРОВЕРЯЮЩИХ И РАЗЛИЧАЮЩИХ
СОВОКУПНОСТЕЙ ВХОДНЫХ НАБОРОВ
В этом параграфе будет рассмотрено решение одной
из важнейших задач тестового диагноза — задачи по-
строения входных наборов, на которых выходной набор
Z" устройства, находящегося в состоянии es, отличается
от выходного набора Z( устройства, находящегося в со-
стоянии et Такие наборы будем называть различающи-
ми (относительно е8 и щ) и обозначать записью A'(s, 0-
Когда одно из технических состояний, например в/,
является исправным состоянием е устройства, разли-
чающие входные наборы называются проверяющими
или обнаруживающими и обозначаются через А(0, s) А
Для обозначения совокупностей различающих входных
наборов (различающих совокупностей) будем использо-
вать фигурные скобки: {A(s, /)} или {А(0, s)}.
Задача построения различающих совокупностей
является обратной задачей диагноза, рассмотренной
в общем виде в § 1-8. Различающие входные наборы
соответствуют элементарным проверкам а разли-
чающие совокупности входных наборов — подмножест-
вам П,; указанных элементарных проверок.
В гл. 1 была рассмотрена задача и приведены алго-
ритмы получения некоторой одной пли совокупности
всех проверяющих либо различающих элементарных
проверок, когда моделью объекта диагноза является
таблица функций неисправностей. Поэтому здесь мы
лишь проиллюстрируем решение этой задачи на приме-
ре простейшего комбинационного устройства (логиче-
ского элемента И), изображенного на рис. 3-10.
1 Подразумевается, что состояние ei при t=0 соответствует
исправному состоянию е устройства.
212
Пример 3-33. Таблица 3-3 является ТФН для рассмагрпваемого
устройства в исправном (столбец у} и в семи неисправных (столбцы
if' —if7) технических состояниях. Таблица задана на полном мно-
жестве входных наборов. Воспользовавшись алгоритмом А1-7 (см.
§ 1-8), построим совокупности всех проверяющих входных наборов
{X(О, S|)} для всех 1=1, 2, .... 7. Ради краткости записи входные
наборы будем обозначать номерами строк ТФН. Тогда {X (О, s0} =
= {А'(0 s3)} = {3}, {Х(0 s2)} = {X(0, s4)} = {0, I, 2}, (Х(0, s5)} =
= {1} и (Х(0, s6)} = {X(0 s7)} = 0. Совокупности всех различаю-
щих входных наборов для всех пар st, s, = I, 2, ..., 7, iff имеют
вид
{A (s„ s2)} = {A (S1, s.)} = {A (s2, s3)} = {A" (s3, s,)} =
= {0,1. 2, 3}, {A(s„ s3)} = {A (s2, Si)} = {A (sjt s7)} = 0,
{A(s., s3)} = {A(s„ s5)} = {1, 3}, {A(s„ s3)} = {A(s„ s,)} =
= {A (s3, S;)} = {A’ (s3, s7)} = {3}, {A (s2, s=)} = {A (s3, s5)} =
= {0, 2}, {A (s2, s3)} = {A (s2, s7)} = {A (?„ s,)} = {A (s„ s7)} =
= {0, 1,2}, {A(S3,Sj)} = {A(s6, s,)} = {I}.
МЕТОД РАЗЛИЧАЮЩЕЙ ФУНКЦИИ
Задача построения проверяющей плп различающей
совокупности наборов значений входных переменных
устройства может быть решена аналитически, если
устройство А во всех технических состояниях задано
с помощью аналитических выражений его выходных
функций. Действительно, различающие наборы двух бу-
левых функций р и fj, т. е. наборы значений входных
переменных, па которых значения функций fl и р раз-
личны, совпадают с рабочими наборами так называемой
различающей функции D[p, р]=р ф f’' = f'f'VPP- Та-
ким образом, если комбинационное устройство, находя-
щееся в техническом состоянии щ, реализует па своих k
выходах функции z'i, ..., ?•/„ а в техническом состоянии
е, — функции г1,, ..., г-'л, то рабочие наборы различаю-
щей функции D [гц, г-й, .... z'u, zih]=D \z\ zi] =
= г‘1фгЛ V • • V г'йфгД составляют совокупность
всех различающих наборов значений входных перемен-
ных устройства xt, .. , хп.
Пример 3-34. Построить по различающей функции совокупность
всех проверяющих входных наборов для устройства рис. 3-1 при
наличии в нем неисправности s={a°, (6,2)’, 6°}.
Выражение функции г, реализуемой устройством в исправном
состоянии, представлено выражением (3-3): z = ab\/ad\/bcd\J
\/ а с b и функции г® — выражением (3-16): zs = cbf d. Вычис-
213
лим различающую функцию и представим ее в совершенной дизъюнк-
тивной нормальной форме:
D [г, zs] - г zs \/ z’s = (ab V a d\J bed \/ ас b )(dc V bd) V
V (a V *)(« V d) (b V~c V d)(a V с V b) (с ftV d) = bed V abd V
V (ob \J b cd\/ ab rd)(c ft у d) = bed \/ abd \/ abc \J ab d =
= abed V abed \f abed V a b c d \J a ft c d \]abc d (3-17)
Шесть конъюнкций выражения (3-17) соответствуют всем шести
входным наборам сети рис. 3-1, на которых обнаруживается задан-
ная неисправность s.
Для устройств большой размерности получение ТФП
и ее обработка, равно как получение функций z‘, zi и
вычисление всех рабочих наборов различающей функ-
ции D [z‘, zi], часто оказываются затруднительными
или даже невозможными. Упрощение может быть до-
стигнуто за счет отказа от требования получения всех
различающих наборов и за счет использования инфор-
мации о структуре устройства.
Рассмотрим более подробно использование аналити-
ческого представления различающих функций при за-
дании комбинационного устройства его структурой для
построения некоторого одного входного набора Х(0, s),
обнаруживающего заданную произвольную (одиночную
или кратную) логическую неисправность s устройства.
Итак, пусть комбинационное устройство А задано
своей логической сетью, не содержащей петель обрат-
ной связи. Входные переменные сети —X], . ., хп, ее
выходные функции — zb ..., Zk. Сеть состоит из N логи-
ческих элементов.
Функцию, реализуемую сетью на выходе логическо-
го элемента тр, обозначим символом t)i. Для обозначе-
ния прямой или инверсной функции, реализуемой сетью
в произвольном узле i сети, будем использовать символ
Wi, т. е. ль ..., Хп, хп, У\, yi, (М j/jv}-
Совокупность {ку} всех входных переменных элемен-
та ijf сети обозначим w{Пусть неисправность s сети
задана совокупностью {тф3 ее неисправных элементов. Как
и прежде, yi (ysi) или z^ (zs7) будут обозначать функцию,
реализуемую исправной сетью (сетью, содержащей неис-
правность s) на выходе элемента т},- или на выходном
полюсе zT соответственно. Аналогично трактуются обо-
значения Wi и zafi, Wt и Wsl{. Исправный элемент еет.и
214
Hi (illi £ {f}s) реализует логическую функцию ij, (1Г^). Ло-
гическая функция неисправного элемента if,- (ifi G {i]}s)
обозначается i]s,-(IF,). Входной набор X (0, s), обнаружи-
вающий неисправность s, должен удовлетворять по
крайней мере одному из k булевых уравнений вида
£> [*т (X), z\ (X)] = (X) z^ (X) V (X) z^ (X) =
= 1, у= 1, 2, ... , k. (3-18)
Условимся для обозначения различающих функций (3-18)
пользоваться более короткой записью вида D [г. ] там, где
это не внесет путаницы. Заметим, что для любой пары
булевых функций j и р справедливы следующие соот-
ношения:
^D[f]=jD[f]-
ID[f] = pDU].
Иаша задача состоит в том, чтобы заменить процеду-
ру непосредственного решения системы уравнений
(3-18) рекуррентной процедурой вычисления одного или
нескольких различающих входных наборов из {У (0, s)}.
В основу этой процедуры положены операции метода
обратной подстановки (см. § 3-1), а также описываемые
ниже операции вычисления различающей функции D[yt]
выхода некоторого элемента по различающим функциям
D [wzJ его входов и функциям tj,- (щ/() и т;’, (U^), реали-
зуемым исправными и неисправными логическими элемен-
тами сети.
Выделим в сети, имеющей неисправность s, все пути,
ведущие от выхода каждого неисправного элемента T)s,-
к выходам сети. Назовем такие пути неисправными.
Переменную узла сети, не принадлежащую неисправным
путям и являющуюся входной переменной элемента т]>,
обозначим w[{, а принадлежащую неисправным путям—иц.
Тогда аналогично Wl{ (Wm^ — совокупность всех входных
переменных элемента тд, не принадлежащих (принадлежа-
щих) неисправным путям.
215
Учитывая введенные выше обозначения, выпишем
следующие очевидные соотношения. В исправной сети
(относительно которой рассматривается неисправность
s) для любого узла I, являющегося выходом элемента
T]i с входными переменными (U/;, Wm),
(a)
(Для неисправной сети прежде всего отметим, что
wsz Тогда при исправном элементе тд имеем:
= Wsm),
(б)
а при неисправном элементе
ysi = 7lsi(Wiit Wsmy
(в)
Как W так и могут {быть пустыми^[совокупно-
стями. При Для случая (б) имеем ysi — yt.
Получим теперь выражение различающей функции D [у,]
через выражения различающих функций D [ш, ] входных
переменных w( элемента т;,. Пусть для всех элементов
сети реализуемые ими функции 7]t-(U7f) и тД(ЙД) представ-
лены в дизъюнктивной нормальной форме.
Прежде всего отметим, что О[и/Д = 0. Рассмотрим
исправный элемент сети, реализующий операцию конъюнк-
ции Д входных переменных совокупности Wt и Wm (индекс
элемента опускается), т. е.
У = 7J (Wt, Wm) = wm. (3-19)
/x /x I in
Аналогично для элемента, реализующего операцию \/>
имеем:
yv = Wm> = V®/V
v v Im
(3-20)
216
Опуская формальные доказательства, основанные на
свойствах различающей функции и использовании соот-
ношения (б), получаем следующие выражения для
О[УЛ1 и D[yv]:
D 1ул]=(Л ад) (Л V Л (V D W); (3-2 О
I т т т
D [yv] = D[yv] = (Л ад) (Л ад, v Ал.) (V D
1т т т
(3-22)
В общем виде для исправного элемента, реализую-
щего произвольную дизъюнкцию конъюнкций VA.
!/VA = А/Л Wm^= V Л адт), (3-23)
где I — текущий индекс конъюнкции, имеем:
D [уул] = D [£vj = D [Д (V WH V V ад,,,)] =
= {Д (V ад/ V V ад,„) V Л (V ад/ V V “<)} X
t I ni t I т
X (V D [V ад/ V V ад»»1)—{Л (V ад/ V V ад™) V
t I т t I tn
V Л (V ад/ V V ^)} {V {(Лад/) X
t I tn t I
X<A®tmy A^/m)(v £[адт])}}- (3-24)
т т т
В излагаемом ниже алгоритме получения обнаружи-
вающих входных наборов Л'(0, s) по заданной сети
устройства исправные элементы обрабатываются по
формулам (3-21), (3-22), (3-24). Для неисправных эле-
ментов берется различающая функция его выхода в виде
D [у г] =yiysi V Vtysi< в которую вместо у, и у г подстав-
ляются правая часть и инверсия правой части выраже-
ния (а), а вместо yst и yst — правая часть и инверсия
правой части выражения (в). Тем самым (как и для
исправных элементов £>[уг] представляется как функция
переменных и ад,.
Пусть C={t]s), g=l, 2, .|С| — множество вы-
ходных элементов, принадлежащих неисправным путям
217
сети. Тогда выполнение условия (3-18) эквивалентно
удовлетворению равенства
= (3-25)
где уе— функция, реализуемая па выходе элемента qg
(выходном полюсе у сети).
Прежде чем описывать алгоритм решения уравнения
(3-25), сделаем несколько замечании. Па каждом шаге
алгоритма рассматривается некоторая булева функция
У, представленная в дизъюнктивной нормальной форме,
и обрабатывается один из дизъюнктивных членов (терм)
Т этой формы. Пусть X — текущий индекс рассматривае-
мой функции Уг н v — текущий индекс обрабатывае-
мого терма 7\; Ух — \J 7\. Общий вид терма Т
V
следующий:
Тv = f\wi f\ wm /\ wsmD
Первой (Я=1) всегда рассматривается функция, пред-
ставляющая левую часть равенства (3-25), при этом
с
Yt=\/D[y"] и 1\ — Tg = D[yf!]. Обработка терма Tv со
₽=1
стоит в сопоставлении его "переменным wi п wm соответ
ствующпх им выходов ло1 нческпх элементов сети, после
чего следует .замена эньх переменных, а также перемен-
ной D [wm] функциями, аргументами которых являются
входные переменные указанных элементов. Замена про-
изводится по следующим правилам:
1. Каждая переменная Wi или win, не являющаяся
входной переменной сети, заменяется правой частью
(или инверсией правой части) выражения (о) для эле-
мента, соответствующего этой переменной.
2. Каждая переменная w&m заменяется правой ча-
стью (или ее инверсией) уравнения (б), когда соответ-
ствующий ей элемент исправен, и уравнения (в), когда
такой элемент неисправен.
3. Переменная D заменяется правой частью
уравнения (3-21), (3-22) пли (3-24) (в зависимости от
функции, реализуемой элементом, соответствующим пе-
ременной wm), когда указанный элемент исправен, или
выражением wmwsm \/ wmwsm, когда элемент неиспра-
Ёён. В последнем случае производится повторная заме-
на переменных wm, wsm и их инверсий wm, wam в соот-
ветствии с правилами 1 и 2.
Блок-схема алгоритма ЛЗ-1 построения хотя бы од-
ного входного набора сети, обнаруживающего заданную
неисправность s, представлена на рис. 3-23. Одна оста-
новка (Конец 1) наступает при первом получении функ-
ции содержащей терм Tv = Д х;, т. е. терм, со-
стоящий только из символов входных переменных х,
сети. Другая остановка (Конец 2) означает, что не су-
АЗ-1 построения проверяющего
алгоритма
Рис. 3-23. Блок-схема
набора А (О, s).
219
шествует ни одного входного набора, обнаруживающего
неисправность s (т. е. неисправность s несущественна).
Проиллюстрируем работу алгоритма АЗ-1 на приме-
ре сети рис. 3-24 (без повторителя во входном узле Хз).
Рис. 3-24. Пример логической сети для построения проверяющего
набора А'(0, s).
Пример 3-35. Пусть в сети рис. 3-24 имеется константная неис-
правность s=2°. Неисправным путям принадлежат элементы 2, 5, 6
и 8. Множество С содержит единственный элемент 8, который испра-
вен и реализует функцию у«,= уиуъучу1-
Полагаем А=1, тогда
УХ = У1 = £)[^].
Единственный необработанный терм = Z)[</S] в У] не является
термом вида А х, и поэтому заменяется по правилу 3 согласно
выражению (3-21)
Ti = D [у8] —'уСу1 (уъ ys V УвбУ‘»)(О [у6] V D [уе])
220
или в дизъюнктивной нормальной форме
Л ГбО [Н V7* "УчУ^У^О [t/s] V
V УчУчУз y*D [г/fij v"b'4^ss'/sei> ['/в]
Увеличиваем Л на 1 и принимаем УХ = У2 = Д.
В форме У2 нет тер лов вида Д xt, а очередным необработанным
является ее первый терм. По правилу 1
Уч = Х2 V^b
Ут = 'х» Х/'уз;
Уз = х, V у-з.
Уз = х4 V Уз
и по правилу 3
D [f/s] = D [(x,i/2)] = Xi(j/2 V ysi) D [«&]•
Так как входные полюсы сети никогда не принадлежат неисправ-
ным путям, условимся не отмечать эти переменные знаком Д.
Тогда
Ti = (х2 V У1)(Хз V V Уз)(Хз \/уг) х, V ° [</2] =
Т> [.'/г](х2 V yi)(x3 V </з) х,</2 ,'/s2 xix2x3//2,vs2 Г> [т/2 J V
V Xi 'll, 'узУз «ДС [!faj V x,x^y3D [1/2I V ХзХ^нУгУ^Т) [уг].
Принимаем Уз — Т,. В форме Уа нет термов вида Д х/, обработке
подлежит ее первый терм. По правилу 1
Уг—х^хз,
по правилу 2
ys2= 1.
по правилу 3
D [.%] = УзУ‘з V Уз yss = Уг = Х2 х3,
т. е.
T’i = XiX2XaX2 Хз1 х2 х3 = 0.
Получение нулевого значения для Д вынуждает перейти к обра-
ботке очередного (второго) терма из У3. Для этого терма Т2 по пра-
вилу 1
Г1 = Xi ха;
рз = х2х4,
что с учетом полученных выше значений для уг, у‘2 и D[ys] дает:
Т-з = Xi Xi Ха Х2 Х4 Х2 X3I Х2 Ха == Xi Х2 Хз Хз.
Полученный терм Тг является термом вида Д х(- и поэтому задает
входной набор 0000 (Xj.^XjXt), обнаруживающий неисправность
221
Пример 3-36. Пусть в сети рис. 3-24 неисправность s состоит
в том, что произошло замыкание (соединение) выходов элементов 1
и 5 и, кроме того, оборвался второй вход элемента 2. Предположим,
что соединение выходов указанных элементов приводит к тому, что
па втором входе элемента 4 и втором входе элемента 8 реализуется
функция t/ii/s. а обрыв входа элемента ИЛИ эквивалентен подаче па
оборванный вход константы 0:
7]S1 (irf ) х, Хз y2;
7js2 (U7J = xa;
Vs (Ц7;) = X, Хз~У2.
Выходы элементов 7, 2, 4, 5, 6, 8 принадлежат неисправным пу-
тям; С = {8}. Полагаем Х = 1; У1 = £>(//»]; 7\ «= D [f/s] =
= D [J/7//4 i/s Уз]- По формуле (3-21) имеем:
Л — У1 (у, Уй Уч V ysi yst ys4)(D [//4] V n[j/s] V о Ьс])*.
Так как T’i-^-O, y2 = T'i. В качестве первого необработанного
терма в У2 выберем терм Т, — у-, уз у-, yeD [jm], обработка которого
дает;
Т, = (Хз v Гз)(Х» v V Уг)(Хз V Уг) Хг (у, \/ у*з) D [j/,] =
= (Хз v {/s)(Xi V {/г)(*4 v Уг) хгух y»iD [f/i].
Так как 7"i=#T), Уз = ^1
Обработаем первый терм У3.
Г! — xlxiXiXiyiysiD [//,].
Гак как yt = xi хз, 7'1 = 0. В У3 выберем для обработки терм
Л = Узу2х2У1Уе1О [</1] =х2х4 х2 Хз х2 х, Хз X
X (*i V хз v ysi) (y>yst V У1 ysi)-
Т2 £0, У4 = Т2.
Обработаем в У4 терм 7’i=X|X2x3X4f/®2t/i'/si:
Т| = Х1 Х2 Хз Хз Х2 Х1 Хз (Х1 V Хз V f/sa) = Xi Хз Хз Хз ф 0.
Полученный терм задает входной набор 0000 (Х1Х2Х3Х4), обнару-
живающий заданную неисправность з.
МЕТОД ПРОВЕРКИ БУКВ ЭКВИВАЛЕНТНОЙ ФОРМЫ
Рассмотренные выше аналитические способы постро-
ения набора Х(0, s), обнаруживающего заданную не-
исправность s, связаны с получением и преобразовани-
* Здесь и далее для более короткой записи терм представ-
ляется в скобочной, а не в дизъюнктивной нормальной форме.
222
ем для каждой неисправности я достаточно сложных
аналитических выражений. Поэтому аналитические ме-
тоды для устройств большой размерности оказываются
громоздкими и неудобными. В значительной мере от
указанных недостатков свободен метод построения одно-
го проверяющего набора Л'(О, s) или их полной сово-
купности {X(0, я)} по эквивалентной форме дерева.
Пусть заданы прямая и обратная эквивалентные
формы функции исправной одповыходной логической
сети (ЭФ и ОЭФ) и для этой же сети, содержащей кон-
стантную неисправность я (ЭФ® и ОЭФ’). Если неис-
правность s существенна, то всегда существует входной
набор Xj такой, что z(X,) =0, a z®(X,) = l, либо такой,
что z(X,)=0, a z®(A'j) = l. В первом случае будем инте-
ресоваться ЭФ функции исправной сети, во втором
ОЭФ. Выявим некоторые свойства неисправности я и
обнаруживающего ее набора ХДО, я) па основе анализа
ЭФ (ОЭФ). Прежде всего, так как на наборе Xj z(Xj) =
= 0 (z(Xj)=0), то каждый терм ЭФ (ОЭФ) равен 0,
т. е. содержит буквы, равные 0. Так как zs(A;) = l
(ze(Xj) = l), то в ЭФ6 (ОЭФ®) функции неисправной сети
по крайней мере одни из ее термов па наборе X, равен
1, т. е. все буквы этого терма равны 1. В § 3-3 было
установлено, что ЭФ4(ОЭФ4) для класса константных
неисправностей может быть получена путем фиксации
по определенным правилам нулями и единицами букв
ЭФ (ОЭФ), при этом каждый терм ЭФ® (ОЭФ®) явля-
ется подтермом соответствующего ему терма в ЭФ
(ОЭФ) * *. Наличие в ЭФ® (ОЭФ®) терма, равного 1 на
наборе Xj, означает, что в соответствующем ему терме
ЭФ (ОЭФ) (обозначим его номером k) неисправность
я нс фиксирует ни одну букву равной 0 *. Из условия
z(Aj)=0 и z®(Xj)=l (z(Xj)— 0 п z8(Xj) = l) следует,
что некоторые буквы терма k ЭФ (ОЭФ), которым на-
бор Xj предписывает значение 0, фиксируются неисправ-
ностью я, равными 1. Обозначим множество всех букв
терма k ЭФ (ОЭФ), которые фиксируются неисправно-
стью я значением 1, через Qi,. Поскольку г®(А,) — 1
(z®(Xj) = l), набор Xj предписывает в терме k ЭФ
1 Заметим, что указанное свойство термов ЭФ’ (ОЭФ’) имеет
место при любом способе фиксации неисправностью s букв
ЭФ (ОЭФ)
* Если г’я! (z’sl), то термом k является любой терм
ЭФ (ОЭФ).
223
(ОЭФ) значение 0 только буквам (необязательно всем),
принадлежащим множеству Qh-
Таким образом, если неисправность s существенна,
то в ЭФ или ОЭФ найдется по крайней мере один терм
k, в котором неисправность $, во-первых, фиксирует не-
пустое множество букв Q/, значением 1, во-вторых, не
фиксирует ни одной буквы терма k значением 0. Для
краткости будем называть такой терм единичным тер-
мом ЭФ (ОЭФ) относительно неисправности s. Набор
Xj, обнаруживающий неисправность s, во-первых, пред-
писывает значение 1 всем буквам /?-го единичного тер-
ма, не принадлежащим множеству Qk, во-вторых, зна-
чение 0 — хотя бы одной букве из множества Qh и,
в-третьих, значение 0 — по крайней мере одной букве
в каждом из остальных термов ЭФ (ОЭФ). Заметим, что
указанные свойства набора X, по отношению ко всем
единичным термам ЭФ и ОЭФ, определяемым заданной
константной неисправностью s, являются необходимым
и достаточным условием принадлежности набора Xj
полной проверяющей совокупности {АДО, s)}.
Таким образом, проверка наличия неисправности s
сводится к проверке подмножества Q'h букв из множе-
ства Q/; с точки зрения наличия фиксации этих букв
значением 1.
Определим формально понятие проверки некоторого
множества Ri, букв /г-го терма эквивалентной формы.
Пусть задана ЭФ (ОЭФ) функции z(z) и пусть
zR (Zpi) — функция, получаемая путем фиксации в /г-м
терме ЭФ (ОЭФ) всех букв множества Rh значением 1.
Будем говорить, что на наборе X, множество Rh букв
Л-го терма ЭФ (ОЭФ) проверяется, если, во-первых,
набор Xj предписывает всем буквам множества Rh зна-
чение 0* и, во-вторых, на этом наборе z(X3j=0 (z(Xj) =
= 0), a zRk(Xj) = 1 {zRk(Xj) = 1). Очевидно, что на на-
боре Xj все термы ЭФ (ОЭФ) равны 0 и в k-м терме
всем буквам, не принадлежащим множеству Rh, пред-
писывается значение 1. Сравнив это определение с рас-
* Если входной набор Xj предписывает входной переменной ха
значение 6 = ) (0), то тем самым в ЭФ (ОЭФ) любой букве, пред-
ставляющей переменную ха(ха) с любым индексом, предписывает-
ся значение 6(6).
224
смотренными выше свойствами наборов из {Л’ (0, s)},
можно заключить, что при Rh — Q'/, набор Xj
обнаруживает неисправность s.
Если для каждого единичного терма ЭФ и ОЭФ по-
строить все наборы, проверяющие проверяемые подмно-
жества Q'h букв, то эти наборы образуют полную про-
веряющую совокупность {X(0, s)}. Заметим, что, как это
следует из § 3-3, способ фиксации букв ЭФ (ОЭФ)
функции z(z) неисправностью s в общем случае не
является однозначным. Это значит, что две такие раз-
ные фиксации могут дать различные единичные отно-
си гелыю s термы ЭФ (ОЭФ) и различные по виду ЭФ8
(ОЭФ8). Но различные эквивалентные формы функции
r"(z ) описывают одно и то же неисправное устройство
1 , и, кроме того, рассмотренный вуше способ провер-
ки букв единичных относительно неисправности s тер-
мов ЭФ н ОЭФ дает полную проверяющую совокупность
{.¥(О, s)}. Поэтому последняя не зависит от выбранного
способа фиксации неисправностью s букв ЭФ (ОЭФ) и
полностью совпадает с проверяющей совокупностью
{Л (О, s)}, полученной любым другим методом, например
методом различающих функций.
Пример 3 37. Дли сети рис. 3-1 неисправность s={a°, (6, 2)1, 6°)
фиш ирмч в ЭФ (17) и в ОЭФ (3 8) буквы «ц, а2, bi, сь di значе-
ппямп О, а буквы oj, «2, ё|, di— значениями 1 (см. пример 3-26).
Запишем ini значения над соответствующими буквами ЭФ и ОЭФ:
00 000 J____ 1_______ 12__)__________
z - Ь, a, V biCidi V "2 с2Ьг V bi V aaO> di V «2 d3;
oi о о о 1 1 ni oi о
J Lo _TL
z = b V bib2d3 V biCzdz V «1 ci Сг V aiCiCzd-z V
о o_i_i_ 0 1
L L L о L L *- !_ L
\/ QtCibz ds \/ (iictzdi у ctidiCzdz tiidibz d3.
11 1 0 1 011
Единичными относительно неисправности s в ЭФ являются тер-
мы 3, 4, 5 и 6, а в ОЭФ — термы 2, 3, 5, 6, 8 и 9 (нумерация термов
идет слева направо). Начнем с проверки буквы а2 единич-
ного терма 3 в ЭФ (<2з = {«г})- Выпишем под буквами
этого терма значения, которые должны быть им предписа-
ны искомым проверяющим набором A'j-e{A'(0, s)}, и тем самым
предпишем входным переменным а, b и с соответственно значения
1 0, 0, что определяет значения всех других букв ЭФ с переменными
а, b и с. Все такие предписанные значения букв назовем обязатель-
ными. Выписанные под формулой z обязательные значения букв
подчеркнуты. Значения остальных входных переменных (в данном
случае переменной d) должны быть выбраны так, чтобы все термы
15—358 225
ЭФ были равны 0. В нашем примере все термы ЭФ равны 0 незави-
симо от значения переменной d. Таким образом, получаем два вход-
ных набора 1000 и 1001 (abed), обнаруживающих неисправность s.
Проверка буквы а2 в термах 4, 5 и 6 ЭФ дает еще один искомый
набор 1010. Найденные три набора составляют подмножество
{Х(0, s)}° обнаруживающих неисправность s наборов, па которых
исправная схема дает на выходе сигнал 0.
Аналогично проверка проверяемых подмножеств букв единич-
ных термов ОЭФ относ 1тельно неисправности s выявляет наборы
подмножества {А'(0, s)}1, па которых исправная схема имеет на
выходе сигнал 1. Заметим, чго термы 2, 4, 5, 7, 8, 9 ОЭФ равны 0
на любом входном наборе. При проверке буквы bt в терме 2 (Q2=
= {61}) положим 5 = 0 (5=1) и d=l. Проставим и подчеркнем
обязательные вхождения букв. Тогда термы 1 и .3 становятся рав-
ными 0, а для равенства нулю терма 6 необходимо, чтобы одна из
переменных а или с равнялась 1, что дает три проверяющих набора
1111, 0111, 1101е{А(0, s)}1. Проверка подмножеств букв
в остальных единичных термах ОЭФ новых проверяющих наборов
не выявляет. Построенные шесть обнаруживающих неисправность s
входных наборов соответствуют наборам совокупности {А(0, s)},
найденным выше па основе различающей функции P[z, zs] (3-17).
В дальнейшем будет показано, что нс всегда прове-
ряемые подмножества Q'h единичных относительно не-
исправности s термов ЭФ (ОЭФ) являются одноэле-
ментными (как в рассмотренном выше примере).
Пример 3-38. В § 3-6 будет рассмотрена избыточная сеть
рис. 3-40, ЭФ которой имеет вид:
1 I 11
z = Uib^Ci \/ а2Ь2 е2\/ ct\ bi<t2b2 \/ cic2.
(1_1 о о I и о I и 1 и о
Неисправность 5='{а'} входного полюса а фиксирует равными 1
буквы щ и а2 единичных термов 1, 2 и 3. В первом и втором термах
множества букв <21 = {щ) п Q2= {«2} не могут быть проверены
(терм С[С2 становится равным 1); в третьем терме пи буква zZj, ин
буква «2 не могут быть проверены поодиночке (щ = 0 не позволяет
предписать 02=1, и наоборот), но множество букв Q3={aia2) про-
веряется на наборе 010 (abc). На этом наборе, как уже отмечалось,
обнаруживается неисправность s.
Для получения хотя бы одного любого проверяюще-
го набора .¥(0, s) достаточно проверить подмножество
букв Q';t хотя бы в одном единичном относительно s
терме ЭФ или ОЭФ. Очевидно, что для удовлетворения
условий проверки заданного подмножества букв /г-го
терма в ЭФ п ОЭФ большой размерности может потре-
боваться значительный перебор вариантов доопределе-
ния букв, не входящих в /е-й терм. Этот перебор можно
исключить, если следующим образом формализовать
процесс проверки букв терма
226
Из сказанного выше следует, что для проверки всех
подмножеств Q'i, букв й-го единичного относительно не
исправности s терма ЭФ пли ОЭФ (неисправность s
фиксирует значениями 1 множество Qi< букв) необходи-
мо одновременно выполнить условия:
1 . Обеспечить равенство х'ь—1 дизъюнкции ин-
версий всех переменных, представленных буквами мно-
жества Qi Тем самым будет обеспечено задание обя-
зательных значений 0 буквам (в конечном итоге вход-
ным переменным, представленным буквами) всех про-
веряемых подмножеств Q'k множества Q/t.
Пример 3 39. Для единичного терма 5 oiCiC2rf2 ОЭФ из приме-
ра 3-37, где Q5= {ui, cJ, получаем: x*s=(«Vc) = '-
2 Задать обязательные значения»! переменным, пред-
ставленным буквами /г-го терма, не принадлежащими
множеству Qk- Это требование можно представить вви-
то равенства х2/( = 1 конъюнкции "/А указанных пере-
менных
Дчч tout же примера 3 34 имеем: х2г, = с</=1.
3 Обеспечить равенство пулю остальных термов ЭФ
(О >Ф) Поскольку но условию I /г-н терм ЭФ (ОЭФ)
нткже р шоп пулю, рассматриваемое условие (обозна-
чим сто гапнсыо р=1) эквивалентно требованию равен-
ствз I функции z(z). Заметим, что для последней может
быть использована любая, в том числе минимальная
форма булевой функции
Продолжая пример 3 39, воспользуемся для функции z выраже-
нием (3 3) и длившем:
р z ab V й d V bi d V й с b = 1.
Удовлетворение всех грех условий состоит в равен-
11 вс I функции х’/|х2/|р, рабочие наборы которой явля
ю гея искомыми проверяющими наборами.
Запершая пример 3-39, получаем:
хцх26р (д\/ c)(cd)(ab V ad\/ bed V а с b) = bed,
откуда следует, что все проверяемые подмножества Qg множества Qs
буки проверяются на наборах 0111 и 1111 (abed).
Полученные указанным образом проверяющие набо-
ры для каждого единичного относительно $ терма ЭФ и
ОЭФ образуют полную проверяющую совокупность
{Х(0, s)}.
15* 227
МЕТОД СУЩЕСТВЕННЫХ ПУТЕЙ
Остановимся теперь на другом подходе к решению
задачи построения проверяющих или различающих сово-
купностей входных наборов. Этот подход в наиболее
явном виде реализует идею метода существенных путей,
изложенную в гл. 1 и состоящую в том, что для обнару-
жения неисправности необходимо и достаточно обеспе-
чить условия ее проявления и условия ее транспортиров-
ки. Формализуем эти условия для одиночных логических
неисправностей логических сетей общего вида (произ-
вольный базис элементов, наличие разветвлений, воз-
можная избыточность сети).
АНАЛИТИЧЕСКИЕ УСЛОВИЯ ОБНАРУЖЕНИЯ НЕИСПРАВНОСТИ
Пусть задано комбинационное устройство без конту-
ров обратной связи, имеющее п входных и k выходных
полюсов и содержащее N логических элементов т)Ь 1 =
= 1, 2, .. ., N. Для элемента гр, имеющего п, входов, на
которых в устройстве реализуются функции yim, т=
= 1, 2, и один выход с реализуемой на нем функ
цией у г, задан список из S, логических неисправностей.
При наличии неисправности х, х=1, 2, элемент
будем обозначать символом ту4;, а реализуемую им логи-
ческую функцию — символом //*,-.
Набор У, (0, х) значений входных функций па
котором y*i(Yi) К,), назовем проверяющим набором
элемента тр- (относительно неисправности х). При пали
чин Pis^l проверяющих наборов /-й, /=1, 2, ..., р,8, на-
бор будем обозначать У, ДО, х) Для m-п компоненты
набора УгДО, х) введем обозначение 6(/’)®гт, по там, где
это не внесет путаницы, будем опускать индексы i, т п х.
Очевидно, б(/) = !, 0.
Условие подачи на элемент тр- сети хотя бы одного
проверяющего набора можно представить в виде
Pis ni
ais = V /\уъ™ = 1, (3-26а)
1=1 ГП=\
где Vim } —yim при 8(/)= И У 1т при 8 (/) = 0.
Можно утверждать, что выполнение равенства a,s =
= 1 является необходимым и достаточным условием про-
явления неисправности х на выходе элемента тр, т. е.
в узле, наиболее близко расположенном к месту возник-
новения неисправности.
228
Подставив в (3-2ба) выражения для функций
, хп), получим функцию UiS, зависящую от
входных переменных сети, на каждом рабочем наборе
которой обеспечивается проявление неисправности s.
Пример 3-40. Если в сети рис. 3-1 одиночная неисправность
s заключается в изменении функции элемента 4 с ИЛИ на И, ю
«н УчУчХ/ УчУ^ = У\а\/ yta — aedy а(с\/ d). На восьми рабо-
чих наборах функции a4s рассматриваемая неисправность s прояв-
ят гея на выходе элемента 4 в изменении «/4=1 на г/"4 = 0.
Рассмотрим более сложный случай проявления не-
исправности.
Пример 3-41. В сети рис. 3-11, как это отмечалось в § 3-2, ко-
роткое ымык.зине диола Д в элементе 11 \ не меняет функционирова-
ния (леменга //|, т. е. yi = ysl=ab, по нарушает функционирование
элемента //2: у2=ас, y’t2 = abc. Указанная неисправность проявляется
па выходе элемента И % на единственном входном наборе 101 (afec);
функция az,—abc зависит не только от входных переменных а и с
>лс мента И2, но также от переменной Ь.
Константные неисправности на соединениях (узлах),
являющихся входами или выходом элемента т}ц будем
сиодпть к логическим неисправностям элемента т]г
(см. § 3-2).
Пример 3-42. Для шести константных одиночных неисправно-
стей входов и выхода двухвходового элемента И имеем следующие
проверяющие наборы и соответствующие функции aia:
S rf/(°, s) («IV °«s
К1)‘ {01} упуа
(/-•’)* {10} Ч1\У\2
(М)“ {"} yalUi
(< {11} ЧПУН
м {(II, 1(1,ПН} ‘Hilin V Ниццу Ииуи
{"} ‘Ihyti
При рассмотрении констан гной неисправности соеди-
нен ня входного полюса с узлом разветвления сети
(узла разветвления сети с выходным полюсом) для еди-
нообразия представления неисправностей условно вне-
сем в неисправное соединение I элемент-повторитель 774,
функции па входе и выходе которого обозначим соответ-
ственно уц и у г. Константная неисправность соединения
i будет рассматриваться как логическая неисправность
элемента Пр
В дальнейшем нам потребуется представление функ-
ции ais в виде ais = ali8 \/ a°is, где a'is(а°<8)— функция,
рабочие наборы которой задают все проверяющие набо-
22
ры неисправности s такие, что yi(Yj) = l, a ysi(Yi)=O
(Уг(Уг)=0, а^(У0 = 1).
Обратимся теперь к условию транспортировки не-
исправности.
Пусть неисправность s проявляется в узле i сети.
Введем понятие функции наличия существенного (чув-
ствительного) пути от узла I, являющегося выходом эле-
мента тр, до выходного полюса у, аргументами которой
являются входные переменные сети. Оборвем условно со-
единение (узел) i и образовавшемуся новому входу сети
сопоставим дополнительную входную переменную уг-
Будем считать, что (Xj) = l, если па наборе Xj зна-
чений входных переменных Xi, ...,хп сети изменение
значения дополнительной входной переменной г/, приво-
дит к изменению значения выходной функции сети;
р (Л/) = 0 в противном случае.
Можно утверждать, что выполнение равенства
k
VPZ=1 (3-266)
7=1
есть необходимое условие транспортировки неисправнос-
ти s элемента т],-, когда контрольными точками являются
выходы Zi, .... г7, .... сегн. При рассмотрении кон-
стантных неисправностей узел I может быть не только
выходом реального элемента сети •»],-, по также выходом
условно поставленного в соединение i повторителя /7,.
Рассматривая совместно (3-26а) и (3-266), можно сде-
лать вывод, что выполнение равенства
k
V = 1 (3-26в)
7=1
является необходимым и достаточным условием обнару-
жения неисправности s элемента т]г- на выходах сети.
Если (3-26в) не выполняется ни на одном из 2” наборов
входных переменных сети, то неисправность s несущест-
венна, так как она не нарушает правильного функцио-
нирования устройства.
Все входные наборы сети, на которых выполняется
условие (3-26в), составляют полную проверяющую со-
вокупность {X (0, s)} входных наборов относительно не-
исправности s. Наборы этой совокупности будем назы-
вать проверяющими наборами сети для неисправности $.
230
Условие проявления одиночной неисправности s доста-
точно четко определяется требованием образования па
входах элемента тц одного из проверяющих наборов
У,;(0, s). Однако условие транспортировки неисправнос-
ти пли, иными словами, условие наличия существенного
пути нуждается в конкретизации.
Рассмотрим один из аналитических методов решения
уравнения = 1, т. е. нахождения всех таких входных
наборов сети, на каждом из которых обеспечивается су-
щественный путь от узла i до выхода у. Этот метод
использует понятие булевой разности (булевой произ-
водной) булевой функции.
Предварительно запишем аналитическое выражение для
функции z(i, реализуемой па выходном полюсе у сети,
когда узел i является входным полюсом сети с дополни-
тельной входной переменной у,. Под булевой разностью
функции (xi,..., хп, уд относительно переменной t/i
понимается следующая функция:
dzii/dyi = zli(x„ ..., хн, /Л)фгг (л-,, ..., хп, у,). (3-27)
Как видно, второе слагаемое в правой части выраже-
ния (3-27) отличается от первого инверсным значением
переменной //, (что соответствует изменению значения
сигнала в узле «)• Из свойства функции «сумма по мо-
дулю 2» следует, что выражение (3-27) равно 1 тогда и
только тогда, когда значения первого и второго слага-
емых различны. Отсюда очевидно, что
Р,, dz^/dyi.
iaMcniM. что понятие булевой! разности функции zyi
по переменной // i оппада< । с понятием различающей
ф\пкц|Н1 /)|2Г|, гели z'(1 zfi (д',, .... ,v„, /у), т. е. пе-
пси равное।ь сос гоп г в вивер тированпн входной перемен-
ной Приведем без доказательств некоторые важные
свойства булевой разности функции f(X) =f(xi,...
... , л*а ,..., хп) попеременной Л'а;
dxa dxa •
2) df(X) df(X) .
dxa dxa
231
3) ^У^- = 0, если f (X) не зависит от х , т. е.
f(x„ ха, .... x„) = f(x„ .... ха, .... Хп);
4) — 1, если f (X) зависит только от ха;
5) =f(X)^eg(X)^e
dg(X).
dxa dxa ’
mm Jsm
dxa dxa
Пример 3-43. Пусть в сети рис. 3-1 необходимо найти входные
наборы, обеспечивающие наличие существенного пути от входа 2
элемента 6 до выхода z. Методом, например, обратной подстановки
найдем выражение
£6г(а, b, с, d, уег) = УегЬ\/ (ad\/ а b с).
Вычислим dze2/dye2. Учитывая свойства 6, 5 и 3 булевой разно-
сти булевой функции, получаем:
в dZeE <-лч d(^b>
— (а V d)(n V b V с) b = ab V bd.
Последнее выражение обращается в I на шести наборах значе-
ний переменных а, 6, с, d: 1100, 1101, 1110, 1111, 0101, Obi 1, каждый
из которых обеспечивает наличие требуемого существенного пути.
Для неисправности s=(6,2)1 условие ее проявления имеет вид:
o62s —yi = а (с \J d) = 1.
Тогда полная проверяющая совокупность {Х(0, s)} может быть
получена согласно условию (3-27):
“essPusz = а (с V d)(ab \/ bd) = ab cd = 1.
Значит, рассматриваемая неисправность обнаруживается на
единственном входном наборе 0101.
Для вычисления булевой разности кроме выражения
(3-27) можно использовать следующее эквивалентное
ему выражение, вычисления по которому в некоторых
случаях оказываются проще:
йг . _
zp.(Xi, .... Хп, 1)фгт/(х„ Хп, 0). (3-28)
232
Из выражения (3-28) видно, что булева разность не
зависит от переменной (z/J, относительно которой она
вычисляется.
Для рассмотренного выше примера 3-43 имеем:
V (« d V a bc)]Q)(a d\/ а b с) =
= b (а V d) (a V b V с) = ab V bd.
Для нахождения совершенной дизъюнктивной нормаль-
ной формы (СДНФ) функции dz_(Jdi/i при условии, что
известна СДНФ функции z можно воспользоваться тем,
что рабочие наборы функции dz^/dtp представляют собой
пары соседних по переменной yt наборов, один из кото-
рых является рабочим и второй — нерабочим наборами
функции zTi. Справедливость этого следует непосредст-
венно из анализа выражения (3-28). Например, если
f (Xi, х2, х3) = XiX2jc3 V V л'1Х2х3, то df/dx2 =
— Х1Х2Х3.
Известны также другие правила получения выраже-
ния булевой разности, однако здесь мы на них останав-
ливаться не будем.
СТРУКТУРНЫЙ подход
Метод существенных путей в аналитическом виде для
схем большой размерности может оказаться громоздким.
Рассмотрим решение задачи задания условий проявления
и транспортировки и, в конечном итоге, построения про-
веряющей совокупности входных наборов для одиночной
неисправности s элемента г|, по структуре сети.
Проявление неисправности х элемента тр- па проверя-
ющем ее наборе У\;(0, $) в двоичной логической сети
состоит в изменении значения сигнала Уг(.Уц) = 1 (0)
в узле i на противоположное у8г(Уц) =0(1). Будем обоз-
начать это изменение символом D (соответственно D).
D-кубом неисправности s элемента тр- назовем (nj+1)-
мерный вектор, образованный проверяющим набором
Уг-Д0, $) и приписанным справа от последнего символом
D (когда ^(Уи) = 1 и ysi(Yij)=0) или D (когда ^(Уъ) =
= 0 и ysi(Yij) — 1). Совокупность проверяющих наборов
{У,3(0, s)/j=A, 2,...,piS} порождает совокупность всех
D-кубов неисправности s элемента гр.
233
Пример 3-44. Гак, для неисправности s, состоящей в преобразо-
вании трехвходового элемента 1], И в элемент ИЛИ существует
шесть проверяющих наборов входных переменных УпУаУа, содер-
жащих одну или две единицы, которые задают шесть D-кубОв неис-
правности s: 100Р, ОЮЛ, 001/Э, 110/J, 011/J и 101Z5.
Введем понятие сжатых D-кубов неисправности s эле-
мента Для этого воспользуемся некоторой минималь-
ной дизъюнктивной нормальной формой (МДНФ) функ-
ции а^Дс/Д), представляющей условие подачи на эле-
мент T)j хотя бы одного обнаруживающего неисправ-
ность $ набора Yi, на котором yi(Yi) = 1 (Уг(Уг) =0).
Условимся обозначать символом ~ (тильда) безразлич-
ное (0 или 1) значение сигнала в некотором узле. Каж-
дой Г-Й КОНЪЮНКЦИИ (r^Pis) МДНФ функции ct'is (ссог<з)
поставим во взаимно-однозначное соответствие п,-мер-
ный вектор R, причем букве конъюнкции соот-
ветствует значение 1 (0) m-к координаты вектора; коор-
динатам вектора, которые соответствуют отсутствующим
переменным в конъюнкции, приписывается значение
Таким образом, каждый такой вектор R представляет
группу проверяющих неисправность s входных наборов
элемента т], (или проверяющий интервал), отличающих-
ся всевозможными совокупностями значений входных
переменных, которым соответствует символ ~ вектора
R. Припишем справа к вектору R символ D(/J), если
вектор R соответствует конъюнкции г функции alis(a°is).
Полученный таким образом (п,+ 1)-мерпый вектор, со-
держащий символы ~, назовем сжатым D-кубом не-
исправности.
Так, для примера 3-44 имеем <4s = a>,-s = ytiyt2 V yi2 уи V
V W’ .Wi (“4s = 0). Три конъюнкции функции o.crs дают три сжатых
/J-куба неисправности: 10 -v D, ~ 10D п 0 •%. 1£).
Таким образом, задание некоторого D-куба неисправ-
ности s является заданием одного из вариантов условия
проявления этой неисправности. Чтобы реализовать это
задание, необходимо найти такой входной набор X сети,
который обеспечивает появление на входах элемента тц
проверяющего набора Уц, образующего выбранный D-
куб неисправности. Говорят, что при этом наборы X и
Y-ij структурно соответствуют друг другу. Если узлу i се-
ти заданием сжатого D-куба неисправности предписы-
вается значение то будем считать, что это значение
обеспечивается любым входным набором X.
234
Транспортировка неисправности s из узла i, где s
проявляется, в контрольную точку у, где s обнаруживает-
ся, состоит в передаче изменений значений входных сиг-
налов на выходы элементов, расположенных на одном
или нескольких путях, соединяющих узлы i и у. Рассмот-
рим один из таких элементов — элемент т)д, через кото-
рый происходит транспортировка неисправности.
Изменение значений входных сигналов элемента гр,
соответствует тому, что на некотором входном наборе
сети Xj его входной набор У/, при исправной сети отли-
чается от его входного набора Ysh при наличии неисправ-
ности s в элементе тр-. Сравним покоординатно наборы
Yh и Уб, и представим их одним набором YDh по следую-
щим правилам:
если = 1 (0), то 6Dhm= 1 (0);
если 6hrn=l(0) И 6shm = 0(l), ТО (Phm=D (D).
Здесь dhm, 6shm и —m-e координаты наборов
Yh, Y3h и набора YDh соответственно, а символ D имеет
тот же смысл, что и прежде.
Набор YDh назовем входным D-набором элемента т]Л.
Входной D набор элемента г]л, представляющий пару
наборов Yh н У8Л таких, что tjh(Yh) =£yh(Ysh), назовем
существенным D-набором. D-кубом элемента (или
просто D-кубом) назовем (пь +1) мерный вектор, обра-
зованный существенным D-набором и приписанным спра-
ва от последнего символом D (когда ун (Yh) = 1 и yh (Ysh) =
=0) или/) (когдаyh(Yh) =0иyh(Ysh) = 1).Входы,которые
в D-кубе элемента представлены координатами со значе-
ниями D и D, принято называть существенными1 входами
относительно данного D-куба, так как одновременное из-
менение значений сигналов (предписанных набором Уд) на
этих входах па противоположные (предписанные набо-
ром Ysu) вызывает изменение значения выходного сигна-
ла элемента. Таким образом, D-куб элемента задает
один из вариантов выполнения условия транспортировки
неисправности через элемент Все возможные вариан-
ты транспортировки любой неисправности s через
исправный элемент логической сети могут быть полу-
чены исходя только из функции, реализуемой элементом
гр,, например, по его таблице истинности путем нахож-
дения всех D-кубов элемента. Для этого необходимо осу-
ществить попарное сравнение каждого рабочего набора
1 Отсюда происходит название «существенный путь».
235
с каждым из нерабочих наборов таблицы. Один из срав-
ниваемых наборов выступает в качестве набора Уд,
а другой — в качестве набора Ysh. При этом в зависимос-
ти от того, какой набор пары — рабочий или нерабо-
чий—принят за набор Yh, каждая пара таких наборов
образует два D-куба элемента, один из которых может-
быть получен из другого заменой всех символов D(D) на
символы D(D). Эти D-кубы будем называть дуальными
относительно друг друга.
Пример 3-45. Пусть табл. 3-1 (без столбца z2) является таблицей
истинности некоторого трехвходового элемента. Проводя указанное
сравнение и выбирая рабочие наборы функции z, в качестве набо-
ра Yh, получаем (пары сравниваемых наборов представлены в скоб-
ках номерами от 0 до 7):
1) (2,0) —GOOD
2) (2,1) — 0DDD
3) (2,3) — 0IDD
4) (2,4) — DDOD
5) (2,5) — DDDD
6) (6,0) —DDOD
7) (6,1) —DDDD
8) (6,3) —DIDD
9) (6,4) — 1D0D
10) (6,5) — 1DDD
И) (7,0) — DDDD
12) (7,1) — DDtD
13) (7,3) — D11D
14) (7,4) — 1DDD
15) (7,5) — 1D1D
Построив для каждого из этих D-кубов его дуальный D-куб,
получим множество всех D-кубов рассматриваемого элемента.
Введем понятие сжатых D-кубов элемента. Как и
прежде, пусть символ ~ означает безразличное (0 или
1) значение сигнала. На множестве всех D-кубов эле-
мента произведем попарное склеивание всех таких D-ку-
бов, которые различаются только в одной координате
значениями 0 и 1, в один D-куб, где эта координата име-
ет значение Назовем сжатым D-кубом элемента D-
куб, хотя бы одна координата которого имеет значе-
ние
Для построенного в примере 3-45 подмножества D-кубов склеи-
ваются следующие пары D-кубов: I и 9, 2 и 10, би 12, 9 и_15, которые
соответственно образуют 4 сжатых D-куба: ~ D0D, ~DDD, DD~D
и 1D-D.
Использование сжатых D-кубов элементов (так же,
как и сжатых D-кубов неисправности), во-первых, позво-
ляет в некоторых случаях более компактно записать
множество D-шубов (D-кубов неисправности) элемента
и, во-вторых, повышает эффективность приводимого ни-
же алгоритма вычисления проверяющего набора Х(0, s).
Нетрудно видеть, что наличие сжатого куба с символа-
ми ~ на некотором подмножестве координат (будем
называть их безразличными) означает наличие D-кубов
236
элемента, отличающихся от рассматриваемого сжатого
D-куба элемента всеми возможными наборами значений
D, D его безразличных координат. Будем считать, что
эти D-кубы поглощаются рассматриваемым сжатым D-
кубом и удалим их из списка D-кубов элемента.
Так, в примере 3-45 сжатый D-куб ~ D0D поглощает два /5-ку-
ба: DD0D и DDQD. Произведя все поглощения, подмножество
/5-кубов, построенное в примере 3-45, можно сократить до семи
D-кубов: ~DOO. -ООО, OlOO, O1DD, OD —О, ОНО и 1O — D.
Очевидно, что символ ~ получил теперь расширен-
ное толкование. Координата с символом ~ может иметь
любое из четырех значений: О, 1, D или D.
Итак, один из вариантов условия транспортировки
неисправности s можно представить заданием одного из
D-кубов на входах п выходах некоторых элементов, при-
надлежащих путям, ведущим из узл"& i в узел у. Необхо-
димыми условиями при этом являются: во-первых, нали-
чие значений D(D) только в узлах, принадлежащих этим
путям, во-вторых, одному узлу может задаваться только
одно из значений D или D, точно так же, как и всем
узлам, соединенным с одним узлом разветвления,
в-третьпх, наличие хотя бы одного D-пути (I, у), т. е.
пути из узла i в узел у, каждому узлу которого приписан
символ D или D, в-четвертых, наличие D-пути (i, h)
в любой узел h, имеющий значение D или D. Назовем
свободными входы элементов D-пути, не принадлежащие
последнему. Тогда для реализации рассматриваемого
варианта условия транспортировки неисправности необ-
ходимо найти такой входной набор X сети, который обес-
печивает появление па свободных входах каждого эле-
мента тр, всех D-путей (i, -р) значений, требуемых D-на-
бором У"/, выбранного D-куба элемента щ (будем
говорить, что при этом наборы X п Ус/, структурно соот-
ветствуют друг другу) ’.
Очевидно, набор X является проверяющим относи-
тельно неисправности s элемента тр тогда, когда он
структурно соответствует как выбранному проверяющему
набору Yfj (0, s) неисправного элемента T]s,-, так и D-на-
борам элементов всех D-путей (i, у). Прежде чем рас-
сматривать способы построения проверяющих входных
наборов сети, введем понятие тупикового D-куба элемен-
1 Если в узле / сети выбранным сжатым О-кубом задано значе-
ние —, то будем считать, что это значение обеспечивается любым
набором X.
237
та, а также понятие операции однозначного распростра-
нения сигналов в сети.
Пусть для элемента щ, имеется входной D-набор YDh,
представляющий пару наборов Yh и Ysh таких, что
yh(Yh) =yh(Ysh). Тупиковым D-кубом элемента т)^ являет-
ся (щ, + 1)-мерный вектор, состоящий из обладающего
указанным свойством D-набора YDh с приписанным спра-
ва от последнего символом 1 (когда ук=\} или 0 (когда
уь—О). Дуальный тупиковый D-куб получается путем за-
мены в заданном тупиковом D-кубе символов D на D, и
наоборот. Входы, которые в тупиковом D-кубс элемента
представлены координатами со значениями D и D, назы-
ваются несущественными, так как одновременное изме-
нение значений сигналов па этих входах па противопо-
ложные не вызывает изменения значения выхода эле-
мента.
Найти тупиковые D-кубы можно по таблице истиннос-
ти элемента путем сравнения всех пар рабочих и всех
пар нерабочих наборов, принимая один набор пары
в качестве набора Yh, а другой — в качестве набора Ysh-
Пример 3-46. Для элемента, рассмотренного в предыдущем при-
мере, принимая первый из указанных в скобках набор в качестве
набора Ул, имеем одну часть всех тупиковых D-кубов:
(2,6) — 75101; (2,7) — D1D1; (6,7) — 11751; (0,1)—OO/JO; (1,4) —DODO; (0,3) — ODDO; (1,5) — DOI о; (0,4) —"D000; (3,4) — DDDO; (0,5) — DODO; (3,5) — DD10; (1,3) — 0D10; (4,5) — 10D0.
Другие тупиковые D-кубы элемента могут быть найдены по-
строением кубов, дуальных по отношению к каждому из указанных
выше.
Аналогично сжатым D-кубам вводятся понятие сжа-
тых тупиковых Д-кубов, а также операция поглощения
кубов.
В подмножестве построенных в примере 3-46 тупиковых D-кубов
склеиваются две пары кубов, образуя два сжатых тупиковых D-куба:
~0D0 и D0~0. Первый из них поглощает куб DODO и куб D0D0
(тупиковый D-куб, дуальный кубу D0D0), второй — кубы D0D0 и
D0D0.
Из физических соображений ясно, что задание тупи-
кового D-куба элемента прекращает передачу изменения
238
значений сигналов со входов на выход элемента (обры-
вает D-путь).
В дальнейшем нам понадобятся сжатые таблицы ис
гинности логических элементов, которые мы будем зада-
вать следующим образом. Представим прямую и обрат-
ную функции, реализуемые элементом, в некоторой ми-
нимальной дизъюнктивной нормальной форме. Каждая
строка сжатой таблицы истинности элемента взаимно-
однозначно соответствует каждой конъюнкции функции
у и у, причем букве ym(ym) конъюнкции соответствует
шачение 1 (0) в столбце ут рассматриваемой строки;
в ее столбцах, соответствующих отсутствующим перемен-
ным в конъюнкции, проставляется символ безразличного
значения Таким образом, каждая строка представля-
ет в общем случае группу входных* наборов элемента
(интервал), отличающихся всевозможными совокупнос-
тями значений 0, 1 входных переменных, которым соот-
ветствует символ ~ . В столбце у проставляется значе-
ние функции у на наборах интервала. Иногда строку
сжатой таблицы истинности элемента будем называть
простым кубом (если опа не содержит символов или
сжатым простым кубом элемента (в противном случае).
Пример 3-17. Для элемента, таблица истинности которого пред-
ставлена табл 3-1 (без столбца г2), прямая п обратная функции
имени соответственно вид:
Zi = XiXn V х2х3;
21 = V *1*з-
Ниже приводится сжатая таблица истинности этого элемента:
Учитывая расширенную интерпретацию символа
сжатые простые кубы элемента могут поглощать тупико-
вые £)-кубы.
Так, например, сжатый простой куб элемента в примере 3-47 —
0~ 10 поглощает два тупиковых £)-куба этого элемента (см. пример
239
3-46) 0D10 и О/Л О. В соответствии с этим полученное в примере 3-46
подмножество тупиковых D-кубов сокращается до четырех кубов:
D\D\. ODDO, DDDO, DDW.
На рис. 3-25 приведены сжатые таблицы истинности
И таблицы D-кубов и тупиковых D-кубов двухвходовых
элементов И, ИЛИ, «сумма по модулю 2», инвертора п
элемента, сжатая таблица истинности которого представ-
лена табл. 3-4. Сжатые таблицы истинности отделены от
таблиц О-кубов двойной линией, одинарная линия в таб-
лицах О-кубов разделяет D-кубы и тупиковые О-кубы.
Перейдем к определению операции однозначного рас-
пространения сигналов в логической сети. Пусть для эле-
ментов сети заданы их сжатые таблицы истинности и
таблицы всех О-кубов. Для обозначения неопределенно-
го или неизвестного значения сигналов на входах или
выходах элементов (в узлах сети) введем символ X.
Значения 1, О, О, D будем называть определенными,
а значение ~—безразличным значением. Назовем
кубом элемента т]< (и< +1)-мерный вектор, первые и, ко-
ординат которого соответствуют входам, а последняя —
выходу элемента, причем каждая 'координата может
иметь значение из множества {1, О, D, D, ~, X}-
Пусть всем входам и выходу элемента т]< приписаны
неопределенные значения X. Выполним замену некото
рых неопределенных значений определенными или без-
различными значениями и назовем результат такой за-
мены исходной фиксацией соответствующих входов и,
возможно, выхода элемента, а в общем случае — узлов
сети. Координаты куба элемента (или входы и выходы
элемента, узлы сети), которым при исходной фиксации
задаются определенные значения, назовем фиксированны-
ми. Суть операции однозначного распространения (ОР)
над элементом т), состоит, во-первых, в проверке физиче-
ской непротиворечивости исходной фиксации и, во-вто-
рых, в определении значений тех нефиксированных коор-
динат, которым непротиворечивая исходная фиксация
однозначно предписывает определенные значения при
произвольных значениях на других нефиксированных
координатах. Обе эти задачи решаются путем сравнения
значений координат заданного исходной фиксацией куба
элемента со значениями соответствующих координат
строк сжатой таблицы истинности^ когда исходная фик-
сация не содержит символов D и D, и строк сжатой таб-
лицы истинности и таблиц всех О-кубов элемента тр- (бу-
240
16—358
Дем все эти таблица называть исходными таблицами;
при наличии в фиксации символов D или D. Строки, для
которых значения всех указанных координат совпадают
со значениями 'координат исходной фиксации, будем на-
зывать непротиворечащими (исходной фиксации); мно-
жество таких строк будем обозначать символом В *.
Если в сжатой таблице или таблице £)-кубов не со-
держится пи одной пепротиворечащей строки (множест-
во В пусто), то исходная фиксация и ее ОР противоре-
чивы. В противном случае (т. е. при непротиворечивости
исходной фиксации или ее ОР) произведем сравнения
значений нефиксированных координат в пеиротивореча-
щих строках (строках множества В). Если определенные
значения одной или нескольких таких координат покоор-
динатно одинаковы во всех строках множества В, то
будем говорить, что это определенное значение или сово-
купность определенных значений нескольких координат
однозначно предписываются {фиксируются) исходной
фиксацией при безразличных (~) значениях других не-
фиксированных и пефиксируемых координатах. В резуль-
тате ОР фиксируемые координаты вместо неопределен-
ных (X) или безразличных (~) значений приобретают
некоторые определенные значения, а другие оставшиеся
координаты (кроме координат, фиксированных исходной
фиксацией) вместо неопределенного значения X при-
обретают произвольное значение В рассмотренном
случае считаем операцию ОР результативной. В случае
отсутствия хотя бы одной фиксируемой определенным
значением координаты считаем операцию ОР безрезуль-
татной.
Пример 3-48. Проиллюстрируем различные исходы ОР для двух-
входового элемента И, исходные таблицы которого, т. е. сжатая
таблица истинности и таблицы D-кубов, даны на рис. 3-25.
а) Исходная фиксация задана кубом Х01 (У\УгУ). По сжатой
таблице истинности находим, что последняя не содержит ни одной
непротиворечащей строки, т. е. строки, в которой значения коорди-
нат совпадают со значениями фиксированных координат в кубе Х01
(множество В строк пусто). Следовательно, исходная фиксация про-
тиворечива.
Ход операции ОР удобно представлять в виде таблицы, в первой
строке которой записана исходная фиксация, затем следуют строки
* Будем считать, что безразличное ~ и неопределенное X зна-
чения координаты совпадают с любым определенным значением этой
же координаты.
242
множества В и, наконец, в последней строке записан исход ОР.
Тогда дчя рассмотренного случая имеем:
б) Исходная фиксация— —Из всех исходных таблиц на-
ходим B={1DD, DL)D, DDO, 0 — 0}. Исходная фиксация непротиво-
речива, однако доопределения значений нефиксированных координат
произвести нельзя (операция ОР безрезультатна). Исход операции
ОР ~ /<Х- Таблица имеет вид:
~ D X
1 D D
D D D
D D 0
0 -х. 0
-х D х
в) Исходная фиксация — XI. Имеется единственная пепротпво-
речащая строка сжатой таблицы истинности: Д={111}. Значит,
исходная фиксация непротиворечива. Анализ значений нефиксирован-
ных координат (т. е. у> и у2) в этой строке показывает, что исход-
ная фиксация однозначно предписывает нм значение 1, т. е. опера-
ция ОР является результативной. Исходом операции является
куб 111. В табличном виде имеем:
Пример 3-49. Для элемента, который рассматривался в приме-
рах 3-45, 3-46 и 3-47, а сжатая таблица истинности и таблица всех
Д-кубов изображена на рис. 3-25, задана исходная фиксация DDXX-
16* 243
По исходным таблицам находим множество непротнворечащих строк
и затем определяем исход операции ОР:
D D X X
-ч. D 0 D
-ч. D D D
D D -ч. D
D D -ч D
Операция ОР результативна и фиксирует выход элемента зна-
чением D при безразличном значении на незафиксированном третьем
входе элемента.
Выполнение операции ОР над сетью заключается
в последовательном выполнении операций ОР над всеми
теми элементами, входы пли выходы которых оказались
фиксированными либо благодаря исходной фиксации,
либо в результате выполнения операций ОР над други-
ми элементами. Операция ОР над сетью заканчивается,
когда выполнены все результативные операции ОР над
элементами сети. При задании исходной фиксации и
в процессе выполнения операции ОР над сетью фиксация
узла, связанного с узлом разветвления некоторым зна-
чением, означает фиксацию этим значением всех узлов
сети, связанных с рассматриваемым узлом разветвления.
Нетрудно показать, что исход операции ОР над сетью не
зависит от выбранной последовательности выполнения
операций ОР над элементами.
В процессе выполнения операции ОР над сетью мо-
жет обнаружиться элемент, для которого подмножество
его фиксированных координат противоречит исходным
таблицам элемента (множество В пусто), или может
обнаружиться узел сети, который фиксируется двумя
различными определенными значениями. И в том, и
в другом случае это будет означать, что исходная фикса-
ция и ее ОР противоречивы.
На рис. 3-26 изображен фрагмент сети с заданной на нем исход-
ной фиксацией (значения 1 и 0 в кружках). Там же в таблицах
показаны результаты выполнения операций ОР над элементами
сети. Сначала обработаны элементы 1, 2, 3, 6 и 7, для которых
фиксированные узлы являются входами или выходами. Результатив-
ные исходы операции ОР (над элементами 2 и 3) определяют новую
исходную фиксацию (дополнительно фиксируются оба входа элемен-
244
I a 4 ii один вход элемента 5) Операции ОР над элементами 4 и 5
дополнительно фиксируют входы элемента 6. Наконец, операция ОР
над элементом 6 показывает, что заданная исходная фиксация про-
тиворечива.
Теперь, используя операцию ОР над сетью, решим
задачу проверки, является ли данный входной набор X
сети проверяющим для неисправности s, вариант условия
проявления которой задан одним из ее D-кубов неисправ-
ности. В этой задаче исходной фиксацией являются зна-
Элемент 1 Элемент Z Элемент 3 Элемент Б
- 7 D X 0 X X 7 X X X X 0
0 1 0 7 0 0 7 1 0 0
7 7 0 0 0 0 — 7 7 /V и 0
X 1 0 X 0 ~ 0 7 ~ 7 I X 0
Элемент? Элемент 4 Элемент 5 Элемент Б
X 0 X 0 1 X 1 X X 7 7 0
0 0 0 ' 0 7 7 7 7 Ф
7 rxj 1 0 1 7 7 7 —
X 0 X 7 ~ 7
Рис. 3-26. Иллюстрация операции однозначного распространения над
сетью.
245
чения сигналов, предписанные D-кубом неисправности s,
а также входным набором X.
Выше было сказано, что набор X является проверяю-
щим, если он, во-первых, структурно соответствует про-
веряющему набору Yij(O, s) элемента зд и, во-вторых,
обеспечивает образование хотя бы одного О-пути (i, у).
Первое условие выполняется, если исходная фиксация
непротиворечива. Второе условие требует, чтобы по за-
вершении операции ОР над сетью хотя бы один выход
сети имел значение D пли D. Еслп исходная фиксация
противоречива пли пи одни выход сети не получил зна-
чения D(D), следует повторить процедуру для другого
.D-куба неисправности s. Если такого О-куба неисправ-
ности нет, набор X не является проверяющим. Очевидно,
что использование сжатого О-куба неисправности позво-
ляет фиксировать меньшее число узлов сети, а потому
возможно более быстро получить искомое решение.
Блок-схема алгоритма АЗ-2, реализующего указанные
действия, представлена на рис. 3-27.
Построение всех наборов проверяющей совокупности
{X(0, s)} можно организовать путем проверки по алго-
ритму АЗ-2 каждого 'из 2П входных наборов сети для
каждого D куба неисправности s. Если совокупность
{Х(0, s)} пуста, то неисправность s несущественна.
Пример 3-50. Пусть в сети рис. 3-24 неисправным узлом i
является входной полюс х3, на котором постоянно закреплено зна-
чение 0, т. е. s = x°3. Рассматривая соединение (узел) как повтори-
тель, получаем D-куб неисправности s в виде 1£){х3|Х3}. Из псех
16 входных наборов проявление рассматриваемой неисправности s
обеспечивает каждый из 8 входных наборов со значением х3=1.
Таблица истинности и таблица /9-кубов двухвходового элемента
ИЛИ приведена на рис. 3-25. Для четырехвходового элемента ИЛИ
эти таблицы имеют аналогичный вид.
Итак, исходная фиксация задается значением D на выходе по-
вторителя входа хз и исследуемым набором на входах сети. Резуль-
таты выполнения операции ОР для всех входных наборов с Хз=1
сведены в табл. 3-5, а для входного набора 0010, кроме того, значе-
ния сигналов в узлах сети показаны па рис. 3-24. Из табл. 3-5 вид-
но, что из восьми наборов, на которых неисправность s проявляется,
только па двух (0010 и 1111) образуется существенный путь от
полюса Хз до выхода г; эти наборы п составляют искомую совокуп-
ность {Х(0, з)}.
Как уже упоминалось, существенный путь (будем
его обозначать записью начального узла i и конечного
узла у в фигурных скобках {i, у}) представляет собой
в общем случае совокупность D-путей (i, у). D-пути, на-
246
247
Т а б л и ц а 3-5
D-пути (х3, 1, 4, г) (х3, 2, 5, г) (хз, 2, 6, г) (Хз, 1, 4)(ХЗ, 7) (х3, 2, 5) (Хз, 1), (хз, 7) .5-.S (9 ‘3 ‘Ех) ‘(I >ех) сч г- (хз, 7) (хз, 7, z)
|О) о о о о о о ci
и 5 ° IQ IQ IQ О [Q [Q о — О Q о — о Q Q — — о о о о Q Q О о — ~ О О
у-, Уз Хч —' О О О — ООО
Уъ Уч Х^ ° " О — ° " О —' 1Q |О) о о IQ IQ о о
4i 'х аЛ IQ IQ о о ]Q |Q о О О О ° ° - - - -
Л Хц У1 |Q |Q IQ |Q о о о о о о „ „ О О - -
Уз Xi Xi 0 0 0 1 1 0 1 1 0 0 0 1 1 0 1 1
Уч Xi х3 о о — — о о — —
*Х lx ХЛ Q Q Q Q Q Q Q Q о о о о — — — —•
*1 Xi Xi X3i Xi 0 0 10 0 0 11 0 110 0 111 10 10 10 11 1110 1111
№ п. и. — СЧ СО 'Ф ЮСОГ^СО
чикающиеся в узле I, но не заканчивающиеся в узле -у,
будем называть тупиковыми.
Существенный путь {t, у}, состоящий из единственного
D-пути (г, у), является простым, в противном случае —
сложным.
В рассмотренном примере сети (рис. 3-24) на входном наборе
1111 образуется простой существенный путь {х3, z}=i(x3, 7, z),
а на наборе 0010 — сложный существенный путь из трех D-путей:
(х3, 1, 4, г), (х3, 2, 5, г), (х3, 2, 6, z). На остальных наборах из
табл. 3-5 все D-пути тупиковые.
Сложный существенный путь всегда содержит так
называемые простые участки. Узел сети принадлежит
простому участку, если через этот узел проходят все
D-пути, образующие сложный существенный путь.
Например, простыми участками сложного существенного пути
{х3, z) на входном наборе 0010 являются узел х3 и полюс z.
В предыдущем параграфе было сделано утверждение
о неизбыточности сетей, не имеющих разветвлений
(деревьев), или эквивалентное ему утверждение об от-
сутствии в деревьях несущественных константных не-
исправностей. Теперь легко показать справедливость по-
следнего утверждения относительно одиночных констант-
ных неисправностей. Действительно, в деревьях фукции,
реализуемые на входах произвольного элемента тр, не
имеют общих входных переменных сети. Так как все
входные переменные логических элементов существенны,
то (при допустимости всех входных наборов сети) на
входах элемента тр- можно обеспечить любой 2 его
входных наборов и тем самым обеспечить проявление на
его выходе любой логической неисправности s. Далее,
в дереве имеется единственный путь от узла i до выхода
z, причем функции, реализуемые на свободных входах
элементов этого пути, также не имеют общих (между
собой и с функциями входов элемента т)г) входных пе-
ременных сети, т. е. на свободных входах каждого эле-
мента пути (i, z) может быть обеспечена любая комби-
нация их значений. Последнее означает, что всегда мо-
жет быть обеспечено условие транспортировки неисправ-
ности от узла i на выход г. Таким образом, оба условия
обнаружения любой одиночной неисправности s в дереве
могут быть выполнены (т. е. неисправность s всегда су-
щественна) .
В алгоритме АЗ-2 основными являются достаточно
простые операции ОР над элементами сети. Однако ал-
249
горитм в общем случае может требовать перебора всех
2П входных наборов для [каждого D-куба неисправности
s. Поэтому применение алгоритма АЗ-2 нецелесообразно
для сетей с большим числом п входов.
Сохранив структурный способ реализации метода су-
щественных путей, решим задачу построения одного про-
веряющего набора Х(0, s) путем направленного вычис-
ления последнего, а не перебором входных наборов сети.
Для удобства изложения процедуры вычисления про-
веряющего набора введем понятие операции расширения
фиксации (кратко операции РФ). Операция РФ над
сетью (над элементом) состоит в принудительном зада-
нии или фиксации значений 1 или 0 некоторым незафик-
сированным узлам сети (входам и выходу элемента).
Как и при операции ОР, фиксация узла сети, соединен-
ного с узлом разветвления сети, некоторым значением,
полученным в результате выполнения операции РФ, пре-
дусматривает фиксацию этим значением всех узлов сети,
соединенных с рассматриваемым узлом разветвления.
Использование операции РФ позволяет заменять одну
фиксацию (когда, например, она противоречива) другой,
а также расширять непротиворечивую исходную фикса-
цию (что необходимо, в частности, когда стоит задача
получения фиксированных значений для всех узлов се-
ти). Число возможных вариантов операции РФ опреде-
ляется числом фиксируемых узлов сети (элемента), каж-
дому из которых независимо от других может быть
придано значение 1 или 0.
Суть алгоритма вычисления проверяющего набора
(блок-схема этого алгоритма АЗ-З представлена на
рис. 3-28) заключается в следующем. Каждый шаг алго-
ритма состоит из операции РФ, в результате выполнения
которой определяется исходная фиксация на данном ша-
ге, из операции ОР по отношению к этой фиксации и
ряда проверок различных условий. Исходную фиксацию
на первом шаге задает £)-куб неисправности s элемента
Т]г сети.
Если операция ОР показала, что исходная фиксация
на l-м шаге непротиворечива, то производится проверка
наличия в сети нефиксированных определенными значе-
ниями узлов.
При наличии нефиксированных узлов выполняется
один из вариантов операции РФ, благодаря чему опре-
250
деляется исходная фиксация для (/+1)-го шага алго-
ритма.
Когда нефиксированных ^злов нет, производится про-
верка наличия символа D(D) хотя бы на одном выходе
сети V (т. е. наличия существенного пути {i, у}).
Рис. 3-28. Блок-схема алгоритма АЗ-З вычисления проверяющего на-
бора Х(0, s).
251
Если существенный путь {i, у} имеется, то работа ал-
горитма закончена — значения сигналов на входах сети
составляют искомый проверяющий набор Х(0, s).
Если существенного пути нет или операция ОР пока-
зала, что исходная фиксация на l-м шаге противоречива,
то необходимо вернуться к выполнению того ближайшего
шага алгоритма, на котором имеется хотя бы один не
использованный прежде вариант операции РФ. При воз-
врате с 1-го шага к выполнению предыдущего (/—1)-го
шага «стирается» фиксация узлов, полученная при вы-
полнении операции ОР и операции РФ на l-м шаге При
наличии неиспользованного варианта операции РФ на
l-м шаге последняя выполняется, что дает новую исход-
ную фиксацию для (/+1)-го шага.
Если в процессе возврата алгоритм вышел на первый
шаг, то проверяется возможность задания нового D-куба
неисправности s. При наличии такого D-куба неисправ-
ности алгоритм применяется повторно, а его отсутствие
говорит о том, что проверяющего набора Х(0, s) не су-
ществует, т. е. неисправность s несущественна.
Алгоритм АЗ-З предполагает наличие некоторой про-
цедуры упорядоченного перебора как вариантов опера-
ции РФ, так п D-кубов неисправности s. Это обеспечи-
вает возможность рассмотрения всех возможных вариан-
тов операции РФ для каждого из возможных D-кубов
неисправности s. Отсюда следует, что по алгоритму АЗ-З
всегда будет получен проверяющий набор Х(0, s), если
он существует.
Процедуру перебора вариантов операции РФ можно
организовать по-разному, наложив на операцию РФ
некоторые специальные требования. Целью большинства
этих требований является стремление исключить из пе-
ребора варианты операции РФ, заведомо не ведущие к
цели, и ускорить получение искомого решения. Напри-
мер, можно расчленить алгоритм АЗ 3 на два последова-
тельно выполняемых этапа: этан задания D-путей (i, у)
и этап реализации D-путсй. Такое расчленение соответст-
вует установлению некоторого порядка в последователь-
ности выполнения операций РФ. Рассмотрим особенно-
сти, вносимые при этом в алгоритм АЗ-З.
Будем считать, что все элементы сети упорядочены по
рангам (см. § 3-1) и пронумерованы в порядке неубыва-
ния рангов. Условимся также, что каждый раз операция
РФ выполняется над одним элементом сети.
252
Первым в алгоритме следует этап задания /5-путей.
Это достигается тем, что на каждом шаге выбираются
варианты операции РФ только над теми элементами,
у которых хотя бы один вход фиксирован символом D
или D, а выходу 'приписан символ X. Будем называть
такие операции D-операпиями РФ. При выполнении
D-операции РФ используется таблица /5-кубов соответст-
вующего элемента. Из таблицы берется /5-куб, /5-набор
которого не противоречит имеющейся фиксации входов
элемента и содержит символы 0(25) только на входах,
зафиксированных этими значениями. О-наборы О-кубов,
удовлетворяющих указанным требованиям, составляют
варианты операции РФ рассматриваемого шага для
незафиксированных входов элементов. Использование
сжатых О-кубов приводит к необходимости включить
безразличное значение ~ в число принудительно зада-
ваемых операцией РФ значений. В качестве обрабатыва-
емого на l-м шаге можно брать необработанный элемент
с наименьшим номером наименьшего либо, наоборот,
наибольшего ранга1. В нервом случае будут постепенно
удлиняться все имеющиеся в сети участки D-путей, что
соответствует стремлению организовать сложный суще-
ственный путь, а во втором удлиняется все время один
и тот же участок О-пути.
За D-операцией РФ на каждом шаге алгоритма сле-
дует операция ОР. Если операция ОР показала противо-
речивость исходной фиксации, то следует вернуться к
выполнению ближайшего шага, имеющего не использо-
ванные прежде варианты D-операции РФ над еще необ-
работанным элементом, выбрать такой вариант, после
чего продолжить процедуру. При отсутствии такой воз-
можности следует задать другой D-куб неисправности з
и повторить процедуру сначала. Если, наконец, других
О-кубов неисправности s нет, то работа алгоритма пре-
кращается: проверяющий набор Х(0, з) не существует.
Если в сети нет элементов, над которыми эту опера-
цию можно было бы выполнять, О-операция РФ невоз-
можна. При этом следует проверить наличие символа
0(25) хотя бы на одном выходе сети. Если такого выхода
сети нет, то надо поступить так же, как в случае проти-
воречивости исходной фиксации. Если хотя бы на одном
1 Будем предполагать, что элементы сети пронумерованы так,
что из двух элементов элемент большего ранга имеет больший номер.
253
выходе сети имеется символ D(D), то необходимо 'перей-
ти ко второму этапу алгоритма — к реализации D-путей.
Второй этап алгоритма выполняется аналогично пер-
вому. Имеющие место особенности состоят в следующем.
Исходной фиксацией на первом шаге второго этапа явля-
ется фиксация, полученная по завершении первого этапа.
Операция РФ па этом этапе выполняется над элемента-
ми, выход которых зафиксирован значением 0 пли 1, а
по крайней мере значение одного из входов не определе-
но, т. е. имеет значение X. Для упорядочения перебора
вариантов операции РФ и возможного ускорения работы
алгоритма целесообразно в качестве обрабатываемого
на /-м шаге брать пригодный для выполнения операции
РФ, не обработанный на втором этапе элемент с наи-
большим номером, т. е. расположенный возможно ближе
к выходам сети. При выполнении операции РФ на этом
этапе использую гея сжагые таблицы истинности элемен-
тов и таблицы их тупиковых D-кубов. Задание одной
строки этих таблиц, не противоречащей имеющейся
фиксации входов и выхода элемента, обеспечивает вари-
ант операции РФ рассматриваемого шага. На каждом
шаге осуществлением операций ОР производится про-
верка непротиворечивости исходной фиксации. Когда
последняя противоречива, производится возврат к вы-
полнению ближайшего предыдущего шага алгоритма,
имеющего не использованные прежде варианты операции
(или D-операции) РФ. Если такого шага среди шагов
второго этапа не оказалось, то снова выполняется пер-
вый этап, т. е. ищется другой вариант задания D-путей
(i, у). Положительным исходом второго этапа алгорит-
ма является отсутствие элементов, которые могут под-
вергаться требуемой операции РФ. Последнее означает
обеспечение условий проявления и транспортировки
неисправности, т. е. построение проверяющего набора
Х>(0, s) или интервала проверяющих входных наборов,
если неопределенное значение X входных полюсов рас-
сматривать как безразличное значение ~
Очевидно, что наличие безразличных ( ~) значений
узлов на втором этапе алгоритма также ускоряет полу-
чение искомого решения за счет уменьшения числа опе-
раций РФ и уменьшения числа возможных противоречи-
вых фиксаций.
Пример 3-51. Построить проверяющий набор для неисправности
s=(4, 2)° сети (рис. 3-29).
254
Для указанной неисправности s имеется единственный D-куб
неисправности DID (eyiy,,). Результаты расчетов (значения сигналов
в узлах сети) сведены в табл. 3-6, в которой пустые клетки соответ-
ствуют значениям X-
Операция ОР шага 1 непротиворечива и дает Za=0 и t/3=~.
D-операцию РФ шага 2 можно выполнять над элементами 6 и 7;
выбран элемент 6 и D-набор DO его единственного D-куба
D0D (у^Уе)- В результате операции ОР шага 2 фиксируется значе-
нием D узел 6 сети. На шаге 3 D-операция РФ проводится над эле-
ментом 7, выбирается вариант D-набора 0D (Ьу^. Операция ОР
этого шага делает t/7=D, t/e=0. После шага 3 D-операция РФ не-
возможна из-за отсутствия в сети элементов, у которых входы фик-
сированы символами D (D), а выходы — символом X. Возвращаемся
на один шаг назад и выполняем шаг 3'—проводим D-операцшо РФ
над элементом 7, выбрав вариант D-набора 1D (&</.;), а также опе-
рацию ОР, которая дает yi=y&=y^ = D. На шаге 4 D-операция
возможна над элементами .9 и /2; выбираем элемент 9 и единствен-
ный пригодный D-набор Dll (ysay5). Операция ОР при этом про-
тиворечива: она требует значения 0 па выходе у5, который уже фик-
сирован значением 1 (в таблице это представлено в виде записи 0/1
для столбца у$ в строке 8). Возвращаемся на один шаг назад и
выполняем шаг 4'-. для элемента 9 пет вариантов D-операцин РФ;
проводим D-операцню РФ над необработанным элементом 12, взяв
D-набор D1 (</I0a) его единственного D-куба и операцию ОР, кото-
рая фиксирует выход z2 значением D и узлы у3, у5 и г, соответствен-
но значениями 1, 0 и 0. На этом первый этап заканчивается — по-
строены D-пути (4, 6, 8, 10, z2) и (4, 1, 8, 10, z2).
855
Таблица 3-6
Узлы и их значения Q QQ
г? о о о о о О о о о О о о о
Q QC1 QQ QQ
Q О О о
? г г ? О QQ QC) QQ
IQ Q QQ QQ QQ
2Ь Q QQ QQ QQ Q4 QQ
О О О о
IQIQ IQ IQ IQ IQ IQ IQ IQ |Q IQ IQ IQIQ
О о О о О о о о о о о о
—< ’
о о о о о о о о о о о о о о
ла г -
О о
•о о о —
о
Операции РФ (D-куб s) ОР D-РФ (для 7)6) ОР D-РФ (для т)7) ОР D-РФ (для я,) ОР D-РФ (для т9) ОР D-РФ (для т)12) ОР РФ (для Т]2) ОР
№ строк — сч СО ю со 1О СО О0 Ь- ОО
№ шагов СЧ СО со ’ф ю
Этапы алго- ритма
256
На шаге 5 второго этапа алгоритма операция РФ может быть
выполнена над элементами / и 2 (их выходы фиксированы значе-
ниями соответственно 1 и 0, а значения входов не определены).
Выбираем элемент 2 и по сжатой таблице истинности из двух воз-
можных для операции РФ выбираем куб ~00 (dcy2). В результате
операции ОР шага 5 узел d фиксируется значением 1. Все узлы
сети фиксированы Поэтому работа алгоритма заканчивается—по-
строен проверяющий входной набор Х(0, s) =11010 (abcde), а по-
лученная на первом этапе алгоритма совокупность £)-путей образует
сложный существенный путь {4, z2).
При выполнении второго этапа алгоритма можно проиллюстри-
ровать преимущества использования в операциях РФ сжатых кубов.
Так, например, если на шаге 5 применять полную таблицу истинно-
сти элемента 2 (а не сжатую) и из трех возможных для операции
РФ кубов выбрать куб ООО (dcy^, то операция ОР этого шага ока-
жется противоречивой. Последнее потребует возврата к элементу 2
и выбора, например, куба 100 {dcy2}, который щаст искомое решение.
Сделаем некоторые замечания относительно возмож-
ных модификации алгоритма АЗ-З. гГри желании полу-
чить полную совокупность {X(0, s)} проверяющих вход-
ных наборов необходимо после получения каждого оче-
редного набора Х(0, s) продолжить работу алгоритма
путем возврата к выполнению ближайшего предыдуще-
го шага, на котором имеются неиспользованные вариан-
ты операции (D-операции) РФ или же варианты зада-
ния D-кубов неисправности s. После исчерпания всех
таких вариантов работа алгоритма заканчивается, а со-
вокупность {Х(0, s)) образуют все полученные наборы
Х(О, s). Из изложенного видно, что алгоритм АЗ-З мо-
жет оказаться достаточно громоздким из-за большого
числа отрицательных исходов его операций и необходи-
мости возвратов к выполнению предыдущих шагов. При-
чем число перебираемых вариантов операции РФ для
«узких» сетей (т. е. сетей с относительно небольшим
числом входов, но большим числом элементов, рангов
и разветвлений) может даже превысить число 2" всех
возможных входных наборов сети. Поэтому для таких
сетей более эффективна, по-видимому, стратегия пере-
бора входных наборов по алгоритму АЗ-2, в то время
как алгоритм АЗ-З целесообразен для обработки «широ-
ких» сетей (с большим числом входов п, но малым чис-
лом рангов и разветвлений).
Обратим внимание на то, что именно наличие в сети
разветвлений является причиной появления отрицатель-
ных исходов операций алгоритма АЗ-З. В деревьях алго-
ритм АЗ-З не будет иметь возвратов вообще. Как уже
отмечалось, это связано с тем, что, во-первых, в дереве
17—358 257
имеется единственный путь от выхода элемента до вы-
хода сети и, во-вторых, функции узлов, не лежащих на
одном пути, не имеют общих переменных (поэтому
операция ОР всегда непротиворечива, а .D-операция РФ
на первом этапе всегда возможна).
В методе существенных путей для случая одиночных
логических неисправностей условие проявления неис-
правности выражается через требования к входным на-
борам неисправного элемента, а условие транспортиров-
ки— через требования к входным наборам некоторых
исправных элементов сети. Обеспечение необходимых
наборов осуществляется последовательным доопределе-
нием значений узлов сети путем выполнения операции
РФ только над исправными элементами.
При построении проверяющего набора Х(0, s) мето-
дом существенных путей для случая кратной неисправ-
ности s = {oi, о2, ..о/} возникают следующие принципи-
альные особенности. Во-первых, проявление неисправно-
сти s состоит в проявлении каждой одиночной неисправ-
ности из некоторого подмножества s" множества s' всех
неисправных элементов (s'^s) таких, что никакие два
из них не лежат на одном пути. Задание условия про-
явления одиночной составляющей неисправности s по-
прежнему состоит в задании проверяющего набора не-
исправного элемента. При этом число вариантов
задания условий проявления кратной неисправно-
сти s определяется числом различных подмножеств s".
Во-вторых, задание условий транспортировки проявлен-
ной неисправности s" помимо задания условий транс-
портировки через исправные элементы (D-кубы исправ-
ных элементов) требует рассмотрения условий транс-
портировки через неисправный элемент (т. е. необходи-
мо вводить понятие D-куба неисправного элемента).
В-третьих, на этапе реализации D-путей требуемые
определенные значения 0 и 1 узлов необходимо обеспе-
чить как в исправной сети, так и в сети, содержащей
неисправность s. Последнее требует введения новой
характеристики — простых кубов неисправных элемен-
тов. Указанные обстоятельства существенно усложняют
алгоритм вычисления проверяющего набора сети и явля-
ются, по-видимому, основной причиной, по которой ме-
тод существенных путей в настоящее время нашел
применение только для случая одиночных неисправно-
стей комбинационных устройств-
258
ПОСТРОЕНИЕ РАЗЛИЧАЮЩЕЙ СОВОКУПНОСТИ
Обратимся к задаче построения различающей сово-
купности входных наборов {A(s, /)} для двух неисправ-
ностей з и I, s=^=t, сети. Для одновыходных комбинаци-
онных устройств полная различающая совокупность
{А(з, /)} может быть построена на основе полных про-
веряющих совокупностей {А(0, s)} и {А(О, t)}. Действи-
тельно, в различающую совокупность {A(s, t)} входят те
наборы из {А(0, s)}, которые не являются наборами
совокупности {А (О, /)}, и наоборот. Формально это мож-
но записать в виде разности объединения и пересечения
множеств:
{X (s, /)} = ({X (0, з)} U (0. /)}) \ № (0, s)} А {X (0, /)}).
(3-29)
Выше было приведено выражение (3-27), представ-
ляющее условия проявления и условия транспорти-
ровки неисправности s элемента тр, обнаруживае-
мой на выходе у. Используя те же обозначения, необ-
ходимое и достаточное условие различения неисправно
сти з элемента тц- и неисправности t элемента
приобретает вид:
k _ _ _ _
(«/< V ₽/т) V («<* V ₽ ,т)1=1 • (3'3°)
Здесь запись als (Д ) означает неудовлетворение условия
проявления (транспортировки) неисправности s. Все
входные наборы сети, при которых выполняется условие
(3-30), составляют полную различающую совокупность
{А(з, /)}. Условие (3-30), эквивалентное (3-29), выде-
ляет в сети по крайней мере один выходной полюс у
и находит такой входной набор, на котором на полюсе
у выполняются оба условия обнаружения неисправности
з, но не выполняется хотя бы одно из условий обнару-
жения неисправности t, или наоборот.
k k
Поскольку условия V a,sp. = 1 ( V адВ. = 1) опреде-
i=i т=1
ляют совокупности (А(0, s)} ({А(0, /)}), то получение
различающей совокупности {A(s, t)}, по-видимому, удоб-
нее осуществлять на основании (3-29) вместо исполь-
зования (3-30).
17* 259
Пример 3-52. Пусть в сети рис. 3 1 рассматриваются две неис-
правности. Неисправность s состоит в изменении функции элемента 7
с ИЛИ на И. Ранее было получено выражение для функции а48 =
=acd V а (с V d). Неисправность t—{6, 2)°, для нее a3t = byi =
— b (а V cd). Выражения для функций 04г и найдем путем полу-
чения выражений z4(a, b, с, d, у<) и z6(a, b, с, d, у3), а затем — бу-
левых разностей dz^dy^ и dz3ldy3:
zt — by., V у. (by d);
г6 = увУ (а V cd)(b yd) = у6у а (с V d)(b у d);
₽4z = dzijdyt — b^(byd)=dy b;
fez = dz6/dyQ = [а (с V d)(b V d)l — a V cd У bd = a V d(by c).
Определим {X (0, s)} и (0, /)}.
“isf iz = 1« cd \, а (с V d)) (d 'v b) = abed \/ abc d Vj
V a bed V ab cd У a b cd.y ab cd ;
(A'(0, s)} = <0111, 1101, 0011, 1001, 1000, 1010};
«e/fez = b (a V cd) [ay d (by c)J == ab у/ bed,
(A (0. /)} = {1100, 1101, 1110, 1111, 0111}.
На основании (3-28) имеем;
{A(S, 7)} = {0011, 1001; 1000, 1010, 1100, 1110, 1111}.
Рассмотренный подход построения различающей со-
вокупности (A(s, /)} можно распространить и на много-
выходные устройства, если номера наборов проверяю-
щих совокупностей {А,(0, s)} и {А(0, 7)} снабжать
индексами номеров выходные полюсов, на которых
обнаруживаются неисправности s и t, что соответствует
замене в (3-29) совокупностей {A(s, t)}, {А(0, s)} и
{А (О, /)} совокупностями (f (s, /)}, (Г(0, $)} и {Г(0, /)}
элементарных проверок. Напомним, что элементарная
проверка определяется (см. гл. 1) значением воздейст-
вия (номером входного набора) и составом контроль-
ных точек (номером выходного полюса). Различающая
совокупность {Г (s, /)} должна содержать те элементар-
ные проверки из {Г (0, л)}, которых нет в {Т (0, t)}, и
наоборот.
Пример 3-53. Если для некоторой сети с тремя выходами Zi, z2
и z3 имеем: {7(0, s)} = {/1, 32, З3, 7Ь 42, 73}, {ЦО, t)} = {22, 23, 32,
43, 73), то на основании (3-29) получаем; (Г (s, <)} = {/ 1, 22, 23,
4i, 42, 43}.
260
3-5. РЕШЕНИЕ ПРЯМЫХ ЗАДАЧ ДИАГНОЗА
ДЛЯ КОМБИНАЦИОННЫХ УСТРОЙСТВ
В настоящем параграфе будет рассмотрено решение
двух задач. Первая задача состоит в выделении из мно-
жества 5 всех заданных неисправностей его подмноже-
ства Sj(SjSS) неисправностей s, обнаруживаемых на
заданном наборе Xj; напомним, что неисправность s
обнаруживается на наборе Xj(s^Sj), если zs(Xj) =^=z,(Xj).
Вторая задача состоит в выделении из множества Рвсех
заданных пар неисправностей его подмножества Pj (Pj^P)
нар неисправностей, различимых между собой на набо-
ре Xj; неисправности пары (s, 1)еР различимы между
собой на наборе Aj((s, t)^Pj), если z“(Zj) #=z((Aj). Обе
задачи относятся к прямым задачам диагноза.
Рассмотренные в § 1-7 алгоритмы решения прямых
задач диагноза по таблице функций неисправностей при-
годны для комбинационных устройств без каких-либо
изменений. Подмножества Sj или Pj формируются пу-
। ем сравнения содержащихся в строке таблицы функций
неисправное гей результатов ksj, Rlj элементарной
проверки nJ (в нашем случае — выходных слов Zj, Zsj,
Z'j, выдаваемых устройством на входном наборе Xj).
Для получения подмножеств Sj или Pj могут быть
использованы различающие функции Z)[z, zs] или соот-
ветственно D[zs, z*j. В подмножество Sj[Pj) включаются
те неисправности s (пары неисправностей s и 1), для
которых различающая функция D[z, zs](Z)[zs, z*]) при-
нимает значение 1 па наборе Xj (см. § 3-4).
Использование таблиц неисправностей и различаю-
щих функций требует полного перебора всех неиоправ-
iioi ।< и или иссд пар iieiiciipaBiiocieii. Рассмотрим иеко-
|<>рыс методы вычисления подмножеств S, и Pj, не тре-
бующие указанного перебора.
МЕТОД ОБОБЩЕННОЙ ФУНКЦИИ ВЫХОДА
Понятие обобщенных функций yi, z^ введено в §3-3.
I lycib для некоторого одновыходного устройства заданы
аналитически (т. е. в виде выражений алгебры а-состоя-
11 пй узлов сети) его обобщенная выходная функция z и
ее инверсия z. Подставим в выражения этих функций
значения входных переменных Xi, .... хп, предписанные
нм входным набором Xj. Получаемые при этом выраже-
261
ния z(Ajj и z(Xj) содержат только символы i“ (а=Н,
1, 0) состояний узлов устройства и представляют собой
задание всех тех одиночных и кратных константных не-
исправностей *, наличие которых в устройстве не изме-
няет исправное значение выхода z и его инверсии z на
наборе Xj. Тем самым, когда Xj является рабочим (не-
рабочим) набором устройства, выражение z(Xj) задает
подмножество Sj необнаруживаемых (Sj обнаруживае-
мых), а выражение z(Xj) —подмножество Sj обнару-
живаемых (Sj необнаруживаемых) неисправностей.
Используем в дальнейшем символы Sj, Sj для обо-
значения логических выражений, задающих соответст-
венно подмножества неисправностей Sj, S}, т. е. когда
Xj — рабочий набор, будем писать Sj=z(Xj) и Sj = z(Xj).
Наоборот, Sj=z(Xj) и Sj=z(Xj), когда Xj — нерабочий
набор.
Пример 3-54. Найдем Sj для сети рис. 3-18 на нерабочем вход-
ном наборе Xj=0010 (akdh). Обобщенная функция z для этой сети
представлена выражениями (3-13). После подстановки в (3-13) зна-
чений входных переменных из заданного набора получаем:
3/ = г (0010) = (а1 1н Зн \Д‘3Н 1н Зн \/
v b‘lH З11 Х/1‘зН Х/3‘) V (Ан сн 2й Зн V
v k°c" 2Н зн V<('2H зн V2’3H va1)^" зн V
V 2‘зн V31) V (Л*3Н V31).
Раскрывая скобки и производя упрощения, получаем:
Sj = З1 V 1‘3Н V2*3H Vft'3H Va‘b' 1H 3H Va‘A‘bH 1Ы Зн V
v 2Н Зн Ан V^°cH 2й Зн Vc°^2H Зн. (3-31)
Выражение S, для необнаруживаемых неисправностей сети
рис. 3-18 может быть получено аналогичной обработкой обобщенной
функции z, заданной выражением (3-15).
Распространение рассмотренного метода на ^многовы-
ходные устройства состоит в получении для каждого
выхода у выражений S^. и STj. и в дополнительных (см. ниже)
1 Более строго здесь следовало бы говорить о технических со-
стояниях устройства, так как выражение z(Xj) содержит конъюнкцию
вида Д'", представляющую исправное состояние. Или, иначе, сле-
дует считать, что множество 3 неисправностей содержит также «ну-
левую неисправность» s0 (см. § 1-7).
262
операциях над этими выражениями. Выражение Sj, за-
дающее неисправности, обнаруживаемые хотя бы па од-
ном выходе устройства, определяется через дизъюнкцию
выражений §
~ k ~
а выражение S, для необнаруживаемых (ни на одном
выходе) неисправностей — через конъюнкцию выраже-
ний S^.:
„ k ~
S,= AS„.
Последние два равенства существенно используют тот
факт, что объединение выражений, задающих подмно-
жества обнаруживаемых (S р и необнаруживаемых (S7/.)
неисправностей для любого у, образует выражение,
задающее множество S всех неисправностей, т. е.
*$т/ V = 1. _
Знание подмножеств Sy/ и S . позволяет вычислить
подмножества пар Р/ различаемых и Р/ неразличаемых
неисправностей. Очевидно, пара неисправностей s и t раз-
личима, т. е. (s, если найдется хотя бы один вы-
ход у такой, что s (ЕЕ S f (или Sif) и / G ST/ (или S
И наоборот, (s, t) (ЕЕ ?i> если s, / (ЕЕ S^. [или (s, t) S(/] для
всех у= 1, 2, ..., k.
Рассмотренный метод вычисления выражений S/ и S/
требует наличия или предварительного вычисления обоб-
щенных прямых и инверсных функций выходов уст-
ройства. Метод вычисления выражений Sj, Sj непосред-
ственно по структуре устройства, когда на входы по-
следнего подан входной набор X,-, изложен ниже.
СТРУКТУРНО-АНАЛИТИЧЕСКИЙ МЕТОД
Основная идея метода состоит в
каждого элемента т)< исправной сети
зуемая им функция, поступающий на
следующем. Для
известны реали-
него входной на-
263
бор Yi, структурно соответствующий набору Xj сети, и
значение выхода t/i на этом наборе. Выведем формулы,
позволяющие вычислять логические выражения Si и S,-,
задающие подмножества Si обнаруживаемых и S, не-
обнаруживаемых на выходе элемента тг)$ неисправностей
по известным выражениям S,m и Sim, задающим под-
множества Sim обнаруживаемых и соответственно
не обнаруживаемых на входам элемента неисправно-
стей на наборе Xj *. Наличие таких формул для эле-
ментов сети и для ее соединений даст нам возможность
воспользоваться методом прямой или обратной подста-
новки и последовательно ранг за рангом вычислить вы-
ражения и для подмножеств неисправностей, об-
наруживаемых и не обнаруживаемых на выходе у на
входном наборе X,- сети.
Рассмотрим некоторый элемент тр сети, для приме-
ра— двухвходовой элемент И реализующий функцию
У1~УаУг2- Обобщенная функция, реализуемая на выходе
элемента, имеет вид:
yi — УнУи1Н V i' • (3-32)
Возьмем некоторый входной набор X, сети и подста-
вим этот набор в обобщенные функции левой и правой
части (3-32). В результате подстановки имеем:
9i (Xj) = yh (Х,) у!г (Х,) /н V i'. (3-33)
Как уже известно, выражение Hi(Xj) для произволь-
ного узла сети I задает множество S; обнаруживаемых
в узле i неисправностей, если набор Xj — нерабочий на-
бор функции yi, и наоборот, когда Xj—-рабочий набор
фунции у i, то выражение yi(Xj) задает множест-
во S; необнаруживаемых неисправностей. Аналогичные
утверждения были сделаны относительно выражения
y(Xj). Если набору X,- на входах (i, 1) и (I, 2) элемента
щ структурно соответствует, например, набор У,=01, то
набор Xj для функций уц и yi является нерабочим, а для
* Здесь и в дальнейшем, где это будет удобно, в обозначениях
вида S,-,-(Si3) будем опускать индекс /, понимая, что соответствую-
щие выражения строятся для зада>нного входного набора Xj.
264
функции уц — рабочим набором. Учитывая сказанное,
выражение (3-33) можно записать в виде
Sz = SI1Sz,tH Vi1- (3-34)
Заметим, что выражение (3-34) справедливо для лю-
бых входных наборов Xj, которым структурно соответ-
ствует набор У, = 01. Аналогично для остальных трех
наборов У, = 00, 10 и 11 соответственно получим:
il; (3-35)
v <1; (з-зб)
•Sz = \/ i (3-37)
Для определения выражений Sj для не обнаружи-
ваемых на наборах 00, 01 и 10 и выражения 5, для об-
наруживаемых на наборе 11 неисправностей можно по-
ступить двояко. Первый путь состоит в обработке
описанным способом инверсии yi обобщенной функции,
реализуемой на выходе элемента т)<, а второй (более
простой)—в инвертировании выражений (3-34) — (3-37).
Во втором случае, например, из (3-34) получаем:
В табл. 3-7 приведены формулы для вычисления вы-
ражений Si и Si для дву^входовых элементов И, ИЛИ
и «сумма по модулю 2», а также для повторителя. По-
следний представляет интерес в связи с необходимостью
рассмотрения входных полюсов сети, а также узлов,
являющихся соединением узлов разветвления с входами
элементов или выходными полюсами сети (т. е. ветвей
разветвлений).
Прежде чем переходить к процедуре построения’выра-
жений и по структуре сети, отметим особенности
вычисления выражений Si и S, для узлов сети, связанных
непосредственно с входными полюсами, а также для вет-
вей разветвлений. Поскольку указанные узлы сети не
являются непосредственными выходами элементов сети,
го вставим в каждый такой узел условно элемент-повто-
265
Т а 6 л и ц а 3-?
Тип эле- мента >7 У1 Sj
«и |.Vj2
0 0 0 'SixSi^ V i1 (sh V S/2)iH V (°
и 0 1 0 Sj,Sj2ZH V Z> (Sj, V Sj2)(H V 4°
1 0 0 Sj,S/2zH v «' (Sj, V Sj2)iH V
1 ) ) (Sj, VSj2)iH v »° Sj,Sj2(H V z*
0 0 0 (Sj, V v SjjSjjZ11 V ‘°
или 0 1 1 Sj,Sj2tH V i° (Sj, V Sj2)zH V z*
1 0 1 ShSlei11 V z° (Sj, V Sj2)zH V 4*
1 1 1 Sj,Sj2!H V i° (Sj, V Sj2)zH V «*
0 0 0 (5/15/2 V 5/i5/a)i^ V (Sj,S/2 V Si,Sj2)zH V 4°
ф 0 1 1 (5/15/2 V 5/15/г)/^ V i° (Sj,Sj2 V Sj,Sj2)zH V z*
1 0 1 (Sj,Sj2 V Sj,s/2)ZH V 4° (Sj,S/2 V Si,Si2)zH V 4*
1 1 0 (Sj,S/2 V Sj,Sj2)/H V i‘ (5/15/2 \/ 5/15/г)^ V
п 0 1 1 1 0 1 Sj,iH V z1 Sj,iH V 4° Sj,(Hv»0 Sj,z’H V 41
ритель. Для входного полюса xt сети (переменные вы-
хода и входа повторителя щ обозначаются соответст-
венно tji и уп) обычно принимают 5^=0 и 5н=1, т. е.
полагают, что нет неисправностей, искажающих входной
сигнал. Тогда приведенные в табл. 3-7 выражения для
повторителя принимают вид:
для Xi = 0 S, = i1, S, = /н V t°;
для Xi = 1 S,- = i°, S(- = iH \Z il.
Узел сети, являющийся входом повторителя, постав-
ленного в ветвь разветвления, отождествляется с соеди-
266
нением сети между входным полюсом или выходом эле-
мента и рассматриваемым узлом разветвления. Как уже
было принято в § 3-3, узлы сети, являющиеся ветвями
разветвлений, получают буквенные обозначения. Пусть,
например, выход элемента тр разветвляется и в его вет-
ви разветвления d условно поставлен повторитель Пц
с выходом d и входом (d, 1). Во всех вычислениях бу-
дем отождествлять узел (d, 1) с выходом элемента тд>
т. е. узлом i((d, 1)=0- Тогда из приведенных в табл.3-7
выражений для повторителя получаем:
для yi r=yd — 0 Sd = Sid4 \/ dl, Sd — Sid4 X/ ;
для yi = yd=\ Sd’= Sid4 V d\ Sd^'Std4 V d'.
При вычислении ST удобнее применять метод обратной
подстановки, поскольку при этом выражения S{ и Si
вычисляются не для каждого узла i сети, а по мере не-
обходимости.
Пример 3-55. Построим выражение S, для сети рис. 3-18 и вход-
ного набора Х;=0010 (akdh'\ методом обратной подстановки. Будем
считать, что буквы a, к, d, h, b и с обозначают выходы повторите-
лей, поставленных в соответствующие соединения.
Для выходного элемента 3 (ИЛИ) на наборе У3=000 (yiy?h)
имеем:
S2 = S3= (S, \/S2 V Sft) Зн V31.
На элемент 1 (И) поступает входной набор Fi = 00 (Х|Х2), по-
этому
S, = S«SjlH V 1' -
Для элемента 2 (ИЛИ — НЕ) У2=01 (x2xs):
S2 = SfSd2H V 2*.
Вычислим необходимые выражения для ветвей разветвления Ь
и с и входных полюсов h, а и d:
Sb = &Ь» v b’; Sc = Sach V c°; Sh = h'; Sa = a'; Sd = /P.
Для входного полюса k
Sk = A1; Sk = k4 V b°.
Осуществив необходимые подстановки, окончательно получим:
Sz = S, = (SaS»lH V 1' V W V 2' V *') 3H V 31 =
267
= {д’ (Skb" v Ь1) 1й VI' V (Skc" V c") V
v 2' V Л1} Зн V з1 = {д’ (k'bH V ь') ’н \/ I1 V
V I(feH V k°) сн V с°] ^2Н V 21 V л1} Зн V З1 =
= a'k'bHlН3Н V д'&’ 1Н3Н v 1 ’Зн V Лнсн2нЗн V
V *VcH2H3H V f W3H V 2' 3H V л'з” v З1 •
Полученное решение, естественно, совпадает с решением (3-31).
Из выражения S, можно получить полный список
обнаруживаемых на наборе Х-, одиночных и кратных
неисправностей. Для этого указанное выражение необ-
ходимо представить в совершенной нормальной форме
путем умножения его термов на дизъюнкции вида (tHV
V i1 V t°) Для отсутствующих в данном терме символов
узлов и последующего раскрытия скобок. Каждый терм
совершенной нормальной формы представляет набор
a-состояний всех узлов сети, т. е задает одну одиночную
или кратную неисправность устройства. Для сокраще-
ния записи можно из этих термов удалить символы
узлов, находящихся в Н-состоянии.
Выражения, задающие одиночные неисправное'*™,
обнаруживаемые (О3) или не обнаруживаемые (<5,) на
наборе X,-, легко получить из соответствующих выраже-
ний S; или Sj для кратных неисправностей, если вос-
пользоваться зависимостью =0 при (а, р)е{0, 1} и
а=^Ь, отражающей условие существования в сети толь-
ко одного неисправного узла.
Из (3-31), например, получим:
O = ^\/V\J ^\Jhx\fd\
Более компактная по сравнению с выражением вида
(3-31) форма задания обнаруживаемых на наборе X;
неисправностей может быть получена через ЭФ и ОЭФ
функции устройства. Рассмотрим такой метод.
МЕТОД ЭКВИВАЛЕНТНОЙ ФОРМЫ
Как уже отмечалось ранее, функционирование
устройства, содержащего произвольную константную
неисправность seS, может быть задано посредством не-
которой фиксации константами букв ЭФ или ОЭФ. За-
268
метим, что обратное в общем случае неверно, т. е. если
ЭФ' (ОЭФ') получена посредством некоторой фиксации
букв ЭФ (ОЭФ), то это не означает, что существует
константная неисправность seS такая, что zs(zs) опи-
сывается ЭФ' (ОЭФ').
Примем для результата некоторой i-й фиксации букв
ЭФ (ОЭФ) обозначение ЭФ* (ОЭФ*). Тогда из сказан-
ного выше следует, что если найти все такие фиксации
букв ОЭФ (ЭФ), при которых на рабочем (нерабочем)
наборе Xj выражения ОЭФ* (ЭФ*) становятся равны-
ми 1, то тем самым будет задано подмножество 5,- не-
исправностей, обнаруживаемых на наборе Xj. Рассмо-
трим правило, по которому можно получить все инте-
ресующие нас фиксации букв например ЭФ. Значение
z=l может быть получено, очевидно, тогда, когда хотя
бы одна конъюнкция ЭФ фактически окажется равной!,
т. е. окажется равной 1 каждая буква этой конъюнкции.
Значение 1 может быть либо предписано букве подан-
ным на устройство входным набором X,, либо присвоено
ей в результате фиксации. При фиксации буквы х зна-
чением 1,0 будем, как и прежде, пользоваться соответ-
ственно обозначениями х1, х°, а при отсутствии фикса-
ции— символом хн. Очевидны следующие равенства:
хн=хн, х’=х°, х°=х1. Обозначим значение буквы х,
предписываемое ей входным набором, символом бж.
Если бЛ = 1, то возможными состояниями буквы х, при
которых ее значение равно 1, могут быть как Н-состоя-
ние (хн), так и 1-состояние (х1). Если 6ж=0, то единст-
венным состоянием буквы х, при котором ее значение
равно 1, является 1 состояние (х1). Предположим вна-
чале, что исследуемая сеть является деревом.
Пример 3-56. На рис. 3-30 изображена древовидная логическая
сеть, эквивалентная форма функции которой имеет вид:
z — d\J а Ь с.
Пусть, например, на входном наборе 1000 (abcd) (z(1000)=0)
рассматривается конъюнкция с5с ЭФ. Выпишем значения ее букв,
предписываемые поданным входным набором:
а*Ь с
0 1 1.
Тогда условие равенства 1 этой конъюнкции в терминах состоя-
ний ее букв принимает вид-
= а (Е>н Vb° )(сН \/с° ) = fl° b° cn V
У/[а0Ь°ск V a°c°bK V e°bHcH = 1. (3-38)
269
Общее условие равенства I выходной функции z на поданном
входном наборе представляет собой дизъюнкцию выражений вида
(3-38), полученных для каждой конъюнкции букв ЭФ. Это условие
и определяет все искомые способы фиксации букв ЭФ. Для рассма-
триваемого примера все способы фиксации букв ЭФ, при которых
на наборе 1000 z=l, определяются выражением
/ (г = 1,1000) = d1 V a°b°c° V д06°сн V «W V я°6Нсн, (3-39)
где символом f (z=l, 1000) обозначена функция a-состояний, за-
дающая условия равенства z=l на входном наборе 1000. Выраже-
ние Sz, задающее множество обнаруживаемых набором Xj = 1000 не-
Рис. 3-30. Пример логической сети без раз-
ветвлений для построения множества не-
исправностей, обнаруживаемых набором Xj.
исправностей, полученное, например, рассмотренным выше методом
обобщенной функции (выкладки здесь опущены), имеет:
Sz = З1 V d‘3H V 2131Г V «VcnlH2H3H v a°b°cHlH2H3H V
V ЛЛЬП1Н2Н3Н V Лнсн1н2нЗн. (3-40)
Покажем теперь, как из компактного выражения (3-39)
может быть получено искомое выражение (3-40). Назовем
совокупность Ха всех букв вида х°г(о, = 0,1) некоторой
конъюнкции выражения (3-39) или (3-40) фиксированной
частью конъюнкции, а совокупность Xй всех букв вида
ее „нормальной11 частью. Будем рассматривать сово-
купность значений сигналов входных полюсов сети, пред-
писываемых им состояниями букв фиксированной части Х~
некоторой конъюнкции выражения (3-39), как исходную
фиксацию узлов дерева.
Осуществим операцию однозначного распространения
(ОР) но отношению к этой фиксации и следующим образом
построим граф G(№) однозначного распространения. Ребрам
графа G(X°) взаимно-однозначно сопоставим узлы
(соединения) исходного дерева, переменные которых
270
D результате операции ОР зафиксированы значениями
О и 1 (эти значения припишем в качестве верхних индек-
сов обозначений соответствующих ребер), а вершинам —
элементы, выходной и входные полюсы сети. Каждый
граф G(A’°) в общем случае 'представляет совокупность
несвязанных .поддеревьев с определенными для них на-
чальными вершинами (соответствуют входным полюсам
исходной сети) и конечными вершинами (соответствуют
либо выходному полюсу, либо элементам, у которых за-
Рис. 3-31. Графы однозначного распространения в сети рис. 3-30 для
примера 3-56.
фиксировано некоторое подмножество входов и не зафи-
ксирован выход).
На рис. 3-31 для фиксированных частей пяти конъюнкций выра-
жения (3-39) изображены соответственно графы G(d'), G(aub°c°),
G(a°b°), G(aoc°) и G(a°).
Определим сечение графа G(X:’) как совокупность его
ребер, удаление которых разрывает все пути от началь-
ных вершин графа в его конечные вершины, причем
каждый путь разрывается не более чем в одном месте.
По каждой конъюнкции (терму) выражения (3-39)
функции a-состояний будем следующим образом строить
совокупность конъюнкций искомого выражения (3-40)
для Sz. Рассмотрим совокупность обозначений всех ре-
бер некоторого сечения графа G(A”), построенного для
рассматриваемого терма из (3-39), как конъюнкцию
соответствующих высказываний; последняя является
фиксированной частью некоторой конъюнкции искомого
выражения (3-40) для Sz. Для получения ее «нормаль-
271
ной» части образуем конъюнкцию обозначений, во-пер-
вых, всех ребер исходного дерева, которые лежа г на
путях от входных полюсов, соответствующих буквам
«нормальной» части рассматриваемого терма из (J-39),
до выходного полюса г, присвоив этим ребрам верхний’
индекс «Н», и, во-вторых, всех ребер графа G(A°), рас-
положенных между рассматриваемым сечением и конеч-
ными вершинами графа, заменив в них верхний индекс
с о=0,1 на «Н». Полученная таким образом конъюнк-
ция состояний узлов дерева является некоторой конъ-
юнкцией искомого выражения <SZ. Все сечения для каж-
дого графа G(X°) определяют все конъюнкции выра-
жения Sz.
Продолжая пример 3-56, находим все сечения графа G(d‘)
(рис. 3-31,а), соответствующего терму d1, который не имеет «нор-
мальной» части. Два сечения этого графа {З1} и (d‘) дают соответ-
ственно две конъюнкции в (3-40): 3‘ и d‘3u. Четыре сечения {З1},
{21}, {1°, а0} и (аиЬ°си} графа (/(bWc0) (рис. 3-31,6) для терма
aWc'’ дают три новые конъюнкции 2*3Я, й°7°2яЗя и й°Ьиси1я2яЗя.
В графе G(auo°) (рис. 3-31,в) для фиксированной части терма а°Ьдсп
единственное сечение (й°, 6и) задает фиксированную часть аиЬ°
искомой конъюнкции. «Нормальная» часть ся рассматриваемого
терма задает «нормальную» часть ся1я2яЗя искомой конъюнкции,
соответствующую ребрам пути в дереве (рис. 3-30) от входного
полюса с до выхода г. Аналогично анализ терма а°сиЬи дает конъ-
юнкцию а°с°6я1я2яЗя. Единственное сечение графа G(a°) для тер-
ма а°6яся (рис. 3-31,6) дает фиксированную часть й° последней
конъюнкции выражения (3-40). Ее нормальная часть 6яся1я2нЗн
соответствует ребрам путей в дереве от входных полюсов Ь и с до
выхода z.
Теперь обратимся к логическим сетям произвольной
конфигурации.
Построим эквивалентное дерево для рассматривае-
мой сети. Как и прежде, выходной узел элементов обо-
значается номером этого элемента, а ветви разветвлений
и узлы, связанные с входными полюсами, получают бук-
венные обозначения. Вершинами эквивалентного дерева
теперь кроме входных полюсов, элементов и выходного
полюса будут и узлы разветвления исходной сети. По-
следние на рисунках будем обозначать зачерненными
кружками без специальных названий. Имея выражение
ЭФ (ОЭФ) дерева, построенного для исследуемой струк-
туры, найдем так же, как это делалось выше, все спосо-
бы фиксаций букв ЭФ (ОЭФ), при которых на нерабо-
чем (рабочем) наборе Xj z= 1 (z= 1).
272
Пример 3-57. Для сети (рис. 3-32) эквивалентное дерево изобра-
жено на рис. 3-33 и ЭФ дерева имеет вид:
z = abictd V ab~b2ct V abiCjC2 . (3-41)
Условие равенства z=l на нерабочем наборе сети Xj=0000
(abed)
f(z= 1,0000) = a'b}c]d' V a’b'cj (b2 V b£) V a'b[c{ (eg V 4‘) =
= «'bjejd1 V a'bjcjbg V о'ь[с[ьН V a'bjcjcg V fl’bjcjeg1 = 1. (3-42)
Для получения конъюнкций искомого выражения Sz
воспользуемся описанной выше методикой построения Sz
для структур типа дерева с единственным отличием, со-
Рис. 3-32. Пример логической сети для построения множе-
ства Sj неисправностей, обнаруживаемых набором Xj.
18—358
273
ётбяЩйМ й том, что все необходимее операции соверШй-
ются не в исходной сети, а в эквивалентном дереве,
в терминал состояний узлов которого записываются по-
строенные конъюнкции. Опустим нижние индексы
в обозначениях «расщепившихся» узлов эквивалентного
дерева. Будем называть полученную таким образом
конъюнкцию и соответствующее ей сечение некоторого
графа G(A"1) запрещенными в следующих двух слу-
чаях. Во-первых, если в конъюнкции содержится пара
букв вида где е — обозначение узла исходной
сети, «расщепившегося» в эквивалентном дереве а, р =
=0,1, Н, а=^=р. Такая конъюнкция соответствует заданию
разных состояний одному и тому же узлу сети, т. е. фи-
зически невозможной устойчивой неисправности. Во-вто-
рых, запрещенной будет считаться конъюнкция, содер-
жащая пару букв вида etf (о, 6 = 0, 1), где е — узел
сети такой, что все пути от узла е до выхода сети z про-
ходят через узел q. Такая конъюнкция соответствует
либо заданию множества неисправностей устройства, за-
даваемого всегда некоторой другой, незапрещенной,
конъюнкцией, либо также соответствует физически не-
возможной неисправности в исследуемом устройстве.
Таким образом, удаление запрещенных построенные
конъюнкций или, что все равно, построение конъюнкций
для незапрещенных сечений всех графов G(A'°) обеспе-
чивает получение искомого выражения Sz.
Проиллюстрируем сказанное на примере 3-57. На рис. 3-34 изо-
бражены графы G(-Y’) соответственно для фиксированных частей
термов о^ЬЦс1^1, сРЬ^с^&г, a'frjcjfrg1 (a'bjcjcg1) и
Девять сечений графа G(a1611c1id1) рис. 3-34,а задают следую-
щие незапрещениые конъюнкции: 51, 21415н, 2*rf14H5H, а1е1412н5н,
a*e1d12H4H5H, аЧ‘4,еИ2в5в, a1l1d‘eII21I4u5H, o’&ic‘41lI1eH2H5H,
a‘b,c1d‘lBeB2B4B5B. В графе G (рис. 3-34,6) сечения, про-
ходящие через пару ребер b‘i, b°2 или пару 1*1, 1°2, и полученные по
ним конъюнкции, содержащие соответственно пары букв 6*6° или
1*1°, являются запрещенными, так как они задают физически невоз-
можные в устройстве неисправности {61, 6°} и {I1, I0}. Сечения,
проходящие через ребра ЬЦ, сЦ, 1°2 или пару ребер Ь°2, 1Ц, и полу-
ченные по ним конъюнкции, содержащие соответственно пары букв
64° или Ь0!1*, также запрещены, поскольку каждое из этих сечений
* Заметим, что все пути от входного полюса Ь до выхода z
в графе исходной сети проходят через узел 1.
274
соответствует заданию двух различных неисправностей в узле 1.
Действительно, задание в ЭД, например, неисправности 64с1] 1°2
эквивалентно заданию в нем неисправности {14, I’a}- Незапрещениые
сечения графа G(a,b,lciib°2) рис. 3-34,6 задают следующую группу
новых конъюнкций выражения Sz: 21314Н5Н, 2,/°Зн4и5н,
211°/ыЗп4и5Е, 216°lEfE3E4H5H, aie>3‘2E4E5H, a‘e‘f»2H3E4E5E,
a'e1l°2EfE3E4H5E, a1e1b°2ElEfE3E4H5H, a1l131eE2E4H5E,
«1l1f°eu2H3H4H5H, a‘&1c134EeE2H4E5E, а‘/?1с1{01ЕеЕ2Е3Е4Е5Е. На
основе анализа нёзапрещенных сечений графа G(a,fc11c4c°2)
Рис. 3-34. Графы однозначного
рис. 3-33 для примера 3-57.
распространения в сети
(рис. 3-34,г) аналогичным образом получаются две новые конъюнк-
ции: 21с°1н/нЗн4н5н и a1e1c°2HlHfH3H4H5H. При обработке терма
alblicliba2 его «нормальная» часть Ьн2 задает во всех конъюнкциях,
соответствующих сечениям графа G(alb1lclt) (рис. 3-34,в), совокуп-
ность букв fcHlHfH3H4H5H (путь в ЭД от Ь2 до z). Поэтому сече-
ния, -проходящие через ребро blt или через ребро I1), и полученные
по ним конъюнкции, содержащие соответственно пары букв Ь*ЬЕ
или 1ЧН, являются запрещенными. Два незапрещенных сечения
18* 275
/
этого графа дают две конъюнкции 2*&н 1 HfH3H4H6H и
a,e,2H&HlHfH3H4H5B. Аналогично анализ терма (соот-
ветствующий граф G(a*61ic1i) изображен_на рис. 3-34,в) дает две
последние конъюнкции выражения S2: 21cBlHfB3B4B5B и
a‘e‘2BcBlBfH3B4B5B.
Таким образом, выражение (3-42), содержащее 5 термов, дало
возможность получить выражение Sz, задающее множество неисправ-
ностей, обнаруживаемых на наборе Xj = 0000, и содержащее
27 конъюнкций.
Множество Oj, одиночных неисправностей, обнаружи-
ваемых на наборе Xj, очевидно, может быть построено
на основе анализа незапрещенных одиночных сечений
всех графов G(Xa) (сечений, проходящих только через
одно ребро графа).
Для рассматриваемого примера одиночные сечения графов
G (Xе) рис. 3-34 дают множество OJ = {51, 21}.
ПОСТРОЕНИЕ МНОЖЕСТВА ПОДОЗРЕВАЕМЫХ НЕИСПРАВНОСТЕЙ
Как уже отмечалось в гл. 1, к прямым задачам ди-
агноза технического состояния относится и задача по-
строения по результатам некоторого эксперимента над
устройством множества S*t подозреваемых неисправно-
стей, т. е. такого множества неисправностей, наличие
которые не противоречит известному поведениию иссле-
дуемого устройства на некоторой данной совокупности Т
входных воздействий (входных наборов). Если экспери-
мент состоит из одной элементарной проверки на вход-
ном наборе Xj, то задача определения подозреваемых
неисправностей S*j очевидным образом сводится к за-
даче построения множества Sj обнаруживаемых неис-
правностей. Для ее решения, например, в рассмотренном
ранее структурно-аналитическом методе построения вы-
ражения Sj(Sj) и в случае одновыходного устройства
при неправильной реакции устройства на набор Xj спи-
сок подозреваемых неисправностей S*j определяется
решением уравнения Sz=l, а при правильной реакции —
решением уравнения Sz=l. Точно так же при использо-
вании аналитического метода обобщенных функций (или
последнего из рассмотренных методов) исследуется со-
ответственно прямая обобщенная функция z или инверс-
ная z (ЭФ или ОЭФ) в зависимости от того, 1 или О
появляется на выходе устройства на рассматриваемом
входном наборе Xj. Наличие в исследуемом выражении
276
конъюнкции, целиком состоящей из букв вида ен, озна-
чает, что исправное состояние устройства ие противоре-
чит результатам эксперимента. Для построения множе-
ства S*t подозреваемых неисправностей по одному из
трех рассмотренных выше методов необходимо произве-
сти логическое перемножение соответствующих аналити-
ческих выражений, полученных для каждого набора
Xj^T, зная реакцию на него исследуемого устройства.
При этом для случая устойчивых неисправностей в по-
лучаемом выражении все термы, содержащие хотя бы
одно произведение вида еае\ где а, р=0,1, Н, а#=р,
а е — узел сети или вход эквивалентного дерева, при-
равниваются нулю. Эти упрощения соответствуют рас-
смотрению устойчивых неисправностей в алгебре a-со-
стояний, введенной в § 3-3. w
Построение множества S*r по результатам экспери-
мента на некоторой заданной совокупности Т входные
наборов рассмотрим на примере использования послед-
него метода, основанного на анализе ЭФ (ОЭФ). Преж-
де всего для каждого набора Х-^Т, на котором иссле-
дуемое устройство выдало реакцию z*(X3), необходимо
получить выражение для функции a-состояний на сово-
купности наборов Т f(z=z*(Xj), Xj}, используя при этом
ЭФ, если z*(Xj) = l, или ОЭФ, если z*(X3)=O. Условия,
при которых соблюдаются равенства z = z*(Xj) для всех
наборов записываются в виде
f{{z = z*(X/)}, 7}= Л F{* = **(*/)> = (3-43)
Упрощение полученного выражения осуществляется
по правилам алгебры a-состояний. При записи каждой
функции a-состояний f{z=z*(Xj), ХД и при получении
выражения (3-43) удобнее более короткая запись этих
функций, которая получается, если использовать соот-
ношения
au\J a
aHV a' = a°;
a1 \/a=cF.
И лишь окончательная ДНФ выражения (3-43)
должна быть записана без инверсий над символами а =
= {0,1,Н}. Правила построения выражения Я*т, задаю-
277
щего множество подозреваемых неисправностей S*r на
основе анализа термов выражения (3-43), остаются точ-
но такие же, как и при построении выражения за-
дающего множества Sj неисправностей, обнаруживае-
Пример 3-58. Для сети рис. 3-32 предположим, что при после-
довательной подаче двух наборов Т = {0000, 1111} на выходе полу-
чены фактические реакции z*(0000) = l, z*(llll)=0. Найдем выра-
жение S*t, задающее множество подозреваемых неисправностей.
Функция f{z*='1,0000} [см. 3-42)] имеет вид:
f{z* = 1,0000} =n1b[cjd! V «‘b}c} (<>Г\/сГ).
Для входного набора 1111 и реакции z*(llll)=0, используя
ОЭФ дерева z=« V&iVCiVd62c2, получаем:
/ {z* = 0,1111} = a° V t>?Vc?V
Тогда
f {z* = 1,0000; z* = 0,1111} = f {z* = 1.0000} f {z* = 0,1111} =
= fl’ftjcjd0 (6^ V $ b(2 ) = Л1 V а'Ь\с\(Рь'2<% V
V а'ь\с\сРь^с^. (3-44)
На рис. 3-35,а изображен граф G(o1felIc1id°c12) однозначного
распространения для фиксированной части первого терма выражения
(3-44). Его «нормальная» часть Ьп2 определяет совокупность букв
6Н1П}Н3Н4П5Н в искомых конъюнкциях, соответствующих всем се-
чениям графа G(al&11c*id°c12). Незапрещениые сечения графа
G(a1b11c*id0c,2) дают следующие конъюнкции выражения 8*т:
2lc1d°bHlnfn3H4H5H и a1e,c1d°2H6HlHfH3H4H5H. Аналогично аиа-
278
ЛйЗ второго терма йыраЖения (3-44) дает граф G(afbilcitdnbi«)
рис. 3-35,6 и две конъюнкции: 216,Д°сн1н/ыЗн4115и и
а|е’6|Ц°2нсн1н/'нЗн4н5н. На рис. 3-35,в изображен граф
G(a16’iCiid°) для третьего терма из (3-44). «Нормальная» часть
6н2сн2 этого терма задает совокупность букв &HcHlHfH3n4H5H
в конъюнкциях, получаемых из анализа сечений графа G(albtic,Id°).
Незапрещеиные сечения графа G(aibilc,ld°) определяют две послед-
ние конъюнкции выражения 8*т- 21d°6HlHfH3H4H5H и
a1e,dt>2H6HcHlHfH3H4H5H.
Таким образом,
S*r = г'с'д'Ф11!11 fH3H4H5rl V /нЗн4н5Н V
V 2'6'АН1Н /»3Н4Н5» V /Н3Н4Н5» V
V 2WW /ИЗН4Р5Н V a‘?^2HfeHCHlH /И3Н4Н5П.
Заметим, что аналитическое представление функций
a-состояний удобнее заменить совокупностью векторов,
представляющих термы этой функции, а операцию пере-
множения функций — операцией попарного пересечения
векторов, соответствующих этим функциям.
Если в выражении S*j, задающем множество подо-
зреваемых неисправностей, положить все буквы вида пн
равными 1, а затем перечислить все встречающиеся
в полученных конъюнкциях состояния соединений сети,
то тем самым будет получено множество О*т одиночных
неисправностей, по крайней мере одна из которых дей-
ствительно имеет место в исследуемом устройстве. За-
метим, что в общем случае |О*т| ^ |О(5*т) |, где
О (S*T) — множество одиночных неисправностей, состав-
ляющих множество S*r всех подозреваемых неисправно-
стей.
Множество О*т в примере 3-58 имеет вид: О*т={с|, bl, с1, d°,
е1, 21}.
Очевидно, что для нахождения действительно имею-
щих место в устройстве константных неисправностей
с целью их устранения выражение для 8*т дает инфор-
мации существенно больше, чем множество О*т.
Так, для рассматриваемого примера 3-58 заведомо существую-
щей неисправностью является неисправность d° (так как опа входит
во все конъюнкции выражения 8*т), а при отсутствии в устройстве
неисправности 21 в ием обязательно присутствует неисправность s=
= {а1, е*}, так как она входит во все конъюнкции выражения 8*т,
содержащие букву 2Н.
Начинать поиск действительно имеющихся в устрой-
стве неисправностей нужно с проверки одиночных не-
исправностей, соответствующих буквам конъюнкции вы-
279
ражения S*T с наиболее короткой фиксированной ча*
стью, как наиболее вероятных. Использование же более
компактной совокупности О*т или O(S*t) требует все-
гда проверки всех составляющих ее одиночных неис-
правностей в произвольном порядке.
Рассмотрим теперь решение задачи построения сово-
купности Oj обнаруживаемых набором Xj одиночных
неисправностей на основе метода существенных путей.
МЕТОД СУЩЕСТВЕННЫХ ПУТЕЙ
Исследуем неисправность s элемента rji на входном
наборе сети Xj по алгоритму АЗ-2 (§ 3-4, рис. 3-27).
Если Xj^X (0, s), т. е. если на наборе Xj неисправность
s обнаруживается, то включим s в множество О, обна-
руживаемых на наборе Xj неисправностей, в противном
случае seOj (Oj — множество не обнаруживаемых на
наборе Xj неисправностей); в обоих случаях перейдем
к исследованию другой неисправности того же или дру-
гого элемента сети. Если число элементов сети N, а эле-
мент ф может иметь Sj логических неисправностей, то
суммарное число одиночных неисправностей сети |О| =
N
= 2 •$<. Таким образом, множество О, может быть по-
/=1
строено |О|-кратным применением алгоритма АЗ-2.
Как следует из сказанного, проверке на выполни-
мость условия транспортировки должен подвергаться
выходной узел каждого элемента т]< сети, на входах ко-
торого на наборе Xj сложится проверяющий набор
К/(О, s) хотя бы для одной его неисправности s. Множе-
ство таких элементов обозначим через Nj.
Рассмотрим два узла й, i2 сети и приведем следую-
щие очевидные утверждения:
1. Если на входном наборе Xj узел i2 принадлежит
простому участку существенного пути {и, у}, то при этом
имеется также существенный путь {i2, у}.
2. Если все пути от узла i2 до выхода у проходят
через узел ii и на наборе Xj нет существенного пути
{й, у}, то при этом также нет существенного пути
{й. ?}
Из первого утверждения следует, что если набором
Xj обеспечен простой существенный путь {i, у}, то тем
самым обеспечен простой существенный путь до выхода
280
у от любого узла, принадлежащего пути {/, у}. Если рас-
сматриваются константные неисправности, то на произ-
вольном входном наборе Xj проявляется неисправность
Г> если о=(0, 1) —значение функции в узле/исправной
сети на наборе Xj. Таким образом, если на наборе Xj
обнаруживается некоторая константная неисправность
узла i и при этом существенный путь {/, у} простой, то
на этом наборе обнаруживается одна определенная не-
исправность любого входа или выхода элемента, при-
надлежащего пути {i’,y}. Сказанное справедливо также
для узлов простых участков сложного существенного
пути {/, у}.
Если взять за основу утверждение 1, то лучшей стра-
тегией при построении подмножества Oj обнаруживае-
мых неисправностей является перебор элементов мно-
жества Nj в порядке неубывания их рангов. При этом
в первую очередь будут определяться наиболее длинные
существенные пути, благодаря чему многие узлы (при-
надлежащие простым участкам этих путей) будут вклю-
чены в множество Oj без дополнительного их рассмотре-
ния.
Однако утверждение 2 делает разумной другую стра-
тегию— перебор элементов множества Nj в порядке
невозрастания их рангов. При этом в первую очередь
будут определяться узлы, через которые проходит наи-
большее число путей. Благодаря этому при отсутствии
существенного пути от рассматриваемого узла до выходов
сети многие узлы (все пути от которых проходят через
рассматриваемый узел) будут исключены из дальнейше-
го рассмотрения, как не принадлежащие множеству О,.
Можно организовать поочередное применение обеих
указанных стратегий так, как это сделано в следующем
примере.
Пример 3-59. Построим подмножество О} константных неис-
правностей узлов сети рис. 3-24, обнаруживаемых на входном набо-
ре Xj= 1011
Множество Nj образуют все узлы сети, так как рассматриваются
константные неисправности. Разобьем множество Nj иа группы узлов
по рангам элементов сети: {хь хг, хз, х4}, {(/, /), (Л 2), (2, /),
(2, 2), (3, /), (3, 2)}, {2}, {(4, /), 1, (5, /), (5, 2), (6, 1), (6, 2), 3,
(7, 2)}, {4, 5, 6, 7}, {8}. Здесь первая цифра в круглых скобках ука-
зывает номер элемента, а вторая — иомер входа элемента.
Очевидно, проверка на наличие существенного пути от узла 8
(выхода z сети) не требуется — такой путь всегда имеется. Осталь-
ные группы узлов будем обрабатывать по алгоритму АЗ-2 в следую-
281
щей последовательности: {хь х2, х3, х4}, {4, 5, 6, 7}, {(/, /), (/, 2),
(2, 1), (2, 2), (3, /), (3, 2)}, {(4, 1), 1, (5, /), (5, 2), (6, /), (6, 2),
3, (7, 2)}, {2}. В результате исследования входного полюса х,
обнаруживается отсутствие существенного пути {х,, z} (D-цепи
обрываются в узле (/, 1), так как х.з=1, и в узле (3, 2), так как
д4 = 1). От входного полюса х2 на исследуемом наборе имеется про-
стой существенный путь {х2(4, 1), 4, z}. Таким образом, неисправ-
ность х*2, а (на основании утверждения 1) также неисправности
(4, 1)1 4° и 3* обнаруживаются; поэтому узлы (4, 1) и 4 исключают-
ся из дальнейшей обработки. Аналогично выясняется отсутствие
существенных путей от входных полюсов х3 и х4 (так как д4=1).
Переходим к исследованию узлов второй группы, которая теперь
состоит из узлов 5, 6 и 7. От всех этих узлов существенный путь
до выхода z отсутствует (так как </4=1); на основании утвержде-
ния 2 существенные пути отсутствуютм от узлов (5, /), (5, 2), (6,1),
(6, 2), 3, (3, /), (3, 2) и (7, 2), которые исключаются из дальнейшей
обработки. Переходим к узлам третьей группы, имеющей теперь вид
{(/, /), (/, 2) (2, 1), (2, 2)}. От всех этих узлов существенный путь
отсутствует. Четвертая группа узлов теперь содержит только один
узел 1, от которого имеется простой существенный путь (/, 4, г),
т. е. неисправность /’ обнаруживается. От узла 2 пятой группы су-
щественного пути нет Итак Оюи = {х'г (4,1)1, I1, 4», 8>}.
3-6. МЕТОДЫ ПОСТРОЕНИЯ ПРОВЕРЯЮЩИХ ТЕСТОВ
ДЛЯ КОМБИНАЦИОННЫХ УСТРОЙСТВ
В этом параграфе рассматривается ряд характерны^
методов построения алгоритмов проверки работоспособ-
ности комбинационных устройств. Как отмечалось в гл. 1,
алгоритм диагноза в общем случае представляет собой
совокупность Т элементарных проверок с некоторой за-
данной безусловной или условной последовательностью
их реализации. Примем здесь обычные предположения
о том, что, во-первых, алгоритмы проверки являются
безусловными алгоритмами с безусловной остановкой и,
во-вторых, составы контрольных точек фиксированы и
одинаковы для всех допустимых элементарных прове-
рок. Тогда задача построения алгоритма проверки рабо-
тоспособности комбинационного устройства состоит
в построении совокупности {X} п входных наборов
устройства, достаточной для обнаружения на заданных
контрольных точках всех существенных неисправностей
устройства из заданного множества S неисправностей.
Совокупность {Х}п принято называть проверяющим или
контролирующим тестом
Заметим, что для неизбыточных комбинационны^
устройств и для класса S константных неисправностей
(в таких устройствах, как это указывалось в § 3-3, нет
несущественных константных неисправностей) тест {Л}
282
проверки работоспособности является также тестом про-
верки исправности. Если несущественные неисправности
являются следствием специально введенной в устройст-
во избыточности (с целью, например, повышения надеж-
ности устройства), то тест проверки работоспособности
не является тестом проверки исправности устройства.
Для построения последнего в этом случае обычно тре-
буется увеличение числа контрольных точек.
Укажем также на то, что, как правило, допустимыми
будем считать все возможные входные наборы устрой-
ства (при п входдх имеется 2П таких наборов).
Начнем рассмотрение с методов построения контро-
лирующих тестов, основанных на перечислении в той или
иной форме неисправностей seS. Поскольку число крат-
ных неисправностей |S| обычно существенно больше
числа одиночных неисправностей |О|, то подобные ме-
тоды целесообразно использовать для случая одиночных
логических неисправностей логической сети комбинаци-
онного устройства.
МЕТОДЫ, ОСНОВАННЫЕ НА ПЕРЕЧИСЛЕНИИ НЕИСПРАВНОСТЕЙ
МЕТОД ПЕРЕБОРА ВХОДНЫХ НАБОРОВ СЕТИ
Метод перебора входных наборов сети основан на
решении задачи построения множества О,- одиночных
неисправностей, обнаруживаемых входным набором Xj
(см. § 3-5). Будем подавать на в,ходы Xi, ..., хп сети
в некоторой произвольной последовательности допусти-
мые наборы Xj, j=l, 2, ..., 2П, и определять для каждо-
го из них множества О3 обнаруживаемых неисправно-
стей. Если подмножество Oj таково, что в нем содер-
жится хотя бы одна неисправность из заданного
множества О неисправностей, не обнаруженная ни од-
ним из поданных ранее входных наборов, то входной
набор Xj включается в тест {Х}п. Для этого на каж-
дом j-м шаге алгоритма строится множество
неис-
правностей, обнаруживаемых совокупностью Tj наборов,
включенных в множество {Х}п. Построение проверяющего
теста {Х}п заканчивается, когда либо все неисправно-
сти из множества О оказались обнаруживаемыми, либо
пока не будут исчерпаны допустимые входные наборы
сети (/=2П). Таким образом, рассмотренная процедура
283
Рис. 3-36. Блок-схема алгоритма АЗ-4 построения проверяюще-
го теста {Х}П методом перебора входных наборов.
284
всегда заканчивается построением совокупности входные
наборов, достаточной для проверки работоспособности
устройства (имеется в виду, что будут обнаружены все
те неисправности из множества О, которые можно обна
ружить путем подачи допустимых воздействий на внеш-
ние входы и проверки ответов устройства на внешних
выходах, т. е. все существенные неисправности). На
рис. 3-36 дана блок-схема алгоритма АЗ-4 построения
проверяющего теста {А} п на основе перебора входных
наборов сети. Разумеется, что построенный по алгорит-
му АЗ-4 тест может быть избыточным, т. е. содержать
по крайней мере один набор, удаление которого из те-
ста (Х}п не лишает укороченный тест свойства обнару-
живать все существенные неисправности устройства.
В основу построения непзбыточного (тупикового)
проверяющего теста {Х}у, по найденному тесту {Х}п
можно положить следующие соображения. Как следует
из предложенной выше процедуры построения прове-
ряющего теста, всякий включенный в тест входной набор
обнаруживает по крайней мере одну неисправность, не
обнаруживаемую ни одним из ранее включенных в тест
наборов. Таким образом, в отношении последнего вклю-
ченного в тест набора можно заключить, что он неизбы-
точен, т. е. его нельзя удалить из теста. Повторим те-
перь процедуру построения проверяющего теста только
на множестве вводных наборов, составляющих ранее
найденный тест {Х)Г1, начав ее с подачи вышеупомяну-
того неизбыточного набора. Остальные наборы теста
{X}п будем подавать, например, в том же порядке,
в каком они были получены при построении {Х}п. В ре-
зультате будет построен проверяющий тест (Х}|Г1 с чи-
слом наборов Ni, меньшим или равным числу наборов
N в первоначальном проверяющем тесте {X} п. В отно-
шении последнего из включеных в тест {Х}|П входного
набора опять будет верно утверждение о его неизбыточ-
ности. Указанную процедуру можно проделать т раз,
где (N—1), и закончить тогда, когда тест {Х}^ со-
стоит из последних наборов ранее построенных т+1
проверяющих тестов {Х}п, {Х)Р, ..., {Х}^. Таким об-
разом, установлена неизбыточность каждого из Nm на-
285
боров теста {Х}^ , откуда следует, что этбт теРт являет-
ся неизбыточным.
Пример 3-60. В табл. 3-8а строки обозначены номерами наборов
некоторого теста {X} п и расположены сверху вниз в порядке их
получения по алгоритму АЗ-4. Неисправностям сопоставлены столб-
цы Oi—о8. Единица в клетке (Xj, of) поставлена тогда и только
тогда, когда неисправность о, обнаруживается па наборе Xj, т. е.
OjeOj.
Таблица 3-8а
Х! о. «3 О1 Ой Ое °’
1 1 1 1 1
2 1 1 1
3 1 1 1
4 1 1 1
5 1 1 1
Заметим, что каждый набор X, в табл. 3-8а обнаруживает, ио
крайней мере, одну неисправность, не обнаруживаемую ни одним из
наборов теста {X} п > предшествующих набору Xj. Последний набор
в совокупности {X}п табл. 3-8а, т. е. набор 5, является неизбыточ-
ным. Применим алгоритм АЗ-4 при условии подачи наборов теста
{X} п в следующем порядке: 5, 1, 2, 3. 4 (см. табл. 3-86).
Таблица 3-86
Х! °1 О, Рз °* Об °в о, Ов
5 1 1 1
1 1 1 1 1
3 1 1 1
4 1 1 1
Набор 2 в новый проверяющий тест {X} 7 не вошел, так как
ранее поданные наборы 5 и 1 обнаруживают все неисправности,
обнаруживаемые набором 2. Набор 4 неизбыточен. Повторим алго-
286
Таблица 3-8в
ритм АЗ-4 на наборах теста {х} П1 в следующей последовательно-
сти: 4, 5, 1, 3 (см. табл. 3-8в).
Набор 3 оказался избыточным и в тест {Х}Пг не вошел. Все
три набора теста {Х}п2 побывали последними в тестах: {X} п
(табл 3-8а), {Х}П1 (табл. 3-86), {X} Пг (табл. 3-8в). Следовательно,
тест ИП2 = {4, 5, 1} неизбыточен.
Процедура построения проверяющего теста методом
перебора входных наборов сети эффективна для логиче-
ских сетей с большим числом элементов и уровней (ран-
гов), но с относительно небольшим числом внешних
входов. Наоборот, для сетей с большим числом входов,
но с относительно небольшим числом элементов и уров-
ней и по-прежнему для случая одиночных неисправно-
стей более выгодным является, по-видимому, метод вы-
числения наборов проверяющего теста {X} .
МЕТОД ВЫЧИСЛЕНИЯ НАБОРОВ ПРОВЕРЯЮЩЕГО ТЕСТА
Метод вычисления наборов проверяющего теста со-
стоит в следующем. Пусть к /-му шагу алгоритма, реа-
лизующего рассматриваемый метод, построена совокуп-
ность Г,-! наборов, включенные в тест (Х}п, и опреде-
лено множество От. j неисправностей, обнаруживаемых
на совокупности Т(при / = 1, Т. }—От_ ( — 0). Для
произвольной не обнаруженной на совокупности Т j_\ не-
исправности $=0,^0 \ОГ вычисляется некоторый об-
наруживающий эту неисправность набор Х^{Х(О, о,)}
с использованием одного из методов построения прове-
ряющей совокупности {X(0, s)}={X(0, о,)} (см. § 3-4).
Затем, если неисправность о{ существенна и, следова-
тельно, набор Х{ существует, то строится совокупность
287
Рис. 3-37. Блок-схема алгоритма АЗ-5 вычисления наборов проверяю-
щего теста {Х}п.
288
6i неисправностей, обнаруживаемых на наборе X,, с ис*
пользованием одного из изложенных_в § 3-5 методов.
Обнаруженные неисправности OTj~OT. , (J Oi исклю-
чаются из исходного списка неисправностей О, а набор
Xi включается в совокупность Т, теста {Х}п *. Процесс
построения теста {X}11 заканчивается, когда на множе-
стве входящих в него наборов обнаруживаются все су-
щественные неисправности сети. На рис. 3-37 изображе-
на блок-схема описанного алгоритма АЗ-5. Построен-
ный тест {Х}п также может оказаться избыточным. Для
построения неизбыточного теста из найденного можно
воспользоваться рассмотренной выше процедурой, осно-
ванной на многоразовом применении алгоритма АЗ-4
к множеству наборов исходного теста Укажем, что
алгоритм АЗ-5 может быть существенно упрощен, если
отказаться от вычисления совокупности (5, неисправно-
стей, обнаруживаемых набором Х.3-. В этом случае тест
{X}п будет представлять объединение наборов ХДХ,е
е{Х(0, о,)}), построенных для всех OjeC Естественно,
что неизбыточность такого теста также не может гаран-
тироваться.
ХАРАКТЕРИСТИЧЕСКИЕ НЕИСПРАВНОСТИ
Очевидно, что сложность обоих рассмотренные мето-
дов построения проверяющего теста {Х}п существенно
зависит от числа |О| неисправностей, относительно ко-
торых строится тест. Поэтому вполне естественно поста
вить следующий вопрос нельзя ли из полного списка О
заданных неисправностей сети выделить некоторое под-
множество 0х неисправностей такое, что тест, построен
ный относительно подмножества 0х, оказался бы те-
стом, достаточным для обнаружения всех существенных
неисправностей из множества О? Если при этом 10х | -С
<С]0|, то это приведет к значительному упрощению
реализации методов, требующих в той или иной форме
перечисления неисправностей. Оказывается, что подмно-
жесто 0х, которое в дальнейшем будем называть под-
множеством характеристических неисправностей сети,
удается выделить в ряде частных случаев структур ком-
* Если неисправность ог оказалась несущественной, то она тоже
исключается из списка неисправностей (?.
19—358 289
бинационных устройств, базисов логических элементов и
классов неисправностей.
В предыдущем параграфе уже отмечалось, что для
случая константных неисправностей сети входной набор
Xit обнаруживающий неисправность в узле I, обнаружи-
вает также некоторые неисправности других узлов сети,
принадлежащих простым участкам существенного пути
(i, у}-
Это свойство наиболее эффективно проявляется в сетях
без разветвлений, т. е. в деревьях, так как в них любой
существенный путь {i, z}, в том числе существенный путь
{хв, z] от входного полюса ха, а^{1, 2, ..., п}, до вы-
хода z всегда простой. Для того чтобы на двух входных
наборах, проверяющих состояние входного полюса ха (т. е.
на выборах, на которых обнаруживаются неисправности
х’а и x’J, проверить состояние всех узлов сети, лежащих
на пути {лв, z}, необходимо, чтобы эти наборы в исправ-
ной сети задавали в любом узле i, принадлежащем пути
{лв, z}, оба значения (0 и 1) соответствующей переменной
yi. Это условие, в частности, выполняется, если наборы
рассматриваемой пары оказываются соседними по пере-
менной ха проверяемого входного полюса, т. е. отличаются
значением только одной переменной ха. Обозначим два
входных набора, проверяющих состояние входного полю-
са ха и соседних по его переменной, через и А'а| на
наборе А'аС(А'а1) х(1 = 0(л‘а= 1). Указанную пару наборов
будем называть выявляющей парой1.
Значения выхода z исправной сети, как и значения
переменных yt узлов пути *{ха, г}, на этих наборах раз-
личны. Заметим, что значения сигналов на входах элемен-
тов пути {ха, z}, но не принадлежащих этому пути, на
наборах Ха0 и Ха1 всегда одинаковы, вне зависимости от
того, какие и сколько устойчивых константных неисправ-
ностей присутствуют в сети. Это связано с неизменностью
значения на наборах Ха0 и Ха1 любой переменной если
Пусть в сети содержится неисправность sa. Здесь
индекс а указывает на то, что среди одиночных неисправ-
ностей, составляющих неисправность sa, имеются не-
1 В § 3-7 будет пояснен смысл такого названия,
290
исправности узлов, принадлежащих пути {л'а, z}. 'Тогда
на наборах и Л"о1 значения выхода z оказываются оди-
наковыми. На этих соображениях основано доказательство
следующего утверждения.
Проверяющий тест {%}п, который построен относи-
тельно одиночных константных неисправностей входных
полюсов сети, не имеющей разветвлений и реализован-
ной в произвольном базисе логических элементов, и со-
стоит из пар соседних по переменным ха, а=1, 2, ..., п
наборов, проверяющих состояние входного полюса ха,
является достаточным для обнаружения любой красной
константной неисправности сети. Так как дерево неиз-
быточно, то тест {Х}П всегда существует. Длина такого
теста дерева с п входами определяется соотношением
л + Г<|ОТП |<2/г.
При некоторых ограничениях на базис логических
элементов и для класса одиночных константных неис-
правностей в дереве требование соседства наборов теста
{X}11, проверяющих состояние входных полюсов, можно
снять.
Пусть логический элемент реализует функцию, для
которой существует дизъюнктивная нормальная форма,
имеющая по крайней мере одну букву, которая входит
в эту форму в некотором одном виде (прямом или об-
ратном). В этом случае будем говорить, что элемент
(или реализуемая им функция) обладает свойством
однородности относительно входов (переменных), кото-
рые представлены в ДНФ буквами в одном виде. Харак-
терным для этих элементов является наличие по край-
ней мере одного входа такого, что на любых двух набо-
рах, проверяющих состояние этого входа, в исправном
элементе на его выходе появляются два различных зна-
чения выходной переменной.
Пример 3-61. Таблица 3-9 является таблицей истинности некото-
рого логического элемента.
Дизъюнктивная нормальная форма функции у имеет вид: у —
= XiX2 Хз V -«1X2X3. Только переменная Xi входит в ДНФ в одном
виде. Неисправность х1, обнаруживается на наборах 1 и 4, на ко-
торых значение выхода исправного элемента равно 0; неисправность
.v°i - па наборах 5 и 8, на которых значение выхода равно 1. Сле-
19* 291
довагелыю, рассматриваемый элемент обладает свойством однород-
ности относительно входа %].
Таблица 3-9
№ Х1 Хц ХЭ У № Xi лга Хз У
1 0 0 о 0 5 1 0 0 1
2 0 0 1 0 6 1 0 1 0
3 0 1 0 0 7 1 1 0 0
4 0 1 1 0 8 1 1 1 1
Элементы булева базиса являются частным случаем
элементов, обладающих свойством однородности относи-
тельно каждого своего входа. При этом для каждого
входа имеется одна пара наборов, проверяющих его со
стояние, на которых выход элемента имеет различные
значения. Наъример, для двухвходового элемента И
с входами XtX2 состояние входа xt может быть проверено
на единственной паре наборов 01 п 11 (г/(01)=0,
у(11) = 1). Так как в тупиковую дизъюнктивную форму
прямой (обратной) функции, реализуемой элементом
простого базиса, каждая входная переменная входит
в одном виде, то элементы простого базиса обладают
свойством однородности также по отношению ко всем
своим входам. Двухвходовый элемент «сумма по моду-
лю 2» не обладает свойством однородности; на наборах
00 и 11, проверяющих состояние каждого одного входа
элемента, его выход имеет одно и то же значение, рав-
ное 0.
Можно утверждать следующее. Любой проверяющий
тест {X}n, построенный относительно одиночных кон-
стантных неисправностей входных полюсов сети, не
имеющей разветвлений и реализованной на логических
элементах, обладающих свойством однородности относи-
тельно хотя бы одного из своих входов, является тестом,
достаточным для обнаружения в сети любой одиночной
константной неисправности.
В рассмотренных случаях одиночные неисправности
входных полюсов составляют множество 0х характери-
стических неисправностей класса О.
292
Обратимся теперь к неизбыточным Сетям с проиЗ-
вольной структурой, реализованным на элементах, обла-
дающих свойством однородности относительно хотя бы
одного из своих входов. Для таких сетей и для случая
одиночных константных неисправностей справедливо
следующее утверждение. Проверяющий тест {Х}п, по-
строенный относительно одиночных константных неис-
правностей входных полюсов и ветвей разветвлений
такой сети, является достаточным для обнаружения
в пей любой одиночной константной неисправное!и.
Указанные неисправности составляют множество 0х
в рассматриваемом случае.
Так как рассматривается неизбыточная сеть, в кото-
рой существенны все одиночные константные неисправ-
ности, то тест {Х}п существует.
Пример 3-62. Для сети рис. 3-1 множество 0х в классе О со
ставляют одиночные константные неисправности узлов {a, b, с, d,
(/, 2), (2, /), (5, /), (6, 1), {6, 2), (7, /)} (назовем их характери-
стическими узлами). Найдем проверяющий тест сети методом пере-
бора ее входных наборов. Будем подавать двоичные входные наборы
в порядке возрастания их десятичного эквивалента. Для определения
множества (5jsOx характеристических неисправностей, обнаружи-
ваемых набором Xj, воспользуемся структурным методом существен
пых путей, описанным в § 3-4 и 3-5. Результаты исследований девя-
ти первых входных наборов отражены в табл. 3-10. Набор 7 в тест
{Х}п не входит, так как все характеристические неисправности,
обнаруживаемые этим набором, обнаруживаются ранее поданным
набором 5. На наборах 1—6, 8 и 9 обнаруживаются все характери-
стические неисправности сети, и, таким образом, эти наборы состав-
ляют проверяющий тест {X}rl для класса одиночных константных
неисправностей. Применение к найденному тесту, например, рассмо-
тренной выше методики построения неизбыточного теста дает тупи-
ковый проверяющий тест {Х}у > состоящий из шести наборов
{Х}" = {2, 3, 5, 6, 8, 9}.
Пример 3-63. Для сети рнс. 3-1 найдем тест {Х}Г1 для класса
одиночных константных неисправностей методом вычисления наборов
проверяющего теста. Исходным множеством неисправностей являет-
ся множество 0х, найденное в предыдущем примере. Для построе-
ния проверяющего набора Х(0, о,), где о,еОх, воспользуемся опи
санным в § 3-4 структурным методом вычисления проверяющего
набора, основанным на идее существенных путей. Построение мно-
жества Oj осуществляется так же, как и в предыдущем примере.
Результаты применения метода представлены в табл. 3-11 На по
строенной совокупности из семи наборов обнаруживаются все ха-
рактеристические неисправности сети. Все наборы 1—7 теста неиз-
быточны.
Рассмотрим способ построения подмножества 0х ха-
рактеристических одиночных константных неисправио-
293
№ *1
abed £1° a1 b° fcl c1 d° JI (1,2)“ (1,2)-
1 0 0 0 0 1
2 0 0 0 1 1 1 1
3 0 0 10 1 1 1 1
4 0 0 11 1 1 1
5 0 10 0 1
6 0 10 1 1 1 1 1
7 0 110
8 0 111 1 1 1
9 10 0 0 1 1
№ Xj 0, Of
a b c d £1° °* t* 00 c* (1.2)“ (1.2)>
1 a° 110 1 1 1
2 a' 0 10 1 1 1 1 1
3 0 0 0 1 1 1 1
4 c° 0 111 1 1 1
5 d* 0 0 10 1 1 1
6 (3.1)' 0 10 0 1
7 (6.1)' 10 11 1
294
Таблица 3-10
0х
(2,1,» (2,1)* (3,1)’ (3,1)* (6,1)’ (6,1)* (6,2)’ (6,2)* (7,1)» (7.1)*
1
1 1
1
1 1
1 1
1 1 1
1 1
1 1
1 1
ох
Таблица 3-11
(2,1)’ (2,1)* (3,1)» (3.1)* (6.1)» (6.1)* (6,2)0 (6,2)* (7,1)» (7,1)*
1 1
1 1 1
1 1
1 1
1
1 1
1 1
295
стей для сетей, содержащих несущественные неисправ-
ности указанного класса, т. е. для избыточных сетей.
Прежде всего заметим, что если сеть, построенная из
элементов, обладающих свойством однородности отно-
сительно хотя бы одного из своих входов, содержит не-
которую одиночную несущественную константную неис-
правность, то она также содержит несущественную
одиночную неисправность некоторого входного полюса
или некоторой ветви разветвления. Справедливость
этого замечания следует из того факта, что если неко-
торая неисправность выхода элемента сети несущест-
венна, то при этом не могут быть существенными обе
неисправности («константа 0» п «константа 1») его вхо-
да, по отношению к которому элемент обладает свойст-
вом однородности (в противном случае обе неисправно-
сти выхода рассматриваемого элемента были бы суще-
ственны).
Итак, пусть имеется избыточная сеть, реализованная
для простоты па элементах, обладающих свойством
однородности по отношению ко всем их входам. Будем
определять множество характеристических неисправно-
стей такой сети постепенно с одновременным построени-
ем множества наборов, проверяющих все существенные
неисправности каждой определенной части множест-
ва 0х. Назовем начальным множеством характеристи-
ческих неисправностей множество Охо одиночных неис-
правностей входных полюсов и ветвей разветвлений
(Ох0 совпадает с множеством 0х для неизбыточных се-
тей).
Построим тест {JQ? относительно множества Охо.
Если каждая неисправность оеОх0> существенна, то
тест {X}'' достаточен для обнаружения любой одиноч-
ной неисправности рассматриваемой сети1. В противном
случае выделим из Ох0 подмножество Охн0 несущест-
венных одиночных неисправностей (OoHsOx0), а также
множество Во элементов сети, у которых по крайней
мере одна неисправность каждого из входов оказалась
несущественной.
Если множество Во пусто, то в сети нет несуществен-
ных одиночных неисправностей, отличных от неисправнос-
1 При этом в рассматриваемой избыточной сети нет несуществен-
ных одиночных неисправностей, но может быть несущественной не-
которая кратная неисправность,
296
Тей, составляющих подмножество ОрН, и тест по*
строенный относительно существенных неисправностей из
множества О^, является достаточным для обнаружения
любой существенной неисправности из множества О (т. е.
О* — множество характеристических неисправностей из-
быточной сети). Если это не так, то для каждого эле-
мента греВо необходимо определить, осуществляется
ли на наборах {X}'1 проверка состояний его выхода.
Эта задача может быть решена, например, с по-
мощью алгоритма АЗ-2 (§ 3-4, рис. 3-27). Затем следует
выделить множество элементов, по крайней
мере одна неисправность выхода которых пе обнаружи-
вается на наборах {X}1 0. Если множество В'о пусто, то
{X}11»—проверяющий тест сети. В противном случае
дополним множество Охн неисправностями выходов
элементов из множества В'о, которые не проверяются
наборами {Х}п0; при этом получим множество неисправ-
ностей 0 х).
Построим входные наборы сети, обнаруживающие
эти непроверенные неисправности (если, конечно, эти
неисправности существенны), и дополним ими тест
{X} о, при этом получим тест {Х}г\ относительно суще-
ственных неисправностей из множества Oxi.
Будем повторять рассмотренную выше процедуру т
раз, исходя из множеств 0х, и {Х}П/, 1=1, 2, ..., т, как
из множеств Ох0 и {X} ° до тех пор, пока множество
непроверенных наборами теста {X}1™ неисправностей
выходов элементов из множества В'т пе окажется пу-
стым. Тогда множество Охт — множество характеристи-
ческих неисправностей сети, а совокупность наборов
{X} т — тест, достаточный для обнаружения всех ее
существенных одиночных неисправностей.
Пример 3-63. Для сети рис. 3-38 в табл. 3-12 представлен тест
(Х}По (наборы 1—5) относительно неисправностей множества Ох0.
Наборов, проверяющих одиночные неисправности (2, У)1 и (2, 2)1,
не существует, т. е. QXHo={(2, /)*, (2, 2)1}; В0={2). Не-
исправность 2° выхода элемента 2 проверяется на наборе 1, а неис-
правность 2* не проверяется ни на одном наборе (1—5)
(В'о= {2}). Добавим неисправность 21 к множеству Охо, образуя
множество 0х], и вычислим набор Х(0, 21) (набор 6); B'i = 0,
поэтому Ox=Oxi и {Х}П={Х)И1 (наборы 1—6).
297
Для построения множества 5х характеристических
кратных константных неисправностей комбинационных
сетей общего вида (произвольный базис элементов, про-
извольная структура, возможная избыточность сети)
обратимся к результатам, полученным в § 3-3. Следст-
вием этих результатов является следующее заключе-
ние. В сети без разветвлений, реализованной в произ-
вольном базисе логических элементов, любая кратная
1
Рис. 3-38. Пример избыточной логической сети
для построения множества Ох характеристиче-
ских неисправностей.
298
Таблица 3-12
о*
°о 2»
(1.2)* (1,2)» (2,1)* (2.1)0 (2.2)* (2,2)° (3.1)« (3.1)0 (3.2)* (3,2)0
1 1 1
1 I
1
1 1
1
константная неисправность s эквивалентна некоторой
кратной константной неисправности входных полюсов
сети. Рассмотренный в § 3-3 способ фиксации неисправ-
ностью s букв эквивалентной формы функции сети
является способом построения искомой эквивалентной s
Рис. 3-39. Иллюстрация разбиения сети рис. 3-1 на максимальные
деревья.
кратной неисправности входных полюсов сети (фикса-
ции буквы ха в ЭФ константой о соответствует неис-
правность хаа). Очевидно, что произвольная сеть с раз-
ветвлениями может быть представлена связанной сово
299
купностью максимальных подсетей без разветвлений.
Входами каждой такой подсети (поддерева) являются
либо неразветвляющиеся входные полюсы исходной
сети, либо ветви узлов разветвлений, а выходом —
выходной полюс сети либо узел разветвления. На
рис. 3-39 пунктирными линиями обведены 4 максималь-
ных поддерева исходной сети рис. 3-1.
Неисправность х’разветвляющегося входного полюса ха
эквивалентна кратной неисправности «константа о» на
всех его ветвях разветвления.
На основании сказанного можно заключить, что лю-
бая кратная константная неисправность произвольной
сети эквивалентна кратной неисправности некоторых
неразветвляющихся входных полюсов и некоторых вет-
вей разветвлений сети. Таким образом, всевозможные
кратные неисправности неразветвляющихся входных
полюсов и ветвей разветвлений сети образуют множест-
во 5х характеристических неисправностей. Узлы сети
рис. 3-1, неисправности которых входят в множество
5х, на рис. 3-39 отмечены крестами.
МЕТОД ЭКВИВАЛЕНТНОЙ ФОРМЫ
Теперь рассмотрим метод построения проверяющего
теста {Х}п для случая одиночных константных неис-
правностей в логических сетях произвольной конфигу-
рации, основанный па исследовании аналитического вы-
ражения прямой или обратной эквивалентной формы
дерева. Например, для непзбыточных сетей, реализован-
ных в простом базисе, один из очевидных способов
использования этого аппарата состоит в применении
алгоритма АЗ-5. При этом для каждой неисправности
строится проверяющий ее набор А; (О, о,-) мето-
дом, основанным на проверке хотя бы одного подмно-
жества Q'h множества Qk букв единичного терма k ЭФ
(ОЭФ), фиксируемых неисправностью о, равными 1
(см. § 3-4). Задача построения совокупности О, не-
исправностей в алгоритме АЗ-5 также решается
с использованием аппарата ЭФ (см. § 3-5). Аналогич-
ным образом может быть построен тест {А} для избы-
точных сетей, реализованных в простом базисе, с одно-
временным получением множества 0х в соответствии
с описанной выше процедурой. Если отказаться от
300
свойства непзбыточностп проверяющего теста {А'}П и
поэтому не решать в алгоритме АЗ-5 задачу построе-
ния совокупности неисправности Oi, то тест{Х}п=
= и Х (0, о,-).
Известен другой способ построения неизбыточного
теста {А'}п, использующий аппарат ЭФ и не требующий
перечисления характеристических неисправностей сети
п анализа фиксаций букв ЭФ (ОЭФ) каждой такой
неисправностью. Рассмотрим этот способ.
Прежде всего напомним и несколько обобщим понятие
проверки буквы di(ai — а,, если о — 1, и ai = а,, если о =
= 0) терма k ЭФ или ОЭФ (в § 3-4 было определено по-
нятие проверки на 1 совокупности Rk букв /г-го терма ЭФ
или ОЭФ). Будем говорить, что буква а’, принадлежащая
/г-му терму выражения ЭФ или ОЭФ, проверяется па 1
(0), если найден такой набор значений входных пере-
менных сети, на котором, во-первых, буква а] прини-
мает значение 0 (1), во-вторых, все остальные буквы
/г-го терма принимают значение 1 и, в-третьих, по край-
ней мере одна буква каждого терма, отличного от /г,
выражения ЭФ или ОЭФ принимает значение 0 (т. е.
такой терм равен 0). Если буква а\ некоторого терма
проверяется па 1 (0), то будем говорить, что в этом же
терме проверяется па 0 (1) буква а{ .
Пример 3-64. ЭФ функции сети рис. 3-4 имеет вид (3-11):
z = V «’Ci V bib? \/ biCi V atbib2 Ci.
0 1 0 0 0 1 0 0 110 1
Для проверки буквы at в первом терме на 1 полагаем входные
переменные а и b равными соответственно 0 и 1 (обязательные
значения букв подчеркнуты); при этом все остальные термы (3-11)
становятся равными 0. Положим входную переменную с, например,
равной 0, тогда все буквы ЭФ функции сети на наборе 010 (abc)
принимают значения, написанные под соответствующими буквами ЭФ
функции z. На наборе 010 кроме проверки на 1 буквы at первого
терма проверяются на 1 буква 6] третьего и буква 5г пятого термов.
Нетрудно показать, что для любой буквы at из ЭФ
можно указать по крайней мере одну букву dt из ОЭФ;
отсюда, в частности, следует, что если на наборе Д'/
301
проверяется на 1 (0) буква dt ЭФ, то в ОЭФ на этом же
наборе Xj проверяется на 0(1) буква а’ хотя бы в одном
терме.
Пример 3-65. На наборе 010 буквы ОЭФ функции сети рис. 3-4
принимают значения, написанные под соответствующими буквами:
2 = dibtbz v ttibiCi V Ю Ьг Ci V bi Ьг Cl.
Ill 110 001 001
Таким образом, в ОЭФ на наборе 010 проверяются на 0 буквы
щ, Ь] и Ь2 первого терма.
Учитывая отмеченную дуальность проверки букв ЭФ
и ОЭФ, в дальнейшем будем говорить о проверке толь-
ко на 1 букв как ЭФ, так и ОЭФ.
Назовем пару букв аа ар(а^=р), содержащихся в тер-
ме ЭФ или ОЭФ, парой букв вида В. Опуская формаль-
ные доказательства, укажем на особенности входных
наборов сети, проверяющих некоторые отдельные буквы
ее ЭФ или ОЭФ.
1. Если на входном наборе Xj проверяется на 1 буква
аа(аа) некоторого терма ЭФ или ОЭФ, не содержащего
пары букв вида В, и при этом нет терма, в котором про-
веряется на 1 буква а?(аХ а^р, то на [наборе Xj в ис-
следуемой сети образуется простой существенный путь
{а, г} от входного полюса а до выхода сети z, причем
этот путь совпадает с путем, ассоциируемым с прове-
ряемой буквой aa(aj и закодированным с помощью
индекса а. Как уже указывалось ранее, на наборе Xj
будут обнаруживаться ровно по одной неисправности
каждого узла сети, принадлежащего этому пути.
Пример 3-66. Для сети рис. 3-1 ОЭФ имеет вид (3-8); па вход-
ном наборе 0111 (abed) получаем:
z = Ьщ2 V btCidi V bibzds \J at Cia2 V ai CiC2d2
oo oil ;o i i loo ioii
V Gi c,b2d3 V aiOidi V«i diC2d2 V «i dibada.
1011 100 1011 toil
Во втором и шестом термах ОЭФ, не содержащих пар букв
вида В, проверяются на 1 соответственно буквы Б1 и ёь Анализируя
поведение сети, устанавливаем, что на исследуемом входном наборе
Xj=0111 образуются простые существенные пути: {Ь, г} = {Ь, 6,9, г)
и {с, г} = {с, 1, 4, 6, 9, z}.
302
2. Если на входном наборе сети Л/ буква аа (аа) про-
веряется на 1 только в одном или нескольких термах ЭФ
или ОЭФ, содержащих пару букв вида В, например
ааа? (а =/=$), то на наборе Ху в исследуемой сети нет су-
щественного пути от входного полюса а до выхода
сети z, т. е. неисправность s=a1(a°) на наборе Xj не
обнаруживается. Однако в рассматриваемом случае на
наборе Xj может образоваться простой существенный
путь, который, во-первых, принадлежит пути, ассоцииро-
ванному с буквой аа, и, во-вторых, начинается в неко-
тором внутреннем узле сети.
Пример 3-67. В примере 3-66 буква <71 проверяется в 8-м н 9-м
термах, содержащих пару букв вида В. Нетрудно убедиться, что на
рассматриваемом наборе Х,=0111 не проверяется неисправность
входного полюса d s=d°, но образуется простой существенный путь,
принадлежащий пути, ассоциируемому с буквой dit и начинающийся
в узле (/, 2), т. е. обнаруживаются определенные неисправности
узлов пути {(/, 2), г}.
3. Если на входном наборе Xj в нескольких термах
ЭФ пли ОЭФ, не содержащих пар букв вида В, прове-
ряются па 1 буквы с одной и той же переменной, на-
пример а (а), но с попарно различными индексами, на-
пример сц, а.2, ..., at, то на наборе Xj образуется
сложный существенный путь от входного полюса а до
выхода сети. Существенный путь {a, z} образован путя-
ми, ассоциированными с проверяемыми буквами а
аа*, aat. Этот путь обладает тем свойством, что от
любого его узла на рассматриваемом наборе Xj обеспе-
чивается существенный путь до выхода сети. Таким
образом, па наборе Xj проверяется некоторая неисправ-
ность любого узла сети, принадлежащего сложному
существенному пути {п, z}. Будем такой существенный
путь называть собственным существенным путем.
Пример 3-68. ЭФ и ОЭФ функции сети рис. 3-40 имеют вид:
Z = О1Й1С1 V ОгЬгСг V (нЬ&гЬг XJ CjCaJ (3-45)
z — at ci V b. Ci V я2 c2 V 62 c2. (3-46)
01 01 01 01
Здесь индексом 1 обозначены пути, проходящие через элемент 2,
а индексом 2 — через элемент 3. На входном наборе 110 (abc) про-
веряются на 1, например, буквы щ и а? ОЭФ (3-46) ; пути, ассоции-
руемые с этими буквами (а, 1, 2, 4, z) и (а, 1, 3, 4, z), составляют
303
сложный существенный путь (cl, 2}, который образуеюя на рассма*
триваемом наборе, причем этот путь является собственным сущест-
венным путем, так как на наборе 110 образуются существенные пути
от всех узлов сложного пути (а, г}, а именно существенные пути
{а, г), {/, г} {(2, 2), г), {(3, /), г}, {2, г), {3, г}.
Для простоты рассмотрим сети, реализованные на
элементах простого базиса. Отмеченные выше особенно-
сти проверки букв ЭФ и ОЭФ дают возможность сде-
лать следующее заключение.
Рис. 3-40. Пример избыточной логической сети
с непроверяемыми по отдельности буквами ЭФ
Если в ЭФ и ОЭФ функции сети, из которых удале-
ны термы, содержащие лары букв вида В (такие ЭФ п
ОЭФ будем называть сокращенными), совокупностью
входных наборов {X} проверена на 1 совокупность букв
такая, что, во-первых, пути, ассоциированные с прове-
ренными буквами, включают все узлы сети п, во-вторых,
проверенные буквы представляют пары букв, в каждую
из которых переменные входят с одним и тем же индек-
сом в прямом и инверсном виде, то совокупность {X}
есть проверяющий тест {X} сети для случая одиночных
константных неисправностей в ней.
Пример 3-69. В табл. 3-13 столбцы (кроме первого) соответст-
вуют термам сокращенных ЭФ и ОЭФ функции сети рис. 3-1 [с л.
(3-7) и (3-8)] а строки — входным наборам. Для проверяемых букв
значения, предписываемые им соответствующими входными набора-
ми, подчеркнуты. Построенная совокупность входных_ наборов про-
веряет следующие буквы ЭФ и ОЭФ ah йц й2; 6ь Ьц сь сц Ь2, Ь2;
й2, й2; d:i, d3; пути, ассоциированные с буквами at, bi, Ci, b2, d2, da,
включают все узлы сети. Наборы табл. 3-13 составляют тест {Х}П
сети.
Для сетей, реализованных в произвольном базисе,
кроме проверки указанной совокупности букв ЭФ и
304
Таблица 3-13
Наборы Термы
ЭФ ОЭФ
abed n, й, bi ct di a-2 c2 O2 di bi fig di </3 ft, o2 &i Ci di a, c, b3
0 10 1 0_1 1 0 I 1 'Л 1 0 0 I 1 0 1 0 0
10 0 0 1 0 ООО 0 1 1 0 1 1 o_i 1 _0 1 I
0 0 11 110 1 0 111 0 0 0 1 oioo 0 0 10 0 0 0_1 1 l_o 1 1 0_l 1 0 0 1 0 0 w _0 1 0 0 1 0 <1 0 i o_ 0 0 1 _0 1 I l_0_l 000 1 1 2. £1 1 1 l_0 1 1 1 1 £1 1110 10 0 0
ОЭФ необходима дополнительная проверка того, чтобы
каждом} узлу исправной сети наборы, обеспечивающие
существенные пути, проходящие через данный узел,
предписывали сигналы 0 и 1.
Так как после построения очередного набора, прове-
ряющего еще пе проверенную букву, по ЭФ (ОЭФ)
легко определить проверяемые этим набором другие
отдельные буквы, то для построения неизбыточного про-
веряющего теста можно воспользоваться описанной
в данном параграфе процедурой. Наоборот, отказав-
шись от получения непзбыточного теста, можно отка
заться от какого-либо анализа графа сети и строить
проверяющий набор для каждого одного вхождения
каждой буквы ЭФ и ОЭФ
К сожалению, изложенные выше относительно про-
стые условия построения проверяющего теста являются
лишь достаточными, но ие являются необходимыми.
Действительно, возможна такая логическая сеть, в ко-
торой неисправность некоторого входного полюса про-
веряется на наборах, каждый из которых образует
сложный существеннуй путь от рассматриваемого полю-
са, не являющийся собственным. Тогда ни одна буква
ЭФ или ОЭФ функции сети, соответствующая этому
полюсу, не может быть проверена, а следовательно, не
будет обнаружена рассматриваемая существенная не-
исправность.
Пример 3-70. Рассмотрим сеть (правда, избыточную), изобра-
женную на рис. 3 40 Нетрудно убедиться, что ни одна буква выра-
20—358 305
Жения (3-45) не может быть проверена на 1. Однако, например, нй
входном наборе 010 (abc) осуществляется проверка неисправности а'.
На этом входном наборе образуется сложный существенный путь
{а, г} от входного полюса а через элементы 2 и 3, причем этот путь
не является собственным, так как на наборе 010 не образуется суще-
ственный путь, например, от узла (2, 2), принадлежащего пути {а, г].
С другой стороны, возможна логическая сеть такая,
что неисправность некоторого ее внутреннего узла (не
являющегося входным полюсом) обнаруживается на на-
борах, каждый из которых не проверяет неисправности
ни одного входного полюса, имеющего путь до рассма-
триваемого узла. В этом случае также не будет прове-
рена ни одна буква аа или аа ЭФ п ОЭФ, с которой
ассоциируется путь, проходящий через рассматриваемый
узел.
Пример 3-71. Для неизбыточной сети рис. 3-41 имеем:
z = а2Ь2 V fliCi V с> V bidi V bi dr,
(3-47)
z = аг «1 Ci bi di \/ аг щ Cibidi V n2ci«ibi di XJ asCiOibidi \/
V b2 ci Ci bi di V Ьг a. Ci bt d, V b2 ски bi di V b2Ciaibidi. (3-48)
Здесь индексом l обозначены пути, проходящие через элемент 1
или 3, а индексом 2 — через элемент 2.
Если в ОЭФ (3-48) удалить термы 3, 4, 6 и 8, которые содержат
пары букв вида В, то в сокращенной ОЭФ не могут быть провере-
ны буквы а2 и Ь2. В то же время на наборе 1111 (abed), на котором
не проверяется неисправность ни одного входного полюса сети, осу-
ществляется проверка неисправностей (2, /)°, (2, 2) °, 2°. Заметим,
что на наборе 1111 проверяются буквы а2 в четвертом и 52 в восьмом
Рис. 3-41. Пример неизбыточной
логической сети с непроверяемы-
ми буквами сокращенной ЭФ.
306
термах несокращенной ОЭФ
(см. проверку букв в термах,
содержащих пары буквы ви-
да В).
Возможны также слу-
чаи, когда неисправ-
ность внутреннего узла
сети проверяется на вход-
ном наборе, на котором
не проверяется ни одна
буква несокращенной ЭФ
и ОЭФ.
Таким образом, невоз-
можность удовлетворения
изложенным выше усло-
виям построения прове-
ряющего теста не озна-
чает, что неисправно-
11003—23
сти узлов, принадлежащих путям, соответствующим не-
проверенным буквам ЭФ или ОЭФ, являются несуще
ственными.
Выходом из создавшегося положения (и при неже-
лании индивидуального рассмотрения фиксации букв
ЭФ и ОЭФ каждой неисправностью огеОх, как это
требуется по алгоритму АЗ-5) является проверка на 1
в каждом /г-м терме ЭФ и ОЭФ всех таких проверяемых
подмножеств его букв, чтобы найденные наборы могли
обнаружить любую неисправность s, относительно кото-
рой терм k является единичным. Заметим, что если
в некотором терме /г ЭФ (ОЭФ) входным набором Xj
проверено на 1 некоторое подмножество его букв, то
набор Xj обнаруживает любую неисправность s, относи-
тельно которой рассматриваемый херм k является, во-
первых, единичным и, во-вторых, множество Qh всех
букв терма k, фиксируемых неисправностью s равны-
ми 1, целиком содержит подмножество Q'h (т. е.
Из сказанного следует, что в каждом терме /г
ЭФ и ОЭФ функции сети следует проверять на 1 не лю-
бое проверяемое множество Q/< его букв, а лишь каждое
такое множество Qh букв, любое подмножество Q'h ко-
торого (Q'^cQ/,) не проверяется. Множество Qi, букв
терма k, каждое подмножество Q'h которого не про-
веряется, назовем ядром терма k.
Таким образом, совокупность входных наборов про-
извольной логической сети, проверяющих на 1 в каждом
терме ЭФ и ОЭФ функции сети все его проверяемые
ядра, является проверяющим тестом сети для случая
кратных константных неисправностей в ней, или полным
проверяющим тестом.
Из сказанного выше вытекает следующая рекомен-
дация для проверки всех проверяемых ядер букв тер-
ма /г, содержащего щ, букв. Вначале необходимо пы-
таться проверить по отдельности каждую его букву и
только, если удалось проверить лишь (пь—2) или менее
букв, переходить к проверке всех пар не проверенных
по отдельности букв терма k, а при наличии не менее
одной тройки попарно непроверяемых букв переходить
к проверкам всех таких троек и т. д.
Пример 3-72. На рис. 3-42 изображен граф некоторого терма 1<
(пк~8) ЭФ или ОЭФ, узлы 1—6 которого условно соответствуют
непроверяемые по отдельности буквам терма, а узлы 7 и 8 — его
проверяемым отдельным буквам. Сплошные (пунктирные) линии на
20* 307
xi Термы
а bed fej а3 bt са d2 bi b2 ds Cl c5 Ct
1 1 0 1 0 1 0 0 1 0 1 1 0 1 1
0 1 1 1 0 0 0 1 1 0 1 1 1 0 0
0 0 0 1 1 2 1 21 1 2 1 12 1
0 1 0 0 0 0 0 0 0 0 1 0 1 0 1
0 0 1 0 1 0 1 1 0 1 0 0 1 0 0
1 1 0 0 0 1 0 0 0 0 1 0 0 1 1
Рис. 3-42. Иллюстрация нахож
дения ядер терма ЭФ (ОЭФ).
графе соединяют пары вершин, ко-
торым соответствуют пары букв,
проверяемые (непроверяемые) в
рассматриваемом терме. Кроме на-
боров, проверяющих отдельные
буквы (соответствующие вершинам
7 и 8) и проверяющих пары букв
(соответствующие парам вершин,
соединенных сплошными линия-
ми), в рассматриваемом терме не-
обходимо проверить, если это ока-
жется возможным, лишь две трой-
ки попарно непроверяемых букв,
соответствующие тройкам вершин
1. 2, 3 и /, 3, 4.
Пример 3-73. Для сети, изо-
браженной на рис. 3-1, в табл. 3-13
представлены три набора 0101, 1000
и ООН, проверяющие по отдель-
ности все .проверяемые буквы
каждого терма ЭФ (3-7). Заметим,
что буква di во втором терме, Ь? в четвертом, с2 в пятом, </2 и d3
в шестом термах ЭФ не проверяются. Пара букв cl^ds в шестом тер-
ме проверяется на наборах 0101 и ООН. Таким образом, на указан-
ных трех наборах проверяются на 1 все проверяемые ядра каждого
терма ЭФ функции сети. В табл. 3-14 выписаны все термы несжатой
ОЭФ (3-8). На первых пяти наборах (см. табл. 3-13) проверяются
все проверяемые ядра термов ОЭФ, за исключением буквы щ в седь-
мом терме, которая проверяется на шестом наборе 1100. Таким
образом, найденные девять наборов представляют тест {X} ц для
случая кратных константных неисправностей сети рис. 3-1 *.
* На самом деле можно показать, что набор 1100 является из-
быточным и, таким образом, тест {Х}п, построенный в примере 3-69
для класса одиночных неисправностей, является тестом п для класса
кратных иепсправпортей,
30§
Таблица 3-1
ОЭФ
dj Ci С-2 Cl 2 «1 Ci di dl d. Сд cij ch bt d3
0 10 1 0 1 1 1 0 1 0 0 0 0 1 0 0 11
1 0 1 1 l_0 1 1 1 0 0 1 9. 1 1 10 11
110 1 1 1 0 1 1 0 0 1 0 0 1 10 0 1
110 0 1 1 1 2. 1 2 1 1 1 0 0 1 1 1 0_
10 10 1 0 0 0 1 о 1 1 1 1 £ 110 0
0 10 0 0 1 1 0 0 1 1 0 1 0 0 0 110
Очевидно, что для непзбыточных сетей п для слу-
чая одиночных константных неисправностей в них такой
способ построения теста может потребовать много
«лишних» вычислений и дать «сильно» избыточный тест
за счет проверки подмножеств букв, фиксация которых
не имеет физической интерпретации на языке одиноч-
ных константных неисправностей, а также за счет мно-
гократной проверки одних и тех же подмножеств букв
в разных термах.
Для случая кратных неисправностей тест, построен-
ный указанным способом, по-видимому, будет менее
избыточным. К другим недостаткам метода построения
проверяющего теста, основанного на проверке букв ЭФ
и ОЭФ, следует отнести большую размерность ЭФ
(ОЭФ) для практических комбинационных устройств и
необходимость получения и анализа не только ЭФ, но
н ОЭФ.
МЕТОД ВЫЯВЛЯЮЩИХ ПАР НАБОРОВ
В ряде конкретных случаев исследования сетей в ре-
зультате правильной реакции сети на наборы проверяю-
щего теста {X} в предположении одиночных констант-
ных неисправностей удается сделать заключение о пол-
ном или почти полном отсутствии в исследуемой сети
кратных константных неисправностей. Такое свойство
специальных наборов теста {Х}п. проверяющего одиноч-
ные неисправности в сети без разветвлении, уже отме-
чалось выше.
sop
Необходимо отметить полезное свойство выявляющей
пары наборов (Ха0 и Ха1), соседних по переменной ха
и проверяющих в предположении одиночных неисправ-
ностей состояние входного полюса ха. Это свойство со-
стоит в возможности выявляющей пары наборов обна-
руживать некоторые кратные неисправности в сети
с разветвлениями.
На основе соображений, сделанных выше относи-
тельно свойств этих наборов для случая сети без раз-
ветвлений, можно заключить следующее. Пусть so —
произвольная константная неисправность сети такая,
что среди составляющих ее одиночных неисправностей
содержится по крайней мере одна неисправность узла1
сети, через который проходят все пути от входного по-
люса х а до выхода сети z (для простоты рассматрива-
ются одновыходные сети).
Тогда на паре наборов X и Xai обнаруживается любая
неисправность sa сети. Действительно, в исправной сети
z(XaD)=^z(Xai), в то время как при наличии в ней не-
исправности sazS“ (A'a0) = zS“(A'ol). Таким образом, правиль-
ная реакция исследуемой сети на наборы Х^ и Xai гаран-
тирует исправность узла i (и, в частности, входного полюса
xj в предположении кратных константных неисправностей.
Иногда будем говорить, что указанные наборы Ха0, Ха1
проверяют исправность узла i (входного полюса ха).
Пример 3-74. Для сети рис. 3-18 следующие пять наборов
составляют множество пар (A’OLo> ^ai) для всех четырех входных
полюсов сети (a k d h):
X, 0x1x00
Хг 1 J 1 j 0 0
X, 0 0 / 0 0
Xi 0 0 10
Хъ 0 1 01
Дугами выделены пары наборов вида (Х^, Xal)(a = /z, k, d, h).
На множестве наборов Xi-j-Xs обнаруживается любая кратная неис-
правность сети, в которую входит хотя бы одна из неисправностей
узлов: а, 1, 3, k, d, 2, h. Для того чтобы построить проверяющий
тест относительно одиночных константных неисправностей, наборы
Xi+Xs необходимо дополнить наборами, обнаруживающими неис-
310
ПравносТи узлов b И с сети рис. 3-18, которые являются ветВЯМй
разветвлений. Поскольку на соседних наборах Л, и Х3, проверяющих
состояние входного полюса k, существенный путь {/г, г] простой,
а узел с принадлежит этому пути, то наборы X, и Х3 проверяют
состояние узла с. Для проверки состояния узла b известными мето-
дами могут быть построены два набора: Лс=1010 и .¥7=1110. Та-
ким образом, на множестве наборов заведомо обнаружива-
ются все одиночные неисправности рассматриваемой сети и все крат-
ные, за исключением кратных неисправностей узлов b и с (на самом
деле в данном примере наборов X\^-Xi достаточно для обнаружения
любых константных неисправностей сети).
В некоторых случаях удается выделить и другие крат-
ные неисправности сети, обнаруживаемые парой соседних
наборов и Ха1. Для этого необходимо сопоставить
конфигурацию подсети [a, z]* и конфигурацию существен’
ного пути {ха, z} на наборах Л'а0 и Xol. Заметим, что на
обоих наборах пары существенный пут*. {ла, z} будет одним
и тем же. Пусть узел i принадлежит простому участку
существенного пути {ха, г} на наборах Хай и Ха1. Будем
называть путем, обходящим узел i, всякий путь в под-
сети {a, z}, начинающийся из узла разветвления j пути
{лк, z}, расположенного между полюсом ха и узлом i,
закапчивающийся на выходе сети z и не содержащий узла i.
Правильные, т. е. различные (0,1 или 1,0), значения сигнала
на выходе сети z на паре наборов Ха0 и ХО1 при неисправ-
ности Г могут быть лишь в случае передачи изменения
сигнала на входном полюсе ха на выход сети по пути,
обходящему неисправный узел i. Причем этот путь стал
«проводящим» вследствие некоторой кратной неисправ-
ности сети, включающей неисправность узла i. Для
простоты ограничимся рассмотрением сетей в булевом
базисе. Заметим, что если в такой сети вершина / при-
надлежит существенному пути {ха, z}, то четность числа
инверсий всех его .D-путей между вершиной j и выход-
ным полюсом z одинакова. Будем называть ее чет-
ностью числа инверсий участка {/', z} существенного
пути. Рассмотрим один частный случай.
Пусть четность числа инверсий в каждом обходящем
узел i пути (/, z) отлична от четности числа инверсий
участка {/, z} существенного пути {ха, г}. Тогда на паре
* Подсетью [a, г] будем называть совокупность полюсов ха, z,
элементов исходной сети, лежащих на всех путях от входного по-
люса ха до выхода z, и связей между ними.
311
наборов Ха0 и Ха1 будет обнаружена любая кратная не-
исправность s‘ сети, содержащая неисправность узла i,
т. е. правильная реакция сети на наборы Ха0 и Ха] озна-
чает исправность узла i в предположении кратных неис-
правностей. Действительно, в силу указанного отличия
четности чисел инверсий реакция схемы с неисправностью s'
на наборах Ха0 и Ха1 либо одинакова, либо различна, но
в последнем случае не может быть правильной, например
z (X 0) = 0, z (X ,) = 1, а / (X 0) = 1, zsi (X ,) = 0.
Распространение полученного результата на сети,
реализованные в простом базисе, трудностей не вызы-
вает, поскольку такая сеть может быть представлена
в булевом базисе без увеличения числа узлов развет-
влений. Заметим, что в рассмотренном ранее случае,
когда узел i является узлом простого участка не только
существенного пути {ха, z}, но и узлом простого участка
всей подсети [a, z]*, вообще нет путей, обходящих
узел к
Пример 3-75. Для сети рис. 3-1 пара соседних по переменной а
наборов Ха0=0001 и Xai = 1001 проверяет состояние входного по-
люса и по простому существенному пути {а, z} = {a, 4, 7, 8, 9, г}.
Единственный обходящий путь (4, 6, 9, z) обходит узлы (7, 7), 7, 8
и не имеет инверсий. Участок {4, 7, 8, 9} существенного пути {а, г}
содержит одну инверсию. Узлы а, 4 и 9 вообще не имеют обходящих
путей. Следовательно, на рассматриваемой паре наборов будет обна-
ружена любая кратная неисправность, содержащая неисправность
хотя бы одного из узлов а, 4, (7, 7), 7, 8 9.
Рассмотрим теперь случай, когда четности чисел инвер-
сий в некотором одном обходящем узел i пути (/, г) и в
участке {/, z} существенного пути {ха, z} совпадают.
Будем искать некоторые условия, при выполнении которых
наличие такого обходящего пути не может привести к пра-
вильной реакции на наборы А'а0 и А"а1 сети, содержащей
неисправность в узле t, и в предположении кратных кон-
стантных неисправностей. Предположим, что в исследуемой
сети па свободном входе некоторого элемента т; обходя-
щего пути (/, z) на наборах Ха0 и Xai образуется одно
и то же значение сигнала, которое однозначно фиксирует
значение выхода элемента тр Это означает, что по обхо-
дящему пути (/, z) на наборах Ха0 и X } не может про-
* Узел с является узлом простого участка подсети fa, z], если
через него проходят все пути от входного полюса ха до выхода Z.
312
изойти передача информации об изменении сигнала
в узле j. Будем говорить, что при этом происходит па-
дежная отсечка обходящего пути (/, z) в исследуемой
сети. Заметим, что в исправной сети в любом обходя-
щем пути всегда найдется элемент т], значения сигналов
на выходе которого на наборах А"а0 и Ха1 одинаковы.
Таким образом, в исправной сети все обходящие пути
отсечены, но задача состоит в обеспечении их отсечки и
в исследуемой сети, если это возможно, т. е. в обеспе-
чении надежной отсечки. В этих условиях правильная
реакция сети на наборы Ха0 и А'а1 гарантирует
исправность узла i в предположении .кратных констант-
ных неисправностей в сети.
Пример 3 76. В сети рис. 3-1 пара соседних наборов Xdo=OOlO
и Xdi = 0011 (a6cd) проверяет исправность входного полюса d по
простому существенному пути {d, z} = {d, 1, 4, 7, <8, 9, z}. Для вхо-
да 2 элемента 1 имеется единственный обходящий путь (d, 3, 5,
3, 9, z) с таким же числом инверсий (одна), как и в участке {d, z,]
существенного пути. В исправной сети значение Ь = 0 на обоих рас-
сматриваемых наборах однозначно фиксирует значением 1 выход
элемента 5 принадлежащего обходящему пути, и, таким образом,
отсекает его
Рассмотрим некоторые условия надежной отсечки об-
ходящего пути на его элементе в исследуемой сети.
Найдем некоторую минимальную совокупность входных
полюсов {х}', на которых значения сигналов, обусловленные
общей частью наборов Ха0 и Ха} в исправной сети, одно-
значно фиксируют значение сигнала некоторых свободных
входов элемента т;х и значение сигнала на его выходе вне
зависимости от значения сигнала на его входе, принадле-
жащем обходящему пути. Тогда условие надежной отсечки
состоит в том, чтобы входные полюсы совокупности {х}'
и каждый узел I всех путей (хр, Л), где Хр£{х}', значе-
ние сигнала которого фиксируется в результате рассмот-
ренного однозначного распространения вплоть до элемен-
та т]}, были исправны. Информация об исправности входных
полюсов {%}' и каждого узла I должна быть предвари-
тельно получена на основе обработки результатов при-
ложения к исследуемой сети некоторой совокупности
входных наборов.
Продолжение примера 3-76. Пусть для обнаружения неисправ-
ностей входного полюса Ь к сети рис. 3-1 были приложены два со-
седних набора Хьо = 0001 и Хы = 0101 (abed), на которые проверяе-
мая сеть дала правильный ответ. Поскольку существенный путь
313
{b, z} = {6, 2, 5, 8, 9, z} — простой и содержит одну инверсию,
а в единственном обходящем пути (Ь, 6, 9, г) инверсий нет, то мож-
но сделать вывод об исправности всех узлов существенного пути
{b, z} и, в частности, входного полюса Ь, входа и выхода элемента 2.
Тогда на рассмотренной в начале примера 3-76 паре наборов, прове-
ряющих входной плюс d, обеспечивается надежная отсечка обходя-
щего пути на элементе 5 благодаря значению Ь=0 на наборах Хао
и Xai и исправности пути (Ь, 2, 5). Правильный ответ на наборах
Xdo и будет гарантировать исправность узлов (/, 7), 1, 4, обхо-
дящий путь которых надежно отсечен. Аналогичным образом на
этих наборах проверяется исправность узлов (7, 1), 7, 8, для кото-
рых другой обходящий путь (кроме отсеченного) (4, 6, 9, г) имеет
иную четность числа инверсий, чем участок {4, 7, 8, 9, z} существен-
ного пути {d, г}.
В табл. 3-15 для.сети рис. 3-1 приведены пары соседних набо-
ров Ха0 и Xai (а = а, Ь, с, d) и указаны простые существенные
пути от входных полюсов сети на этих наборах. На каждой паре
наборов Ха0, Xai галочками отмечены узлы, исправность которых
гарантируется при правильных ответах сети на этой паре наборов
в соответствии с изложенными выше правилами. Заметим, что на
последней паре наборов 0100 и 0101 обходящий путь (d, 1, 4, 7,
8, 9, z), имеющий ту же четность числа инверсий, что и участок
существенного пути {d, 3, 5, 8, 9, z}, надежно отсечен благодаря
значению c=«/i=0 и исправности узла с (которая была установле-
на в результате правильного ответа сети на наборы Лсо=(0101 и
ХС1 = 0111). Обходящий путь (d, /, 4, 6, 9, z) имеет четность числа
инверсий, отличную от четности числа инверсий параллельного уча-
стка рассматриваемого существенного пути. Поскольку в каждом
столбце табл. 3 15 имеется отметка (галочка), т. е. исправность
каждого узла сети гарантируется, совокупность семи наборов 0001,
1001, 0011, 0111, 0101, 0010, 0100 является полным проверяющим
тестом {Х}п сети для случая константных неисправностей.
Рассмотрим еще один прием надежной отсечки неко-
торого обходящего узел i пути (/, z). Пусть по-прежне-
му этот путь — единственный из всех обходящих узел i
путей, требующий надежной отсечки. Построим, напри-
мер, на наборе Ха1 в исправной сети все D-пути, на-
чинающиеся из полюса Ха> в том числе и тупиковые D
пути (см. § 3-4). Предположим, что на координатах
элемента т;х булева базиса рассматриваемого обходя-
щего пути сложился тупиковый D-куб, имеющий на
одной входной координате mi символ D{D), на другой
m2 — символ D(D) и на выходной и остальных входных
коорднатах — константы 0 или 1, причем вход mt с сим-
волом D(D) принадлежит рассматриваемому обходяще-
му пути. Выделим свободный вход mz элемента i)X1
имеющий символ D(D)
314
Таблица 3-15
> > > > > >
Со > > > >
> >
> V
(7. 1) | > >
(S. Л | V
> >
м- > >
Со >
CN >
- > >
| (г ‘з) >
| (I '£) >
| (/ 'г) Л
(1,П | Л
43 Л >
>
•е> > >
е >
Существенный путь {а, 4, 7, 8, 9, z} {6, 6, 9, 2} {Ь, 2, 5, 8, 9, 2} {с, 1, 4, 6, 9, 2} {d, 1, 4,17, 8, 9, Z} {d, 3, 5, 8, 9, 2}
| Р о q v 0 0 0 1 10 0 1 0 0 11 0 111 0 0 0 1 0 10 1 0 10 1 0 111 0 0 10 0 0 11 0 10 0 0 10 1
315
Предположим известным, что в исследуемой Сети на
паре входных наборов Ха1 и Ха0 на выделенном свободном
входе т2 элемента т)х имеют место соответственно значения
О и 1 (1 и 0). Тогда возможны два случая. В первом слу-
чае в исследуемой сети на входе т, элемента цх, принад-
лежащем пути (/, z), на наборах Ха1 и Ха0 образуются
соответственно значения 1 и 0 (0 и 1). При этом значения
сигналов на выходе элемента т;х будут одинаковы и обхо-
дящий путь надежно отсечен. Во втором случае значения
сигналов на входе trh элемента т]х одинаковы, например,
при наличии константной неисправности узла участка (j, к)
рассматриваемого обходящего пути (/, z). Очевидно, что
в этом случае путь (/, z) отсечен1. Для реализации условия
надежной отсечки найдем некоторую минимальную сово-
купность входных полюсов {%}', на которых значения сиг-
налов, обусловленные обдей частью наборов Xa0 и Xaif
такие, что при рассмотрении их и значения D(D) на вход-
ном полюсе ха в качестве исходной фиксации операция ОР
фиксирует значением D (D) свободный вход т2 элемента т]х.
Тогда условие надежной отсечки состоит в исправности
всех входных полюсов {х}', входного полюса ха и узлов
всех путей (ло, Я) и (хр, Я), где л?£{х}', значения сигна-
лов которых фиксируются вплоть до элемента т;х в резуль-
тате рассмотренной операции ОР.
Пример 3-77. В сети рис. 3-43 на паре соседних наборов X2i = 11101
и %2о= 10101 (Х1Х2Х3Х4Х5) обеспечивается проверка исправности вход-
ного полюса х2 по простому существенному пути {х2, z} = {х2, 1, 5,
7, 8, г], выделенному на рисунке жирной линией. Для узла (5, 2)
имеются два обходящих пути: (хг, 2, 6, 8, г) и (1, 4, 6, 8, z). Пер-
вый путь не требует отсечки, так как он и участок {х2, г} сущест-
венного пути имеют разные четности чисел инверсий. Второй обхо-
дящий узел (5, 2) путь, выделенный пунктирной линией, требует
надежной отсечки. Изобразим на рис. 3-43, например на наборе Х21,
все D-пути (в том числе п тупиковые) от входного полюса х2. На
элементе 6 (И) образуется тупиковый D куб DD0. Сигнал I) на сво-
бодном входе элемента 6 является следствием ОР исходной фикса-
ции x2 = D, х5=1. Таким образом, для надежной отсечки обходящего
1 При этом значение сигнала на выходе элемента т1Х может ме-
няться на наборах А'а0 и Ха}, так как через элемент т;х проходит
еще один обходящий узел i путь, но по условию только один рас-
сматриваемый обходящий узел i путь (/, z) имеет ту же четность
числа инверсий, что и участок {/, г} существенного пути.
316
пути (J, 4, 6, 8, z) достаточно предварительно установить Исправ-
ность входных полюсов X?, х5, входов и выхода элемента 2 На паре
наборов 01011, 00011, проверяющих исправность входного полюса
по простому существенному пути {х2, 2, 6, 8, г}, при правильном
ответе сети устанавливается исправность узлов х2 (2, 1) и 2, так как
в обходящих узлы (2, 1) и 2 путях (л_2, 1, 4, 6, 8, г) и (х2, /, 5, 7,
8, г) инверсии пет, тогда как в участке {х2,г} существенного пути есть
Рис. 3-43. Пример логической сети, иллюстрирующей один вариант
надежной отсечки обходящего пути.
одна инверсия. Аналогично на паре наборов 01101, 01100, проверяю-
щих исправность входного полюса х$ по простому существенному
пути {х5, 2, 6, 8, z}, при правильном ответе сети устанавливается
исправность входного полюса и узла (2, 2). Таким образом, пра-
вильные ответы сети на рассмотренные в начале примера наборы
Х21 = ПЮ1 и Х20= 10101 гарантируют исправность узла (5, 2).
Рассмотренные выше примеры не исчерпывают всех
случаев, позволяющих сделать заключение об отсутст-
вии в сети некоторых кратных неисправностей в резуль-
тате правильных ответов исследуемой сети на наборы,
построенные для обнаружения одиночных неисправно-
стей. Но все они связаны с определенными свойствами
структуры исследуемой сети, конфигурацией существен-
ных путей на рассматриваемых входных наборах и др.;
эти свойства, очевидно, могут отсутствовать в общем
случае. Например, когда все входные полюсы развет-
вляются и для каждого входного полюса ха все пути
(ха, z) имеют одинаковую четность числа инверсий,
317
рассмотренные выше частные приемы обнаружений
кратных неисправностей уже не работают. Представляет
интерес описанный в литературе1 пример неизбыточной
сети, в которой можно указать некоторую кратную кон-
стантную неисправность s такую, что ни один из набо-
ров, обнаруживающих ее, не обнаруживает ни одной из
составляющих ее одиночных неисправностей о4, т. е.
для обнаружения неисправности s требуются «специаль-
ные» входные наборы.
3-7. ПОИСК НЕИСПРАВНОСТЕЙ В КОМБИНАЦИОННЫХ
УСТРОЙСТВАХ
В настоящем параграфе рассматриваются методы
построения диагностических тестов для решения задачи
поиска неисправностей в комбинационных устройствах.
Предварительно заметим, что в принципе задачи по-
строения диагностического теста и поиска неисправно-
стей в комбинационных устройствах могут быть решены
с помощью таблиц функций неисправностей и таблиц
покрытий. Однако такой подход часто оказывается
практически неприемлемым из-за больших размеров
этих таблиц. Часто решают задачу поиска неисправно-
стей с использованием диагностических словарей. Пол-
ный диагностический словарь должен содержать значе-
ния выходов комбинационного устройства при всех воз-
можных неисправностях на всем множестве входных
наборов устройства. По совпадению фактических выход-
ных значений испытуемого устройства со значениями,
записанными в диагностическом словаре, определяют
техническое состояние испытуемого устройства. По су-
ществу, полный диагностический словарь есть не что
иное, как таблица функций неисправностей. Имеется
довольно обширная литература по автоматическому со-
ставлению и использованию диагностических словарей.
Эти вопросы останутся вне рамок нашего рассмотрения.
Для случая одиночных неисправностей задача на-
хождения входного набора, различающего пару разли-
чимых неисправностей, может быть решена методом
существенных путей при задании устройства своей
структурой. Идея такого подхода была изложена в гл. 1,
необходимые и достаточные условия различения двух
1 См. замечания по библиографии.
318
неисправностей в терминах их проявления и транспор-
тировки сформулированы в § 3-4. Объединение входных
наборов, различающих все пары различимых одиночных
неисправностей, образует диагностический тест. Мы не
будем рассматривать этот метод более подробно, по-
скольку, во-первых, возможность построения диагности-
ческого теста путем рассмотрения всевозможных пар
одиночных неисправностей очевидна ,и, во-вторых, такой
подход даже при наличии простых методов выделения
по структуре заведомо неразличимых неисправностей
весьма трудоемок уже для небольших комбинационных
устройств.
Для того чтобы избежать перечисления пар всех не-
исправностей при построении диагностического теста,
можно воспользоваться следующей условной процедурой.
В качестве начальной части диагностического теста
используется проверяющий тест устройства. Если реали-
зация проверяющего теста показывает, что устройство
неисправно, то одним из методов, описанных в § 3-5,
определяется множество одиночных подозреваемых
неисправностей устройства, выделяемых проверяющим
тестом. Если полученная при этом глубина поиска неис-
правностей недостаточна, то можно выбрать какую-либо
пару подозреваемых неисправностей и найти в соответ-
ствии с рекомендациями, данными в § 3-4, входной па-
бор Xi (если он существует), различающий эту пару
неисправностей. Реализация набора Xi уменьшит число
подозреваемых неисправностей, по крайней мере, на
одну. Если различающего входного набора для выбран-
ной пары неисправностей не существует, то они нераз-
личимы. Аналогично можно найти входные наборы Xz,
Х3 ... и т. д., различающие все другие пары различимых
неисправностей из числа подозреваемых. Обычно услов-
ные диагностические процедуры оказываются короче
безусловных. Однако на каждом шаге эксперимента они
требуют анализа ответов устройства и принятия реше-
ния о том, какие входные наборы подавать на следую-
щем шаге.
Решение задачи построения диагностических тестов
для поиска кратных неисправностей (для краткости бу-
дем называть такие тесты полными диагностическими)
методами, требующими хотя бы частичного перечисле-
ния пар неисправностей, практически неприемлемо даже
для не очень сложных устройств. Причиной этому
319
является весьма большое число возможных кратных нс*
исправностей.
Рассмотрим методы построения алгоритмов поиска
кратных неисправностей, не требующие перечисления
последних.
Пусть задано комбинационное устройство в виде
одновыходной логической сети. Всем ветвям разветвле-
ний логической сети сопоставлены различные буквы.
Логическую сеть, в которой буквы, приписанные пераз-
ветвляющимся входным полюсам и ветвям разветвле-
ний, рассматриваются как независимые переменные
логической сети, назовем моделью М. В § 3 6 показано,
что любая кратная константная неисправность произ-
вольной сети может быть эквивалентно представлена
через задание а-состояний 0,1, Н независимых перемен-
ных модели М.
С введением модели М задача определения техниче-
ского состояния комбинационного устройства сводится
к задаче определения a-состояния модели М, т. е.
а-состояний всех ее независимых переменных
СТРУКТУРЫ ТИПА ДЕРЕВА
Сначала найдем решение задачи определения а со
стояния модели М для важного частного случая — для
логических сетей вида дерева в произвольном базисе.
Класс рассматриваемых неисправностей — константы 1
и 0 на входах и выходах логических элементов.
Пусть дерево реализует функцию z(xit х2....хп).
Независимыми переменными модели М для этой сети
являются входные переменные х(, х2, ..., хп
Вычислим булеву производную ^=z(xt, хг, ..., Xi,...
..., xn)®z(Xi, •••> л'> •••> х«) и запишем ее в форме ло-
гической суммы импликантов //, /=1, 2, ..., s:
^=/. VAV-V/- (3-49)
В § 3-4 показано, что булева производная dzldx, не
зависит от переменной xt. Конъюнкцию переменных 6^.—
= х”1' ... х°^~'х°^' (без переменной л-,) будем назы-
320
вать представителем импликанта Ij, если 1,~\ при
sv = 1. Здесь сй = 0,1 и
xi
ak I Xk, если Ofc = 1,
Xk I Xk, если ofe = 0.
Найдем совокупность представителей {s’*, es*, s1*},
1 < r < s, импликантов /, из (3-49) такую, что для каждого
импликанта // найдется его представителье**., &(Е{1,2,
Далее из каждого представителя ekx образуем пару со-
седних по переменной х£- входных наборов:
.»-J " V
" 1 Х1,\’.
что сокращенно будем записывать как ex=(xis.kx, xiekx)~
— 5* ekx. Входные наборы пары е^, соседние по перемен-
ной Xi, в § 3-6 были названы выявляющими. Поясним
теперь смысл этого определения. Будем говорить, что
па множестве наборов Т выявляется a-состояние 0,1
или Н переменной х„ если все векторы функции «-со-
стояний па множестве наборов Т, соответствующие ее
термам (см. § 3-5), имеют для переменной х,- одно а-
состоянпе — 0,1 или Н соответственно. Это означает,
что на множестве наборов Т можно сделать однознач-
ное заключение об a-состоянии переменной х;.
Рассмотрим объединение пар выявляющих наборов Тх ~
Г
= Н 8„ sfe. для одной переменной х,. Можно показать,
Л=1 » ‘
что Тх является совокупностью пар входных наборов,
выявляющих а-состоянпе Н переменной х, дерева, если
все множество входных наборов выявляет а-состояние
Н переменной х,. Объединение
п
совокупно-
стей ТXl для всех п входов х,- является полным диагно-
стическим тестом для дерева.
Для удобства ссылок описанную процедуру будем
именовать алгоритмом АЗ-6.
Пример 3-78. Найти по алгоритму АЗ-6 полный диагностический
тест для трехвходового одноэлементного дерева, реализующего
функцию 2=7, 72Хз V Х2 (Л1фХ,)_
21—358 321
Для построения теста вычисляем булевы производные по пере-
менным X], х2, х3, затем находим представителен импликантов про-
изводных и, наконец, пары выявляющих наборов. Результаты этих
операций сведены в табл. 3-16.
Т аб лица 3-16
i dzfdxi sx- ч
1 Хг\/Хз X2X3 (X2X3» X2X3) X2X3 = Л1 III он
2 Х1\/Хз X1X3 (Л'1 Хз» Х1Х3) 6, Х1Хз = • 011 001
3 Xi\/Xi Л1X2 (Xi Х2» Х1Х2) 6r XiXa = . лэ он 010
Объединение Т v пар е„ выявляющих наборов дает искомый
Л;
полный диагностический тест, содержащий четыре входных набора:
001, 010, ОН, 111.
Выбор других возможных представителей импликантов булевых
производных, приведенных в круглых скобках в столбце еж_ таблицы,
дает полный диагностический тест из шести входных наборов: ООО,
001, 010. 101, НО, 111.
Изложенный метод очень удобен при построении
полных диагностических тестов для древовидных сетей
простого базиса. Дерево обладает следующими двумя
свойствами:
1) функция г(Х1, ..., Х{, ,.хп), реализуемая дере-
вом, может быть представлена в нормальной форме,
в которой одна п та же буква встречается либо только
в прямом, либо только в инверсном виде;
2) существует бесповторпая скобочная форма пред-
ставления фуНКЦИИ 2. ФуНКЦИЮ Z(X1, ..., Xj, .... хп)
всегда можно представить в виде
Z = kiXi V кг ИЛИ Z = ktXi V kt, (3-50)
где ki, fa, fa, /г4 — некоторые булевы функции, не зави-
сящие от переменной х,-. Будем искать диагностический
322
тест отдельно для каждой независимой переменной х,
дерева. Из (3-50) следует, что
dz[dXi=k\kz или dz!dXi=kzkb.
Благодаря указанным выше свойствам всегда суще-
ствует один представитель всех импликантов булевой
производной dz]dXi. Для получения этого представителя
следует составить конъюнкцию из переменных функции'
/гД/гз) в том их виде, в каком они входят в выражение
для функции ki(ks). Дополнив эту конъюнкцию инвер-
сиями переменных функции fe(&4), получим коиыонк-
цию, которая является представителем всех нмпликап-
тов функции dzjdxi.
Отыскание набора, представителя всех импликантов
функции dzjdxi, можно производить ^непосредственно по
логической сети дерева согласно следующему алгоритму
АЗ-7. Выбираем вход Xi. Выделяем элементы, лежащие
на пути от выбранного входа х{ до выхода сети. При-
сваиваем всем, не входящим в выбранный путь входам
этих элементов значения 0 или 1, обеспечивающие су-
щественность пути от Xi до выхода сети (см. § 3-4).
Распространим эти значения до входов сети по следую-
щему правилу. Если выходу элемента присвоено значе-
ние 1 (0), то всем неинвертируемым входам этого эле-
мента присваиваются значения 1 (0).
Всем инвертируемым входам элемента присваиваются
значения 0 (1). По достижении всех входных полюсов
(кроме xi) получаем входной набор е*, являющийся пред-
ставителем всех импликантов функции dzldxi. Далее из
представителя е* образуем пару ех соседних по перемен-
ной xt выявляющих наборов S е. Объединение последних
xi xi
п
и S s является полным диагностическим тестом. Длина
i=i х‘ xt
этого теста не превосходит 2ц, где п — число входов
древовидной сети.
Помимо нахождения представителей импликантов
для булевых производных dzldx.-, в следующем разделе
нам потребуется находить представителей импликантов
для функции z(z), реализуемой древовидной сетью.
В случае сети в произвольном базисе для этого следует
получить некоторую импликантную форму функции
z(z) и найти совокупность представителей всех ее
21* 323
ймпликантов. В случае логической сети в простом базй-
се следует .приписать выходному полюсу сети, реали-
зующей функцию z, значение 1 (О) и распространить
это значение ко входам дерева способом, указанным
выше. По достижении всех входных полюсов получаем
входной набор ez (в-), являющийся представителем всех
импликантов функции z(z).
Рис. 3-44. Пример древовидной (бесповторной)
логической сети для построения полного диаг-
ностического теста.
Пример 3-79. Построить по алгоритму АЗ-7 полный диагности-
ческий тест для сети рис. 3-44.
Начнем с построения пары тестовых наборов для переменной Xj.
Выделяем элементы 1, 3, 5, лежащие на пути от Xi до выхода
г сети. Присваиваем входам этих элементов, не входящим в выде-
ленный путь, значения, обеспечивающие существенность пути: х2=1,
xs=l, с=1. Распространяем эти значения до входов сети: а) х4 = 0,
d=0; б) х5=1, хе=1. Искомая пара соседних по переменной Xi на-
боров
Х1 Х2 Хз X* Xs х6
( 0 1 1 0 1 1
С xi~ ( I I 1 О I 1 .
Аналогично ищутся пары наборов для остальных входных пере-
менных сети:
( 101011 J 000011
( 1110 11, ( 0 0 10 11,
f 110000 I I 1 О 1 0 1
I 110 10 0, \ 110111,
J 110 110
е*‘— I 110 111.
Удалив повторяющиеся наборы, получим полный диагностиче-
ский тест из десяти наборов: 000011, 001011, 011011, 101011, 110000,
110100, 110101, 110110, 1110111, 111011.
324
ПРОИЗВОЛЬНЬ1Е логические сети
Пусть в заданной одновыходной сети выдёлены всё
ее максимальные древовидные подсети. Выходами таких
подсетей являются либо внешние выходы исходной сети,
либо выходы элементов, соединенных с узлами развет-
влений, а входами —либо неразветвляющиеся входы
сети, либо ветви разветвлений. Узлы разветвлений бу-
дем обозначать буквами без индексов, а ветви развет-
влений— теми же буквами с нижними числовыми
индексами. Древовидным подсетям присвоим ранги по
следующему правилу. Ранг 1 имеет .подсеть, ближайшую
к выходу сети. Подсеть имеет ранг /+1, если макси-
мальный ранг подсетей, непосредственно связанных с ее
выходом, равен /. »
Основу метода построения полного диагностического
теста для произвольной сети составляет многократное
применение к выделенным подсетям алгоритмов АЗ-6
или АЗ-7 построения таких тестов для древовидных се-
тей, т. е. тест для произвольной сети .получается суперпо-
зицией тестов для ее древовидных подсетей.
Приведем последовательность операций алгоритма
АЗ-8 построения полных диагностических тестов для
произвольных одновыходных логических сетей.
1. Выделить древовидную подсеть ранга 1 и по алго-
ритму АЗ-6 (при произвольном базисе) или АЗ-7 (при
простом базисе) построить для каждого ее входа xit
i = 1, 2, ..., т, пары выявляющих наборов ех.~^х.еХ[-
2. В выявляющих наборах, полученных в п. 1, заме-
нить по указанным ниже правилам все символы Xi пере-
менных, представляющих ветви разветвлений, символа-
ми х соответствующих им узлов разветвлений.
Эта операция необходима в связи с тем, что выяв-
ляющие наборы представлены в терминах входных пе-
ременных подсети ранга 1, а конечной целью алгоритма
является получение выявляющих наборов в терминах
входных переменных сети.
а) Если выражение для ех. содержит символы Xj (Xj)
.своего0 узла разветвления х, то последние удаляются из
ег, а вместо 6, записывается символ б*.
б) Если е содержит символы ук или yk всех ветвей
.чужого" узла разветвления у, то вместо всех симво-
325
лов в прямом (инверсном) виде записывается один сйм*
вол у (у) в прямом (инверсном) виде. Символ 8„ заменяет-
ся на 8Д.
в) Если ех содержит символы у, и yt „чужого" уз-
ла разветвления у, то ех заменяется двумя выражениями:
одно из них е* получается из е заменой всех символов
У! и yi на один символ у, а второе е2л — заменой на один
символ у.
Правила „б“ и „в“ применяются к выражениям ех, а
1.2
также е многократно до тех пор, пока такое применение
возможно.
3. Выделить все древовидные подсети ранга 2 и
к каждой из них применять операции п. I. Пусть для
подсети, выходом которой является узел разветвления
х, операции п. 1 привели к получению пар выявляю-
щих наборов.
Заменить каждый символ бж в выражениях, получен-
ных в п. 2 для пар выявляющих наборов, последователь-
но каждым из выражений для пар выявляющих набо-
ров, полученных в п. 3
4. По выражениям |для е , полученным в п. 3, выде-
xi
лить переменные у (у), представляющие узлы разветвлений,
являющиеся выходами древовидных подсетей ранга 2.
Для каждой такой подсети вычислить некоторое импли-
кантное выражение реализуемой на ее выходе функции
у (у) и найти совокупность представителей импликантов.
Пусть для функции у(у) получено представителей
импликантов.
Заменить каждый символ у (у) в выражениях, полу-
ченных в п. 3 для пар выявляющих наборов, последо-
вательно каждым из представителем пмпликан-
тов функции у (у).
5. К выражениям для е^, полученным'[в п. 4, приме-
нить операции п. 2, после чего применить операции
пп. 3 и 4 к древовидным подсетям ранга 3 и т. д. до тех
пор, пока все выражения для eXl не окажутся представ-
ленными в терминах входных переменных исходной
сети.
326
Переходя к обычной двоичной записи входных набо-
ров, получаем совокупность выявляющих входных набо-
ров, которая образует полный диагностический тест для
сети в целом. Доказательство этого факта можно найти
в литературе, приведенной в библиографической справ-
ке настоящей главы.
Рис. 3-45. Пример логической сети для построения полною
диагностического теста.
Пример 3-80. Построить по алгоритму АЗ-8 полный диагностиче-
ский тест для сети рис. 3-1. Эта сеть вместе с необходимыми для
данного метода обозначениями приведена па рис. 3-45.
Сеть состоит из двух максимальных древовидных подсетей: ран-
га 1 с выходом z и входами bt, Ьг, dz, qi, qz и ранга 2 с выходом q
и входами а, с, dt.
Применяя алгоритм АЗ-7 для подсети ранга I, получим следую-
щую совокупность пар выявляющих наборов:
eb, = Sb, Q^bid-;
cq, = S<u b'O-^dz',
bs * 9i-
По правилу „а“, п.2 алгоритма АЗ-8 получаем:
% = ^bq^zd-z-,
cba =bi,dzqz q\\
cd, = Sd.b^2 q> b, <
Cn = ^qbibzdz',
Чу
= b(lbl <h.
327
По правилу «б»
eb, = sbqd2\
еЬ, =
= ^ab2bi q\
<‘Qi = Mck;
cqt ~ rfz"
По правилу «в» «расщепляется» только пара et,
е',3 = ^bq;
</, = 5‘'h V-
В соответствии с п. 3 алгоритма АЗ-8 для древовидной подсети
ранга 2 с выходом q находим три пары выявляющих наборов отно-
сительно каждого из ее входов с, с, dt;
с а = bnc di‘,
с с = Sr/rdi;
се, = s,i,ae-
Подставляя эти выражения в е(?] и вместо 6д, получаем:
— Вас dMi",
е^ = bcdiabda;
= cbdz>
еп = йдС d\ b d?*,
Ч*
el. = Scadtdib’,
42 -
=\acbdi
Согласно n. 4 алгоритма АЗ-8 находим представителей импли-
кантов выражений для функции q, реализуемой на выходе подсети
ранга 2, и для ее инверсий q. Такие представители единственны:
= acdi;
е— = а с di.
Подстановка Ед и е_ вместо символов q и q в выражения для
пар выявляющих наборов дает:
eb =bi>acdid2;
с dids;
а с
е\ ~ ^db а с
328
Повторное применение правил «а», «б» и «в» п. 2 даст:
6Ь1 —* ^a^cd't e\ = babc d; 41 e\ = bab c d; 4л
elb = Ььа с d; = babc d; e3 = bca bd-, 42
eL =eb^cd- e3 =bcabd; 41 Д = Sea b d; 4л
ed,= c b’ = S'*7 c b> = bdabc\ e\ = Ьйа be. <z»
Все пары выявляющих наборов представлены в терминах вход-
ных переменных сети, поэтому процесс вычислений на этом заканчи-
вается. Представляя пары выявляющих наборов в двоичной записи
п исключая повторяющиеся наборы, получаем искомый тест: 0000,
0001, 0010, ООП, 0100, 0101, ОНО, 0111, 1000, 1011, 1100, 1101, 1111.
ДЕШИФРАЦИЯ РЕЗУЛЬТАТОВ ДИАГНОСТИЧЕСКОГО ТЕСТА
Алгоритм АЗ-8 позволяет решить лишь часть общей
задачи поиска неисправностей, а именно, построить со-
вокупность входных наборов, достаточную для макси-
мально возможного различения неисправностей комби-
национного устройства. Другая, зачастую более слож-
ная часть упомянутой общей задачи заключается
в дешифрации результатов диагностического экспери-
мента над комбинационным устройством, т. е. в указа-
нии характера или места неисправности. В § 3-5 изло-
жено решение этой задачи на языке эквивалентных
форм, а также методом обобщенных функций. Оба эти
подхода сопряжены со значительными объемами вычис-
лений, а при работе с ЭФ (ОЭФ), кроме того, требуется
дополнительная обработка результатов с целью исклю-
чения (см. § 3-5) физически невозможных неисправно-
стей устройства из числа подозреваемых.
В модели М все (одиночные и кратные) константные
неисправности устройства задаются через неисправно-
сти ветвей разветвлений и неразветвляющихся полюсов.
Поэтому при построении обобщенной функции z выхода
устройства (или ее инверсии z) можно ограничиться
заданием обобщенных функций вида у=ууп V у1 или
у=ууп\/ у° только для ветвей разветвлений и нераз-
ветвляющихся входных полюсов. Получаемые при этом
обобщенные функции z и z (будем называть их сокра-
щенными) имеют более короткие записи, что уменьшает
объемы вычислений при выделении подозреваемых не-
исправностей.
329
Физически невозможные неисправности при работе
с обобщенными (в том числе сокращенными) функция-
ми не попадают в число подозреваемых, потому что
«расщепление» внутренних узлов разветвлений не со
провождается «расщеплением» входов, как это имеет
место при построении ЭФ или ОЭФ, а «расщепление»
входных полюсов разветвлений не может привести к по-
явлению физически невозможных неисправностей в чис-
ле подозреваемых даже при работе с ЭФ и ОЭФ.
Отметим еще одно обстоятельство, позволяющее
в ряде случаев дополнительно упрощать записи сокра-
щенных обобщенных функций.
Выделение неисправностей, обнаруживаемых на
входном наборе X; (подозреваемых в устройстве после
подачи этого набора и получения неправильной реак-
ции) по обобщенной (в том числе сокращенной) функ-
ции z или z, требует только подстановки вместо симво-
лов входных переменных их значений предписываемых
наборов Xj. Эта простота достигается за счет того, что
в записи функций 2, z введены символы а-состояний
узлов (полюсов) сети. Эквивалентная форма для z и
ОЭФ для z не содержит символов а-состояний узлов и
полюсов сети и поэтому, вообще говоря, проще пред-
ставлений обобщенных функций z и z. Платой за эту
простоту является необходимость более сложной обра-
ботки ЭФ или ОЭФ при выделении подозреваемых не-
исправностей: для каждой переменной по предписанно-
му ей входным набором Xj значению необходимо опре-
делять возможные ее а-состояния.
Рис. 3-46. Пример логической сети для иллюстрации
дешифрации результатов диагностических экспери-
ментов.
330
Имеется возможность перераспределять указанные
преимущества и недостатки эквивалентных форм и
обобщенных функций путем задания выходных функций
устройства и их инверсий в смешанной форме, в кото-
рой ветви некоторых узлов разветвлений (например,
всех внутренних узлов разветвлений) представлены их
обобщенными функциями через a-состояния, а ветви
остальных узлов разветвлений (например, всех раз-
ветвляющихся входных полюсов) и неразветвляющиеся
входные полюсы представлены реализуемыми в них
функциями в ЭФ или ОЭФ. Проиллюстрируем использо-
вание смешанной формы задания выходных функций
примером.
Пример 3-81. Выделить множество подозреваемых неисправно-
стей в устройстве, структурная модель М недорого дана на рис. 3 46,
по результатам следующего эксперимента:
а 6 с Z*
ООО 0 0.1 0 1 0 0 1 1 1 0 0 1 0 0 1 0
Единственный внутренний узел разветвления у представим обоб-
щенными функциями его ветвей:
7 = У'У" V </’; Уг = \J Ут
Уг = У^ Х/У°; Уг = Уг У% V У<2 .
Методом прямой или обратной подстановки построим смешанную
форму прямой & и инверсной г функций выхода сети.
z = а V 6i ({/J V И’ с0) (Уг V ^2 (6г 7)) =
= a bi с£ V a Ь,у2 V a btb2Ciy£ V a y^cs V V
V ау^Ьгс, y/atffbzCiCz V «^62Ci у2 V atff#btcr,
z~ = а\/ b,y\ V 617/ 62 V 617* ci V сеУг V c^2 62 V «2^ ci-
Приведем результаты анализа двух первых термов формы & на
входном наборе ООО (выход при этом равен 1). В первом терме
аЪ\с2 обрабатываются все буквы обычным для ЭФ образом, так, как
описано в § 3-5:
а 6[ с2 -» я0 б)1 с2 = а' б{ с2 .
331
Таблица 3-17
Группа Входной набор.
строк ь, С1 Ci Ух Ул Значение вы-
хода
1 т 1 "7 — — 1 — о ООО
7 7 1 1 н Z* = 1
1 1 — — — О О
I — 1 1 — О II
1 — 1 1 л н —
1 — I 1 — н О
1 — 1 1 — н н
1 1 1 Л — — 1 и — 0 0 1 z* = О
2 — 1 — О — н —
— — — — О — 1
— — “Г — "Q — н
— — — — О О — н
л 1 л — — н к о 1 1
1 7 л — II — II
3 1 — л — н О н
1 "7 —• О н — н
1 — — О н О н
I — 1 1 н н 1
1 7) 0 О — — 1 н — 0 1 0 z* = 0
4 — О — 1 н
— — О 7 1 1 — н и
Л н — н 1 1
5 1 н л — н 1 н —
1 н — О н 1 н
1 н О — н н 1
332
Продолжение табл. 3-17
Группа строк а bl ь, С2 Входной набор. Значение вы- хода
Т Н 0 н н н
5 1 Н т н н 1
1 Н "Т "Г н н н
1 Н — 0 н н н
л 0 —. 0 — — 0 1 1
1 0 — — — 0
1 0 “б "б — — н Z* = 1
т — — — 0 0 —
6 1 — — — — 0 • 0
1 “б "б 0 н
1 0 0 0 н
1 — 0 0 — н 0
1 — “б 0 — II н
7 “Г II н II н н н —
"0 ___ — . 100
— 1 — —- — 1 —
— 1 "Г — — н — z* = 0
8 — 1 — 1 — н —
— — — — 1 — 1
— — 1 — 1 — н
— — — т 1 — и
9 II и II и н II н
Во втором терме abiy°2 обрабатываются только буквы а и Ei,
так как переменная у2 уже представлена своим а-состоянием:
.,0 ~0~.(Г„0 I <,1 „О
Аналогично обрабатываются на наборе ООО остальные термы
функции £. Результаты этой обработки представлены в векторной
форме группой строк 1 в_табл. 3-17. Значениями компонент векторов
являются символы 0, 1, 0, 1, Н а-состояиий, а прочерк означает до-
пустимость любого a-состояния, а=0, 1, Н.
Группа строк 2 является результатом обработки термов функ-
ции & на наборе 001. Результатами попарного логического перемно-
жения векторов групп строк 1 и 2 является группа строк 3.
333
После получения векторов а-состояний для функции z на набо-
ре 010 (группа строк 4) снова выполняется перемножение этих век-
торов, на векторы группы строк 3 и т. д. до получения окончательно-
го результата, которым в данном случае оказалось исправное состоя-
ние сети.
Заметим, что при задании сети на рис. 3-46 с по-
мощью ЭФ и ОЭФ «расщепление» внутреннего узла у
проявилось бы в «расщеплении» переменных Ьг (на b'z
и Ь"2) и Ci (на с\ п c"i). Окончательным результатом
обработки ЭФ и ОЭФ явилась бы табл. 3-18, содержа-
щая четыре вектора а-состояпип, из которых три
последних представляют физически невозможные неис-
правности (переменные Ь'\ и Ь"2, а также с'\ и c"j не
могут находиться в разных «состояниях).
Т а б л и ц а 3-18
а ь, 6/ ьа"
н н н И II н н
н н 1 Н н н н
и н н н н 1 н
и н 1 (1 н 1 и
Изложенная выше процедура построения полного диаг-
ностического теста предусматривает получение группы
{пх } пар выявляющих входных наборов раздельно для
каждой ветви разветвления и неразветвляющихся вход-
ных полюсов. Организуем процесс реализации теста
в виде последовательности подачи на устройство группы
{>%} пар выявляющих наборов со сравнением факти-
ческих значений z* выхода устройства для каждой от-
дельной пары из {пт }. Если такой подход дополнить
некоторыми операциями анализа структуры устройства,
то в ряде случаев можно значительно упростить про-
цедуру дешифрации результатов реализации полного
диагностического теста. Определим эти операции ана-
лиза.
Пусть имеется пара входных наборов Хь Х2. Назовем
выделенными входные полюсы устройства, на которых
значения сигналов на наборах Xi и Х2 различны. Мно-
жество путей в сети, ведущих от выделенных входных
334
полюсов до выхода, и таких, что во всех им принадле-
жащих узлах на наборах Xi и Х2 значения сигналов
различны, назовем динамическим путем на паре набо-
ров Xi, Х2 и обозначим записью £>(Xi, Х2). Участок ди-
намического пути называется простым, если он принад-
лежит каждому пути последнего. Простой динамический
путь состоит только из простых участков.
Интересующие нас операции анализа логической
сети заключаются главным образом в определении кон-
фигурации динамических путей исследуемой сети па
парах выявляющих наборов. В результате анализа мож-
но сделать вывод о том, что некоторая переменная у,
модели М находится в Н-состояпни, если выполняется
одно из следующих условий:
1) На паре выявляющих наборе^ (Xk, Xi) из {tn }
узел z/j принадлежит простому участку динамического
пути D (Xh, Xi) и выход устройства принимает разные
значения z* (Xk) =^z* (Xi).
2) На паре выявляющих наборов Xk, Xi из {tn }:
а) узел разветвления у, к которому относится у,, при-
надлежит простому участку динамического пути D
(Xh, Xi); б) в любом пути от tp до выхода z, принадле-
жащем динамическому пути D (X/t, X/), содержится чет-
ное (нечетное) число инверсий; все пути от других
(отличных от tp) ветвей узла у до выхода z либо заве-
домо не принадлежат динамическому пути D (Xk, X,),
либо содержат нечетное (четное) число инверсий;
в) узел у принимает значение 0 па наборе У/, и значе-
ние 1 на наборе X/, y*(Xk)=0 и у' (Х,)~[. (Аналогично
это условие формулируется для случая, когда y*(Xk) = l
и у* (Xi) =0); г) выход сети принимает значение 0 (1) иа
наборе X/t и значение 1(0) иа наборе X/, z*(X/,) =0 п
z* (A'z) = 1 (z* (Хи) = 1 и z* (X/) =0).
3) Узел разветвления у содержит две ветви у; и ур
а) на всех парах выявляющих наборов из {tn } и {tn^.} не
существует динамического пути от выделенных входных
полюсов до выхода z, идущего в обход узла у, б) зна-
чение выхода устройства одно и то же на наборах каж-
дой отдельной пары выявляющих наборов из {tn };
S/j
в) существует пара выявляющих наборов (Xk, Xi) из
на которой значения выхода устройства различ-
335
пы, 2* (Xk) =£z* (Xi). Заметим, что условие 3 охватывает
случай, когда ветвь у2 избыточна.
Приведем еще два условия (4 и 5), при удовлетво-
рении которых можно сделать вывод о том, что узел г/,
в испытуемой сети либо неисправен (фиксирован одной
из констант 0 или 1), либо переменная у,- несущест-
венна.
4) На всех парах выявляющих наборов из {пг .} не
-У
существует динамического пути, идущего в обход узла
Уз, и значения выхода устройства одинаковы для каж-
дой отдельной пары наборов из {п^,}.
5) На всех парах выявляющих наборов из {пг } не
у i
существует динамического пути, идущего в обход узла
разветвления у(у^ является ветвью этого узла); в любом
пути от узла у до выхода сети одинаковое число инвер-
сий; значения выхода сети одинаковы на наборах каж-
дой отдельной пары из {ш^}'
Порядок проверки выполнимости условий 1—5 мо-
жет быть любым и, более того, условным: некоторые
условия могут удовлетворяться только после установле-
ния факта выполнения других условий. Условия 1—3
даюг возможность исключать из дальнейшего рассмо-
трения независимые переменные модели М, оказавшие-
ся в Н-состоянии. Условиями 4 и 5 также можно вос-
пользоваться для той же цели тогда, когда имеется
возможность не детализировать вид константной неис-
правности (0 или 1) узла у, (возможная в этом случае
несущественность переменной yj не приведет к каким-
либо ложным выводам, а лишь сделает безрезультатной
попытку устранения несуществующей неисправности
в узле yj).
Пример 3-82. Для сети рис. 3-45 в табл. 3-19 заданы совокупности
пар выявляющих наборов (эти совокупности были построены в приме-
ре 3-80) и фактические значения выхода z*, полученные в результате
реализации полного диагностического теста (значения выхода
исправной сети z будут использованы в дальнейшем при построении
полного проверяющего теста). Определить техническое состояние
(подозреваемые неисправности) сети с использованием условий 1—5.
Определяем, что в Н-состоянии по условию 1 находится пере-
менная а, по условию 2 — Ь, и вновь по условию 1 — q2, а условие 4
выполняется для переменной с. Эти результаты формально можно
записать в виде следующей системы равенств:
336
a} = a11 = 0;
b?=l; b{ = b°=0;
?2 = 1 ’ ?2 = ?2 =
CH \J c' Vc°= 1.
(3-51)
Так как условия 1—5 выполняются не для всех независимых
переменных модели Л1 устройства, необходимо продолжить дешифра-
цию одним из общих методов с учетом, однако, приведенной выше
системы равенств (3-51).
Представим выходную функцию г и ее инверсию г в смешанной
форме при условии задания обобщенными функциями только ветвей
9) и внутреннего узла разветвления q.
С учетом третьей строки системы равенств (3-51) обобщенные
функции для переменной <?2 упрощаются:
?2 == 4^2 \
Яг = Я <72* .
Тогда
г = abaft V bxcdxft V btq\ V " b.,c<ft \/
V « М,?'1 V «"с d^1 V « М2</2;
z = aq\ V Я^с V <7i'M2 V <71’ Mid/z V
V q^b2 cd2 а V а Ь{\/ djcbt V bjb^.
Дешифрация выполняется на наборах полного диагностического
теста (в табл. 3-19 эти наборы отмечены знаком V)- Для иллю-
страции приведем результаты дешифрации по двум первым термам
функции z на двух наборах.
На наборе 1111 (bead}
biCdig'1 -» b” c' d{ eft .
На наборе 0000 (bacd)
0;
bjcrfj^1 -> 0.
Заметим, что без учета системы .равенств (3-51) для указанных
термов и наборов были бы получены выражения
аи Ь? <7» = (дн V «’ )(bH V Ь‘) <7? . b\c^d{<// = X
X rf? <?V> и bjc'djt// соответственно.
Окончательные результаты дешифрации в векторной форме при-
ведены в табл. 3-20.
22—358 337
Таблица 3-19
Группы наборов b а с d Z* Z
V о 1 V 1 1 1 1 1 1 0 1 0 1
V о о 0 0 1 1
V 1 0 V 0 0 0 0 0 1 1 0 1 1
V 1 о 0 1 I 0
0 0 0 0 1 1
0 0 0 1 0 1
w 1 0 0 0 1 1
1 0 0 1 1 0
1 0 0 1 1 0
V 1 1 0 1 1 1
V 1 1 0 0 1 1
{жм 1 0 V 1 0 0 0 1 1 1 1 1 1
1 0 0 1 1 0
V 1 о 1 0 1 1
1 0 1 1 1 1
V 0 0 1 0 1 1
0 0 0 0 1 1
V о о 1 1 0 0
0 0 0 1 0 1
{Ж)1д2} V 0 • 0 0 0 0
0 0 0 0 1 1
0 0 1 0 1 1
0 0 1 1 0 0
1 0 1 0 1 1
W 1 0 0 0 1 1 1 0 1 1 1 1
0 0 1 1 0 0
1 0 0 0 1 1
1 1 0 0 1 1
{ЯЛа} 1 0 1 1 0 1 0 1 1 1 0 1
0 0 0 0 1 1
0 1 0 0 0 0
0 0 0 1 0 1
0 0 1 1 0 0
{Ж-} 1 0 1 0 0 1 1 1 1 1 0 1
0 0 0 0 1 1
0 0 1 0 1 1
338
Таблица 3-20
а bl <?а с d,
н н н н н н н н н н н н н н н н н н т 1 1 0 1 1 1 1 н н 1 1 0 I 1 н н 1 н н 7 н н 7
Укажем на другую возможность использования слу-
чаев выполнения условий 4 и 5. Узлы, для которых это
имеет место, либо неисправны, когда они фиксированы
константами 0 пли 1, либо исправны, когда они несу-
щественны. Из-за возможной несущественности пере-
менной нельзя дать точного заключения о техническом
состоянии проверяемого узла. Чтобы убедиться в дей-
ствительном состоянии таких узлов, необходимо прове-
рить их с помощью щупа или, например, вольтметра,
осциллографа и т. п. Проверим физически состояния
таких узлов и при необходимости устраним их неисправ-
ности. После этого повторно обратимся к условиям
1—5 для тех переменных (узлов), a-состояния которых
еще не определены и т. д. до тех пор, пока либо ни одно
из условий 1—5 не будет выполняться ни для одной
переменной и при этом не будет непроверенных физиче-
ски узлов, для которых удовлетворяется условие 4 или
5, либо не станут известными a-состояния всех перемен-
ных модели М.
Продолжение примера 3-82. Пусть в рассматриваемой сети
имеется кратная неисправность qt=b2=c=l. Эта неисправность
относится к числу подозреваемых, указанных в табл. 3-20, и поэтому
пе противоречит приведенным в табл 3-19 фактическим значениям
выходной функции г*.
* Первая проверка условий 1—5 показала, что условие 4 выпол-
няется для переменной с. После физической проверки этого узла и
устранения его неисправности получаем сн = 1. Повторное обраще-
ние к условиям 1—5 показывает, что удовлетворяются условие 1
для переменной d2 (dH2=l) и условие 4 для переменной qt. Про-
верив узел q\ .и устранив его неисправность, принимаем <7Н| = 1,
после чего находим, что условие 4 выполняется для переменной 62-
После проверки и устранения неисправности узла Ь2 принимаем
6Н2=1 и снова проверяем выполнение условий 1—5. Находим, что
по условию 1 узел d, исправен (dHi = 1). Таким образом, чередова-
ние операций дешифрации и устранения неисправностей узлов, для
которых выполнялось условие 4 или 5, в данном случае позволило не
22* 339
только определить имевшее место до начала эксперимента техниче-
ское состояние устройства, но также восстановить его исправное
состояние
СВЯЗЬ ДЕШИФРАЦИИ РЕЗУЛЬТАТОВ ДИАГНОСТИЧЕСКОГО
ЭКСПЕРИМЕНТА С ПОСТРОЕНИЕМ ПРОВЕРЯЮЩЕГО ТЕСТА
В заключение параграфа рассмотрим применение
изложенных результатов к построению полных прове-
ряющих тестов. Для наглядности ограничимся простым
базисом.
Вопросы дешифрации результатов диагностических
экспериментов оказываются весьма близкими к вопро-
сам построения полного проверяющего теста. В частно-
сти, условия 1—3 позволяют после реализации диагно-
стического теста на испытуемом устройстве отбирать
для последующей дешифрации только некоторые набо-
ры теста. Предположим, что испытуемым является
исправное устройство. Поскольку ответы исправного
устройства на наборы полного диагностического теста
известны, то, принимая эти ответы в качестве результа-
та предполагаемого диагностического эксперимента над
исправным устройством, можно заранее отобрать из
полного диагностического теста входные наборы, кото-
рые позволяют полностью дешифрировать эти результа-
ты. После дешифрации результатов получим, что испы-
туемое устройство исправно или находится в одном из
технических состояний, неотличимых от исправного.
Последнее означает, что отобранные входные наборы
образуют полный проверяющий тест.
Естественно, что полный диагностический тест
является и полным проверяющим тестом. При сравне-
нии па уровне минимальных форм длина диагностиче-
ского теста заведомо не меньше длины проверяющего
теста. Обычно диагностический тест намного длиннее
проверяющего, поэтому в «чистом виде» полный диагно-
стический тест для цели проверки может быть сильно
избыточным. Ниже будет дан способ сокращения этого
теста до полного проверяющего на основании изложен-
ных выше условий 1—3. Сами условия 1—3 при этом
следует несколько изменить, а именно, следует под зна-
чениями выхода устройства понимать значения выхода
исправного устройства, кроме того, в условии 2 пункты
«в» и «г» следует заменить на один пункт «в» — выход
исправного устройства принимает различные значения
340
иа паре наборов (Xk, Xi). Теперь условия 1—3 позволя-
ют сократить полный диагностический тест Т без потери
полноты проверки исправности устройства.
Назовем пары выявляющих входных наборов (Хи,
Х^), удовлетворяющие условиям 1,2, отмеченными.
Справедливо следующее утверждение. Если для всех
переменных модели М существуют отмеченные пары, то
эти пары входных наборов образуют полный проверяю-
щий тест. Действительно, по правильной реакции выхо-
да испытуемого устройства на отмеченных парах вход-
ных наборов заключаем согласно условиям 1, 2, что все
переменные модели М находятся в Н-состоянии. По-
следнее означает, что логическая сеть испытуемого
устройства исправна и, кроме того, неизбыточна. Сле-
довательно, отмеченные пары входных наборов образу-
ют полный проверяющий тест.
Сложнее обстоит дело, если не удается найти отме-
ченные пары входных наборов для всех переменных
модели М. Сформируем множество Тп входных наборов
следующим образом. Включим в множество Тп все от-
меченные пары выявляющих входных наборов. Кроме
того, включим в множество Тп все пары выявляющих
входных наборов для тех переменных модели М, для
которых не удалось найти отмеченные пары. Невозмож-
ность отыскания отмеченных пар может быть вызвана
как наличием избыточности в исходной сети, так и
трудностью анализа выполнимости условий 1,2. Можно
показать, что множество Тп является полным проверяю-
щим тестом произвольной (в том числе и избыточной)
сети. Полный проверяющий тест может быть получен
без предварительного построения полного диагностиче-
ского теста по следующей упрощенной процедуре.
1. Выбирается неразветвляюшпйся входной по-
люс Х{.
2. Находится пара (Хи, Xt) выявляющих наборов
для Xi. Если все пары исчерпаны, выбирается следую-
щий неразветвляющийся входной полюс.
3. Моделируется поведение исправного устройства на
наборах Хи, Xi.
4. Проверяется, выполняется ли условие 1 для х<.
Если да, то пара наборов (Хи, Xi) включается в тест, и
осуществляется переход к п. 1.
Если нет, то осуществляется переход к п. 2.
341
Использовав все перазветвляющиеся входные полю-
сы, следует переходить к построению пар выявляющих
наборов для переменных модели М, принадлежащих
разветвляющимся входным полюсам, начиная с наибо-
лее близких к выходному полюсу схемы. Повторяются
пункты 2,3,4 с проверкой выполнимости условий 1, 2,3.
После этого осуществляется переход к рассмотрению
«внутренних» переменных модели М.
Пример 3-83 Построим полный проверяющий тест для сети
рис. 3-45.
Начнем с переменной а. Находим первую пару выявляющих
входных наборов: (1000, 1100) (bacd). Моделируем поведение исправ-
ного устройства на наборах этой пары: z (1000)= г (1100) =1. Уело
вие 1 пе соблюдается.
Находим следующую пару выявляющих входных наборов (1001,
1101). Для этой пары z (1001) =0, z (1101) == 1.
Условие 1 выполнено. Включаем наборы 1001, 1101 в тест Тп.
Аналогично убеждаемся, что пара 0001, 0011 удовлетворяет усло-
вию 1 для переменной с, а пары 0111, 1111; 0001. 0001 -условию 2
для переменных 6] и Ь2 соответственно. К настоящему моменту уже
выяснено, что в случае правильного ответа испытуемого устройства
на отобранных входных наборах переменные а, с, bi, b2 модели М
находятся в Н-состоянин. Рассмотрим переменную dt. Находим для
нее пару выявляющих входных наборов: 0010, ООП, г (0010) =1,
г (0011) =0. На данной паре наборов узел d2 не входит в динами-
ческий путь D (0010, ООН), так как сигнал 0 на входе b блокирует
через исправный узел Ь2 распространение изменений сигнала от вхо-
да d через узел d2. Следовательно, для d\ выполнено условие 1
Включаем наборы 0010, ООН в тест 7',,. Аналогично определяем, что
на парах выявляющих наборов 1000, 1001; 1001, 1101; ООП, 0001 вы-
полняется условие 1 для переменных d2, qt, q2 соответственно. Уда-
лив из Тп повторяющиеся наборы, получим полный проверяющий
тест для сети рис. 3-45 из восьми наборов; 1111, 1101, 1001, 1000,
0111, ООП, 0010 0001 Проверяющий тест для одиночных неисправ
ностей этой же сети, найденный в примере 3-69, также состоит из
восьми наборов.
Нетрудно заметить, что состав и длина теста Тп мо
гут зависеть от порядка получения пар выявляющих
входных наборов.
Построенный тест обладает одной интересной осо-
бенностью. При проверке исправности состояний узлов
хг исследуемого устройства па паре выявляющих набо
ров «активизируется» минимально возможная часть
сети. При этом, вообще говоря, уменьшается число не
исправностей, обнаруживаемых на данной паре вход-
ных наборов, по сравнению с любой другой парой не-
выявляющих наборов, проверяющих исправное состоя-
ние узла xi. Последнее обстоятельство может привести
342
к избыточности теста. С другой стороны, благодаря это-
му построенный проверяющий тест обладает хорошими
диагностическими свойствами
ЗАМЕЧАНИЯ ПО БИБЛИОГРАФИИ
Комбинационные устройства, основные определения
п описание их моделей — функциональной и структур-
ной, изложенные в § 3-1, основаны на фундаментальных
работах по теории дискретных устройств [Л. 30, 31, 6].
Структурно-аналитический аппарат эквивалентной фор
мы (ЭФ) описания функционирования комбинационного
устройства в произвольном базисе [Л. 33] по существу
совпадает с аппаратом эквивалентной нормальной
формы, введенным впервые Армстронгом для пеизбы-
точных сетей в простом базисе [Л. 32]. Различные фи-
зические характеристики информационных сигналов
в более сложных моделях комбинационных устройств и
неисправности в них исследованы, например, в [Л. 34,
35, 36].
Помимо табличного [Л. 9] и структурного [Л. 37]
способа задания функционирования неисправного
устройства в § 3 3 основной упор сделав иа аналитиче-
ские методы решения этой задачи в случае константных
неисправностей [Л. 38—40 и 33]. Подж [Л. 38] для
этого исследует обобщенную функцию, реализуемую
устройством; в [Л. 39—41] рассматриваются способы
фиксации неисправностью букв выражения ЭФ (ОЭФ)
функции исправной сети. Для этих же целей в [Л. 41]
используется скобочная форма функции выхода, а, на-
пример, в [Л. 42]—дизъюнктивная нормальная форма.
К сожалению, во многих работах, использующих неко-
торое аналитическое выражение функции выхода
исправной сети, отсутствует четкая связь между не-
исправностью логической сети и способом преобразова-
ния ею исходного выражения. Фридман [Л. 43] наибо-
лее подробно рассмотрел избыточные логические сети
и некоторые интересные особенности обнаружения неис-
правностей в них.
Впервые в отечественной литературе задачи построе-
ния проверяющих и различающих совокупностей, а на их
основе задачи построения проверяющих и диагностиче-
ских тестов были строго сформулированы и решены на
языке таблиц функций неисправностей (ТФН) в [Л 44].
Наиболее полно этот аппарат использован для целей
343
технической диагностики в [Л. 4]. Методы построений
и исследования ТФН, ставшие уже классическими, рас-
сматриваются в гл. 1, а в § 3-4 исследуются аналитиче-
ские [Л. 45, 49] и структурные [Л. 51] методы построе-
ния проверяющих и различающих совокупностей. Метод
различающей функции с использованием структуры про-
веряемой сети для построения некоторого входного
набора, обнаруживающего заданную произвольную
(одиночную или кратную) логическую неисправность,
рассмотрен в [Л. 45]. Первые упоминания, связанные
с идеями метода существенных путей (по отношению
к двухуровневым сетям), по-вндпмому, относятся к ра-
боте Элдреда [Л. 46]. Он же был одним из первых
исследователей, обративших внимание на важность
диагноза технического состояния аппаратуры вместо
практиковавшейся проверки отдельных алгоритмов, вы-
полняемых объектом. Армстронг в [Л. 32] ввел понятие
простого существенного (чувствительного) пути. Необ-
ходимые и достаточные условия проверки заданной оди-
ночной логической неисправности и различения пары
таких неисправностей определены в [Л. 47, 48].
В 1959 году Акерс определил [Л. 49] понятие булевой
разности (производной). В последующих работах, на-
пример группы Селлерса [Л. 50], этот аппарат исполь-
зуется для анализа ошибок в дискретных устройствах.
По существу булева разность является аналитической
записью условия наличия существенного пути от задан-
ного узла до выхода сети В [Л. 51] Рот наиболее алго-
ритмично реализовал идеи метода существенных путей
для структур произвольной конфигурации, построенных
в произвольном базисе элементов, для случая одиноч-
ных логических неисправностей. В этой работе он реша-
ет две задачи: вычисление набора, обнаруживающего
заданную неисправность, и определение множества не-
исправностей, обнаруживаемых заданным набором.
Комбинация решений этих задач составляет стратегию
построения проверяющего теста сети, описанную в § 3-6.
Несмотря на то что алгоритмы Рота запрограммирова-
ны на языке APL и являются одними из первых машин-
ных программ в технической диагностике, они малоэф-
фективны для устройств с большим числом элементов
и рангов.
Правила фиксации неисправностью букв ЭФ (ОЭФ)
функции логической сети [Л. 39, 40, 33] и определение
344
понятия проверки множества букв в терме [Л. 39] со-
ставляют описанный в § 3-4 метод построения прове-
ряющей совокупности на основе анализа ЭФ и ОЭФ
функции сети.
Структурно-аналитические методы построения мно-
жества неисправностей, обнаруживаемых на заданном
наборе, основанные на [Л. 38, 52, 53], описаны в § 3-5.
Более компактное представление искомого множества
дает метод Пархоменко [Л. 33], исходящий из пред-
ставления любой константной неисправности сети по-
средством фиксации букв ЭФ (ОЭФ) исправной сети.
Использованное в § 3-4 и 3-5 понятие однозначного
распространения от исходной фиксации [Л. 54] впер-
вые неформально было определено Ротом в [Л. 51].
В этой же работе Рота структурным алгоритмом
«test — detect» строится множество Oj неисправностей,
обнаруживаемых набором Xj, и дано одно условие, по-
зволяющее в некоторых случаях избежать в алгоритме
полного перебора всех неисправностей из полного
списка О.
Методы построения проверяющего теста комбина-
ционного устройства, основанные на задании списка
неисправностей S и описанные в § 3-6, могут быть упро-
щены при замене множества S множеством Sx характе-
ристических неисправностей устройства, определенных
в [Л. 48, 57]. Метод Армстронга [Л. 32], основанный
на проверке отдельных букв ЭФ и ОЭФ функции сети,
не всегда приводит к построению проверяющего теста.
Соответствующий пример для избыточных сетей дан
в [Л. 55] Шнейдером, а для неизбыточных — в [Л. 39]
Чипулисом. В [Л. 39] и [Л. 56] для обнаружения всех
одиночных и кратных константных неисправностей Чи-
пулис проверяет все проверяемые подмножества букв
термов ЭФ и ОЭФ функции сети. В [Л. 58, 59] иссле-
дуются отдельные приемы, позволяющие в некоторых
случаях по результатам правильной реакции устройства
на наборы, проверяющие его одиночные константные
неисправности, делать заключение об исправности от-
дельных узлов сети в предположении кратных констант-
ных неисправностей. Тем не менее Чипулис показал
в [Л. 60], что в общем случае для обнаружения крат-
ных неисправностей могут быть необходимы специаль-
ные наборы.
345
В [Л 61—63] рассмотрены вопросы построения
диагностических словарей и использования их для по-
иска неисправностей в блоках цифровых устройств
вплоть до ЦВМ в целом. В этих работах решались за-
дачи автоматизации составления диагностических сло-
варей, повышения разрешающей способности последних
с учетом возможной неполноты их и достоверности кон-
троля. В [Л. 47] предложен метод существенных путей
для нахождения входного набора, различающего задан-
ную пару неисправностей. В [Л. 64] та же задача ре-
шается на языке £)-кубов. В [Л. 65, 66] предложены
условные и безусловные процедуры построения тестов
для поиска одиночных неисправностей. В [Л. 38] впер-
вые введена структурно-аналитическая модель функцио-
нирования комбинационного устройства в предположе-
нии, что в нем возможны кратные неисправности.
В [Л. 52, 53] идеи, предложенные в [Л. 38], распрост-
раняются па класс неисправностей типа сбоев п на
устройства с памятью. Работа [Л. 40] использует ЭФ
функции сети для выделения множества подозреваемых
неисправностей в заданном диагностическом экспери-
менте. В [Л. 33] предложен метод расшифровки диагно-
стических экспериментов алгеброй а-состояний при за-
дании устройства ЭФ и ОЭФ. Впервые задача построе-
ния полного диагностического теста для логических
сетей вида дерева, построенных в базисе из элементов
И, ИЛИ, ИЕ, решена в [Л. 66]. В [Л. 67] решена за-
дача построения полных диагностических тестов для
деревьев в произвольном базисе. Решение задачи пост-
роения полного диагностического теста для комбина-
ционных устройств произвольной структуры, построен-
ных в произвольном базисе, изложено в [Л 69]
ГЛАВА ЧЕТВЕРТАЯ
ДИСКРЕТНЫЕ ОБЪЕКТЫ ДИАГНОЗА С ПАМЯТЬЮ
Одно из принципиальных отличий дискретны^
устройств с памятью от комбинационных состоит в том,
что их выходные функции зависят не только от входных,
но также от внутренних переменных, представляющих
память устройства. Физически память может быть реа-
лизована при помощи специальных элементов памяти
(например, триггеров), обратных связей, при помощи ко-
346
горых образуются контуры из логических элементов И
элементов памяти, или, наконец, временных задержек.
В соответствии с этим внутренние переменные сопостав-
ляют обычно выходам триггеров или временных задер-
жек, либо выходам элементов, охваченных обратной
связью.
4-1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИСПРАВНЫХ ДИСКРЕТНЫХ
УСТРОЙСТВ С ПАМЯТЬЮ
Общепринятой математической моделью устройства
с памятью является абстрактный или структурный ко-
нечный автомат. В конечном
делить комбинационную
часть и память так, как это
показано па рис. 4-1. На
этом рисунке автомат дан
в однолинейном представле-
нии. Обозначения па рисун-
ке следующие: X — внешний
входной сигнал автомата,
Z — внешний выходной сиг-
нал автомата, W вход-
ной сигнал памяти, У вы-
ходной сигнал памяти (или
внутренний входной сигнал
автомата).
автомате всегда можно вы-
Рис. 4-1. Однолинейное пред-
ставление автомата.
АБСТРАКТНЫЙ КОНЕЧНЫЙ АВТОМАТ
Однолинейное представление (рис. 4-1) соответствует
рассмотрению дискретного устройства с памятью как
абстрактного конечного автомата. При этом предпола-
гается, что намять автомат реализована па задержка^,
каждая из которых задерживает сигнал иа одно и то же
время т. Если изменение значений входного сигнала про-
исходит одновременно с изменением выходного сигнала
памяти через интервалы времени т, то абстрактный авто-
мат является синхронным, а интервал времени т назы-
вается тактом синхронизации. В теории абстрактных
автоматов принято называть внешний входной сигнал X,
внешний выходной сигнал Z, выходной сигнал памяти У
соответственно входным, выходным символом и симво-
лом внутреннего состояния или кратко состоянием. Со-
вокупность различных вводных, выходных символов и
347
символов состояний принято называть Соответственно
входным алфавитом, выходным алфавитом и алфавитом
состояний автомата.
В соответствии с принятой идеализацией функциони-
рование исправного абстрактного конечного автомата
может быть задано двумя зависимостями:
2 D (4-П
и
= YJ, (4-2)
где Zv, Yv — символы алфавитов: входного {А-}, выходного {Z}
и состояний {У} соответственно, а нижние индексы v и v+1 являют-
ся номерами настоящего (текущего) и следующего тактов.
Для функций возбуждения можно записать:
У,). (4-3)
Кроме того, в данном случае
Г»+1=^.
Зависимости (4-1) и (4-2) описывают автомат Милн, когда вы-
ходные сигналы зависят как от входных сигналов, так и от выходных
сигналов памяти, т. е. состояний. Известны также автоматы Мура,
у которых выходные сигналы определяются только состояниями
автомата. Заметим еще, что комбинационное устройство можно
рассматривать как вырожденный случай автомата с памятью, когда
выходной сигнал Z последнего зависит только от внешних входных
сигналов Z.
Задание автомата зависимостями (4-1) и (4-2) соответствует
перечислению всех возможных пар «входной сигнал — состояние» и
сопоставлению этим парам выходных сигналов и состояний. Это
часто делают в табличной, графической или матричной форме.
Пример 4-1. Примером задания абстрактного автомата с вход-
ным алфавитом {A} = {Aj, Х2], выходным алфавитом {Z) = {Z|, Z2}
и алфавитом состояний {У} = {У1, У2, У3, У4, У5} в табличной форме
является табл. 4-1, называемая таблицей переходов — выходов авто-
мата.
Строки таблицы соответствуют состояниям входов (символам
входного алфавита, входным наборам) автомата в настоящий мо-
Таблица 4-1
>4+1/2» {У»}
1 2 3 4 5
И4 1/Z, 4/Z2 l/z, 5/Z2 5/Z, 1/Z2 3,/Zt 4/Z2 2/Zs 5/Z2
348
мент времени v, а столбцы — со-
стояниям автомата из алфавита
{У} в тот же момент времени (в
табл. 4-1 вместо символов Уь
У2, • > Уб приведены индексы 1,
2, ..5). В таблицах переходов —
выходов в шапке боковика указы-
вается содержимое клеток табли-
цы, а именно состояния автомата
в момент .времени v+1, п (через
косую черту) выходные состояния
(выходные символы) в момент v.
По таблице переходов — выходов
легко проследить все возможные
переходы из одного состояния ав-
томата в другое, а также имею-
щие при этом место состояния вы-
ходов (символы выходного алфа-
вита, выходные наборы) Напри-
мер, автомат, находящийся в дан-
ный момент в состоянии 3, под
воздействием входного символа
Х\ перейдет в состояние 5 и при
этом выдаст выходной символ Zb
Рис. 4-2. Граф переходов—вы-
ходов автомата, рассмотренно-
го в примере 4-1.
а под воздействием входного сим-
вола Х2 перейдет в состояние 1 и выдаст выходной символ Z2.
Графической формой задания автомата является его граф пере-
ходов— выходов пли сокращенно — граф переходов. Для рассмо-
тренного в примере 4-1 автомата такой граф представлен на рис. 4-2.
Вершины графа переходов — выходов соответствуют состояниям
автомата, а дуги — возможным переходам из состояния в состояние
(по направлению стрелок). Каждой дуге приписан входной символ,
при подаче которого осуществляется соответствующий переход,
а также (через косую черту) — выходной символ, выдаваемый при
этом автоматом.
Таблица 4-2
/z, O'v+l}
1 2 3 5
{Ч 1 x,/z, *2/Z2
2 A’i/Zi
3 x2/z2
4 A'i/Zs X2/Z2
5 X,/Z2 X2/Z2
Примечание. В шапке боковика указано содержимое клеток таблицы:
входной символ и (через косую черту) выходной символ в момент времени v.
349
Матричной формой заданий автомата является его матрица
переходов — выходов. Матрица переходов — выходов автомата из
примера 4-1 представлена табл. 4-2.
Это квадратная матрица, порядок которой равен числу состоя-
ний автомата. Каждому состоянию в момент времени v сопоставля-
ется строка матрицы, а в момент v+1 —ее столбец. На пересечении
строки i н столбца j ставится либо пара вход—выход (входной —
выходной символы), когда в автомате имеется переход из состояния
У; в состояние Yj, либо ничего не ставится, когда такого перехода
нет. Очевидно, все три рассмотренные формы задания автоматов
эквивалентны.
Различают устойчивые и неустойчивые состояния
автомата. Автомат находится в устойчивом состоянии Уг
относительно входного символа Х„ если при этом вход-
ном символе состояние автомата пе меняется, т. е. в мо-
мент v и в момент v+1 остается равным У,. В противном
случае состояние У,- неустойчиво.
Рассмотренный выше автомат имеет устойчивое со-
стояние 1 на вводном символе Лл, а также состояния 4-
и 5 на входном символе Х2. По таблице переходов — вы-
ходов устойчивые состояния находятся путем просмотра
ее столбцов: состояние, указанное в клетке некоторого
столбца таблицы, устойчиво, если оно совпадает с со-
стоянием, которому соответствует данный столбец. На
графе переходов — выходов устойчивым состояниям со-
ответствуют вершины, имеющие петли, а в матрице пе-
реходов— выходов устойчивыми являются состояния
с непустыми диагональными клетками.
Различают инициальные и неинициальные автоматы.
Для первых задано одно начальное состояние, а у вто-
рых может быть любое начальное состояние С физиче-
ской точки зрения инициальный автомат требует наличия
цепи установки его в начальное состояние по специаль-
ному сигналу. У неинициальных автоматов цепей уста-
новки в начальное состояние нет.
СТРУКТУРНЫЙ КОНЕЧНЫЙ АВТОМАТ
Рассмотренная однолинейная блок-цхема рис. 4-1 и
таблицы, графы и матрицы переходов — выходов пред-
ставляют абстрактный конечный автомат, у которого
входные, выходные сигналы и состояния представляются
символами. Такое представление является полезным при
рассмотрении общих вопросов теории автоматов и тео-
350
рии экспериментов над автоматами. Однако для решения
ряда конкретных практических задач синтеза, анализа
или диагноза технического состояния реальных дискрет-
ных устройств пользоваться моделью в виде абстрактно-
го автомата не всегда удоб
но. Рассмотрим другую мо-
дель, более детально описы
вающую дискретное устрой-
ство с памятью, — структур-
ный конечный автомат.
Блок-схема структурного
автомата с разбиением его
на комбинационную часть и
память показана на рис. 4-3.
Автомат имеет п внешних
входов, которым сопоставле-
ны входные переменные Xi,
х2, ., Хп, k внешних выхо-
дов с соответствующими им
Рис. 4-3. Блок-схема структур-
ного автомата.
выходными функциями Z1,
на которых реализуются
z2, . .., zft, / входов памяти,
функции возбуждения wt, w2, . .., wf, и, наконец, tn вы-
ходов памяти, которым сопоставлены внутренние пере-
менные iji, у2, . . ут- Для исправного структурного авто-
мата вместо (4-1), (4-2) и (4-3) имеем-
= У) (4-4)
для всех i = 1,2....k,
У) (4-5)
для всех / = 1,2, ..., т,
wgv = fwg(Xv, У) (4-6)
для всех g—1,2, ..., I.
В этих формулах ^ = {ль, х2,.......... и У =
— У2у, —» ут}-
Переход от абстрактного автомата к структурному
состоит в кодировании входных, выходных символов и
символов состояний абстрактного автомата наборами
значений соответственно входных переменных, выходных
функций и внутренних переменных структурного автома-
та. Очевидно, что для кодирования N разных символов
необходимо не меньше log2A двоичных переменных или
функций.
351
Пример 4 2. Для кодирования двух символов входов абстракт-
ного автомата, рассмотренного в примере 4-1, достаточно одной
входной переменной хь если значение xt = 0 обозначить а значе-
ние Xi = l — через Х2. Кодирование его выходных символов требует
также одной выходной функции zt, а символов состояний — трех
внутренних переменных у\, у2, Уз- Пусть принято следующее коди-
рование:
V1 Z1 </i.Va.Va
0— Л, 0— Zj ООО — У!
1 — Х2 1 — z2 001 — у2 010 —Уз 011 — У4 100-У6
Тогда вместо таблицы переходов — выходов абстрактного авто-
мата (табл. 4-1) получаем таблицу переходов — выходов структур-
ного автомата в виде табл. 4-3.
Таблица 4-3
yi’y^y^lZi УъУъУъ
ООО 0)1 010 011 100
Х1 0 000/0 000/0 100/0 010/1 001/1
1 011/1 100/ 1 000/ 1 011/1 100/1
В этой таблице ради упрощения при обозначениях переменных и
функций индекс v опущен, а индекс v+1 заменен штрихом.
Пользуясь таблицей переходов — выходов структурно-
го автомата, зависимости (4-4) — (4-6) легко задать та-
блицей истинности, в которой значениями независимых
переменных являются значения входных переменных
(xi), а также внутренних переменные (t/i, у?, у3) в мо-
мент времени v, а значениями функций — значения вну-
тренних переменных (z/'i, y'z, у'3) в момент времени v+1
и значения выходных функций (Zi) в момент времени v.
Заметим, что так построенная таблица истинности мо-
жет содержать меньше чем 2"4"1 строк в связи с тем, что
некоторые комбинации значений ее независимых пере-
менных могут отсутствовать в таблице переходов — вы-
ходов. Для абстрактного автомата, рассмотренного
в примере 4-1, и соответствующего ему структурного
автомата из примера 4-2 таблица истинности (табл. 4-4)
построена по табл. 4-3,
352
Таблица 4-4
*1 У1 У 2 Уъ У\ У'* //'в Z1 *1 Уг У* Уъ 0 \ У 'а У'* Zi
0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 1
0 0 0 1 0 0 0 0 1 0 0 1 1 0 0 1
0 0 1 0 1 0 0 0 1 0 1 0 0 0 0 1
0 0 1 1 0 1 0 1 1 0 1 1 0 1 1 1
0 1 0 0 0 0 1 1 1 1 0 0 1 0 0 1
От таблицы истинности нетрудно перейти к тем или
иным формам представления булевых функций. В част-
ности, ио табл. 4-4 для .примера 4-1 ji 4-2 получаем сле-
дующие дизъюнктивные нормальные формы:
z,=v х,уГугу» v
y'l = х,у,у2уг V х2у2у2у» V ХхУ^Уз-,
у'2 = х,у,угузу х^у2у» V х^у,у2у3,
у'з = ~х,у3у2у3 V Хху,у2уУ Хху2у2уг.
Эти формы являются явным заданием зависимостей
(4-4) и (4-5).
Таблица истинности или соответствующая ей систе-
ма булевых выражений являются описанием комбина-
ционного эквивалента автомата с памятью. Такое пред-
Г; хг ХП У, Ком 6ин а. - ционная часть ! : Z й 2 К Память — у!
Уг . , — y'z
Ут v,i &
Рис. 4-4. Комбинационный эквивалент автомата.
ставленпе конечного автомата его комбинационным
эквивалентом соответствует условному разрыву обратных
связей автомата на выходах памяти. Представление
автомата рис. 4-3 в виде комбинационного эквивалента
изображено на блок-схеме рис. 4-4.
23—358 353
Различают полностью определенные и не полностью
определенные автоматы с памятью. Автомат является
полностью определенным, если его поведение определено
для всех 2" входных наборов (для всех символов вход-
ного алфавита) и для всех внутренних состояний, т. е.
для каждого входного набора (входного символа) и
каждого состояния определены как перевод в следую-
щее состояние, так и значения всех его выходов (вы-
ходной символ). В противном случае автомат является
не полностью определенным. Следовательно, таблица
переходов - выходов полностью определенного автомата
имеет число строк, равное 2'1 (мощности входного алфа-
вита), и не содержит хотя бы частично не заполненных
клеток.
ЛОГИЧЕСКАЯ СЕТЬ
Рассмотрим теперь структурное представление ди-
скретного устройства с памятью в виде логической сети
(схемы). В § 3-1 было введено понятие правильной логи-
ческой сети, задающей комбинационное устройство. Рас-
пространение этого понятия на устройства с памятью со-
стоит в том, что, во-первых, базис сети может содержать
элементы памяти (задержки, триггеры) и, во-вторых,
среди k выходные функций, реализуемых на выходных
полюсах сети, найдется хотя бы одна, существенно зави-
сящая от внутренних переменных сети, сопоставленных
выходам элементов памяти или выходам элементов,
охваченных обратными связями. Частным случаем логи-
ческих сетей с памятью являются логические сети без
обратных связей.
Комбинационная часть автомата всегда может быть
представлена многовыходной логической сетью, входами
которой являются внешние входы xt, xz, ..., хп автомата
и выходы z/i, у2, . . ., ут памяти, а ее выходами — внеш-
ние выходы Zi, 22, . . ., zh автомата и входы Wi, ьу2, , Wi
памяти. Поэтому все свойства и особенности логических
сетей, а также способы получения их аналитических
описаний в виде различных прямых и инверсных форм
булевых функций, изложенные ранее, в гл. 3, для комби-
национных устройств, остаются в силе при рассмотрении
комбинационных частей автоматов. Подчеркнем, что
условный обрыв всех внешних обратных связей позволя-
ет выполнять ранжирование элементов логических сетей
с памятью.
354
Получение аналитиче-
ских описаний логических
сетей с памятью рассмо-
трим для двух случаев,
определяемых способом
реализации памяти авто-
мата. Когда память реа-
лизована на временных
задержках (с обратными
сязями или без них) или
при помощи контуров об-
ратных связей, охваты-
вающих логические эле-
менты, аналитические
описания логических се-
тей с памятью могут быть
получены темп же мето-
6)
Рис. 4-5. Способы представления
памяти в комбинационном эквива-
ленте автомата.
дамп, которые применимы
для комбинационных ло-
гических сетей. В этом
случае блок памяти авто-
мата содержит не связанные между собой времен-
ные задержки (рис. 4-5,а) либо прямые соединения
(рис. 4-5,6). Примем предположение, что задержки
и прямые соединения блока памяти являются повторите-
лями, т. е. yi=Wi для всех 1=1, 2, ..., т=1, и оборвем
(условно) соединения сети па выходах блока памяти.
Это ведет (см. рис. 4-4) к замене блока памяти блоком
повторителей, а логической сети с памятью — комбина-
ционной логической сетью без обратных связей с вход-
ными полюсами xt, . . ., xn, z/i, ..., ут и выходными по-
люсами Zt, . . ., zh, y't, .. ., у'т. Для описания такой сети
могут быть использованы все те методы и приемы, кото-
рые были рассмотрены в предыдущей главе.
Таблица 4-5
*1 *2 V У* Z *1 Хя у У* г
0 0 0 0 0 1 0 0 0 0
0 0 1 0 0 1 0 1 I 1
0 1 0 0 0 1 1 0 0 0
0 1 1 0 0 1 1 1 1 1
355
Пример 4-3. На рис. 4-6,а представлена некоторая логическая
сеть с обратными связями, а на рис. 4-6,6 — соответствующая ей
комбинационная логическая сеть, построенная в предположении
обрыва обратной связи — соединения выхода элемента 3 с входами
элементов 1 и 2. Оборванное состояние заменено повторителем, вход
которого обозначен W, а выход — у'. При выбранном способе обры-
ва получилась комбинационная структура, описываемая таблицей
истинности (табл. 4-5).
Рис. 4-6. Сеть к примеру 4-3 и ее комбинационные эквива-
ленты.
Дизъюнктивная нормальная форма функции, реализуемой этой
структурой, имеет вид:
z = XiX2y \J xix2y = х,у.
ЭФ и ОЭФ соответственно имеют вид:
г = (Уг у Х2У1) = Х1У2 v х,х2уг,
~z= X! \/ у, ys 'V Х^ Уе-
Если разорвать соединение выхода элемента 2 с входом эле-
мента 3, то получим структуру, представленную на рис. 4-6,в. Как
356
ппдпо из рис. 4-6, обрыв обратных связей в разны?; точках контура
приводит к получению различных структур комбинационных логиче-
ских сетей.
ЛОГИЧЕСКИЕ СЕТИ С ТРИГГЕРАМИ
Перейдем к получению аналитических описаний логи-
ческих сетей, память которые реализована на специаль-
ных элементах — триггерах. На рис. 4-7 приведена схема
широко распространенного двухвходового триггера из
двух логических элементов
ИЛИ— НЕ, охваченных об-
ратной связью. Выберем в
качестве внутренней пере-
менной триггера переменную
pi, сопоставленную соедине-
нию между выходом элемен-
та 1 и входом элемента 2.
При этом таблица перехо-
дов — выходов триггера име-
ет вид табл. 4-6а.
Таблица 4-6а Таблица 4-66
Р1ЧУ1У* Р1 Pi'IUiVt А
° 1 > 0 1 1
00 0/01 1/10 со — —
W1W2 01 1/10 1/10 01 1/10 1/10
10 0/01 0/00 10 0/01 0/00
11 0/00 0/00 11 0/00 0/00
Из табл. 4-6а получаем аналитические выражения для
выходных функций yit)2 и внутренней переменной р'г.
у,= Xi = (Л V Wl’
у2 = ptw2.
Анализ работы рассматриваемого триггера с учетом
временных задержек логических элементов показывает,
что когда входной набор 11 .(аца^), который однозначно
устанавливает выходной набор 00 (ур/г), изменяется на
входной набор 00, возможно неоднозначное поведение
ipmrepa (разные физические экземпляры триггера бу-
дут вести себя по-разному). Если, например, задержка
357
Элемента / меньше задержки элемента 2, то при указан-
ном изменении сигналов на входах будет получен выгод-
ной набор 10 (У1У2) В противном случае выходной набор
будет 01. В связи с этим при проектировании устройства
с памятью считают входной набор 00 запрещенным, что
соответствует описанию триггера рис. 4-7 таблицей пе-
реходов выходов, заданной табл. 4-66 с прочерками
в строке 00.
В ряде случаев может оказаться необходимым более
детальное описание поведения триггера, когда каждому
соединению контура обратной связи сопоставляется своя
независимая внутренняя переменная. Учет всех возмож-
ных комбинаций значений этих переменных позволяет
рассмотреть переходные режимы работы контура и бо-
лее точно выявить возможные неоднозначности состоя-
ний триггера и переводов между ними. Для триггера
рис. 4-7 при указанных условиях получаем таблицу пе-
реходов— выходов в виде табл 4-6в.
Таблица 4-6в
P\Pi
00 1 01 10 11
00 — 01 10 —
W1W2 01 10 00 10 00
10 01 01 00 00
11 00 00 00 00
В клетках этой таблицы приведены только значения
выходов yt и у2, так как при данном рассмотрении p'i —
=yi и р'ъ=уг. Прочерки в двух клетках таблицы про-
ставлены по соображениям, подобным тем, которые бы-
ли приведены ранее, при построении табл. 4-66. Анали-
тические выражения выходных функций триггера сле-
дующие:
У1 = р'1 = PnWP,
У2 = р\ = P1W2.
Аналогично описанному могут быть рассмотрены
другие виды триггеров с потенциальным управлением.
Более того, такому рассмотрению могут подвергаться
любые одиночные и взаимосвязанные контуры обратных
358
связей. Однако для триггеров как типовых элементов
памяти предварительное получение описания н,х поведе-
ния оправдано, чего нельзя сказать о контурах обратных
«.вязей, многообразие которых чрезвычайно велико. По-
этому описание контуров обратных связей обычно вы-
полняется в процессе описания устройства в целом.
Возможные неоднозначности поведения контуров вы-
являются в процессе анализа устройства на наличие
в нем состязаний. Для этого используется так называе-
мое троичное моделирование, о котором будет сказано
ниже.
Итак, .пусть для реализации памяти автомата исполь-
зуются триггеры. Тогда возможны два способа получе-
ния аналитических описаний логической сети, представ-
ляющей такой автомат Первый способ состоит в пред-
ставлении каждого триггера сетью из логических эле-
ментов, охваченных обратными связями, и в вынесении
этих элементов из блока памяти в комбинационную
часть автомата. Это равносильно переходу к логической
сети, в которой память реализована обратными связями.
О получении аналитических описаний таких сетей речь
шла выше.
Можно, однако, не производить указанного преобра-
тованпя элементов памяти, а поступить следующим об-
разом. Построим аналитическое описание комбинацион-
ной части автомата. Это описание содержит наряду с вы-
ражениями для выходных функций Zi, . .., Zh выражения
для функций возбуждения Wi, w2, ., Wj, зависящих от
переменных х1( . хп, щ, .. ., ут Выпишем затем фор-
мулы для реализуемых триггерами функций. Аргументами
последних являются функции возбуждения wit а так-
же внутренние переменные р, триггеров. После подста-
новки в эти формулы вместо символов Wt представляю-
щих их выражений будет получено искомое описание
<01 и Заметим, что в ряде случаев по комбинационной
части автомата потребуется строить как прямые, так и
обратные формы для функций Wt.
Пример 4-4. На рис. 4-8,а приведен пример логической сети
( триггером (элементы 4, 5) и обратной связью, охватывающей все
леменгы сети. На рис. 4 8,6 приведена комбинационная логическая
с<>|., полученная из данной сети путем обрыва соединения выхода
k mvhi.i 5 с элементами 4 и 1. Дизъюнктивные нормальные формы
'|>\||кцпп. реализуемых сетью, имеют вид:
(4-7)
(4-8)
359
z = a y\J су,
у' = ab c\J by V ас У-
Рис. 4-8. Сеть к примерам 4-4 и 4-5.
При рассмотрении триггера как элемента памяти, описываемого
таблицей переходов — выходов или соответствующими зависимостя-
ми выходов от входов, получим структуру, изображенную на
рис. 4-8,в. Триггер пусть описывается таблицей 4-6в. Тогда имеем:
Wi = а с у; w, = а V с \J у;
w2 = с b V У b\ w2 — с у\/ Ь;
z = p'i — р2 ui1 = р2а\/ р2с \/ р2у;
У' = р'г — piWi = pi с y\J -p2b.
СОСТЯЗАНИЯ И ТРОИЧНОЕ МОДЕЛИРОВАНИЕ
Реальные дискретные устройства с памятью, как и
комбинационные устройства, могут иметь такие соеди-
нения их элементов, которые не удовлетворяют формаль-
ному определению правильной логической сети. В таких
360
случаях необходимы либо искусственные приемы, де-
лающие возможным использование логической сети как
модели устройства, либо применение других более под-
ходящих моделей.
В дискретных устройствах в процессе их работы мо-
гут возникать непредусмотренные кратковременные им-
пульсные сигналы в моменты переходов от одного
входного набора или внутреннего состояния к другому.
Это явление в теории релейных устройств получило на-
звание состязаний. Физическая причина состязаний со-
стоит в различных временах прохождения но цепям
устройства сигналов, поступающих па различные выходы
одного и того же логического элемента или элемента
памяти.
При рассмотрении комбинационных устройств мы не
уделяем внимания состязаниям в связи с тем, что по-
следние не мешают делать правильные выводы о техни-
ческом состоянии таких устройств в предположении на-
личия в них правильных устойчивых неисправностей.
Действительно, возникший в комбинационном устройстве
кратковременный импульс нигде не заномппастся, а его
появление в контрольных точках «фильтруется» тем, что.
измеряются только установившиеся значения выходных
сигналов. Этого нельзя сказать о состязаниях в устрой-
ствад с памятью. Возникающие в них импульсы могут
поступать на входы триггеров или логических элементов,
охваченных обратной связью, и таким образом могут
запоминаться, т. е. изменять непредвиденным образом
внутренние состояния устройства. Состязания могут
привести к нарушению алгоритма функционирования
устройства с памятью, а при диагнозе — к неправильным
выводам о его техническом состоянии.
Для выявления состязаний в комбинационном уст-
ройстве (в комбинационной части устройства с памятью)
обычно выполняют специальный анализ логической сети
в предположении, что сигналы на полюсах и в узлах
сети могут принимать одно из трех возможных значе-
ний: 0, 1 или 1/2. При этом 0 и 1 являются «обычными»
определенными значениями сигналов, а 1/2 означает ли-
бо изменение сигнала с 0(1) на 1(0), либо может трак-
товаться как неопределенное (0 или 1) значение. Такой
анализ называют троичным моделированием.
При троичном моделировании каждый раз рассматри-
вается пара входных наборов и Х2 и определяется
361
йбзможность появления состязаний в устройстве прй
переходе от одного из этил наборов к другому. По набо-
рам и Х2 строится переходный троичный набор Ал, 2,
у которого входные переменные имеют значение 1/2, если
их значения в наборах и Х2 различны; значения дру-
гих переменных набора Xli2 совпадают с их значениями
в наборах Xt и Х2. Всем внутренним узлам и выходным
полюсам логической сети устройства приписываются зна-
чения 1/2. После этого на входы устройства подаются
последовательно наборы Ал, Х12, Х2. Для каждого вход-
ного набора и набора значений внутренних переменных
Y=yi, Уг, > Ут, установившегося в результате подачи
предыдущего входного набора (для первого набора А\
Таблица 4-7 Таблица 4-8
И ИЛИ-НЕ
AJj Хл У Xi Xi У
0 0 0 0 0 1
0 1/2 0 0 1/2 1/2
0 1 0 0 I 0
1 0 0 1 0 0
I 1/2 1/2 1 1/2 0
1 1 1 1 1 0
1/2 0 0 1/2 0 1/2
1/2 1 1/2 1/2 1 0
1/2 1/2 1/2 1/2 1/2 1/2
этими значениями являются значения 1/2), вычисляются
значения во всех узлах сети. Такой троичный расчет сети
с памятью имеет две особенности. Первая из них опре-
деляется наличием значения 1/2 сигналов и состоит
в умении вычислять троичные значения выходных функ-
ций логических элементов п элементов памяти в слу-
чаях, когда на их входы подаются неопределенные зна-
чения 1/2. Для каждого типа элемента могут быть
построены соответствующие таблицы, подобные приве-
денным в качестве примера табл. 4-7 и 4-8 для двухвхо-
довых элементов И и ИЛИ — НЕ.
Вторая особенность состоит в том, что при расчете
значений в узлах может потребоваться многократная
362
обработка одних и тех же элементов, охваченных кон-
турами обратной связи, до тех пор, пока не будут полу-
чены установившиеся значения (0, 1 или 1/2) во всех
узлах сети. В результате троичного моделирования на
наборах Xi, Xi, 2 и Х2 каждому узлу и полюсу сети ока-
жется приписанной последовательность из тре,х устано-
вившихся троичных значений сигналов. Последователь-
ности <0,0,0> * или <1,1,1 > свидетельствуют о том,
что в соответствующем узле устанавливается определен-
ное значение и состязания при переходе от X, к Х2 пе
возникают. Признаком возможного появления статиче-
ских состязаний являются последовательности вида
<0,1/2,0> пли <1,1/2,1 >, а динамических состязаний—
последовательности <0,1/2,1> или <1,1/2,0>. Другие
виды последовательностей (например, <0,1/2,1/2> или
< 1,2,1/2,1,2>) говорят либо о неопределенности значе-
ний сигналов, либо о наличии генераторного режима
в контуре обратной связи.
Пример 4-5. Выполнить троичное моделирование для устройства
рис. 4-8 на входных наборах XI = 101 (abc) и Х2=010 (аЬс)
Строим промежуточный набор X,. 2=1/2 1/2 1/2. Результаты вычис-
ления значений сигналов в узлах /—5 па каждом наборе представле-
ны в табл. 4-9.
Т а б л и ц а 4-9
а Ъ С / 2 3 4 5 *
1 0 1 1/2 1/2 1/ 2 \/2 1/2
1 0 1 0 0 1 1/2 0
1 0 1 0 0 1 1 0
1/2 1/2 1/2 0 0 1 1 0
1/2 1/2 1/2 1/2 1/2 1/2 1/2 0
1/2 1/2 1/2 1/2 1/2 1/2 1/2 1/2
0 1 0 1/2 1/2 1/2 1/2 1/2
0 1 0 1/2 0 0 1/2 1/2
При вычислениях использовались табл. 4-7 п 4-8. На наборах 101
п 1/2 1/2 1/2 установившиеся значения сигналов получены после
двух просчетов, а на наборе 010 — после одного. Анализируя после-
до па гсльности установившихся значений, получаем следующие ре-
зультаты: при подаче на устройство последовательности наборов
* Условимся последовательности входных, выходных символов и
символов состояний обозначать угловыми скобками < >.
363
<%1Х2> статические состязания возможны в узле 2, а динамиче-
ские— в узле <?; узлы 1, 4 и 5 имеют неопределенные значения сиг-
налов.
4-2. НЕИСПРАВНЫЕ ДИСКРЕТНЫЕ УСТРОЙСТВА
С ПАМЯТЬЮ И ИХ МОДЕЛИ
В этом параграфе рассматривается функциональный
подход к решению задач диагноза, когда задано только
правильное функционирование автомата на заданном
множестве входных последовательностей. Описываются
модели исправных и неисправных дискретных устройств:
логическая сеть с элементами памяти, абстрактный авто-
мат, таблица функций неисправностей, а также — неис-
правности и их модели. Приводится способ перевода от
наиболее распространенного задания дискретного уст-
ройства в виде логической сети или аналитического опи-
сания к таблице переходов — выходов.
Способы задания неисправных комбинационных
устройств, рассмотренные в гл. 3, полностью распростра-
няются на комбинационные части устройств с памятью.
Поэтому здесь будет обращено внимание в основном на
специфику задания неисправных дискретных устройств,
определяемую наличием у них памяти.
В первую очередь следует расширить понятие пра-
вильной неисправности, распространив его па случаи,
когда неисправности превращают исправное устройство
с памятью в комбинационное. Эю возможно потому, что
при этом сохраняется условие описания неисправного
устройства А{ моделью, принятой для описания исправ-
ного устройства А, так как комбинационное устройство
является вырожденным устройством с памятью, имею-
щим единственное внутреннее состояние.
Как уже отмечалось, функциональным описанием ди-
скретного устройства с памятью является таблица пере-
ходов выходов или эквивалентные ему описания в ви-
де графа, матрицы переходов — выходов, таблицы
истинности (пли ее части) комбинационного эквивалента
либо, наконец, системы булевых выходных функций и
внутренних переменных. Чаще всего мы будем пользо-
ваться таблицей переходов — выходов.
В § 3-2 была обсуждена постановка задачи проверки
работоспособности (или исправности) комбинационного
устройства на заданном множестве {Лф, входных наборов
в рамках функционального подхода. Рассмотрим анало-
364
। нчиую „остановку применительно к устройствам с па-
мятью.
В распоряжении исследователя имеется некоторое
устройство Л*, являющееся, быть может, неисправной
модификацией исправного устройства с памятью А. Воз-
можные неисправности устройства А—правильные. Из-
вестно функциональное описание устройства А в виде
таблицы переходов — выходов абстрактного или струк-
турного автомата. Задано некоторое конечное множество
{<Х;>фз, 1=1, 2, .... N, допустимых входных последо-
вательностей (/ — порядковый номер последовательно-
сти, j — порядковый номер входного набора в последо-
вательности), т. е. последовательностей входных набо-
ров, подача которых на рассматриваемое устройство до-
пустима. Ставится вопрос: что можйо сказать о техни-
ческом состоянии устройства А*, если имеется возмож-
ность наблюдать (измерять, контролировать) только вы-
ходные последовательности выдаваемые устрой-
ством в ответ на допустимые входные последовательно-
сти <Х;>7 из множества {<Хд>г}я.
Назовем процесс подачи входных последовательно-
стей, наблюдения соответствующих им выходных после-
довательностей и вывода заключений, основанных на
этих наблюдениях, экспериментом пад устройством (над
автоматом).
Поведение устройства с памятью зависит не только
от значений входов, но также от его состояний. Иными
словами, одно и то же устройство в ответ на одну и ту
же входную последовательность может выдавать различ-
ные выходные последовательности в зависимости от то-
го, в каком начальном состоянии находится устройство
в момент подачи первого входного символа (входного
набора) рассматриваемой входной последовательности.
При функциональном подходе состояния устройства ис-
следователю неизвестны, так как внутренние переменные
недоступны для наблюдения.
Пусть исправное устройство А имеет М состояний Yh,
h=l, 2, . . ., М. Тогда в исправном устройстве, не имею-
щем установки в начальное состояние (в неинициальном
автомате) для входной последовательности <Х,>/ на-
чальным состоянием Унач может оказаться любое из М
состояний множества {Уд} всех возможных состояний
устройства. Следовательно, каждой подаваемой на ис-
правное устройство А входной последовательности {Aj}(
365
можно сопоставить М выходных последовательностей
Выходные последовательности <Zj>//, будем
называть правильными. При заданной входной последо-
вательности {<%;>/ правильные выходные последова-
тельности нетрудно получить по таблице переходов -вы-
ходов исправного устройства.
Исходя из указанной зависимости поведения устрой-
ства с памятью от его начального состояния, ответ на
поставленный выше вопрос состоит в следующем. Если
хотя бы одна полученная при эксперименте над устрой-
ством Л* выходная последовательность <Z*j>//1, /=1,
2, . . ., N, не совпадает ни с одной из М правильных по-
следовательностей h = \, 2, ..., М, то исследуе-
мое устройство неисправно (и неработоспособно на мно-
жестве {<Х,>/}л заданных входных последовательно-
стей). Однако в противном случае (даже тогда, когда
каждая из N выходных последовательностей
совпадает с какой-либо из М соответствующих ей пра-
вильных последовательностей <Z,->;/l) об исправности
или работоспособности устройства ничего сказать нель-
зя— оно может оказаться как исправным (работоспо-
собным), так и неисправным (неработоспособным).
Полученные выводы остаются в силе также для ини-
циальных автоматов, если оставаться в рамках функцио-
нального подхода. Отличие здесь заключается только
в меньшем числе необходимых сравнений фактических
выходных последовательностей <Z*j>( с правильными
выходными последовательностями, так как при каждом
сравнении имеется лишь одна (вместо М для неиници-
ального автомата) правильная выходная последователь-
ность <Zj>;.
Рассмотренная постановка задачи характерна для
проверки правильности функционирования устройства
с памятью, когда множество {<Х)>/}3 образуют рабочие
входные последовательности устройства, т. е. те после-
довательности, которые подаются на него в процессе
функционирования. При решении задач проверки рабо-
тоспособности, исправности пли поиска неисправностей
ограничиться функциональным описанием устройств
с памятью в большинстве случаев нельзя.
При задании устройства с памятью логической сетью
его неисправности состоят либо в нарушении функцио-
нирования хотя бы одного логического элемента или эле-
мента памяти сети, либо в искажении связен сети. Су-
366
Шественными для устройств с памятью в отличие от ком-
бинационных устройств являются изменения величин
временных задержек логических элементов, а также за-
держек, вводимых в качестве элементов памяти или
в целях исключения состязаний. Причина состоит в том,
что как «малые» изменения величин задержек, так и
обрывы или короткие замыкания элементов, реализую-
щих задержки, могут приводить к искажению переходов
п выходных функпий устройств с памятью.
Неисправности типа обрыва элементов, реализующих
задержки, хорошо представимы моделью константных
неисправностей При формализации решения задач об-
наружения и особенно поиска неисправное гей тина «ма-
лых» изменений и коротких замыканий элементов, реа-
лизующих задержки, в общем случде требуются более
точные описания неисправных устройств, чем при рас-
смотрении логических неисправностей. Частым следстви-
ем неисправностей временных задержек являются со-
стязания, приводящие к неправильной работе памяти
устройства. Состязания могут возникнуть также вслед-
ствие появления в устройстве константных неисправно-
стей, в частности, таких, которые ликвидируют структур-
ную избыточность, введенную специально с целью
исключения состязаний.
Рассмотрение неисправностей триггеров можно орга-
низовать как на физическом, так и на логическом уров-
не, подобно тому, как это подробно было изложено для
логических элементов в § 3-2. Для описания неисправ-
ных модификаций триггера можно использовать как
таблицы (графы, матрицы) переходов — выходов, так и
таблицы состояний комбинационных эквивалентов. Со-
поставление описаний исправного триггера и его неис-
правных модификаций позволяет определить существен-
ные и несущественные неисправности триггера. Пусть,
например, исправный и неисправный" триггеры заданы
таблицами переходов выходов. По аналогии с логиче-
ским элементом функционирование триггера описывает-
ся функцией выхода Если сопоставление функций выхо-
да исправного и неисправного триггеров показывает, что
они различны, то неисправность существенна. Это зна-
чит, чю существует хотя бы одна входная последова-
тельность, ответы на которую исправного и неисправного
триггера различны. Если неисправность не изменяет вы-
ходную функцию, то она несущественна.
367
Заметим, что из-за большой сложности анализа
устройств с памятью на практике часто рассматривают
триггер как функциональный элемент и ограничиваются
классом константных неисправностей на его входах и
выходах. При этом число рассматриваемых неисправно-
стей может оказаться меньше, чем при рассмотрении
триггера как логической сети, поскольку при рассмотре-
нии триггера как функционального элемента констант-
ные неисправноегн внутренних соединений триггера не
учитываются.
В рамках классической теории экспериментов над
автоматами математической моделью устройства с па-
мятью является обычно абстрактный конечный автомат.
При этом неисправности устройства интерпретируются
как искажения выходных символов автомата или пере-
ходов между его состояниями Очень часто невозможно
однозначно указать места возникновения физических
неисправностей в устройстве, вызывающих данное нару-
шение переходов между состояниями абстрактного авто-
мата. Это ограничивает применение модели абстрактного
автомата задачами проверки работоспособности, пра-
вильности функционирования и иногда исправности
устройств.
Прежде чем перейти к рассмотрению моделей i-не-
исправных устройств с памятью, сделаем несколько
замечаний. Будем предполагать, чго все неисправности
являются правильными. Под элементарной проверкой
устройства с памятью будем понимать подачу на его
входы (основные и, возможно, дополнительные) после-
довательностей входных наборов и наблюдение ответ-
ных выходные последовательностей на контрольных точ-
ках, в число которых входят все основные и могут вхо-
дить дополнительные выходы устройства. Как правило,
будем считать, что составы контрольных точек фиксиро-
ваны и одинаковы для всех элементарных проверок.
В этом случае вместо множества П допустимых элемен-
тарных проверок можно рассматривать множество
{<Х7>г} входных последовательностей. Если на вход-
ные последовательности не наложены никакие ограниче-
ния, их число бесконечно, а длина может меняться от 1
до бесконечности. Поэтому прямое перечисление вход-
ных последовательностей при задании автомата в общем
случае невозможно. В то же время таблица переходов—
выходов автомата описывает в компактной форме все
368
(в гом числе бесконечные по длине) возможные входные
последовательности автомата Будем предполагать, что
никакие ограничения на входные последовательности не
накладываются (все последовательности допустимы)
В тех случаях, когда это не так, будем делать специаль-
ные оговорки.
Задание устройства с памятью как объекта диагноза
его явной моделью (W, {Ч7'}) в виде таблицы функций
неисправностей будет рассмотрено в следующем пара-
графе.
Чаще всего дискретное устройство с памятью, как и
комбинационное, задается своей структурой (функцио-
нальной схемой, логической сетью) и реже — аналити
ческпм описанием Таблицы переходов — выходов для
реальных устройств задаются очень "редко и, как прави-
ло, для исправных устройств. Рассмотрим, как построить
таблицы переходов выходов структурного и абстракт-
ного автоматов для устройства с памятью, заданного
аналитически или логической сетью.
Когда устройство задано аналитически, построение
структурной таблицы переходов выходов состоит
и вычислении значений выходных функций z и внутрен-
них переменных у' для каждой пары входной набор—
внутреннее состояние (Xj, Y(1), j=l, 2, ..., 2"; /г=1, 2. . .
. . ., 2m.
Пример 4-6. Вычислить значения выходной функции z и вну-
тренней переменной у' по формулам (4 7), (4-8), описывающим
функционирование устройства рис. 4-8, а на входном наборе
ООО (abc) при внутреннем состоянии 0 (т/):
z (ООО) = c^Vc7=l-lV°-1 = l;
у' (ООО) = яЬ7 V by\J ас~у =0-0-1 V 0-0 V 0-1 • 1 = 0.
Выполнив аналогичные вычисления для остальных пар (Xj, Ул),
получим структурную таблицу переходов — выходов, представленную
табл. 4-10.
Когда устройство задано логической сетью, можно
либо сначала получить аналитическое его представление
(методом прямой или обратной подстановки, как было
итожено в § 3-1 и 4-1) и затем поступить так, как
н примере 4-6, либо вычислять значения выходов и вну-
ipeiiinix переменных непосредственно по структуре.
Пример 4-7. Вычислить значение функции z и внутренней пере-
Mi иной // по структуре устройства рис. 4-8,а на входном наборе 101
(«(’<) и при «/=0. Будем вычислять значения на выходах элементов
° I -358 369
В порядке их номеров. Для элементов 1, 2, 3, 4, 5 соответственно
имеем:
У1 = с V У = 1 V 0 = °; Уг = ayt = 1-0 = 0;
Уз = bVl/i - 0V0 = 1;
г = Уг\/У = 0 V 0 = 1;
у' = у$ — yi V Уз = 1 V 1 = °-
Построение таблицы переходов — выходов абстракт-
ного автомата по заданной таблице структурного авто-
Таблнца 4-10
U'/з У
0 1
0 0 0 0/1 0/0
0 0 1 0/1 0/0
0 1 0 0/1 1/0
0 1 1 0/1 1/0
1 0 0 1/0 0/0
1 0 1 0,1 0/0
1 1 0 1/0 1/0
1 1 1 0/1 1/0
мата состоит в кодировании входных наборов, наборов
внутренних переменных и выходных наборов символами
входного алфавита, алфавита состояний и выходного
алфавита абстрактного автомата.
Пример 4-8. По табл. 4-10 построить абстрактную таблицу пере-
ходов — выходов устройства рис. 4-8,я. Примем следующее кодиро-
вание:
а b с У Z
0 0 0 — X, 0 —У, 0 — Z1
0 0 1 — Хг 0 1 0 — X-t 0 1 1 — Хг 1 0 0 — Х5 1 0 1 — X, 1 1 0— х7 1 1 1—X, 1 — у2 1 — z2
Искомой является табл. 4-11.
Построение таблицы переходов — выводов неисправ-
ного устройства с некоторой неисправностью i произво-
дится таким же образом, если известна логическая сеть
или аналитическое описание устройства с i-й неисправ-
ностью.
370
Логическая сеть неисправного устройства с памятью
А‘ может быть получена из логической сети исправного
устройства А изменением функциональных свойств логи-
ческих элементов, элементов памяти или связей, опреде-
ляемых наличием в устройстве неисправности s,.
Таблица 4-11
Y'/Z {r}
Yxx
X, Yx/Zi Yx/Z,
Х2 Yx/Zi Yx/Zx
А'з Yi/Zx
{X} Xt Yx/Z2 YilZx
X5 Yi/Zx Yx/Zx
x. Yx/Z2 Yx/Zx
X-, YijZx Yi/Zx
Xt Yx/Z2 Yi/Zx
Таким образом, можно говорить о явной графической
модели вида (Л, (Л’}) и от нее перейти к явной аналити-
ческой модели (F, {F’}), получив аналитические описания
всех i-неисправных устройств. Наконец, вычислив значе-
ния выходных функций и внутренних переменных на
каждом входном наборе X, при каждом состоянии У/(,
можно перейти от указанных моделей к совокупности
таблиц переходов — выводов исправного и всех t-неис-
правных устройств. Все перечисленные явные модели
громоздки и поэтому неудобны. Однако в следующем
параграфе для изложения основных результатов теории
экспериментов над автоматами мы все же воспользуемся
явной моделью.
si
Структурная неявная модель вида (Л, S, Л — А1),
представляющая собой задание логической сети исправ-
ного устройства А, класса неисправностей 5 и правил
получения для каждой s,eS логической сети i-неисправ-
ного устройства Л’, будет использована в дальнейшем
при описании методов построения проверяющих входных
последовательностей.
24* 371
Для дискретных устройств с памятью, так же как
и для комбинационных устройств (см. гл. 3), можно исполь-
зовать аналитические неявные модели вида (F, X, X X У,
_ S,, ххг Sj, XXY
F------*F, Г')или(Г, X, Xy^Y, F-----<F‘). Здесь X
множество наборов значений входных и внутренних пе-
ременных устройства. Применительно к устройствам
с памятью можно рассматривать также табличную неяв-
ную модель, в которой исправный автомат задан своей
таблицей переходов — выходов, а возможными неисправ-
ностями являются искажения значений выводов или пе-
реходов между состояниями. Такая модель будет ис-
пользована при описании методов построения проверяю-
щих тестовых последовательностей.
4-3. ОСНОВЫ ТЕОРИИ ЭКСПЕРИМЕНТОВ НАД АВТОМАТАМИ
Не задаваясь целью детального и строго формально-
го изложения результатов теории экспериментов над
автоматами, мы ограничимся здесь рассмотрением толь-
ко основных понятий и постановки задач в рамках ука-
занной теории.
Характерным для классической теории экспериментов
над автоматами является использование функциональ-
ного подхода, когда автомат задается таблицей перехо-
дов— выводов (или какой-либо другой эквивалентной
ей формой задания), а доступными для эксперимента
являются только внешние входы и выходы автомата.
Следует отметить, что последнее условие проведения
эксперимента не является ограничением, так как введение
дополнительных входов и выводов в исходный автомат
всегда может быть интерпретировано как переход к рас-
смотрению другого автомата с расширенными входным
и выходным алфавитами.
ОСНОВНЫЕ ПОЛОЖЕНИЯ И ПОСТАНОВКА ЗАДАЧ ДИАГНОЗА
Пусть исправный автомат Л и все его i-неисправные
модификации /1* при заданном классе X рассматривае-
мых неисправностей представлены своими таблицами Ч7,
4я переходов — выходов. Присвоим автомату А номер
i=0, включив его тем самым в множество автоматов А*,
считая, что i=0, 1, ..., |Х|. Объединим эти таблицы
в единую таблицу — таблицу функций неисправностей,
372
в которой автомат Ai, 1=0, 1, . .|S|, имеет внутрен-
них состояний Ylh, h = 0, 1, ..М{, образующих множест-
во {Уф, а входной алфавит {X} состоит из /V входных
символов Xj, j=l, 2, ..N<Z2n, где п — число входных
полюсов автомата. Автомат Аг, находящийся в состоянии
Уг\, в ответ на подачу на него входного символа X,- пере-
ходит в состояние У’/ij и выдает выходной символ Zjh-
Пусть множество {У} является объединением множеств
Is!
{У*} состояний всех автоматов Л*{У} = (J {У‘}. Тогда
£=0
таблицу функций неисправностей можно рассматривать
как таблицу переходов — выходов некоторого автомата
А с множеством {У} состояний и тем же входным алфа-
витом {X}. Выходной алфавит {Z} автомата А является
объединением выходных алфавитов автоматов Л*.
Запись Лг/У’л. означает, что автомат Лг находится
в состоянии Yih- Два состояния: У1 автомата At и У2
автомата Лг—называются эквивалентными, У1 = У2, если
при подаче на автоматы A^Yt и Л2/У2 любой входной
последовательности оба автомата выдают одинаковые
выходные последовательности; в противном случае со-
стояния У1 и У2 различимы (неэквивалентны). Определе-
ние эквивалентности состояний справедливо также для
одного и того же автомата. Автомат At эквивалентен
автомату Аг, At=A2, если каждому состоянию У/,, /г =
= 1, 2, .. ., Mi, автомата At соответствует по крайней
мере одно эквивалентное состояние автомата А2, и нао-
борот. Автомат, для которого не существует меньшего
по числу состояний эквивалентного ему автомата, назы-
вается минимальным. Автоматы называются сравнимы-
ми, если они имеют одинаковые входные алфавиты
Автомат At называется сильносвязным, если существует
входная последовательность, переводящая автомат A\/Yi,
в At/Yi,, где Yk и У/,— любые два состояния автомата At,
причем k может равняться h. Обратимым называется
автомат, который из любого состояния можно перевести
в начальное подачей на него некоторой входной после-
довательности <Х;>г, где I — номер последовательно-
сти. В общем случае среди автоматов A*, t=0, 1, . .., |S|,
могут оказаться эквивалентные; автоматы А1 могут быть
не минимальными, а среди состояний из множества {У}
могут быть эквивалентные состояния. Автомат А, задан-
ный описанной таблицей функций неисправностей, часто
373
называют расщепляемым автоматом. Смысл этого терми-
на состоит в том, что в автомате А нет переходов между
состояниями Yih, и состояниями yj/i при i#=/ составляю-
щих его автоматов А{ и ЛЛ
Методика решения задач диагноза технического со-
стояния по таблице функций неисправностей была рас
смотрена достаточно детально в гл. 1. В § 1-9 дано пред-
ставление алгоритмов диагноза графами-деревьями. Из-
ложим особенности указанной методики и графического
представления алгоритмов диагноза применительно
к таблице функций неисправностей, задающей расщеп-
ляемый автомат А.
Будем рассматривать задачи тестового диагноза тех-
нического состояния автоматов. Пусть А*— автомат, над
которым производится эксперимент; но постановке зада-
чи А* является одним из автоматов Л(»=0) или А‘,
1=1, 2, .. ., |S|. Под элементарной проверкой будем по-
нимать подачу входной последовательности <Х,>г дли-
ны 1 или больше на входы автомата А*/У*п и измерение
ответной выходной последовательности
Тогда задача построения алгоритма проверки исправ-
ности (работоспособности) автомата состоит в том, что-
бы найти такую последовательность (или совокупность
последовательностей) элементарных проверок, реализа-
ция и анализ результатов которых позволяют установить,
является автомат А* автоматом А (либо одним из авто-
матов А\ эквивалентных автомату Л) или же А*=/=А.
Задача поиска неисправностей состоит в нахождении по-
следовательности (или совокупности последовательно-
стей) элементарных проверок, в результате реализации
которой устанавливается, каким из автоматов А\ i=
=0, 1, . . ., |S|, является автомат А* (с точностью до
эквивалентности автоматов Л'). Из приведенных опреде-
лений следует, что наличие эквивалентных автоматов
среди автоматов Л, Л* влияет только на достижимую
глубину диагноза. Поэтому ради простоты дальнейшего
изложения будем считать, что таблица функций неис-
правностей не содержит эквивалентных автоматов. Дру-
гие случаи необходимости учета эквивалентности авто-
матов будем оговаривать особо.
Как следует из сказанного, особенность таблицы
функций неисправностей автоматов состоит в том, что
требуется различать между собой не пары ее столбцов,
а пары групп столбцов. Причем каждая группа столбцов
374
представляет таблицу переходов — выходов одного из
автоматов А или Л*. Для каждого из автоматов А\ 1=
=0, 1, .... |S| предполагаются известными подмножест-
ва {У7нач}<={У*} их допустимых начальных состояний, т. е.
состояний, в любом из которых может находиться авто-
мат Л’ перед реализацией любого эксперимента над ним.
Объединение подмножеств {У’нач} дает подмножество
{УНач}с{У} допустимых начальных состояний расщепляе-
мого автомата Л,{Унач}= U {^'нач}.
»=0
Подмножество возможных конечных состояний авто-
мата Л‘, в любом из которых может оказаться этот авто-
мат после подачи на него некоторой входной последо-
вательности <Х/>/, обозначим записью {УгКОп}г Объеди-
нение и {У’кон}/ Дает подмножество {УКОн}/ возможных
i=0
конечных состояний расщепляемого автомата Л относи-
1$1
тельно последовательности <Х;>(, {УКОц}/ = (J {УСон}/.
i=0
Для того чтобы различить автоматы Ai, i=0, 1, ...
. . ., |S|, необходимо построить и затем реализовать не-
которую последовательность или совокупность последова-
тельностей {<Xj>i} входных символов (входных набо-
ров), в ответ на которую различаемые автоматы выдают
разные последовательности или совокупности последова-
тельностей {<Z’j>/} выходных символов (выходных
наборов). Придать входной последовательности <_Xj<Zi
свойство различать автоматы Л‘ можно различными спо-
собами.
Можно, например, потребовать, чтобы последователь-
ность <Х,->/ давала возможность построить таблицу Ч’*
переходов — выходов исследуемого автомата Л*. Путем
последующего сравнения таблицы Чг* с таблицами 4й
переходов — выходов различаемых автоматов А‘ уста-
навливается, каким из автоматов Л’ является автомат
А*. Сложность решения задачи различения таким спо-
собом весьма высока (необходимы последовательности
<Xj>; большой длины), если не предусмотрены спе-
циальные меры по непосредственной установке и кон-
тролю состояний автомата, о чем будет идти речь в кон-
це этого параграфа Кроме того, при указанной поста-
новке задачи различения автоматов пути ее решения
375
Известны только для узких классов автоматов А\ удов-
летворяющих достаточно жестким ограничениям, напри-
мер, если автоматы составляют класс сильносвязных
автоматов и есть возможность наблюдать состояние
автомата (измерять значения внутренних переменных).
Тогда алгоритм снятия таблицы переходов — выходов
автомата этого класса состоит в определении всех пере-
ходов из каждого состояния под воздействием каждого
входного символа и соответствующих этим переходам
выходных символов.
Более рациональным является решение задачи раз-
личения автоматов путем придания входной последова-
тельности либо свойства определения подмноже-
ства {Т*Нач}гС={Унач} начальных состояний расщепляемого
автомата А, т. е. состояний, в одном из которых факти-
чески находился автомат А в момент подачи первого
символа последовательности <%•;>/, либо свойства опре-
деления подмножества {У*Кон}г^{У} конечных состояний
расщепляемого автомата А, т. е. состояний, в одном из
которых фактически окажется автомат А после подачи
последовательности <Aj>;.
В первом случае последовательность <Xj>; называ-
ют отличительной1 относительно подмножеств
{У*нач}г Найдя подмножество {У*пач}г, выполняют опера-
цию пересечения его с множествами {У’нач} допустимых
начальных состояний каждого из автомата А*. Исследуе-
мый автомат А* является одним из тех автоматов /В, для
которых это пересечение не пусто, {У*Нач};П {Угнач}=И=0-
Во втором случае последовательность <Xj>; назы-
вают установочной относительно подмножества {У*кон}г-
Аналогично первому случаю непустые пересечения полу-
ченного подмножества {У*КОн}г с множествами {У’кон}; со-
стояний указывают автоматы А{, одним из которых явля-
ется автомат А$, {У^кон}; {Y^koh}i=A=0-
ДЕРЕВО ПРЕЕМНИКОВ
В основе методов построения как отличительных, так
и установочных входных последовательностей лежит по-
нятие дерева преемников. Начнем рассмотрение понятия
с некоторых определений. Для иллюстрации будем обра-
1 В литературе иногда ее называют диагностической.
376
щаться к автомату Ai, таблица переходов — выходов и
граф переходов — выходов которого представлены соот-
ветственно табл. 4-12 и рис. 4-9.
Та блица 4-12
+ 1 /
1 n 3 4 1 5
А'1 2/1 1/1 5/0 2/0 4/1
И,} ЛЛ2 1,0 3/0 3/1 1,0 5/0
Автомат А имеет пять состояний, обозначенных циф-
рами 1, 2, . . ., 5, входной алфавит {Х±, Х2} и выходной
алфавит {1,0}. л
Преемником состояния Y^ автомата относительно
входной последовательности <А',>( называется состоя-
ние У/,/, в которое переходит автомат, находящийся в со-
стоянии Уд, под воздействием последовательности
Рис. 4-9. Граф переходов—выходов автомата,
таблица переходов—выходов которого представ-
лена табл. 4-12.
Например, состояние 3 автомата А является
преемником состояния 1 относительно входной последо-
вательности <A'i, Х2> или, короче, <Xi, Х2>-преемни-
ком состояния 1. Совокупности состояний автомата бу-
дем называть Y-множествами. Элементы У-множества не
377
обязательно различны. У-множество, содержащее един-
ственный элемент, называется простым, а содержащее
несколько одинаковых элементов, — кратным. У-множе-
ство однородно, если все его элементы одинаковы.
Дерево преемников представляет собой ориентиро-
ванный граф. Начальной вершине графа (единственной
вершине нулевого ранга, или корню дерева) поставлено
в соответствие исходное множество {УНач}о допустимых
{>,2,ЗД5}
,—5—1—*—,
{|,ЗЛ5}{з}
X, | Х2 X, ! Xz
I------------1 I---1--------1
{i,z}(z}M {з,1,|)(з,з} {г.2,ВД{з} {и,5}[з}{з}
х, I Х2 х, | Х2 X; I х2 X, I хг
। к Щ I-----------1 I-----------1
{2,|}{|}{2}{г} {|,3}{3}{V}{5}{2,2}{4}{5} {3}{u}{5}{3} {з,з,1}{5}{5} {zx,v}{5}[5) {и,5){з}{з}
Рис. 4-10. Дерево преемников к примеру 4-9.
начальных состояний автомата. Ветвям дерева при-
писаны символы входного алфавита автомата. При
мощности входного алфавита, равной а, из каж-
дой вершины (кроме конечных, пли висячих, вер-
шин) дерева исходит а разных дуг. Следователь-
но, пути в дереве 'представляют входные после-
довательности. Имеется а'~ путей длины г, начинаю-
щихся в корне и заканчивающихся в вершинах г-го ран-
га дерева. Каждой вершине дерева поставлены в соот-
ветствие группы У-множеств состояний автомата. Корню
дерева, как указывалось, поставлено в соответствие У-
множество {УНач}о допустимых начальных состояний авто-
мата. У-множества, поставленные в соответствие вну-
тренним и висячим вершинам дерева преемников, нахо-
дятся следующим образом. Пусть путь, начинающийся
в начальной вершине и заканчивающийся в некоторой
внутренней или висячей вершине дерева, представляет
входную последовательность <Aj>/. Найдем для каж-
дого начального состояния У/( нач^{Унач}о его преемника
Yhi относительно последовательности <Xj>; и выходную
последовательность </;>//,. Объединим состояния-пре-
емники в У-множества по следующему правилу. Два со-
стояния-преемника Yhi и Ygi принадлежат одному и тому
же У-множеству тогда и только тогда, когда соответст-
378
вующпе выходные последовательности <Zj>№ Й
<Zj>ig одинаковы.
Пример 4-9. Построить дерево преемников для автомата .41
(рис. 4-9, табл. 4-12) при допустимом множестве начальных состоя-
ний {Унач}о^ {1* 2, 3, 4, 5}.
Четыре первых ранга дерева преемников показаны на рис. 4-10.
Информация для построения дерева берется из таблицы переходов —
выходов автомата. Разберем детально построение левого пути дере-
ва, представляющего последовательность <Xi, Хь Х]> (другие пути
строятся аналогично) *. Корню дерева поставлено в соответствие
У-мпожество {УНач}о- Из корня исходят две ветви и Х2, пред-
ставляющие символы входного алфавита. Первая последователь-
ность <Xi>i длины 1 дает следующие выходы и состояния преем-
ника:
Yh < X, >lft Yh..
1 I 2
2 I 1 *
5 1 4
3 0 5
4 0 2
На основании полученных значений выходной последовательно-
сти <Zi>ii, первой слева вершине первого ранга следует сопоста-
вить два У-множества: {2, 1, 4} п {5, 2}. Из этой вершины также
исходят две ветви X] и Х2.
Определение У-множеств очередного г-го (в данном случае вто-
рого) ранга можно выполнить путем рассмотрения входных последо-
вательностей длины г при исходном множестве {УНач}о допустимых
начальных состояний или последовательностей длины 1, приняв в ка-
честве начальных состояния У-множеств, поставленных в соответст-
вие вершинам предыдущего (г—1)-го (в данном случае первого)
ранга. Воспользуемся вторым, более простым способом, который для
последовательности <Xi>i дает:
Yh Zi ih
2 1
Ум
1
4 0 2
5 1 4
2 1 1
Получаем три У-множества: {1,
последовательностью <ХЬ Xi>.
2}, {2}, {4, 1}, порождаемые
1 Номер последовательности будем опускать в тех случаях,
когда он не имеет значения.
379
Наконец, для
<Xi>! получаем:
ранга 3 при бездействии последовательности
Yh <Л >ih Yhi
1 1 2
2 1 1
2 1 1
4 0 2
1 1 2
Имеем четыре У-миожества {2, 1}, {1}, {2}, {2}, порождаемые
последовательностью <Xj, Хь Xj>. Остальные ветви преемников
рис. 4-10 построены аналогично.
Дерево преемников в принципе можно продолжать
бесконечно, однако для интересующих нас целей по-
строения отличительных и установочных входных после-
довательностей в этом, оказывается, нет необходимости,
так как требуемую информацию о поведении автомата
можно представить деревом с путями конечной длины.
В зависимости от правил усечения путей дерева преем-
ников можно получить либо отличительное, либо уста-
новочное дерево.
ПОСТРОЕНИЕ ОТЛИЧИТЕЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Отличительное дерево есть дерево преемников, в ко-
тором вершина ранга г является висячей, если: а) ей
поставлена в соответствие группа У-множеств, содержа-
щая хотя бы одно кратное У-множество; б) ей постав-
лена в соответствие группа У-множеств, поставленная
в соответствии какой-то вершине ранга меньше г; в) сре-
ди вершин ранга г имеется хотя бы одна, которой постав-
лены в соответствие только простые У-множества. В по-
следнем случае все вершины ранга г являются висячими.
Пример 4-10. Построить отличительное дерево для автомата Ai
(табл. 4-12, рис. 4-9). Отличительное дерево для автомата Аь пред-
ставленное па рис. 4-11, получено путем построения дерева преемни-
ков и обрыва его ветвей по приведенным выше правилам. Ветви,
соответствующие входным последовательностям <Х2>, <Х]Х2> и
<ХЬ Хь Х2>, оборваны по правилу «а». Ветвь, соответствующая
последовательности <ХЬ Xlt Хь Х[>, оборвана по правилу «б»:
группа У-множеств {2, 1}, {1}, {2}, {2} ранга 4 совпадает с группой
У-множеств ранга 3. Ветви, соответствующие последовательностям
(Хь Xi, Хь Х2, X]) и <ХЬ Хь X], Х2 Х2>, обрываются по правилу
«в», так как каждая из них оканчивается группой простых У-мно-
жеств.
380
Отличительным входным последовательностям соот-
ветствуют пути (от корня до висячей вершины) отличи-
тельного дерева, заканчивающиеся вершинами, которым
сопоставлены только простые У-множества. Действитель-
но, при этом число простые У-множеств в конечных вер-
шинах путей равно числу допустимых начальных состоя-
ний автомата и, кроме того, разным простым У-множе-
ствам соответствуют разные выходные последовательно-
сти, каждая из которых, следовательно, соответствует
«своему» начальному состоянию.
{«И
!_______±.________I Лг
{гллНьг}
---1
{w№}
{2,;}{1}{г}{г} {|,з){з}{ы}
{ЗД}{5,3}
HOW {зл}{»}{г}{г>
Рис. 4-11. Отличительное дерево к примерам 4-10 и 4-11.
В теории экспериментов над автоматами различают
безусловные и условные, простые и кратные эксперимен-
ты. Определение безусловного и условного экспериментов
над автоматом совпадают с соответствующими определе-
ниями условного и безусловного алгоритмов диагноза,
данными в гл. 1. При простом эксперименте требуется
единственный экземпляр исследуемого автомата, а при
кратном — два или больше. Практическая интерпретация
кратного эксперимента, когда физически имеется един-
ственный экземпляр устройства, возможна при условии
гарантированной установки устройства в одно и то же
начальное состояние.
Отличительное дерево рассмотренного выше вида
естественным образом представляет простые безуслов-
ные отличительные эксперименты над автоматом. Не-
трудно показать, что все представляемые деревом отли-
381
чительные последовательности являются безусловными
последовательностями минимальной длины. При реали-
зации безусловного отличительного эксперимента па ис-
следуемый автомат А* подается безусловная отличи-
тельная последовательность <Х;>/ и фиксируется от-
ветная выходная последовательность <Z*j>;. Затем
производится сравнение последовательности <Z*3>i
с возможными выходными последовательностями, кото-
рые предварительно определяются по отличительному де-
реву и по таблице (графу) переходов—выходов автома-
та для соответствующего отличительного пути. В зависи-
мости от способа сравнения безусловная отличительная
последовательность может быть реализована как после-
довательность с безусловной остановкой (когда сравне-
ние выполняется один раз после реализации всей после-
довательности или с условной остановкой (когда
сравнение выполняется многократно после реализации
каждого очередного символа из <Xj>/).
Пример 4-11. Построить простой безусловный эксперимент для
автомата Ал (табл. 4-12, рис. 4 9) с безусловной и с условной оста-
новкой. Выберем на отличительном дереве (рис. 4-11) отличительный
путь, определяемый последовательностью <Xj>i = <Xi, Xt, Хл,
Х2, Xi>. В табл. 4-13 представлены выходные последовательности,
выдаваемые автоматом й]/1, ,<4i/2, Ai/3, At/4, AJ5 соответственно
в ответ на <Xj>i.
Таблица 4-13
Начальное состоя-
ние
(Zj>lftnpH <Ху>,
1
2
3
4
5
<1 I 1,0,0>
<1,1,1,0,1>
<0.1,0,0,0>
<0,1,1,0,0>
<1,0,1.0,1>
Последовательности построены по графу переходов — выходов
рис. 4-9. Как видно из табл. 4-13, каждому начальному состоянию
соответствует своя выходная последовательность. Пусть в результате
эксперимента с безусловной остановкой над автоматом А* получена
выходная последовательность <Z*j>1x=<0, 1, 0, 0, 0>. Сравнивая
с последовательностями табл. 4-13, находим, что автомат
А* есть автомат AJ3. При реализации эксперимента с условной
остановкой требуется подача на автомат А* только трех первых
символов последовательности <Xj>i, при этом выходная последо-
382
вательность <Z*j>ift = <0, 1, 0> однозначно указывает, что иссле-
дуемый автомат находится в начальном состоянии 3.
Известно, что при числе допустимых начальных со-
стояний автомата, большем двух, задача различения
автоматов простым безусловным отличительным экспе-
риментом не всегда имеет решение. Формальным при-
знаком этого является отсутствие в отличительном дере-
ве висячих вершин, которым поставлены в соответствие
только простые У-множества. В таких случаях можно
попытаться воспользоваться простым условным экспери-
ментом.
Особенность простого условного эксперимента состо-
ит в том, что подаваемая па автомат Л* отличительная
последовательность формируется в процессе эксперимен-
та над автоматом. Очередной входной символ последо-
вательности назначается в зависимости от результатов
анализа выходной последовательности, полученной в от-
вет на ранее поданную входную последовательность.
Простой условный эксперимент всегда является экспе-
риментом с условной остановкой.
Пример 4-12. На рис. 4 12 приведен граф переходов-—выходов
некоторого автомата А2. При допустимом множестве начальных со-
стояний {Унач}о = {1, 2. 3, 4} простой безусловный отличительный
383
эксперимент для Д2 не существует. Однако условный отличительный
эксперимент позволяет определить начальное состояние Подав вход-
ную последовательность <Xt, Х2> и получив выходную последова-
тельность <1, 0> или <il, 1>, определяем, что в первом случае
начальным состоянием может быть 1 или 2, а во втором 3 или 4
Эту информацию используем при назначении следующего входного
символа. При выходной последовательности <1, 0> назначен Xt,
а при <1, 1> — Х2 и затем Хц В результате в первом случае по-
даем <Х[, Х2, Xi> и получаем <1, 0, 1>, если начальное состоя-
ние 1 и <1, 0, 0>, если начальное состояние 2. Во втором случае
подаем <Xi, Х2, Х2, Xi> и получаем <1, I, 0, 1>, если начальное
состояние 3 и <1, 1, 0, 0>, если начальное состояние 4.
Необходимое условие, при котором возможно суще-
ствование решения задачи определения начального со-
стояния автомата простым условным экспериментом,
состоит в следующем: в отличительном дереве для каж-
дого допустимого начального состояния найдется путь,
заканчивающийся внутренней или висячей вершиной,
которой сопоставлена группа У-множеств, содержащая
простое У множество, причем каждому начальному со-
стоянию соответствует свое У-множество. Указанное
условие не является достаточным. Действительно, успеш-
но воспользоваться простым условным экспериментом
удается тогда, когда в ответ на последний символ вход-
ной последовательности, представляющей эксперимент,
автомат выдает выходное значение, которому соответст-
вует в отличительном дереве простое У-множество. Яспо,
что в общем случае это не всегда возможно: в процессе
реализации входной последовательности может быть по-
лучено значение, которому соответствует непростое У-
множество висячей вершины дерева.
Кратный эксперимент над автоматом используется
тогда, когда простой (условный и безусловный) экспе-
римент не позволяет решить отличительную задачу.
Кратный эксперимент, длина которого больше 1, всегда
условный.
В основе организации кратного эксперимента лежат
следующие соображения. Пусть задано исходное множе-
ство {УНач}п, содержащее несколько допустимых началь-
ных состояний автомата. Выделим из множества {УНач}о
два (любых) состояния Yh и Yg и построим для них от-
личительную безусловную последовательность <Xj>hg-
Такая последовательность всегда существует, если Yh и
Yg неэквивалентны. Минимальную по длине последова-
тельность <Xj>hg можно получить из отличительного
дерева, построенного в предположении, что допустимыми
384
начальными состояниями являются состояния Yh и Yg.
Затем вычислим по таблице переходов — выходов выход-
ные последовательности <Z;>fe для каждого A/Y, где
У/4е{Унач}о, выдаваемые автоматом А в ответ на <Xj>hg-
Используем эти выходные последовательности в качест-
ве признака разбиения множества {УПач}о на классы.
В один и тот же класс включаются все те состояния из
{Упач}о, для которых выходные последовательности
<Zj>ft совпадают.
Описанные операции можно представить графически
в виде фрагмента отличительного дерева кратного экс-
перимента. Если возникает задача построения полного
дерева кратного эксперимента, то из выделенных клас-
сов допустимых начальных состоянии отбираются не пу-
стые и нс одноэлементные. Каждый ха кой класс пооче-
редно принимается в качестве нового исходного множе-
ства допустимых начальных состояний и по отношению
к нему повторяются все изложенные выше операции
(выбирается пара начальных состояний, строится для
нее простая безусловная отличительная последователь-
ность, находятся выходные 'последовательности и, нако-
нец, производится разбиение исходного допустимого мно-
жества на классы). Процесс продолжается до тех пор,
пока не окажется, что все полученные в результате раз-
биений классы либо одноэлементные, либо пустые.
Пример 4-13. Построить полное отличительное дерево кратного
эксперимента для автомата А2 (рис. 4-12) при {Уцач}о= {7, 8, 9, 10}.
Отнесем {Упач}о к нулевому рангу н обозначим {УПач}о|- Обозначим
первую копию автомата А2 через Л(1), вторую — через Л (2) и т. д.
Пусть первой подается (рис. 4-13) отличительная последовательность
<Xj>7 8=<Х2, Х,>. Для удобства в прямоугольниках-вершинах
дерева указаны не только {УНач}, но также номер копии автомата
и отличительная последовательность <Xj>hg, а рядом с дугами
дерева — ответные выходные последовательности <Zj> При подаче
<Х3'>7 8 на первую копию А (1) 'возможны три выходные последо-
вательности: <0, 1> при начальном состоянии 7, <0, 0> при на-
чальном состоянии 8 и <1, 1> при начальных состояниях 9 пли 10,
выделяющие три класса допустимых начальных состоянии. Класс
{9, 10} — не одноэлементный. Для его разбиения требуется вторая
копия Л (2). При подаче на Л (2) последовательности <Х^> опреде-
ЛЯвМ ^нач== 9 (при <Zj>9=1) или Унач = 10 (при <Z;>I0 = 0).
Кратность эксперимента (число требуемы,х копий
автомата) зависит от выбора пар состояний Yh и Уg, для
которых строятся отличительные 'последовательности.
Полное отличительное дерево кратного эксперимента со-
держит все возможные исходы последнего, но 'построение
25—358 385
его может оказаться громоздким. Иметь полное отличи-
тельное дерево кратного эксперимента заранее (до про-
ведения эксперимента) необязательно, если имеется воз-
можность строить его в процессе реализации экспери-
мента. При этом каждый раз строится одна ветвь дерева
(простая безусловная отличительная последователь-
Рис. 4-13. Отличительное дерево автомата (кратный эксперимент)
к примеру 4-13.
ность), которая соответствует наблюдаемому исходу
эксперимента на данном шаге. Начальная (первая) от-
личительная последовательность, естественно, назначает-
ся предварительно.
ПОСТРОЕНИЕ УСТАНОВОЧНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Перейдем теперь к рассмотрению установочных де-
ревьев. Установочное дерево есть дерево преемников,
в котором вершина ранга г является висячей, если: а) ей
поставлена в соответствие группа У-множеств, сопостав-
ленная также некоторой вершине ранга меньше г;
б) среди вершин ранга г имеется хотя бы одна, которой
386
поставлена в соответствие группа, содержащая только
однородные /-множества. В последнем случае все вер-
шины ранга г являются висячими.
Пример 4-14. Построить установочное дерево для автомата /1|
рис. 4-9 в предположении, что допустимое множество начальных
состояний {УНач}о= {1, 2, 3, 4}. Строим дерево преемников
(рис. 4-14). На втором ранге дерева получаем две висячие вершины,
которым поставлены в соответствие группы, содержащие только
однородные У-множества. Эти вершины принадлежат путям (Л'2, Xi)
и (Х2, Х2). По правилу «б» па этом построение дерева заканчи-
вается.
{Z,i} {5, г}
X, | А
{>,г,з,ч}
I -|
{’.2}{3}{1} {3,l}{j,3}
{г,г}{5}(5} г {;,|}{з}{з}
{1.3,1} {з}
xi | *г
Рис. 4-14. Установочное дерево автомата к при-
меру 4-14.
Установочным входным последовательностям соответ-
ствуют пути установочного дерева, начинающиеся у кор-
ня дерева и заканчивающиеся вершинами, которым
поставлены в соответствие только однородные /-множест-
ва (в примере 4-14 установочными являются последо-
вательности <Х2, Xi> и <Xz, Хг>). Действительно, при
этом разным однородным /-множествам соответствуют
разные выходные последовательности, каждая нз кото-
рых тем самым однозначно определяет «свое» конечное
состояние автомата.
Установочная задача, как п рассмотренная ранее от-
личительная, может решаться при помощи простых без-
условных и условных экспериментов, к рассмотрению
которых мы и перейдем. Нужды в рассмотрении кратиыд
экспериментов для решения установочной задачи нет,
так как известно, что эту задачу всегда можно решить
простым (даже безусловным) экспериментом.
Установочное дерево рассмотренного выше вида
естественным образом представляет простые безуслов-
ные эксперименты над автоматом, причем это дерево
представляет все установочные последовательности ми-
25* 387
нимальной длины. Реализация простого безусловного
устано!вочного эксперимента ничем не отличается от опи-
санной ранее реализации простого безусловного
отличительного эксперимента.
Пример 4-15. В табл. 4-14 приведены: установочная последова-
тельность <Xj> = {X2. -^1} Для автомата At (рис. 4-9) при
{Унач}о={1, 2, 3, 4}, выходные последовательности <Z3->h для
начальных состояний Уп=1, 2, 3, 4 и конечные состояния Ye, в ко-
торые переходит автомат после подачи последовательности <Xj>.
Таблица 4-14
Начальное состояние <Z;> h при (Ху) = (Х2, Х,> Конечное состояние Kg
1 0,1 2
2 0,0 5
3 1,0 5(3)
4 0,1 2
Таблица составлена для безусловного установочного эксперимен-
та с безусловной остановкой. Реализация эксперимента с условной
остановкой позволила бы ограничиться подачей только одного вход-
ного символа Х2 в случае получения ответного выходного символа 1
(при этом конечным состоянием автомата было бы состояние 3, ука-
занное в скобках в третьей строке табл. 4-14).
Получение установочных последовательностей мини-
мальной длины требует построения полного установоч-
ного дерева. Если отказаться от требования минималь-
ности длины установочных последовательностей, то
установочное дерево можно построить более простым
способом. Этот способ состоит в следующем.
В строящемся дереве преемников группы У-множеств,
содержащие хотя бы одно неоднородное У-множество,
поочередно принимаются в качестве исходных множеств
допустимых начальных состояний. Выбирается любое
неоднородное У-множество группы (иа нервом шаге им
является множество {УП11ч}о) н в нем- любая пара раз-
личных состояний, скажем, Ул и Yg. Относительно этой
пары состояний строится простая безусловная отличи-
тельная последовательность <Xj>hg (подобно тому, как
это делалось при организации кратного отличительного
эксперимента). По ответным выходным последователь-
ностям определяются <%;>71е-преемники состояний рас-
сматриваемой группы У-множеств. Описанный процесс
388
повторяется до тех пор, пока все У-множества дерева
не окажутся однородными. Так построенное установоч-
ное дерево называют регулярным.
Пример 4-16. На рис. 4-15 представлено регулярное установочное
дерево автомата Л2 рис. 4-12, построенное при {УНач}о = {7, 8, 9, 10}.
В прямоугольниках-вершинах дерева указаны в качестве начальных
состояний неоднородные У-.множества, а также входные последова-
{Ук<7н} = {Г0,/0} \0„=3
Рис. 4-15. Регулярное установочное дерево автомата к примеру 4-16.
тельности <Xj>hg, различающие выбранные пары состояний Yh и
Yg из этих У-.мпожеств. Рядом с ветвями дерева указаны выходные
последова гелыил тп <7 >, выдаваемые автоматом под воздействием
входных последовагсльпостей А;>,,г. Например, иа ранге 0 из
множества {Упач}о={7, 8, 9, 10} выбрана пара состояний 7, 9 и раз-
личающая ее последовательность {A'J. При этом автоматы Л2/7,
Л2/8, Л2/10 переходят соответственно в состояния {Упач}п =
= {2, 2, 9} и выдают выходную последовательность <Zj>7, 8, ю =
= <0>, Л2/9 переходит в состояние 10 и выдает <Zj>9=<1>.
Далее из неоднородного У-множества {Унач}п={2, 2, 9} выбираются
пара 2, 9 и отличительная последовательность <Х3->2|9 = <ХЬ Х2>.
Полная установочная последовательность <ХЬ Xi, Х2>, таким обра-
зом, состоит из отличительных последовательностей <Х\> и
<ХЬ Х2>. В табл. 4-15 для рассмотренного дерева приведены для
каждого начального состояния ответная выходная последователь-
ность на полную входную установочную последовательность
<ХЬ Xi, Х2> и конечное состояние автомата.
389
Г а б ли ц а 4-15
Начальное состояние {Zj)h при (Ху) = = (Xi, *1, Х2> Конечное состояние Y&
7 0,1,0 10
8 0,1,0 10
9 1,0,1 3
10 0,1,1 3
Способы построения простых условны,х установочных
экспериментов мало чем отличаются от рассмотренных
выше способов построения простых условных отличи-
тельных экспериментов, поэтому они детально рассма-
триваться пс будут, а лишь иллюстрируются примером.
Суть условного эксперимента состоит в том, что по по-
лученной выходной последовательности выделяется на
каждом шаге только одна ветвь дерева.
Ранги.
{Уи«н}={'0.'0) {Уком}={3}
Рис. 4-16. Установочное дерево автомата к примеру 4-17.
Пример 4-17. Построить простой регулярный условный устано-
вочный эксперимент для автомата Д2 рис. 4-12 при условии, что
{УВач}о= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Выберем произвольную отли-
чительную последовательность, например <Xj>?,e= <Уг, Xi>, для
произвольной пары состояний 7, 8. Предположим, что при подаче
этой последовательности на испытуемый автомат получена выходная
последовательность <0, 0>. Эта выходная последовательность соот-
ветствует У-множеству, равному {2, 2, 9}, которое является .множе-
390
ством {Х2, Aj}-преемников множества {УНач}о (рис. 4-16). Следова-
тельно, можно сделать вывод, что после подачи последовательности
<Х2%1> автомат Д2 может оказаться только в состоянии 2 или 9
Поэтому далее имеет смысл рассматривать в качестве нового мио
жества начальных состояний только У-множество {2, 2, 9}. Подаем
на автомат <Xj>2. 9= <Xt, Л'2>. Предположим, что при этом по-
лучаем выходную последовательность <1, 1>, которая однозначно
определяет переход автомата в состояние 3.
Отличительные и установочные эксперименты фор-
мально предназначаются для определения начального
или конечного состояний автомата, заданного своей таб-
лицей переходов выходов. В качестве такого автомата
можно рассматривать как исправный А или любой не-
исправный А' автомат, так и расщепляемый автомат А.
Первому случаю, по существу, посвящено все предыду-
щее рассмотрение. Особенность второго случая состоит
в том, что нас не интересует начальное или конечное
состояние расщепляемого автомата Л, а требуется узнать,
либо каким из автоматов А или Л’ является исследуе-
мый автомат Л* (задача поиска неисправного автомата),
либо еще проще является или пе является автомат 1*
автоматом А (задача проверки работоспособности или
исправное in автомата). Поэтому в задаче поиска пенс
нравного автомата достаточно построить эксперимент,
позволяющий выделить подмножество начальных или
конечных состоянии расщепляемого автомата А, все из
КОТОрЫХ, ОДНаКО, ЯВЛЯЮТСЯ СОСТОЯНИЯМ 11 одного и того
же автомата А или Л‘. В задаче проверки работоспо-
собности автомата эксперимент должен выделить под-
множество состояний, которые либо принадлежат только
автомату Л, либо являются состояниями автоматов Л',
4=1, 2, . . , |S|.
Указанная особенность, имеющая место при рассмо-
трении расщепляемого автомата А, соответствует воз-
можности проведения диагноза с меньшей глубиной
Формально это может быть учтено через изменение ира
вил усечения ветвей дерева преемников при построении
отличительны^ или установочных деревьев. Необходимо,
во-первых, исключить правило «а» для отличительных
деревьев, согласно которому требовалось отсечение вет-
вей с вершинами, которым сопоставлено хотя бы одно
кратное У-множсство. Это следует из того, что в расщеп-
ляемом автомате А переходы между состояниями, при-
надлежащими разным автоматам A’. i—О, 1........... |S|,
невозможны, и поэтому начальные состояния, преемни-
391
ками которых являются состояния кратного У-множест-
ва, всегда принадлежат одному и тому же автомату А
или Ai. Правило «б» для отличительного дерева и такое
же правило «а» для установочного дерева остаются в си-
ле, так как целью их применения является исключение
повторяющихся частей деревьев. Наконец, правило «в»
для отличительного дерева и правило «б» для установоч-
ного дерева должны быть переформулированы следую-
щим образом: вершина ранга г отличительного или уста-
новочного дерева является висячей, если среди вершин
ранга г имеется хотя бы одна, которой сопоставлена
группа У-множеств такая, что каждое из ее У-множеств
содержит состояния только одного из автоматов А или
А* (при решении задачи поиска неисправного автомата),
либо такая, что все ее У-множества, содержащие состоя-
ния автомата А, не содержат пи одного состояния авто-
матов А\ t=l, 2....|S| (при решении задачи проверки
работоспособности автомата).
УЧЕТ ОСОБЕННОСТЕЙ РЕАЛЬНЫХ УСТРОЙСТВ ПРИ РЕШЕНИИ
ЗАДАЧ ДИАГНОЗА
Описанные выше способы решения задач тестового
диагноза: проверки исправности или работоспособности
и поиска неисправностей с использованием отличитель-
ных и установочных последовательностей сложны
(точнее, громоздки) и приводят к получению экспери-
ментов большой длины. Причем длина эксперимента бы-
стро растет при увеличении числа Mj состояний и мощ-
ности |S| класса неисправных автоматов.
Сложность диагноза абстрактного автомата метода-
ми классической теории экспериментов является следст-
вием того, что исследователю ничего не известно о вну-
треннем строении автомата. Исследователь может рас-
полагать той информацией, которую он получает при
подаче входной последовательности п наблюдении вы-
ходной. Достаточно сделать некоторые дополнительные
допущения, и задача значительно упрощается. Допу-
стим, например, что для исправного автомата А преду-
смотрена возможность установки его в начальное со-
стояние, которая устанавливает каждый из неисправных
автоматов Л1’ соответственно в некоторое определенное
известное для этого автомата начальное состояние, не-
зависимо от того, в каком состоянии находился автомат
392
цо установки. Такая установка в реальных устройствах
обычно предусматривается и осуществляется по отдель-
ной независимой системе каналов, причем сигналы уста-
новки действуют непосредственно на элементы памяти,
состояния которых формируют состояние автомата.
Тогда нахождение установочного эксперимента сущест-
венно упрощается, так как допустимое множество на-
чальных состояний расщепляемого автомата будет
состоять из |S | +1 начальных состояний автоматов
{Л, Л1,..., Л5,1}. Очевидно, если средн этих состояний
нет эквивалентных, то задача диагноза всегда разреши-
ма при помощи установочного эксперимента, причем
этому эксперименту предшествует установка в началь-
ное состояние.
Кроме того, многократное применение установки
в начальное состояние позволяет использовать кратный
эксперимент. Введение установки в начальное состояние
можно интерпретировать как дополнение таблицы пере-
ходов — выходов специальным столбцом, озаглавленным
входным символом, подача которого переводит автомат
из любого состояния в начальное. Иначе говоря, вход-
ной алфавит расширился, в пего включен дополнитель-
ный символ, который не влияет на работу автомата,
а используется только для установки в начальное со-
стояние. Можно предусмотреть не одну установку, а не-
сколько различных, каждая из которых устанавливает
автомат в определенное состояние.
Если бы исследователь имел возможность непосред-
ственно наблюдать, в каком состоянии находится
автомат, то ие надо было бы выполнять операции по
построению и реализации отличительных пли установоч-
ных последовательностей, которые к тому же могут
иметь большую длину. В реальных устройствах непо-
средственно наблюдать состояние можно путем измере-
ния состояний элементов памяти. В терминах абстракт-
ного автомата это можно интерпретировать как расши-
рение выходного алфавита. Рассмотрение указанных
возможностей на уровне абстрактных автоматов можно
использовать для синтеза устройств с учетом удобства
диагноза их технического состояния. Можно ставить
задачу дополнить исходную таблицу переходов — выхо-
дов автомата таким образом, чтобы, не изменяя рабо-
чего алгоритма функционирования автомата, обеспе-
чить возможность проведения диагноза с требуемой
393
глубиной. Такое преобразование автомата можно про-
изводить до тех пор, пока исследователь не будет иметь
возможность устанавливать автомат в любое состояние
и измерять состояния всех его элементов памяти (точ-
нее, значения всех внутренних переменных автомата).
Рассмотрим более детально этот предельный случай.
Формулировка задач диагноза н модель устройства
остаются прежними. Задан полностью определенный
исправный автомат А и множество S его возможных
неисправностей. Каждой неисправности SieS соответст-
вует автомат A*, i=l, 2, ..., |S|. Объединение А и всех
Л’ образует расщепляемый автомат А. Два состояния
разных автоматов А> и А'1, I, йе{0, одина-
ковые по составу и значениям внутренних переменных,
будем называть одноименными. Число пеоднопмепиых
состояний расщепляемого автомата А обозначим сим-
волом 7ИН. Два автомата Л!' и Ак назовем совместимыми
по состояниям и переходам, если для каждого состояния
одного автомата найдется одноименное состояние
в другом автомате, и наоборот, н если автоматы из
одноименных состояний при подаче любого входного
символа переходят снова в одноименные состояния и
при этом выдают одинаковые выходные символы.
Тогда неисправность существенна, если соответст-
вующий ей автомат А' несовместим с Л; две неисправ-
ности Si и s/i различимы (неразличимы), если соответст-
вующие им автоматы Л' и Ак несовместимы (совме-
стимы) .
Введем в рассмотрение следующие три операции над
автоматами: а/,— подать на автомат сигнал установки
в состояние У/,е{У}, йе{1, 2, ..., Мп}; bg — определить,
является ли фактическое состояние автомата У*е{У}
состоянием Уйе{У); операция Ье имеет положительный
исход при Y*=Yg и отрицательный — в противном слу-
чае; Xj — подать на автомат входной символ (набор) Xj,
/е{1, 2, ..., N}, где N — число символов входного алфа-
вита, и определить ответный выходной символ (на-
бор) Zj.
Последовательность таких операций назовем
обобщенным экспериментом над автоматом. Специально
организованный обобщенный эксперимент позволяет
построить таблицу переходов выходов исследуемого
автомата Л *. Примером одной из возможных организа-
ций условного обобщенного эксперимента является
394
Рис. 4-17. Блок-схема алгоритма А4-1 (алгоритма условного обоб-
щенного эксперимента)
395
алгоритм А4-1, блок-схема которого представлена на
рис. 4-17. Для каждого состояния Yh автомата А* и
входного символа X; фиксируется содержимое соответ-
ствующей клетки (Xj, Yh) таблицы переходов—выходов:
состояние Yg, в которое переходит автомат из Yh под
воздействием Xj, и выходной символ Z,h. Для этого про-
изводим установку А* поочередно в каждое из его со-
стояний с помощью операции а/„ начиная с /i=l и кон-
чая h=Mn. Если операция Ьц показывает, что Yh отсут-
ствует в А*(У*=#У/1), то увеличиваем h на единицу и
производим установку в следующее по порядку состоя-
ние, пока нс получим /г = Л41Г. Если состояние У/, входит
в множество состояний A* (Y* = Yh), то подаем первый
входной символ Xj(/ = 1) и проверяем с помощью опе-
рации bg, в какое состояние перешел Д*/УЛ под воздей-
ствием Xj. Это осуществляется перебором всех значений
g и сравнением У* с Yg. При У*=А=УК увеличиваем g
на 1, при Y*—Yg определяем ZjZl п печатаем результат
YglZjh в клетку таблицы переходов—выходов, располо
женную на пересечении строки Xj и столбца Уй. Затем
переходим к подаче следующего входного символа Xj+i,
выполняя предварительно установку снова в Ул (опера-
ция ah), и так до тех пор, пока не переберем все симво-
лы входного алфавита (j—N). Этим заканчивается по-
строение столбца таблицы переходов—выходов. Если
h=A=Mlt, то увеличиваем h на единицу и повторяем опи-
санную процедуру для У/i+i.
Пример 4-18. Пусть из двух триггеров 1\ и Т2 построен двухраз-
рядный кольцевой регистр сдвига. Выходной сигнал снимается
с триггера Т2. Когда триггер Тг изменяет свое состояние с единицы
на нуль, исправный регистр выдает выходной сигнал, равный едини-
це, в остальных случаях этот сигнал равен нулю. Входной алфавит
автомата, описывающего регистр, состоит из двух символов: Хо=О
и Xi = l. Пусть в регистре появилась неисправность, состоящая
в том, что выходной канал соединен с выходом триггера 7'1 вместо
Г2- Графы переходов исправного регистра (автомат Д) и неисправ-
Рис. 4-18. Графы переходов исправного Д и неисправного А' автома-
тов к примеру 4-18.
396
кого (автомат А‘=А') приведены на рис. 4-18. Состояния 1 и Г
есть 01 (Ti, Т2), а состояния 2 и 2'— 10. При заданной неисправно-
сти пары состояний 1 и 2', а также 2 и Г — эквивалентны, следо-
вательно, автомат А эквивалентен автомату А'. Различить эти
автоматы при помощи классических экспериментов нельзя. Однако
благодаря тому, что указанные эквивалентные состояния не являют-
ся одноименными, обобщенный эксперимент, состоящий ив операций
<01, 61, Х1>, позволяет обнаружить рассматриваемую неисправность
(для автомата А будет получено Zi = 0, а для А1—2t — l).
Реализация операций аь и bg требует дополнитель-
ной аппаратуры (цепи установки, вывод дополнитель-
ных контрольных точек), но расширяет класс автома-
тов, диагноз технического состояния которых возможен
с требуемой глубиной. Обобщенные эксперименты обыч
но короче, чем классические. В рассмотренной постанов-
ке задачи предполагается, что дополнительные цепи
установки и контрольные точки предусмотрены в авто-
мате заранее п для всех его элементов памяти или кон-
туров обратных связей. В общем случае это, по-видимо-
му, необходимо. В конкретных же случаях можно при
сохранении требуемой глубины диагноза уменьшить
число дополнительных цепей установки и контрольных
точек, определяя их необходимость в процессе построе-
ния эксперимента над автоматом.
Это, в частности, можно сделать, если эксперимент
строится шаг за шагом ио структурной таблице перехо-
дов—выходов расщепляемого автомата. Пусть преду-
смотрена установка (операция апач) автоматов А', I—
= 0, 1, ..., |S|, в известные их начальные состояния
К’нач, У{наче{У}, причем цепи этой установки абсолютно
надежны (не требуется проверки правильности установ-
ки, т. е. проведения операции йП0<1). Предположим так-
же, что все автоматы А' являются синхронными или все
их состояния устойчивы. Первой в искомый эксперимент
включается операция аНач, а затем последовательно —
операции типа Л;. Значения выходов Z’j, получаемые
при выполнении операций Л,, используются в качестве
признаков разбиения множества автоматов А на классы
и подклассы. Поэтому в указанную последовательность
операций Xj в качестве очередных включаются только
те операции, которые дают результативные разбиения.
При отсутствии таких операций повторно берется опе-
рация Пцач, формируется новая последовательность ре-
зультативных операций Xj и т. д. до тех пор, пока не
окажется, что все операции Х3 являются безрезультат-
ными. Если к этому времени требуемая глубина диагно-
397
за еще не достигнута, го к числу контролируемых вы-
ходов добавляется один дополнительный выход, после
чего описанный процесс повторяется. Допустимое число
дополнительных выходов q задается заранее. Если и
после добавления q выходов глубина диагноза недоста-
точна, то добавляется операция типа аи установки
устройства в некоторое состояние Yjlt отличное от на-
чального. Допустимое число d таких установок также
задается заранее. Если после введения дополнительных
установок заданная глубина диагноза все еще не до-
стигнута, то необходимо рассмотреть возможность уве-
личения заданных значений q и d. Заметим, что исполь-
зование в качестве дополнительных контрольных точек
выходов всех элементов памяти (контуров обратных
связей) соответствует использованию операции типа bg.
4-4. ПОСТРОЕНИЕ ПРОВЕРЯЮЩИХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
ПО НЕЯВНЫМ МОДЕЛЯМ
В § 4-3 рассматривались способы построения прове-
ряющих последовательностей при использовании явных
моделей. Рассмотрим теперь методы решения задач
проверки дискретных устройств, использующие неявные
модели.
ПОСТРОЕНИЕ ПРОВЕРЯЮЩЕЙ ПОСЛЕДОВАТЕЛЬНОСТИ
ПО ТАБЛИЦЕ ПЕРЕХОДОВ—ВЫХОДОВ
Одним из видов неявной модели является таблица
переходов—выходов исправного автомата. Моделью
неисправности является любое искажение таблицы пе-
реходов—выходов, вызванное неисправностью устройст-
ва. В этом случае проверка исправности состоит в про-
верке соответствия работы автомата, над которым про-
водится эксперимент, таблице переходов — выходов за-
данного исправного автомата.
Рассмотрим принцип построения проверяющей после-
довательности для наиболее простого случая, когда:
1) исправный автомат минимальный, сильносвяз-
ный;
2) рассматриваются неисправности, которые не уве-
личивают числа состояний в неисправном автомате по
сравнению с исправным;
3) проверяемый автомат имеет решение отличитель-
ной задачи относительно каждого допустимого началь-
398
пого состояния из Множества {У1, Уз, - -Ум}, где Л4 —
число состояний автомата.
Заметим, что под существованием решения отличи-
тельной задачи подразумевается существование отличи-
тельной относительно любого состояния Yh последова-
тельности Rh- Эта последовательность может быть
условной (условный отличительный эксперимент), по-
строенной при предположении, что перед началом экспе-
Рис. 4-19. Последовательность L} и фрагменты последовательностей
Г.2 и L3.
399
римента автомат находится в состоянии У/„ или без-
условной. В первом случае при получении ожидаемого
ответа автомата на Rh можно утверждать, что перед по-
дачей Rh автомат находился в Уд.
В противном случае можно только сделать вывод,
что начальным состоянием автомата было не Yh- Во
втором случае ответ автомата на Rh точно укажет, в ка-
ком начальном состоянии находился автомат перед по-
дачей Rh.
При этих условиях проверяющая последовательность
L состоит из трех частей (рис. 4-19). Первая часть £i
устанавливает исправный автомат в исходное состоя-
ние У1. Последовательность £t состоит из двух подпо-
следовательностей: L\ — установочной (всегда может
быть найдена), которая устанавливает автомат в изве-
стное состояние YЁ, и условной последовательности £"i,
переводящей автомат из Yg в исходное состояние У1.
Установочная подпоследовательность L\ строится мето-
дами, изложенными в § 4-3. Подпоследовательность L"i
определяется по таблице исправного автомата с учетом
того, в какое конкретное состояние Yg из множества
допустимых состояний {У1, Уа, .. Ум} перешел автомат
под действием L\. Подпоследовательность L"\ сущест-
вует, так как автомат сильносвязный. Последователь-
ность £i=<£'i, £"i>.
Вторая часть £2 последовательности L обеспечивает
установку автомата в каждое из его состояний и про-
верку правильности этой установки. Обозначим конечное
состояние, в которое переходит автомат из Yh в ре-
зультате подачи на него отличительной последователь-
ности Rh, символом qi,- Записью Т(qh, Yh) будем обозна-
чать входную последовательность, переводящую авто-
мат из состояния q/t в некоторое состояние Yr. Тогда
последовательность £2 имеет вид:
£,= <£., £(?,, У2), К2, Т (q2, У,), ...
ПЯьЛ), Rh. T(qhYh^, ..., RM, T(qMYt), Rt>.
Фрагмент последовательности L-> представлен на
рис. 4-19,6. В начале £3 стоит отличительная последова-
тельность Ri, так как в результате реализации подпо-
следовательности £"] автомат был переведен в состоя-
ние У] *, и надо убедиться, что он действительно нахо-
* Если автомат имеет безусловную отличительную последова-
тельность, то индекс при R можно опустить.
400
Ц1тся в этом состоянии. ,/?1 в конце L2 проверяет при
вильность перехода автомата в Yt под воздействием
Tiq^Yt). В последовательности L2 подпоследователь-
ности Т обеспечивают установку автомата в каждое из
его состояний, а подпоследовательности R — проверку
правильности этой установки.
Третья часть L3 последовательности L служит для
проверки правильности каждого перехода автомата из
каждого его состояния Yh, h=\, 2, ..., М тюц воздейст-
вием каждого входного -символа Xj, /=1, 2, ..N,
где N — число входных символов. Обозначим через Yhj
состояние автомата, в которое он переходит из состоя-
ния Yh при подаче входного символа XСоответственно
будем приписывать двойной индекс hj отличительной
относительно Y/,j последовательности Rhj и состоянию
qhi, в которое переходит автомат из Yhj под воздействи-
ем Rhj. Тогда с учетом обозначений, принятых при по-
строении L2, последовательность L3 имеет вид:
L3=CT(qi, YM)....... Т (qh lN, Y/t l), Rh_it T^YJ
•^1’ ^/>1’ ЪЛ -^2’ ^/12’
^/i—|)’ |» RhN-l’
T<4hN-v Кл-р T(qh_x, ^)> ^).-
RM—1> (?M-P
На рис. 4-19,e изображен фрагмент последователь-
ности L3, иллюстрирующий проверку всех переходов по
Xj, j=l, 2, ..., N, из состояния Yh. Правильность пере-
хода по каждому символу Xj проверяется отличитель-
ной последовательностью Rhj, затем осуществляются пе-
реход в Ул-i, проверка этого перехода и, наконец, снова
переход в Yh. Переход из У/»_i в Ул (последовательность
Rh-i, T(qh-iYh)) всегда происходит правильно, так как
был проверен раньше при реализации последователь-
ности L2.
При принятых ограничениях описанный метод позво-
ляет определить по проверяющей последовательности
L=Lt, L2, L3 и ответам автомата на эту последователь-
ность, соответствует или нет таблица переходов—выхо-
дов испытуемого автомата таблице переходов—выходов
исправного автомата. Длина проверяющей последова-
тельности L, построенной по этому методу, примерно
равна NM3.
2(>—358 401
Пример 4-19. Минимальный сильносвязный автомат А3 задан
графом переходов — выходов (рис. 4-20). Отличительной является
последовательность <Х2, Х2>. Ответы автомата на эту последова-
тельность в зависимости от его начального состояния приведены
в табл. 4-16.
Таблица 4-16
5нач <Z> ^кон
1 hl 3
2 1,0 1
3 0,1 2
переходов
Рис. 4-20. Граф
автомата к примеру 4-19.
Установочной является последовательность <Х]>. Следователь-
но, Г/1 = <-М>. Предположим, что испытуемый автомат в ответ
на подачу последовательности <Xi> выдал выходной сигнал 0.
Обращаясь к графу переходов — вы-
ходов рис. 4-20, находим, что авто-
мат теперь находится в состоянии 2,
поэтому L//i = <X2, Х2>. Подпоследо-
вательность L" переводит Аз в со-
стояние 1, с которого начинаются об-
ход и проверка состояний и перехо-
дов при помощи последовательностей
L2 и L3. Проверяющая последователь-
ность L=iLiL2L3 приведена в табл.
4-17 как в общих обозначениях, так
и во входных символах. Две по-
следние строки содержат значения
выхода Z и номера состояний У ис-
правного автомата А3. Заметим, что
во время проведения эксперимента
над испытуемым автоматом Д* све-
дения о его состояниях отсутствуют,
выхода исправного автомата Z с фа-
Любое несовпадение значений
ктическими значениями Z* говорит о неисправности испытуемого
автомата.
Последовательность построена формально в соответ-
ствии с изложенным методом и состоит из 55 символов.
Эта последовательность избыточна. Действительно, если
ответы проверяемого автомата на последовательность
<Li, L2> совпадают с ответами исправного автомата,
то можно заключить, что в проверяемом автомате А*
есть три такие состояния 1*, 2*, 3*, что ответы .4*/!*,
А*{2* и Д*/3* на последовательность <Х2, Хг> совпа-
дают с соответствующими ответами автомата А3. Теперь
остается проверить правильность всех переходов из
каждого состояния. Но некоторые переходы оказались
402
Т г б л и ц a 4-17
J ьГ 6 1
с? >< >< о СО
>< — CN
сч >< о со'
е£ >< >< о сч
со >< СО
с£ £ >< о сч
>? >< — СО
(1‘г)1 >< о со
с? >< ч о сч
со ссГ Q
С? СТ <3 X >< 2,3
сч >< о 3,1
<£ СТ СТ X X о 1,2
7(1,3) >< —' СО
е? >< >< со
еТ ссГ >< о сч
с? >< ч —’ 2.3
-4 >< о СО
-Г >< о О1
-4 N
26*
403
уже проверены. Например, рассмотрим часть последова-
тельности L2, равную </?3, Т(2, 1)>. Ответ испытуемо-
го автомата на последовательность /?3 говорит о том,
что автомат Л* перед подачей последовательности /?3
находился в состоянии 3*, соответствующем состоя-
нию 3 автомата Л3. Ответы на второй символ последо
вателыюсти Rs и первый символ последовательности
Т(2, 1), составляющих последовательности <Х2, Хг>,
говорят о том, что перед подачей последовательности из
этих двух символов автомат А* находился в состоя
нии 1*, соответствующем состоянию 1 автомата А3. По
этим ответам можно сделать заключение, что автомат .4*
под воздействием символа Х2 перешел из состояния 3*
в состояние 1* и выдал выходной символ Z=0, т. е. пе-
реход по Х-> из состояния 3* в состояние I* проверен и
проверять его в дальнейшем не имеет смысла.
Изложенные выше соображения послужили основой
для создания методов построения проверяющей после-
довательности возможно меньшей длины.
Рассмотрим один из таких методов. Последователь-
ность L начинается установочной последовательностью.
Далее к установочной последовательности добавляются
безусловные отличительные последовательности R, R ...
до тех пор, пока ответы исправного автомата на очеред-
ную последовательность R не повторятся. Как только
ответ повторится, что говорит о том, что исправный
автомат снова попал в некоторое состояние Ул, к полу-
ченной последовательности добавляется первый вход-
ной символ Xi и затем снова повторяются последова-
тельности R до очередного повторения ответа. Если
в построенной последовательности был уже реализован
переход из некоторого состояния Ул по входному сим-
волу Xi, то реализуется переход из Yh по входному сим-
волу Хг, т. е. добавляется Х2, и т. д. Процесс построения
последовательности L заканчивается тогда, когда в ней
будут реализованы переходы для каждого состояния по
каждому входному символу. Если после очередного по-
вторения ответа автомата Л па последовательность R
автомат оказался в некотором состоянии У/г, для кото-
рого уже реализованы переходы по всем входным
символам, осуществляется переход в состояние YE. для
которого реализованы переходы еще не по всем вход-
ным символам, с целью реализации перехода из этого
состояния Yg по очередному входному символу. После-
404
11031—2э
довательность, обеспечивающая переход в состояние Уе,
формируется из частей уже построенной последователь-
ности таким образом, чтобы переход в испытуемом
автомате происходил по уже проверенным путям в гра-
фе переходов — выходов. Поскольку исправный автомат
сильносвязный и минимальный, то этот процесс всегда
сходится, т. е. проверяющая последовательность L всег-
да может быть построена описанным способом.
<х2> <Х2>
<7> <1> (0,1)
<Х2>
<1>
Рис. 4-21. Смена состояний автомата рис. 4-20 при реализации про-
веряющей последовательности.
Продолжение примера 4-19. Построим по описанному способу
проверяющую последовательность для автомата из примера 4 19.
На рис. 4-21 представлен граф, иллюстрирующий последовательность
переходов исправного автомата Аг при подаче проверяющей после-
довательности. Вершины графа соответствуют состояниям автомата,
каждое из которых повторяется на графе столько раз, сколько раз
в него осуществляется переход при реализации проверяющей после-
довательности. Дута между соседними состояниями Ут и У,, обо-
значена входной последовательностью, подача которой обеспечивает
переход из Ут в У„, и соответствующей ей выходной последова-
тельностью. Под воздействием установочной последовательности
<Xi> автомат Л3 переходит в состояние 2, затем подается последо-
вательность R = <Xi, Х2> четыре раза. Соответственно автомат А3
переходит из As/2 в Д3/1, в As/3, в А3/2 и, наконец, в Л3/1. После
четвертого приложения отличительной последовательности R ответ-
ная выходная последовательность, равная <1, 0>, совпадает с той,
которая была после приложения последовательности R первый раз.
Поэтому можно сделать вывод, что автомат Л3/2 перешел в Лз/1.
Теперь проверяется переход Д3/1 по входному символу Х} подачей
последовательности <XrR>. По ответной выходной последователь-
ности <1, 0, 1> определяется, что автомат переходит в A-J2. Про-
405
веряется переход из Л3/2 по Xi и т. д. После проверки перехода
из Л3/1 по Х2 автомат As оказался в состоянии 1, переходы из ко-
торого по всем символам входного алфавита уже проверены. Тогда
автомат А3[1 переводится в /13/2 по проверенному уже переходу
входным символом Х2 и т. д. Проверяющая последовательность, по-
строенная по второму способу, имеет длину 30 символов, т. е. суще-
ственно меньше, чем построенная по первому способу.
ТРОИЧНОЕ МОДЕЛИРОВАНИЕ ИСПРАВНОГО И НЕИСПРАВНОГО
УСТРОЙСТВ
Как упоминалось ранее, часто в качестве неявной
модели объекта диагноза используется логическая сеть,
а рассматриваемые неисправности ограничиваются
классом одиночных константных неисправностей. Рас-
смотрим при этих условиях некоторые методы решения
прямой и обратной задач диагноза.
Задача нахождения совокупности неисправностей,
обнаруживаемых данной входной последовательностью,
решается обычно троичным моделированием логической
сети исправного устройства и сетей его неисправных
модификаций; неисправные сети получаются путем вне-
сения соответствующих константных неисправностей
в исправную сеть. Заметим, что принципиально этот
метод пригоден для любых, в том числе логических не-
исправностей.
Будем рассматривать общий случай, когда началь-
ное состояние исправного устройства и его неисправных
модификаций неизвестно. До начала моделирования
входным и выходным полюсам, а также внутренним
узлам (следовательно, и узлам, представляющим вну-
тренние переменные у\, у2, .., ут) структуры задаются
неизвестные значения 1/2 (см. § 4-1).
Моделирование начинается с того, что берется пер-
вый входной набор заданной последовательности и
на этом наборе методом прямой подстановки (см. гл. 3)
вычисляются значения внутренних узлов и выходных
полюсов исправного А и i неисправных Л’ устройств.
Операции прямой подстановки выполняются поэлемент-
но с использованием троичных таблиц истинности эле-
ментов сети. На данном шаге процесса моделирования
обрабатывается один из элементов, значения входов
которых изменились на предыдущих шагах. Признаком
окончания моделирования является отсутствие таких
элементов. Первыми обрабатываются элементы, входа-
ми которых являются входные полюсы сети. Заметим
406
также, что при моделировании неисправных устройств
влияние неисправности учитывается только в направле-
нии распространения сигналов в сети.
По окончании моделирования сетей на наборе Aj по-
лученные значения выходов исправного устройства Л
сравниваются со значениями выходов каждого из неис-
правных устройств А‘. Неисправность OteO (или
eS) обнаруживается, если хотя бы один выход уе
<={1, 2, ..., k} имеет определенные (0 или I) значения
в А и в Л‘ и эти значения различны. Устройства А‘,
неисправности которых обнаруживаются па данном на-
боре, из дальнейшего моделирования могут быть исклю-
чены. Полученные значения внешних полюсов и вну-
тренних узлов сетей А и А' сохраняются (запоминают-
ся). Заметим, что достаточно было бы запомнить
значения выходов элементов памяти и контурных эле-
ментов, однако при этом потребовалось бы предвари-
тельное выделение контуров сети.
Затем по набору А, и по второму набору Х2 после-
довательности формируется промежуточный набор Ai,2
(см. § 4-1). Моделирование на наборе Ai,2 выполняется
аналогично описанному для набора А4, с учетом, одна-
ко, зафиксированных значений внутренних переменных.
Сравнение значений выходов сетей при этом не произво-
дится. Полученные новые значения полюсов и узлов
сети запоминаются.
Далее выполняется моделирование на наборе Х2
(также с учетом полученных на наборе А\2 значений
внутренних переменных), по окончании которого произ-
водится сравнение значений выходов. Неисправные
устройства, неисправности которых обнаруживаются на
наборе А2, из дальнейшего рассмотрения исключаются.
После этого последовательно выполняется моделиро-
вание на промежуточном наборе Хг, 3, затем на наборе
А3 и т. д. до тех пор, пока либо нс будет промоделиро-
вана вся заданная последовательность входных набо-
ров, либо не будут обнаружены все заданные неисправ-
ности.
В описанном процессе моделирования на каждом
одном наборе моделируются все сети. Возможна другая
организация процесса, когда каждая одна сеть модели-
руется на всей последовательности наборов. В послед-
нем случае возможна экономия памяти.
407
Пример 4-20. На рис. 4-22 представлена логическая сеть с обрат-
ными связями. Рассматриваются одиночные константные неисправ-
ности на входах сети и выходах элементов. Пусть задана последова-
тельность входных наборов <%.,•>= <001 (abc), 010, 100, 000, ОН,
111>. С помощью моделирования определить неисправности, обна-
руживаемые на этой последовательности.
Рассмотрим моделирование исправного устройства и устройства
с неисправностью а1 на первых двух наборах последовательности
-Х\ = 001 и Х2 = ою. Всем узлам и полюсам сети присваиваем значе-
ние 1/2. Список элементов сети, значения входов которых изменяются
Рис. 4-22. Сеть с обратными связями к примеру 4-20.
в процессе моделирования, назовем для удобства списком d. На
каждом шаге процесса обрабатывается и затем вычеркивается пер-
вый элемент списка d. Если значение выхода обрабатываемого
элемента изменилось, то в список d добавляются не содержащиеся
в нем элементы, входами которых является указанный выход; в про-
тивном случае это не делается.
При подаче набора Xi = 001 исходный список d образуют эле-
менты /, 2, 3, 4. Для элемента 1 по его троичной таблице истинно-
сти (табл. 4-8) находим значение yi = 0 его выхода; список d приоб-
ретает вид {2, 3, 4}. Аналогично для элемента 2 у2= I в список d
добавляется элемент 5: {3, 4, 5}. Далее: #3 = 0, {4, 5}\ у4=1, {5, 7};
^5 = 0, {7, 6}; s/7 = 0, {6, /}; у6=1, {], 7}; tJl=0, {7}; у7 = 0, {0}.
Получение пустого списка, d служит признаком окончания моделиро-
вания. Полученные значения узлов и полюсов приведены в левой
части первой строки табл. 4-18.
Аналогично проводится моделирование на промежуточном набо-
ре Х12 = 0 1/2 1/2. При подаче этого набора меняются значения
входных полюсов b и с, поэтому в исходный список d входят эле-
менты /, 2, 4. Вычисляем значения выходов элементов и списки d:
Ух = №, {2, 4, 3}; у2=1, {4, 3}; ^,=11/2, {3, 7}; f/3=0, {7}; f/7=0,
{0}. Обработка элементов 5 и 6 не понадобилась, так как значения
408
их входов на наборах Xi и Xi, 2 оказались одинаковыми. Результаты
моделирования помещены во второй строке табл. 4-18.
Для набора Х2=010 исходный список d содержит элементы
1, 2, 4. Вычисления дают: yi=l, {2, 4, 3}; #2=1, {4, 3}; #4 = 0,
{3, 7}; #3 = 0, {7}; #7 = 0, {0}. Результаты помещены в третьей
строке табл. 4-18.
При неисправности щ значение 1 зафиксировано на входном
узле а, остальные входы принимают значения, задаваемые входными
наборами, т. е. фактически в данном случае вместо наборов 001,
010 на входах образуются наборы 101 и ПО, на которых и выпол-
Т аблица 4-18
Входные наборы Значения в узлах сети исправного устройства Зиапепия в узлах сети устройств с неисправностью
и b с 1 2 3 4 5 6 7 1 2 3 4 б 6 7
0 0 1 0 1 0 1 0 1 0 0 Г 0 1 0 1 0
0 1 2 1/2 1 2 1 0 1/2 0 1 0 1/2 1/2 1/2 1,2 1 2 1/2 1/2
0 1 0 1 1 0 0 0 1 0 1 2 0 1 /2 0 1/2 1/2 1 '2
няется моделирование описанным выше способом (промежуточным
является набор 1 1/2 1/2). Результаты моделирования помещены
в правой части табл. 4-18. Из этой таблицы видно, что неисправность
й1 не обнаруживается па наборах Х] = 001 и Х2=010, так как на
выходных полюсах в узлах 3 п 6 (г{ и z2) па наборе X! при наличии
неисправности а=1 получены значения 0 и I, совпадающие с соот-
ветствующими значениями левой части табл. 4-18, а на наборе Х2—
значения 1/2. Заметим, что если провести двоичное моделирование
(без учета состязаний) на тех же наборах Х1=001, Х2=010, то по-
лучим при исправном устройстве
а b с 1 2 3 4 5 6 7
0 0 10 10 10 10
0 10 1 1 0 0 0 1 0
и при неисправности а1
abc/234567
0 0 10 10 10 10
0 10 10 10 0 10
Полученные значения в узле 3 (zj различны в исправном и
в неисправном устройствах на наборе Х2=010. Отсюда можно было
бы сделать неверный вывод, что неисправность а1 обнаруживается
последовательностью <ХЬ Х2>. Однако, как показывает троичный
расчет, из-за состязаний можно получить в узле 3 (zp при неисправ-
ности а* значения, совпадающие со значениями в исправном устрой-
стве.
В табл. 4-19 приведены результаты троичного моде-
лирования выходных значений сети (рнс. 4-22) для всех
заданных неисправностей на заданной входной последо-
вательности. Результаты моделирования на промежу-
409
Таблица 4-1д
-
tT 0 1/J 0 1/2 1 1/2 0 1/2 0 1/2 1 1,2 табл. 4-
°, | 'г 'г ' эпнзжъ 0 0 1 0 I 0 1 0 I 0 1 0
0 1 0 1 0 1 0 1 0 1 0 0 Предо.
с» 21 23 0 1,2 0 1 2 1 '2 1, 2 0 1/2 0 1/2 1'2 1,2
0 1/2 0 1/2 1/2 1 2 0 1,2 0 1/2 0 0
| гг 'г 1 0 1 0 3/1 0 6. I 3 '1 I 0 I 0
е 5г ’г 0 1 1'2 1/2, 1/2 1/2 1/2 1,2 0 0 0 0
а <Т 0 1 0 1 0 1/2 0 1/2 0 1/2 0 1/2
Исправное ус- ус тройство гТ 0 1 0 1 1/2 1,2 0 1/2 0 1/2 0 0
Входные наборы а b с 0 0 1 0 1 0 1 1 0 ООО 0 1 1 1 1 1
410
точных наборах в таблице не представлены. Как видно
из таблицы, неисправности 2°, 3l, 51, 6°, 71 обнаружи-
ваются на наборе Xi—001, а Ь°, 21, I1, 5°, 61 — на наборе
Л6= 111. Остальные неисправности на заданной последо-
вательности не обнаруживаются. Прочерк в таблице па
пересечении строки Х3- и столбца означает, что не-
исправность а=0,1, на входном наборе Xj не моде-
лировалась, так как была обнаружена на одном из пре-
дыдущих наборов.
Моделирование может быть использовано для пост-
роения проверяющих последовательностей путем слу-
чайного выбора входных наборов. Эффективность тако-
го способа, однако, уменьшается по мере сокращения
числа оставшихся необнаруженным*! неисправностей,
так как увеличивается вероятность того, что очередной
набор окажется безрезультатным. В этом случае целе-
сообразно обратиться к решению обратной задачи диаг-
ноза— к целенаправленному вычислению последова-
тельности, обнаруживающей заданную неисправность.
Рассмотрим два подхода к решению этой задачи —
«комбинационный» и «автоматный». Ограничимся клас-
сом одиночных константных неисправностей.
ПОСТРОЕНИЕ ПРОВЕРЯЮЩЕЙ ПОСЛЕДОВАТЕЛЬНОСТИ
ПО КОМБИНАЦИОННОМУ ЭКВИВАЛЕНТУ
Комбинационный подход основан на преобразовании
последовательного устройства путем условного обрыва
обратных связей (в том числе в триггерах) в комбина-
ционный эквивалент. Это преобразование было рассмо-
трено в § 4-1 (см. рис. 4-1, 4-3—4-5). При необходимо-
сти (/?^>2) такие эквиваленты (копии) соединяются по-
следовательно в итеративную сеть так, как показано
в однолинейном представлении па рис. 4-23. Нижние
индексы при символах векторов входных X, внутренних
Y и Y' и выходных Z переменных являются номерами
копий и одновременно номерами тактов работы устрой-
ства А, как автомата с памятью. Для копии v, v=l,
2, ..., р, вектор Yv задает состояние автомата в настоя-
щий момент времени v, а вектор Y'v—в следующий
момент времени v + 1, = Для итеративной
сети внешними входами являются входы X всех копий и
411
Входы Yi первой копии, а внешними выходами — выходы
Z всех копий и выходы Y'p последней копии.
К построенной таким образом итеративной сети мо-
жет быть применен описанный в § 3-4 метод существен-
ных путей для построения входных последовательностей,
обнаруживающих заданную неисправность. Имеющиеся
при этом особенности и ограничения состоят в сле-
дующем.
Рис. 4-23. Итеративная сеть.
Одиночная неисправность исходного устройства А
представляется р-кратпон неисправностью итеративной
сети (каждая копия содержит одну одиночную не
исправность1). Контрольными точками являются внеш-
ние выходы Zp последней копии. Начальное состояние
устройства предполагается неизвестным, поэтому обя-
зательным условием является получение безразличных
значений (~) на входах Yi первой копии. Искомой про-
веряющей последовательностью <Х3> является после-
довательность входных наборов <Хи Х2, ..Хг> длины
Случай /<р имеет место для асинхронных
устройств при наличии неустойчивых состояний (при
этом некоторые соседние копии будут иметь одинаковые
входные наборы Xj).
Таким образом, для построения итеративной сети
требуются выделение в исходной сети устройства эле-
ментарных контуров 2 и определение совокупности точек
условных обрывов обратных связей. Эти точки являются
выходами контурных элементов (логических элементов,
принадлежащих контурам) п определяют состав вну-
тренних переменных щ, у?, • - ., у™. Известен ряд мето-
дов решения этих задач.
1 Особенности обнаружения кратных неисправностей описаны
в гл. 3.
2 Под элементарным контуром или, сокращенно, контуром в сети
понимается такая последовательность элементов 1, 2, ..., п, когда
выход каждого предыдущего элемента соединен с входом последую-
щего, а выход н-го элемента со входом I-го и при этом ни один
элемент не входит в последовательность более одного раза.
412
Задачу выделения элементарных контуров решают
обычно в два этапа Сначала выделяют в сети так на-
зываемые максимальные сильносвязные подсети МССП,
т. е. подсети, для которых справедливы два утвержде-
ния, во-первых, для каждой упорядоченной пары их
узлов имеется хотя бы один путь по направлению рас-
пространения сигналов, соединяющий первый узел пары
со вторым; во-вторых, они не являются частью (под-
сетью) никакой другой МССП. Выделение МССП мож-
но осуществить, выполнив следующие две операции.
Сначала из сети последовательно удаляются элементы,
все входы (или выходы) которых являются внешними
входами (выходами) исходной сети или подсети, полу-
ченной после удаления некоторых элементов. Вторая
операция состоит в выборе любого ""одного элемента по-
лученной подсети, в определении для этого элемента
множества всех его последователей (элементов, к кото-
рым ведут пути от выхода выбранного элемента в на-
правлении распространения сигналов) и множества всех
его предшественников (элементов, от выходов которых
имеются пути ко входам рассматриваемого элемента)
и, наконец, в нахождении пересечения указанных мно-
жеств. Непустое пересечение вместе с рассматриваемым
элементом образует МССП. Над подсетью, полученной
после удаления из нее элементов выделенной МССП,
снова выполняются описанные операции и т. д.
Очевидно, все элементарные контуры содержатся
в выделенных МССП. Выделение элементарных конту-
ров состоит в получении для каждого контура списка
входящих в него элементов. Эта задача решается систе-
матическим просмотром всех путей в МССП и выделе-
нием среди них замкнутых элементарных путей.
Задачу определения точек условного разрыва обрат-
ных связен можно решать при разных предпосылках.
Наиболее простым является выбор в каждом элементар-
ном контуре любой одной точки разрыва. При желании
получить минимальное число разрывов потребуется пе-
ребор возможных вариантов. Наконец, можно приме-
нять различные эвристические процедуры с учетом тех
или иных физических соображений: например, в первую
очередь разрывать обратные связи в триггерах или в тех
узлах, которые являются выходами контуров и располо-
жены наиболее далеко (в направлении распространения
сигналов) от входов сети. Заметим, что для построения
413
итеративной сети как модели выбор точек разрывов
обратных связей не играет принципиальной роли в том
смысле, что при любом выборе проверяющая последова-
тельность будет построена, если она может быть по-
строена по этому методу, хотя разные варианты выбора
могут давать разные последовательности по составу и
числу входящих в них наборов.
Построение проверяющей последовательности начи-
нают с рассмотрения итеративной сети, содержащей
единственную копию (,о=1). На сети ищутся условия
образования существенного пути {г, -у} от неисправного
узла i до хотя бы одного внешнего выхода у, у= 1, 2, ...
..., k, при у$= ~ для всех р=1, 2, ..т. Если сущест-
венный путь {г, у} построен, то соответствующий вход-
ной набор образует искомую входную последователь-
ность <ХР> длины 1. Если при указанных условиях
существенный путь {i, у} построить не удается (не удов-
летворяются условия проявления или условия транспор-
тировки неисправности), то переходят к рассмотрению
итеративной сети из двух копий (р—2) и т. д.
При числе копий р 2 следует рассматривать варианты
образования существенных путей {is, ур} как от неисправ-
ного узла iv одной копии v, 1 < v < р, так и от неисправ-
ных узлов нескольких копии до внешнего выхода у?, по-
следней копии р. Иными словами, существенный путь
может быть не только сложным, но может иметь не-
сколько начальных вершин, а передача значения D(D)
может происходить через неисправный элемент.
На втором этапе алгоритма—этапе доопределения
значений сигналов в узлах сети до ее входов — необхо-
димо, во-первых, обеспечить безразличные значения
(~) всех внутренних переменных у^, где второй
индекс при у — номер копии, на входах первой копии
(,о=1) и, во-вторых, учитывать наличие неисправного
узла в каждой обрабатываемой копии. Первое требова-
ние удовлетворяется путем выбора подходящих вариан-
тов операции расширения фиксации (см. гл. 3), а не-
исправные узлы учитываются следующим образом.
Если в результате очередной операции над элемен-
тами сети в неисправном узле i будет получено значе-
ние 0 или D при неисправности Iе либо значение 1 или
D при неисправности г1, то никаких действий по учету
влияния неисправности предпринимать не надо. В про-
414
тивном случае (в узле i получено значение 1 или D при
неисправности 1° либо значение 0 или D при неисправ-
ности z1) необходимо моделирование работы исправной
и неисправной сети на полученной последовательности
входных наборов. Если при моделировании значения
в контрольной точке у для исправной и для неисправной
сетей различны, то последовательность является прове-
ряющей; при одинаковых значениях в узле у следует
искать другую проверяющую последовательность.
Для синхронных устройств приведенных выше усло-
вий построения проверяющих последовательностей до-
статочно, если предположить, что имеется возможность
контролировать значения выходов устройства в каждом
такте синхронизирующей последовательности Для асин-
хронных устройств необходимо вьПюлненве двух сле-
дующих дополнительных требований.
Ради удобства измерений необходимо (или, во вся-
ком случае, желательно), чтобы значения выходов уР
(выходов, которыми заканчиваются существенные пути)
были устойчивыми. Это требование будет удовлетворе-
но, если в последней копии р для каждой пары внутрен-
них входных у?р и выходных |3 = 1, 2, . , т, пере-
менных выполняется одно из следующих условий:
если У₽г=1(°)> то 1(0);
если y?p = D(D), то у'рр
D(D), если у},
1, 0, D(D) в противном слу-
чае;
если У?р = ^, то Урр=1, 0, D, D,^.
Условие у?р = урр = D (D) гарантирует устойчивость
существенного пути {i, у}, проходящего через узел (узлы) р
копии р.
В сжатой форме приведенные условия будем пред-
ставлять записью
(4-9)
При /2—1 условие (4-9) удовлетворяется „автомати-
чески", благодаря тому, что у$р = ^для всех [3, а при
р^2 требуется специальная его проверка.
Второе дополнительное требование следует из того,
что для обеспечения правильной работы в асинхронных
415
устройствах смена входных наборов должна происхо-
дить только в устойчивых состояниях. Для наших целей
это требование может быть ослаблено: достаточно, что-
бы для каждой копии v<p — такой, что Xv=£Xv,lt удов-
летворялось условие
юэй. (4-ю)
аналогичное условию (4-9).
Заметим, что для первой
имеет место, для других
проверка.
копии это условие всегда
копий необходима его
Рис. 4-24. Логическая сеть к примеру 4-21.
Пример 4-21. Для устройства, заданного логической
сетью рис. 4-24, построить входную последовательность,
обнаруживающую неисправность 6°. Для логических
элементов сети заданы пх сжатые таблицы истинности,
таблицы Д-кубов неисправностей и таблицы Д-кубов
(в том числе тупиковых Д-кубов элементов). Для части
элементов сети рис. 4-24 эти таблицы приведены в гл. 3,
для других могут быть построены по правилам, изло-
женным в § 3-4.
Определим точки разрывов обратных связей. Эле-
ментов, все входы или выходы которых являются внеш-
ними, в сети рис. 4-24 нет. Сеть содержит две МССП:
{6, 7, 8, 9} и {10, 11}. Первая из них состоит из двух
элементарных контуров {7, 8} и {6, 8, 9}, а вторая сама
является элементарным контуром {10, 11}. Разорвем
каждый контур в отдельности на верхних входах эле-
416
ментов 6 и 10 и на нижнем входе элемента 7. Точкам
разрывов соответствуют переменные 1/8, ув, уц и y's,
y's, у'ц.
Ограничиться одной копией (р=1) нельзя, так как
проявление неисправности 6° требует задания на эле-
менте 6 единственно возможного Д-куба неисправно-
сти 2, 6), который предписывает значение 1
внутренней переменной ys.
Две копии (,о = 2) позволяют найти последователь-
ность, обнаруживающую неисправность 6°. На рис. 4-25
представлена соответствующая итеративная сеть,
в узлах которой указаны значения сигналов, получен-
ные в результате расчета. Проверяющая последователь-
ность состоит из двух входных наборов:
1 2 3 4 *5
1 ~ 1 1
Х2= 1 1 0 0 0,
причем набор Xi определен не полностью.
Получение не полностью определенных входных на-
боров является характерным при построении тестовых
последовательностей по логической сети устройства.
Для асинхронных устройств доопределение таких набо-
ров следует выполнять так, чтобы смежные в последо-
вательности наборы отличались значениями как можно
меньшего числа переменных. При этом уменьшается
опасность возникновения состязаний из-за невозможно-
сти практически обеспечить строго одновременное изме-
нение значений нескольких входных переменных. Заме-
тим, однако, что при любом способе доопределения
полученная входная последовательность должна подвер-
гаться троичному моделированию на предмет выявления
недопустимых состязаний. Если состязания вызваны
тем, что не обеспечивается одновременное изменение
значений нескольких переменных в двух смежных набо-
рах Xv и последовательности, то следует устра-
нить это требование введением в последовательность
дополнительных наборов. Дополнительные наборы Ха,
Хъ, ..., Хт должны быть такими, чтобы в последователь-
ности Xv, Ха, Хь, ..., Xr, X любые два смежных
набора были соседними по единственной переменной.
После введения дополнительных входных наборов надо
проверить, является ли полученная последовательность
тестовой, и провести повторно троичное моделирование.
27—358 417
Рис. 4-25. Две копии логической сети, изображенной на рис. 4-24.
418
Следуя указанной выше рекомендации, в нашем при-
мере неопределенности в наборе Xi на полюсах 2 и 4
следует заменить определенными значениями 1 и 0 из
набора Хг. Тогда Xi=11101. Результаты моделирования
на входных наборах Xi и Х2 представлены в табл. 4-20.
Таблица 4-20
Входные наборы Исправное устройство
/ 2 3 4 5 6 7 8 9 10 11
1 1 1 0 1 1 0 1 1 0 0
I 1 1/2 0 1/2 1 0 1 1 0 1/2
А 2 1 1 0 0 0 1 0 1 1 0 1
Входные Неисправное Устройство
наборы 1 2 3 4 5 6 7 8 9 10 11
xt 1 1 1 0 1 0 0 1 1 0 0
А\,2 1 1 1/2 0 1/2 0 0 1/2 1/2 1/2 1/2
1 1 0 0 0 0 0 0 0 1/2 1/2
Из таблицы видно, что в неисправном устройстве
возможны критические состязания (значения 1/2 в узлах
10 и 11 на наборе Х2), которые могут воспрепятствовать
уверенному обнаружению неисправности 6° на выходе z.
Причиной состязаний является одновременное измене-
ние входных переменных 3 и 5 при переходе от набора
Xi к набору Xz. Введем между Xt и Х2 дополнительный
набор Ха—11001, т. е. перейдем к последовательности
<X.j, Ха, Х2> длины 3. Анализ итеративной сети из
трех копий показывает, что последовательность <Ai,
Ха, Х2> обнаруживает неисправность 6° на выходе z.
В условной форме результаты этого анализа представ-
лены на рис. 4-26,а. На этом рисунке для каждой копии
указаны значения входных переменных, а также значе-
ния внутренних переменных на входах и выходах копии.
Результаты троичного моделирования сети рис. 4-24
на последовательности <Xi, Ха, Х2> представлены
в табл. 4-21. Из таблицы видно, что недопустимые со-
стязания теперь не возникают (выход 11 имеет на набо-
ре Х2 определенные значения: 1—в исправном и 0—•
в неисправном устройстве).
27* 419
Копия! Копия2 КопияЗ
Рис. 4-26. Итеративные сети к примеру 4-21.
420
Таблица 4-21
Входные наборы Исправное устройство
1 2 3 4 5 6 7 8 9 10 11
Xi 1 1 1 0 1 1 0 1 1 0 0
Xt,a 1 1 1/2 0 1 1 0 1 1 0 0
Ха 1 1 0 0 1 1 0 1 1 0 0
Ха,2 1 1 0 0 1/2 1 0 1 1 0 1/2
Хг 1 1 0 0 0 1 0 1 1 0 1
Входные Неисправное устройство
наборы 1 2 3 4 5 6 7 8 9 10 11
Xi 1 1 1 0 1 0 0 1 1 0 0
хиа 1 1 1/2 0 1 0 0 1/2 1/2 1/2 0
Ха 1 1 0 0 1 0 0 0 0 1 0
Ха,2 1 1 0 0 1/2 0 0 0 0 1 0
xt 1 1 0 0 0 0 0 0 0 1 0
Как отмечалось выше, тестовая последовательность
асинхронного устройства должна удовлетворять усло-
вию (4-9) для последней копии р, а также условию
(4-10) для каждой копии v, ve{2, 3, р—1}, такой, что
Выполнения этих условий (как, впрочем,
и условия соседства по единственной переменной смеж-
ных наборов) можно пытаться достичь в процессе
построения тестовой последовательности. Другой путь
состоит в построении тестовой последовательности без
учета условий (4-9) и (4-10) с последующей ее провер-
кой на удовлетворение этих условий. Если результат
проверки окажется отрицательным, то следует найти
другой вариант (если он имеется) последовательно-
сти и т. д.
Вернемся к примеру 4-21. Обращаясь к рис. 4-26,а,
находим, что копии 2 и 3 должны удовлетворять (Ха=^='
и р = 3), но не удовлетворяют условиям (4-10)
и (4-9):
для копии 2 011 (г/n, ys, у8) ФО £)£)(«/„, y’s, у’&)
и для копии 3 QDD^DDD.
421
На копию 2 поступает входной набор Ха= 11001, ко-
торый переводит ее из состояния ОН в состояние ODD.
В исправном устройстве (при этом 0 = 1) состояние
копии 2 будет устойчивым, а в неисправном устройстве
D = 0— неустойчивым. Приняв состояние ODD в качест-
ве начального, методом прямой подстановки (прямым
двоичным моделированием) определим следующее со-
стояние копии 2 при неизменном входном наборе Ха.
Это состояние равно ODD, т. е. устойчиво (как в исправ-
ном, так и в неисправном устройствах), поэтому моде-
лирование прекращаем. Копия 2 «расщепляется» на две
копии — копию 2 и копию <3 (см. рис. 4-26,6) с одним и
тем же входным набором Ха, но разными начальными
состояниями 011 и ODD.
Аналогично поступаем с копией 3 (рис. 4-26,а), кото-
рая «расщепляется» также на две копни 4 и 5
(рис. 4-26,6) с входным набором Х2 и начальными со-
стояниями ODD и DDD соответственно. Заметим, что
копия <3 на рис. 4-26,а будет находиться в устойчивом
состоянии при неисправном устройстве и в неустойчи-
вом— при исправном.
Таким образом, окончательно получена тестовая по-
следовательность из трех наборов <Xi, Ха, Х2>, при
подаче которой на устройство произойдет следующая
смена его состояний:
— -v -> 011 — ODD — ODD DDD DDD.
На рис. 4-26,6 в обозначениях, введенных в § 1-8,
отображены условия проявления и транспортировки не
исправности 6° на входной последовательности <.Xi, Ха,
Хг>- В копии 1 неисправность не проявляется и не
обнаруживается — происходит установка устройства
в требуемое состояние 011. В копии 2 неисправность
проявляется и транспортируется на выходы у'9 и y's.
В копии <3 происходит то же, что и в копии 2, и, кроме
того, неисправность запоминается в контуре {6, 8, 9} (см.
рис. 4-24), о чем говорит наличие существенного пути
от входа у9 к выходу у'9. Существенный путь от входа
Ув копии 3 (и последующих копий 4 и 5) прерывается,
так как на элемент 7 (рис. 4-24) поступает тупиковый
D-куб (на входе 4 значение 0). В копии 4 неисправность
транспортируется в контрольную точку z(y'n). Наконец,
422
в копии 5 происходит то же, что в копии 4, и, кроме
того, неисправность запоминается в контуре {10, 11}
(рис. 4-24).
ПОСТРОЕНИЕ ПРОВЕРЯЮЩЕЙ ПОСЛЕДОВАТЕЛЬНОСТИ
ПО ЛОГИЧЕСКОЙ СЕТИ
Перейдем теперь к изложению «автоматного» под-
хода к построению проверяющих последовательностей.
Как отмечалось, при этом подходе построение последо-
вательности ведется по логической сети исправного
устройства без разрыва контуров обратных связей. Эле-
менты памяти (например, триггеры), а также контуры
могут обрабатываться либо как отдельные элементы,
заданные их таблицами переходов-жвыходов, либо как
логические подсети с обратными связями.
Введем несколько понятий и определений. Соедине-
ние входа элемента контура с выходом другого элемен-
та контура назовем контурным узлом, а переменную, со-
поставленную этому узлу,—контурной переменной. Зна-
чение контурной переменной узла у в настоящий момент
времени будем обозначать символом у, а в следующий
момент времени — символом у'. Пеконтурные входы
(переменные) элементов контура назовем внешними его
входами (переменными). Совокупность значений одной,
нескольких или всех контурных переменных назовем
состоянием о контура, а совокупность значений внеш-
них переменных - входным набором контура. Соедине-
ния выходов элементов контура со входами элементов,
не принадлежащих этому контуру, или с выходными по-
люсами сети назовем выходами данного контура.
Входной набор контура называется устанавливаю-
щим в о, если его подача на контур переводит послед-
ний в состояние о независимо от начального состояния
Овач, в котором находился контур в момент подачи
набора.
Говорят, что контур, на который подан устанавли-
вающий входной набор, находится в псевдоконтурном
режиме. В этом режиме хотя бы одна контурная пере-
менная несущественна, т. е. изменение значения такой,
как, впрочем, и любой контурной переменной у не вызы-
вает изменения значения переменной у'. Состояние о
в псевдоконтурном режиме всегда устойчиво, однако при
переходе из онач в о контур может проходить через не-
423
устойчивые состояния, число которых зависит от состоя-
ния Пнач’
Возможны два других режима работы контура,
когда все его контурные переменные существенны, т. е.
изменение значения переменной у в любом контурном
узле вызывает изменение значения переменной у'. Один
из этих режимов называют режимом запоминания, ха-
рактеризующимся тем, что в нем состояние контура
устойчиво. В другом режиме — режиме генерации —
состояние контура неустойчиво, т. е. происходит непре-
рывная смена одного состояния другим. Режим генера-
ции стабилен в контурах с нечетным числом инверсий
контурных переменных. При четном числе инверсий
в контуре для обеспечения стабильности режима гене-
рации необходимы специальные меры (например, внеш-
няя синхронизация, согласование величин задержек
в элементах контура); в противном случае из-за нера-
венства задержек в элементах контура генерация либо
не возникает совсем, либо самопроизвольно прекра-
щается — контур бесконтрольно переходит в одно из
своих устойчивых состояний.
В контурах из логических элементов простого бази-
са число инверсий контурной переменной не зависит от
входного набора контура. В контурах произвольного
базиса число инверсий может зависеть от поданного на
контур входного набора, например, при одном входном
наборе элемента контура этот элемент может инверти-
ровать контурную переменную, на другом — не инверти-
ровать.
Входной набор, при подаче которого контур оказы-
вается в режиме запоминания или генерации, называют
нейтральным. Для элементарного контура, состояние
которого задается единственной контурной переменной,
нейтральные наборы для режимов запоминания и гене-
рации всегда различны. Когда состояние контура опре-
деляется несколькими контурными переменными, один и
тот же набор может устанавливать контур как в режим
запоминания, так и в режим генерации, в зависимости
от начального состояния (тпач 'контура. В таких случаях,
называя входной набор контура, следует делать соот-
ветствующие оговорки.
Когда начальное состояние <тнач контура неизвестно,
а запомнить необходимо определенное состояние о, по-
424
даче на контур нейтрального набора должна предше-
ствовать подача устанавливающего в о набора.
Условия существования описанных выше режимов
контура можно получать из его аналитического описа-
ния. По логической сети для любого контурного узла у
элементарного контура получают булево выражение,
имеющее в общем случае следующий вид:
у'=Ау\/ By\JC. (4-11)
Здесь у — значение контурной переменной в настоя-
щий момент времени, а у' — в следующий момент вре-
мени; А, В, С — булевы функции от внешних перемен-
ных и, возможно, других контурных переменных кон-
тура.
Инвертируя правую часть (4-1Ц, находим выраже-
ние для инверсного значения контурной переменной:
tf = ACy\jBCy\/ABC. (4-12)
Переходя к совершенной дизъюнктивной нормальной
форме, выполняя поглощения и другие упрощения, вме-
сто (4-11) и (4-12) получим соответственно:
у’ = АВС у V АВС у V АВС \/ С; (4-13)
у’=АВСу \J ABCy\J АВС. (4-14)
Члены АВС, С и АВС определяют псевдоконтурные
режимы, поскольку эти члены однозначно определяют
значение у'(у') независимо от значения у'_ в предыду-
щий момент времени, т. е. от у. Член АВС определяет
режим запоминания, так как сохраняет прежнее значе-
ние у'—у(у' = у) и создает условия, при которых пере-
менная у существенна. Член АВС определяет режим
генерации, так как вызывает непрерывное изменение
переменной у через интервалы времени, определяемые
суммарной задержкой элементов контура {у'—АВСу).
От выражений вида (4-13) и (4-14) нетрудно перей-
ти к таблицам переходов, что иллюстрируется следую-
щим примером.
Пример 4-22. Построить таблицы переходов для контура
{10, 11*} сети (рис. 4-24).
* Здесь и в дальнейшем контур будем обозначать как множе-
ство {а, Ь ... }, где а, Ь ... — номера элементов, образующих контур.
425
Входными переменными контура являются входная х5 и вну-
тренняя ув переменные сети. Контурные узлы — ухо и уц.
Пусть состояние контура определяется одной контурной пере-
менной узла ум. Из анализа сети получаем:
У'10=УяУ ю V
у'ю—х5ую V Ув-
В соответствии с (4-13) и (4-14) А — уа, В=0, С&=х6уа. Таб-
лица переходов имеет вид:
Таблица 4-22
У'ю J/10
0 1
00 пи ш
хвУа 01 10 ПЙ 1 0 ш
11 ПИ 0
Устойчивые состояния контура, т. е. состояния, которые не изме-
няются при воздействии данного набора значений входных перемен-
ных х$уа, отмечены в таблице прямоугольниками. Нейтральным набо-
ром, задающим контуру режим запоминания, является набор
СО (х5, уа). Имеются два набора, устанавливающих контур в 0 (01
и 11), и один набор, устанавливающий в 1 (10). Режим генерации
при рассматриваемом задании состояния контура одной переменной
Ую (при этом значение другой контурной переменной у1Х определя-
ется однозначно значениями х5 и Щс) невозможен.
Приведенная таблица как модель предполагает, что временная
задержка элемента 10 контура больше задержки элемента 11 и
поэтому недостаточно точно отражает работу реального устройства.
Например, в рассматриваемом контуре переход от входного набо-
ра 11 (х5, уа) к набору 00 может приводить к неопределенности —
в зависимости от соотношения задержек элементов контура пере-
менная ую может принимать разные значения: 0 или 1.
Построим таблицу переходов при задании состояния контура
•обеими контурными переменными yi0 и уц. Анализ сети дает:
у'ы = Уч Уи\ у'= Х-„ ухо\
У'io = Ув\/Уи\ У’и = XsV У10-
Теперь таблица переходов содержит четыре столбца (табл 4-23)
Входные наборы 01, 10 и 11 (х5, уа) являются устанавливающи-
ми в состояние 01, 10 и 00 (у1В, уп) соответственно. Действительно,
например, набор 01 (х5, уа) из любого начального состояния уста-
навливает контур в состояние 01 (г/ю, Уп); состояние 01 устойчиво
при входном наборе 01 (х5, уа), из состояний 10 и 11 (yi0, Уи) при
входном наборе 01 (х5, уа) контур переходит в состояние 00 (r/ю, Уп),
из которого переходит в состояние 01, так как состояния 10, 11 и
426
Таблица 4-23
У,юУ,и
03 01 10 11
00 11 |оГ| llol 00
01 01 |оГ| 00 00
Х$уя 10 10 00 0 00
11 181 00 00 00
00 неустойчивы при входном наборе 01. На нейтральном входном
наборе 00 теоретически возможны как режим запоминания (когда
начальными состояниями являются 01 или 10), так и режим генера-
ции (когда начальным является состояние 00 или 11). Заметим, что
реально стабильный режим генерации в рассматриваемом асинхрон-
ном контуре не наступит — контур самопроизвольно перейдет
в устойчивое состояние 01 или 10 (окажется в режиме запоми-
нания)
До сих пор режимы работы контура рассматрива-
лись в предположении, что контурные переменные прини-
мают определенные значения 0 и 1. Однако все сказан-
ное о режимах работы контура остается справедливым
также для случая, когда значениями контурных пере-
менных могут быть также значения D, D. В этой связи
для наших целей важно отметить следующее свойство
элементарного контура, находящегося в режиме запоми-
нания. В этом режиме образуется замкнутый существен-
ный путь, проходящий через все контурные узлы. Гово-
ря формально, в режиме запоминания может храниться
значение D(D). При этом все контурные узлы имеют
значение D(D), или, другими словами, контур находит-
ся в состоянии од.
Для элементов памяти и контуров обратных связей
можно построить таблицы D-кубов неисправностей и
D-кубов элементов аналогично тому, как это было опи-
сано в § 3-4 для логических элементов. Регулярная
процедура построения D-кубов заключается в представ-
лении заданного таблицей переходов—выходов элемента
памяти (или контура) его таблицей истинности и в по-
парном сравнении строк последней. В дополнение
к классификации D-кубов, введенной при рассмотрении
логических элементов, введем следующие определения.
427
D-куб элемента называется внешним (внутренним), если
значение D(D) кроме выходных переменных имеют
только входные переменные (только внутренние или
контурные переменные) элемента памяти или контура.
Если значения D(D) имеют хотя бы одна входная и
хотя бы одна внутренняя (контурная) переменная, то
D-куб называется смешанным. Внешние D-кубы делят
на безусловные и условные. Безусловный внешний D-
куб является сжатым D-кубом, в котором все внутрен-
ние переменные имеют значение В условном внеш-
нем D-кубе хотя бы одна внутренняя переменная имеет
определенное значение (1 или 0). Наконец, различают
устойчивые и неустойчивые D-кубы. Устойчивым являет-
ся D-куб, значения (1, 0, D, D) переменных которого
задают устойчивое состояние элемента памяти или кон-
тура. В противном случае D-куб неустойчив — при неиз-
менных входных значениях он переходит в некоторый
другой D-куб.
Пример 4-23. Построить D-кубы для контура (10, 11} сети
рис. 4-24.
Таблица 4-24
№ п.п. ХЪ Ун 1/10 Уп Z1O 2ц
1 0 0 0 0 11
2 0. 0 0 1 01
3 0 0 1 0 10
4 0 0 1 1 00
5 0 1 0 0 01
6 0 1 0 1 01
7 0 1 1 0 оо
8 0 1 1 1 00
9 1 0 0 0 10
10 1 0 0 1 00
11 1 0 1 0 10
12 1 0 1 1 00
13 1 1 0 0 00
14 1 1 0 1 00
15 1 1 1 0 00
16 1 1 1 1 00
428
Таблица 4-25
Номер строки D-кубы неисправностей Типы £>-кубов
х$ Уъ Ую Уи Zio 2ц
1 0 0 0 0 D I 0 0 0 0 1 D 0 0 0 ODD Условные
(13,14,15,16) 1 1 -х, -v D 0 1 1 ~ -X. 0 D 1 1 ~ ~ D D Безусловные
Пусть выходами контура являются узлы 10 и 11, т. е. выход-
ными функциями Ию и 2ц являются контурные переменные у'ю и
у'и соответственно. Это позволяет рассматривать табл. 4-23 как
таблицу переходов — выходов контура. Таблица 4-24 является таб-
лицей истинности комбинационного эквивалента контура.
Ради экономии места не будем выписывать все возможные D-ку-
•бы контура, а ограничимся только характерными D-кубами в соот-
ветствии с приведенной выше их классификацией.
Таблица 4-26
Номер строк D-кубы контура Типы D-кубов
*5 У9 Ую У и Й’ю 21 >
1 — 5 _0 D 0 0 D 1 Внешние условные
6 — 10 D D 0 1 0 D
2 —3 0 0 D D D D Внутренние нетуппко-
1 — 3 0 0 D 0 1 D вне
5 — 6 0 1 0 D 0 1 Внутренние тупиковые
15 — 16 1 1 1 D 0 0
1 — 6 0 D 0 D D 1 Смешанные нетупико
5 — 10 D D 0 D 0 D вне
7 2 — 16 — 5 D 0 1 D 1 0 D D 0 0 0 1 Смешанные тупиковые
429
В табл. 4-25 приведены примеры D-кубов неисправностей кон-
тура, а в табл. 4-26 — D-кубов контура. В первом столбце этих
таблиц указаны строки (группы строк) табл. 4-24, порождающие
соответствующие D-кубы. Из приведенных D-кубов устойчивым
является, например, внутренний D-куб 00DDDD. Неустойчив вну-
тренний тупиковый D-куб 111D00. Неустойчивым в неисправном и
устойчивым в исправном состоянии является внешний условный
D-куб DD010D. Наконец, неустойчив в исправном и устойчив в не-
исправном состоянии D-куб 010D01 (внутренний тупиковый).
Теперь можно описать алгоритм, реализующий
«автоматный» подход к построению проверяющих после-
довательностей. При описании основное внимание бу-
дет уделено особенностям, отличающим этот алгоритм
от алгоритма АЗ-З (см. гл. 3), реализующего метод су-
щественных путей для комбинационных устройств.
Задана логическая сеть устройства с памятью. По
сети определены ее элементарные контуры. Для логи-
ческих элементов и для элементов памяти сети имеются
таблицы D-кубов неисправностей и D-кубов элементов.
Те контуры, для которых построены таблицы D кубов,
рассматриваются как элементы памяти. Другие контуры
обрабатываются как подсети из логических элементов.
Задана одиночная константная неисправность узла I.
Сначала задаются на сети условия проявления неис-
правности. Это делается, как обычно, путем задания
D-кубов, неисправности на логическом элементе, эле-
менте памяти или, наконец, на внешнем входе сети.
Если неисправным является выход элемента памяти, то
в первую очередь следует использовать безусловные
D-кубы неисправности. При использовании условного
D-куба неисправности фиксируется начальное внутрен-
нее состояние (обозначим его символом Уп), предписы-
ваемое исправному элементу памяти выбранным D-ку-
бом. Задаваемые D-кубами неисправности значения
в узлах сети будем относить к моменту времени t. В на-
чальное состояние Уы элемент памяти должен быть уста-
новлен заранее в момент времени меньше t.
После этого переходят к заданию на сети условий
транспортировки неисправности, т. е. к организации су-
щественного пути {i, у} от неисправного узла i до одно-
го из внешних выходов у, также в момент времени t.
Если простой или сложный путь {1, у} не содержит эле-
ментов памяти и контуров обратных связей, то условия
транспортировки задаются так, как было описано
в гл. 3 для комбинационных устройств. При наличии
в пути {i, у} элементов памяти (в том числе принадле-
430
жащих контурам) на последних задаются в первую
очередь внешние безусловные D-кубы; если таких
D-кубов нет или их задание невозможно из-за противоре-
чий, то используются внешние, а затем и смешанные
условные D-кубы. В последних случаях также фикси-
руются начальные состояния Уп, в которые должны быть
установлены элементы памяти в момент времени мень-
ше t.
В контурах условия транспортировки задаются
D-кубами контурных логических элементов и контурных
элементов памяти. Если при этом потребуется задание
контуру режима запоминания, то фиксируются началь-
ные значения у„ всех контурных узлов с тем, чтобы
установить эти значения в момент времени меньше t.
После задания условий проявления и транспортировки
неисправности выполняются операции ОР над элемен-
тами сети. Признаком задания контуру режима запо-
минания при организации существенного пути служит
возникновение одного из противоречий вида О— D(D)
или 1—D(D) на контурном узле. Это противоречие раз-
решимо и устраняется предварительной установкой на-
чальных значений у„ всех контурных узлов в момент
времени меньше t.
Задание D-куба неисправности и D-кубов элементов
на сетях с памятью выполняется так, как в комбина-
ционных сетях. Относительно же операции ОР над кон-
турными элементами сети сделаем следующую оговор-
ку. Пусть имеется возможность выполнить операцию ОР
над контурным элементом, контурный вход которого
имеет значение 1,O,D или D, такую, результатом которой
является задание контурному выходу элемента одного
из указанных значений. Рекомендуется эту операцию
ОР выполнять одновременно с операцией РФ или
D-операцией расширения фиксации (РФ или D-РФ, см.
гл. 3) такой, которая задает неконтурным входам эле-
мента значения, однозначно определяющие на контурном
выходе значение, предписываемое ему операцией ОР,
при безразличном значении ~ контурного входа. Та-
кую обобщенную операцию будем кратко обозначать
ОР + РФ илиОР-^-РФ. Выполнение обобщенной опера-
ции возможно только тогда, когда хотя бы один некон-
турный вход элемента имеет значение X или
Например, пусть на контурный вход а контурного
трехвходового элемента И подано значение 0, а на его
431
неконтурные входы b и с — значения X и 1 соответст-
венно. Операция ОР определяет значение выхода у=0.
Значение у=0 также однозначно определяется при за-
дании неконтурному входу b значения 0 при безразлич-
ном значении ~ контурного входа а. Обобщенная опе-
рация ОР + РФ, следовательно, состоит в задании на
элементе куба 0010 (а, Ь, с, у).
Рассмотренная рекомендация по замене операции
ОР обобщенной операцией ОР + РФ (Р-РФ) не являет-
ся обязательной. Эта замена лишь отражает стремление
задать контурам псевдоконтурпый режим, т. е. исклю-
чить необходимость предварительной установки в на-
чальные состояния обрабатываемых контуров за счет
обеспечения несущественности контурных входов их
элементов. Следует иметь в виду, что при этом, во-пер-
вых, не учитывается то, что задание определенных зна-
чений на некоптурных входах элемента может в даль-
нейшем потребовать предварительной установки в на-
чальные состояния некоторых других контуров, и,
во-вторых, не учитывается возможность, быть может,
более удачного обеспечения несущественности контур-
ных входов других элементов обрабатываемого контура.
Иными словами, алгоритм должен в процессе перебора
допустимых вариантов предусматривать возможность
отказа от замены операции ОР обобщенной операцией
ОР + РФ (D-РФ) над контурными элементами сети. Не
имеет смысла, в частности, выполнять обобщенную опе-
рацию ОР + РФ (О-РФ) больше чем над одним контур-
ным элементом одного и того же элементарного кон-
тура.
Отметим еще одну особенность алгоритма, связан-
ную с наличием контуров в сети. Рассмотрим некоторую
МССП сети, все элементы которой обработаны, благо-
даря чему определены значения (0, 1, D, D, ~) всех
внутренних узлов и внешних входов МССП в момент
времени t. Часть внутренних узлов МССП может требо-
вать предварительной установки их значений. Совокуп-
ность внутренних узлов МССП, значения которых не
определяются однозначно значениями внешних входов
МССП, можно определить путем моделирования работы
МССП. При этом внешним входам МССП задаются
предписанные им значения, а всем внутренним узлам —
значения X- Внутренние узлы, в которых после модели-
рования сохранились значения X, образуют множество
432
{ун} узлов, требующих предварительной установки в мо-
мент времени меньше t. Описанную операцию будем
называть операцией анализа контурных сигналов (со-
кращенно АКС).
Предположим, что существенный путь {i, у} построен.
В процессе обработки сети могли использоваться не-
устойчивые D-кубы и кубы элементов памяти ’, а также
могли оказаться неустойчивыми состояния контуров1 2.
Поэтому необходимо выполнить прямое моделирование
сети с целью определения, окажется ли устойчивым
значение D(D) в узле у. По существу, моделированию
должна подвергаться только та минимальная часть
сети, на узлах которой оказались заданными или вычис-
ленными значения сигналов 1, О, D, D, Следствием
выделения этой части сети является выделение ее внеш-
них входов — узлов, которые являются либо выходами
элементов, у которых все входы имеют значения X,
либо внешними полюсами сети.
Обозначим совокупности требующих предварительной
установки в момент времени меньше t начальных 'состоя-
ний элементов памяти записью {KH}<Z и значений контур-
ных переменных — записью Моделирование начинают
с задания начальных состояний {Ун}^ и значений
После этого подают на внешние входы выделенной ча-
сти сети предписанные им значения, а неисправному
узлу задают значение D(D). Затем такт за тактом
выполняют непосредственно моделирование. Если
устойчивое значение D или D на узле у не получено, то
строят новый вариант существенного пути {i, у). В про-
тивном случае переходят ко второму этапу алгоритма —
до определения значений в узлах сети и на входных
полюсах.
Прежде чем перейти к описанию операций второго
этапа алгоритма, остановимся па случаях, когда не
удается реализовать ни один из возможных вариантов
образования существенных путей от узла i до хотя бы
одного из выходных полюсов у, у=1, 2, ..., k. Это мо-
жет иметь место либо в результате неразрешимых про-
1 Кубом элемента памяти называется комбинация значений вход-
ных, выходных и внутренних переменных.
2 Заметим, что неустойчивые D-кубы неисправностей, D-кубы и
кубы элементов следует использовать только в крайнем случае, когда
задание устойчивых D-кубов невозможно.
28—358 433
тиворечий, либо из-за неустойчивости значений D(D) на
выходном полюсе у. В обоих случаях необходимо про-
верить наличие элементов памяти или контурных эле-
ментов в путях (i, у). Если таких элементов ни в одном
пути (i, у) нет, то рассматриваемая неисправность
узла i несущественна. В противном случае переходят
к попыткам реализации условий проявления и транспор-
тировки неисправности с промежуточным запоминанием
значения D(D) на элементах памяти или в контурах.
Для этого в качестве контрольных точек принимают
принадлежащие путям (i, у) выходы элементов памяти
и выходы первых на этих путях (в направлении рас-
пространения сигналов) элементов контуров. Указанные
элементы памяти, первые элементы контуров, а также
контуры, в которых выделены первые элементы, будем
называть p-элементами и р-контурами соответственно.
Затем применяют описанную процедуру для построения
существенных путей {i, р} при обязательном условии
задания p-элементу памяти или р-контуру либо режима
запоминания, либо режима установки в такое состояние
Ср, при котором выход p-элемента имеет значение 0(D).
Для элементарных контуров состоянием о₽ всегда явля-
ется состояние <rD; для элементов памяти в общем случае
это условие необязательно. Если p-контуру или р-элемен-
ту памяти задается режим запоминания состояния ар ,
то фиксируется необходимость предварительной их уста-
новки в это состояние.
Если существенный путь {«, р) построен, то переходят
к попыткам построения существенного пути {р, -у), при-
нимая узел р за место проявления неисправности, сохра-
няя или задавая режим запоминания состояния на
P-элементе памяти или p-контуре и относя получаемые
при этом значения в узлах сети к моменту времени ti>t.
Если существенный путь {i, р} не удалось построить ни
для одного узла р, то неисправность узла i несуществен-
на. Если построить путь {р, у] не удается, необходимо
проверить и использовать возможность реализации этого
пути с повторным промежуточным запоминанием. При
этом поступают так, как описано выше, с выделением
момента времени fe>A и т. д.
Для простоты изложения в дальнейшем при рассмот-
рении вопросов, связанных с проявлением и транспорти-
ровкой неисправности с промежуточным запоминанием,
434
будем предполагать, что имеется единственное промежу-
точное запоминание для т. е. существенный путь
состоит из двух участков: {i, £} и {0, у}.
При дальнейшем изложении сначала будем считать,
что построен существенный путь {*, у}. Об особенностях
работы алгоритма для случая транспортировки неис-
правности с промежуточным запоминанием будет сказа-
но в конце описания алгоритма.
На втором этапе алгоритма используются операции
РФ (£>-РФ) и ОР, а также при необходимости — обоб-
щенная операция ОР + РФ (£)-РФ) и операция АКС.
Исходной фиксацией значений сигналов в узлах сети
являются значения, полученные в результате построения
существенного пути {i, -у} и отнесенные к моменту време-
ни t. При обработке элементов памяти и контурных эле-
ментов следует соблюдать правила и рекомендации, из-
ложенные выше при описании первого этапа алгорит-
ма— этапа построения существенных путей. Речь идет
о первоочередном задании на элементах памяти безус-
ловных кубов, об использовании обобщенной операции
ОР-рРФ (£)-РФ) над контурными элементами, а также
операции АКС.
Успешным завершением второго этапа алгоритма для
момента времени t является получение входного набора
X(t). Если все возможные варианты доопределения ока-
зались противоречивыми (набор X(t) не построен), то
возвращаются к первому этапу алгоритма, выбирают
другой вариант существенного пути {i, у} и снова выпол-
няют доопределение при новой полученной исходной
фиксации.
Когда входной набор X(t) получен, выполняется про-
верка, зафиксированы ли в процессе работы алгоритма
(на первом и на втором его этапах) внутренние состоя-
ния {Ун}<г элементов памяти или значения контурных пе-
ременных {yui<t, требующие предварительной установки
в момент времени меньше t. После этого моделируется
работа сети на наборе X(t) (с предварительным зада-
нием, если это необходимо, исходных состояний {FH}<Z
элементов памяти и значений контурных переменных
с Целью проверки устойчивости значения £)(£))
в контрольной точке у. Если устойчивость не достигнута,
то рассматривают новый вариант доопределения. В про-
тивном случае при условии, что{Уи}<г= 0 и {yH}<f = 0,
•28* 435
поиск других вариантов прекращают — построена про-
веряющая последовательность <X(rf)> длины 1. Если
последнее условие не выполняется, то поступают следу-
ющим образом.
На входы тех элементов памяти, которые требуют
предварительной установки в состояние Ун, подают их
устанавливающие в Ун входные наборы. Полученные при
этом значения входов элементов памяти, а также значе-
ния контурных переменных {Ун}^ относят к моменту
времени t—1 и принимают в качестве исходной фикса-
ции, после чего снова выполняют второй этап алгоритма.
Если из-за противоречий подача устанавливающего
в Ун набора на некоторый элемент памяти невозможна,
то следует попытаться сохранить на нем режим запоми-
нания, отнеся установку в состояние Ун на момент вре-
мени < (/—1). Аналогично следует поступать, когда про-
тиворечия не позволяют задать некоторому контуру псев-
доконтурный режим — в момент времени t—1 сохраняет-
ся режим запоминания, а подача устанавливающего на-
бора переносится на момент времени < (/—1).
При доопределении значений сигналов в моменты
времени меньше t следует учитывать особенности работы
с неисправным узлом i, указанные ранее, при описании
построения проверяющих последовательностей на основе
«комбинационного» подхода.
Уснешное^доонределение значений узлов сети в момент
времени t — 1 дает входной набор X (/ — 1). Проверяется
наличие состояний {Ун}<(г_1) элементов памяти, а также
контурных переменных {ун}< (Z_1)f требующих предвари-
тельной установки в момент времени <(/—1), и выпол-
няется моделирование работы сети на наборе X(t—1).
При X(t—l)=X(t) целью моделирования является про-
верка устойчивости значения D(D) в контрольной точке
у, а при X(t—l)^=X(t)—проверка устойчивости исход-
ной фиксации значений в узлах сети для момента време-
ни t—1. При отрицательном исходе моделирования ищут
новый вариант доопределения для момента времени
t— 1.
При положительном исходе и при условии, что
{Ун}< (<21)= 0 и (z-i)—0» выполнение алгоритма
прекращают — построена входная последовательность
<^Х (I — 1), X (/)>• длины 2. Если же {Ун}< =И= 0 или
436
{y»}<(i—i)¥z0> то набор Д’ (Z — 1) запоминается, после
чего выполняется этап доопределения для момента време-
ни t — 2 и т. д.
Если все возможные варианты доопределения для мо-
мента времени t — I при Z>0, где Z = О, 1, 2 оказа-
лись нереализуемыми или [Уи}(/ = {yH}>(Z_Z) и {ун}(/ /) =
= {ун}> (Z_Z), т- е- совокупность значений {Ун} и {ун} по-
вторилась, то возвращаются назад и ищут другой ва-
риант доопределения для момента времени >(t—I).
Если это невозможно даже для момента времени t, то
ищут новый вариант существенного пути {/, у}.
Признаком успешного окончания работы по описан-
ному выше алгоритму всегда является получение для
момента времени t—I, 1=0, 1, 2 . . ., входного набора
X(t—Z), обеспечивающего устойчивость либо значения
D(D) в контрольной точке [когда X(t—l)=X(t—1+
+1) = ... =Х (Z)], либо исходной фиксации для ближай-
шего следующего момента времени Z—1 + г, г=1, 2, 3 ....
Z>r^= 1 [когда X(t—l)TtA(Z—l + r-j-l)] при условии,
что {Ун}<(,_/) = 0 и M<(Z_Z)=0.
В заключение полученная входная последователь-
ность <X(t—ZMaiKC), .... A('Z—I), .... X(Z)>, где 1макс —
максимальное значение Z, проверяется на отсутствие не-
допустимых состязаний методом троичного моделирова-
ния.
Если условия транспортировки неисправности реали-
зуются с промежуточным запоминанием (см. выше), то
второй этап алгоритма начинают для момента времени
Zj, для которого исходной фиксацией являются значения
в узлах сети, задающие последний участок существенно-
го пути {р, у} и режим запоминания состояния о₽ на
p-элементе памяти или в р-контуре.
Задание режима запоминания состояния ^-элементу
памяти состоит в подаче иа него нейтрального набора
с определением начального состояния YH. Состояние Ун
определяется следующим образом. D-куб элемента па-
мяти, задающий состояние о расщепляется на два ку-
ба—один из них получается заменой в D-кубе значений
D(D) значениями 1(0), а второй — значениями 0(1). При
этом вместо одного входного набора XD и одного состоя-
ния 0^ исходного D-куба в общем случае (когда D-куб
смешанный) получаем два входных набора Xi и Хо и два
437
состояния oi и оо. По таблице переходов элемента памя-
ти производится проверка, какими наборами являются
Xi и Хо. Если оба эти набора — устанавливающие, то
предварительное задание начального состояния Ун не
требуется. Если же один из наборов, скажем Xi, являет-
ся нейтральным, а второй (Хо) —устанавливающим, то
предварительная установка элемента памяти необходи-
ма, причем Ун— oi. Случай, когда оба разных набора Xi
и Хо являются нейтральными, возможен при внешнем
исходном D-кубе. При этом Ун=О1=о0-
Задание режима запоминания состояния oD р-кон-
туру состоит в подаче на его контурные элементы D-ку-
бов, обеспечивающих непротиворечивое получение значе-
ний D(D) во всех контурных узлах, с определением на-
чальных значений ув всех контурных переменных. Значе-
ния ув находятся следующим образом. Состояние on
расщепляется на два состояния: ot и о0. Для получения
состояния Oi значения D(D) в <ти заменяются значения-
ми 1(0), а для получения Оо — значениями 0(1). Затем
выделяется p-элемент контура и находится значение его
контурного входа у$, предписываемое подаваемым на
элемент D-кубом неисправности или D-кубом элемента,
реализующим условия задания существенного пути {i, р}.
Начальными значениями уа контурных переменных могут
быть значения, определяемые либо тем состоянием oi
или Оо, у которого значение контурной переменной у в
совпадает с найденным ее значением, либо состоянием
Ods, получаемым из ов заменой значения D(D) контур-
ной переменной ув найденным ее значением.
После построения входного набора Х(Д) и проверки
устойчивости значения D(D) в узле у переходят к реа-
лизации второго этапа алгоритма для момента времени
ti—1. При этом исходную фиксацию составляют: значе-
ния в узлах сети, задающие существенный путь {i, р} и
режим установки в состояние щ, oG или ons p-элемента
памяти или p-контура; значения, которые необходимы
для задания состояний {Ун}<ц других элементов памяти;
значения {y^<tt контурных переменных других контуров.
Далее выполняются операции алгоритма так, как описа-
но выше. При разрешении противоречий, связанных
с заданием режима установки p-элементу памяти или
p-коптуру, следует следить за тем, чтобы режим запоми-
нания состояния о сохранялся вплоть до момента вре-
438
мени ti—l—t, в который реализуются условия образова-
ния существенного пути {г, р).
Пример 4-24. Задана логическая сеть устройства с па-
мятью (рис. 4-27), таблицы сжатых кубов и D-кубов эле-
ментов сети. Для логических элементов данной сети
таблицы D-кубов были приведены в гл 3, а для элемен-
Рис. 4-27 Логическая сеть к примеру 4-2ч.
та памяти можно пользоваться табл. 4-25 и 4-26 с соот-
ветствующим переименованием переменных или пост-
роить соответствующие D-кубы по табл. 4-24, если они
отсутствуют в табл. 4-25 и 4-26. Требуется построить
проверяющую последовательность, обнаруживающую не-
исправность 6°.
В сети имеются две МССП, каждая из них содержит
по одному элементарному контуру: {б, 7, 6} и {9, 10, 11}.
Результаты обработки сети будем заносить в
табл. 4-27. Задаем D-куб неисправности на элементе
6—11D (2, 8, 6) (строка 1 табл 4-27).
Переходим к заданию условий транспортировки не-
исправности на выход z устройства (узел 12}. Для этого
последовательно задаем D-кубы элементов 7 и 8 (выпол-
няем D-операции РФ). Этим операциям соответствуют
строки 2 и 3 табл. 4-27.
В контурном узле 8 контура {б, 7, 8} получено проти-
воречие (1 на входе элемента б и D на выходе элемента
8). Других вариантов D-кубов неисправности для эле-
мента б, а также других вариантов организации суще-
ственного пути в пределах контура нет. Следовательно,
реализация условий проявления и транспортировки не-
исправности на выход 12 в один такт невозможна, не-
обходима предварительная установка состояния или ops,
или Оо, или oi в контуре {б, 7, 8}
439
Таблица 4-27
° Этап Момент времени Номер строки Операция (номер элемента) Узлы и их значения
алго- ритма 1 2 3 4 5 6 7 8 9 10 11 12 13 14
\ t \ 2 3 Задание D-куба неисправности (6) П-РФ (7) О-РФ (8) 1 1 1 1 0 0 D D D D D 1 1 1/D
1 /1 4 5 6 7 8 9 D-РФ (б) D-РФ (7) D-РФ (8) D-РФ (9) D-РФ (10) D-РФ (11) 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 D D D D D D D D D D D О D D D D D D D D D D 0 0 0/D
h 10 И 12 13 О-РФ (9) D-РФ (10) D-РФ (11) D-РФ (12) 0 0 0 D D D D D D D D D D D О D D D D D D
— 14 15 16 17 18 19 Моделирование 0 0 0 0 1 1 0 0 0 0 D D D D 0, D 0, D 0, D D D D IQ IQ IQ _-|Q> IQ 1Q 0 0 0 D D D 0 0 D D 1 1 D D О 0 0 0 D D
Продолжение табл. 4-27'
Этап алго- ритма Момент времени Номер строки Операция (номер элемента) Узлы и их значения
1 2 3 * 5 6 7 8 9 10 и 12 13 14
ts 20 Исходная фикса- 1 1 0 0 0 D D D D D D D
ция
21 Исходная фикса- 1 1, о 1, D 1 0, D 1, D 0
ЦИЯ
22 ОР (9) 1 1, D 1, D 1 0, D/1 1, D 0
23 Исходная фикса- 1 D D D 0, D 1, D 0
ЦИЯ
Лиакс —1 24 ОР (9) 1 D D D D 1, D 0
25 ОР (10) 1 D D D D D 0
2 26 ОР (11) 1 1 D О D D D 0
27 D-РФ (8) 1 1 1 D D D D D 0
28 D-РФ (7) 1 0 1 1 D D О D D 0
29 D-РФ (6) 1 1 0 1 1 D D ’ D D О 0
30 Исходная фикса- 1, D 1, D 1
ция
31 ОР (9) 1,0 1, о 1 1
/ О 32 ОР (10) 1, о 1, о 1 1 0
шакс — 33 РФ (8) 1 1, D 1 1 1 0
34 РФ (7) 1 1 1, D 1 1 1 0
35 РФ (6) 1 1 1 D 1 1 1 0
Выходом p-элемента является узел 6. Значит, задание
существенного пути {», р}={6, 6} сводится к заданию
условий проявления неисправности узла 6, т. е. к подаче
на элемент 6 D-куба неисправности 11 D (2, 8, 6) с по-
следующим запоминанием oD в контуре {6, 7, S}.
Имеем:
aD—DDD(6, 7, S);
111;
с„ = ООО;
ys^=.ys= 1.
Следовательно, начальные значения уа контурных
переменных определяются состоянием <rt=lll или со-
стоянием D.DI. Запоминаем обязательное значение у8= 1
и возможные значения для ув и у1 и относим их к момен-
ту времени 1.
Теперь переходим к попыткам организации сущест-
венного пути {р, у}={6, 12} в момент времени ti>t.
В контурных узлах 6, 7, 8 задаем значения D, т. е. по-
даем на элементы 6, 7, 8 соответствующие D-кубы (см.
строки 4, 5, 6 табл. 4-27). Затем задаем последовательно
D-кубы элементов 9, 10 и И (строки 7, 8, 9). В контур-
ном узле 11 получено противоречие (0 на входе элемента
9, который соединен с выходом элемента 11, задан вы-
бранным для элемента 9 D-кубом, a D на выходе элемен-
та И получили при выборе D-куба для элемента 11}.
Других, непротиворечивых вариантов организации суще-
ственного пути через контур {9, 10, 11} нет—необходима
предварительная установка состояния или ans, или оо,
или о, в этом контуре с последующим запоминанием gd
в контуре {9, 10, 11}.
Выходом (3-элемента является узел 9. На (3-элемент
подается D-куб элемента ODD (//, 8, 9).
Имеем:
GjD=DDD (9, 10, //);
01=101;
Оо=010;
442
Значит, значения t/„ контурных переменных в момент
времени_/1 определяются состоянием оо=010 или состоя-
нием DDQ. Запоминаем эти значения и переходим к орга-
низации существенного пути {р, у}={9, 12} в момент вре-
мени
В контурных узлах 9, 10, И задаем значения D, D, D
соответственно, т. е. подаем необходимые D-кубы на эле-
менты 9, 10 и 11 (строки 10, 11, 12 табл. 4-27). Теперь
задаем D-куб элемента памяти. Для него безусловных
D-кубов нет, выбираем единственный устойчивый внут-
ренний D-куб 0 DDDD (5, 11, 13, 14, 12), обеспечиваю-
щий проведение значения D со входа элемента 11 па вы-
ход элемента 12 (строка 13). Проверяем, требует ли этот
D-куб предварительной установки элемента памяти в на-
чальное состояние Ун.
Имеем:
Xd = QD(5, 11); cd = DD;
Х, = 01; с, = 01;
Л’(| = 00; о0 = 10.
Обращаясь к таблице переходов — выходов элемента
памяти (табл. 4-23), находим, что набор ^=01 является
устанавливающим в состояние oi=01, однако ^=00
является нейтральным набором. Поэтому требуется
предварительная установка в состояние Ун=оо— Ю в мо-
мент времени меньше t2. Находим устанавливающий
в состояние 10 входной набор Xn=10(5, 11) и запоми-
наем его.
Прежде чем переходить ко второму этапу алгоритма,
для момента времени <2, проверим устойчивость значения
D на выходе у=12. Для этого выделяем подсеть, со-
стоящую из элементов 9, 10, 11 и 12 (именно на этой
подсети задан существенный путь {р, ?}={Р, 12} в мо-
мент времени t2). Внешними входами подсети являются
узлы 4, 5 и 8. Задаем значения г/э={0, D), у)0={1, D},
Уи=0 контурных узлов контура {9, 10, 11} и значения
Хп=10 (5, 11) на входах элемента памяти. Напомним,
что эти значения должны быть заданы в момент времени
<t2. Противоречий нет, можно выполнять моделирова-
ние.
Результаты моделирования представлены в строках
14—19 табл. 4-27. В строке 14 заданы начальные значе-
443
ния {г/н} и Хп. Строка 15 представляет установку элемен-
та памяти в состояние 10 (13, 14). Затем в строке 16 за-
фиксирована подача значений 00 D (4, 5, 8) на внешние
входы подсети. Остальные строки отражают изменения
сигналов в узлах подсети под влиянием поданных вход-
ных значений. Строки 18 и 19 одинаковы, что служит
признаком окончания моделирования. Следовательно,
значение D на выходе элемента 12 устойчиво. Устойчи-
вость D в узле 8 обеспечивается режимом запоминания
в контуре {6, 7, 8}.
Исходной фиксацией для второго этапа алгоритма
в момент времени t2 являются значения в узлах 4, 5,
8—12, указанные в строке 13 табл. 4-27 (эти значения
задают существенный путь {9, 12}), а также значения
в узлах 1, 2, 3, 6, 7 и 8, указанные в строке 6 той же
таблицы (эти значения задают режим запоминания со-
стояния в контуре {6, 7, 8}, а следовательно, и существен-
ный путь {6, 8}). Исходная фиксация (см. строку 20
табл. 4-27) непротиворечива. Никакие операции по до-
определению значений в узлах сети не требуются, так
как значения всех узлов определились в результате вы-
полнения первого этапа алгоритма. Получен входной на-
бор X(t2) —11000 (/, 2, 3, 4, 5). Моделирование работы
сети на наборе X(t2) показывает, что значение D на вы-
ходе элемента 12 устойчиво (результаты этого модели-
рования не приводятся).
Целесообразно попытаться установить одновременно
все значения {г/н} и {Ун}, определенные при построении
существенного пути {6, 12} (несмотря на то, что этот путь
определялся последовательно по частям). Если после
рассмотрения всех вариантов доопределения (установки)
окажется, что этого сделать нельзя за любое заданное
число тактов (с помощью последовательности любой за-
данной длины), тогда следует перейти к передаче D(D)
по шагам с промежуточным запоминанием.
Для реализации этой попытки полагаем t=t!=t2=
='^макс, а предварительную установку требуемых значе-
ний относим к моменту ^мяко—1- Исходную фиксацию
для момента времени ^Макс—1 задают значения 1, (/, D),
(1, D), 1, (0, D), (1, D), 0 (5, 6, 7, 8, 9, 10, 11). ОР(9)
(строка 22) показывает, что эта фиксация противоречива
в узле 9, так как 1 в узле 8 однозначно определяет зна-
чение 1 в узле 9 вместо требуемого 0. В этом случае
установку части контуров или элементов памяти необхо-
444
димо отнести к моменту времени /маКс—2. В общем слу-
чае необходим перебор вариантов совокупностей конту-
ров и элементов памяти, установка которых относится
К /макс 2. Отнесем к моменту /ма.кс—2 установку конту-
ра {6, 7, S}. Тогда для /макг—1 имеем исходную фикса-
цию 1, D, D, D, (О, D), (1, D)0 (5, 6, 7, 8, 9, 10, 11), за-
писанную в строке 21. Выполняя операции ОР и D-РФ
над элементами 9, 10, 11, 6, 7, 8 (строки 24—29), полу-
чаем X(fMa'KC—1) = 11011 (1, 2, 3, 4, 5). Для момента вре-
МеНИ £макс—2 исходная фиксация (1, D), (1, D), 1 (6, 7,8)
записана в строке 30. Выполняем операции ОР и РФ
(строки 31—35). При выполнении РФ (5) из двух воз-
можных значений 1, D узла 7 при выборе куба исполь-
зуется значение 1, т. е. то, которое обеспечивает обяза-
тельное значение 1 в узле 8. Для элемента 6 операция
РФ (6) состоит в выборе D-куба неисправности, посколь-
ку в момент времени /макс—2 обеспечиваются условия
проявления неисправности, которые сохраняются в мо-
менты Времени /макс—1 И /макс- НабоЦ -^(/макс 2) —
= 111-------(/, 2, 3, 4, 5).
Поскольку наборы, полученные для моментов време-
ни /макс, /макс 1 И /макс” 2, НеОДИНЗКОВЫ, ЛГ (’/макс)
^-^(/макс—1)¥=-^(/ма’кс—2), то после получения каждого
набора проводится моделирование, чтобы убедиться
в устойчивости состояния сети перед подачей набора
-^(/макс) и Х(/макс—1)- В примере использовались только
устойчивые кубы, D-кубы и D-кубы неисправности, по-
этому все указанные состояния устойчивы, что и показа-
ло моделирование, результаты которого здесь не приво-
дятся.
Таким образом, построена входная тестовая последо-
вательность <^А^(/макс—2), X(/макс 1)> -^(/майс)>- Про-
верка на отсутствие недопустимых состязаний требует
троичного моделирования работы сети на этой последо-
вательности, а при использовании неустойчивых кубов,
D-кубов и D-кубов неисправности — специального моде-
лирования. Результаты моделирования здесь не приво-
дятся.
Заметим, что если в сети рис. 4-27 в соединение вы-
хода элемента 8 со входами элементов 9 и 10 вставить
инвертор, то противоречие, указанное в строке 22, в узле
9 не возникнет и тестовая последовательность будет со-
стоять из двух наборов Х(/ма'кс—1) = 11111 (/, 2, 3, 4, 5)
иХ(/макс) = П000.
445
Изложенный метод учитывает возможные состяза-
ния на входах контурных элементов и элементов
памяти, т. е. при переходе от одного входного на-
бора контура к другому, посредством установки
контуров и элементов памяти в определенное со-
стояние с последующим его запоминанием. Если
такие состязания не учитывать, то увеличивается
вероятность получения последовательности, при
подаче которой возможны недопустимые состязания.
Например, приведенная выше последовательность из
двух наборов является тестовой и для сети рис. 4-27, но
только при условии, что при переходе от Х(/манс—1)
к X(ZMattc) раньше изменится значение в узле 8, чем
в узле 4. В противном случае использование последова-
тельности может привести к неверному выводу. Резуль-
тат может быть искажен за счет состязания на входах.
При этом надо помнить, что состязания в сетях, подклю-
ченных к входам контурных элементов, не учитываются
в процессе построения последовательности, а выявляются
при троичном моделировании.
ЗАМЕЧАНИЯ ПО БИБЛИОГРАФИИ
Основы теории конечных автоматов изложены в [Л. 3,
6, 71, 72]. В этих работах сформулированы основные по-
ложения теории и определения, рассмотрены методы
анализа и синтеза автоматов как моделей дискретных
устройств, описаны различные формы представления ко-
нечного автомата (таблица переходов — выходов, граф
переходов — выходов, матрица переходов — выходов).
В [Л. 70] впервые указывается на возможность использо-
вания эксперимента над автоматами для целей диагноза
технического состояния дискретного устройства. В [Л. 3]
излагаются основы теории экспериментов над конечными
автоматами и развивается идея использования экспери-
ментов для диагноза технического состояния дискретного
устройства. Описываются методы построения проверяю-
щего и диагностического эксперимента для заданного пе-
речня неисправностей. Каждая неисправность задается
в явном виде — таблицей переходов — выходов устройст-
ва с данной неисправностью. Метод построения проверя-
ющей и диагностической последовательности, использую-
щий аналогичную постановку задачи, и его реализация
в виде программы для ЭВМ изложны в [Л. 74]. Задача
446
Построения последовательности решается путем пооче-
редного моделирования при помощи ЭВМ поведения
исправного и каждого неисправного устройств, заданных
таблицами переходов — выходов, на каждом из входных
наборов и выбора на каждом шаге алгоритма одного
входного набора по информационному критерию.
Выбранные наборы составляют искомую последова-
тельность.
Для абстрактного конечного автомата метод построе-
ния проверяющей последовательности, обнаруживающей
любую неисправность, которая изменяет таблицу пере-
ходов— выходов, т. е. последовательности, позволяющей
проверить соответствие таблицы переходов — выходов
испытуемого устройства таблице переходов — выходов
исправного, по-видимому, впервые -изложен в [Л. 75].
Дальнейшие исследования показали, что длина последо-
вательности, получаемой по этому методу, может быть
уменьшена. Метод, позволяющий получить более корот-
кую проверяющую последовательность при тех же усло-
виях, изложен в [Л. 76]. Использование структурной таб-
лицы переходов — выходов, а также возможности рас-
ширения входного и выходного алфавита для целей
диагностики дискретных устройств описаны в
[Л. 77, 78].
В [Л. 77] .введено понятие обобщенного эксперимента и
указаны дополнительные возможности для диагноза тех-
нического состояния устройства, которые дает использо-
вание обобщенного эксперимента. В [Л. 78] описан один
из алгоритмов, в котором используется расширение вход-
ного и выходного алфавита структурного автомата по
мере необходимости в процессе построения проверяю-
щей последовательности.
Основные понятия, определения и основы теории ло-
гических сетей изложены в [Л. 73, 30]. Методы построе-
ния последовательности, обнаруживающей заданную не-
исправность, а также решение вспомогательных задач
(установки элементов памяти сети в заданное состоя-
ние при неизвестном начальном состоянии и пере-
вода из одного состояния в другое) описаны в
[Л. 79—88].
В (Л. 79] впервые решается задача построения по ло-
гической сети и функциям элементов входной последова-
тельности, устанавливающей элементы памяти сети в за-
данное состояние при произвольном начальном состоя-
447
нии, т. е. независимо от начального состояния, и описы-
вается применение принципа существенных путей к сетям
с памятью.
В [Л. 84] рассматривается сеть, которая условно
построена из исправной сети и сети с данной не-
исправностью путем непосредственного соединения одно-
именных входов исправной и неисправной сетей. При
этом каждая пара одноименных выходов подается на
входы двухвходового элемента сравнения, реализующего
функцию «исключающее ИЛИ». Задача нахождения про-
веряющей последовательности сводится к нахождению
такой последовательности, на последнем наборе которой,
по крайней мере, на выходе одного из элементов сравне-
ния появляется значение «единица». В остальных рабо-
тах этой группы построение последовательностей основа-
но на принципе существенных путей. В [Л. 81] изложен
комбинационный подход к построению проверяющей по-
следовательности, основанный на представлении логиче-
ской асинхронной сети с памятью в виде итеративной
комбинационной сети, состоящей из ряда копий. В [Л. 80,
82] описаны методы построения последовательности,
основанные на непосредственном анализе исходной асин-
хронной сети с элементами памяти без обратных связей
[Л. 80] и для сетей общего вида с обратными связями
(Л. 82].
Особенность метода, изложенного в [Л. 83], состоит
в основном в выделении некоторых определенных частей
сети при анализе и расширении набора символов, обозна-
чающих значения сигналов в узлах сети, например, для
учета изменения сигнала с 0 на 1 и наоборот. В основу
метода заложен принцип существенных путей.
В [Л. 85] излагается разновидность метода сущест-
венных путей для синхронных сетей без обратных связей
с триггерами в качестве элементов памяти. По этому ме-
тоду построение существенного пути начинается от вы-
хода устройства, а не от места неисправности.
Основное отличие метода [Л. 86] от остальных работ,
основанных на принципе существенных путей, состоит
в том, что метод пригоден для построения последователь-
ности, обнаруживающей заданную краткую константную
неисправность, а не только одиночную. В [Л. 87, 88] рас-
сматриваются некоторые вопросы и особенности построе-
ния проверяющих последовательностей для одиноч
ных неисправностей по методу существенных путей
448
для синхронных сетей с памятью без внешних обратных
связей.
Теория и метод троичного моделирования изложены
в [Л. 35]. Несколько способов учета состязаний в процес-
се построения проверяющей последовательности для се-
тей с памятью описаны в [Л. 89]. С методами построения
проверяющих последовательностей посредством модели-
рования работы исправного и неисправных устройств на
входных последовательностях можно ознакомиться по
[Л. 90].
29—358
Список литературы
Глава первая
1. Берж К. Теория конечных графов и ее применения. М.,
Изд-во иностр, лит., 1962. 320 с.
2. Введение в техническую диагностику. М., «Энергия», 1968.
224 с. Авт. Г. Ф. Верзаков, Н. В. Киншт, В. И. Рабинович, Л. С. Ти-
монен.
3. Гилл А. Введение в теорию конечных автоматов. М., «Нау-
ка», 1966. 272 с.
4. Карибский В. В., Пархоменко П. П., Согомонян Е. С. Техни-
ческая диагностика объектов контроля. М., «Энергия», 1967. 80 с.
5. Колдуэлл С. X. Логический синтез релейных устройств. М.,
Изд-во иностр, лит., 1962. 740 с.
6. Миллер Р. Теория переключательных схем. М., «Наука»,
1970, т. 1, 416 с„ т. 2, 304 с.
7. Миронов Г. А. Испытательные программы для контроля циф-
ровых машин. Под ред. Н. А. Криницкого. М., «Наука», 1964. 267 с.
8. Пархоменко П. П. Основные задачи технической диагности-
ки. — «Труды I Всесоюзного совещания по технической диагности-
ке». М., «Наука», 1972, с. 7—22.
9. Пархоменко П. П. О технической диагностике. М., «Знание»,
1969. 64 с.
'10 . Селлерс Ф. Методы обнаружения ошибок в работе ЭЦВМ.
М., «Мир», 1972. ЗЮ с.
11. Яблонский С. В., Чегис И. А. О тестах для электрических
схем. — «Успехи математических наук». 1955, вып. 4(66), № 10,
с. 182—184.
Глава вторая
12. Блинов И. Н., Мозгалевский А. В. Выбор параметров для
автоматического обнаружения неисправностей. — «Автоматика и
телемеханика», 1965, № 10, с. 1809—1812.
13. Бритов Г. С., Мироновский Л. А. Диагностика линейных
систем автоматического регулирования. — «Известия АН СССР.
Техническая кибернетика», 1972, № 1, с. 76—83.
14. Brule J. D., Johnson R. A., Kletsky Е. J. Diagnosis of equip-
ment failures. — «IRE Transaction», 1960, vol. RQC-9, p. 23—34.
15. Гельфандбейн Я. А. Методы кибернетической диагностики
динамических систем. Рига, «Зинатне», 1967. 542 с.
16. Евланов Л. Г. Контроль динамических систем. М., «Наука»,
1972. 423 с.
17. Ицкович Э. Л., Трахтенгерц Э. А. Алгоритмы централизо-
ванного контроля и управления производством. М., «Советское
радио», 1967. 352 с.
450
18. Карибский В. В. Анализ систем для контроля работоспособ-
ности и диагностики неисправностей. — «Автоматика и телемеха-
ника», 1965, № 2, с. 308—314
19. Ксенз С. П. Поиск неисправностей в радиоэлектронных си-
стемах методом функциональных проб. М., «Советское радио»,
1965. 135 с
20. Маркович 3. П., Осис Я. Я- Порядок составления граф-мо-
дели сложного объекта технической диагностики. — В кн.: Кибер-
нетика и диагностика. Рига, «Зинатне», 1968, вып. 2, с. 19—32.
21. Методы неразрушающих испытаний. Под ред. Шарпа М.,
«Мир», 1972. 494 с.
22. Автоматический поиск неисправностей. Л., «Машинострое-
ние». 1966. 264 с. Авт.: А. В. Мозгалевский, Д. В. Гаокаров,
Л. П. Глазунов, В. Д. Ерастов.
23. Мэзон С., Циммерман Г. Электронные цепи, сигналы и си-
стемы. М., Изд-во иностр, лит., 1963. 619 с.
24. Павлов Б. В. Кибернетические методы технического диагно-
за. М., «Машиностроение», 1966. 151 с
25. Ratnomoorthy С. V. A structural theory of machine diagno-
sis. Spring Joint Computers Conference, AFIPS Conf. Proc., 1967,
vol. 30, p. 743—756.
26. Селезнев В. П. Навигационные устройства. М., Оборонгиз,
1961. 612 с
27. Сердаков А. С. Автоматический контроль и техническая
диагностика. Киев «Техшка», 1971. 242 с
28. Согомонян Е. С. Контроль работоспособности и поиск не-
исправностей в функционально связанных системах. — «Автоматика
и телемеханика», 1964, № 6, с. 980—990.
29. Физико-технические методы неразрушающего контроля эле-
ментов и приборов электронной техники. (Сборник по обмену опы-
том). М., НТО радиотехники, электроники и связи им. А. С. По-
пова, 1969. 104 с.
Глава третья
30. Кобринский Н. Е., Трахтенброт Б. А. Введение в теорию
конечных автоматов. М., Физматгиз, 1962. 404 с.
31. Поспелов Д. А. Логические методы анализа и синтеза схем.
М., «Энергия», 1968. 328 с.
32. Armstrong D. В. On finding a nearly minimal set of fault
detection tests for combinational logic nets. — «IEEE Transactions
on Electronic Computer», 1966, vol. EC-15, № 1, p. 66—73.
33. Пархоменко П. П. Диагноз технического состояния дискрет-
ных устройств методом выделения подозреваемых неисправностей.
Комбинационные устройства. Устойчивые неисправности. — «Авто-
матика и телемеханика», 1971, № 6, с. 126—137.
34. Рабинович 3. Л. О некоторых методах описания схем с уче-
том физических характеристик информационных сигналов. — «Вы-
числительные системы», Новосибирск, 1968, вып. 7, с. 13—19.
35. Eichelberger Е. В. Hazard detection in combinational and
sequential switching circuits. — «IBM Journal of Research and De-
velopment» 1965, vol 9, № 2, p. 90—99.
36. Томфельд Ю. JI. О логических состязаниях в неисправных
схемах. — «Труды Международного семинара по прикладным аспек-
там теории автоматов». Варна, Болгарская Академия наук. Инсти-
тут технической кибернетики, 1971, с. 420—429.
29* 451
37. Скляревич А. Н. Метод отыскания схемы функционирования
комбинационного автомата при появлении комплекса неисправно-
стей. — «Автоматика и вычислительная техника», 1969, № 5,
с. 30—36.
38. Poage J. F. Derivation of optimum tests to detect faults in
combinational circuits. Symposium on Mathematical Theory of Auto-
mata, Polytechnic Institute of Brooklyn, April 24, 25, 26, 1962.
39. Чипулис В. П. О построении тестов для контроля комби-
национных схем. — «Автоматика и телемеханика», 1970, № 10,
с. 172—177.
40. Гольдман Р. С., Чипулис В. П. О диагностике неисправно-
стей комбинационных схем —«Автоматика и телемеханика», 1971,
№ 3, с. 114—119.
41. Коган И. В., Стерликова Л. Н. Вопросы построения полных
тестов для бесповторных скобочных формул. — «Труды I Всесоюз-
ного совещания по технической диагностике» М., «Наука», 1972,
с. 167—169.
42. Казначеев В. И. Использование инверсных преобразований
функций алгебры логики при построении тестов комбинационных
схем. — «Труды I Всесоюзного совещания по технической диагно-
стике». М., «Наука», 1972, с. 189—191.
43. Friedman A. D. Fault detection in redundant circuits. — «IEEE
Transactions on Electronic Computers», 1967, vol. EC-16, Me 2,
p. 99—100.
44. Чегис И. А., Яблонский С. В. Логические способы контроля
работы электрических схем. — «Труды Матем. ин-та им. В. А. Стек-
лова». Изд-во АН СССР, 1958, т. 51, с. 270—360.
45. Amar V., Condulmari N. Diagnosis of large combinational
networks. — «IEEE Transactions on Electronic Computers», 1967,
vol. EC-16, № 5, p. 675—680.
46. Eldred R. D. Test routines based on symbolic logic state-
ments. — «Journal of ACM», 1959, vol. 6, Me 1, p. 33—36.
47. Горовой В. P. К вопросу диагностики комбинационных ре-
лейных устройств. — «Автоматика и телемеханика», 1968, Me 11,
с. 149—155.
48. Халчев В. Ф. Построение проверяющего теста для комби-
национных схем. — «Автоматика и телемеханика», 1970, Me 10,
с. 166—171.
49. Akers S. В. On a theory of Boolean functions. — «Journal
SIAM», 1959, vol. 7, Me 4, p. 487—498.
50. Sellers F. F., Hsiao M. Y., Bearnson L. W. Analyzing errors
with the Boolean difference. — «IEEE Transactions on Computers»,
1968, vol. C-17, № 7, p. 676—683.
'51 . Roth J. P., Bouricius W. G., Schneider P. R. Programmed
algorithms to compute tests to detect and distinguish between failu-
res in logic circuis. — «IEEE Transactions on Electronic Computers»,
1967. vol. EC-16, Me 5, p. 567—580.
'52 . Ермилов В. А. Метод отбора существенных неисправностей
для диагностики цифровых схем. Общие выражения для неисправ-
ностей, возможных при эксперименте. — «Автоматика и телемеха-
ника», 1971, Me 1, с. 159—167.
53. Ермилов В. А. Метод отбора существенных неисправностей
для диагностики цифровых схем. Выражения для одиночных крат-
ковременных неисправностей, возможных при эксперименте. —
«Автоматика и телемеханика», 1971, № 3, с. 107—113.
452
54, Жуков М. В., Халчев В. Ф,, Чудин А. А. Метод определе-
ния непротиворечивой фиксации значений переменных в узлах ком-
бинационных схем. — В кн.; Техническая диагностика (Управление
и информация. Вып. 4). Владивосток, 1973, с. 156—175.
55. Schneider Р. R. On the necessity to examine D-chains in diag-
nostic test generation — an example. — «IBM Journal of Research and
Development», 1967, vol. 11, № 1, p. 114—115.
56. Чипулис В. П. О построении полных контролирующих тес-
тов. —«Автоматика и телемеханика», 1971, № 11, с. 159—163.
57. Bossen D. С., Hong S. J. Cause-effect analysis for multiple
fault detection in combinational networks. — «IEEE Transactions on
Computers», 1971, vol. C-20, № II, p. 1252—1257.
58. Yau S. S., Yu-Shan Tang. An efficient algorithm for genera-
ting complete tests sets for combinational logic circuits. — «IEEE
Transactions on Computers», 1971, vol. C-20, № 11, p. 1245—1251.
59. Коган И. В. Условия контролируемости комбинационных
схем относительно константных неисправностей. — В кн.: Техниче-
ская диагностика (Управление и информация. Вып. 4). Владивос-
ток, 1973, с. 128—155.
60. Чипулис В. П. О проверке схем при сочетании неисправно-
стей. — «Автоматика и телемеханика», 1972, № 9, с. 173—174.
61. Chang Н. Y., Thomis W. Methods of interpreting diagnostic
data for locating faults digital machines. — «BSTJ», February 1967,
vol. 46, № 2, p. 289—317.
62. Гробман Д. M. Программный контроль и диагностика не-
исправностей ЦВМ.-—В кн.: Диагностика неисправностей вычисли-
тельных машин. М., «Наука», 1965, с. 7—22.
63. Вейцман И. Н., Синельников В. Е., Флеров А. Б. Диагно-
стирование неисправностей в блоках вычислительных устройств. —
«Вопросы радиоэлектроники. Серия ЭВТ», 1973, вып. 8, с. 46—59.
64. Roth Р. J. Ап algorithm to compute a test to distinguish bet-
ween two failures in a logic circuit. — «Proc, of the 1970 IEEE In-
ternational Computer Group Conference», 1970, p. 247—249.
65. Hornbuckle G. D., Spann R. M. Diagnosis of single-gate
failures in combinational circuits. — «IEEE Transactions on Compu-
ters», March 1969, vol. C-18, Ke 3, p. 216—220.
66. Stephen Y. H. Su, Yun-Chung Cho. A new approach to the
fault location of combinational circuits. — «IEEE Transactions on
Computers», January 1972, vol. C-21, We 1, p. 21—30.
67. Гольдман P. С., Чипулис В. П. Диагностика бесповторных
комбинационных схем. — В кн.: Дискретный анализ. Новосибирск,
1969, вып. 14, с. 3—15.
68. Каравай М. Ф. Диагноз кратных неисправностей древовид-
ных схем произвольного базиса. — «Автоматика и телемеханика»,
1973, We 1, с. 173—181.
69. Каравай М. Ф. Построение теста для поиска кратных не-
исправностей комбинационных устройств произвольного базиса. —
«Автоматика и телемеханика», 1973, We 4, с. 164—179.
Глава четвертая
70. Мур Э. Ф. Умозрительные эксперименты с последователь-
ностными машинами. — В кн.: Автоматы. Под ред. К. Э. Шеннона
и Дж. Маккарти. М., Изд-во иностр, лит., 1956, с. 179—210.
71. Глушков В. М. Синтез цифровых автоматов. М., Физматгиз,
1962. 476 с.
453
TL Логика. Автоматы. Алгоритмы. М., Физматгиз, 1963. 556 с.
Авт.: М. А. Айзерман, П. А. Гусев, Л. И. Розоноэр, И. М. Смир-
нова, А. А. Таль.
73. Burks A. W., Wright J. В. Theory of logical nets. — «Proc.
IRE», 1953, vol 41, p. 1351—1365.
74. Seshu S. On an improved diagnosis program. — «IEEE Tran-
sactions on Electronic Computers», February 1965, vol. EC-14,
p. 76—79.
75. Hennie F. C. Fault detection experiments for sequential cir-
cuits. — «Proc, of the 5 Annual Symp. on Switching Theory and Lo-
gical Design», 1964, vol. S-164, p. 95—110.
76. Груиский И. С. Контрольный эксперимент с сильносвязным
диагностируемым автоматом. — «Автоматика и телемеханика»,
1972, № 3, с. 138—141.
77. Карибский В. В., Пархоменко П. П., Согомонян Е. С. Воп-
росы контроля работоспособности и поиска неисправностей в конеч-
ных автоматах.—«Доклады АН СССР», 1965, т. 161, № 1, с. 59—62.
78. Карибский В. В., Пархоменко П. П., Согомонян Е. С. Ме-
тод построения проверки устройств с памятью, описываемых мо-
делью конечного автомата. — «Автоматика и телемеханика», 1969,
№ 2, с. 77—81.
79. Карибский В. В. Об установке элементов памяти в задан-
ные состояния и обнаружении неисправности в дискретном устрой-
стве. Техническая диагностика. — «Труды I Всесоюзного совещания
по технической диагностике». М., «Наука», 1972, с. 218—223.
80. Карибский В. В. Построение входной последовательности,
обнаруживающей заданную неисправность дискретного устрой-
ства.— «Автоматика и телемеханика», 1972, № 5, с. 153—162.
81. Putzolu G. R., Roth J. Р. A heuristic Algorithm for testing of
asynchronous circuits. — «IEEE Transactions Computers», June 1971,
vol. C-20, № 6, p. 639—647.
82. Карибский В. В. О методе «существенных» путей для ди-
скретных устройств с обратными связями. — «Автоматика и теле-
механика», 1973, Ks 8, с. 126—137.
83. Kriz Т. A. A path sensitizing algorithm for diagnosis of bi-
nary sequential logic. — «Proc, of the 1970 IEEE International Com-
puter Group Conference», June 1970, № 4, p. 250—257.
84. Гробман Д. M. О построении тестов для схем с элементами
памяти. — «Труды II Всесоюзного совещания по технической диаг-
ностике. Известия ЛЭТИ им. В. И. Ульянова (Ленина)», 1972,
вып. 118, ч. 1, с. 79—82.
85. Плитман А. Д. Об одном методе обнаружения одиночных
неисправностей в схемах с памятью. — «Автоматика и телемеха-
ника», 1972, № 10, с. 166—173.
86. Ведешенков В. А., Плитман А. Д., Сорокин Г. К. Об обна-
ружении кратных неисправностей в конечных автоматах «Труды
II Всесоюзного совещания по технической диагностике. Известия
ЛЭТИ им. В. И. Ульянова (Ленина)». 1972, вып. 118 ч. I,
с. 93—97.
87. О построении проверяющих тестов для дискретных
устройств с элементами памяти. Техническая диагностика. — «Тру-
ды I Всесоюзного совещания по технической диагностике». М.,
«Наука», 1972, с. 224—227. Авт.: А Ф Волков, В. А. Ведешенков,
А. В Тюрин, А. Д. Плитман, А. Т. Андреева.
454
88. Структурный метод построения проверяющих тестов ДЛй
дискретных устройств с памятью. «Труды II Всесоюзного совещания
по технической диагностике. Известия ЛЭТИ им. В. И. Ульянова
(Ленина)». 1972, вып. 118, ч. 1, с. 82—85. Авт.: А. Ф. Волков,
В. Д. Зенкин, А. В. Тюрин, Э. Я. Меттер.
89. Карибский В. В. Учет состязаний на входах элементов при
построении проверяющей последовательности. — «Автоматика и те-
лемеханика», 1973, № 9, с. 152—164.
90. Чжен Г., Мэннинг Е., Метц Г. Диагностика отказов цифро-
вых вычислительных систем. Пер. с англ, под ред. И. Б. Михай-
лова. М., «Мир», 1972. 232 с.
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
А
Автомат абстрактный 347, 348
— асинхронный 347
— инициальный 350
— исправный 364, 369
— минимальный 373
— неинициальный 350
— неисправный 364, 369
— обратимый 373
— определенный не полностью
354
------ полностью 354
— расщепляемый 374
— сильносвязный 373
— синхронный 347
— совместимый 394
— сравнимый 373
— структурный 351
— эквивалентный 373
Алгебра а-состояний 199
Алгоритм диагноза 14, 74
------- безусловный 77
— - условный 78
— — с безусловной останов-
кой 78
—-----условной остановкой
79
— тривиальный 48
— функционирования 10
Алфавит 347
а-состояние 198, 199
Б
Базис 166
— булев 174
— простой 175
Блок логической модели одно-
канальный 116
— — — многоканальный 116
------обобщенный 132
Буква ЭФ 177
Буквенное предложение 201
Булева разность (производная)
231, 232
456
В
Вес технического состояния 81
Ветвь разветвления 167, 198,
265
Воздействие 29
— рабочее 20
— тестовое 20
Входы объекта дополнительные
20
-----основные 20
Выход обязательный логической
модели 133
— разветвляющий блока логи-
ческой модели 124
Выходы объекта дополнитель-
ные 21
-----основные 21
Выходные функции 32
Г
Генетика техническая 9
Глубина диагноза 12, 42
— поиска 12
Граф ОР 270
— переходов-выходов 349
— причинно-следственных свя-
зей 142
--------с неисправностями 148
Д
Дерево 175, 376
— отличительное 380
— преемников 376
— регулярное 388, 289
— установочное 386, 389
— эквивалентное 175
Дешифрация результатов диаг-
ностического эксперимента
329
Диагноз 8
— технического состояния 11
Диагностика 8
— техническая 8, 14
Диагностический словарь 318
Д-куб неисправности 233, 429
— сжатый 234
— элемента 235, 428
----внешний безусловный 428
----внутренний условный 428
----неустойчивый 428
----сжатый 236
— — смешанный 428
— — тупиковый 238
-------сжатый 238
----устойчивый 428, 430
Длина алгоритма диагноза 82
— последовательности 406
Д-операция РФ 253
---- путь 237
-------тупиковый 248
3
Задача анализа модели обрат-
ная 62. 70
-------прямая 53, 70
— генеза 8
— диагноза 8
----обратная 62, 406
— отличительная 380
— прогноза 8
— прямая 52, 261, 276, 406
Значение воздействия 29, 35
— обязательное буквы ЭФ
225
— ответа 29
И
Искажение связей 186, 188
Источник воздействий 21
Исходная фиксация 240
----противоречивая 242, 244
К
Комбинационный эквивалент
автомата 353
Компонента объекта 92
Контрольная точка 21, 90, 368
Контур обратной связи (эле-
ментарный) 412
Куб 427
— элемента простой 239
---сжатый 239
М
Матрица переходов-выходов 350
Метод вычисления подозревае-
мых технических состояний
59
----различающих элементар
ных проверок 66
— подстановки обратной 170,
369
Метод подстановки прямой 170,
369
— последовательного восста
новления 140
— существенных путей 228, 258
Моделирование
— двоичное 409
— троичное 361, 406
Модель логическая 94
-----обобщенная 132
----- правильная-95
— математическая двоичная
51, 80
----- неисправности 33
— объекта исправного 32
----- неисправного 33
--------диагноза неявная 30,
33, 52, 194, 197
— — эквивалентная явная
30, 33, 52, 194, 195, 197
Модель М 320
— независимая переменная 320
— физическая 22, 37
Модификация неисправная 365,
367
Н
Набор дополнительный 417
— избыточный, неизбыточный
285
— разделяющий 117
Наборы входные 423
— контура 423
— нейтральные 424
— обнаруживающие (для се-
ти) 212
— проверяющие (для сети)
212, 230
----- для элемента 228
— различающие 212
— смежные 417
— устанавливающие 423
Неизбыточность деревьев 212,
248, 291
Неисправность доминирующая
141, 203
— константная 193, 406
— кратная 32, 193
— логическая 193
— логического элемента 185
— неправильная 184, 185 191
— несущественная 192, 230
— неустойчивая 194
— одиночная 32, 193, 406
— подозреваемая 59 276
— правильная 184, 185, 364
— существенная 192
457
Неисправность устойчивая 194
— физическая 28, 183, 186, 188
— характеристическая 289, 292,
293, 298
О
Область допустимых значений
параметра 93
Объект без памяти 31
— гибридный 5, 31
— диагноза 8, 27
---многорежимный 96
---однорежимный 96
— дискретный 5, 31, 346
— комбинационный 31
—- непрерывный 5, 31, 90
— последовательностный 31
•— с памятью 31, 346
Операция однозначного распро-
странения (ОР) —244, 431
------- безрезультатная 242
------- над элементом 240
------- противоречивая 242,
244
—------результативная 242
— расширения фиксации (РФ)
250, 431
— Д-расширения фиксации
Д—РФ 431
Определяющий столбец—141
Ответ объекта 29
Отмеченные пары выявляющих
наборов 341
Отсечка обходящего пути 313
П
Память 346
Пара букв вида В 302
— наборов выявляющая 290,
310, 321
Параметры внутренние 28
— входные 28
— выходные 28
— контролируемые 90
Переменные входные 32, 351
— выходные 32, 351
— контурные 423
Подсеть сильносвязная 413
---максимальная 413
Подстановка обратная 170, 369
Подсхема максимальная древо-
видная 318
Подход структурный 53, 51
— функциональный 163, 364,
365
Поиск неисправностей 11, 318,
374, 391
458
Последователь 413
Последовательность входная
365
— выходная 365
— отличительная 376
----безусловная 381, 382
---- условная 383
— проверяющая 411
— условная 381
— установочная 376
Представитель импликанта 321
Представление однолинейное
347
Предшественник 413
Преемник 377
Прогностика техническая 19
Проверка исправности 10, 282,
374, 391
— правильности функциониро-
вания 10
— работоспособности 10, 282,
374, 391
----элементарная 368, 14, 29,
49
---- безрезультатная 58
----допустимая 14, 34
----обнаруживающая 62, 7
----разлагающая 62, 71
Процедура условная диагности-
ческая 319
Прямая 170, 369
Путь, ассоциированный с бук-
вой ЭФ 177
— динамический 335
— обходящий 311
— существенный 67, 230, 246
----простой 67, 248
----сложный 67, 248
----собственный 303
Р
Разбиение множества техниче-
ских состояний 54, 76
Ранг дерева 378
Ранжирование логической сети
168
— генерации 424
Режим запоминания 424
— псевдоконтурный 423
Результат диагноза 8, 21
— элементарной проверки 14,
29
с
Сбой 194
Свойство обнаружения неис-
правности 41
— однородности функции (эле-
мента) 291
— различения неисправностей
41
Сеть 167, 354
— логическая 167, 354
----- избыточная 208
----- итеративная 411
-----правильная 167, 172
----- эквивалентная 173
Сечение графа ОР 271
--------запрещенное, незапре-
щенное 274
Символы алфавита 347
Система диагноза 13
-----тестового 13, 19, 36
-----функционального 13, 19,
38
— управления диагностическая
25
Совокупность контрольных то-
чек проверяющая 122
--------различающая 127
— элементарных проверок ми-
нимальная 44
-------- неизбыточная 44
-------- полная 44
Соединение сети 198
— некорректное 181
Состояние 181
— автомата 347
----- конечное 375
----- начальное 375
----------неустойчивое 350
----- устойчивое 350
— контура 423
— объекта исправное 28
----- неисправное 28
— техническое 11, 28
Состояния автомата
-----допустимые 375
-----конечные 375
----- начальные 375
-----неэквивалентные 373
-----одноименные 394
----- эквивалентные 373
— технические необнаруживае-
мые 56
-----неразличаемые 54
-----обнаруживаемые 56
-----подозреваемые 57
-----различаемые 56
Состязания 360, 361
— динамические 363
— статические 363
Средства диагноза 13, 83
----аппаратурные 15, 83
—-------автоматизированные
15, 84
--------автоматические 15, 84
--------внешние 15, 83
--------встроенные 15, 84
--------ручные 15, 84
--------специализированные 5,
84
--------универсальные 15, 84
----программно-аппаратур-
ные 86
----программные 15, 85
Структура объекта 28, 92
Схема функциональная объекта
диагноза 93
Т
Таблица истинности 187, 352
----сжатия 239
---- троичная 362
— переходов-выходов 348
----абстрактная 348, 352
---- структурная 352
— функций неисправностей 40,
195, 372
Терм (конъюнкция) ЭФ 177
----единичный 224
----запрещенный 274
----незапрешенный 274
Триггер 357
Текст диагностический 318, 319
----полный 319
— избыточный, неизбыточпый
(тупиковый) 285
— проверки исправности 282
---- работоспособности 282
— проверяющий (контроли-
рующий) 282
----полный 307
Триггер 357
У
У-множество 377
— кратное 378
— однородное 378
— простое 377
Узел сети 198
Управляемый разрыв 135
Условие обнаружения пепспрлп-
ности 68, 230
459
Условие проявления Неисправ-
ности 67, 228, 430, 431, 434
— различения неисправностей
68, 259
— транспортировки неисправ-
ности 67, 230, 430, 431, 434
Устройство дискретное с па-
мятью 346
— исправное (при функцио-
нальном подходе) 184, 187
— неисправное (при структур
ном подходе) 185
----- (при функциональном
подходе) 184, 187
Участок простой динамического
пути 335
-------сложного существен-
ного пути 248
Ф
Фиксация неисправностью букв
ЭФ 204, 206
Форма скобочная 173
— смешанная 331
— эквивалентная (ЭФ) пря-
мая, обратная 176
-----сжатая 181
-----сокращенная 304
Функция обобщенная 199
-----сокращенная 329
— различающая 213
Функция условий работы блока
объекта диагноза 94
Ц
Цена алгоритма диагноза 82
— элементарной проверки 81
Ч
Часть конъюнкции терма нор-
мальная 270
------- фиксированная 270
Э
Эксперимент 365, 381
— безусловный 381
— кратный 381, 384
— обобщенный 394
— отличительный 381
— простой 381
— условный 381, 383
Элемент логический 166, 169
--- простой 174
— памяти 346
— коммутирующий 117
Этап производства 9
— хранения 10
— эксплуатации 9
Я
Ядро терма ЭФ 307
ОГЛАВЛЕНИЕ
Предисловие . «’
Введение . . . ... В
Глава первая. Основные задачи технической диагностики 18
1-1. Системы диагноза технического состояния 19
1-2. Диагностические системы управления 25
1-3. Объекты диагноза............................... 27
1-4. Математические модели объектов диагноза . . 30
1-5. Функциональные схемы систем тестового и функ-
ционального диагноза .... ... 30
1-6. Таблица функций неисправностей . 40
1-7. Прямые задачи диагноза ... . . 52
1-8. Обратные задачи диагноза . 62
1-9. Алгоритмы диагноза .... 74
1-10. Способы и средства реализации алгоритмов диаг-
ноза ........................................... 83
1-11. Об организации процессов диагноза . . .87
Замечания по библиографии . 89
Глава вторая. Непрерывные объекты диагноза 90
2-1. Построение логических моделей непрерывных объек-
тов диагноза.................................... 92
2-2. Анализ логической модели, построение таблиц функ-
ций неисправностей .... 105
2-3. Построение проверяющих совокупностей контроль-
ных точек......................................121
2-4. Построение различающих совокупностей контроль-
ных точек......................................127
2-5. Графы причинно-следственных связей .... 142
2-6. Диагноз технического состояния объекта с учетом
возможных неисправностей датчиков .... 150
2-7. Диагноз технического состояния непрерывных объек-
тов, содержащих обратные связи . 155
2-8. О физических методах диагноза технического со-
стояния объектов . . . . 158
Замечания по библиографии...................... 1<>1
Глава третья. Дискретные комбинационные объекты
диагноза . . .................... . 1<>-’
3 1. Исправные комбинационные устройства и их мате
магические модели .... ...
Функциональный подход . . . 1<> *
Структурный подход ... 11 < >
Скобочная форма.......................... 1/1
Эквивалентная форма функции логической сети 1 /1
П>1
3-2. Неисправности комбинационных устройств . . . 183
3-3. Виды и методы построения математических моде-
лей неисправных комбинационных устройств . . 194
Явные модели..................................195
Неявные модели................................197
Метод обобщенной функции выхода . . 197
Метод эквивалентной формы ... . 203
3-4. Построение проверяющих и различающих совокуп-
ностей входных наборов.........................212
Метод различающей функции........................213
Метод проверки букв эквивалентной формы . 222
Метод существенных путей . . . 228
Аналитические условия обнаружения неисправно-
сти ...........................................228
Структурный подход......................... . 233
Построение различающей совокупности . . . 259
3-5. Решение прямых задач диагноза для комбинацион-
ных устройств............................ 261
Метод обобщенной функции выхода..................261
Структурно-аналитический метод . 263
Метод эквивалентной формы . . . . . 268
Построение множества подозреваемых неисправно-
стей ........................................... 276
Метод существенных путей.........................280
3-6. Методы построения проверяющих тестов для ком-
бинационных устройств . . 282
Методы, основанные на перечислении неисправностей 283
Метод перебора входных наборов сети . . . 283
Метод вычисления наборов проверяющего теста 287
Характеристические неисправности . . 289
Метод эквивалентной формы . . 300
Метод выявляющих пар наборов.....................309
,3-7. Поиск неисправностей в комбинационных устрой-
ствах ......................................... ... 318
Структуры типа дерева . . . 320
Произвольные логические сети.....................325
Дешифрация результатов диагностического теста . 329
Связь дешифрации результатов диагностического
эксперимента с построением проверяющего теста . 340
Замечания по библиографии . .... 343
Глава четвертая. Дискретные объекты диагноза с па-
мятью ..............................................346
4-1. Математические модели исправных дискретных
устройств с памятью .... . 347
Абстрактный конечный автомат . . 348
Структурный конечный автомат . . 350
Логическая сеть .... .... 354
Логические сети с триггерами ... . 357
Состязания и троичное моделирование ... 360
4-2. Неисправные дискретные устройства с памятью и
их модели......................................364
4-3. Основы теории экспериментов над автоматами . . 372
Основные положения и постановка задач диагноза 372
Построение отличительных последовательностей . 380
462
Построение установочных последовательностей . . 386
Учет особенностей реальных устройств при решении
задач диагноза ..................................392
4-4. Построение проверяющих последовательностей по
неявным моделям ................................398
Построение проверяющей последовательности по
таблице переходов — выходов.......................398
Троичное моделирование исправного и неисправного
устройств.........................................406
Построение проверяющей последовательности по
комбинационному эквиваленту.......................411
Построение проверяющей, последовательности по
логической сети .... . 423
Замечания по библиографии . ... 446
Список литературы...........................................450
Алфавитный указатель ... ....................456
Вячеслав Владимирович Карибский
Павел Павлович Пархоменко
Егор Сергеевич Согомонян
Виктор Феодосиевич Халчев
Редактор
Редактор издательства
Оформление художника
Технический редактор
Корректор
Основы
технической
диагностики
А. В. Северяков
Г. В. Лихачева
Л. В. Иванова
И. А. Володяева
Сдано в набор 27/VIII 1975 г. Подписано к печати 8/IV 1976 г. Т-06939
Формат 84Х108'/в2 Бумага типографская № 2 Усл. печ. л. 24,36
Уч.-изд. л. 25,41 Тираж 12 000экз. Зак. 358 Цена 1 р. 86 к.
Издательство «Энергия», Москва, М-114, Шлюзовая наб. 10
Московская типография № 10 Союзполнграфпрома при Государ-
ственном комитете Совета Министров СССР по делам изда
тетьств, полиграфии и книжной торговли. Москва. М-11-1,
Шлюзовая наб,, 10-