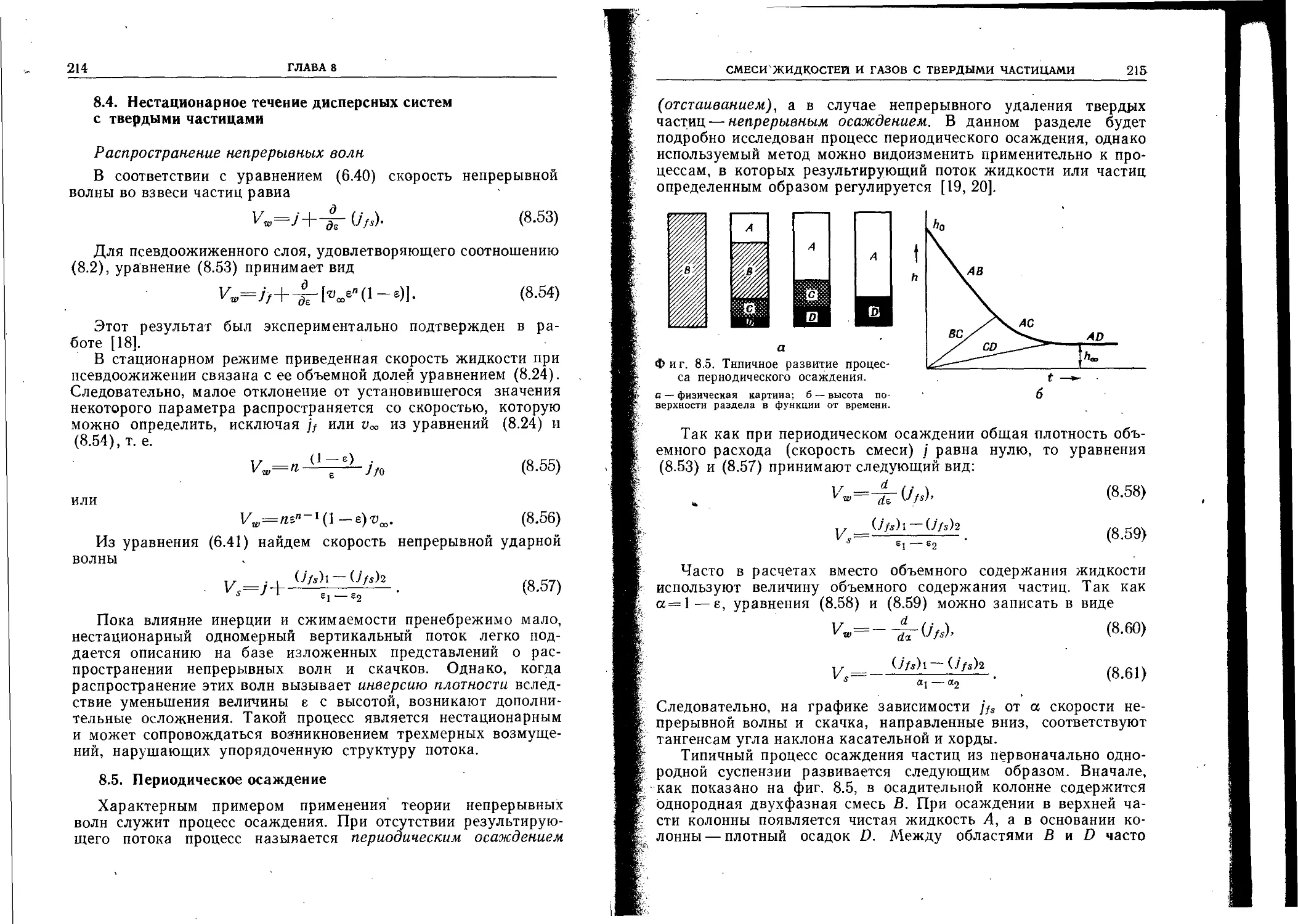
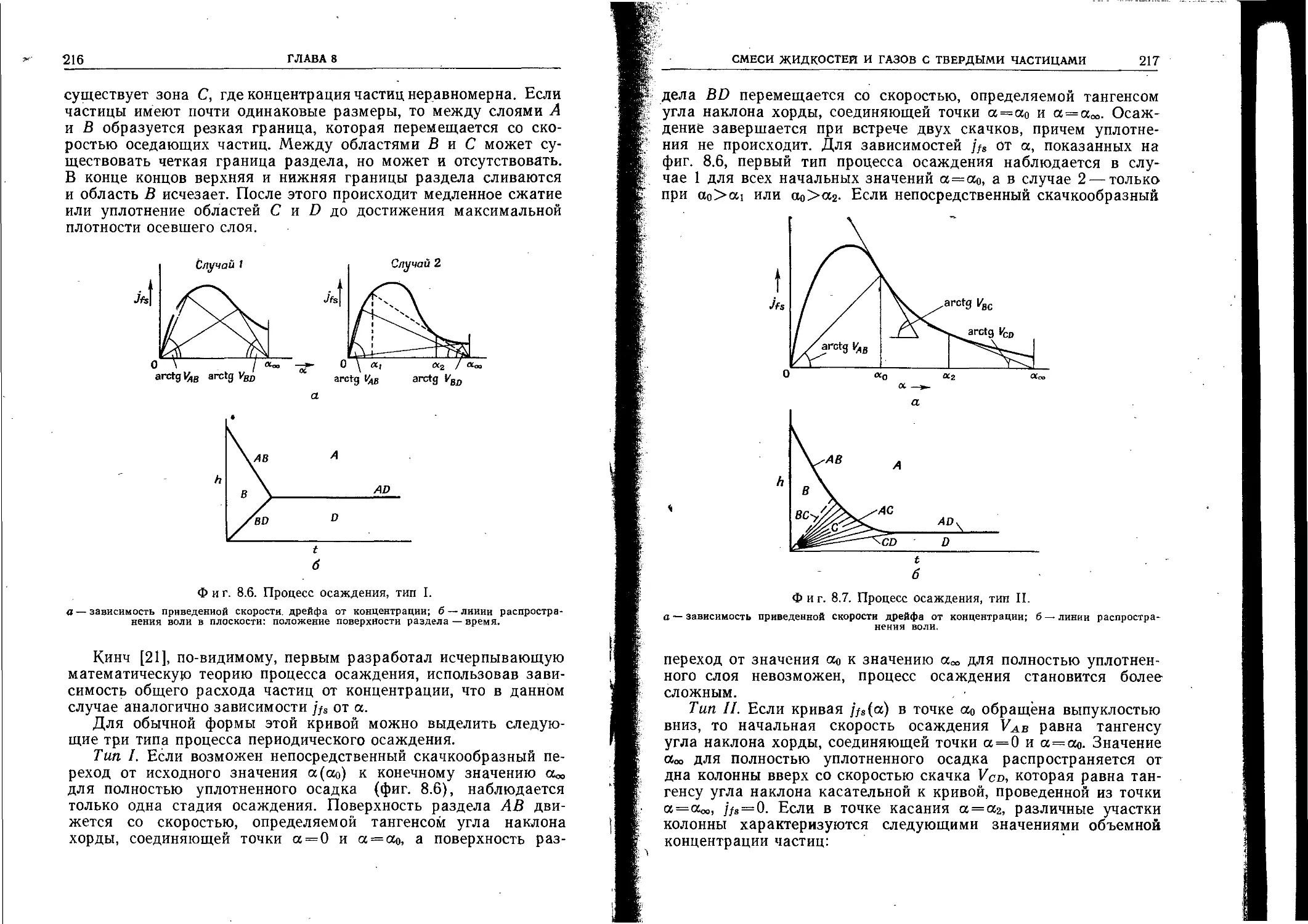
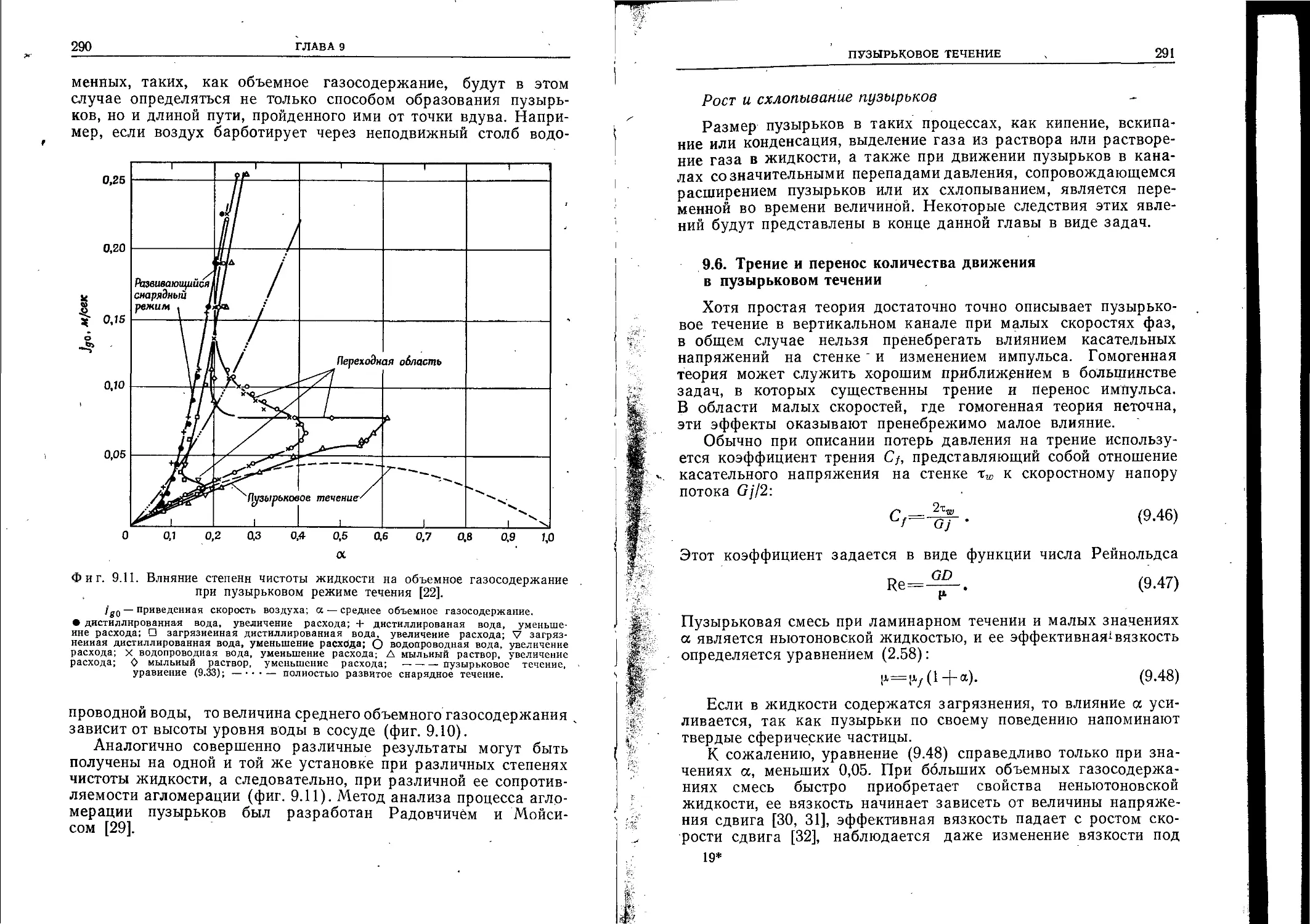
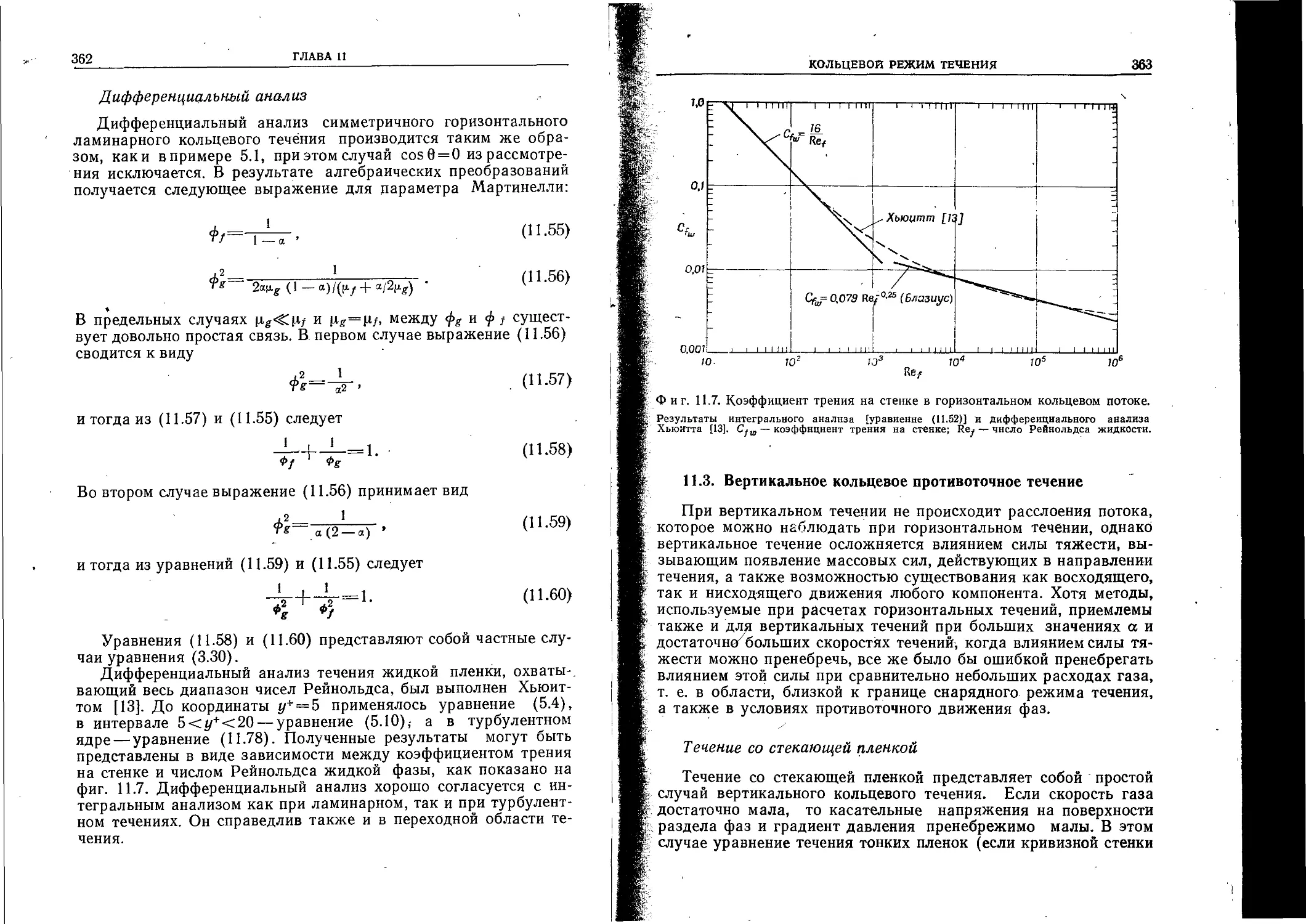
Author: Уоллис Г.
Tags: движение жидкостей гидродинамика теплотехника химические технологии
Year: 1972
Similar
Text
ONE-DIMENSIONAL
TWO-PHASE FLOW
GRAHAM B. WALLIS
Associate Professor of Engineering
Thayer School of Engineering
Dartmouth College
McGRAW-HILL BOOK COMPANY
NEW YORK * ST. LOUIS * SAN FRANCISKO
LONDON * SYDNEY * TORONTO * MEXICO * PANAMA
(
Г. УОЛЛИС
ОДНОМЕРНЫЕ
ДВУХФАЗНЫЕ
ТЕЧЕНИЯ
Перевод с английского
кандидатов техн. наук В. С. ДАНИЛИНА
н Ю. А. ЗЕЙГАРНИКА
Под ред. проф. И. Т. АЛАДЬЕВА
' У-б'
D
ИЗДАТЕЛЬСТВО «МИР»
Москва 1972
5Ч5МЪМ
УДК 532.529.5
Эта книга является фундаментальным курсом по
гидродинамике двухфазных сред. В разделе, посвященном аналитическим
методам, рассмотрены различные модели двухфазных потоков,
расчет гидравлического сопротивления каналов, напряжений
трения, фазовых превращений; анализируются волновые явления
в двухфазных потоках различных структур и релаксационные
процессы, а также поверхностные явления. Раздел, отведенный
практическим приложениям, включает широкий круг вопросов по
анализу и расчету двухфазных потоков различных структур в
конкретных технических условиях (суспензии, а также пузырьковые,
снарядные, кольцевые и дисперсные течения). Содержание книги
позволяет характеризовать ее одновременно как учебное пособие,
справочное руководство, обзор современного состояния вопроса
и пособие для исследователей.
Книга адресована инженерам-теплотехникам, инженерам —
исследователям в области гидродинамики и теплотехники,
химической технологии, ядерной энергетики, пневмотранспорта и других
областей техники, студентам старших курсов и аспирантам.
Редакция литературы по новой технике
ИВД- Й8Л972
Г. УОЛЛИС
Одномерные двухфазные течения
Редактор О. Прядкина
Художник Э. Эрман Художественный редактор Я. Блинов
Технический редактор Я. Толстякова
Сдано в набор 18/П 1972 г. Подписано к печати 9/Х 1972 г. Бумага № 2
60X90Vi6=13,75 бум. л. Печ. л. 27,50. Уч.-изд. л. 25,17. Изд. № 20/6346.
Цена 2 р. 72 к. Зак. 162.
Издательство «Мир», Москва, 1-й Рижский пер., 2.
Ленинградская типография № 8 Главполнграфпрома Комитета по печати
прн Совете Министров СССР. Ленинград, Прачечный пер., 6
ОТ РЕДАКТОРА РУССКОГО ИЗДАНИЯ
Учение о течении двухфазных сред в каналах и связанных
с этим процессах — гидродинамика двухфазных течений —
сравнительно молодая наука. Она является разделом механики
жидкостей и газов и опирается на ее принципы и методы. В
настоящее время гидродинамика двухфазных течений находится, по-
видимому, в начальной стадии становления.
Между тем такие течения часто встречаются в природе и
широко используются в различных областях техники, но из-за
отсутствия теории приходится довольствоваться
экспериментальными исследованиями с ограниченным эмпирическим анализом
их результатов. В настоящее время имеются данные по
гидродинамике многих процессов, протекающих в конкретных
условиях. Систематизация данных и их анализ являются
важными этапами исследований. Эта работа уже начата и частично
выполнена. В вышедших в последние годы монографиях и
учебных пособиях [1—7, 9, 10] содержатся обзоры современного
состояния вопроса и анализ отдельных процессов,
преимущественно эмпирическими методами, а также методами подобия и
размерностей.
В некоторые из этих работ включены лишь элементы
аналитического исследования отдельных процессов гидродинамики
двухфазных течений без последовательного применения
аналитических методов. Пожалуй, только в «Гидродинамике
суспензий» А. Фортье [8] аналитические методы используются широко
и логически последовательно. Но эта книга посвящена только
течению одного вида двухфазных сред-—суспензий, т. е.
взвесей твердых частиц в жидкостях. Гидродинамика суспензий хотя
и сложнее динамики однофазных сред, все же гораздо проще
динамики газо-жидкостных смесей, изобилующей разнообразием
форм течения и включающей процессы дробления, испарения и
конденсации, что существенно усложняет анализ.
В предлагаемой вниманию читателей книге Г. Уоллиса
«Одномерные двухфазные течения» излагаются основы методов
анализа двухфазных течений. Хотя здесь рассматривается течение
различных двухфазных сред, основное внимание уделяется
течению газо-жидкостных смесей. Из двух возможных теоретических
подходов — статистического, основанного на исследовании
динамики одиночных дискретных частиц, составляющих систему,
6 ОТ РЕДАКТОРА РУССКОГО ИЗДАНИЯ
с последующим изучением системы, содержащей множество
таких частиц, н феноменологического, использующего
представление о непрерывной среде, — автор применяет только, последний.
В этом случае важен вопрос об осреднении физических
характеристик течения в пространстве н времени. В книге
рассматриваются только пространственные изменения в направлении
течения, а физические характеристики течения в двух других
направлениях принимаются постоянными или известными.
Книга написана на основе прочитанного автором курса
лекций. В ией предлагается много интересных задач для
самостоятельного решения. Некоторые из них решены автором, и
последовательный ход решений приведен в книге. Как учебное
пособие книга имеет определенные методические достоинства.
Книга состоит из двух частей: в первой излагаются
аналитические методы, а во второй — их применение к конкретным
техническим задачам. Прн использовании аналитического метода
рассматриваются две основные модели течения: гомогенная и
раздельная. Затем эти модели усложняются путем сокращения
ограничений н учета других факторов, например профилей
скоростей и концентраций фаз. Рассматривается также модель
течения, которую автор назвал моделью потока дрейфа. Эта модель
мало известна в литературе, но полезна, в особенности при
исследовании раздельного течения. Одна из глав аналитического
раздела посвящена нзложеиню теории непрерывных и динамических
волн. Это также мало известное и почти не используемое
средство анализа. Автор показывает, что теория волн особенно
полезна и эффективна прн исследовании неустановившихся
течений, т. е. переходных процессов.
Во второй части рассматриваются конкретные формы
(режимы) течения: твердых частиц в жидкостях н газах,
пузырьковое, снарядное, кольцевое и дисперсное течения.
В книге рассмотрен широкий круг вопросов двухфазной
гидродинамики. Некоторые из них изложены очень кратко и даже
поверхностно," но в целом книга представляет собой
значительный вклад в изучение гидродинамики двухфазных, систем и,
можно думать, будет встречена с интересом нашей научной и
инженерной общественностью,
И. Аладьев
Литература
1. Кутате л а дзе С. С, Стырикович М. А., Гидравлика газо-жид-
костных смесей, Госэнергоиздат, 1958.
2. Петров П. А., Гидродинамика прямоточного котла, Госэнергоиздат,
3. Pay шеибах Б. В., Бел ый С. А., Беспалов И. В., Борода-
чев В. Я, Волынский М. В., Прудников А. Г., Физические
осот РЕДАКТОРА РУССКОГО ИЗДАНИЯ
if
новы рабочего процесса камер сгорания воздушно-реактивных
двигателей изд-во «Машиностроение», 1964-
Ву.тис Л. А., Кашкаров В. П., Теория струи вязкой жидкости,
иза-во «Наука», 1965. ^ „
Дейч ME., Филиппов Г. А„ Газодинамика двухфазных струй,
ГамГе^Т'Жшарня Г. Э., Семенов Н. И.. То,.г..А.А.
Гидродинамика газо-жидкостных смесей в трубах, изд-во «Недра», 1969.
То и г Л., Теплоотдача при кипении и двухфазное течение, изд-во «мир»,
Фортье А., Механика суспензий, изд-во «Мир», 1970.
CovC Гидродинамика многофазных систем, изд-во <Мир», 1971.
Hewitt G F„ Hall-Taylor N. S., Annular two-phase Flow, Pcrga-
mon Press, 1970 (готовится к изданию в изд-ве «Энергия»).
Ж,
ПРЕДИСЛОВИЕ АВТОРА
Цель книги — дать полное изложение основных методов
исследования одномерных двухфазных течений и показать, как
эти методы могут быть использованы для решения широкого
круга практических задач. Тематика настоящего исследования
имеет огромное значение для многих традиционных
технических дисциплин. Данный раздел гидромеханики достиг уровня
развития таких самостоятельных дисциплин, как гидродинамика
сжимаемых сред или теория пограничного слоя. Со" временем
некоторые более простые вопросы следовало бы ввести в
студенческие курсы.
Так как рассмотрение всех аспектов двухфазных течений
потребовало бы очень большого объема книги, пришлось
ограничиться анализом течений, которые в существенной степени
являются одномерными, т. е. течениями в трубопроводах и
каналах или на протяженных поверхностях. Использование
профилей скорости и концентрации допускает изменение параметров
в поперечном направлении. Неодномерные эффекты вводятся,
только когда это необходимо, для дальнейшего развития
формулировки одномерных допущений или при использовании данных,
требуемых для адекватной постановки задачи. Например, для.
пузырька, поднимающегося в жидкости, не рассматриваются
двумерные поля внутреннего и внешнего течения, но делается
ссылка на результирующую зависимость скорости от диаметра.
Конечно, многие одномерные уравнения и методы легко
представить в общей форме, заменяя в математических
формулировках скалярные величины на векторные.
Для краткости основное внимание сосредоточено почти
исключительно на гидродинамических аспектах двухфазных
течений. Процессы тепло- и массообмена, а также механизмы
образования зародышей-при фазовых превращениях подробно
не рассматриваются. Поэтому читателю, интересующемуся
соответствующими вопросами кипения, конденсации, вскипания
(мгновенного парообразования), замерзания, горения и течений
с химическими реакциями, может потребоваться дополнительная
информация.
Большинство аналитических выводов отобрано, исходя из их
общности и целесообразности применения при определении
параметров, представляющих интерес в инженерных приложениях.
ПРЕДИСЛОВИЕ АВТОРА
9
впичными переменными являются изменение давления и плот-
"сти вдоль канала, расход при истечении из сосудов, толщина
"йдкой пленки, пространственные изменения концентраций фаз,
руктура потока и факторы, ухудшающие совершенство обору-
"довайия.
Книга рекомендуется в качестве учебника для студентов
йверситетов, а также как справочное руководство для инже-
ров и исследователей. Она разделена на две части. Часть I,
'^держащая гл. 1—7, посвящена аналитическим методам,
находящим широкое и достаточно общее применение. Эти методы
поясняются примерами из различных областей техники. При
хом основное внимание уделяется их общности, освоению клю-
шх концепций и развитию аналитического мышления, усвое-
материала и его доступности.
^Часть II содержит материал, связанный с конкретными соче-
1-аиши фаз, режимами течения и практическими
приложении. Например, в гл. 8 специальные разделы посвящены воп-
ам псевдоожижения и осаждения. Каждой из основных
уктур газо-жидкостных потоков посвящена целая глава. Все
етоды, описанные в ч. I, используются в ч. II в соответствую-
их ситуациях. Рассматриваются конкретные расчетные ме-
оды, корреляции, границы режимов течения и специфические
обенности некоторых систем. При этом основное внимание
цяется определению важнейших для технических приложе-
g параметров.
„«■"■Достаточно подробно однофазные течения рассматриваются
^"ИщЬ в гл. 6 для объяснения основных положений распростра-
*я. волн и их взаимодействия. Многие учебники по гидроме-
ке в этом отношении несовершенны. Лишь в некоторых из
упоминается о непрерывных волнах. В большинстве же не
ано, что упругие и гравитационные волны относятся к об-
"у классу динамических волн, вызванных силами, которые
лбвлены некоторой формой градиентов концентрации.
t ^Чтобы не перегружать книгу, многие теоретические выводы
%е.ны в раздел задач, где показан путь решения или приво-
ответ, но подробности вывода опущены. Не рассматри-
Ея также многие интереснейшие аспекты неодномерных
гофазных течений, за исключением тех случаев, когда они
-значительной степени способствуют более полному описанию
"нкретных явлений.
Предполагается, что читатель знаком с основами гидромеха-
ки и термодинамики, а также с методами вывода уравнений
«ранения для соответствующего контрольного объема. Выводы
'ундаментальных теорем не приводятся и в большинстве случаев
гспользуются только конечные результаты. Для студентов, не
-звакомых с конкретными формами некоторых соотношений,
" 10
ПРЕДИСЛОВИЕ АВТОРА
может оказаться полезным вывести их и убедиться в их
справедливости.
С академической точки зрения книга, возможно, слишком
велика для отдельного курса. Части I и II можно использовать
для двухсеместрового дополнительного курса для аспирантов,
специализирующихся в области прикладной механики,
строительной промышленности и химической технологии, или ввести
в курс гидромеханики с гибкой учебной программой. Более
элементарный курс, подходящий, возможно, для факультативного
чтения студентам старших курсов вслед за общим курсом
гидромеханики, может включать гл. 1—4 с привлечением материала
из гл. 8—12. Более сложные вопросы распространения во,лн,
нестационарного течения, профилей скорости и поверхностных
явлений можно оставить для следующего курса. Хорошо
подготовленным студентам, интересующимся общими
теоретическими положениями, рекомендуется детально изучить ч. I,
оставив ч. II для самостоятельного чтения.
Для инженеров и исследователей ч. I служит теоретическим
фундаментом, позволяющим охватить проблему в целом и,
возможно, расширить сферу интересов. Часть II содержит решения
многих конкретных практических задач.
Я не пытался писать книгу влформе научной или
технической хроники, вследствие чего из рассмотрения исключены
вопросы, кто, что, когда и как сделал. Книга задумана так, чтобы
ею можно было пользоваться без частого обращения к другим
опубликованным работам. Библиографический материал
упоминается только там, где необходимо обращение к другим
источникам, или с целью привлечения внимания читателя к более
конкретной подробной информации.
Текст книги написан на основе конспектов лекций,
прочитанных совместно с Дж. Г. Коллье в Дартмутском колледже (1965,
1966, 1968 гг.), Университете в Глазго (1967г.) иСтэнфордском
университете (1967 г.). Этот материал был существенно
переработан для более удобного использования студентами и
читателями, не знакомыми с рассматриваемой областью.
Дополнительно были введены примеры и задачи, поясняющие физический
смысл теоретических положений и содействующие их
сознательному практическому применению.
Выбор обозначений был сделан главным образом при
обмене мнениями с доктором Новаком Зубером в 1964 г., когда
мы попытались составить последовательную систему из
множества символов, используемых многими авторами в разных
областях.
Грэхем. Б, Уоллис
ОБОЗНАЧЕНИЯ
А — площадь; константа; коэффициент;
а — коэффициент усиления в уравнении (6.124);
константа или коэффициент; ускорение;
В — общая массовая сила; коэффициент ослабления;
константа или коэффициент; поправочный коэффициент;
Ъ — массовая сила на единицу объема; ширина;
индекс; константа;
С — константа; коэффициент присоединенной массы;
Со — коэффициент сопротивления; '
Cf—коэффициент трения (см. сноску на стр. 39);
Со — определяется в уравнении (4.21);
Си Сг — поправочные коэффициенты;
с — скорость динамической волны относительно
средней или среднемассовой скорости; скорость звука;
удельная теплоемкость; коэффициент уплотнения;
са — мольная концентрация неконденсирующегося газа;
сс — скорость упругих волн;
cCh, ccs — волновые скорости в гомогенном и расслоенном
потоке;
£р — удельная теплоемкость при постоянном давлении;
с„ — удельная теплоемкость при постоянном объеме;
D — диаметр трубы;
Db — диаметр пузырька;
Da — диаметр капли;
Do—диаметр отверстия;
3) — диссипация энергии в единице объема;
d — диаметр частицы; дифференцирование;
dA — элемент поверхности;
dr — элемент объема в окрестности радиус-вектора;
д — частное дифференцирование;
Е — определяется уравнением (8.80); унос;
е — основание натурального логарифма; внутренняя
энергия единицы массы;
F — сила на единицу объема всей области течения;
сила; функция, определяемая по уравнению (1.1.25);
f — сила на единицу объема компонента;
G — плотность потока массы (массовая скорость);
g — ускорение силы тяжести;
Н — высота; знак касательного напряжения;
h — энтальпия; коэффициент теплоотдачи; высота;
/ — плотность объемного расхода (приведенная
скорость) ;
или /2 1 — плотность потока дрейфа (приведенная скорость
дрейфа);
К — константа; параметр [уравнение (5.49)]; отношение
скоростей [уравнение (8.125)];
S2
•^
ОБОЗНАЧЕНИЯ
k — константа; коэффициент теплопроводности;
ks — шероховатость;
L — длина; параметр, характеризующий тепловое
запаздывание [уравнение (8.126)];
/ — длина пути перемешивания;
In — натуральный логарифм;
М — массообмен в единице объема за единицу времени;
М — число Маха;
т— плотность потока массы при кипении или
конденсации; индекс; отношение массовых расходов; доля
поперечного сечения, занятая жидкостью в области
цилиндрической части пузыря при снарядном
режиме течения; коэффициент;
N — безразмерная обратная вязкость; индекс;
п — показатель степени в корреляционных
соотношениях; отношение скоростей;
' р — давление;
Ар — падение давления;
Р — периметр;
Q — объемный расход;
q — объемный расход на единицу ширины;
qe — плотность теплового потока;
R — радиус; радиус кривизны; газовая постоянная;
г —радиус;
г — радиус-вектор точки в пространстве;
го — радиус трубы или канала;
гг — параметр, определяемый в уравнении (3.37);
5 — мощность источника массы;
s — энтропия;
Т — температура;
AT — разность температур;
/ — время;
U — скорость волны;
и — скорость волны относительно Vo; локальная
скорость;
и* —скорость трения (динамическая скорость);
«о — характерная поперечная скорость в модели рей-
нольдсова потока;
Vi, V2 — истинные скорости компонентов;
V — средняя скорость; скорость однофазного потока;
Vo — средневзвешенная скорость [уравнение (6.75)];
Vi, Vz — невозмущенные скорости компонентов;
Vs — скорость ударной волнБ1;
Vw — скорость непрерывных волн;
v — средняя скорость однофазного потока;
vi2 — относительная скорость;
ОБОЗНАЧЕНИЯ 13
V\.j — скорость дрейфа компонента 1 относительно
скорости смеси;
vw — скорость непрерывных волн относительно средней
или среднемассовой скорости;
v — удельный объем;
У—объем;
W — массовый расход;
w — работа;
wa— механическая работа;
wx-—работа сил трения;
X— обобщенная координата для процесса осаждения
[уравнение (8.68)]; параметр Мартинелли
[уравнение (3.31)];
х — расходное массовое паросодержание или
газосодержание [уравнение (1.7)];
У — обобщенная координата для процесса осаждения;
у — пространственная координата; расстояние от стенки;
z— координата в направлении движения;
а—.истинное объемное паро- или газосодержание;
объемная доля компонента 2;
Р — краевой угол (градусы); угол скачка уплотнения;
мощность источника массы на единицу длины;
безразмерная величина падения давления;
Y — показатель изоэнтропы;
/ б—толщина пленки; отношение объемных расходов;
малое изменение параметра;
А — отрицательное приращение;
V — оператор градиента; дивергенция;
е — объемная доля компонента 1; рейнольдсов поток;
I — доля диссипированной энергии, переданная
компоненту 2;
у\ — предельная вязкость при высокой скорости сдвига;
доля силы, обусловленная фазовым переходом и
действующая на компонент 2;
0 — угол относительно вертикали; угол клина;
к — длина волны; параметр, определяемый уравнением
(10.57);
ц — вязкость;
v = n/p — кинематическая вязкость;
р — плотность;
о — поверхностное натяжение;
г — касательное напряжение;
Ф — тепловой поток; функция; потенциал скорости;
Ф^Фе — параметры Мартинелли, определяемые
уравнениями (3.24) и (3.25);
14 ОБОЗНАЧЕНИЯ
Ф — коэффициент формы;
(о — частота;
Q — поправочный коэффициент (фиг. 3.13); частота
реакции, определяемая уравнением (2.92);
г|з — функция, определяемая уравнением (8.18);
Г — массовый расход на единицу ширины.
ИНДЕКСЫ •
1 —компонент 1; состояние 1; положение 1;
2 — компонент 2; состояние 2; положение 2;
а — воздух;
А — ускорение;
b — пузырь;
с — непрерывная фаза; кривизна; ядро кольцевого
потока;
d— капля; дискретная фаза;
е — выход; эффективное значение;
f — жидкость или непрерывная среда;
F — трение;
g— газ;
G — гравитационная составляющая;
i — компонент г; поверхность раздела; вход; внутренняя
область; отклонение; квантовое состояние;
j — величина, взятая относительно или относящаяся
к среднеобъемному расходу;
т — параметр смеси для гомогенного потока; значение
на оси трубы для однофазного потока;
п, N — нормаль;
р— труба; частица;
s — твердое тело; снарядный режим; скачок, энтропия;
t — тангенциальная составляющая; турбулентный
режим течения;
w — волна; стенка;
оо — одиночная частица; капля или пузырек в
бесконечной среде; предельное значение;
ТР — двухфазный;
е — при концентрации непрерывной фазы, равной е;
8 — при угле с вертикалью, равном в;
О —начальное или граничное значение; отверстие,
внешняя часть; нулевое расходное массовое
газосодержание (паросодержание); нулевой расход;
торможение; значение, взятое относительно неподвижной
жидкости или частицы.
Замечание. Нижние индексы в гл. 6 означают
частные производные, а нижние
индексы за скобками, содержащими
ОБОЗНАЧЕНИЯ 15
частные производные, означают
величины, которые остаются
постоянными.
* — безразмерный параметр; значение параметра
в точке, где число Маха равно 1;
' — модифицированная форма; возмущенное значение;
параметр в новой системе отсчета;
Н безразмерная форма профилей скорости.
БЕЗРАЗМЕРНЫЕ КОМПЛЕКСЫ
Fr — число Фруда;
М — число Маха;
Nu — число Нуссельта;
Рг — число Прандтля;
Re — число Рейнольдса;
We — число Вебера;
Dpf[Dg(Pl-P2)]''*
NJ=:
NAr=-
#bo=l
»f2g'4Pf-PeVh
gR2(pf — pg)
■число Архимеда;
— число Бонда;
„ , g°2(P/-Pg)_4HCJIQ Этвеша;
Ео а
ЯП*
/
/
Ар*
сг3р
свойства;
ifp/h
комплекс, характеризующий, физические
} [gD(Pf-Pe)Yh '
'/2
[^(Р/-Р*)Г'* '
f D2g(Pf-pg) '
— (dp/dz) — pgg cos 0
g(pf — Pe)
a \ pf I
16 ОБОЗНАЧЕНИЯ
НЕКОТОРЫЕ СОКРАЩЕНИЯ, ИСПОЛЬЗУЕМЫЕ
В ЛИТЕРАТУРЕ
АЕС U. S. Atomic Energy Commission — Комиссия по
атомной энергии США;
AEEW Atomic Energy Establishment, Winfrith, UKAEA —
Центр по атомной энергии, Уинфрит, Великобритания;
AERE Atomic Energy Research Establishment, UKAEA —
Научно-исследовательский институт атомной энергии,
Харуэлл, Великобритания;.
ANL Argonne National Laboratory—Аргоннская
национальная лаборатория, США;
CISE Centro Informazioni Studi Esperienze, Milan, Italy —
Информационный центр научных исследований,
Милан, Италия;
EURAEC Euratom-Atomic Energy Commission Joint Program —
Объединенная программа Комиссии по атомной
энергии Евратома;
NYO New York Operations Office of U. S. Atomic Energy
Commission — Нью-Йоркское управление Комиссии по
атомной энергии США;
UKAEA United Kingdom Atomic Energy Authority —
Управление по атомной энергии Великобритании.
Часть I
АНАЛИТИЧЕСКИЕ МЕТОДЫ
\% Заказ М> 162
I I
$
1
ВВЕДЕНИЕ
1.1. Что такое двухфазное течение?
Фазой называется одно из состояний вещества, которое
может быть газообразным, жидким или твердым. Многофазное
течение— это совместное течение нескольких фаз. Двухфазный
поток представляет собой простейший случай многофазного
течения.
Для характеристики потока, фазы которого не состоят из
одного и того же химического вещества, иногда используется
термин двухкомпонентный. Например, паро-водяной поток
является двухфазным, в то время как течение воздухо-водяной
смеси — двухкомпонентное. Некоторые двухкомпонентные потоки
(главным образом жидкость — жидкость) состоят из одной фазы,
но их часто называют двухфазными, отождествляя фазы с
непрерывным или дискретным компонентом.
Так как математические методы, с помощью которых
описываются двухфазные или двухкомпонетные течения, идентичны,
выбор определений практически не имеет значения. Поэтому
в данной книге оба термина будут использоваться
преимущественно как синонимы').
Можно привести множество типичных примеров двухфазных
течений. Некоторые из них, например туман, смог, дым, дождь,
облака, снег, айсберги, зыбучие пески, пыльные бури и грязь,
встречаются в природе. С другими процессами, в том числе
кипением воды, заваркой чая, взбиванием яиц, перемешиванием
салата, намазыванием джема, взбиванием крема,
размешиванием сахара и закручиванием спагетти, мы часто встречаемся на
кухне и в столовой.
Некоторые бытовые процессы включают последовательное
изменение структуры двухфазного потока. Например, в
кофеварке вода кипит сначала с образованием пузырьков пара,
затем паровых или жидких полостей, после чего поднимается по
■' Определение фаз, а также двухфазных и двухкомпонентных течений,
данное автором, не является достаточно строгим и общим. В многофазных
системах обязательно наличие поверхностей раздела, на которых свойства
изменяются скачкообразно, что" существенно отличает эти системы от
многокомпонентной среды (однофазной), где таких скачков нет. Последнее
заметно сказывается на математических методах описания многофазных
систем, поэтому вряд ли удачно использование терминов «двухфазный» и
«двухкомпонентный» в качестве синонимов (возможно, за исключением
квазигомогенных систем). — Прим. перев.
2*
20
ГЛАВА 1
центральной трубке, просачивается через слой молотого кофе иг
в конце концов по каплям вытекает в чашку. Когда пиво
выливается из бутылки, скорость ее опорожнения ограничена
скоростью роста пузырей в горлышке при снарядном течении;
затем образование зародышей газовой фазы благодаря дефектам
стеклянных стенок приводит к вспениванию свободной
поверхности. Изготовление хлеба и торта начинается процессом
.многофазного смешения; дальнейшее приготовление
сопровождается выделением пузырьков, если только не забыты
соответствующие компоненты, и наконец потребление — один из самых
обычных многофазных процессов.
Искусное сочетание букета, структуры и температуры,
характеризующее качественный «Мартини», — результат умелого
управления двухфазными химико-технологическими процессами.
Биологические системы содержат очень мало чистых
жидкостей. Многофазные жидкости организма, такие, как кровь,
сперма и молоко, состоят из различных клеток, частиц или
взвешенных капель. Для них справедливы почти такие же
уравнения, что и для красок, чернил, паст и суспензированного
ядерного топлива.
Другой пример можно привести из знакомой области
противопожарной техники. Почти все без исключения способы
тушения огня включают использование многофазных систем — брызг,,
струй, пены или порошков. Даже при рассмотрении
огнетушителей на чистом газе нельзя не учитывать мгновенного
испарения, происходящего при истечении газа из баллона под высоким
давлением. Более того, само пламя, являющееся обычно
результатом реакции между твердым или жидким топливом и
кислородом воздуха, образует дым и пар, которые невидимы, если
только они не двухфазные, и вызывают смерть вследствие
раздражения носоглотки прежде, чем жертва погибнет в собственных
многофазных выделениях. В бойлерах, автомобильных
двигателях и ракетах специально предусматривается сгорание
двухфазных дисперсных систем.
Столь же разнообразны примеры из промышленности.
Свыше половины предприятий химической промышленности
имеет дело с многофазными течениями. Многие промышленные
процессы, например производство энергии, охлаждение и
дистилляция, зависят от испарительных и конденсационных
циклов. Эффективность опреснительных станций ограничена
уровнем развития технологии двухфазных систем. Выплавка стали,
производство бумаги и пищи включают некоторые узловые
процессы, которые зависят от правильного функционирования
оборудования, использующего многофазные системы. Многие
проблемы очистки воды и воздуха обусловлены некоторыми
необычными свойствами двухфазных течений.
ВВЕДЕНИЕ v 21
1.2. Методы анализа
Двухфазные течения подчиняются всем основным законам
гидромеханики. Однако уравнения более сложны и более
многочисленны, чем в случае однофазных течений.
Как будет показано ниже, методы анализа одномерных
течений разделяются на несколько классов в порядке возрастания
их сложности в зависимости от объема информации,
необходимой для описания течения.
Корреляции
Корреляция экспериментальных данных в виде функции
выбранных переменных представляет обычный способ получения
требуемых уравнений посредством минимума аналитических
операций. Самые простые корреляции — это математические
операции, легко выполняемые современными вычислительными
машинами, в то время как в более совершенных методах
используется анализ размерностей или объединение нескольких
переменных в комплексы на определенной логической основе.
Одно из преимуществ корреляционных формул — простота их
использования. Пока они применяются для условий,
аналогичных тем, в которых были получены исходные данные, они
могут' быть вполне удовлетворительными в пределах
статистического разброса данных, который обычно известен. Однако они
могут привести к ошибочным результатам, если используются
без разбора. Более того, поскольку корреляционные зависимости
почти не вскрывают сущности явлений, они не указывают путей
повышения эффективности или увеличения точности расчета.
В данной книге корреляции, не обладающие требуемой
общностью результатов, как правило, не приводятся. Используемые
корреляции даются в безразмерном виде и имеют
определенную теоретическую базу или же подтверждаются
многочисленными данными.
Простые аналитические модели
Для обработки экспериментальных результатов и оценки
расчетных параметров могут оказаться вполне пригодными
очень простые аналитические модели. Например, в гомогенной
модели смесь компонентов считается некоторой
псевдонепрерывной средой с усредненными свойствами, а структура потока
подробно не рассматривается. Взвесь капель в газе, пена или
расслоенное течение газа над жидкостью в этом смысле совер-
1 щенно идентичны. В модели раздельного течения потоки
каждой фазы рассматриваются самостоятельно. Записываются
>«*
22 ГЛАВА 1
уравнения для каждой фазы и учитывается межфазное
взаимодействие. В модели потока дрейфа внимание сосредоточено
на характерном относительном движении фаз.
Каждой из этих элементарных моделей посвящены
отдельные главы ч. I, и они широко используются в ч. II данной
книги.
Интегральный анализ
Интегральный анализ в рамках одномерной схемы
начинается с допущения о виде некоторых функций, описывающих,
например, распределение скорости и концентрации в канале.
Затем эти функции приводятся к виду, удовлетворяющему
соответствующим граничным условиям и основным уравнениям
гидромеханики в интегральной форме. Аналогичные методы
достаточно широко используются при анализе однофазного
пограничного слоя.
Дифференциальный анализ
В дифференциальном анализе поля скоростей и концентраций
описываются с помощью соответствующих дифференциальных
уравнений. Обычно, следуя одномерной схематизации течения,
уравнения записывают для средних по времени величин, как и
в теории турбулентности однофазной среды. В более
сложных модификациях теории может даже учитываться временная
зависимость.
В данной книге будет показана взаимосвязь аналитических
методов различных уровней. Обычно более сложные теории
позволяют учесть дополнительные эффекты и определить
поправочные коэффициенты, которые могут быть использованы в
более простых теоретических методах для повышения их точности.
Кроме того, сложная теория может выявить аналитические, а не
эмпирические связи между важнейшими переменными. Таким
образом, рассмотренные аналитические методы образуют
пирамиду, в основании которой лежат более широкие и общие
теории, поддерживающие более приближенные и элементарные
методы.
Универсальные явления
Кроме рассмотренной последовательности аналитических
методов, существует класс очень действенных способов
исследований, основанных на универсальности некоторых явлений, не
зависящих от режима течения, аналитической модели или
характеристик рассматриваемой системы. Типичными примерами
ВВЕДЕНИЕ
23
таких методов служат различные теории волнового движения и
экстремальные методы определения координат предельных
состояний системы. Эти концепции используются в различных
главах книги, содействуя их объединению на основе единой
логической схемы. Их истолкование будет углубляться по мере
рассмотрения каждой новой задачи.
1.3. Режимы течения
Увеличение точности результатов достигается обычно путем
усложнения методики. Объем информации, необходимый для
проведения подробного исследования двухфазных течений,
часто неоправданно велик. Например, для анализа движения
одиночного пузырька газа, всплывающего в неподвижной жидкости,
приходится учитывать следующие эффекты: 1) инерцию газа и
жидкости; 2) вязкость газа.и жидкости; 3) разность
плотностей и подъемную силу; 4) поверхностное натяжение и
загрязнение поверхности. Последний из указанных факторов
определить чрезвычайно сложно, так как «загрязнение» может быть
обусловлено различными причинами — просто грязью,
растворенными веществами или же поверхностноактивными агентами.
Тепло- и массообмен также влияют на движение пузырька.
В качестве первого этапа решения этой задачи, возможно,
следует выделить различные режимы, для каждого из которых
будут иметь преобладающее влияние те или иные
геометрические и динамические параметры.
При определении режима течения необходимо описание
морфологического распределения компонентов, или структуры
потока. Структура потока часто становится очевидной из
визуальных или фотографических наблюдений, но это не адекватно
полному определению режима течения из-за наличия
дополнительных отличительных- критериев, например, относительного
влияния различных сил или различий между ламинарным и
турбулентным течениями. Чтобы упорядочить терминологию,
ограничим классификацию морфологической структурой течения
газо-жидкостных систем (например, пузырьковая, снарядная,
кольцевая и.дисперсная) и проведем дальнейшее деление
каждой структуры на несколько режимов.
Течения смешанной структуры, обычно характерные для
области перехода, обозначаются сложным термином (например,
«снарядно-кольцевая» и «дисперсно-кольцевая» структуры
течения). Возможно использование некоторых синонимов (например,
«туман», или «водяная пыль», вместо «дисперсного» потока).
В качестве иллюстрации сложности двухфазных течений на
фиг. 1.1 показана последовательная смена структур потока
в испарительном канале по мере увеличения паросодержания.
24
ГЛАВА 1
О о О
оо о о Оо
» • • » • о
Пар
\i
Капли
Дисперсно - нольцевая
Очевидно, что для каждого участка испарителя требуется свей
метод анализа и, кроме того, необходимо исследовать вопрос
о развитии последующего режима из
предыдущего.
Многими авторами были
предложены диаграммы структур и режимов
течений, области которых наносятся
на график с двумя независимыми
координатами. Для рассматриваемого
испарительного канала и конкретных
компонентов в качестве независимых
координат можно выбрать расходы
этих компонентов, как показано на
фиг. 1.2 и 1.3- Но так как режим
течения определяется множеством
переменных, двумерная диаграмма не
обладает достаточной общностью
представления. Критерии для границ режимов,
S„ если они известны, будут подробно
СнаряЭио-южчеюя рассмотрены -в дальнейшем при
.анализе каждого из режимов. Если для
^.^ конкретных случаев указанные кри-
[\ терии представляются на двумерном
I 1 Снсюядная графике, то области отдельных
режимов сильно изменяются по форме и
размерам с изменением таких
параметров, как давление или диаметр ка-
Пузырьково-снарядиая нала- ПРИ некоторых сочетаниях
параметров соответствующие режимы
вообще отсутствуют на диаграмме.
Кольцевая
Снарядная
4
Пузырьковая
Жидкость
Фиг. 1.1. Приближенная последовательность
структур потока в вертикальной испарительной
трубе.
•Фиг. 1.2. Границы режимов течения для вертикального восходящего потока
воздуха и воды при давлении 1,05 ала в трубе диаметром 25,4 мм, полученные
иа основании используемых в работе уравнений.
•Фиг. 1.3. Различные режимы кольцевого течения для однонаправленного
восходящего потока воздуха и воды в трубе диаметром 31,8 мм при давлении
1,05 ата [1].
□ снарядный и пеииый поток; • переходная область; кольцевой поток: О
поверхность не смачивается, V отсутствие воли возмущений, V нерегулярные волны возмущения,
А волны возмущения н мелкая рябь, Д волны возмущения и крупная рябь.
\ ГО
Приведенная скорость воды jf, м/сек
Расход воды, г/сек
I
26 ГЛАВА 1
1.4. Система обозначений
Прежде чем приступить к исследованию двухфазных
течений, необходимо уточнить терминологию. Хотя подробный
список обозначений приводится в начале книги, возможно,
потребуются некоторые пояснения. Кроме того, усвоение простых
соотношений между некоторыми параметрами облегчит
использование аналитических методов.
Простые обозначения
Два компонента обычно различаются между собой
индексами 1 и 2, или / и g — для газо-жидкостной системы, или / и
5 — для системы жидкость — твердые "частицы. Компонентом 2
обычно считается дисперсная фаза или более легкая фаза в
случае расслоенного течения.
Общий массовый расход (кг/сек) обозначается W. Общий
расход равен сумме расходов компонентов
W=W!+W2. (1.1)
Объемный расход (м3/сек) обозначается Q. Очевидны
следующие соотношения:
Q=Qi+Q2, (1.2)
Q2=^L. (1.4)
Каждая область поля течения заполнена каким-либо из
компонентов. Если через а обозначить часть элементарного объема,
которую занимает в некоторый момент времени компонент 2,
то, если элемент выбран достаточно малым, а может быть
равным только 0 или 1. Однако для большинства целей объем
выбирается значительно большим, чем размер частиц дискретной
фазы (пузырьков или капель), поэтому а представляет собой
среднюю объемную концентрацию. Обычно для исключения
влияния местных пульсаций а измеряется как средняя величина по
всему поперечному сечению канала на достаточной длине. Таким
образом, если труба длиной L и поперечным сечением А
внезапно перекрывается запорными вентилями на ее концах, то
можно исследовать состав смеси и определить общий объем У2,
который занимает компонент 2. Тогда среднее значение а равно
<«>ЧЬ (1.5)
ВВЕДЕНИЕ
27
Часто невозможно измерить (а) на длинном участке трубы
из-за неоднородности потока. В этом случае большое число
мгновенных значений на длине 6Z. дают среднее значение а в
данном месте. Осредненное значение а по объему и времени равно
)dr)dt
Обычно символ а используется для обозначения средней
объемной концентрации без точного указания о способе осреднения.
Поэтому в тех случаях, когда важны периодические явления или
неравномерность концентраций, необходима особая
осторожность. В газо-жидкостных системах через а обычно обозначается
истинное объемное газосодержание, или объемная концентрация
газа.
Во многих случаях, особенно в задачах, связанных с
кипением или конденсацией, желательно знать часть общего
массового расхода через заданное сечение, приходящуюся на
каждый из компонентов. Поэтому расходное массовое
газосодержание (паросодержание) определяется как
*=%- ■ (1".7)
Очевидно, в случае нестационарного или неоднородного потока
величину х -следует осреднить. Среднее значение берется для
выделенной поверхности за некоторый период времени, поэтому
/г\ \GjdAdt (Л Rv
<Х>- lOdAdt ' (L8)
Плотность объемного расхода, или приведенная скорость
(м/сек), обозначается /. В действительности это векторная
величина, однако в данной книге / будет использоваться
исключительно для^обозначения скалярной составляющей в направлении
движения вдоль трубы или канала. Приведенная скорость
следующим образом связана с локальной концентрацией и
истинными скоростями компонентов (фаз):
7i=(l—a)^i> (1.9)
_ h=w2. (1.10)
Скорость смеси равна
7=Л+72. (1.П)
Очевидны следующие соотношения:
Q^J.dA, (1.12)
Q2=$J2dA. (1.13)
28л
ГЛАВА 1
Среднее значение приведенной скорости компонента 2 через
сечение площадью А равно
<Л> = -^. (1.14)
Если изменения в поперечном направлении не рассматриваются,
то скобки в уравнении (1.14) обычно опускают.
Плотность потока массы (массовая скорость) обозначается
<2 (кг/м2 • час). Для малого элемента, в пределах которого
плотность каждого компонента можно считать постоянной,
Oi=Pi7'n (1.15)
Q2=p2y'2, (1.16)
0=0,4-02. . (1.17)
Среднем ассовая плотность потока компонента 2 через сечение
площадью А определяется следующим образом:
<02> = ^-. 0.18)
v Хотя в наиболее общем описании течения двухкомпонентной
феды необходимо учитывать изменение всех рассмотренных
величин в трехмерной системе координат и во времени, мы в
основном ограничимся допущениями об одномерности потока и
<уудем использовать только средние по сечению канала величины.
В тех случаях, когда параметры претерпевают значительные
изменения по поперечному сечению канала, данная схема
становится несостоятельной и необходим более подробный анализ.
Ниже дается сводка некоторых полезных соотношений для
одномерного течения
<?1
А '
02
А '
Oi + Ог
А
h
1—а '
h
а '
wl
А '
Щ
А '
(1.19)
(1.20)
(1.21)
(1.22)
(1.23)
(1.24)
(1.25)
ВВЕДЕНИЕ
29
W\=QlPl>
^2=Q2p2)
h — Qi _
», 1
h 0г
Gi Wx 1
Щ
Go
W-,
Из уравнений (1.26) — (1.29) следует
1 —x I/, pi 1 —a.
Относительная скорость определяется как
^21 = (^2 — *>l) = — *>12.
(1.26)
(1.27)
(1.28)
(1.29)
(1.30)
(1.31)
Скорость дрейфа определяется как разность между скоростью
компонента и скоростью смеси
(1.32)
(1.33)
vlJ=v1-j>
V2j = V2-j.
Плотность потока (приведенная скорость) дрейфа представ-
I; ляет собой плотность объемного расхода компонента через
поверхность, движущуюся со скоростью смеси, т. е.
j21=a(v2—f), (1.34)
y12=(l-«)(*i-A (1-35)
Подставляя (1.11) и (1.34) и используя соотношение (1.10),
получим
к \=к — а Ui+Ji)=h (1 - а) - «А •
Аналогично
t У1 з=У1« — (1 — «) /2- (1 -37
Следовательно,
(1.38)
(1.36)
У2 1
-/12.
га симметрия является важным и полезным свойством приве-
енной скорости дрейфа.
.%,£ Подставляя в соотношение (1.37) выражения для /i и /г из
■a:'f§|.22) и (1.23), получим
)х 2=<* (1 - «) (*>, - w>) = a0 - а) "0\ 2-
(1.39)
4ЙЕк:'
30
ГЛАВА 1
Сл.еД°вательно> приведенная скорость дрейфа
пропорциональна относительной скорости. В записанных выше уравнениях
може*" быть использована любая система единиц при
соблюдений условий совместимости и последовательности.
Скорости, характеризующие течение в целом, например
скорости волн, обозначаются прописными буквами с
соответствующими нижними индексами.. Например, скорость непрерывных
волн обозначается Vw, скорость ударной волны Vs-
Свойства
Чтобы различить обозначения объема и скорости, первый
набран рукописными буквами. Таким образом, объем пузырька
обозначается как Ть, а удельный объем газа vg. Заметим, что
Vfg означает скорость жидкости относительно газа, a vjg —
изменение удельного объема при испарении. В случае описания
термодинамических свойств индексация противоположна, т. е.
vfg=vg—vf Hhfg = hg — hfil.
При обозначении свойств, таких, как плотность р и вязкость
(х, не должно возникать затруднений. Поверхностное натяжение
обозначается а и имеет размерность силы на единицу длины.
Энтальпия и коэффициент теплоотдачи обозначены символом h,
но их различие очевидно из текста.
Падение давления
Падение давления в трубе обозначается Ар. С другой
стороны, dp/dz характеризует скорость роста давления вдоль
оси z. Следовательно, если z — координата, направленная вдоль
оси трубы и отсчитываемая в направлении течения, то падение
давления на участке длиной L будет равно
£
Ap=-I-g-flfe. (1-40)
о
Координаты
Так как символ х уже выбран для обозначения паросодержа-
ния, его не следует использовать для обозначения координаты.
В общем случае z будет соответствовать координате,
измеряемой в направлении потока, а у — координате, отсчитываемой от
границы, например стенки. Расстояние от оси трубы по радиусу
будет обозначаться через г.
') Во избежание возможной путаницы в обозначениях v и v в качестве
основной переменной чаще всего удобнее использовать плотность, а не
удельный объем.
ВВЕДЕНИЕ
31
Единицы
Все уравнения записываются в совместимой размерной
форме и пригодны для использования любой из принятых систем
единиц. Всюду опущены коэффициенты, представляющие собой
соотношения между различными общеупотребительными
единицами.
IS
Задачи
1.1. Пузырьковая смесь течет по трубе диаметром 25 мм. Расход газа
0,85 м3/мин, а скорость пузырьков, определенная фотографическим методом,
составляет 30 м/сек. Каково объемное газосодержание? Чему равна скорость
жидкости, если ее расход составляет 0,14 мъ/мин>
1.2. По трубе диаметром 32 мм течет смесь воздуха при температуре 21° С
и давлении 1,4 ата с расходом 136 кг/час и воды с таким же расходом.
Чему равна общая плотность объемного расхода у? Каковы средние
скорости каждой фазы, если приведенная скорость дрейфа jg/ равна 3 м/сек?
1.3. Паро-водяная смесь с паросодержанием 1 % при атмосферном давлении
поднимается по вертикальной трубке кофеварки. Измеренное объемное паро-
содержаиие равно 80%. Каково отношение средней скорости пара к средней
скорости воды?
1.4. В некоторой Системе из жидкости с твердыми частицами (плывун)
приведенная скорость дрейфа связана с объемной концентрацией жидкости в
соотношением
i
jfs = 1,515е3 (1 — е) м/сек.
Чему равна величина 8, если восходящий поток жидкости через
стационарный слой частиц //=0,305 м/сек? Если сферические частицы имеют
случайную упаковку с плотностью упаковки бо=0,4, то является ли
рассматриваемая система «псевдоожижеииой» или же частицы покоятся одна на другой?
1.5. Выразить G через паросодержание, скорости фаз и их плотности.
1.6. Выразить у через массовые скорости каждой фазы, диаметр трубы и-
плотности фаз.
1.7: Показать, что приведенная скорость дрейфа не зависит от движения
наблюдателя.
1.8. Показать линии постоянных значений /, G и х на графике зависимости
h от /1 Для заданных свойств фаз. Можно ли нанести линии a=const?
Почему нельзя?
1.9. На графике зависимости /2 от y'i показать линии a = const, если
а) Vi/v2 = const; б) vt 2=const, в) y'i2=const; г) /i2=£a(l—a)".
1.10. Выразить плотность потока количества движения для одномерного
течения через G, х, а и плотности фаз. При каком значении а плотность
потока количества движения будет минимальна, если G и х — постоянны? При
каком значении а величина G будет максимальна, если х и плотность
потока количества движения заданы?
1.11. Решить задачу 1.10, используя вместо потока, количества движения
поток кинетической энергии.
1.12. Показать, что при течении ■ несжимаемой среды в канале постоянного
сечения у не зависит от координаты, хотя потоки отдельных фаз могут
Изменяться.
,t,13. Показать, что приведенная скорость дрейфа равна нулю при а=0 и
« = 1.
1.14. Доказать, что j2v{ 2 = v2v^.
32 глава l
1.15. Бутылка наполняется до краев пенящимся пивом. После отстаивания
до прекращения выделения пузырьков бутылка оказалась заполненной
на 70%. Чему равно первоначальное объемное газосодержаиие? Вычислить
массовое газосодержание смеси, вытекающей из крана.
1.16. Определить максимальное значение а для устойчивой засохшей пеиной
структуры (так что жидкие пленки имеют толщину в несколько молекул),
образованной пузырьками диаметром 1 мм.
1.17. Какое значение а соответствует плотной упаковке множества сфер?
1.18. Вода под давлением 70 ата поступает в прямую испарительную трубу.
Чему равны объемное паросодержание и гыготиость потока количества
движения при л:=0, 0,1 и 0,5, если отношение скоростей vejvf постоянно и равно
2,5, а плотность потока массы 10е кг/м2 • час?
1.19. В некотором режиме движения вертикального потока относительная
скорость постоянна и равна va. На графике зависимости /i от /г нанести
линии <z=const. Показать, что эти линии огибаются некоторой кривой в
квадранте, соответствующем противоточному движению. За этой огибающей,
называемой линией «захлебывания», существование .данного режима невозможно.
Показать, что уравнение линии «захлебывания» имеет вид
I'/ij. ;'/>_ „V.
Л тУг -"о •
Литература
1. На 11-Taylor N.. Hewitt G. F.. AERE-R3952, UKAEA, 1962.
2
ГОМОГЕННОЕ ТЕЧЕНИЕ
2.1. Введение
Теория гомогенного течения дает простейший метод
исследования двухфазных (или многофазных) течений. В ней
определяются соответствующие средние свойства и смесь
рассматривается как некоторый квазиконтинуум, который описывается
уравнениями однофазной среды. При этом могут использоваться все
обычные методы гидромеханики.
Для анализа необходимы средние параметры: скорость,
термодинамические свойства (например, температура и плотность)
и переносные свойства (например, вязкость). Эти кажущиеся
свойства являются средневзвешенными и не обязательно
соответствуют свойствам отдельной фазы. Определение
соответствующих свойств очень часто следует начинать с более сложных
уравнений и приведения их к виду уравнений однофазного
потока. Например, эффективную вязкость эмульсии можно
определить из анализа трехмерного поля течения двух компонентов.
В другом случае кажущиеся свойства смеси газа с частицами
находят из отдельных уравнений для каждого компонента,
допуская наличие некоторого класса подобных решений (гл. 8,
стр.235).
Различие скоростей, температур и химических потенциалов
фаз обычно обусловливает взаимный обмен количеством
движения, теплом и массой. Часто эти процессы протекают очень
быстро, особенно в тех случаях, когда одна из фаз тонко
диспергирована в другой, и тогда можно сделать допущение о
достижении равновесия. В этом случае средние значения скоростей,
температур и химических потенциалов для обеих фаз равны.
Результирующие уравнения просты по форме и в употреблении,
'однако во многих случаях целесообразно проверить
справедливость допущений о равновесии путем использования более
точных методов, которые будут изложены в последующих главах,
, или путем детального анализа других процессов обмена, которые
va. данной книге не рассматриваются. Равновесная теория
становится неточной в условиях резкого ускорения и изменения
давания, например при определении расхода вскипающей паро-во-
геой смеси через короткие сопла или диафрагмы. Для этого
обходимо рассмотреть скорости зарождения пузырьков и их
_ст в перегретой жидкости. Неравновесные эффекты также
'"!Я1*еют место при конденсации переохлажденного пара в высоко-
3 Заказ № 162
' 34
ГЛАВА 2
скоростных потоках или при сгорании частиц твердого топлива
в сопле ракетного двигателя.
Неправомерность теории гомогенного течения в некоторых
случаях вполне очевидна. Например, противоточное
вертикальное течение, обусловленное силой тяжести, действующей на фазы
с различной плотностью, не может быть описано с
использованием соответствующей «средней» скорости.
В данной главе будет изложена теория гомогенного течения,
подкрепленная достаточным количеством примеров,
иллюстрирующих соответствующие методы. Частные и конкретные
приложения будут даны в последующих главах.
2.2. Одномерное стационарное гомогенное равновесное
течение
, Основные уравнения одномерного стационарного гомогенного
равновесного течения в канале имеют следующий вид:
уравнение неразрывности
W/=pmt)A=const, • (2.1)
уравнение количества движения
Ш11Г--А^ПГ- P*w-APmg cost, (2.2)
уравнение энергии
■4fr;-£-«'-B-(*+-T-+№)- <2-3>
В этих уравнениях А и Р — соответственно площадь сечения
и периметр канала, %w—среднее касательное напряжение на
стенке, dqe\dz — тепловой поток на единицу длины канала, zg —
вертикальная координата и 0 — угол наклона канала
относительно вертикали. В большинстве случаев в уравнении энергии
члены, связанные с работой, принимаются равными нулю. Если
представляет интерес только изменение величин между
характерными точками канала, можно воспользоваться уравнениями
движения и энергии в интегральной форме.
Уравнение (2.2) часто записывается в явном виде
относительно градиента давления, т. е.
Три члена в правой части этого уравнения можно
рассматривать как составляющие градиента давления, обусловленные
трением, ускорением и силой тяжести. Так как инженеры (бу-
ГОМОГЕННОЕ ТЕЧЕНИЕ
35
дучи пессимистами) интересуются в основном потерями
давления, обычно принимаются следующие определения:
4rL = P^cos9. (2.7)
\ dz /a
Следовательно, градиент давления в целом равен сумме
отдельных составляющих, т. е.
&=№Мж1+Ш„- <2-8>
Помимо приведенных выше уравнений мы обычно
располагаем, некоторой информацией об уравнении состояния
компонентов. Например, для паро-водяной смеси могут быть
использованы термодинамические таблицы или диаграмма Молье. Для
смеси газ-а с твердыми частицами можно вывести уравнение,
эквивалентное уравнению состояния, при допущении о равновесии
между компонентами или других допущениях.
Среднюю плотность среды1' можно выразить различными
способами. В функции от объемного газосодержания а она
записывается следующим образом:
P»=«P2 + (1-«)Pi. (2.9)
в то время как в функции от массового газосодержания
аддитивными величинами будут удельные объемы, т. е.
— =— + -^—-. (2.10)
Масса каждого компонента в единице объема в функции от а
или х может быть определена из следующих соотношений:
•*Рт = аР2, (2.11)
(l-JC)pm = (l-a)p,. (2.12)
Для гомогенного стационарного потока при равенстве скоростей
фаз объемное и массовое газосодержание соответственно равны
°2 - h (2.13)
(2.14)
•> Плотность смеси.
3*
" <?1 + <?2 —
Х Wi + W2~
— Прим. ред.
J
G2
G
36
ГЛАВА 2
Простым примером гомогенного течения может служить изо-
энтропическое расширение паро-водяной смеси в сопле без
трения и теплообмена со стенками. Конечное состояние в процессе
расширения в заданном интервале давлений при постоянной
энтропии можно определить по диаграмме Молье.
Следовательно, можно найти перепад энтальпий и конечную плотность.
Скорость истечения определяется затем как интеграл уравнения
(2.3), а площадь сечения вычисляется по уравнению (2.1).
Методика расчетов точно такая же, как и при расчетах процесса
расширения сухого пара. Однако возможны неточности,
обусловленные эффектами неравновесности. При быстром расширении
вода и пар не находятся в тепловом равновесии и имеют
различные скорости. Трение и теплообмен между фазами также
приводят к необратимости, что не соответствует допущению
о постоянстве энтропии.
Пример 2.1. Сухой насыщенный пар из большого сосуда под давлением
7,03 ата расширяется через адиабатическое сопло без треиия до давления
1,05 ата. Чему равны скорость и массовая скорость на срезе сопла?
Решение. Из таблиц для водяного пара для рассматриваемого изоэнтропи-
ческого расширения находим, что влажность на срезе сопла равна
10,7%. Следовательно, удельный объем и энтальпия на срезе равны
ve=0,893 • 1,642+0,107-0,00104=1,47 м3/кг, he = 639,3 — 0,107 • 538,7 =
=581,7 ккал/кг. Энтальпия на входе в сопло равна й*=659,9 ккал/кг.
Пренебрегая гравитационными членами в уравнении (2.3), для
адиабатического истечения получим
• =fti — he = 78,2 ккал/кг.
2
Следовательно,
ve = 91,53 l/78j = 810 Ml сек.
Массовую скорость определим из уравнения (2.1)
Jl = -^ = -^£-=551 кг/м2- сек.
A ve 1,47
Пример 2.2. Вывести уравнения расширения газа, содержащего взвешенные
мелкие твердые частицы (в рамках одномерной схемы без учета трения).
Считать, что поток является гомогенным, скорости фаз одинаковы, и
рассмотреть два предельных случая термического поведения системы:
1) между газом и частицами нет теплообмена, 2) процесс расширения
характеризуется полным тепловым равновесием между компонентами.
Используя полученные результаты, вычислить скорость на срезе сопла,
давление торможения на входе в сопло и температуру газа на срезе
при расширении смеси, состоящей из песка (удельная теплоемкость
0,21 ккал/кг • град) и воздуха в соотношении 2:1, до числа Маха,
равного 2, при давлении 1,05 ата. Температура торможения на входе в
сопло равна 815,6° С.
Решение. Простейший метод решения состоит в выводе уравнений состояния
и адиабатического расширения для псевдогаза, эквивалентного
рассматриваемой смеси газа с частицами песка.
ГОМОГЕННОЕ ТЕЧЕНИЕ
37
Обозначим температуру воздуха через 7" и присвоим параметрам
воздуха индекс а.
Для 1 кг чистого воздуха уравнение состояния имеет вид
Pa*a = RaT. (2.15)
Если плотность частиц много больше плотности воздуха и двухфазная
смесь содержит m килограммов частиц на килограмм воздуха, то
кажущаяся плотность (или удельный объем) среды будет связана с
плотностью (или удельным объемом) воздуха следующим приближенным
соотношением (см. задачу 2.1):
J- = -^S- = \+m. (2.16)
Pa v
С использованием соотношения (2.16) можно переписать уравнение (2.15)
в таком виде, чтобы получить уравнение состояния для псевдогаза,
эквивалентного смеси газа с частицами, которое имеет вид
pv= , fa T. (2.17)
* 1 + тп '
Следовательно, влияние частиц сводится просто к изменению
соответствующего значения R в уравнении состояния совершенного газа.
Процесс расширения будет зависеть от теплообмена между фазами.
Если между воздухом и частицами нет теплообмена и трения (так как
предполагается, что оии имеют одинаковые скорости), то расширение
воздуха будет изоэитропическим в соответствии с законом
pv/ = const. (2,18)
Так как 1 + m в (2.16)—величина постоянная, то (2.18) эквивалентно
соотношению
pva=* const. . (2.19)
Таким образом, при отсутствии теплообмена смесь ведет себя как псев-
догаз с тем же показателем изоэитропы \а, что и у чистого воздуха, ио
с другим значением R=Raf(l+m).
С другой стороны, если газ и частицы все время находятся в тепловом
равновесии, то общая энтропия смеси остается постоянной. Если частицы
имеют удельную теплоемкость с, то приращение их энтропии,
соответствующее передаче воздуху dQ количества тепла, будет равно
dsp = £н = с/и-=— (на 1 кг воздуха), (2.20)
а приращение энтропии воздуха будет равно
dSa=W- = cpa^£— RaJf. (2.21)
Суммируя (2.20) и (2.21), получим
dsa + dsp = -^- {с ^ + тс) — 1*а-Ц- = о. (2.22)
Следовательно, псевдогаз подчиняется закону расширения
r-y»-WT== const, (2.23)
38
ГЛАВА 2
где
J^zl- _ Ra (2.24)
Т Сра + тс '
Решая уравнение (2.24) относительно \ и используя соотношение #а =
= Сра — С„а, ПОЛуЧИМ
Сра + ШС
Cva + тс
(2.25)
Этот результат можно было бы получить также, если учесть, что
эффективные удельные теплоемкости смеси при постоянном давлении и по
стоянном объеме равны соответственно
Сра 4- тс Cva _j_ тс
1 4- rn I + it
Следовательно, влияние теплообмена сводится к модификации
показателя изоэнтропы в соответствии с уравнением (2.25). Таким образом,
псевдогаз, эквивалентный исходной смеси, характеризуется параметрами
R=*Ral{l + т) и \, определяемым по уравнению (2.25), ио в других
отношениях подчиняется всем хорошо известным соотношениям
газодинамики одномерных течений, которые приводятся в обычных учебниках,
например [1]. Другим путем эти результаты можно получить из
уравнений (2.1)—(2.3) без учета гравитации, трения и теплообмена с
окружающей средой.
В рассматриваемом числовом примере псевдогаз характеризуется
следующими величинами параметров:
994
R = ~ ' = 9,78 м/град и ^=1,4—при допущении 1;
0,241+2-0,21 , ,,,
~ — !— =— = 1,11 при допущении 2.
1 0,173 4-2-0,21
Давление торможения определяется по формуле
А-лО+^Мг)™1-0, (2.26)
а конечная температура воздуха на срезе сопла — по формуле
Те = 7-0 (1 + ^- М^~'. (2.27)
Скорость на срезе сопла равна
ve = UeVWr~e. (2.28)
Подставляя соответствующие значения, получим
1.. При отсутствии теплообмена между компонентами
Р0 = 8,23 ата, ' Ге = 333,2°С, Ve = 570 м/сек.
2. При тепловом равновесии между компонентами
Р0 = 7,7 ата, Ге = 619°С, Ve = 617 м/сек.
Уточнение уравнения движения
Уравнение движения можно рассмотреть более подробно,
выразив касательное напряжение на стенке через коэффициент тре-
ГОМОГЕННОЕ ТЕЧЕНИЕ
39
ния и средний гидравлический диаметр канала Di. Средняя
величина касательного напряжения равна
rw=Cf-t-Pmv*, (2.29)
а градиент давления, обусловленный силами трения, имеет вид
-(-si=2C'p«-2T- " (2-30)
Удобную для анализа модификацию уравнения (2.30) можно
получить, подставляя соответствующие выражения для объемного
и массового расхода
v=j= Ql + °2 , (2.31)
Рш,=0=^, (2.32)
тогда
-№,-*£-■ <2-33>
В качестве переменных можно выбрать также удельные
объемы компонентов и массовое газосодержание. Из уравнений
(2.10) и (2.32) получим
v=-£-=G[xV2+(l-x)Vl] = G(Vl + xVld. (2.34)
Подстановка (2.31) и (2.34) в уравнение (2.30) дает
A-¥)r = ^Tr-{vi + Xvi^ (2'35)
Так как массовый расход постоянен и скорости фаз одинаковы,
то градиент давления, обусловленный ускорением, в
соответствии с (2.6) равен
О-ЗГ- (2.36)
Подставляя v из (2.1) в (2.36), получаем-
г(-П-°тЬ£)- е-»)
1 В американских и английских работах перепад давлений, связанный
с трением, часто определяют по формуле Фаннинга &p=Cf(l[Dh) (pmV2/2),
где Dh=flP — гидравлический диаметр, f — сечение канала, Р — его периметр.
В связи с этим величина коэффициента треиия С/ (иногда его называют
фактором трения) оказывается в 4 раза меньше, чем в расчетах, использующих
Dh—iflP (как это принято в отечественной литературе). — Прим. перев.
\ dz )л
40
ГЛАВА 2
Выполняя дифференцирование, находим
-(JEA =02—(—\- — 4-4^. (2-38)
\ dz )А и dz I ы ) ы A dz
Далее, дифференцируя (2.10), получаем
(2.39)
или в функции удельных объемов фаз
Для однокомпонентной смеси (например, для паро-жидко-
стной среды) vj и vg зависят только от давления. Аналогично
для двухкомпонентной смеси vx и v2 можно представить в виде
функции давления, если термодинамический процесс известен.
Тогда уравнение (2.40) можно переписать в виде
" -£Ш—.■£-+4М+<1-*»^]- (2-41>
Из уравнения (2.38) можно получить выражение для падения
давления из-за ускорения в функции массового газосодержания,
расхода и переменных свойств
-mro-i-.-s+^i'-^+o-^-s-]-
При подстановке р™. из уравнения (2.10) в уравнение (2.7)
можно определить падение давления, обусловленное силой
тяжести, в функции от массового газосодержания
-(lL) =gcos%-±—. (2.43)
\ dz /a s vt 4- xvt 2
Подставляя (2.35), (2.42.) и (2.43) в (2.8), после
соответствующих преобразований получим следующее выражение для
градиента давления:
dp
~~ dz ~~~
2Cf dx . 1 dA , gcosO
-gi- 02(гг, + x»t 2) + QSiri 2 ^r - G2 (irx+Xtr! 2> X ^T + ^ + ^ 2
(2.44)
ГОМОГЕННОЕ ТЕЧЕНИЕ
41
к.
Возможны другие варианты этого уравнения, если использовать
другие переменные. Однако форма уравнения сохранится и
физический смысл каждого члена не изменится. Действительно,
любой аналитический метод исследования одномерного
стационарного течения в конечном счете приводит к следующей форме
уравнения:
dx . л 1
dp
cF + cx
dz
■ + С
A A dz
dA n .
-йТ + ceS cos I
dz
1—M2
(2.45)
В этом уравнении Ср, Сх, С а и Cg — так называемые
коэффициенты влияния, учитывающие соответственно вклад трения,
фазовых превращений, изменения площади сечения и силы тяжести
в величину градиента давления. Величина М2 в знаменателе
имеет такой же смысл, как и квадрат числа Маха
для'однокомпонентной, среды. Сравнивая уравнения (2.44) и (2.45) с учетом
(2.32), находим выражение для скорости распространения
упругих волн в гомогенной двухфазной смеси в виде
■ ы [х -
dp
(1-Х)
dp
(2.46)
Другой, более прямой вывод этого уравнения будет представлен
в гл. 6. С использованием (2;9), (2.11) и (2.12) можно получить
выражение для с в функции а
С={[вр2+(1-в)р1][вр2(-^-) + (1-в)р1(_^.)]р.
(2.47)
Псевдозвуковые скорости для чистых компонентов в таком же
термодинамическом процессе, как и для двухфазного потока,
можно определить следующим образом-;
Сх
(2.48)
Используя эти определения, преобразуем уравнение (2.47) к виду
«2
= [ap2+(l-a)pi]
Р2С2
hC\
(2.50)
При piCi23>p2c22 и pi^>'p2 (например, для водо-воздушной смеси
при атмосферном давлении) это уравнение сводится к
приближенному выражению
Р2 62
Pi я (1-я)
(2-51)
42
ГЛАВА 2
Очевидно, скорость звука в гомогенной смеси может быть
много меньше, чем в чистом газе. Минимум достигается при
а = '/2, и в смеси воздуха с водой при атмосферном давлении
скорость звука оказывается равной ~21 м/сек.
Обычно изменение массового паросодержания
рассчитывается по уравнению энергии в предположении, что подведенное
тепло затрачивается на испарение. Однако если происходит
достаточно бурное «вскипание»1' вследствие падения давления, то
массовое паросодержание определяется не только энтальпией,
и в этом случае более точным будет' следующий путь. Пусть
массовое паросодержание является функцией энтальпии и
давления. Тогда для заданной термодинамической системы
x=x(h, p). (2.52)
Дифференцируя, получим
dx I дх \ dh .1 дх \ dp (Г) ^-о\
Кроме того,
(-ж),=тЬ- (2-54)
Теперь уравнение (2.44) принимает вид
dp =
dz .
^Lni,... j_ „.. .ч , ni VA2 dh пл fmm_ j_ _ _ч 1 rjA_ , gcos9
'&->t ~« «"19 dh _„ . , N 1 rdA
_L02 (tr, + хщ 2> +0»-^ -5- -02И + ^, 2) -g-gr +
v±+jXV\2
(2.55)
Возможны многие другие формы уравнения (2.55), если
использовать в уравнении (2.52) другие термодинамические
свойства.
Практически условие равенства числа Маха единице с
большой вероятностью определяется уравнением (2.46), а не
аналогичным результатом, который можно было бы получить,
используя весь знаменатель уравнения (2.55). Это связано с
эффектами неравновесности, которые препятствуют быстрому
протеканию фазовых превращений, вызываемых внезапным
изменением давления.
.'' Термин вскипание обычно используется для описания процесса
парообразования, вызванного падением давления, в то время как кипение
относится к парообразованию вследствие подвода тепла.
ГОМОГЕННОЕ ТЕЧЕНИЕ ' - 43
Если кинетическая энергия потока достаточно велика, то
градиент энтальпии нельзя рассчитывать непосредственно из
уравнения энергии, и уравнение (2.55) приобретает более сложный
вид (см. задачу 2.25).
Неравновесные эффекты, связанные с фазовыми
превращениями, можно исследовать, заменяя уравнение (2.52) некоторым
уравнением эффективного термодинамического процесса, либо
путем простого допущения об образовании некоторой доли
равновесного количества пара, либо путем более тщательного
анализа,' когда действительное паросодержание рассматривается
в связи с неравновесными процессами тепло- и массообмена [14].
2.3. Коэффициент трения для гомогенного течения
Ламинарное течение
Были предложены различные методы расчета коэффициента
трения в двухфазном гомогенном потоке Cf, который входит
в уравнения (2.44) и (2.55) только как эмпирический параметр.
Для ламинарного течения простейший метод состоит в
определении соответствующей «эффективной вязкости» смеси.
Например, теоретическое решение для взвеси жидких сферических
частиц при низких концентрациях имеет вид
P=ft(l-b2,5« ^Г )' (2.56)
где индекс 1 относится к непрерывной фазе. Если взвесь состоит
из твердых частиц, то величина ц,2 очень велика, и уравнение
(2.56) сводится к уравнению Эйнштейна [3]
l*=,i,(l + 2,5a). ' (2.57)
Для взвеси, содержащей пузырьки газа с малой вязкостью,
получим
1*=М1+«). (2-58)
К сожалению, уравнения (2.56) — (2.58) применимы только при
концентрациях до 5%, когда изменение вязкости невелико.
Предлагались различные реологические модели, соответствующие
большим значениям а и частицам различных размеров и форм;
они будут рассмотрены в следующих главах. Многие
двухфазные смеси являются неньютоновскими жидкостями.
Часто детальная структура двухфазного потока неизвестна
и нельзя определить идеализированную реологическую модель
течения. Сталкиваясь с необходимостью выбора соотношения
для вязкости, многие исследователи принимали средние
значения, удовлетворяющие предельным случаям, когда отсутствует
44
ГЛАВА 2
одна из фаз. Ниже приводятся некоторые часто используемые '
соотношения для газо-жидкостных потоков
_L = JL _|__Lz£. (Макадаме [4]), (2.59)
ц=Х(АгН-(1 — х) ^ (Чиккити [5]), (2.60)
^Jj-^+Jj-^ (Даклер[6]). (2.61)
Во многих случаях целесообразно установить соотношение
между вязкостью, коэффициентом трения и потерями давления
на трение для двухфазного потока и соответствующими
величинами для однофазного потока одной из рассматриваемых фаз.
Например, для ламинарного течения из уравнения (2.59)
получим
тН^+(1-*>Г- " (2-62)
Если обозначить индексом /0 случай, когда по трубе течет
жидкость с той же самой массовой скоростью, что и при совместном
течении фаз, то для ламинарного потока без фазовых
превращений, используя уравнение (2.62), получим
-т--тг„[х+<н- #+*£- or- <2-бз)
Отношение градиента давления, обусловленного трением, для
двухфазного потока к такому же градиенту давления для
соответствующего однофазного потока известно как параметр
двухфазности и обозначается <j>2 с соответствующим, индексом,
например
тг'° —{dp/dz)p v
Если можно определить ф2/0, первый член в числителе уравнений
(2.44) или (2.55) можно заменить в соответствии с
соотношением
-^- О2(,;Н-*Л)=^ -^ ОЧ. (2.65)
Турбулентное течение
Коэффициент трения для однофазного турбулентного течения
обычно представляют в виде функции от числа Рейнольдса и
шероховатости трубы. За исключением предельных случаев, дей-
ГОМОГЕННОЕ ТЕЧЕНИЕ
45
ствительная величина отличается не более чем вдвое от
значения С/?«0,005, которое дает грубая оценка. В промышленных
условиях трубы подвержены коррозии, деформации, на их
стенках образуется накипь, в связи с чем погрешность
определения потерь давления для однофазного потока часто достигает
25%, так что не приходится ожидать более точного соотношения
для двухфазного потока.
0,0076
§ 0,0050
к
к
□1 ••
g On.
_° ■ а
0
■ V
V
♦
1
л
■
0
а
■
V
-
1
V
0
♦
1
а|
■
•а
а
V
1
л
к |
а
•
1
1 к
0
■
□
1
Массовый расход газа, г/сек
к 1,895
, 4,171
Тернер
i
• 3,88
к 5,40
л 7,30
Мейер
о
а
■
V
1
1
а
111
23,95
•
1
1
i
1
■
!
го зо 40
Расход жидкости Wf, г/сек
50
Фнг. 2.1. Коэффициент трения для гомогенной системы при
дисперсно-кольцевом режиме течения [7].
Мейер и Тернер; медная трубка с внутренним диаметром 13,9 мм; р=1 атм;
восходящий однонаправленный водо-воздушный поток.
Наиболее употребительны три способа оценки коэффициента
трения для двухфазного турбулентного потока.
1. Принимается постоянное значение для всех условий.
Хорошие результаты дает величина
=0,005.
(2.66)
На фиг. 2.1 приведены некоторые данные для дисперсно-
йсольцевого течения с большой скоростью. В этих условиях
значительная часть жидкости уносится в ядро потока в виде капель
теория гомогенного течения дает приемлемое приближение.
2. Используется коэффициент трения, рассчитанный для
некоторого эквивалентного однофазного потока. Например, дляпа-
ро-водяной смеси с низким паросодержанием можно принять
46
ГЛАВА 2
тот же коэффициент трения, что и для потока чистой жидкости
при одинаковых массовых скоростях (жидкость — пар).
Соответствующее число Рейнольдса равно
Re,=
GD
v-f
(2.67)
причем легко показать, что
^0=1+X^_!J. (2.68)
Этот метод был использован Макадамсом и др. [4], а также
Оуэнсом [8]. Типичные результаты приведены на фиг. 2.2. При
50
40
за
2 с
<8|
~ го
J? E
I
П 1 1 I I I
Массовое паросодержание т.
о 0 -0.1
л 0,12 -0,2
а 0,3 - 0,5
3 4 6 8 Ю 20 30
Измеренные значении градиента давления
в двухфазном потопе ,ата Iм
40 50
Ф н г. 2.2. Сравнение расчетных н измеренных значений градиента давления
в двухфазном потоке, движущемся по трубке с внутренним диаметром 2,0 мм
и длиной 762 мм [8].
Вода под давлением от 5,0 до 26,3 ата при массовом содержании пара о.т 4 до 50%.
высоких паросодержаниях, приближающих смесь к чистому пару,
становится целесообразной замена (2.68) аналогичным
выражением для потока одной только паровой фазы.
3. По одному из соотношений для эквивалентной вязкости
смеси определяется число Рейнольдса и используется
зависимость от него коэффициента трения однофазного потока. На-
ГОМОГЕННОЕ ТЕЧЕНИЕ
47
пример, уравнение Блазиуса для течения в гладких трубах
имеет вид
C^O^Re-0'25. ' (2.69)
Используя соотношение (2.59) и определение фу0 (2.64),
нетрудно получить
Ф/о=
1 + xl-^- 1
1+Х
tV
v-g
1
-v«
(2.70)
Результаты расчетов по формуле (2.70) для воды приведены
в табл. 2.1. Аналогичные таблицы для быстрой оценки
расчетных параметров можно составить также для криогенных
жидкостей.
Таблица 2J
Значения параметра ф'10 для паро-водяной смеси, вычисленные
по формуле {2.70) для гомогенной модели
X, %
1
5-
10
20
30
40
50
60
70
80
90
100
Давление, ата
1,035
16,21
67,6
121,2
212,2
292,8
366
435
500
563
623
682
738
7,03
3,40
12,18
21,8
38,7
53,5
67,3
80,2
92,4
104,2
115,7
127
137,4
35,15
1,44
3,12
5,06
7,8
11,74
14,7
17,45
20,14
22,7
25,1
27,5
29,8
70,3
1,19
1,89
2,73
4,27
5,71
7,03
8,30
9,50
10,70
11,81
12,9
13,98
105,3
1,10
1,49
1,95
2,81
3,60
4,36
5,08
5,76
6,44
7,08
7,75
8,32
140,6
1,05
1,28
1,56
2,08
2,57
3,04
3,48
3,91
4,33
4,74
5,21
5,52
176,2
1,04
1,16
1,30
1,60
1,87
2,14
2,41
2,67
2,89
3,14
3,37
3,60
210,9
1,01
1,06
1,13
1,25
1,36
1,48
1,60
1,71
1,82
1,93
2,04
2,14
225,6
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
Другой способ расчета потерь давления на трение состоит
в том, что вместо коэффициента трения вводятся соотношения
для параметра двухфазности. Подробно этот метод будет
рассмотрен в следующей главе. Для частного случая течения
кипящей воды результаты такого корреляционного метода,
предложенного Мартинелли и Нельсоном [9], приведены в табл. 2.2
для сравнения с данными расчета по формуле (2.70).
Существует достаточно заметное рассогласование данных
двух таблиц. Какие из них являются более точными, зависит от
режима течения. Метод Мартинелли—Нельсона обычно дает
лучшие результаты для потоков с раздельным течением фаз, в то
время как теория гомогенного течения более приемлема для
48 ГЛАВА 2
Таблица 22
Значения параметра Ф?0для паро-водяной смеси,
вычисленные по эмпирической формуле Мартинелли
X, %
1
5
10
20
30
40
50
60
70
80
90
100
1,035
5,6
30
69
150
245
350
450
545
625
685
720
525
7,03
3,5
15
28
56
83
115
145
174
199
216
210
130
35,15
1,8
5,3
8,9
16,2
23,0
29,2
34,9
40,0
44,6
48,6
48,0
30,0
Давление
70,3
1,6
3,6
5,4
8,6
11,6
14,4
17,0
19,4
21,4
22,9
22,3
15,0
105,3
1,35
2,4
3,4
5,1
6,8
8,4
9,9
11,1
12,1
12,8
13,0
8,6
ата
140,6
1,2
1,75
2,45
3,25
4,04
4,82
5,59
6,34
7,05
7,70
7,95
5,90
176,2
1,1
1,43
1,75
2,19
2,62
3,02
3,38
3,70
3,96
4,15
4,20
3,70
210,9
1,05
1,17
1,30
1,51
1,68
1,83
1,97
2,10
2,23
2,35
2,38
2,15
225,6
1,00
1,00
1,00
1,00
1,00
1,00
1,00
1,00
1,00
1,00
1,00
1,00
дисперсных систем. Для примера на фиг. 2.3 показано, как по
мере увеличения массовой скорости движущейся с высокой
скоростью паро-водяной смеси, т. е. с увеличением уноса жидко-
ГООг
•е
N.
Метод|
Мартинелли- Нельсона
Гомогенная модель
0,001
0,01 0,1
Массовое паросодержание ос
Фиг. 2.3. Параметр Фу0 в зависимости от массовой скорости потока воды
в трубке с внутренним диаметром 5 мм при давлении 70,3 ата [10].
Обозначение
О, 103 кг /м2- сек
0
4,37
Д
3,35
О
2,455
D
1,75
V
1,14
ГОМОГЕННОЕ ТЕЧЕНИЕ 49
cthv экспериментальные данные отклоняются от результатов
расчета по методу Мартинелли — Нельсона в сторону гомогенной
модели.
Пример 2.3. Вывести уравнение для падения давления при гомогенном
течении паро-водяной смеси в круглой трубе постоянного сечения с
равномерным тепловым потоком. Пренебречь членами кинетической и
потенциальной энергии, а также эффектами вскипания и сжимаемости (эти
допущения справедливы только при высоких давлениях н низких
скоростях, когда общий перепад давления мал по сравнению с абсолютным
давлением). Считать коэффициент трення постоянным.
Решение. Сначала установим связь между скоростью подвода тепла на
единицу длины и тепловым потоком в виде
А=*/)Ф, ^ (2.71)
где у—плотность теплового потока.
Используя определение G и имея в виду, что W — постоянная
величина, -с учетом сделанных допущений получим
dh __ 4ф
~~dT~~ GD '
(2.72)
Пренебрегая вскипанием н сжимаемостью, при подстановке (2.72)
в (2.55) получим
dp 2С/ _„ . _9 vfg 4Ф gcosB "/0,,л
j = —ft~ О2 (У/ т xvfg) 4- и2 -г т=ггг т -—£-; . (2.73)
dz D v ' 1S' ' hfg GD vj -f. xvfg v '
Если изменение давления мало, то энтальпия смеси определяется
уравнением
h = hf + xhfg. (2.74)
Из (2.72) н (2.74) следует
dx _ 4ф ,07,х
1F~ GDhtg- KZJb)
Так как у — константа, уравнение (2.75) можно проинтегрировать от
. начального значения х, до некоторой точки г, что дает
*в"+-о?^тг- (2J6)
Подставляя (2.76) в (2.73), обозначая плотность на входе через р< и
выполняя интегрирование по всей длине трубы L, в конечном счете
получим
D ?l \ D J ■' hfg hfg D
GhfgD I 4*rfgH 4Z, \
4- g cos В — In 1 +-pm rrl- \/-u)
^vfg - \ Ghfg D ]
В частном случае лч = 0 зависимость от массового паросодержания при
z=L имеет другой вид:
4 Заказ № 162
50 ГЛАВА 2
Эта задача подробно была исследована Оуэнсом [8]. Используя
уравнение (2.77), важно проверить справедливость сделанных допущений, так
как влняине сжимаемости и кинетической энергии быстро возрастает
с увеличением расхода, а в тех случаях, когда существенно
относительное изменение давления, необходимо учитывать эффект вскипания.
Пример 2.4. Вода с массовой скоростью С/=271,2 кг/м2-сек подается в
нижнюю часть вертикальной трубы диаметром 12,7 мм и длиной 1,515 м.
К трубе без потерь подводится тепловой поток 6,304-105 вт/м2.
Рассчитать падение давления в испарителе при начальном давлении а) 25 ата,
б) 70 ата. Принять коэффициент трения постоянным и равным 0,005.
Решение. В рамках теории гомогенного течения решение сводится просто
к использованию уравнения (2.77).
а) нз термодинамических таблиц при давлении 25 ата находим
v/g = 0,0815 м3\кг, v,=0,001195 м3\кг, hfg = 1,847- 10е дж/кг.
Из уравнения (2.77) получим
то 1П Л 2. 1,515-0,005. 271,22. 0,001195 ,
Ар =1,02. 10-6 [ • .___, + .
(2 ■ 1,515)2 ■ 0,005 - 271,2 - 6,304 • 1Q5 . 0,0815
+ 0,01272 • 1,847 • 106 +
271,2 • 6,304 • 105 . 0,0815 ■ 4 • 1,515
+ 1,847- 106 . 0,0127 +
9,8 - 271,2- 1,847- 1Q6 • 0,0127
+ 4 • 6,304 • 105 . 0,0815 Х
V! (\ 6'304 ' 105 - °'0815 " 4 - 1'515 W — '
Х \ + 271,2.1,847.106.0,001195.0,0127 )\~
=0,00107 + 0,0219 + 0,0367 + 0,01156 = 0,07123 ата.
Так как эта величина мала по сравнению с 25 ата, то допущение о
постоянстве свойств жидкости справедливо.
Проверим также влияние сжимаемости и убедимся, что пар на
выходе нз испарителя не перегрет.
Массовое паросодержанне на выходе в соответствии с уравнением
(2.76) равно .
_ ф 4Z, _ 6,304.105.4-1,515
Хе~ Ghfg D 271,2 • 1,847 • 106 • 0,0127 ~ '
Проверим влияние сжимаемости и вскипания, оценив члены в
знаменателе уравнения (2.55). Из термодинамических таблиц находим
fog
dp
dv-f
Sf
дх
Jp~
= —3,38 • Ю-з (Мз/кг)/ата,
0 при jc= 1,
(-?£-] = —0,553 • 10-2 aTa-i при х = 0,
\ др )п
дх ^ =—0,285- 10-2 ш-1' при л: = 0,5.
др )н
ГОМОГЕННОЕ ТЕЧЕНИЕ
51
Наибольшее численное значение суммы, заключенной в скобки в
знаменателе уравнения (2.55), будет прн д:=0,6. Величина знаменателя
в целом равна'>
1 — 271,22 - 0,6 • 3,38 • 10-3 - ' = о,9985.
0,981 - IIP
Таким образом, сделанные допущения справедливы. Однако, если G и ф
увеличить в 10 раз, знаменатель станет равным 0,85; так что его нельзя
уже будет приравнять к единице, не внося существенной погрешности.
б) при начальном давлении 70 ата значения требуемых параметров
равны ^/£=0,0265 м3/кг, ir/=0,00135 м3/кг, h1g = 1,517 • Ю6 дж/кг.
Подставляя, как и ранее, числовые значения, получим
л„ лп-гко °-0265 1,847-106 --,...
АрА = 0,0368 - -р^ • {5ПЮ6 = 0,01456 ата,
' л ллл.пс 0,00135 , „„001 0,0265 1,847-106
А^ = 0,00106 ■ -тш + 0,0221 • -^ ■ 1Ш Ю6 =
= 0,00992 ата,
Арп = 0,0078 In 17,3 = 0,02223 ата.
Следовательно, суммарное падение давления равно 0,01456+0,00992+
+ 0,02223 = 0,04671 ата.
Пример 2.5. Воздух и вода при температуре ^=21° С движутся по вертикальной
трубе диаметром 24,8 мм. Расходы фаз №/=0,457 кг/сек и Wg =
=0,00852 кг/сек, давление на выходе 1,033 ата, а давление на расстоянии
0,456 м вверх по" потоку составляет 1,054 ата. Как это согласуется
с результатами теории гомогенного течения прн С/=0,005?
Решение. Так как падение давления незначительно, будет справедливым
допущение о постоянстве свойств при расчете падения давления
из-за ускорения и потерь давления на тренне. Падение давления
из-за ускорения обусловлено расширением газа. Так как Wj^>Wg, то
термодинамический процесс близок к изотермическому (см. пример 2.2).
Сначала запишем в удобной форме уравнение (2.44),
воспользовавшись выражениями (2.31) и (2.32) и исключив х с помощью
соотношений (2.11) н (2.12). Так как изменение ^сечения н массового паросодер-
жання, а также сжимаемость жидкости равны нулю, то
_ dp_ __ ZC/jG/D +- g cos 8 [apg + (1 — a) P/]
dz ~~ 1 +- Gjgfg (dv-g/dp)
В условиях изотермического расширения газа
dvg = 1_
dP ~ P?g'
(2.79)
(2.80)
■') Автор пренебрегает третьим членом в знаменателе уравнения (2.55)
ввиду его малости по сравнению с первым, а второй член равен нулю, так
как dvf/dp~0. — Прим. перев.
4*
52 ГЛАВА 2
Требуемые для расчета переменные определяются следующим образом;
j = j = 15,34 Mjсек,
G = —'—. — = 955 «г/ж2 • сек,
А
s -- 0,939.
Qf + Qg
Сделав необходимые подстановки в уравнение (2.79), получим
-- dp- =0,0141 ата/м.
dz
Так как градиент давления очень мал, то скорость вдоль канала
почти не меняется и суммарное падение давления находится путем
умножения полученного градиента на длину, т. е.
Ар = 0,0141 • 0,456 = 0,00643 ата.
Ошибка в определении падения давления обусловлена главным
образом неточной оценкой объемной доли жидкости, которая дается в
рамках теории гомогенного течения при заданных значениях расходов фаз.
В действительности структура потока снарядная или кольцевая н газ
движется намного быстрее, чем жидкость. Экспериментально
определенная объемная доля жидкости оказывается равной 0,23, что намного
больше значения 0,061, вычисленного по теории гомогенного течения.
Ошибку такого порядка следует ожидать во всех случаях, когда данная
теория используется при анализе режимов, к которым она не применима.
В рассматриваемом случае более подходящей оказывается модель
раздельного течения фаз. Теория снарядного течения нлн теория,
применимая к переходной области между снарядным и кольцевым режимами,
как будет показано в гл. 10 и 11, оказывается еще более точной.
Во многих случаях решение задачи не удается получить
в окончательном виде. Тогда уравнения типа (2.55) и (2.79):
представляют в виде конечных разностей и используют
численные методы интегрирования.
Заметим, что, подставляя (2.80) в знаменатель уравнения
(2.79), можно показать, что квадрат числа Маха для
изотермической гомогенной газо-жидкостной системы равен
М2=-^-. (2.81)
2.4. Падение давления в коленах, тройниках,
диафрагмах и т. д.
Обычный метод расчета падения давления однофазного
потока в арматуре трубопроводов состоит в замене данного
элемента арматуры участком трубы эквивалентной длины. Так
ГОМОГЕННОЕ ТЕЧЕНИЕ 53
же можно поступить и при расчете двухфазного потока. В этом
случае эквивалентные длины труб оказываются несколько
большими.
Некоторые задачи, связанные с определением перепада
давления в соплах и диафрагмах, будут рассмотрены в конце этой
главы.
2.5. Нестационарное течение
Теория гомогенного течения может „быть распространена на
случай нестационарного течения путем введения в уравнения
неразрывности, движения и энергии членов, зависящих от времени.
Для одномерного течения эти уравнения в дифференциальной
форме имеют следующий вид:
уравнение неразрывности
<Эрл
dt
уравнение движения
dv
+-s-M=°-
I dv , dv \
p» (-*-+*-ЗГГ
dp
dz
•Pm£COS9—_-tw,
(2.82)<
(2.83).
уравнение энергии
d г / . «2
~di
М*+-?)]+-^М*+т)Ь
~ТГТ—£-J-IW«»e- (2-8*
dw \
— 1 — i
Эти уравнения можно комбинировать различными способами,
выбор которых определяется целью исследования. Весьма
полезный способ состоит в подстановке тождества
Pme=Pm?i-P (2.85}
в уравнение (2.84) и последующем дифференцировании,
приводящем к
д?г>
dt
dv
d (pmtQ
dz
dv
(*+4)[-
При использовании (2.82) и (2.83) получаем
1 i ( dh , dh \ .
■]+р»Ьг+г'-зг) +
■*"'в)-45-+:И-*
dw
dz
). (2.86)
dh , dh 1 / dp
dt ~*V dz ~ ?m X~dT
-v
dz
■) + V
P z„
?m
Mm X
dqe
dw
dz
dz
(2.87)
54
ГЛАВА 2
Применение этого уравнения можно проиллюстрировать на
примере потока в прямой испарительной трубе при высоком
давлении, когда члены, соответствующие изменению давления и
вязкой диссипации, во время неустановившегося режима малы по
сравнению с другими членами уравнения энергии. Пусть диаметр
трубы равен D, тепловой поток на стенке <j>, а механическая
работа равна нулю. Тогда уравнение (2.87) принимает вид
dh . dh 1 4ф А) QQ\
~л1 \~1>-а— = гГ • (2.00)
dt ' dz fm D v
Если изменение давления и его влияние на свойства
незначительны, энтальпию и плотность можно представить следующим
■образом:
h = hf-^xhfg, • ' (2.89)
J-=v+Xv,e. (2.90)
Подстановка (2.89) и (2.90) в (2.88) дает
где
°~5£- <2:92>
Уравнение (2.91) представляет собой уравнение
распространения для расходного Массового паросодержания и может быть
проинтегрировано для получения динамической характеристики
канала теплообменника. Левая часть уравнения является
субстанциональной производной по времени от расходного
массового паросодержания и характеризует скорость изменения
паросодержания данного элемента жидкости (лагранжева система
отсчета). Величина Q имеет размерность, обратную времени, и
может быть названа частотой реакции. Если известен момент
времени /0, в которой элемент жидкости начал испаряться, то
уравнение (2.91) можно проинтегрировать, что дает
x(t, 'o) = -^-(*B('-'°,-l). (2-93).
Следовательно, массовое паросодержание в данном элементе
жидкости увеличивается во времени по экспоненциальному
закону. Дальнейший анализ в этом направлении приводит к
определению характеристики переходного режима парогенераторов
и конденсаторов [11].
ГОМОГЕННОЕ ТЕЧЕНИЕ
55.
Задачи
2.1. Вывести уравнение (2.16) из (2.10) н определить условия, при которых
погрешность уравнения (2.16) не превышает 5%.
2.2. Решить пример 2.2, если требуемая скорость на выходе равна
а) 300 м/сек, б) 450 м/сек и в) 850 м/сек.
2.3. Полагая, что гомогенный двухфазный поток между параллельными
пластинами состоит из большого числа параллельных слоев двух фаз,
ориентированных вдоль пластин, показать, что эквивалентная вязкость определяется
соотношением
1 _ а 1—а
{* ~ Р-2 ~ Pi
2.4. Решить задачу 2.3, если слои жидкости ориентированы перпендикулярно»
пластинам, н показать, что
2.5. Сравнить значения эквивалентной вязкости, определенные по
уравнениям (2.59)—(2.61), с результатами решения задач 2.3 и 2.4 для паро-водя-
нон смеси при расходном массовом паросодержанин 0,1, 1 и 10$) н
давлениях 0,7, 7 н 70 ата.
2.6. Определить коэффициент трення для водо-воздушного потока,
движущегося по трубе диаметром 50,8 мм при температуре 21° С и давлении 2 ата,
используя различные методы, рассмотренные в книге, при следующих
условиях:
jf, м/сек
jg, м/сек
0,3
3
3
3
3
0,3
30
3
3
30
70
70
2.7. Неподвижный пыльный воздух захватывается трубкой Пито (полнога
напора), закрепленной на джипе, пересекающем пустыню со скоростью
80 км/час. Весовые, доли песка и воздуха равны. Каково измеряемое
давление торможения? Четко сформулировать все сделанные допущения.
2.8. Вертикальный рабочий участок трубы установлен в экспериментальном
водяном контуре высокого давления. Труба внутренним диаметром 10 мм
н длиной 2' м равномерно обогревается источником мощностью 100 кет.
Насыщенная вода поступает на вход при давлении 70 ата; расход воды
равен 0,126 кг/сек. По различным уравнениям, приводимым в книге,
рассчитать потери давления на тренне, под действием силы тяжести н из-за
ускорения, а также полный перепад давления. Сравнить расчетные значения
полного перепада давления с измеренной величиной, равной 0,56 ата.-
2.9. Определить критическую массовую скорость паро-водяной смеси при
расходном массовом паросодержанин 26,9% и давлении 8,8 ата. Измеренное
значение равно 6180 кг/м2 • сек.
2.10. Водо-воздушная смесь истекает из большого бака через суживающееся
сопло с площадью выходного сечения 6,45 см2. Расход воздуха 1,3 г/сек,.
расход воды 4,5 кг/сек, причем фазы полностью перемешаны. .Температура
равна 21° С, а внешнее давление 1,03 ата. Чему равно давление в баке?
(Использовать уравнение Бернулли для гомогенной смеси н пренебречь
трением на стенках, а также влиянием силы тяжести.)
2.11. Рассмотреть процесс нзоэнтропического адиабатического гомогенного
равновесного истечения испаряющегося жидкого углекислого газа из большого
56 ГЛАВА 2
цилиндрического баллона, в котором он хранился под давлением 70 ата и
температуре 27° С. Определить расходное массовое паросодержанне, скорость,
плотность и массовую скорость в функции давления. Каково критическое
давление, при котором происходит запирание? Принять, что запирание
потока соответствует максимуму массовой скорости.
2.12. Рассмотреть ннзкоскоростной ламинарный поток газо-жндкостной смеси
в горизонтальной трубе. Пусть объемный расход газа равен Qg, а объемный
расход жидкости Q/. Падение давления в трубе чистой жидкости Ар/, а
падение давления двухфазного потока АрТр. Используя уравнение (2.58),
показать, что при p/^>Pg
ЬРтр , = 2<?g
Д/>/ Q/ '
2.13. Если жидкость загрязнена, то мелкие пузырьки газа ведут себя
подобно твердым сферическим частицам. Решая для этого случая задачу 2.12
н используя уравнение (2.57), показать, что
А'гя 1=3,5Q*'
А/7 ' Q/ '
2.14. Решить задачу 2.12 для турбулентного течения, принимая коэффициент
трення таким же, как н для чистой жидкости. Подсказывают ли решения
задач 2.12—2.14 метод представления данных для двухфазных потоков? (см.
работу [12].)
2.15. Шлам из частиц угля в воде перекачивается по горизонтальной трубе
диаметром 50 мм на расстояние 30 м со средней скоростью 3 м/сек. Шлам
является неньютоновской жидкостью с предельной- вязкостью при больших
скоростях сдвига 0,015 кг/м-сек. По объему шлам состоит на 45% из частиц
угля с плотностью 1350 кг/м3. Измерения, проведенные в той же трубе для
однофазного потока, привели к следующей зависимости коэффициента тре-
лня при турбулентном режиме течения:
Cf = 0,026 Re~0-12.
Чему равно падение давления? Как изменятся результаты, если число Рей-
нольдса определять не по предельной вязкости шлама, а по вязкости воды
при температуре 21° С?
2.16. Предполагается, что интенсивность гидравлического удара в
гидравлических линиях можно значительно уменьшить путем растворения в жидкости
воздуха в виде мелких пузырьков. Проанализировать возможности' зтой
идеи.
2.17. Вывести уравнения, описывающие течение адиабатически сжимаемого
потока запыленного газа в длинном горизонтальном трубопроводе, принимая
коэффициент трения постоянным (т. е. уравнение линий Фанно).
2.18. Вывести уравнения, описывающие течение запыленного газа в длинном
трубопроводе без трення, но с постоянным тепловым потоком на стенке
(т. е. уравнение линий Релея).
2.19. Объединить решения задач 2.17 и 2.18, чтобы получить соотношения
для прямого скачка уплотнения-в гомогенном потоке» запыленного газа.
2.20. Проанализировать двухфазное течение в сопле, показанном на фиг. 2.4.
Для несжимаемого гомогенного потока без фазовых превращений показать,
что
А — Рч -■
°\ Ах (А,
Р\—Рз-
1 1+х|_^_1
р/ л2 \ А2
~ 2Р/ [ А2 1)
1+-
•{-
V ?g
»* /J
ГОМОГЕННОЕ ТЕЧЕНИЕ
57
Как изменятся эти результаты, если сопло будет с острыми кромками,
вызывающими сужение струн?
2.21. На фнг. 2.5 схематически изображен предполагаемый способ
регулирования расхода нефти через регулирующее сопло-вентнль путем изменения
расхода воздуха, подаваемого через гребенку медицинских игл. Каково
соотношение между расходами воздуха и нефти Wg и W{i
Фнг. 2.4. Истечение
газо-жндкостной смеси нз сопла (задача 2.20).
2.22. Днл [13] измерил падение давления Ар при обтекании трубного пучка
двухфазным потоком. Его результаты были представлены в виде зависимости
Ap/Apg* от QtPfKQf +Qg) (>g, где Apg* —- падение давления при таком же
расходе Wf + Wg чистого газа. Показать, что теория гомогенного течения
при значении коэффициента трення, равном коэффициенту трення для
чистого газа, дает достаточно хорошее совпадение с данными, представленными;
на фнг. 2.6.
у/////,
Нефть
W(
Воздух \Wg
Фнг. 2.5. Регулирующее сопло-вентиль для двухфазного потока.
Температура и давление торможения нефти и воздуха равны 38° С и 28 ата. Принять,
что запирание происходит в горле, где Л*=0,645 см2.
2.23. Показать, что уравнение распространения для объемной концентрации,,
аналогичное уравнению (2.91), имеет внд
■ + w-
да
dz
Че
■ + (1
-.,]
Q.
Показать, что если t0 — момент начала испарения элементарного объема
жидкости ни — постоянная величина, то плотность этого элементарного объема
жидкости спустя время t будет равна
Р if, *о) = 9/е'
-s (<-<„)
2.24. Вывести соотношения для прямого скачка уплотнения в
изотермическом гомогенном пузырьковом'потоке (см. гл. 9).
2.25. Уравнение' (2.55) непригодно для расчета градиента давления в
испарителе, если кинетическая энергия жидкости достаточно велика, так как
в этом случае энтальпию нельзя определять непосредственно из теплового.
58
ГЛАВА 2
10°
ю-'
ю-2
т~3
i9 о
* 2*^°
О
°v
о Воздух-вода,1 опт, Pg/Pf =0,0072
п Пеитаи-пеитаи,44атн, p„/pf = 0,0212
\ 1 ■ 1
)
тога-
ю°
Qf
ю1
ю2
ю3
Pf
Qf+Qg Рэ
Фнг. 2.6. Корреляция Дила [13] для падения давления в турбулентном
горизонтальном двухфазном потоке при поперечном обтекании трубного пучка,
расположенного под углом 45° (задача 2.22).
баланса. Используя уравнение энергии, показать, что при равенстве нулю
потенциальной энергии н технической работы уравнение (2.55) принимает вид
2C/G2
dp
D?„
+
Gv21 dqe
G2 dA
h2\A dz Afm dz
Ф+.;
i cos 8
dz
>+<*[*£+<■-*>-£+•»(-£).]•
где
1
1 +G2v21/A2ipm
Каково условие запирания в этом случае?
2.26. Сравнить порядок величии различных членов в уравнениях (2.44) н
(2.55) для вертикального восходящего потока паро-водяной смеси при
массовом паросодержанни 10%, массовой скорости G = 5 • 10е кг/м2 • час и
плотности теплового потока на стенке 3 • 10б ккал/м2 • час в трубе диаметром 25 мм
с конусностью 1 : 100 при давлениях 0,1, 1, 10 и 100 ата. Будет лн для всех
этих условий иметь значение уточнение, сделанное в задаче 2.25?
2.27. Исследовать влияние вдува мелких твердых частиц в горячий газ перед
его расширением в сопле на тягу ракетного двигателя.
2.28. Какова скорость опорожнения корпуса ядерного реактора с
насыщенной водой под давлением 140 ата через отверстие диаметром 25 мм с
скругленными кромками? Принять условия запирания для изоэнтропйческого
адиабатического гомогенного истечения и рассмотреть следующие случаи: а)
равновесное течение; б) в потоке содержится только половина количества пара,
характерного для равновесного процесса; в) количество пара равно 0,1 от
значения для равновесного процесса; г) парообразования не происходит.
2.29. Вода и воздух движутся вверх по вертикальной трубе диаметром 50 лш
и длиной 3 м и вытекают в атмосферу с давлением 1,033 ата. Считая
поток гомогенным и изотермическим при температуре 21° С, рассчитать
давление на входе для следующих измеренных плотностей объемных расходов при
атмосферном давлении:
ГОМОГЕННОЕ ТЕЧЕНИЕ
59
jf, м1 сек
jg, м/сек
0,15
0,3
0,3
0,6
3
0,6
4,5
3
9
9
10,5
10,5
12
12
12
18
При каких условиях поток в выходном сеченнн запирается? Чему равно
давление на выходе в условиях запирания? Использовать численный метод
решения.
D
Фиг. 2.7. Демонстрационный эрлифт
(задача 2.30).
н
Вода
при
21°С \
1
oVoVo
°o0oO°°°°
«0000°
OOO
o0o
О oO
"."о"
о
°°o° о о о
0°00o0°
о оo0o°
S°oo
^- Стекающая
пленка
T Подъемная
-"-" труба
1
h
JflU
Bap6omep''Y
\W9
Воздух j
?рц2ГС
2.30. На фиг. 2.7 показано устройство демонстрационного лабораторного
эрлифта. Определить падение давления в подъемной трубе в зависимости
от расходов воды н воздуха Wf н Ws. Каково соотношение между Wg и Wf,
если £)=0,1 м, Л = 0,3 м, а #=0,6 м. При каких условиях мощность,
затрачиваемая на привод воздушного компрессора в расчете на 1 кг нагнетаемой
воды, будет минимальна?
2.31. Решить задачу 2.30 для случая, когда Л= 15 м, #=30 м, а диаметр
трубы увеличен до 150 мм. Использовать численный метод решения.
2.32. В условиях быстропротекающих процессов термодинамическое
равновесие, которому соответствует уравнение (2.52), не достигается. Принять, что
при быстром расширении энтальпия остается постоянной, а расходное
массовое паросодержанне является некоторой функцией времени, т. е.
х = х(р, t).
Проанализировать соотношения для одномерного течения, принимая для
указанной функции некоторые простые выражения, например степенной закон,
экспоненциальный закон, разложение в ряд и т. д.
Литература
1. Shapiro A. H., The Dynamics and Thermodynamics of Compressible
Fluid Flow, The Ronald Press Co., N. Y., 1953.
2. T ay lor G. I., Proc. Roy. Soc. (London), A148, 141 (1932).
3. E i n s t e i n A., Ann. Phys., 4, 289 (1906).
4. McAd ams W. H. et al., Trans. ASME, 64, 193 (1942).
^50 ГЛАВА 2
5. CicchittiA. et al„ Energi Nucl., 7, № 6, 407—425 (I960).
6 Dukler A. E. et al., A. I. Ch. E. J., 10, № 1, 38—51 (1964).
7. Meyer P. E., Wallis G. В., АЕС Rept NYO-3114-10, Sept. 1965.
8. Owens W. L., Jr., Am. Soc. Mech. Engrs, paper 41, vol. 2, 1961,
pp. 363—368.
9 Martinelli R. C, Nelson D. В., Trans. ASME, 70, 695 (1948).
10. M u s с e 11 о 1 a M., UKAEA Rept AEEW-R284, 1963.
11. Уоллис, Хнслн, Труды амер. общ-ва инж.-мех., серия С,
Теплопередача, № 3, 166 (1961).
12. Wallis G. В., Am. Soc. Mech. Engrs, paper 38, vol. 2, 1961, pp. 330—
340
13. Diehl J. E., Unruh С H., Am. Soc. Mech. Engrs, paper 58-HT-20, 1958.
14. Simpson H. C, Silver R. S., Symp. Two-phase Fluid Flow, London
Inst. Mech. Engrs, 1962, pp. 45—56.
3
РАЗДЕЛЬНОЕ ТЕЧЕНИЕ
3.1. Введение
В модели раздельного течения фазы могут иметь разные
свойства и скорости. Эта модель может быть исследована методами
различной степени сложности. Наиболее детальный анализ
основан на использовании уравнений неразрывности, движения и
энергии отдельно для каждой фазы, причем эти шесть
уравнений решаются совместно с уравнениями, описывающими
характер взаимодействия фаз между собой и со стенкой канала. В
простейшем случае допускается несоответствие только по одному из
параметров фаз, например по скорости, а уравнения сохранения
t записываются для среды в целом. Если число переменных,
подлежащих определению, превышает имеющееся количество
уравнений, вводятся корреляционные зависимости или упрощающие
предположения.
3.2. Стационарное течение, при котором фазы
рассматриваются совместно, но допускается несоответствие
их скоростей
Предположим, что одно из допущений теории гомогенного
равновесного течения опущено с тем, чтобы учесть различие
скоростей фаз. Теперь можно вывести уравнения неразрывности
движения и энергии для одномерного стационарного течения,
используя две скорости: V\ и v2. С другой стороны,
дополнительная степень свободы системы может быть учтена путем введения
в уравнения как объемного, так и массового паросодержания.
Далее будут рассмотрены некоторые из наиболее
целесообразных форм этих уравнений.
Уравнение неразрывности
Обычно подвод массы извне в поток не производится и
общий массовый расход остается постоянным. Следовательно,
W=Wi-\-W2=const. (3.1)
При отсутствии фазовых превращений Wi и №2 постоянны.
Массовый расход можно выразить в функций других пере-
\ менных многими способами. Например, если площади попереч-
62
ГЛАВА 3
ного сечения потоков фаз равны Л1 и Л2, то
U^p^A. (3.2)
W2=?2v2A2. (3.3)
Плотности потоков массы каждой фазы (массовые скорости)
в соответствии с соотношениями, выведенными в гл. 1, равны
Gi=Pi«i(l-«). (3-4)
G2=p2v2a'. (3.5)
Используя определение х, из двух предыдущих уравнений можно
получить два различных выражения для общей плотности
потока массы (массовой скорости) смеси
0=Р1^Т
0=р2'У2 —.
(3.6)
(3.7)
Уравнение движения
Используя соотношения между а, х, G, vu v2 и другими
переменными, можно получить множество различных форм
уравнения движения'. Например, один из вариантов уравнения
стационарного течения в круглой трубе имеет вид
dp
dz
D
+ 0-|-[x«2+(l-x)«1] + [aP2+(l-a)pI];cos9.
dz
(3.8)
Уравнение энергии
Уравнение энергии обычно записывается с использованием
массового паросодержания х:
W \
dqe
dz
dz
dz
[^+(1-*)*,] +
dz
-a-*)-r-
+ gcos9. (3.9)
Для решения приведенной выше системы уравнений, помимо
зависимостей между термодинамическими свойствами, требуется
еще два дополнительных соотношения. Хотя целесообразнее
было бы вывести эти соотношения из анализа течения каждого
компонента в отдельности, общий метод состоит в
использовании эмпирических зависимостей для т№ и а в функции" от
расходов, свойств жидкости и геометрии. Поэтому метод
решения определяется главным образом видом этих зависимостей.
РАЗДЕЛЬНОЕ ТЕЧЕНИЕ
63
Когда эмпирические соотношения используются для
заполнения пробелов в теории, следует помнить, что все они обычно
справедливы для условий адиабатического течения с малыми
градиентами давления. При больших скоростях фазовых
превращений и больших ускорениях потока они могут давать
значительную ошибку.
Общий метод корреляции напряжений трения на стенке
в случае газо'-жидкостных потоков был разработан Мартинелли
и др. [1, 2]. Действительное напряжение трения в случае
двухфазного потока представляется как произведение <f>2 на значение
касательного напряжения для соответствующего однофазного
потока. Например, один из методов, упомянутых в предыдущей
главе, связывает величину действительного напряжения трения
на стенке с его значением, которое имело бы место при течении
одной только жидкости с расходом, равным расходу сме'си.
Такой подход оправдан для процессов кипения и конденсации.
Определяя (Cf)f0 как коэффициент трения, соответствующий
потоку одной только жидкости, получим
-№г-2£*£&-. (а.о,
Корреляционное уравнение для объемного паросодержания
парожидкостной смеси данного вещества часто представляют
в виде
а = а(р, х). (3.11)
В этом случае эквивалент уравнения (2.44) имеет вид
__ dp /2(C/)/qG2"Wo ,r2dx_i (2xvg _ 0 1-х
dz —\ D *~U dz \\ T~ Z 1—a '
, I да \ Г (1-Х)» X2 1 J
02 dA r x2 , (1— лг)2 ]
dz
+««-(^.+-^))(ч-о"{4^+-
При решении уравнений, подобных этому, приходится
использовать численные методы.
Знаменатель уравнения (3.12) можно приравнять нулю для
определения условия запирания потока при отсутствии вскипа-
64 ГЛАВА 3
ния. С учетом уравнений (3.6) и (3.7) это условие можно
представить в следующем виде:
«"-f + O—J-f + l-^-LM-P^)-!. (3-13)
Однако это уравнение не обладает требуемой общностью, так
как член (да/др)х обычно определяется из корреляционных
уравнений, справедливых для умеренных значений градиентов
давления, когда силы трения преобладают над инерционными членами.
Более строгий анализ, ,в котором отдельно рассматриваются
уравнения движения каждой фазы, будет приведен позднее
(см. стр. 88). Если преобладают инерционные члены, то условие
запирания имеет вид
1_а / ' 'WO. (3.14)
Уравнения (3.13) и (3.14) дают сходные результаты только
в частном случае
Pgv2g=?fv2f. (3.15)
«•
Пример 3.1. Рассмотреть процесс течения вскипающей жидкости в сопле.
Пусть в начальном состоянии жидкость является насыщенной и ее
кинетическая энергия пренебрежимо мала, а массовое паросодержание в
области меньшего давления равно х. Считать течение адиабатическим,
равновесным н пренебречь влиянием силы тяжести. Чему равна
максимально возможная массовая скорость в сечении с паросодержаннем х?
Решение. Пусть перепад энтальпий между начальным и конечным состоянием
равен ДА. С учетом сделанных допущений из уравнения (3.9) получим
2Ah = xv2g + {l—x)v2f. (3.16)
Плотность потока массы можно выразить в зависимости от х, исключая
а с помощью уравнений (3.6) и (3.7):
a=(_JL-+±Z±\-\ (3.17)
\?gvg PfVf >
Обозначая i>g/i>/=n и исключая vf из уравнений (3.16) и (3.17), получим
2 ДЛО-2 = (— + '~Х V8 (х«2 + 1 - х). (3.18)
\n?g Р/ /
Если термодинамический процесс известен, то ДА и х определены, и
уравнение (3.18) можно использовать для исследования влияния п на
плотность потока массы G. В частности, G будет иметь максимум при
0 = -4-(2AhG-2) = 2nx(-^ + -^^-)2 -
dn ч ' V. Щг р/ )
-2(J«ia+l-*)-^—(-г- + -Ц:£-). (3-19)
РАЗДЕЛЬНОЕ ТЕЧЕНИЕ , 65
т. е. когда
\ n?g ?f MP/ n2?g)
(3.20)
Член в первых скобках не может быть равен нулю, н единственное
нетривиальное решение уравнения (3.20) имеет вид
Лз =
Р/
?g
или
vf
1L
?g
(3.21)
Следовательно, максимальное значение G в соответствии с уравнением
(3.18) будет равно
(2 ДА)''*
{-'макс — "
[О-*)!$'+xl?W*
(3.22)
Незначительные отклонения величины п от значения, определяемого
уравнением (3.21), оказывают очень слабое влияние на величину G.
Если запирание определяется максимально возможным расходом
через выходное сечение данного сопла, то можно показать, что оно
происходит при G, определяемом уравнением (3.22). Как видно из фиг. 3.1,
3 >о<
43
ю-
1 1 1 1 1111
= х=0,2 . у
У
- У
1 1 1 ММ
1 1 1 1 11II.
/;У
КХ'=0,4
i i i
\
-
Z
1 1117
ю
100
,ата
100
Фнг. 3.1. Сравнение измеренных массовых скоростей паро-водяной смесн
в режиме запирания с расчетами по уравнению (3.22) для двух интервалов
паросодержання х [13].
Муди [3] довольно успешно использовал уравнение (3.22) для сравнения
с имеющимися данными для. паро-водяных потоков. Так как в
термодинамическом процессе х изменяется не очень сильно и величина ДА
максимальна для изоэнтропического процесса, то максимальное
значение G соответствует случаю обратимого и изоэнтропического вскипания.
На графиках, показанных на фиг. 3.1, по оси абсцисс отложено
измеренное давление рт на срезе сопла. Так как поток был заперт, то это
давление не было равно давлению окружающей среды. На фнг. 3.2
приведены значения рт в функции от начальных параметров торможения
Ра и А0, полученные из дополнительного условия максимума величины G
в функции давления р2 в соответствии с зависимостью (3.22). Таким
образом, рт соответствуют следующему условию:
-Ц-=0 при ъ=рт. (3.23)
5 Заказ К» 162
66
ГЛАВА 3
Если противодавление меньше рт, то считается, что поток заперт, и G
определяется из уравнения (3.22) с использованием термодинамических
свойств, соответствующих рт- В' общем теоретические значения,
приведенные на фиг. 3.2, имеют тенденцию к превышению данных,
полученных Фауске [4], который нашел, что приближение (рт1ро) «0,55 является
достаточно точным.
200
200 300 400 500 600 700
Энтальпия торможения h0, -ккал/кг
Фиг. 3.2. Местное статическое давление и параметры торможения при
максимальном расходе паро-водяной смеси в функции начальных параметров
торможения [3].
Несмотря на привлекательность данного метода анализа, теория
максимального расхода при заданной кинетической энергии (или
соответственно минимума кинетической энергии при заданном расходе)
совершенно некорректна в деталях. В потоке образуется намного меньше
пара, че,м это следует из сделанного допущения о равновесии.
Отношение скоростей, вычисленное по уравнению (3.21), не является точным.
Использование уравнений (3.22) и (3.23) оправдано тем, что они
определяют максимум максимумов, который не очень чувствителен к
исходным допущениям.
РАЗДЕЛЬНОЕ ТЕЧЕНИЕ
67
Определение касательного напряжения на стенке
и объемного газосодержания
Уравнения (3.1), (3.8) и (3.9) в общем случае не могут быть
решены без дополнительных соотношений для касательного
напряжения на стенке (или потерь давления на трение) и
объемного газосодержания. Один из возможных путей состоит в
использовании допущений теории гомогенного течения, при этом
рассматриваемые уравнения сводятся к уравнениям, полученным
в предыдущей главе. Другой способ, свойственный модели
раздельного течения, связан с корреляционным методом,
разработанным Мартинелли и др. [1, 2] в период 1944—1949 гг.
Возможно, наиболее простым оказывается соотношение для
потерь давления на трение. Предполагается, что при заданных
расходах газа и жидкости известен способ определения
градиентов давления, которые имели бы место при течении по трубе
только одной из фаз. Обозначим эти градиенты давления как
(dp/dz)g и (dp/dz)f. Теперь определим новые переменные в
функции отношения действительного градиента давления dp/dz при
отсутствии фазовых превращений, ускорения и массовых сил
к величине градиента давления для каждого компонента в
отдельности, т. е.
Если нет потока газа, то
1
л2 =1. -fr=0. (3.26)
Аналогично если нет потока жидкости, то
-Г=1' -т-=0- С3-27)
4 4
В критической точке, где фазы неразличимы, соотношение
между j>f и j>g принимает вид
ф. ф
А ' (3.28)
g
для ламинарного потока и
ШЧ(-£Г-. <^>
5*
68
ГЛАВА 3
для турбулентного потока, подчиняющегося закону Блазиуса для
гладких труб.
Очень простую модель раздельного течения можно также
получить, исходя из предположения о том, что обе фазы
движутся без взаимодействия в двух горизонтальных разделенных
цилиндрах и что суммарное сечение этих цилиндров -равно
сечению данной трубы. Потери давления в каждом из
воображаемых цилиндров такие же, как и в реальном потоке, и
обусловлены только трением, причем они рассчитываются по теории Ъд-
Щ
Фиг. 3.3. Корреляционная схема Мартинелли на основе уравнения (3.30).
нофазного течения. Эта модель раздельного цилиндрического
течения [5] напоминает исходную модель Мартинелли, однако
обладает тем преимуществом, что может быть аналитически
исследована до конца, в то время как модель Мартинелли
ограничена полуэмпирическим решением. Результатом такого
подхода является соотношение (см. задачи 3.3, 3.4 и 5.12, а также
пример 3.2)
/ 1 \1/« / I \1/Л
Ы) +Ы) -1- (з-зо)
где п=2 для ламинарного течения; л = 2,375—2,5 для
турбулентного течения при использовании коэффициента трения; п =
=2,5—3,5 для турбулентного течения, рассчитываемого по
теории пути перемешивания. Уравнение (3.30) согласуется с
уравнениями (3.26) — (3.29), как это видно из фиг. 3.3.
Уравнение (3.30) определяет однопараметрическое
семейство кривых, которые можно использовать при анализе
экспериментальных данных.
РАЗДЕЛЬНОЕ ТЕЧЕНИЕ 69
Пример 3.2. Разработать модель раздельного цилиндрического
турбулентного течения, считая коэффициент трения для каждой фазы постоянным.
Решение. Пусть движущийся газ имеет форму цилиндра радиусом rg, а
жидкость— цилиндра радиусом rj.~ Следовательно, объемные концентрации
газа и жидкости равны
г2 г2
где г0—действительный радиус трубы.
Градиент давления газа в воображаемом цилиндре равен
dp
dz
-С/Р (*')*-
rg М « )
Cftg?g 1
ГО а'*
и цмеет то же значение, что и действительный градиент давления.
Первый множитель в правой части идентичен (—dp/dz)g;
следовательно, из уравнения (3.24)
Л2- l
Аналогично для жидкости
*2
1
Pf (!-«)•/•
Исключая а из этих выражений, получим
что соответствует уравнению (3.30) при и=2,5.
Чтобы устранить неизвестный градиент давления из обоих
корреляционных параметров, целесообразно ввести новую
переменную в виде их отношения, т. е.
Ф2„ (dp/dz)f
*--$-тщ- (3-31)
Величина X2 показывает, в какой степени поведение двухфазной
смеси ближе к жидкости, чем к газу. Таким образом, можно
ожидать существования некоторой зависимости между X2 и
объемным газосодержанием, как это показано на фиг. 3.3. Из-за
значительно большего удельного объема газа изменение
объемного газосодержания несимметрично относительно Х=1, и, как
следует из графика, при понижении давления соответствующие
прямые имеют больший угол наклона.
Так как падение давления можно рассчитать по теориям
ламинарного и турбулентного течения как для жидкости, так и для
газа, то возможны четыре различные комбинации. В кольцевом
потоке течение газа редко бывает ламинарным, если поток
70
ГЛАВА 3
жидкости турбулентный, и поэтому такое сочетание не вызвало
интереса. На фиг. 3.4—3.6 представлены данные Мартинелли
для низких давлений, соответствующие остальным трем
комбинациям потоков; там же приведены корреляционные кривые.
Как видно из фиг. 3.7, удовлетворительное согласие для всех
режимов течения обеспечивается с помощью уравнения (3.30)
при п = 3,5; для турбулентного режима лучшее совпадение дает
значение п = 4.
т—i и i i in .—i—i i м 111
II I i i i i l I I I l i i i i 'I l l I I i i I I I I I I | i i l l i II
0,07 0,1 i ю too
X
Фиг. 3.4. Сравнение потерь давления, рассчитанных по уравнению (3.30) при
п =4, с экспериментальными данными Мартинелли для
турбулентно-турбулентного потока [5].
ф — безразмерные потери давления; X — параметр Мартинелли. соотношение
Мартинелли [1]; • уравнение (3.30), я=4; • экспериментальные данные.
На фиг. 3.8 показана эмпирическая зависимость Мартинелли
для объемного газосодержания при низких давлениях.
Корреляционная кривая очень хорошо описывается
уравнением
а = (1+Х0'8)-0'378. (3.32)
Хотя соотношение Мартинелли было получено в
специфических условиях горизонтального течения без фазовых
превращений и значительных ускорений, им часто пользуются при
расчете объемного газосодержания и потерь давления на трение,
вводя его в уравнение (3.12), даже если указанными и другими
дополнительными эффектами пренебречь нельзя. Такая
операция приводит к прогрессивно увеличивающейся погрешности,
так как составляющая потерь давления на трение уменьшается
100
Фиг. 3.5. Сравнение потерь давления, рассчитанных по уравнению (3.30)
при и=3,5, с экспериментальными данными Мартинелли для вязкого потока
жидкости и турбулентного потока газа [5].
ф„— безразмерные потери давления; X — параметр Мартинелли. соотношение
Мартинелли [1]; уравнение (3.30), л=3,5; ■ экспериментальные данные.
ТОО
Фд
Ю-
'1 ' т—i-i-i 1 1 1
1
1—1—гтТТТТ
i i i i i 111
i ' ii
i i i i i 111
i i i i i ш
1 Г" Г 1 1 11*
i i i i i 111
0.07
0,1
ю
100
Фиг. 3.6. Сравнение потерь давления, рассчитанных по уравнению (3.30),
с экспериментальными данными Мартинелли для вязко-вязкого течения [5].
соотношение
ф^—безразмерные потери давления; X — параметр Мартинелли;
Мартинелли [1]; уравнение (3.30), я=2,75; - - - - уравнение (3.30), я=3,5;
■ экспериментальные данные.
s
100
10
II1
_
-
-
~
z
~i
1 1 1 1 1 II
1 1 1 ! 1 1 1
..,._
1 1 1 1 1 1 II
•\ ' \ 1 1 1 1 1 1
1 1
■ *d?
i i 11 и
jjv
III!
1 III 1 yi
У
, /
У-
Г
:
i .i i i 1111
o\ol
0,1
1
X
10
too
Фиг. 3.7. Сравнение потерь давления, рассчитанных по уравнению (3.30)
при я=3,5, с экспериментальными данными Мартинелли для всех режимов
течения [5].
ф — безразмерные потери давления; X — параметр Мартинелли; уравнение (3.30),
л=3,5; • экспериментальные данные.
100
Фиг. 3.8. Соотношение Мартинелли для объемного газосодержания [1].
(1 — а) — объемная концентрация жидкости; X — параметр Мартннеллн.
РАЗДЕЛЬНОЕ ТЕЧЕНИЕ 73
пропорционально другим членам. Соотношение Мартинелли по
существу устанавливает баланс касательных напряжений и
потерь давления. Если значительны массовые и инерционные силы,
требуются более точные методы анализа.
Пример 3.3. Решить пример 2.5, используя соотношения Мартинелли—Лок-
карта.
Решение. Число Рейнольдса, вычисленное для условий течения в трубе одной
только жидкости, равно 23 000; следовательно, поток жидкости
турбулентный и коэффициент трения равен 0,005. Тогда градиент давления
будет равен
( dp \ 2 • 0,005 . 94,52 . 1,р
- \-t)f = 2Д8 = З6 duH'CMZ-
Аналогично для потока газа число Рейнольдса оказывается равным
24 000; следовательно, коэффициент трения можно принять равным
0,005 и градиент давления будет равен
■(■
dp \ 2 • 0,005 • 1,7652 . о,80 • Юз ,„ , , ,
1 — =10 дин/смл.
dz jg 2,48
Теперь можно вычислить параметр Мартинелли Xtt
Udp,dz)fVI, /36 У/*
Xtt'V¥pWh\ -VW) -1,897-
Из фиг. 3.4 и 3.8 находим
0^ = 6,0, 1—<х = 0,29.
Вычислим теперь потери давления на трение
АРр=ф1[—%-) £ = 36 • 10 • 45,6 • 1,02 • 10-6=0,0165 ата.
Падение давления под действием силы тяжести
Ара = 9,8 ■ 102(0,29 ■ 1 + 0,71 • 1,25 • 10-3) . 45,6 • 1,02 • 10-6 = 0,01325 яга.
При расчете падения давления из-за ускорения возникают
трудности, связанные с большой чувствительностью этой величины к точности
вычисления малых изменений а. Однако маловероятно, чтобы эта
величина превысила падение давления из-за ускорения в гомогенном потоке.
Поэтому можно воспользоваться формулой (2.79) из примера 2,5, которая
дает завышенное значение Ар:
0,0165 + 0,01325 -поо,
Д/,== —ош =°'0337 ата-
Обе рассчитанные величины — объемная концентрация и потери
давления— превышают измеренные значения (0,23 и 0,02Г ата). Это
обусловлено тем, что фактический режим течения — снарядно-кольцевой,
причем жидкие прослойки движутся со скоростью газа, и, следовательно,
объемная концентрация жидкости будет меньше. В примере 10.5 будет
показано, как получить точное решение.
74
ГЛАВА 3
Течение паро-водяной смеси в прямых трубах
По-видимому, вследствие большого практического значения
течение паро-водяной смеси исследовалось в большей мере, чем
любой другой двухфазной системы. Имеются детально
разработанные соотношения на основе метода Мартинелли и созданы
удобные таблицы и номограммы. Значения величины ф/02,
входящей в соотношения Мартинелли—Нельсона, уже были
приведены в табл. 2.2. На фиг. 3.9 представлен график, позволя-
0 20 40 60 80 ЮО
Фиг. 3.9. Объемное паросодержание в зависимости от массового паросодер-
жания паро-водяного потока при различных давлениях [2].
а — объемное паросодержание; ж —массовое паросодержание.
ющий быстро найти объемное паросодержание в зависимости,
от массового паросодержания и давления. Эти эмпирические
соотношения совместно с уравнением (3.12) и допущением о
тепловом равновесии позволяют путем численного интегрирования
определить падение давления.
Во многих случаях возможны значительные упрощения.
Например, для прямой трубы постоянного сечения (т. е. при
постоянном G) интегрирование уравнения (3.8) дает
L
Д/?=4" \twdz + G [xvg+(\ -x)vf]o +
о
L
+ g-COs9j[ap^+(l-a)P/]fife. (3.33)
о
РАЗДЕЛЬНОЕ ТЕЧЕНИЕ
75
При постоянном тепловом потоке, а также постоянных
величинах механической работы, кинетической и потенциальной
энергии уравнение (3.9) для двухфазной области принимает
вид
dx
4Ф
dz
DQh
■fs
(3.34)
т. е. массовое паросодержание линейно увеличивается с
расстоянием. Принимая х = 0 при z = 0, считая коэффициент CfQ посто-
юоо
Ю 100
Давление, ата
Фиг. 3.10. Параметр ~Ф^0 [уравнение (3.36)] в зависимости от давления и
конечного массового паросодержания паро-водяной смеси [2].
янным и используя уравнения (2.5) и (3.10) при допущении
о постоянстве свойств, получим уравнение (3.33) в виде
L
+ £COs9j[(l-a)p/-r-ap^]fite. (3.35)
о
Члены, заключенные в фигурные скобки, могут быть рассчитаны
корреляционным методом Мартинелли—Нельсона. Результаты
расчета первых двух членов уравнения (3.35) представлены
* 76
ГЛАВА 3
на фиг. 3.10 и 3.11 в виде параметров
<£/о=— J ф/odx
(3.36)
г2=-
Р/
*2 Р/
(1
Рг
;?--•]■
(3.37)
Последний член в уравнении (3.35) можно вычислить, выполняя
интегрирование данных, полученных с помощью фиг. 3.9. Такое
Ю '00
Давление7ата
500
Фиг. 3.11. Параметр г2 [уравнение (3.37)] в зависимости от давления и
конечного массового паросодержания паро-водяной смеси [2].
графическое представление параметров обеспечивает очень
быстрый способ определения потерь давления при течении
пароводяной смеси.
Другие (в целом более точные) значения параметров ф/0 .
ф/02, а и руг2 для воды при высоком давлении были получены
Томом [6] при использовании гораздо большего количества
данных, чем в исходном соотношении Мартинелли—Нельсона. Эти
результаты приведены в табл. 3.1 и 3.2.
Таблица 3.1
Уточненные значения параметров Мартинелли по данным Тома [6]
Массовое
паросодер-
1
5 '
10
20
30
40
50
60
70
80
90
100
Давление, arfl
17
j.2
Ф/0
2,12
6,29
11,1
20,6
30,2
39,8
49,4
59,1
68,8
78,7
88,6
98,86
^2
*/о
1,49
3,71
6,30
11,4
16,2
21,0
25,9
30,5
35,2
40,1
45,0
49,93
42
Ф/0
1,46
2,86
4,78
8,42
12,1
15,8
19,5
23,2
26,9
30,7
34,5
38,30
I2
1,11
2,09
3,11
5,08
7,00
8,80
10,6
12,4
14,2
16,0
17,8
19,65
88
Ф/0
1,10
1,62
2,39
3,77
5,17
6,59
8,03
9,49
10,19
12,4
13,8
15,33
I2
Ф/о
1,03
1,31
1,71
2,47 ,
3,20
3,89
4,55
5,25
6,00
6,75
7,50
8,165
147
А2
Ф/0
1,21
1,48
2,02
2,57
3,12
3,69
4,27
4,86
5,45
6,05
6,664
12
Ф/о
1,10
1,21
1,46
1,72
2,01
2,32
2,62
2,93
3,23
3,53
3,832
210
а2
Ф/о
1,02
1,08
1,24
1,40
1,57
1,73
1,88
2,03
2,18
2,33
2,480
"а2
Ф/о
1,06
1,12
1,18
1,26
1,33
1,41
1,50
1,58
1,66
1,740
Таблица 3.2
Уточненные значения параметров Мартинелли по данным Тома [6]
Массовое
паросодер-
1
5
10
20
30
40
50
60
70
80
90
100
Давление, ата
17
а
0,288
0,678
0,816
0,910
0,945
0,964
0,975
0,984
0,990
0,994
0,997
1
Hff
0,4125
2,169
4,620
10,39
17,30
25,37
34,58
44,93
56,44
69,09
82,90
98,10
42
а
0,168
0,512
0,690
0,833
0,895
0,930
0,952
0,967
0,979
0,988
0,995
1
Гг9/
0,2007
1,040
2,165
4,678
7,539
10,75
14,30
18,21
22,46
27,06
32,01
37,30
88
а
0,090
0,340
0,521
0,710
0,808
0,866
0,908
0,936
0,959
0,976
0,989
1
г2Р/
0,0955
0,4892
1,001
2,100
3,292
4,584
5,958
7,448
9,030
10,79
12,48
14,34
147
а
0,0476
0,207
0,355
0,553
0,679
0,767
0,832
0,881
0,920
0,952
0,978
1
Hff
0,0431
0,2182
0,4431
0,9139
1,412
1,937
2,490
3,070
3,678
4,512
5,067
5,664
210
а
0,0213
0,102
0,193
0,350
0,480
0,589
0,682
0,763
0,834
0,895
0,951
1
r%ff
0,0132
0,0657
0,1319
0,2676
0,4067
0,5495
0,6957
0,8455
0,9988
1,156
1,316
1,480
78
ГЛАВА 3
Дальнейшая разработка этого метода Барокши :[7] сделала
возможным его использование для других жидкостей в широком
диапазоне массовых скоростей. Параметр ^>/02 в этом случае
представляется как функция комплекса, определяемого
физическими свойствами фаз, (n//ng)°'2/(p//pg), для заданного значе-
Ю~5
Натрий.
10
w-3 /о-2
WflMf*KPtlPg)
зоо юоо ноо
10'
540 600
Ру(шЯш| "Г. |
315
Ртуть.'С i
, !
700
600
1
400
1,
900 10001100
800 900 ЮОО
i l l
500 600 700 760
1 III
50 100
Bob-c'lL
ио
_|—
200
374
I
Фиг. 3.12. Соотношение Барокши [7] для параметра Ф/q2 при G= 1360 кг/м2 • сек.
ния G=1360 кг/м2-сек (фиг. 3.12). Для получения величины
фт2, соответствующей другим массовым скоростям, данное
значение j>f02 умножается на поправочный множитель Q, значения
которого приведены на фиг. 3.13. Причудливый характер кривых
фиг. 3.13 дает отличный повод для насмешек тем скептикам,
которых не воодушевляют эмпирические методы. Однако при
отсутствии лучшей информации они все же позволяют инженеру-
проектировщику определить рабочие характеристики.
1,6
1,4
1.2
1.0 -
0,8 -
0.4
18
1,6
2
7,4
12
1.0
0,8
0,6
-
-
-
I
сек
Л
ТО
О
00
ч>
II
у>
си
? i
8
о
ч
II
to
I
I
f^=^sr—
аГ——
80
80
60_^—-
I
I
Паросодержание, %
■==—~—— ГО__ У,
20 ' *~~~~-^~^£^'
100
^__4(Г"ч-->. j><^
20 J^>>^^^—С~*
S2^^^^
1
1 л
Л\20
/ Ю\
// 5,4о\\
60 \\
во =*^;
5 У////
, отп40 3о60
-
V -
ш-
—
0,0001
0,00! 0,01
(н/РдРУШРд)
Фиг. 3.13. Прправочный множитель Q для соотношения Барокши,
учитывающий влияние массовой скорости, в зависимости от безразмерного
комплекса (Hf/Hg)°'2/((p//pg) [7].
80
ГЛАВА 3
3.3. Одномерное раздельное течение, при котором фазы
рассматриваются в отдельности
Чтобы уменьшить число эмпирических соотношений,
используемых для расчета раздельного течения, необходимо увеличить
число исходных уравнений. Для этого достаточно вместо
использования только уравнений для смеси в целом сформулировать
законы сохранения для каждого компонента в отдельности.
Таким образом, увеличение точности метода достигается ценой его
усложнения.
На данной стадии целесообразно сохранить самую общую
форму используемых уравнений, которая будет служить основой
для обобщенного представления в последующих главах. Это
потребует введения некоторых символов и использования концепций,
которые могут показаться весьма абстрактными, причем их
смысл трудно уяснить без анализа более конкретных случаев.
Для облегчения усвоения материала будут рассмотрены
соответствующие примеры.
Уравнения неразрывности
Уравнения сохранения массы, или неразрывности, можно
записать в следующей достаточно общей дифференциальной форме:
-^- [Pi (1 — «)] + V [Pl (1 — <х) vt] =5-! 2+^, (3.38а)
-^-(p2a)+V(p2aV2)=-S12+S2, (3.386)
где Si 2 — изменение массы за счет фазовых превращений в
единице объема потока; Si и S2— изменения массы от внешних
источников — обычно равны нулю.
Для одномерного потока после интегрирования по сечению
канала уравнения (3.38) приобретают вид
-!L-[Pl(\-*)A]+-^[PlQ-*)vlA]*=§(S12+S1)dA, (3,39а)
-^-(p2eA)+-^-[p2a«2A]=J(-512+52)rfA. - (3.396)
Соответствующие интегральные формы этих уравнений можно
получить точно таким же способом, как и в случае
однофазного потока.
РАЗДЕЛЬНОЕ ТЕЧЕНИЕ 81
Уравнения движения
Уравнения импульса, или движения, или закон Ньютона, для
обеих фаз трехмерного потока можно записать в следующей
достаточно общей векторной форме:
pi(T+viVV')=bi+f'~v^ (3-40а>
P2(^r+v2W2) = b2+f2-Vp, (3-406)
где bi и Ьг-—массовые силы, действующие на единицу объема
каждого компонента, а Vp— некоторый средний градиент
давления, или объемное напряжение, которое определяется видом
системы и обычно равно термодинамическому давлению одной
или обеих -фаз. Величины fi и f2 введены для обозначения
остальных сил. Так как уравнения (3.40 а) и (3.40 6)
выражают баланс сил (или количества движения), то величины
/вводятся в общем виде, а способ их определения будет зависеть от
конкретного режима течения и условий задачи.
Например, если уравнения (3.40 а) и (3.40 6) применяются
к элементу несжимаемой ньютоновской жидкости, состоящей
только из одного компонента, который не испытывает фазовых
превращений, то получается результат, характерный для
обычного вязкого течения:
fi=PiV2v„ (3.41а)
f2=[x2V2v2. (3.416)
Для получения квазинепрерывной модели двухфазного
течения f обычно рассчитываются для элемента, большего, чем
частицы, капли или пузырьки. В этом случае f представляет
собой полную усредненную поверхностную силу,_ Детствующую на
единицу объема грвдьПГ неучитываемую градиентом "давления.
Составляющие силы f: сопротивление, эффекты присоединенной
массы при относительном движении, взаимодействие между
частицами, изменение импульса из-за конденсации или испарения
и т. п. Определение f в некоторых случаях требует особой
осторожности. Например, большинство сил «сопротивления»,
действующих на взвешенные в потоке частицы, определяется
экспериментально и включает совместное влияние Vp и f; кроме
того, фазовые превращения изменяют гидродинамическое
сопротивление, а при изменении внешних сил изменяется форма
пузырьков или капель и, следовательно, сила сопротивления.
6 Заказ М> 162
82
ГЛАВА 3
Величины Fi и F2 эквивалентны силе f, но относятся к
единице объема не фазы, а всего потока, т/е.
/=Wi(l-«), (3.42)
F2=/2a. (3.43)
Если эти силы целиком обусловлены взаимным гидравлическим
сопротивлением, то, поскольку действие и противодействие
равны,
F, = -F2=Fl2. (3.44)
В случае одномерного течения уравнения (3.40а) и (3.406)
в проекции на ось, совпадающей с направлением движения,
принимают следующий вид:
Пример 3.4. В кольцевом потоке жидкость движется в виде пленки по стенке
трубы, а поток газа занимает центральное цилиндрическое ядро. Пусть
диаметр трубы равен D, а касательные напряжения на поверхности
раздела фаз и на стенке равны соответственно т, и т». Для
вертикального симметричного потока (положительное направление движения —
вверх) записать выражения для величин Ff, Fg, ff, fg, bf и bg, т. е.
вывести уравнения движения.-
Решение. Диаметр газового ядра потока равен DY&", где а — истинное
объемное газосодержание. Следовательно,
„ —zi%D Ya 4х; уа
е 7tD2/4 D
_ T,itD Ya — zw%D __ 4 (тг Ya — zw)
t~ 7tD2/4 , — D
Соответствующие значения ff и fg равны
Ff 4 (т, V^~ - т J
// =
fg =
1—<x D(l—<x)
Fg 4t,-
Кроме того,
dY*'
b/ = -?fg
bg = -?gg-
РАЗДЕЛЬНОЕ ТЕЧЕНИЕ 83
Таким образом, уравнения движения (3.45) и (3.46) для
рассматриваемого случая имеют вид
4хг dp
?g
dvf
dt
dvg
+
+
Vf
Vg
dvf
dz
dvg
ft?
DYa
dz
Пример 3.5. Уравнение Кармана — Козени для потерь давления на трение
при вязком течении сквозь плотный слой сфер диаметром d при
истинной объемной концентрации жидкости е имеет вид
дР \ _.1йп ^'/о 0-£)2
•(*■),-•»
<Р
где //о — приведенная скорость жидкости относительно частиц. Для
обозначения объемной концентрации жидкости использован символ е, так как а
обычно используется для обозначения истинной объемной концентрации
дискретной фазы. Вывести выражения для величий ff и fs. Индексы
•| и s относятся соответственно к жидкости и частицам. Чему равны
составляющие силы fs, обусловленные действием жидкости и
действием частиц?
Решение. Так как мы рассматриваем только потери давления на трение,
то инерционные и гравитационные члены из уравнений (3.45) и. (3.46)
исключаются, что дает
'-'-№).
Сила f3, действующая на частицы, суммируется из двух сил: силы,
обусловленной действием жидкости (fs)t, и силы, обусловленной действием
частиц (fs)s. Таким образом,
/* = (/*)/ + (/*)*•
Сила взаимодействия между жидкостью и частицами "определяется,
уравнением (3.44). Следовательно,
/> = //* =-(A)/О-*)-
Используя эти соотношения, получим
180М/0 (1-е)2
// = "
rf2 e3
(Л)/—180—52 i2—'
If \ — ion ^^° 1~S
После того как величины f определены, их можно использовать при
решении более сложных задач (встречающихся при расчетах
псевдоожижения и уплотнения слоев), когда другими членами в уравнениях (3.45)
и (3.46) пренебречь нельзя.
Пример 3.6. В псевдоожиженном слое частицы взвешены в восходящем
потоке жидкости и взаимодействие между частицами пренебрежимо мало.
6*
84 ГЛАВА 3
Используя результаты, полученные в предыдущем примере, вывести
выражение для приведенной скорости жидкости, при которой
происходит псевдоожижение слоя с объемной концентрацией жидкости е.
Каков в этом случае градиент давления в слое?
Решение. Условие псевдоожижения имеет вид
(/»), = 0.
Используя уравнения (3.45) и (3.46) без инерционных членов, получим
Путем совместного решения этих уравнений находим
d2g (.9s — Р/) ез
J/0-
180^ 1
~4г=^[ер/+(1-£)р*]-
Таким образом, градиент давления в слое оказывается равным просто
его весу (частиц и жидкости) на единицу высоты слоя.
3.4. Течение с фазовыми превращениями
В данном разделе будут выведены общие уравнения
одномерного раздельного движения в канале при наличии
фазовых превращений. В отношении величин f для большей
определенности примем, что силы сопротивления стенок канала
движению компонентов 1 и 2, приходящиеся на единицу объема
потока, равны соответственно FWi и FW2. Пусть сила
взаимодействия компонентов F12 действует на компонент 1 в направлении
движения, а на компонент 2 в противоположном направлении.
Так как компоненты имеют различные скорости, любое фазовое
изменение приведет к изменению количества движения.
Массовая скорость фазовых превращений на единицу длины равна
Wdx/dz, а изменение скорости равно Vi—vi. Следовательно,
сила, с которой связано увеличение количества движения из-за
фазовых превращений, приходящаяся на единицу объема
канала, будет равна
(^—Oi)-x-§-=(^-^)0-S-- (3-47)
Из приведенных рассуждений неясно, какую часть этой силы
следует приписать потоку каждого из компонентов.
Действительно, это распределение будет зависеть от типа процесса
(например, кипение или конденсация) и характера взаимозависи-
РАЗДЕЛЬНОЕ ТЕЧЕНИЕ 85
мости между процессом фазовых превращений и
гидродинамическим механизмом, обусловливающего появление силы Fi %•
Например, сила сопротивления, действующая на испаряющуюся
каплю, будет зависеть от скорости ее «испарения».
Чтобы сохранить общность формулировок, обозначим через
т] часть полной силы, определяемой уравнением (3.47), которая
соответствует потоку компонента 2; тогда доля этой силы 1 —
tj характеризует поток компонента 1. Выбор величины ц для
разных систем может быть различным.
Таким образом, если массовые силы связаны только с
гравитацией, уравнения движения для стационарного течения имеют
следующий вид:
Pi«i
Р2^2
dv\
dp
dz
dv2
dz
dp
Pig" COS S
dz
dz
Pag" C0S6
| ^12—Fw\
1 1—a
^12 + Fw4
1--Ч
1 —a
- 1 Л».
(Vt-vJQ
dx
~dz~
(3.48)
(Vi — vJQ
dx
dz
(3.49)
Уравнения (3.48) и (3.49) можно объединить несколькими
способами. Особенно удобны следующие два:
1. Умножим уравнение (3.48) на 1—а, а уравнение (3.49)
на а и сложим их. В результате получим уравнение движения
смеси, которое можно было бы получить, рассматривая баланс
количества движения для обоих компонентов совместно:
(l-a)p^^L
ip2v2 ■
dvn
dp
dz
dz
-g-COs6[Pl(l-a) + p2a] —
-(F^ + F^-^-v^Q
dx
IF
(3.50)
Далее, если последний член правой части перенести в левую
часть и использовать уравнения (3.2) — (3.5), а также (3.47),
то будет получено уравнение
1 d , Т17, _. , TV7 „ ч jip_
dz
A dz
■ (Wxvx+W2v2) = -
■gCOs6[Pl(l—a) + p2a]-
(3.51)
выражающее баланс количества движения для смеси в целом.
2. Вычтем уравнение (3.49) из (3.48), тогда
Pi*»i
~~dz~~
■Рг^г
dv2
dz
Pi)L
= g-cos6(p2-
/?12 n ^L. (
u dz V
w\
wl
a(l-a)
(Z>2-*>,)• С3'52)
86 ГЛАВА 3
Это уравнение не содержит градиента давления и может
рассматриваться как уравнение относительного движения, так как
оно характеризует разность скоростей увеличения кинетической
энергии фаз.
Обычно в контакте со стенкой находится только один
компонент, и соответствующее касательное напряжение на стенке
можно вычислить корреляционным методом. Сила
взаимодействия между компонентами является функцией относительной
скорости и также может быть определена. Однако точное
решение полученных уравнений очень часто связано с огромными
трудностями.
Пример 3.7. Используя корреляционную схему Мартинелли для газо-жид-
костного потока, вывести выражения для величин Ffg и FWf, если
Fwg=0, так как жидкость смачивает стенку канала по всей длине
(кольцевое течение).
Решение. Соотношение Мартинелли устанавливает баланс между
величинами F и градиентом давления, так как влияние инерции, гравитации и
фазовых превращений не учитывается. Поэтому из уравнений (3.48) и
(3.49) следует
F - FfS dp_
wf~
dz
Представляется более целесообразным выразить силу, действующую на
жидкость, через свойства жидкости, а силу, действующую на газ, через
свойства газа. Используя уравнения (3.24) и (3.25), получим
Если ФУ и Фг2 определяются по соотношению Мартинелли как
функции а, то FWf и Ffg могут быть выражены как функции известных
параметров, а значение а следует определить из решения уравнений (3.48) и (3.49),
даже если нельзя пренебречь влиянием силы тяжести и инерции.
Уравнения количества движения можно объединить с
уравнениями неразрывности, чтобы получить обычное
газодинамическое уравнение. Рассмотрим вначале компонент 2. Напишем
тождество
№ dz 2 dz V2 dz ■ (6-b6>
Изменение плотности второй фазы обычно связано с изменением
давления и характером термодинамического процесса, в
котором участвуют компоненты. Например, для чистого вещества
в равновесных условиях плотности фаз зависят только от
давления.1 Для системы, состоящей из газа и частиц, как это было
РАЗДЕЛЬНОЕ ТЕЧЕНИЕ
87
показано в примере 2.2, можно использовать уравнение
состояния для псевдогазовой среды.
В любом случае можно записать
^=АР1£- - (3.54)
dz др/д?2 v '
при условии, что др/дрг определяется исходя из заданных
условий.
Определим псевдозвуковую скорость с2 для компонента 2
по уравнению
«!=-&■ (3-55>
Объединяя уравнения (3.53) — (3.55) и используя затем
уравнение (3.49), после преобразований получим
+ Fl2 + Fw2 +j_(V2_Vi)GA>Li (3.56)
Перепишем уравнение (3.3) в виде
Wx=Aap2v2. (3.57)
Дифференцируя последнее, получим
1 dx 1 dA 1 da 1 d (f2v2)
x dz A dz ' a dz ■ р2г>2 dz
(3.58)
Исключим d(p%v2)/dz с помощью уравнений (3.56) и (3.58).
Тогда
dp 1 (л v* \ 1 dx 1 da. 1 dA ,
dz п ,,2 I е2 I х dz a dz A dz
hv2 \ С2
[p2gcos6 + f" + y"'a + 3-iv2-Vl)Q*L]. (3.59а)
Аналогичное уравнение для другой фазы будет иметь вид
,.2
dj> ]__(■, _ _^i_ \ 1 dx . 1 da 1 dA
dz p v2 I c2 1 ! —x dz ~ 1 — a dz A dz
1
. ^kcose-^^L+i^K-.OG^]. (3.596)
Приведенные выше уравнения напоминают общие уравнения
одномерного стационарного однокомпонентного потока, за
исключением эффектов фазовых превращений и наличия дополни-
88 ГЛАВА 3
тельной степени свободы, связанной с переменной величиной а.
Запирание отдельных компонентов происходит при vi = ci или
02 = С2, но это не обязательно соответствует «запиранию» общего
потока, так как величина а не связана однозначно с
локальными условиями.
Для исследования условий запирания потока в целом
исключим da/dz с помощью уравнений (3.57) и (3.58), что дает
dp
dz
P2*l
1 -
«I
1—а
Pi^l
1 -
«?
1 dA
A dz
wl
w\
-gcosi
dx
П
1—а
h^2
Plw?
dz
2 I
2
1 —a
+ /=".
1 2
1
■0(г»2-г»,)
1-4
Pl«?
Pi»?
P2W2
(3.60)
Так как f[2H dx/dz не зависят от градиента давления,
условие запирания имеет вид
1-
hvt
1 -
$
Р,«?
1
«?
=0.
(3.61)
Все множители, кроме заключенных в скобки,
положительны, поэтому одно из отношений, либо М22 = с>22/с22, либо Mi2 =
= Vi2/ci2, должно быть меньше единицы, в то время как другие
больше единицы. Таким образом, один из потоков является
сверхзвуковым, а другой — дозвуковым.
Условия запирания существенно меняются, если происходит
вскипание (фазовое превращение, обусловленное изменением
давления). Этот эффект требует введения зависимости членов
с dxjdz в правой части уравнения (3.60) от градиента давления.
В общем случае если термодинамический процесс известен
{или постулируется), то величина дх/др может быть определена
dx __ dx dp
dz ' ,др dz
(3.62)
Объединяя уравнения (3.62) и (3.59 а), получим условие
запирания при вскипании
hv2
■(1-м!)-
1
piwi
■ 0-м?)-
дх
др
1—a
1— X
-hG(v2-v{)
1-7,
Pi«?
P2^
=0. (3.63)
РАЗДЕЛЬНОЕ ТЕЧЕНИЕ 89
Этот результат зависит от величины ц, за исключением
случая
Р1г»2=р2г»22. (3.64)
3.5. Течение с преобладанием инерционных сил
В тех случаях, когда двухкомпонентный раздельный поток
быстро разгоняется в сопле, в уравнениях (3.48) и (3.49)
преобладают инерционные члены и члены, связанные с перепадом
давления. В этом случае изменение скоростей компонентов
может быть взаимосвязанным. Например., для стационарного
одномерного потока без фазовых превращений при f = 0
dp dv\ dvo /о «г-ч
В частности, если начальные скорости компонентов малы и
изменение плотности незначительно, скорости истечения при
расширении связаны простым соотношением
V2
= Vf- ■ (3-66)
Это выражение не является универсальным, но дает хорошее
приближение в условиях быстрого расширения при низких
числах Маха.
Пример 3.8. Воздух и вода вытекают из большого бака через сужающееся
сопло с площадью выходного сечения 6,45 см2. Расходы фаз, измеренные
при атмосферном давлении, составляют 32,77-10"3 м3/сек (воздух) и
0,442-Ю-8 м?/сек (вода). Чему равно давление в баке и скорости
истечения компонентов, если противодавление равно атмосферному
(1,033 ата), а температура равна 21°С. Трением иа стенках пренебречь.
Решение. Задача в сформулированном выше виде является неопределенной
вследствие отсутствия информации о методе смешения компонентов и
результирующей структуре потока. Приходится ограничиться
рассмотрением двух предельных случаев: 1) между компонентами отсутствуют
силы взаимодействия (т. е. fi=f2 = 0); 2) силы взаимодействия между
компонентами столь велики, что относительное движение компонентов
отсутствует (т. е. поток является гомогенным).
Принимая первое допущение, воспользуемся уравнением (3.65) и
вначале пренебрежем изменением плотности воздуха (в дальнейшем при
необходимости это можно будет учесть). Интегрируя уравнение (3.65),
получим
р,!»2 poll2,
Д/>=-^=^. (3.67)
90
ГЛАВА 3
Пусть индекс 2 относится к воздуху, причем его объемная концентрация
в выходном сечении сопла равна а. Как обычно,
— т*
V2-
н
а
Подстановка (3.68а) и (3.686) в (3.67) дает
Pitf
hJl
откуда
( 1 _ а)2 а2 '
a h \ Р2 /
" Р2
Следовательно,
У2 Г Р2 /
По условиям данной задачи
у, = 0,685 м1 сек, h = 50.8 м1сек>
р, = 103 жг/^з, Р2 = 1,22 кг/л3.
Следовательно,
- = 0,72
1
1 +(0,685/50,8) (103/1,22)'
Полетами эти значения в (3.68а) и (3.686), получим
Щ-
0^- = 2,45 м\сек, v2 = ^r = 70,5 м/сек.
0,Jo
0,72
1,22 ■ 70,52 f 02 1q_5_oj0309 ama.
(3.68а)
(3.686)
(3.69)
(3.70)
(3.71)
Тогда падение давления по формуле (3.67) составит
д^_ Ю3-2,452 iQ2 10_5 = оозоб а/ия
или (для проверки)
с постоянным сечением принимает вид
^ dv __j£_ (3.72)
а <fe ~ dz '
РАЗДЕЛЬНОЕ ТЕЧЕНИЕ
9!
илн при использовании уравнения (2.32)
«--£-—-£■ <3-га>
Принимая на время, что среда несжимаема, и выполняя интегрирование,
получим уравнение Бернулли для гомогенной смеси
-±-?mv2 = Ap. {3.74 >
Записывая уравнение (3.74) через / и G, находим
JG 51,485 (50,8 • 1,22 + 0,685 • Iff») , ло п1по
Ар= -+<у-= - = —- 1,02 • 10-5 = 0,192 ama.
Видно, что результаты, полученные двумя методами, значительно
отличаются друг от друга. Так как соответствующей организацией
смешения жидкостей обеспечивается почти любой' перепад давления в
указанном диапазоне, то, очевидно, имеются широкие возможности
проектирования устройств на двухфазных потоках. Например, если по
экономическим соображениям необходимо обеспечить минимальный перепад
давления, то, по-видимому, выгодно предусмотреть разделение воздуха и
воды в баке таким образом, чтобы поверхность раздела находилась на
уровне сопла и в нем осуществлялось расслоение течения с небольшим
трением между компонентами. С другой стороны, если требуется
большой перепад давлений (например, для ограничения утечек нз сосуда),
следует организовать тщательное смешение компонентов с образованием
смеси, близкой к гомогенной. Вряд ли при таких высоких объемных
газосодержаниях пузырьковый поток будет устойчивым. По-видимому,,
необходимо создание капельной дисперсной среды. Скорости воздуха,
полученные в данном примере, достаточны для эффективного распыления.
Пример 3.9. Проанализировать расслоенное течение воздуха и воды в сопле
Лаваля, если процесс изоэнтропический и адиабатический. Пренебречь
трением, фазовыми превращениями и уносом капель. Показать, в част-
-ности, каким образом максимально возможный расход воздуха связан
с расходом воды при заданных начальных условиях и геометрии горла.
Решение. Максимальный расход будет определяться условиями запирания
общего потока в хорле.
Пусть начальные параметры торможения равны р0/ для жидкости
и pog, Tog для газа.
Так как вода несжимаема, то справедливо уравнение Бернулли, и
ее скорость в сечении с давлением р будет равна
Соответствующий расход через единицу площади определяется
следующим образом:
^-=[2(А>/-/>)Р/]Ь. (3.76)
Так как W) — константа, дифференцируя уравнение (3.76), получим
92
ГЛАВА 3
Газ будет изоэнтропически расширяться в сопле, изменение сечения
•которого определяется разностью между общей площадью и сечением,
занятым жидкостью. В функции от местного давления это сечение
определяется хорошо известным уравнением [8]
Ут0.
Og / POg
W„
Pog
1/Т
2т
#g(7-l)
1
р \(т-1)/т1"
Pog)
(3.78)
где v — показатель адиабаты для газа.
С помощью уравнений (3.76) и (3.78) можно определить
зависимости между расходами и общей площадью сечения канала. При
запирании в горле газ имеет сверхзвуковую скорость, а жидкость — дозву-
Фиг. 3.14. Раздельное течение газа и жидкости в сопле Лаваля в режиме
запирания.
ковую. Изменение площади по длине сопла показано на фиг. 3.14.
Заметим, что давления торможения обоих, потоков не обязательно
одинаковы, хотя локальные давления предполагаются равными.
Из уравнения (3.59а) следует, что уравнение для газа,
соответствующее уравнению (3.77), имеет вид
dAg I dA l 1 da ^ 1^ (i_M|)jgg.. (3.79)
1
dz
A dz
dz
*A
dz
Считая воздух совершенным газом, можно заменить pgvg2 на yp№g2,
что, как обычно, дает
1
dAc
dz
_1_
М?
— 1
1 dp
IP dz
В горле dA/dz равно нулю. Следовательно,
dA,
■ +
dA
£_ = 0.
(3.80)
(3.81)
dz dz
Из уравнений (3.77) и (3.80) получаем уравнение (3.61) в другом виде:
1 Л , 1А/
№
1 +
2 (Poftp—!)
= 0.
(3.82)
РАЗДЕЛЬНОЕ ТЕЧЕНИЕ 93
Далее, если А* —площадь горла, то
Af + Ag = A*.
Исключая Ag из уравнений (3.82) и (3.83), получим
Af = A*
1 +
2(1-1/м2)(» lp-l)
Кроме того, из уравнения (3.76) имеем
Af=Wf[29f(pof-
Р)У
■Ч*
(3.83)
(3.84)
(3.85)
Совместное решение уравнений (3.84) и (3.85) дает значение
давления в горле и площадь сечения, занимаемого жидкостью. Путем
подстановки в соответствующие уравнения можно определить другие
переменные.
Увеличение Wf
Фиг. 3.15. Результаты совместного решения уравнений (3.84) и (3.85)
из примера 3.9.
Графический метод представления результатов показан на фиг. 3.15.
В соответствии с уравнениями (3.84) и (3.85) строятся зависимости Af
от р. Уравнение (3.84) не содержит расхода жидкости. Mg является
функцией только отношения давлений в газовом потоке в соответствии
с уравнением
•е-т^т-Г""-']-
В уравнении (3.84) площадь-Л/ равна нулю, если Мг2=1, и это
соответствует запиранию только газового потока. Если М.е> 1 и
возрастает, то р уменьшается, а Л/ возрастает.
С другой стороны, в соответствии с уравнением (3.85) Af возрастает
с увеличением р. С увеличением Wf точка пересечения кривых
смещается влево. В пределе жидкость целиком заполняет канал, давление
в горле равно нулю и газовый поток отсутствует.
Зная р a Ag из фиг. 3.15, по уравнению (3.78) можно найти расход
газа.
94
ГЛАВА 3
Простейший метод определения геометрического места
максимальных расходов состоит в использовании в качестве параметра давления
в горле. Сначала по уравнению (3.84) рассчитывается величина Af,
затем по уравнению (3.85) вычисляется Wf, по (3.83) определяется Ag
и по (3.78) — Wg.
3-ю<]
2-10'
^ he
2000
Wg
-rj-, кг/мг- сек
Фиг. 3.16. Соотношение критических расходов воздуха и воды при
расслоенном течении и одинаковом полном давлении (а>/=/)о«)-
V=-l,4, i?„=29,34 м[град, Г0=2Г С, р/ = 103 кг!м3, (Mg)t — число Маха газовой фазы,
а, — объемное газосодержание и Л* — площадь горла сопла в режиме запирания общего
потока.
■'«■
Допустимые значения расходов находятся слева от линий,
показанных на фнг. 3.16, где указаны границы, рассчитанные описанным выше
способом.
Этот метод решения можно сравнить с аналогичным методом
исследования раздельного совместного течения газов [9].
РАЗДЕЛЬНОЕ ТЕЧЕНИЕ
95
3.6. Применение принципа возрастания энтропии
к расчету коэффициента т]
До сих под мы преднамеренно обходили вопрос о величине
ч, связанной с эффектами фазовых превращений компонентов,
считая ее такой переменной, которую можно выбрать в
соответствии с рассматриваемыми условиями. Особенно интересный
анализ обусловлен требованием изоэнтропийности потока [10].
Это дает возможность определить конкретное значение у\. Когда
потребуется раскрыть физический смысл результатов, будем
называть фазы «жидкостью» и «газом».
Сначала, пренебрегая технической работой и работой сил
трения, запишем уравнение сохранения энергии для системы
в целом
(3.87)
Если через 5S обозначить прирост энтропии на единицу
длины из-за необратимых процессов и теплообмена, то баланс
энтропии для стационарного одномерного потока будет иметь
вид
Ss=W-§r[xs2+(l-x)s1]. (3.88)
Преобразуем уравнение (3.51), используя определение х,
G~£r[^2+(l-^)%] = --^--i§rcose[ap2+(l-a)p1]-
-(^+^2)- (3,89)
Из термодинамики известно, что для гомогенного чистого
вещества в состоянии равновесия
Tds^dh—-dp. (3.90)
Более того, для двухфазной смеси
Td[xs2+(l-x)s1]=d[xh2 + (\-x)hl]-fe+-±==f-)dp.
(3.91)
Хотя^уравнение (3.91) обычно выводится для частного
случая гомогенной смеси, оно тем не менее является
алгебраическим соотношением между термодинамическими свойствами,
которое справедливо для любого изменения состояния при
условии фазового равновесия. Следовательно, можно разделить
95 глава з
уравнение (3.91) на dz, а затем, подставляя необходимые
величины из уравнений (3.87) — (3.89) и используя соотношение
между х и а, в конечном счете получить
TSX=
dq,
dt
--\-*(\-*)(v2-vx)A j^cos6(Pl-p2)+
_, ./ 1 \\ dx dv22 d^l)
+
+ GA(Fwl + Fw2)(f+-^f-). (3.92)
Последний член в уравнении (3. 92) можно преобразовать
следующим образом:
QA(Fwl + Fj)(-± + ±=f-) = A [az>2 + (l -«)*>,] (Fwl + Fw2)=
= [vt+a (v2 - г»,)] AFwl + [v2- (1 - a) (v2 - vx)\ AFw2=
=VlAFwl+v2AFw2+Aa(l -«^-^(-^L—*?-). (3.93)
Объединяя уравнения (З. 92) и (3. 93), получим
TS,
dqe
dt
-vlAFwl-\rv<iAFtia-\-
+-
+ a(l-a)(7»2-z»1)^{gcos9(Pl-p2)-f-i^
«Й
+
dx
dz
Щ
dz
dv{
dz
(3.94)
В уравнении (3.94) учитываются четыре различных причины
прироста энтропии: 1) теплообмен, 2) трение жидкости о стенки,
3) трение газа о стенки, 4) относительное движение.
Прирост энтропии вследствие относительного движения
представляет собой новое явление для тех, кто обычно занимается
однофазными потоками, и поэтому часто не учитывается.
В уравнении (3. 94) этот механизм прироста энтропии
представлен последним членом, который равен нулю только при
нулевом значении одного из сомножителей. Рассматривая
сомножители по порядку, получим следующие условия отсутствия
прироста энтропии вследствие относительного движения:
а=0 —однофазный поток жидкости,
(1—а)=0—однофазный поток газа,
v2—vl—-гомогенный поток.
РАЗДЕЛЬНОЕ ТЕЧЕНИЕ 97
Единственное нетривиальное решение имеет место при
равенстве нулю множителя, заключенного в фигурные скобки, откуда
после преобразований получим
p^i dz -hgpicoso-t- 2 1_e dz _f- ,__a —
= №-^ + gP2cos6+4 Qto-^ -g-+-^f-. (3.95)
Чтобы раскрыть физический смысл уравнения (3.95), обозначим
обе части его через X, умножим' левую часть на 1—а, правую на
а и сложим их. В результате получим
1 /1 \ йЩ i dv2 , - . „ dx .
+ ^cos6[(l-a)Pl + ap2]+Fa,1 + ^2. (3.96)
При сравнении с уравнением (3.50) получается простое
соотношение
Х=--^. (3.97)
Следовательно, уравнение (3.95) эквивалентно уравнениям
движения каждой фазы при отсутствии трения между ними,
т. е.
№-^— ■g-P^co.8-^—т "'V"' -£-• (3-99)
Таким -образом, очевидно, что для постоянства энтропии сила,
представленная уравнением (3.47), должна быть разделена
между компонентами поровну, причем каждый из компонентов
испытывает силу реакции, равную —'/г G(v2—Pi) (dx/dz) на
единицу объема канала. Так как члены в уравнениях движения
представляют собой силы, отнесенные к единице объема
соответствующего компонента, эти силы нужно разделить на
объемную концентрацию каждого из них.
Следовательно, для изоэнтропического потока следует
выбирать величину ri равной 7г- Полученное уравнение применимо
в равной степени к процессам испарения и конденсации и
абсолютно симметрично. На первый взгляд может показаться
весьма странным, что силу реакции, обусловленную испарением,
следует делить между жидкостью (или твердыми частицами) и
паром. Большинство авторов обычно приписывают всю силу
реакции потоку пара при испарении и потоку жидкости при
конденсации. Однако объяснение следует искать в двумерных
эффектах, которые не учитываются при одномерной идеализации.
7 Заказ № 162
98 ГЛАВА 3
Действительно, локальные скорости потоков' пара и жидкости,
тангенциальные к поверхности раздела, будут одинаковыми,
а скорость в поле течения будет изменяться. Если можно было
бы получить решение для трехмерной задачи в общем виде, это
расширило бы наше представление об обратимых процессах
испарения и конденсации.
Условие равного распределения между компонентами силы,
определяемой уравнением (3.47), можно получить также из
рассмотрения обратимости. Если сила не будет распределена
поровну, то уравнения для случаев испарения и конденсации
будут различными и систему нельзя будет вернуть в исходное
состояние путем противоположного обратимого процесса.
Описательно этот результат можно сформулировать
следующим образом: если вы намерены использовать одномерную
модель течения и удовлетворить требованию постоянства
энтропии системы, то для соблюдения совместимости всех
уравнений вы должны учесть последние члены в уравнениях (3.98)
и (3.99).
Предположим теперь, что между потоками пара и жидкости
происходит необратимый обмен количеством движения. Этот
процесс можно представить аналогично предложенному Рей-
нольдсом [17] для описания турбулентного обмена импульсом
массы М в единице объема за единицу времени, которая
последовательно входит в контакт с паром и жидкостью и делит
импульс с каждой из фаз. Результирующая сила в направлении
движения для жидкости равна
F,2={v2-v,)M, (3.100)
а соответствующая сила для газа равна
-Fl2=-(v2-vl)M. (3.101)
Общая сила, действующая на жидкость в единице объема
потока и обусловленная относительным движением, при
допущении, что процессы обратимого и необратимого переноса
импульса можно представить линейной функцией, равна
(v2 - vt) \м - -J- G (dxldz)]
и аналогично для газа
(*»2-*»1)[--М—j-G (rfx/dz)l.
Другой способ описания состоит в рассмотрении потоков
массы и импульса через поверхность раздела фаз. Если
периметр поверхности раздела равен Pt в трубе с сечением А, то
площадь поверхности на единицу объема составляет Pi/А. Если
РАЗДЕЛЬНОЕ ТЕЧЕНИЕ 99
через е0 обозначить необратимый рейнольдсов поток *> через
единицу площади поверхности раздела фаз, то
в„=4г- (ЗЛ02)
Массовая скорость испарения с единицы поверхности
раздела фаз равна
т=-р^-£-=т1ш2=—т21. (3.103)
Результирующие силы, действующие на жидкость и пар в
единице объема, теперь можно записать в виде
Ъ = -(Ъ—Ог)-%-(*о+-!!г), (3-105)
Разделим уравнения (3.104) и (3.105) соответственно на
1—а и а, чтобы определить силы, приходящиеся на единицу
объема каждого компонента, и, подставляя результаты в
уравнения движения (3.98) и (3.99), получим
dv\ dp 0 Fwi
Pi
Л(1
^(Ч—оМ^—т)' (3.106)
dvn dp 0 Fw?
P2*2^?-=--2f—Panose f-
^(*2-*.)(*«> +it). С3--107)
Эти уравнения симметричны и применимы для процессов
фазовых превращений в любом направлении в зависимости от знака
т. Последний член в каждом уравнении можно рассматривать
как соответствующим образом модифицированное выражение
для межфазного касательного напряжения (и обмена
импульсом), которое обусловлено фазовыми превращениями. Другой
вывод этих же самых результатов будет дан в гл. 7.
Интерпретация полученных результатов представляет
интерес с точки зрения термодинамики необратимых процессов.-Член,
содержащий т, связан с упорядоченным массообменом и не
') Понятие рейнольдсова потока впервые было предложено Рейнольдсом
в 1874 г. [17]. Оно использовалось Нуссельтом [18], Сильвером [19—21] и
особенно широко — Сполдингом [11] при исследовании проблем горения
и совместного тепло-,и массообмена. В приложении к двухфазным потокам
это понятие используется сравнительно недавно [10, 22—24]. К сожалению,
во многих учебниках данный вопрос не рассматривается.
7*
100 ГЛАВА 3
дает вклада в прирост энтропии. Однако рейнольдсов поток
ео является мерой внутреннего хаотичного массопереноса,
необратимости и возрастания энтропии. Например, подставляя
уравнения (3.106) и (3.107) в (3.94), получим
^=Т + ^ч + ^-2+(«2 ~ *>i)2 %Pf (3.108)
Заметим, что в уравнении (3.108) члены, связанные с
касательными напряжениями, на стенке, не обязательно
положительны. Так, при вертикальном снарядном течении второй член
может быть отрицательным, в то время как третий член равен
нулю. Однако, согласно второму закону термодинамики,
последний член должен быть достаточно большим, чтобы
результирующая диссипация оказалась положительной.
По-видимому, аналогичным путем можно объяснить
приращение энтропии вследствие энерго- и массообмена между фазами
при конечной разности температур и потенциалов Планка.
Такой подход дает возможность распространить методы Сполдинга
[11] на двухфазные течения и разработать очень эффективный
метод анализа таких процессов, как многокомпонентные
химические реакции, горение, а также других практически важных
задач. Понятие рейнольдсова потока, по-видимому, может быть
ключевым в таком обобщенном анализе.
Последний член в уравнении (3.108) можно рассматривать
как силу (на единицу объема), равную (v2—Vi)eoPi,
умноженную на разность скоростей v2—v\, что соответствует обычным
представлениям о возрастании энтропии в линейных системах.-
Так как приращение энтропии из-за межфазного трения
(в потоке с одинаковыми начальными скоростями фаз) равно
нулю в двух предельных случаях: при ео = °о (гомогенный
поток) и при 8о = 0, очевидно, оно имеет максимум где-то между
этими значениями. Например, при расширении двух
несжимаемых жидкостей из состояния покоя при отсутствии фазовых
переходов, гравитации и трения на стенках приращение
энтропии будет равно нулю либо при t>iA>2 = l, либо в соответствии
с уравнением (3. 66) при V\lv2 = (рг/pi)1/2-
3.7. Уравнения энергии
Общее уравнение сохранения энергии фаз при одномерном
течении можно сформулировать, рассмотрев некоторый
контрольный объем канала длиной dz. Например, для компонента 2
д
dt
Лар2 е
-~[AaP2v2{h+v22)} =
=^(Че+Ят -•*>,- «О А - A?2*v2g cos 6, (3.109)
РАЗДЕЛЬНОЕ ТЕЧЕНИЕ 101
где qe, </т,—ws и хюх — соответственно средние скорости
притока энергии в единицу объема канала вследствие тепло- и
массообмена, механическая работа и работа сил трения. Так как
указанные процессы могут протекать при взаимодействии
компонентов между собой и каждого из них со стенкой канала, то
формулировка уравнения в общем виде становится чрезвычайно
сложной. Ввиду того что данная книга посвящена прежде всего
проблемам гидромеханики, а не тепло- и массообмена, мы не
будем рассматривать и выводить уравнение энергии в общем
виде. В соответствующих случаях будут приняты необходимые
упрощения.
Пример ЗЛО. Каков вид уравнения, описывающего изменение внутренней
энергии твердых частиц в одномерном стационарном потоке газа?
Пренебречь тепло- и массообменом, трением на стенках и механической
работой.
Решение. Будем считать частицы компонентом 2. Так как поток
стационарный и массообмен отсутствует, то
4p2w2=W2 = const. (3.110)
Уравнение (3.109) в данном случае принимает вид
р2аг;2
^(fh+^-l+gcosi
~qe~w. (3.111)
Так как частицы несжимаемы и единственной массовой силой является
сила тяжести, то уравнение (3.46) можно представить в виде
^ d
-.+ g-cos6+—-{pv2)
Р2
dz 2 ^s ' dz
= h. (3.112)
Объединяя уравнения (3.111) и (3.112) и используя термодинамическое
соотношение /t2—e2+pv2, получим
! de2 , /о \
?2«V2[-4r+-^-) = qe-™x (з.цЗ)
или с учетом уравнения (3.43)
7 — W — F~V~
(3.114)
de2 9e-wz~F2v2
dz P2<W2
Если члены, характеризующие механическую работу wx и F2V2, малы
по сравнению с членом, характеризующим теплообмен qe, то при qe,
вычисленном по теории теплообмена, нетрудно определить величину
den/dz. В частности, если коэффициент конвективного теплообмена между
частицами и жидкостью равен ft, температуры равны Т\ и Гг, а
сферические частицы имеют диаметр d и постоянную удельную теплоемкость
сг, получим
^А^-Га^-даг (3-115)
И, следовательно,
J*ZjL= 6* (Г,-Г2)• 3.116)
dz c2?2v2d
102 " ГЛАВА 3
В общем случае wx и F2V2 не обязательно малы и не обязательно
равны по величине и противоположны по знаку, как это показано в
следующем примере, поэтому вывод энергетических соотношений может
быть достаточно сложным.
Пример 3.11. Рассмотреть одномерное стационарное течение без массообмена.
Принять, что механическая работа и теплообмен отсутствуют, но учесть
силу взаимодействия между компонентами Fi 2 на единицу объема
потока (действующую на компонент 1 в направлении его движения).
Проанализировать уравнения энергии' для компонентов, лренебрегая силой
тяжести.
Решение. В правой части уравнения (3.109) остается только один член,
обусловленный работой сил трения, а также его аналог для другой фазы.
Для рассматриваемых условий получим
PI О -«) "1 -£-(*!+ -5-] = -»,,• (3-117>
dz
'«?
PijMb-jj- |*2 +-y-)= WrT ' (ЗЛ18)
Заметим, что скорость, с которой компонент 2 производит работу,
равна Fi 2V2. Однако компонент 1 воспринимает только часть этой работы,
равную F\ 2t»i. Следовательно, из-за относительного движения происходит
«диссипация» работы, равная для единицы объема
2> = Fl2(v2 — vi). . (3.119)
Эта диссипация равна произведению скорости прироста энтропии на
температуру и проявляется в виде «тепла», однако в рамках данного
анализа нельзя ответить на вопрос, как распределить эту энергию между
уравнениями (3.117) и (3.118), чтобы сохранить баланс.
Один из способов преодоления этой трудности заключается в
усложнении исследования путем введения дифференциального анализа, не
допускающего разрыва непрерывности в скорости. Это приводит к
исследованию трехмерных полей температуры и скорости, «коэффициента
восстановления» и других величин и явлений, выходящих за рамкн
одномерного анализа.
Более простое решение состоит в распределении диссипируемой
энергии между компонентами, как в случае подвода энергии от
источника тепла, т. е.
d ( $\
dz
d
P2<W2 —£
( 4 \
I /*2+ -5- l=— Fl2v2 + (1 —Z)Fl2(v2 — vi), (3.121)
где £ — просто удобный параметр, который выполняет такую же
функцию, как и параметр г) в уравнениях (3.48) и (3.49).
Заметим, что правые части уравнений (3.120) н (3.121) можно
представить как произведение силы на некоторую; средневзвешенную
скорость £»2+(1—£)»i, которую можно рассматривать как эффективную
скорость на поверхности раздела фаз.
При одновременном протекании процессов обмена теплом, массой
и количеством движения строгий анализ процессов энергообмена очень
усложняется. Удобным способом упрощения задачи служит модель рей-
нольдсова потока, которая будет рассмотрена в гл. 7.
- РАЗДЕЛЬНОЕ ТЕЧЕНИЕ 103
Задачи
3.1. Для контрольного объема одномерного потока вывести уравнения
количества движения для компонента 2 в виде
-щ- (tW2^) + -^ (Р2«Ф0 = AF'2 + *АЬ2,
где Fz — общая результирующая поверхностная сила, действующая на
компонент 2 в единице объема канала.
Объединить это уравнение с уравнением неразрывности и получить
уравнение (3.406). Как объяснить появление кажущейся составляющей силы,
обусловленной фазовыми превращениями?
3.2. Доказать, что для модели раздельного течения в цилиндрах при
ламинарном режиме в уравнении (3.30) /1=2.
33-. Доказать, что для модели раздельного течения в цилиндрах при
турбулентном режиме п=2,5, если коэффициент трения принимается постоянным,
и га=2,375, если применяется уравнение Блавиуса.
3.4. Решить задачу 2.10, используя модель раздельного течения.
3.5. Рассмотреть гомогенный поток с постоянным коэффициентом трения.
Выразить потери давления на трение в функции параметров Мартинелли.
Для различных отношений плотностей фаз построить зависимость Фе от X и
сравнить ее с представленной на фиг. 3.4.
3.6. Решить задачу 3.5, используя другие допущения относительно
коэффициента трення для ламинарного и турбулентного потоков.
3.7. Используя результаты, полученные в примере 3.6, а также уравнения
(3.48) и (3.49), показать, как распространить корреляцию Мартинелли на
вертикальный поток, если влиянием инерции и фазовых превращений можно
пренебречь. Какие из кривых, постоянных а или постоянных dp/dz, будут
выглядеть аналогично зависимости (dp/dz) g от (dp/dz) ft
3.8. Для течения в прямой трубе можно начать анализ не. с уравнения
энергии, как это сделано в примере 3.1, а с уравнения количества движения.
Показать, что если суммарная сила трения на стенке, деленная на площадь
поперечного сечения трубы, равна F, то
Ьр— F = G [xvg — (1 — х) Vf].
Используя уравнение неразрывности, показать, что G имеет максимум при
1/2
заданном значении F, если Vg/vf=(pflpg) . Кроме того, показать, что
наибольшее из максимальных значений G соответствует случаю F=0, т. е. изо-
энтропическому течению. Каков этот абсолютный максимум величины G
в функции от Кр и х?
Сравнить расчетные величины этого максимума с результатами расчета
в примере 3.1 для конкретных случаев истечения насыщенной воды.
Результаты не должны сильно различаться.
Эта модель минимального потока количества движения впервые была
предложена Фауске [4].
3.9. Вместо того, чтобы искать максимум величины G в функции отношения
Vg/vf для заданных потоков количества движения или энергии, возможно,
целесообразнее решить совместно уравнения количества движения и энергии.
Сделать это, представив зависимости G от vg/Vf для расчетов по величине
энергии и по величине количества движения (пример 3.1 и задача 3.8). Какова
разница в типичном случае расширения насыщенной воды от давления 140,6 до
84,4 ата, если результаты определяются по пересечению этих кривых или
по их максимумам?
ЗЛО. При каком значении п в зависимости от давления уравнение (3.30)
наилучшим образом описывает эмпирические кривые, представленные на
фиг. 3.17? Представить результаты в виде функции п от приведенного
104 ГЛАВА 3
давления (давления, отнесенного к критическому), т. е. обработать результаты
в виде, облегчающем экстраполяцию данных для других жидкостей.
3.11. По горизонтальному трубопроводу внутренним диаметром 200 мм,
длиной 3,45 м, иа входе которого давление равно 72 ата, пропускается
870 м3/сутки нефти и 6,4 кг/сек газа. Температура в трубопроводе равна
26,7° С. Плотность и вязкость нефти равны соответственно 0,779 г/см3 и
0,574 спз. Плотность и вязкость газа равны соответственно 55,7 кг/м3 и
0,014 спз. Определить потери давления в этом трубопроводе. Измеренное
значение равно 2,25 ата.
3.12. а) Определить критический расход паро-водяной смеси с паросодержа-
нием 26,9 вес. %, истекающей из горизонтальной трубы внутренним
диаметром 6,83 мм под давлением 8,8 ата. Сравнить полученную величину с
экспериментальными данными Фауске [12] (6,18- 103 кг/м2-сек).
Фиг. 3.17. Эмпирическая зависимость параметра Ф/ от давления и X для
воды [2].
б) Рассчитать распределение давления на конечном участке трубы длиной
1,22 м при массовой скорости смеси 6,18- 103 кг/м2 -сек. и сравнить результат
с экспериментальными данными Фауске [12], представленными на фиг. 3.18.
Начальное давление 24,6 ата, массовое паросодержание на входе 19,04 вес. %.
'Принять, что из-за тепловых потерь энтальпия жидкости в трубе уменьшается
на 4,56 ккал/кг на 1 м длины трубы. Для определения потерь давления на
трение использовать корреляцию Барокши.
3.13. Решить задачу 2.29, используя корреляцию Мартинелли.
3.14. Решить задачу 2.20, используя модель раздельного течения и
соответствующие допущения.
3.15. Решить задачу 2.30, используя корреляцию Барокши.
3.16. Рассмотреть процесс конденсации в круглом канале диаметром D.
Считать, что пар не соприкасается со стенкой и пленка конденсата
настолько тонка, что Vf<^Vg и а~\. С помощью уравнения (3.59) показать,
что градиент давления равен
,й , „,2 Г 1 dA ..... \ dx . 2С/« ]
в g- cos о + р 1Г„\ — —; \- (1 -4- тЛ : =г—
__rf£__ *g* г?г[ A dz ^у ^ |; х dz ^ D J
_ dz ~ 1 _ м|
где Cfi — определяемый соответствующим образом коэффициент трения на
поверхности раздела фаз.
РАЗДЕЛЬНОЕ ТЕЧЕНИЕ
105
Вычислить градиент давления для восходящего потока пара при
температуре 32° С и скорости 150 м/сек в прямой вертикальной трубе диаметром
25 мм, если C/i=0,005, а массовая скорость конденсации равна
1,36-Ю-3 г/см2-сек. Рассмотреть два предельных случая: г|=0 и т] =0,5,
Каким будет градиент давления, если труба расширяющаяся, так что
dD/dz=0,05?
Решить ту же самую задачу при скорости пара 300 и 450 м/сек.
3.17. Рассмотреть процесс равномерной конденсации в прямой
горизонтальной трубе при низких значениях числа Маха. Принять допущение о
постоянстве свойств и считать, что в трубе длиной L скорость пара на входе Vi,
30
а
Е
а
i го
w.10
a
Е
а
О 250 500 750 1000 12S0
Длина рабочего участка,мм
Фиг. 3.18. Изменение давления вдоль трубы при вскипании [12].
а на выходе V2. Используя решение задачи 3.16, показать, что
восстановление давления равно [23]
1
-
1
1
6180 кг/мг-сек
-
V
Критическое давление —*
Конец трубы"
1 1
Р2 — Р\
= 0+4)
Показать, что если труба короткая и конденсация полная, то расчетное
восстановление давления будет равно
Й-Р1=(1+ч) 4itgV\-
Используя уравнение Бериулли для центральной линии тока пара,
показать, что этот результат справедлив только при условии, что скорость на
центральной линии тока в (1 + г|) раз больше средней. Согласуется ли это
с обычными профилями скорости для турбулентного потока, если г| = У2?
3.18. Последний член в уравнении (3.106) можно представить таким образом,
чтобы продемонстрировать влияние модифицированного касательного
напряжения на поверхности раздела, обусловленного фазовыми превращениями.
Показать, что это касательное напряжение равно
*l = (V2 — Щ
\ ( т
Если испарение происходит достаточно быстро, то т/2 может быть больше,
чем во. Отрицательное касательное напряжение, по-видимому, не имеет
смысла, так что при высоких массовых скоростях испарения должно выполняться
106L
ГЛАВА 3
тождество (во—т/2) = 0. При таких больших скоростях испарения члены,
связанные с инерцией и фазовыми превращениями, намного больше членов,
обусловленных трением и массовыми силами. Показать, что в этом случае
для газо-жидкостного потока уравнения (3.106) и (3.107) принимают вид
dVf
W dz ~
dvg
?Svg d2 -
dp
dz '
dp
dz
vg — vf n. dx
G-—
a dz
Показать, что при испарении в прямом канале (G=const) при условии
р/=const
d \ tt* 1 (J—r)2 (1—*)2l 22
~di~[~9? 2" (l-a)2 + i_« J-°- (3-Ш>
Этот результат был получен Леви при использовании модели обмена
количеством движения, которая вполне применима для условий быстрого
испарения в трубах. (Это эквивалентно допущению т) = 1.)
Показать, что для малых значений х при вскипании или испарении из-
исходного жидкого состояния
vf ~\2 ?g J ■
Проинтегрировать уравнение (3.122), начиная с х=0, и вывести
соотношение между х и а для любого сечения канала.
3.19. Условие запирания при вскипании определяется уравнением (3.62).
Принять, что приближенно выполняется условие (3.63), так что
действительное значение т] ие играет роли. Кроме того, принять, что в газо-жидкост-
ном потоке р/3>р« и cf2~^.cg2. Показать, что массовая скорость
определяется выражением [10]
G2 = /—— — 2 — —
\ р2ас2 др арг
причем а определяется по уравнению (3.71).
3.20. Используя результаты решения задачи 3.19, определить максимально
возможные значения массовой скорости воды в функции от давления при
*=0,03; 0,1; 0,5 и 0,8. Результаты должны совпадать с данными Леви [14],
представленными на фиг. 3.19.
3.21. При расширении из полностью заторможенного состояния при
постоянстве свойств и нулевой гравитации приращение энтропии равно нулю, если
1/2
по всей длине канала у1/у2=1 (гомогенный поток) или yi/i>2=(p2/Pi)
(раздельное течение без трения). Зиви [15] утверждает, что максимальная (он
называет это минимумом) скорость возрастания энтропии имеет место, если
1/3
повсюду Vi/v2= (рг/Pi) . Согласны ли вы с этим?
3.22. Показать, что при раздельном течении
а) Возрастание энтропии, приходящееся на единицу объема и связанное
только с эффектами на поверхности раздела фаз, равно
s,_Jfca_!fl2 + 0
-£-[<'-> •' + «-!LHL]}-
Показать, что увеличение энтропии из-за фазовых превращений зависит от
разницы между «скоростью поверхности раздела», (1—11)41+1142, и
среднеарифметической скоростью фаз (i>i + Чг)/2.
РАЗДЕЛЬНОЕ ТЕЧЕНИЕ
107
10
1
0,7
L i i 11 гг
i < i
\
1 1 1 1 1 1 11
X = 0,7 ../
У/
S'.j
ш •'/ Я, = 0,2
-Г ■ /
г i iiii.il
Ю3 (с
1
у
Mill 1—1 1
-
4
10d
Критический раскод, кг/мгсек
Фиг. 3.19. Критические расходы паро-водяной смеси.
Расчетные данные заимствованы из работы [14]. Точки соответствуют экспериментальным
данным. Эти данные должны совпадать с решениями задач 3.19 и 3.20.
б) Приведенное выше уравнение преобразуется к виду
Уч — У\
■[F» + a-§-to-* )("-г)]-
Показать, что приращение энтропии из-за фазовых превращений равно нулю
•foQH Л '2' И ЧТ0 При испаРеиии Ч > '/г, а при конденсации ц < '/2
6.26. Показать, что силы межфазного взаимодействия, приходящиеся на
единицу объема, которые входят в уравнения (3.48) и (3.49), можно
представить в виде v
dx
~Iz~'
Fx = |>i 2 + (ч- -у") (** - »i) G -g-] - -±- (V2- щ) Q
108 ГЛАВА 3
Показать, что прирост энтропии зависит от «несимметричных» сил, которые
действуют в противоположных направлениях на компоненты 1 и 2, и не
зависит от «симметричных» сил. Показать, что рейнольдсов поток во
пропорционален «несимметричной» составляющей силы, в то время как массовая
скорость т пропорциональна симметричной составляющей. Связать это
с общей идеей обратимости в термодинамике.
3.24. Каким образом связаны между собой величины г| и £ в примере 3.11?
Одинаковы ли две скорости иа поверхности раздела:
С«2 + (1 — С) Vi и гр2 + (1 —- rj) vi ?
Как связаны эти скорости с пограничным слоем или явлениями смешения на
каждой из сторон поверхности раздела?
3.25. Вертикальный рабочий участок трубы установлен в экспериментальном
водяном контуре высокого давления. Труба внутренним диаметром 10 мм и
длиной 4 м равномерно обогревается по всей длине. Определить падение
давления на рабочем участке трубы в зависимости от расхода воды,
имеющей на входе в рабочий участок температуру 205°С и давление 70 ата.
а. Рассчитать падение давления в рабочем участке для расхода воды
2 г/мин и подводимой мощности 100 кет, используя 1) гомогенную модель;
2) модель Мартинелли—Нельсона; 3) соотношение Тома; 4) соотношение
Барокши.
б. Определить падение давления в зависимости от соотношения
расходов в диапазоне от 2 до 15 г/мин для подводимой мощности 100 и 200 кет,
используя: 1) соотношение Мартинелли—Нельсона; 2) соотношение Барокши.
3.26. Смесь воды и воздуха течет по гладкой горизонтальной трубе длиной
106 л и внутренним диаметром 25 мм. Расходы воды и воздуха равны
соответственно 125 и 2 г/сек. Давление на выходе из трубы равно 1 атм. Система
изотермическая, причем температура равна 20° С. Рассчитать падение
давления в трубе, используя соотношение Локкарта—Мартинелли.
3.27. Показать, что для раздельного течения двух несжимаемых жидкостей
в сопле
Д///г=Д/?'/г + Д/?2/г,
где Api и Др2 — падение давления. при движении по соплу только одного
компонента. Сравнить этот результат с уравнением (3.30) и соотношением
Мартинелли.
(Мэрдок [16] нашел, что для водо-воздушной и паро-водяной смесей
Ар1'2=1,26Дру8 + ^'2.)
3.28. Одномерная модель течения не учитывает изменения переменных по
сечению канала. В результате из-за различных способов «осреднения» при
интегрировании по сечению канала вводятся ошибки. Показать, какие следует
ввести поправочные коэффициенты в уравнения, используемые в тексте,
с тем чтобы учесть эти эффекты. Исследовать возможности улучшения
теории-таким способом.
3.29. Решить задачу 2.9, используя: а) теорию минимального потока
кинетической энергии из примера 3.1; б) теорию минимального потока количества
движения из задачи 3.8; в) модель обмена количеством движения из задачи
3.18 и г) результаты решения задачи 3.19.
3.30. Решить пример 3.9 для случая: а) двух несжимаемых жидкостей;
б) двух сжимаемых газов и в) многофазного потока из п сжимаемых
жидкостей [9].
РАЗДЕЛЬНОЕ ТЕЧЕНИЕ
109
3.31. Решить пример 3.5 для случая вертикального потока. Показать, что
о- учетом силы тяжести выражения для ft н (f,)f остаются неизменными, но
(fs)s = (?s — 9f)g— ^2 ^~~ •
Показать, что этот результат согласуется с решением примера 3.6.
Литература
1. L о с k h а г t R. W., М а г t i п е 11 i R. С, Chetn. Eng. Progr., 45, 39 (1949)
2. Martinelli R. С, Nelson D. В., Trans. ASME, 70, 695 (1948).
3. Муди. Труды амер. общ-ва инж.-мех., серия С, Теплопередача, № 1
160 (1965). И '
4. F a u s к е Н. К., ANL Rept 6633, 1962.
5. Turner J. M., Ph. D. thesis, Dartmouth College, Hanover, N. H., 1966,
см. также Turner J. M., Wall is G. В., Rept NYO-3114-6, 1965;
Turner J. M., W alii s G. В., АЕС Rept NYO-3114-14, 1966.
6. Thorn J. R. S., Intern. J. Heat Mass Transfer, 7, 709—724 (1964)
7. Baroczy С J., A. I. Ch. E. J. preprint № 37, 8th National Heat
Transfer Conf., Los Angeles, Calif., 1965.
8. Shapiro A. H., The Dynamics and Thermodynamics of Compressible
Fluid Flow, The Ronald Press Co., N. Y., 1953.
9. Бернстейн, Хевнер, Хейзер, Труды амер. общ-ва инж.-мех.
серия Е, Прикладная механика, Ш з, 99 (1967).
10. Wallis G. В., Intern. J. Heat Mass Transfer, 11, 445—472 (1968).
11. Сполдинг Д. Б., Конвективный массоперенос, изд-во «Энергия», 1965.
12. Fauske H. K-, Inst. Mech. Eng. Symp. Two-phase Flow, paper 10, Feb.
13. Levy S., Trans. ASME J. Heat Transfer, 82, 113—124 (1960).
14. Лев и, Труды амер. общ-ва инж-мех., серия С, Теплопередача, ЛР> 1,
64 (1965).
15. 3 и в и, Труды амер. общ-ва инж.-мех., серия С, Теплопередача, № 2
139 (1964). " '
16. Мэрдок, Труды амер. общ-ва инж-мех., серия D, Техническая
механика, №4, 8 (1962).
17. Reynolds О., Proc. Lit. Phil. Soc, England 14 7—12 (1874)
18. N u s s e 11 W., Z. Ver. Deut. Ing., 60, 102—107 (1916)
19. S i 1 v e r R. S., Nature, 165, 725 (1950).
20. Silver R. S., Fuel, 32, 121—150 (1953).
21. Silver R. S., Proc. 3rd Intern. Heat Trans. Conf., A. I. Ch. E., N. Y.
1966. ' ' '
22. Silver R. S., Proc. Inst. Mech. Engrs, 178, 339—376 (1963).
23. Wall is G. В., Proc. Inst. Mech. Engrs, 180, 27—35 (1965—1966)
24. S i 1 v e r R. S., W a 11 i s G. В., Proc. Inst. Mech. Engrs, 180 ' 36—40
(1965—1966).
МОДЕЛЬ ПОТОКА ДРЕЙФА
4.1. Введение
Модель потока дрейфа представляет собой по существу
модель раздельного течения, в которой нас интересует не движение
отдельных фаз, а их относительное движение. Хотя
теоретический подход может быть достаточно общим, эта модель
особенно полезна в тех случаях, когда относительное движение
определяется несколькими ключевыми параметрами и не зависит от
расходов фаз. Например, в пузырьковых потоках, движущихся
с низкими скоростями в вертикальных трубах большого сечения,
относительное движение между пузырьками и жидкостью
определяется балансом сил сопротивления и выталкивания, который
зависит от объемной концентрации, а не от расходов. Теория
потока дрейфа широко используется при исследовании
пузырьковых, снарядных и капельных течений газо-жидкостных систем,
а также взвесей твердых частиц в жидкости типа псевдоожиж-
женных слоев. Эта модель служит отправным пунктом для
распространения теоретических методов на потоки, в которых
существенны эффекты неодномерности, например изменение
плотности и скорости по сечению канала. Она также служит
основой для быстрого решения нестационарных задач осаждения и
осушения пены.
4.2. Общая теория
Понятие плотности потока дрейфа (приведенной скорости)
/21 было введено в гл. 1, где было показано, что это плотность
объемного расхода (приведенная скорость) каждого компонента
через поверхность, движущуюся со скоростью смеси /. С
помощью уравнения (1.39) этот расход можно выразить через
относительную скорость
Л1 =«21*0—*) ' (4Л)
или с помощью уравнения (1.36) представить в виде зависимости
от приведенных скоростей компонентов
/2i=0-*) Л-«Л- (4-2)
Так как /=/i + /2, то возможны и другие формы записи урав-
нения (4.2): yI=(i _«)у_уа1, (4.3)
/V=*/'+Ai- (4.4)
МОДЕЛЬ ПОТОКА ДРЕЙФА 111
Согласно уравнению (4.3), приведенная скорость компонента 1
равна сумме его объемной концентрации, умноженной на сред-
необъемную скорость смеси, и приведенной скорости дрейфа
(—/г 1 =/i 2) • Уравнение (4.4) аналогично описывает движение
компонента 2. Следовательно, поток дрейфа аналогичен
диффузионному потоку в процессе молекулярной диффузии газов, что
открывает удобный путь модификации теории гомогенного
течения с учетом относительного движения. Действительно, все
характеристики потока, например объемное газосодержание,
среднюю плотность и поток количества движения, можно выразить
через их значения для гомогенного потока путем введения
поправочных коэффициентов или дополнительных членов,
зависящих только от отношения /21 к приведенным скоростям
компонентов. Например, объемное газосодержание а в соответствии
с уравнением (4.2) равно
«Н^-тг)- <4-5>
а средняя плотность рт равна
Pm=Jm+Jm_+{pi _ р2) -Al-. ' (4.6)
При /2 1 = 0 получаются результаты для гомогенного потока.
4.3. Режимы течения без трения на стенках
с преобладающим влиянием силы тяжести
Теория потока дрейфа особенно удобна при анализе режимов
течений, в которых гравитационные (или некоторые другие
массовые силы) уравновешиваются градиентом давления и силами
взаимодействия между компонентами. При этом для
вертикального потока уравнения (3.45) и (3.46) сводятся к следующим:
0=-g-*P.+-£b (4-7)
O—g-ет.--^- (4-8)
Вычитая уравнение (4.8) из (4.7), получим
F12=<x(l-a)£(Pl-p2). (4.9)
При отсутствии влияния стенки сила взаимного сопротивления
Fi 2, приходящаяся на единицу объема, оказывается функцией
свойств компонентов, их структуры, объемного содержания и
относительного движения. Следовательно, для данной системы
Fi 2 — функция только а и /г ь Тогда с учетом уравнения (4.9)
112 ГЛАВА 4
h 1 будет зависеть только от а и свойств системы, так что можно
написать
72 1—Ai (а> свойства системы). (4.10)
Очевидно, что при конечной относительной скорости с учетом
уравнения (4.1) мы должны получить /2i-»-0 при а = 0 и а=1.
Пример 4.1. Используя результаты решения примера 3.4, найти соотношение
между jSf и е Для вертикально движущейся системы, состоящей из
жидкости н твердых частиц, к которой применяется уравнение Кармана—
Козеии.
Решение. Пусть компонент 1 —жидкость и 8=1 —а.
Из примера 3.4 имеем
где jfo—приведенная скорость жидкости прн /s=0. Следовательно, из
уравнения (4.2) получим
7,/ = -<1-«)7/о. (4-12)
Объединяя приведенные выше соотношения с уравнением (4.9),
получим
<Pg(p,-P/)«' 4
Jsf 180ц/ V
Это уравнение применимо к плотным слоям при значениях в до 0,6.
Прн больших значениях е полученное выражение для /./ несправедливо,
так как эта величина при е=1 не стремится к нулю.
Было условлеио, что положительному значению соответствует
движение вверх. Отрицательная величина /,у означает, что прн ps > р/
частицы имеют приведенную скорость дрейфа, направленную
противоположно средней скорости движения.
Применяя уравнение (4.10) к данной системе, можно
построить зависимость j2i от а (фиг. 4.1). Далее, если для заданных
условий известны объемные расходы Qi и Q2, то по1 формулам
(1.19) и (1.20) можно определить ]\ и /2, а с помощью
соотношения (4.2) —найти линейную зависимость между /г i и а.
Действительно, уравнение (4.2) изображается на фиг. 4.1 прямой,
соединяющей точки а=0, /21 =7*2 и а = 1, /2i=—/i. Точки пересечения
этой прямой с кривой, описываемой уравнением (4.10),
определяют реальные значения а [1—3].
Такой графический метод решения уравнений (4.2) и (4.10)
особенно удобен как наглядный способ определения влияния
расходов Qi и Q2, так как поведение фаз в случаях
однонаправленных и противоположно направленных течений в любом
направлении можно определить простым смещением прямой линии.
Фиг. 4.1 построена для частного случая мелких пузырьков,
взвешенных в жидкости, движущейся в вертикальной трубе.
МОДЕЛЬ ПОТОКА ДРЕЙФА 113
В этом случае для однонаправленного движения вверх или вниз
решение имеется всегда; для противотока с нисходящим
движением газа решения не существует, в то время как для проти-.
вотока с восходящим движением газа в зависимости от
расходов фаз возможны либо два решения, либо ни одного. Для
взвеси твердых частиц в
ЖИДКОСТИ фуНКЦИЯ /2 1 ОТ
а резко обрывается в
точке, соответствующей
хаотическому
нагромождению частиц с
образованием плотного слоя. Если
обозначить объемную
концентрацию частиц через а,
то, как видно из
типичных данных (фиг. 4.2),
а имеет некоторое
максимально возможное
значение. На этом графике
приведенная скорость
дрейфа представлена
в безразмерном виде пу-
Фиг. 4.1. Графический
метод решения уравнений (4.2)
и (4.10).
J21
к
0
®//
^^
\ Уравнение (4.10)
>. \ 7
ос ^v
~Uth
-(jt)z
Уравнение (4.2)
-U,)i
(Г) Однонаправленное движение
© Противоток
© Точка „захлебывания"
@ Нет решения
тем деления ее на предельную скорость осаждения одиночной
частицы и,» в бесконечном объеме жидкости. Показанная кривая
описывается типичным корреляционным уравнением,
справедливым для большого числа экспериментальных данных:
-Ai_=a(l-a)-> (4.14).
где п — некоторая функция определенного соответствующим
образом числа Рейнольдса, причем для систем жидкость—твердые
частицы среднее значение п равно 3- В общем случае а означает
объемную концентрацию дискретного компонента.
Действительное значение аМакс, при котором частицы
приходят в соприкосновение, зависит от их формы и характера сил
взаимодействия. В предельном случае коагулирующей взвеси
«макс может быть меньше 0,1. Для твердых сферических частиц
8 Заказ № 162
114 ГЛАВА 4
величина аМакс обычно заключена в диапазоне 0,58—0,62 и
зависит от способа упаковки. При встряхивании слоя или
вибрации могут быть получены более высокие значения аМакс- Кривая
зависимости /Ww». от а, показанная на фиг. 4.2, характеризует
баланс гидродинамического сопротивления и выталкивающей
силы. Величина аМакс соответствует точке, в которой становятся
0.T2S
0,100
0,075
0,050
0.1
0 0,7 0,2 0,3 0,4 0,5 0,6
ос
Фиг. 4.2. Зависимость безразмерной плотности потока дрейфа от объемной
концентрации частиц при псевдоожижении различных материалов водой [4].
Обозначение
X
о
о
о
д-
Материал
Частицы
катализатора
То же
Стекло
*
Свинцовая
дробь
Диаметр, мм
3,28
4,42
5
0,51
1,28 '
Обозначение
V
>
<
+
|
Материал
Морской
песок
То же
Дробленая
порода
Уравнение
(4.14)
Диаметр, мм
0,37
0,55
1,00
1,41
и = 3
значительными силы взаимодействия между частицами. Если а
достигает аМакс, то необходимо вернуться к уравнениям (4.7) и
(4.8), чтобы включить в них члены, характеризующие
взаимодействие между частицами. В случае абсолютно недеформируе-
мых и несжимаемых частиц плотный слой частиц с
концентрацией амакс должен удерживаться либо сверху, либо снизу, что
зависит от значения /2 i/vco. Для легко деформируемых частиц,
таких, как пузырьки, силы взаимодействия могут быть настолько
малыми, что уравнение (4.14) будет достаточно точным вплоть
до значений а, близких к единице.
Частицы,
поддерживаемые
Сверху
Частицы в
начальной стадии
псевдоожижения
V
Частицы,
поддерживаемые
' снизу
МОДЕЛЬ ПОТОКА ДРЕЙФА 115
Предельное состояние противоточного движения называется
«захлебыванием» и соответствует точке касания линии,
описываемой уравнением (4.2), и кривой, определяющей зависимость
J21 от а. Если при достижении этой точки увеличить расход
какой-либо фазы, решение для стационарного потока оказывается
невозможным и должны произойти соответствующие изменения
в системе (изменение режима течения или отвод избытка
вещества на концах канала).
Кривую /21 (а) можно построить по ее касательным, если
известны соответствующие расходы в точках «захлебывания».
0,03
Jzj
Вада,м/сек
0,02
J
о,ог
0 0,5 /
а
Фиг. 4.3. Построение графика зависимости плотности потока дрейфа от
концентрации по данным работы [5] для режима «захлебывания».
На фиг. 4.3 этот метод использован применительно к данным
Блендинга и Эльгина [5], полученным в режиме «захлебывания»
для жидко-жидкостной системы (вода—нефть) в вертикальной
трубе.
Другой путь представления различных режимов движения
предусматривает запись уравнения (4.2) в виде
Для данной системы последний член этого уравнения является
функцией: только'а. Следовательно, линии a = const на графике
зависимости /2 от /i будут прямыми с наклоном а/(1 — а). Точки >
пересечения осей будут соответствовать значениям /21/(1 — а) и
—/21/а. На фиг. 4.4, представляющей график такого типа,
указаны области различных режимов движения в соответствии
i с функцией /21(a), показанной на фиг. 4.1. Полученные выводы
иллюстрируются на фиг. 4.5, где представлены данные работы
[6] для пузырькового газо-жидкостного потока.
8*
0,03
- 0,02
0,01
-j, Нефть,
м/сек
Однонаправленное
движение вверх
Ограниченная область
противотока
Однонаправленное
движение вниз
Область
нереализуемых
режимов
Фиг. 4.4. Области различных режимов движения для одномерного
вертикального потока в зависимости от плотностей объемных расходов компонентов при
условии, что плотность потока дрейфа зависит только от а, но не зависит ии от
U, ни от ;2.
Показан частный случай pi > р2.
10 20 50 ЛОО
Приведенная скорость жидкости j,,см/сек
• а = 0,10
х ос = 0,15
о а = 0,20
+ а = 0,25
Фиг. 4.5. Данные работы [6] для пузырькового потока в вертикальных трубах
сечением 8 и 10 см2.
МОДЕЛЬ ПОТОКА ДРЕЙФА Ц7-
Используя уравнение (4.14) и геометрический метод
определения точки «захлебывания»,'представленный на фиг. 4.1, легко
показать, что соответствующие расходы в точке «захлебывания»
в параметрическом виде выражаются в функции от а
следующими уравнениями;
Л=Л1-«-^=«2*»л(1-«)»-1. (4.16)
Л = -Л1-(1-«)-^=-0-««)^(1-«)л- . (4.17)
Пример 4.2. Для пузырькового режима течения некоторой смеси было
найдено, что п—% и v^ =0,305 Ml сек. Каково соотношение между Qf и Qg
для режима «захлебывания» в вертикальной трубе диаметром 152,4 мм?
Решение. Используя заданные значения п и v^ и считая газ компонентом 2,
находящимся в дискретном состоянии, из уравнений (4.16) и (4.17)
получим
jg = 0,71<х2 (1 — а) м1 сек,
if = —0,305 (1 — 2а) (1 — а)2 м(сек.
Площадь поперечного сечеиия трубы равна я/4 • 0,15242 = 1,82 • 10";2 ж2.
Следовательно, Q/=0,334// м^/мин и Qg=0,334/g м3/мин. Ниже
приводятся расчетные значения для точек «захлебывания».
а
Q/, м31мин
Qg, м3/мин
0
0,334
0
0,1
0,2165
0,00594
0,2
0,1245
0,0215
0,3
0,0653
0,0422
0,4
0,0241
0,0639
0,5
0
0,0835
Предполагается, что не происходит агломерации пузырьков,
приводящей к изменению режима течения.
4.4. Уточнения упрощенной теории
Упрощенная теория одномерного течения с преобладающим
влиянием сил тяжести не учитывает изменения концентрации и
скорости по сечению канала. Величины a, uiHu2, /i и /2 являются
средними по сечению. Уравнения неразрывности и движения,
записанные через эти средние значения, в общем случае не
идентичны строгой записи этих уравнений через соответствующие
интегралы по сечению потока (например, произведение средних
значений не равно среднему значению произведения). Так,
поток количества движения в трубе с некоторым распределением
скоростей, но равномерной плотностью равен
р §v2dA=Ap<.v2}, (4.18)
118 ГЛАВА 4
однако это выражение не эквивалентно выражению
AJJvdA\2=AP(vy, (4.19)
где скобки ( ) означают среднее значение по сечению,
определяемое уравнением
<АГ>=1™-
(4.20)
Аналогично тому, как в случае однокомпонентного потока
отношение уравнений (4.18) и (4.19) обычно записывается в виде
некоторого поправочного коэффициента к одномерной теории,
в случае течения двухкомпонентной среды отношение
соответствующих интегралов также используется для определения
параметров, равных единице для истинно одномерного потока и не
сильно отличающихся от единицы в общем случае.
Особенно полезен параметр распределения С0, введенный Зу-
бером и Финдлеем [7], который определяется как
С0 представляет собой отношение среднего значения
произведения приведенной скорости на концентрацию к произведению
средних значений этих величин.
Удобное определение средней скорости фазы 2 следует из
уравнения (1.23)
^=-Йг- (4.22)
Выполнив в уравнении (4.4) почленное осреднение по сечению
канала, получим
0'21> = 0'2> -<<*/>• (4.23)
Объединяя уравнения (4.21) —(4.23), имеем
^2=С0</> + -^-. (4.24)
Заметим, что уравнение (4.23) является строгим для средних по
сечению канала величин. Однако величина и2 в уравнении (4.22)
в общем случае не равна (v2), так как последняя связана в
общем случае с распределением приведенной скорости и объемной
концентрации уравнением
о2>=
=(£)■ (4-25)
МОДЕЛЬ ПОТОКА ДРЕЙФА
119
Обычно удобнее пользоваться средней скоростью v2, а не (иг).
так как первая через уравнение (4.22) непосредственно связана
с объемным расходом Q2 и средней объемной концентрацией (а).
(а) — удобная величина средней объемной концентрации, так
как она без труда определяется иЗ простого эксперимента,
заключающегося в мгновенном отключении некоторого участка
канала и определении части общего объема, занимаемой
компонентом 2. Величину (а) также определяют методами v-просвечи-
вания.
Справедливы следующие уравнения, записанные через
объемные расходы Qi и Q2:
Q1 + Q2
</>■-
(4.26)
(4.27)
(4.28)
С учетом уравнений (4.22), (4.25) и (4.26) уравнение (4.24}
можно представить в виде
«D А
-С0
Q1 + Q2 1 </2i>
A "г" <ot>
(4.29)
Следовательно, среднеобъемное значение а равно
Q2 — А </2 1>
<а> =
С0 (Qt + Q2)
(4.30)
Если (jii) мало по сравнению с QilA, то уравнение (4.30)
сводится к следующему:
<а>=-?гГ
Q2
С0 Qa + Qi
(4.31)
Второй сомножитель в уравнении (4.31) одинаков с
получаемым в рамках теории гомогенного течения. Таким образом,
влияние изменения концентрации (без влияния относительной
скорости) учитывается умножением средней концентрации,
рассчитанной по теории гомогенного течения на поправочный
коэффициент 1/Со. Этот поправочный коэффициент равен параметру К,
который использовал Бэнков [8], и параметру Арманда [9],
используемому в советской литературе.
Величина (/21) в общем случае не может быть вычислена,
если неизвестна зависимость /г i от а, а также изменение а по
сечению канала. Однако в двух случаях возможны упрощения.
120
ГЛАВА 4
Случай 1. /2i не зависит от а, т. е.
/2,=const. (4.32)
Следовательно, среднее значение /г i равно этой константе.
С л у ч а й 2. /2 1 линейно зависит от а, т. е.
/ai=A+M, (4-33)
где £о-и Ь\ — константы.
В этом случае
<Л1> = *<ггА<«>> (4-34)
:и уравнение (4.30) принимает вид
<">-отта- • <4-38>
Уравнение (4.35) применимо, например, к таким режимам
течения газо-жидкостных систем, как снарядный или пузырьковый
ленно-турбулентный.
Заметим, что рассматриваемые выше локальные приведенные
скорости / имеют смысл средних по времени объемных расходов
через данное сечение. Если изменение потоков во времени
велико, необходимы более сложные уравнения.
Пример 4.3. Важным приложением упрощенной теории одномерного потока
дрейфа является анализ экспериментальных данных. Рассмотрим
применение этого метода к данным Смиссерта [10], полученным для потока
водо-воздушной смеси в вертикальной трубе диаметром 50,8 мм. Нижний
индекс 1 относится к воде, индекс 2 — к воздуху.
Вначале исходные данные используются для определения /2 i по
уравнению (4.2). Полученные результаты представляются (фнг. 4.6) в виде
функции от а для наименьшего и наибольшего расходов жидкости.
Допущение о том, что /2 1 зависит только от а, вполне приемлемо, ио
наблюдается заметное смещение точек при изменении /ь Кроме того,
значение /21 при а=0,8, по-видимому, завышено.
Объяснение этим результатам можно найти из анализа влияния
параметра С0. Уравнение (4.22) в сочетании с уравнением (4.24) дает
к 1 = (• — С0а) к — QWi- (4.36)
Для удобства записи знак осреднения опускается. Теперь заметим, что
большие значения /21 на фиг. 4.6 соответствуют большим значениям
/2 ( = 10 м/сек). Чтобы при таких расходах величина /21 оставалась
небольшой, величина' 1—С0а должна стремиться к нулю. Следовательно,
а приближается к величине 1/Со. Обратившись вновь к фиг. 4.6, ■
заметим, что предельное значение а равно примерно 0,8; и ему
соответствует значение С0 около 1,25.
Подставляя С0=1,25 в уравнение (4.36) и производя пересчет /21
для всех экспериментальных данных, получим данные, представленные
на фиг. 4.7. Экспериментальные точки располагаются около прямой
линии, величина /] не оказывает систематического влияния, а /21 не
достигает слишком больших значений.
Располагая этими экспериментальными данными и используя
параметр Со, найдем величину показателя степени п в уравнении (4.14).
МОДЕЛЬ ПОТОКА ДРЕЙФА
121
Построив зависимость /2 i/a от 1 — а в логарифмическом масштабе, мы
должны получить линию, имеющую наклон п, причем при а=0 значение
функции равно !)ю. Из фиг. 4.8 видно, что п близко к нулю, а величина
v^ составляет около 0,37 м/сек. Изменение режима течения
обнаруживается при значениях а, близких к 0,8. Разброс точек того же порядка,,
что и погрешность экспериментальных данных.
Фиг. 4.6. Данные работы [10], представленные в виде зависимости плотности
потока дрейфа от концентрации при С0=1.
В рассмотренном примере способ введения компонентов определял
некоторый диапазон размеров пузырьков, обусловивший постоянное
значение fa, • Это дало возможность обработать все данные, используя
только один параметр Со. Результаты, приведенные в работе [10] для
азотно-ртутной смеси, обнаруживают отчетливую зависимость v^ от /ь.
хотя среднее значение v^ =0,76 м/сек отличается от всех полученных
значений не более чем на 10%.
Так как возможны вариации трех параметров (С0, v^ и п), то при
обработке экспериментальных данных рассмотренным способом без учета
структуры потока или других важных параметров, например размеров-
пузырьков, имеется опасность получения ошибочных результатов.
Естественно, что наилучшим методом будет такой, в котором выполняются-
дополнительные независимые измерения этих параметров. К этому-
]
О 0,2 0,4 0,6 0,8
а
Фвг. 4.7. Скорректированные данные фиг. 4.6 при С0=1,25.
',о
8 0,3
0,1
п—I' I Mir
^£3£^
fg °
аоз
Вероятное
-«*
изменение
режима
п = 0
о 0,030
« 0,07!
.=, 0,092
О 0,122
v 0,183
д* 0,244
а 0,305
I i i i i i I I
0,1
7.0
1-ос
Фиг. 4.8. Определение я по данным фиг. 4.7.
МОДЕЛЬ ПОТОКА ДРЕЙФА 12&
вопросу мы еще вернемся в следующих главах при подробном
рассмотрении конкретных режимов течения.
Способ представления данных иа фиг. 4.7 и 4.8 отражает реальный
разброс и не преувеличивает возможностей корреляционного метода.
Во многих публикациях при сравнении экспериментальных данных с
корреляционными зависимостями создается иллюзия уменьшения разброса.
4.5. Условия выбора знаков и идентификация
компонентов 1 и 2
Так как скорости и потоки компонентов в одномерном
течении могут быть либо однонаправленными, либо противоположно-
направленными, необходимо условиться относительно знаков.
При этом выбор системы отсчета не имеет значения.
Обычно нас интересует движение и концентрация одного из
компонентов в большей мере, чем другого. Действительно, до-
сих пор мы «выделяли» компонент 2, оперируя его объемной
концентрацией а, и не рассматривали концентрацию от 1 до 1 — а.
К тому же при анализе мы предпочитали использовать величину
/гь а не /i 2, хотя определяющие уравнения абсолютно
симметричны. И наконец, мы приняли, что компонент 2 имеет
дискретную структуру. Все эти действия продиктованы тем
обстоятельством, что относительную скорость и21 или предельную скорость.
и» обычно предпочитают рассматривать как скорость частицы
в жидкой среде, а не как скорость жидкости, при которой
частица будет неподвижна. Поэтому обычно удобно выбирать знак
таким образом, чтобы скорости отсчитывались в положительном
направлении дрейфа компонента 2, при этом величина /2i будет
положительной. В другом случае, когда для определения /21
рассматривается баланс сил (пример 4.1), может оказаться
целесообразным выбор положительного направления, совпадающего,
•с направлением гравитационного поля.
В следующих главах иногда будет удобно использовать
обратную систему, если нас интересует движение непрерывного-
компонента, например при течении жидкости через почти
неподвижный псевдоожиженный слой частиц. С этой целью мы
определим е как объемную концентрацию непрерывного компонента,
т." е.
. е=1-а, (4.37)
и будем оперировать величиной ]\ 2, а не /гь Аналитический
метод при этом остается неизменным.
4.6. Нестационарное течение
Плотность потока дрейфа является очень полезным
параметром при анализе нестационарных течений с помощью теорий
волнового движения, которые будут рассмотрены в гл. 6.
^24 ГЛАВА 4
Задачи
4.1. Используя модель потока дрейфа, показать, что средние скорости фаз
равны
V\ = —; , Vf = .
Вывести выражение для потока количества движения при одномерном
течении в канале.
4.2. Воздух и вода движутся по вертикальному каналу при температуре
21° С и давлении 2,5 ата. Зависимость плотности потока дрейфа от объемного
газосодержания имеет вид
jgf = 0,244а (1 — а)2 м/сек.
Чему равно объемное газосодержание для следующих значений // и jg:
jp м/сек 0,152" 0,305 0,152 0,71 1,525
jg, м/сек 0,152 0,152 0,305 0,71 1,525
Сравнить для этих условий поток количества движения и объемное
газосодержание, рассчитанные по теории дрейфа со значениями этих
величин, вычисленных для модели гомогенного потока и с использованием
соотношения Мартинелли для трубы диаметром 50 мм.
4.3. Воздух равномерно барботирует через слой покоящейся воды. Каково
соотношение между плотностью объемного расхода воздуха и объемным
газосодержанием, если /g/=o00 а (1 — а)2? Каков физический смысл двух
возможных значений газосодержания? Каким образом зависит высота столба
двухфазной смеси при барботаже от расхода воздуха, если глубина слоя
воды без пузырьков равна 1 л и ош =0,25 см/сек} Когда наступит
«захлебывание»?
4.4. Построить кривые /2 от а в зависимости от j\ и /i от а в зависимости
от j3 для плотности потока дрейфа, соответствующей уравнению (4.14).
Определить условия «захлебывания» для однонаправленного и противоточиого
движения.
4.5. Показать на графике, каким образом объемная концентрация зависит
от расхода жидкости в псевдоожиженном слое при различных потоках
частиц, направленных как вверх, так и вниз. Какие области графика
соответствуют однонаправленному и противоточному движению вверх и вниз?
В какой части графика а=амакс, если движение частиц не ограничено ни
концами, ни стенками канала?
4.6. Эксперименты с водо-воздушной смесью в режиме «захлебывания» дали
следующие результаты:
— jf, см/сек 0 1_2 4 5 9 -11 15 18
jg, см/сек 12 10 9 7 6 4 3 2 1
Вывести зависимость jgf от а. При каких значениях v и п уравнение
(4.14) дает «наилучшее» совпадение с экспериментом?
4.7. Как изменится графический метод, показанный на фиг. 4.1, в
предельном случае гомогенного потока с »i = »2?
4.8. Один из способов определения величин С0 и /г1 состоит в построении
зависимости /г/а от /. При каких значениях п в уравнении (4.14) эта
зависимость будет линейной? Какие характеристики этой линии будут
определять С0 и Oqo ? Как в этом случае будет зависеть от а скорость дрейфа
i>2j компонента 2?
?
МОДЕЛЬ ПОТОКА ДРЕЙФА 125
4.9. Для пузырькового пенно-турбулентного течения и для снарядного
течения vgj приблизительно постоянна. Показать, что для изотермического
течения условие запирания имеет вид
Показать, что при одинаковых массовых скоростях компонентов давление,
при котором наступит запирание, в этом случае будет меньше, чем для
гомогенного потока. Считать С0=1.
4.10. Решить задачу 4.9, считая Со константой, не равной 1.
4.11. При наличии дрейфа различные выражения для потерь давления на
трение в гомогенном потоке не идентичны; в частности, можно выбирать
из соотношений
2C/G2 2CfGJ 2Cf?mj*
D?m ' D ' D ■
Сравнить эти выражения, записав их через /21 и потоки каждого
компонента. При каких условиях эти соотношения наиболее чувствительны к
сделанным допущениям?
4.12. Если существует дрейф, то истинный поток количества движения
отличается от его значения, определяемого теорией гомогенного течения.
Выразить поток количества движения через отношения /2i к плотностям объемного
расхода компонентов и отношения их массовых скоростей к суммарной
массовой скорости. Показать, что соотношение между потоками количества
движения для течения при наличии дрейфа и без него
GlKl+j2dJi) + G2!(\-j2l/J2)
Gi + G2
4.13. Исходя из уравнений (3.39а) и (3.396), а также используя определение
Q в уравнении (2.92), показать, что при наличии дрейфа уравнение скорости
распространения объемной концентрации паро-жидкостного потока при
постоянных свойствах жидкости имеет вид
Если jgf — функция только а и свойств системы, показать с помощью
соотношения
д . __да д '.
dz Jgf~ dz ~d^Jsf
что изменения объемной концентрации распространяются со скоростью
непрерывной волны
vw = J + -fo-Ugf).
причем концентрация экспоненциально возрастает со временем.
4.14. Вывести соотношение между /2, и а, используя данные,
представленные на фиг. 4.5. Объяснить его характер.
4.15. Решить задачу 2.30, если /g/=0,305a м/сек.
4.16. Решить задачу 2.31, если /g/=0,305a м/сек.
4.17. Каково соответствие между линиями, показанными на фиг. 4.4, и
результатами а) теории гомогенного течения; б) корреляционного метода
Мартинелли для вязко-вязкого течения?
126
ГЛАВА 4
4.18. В условиях кипения с иедогревом в вертикальном восходящем потоке
Со может быть меньше единицы (почему?), в то время как величина jef
положительна. Исследовать, при каких условиях объемное паросодержание
в канале может превышать значения, определяемые по теории гомогенного
течения. .
4.19. Найти величину Со, если а и / изменяются по сечению круглой трубы
по степенному закону. Какой диапазон значений приемлем при различных
условиях?
4.20. Принять, что вводимые в вертикальную трубу пузырьки имеют
различные размеры. Каким образом можно уточнить теорию потока дрейфа через
соответствующие средние величины, если известны функции распределения
пузырьков по размерам и зависимость jei от размера пузырька и локальной
величины а?
Литература
1 W а 11 i s G В., Paper № ЗЙ, Proc. Intern. Heat Transfer Conf., ASME,
Boulder, Colo., vol. 2, 1961, pp. 319—340.
2 W a 11 i s G. B./-Symp. Interaction Fluids Particles, Inst. Chem. Engrs.„
London, 1962, pp. 9—16.
3. W a 11 i s G. В., Symp. Two-phase Flow, Inst. Mech. Engrs, paper № 3,
4. Wil'hTlm R. H., Kwauk M., Chem. Eng. Progr, vol. 44, 1948, pp.201—
217
5 В Ian din g F. H., Elgin J. C, Trans. A. I. Ch. £., 38, 305-335 (1942).
6 Deruaz R., ANL transl. 61, 1964 (from the French, Centre D'Etudes
Nucleases de Grenoble, note TT № 165, April 1964).
7. Зубер, Финдлей, Труды амер. общ-ва инж.-мех., серия С, Теплопере-
8 B^nkoff S. G., Trans ASME J. Heat Transfer, ser. C, 82, 265 (1960).
9. Арманд А. А., Изв. ВТИ, № 1, 16 (1946).
10. S m i s s a e r t G. E., ANL Rept 6755, 1963.
5
ПРОФИЛИ СКОРОСТИ И КОНЦЕНТРАЦИИ
5.1. Введение
Дальнейшее углубление анализа, выходящее за рамки
упрощенных моделей гомогенного и раздельного течений, связано
с рассмотрением профилей скорости и концентрации по сечению
канала. Такое рассмотрение еще соответствует
квазиодномерному описанию течения, так как допускается различие
локальных скоростей фаз только в основном направлении движения.
Любое движение поперек канала либо не принимается во
внимание, либо учитывается введением таких параметров, как
«коэффициент турбулентной диффузии», характеризующий
турбулентное перемешивание. В турбулентном потоке профили
скорости и концентрации являются осредненными за достаточно
длительный промежуток времени.
Профили скорости и концентрации нужны главным образом
для обоснования введения поправочных коэффициентов в
простые соотношения, используемые в моделях гомогенного и
раздельного течений для повышения их точности. В ряде случаев,
например для коэффициента трения и параметров двухфазно-
сти, можно получить аналитические зависимости, не
ограничиваясь эмпирическими результатами предыдущих глав. Эта
теория может оказаться полезной также при выводе некоторых
безразмерных комплексов.
5.2. Общие соображения
Понятие профилей скорости для однофазного потока стало
привычным. Некоторые простые случаи, например течения в
круглых трубах, исследованы очень подробно.
В двухфазных потоках ситуация значительно сложнее по
следующим причинам:
1. Концентрация дискретной фазы может быть
неравномерной и несимметричной. В горизонтальных трубах возможно
отложение взвешенных частиц. Жидкие пленки прилипают
к стенкам, и в нижней части трубы они толще, чем в верхней.
Пузырьки всплывают преимущественно по центральной области
сечения вертикальной трубы. Группы больших пузырей
вызывают значительные периодические изменения концентрации.
2. «Концентрация» не всегда является характеристикой,
пригодной для описания локальных свойств двухфазной системы.
128
ГЛАВА 5
Крупные частицы могут оседать на дно трубы, в то время как
мелкие частицы остаются взвешенными. Очень мелкие частицы
(диаметром менее 1 мк) движутся вдоль линий тока жидкости,
в то время как крупные либо лишь незначительно отклоняются
при движении по каналу установки, либо многократно
сталкиваются с ограничивающими поток стенками. Одновременно
могут существовать несколько видов течения — в виде капель,
пузырей И пленки жидкости.
Ф и г. 5.1. Распределение скоростей
газа и частиц в канале [1].
Скорости газовой фазы
^ - чистый воздух
4,97 |
W
g
W,
= 8,13
g
Стеклянные
частицы
Скорости, твердой фазы
W,
-Д-
Wg
■ = 4,97
^
= 8,13
Стеклянные
частицы
30 40
Радиус.мм
1±
W,
Wa
= 0,249
-=0,551
: 0,876
Частицы
окиси магния
3. Хотя на поверхности раздела фаз нет относительного
движения, оно возможно в масштабе, превышающем расстояние,
для которого имеет смысл допущение о сплошности среды.
Например, средняя скорость капли во взвеси не обязательно равна
скорости несущей жидкости. Таким образом, как показано на
фиг. 5.1, существуют профили скорости для каждой фазы.
Общее решение таких задач практически невозможно.
Рассмотрение всех работ, выполненных в этой области, само по
себе потребовало бы объема целой книги. Поэтому в данной
главе будут получены только некоторые простые результаты,
расширяющие рамки моделей гомогенного и раздельного
течений и дающие материал, который будет полезен для
использования в следующих главах.
Профили скорости и концентрации можно исследовать как
дифференциальными, так и интегральными методами. В
первом случае значения скоростей и концентрации определяются
ПРОФИЛИ СКОРОСТИ И КОНЦЕНТРАЦИИ 129
из решения дифференциальных уравнений, полученных путем
рассмотрения малых элементов поля течения. Во втором случае
форма профилей задается, а динамические и геометрические
условия удовлетворяются соотношениями в интегральной форме.
5.3. Дифференциальный анализ
Профили скорости в однофазном потоке
В однофазном потоке концентрация обычно постоянна по
всему сечению канала. Свойства жидкости могут меняться по
нормали к направлению Потока из-за изменений температуры и
состава, однако обычно в уравнениях используются
соответствующие локальные значения вязкости и плотности.
В хорошо известном методе «универсального» профиля
скорости в круглых трубах сначала из баланса сил вычисляют
распределение касательных напряжений, затем устанавливают их
связь с градиентами скорости и наконец интегрированием этих
градиентов находят профиль скорости [2]. При этом
используются такие параметры, как скорость трения !> и *, а также
безразмерные величины скорости и расстояния от стенки:
=(^-)72. (5Л)
й+=-^г, (5.2)
ра*у
й* = |
iH-=-
(5.3)
Принимается, что вблизи стенки течение является ламинарным
и касательное напряжение связано с профилем скорости
уравнением
-=.-£-• (5-4)
Для течения в круглой трубе с постоянной плотностью
приближенное решение для малых значений у имеет вид
а+=у+, (5.5)
причем экспериментальным путем установлено, что оно
справедливо до г/+?»5.
Для области турбулентного течения существует много
различных соотношений для выражения зависимости между
'' Динамическая скорость. — Прим. перев.
9 Заказ № 162
130 ГЛАВА 5
касательным напряжением и градиентом скорости. Пожалуй,
наиболее простое из них имеет вид
dv
Z = ^-dJ
dy
(5.6)
где / — длина пути перемешивания, введенная Прандтлем [3].
Если принять линейную зависимость / от г/, то
l=ky. (5.7)
При использовании этих уравнений для круглых труб
получается безразмерный логарифмический профиль скорости
и+=^-1пу+ + С. (5.8)
Эмпирическим путем найдено, что &«=;0,4, С»5,5 и что
уравнение (5.8) справедливо для г/+>30.
В области от у+—Ь до г/+=30 располагается промежуточный
слой, в котором касательное напряжение описывается
уравнением
х=((х+вр)-^-, (5.9)
где е определяется [4] как
s=n*vy(\-e-*n*vyl»), (5.10)
причем п — эмпирическая безразмерная константа,равная ~0,1.
Если рассматривается течение неньютоновской жидкости, то
решение для ламинарного режима можно получить, заменяя
уравнение (5.4) соответствующим соотношением между
касательным напряжением и скоростью деформации.
Профили скорости в двухфазном потоке
Рассмотренные выше методы можно применить к
двухфазным (или многофазным) потокам только при условии их
локальной гомогенности. Тогда определяется общий для обоих
компонентов профиль скорости. Для решения уравнений требуется
знать профили величин р, ц и /. Обычно плотность гомогенного
потока и эквивалентную вязкость находят в виде функций от
объемного газосодержания а методами, изложенными в гл. 2.
Таким образом, определение режима течения в зависимости от
профиля концентрации и свойств компонентов дает возможность
рассчитать р и ц в любой точке. Вычисление пути
перемешивания связано с большими трудностями, так как для двухфазных
потоков пока еще не получено универсального эмпирического
соотношения. Пути перемешивания для двухфазных сред иногда
больше, а иногда меньше, чем для однофазных. Например,
исследования газового ядра при кольцевом течении [5] показали,
ПРОФИЛИ СКОРОСТИ И КОНЦЕНТРАЦИИ
131
что уравнение (5.8) приемлемо и для двухфазных потоков, но
величина k уже не является константой, а зависит от расходов
(фиг. 5.2). Профили скорости газа заметно отличаются от соот-
вествующих профилей для однофазного потока (фиг. 5.3) в про-
Ф н г. 5.2. Профили скорости газа при дисперсно-кольцевом течении [5].
W, г/сек
37,8
63,0
37,8
W*, г I сек
63,0
6,3
157,5
Левая часть
▼
♦
Правая часть
V
О
D
тивоположность результатам, показанным на фиг. 5.1 и
полученным для систем газ—твердые частицы. Исследования такого
типа пока еще не позволяют сделать общих заключений.
В любом случае можно разработать расчетную схему, в
которой будет использована доступная информация об изменении
свойств и пути перемешивания по сечению канала. Для осесим-
метричного установившегося течения без расслоения фаз
распределение касательных напряжений в круглой трубе,
наклоненной под углом 8 к вертикали, находится из баланса сил,
действующих на цилиндр радиусом г, показанный на фиг. 5.4.
:_£-(.
dp
dz
P2g
cos б) - g (p' -£> cos 6 J (1 - a) 2r dr. (5.11)
Введем безразмерные параметры
* 4т
£>g(Pl — P2)
(5.12)
Ар*
— (dp'dz) — p2ff cos 6
£(Pi — P2)
(5.13)
0,4 0,6
У/0
&
V
Фиг. 5.3. Влияние расхода воды на профиль скорости воздуха при дисперсно-
кольцевом режиме течения [5].
X
О
д
п
W„=63 г /сек
Wf, г!сек
0
3,78
25,2
63,0
126,0
р , 10 г/см3
1,44
1,45
1,55
1,70
1,89
г=У±
t t
р + Ър
±=bk
t t
Фиг. 5.4. К выводу уравнения (5.11). Баланс сил, действующих на
элементарный цилиндр.
ПРОФИЛИ СКОРОСТИ И КОНЦЕНТРАЦИИ 133
2г
(5.14)
D
и запишем уравнение (5.11) в безразмерном виде
г*
т*=г* Д/7* - ^Д- J (1 — a) 2r* rfr*. (5.15)
о
Это распределение касательных напряжений заметно
отличается от линейного профиля для однофазного потока. Так как
в уравнении (5.15) содержатся два конкурирующих члена, то
в зависимости от структуры потока возможны любые профили:
с максимумами и минимумами, переменного знака и кривизны.
Следуя Тернеру [6], запишем уравнения (5.4) и (5.6) в
безразмерном виде, используя следующие параметры:
*! = № (бЛб)
^=J77~[^(P<-P2)]'/2> (5Л7>
* v V?l
/•=ТГ- (5.19).
Индекс / относится к любой фазе, причем индекс фазы
выбирается таким образом, чтобы pi>p2. Свойства или параметры
без индексов означают среднюю локальную величину для
гомогенной системы. Для ламинарного течения уравнение (5.4)
принимает вид
dv*i _ NRi
■ т-
. (5.20)
dr* 8
а для турбулентного течения из уравнения (5.6) следует
-£__«Ч,Т.. (5.21)
где Н означает знак касательного напряжения.
^Параметр N в уравнении (5.20) является функцией
локальной вязкости и плотности гомогенной среды и может быть
представлен в виде
"-*(*■)"*?-".(■£)"■?• (S-22>
С помощью уравнения (2.9) величина Ri может быть
представлена как функция локального значения а и отношения
плотностей pi/p2.
Из любого уравнения (2.56)—(2.61) отношение ц/ц* можно
134
ГЛАВА 5
выразить в виде функции а и отношения коэффициентов
вязкости p-i/p.2- Кроме того,
±!_ = Ж(Ж.\41 (523)
to Ni \ P2 /
Объединяя эти результаты, в конечном итоге получим, что N
является функцией Ni, N2, pi/рг и а.
Профиль скорости определяется путем интегрирования
уравнений (5.20) и (5.21) с использованием уравнения (5.15) и
данных об изменении а и /* в зависимости от радиуса г*.
Плотность объемного расхода каждой фазы в безразмерном виде
находится интегрированием профиля скорости, т. е.
fi = $aiV'l2r'dr, (5.24)
о
где а, — объемная концентрация фазы i и
У*=Лр'/г[£-£>(Р.-р2)Г,/2- (5-25)
В общем случае, если режим течения таков, что локальное
значение а можно выразить через среднее значение (а), имеем
j*=j*(Ap*, <а>, ~, Nu N2, б). (5.26)
Пример 5.1. Вывести выражения для //* и jg* для ламинарного
вертикального кольцевого потока газо-жидкостной смеси.
Решение. Для вертикального потока cos 0 = 1. Так как поток кольцевой,
локальное значение а равно единице в газовом ядре и нулю в жидкой
пленке. Следовательно, в зависимости от общего объемного
газосодержания уравнение (5.15) принимает вид
для газового ядра х* = г* Др*, (5.27)
г*
для жидкой пленки т* == г* Др* ^- \ 2яг* dr*. (5.28)
YT
Интегрируя уравнение (5.28), получаем для пленки
х* = /-»(Др»—1)+-^-. (5.29)
Подставляя (5.29) в (5.20), при i=f находим
dv*. N/
[г* (Ар*-!)+-£-]• (5-3°)
dr* 8
Интегрирование от г* до стенки, где г*=1, о/*=0, дает
Nf
(Ар*—1) (1 — г*2)
- a In Г* .
(5.31)
Так как а, = 1 в пленке и а,=0 в ядре, то путем подстановки
полученного значения Vf* в (5.24) и последующего интегрирования находим
ПРОФИЛИ СКОРОСТИ И КОНЦЕНТРАЦИИ 135
У/ = -35-{(Др*-1)(1-=')2 + 2а[(1-а)+а1па]}. (5.32)
Скорость, иа поверхности раздела фаз определяется из уравнения (5.31)
при г*2=а и может быть выражена через безразмерную скорость газа
vg* умножением на квадратный корень из отношения плотностей, т. е.
(vs)i = ~w(-^) [(AP*-l)(l-«)-«ln«]. (5.33)
Подставляя теперь (5.27) в (5.20) найдем, что в газовом ядре
dv* Ng
— *- — ^г*Др*. (5.34)
dr* 8
v„
Интегрируя от г* до У~а и используя (5.33), получим следующее
выражение для профиля скорости газа:
Ng Nf I ?g \Ч*
"* W Ap*ir*2-a)+-w(-^-) [(AP*~ l)d-«)-«In»].
(5.35)
Подставляя (5.35) в (5.24) и учитывая, что а, = 1 в ядре и а*==0
в пленке, в итоге получим
Ng ( Nf I fs \'h )
jg=^r r2A/>*+2aTv7ii7/ [(Ap*-i)(i-«)-ain«]-j.
(5.36)
Уравнения (5.32) и (5.36) соответствуют частным случаям уравнения
(5.26).
Для конкретного сочетания компонентов и режима течения
в трубе заданных размеров уравнение (5.26) описывает два
безразмерных расхода /* и /* как функций Ар* и {а). Если Ар*
и (а) определяются по известным значениям расходов, эти два
уравнения должны решаться совместно.
Даже если невозможно получить теоретического решения
этих уравнений, используемые безразмерные параметры могут
служить основой рациональной корреляционной схемы анализа
экспериментальных данных. При необходимости безразмерные
параметры можно объединить в новые комплексы.
Пример 5.2. В модели раздельного течения для кольцевого вертикального
потока предлагается определять коэффициент трения на стенке по
корреляционной зависимости от числа Рейнольдса для жидкой пленки
Re/=/iP/D/n/. Показать, как такое выражение связано с уравнением
(5.26).
Решение. Число Рейнольдса легко выразить через безразмерные параметры
следующим образом:
Ref = j*Nf (5.37)
Из уравнения (5.15) следует, что безразмерное касательное напряжение
на стенке ти* равно
<, = V -(•-«)• (5.38)
136
ГЛАВА 5
Коэффициент трення на стенке можно записать следующим образом:
с/" —w £— ~ 77** • '
1 2?fJf 2jf
Следовательно,
с*= [*/>•-<»-JH1-)». (М0)
4/f
Таким образом, выражение для Cfm в виде функции от Re/
предполагает наличие связи между //*, Nf, Ар* и а и является частным
случаем уравнения (5.26).
5.4. Интегральный анализ
В интегральном анализе форма профилей скорости и
концентрации не вычисляется, а задается. Неизвестные параметры
определяются либо эмпирически, либо из профилей,
удовлетворяющих определенным интегральным уравнениям и граничным
условиям. Известным примером из области однофазных течений
может служить интегральный метод Кармана для пограничного
слоя. Этот метод широко не использовался для
двухфазных течений, и пока получены только немногие полезные
результаты.
Модель переменной плотности, предложенная Бэнковым
для течения в круглых трубах, основана на допущении о
локальной гомогенности потока и отсутствии относительного
движения. Принимается, что скорость и концентрация изменяются
по степенному закону, т, е.
■(*-)""■
(5.42)
где vm и am — значения на оси трубы, у — расстояние от стенки
и го — радиус трубы. Из уравнения (1.6) найдем среднее
значение а, равное
Массовая скорость фазы 2 составляет
C2=-^rJ ™P£*(r0-y)dy = amvmP2(m + n + mn){n+m + 2nm),
(5.44)
ПРОФИЛИ СКОРОСТИ И КОНЦЕНТРАЦИИ
137
а массовая скорость фазы 1 равна
Го
G, = —г f (l-a)x>p,2ic(r0-y)rfy=
"'"о о
_ Г 2от2 2w2OT2 ]
<*ЛР1 [ (1 + От) (1 + 2ОТ) ат (ОТ + П + ОТЛ) (Л +-Я» + 2ЯОТ) J •
(5.45)
Так как
G, 1
G2 jt
то, объединяя уравнения (5.44) и (5.45), получим
. i__p2_ 1—- -V (от + » + я?и) (я + т + 2гс/и)
"+" Р1 JC _ П2(1+от) (1 +2OT)am
(5.46)
(5.47)
Исключая ат из (5.43) и (5.47), в конечном счете найдем, что а
и х связаны следующим соотношением:
К
1 + (P2/Pl) [(1 -*)/*]
где
(5.48)
1С— 2(т + п + тп) (т + п + 2тп) /^ ла\
(л + 1)(2я+1)(л1 + 1)(2«+1) • ^°-^}
В широком диапазоне значений п от 0,1 до 5 и т от 2 до 7 К
изменяется только в пределах от 0,5 до 1.
Соотношение (5.48) при использовании соотношения
iS"i=£- = A- (5.50)
Pi х j2 ^ >
принимает вид
откуда ясно, что параметр К тождественно равен обратной
величине параметра С0, который был введен в гл. 4. Эти
результаты дают возможность уточнить теорию гомогенного течения,
чтобы учесть двумерные эффекты.
Преимущество модели такого типа заключается в том, что
ее можно использовать при выводе выражений для различных
величин, например потоков количества движения и
кинетической энергии, в функции от параметров тип. Кроме того, так
как всегда а=0 при г/ = 0 (т. е. фаза I должна смачивать стенку),
то касательное напряжение на стенке можно связать
138
ГЛАВА 5
с градиентом скорости на ней. Однако форма уравнений (5.41),
(5.42), а также допущение о «локальной гомогенности»
ограничивают число режимов, для которых применим этот метод.
Параметр К является основным для различных соотношений
между истинным объемным и массовым расходным
газосодержаниями в газо-жидкостных потоках.
Пример 5.3. Показать, что если К=const, то при увеличении х в испарителе
а стремится к некоторому предельному значению. Как получить большее
значение Ю
Решение. По мере увеличения х отношение (1-х:)/л; стремится к нулю,
и из уравнения (5.48) следует, что а стремится к пределу, равному К-
При превышении этого значения должен произойти переход к режиму
течения, которому соответствует новое значение Д.
Уравнение (5.41) может оказаться полезным даже в том
случае, когда уравнение (5.42) абсолютно неприменимо, например
в случае кольцевого газо-жидкостного потока. Будем
рассматривать жидкую пленку как часть эквивалентного однофазного
потока, заполняющего трубу. Для турбулентного потока при
малых числах Рейнольдса т~7, и найденная интегрированием
средняя скорость эквивалентного однофазного потока, равна
v=-&-om. (5.52)
При объемном газосодержании а средняя скорость в жидкой
пленке будет равна
''"=1(ЬГ "" ГЧ-^ГМг.-^У, (5.53)
откуда
49
(i->m8/'(i+4-*^)
t~~ 60 т ' 1-я
(5.54)
Следовательно, с учетом выражения (5.52)
Коэффициент трения на стенке определяется из теории
однофазного течения как функция v, и касательное напряжение на
стенке равно
^ = CfwJL?f:b2. (5.56)
ПРОФИЛИ СКОРОСТИ И КОНЦЕНТРАЦИИ 139
Теперь, используя уравнения (5.55) и (5.56), можно связать
касательное напряжение на стенке со средней скоростью
жидкости и даже рассчитать его, если известно объемное
газосодержание. Подробнее этот метод будет рассмотрен в гл. 11.
5.5. Более сложные методы анализа
Профили скорости и концентрации в полностью развитом
стационарном потоке являются, по-видимому, простейшими
примерами двумерных эффектов. Из многочисленных более сложных
явлений, имеющих большое практическое значение, отметим
следующие: двухфазные струи, развитие профилей на начальных
участках трубопроводов, пограничный слой при пленочном
кипении и конденсации, абляцию и горение, течение в
криволинейных каналах и центробежных сепараторах, волновые
явления на поверхности раздела фаз, процессы дробления капель и
движение больших пузырей в каналах и соплах.
Подробный вывод уравнений, в должной мере отвечающих
поставленным задачам, выходит за рамки данной книги. Однако
результаты исследований многомерных течений будут часто
использоваться в теории одномерных течений. Так:, например, мы
не приводим аналитического вывода уравнения, описывающего
увеличение скорости большого пузыря при его движении по
вертикальной трубе, однако конечные результаты будут
использованы достаточно широко.
Задачи
5.1. Вывести уравнение (5.8) из уравнений (5.6) и (5.7), используя закон
распределения касательных напряжений для течения однофазной жидкости
постоянной плотности в круглой трубе.
5.2. Показать, как распределение касательных напряжений в вертикальном
кольцевом газо-жидкостном потоке зависит от величин Др* и а.
5.3. Вывести уравнение (5.51) из уравнений (5.41) и (5.42), используя
определение параметра С0 из гл. 4 [уравнение (4.21)]. Показать, что С0=К'1.
5.4. Вычислить параметр К для я=0,1; 1; 5 и т = 2; 4; 7.
5.5. Показать, что безразмерная величина падения давления
g(?f — 9g)
для газо-жидкостного потока в вертикальной трубе равна показаниям
дифференциального манометра, подключенного к трубе единичной длины,
содержащей жидкость с плотностью р/ под слоем газа с плотностью pg.
5.6. Какой безразмерный комплекс определяет увеличение скорости
большого пузыря газа в невязкой жидкости?
5.7. Какой безразмерный комплекс определяет увеличение скорости большого
пузыря газа в очень вязкой жидкости?
5.8. Объединить результаты решения задач 5.6 и 5.7 и показать, что
увеличение скорости пузыря в жидкости с любой вязкостью можно представить
140
ГЛАВА 5
зависимостью Vb* от Nf, где Уь* — безразмерная скорость пузыря, равная
^=мр/)'/2№(р/-дг'А.
Какое соотношение между Nf и Vb* характерно для пузыря в вязкой
жидкости?
5.9. Для газо-жидкостного вертикального восходящего потока До*
определяется соотношением
д * =_ —dPldz — Pgg
Р ~ giff — 9g)
Рассмотреть ламинарное или турбулентное течение одного только газа или
одной только жидкости в вертикальной трубе. Исходя из обычных
соотношений ламинарного течения и при заданном коэффициенте трения
турбулентного течения получить следующие выражения, связывающие Др* с другими
безразмерными параметрами (ось координат г направлена вверх):
а) ламинарный поток одной только жидкости
327*,
Ар*=\ -| '— •
Nf
б) ламинарный поток одного только газа
* = -»?-•
в) турбулентный поток одной только жидкости
Ар*=\+2С//;
г) турбулентный поток одного только газа
Ар =2CfJg.
5.10. Согласно Арманду [10], /С=0,833 для горизонтального потока. Найти
зависимость объемного паросодержания от массового паросодержаиия для
паро-водяной смеси при давлениях 35, 70 и 140 ата и сравнить полученные
результаты с результатами расчетов методами Мартинелли и Тома.
5.11. Выполнить интегральный анализ характеристик жидкой пленки в
ламинарном кольцевом потоке, исходя из распределения скорости для
однофазного потока
•-*['-(v)"]-
Показать, что о/=о (1—а) и, следовательно, параметр Мартинелли Ф/
равен -"
1
5.12. Принимая величину пути перемешивания постоянной, проинтегрировать
уравнение (5.6) для однофазного потока и показать, что
Др* = (7/*у*)2
и, следовательно,
,.. (2С/>'/г.
ПРОФИЛИ СКОРОСТИ И КОНЦЕНТРАЦИИ 141
Выполнить такой же анализ для модели раздельного цилиндрического течения,
принимая, что /* имеет одинаковое значение в обоих цилиндрах, равное пути
перемешивания в однофазном потоке. Показать, что в этом случае п=3,5
в уравнении (3.30). -
5.13. Уравнения (5.32) и (5.36) можно использовать для построения
зависимости //* от \g* при постоянных значениях а. Показать, что линии
a=const прямые. Каково геометрическое место точек Ap*=const? Каково
геометрическое место точек «захлебывания»? Сравнить результаты с данными,
приведенными на фиг. 4.4.
Для потока воздуха и воды прн температуре 21° С и давлении 1,05 ата
в трубе диаметром 25,4 мм определить Nf, Ng и р«/р/. Сравнить
зависимость //* от je* с данными для пузырькового потока, приведенными на
фиг. 4.5.
5.14. Вывести выражение для потока количества движения в трубе, исходя
из модели Бэнкова. Сравнить результаты с теорией гомогенного течения.
5.15. Используя результаты примера 5.2, вывести соотношения между jf*,
Nf, Др* и а для горизонтального потока, если связь между коэффициентом
трения С/ для однофазного потока и числом Реннольдса р/о£)/ц/ выражается
уравнением Блазиуса
1 \ «V
Показать, что полученные зависимости почти совпадают с результатами
расчетов в предположении, что коэффициент трения на стенке, определяемый
уравнением (5.39), связан с числом Рейнольдса для пленки Re/ аналогичным
уравнением
г л (WfD-VU
С^=А{-7Г) ■
5.16. Решить пример 5.1 для случая горизонтального течения. Показать, что
32У* Nf ( ?g)'u ,. ,
е =a2-L 2 - a(l— <*),
Ng Ар* + Ng \ Р/ I
32/
/
NfAp*
• = (l-a)2
Левые части этих уравнений — не что иное, как параметры Мартинелли для
вязкого течения. Для различных значений |Х//|хв вывести соотношения между
Фf и <£g., « и X и сравнить результаты с данными фиг. 3.6 и 3.8.
5.17. Провести дифференциальный анализ ламинарного газо-жидкостного
потока в горизонтальных, вертикальных и наклонных трубах, используя
уравнение (5.42), а также локальные значения плотности и вязкости из гл. 2.
5.18, Показать, что для течения жидкости с постоянными свойствами без
трения между параллельными пластинами, расположенными на расстоянии
2а, при равномерной конденсации на них с массовой скоростью m осевой
и радиальный профили скорости соответственно описываются уравнениями [9]
mm icy
" — -cos—-
2a?g 2а
142
ГЛАВА 5
где г — осевая координата, а у отсчитывается от центральной линии по
нормали к пластинам. Как изменяется давление в функции г и у? Показать, что
линии тока направлены по нормали к стенкам и что скоростной напор на
центральной линии вдвое больше среднего. Получить последний результат,
используя общее уравнение баланса количества движения, и сравнить с уравнением
Бернулли для центральной линии тока.
5.19. Показать, что решение уравнения (5.18) для малых значений z является
аппроксимацией решения уравнения для потока с потенциалом скорости
т , -кг яу
Ф = сп -=— cos ——- .
fg 2а la
Показать, что это решение описывает безвихревое течение, в то время как
решение задачи 5.18 относится к потоку, в котором элементы жидкости
имеют постоянную скорость вращения. Определить поле давлений в канале.
5.20. Показать, что течение без трения в трубе радиусом г0 с равномерной
конденсацией на стенках можно представить полем скоростей [9]:
■птг яг2
• cos -
Wo " 1r\
v-J^Lsin.
9gr 2гг0
Построить распределение скоростей и сравнить его с результатами Олсона
и Эккерта [8]. Показать, что скоростной напор на оси вдвое больше
среднего. Определить поле давлений в функции гиг.
5.21. Как использовать решения задач 5.18—5.20 для описания обратимых
процессов испарения и конденсации в канале? Эти результаты могут иметь
практическое значение при разработке эффективных двухфазных сепарацион-
ных устройств для дистилляции, обессоливания и очистки воды и для
повышения термодинамической эффективности установок, использующих процессы
испарения и конденсации (например, холодильников и энергетических
установок) .
5.22. Показать, каким образом при конденсации иа стенках канала можно
получить положительные, отрицательные или нулевые значения касательного
напряжения на стенке в зависимости от профиля скорости. -•>
Литература
1. Soo S. L., Тгегек G. J., Dimick R. С, Hohnstreiter G. E., Ind.
Eng. Chem. Fundamentals, 3, 98—106 (1964).
2. Ш л и х т и н г Г., Теория пограничного слоя, изд-во «Наука», 1969.
3. Prandtl L., Essentials of Fluid Dynamids, Blackie, Ltd., Glasgow, 1952,
p. 118, (перевод с нем. „Fflhrer durch die Stromungslehre", 3rd ed., Vie-
weg, Braunschweig, 1949).
4. Deissler R. E., NACA Tech. Notes, № 2129, 1950; № 2138, 1952;
№ 3145, 1959.
5. G i 11 L. E, H e w i 11 G. F., L а с е у P. M. C, Chem. Eng. ScL, 19,
665 (1964).
6. Turner J. M., Ph. D. thesis, Dartmouth College, Hanover, N. H., 1966.
7. Bankoff S. G., Trans. ASME, J. Heat Transfer, ser. C, 82, 265 (1960).
8. О л с о н Р. М., Э к к е р т Э. Р. Г., Труды амер. общ-ва инж.-мех., сер. Е,
Прикладная механика, № 1, 7 (1966).
9. У о л л и с Дж., Труды амер. общ-ва инж.-мех., сер. Е, Прикладная
механика, № 4, 261 (1966).
10. А р м а н д А. А, Изв. ВТИ, № 1, 16 (1946).
ч
6
ОДНОМЕРНЫЕ ВОЛНЫ
6.1. Введение
Эта глава посвящена развитию теории одномерных волн
применительно к однофазным и двухфазным течениям. Однофазные
течения приходится рассматривать потому, что многие
результаты, необходимые для дальнейшего изложения, как это ни
странно, не содержатся ни в одном из хорошо известных курсов
по данной теме. Так как для большинства читателей принципы
теории окажутся новыми, для иллюстрации физического смысла
математических уравнений будет рассмотрено достаточное число
примеров.
Теория волн является очень действенным методом
исследования нестационарных течений и переходных режимов. С
помощью этой теории объясняются такие явления, как запирание
и «захлебывание», которые ограничивают эффективность
установок. В некоторых случаях изменения режимов течения могут
быть связаны с неустойчивостью, обусловленной усилением волн.
Волны могут переносить либо непрерывные изменения
некоторых значений параметров, либо ступенчатые, изменения или
конечные разрывы. Последний тип волн будем называть ударными
волнами или скачками. Существует множество видов волн и
скачков, которые определяются вызывающими их физическими
процессами. Два наиболее важных вида волн: непрерывные >>
и динамические. Непрерывные волны представляют собой
квазистационарное явление и наблюдаются всякий раз, когда
имеется зависимость между расходом и концентрацией 2К Одно
'' Я впервые услышал о «непрерывных волнах» непосредственно от
одного из участников семинара в Массачусетсом технологическом институте,
на котором этот термин использовал проф. Шапиро. Он не только
нагляднее, чем термин «кинематические» волны, который применили Лайтхилл
и Уитхэм для обозначения того же явления, ио и, кроме того, его труднее
спутать с «динамическими» волнами. Для понимания того, что
распространяется, необходимо очень простое представление о непрерывности, однако
потребовалось много времени, чтобы этот вопрос был введен в элементарные
курсы гидродинамики.
2> Например, уравнение неразрывности в этом случае можно
преобразовать следующим образом:
д(?А) д(?сА)
dt "*" дг ■ '
(см. продолжение сноски на следующей странице)
144
ГЛАВА б
установившееся значение просто переходит в другое при
отсутствии динамических эффектов, связанных с инерцией или
импульсом. С другой стороны, возникновение динамических волн
связано с существованием сил, которые ускоряют вещество
в волне вследствие градиентов концентрации. Так как плотности
фаз и их объемные содержания представляют собой формы
концентрации, в пределах двух основных классов волн
насчитывается много других типов волн. Кроме того, процесс
взаимодействия между различными волнами определяет те из них (если
они имеются), которые оказывают преобладающее влияние на
движение и, следовательно, определяют устбйчивость течения.
Многие волновые явления в двухфазных средах, в
особенности поверхностные волны, по своей природе являются двух-
и трехмерными и в этой главе не рассматриваются.
6.2. Непрерывные волны в однофазном потоке
Непрерывные волны возникают всякий раз, когда
установившийся равновесный расход вещества зависит от имеющегося
количества этого вещества. Например, расход воды в реке
зависит от ее глубины, поток автомобилей на шоссе — от плотности
движения, а скорость, с которой доктора осматривают
пациентов,— от числа ожидающих за дверью. Конкретнее, расход на
единицу ширины вязкой жидкой пленки, стекающей по
вертикальной стенке, в зависимости от ее толщины определяется
уравнением
*= щ ' (6Л)
где q — расход, а б—толщина, т. е. количество имеющейся
жидкости.
Для общности изложения и для расширения возможностей
дальнейшего анализа, примем, что расход выражается неким
соответствующим параметром /. Обозначим количество вещества
через некоторую обобщенную переменную а, которую" будем
называть концентрацией. Концентрация а может выражаться
в любых единицах, соответствующих определению /, например
д(?А) , d(fcA) д(?А) п
dt ^ д(?А) дг
д(?А) д(?А)
"г у -и
dt ^ w dz — '
где
. д(?сА) _ д(с)
Vw~ д(9А) -с+?л д(РА)
— скорость переноса постоянного значения р [см. далее формулы (6.3) и
(6.22)]. — Прим. перев.
\
ОДНОМЕРНЫЕ ВОЛНЫ 145
в кг/м, м3/м3, числом молекул в единице объема, числом
автомобилей на милю, глубиной жидкости, числом пациентов на
кабинет и т. д. Единственно, что при этом требуется, это чтобы
величина j была функцией от а и равнялась произведению V на а,
где V— средняя скорость.
Скорость непрерывной волны выводится из условия
неразрывности вещества, проходящего через контрольный объем,
движущийся со скоростью волны и ограниченный линиями аа и bb на
фиг. 6.1, где показана волна, распространяющаяся со скоростью
Ъ
Ь
Фиг. 6.1. Распространение непрерывной волны.
Yw из области с концентрацией а в область, где концентрация
равна а + ба. Относительно фронта волны приток и сток
вещества равны. Следовательно,
j-*Vw=J+By -V9(* + 8а), (6.2)
откуда
^=Щ- (6-3)
Если в волне происходит конечное изменение концентрации,
то из тех же соображений получим
vH-£=£)f- (6-4)
Нижние индексы относятся к областям перед фронтом волны и
за ним. Такую волну будем называть непрерывной ударной
волной. Нижний индекс f означает, что по обе стороны от волны
поддерживается равенство сил и что влияние инерции отсутствует.
Непрерывные волны часто наблюдаются, например, в таких
системах, где гравитационные силы уравновешиваются силами
сопротивления. Исключая из уравнения (3.45) инерционные
члены и градиент давления, получим для однофазного потока
/+£=0. (6.5)
10 Заказ № 162
I
I
а
146 ГЛАВА б
Если b — постоянная массовая сила, то сила сопротивления на
единицу объема также должна быть постоянной, так как поток
не ускоряется. Тот факт, что ;' является функцией а, означает,
что эта постоянная сила сопротивления является одновременно
функцией ;' и а. Действительно, для конкретных систем закон
сопротивления может быть определен зависимостью
/=/(/, «)• (6-6)
С другой стороны, так как
j=*V, (6.7)
уравнение (6.6) эквивалентно уравнению
f=f(V, «). (6.8)
Используя уравнение (6.7) из уравнения (6.3), можно
получить другой вид выражения для скорости непрерывной волны:
'^-^«(-зг)/ <6-9>
откуда следует, что скорость волны превышает среднюю
скорость на величину a(dV/da)f. Преимущество этого выражения
состоит в том, что результат не зависит от единиц измерения а.
Если соотношение (6.8) известно в явном виде, можно
написать
( да )f
{dfjda)v
W/dV)a
(6.10)
Объединяя уравнения (6.9) и (6.10) и используя индексы,
относящиеся к частным производным, получим
V„=V-4^-. (6.11)
J v
Физический смысл полученных результатов поясняется
следующими примерами.
Пример 6.1. Определить скорость непрерывной волны для вязкой жидкости,
стекающей по вертикальной стенке. Показать, что эта скорость в три
раза больше средней скорости. Определить профиль поверхности пленки,
стекающей по стенке опорожняемого через дно сосуда, который в
начальный момент был заполнен жидкостью.
Решение. Величина б соответствует количеству жидкости иа единицу
ширины и может быть отождествлена с величиной ос. Расход на единицу
ширины q может быть отождествлен с /. Из уравнения (6.7) находим
среднюю скорость жидкости
у = Л_= *<р/-р«>" . (6.12)
$ 3flf
ОДНОМЕРНЫЕ ВОЛНЫ
147
Скорость непрерывной волны определяется из (6.3), что дает
_dq_ g(?f-?g)V
Vw~ db ~ (1, • {ЬЛ6>
Из уравнений (6.12) и (6.13) следует, что-
VW = ZV. (6.14)
Так как сосуд опорожняется, то непрерывные волны 'будут
переносить соответствующие значения толщины пленки, причем каждая будет
распространяться со своей скоростью в соответствии с уравнением (6.13).
Если в начальный момент опорожнения ^=0 при z=0 поверхность
плоская, то отсюда, начиная с этого момента, распространяются волны, соответ-
-^
'/
/
'>
/
V
н
/
/
/
/
1
в, '
«2
w
\
щ
'
У
t = 0
VwJ
Фиг. 6.2. Стекание жидкой пленки по стенке прн опорожнении сосуда.
а — профиль поверхности плеикн по истечении времени t; б — положения волн в
плоскости zt.
ствующие всем значениям б. При дальнейшем движении в соответствии
с уравнением (6.13) большие значения б будут переноситься быстрее.
Спустя время t волна пройдет расстояние
z=V„t,
(6.15)
и положение каждой волны в плоскости zt можно изобразить прямой
линией (фиг. 6.2, б).
Подставляя выражение для V из (6.13) в (6.15), получим уравнение
поверхности в момент времени t (которое было выведено в работе [2]
и представлено на фиг. 6.2, а)
g(P/— 9g)t
V-f
82.
(6.16)
Пример 6.2. Вязкая жидкость стекает по стеике с постоянным расходом,
соответствующим толщине бь Расход мгновенно снижается до нового
значения, соответствующего при стационарном течении толщине бг.
Показать, что происходит с профилем поверхности жидкости.
Решение. Как и в предыдущем случае, от точки z=0 будут распространяться
волиы, однако теперь они будут соответствовать значениям б,
заключенным между 6i и бг- Начальное ступенчатое возмущение будет
распространяться вдоль стенки (фнг. 6.3).
10*
148 ГЛАВА б
/
/
/
/
/
/
/
/
/
•
/
/
/
/
/
S
•
/
/
?
S
/
/
sz
8
Si
v
^v
*
Значения S
между S, и 8г
Фиг. 6.3. Характер стекающей жидкости пленки после внезапного уменьшения
расхода.
а — профиль поверхности по истечении времени t; б — положения волн в плоскости zt.
Два предыдущих примера прказывают, каким образом
движение непрерывных волн дает возможность переносить
«конечные условия» по потоку. Этот механизм является общим. Если
непрерывные волны не распространяются таким образом, то
конечные условия не могут оказать никакого влияния.
Предельные условия достигаются, когда непрерывные волны
останавливаются, что в случае упругих волн аналогично запиранию,
когда число Маха достигает единицы.
Пример 6.3. Коэффициент трення при турбулентном течении стекающей
жидкой пленки приблизительно постоянен. Каково соотношение между
скоростью непрерывной волны н средней скоростью жидкости?
Решение. Касательное напряжение на стенке равно
%, = <?/• V2PV2.
(6.17)
Отождествляя толщину пленки б с концентрацией, получим следующее
выражение для силы, приходящейся на единицу объема:
/ = -
Из уравнения (6.11) следует
V,
CffV2
28
(6.18)
откуда
ЗУ
2
(6.19)
Следовательно, скооость волны в полтора раза больше средней скорости.
V
ОДНОМЕРНЫЕ ВОЛНЫ 149
Образование непрерывных ударных волн
Когда быстрая непрерывная волна догоняет более
медленную, они сливаются с образованием скачка. В плоскости zt этот
процесс изображается пересечением линий распространения волн
с образованием некоторой новой линии, имеющей
промежуточный наклон. Чтобы скачок сохранял крутой фронт и не
вырождался в серию более слабых скачков и волн, непрерывные волны
должны приближаться к скачку с обеих его сторон. По этим
эффектам судят, будет ли образовавшийся скачок устойчивым, и
Фиг. 6.4. Определение направления распространения устойчивого скачка
по кривой расход — концентрация.
если да, то в каком из направлений, 1 или 2, он будет
распространяться в жидкости. По уравнению (6.4) направление движения
скачка определить нельзя.
Для примера на кривой зависимости / от а (фиг. 6.4, а)
показан непрерывный скачок. В соответствии с уравнением (6.4)
скорость скачка характеризуется наклоном хорды, соединяющей
точки 1 п 2. Соответствующие скорости непрерывных волн в
жидкости, примыкающей к скачку, определяются наклонами
касательных к кривой в точках / и 2. Если скачок устойчив, то
состояние 2 должно иметь место на его положительной стороне,
как это видно из фиг. 6.4, б.
Пример 6.4. Экспериментально установлено, что на длинных ровных
участках автострады имеется определенное соотношение между числом
автомобилей на милю (концентрацией) а и числом автомобилей в час /.
Движения иет, если нет автомобилей (ос=0) или если автомобили стоят
вплотную друг к другу (ос=аМакс). При некотором промежуточном
значении ос имеется максимум потока /макс- Предположим, что долгое
время по автостраде движется стационарный поток автомобилей,
равный /1</макс и в точке z0 происходит авария, временно снижающая
150
ГЛАВА б
допустимый поток автомобилей в окрестности этой точки до значения
/2</ь Что произойдет и как можно описать развитие событий с
помощью зависимости / от ос?
Решение. На фиг. 6.5, а показана зависимость / от а. Так как стационарный
поток /i существовал в течение длительного времени, то он, по-вндимому,
распространился в направлении движения и, следовательно, соответство-
«•2 *< <*2
ее
а
6
Фиг. 6.5. Временное изменение плотности движения на шоссе.
На фнг. 6.5, б скачки показаны жирными линиями, а непрерывные волны — тонкими.
вал меньшему из двух возможных значений ос (характеризуемому
положительным наклоном кривой). Когда авария снижает поток до
величины /г, новое значение ос распространяется по автостраде в
отрицательном направлении — назад. Следовательно, в точке, изображающей
новую ситуацию, кривая должна иметь отрицательный наклон и
величине /2 должно соответствовать большее из двух значений ос. Условия
существования устойчивого скачка между oti и а2 удовлетворяются, и
эта волна движется по автостраде назад с отрицательной скоростью Vs,
показанной иа фигуре. В момент времени /' (после восстановления
движения) исходный скачок в месте происшествия расщепляется на
непрерывные волны, соответствующие сплошному спектру значений а. Волны,
ОДНОМЕРНЫЕ ВОЛНЫ 15!
соответствующие значениям а слева от максимума кривой,
распространяются вперед, а соответствующие величинам справа от максимума —
назад. Самая быстрая волна, распространяющаяся вперед, соответствует
«=«2', так как это значение характеризует плотность движения,
которая установилась при потоке /2 за местом происшествия. Самая быстрая
из волн, движущихся назад, соответствует величине ос2 — бос и
распространяется против движения по автостраде до слияния со скачком в
момент времени t = t". По мере наложения последующих волн скачок
«ослабляется», разворачивается в плоскости tz и асимптотически вырождается
в бесконечно малую непрерывную волну, соответствующую величине а^
Веер волн между ос2' и ось показанный иа фнг. 6.5, б, в конце концов
сливается со скачком между <хг' и ос', который двигался в направлении
движения на автостраде от места происшествия.
Плотность движения в зависимости от t и z легко определяется из
фнг. 6.5, б. На больших свободных участках графика плотность
постоянна, в то время как в области, занятой веером линий, плотность
непрерывно изменяется.
Устойчивость непрерывных волн
Пока длина волны достаточно велика, всегда можно выбрать
сечения аа и ЬЬ на фиг. 6.1, достаточно удаленные от крутого
волнового фронта, так что поток можно считать стационарным.
Однако в рамках анализа квазистационарного течения,
постулирующего баланс результирующих сил, действующих на поток
вещества, невозможно учесть ускорение, которое должно иметь
место на каком-либо участке волны. Для учета этого ускорения
следует выбрать другой механизм процесса. Во многих случаях
такой механизм может быть обусловлен силами,, вызванными
градиентами концентрации (т. е. эффектом сжимаемости).
Влияние градиента концентрации обычно исследуется при
рассмотрении динамических волн.
Влияние источника массы
Теория непрерывных волн требует соответствующей
модификации в тех случаях, когда имеется источник массы,
добавляемой к потоку (например, поступление воды из притоков реки,
приток автомобилей на автостраду на перекрестках, конденсация
на жидкой пленке). Для этого случая видоизменим фиг. 6.1,
включив источник массы р на единицу длины, и рассмотрим
стационарный контрольный объем длиной Ьг, показанный на
фиг. 6.6. При надлежащем выборе единиц измерения р получим
откуда
да , dj a
dt "•" дг ?ш
(6.21)
152 глава в
Если / — функция а, то (dj/dz) можно заменить на (dj/da)X
X (da/dz) и, используя уравнение (6.3), получить
а* , ,, да „ (622)
dt
V™ dz ~
Левая часть уравнения (6.22) представляет собой полную про-
-j+S; Фиг. 6.6. Контрольный объем при наличии
источника вещества с расходом {$ на
единицу длины.
IV/V/V/.
изводную по времени от а для системы координат, движущейся
со скоростью Vw Следовательно,
da \
dt |движение со
'скоростью V
(6.23)
При р = 0 непрерывные волны переносят постоянные значения а,
что было рассмотрено ранее. В других случаях рост или
затухание волн будет определяться знаком р.
Пример 6.5. Решить пример 6.1 для условий равномерной конденсации на
поверхности пленки с постоянной скоростью (объем конденсата на
единичной площадке в единицу времени).
Решение. Отождествим а с толщиной пленки д. Тогда для данной волиы
уравнение (6.23) примет вид
do
dt
= Р.
(6.24)
Так как р — константа, то интегрирование уравнения (6.24) дает
o-o0 = fi(*-*0), (6.25)
где индекс 0 означает начальные условия, которые служат для
определения волны.
Так как скорость волны равна Vw, то нз уравнения (6.13) для
данной волны находим
dz J g(p/~ Pg)82
dt ~ u,
Объединяя (6.24) и (6.26), получим
do __ dbjdt __
Pn
dz
dz/dt g(?/ — ?g)
82,
(6.26)
(6.27)
ОДНОМЕРНЫЕ ВОЛНЫ 153.
а после интегрирования
g- = P(z —z0). (6.28>
Уравнение (6.28) определяет траекторию волны в плоскости bz.
Исключая 6 из (6.25)—(6.28), получим уравнение линии распространения волиы
. в плоскости zt в функции начальных параметров, а именно
Po+^(^-g]3=8o3+3;p(p(;rg • (6-29)
С другой стороны, исключая б0 нз (6.25) и (6.28), определим б в функ-
• цин z в данный момент времени, т. е. профиль поверхности
0з=[о-р(;-гЬ)]з+ ^ГрУ • (6-3°>
Условиям данной задачи удовлетворяют два семейства волн: волны,
начинающиеся в момент t0=0 из точки z0=0 при всех значениях б,
н волны, начинающиеся в последующие моменты времени из точки
z0=0 прн значении б0=0. Для первого семейства нз (6.28)—(6.30) имеем
b3 = bl + —-S _.. (6.31)
0 g(9f — ?g) '
Линия распространения волны в плоскости zt описывается уравнением,
а профиль поверхности — уравнением
^3=(8-^)3+Т(^г- <6-33>
Линии распространения воли и профиль поверхности для второго
семейства волн совпадают-и описываются одним уравнением
8з=__М* (6.34),
g(tf — tg) '
которое является уравнением профиля пленки в конечном
установившемся состоянии. В плоскости zt линии распространения волн
параллельны, и нз (6.29) следует
'-»+[«<,/*.> Л"- <"»>
Эти результаты представлены на фнг. 6.7.
154 ГЛАВА 6
z=o?
Уравнение (6.31)
Уравнение (6.34-)
~р, Уравнение (6.35)
Уравнение (632)
Уравнение (6.33)\
а
■4> и г. 6.7. Неустановившийся процесс стекания пленки вязкой жидкости при
равномерной конденсации иа ией.
,а — профиль поверхности и линии распространения волн, б — линии распространения волн.
6.3. Непрерывные волны в потоке несжимаемой
двухкомпонентной среды
Рассмотрим течение двух несжимаемых компонентов 1 и 2
в канале постоянного сечения. Из условия неразрывности потока
.следует, что общий расход и, следовательно, среднее значение
плотности объемного расхода ;* постоянны по всей длине канала
(однако возможно их изменение во времени, связанное с
изменением конечных условий). Обозначая плотности объемного
расхода (приведенные скорости) компонентов через j\ и /г,
постучим
j = jl + h; (6-36)
Пусть объемная концентрация компонента 2 равна а. Как и
ранее, условие равновесия имеет вид
/(7*i. Л. a)=const. (6.37)
Метод, использованный при выводе уравнений (6.3) и (6.4),
-можно применить и в данном случае для определения
скоростей непрерывной волны и скачка соответственно:
М^),гЫЫ/ (6-38>
у г «»)■-<ШЛ _[<*)■-»■), 1 (639)
Чтобы пояснить смысл уравнений (6.38) и (6.39),
представим уравнение (6.37) в виде графической зависимости а от /2
одномерные волны 155
для разных значений ]\ (фиг. 6.8). Например, для газо-жид-
костного потока это будет зависимость истинного объемного
газосодержания от расхода газа при разных расходах жидкости.
Переход от точки / к точке 2 через фронт волны в соответствии
с уравнением (6.36) должен осуществляться вдоль линии
/i+/z=const. Тогда уравнения (6.38) и (6.39) непосредственно
определяют требуемые скорости волн. Графически скорости
непрерывной волны и скачка изображаются соответственно
углами наклона касательных и хорд к кривой /i+/2=const.
Ф н г. 6.8. Непрерывные волны в
потоке несжимаемой двухкомпонентной
среды.
Скорость непрерывной волны определяется
тангенсом угла наклона касательной к
кривой /i + /i»const. Скорость скачка равна
тангенсу угла наклона хорды, соединяю-
щей-соответствующие точки этой же кривой.
Существенная модификация этого метода связана с
использованием плотности потока дрейфа (приведенной скорости) /2i,
которая была введена в гл. 4.
Подставляя уравнение (4.4) в уравнения (6.38) и (6.39),
получим
<ЭУ21 \
h./'
V,.
--J-
да
(6.40)
V,
- /_1_ Г (721 )l~ (72l)2 1
L «1 — 02 \j,f'
(6.41)
Уравнения (6.40) и (6.41) справедливы всегда. Особенно
полезны они в тех случаях, когда приведенная скорость дрейфа
является функцией только концентрации и не зависит от общего
расхода. При этом скорости волны отличаются от среднеобъем-
ной скорости на величину, которая зависит только от а и свойств
системы. Тогда соотношение между /21 и а выполняет ту же
самую функцию для двухфазного потока, как и зависимость / от
а — для однофазного. Как и ранее, скорости волны и скачка
можно представить углами наклона касательных и хорд.
156
ГЛАВА б
В следующих главах теория непрерывных волн будет
использована для анализа характеристик нестационарного
одномерного движения в барботажных колоннах для исследования
пенной структуры, а также процессов осаждения и псевдоожижения.
Пример 6.6. Экспериментально установлено, что выражение для je/ в барбо-
тажной колонне имеет вид
Jg/ = Va>a^-^2- (6'42)
Известно также, что при ос > 7г пенная структура крайне неустойчива
и происходит быстрое разрушение и слияние пузырьков.
Вертикальный сосуд постоянного диаметра заполнен жидкостью до
высоты Н. Затем через него пропускают газ с приведенной скоростью
jg^v^/S. Какова высота столба газо-жидкостной смеси? Сколько
времени потребуется для установления нового режима во всей колонне прн
незначительном изменении расхода газа?
Решить эту же задачу прн jg=v!X1l4.
Решение. Так как //=0, то, считая газ компонентом 2, из уравнения (4.2)
получим
Jg/=0~a)Jg. (6.43)
Объединяя уравнения (6.42) и (6.43), находим
Jg=v„av-a)- <6Л4>
Уравнение (6.44) -при ■ jg = v00 /8 имеет решение a='/2±V2A- Обычно
меньшее значение соответствует основанию колонны, а большее — ее
вершине (так как непрерывные волны распространяются от концов).
Однако пеиа настолько неустойчива, что, по-видимому, имеет смысл только
значение ос='/2—V2U. Так как количество жидкости постоянно,- то
высота столба газо-жидкостной смесн Н' определяется из выражения
#' —Я
Я'
Следовательно,
Я' = -Д—= Я/_, =1,17Я. (6.45)
Если расход газа меняется незначительно, то новые условия будут
распространяться со скоростью непрерывной волны в соответствии с
уравнением (6.40). Так как /=/«, то с учетом уравнения (6.42) получим
^„=./,+Чво-вм,-3в>- (6.46)
Следовательно, для заданного значения ]Й и расчетного ос имеем
V =0,605i» . (6.47)
да оо у '
Время прохождения волиы через всю колонну н установления
нового значения ос равно
И' Я
-£— = 1,935-^-. (6.48)
ОДНОМЕРНЫЕ ВОЛНЫ
157
При jg — v^fi мы получили бы решение уравнения (6.43) в виде
a='/2, т. е. результат, соответствующий режиму «захлебывания» ■>. При
этом из уравнения (6.46) следует, что Vw=0, т. е. волны вообще не
могут распространяться, что объясняет механизм «захлебывания».
6.4. Динамические волны
Динамические волны в однокомпонентном потоке
Динамические волны образуются всякий раз, когда
результирующая сила, действующая на поток вещества, обусловлена
градиентом концентрации. Обозначим эту силу, приходящуюся
Скорость волны с относительно жидкости ,
|/=<0
-. «* .
1*<*
-SV
Фиг. 6.9. Распространение динамической волны.
на единицу объема, через f. В рамках линейной зависимости
эта сила, вызванная градиентом концентрации da/dz, равна
/=
а/
д (да/дг)
да
dz
(6.49)
Используя нижний индекс для обозначения производной
и заменяя da/dz более общим символом Va, можно
представить уравнение- (6.49) в следующем виде:
/=Л.-аг- (6-5°)
Рассмотрим случай, показанный на фиг. 6.9, когда
динамическая волна перемещается со скоростью с относительно
неподвижной жидкости или частиц. Волна будет неподвижна, если
всей системе сообщить скорость —с. Тогда уравнения нераз
рывностн и движения для волны примут соответственно
следующий вид:
da
~dz~
dV
dz
=0
(6.51)
(6.52)
!) В этом случае правильнее было бы говорить о смене режима работы
колонны, а не о «захлебывании».— Прим. перев.
158
ГЛАВА б
Исключая dV/dz и da/dz из уравнений (6.51) и (6.52), получим
с2=-^-. (6.53)
Следовательно, скорость волны определяется выражением
C=±(-Z£l)''\ (6.54)
Динамические волны распространяются со скоростью с
относительно жидкости в обоих направлениях, в то время как
непрерывные волны движутся только в одном направлении. Вообще
условием существования волн является отрицательное значение
величины /ve. Физически это означает, что рассматриваемая
система оказывает сопротивление при сжатии или расширении
(в противном случае в условиях постоянного давления
окружающей среды она бы катастрофически взрывалась или
сжималась).
Примеры динамических волн в однокомпонентном потоке
Длинные волны в канале постоянной ширины. Концентрацию
можно выразить через объем, приходящийся на единицу
ширины и на единицу длины, т. е. через глубину. Следовательно,
а можно отождествить с глубиной слоя воды у в канале, т. е.
а=у. (6.55)
Нетрудно показать, что сила, действующая на вертикальный
слой жидкости шириной b вследствие малого изменения
глубины 6у, равна
F=-?gyb(by). (6.56)
Следовательно, средняя по сечению сила, приходящаяся на
единицу объема, равна
/=1^Г=-Р^' (6-57)
откуда, используя (6. 50), получим
/V.=-P£. (6-58)
Подстановка уравнений (6.58) и (6.55) в (6.54) дает хорошо
известный результат
c=±(gy)'h. (6.59)
Волны в однородной сжимаемой жидкости. Обычно
концентрация выражается как масса вещества в единице объема, т. е.
а=Р. (6.60)
ОДНОМЕРНЫЕ ВОЛНЫ
159
Сила, действующая на элемент жидкости единичного объема,
равна
/—-§-=---£-&• <6-6»
откуда с учетом (6.50) следует
Последующая подстановка уравнений (6.62) и (6.60) в (6.54)
приводит к известному выражению
с
= +«£-Y
± (-£)"'■ (6.63,
Производную др/др следует вычислять для конкретного
процесса. В газах обычно происходит изоэнтропический процесс,
однако в некоторых случаях возможны другие процессы,
например изотермический.
Динамические волны в потоке несжимаемой
двухкомпонентной среды в канале постоянного сечения
Рассмотрим стационарное движение двух компонентов со
скоростями vi и Vz в прямом канале постоянного сечения. Чтобы
динамическая волна стала неподвижной, сообщим всей системе
скорость —U. В новой системе отсчета скорости компонентов
будут следующими:
v[=vx-U, (6.64)
1)2 = 1)2— U. (6.65)
Уравнения неразрывности примут вид
^-[г,;(1--а)]=0. (6.66)
d
dz
[г»2*]=0, , (6.67)
а уравнения движения в соответствии с уравнениями (3.45) и
(3.46) станут.следующими:
P^^-=-^F+/1 + 6I. (6.68).
Р2*2-^т=--|г+Л + б2. (6-69)
160
ГЛАВА 6
Вычитая (6.69) из (6.68) , получим
i i
piv'l4I—p2V2-jj-=fi-f2-\-bl-b2. j (6.70)
Динамические волны будут существовать в случае, когда
правая часть уравнения (6.70) линейно зависит от градиента
концентрации, т. е.
/1-/2+&i~62=-/vaJ^. (6-71)
Подставляя уравнение (6.71) в (6.70) и исключая dv'Jdz и
dv'Jdz с помощью уравнений (6.66) и (6.67), получим
•££•+-*£-+/,.-о. «ш>
Выражая v[ и v'% через исходные скорости с помощью
уравнений (6.64) и (6.65), получим квадратное уравнение
относительно U:
v* (т^г+^) - ™ (т^+-^)+л^г +#+А -=о.
(6.73)
откуда
V\9l i "292 , Г — Р1Р2 (^1 — V2)2 _ ( Р1 . h_) f ]''г
I— а "*" а —[ а(1— а) , \1—a a/ V"J
Pl/(1—а) +Р2/«
(6.74)
Вводя средневзвешенную скорость (которая не равна
скорости центра тяжести)
»Л>— Р1/(1_.) + й/. 1Ь'7&)
и скорость динамической волны
С=+( -^l-^)2 _f У/2С PJL Ll2_\-,/2 (676)
С ±U/p2+(I-a)/p, VJ \l_a+aj ' 10-'°>
приведем уравнение (6.74) к виду
(j=V0±c. (6.77)
Следовательно, динамические волны движутся относительно
средневзвешенной скорости Vo со скоростью ±с, определяемой
уравнением (6.76).
Из уравнения (6.76) можно заключить, что fVa должна быть
не только отрицательной, но и достаточно большой величиной,
чтобы подавить возмущающее действие относительного
движения.
U= '
ОДНОМЕРНЫЕ ВОЛНЫ
161
Пример динамических волн в потоке несжимаемой
двухкомпонентной среды в прямоугольном
горизонтальном канале
Рассмотрим поток двух жидкостей, имеющих скорости vi и
V2 в горизонтальном канале постоянной ширины глубиной Н.
Массовые силы в направлении потока отсутствуют, однако
изменение гидростатического давления по сечению канала под
действием градиента концентрации вызывает увеличение сил f
в направлении движения, хотя эти силы не входят в средний
градиент давления.
*-1>2
Фиг. 6.10. Распространение динамической волны при расслоенном течении
двух несжимаемых компонентов в горизонтальном канале.
Обозначим давление в верхнем слое канала через р. Тогда
результирующая сила, действующая на единицу ширины
элемента более легкой жидкости (заштрихованная, область на
фиг. 6.10), равна
Fl=(\-a)Hbp, (6.78)
а результирующая сила, действующая на единицу ширины
элемента более тяжелой жидкости, равна
F2 = atf [8/>-£(p2-Pl)//8a].
(6.79)
Вычитая общую силу, действующую на единицу объема
жидкости 2, из соответствующей силы, действующей на единицу
объема жидкости 1, получим
Ьр0— а) Я
Ч.Н
/'-/»= ZW-^h -igb-ifr-gfe-P.)"*»]. (6-80)
Следовательно,
И Заказ № 162
/i-/2 = (P2-Pi)£#-
дг
(6.81)
162
ГЛАВА б
В соответствии с (6.71) величина fVa равна
/va = -(p2-Pl)£//. (6.82)
Из (6.76) получим скорость динамических волн
относительно Vo
Видно, что относительная скорость оказывает возмущающее
влияние, так как она вызывает уменьшение скорости
динамической волны. Действительно, при достаточно высокой относительной
скорости с2 становится отрицательной величиной и поток
оказывается неустойчивым. Это происходит при
(^-^)2>(P2-Pi)^//(^+1^L). (6.84)
Эти уравнения непригодны при длинах волн, меньших, чем
размеры канала, так как становится несправедливым одномерное
приближение. Можно показать, однако, что они являются
предельными в решении двумерной задачи при больших длинах
волн [3].
Дальнейший анализ расслоенного течения жидкостей развит
Лонгом [4—6]. Особый интерес представляет его исследование
одиночных волн с профилем гиперболического секанса. Введем
следующие обозначения для волн с амплитудой б:
Н
(6.85)
yWip'i/2[^(p2-Pi)rV2, (6.86)
У2=У'2р2/2 [gfffa- Р,)Г,/г. (6.87)
Условие пересечения волн, полученное Лонгом, имеет вид
;*2 / ** \ -*2 / \
7I^(i-rb)+-s-(>+-T-)-'- <**»
Условие, при котором уравнение (6.88) удовлетворяется для
всех значений б*, т. е. для волн любой амплитуды, записывается
в виде
.*2 .*2
(I—a)4 ^"^Г- (6-89)
При этом уравнение (6.88) сводится к следующему:
h
(I-a)
ОДНОМЕРНЫЕ ВОЛНЫ 163
Если теперь в уравнении (6.90) изменять а, то будут
получены результирующие зависимости между /i и /2 в виде эллипса,
ограничивающего область допустимых расходов. Границы этой
области определяются дифференцированием уравнения (6.90) по
а, откуда .« .«
TT^F-4—0' <6-91>
что идентично уравнению (6.89). (Было бы нелогично, если бы
это оказалось не так!)
Исключая а из (6.90) и (6.91), получим
/1
''•+/?'•= 1. (6.92)
Это уравнение устанавливает максимально возможные
расходы компонентов, не вызывающие образования стационарных
волн неопределенной амплитуды. Таким образом, уравнение
(6.92) определяет геометрическое место точек расходов при
«захлебывании».
Проведенный анализ интересен тем, что он обнаруживает
примечательное соответствие между уравнением (6.92) и
эмпирическими корреляционными формулами для режимов
«захлебывания» при вертикальном кольцевом течении (гл. 11), хотя в
последнем случае динамика процесса имеет совершенно иной
характер и сила тяжести не действует непосредственно на
межфазную поверхность как восстанавливающая сила.
Влияние сжимаемости на динамические волны
в потоке двухкомпонентной среды
Если влияние сжимаемости значительно, распространение
динамических волн зависит от градиентов трех «концентраций»:
плотностей обоих компонентов и объемной концентрации одного
из них.
Тогда уравнения неразрывности (6.66) и (6.67) принимают
вид
JL[t,;Pl(l-«)]=0, (6.93)
-|r(w)=0. (6.94)
.Изменения плотности связаны с изменением давления
следующим образом:
_d^=dp!dz_ (05)
dz dpidpi x '
J*L= dPljz ' (6.96)
dz др,др2
11*
164
ГЛАВА 6
Из (6.93) и (6.95) следует
1 йУ\
„' dz
da
1
dp.
1 — a dz
Pl(<WPi) dz
и аналогично из (6.94) и (6.96)
dv<,
1 da
dz
a dz
1 dp
P2 (<*p/dp2) ^
=0.
(6.97)
(6.98)
С учетом сделанного допущения о том, что силы f в
уравнениях (6.68) и (6.69) зависят от градиента концентрации, и
исключая массовые силы, получим
, dv.
Vlca
da
<*Р
df„
Рг^г
lv» dz
da
dz
"■/" 2ua
dz
dp
2v" dz
dz
=0,
=0.'
(6.99)
(6.100)
Система уравнений (6.97) — (6.100) содержит четыре
неизвестных и совместима только при условии
1
—1
v'\
0
1^1
0
\J
1
v2
0
P2^2
1 —a
1
a
/lyct
/ 2va
Pi (.dp(dfi)
1
P2 (dpidf2)
=0. (6.101)
Вычислив определитель, после умножения на i^ и о£
получим
P2U2J
/*. U
dp/dpi
I /ic«
Piu?
1
dp/dp2
(6.102)
Если сжимаемость равна нулю, получим предыдущий
результат,, т. е. уравнение (6.72). С другой стороны, если можно
пренебречь силами f (как, например, при расслоенном течении
с низкой относительной скоростью), то полученное уравнение
Р2и2
1
др/д?2
Pi»i
1
<?p/<?Pi
=0
(6.103)
находится в соответствии с уравнением (3.61).
ОДНОМЕРНЫЕ ВОЛНЫ 165
Если относительная скорость равна нулю и оба компонента
имеют скорость v', уравнение (6.103) сводится к следующему:
a 1 — а
•о = ^ ?±~. . (6.104)
■ + ■ ■
p2(dp/dp2) Vi(dp/d?i)
Следовательно, упругие волны распространяются со скоростью
U= V ± ccs, (6.105)
где ccs — скорость распространения упругих волн в расслоенном
потоке без скольжения фаз. Из уравнений (6.104) и (6.105)
следует
+ '
Р2 Pi
+ '
(6.106)
р24 ?А
где с^ и <?г—скорости распространения упругих волн в каждом
компоненте. В соответствии с уравнением (6.106) скорость волны
заключена между а и с2.
Следует подчеркнуть, что скорость ccs не является скоростью
распространения упругих волн в гомогенной смеси, в которой
отсутствие относительного движения компонентов обусловлено
силами их взаимодействия. Если силы f в (6.68) и (6.69) равны
нулю, то эти уравнения не могут удовлетворять одновременно
условиям v[ = v'2 и dv[/dz = dv'2/dz. Следовательно, в истинно
гомогенном потоке должны существовать значительные силы
межфазного трения. При отсутствии других внешних сил
/,ei— a) + /2a=0, (6.107)
так как действие и противодействие компонентов равны и
противоположны по направлению. Рассматривая поток как
гомогенный и суммируя (6.68) и (6.69), предварительно умноженные
на 1 — а и а соответственно, в пренебрежении массовыми силами
получим обычное уравнение движения жидкости со средней
плотностью рт, аналогичное уравнению (2.9):
[(1 - a) Pl +ap2] v' -g-= - М-. (6.108)
Считая поток гомогенным и исключая da/dz из (6.97) и
(6.98), получим
1 dv' , dp J" е j_ 1 —
v' dz ' dz
I Pl (dp/dp,) + P2(dp/<?P2) J-°' (6,1°9)
166 ГЛАВА б
В соответствии с уравнением (2.50) из (6.108) и (6.109)
непосредственно следует, что
*>Г=<4=|[ар2 + (1-а)Р1] /-Lr^—V))-'. (6.110)
где Сед — скорость распространения упругих волн в истинно
гомогенной смеси. В отличие от ccs значение ссл не обязательно
заключено между Ci и сг и при некоторых условиях может быть
значительно меньше значения каждой из этих скоростей. Если рг
намного меньше pi и с\ меньше с\, то уравнение (6.110) можно
упростить:
^=-*^г (бл11)
Следовательно, скорость сск минимальна при а=7г:
(cchhm=2c2(f)'h. (6.112)
Например, для водо-воздушной смеси при атмосферном давлении
Ci~336 м/сек, p2/pi = 0,0012 и (ссь)мин~23 м/сек.
Если для двухкомпонентной смеси известна только величина
объемного газосодержания, то, очевидно, возникает вопрос,
какое из выражений, (6.106) или (6.110), использовать в расчетах
или принять некоторое компромиссное решение. Можно ожидать,
что выражение (6.106) более подходит для однородной
мелкодисперсной пузырьковой смеси, в то время как выражение
(6.110) применимо при раздельном движении
невзаимодействующих компонентов. При некотором промежуточном значении
сил сопротивления они, по-видимому, будут зависеть от
амплитуды и частоты волн и, следовательно, скорость волны будет
функцией этих переменных, а также свойств компонентов. В
настоящее время информация об этом явлении очень ограничена.
Пример 6.7. В работе [7] получено следующее уравнение для скорости звука
в пузырьковой смеси:
'c = -^t±.HgRT)4\ (1)
где
Qg
'=ТЗГ.' (2)
* = ТТ]Г^' (3>
ОДНОМЕРНЫЕ ВОЛНЫ
167
и Rg — газовая постоянная. Вывести это уравнение, используя
выражение (6.110). ' v
Решение. Пренебрежем сжимаемостью жидкости, считая, что PiCi2^>p2c22, и,
вводя соответствующие обозначения для газа и жидкости,
перепишем (6.110) в виде
' * = -%*-' (5)
где
?m = a?g + (l— <*)Р/. (6)
Истинное объемное газосодержание в гомогенном потоке связано
с отношением объемных расходов компонентов следующим образом:
__ Qg _ Ь
а~ Qf + Qg ~~ 1+5 ' (7)
Отношение массовых расходов выражается через газосодержание
в виде
Wg apg
р = "й7"= (i-«)p/ ' (8)
С использованием (6) и (8) получим
?т = a?g ~
Подставив затем (7) и (9) в (5), найдем
1 +8
?m = «?g—P-. (9)
Для адиабатического распространения упругих волн в чистом газе
имеем
4=W- (11>
Подстановка уравнения (11) в (10), извлечение квадратного корня
и привлечение уравнения (3) дают в итоге требуемый результат
с-
1 + 5
= — (T*WV'. (12)
В соответствии с работой [7] нетрудно установить, что удельные
теплоемкости смесн в условиях теплового равновесия равны
г ч + Kg .„.
°р =—ГТГ-' ( }
- - Cf+Kg (14)
*»- 1 + р
Показатель изоэнтропы для расширения двухфазной смеси в
условиях полного теплового равновесия равен
т>г= ср = Cf + Ks •
Cv С J + $Cvg К '
168
ГЛАВА 6
Это уравнение идентично (2.25) из примера 2.2. Следовательно,
уравнение (12) будет справедливо только при отсутствии теплообмена
между фазами; если в системе поддерживается равновесие, в
уравнении (15) следует заменить у' на yg.
Влияние фазовых превращений
Если при распространении волны происходят фазовые
превращения, то ее скорость зависит от степени приближения к
равновесию. Например, для гомогенной системы в виде мелкодис-
1 I М 1111
р,ата
0,00001
0.0001 0,001 0,01
Паросодержание, х
I i i i inn
ОЛ
Фиг. 6.11. Теоретические значения скорости звука в равновесной гомогенной
паро-водяной смеси [8].
персного паро-водяного потока величина др/др может быть
определена из термодинамических таблиц или диаграмм, и скорость
звука изменяется, как показано на фиг. 6.11. В реальных
условиях имеют место многочисленные эффекты неравновесности,
усложняющие работу таких систем, как испарители мгновенного
вскипания низкого давления. Существенное влияние оказывают
также поверхностное натяжение и процесс зародышеобразования.
6.5. Взаимодействие динамических и непрерывных волн
Однофазный поток
Во многих практических случаях динамические и
непрерывные волны существуют одновременно. Условием одновременного
существования обоих видов волн является зависимость силы,
ОДНОМЕРНЫЕ ВОЛНЫ 169
приходящейся на единицу объема и действующей на жидкость
или частицы, от всех трех переменных—скорости, концентрации
и градиента концентрации, т. е.
Для однородного стационарного потока, движущегося с
постоянной скоростью, условие равновесия имеет вид
/+*=0, -£-=0. (6.114)
Уравнения неразрывности и движения для нестационарного
потока записываются в виде
»(тг+^тг)-/+»- <б-»6>
Рассмотрим первоначально стационарное течение, для
которого справедливо уравнение (6.114), причем концентрация а
повсюду постоянна, а система координат выбрана таким
образом, что У = 0. При малых отклонениях величин а' и у от
равновесных значений уравнения (6.115)" и (6.116) принимают
следующий вид:
-£- + «-5Г=0, , (6.117)
р-^-=Аг'+Аа'+/у*-£-. (6Л18)
где нижние индексы, как и ранее, означают частные производные.
Дифференцируя (6.118) поз и исключая v с помощью (6.117),
получим
P-^-+«A.-Sf-A-^-+.A-^=o. (6.П9)
Используя полученные ранее результаты, можно определить
следующие величины, идентичные скоростям распространения
динамических и непрерывных волн относительно средней
скорости: _
■vw= V„ - К= - А-а, (6.120)
J V
c=(-^-u]'\ (6.121)
170 ГЛАВА 6
Поскольку в любой предполагаемой системе f отрицательна
(в противном случае частицы беспредельно ускорялись бы),
можно ввести величину
Д=_^2_, (6.122)
Р
которая положительна и характеризует «демпфирование».
С помощью (6.120) —(6.122) уравнение (6.119) можно
представить в следующем виде:
f)2a'
дР
°г?ёг+в{^+*-^У°- . <6'123>
Физический смысл уравнения (6.123) наиболее наглядно
раскрывается при введении выражения
а =апе
at + ш (t-z/U) (6.124)
которое соответствует волне с частотой со/2я и скоростью U,
причем ее усиление или ослабление во времени зависит от
знака а. По определению, величины а и со действительные.
Подстановка выражения для а', разделение действительной и
мнимой части и решение относительно я и со2 дают
a=4("wL-1)' , (6Л25)
я В2 tj-U2 (6Л26)
Из уравнения (6.126) видно, что величина со2 будет
положительной только при условии, что значение U2 заключено между
значениями v2 и с2. Следовательно, если v2w>c\ то для волн,
движущихся в направлении vw, отношение vw/U будет больше
единицы, и такие волны будут усиливаться. С другой стороны,
если v2 <с2, отношение vw/U всегда меньше единицы, и все
волны будут затухать. Таким образом, устойчивость течения
полностью определяется соотношением величин скоростей
динамических и непрерывных волн, т. е. с и vw. Если непрерывные волны
обгоняют динамические, то течение неустойчиво. Так как
система координат выбрана так, что У = 0, величина vw должна
быть выражена относительно средней скорости.
Известной иллюстрацией полученных выводов служит
аналогия с потоком транспорта. Лайтхил и Уитмен [1] показали, как
можно использовать теорию непрерывных волн для описания
нестационарного движения в стационарном потоке транспорта,
и их выводы наводят на мысль, что в некоторых случаях
возможна неустойчивость движения, подобная «скатывающимся»
ОДНОМЕРНЫЕ ВОЛНЫ 171
волнам. Происходящее можно понять, рассматривая
динамические волны, обусловленные реакцией водителя (и состоянием
тормозов и педали подачи газа) на изменение локальных
градиентов концентрации. Если тормоза плохие, поверхность дороги
скользкая или видимость ограничена из-за густого тумана, то
скорость динамической волны уменьшается. Если она становится
"меньше скорости непрерывной волны, то в результате
произойдет скопление большого числа автомобилей. Аналогичный
эффект будет иметь место и при нормальных условиях, если
водители спешат и сокращают интервалы между движущимся
транспортом, так что скорость непрерывной волны превышает скорость
динамической волны. Опытный водитель интуитивно будет
менять скорость и расстояние, отделяющее его от других
автомобилей, так что скорость динамической волны всегда будет
служить «фактором безопасности» в большей мере, чем локальная
скорость непрерывной волны.
В тех случаях, когда имеет место только один из видов
волнового движения, уравнения (6.125) и (6.126) дают обычные
результаты. Например, если 5 = 0, все частоты волн возможны
только при c2 = U2; в этом случае а = 0 и, следовательно, не
происходит ни усиления, ни ослабления волн (динамические волны).
С другой стороны, если со становится очень малой величиной
(длинные волны), то v2w =£/2, и волны без изменений
распространяются со скоростью vw, так как в соответствии с
уравнением (6.125) а = 0 (непрерывные волны).
Пример 6.8. Исследовать устойчивость длинных одномерных воли в вязкой
пленке жидкости, стекающей по наклонной пластине.
Решение. Пусть пластина наклонена к вертикали под углом 9.
Составляющие силы тяжести в перпендикулярном и продольном направлениях
к пластине равны соответственно g sin 0 и g cos 9. Подставляя эти
значения в (6.12), (6.13) н (6.59), при толщине пленки б получим
£cose(P/ — р^)52
V= 3^ ' (6Л27)
P-COS6 (о, — р.) 52
* U V" , (6.128)
c = ±(5g-sin8)'^. (6.129)
Неустойчивость возникает, когда скорость непрерывных волн
превышает скорость динамических волн, распространяющихся по потоку,
т. е. п£ш
Vw > V + с. (6.130)
Подставляя выражения для Vw, V и с из (6.127)—(6.129) в
неравенство (6.130), получим следующее условие неустойчивости:
2g-cose(P/ — Р^)82
rg, >(8£-sin6)'/*. (6.131)
3(Х/
172
ГЛАВА 6
С другой стороны, используя уравнение (6.127), после
перегруппировки членов -получим
4Vb(?f-9g)
ft
>3tg6. (6.132>
Левая часть неравенства (6.132) представляет собой обычное
выражение для числа Рейнольдса стекающей пленки при p?^>pg.
С помощью более точного метода Брук [9] получил в правой части
неравенства (6.132) вместо 3 коэффициент 10/3.
Неустойчивость проявляется в виде скатывающихся волн,
аналогичных наблюдаемым во время дождя на окнах и наклонных участках улиц
или на окрашенных стенах со слишком толстым слоем краски.
Поток двухкомпонентной несжимаемой среды
Рассмотрим течение двухкомпонентной несжимаемой среды
в канале постоянного сечения без фазовых превращений.
Уравнения неразрывности для компонентов записываются в виде
-£-+**-*-+»-£-=<>.. <6ЛЗЗ>
--£--^-£-+<1-«>-£-=°- <6Л34>
Как обычно, уравнения движения представим в виде
Р. (-^ + ".-^) = --& + '. + /- <6Л35>
Ра(-^+^-5-) = --^+*а+/, (6.136)
Вычитая (6.136) из (6.135), получим
Р.(^+".^)-Р»(^+^Н-^+/.-/* (6-137)
Правую часть уравнения (6.137) можно заменить новой
переменной
/=-[(ft1-ft2)+(/1-/2)]. (6Л38)
причем f является функцией скоростей обоих компонентов,
концентрации и ее градиента (и, возможно, также других
производных скорости или концентрации), т. е.
f=f(vu v2 a, -*- и т. д.).' (6.139)
Рассматривая малые возмущения величин vi, 02, о/, 8f в
однородном стационарном потоке с параметрами Vi, Vz, а и остав-
ОДНОМЕРНЫЕ ВОЛНЫ
173
ляя в уравнениях (6.133), (6.134) и (6.137) только члены
первого порядка малости, получим
да' . , , да' . dvn n ,„ . .„.
тг+к>-аг+"-&-=0' (ьчо>
«■■О + ^^-^+^тМ—V. (W42)
Величины oi и v% можно исключить из этих уравнений путем
дифференцирования уравнения (6.142) по г и подстановки
выражений для их производных из (6.140) и (6.141). В результате
получим
д*а
дР
' ( Pi , Р2 \ 1 о д2*' ( ViPi | V292 \ |
! \l_a"T" a Jl* dzdt \ 1— a ' а ^"Г
+Щ^+Щ = ^- («43)
Величина б/ является суммой членов, характеризующих
вклад возмущений каждого параметра:
5/=A«'+/^i+/^2+/va^-. (6.144)
Дифференцирование уравнения (6.144) по z и подстановка
выражений для dvijdz и dvzldz из (6.140) и (6.141) дают
d{bf) _^ дх' I /„, **Л,_Ы_(Г | v\fy. V* \ ,
d? <Й \1—а а/"Т"аг\-/,х'1_1—a a /"+".
+A.-S-. (6.145)
Уравнение (6.145) можно привести в соответствие с общей
теорией непрерывных волн, если представить f в виде функции
скорости одного из компонентов и суммарной плотности
объемного расхода (приведенной скорости смеси) /.
Тогда
f=f'(V2,J,a), (6.146)
где -
J=Vi(l-a)-[-Vfi. (6.147)
ГЛАВА 6
Производные в уравнении (6.145) можно вычислить с учетом
(6.146) следующим образом:
df , df
dj '
Подставляя (6.148) —(6.150) в (6.145), получим
djbf) да' /1 df \ , д^_1дГ___У^дГ_
Щ dt \ к dv2 I'' dz \ да a dv2
(6.148)
(6.149)
(6.150)
■)+/
д®а'
Voc dz2 '
(6.151)
д(Ь/) __ 1 df
dz a dv2
da'
Ш'
dt
dz
Vo—a
fa
A
f2
#>a
+ /«.-£- (6Л52)
Множитель, на который умножается да'/dz в (6.152), с помощью
(6.146) можно представить в виде
. *+'№),..,-*-<™/-.,-ИН,- <6Л53)
Нетрудно заметить, что он представляет собой скорость
непрерывной волны Vw, для которой ранее было получено
уравнение (6.38).
Уравнения (6.152) и (6.153) можно подставить в (6.143), что
дает
&а'
дР
Величина Vo является средневзвешенной скоростью, которая
равна [см. уравнение (6.75)]
Кп =
ViPl/( 1 — а) + V№la
(6.155)
'о— pi/(1 —«) + р2/«
а введенные параметры А и В определяются соотношениями
В =
Р1/(1—<*) +Р2/а
Pl/(1— а) + Р2/а
(6.156)
(6.157)
ОДНОМЕРНЫЕ ВОЛНЫ
175
*
Смысл уравнения (6.154) раскрывается при подстановке
выражения
aat + l«{t-4U) (6Л58)
=апе
и определении всех скоростей волн через Vo, т. е.
U=VQ+u,
(6.159)
(6.160)
Введем новую величину, которая определяется как квадрат
скорости динамической волны, вычисляемой по уравнению (6.76):
с2=1/02-Л.
В итоге получим
а=
В
')•
В2 Ц1 vl — и?
4 м2 м2 — с2
(6.161)
(6.162)
(6.163)
Качественные выводы, которые следуют из уравнений (6.162)
и (6.163) для двухкомпонентного потока, абсолютно идентичны
выводам, сделанным из анализа уравнений (6.125) и (6.126) для
однокомпонентного потока. Динамические волны движутся со
скоростью ±с относительно средневзвешенной скорости Vo,
определяемой уравнением (6.155). Неустойчивость наступает при
v2w >c2, т. е. когда волны возрастают в направлении vw со
скоростью, описываемой уравнением (6.162). При отрицательном
значении с2 поток всегда неустойчив.
6.6. Динамические ударные волны
Теорию динамических ударных волн можно развить, исходя
из уравнений неразрывности, движения и энергии для
поверхности с конечными разрывами. Прямой скачок уплотнения
в газодинамике и гидравлический прыжок в гидравлике
представляют собой конкретные примеры динамических ударных
волн.
Прямые скачки уплотнения
Рассмотрим стационарный прямой скачок в двухкомпонент-
ном газо-жидкостном потоке, показанный на фиг. 6.12.
Уравнение неразрывности для скачка имеет простой вид:
01=02
(6.164)
176
ГЛАВА б
Уравнения количества движения и энергии соответственно
запишем в виде
Рх +(0/v/-\-Ggvg)1=p2+(GfVf+Ggvg)2, (6Л65)
+Gs{hs+4-)\- <блбб>
Термодинамические соотношения между давлением,
энтальпией и плотностью позволяют осуществить дальнейшие
преобразования.
Gf, — \ \ *■ 6f2
G9l - ) <~е3г
% *- ^V9z
Фиг. 6.12. Прямой динамический скачок уплотнения в двухфазном
газогжидкостном потоке.
Подробное решение этих уравнений будет приведено в
последующих главах. Однако в качестве примера рассмотрим
решение для простого случая ударной волны в гомогенном
изотермическом потоке, когда только один из компонентов является
сжимаемым и подчиняется законам идеального газа. Обозначим
сжимаемый компонент индексом g, а другой — индексом f (хотя
это могут быть и твердые частицы).
В этом случае уравнение (6.165) принимает вид
px + Gj,=p2+Gj2. (6.167)
Кроме того, так как сжимаемым является только газ,
h-Ji=Ugh-Ug)i- (6-168)
Объединяя (6.168) и (6.167), получим
Pl-P2=Q\Ug)2-Ug)il (6.169)
Далее, для изотермического потока газа
P1Ug)l=P2(Jgh- (6.170)
Из уравнений (6.169) и (6.170) получим
Pi=QUgh, (6-171)
P2=0(Jg)u (6-172)
ОДНОМЕРНЫЕ ВОЛНЫ 177
С учетом (2.81) числа Маха до скачка и за ним в изотерми*
ческом потоке гомогенной среды будут равны
М?= _*п , (6.173)
Ма=
Рх
О Ugh
Pi
(6.174)
Из (6.171) — (6.174) следует удобное и простое соотношение
М,
Ug)
g>x
Р2
Щ
Ugh
р\
(6.175)
Эддингтон [10] получил подтверждение этих результатов при
исследовании газо-жидкостных потоков с объемным
газосодержанием до 50%.
Косые скачки уплотнения
Косые скачки обычно исследуются путем разложения
результирующего движения вдоль и перпендикулярно фронту волны.
Рассмотрим, например, косой скачок уплотнения в
изотермическом гомогенном потоке, показанный на фиг. 6.13.
AJ'w
Фиг. 6.13. Косой динамический скачок уплотнения в двухфазном потоке.
Вдоль фронта волны скорость постоянна, поэтому
ylCosp=y2cos(p —6).
(6.176)
По нормали к фронту волны из треугольников скоростей
получим
У,81пр=У,лг, (6.177)
Л sin №-9)=/^. (6.178)
12 Заказ №. 162
178
ГЛАВА 6
Из уравнения (6.175) следует, что в направлении,
нормальном к фронту волны,
мЬш2р=М?„=4г^= ,(^ . (6.179)
(Jg)2N hN ] fN
Исключая J2N из уравнений (6.178) и (6.179), получаем
выражение
-^7-hNCtg^tg^-B)-jfN. (6.180)
Mf sin2 p
Имея в виду, что все скорости, перпендикулярные фронту
волны, равны скоростям набегающего потока, умноженным на
sin P, путем преобразования уравнения (6.180) можно получить
следующую неявную зависимость для угла наклона скачка
в функции от известных параметров набегающего потока и угла
клина 8:
g .—-А-^лсйс.п й +гт (d _ m _ cin2 t
- cos « sin «tg («- 9) -sin2 p. (6.181)
Соотношения для других параметров, представляющих
интерес, например для отношения давлений, можно получить, если
использовать значение р и рассмотреть поток, нормальный
к волне.
Полученные результаты хорошо подтверждаются данными
Эддингтона [10].
Релаксация
Так как скорости и термодинамические свойства изменяются
в скачке очень быстро, для достижения нового состояния
равновесия между фазами требуется значительное время. Механизм
возврата к равновесному состоянию известен как релаксация.
Если релаксация происходит медленно, общая толщина скачка
может быть значительной.
Рассмотрим для примера взвесь мелких твердых сферических
частиц в жидкости. Пусть концентрация их такова, что за время
установления равновесия свойства жидкости, ее скорость и
температура остаются постоянными. Обозначив параметры частиц
индексом s и рассматривая процесс для отдельной частицы
(система координат Лагранжа) в ускоряющемся ламинарном
потоке, получим
J^J5r=3ir'V^-^)' (6Л82)
ОДНОМЕРНЫЕ ВОЛНЫ 179
откуда
■|^^=к-^- (6Л83>
Следовательно, постоянная времени процесса релаксации
скорости для частицы равна
Аналогично для термической релаксации получим
"'Т*' °т = 2тсV (те ~ т*)> ' (6Л85)
и постоянная времени процесса термической релаксации будет
равна
^r=^|£i-. (6.186)
Например, для частиц алюминия (ps = 2,71 г/см3, cs —
= 0,21 ккал/кг • град) диаметром 0,025 мм, взвешенных в воздухе
с температурой 20° С, /„=5,45 мсек и £г=4,93 мсек. За это время
при скорости газового потока около 300 м/сек частица пройдет
путь более метра.
Задачи
6.1. На автостраде соотношение между / (автомобилей в час) и а
(автомобилей на милю) имеет вид
y = -g-(120 -a).
Какова предельная скорость? Какова максимальная пропускная способность
■автострады? Что произойдет, если поток в 1000 автомобилей в час
задержится у светофора на 2 мин, после чего движение возобновится?
6.2. Какова максимальная пропускная способность автострады в задаче 6.1,
если светофор действует непрерывно, причем красный и зеленый сигналы
чередуются с интервалами 1 мин?
■6.3. Уравнение задачи 6.1 относится к одному ряду трехрядной автострады.
Как далеко против движения по шоссе распространится влияние аварии,
в результате которой одни из рядов перекрывается на полчаса, если общий
поток 4000 автомобилей в час?
6.4. Одной из обязанностей декана факультета в колледже является
ознакомление членов факультетского совета с документами, которые
рассылаются в алфавитном порядке. Если скорость, с которой каждый из
профессоров знакомится с документами, пропорциональна получаемому количеству
документов в некоторой степени п., что произойдет, если:
а) декан начал рассылку документов в понедельник?
б) один из членов факультетского совета отсутствует в течение месяца?
Существует ли некоторое наиболее предпочтительное значение п?
6.5. Показать, что если расход жидкости из примера 6.2 внезапно увеличить
до начального значения, то образуется скачок. Каким образом следовало бы
12*
180
ГЛАВА б
изменить расход жидкости, чтобы с течением времени изменение б
распространялось от верха стенки в виде треугольной симметричной • волны? Как
будет меняться форма этой волны при ее движений? Когда образуется
первый скачок?
6.6. Решить пример 6.3, используя вместо уравнения (6.11) уравнение (6.3).
Каков будет результат, если коэффициент трения пропорционален числу
Рейнольдса в степени —га?
6.7. Показать, что между двумя точками на кривой зависимости / от а не
может существовать устойчивый непрерывный скачок, если линия,
соединяющая эти точки, пересекает данную кривую в некоторой промежуточной
топке.
Режим 1 Режим 2
Ф иг. 6.14. Два режима течения жидкой пленки внутри вращающегося цилиндра
(задача 6.13).
6.8. Вывести соотношения теории непрерывных волн для однофазного потока
в канале переменного сечеиия. Показать, что увеличение сечения вызывает
ослабление волн и наоборот.
6.9. Показать, что при постоянном коэффициенте трения стекающая
турбулентная пленка неустойчива, если
ctge>2C/.
6.10. Используя решение задачи 6.9, найти критическое число Фруда для
образования белых пенистых волн в реках.
6.И. Решить задачу 6.9, если коэффициент трения пропорционален числу
Рейнольдса в степени —п.
6.12. Вывести соотношение между расходом жидкости и толщиной
ламинарной жидкой пленки на приводном ремие единичной ширины, движущемся
вертикально со скоростью V. Каков максимально возможный расход? Для
расходов, меньших максимального, существуют два возможных значения
толщины пленки [11]. Какова будет толщина пленки перед препятствием в виде
острой кромки, расположенной перпендикулярно потоку и за ннм? Почему?
6.13. Рассмотреть течение жидкой пленки на внутренней стенке вращающегося
цилиндра. Считая скорость цилиндра равной V н учитывая только силы
тяжести и вязкости, вывести соотношение между расходом жидкости на
единицу ширины при круговом движении и толщиной пленки в" различных
точках по окружности цилиндра. Считать течение ламинарным. Показать,
что в зависимости от количества жидкости в цилиндре возможны две
конфигурации жидкой пленки (фиг. 6.14). Какова причина изменения
конфигурации пленки? В какой точке при втором режиме течения скорость
непрерывной волны равна нулю? Чему равно критическое количество жидкости,
необходимое для наступления второго режима, в зависимости от размеров
цилиндра и свойств жидкости?
ОДНОМЕРНЫЕ ВОЛНЫ 181"
6.14. Решить задачу 6.13 для турбулентного течения при постоянном
значении Су. При каких условиях будут существенны центробежные и
инерционные силы?
6.15. Чему равна скорость непрерывной волны при течении гомогенной
несжимаемой двухфазной смеси в канале постоянного сечения?
6.16. Пар конденсируется с постоянной скоростью на внутренней поверхности
вращающегося барабана, и пленка жидкости удаляется на периферийных
участках (вращающихся вместе с барабаном), расстояние между которыми/,
много меньше радиуса барабана. При вращении барабана пленка конденсата
колеблется между участками удаления конденсата. Если пленка ламинарная
и инерционные и центробежные силы малы, то, заменяя синусоидальное
гравитационное поле (вдоль пленки) прямоугольной волной, показать, что
а. Существуют три или четыре вида волн на поверхности пленки в
зависимости от того, будет ли период полуоборота Т больше или меньше, чем
Г ЗЬщг Т/з
Tc±2g$4?f~?g) \ •
б. Безразмерная средняя толщина пленки 6/L может быть представлена'
в виде функции от TjTc и рГ/L.
в. Скачок не образуется.
Представить различные режимы движения волн в плоскостях гб и zt и
подробно объяснить полученные характеристики.
6.17. Построить зависимость от а скорости распространения упругих волн
в гомогенной водо-воздушной среде при температуре 2ГС и давлении!, 7
и 70 ата.
6.18. Согласно уравнению (6.92), вследствие роста стационарных волн
возможно «захлебывание». В соответствии с уравнением (6.84) движущиеся
волны тоже могут быть неустойчивыми. Получить с помощью уравнения
(6.84) нижние пределы расходов, при которых еще не наступает
«захлебывания» в длинном горизонтальном канале. В коротких каналах только почти
неподвижные волны будут расти в достаточной для наступления «захлебы-,
вания» степени.
6.19. Подставить выражение
в уравнение (6.123) и решить его относительно а' и а/. Дать физическое
объяснение результатов и сравнить полученные уравнения с (6.125) и (6.126).
Изменится ли условие устойчивости?
6.20. Для жидкой пленки на вертикальной поверхности с=0 и движение
всегда неустойчиво. Рассмотреть турбулентную стекающую плёнку, по
которой распространяются возмущения с длиной волны Х,=2гог6. Показать, что
если га достаточно велико для использования одномерного приближения, та
значение U, определяемое из выражения (6.126), равно
Показать, что при га=10 и Су=0,01 волна увеличится в е раз на расстоянии,,
в 92 раза превышающем толщину пленки.
6.21. Решить задачу 6.20 для ламинарного течения и показать, каким
образом усиление волны зависит от числа Рейнольдса.
6.22. Прямой скачок уплотнения перемещается со скоростью 70 м/сек, а
параметры в неподвижной водо-воздушной смеси перед ним равны: р = 1,05 ата,
7,=24°С
и се=0,3 (се — объемное газосодержание). Каковы условия за скачком?
Какие значения риа установятся вблизи неподвижной стенки при
нормальном отражении такого скачка?
182 ГЛАВА 6
6.23. Поток гелия и воды при а='/2> Г=38°С и р=1,4 ата набегает на клии
с углом 29=60°. Определить угол наклона скачка и давление за ним. Скорость
набегающего потока 120 м/сек.
6.24. Используя определение режима «захлебывания», данное в гл. 4,
показать, что в точке «захлебывания» скорость непрерывной волны всегда равна
нулю.
6.25. Показать, что при течении двухфазной смеси с постоянными свойствами
в канале постоянного сечения при наличии фазовых превращений скорость
распространения непрерывных волн такова, что
( (движение со __ I * Л- (\ a\\Q
dt /скоростью Vw [ vfg ^ v "J '
где Й определяется выражением (2.92). Сравнить этот результат с
уравнением (6.23).
6.26. Можно определить следующие четыре числа Маха, представляющие
совой отношения скоростей фаз к скоростям динамических и упругих волн:
m
dx~ Viu-*)i9i]7^a ' d2~V(-«/p2)/2J'
м,= »L_ . м2=- «*
У др1д?\ У др!д?2
Показать, что (6.102) можно представить в виде
1-М2- , 1-а 1-М,*
P2t»2 1-г1/Мл р,», 1 — 1/М
= 0
d\
и что при выполнении соотношения (6.107) оно сводится к следующему:
! — М22 _, /1 ч 1—М,"
2 .+ (1—а) L_ = 0.
1-М« 1-Мд
6.27. Показать, что если относительная скорость в расслоенном потоке мала
по сравнению С\ и с2, то скорость волны равна
^/P2 + ^(l-g)/Pl
«/pa + (l-«)/Pi ± "•
6.28. Вывести уравнение (6.88), исходя из уравнения Бернулли и условия
равенства давлений на поверхности раздела.
6.29. Показать, что результаты, полученные в этой главе для двухкомпонеит-
ных потоков, при наличии только одного компонента сводятся к известным
результатам для однокомпонентных сред.
6.30. Система, описанная в примере 6.6, в начальный момент времени
состоит из слоя чистой жидкости глубиной Я. Внезапно вводится воздух с
плотностью объемного расхода jg^v^/8, которая поддерживается постоянной.
Описать происходящий процесс, если не происходит разрушения и слияния
пузырьков. Система расширяется вверх и достигает высоты, в несколько раз
большей Я, где предусмотрен переток образовавшейся пены. Существуют по
крайней мере три стадии этого процесса.
6.31. При каких условиях непрерывные волны могут быть обусловлены
расходом, зависящим не от концентрации, а от термодинамической плотности?
Вывести соотношения теории непрерывных волн для случая, когда расход
определяется как плотностями, так и объемной концентрацией.
ОДНОМЕРНЫЕ ВОЛНЫ 183.
6.32. При снарядном режиме течения последовательно чередуются большие
цилиндрические пузыри газа и жидкие пробки. Какова средняя скорость-
звука [12] при такой структуре? В каком соответствии находится этот
результат с данными для гомогенного течения и раздельного течения
[уравнения (6.110) и (6.106)]? Всегда ли скорость звука при снарядном режиме
больше, чем при других режимах?
6.33. а. Используя уравнения (6.164)—(6.166), вывести соотношения для
динамических ударных волн в равновесном однокомпонентном паро-жндкост-
ном потоке.
б. Движущийся по каналу пар при давлении 0,7 ата и сухости 10%
встречает стационарную динамическую ударную волну. Определить скорости
по обе стороны волны в функции от давления за ней.
6.34. а. Используя уравнения (6.164) — (6.166), показать, каким образом
можно исследовать «скачки конденсации», возникающие при образований-
зародышей в высокоскоростном потоке переохлажденного пара.
б. Решить задачу 6.336, если пар сухой и переохлажденный, но имеет
энтальпию, соответствующую сухости 90%. Как будет отличаться решение-
этой задачи от решения задачи 6.336? Принять, что за скачком существует
термодинамическое равновесие.
Литература
• 1. Lighthill M. J., Whit ham Q. В., Proc. Roy. Soc. (London), 229A
281 (1955).
2. Jeffreys H., Proc. Cambridge Phil. Soc, 26, 204—205 (1930).
3. Л а м б Г., Гидродинамика, Гостехиздат, 1947.
4. LongR. R., Tellus, 5, № 7, 42—57 (1953).
5. LongR. R., Tellus, 6, № 2, 97—115 (1954).
6. LongR. R., Tellus, 8, № 4, 460—471 (1956).
7. H u e у С. Т., В г у a n t R. A. A., ASME paper 65-WA/FE-S, 1965.
8. К а г р 1 u s Н. В., Rept № С00-248, Armour Res. Found., June 1958.
9. Brooke В. Т., /. Fluid Mech., 2, 554 (1957).
10. E d d i n g t о п R. В., AIAA paper 66-87, 1966.
11. Van Rossum J. J., Appl. Scl. Res., sec. A, 7, 121—144 (1958).
12. Henry R. E., Fauske H. K-, Trans. Am. Nucl. Soc, \\, № I 364 (June
1968).
7
ЯВЛЕНИЯ НА ПОВЕРХНОСТИ РАЗДЕЛА ФАЗ
7.1. Введение
На границе твердой поверхности и жидкости, а также на
поверхностях раздела жидкой и газообразной фаз происходят
весьма интересные процессы, включающие множество
физических и химических эффектов. Например, присутствие очень малых
загрязнений может чрезвычайно сильно повлиять на условия
начала процессов конденсации и кипения, устойчивость пенных
образований, волнообразование на поверхности озер, а также
«запотевание» зеркальных поверхностей и очков.
Для анализа двухфазных течений очень важно, каким
образом поверхностные явления учитываются в граничных условиях,
которым должны удовлетворять различные уравнения. При
анализе однофазных течений обычно считают, что поля напряжений
и скоростей не имеют разрыва. В двухфазных потоках возможно
скачкообразное изменение составляющих скорости и
напряжения на поверхностях раздела фаз.
7.2. Граничные условия для скорости
Если на поверхности раздела не происходит фазового
превращения или массообмена, то условия совместимости профилей
скоростей остаются одинаковыми для однокомпонентного и двух-
компонентного течений. Однако при наличии фазового превраще-
Ф и г. 7.1. Граничные условия для
скорости на поверхности раздела фаз.
ния возможно появление конечной скорости через поверхность
раздела. Этот поперечный поток должен удовлетворять условию
неразрывности, поэтому если на поверхности раздела
происходит изменение плотности, то оно непременно сопровождается
изменением скорости. В результате для изображенной на
фиг. 7.1 поверхности раздела должны удовлетворяться
следующие условия:
<<vz„
Фаза 2
■*-vzt
Фаза J
-*- "it
"ш
ЯВЛЕНИЯ НА ПОВЕРХНОСТИ РАЗДЕЛА ФАЗ
185.
1. Неразрывности касательных скоростей
2. Неразрывности плотности потока массы в поперечном
направлении
Pl«lAf = P2«2Af=W. (7.2)
где т — плотность потока массы через поверхность раздела в
направлении нормали к ней. Обычно считают, что средняя скорость
движения вещества в процессе фазового превращения
направлена перпендикулярно поверхности раздела.
Если поверхность раздела перемещается, то скорость ее
движения просто накладывается на указанные выше скорости.
7.3. Граничные условия для напряжения
Влияние поверхностного натяжения
Условие неразрывности напряжения при переходе через
поверхность раздела видоизменяется под действием
поверхностного натяжения. Если поверхность раздела криволинейная,
то значения давления по разные стороны от нее отличаются на
величину
A-A=ehb+T5-)' (7-3>
где Ra и Rb — радиусы кривизны поверхности раздела в двух
взаимно перпендикулярных направлениях (фиг. 7.2).
Фиг. 7.2. Граничное условие для да
вления на поверхности раздела фаз
Ra и Rь — радиусы кривизны в двух вза
имно перпендикулярных направлениях.
Если поверхностное натяжение постоянно на всей
поверхности раздела, то при переходе через нее касательные напряжения
будут изменяться непрерывно. Однако при наличии загрязнений,
пыли, поверхностно активных веществ или же градиентов
температуры вдоль поверхности раздела на ней могут возникнуть
градиенты поверхностного натяжения. В этом случае
касательные напряжения на поверхности раздела будут иметь скачок,
равный по величине градиенту поверхностного натяжения.
«86
ГЛАВА 7
Таким образом,
t1+Vo=t2. (7.4)
Справедливость уравнения (7.4), записанного в векторном виде,
подтверждается с помощью фиг. 7.3, на которой изображен
элемент поверхности раздела, причем направление оси х совпадает
•с направлением Va. Сила, действующая со стороны первой
жидкости, равна xidxdy, а со стороны второй жидкости — соответст-
гвенно —x-idxdy.
©
(Ч)х-* 7"-
фиг, 7.3. Граничные условия для касательных напряжений на поверхности
раздела фаз.
Сила поверхностного натяжения равна —ady+ (a+Vadx)dy.
Из баланса сил в направлении оси х следует
KL+Va-(,2),=0, (7.5)
■а в направлении оси у, перпендикулярной х,
'Ы-Ы=0. ' (7.6).
Уравнения (7.5) и (7.6) представляют собой скалярные
составляющие уравнения (7.4).
Если поверхность раздела двух фаз соприкасается с твердой
поверхностью или какой-либо третьей жидкостью, то все три
результирующие межфазные натяжения должны
уравновешиваться в точке их пересечения. Например, в случае касания
трех мыльных пузырей три поверхности должны сходиться под
утлом 120° друг к другу. Если газ и жидкость находятся в
контакте с плоской твердой поверхностью, то в этом случае краевой
угол определяется как угол между поверхностью раздела
жидкость— газ и твердой поверхностью, причем отсчет ведется со
стороны жидкости. Из условия равновесия поверхности раздела
(или из эквивалентного условия минимума энергии)
cosp=8w~8'/ • (7.7)
"fe
Краевой угол довольно изменчив; он с трудом
воспроизводится при измерениях, поскольку зависит не только от
появления НА ПОВЕРХНОСТИ РАЗДЕЛА ФАЗ 187
верхностного натяжения, но также и от небольших
изменений в чистоте и микрошероховатости твердой поверхности.
Местное окисление поверхности или наличие на ней
адсорбированных газов также может оказать существенное влияние на
величину краевого угла. Краевые углы, образующиеся во время
прямого и возвратного движений мениска (поверхности раздела),
могут сильно отличаться друг от друга, особенно если эти
перемещения осуществляются достаточно быстро.
Поверхностное натяжение играет чрезвычайно важную роль
в определении гидродинамических и теплообменных
характеристик газо-жидкостных систем. Волнистость и устойчивость
поверхности раздела фаз, образование, унос и дробление пузырей и
капель— все эти процессы определяются поверхностным
натяжением. Зарождение пузырей при кипении зависит отусловий роста
очень мелких пузырьков в углублениях или трещинах в
поверхности нагрева и выхода пузырька из них. Капельная
конденсация также в значительной мере определяется величиной
краевого угла.
Пример 7.1. Чему равна разность давлений внутри и вне парового пузырька
радиусом 2,54 мк, если 0=58,9 дин/см?
Решение. Поскольку кривизна поверхности раздела одинакова .во всех
направлениях, уравнение (7.3) принимает вид
2а
Р2 — Р\ =
поэтому
2 • 58 9
Р%-Р\= 254 . t'o-4 • 1,02 - 10-6 = 0,472 ата.
Пример 7.2. Рассмотрим устойчивость плоской горизонтальной поверхности
раздела между жидкостями плотностью pi и р2. Пусть р! — плотность
верхней жидкости, и пусть pi > p2. Как будет вести себя поверхность
раздела при воздействии малого синусоидального возмущения вида
Ti=Tiosin (2nz/L)? Будет „возмущение усиливаться или затухать?
Решение. Так как т) мало, то кривизна поверхности раздела описывается
следующим соотношением:
1 d\ 4*2 2V
т=-ш-^—тг^^—г-
Изменение давления при переходе через поверхность раздела составляет,
согласно уравнению (7.3),
4aic2 2nz
Р\ — Р2 = L2 По sin
Избыточное гидростатическое давление, обусловленное возмущением
поверхности раздела, равно
g(.H — P2>1loSin—7—.
J 88
ГЛАВА 7
Приложенное возмущение, будет ослабляться, если р\—р2 превышает
избыток гидростатического давления, т. е. если
4оя2
L2 >g(Pl — P2).
или, другими словами,
L<I* = 2KVlFb=&- (7-8>
Таким образом, существует некая критическая длина волны Lc,
определяемая уравнением (7.8). При длине волны, большей критической, приложенное
возмущение усиливается. Анализ скорости нарастания этого возмущения,
проведенный с учетом влияния сил инерции, показывает, что наибольшей
скорости роста возмущения соответствует длина волны L=yr3Lc.
Рассмотренное выше явление известно как неустойчивость Тейлора [1].
7.4. Влияние фазовых превращений на величину
напряжений на поверхности раздела
Если на поверхности раздела происходит изменение фазового
состояния вещества, то оно сопровождается переносом массы
через эту поверхность. При этом если оба компонента не
перемещаются с одинаковой скоростью, то одновременно с
переносом массы может происходить перенос количества движения.
Нормальная составляющая скорости испаряющегося или
конденсирующегося пара изменяется, как это следует из уравнения
(7.2), при переходе через поверхность раздела фаз. Давление,
действующее со стороны пара на жидкость в процессе
испарения или конденсации, равно
(kp)N=m (vgN — vfN)=m2vfg. (7.9)
Обычно этот эффект несуществен.
Влияние фазового превращения на касательные напряжения
определить труднее. В условиях ламинарного течения на
плоской пластине при наличии конденсации задача аналогична
рассмотренному Шлихтингом [2] отсасыванию пограничного
слоя. Эта задача имеет асимптотическое решение, в котором
влияние вязких сил трения на поверхности исчезает и
сохраняется только член, учитывающий перенос количества движения,
т. е. если разность скоростей потоков равна va, то касательное
напряжение на поверхности раздела фаз определяется
следующим образом:
xK=mv12. (7.10)
Очевидно, действие этого касательного напряжения на
жидкость в процессе конденсации и на газ в процессе испарения
таково, что конденсацию уже нельзя считать просто
«отрицательным испарением». Качественно это проявляется в том, что
ЯВЛЕНИЯ НА ПОВЕРХНОСТИ РАЗДЕЛА ФАЗ
189
при конденсации уменьшаются вязкие касательные напряжения,
действующие на газовый поток, а при испарении уменьшаются
касательные напряжения, действующие на жидкостный поток.
На основе представлений о рейнольдсовом потоке,
изложенных в гл. 3, в работе Силвера и Уоллиса [3] предложена простая
модель расчета касательного напряжения на поверхности
раздела фаз в турбулентном расслоенном газо-жидкостном потоке
при наличии фазовых превращений. Согласно этой модели, при
отсутствии фазовых превращений касательное напряжение на
поверхности раздела обусловлено столкновением с повёрхно-
V-
\Uo-VgN
\"0 + "дЫ
Газ
Жидкость
Фиг. 7.4. Рейнольдсов поток при наличии фазового превращения [3].
стью частиц жидкости из основного потока и их отражением
обратно после передачи части их количества движения стенке.
Если с единицей поверхности в единицу времени сталкивается
масса жидких частиц е0, то касательное напряжение
определяется следующим образом:
то=ео(^-^/)- (7.11)
В рамках элементарной модели можно представить, что этот
поток массы образуется двумя потоками: движущимся по
направлению к стенке и движущимся в обратном направлении.
Каждый из этих потоков занимает половину сечения и движется
со средней скоростью «о (фиг. 7.4). Для потока пара
V2«oPe-
(7.12)
Пусть теперь имеется дополнительный поток массы т,
обусловленный наличием фазового превращения и направленный от
жидкости к газу. Этот поток можно учесть наложением
скорости, определенной из уравнения (7.2), на принятую выше
картину турбулентных перемещений. Поток, движущийся в
направлении поверхности раздела со скоростью «о, теперь будет иметь
скорость «о—vgN, тогда как поток, движущийся в обратном
направлении, приобретает скорость ua+vgN. Масса пара,
передающего количество движения газовому потоку, отнесенная
j9Q ГЛАВА 7
к единице поверхности, составит lkpg{u0+vgN), тогда как
результирующий поток, передающий импульс жидкости, равен
всего лишь V2Pg («о — vgN).
Если принять, что переносимая масса в исходный момент
находится в равновесии с потоком, из которого она поступает, то
силы «торможения», действующие на газовый и жидкостный
потоки, отнесенные к единице объема канала, могут быть
записаны следующим образом:
Ff=Pi{vg—Vf) •-^-?g(uQ-vgN), (7.14)
где Pi — периметр поверхности раздела.
Если выразить Fg и Ff через 8о и т, то
F^-P^-v,)^^), (7.15)
/V=P>,-<V)(e0-^-). (7.16)
Если на поверхности раздела фаз происходит не кипение, а
конденсация, то знаки при т в приведенных выше уравнениях
просто изменятся на обратные. Поэтому параметр т можно
заменить на параметр trifg, обозначающий поток испаряющейся
массы, причем trifg может быть либо положительной, либо
отрицательной величиной.
Обозначим газовую фазу индексом 2. Подставим в
уравнения (3.45) и (3.46) выражения из уравнений (3.42) и (3.43) и
добавим силы FWf и Fwg,' учитывающие касательные напряжения
на стенке. В результате получим уравнения движения для
установившегося течения в следующем виде:
dvf dp fi Pwf . Pi(vg — vf) I mfg \
(7.17)
dVg dp 0 Fwg Pi(vg — Vf) I mfg \
(7.18)
p*0
Эти выражения идентичны уравнениям (3.106) и (3.107).
Иногда бывает удобно разделить массовый поток на две
составляющие: «переносную» и «циркуляционную», так как для
потока т не обязательно должны соблюдаться условия
равновесия на стенке (например, в случае вдува через щели). Цир-
ЯВЛЕНИЯ НА ПОВЕРХНОСТИ РАЗДЕЛА ФАЗ
191
куляционный, или перемешивающий, поток при фазовом
превращении в любом направлении равен
т
(7.19)
Этот поток уменьшается с ростом интенсивности кипения и
конденсации. Уравнения (7.15) и (7.16) получаются путем
добавления т к соответствующему потоку.
Фиг. 7.5. Вдув газа в турбулентный пограничный слой.
Сравнение даииых из работы Кутателадзе н Леонтьева [4] с различными теориями.
Касательные напряжения на стенке в развивающихся
турбулентных пограничных слоях при наличии массообмена или вдува
газа претерпевают аналогичное изменение. Кутателадзе и
Леонтьев [4] приводят уравнение, справедливое для случая вдува
газа того же молекулярного веса, что и основной поток. Это
уравнение в принятых нами обозначениях имеет следующий вид:
т
4е,
■)*(»■
т \—
4е0
г
(7.20)
Оно графически представлено на фиг. 7.5, где сопоставляется
с результатами других авторов, исследовавших течения на
проницаемой плоской пластине. Для удобства сравнения уравнение
(7.19) представлено в виде.
-=1
(7.21)
192
ГЛАВА 7
На фиг. 7.5 также представлено уравнение, выведенное на базе
более сложного анализа Силвером и Уоллисом [3]:
Лт-=е-йЧ2-1 (7.22)
ео
и уравнение, заимствованное из книги Сполдинга [5]:
1ш-=Л-(ейч*-\)-1ш (7.23)
Весьма удивительно, что рейнольдсова модель потока дает
приемлемые результаты также в случае ламинарного
пограничного слоя [7]. Она эффективна и при расчете влияния фазового
превращения на коэффициенты тепло- и массоотдачи на
поверхности раздела фаз. Например, испаряющиеся капли стремятся
«экранировать» себя от теплообмена с окружающим газом. При
числах Прандтля и Шмидта, близких к единице, отношение
Sm/so равно отношению коэффициентов тепло- и массоотдачи при
наличии испарения к соответствующим значениям этих
коэффициентов при отсутствии испарения. Многие приложения теории
потока Рейнольдса рассмотрены в книге Сполдинга [5].
Значение е0 обычно определяется через параметры
однофазного течения при тех же условиях. Например, при течении
в трубе касательное напряжение может быть определено через
коэффициент трения
Тогда из уравнений (7.11) и (7.12) получаем
eQ^±-CfP(vg-vf), (7.25).
«о=С, («,-«,). (7.26)
Отсюда следует, что С/ можно рассматривать как отношение
скорости перемешивания и относительной скорости.
С другой стороны, турбулентное перемешивание можно
охарактеризовать, используя понятие скорости трения
(динамической скорости)
и*=(^у/г. (7.27)
Очевидно, что и* и «о связаны соотношением
-!$-=УЩ. (7.28)
В общем случае и* характеризует пульсации скорости в
основном потоке, а и0 представляет собой соответствующую усреднен-
ЯВЛЕНИЯ НА ПОВЕРХНОСТИ РАЗДЕЛА ФАЗ 193
ную скорость, характеризующую процесс смешения в
пограничном слое в целом.
Если на поверхности жидкой пленки образуются волны, то
значение ео увеличивается пропорционально величине
коэффициента трения на поверхности раздела фаз.
7.5. Другие эффекты
В настоящей работе не рассматриваются вопросы
термодинамики двухфазных сред и явления переноса, связанные с
поверхностными явлениями. Читатели могут найти их в книге Дэ-
виса и Риделя [б]. Поверхностные электрические и адгезионные
.эффекты при необходимости могут быть включены в общую
теорию одномерных течений путем введения соответствующих
дополнительных составляющих к силам fi и /г в уравнениях
движения (3.40). Некоторые другие явления будут рассмотрены
в следующих главах.
Задачи
7.1. Вычислить значения т, VfN н vgn в уравнении (7.2) для случая
испарения с поверхности воды при давлениях 0,1, 1, 10 и 100 ата, соответствующие
следующим плотностям теплового потока на поверхности: 104, 105 и
10е ккал/м2 • час.
7.2. Определить разность давлений в уравнении (7.9) для условий задачи
7.1.
7.3. Жидкость под действием снл поверхностного натяжения засасывается
в длинную прямую горизонтальную капиллярную трубку, на обоих концах
которой поддерживается одинаковое давление. Показать, что расстояние,
на которое поверхность раздела проникает в трубку за время г, определяется
соотношением ,
_/ DatcosfL УU
7.4. В кольцевом вертикальном газо-жидкостном потоке поверхностное
натяжение влияет на динамические волны. Считая пленку тонкой и учитывая
перепад давлений, обусловленный поверхностным натяжением, показать с
помощью уравнения (6.158), что уравнение (6.162) остается неизменным, а
уравнение (6.163) принимает вид
"2 | 2 _ 2 , Дз(4/£>2^(о2/£/2) | _ 52 VJ — U2
U2 \ 4[Р*/« + Р//0-«)] J 4 «2 '
Показать, что спектр длин волн в этом случае неустойчив. Какова
наименьшая длина волны, обладающей способностью к дальнейшему росту? Какова
длина наиболее быстро растущей волны?
7.5. Если капля испаряется в среде сильно перегретого пара, то температура
ее поверхности близка к температуре насыщения, а скорость испарения
регулируется интенсивностью теплоотдачи от пара к капле. Показать из
уравнения баланса энергии, что
sm __ hfs m
Ч СрЬТ е0
13 Заказ № 162
194
ГЛАВА 7
где ДГ — перегрев пара, а ср — его удельная теплоемкость. Решая это
уравнение совместно с уравнением (7.21), показать, что массовая скорость
испарения равна
СрДГео J
m =: .
hfg l +0,5cpAT/h/g
и что второй множитель характеризует снижение эффективной теплоотдачи
вследствие массопереноса. Насколько велико влияние этого фактора для
а) воды, присутствующей при давлении 70 ат в паре, перегретом на
110° С?
б) капли бензина прн давлении 1,033 ат, находящейся в пламени,
имеющем температуру 1100° С?
7.6. Используя рейнольдсову модель потока, найти соотношение между
мольной концентрацией неконденсирующихся газов (с0) w вблизи поверхности
конденсации и их концентрацией в невозмущенном потоке (ca)s- Массовая
скорость конденсации т. Показать, что любое из уравнений (7.21)—(7.23) дает
следующее соотношение [7]:
(св)«
■=1-1 f- -rj-l + Члены высшего порядка.
7.7. Поток воздуха обтекает плоскую пластину, расположенную параллельно
основному потоку. Температура основного потока 21° С, давление 1,033 ата,
скорость невозмущенного потока 0,7 м/сек. Представить графически
касательное напряжение в функции расстояния от передней кромки пластины, если
воздух вдувается равномерно через поверхность пластины со скоростью
0,003 м/сек.
7.8. Бумага, протягиваемая над нагретым твердым цилиндром, высушивается
с массовой скоростью испарения воды 100 кг/м2-час. Предполагается, что если
обдувать слой бумаги струями воздуха, то это приведет к увеличению
скорости сушки. При каком коэффициенте массоотдачи струи становятся
эффективными? (Указание. Сначала следует связать коэффициент массоотдачи с и0.)
7.9. При выводе уравнений (7.15) и (7.16) скорость поверхности раздела
была принята равной скорости жидкости. Однако в общем случае
изображенная на фиг. 7.4 картина будет иметь место по обе стороны от
поверхности раздела, где e0g и во/ — рейнольдсовы потоки в паре и жидкости
соответственно. Показать, что в этом случае
_ (% — «/) (Bog + m/2) (ео/ + m/2)
Far Pi
g~
Ff = Pi
4g + e0/
(Vg — vf) (s0g. —m/2) (e0/ — m<2)
eog- + eo/
и что уравнения (7.15) и (7.16) будут справедливы с точностью до первой
степени т/го, если е0 выбрать в соответствии с соотношением
Какова скорость поверхности раздела фаз?
7.10. Определить скорость вдува воздуха, при которой сопротивление трения
на плоской пластине, расположенной параллельно основному потоку, равно
ЯВЛЕНИЯ НА ПОВЕРХНОСТИ РАЗДЕЛА ФАЗ 195
нулю. Скорость основного потока 70 м/сек, давление 1,05 ата, температура
27° С.
7.11. При какой массовой скорости испарения касательные напряжения на
поверхности гладкой пленки воды на стенке трубы диаметром 25 мм,
через которую со скоростью 30 м/сек течет насыщенный пар при давлении
35 ат, станут равными нулю?
7.12. Какова величина коэффициента теплопередачи через горизонтальную
ламинарную пленку конденсата при расходе жидкости через нее, равном Г
(кг на 1 час н 1 ж ширины) и скорости vg ;§> Vf, если массовая скорость
конденсации такова, что ш^>8о?
7.13. Используя результаты решения задачи 7.12, определить, как меняется
толщина пленки и коэффициент теплоотдачи вдоль координаты z для
изображенного на фиг. 7.6 случая. Физические свойства и величину пг принять
постоянными. Как влияет расстояние между пластинами b при заданном
расходе пара на величину коэффициента теплоотдачи?
V///////////////////////////
\ .
Фиг. 7.6. Схема течения к задаче 7.13. т , "■"6"Ka -~. ■
^777777777777777777777777777,
7.14. Почему у простуженных детей более затрудненное дыхание, чем у
взрослых людей?
7.15. Решить задачу 7.3 для случая вертикального расположения трубы.
7.16. С помощью рейнольдсовой модели потока показать, что приближенное
выражение для минимальной скорости переноса, предотвращающей
осаждение частиц из потока суспензии в горизонтальной трубе, записывается
следующим образом: >
v
С/
Показать, что при С/=0,005 условие минимума скорости переноса имеет вид
v —™--- -««,
и*
■ 7.17. а. В некотором объеме воды, в котором существует градиент
температуры, находится неподвижный пузырь воздуха. Градиент температуры
вызывает изменение поверхностного натяжения около пузыря, что сопровождается
появлением конвективных токов в жидкости. Каково направление действия
на пузырь результирующей силы?
б. Будет ли пузырь под действием этой силы перемещаться в
направлении градиента температуры или в обратном направлении? Согласуется ли
направление движения с требованием «минимума ' энергии», необходимого
Для равновесия.
в. Объяснить, каким образом под действием градиента температуры
газовый пузырь может удерживаться на обращенной вверх поверхности.
7.18. Рассмотреть задачу 7.1 применительно к случаю образования парового
пузыря в воде при атмосферном давлении. С помощью таблиц водяного пара
определить величину перегрева жидкости, необходимого для поддержания
пузыря в равновесии.
13*
196
ГЛАВА 7
Литература
1. Taylor G. I., Proc. Roy. Soc. (London), A201, 192 (1950).
2. Ш л и х т и н г Г., Теория пограничного слоя, изд-во «Наука», 1969.
3. Silver R. S., Wal lis G. В., Proc. Inst. Mech. Engrs, 180, part 1, 36—40
(1965—1966).
4. Кутателадзе С. С, Леонтьев А. И., Турбулентный пограничный
слой сжимаемого газа, изд-во СО АН СССР, 1962.
5. С по лд инг Д. Б., Конвективный массоперенос, изд-во «Энергия», 1965.
6. D a v i e s J. Т., R i d е а 1 Е. К-, Interf acial Phenomena, 2nd ed., Acad. Press
Inc., N. Y., 1963.
7. Wal lis G. В., Intern. J. Heat Mass Transfer, 11, 445—472 (1968).
Часть II
ПРАКТИЧЕСКИЕ ПРИЛОЖЕНИЯ
8
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ
'Ч*.1
8.1. Введение
Примером двухфазной системы является суспензия,
состоящая из жидкости и взвешенных в ней твердых частиц. Из-за
отсутствия влияния поверхностного натяжения, дробления и
деформации такая система обычно проще для исследования, чем
соответствующие газо-жидкостные или жидкостно-жидкостные
дисперсные системы. Несмотря на это, иа практике возникают
осложнения, обусловленные такими факторами, как широкий
спектр размеров и'форм частиц, неоднородность структуры
потока, агломерация и силы взаимодействия между частицами.
В качестве технических приложений можно упомянуть раз-1
личные технологические процессы и аппараты: псевдоожиженные
слои для обогащения урановой руды, формовка строительных
каркасов, пластиковые покрытия; отстойники, фильтрующие
слои, потоки грунтовых вод к скважинам, уплотнение грунта;
пневмо-и гидротранспортеры; плазменное распыление, очистка
пескоструйным аппаратом, выхлопные струи ракетных
двигателей, содержащие продукты сгорания или несгоревшие частицы
металлических добавок; течение красок, шлама, печатной краски,
мыла и бумажной пульпы.
В данной главе мы рассмотрим различные режимы течения
смесей жидкости с твердыми частицами, каждый из которых
определяется балансом между несколькими силами. Например,
динамика процесса осаждения определяется соотношением
между подъемной силой и силой сопротивления, в то время как
доминирующими силами в высокоскоростном потоке в сопле
являются силы давления, инерции и межфазного сопротивления.
Здесь не будут рассматриваться многочленные общие уравнения,
практически не позволяющие получить решение. Читателю,
интересующемуся более сложными системами, не рассматриваемыми
в данной главе, рекомендуется применить общие методы,
изложенные в ч. I книги, к конкретным исследуемым задачам.
8.2. Одномерный вертикальный поток однородной
несжимаемой дисперсной системы без трения на стенках
Общая теория однородного стационарного течения
Рассмотрим стационарное течение смеси жидкости с
твердыми частицами в вертикальном канале постоянного сечения.
200 ГЛАВА 8
Если скорости достаточно малы, а размеры канала достаточно
велики, можно пренебречь трением на стенках, и считать, что
общее движение относительно канала не оказывает влияния на
относительное движение частиц и жидкости. Следовательно, для
данной системы относительное движение зависит только от
локальной концентрации, свойств и гравитационного поля, но не
зависит от результирующих расходов компонентов. Убедительное
подтверждение справедливости этого допущения было получено
экспериментально Лапидусом и др. [1, 2].
В соответствии с изложенным в гл. 4 можно определить
приведенную скорость дрейфа jfs, которая зависит только от
концентрации. Обозначив объемную концентрацию жидкости
(истинное объемное содержание жидкой фазы) 'через е,
получим, как и ранее, '
/'/*=(!-е)/7-*Л. (8-1)
где индекс / относится к жидкости, as — к частицам, причем
положительное направление давижения — вверх. Для описания
систем, состоящих из жидкости с твердыми частицами, обычно
используют величину е, хотя можно пользоваться и значением
а=1—е.
С учетом того, что е относится к непрерывной фазе,
эмпирическое соотношение (4.14) записывается в виде
//,=«.«" (1-*). (8.2)
где Voc — предельная скорость осаждения одиночной частицы
в бесконечно большом объеме неподвижной жидкости. Если,
из исходных соотношений можно определить значения у», и п, то
все аналитические методы, изложенные в гл. 4, применимы и
в данном случае.
Конечная скорость осаждения одиночной частицы
Конечная скорость осаждения одиночной частицы
определяется из баланса сил тяжести-и сопротивления. Например, для
сферической частицы диаметром d
Т- d*S (Р/ - Р,)=CDm -\&\ Pfvl, (8.3)
где Cd<x, — коэффициент сопротивления, зависящий от числа
Рейнольдса Re*,, определяемого как
v dp,
Re-^V^ ' (8'4)
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ
201
Упрощая уравнение (8.3) и используя (8.4), чтобы исключить
v<x>, получим
r D 2 _ 4 d3?fg(?s — ?f)
$
(8.5)
Следовательно, величина Cn<x>Re2 не зависит от v*, и может
оо
быть рассчитана непосредственно по известным параметрам.
ю1
!07 —
10'
10s-
ю<
4
10'
10'
ю1
ю°
ю-
*■ /
10'г 10'' 10° 10'
Re»
Ю2
ю3 ю4
Фиг. 8.1. Изменение величины С Re2 в зависимости от Re_ для сфери-
Deo оо ""
ческих частиц [3].
Так как CD°° является функций Re*,, то CDooRe^ можно
выразить аналитически или графически [3] в функции Re*, (фиг. 8.1).
Используя это соотношение и уравнение (8.5), можно найти Re*,
и, следовательно, Уоо.
В большинстве практических случаев для систем жидкость —
твердые частицы число Рейнольдса меньше 1000. В этом случае
зависимость коэффициента сопротивления от числа Рейнольдса
202
ГЛАВА 8
можно представить в следующем виде:
CDM=~-(l+0,15Re°o;687). (8.6)
оо
Для чисел Рейнольдса, больших 1000, коэффициент
сопротивления приблизительно постоянен и равен
CDm=0,44. (8.7)
Модификация этих уравнений для несферических частиц
рассмотрена Хейвудом [5].
Правую часть уравнения (8.5) удобно выразить через
безразмерную обратную вязкость Nf (иногда называемую числом
Грасгофа), тогда
CDxRel = ~N2f. (8.8)
Определение показателя степени п
Ричардсон и Заки [6] установили, что показатель степени п-
в уравнении (8.2) зависит прежде всего от числа Рейнольдса,
определяемого уравнением (8.4). Кроме того, следует ввести
поправочный коэффициент, выраженный через отношение
диаметра частицы d к диаметру трубы D. Корреляционные формулы
Ричардсона и Заки для широкого диапазона чисел Рейнольдса
имеют следующий вид:
ReGO<0,2
0,2<ReM<l
1< Re» < 200
200<Reoo<500
500 < ReM
«=4,65+19,5-^,
n=(4,35+17)5-g-)Re»°'03.
n=(4,45+18-g-) Re"0'1,
re=4,45Re-°'I(
re=2,39.
(8.9a)
(8.96)
(8.9b)
(8.9r)
(8.9д)
Намного большие значения п могут быть получены для
конгломератов частиц [7]. Это относится к частицам микронных
размеров и особенно к частицам несимметричной формы, когда они
самопроизвольно объединяются в устойчивые хлопьевидные
комплексы. В таких случаях целесообразно экспериментально
определять приведенную скорость дрейфа в зависимости от
концентрации.
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ 203
Силы, действующие на частицы и жидкость
Рассмотрим множество неподвижных частиц в
горизонтальном потоке жидкости, причем сила, действующая на частицу,
выражается через скорость жидкости, свойства и концентрацию
(фиг. 8.2). Общая сила, необходимая для удержания частицы
объемом 7°р, равна
(8.10)
'"-»%(/.-£■)•
где fs — сила, определение которой было дано в гл. 3. Силу F'
можно выразить через приведенную скорость жидкости и свой-
а Ъ
1-
Приведеннал*
скорость
жидкости
Jfo *.
Давление р 1-
г'
О-»2- о о о
о о о
о о о о
о о о
Yz
»|
I- Давление p+Sp
Фиг. 8.2. Силы, действующие на множество частиц.
Частица удерживается в потоке силой F', направленной против силы сопротиаления
потока жидкости.
ства, если ввести определение коэффициента сопротивления для
заданного е:
F'
(CD\-
1!2?//0А.
(8,11)
где Лр — характерное поперечное сечение частицы, //о —
приведенная скорость жидкости. Коэффициент сопротивления
учитывает влияние как градиента давления, так и сил, входящих в /„.-
Объем среды, заключенный между линиями аа и ЬЬ
(фиг. 8.2), должен находиться в равновесии. При этом не
происходит изменения количества движения жидкости, а
«концевые эффекты» можно свести к минимуму, выбирая объем
достаточно большим. Так как внешняя сила, действующая на частицу,
уравновешивается градиентом давления, то
/=■'(!-б) =
(8.12)
Индекс F означает, что градиент давления обусловлен только
трением. Сила сопротивления, действующая на частицу, должна
быть равна и противоположно направлена силе сопротивления,
204 ГЛАВА 8
действующей на жидкость. Следовательно (как и в примере 3.4),
^ = е/,= -(1-е)/,. (8.13)
Полезным параметром является также величина
//.=//-/,- (8Л4)
Объединяя уравнения (8.10) — (8.14), можно получить
следующие соотношения между силами:
-V--(t'ni.T pfj/o-f- п=тл~гг/^—
= -//.= -77ПГЛ-- С8'15)
// _ /, _ # _ {>
8(1_.)
Если коэффициент сопротивления (Св)е может быть
определен как функция объемного содержания жидкости и ее свойств,
то все рассмотренные силы могут быть рассчитаны.
Например, для спокойного псевдоожиженного слоя, в,
котором действие сильк тяжести на частицы уравновешивается
восходящим потоком обтекающей их жидкости, уравнения (3.45) и
(3.46) сводятся к следующему:
4г=-£р/+//=-£р,+л- (зле)
Объединяя (8.15) и (8.16), получим
vP
g(?s — ?/)-J-
(CD).= i^T"- (8-17)
Согласно экспериментальным данным Роу [8], (CD)e можно
представить в виде произведения двух функций, одна из которых
зависит только от объемного содержания, а другая — от числа
Рейнольдса:
(CD).=CDM*). (8.18)
Величина г|з(е) представляет собой отношение силы
сопротивления, действующей на одну из множества частиц, к силе
сопротивления такой же одиночной частицы в потоке жидкости,
движущейся с той же относительной приведенной скоростью.
Величина CDs определяется как функция «приведенного» числа
Рейнольдса по обычным зависимостям, например по уравнениям
(8.6) и (8.7), в которых число Рейнольдса должно быть
определено по уравнению
Re,=-^. (8Л9)
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ
205
Условие равновесия для сферической частицы,
эквивалентное (8.8), теперь принимает вид
(CD)eRe^=4^/.
(8.20)
Для частицы, находящейся в равновесии, из уравнений (8.20)
и (8.5) следует
CDa> Re2„=(CD). Re?.
(8.21)
■ Выражая коэффициент сопротивления с помощью уравнений
(8.6) и (8.7) и подставляя (8.18) в (8.21), получим
для Re < 1000
Reoo(l+0)15Re?87)=^(e)Re,(l+0,15Re?'687), (8.22)
для Re> 1000
ReL=<Ke)Re?. (8.23)
Для жидкости с заданными свойствами уравнения (8.22) и
(8.23) определяют связь между £/«,, е и //о и могут быть
использованы для определения величины //s.
Из сравнения уравнений (8.22) и (8.23) с корреляционными
формулами Ричардсона и Заки (8.9) с использованием (8.1) и
(8.2) следует
//0=^"- (8.24)
Умножим теперь уравнение (8.24) на Pfd/Uf и получим
Re,= Re е«.
(8.25)
При числах Рейнольдса, больших 1000, из (8,23) и (8,25)
следует, что
ф(е) = е-2л, (8.26)
тогда из (8.9д) имеем
ф(в)=е-4'78. (8.27)
С другой стороны, при очень малых числах Рейнольдса из (8.22)
и (8.25) следует
ф(е) = е-«, • (8.28)
тогда из (8.9а) имеем
^(е^е-4'65. (8.29)
Компромиссная зависимость между (8.27) и (8.29) имеет вид [9]
ф(е) = Е
-4,7
(8.30)
Справедливость уравнения (8.30) можно проверить в
широком диапазоне чисел Рейнольдса, если возвести уравнение (8.25)
206
ГЛАВА 8
в степень 4,7/п и умножить полученный результат на (8.22),
что дает
Ren-4,7/n)(l+0)15Re0,687)=Re(,-4,7/n)(l+0)15Re0,687)i (ggi)
Очевидно, уравнение (8.31) не может точно выполняться
в широком диапазоне чисел Рейнольдса. Однако для
рассматриваемых частных значений параметров можно потребовать, чтобы
функция числа Рейнольдса, определяемая уравнением (8.31),
была приблизительно постоянной. Тогда, дифференцируя (8.31),
получим
(l -Ц) Re-4'7/n + 0,15(l,687 -Ц-) Re,
откуда
l+0,15Re^687
1 + 0,25.3Re^687 *
(0,687-4,7/л)
«=4,7
=0, (8.32)
(8.33)
Сравнение величин п, вычисленных по формуле (8.33), с
данными Ричардсона и Заки приводится в табл. 8.1. Значение п для
Re =1000 получено из (8.26) и (8.30).
Таблица 8.1
Сравнение значений п, вычисленных
формулам (&33) и (8.9)
Я'оо
Ричардсон и Заки,
формула (8.9)
Формула (8.33)
0
4,65
4,7
0,2
4,65
4,65
1
4,35
4,31
10
3,53
3,65
по
100
2,8
3,05
1000
2,39
2,35
Совпадение результатов свидетельствует, что уравнение
(8.30) является приемлемой аппроксимацией.
Тогда уравнение (8.15) для сферических частиц примет вид
f -4,7 п О
-J fs £ uDi"4"
(У/о
(8.34)
и все силы могут быть рассчитаны по известным параметрам.
Для частицы, находящейся в равновесии в гравитационном
поле, уравнение (8.20) становится явным относительно
объемного содержания жидкости
.4,7 __ 3 CDs Re,
* —4 jji — - (8-3о>
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ 207
. В системе с движущимися частицами величина, //о связана
с относительной скоростью и приведенной скоростью дрейфа
следующим соотношением:
У/о=т^7=^- (8.36)
Например, уравнение (8.34) при введении относительной
скорости принимает вид
/„ = _.-*■'C^-J-2^- (8-37>
Это уравнение аналогично полученному Зубером [52] для
ламинарного режима течения дисперсной двухфазной среды, в
котором е содержится в степени —2,5.
8.3. Однородное псевдоожижение
Если частицы данного размера вводятся в вертикальный
цилиндр и жидкость с более низкой плотностью принудительно
движется вверх с достаточно высокой скоростью, то частицы
переходят в псевдоожиженное состояние; иными словами, они
больше не соприкасаются друг с другом, а поддерживаются
потоком жидкости и имеют свободу перемещения..
При однородном псевдоожижении частицы равномерно
распределены в расширяющейся смеси. При некоторых условиях.не
может быть достигнуто однородное псевдоожижение частиц и
жидкость либо просачивается по каналам с низким
сопротивлением или образует пузыри, которые растут в слое подобно
пузырям газа в жидкости.
Минимальная скорость псевдоожижения
.Приведенная скорость жидкости, при которой начинается
переход слоя в псевдоожиженное состояние, обычно называется
минимальной скоростью псевдоожижения. При минимальной
скорости псевдоожижения силы сопротивления и давления,
действующие на частицу, становятся равными их весу.
Следовательно, уравнение (8.35) справедливо для начала
псевдоожижения и процесса расширения слоя, пока распределение частиц
остается равномерным.
Величина е для беспорядочной упаковки сферических частиц
равна 0,4. Тогда величина е4,7 равна 0,0135 или '/74 и
минимальная скорость псевдоожижения в неявном виде определяется из
уравнения (8.35)
(CDaR£)mf=0№Nf. (8.38)
208 ГЛАВА 8
Зная величину CusRe^, с помощью фиг. 8Л или уравнений
(8.6) и (8.7) находим Res и из уравнения (8.19) определяем
минимальную скорость псевдоожижения.
Коэффициент в (8.38) хорошо согласуется со значением
0,0195, приведенным в работе [8], а также с результатами работ
[10,11].
Величина е, при которой приходят в соприкосновение
несферические частицы, может достигать 0,8. Если известны
соответствующие данные об упаковке таких частиц, то для определения
минимальной скорости псевдоожижения можно использовать
(8.35).
Падение давления в псевдоожиженном слое
Неподвижный слой. Потери давления на трение в неподвижном
слое частиц можно определить обычным методом, вводя
коэффициент трения С :
где Ат — общая площадь поверхности частиц, а Та —
соответствующий объем потока. Для сферических частиц диаметром d
отношение TJAt равно
^=т^т4- <8-40>
Для несферических частиц часто вводится коэффициент
формы Ф
J^=J ! L (8.41)
Ат Ф 1 —е 6 • V * >
Средняя скорость в слое связана с приведенной скоростью
соотношением
•ot=~- • (8-42)
Подставляя (8.40) и (8.42) в (8.39) и вводя новое определе-
3CJ
ние коэффициента трения С/ =—~—, получим
-Ш„=2С/4^. (8.43)
Для несферических частиц вместо d подставляется отношение
d/Ф.
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ 209
Коэффициент трения, содержащийся в (8.43), обычно
выражается в зависимости от числа Рейнольдса, определяемого через
•среднюю скорость жидкости [из (8.42)] и среднюю
гидравлическую глубину слоя [из (8.40)], т. е.
Re/= <^L_
I (1— S)(X/
(8.44)
Заметим, что Re/ отличается от числа Рейнольдса,
определяемого уравнением (8.19).
Ref
6 IOO 2
PfJfod
■Фиг. 8.3. Коэффициенты трения при течении в пористых средах в сравнении
с данными Эргана [17] [уравнение (8.46)] и корреляцией
Симпсона—Роджера [16] (заимствовано из работы [17]).
При малых числах Рейнольдса (Re/<10) из уравнения
Кармана—Козени [12, 13] для ламинарного потока следует, что
С,
90
Re/
(8.45)
Это значение заключено между значениями 75 в уравнении
Блейка—Козени [14] и 100, которое рекомендует Лева [15].
Зависимость С/ от Re/ при более высоких числах Рейнольдса
приведена на фиг. 8.3. Она сравнивается с корреляцией
Симпсона и Роджера [16] и следующим уравнением Эргана [17]:
75
Re/
-0,875.
(8.46)
14 Заказ .4» 162
210 ГЛАВА 8
Начальная стадия псевдоожижения. В начальной стадии
псевдоожижения жидкость только поддерживает частицы. Из (8.14) —
(8.16) следует, что
-Ш,=а-')*(р.-р/>- <8-47>
Подставляя (8.44) и (8.45) в (8.43), получим
СМ=2{'-*)* К (8-48)
Уравнение (8.48) напоминает (8.38), однако оно было
получено совершенно другим путем. Считая, что в начальной стадии
псевдоожижения 8=0,4, приведем (8.48) к следующему виду:
N2f=\\,25CfRe}, (8.49)
и тогда (8.38) принимает вид
N}=55,5CDsRel. (8.50)
С учетом'уравнений (8.19) и (8.44) при е=0,4 получим
Re/=-|r- (8-51)
Для ламинарного потока CDs = 24/Res, C/ = 90/Re/ и правая часть
(8.49) оказывается равной 1690 Res, в то время как правая часть
(8.50) равна 1330 Res. Сравнение результатов двух
рассмотренных методов в широком диапазоне чисел Рейнольдса приводится
в табл. 8.2.
Таблица 8.2
Сравнение аначений Щ
для начальной стадии псевдоожижения,
рассчитанных по формулам (8.49) и (8.50)
Re*.
880800-0
Формула (8.49)
Симпсон —
Роджер [16]
16,9
1690
1,83- 104
1,7- 105
1,35- 106
6,75 • 106
2,20- 107
7,7- 107
Эрган [17]
14,1
1410
1,73 • 104
1,62- 105
1,38- 106
7,23- 106
2,8 • 107
10,9- 107
Формула (8.50)
13,3
1530
2,30. 104
2,14- 10^
1,72 • 106
7,78 • 106
2,44- 107
9,76 • 107
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЁРДЫМИ ЧАСТИЦАМИ 211
Как видно, эти два метода дают достаточно близкие
результаты в пределах точности, с которой обычно известны величины
С/ и Сд.
Псевдоожиженное состояние. В псевдоожиженном состоянии
условие равновесия для элемента горизонтального слоя имеет
вид
dp
dz
=.?[6Р/+П-6)Р*].
(8.52
откуда при известном значении е можно найти градиент
давления.
Фиг. 8.4. Суммарные потери
давления на трение в
псевдоожиженном слое в зависимости от
приведенной скорости жидкости.
ПссвВоожиженный спой
ш
ч
jf —
Для псевдоожиженного слоя в прямом вертикальном канале
общие потери давления на трение постоянны и равны
погруженному весу всех частиц слоя, разделенному на общую площадь
поперечного сечения. Кривые зависимости суммарных потерь
давления на трение от приведенной скорости жидкости
аналогичны показанной на фиг. 8.4. Точка провала кривой
соответствует началу псевдоожижения.
Порядок расчета однородных псевдоожиженных слоев
■ Неподвижный слой (без результирующего движения частиц).
Если известны свойства частиц и жидкости и определена
приведенная скорость жидкости, то простейшие расчетные операции
для сферических частиц выполняются в следующей
последовательности:
1. Из (8.19) определяется Res.
2. Для расчета CDs в (8.6) и (8.7) вместо Re«, подставляется
Res.
3. Определяется величина CDsRe2.
4. По вычисленной величине CDsRe2 из (8.35) определяется е.
Если величина е заключена в пределах от 0,4 до 1, то слой
сферических частиц является псевдоожиженным; для несфе-
14*
212 ГЛАВА 8
рических частиц, требуется дополнительная информация о
значении е в плотном слое.
5. Если слой псевдоожиженный, то градиент давления
рассчитывается по уравнению (8.52). Если слой непсевдоожижен-
ный, то число Рейнольдса Re/ определяется из (8.44), после
чего по фиг. 8.3 находится величина С/. Затем по уравнению
(8.43) рассчитывается (dp/dz)F, а для определения
результирующего градиента давления к этой величине добавляется
гидростатический градиент pfg.
Если частицы несферические, то вид уравнений остается
неизменным, однако, как показано Хейвудом [5], необходимо
введение поправочных коэффициентов.
Подвижный слой (частицы имеют результирующее движение).
Слой должен быть псевдоожиженный. Наиболее простой
является корреляция Ричардсона и Заки.
1. По (8.5) определяется CDooRe^.
2. По (8.6), (8.7) или по фиг. 8.1 находится Re,*,.
3. По (8.4) вычисляется у».
4. По (8.9) вычисляется п.
5. По (8.2) определяется jfs и с помощью (8.1) и методов гл. 4
находится е. По (8.52) рассчитывается градиент давления.
Если предполагается, что трение на стенках значительно, его
вычисляют по теории гомогенного течения и суммируют с
падением давления под действием сил тяжести.
Пример 8.1. Вода при температуре 20° С движется вверх по вертикальной
трубе сечением 6,45 см2; объемный расход воды 1,84 смг/сек. В трубе
находится медная дробь диаметром 0,0254 см. Будет лн слой частиц
псевдоожиженный? Определить градиент давления и объемное
содержание жидкости. Исходные данные: .0=2,87 см, (х/ = Ю-2 г/см-сек, ps =
= 8,92 г/см3, р,= 1,00 г/см3.
Решение. Приведенная скорость жидкости в трубе равна
Qf 1 84
JfO = ~j[- = -glT = 0-285 см1сек- 0>
По формуле (8.19) получим
_ *Jm _ 0,0254 • 0,285 ■ 1,0
Re,-——— т 0,725. (2)
Из (8.6) следует, что
CD, = 37.1. (3)
Используя уравнения (2) и (3), получаем
CDs Re* = 37,1 - 0.7252 = 19,5. (4)
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ 213
Используя уравнение (8.35) и определение величины Nf, находим
.4,7 _J CDsReyf __адв.; 19,5,0,012 _oou5) (5)
4 Р/ d?g (9s—?f) 0,0254s ■ 981 • 7,92
следовательно,
е = 0,01151/4-7 = 0,385. (6>
Так как эта величина меньше обычного значения для беспорядочной
упаковки сфер (е=0,4), то слой не будет псевдоожиженный.
Для расчета величины CdsR&s можно использовать также
формулу (8.38), которая справедлива для начала псевдоожижения:
(Co,r.;)./=o.o„ ц*";-'" -
0,018 ■ 1 ■ 0,02543 • 981 • 7,92 _ 22
0,012
Так как значение, определяемое уравнением (4), меньше этой величины,
слой не является псевдоожиженный.
Следовательно, объемная доля жидкости до начала псевдоожижения
составляет около 0,4.
Потери давления расчитываются по формуле (8.43). Вначале
определим число Рейнольдса по формуле (8.44)
_ d?fJ/o 0,0254 • 1 ■ 0,285 _ , „,
*е/= (1_.)(1/ =—ox~aoi— = 1'21- (8>
Далее по формуле (8.45) находим
С,—J°—-?°- (9>
Lf~ Re, _ 1,21 W
и, используя формулу (8.43), получаем
SC/Z/od-6)
\ dz )р
йГеЗ
2 • 90 • 1 • 0,0813 ■ 0,6
1,21 • 0,0254 ■ 0,064
= 4460 г/см? • сек?. (10)
Добавляя гидростатический градиент ptg, определим общий градиент
давления
dp
dz
: 4460+ 981 =5441 дин/см^. (Ц)
Для проверки рассчитаем,' каким был бы градиент давления, если бы
слой находился в начальной стадии псевдоожижения. По формуле (8.52)
находим
-^f- = S t£P/ + О — е) Pil =981 (°.4 • 1 + 0,6 • 8,92) =5640 дин/см*. (12)
Так как градиент давления, вычисленный по условиям данной
задачи, меньше вычисленного по формуле (12), рассматриваемый слой
не является псевдоожиженный, что согласуется с результатами,
полученными на основе (6) и (7).
214 ГЛАВА 8
8.4. Нестационарное течение дисперсных систем
с твердыми частицами
Распространение непрерывных волн
В соответствии с уравнением (6.40) скорость непрерывной
волны во взвеси частиц равна
Для псевдоожиженного слоя, удовлетворяющего соотношению
(8.2), уравнение (8.53) принимает вид
^=У/ + -й-Ке-(1-е)]. (8.54)
Этот результат был экспериментально подтвержден в
работе [18].
В стационарном режиме приведенная скорость жидкости при
псевдоожижении связана с ее объемной долей уравнением (8.24).
Следовательно, малое отклонение от установившегося значения
некоторого параметра распространяется со скоростью, которую
можно определить, исключая // или vx из уравнений (8.24) и
(8.54), т. е.
Vw=n-^^-jf0 (8.55)
или
Vw=m»-4\-e)vco. (8.56)
Из уравнения (6.41) найдем скорость непрерывной ударной
волны
^_.+ Uf.)i-ih.h (8>57)
Пока влияние инерции и сжимаемости пренебрежимо мало,
нестационарный одномерный вертикальный поток легко
поддается описанию на базе изложенных представлений о
распространении непрерывных волн и скачков. Однако, когда
распространение этих волн вызывает инверсию плотности
вследствие уменьшения величины е с высотой, возникают
дополнительные осложнения. Такой процесс является нестационарным
и может сопровождаться возникновением трехмерных
возмущений, нарушающих упорядоченную структуру потока.
8.5. Периодическое осаждение
Характерным примером применения' теории непрерывных
волн служит процесс осаждения. При отсутствии
результирующего потока процесс называется периодическим осаждением
СМЕСИЖИДКОСТЕИ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ
215
(отстаиванием), а в случае непрерывного удаления твердых
частиц — непрерывным осаждением. В данном разделе будет
подробно исследован процесс периодического осаждения, однако
используемый метод можно видоизменить применительно к
процессам, в которых результирующий поток жидкости или частиц
определенным образом регулируется [19, 20].
Л.
\/4В
ВС/
/ CD
^АС
S^**
AD
*.
Фиг. 8.5. Типичное развитие
процесса периодического осаждения. t —»- ■
а — физическая картина; б — высота по- ' 6
верхности раздела в функции от времени.
Так как при периодическом осаждении общая плотность
объемного расхода (скорость смеси) ;' равна нулю, то уравнения
(8.53) и (8.57) принимают следующий вид:
Vw—-irUfs)'
v,=
(Jfs)l — (jfs)2
(8.58)
(8.59)
Часто в расчетах вместо объемного содержания жидкости
используют величину объемного содержания частиц. Так как
а=1—е, уравнения (8.58) и (8.59) можно записать в виде
V„=-4-(/„), (8.60)
da
V,
Я] 0t2
(8.61)
Следовательно, на графике зависимости jfS от а скорости
непрерывной волны и скачка, направленные вниз, соответствуют
тангенсам угла наклона касательной и хорды.
Типичный процесс осаждения частиц из первоначально
однородной суспензии развивается следующим образом. Вначале,
как показано на фиг. 8.5, в осадительной колонне содержится
однородная двухфазная смесь В. При осаждении в верхней
части колонны появляется чистая жидкость Л, а в основании
колонны— плотный осадок D. Между областями В и D часто
216 ГЛАВА 8
существует зона С, где концентрация частиц неравномерна. Если
частицы имеют почти одинаковые размеры, то между слоями А
и В образуется резкая граница, которая перемещается со
скоростью оседающих частиц. Между областями В а С может
существовать четкая граница раздела, но может и отсутствовать.
В конце концов верхняя и нижняя границы раздела сливаются
и область В исчезает. После этого происходит медленное сжатие
или уплотнение областей С и D до достижения максимальной
плотности осевшего слоя.
Случай i
Случай 2
О \ / <*<»
arctglfcg arctg VBD
«2
AD
t
6
Фиг. 8.6. Процесс осаждения, тип I.
а — зависимость приведенной скорости, дрейфа от концентрации; б — линии распростра
нения воли в плоскости: положение поверхности раздела — время.
Кинч [21], по-видимому, первым разработал исчерпывающую
математическую теорию процесса осаждения, использовав
зависимость общего расхода частиц от концентрации, что в данном
случае аналогично зависимости jfS от а.
Для обычной формы этой кривой можно выделить
следующие три типа процесса периодического осаждения.
Тип I. Если возможен непосредственный скачкообразный
переход от исходного значения а(ао) к конечному значению а»
для полностью уплотненного осадка (фиг. 8.6), наблюдается
только одна стадия осаждения. Поверхность раздела АВ
движется со скоростью, определяемой тангенсом угла наклона
хорды, соединяющей точки а = 0 и а = ао, а поверхность раз-
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ
217
дела BD перемещается со скоростью, определяемой тангенсом
угла наклона хорды, соединяющей точки а=ао и а=а0О.
Осаждение завершается при встрече двух скачков, причем
уплотнения не происходит. Для зависимостей //s от а, показанных на
фиг. 8.6, первый тип процесса осаждения наблюдается в
случае 1 для всех начальных значений а=ао, а в случае 2 — только
при ao>ai или a0>a2- Если непосредственный скачкообразный
\-АВ
В \
ВСу/£>>ь
А
^АС
~~<CD
AD^
D
t
б
Фиг. 8.7. Процесс осаждения, тип II.
■ зависимость приведенной скорости дрейфа от концентрации; б — линии
распространения воли.
переход от значения осо к значению а^ для полностью
уплотненного слоя невозможен, процесс осаждения становится более
сложным.
Тип //. Если кривая //s(a) в точке осо обращена выпуклостью
вниз, то начальная скорость осаждения Vab равна тангенсу
угла наклона хорды, соединяющей точки а = 0 и а=ао. Значение
а» для полностью уплотненного осадка распространяется от
дна колонны вверх со скоростью скачка Vcd, которая равна
тангенсу угла наклона касательной к кривой, проведенной из точки
a=aoo, //s = 0. Если в точке касания а = аг, различные участки
колонны характеризуются следующими значениями объемной
концентрации частиц:
218
ГЛАВА 8
область А — чистая жидкость, а = 0;
область В — начальное значение концентрации а = ао;
область С — промежуточная концентрация от ао до а2;
область D — конечная концентрация осадка а».
Так как на границе раздела ВС не происходит
скачкообразного изменения объемной концентрации частиц, эта поверхность
Фиг. 8.8. Процесс осаждения, тип III.
■а — зависимость приведенной скорости дрейфа от концентрации: б — линии
распространения волн.
практически может не наблюдаться. Когда верхняя граница
области С, перемещающаяся со скоростью непрерывной волны,
соответствующей значению ао, достигает границы АВ, область В
исчезает и скачок начинает усиливаться и замедляется. В любой
последующий момент времени значения а непосредственно
за скачком определяются непрерывной волной, достигающей
в данный момент поверхности раздела. Это уплотнение области С
продолжается до совмещения поверхностей раздела АС и CD
и завершения процесса осаждения. Перемещения поверхностей
раздела и всех непрерывных волн в области С для этого вида
осаждения показаны на фиг. 8.7.
Тип III. Если кривая jfS в точке ао обращена выпуклостью
вверх (фиг. 8.8), то между областями В и С имеет место ска-
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ 219
чок объемной концентрации частиц и образуются три
отчетливые поверхности раздела. Объемная концентрация у верхней
границы области С определяется точкой касания касательной,
проведенной из точки а0, так как в данном случае наиболее
быстрая непрерывная волна в области С фактически не отстает от
скачка ВС, который поэтому не усиливается и не ослабляется.
Когда поверхности раздела АВ и ВС совместятся, область В
исчезает, и в дальнейшем происходит уплотнение области С до
полного завершения осаждения. Перемещение поверхностей
раздела для этого типа процесса осаждения показано на фиг. 8.8.
«Обобщенный» анализ процесса периодического
осаждения [7]
Пусть Vs — скорость скачка между чистой жидкостью и
верхней границей области оседающих чяптиц. На графике //Да)
скачок изображается хордой, соединяющей точки а=0, а=а, и
движется со скоростью ;>s/a. В момент времени t положение
непрерывной волны, распространяющейся от основания осевшего
слоя, определяется соотношением
h=Vwt (8.62)
и изображается в плоскости М, исходящей из начала координат
линией распространения волны с наклоном Vw. Так как для
заданной системы жидкость—частицы Vs и Vw завиеят только от а,
эти величины можно рассматривать в функции одна "от другой.
Следовательно, для всех процессов осаждения тангенс угла
наклона касательной к криволинейному участку в плоскости ht
в точке пересечения с прямой, проведенной из начала координат
и имеющей тангенс угла наклона Vw, будет равен Vs. Поэтому
все кривые для различных начальных высот и концентраций
имеют одинаковую форму и их можно совместить, умножив
ординату и абсциссу на соответствующий множитель. Таким
множителем является величина 1/Аоао (где h0 —
начальная высота), при этом все кривые по завершении
осаждения пройдут через точку 1/а«,. На полученной кривой будут
расположены все точки, характеризующие стадию уплотнения.
Начальной стадии, когда скорость осаждения постоянна,
соответствует постоянное значение Vs, т. е. касательная к кривой,
которая пересекает линию / = 0 в точке 1/а0. Если кривая jfS имеет
перегиб, то Vw проходит через максимум и обобщенная кривая
осаждения состоит из двух ветвей, сходящихся в точке
возврата. Если ао меньше значения, соответствующего
максимальной величине Vs, начальная стадия осаждения представлена
касательными к нижней ветви и происходит осаждение типа III.
Если линия, соответствующая начальной стадии, пересекает
220 ГЛАВА 8
горизонтальную прямую 1/а«>, представляющую конечное
состояние, раньше, чем верхнюю ветвь, происходит осаждение типа I.
Три основных типа процесса осаждения в виде обобщенной
зависимости Y=h/hoao от X=t/h0ao показаны на фиг. 8.9.
Фиг. 8.9. Обобщенное изображение процесса периодического осаждения [7J.
Взаимосвязь зависимостей jfS от а и Y от X обнаруживается
из следующих тождеств:
/V ™ зз j у
V ^-UlL^JL
Vw da X '
(8,64)
Касательная к кривой X от Y пересекает ось Y в точке
у-х4г=^Г' . (8-65)
а ось X в соответствии с уравнением (8.63) —в точке 1///«-
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ 221
Подставляя уравнения (8.63) и (8.64) в уравнение (8.65),
получим
откуда
X
JfS
djfs
da
1
X
-J/s-
dj/s
da
(8.66)
(8.67)
и, следовательно, величина l/JC определяется пересечением
касательной к кривой jfS с линией а=0. Согласно уравнению (8.64),
пересечение ее с осью а происходит в точке 1/У.
Jh
■t
Ф н г. 8.10. Взаимосвязь функций X (К) и jf, (a).
Эти интересные дополнительные геометрические соотношения
(фиг. 8.10) значительно упрощают построение одной кривой
по известной другой. Каждая кривая содержит более чем
достаточную информацию для построения другой кривой, так как
координаты любой точки и наклон касательной в ней известны.
Если jfS задается в обычной форме, соответствующей
уравнению (8.2), то координаты обобщенной кривой процесса
осаждения в параметрическом виде будут следующими:
Л"=[яг»ва2(1-а)«-1]-1, (8.68)
(л 4- 1)я— 1
Г = -
(8.69)
222 ГЛАВА 8
Для процесса осаждения типа III часто более точным
оказывается построение начала процесса в виде прямой линии,
соединяющей точки 1/cto и l///s на соответствующих осях, если точка
касания касательных с нижней ветвью расположена значительно
ниже оси X.
4
X, мин/см.
Фиг. 8.11. Изображение процесса осаждения в плоскости X—Y при различных
начальных концентрациях и одинаковых положениях поверхностей раздела [7].
Рассмотренный метод был видоизменен Уоллисом [7],
представившим данные работы [22] в виде зависимостей Y от X.
Типичные результаты такой обработки данных приведены
на фиг. 8.11. Для мелких частиц неправильной формы,
использованных в этих экспериментах, значение п заключено между
20 и 30, что указывает на значительное влияние образования
конгломератов частиц.
Диапазоны начальных значений а, соответствующие трем
типам процесса осаждения, показаны в координатах а — jfS и
X—Y на фиг. 8.12. Если справедливо уравнение (8.2), то перегиб
функции jfS(a) и точка возврата в плоскости X—Y имеют
координату
*,~-ЛТГ' (8-70)
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ 223
причем
«„(1+л) + [а^(1+л)2 —4пя ]'/.
2 Ъ1
(8.71)
Пример 8.2. Рассмотреть процесс осаждения сферических стеклянных частиц
диаметром 0,0254 см в 90%-ном растворе глицерина при температуре
Течка перегиба
Фиг. 8.12. Изображение различных типов процесса осаждения в зависимости
от начальной концентрации в плоскостях jf,—а и X—Y.
20° С в вертикальной трубе диаметром 10 см. Описать развитие
процесса при исходной высоте смеси 100 см н начальных концентрациях
а0=0,1; 0,2; 0,3; 0,4 и 0,5. Чему равно время осаждения в каждом
случае?
Решение. Вначале, следуя стандартной методике и используя параметры v
и я, определим зависимости //«(а) н Y(X).
Следующие данные заимствованы нз книги "Handbook of Chemistry
and Physics" (The Chemical Rubber Company, Cleveland, Ohio):
(a/ =s=2,19 г (cm ■ сек, р^ = 2,32 г/см5,
р/= 1,23 г/смЗ.
224
ГЛАВА 8
Используя уравнение (8.5), получим
С Re2 __ 4 0,02543 . 1,23 ■ 981 • 1,09
CDco Кес° — "3 2JCJ2 — U,UOt>-
По формуле (8.6) с учетом (1) найдем
Re
CDoo *e~
24
= 2,5- 10-4;
тогда из (8.4)
Яе^/ 2,5 • 10-4.2,19 ПП1,„
"- = ^^7" = Р.0254.1.23 = °'01753 в^ввк'
а из (8.9а)
п = 4,65 + 1 %bdlD = 4,70.
Объединяя результаты (3) и (4) с (8.2), получим
jfs = 0,01753а (1 — а)4-7 см/сек.
Теперь по формулам (8.68) и (8.69) найдем X яУи построим зави
симость, показанную на фиг. 8.13.
70
(1)'
(2*
(3),
(4).
(5).
2 -
\*г'°
-\
^0=* \
"IZ-2
N
\
\ \
\ \
\ \
\ \
-
-
-
1
/_?"_
Y к4-
0 0.5 1,0
Х,10~3сех/ал
Фиг. 8.13. Зависимость У (X) для примера 8.2.
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ 225
Конечное значение а в осадке сферических частиц составляет — 0,6,
откуда 1 /а тс = 1 /0,6 = 1,667.
По формулам (8.70) и (8.71) найдем а г=0,35 и а2=0,43.
Следовательно, в интервале значений 0,43 > а0 > 0,35 будет иметь место
осаждение типа II.
Нижняя граница процесса' осаждения типа III определяется
построением касательной к нижней ветви функции У (X), которая проходит
почти через точку пересечения верхней ветви с прямой l/a^. Поэтому
осаждение типа III будет иметь место в интервале значений 0,22 < a < 0,35.
Фиг. 8.14. Положение поверхностей раздела в зависимости от времени для
примера 8.2.
Таким образом, осаждение типа I будет наблюдаться при а0=0,1,
0,2 и 0,5; типа И —при а0=0,4 и типа III —при а0=0,3.
Для построения графика h (t), характеризующего перемещение
поверхностей раздела, ординаты и абсциссы фиг. 8.13 следует умножить
на соответствующие значения ft0ao- Результирующие кривые показаны иа
фиг. 8.14. Общее время осаждения равно
<*0
0,1
' t, час 2,18
0,2
3,06
О.з
4,55
0,4
6,07
0,5
7,00
8.6. Силы взаимодействия между частицами
Ранее было сделано предположение, что процесс осаждения
заканчивается в момент, когда частицы наслоятся друг на друга
(a = a«,). В действительности, если частицы (или слой, образо-
15 Заказ № 162
226
ГЛАВА 8
ванный множеством частиц) способны деформироваться под
напряжением сжатия, возможно дальнейшее уплотнение слоя. Сила
сопротивления этому сжатию определяется зависимостью между
напряжением и деформацией для данной структуры слоя.
Результирующая сила, действующая на частицу в таком слое
вследствие сжатия, будет зависеть от градиента концентрации
и, возможно, от других переменных.
Чтобы охарактеризовать силы взаимодействия между
частицами, рассмотрим статические условия, когда множество частиц
подвергается сжатию в горизонтальном направлении силой F',
действующей по площади А. Допустим, что для частиц можно
определить некоторое среднее значение горизонтальной
составляющей напряжения os. Тогда из баланса сил относительно
вертикальной плоскости получим соотношение
pe + e,(l-e)=-J-, (8.72)
которое можно привести к виду
К-/>)(1-б)+р=-^-. (8.73)
Первый член этого уравнения можно использовать для
определения давления частиц ps, которое следует добавить к
давлению жидкости, чтобы найти общую силу, действующую на
единицу площади. Тогда
А=(°,-/>)(!-*). (8.74)
При наличии градиента концентрации разность давлений
частиц равна —dps на расстоянии dz. Однако частицы занимают
только часть 1 — е от всего объема. Следовательно, вклад сил
взаимодействия частиц в силу /„ равен —1/(1 — е) (dpsfdz). Если
FfS, как обычно, означает силу, обусловленную движением
жидкости, то для статических условий и горизонтального
расположения системы уравнения (3.45) и (3.46) примут вид
0=-*+^. (8-75)
0=
dz
dp Ffs 1 dps
dz 1 — e 1 — e dz
Исключая Ffs, получим
(8.76)
-£ + -£--* -(8.77)
причем это уравнение можно было бы вывести из (8.73) и (8.74),
так как F'/A — константа.
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ 227
Обычно ps является функцией е, которую можно определить
экспериментально, и для большинства систем это давление не
зависит от давления жидкости, так как между частицами
имеется единственная точка касания, а гидростатическое давление
действует по всей их поверхности. Однако если сжимаемость
самих частиц значительна (например, пузырьки газа), то ps будет
зависеть как от е, так и от р [87]. Эмпирическое уравнение,
часто используемое для волокнистых материалов, имеет вид
р?=В(\-в). (8.78)
Последний член уравнения (8.76) для удобства можно
переписать в виде
* (8.79)
dps
1-е dz
где
1
1 — е
1
dps de
де dz
dPs
г? de
dz
1
(8.80)
эквивалентна величине f ,, введенной в гл. 6 и выражающей
влияние градиента концентрации на силу, действующую на
частицы.
Пример 8.3. При фильтрации волокнистого материала жидкость протекает
через волокнистый слой, который удерживается пористой стенкой. Как
изменяются объемная концентрация и давление в этом слое? Считать,
что применимо уравнение Кармана—Козени, что 1—8 мало и слой
накапливается столь медленно, что течение можно считать стационарным.
Решение. Используя величину приведенной скорости жидкости //о из
примера 3.5, получим
Из уравнений (8.75)—(8.78) и (8.81) следует, что
dps _ 180М/о „2N /8 82)
dz ~~~ d?BW ■ Р° • v • >
Так как 1—8 мало, будем считать, что е=1, и проинтегрируем урав-
. нение (8.82) при р«=0 в точке z=0, что дает
pV-W) = {\_W)Cz, (8.83)
где
180fV/o_ (884)
Для определения изменений объемной концентрации с расстоянием
подставим (8.78) в (8.83), откуда
(\—e\U-W)/N = . (\—1N)Cz (g85
У1 е> д(1-2ЛГ)/ЛГ • V • /
15*
223 ГЛАВА 8
Так как для волокон ЛАда'Д, результирующие распределения давления
и объемной концентрации будут такими, как показано на фиг. 8.15.
Чистая _«
жидкость
0-£)и
у Пористая
Фиг. 8.15. Изменение объемной концентрации и давления в волокнистом слое
при фильтрации волокнистого материала из суспензии.
Из (8.85) нетрудно определить соотношение между средней
концентрацией частиц в слое и концентрацией на стенке:
1—2N
(1-0
1— N
(1— е)ш-
(8.86)
Следовательно, с учетом (8.77) и (8.78) можно получить следующее
соотношение между суммарным падением давления в слое и средней
4 6 10 2 < f ff 2
Др, ps, см еод. ста.
Фиг. 8.16. Фильтрация через волокнистый слой [23].
Др— суммарное давление; ps — уплотняющее давление; (1 — е) р, — плотность
волокнистого слоя, г}смъ\ 1 — однородная плотность волокнистого слоя при механическом
уплотняющем давлении р3; 2 — расчетная суммарная плотность слоя при падении
давления 4р.
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ 229
объемной концентрацией частиц:
В (1-0= \J£ Ар". (8.87)
Концентрация (1 — е) пропорциональна плотности слоя. Поэтому кривая
зависимости падения давления от плотности для рассматриваемого слоя
будет смещена от кривой зависимости уплотняющего напряжения от
плотности, причем это смещение определяется коэффициентом
(1—2Л/)/(1 — N). На фиг. 8.16 показаны типичные данные для #=0,225.
Значение коэффициента (1—2Л/)/(1—N) равно 0,71.
Другой вывод [23] основан на модификации уравнения Кармана—
Козеии для волокнистого слоя, предложенной Дэвисом [24]; при этом
уравнение (8.81) содержит множитель (1 — г)1 ■ в данном случае
полученное обычным путем результирующее уравнение имеет вид
в (^=4^§-А^- <8-88>
При JV=0,225 имеем (1 — 1,5JV)/(1 — 0.5JV) =0,75, и поэтому различие
между результатами, полученными этими двумя методами, трудно
проиллюстрировать на фнг. 8.16.
8.7. Нестационарный поток при наличии сил
взаимодействия между частицами
Поведение осадка, уплотняющегося до значений а, больших
осоо, можно описать с помощью уравнений (3.45), (3.46), опустив
инерционные члены и включив силы взаимодействия между
частицами. Тогда
о=--£-р/*+^. <8-89>
°=--Й--р*--ё-+*-!-. (8-9°)
Исключая из этих уравнений др/dz с использованием (8.15),
получаем д.
(P,-P/)ff=£-£--//,- (8.91)
Величина ffS является функцией расходов и объемной
концентрации. Обычно величину / можно определить тем или иным
способом (например, при периодическом осаждении и уплотнении
грунта / = 0) и //5 удобно представить в следующем виде:
//,=//,(/. it- e)- (8-92)
Уравнения неразрывности для жидкости и смеси в целом (при
условии несжимаемости) имеют вид
-Й-+т=° (8-93)
и
j=const.
(8.94)
230 ГЛАВА 8
Теперь уравнения (8.91) — (8.94) можно решить совместно.
Дифференцируя уравнение (8.91) по г и используя (8.92) и
(8.94), находим
аге , дЕ ( de \2 \( dffs \ djf I dffs \ дв
Е-
djf /j dz
Д]=0. (8.95)
А?2 ' dz \ dz
Исключая djf/dz из (8.93) и (8.95), получим
J2^ дЕ I ds )2 ( dffs \ Г дл (df/s!ds)j d, I
h dz* +-згЬг) +[-Tir)ji-dT— (df/s!djf)j -дг\=°- (8-96>
Если Е = 0 или частицы не соприкасаются друг с другом,
последний член уравнения (8.96) легко представить в виде
уравнения, описывающего распространение непрерывных волн в
процессе осаждения.
Если Е — константа, то уравнение (8.96) по форме
аналогично уравнению диффузии, так как величина dffs/djf
отрицательна, и его можно уподобить хорошо известному уравнению
уплотнения грунта [59]
Л2е fie
c4zT—W-> (8.97)
где с — коэффициент уплотнения. Очевидно, теория Терзахи
является разумной аппроксимацией только в тех случаях, когда
диффузия изменения величины е оказывает определяющее
влияние на движение непрерывных волн.
8.8. Устойчивость псевдоожиженных систем
Устойчивость псевдоожиженных систем можно исследовать,
используя теоретический метод, описанный в разд. 6.4. Скорость
непрерывной волны определяется уравнением (8.53), а скорость
динамической волны — уравнением (6.76). Заметим, что до тех
пор, пока величина (—fvo), которую можно рассматривать как
обратную сжимаемость, имеет по крайней мере такую же
величину, как и член
?(?s (Vf — Vs)2
а(1— ос) ffl(l —ay+fs/a '
скорость динамической волны является мнимым числом и
система всегда неустойчива.
К сожалению, в настоящее время нет достаточных данных
для надежного расчета эффективной сжимаемости псевдоожи-
женного слоя [26].
Обычный метод исследования основан на пренебрежении
величиной fvcc. Это приводит к выводу, что при отсутствии огра-
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ 231
ничений [26—29] все псевдоожиженные системы неустойчивы.
Однако скорость роста возмущений сильно зависит от свойств
системы.
Скорость роста возмущений можно определить как функцию
от длины волны с использованием уравнений (6.162) и (6.163).
Подробности такого расчета предусмотрены в задаче 8.24.
Установлено, что быстрее всего усиливаются волны минимальной
длины. Так как размеры волн, по-видимому, должны несколько
превышать размеры отдельных частиц, считается, что
приемлемая наименьшая длина волны в 20 раз больше диаметра частицы;
из этого условия рассчитывается расстояние L, на котором
возмущение усиливается в е раз. Результаты таких расчетов
представлены в табл. 8.3, причем они близки к данным, полученным
Таблица 8.3
Расчеты устойчивости по данным работы [30]
Среда
Вода
Воздух
Частицы
Стеклянные шарики
То же
Частицы катализатора
То же
Стеклянные шарики
Свинцовая дробь
Стеклянные шарики
То же
Частицы катализатора
То же
Стеклянные шарики
Свинцовая дробь
d, см
0,029
0,051
0,336
0,458
0,518
0,128
0,029
0,051
0,336
0,458
0,518
0,128
tsltf
2,5
2,5
1,6
1,6
2,5
10,8
2000
2000
1300
1300
2000
9000
Fr
0,00052
0,00067
0,00088
0,0099
0,036
0,13
1,1
2,03
10,0
13,0
40,0
85,0
L/Ш
342
266
12,0
10,6
4,92
2,28
0,66
0,54
0,40
0,39
0,36
0,34
L, см
99
136
40
49
26
29
0,2
0,3
1,3
1,8
1,9
0,4
Джексоном [29]. В таблице приводятся также значения числа
Фруда
Ъ=%~> (8-98)
которое в работе [30] предлагается рассматривать как критерий
устойчивости системы.
Если расстояние L мало, то волны быстро усиливаются и
порождают трехмерные возмущения, обусловленные инверсией
плотности. В слое образуются пузырьки ожижающего агента,
которые поднимаются через этот слой подобно пузырькам газа
в жидкости.
232 ГЛАВА 8
v 8.9. Течение систем газ—твердые частицы
Исследование сжимаемых потоков газа со взвешенными
частицами приняло широкий размах в связи с развитием ракетной
техники. Необходимость высокой точности при определении
тяги требует разработки теоретических методов анализа сильно
ускоряющихся потоков при высоких числах Маха. Поэтому
большую часть публикаций составляют работы, связанные
с изучением течений в соплах при сверхзвуковых скоростях.
Для ознакомления с современным состоянием вопроса
заинтересованному читателю будут полезны обзорные статьи
[31—33].
Одномерное установившееся течение
Одномерное установившееся течение описывается системой
из обычных пар уравнений сохранения массы, количества
движения и энергии. Исследование задачи в общем виде
чрезвычайно сложно, но во многих случаях обосновано пренебрежение
следующими эффектами и величинами:
1) тепло-массообменом и обменом количеством движения со
стенками сопла;
2) силами взаимодействия между частицами и их тепловым
(броуновским) движением;
3) влиянием множества частиц на силы сопротивления;
4) эффектом присоединенной массы;
5) градиентом температуры внутри частицы;
6) фазовыми превращениями и химическими реакциями;
7) излучением;
8) диссоциацией, ионизацией и «неидеальностью» газа;
9) объемом, занимаемым частицами;
10) вкладом среднего градиента давления в силу,
действующую на частицу (по сравнению с вязким сопротивлением);
11) двух- и трехмерными эффектами;
12) изменением формы и размеров частиц;
13) силой тяжести.
Если какое-либо из сделанных допущений несправедливо,
необходима соответствующая модификация метода.
Уравнения неразрывности имеют вид
P^,A=W,=const, (8.99)
H^=const. (8.100)
Общее для обоих компонентов уравнение движения
записывается следующим образам:
^-^+^-Й-М4Н0. (8.101)
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ 233
причем уравнение движения только для частиц имеет вид
V,
dv.
CDh
dz
d?s
(vg-vs)\vg
(8.102)
где T'g
Общее уравнение энергии для газа и частиц записывается
следующим образом:
Ws (К + -rty+Ws (а,+4-^)= ^Ао+ ^Ао. (8-103)
где индекс 0 означает условия торможения.
Если частицы несжимаемы, то в соответствии с примером
(3.10) уравнение теплового баланса для них имеет вид
v.^SrM-T.), (8.104)
эквивалентная температура газа для расчета
теплообмена с частицей, не всегда равная температуре газа, так как
в слое газа, окружающем частицу, происходит вязкая
диссипация энергии. Если относительная скорость велика, можно
принять, что Т/ равна температуре торможения в относительном
движении. Однако в большинстве практически важных случаев
этот эффект незначителен, и можно считать, что Т =Tg.
При малых числах Рейнольдса и Маха применимы обычные
уравнения для сопротивления и теплоотдачи при ламинарном
режиме течения:
——З^-К-^. (8.106)
v
s dz
dTs
dz
<&9,
(8.106)
где cs — удельная теплоемкость частиц.
Выражая энтальпию через температуру и считая свойства
постоянными, перепишем (8.103) в виде
Wt\c„Tg-
«*
(8.107)
Кроме того, уравнение состояния для газа устанавливает
связь между изменениями давления, температуры и плотности
Р=Р&Тв- (8Л08)
Уравнения (8.99), (8.101)^—(8.104) и (8.108) образуют
систему из шести уравнений с шестью неизвестными Tg, Ts, vs, vg,
p и рг (предполагается, что расходы и геометрия канала
заданы), которая может быть решена различными методами.
234 ГЛАВА 8
1+1Я, '
Cpg -\- mscs
1 +/ns
Cpg + mscs
Гомогенное равновесное течение
Один из наиболее простых результатов получается при
допущении, что межфазный обмен количеством движения и энергией
происходит настолько быстро, что на всем протяжении канала
температуры и скорости компонентов равны. Тогда уравнения
(8.105) и (8.106) сводятся к следующим:
vs=vg, (8.109)
Ts=Tg. (8.110)
Подстановка этих уравнений в другие уравнения системы
приводит к результатам, которые были получены ранее при
решении примера 2.2. Смесь ведет себя как псевдогаз,
обладающий следующими свойствами, зависящими от массовой доли
частиц:
* (8.111)
(8.112)
При этом можно использовать все общепринятые уравнения
для одномерного сжимаемого течения, заменяя соответствующие
свойства газа приведенными выше свойствами псевдогаза.
Скорость звука равна
c=ViWr, (8.114)
т. е. она меньше скорости звука в чистом газе. Эквивалентное
число Маха равно
М=-£. (8.115)
Предельные случаи неравновесного течения
Принимая, что теплообмен и обмен количеством движения
в каждом сечении либо полностью завершены, либо полностью
отсутствуют, можно получить следующие три простых результата
[34]. Смесь ведет себя как псевдогаз с указанными выше
свойствами.
Динамическое равновесие, тепловая изоляция. Так как
частицы не участвуют в теплообмене, их температура остается
постоянной. Тогда
Ts=const. (8.116)
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ
235
Так как из-за наличия частиц эффективная плотность газа
возрастает, но другие эффекты отсутствуют, газовая постоянная
и удельная теплоемкость псевдогаза определяются следующим
образом:
*'=-TW' (8.П7)
С'=^Т1^- (8-ш)
Показатель изоэнтропы не изменяется и имеет такое же
значение, как и для чистого газа:
T'=V (8.119)
Скорость звука определяется температурой газа, т. е.
c=VTWTg. (8.120)
Тепловое равновесие, динамическая изоляция. В этом
случае частицы движутся с низкой скоростью и действуют на газ
как источники тепла. Для получения приемлемого решения
следовало бы видоизменить допущения 9 и 10, однако предельное
условие имеет вид
^=const. (8.121)
Происходит расширение только газовой фазы, обладающей
следующими свойствами:
R'=RK. (8Л22)
Cp^Cpg + MsP» (8.123)
Тепловая и динамическая изоляция. Газ не взаимодействует
с частицами и расширяется таким образом, как если бы он был
«чистым». Как и ранее, для получения приемлемых выводов
о движении частиц следует видоизменить допущения 9 и 10.
Анализ рассмотренных предельных случаев показывает, что
во многих практических случаях определяемые характеристики
системы сравнительно слабо зависят от сделанных допущений.
Однако, если требуется большая точность, необходимо
усложнить анализ.
Подобные решения для постоянного запаздывания
Принимая, что отношения скоростей и температур
компонентов постоянны, можно получить семейство точных решений для
ламинарного режима. Допустим также, что обе фазы имеют
236
ГЛАВА 8
одинаковую температуру торможения Т0 в состоянии покоя.
Следуя Клигелю [35], введем следующие параметры:
*НГ' <8Л25>
T0—Ts
L= ° ' . (8.126)
'о—1 g
Тогда уравнения (8:105) и (8.106) примут вид
dvg __ 18ttg i _ /с
dz — di9s К '
dTg l2kg(TQ-Tg) \_L
(8.127)
~ST~ t^^ K.L '• (8.128)
Уравнение энергии (8.107) можно привести к следующему виду:
То-Тк=4- l+/nsK\ . (8.129)
0 г 2 cpg + mscsL v '
Дифференцируя (8.129), получим
1 dTg 2 dvg
(8.130)
TQ—Tg dz vg dz *
Подстановка (8.130) в (8.128) дает
-тЕ-=-мЛ—ЧтА- (8.131)
dz d2pscs KL v '
Согласно уравнениям (8.127) и (8.131), скорость газа, а
следовательно, и скорость частиц линейно увеличиваются вдоль
сопла. Кроме того, поскольку оба выражения должны быть
совместимы,
c^g I l/L — l . ,я 1Ч9ч
—kg-=^- 1//C— 1 - (8'ld2)
Левая часть уравнения (8.132) является аналогом числа
Прандтля, в котором удельная теплоемкость газа заменена
удельной теплоемкостью частиц. Этот параметр определяет связь
между тепловым и скоростным запаздываниями.
Дальнейший анализ основан на использовании уравнений
движения и неразрывности. С помощью уравнений (8.99),
(8.125) и (8.126) уравнение (8.101) приводится к виду
' РЛ-^г(1+т^) + -^=°- (8-133)
Это уравнение представляет собой уравнение количества
движения для одномерного потока псевдогаза плотностью
Р'=(1+msK)Pg. (8.134)
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ
237
Этот псевдогаз подчиняется уравнению состояния идеального
газа, эквивалентному (8.108), если его температура равна
температуре газа, и характеризуется следующим значением газовой
постоянной:
Уравнение (8.129) представляет собой уравнение энергии для
псевдогаза с удельной теплоемкостью
ср= \+msK2 • (8Л36)
Из (8.135) и (8.136) следует, что удельная теплоемкость при
постоянном объеме равна
cpg + mscsL Rg
С"= 1+Я/2 --l+msK- (8Л37)
Следовательно, отношение удельных теплоемкостей
(эффективный показатель адиабаты) для смеси равно
1- \ + m^ Ir—rV. (8.138)
1 + msK Cpg + mscsL J y '
Двухкомпонентный поток можно теперь считать
псевдогазом, обладающим указанными выше свойствами и
имеющим общий массовый расход Ws + Wg. В этом случае
пригодны все обычные соотношения для одномерного газового
потока.
Если требуется рассчитать сопло на основе приведенных
результатов, необходимо выполнить следующие операции. Вначале
произвольно задается величина К. Значение L находится из
выражения (8.132). Затем можно определить все свойства
псевдогаза и найти изменение площади сечения, а также скоростей
в функции от давления при заданных начальных условиях и
расходах компонентов. Однако форма сопла не является
произвольной, так как уравнением (8.129) координата z сопла
связана с другими параметрами потока. Таким образом, сопло,
рассчитанное для конкретных начальных условий, расходов и
значений К, будет иметь определенную геометрию. Изменение К
приведет к изменению геометрии сопла, причем для заданной
скорости истечения меньшим значениям К будут соответствовать
более короткие сопла.
238
ГЛАВА 8
Метод малых возмущений
Метод исследования течений при малых отклонениях от
равновесия может быть развит на основе уравнений, записанных
в функции отклонений от параметров гомогенного течения
[36, 37].
Исходными являются уравнения (8.105) и (8.106),
определяющие тепловое и динамическое запаздывание. Если ввести
«характерные» значения скорости vc, длины Lc и температуры
Тс, то можно записать следующие соотношения:
(8.139)
(8.140)
(8.141)
d2?svc
18it.gLc
d2?scsvc
vs
vc
vs
d (vs!vc)
d (zlLc)
d{TsITc)
vg
vc
Tg
Vs
Vc
Ts
vc d (zjLc)
Безразмерные параметры
d2?sVc
18(j.gZ.c
d2cspsVc
\2KgLc
(8.142)
характеризуют отклонения скорости и температуры от
соответствующих значений для равновесного гомогенного потока. Если
эти параметры малы, их можно использовать для анализа
распространения возмущений. Кроме того, отношение
рассматриваемых величин
гт 3 pgCs K '
обычно близко к единице. Величина параметров е„ и ет может
также служить для оценки применимости допущения о
гомогенном равновесном течении.
Скачки уплотнения
При течении смесей газа с частицами возникают как прямые,
так и косые скачки уплотнения. В зависимости от того,
достигает ли поток скорости распространения упругих волн в
гомогенной среде или скорости звука в чистом газе, могут
наблюдаться (по меньшей мере) скачки уплотнения двух типов.
Скорость распространения упругих волн в гомогенной среде
равна
c'=VJWT, - (8.144)
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ
239
где R' и у' определяются уравнениями (8.111) и (8.113). С
другой стороны, скорость звука в чистом газе равна
c*=Vl*K*Te-
(8.145)
Введем числа Маха, основанные на каждой из указанных
скоростей:
М' =
М.
с
v
(8.146)
(8.147)
«Слабый» скачок уплотнения характеризуется такими
условиями в набегающем потоке: М'>1, Mg<l. В этом случае
Скачок уплотнения
Набегающий поток
Ч,
Зона релаксации
Фиг. 8.17. Изменение давления и скорости в «сильном» хкачке уплотнения
в двухфазном потоке.
в скачке происходит довольно плавное изменение параметров.
«Сильный» скачок возможен только при Mg>l. Газ
претерпевает в прямом скачке такие же изменения, как и при
f однофазном течении, а за скачком существует зона релакса-
' ции, где частицы и газ приходят в состояние равновесия. В
каждом случае конечное состояние определяется теорией
гомогенного течения.
На фиг. 8.17 приводится схема сильного прямого скачка
уплотнения. Условия перед скачком обозначены индексом 1,
а за скачком — индексом 2; конечному состоянию соответствует
индекс 3.
При переходе через фронт скачка газ подчиняется
обычным уравнениям газодинамики, а частицы сохраняют свою
скорость и температуру неизменными. В частности, выполняются
240 - ГЛАВА 8
соотношения
или
м^=
Mgl + 2/(Tg-l)
2Tg
ж=1+-ЛМмк-1),
Pi ' fg + 1
P2—Pl =
(*>g)2*V
(fg)2 _
«1 ~~
2(?g)l^ ^
Tg+1
M»,
Tg + 1 +1f+l
Tg+1
Mg.
(8.148)
(8.149)
(8.150)
(8.151)
(8.152)
Точно такие же уравнения с использованием соотношения
(8.146) для числа Маха, а также соотношений (8.111) и (8.113)-
М,'>1
Фиг. 8.18. Изменения температуры и скорости в «слабом» скачке уплотнения
в двухфазном потоке.
для газовой постоянной и отношения удельных теплоемкостеи
применимы для расчета изменения параметров между
состояниями 1 и 3.
Так как "Vg>"V' и М^>Мгь из соотношений (8.150) и (8.152)
ясно, что конечная скорость в состоянии 3 меньше скорости
в состоянии 2, а конечное давление выше давления в
состоянии 2.
Торможение частиц и газа вызывается непрерывным ростом
давления в зоне релаксации. Однако на начальном участке
этой зоны под действием сил сопротивления частиц, обладающих
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ
241
большей скоростью, скорость газа может возрастать.. Для
слабого скачка между состояниями 1 и 3 справедливы
аналогичные уравнения, однако в этом случае отсутствует начальный
разрыв значений параметров газовой фазы (фиг. 8.18).
Зона релаксации
В зоне релаксации за скачком уплотнения параметры
меняются непрерывно [3], причем силы сопротивления и теплообмен
между частицами и газом определяют скорость приближения
системы к равновесию [38—40].
5
4
?з
1
^
1
!
-—
1
/
-
1
1,1
1,0
,0.9
0,8
0,7
0,6
1
ш
И
i
i
• i
1
-
i
г,см
а
г 4
Z,CM
б
1,2
Ю
8
0.4
2 4
г,см
в
Фиг. 8.19. Изменение скоростей и температур газа и частиц за «сильным»
скачком уплотнения; Mgi= 2 [39].
а — изменение скорости в зависимости от расстояния г; 6 — изменение температуры
в зависимости от расстояния г; в — изменение давления в зависимости от расстояния г.
Индексы 1, 2 и 3 относятся соответственно к частицам с радиусами 0,5, 1,5 н 2,5 мкм.
В анализе Кэррье [38] пространственная координата была
исключена путем использования отношения уравнений (8.105)
и (8.106), так что
dTs
dv.
2k„
Зс
sPg
Va- — V.
(8.153)
16 Заказ № 162
242 ГЛАВА 8
Во многих практических случаях коэффициент 2/3(kg/cslig)
близок к единице. Действительно, соотношение, аналогичное
1,20
1.16
8 U2
н
1,08
1,04-
1,00
щ^'
1
1
*\\^*
1
VvX/Ъ
1
1
1
f
10
IS 20
Z,CM
a
25
30
36
40
100
0,96
S0,92
и
N
0,84-
0,80
10
IS
20
г,см
6
25
30
35
40
Фиг. 8.20. Изменение скоростей и давлений в «слабом» скачке; Mgi = 0,91,
М, = 1,1 [39].
а — изменение скорости в зависимости от расстояния г; б — изменение давления в
зависимости от расстояния г.
Индексы 1, 2 и 3 относятся соответственно к частицам с радиусами 0,5, 1,5 и 2,5 мкм.
(8.153), приближенно выполняется в широком диапазоне чисел
Рейнольдса, что обусловлено взаимосвязью процессов обмена
количеством движения и теплом.
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ 243
Так как А — константа, то, исключая давление и плотность
газа с помощью уравнений (8.99), (8.108) и (8.101), получим
^^+^+*л-йг-!Н>- (8Л54)
После интегрирования находим
WKvK+ Ws*s+ ^^=const. (8.155)
Уравнение (8.155) определяет зависимость Tg от vs и vg.
Уравнение (8.107) характеризует зависимость Ts от этих же
скоростей. Подстановка. Tg и Ts в (8.153) приводит в конечном
счете к дифференциальному уравнению, определяющему связь
между vs и vg, которое можно решить численным методом.
Затем, принимая любую из скоростей в качестве независимой
переменной, с помощью уравнения (8.105) можно определить г,
а затем в функции от координаты найти все остальные
параметры.
Подробное изложение такого метода, интегрирования и
результаты некоторых численных расчетов приводятся, например,
Крайбелом [39]. Он рассмотрел также случай такого
распределения частиц по размерам, когда 70% частиц имеют средний
диаметр, 12% частиц имеют диаметр,, равный 7з среднего, а
диаметр оставшихся 15% частиц равен 5/з среднего. Эти группы
частиц отмечены индексами 1, 2 и 3 на фиг. 8.19 и 8.20, где
показаны зоны релаксации за сильным и слабым скачками
уплотнения. Размер частиц типичен для ракетных топлив, и
средний диаметр равен 3 мк. Заметим, что протяженность зоны
релаксации составляет несколько десятков миллиметров. Для
частиц, больших в 10 раз, общая толщина скачка может быть
около метра.
Косые скачки
Связь между параметрами потока перед косым скачком и за
ним можно получить обычным путем, рассматривая проекций
движения на направления, нормальное и касательное к фронту
скачка. В зоне релаксации линии тока частиц и газа
искривлены. При обтекании клина, например,, вблизи его передней
кромки не успевает установиться равновесие и угол наклона
скачка определяется только параметрами газа. В удаленной
области угол наклона приближается к углу наклона
равновесного потока. Каким образом происходит переход из одной
области в другую, пока не ясно.
16*
244 ГЛАВА 8
Двух- и трехмерные эффекты
Для анализа неодномерных двухфазных течений уравнения
сохранения можно представить в векторной форме. Эти
уравнения можно решить численным способом, используя метод
«характеристик», образующих сетку для численных расчетов [41,42].
В качественном отношении запаздывание частиц по скорости
и температуре такое же, как и при одномерном течении, с той
лишь разницей, что в данном случае относительная скорость
Увеличение,
диаметра частиц
Фиг. 8.21. Траектории частиц в сопле Лаваля, иллюстрирующие влияние
двумерных эффектов на предельное положение линий гока частиц разных
размеров, начинающихся вблизи стенки.
должна быть представлена в векторной форме. Например, при
повороте газового потока частицы будут сохранять
прямолинейное движение до тех пор, пока вследствие относительной
скорости в поперечном направлении не возникнет сила
сопротивления, достаточная для возвращения их к линиям тока газа.
Таким образом, в сопле Лаваля частицы стремятся удалиться
от стенок и сконцентрироваться вблизи оси, причем с
увеличением размеров частиц этот эффект усиливается (фиг. 8.21).
Аналогичное явление наблюдается в зоне релаксации за
двумерными скачками уплотнения, при столкновении струй с
препятствием, при обтекании криволинейной поверхности и т. д.
Другие эффекты
Если выполняются не все условия, указанные на стр. 232, то
можно привести многочисленные примеры дополнительных
эффектов, сопровождающих реальные течения. Некоторые полезные
работы по этому вопросу упомянуты в списке литературы [43].
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ 245
8.10. Дополнительные силы, действующие в быстро
ускоряющихся потоках
Присоединенная масса
При ускорении частицы относительно окружающей жидкости
вокруг нее формируется двумерное поле течения, которое
характеризуется определенной кинетической энергией. Следовательно,
помимо работы, затрачиваемой непосредственно на ускорение
самой частицы, для ее движения требуется еще некоторая
дополнительная работа. Этот избыток энергии можно связать
с некоторой дополнительной силой, приложенной к частице.
Таким образом, для -движения сферической частицы в большом
объеме покоящейся невязкой жидкости с ускорением а
необходима сила
F' = 46Kd*(Ps+-?f)a, (8.156)
т. е. движение частицы таково, как если бы она обладала
некоторой дополнительной «присоединенной массой», равной
половине массы вытесняемой жидкости.
' Частицы других форм характеризуются различными
величинами присоединенной массы. В общем случае можно считать,
что истинную массу частицы следует увеличить- в l + Cp//ps раз.
Например, С-=112 для сферы, С = 1/ь для эллипсоида вращения
с отношением осей 1 :2, ориентированного по потоку, и С=0,045
для эллипсоида с отношением осей 1 :6 [44]. 'Следует ожидать
также, что на величину коэффициента Сбудут влиять соседние
частицы, т. е. он будет зависеть также и от концентрации а.
Зубер [52] полагает, что для потока взвеси частиц
присоединенную массу следует умножить на коэффициент (1+2ос)/(1—а).
Эффект присоединенной массы состоит в необходимости
включения дополнительной составляющей в силу /,
рассмотренную в гл. .3. При использовании системы координат, связанной
с частицей, эта сила оказывается пропорциональной
относительному ускорению, т. е.
/,= -//Т^=-сР/[4-<*'-*/> + *'-Е-<г''-г''>]- (8Л57>
Эта сила приводит к уменьшению скольжения. Например,
используя уравнения (3.45), (8.15), (8.36) и (8.157), можно
получить следующее уравнение восходящего движения частицы
246 ГЛАВА 8
в стационарном потоке:
ч, 0 -dvs _ „. dp 3e3(cd)£ Р/ К -у/) \vs-v/\
_ ■ d(v, — v<\
~CP/vs Ksdz f) . (8.158)
В быстро ускоряющемся потоке последний член в правой
части может быть достаточно большим по сравнению с членом
в левой части этого уравнения, если
Cff I dvf
?s
1-^г)^0'1- (8.159)
Для твердых частиц, взвешенных в газах, вследствие малого
значения отношения плотностей этот эффект обычно незаметен,
если только vs не проходит через максимум или минимум.
Однако при течении жидких суспензий в соплах этим эффектом
пренебрегать нельзя.
Предположим, что в уравнении (8.158) доминируют члены,
характеризующие градиент давления и инерцию, т. е.
dvs dp „ d{vs — vf)
•°*.-аГ=- -&— CpfVs аг^ ■ (8.160)
Используя уравнение (8.157), запишем эквивалентное
уравнение для жидкости в следующем виде:
dvf dp , l — s ~ d(vs — vf)
vfb-4T = --£+-^C9fvs L-JL. (8.161)
Исключая градиент давления путем вычитания (8.161) из
(8.160), получим
dvs dvf с d(vs — vf)
vsPs-aF—bPf~ar-~ — p^s 1ГХ-. (8.162)
Объединяя члены, содержащие dvs/dz и dvf/dz, после деления
на pfVs получим
Hj-+-f)3H3~t4)^-. (8Л63)
откуда
dvs Vflvs + С/г
dvf. — ?s/9/ + C/e • (8Л64)
Если Сие постоянны, как в потоке несжимаемой среды без
деформации частиц, то уравнение (8.164) принимает вид
dVe Vf , ,
-d^=ait+b' (8Лб5)
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ 247
Обозначая
(8.166)
Vf
приведем уравнение (8.165) к виду
(8.167)
1 dvf _л
Vf dn я2 — Ъп — а
Если корни знаменателя правой части этого уравнения равны
«1 и —п2, то после разложения на сомножители и
интегрирования получим
V
--(ю/)0(п-п1)-п'ап'+пд(>1 + >12Гп>Кщ+Пг), (8.168)
где (vf)o — константа интегрирования.
Так как Vf в процессе ускорения возрастает, то из уравнения
(8.168) следует, что величина п должна стремиться к величине
Mi, т. е.
п-*п1 = — 2 • (8.169)
Уравнение (8.169) определяет максимальное значение
отношения скоростей при быстром ускорении потока.
Пример 8.4. Каково предельное отношение скоростей фаз при ускоренном
течении по соплу жидкости, содержащей небольшое количество
сферических пузырьков газа низкой плотности?
Решение. Via условия задачи следует, что
2 р/
Тогда, сравнивая (8.164) и (8.165), получим
а = 2, 6=1.
Подставляя эти значения в (8.169), определим
«1 = 2, '
что соответствует предельному значению коэффициента скольжения
Vgjvf. Влияние члена, характеризующего силу сопротивления в
уравнении (8.158), сказывается в том, что коэффициент скольжения всегда
будет несколько меньше этого предельного значения.
Сила Бассе
При ускорении частицы относительно жидкости вокруг нее
формируется не только потенциальное, но и вязкое поле
течения. Так как вязкие эффекты, например рост пограничного слоя,
описываются уравнениями диффузии, мгновенное поле течения
оказывается зависящим от всей предыстории движения частицы
248 ГЛАВА 8
л рассчитать его довольно трудно. Для ламинарного режима
течения Бассе [45] получил следующий результат:
и
fs
Y~i
fitf'
-Л'.
(8.170)
где f — фиктивная переменная, позволяющая учесть движение
частицы между моментом to и настоящим моментом времени t.
В частности, для случая линейного изменения vs — Vf в
интервале от to до t найдено (см. задачу 8.34), что отношение силы
Бассе к силе сопротивления при стационарном режиме течения
равно d/invft. Зубер [52] предположил, что для частицы,
входящей в состав взвеси, эту силу следует увеличить в (1—а)-2'5 раз,
что, по-видимому, переоценивает эффект присутствия соседних
частиц.
8.11. Характеристики трения для суспензий
Характеристики трения для жидкости определяются связью
между касательными напряжениями и скоростями деформации
сдвига. Для ламинарного
'oil ггп i ггп i пи \у м 11 /л одномерного течения
ньютоновской жидкости
справедлива простая линейная
зависимость, определяющая
вязкость, т. е.
(1,=
dv/dy
(8.171)
ю~* ю~
т, 0,4 кг/см2
Многие суспензии не
подчиняются такой зависимости
и должны исследоваться
реологическими методами
для ньютоновских
жидкостей. В качестве примера
на фиг. 8.22 приведена
типичная диаграмма
касательных напряжений для взвеси
частиц окиси тория.
Фиг. 8.22. Диаграмма
касательных напряжений для взвеси частиц
окиси тория [47].
dv!dr — скорость деформации сдвига;
X — касательное напряжение.
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ
249
Используя методы, изложенные в гл. 5, по известному
распределению касательных напряжений можно рассчитать
градиенты скорости и, выполнив интегрирование по сечению канала,
определить профиль скорости для ламинарного потока.
При малых значениях объемных концентраций частиц взвесь
сферических частиц по своим характеристикам близка к
ньютоновской жидкости, причем отношение вязкости смеси к вязкости
жидкости можно выразить через а. Например, уравнение
Эйнштейна [46] для ос<0,05 имеет вид
,1=11,(1 + 2» (8.172)
и является пределом для уравнения, предложенного в работах
[83, 86]:
?=ь (1- а)"2'5, (8.173)
или эквивалентного выражения
(А=(А/е-2'5. (8.174)
Уравнение, содержащее другой коэффициент, было получено
в работе [49]:
(,=^(1+5», (8.175)
причем имеются экспериментальные подтверждения, что
уравнение Эйнштейна действительно занижает эффективную вязкость
смеси.
Были предприняты попытки получить аналогичные
результаты для несферических частиц [50] и осуществить разложение
в ряд по более высоким степеням ос. Однако по данным
различных авторов значения коэффициентов сильно различаются.
Большинство неньютоновских суспензий обладает некоторой
предельной вязкостью ц при больших скоростях сдвига,
которую можно связать простым соотношением с вязкостью
жидкости и концентрацией частиц.
Предельную вязкость неньютоновских суспензий часто
рассчитывают по следующей корреляционной зависимости [51]:
7)=^**. (8.176)
Одна из таких зависимостей показана на фиг. 8.23.
Коэффициент k определяется свойствами частиц, и в общем случае он
больше, для мелких частиц, которые коагулируют и вызывают
увеличение вязкости за счёт сил взаимодействия. Например, по
данным Томаса [51], величина k для водных суспензий
достаточно точно определяется уравнением
А=2,5+-^-Ф, (8.177)
250 ГЛАВА 8
где d — диаметр частицы в микронах, а Ф — коэффициент
формы, равный единице для сферических частиц. При низких
значениях концентрации крупных частиц k становится равным 2,5
и уравнения (8.172), (8.173) и (8.176) дают приблизительно
одинаковые результаты.
О 0,05 0,)0 0,75 0,20 0,25
■Фиг. 8.23. Влияние объемной концентрации частиц на предельную вязкость
при больших скоростях сдвига [51].
а — объемная концентрация частиц.
Обозначение
V
' а
о
•
л
Вещество
Двуокись титана
Графит
Окись тория
Окись тория
Каолин
Диаметр
частиц, мкм
0,40
2,35
0,74
1,35
2,85
Некоторые другие модели для расчета вязкости суспензий
были рассмотрены Зубером [52], а исчерпывающий обзор работ
по этому вопросу выполнен Рутгерсом [53, 54].
Ламинарное течение
При ламинарном режиме течения ньютоновской жидкости
в круглой трубе касательное напряжение на стенАе связано
с вязкостью следующим уравнением:
от/
*ш=Р-ТГ> (8.178)
а градиент давления равен
-(й^- <8-179>
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ 251
Эквивалентные соотношения для неньютоновской жидкости
зависят от ее конкретных реологических свойств. Однако можно
ввести эффективную вязкость, определяемую соотношением
Ре
8V/D
(8.180)
Тогда уравнение (8.171) заменяется некоторым соотношением
для «псевдонапряжений», которое выражает связь между
касательным напряжением на стенке
и скоростью сдвига у стенки
при том же общем расходе
ньютоновской жидкости. Некоторые
типичные результаты показаны
на фиг. 8.24. При изменении
диаметра трубы или скорости
соотношение между касательным
напряжением на стенке xw и
эффективной скоростью деформации
сдвига 8V/D для данной смеси
жидкости с частицами сохраня-
Ф и г. 8.24. Диаграмма
«псевдонапряжений» для концентрированных суспензий
Th02 [47].
С изменением диаметра трубы данные для
ламинарного и турбулентного режимов
соответственно совпадают. 8V/D — эффективная
скорость деформации сдвига; ти — касательное
напряжение на стенке.
Обозначение
О
Д
а
л
к
ш
Диаметр трубы,
мм
3,15
8,07
26,10
3,15
8,07
26,10
Свойства
суспензии
сс=0,10
1=5,7 спз
сс=0,16
4=10,1 спз
' 2 4 6 8 10
ш, 0,488-Ю-3 кг/см2
ется неизменным, пока поток остается ламинарным. Поэтому
диаграмма «псевдонапряжений» может быть использована при
расчете падения давления для ламинарного потока.
Другой метод состоит в использовании зависимости
коэффициента трения от числа Рейнольдса, выраженного через
эффективную вязкость. Коэффициент трения определяется
соотношением
С,=
42?mV2
(8.181)
252
ГЛАВА 8
Тогда из уравнения (8.180) получим
С/=Ж- (8Л82)
где Rem определяется по эффективной вязкости
Rem=^^. ' (8.183)
re
При использовании этого метода для определения це все же
необходима диаграмма «псевдонапряжений». Когда справедлива
аппроксимация, базирующаяся на квазиньютоновском описании
поведения системы, ц и це идентичны. Переход к турбулентному
режиму течения в круглых трубах происходит при ReTO>2500.
Если можно установить реологические соотношения между
напряжением и скоростью деформации, то для ламинарного
потока в принципе можно точно рассчитать падение давления
в зависимости от расхода. Однако на практике реологические
характеристики не всегда объяснимы и столь своеобразны, что
исключают возможность проведения рационального анализа,
основанного на первом законе механики [50]. Обычно ограничиваются
попыткой согласовать экспериментальные данные с
соответствующей математической моделью. Так как инженерные приложения
любой теории обычно ограничены определенным интервалом
скоростей сдвига, для этой цели обычно используется любая из
подходящих к данному случаю кривых.
Чаще всего употребляются следующие соотношения:
а) степенной закон
*=*(--£-)". (8-184)
б) соотношение Бингэма [55]
т=ту+г(—%-) ПРИ *>V (8.185)
-^=0 при x<v
\
в) соотношение Кассона [56]
~ .vw/4-n--£)],'\ <8-186>
г) соотношение Ри и Эйринга [57]
«c(-S-)+t««"(-t-£-)- <8-187>
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ 253
Соотношение Бингэма справедливо для многих пластических
жидкостей. Соотношение Кассона дает хорошие результаты
применительно к крови [58], чернилам [56] и угольным
суспензиям [59], причем для взвеси частиц окиси тория,
исследованной Томасом, эта формула дает лучшие результаты, чем
модель, предложенная первоначально самим Томасом [47].
Соотношение Ри—Эйринга наиболее эффективно для множества данных
(так как включает три константы, значения которых можно
соответствующим образом подобрать), однако оно неудобно
для использования в аналитическом исследовании.
Общее уравнение с тремя произвольными константами,
которое сводится в конкретных случаях к моделям а—в, имеет
следующий вид:
тЯ,=т»+А(_-^-)", (8.188)
причем с помощью этого уравнения можно удовлетворительно
описать большинство экспериментальных данных.
Турбулентное течение
Из-за высоких местных скоростей деформации в
турбулентных потоках введение эффективной вязкости не позволяет точно
описать распределение сил в заданной области течения. Лучшая
аппроксимация обычно достигается при использовании числа
Рейнольдса, вычисляемого по предельной вязкости при больших
скоростях сдвига, т. е.
Re,=-£aJ^-. (8.189)
Такого рода зависимость коэффициента трения от числа
Рейнольдса показана на фиг. 8.25. Так как эффективная
вязкость при ламинарном течении может быть во много раз больше
предельной вязкости, линии для ламинарного потока на таком
графике смещаются.
Интересным и важным эффектом, наблюдаемым во взвесях
волокон или длинных цепей молекул, является снижение
сопротивления при турбулентном течении [48, 61—64]. По-видимому,
степень турбулентности снижается из-за демпфирующего
действия волокон на структуру вихрей. В практических случаях для
снижения потерь давления в трубопроводах иногда
экономически выгодно добавлять в жидкости частицы в виде волокон
или полимеры.
*■ 254
ГЛАВА 8
10'
ю-
1,5-103
Число Рейнольдса -УВ.
Фиг: 8.25. Коэффициент трения для концентрированной суспензии ТЬОг [48].
Для разных диаметров трубы данные для турбулентного режима совпадают.
Обозначение
О
■ Л
D
•
А
■
Диаметр
трубы, мм
3.15
8,07
26,10
3,15
8,07
26,10
Свойства
суспензии
а = 0,10
*1 = 5,7 спз
а = 0,16
тг) = 10,1 спз
Пневмотранспорт
Исследование потоков частиц, взвешенных в газе и имеющих
размеры выше нескольких микрон, гораздо сложнее, чем анализ
движения жидких суспензий: частицы в трубе «витают»,
одновременно существует множество различных режимов течения и
приобретают значение, например, такие параметры, как коэф-
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ 255
фициент восстановления при ударе частиц. Предлагались
многочисленные эмпирические соотношения, однако лишь немногие из
них являются достаточно общими.
8.12. Неравномерное распределение частиц
В предыдущих разделах данной главы было принято, что
частицы равномерно распределены по всему полю течения.
Теперь кратко рассмотрим некоторые случаи, когда это допущение
неприменимо. Для удобства можно выделить три общих класса
неоднородных течений:
1. Расслоенное течение, при котором частицы
концентрируются в слоях или кольцевых областях, что обусловливает
неравномерное распределение в поперечном сечении трубы.
2. Периодическое течение, при котором концентрация
изменяется вдоль трубы.
3. Агрегативное течение, при котором частицы или жидкость
в потоке стремятся образовать многочисленные дискретные
области высокой концентрации.
, Часто обнаруживается близкое сходство таких течений
с.аналогичными течениями газо-жидкостных систем.
Расслоенное течение
Гравитационные эффекты. Простейшим примером потока
с расслоением является горизонтальный поток, в котором под
действием силы тяжести более тяжелый компонент
концентрируется у дна канала. Степень происходящего расслоения
определяется балансом между выталкивающей силой, действующей
на частицу, и силами, обусловленными движением частицы
относительно жидкости. Этот баланс обычно выражается через
отношение конечной скорости осаждения vx к скорости трения на
стенке и*, определяемой уравнением (7.27). Распределение
концентрации при этом часто представляют в виде зависимости
а/(а) от Voo/u*.
По данным Томаса [65], значение Vcju*— 0,2 определяет
границу режимов, при которых частицы скапливаются на дне трубы
или преимущественно движутся в виде суспензии.
Соответствующие значения, рассчитанные по теории рейнольдсова потока
(задача 7.16), заключены между 0,1 и 0,15. Рассмотренные
простые соотношения, однако, не отражают фактической взаимосвязи
поведения частиц и профиля скорости. Очень мелкие частицы
погружены в пограничный слой, где скорость потока намного
меньше, чем и*, в то время как на очень крупные частицы
действуют подъемная сила и сила сопротивления,
определяемые взаимодействием с потоком, имеющим среднюю скорость
256
ГЛАВА 8
движения. В общем случае поведение достаточно мелких частиц,
погруженных в пограничный слой, при условии минимальной
скорости переноса описывается законом Стокса (Reoo<l) и
критическая величина и* для неконцентрированной суспензии (и*)
равна [65]
^н.=0,01 (J^L) ' \ (8.190)
Для более крупных частиц (Re<x,>l) применяется соотношение
вида
который свидетельствует о существенном влиянии отношений
диаметров и плотностей.
Приведенные уравнения относятся к суспензиям с бесконечно
малой концентрацией частиц, т. е.. <х=0. При значительной
концентрации частиц скорость трения у стенки при минимальной
скорости переноса и* можно найти из следующей
корреляционной зависимости [65]:
-^=1+2,8 (-V) V''. (8.192)
"о \ "о J
Влияние отношения плотностей в уравнении (8.191)
сказывается в увеличении vx/u* для систем газ — твердые частицы.
Это означает, что малая концентрация частиц сильно
отражается на результатах расчетов по уравнению (8.192). Кроме того,
минимальная скорость переноса жидкости становится
соизмеримой с конечной скоростью осаждения частиц, в то время как в
системах жидкость — твердые частицы она намного больше этой
скорости. Это возможно только при «витании» частиц в трубе,
когда они приобретают скорости, соизмеримые со скоростями
невозмущенного потока. Как только частицы оседают, их
перемещение становится затруднительным и они начинают
заполнять трубу, на порядок увеличивая падение давления. Этот
«скачок» является важной границей режимов работы
пневмотранспортеров [66].
Аналогичные методы применимы при исследовании эрозии,
а также переноса ила и песка в речных наносах [67, 68].
Неравномерная радиально-симметричная концентрация.
Даже при отсутствии или пренебрежимо малом влиянии
гравитации возможны достаточно большие изменения концентрации
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ 257
частиц поперек канала^ Например, при вязком течении Пуазейля
в трубе малого диаметра частицы концентрируются в кольцевой
зоне, расположенной от оси трубы на расстоянии, равном ~0,6
радиуса трубы, причем ядро потока содержит сравнительно мало
частиц [69].
Каналообразование или фонтанирование в псевдоожижен-.
ных слоях. Эффекты неравномерности в псевдоожиженных
слоях могут вызываться соответствующей организацией ввода
жидкости. Например, если жидкость вводится в центре
вертикальной колонны в виде высокоскоростной струи, может
установиться один из видов кольцевого противоточного движения,
когда неконцентрированная смесь жидкости с частицами в
центре движется вверх, а плотный поток смеси вблизи стенки
направлен вниз. Поведение таких систем описано Лева [15].
Периодическое течение
Образование пробок. Значительные изменения
концентрации частиц вдоль канала могут быть обусловлены ростом
возмущений, рассмотренных в разд. 8.8, а также турбулентностью
и другими трехмерными возмущениями,
нарушающими простую одномерную
структуру потока.
Так как неустойчивость наблюдается
при многих длинах волн, при
образовании пробок не существует простого
периодического изменения структуры.
Отдельные пробки образуются, растут,
сжимаются и непрерывно догоняют
друг друга (фиг. 8.26). Если пробки
принимают форму двумерного пузыря, такое
течение может быть исследовано
методами, описанными в гл. 10 [70].
* Фиг. 8.26. Образование пробок в псевдоожижен-
Г ном слое.
Стеклянные сферические частицы в трубе диаметром
2,54 см.
Образование волн в расслоенном потоке. В горизонтальных
грубах, когда жидкость протекает над слоем плотных частиц,
можно наблюдать периодическое образование волн или дюн,
медленно перемещающихся в направлении движения жидкости
17 Заказ № 162
Ш
*
<fcam«4»,
падающие
вида
258
ГЛАВА 8
(фиг. 8.27). Эти волны, по-видимому, являются результатом
неустойчивости Гельмгольца (вызванной относительным
движением) и могут быть описаны с помощью соотношения [71]
(или конгломератов) частиц вы-
диаметром В и со скоростью Uj
при длине волны К, причем
частицы имеют плотность ps и
диаметр d, а скорость и
плотность жидкости равны vf и р/.
Подобные явления
характерны также для речных
наносов, песчаных дюн и снеговых
заносов.
Агрегативное течение
Флоккуляция. Очень мелкие
частицы (диаметром до 100 мкм
и менее) или частицы
неправильной ветвистой формы
Фиг. 8.27. Периодические
нестационарные явления, наблюдаемые при
течений взвесей сферических частиц
в горизонтальных трубах [71].
стремятся к образованию конгломератов или хлопьев, которые
не разрушаются при движении в окружающей жидкости. Хлопья
удерживаются силами взаимодействия между частицами. Из-за
рыхлой структуры конгломератов жидкость может двигаться не
только вокруг, но и сквозь них. Флоккуляция является одной из
причин неньютоновских характеристик.суспензий.
Для хлопьевидных суспензий приближенное значение п
в уравнении (8.2) обычно очень велико (например, в работе [7]
приводятся значения от 20 до 30). Кроме того, п не является
постоянной величиной для всего диапазона концентраций, так
как размеры конгломератов зависят от концентрации.
Один из эффектов флоккуляции проявляется в том, что
осаждение завершается при низких значениях е. Осадок представляет
собой пористую массу, состоящую из частиц, удерживаемых
силами взаимодействия в рыхлой структуре. Дальнейшее
справедливого для скоплений
сотой Н, движущихся в трубе
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ 259
уплотнение возможно только при разрыве связей между
хлопьями и вытеснении жидкости через слой окружающих ее
частиц.
Образование пуз'ырей. В тех случаях, когда ожижающим
компонентом смеси является газ, а частицы достаточно крупные
или плотные, можно наблюдать явление, обратное флоккуляции,
а именно образование пузырей газа, не содержащих
частиц.-Причины образования таких пузырей до конца еще не ясны.
Возможно, они являются результирующим трехмерным эффектом
неустойчивости одномерной
структуры (стр. 231).
Много исследований было
посвящено изучению явления
образования пузырей в больших слоях, псев-
доожиженных газом [72—78].
Форма такого пузыря показана на
фиг. 8.28. Подъем пузырей
происходит почти так же, как и всплытие
газовых пузырьков в жидкости при
отсутствии вязкости и
поверхностного натяжения. Действительно,
скорость подъема пузыря газа в на-
Ф и г. 8.28. Фотография двумерного пузыря
в псевдоожиженном слое [78].
чальной стадии ожижения при низкой плотности газа
определяется по уравнению, аналогичному уравнению Дэвиса и
Тейлора [79] для пузырьков газа (константа уравнения несколько
изменяется), а именно [80]
vb=0,7lguT^'. (8.194)
Если плотность газа значительна, это уравнение принимает вид
р>=0'71^,/,уУ'Ь(р!-р7)-оГ- (8Л95)
Поверхность пузыря непроницаема для жидкости, и,
действительно, в пузыре наблюдается непрерывная циркуляция газа,
направленная вверх к его лобовой части и вдоль боковой
поверхности вниз к кормовой части. Эта циркуляция препятствует
схлопыванию пузыря.
1 Хотя газовые слои обычно содержат пузыри, а в суспензиях
их нет, все же существует непрерывный переход от одного вида
17*
260 ГЛАВА 8
ожижения к другому [16, 81]. Образование пузырей может
происходить при ожижении свинцовой дроби водой, а с другой
стороны, в смеси легких сферических частиц с воздухом при
достаточном давлении пузыри не образуются.
Простой, но приближенный критерий вероятности
образования пузырей был предложен в работе [30], авторы которой
использовали число Фруда для частицы, определяемое по
уравнению (8.98). Равномерное псевдоожижение характеризуется
числами Фруда меньше единицы, а при больших числах Фруда
происходит образование пузырей. С другой стороны, Джексон
' [77] предположил, что скорость усиления одномерных
возмущений (табл. 8.3) можно использовать для оценки вероятности
образования пузырей. Подобное исследование было проведено
также Пигфордом [82] и Смитом [27].
В работе [81] граница этих режимов устанавливается путем
рассмотрения условий, при которых пузырь может
разрушиться. В этой работе показано, что, если циркуляция
жидкости у кормовой части пузыря происходит достаточно
интенсивно, частицы могут уноситься жидкостью и заполнять пузырь
снизу. Приближенное условие наступления такого режима имеет
вид
•о „>■*„. ^ (8.196)
Так как скорость пузыря определяется уравнением (8.194),
с помощью соотношения (8.196) можно получить следующее
условие нарушения устойчивости пузыря:
V Г 1 е. Т/г/ да'/з V/г
m < 0,71 [р-
(8.197)
(gd)'h ' l?sl(.?s— ?/)— £о.
Следовательно, число Фруда является основным фактором,
определяющим отношение максимального диаметра устойчивого
пузыря к диаметру частицы.
8.13. Теория фильтрации
Трехмерное течение жидкости через пористые среды
встречается в фильтрационных аппаратах, при выщелачивании, в оса-
дительных колоннах и многих процессах строительной техники
(например, течение грунтовых вод к скважинам, просачивание
через дамбы и уплотнение грунта).
Как обычно, теория процесса включает два уравнения
неразрывности и движения. В простейшем случае течение
стационарно, жидкость несжимаема, пористая среда гомогенна и
инерционные члены пренебрежимо малы. Уравнение неразрывности
для жидкости имеет вид
V • j/=0, (8.198)
где у — вектор.
смеси жидкостей и газов с твердыми частицами 261
Уравнение (3.45) в векторной форме записывается
следующим образом:
'-ЧР-Р#Ъ-Ь=0, (8.199)
где к — единичный вектор, направленный вверх.
Величину if можно определить через j/, а также через
свойства жидкости и частиц (так как структура пористой среды
неизменна). Для ламинарного течения в соответствии с примером
8.3 при js = 0 получим
180ц.,
f/=-w0-£)i/- (8-20°)
Коэффициент проницаемости Дарси равен
gof rf2e2
*—isff/a-o • <8-201)
Если определить негидростатическое давление р' как
p'^pA-gz, (8.202)
то, используя уравнения (8.200) и (8.201), получим
-if=-xJ/- (8-203)
Объединяя этот результат с (8.198), находим
VV=0. (8.204)
Следовательно, изменение давления описывается уравнением
Лапласа, причем поток жидкости всюду пропорционален
отрицательному градиенту давления. Для решения конкретных за-
, дач могут быть использованы все обычные методы теории
потенциального течения. Обзор работ европейских исследователей
по этому вопросу содержится в книге Егера [84], где приводятся
также примеры использования различных приближенных
методов.
Для турбулентных течений лучше использовать численные
методы "расчета.
Приближенное решение для нестационарного потока было
получено Терзахи [25],, который модифицировал уравнение
(8.204) следующим образом:
где с определяется как коэффициент уплотнения. Хотя эта
теория до сих пор используется во многих учебниках по механике
грунтов, она, как было показано при анализе уравнения (8.97),
не вполне корректна.
262
ГЛАВА 8
'Задачи
8.1. Сравнить конечную скорость осаждения дроби в воздухе и воде, если
d=2 мм. Произвести расчет для свинцовой дроби (ps = ll,2 г/см3) н для
пластиковой дроби (р3 = 1,76 г/см3).
8.2. Чему равны значения п в уравнении (8.2) для систем жидкость —
твердые частицы, рассмотренных в задаче 8.1?
8.3. Вместо дифференцирования уравнения (8.31) использовать уравнения
(8.22) и (8.30) для определения наилучшего значения п в корреляции
Ричардсона и Заки как функции от числа Рейнольдса.
8.4. Вывести общее безразмерное соотношение между приведенной скоростью
дрейфа и концентрацией, используя величины Nf, e и число Рейнольдса
R<zfs = Pfjfsd[\if.
8.5. В работе [9] получено следующее общее соотношение для минимальной
скорости псевдоожижения:
(Res)m/ = (33,72 + 0,0408Л^)'/г— 33,7.
Сравнить этот результат с приведенными в книге теоретическими
соотношениями.
8.6. В работе [85] приводится следующее уравнение для массовой скорости
жидкости в начальной стадии псевдоожнжения:
ая, = 1,355- 105 "tfb-'f)
(размерности величин: G — кг/м2-час; d — м; р — кг/м3; ц — кг/м • час).
Сравнить это уравнение с приведенными в книге.
8.7. Рассчитать минимальные скорости псевдоожижения стеклянных шариков
(ps=2,5 г/см3) в воздухе и воде и сравнить результаты с
экспериментальными данными работы [8]. Условия атмосферные: 20° С и 1 атм
Ожижающая среда
Воздух
Вода
d, см
0,0083
0,0273
0,065
0,065
1,2
Измеренное зиаче-
™е Uh) mf см'сек
0,823
7,01
30,5
0,597
10,12
8.8. По мере движения воздуха через псевдоожиженный слой последний
расширяется. Показать, каким образом в коническом аппарате можно
организовать такой слой, частицы которого по всей глубине аппарата
находились бы в состоянии начального псевдоожижения. Рассчитать такой слой для
частиц диаметром 0,6 мм и плотностью 2,6 г/см3 при условии^ что верхнее
основание конического аппарата сообщается с атмосферой и имеет площадь
0,2 м2, а глубина слоя равна 0,9 м.
8.9. Воздух прн температуре 21° С движется через слой медной дроби
диаметром 0,065 см, имеющий постоянное потхеречное сечение. Измеренная на
выходе из слоя скорость воздуха при давлении 1 атм равна 1 м/сек.
Определить глубину псевдоожижения этого слоя.
8.10. По вертикальному каналу диаметром 0,7 м с помощью сжатого воздуха
при давлении 3,5 ата и температуре 40° С необходимо транспортировать зерно
диаметром 6 мм. Экспериментально установлено, что во избежание
возможной неустойчивости потока объемная доля зерен в канале не должна
превышать 0,05. Определить скорость воздуха, необходимую для транспортировки
100 т зерна в час. Кубометр плотного слоя зерна весит 800 кг.
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ 263
8.11. Цилиндрический фильтр, установленный в трубопроводе сжатого
воздуха, состоит из спекшихся сферических частиц диаметром 0,5 мм, объемная
доля которых равна 0,3. Размеры фильтра: толщина — 6 мм, диаметр —
150 мм, длина 200 мм. Чему равно падение давления на фильтре при
объемном расходе воздуха 1 нм3/мин, если начальные параметры воздуха 7,0 ат
и 32° С? Каковы возможные отклонения от этой величины падения давления,
если при изготовлении фильтра допуск по величине объемной доли частиц
составляет ±10%?
8.12. Сравнить результаты расчетов по уравнениям (8.48) и (8.35) как для
малых, так и для больших чисел Рейнольдса в диапазоне объемной
концентрации 0,3 < е < 0,6. Как зависят результаты расчетов от выбора уравнения,
Фиг. 8.29. Объемная концентрация частиц а в псевдоожиженной системе в
зависимости от приведенной скорости жидкости }}.
is — линии постоянных приведенных скоростей частиц.
если для указанного диапазона е используются методы, изложенные в гл. 4?
8.13. Руда с плотностью 2,24 г/см3 и средним размером частиц 0,1 см
обогащается при противоточном движении кислоты (р/ = 1,04 г/см3, \х.) =
=0,3 кг/м-час) в цилидре диаметром 1,8 м. Найти предельное отношение
расходов компонентов, при котором наступает «захлебывание».
8.14. Показать, что зависимость объемной концентрации частиц в
псевдоожиженной системе от приведенной скорости жидкости при разных расходах
восходящего и нисходящего потоков частиц может быть представлена
графически (фиг. 8.29). Установить по графику направление потока частиц,
точки, соответствующие «захлебыванию», и конечную скорость осаждения
частиц.
8.15. Объединить результаты решения задачи 8.14 с теорией падения
давления в плотном слое и методом расчета трения на стенке для гомогенного
потока с целью получения зависимостей градиента давления от приведенной
скорости, аналогичных показанным на фиг. 8.30. Объяснить характерные
особенности полученных кривых.
8.16. Окись тория с плотностью 9,5 г/см3 входит в состав водной суспензии
(температура воды 25° С, диаметр частиц 10 мкм и их концентрация 500 г/л).
Литр такой смеси заливается в вертикальный цилиндр диаметром 5 см, после
чего происходит осаждение. Описать дальнейшее поведение системы.
8.17. Некоторая флоккулирующая суспензия подчиняется уравнению
jfs = 0,00305а (1 — а)Ю м/сек.
Осаждение завершается при а=0,5. Описать процесс осаждения для такой
суспензии при а0=0,01, 0,05, 0,1, 0,15 и 0,2.
264 ГЛАВА 8
8.18. Вывести уравнение (8.71).
8.19. Стационарный псевдоожиженный слой состоит из частиц катализатора
(af=0,4 см, ps = 1,6 г/ем3), взвешенных в воде, заполняющей трубу
диаметром 10 см, причем е=0,8. Описать поведение системы при резком
уменьшении расхода воды вдвое.
8.20. Проинтегрировать уравнение (8.82), если I—е не очень малая
величина. Какая ошибка вызывается допущением о малости 1—е при Af=0,25
для следующих значений 1 —е: 0,002, 0,01, 0,05 и 0,1?
8.21. На фильтре образуется волокнистый слой, падение давления на котором
равно 0,07 ат. Какова среднеобъемная плотность волокнистого слоя, если
соотношение для уплотняющего напряжения имеет вид ps=560 (1—е)4 ат?
8.22. Показать, что, если частицы не соприкасаются, уравнение (8.96) соот-
Ф и г. 8.30. Градиент давления в псевдоожиженной системе — dp/dz в
зависимости от приведенной скорости жидкости />.
js — линии постоянных приведенных скоростей частиц.
ветствует непрерывным волнам. Показать, что при использовании уравнения
Кармана—Козени скорость непрерывной волны втрое больше скорости
жидкости.
8.23. При каких условиях уравнение (8.97) будет достаточно точным, если
в уравнении (8.96) £'=const?
8.24. Получить результаты, представленные в табл. 8.3, принимая / =0
п=3, ff3cvoc (vf — us)1'5 и е=0,4.
8.25. Рассчитать сопло для пескоструйного аппарата, обеспечивающее расход
песка 0,4 кг/мин (d=0,5 mm, ps=2,40 г/см3) при скорости на срезе 120 м/сек,
если к аппарату подводится сжатый воздух под давлением Pog=7 ат и
температуре Г0г=21°С.
8.26. Одиночная частица песка (d=0,5 мм, р„=2,4 г/см3) вводится в
воздушный поток с параметрами 93° С н 1,4 ата при скорости 300 м/сек. Какое
расстояние пройдет частица, прежде чем приобретет скорость 240 м/сек?
8.27. Насадок для плазменной струи рассчитан для работы на азоте при
5000° К (М-г—10-3 г/см-сек, pg==3-10~5 г/см3) и никелевых частицах (р„ =
=8 г/см3). Какая длина требуется для ускорения частиц диаметром 10 мк
до скорости 700 м/сек, если сопло рассчитано для K=lk? Какое время тре-
будется частице для ускорения от 6 до 600 м/сек? Рассчитать изменение
энтальпии частицы за это время, если kg~\Q-3 кал/см- сек- град. Будет ли
частица испаряться?
8.28. Показать, что если рассмотренные в задаче 8.27 частицы настолько
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ
265
велики, что их скорость мала, а скорость плазмы постоянна, то изменение
дх энтальпии на расстоянии z равно
AA_4Mf (* tvMv*
V-g \ d fsdvg) '
г-де ДГ —■ средняя разность температур частиц и плазмы.
■8.29. В сопле длиной 0,3 м, работающем на воздухе при температуре 260° С
и скорости на срезе около 300 м/сек, ускоряются алюминиевые частицы
плотностью 2,7 г/см3 (и удельной теплоемкостью 0,2 ккал/кг-град). Каков
должен быть размер частиц, чтобы е„ и ет, определенные по уравнениям
(8.141) и (8.142), были «малы»?
8.30. В запыленном воздухе образовался стационарный скачок уплотнения.
Условия в набегающем потоке: и=600 м/сек, ms = \, Г=200°С, ps = 3,2 г/см3,
£„=0,2 ккал/кг ■ град и d=l0 мк. Какова структура скачка?
8.31. Решить задачу 8.30 при и=370 м/сек.
8.32. Каково влияние эффекта присоединенной массы на динамические волны
в двухфазном потоке? Определить максимально возможное отклонение
скорости распространения упругих волн от теории гомогенного течения для
воздухо-водяной смеси при а='/2 и С='/2.
8.33. При каких условиях последний член уравнения (8.158) может стать
больше члена, обусловленного сопротивлением. Выполнить численные расчеты
для типичных случаев.
8.34. Доказать, что если в системе координат, связанной с частицей,
относительная скорость линейно возрастает со временем, то отношение силы Бассе
к силе сопротивления частицы в стационарном ламинарном потоке равно
d/ ynvft. Объяснить физический смысл этого результата, используя простое
понятие диффузии. Для каких размеров частиц в воздухе при атмосферных
условиях сила Бассе может быть значительна^ если ^=0,01 сек?
8.35. Суспензия содержит 40% частиц угля с плотностью 1,35 г/см3,
взвешенных в воде при температуре 21° С, и подчиняется уравнению Кассона,
причем ts=4,4-10"2 г/см2, а г| = 7,28 • Ю"2 г/см- сек. Построить диаграмму
«псевдонапряжений» для ламинарного потока. Чему равны потери давления на
трение при скорости потока 0,3 м/сек в трубе диаметром 25 мм и длиной
30 м?
8.36. Угольная суспензия, рассмотренная в задаче 8.35, течет по трубе, для
которой данные для однофазного турбулентного потока описываются корре-
' ляционным уравнением Cf=0,026Re~0>12. Чему равно падение давления при
скорости потока 3 м/сек в трубе диаметром 25 мм и длиной 30 м?
8.37. Флоккулирующая суспензия транспортируется- на станцию, химической
переработки при температуре 90° С. Чему равно падение давления при
движении вверх по вертикальной трубе диаметром 25 мм и длиной 30 м, если
расход равен 104 кг/час, диаметр частиц 1 мкм, плотность ps=6,4 г/см3 н
суспензия состоит из 0,3 кг частиц на I кг воды?
8.38. Какова минимальная скорость переноса в пневмотранспортере для
зерна (р«=1,2 г/см3, d=& мм), если диаметр трубы равен 36 см, давление
14 ата, температура 21° С, при а) низкой концентрации зерна? б) при а=0,1?
8.39. Наносы в реке состоят из частиц ила, причем d=l00 мкм, ps=2 г/см3.
При какой скорости течения начнется разрушение слоя? Если русло реки
выложено галькой диаметром 1 см, какую скорость можно считать
допустимой во время весеннего половодья?
8.40. Для расчета минимальной скорости переноса больших частиц в
длинных трубах предложена корреляционная формула
„_ J#*(P,-P/)"|''»
Сравнить это выражение с предложенными в книге.
266
ГЛАВА 8
8.41. Характер циркуляции газа в пузыре, поднимающемся в псевдоожижен-
ном слое, зависит от отношения Vbljfo- Каково это отношение при
псевдоожижении свинцовой дроби диаметром 0,25 мм атмосферным воздухом, если
7°ь = 1,639 л>
8.42. Каким образом видоизменяется теория возрастания энтропии,
изложенная в гл. 3, с учетом эффекта присоединенной массы? Показать, как можно
модифицировать уравнение (3.87) для учета кинетической энергии,
связанной с трехмерным полем течения вокруг частиц, движущихся относительно
жидкости. Эта кинетическая энергия не диссипирует и может быть
восстановлена. Какова в этом случае корректная форма записи уравнений (3.106) —
(3.108)?
Литература
1. Lap id us L., Elgin J. C, A. I. Ch. E. J., 3, 63 (1957).
2. Lapidus L., Quinn J. A., Elgin J. C, A. I. Ch. E. J., 7, 260 (1961).
3. Rowe P. N., Trans. Inst. Chem. Engrs, 39, 175 (1961).
4. Schiller L., Neumann A., Z. Ver. Deutsch. Ing., 77, 318 (1935).
5. H e у w о о d H., Symp. Interaction Fluids Particles, Inst. Chem. Engrs,
London, 1962, pp. 1—8.
6. Richardson J. F., Z a k i W. N., Trans. Inst. Chem. Engrs, 32, 35—53
(1954).
7. W a 11 i s G. В., Symp. Interaction Fluids Particles, Inst. Chem.""Engrs,
London, 1962, pp. 9—16.
8. Rowe P. N., H e n w о о d G. A., Trans. Inst. Chem. Engrs, 39, 43—54
(1961).
9. Wen С Y., Yu Y. H., Chem. Eng. Progr. Symp., ser. 62, 62, 100—11!
(1966).
lO.'P inch beck P. H., Popper F., Chem. Eng. Sci., 1, 57 (1956).
11? Van Нее r den D., Nobel A. P. P., van Krevelen D. W., Chem.
Eng. Sci., 1, 63 (1951).
12. Carman P. C, Flow of Gases through Porous Media, Butterworth
(Publishers), Ltd., London, 1956.
13. Carman P. C, Fluid Flow through Granular Beds, Trans. Inst. Chem.
Engrs, 15, 150—166 (1937).
14. Blake F. E., Trans. Am. Inst. Chem. Engrs, 14, 415 (1922).
15. Лева М., Псевдоожижение, Гостоптехиздат, М., 1961.
16. Simpson H. С, Rodger В. W., Chem. Eng. Sci., 16, 179 (1962).
17. E r g u n S., Chem. Eng. Progr., 48, 93 (1952).
18. S 1 i s P. L., W i 11 e m s e Th. H., Kramers H., Appl. Sci. Res., A8,
209 (1959).
19. Shannon P. Т., Tory E. M., Ind. Eng. Chem., 57, 18—25 (1965).
20. M о n t с r i e f f A. G., Trans. Inst. Mining Metal, 73, part 10, 729—759
(1963—1964).
21. Kynch G. J., Trans. Faraday Soc, 48, 166—176 (1952).
22. E g о 1 f С. В., М с С a b e W. L., Trans. Am. Inst. Chem. Engrs, 33, 630
(1937).
23. Han S. Т., I n g m a n s о п W. L., TAPPI, 21st Eng. Conf., Boston, Mass.,
50, № 4, 176—180 (April 1967).
24. Davis С N., Proc. Inst. Mech. Engrs, Bl, 185 (1952).
25. Terzaghi K-, Theoretical Soil Mechanics, chap. 13, Wiley Inc., N. Y.,
1943.
26. W a 11 i s G. В., One-dimensional Waves in Two-component Flow, UKAEA
Rept, AEEW-R162, 1962.
27. Smith J. L., Massachusetts Institute of Technology, 1963,
неопубликованная работа.
СМЕСИ ЖИДКОСТЕЙ И ГАЗОВ С ТВЕРДЫМИ ЧАСТИЦАМИ 267
28. Murray J., J. Fluid Mech., 21, 465—493 (1965).
29. Jackson R., Trans. Inst. Chem. Engrs, 41, 13—21 (1963).
30. Wilhelm R. H., Kwauk M., Chem. Eng. Progr., 44, 201 (1948).
31. Клигель, Вопросы ракетной техники, № 10, 3 (1965).
32. X о г л а н д, Ракетная техника, № 5, 3 (1962).
33. Soo S. L., A. I. Ch. E. J., 7, № 3, 384—391 (1961),
34. А льтман, Картер, Процессы горения, Физматгиз, М., 1961.
35. К 1 i e g е 1 J. R., IAS paper № 60-65, 1960.
36. Рэнни, сб. «Детонация- и двухфазное течение», изд-во «Мир», 1966,
■ стр. 121.
37. Марбл, Ракетная техника и космонавтика, № 12, 95 (1963).
38. С а г г i e r G. F, /. Fluid Mech., 4, 376—382 (1958).
39. К р а й б е л, Труды амер. общ-ва инж.-мех., серия D, Техническая
механика, № 3, 24 (1961).
40. R u d i n g e r G., Phys. Fluids, 7, 658—663 (1964).
41. К л и г е л ь, Н и к е р с о н, сб. «Детонация и двухфазное течение», изд-во
«Мир», 1966, стр. 183.
42. N i с k e r s о n G. R., К 1 i e g е 1 J. R, TRW Rept 6120-8345-MU000,
May 1962.
43. Бойер, Гранди, сб. «Детонация и двухфазное течение», изд-во «Мир»,
1966, стр. 78/
Уильяме, там же, стр. 103;
М о р г е н т а л е р, там же, стр. 155;
Marble F. E., Phys. Fluids, 7, № 8, 1270—1282 (1964);
Бэйли, Нильсон, Серра, Щупник, Ракетная техника, № 6, 56
(1961);
Рудингер, Ракетная техника и космонавтика, №7,3 (1965);
Ru dinger G., Chang A., Phys. Fluids, 7, 1747—1754 (1964);
Gilbert M., All port J., Dun lap R., Am. Rocket Soc. J., 1929—1930
(1962).
44. Prandtl L., Essentials of Fluid Dynamics, Blackie, Ltd, Glasgow, 1952,
p. 342.
45. Basset А. В., Hydrodynamics, Dover Publications, Inc., N. Y., 1961, p. 270.
46. Einstein A., Ann. Phys., 4, 289 (1906).
47. Th о m a s D. G., A. I. Ch. E. J., 6, № 4, 631—639 (1960).
48. T h о m a s D. G., A. I. Ch. E. J., 8, 266—278 (1962).
49. H a p p e 1 J., /. Appl. Phys., 28, 1288—1292 (1957).
'50. Реология. Теория и приложения, ИЛ, 1962.
51. Thomas D. G., A. I. Ch. E. J., 7, № 3, 431—437 (1961).
52. Zuber N., Chem. Eng. Sci., 19, 897—917 (1964).
53. R u t g e r s R., Rheol. Acta, 2, № 4, 305—348 (1962).
54. RutgersR, Rheol. Acta, 2, № 3, 202—210 (1962).
55. Bingham E. C, Fluidity and Plasticity, McGraw-Hill, N. Y., 1922.
56. С a s s о п N., Rheology of Disperse Systems, С. С.. Mill, ed., Pergamon
Press, N. Y., 1959.
57. Ри, Эй ринг, Реология. Теория и приложения, ИЛ,'1962.
58. Charm S. E., Kurland G. S., Brown S. L., ASME Biomed. Fluid
Mech. Symp., Denver, Colo., 1966, pp. 89—93.
59. Huff W. R., Hold en J. H., Phillips J. A., U. S. Bureau of Mines
Rept RI6706, 1965.
60. T h о m a s D. G., Paper № 64, Progr. Intern. Res. Thermodyn. Transport
Properties, ASME, 1962.
61. Daily J. W., Bugliarello G., TAPPI, 44, 497—512 (1961).
62. Bugliarello G., Daily J. W., TAPPI, 44, 881—893 (1961). •
63. Mih W., Parker J., TAPPI, 21st Eng. Conf., 50, № 5, 237—246 (1967).
64. Savins J. G., Soc. Pet. Eng. J., 4, № 3, 203—214 (1964).
65. T h о m a s D. G„ A. I. Ch. E. J., 8, 373—378 (1962).
268
ГЛАВА 8
66. Zenz F. A., Ind. Eng. Chem., 41, 2801—2806 (1949).
67 Чоу В. Т., Гидравлика открытых каналов, Стройиздат, 1969.
68 Kennedy J. F., /. Boston Soc. Civil Engrs, 52, 247—266 (1965).
69. Segre J., Silberberg A., /. Fluid Mech., 14, 136—157 (1962).
70. О r m i s t о n R. M., Mitchell F. R. G., Davidson J. F., Trans. Inst.
Chem. Engrs, 43, 209—216 (1965).
71. T h о m a s D. G., Science, 144, 534—536 (1964).
72. Rowe P. N., Chem. Eng. Progr. Symp., 58, 42 (1962).
73 Rowe P. N., Partridge B. A., UKAEA Rept AERE-R4660, 1964.
74. Harrison D., Leung L. S., Trans. Inst. Chem. Engrs, 40, 146 (1962).
75 Davidson J. F., Paul R. C, Smith M. J. S., Duxbury H. A.,
Trans. Inst. Chefn. Engrs, 37, 323 (1959).
76. Murray J. D., Harvard Univ., Cambridge, Mass., NSF Grant GP-2226,
1963.
77 Jackson R., Trans. Inst. Chem. Engrs, 41, 22—28 (1963).
78. Rowe P. N., Partridge B. A, L у a 11 E„ UKAEA Rept AERE-R4543,
1964
79. DaviesR. M., Taylor G. I., Proc. Roy. Soc. (London), 200, 375 (1950).
80. Дэвидсон, Харрисон, Псевдоожижение твердых частиц, изд-во
«Химия», 1965.
81. Harrison D., Davidson J. R., DeKock J. W., Trans. Inst. Chem.
Engrs, 39, 202 (1961).
82. Pigford R. L., Massachusetts Institute of Technology, 1959,
неопубликованная работа.
83. Roscoe R., Brit. J. Appl. Phys., 3, 267 (1952).
84. Jaeger C, Engineering Fluid Mechanics, St. Martin's Press, Inc., N. Y.,
1957.
85. Frantz J. F., Chem. Eng. Proc. Symp. ser. 62, 62, 29 (1966).
86. В r i n k m a n H. G„ /. Chem. Phys., 20, 571 (1952).
87. Taub P. A., /. Fluid Mech., 27, 561—580 (1967).
9
ПУЗЫРЬКОВОЕ ТЕЧЕНИЕ
9.1. Введение
Для пузырькового течения характерно присутствие отдельных
пузырьков в непрерывной жидкой среде. Имеется много типов
пузырькового течения. Область объемных газосодержаний,
соответствующих пузырьковому течению, простирается от одиночного
изолированного пузырька в большом объеме жидкости до
квазисплошного течения пены, когда на долю жидкости приходится
менее 1% объема среды. Взаимодействиями между силами
поверхностного натяжения, вязкости, инерции и подъемными
силами обусловлен целый ряд эффектов, часто проявляющихся
в различной форме пузырьков и траекторий их движения. Режим
течения, при котором размеры пузырей столь велики, что они
приобретают цилиндрическую форму и почти полностью
заполняют объем канала, называется снарядным и будет рассмотрен
в следующей главе.
В технике пузырьковое течение можно наблюдать в барбо-
тажных колоннах, в испарителях, работающих при высоких
давлениях, в поверхностных дистилляторах, пенных огнетушителях,
в производстве пива, шампанского и мороженого, в криогенике,
флотации (удалении примесей), в сточных трубопроводах
стиральных машин, при мгновенном вспенивании во время
шевингования, в системах обеспечения дыхания под водой и
регулировании волн в портах.
9.2. Образование пузырьков
Стабилизированный равновесный пузырьковый режим
течения встречается весьма редко. Газовые пузырьки,
присутствующие в жидкостях, обычно стремятся слиться друг с другом,
в результате чего пузырьковая структура теряет свою
«однородность». Если в канале происходит испарение или
конденсация, мелкие пузырьки могут существовать в потоке лишь -как
некая переходная структура. По этим причинам особенно важно
иметь представление о возможных способах образования
пузырьков. Кроме того, размер пузырьков оказывает влияние на
динамику пузырьковой смеси и потому часто должен быть определен
через соотношения, описывающие механизм образования
пузырьков. Несмотря на большое число работ, посвященных данному
270 ГЛАВА 9
вопросу, всеобщее признание получили всего лишь несколько
соотношений для расчета размера пузырька. Ниже будут
приведены некоторые наиболее простые из этих соотношений.
Образование пузырьков в отверстии
Одним из наиболее простых способов образования пузырьков
является вдув газа в неподвижную жидкость через обращенное
кверху круглое отверстие. Если принять, что в отверстии
радиусом R0 находится приблизительно сферический пузырек
радиусом Rb, связанный с этим отверстием цилиндрической шейкой,
то наибольший размер пузырька, определяемый из условия
статического равновесия, будет равен
4/3^k(P/-pff) = 2^0a. (9.1)
Радиус пузырька, который образуется при вдуве газа через
небольшое отверстие с малыми расходами, приближенно
вычисляется следующим образом:
На основе экспериментальных данных Кутателадзе и Стырико-
вич [1] предложили соотношение
которое перестает быть справедливым, когда диаметр отверстия
становится соизмеримым с радиусом пузырька, т. е. когда
«°>°'s[w^f' <9-4)
Если образование пузырьков происходит с конечной
скоростью, то на этот процесс оказывают влияние многие факторы.
В частности, весьма существенными являются все свойства газа
и жидкости, а также конструктивные особенности отверстия
и способ подвода газа. В работе Джексона [2] дается обзор
литературы по данному вопросу и показано, что в общем
случае процесс образования пузырьков чрезвычайно сложен.
С увеличением расхода газа через отверстие размер
пузырьков сначала также возрастает, поскольку по достижении
размера, определяемого уравнением (9.3), пузырьку требуется
еще некоторое время, чтобы оторваться от отверстия. Для
системы, в которой расход газа через отверстие поддерживается
постоянным, можно рассчитать отрывной размер пузырьков, если
известно время, в течение которого пузырек остается прикреп-
ПУЗЫРЬКОВОЕ ТЕЧЕНИЕ 271
ленным к отверстию [3]. Дэвидсон и Харрисон [4] рассчитали
это время из уравнения движения всплывающего пузырька и
получили следующее выражение для объема пузырька в момент
его отрыва в невязкой жидкости:
Th
= 1,138--^-
g'
(9.5)
где Qg — объемный расход газа через отверстие. На фиг. 9.1
результаты расчета по уравнению (9.5) сравниваются с
имеющимися данными для воды в широком диапазоне размеров
отверстий. Расхождение теории и опытных данных при малых
расходах газа обусловлено приближением к предельному
квазистатическому случаю, для которого справедливо уравнение (9.3).
Более общее решение в виде степенной зависимости скорости
роста пузырька рассматривается в задачах 9.3—9.6. Дэвидсон
и Шюлер [5] провели аналогичные расчеты для вязких
жидкостей и получили следующее выражение:
Th
£■)""[
l5y.fQg
1ЭА
2£(р/— ?g)
(9.6)
Когда скорость газа велика, поток количества движения из
отверстия становится существенным и объем пузырька
определяется из следующего уравнения:
(36^)'/з
2^(Р/-^) уч,_
^v-fQg
-* Ь ,
lofV
(9.7)
где А0— площадь сечения отверстия.
При достаточно большой скорости газа в устье отверстия
образуются уже не отдельные пузыри, а истекает струя газа,
которая в последующем дробится на отдельные пузырьки.
Условие формирования газовой струи записывается следующим
образом [1]:
■V?g
[g° (р/ — ?g)]
> 1,25
g(?f~?g)Rf>
'/г
(9.8)
где vg — скорость газа в отверстии. Радиус образующихся таким
•путем пузырьков приблизительно в два раза больше радиуса
отверстия.
В промышленных установках пузырьки обычно образуются
с помощью группы отверстий или пористой пластины. В этом
случае теория образования пузырьков в одиночном отверстии
полезна лишь как первое приближение.
100
TOOO
юооо
Фиг. 9.1. Объем пузырей, образующихся при вдуве газа в невязкие жидкости
через погруженные в них отверстия и сопла [4].
Уолтере (воздух-во- т ба d=[2J MM
Труба d= 19,05 мм
Труба d=25,i мм
Колдербенк (воздух— Капилляр 0,265 см
вода) Щели шириной 1,59—6,35 мм
ван-Кревелен и Хоф-
тицер
(воздух—вода)
ван-Кревелен н Хоф-
тицер
(водород—вода)
Капилляр 0,23 см
Капилляр 0,23 см
Дэвидсон и Амнк Отверстие #=0,48 см
Шюлер Отверстие d=0,I5—0,25 см
I О расчетное значение
I • эксперимент
D расчетное значение
■ эксперимент
Д расчетное значение
А эксперимент
X
♦
О
v
ПУЗЫРЬКОВОЕ ТЕЧЕНИЕ 273
Образование пузырьков вследствие неустойчивости
по Тейлору
В определенных условиях пузырьки могут образовываться
путем отрыва от газовой или паровой подушки над пористой или
нагретой поверхностью. Непрерывный процесс образования этих
пузырьков не идентичен классическому случаю «неустойчивости
по Тейлору» [6] менее плотной жидкости, расположенной ниже
жидкости с большей плотностью, однако величина пузырьков
характеризуется в этом случае тем же самым безразмерным
параметром
Зубер [7] распространил теорию неустойчивости Тейлора
на случай непрерывного образования пузырьков с поверхности
паровой пленки, что используется при описании пленочного
кипения.
Образование пузырьков путем испарения
или массопереноса
Пузырьки могут также образовываться путем испарения
жидкости или высвобождения растворенного в жидкости газа
(например, в пиве, содовой воде, шампанском). Эти пузырьки
образуются практически в одних и тех же центрах парообразования,
которыми служат либо примеси, взвешенные в жидкости, либо
углубления, царапины или раковины в стенках сосуда. Особый
интерес представляет формула, полученная Фритцем [8], для
эквивалентного отрывного диаметра пузырька (т. е. диаметра
сферы того же объема), образующегося на горизонтальной
поверхности. Если р — краевой угол в градусах, то
эквивалентный диаметр равен
rf=0'0208pb(i7^r- (9Л0)
Это уравнение справедливо только для квазистатического
состояния системы и недостаточно корректно описывает поведение
пузырьков, образование которых протекает весьма быстро, как,
например, при кипении.
Влияние касательных напряжений на размер пузырька
В случае вынужденной конвекции или механического
перемешивания жидкости размер пузырьков определяется
касательными напряжениями. Эти напряжения оказывают влияние как
на размер пузырьков, сместившихся от точки их зарождения, так
18 Заказ № 162
274
ГЛАВА 9
и на максимальные размеры пузырьков, которые неподвижны
в поле течения. Можно полагать, что критический размер
пузырька в обоих случаях определяется балансом сил
поверхностного натяжения и сил, действующих на него со стороны
жидкости, т. е. надлежащим образом выбранным числом Вебера.
Этому вопросу посвящено ограниченное число заслуживающих
внимание работ, однако для оценки размера пузырьков может
оказаться полезной формула Хинце [9]
а=0,725(^(^У'\ (9.11)
где Р/М — диссипированная механическая мощность, отнесенная
к единице массы.
9.3. Одномерное вертикальное течение пузырьковой смеси
при отсутствии касательных напряжений на стенке
Так как касательные напряжения на стенке малы, а профили
концентраций и скорости приблизительно постоянны, методика,
описанная в гл. 4, может быть использована для анализа
пузырькового течения в вертикальной трубе.
Основная задача заключается в отыскании соответствующего
выражения для приведенной скорости дрейфа jgf в функции
основных параметров. Для большинства практических целей
хорошим приближением может служить эмпирическое уравнение
(4.14):
Jgf=va>*Q-*)a- (9Л2)
Теперь остается лишь выразить и<х> и п через свойства жидкости
и размер пузырьков.
Скорость подъема одиночных пузырьков
Зависимость предельной скорости подъема одиночного
пузырька Уоо от свойств жидкости была найдена экспериментально
Пиблсом и Гарбером [10], ХейберманомиМортоном [11], а также
многими другими исследователями. На фиг. 9.2 показана
зависимость скорости подъема в воде пузырьков воздуха от их
размеров. Достаточно точное выражение для скорости подъема
самых мелких пузырьков, форма которых близка к идеально
сферической, поскольку определяется в основном силой
поверхностного натяжения, получается из решения Стокса [12]
ПУЗЫРЬКОВОЕ ТЕЧЕНИЕ 275
Это уравнение справедливо для твердых сфер, и, следовательно,
считается, что скорость жидкости на поверхности пузырька
стремится к нулю. Для жидких сфер с деформируемой поверхностью
50
40
30
20
1
=1 8
6
5
4
3
2
1
-
„
_- х
-
у
- У
Л
i i
X
вя)
у/
i l
I I
&1
i
11
С
•Г*^
1 I I I
1 1 1 1 1 II 1
*"**<5Й0о Jt* х ^гРО^
D
1 1 1 1 1 1 1
>**£-
л^^'
*^.
_
■
■
-
-
-
i i .
0,01
0,02
0,04 0,06 0,1
0,2
fit, СЛ
0,4 0.6 0,8 1,0
2,0
4,0
Фиг. 9.2. Предельная скорость подъема пузырьков воздуха в фильтрованной
или дистиллированной воде в зависимости от их размера [11].
- эквивалентный радиус.
(9.15)
и вязкостью жидкости ^ff Адамар [13] и Рыбчинский [14]
получили следующее уравнение:
d2g{9f-9g)3yg + 3y 9
Если Hg<giHf, то (9.14) сводится к виду
d2g (Р г — 9g)
V™~ 12(1/
При полном отсутствии загрязнений, которые имеют
тенденцию накапливаться на поверхности пузырька и оказывают
определенное сопротивление действию касательных напряжений,
можно экспериментально получить значения Уоо, соответствующие
уравнению (9.15). Однако в большинстве практических случаев
всегда имеются загрязнения, вследствие чего скорость подъема
пузырька заключена между значениями, определяемыми
уравнениями (9.13) и (9.15).
В другом предельном случае, когда размеры пузырьков очень
велики, влиянием поверхностного натяжения и вязкости можно
18*
276
ГЛАВА 9
пренебречь, и скорость подъема пузырька определяется
выражением Дэвиса и Тейлора [15],
•Оа>=-\-УЖ, (9-16)
где ^с — радиус кривизны в окрестности «вершины» пузырька.
Пузырь при этом обычно имеет приблизительно сферическую
головную участь с углом охвата примерно 100° и относительно
плоскую кормовую часть.
Уравнение (9.16) можно записать с использованием в
качестве переменной объема газа, содержащегося в пузырьке, 7°ь:
•о<ю=О,79(^;/0,/*. (9.17)
С другой стороны, можно определить эквивалентный радиус
пузырька Rb как.радиус сферического пузырька, имеющего тот
же объем:
П=4/з^б- (9-18)
Тогда скорость подъема пузырька запишется следующим
образом:
v~=Vgb- (9-19)
Для пузырьков промежуточного размера существенны силы
инерции жидкости, ее поверхностное натяжение и вязкость,
чистота, а также то обстоятельство, происходит ли подъем
пузырьков по прямой линии, совершают ли они
возвратно-поступательные перемещения или же движутся по спиральной траектории.
В литературе имеется много соотношений для скорости подъема
пузырька, но, возможно, наиболее универсальными являются
соотношения Пиблса и Гарбера [10], приведенные в табл. 9.1.
Эти соотношения соответствуют случаю пренебрежимо малой
плотности газа по сравнению с плотностью жидкости. Диапазон
применимости каждого уравнения определяется с помощью
следующих безразмерных комплексов:
Re„- 'Z , (9.20)
G, = -5—J-
(9.22)
Следует отметить, что в области 4 скорость подъема пузырька
не зависит от его размера. Гармати [16] полагает, что для этой
ПУЗЫРЬКОВОЕ ТЕЧЕНИЕ
277'
Таблица 9.Г
Предельная скорость подъема одиночных газовых пузырьков
в жидкости [10]
Область
Предельная скорость
Диапазон применимости
2Rl(?f_9g)g
9ц
v =Q,33g'
0,76
/
ру \0,52
/?!■"
V = 1
■*ш
50
(ga\0,25
Re„<2
2<Reu<4,02Of0'0214:
4,02Gr°'2,4<Reft<
<3,10G70'25
16,32G?'144<G2<5,75
3,10Gf0,25
5,75 <G2
3,10Gr°'25<Re»
области следует принять величину постоянной в уравнении
равной 1,53, а не 1,18. Верхняя граница области 4 достигается при
-скорости подъема пузырька, сравнимой со значением,
полученным с помощью выражения (9.19), т. е.
R">2[-wT (9-23>
определяет область 5, в которой справедливо уравнение (9.19).
Пример 9.1. Рассчитать скорость подъема в воде пузырьков воздуха,
эквивалентный радиус которых равен 0,2, 0,5 и 2 см, если ст=70 дин/см,
р/ = 1 г/см3, ц/ = 0,01 «з и g=981 см/сек2.
Решение. Из уравнения (9.21) при заданных значениях физических параметров,
получим
Ol=^W!i = 2,86.10-n.
Тогда 4,02 G, °-214=715 и 3,1 Gr°-25= 1340.
Кроме того, из уравнения (9.23) имеем
.g?f
■Г-*
51 см.
Чтобы определить область табл. 9.1, соответствующую
происходящему процессу, воспользуемся графиком, представленным на фиг. 9.2,
и с его помощью найдем первое приближение для скорости пузырька*
278 ГЛАВА 9
а следовательно, и для числа Рейнольдса, определяемого
уравнением (9.20). В результате получим
Rb, см
vb, см/сек
Reft
Область
0,2
25
1000
3
0,5
25
2500
4
2,0
40
16 000
5
Расчетные значения скорости пузырька, согласно уравнениям,
приведенным в табл. 9.1, и уравнению (9.19), будут следующими:
Rb = 0,2 см
Rb = 0,5 см
Rb = 2 см
Сравнение с данными фиг. 9.2 указывает на хорошее согласование
с экспериментом, а также свидетельствует о том, что в области 4 более
точные результаты получаются при использовании значений постоянной,
предложенной Гармати.
Влияние стенок
Если пузырек всплывает в сосуде конечных размеров, то его
скорость в общем случае оказывается меньше рассчитанной по
формулам табл. 9.1. Для трубы диаметром D отношение
скорости подъема пузырька Vb к соответствующей скорости в
бесконечно большом объеме v,*, может быть выражено в виде
функции от d/D, где d = 2Rb.
Коллинз [17] исследовал движение больших пузырей в
условиях, соответствующих области 5, когда можно пренебречь
вязкостью. Полученные им данные'достаточно хорошо описываются
следующими уравнениями:
4-<0,125, -^-=1, (9.24)
оо
0,125 <^<0,6, -^=i)i3e-d/D, (9.25)
оо f
0,6 <4. -£-=0.49б(4}",\ (9.26)
Уравнение (9.26) эквивалентно уравнению (10.5), описывающему
скорость подъема пузырей в невязкой жидкости при снарядном
течении.
v = 1,35 [-тгя-1 2=25,2 см/сек,
со \ 0,2 /
v =1,18
со
НЛН
1,53
(981 • 70):
74 =
19,1 см/сек,
24,8 см/сек,
v =1,00 (981 • 2) /г = 44,3 см/сек.
Чг — <
ПУЗЫРЬКОВОЕ ТЕЧЕНИЕ
279
Аналогичные поправки можно получить и для случая подъема
пузырьков в вязких жидкостях. В работе Ладенбурга [18]
пузырьки отождествлялись с твердыми сферами. Для этих условий
получено следующее соотношение:
-?-=(!+ ТГ-Г- <9-27>
оо
Для жидких сфер при (iff-Cn/ Эдгар [19] получил уравнение
tMi + T-)"1- <9-28)
оо
Если отношение d/D превышает примерно 0,6, то в этом случае
реализуется снарядное течение. В этих условиях справедливо
уравнение
-Й-=0,12 (-J-)-*. (9.29)
Приемлемое совпадение с выражением (9.28) дает
А-=1—*/£-. (9.30)
оо
При d/D = 0,6 кривая, описываемая этим выражением, касается
кривой (9.29). Соотношением (9.30) можно пользоваться для
оценки скорости пузырьков при d/D<0,6.
Влияние вибраций
Если пузырек находится в вибрирующем вертикальном столбе
жидкости, то в этом случае на него действует опускная сила,
противодействующая подъемной. При определенных условиях
пузырек будет устойчиво колебаться около некоторого среднего
положения или даже перемещаться вниз [20, 21, 50].
Влияние объемного газосодержания
Влияние объемного газосодержания удобно учитывать с
помощью уравнения (9.12). В этом случае нужно только получить
соответствующие значения для показателя степени п.
В работе [22;] делается простое допущение, что изменение
относительной скорости с объемной концентрацией газа
происходит по линейному закону, и рекомендуется значение п,
равное 2. Если при этом принять величину скорости подъема
одиночного пузырька по Пиблсуи Гарберу (область 4 табл. 9.1), то
y./=l,18*(l-a)2p7v,[aStP/-P,)],/'- (9-31>
280 ГЛАВА 9
С учетом рекомендации Гармати относительно величины
постоянной в уравнении (9.31) указанное выражение примет вид
jgf= 1,53а (1 - а) V'/2 [°g (P/ - Р,)1,/4• <9-32>
На фиг. 9.3 результаты расчетов по уравнениям (9.31) и
(9.32) сравниваются с экспериментальными данными работы
0,08
0,06 -
0,04
0,02
по
д
Точки
захлебывание'
Фиг. 9.3. Сравнение результатов расчета по уравнениям (9.31) и (9.32) с экспе-.
риментальными данными Шульмана и Молстеда для системы воздух—вода
при вертикальном пузырьковом течении [23].
-if, м/сек
О 0,6137 0,0271 0,0405
V
0,0543 0,0677
уравнение (9.31);
уравнение (9.32).
123] для противотока воздуха и воды. И на этот раз при
использовании постоянной Гармати получены лучшие результаты, что
дает основания рекомендовать эту постоянную для газо-жид-
костных систем. Для систем жидкость — жидкость лучшие
результаты дает уравнение (9.31).
Данные на фиг. 9.3 представлены в тех же координатах,
что и на фиг. 4.1. Данные, соответствующие стационарным
режимам, обозначены точками, а условия «захлебывания» представ-
ПУЗЫРЬКОВОЕ ТЕЧЕНИЕ 281
лены касательными. Отклонение экспериментальных данных от
теоретической кривой для пузырькового течения происходит
приблизительно при а=0,3 вследствие «захлебывания» и
соответствующего изменения режима течения. Новый режим течения
характеризуется очень большими пузырями, а суммарная
площадь поверхности раздела газ — жидкость выше точки
«захлебывания» существенно снижается. Так, Шульман и Молстед [23]'
обнаружили резкое уменьшение коэффициентов массообмена
в указанных на графике точках «захлебывания» течения.
Во многих практических приложениях газ (или легкая
жидкость) барботирует через неподвижную жидкость. В этом
случае из уравнений (9.31) и (4.7) следует
/eo=U8a(l-a)p7,/4°£tP/-P,)],/4- . (9-33>
На фиг. 9.4 результаты расчета по этому уравнению
сравниваются с экспериментальными данными Кутателадзе [24] по бар-
ботажу воды через слой ртути. «Захлебывание» и изменение
режима течения происходит при а = 0,4, вблизи максимума кривой.
Показатель п не всегда точно равен 2, хотя при низких
значениях а, т. е. в области, где в основном применяется теория
пузырькового течения, это изменение не очень существенно. Гей-
лор, Роберте и Пратт [25], исследовавшие системы жидкость —
жидкость для области 1 табл. 9.1, получили п = 2. Майлс, Шед-
ловски и Росс [26] получили я =1,6—1,9 для устойчивых пен
при больших значениях а. В работе Зубера и Хенча [27]
приводятся данные дальнейшего аналитического и экспериментального-
исследования пузырькового режима течения. Для различных
областей табл. 9.1 авторы рекомендуют следующие значения, п:
Область 1 я = 2,
Область 2 п = 1,75,
Область 4 п= 1,5.
Если размер пузыря больше определяемого по соотношению
(9.23), то существенную роль играют эффекты, связанные
с трехмерностью течения, и происходит интенсивный захват
и унос; пузырей в следе предыдущего крупного пузыря. В
результате такого «кильватерного» движения пузырей происходит
увеличение относительной скорости с увеличением числа
находящихся в потоке пузырей. В связи с этим показатель степени п
в уравнении (9.12) становится меньше 1. Течение сильно турбу-
лизируется и принимает нестационарный характер. Это течение,
названное Зубером пенисто-турбулентным, по-видимому,
представляет собой некий переходный режим между «идеальным
пузырьковым течением», в котором подъем пузырьков происходит
?м
Изменение режима
течения вследствие
.захлебывания"
5-
1
-
-
к
к/.«
/ь. о о
1
1
к^
т kjf^
а
1
1
4
а
am д
jt. (
Изменение ре
течения вела
„захле6ыеан1
i
О
°
жима _
сгаеие
1Я"
'
1 -
0,1
0,2
0.3 04
a
0,5 0,6 0,7
Фиг. 9.4. Данные по барботажу воды через ртуть при различных
геометрических характеристиках отверстий [24].
приведенная скорость воды; а — объемное содержание воды;
j — приведенная скорость воды; и, — ииссииис tuA^mannt п"м"', уравнение
(9 33)- о —степень перфорации пластины 33%, начальная высота Л„=55 мм, диаметр
отверстия do: • О 10 мм; □ ■ 5 мм: АД 3 мм; б — диаметр отверстия а\-Ъ
««.начальная высота Л0=155 см; степень перфорации пластины: «О
44,5%; ■ П 32,3%; АД 12,5%
ПУЗЫРЬКОВОЕ ТЕЧЕНИЕ 285
равномерно и стационарно, и снарядным течением, при
котором труба заполнена большими пузырями, следующими друг
за другом в следе предыдущего пузыря. В пенисто-турбулентном
течении существенную роль играет процесс агломерации
пузырей, поскольку пузырь, находящийся в следе предыдущего
пузыря, движется быстрее своего «лидера» и в конце концов
сливается с ним. Стационарное состояние не достигается до тех пор,
пока не завершится слияние пузырей, а для этого может
потребоваться канал значительной длины.
Согласно Зуберу [27|], при пенисто-турбулентном течении
скорость движения пузырей относительно среднеобъемной скорости
смеси равна скорости, характерной для области 4 табл. 9.1, т. е.
iV, = 1,53
Jgi
9}
(9.34)
i%,o
ю,о
ii
а»
.8,0
6,0
4,0
2.0
I '■■
-
-
-
i
К I
I
•
op
1
1
1
k/
4V=»,2
1
k/
-
-
-
SosSyxo - водяные смеси
i i
о 0
° 3,04
♦ 6,10
u 9,IS
• 12,20
* 78,30
■ 24,40
• 30,45
0 - 6,08 en
i i
i
-
2,0
4,0 6,0
j, м/сек
8,0
10.0
Фиг. 9.5. Сравнение результатов расчета по уравнению (9.36) с
экспериментальными данными [28].
vg — истинная скорость газа; / суммарная приведенная скорость.
•284
ГЛАВА 9
Соответствующее выражение для скорости дрейфа имеет вид
"g (р/ — ?g)
jgf= l ,53a
?f
(9.35)
при этом п = 0.
Модификации простой теории, учитывающие
изменения концентрации и скорости
Изменения концентрации и скорости движения пузырьков
можно учесть по описанному в гл. 4 методу Зубера [28]^
Например, если использовать параметр Со из уравнения (4.24), то для
пенисто-турбулентного пузырькового течения получим
ag(?f — ?gY
vg=CJ+\,53
?f
(9.36)
На достаточном удалении от места вдува пузырей при этом
режиме течения значение Со обычно заключено в диапазоне от
1,0 до 1,5," а наиболее вероятное значение Со равно примерно
1,2. На фиг. 9.5 расчеты по этой теории сопоставляются с
некоторыми экспериментальными данными. В используемых на этом
графике координатах Со определяется как тангенс угла наклона
кривой, а величина vg, равна отрезку, отсекаемому этой кривой
на оси ординат.
9.4. Нестационарное течение
При анализе нестационарных течений удобно одновременно
использовать теорию распространения непрерывных волн и
соответствующие выражения для скорости дрейфа. Методы расчета
аналогичны описанным в предыдущей главе.
Рассмотрим, например, дренаж влаги из пены, первоначально
равномерно распределенной в вертикальной трубе. Поскольку
величина а близка к единице, удобно использовать в качестве
параметра объемное влагосодержание е.
Пусть начальное значение е равно е0. Как только начинается
процесс дренирования пены, от верхнего и нижнего концов
трубы, где заданы граничные условия, распространяются волны.
На верхнем графике фиг. 9.6 процесс дренирования
представлен в координатах: приведенная скорость дрейфа — объемное
влагосодержание, а на нижнем — координата — время.
Условия устойчивого скачка влагосодержания
удовлетворяются на нижней границе пены. Поверхность раздела,
образующаяся в процессе дренирования, поднимается вверх со
скоростью vs; ниже этой поверхности расположена чисто жидкая
ПУЗЫРЬКОВОЕ ТЕЧЕНИЕ
285
фаза. На верхней границе пены не может быть никакого скачка,
так как кривая jgf в этой зоне обращена выпуклостью вниз.
Следовательно, непрерывные волны, соответствующие спектру
значений влагосодержания от е = 0 до е=е0, будут
распространяться вниз, в зону существования пены, каждая со своей
собственной скоростью. Как это видно на фиг. 9.6, процесс
дренирования протекает в две стадии.
Фиг. 9.6. Диаграммы дренирования первоначально равномерно
распределенной пены.
Стадия 1. Сначала скачок влагосодержания от е = ео до е — \
распространяется вверх от нижней границы пены, а
непрерывные волны распространяются вниз через пену от верхней ее
границы. На этой стадии скорость дренирования влаги из пены
определяется скоростью распространения скачка
влагосодержания и является постоянной величиной.
Стадия 2. Когда первая непрерывная волна, соответствующая
влагосодержанию (е0— бе), достигнет поверхности раздела фаз,
газосодержание над поверхностью скачка начнет увеличиваться,
интенсивность скачка нарастает, а скорость его движения вверх
уменьшается. В любой последующий момент времени
влагосодержание над поверхностью раздела определяется тем
значением е, для которого время, отсчитываемое от начала процесса,
оказывается достаточным, чтобы соответствующая волна непре-
286 ГЛАВА 9
рывности распространилась от верха пены до поверхности
раздела.
Указанные процессы напоминают перевернутую картину
осаждения третьего типа и могут быть изображены в
универсальных ХУ-координатах, как это показано на фиг. 9.7, а также
описаны уравнениями (8.68) и (8.69). Значение а«х> по окончании
дренирования практически равно единице.
<|^ 1
II
>-
\
I
1-Ео
Ео
Фиг. 9.7. Диаграмма дренирования пены в координатах XY.
Для удобства сравнения с фиг. 9.6 ось У направлена вниз.
Если высоту зоны, заполненной жидкой фазой, в любой
момент времени стадии 2 обозначить через h, а поперечное сечение
трубы — через А, то количество дренированной жидкости будет
равно A (ho — К), а количество жидкости, оставшейся в пене,
Ah0B0-A{h^h)=Ah(p.u[1^--\)=Ah0%{Y-\), (9.37)
где Afloat — начальное содержание газа в пене. Переписав
уравнение (8.69) в функции е, получаем
(К-1)=-
■(л + 1)в
1 =
s(w— 1) — /и2
л (l-^s л(1-в)2 ■ (9-38>
При малых значениях е в качестве приемлемого приближения,
определяющего количество оставшейся в пене влаги, можно
использовать выражение, полученное из (9.37) и (8.38),
(v4Vo)e(«— 1)
Tf=-
(9.39)
где е — влагосодержание непосредственно над границей чисто
жидкой (дренированной) фазы.
Такое количество влаги остается по истечении времени t,
определяемого через параметр X:
t—XaQhu — n(1_e)2sn-il,
E"-if.
(9.40)
ПУЗЫРЬКОВОЕ ТЕЧЕНИЕ 287
Когда в этих уравнениях е равно е0, начинается стадия 2.
Стадия 1 в плоскости h — t описывается прямой, соединяющей
точку, характеризующую начальные условия, и точку начала
стадии 2.
Пример 9.2. Авторами работы [26] проведены опыты с однородной пеной,
полученной из 0,24%-ного раствора лаурилсульфата натрия. Опыты
проводились в вертикальной колонне диаметром 3,2 см. Данные
эксперимента по стационарному дренированию жидкости через неподвижную
пену описывались следующим уравнением:
у = 0,24л:1'8,
(9.41) 200
где у — расход жидкости через
пену в см3/мин, ах — объем жидкости
во всех 295 см3 пены.
Авторы также исследовали
нестационарный процесс, реализуемый
при внезапном перекрытии линии
подачи жидкости, фиксируя
количество оставшейся в пене влаги в
функции времени. Требуется получить
расчетным путем их данные, если
в начальный момент в объеме 295 см3
пены было равномерно
распределено 6,9 см3 влаги.
Ф и г. 9.8. Сравнение расчетных и
экспериментальных данных по дренированию
пены (для примера 9.2).
О экспериментальные данные [26]; теория.
!50
| ЮО
50-
2 4 6 8
Количество жидкоЬтли в пеие,см3
Решение. В используемых нами обозначениях уравнение (9.41) принимает вид
-7/0=13,9еЧ (9.42)
при этом скорости измеряются в см/сек. Подставляя уравнение (9.42)
в уравнение (4.7), получаем прн jg=0
yV/=13,9s,-8(l —s). (9.43)
Следовательно, v„, =13,9 см/сек, аи = 1,8, Л0аоЛ0=295 — 6,9=288,1 см3,
а а0Л0=288,1/8,05 = 35,8 см. Подставляя этн значения в (9.39) н (9.40),
получаем
У/=128е см?, (9.44)
(9.45)
<= 1,432s-0'8. сек,
Теперь подставим значение е0=6,9/295=0,0234 в (9.44) и (9.45) н
определим условия завершения стадии 1
■Vt = 3,0 см? и t--
:28,8 сек.
Стадия 1 описывается прямой, соединяющей начальную точку с
полученной точкой.
На фнг. 9.8 расчеты для обеих стадий процесса сравниваются с
экспериментальными данными.
288 ГЛАВА 9
t 9.5. Некоторые специальные вопросы, связанные
с пузырьковым течением
Размер пузырьков
Для практических приложений очень важно определить
размер пузырька, так как приведенные в разд. 9.2 простые урав-
25
го
»5
Пенисто
турбулентный
режим в
ъ
I
I4
Идеальный пузырьковый
режим
0,2
0,3
0,4
0,5
ос
Фиг. 9.9. Влияние условий ввода воздуха на величину-объемного
газосодержания при пузырьковом режиме течения [27].
1е0— приведенная скорость газа.
Характеристики перфорированных пластин
Обозначение
•
О
О
X
Число отверстий
1
49
100
289
Диаметр, мм
4,06
4,06
1,52
0,41
Шаг, мм (отверстия
расположены
по вершинам квадрата)
6,25
9,50
6,25
нения не применимы к сложным геометриям большинства
промышленных установок. Кроме того, размер пузырька является
важной переменной при расчете скорости его подъема
ПУЗЫРЬКОВОЕ ТЕЧЕНИЕ 289
с помощью табл. 9.1, а также при определении показателя п
в уравнении (9.12). По размеру пузырька можно также
установить, имеем ли мы дело с идеальным барботажем или же
с пенисто-турбулентным режимом течения. На фиг. 9.9
представлены данные, показывающие чрезвычайно сильное влияние
условий ввода воздуха. При одинаковых суммарных расходах
воздуха, вдуваемого в столб воды через разные
перфорированные пластины, получаются совершенно различные результаты.
Агломерация и дробление пузырьков
Если не принимать специальных мер, таких, как добавка
в жидкость поверхностно активных веществ, то пузырьки при
соприкосновении будут сливаться. Если размер введенных в си-
0 0,1 0,2 0,3 0,4 у
.ОС
Фиг. 9.10. Влияние агломерации на среднее объемное газосодержание при
барботаже воздуха через слои водопроводной воды разной высоты [22].
/go — приведенная скорость воздуха; а — среднее объемное содержание воздуха.
Начальная высота слоя жидкости: X 0,305 м, О 0,61 м, Д 0,915 м, идеальное пузырьковое
течение, уравнение (9.33); — ... — полностью развитое снарядное течение.
стему пузырьков меньше максимального устойчивого размера
для существующего поля касательных напряжений [уравнение
(9.11)], то происходит агломерация таких пузырьков. Размер
пузырьков, а следовательно, и значения зависящих от него пере-
19 Заказ № 162
290 ГЛАВА 9
менных, таких, как объемное газосодержание, будут в этом
случае определяться не только способом образования
пузырьков, но и длиной пути, пройденного ими от точки вдува.
Например, если воздух барботирует через неподвижный столб водо-
Фиг. 9.11. Влияние степени чистоты жидкости на объемное газосодержание
при пузырьковом режиме течения [22].
'«о- приведенная скорость воздуха; а — среднее объемное газосодержание.
• дистиллированная вода, увеличение расхода; + дистиллированая вода,
уменьшение расхода; О загрязненная дистиллированная вода, увеличение расхода; V
загрязненная дистиллированная вода, уменьшение расхода; О водопроводная вода, увеличение
расхода; X водопроводная вода, уменьшение расхода; Д мыльный раствор, увеличение
расхода; О мыльный раствор, уменьшение расхода; пузырьковое течение,
уравнение (9.33); —.._ полиостью развитое снарядное течение.
проводной воды, то величина среднего объемного газосодержания
зависит от высоты уровня воды в сосуде (фиг. 9.10).
Аналогично совершенно различные результаты могут быть
получены на одной и той же установке при различных степенях
чистоты жидкости, а следовательно, при различной ее
сопротивляемости агломерации (фиг. 9.11). Метод анализа процесса
агломерации пузырьков был разработан Радовчичем и Мойси-
сом [29].
ПУЗЫРЬКОВОЕ ТЕЧЕНИЕ
291
Рост и охлопывание пузырьков
Размер пузырьков в таких процессах, как кипение,
вскипание или конденсация, выделение газа из раствора или
растворение газа в жидкости, а также при движении пузырьков в
каналах со значительными перепадами давления, сопровождающемся
расширением пузырьков или их схлопыванием, является
переменной во времени величиной. Некоторые следствия этих
явлений будут представлены в конце данной главы в виде задач.
9.6. Трение и перенос количества движения
в пузырьковом течении
Хотя простая теория достаточно точно описывает
пузырьковое течение в вертикальном канале при малых скоростях фаз,
в общем случае нельзя пренебрегать влиянием касательных
напряжений на стенке ~ и изменением импульса. Гомогенная
теория может служить хорошим приближением в большинстве
задач, в которых существенны трение и Перенос импульса.
В области малых скоростей, где гомогенная теория неточна,
эти эффекты оказывают пренебрежимо малое влияние.
Обычно при описании потерь давления на трение
используется коэффициент трения С/, представляющий собой отношение
касательного напряжения на стенке xw к скоростному напору
потока Gj/2:
C,=-|f- • (9.46)
Этот коэффициент задается в виде функции числа Рейнольдса
Re=—. (9.47)
Пузырьковая смесь при ламинарном течении и малых значениях
а является ньютоновской жидкостью, и ее эффективная! вязкость
определяется уравнением (2.58):
!*=!*, (1+а). (9.48)
Если в жидкости содержатся загрязнения, то влияние а
усиливается, так как пузырьки по своему поведению напоминают
твердые сферические частицы.
К сожалению, уравнение (9.48) справедливо только при
значениях а, меньших 0,05. При больших объемных
газосодержаниях смесь быстро приобретает свойства неньютоновской
жидкости, ее вязкость начинает зависеть от величины
напряжения сдвига [30, 31], эффективная вязкость падает с ростом
скорости сдвига [32], наблюдается даже изменение вязкости под
19*
292
ГЛАВА 9
действием электрического поля [33]. Пенные образования при
больших объемных газосодержаниях обладают значительной
упругостью; пузырьки в этом случае ведут себя подобно атомам
в кристалле. Например, при течении пенистого пива по
пластмассовым трубкам все пузырьки движутся с одинаковой
скоростью, а область действия касательных напряжений ограничена
тонкой пленкой жидкости на стенке трубки.
Для турбулентного течения удовлетворительные результаты
получаются при расчете числа Рейнольдса по вязкости жидкой
фазы и использовании расчетных соотношений для однофазного
потока. При значениях чисел Рейнольдса до 105 хорошим
приближением является С/^0,005. Мейер [30] обнаружил, что
данные Роуз а и Гриффитса [34] ложатся вокруг этого значения С/
с разбросом точек, имеющим случайный характер, причем
максимальное отклонение составляет 25%. Поток импульса также
можно рассчитать с помощью теории гомогенного течения с
точностью примерно 20%. Если приведенные скорости компонентов
не очень велики по сравнению со скоростью дрейфа, то более
точные результаты для вертикального течения получаются при
расчетах с учетом поправки, полученной при решении
примера 4.1:
J\ l + hi/Ji ^ 1-72 1/72 Г
Пример 9.3. Вода и воздух движутся вверх по вертикальному каналу.
Значения плотностей фаз и приведенных скоростей следующие: р/=1 г/см3,
Рв =0,002 г/см3, jf=20 см/сек, /g=50 см/сек. Приведенная скорость дрейфа
определяется соотношением
jgf = 20а (1 — я)2 см /сек.
Каким должен быть поправочный множитель к величине потока
импульса, вычисленного по гомогенной теории, чтобы получить правильное
значение?
Решение. Поток импульса, рассчитанный по гомогенной теории, определяется
в виде jG, а искомый поправочный множитель — в виде
Gf Gg
7 +■
0(1 +jgf/jf) G(l-jg/ljg) •
С помощью уравнения (4.2) и заданных значений // и jg находим
а=0,25 и jgf=2,8 см/сек. Массовые плотности потока компонентов
соответственно равны
Gf = pfjf = 20 г/см2 ■ сек,
Gg = fgjg = 0,1 г/см2 ■ сек,
а искомый поправочный множитель
20 ■+„ °-' =0,878.
20,1(1+0,14) ч 20,1(1—0,056)
ПУЗЫРЬКОВОЕ ТЕЧЕНИЕ 293
9.7. Скорость звука в пузырьковых смесях
Скорость звука в пузырьковой смеси может быть рассчитана
с помощью уравнений, выведенных в гл. 6. В случае небольших
пузырьков, плотность которых значительно меньше плотности
жидкости, приближенно справедливо допущение о гомогенности
среды, и для определения скорости звука можно воспользоваться
уравнением (6.110), т. е. уравнением Вуда [35]:
с2_ J (9.49)
[»?g + (1 - «) ?/\ [*l?gcg + (1 - «)/Р/С/1 '
Для воздухо-водяной смеси при температуре 15,5° С и
адиабатическом процессе cg = 340 м/сек, с/= 1460 м/сек, a pg/p/=0,0012.
При а>10_3 хорошим приближением служит следующее
выражение:
(9.50)
[a(I-a)p,/p,]'/»
Минимум с имеет место при a = 0,5.
Из-за нестационарности тепловых эффектов, сопутствующих
прохождению волны, не всегда ясно, какой процесс следует
выбрать для расчета величины др/др в газе. При быстром сжатии-
и расширении можно ожидать, что процесс протекает
адиабатически. В этом случае
cl=4gReT. (9.51)
При медленном изменении параметров наиболее вероятен
изотермический процесс, т. е.
cg=RgT. (9-52)
При высоких частотах процесс должен приближаться к
адиабатическому, а при низких — к изотермическому [36, 37].
На фиг. 9.12 результаты расчета по уравнениям (9.51) и
(9.52) сравниваются с экспериментальными данными при
атмосферном давлении и умеренных частотах.
Если размер пузырьков мал, то их эффективная сжимаемость
изменяется под действием поверхностного натяжения. Для
определения скорости звука в этом случае следует [38] ввести в
выражение (9.50) множитель
(14-- * Vй
\ ^ 3pR„ + 4s )
где Rb — радиус пузырька, а р — давление. Для очень мелких
пузырьков этот множитель достигает своего предельного
значения 0,82. При больших частотах (выше —1 кгц), сравнимых
294
ГЛАВА 9
с собственной частотой пульсаций пузырьков [39],
определяемой [50] в виде (3yp/pfR2b)'k, возникают некоторые резонансные
явления.
/оо
до
80
70
^ .
^ 60
60
40
30
го
ю
О 0,2 0,4 0,6 0,8 1,0
ОС
Фиг. 9.12. Скорость звука с в пузырьковой смеси воздуха н воды при
атмосферных условиях [36, 37].
X 1 кгц; □ 0,5 кгц (данные работ [36, 37]); О экстраполяция на нулевую частоту;
■ изотермический процессу адиабатический процесс.
9.8. Границы пузырькового режима течения
Нижнего граничного значения объемного газосодержания для
пузырькового течения при однонаправленном движении двух
фаз не существует. На практике пузырьковый режим течения
нарушается по одной из двух причин:
1) из-за слияния пузырей при их образовании или в процессе
их движения по каналу;
2) вследствие специфических особенностей процессов вдува
и генерации газовой или паровой фазы и их динамического
взаимодействия с течением в канале.
I i 1 1 1 "'I """I 1 ' 1" |
1
J
!■ !
!
\ /
°v\ //
- о\ \ / /
°\ ^— —-^ ^s
° о
1
ПУЗЫРЬКОВОЕ ТЕЧЕНИЕ
295
Оба упомянутых выше процесса довольно своеобразны.
Скорость слияния пузырьков очень чувствительна к наличию
примесей, пусть даже в очень небольших количествах (фиг. 9.11).
Градиенты скорости и турбулентность вызывают увеличение
скорости слияния небольших пузырьков и, следовательно,
агломерацию, одновременно способствуя отрыву друг от друга
пузырьков большего размера. В инженерной практике иногда
используют очень приближенное эмпирическое правило, согласно
которому переход от пузырькового течения к снарядному течению
в «чистых» жидкостях происходит при величине объемного
газосодержания 10%, в то же время в работе Роуза [34] отмечалось
существование пузырькового режима в водопроводной воде при
60%-ном объемном газосодержании. Кроме того, имеются
вспенивающие вещества, с помощью которых можно обеспечить
пузырьковый режим течения по существу до 100% объемного
газосодержания.
Второй случай нарушения пузырькового режима течения
часто нельзя проанализировать без рассмотрения характеристик
всей системы в целом. Например, в трубе парогенератора
пузырьковое течение может смениться снарядным вследствие
подавления значительного числа центров парообразования, так
что пар будет образовываться в виде нескольких пузырей
большого размера вместо множества мелких пузырьков. Аналогично,
если газ вводится в поток жидкости через пористую поверхность,
то при определенных условиях на поверхности инжектора
происходит переход от режима генерации небольших пузырьков
к образованию газовой «подушки», которая периодически
разрушается с образованием отдельных пузырей в форме "снарядов
[22]. Только в некоторых специфических случаях, когда
предельные условия могут быть зафиксированы (возможно, в режиме
«захлебывания» течения), оказывается возможным описать этот
переход аналитически.
По чисто теоретическим соображениям должна существовать
возможность точного определения предельного устойчивого
распределения размеров пузырей (если такое вообще существует)
в очень длинном канале на достаточном удалении от точек ввода
всех фаз. Однако в большинстве практических случаев
пузырьковый режим течения никогда не бывает «полностью развитым»
и всегда испытывает влияние входных условий.
Пример 9.4. Воздух и вода движутся вверх в вертикальной трубе диаметром
50,8 мм и длиной 3,05 м. Смесь истекает в среду с давлением 1,033 ата.
Считая режим течения пузырьковым и принимая температуру смеси
равной 21° С рассчитать давление на входе в трубу для следующих
значений приведенных скоростей фаз, определенных при атмосферных
давлении н температуре:
296 ГЛАВА 9
jf
Jg<
м/сек
м/сек
0,152
0,305
0,305
0,61
3,05
0,61
4,58
3,05
9
9
15
15
9,75
9,75
10,4
10,4
11
11
0
0
11
11
6
6
12,2
12,2
Решение. Так как размер пузырьков не задан, то следует выбрать область
,, режимов, в которой происходит процесс согласно табл. 9.1, и
соответствующие значения показателя степени п в уравнении (9.12). Если не
принималось никаких специальных мер для образования мелких
пузырьков, то наиболее вероятным режимом, по-видимому, будет
пенисто-турбулентный, н для определения скорости vgj следует использовать
уравнение (9.34). Подставляя в него значения физических параметров воды и
воздуха при температуре 21° С, получаем
vsi = 0.25 м/сек, (1)
откуда
jgf = 0,25а. (2)
Подставляя это выражение в уравнение (4.5) и решая его
относительно а, находим
Jg
jf + Jg + Vgj
(3)
Так как давление вдоль трубы изменяется, то будет меняться и
величина je. Для изотермического процесса расширения
J*=-fu*\
а'
(4)
где ра — атмосферное давление, a (jg)Pa —заданная приведенная
скорость газа.
Дополнительные трудности возникают в том случае, если на выходе
из канала достигается скорость звука, т. е. происходит запирание
канала; при этом давление на выходе не обязательно равно давлению
окружающей среды.
Определим три составляющие градиента давления.
/. Составляющая, связанная с ускорением потока:
\ dz)A
Ов
dv.
s
+ Gf
dvf
Je-dT^"f^r'
ve и v/ определяются подстановкой уравнения (3) в (1.22) и (1.23)
Vg=jf + Jg + Vgj,
Jf + jg + vgj
Jf -Г Vgj
Вдоль канала изменяется только величина jg; следовательно,
Jvg djg
dz dz '
dVf djg
Jf
dz
dz jt + Vgj
(5)
(6)
(7)
(8)
(9)
ПУЗЫРЬКОВОЕ ТЕЧЕНИЕ
297
С учетом (8) и (9) уравнение (5) принимает вид
JUL) JaK + a, .3! )-%*-• (.0)
dz I a \ g r Jf + vgjl dz
Если длина выбранного участка достаточно мала, то производную dje/dz
можно найти дифференцированием уравнения (4), т. е.
dJg —a \ P°dP (П)
dz KJg'Pa p2 dz *
Из уравнений (10) и (11) получаем
2. Составляющая, связанная с потерями на трение:
Соответствующие значения входящих в уравнение (13) величин равны
С/=0,005, £>=50,8 мм,
а = ?gJg + ?fJf- С14)
J = Jf + Jg- (15)
3. Составляющая, связанная с действием силы тяжести:
-(■^)0 = ^Яр* + (1-я)р/]- (16)
Из уравнений (12)—(14) получается обычное выражение для dpldz
dp 2CfGjlD + g [a9g + (1 - a) P/]
dz l-(Ge + Gfjf/Uf + vgj)) (jg)p PalP2 '
(17)
Второй член в знаменателе уравнения (17) играет ту же самую
роль, что н квадрат числа Маха в уравнении (2.45). Если этот член
, больше единицы, то градиент давления меняет знак и течение должно
<5ыть сверхзвуковым. Обычно этого не происходит, и давление иа выходе
изменяется до момента запирания канала при числе Маха, равном единице.
Условия запирания следующие:
P* = P°WPa{ae + Gfjp^)> <18>
где ре — давление на выходе нз канала.
Методика решения задачи следующая. Труба делится на отдельные
участки и расчет давления ведется, начиная с выходного сечения трубы.
Прежде всего по уравнению (18) рассчитывается давление на выходе
из трубы, при котором произойдет ее запирание. Если оно меньше ра,
то давление на выходе будет равно атмосферному; если же оно
превышает ра, то произойдет запирание канала и давление на выходе
берется равным рассчитанному по уравнению (18). Значение а
определяется по уравнению (3), а —dpldz по уравнению (18). Тем самым
определяются значения р, a, js и / в начале последнего участка, после чего
298 ГЛАВА 9
указанная процедура повторяется, пока не будут определены искомые
параметры на входе в трубу.
Рассматриваемая задача была'решена на вычислительной машине.
Результаты расчетов приведены в табл. 9.2. Следует отметить, что при
малых расходах преобладает составляющая градиента давления,
обусловленная силой тяжести, а при больших расходах—составляющие,
связанные с ускорением и трением.
Таблица 9.2
Составляющие градиента давления, а также значения давления
на входе и выходе по результатам решения примера 9.4
jp м/сек
0,152
0,305
3,05
4,57
9,15
9,76
10,4
и.о
11,6 ,
12,2
Jg, м/сек
0,305
0,61
0,61
3,05
9,15
9,76
10,4
11,0
11,6
12,2
АРас ат
0,00003
0,00013
0,00428
0,400
0,489
0,585
0,654
0,691
0,728
0,835
Др j, ат
0,00021
0,00112
0,0659
0,1954
0,7759
0,8866
0,9787
1,075
1,176
1,280
4.Pg., ат
0,1790
0,1502
0,2627
0,200
0,198
0,202
0,206
0,210
0,214
0,217
Ре, ат
1,033
1,033
1,033
1,033
1,033
1,033
1,07
1,14
1,21
1,24
p., at
1,215
1,185
1,367
1,469
2,517
2,708
2,907
3,114
3,326
. 3,575
Примечания: Др — падение давления из-за ускорения; Др* — потери давления иа
трение; 4р — падение давления вследствие преодоления силы тяжести; р — давление в выходном
сечении канала; р, — давление во входном сечении канала.
9.9. Изотермическое гомогенное течение
газо-жидкостных смесей в прямых трубах
Вместо численных методов решения, как в примере 9.4, часто
удобнее пользоваться аналитическими выражениями для
зависимых переменных. Эти уравнения могут быть выведены с
помощью гомогенной теории, если рассматривать пузырьковую
смесь как псевдогаз с соответствующими физическими
свойствами.
Так как пузырьковый режим течения не существует при
больших объемных газосодержаниях, а плотность жидкости обычно
значительно больше плотности газа, то почти весь поток массы
приходится на долю жидкой фазы и результирующее течение
по существу является изотермическим. Итак, хотя в принципе
было бы интересно получить точные решения для общего случая
пузырькового течения, допущение постоянства температуры
обычно вполне оправдано.
На данной стадии пренебрежем влиянием фазовых
превращений, поскольку они усложнили бы анализ.
ПУЗЫРЬКОВОЕ ТЕЧЕНИЕ 299
Тогда, как обычно, выражение для градиента давления в
прямой трубе, расположенной под углом 8 к вертикали, будет
иметь вид
dp __2CfjG/D + (G/j) g cos 6
—dT l-jgGlp • <9-М>
Число. Маха для изотермических условий равно
М2=^-. (9.54)
Обозначим параметры, при которых число Маха равно единице,
звездочкой. Тогда из уравнения (9.54) следует
p*=fgQ. (9.55)
Из соотношений, описывающих изотермическое расширение газа
в канале постоянного сечения, имеем
(9.56)
(9.57)
(9.58)
(9.59)
Подставляя в (9.53) выражения для переменных /, р, jg, dp/dz
в функции числа Маха, получаем в итоге
Решая
Проди
совместно
-#-■
_ ^
Jg '
уравнения (9.54) — (9.5
Р=
Jg=
фференцируем уравнение
1
Р
dp _
dz
P*
M '
= M/J.
(9.57)
1 tfM
M dz
rfM i_M2_2C/ s*M+l . gcos8
dz M2 — D 6* +y2B*(l+Mo*)
(9.60)
где б =jg/jf (пример 6.7) и
8*=^. (9.61)
Из уравнения (9.60) видно, что и трение, и сила тяжести в
восходящем потоке действуют в одном направлении, стремясь
приблизить число Маха к 1. Это следует из того, что величина
dM./dz положительна при М<1 и отрицательна при М>1.
Очевидно, однако, что в нисходящем потоке трение и сила тяжести
действуют в противоположных направлениях, что может
300
ГЛАВА 9
привести к плавному переходу через М=1 при
i^f- (1+s*)2=~gc°s6 • (9-62>
Поскольку в этом случае правая часть уравнения (9.60) при
М>1 положительна, а при М<1 отрицательна, то скорость
течения должна изменяться от сверхзвуковой до дозвуковой при
непрерывном уменьшении числа Маха.
Уравнение (9.60) можно проинтегрировать, получив при этом
в явном виде довольно сложное уравнение для изменения числа
Маха с расстоянием. В этом случае давление и массовая скорость
газовой фазы повсюду определяются из уравнений (9.57) и (9.58).
При горизонтальном течении интегрирование упрощается.
Оно дает уравнение «линии Фанно» для пузырьковой смеси.
Уравнение (9.60) для этого случая можно записать через
элементарные дроби
^.Л_«[^-^-*^р.]. (9.63)
После интегрирования оно принимает вид
2С/"£!^=8*(-Ж- l) + 8*2lnM-(l-8**)lniL+^r. (9.64)
Полученное соотношение согласуется с данными Хьюи [40, 41].
9.10. Изотермическое гомогенное течение при изменении
только площади поперечного сечения канала
Если в уравнении движения существенны только члены,
учитывающие изменение количества движения, то оно принимает
вид
- -%-=°Ъ- (9-65)
В большинстве случаев при пузырьковом течении поток массы
почти полностью приходится на долю жидкой фазы, и тогда
Кроме того, для изотермического течения с параметрами
торможения ро и б о
-v=^- (9-67)
Подставляя (9.67) в (9.66), а результат в (9.65), получаем
dP (л 1 * Р0 \_„ ; dJ
dz
(1 + 8о^) = Р/У#. , (9.68)
ПУЗЫРЬКОВОЕ ТЕЧЕНИЕ .301
Если это уравнение проинтегрировать от условий
торможения до некоторого текущего значения р, то, как показали Танг-
рен, Додж и Зайферт [42], будет получено в явном виде
уравнение скорости течения в функции отношения давлений
?/Р
2Л>
■ = 1
Р
Ро
A In ■
Ро
(9.69)
Уравнения (9.66) и (9.67) можно также подставить в (9.54) и
получить
М2=
?/Р
Роьо
1 +
Роьо
(9.70)
Исключив из уравнений (9.69) и (9.70) параметр /2, получим
выражение для числа Маха в зависимости от отношения
давлений
М2=
_2_
l-k-b*ir)(l + -&F- <9J1>
При числе Маха, равном 1, р = р*, и из уравнения (9.71) можно
найти отношение р*/ро. В табл. 9.3 представлены некоторые
результаты расчетов этого параметра.
Таблица 9.3
Отношение р*/ро в сопле как функция отношения
приведенных скоростей газовой и жидкой фаз
(при параметрах торможения) и объемного
газосодержания для- пузырькового течения [42]
а0
So
Р*/Ро
0,67
2
0,55
0,5
1
0,52
0,333
0,5
0,46
0,2
0,25
0,39
0,091
0,1 .
0,30
0,05
0,05
0,25
Если известна зависимость отношения, давлений от числа
Маха, то с помощью соотношений, которые легко выводятся из
условия изотермичности течения, можно определить значения
ряда других полезных переменных. К числу таких соотношений
относятся
м=4-=
в*
А*
А
(9.72)
На фиг. 9.13 представлены результирующие зависимости
числа Маха, отношения давлений, отношения скоростей и
отношения плотностей от геометрии сопла.
Xs
32.
2.8
2.4
Г
'.2
0,4-
■II 1 1
_
»0=0,05-
0.Ю-
0,25-
0,50-
-
Jill
" -
jfi'Ш-К00
Ш/—2,00
W ~
zpo^jL~o,os
wJm-o,\o
^Я%Г^0,25
~ ^&^^-0,ЬО
^**\ i i i i i i i
*6
2fi
2.4
0,2
Суживающаяся
°-6SM '-°
0.6 0,2 0
Расширяющаяся |
Горло
а
2.0
1,6
*
1,2 =:
0.8
0,4
1 1 1 1
:==:==^<^
ziit^^,
0,25//^
0.10 У
0.05
0,2
0
1 1 1 1
1 1 1 1
= 2.00
1.00
-0,50
к,0,05
ISC'0-'0
5^%v
,50 ^^ч
;,оо-^^
2,00 ^^^.~
i i i гЧ
о ол
0.6,
■ '.О
0,6
0,2 О
Суживающаяся Расширяющаяся
Горло
в
1,6
1,2
0,8
0,4
1
~
-
-
^^^
—
-
-
1
\ ' '
0,26 -_
0.10 —
0,05 -
1 1 1
1 1 "1 '1
^*о=0,06
^0,10
^-0£0
^1,00
^2,00
^у 2,00
«К Л00
1 1^^
—
-
-
_
_
-
-
-
О 0.2
0.6
/f/A
1,0 0,6 0,2 О
Суживающаяся Т Расширяющаяся
' * часть " часть " *"1
Горло
6
2,0
',6
1,2
}
5-
0,8
0,4
1 1 1 1
-
—
-
г\
1 1 1 1
«0=2,00^
0.05^1 ^
,^^~S^~- Uoo
Г ^ 2,00 '
1 1 1 1 1
ч0,25
ч0,10
0,05
1 1
-
-
-
1
О 0,2
0,6
А/А
1.0 0,6 0,2 О
Суживающаяся Расширяющаяся
Гор^
Фиг. 9.13. Характеристики сопел при изотермическом пузырьковом течении
без трения [42].
ПУЗЫРЬКОВОЕ ТЕЧЕНИЕ 303
Площадь горла сопла в функции параметров на входе в сопло
определяется из уравнения (9.54) приМ = 1
JgG*_Q*gW (Qg)0Wpo
1 р Л*2р* Л*2р*2 ' [У.Ю)
откуда
m"--
Качественно процессы истечения пузырьковых сред из сопел
и методы решения практических задач очень сходны с
аналогичными задачами однофазных течений, рассмотренными в работе
Шапиро [43].
Использование уравнений движения для каждого
компонента
Хотя допущение о гомогенности потока вполне приемлемо для
большинства задач, оно все же может оказаться ошибочным
в том случае, когда под действием массовых сил или
ускоряющего поля возникает значительная относительная скорость фаз
(«скольжение»). Ранее уже было показано, как с помощью
модели потока дрейфа можно учесть скольжение в
низкоскоростном вертикальном потоке. Если же ускорение существенно
(в соплах оно может во много раз превышать величину g), то
уравнения движения следует рассматривать отдельно для
каждого компонента [уравнения (3.45) и (3.46)].
Когда силы / не очень велики, то, очевидно, при заданном
градиенте давления газ будет разгоняться значительно быстрее
жидкой фазы, чем и обусловливается отклонение от допущения
о гомогенности течения. Сила f состоит по крайней мере из трех
составляющих: силы сопротивления, силы, связанной с
присоединенной массой, и силы Бассе. Характер взаимодействия этих
сил пока еще не изучен в подробностях. Присоединенная масса,
как показано в примере 8.4, ограничивает верхний предел
отношения Vg/vf величиной, равной примерно 2. Измеренные Мюиром
и Эйхорном [44|] значения vg/vf при течении высокоскоростных
потоков в соплах заключены в пределах от 1,1 до 1,8.
9.11. Ударные волны
Согласно Эддингтону [45}, как прямые, так и косые скачки
уплотнения в пузырьковых потоках могут быть описаны с
помощью изотермической гомогенной теории, представленной
в разд. 6.6. Соотношения для прямого скачка уплотнения можно
304 ГЛАВА 9
получить непосредственно из уравнения (6.175):
M?=-L=<^=^L»L-. (9.75)
Толщина ударной волны определяется рассмотренными в гл. 8
процессами релаксации. Равновесие в данном случае наступает
значительно быстрее, чем при течении смеси газа с твердыми
частицами. Типичные измеренные значения толщины ударной
волны составляют примерно 25 мм.
Задачи
9.1. В воде при температуре 20е С очень медленно образуется пузырек
воздуха. Каков его отрывной диаметр, если а) он образуется в обращенных
устьем вверх несмачиваемых отверстиях радиусом 0,1, 0,5, 1 и 2 мм; б)
отверстие, в котором происходит образование пузырька, представляет собой
углубление в смачиваемой поверхности, а краевой угол р равен 30, 60, 90
или 120°?
9.2. Рассчитать равновесный размер пузырька в миксере для сбивания
сливок, содержащем 1 л жидкости, если мощность двигателя Ув л. с.
9.3. С учетом присоединенной массы показать, что уравнение движения
сферического пузырька, свободно растущего в невязкой жидкости,
имеет следующий вид [4]:
n^/-?g)g = ^r [Vb (?g + >/2Р/) —-] ■
Объяснить, почему во время роста пузырька появляется дополнительная
сила fg.
9.4. Рост пузырька в задаче 9,3 происходит по закону "Vb=Ata, где А и
а — постоянные, a pg<g pf. Показать, что в этих условиях центр пузырька
за время t переместится на расстояние
г— \-r-gt2-
а + 1 s
9.5. Показать, что если пузырек в задаче 9.4 растет в устье отверстия, со
стороны которого на него не действует никаких сил, а отрыв пузырька
происходит при z=Rb, то его объем в момент отрыва равен
]1/(б-о)
■[(■i-гтм
Показать, что это уравнение согласуется с уравнением (9.5) при а=\. Что
произойдет, если а=6?
9.6. Если рост пузырьков происходит в условиях нестационарного тепло-
нли массообмена, то их радиус увеличивается пропорционально корню
квадратному из времени. Пузырек зарождается в перегретой жидкости путем
пропускания импульса тока по нагретой проволоке. Рост пузырька
описывается уравнением Rb=2t'12, где Rb выражен в см, а / — в сек. Каков
объем пузырька в момент его отрыва от проволоки?
9.7. Решить задачи 9.3 и 9.4 при условии, что пузырек растет в очень вязкой
жидкости. Принять, что скорость движения пузырька постоянна и равна
предельной скорости. Показать, что при а = 1 решение имеет вид уравнения (9.6).
9.8. Каков максимальный объем пузырька, который можно выдуть из
данного отверстия в вязкую жидкость, если справедливо уравнение (9.7)? Рас-
ПУЗЫРЬКОВОЕ ТЕЧЕНИЕ 305
считать этот объем для случая вдува воздуха в патоку через отверстие
диаметром 6,35 мм (p_f = l,2 г/см3, jn_f = 1000 пз).
9.9. Решить пример 9.1 при Rb =0,005, 0,05, 0,1, 0,3 и" 1,0 см.
9.10. Решить пример 9.1 и задачу 9.9, если жидкость—анилин с р/ = 1,02 г/сж3,
ц/=2,93 спз, а=41,7 дин/см.
9.11. Пузырек образуется в столбе пересыщенной двуокисью углерода воды.
Верхний конец столба высотой 30,5 м открыт. Согласно данным работы [49],
0,25
С 0,20
0,15
А 1 1 1 1 |
° ° о
Е
1 i i i I I
1 1 1 1 1 1 II
*9 ^
S о.й
о
ч:
i i i 11111
о
А
0,003
0,01
0,1
jgO. м/сек
а
0,25
0,20
0,15
л 1Л
i 1 1 1 П
О О
о
о
8
1 1 1 1 1 1
I i i i i i i i
°8
° о
О
о
о
о
о
1 1
* о о
О о
. °о о
i 1 0| | | |
о
0.003
0,01
о.т
j 0,м/сек
б
Фиг. 9.14. а — скорость движения пузырьков; б — скорость дрейфа при бар-
ботаже газа через неподвижную жидкость 146].
v„ — скорость пузырьков; о„- — скорость дрейфа; /^ — приведенная скорость газа.
коэффициент массоотдачи к всплывающим пузырькам не зависит от их
диаметра, так что массовая скорость выделения газа постоянна. Приняв массовую
скорость выделения газа равной 10~4 г/см2-сек, рассчитать объем пузырька
и скорость его подъема в различных точках столба воды, если пузырек
образуется в основании столба и его диаметр равен 10 мк. Испарением в пузырек
пренебречь, но учесть изменение гидростатического давления и действие сил
поверхностного натяжения. -
9.12. В работе Никлина [46] была определена зависимость скорости дрейфа
vgj пузырьков воздуха в неподвижной воде от приведенной скорости газа.
Полученные им результаты представлены на фиг. 9.14. Найти связь между
20 Заказ №. 162
306 ГЛАВА 9
jgf и а, а также между »м и п; объяснить существование минимума vgj.
9.13. В работе [47] исследовано однонаправленное течение воздухо-водяной
смеси по вертикальной трубе диаметром 5,3 см. Результаты этого
исследования приведены на фиг. 9.15, а. Используя данные фиг. 9.15, а, рассчитать п,
vco • vei и /*/ в функции а. Какой режим пузырькового течения будет иметь
место? На фиг. 9.15,6 представлена зависимость vgj от а. Каковы будут
значения от и п, если воспользоваться данными этого графика?
Согласуются ли выводы, следующие из этих двух графиков?
25
20
£
Г5
10
о
0.1
а
6
0.2
0.3
Фиг. 9.15. Некоторые экспериментальные данные для вертикального
пузырькового течения [47].
О экспериментальные данные.
9.14. Смесь воздуха и бензола (а=28,8 дин/см, р/=0,875 г/см3, ц/ = 0,647 спз)
движется вверх по вертикальной трубе диаметром 25,4 мм. Расходы фаз
составляют соответственно 0,454 и 454 кг/час. Диаметр пузырьков в нижней
части трубы, где давление 3,52 ата, а температура 15е С, равен 2 мм.
Рассчитать изменение объемного газосодержания и давления с высотой. Какой
длины должна быть труба, чтобы снизить давление до атмосферного?
9.15. Решить задачу 9.14 при десятикратном увеличении расходов обеих фаз.
9.16. Цепочка пузырьков воздуха радиусом Rb = \2,7 мм поднимается вверх
в неподвижной жидкости, заполняющей вертикальную трубу диаметром
50 мм. Какова их скорость а) в глицерине при 20° С и б) в воде при 20° С?
Каков расход газа в каждом случае, если расстояние между пузырьками
в цепочке составляет 76 мм>
9.17. Длинная вертикальная труба частично заполнена чистой воДой. Высота
столба воды 50 см. Вода содержит сильно вспенивающее вещество. В
основание столба внезапно подводится воздух с приведенной скоростью 3 см\сек.
ПУЗЫРЬКОВОЕ ТЕЧЕНИЕ 307
Каждый образующийся пузырек имеет объем 0,002 смъ. Показать, что
графики, представленные иа фиг. 9.16, качественно описывают поведение
системы. Выделить на графиках различные стадии процесса и рассчитать
характерные значения параметров. Какие режимы, если таковые существуют,
физически невозможны или неустойчивы?
9.18. Какова скорость звука в смеси водорода с воздухом при давлении
70 ата, температуре 21е С и средней плотности смеси 0,64 г/см3?
9.19. Решить задачу 9.18, если давление 0,35 ата, а радиус пузырька 1 мм.
9.20. Решить пример 9.4 для случая горизонтального течения.
Фиг. 9.16. Диаграмма неустановившегося процесса барботажа в системе,
описанной в задаче 9.17.
9.21. Через бак диаметром 0,3 м, содержащий 76 л воды при температуре
20° С, должен барботировать воздух с расходом 0,095 нмг1мин. Конструктор
может выбирать число сопел или отверстий для вдува воздуха, а также их
диаметр. Показать, как зависят следующие параметры от конструктивных
характеристик системы вдува: а) объемное газосодержание, б) время
пребывания пузырей в жидкости, в) суммарная поверхность раздела фаз в баке,
г) предельные значения параметров, соответствующих режиму барботажа.
9.22.'Шульмаи и Молстед [23], исследовавшие пузырьковое течение при
противоточиом движении фаз в колонне диаметром 100 мм, обнаружили,
что «захлебывание» происходит прн следующих массовых скоростях воды
и.двуокиси углерода:
—Wf, кг/м2 • час
Wg, кг/м2 • час
73200
185
48 800
205
24 400
234
Сравнить эти данные с теоретическими значениями.
20*
308
ГЛАВА 9
9.23. Вывести уравнение (9.72).
9.24. Показать, что при изотермическом гомогенном течении в сопле при
отсутствии потерь на трение
-7141И'4)!-^[ст('4)]=
1 dm M2(l + l/8>
— М2 dz 2(1 +M2/S)
и что это уравнение вместе с (9.72) может служить основой для численных
расчетов всех переменных в функции б* и М.
9.25. Как зависит расход жидкости через регулирующее сопло-вентиль
заданной геометрии при заданных параметрах торможения на входе от
величины б0? Вывести соотношение между Wf И Wg для такого сопла-вентиля,
описанного в задаче 2.21. Спроектировать вентиль такого типа для
регулирования с помощью сжатого воздуха расхода нефти (плотностью
960 кг/ж3) в диапазоне от 1 до 10 т)час при температуре 15,5° С и
давлении 7 ата.
9.26. Считая отношение (1 — а)/С в сопле постоянным (С— коэффициент
присоединенной массы), показать, что предельное значение отношения vg/vf
в ускоряющемся пузырьковом потоке равно
vg = 2(1—а)
vf ~ УС2+ 4С(1 — а) — С
Показать, как отношение скоростей зависит от среднего объемного
газосодержания, считая, что С = '/2-
Если пузыри принимают форму эллипсоидов с отношением осей 1 :6,
то величина С падает до 0,045. Как это сказывается на отношении скоростей?
9.27. Показать, что отношение скоростей при переходе через прямой/скачок
уплотнения в пузырьковой смеси в функции параметров течения перед скачком
описывается соотношением
к ___ Щ+h
h m;_(i + »,) •
9.28. Вода и воздух подаются в экспериментальное сопло Л аваля при
давлении 7 от и температуре 21° С. Расход воды 2,83 м3/мин, расход воздуха
5,66 нм3/мин. Каково сечение горла в случае запирания канала? При какой
площади выходного сечения в сопле возникают скачки уплотнения, , если
истечение происходит в атмосферу с давлением 1,033 ата? Построить
кривую изменения давления по длине сопла в функции площади поперечного
сечения канала для различных значений выходного сечения сопла. Какова
максимальная тяга сопла?
9.29. Проанализировать силы, действующие на пузырьки в одномерном
потоке. При каких условиях течение определяется балансом между а) силой
тяжести и силой сопротивления, б) силами инерции и давления, в) силой
давления и силой Бассе, г) силой поверхностного натяжения и
подъемной силой?
9.30. Показать, что если Твлагосодержание в в уравнениях (9.39) и (9.40)
считать малой величиной, то при этом вносится ошибка, ведущая к
занижению продолжительности стадии 1 процесса дренирования влаги. Показать,
что стадия 1 в примере 9.2 действительно кончается в момент t=30 сек,
когда из пены дренируется 3,87 см3 жидкости.
9.31. Бутыль с пивом резко встряхивается, после чего ее содержимое
выливается в длинный прямой вертикальный сосуд. Описать происходящий про-
ПУЗЫРЬКОВОЕ ТЕЧЕНИЕ , 309
цесс, если начальное объемное газосодержание смеси составляет 80% и по
прошествии первых нескольких секунд пузырьки не образуются и не схлопы-
ваются.
9.32. Решить задачу 9.31 при начальном объемном газосодержании 30%.
9.33. Согласно данным работы [48], размер пузырьков, образующихся в
отверстиях сопел в установках с псевдоожиженным слоем, описывается
уравнением (9.5). Рассчитать объемное газосодержание в функции числа сопел,
если слой стеклянных шариков диаметром 0,01 см приводится в псевдоожи-
женное состояние путем вдува воздуха при нормальных давлении' и
температуре с приведенной скоростью 3 см/сек. Толщина слоя 3 м. Принять, что
все избыточное количество воздуха сверх необходимого для обеспечения
псевдоожижениого состояния идет на образование пузырьков.
Сформулировать остальные сделанные допущения.
Литература
-139 (June 1956).
твердых частиц.
Trans. Inst. Chem. Engrs, 38,
Progr.,
' W.,
49, 88
Model
L., Morton R. K-, Taylor D.
and Physical Papers, vol. 1,
1. Кутателадзе С. С, Стырикович М. А., Гидравлика газо-жидко-
стных систем, Госэиергоиздат, М.—Л., 1958.
2. Jackson R., Chem. Eng., 42, 107—118 (May 1964).
3. S i e m e s W., К a u f m a n n J. F., Chem. Eng. Sci., 5, 127-
4. Д э в и д с о н И. К., X а р р и с о н Д., Псевдоожижение
изд-во «Химия», 1965.
5. Davidson J. F., Sch filer В. О. G
144—154, 335—342 (1960).
6. Taylor G. I., Proc. Roy. Soc. (London), A210, 192 (1950)
7. ZuberN, AEC Rept U-4439, 1959.
8. Fritz W, Physik. Z., 36, 623 (1933).
H i n z e J. O., A. I. Ch. E. J., 1, 289 (1955).
Peebles F. N., G a r b e r H. .L, Chem. Eng.
Haberman W "
802, 1953.
Stokes G. G., Mathematical
Uriiv. Press, London, 1880.
13. H a d a m a r d J., Compt. Rend. Acad. Sci. Paris, 152, 1735—1738
14. Rybczynski W., Bull. Acad. Sci. Cracovie, A, 40—46 (1911).
15. Da vies R. M., Taylor G. I., Proc. Roy. Soc. (London), 200,
375—390 (1950).
Harmathy T. Z, A. I. Ch. E. J., 6, 281 (1960).
С о 11 i n s R., /. Fluid Mech., 28, part 1, 97—112 (1967).
LadenburgR., Ann. Phys., 23, 447 (1907).
Edgar С. В., Jr., AEC Rept № NYO-3114-14 by G. B. Wallis, 1966, pp. 19—
21.
J a m e s о n G. J., Chem. Eng. Sci., 21, 35—48 (1966).
Jameson G. J„ Davidson J. F., Chem. Eng. Sci., 21, 29—34 (1966).
Wallis G. В., Intern. Heat Transfer Conf, Paper № 38, Boulder, Colo.,
ASME 1961
23. Shul'manH. L., Mo 1st ad M. C, Ind. Eng. Chem., 42, p. 1058 (1950).
24. Кутателадзе С. С, Москвиче в а В. Н., ЖТФ, 29, № 9, 1135—
1141 (1959).
Ga у lor R., Roberts N. W., Pratt H. R. С, Trans. Inst. Chem.
Engrs, 31, 57 (1953).
M i 1 e s G. D., ShedlovskyL, RossJ., /. Phys. Chem., 49, 93 (1943).
Zuber H., Hench J., Rept № 62GL100, General Electric Co.,
Schenectady, N. Y., 1962.
3 у б е р Н., Труды амер. общ-ва инж.-мех., серия С, Теплопередача, № 4,
стр. 29 (1965).
9.
10.
11.
12.
16.
17.
18.
19.
20.
21.
22.
25.
26.
27.
28.
-97 (1953).
Basin Rept'
Cambridge
(1911).
ser. A,
* 310 ГЛАВА 9
29. R a d о v с i с h N. А., М о i s s i s R., Rept № 7-7673-22, Dep. Mech. Engrs,
Massachusetts Inst. Techn., 1962.
30. Meyer P. E., Wallis G. В., AEC Rept № NYO-3114-12 (EURAEC
1530), 1965.
31. Penny W. G., Blackman M., Note 282, Ministry of Home Security,
Great Britain, 1943; см. также Hermans J., Flow Properties of Disperse
Systems, North-Holland Publ. Co., Amsterdam, 1953.
32. Sibree Т. О., Trans. Faraday Soc, 31, 325 (1943).
33. Raza S. H., Mars den S. S., Soc. Pet. Engrs J., 359—368 (December
1967).
34. Rose S. C, Jr., Griffith P., Rept 5003-30, Mass. Inst. Techn., 1964.
35. В у д А., Звуковые волны и их применения, Гостехтеоретиздат М.—Л.,
1934.
36. Karplus H. В., Rept COO-248, Armour Res. Found., June 1958.
37.-Gouse S. W., Jr., Brown G. A, E. P. L. Rept DSR 8040-1, Mass. Inst.
Techn, April 1963.
38. Marchal R., Compt. Rend. Acad. Sci., 254, 2524—2526 (1962).
39. Silberman E, /. Acoust. Soc. Am., 29, № 8, 925—933 (1957).
40. Hue у С. Т., Bryant R. A. A, A. I. Ch. E. J., 13, № 1, 70—76 (1967).
41. Huey С. Т, Can. J. Chem. Eng., 44, № 6, 313—321 (December 1966).
42. Tangren R. F., Dodge С H., S e i f e r t H. S., /. Appl. Phys., 20, № 7,
637—645 (1942).
43. S h a p i г о А. Н, Dynamics and Thermodynamics of Compressible Fluid
Flow, Ronald Press Co, N. Y, 1953.
44. M u i r J. F, E i с h h о г п R, JSME Semi-Intern. Symp, Tokyo, September
1967, pp. 81—92.
45. Eddington R. B, AIAA Paper 66-87, 1966, см. также Rept32-1096,JPL,
Calif. Inst. Techn, 1967.
46. N i с k 1 i n D. J, Chem. Eng. Sci., 17, 693—702 (1962).
47. Marrucci G, Gioia F, Chim. Ind., Italy, 45, № 10, 1205—1211 (1963).
48. Harrison D, Leung L. S, Trans. Inst. Chem. Engrs, 39, 409 (1961).
49. Calderbank P. H, Moo-Young M. B, Chem. Eng. Sci., 16-39—54
(1961).
50. Ф о с т е р Дж, Б о т т с А, Б а р б и н А, В а х о н Р, Труды амер. общ-ва
инж.-мех., серия D, Теоретические основы инженерных расчетов, № 1,
137 (1968).
10
СНАРЯДНОЕ ТЕЧЕНИЕ
10.1. Введение
Снарядное течение характеризуется последовательным
прохождением по каналу одиночных больших пузырей,
занимающих почти все его поперечное сечение. В
качестве примера можно упомянуть течение га- г
зо-жидкостной смеси в соломинке, когда бокал
уже почти пуст; течение в «стояке»
кофеварки; течение в горловине слишком быстро
опорожняемой бутылки.
Характерный вид пузыря при снарядном
течении в вертикальной трубке, полученном
в лабораторных условиях, показан на фиг. 10.1.
Фиг. 10.1. Снарядоподобный пузырь, всплывающий
в глицерине в вертикальной трубке.
10.2. Общая теория
Динамика пузыря
Если удается описать динамику типичного одиночного
пузыря, то можно рассчитать и некоторые интегральные
характеристики снарядного режима течения. По-видимому, это лучше
всего сделать, рассмотрев единичную ячейку, состоящую из
одного пузыря и части жидких пробок по обе стороны от него, как
показано на фиг. 10.2. При заданной величине суммарного
объемного расхода скорость смеси (средняя плотность суммарного
объемного расхода) / определяется из простого соотношения
,_«^. „„.I,
312
ГЛАВА 10
Динамика рассматриваемого пузыря определяется этой
скоростью, соответствующим профилем скоростей, длиной пузыря,
геометрическими характеристиками трубки и свойствами
жидкости. Без учета влияния следа предыдущего
пузыря профиль скорости в жидкой пробке
будет зависеть от шероховатости трубки и
числа Рейнольдса
э ..
I.
J/
Re,=
JD?f
*f
(10.2)
Следовательно, динамика пузыря зависит
от /, а не от приведенных скоростей jg и jf
газовой и жидкой фаз. Кроме того, так как
каждая единичная ячейка, показанная на
фиг. 10.2, независима, динамика пузыря не
связана с объемным газосодержанием а.
Фиг. 10.2. «Единичная ячейка», рассматриваемая при
анализе снарядного течения.
Скорость пузыря
Согласно изложенному выше, скорость пузыря является
функцией средней плотности суммарного объемного расхода /,
геометрии трубки, свойств жидкости и поля массовых сил. Почти
во всех- случаях длина пузыря не является существенной
переменной, так как его движение полностью определяется
динамикой его носовой и хвостовой частей.
Скорость дрейфа газовой фазы равна разности скорости
пузыря и скорости смеси
vg}=vb-j. (10.3)
Следовательно, скорость дрейфа также не зависит от объемного
газосодержания, но зависит от /, а не от jg и jf.
Объемное газосодержание
Величина объемного газосодержания, или средняя объемная
концентрация газа, может быть выведена из уравнения (1.10),
если известны скорость пузыря и приведенная скорость газовой
фазы ,•
«~. (Ю.4)
СНАРЯДНОЕ ТЕЧЕНИЕ 313
Падение давления
Падение давления удобно представить в виде трех
составляющих:
. 1) падения давления в жидкой пробке;
2) падения давления на концах пузыря;
3) падения давления вдоль пузыря.
Обычно вязкость и плотность газа значительно меньше, чем
у жидкости. В этом случае газ в пузыре по существу находится
при постоянном давлении. Пузырь имеет приблизительно
цилиндрическую форму, и поверхность раздела газ—жидкость имеет
постоянную кривизну. Поэтому давление вдоль пузыря не
уменьшается и третья из перечисленных выше составляющих равна
нулю.
Падение давления в пробке жидкости (первая составляющая)
может быть рассчитано по обычной методике для однофазного
течения.
Падение давления на концах пузыря (вторая составляющая)
должно быть определено через основные параметры течения.
10.3. Вертикальное снарядное течение
Скорость подъема одиночных пузырей
в неподвижной жидкости
Всплытие пузыря в* более плотной жидкости происходит под
действием подъемной силы. Скорость Uoo, с которой одиночный
пузырь всплывает в неподвижной жидкости, определяется
взаимодействием подъемной силы и других сил, действующих на
пузырь и зависящих от его формы и характера движения. Если
вязкостью газа или пара в пузыре можно пренебречь, то, кроме
подъемной силы, существенными оказываются, только три силы:
инерция жидкости, вязкость жидкости и поверхностное
натяжение. Соотношение между подъемной силой и этими тремя силами
может быть выражено через три безразмерных комплекса
DgiSf-ъУ 02*<Р/-р,)' D*gtij-fg)'
где D — характерный размер поперечного сечения канала.
Общее решение задачи представляет собой функцию этих трех
параметров, которые могут быть тем или иным образом
скомбинированы в виде новых безразмерных величин. Так как длина
пузыря больше диаметра трубы, то она не влияет на скорость
подъема пузыря. С другой стороны, из уравнений (9.26) и (9.29)
следует, что эквивалентный диаметр пузыря должен превышать
60% диаметра трубы.
314 ГЛАВА 10
Наиболее простые решения получаются в том случае, если
движение определяется только одним безразмерным комплек-
« сом. Ниже дается анализ этих предельных случаев.
Случай преобладающего влияния инерционных сил. Если
можно пренебречь вязкостью и поверхностным натяжением, то
скорость подъема пузыря определяется исключительно первым
из трех безразмерных комплексов. Таким образом,
^=klPJ^[gD(Pf-?g)}''\ (10.5)
Приближенные аналитические решения этой задачи для
снарядного режима течения в цилиндрическом канале были получены
в работах [1, 2]. Для круглых труб получены следующие
значения постоянной ki:
£,=0,351 (работа [1]), (10.6)
£,=0,328 (работа [2]). (10.7)
Экспериментальным путем получено чуть отличающееся
значение постоянной ki = 0,346. Это значение близко к значению
ki=0,345, полученному в ряде опытов Уайта и Бердмора [3].
Таким образом, предпочтительным является значение
£,=0,345. (10.8)
Если измерить скорость подъема пузыря в трубе с открытым
верхним концом, то достаточно явно обнаружится зависимость
скорости от длины пузыря, что обусловлено расширением газа
при подъеме пузыря под действием градиента гидростатического
давления. Благодаря этому расширению величина / перед
пузырем не равна нулю и скорость подъема пузыря увеличивается за
счет движения жидкости перед ним. Никлин [4] измерял время
прохождения пузырей различной длины в закрытых сверху
трубах, исключающих возможность движения жидкости перед
пузырем. Он показал, что скорость подъема пузыря относительно
неподвижной жидкости действительно описывается уравнениями
(10.5) и (10.8) и не зависит от длины пузыря.
Гриффите [5] исследовал снарядное течение в трубах с
некруглым поперечным сечением. В прямоугольных каналах со
сторонами Db и Ds более существенное влияние оказывает
больший размер Ъь, и его следует использовать в качестве
характерного размера для подстановки в уравнение (10.5). Константа ki,
представленная в виде функции отношения Ds/Db:
*!=0,23+0,13-5*-, (10.9)
хорошо согласуется с данными, полученными Гриффитсом.
Предельный случай Ds/Db ->■ 0 согласуется с теоретическими
расчетами Биркхофа и Картера [6] для плоских двумерных пузырей.
СНАРЯДНОЕ ТЕЧЕНИЕ
315
В работе Гриффитса приводятся также данные по скорости
подъема пузырей в кольцевых каналах и трубных пучках.
Характерным размером кольцевых каналов, используемым для
подстановки в уравнение (10.5), является наружный диаметр D0.
На фиг. 10.3 представлена зависимость коэффициента ki of
отношения внутреннего диаметра канала к наружному Di/D0.
Из рассмотрения этого графика можно сделать важный вывод:
чем меньше ширина кольцевой щели, тем больше скорость
подъема пузыря. В предельном
случае Di = D0 значение постоян- о,в
ной k\ приблизительно равно
£,=0,23 ]/т7. (10.10) *•
Фнг. 10.3. Зависимость
коэффициента k\ от геометрии канала [5].
' — трубные пучки; 2 — кольцевой канал:
3 — прямоугольный канал; OtID0 — для
кольцевого канала; (1 — Dh/D0) — для
грубиых пучков; DJDb — для
прямоугольного канала; Dh — гидравлический
диаметр.
0.4
0,21
0,2 0,4 0,6 Q8
VA>. 1-Dh/D0),DS/Db
',0
Это значение можно получить и из уравнения (10.9) для
плоского пузыря, охватывающего кольцевую щель, считая, что
вся жидкость собирается на одной стороне щели.
Симметричные пузыри в кольцевых каналах обычно не
наблюдаются.
В трубных пучках в качестве характерного размера лучше
взять диаметр обечайки D0, а не диаметр отдельных труб.
Экспериментальные данные, подтверждающие существование снаря-
доподобных пузырей в трубных пучках, содержатся в статье
Гриффитса [5].
Следует напомнить, что приведенные выше уравнения
справедливы, только когда можно пренебречь влиянием сил
поверхностного натяжения и сил вязкости. Границы их применимости
будут рассмотрены позднее.
Случай преобладающего влияния вязких сил. Если в
потоке преобладают силы вязкости, то уравнение,скорости подъема
пузыря легко выводится из соответствующего безразмерного
комплекса
v„=k0
gD4?f-?g)
(10.11)
Экспериментальные данные подтверждают это уравнение
•для случая вертикальных круглых труб при следующих
316
ГЛАВА 10
значениях k^:
£2=0,010 (работа [7]), " (10.12)
^=0,0096 (работа [3]). (10.13)
Случай преобладающего влияния сил поверхностного
натяжения. Силы поверхностного натяжения преобладают в том
случае, когда пузырь вообще не движется. Поверхность раздела
фаз в статических условиях принимает такую форму, при
которой гидростатические силы полностью уравновешиваются силами
поверхностного натяжения. В случае вертикальных круглых
труб подобное равновесие имеет место {8, 9] при
JVEg- gDHV~?g) <3,37. (10.14)
Этот безразмерный комплекс был назван Гартмати [Ю]^лислом
Этвеша.
Иногда используют и другую перемтнулйг-назьГваемую
числом Бонда и определяемую как
. „fc=**(P/-P«>=J^,. (10Л5)
Общий случай. Поскольку в общем случае решение
описывается тремя параметрами, то его можно представить в виде
графика на плоскости, взяв в качестве переменных любые два
безразмерных комплекса и рассматривая при этом третий
независимый безразмерный комплекс как параметр. Выбор
комплексов в том или ином качестве диктуется только соображениями
удобства. Например, определяемая уравнением (10.5)
безразмерная скорость пузыря ki равна 0,345 согласно (10.8) и может
быть представлена в функции безразмерной обратной
вязкости Nf
[£%(?/■ — Pp-)P/]Vi
Nt= — ■ (10.16)
Комплекс Nf получается путем исключения Voo из двух первых
безразмерных комплексов. Весьма удобный третий независимый
параметр определяется путем исключения v<x> и D. Полученное
при этом число Архимеда зависит только от свойств жидкости
и ускорения силы тяжести и является величиной, постоянной для
данной жидкости при заданной температуре. Таким образом,
А^АГ= ,,,„ " ■ (ЮЛ/)
На фиг. 10.4 экспериментальные данные представлены в виде
перечисленных выше комплексов. Видно, что при этом удов-
СНАРЯДНОЕ ТЕЧЕНИЕ
317
Ю'
/с,= 0,345 (Ю.в)
Соотношение(Ю. 19)
Юч
10°
Фиг. 10.4. Скорость подъема пузыря при снарядном режиме течения [7].
kt — безразмерная скорость пузыря; N, — безразмерная обратная вязкость.
Результаты настоящей работы: D вода, NAl=2 ■ UP; А 50%-ный глицерин, JVAr-8 • 103;
Т 70%-ный глицерин; Л?Дг=6,9 • 102; • 89%-ный глицерин, WAr = 14; О 95%-иый глицерин,
ЛГДг=2,2; О 5000 вискасил, WAr = l,23- Ю-3; V 10 000 внскасид, ЛГДг=3,08 • 10-4; Д 30 000 ви-
скасил, JVAr=3,42 • 10-5; О 60 000 вискасил, WAr=8,55 • Ю-6; Ш результаты Думитреску,
вода; ф результаты Гриффитса и Уоллиса, вода.
летворяются асимптотические решения, эквивалентные
уравнениям (10.8), (10.12) и (10.14). Эти решения следующие.
Область преобладающего влияния инерционных сил
• Nf > 300, 7VE6>100,
£1=0,345.
Область преобладающего влияния сил вязкости
Nf<2, 7VE6>100,
A1=0,01^V/. (10.18)
Область преобладающего влияния сил поверхностного
натяжения
JVE6<3,37,
7V2=6,27VAr.
(10.19)
318
ГЛАВА 10
Использовались также и другие методы графического
представления результатов с помощью различных комбинаций
безразмерных параметров. Уайт и Бердмор [3J ввели комплекс,
учитывающий свойства жидкости:
Г=-^-. (10.20)
Если плотность газа мала по сравнению с плотностью жидкости,
то в этом случае Y=l/N^. На фиг. 10.5 представлена
зависимость ki от А/ео с У в качестве параметра.
°'401 мим—:—i—i—i i i м 11 1—i—i i ми
Фиг. 10.5. Данные фиг. 10.4, представленные в виде зависимости k\ от Л/вб
с У в качестве параметра [3].
Приведенное ниже уравнение (10.21) в соответствующих
условиях сводится к уравнениям (10.8) и (10.11)
^=0,345 (l-e-0'01^/0'345). (10.21)
Уравнение (10.21) дает хорошее приближение также и при
промежуточных значениях Nf, указанных на фиг. 10.4, когда
влияние поверхностного натяжения пренебрежимо мало.
СНАРЯДНОЕ ТЕЧЕНИЕ 319
Влияние поверхностного натяжения можно учесть
алгебраически путем модификации уравнения (10.21):
ft1=0,345(l -e-*filNf/**s)(l _е(з.з7-лгЕб)/т)) (Ю>22)
где т является функцией Nf и принимает следующие значения:
TV/> 250, да=10,
18 < Nf < 250, т=69Л70,35, (Ю-23)
Nf<\8, т=25.
Уравнение (10.22) представляет собой общее соотношение для
скорости подъема пузыря, в котором учитываются все
определяющие этот процесс параметры.
В области слабого влияния сил вязкости, т. е. в случае
больших значений Nf, из уравнений (10.22) и (10.23) следует
£, =0,345 [l-eP'87-^)/10]. (ю.24)
Это соотношение объединяет данные, используемые в работе Ма-
сика и Петраша [11], и согласуется с их уравнением, в котором
в качестве независимой переменной фигурирует число Бонда:
*, =0,34 Г1-4
0,84 \Nbo /4>7
(10.25)
Форма пузыря при разных режимах различна. В вязкой
жидкости (Nf<2) носовая и хвостовая части пузыря скруглены,
а течение в следе ламинарное, тогда как в жидкости с
незначительной вязкостью (Nf>300) хвостовая часть пузыря плоская,
а течение в следе турбулентное.
Пример 10.1. Какова скорость подъема пузыря при снарядном режиме
течения в круглой вертикальной трубе диаметром 2 см, если плотность газа
равна 10 3 г/см3? Физические параметры жидкости следующие: р, = 1 г1см3
а=100 дин/см, ц/=1 из.
Решение. Прежде всего нужно рассчитать следующие безразмерные
комплексы, пренебрегая плотностью газа по сравнению с плотностью жидкости:
_ gD2?f _ 981-22.1
ЛЕб~ „ Too -39'2-
gl*D*l*tf ад,'/. . 23/* . I
Nf=r
"М* _.■■ ioo3/2 • l'fr „
АГ_ $gu ~ 12.981*'. '
r=-L=io-3.
320 ГЛАВА 10
Из уравнения (10.22) и (10.23) имеем
69 ,с
т= ——-=15,
kx = 0,345 (1 - е-0'*8'0-™) (1 - e(3.37-39,2)/i5) = o29i
а из уравнения (10.5)
ит = 0,29 • \~'1г [981 • 2 • 1],/г = 12,7 см/'сек.
С другой стороны-, из фиг. 10.5 следует, что £i = 0,26, a v =11,4 см\сек.
Использование скорости пузыря в модели потока дрейфа
Приведенная в гл. 4 методика может быть использована
также применительно к снарядному режиму течения, поскольку
в этом случае влияние касательных напряжений на стенке на
динамику пузыря мало. Это приблизительно справедливо при/
значениях Nf, больших 300, а также когда потери давления hj
трение, рассчитанные по теории гомогенного течения, малылю-
сравнению с составляющей падения давления под действием
силы тяжести.
В разд. 10.2 было показано, что скорость дрейф^г^/ не
зависит от а, а является функцией /. Однако в одномерных течениях
при отсутствии касательных напряжений на стенке скорость
дрейфа не зависит от /, а является функцией а. Оба этих
условия удовлетворяются только при ugj=const. Значение этой
постоянной можно вычислить из рассмотрения частного случая
движения одиночного пузыря в неподвижной жидкости, когда
^=г\„. . (10.26)
отсюда для всех значений та
JgfTav-m <10-27)
Скорость пузыря при наличии результирующего потока
находится из уравнения (10.3):
*»=У + *„. (Ю.28)
Величина среднего объемного газосодержания определяется из
уравнения (10.4)
<a> = 7J4^"- (10-29)
S со
Уравнение (10.29) можно записать через объемные расходы
фаз [12]
<'>=<?/ + <£W- (1°-30)
СНАРЯДНОЕ ТЕЧЕНИЕ
321
Если исходить из допущения о пренебрежимо малом влиянии
касательных напряжений на стенке, градиент давления при
отсутствии ускорения потока запишется следующим образом:
dp
^Г=£ [Р/(!-*) +р£аЬ
(10.31)
Этот градиент давления можно рассчитать, используя значение
а, определенное по уравнению (10.29).
f
!ЧМ
Развитие упрощенной теории
В действительности скорость дрейфа пузыря не является
строго постоянной величиной, так как на нее оказывает влияние
профиль скорости в пробке жидкости, который зависит от /, или,
-точнее, от числа Рейнольдса, рассчитанного по уравнению (10.2).
На профиль скорости оказывает также влияние след
предыдущего пузыря. Эти эффекты можно учесть введением поправочных
множителей к выражению (10.28), а именно
vb=CJ+C2va. (10.32)
Коэффициент С\ учитывает отличие средней плотности
объемного расхода от средней скорости жидкости, а коэффициент
Сг — действительный профиль скорости. Поправочный
множитель С\ в целом оказывает на уравнения такое же влияние,
как и коэффициент С0 в уравнении (4.24), хотя физические
процессы, с которыми связано появление этих коэффициентов,
не идентичны.
В случае полностью развитого турбулентного течения в
жидкой пробке (число Рейнольдса больше ~8000) результат
получается довольно простым. Скорость пузыря равна vx
относительно приблизительно постоянной скорости в турбулентном
ядре [4]. Для круглой трубы и полностью развитого течения
Re, > 8000, С1 = 1,2> С2=1. (10.33)
В работе [5] приводятся соответствующие значения
коэффициента Ci для прямоугольных и кольцевых каналов при больших
числах Рейнольдса. Эти данные представлены на фиг. Л0.6.
До сих пор еще не существует общепринятых соотношений
для d и Сг в ламинарной области течения. Гриффите и Уоллис
[12] построили зависимость коэффициента С2 от числа
Рейнольдса, однако им не удалось разделить влияние двух
поправочных множителей. При больших скоростях коэффициент d,
по-видимому, достигает предельного значения 2,27,
определенного Тейлором [13] при анализе горизонтального течения.
Влияние следа предыдущего пузыря на скорость подъема
следующего за ним пузыря было учтено Мойссисом [14], который
для круглой трубы получил зависимость коэффициента Сг от
21 Заказ №162
322
ГЛАВА 10
отношения расстояния между пузырями Ls (длины жидкой
пробки) к диаметру трубы D
C2=l + 8e-l'06LslD. (Ю.34)
Это означает, что последующий пузырь стремится догнать
предыдущий и слиться с ним. Поэтому снарядное течение никогда
не бывает полностью развитым и устойчивым, хотя в конце
концов длина пузырей становится столь большой, что
вторым членом в уравнении (10.34) можно пренебречь. На
входном участке трубы, а также
в области перехода
пузырькового течения в снарядное
или же в случае
непрерывного образования
IJ0
1,26
1,22 h
I
1,18
1,14
1,10
с 1 1
-
-
-1
-
1 r/*Z
-5
i i
1 "Г" I
^3
4
I i i
1
2N
5-
1
-
*
-
-
-
-
О 0,2 0,4 0JB ОД
Di/D0,(l-Dh/D0),DS/Db
1,0
\
Фиг. 10.6. Изменение
коэффициента Ci в зависимости от
геометрии канала [5].
/ — круглая труба, асимптота;
2—квадратный канал; 3 — прямоугольные
участки; 4 — кольцевой канал и трубные
пучки; 5 — параллельные плоскости;
Di/D0 — для кольцевого канала;^!,^»-
— DhID0) — для^~Ттубны*----Т1учков;
DJDb — для прямоугольного канала.'
пузырьков в процессе кипения взаимодействием между ними
пренебрегать нельзя. Уравнением (10.34) довольно неудобно
пользоваться на практике, поскольку длину пробки Ls нельзя
выразить только через суммарные расходы компонентов. В
каналах, в которых происходит кипение, с достаточной точностью
можно принять [5]
С2=1,6. (10.35)
С учетом коэффициентов d и Сг можно несколько
модифицировать уравнение (10.30), получив при этом более точное
уравнение для среднего объемного газосодержания
<а>:
Qg
Сх (Q/ + Qg) + C2Ava
(10.36)
Величину поправки к уравнению (10.31), которую
необходимо вводить в случае значительных касательных напряжений
на стенке, довольно трудно определить. Среднее значение каса
тельных напряжений может быть как положительным, так и
отрицательным, так как в действительности часть жидкости вокруг
СНАРЯДНОЕ ТЕЧЕНИЕ 323
пузыря стекает вниз по стенке. Возможный путь решения состоит
в определении касательных напряжений в жидкой пробке, исходя
из величины коэффициента трения для однофазного течения,
рассчитанного по суммарной приведенной скорости /:
**=Cf± Pff, (10.37)
где Cf — обычная функция Re,. Приближенно можно принять,
что часть длины трубы (1—а) занята жидкими пробками,
поэтому если пренебречь величиной касательных напряжений на
стенке вокруг пузыря, то уравнение (10.31) с учетом
гидравлического сопротивления течению жидких пробок примет вид
—2-=g[P/(l-*) + P^] + (l-*)C,-^-. (10.38)
Если плотность газа значительно меньше плотности
жидкости, то в этом случае
.Р»«(1-«)Р/. (Ю.39)
и последний член в уравнении (10.38) можно представить в виде
[-*),-*¥- (10.40)
Это выражение можно рассматривать как составляющую
градиента давления, обусловленную трением, в гомогенном потоке,
в котором средняя плотность рассчитывается, исходя из
величины объемного газосодержания, определенного по (10.30).
Поэтому методика, использованная во второй части примера 9.4
для пузырькового течения, с известным приближением
применима и к снарядному режиму течения.
Поправка для длинных пузырей
' Если длина пузырей велика (например, больше 15
диаметров), то в пленке, окружающей пузырь, содержится большое
количество жидкости. Для чисто потенциального течения скорость
жидкости относительно пузыря в направлении, противоположном
его движению, на расстоянии h от его носка равна i2gh. Однако
в конечном счете достигается некая предельная скорость, при
которой вес пленки полностью уравновешивается касательными
напряжениями на стенке. В этом случае пленка стекает с
постоянной скоростью и имеет постоянную толщину; оба эти
параметра можно рассчитать по теории стекающей пленки. Так как
вес пленки полностью уравновешивается касательными
напряжениями на стенке, то жидкость, содержащаяся в пленке, не
оказывает никакого влияния на величину суммарного градиента
21*
324 ГЛАВА 10
давления. Кроме того, длина пробок жидкости также
уменьшается за счет жидкости, содержащейся в пленке. Оба эти эффекта
можно учесть, если условно принять жидкость, содержащуюся
в пленке, за газ и соответствующим образом скорректировать
величину объемного газосодержания, входящую в уравнение
(10.38). Для длинного цилиндрического пузыря, окруженного
пленкой толщиной 6 (фиг. 10.7),
отношение объема пузыря к
объему трубы равно
л\
__.....!-
L:
Of
}
V — V2gh (относительно
пузыря)
-8а, (асимптотическая
— толщина)
D — 25 \2
\CL~iA
Теперь эффективное объемное
газосодержание, используемое при
расчете падения давления по
уравнению (10.38), следует
представить в виде
а'=а(1-т9~2- (10-41)
Толщина пленки
рассчитывается следующим образом. Рас-
Фиг. 10.7. Стенание пленки вокругдлйн-
ного пузыря в вертикальнЫ^трубе.
смотрим сечение трубы через цилиндрическую часть пузыря,
изображенного на фиг. 10.7. Скорость движения газа вверх
в центре трубы равна скорости пузыря, поэтому
(10.42)
vg=v„
Для невязких пузырей и турбулентного режима течения (Rej>
>8000) из (10.32) и (10.33) следует
vg=\,2j + 'oat. (10.43)
Расход газа через поперечное сечение трубы равен
Qg-=^-vg{D-2bf. (Ю.44)
Пусть расход жидкости, стекающей вниз, в рассматриваемом
сечении будет Q'. Так как из условия неразрывности суммар-
СНАРЯДНОЕ ТЕЧЕНИЕ
325
ный объемный расход через любое поперечное сечение трубы
постоянен, то
Qe-Q'f=Q-^-J. (Ю.45)
Из уравнений (10.43) — (10.45) следует, что приведенная
скорость жидкости, стекающей вниз, будет равна
А=1&г=иМ+,0*>)(1--ТгУ-1- :(10-46)
Теперь величину Q' можно связать с толщиной пленки б с
помощью соотношений теории стекающей пленки (гл. 11). Затем,
решая совместно уравнение (10.46) и уравнения стекающей
пленки, можно определить б.
Теория справедлива лишь при Afy>300. В этих условиях
скорость пузыря определяется уравнением (10.5) и равна
г-м=0,345Р7,/2 [gD (Р/ - р,)] ч\ (10.47)
[Заметим, что аналогичная методика может быть применена и
к случаю движения пузырей в вязких жидкостях, так как можно
вывести уравнение, которое заменило бы уравнение (10.43) при
4tej<8000.]
Используя соотношение /'/Уоо = /*70,345, приведем уравнения
движения стекающей пленки (11.68) и (11.76) к более удобному
виду
" Rer = y;'yV/=-^-0,345yV/, (10.48)
оо
Rer < 3500 ^-=3,85^ (-^-)3, (10.49)
ОО
3500 < Rer < 30000 -^-=190 (-^-)Vl. (10.50)
оо * ^
Разделив обе части уравнения (10.46) на Уоо, получим
л-[1Л++1){1-»х-+: 00.5.)
ОО \ ОО / \ / 00
Теперь нужно совместно решить уравнения (10.49) — (10.51).
Графическое решение представлено на фиг. 10.8. С помощью
уравнения (10.51) построена серия кривых зависимости j'/va> от
б ID при различных значениях j/vv,. Точка пересечения кривых,
соответствующих уравнениям (10.49) и (10.50), дает значение
8/D. Подставляя его в выражение (10.41), получим
модифицированное значение а, которое подставляется в (10.38). В общем
326
ГЛАВА 10
случае (10.38) дает завышенные значения градиента давления.
Если же в него подставить модифицированное значение а,
рассчитанное по (10.41), то оно даст заниженное значение
градиента давления.
Падение давления из-за ускорения рассчитывается так же,
как и при пузырьковом режиме течения, что и было
проиллюстрировано в примере 9.4. Однако поскольку снарядный режим
Фиг. 10.8. Графический способ определения толщины пленки вокруг пузыря
при снарядном течении. у/
течения не является в такой же степени гомогенным^ как
пузырьковый режим, то условие запирания канала, описываемое
уравнением (18) в примере 9.4, при снарядном режиме течения,
возможно, будет ошибочным. Кроме того, поскольку часть жидкости
движется в пробках со скоростью /, а остальная часть жидкости
движется вниз в стекающей пленке, допущение о постоянной
скорости жидкой фазы не является корректным. В этой области
целесообразны дальнейшие исследования.
Пример 10.2. Рассчитать средний градиент давления в вертикальной нефти-
ной скважине дли следующих условий: Q/ = Qg=35,4 л/сек, D = \5 см,
(Х/ = 1 из, а=25 дин/см, р/=0,85 г/см3, pg=0,0025 г/см3. Местное давление
равно 4,2 ата.
Решение. В вертикальной трубе большой длины образуются снаридоподоб-
ные пузыри. Кроме того, если протиженность трубы достаточна для
того, чтобы происходила агломерации снарядов, то эти пузыри могут
быть очень длинными. Поэтому в зависимости от конструкции скважины
СНАРЯДНОЕ ТЕЧЕНИЕ 327
величина градиента давления должна быть заключена между значениями,
полученными с помощью уравнении (10.38) при подстановке в него а
из (10.36) и из (10.41). При этом снарядное течение предполагаетси
полностью развитым, и никаких поправок с помощью уравнении (10.34)
не» вводитси.
Сначала определим соответствующие безразмерные комплексы
„/В*1У'.15'/-.0.8Б=Ж01
*E,= 981-g-°'85=7250,
_ 25^-0,85'/*
Аг_ 18.981'/. "
Из фиг. 10.4 находим ki = 0,345, так что
vm = 0,345 (981 • 15)'/г = 42 см /сек.
Площадь поперечного сечения трубы равна
Л =4- • 152=177 см*.
4
Затем определим приведенные скорости нефти и газа
Q/ 35400 опл ,
Jf — -г- ~ —Tff— = 200 см/сек,
Qg 35400- опл ,
Уг=—т-=—р=—=200 см /сек
и число Рейнольдса для жидкой пробки
;■ tfJ£_± 085^400^ = 51(Ю
' V-f 1
Теперь надлежит решить, как вести дальнейшие расчеты, так как
при числах Рейнольдса, меньших 8000, не существует методов расчета
коэффициентов С\ и С2. Единственно возможным путем явлиется
использование теории, разработанной для турбулентного режима течении в
предположении, что нносимая при Re=5100 ошибка незначительна. Тогда
величина <а> из уравнении (10.36) при (^ = 1,2 и С2=1 будет равна
35400
<а> — 1,2 ■ 70 800 + 42 ■ 177 ~ 0,,i84-
Дли гладких труб-при Re=5100 коэффициент трении равен 0,009. Тогда
сумма составлиющих градиента давления, обусловленных силой тяжести
и трением, в (10.38) будет равна
— dp -^981 (0,85 • 0,616 + 0,0025 • 0,384) +
dz
+ 0-61620'009 0,85-4002 .-А-=513 +100 = 613 дин/см*.
328
ГЛАВА 10
Поправка на величину потерь давления из-за ускорения потока
находится с помощью уравнения (17) из примера 9.4. Знаменатель этого
уравнения с достаточной точностью равен
' ! "fy* _l 0.85-2003 _
' (jf + vjp ~ 242-4,2.103.981 '
Тогда градиент давления примет следующее значение:
dp 613
-ЧГ = оМз=шдин!см3-
Чтобы ввести поправку на длину пузыря, обратимся к фиг. 10.8.
400
При //оет = -j- = 9,5 и N=1440 по графику находим 6Д>=0,0485. Тогда
по уравнению (10.41) получаем скорректированное значение объемного
газосодержании
- . 0.384
= 0,471.
Если подставить это значение в (10.41), то расчетная величина
градиента давления уменьшитси на величину отношении (1—а')/(1 — а):
[1 —2 (0,0485)] 2
1чение в (10
:и на величи
dp = (618) (0,529)
dz ~ 0,616
531 дин/см3.
заключена между
ению.
Следовательно, искомаи величина градиента давлении
531 и 618 дин/см3; по-видимому, ближе к нижнему зна!
Вязкие эффекты
При Nf<300 или при Rej<8000 существенную роль начинают
играть вязкие эффекты и приведенные выше уравнения
становятся неточными. В настоящее время эти явления недостаточно
исследованы. Однако поскольку влияние подъемных. сил мало
по сравнению с влиянием вязких сил и сиЛуПоверхностного натя-%
жения, то данные, которые будут приведены в разд. 10.4, с
известным приближением мджщ считать справедливыми. Эти
данные следует использовать в том случае, когда величина у»,
рассчитанная по уравнению (10.22), значительно меньше /,
например при
•^-<0,1. (10.52)
10.4. Горизонтальное снарядное течение
Скорость пузырей
В условиях горизонтального течения скорость дрейфа,
обусловленная действием подъемных сил, равна нулю. Поэтому
параметр г)» теряет смысл. Однако средняя скорость движения
пузырей отличается от средней скорости жидкости. Это стано-
СНАРЯДНОЕ ТЕЧЕНИЕ
329
вится очевидным при "рассмотрении фиг. 10.9. Поскольку вдоль
пузыря давление постоянно, то пленка жидкости на стенке по
существу неподвижна. При средней толщине этой пленки б
площадь поперечного сечения, занимаемая пузырем, равна
А
ь~
= тг
(^-§)2. (10.53)
Из условия неразрывности приведенной скорости в этом сечении
следует
или в случае тонкой пленки
"*~ (1 + -Z?-)/- (Ю-55)
Следовательно, оь>/.
\
А
Фиг. 10.9. Горизонтальное снарядное течение.
Весьма полезным параметром, характеризующим долю
поперечного сечения, занятую жидкостью, на участке трубы, где
находится пузырь, является
w=l--^- = l—f-. (10,56)
При отсутствии влияния вязких и инерционных сил в газовой
фазе, а также в условиях независимого движения пузырей
можно представить параметры, определяющие скорость движения
пузыря, в виде следующих безразмерных комплексов:
j jD iv-f (Р/ — ?g)gD2
Первый безразмерный комплекс представляет собой отноше:
ние скорости жидкости в пробке к скорости пузыря, второй
комплекс— это число Рейнольдса для жидкости в пробке, третий
характеризует соотношение вязких сил и сил поверхностного
натяжения, и четвертый — соотношение подъемных сил и сил
поверхностного натяжения. Фактически последние три комплекса
аналогичны комплексам, описывающим соотношение
инерционных, вязких, подъемных сил и сил поверхностного натяжения
330
ГЛАВА 10
в случае вертикального течения. Первый комплекс является
величиной, обратной Ci.
Можно объединить второй и третий комплексы, получив при
этом не зависящий от скорости параметр, постоянный для
данной жидкости и данной трубы, а именно
^
D?fa
(10.57)
Суо [15|] провел экспериментальное исследование снарядного
течения при
(Р/ — ?g)gD2
<0,88,
(10.58)
когда расслоение потока было несущественным и влиянием
подъемных сил можно было пренебречь. Полученные им данные
'.2
1.0
J
"ь
0,8
0,6
-
-
т
1
\ =
А =2,7-
i
i
,5 • ГО"*
o-s/
-|
1
,А
1
=3.4 • Ws
\ Очень большое
\ значение А
\ 1 ,
-
_
-
т
32
48
64
#'хДз
Фиг. 10.10. Отношение скоростей j/Vb в зависимости от параметра /ц//сг [15],
снарядное течение; пузырькоао-снарядное течение.
представлены на фиг. 10.10 в "виде соотношения приведенных
выше безразмерных параметров/Из графика видно, что при
очень малых скоростях пробку жидкости и пузырь движутся
с одинаковой скоростью. Приэтом, согласно уравнению (10.55),
пленка жидкости вокруг пузырей будет очень тонкой. При
больших скоростях и больших числах Рейнольдса отношение j/vb
стремится приблизительно к 0,84, т. е.
vh
U9/.
(10.59)
Значение коэффициента в выражении (10.59) очень близко к
эквивалентной величине (Ci=l,2) для вертикального течения при
больших числах Рейнольдса. Числа Рейнольдса Re,,
соответствующие достижению асимптотического значения на фиг. 10.8,
равны приблизительно 3000. Поэтому при Rej>3000 справед-
СНАРЯДНОЕ ТЕЧЕНИЕ 331
ливо простое выражение для скорости пузыря через суммарный
объемный расход фаз
^=1,2^^. (10.60)
Кривые на фиг. 10.10, отвечающие большим значениям X,
соответствуют режиму, при котором влияние сил инерции
пренебрежимо мало, и движение определяется соотношением между
силами вязкости и силами поверхностного натяжения.
Полученные для этого случая данные {13] могут быть описаны
следующим эмпирическим уравнением:
m=0,56(l-e-2'64(^s)0'567), (10.61)
которое при малых циь/о сводится к
OT^1(48(J^)0-567. (Ю.62)
Уравнение (10.62) дает промежуточные значения т между
рассчитанными по уравнению Брезертона [8]
т=2,68(-^у/з (10.63)
и Фейрбразера и Стабса [16]
от=1)0(^),/г. (10.64)
Уравнение (10.62) точнее описывает данные Брезертона, чем
(10.63) и (10.64).
Параметр т оказывается весьма полезным, если нужно
рассчитать толщину жидкой пленки вокруг пузыря. Однако сама
форма уравнений (10.61) и (10.64) требует применения метода
последовательных приближений, так как величина ьъ обычно
неизвестна. Другое выражение, определяющее С4 с точностью
2%, имеет вид
C^l + l^d-e-3'8^^0'8). (10.65)
Если требуется определить точное значение т, то уравнение
(10.61) следует использовать после определения величины ьъ
с помощью уравнения (10.65).
Если С4>2, то пузырь движется со скоростью,
превышающей скорость жидкости в пробке на оси трубы. Поэтому
характер течения жидкости относительно пузыря будет совершенно
различным [21, 26] в случаях Сх<2 и Cj>2.
332
ГЛАВА 10
Объемное газдсодержание
Величина объемного газосодержания а определяется по
выражению (10.4), куда подставляется скорость движения
пузыря, найденная описанным выше способом. При достижении
асимптотического предела, т. е. при числах Рейнольдса больше
3000, из выражений (10.60) и-(10.4) получается простое
соотношение
a=0'84l^FQ7' (10-66)
которое можно сравнить с (4.31). Оно также хорошо согласуется
с экспериментальными данными Арманда [17].
Падение давления
Падение давления в жидкой пробке может быть рассчитано
по методике, принятой для однофазного течения. Падение
давления вдоль цилиндрической части пузыря равно нулю. Поэтому
следует учесть только дополнительное падение давления в
каждом пузыре вследствие сопротивления его носовой и хвостовой
частей. Так как один и тот же расход газа в одной и той же
трубе может быть достигнут при различном числе пузырей, то
падение давления нельзя рассчитать до тех пор, пока длина
пузыря не будет задана независимым образом.
Падение давления на один пузырь при малых числах Re3-
можно описать следующими соотношениями [15]:
Re,-< 270, APb=3^L> (10.67)
270 < Re, < 630, Apb=0,№pfv2b. (10.68)
Внезапный переход при Rej = 270 от соотношения (10.67),
характерного для чисто вязкого течения, к соотношению (10.68),
типичному для чисто инерционного течения, необычен, так как
в этой точке не происходит резкого изменения динамики потока.
По-видимому, смысл приведенных неравенств в том, что при
малых числах Рейнольдса справедливо соотношение (10.67), а при
больших—(10.68). Падение давления на один пузырь
приблизительно равно падению давления на длине, равной примерно
4 диаметрам трубы. Тогда приближенное соотношение для
типичной единичной ячейки трубы, включающей один пузырь
и одну жидкую пробку, при всех значениях числа Рейнольдса
будет иметь следующий вид:
Д^=4С/^-Р//^±^) (10.69)
СНАРЯДНОЕ ТЕЧЕНИЕ
333
где Ls — длина жидкой пробки, а выражение для среднего гра-
л.диента давления можно будет записать следующим образом:
л.
dp
1С
f?fJz
LS + 4D
dz
D
Ls + J-b
(10.70)
Расчет последнего отношения в уравнении (10.70) зависит от
условий задачи. Возможно, будет известен объем Уь каждого
■'.'пузыря. Тогда, зная объемное газосодержание, можно
определить длину единичной ячейки
£,+£»==-
Аа.
(10.71)
Так как 1/Ci определяет долю поперечного сечения, занятую
пузырем, то с учетом выражения (10.54) получаем хорошее
приближение для длинных пузырей
(10.72)
Подставляя уравнения (10.71) и (10.72) в (10.70), имеем
dp ICftfp
dz
D
/1 r.4DA\
Так как
Си
(10.73)
(10.74)
уравнение (10.73) может быть записано через приведенные
скорости и коэффициент Ci
dp
dz
D
ADA
ГьСх
h
(10.75)
10.5. Снарядное течение в наклонных трубах
Снарядное течение в наклонных трубах было исследовано
Рунге [18]. При описании этого режима течения используются
те же параметры, что и в случае вертикального течения. К ним
следует добавить только угол 8 между осью трубы и
вертикалью. Для каждого значения 8 скорость подъема пузыря
характеризуется серией кривых, аналогичных приведенным на
фиг. 10.4, т. е. для описания такой четырехмерной поверхности
понадобится комплект графиков.
Предположим, например, что скорость пузыря приведена
к безразмерному виду и представлена в виде параметра ki.
В общем случае
k^kx[Nf, Nm, в]. (Ю.76)
334
ГЛАВА 10
ад
!,5
',2
Hi.
14.
0.8-
ОД
ь
1 1 1 1 1 1
-
1 1
о Nf = 23 130
♦ Nf = 24
» /Vf = 76,7
о Nf = 0,36
I i
I 1
/VES > 700
I
' "
N. -
-
75
30
4S
в, град
60
75
90
2,0
7,6
1,2-
0,8
0,4
/Vf =72 625
Nf=10 4H0
Nf=900
Nf = ZZ4
Nf= 45
76
30
45
в, град
б
60
75
ВО
Фиг. 10.11. Скорость подъема пузырей при
6 — угол относи
Проще и удобнее представить скорость пузыря в наклонной
трубе в относительном виде, разделив уравнение (10.76) на
величину ki, которая соответствует случаю движения пузыря и той
же жидкости в вертикальной трубе и которую можно рассчитать
по соотношениям, приведенным в разд. 10.3. Исключая общие
параметры, получим
"Л" г
AW)
»» *. ("„ N™ °)
(10.77)
СНАРЯДНОЕ ТЕЧЕНИЕ
335
2,0
t
7,6
1,2
0.8
0,4
I
-
I
I
т
7
О
д
о
I
I
■^г" У'"5!)™*
Nf = 7260
Nf = 7230
Nf= 700
Nf = 775
Nf = 35
I
I I
40 < NEb < 50
I I -
-
~
-
30
45
9, град
в
60
76
30
2,0
',S
1,2
0,8
0,4h
> 76 30 45 60 75 SO
t7, град
. г
Нарядном течении в наклонных трубах [18].
ьно вертикали. ■ . . •
где Уе—«скорость пузыря в наклонной трубе. Из уравнения
(10.77) следует, что отношение скорости пузыря в наклонной
трубе к его скорости в вертикальной трубе можно представить
в виде функции от Nf, A/e6 jh 8.
В работах [18, 19]^четырехмерная поверхность, описываемая
уравнением (10.77), в выбранных диапазонах чисел Этвеша была
аппроксимирована серией кривых, представленных на фиг. 10.11.
Эти графики вместе с соотношениями разд. 10.3 можно исполь-
1
1
1
о
т
о
д
7
1
1
Nf = 4460
Nf = 410; 100
Nf= 20
Nf= 72
Nf = 8,2
I
1
20 < Ntb < 30
1
-
-
-
336 ГЛАВА 10
зовать для расчета, скорости подъема пузырей в неподвижной
жидкости в-наклонных трубах в широком диапазоне реальных
условий с погрешностью, не превышающей 10%.
Характерно, что скорость пузыря в наклонных трубах
оказывается в общем случае выше, чем в вертикальных трубах того
же диаметра. В невязкой жидкости пузырь поднимается быстрее
в наклонной трубе, чем в вертикальной, даже если ось трубы
наклонена к горизонтали всего на 2—3°. Поэтому нужно
принимать специальные меры,
чтобы в соответствующих
конструкциях
«горизонтальные» трубы были точно
ориентированы.
На фиг. 10.12 показано,
как изменяется форма
воздушных пузырей,
всплывающих в глицерине, при
изменении угла наклона трубы.
Фиг. 10.12. Пузыри прн
снарядном течении в наклонных трубах.
Если труба расположена почти горизонтально, то пузырь
как бы скользит вдоль верхней поверхности, трубы. Пленка
жидкости над верхней частью пузыря может быть очень
тонкой, и если краевой угол велик, то на поверхности трубы
могут появиться сухие пятна. Это особенно важно учитывать при
проектировании парогенераторов, так как испарение тонкой
пленки в верхней части пузыря может привести к местному
перегреву трубы и выпучиванию ее стенок.
Пример 10.3. Решить пример 10.1 для значений 0, равных 30, 60 и 80°.
Решение. Величина NEU наиболее близка к диапазону значений этого числа,
представленному на фиг. 10.11, е. При Nf=8B приближенные значения
11 е ^со Для данных углов наклона трубы 'будут следующими:
в, град
30
1,2
60
1.2
80
1,0
Принимая для вертикальной трубы среднее из полученных в
примере 10.1 значений v^, находим соответствующие значения i>9, равные
14,4, 14,4 и 12,0 см/сек.
СНАРЯДНОЕ ТЕЧЕНИЕ 337
10.6. Границы снарядного режима течения
Практически не существуют нижние предельные значения
•среднего объемного, газосодержания, расходного массового
газосодержания или расходов фаз, при которых можно получить
снарядный режим течения: Пузырьковый режим течения при малых
скоростях движения фаз вследствие агломерации всегда
стремится перейти в снарядный режим. При объемных
газосодержаниях ниже примерно 10% этот процесс протекает
относительно медленно и пузыри, типичные для снарядного режима
течения, наблюдаются лишь в очень длинной трубе. При наличии
в жидкости загрязнений пузырьковый режим течения может
затянуться.
Если затормозить движение длинных пузырей, остановив
течение смеси в горизонтальной трубе небольшого диаметра (или
в условиях нулевой гравитации), то они разобьются на более
мелкие пузыри длиной примерно в 2—3 диаметра трубы [20,21].
По-видимому, такая неустойчивость возможна также и при
очень низких значениях приведенной скорости /. Однако она не
приводит к изменению режима течения, а просто накладывает
некий верхний предел на длину устойчивого пузыря. Длинные
пузыри могут также дробиться при прохождении через
-различного рода сужения [21].
Действием' на пузырь касательных напряжений со стороны
жидкой фазы, а также лобового сопротивления обусловлено
наличие верхней границы снарядного режима течения. Одна из
границ этого режима определяется условиями, при которых
длинный пузырь в результате относительного движения
окружающей жидкости будет дробиться на более мелкие пузыри.
При разрушении пузыря в очень вязкой жидкости в его
хвостовой части образуются длинные нитеобразные струи, которые
в свою очередь дробятся на мелкие пузыри. С другой стороны,
при больших числах Рейнольдса происходит отрыв жидкой
фазы в хвостовой части пузыря с образованием сильно
возмущенного следа, в который уносятся мелкие пузыри. В работе
>Суо [15] приводится условие существования этого процесса в
горизонтальном потоке
-^—>1,1 • 106. (10.78)
Смена режима течения происходит постепенно, и длинные
пузыри, сопровождаемое небольшими пузырями, могут
наблюдаться в некотором диапазоне расходов.
Для вертикального течения получены аналогичные условия
смены режима течения. При больших числах Рейнольдса
относительная скорость между газовой и жидкой фазами непрерывно
22 Заказ № 162
338
ГЛАВА 10
возрастает вдоль пузыря до тех пор, пока под действием
касательных напряжений на стенке жидкая пленка не достигнет
предельной скорости. Поэтому условие дробления пузыря под
действием относительной скорости между .жидкой пленкой и
газовым пузырем является условием, определяющим максимальную
устойчивую длину пузыря, но не условием ликвидации
снарядного режима течения. С практической точки зрения длинный
пузырь с большим числом небольших пузырьков в следе ведет
себя подобно эквивалентному большому пузырю, поскольку
динамика носовой части пузыря определяет скорость дрейфа,
а большой пузырь и его след движутся вместе.
Противоточное движение газового ядра пузыря и жидкой
пленки рассматривается Никлином и Дэвидсоном [22] как
возможная причина «захлебывания» и последующего образования
больших неустойчивых волн на поверхности раздела фаз. В
момент «захлебывания» сила трения между газом и жидкой
пленкой по существу равна нулю. При толщине жидкой пленки б
площадь поперечного сечения, занятая газом, и расход газа
в ядре будут равны соответственно
Л»=Ч4-8)2 <10-79)
и \ '
Q'g=Abvb, (10.80)
где скорость у& рассчитана по уравнению (10.3) и является
функцией /, а не // и jg. Расход жидкости в пленке, стекающей
вниз, равен
. Q',=Abvb-Aj. (10.81)
Соотношение между Q' и Q', при котором наступает
«захлебывание», можно получить экспериментально или из уравнений,
которые будут приведены разд. 11.4. Предположим, что
геометрическое место точек, соответствующих «захлебыванию»,
описывается кривой, изображенной на фиг. 10.13. При заданной
величине / и толщине 6, используемой в качестве параметра,
уравнения (10.80) и (10.81) имеют вид прямых с наклоном —1,
проходящих через точку с координатами Qf, Qg, определяемыми
величиной расходов компонентов потока.
Асимптотическое значение толщины пленки б<х. находится,
как и ранее, из (10.41), (10.50) и (10.51). Если величина б, при
которой прямая пересекается с кривой «захлебывания», меньше
б с», то неустойчивое состояние не наступает. С другой стороны,
если пересечение прямой с кривой «захлебывания» происходит
при б>б<х>, то «захлебывание» наступает по достижении
последнего значения.
СНАРЯДНОЕ ТЕЧЕНИЕ
''339
Рассмотрим, например, случай Д/>>300 и Rej>8000. Из
уравнения неразрывности следует, что направленная вверх
приведенная скорость газа в пузыре при предельной толщине пленки
равна
fg=J+j'f, (Ю.82)
поскольку /' отсчитывается вниз (для удобства правила знаков
не соблюдаются). Эти значения /' и /' могут быть теперь
сопоставлены с соответствующими корреляционными уравнениями
для скорости «захлебывания» стекающих пленок. При Nf>300
Линия
„захлебывания"
-Qf
Qf a Qg лежат на этой прямой
^Направление уменьшения 8
Фиг. 10.13. Определение максимальной устойчивой длины пузыря по теории
Никлина и Дэвидсона.
и условиях, при которых предельное состояние достигается только
в жидкой пленке, таким уравнением может служить
h +J/ =1. (Ю.83)
Из определений безразмерных комплексов находим
. _ 0,35у)
Jr-
/,=0
,3451/ ?sJg .
(10.84)
(10.85)
Кроме того, уравнение (10.82) можно привести к безразмерному
виду
J ОО ОО 00
Предположим теперь, что в начале расчета были известны
параметры j/Vcc, Pf/pg и Nf. Сначала нужно решить уравнения
22*
340
ГЛАВА 10
/
(10.49) — (10.51) относительно j'/vx. Затем, используя
полученное значение j'Jvoo, из (10.86) можно определить j'/v<x>. После
этого с помощью (10.84) и (10.85) рассчитываются значения /*
и /* и определяется левая часть уравнения (10.83). Если она
будет больше единицы, то произойдет «захлебывание» течения,
в противном случае стекающая пленка будет устойчивой.
Условие начала «захлебывания» при предельной толщине жидкой
100
■ю
I I i in
Mill
п—I—I ми
Турбулентное течение
Яег=ЗВ00 ■
' i i i i I
' 'I'll
100
1ОО0
Nf
10000
lOOOOO
Фиг. 10.14. Расчет критического значения j/v , при котором происходит
«захлебывание» в условиях снарядного режима течения [22J.
пленки достигается, если удовлетворяется уравнение (10.83). Тем
самым фактически задается некоторое соотношение между
первоначально выбранными параметрами j/Va,, PtlPg и Nf.
Описанные выше расчеты были проведены Порто [23].
Результаты этих расчетов представлены на фиг. 10.14. Этот график
позволяет определить максимально допустимую величину j/voo
для заданных значений Ур//рг и Nf.
Настоящая теория позволяет рассчитать момент наступления
«захлебывания», если достигнута предельная толщина пленки
боо. Для не очень длинных пузырей «захлебывание» наступает
при больших значениях j/vx и значениях б, превышающих
асимптотическое.
На фиг. 10.15 результаты таких расчетов сравниваются с
данными Говье и Шорта [24] для переходной области между
снарядным и «пенистым» режимами течения при приведенных ско-
СНАРЯДНОЕ ТЕЧЕНИЕ
34»
ростях течения жидкой фазы менее // = 0,3 м/сек. Согласование
представленных данных позволяет сделать вывод, что
вспенивание вызвано дроблением нижних концов длинных пузырей в
результате «захлебывания». Маловероятно, что пенообразование
может повлиять на уравнения, описывающие объемное
газосодержание и падение давления при снарядном режиме течения.
Однако оно может существенно повлиять на массообмен в
системе за счет увеличения площади поверхности раздела фаз.
20
и»
Ю
" "d =3SMM,N_=_23000
Dj63fiMMJi=B!^0
Теория турбулентного течения пленки
/„-.-— ~Dj63fiMMjizB.°£9--
0,2
0,4 0,6
jf, м/сек
0,8
1.0
Фиг. 10.15. Сравнение расчетных данных, представленных на фиг. 10.14, с
экспериментальными данными Говье и Шорта [24] по переходу от снарядного
течения к пенистому при малых расходах жидкости.
Если плотность суммарного объемного расхода увеличится
сверх предельного значения, определяемого по фиг. 10.14,.
то точка «захлебывания» сместится вверх по пузырю и в конце
концов жидкая пленка совсем перестанет стекать вниз.
Предельное значение / равно приведенной скорости газа:
в точке Q' =0 на кривой «захлебывания». Это условие лежит
в основе критерия Уоллиса [25], определяющего переход к чист
кольцевому режиму течения без нисходящих токов жидкости:
J^=0,9[gD(?/-?e)]'h. (10.87)-
При скоростях, меньших рассчитанной по уравнению (10.87),
происходит непрерывное перекрытие центрального газового ядра
жидкими пробками и разрушение последних вследствие
последовательной смены процессов «захлебывания» течения и
агломерации пузырей. Такое, течение называется снарядно-кольцевым и
является промежуточным между чисто снарядным течением и
течением, характеризуемым непрерывным движением жидкой
пленки. Этот вопрос будет рассмотрен в следующей главе.
Пример 10.4. Проверить, произойдет ли «захлебывание» в стекающей вокруг
. Пузырей пленке при принятых в примере 10.2 условиях.
Решение. Из фиг. 10.14 при V^7p7=18,5 и #,= 1440 находим критическое
значение jlvm, приблизительно равное 16. При принятых в примере 10.2
342 ГЛАВА 10
условиях j/v^ =400/42=9,5. Так как эта величина меньше критического
значения //от , то «захлебывании» не произойдет.
Пример 10.5. Решить пример 2.5, используя теорию снарядного течении.
Решение. Исходя из заданных параметров, находим 0^=0,17 м/сек, Ci = 1,2,
Сг=1. Затем с помощью выражения (10.36) вычислим
■jg _ 14,4
1.2У + »
1,2- 15,3+0,17
= 0,773.
Величина объемного влагосодержания
1 —<х = 0,227
хорошо согласуется с экспериментальным значением 0,23.
Составляющие потерь давления на ускорение и трение вычис-
ляютси по уравнению (10.38) н равны 2,3 • 10~2 и 2,2 • 10~2 ат/м
соответственно. Суммируя эти величины и умножай сумму на 0,457 м, находим
Д/>=2,06-10~2 ат. Составляющая потерь давления на ускорение,
вычисленная по гомогенной теории, дающей завышенные значения, равна
Др=2,06- 10~2/0,864=2,38 • Ю-2 ат. Экспериментальное значение Д/>
заключено между этими двумя расчетными величинами.
Если ввести попранку на большую длину пузырей, то расчетное
падение давления уменьшится примерно на 40%. Этот результат будет
явно ошибочным, и причина станет ясной, если обратиться к фиг. 10.14.
Так как j/v^ =90, то произойдет «захлебывание» течении и в потоке
останутся только короткие пузыри.
10.7. Пульсация давления при снарядном течении
Уравнения (10.38) и (10.75) дают среднее значение градиента
давления. Однако давление вдоль пузыря по существу постоянно.
Поэтому действительное распределение давления на протяжении
CZ)
Мгновенное
/значение
./ давления
Координата г -
Фиг. 10.16. Средняя и переменная составляющие падения давления при
снарядном течении.
нескольких единичных ячеек подобно показанному на фиг. 10.16,
т. е. на средний градиент давления накладывается
приблизительно треугольная или пилообразная составляющая. В
результате при снарядном течении двухфазной смеси возможны
пульсации давления.
СНАРЯДНОЕ ТЕЧЕНИЕ . 343
Задачи
10.1. Некая силиконовая жидкость имеет вязкость 5000 спз, поверхностное
натяжение 21 дин/см и плотность 1 г/см3. Какова скорость подъема пузырей
при снарядном течении в вертикальных трубах диаметром 2,5, 13, 130 и
610 мм? Жидкость считается неподвижной.
10.2. Когда длинный пузырь поднимается н закупоренной снизу трубе, та
> приведенная скорость / перед пузырем не равна нулю вследствие расшире-
* ния газа, обусловленного градиентом гидростатического давления. Пузырь
объемом 160 см3 вдувается в столб воды высотой 30 м, заключенный в трубе
диаметром 25 мм. Каково время подъема этого пузыря на поверхность?
Температура воды 21°С. Труба закупорена снизу, а верхний ее конец сообщается
с атмосферой.
10.3. Показать с помощью уравнения (5.32), что толщина жидкой пленки
вокруг пузыря, всплывающего в неподвижной вязкой жидкости, составлиет
~40% радиуса. Какова величина ошибки, вносимой при использовании
уравнения (11.69), не учитывающего кривизну трубы?
10.4. Каков минимальный размер трубы, заполненной водой, в которой при
температуре 21° С могут всплывать большие пузыри воздуха а) на земле,,
б) в космическом корабле при g=3-10~5 ж/сек2?
10.5. Вода при давлении 70 ата медленно испаряется в длинной вертикальной
трубе диаметром 12,7 мм. Рассчитать объемное паросодержание в функции
длины канала, если массовая скорость 0=4,9 • 105 кг/м2-час, плотность теп-
' лового потока ^=2700 ккал/м2-час, вода на входе в трубу нагрета до
температуры насыщения. Какова длина участка трубы, на котором будет
сохраняться снарядный режим течения?
10.6. Решить задачи 2.30 и 2.31, считай, что преобладает снаридный режим
течения.
10.7. Решить задачу 4.2 для случая снарядного режима течения.
10.8. Рассчитать среднеквадратичную величину пульсаций давления при
течении смеси воздуха н воды в вертикальной трубе диаметром 25,4 мм при
давлении 2 ата и температуре 10° С. Расходы фаз равны №/=4,5- 103 кг/часу
1^=9 кг/час. Объем каждого пузыря 16 см3.
10.9. Большой пузырь вдувается в нижнюю часть трубопровода диаметром-
0,9 м и длиной 3200 м, имеющего перепад высот 305 м. Как долго будет
пузырь перемещаться по трубе, прежде чем он достигнет закрытой задвижки
в верхней части трубопровода?
10.10. Горизонтальная труба диаметром 9,5 мм заполнена жидким металлом-
(<т=300 дин/см, ц/=0,02 из, р/=5 г/см3). Через трубу пропускается га»
для охлаждения металла и образования на стенках трубы затвердевшей
фазы в виде равномерной пленки толщиной 0,13 мм. Каков должен быть
расход газа?
10.11. Цепочка пузырей объемом 1 см3 каждый вдувается с частотой 5 ру-
зырей в 1 сек в поток глицерина (р/=1,26 г/см3, ц/=700 спз, сг=63 динГсм),.
движущийся с расходом 10 см3/сек по горлзонтальной трубке диаметром
5 мм. Каковы длина пузырей, скорость их движения, толщина пленки вокруг
пузырей и падение давления?
10.12. .Определить скорость течения вермонтской кленовой патоки (р/-=
— 1,42 г/см3, ц/ = 10 000 спз, сг=77 дин/см) из банки емкостью 4,5 л через-
сливной носик диаметром 25,4 мм, наклоненный под углом 45° к горизон-
> тали.
10.13. Рассчитать изменение толщины пленки вокруг длинного пузыря в
горизонтальной трубе в функции диаметра трубы, расстояния от носовой
части пузыря, / и свойств жидкости. Использовать данные теории стекающих
пленок.
10.14. С помощью уравнения (10.51) объяснить, почему линии постоянных
значений j/v на фиг. 10.8 практически сходятся в одной точке. Показать,.
344 ГЛАВА 10
что точка пересечения, имеет приблизительно координаты (o/D = 1l24,
yl/tioo=5/6). При каком значении Nf толщина пленки вокруг пузыря не
будет зависеть от у?
10.15. Нарисовать линии тока в жидкой пробке, если С\ < 2 и С\ > 2 при
ламинарном течении. Проанализировать качественно явления, которые могут
наблюдаться в этих двух случаях.
10.16. Пусть длинные пузыри движутся в вертикальной парогенерирующей
трубе. Для расчета толщины стекающей пленки вокруг пузыря можно
использовать фиг. 10.8. По мере стекания по стенке трубы пленки жидкость
испаряется. Показать, что максимально возможная длина пузыря при
условии, что пленка не высыхает, прежде чем достигнет конца пузыря,
определяется по формуле
Определить Ьь для течения паро-водяной смеси при давлении 20 ат в трубе
диаметром 13 мм, /=0,3, 3 или 15 м/сек и Ф = 3- 106 ккал/м2 • час.
Литература
1. Dumitrescu D. Т., Z. Angew. Math. Mech., 23, № 3, 139 (1943).
2. D a v i e s" R. M., Taylor G. I., Proc. Roy. Soc. (London), 200A, 375—390
(1950).
3. White E. Т., В ear dm ore R. H., Chem. Eng. ScL, 17, 351—361 (1962).
4. N i с k 1 i n D. J., Wilkes J. O., Davidson J. F., Trans. Inst. Chem.
Engrs, 40, 61—68 (1962).
5. Griffith P., ASME paper № 63-HT-20, Nat. Heat Transfer Conf., Boston,
Mass, 1963.
6. Birkhoff G, Carter D, /. Rat. Mech. Anal., 6, № 6, 769—780 (1957).
7. Wallis G. B, Rept 62GL130, General Electric Co, Schenectady, N. Y,
1962.
8. Bretherton F. P„ /. Fluid Mech., 10, 166 (1961).
9. Hattori S, Rept. Aeronaut. Res. Inst. Tokyo Imp. Univ., № 115, 1935:
10. H a r t m a t h у T. Z.,-A. I. Ch. E. J., 6, 281 (1960).
11. Ma si с a W. J, Petrash D. A, NASA Rept TN D-3005, 1965.
12. Гриффите П, У о л л и с Г, Труды амер. общ-ва инж.-мех., серия С,
Теплопередача, № 3, стр. 99 (1961).
13. Taylor G. I, /. Fluid Mech., 10, 161—165 (1961).
14. М о й с с и с Р, Гриффите П, Труды амер. общ-ва инж.-мех., серия С,
Теплопередача, № 1, стр. 38 (1962).
15. Suo M, Griffith P, ASME, paper № 63-WA-96, 1963.
16. Fairbrother F, Stubbs A. E, /. Chem. Soc, 1, 527—529 (1935).
17. Ар м а н д А. А, Изв. ВТИ, № l, CTp. 16—23 (1946).
18. Runge D. E, Wallis G. B, AEC Rept NYO-3114-8 (EURAEC-1416),
1965.
19. Wal lis G. B, AEC Rept NYO-3114-14 (EURAEC), 1966.
20. Griffith P, Lee K. S., ASME paper № 63-WA-97, 1963.
21. Goldsmith H. L, Mason S. G, /. Colloid, ScL, 18, 237—261 (1963).
22. N i с k 1 i n D. J, Davidson J. F, Paper № 4, Two-phase Flow Symp,
Inst. Mech. Engrs, London, 1962.
23. P о r t e о u s A, Dartmouth College, Hanover, N. H. (неопубликованная
работа, 1966).
24. Govier G. W, Short W. L, Can. I. Chem. Eng., 36, № l, 195 (1958).
25. W a 11 i s G. B, Rept AEEW-R 142, Atomic Energy Establishment, Win-
frith Heath, England, 1962.
26. Cox B. G, /. Fluid Mech., 20, part 2, 193—200 (1964).
11
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ
11.1. Введение
При кольцевом режиме течения по стенке трубы движется
жидкость в виде пленки, а в центральной части трубы газ
образует «ядро» потока. Если в газовом ядре распределено
значительное число унесенных капель жидкости, то в таком случае режим
течения называется дисперсно-кольцевым. Его можно
рассматривать как переходный режим от кольцевого режима течения
к дисперсному, при котором вся жидкость полностью
распределена в газовом потоке в виде мелких капель.
Расслоенный режим течения, наблюдаемый в горизонтальных
или наклонных трубах, в известной мере подобен кольцевому
течению, поскольку оба компонента движутся рядом, не
смешиваясь друг с другом. Отсутствие симметрии в расслоенном потоке
затрудняет его анализ, хотя некоторые основные методы расчета
в равной степени применимы как к кольцевому, так и к
расслоенному режимам течения.
Кольцевое течение преобладает в испарителях, трубопроводах
природного газа, системах парового обогрева.
^ Теории кольцевого режима течения наглядно демонстрируют
последовательное усложнение аналитических методов, о которых
говорилось в гл. 1. Отдельные соотношения, простые модели,
интегральные и дифференциальные методы расчета могут быть
систематизированы по степени их сложности. Так как каждый
из указанных методов анализа может быть применен к течению
как жидкой, так и газовой фазы, то в принципе возможны
многочисленные комбинации.
В дальнейшем особое внимание будет уделено вопросу
Взаимосвязи методов анализа различной степени сложности.
Обычно более сложный анализ дает метод расчета эмпирических
постоянных, используемых в простых моделях, или поправочных
множителей, с помощью которых можно достигнуть большей
точности.
Горизонтальное и вертикальное течения будут рассмотрены
отдельно. Однако, когда это возможно, будут получены общие
методики расчета, применяемые к течению с любой ориентацией
в пространстве.
346
ГЛАВА 11
11.2. Горизонтальное течение
Границы кольцевого и расслоенного режимов
при горизонтальном течении
Границы различных режимов при горизонтальном течении
еще недостаточно точно определены. Простая диаграмма Бей-
кера [1], приведенная на фиг. 11.1, может дать общее
представление о расположении областей существования различных режи-
jo"' / /о ;<г ю3 to*
Gf\+/6g
Фиг. 11.1. Диаграмма Бейкера режимов адиабатического горизонтального
двухфазного двухкомпонентного течения [1].
р„ и Ру — в кг/м3, G, и G„ — в ке/мг ■ час. О-в дин/см, ц, — в спз.
' Ч(*)ШГ- -[(?Ш"П"'
В правом нижнем углу диаграммы представлен режим расслоенного течения с жидкими
перемычками.
мов, однако она не учитывает всех существенных параметров.
Вместе с тем путем простых рассуждений можно заключить, что
большие расходы газовой фазы ведут к более интенсивному
уносу капель, а при больших расходах жидкости наблюдается
тенденция к переходу к пузырьковому или снарядному течению,
что отражено на представленной диаграмме.
Параметр, отложенный на диаграмме Бейкера по оси ординат,
имеет размерность, но не имеет в представленном виде
физического смысла1'. Однако в нем содержится произведение (p'tjg),
•> Используемые Бейкером комплексы X и \|) являются безразмерными.
С этой целью pg, pt, [i/ и а нормированы относительно плотности воздуха
(1,21 кг/м3), плотности воды (1000 кг/м3), вязкости воды (1 спз) и ее
поверхностного натяжения (73 дин/см) при нормальных условиях. — Прим. перев.
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ 347
характеризующее инерционные силы газовой фазы. Можно
ожидать, что соотношение между этой силой и силой тяжести
определяет переход к расслоенному режиму течения. Это
соотношение, по-видимому, можно представить в безразмерном виде
Jl=JgpJ'[gD(9f-pg)]-,h. (11.1)
Для рассмотренных Бейкером диаметров труб значения /*
на границах между расслоенным и волновым течениями, а также
между кольцевым и снарядным течениями заключены в
пределах 0,25—1,0.
Граница дисперсного режима течения определяется
механизмом уноса капель. Было обнаружено, что она практически не
зависит от ориентации трубы и определяется прежде всего
силами взаимодействия газового потока с волновой поверхностью
раздела фаз. Образование волн на поверхности определяется
соотношением сил поверхностного натяжения, вязкости и инерции.
Для систем воздух—вода при атмосферном давлении
критическая скорость газа, при которой начинается унос капель,
составляет примерно 20 м/сек, за исключением случая очень
малых расходов жидкой фазы, когда силы вязкости в тонкой пленке
жидкости препятствуют образованию больших волн на
поверхности пленки. Поскольку влиянием сил вязкости в жидкой фазе
можно пренебречь [2], критическая скорость газа будет
определяться уравнением
-^-(—У/г=2,5- 10"4. (11.2)
Это уравнение согласуется с диаграммой Бейкера в
представленном на ней диапазоне изменения параметров. Более подробный
анализ уноса капель будет дан в гл. 12.
Корреляции
Приведенные в гл. 3 корреляции для раздельного течения
фаз применимы для горизонтального кольцевого и расслоенного
режимов течений. В частности, с помощью соотношения Марти-
нелли, уравнения (3.30) при л = 3,5 и уравнения (3.32) можно
очень быстро рассчитать составляющую градиента давления,
обусловленную трением, и величину объемного газосодержания
Для этой цели можно использовать также фиг. 3.4—3.8.
Введенные Мартинелли параметры > » f ? и I весьма полезны при
расчетах по более сложным методикам.
348
ГЛАВА 11
Раздельное течение. Модель кольцевого течения %
Как и в примере 3.3, уравнения движения одномерного колв*
цевого течения можно вывести, используя усредненные значения
касательных напряжений на поверхности раздела фаз и на
стенке. Для стационарного горизонтального течения без
ускорения из баланса сил для газового ядра и всего потока в целом
соотношения между этими касательными напряжениями и
градиентом давления имеют вид
dp 4т,-
(11.3)
— -н- • О1-4)
dz D к . '
dp _ 4тд,
Касательные напряжения на поверхности раздела фаз
Касательные напряжения на поверхности раздела фаз,
вероятно, зависят от разности между скоростью газа и некоторой
характерной скоростью поверхности раздела. Если скорость газа
значительно больше скорости жидкости, то последней можно
пренебречь, и тогда, как обычно,
**=(£/)/-§-р^*=——& • О1-5)
Если тот же поток газа заполнит все сечение трубы, то
касательное напряжение на стенке будет следующим образом
определяться через коэффициент трения (Q)g:
*»g=(Cf)e-TPeff С11-6)
Соответствующий градиент давления будет равен
*ы_ 4cf)g?g4
dz ).— D ~ D
dpj\ _
(11.7)
Решая совместно уравнения (11.3), (11.5) и (П.7) с учетом
уравнения (3.24), определяющего параметр ф2, получим
выражение
(Cf)t=a'yag(Cf)e, (11.8)
из которого становится ясным физический смысл параметра
Мартинелли <j>g2.
Иногда используется другой параметр — приведенный
коэффициент трения газовой фазы, который определяется таким
образом, что при течении по трубе одной только газовой фазы
кольцевой режим течения 349
с тем же расходом, что и в двухфазном потоке, градиент
давления сохраняется таким же, как и в двухфазовом потоке.
Обозначим этот коэффициент через (Cj)sg, тогда
Связь между (Cf)Sg и (Q)j весьма простая:
(С) --^
-ФАСА
/>g-
(11.10)
Выражение для (Q)< в явном виде через измеряемое
величины следует непосредственно из уравнений (11.3) и (11.5):
V*
На фиг. 11.2 представлен график, качественно
иллюстрирующий зависимость коэффициента трения на поверхности раздела
/-а
Фиг. 11.2. Гидравлические характеристики различных режимов течения [2].
Качественная зависимость эффективного коэффициента трения на поверхности раз-
от объемного влагосодержания (I —а).
дела фаз
2Р„;
S'g
фаз от объемного влагосодержания для восходящего,
горизонтального и нисходящего течений. С помощью этого графика
удобно анализировать различные режимы течений [3]. В
горизонтальном или нисходящем потоке при малых скоростях газа
350
ГЛАВА II
поверхность жидкой пленки гладкая и величина коэффициента
трения приблизительно та же, что и в гладких трубах. При
скорости газа больше критической начинается волновое движение
пленки и величина коэффициента трения резко возрастает до
некоторого максимального значения, после которого она следует
кривой, обозначенной на графике как кольцевое течение с
«волновой поверхностью раздела». При больших скоростях газа
происходит срыв верхушек волн и унос капель, приводящий к
увеличению плотности ядра потока. При этом коэффициент трения
возрастает приблизительно пропорционально отношению pdpg,
где рс в данном случае представляет среднюю плотность ядра
потока, которое считается гомогенным.
При очень больших расходах обеих фаз почти вся жидкость
в потоке распределена в виде мелких капель. В этом случае
градиент давления и объемное газосодержание определяются по
теории гомогенного течения. Так, градиент давления равен
«Р-2^. (11.12)
dz
В гомогенном потоке объемное влагосодержание определяется
по формуле
1-а=-г47-. (11.13)
Jf + Jg
В кольцевом потоке объемный расход газовой фазы обычно
значительно больше расхода жидкой фазы, поэтому эти уравнения
могут быть приближенно записаны в виде
1_a^4^=j£.^. (Ц.15)
Jg ?/ Gs
Подставляя (11.15) в (11.14), находим
Поскольку величина коэффициента трения в гомогенном потоке
почти не отличается от коэффициента трения (Cf)g при течении
по трубе одной только газовой фазы, то можно воспользоваться
уравнением (11.16) для определения эффективного значения
коэффициента трения на поверхности раздела фаз в гомогенном
потоке
-g-f^-lCAK-^O-)]-"-- <"-17>
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ 351
Для системы воздух—вода при атмосферном давлении p//pg~
«800, поэтому в случае гомогенного течения величина,
определенная уравнением (11.17), очень быстро растет с увеличением
(1—а), что хорошо видно из фиг. 11.2. Видна также тенденция
кривых с увеличением расхода жидкой фазы и доли уноса капель
смещаться в сторону линии, соответствующей гомогенному
течению.
В вертикальном потоке касательные напряжения на
поверхности раздела фаз должны компенсировать действие силы тяжести
на жидкую пленку и обеспечивать ее вертикальное движение.
Кроме того, любые жидкие пробки или находящиеся в потоке
капли вносят дополнительный вклад в гравитационную
составляющую градиента-давления в ядре потока. Таким образом, при
малых расходах газовой фазы в области снарядного режима
течения величина коэффициента трения, рассчитанная по
уравнению (11.11), заметно больше, чем для кольцевого режима
течения. При более низких расходах жидкой фазы эта разница
обнаруживается лишь при объемном влагосодержании более 0,2. При
больших расходах жидкости область перехода от снарядного
режима течения к дисперсно-кольцевому становится «размытой» и
наблюдается общее смещение кривых в сторону линии
гомогенного течения.
В основу простого анализа кольцевого течения с волновой
поверхностью раздела фаз положен график зависимости
коэффициента трения на поверхности раздела фаз от безразмерной
толщины пленки (фиг. 11.3). Экспериментальные точки
группируются около прямой, описываемой уравнением
(^=0,005(1+300-^-). (11.18)
Для течения тонких пленок в трубах это уравнение
приблизительно совпадает с следующим выражением:
(СД.=0,005 [1+75(1 -о)]. (11.19)
Уместно отметить, что соотношения Никурадзе [4] и Муди [5]
для Cf в шероховатой трубе могут быть аппроксимированы
уравнением
С, «* 0,005(1+75-**-V (11.20)
которое справедливо в диапазоне значений 0,001 <ks/D<0,03,
где ks — размер зерен так называемой песчаной шероховатости.
Согласно (11.18), волновая кольцевая пленка приблизительно
эквивалентна песчаной шероховатости, в четыре раза
превосходящей толщину этой пленки.
352
ГЛАВА 11
С помощью уравнений (11.19) и (11.11) получим следующее
выражение для градиента давления в горизонтальном потоке:
dP\
dz ]p
10
_2 ?.gJg 1+75(1
■а)
D
(11.21)
С помощью уравнения (11.19) можно также получить
аналитическое выражение для параметра Мартинелли <f>/ . Если при-
0,0750
0,0625
0,0500
J 0,0375
0.0250
0,0725
0,005
-
~
^а°
1
ь 0^\
9^»»
Л™
1
1
Д ^r
д ^ЛЭ
* Л\ '
дР^" •
. •
г
д
Й^ДД
—т-
9^ о
1
0
с
-
■
0.01
0.02
S/D
0,03
0,04
Фиг. 11.3. Сравнение результатов расчета по уравнениям (11.18) и (11.19)
с экспериментальными данными для воздухо-водяных смесей [3].
О Мартннелли, горизонтальная труба, d=25,4 мм; • Даклер, вертикальная труба, d"
=25,4 мм; А Чей Ше-фу, вертикальная труба, d=50,8 мм; □ Чарвониа, вертикальная
труба, d=76,2 мм; —уравнение (11.18); уравнение (11.19). (С{){ коэффициент
трения на поверхности раздела фаз; б/D — безразмерная толщина пленки.
нять (C/)g~0,005, то из уравнений (11.8) и (11.19) следует
1+75(1—а) у/г
и-
(11.22)
Соответственно приведенный коэффициент трения газовой
фазы запишется следующим образом:
(^=0,0051+75 <;,-'>.
(11.23)
Более простое выражение, дающее практически те же результаты
при значениях (1 —а) до 0,1, имеет вид
(C/)w=0,005 [1+90(1-а)].
(11.24)
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ ф 353
Легко также запомнить мнемоническое правило, согласно
которому с ростом влагосодержания потока на 0,1 градиент давления
0,06 г
0
0
0,005
0,02
0.0J
OfiA
0,015
0.06
0,02
0,08
0,025
0,10
0,03 S/D
0,12 Г-а
Фиг. 11.4. Сравнение результатов расчета по уравнению (11.24) с
экспериментальными кривыми [6] для вертикального нисходящего течения.
(Cf)sS — приведенный коэффициент треиия.
увеличивается в 10 раз. Расчеты по приведенному выше
уравнению сравниваются на фиг. 11.4 с экспериментальными
кривыми [6].
Пример 11.1. Смесь воздуха и воды движется по горизонтальной трубе
диаметром 25,4 мм. Массовый расход газа составляет 136 кг/час, pg =
= 1,6 кг/м3. Рассчитать с помощью уравнения (11.21), а также уравнений
(11.24) и (11.9) градиент давления, если объемное газосодержание
потока составляет 90%.
Решение. Площадь поперечного сечения равна
ъ -2,542
= 5,07 см2,
тогда
Jg:
4
136 • 104
46,7 MJceK.
3600 • 1,6 • 5,07
а) С помощью уравнения (11.21) получаем
/ dp\ 10-2.1,6-46,72.8,5 .... ,
(- ЧГ)F = 9,81 -2,54 -0,768- 102 -0-155 «У*.
б) Приведенный коэффициент [уравнение (11.24)] равен
(Cf)
sg-
: 0,05,
23 Заказ № 162
354
ГЛАВА 11
тогда из (11.9) находим
^£-^0.05 Л." Ч6;46'Л =0.140 ат/м.
dz
9,81 • 2,54 • 102
7, Г 1L
[ ve(ve — vA
Эти выражения для коэффициента трения на поверхности
раздела фаз можно сравнить также с корреляционной формулой
Леви [7], записанной через функцию F'
XU R, (11.,25)
vg(vg — vf) (?f — ?g) J
где # — эмпирическая функция отношения плотностей,
достаточно точно описываемая выражением [3]
(11.26)
Принимая следующие допущения, вполне приемлемые в
настоящей теории:
Р/»Р*г>
получаем из (11.25) и (11.26)
F' =
*?А
В то же время из (11.5) следует
F' =
-fi
8
(11.27)
(11.28)
Леви связал величину F' с отношением средней толщины
пленки к радиусу трубы. С учетом соотношения (11.28) корреля-
0.2
-— 0.1 -
-от -
0,04
0,02
0,004
0,0 J
ао2 от
2S /О
Фиг. 11.5. Сравнение расчетов по соотношению Леви и уравнению (11.18)
с экспериментальными данными для горизонтального течения.
соотношение Леви [7j: настоящая теория, уравнение (11.18); данные Уикса
и Даклера [8], труба, D = 25,4 мм; 26/D — отношение толшииы пленки к радиусу трубы.
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ 355
ция Леви и зависимость на фиг. 11.3 устанавливают связь между
одними и теми же параметрами. Поэтому обе теории можно
непосредственно сравнить, подставляя уравнение (11.18) в (11.28).
На фиг. 11.5 результаты расчета по соотношению Леви и
уравнению (11.18) -сравниваются с экспериментальными данными
Уикса и Даклера [8].
Касательные напряжения на стенке
Выполнив аналогичные выкладки для жидкой фазы, получим
уравнение, эквивалентное (11.8):
(С/)и,=(1-а)2^(С/)/, (11.29)
где (С/)№ — коэффициент трения на стенке для жидкой пленки,
a (Cf)f — коэффициент трения при течении по трубе одной только
жидкой фазы. Можно ожидать, что (Cf)w~ (С/)/, поскольку
шероховатость стенки трубы в обоих случаях одинакова. Тогда
из уравнения (11.29) можно получить следующее выражение для
Ф/^-Г^Т- (ИЗО)
Многочисленные исследования показали, что выражение (11.30)
является приближенным. .Оно согласуется также с результатами
интегрального анализа, который будет представлен позднее.
Кроме<гого, будет показано, что коэффициент трения на стенке
описывается почти такой же зависимостью от числа Рейнольдса
жидкости, как и при однофазном течении, за исключением пере-.
ходной области от ламинарного режима течения к
турбулентному. Число Рейнольдса жидкости определяется следующим
образом:
?fJfD
Re,=-^-. ' (И.31)
В общем случае из (11.4) следует
где для ламинарного течения
(C/L=4eV' (1L33)
а для турбулентного течения в качестве простого первого
приближения (Cf)w можно принять, как обычно, равным 0,005.
23*
356 ГЛАВА 11
Расчет градиента и объемного газосодержания
Приведенные выше соотношения позволяют рассчитать
касательные напряжения на поверхности раздела фаз и на стенке,
входящие в соотношение (11.3) и (11.4). Затем эти два
соотношения можно решить совместно и определить градиент давления и
объемное газосодержание. Например, при определении величины
объемного газосодержания для турбулентно-турбулентного тече-
Фиг. 11.6. Сравнение результатов расчета объемного влагосодержания по
уравнению (11.35) с эмпирическими результатами Мартинелли.
(1 _ а) — объемное влагосодержание; X — параметр Мартинелли; результаты
Мартинелли [9]; уравнение (11.35).
ния мы исключаем из уравнений (11.32) и (11.21) (dp/dz)p
и в итоге получаем
(1_а)2 [1+75(1-а)] _ Wt .
(11.34)
Если ввести параметр Мартинелли, то как для ламинарного, так
и для турбулентного течения жидкости можно написать
(1-<*)2[1 +75(1—а)]
--Х2
(11.35)
На фиг. 11.6 результаты расчета по уравнению (11.35)
сравниваются с эмпирической кривой Мартинелли.
На практике величину X2 легко рассчитать по известным
параметрам, после чего с помощью уравнения (11.35) можно
определить а. Градиент давления легче всего рассчитать, подставляя
это значение а в выражение (11.30).
кольцевой режим течения
357
Пример 11.2. Решить пример 3.3, используя уравнения (11.35) и (11.30), для
случая горизонтального течения. Расход жидкости уменьшен в 3 раза.
Решение. Число Рейнольдса жидкости равно 23000/3=7700, т. е. течение
турбулентное, и величина коэффициента трения, определенная по
диаграммам однофазного течения, равна 0,009. Вычислим составляющую
градиента давления, обусловленную трением, для жидкой фазы:
(-£),-
2 • 0,009 • 31,52 • 1,0
2,48
= 7,2 дин/см^.
Градиент давления для газовой фазы, как и раньше, равен 9,4 дин/см3,
поэтому
7,2
9,4
*2 =
= 0,766.
Решая уравнение (11.35) методом последовательных приближений,
получаем (1 — а) =0,18. Тогда из выражения (11.30)
ФГ-
= 5,55
0,18
и градиент давления в двухфазном потоке будет равен
dp
dz
■■ Ф) ( ~) = 5,552 . 7,2 = 222 дин/см*.
Обобщение полученных уравнений
Полученные выше выражения для касательных напряжений
]на стенке и на поверхности раздела фаз могут быть подставлены
;в общие уравнения, приведенные в примере 3.3, что позволит
рассмотреть кольцевое течение с учетом массовых сил,
изменения сечения, фазовых переходов и сжимаемости среды.
Применение этого метода к некоторым частным случаям будет
рассмотрено позднее.
J Дальнейшее усовершенствование теории
До сих пор учитывалось влияние только основных
переменных на динамику кольцевого течения. Был рассмотрен баланс
. между преобладающими силами без учета вторичных эффектов.
^.Однако в общем случае имеется по крайней мере семь
различных взаимодействующих сил, обусловленных градиейтом
давления, подъемной силой, поверхностным ' натяжением, инерцией и
Вязкостью каждой фазы. Полного описания совместного влияния
„этих сил пока еще не существует, однако в последующих
нескольких разделах будет рассмотрен ряд методик, которые могут
служить примером успешной модификации простой теории,
позволяющей получить более точные, но в то же время более
сложные теоретические модели процесса. Дальнейшие модификации
'еории будут рассмотрены при анализе вертикального кольцевого
:течения.
358 ГЛАВА 11
Интегральный анализ
При интегральном анализе кольцевого режима течения
задается профиль скорости в потоке. Затем этот профиль
интегрируется на участках сечения трубы, занятых каждой фазой, чтобы
определить расходы фаз. Величины касательных напряжений
на стенке и на поверхности раздела фаз связываются с
профилем скорости с помощью уже известных соотношений
однофазного течения. Из-за сложностей, вносимых граничными
условиями для газового потока на волновой поверхности раздела
фаз, этот метод рекомендуется использовать при анализе течения
жидкой пленки в симметричном кольцевом потоке.
Жидкая пленка
При однофазном течении жидкости со средней скоростью v,
когда жидкость заполняет все сечение трубы, градиент
давления, обусловленный трением, определяется по формуле
где коэффициент трения С/ является функцией числа Рейнольдса
Rem=^f. (И.37)
Предположим теперь, что только часть сечения трубы от стенки
до радиуса faro занята этим однофазным потоком, а остальное
сечение трубы заполнено газом либо газовым ядром со
взвешенными в нем каплями или даже вспененной жидкостью или просто
пенной структурой. Если профиль скорости в жидкой фазе
описывается функцией и(г), то тогда приведенная скорость жидкости
в данном канале будет равна
jf^-L^ J 2ur«ofr="J2r*Hflfr*. (11.38)
Для ламинарного течения
а=2г>(1 -г*2) (11.39)
и уравнение (11.38) окончательно принимает вид
jf=(l-afv. (11.40)
С другой стороны, при турбулентном течении, когда профиль
скорости описывается степенной функцией с показателем сте-
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ
35Э>
пени 77,
60 -.
в=-5-5(1-гУ. (11.41)
Подставляя это выражение в уравнение (11.38), получаем
jf=(\-yZy''(\+±-yiyb. (11.42)
Оба уравнения (11.40) и (11.42) можно представить в общем
виде
jf=j(a)Vi
(11.43)
где / (а)— некоторая функция а, которая может быть получена
i при любом допущении относительно конкретного вида профиля
скорости.
Если в двухфазном потоке известны // и /, то можно
рассчитать v и затем подставить найденное значение в уравнения
(11.36) и (11.37), чтобы получить градиент давления.
Упомянутые выше величины легко связать с параметром
i Мартинелли для жидкой фазы j>f. Для ламинарного течения
("&),
dp)
dz )f
= Z)2
* (11.44)
Z)2
(11.45)
Сравнивая уравнения (11.40), (11.44) и (11.45), находим
Л
ф}-
( dz ),
^откуда
(-*),
Ь=-г^г
(1-а)2 '
(11.46)
(11.47)
Для турбулентного течения из уравнения Блазиуса [10]
(совместимого с законом '/7 для профиля скорости) имеем
C/=0,079Re-°'25.
Подставляя это выражение в (11.36), получаем
(-
dp \ __ 0,158P/t>2 / V-f
dz jP
D
\vD9f
(11.48)
(11.49)
360 ГЛАВА 11
Чтобы определить ' величину (dp/dz)F с помощью уравнения
(11.42), заменим v в (11.49) на jf. Затем, рассчитывая вновь
параметр ф;, получим [11, 12]
*/= Г"5—8 w-- О1-50)
(1_1^Г)(ц-8-/«-)'■
Данные табл. 11.1 свидетельствуют о том, что в большинстве
практических задач расхождениями между уравнениями (11.47)
и (1Г.50) можно пренебречь и что уравнением (11.47) можно
пользоваться как в случае ламинарного, так и в случае
турбулентного течений жидкой пленки. В этой же таблице для
сравнения приведены значения параметра ф{ и параметра фщ,
рассчитанного Мартинелли для турбулентно-турбулентного течения.
Таблица И. 1
Сравнение результатов расчета параметра Ф;
по уравнениям (11.47) и (11.50) и параметра Мартинелли <t>ftt
для турбулентно-турбулентного течения Jill
а
0,96
0,95
0,91
0,86
0,81
0,77
0,69
0,60
0,52
0,47
0,34
0,24
0,16
0,10
*/«
24,4
18,5
11,2
7,05
5,04
4,20
3,10
2,38
1,96
1,75
1,48
1,29
1,17
1,11
Ь=^га
25,0
20,0
ИЛ
7,14
5,26
4,35
3,23
2,5
2,08
1,89
1,52
1,32
1,19
1,11
Ошибка,
%
2,5
. 8-!
—0,9
1,0
4,4
3,6
4,2
5,0
6,1
8,0
2,7
2,3
1,7
0
о _ »
*' (,_/a)(1 + -i^y/8
25,7
20,5
11,4
7,32
5,39
4,45
3,29
2,55
2,12
1,92
1,53
1,33
1,20
1,12
Ошибка,
%
5,1
9,8
1,8
3,7
6,5
5,6
, 5,8
6,7
7,6
8,9
3,3
3,0
2,5
0,9
Этот анализ должен был подтвердить правомерность
применения уравнения (11.30) как для ламинарного, так и для
турбулентного горизонтальных кольцевых течений. Кроме того, с пбмо-
щью уравнения (11.43) уравнение (11.49) может быть
преобразовано в выражение для коэффициента трения на стенке
(Cf)w=0,079ReJlf* (1~ta)2 ■ (11.51)
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ 361
Согласно данным табл. 11.1, /7/» почти идентично (1—а), если
профиль скорости описывается законом 77, и тогда (11.51)
сводится к уравнению
(C/)w=0,Q79Ref'\
(11.52)
из которого следует, что коэффициент трения на стенке в
двухфазном потоке может быть описан уравнением Блазиуса, если
число Рейнольдса рассчитывать по приведенной скорости
жидкой фазы // [уравнение (11.31)]. Тем самым делается шаг вперед
по сравнению с простым допущением, что коэффициент (Cf)w
всегда равен 0,005.
Газовое ядро
Случай вязкого течения газового ядра потока представляет
незначительный практический интерес. Действительно,
интегральный^ анализ дает точно такой же результат, что и более
фундаментальный дифференциальный анализ, представленный в при-
. мере 5.1.
Решение для турбулентного течения газового ядра,
полученное Тернером [11] при сравнительно больших толщинах пленки,
не очень сильно отличается от расчетов по уравнению (11.22).
Тернер принимал закон 1h для профиля скорости газа, используя
отношение радиуса к полному радиусу трубы. Кроме того, требо-
" валось равенство скоростей жидкости и газа на поверхности
раздела фаз. Скорость жидкости на поверхности раздела фаз в свою
^очередь определялась, исходя из допущения о справедливости
закона lh для профиля скорости в жидкой пленке.
Полученное Тернером выражение, эквивалентное (11.43),
имеет вид
/г=г{1-(1-к«-)'"(и-4^)-
оответствующее выражение для фг записывается следующим
бразом:
^={i-(i-i/;)8'-(i+4-v^)-
- 0,817
(11.54)
362 ГЛАВА 11
Дифференциальный анализ
Дифференциальный анализ симметричного горизонтального
ламинарного кольцевого течения производится таким же
образом, каки впримере 5.1, при этом случай cos 0 = 0 из
рассмотрения исключается. В результате алгебраических преобразований
получается следующее выражение для параметра Мартинелли:
Фг=-т±г- (1L55)
*'= 2а^(1-а)/([х/+а/2^) " (И'56)
В предельных случаях |лё<Сц/ и y,g=Hf, между <j>g и ф /
существует довольно простая связь. В первом случае выражение (11.56)
сводится к виду
<&=-*-. . о1-57)
и тогда из (11.57) и (11.55) следует
1 ' ' =1. (11.58)
Во втором случае выражение (11.56) принимает вид
а(2 — а) '
и тогда из уравнений (11.59) и (11.55) следует
tf=T75Z^T. <П-59>
1,1 1. (11.60)
*g */
Уравнения (11.58) и (11.60) представляют собой частные
случаи уравнения (3.30).
Дифференциальный анализ течения жидкой пленки, охваты-,
вающий весь диапазон чисел Рейнольдса, был выполнен Хьюит-
том [13]. До координаты г/+ = 5 применялось уравнение (5.4),
в интервале 5<г/+<20 — уравнение (5.10),- а в турбулентном
ядре — уравнение (11.78). Полученные результаты могут быть
представлены в виде зависимости между коэффициентом трения
на стенке и числом Рейнольдса жидкой фазы, как показано на
фиг. 11.7. Дифференциальный анализ хорошо согласуется с
интегральным анализом как при ламинарном, так и при
турбулентном течениях. Он справедлив также и в переходной области
течения.
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ
363
Фиг. 11.7. Коэффициент трения на стенке в горизонтальном кольцевом потоке.
Результаты интегрального анализа [уравнение (11.52)] и дифференциального анализа
Хьюитта [13]. Cfw — коэффициент трения на стенке; Re^ — число Рейнольдса жидкости.
11.3. Вертикальное кольцевое противоточное течение
При вертикальном течении не происходит расслоения потока,
которое можно наблюдать при горизонтальном течении, однако
вертикальное течение осложняется влиянием силы тяжести,
вызывающим появление массовых сил, действующих в направлении
течения, а также возможностью существования как восходящего,
так и нисходящего движения любого компонента. Хотя методы,
используемые при расчетах горизонтальных течений, приемлемы
также и для вертикальных течений при больших значениях а и
достаточна больших скоростях течений, когда влиянием силы
тяжести можно пренебречь, все же было бы ошибкой пренебрегать
влиянием этой силы при сравнительно небольших расходах газа,
т. е. в области, близкой к границе снарядного режима течения,
а также в условиях противоточного движения фаз.
Течение со стекающей пленкой
Течение со стекающей пленкой представляет собой простой
случай вертикального кольцевого течения. Если скорость газа
достаточно мала, то касательные напряжения на поверхности
раздела фаз и градиент давления пренебрежимо малы. В этом
случае уравнение течения тонких пленок (если кривизной стенки
364 ГЛАВА 11
можно пренебречь) имеет следующий вид:
*=£(Р/-Р,)(8-У), 01.61)
где б — толщина пленки, а у — расстояние от стенки.
Для ламинарного течения уравнение (11.61) принимает вид
b-^—S(?f-?g)^-y). ., (П.62)
В результате интегрирования получаем
V-/0
=£(Р/-Р,)(8у-Нг)- (И-63>
Повторное интегрирование по толщине пленки дает объемный
расход жидкости на единицу ширины пленки [14]
Ь= з^ • 01.64)
Соответственно массовый расход жидкости на единицу ширины
пленки, обычно обозначаемый буквой Г, равен
T=Pfqf. (11.65)
Полный объемный расход жидкости в тонкой пленке,
стекающей по стенке трубы диаметром D, составит
Q/=-3 ^——' ( }
а приведенная скорость жидкости // будет равна
'/=НГ Vp • (11-67)
Уравнение (11.67) можно записать в эквивалентном виде
//=-W^-)8- о1-68)
Число Рейнольдса пленки можно определить в виде
Rer=-^-, (11.69)
а безразмерную толщину пленки — в виде
f —
S*= s KVf 2,g) xf . (11.70)
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ
абб
Для круглой трубы (11.69) и (11.70) эквивалентны следующим
уравнениям:
J/?fD
Rer
Iх/
-flNt.
v=±.Ny*.
(11.71)
(11.72)
Тогда выражение (11.64) можно записать в виде
8*=0,909Rer/3. (11.73)
Графическое представление экспериментальных данных в виде
зависимости б * от Rer позволяет установить соответствие
юо
Фиг. 11.8. Влияние числа Рейнольдса на толщину стекающей пленки при
нулевых касательных напряжениях на поверхности жидкости [15].
6* — безразмерная толщина пленки; Rer — число Рейнольдса.
с результатами расчета по уравнению (11.73) вплоть до значений
Rer=1000 (фиг. 11.8). При больших значениях числа Рейнольдса
пленка становится турбулентной, и для ее описания необходимо
другое соотношение. Линия, вблизи которой группируется
большая часть экспериментальных данных на фиг. 11.8, описывается
уравнением
B'^.llSRer'6. (11.74)
В работе Белкина и др. [15] предложено другое соотношение:
8*=0,3l5(Rer-/C;)2/3, (11.75)
•366
ГЛАВА И
где С/ — соответствующий коэффициент трения. При С/=0,008
это соотношение принимает вид
§*=0,063Rer/3. (11.76)
Результаты расчета по соотношению (11.76) также
представлены на фиг. 11.8. Они хорошо согласуются с
экспериментальными данными Белкина.
Выражение (11.76) предпочтительнее, поскольку в сочетании
с выражениями (11.71) и (11.72) оно позволяет исключить
вязкость как параметр, и тогда
^-=0,063у;/3. (П-77)
С другой стороны, (11.74) выражает обычную зависимость
коэффициента трения от числа Рейнольдса в степени —0,2.,
Пример 11.3. Вода при температуре 21° С стекает вниз по вертикальной
поверхности с расходом 14,9 кг]мин на 1 м ширины поверхности. Какова
толщина пленки?
Решение. Вязкость воды при 21° С равна 3,72 кг/м-час. Расход в час на
единицу ширины равен 890 кг/м-час. Из (11.69) имеем
т. е. течение все еще ламинарное, и поэтому для определения толщины
пленки следует использовать уравнение (11.73). Тогда безразмерная
толщина б* будет равна
5* =0,909 • 960,/з=8,96,
и из (11.70) находим
^8-96( 10002 ■9,8202.36002)'/3 = 4-25-10"4 М-
Дифференциальный анализ стекающих пленок в условиях
однонаправленного движения фаз был выполнен Даклером [16].
В этом анализе до. г/+ = 20 использовались уравнения (5.9) и
(5.10), а при больших значениях у+ коэффициент турбулентной
вязкости определялся по выражению Кармана
у+>20 «_0,13(^)'(^)-!. (11.78)
Используя эти соотношения и следуя описанной в гл. 5 общей
схеме расчета, можно вывести выражения для профиля скорости
и толщины пленки. На фиг. 11.9 приведены полученные
расчетные зависимости б* от Re/ для различных значений
безразмерного параметра |3, характеризующего величину касательных на-
КОЛЬЦЕВОИ РЕЖИМ ТЕЧЕНИЯ
367
пряжений на поверхности раздела фаз. В случае нисходящего
течения в трубах |3 определяется соотношением
-Р=^У3^-- (П.79)
Относительная роль касательных напряжений на поверхности
раздела фаз и силы тяжести характеризуется отношением 4J3/8*,
юо юоо юооо юоооо
Фиг. 11.9. Безразмерная толщина пленки б* в зависимости от числа
Рейнольдса Re/ при различных значениях параметра Р, характеризующего
величину касательных напряжений на поверхности жидкости [16].
которое в случае тонких пленок эквивалентно —Ар*/(1—а) и
определяет изменение касательных напряжений по толщине
пленки.
Устойчивость стекающих пленок
На вертикальной поверхности восстанавливающая сила для
длинных волн и, следовательно, скорость динамической волны
равны, нулю. Однако скорость непрерывных волн, как и в
примере 6.1, равна
Vw=3vf. (11.80)
Это соотношение было получено Бенджамином [18], и оно вполне
согласуется с соотношением Капицы [19] и Портальского [20]
1^ = 2,50,.
Поскольку скорость непрерывных волн является конечной
величиной, а скорость динамических волн равна нулю, то, согласно
уравнению (6.132), течение стекающих пленок всегда будет
неустойчивым, за исключением случая коротких волн, когда
368
ГЛАВА И
поверхностное натяжение оказывает стабилизирующее
воздействие на пленку. Этот вывод был сделан Бенджамином [18],
который также показал, что темп нарастания неустойчивости
в сильной степени зависит от числа Рейнольдса. Некоторые
авторы утверждают, что имеется «критическое число
Рейнольдса», по достижении ' которого начинается неустойчивое
течение пленки. Однако весьма вероятно, что при малых числах
Рейнольдса темп нарастания возмущений столь мал, что
в реальных установках ограниченных размеров заметное
усиление возмущений просто не обнаруживается.
Фиг. 11.10. Запись показаний
датчика электросопротивления,
иллюстрирующая нарастание
неустойчивости стекающей пленки в трубе
диаметром 31,75 мм и длиной
0,915 м.
а — верхняя часть трубы; б — нижняя
часть трубы, расход воды 136 кг/час;
скорость волны 0,365 м/сек; расход
воздуха 0,142 нм?1мин.
Хьюитт и Уоллис [21] провели эксперименты, в которых
амплитуда волн в стекающей пленке измерялась вблизи верхнего
и нижнего концов вертикальной трубы диаметром 31,75 мм и
длиной 0,915 м. Происходящее на этой длине усиление волн ясно
видно на фиг. 11.10, где представлена запись изменения по
времени толщины пленки в двух указанных сечениях. Данные
получены путем измерений местной электропроводности участка
трубы в продольном направлении. Проводимость воды
обеспечивалась добавкой в нее небольшого количества соли. Хотя
в нижней части трубы пленка имела явно выраженную волновую
поверхность, уравнение (11.73) все еще оставалось справедливым
для описания средней толщины пленки.
Практически, как показано в задаче 7.4, имеется целый спектр
длин волн и частот, при которых течение всегда неустойчиво, и
все эти волны, как это следует из уравнения (6.126), движутся
со скоростью, меньшей vw. Взаимодействие таких волн носит
довольно неупорядоченный характер. Хьюитт и Уоллис [21]
показали, что можно зафиксировать много разных значений скорости
волны, если стекающая пленка подвергается воздействию
отдельных единичных возмущений. Приведенная на фиг. 11.10
запись также свидетельствует об отсутствии какой-либо
преобладающей длины волны.
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ 369
11.4. «Захлебывание»-'
Если в центре вертикальной трубы снизу вверх движется газ,
а по стенкам стекает вниз пленка жидкости, то на поверхности
этой стекающей пленки возникают касательные напряжения,
Расход газа, кг/час
Фиг. 11.11. Гидравлические характеристики течения вблизи границы
однонаправленного и противоточного течений [22].
Полное давление 1,4 ата; диаметр трубы 31,75 мм.
которые стремятся задержать ее движение. Пока пленка
сравнительно гладкай и устойчивая, касательные напряжения обычно
малы, и толщина пленки, а следовательно, и объемное
газосодержание по существу остаются такими же, как и при отсутствии
в центре трубы газового йотока [21, 28]. Однако, начиная
24 Заказ № 162
370 ГЛАВА 11
с некоторого расхода, газа при заданном расходе жидкости,
на поверхности раздела фаз возникают очень большие волны,
течение в целом становится хаотическим, градиент давления газовой
фазы заметно возрастает (фиг. 11.11) и жидкость выплескивается
через верхнюю часть трубы. Этот процесс известен как
«захлебывание» течения. В отличие от аналогичных явлений при
дисперсных режимах течения жидкой или газовой фазы
«захлебывание» при кольцевом режиме течения не соответствует границе
плавного изменения режима течения, а обусловлено внезапным
и резким возникновением неустойчивого течения,
сопровождающимся увеличением градиента давления на порядок.
Эмпирические соотношения для режима «захлебывания»
Турбулентное течение обоих компонентов. Пусть приведенные
скорости направленного вверх газового потока и направленного
вниз потока жидкости равны jg и jf. Эмпирическое соотношение
для «захлебывания» можно получить следующим образом. Про-
тивоточное движение газовой и жидкой фаз поддерживается
подъемной силой, обусловленной разностью плотностей газа и
жидкости. Расходы фаз можно связать с толщиной пленки через
уравнения движения, в которых движущая подъемная сила
уравновешивается силами трения в жидкой пленке. По аналогии с
однофазным турбулентным течением можно принять, что
усредненные турбулентные касательные напряжения связаны с
усредненными потоками количества движения компонентов, а именно
с параметрами pgp/a и р//2,/(1—а). Безразмерные комплексы,
связывающие эти потоки количества движения с
гидростатическими силами, записываются следующим образом:
fr-=JfPTisD(pf-pg)]-^ (П.82)
В эти комплексы ни в каком виде не входит зависимая
переменная а.
Тогда в случае пренебрежимо малого влияния других сил,
таких, как вязкость и поверхностное натяжение, можно найти
общее выражение, описывающее процесс «захлебывания» через
указанные выше безразмерные параметры. Эта гипотеза
убедительно подтверждается результатами всестороннего исследования
процесса «захлебывания» в насадочных колоннах. Например,
Лобо и др. [23], а также Шервуд и др. [24]
представили'экспериментальные данные в виде зависимости
А* М- $* от Щ^]'\ (11-83)
g FZ P/ ' ; Jg\9g)
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ 371
где a/F3 — характеристический параметр, определяемый как
суммарная площадь поверхности насадки, деленная на полный
объем потока.
Первый параметр идентичен /'* , а второй ////'*, если, как
обычно, сделать допущение, что (р/ — Pg)~P/, a а/F3
рассматривать как величину, обратную характерной длине D. После
замены координат кривые Лобо и Шервуда могут быть
представлены на графике в виде зависимости }*f от j*-, как на фиг. 11.12.
0,8
0,6
tig
0,4
0,2
— х
\
О
-
i
i
8\
X Jk
* xV
1
■т
Чо
х^^
х\«
1
1
-
-
1
0,2
0,4
0,6
0.8
Фиг. 11.12. Соотношения Шервуда [24] и Лобо [23] для «захлебывания»
течения в координатах 1/ j„ и 1/ L '
О — точки на кривой Шервуда; X точки на кривой Лобо; уравнение (11.84).
Обе кривые достаточно точно описываются уравнением
А1г+К'г=0,775.
(11.84)
Вид этого уравнения позволяет провести сравнение с данными
Делла и Прэтта [25], определивших расходы при
«захлебывании» в насадочных колоннах для различных комбинаций
жидкость—жидкость. Данные по «захлебыванию», нанесенные
'А V.
на график в координатах /'*
/
ложатся на прямые,
отсекающие на осях координат приблизительно равные отрезки.
Окончательное выражение имеет вид
>+°^(m-tr-4
?jl
ji,
g(?c—?d) F3
(11.85)
24*
372 ГЛАВА 11
где индексы end относятся к непрерывной и дискретной фазам.
Если помимо других параметров включить в коэффициент С
влияние поверхностного натяжения, то, умножив уравнение
(11.85) на j*'^ получим
yf* + 0,835y*V*=C. (11.86)
Подобие уравнений (11.86) и (11.84) очевидно.
Введенный Шервудом и Лобо поправочный множитель к /*,
учитывающий влияние вязкости и равный отношению вязкостей
в степени Vio, для большинства жидкостей несуществен.
Аналогично поверхностное натяжение входит в уравнение (11.85)
в степени 7i6, т. е. его влияние тоже незначительно.
Соотношения для «захлебывания» в вертикальных трубах
напоминают уравнения (11.84) и (11.86) и могут быть записаны
в общем виде следующим образом [26]:
f^mjf^C. (11.87)
В случае турбулентного течения т=1. Величина С зависит
от конструктивного выполнения концов труб, а также способа
подачи и отвода жидкости и газа. Для труб с острыми выходными
кромками С = 0,725; если же концевыми эффектами можно
пренебречь, то 0,88 < С <1 [27, 20]. В наклонных трубах расходы
в точках «захлебывания» могут быть значительно большими.
Во многих экспериментах в режиме «захлебывания»
течения наблюдался гистерезис. Например, если в вертикальной
трубе существует гладкая пленка, то расход газа, при котором
начинается «захлебывание» течения, совпадает с расходом
газа, вызывающим волны большой амплитуды. С
образованием этих волн происходит разрушение всей пленки, которая
сморщивается и покрывается волнами, амплитуда которых
в несколько раз превышает толщину пленки. Чтобы пленка
вновь стала гладкой, расход газа необходимо снизить до
значительно более низкого уровня, чем при возникновении волн.
Как показано на фиг. 11.13, петля гистерезиса, по-видимому,
ограничена значениями С=0,88 и С=\.
Обнаружено также, что после осушения трубы для
восстановления нисходящего течения жидкой пленки расход газа
следует уменьшить ниже значения, характерного для труб с
острыми кромками [27]:
У'^— 0,5. (11.88)
Вязкий режим течения жидкой пленки. Если жидкость
очень вязкая, то член, характеризующий инерцию жидкости,
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ 373
в уравнении (11.83) должен быть заменен членом,
пропорциональным силам вязкости. Отношение вязкой и подъемной сил
определяется выражением
Jf
V-fJf
(11.89)
N/ gD4?f~?g)
В работе [26] приведено соотношение для «захлебывания»
т.о.
Фиг. 11.13. Скорости «захлебывания» при течении воздухо-водяной смесит
в вертикальных трубах при минимальных концевых эффектах.
Все данные получены прн атмосферном давлении. О диаметр 25,4 мм, «короткая
колонна»,' подвод воздуха через отверстие со скругленными кромками [28]; X диаметр»
25,4 мм, колонна средней длины; подвод воздуха через отверстие со скругленными
кромками [28]; Л диаметр 31,75 мм, подвод н отсос воды через пористые стенки (в этих
точках с увеличением расхода начинается «захлебывание» течения) [21]; □ диаметр
31,75 мм (в этих точках с уменьшением расхода прекращается «захлебывание» течения;
[21]; + диаметр 19 мм [29], начало «захлебывания»; v диаметр 19 мм [29], конец
«захлебывания».
в условиях волнового течения пленки в трубах с гладкими
кромками при
4h+v Ы
=0,725.
(11.90)
В общем случае условие «захлебывания» для любого
значения вязкости жидкости описывается уравнением (11.87), где т
374
ГЛАВА 11
и С, как это показано на фиг. 11.14 и 11.15, являются функциями
Nf. Уменьшение коэффициента С для вязких жидкостей до
значено ооо
Фиг. 11.14. Коэффициент т в уравнении (11.87) в зависимости от
безразмерного комплекса Nf [26].
ния, характерного для труб с острыми кромками при движении
в них невязкой жидкости, вероятно,.связано с концевыми
эффектами [34].
аэ
0,8
0.7
—• — *■
* У...
/
Ж Х- X х——* —
10 30
100
300 1000 3000 10000
Фиг. 11.15. Коэффициент С в уравнении (11.85) в зависимости от
безразмерного комплекса Nf [26].
На фиг. 11.16 некоторые экспериментальные данные по
«захлебыванию» течения сравниваются с результатами расчета по
уравнению (11.87).
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ
375
Фиг. 11.16. Скорости «захлебывания» в смесях водных растворов глицерина и
этиленгликоля с воздухом при атмосферном давлении в условиях противоточ-
ного -движения фаз в вертикальной трубе диаметром 19 мм [26].
Сравнение экспериментальных данных с результатами расчета по сравнению (11.87) при
m и С с фиг. 11.14 и 11.15.
Жидкость
Глицерин
99% + 1%
95%
90%
80%
75%
70%
60%
50%
33%
Вода
Этнленгликоль
Обозначение
О
□
Л
О
0
V
•
ш
А
♦
Т
Вязкость прн
10°С, спз
3000
1270
498
116
60
39
17
9
4
1
~30
Nf
3,4
8,2
21
90
160
250
560
1000
2200
8200
300
Пример 11.4. Воздух и вода движутся в вертикальной трубе диаметром
50,8 мм в' режиме противотока. Каков максимально допустимый расход
жидкости, если Wg=9\ кг/час? pg=l,6 кг\мъ; р/=1000 кг\мъ; ц/=
=3,72 /te/м ■ час.
Решение. Поперечное сечение трубы равно
«• 5о,8;. ю-» = 0_з ^
Теперь вычислим приведенную скорость газа jg:
91
Jz = 5- = 7,75 м/сек.
s 3600 • 1,6 • 2,04 • Ю-3
,.. 376 ГЛАВА 11
Из уравнения (11.81) имеем
f = 7,75 f '"6 з зГ = °'43-
g \9,8- 50,8 • 10~3 • 103 J
Допустим, что концевые эффекты сведены к минимуму и что вся
предыстория течения позволяет принять максимальное значение С равным
■единице.
Так как / =0,655, из (11.87) следует
mj,"h =C —/*v' = l —0,655=0,345.
Из (10.16) находим
_ [(50,8 ■ IP"3)3 ■ 9,8 • (Ю3)2]'^ _
N* ~ 3,72/3600 3'5 - Ш ■
Тогда из фиг. 11.14 т=\, и, следовательно //* = 0,3452=0,119. Далее
из (11.82) находим максимальное значение //
//= (9.8 • 50,8 • 10-3)'/2 .0,119=0,0845 м1сек,
Следовательно, максимально возможный расход жидкости равен
//Р/Л =0,0845 • 103 • 2,04 • 10"3 • 3600=615 кг/час.
Расчет «захлебывания» на основе модели раздельного
цилиндрического течения [11]
Модель раздельного цилиндрического течения была
рассмотрена в гл. 3. Эта модель, безусловно, лишь приблизительно
описывает действительную геометрию течения в трубе, и все же
именно она является теоретической основой очень удачных
соотношений Мартинелли для горизонтального кольцевого и
расслоенного течений. Несмотря на ее недостатки, следует отметить, что
•единственный аналитический вывод уравнения (11.87) получен
на основе этой модели.
Весьма вероятно, что такая модель в наибольшей мере
отвечает процессам, происходящим в насадочных колоннах, так как
.в этом случае она описывает возможную конфигурацию течения.
Аналогичный анализ приведен также в работе Делла и
Прэтта [25].
Турбулентное течение. Если модель раздельного
цилиндрического течения использовать для анализа вертикального
течения, то необходимо учесть влияние силы тяжести. Тогда сила,
действующая на единицу объема газа, будет равна —dp/dz —pgg
вместо —dp/dz, а сила, действующая на единицу объема
жидкости, будет равна —dp/dz—pfg; (координата z в данном случае
■отсчитывается в вертикальном направлении).
Используя уравнение (5.6), результаты решения задачи 5.12
м принимая допущение о постоянстве длины пути перемешивания
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ 377
в каждом цилиндре, получаем
fg=JjL.Lp'Ua'n (Ц.91)
у;=^(1-Д^)*/.(1 _«)'/', (п.92>
где a = r2g/r20, 1—a = r2f/rz0, rg и г/—радиусы разделенных
цилиндров, а // и lg — безразмерные величины, нормализованные
относительно размеров каждого цилиндра или относительно
диаметра всей трубы. В первом случае
а во втором
lg=lf=V. (11.94)
В момент начала «захлебывания» степень турбулентности во
всем поле течения чрезвычайно возрастает. Длина пути
перемешивания, в обычных условиях применимая лишь для -ядра
потока, в данном случае может быть принята для всей трубы.
Согласно Никурадзе [30], эта длина для ядра потока равна
0,14г0 и вполне может быть аппроксимирована выражением
1' = Ц-. (11.95)
Подставляя выражение (11.95) в уравнения (11.91) и
(11.92), получаем
rg=Lp*'\al\ (11.96)
У; = (1-Л/>*),/2(1-«)л/2, (П-97)
где п принимает значение 3,5 либо 2,5 в зависимости от того,
какое соотношение, (11.93) или (11.94), будет справедливым,
и имеет тот же смысл, что и /гв уравнении (3.30).
Исключая Ар* из уравнений (11.96) и (11.97), получаем
соотношение
.*2 .*2
напоминающее уравнение (6.90). Огибающая семейства
кривых, описываемых уравнением (11.98) при различных
значениях а, имеет следующий вид:
/;/(" + ,)+yf(" + ,,= l. (11.99)
378
ГЛАВА 11
Уравнение (11.99) согласуется с уравнением (11.87) при т=\
и п, равном некоторому промежуточному значению,
а именно 3.
Вязкое течение жидкой пленки. В случае вязкого течения
жидкой фазы уравнение (11.97) заменяется следующим:
^=-|f(i-a)2(i-A/>*). (li.ioo)
Исключая а из уравнений (11.96) и (11.100), получаем
J \1/л
Ар*
+
згу:
N/(1— Ар*)
Чг
= 1.
(11.101)
Продифференцируем уравнение (11.101) и найдем уравнение
огибающей
..2/"
2,8
(11.102)
(1 — Ар*)*'* ~л"(Др*)(1 + 1/в'
Уравнения (11.101) и (11.102) не имеют простого решения,
однако /* и /* могут быть выражены в функции Ар* в
параметрическом виде:
5,6
\Nf
2 + (n —2) Ajp*
Г nAp*
I 2 + (n
,*(! + !/«)
■ 2) Д/>* J
л/4
(11.103)
(11.104)
Для различных значений Ар* с помощью уравнений (11.103)
и (11.104) вычисляются/* и/* совокупность которых дает
кривую «захлебывания» течения. Эти величины в последующем
могут быть- использованы для определения значения С,
которое будет согласовываться с левой частью уравнения (11.91).
В табл. 11.2 приведены значения С при л = 2,5 и л=3,5. Как
можно видеть, С практически является постоянной величиной.
Таблица 11.2
Значения С при «захлебывании» течения. Расчет с использованием
модели раздельного цилиндрического течения (вязкое течение пленки,
турбулентное течение газового ядра)
&р*
С (я=2,5)
С (л=3,5)
0
1
1
0,1
0,987
0,876
0,2
0,956
0,853
0,3
0,929
0,826
0,4
0,91
0,816
0,5
0,899
0,821
0,6
0,893
0,837
0,7
0,900
0,863
0,8
0,920
0,897
0,9
0,951
0,941
1,0
1
1
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ
379
11.5. Вертикальное восходящее однонаправленное
кольцевое течение
Границы вертикального кольцевого режима течения
Существуют два механизма, определяющих границы
вертикального кольцевого течения:
■. 1) «перекрытие» газового ядра жидкостью из пленки с
последующим переходом кольцевого режима течения в
снарядный;
2) унос капель с поверхности пленки с последующим
переходом, от кольцевого режима течения к
дисперсно-кольцевому.
При определенных сочетаниях свойств жидкости и размера
трубы эти два критерия могут перекрывать друг друга, т. е.
идеальное кольцевое течение практически не существует.
Переход от снарядного режима течения к кольцевому.
Существуют различные методы определения условий перехода от
снарядного режима течения к кольцевому, что создает
отличные объективные возможности для анализа соотношений,
определяющих границы режимов течения.
К этим методам относятся:
1. Определение критериев восходящего и нисходящего
течений жидкой пленки в функции расхода газовой фазы.
2. Определение условий, при которых в газовом ядре
исчезают жидкие перемычки.
3. Измерение путем отбора проб относительного расхода
жидкости на оси трубы в функции расходов фаз.
4. Сравнение экспериментальных и расчетных значений
объемного газосодержания в момент смены режимов течения.
5. Измерение падения давления.
Все эти методы будут рассмотрены по порядку и
сопоставлены с количественными расчетными критериями.
Критерии восходящего и нисходящего течений в жидкой
пленке. Если на стенке вертикальной трубы образуется пленка
жидкости, например, путем впрыскивания через пористую
спеченную металлическую пробку, то эта пленка в зависимости
от расходов газовой и жидкой фаз может либо стекать вниз,
либо двигаться вверх, либо может разделиться и частично
двигаться вверх, а частично стекать вниз. Нисходящее течение
пленки ограничено «захлебыванием». При заданном расходе
восходящего потока газа имеется максимально возможное
значение расхода нисходящего потока жидкости, и наоборот.
Расход газа, при котором невозможно нисходящее течение
380 ГЛАВА 11
жидкости, является одним из вероятных критериев верхней
границы снарядного режима течения при малых расходах
жидкости.
В реализованном интервале значений постоянной С
в уравнении (11.87) предельный расход газа, при котором
жидкость не стекает вниз по стенке, определяется
соотношениями
0,5<yg<l. (11.10'5)
Верхнее значение /* достигается при минимальном влиянии
концевых эффектов.
Характерные результаты представлены на фиг. 11.11. Они
получены при подаче воды в вертикальную трубу через
пористый участок стенки и при непрерывном увеличении расхода
восходящего потока воздуха. При малых расходах воздуха вся
жидкость стекает вниз. После «захлебывания» течения часть
воды начинает двигаться вверх, и в конце концов
достигаются условия, при которых вся вода движется вверх.
Фиксируя условия, при которых вся вода будет двигаться вверх,
можно определить нижнюю границу однонаправленного
течения.
При очень малых расходах жидкости заштрихованная
область на фиг. 11.11 становится узкой, так как, если
впрыскивать жидкость в трубу при условиях, соответствующих концу
кривой «захлебывания», когда жидкость не может стекать
вниз, единственно возможным для жидкости в этом случае
останется движение вверх. Экспериментальные данные как для
вязких, так невязких жидкостей [31] описываются уравнением
fg^f 0,9. (11.106)
При меньшем расходе газа часть жидкости стекает вниз,
а при большем часть жидкости непрерывно движется вверх.
Если жидкость в пленке стекает вниз и не имеет возможности
выливаться из нижней части трубы, то в этом случае в канале
будут образовываться жидкие пробки.
Следует также отметить, что в широком диапазоне
расходов жидкой фазы уравнение (11.106) приблизительно
согласуется с границей «запрещенной области», показанной на
фиг. 11.24.
Перекрытие газового ядра потока жидкими «перемычками».
Появление жидких перемычек в поперечном сечении может
быть зафиксировано с помощью электроконтактного зонда,
подобного разработанному Гриффитсом [32] и использованному
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ
381
Гриффитсом и Хеберстро [33], а также Бреннером [35]. Зонд
в виде проводящего наконечника, укрепленного на
изолированном стержне, помещают в ядро двухфазного потока. Если
электропроводность жидкости сильно отличается от
электропроводности газа, то по величине измеренного электрического
сопротивления между концом зонда и стенкой трубы можно
определить, перекрыто сечение трубы жидкостью или нет.
Такой метод определения условий смены режимов течения
довольно произволен, поскольку имеется весьма широкая
область течения, в которой жидкие пробки становятся
небольшими и довольно далеко отстоят друг от друга, однако
полностью не «исчезают. Экспериментальные данные Гриффитса,
Хеберстро и Бреннера описываются следующими
соотношениями:
У;<1,5 £=0,9+0,6./;, (11.107)
У/>1,5 /g=(7+0,06-^)yy. (11.108)
Измерения уноса капель жидкости с помощью
зонда-пробоотборника. Другим способом определения наличия жидких
перемычек в газовом ядре является отбор проб из потока с
помощью зонда, установленного на оси трубы. Этот
зонд-пробоотборник фиксирует как жидкие перемычки, так и унос
капель жидкости. Он не собирает никакой влаги в случае
«идеального» кольцевого течения, при котором вся жидкость
течет по стенке трубы. С помощью зонда можно определить
приведенную скорость жидкости (//)сь вблизи оси трубы,
которую можно сопоставить со средней приведенной скоростью
жидкой фазы jf. В случае снарядного течения (jf)cL может
значительно превосходить //, поскольку жидкость в пробках
может двигаться вверх, а в пленке жидкости вокруг пузыря —
вниз. Поэтому скорость жидкой фазы в центре трубы будет
иметь максимум, а на стенке трубы она будет отрицательной.
На фиг. 11.17а приведены данные по уносу капель
жидкости при течении смеси воздуха и воды при атмосферном
давлении. Унос не наблюдался только в ограниченном диапазоне
скоростей газа при малых расходах жидкости. При малых
расходах газа унос связан с наличием жидких перемычек,
тогда как при больших расходах газа он связан с наличием
в потоке капель. Экстраполируя на ось абсцисс часть
графика, относящуюся к ^снарядному течению, можно определить
нижнюю критическую скорость газа, при которой происходит
переход от снарядного течения к кольцевому. Уравнение линии
перехода имеет вид
у;=0,4+0,бу;. (11.109)
I
382 ГЛАВА 11
'80| I I I I ']. I I ! ■
Ф иг. 11.17а. Унос капель жидкости в зависимости от расходов воды и воздуха
при восходящем кольцевом течении [35].
Внутренний диаметр трубы 25 мм; внутренний диаметр зоида 4,7 мм.
Эта кривая проходит значительно ниже линии перехода,
определенной с помощью электроконтактного зонда.
Сравнение экспериментальных и расчетных значений
объемного газосодержания. Основной целью выявления границы
перехода между любыми режимами течения является
определение условий, по достижении которых вместо одной теории
следует применять другую. Следовательно, условия перехода
от снарядного течения к кольцевому определяются точкой
пересечения расчетных кривых, соответствующих теориям снарядного
и кольцевого течения. Например, согласно теории снарядного
течения, величина объемного газосодержания в турбулентном
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ
383
Фиг. 11.176. Падение давления Ар* в зависимости от приведенной скорости
воздуха /V при постоянных значениях приведенной скорости водЬ1 ; *.вос.
ходящее кольцевое течение, однонаправленное движение фаз [351 '
Все параметры в безразмерном виде. Первая колонка данных относится % Tnvfi
метром 19 мм, вторая — к трубе диаметром 25,4 мм. 'РУре диа-
потоке, определенная по уравнению (10.36), равна
1.2 (У/ + Jg) +0,345 VgD(r/-tg)/9f
Это соотношение можно переписать следующим образом-
(11.110)
Соотношение для объемного газосодержания в восходящем
кольцевом потоке (оно будет*выведено позднее) имеет вид
1—2,85(1—а)
Jf
2,85(1—а)
= 0,775.
(11.112)
384
ГЛАВА 11
На фиг. 11.18 результаты расчета, полученные по этим двум
соотношениям, сравниваются с экспериментальными данными,
полученными при течении воздухо-водяного потока в трубе
диаметром 25,4 мм [35]. Экспериментальные данные для
снарядного течения имеют большой разброс вследствие того, что
объемное газосодержание определялось путем отсечки
быстродействующими запорными клапанами участка трубы и ре-
0,7
0,6
0,5
0,4
0,3
0,2
0,7
1111
S
--ХХХ
1
V *
\ „
X XX X
■Л х х
Ч хх X
** *-t *й^
XX ^* ^i -
* „"*2хх
X X х X X
X
1 1 1 1
1111
4 точки
Ч. »
4 точки
i i i i
! 1 1 1
3 точки
/
—* 1-
1 1 I I
1 ■■
-
~
.
-
"
, 5 точек
/ 5 точек -
5 точек . / •-
4 точки
i i i > i i i i I i
0,5
1,0
7,5
2,0
Л
Фиг. 11.18. Объемное влагосодержание в области перехода от снарядного
режима течения к кольцевому [35] при //* = 0,53.
кольцевое течение, соотношение (11.112); снарядное точение,
соотношение (11.111).
зультат, естественно, зависел от количества пузырей,
«захватываемых» при этой операции. Экспериментальные данные,
относящиеся к кольцевому режиму течения, группируются
вокруг расчетной кривой. Теоретические кривые пересекаются
в точке, характеризуемой величиной объемного влагосодержания
1—а = 0,2, при этом значения /* и /* приблизительно
согласуются с уравнением (11.109). Из уравнения (11.112) следует, что
действительная кривая, соответствующая (1—а) =0,2,
описывается соотношением
у;=о,зз+о,75у;. (п.пз)
Измерения падения давления. Некоторые исследователи,
например Говье и др. [36—38], полагали, что границы режимов
течения соответствуют максимумам или минимумам измерен-
КОЛЬЦЕВОИ РЕЖИМ ТЕЧЕНИЯ
385
ного падения давления. Эту гипотезу можно сопоставить с
результатами других методов, используя данные, подобные
приведенным на фиг. 11.176.
Расчеты с помощью этого метода не являются достаточно
точными, поскольку в ряде случаев кривые в области
максимумов и минимумов довольно плоские. Однако порядок
рассчитанных величин правильный. Это свидетельствует о том, что ход
кривой падения давления тесно связан с изменениями режима
течения.
Обсуждение. Из всех методов расчета границ между
кольцевым и снарядным течениями наиболее привлекателен с
инженерной точки зрения метод, описанный в разделе «Сравнение
экспериментальных и расчетных значений объемного
газосодержания», который основан на определении параметров точки, по
достижении которой вместо одной теории следует использовать
другую. Результаты расчета по этому методу согласуются с
измерениями уноса зондом-пробоотборником с последующей
экстраполяцией экспериментальных кривых, приводящей к
известной идеализации процесса. Указанный метод позволяет
произвести оценку условий, при которых влияние жидких пробок на
динамику течения газо-жидкостной смеси в целом мало.
Метод измерений с помощью электроконтактного зонда дает
завышенные примерно на 50% значения скорости газа, так как
случайные жидкие перемычки еще долго существуют после того,
как они уже перестали определять режим течения.
Область, заключенная между кривыми, описываемыми
уравнениями (11.109) и (11.107), может рассматриваться как
переходная от снарядного режима течения к кольцевому, причем этот
переход происходит постепенно.
Переход к дисперсно-кольцевому режиму течения. В
высокоскоростном кольцевом потоке обычно наблюдается
значительный унос жидкости в газовое ядро. Если этот унос измеряется
с помощью пробоотборника, регистрирующего массовый расход
жидкости через площадку а в центре трубы Wf, то можно
определить параметр, который приблизительно соответствует доле
унесенной жидкости
E=lL A= Uf)CL (Ц.114)
Wf a jf
Для чисто гомогенного и одномерного течения £ = 1;. для
чисто кольцевого режима течения Е = 0.
Согласно фиг. 11.17а, имеется весьма узкий диапазон
расходов, в котором унос капель мал. Фактически в большинстве
кольцевых течений содержится некоторое количество унесенных
капель, и поэтому эти течения можно условно рассматривать как
25 Заказ № 162
386 ГЛАВА 11
бы состоящими из двух фаз: гомогенного тумана и жидкой
пленки.
Расчет уноса более подробно будет рассмотрен в следующей
главе.
Соотношения для определения объемного
влагосодержания и падения давления
Соотношение Дармутского колледжа [35]. Соотношение
Дармутского колледжа было выведено на основе гипотезы о
существовании такого кольцевого течения, в котором вязкие силы
И силы поверхностного натяжения малы, а динамика жидкости
определяется соотношением гидростатических и инерционных сил
в газовой и жидкой фазах. Эта гипотеза частично основана на
наблюдении, что жидкая пленка имеет явно выраженную
волновую поверхность и что профильное сопротивление пленки
намного превосходит сопротивление трения на поверхности
раздела. В результирующее соотношение входят параметры /* и
/*, которые уже использовались ранее в формулах для расчета
«захлебывания». Если данные, полученные в экспериментах
с воздухо-водяной смесью в трубе диаметром 25,4 мм,
представить в координатах /* — /* (фиг. 11.19), то оказывается, что
линии постоянного значения объемного влагосодержания являются
прямыми, касательными к кривой «захлебывания». Уравнение,
описывающее эти линии, имеет вид
.* .*
1—2,85^(1 —«) 2,85(1-а) =°.775- (11.П5)
-Более точные данные последующих экспериментов [11]
указывают на некоторые отклонения от линейности кривых
постоянного объемного влагосодержания. Согласно этим данным,
уравнение, описывающее линии постоянного объемного
влагосодержания, имеет следующий вид:
£-*-=! (11.116)
1—3,1(1— а) 3,1(1—а)
и справедливо только в диапазоне значений /'* и j*,
приведенных на графике, когда унос капель ниже ~20%.
Модифицированное соотношение Мартинелли [И].
Соотношение Мартинелли первоначально было получено для
горизонтального течения и не применимо для вертикального течения,
поскольку не учитывает влияния силы тяжести. Однако его можно
использовать при достаточно больших скоростях
(приблизительно при \*~>2), при которых касательные напряжения опре-
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ 387
деляют динамику течения пленки. При меньших скоростях более
точные результаты получаются, если следовать описанной в
примере 3.7 методике определения сил трения в двух потоках. При
Обозначение
О
«
+
Л
а
т
0
в
А
•
V
в
1-а.
0,200
0,175
9,1625
0,1500
0,1375
0,125
0,1125
0,100
0,0675
0,075
0,0625
0,050
Линия „захлебывания'
уравнение(11.87),
т = 7, С = 0,88
Фиг. 11.19. Линии постоянного объемного влагосодержания при кольцевом
• течении воздухо-водяной смеси [35].
ig*, if* — безразмерные приведенные скорости газа и жидкости соответственно.
отсутствии ускорения потока или фазовых превращений
уравнения движения для газового ядра и потока в целом записываются
следующим образом:
-2-+P«S+tf(--&),=0' (".117)
-#-+*[«Р,+(1-«)Р/] + */(—#-),=0. (11.118)
25*
ГЛАВА 11
0.04
о*о' 0,08 0.09 0,Ю 0.11
0,12 7-ос = 0J3
0,03
лРэ
0,14
0,15
0,02
0,01
Геометрическое
место точек
„захлебывания"
0,16
0.005
-Л 1 1 L.
0,010
-1 L
Фиг. 11.20. Определение объемного влагосодержания и падения давления по
модифицированному соотношению Мартинелли [11, 35].
ДР«* ~ безразмерное падение давления для газа; Др/* — безразмерное падение давления
для жидкости.
Если использовать следующие выражения для падения давления
на трение:
Ар'
Ар
(-dpldz)g
{-dp]dz)t
f~ gitt-tg) '
(11.119)
(11.120)
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ
389
то уравнения (11.117) и (11.118) примут вид
Ap*=<$>\Ap*g, (11.121)
АР*=^Ар;+(1-«). (П.122)
Считая <f>f и ф„ известными функциями а, можно решить
систему уравнений (11.121) и (11.122), получив в итоге Ар* и а
в функции Ар* и Ар* ' как это было сделано Тернером [11, 35],
который принял <f>f =1/(1 — а) и использовал эмпирическое
выражение </>g. Ревультаты приведены на фиг. 11.20. С
помощью этой диаграммы можно быстро определить Ар* и а. Линии
постоянного объемного влагосодержания на графике — прямые,
а их огибающая является геометрическим местом точек,
соответствующих «захлебыванию» течения.
Простые модели течения
Модель раздельного цилиндрического течения. Модель
раздельного цилиндрического течения для вертикального потока
■ может быть получена точно таким же образом, как и для
горизонтального. Составляющая градиента давления, обусловленная
трением, для газового цилиндра будет равна — {dp/dz+pgg),
а для жидкого —(dp/dz+pfg). В случае однонаправленного
движения газовой и жидкой фаз эта модель справедлива при
—dp/dz>pfg, а в случае противоточного движения фаз — при
—dp/dz<pfg. Она позволяет получить приемлемые соотношения
для расчета «захлебывания» течения.
Модель гомогенного течения. В работе [39] предпринята
попытка использовать модель гомогенного течения в качестве
основы при выводе соотношения для составляющей градиента
давления, обусловленной трением, в дисперсно-кольцевом потоке.
Для надлежащей проверки теории прежде всего надо оценить
диапазон расходов, в котором режим течения был именно
дисперсно-кольцевым, а не каким-либо другим, например
снарядным. Если имелись данные по величине уноса, граница режима
течения определялась следующим требованием: унос,
измеряемый зондом-пробоотборником, должен превышать 20% и лежать
правее соответствующих минимальных значений на графиках
' типа фиг. 11.17а. Если же авторы не приводили значений уноса,
то существование дисперсно-кольцевого режима течения
определялось требованием: приведенная скорость газа (или пара)
должна быть выше значений, соответствующих линиям перехода
от снарядного режима к кольцевому [соотношения (11.107)
и (11.108)], а также выше критической скорости газа, при
которой начинается унос капель жидкости [2], [уравнение (11.2)].
390
ГЛАВА 11 !
Во всех случаях гомогеннвя теория обеспечивая^? Вбйее точный
расчет потерь давления на трение, чвм.<аей^кошейЙе Мартинелли.
С другой стороны, соотношение МартЩ^ЯИ дает более точные
значения а по сравнению с теорией гомогенного течения.
Коэффициент трения, рассчитанный по гомогенной теории, очень
близок к 0,005 для всех рассмотренных данных.
С помощью гомогенной модели можно получить'более точные
соотношения, если ввести поправочный множитель, учитывающий
влияние поверхностного натяжения. Введение такого множителя
оправдано определяющим влиянием поверхностного натяжения
на устойчивость пленки, шероховатость поверхности раздела фаз
и унос капель. Например, соотношение Миланского
информационного центра научных исследований (CISE) [40] для расчета
составляющей градиента давления, обусловленной трением,
представляет собой по существу модифицированное уравнение
для гомогенного течения
\ dz )f
GI,4-0,86g0,4
Ж2
(11.123)
где 7°— усредненное значение удельного объема гомогенной
смеси. Было найдено, что поверхностное натяжение является
значительно более существенной переменной, чем вязкость
любого компонента или любым образом определенная средняя
вязкость смеси. В работе [41] также отмечается существенное
влияние поверхностного натяжения на величину эффективного
коэффициента трения в гомогенном потоке.
Модель раздельного течения.. Модель раздельного течения
может быть получена с помощью выражений для касательных
напряжений на стенке и поверхности раздела фаз, выведенных
в разд. 11.3. Из рассмотрения фиг. 11.21 следует, что уравнение
(11.18) применимо как к вертикальному, так и к
горизонтальному течениям.
В работе [3] были получены простые соотношения в
предположении, что коэффициент трения для однофазного
турбулентного течения как жидкой, так и газообразной фаз равен 0,005.
Если пренебречь влиянием сжимаемости, относительной
скорости и уноса, то уравнениям (11.121) и (11.122) будут
эквивалентны следующие уравнения:
А^Ю-у;^75,^-*) ,
(11.124)
Ар*=-
10-
(1-а).
(11.125)
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ
391
С другой стороны, в случае ламинарного течения
^ =и f
где
^•="(1^+0,684 (1-«),
32у/;х/ _ 32/7
Jf~ D2g(9f-Pg) ~ Nf •
(11.126)
(11.127)
Поправочный множитель 0,684 в (11.126) учитывает кривизну
профиля скорости и может быть определен путем
дифференциального анализа.
0.2
0,1
£ 0.08
о
V О.06
и.
0,04
I I I III 1 | I 1 I I I 1 "<S>j
0,002
0,004
0,007 0,01 0,02
2S/D
0,04 0,07 0,1
0,2
Фиг. 11.21. Сравнение результатов расчета по уравнению (11.18) и
соотношению Леви [3, 7] с экспериментальными данными Миланского информационного
центра научных исследований (CISE) для вертикального течения.
Эксперименгальные данные C1SE- С вода в трубе диаметром 25 мм; □ вода в трубе
диаметром 15 мм; Д спирт в трубе диаметром 15 мм; уравнение (11.18);
—. соотношение Левн [7]; 26ID — отношение толщины жидкой пленки к радиусу
трубы.
На фиг. 11.22—11.24 представлены результаты расчетов по
уравнениям (11.124) и (11.125) для турбулентно-турбулентного
режима течения. Следует отметить ряд важных моментов.
Из фиг. 11.22 видно, что характер течения чрезвычайно резко
изменяется, когда /* становится меньше ~1. При /*<0,95
нисходящее течение невозможно; при /*, немного меньших 0,95, для
обеспечения восходящего течения требуются- большие объемные
влагосодержания (1—а). (В действительности имеется
небольшая область существования восходящего течения вблизи начала
координат, однако значения /* в этой области ниже 0,01.)
Практически величине /* =0,9 соответствует такое состояние, когда
тонкие пленки стекают вниз, а толстые движутся вверх.
Результирующее восходящее течение жидкости может иметь вид
392
ГЛАВА II
ПО
поверхности тонкой сте-
При /* <0,9 волны обычно достаточно высоки,
движущейся вверх толстой пленки
кающей пленки
чтобы временами перекрывать сечение трубы и вызывать переход
к снарядному режиму. Это заключение согласуется с эмпиричес
ким соотношением (11.106).
Фиг. 11.22. Зависимость безразмерной приведенной скорости жидкости //* от
объемного влагосодержания 1—а при различных значениях безразмерной
приведенной скорости газа jg*. Расчет по уравнениям (11.124) и (11.125) для
турбулентной пленки [3].
В случае ламинарного течения жидкости картина качественно
остается той же самой, только переход к снарядному режиму
течения происходит при/*=» 0,8.
Те же самые выводы можно сделать из рассмотрения
зависимостей падения давления Ар* от /* при малых приведенных
скоростях течения жидкой фазы (фиг. 11.24). При скоростях газа
/* " меньших 0,8—1, падение давления резко возрастает и
имеется некоторая «запрещенная область», в которой решения для
Ар* вообще не существуют. Поскольку располагаемый напор
зачастую определяется внешними характеристиками системы, то
наличие этой «запрещенной» области вызывает значительные
практические трудности. При попытке саботать в этой области возни-
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ 393
кает либо новый режим течения, либо неустойчивое состояние,
сопровождающиеся сильными колебаниями рабочих параметров
-системы. Кроме того, при расходах газа, пересекающих эту
область в диапазоне малых расходов жидкой фазы, при заданном
расходе жидкости возможны три решения для падения
давления. Довольно небольшие пульсации любого параметра могут
Фиг. 11.23. Безразмерное падение давления Др* в зависимости от безразмер_-
ной приведенной скорости газа jg* при различных значениях безразмерной
приведенной скорости жидкости //*. Расчет по уравнениям (11.124) и
(11.125) [3].
привести к скачкообразному переходу от малого перепада
давления к большому.
Сама величина минимального падения давления при
постоянном расходе жидкости также является весьма существенным
параметром с точки зрения устойчивости системы, в которой
регулируются давление и расход жидкости. Если уменьшить расход
газа ниже значения, соответствующего минимальному падению
давления, то расход газа будет уменьшаться и далее, пока вся
394 глава н
труба не заполнится'жидкостью. .Из рассмотрения фиг. 11.23 и
11.24 следует, что при Ар*, меньших 0,3, максимальная скорость
жидкости при заданном падении давления достигается при /*«*
«1,1.
о\ 1 1 I
ио us го
Фиг. 11.24. Область малых значений )t* на фиг. 11.23 (увеличенный масштаб).
Пример 11.5. Решить пример 11.2 для случая вертикального течения. При
решении использовать: а) модифицированное соотношение Мартинелли
и фиг. 11.20; б) уравнение (11.115) и фиг. 11.19; в) модель раздельного
течения.
Решение, а. Из примера 11.2 имеем (—dp/dz)f=7,2 дин/см3 и (—dp/dz)<-g=
=9,4 дин/см3. Из уравнений (11.119) и (11.120) следует
^=ш=9'6 •10_3; д^м=7-35 • 10~3-
Из фиг. 11.20 1—а=0,176, Др*=0,42.
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ 395
б. Значения \Й и // соответственно равны 14,4 и 0,314 MJceK. Тогда,
согласно (11.81) и (11.82), значения je* и //* будут равны
f e ,4,4 I !* Г)Ч'= 1,015.
s [ 24,8 • Ю-3 • 9,8 • 103 J
/ =,0,314/ f гУ/г = 0.636.
f \ 24,8 • Ю-3 • 9,8 • 103 /
Из фиг. 11.19 1—а=0,175.
в. Используя полученные выше значения jg* и //*, из фиг. 11.22 и
11.23 находим 1 — а=0,205 и Др*=0,3.
Поскольку рабочая точка близка к границе между снарядным и
кольцевым течениями и к минимальному значению падения давления,
на фиг. 11.23, соответствующему нулевым касательным напряжениям на
стенке, то, по-видимому, расчет с использованием модели раздельного
течения менее точен, чем расчеты по методам «а» и «б».
Пример 11.6. Решить пример 2.5 с помощью теории кольцевого течения.
Решение. Значения jg* и //* равны
/,= 14,4 ( ''22 з зГ- LOIS,
s V 9,8 - 24,8 • 10~3 • 103 /
>^=<^мв(-58тwтl5г),/,=,■в,•
Онн выходят за пределы значений, указанных на фиг. 11.19. Из
соотношений (11.108) и (11.109) следует, что рассматриваемый режим
соответствует переходной области между снарядным и кольцевым
течениями. Если принять, что в этой области справедливо уравнение (11.116),
то получим
1,015 1,91
1_3,1 (1 —а) 3,1 (1—а) — '
откуда 1—а=0,232, что близко к экспериментальному значению.
По фиг. 11.23 можно определить Др*«0,66. Тогда падение давления
будет равно 0,66 • 103 • 10"4 • 0,457=0,0302 ат. Полученное значение
является завышенным, по-видимому, вследствие того, что не была учтена
кривизна профиля скорости или вероятное изменение направления
течения жидкой пленки.
■Уточнение модели раздельного течения [3]
Точность модели раздельного течения можно повысить
многими методами, в которых учитываются дополнительные
явления. В большинстве случаев общий вид соотношений остается
неизменным и лишь вводятся различные поправочные множители,
зависящие от дополнительно рассматриваемых параметров.
Жидкая пленка. С помощью изложенной в гл. 5 методики
можно выполнить дифференциальный анализ уравнений
усредненного по времени течения жидкой пленки. В примере 5.1
получены результаты для ламинарного течения в пленке. В диапазоне
значений 0<(1—а)<0,2, характерном для кольцевого режима
396 ГЛАВА II
течения, падение давления с допустимой степенью точности
можно определить по соотношению (11.126).
Анализ течения пленки, содержащей ламинарный,
промежуточный и турбулентный слои, был выполнен Хьюиттом [42].
Некоторые из использованных им параметров и их эквиваленты «
в используемых в настоящей работе обозначениях приведены
в табл. 11.3. Там же указан физический смысл этих параметров.
Результаты могут быть представлены графически в виде
зависимости коэффициента трения на стенке от числа Рейнольдса
для различных значений других параметров, как это показано
на фиг. 11.25 и 11.26.
- 1 1 1 1 11II
1 1 ! 1 1 1 1 1
I I mm
1
1 1 1 1 1II
1 1 1 М III
& □
200 75
II 1 1 1 1 111
1 1 II 1 1ТТ
о Обоэжпонце
20 0 Z
— Горизонтальное
течение
1 1 .1 1 i i м
''1—: 1 1- I I I Mil 1 1 I I I III!—1_J ' i I i i ill i i .l,i.
Ю Ю3 ю4 10s юв
Ref
Фиг. 11.25. Коэффициент трения на стенке в вертикальном потоке при Re*= oo
Расчет на основе дифференциального анализа Хьюитта [42].
^„ — коэффициент трения на стенке; Re^ — число Рейнольдса.
Таблица 11.3
Некоторые безразмерные параметры, используемые Хьюиттом
в безразмерном анализе течения жидкой пленки
в кольцевом потоке [42]
Хьюитт
Настоящая
книга
Физический
смысл
W+
Re/
Скорость
дг73 д/>*
/ 4
Падение
давления
М
/ D
Толщина
пленки
1/аЗ
Lp*
1—а
Кривизна
профиля
касательных
напряжений
Re*
^ [А/**-(1-«)]'/,
4
Касательное напря-
. жение на стенке
Линии постоянных значений р соответствуют постоянным
падениям давления при различных расходах жидкости. При ма-
КОЛЬЦЕВОИ РЕЖИМ ТЕЧЕНИЯ 397
лых расходах пленка тонкая, профиль касательных напряжений
в ней приблизительно линейный, а полученные результаты
согласуются с кривой для горизонтального течения. С увеличением
расхода жидкости профиль касательных напряжений искажается
под действием силы тяжести и в конце концов величина
касательного напряжения на стенке, а следовательно, и коэффициент
трения резко уменьшаются. Число Рейнольдса жидкой фазы в точке
7.°F
0,01 г
0,001
Фиг. 11.26. Коэффициент трения на стенке в вертикальном потоке при Re* =
= 1000 [3]. Расчет на основе дифференциального анализа Хьюитта [42].
Суш — коэффициент трения на стенке; Re^ — число Рейнольдса.
нулевых касательных напряжений на стенке может быть связано
с величиной р следующими приближенными соотношениями [3]:
(11.128)
(11.129)
Вязкие эффекты и нелинейность профиля касательных
напряжений обычно учитываются введением в уравнение (11.125) двух
поправочных множителей
, „2
^CfwJf
Re7 < 300, ■p=l,2Re>/',
2000 < Re/ < 20000, p=0,13Re//3.
Ар*
■B(l-a),
(11.130)
(1_«)2
где С. —коэффициент трения в случае линейного профиля
касательных напряжений, определяемый, как и при
горизонтальном течении, по "фиг. 11.7. Параметр В учитывает кривизну
398
ГЛАВА П
профиля касательных напряжений. Ниже приводятся значения В,
обеспечивающие согласование уравнения (11.130) с
результатами Хьюитта при различных числах Рейнольдса [3]:
Re, < 1000, В =0,684,
1000 < Re, < 8000, £=0,193Re?'183,
Re/>8000, Въ\. (11.131)
Эти уравнения представляют собой просто одно из приближений
.к общей функции, связывающей Ар*, 1 — а, /* и. Re/, которое
дает точные предельные значения при ламинарном течении или
в случае горизонтального потока. Наибольшая ошибка
получается вблизи точки нулевых касательных напряжений на стенке.
Газовое ядро. При анализе течения газового ядра, в
результате которого было получено уравнение (11.124),
пренебрегали следующими факторами: уносом жидкости, скоростью
границы раздела газ—жидкость, вязкостью газа и его
сжимаемостью.
Влияние уноса жидкости приблизительно можно учесть, если
рассматривать ядро потока как гомогенную смесь газа и капель.
Пусть массовый расход газа равен Wg, жидкости в пленке Wf и
унесенных капель We. Тогда суммарный массовый расход в ядре
потока равен
Wc=Wg+We. (11.132)
Средняя плотность ядра потока приблизительно составит (при
Pf>pg)
РС=^Р*. (11.133)
Следовательно, величина /* возрастает в {WJWgY12 раз.
Что же касается влияния скорости поверхности раздела фаз
на течение газового ядра, то неясно, какую скорость следует
использовать: среднюю скорость жидкости, скорость волн на
поверхности или усредненную по времени скорость. Так как в
большинстве случаев пленка тонкая и касательное напряжение в ней
приблизительно постоянное, то вполне допустимо считать, что
скорость поверхности раздела будет в 2 раза больше средней
скорости жидкости.
При таких допущениях касательное напряжение на
поверхности раздела определится следующим образом:
4t = 2C/tpe(vg-2v,)*.
(11.134)
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ 399
Отношение скоростей можно выразить через расходы:
У, Wf 9ga
-vj- р,(1-«) Wg • (11Л*>
Подставляя (11.135) в (11.134), получим выражение для
касательного напряжения на поверхности раздела фаз.
Следовательно, поправочный множитель к Ар* в уравнении (11.124)
будет равен
W, ?g а \а .
1-2-
wg P/ ' —а
Вязкость газового ядра влияет на течение в пограничном слое
вблизи поверхности раздела, а тем самым и на величину
касательных напряжений на этой поверхности. В данном случае в
качестве приемлемого приближения можно использовать значение
коэффициента трения для газового потока в трубе вместо
постоянного, значения 0,005 в уравнении (11.19). При числах
Рейнольдса до 10е можно использовать уравнение Блазиуса
(С,)г=0,079 (Re^r0'25. (11.136)
При этом число Рейнольдса для газа рассчитывается по
суммарному массовому расходу в ядре и вязкости газа, т. е.
R..--^^-. 0U37)
1tD|i
■g
-,—0,25
С учетом всех этих поправочных множителей уравнение
(11.121) принимает вид
(11.138)
На фиг. 11.27 представлены характерные результаты
последовательного умножения экспериментальных значений
приведенного коэффициента трения, полученных Джиллом и Хьюиттом
[43], на указанные выше поправочные множители.
На фиг. 11.28 показаны результаты применения всех этих
поправочных множителей к данным, полученным "в экспериментах
с двумя различными системами впрыска жидкости. Поправки
вводились к падению давления, определенного Джиллом и
Хьюиттом, вычитанием из полного падения давления составляющей
падения давления из-за ускорения.
С учетом сжимаемости газа изменяются уравнения (11.124) и
(11.125), поскольку ускорение газового ядра отражается на
балансе количества движения каждой фазы. Так как величина
1 — а мала и по существу постоянна, обычно достаточно
умножить рассчитанный градиент давлений в обоих уравнениях на
■* 400
ГЛАВА И
5 -
—..|«л/
•
'
-
д
5
э
X
д .^
^^ + +
0 о
+
о
Wg = 136 кг/час
Многоструйный
X
X
д -^
■^ Д
+ 4-
+
О
О
(возЭух)
инментор
0,02
0,03
0.04
.' -а.
Фиг. 11.27. Результаты последовательного введения поправочных множителей
к экспериментальным данным Джилла и Хьюитта [43] по (Cf)sgl(Cf)g в
функции объемного влагосодержания [3].
Три поправочных множителя, входящие в уравнение (11.138):
Г *ftf I2 _0 25
ai = WJW ■ а2= 1—2 — - ; а3=0,079 Re_ ' /0,005.Прямая линия описывается
eg' [ WgPj(l — a) J & I
модифицированным уравнением (11.24): (Cf)ag=(Cj)g [1+ 90(1 — а)]. X
экспериментальные данные без поправок, 1=1; О экспериментальные данные с учетом поправки на
унос, |=ai; + экспериментальные данные с учетом поправок на унос и относительную
скорость, 4=ai<22; д экспериментальные данные с учетом поправок на унос,
относительную скорость и число Рейнольдса газа, %=aia2a3.
1/(1—М2), где Мс — изотермическое число Маха для ядра
потока, обычно определяемое как
,2 _ . aje We + Wg) Qg
Mi
(11.139)
a2/? a?A2p
Иногда удобно использовать в расчетах модифицированную
безразмерную приведенную скорость ядра потока
Jc = Jg
и безразмерное давление
s\Wg)
(11.140)
(11.141)
gD(f/—?g)
В этом случае квадрат числа Маха ядра потока выражается сле-
Мс=Х^-. (11.142)
дующим образом:
;2л*
&р
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ 401
6 -
ее
3-
Обозначение
Wg,ta/4ac
Устройство Ли
иода жидкости
+
МО
X
230
Щеле
о
320
д
90
v
140
Фс
>
то
<
230
а
а
270
0,05
1-е
Фиг. 11.28. Отношение приведенного коэффициента трения к коэффициенту
трения газа в зависимости от объемного влагосодержания [3]. Расчет по
данным Джилла и Хьюитта [43] с учетом всех поправочных множителей в
уравнении (11.138).
• Вертикальное восходящее течение смесн воздух—вода, Д=31,7 мм.
Пример 11.7. Джилл и Хьюитт [43] измерили толщину пленки и градиент
ч. давления в восходящем однонаправленном кольцевом потоке. Типичные
экспериментальные данные: №g=136 кг/час; Wf = 2\2 кг/час;
= 1,32 кг/м3; р/ = 1010 кг/л3; p,g=0,063 кг/м-час; р,/=3,89 кг/м
№е=242 кг/час; 6=0,27 мм; .0=31,7 мм; —dp/dz=381,9 кг1м2-м.
внить эти данные с теоретическими расчетами.
Решение. Число Рейнольдса жидкой пленки равно
4Wf 4 • 212
Ref=^-= _,n,Z ,lt ,„» =2180.
P* =
• час;
Срл-
IcDfA/
■к (31,7 • 103) • 3,89
По этому значению Re/ из фиг. 11.25 и уравнения (11.131) находим
(Су„)'=0,015 и Я=0,79.
Расчетные значения //* и /с* равны соответственно 0,133 и 3,94.
Из (11.137) получаем Re*=2,4 • 105, р*=360, а 2WtpglWgpf=0,004.
Согласно уравнению (11.142), Мс2=0,043. Тогда уравнения (11.130) и
(11.138) с учетом всех поправочных множителей примут вид
Ар* (1-0,043) =-2= !1__ +0,79(1-а),
Ар*( 1—0,043) =0,112
(!_«)»
1 +75(1—a) t
Чг
4 • 10~ла
1—а
Решая эти уравнения совместно, находим Др* и а. В результате
1 — а=0,038, а Др*=0,40, что согласуется с экспериментальными
значениями 1—а=0,034 и Др*=0,38.
26 Заказ № 162
402
ГЛАВА It
Поверхность раздела газ—жидкость. На поверхности
раздела газ—жидкость в кольцевом потоке возможны различные
режимы. Очень тонкие пленки — гладкие, тогда как на толстых
образуются большие волны возмущения. Между этими двумя
предельными режимами заключена область малых волн, или ряби.
Значения Cf для гладкой трубы
i ■ i I i 1 1 '
О 1 2 3 4 5 6
(S/D)x703
Фиг. 11.29. Влияние волнистости поверхности раздела на величину
коэффициента трения [3]. Расчет по данным Ширера и Неддермана [44].
Диаметр трубы 31,7 мм, восходящее течение воздухо-водяной смеси. Cf f — коэффициент
треиия на поверхности раздела.
Удары капель о поверхность раздела фаз и унос изменяют
картину течения при больших скоростях газа. Эти различия в
режимах течения должны сказаться на величине коэффициента трения
на поверхности раздела и, возможно, также на характере течения
обеих фаз. .
Указанные эффекты иллюстрируются на фиг. 11.29, где
результаты расчета по уравнению (11.18) сравниваются с
некоторыми данными Ширера и Неддермана [44] для восходящего
однонаправленного кольцевого течения. Из фиг. 11.29 ясно видно,
что кольцевое течение, описываемое уравнением (11.18),
характеризуется наличием волн возмущения; значения коэффициента
трения в области ряби и гладкой пленки ниже. Каждая серия
приведенных экспериментальных точек соответствует
постоянному расходу газа.
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ 40$
На фиг. 11.4 были приведены данные из работы [6] для
нисходящего течения, представленные в виде зависимости
приведенного коэффициента трения от 6/D для различных массовых
скоростей жидкой фазы. Эти данные согласуются друг с другом
и приблизительно с уравнением для кольцевого течения с
волновой поверхностью пленки в области, которую авторы
классифицируют как «дисперсно-кольцевое течение». По-видимому,
возникновение волн возмущения совпадает с появлением уноса.
Аналогичные результаты описывались в работах [41, 45],
авторы которых обнаружили сильное влияние^ поверхностного
натяжения.
Отсюда следует, что область применения уравнения (11.18),
по-видимому, ограничена режимом течения с большими волнами
возмущения. Для обеспечения большей точности расчетов
течения в области ряби или гладкой пленки необходимы новые
расчетные соотношения, а также критерии для определения
режима течения пленки. В работе Ширера wНеддермана [44]
указывается на влияние расходов газовой и жидкой фаз, вязкости,
плотности, а также поверхностного натяжения и диаметра трубы.
Совместное влияние всех этих параметров в общем виде пока
еще не определено.
Дополнительные эффекты
Кроме только что описанных явлений, имеются еще два,
которые затрудняют проведение точных расчетов. Речь идет о
входных эффектах и уносе капель. На одной и той же установке
могут быть получены совершенно разные результаты, если
изменится способ ввода фаз. В предельных случаях жидкость
вводится либо в виде пленки на стенке трубы, либо в виде
диспергированных капель небольшого размера. Например,
приведенные на фиг. 11.30 данные по падению давления Др* для этих
двух случаев различаются в 2 раза. Влагосодержание в ядре
потока вследствие уноса капель может не достичь равновесного
значения на расстоянии ~200 диаметров от входа. Даже в
случае равновесия отсутствуют надежные методы расчета уноса.
Описанный в следующей главе метод (разд. 12.10) дает лишь
первое приближение.
Изменяющаяся доля уноса приводит к дополнительным
эффектам, обусловленным массообменом между кольцевой пленкой
и газовым ядром, а также влияет на величину членов,
характеризующих ускорение потока и потери на трение.
В инженерных расчетах, возможно, целесообразно принять
долю уноса в качестве зависимой переменной, оценить ее
влияние на характеристики течения и изыскать способы ее
регулирования с помощью соответствующих технических устройств на
26*
404
ГЛАВА 11
входе, а также в самом дотоке, например, с помощью
заверителей.
Задачи
11.1. Смесь воздуха и воды движется по горизонтальной трубе диаметром
25,4 мм при температуре 21° С и давлении 7 ата. Расход каждого
компонента 450 кг/час. Каким будет при этом режим течения? Рассчитать падение
давления в функции количества жидкости, унесенной в виде капель, и
сравнить результаты с расчетом по уравнению (3.30) при л=3,5. ,
11.2. Рассчитать с помощью уравнения (11.8) и соотношений Мартинелли
отношение (С/),/(С/)в. Сравнить результат с рассчитанным по
уравнению (11.23) значением, подставив в это уравнение вместо 0,005
коэффициент (Cf)g.
a4j;
Фиг. 11.30. Сравнение теории и
экспериментальных данных двух
разных исследований прн одних и
тех же расходах, но разных
способах ввода жидкости.
теория ламинарной пленки,
уравнение (11.126); теория
турбулентной пленки, уравнение (11.125);
Д экспериментальные данные [52], /«***
«=1,9, форсунка; О
экспериментальные данные [50], /в*»2.0, кольцевая
щель. Оба эксперимента проведены
с воздухом и водой в вертикальной
трубе диаметром 31,7 мм примерно
прн атмосферном давлении. Унос не
измерялся.
11.3. Сравнить уравнение (11.20) с диаграммами для расчета коэффициента
трения в однофазном потоке.
11.4. Нефть (р/=780 кг/м3, Ц/=0'6 спз) и природный газ (pg=56 кг/м3,
p,g=0,014 спз) движутся при давлении 70 ата по горизонтальному
трубопроводу диаметром 200 мм. Градиент давления поддерживается равным
0,7 ата/км, хотя отношение расходов компонентов может изменяться из-за
изменений условий на входе. Рассчитать соотношение между расходами
в указанных условиях.
11.5. Если профиль скорости в турбулентном потоке описывается степенным
законом с показателями степени 1 /п, то выражение С/=Л (Rem) ~~ ,^п+1>
эквивалентно (11.48). Какой вид имеет зависимость <j>f от л?
Сравнить-результаты с данными табл. 11.1 при п—5, 9 и 19. Каково предельное выражение
для Ф при п —»- оо?
11.6. Сравнить уравнение (11.54) с соотношением Мартинелли и
уравнением (11.22) при характерных значениях отношения вязкостей и плотностей
фаз.
11.7. Вывести уравнения (11.55) и (11.56) и сравнить (11.56) с другими
соотношениями, связывающими Фе и а.
11.8. Оценить по степени сложности различные анализы течения жидкой
пленки в горизонтальном кольцевом потоке. При каких условиях
целесообразно использовать более сложные теории? Какова разница в результатах
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ 405
расчетов толщины пленки по наиболее сложной теории при Re/=10e;
—(rfp/dz)j,=2,3- 10-2 ат/м; (—dp/dz),=2,3 • 10~4 ат/м?
11.9. Какова толщина пленки воды, стекающей по вертикальной стенке при
температуре 20° С и следующих значениях расходов: 10-1 и Ю-4 нм3\м">
11.10. Каковы скорости непрерывных волн при условиях задачи 11.9?
11.11. Сравнить уравнения (11.68) и (5.32) при Др*=0. При каких значениях
6/D расчет толщины пленки дает ошибку в 10% из-за пренебрежения
кривизной поверхности трубы при заданном расходе жидкости?
11.12. Сравнить кривые «захлебывания» течения, рассчитанные по
уравнениям (11.116), (11.124) и (11.125), с результатами расчета по
модифицированному соотношению Мартинелли на фиг. 11.20.
11.13. 99%-ный глицерин стекает вниз в вертикальной трубе диаметром 19 мм
при температуре 10° С. Объемный расход глицерина 2 см3/сек. Каков
максимально допустимый расход воздуха в условиях противоточного движения
при давлении 1 ат?
11.14. Сравнить соотношения, описывающие границу кольцевого режима
(«захлебывание») при очень малых расходах газовой фазы, с- условиями,
при которых снарядоподобный пузырь будет находиться в состоянии покоя
в вертикальной трубе.
11.15. Ширер и Дэвидсон [46] проанализировали образование волн на
внутренней поверхности трубы, соответствующих режиму «захлебывания». В
качестве определяющих параметров ими были выбраны число Вебера,
Рг/«2о7о", Re и параметр У, рассчитанный по уравнению (10.20). Показать,
что их результирующая формула, а также уравнения, представленные
в разд. 11.4, являются частными случаями общей зависимости от jg*, if*,
Nt, NE0.
11.16. Вертикальная труба диаметром D и длиной L закупорена в нижней
своей части, а сверху соединяется с большим объемом жидкости малой
вязкости, находящейся при температуре насыщения. Показать, что
максимальное значение теплового потока при равномерном обогреве стенки трубы без
ее перегрева составляет
д _,„ hfgD3'*l9gg(Pf-9g)Y'*
»"макс — t" ~f~ ГТ7Т5 '
£[1+(Рг/Р/)Л]2
где С = '/в для трубы с острыми кромками в верхней ее части и С='/4 для
трубы со скругленными кромками [47].
11.17. Предположим, что в результате гидравлического прыжка на
поверхности стекающей пленки в трубе образуется очень большая волна. Показать,
что решение для потенциального течения невязкой жидкости за волной при
противоточном движении фаз может быть записано в виде функции от //*
и /«*■
11.18. Определить соотношение между массовой скоростью G, массовым паро-
содержанием х и давлением р на границе между снарядным и кольцевым
режимами течения воды в вертикальной трубе диаметром 38 мм.
11.19. Сравнить соотношения между //*• и jg* при постоянных значениях
объемного газосодержания воздухо-водяной смеси в вертикальной трубе
диаметром 31,7 мм при давлении 1,40 ата и температуре 21° С, воспользовавшись
следующими уравнениями:
а) (11.116);
б) (11.121), (11.122) н фиг. 11.20;
в) (11.124) и (11.125) или (11.126) в зависимости от характера течения
(ламинарное или турбулентное);
г) (11.124) и (11.125) с учетом поправок на относительную скорость,
значения чисел Рейнольдса газовой и жидкой фаз и сжимаемость;
д) дополнительно к поправкам, перечисленным в предыдущем пункте,
учесть унос 20% влаги.
406
ГЛАВА 11
11.20. Показать, что минимум падения давления, рассчитанный по уравнению
(11.126), при заданном расходе жидкости почти совпадает с точкой нулевых
касательных напряжений на стенке. Сравнить с результатами расчета по
уравнению (11.128).
11.21. Сравнить минимум падения давления, рассчитанный по уравнению
(11.125), с результатами расчета по уравнению (11.129) и показать, что
результаты будут одинаковыми, если коэффициент трения на стенке взять
равным 0,01 вместо 0,005.
11.22. Соловьев и др. [48] обнаружили, что при графическом представлении ■>
зависимости Ар*/(Ар*) мин от /г*/(/г*)мин получается универсальная кривая
для всех расходов жидкости в восходящем кольцевом потоке с ламинарной
пленкой. Проверить это для значений /'/*, равных 10~5, 10~4, Ю-3 и 10_г
с помощью уравнений (П.123) н (11.125).
11.23. Показать, что переход от нисходящего к восходящему течению вязкой
жидкой пленки происходит примерно при /й*=0,8.
11.24. Хартли и Роберте [49] получили следующее соотношение для
коэффициента трения на поверхности раздела фаз в кольцевом потоке:
<С,),-(С,),-1.5[-£-.±- У-щ^\-
Сравнить его с соответствующими соотношениями в данной книге.
Таблица 11.4
F-
"3
о
<
0,89
8,96
6,99
3,75
2,42
CJ
в
а*
а
139,0
122,5
232,5
304,0
136,6
"3
а*
0
503,9
172,1
0,73
69,5
"*
а
О.
1,22
1,38
1,41
1,41
1,29
'ч
РЛ
о.
1013
1013
1013
1013
1013
<3
3,81
3,77
3,99
3,72
3,90
/час
а
9,08
858,1
168,4
8,35
89,4
*5
во"
0,114
0,444
0,226
0,063
0,203
«У
<3
j°
0,064
0,064
0,064
0,064
0,063 .
11.25. В табл. 11.4 приведены некоторые характерные экспериментальные
данные, полученные Джиллом и Хьюиттом [43] для восходящего дисперенсг-
кольцевого течения в трубе диаметром 31,7 мм. Сравнить эти данные с
расчетными значениями, сделав при этом необходимые поправки и допущения.
We — расход жидкости, унесенной в виде капель;. Wj — расход в жидкой
пленке.
11.26. В табл. 11.5 приведены некоторые экспериментальные данные [50],.
полученные при исследовании восходящего кольцевого течения воздухо-во-
дяной смеси в вертикальной трубе диаметром 31,7 мм. Сравнить эти
данные с
а) результатами расчета по уравнениям (11.115) и (11.116);
б) фиг. 11.20;
в) результатами расчета по уравнениям (11.124), (11.125) и (11.126);
г) моделью раздельного течения с учетом всех эффектов;
д) результатами расчета по «немодифицированному» соотношению Мар-
тинелли, приведенному в гл. 3;
е) теорией гомогенного течения.
Средние значения свойств, не приведенных в таблице: цв=997 кг/м3,
Р/=0,064 кг/м-час.
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ 407
Таблица 11.5
W , кг/час
90,66
90,66
90,85
91,07
93,71
93,71
94,57
95,36
96,11
96,07
93,30
94,30
112,7
115,4
115,5
Н6,9
116,1
117,9
118,3
119,2
120,6
120,6
119,7
121,9
Wj, кг/час
35,4
43,5
68,3
85,8
134,2
178,6
222,1
326,2
382,1
440,8
290,4
. 524,8
18,0
43,6
68,0
89,2
137,2
183,6
226,9
285,2
843,0
388,4
464,9
584,3
Pg., кг/л3
1,24
1,24
1,24
1,27
1,31
1,32
1,35
1,38
1,39
1,40
1,36
1,43
1,26
1,28
1,28
1,30
1,32
1,35
1,38
1,40
1,44
1г44
1,47
1,54
|)у (средняя
вязкость
воды), кг/м-час
3,52
3,78
3,84
4,02
3;99
3,87
3,93
4,01
4,01
4,05
3,81
3,86
3,44
3,62 .
3,73
3,84
3,80
3,75
3,83
3,84 .
3,90
3,95
3,96
3,99
i-«, %
2,76
2,91
3,39
3,70
4,21
4,89
5,38
6,66
8,06
7,37
5,95
8,48
1,73
2,13
2,46
2,78
3,18
3,58
4,09
4,47
4,94
5,57
6,14
6,86
Градиент
давления,
10—' ат/м
6,702
7,488
9,482
10,05
14,45
17,42
19,78
26,94
29,12
31,65
24,14
34,88 "
• 5,434
- 10,51
13,21
15,33
20,14
25,18
30,54
33,44
37,79
39,50
44,91
49,42
11.27. В вертикальном эрлифте требуется обеспечить максимально возмож-
вый расход жидкости при заданном градиенте давления. Жидкость—вода
при температуре 21° С, градиент давления 0,03 ат/м, диаметр трубы. 76 мм.
Какой понадобится расход воздуха при давлении 1,4 ата> Каков к. п. д.
эрлифта, если под этим подразумевать потенциальную энергию, сообщенную
воде, приходящуюся на единицу энергии, затрачиваемой на прокачку
воздуха?
11.28. Полный интегральный - анализ горизонтального кольцевого течения
с гладкой поверхностью раздела газ—жидкость может быть выполнен [51]
с помощью уравнений (11.46) и (11.50) в сочетании с соответствующими
выражениями для 4>g, полученными при допущении, что газ течет в гладкой
трубе диаметром D Ya. Не пренебрегая скоростью поверхности раздела фаз,
получить выражения для <j>g для ламинарного и турбулентного режимов
течений, подчиняющихся закону Блазиуса. Вывести выражения для Фе и се
в зависимости от X для четырех сочетаний ламинарного и турбулентного
течения каждого компонента. Сравнить с соотношениями Мартинелли.
Данная теория не очень точна, так как она не учитывает волнового
характера поверхности раздела. -
11.29. Сравнить кривую «изменение направления течения на противоположное»
на фиг. 11.11 с границей «запрещенной области» на фиг. 11.24. Каков эффект
учета (с целью получения более точных расчетов) значений чисел Рейнольдса
газовой и жидкой фаз, относительной скорости, профиля касательных напряжений?
408 ГЛАВА П
11.30. В кольцевом потоке jg обычно значительно больше j/. В этом случае
скорость непрерывных воли приблизительно определяется в виде
^=[d(l-a)J//
Показать, что скорость непрерывной волны может быть представлена в
безразмерном виде следующим образом:
С помощью фиг. 11.22 сравнить Vm* с безразмерной скоростью жидкости
Vf*=ji*/(l — а). Прн каких условиях скорость волн будет больше скорости
жидкости?
Литература
1. Baker О., Oil Gas J., 53, № 12, 185—190, 192, 195 (July 1954).
2. Steen D. A., M. S. Thesis, Dartmouth College, Hanover, N. H., 1964;
см. также Steen D. A., Wall is G. В., АЕС Rept NYO 3114-2, 1964.
3. W a 11 i s G. В., Papers № 69-FE-45, 69-FE-46, ASME Appl. Mech. Fluids
Engrs. Conf., Northwestern Univ., June 1969; см. также Уоллис Г.,
Труды амер. общ-ва инж.-мех., серия D, Теоретические основы
инженерных расчетов, № 1 (1970).
4. N i k u r a d s e J., Forschungsheft, 301 (1933).
5. Mo о d у L. F., Trans. ASME, 66, 6-71 (1944).
6. Чен Ше-фу, Ибеле У./ Труды амер. общ-ва инж.-мех., серия С,
Теплопередача, № 1, стр. 116 (1964).
7. Levy S., Intern. J. Heat Mass Transfer, 9, 171—188 (1966).
8. Wicks M., Dukler A. E., A. I. Ch. E. I., 6, 463—468 (1960).
9. Lockhart R W., Mar tine Ш R. C, Chem. Eng. Progr., 45, 39 (1949).
10. Blasius H., /. Forschungsheft, 131 (1913).
11. Turner J. M., Ph. D. Thesis, Dartmouth College, Hanover, N. H., 1966.
12. Ар м а н д А. А., Изв. ВТИ, № 1, 16—23 (1946).
13. Hewitt G. F. (неопубликованная работа, 1967).
14. Nuss elt W., Z. Ver. Deutsch. Ing.,b0, p. 541 (1916).
15. В el kin H. H., MacLeod A. A., Monrad С. С, Rothfos R. R.,
A. I. Ch. E. I., 5, 245—248 (1959).
16. Dukler A. E., Chem. Eng. Progr. Symp. Ser., 56, № 30, 1—10 (1960).
17. Von К а г ш а п Th., NACA Rept. TM 611, 1931.
18. В e n i a m i п Т. В., /. Fluid Mech., 2, 554 (1957).
19. Капица П. Л., ЖЭТФ, 18, вып. 1, 3—18 (1948).
20. Т a i 1 b у S. R., Р о г t а 1 s k i S., Trans. Inst. Chem. Engrs., 38, 324—330
(1960).
21. Hewitt G. F., Wallis G. В., Multi-Phase Flow Symp., ASME,
November 1963, 62—74.
22. Hewitt G. F., L а с е у P. M. C, N i с h о 11 s В., Symp. Two-Phase Flow,
Exeter, England, vol. 2, June 1965, B401—B419.
23 L о b о W. E., Friend L., H a s h m a 11 F., Z e n z F., Trans. A. I. Ch. E.,
41, 693—710 (1945).
24. S h e r w о о d Т. К-, Shipley G. H., H о 11 о w а у F. A. L., Ind. Eng.
Chem., 30, 765 (1938).
25 Dell F. R„ Pratt H. R. C, Trans. Inst. Chem. Engrs., 29, 89—109 (1951).
26. Wallis G. В., Rept General Electric Co., 62GL132, Schenectady, N. Y.,
1962.
КОЛЬЦЕВОЙ РЕЖИМ ТЕЧЕНИЯ
409
27. W a 11 i s G. В., UKAEA Rept AEEW-R123, 1961.
28. N i с к 1 i n D. J., Davidson J. F., Paper № 4, Symp. Two-Phase Flow,
Inst. Mech. Engrs., London, February 1962.
29. Wallis G. В., Steen D. A., Brenner S. N., AEC Rept NYO-10, 487,
EURAEC 890, July 1963.
30. Nikuradse, 7. Forschungsheft, p. 356 (1932).
•31. W al 1 i s G. В., UKAEA Rept AEEW-R142, 1962.
32. Griffith P., Argonne Natl. Lab. Rept ANL-6796, 1963.
33. G r i f f i t h P., H a b e r s t г о h R. D, Rept 5003-28, Mech. Eng. Dep„ Mass.
Inst. Techn., 1964.
34. С 1 i f t R., P r i t с h a r d C. L., N e d d e r m a n R. M., Chem. Eng. Sci., 21,
87—95 (1966).
35. Wallis G. В., АЕС Rept NYO-3114-14, EURAEC 1605, 1966.
36. G о v i e r G. W., Radford B. A., Dunn J. S. G., Can. J. Chem. Eng.,
35, 58 (1957).
37. Govier G. W., Short W. L., Can. J. Chem. Eng., 36, 195 (1958).
38. Brown R. A. S., Sullivan G. A., Govier G. W., Can. J. Chem. Eng.,
38, 62 (1960).
39. Wallis G. В., Meyer P. E., AEC Rept NYO-3114-10, EURAEC 1480,
September 1965.
40. С as agr ande I., Cravarolo L., H ass-id A., Pedrocchi E.,
CISE R-73, Milan, 1963.
41. Be r gel in O. P., Kegel P. K., Carpenter F. G., Gazley C, Heat
Transfer and Fluid Mech. Inst., Berkley, Calif. 1949.
42. H e w i 11 G. F., UKAEA Rept AERE-R3680, 1961.
43. G i 11 L. E, H e w i 11 G. F, UKAEA Rept AERE-R3935, 1962.
44. Shearer С J., N e d d e r m a n R. M., Chem. Eng. Sci. 20, 671—683
(1965).
45. Dukler A. E., Ph. D. Thesis, Univ. of Delaware, 1951.
46. Shearer С J., Davidson J. F., /. Fluid Mech., 22, part 2 321—335
(1965). - ■ p
47. G а ш b i 11 W. R., Oak Ridge Natl. Lab., Tennessee, 1964. (частное
сообщение).
48. Соловьев А. В., Преображенский Е. И., Семенов П. А.,
Химическая промышленность, № 8, 41—44 (1966).
49. Hartley D. E., Roberts D. С, Queen Mary College, London, Nuclear
Research Memo Q6, May 1961.
50. Hewitt G. F., King I., Love grove P. C, UKAEA Rept AERE-R3764,
1961.
51. Levy S., 2nd Midwest Conf. Fluid Mech., p. 337, 1952.
52. Bennett J. A. R., Thornton J. D., UKAEA Rept AERE-R3195, 1965,
v
12
ДИСПЕРСНОЕ ТЕЧЕНИЕ
12.1. Введение
Поведение капель, взвешенных в жидкости, во многих
отношениях аналогично поведению газовых пузырьков.
Действительно, многие уравнения, которые будут выведены в настоящей
главе, аналогичны соответствующим уравнениям из гл. 9.
Качественные различия между поведением капель и
пузырьков наиболее заметны при большой разнице плотностей
компонентов потока, например, в газо-жидкостных системах при
низком давлении. При пузырьковом течении основная часть
инерционных сил приходится на непрерывную фазу, вследствие чего
силы сопротивления, действующие на пузырьки, оказываются
значительными по сравнению с их импульсом. Поэтому пузырьки
в условиях вынужденной конвекции следуют за течением
окружающей жидкости, почти полностью совпадая с ним. Для капель,
однако, требуется участок значительно большей протяженности,
чтобы их движение совпало с движением окружающего газа.
По этой причине модель гомогенного течения обычно лучше
описывает пузырьковое течение, нежели дисперсное. Дисперсно-
кольцевой режим также не имеет аналога в пузырьковом
течении.
12.2. Образование одиночных капель
Образование капель в устье отверстия в квазистатических
условиях представляет собой обращенную задачу образования
пузырей. Поэтому радиус капли будет определяться соотношением,
аналогичным (9.3):
где индекс 2 относится к дискретному компоненту. Аналогично,
если капли образуются в процессе конденсации на обращенной
вниз горизонтальной поверхности, например, потолке, то радиус
капель определяется длиной волны, характерной для
неустойчивости Тейлора. Поэтому из уравнения (9.9) следует
«-""[-теЬйгГ- <12-2)
ДИСПЕРСНОЕ ТЕЧЕНИЕ 411
С увеличением скорости истечения жидкости из отверстия
вследствие сравнительно высокой плотности жидкой фазы
критическая скорость, определяемая уравнением (9.8), будет вскоре
превзойдена и образование капель будет происходить путем
дробления истекающей струи жидкости. Эта классическая задача
была исследована Релеем [1], который показал, что течение
такого рода струй всегда неустойчиво и что длина волны,
соответствующая наиболее неустойчивому режиму течения, примерно
в 4,5 раза больше диаметра струи, если плотностью окружающей
среды можно пренебречь. При дроблении струи указанным
путем радиус образующихся капель приблизительно равен
Rd^l,9R0- (12.3)
Дальнейший рост скорости струи приводит к более резко
выраженной неустойчивости вследствие движения относительно
окружающей жидкости. В результате струя становится сильно
неустойчивой уже вблизи устья отверстия и распадается, образуя
расходящийся поток очень мелких капель. Этот процесс
называется распылением.
12.3. Распыление
В большинстве случаев процесс распыления заключается
в образовании множества мелких капель жидкости путем
дробления сплошной струи жидкости. Дробление обычно происходит
под действием аэродинамических сил, обусловленных
относительным движением фаз. Могут также использоваться
механические, центробежные, электрические и ультразвуковые силовые
поля.
Основным безразмерным параметром, характеризующим
устойчивость одиночной капли, является число Вебера,
рассчитываемое по относительной скорости и плотности газа [2—8]:
We=J^i_£ ti (12.4)
о
Для невязких жидкостей критическое число Вебера, по
достижении которого начинается дробление капель, равно примерно 12.
Вязкость жидкости, по-видимому, оказывает
стабилизирующее действие, которое можно охарактеризовать с помощью
параметра устойчивости [i2f/pfda. Данные исследований [5—7] при
значениях параметра устойчивости, меньших пяти, достаточно
хорошо описываются уравнением
We
-4+(.
„2 \0,36
Р/
аГо
(12.5)
... 412
ГЛАВА 12
Наличие в параметре устойчивости вязкости жидкости позволяет
предположить, что неустойчивость возникает в виде
динамических пульсаций формы капли! Однако на конечной стадии
процесса дробления капля «продавливается» и превращается вбал-
лоноподобную под действием скоростного напора в точке
торможения. В конце концов капля разрывается, образуя кольцо более
мелких капель [4, 9].
Если капля вводится в поток газа при больших значениях
числа Вебера, то в результате последовательного ее дробления
образуется множество мелких капель. В этих условиях
выражение для окончательного размера капель имеет вид [7]
ш°
'°'25=-^S^+0,315 №* (CD)0 (Wetf125 In A
(We)g.« +°'315l^7,.) (^)o(We)r°ln-^, (12.6)
где индекс 0 относится к начальным условиям.
Широко используемое уравнение для расчетов среднего
размера капли при дроблении ее окружающим воздухом имеет
следующий вид [10]:
где vo — начальная относительная скорость. Недостаток этого
уравнения в том, что оно не безразмерное, а поэтому при
расчетах следует внимательно относиться к используемым единицам
измерений. Здесь р/ выражено в г/см3, vo — в м/сек, d— в мк, а —
в дин/см и (А/ — дин ■ сек/см2.
Пример 12.1. Сравнить рассчитанные по уравнениям (12.5) н (12.7) размеры
капель при распылении бензина (а=28,8 дин/см, р/ =0,875 г/см3, щ =
=0,647 спз) в карбюраторе. Скорость воздуха 76,3 м/сек, отношение
массовых расходов воздух—горючее 18.
Решение. При первой оценке величины d пренебрегаем влиянием параметра
устойчивости в уравнении (12.5). В итоге получаем
12-28,8 _с 1П_з
76302 . 1,21 . Ю"
= 5 - 10 й см. -
Параметр устойчивости оказывается равным 0,012, так что поправка
на вязкость жидкости пренебрежимо мала.
Члены, стоящие в правой части уравнения (12.7), равны
л Г 28,8 _
У 0,875 ~'
cnJ(0,647.1Q-2)2l0-225 I IP3 ■ 1,21 У'5 пм
597 L 28,8 ■ 0,875 J • ( 18 • 875 ) =0-63^-
: 44 МК,
-2\2 10,225 / 1ПЯ . 1 OI \1,5
Следовательно, расчетный размер капли равен — 4,5 • 10~3 см
ДИСПЕРСНОЕ ТЕЧЕНИЕ
413
Практически размер капли точно не может быть рассчитан,
так как процесс распыления зависит от многих нерегулируемых
переменных, как степень турбулентности течения в струе,
шероховатость канала или отложения грязи в сопле.
12.4. Спектры размеров капель
С помощью уравнений (12.5) и (12.7) можно рассчитать
только средний размер капель. Имеется много возможных
способов определений «среднего» диаметра капель. Наиболее
распространенным является способ определения среднего диаметра по
отношению объема к поверхности
макс
j" (&p(d)dd
j cPp (d) dd
о
где р (d)— плотность вероятности размера капли в интервале d
и d+dd. Капля, диаметр которой равен определенному .выше
среднему диаметру, имеет то же отношение поверхности к
объему, что и поток капель в целом.
Чтобы найти корреляционные выражения на основе
экспериментальных данных, было предложено много различных
статистических распределений капель по размерам. Многие авторы
использовали нормальное и логарифмически нормальное
распределения, которые обычно применяются при описании структуры
грунтов и размолотых частиц [12—14].
Функция распределения Нукиямы—Танасавы [15] имеет вид
p(d)=Adme-bdn, (12.9)
где А и Ъ — нормирующие множители, а, т и п — обычно целые
числа, которым иногда можно придать физический смысл. Очень
часто одни и те же экспериментальные данные с равным успехом
описываются любыми из этих распределений [16].
Уравнение (12.9), как это показано в работе [17], можно
получить с помощью известного в статистической механике
«формализма Джейнса». При этом принимается, что «состояния»
капель квантуются и могут быть охарактеризованы индексами 1,
2, 3, ... Обозначая одно из этих состояний через i, а вероятность
этого состояния через ри имеем, поскольку капля находится
в некотором состоянии,
2А = 1. (12.10)
Кроме того, считается, что среднее значение диаметра капель,
возведенное в некоторую степень п, известно из физических
414 ГЛАВА 12
соображений. Обычно, когда известен средний объем капель,
л = 3, а когда задана средняя поверхность капель, л =2.
Различным способам распыления соответствуют разные значения п.
Обозначая среднее значение через (dn), получим
ЪрА={йп). (12.11)
Применяя принцип «максимума энтропии», находим, что
плотность вероятности пребывания капли в i'-м состоянии при
отсутствии какой-либо дополнительной информации определяется
соотношением
Pi=Ae~b^1. . (12.12)
Чтобы решить это уравнение относительно плотности вероятности
распределения капель по размерам, нужно связать квантовые
состояния i с геометрическими характеристиками капель.
Согласно одной из моделей, i—число молекул в капле. В этом
случае квантование очевидно:
ioodz. (12.13)
С другой стороны, можно предположить, что основным
эффектом процесса образования капли является создание поверхности.
Если квантовые состояния отражают различные уровни
поверхностной энергии, то
icod2. (12.14)
В общем случае при чисто эмпирическом подходе можно принять
ioodm+\ (12.15)
Число состояний столь велико, что можно рассматривать
распределение как непрерывное:
pidi=p{d)dd. (12.16)
Подставляя (12.16) в (12.12) и используя (12.15), получаем
обобщенную функцию распределения Нукиямы—Танасавы
p(d)^=(m+l)dmAe-bd", (12.17)
которую можно привести к безразмерному виду, как в работе
Шапиро [18], используя диаметр d'', при котором р (d) имеет
максимум. Дифференцируя уравнение (12.17), получаем
■^р-=(т+\) A (md™-1 -brid^"-1) e-bd", (12.18)
откуда
*=-дяг. (12Л9)
ДИСПЕРСНОЕ ТЕЧЕНИЕ
415
Обозначая безразмерный диаметр через
d* = -£r, (12.20)
с помощью уравнения (12.19) находим
от
bdn^^-d*». (12.21)
Теперь следует использовать ограничение, накладываемое
уравнением (12.10). Если число квантовых состояний велико, то
сумма может быть заменена интегралом
со со
\Pidi=\p{d)dd=\. (12.22)
о о
Это соотношение вместе с (12.18) дает возможность определить
постоянную
A=irh-(Jd,,e~*^dd) • (12-23)
При заданных значениях тип можно определить & и Л и
получить функцию распределения в целом.
Так как р (d) имеет размерность d_1, то с. учетом (12.16)
можно определить безразмерную плотность вероятности
следующим образом:
p*^d'p{d). (12.24)
Наиболее употребляемые значения, показателей степени
в уравнении Нукиямы—Танасавы: т = 2 и л = 1. Они
соответствуют квантованию на основе объема капли и заданной величине
среднего диаметра капли. В этом случае уравнение (12.17) вбез-
размерном виде записывается следующим образом:
p*=4d**e-2d\ (12.25)
Чтобы можно было пользоваться этим уравнением, должна
быть известна величина d'. Простой способ определения d'
предложил Маквин [19], который обнаружил, что для большого числа
экспериментальных данных справедливо соотношение
d'=Q. (12.26)
где характерный диаметр do определяется либо по уравнению
(12.5), либо по (12.7).
Имеется и другое соотношение для безразмерной плотности
вероятности р* [18]
p*=lfe-"4\ (12.27)
=-416
ГЛАВА 12
Оно дает численные значения р*, не очень сильно отличающиеся
от результатов расчета по (12.25), однако более удобно для
решения задач массообмена и испарения.
12.5. Предельная скорость одиночных капель
в гравитационном поле
Поведение капель небольшого размера при числах Рей-
нольдса меньше 1 подчиняется уравнению Адамара—Рыбчин-
ского (9.14), только роль компонентов в потоке меняется. Если
использовать индексы 1 и 2 для обозначения соответственно
непрерывного и дискретного компонентов, то уравнение (9.14)
принимает вид
v 1_ <%|Р2_Р11 Зкз + з»ч т ■ (12<28)
При наличии поверхностно активных веществ поверхность
капли не является полностью неупругой, и уравнение (12.28)
должно быть модифицировано способом Левича [20].
Пока форма капли определяется силами поверхностного
натяжения, капли будут приблизительно сферическими, и для
определения их- предельной скорости можно будет использовать
уравнение (8.5) и методы гл. 8. При числах Рейнольдса
выше 1000 (например, в случае движения капель ртути в
воздухе) значение коэффициента сопротивления заключено в
пределах от 0,4 до 0,5 и предельная скорость примерно равна
^ = l,7(gd|pp2~Pll)1/2. (12.29)
Верхняя граница предельной скорости, рассчитываемая по
уравнению (12.29), определяется условием устойчивости капли (12.5).
Сравнивая эти два уравнения для случая невязкой жидкости,
находим, что максимальный радиус устойчивой капли
приблизительно равен
«--(ттйЬйгР-' - е2-30*
Этот критерий не применим к пузырям, размер которых может
быть неопределенно большим, как в случае выделения пузырей
при подводных взрывах.
Если же величина поверхностного натяжения недостаточно
велика, то уже до достижения условий, определяемых
уравнением (12.5), возможно заметное отклонение от правильной
формы капли. Для деформированных плоских капель
предельная скорость их движения почти не зависит от размера капель и
определяется уравнением, аналогичным уравнению Пиблса и
ДИСПЕРСНОЕ ТЕЧЕНИЕ
417
Гарбера для области 4 табл. 9.1:
4g(P2-Pl)° у/^ (12>31)
cdPi J
Левич [21] рекомендует принять Св^1. Следовательно,
^=1,4рГ'/г[;?(Р2-р1)«]'/4. (12.32)
Это уравнение дает некоторое промежуточное значение
предельной скорости движения капель, заключенное между значениями,
определенными по уравнениям Гармати, а также Пиблса и
Гарбера для деформированных пузырей. Область применимости
уравнений (12.32) примерно совпадает с областью 4 табл. 9.1.
12.6. Одномерное вертикальное дисперсное течение
без трения на стенке
Приведенные в гл. 4 методы можно использовать для расчета
течений с взвешенными в потоке каплями, если известно
выражение для скорости дрейфа. Эта задача не подвергалась столь
детальному анализу, как эквивалентная задача о пузырьковом
режиме течения, однако имеются данные, весьма убедительно
свидетельствующие о прямой аналогии между этими двумя
режимами течений. Например, достаточно полное исследование
Прэтта и.др. [22] жидкостно-жидкостной экстракции в брызгаль-
ных установках и насадочных колоннах показало, что
относительная скорость капель в жидкости определяется следующим
соотношением:
*>21 = (1-*)*>„•- (12.33)
Подставляя это значение в уравнение (4.1), получим
Л1=*>„«0-«)2. (12.34)
Это соотношение весьма точно описывает экспериментальные
данные, если характерный размер проходного сечения насадки
колонны превышает величину
^=2Л211^)ТГ- ' 02-35)
Из сравнения уравнений (12.35) и (12.30) следует, что уравнение
Прэтта справедливо, если диаметр капель определяется
условиями устойчивости, а не способом образования капель или
размерами установки. В этом случае, пока вязкие силы
незначительны, уравнение (12.32) справедливо и может быть
подставлено в (12.34), откуда
у21 = 1,4а(1-а)2Рг'/г[ё-(р2-р1)°]'/<. (12.36)
Предложенное Уоллисом [23, 24] уравнение совпадает
с (12.36), за исключением числовой константы. В уравнении
27 Заказ М 162
418
ГЛАВА 12
Уоллиса вместо 1,4 стоит константа 1,18, взятая из работы
Пиблса и Гарбера.
Гейлор, Роберте и Прэтт [25] также отмечают, что уравнение
типа (12.34) будет справедливым в вязкой области, для которой
конечная скорость рассчитывается по (12.28).
12.7. «Захлебывание» в дисперсном потоке
Разработанный в гл. 4 анализ справедлив независимо от того,
какой из компонентов образует диспергированную фазу;
следовательно, можно ожидать аналогичных результатов для
капельного и пузырькового режимов, что иллюстрируется на фиг. 12.1,
Фиг. 12.1. Данные по «захлебыванию» течения для взвеси капель воды в
нефти и наоборот [26].
где показано, что экспериментальные данные Блендинга и Элд-
жина [26] по «захлебыванию» для взвеси капель нефти в воде и,
наоборот, капель воды в нефти графически представляются
одинаково (см. фиг. 4.3).
Уравнения Торнтона и Прэтта [27] для расчета
«захлебывания» течения идентичны уравнениям (4.16) и (4.17) при п = 2.
В некоторых других соотношениях для «захлебывания»
течения, имеющихся в литературе [28, 29], используется понятие
характеристической скорости vo:
v^=\j^+\hV\ (12-37)
ДИСПЕРСНОЕ ТЕЧЕНИЕ 419
Данное соотношение является следствием допущения, что
относительная скорость vn не зависит от концентрации фаз, т. е.
Скорость vo может быть определена путем построения
огибающей линий постоянного значения а во втором квадранте
(задача 1.19). Полученный результат является промежуточным
между соответствующими значениями для идеального
дисперсного потока и пенисто-турбулентного течения, рассмотренного
в гл. 9. Его можно использовать в качестве общего соотношения,
приближенно отвечающего обоим возможным случаям. Скорость
vo можно принять равной Voa и рассчитывать по уравнениям,
приведенным в разд. 12.5.
Сравнение уравнения (12.37) с выражениями (11.84) и-
(11.87), описывающими условия «захлебывания» в кольцевом
потоке, весьма интересно. Во многих насадочных колоннах,
например, точка «захлебывания»"определяется уравнением (11.86),
а не (12.37), что обусловлено слиянием'капель и образованием
сплошных струй жидкости. В любом случае квадратные корни
из приведенных скоростей фаз связаны между собой линейной
зависимостью.
12.8. «Ожижение» дисперсной системы
Если представить, что дисперсная система «ожижена» точно
таким же образом, как и псевдоожиженный слой твердых частиц,
и использовать для описания этой системы уравнения (12.36) и
(4.2), то в итоге получим следующее выражение:
y1 = -l,4(l-a)2prvM^(P2-Pi)],/4, (12.39)
спрайедливое при условии, что слияния капель не происходит,
Кроме того, если слияние капель предотвращается наличием
поверхностных загрязнений, то уравнение (12.39) будет
справедливо во всем диапазоне изменения а. Поскольку полностью
предотвратить слияние капель невозможно, имеется очень мало
экспериментальных данных, подтверждающих это утверждение. Тем
не менее результаты опытов Кутателадзе [30], исследовавшего
барботаж воды через слой ртути, не очень сильно расходятся
с теоретическими расчетами (фиг. 12.2). После ожижения в
течение некоторого периода времени размер капель, по-видимому,
уменьшается и экспериментальные данные располагаются вдоль
нижней кривой.
Можно ожидать изменения характера течения в точке, где
наступает «ожижение» капель, и они уже более не находятся в
контакте друг с другом. Для сферических частиц этот момент
27*
420
ГЛАВА 12
наступает обычно при ct~0,6 или, более точно, если исходить
из данных фиг. 4.2, при 1 — а = 0,38. Подетавляя это значение
в уравнение (12.39), получаем выражение для минимальной
скорости «ожижения»
C/i)«I=0,2Pr,/,te°(p2-Pi)],/4. - (12.40)
Уоллис [24] экспериментально проверил это уравнение. В его
экспериментах воздух барботировал через различные жидкости,
О 0,1 0,2 0,3 0,4 0,5 0,6
Среднее объемное содержание воды
Ф н г. 12.2. «Ожижение» капель ртути в воде [30].
/— пузыри воды в ртути; //, ///, IV — различные режимы течения капель ртути в воде;
ОПЛ — увеличение /i; • Шл—уменьшение /,; А — переход от пузырьковой
структуры к взвеси капель; В — диспергированная ртуть.
причем ввод воздуха осуществлялся через пористую
поверхность. Было установлено, что начало образования взвеси капель
вблизи поверхности приходится на значение а, близкое к
расчетному. При приведенных скоростях газа, превышающих
рассчитанные по уравнению (12.40) значения, наблюдался конусо^
образный поток капель над неглубоким слоем жидкости, через
который вдувался газ.
ДИСПЕРСНОЕ ТЕЧЕНИЕ
421
12.9. Падение давления при вынужденной конвекции
Изложенная в разд. 9.6 методика расчета с известным
приближением применима и в случае дисперсного течения при
вынужденной конвекции. Однако при этом для системы
газ—жидкость аналогия не должна заходить слишком далеко, поскольку
времена релаксации и средние длины свободного пробега для
капель будут значительно больше, чем для пузырей при
пузырьковом течении, вследствие чего наблюдается тенденция к
выпаданию капель на стенки канала.
Например, эффективная вязкость эмульсии при ламинарном
течении может быть рассчитана независимо от того, какая из фаз
находится в диспергированном состоянии, по формуле
,=,^1+2,5а—-^-_j, (12.41)
где индексом 1, как обычно, обозначена непрерывная фаза. При
турбулентном течении приемлемые результаты дает гомогенная
модель течения, причем коэффициент трения в двухфазном
потоке следует рассчитывать по числу Реинольдса, определяемому
по суммарному массовому расходу обоих компонентов и
вязкости газовой фазы:
Re= —. (12.42)
Для системы газ—жидкость сложность расчета состоит
обычно в том, что жидкость как бы прилипает к стенке канала,
так что капли, ударяющиеся о стенку, сливаются друг с другом,
образуя кольцо жидкости. Таким образом, в действительности
никогда не достигается идеальный дисперсный режим течения,
а реализуется своего рода «гибрид» — дисперсно-кольцевое
течение. Наличие кольцевой пленки жидкости приводит к
следующему:
1) уменьшается плотность в гомогенном ядре потока;
2) уменьшается эффективное проходное сечение ядра потока;
3) на поверхности жидкой пленки образуются волны,
увеличивающие эффективную шероховатость стенки;
4) в результате непрерывного обмена жидкостью между
пленкой и ядром потока (осаждение и унос капель) может
возникнуть значительный поток количества движения, что
сказывается на величине касательных напряжений.
Указанные выше эффекты все еще недостаточно ясны. Однако
описанные в разд. 11.5 методы могут быть использованы для
расчета макроскопических переменных, таких, как толщина пленки
и падение давления.
422 ГЛАВА 12
12.10. Унос
Качественные наблюдения
Пусть жидкая пленка стекает вниз по стенке вертикального
канала или течет по дну горизонтального или наклонного канала.
Затем предположим, что газ движется вниз над поверхностью
пленки в том же самом канале. Что произойдет с увеличением
скорости газа?
Прежде всего при малых скоростях газа его действие на
пленку незначительно. Однако в соответствии с анализом,
приведенным в разд. 6.4, с ростом относительной скорости в пленке
возникают возмущения. В частности, с2 в уравнении (6.83) с
ростом относительной скорости, оставаясь отрицательной, растет по
абсолютной величине, разность vz /и2—1 в уравнении (6.163)
возрастает, а следовательно, возрастает и значение а в
уравнении (6.162). В горизонтальных или наклонных каналах сила
тяжести действует как восстанавливающая сила, затягивающая
начало заметной волновой активности. Первые волны
представляют собой небольшую рябь, бегущую в направлении движения
пленки. С увеличением скорости газа растет амплитуда этой ряби
и вскоре появляются трехмерные возмущения. Поверхность
раздела фаз приобретает «насеченную» в поперечном направлении
структуру, аналогичную волнам, возникающим^ при легком
шквалистом ветре на реках или озерах [23,33].
При скорости газа, примерно вдвое превышающей требуемую
для возникновения подобной волновой структуры, появляются
первые скатывающиеся волны, которые имеют значительно
большую амплитуду и скорость, чем предыдущие, и как бы
перекатываются через более равномерные волны малой амплитуды. Фронт
скатывающихся волн довольно крутой, а между гребнями
расположена довольно протяженная область сравнительно
спокойной жидкости. Эти волны были исследованы в ряде
теоретических и экспериментальных работ [34—37].
При довольно большой скорости газа силы сопротивления,
действующие на верхушки гребней скатывающихся волн,
достаточны для того, чтобы сорвать с них капли жидкости, которые
уносятся затем в газовый поток. Началу уноса обычно
предшествует появление «белых барашков», бегущих по поверхности
пленки. Дальнейшее увеличение расхода газа приводит к
возрастанию уноса и уменьшению толщины пленки вследствие потерь
массы и увеличения касательных напряжений на поверхности
раздела фаз, а следовательно, и возрастания скорости жидкости.
Представленные на фиг. 12.3 экспериментальные данные
разграничивают области с различной волновой активностью на
поверхности жидкой пленки. Исследовалось течение воздуха над
24
2 18-
12
а 6
6 8 ГО 12 14
Расход живности, л/мии
16
18
Фиг. 12.3. Области различной волновой активности на поверхности жидкой
пленки в расслоенном воздухо-водяном потоке [33].
Горизонтальный канал шириной 305 мм и высотой 127 мм.
I — начало уноса капель; 2 — появление скатывающихся воли; 3 — появление «насечек» на
поверхности пленки; 4 — возникновение рябн.
'7,5
75
ТО
>5
1 1 1
Расход воды, мл/мин
х 855
о Г 695
• 2480
* 3232
° 3980
_
-
_
1 1 '■
а
д
•
\
1
*
2. Г
• X
?
I,
1
а
д
•
о
X
1
а
О
X
□
8
•
-
-
_
_
20 22 24 26 28 30
Скорость воздуха , м/сек
32
34
Фиг. 12.4. Данные по уносу в нисходящем потоке воздухо-водяной смеси [36].
Труба диаметром 101,6 мм; отбор проб в центре трубы; однонаправленное течение.
424
ГЛАВА 12
поверхностью воды в горизонтальном канале шириной 305 мм я
высотой 127 мм. Из приведенных данных видно, что при
достаточно больших его значениях расход жидкости оказывает слабое
влияние на значения параметров, при которых происходит смена
режимов.
Начало уноса капель можно определить путем регистрации
выпадения капель на несмоченные стенки канала или путем
обнаружения капель в газовом
потоке. Более точные
измерения получаются путем отбора
проб из заданного сечения
газового потока с помощью
зонда-пробоотборника с
последующим измерением отобранного
количества влаги.
В качестве примера на
фиг. 12.4 представлены данные
Стина [36] по уносу в
вертикальной трубе диаметром
101,6 мм, а на фиг. 12.5 —
результаты Уоллиса [38],
полученные в вертикальной трубе
диаметром 22,2 мм. По оси
ординат на этих графиках
отложена величина уноса, рассчи-
Фиг. 12.5. Данные по уносу в
нисходящем потоке воздухо-водяной
смеси [38].
Труба внутренним диаметром 22,2 мм и
длиной 1800 мм; диаметр отверстия зонда-
пробоотборлика 2,39 мм; зоид имеет
резиновый иосок.
Приведенная скорость возЗуха j.^/ceit
тайная по уравнению (11.114). Отложенные по оси абсцисс
значения скорости воздуха представляют собой приведенную
скорость jg. Снижение критической скорости газа, при которой
начинается унос, наблюдаемое на фиг. 12.5 при больших
расходах жидкости, возможно, связано с уменьшением проходного
речения газового потока из-за возрастания толщины жидкой
пленки.
Характерно, что величина критической скорости газа на обоих
графиках слабо зависит от размеров канала, его ориентации и
расхода жидкости.
ДИСПЕРСНОЕ ТЕЧЕНИЕ 425
Соответствующие данные по величине уноса в восходящем
вертикальном потоке уже были приведены на фиг. 11.17.
Существование в потоке жидких перемычек затемняет картину и не
позволяет, за исключением случая очень малых расходов
жидкости, точно определить критическую скорость газа,
соответствующую неустойчивости пленки.
Влияние условий на входе в канал и длины трубы
Представленные на фиг. 12.4 экспериментальные данные были
получены при соблюдении тщательных мер по предотвращению
уноса в местах ввода воды и воздуха в установку. Поэтому эти
данные могут служить критерием устойчивости пленки. Однако
Расстояние от входа, м
Фиг. 12.6. Суммарный расход воды в виде унесенных капель в центральной
части трубы в функции расстояния от входа в трубу [AERE-R3954].
Диаметр трубы 31,7 мм, диаметр центральной части 26,7 мм.
во многих практических случаях эффект неустойчивости пленки
полностью скрадывается уносом на входе в установку. Поскольку
движущиеся вмесхе с газом капли имеют большую осевую и
малую радиальную скорости и поскольку удар капли о жидкую
пленку сопровождается всплеском жидкости, то требуется очень
большая длина канала для подавления влияния входных
условий [39]. На примере экспериментальных данных [40] (фиг. 12.6
и 12.7) можно проследить изменение суммарного количества
унесенной влаги и профиля массовой скорости вдоль, трубы
диаметром 31,7 мм на расстоянии 5,3 м. За начало координат
выбиралась точка ввода жидкой пленки на стенку трубы.
426
ГЛАВА 12
WO
S 80
60
40
20
Высота, М.
* 0,152
*M 61
о 1,07
* 1,52
d 1,38
т2,46
♦ 2.Э2
• 3,38
л 3,84
О 4.4
v4,85
■ 5.31
Фиг. 12.7. Профили массовой скорости воды в функции расстояния от входа
в трубу [AERE-R3954].
Определение критической скорости газа
Критическая скорость газа, при которой начинается унос,
может быть определена, если унос связан только с устойчивостью*
пленки, а не с какими-либо другими факторами. Точное
определение этой скорости не столь простое дело, как это кажется на
первый взгляд. Поскольку нулевой унос не может быть измерен,
то в качестве критической скорости принимается скорость, при
которой впервые появляется заметное количество влаги. Если
обратиться к фиг. 12.4, то можно видеть, что при расходе воды
855 мл/мин значения критической скорости будут равны 19,8,
22,9 и 26 м/сек в зависимости от точности измерений
(соответственные значения доли уноса 0,1, 1,0 и 2,5%)- Скорости
турбулентных пульсаций в жидкости и газе имеют статистический
характер так же, как и спектр волн на поверхности раздела фаз.
Случайная комбинация этих параметров может обусловить унос
ДИСПЕРСНОЕ ТЕЧЕНИЕ
427
капли при весьма низких скоростях газа. Тем не менее почти все
экспериментальные данные указывают на существование
следующих характерных областей зависимости доли уноса от
скорости газа (фиг. 12.8):
1. Область пренебрежимо малого уноса.
2. Область медленного нарастания уноса; кривая обращена
выпуклостью вниз.
120
100
80
о БО
40
20
' 1
-Расход жидкости,мл/мин
х 415В
а 3036
л 2060
• 7700
о 328
„
- J
д s//
7
г— Д
X
/
S Л 1
/У
г>
в a z
D
*' -J
X * * X
j~.—а
+
+ +
+ +
''о °
_
70
20
30
jg,M/ceK
40
50
60
Ф и г. 12.8. Унос в зависимости от приведенной скорости воздуха при
различных расходах жидкости [36].
Силиконовая жидкость QESF-96/5; а=20 дин/см; v—5 ест
3. Область приблизительно линейной зависимости доли уноса
от скорости газа; в, этой области интенсивность уноса с
увеличением скорости газа все время возрастает.
. 4. Область насыщения — при больших скоростях газа доля
уноса достигает своего предельного значения.
В данном случае в качестве критической скорости
произвольно берется скорость газа в точке пересечения с осью абсцисс
экстраполированного участка линейного изменения доли уноса.
Расчет критической скорости газа
Имеется довольно много конкурирующих корреляционных
формул [37, 39, 41—44] для определения начала уноса капель,
однако пока еще не получено единого обобщенного выражения.
В опытах Стина [36] изменялось давление газа, при этом было
обнаружено, что критическая скорость примерно обратно
пропорциональна корню квадратному из плотности газа (фиг. 12.9).
Также было установлено, что вязкость жидкости не оказывает
428
ГЛАВА 12
существенного влияния при превышении критического расхода
жидкости (фиг. 12.9). Что же касается поверхностного
натяжения, то оно оказалось очень существенным параметром,
поскольку оно почти пропорционально критической скорости.
60
40
I
го
1 1 '•
Давление на выходе ,атм
о ;
о 3
* 4
-
'+& У
, а. ^<Ж/ Л /
ill
/ д д
и/
и / ^
и / т
у/
о /
I
1
дА у °
-
1
/5
30
45
j3,M/cex
60
75
Фиг. 12.9. Влияние давления на унос [36].
Расход воды 1,14 л/мин.
На основе анализа экспериментальных данных Стин предложил
следующий критерий, определяющий начало уноса:
* г ' *' 1 =ТС2> 2,46 • 10"4. (12.43)
Это уравнение не является универсальным, оно дает
неправильные результаты в том случае, если жидкость занимает
значительную часть канала или если влияние вязких сил в жидкости
существенно.
Параметр Стина лежит в основе приближенной
корреляционной формулы для определения равновесной доли уноса
в.длинных трубах. Эта формула была выведена Уоллисом [43] и
представляет собой модификацию метода Палеева и Филипповича
[44]. Соответствующая расчетная кривая приведена на фиг. 12.10.
Эта кривая согласуется с большинством опубликованных данных
по уносу с толстых пленок при общей доле уноса менее 50%.
Выше этого значения многочисленные вторичные эффекты, как
длина трубы, методика эксперимента и т. д., обусловливают
значительный разброс экспериментальных данных. Тонкие вязкие
пленки более устойчивы (фиг. 12.8) и характеризуются меньшим
уносом, чем определенный по фиг. 12.10.
ДИСПЕРСНОЕ ТЕЧЕНИЕ
429
во
60
о"
J 40
20
Z-I0"4 4 6 8 Ю 12 14-Ю"4
ТС2
Фиг. 12.10. Корреляционная кривая Уоллиса [43] для равновесного уноса.
vg*g ( 9е X'2
л2 = I — I — безразмерная скорость газа.
Распределения концентрации капель и скорости в потоке
Профили концентрации капель и скорости были тщательно
измерены в Харуэлле [40, 45] и CISE [46]. Согласно данным,
полученным в Харуэлле, концентрация капель по существу
постоянна по всему сечению потока. Соответствующие профили
скорости с ростом уноса (фиг. 5.2) все в большей степени
приближались к параболе. Профили скорости хорошо согласуются с
уравнением (5.8); исключение составляет лишь величина постоянной
k, которая уменьшается от 0,4 до 0,1 в случае наибольшей
концентрации капель. При описании профиля скорости степенным
законом при наличии уноса потери скорости приблизительно
пропорциональны квадрату радиуса, т. е. картина такова, как если
бы произошла «ламинаризация» течения; при этом тонкая
взвесь капель напомина'еТ классическую кинетическую модель
совершенного газа.
Задачи
12.1. Вода конденсируется на горизонтальном потолке камеры при
температуре 32° С. Каков размер капель," отрывающихся от поверхности?
12.2. Через садовый рукав с разбрызгивающей головкой, имеющей 30
отверстий диаметром 1,6 мм, пропускается 18 л/мин воды. Рассчитать размер
капель а) в неподвижном воздухе и б) при скорости ветра 96 км/час.
12.3. Через небольшое отверстие в топливном баке самолета, летящего на
высоте 6 км над уровнем моря со скоростью 900 км/час, вытекает топливо
Определить размер образующихся капель.
430
ГЛАВА 12
12.4. Каков максимальный устойчивый размер . падающих дождевых капель'
Какова их предельная скорость?
12.5. Каков максимальный устойчивый размер капель ртути, опускающихся
12.6. На электростанции должен быть установлен противоточный скруббер
для очистки дымовых газов. Скорость газов 3 м/сек, температура 260° С
При каком размере капель они будут двигаться вниз в нижней части
скруббера!1 Чему равна направленная вниз максимальная скорость впрыскивания
капель через сопловые отверстия, если их температура постоянна и равна
Ш С и капли -не должны дробиться потоком газа?
12.7. Эксперименты показали, что капли горючего диаметром более 15 мкм
не смогут «обогнуть поворот» в точке, где карбюратор автомобиля
соединяется с впускным трубопроводом рабочих цилиндров, и будут оседать на
стенках. Это затрудняет выполнение карбюратором функций
распылительного устройства и увеличивает время задержки реакции двигателя-на
изменение положения дроссельной заслонки. Определить долю поданного в
карбюратор горючего, которое осядет на стенку, в функции отношения
расходов воздух—горючее и скорости воздуха в точке впрыскивания горючего
в карбюратор.
12.8. Сравните уравнения (12.25) и (12.27) с нормальным и логарифмически
нормальным распределением плотности вероятности
а У 2тс
p(d)= !__,Г0"<*-Ш 3)/2 I"2 °
Ino-yTS"
тде d — средний диаметр, а 0 —дисперсия.
12.9. Спектр размеров капель может быть измерен с помощью
высокоскоростной фотографии. К сожалению, этот метод позволяет получить только
мгновенную картину в данном сечении, а не действительный спектр размеров
капель, если капли движутся с разными скоростями. Показать, как
исказится спектр, если: а) капли ускоряются высокоскоростным потоком газа и
■фотография сделана в момент, когда этот процесс еще ие завершился, i.
v б) капли падают в неподвижном воздухе с конечными скоростями.
Фотографии дают картину в сечении, перпендикулярном направлению
движения.
12.10. «Ожижение» капель жидкости является возможной причиной
достижения критической плотности теплового потока при кипении в условиях
естественной конвекции на горизонтальной пластине. С помощью
уравнения (12.40) вывести соотношение для критической плотности теплового
потока, приняв, что все тепло, подведенное к поверхности, идет на образование
лара вблизи поверхности и что температура жидкости равна температуре
насыщения. Кутателадзе [47] эмпирическим путем определил, что постоянная
в уравнении (12.40) равна 0,16.
12.11. Газ барботирует через неподвижный объем жидкости. Сравнить
значение приведенной скорости газа при «захлебывании» пузырькового течения
-с соответствующим значением приведенной скорости при «ожижении» капель.
12.12. При каком диаметре капель и значениях показателя степени п
уравнение (4.14) будет согласовываться с правой ветвью кривой на фиг. 12.2?
12.13. Сравните корреляционную формулу для определения уноса (фиг. 12 10)
с данными фиг. 12.5, 12.8, 12.9 и 11.17.
12.14. Паро-водяная смесь при давлении 35 ата течет в вертикальной трубе
диаметром 25,4 мм. Определить равновесную долю уноса при дисперсно-
кольцевом режиме течения как функцию массового паросодержания и мас-
ДИСПЕРСНОЕ ТЕЧЕНИЕ 431
Таблица 12.1
Данные работы [49] по уносу и падению давления
(We + Wt — полный расход воды)
кг/час,
18,2
22,7
27,2
31,8,
we+wf,
кг/час,
45,4
104
45,4
104
45,4
104
45,4
104
Расстояние от инжектора, мм
152
0,36
2,59
0,54
4,59
0,73
4,54
1,14
5,77
762
1,50
3,90
2,36
6,81
4,04
10,6
5,81
17,2
1816
1,82
5,81
3,28
10,8
6,58
20,3
9,85
30,4
2730
2,27
7,26
3,54
13,5
6,54
23,9
11,0
38,9
3581 •
2,04
9,49
3,95
16,9
8,54
32,0
12,8
4572
2,32
11,1
5,04
9,13
15,4
5486
2,58
15,4
6,22
13,6
а — Данные по уносу. (В таблице приведены значения We в /сг/час.)
we>
кг/час
18,2
22,7
27,2
31,8
we+wf
кг/час
45,4
104
•45,4
104
45,4
104
45,4
104
229
2,783
2,761
2,769
2,726
2,756
2,710
2,742
2,686
686
2,715
2,645
2,686
2,592
2,655
2,532
2,611
2,496
Расстояние от инжектора, мм
1740
2,574
2,371
2,514
2,254
2,402
2,094
2,308
2,935
2654
2,431
2,127
2,352
1,959
2,224
1,798
2,091
1,604
3505
2,348
1,928
2,209
1,720
1,996
1,478
1,866
4496
2,224
1,647
1,986
1,784
1,560
5410
2,089
1,402
1,416
1,513
б — Данные по падению давления. (В таблице приведены значения давления в ата.)
сового расхода. С помощью полученных значений рассчитать увеличение
эффективной плотности парового ядра, обусловленное присутствием в нем.
капель жидкости.
12.15. Определить минимальную скорость ветра, при которой наблюдается'
срыв брызг соленой воды с верхушек волн при шторме.
12.16. На фиг. 12.11 приведены данные работы [48] по уносу в смесях
воздух—этиловый спирт и воздух—вода при кольцевом течении в трубках
диаметром 6 и 12 мм. Показать, что эти данные в принципе согласуются с
кривой фиг. 12.10, однако действительные значения уноса лежат ниже.
Проанализировать возможные причины этих расхождений. В расчетах принять
температуру смеси равной 20° С. При этом соответствующие физические
параметры равны: ця=0,018 спз, р/=1 г/см3, 0=72,8 дик/сж. для воды и pt —
=0,79 г/см3 и 0=22,3 дин[см для спирта; рс и /с — соответственно плотность-
и приведенная скорость ядра потока, которое считается гомогенной смесью-
капель и газа.
- 432
ГЛАВА 12
10" 5 10s
Рс]с,г/См-Свк2
Фиг. 12.11. Данные работы [48] по уносу.
Юв
w,
<!-£) =
we+wf
-доля жидкости в пленке, рс2 — поток количества движения в ядре.
+ вода, трубка диаметром 12 мм; О вода, трубка диаметром 6 мм; • спнрт, трубка
диаметром 12. мч.
12.17. Одна из трудностей, связанных с расчетом уноса, состоит в том, что
равновесное состояние никогда не достигается, поскольку вследствие
падения давления или фазового превращения приведенная скорость газа
вдоль канала непрерывно возрастает. Указанный эффект иллюстрируется
табл. 12.1, где представлены некоторые экспериментальные данные работы [49]
для случая течения воздухо-водяных смесей в трубе диаметром 9,5 мм.
Сравнить эти данные с кривой на фиг. 12.10. Показать, что экперименталь-
ные кривые по мере усиления неравномерности смещаются вправо.
Литература
1. Rayleigh, Proc. London Math. Soc, 10, 1 (1878); Proc. Roy. Soc.
(London), 29, 71 (1879); Phil. Mag., 34, 177 (1892); см. также Ламб Г.,
Гидродинамика, изд. 6, ОГИЗ, Гостехтеоретиздат, М., 1947.
2. Lewis Н. С, Edwards D. G., Goglia M. J., Rice R. I.,
S m i t h L. W., Ind. Eng. Chem. 40, № 1, 67 (1948).
3. H a a s F. C, A. I. Ch. E. J., 10, M920—M924 (1964).
4. P г a n d 11 L., Essentials of Fluid Mechanics, Blackie Ltd., Glasgow, 1953,
p. 328.
5. H i n z e J. O., Appl. Sci. Res., Al, 263—272 (1948).
6. H i n z e J. O., Appl. Sci. Res., Al, 275—288 (1948).
7. I s s h i k i M. N.. Rept 35, Trans. Tech. Res. Inst., Tokyo, Japan, July 1959.
8. Dicker son R. A, Coultas T. A., AIAA paper № 66-611, June 1966.
9. G i f f e n E., M u г a s z e w A., The Atomisation of Liquid Fuels, Chapman
and Hall, Ltd., London, 1953.
10. N u k i у a m a S„ T a n a s a w a Y., Trans. Soc. Mech. Engrs (lapan), 4,
№ 14, 86 (1938).
11. S a u t e r J., NACA Rept TM-518, 1929.
12. Soo S. L., Ind. Eng. Chem. Fundamentals, 4, 426—433 (1965).
13. Kliegel J. R., Intern. Symp. Combust., 9th, Academic Press, Inc., N. Y.,
pp. 811—826, 1963.
ДИСПЕРСНОЕ ТЕЧЕНИЕ
433
14. Dallavalle J. M., Micrometrics, Pitman Publishing Co., N. Y., 1943.
15. Nukiyama S., Tanasawa Y., Trans. Soc. Mech. Engrs (lapan), 5,
№ 18, 63 (1939).
16. I n g e b о R. D., NASA Transl. D-290, June 1960.
17. Трайбус M, Термостатика и термодинамика, изд-во «Энергия», М,
1970.
18. Shapiro A. H., Erickson A. J., Trans. ASME, 79, 775 (1957).
19. Mac Ve an S. S, Dartmouth College, Hanover, N. H., 1967
(неопубликованная работа).
20. Левич В. Г., Физико-химическая гидродинамика, изд. 2 (дополн.), Физ-
матгиз, М., 1959, стр. 407.
21. Левич В. Г., там же, стр. 429.
22. Pratt H. R. С. et al., Trans. Inst. Chem. Engrs, 29, 89—148 (1951); 3»,
57-^93, 289—326 (1953); 35, 267—342 (1957).
23. W a 1 1 i s G. В., дискуссия по докладу № 27, Intern. Heat Transfer ConL,
Boulder, Colo, ASME, 1962, D-70—D-72.
24. W a 11 i s G. B, Paper № 3, Two-Phase Fluid Flow Symp., Inst. Mech.
Engrs, London, 1962.
25. G а у 1 о r R, Roberts N. W., P r a 11 H. R. C, Trans. Inst. Chem. Engrs,
31, 57—68 (1953).
26. В 1 a n d i n g F. H, Elgin J. C, Trans. A. 1. Ch. E., 38, 305—338 (1942).
27. Thornton J. D, Pratt H. R. C, Trans. Inst. Chem. Engrs, 31, 289—
326 (1953).
28. Elgin J. C, Browning F. M., Trans. A. I. Ch. E., 31, 639 (1935);
32, 105 (1936).
29. Crawford J. W.; Wilke С R., Chem. Eng. Progr., 47, 423 (1951).
30. Кутателадзе С. С, Москвичева В. Н, ЖТФ, 29, № 9, 1135—
1141 (1959). -
31. Tayl or G. I., Proc. Roy. Soc. (London), A148, 141 (1932).
32. Hanratty T. J., EngenJ. M„ A /. Ch. E. /, 3, 229—304 (1957).
33. Wallis G. B, Turner J. M, Bemberis I, Kaufman D, AEC,
Rept NYO-3114-4, 1964.
34. Hanratty T. J., Hershman A., A. I. Ch. E. I., 7, 488—497 (1961).
35. Chung H. S, M u r g a t г о у d W, Symp. Two-Phase Flow, Exeter,
England, vol. 2, June 1965, A201—A214.
36. S t e e n D. A, W a 1 1 i s G. B, AEC Rept NYO-3114-2, 1964.
37. Van Ros sum J. J., Chem. Eng. Sci., 11, 35—52 (1959).
38. Wallis G. В., Rept 62GL127, General Electric Co, Schenectady, N. Y,
1962.
39. Wicks M, Dukler A. E, A. I. Ch. E. J., 6, 463—468 (1960).
40. Gill L. E, Hewitt G. F, Hitchon J. W, UKAEA Rept AERE-R3954,
1962.
41. Живайкин Л. Я, Химическое машиностроение, № 6, стр. 25 (1961).
42. Мо ж а р о в Н. А, Теплоэнергетика, 4, стр. 60 (1961).
43. Wal lis G. В, дискуссия к [44], Intern. J. Heat Mass Transfer, 11, 783—
785 (1968).
44. P a 1 e e v I. I, F i 1 i p p о v i с h B. S, Intern. J. Heat Mass Transfer, 9,
1089—1093 (1966).
45. Gill L. E, Hewitt G. F, Lace у P. M. C, UKAEA Rept AERE-R3955,.
1963.
46. Cravarolo L, Hassid A, Pedrocchi E, CISE R-109, Italy, 1964.
47. Кутателадзе С. С, Изв. АН СССР, ОТН, № 4, 529—536, (1951).
48. Minh Т. Q, Huyghe J. D, Symp. Two-phase Flow, Exeter, England,
vol. 1, June 1965, C201—C212.
49. С о u s i n s L. B, Denton W. H, Hewitt G. F, Symp. Two-Phase
Flow, Exeter, England, vol. 2, June 1965, C401— C430.
28 Заказ № 162
НЕКОТОРЫЕ ТЕРМИНЫ, ИСПОЛЬЗУЕМЫЕ В АМЕРИКАНСКОЙ
ЛИТЕРАТУРЕ ПО ДВУХФАЗНЫМ ТЕЧЕНИЯМ
Apparent mass — присоединенная масса
Batch sedimentation — периодическое осаждение (результирующий поток от
сутствует)
Bed fluidizied — псевдоожиженный слой
— packed — плотный слой
Body force — массовая сила
Bubble — барботировать
Compound chocking— запирание общего потока
Condition of minimum transfer — условие минимума скорости переноса
Continuous thickening — непрерывное осаждение
Drift flux—плотность потока дрейфа, приведенная скорость дрейфа
Drift flux model — модель потока дрейфа
Drift velocity — скорость дрейфа
Entrainment — унос капель
Flashing — вскипание (в результате падения давления)
"Flooding" —«захлебывание» течения
Flow annular — кольцевое течение
■— annular-mist — дисперсно-кольцевое течение
— bubbly — пузырьковое течение
— churn-turbulent — пенисто-турбулентное течение
— climbing film — течение с восходящей пленкой
— drop — дисперсное течение
— drop-annular — дисперсно-кольцевое течение
— falling film — течение со стекающей пленкой
— fog—дисперсное течение
— froth — пенистое течение
— homogeneous — гомогенное течение
— mist — дисперсное течение
— plug — расслоенное течение с перемычками
— separated — раздельное течение
— slug — снарядное течение
— stratified — расслоенное течение
Fluidization — псевдоожижение
Friction velocity — динамическая скорость, скорость трения
Interface velocity — скорость поверхности раздела
Mass flux — плотность потока массы, массовая скорость
КРАТКИЙ СЛОВАРЬ ТЕРМИНОВ
Overall volumetric flux — скорость смеси
Quality — расходное массовое газосодержание (паросодержаиие)
Recirculating (mixing) flux —циркуляционный (перемешивающий) поток
Relative velocity — относительная скорость
Reynolds flux model — Рейнольдсова модель потока
Saturated water — насыщенная вода
Separate cylinders model — модель раздельного цилиндрического течения
Slug — снарядоподобньгй пузырь, в вертикальном потоке осесимметричный;
в горизонтальном — асимметричный неправильной формы (напоминает
раковину улитки), смещенный к верхней образующей канала
Superficial — величина, отнесенная к полному сечеиию трубы (приведенная
величина)
Superficial friction factor — приведенный коэффициент трения
Total mass rate — общий массовый расход
Void fraction — средняя объемная концентрация, истинное объемное
газосодержание (паросодержаиие)
Volumetric flux — плотность объемного расхода, приведенная скорость фазы
Volumetric rate — объемный расход
Waves compressibility — упругие волны
— continuity — непрерывные волны
— dynamic — динамические волиы
— interfacial — поверхностные волны
— ripple —■ мелкомасштабные волны (рябь)
— roll — скатывающиеся волны
28*
предметный указатель
Агрегативиое течение 255, 258—260, 265
Варокши соотношение 78
Бассе сила 247, 248
Возрастание энтропии 95, 100, 106, 107
Волны 143
— в кольцевом- потоке 402
— —расслоенном потоке 161
— динамические 143, 157, 159, 163, 193 367
ударные 175
— непрерывные 125, 143, 151, 154, 214, 284,
367
ударные 145, 149, 214
— скатывающиеся 170, 172
— ударные 143, 175, 238—244, 303
— упругие 41, 338
— устойчивость 149, 151, 170, 175
Вскипание 42, 64, 88, 105
Вязкость двухфазной смесн {эффективная
вязкость смеси, эквивалентная вязкость
смесн) 43, 55, 249
Гомогенное течение 21, 33, 389, 390
волны 165
изотермическое 298
равновесное 34, 234
ударные волны 176
— образование 410
— «ожижение» 419
— спектры размеров 413
Касательные напряжения на поверхности
раздела фаз 188, 347, 348
иа стенке 39, 62, 67, 348, 355
— — распределение 131'
Кольцевое течение 82. 134, 345
границы режима' 346, 379—385
дифференциальный анализ 362
«захлебывание» 369—378
интегральный анализ 358
• объемное газосодержание 356, 382,
386—404
падение давления 356, 384—404
поверхность раздела 402
■ протнвоточиое 363
Комплекс, определяемый физическими
свойствами фаз 78
Комплексы безразмерные 127, 135, 316, 319,
396
Конденсация 98, 105, 152, 188
Концентрации профиль 117, 127, 429
Координаты 30
Корреляция 21, 347
Коэффициент трения 43—45, 47, 351, 396
— уплотнения 230, 261
— формы 208
Коэффициенты влияния 41
Краевой угол 186
Критическая скорость газа, вызывающая
уиос капель 426
Давление частиц 226
Движения уравнения 39, 62, 81, 85
Дисперсное течение 410
— — вертикальное 418
«захлебывание» 418
падение давления 421
Дифференциальный анализ 22, 129, 362
Длина пути перемешивания 130
Дренаж влаги из пены 284
Единицы 31
Мартниелли соотношение 47, 67, 69, 360,
386
Массовые силы, действующие на-
компоненты смеси 81, 97, 111, 190, 203
Маха число 41, 42, 52, 182, 239, 299, 400
Минимальный поток количества движения
103
Минимум кинетической энергии 66
Модель обмена количеством движения 106
— переменной плотности 136
— потока дрейфа 22, ПО, 320
— раздельного цилиндрического течения
68, 376, 389
Жидкая пленка вокруг длинного пузыря
в вертикальной трубе 324. 331
кольцевое течение 358, 379, 395
конденсация 152
иа внутренней стенке вращающегося
цилиндра 180
стекающая 146, 147
устойчивость 171, 180
Запирание 58, 63, 88, 106
— компонентов 88
«Захлебывание» 115, 163, 281, 338, 369—378,
418
Ииверсня плотности 214
Интегральный анализ 22, 136, 358
Испарительная труба 50
Испарительный канал 23
Капля, испарение 193
— предельная скорость 416
Неконденсирующийся газ 194
Неравновесные эффекты 33
Неразрывности уравнения 80
Нестационарное течение 53, 214, 229, 284
Неустойчивость Тейлора 188, 273
Образование пробок в псевдоожижеииых
слоях 257
Объемное газосодержание (паросодержа-
ние) истинное 27, 63, 67, 72, 74; см.
также Кольцевое течение, Пузырьковое
течение, Снарядное течение
-Осаждение непрерывное 215
— периодическое (отстаивание) 215
Относительная скорость 29, 112
Ладение давления (граднеит) 30, 40, 58
в псевдоожижениом слое 208—211
суспензиях 248—255
■ вследствие треиня 35, 39, 47, 63, 67,
73
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
437
из-за ускорения 35, 40
под действием силы тяжести 35, 40;
см. также Дисперсное течение,
Кольцевое течение, Пузырьковое течение,
Снарядное течение
Параметр двухфазности 44, 47, 48
— Мартинелли 352, 359, 360. 362
— распределения 118
Паро-водяная смесь 49
течение 74
Пей а 284
Периодическое осаждение 214—225
— течение 255, 257
Плотность объемного
расхода-"{приведенная скорость) 27
— потока дрейфа (приведенная скорость
дрейфа) 29, 114, 200, 284
Плотный слой 83, 112, 207, 260
Пневмотранспорт 264
Поверхностное натяжение 185
Поверхность раздела 184
граничные условия 184—188
— — касательные напряжения 348, 398
коэффициент треиня 350
скорость 106, 398
Пористая среда 83, 112, 208, 260
Приведенный коэффициент трения
газовой фазы 348, 352
Присоединенная масса 245
Противоточцое течение 34, 113, 363
Псевдогаз 36, 37, 234, 237, 298
Псевдоожижеиие 83, 204—214, 263, 419
— устойчивость 230
Пузырьки 23, 112, 274
— агломерация 283, 289
— зарождение 187 ,
— образование 269—274
в псевдоожижеииых слоях 259
— скорость подъема 274—284
Пузырьковое течение 117, 269
вертикальное
в соплах 300
трубах 298
границы режима 294
— — идеальное 281, 289
нестационарное 156
объемное газосодержаиие 279
падение давления 291, 296, 297
поток количества движения 291
скорость звука 166, 293
ударные волны 303
Раздельное течение 21, 61, 348, 390
Распределение частнц 265
Распыление 411
Расслоенное течение 255—257
Расходное массовое газосодержание (па-
росодержание) 27
Режимы течения 23 ■
границы 24
диаграммы 24
с преобладающим влиянием силы
тяжести 111
Рейнольдсов поток 99, 189
Релаксация 178, 241
Сжимаемость псевдоожижеиного слоя 230
Силы взаимодействия между частицами
83, 114, 225—229
Система жидкость — жидкость 115, 281,
418
■ твердые частицы 199
— обозначений 26
«Скачок» давления 256
Скорость дрейфа 29
— звука 41, 165, 166, 168
— относительная 29
— переноса минимальная 195, 256
— поверхности раздела 106, 135, 194, 399
— предельная 113, 200, 275, 416
— профили 117, 127, 129, 426
— трения (динамическая скорость) 129, 192
Снарядное течение 279
в наклонных трубах 333
границы режима 337, 379
длинные пузыри 323
единичная ячейка 311, 320, 332
максимальная длина пузыря 338
объемное газосодержаиие 279
падение давления 313, 323, 326, 332,
342
— — скорость подъема одиночных
пузырей 313—320, 328—333
Средняя объемная концентрация 27
— плотность 35
Структура потока 23
Течение в сопле 56, 89—94, 108, 232—237,
247, 301 .
— систем газ—твердые частицы 36, 101, 232
Унос капель 347, 381, 398, 422
Упругие волиы 41, 165
Уравнение распространения объемной -
концентрации 57, 125
расходного массового даросодержа-
иия 54
Условия выбора знаков 123
Фазовые превращения 84
Фильтрация 227
Флоккуляцня (образование конгломератов
частнц) 202, 222, 258
Частицы, предельная скорость осаждения
200
— коэффициент сопротивления 202, 203
— действующая сила 203
Частота реакции 54
Энергии уравнения 34, 62, 100
Эрлифт 59
ОГЛАВЛЕНИЕ
От редактора русского издания 5
Предисловие автора °
Обозначения '*
Часть I. аналитические методы 17
Глава 1. Введение *9
1.1. Что такое двухфазное течение? 19
1.2. Методы анализа • 21
1.3. Режимы течения 23
1.4. Система обозначений 26
Глава 2. Гомогенное течение
33
2.1. Введение • • 33
2.2. Одномерное стационарное гомогенное равновесное течение . . 34
2.3. Коэффициент трения для гомогенного течения 43
2.4. Падение давления в коленах, тройниках, диафрагмах и т. д. 52
2.5. Нестационарное течение . . 53
Глава 3. Раздельное течение 61
3.1. Введение 61
3.2. Стационарное течение, при котором фазы рассматриваются
совместно, но допускается несоответствие их скоростей... . . 61
3.3. Одномерное раздельное течение, при котором фазы
рассматриваются в отдельности °*J
3.4. Течение с фазовыми превращениями 84
3.5. Течение с преобладанием инерционных сил °9
'3.6. Применение принципа возрастания энтропии к расчету
коэффициента Г) "5
3.7. Уравнения энергии 1°°
Глава 4. Модель потока дрейфа НО
4.1. Введение JjJJ
4.2. Общая теория 110
4.3. Р.ежимы течения без трения на стенках с преобладающим
влиянием силы тяжести JJ1
4.4. Уточнения упрощенной теории Ц7
4.5. Условия выбора знаков и идентификация компонентов 1 и 2 123
4.6. Нестационарное течение 123
Глава 5. Профили скорости и концентрации 127
5.1. Введение }27
5.2. Общие соображения 1*'
5.3. Дифференциальный анализ 129
5.4. Интегральный анализ .. . ■ J*
5.5. Более совершенные методы анализа 139
\
ОГЛАВЛЕНИЕ
439
Глава 6. Одномерные волны 143
6.1. Введение 143
6.2. Непрерывные волны в однофазном потоке 144
6.3. Непрерывные волны в потоке несжимаемой двухкомпонент-
ной среды , . . ." 154
6.4. Динамические волны 157
6.5. Взаимодействие динамических и непрерывных волн 168
6.6. Динамические ударные волны 175
Глава 7. Явления на поверхности раздела фаз 184'
7.1. Введение 184
7.2. Граничные условия для скорости 184
7.3. Граничные условия для напряжения 185
7.4. Влияние фазовых превращений на величину напряжений на
поверхности раздела .... 188
7.5. Другие эффекты 193
Часть II. ПРАКТИЧЕСКИЕ ПРИЛОЖЕНИЯ . . ' 197
Глава 8. Смеси жидкостей и газов с твердыми частицами 199
8.1. Введение 199
8.2. Одномерный вертикальный поток однородной несжимаемой
дисперсной системы без трения на стенках 199
8.3. Однородное псевдоожижение 207
8.4. Нестационарное течение, дисперсных систем с твердыми
частицами 214
8.5. Периодическое осаждение 214
8.6. Силы взаимодействия между частицами 225
8.7. Нестационарный поток при наличии сил взаимодействия
между частицами / 229
8.8. Устойчивость "псевдоожиженных систем 230
8.9. Течение систем газ—твердые частицы 232
8.10. Дополнительные силы, действующие в быстро ускоряющихся
потоках . 245
8.11. Характеристики трения для суспензий '. . . 248
8.12. Неравномерное распределение частиц 255
8.13. Теория фильтрации 260
Глава 9. Пузырьковое течение 269
9.1. Введение 269
9.2. Образование пузырьков 269
9.3. Одномерное вертикальное течение пузырьковой смеси при
отсутствии касательных напряжений на стенке . 274
9.4. Нестационарное течение .' 284
9.5. Некоторые специальные вопросы, связанные с пузырьковым
течением 288
9.6. Трение и перенос количества движения в пузырьковом течении 291
9.7. Скорость звука в пузырьковых смесях 293
9.8. Границы пузырькового режима течения 294
9.9. Изотермическое гомогенное течение газо-жидкостных смесей
в прямых трубах 298
9.10. Изотермическое гомогенное течение при изменении только
площади поперечного сечения канала 300
9.11. Ударные волны ' 303
/
440 ОГЛАВЛЕНИЕ
Глава 10. Снарядное течение 311
10.1. Введение 311
10.2. Общая теория ' 311
10.3. Вертикальное снарядное течение 313
10.4. Горизонтальное снарядное течение 328
10.5. Снарядное течение в наклонных трубах 333
10.6. Границы снарядного течения 337
10.7. Пульсация давления при снарядном течении . 342
Глава 11. Кольцевой режим течения 345
11.1. Введение 345
11.2. Горизонтальное течение 346
11.3. Вертикальное кольцевое протнвоточное течение 363
11.4. «Захлебывание» 369
11.5. Вертикальное восходящее однонаправленное кольцевое
течение 379
Глава 12. Дисперсное течение 410
12.1. Введение 410
12.2. Образование одиночных капель 410
12.3. Распыление 411
12.4. Спектры размеров капель 413
12.5. Предельная скорость одиночных капель в гравитационном поле 416
12.6. Одномерное вертикальное дисперсное течение без трения
на стенке 417
12.7. «Захлебывание» в дисперсном потоке 418
12.8. «Ожижеиие» дисперсной системы 419
12.9. Падение давления прн вынужденной конвекции 421
12.10. Унос 422
Некоторые термины, используемые в американской литературе по
двухфазным течениям 434
Предметный указатель 436
УВАЖАЕМЫЙ ЧИТАТЕЛЬ!
Ваши замечания о содержании книги, об
оформлении, качестве перевода н другие просим
присылать по адресу: 129820 Москва, И-110, 1-й Рижский
пер., д. 2, издательство «Мир».
i