Author: Иевлев В.М.
Tags: движение жидкостей гидродинамика теплофизика
ISBN: 5-02-006735-0
Year: 1990
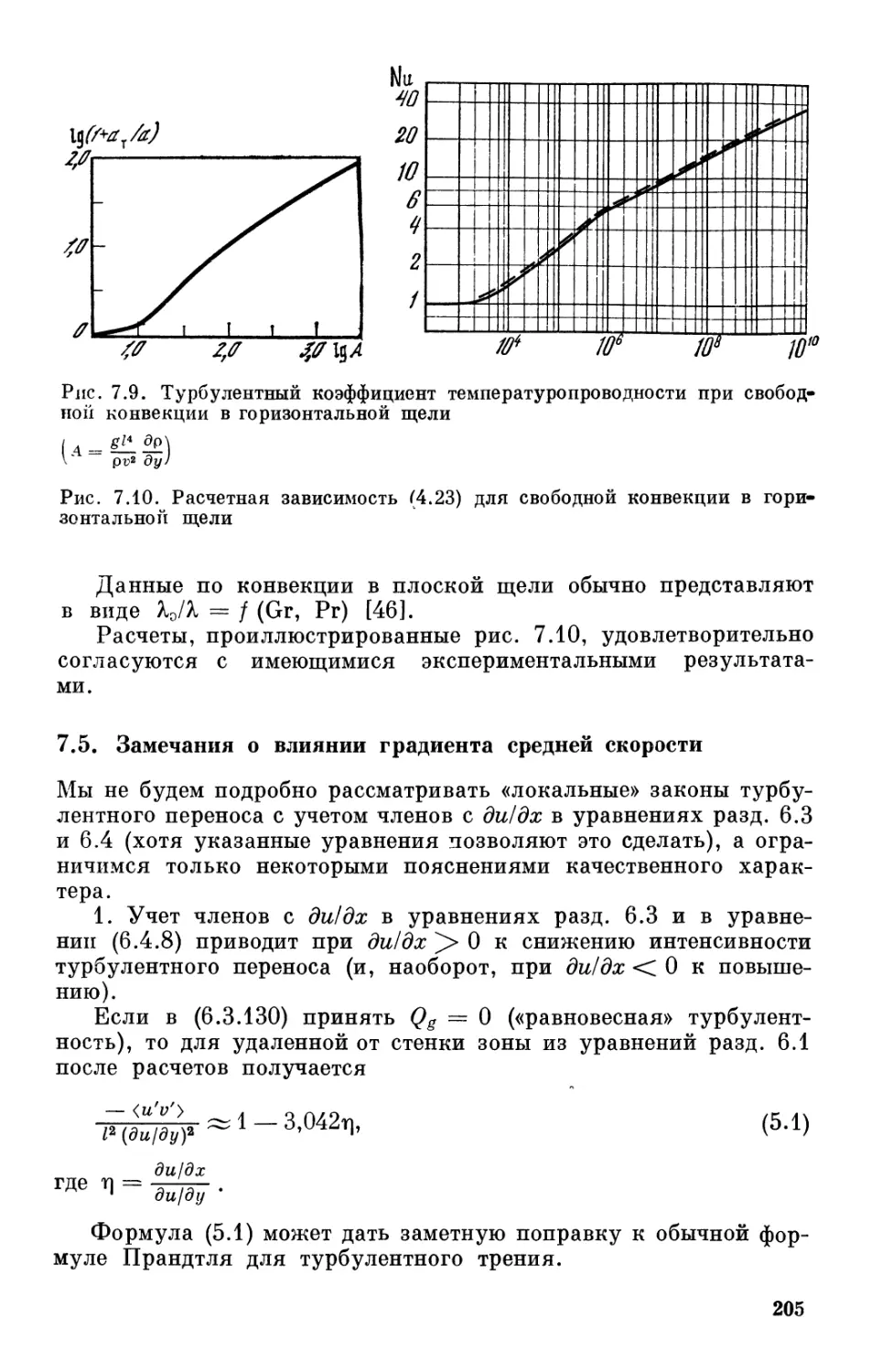
Text
АКАДЕМИЯ НАУК СССР
Отделение
физико-технических проблем энергетики
В. М. ИЕВЛЕВ
ЧИСЛЕННОЕ
МОДЕЛИРОВАНИЕ
ТУРБУЛЕНТНЫХ
ТЕЧЕНИЙ
Ответственный редактор
академик В. И. СУББОТИН
Москва «Наука»
1990
УДК 532.517.4
Численное моделирование турбулентных течений/ В. М. Иевлев—
М.: Наука, 1990.- 216 с. - ISBN 5-02-006735-0.
В монографии рассмотрены два взаимосвязанных подхода к по-
построению теории турбулентности. Часть I посвящена прямому чис-
численному моделированию крупномасштабной турбулентности. Харак-
Характеристики ее получены путем статистической обработки результатов
расчетов («численных экспериментов»). Даны методики расчетов одно-
однородной магнитогидродинамической турбулентности и однородной
турбулентности в стратифицированной среде в поле силы тяжести.
В части II развиты полу эмпирические методы теории, основанной
на принципе «локального подобия» в явлениях турбулентного пере-
переноса. Эта теория позволяет решать большое число практически важ-
важных задач, причем формулы теории уточняются на основе численного
эксперимента, описанного в части I.
Для научных работников, инженеров и студентов в области гид-
гидродинамики и теплофизики.
Ил. 31. Табл. 2. Библиогр. 49 назв.
Рецензенты:
доктор физико-математических наук А. А. ПАВЕЛЬЕВ,
доктор физико-математических наук А. С. ХОЛОДОВ
тт 2004030000-252
042@2)-90 583-90 1 полугодие
ISBN 5-02-006735-0 © Издательство «Наука», 1990
ВВЕДЕНИЕ
Турбулентное движение является наиболее распространенной фор-
формой движения жидкостей и газов в природе и в технических устрой-
устройствах. Однако удовлетворительных (т. е. достаточно универсаль-
универсальных и обоснованных) методов расчета турбулентных течений не
существует, несмотря на уже более чем вековую историю развития
исследований турбулентности и большое число работ в этом на-
направлении, публикуемых ежегодно. Это объясняется двумя при-
причинами:
прежде всего сложностью самого явления;
ограниченностью возможностей того направления в теории тур-
турбулентности, которое сейчас является преобладающим.
Очевидно, необходимы новые подходы при построении теории
турбулентности. В настоящее время в качестве основы для этого
чаще всего используются уравнения для моментов пульсирую-
пульсирующих величин. В теории однородной турбулентности, где достигнуты
наибольшие успехи, применяются уравнения для двухточечных
моментов [1—2], а в теории неоднородной турбулентности — в боль-
большинстве случаев только уравнения для одноточечных моментов
[2—4]. Эти уравнения являются незамкнутыми, они замыкаются
приближенно с помощью различных гипотез (интуитивного ха-
характера, основанных на соображениях подобия или на экспери-
экспериментальных данных). В приближенные выражения, замыкающие
уравнения для моментов, входит обычно некоторый масштаб тур-
турбулентности I. Получение уравнения для I является всегда одной
из наиболее сложных задач полуэмпирических теорий. Дело в том,
что масштаб Z, конечно, не может быть определен только через од-
одноточечные моменты, так как он сам является мерой расстояния
между точками в потоке, на котором существует еще заметно от-
отличная от нуля корреляция турбулентных пульсаций. Поэтому
при получении уравнения для масштаба I поступают обычно одним
из двух способов: либо записывают уравнение для двухточечных
моментов поля скоростей и затем интегрируют это уравнение по
расстоянию между точками, либо записывают уравнение для дис-
диссипации энергии 8 и приближенно определяют отдельные члены
этого уравнения через масштаб I и другие величины. В обоих слу-
случаях приходится делать много предположений достаточно произ-
произвольного характера, не обоснованных в необходимой мере экспе-
экспериментальными данными *.
1 Используется еще и третий способ: в ряде работ вид уравнения для I
просто постулируется, при этом используются аналогия с видом уравне-
уравнений, получаемых указанными способами, а также соображения теории
размерностей.
Одной из первых работ, в которой была предпринята попытка
построения теории турбулентности и результаты которой затем
использовались (и используются сейчас) во многих других иссле-
исследованиях, является работа Ротта [5]. Методы расчетов для различ-
различных практически важных задач, основанные на полуэмпирических
теориях с использованием уравнений для моментов, подробно раз-
разработаны Сполдингом [6—7]. По-видимому, одна из наиболее удач-
удачных и полных теорий, основанная на использовании трех уравне-
уравнений для одноточечных моментов и уравнения для масштаба тур-
турбулентности, разработана В. Г. Лущиком, А. А. Павельевым,
А. Е. Якубенко [8, 9].
Следует отметить, что уравнение для масштаба I в теориях рас-
рассматриваемого типа вызывает сомнение не только из-за произволь
ности и недостаточной экспериментальной обоснованности выра-
выражений для отдельных членов, но и по причинам более принципиаль-
принципиального характера — вероятно, существует некоторый механизм огра-
ограничения максимального масштаба вихрей вследствие прямого влия-
влияния стенки (через поле давлений). Формально это проявляется
в том, что при интегрировании уравнения для двухточечных мо-
моментов поля скоростей по расстоянию между некоторыми точками
М и Мг, удаляющимися друг от друга в направлении нормали
к стенке, один из пределов интегрирования определяется, есте-
естественно, попаданием точки М или Мг на стенку. В проинтегри-
проинтегрированном уравнении при этом появляются члены вида <РСт (^дуУ
и <тст (vt)yy [10], где Рст и тст — пульсации давления и напряже-
напряжения силы трения на стенке (в некоторой точке Мст), а (иг)у — пуль-
пульсация скорости в точке, находящейся на расстоянии у от стенки,
на нормали к ней, проходящей через точку МСт- Величины
<РСт (^-)у> и <тст (Vi)yy могут быть отличны от нуля даже при
больших расстояниях от стенки г/, так как в пристеночном логариф-
логарифмическом слое масштаб турбулентности I возрастает пропорцио-
пропорционально у. Надежных экспериментальных данных по величинам
СРст (Vi)'y> и <Тст {Vi)yy не существует. В большинстве теорий пря-
прямое влияние стенки на масштаб I не учитывается 2.
Из-за указанных трудностей получения уравнения для Z,
ненадежности этого уравнения, а также в связи с возможным пря-
прямым влиянием на I расстояния до стенки во многих случаях раз-
развиваются и успешно применяются полу эмпирические теории,
в которых I определяется не по дифференциальному уравнению,
а с помощью алгебраической формулы, ставящей его в зависимость
только от геометрических факторов (расстояния до стенки, формы
канала) независимо от режима течения жидкости. При этом одно-
одноточечные моменты поля скоростей (в частности, компоненты напря-
напряжений Рейнольдса) могут определяться с помощью как дифферен-
дифференциальных уравнений, так и алгебраических формул (для развитой
«равновесной» турбулентности).
2 Попытка такого учета сделана в [11].
Кроме уравнений для моментов, основой полуэмпирических
теорий турбулентности могут являться уравнения для плотностей
вероятностей различных значений пульсирующих величин в од-
одной или нескольких точках потока [10—14]. Эти методы родственны
методам, в которых используются уравнения для моментов, но
имеют ряд преимуществ [11].
Полуэмпирические теории турбулентности применяются глав-
главным образом для течений типа пограничного слоя (пристеночных
и струйных). Задачи со сложной геометрией (пространственные
течения, отрывные течения и др.) с помощью полуэмпирических
теорий практически не рассчитываются. Такая недостаточная
универсальность полуэмпирических теорий определяется, с одной
стороны, тем, что в механизме турбулентного переноса существен-
существенную роль играют крупные вихри, размер которых соизмерим с по-
поперечными размерами потока. Эти вихри, естественно, не являются
универсальными, их характеристики существенно зависят от гео-
геометрии задачи и от режима течения. Все это плохо учитывается
имеющимися полуэмпирическими теориями, в особенности для
потоков со сложной геометрией. С другой стороны, недостаточная
универсальность полуэмпирических теорий часто определяется
отсутствием необходимых детальных экспериментальных данных.
Поэтому очень полезно провести прямое численное моделирование
крупномасштабных турбулентных движений (численный экспе-
эксперимент) 3.
Работы в этом направлении в последние годы развиваются в раз-
различных странах (см., напр., обзоры [15—18]). Выполнены соответ-
соответствующие расчеты для течений в каналах и для изотропной турбу-
турбулентности, причем рассмотрены как крупномасштабное поле пуль-
сационных скоростей, так и крупномасштабные пульсации темпе-
температуры.
Не ставя себе целью проведение полного обзора работ в обсуж-
обсуждаемом направлении, укажем все же некоторые наиболее существен-
существенные результаты.
Первой работой по численному моделированию крупномасштаб-
крупномасштабной турбулентности в канале является [19]. В работе [20] впервые
введена модель для «подсеточной» турбулентности и выполнен
переход к цилиндрической геометрии.
Следует отметить, что в работах [18—20] тонкий пристеночный
слой не рассчитывался, а при расчетах «ядра потока» граничные
условия формулировались в логарифмической области. Это, ко-
конечно, уменьшает строгость и информативность теории, но дает
возможность упрощенно рассмотреть целый ряд более сложных
задач. Так, в [18] рассмотрена и тепловая задача, и случай шеро-
шероховатости стенки, и течение жидких металлов.
Очень детальное изучение течения в канале, включая присте-
пристеночный слой, приведено в работе [21]. Получено хорошее согласо-
согласование с опытными данными. При этом мелкомасштабная «подсеточ-
3 Это и есть тот новый подход, о необходимости которого шла речь.
ная» турбулентность определялась с использованием эмпирических
констант. В работе [22] дано сравнение различных методов описа-
описания подсеточной турбулентности. Во всех случаях при этом ис-
используются эмпирические константы. В работе [23], посвященной
пульсациям температуры, также применяются аналогичные ме-
методы описания подсеточной турбулентности.
В СССР наибольшие успехи в численном моделировании крупно-
крупномасштабной турбулентности достигнуты О. М. Белоцерковским
[24—26]. Развиваемые далее в этой книге подходы сформировались
у автора как под влиянием его собственным работ, так и в резуль-
результате обсуждений с О. М. Белоцерковским. При этом делается по-
попытка описания подсеточной турбулентности без эмпирических
констант и исследуется ряд новых задач (часть из них рассматри-
рассматривается только методически: большая трудоемкость расчетов не
позволила выполнить их для всех рассмотренных случаев).
Книга состоит из двух частей. Часть I посвящена прямому чис-
численному моделированию крупномасштабной турбулентности; часть
II — развитию полуэмпирических методов, позволяющих решать
большое число практически важных задач. Эти части взаимосвя-
взаимосвязаны: материалы части I могут использоваться как «эксперимен-
«экспериментальный материал» (данные «численного эксперимента»), необхо-
необходимый для проверки и уточнения полуэмпирических методов
части II; а материалы части II подсказывают форму, в которой
удобно представлять (аппроксимировать) результаты расчетов
различных задач в части I с целью их обобщения и дальнейшего
практического использования.
В части I решаются задачи только для несжимаемой жидкости.
Однако использование принципа «локального подобия» дает воз-
возможность перенести результаты расчетов этой части на случай те-
течения газов.
Автор считает своим приятным долгом выразить благодарность
Е. 3. Лейбову, который принял на себя труд по рабочему про-
программированию, отладке программ и по расчетам для части I книги,
а также Н.Н.Баранову, Ю.Г.Туманову и Ю. С. Мелешкову
за большую помощь по подготовке рукописи к изданию.
ЧАСТЬ ПЕРВАЯ
ПРЯМОЕ ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ
КРУПНОМАСШТАБНОЙ ТУРБУЛЕНТНОСТИ
ГЛАВЛ^ПЕРВАЯ
ПОСТАНОВКА ЗАДАЧИ.
НЕКОТОРЫЕ ПРИНЦИПИАЛЬНЫЕ ВОПРОСЫ,
СВЯЗАННЫЕ С КОРРЕКТНОСТЬЮ ПОСТАНОВКИ
И С ВОЗМОЖНЫМИ МЕТОДАМИ ЕЕ РЕШЕНИЯ
1.1. Постановка задачи прямого численного моделирования!
крупномасштабной турбулентности
и используемые уравнения
Полное прямое численное моделирование турбулентности должно
было бы включать в себя расчет эволюции во времени поля «ис-
«истинных» г скоростей, давлений и других параметров потока,
а затем статистическую обработку полученных результатов, т. е.
определение распределения вероятностей различных значений
пульсирующих величин во всех точках потока, моментов различ-
различного порядка и т. д. Однако такая постановка задачи является
нереальной — и не только по техническим причинам (т. е. из-за
недостаточной мощности вычислительной техники), но и по при-
причинам принципиальным. Дело в том, что мгновенные значения сил,
действующих на каждую частицу в потоке, являются случайными
величинами и вследствие неустойчивости движения не могут быть
определены заранее. Это прршципиально не позволяет определить
эволюцию истинного поля скоростей и давлений. Именно поэтому
речь идет не о полном численном моделировании «истинного» поля,
а только о численном моделировании крупномасштабных турбу-
турбулентных пульсаций. Что под этим понимается и насколько коррект-
корректна соответствующая постановка задачи, требует особого поясне-
пояснения.
Запишем уравнения движения среды в следующем виде:
dvt/dt = Ft, i = i, 2, 3; дик/дхк = 0. A.1)
Здесь Ft — сила, действующая на жидкую частицу, отнесенная
к единице объема массы жидкости (т. е. ускорение). При исполь-
использовании уравнений Навье—Стокса
F — * др 1у * (А 9\
дх.
1 Слово «истинных» заключено в кавычки потому, что в действительности
будет определяться неистинное поле (см. ниже).
Для идеальной среды (модель такой среды часто может исполь-
использоваться для расчета движения крупных вихрей при больших чис-
числах Re) в формуле A.2) член с вязкостью опускается. В других
случаях выражение для Ft может быть более сложным (например,
включать в себя объемные силы электромагнитного происхож-
происхождения для случая магнитогидродинамических задач или архиме-
архимедовы силы при движении страцифицированных сред).
Выделим в потоке произвольную группу из п точек. Введем
в рассмотрение тг-точечную плотность вероятности различных зна-
значений скоростей в выделенных точках. Уравнение для /п имеет
следующий вид [11] 2:
Здесь верхний индекс у соответствует номеру точки; символ <( У а
отмечает условные математические ожидания при Ап = const, где
Ап — совокупность скоростей \W во всех выбранных п точках.
Таким образом: (F\ У а —это условное математическое ожидание
(среднее значение) i-й компоненты силы Ft, действующей на едини-
единицу массы жидкости в точке у при заданных значениях скоростей
во всех точках выбранной группы. Обратим внимание на то, что
в уравнения A.3) для /п входит только осредненное значение сил
<\^гУап и не входит истинное значение случайных сил Ft. Поэтому
для определения всех статистических характеристик потока (а все
w-точечные статистические характеристики определяются через /п)
достаточно знать только осредненное значение сил.
Уравнение A.3) представляет собой уравнение Лиувилля для
плотности распределения п «квазичастиц» в бтг-мерном фазовом
пространстве, координатами которого являются координаты и
скорости всех п «квазичастиц». Каждая из «квазичастиц» подчинена
следующим уравнениям движения:
^ = <Hv)>An. A.4)
Эти уравнения отличаются от исходных уравнений A.1) за-
заменой случайной силы Ft в правой части A.1) величиной </^j>a ,
т. е. средним значением этой силы при заданных скоростях во всех
п точках. Таким образом, если проводить расчет эволюции поля
скоростей с заменой в A.1) случайных сил Ft осредненными зна-
значениями (FtyA , то получится поле скоростей, отличающееся, ко-
конечно, от истинного, но имеющее одинаковые с ним статистические
характеристики (т. е. одинаковые /п).
* В работе [11] соответствующее уравнение приведено в более общем виде:
рассматривается не только плотность вероятности /п различных значений
скоростей, но и плотность вероятности совместного распределения ско-
скоростей и других пульсирующих параметров в п точках.
Это принципиальный результат, так как величины (FtyA опре-
определяются скоростями в выбранной группе п точек, а величины Ft
являются случайными. Далее группа из п точек, о которой шла
речь, будет отождествляться с центрами ячеек трехмерной расчет-
расчетной сетки. Чтобы рассмотреть динамику именно крупных вихрей,
оставаясь в рамках реальных возможностей ^ля вычислительных
машин, целесообразно выбирать размеры ячеек расчетной сетки
в несколько раз меньшими предполагаемых размеров крупных вих-
вихрей (но, конечно, размеры этих ячеек много больше, чем размеры
наиболее мелких вихрей при больших числах Re).
Силы <7^>a определяются мелкомасштабной («подсеточной»)
турбулентностью. Так как в уравнения входят только условные
средние значения (математические ожидания) этих сил, а не ис-
истинные силы, при расчетах крупномасштабного турбулентного
движения выражения для членов уравнений, зависящих от под-
подсеточной турбулентности, могут определяться через скорости
крупновихревых пульсаций. Это и создает принципиальную воз-
возможность численного моделирования крупномасштабной турбу-
турбулентности.
Процедура получения уравнения для крупномасштабной тур-
турбулентности может быть различной. Во всех случаях в качестве
исходных используются уравнения Навье—Стокса и уравнение
неразрывности. Далее, в соответствии с [27], могут быть введены
величины, «сглаженные» с помощью функции-фильтра. Так, если
/ (х, t) — любая из величин, характеризующих течение (напримерг
мгновенное значение любой компоненты локальной скорости или
величина давления р), то «сглаженное» значение / (обозначим его /)
определяется следующим образом:
,*)dx'- A.5)
Получили распространение два вида фильтров G:
а) гауссовский фильтр, имеющий для изотропного случая такой
вид:
G(х — х') = (/6 /У* • Да)з еХр [- 6 (хг- XiflMl A.6)
здесь Аа — длина, пропорциональная шагу решетки расчетной
сетки h (часто принимают AJh = 2);
б) фильтр типа «ящик»:
ГA/АаJ при |*-|<а/,
\ Л . ,. A.7)
I 0 при \х — я'|>Д/2 v ;
Выражение A.7) записано для изотропного случая. В ряде ста-
статей для такого фильтра также принимают AJh = 2.
Обозначим
/' = /-/. A.8)
9
Величины /' определяются, очевидно, мелкомасштабной тур-
турбулентностью.
Применяя преобразование A.5) к исходным уравнениям
(Навье—Стокса и неразрывности) и используя A.8), можно полу-
получить уравнения для крупномасштабного движения, в которые будут
входить также члены, зависящие от величин со штрихом (т. е. от
мелкомасштабной турбулентности). Именно по этим уравнениям
и проводится расчет.
Другой метод получения уравнений для крупномасштабной
турбулентности, впервые примененный в [28] (и независимо в не-
несколько другом виде использовавшийся нами), состоит в интегри-
интегрировании исходных уравнений по объемам ячеек расчетной сетки,
т. е. в составлении уравнений баланса (количества движения,
массы) для каждой ячейки. Хотя такой «фильтр» совпадает с A.7)
дри Да = h, использование балансовых соотношений имеет, по
нашему мнению, несомненные преимущества, состоящие в том, что
упрощаются выражения для «штрихованных» членов и величины
со штрихом приобретают более ясный смысл (см. гл. 2), что об-
облегчает формулировку гипотез, описывающих мелкомасштабную
турбулентность.
В связи со сказанным будут использоваться уравнения, осред-
ненные по объемам ячеек расчетной сетки, поэтому, например,
рассчитываемые скорости ut — это средние по ячейкам расчетной
сетки.
Силы взаимодействия между жидкостью в ячейках, зависящие
от мелкомасштабной («подсеточной») турбулентности, при этом
должны быть определены приближенно.
1.2. Замечания о требованиях к точности описания
мелкомасштабной турбулентности
Есть основание надеяться, что некоторая неточность в описании
мелкомасштабной турбулентности не сильно скажется на характе-
характеристиках крупных вихрей и что само описание мелкомасштабной
турбулентности может быть универсальным.
Эти основания базируются на следующем: 1) как известно,
в турбулентных потоках происходит перенос диссипируемой энер-
энергии от крупных вихрей к мелким, поэтому можно ожидать, что
влияние характеристик крупномасштабного турбулентного дви-
движения на мелкомасштабное должно быть большим, а обратное влия-
влияние — значительно меньшим; 2) как известно, при больших
числах Re характеристики турбулентности для разных типов те-
течений оказываются от них мало зависящими. Это означает, напри-
например, что, если вязкость жидкости изменится в несколько раз (и в со-
соответствующее число раз изменится число Re), характеристики
крупных вихрей сохранятся неизменными (тогда как мелкомас-
мелкомасштабная турбулентность, конечно, при изменении вязкости сильно
изменится); 3) при существенном различии спектра крупномас
10
/0
/0
/0
,-г
4—7*
» » 1» ^
/0~* /tf~z
Рис. 1.1. Спектр продольной составляющей турбулентных пульсаций для
различных течений (по: [15])
Ф — безразмерная спектральная [плотность * энергии; [Ф = Ei/iev6I^; К — волновое
число; Kfc — максимальное значение волнового числа; К-^ = 1/6, где 6 — масштаб
А. Н. Колмогорова
штабных пульсаций для разных случаев течений спектр мелкомас-
мелкомасштабных (высокочастотных) пульсаций сохраняется практически
универсальным (рис. 1.1); 4) в работах [11, 18] показано, что из
уравнения для плотности вероятности fn при подстановке в него
приближенных выражений для (Рг}Ап, удовлетворяющих некото-
некоторым требованиям, получаются точные уравнения Фридмана—Кел-
Фридмана—Келлера для всех т точечных моментов, где т <^ п.
Высказанные предположения подтверждаются данными рабо-
работы [22], в которой приведено прямое сравнение разных методов
описания подсеточной турбулентности. Показано, что при изме-
изменении параметров всех использованных моделей в некоторых пре-
пределах характеристики крупномасштабного движения получаются
практически одинаковыми для всех случаев.
Из изложенного, конечно, не следует, что с описанием подсе-
подсеточной турбулентности можно обращаться слишком вольно;1 этот
вопрос требует постоянного внимания.
1.3. Роль и место прямого численного моделирования
в ряду других подходов к решению задач
теории турбулентности
Так как прямое численное моделирование турбулентности требует
проведения значительно более сложных и трудоемких расчетов,
чем решение задач с помощью полуэмпирических теорий турбу-
турбулентности, то те практически важные задачи, которые можно ре-
решить с помощью полуэмпирических теорий, так и нужно решать
{т. е. с помощью этих полуэмпирических теорий). Прямое числен-
численное моделирование необходимо для следующих целей:
накопление «экспериментального» материала (т. е. данных
«численного эксперимента») для проверки и совершенствования
полуэмпирических теорий или, может быть, построение формул,
аппроксимирующих результаты прямых расчетов. В связи с этим
целесообразно рассчитать в первую очередь целый ряд типовых
задач, позволяющих уточнить разные стороны механизма турбу-
турбулентного движения. Методике именно таких расчетов и посвящена
в основном часть I монографии (поэтому в ней рассмотрение огра-
ограничено только случаем несжимаемой жидкости);
самостоятельное решение таких практически важных задач,
которые нельзя решать с использованием полуэмпирических ме-
методов (задачи со сложной геометрией);
прояснение отдельных сторон механизма турбулентного дви-
движения в различных случаях;
Сказанное свидетельствует, что полуэмпирические методы рас-
расчета должны развиваться и совершенствоваться параллельно с раз-
развитием прямого численного моделирования турбулентности.
Об этом уже шла речь во Введении к монографии в связи с обсуж-
обсуждением взаимосвязей ее первой и второй частей.
1.4. О начальных и граничных условиях
При прямом численном моделировании крупномасштабной тур-
турбулентности всегда решается трехмерная нестационарная задача,
но получаемые при этом мгновенные поля скоростей и давлений
представляют интерес, конечно, только как материал для стати-
статистической обработки и в ряде случаев для качественного анализа
характера движений.
Конечными результатами расчетов являются различные ста-
статистические характеристики турбулентного потока, поле которых
может быть и не трехмерным, и статистически стационарным. Тем
не менее для решения и таких задач (статистически стационарных
и нетрехмерных) начальные и граничные условия должны задавать-
задаваться для полной трехмерной нестационарной задачи.
Что касается начальных условий, то можно ожидать, что их
влияние практически не будет сказываться на конечном статисти-
статистически стационарном состоянии потока (вследствие неустойчивости
12
течения и нелинейности задачи). Имеющиеся в литературе резуль-
результаты расчетов подтверждают это (см., напр.: [21]) х.
Граничные условия можно разбить на три группы:
1. Условия на таких границах, где они могут быть сформули-
сформулированы достаточно точно. Сюда относятся условия на стенке (по
крайней мере гладкой) и условия на границах соприкосновения
различных слоев жидкости друг с другом.
2. Условия на краях области расчетов вдоль однородных ко-
координат (например, в продольном направлении при течении в бес-
бесконечно длинном цилиндрическом канале или по любой координате
в случае однородной турбулентности в жидкости, заполняющей
все пространство). Реальное течение вдоль этих координат пред-
предполагается распространяющимся на бесконечно большое расстоя-
расстояние, а область, в которой проводятся расчеты, естественно, конеч-
конечна (и не может быть очень большой). Если длина области расчетов
значительно (хотя бы на порядок) превышает размер основных
крупных энергонесущих вихрей (а так и должно быть), то при фор-
формулировке приближенных граничных условий турбулентное те-
течение по однородным координатам может считаться периодиче-
периодическим (с периодом, равным длине области расчетов). Это внесет
только небольшое искажение в спектр турбулентности в несуще-
несущественной очень низкочастотной части спектра.
3. Некоторые эффективные граничные условия на границе тон-
тонкого пристеночного слоя жидкости с течением в «ядре потока»,
т. е. вдали от стенки. Эти условия должны использоваться при
расчетах только пристеночного слоя, без расчетов «ядра потока».
Конкретная формулировка начальных и граничных условий
приводится далее отдельно для различных задач.
Для других типов граничных условий, особенно по однородным
координатам, должен быть рассмотрен вопрос о необходимости
расширения расчетной области.
ГЛАВА ВТОРАЯ
МЕТОДИКА И РЕЗУЛЬТАТЫ РАСЧЕТА
ОДНОРОДНОЙ ТУРБУЛЕНТНОСТИ
ПРИ БОЛЬШИХ ЧИСЛАХ Re
2.1. Вводные замечания
В этой главе рассматривается однородная турбулентность в не-
несжимаемой жидкости при нулевой средней по всему объему жид-
жидкости скорости. Начальное состояние движения жидкости может
1 Но время достижения стационарного состояния от начальных условий
будет, конечно, зависеть. Поэтому желательно задавать эти условия так,
чтобы они были (по своим статистическим характеристикам) близки к ожи-
ожидаемым конечным.
13
быть неизотропным. Число Рейнольдса предполагается очень боль-
большим даже для пульсаций скорости порядка размера ячеек расчет-
расчетной сетки, так что членами с вязкостью в уравнениях можно пре-
пренебречь (они буду вначале сохранены при общих преобразованиях
уравнений, а затем опущены). Рассмотрение проводится в декар-
декартовой системе координат с осями хг, х2, х3; компоненты скорости
соответственно ии и2, и3\ давление р и плотность жидкости р.
Иногда оси будут обозначаться х = х^у = х2, и z = x3, а скорости
Up, uyi u2. Расчетная сетка имеет прямоугольные ячейки с разме-
размерами Ах, Ау, Аг (постоянными по объему).
Методика расчета в этой главе описана подробно, с различными
деталями. Это сделано потому, что аналогичная (в основном) ме-
методика используется и в следующих главах, где она изложена уже
менее подробно.
2.2. Исходные уравнения
Уравнения движения несжимаемой жидкости имеют вид
диг . д(игик) __ 1 dp &U. диг^
dt "• дхи р ахх *~ дхпдхи ' дхк ' У '
Как обычно, по повторяющимся индексам здесь предполагается
суммирование.
Интегрируя эти уравнения по любому объему V с неподвижной
границей S, получим (что можно, конечно, написать сразу, без
дифференциальных уравнений):
(щип)8 &S = jr§
B.2)
B.3)
Здесь ип — скорость по направлению внешней нормали к поверх-
поверхности S в каждой точке этой поверхности; индекс s отмечает ве-
величины на поверхности; п — единичный вектор по внешней нор-
нормали к поверхности; kt — единичный вектор вдоль оси xt.
Выберем с качестве объема V ячейку расчетной сетки. Запишем
для любой величины /:
J fdV = fAxAyAz,
(V)
где справа / — среднее по объему ячейки значение / (знак осред-
осреднения опущен).
Обозначим для какой-либо ячейки х± — левую границу этой
ячейки по оси х, х2 (х2 = х± + Ах) — правую границу; соответ-
14
ственно у± и у2 по оси у и zt и z2 по оси z. Представим поверхностный
интеграл от любой величины / по грани ячейки (например, по
грани х = х2) следующим образом:
2/2
где </>Х2 — среднее по грани х = х2 значение величины /. Анало-
Аналогично вводятся средние по другим граням величины.
С учетом этого из уравнения B.2) для ut = ux получим (после
деления на AxAyAz):
_ X XI X Х±_ _^ У 3/1 У 1/2 _|_
Ах
Да: \\ 5х /*i \ дх /**) ~^ Ау \\ ду
Аналогичные уравнения получаются для иу и uz.
Из B.3) получим
(ЦЛ-<ЦЛ , <Уу.-<Уу1 , <Vz.-^Vzt = 0 B5)
Ах """ Аг/ ' Az • V " /
В каждой точке, например на грани ячейки у = у2, скорость
ut = (иду=у* (в любой фиксированный момент времени) можно
представить в виде
где, очевидно, (щ)у=У2 представляет собой отклонение скорости
в точке от средней по грани, так что (щУУ2 = 0.
В B.4) входят парные произведения скоростей — величины
типа (ихиУУУ2, для которых получается:
и т. п.
Выражения такого типа будут использованы в дальнейшем.
Если </>х — среднее по поверхности х = const внутри ячейки *
значение какой-либо величины /, то, очевидно;
х2
<!*,. B.6)
где слева — среднее по объему значение /.
То есть по поверхности, получающейся при сечении ячейки плоскостью
х = const.
15
Если аппроксимировать распределение </)х в районе рассмат-
рассматриваемой ячейки и соседней с ней ячейки справа линейной зависи-
зависимостью (т. е. </>х х А + Вх), то с учетом B.4), в частности, по-
получится
</>*, = (/ + /прав)/2, B.7)
где /прав — среднее значение / по объему соседней (справа) ячейки.
По формулам типа B.7) будут определяться средние значения щ и р
на гранях ячеек.
2.3. Аппроксимация отдельных членов уравнений
и получение сеточных уравнений
Отметим все величины в какой-либо ячейке индексом п, /тг, д,
соответствующим номеру ячейки (где п — номер участка вдоль
оси х; т — вдоль оси у; q — вдоль оси z). Отметим средние величи-
величины на грани х = х± ячейки индексом п — V2, m, q\ на грани х = х2
индексом п + V2, m, q; на грани у = yi индексом п, т — 1/2, q
и т. п. С учетом указанных в разд. 2.2 преобразований и обозна-
обозначений из B.2) (т. е. из уравнений типа B.4)) получается
d (Щ)п9 т, q/At = (Мг)П) w, q + (Л^п. m, qr C.1)
ГДе (Мг)П) m,q = (Рг)П-1/2, m, q + {Fijn+tf^ m> q + (Oi)n, WI-V2» Я. —
— (Фг)п, w+Vf, Я. + (Qi)n, m, q-V2 — (Qi)n, m, q+y2- C.2)
Величина (Мг)п, w, q определяется конвективными и вязкими
членами уравнения B.2); величины Ft, Фи Qt имеют смысл сил,
действующих на единицу массы жидкости в рассматриваемой ячей-
ячейке со стороны соседних ячеек (при индексе п — V2, m, q — со
стороны ячейки п — 1, иг, q; при индексе и, /гг, q + 1/2 — со сторо-
стороны ячейки п, т, q + 1 и т. п.); величина Rt — это сила, связанная
с градиентом давления1. Указанные величины определяются сле-
следующим образом:
(Rx)n, т, q = 2рДя (Рп~*> ™» Q. Рп+Ъ ™, q)? C-3)
(Ry)n, т, q=
(Fi)n-y2, m, q = ^Дд [(^г)п-1, m, q Ч" (^г)п, m,g][(^jc)n-l, m, q +
+ (ux)n, m, q] + -J^2~ [{ui)n-1, m, q — (щ)п, m, q] +
+ "AT <^4>n-V2, m, q, C.6)
* Речь идет о сумме обычного, гидростатического давления и «турбулент-
«турбулентного давления», связанного с подсеточной турбулентностью (см. ниже),
16
m,q ?д^~ [(ui)n, m, q + (Ui)n+1, m, q][(ux)n, m, q
(^x)n+1, чп, q] + Д(Г2 [(ui)n, m,q — (щ)п+1, т, q]
<UiUx>n+V2, m, q, C.7)
п, m-V2, q = 4Ду [(^i)n, m-1, q
(^у)п, m, q] + -дТГ [(^i)n, rn-1, g — (^i)n, m, q] +
C-8)
m, q + (^i)n, m+1, q][(^y)n, w, q
(^y)n, m+X, q] + ~др~ [(^i)^, m, q — (ui)n, m+1, q] +
C.9)
m, q-1 + (ui)n, m, q][(^)n, rn, q-1
V
\Цг)п, m, qj H д^2~~ L(^ibi, m, q-1 — (^i/n, m, qj ~T"
4f <^>^ ",«-»/„ (зл°)
i
m, q ~ V^iM» m, q+lJLV^M, m, q
C-11)
+ (Uz)n, m, q+l] + -др- [(wi)rt, m, q — (wi)n, m, q+l] +
, w,
Из уравнения неразрывности B.3), т. е. из уравнения B.5),
для ячейки /г, иг, g с учетом введенных обозначений и принятых
определений получается
1 1
дж l(ux)n+l, m,q \их)п-1, ?n, qj Н д^~ [(^y)n, rn+1, q
— (Uy)n, m-1, q] + "JJ- [Ып, m, q+l — (az)n, m, q-l] = 0. C.12)
2.4. Граничные условия
Так как для рассматриваемой задачи (однородная турбулентность
в безграничном пространстве) необходимо выделить для расчетов
конечную область пространства, то вопрос о формулировке гранич-
граничных условий для выделенной расчетной области не является три-
тривиальным. Можно приближенно предполагать, что течение жидко-
жидкости является периодическим с периодами по осям х, ynz, равными
размерам выделенной расчетной области по этим осям. Погреш-
Погрешность от такого предположения будет, по-видимому, небольшой,
17
если размеры рассчитываемой области значительно превосходят
размеры крупных турбулентных вихрей.
Обозначим Nx — общее число участков длиной Ах, на которые
разбивается ось х в пределах рассчитываемой области; общие числа
участков вдоль осей pz обозначим Ny и Nz соответственно.
Все расчеты проводятся для ячеек п, т, q, где п = 1, 2, . . ., Nx;
т = 1, 2, . . ., Ny; q = 1, 2, . . ., Nz. Из приведенных ранее формул
(и из дальнейшего материала) видно, что для расчетов при п = 1
необходимо знать величины при п = 0 и п = —1; для расчетов
при п = Nx необходимо знать величины при п = Nx + 1 и п =
= Nx + 2 1. Аналогично обстоит дело для крайних ячеек вдоль
осей у и z. Исходя из условий периодичности, принимаем для любой
величины /:
_ /*ч /^ /Л . Для любых т,
m,q— \J)l, т, g» \J)Nx+2, т, q = GJ, т, q,)
(/)n, 0, g = (/)я, iV , qi (/)n, -1, q = (/)n, N -1, g> 1
/л ,x\ /л /л . Для любых тг, g
Wn, iV^+1, q = (/jn, 1, q» (j)n, Ny+2, q — (T)n, 2, g, j
D.1
(/)n, m, о = (/)n, ?n, Nzi (/)n, m, -1 = (/)n, w, iV^-1? 1
/a _ a\ a\ — a\ . Для любых п, т
\j)n, m, Nz+1 — \J)n, m, Ъ \I)n, m, Nz+2 — \J)n, m, 2?J
Это и есть граничные условия. Ниже во всех расчетах будет
приниматься
Nx = Ny = Nz = N. D.2)
2.5. Начальные условия
Начальное поле скоростей должно удовлетворять уравнению
неразрывности; кроме того, должны удовлетворяться требования,
чтобы средняя по всему объему скорость и средний момент коли-
количества движения равнялись нулю, средние по объему значения
величин <i4>, (i?y} и <i4> должны быть заданы, а средние значения
(utUjy при i Ф j должны равняться нулю; должны быть заданы,
наконец, определенные «масштабы» движения («размеры вихрей»)
по всем осям. В пределах удовлетворения этих требований началь-
начальное поле скоростей может задаваться произвольно. Удобно задать
это поле периодическим (аналогия с действием решетки), имея
в виду, что при дальнейшем развитии турбулентного течения
скорости должны приобрести случайный характер. Однако не
исключено, что при разумном времени счета поле скоростей еще
не станет полностью случайным и будет иметь большую периоди-
периодическую составляющую. В связи с этим ниже предлагаются два ва-
варианта формулировки начальных условий: задание периодического
1 См., напр.: B.10.4).
18
поля скоростей и задание случайного начального поля скоростей.
Опыт расчетов должен показать, какой вариант удачней.
Периодические начальные условия. Можно принять например,
следующее начальное распределение скоростей их = ии иу = иг
и uz = и3:\
ut = At sin Zc^-sin k2x2'Sm k3x3 + Mt cos /b^-cos k2x2»
•cos k3x3 + a4 sin ft^'Sin S2x2-sin frg^g + /zij cos к\Х^*
•cos S2^2«cosS3^3, E.1)
u2 = ZJ sin /c^'Sin fc2;z2'Cos fcg^g + H2*cos й^-cos &2;r2«
• sin feg^g + d2 sin й^-sin S2a;2»cos ftg^g + h2 cos й^-
•cos A^2«sin SgX3, E.2)
w3 = 5g sin A^'cos A:2a;2-sin ftg^g + b2 sin ^^'Cos k2x2*
• sin k3x3. E.3)
Величины /cf и kt должны быть выбраны так, чтобы в размер
рассчитываемой области вдоль каждой оси укладывалось целое
число периодов. Например, если размер рассчитываемой области
вдоль оси х% равен Ln то можно выбрать kt = 2nni/Li,ki = 2nnt/Li7
где щ и щ — целые числа. Мы будем принимать kt ^> kt (так что
члены с кг в E.1)—E.3) дают «мелкомасштабные возмущения»).
Величина щ, по-видимому, должна быть не меньше 4 или 5, а п%
в 3—4 раза больше.
Распределения E.1)—E.3) удовлетворяют уравнению нераз-
неразрывности, если:
= k2D2 + k3B3,
E.4)
+ k3b3;
IX/ ^t.
ha
легко
Al
Dt
lt = k2H2,
проверить,
+ Ml + aj
_L I72 _J_ ^2
~t~ ^2 I" «2
Wi = Й:
ЧТО
+ ml =
E.5)
Ъ\ = 8<>2з>,
= <и2и3> = 0.
Здесь знаком < > отмечены средние по объему величины.
Удобно выделить отдельно «мелкомасштабную» часть начальных
возмущений. Для этого запишем (для начального момента t — 0):
О;> = <гг?>кр + <И?>мелк- E-6)
С учетом E.5):
А\ + Ml = 8 <M;>Kp, at + ml = 8 <^>мелк,
^ + Я^ = 8 <a2>KP, d\ + ^ = 8 <^22>мелк, E.7)
19
Из E.4) и E.7) получается:
x E.8)
D2 = Щ(к2к3В3)]{к\ фЬкр - к\ <^>кр - к\ <^>кр}, E.9)
-?>22 , E.10)
Аг = (к2/кг) Н2, Мг = (кф^ D2 + (ка/кг) В3 E.11)
и аналогичные формулы для мелкомасштабных возмущений:
E.12)
- к\ <и|>мелк - Ц <^>мелк}, E.13)
h2 = /8<^>мелк-й22 , E.14)
ai = (h/h) h2, m1 = (k2/h) d2 + (V/7x) 68. E.15)
Примечание. Если /^ = 0, то формула E.11) не пригодна; этот
случай возможен для принятой аппроксимации скоростей только
при к2 l/A<W2}Kp = k3 Y<ulyKp; при этом
В3 = V8 <i4>Kp, D2 = - /8 <wi>Kp, Я2 = 0 E.16)
и уравнение E.9) удовлетворяется. Аналогичное примечание спра-
справедливо и для мелкомасштабных возмущений.
Далее мелкомасштабные возмущения будут во всех случаях
предполагаться изотропными, т. е. будет приниматься
кг = к2 = Е3 = Й, <а1>меЛк = <^2>мелк == <^з>мелк = TF2. E.17)
При этом из E.12)—E.15) получается
Ь3 = WY8, d2 = -WY2, h2 = TF|/6, E.18)
Введем также обозначение
V8 {<^21>кр + <ul>KP + <м|>кр>*==о = «о- E.19)
Для иллюстрации рассмотрим несколько примеров задания
начальных условий:
1) к± = к2 = к3 = к, <i4>Kp = <1^>кр = Оз>кР = и20.
При этом В3 = и0 /8, D2 = — w0 У2, Я2 = щ /6, ЛА = и0
Mi = w0 У2. Можно принять, например: А: = 3&, PF = 0Ди0.
При таких начальных условиях должна формироваться изотроп-
изотропная турбулентность.
2) kt=k2=k3 = к,
20
<(ui> больше <М2>Кр и имеет максимальное значение, допускаемое
принятой аппроксимацией скоростей.
Из E.9) видно, что при увеличении <i4>Kp увеличивается D2\
максимальное значение D2, согласно E.10), соответствует Н2 = 0.
При этом
В3=Р2 = У'8 <ц»>кр -
= 2 /8
тогда получается <uf>Kp = 4 <i4>kP = 4 <и|>кР. Отсюда следу-
следует, что
<^2>нр = <У3>кр = Мо/2, <м?>кр = 2u5f B3=D2 = 2и0, Н2 =
= ^! =0, Мх = 4и0.
Можно по-прежнему принять к = 3&, W — 0,lu0. Эти началь-
начальные данные позволят сформировать неизотропную турбулентность
с одинаковым масштабом по всем осям.
3) кх = к2 — к3 = к, <^2>кР = <"з>кр = 3/2*4 <^1>кР = 0.
Из E.8)—E.11) при этом получается:
В3 = 2 ]/3u0, D2 = -2 /Зи0, Н2 = 0, At= 0, М, =
= 0.
Но-прежнему примем к = ЗА:, W — 0,lw0. Это также случай
неизотропной, но близкой к плоской турбулентности.
4) к2 = к3 = 2А, <U2>Kp = <Из>кР = V4
При этом <z4>Kp =
В этом случае к2 =
т. е. формируется неизотропная турбулентность, но с пульсацион-
ными скоростями по различным осям, пропорциональными мас-
масштабам турбулентности по этим осям.
Из E.8)—E.11) получается:
В3 = 2и0, D2 = -и0, Н2 = и3 УЗ, А, = 2 УЫ0, Mi = 2щ.
Для мелкомасштабных возмущений примем к = Ък2 = 6/с,
W = 0Ди0.
5) к2 = к3 = /с, ki = 2к, <^2>кР = <^з>кр = 4 <^i>Kp, при
этом <Mi>Kp = V3
p Р р ]
Как и в предыдущем случае: kt Y^ul}^ = к2 У <и2>кр =
== к3 У <1^з>кр (т. е. скорости пропорциональны масштабам по
различным осям), но масштаб (и скорость) по оси xt здесь меньше,
чем по осям х2 и х3 (в отличие от предыдущего примера).
Получается: В3 = щ уЩ^, D2 = —щ У%, Н2 = щ ]/Т
4 = щ У%.
21
Можно принять ft — ЗА, W = О,1ио.
6) <wI>kp = <^2>кР = <^з>кР = *4, А2 = А3 = к, АА = А/2.
Это случай с одинаковыми скоростями по всем осям, но с раз-
различными масштабами.
Из E.8)—E.11) получается:
В3 = и0 Y8, D2 = -7ио//8, Я2 = и0 /*%", Л4 = и0 f *%;
Mi = uo//2.
Примем: ft = ЗА, W = 0,1и0.
7) к2=к3 = к, к?= 0, <u2x>Kp = 0; <i4>Kp = <^з>кр = 3/2u20
(плоский случай).
С учетом E.16) получается:
Примем /.Л = ЗА; интересно рассмотреть два случая: W = 0,1
и |^ = 0,01гг0.
8) к± = А3/2, А2 = 2А3, <^>кр = 4 <^>кр, <^>кр = V4
Это случай различия скоростей по всем осям, причем масшта-
масштабы изменяются пропорционально скоростям. Получается:
Н2 =
Можно принять ft = ЗА2 = 6А3, PF = 0,1и0.
Таким образом, могут быть сформулированы самые разно-
разнообразные начальные условия. Расчеты этих примеров, по-види-
по-видимому, дадут возможность прояснить особенности турбулентного
обмена и диссипации энергии и уточнить полуэмпирические тео-
теории. Однако результатов расчетов, охватывающих такой широ-
широкий круг начальных данных, пока нет; из-за большой затраты ма-
машинного времени на расчеты они могут быть получены только
в будущем.
При выборе величин кг необходимо учитывать, что период 1г
рассматриваемых функций [в E.1)—E.3)] вдоль оси хг равен lt =
= 2n/kt. В длину рассчитываемой области должно входить целое
число периодов (минимум 4 или 5). Если принять, что каждый
период должен охватывать минимум 8 ячеек, то общее число участ-
участков вдоль каждой оси должно быть минимум 32 -г- 40. В дальней-
дальнейшем будут приниматься именно такие N. Отдельные расчеты вы-
выполнялись, правда (с методической целью), и при других N, но
22
всегда выбиралось JV, кратное 4 (это, конечно, не обязательно, но
существенно для вида некоторых последующих формул).
При расчетах начальных значений (ut)n, w, q во всех ячейках
можно, по-видимому, приближенно вместо средних по объему
ячеек значений скоростей принимать скорости в центрах ячеек,
вычисляемые по E.1)—E.3). При этом возможно небольшое нару-
нарушение уравнения неразрывности B.5), однако при принимаемом
далее методе выполнения шагов по времени и определения дав-
давления (см. ниже) это нарушение ликвидируется на первом же вре-
временном шаге.
Координаты центра ячейки п, т, q, которые должны подстав-
подставляться в E.1)—E.3) для определения (иг)п,т1Я, равны:]
хг = Ах {п — V2), х2 = Ау (т — V2), х3 = Az (q — V2).
Для расчета поля давления при t = 0 целесообразно задать
во всех ячейках для начала итерационного процесса р = 0.
Задание в качестве начальных условий случайного поля ско-
скоростей. Можно задать поле скоростей как поле ротора некоторо-
некоторого вектора А, приобретающего случайные значения в определен-
определенной группе регулярно расположенных ячеек расчетной сетки (при
этом будет удовлетворяться уравнение неразрывности, так как
divrot A = 0). Если, например, в ЭВМ могут вырабатываться
случайные числа ?, распределенные равномерно в интервале 0 -ч-
-г-1, то для задания поля с (иьу = 0 можно принять
At = MS-0,5), E.20)
где at = const.
Расстояния между ячейками расчетной сетки, в которых «ра-
«разыгрывается» At по E.20), определяют начальный масштаб тур-
турбулентности. Можно взять эти ячейки через 8 н- 10 шагов сетки
Ах, Ау и Az, а масштабы турбулентности по различным осям ко-
координат регулировать выбором шагов расчетной сетки. В каждой
из этих ячеек трижды выбирается случайная величина ? и опреде-
определяются Аг, А2 и А3 по E.20). Таким образом, эти величины в вы-
выбранных ячейках являются независимыми. Величины A t в проме-
промежуточных ячейках определяются путем интерполяции по како-
какому-либо закону между значениями At, «разыгранными» в выбран-
выбранной группе ячеек. Это создает некоторую «корреляцию» между А\
в ближайших соседних ячейках, что важно для определения мас-
масштаба турбулентности. Однако спектр полученной таким путем
начальной турбулентности будет сильно отличаться от реально
наблюдаемого спектра. Дело в том, что в турбулентном потоке от-
отношение разности скоростей в каких-либо двух точках Аи2 к рас-
расстоянию между этими точками г растет с его уменьшением (если
не влияет вязкость жидкости). Это соответствует, в частности,
«закону 2/3» А. Н. Колмогорова.
При определении At описанным методом (путем интерполяции
между «разыгранными» At) величина AUJr не возрастает при
23
уменьшении г, т. е. в полученном описанным путем поле скоростей
мала интенсивность мелкомасштабной турбулентности. Для
частичного исправления этого можно принять At = А^ = А^\,
где А^ определять описанным методом, а А[2) разыгрывать в каж-
каждой ячейке расчетной сетки. После такого определения поля Аг
можно найти поле u = rot А. Метод может быть, конечно, осно-
основан и на использовании случайной величины ? с другим законом
распределения.
Случайные величины ? можно «генерировать» на ЭВМ различ-
различными способами. Если имеется какая-либо отработанная програм-
программа выработки случайных величин, нужно, конечно, воспользо-
воспользоваться ею.
Мы применяли метод «генерации» псевдослучайных величин,
основанный на вычислении величин типа ? = h — entier h, где
h — иррациональное число, образуемое сложением некоторых
других иррациональных чисел. Удовлетворительность этого ме-
метода проверялась экспериментально. Соответствующие вычисле-
вычисления показывают, что коэффициенты at в E.20) при расчете А^
нужно задавать такими:
п1 = 5 V <и23>Ау2 + <и|> Az2 — <и|> Ay2Az2/Ax2, E.21)
а2 = 5 У<цЬ Az2 + <и\У Ах2 — <mJ> Ax2Az2/Ay2, E.22)
а3 = 5 Y<u22> Ах2 + <и?> Az/2 — <uj> Ax2Ay2/Az2. E.23)
Здесь <z4>, <^2> и (ц1у — величины <г4>, которые желательно по-
получить после определения исходного случайного поля скоростей.
При расчете А^ все величины at должны быть уменьшены пример-
примерно в 2 раза.
Формулы E.21)—E.23) не обеспечивают точного получения
необходимых <i4>, не позволяют приблизиться к ним. Величины
А\х) по E.20) удобно определять всегда в одних и тех же точках.
Мы это будем делать в ячейках, в которых п, т, q = 8, 16, 24, . . .
. . ., N1. При этом масштабы турбулентности будут определять-
определяться выбором Ах, Ау и Az.
Величину А\х) в промежуточных точках определим, как ука-
указывалось, с помощью какой-либо интерполяции между «разыг-
«разыгранными» А?\ После такого определения поля А^\ разыгрыва-
разыгрывания А^ и определения At — А^ + А\2) компоненты скорости
вычисляются следующим образом:
m,q — 2Ai
Из)п, m+i, q (^з)п, m_i, q
щ
1 Напомним, 4то, как указывалось, N будет выбираться всегда кратным 4,
24
\Ц2)п, т,д
rn, д ~~ (Аз)П-1, т, д
\из)п, т,д —
Можно было бы еще дополнить программу вычислением <^х)>,
<2> и <(w3)> (которые должны быть близки к нулю) и корректиров-
корректировкой всех иг путем вычитания из них (игу. Однако особой необхо-
необходимости в этом нет. Такая процедура периодически проводится
в ходе дальнейших расчетов (см. общую программу).
С описанным методом задания начальных условий можно рас-
рассчитать такие же примеры, какие были перечислены в разделе
0 периодических граничных условиях. Расчеты проводили с при-
применением обоих вариантов задания начальных условий. Однако
при реально ограниченном (но достаточно большом) времени сче-
счета задание периодических граничных условий оказалось неприем-
неприемлемым, так как сохранялась соответствующая периодическая со-
составляющая в спектре турбулентности. В связи с этим далее ис-
использовалось задание только случайного поля скоростей. Воз-
Возможно, что при увеличении времени счета могут использоваться
и периодические граничные условия. Кроме того, исследование
динамики «размывания» дискретных составляющих в спектре пред-
представляет самостоятельный интерес.
2.6. Приведение уравнений к безразмерному виду
Для приведения уравнений к безразмерному виду выберем неко-
некоторые характерные значения скорости г/хар и длины Zxap, где
Ихар и /хар — постоянные величины. Примем: A^)безразм = utluxdiV,
(#г)безразм = a^/Zxap- Примем также: ^безразм = *Mxap/kap« Рбезразм =
= р/рц|ар; еСЛИ СОХраНЯЮТСЯ ЧЛеНЫ С Vx, TO V6e3pa3M = v/ZXap^xap.
Легко проверить, что если во всех приведенных уравнениях
и формулах перейти к безразмерным величинам, то выражения
сохранят прежний вид, только исчезнет плотность р. Индекс «без-
разм» мы будем опускать г. Тогда, полагая р = 1, можно считать
все приведенные формулы записанными в безразмерном виде.
Выберем в качестве Zxap величину шага вдоль оси х. Тогда
в безразмерных уравнениях Ах = 1, а А г/ и Аг представляют со-
собой отношение шагов по осям у и z к шагу по оси х. Выберем в ка-
качестве ихар введенную по E.19) величину и0 — среднеквадратич-
среднеквадратичную скорость крупномасштабных возмущений при t = 0. Тогда
при задании начальных условий в безразмерном виде в формулах
разд. 2.5 нужно полагать и0 = 1.
1 Величина %езразм в РяДе случаев будет обозначаться просто t, а в ряде
случаев — символом г.
25
2.7. Определение членов уравнений,
зависящих от мелкомасштабной турбулентности
В уравнения C.6)—C.11) входят члены типа (щщУ, определяе-
определяемые мелкомасштабной («подсеточной») турбулентностью. Эти чле-
члены могут быть вычислены лишь приближенно, на основании ка-
каких-либо гипотез, правильность которых подтверждается только
сопоставлением результатов расчетов с опытными данными.
Рассмотрим вначале для примера один из «турбулентных» чле-
членов, например: A/Д#) (uiUxyn-i/2i m, q в C.6). Он описывает ско-
скорость изменения величины (u;)n, m, q под влиянием турбулентного
взаимодействия между ячейками п, т, q и п — 1, m, q.
Примем следующую гипотезу: указанное турбулентное взаимо-
взаимодействие должно быть таким, чтобы стремилась к нулю i-я компо-
компонента скорости, определяемая деформацией жидкости в рассмот-
рассмотренной области потока (пояснения см. ниже).
Компонента аы тензора скоростей деформаций жидкости рав-
равна [20]:
-.-4-(¦?+-?)• <7Л>
Скорость в окрестности какой-либо точки с координатами (хтH,
определяемая деформацией жидкости, вычисляется по выражению
[29]:
G.2)
где гт = хт (хт)о.
Деформационные скорости (*Одеф и (их)деф в центре ячейки
ft, m, q относительно центра ячейки п — 1, т, q, согласно G.2),
равны:
(^г)деф n, m, q отн n-1, m, q ~ (aioc)n-V2» rn, q&Xr
(^х)деф п, m,q отн n-1, m, q ~ \ахх)п-*/2, т, q&%'
В соответствии со сформулированной гипотезой примем при
i Ф х:
д \Цг^х/п-г12, m, q ^^^ «^ (^г/Деф п, т, q отн л-1, m, q X
' ^ , mt q отн п-Х, т, q I
где А = const.
Используя G.3), находим при i Ф х:
¦д^- <и}и?VVa, tn, q = — A (aix)n_i/2, m, дДо: | Kx)n-v2, m, g I • G-4)
При i = х, кроме «турбулентного трения», нужно учитывать
еще «турбулентное давление», и тогда для любого i примем следую-
26
щее приближенное выражение:
-д~ <Wi^x>n-Va, m, q = — A (aix)n_i/,, m, qAx | (a^Jn-i/,, m,q\
+ (pT)n-Vt. m, q^ix- G-5)
Здесь рт — «турбулентное давление», создаваемое подсеточной
турбулентностью; величина А = const ^> О, если влиянием моле-
молекулярной вязкости можно пренебречь.
Аналогично G.5) записываются выражения для других «тур-
«турбулентных членов», например:
1 1 1
/77.71 \ л, — Л In \ , v
д \и/%Ы/у/п, m—*/2, g — •?*• x^iy/7i, т—V2» g ^
X &У | (ayy)n,:m-t/2, q | + (Рт)п, m-V2, Aj/i G.6)
1 11
\ 1гтМ. w; q+1/2uiz
и т. п.
Величины аы для расчетов по формулам типа G.5) и G.6) мож-
можно приближенно определить с помощью конечно-разностной апп-
аппроксимации G.1) с использованием средних по объему ячеек ско-
скоростей вместо скоростей в центрах ячеек. При этом производные
в G.1) определяются так:
(и ) — (и )
v Куп, m, g v fr/n-1, m, g
Ox Jn-i/i, m,q Az '
_ (цк)п, т+1, q - (икК т, q
ду )п, т+1/2, g Аг/
ц?с j ^^_^ ^цКут7+1, m-V2, g уц?с'п-1, т+1/г, g
^^ /п, т-1/2> q Az
1, m-l, g ~ (^fc)n-l, m, q (^fc)n-l, m-l, g
и т. п.
С учетом G.7) и G.1) из G.5), G.6) и аналогичных им формул
получается:
\UyUx)n_i/2i w> q = 2~" | \их)п, m, g — (^х)п-1, m, g | \(^j/)n, m, g
Ax
— (uy)n-l, m, g + ^д [(^x)n, m+1, g + (^зс)п-1, m+1, g
— (^х:)г7, m-l, g — 0^c)n-l,>i-l, g]}* G-8)
<&2^x)n-V2, w, g -~ J- I {ux)n, m, q \ux)n-l, m, g [{(^n, m, g
Ax
— (^z)n-l, m, q ~\ ?д^~ L(w'x)n, m, g+1 T" \ux)n-l, w, g+1
— {lix)n1 m, g-1 — (ux)n-l, m, g-l]}» G-9)
27
и*J>п-1/2, m,q=—A\ (Ux)nt m,q — (ux)n-l, m, q [ X
X [{Ux)n, m, q — Wn-1, m, q] + (^x)n-V,, m, q> G-10)
хи>уУп> m-l/2, g= g" I \иУ'п> m>Q (uy)n, тп-l, q | X
х:)п, m,q — (^x)n, m-1, q + ^д^ I (uy)n+l, in, q + (^y)n+l, m-1, q
— (uy)n-l, m, q — (Uy)n-l,m-l,q | j , (• -
Uy/n, m-V2»Q == 2~ I \^1/)л,тп, q — \uy)n, m-1, q | "{(^z/n, m, q
— (^z)n, w-3, q H / д L(^1/)m> wi, q+1 4~ v^yjn, m-1, q+1
)n, m,q-l — (Uy)n, m-1, g-l]| , G •
, m-V2, q — — ^1 (^l/)n, m, g — (^y)n, m-1, q \ [(uy)n, m, q —
Uy)n, m-1,q] + (Рт)п, m-V2, q» G-1
t m, g_i/2 = ^~ I (Uz)n, m, q — \uz)n, m, q-1 | jv^x/A, in, q
)n, m, q-1 + ^ду [(^z)n+l, m, q ~\~ (uz)n+l, m,q-l —
— (Mz)n_lf m,q —K)n-l,m,q-l
\UyUz/n, m, q-1/2 ~ o~ | (^z)n, m, q — (^z)n, m, q-3 | i (^j//n, ?7г, q
— (uy)n, in, q-1 + ?д7" [(W-z)n, m+1, q
-1, q — K)n, m-1, q-l]j , G-15)
((игJУп, m, q-*/2 ~ — A I (az)n,[m, q — (^z)n, m, q-1 | [(uz)n, m,q —
— (Uz)n, m, q-l] + (Рт)п, m, q-*/2- G.16)
Формулы для (щихУп+Уь, m q получаются из G.8)—G.10) путем
замены во всех индексах п на п + 1; формулы для (щиууПу m+y«, q —
из G.11)—G.13) заменой во всех индексах m на тп + 1; формулы
для (щи'гУп, m, q+v2 получаются из G.14)—G.16) заменой во всех
индексах g на q + 1. Все эти формулы должны использоваться для
расчетов величин по C.6)—C.11).
Заметим, что «турбулентные члены» с коэффициентом А обра-
обращаются в нуль не только для безградиентного течения, но и для
вращательного движения жидкости (как твердого тела).
Величина А при начале расчета должна задаваться, а затеме
в ходе расчетов, она определяется; определение величины рт н,
требуется (см. ниже).
Принятые выражения для турбулентных членов аппроксими-
аппроксимируют (скорее, не средние значения соответствующих величин по
граням ячеек, а математические ожидания этих средних значе-
28
ний при заданных скоростях в ячейках). Такая замена сил допус-
допустима (см. разд. 1.1). Выражения для турбулентных членов можно
было бы выбрать и другие, но, как отмечалось в разд. 2.1, харак-
характеристики крупных вихрей, вероятно, не будут очень чувствитель-
чувствительны к некоторым погрешностям в описании мелкомасштабной тур-
турбулентности.
Для (щщУ выражения G.8)—G.11) далее удобно будет записы-
записывать в следующем виде:
<^i^3c)n-V2, m, q = (Щх)п-У2. m, q + (Рт)п-Ч2, т, q$ix-> G-17)
(ЩКуУп, m-V2, q = (®iy)n, т-»/2> Q + (Рт)п, m-Vi. q^iy G.18)
И Т. Д.
Величины (огх, (uiy и о)г2 определяются в соответствии с G.6)
[см. также: G.8)—G.16)].
Ясно, что в уравнение количества движения C.1) давление р
входит в сумме с /?т, т. е. имеется в виду суммарное давление
Рх = Р+ Рт. G.19)
Только эта величина р% далее и будет определяться (отдельно
р и рт не определяли). Чтобы не переписывать уравнения, мы вмес-
вместо jps оставим обозначение р. Тогда уравнение C.1) сохраняет
прежний вид, но в выражения C.6)—C.11) в правой части вместо
(ц1иху нужно записать со^, вместо (и\иуу — со^ и вместо (uiUzy —
величину (дB.
2.8. Порядок выполнения шагов по времени
при расчете полей скоростей и давлений
При интегрировании уравнений по времени будет использована
методика [24].
Используя явную схему, получаем из C.1):
{UifnX q ~ (Щ)п, т,и + (Мг)п, т,дДт + (ityn, m, дАт. (8.1)
Здесь верхним индексом т + Ат отмечены величины в момент
t = т + Ат; величины в момент t = т записаны без верхнего ин-
индекса.
Обозначим
(«i)n, w,q = (И{)п, m,q + (Мг)п, m,gAt. (8.2)
При этом (8.1) примет вид
{UifnXq = Bi)n. m,g + (^)n,[m, QAx. (8.3
Применим уравнение неразрывности C.12) к моменту г + Ат
подставляя в C.12) скорости в виде (8.3). Получится
1 1
"д^Г [(Ux)n+l, m,q — (#x)ri-l, m, fl] H" "дГ" [(^у)п, тм+1, q — (^2/)n, m-1, g] +
29
~Ь ~д^" [{™х)п+1, m,q (Rx)n-1, m, q] +
Н д7~ l\Ry)n, m+1, g — (Ry)n, m-1, g] +
4 -д7~ [(#z)n, m, g+1 — (-#x)n, m,|g-l] = 0.
Подставим сюда i?x, i?y и i?z из C.3)—C.5) (с учетом того, что
р = 1) и запишем получающееся уравнение в виде, разрешенном
относительно pn,m,q:
Рп, т, q = [ 1/(-д^5- + -д^2 + -д^г] J { 2Д^Г (Pn+2, m, g + Pn-2, m, q) +
1
л, w-2, g) + 2Д22 (Pn,m,[q+2
п-1, m, g (Mx)n+1, w, q]
n, m-1, g (^y) n, m+1, g]
Возможен следующий порядок расчетов.
1. Определение (St)nimtq во всех ячейках по (8.2).
2. Определение рПу т> q во всех ячейках с помощью метода ите-
итераций, основанного на уравнении (8.4). При этом должно быть за-
задано исходное поле давлений (в качестве которого можно принять
откорректированное описываемым далее методом распределение
р в предыдущий момент времени).
3. Определение (игI*т, g в следующий момент времени по (8.3)
[где Rt определяется по C.3)—C.5)]. Ясно, что получающееся
поле и\+Ах удовлетворяет уравнению неразрывности.
2.9. Определение коэффициента А в формулах
для мелкомасштабной турбулентности
Рассмотрим наряду с принятой расчетной сеткой сетку с вдвое
более крупными ячейками вдоль каждой оси г. Обозначим номер
какой-либо крупной ячейки а, |3, у (а, |3 и у — номера соответ-
соответственно вдоль осей х, у и z). Величины а, C и у изменяются
в пределах от 1 до N12 (принимается Nx = Ny = Nz = N).
В ячейку с номером а вдоль оси х входят ячейки исходной (более
мелкой сетки) сд = 2а — 1 и?г = 2а (так что п изменяется
в пределах от 1 до N). Аналогично связаны номера ячеек тир
и q и у. Таким образом, в одну ячейку а, |3, у крупной сетки вхо-
входят следующие восемь ячеек исходной сетки:
При этом предполагается, что эти крупные ячейки остаются в несколько
раз меньше размеров крупных турбулентных вихрей.
30
n m q n m q
2а — 1 20 — 1 2у — 1 2а 20 — 1 2у — 1
2а — 1 20 27 — 1 2а 20 2у— 1
2а —1 20 2y 2а 20 2у
2а — 1 20 — 1 2у 2а 20 — 1 2у
Обозначим как аа> р, v совокупность этих ячеек. При этом сим-
символ 2 будет означать суммирование аа, р, v по всем перечисленным
восьми ячейкам.
Если среднее значение по ячейке я, т, q любой из величин
Ш или р обозначать /„, m,g, то /а,р, Y — среднее значение той же
величины по объему крупной ячейки а, C, 7- Ясно, что
1 vn
Средние значения гг^, и^ и и\ по всему объему рассчитываемой
зоны течения жидкости обозначим <ЦхУ, <z4> и ^Х Эти величи-
величины можно рассчитать, используя более мелкую (исходную) и бо-
более крупную расчетные сетки. Причем
(м|)п, m,q Ж (^ж)п. rn,g + 72 [<(^xJ>n+V2, тп, 9 + <(*4J>n-V2, w, g],
(^?/)n, m, q + V2 [<(a?/J>n, tn+Vi, 9 + ((иуJУп, m-Vi, g]'
(иг)„, Wf g + V2 [<(^J>n, m, g+V2 + <(^J>n, m, g-vJ«
n, m
п, m
(9.2)
Здесь величины в квадратных скобках определяются по G.8),
G.12), G.16) и по аналогичным формулам с увеличенными на 1 соот-
соответственно п,т и q. Используя эти формулы и учитывая что
^ ^(и1)п,т,а и т. п. (для <i4> и (и\у), получаем:
(n, m,q)
> = -i- ^^ )^ {(ЦхJ , w, g_ (Л/2) [(^)Л, т, q- (Ux)n-lt m, g] X
(n, w, g)
X I (Ux)n, m,q — K)n-1, m, g | — D/2) [(мх)Л+1, m, g — K)n, m, g] X
X I (^x)n+l, m,q — (ux)n, m, g | + (Рт)п+»/2. m, g + (Рт)п-У2, m,q),
(9.3)
^ (K)n, m, g —D/2) [(и„)п, w, e— (uy)n, m_i, g] X
i, m, g)
X I (Uyjn, m, q \uy)n, m-1, g | D/^) 1(^^O1, m+1, g — \uy)n, m, g] X
X I (Uy)n, m+1, q \uy)n, m,q\ Ч~ \Рт)п, rn-1/* о "^ \Рт)п, m+V2, g}?
(9.4)
31
(n, m, g)
X | (U2)nt m,q — (Uz)n, m, g-11 —(A/2) [(uz)n, w, q+1 — (uz)n, m, g] X
X | (uz)n, m, g+l —' (Uz)n, m, g | + (Рт)п, m, g-V2 + (Рт)п, m, q+vJ*
(9.5)
При использовании крупной сетки справедливы соотношения,
аналогичные (9.2):
(п1)а, р, у ~ (Йх)а, E, V + 7г [<^J>a+V2, 3, V + <(^J>a-V2, p, у]г
D)а, Р, V ~ (йу)а, р, V + V2 [<4J><х, P+V., V + <DJ>а, Р-1, vl (9-6)
(й1)а, р, у Ж (Й2)«, р, v + V2 [<("zJ>a, 3, v+V. + <Ы>а, р, v-vJ«
Величина (и%У может быть найдена по формуле
(a, p, v) (a, p, v)
формулы для <и?УУ и (и\У аналогичны. Отметим величины <гг|>,
1 и <wl>, найденные с использованием крупной сетки, верхним
индексом «кр».
Величины, стоящие в (9.6) в квадратных скобках, определяют-
определяются по формулам, подобным G.8), G.12) и G.16), но с заменой ut
на пг, п на а, т на Р и q на у.
С учетом сказанного получаются следующие выражения, ана-
аналогичные (9.3)—(9.5):
(a, p, v)
-g- №x)a, p, v — (Й*)а-1, р, 7] | (»х)а, р, у — (»x)a-l, p, Y I ~
J- [(Йх)а+1, р, V — (йх)а, p. vl I (Йх)а+1, Р. V — (пх)а, р, V |} f (9'7)
(а, р, V)
" [(й2/)а, Р, V — (^у)а, р-1, vl I (йу)а, р, V ~ (пу)а, р-1, V I -
4" Кй»)а» Р+1» V — (б1/)а. P. vl I (иу)а, р+1, v — (йу)а, р, v |}' (9-8)
(а, р, у)
2" [("«)«, р, V — (»г)а, р, V-l] I (^)а, p,]v — (йг)а, р, V-l I ~
Y [(Й*)а, Р, V+1 — (ttz)a, р, v] I (»«)«. P. Y+1 — (»*)а, р, 7 |} • (9-9)
32
Естественно потребовать, чтобы величины энергии турбулент-
турбулентного движения, найденные с использованием более мелкой и бо-
более крупной сеток, были бы максимально близки друг к другу.
Для формулировки этого требования введем в рассмотрение ве-
величину П, определяемую так:
П = {<и|> + <и*> + <и|> - <*4>кр - <4>кр - <и!>кр>а- (9.Ю)
Стоящая в фигурных скобках в (9.10) величина лииейно зави-
зависит от А [см.: (9.3)—(9.5) и (9.7)—(9.9)]. Введем следующие обо-
обозначения:
<и*> + <4> + <иЪ — <и?>кр — <4>кр — <и!>кр = ос — Ау.
(9.11)
После соответствующих преобразований для а и у получаются
такие выражения:
а== Туз~{ У^ /^ /^ KUxfn, w, q -f (uy)n, m, q + (иг)п, m, q] —
( )
(n, m, q)
}(9Л2)
(a, p, v)
(n, m, V
— (^x)n-l, m, q | + [(^x)n+l, m, q — (ux)n, m, q] \ (^x)n+l, m,q —
— (ux)n, m, q I + [(uy)n, m,q — (uy)n, m-1, q] \ {uy)n, m, q
— \uy)n, m-1, q I ~Ь Y\uy)n, m+1, q — \uy)n, m q\ \ tyy)n, m+1, q
— \uy)n, m, q I -\~ [\Uz)n, m, q \uz)n, m, q-l\ \ \uz)n, m, q
— (uz)n, m, q-X | + [(Uz)n, m, q+1 — (uz)n, m, q\ \ (uz)n, m, q+1 —
— (Uz)n9 m, q |} — fi j
(a,
— fe)a-1, |3, v] I (»x)a, p, V — (^x)a-l, p, v I + [(йх)а+1, р, v-
— fe)c6, p, vl I (^x)a+l, p, v — (^x)a, p, v I + t(^l/)a, p, V —
— (Uy)a, |3-1, у] | (^)a, |3, v — (^y)a, |3-1, v I + t(^y)a, |3+1, V ~"
— (^y)a, |3, v] I («y)a,!p+J, V ~ (йу)а, p, V I + [(йг)а, |3,> —
— (Й2)а> C, v-l] | (»z)a, |3, v — (»z)a, |3, v-X l]+ [(йг)а, p, v+1 —
— (»z)a, p, y] I (»z)a, C, v+1 ~ (uz)a, p, v l>- (9ЛЗ)
С учетом (9.11) выражение (9.10) для П приобретает такой вид:
П = (а — АуJ. (9.14)
2 В. М. Иевлев 33
Определим А из условия достижения минимума П, т. е. примем
дП/дА = — 2 (а — Ау) у = 0. (9.15)
Отсюда получается А = а/у. (9.16)
При этом Пт1П = 0, и энергия турбулентности, определяемая
с использованием мелкой и крупной расчетных сеток, одинакова
при выполнении (9.15).
Вычисления А можно производить не на каждом шаге по вре-
времени, а, например, через 10—20 шагов, считая на протяжении этих
шагов А = const.
Первый расчет А нужно проводить только после вычислений
полей скоростей на протяжении нескольких десятков временных
шагов; до этого должно приниматься заранее заданное значение
А = const. Такое требование связано с тем, что начальный спектр
турбулентности задается «неравновесным» (в частности, не удов-
удовлетворяется «закон 2/3» А. Н. Колмогорова). Это может повлиять
на величину А.
2.10. Определение статистических характеристик
турбулентности
Как уже указывалось в гл. 1, целью расчетов является определе-
определение не поля скоростей и давления, а различных статистических
характеристик этого поля. Представляет интерес определить,
в частности, следующие величины.
1. Величины <и?>, <и?>, <"з>, <и}>/<и!>2, <*4>/<*4>2, <Из>/<и?>2,
<Р>(<> <!> <»
Заметим, что внутри любой ячейки п, т, q:
ui — (ui)n, m, q + Щ,
где (иг)п, m,q — среднее по объему ячейки значение скорости.
Поэтому величины (ц\У, (и\) и др. должны содержать слагаемые,
определяемые мелкомасштабной турбулентностью. В частности,
нужно принимать
N N N
<«'> = тот ? У\ УдD,»,8 + Й2)п,т,!д}- (Ю.1)
у n=l m=X q=l
где ((щJУп, m, q определяется по методу, изложенному в разд. 2.9.
Здесь везде знак < > означает осреднение по всей рассчитываемой
области, так что для любой величины / имеем
Нужно писать р — <р>, а не р, но при р — 0 в начале итерации при
t = 0 должно быть <р> ж 0. Далее по ходу расчетов будет производиться
корректировка р с цет<ъю обеспечения всегда <р> ^ 0.
34
Мелкомасштабные добавки при выборе не слишком крупной
расчетной сетки невелики. При вычислении <i4> они будут очень
приближенно учитываться, а при вычислении других средних ве-
величин учитываться не будут. Это может привести к погрешности
в расчете, например, <i4>, но вряд ли даст большую погрешность
в расчете <г4>/<г4>2, если и в знаменателе (uf) определять без
мелкомасштабной части.
2. Различные коэффициенты корреляции скоростей и давле-
давлений и масштабы турбулентности. Их много, и мы ограничимся
в дальнейшем только следующими:
N-r N N
N N N
N—r N
NV Nz
l m=l-fr q=l
N N N-r
{E I Z [()П' т' 3 (Щ)п>
2N NlNz-r)<u\> {E, I Z,
x У z } n=l m=X q=l
N N N
^ ^ } (Ю.5)
n=l m=l q=l-{-r
Здесь г — фиксированное целое число, так что Rix зависит от рас-
расстояния между точками г Ах.
В формулах A0.3)—A0.5) (как и в дальнейших расчетах) при-
принято Nx = Ny = Nz = N; в правых частях этих формул сумми-
суммирование по индексу i не предполагается (так что этот индекс имеет
только такое же значение, как и в стоящих в левой части величи-
величинах Rix, Riy и Riz).
Расчеты должны быть выполнены для г = 1, 2, . . ., N12 (при
г ^> N12 приходится выходить за пределы рассматриваемой об-
области течения). Должны быть определены также масштабы тур-
турбулентности (размеры крупных вихрей). Определим три мас-
масштаба:
2* 35
Rlz + ^Ц_ Е
Л
J
В конечно-разностном виде запишем эти выражения следую-
следующим образом:
L
i
2 r=
Здесь индексы гиг — 1 отмечают значение г, при котором берут"
ся соответствующие коэффициенты корреляции. Величина rmax,
как указывалось, не должна превышать N/2, но может быть
и гтах < N12, если при г = гтах коэффициенты корреляции по
абсолютной величине меньше некоторой заданной нормы. Если
при г = N12 коэффициенты корреляции велики (по абсолютной
величине), то расчеты lt производить нельзя: необходимо либо из-
изменить начальные условия (уменьшить масштаб), либо увеличить
рассчитываемую область.
3. Диссипация энергии 8, которую можно найти так:
8 - ^ {«Х> + \У » К
A0.10)
Для приведения к безразмерному виду величину 8 можно раз-
разделить на
3E
Полезно найти также скорости изменения энергии пульсаций
по различным осям, т. е. величины
(О?>х-Лт — <*4>T+At) /|/DЛт <ц\Уи) (без суммирования по
индексу i)
A0.11)
для i = х, у, z.
К статистическим характеристикам турбулентности относится
также ранее определенный коэффициент А,
Все указанные величины должны определяться, конечно, не
на каждом временном шаге. Они могут быть при необходимости
разбиты на группы, определяемые чаще и реже.
Статистические величины должны выводиться на печать, дисп-
дисплей, графопостроитель; некоторые из них — запоминаться.
2.11. Укрупненная блок-схема программы расчетов
Общий порядок расчетов может соответствовать укрупненной
блок-схеме программы, представленной на рис. 2.1. Схема явля-
является укрупненной потому, что большая часть ее элементов долж-
должна быть представлена в виде отдельных блок-схем. Это и делается
в последующих параграфах.
Приведем некоторые пояснения к блок-схеме программы.
1. В качестве исходных данных должны быть заданы: N (це-
(целесообразно принять N > 40; если не хватает возможностей ЭВМ,
то N = 32 или в крайнем случае 24); Ах, Az/, Az (при принятой
характерной длине Ах = 1); Ат (можно принять Ат = 0,02 -т-
-г- 0,03 — см. разд. 2.16); величины кх, к2, к3 и Aj, A2, /г3, необхо-
необходимые в случае задания периодических начальных условий, вхо-
входящие в формулы E.1)—E.3) (целесообразно связать kt с Axt,
приняв kt = тс/ААхг; при этом период изменения скорости при
t — 0 делится на 8 участков; если kt = 0, то Axt можно выбрать
независимо; кг должно быть в целое число раз больше кь)\ коэф-
коэффициенты Aj, М-l, D2, H2,B3, я1? тг, d2, h2, Ъ3, входящие в те же
формулы E.1)—E.3) и необходимые при задании периодических
начальных условий, или формулы для их определения (см.
разд. 2.5); начальные значения <гг|>, <z4> и <м|> в случае задания
случайного начального поля скоростей, нужные для вычислений at
по E.21)—E.23) х; начальное значение коэффициента А; У — но-
номер шага по времени, при котором впервые подсчитываются ста-
статистические характеристики турбулентности и коэффициент А;
As — число шагов по времени, через которое снова подсчитывают-
подсчитываются Л, и статистические характеристики турбулентности 2; sH0H —
номер шага по времени, при достижении (или превышении, но не
более чем на As) которого расчет заканчивается; различные нор-
1 Напомним, что начальные масштабы турбулентности задаются в этом слу"
чае выбором величин Ау и Az (см. разд. 2.5).
2 Часть характеристик можно считать через 2As или даже еще реже,
37
("Ввод"
исходных данных
H
Программа № 1: Опре-
Определение исходных
скоростей
Программа № 2. Опреде-
Определение всех {Щ)п,т,я\
Корректировка Ат
Програмхма № 3: Опреде*
ление давления р
Программа № 4 Опреде-
Определение новых (ы,-)я. »п (/
©
Увеличение номера S ша-
шага по времени на 1
Увеличение
s на As
Программа №5 Расчет
всех (и? >
Программа № 7:
Програ?лма№6.
Определение А,
статистических
величин поля ско
ростей, проверки
Определение (р 2 >
6 и 6Ь проверка <р)
Вывод <р2> ей б,-
[Вывод А,
—I статистических
За кл ючительный
Рис. 2.1. Укрупненная блок-схема программы расчетов
мы для проверки контрольных условий. В ячейку номера времен-
временного шага s должен быть записан нуль.
При более детальном программировании в зависимости от ти-
типа ЭВМ и варианта программы могут потребоваться и другие ис-
исходные данные.
3S
2. Программы№1—7 (поз. 2—5, 8, 11, 13 блок-схемы) состав-
составляются на основе приведенных формул. Ниже блок-схемы этих
программ рассматриваются более подробно.
3. Смысл операций проверки условий, указанных в поз. 7, 9,
10, 15 блок-схемы, состоит в том, что до достижения номера шага
s — I происходит повторяющийся расчет шагов по времени (цикл
замыкается после проверки условия 7). При достижении s = s — 1
вычисляются средние по всему объему значения <м?>, (м1У и <^з)
(поз. 8 блок-схема); они затем понадобятся для расчетов скорос-
скорости диссипации энергии на временном шаге s по формулам A0.10)
и A0.11). После вычисления (щ} проверка поз. 9 дает ответ «да»
(так как s = s — 1) и проводится расчет следующего временного
шага (s = б). При этом также определяется <и?> (поз. 8), провер-
проверка поз. 9 дает ответ «нет», а проверка поз. 10 — ответ «да». Пос-
После этого определяются статистические характеристики поля ско-
скоростей турбулентности (но не поля давления), выводятся на пе-
печать, дисплей, графопостроитель (поз. 11 и 12) и расчет временно-
временного шага снова повторяется (делается шаг .9 = и + 1). На этом вре-
временном шаге проверка по поз. 7 дает ответ «да» и снова проводит-
проводится расчет всех <м?> по поз. 8 — это необходимо для расчетов дис-
диссипации энергии по формулам A0.10), A0.11). Проверки по поз. 9
и 10 дают ответ «нет» (так как s = ь• + 1), и происходит переход
к поз. 13: определяются скорости диссипации энергии на преды-
предыдущем временном шаге (s = s) по формулам A0.10) и A0.11) и оп-
определяется величина </?2> (и, если нужно для контроля,— величи-
величина <р» на том же временном шаге s = I 3. Эти величины выводят-
выводятся на печать, дисплей, графопостроитель (поз. 14).
4. Если не удовлетворяется условие s ^ sK0Ei (поз. 15), то
происходит увеличение величины s по поз. 16 и все расчеты пов-
повторяются с новым s 4. Если условия поз. 15 удовлетворяются, то
производится вывод на печать, дисплей, графопостроитель заклю-
заключительных величин, характеризующих турбулентность (напри-
(например, зависимостей различных статистических характеристик тур-
турбулентности от времени) и выполнение программы заканчивается
(поз. 17 и 18).
В памяти ЭВМ остаются записанными поля скоростей и давле-
давлений на последнем рассчитанном шаге, величины А, Ах, Аг/, Az,
At и др. При необходимости расчет можно продолжить, начиная
с поз. 3 блок-схемы, используя эти данные как исходные. Нужно
перед этим записать снова номер временного шага s = 0 ж, если
3 Давление р по поз. 4, определяемое на временном joiare * = s + 1, отно"
сится к предшествующему временному шагу s = 7.
4 Как уже указывалось, для экономии машинного времени можно разбить
статистические характеристики турбулентности на группы: часть из них
определять при каждом s = s, а другую часть, например, через раз (т. е.
при каждом четном или каждом нечетном номере расчета статистических
характеристик турбулентности). Такая разбивка статистических харак-
характеристик на две группы использовалась при расчетах.
39
требуется, подкорректировать величины i, As, sKOfI, At, и, может
быть, А.
В связи с этим, а также в связи с возможными другими
заданиями исходных данных программу № 1 (поз. 2) целесооб-
целесообразно сделать отдельной.
Во многих случаях (при недостаточном объеме оперативной
памяти ЭВМ, при необходимости дополнительного контроля
и корректировки хода вычислений) блок-схема программы долж-
должна в себя дополнительно включать обмен данными с внешней па-
памятью машины.
Заметим, что рассматриваемая программа не включает в себя
вычисление каких-либо средних значений произведений давле-
давления и функций от скорости. Для вычисления этих величин потре-
потребовалось бы почти удвоение объема памяти машины, так как нуж-
нужно было бы сохранять в памяти поля скоростей одновременно для
двух временных шагов.
2.12. Порядок и блок-схема программы расчета
начального поля скоростей
(программа № 1 на рис. 2.1)
В разд. 2.5 было приведено два варианта задания начальных ус-
условий. В соответствии с этим проводится рассмотрение отдельно
для каждого из этих вариантов.
Периодические начальные условия. Как указывалось в разд. 2.5,
исходные скорости определяются по формулам E.1)—E.3). Все
коэффициенты в этих формулах должны быть заданы или рас-
рассчитаны заранее в соответствии с разд. 2.5. Целесообразно опре-
определить (как уже отмечалось в разд. 2.11), не равные нулю кп
так:
A2.1)
Величины lt принимаются одинаковыми, т. е. кг = к2 = к3 =
= /с, а к должно в целое число раз превосходить все kt (см. при-
примеры в разд. 2.5).
Записывая в E.1)—E.3) в качестве координат xt координаты
центра участка гс, т, q (т. е. хг = Ах (п — У2), х2 = Ау (т —
— У2) и х3 = Az (q — У2)» гДе ^х — 1)» получаем:
\ul)n, m, q —
= Аг sin [к±Ах(п — 72)] sin [к2Ау (т — 72)] sin [k3 Az (q — 1/2) +
+ Мх cos [к±Ах(п — V2)] cos [К^У (т — V2)] cos [K^z {Я. — V 2)] +
+ ах sin [кАх (п — г/2)] sin [My (m — 72)] sin [Mz (q — г/2)] +
+ т1 cos [кАх (п — 1/2)] cos [кАу (т — г/2)] cos [kAz (q — у2)],
A2.2)
(и2)п, т, q = D2 sin [k±Ax (n — 72)] sin [k2Ay (m —1/2)] X
X cos [k3Az (q — 72)] + #2cos [k±Ax (n — 72)] X
40
X cos [k2Ay (m — V2)] sin [k3Az (q — 72)] +
4- d2 sin [kAx (n — V2)] sin [k&y (m — V2)] cos [k^z (Q — V2)] +
-j- ho cos [kAx (n — V2)] cos [kAy (m — г/2)] sin [JiAz (q — 72)],
A2.3)
n,q = B3 Sin [^Дх (fl — 1/2)] COS [/c2 Д# (ttl —
- V2)] sin [/c3Az (q - y2)] + 63 sin [kAx (n - V2)] cos [kAy (m -
- V2)] sin [lAz (q - y2)]. A2.4)
На рис. 2.2, а представлена блок-схема расчета по этим фор-
формулам 2. В ней учитывается периодичность функций A2.2)—
A2.4): их период по индексам п, т и q равен 8, если использовать
A2.1) и если Тс в целое число раз превосходит все kt. Если какое-
либо из kt равно нулю, а другие выбраны по A2.1), то приведен-
приведенной схемой программы также можно пользоваться. Если вместо
A2.1) принимается, например, kt = n/5Axt или кь = п/ЗАхп
то периоды по индексам становятся соответственно равными 10
или 6. С учетом этого должна быть изменена схема программы
(при сохранении ее общей структуры). Сделаем некоторое заме-
замечание, относящееся к индексации величин. Это замечание может
быть существенным не только для расчетов начального поля ско-
скоростей, но и для расчетов на любом временном шаге.
При расчетах начального поля скоростей, а также в дальней-
дальнейшем при расчетах поля давления и при расчетах полей' скоростей
на каждом временном шаге необходимо проводить перебор раз-
различных значений индексов п, т, q, чтобы сделать расчеты для
всех ячеек расчетной сетки. В блок-схеме детали э^ого перебора
по индексам не показаны, так как при записи программы на ка-
каком-либо алгоритмическом языке просто указывается, что расче-
расчеты должны быть выполнены для всех заданных значений индек-
индексов, а порядок реализации этого затем определяется транслятором.
Но перебор по индексам (с контролем на каждом шаге того, дос-
достигнуты ли уже предельные значения индексов) составляет зна-
значительную часть объема рабочей программы.
Для экономии машинного времени может оказаться выгодным
в связи с этим перейти к одноиндексной системе. Такой индекс
(обозначим его к) можно определить, например, так:
к = п + N (т - 1) + N2 (q — 1). A2.5)
При N = 40 эта формула приобретает следующий вид:
к = п + 40 (т - 1) + 1600 (q - 1). A2.6)
Если перебирать п от 1 до 40 2 при т, q = const, затем увели-
увеличить тна1и снова перебрать п и так далее до т = 40, после чего
1 В A2.2)—A2.4) входят аргументы &0Дя (п — V2), к2Ау (т — V2) и kzAz (q —
— V2). Если в них подставить кг из A2.1), то они приобретут вид (л/4)(я —
— V2); {л/А)(т — V2); (я/4)(q — V2), что и учтено в блок-схеме.
2 При N = 40.
41
Для я j, т,, q
i от 1 до 8:
расчет sin [Gг/4) ^ -
sin [GT/4) (m,
sin [Or/4) (g, -
sin [fc Дх (я, -
sin [k Ду (ml -
sin [k Az (q, —
Затем расчет
()„, Wl „, ,
-1/2)]
-1/2)],
1/2)],
-1/2)],
1/2)],
(«3)«,.«
-l/2)];cos[Gr/4)(«1-l/2)];
, cos [(ж/4) (mj-1/2)];
cos[(x/4)((jf1 —1/2)];*)
cos[kAx(nx -1/2)];
cos[kAy(ml-l/2)),
zos[kAz(qi ~ 1/2)],
' Q '
^'V™ С12-2) ^ A2.4)
Для a1 , a2 > аз от О до 4 и каждого
ni,mi,<?i расчет п= я, *¦ 8aj , m - m
<?=<?, +8ая
Запись всех (u,),; ,„ 7 в оперативную
память ЭВМ, исходл из услозия.
("|)и ,„.„=(«/)„ ,,, ,,
+ 8as >
Переход к следующему этапу общей программы
Определение а,A),а2B),ai3) по E.21) - E.23)
Для сх, р, 7 от 1 до N/8
1) определение n, m, q по A2.12),
2) для каждой ячейки я, т, q с величинами
гс, /гг, <7, найденными по A2.12), определение
три раза величины ? по A2.10) и A2.7);
3) с каждым из найденных по п. 2 значени-
значением ? определение Л/1 > = (A/)/i°wl_ q no E.20)
с присвоением индексу i последователь-
последовательно значений 1, 2,3
©
©
Для я, m, <? от 1 до iV
1)
2)
3)
определение Я!, т
определение ah bh
A2 16) - A2.23);
определение (Л,)\1
i= 1,2,3)
1, Яи п
с,-, <?,-, г,
In <? ПО
г, гп2, Яг
, S{, fj, hi
A2.15)
по A2.13);
по
(для
Определение а\2) =1Aafl\ для каждой ячейки п, т,
q определение три раза величины ? по A2.10) и
A2 7); определениеЛ;<2> поE.20).Л,-по A2.11)
Расчет
E.24)
иО,,. ,м.«,, ("г)„, «, , , ("з)
E 2G) (для п, т, q от
©
©
Переход к следующему этапу
общей программы
Рис. 2.2. Блок-схема программы Л» 1 для
вариантов периодического (а) и случайно-
случайного (б) начального поля скоростей
увеличить q на 1 и снова
делать такие же переборы,
пока не будут достигнуты
п = 40, т = 40, q = 40,
то величина &, определяе-
определяемая по A2.6), будет пос-
последовательно принимать
все целые значения от 1
до 64 000. Таким образом,
все ячейки /расчетной сет-
сетки оказываются последо-
последовательно пронумерован-
пронумерованными. Для перехода к од-
ноиндексной системе нуж-
нужно, конечно, переписать
все расчетные формулы с
использованием индекса к.
Мы этого делать не будем,
чтобы не усложнять изло
жение материала (но при
программировании такой
прием можно использо-
использовать).
Функции A2.2)—A2.4)
не изменяются при замене
п ->- п +8а4, т-^т+8а2,
q->q+8as, где а4, а2, аз-
целые числа.
В связи с этим можно
перебирать п, т, q только
в пределах 1, . . ., 8, а
полученные по A2.2) —
A2.4) величины (и4)п,т.д
записывать при каждом
заданном наборе п, т, q
во все ячейки с любым
набором a1,a2,a3i гДе все
at могут иметь значения
0, 1, 2, 3, 4, так что нуж-
нужно производить еще пере-
перебор а4, а2, а3. Это учиты-
учитывается представленной на
рис. 2.2 блок-схемой.
Случайное начальное поле скоростей. В разд. 2.5 указывалось,
что мы примем метод «генерации» псевдослучайных величин |,
необходимых для расчетов, основанный на формуле
l = h — entier h, A2.7)
где h — иррациональное число, образуемое сложением некоторых
42
других иррациональных чисел. Можно задать произвольно два ир-
иррациональных числа (например, I и я), которые мы обозначим yf
и у2, и вычислить вначале h по формуле
h = BiVi + S2y2, A2.8)
где Bi я В2 — произвольные целые числа. С таким h можно найти
| по A2.7), обозначим его ^. Далее можно при вычислениях сле-
следующего значения ? (обозначим его ?2) применить формулу
h = Biyi + В2у2 + B&i, A2.9)
где В3 также целое число. Этот процесс далее может повторяться
при вычислении каждого нового ?, так что при определении
(п + 1)-го значения ? (?n+i) можно принять
h = SiYi + В2у2 + В31п, A2.10)
а затем определить ? = ?п+1 по A2.7). Величины Ви В2, Вд мож-
можно принимать разными для различных групп ячеек расчетной
сетки.
Случайные значения А^ «разыгрываются» в ячейках, в кото-
которых тг, га, q — 2, 16, 24, . . ., iV/8, а в промежуточных ячейках оп-
определяются с помощью интерполяции между «разыгранными»
А^\ Случайные значения А^ «разыгрываются» в каждой ячейке
расчетной сетки (с вдвое меньшими величинами at в E.20) 3), а за-
затем определяются Аь\
At = А{Р + А?\ A2.11)
Номера ячеек, в которых «разыгрываются» А^\ можно пред-
представить в виде
п = 8а, т = 8р, q = 87, A2.12)
где а, р, у = 1, 2, . . ., ЛГ/8.
Для любой ячейки n, m, g обозначим:
щ = 8entier (n/8), m^ = 8entier (m/8), qt =
= 8entier (g/8), A2.13)
^2 = ^i + 8, m2 = mi + 8, q2 = qt + 8.
Во всех ячейках, в которых индексы /г, етг, g составлены из чи-
чисел щ, rrii, Qi, n2, m2, q2, величины А^ разыгрываются, т. е. эти
ячейки относятся к типу A2.12). Очевидно, что
[щ < п < п2, \rrii < т < т2, [qt < q < q2, ; A2.14)
т. е. ячейка /г, га, g находится в окружении ячеек, в которых лю-
любой из индексов равен соответственно тг4, га4, ^4 или тг2, W2» ^2*
Величину (A\1))rii W) 3 определим с помощью интерполяции
8 Мы далее обозначим at в E.20) символами а№ и aW и примем а& =
43
«разыгранных» Аг между указанными ячейками (в которых лю-
любой из индексов равен соответственно тг4, лтг±, qt или /г2, т2, q2).
Интерполяцию будем производить по формуле
(Ai )л, m, q — d\ + Ъ{ (п — П-^) + С{(т — ГП^) -f- gi{q — g2) +
4 гг (« - л2) (т — тг) -т- «i (п — их) (^ — д±) +
+ А (т — т2) (g — g2) + h (п — пг) (т — тх) (q — qx). A2.15)
Приравнивая здесь /г, т и q величинам щ, ml1 gb n2, m2, q2
соответственно, можно найти все коэффициенты. Получается:
аг — (Аг),}1 ?;,l? gi, A2.16)
<Ч, r»t, qt — (А{)(п1 Wl, 9l], A2.17)
:i.m,,gi — V~iMf ir.,,*], A2.18)
:i,«J» A2.19)
A2.20)
qt (^
A2.21)
A2.22)
~Г \^г)п2, mt, qt ~t К^Ч/ъ, m2, gt ~T V^i
(^i)n,, Шоу qi \Ai)n2, ml5 g2 (^i)ni, «i2i 9a (-^i)«t» ^i> Qi\'
A2.23)
При известных 4f скорости находятся по формулам E.24) —
E.26).
Блок-схема программы расчета случайного начального поля
скоростей представлена на рис. 2.2, б.
2.1 Я. О программе определения Ut
^программа № 2 на рис. 2.1)
Это наиболее сложная программа. Проблема состоит в том, что
величины (ui)lly m,q нельзя сразу же записывать в ячейки памя
тв. занятые (Mj)n, m,q» так как при расчетах (ut)n,mtq исполь
зуются величины ut в соседних точках и так как величины щ прг
п. /п пли q = 1 нужны для расчетов при п, т или q = N (в связи
с условиями периодичности). В то же время запись (щ)п>т,(
полностью в свои дополнительные ячейки памяти потребовала бк
почти удвоения необходимого объема памяти ЭВМ.
44
Другая проблема состоит в том, что величины Ft, Фг и Qir
вычисляемые по C.6)—C.11) с учетом G.8)—G.16), целесооб-
целесообразно (по крайней мере временно) сохранять в памяти ЭВМ, так
как эти величины (пропорциональные силе взаимодействия между
жидкостью в различных ячейках расчетной сетки) используются
повторно при расчетах для соседних ячеек («действие равно про-
противодействию»). В связи с тем, что этих величин много (9 для каж-
каждой ячейки), а соседние ячейки перебирать все подряд очень гро-
громоздко (их число «размножается» по осям xt, x2, х3, т. е. по индек-
индексам п, т, q), а также в связи с указанной необходимостью сохра-
сохранять в памяти величины при п, т или q — 1 до расчетов при п,
т или q = N проблема объема памяти ЭВМ для этих величин тоже
очень важна.
Предлагаемый порядок расчетов позволяет ограничиться до-
дополнительным объемом памяти, составляющим около 10% от ос-
основного объема памяти для записи полей ut и р.
Для четкости дальнейшего изложения полезно переписать здесь
некоторые формулы для величин Qt1 Ft и Ф?, уже приводившиеся,
но состоящие из частей, рассмотренных в разных разделах [фор-
[формулы C.6)—C.11); турбулентные члены в них, т. е. формулы
G.8)—G.16) и аналогичные формулы с увеличением п, т или q
на II1:
(^l)Vs. m,q = ?д7 [(U^N, m,q+ (^i)l, m, qf—
- A [{Ul)h m, q - (Ul)N, n, „] f A3Л)
)V2, m,q = ?д^г [(u2)n, m,q+ (U2)l, m, q] [(^l)iV, m, q + (^l, m, q] —
_ , rr+1, q + (ul)N, m+1, q ~ ("Ol, m-1, q ~~ (U^N, m-1, q
2 X
H д^ J I (Ulh, m,q — (^i)iV, m, q |, A6
Чг,т,Ч = 4дТ [(Ua)N,m,q-r- (u3)l, m, q] [(^l)iY, m, q+ (^i)l, m,q]—
, g+l "Г (u*)n, m,q+l— (^l)l, m, g-1 ~" (^)iV, m
A_
2 1 4Az
()l, m, g
Л /
2 1
T (^i)rz,X, gj [(^)n, N, g "f
)п+1, iV, g — (ца)л-1,1, g ~ (
Одновременно индексы х, у, z будут заменены на 1, 2, 3 соответственно.
Члены с v опускаются. В формулах опущена величина рт, так как она
входит в состав суммарного давления р2 (см. разд. 2.3).
45
(Ф2)п, V,, q = Щ- [Юп, ЛГ, g -+ (и2)л> 1, д]2 +
+ -д^ [Ып, 1, g — (И2)п, iV, g]2 —
— -^" [Wn, 1, g — Wn, ЛГ, q] | (и)Л, 1, q ~ (и2)*. N,[q |> A3*5)
(Ф3)п, i/f, g = Щ- [(U3)n, N, q + (Щ)п, 1, q] [WB) iV, g + (W2)n, 1, g] ~
A ( 1
2~ Ь4ЛТ KM2)n, 1, q+l+ (^2)n, iV, g+1— (M2)n,l,g-1—(^2)", N, q-l\~~
+ -^T [Wn, 1, g — (W3)n, N, g]} I Wn, 1, g — W,i, iV, g |, A3-6)
\
(Ql)n, m, V2 ^ Д7 [(а1)п, m, N + (^l)^, m, l] [(^з)гс, m, iV + (^з)п, m, l] —
-1, т, 1
), т,
Ып, т, 1 — Юп, т, iv]| | (^з)п, т, 1 — (Щ)п, т, iV |, A3.7)
4Л1Г Ка2)п, т,Д + (
1
п, т-1, 1 — (^з)п т-1,
~Д7 t(W'2)n, т, 1 — Юп, т, ЛГ]| | (М8) п.тД- ("з)п,,»п, N I
)п, т, V. = 4Д7 [(^з)п, т, JV + (^з)п, т, l]2 —
д7 [Юп, т, 1 — (И8)п, т, iv] | (^з)п, т, 1 — (u>3)n,m,N |r A3.9)
+V2, т. g =
, m, g
ЛГ" [(Ul)n+1' т' Я (^l)ttt т' «J I (Ul)n+1, m, g (^ljn, m, g |?
A3.10)
)n, m,g
, m, g
+ <и) 1 А { * Uu ) 4- (и \
— (ul)n+l, m-1, q — (ul)n, m-1, g] +
\ ]
H д^" L\^2/w+l, m, g (^2/w., m, gj Г | \^l)n+lt m, g (^l/n, m, g |?
A3.11)
)п+1/г, т, q — ^д-JT [(из)п, m,q + (^з)п+1, m, q] [(ul)n, m,q ~Г
А Г 1
+ (^l)n+l, m, q] 2~ \4АГ KMl)n+1» m' Я+1 + (^l)n. m, q+l ~
— (ul)n+l, m,q-l — (ul)n, m, q-l] +
H д^~ L(^3/n+l, m, g (^з)п, m, grj г | (^i)n+l, m, q — (ui)n,vi,q \i
A3.12)
Л Г 1
"i (^2)n, m+1, qj 2" |4Д? L(^2/n+l, m+1, q H~ (^2)^+1, m, q —
(^2/n-l, m+1, q — (^2O1-1, m, q] ~Ь
1 1
H дТ~ L(^l)n, m+1, q (^l)n, m, qjr I (^2/n, m+1, q (^2/n, m, q |»
A3.13)
(Ф2)п, m+y2, q = ^д— [(W-2)n, m>q + {u?)n, m+1, q]2 +
д7~ L(^2)n, m+1, q \U2/n, m, qj | (^2/n, m+1, q (^2/n, m, q \ъ
A3.14)
)п, m+V2» 3 =
, m, q
, m, q
А Г 1
(^2)n, m+1, q] 2" {
— (^2)n,;m+l, q-l — (U2)n, m, q-l] +
H д^" К^з)п, m+1, q (^з)п, m, qj г | \U2/n, m+1, q (^2/n, m, q |>
A3.15)
(Vl)n,m,q+V2 = Д7 [(^l)n, m, q + (ul)n, m, q+l] [(^3)n,m,q +
A { 1
(^З/п, m, q+l] 2~14A^" L(^3)n+1' m'
214A^ ~ (^з)п+1, m, q —
— (^з)п-1, m, q+l — (^з)п-1, т, q] +
+ ~д7 [(ul)n, m, q+l — (^l)n, m, q]j | (^з)п, m, q+l (^з)п, m, q |?
A3.16)
(x 2/n, m, q+V2 == 4Д7" L(^2/n, m, q ~Ь \U2)n, m, q+l] 1(^з)п, m, q +
A [ 1
+ (^з)п, m, q+з] g~ 14Ау" К^зO1' m+1» 5+1 ~t~ v^3/n» m+1, q —
(^3/n, m-1, q+l — \из)п, m-1, q] H~
1 1
+ "д^- [(U2)n, m, q+l — (^2)n, m, q]| | (^з)п, m, q+l — (^з)п, m, q |»
A3.17)
47
[U) H (*b) j
((?з)п, m, g+V2 ^ Д7 [\U3)n, m,q H (*<b)n, w, g+lj
TT~ 1(^3/^, m, g+1 v^3/n, m, gj | (^з)?г, m, g+1 (^3/n, m, q ]
A3.18)
, m,q = (^i)n-V*. w,« — (^i)n+V2, w, g = (^i)o< -3)+V2> w> « —
(^)n+V2,m,q, A3.19)
, rn,q = (Фг)п, m-Vs. 5 — (Фг)т7, ™+'/2, 9 =
(&i)nt (w-D+V., g — (Фг)н, m+V2. 5' A3.20)
, m, g = (ft)n, m, g-V2 — (^?i)n, m, g+V2 =
m, g = (A)iV-V2, m, g — (^г) /2, тп, дт A3.22)
N. g - (Фг),, N-v, g - (Фгк V,. «, A3-2:5)
п, m, g + (АФ|)п, п., д + (Aft)n, tn, g- A3.25)
Последняя формула совпадает с C.2).
При записи приведенных формул учтены граничные условия
(периодичность), т.е., например, вместо (ut)n-lt m%q при п — 1
записано (щ)я, m,g и т.п. Для составления блок-схемы прог-
программы укажем общую последовательность расчетов.
1. Расчет начинается при п, т, q = 1. Вначале при сохранении
q = 1 последовательно перебираются все /г и /тг и определяются
величины (<?j)n,w,v. Для всех ^ = 1, 2, 3 [по: A3.7) — A3.9)].
Эти величины записываются в специально отводимые для них
ячейки памяти ЭВМ. Таким образом, для этого требуется 3 /Vм
ячеек памяти (кроме 4iV3 основных ячеек памяти, в которых за-
записаны поля ut и /?, и кроме, конечно, небольшого числа ячеек
для записей промежуточных результатов расчетов). Одновремен-
Одновременно эти же величины записываются в ячейки, которые в дальней-
дальнейших расчетах будут предназначаться для (Qt)nt m, q+i/t. Для это-
этого требуется еще 3iV2 ячеек памяти.
2. Затем снова перебираются все пит при q — const (=1) 2
и при каждом пит определяется по A3.16)—A3.18)
(Qt)n, m, g+v* = (Qdn, m, »/i (для всех ^ = 1» 2? 3). Определяется
разность A3.21): (Qt)n, m, g-v, — (Qth, m,g+v2 = (А<??)?г, w, g (т. е.
при g = 1 разность ((?f)n, m, v, — (<?i)n, m, з/2 = (A(?i)n, m, i). Эта
разность — величина (AQi)n> т$1 — записывается в свои ячейки
памяти. Для этого требуется еще 3iV2 ячеек. Что касается
величин (Qi)n, т, g+v2» то они после вычисления и записи AQt при
каждом пит записываются в ячейки для (Qt)n, r,%, g+v«» B которых
ранее (в п. 1) была продублирована запись (Qi)n,m,y2-
2 Такие же расчеты будут выполняться и при других q — const.
48
Таким образом, после этих расчетов оказываются записанными
ВеЛИЧИНЫ (Qi)n, m, Vt» (&Qi)r>, w, 1 И (Qi)n, vi, g+Vo = {Qi)n, m, »/a (BCe"
ro 9iV2 ячеек памяти).
3. Далее определяются и (запоминаются) величины (i^)v2>i. i
[по: A3.1)—A3.3I. После :>того при сохранении т, q = 1 после-
последовательно проводятся расчеты для всех п величин (/^n+v» i, i
[по: A3.10)—A3.12)] и величин (AFf)n,lfl [по: A3.19I. В этой
формуле величины (Ff)rt_i/2,i, x равны запомненным ранее (для
Ипрсдыд = п — 1) величинам (Л)ппредыд+»/2, i, i. Величины (А^)п, i, i
суммируются с ранее найденными (в п. 2) величинами (Д(^)п, i, i
и суммы AFt + A^? записываются в тех же ячейках, где были
записаны AQi. Величины {Рг)п+у2У i,i запоминаются временно,
только до расчетов при следующем п.
Так, расчеты проводятся до п = iV — 1 (включительно). При
п = JV расчеты Fi проводить не нужно, так как при этом
(FJn-Va» 1' 1 берется (как и при других п) из расчетов (Ft)n+i/2, i, i
для предыдущего п (т. е. п = iV — 1), a (/^)n+v2, 1,1 ==
= (Ft)N+i/2t l, l = (^i)v2, i, i в силу периодичности граничных усло-
условий [см.: A3.22)]. Величины (Ft)i/t,i,i сохранялись в памяти
(см. начало этого пункта). При п = N также вычисляются и за-
запоминаются AFt + AQt, после чего ячейки для промежуточной
записи Ft могут использоваться для других целей.
4. После указанного в п. 3 прохода всех п при т = 1, q = 1
повторяются такие же расчеты с проходом всех п при т = 2, q =
= 1, далее при т = 3, g = 1 и так далее, до иг — 40, q = 1. В ре-
результате оказываются записанными все величины (AFf)n, w, г +
+ (Д(^) га,г (в ячейках, где после п. 2 были записаны
)
5. Следующие расчеты проводятся также при q = 1, но с по-
последовательным изменением индекса т от 1 до iV при фиксирован-
фиксированном я, затем с таким же «проходом» по т при следующем п и т. д.
Начинаются этк расчеты снова при п, т, q = 1. При этом оп-
определяются все три величины (OJi. v2, i [no: A3.4) —A3.6I, все
(ЛФ«I,1,1 =@;)i,^,i-@;)i,vo,i[no: A3.20)], суммы (AO,)i, 1,1 -
+ (A^)i,i,i + (A^)i,i,i = (Mt)ltXtl [см.: A3.25)] и величины
("i)i, i, i [по: (9.2)]. Величины (u'Ji, i, i записываются в те же ячей-
ячейки, где были ранее записаны (A/^)i, i, i + (AQdi, i, i-
Далее такие же расчеты проводятся, как указывалось, после-
последовательно для всех т при сохранении п, q = 1. При этом при
каждом т вычислять (Ф^)п, т-у2, q нет необходимости, так как
эти величины равны (Of)n, глпр'едыд+1/,,<|» гДе ^предыд = т — 1. Поэ-
Поэтому при каждом m вычисляется только (Oj)i, n?+Vi, i (a затем
АФ^ и /7г). При /тг = Л^ Ф^ рассчитывать не нужно, так как
(Ф*)к, N+yt, q = (Ф*)ч, v8. «» а величины (Ф*К, v8, g сохранялись
в памяти с начала расчетов по этому пункту. Для промежуточ-
промежуточных запоминаний Фг можно использовать те же ячейки, которые
ранее использовались для Ft.
После расчетов для всех п оказываются найденными все
(Sl)n, т, 1.
49
6. Далее проводятся такие же расчеты, как было указано
в п. 2—5 (и в той же последовательности), но для q = 2 и затем
для q = 3. При этом величины (wjn, m> q записываются каждый
раз в новые ячейки памяти, так что требуется еще 6iV2 таких яче-
ячеек. Величины (Qi)n, m,q+y2 записываются при каждом q в одни
и те же ячейки.
7. При q > 4 расчеты также проводятся в указанном в п. 2—5
порядке, но перед расчетами для каждого q производится перенос
величин (м?)Л, m,q-2 B ячейки памяти ЭВМ, где записаны скорости
(Ui)n,m,q-2- ОсВОбоЖДаЮЩИвСЯ ОТ («Qn, m, q-2 ЯЧвЙКИ ИСПОЛЬ-
зуются для записи (^)д, m> q (при рассматриваемом q).
Таким образом, после окончательных расчетов для какого-
либо q > 4 (кроме q = N) оказываются записанными в дополни-
дополнительных ячейках памяти величины (Qi)n,m,i/2 (согласно п. 1),
(Qt)n4m,q+i/t, («i)n, тп.Ь (М|)п, т, q, («j)n, m, g-1 ~ ВСвГО 15 iV2 ВвЛИ-
чин 3. Для всех q от 2 до q — 2 (включительно) величины at
оказываются записанными в соответствующих ячейках для щ.
8. При q = N вычисления упрощаются, так как не нужно оп-
определять (Qi)n, m, N+4f Вместо этого используются ранее запом-
запомненные (по п. 1) величины (Qi)n,m,v2 [см.: A3.24)J. Другие рас-
расчеты, аналогичные указанным в п. 2—5, должны выполняться.
После расчетов при q = N величины ut для q — 1, N — I и N
записываются в ячейки вместо соответствующих {ut)n} m, q; за-
занятые этими пь ячейки, а также ячейки памяти, занятые всеми Qt,
освобождаются.
Таким образом, в результате выполнения расчетов вместо всех
(ut)n, m, q записываются (ui)nt m, g, а дополнительно использо-
использованные 15 N2 ячеек памяти ЭВМ освобождаются 4.
На рис. 2.3 приведена укрупненная блок-схема программы,
соответствующая описанному порядку расчетов.
Для удобства записи в блок-схеме применены такие обозначе-
обозначения:
1) ячейки памяти ЭВМ, используемые для запоминания
(Qi)n,m,i/2, названы ячейками А;
2) ячейки памяти, используемые для запоминания (Qi)n, m, g+v2»
названы ячейками В;
3) ячейки памяти ЭВМ, используемые для запоминания
( () (A^) (A^)
(&), т, q, (AQdn, m, q + (ДЛ)п, m, g, (A^,)n, m, q + (A^,)nf m, q +
+ (АФ*)П, m, q = (Мг)п, w, q и для временного запоминания (?f)n, Wf q
при q = 1, названы ячейками С; ячейки памяти, используемые
для запоминания таких же величин при q = 2 (и других чет-
четных #), названы ячейками D; ячейки памяти, используемые для
тех же целей при q = 3 (и других нечетных q), названы ячейками Е\
4) ячейки памяти, используемые для запоминания всех вели-
величин (ut)n, m, g, названы ячейками U;
3 По отношению к основному объему памяти для записей полей щ и р D/V3)
это составляет долю 15W2/4/V3 = 15/4/V (около 10% при N = 40).
4 Из дальнейшего будет ясно, что их с избытком хватает для других частей
программы.
50
Для п, т от 1 до N:
расчеты всех (?,)„,,„, ,/2 по A3.7) - A3.9);
запоминание в ячейках памяти Л и дублирова-
дублирование запоминания в ячейках В
©
Задание q - 1
\
Для п, т от 1 до N и <? = const расчеты (Q,)n m (/+ , /2
по A3.16)^A3.18) и (AQX.m.q по A3.21) при q <N;
запоминание (AQt)n>m q в ячейках С (при
^ = 1), D (при четных q) или Ь1 (при нечетных q,
кроме g = 1); запоминание (QX,m,q + 1/2 в ячейках В
Задание т = 1
Расчет 0Р,I/2)„,„ по A3.1) * A3.3)
и запоминание в ячейках F
Увеличение
m на 1
Для п от 1 до iV и m, g = const:
Расчет (F.^ + i^.w.g гю A3.10) + A3.12);
{AF,)n m q по A3.19) при п <А^или по A3.22) при п = N;
HiAFt'+bQX.m.q-
Запоминание (AF, + AQ,)n m q в
ячейках С (при <? = 1),D (при чет-
четных q) или ? (при нечетных q, кроме q = 1)
Рис. 2.3. Блок-схема программы расчета и, (про-
(программа № 2 на рис. 2.1)
1
Задание п = 1
Расчет (Ф,);1| 1/2</ по A3.4) + A3.6) и
запоминание в ячейках F
©
Для т от 1 до N:
расчет (ФД, ш + ,/2.4/ по A3.13) + A3.15);
расчет (ДФ,)„ ,„<ч по A3.20) при m<Nили
по A3.23) при т =iV; расчет (AQ, + Д^ + ДФ,)Я,,„ >q -
= ШХ т,ч и затем расчет (иХ,т,ч по (9.2) с
запоминанием в ячейках С (при q = 1),D (при четных д)
или ?" (при нечетных q, кроме 1)
Для /г, т от 1 до N пе-
перенос величин (ы^)и>,„(
,, ,
из ячеек С, D, Е в
ячейки U
©
Возвращение к (V) нет
Вози ращение г Bj
Для /г, т от 1 до ЛГ:
перенос запомненных
величин (и,)п т>д_2 из
ячеек D (при четном q)
или ? (при нечетном q)
в ячейки U
5) ячейки памяти, используемые для величин (/^)i/2,m, q и
^п, у2, qi названы ячейками F.
2.14.0 программе определения давления
(программа № 3 на рис. 2.1)
Расчеты проводятся методом итераций с использованием уравне-
уравнения (8.4). Излагаемая схема построения программы основывается
на методе верхней релаксации [30J. Перепишем уравнение (8.4)
в следующем виде:
P,i, т, q — #i (p7i+2, т, q ~Т Рп-2, т, q) "Г &2 \Рп, т+2, q I Рп, т-2, q)~\~
"Г % (Рп, т, д-,2 Н" Рп, т, д-2) + $Ч т, q, A4.1)
где at =
Х
{"XT [(^i)^-l, m, q —(S^n+i, тп, g]
Первые расчеты выполнялись при использовании для итера-
итераций уравнения A4.1): в правую часть этого уравнения при этом
подставляются известные значения давлений, а определяемое по
A4.1) pn,m,q помещается сразу же в соответствующую ячейку
памяти ЭВМ вместо ранее записанной в этой ячейке величины.
Так, производится обход всех ячеек (метод Зейделя [30]). Однако
необходимое число итераций для метода Зейделя получается
большим (но, вообще говоря, вполне приемлемым). Это число мож-
можно несколько сократить, используя другие, более эффективные
методы. Особенно удобно применить метод верхней релаксации
[30]; при этом процедура расчетов остается почти такой же, как
и в методе Зейделя, но число итераций сокращается. Для проведе-
проведения итераций по этому методу запишем вместо A4.1) следующее
соотношение:
НОВ /л \
Рп, m, c=- I1 — Ю; рп, т, q -f <uO<iPn+2, m, q ~T ®alPn-2, m.qT
tt> m-2, q ~t~ ®&зРп, m, q+2 —
Wf q. A4. j-)
Здесь в правой части находятся все известные (записанные
i памяти машины) давления; определяемое по A4.4) новое давле-
давление р1™вт, q сразу же записывается в соответствующую ячейку
памяти машины вместо записанного ранее там pn,m,q- Таким
52
образом, производится расчет последовательно для всех ячеек
расчетной сетки.
В A4.4) со — итерационный параметр, определяемый в рас-
рассматриваемом нами случае следующим образом:
со = 2/[1 + sin Bn/N)], A4.5)
где N — число участков расчетной сетки в одном направлении.
Таким образом, итерационный процесс состоит в том, что за-
задается некоторое исходное поле pn,in,q<> затем в каждой ячейке
расчетной сетки определяется pl™Bm%q [по: A4.4)] и записывается
в память ЭВМ вместо исходного рп% ш, q в этой ячейке. Так, по-
последовательно производится расчет для всех ячеек расчетной сет-
сетки. Затем такой же процесс повторяется: по A4.4) определяются
все Pn,m,q с использованием ранее найденных в качестве исход-
исходных и так далее до получения некоторого заданного малого раз-
различия между рп, m, q для двух последовательных итераций.
В уравнение A4.4) входят только четные или только нечетные
значения первых, вторых или третьих индексов при давлении.
Поэтому все ячейки расчетной сетки могут быть разбиты на
8 групп, в каждой из которых итерационный процесс расчетов
pn,m,q проводится независимо (независимо от величин р в ячей-
ячейках других групп). Если условно обозначить четные индексы сим-
символом «ч», а нечетные символом «н», то индексы при давлениях
в указанных восьми группах ячеек будут такими (номер группы
обозначим х):
х 123 4 5678
индекс ч, ч, ч н, ч, ч ч, н, ч ч, ч, н ч, н, н и, ч, н н, н, ч н, н, н
Представим индексы п, т, q в виде
п = 2а — аи m = 2р — р^ q = 2у — Vi- A4-6)
Для каждой из групп ячеек расчетной сетки а, |3, у могут иметь
любые значения от 1 до N12, а а4, р4, Yi имеют значения 1 или О,
распределенные по группам следующим образом:
х 12 3 4 5 6 7 8
ссх 0 10 0 0 111
Pi 0 0 10 10 11
Ti 0 0 0 1110 1
После окончания расчетов давления для какой-либо из ука-
указанных групп ячеек целесообразно скорректировать исходные ве-
величины рП} m> q в ячейках следующей группы, для которой пред-
предстоят расчеты.
Для проведения этой корректировки воспользуемся следую
Щими соображениями.
Уравнение (8.4) [и соответственно A4.1)] является конечно
разностной аппроксимацией уравнения
_^— = -L!^]L. A4.7)
дх]гдхк Дт дхк v
53
При этом аппроксимация левой части (лапласиана давления)
проведена (точнее, получилась) на сетке с удвоенными шагами
2Д#, 2Ау и 2Az [именно поэтому в A4.1) входят только четные или
только нечетные индексы]. Если в A4.7) для аппроксимации
д2р/дхчдхк воспользоваться не удвоенной по шагам, а основной
расчетной сеткой, то вместо F.4) получится
Рп, m, q — ai \Рп+1, т, q ~\г Рп-1, т, q) ~Г а2 \Рп, т+1, q ~\~ ' п, т-1, q) i
+ а3 (pn> w, q+1 + PUi т, g_x) + Fn, mt g/4, A4.8)
где ai, a2, a3 и Р прежние [определяемые по: A4.2) и A4.3)].
Итерационные расчеты нужно проводить по A4.4), так как
именно при этом обеспечивается удовлетворение уравнения не-
неразрывности (см. разд. 2.6). Однако pUi mtq для начала итерации
целесообразно определять по A4.7). При этом при расчетах по
A4.8) Рп, w, q для каждой из указанных групп ячеек в правой
части используются давления только в ячейках других групп,
поэтому итерации по A4.8) для каждой группы проводить нельзя
(проводится только один раз расчет исходных pni m, g). При рас-
расчетах для первой группы ячеек (х = 1) в правой части A4.8) ис-
используются давления, которые были на предыдущем временном
шаге (а на первом шаге р = 0). Однако уже при к = 2 два давле-
давления в правой части A4.8) являются правильными (они определе-
определены расчетами при к = 1). Для последней группы (к — 8) в пра-
правой части формулы A4.7) стоят только величины давления в тех
ячейках, для которых расчет уже проведен. Это должно позволить
улучшить исходные данные и уменьшить число итераций.
Самым сложным является вопрос о выборе обоснованных тре-
требований к точности определения р (определяющей окончание ите-
итераций). Приведем по этому поводу только качественные сообра-
соображения. Погрешность 8р в величине давления вызывает такого же
порядка погрешность в величине силы Rt в уравнении количества
движения [см.: C.3) — C.5)], где р = 1, Ах = 1, а Ау и Az также
чаще всего порядка 1:
8R « 8р.
Если размеры ячеек сетки очень различны по разным осям
и если I — наименьший из шагов сетки, то точнее будет написать
[см.: C.3) - C.5I:
8R х 8р/1.
Из (9.3) видно, что погрешность в скорости 6и, возникающая
на очередном временном шаге из-за погрешности в давлении, оп-
определяется по порядку величины так:
8U « Ar8R ж Ах8р/1. A4.9)
Конвективные члены в уравнении количества движения при-
приводят к тому, что скорость жидкости изменяется на величину по-
порядка разности скоростей в соседних ячейках Аи за время поряд-
54
ка продвижения жидкости на длину ячейки, т. е. порядка Ни г.
За один временной шаг Ат изменение скорости по порядку вели-
величины составит АиАти/L Отнесем погрешность A4.9) к этому из-
изменению скорости и обозначим их отношение 8, получим
6 ж 8р/(Аии).
Размер ячеек в несколько раз (в ~5 -.- 8 раз) меньше размера
крупных вихрей, поэтому Аи соответственно меньше скорости
пульсационного движения U. Обозначим Аи = \iu, где \i, по-ви-
по-видимому, составляет 0,2 -г- 0,3. С учетом этого получится
). A4.10)
В исходных данных для рассматриваемых здесь задач прини-
принималось иисх ~ 1, но с ростом времени и должно снижаться, так
что и2 в A4.10) может быть значительно меньше 1.
Если принять, что допустимая погрешность в расчете измене-
изменения скорости на каждом шаге Ат (е) составляет несколько про-
процентов от величины этого изменения и если вести расчет по вре-
времени до снижения и2 до уровня ~0,1, то из A4.10) получится до-
допустимое значение jj
8рх 10. A4.11)
Заметим, что погрешности в расчете давления не приводят
к накапливанию ошибок, создающих невязку в удовлетворении
уравнения неразрывности, так как для принятой методики рас-
расчета на каждом временном шаге погрешности в соблюдении урав-
уравнения неразрывности устраняются (см. разд. 2.8). Поэтому по-
погрешности в давлении 8р приводят только к дополнительному
«турбулизирующему возмущению», которое будет (как и все тур-
турбулентные движения' вообще) подвергаться диссипации. В связи
с этим можно ожидать, что возмущения в несколько процентов
от изменения скорости на каждом шаге (т. е. в доли процента от
разности скоростей в ячейках Аи) совершенно незначительно ска-
скажутся на статистических характеристиках турбулентного движе-
движения. Может быть, поэтому норма A4.11) является слишком жест-
жесткой. Это еще недостаточно проверено при расчетах.
Практически вместо погрешности 8р будет использоваться раз-
разность давлений в двух последовательных итерациях (что, конечно,
не одно и то же; видимо, погрешность больше этой разности).
Таким образом, расчет должен вестись до тех пор, пока раз-
разность давлений для двух последовательных итераций для всех
ячеек расчетной сетки не станет меньше некоторой заранее зада-
задаваемой величины 6р. Для приводимых расчетов мы будем прини-
принимать для 8р норму A4.11) или максимум — в 2 ч- 3 раза боль-
большую величину.
В формуле A4.4) содержится величина Fnt m,q, определяе-
определяемая по A4.3). Эта величина не изменяется при итерациях, поэтому
Напомним, что все представляется в безразмерных величинах.
55
ее целесообразно рассчитать заранее. Число необходимых для
этого ячеек памяти ЭВМ в 8 раз меньше общего числа ячеек рас-
расчетной сетки (так как эти ячейки разбиты на 8 групп и величина F
должна вычисляться и запоминаться отдельно для каждой груп-
группы), т. е. оно составляет N3/8 = 8000 (для N = 40). Это меньше,
чем использовалось для описанных в разд. 2.13 расчетов (там тре-
требовалось 15N2 ячеек памяти, т.е. при N = 40 24 000 ячеек, кото-
которые до начала расчетов давления освобождаются).
На рис. 2.4 показана блок-схема программы расчета давления,
учитывающая изложенные соображения. Ячейки памяти ЭВМ^
предназначенные для записи Fn% w, q, обозначены на схеме «ячей-
«ячейки А» (их всего 1/87V3); предназначенные для записи всех рп% m,q —
«ячейки В» (их количество равно Л3). В приведенной блок-схеме
имеются два близких по содержанию этапа 2 и 3. Это сделано
для того, чтобы сократить объем вычислений при проведении каж-
каждой итерации: если контроль | Ар | < 8р в какой-либо ячейке
расчетной сетки дает отрицательный результат, то далее этот
контроль во всех остальных ячейках не проводится (до следующей
итерации), т. е. расчетный цикл замыкается по другому пути. Так
как ячеек расчетной сетки много, то экономия в объеме вычисле-
вычислений представляется оправданной, даже если она достигается це-
ценой некоторого увеличения объема программы.
Вывод на печать и дисплей величин % (номер группы ячеек
расчетной сетки), / (число итераций, оказавшихся необходимыми
Рис. 2.4. Блок-схема программы расчета давления (программа № 3 на
рис. 2.1)
Определение со по
A4.5), а,-по A4 2)
Задание х= 1,0^ ,
Pi у Ti = 0> задание 5р
0
Расчет для а, /3, 7 от 1 до N/2.
п,т, q по A4.G), Fnm q -A4 3) (и
запись в ячейки А); исходных/?,, m<q
по A4.8) (и запись в ячейки В)
Запись; = 1 (номер итерации)
©
Для а, в, у от 1 до ЛГ/2:
1) определение ри ,„ (/ = рп „!(. (нов) по
A4 4) и запись каждого р„ ,„ , но
вспомогательную ячейку памяти,
2) определение разности Ар между
Рп m,q (нов) и исходным рп mq и затем
перенос р„
Pn.m.q
(нов) в ячейку памяти В на место
©
*© л®
Переход к следующей
точке перебора
по a,fi, у
Выводя,;, s на
печать и дисплей I
Определение р„ „;> q = рп т q
(нов) по A4.4) и запись в
ячейку В
Задание ,? = 7;
Переход к сле-
следующей точке
перебора по
(Задание 2:= 8;
0
Переход к следующему этапу программы
57
для достижения | Ар | ^ 8р во всех ячейках) и s (номер времен-
временного шага) сделан для того, чтобы можно было контролировать
скорость сходимости итерационного процесса. Если она окажется
плохой, то придется либо усовершенствовать методику проведе-
проведения итераций (такие пути есть, но программа при этом услож-
усложняется), либо более подробно рассмотреть вопрос о возможности
увеличения 8р (либо сделать и то и другое) 2.
После накопления дополнительного опыта расчетов от вы-
вывода х, / и s можно будет отказаться.
2.15. О программе расчета (Ui)n>ni>q
(программа № 4 на рис. 2.1)
Перепишем уравнение F.3) для (м*)иТг»г, я» подставив в него R.
из C.3) — C.5). Учтем при этом, что в безразмерных уравне-
уравнениях р = 1, а верхний индекс т + Дт опустим. Получаются сле-
следующие соотношения:
K)n, m, q = (?i)n, m, q + (Дт/2Дж) (/?n-l, m, q — Pn+l,m, g), A5-1)
(U2)n, m,q= (S2)n, m, q + (Ax/2Ay) (рп, m-l,q ~ Pn, m+1, g), A5-2)
(^з)п, w, q = (M3)n, w, « + (AT/2AZ) (prJ, m, q-i — pnt m,q+l)- (lS-i))
Все стоящие в правых частях этих уравнений величины уже
вычислены на предыдущих этапах расчетов.
Блок-схема программы расчетов (^)n,m,q настолько элемен-
элементарна, что нет смысла изображать ее в виде рисунка: величины
(Щ)п, т, g, (U2)n,m,q И (u3)n, m, q ВЫЧИСЛЯЮТСЯ ПО A5.1) — A5.3)
для всех тг, яг, q от 1 до iV, и результаты вычислений запоминают-
запоминаются в отведенных для (г^)п, m,q ячейках памяти ЭВМ (вместо ра-
ранее записанных там (мг)„, m, q).
2.16. Выбор шага по времени
Учтем два ограничения максимально допустимой величины шага
по времени Дг.
1. Для обеспечения хорошей точности расчетов потребуем,
чтобы за каждый временной шаг изменения скорости в какой-либо
(типичной) ячейке расчетной сетки ди было мало по сравнению
с характерной величиной разности скоростей в соседних ячей-
ячейках Аи. Для оценки порядка величины Д? можно считать, что ско-
скорость в какой-либо ячейке изменяется на величину, соизмеримую
с Дм, за время hi (Аи), где h — шаг расчетной сетки (Д^, Ау или
Az). Если обозначить \i = 8u/(Au), то по порядку величины можно
считать
2 Фактически потребовавшееся число итераций см. в разд. 2.18. Оно велико,
но все же приводит к приемлемому времени расчета.
58
At/W(Au)] ж щ A6.1)
т, е. At ~ М< hl{Au).
При принятых в этой главе характерных масштабах длины
0 скорости (для приведения уравнений к безразмерному виду) по-
получается h ж 1 (точнее, Ах = 1, а Дг/ и Az могут отличаться от 1,
но, как правило, не на порядок величины) и Аи < 1 г. Обозначая
1/Дм = к, получим
At^kii. A6.2)
Если допустить, например, чтобы было 8и/Аи — \i = 0,01 -ч-
_~ 0,02 (т. е. изменение скорости на каждом временном шаге
в среднем на 1 -~ 2% от Да) и учесть, что величина к не превос-
превосходит, по-видимому, нескольких единиц, то из A6.2) получится
Д* ^ 0,05-ь 0,1. A6.3)
С ростом t (т. е. номера шага по времени) допустимое At может
увеличиваться, так как падает Аи и растет к = 1/Дц в A6.2).
2. Для формулировки второго ограничения величины At
рассмотрим уравнение, определяющее скорость изменения кине-
кинетической энергии турбулентности. В качестве исходного исполь-
используем уравнение количества движения в форме C.1):
d (Щ)п, т, q/dt = (Mt)n, m, q -f (#<)u, m, q = (Gt)n, m, q- A6.4)
Отсюда при принятой явной схеме интегрирования по времени
получается
(Udtm!q = (Щ)п, mtq + (Gt)n9 m, &. A6.5)
Используя A6.5), найдем
У У У IV^ifn, m, q \U>i)n, m , q v^i)v, in, q {^i/n, m, q\ —
?*mJ Ac,r^J /-SJ
(w, m, q)
= 2M У У У\щ)П9 m,q(Gt)n, ж, q +
«ли шпане «пай
(n, m, <з)
i"'•q' A6'6)
(n, m, g)
Здесь, как обычно, по координатному индексу i предполагается
суммирование.
Правая часть здесь содержит квадратичный по Д? (второй)
член, который всегда положителен и, следовательно, дает увели-
увеличение кинетической энергии турбулентности. Ясно, что это свя-
связано с погрешностью конечно-разностного метода расчета.
Чтобы подтвердить это, заметим следующее.
1 Напомним, что при t = 0 принято и zz 1, а так как размеры ячеек расчет-
нон сетки меньше размеров крупных вихрей, до Аи < и (но не в очень боль-
большое число раз); при t ф 0 величина Аи меньше, чем при t = 0.
59
Если записать дифференциальное уравнение для квадрата сксь
рости жидкости (UiUf), затем аппроксимировать члены этого урав-
уравнения конечно-разностными выражениями и записать выраже-
выражение для (UiUi)t+At — (utUi), используя явную схему интегрирова-
интегрирования по времени, то получится выражение, аналогичное A6.6),
но без последнего члена 2.
Чтобы погрешность расчета диссипации энергии турбулент-
турбулентности была небольшой, последний член в A6.6) должен быть мал
по сравнению с первым членом в правой части этого уравнения,
т. е. должно быть
A6.7)
(л, пг, q)
Отсюда допустимая величина At получается равной
А* = i?v ^ ,' A6*8)
Zj2j 2ll(Gi)n, m, q (Gt)n, m, q
(н, »i, q)
Чтобы определить диссипацию энергии с точностью до несколь-
нескольких процентов, можно принять 8 = 0,03 -ч- 0,05.
Расчет At по A6.8) не нужно, конечно, проводить на каждом
временном шаге.
При выполнении расчета At по A6.8) на каком-либо временном
шаге величину (Мг)п,[ПуЯ [необходимую для расчета (G$)n, m,q
по A6.4)] можно найти по C.2), зная скорости в каждой ячейке
расчетной сетки, а величину (Ri)n,m,q [также входящую в A6.4)]
приходится определять приближенно, используя при вычислении
Rt [по: C.3) — C.5)] величины (pi)n,m,q на предыдущем времен-
временном шаге (которые при принятой схеме расчета записаны в памя-
памяти ЭВМ). Однако вряд ли это существенно, так как речь идет
только об оценке допустимой величины At и так как за один вре-
временной шаг все параметры потока изменяются мало.
Должны учитываться оба указанных вида ограничений для At4
т. е. для At должна приниматься меньшая из величин, определяе-
определяемых по A6.2) или A6.3) и A6.8). Расчеты показывают, что более
жестким оказывается ограничение по A6.8).
Проиллюстрируем сказанное примерами. По описанной мето-
методике рассчитывали случаи изотропной турбулентности. Началь-
Начальное поле скоростей задавали случайным (см. разд. 2.5) с интеграль-
интегральным масштабом турбулентности, превышающим размер ячейки
расчетной сетки в 3—4 раза. Зона расчета 40 X 40 X 40 ячеек.
Разница описанной здесь процедуры преобразований и той процедуры, ко-
которая привела к A6.6), состоит в том, что здесь в качестве аппроксимируе-
аппроксимируемого дифференциального уравнения используется уравнение для иьиь, а при
получении A6.6) применено уравнение A6.4), полученное из уравнения
для ut.
60
?
! I I 1 I
I I I I I I I I I I I I
/ / / 4- f
Рис. 2.5. Зависимость энергии турбулентности от времени
Jf
Рис. 2.6. Зависимость допустимых значений At от времени I
при 8 = 0,04
При этих расчетах, носящих методический характер, величину А
в формулах для мелкомасштабной (подсеточной) турбулентности
не рассчитывали по методике, изложенной в разд. 2.9, а заранее
задавали.
На рис. 2.5 изображена зависимость энергии турбулентности Е
от времени (безразмерного, конечного), рассчитанная при А =
= 0,02 и одинаковых начальных условиях, но с разными шагами
по времени At. При больших Аг наблюдается рост Е, что опреде-
определяется, конечно, последним членом в A6.6), т. е. погрешностью
конечно-разностного метода расчета по принятой методике. Из
рисунка видно, что величина At должна приниматься не больше
чем 0,02 (между случаями Д? = 0,02 и 0,01 разницы уже почти
нет). Это ограничение более сильное, чем по A6.3).
На рис. 2.6 построена завиерхмость допустимых At, определен-
определениях по A6.8) при 8 = 0,04, от времени t. Из него следует, что до-
допустимые значения Д? еще меньше, чем величина, получающаяся
йз анализа рис. 2.5 (но не сильно отличаются от нее). Они значи-
значительно меньше, чем устанавливается по норме A6.3).
С учетом изложенного можно рекомендовать принимать вна-
вначале Дг = 0,01 -т- 0,02, а затем (после нескольких десятков или
61
сотен шагов по времени) проводить расчет по A6.8) и, если буде-j
необходимо, корректировать At; еще через несколько десятков ща,
гов эта процедура может повторяться.
2.17.0 программах расчетов
статистических характеристик турбулентности
1. Осреднение по объему любой величины, которая известна (или
может быть найдена) в каждой ячейке расчетной сетки, произ-
производится по формуле A0.5). С осредненными величинами затем
могут выполняться различные операции (например, осредненная
по объему величина <г4> может быть разделена на <г/?>2 и т. п.).
Значительная часть (но не все) указанных в разд. 2.10 статисти-
статистических характеристик турбулентности представляет собой вели-
величины, осредняемые по A0.5).
Программа таких вычислений очень проста: последовательно
определяется /n, m, qx для каждой ячейки расчетной сетки (т. е.
для п, т, q от 1 до N), найденная величина сразу же прибавляется
к сумме ранее определенных fn,m,qj—и так в конце концов на-
находится сумма /п, т, q для всех ячеек, которая делится на 7V3
для определения </>.
2. Близки по структуре вычислений к указанным расчеты
коэффициента А по формулам разд. 2.9.
Различие состоит в том, что суммирование производится не
только по ячейкам п, т, q, но и по крупным ячейкам, имеющим ин-
индексы а, |3, у, изменяющиеся в пределах от 1 до N12. При расче-
расчетах для крупных ячеек производится последовательный перебор
всех индексов а, |3, у, для каждого набора этих индексов (т. е.
для каждой крупной ячейки) вычисляются (йг-)а, p,v и (р)а, р, v
по (9.1), затем для каждой ячейки п, т, q, входящей в ячейку а,
Р, у, вычисляются члены в формулах для а, |3, у, ах, рх, уг, стоя-
стоящие под знаком 2 2> и рассчитываются сами суммы 2 '•> пос"
ле этого определяются для каждой ячейки а, |3, 7 величины, стоя-
стоящие в формулах (9.12)—(9.14) под знаком 2j 2j 2j и эти величины
а, E, у
складываются с ранее рассчитанными соответствующими сумма-
суммами для других ячеек. Так, после перебора всех индексов а, |3, у
определяются S S 21 по всем ячейкам. Вычисление а, C, у
а, |э, y
по (9.12)—(9.14) никаких пояснений, по-видимому, не требует.
Расчет завершается определением А по (9.16).
3. Для расчетов коэффициентов корреляции можно восполь-
воспользоваться формулами A0.6)—A0.8). Перепишем их в несколько
1 f(n, m, q) может быть любой из величин, указанных в разд. 2.10, из числа тех
параметров, средние значения которых необходимо определить.
2 При этом п приобретает значения 2а — 1 и 2а; т — значения 20 — 1
и 2р и q — значения 2у — 1 и 2у.
62
измененном виде (и с заменой индексов х, z/, z на 1, 2, 3):
N N-r
R
г гн, g=l /г=1
? Юп, ы.дЫ»-г,77.,д]|, A7.1)
п=1+г
iV ЛГ—г
A7.2)
?n=-l+r
3 N-r
1 n, m=-l
N
A7.3)
В этих формулах суммирование по i не предполагается. Здесь,
как принято нами, учтено, что Nx = Ny — Nz = TV. Расчеты по
A7.1)—A7.3) целесообразно проводить, как уже указывалось
в разд. 2.10, для г = 1,2, . . ., Л72 (для больших г i?^- может воз-
возрастать или колебаться из-за периодичности граничных условий).
На рис. 2.7 приводится блок-схема программы расчета Rtl. Блок-
схемы программ расчетов Ri2 и Ri3 имеют полностью аналогичный
вид, но индексы п и т и соответственно, п и q меняются местами
[это видно из формул A7.1)—A7.3)].
4. Масштабы турбулентности рассчитываются по формулам
A0.10)—A0.12).
Введем обозначения:
A7.4)
A7.5)
A7.6)
Здесь индекс г отмечает, что коэффициенты корреляции берутся
цРи заданном значении г; (Ru)r — это коэффициент корреляции
Компоненты скорости ut в какой-либо точке М и перпендикуляр-
перпендикулярен к оси хг компоненты скорости в точке, расположенной на
Расстоянии rAxt от точки М вдоль оси хг (так что обе точки, в ко-
63
Исходное г = 1; во вспомогательных
ячейках памяти Аг, А2, А3 записан О
Для т, q от1 до/^и для л от 1 ppN —г:
определение для i = 1 (u,-),,( т. „ • (w,)n+r,m,
сложение этой величины с записанной в
ячейке Л х и запись в ту же ячейку.
Затем то же для i = 2 и / = 3 (с
записью в ячей ка А2 и А 3)
0
Для т, q от 1 до N и для п от 1 + г до JV;
Определение для i = 1 (и,)„# „,(, • (щ)п_г> „,, q ,
сложение jtoh величины с записанной в ячей
ке A i и запись в ту же ячейку, затем то же
| для i = 2 и 1 = 3 (с записью в ячейки А2 и Л3)
торых берутся скорости
для вычисления Rlt, рас-
располагаются на одной ли-
линии, параллельной оси xt),
С учетом A7.4)—A7.6)
перепишем формулы
A0.10), A0.11) для lt в
следующем виде:
Деление записанного в ячейках Л,
числа на 2 (.V - r)Ar2<uf-2> (для /=1,2, 3),
т.е вычисление i?,i по A7.1).
Ли и г должны сохраняться в памяш ЭВМ
{ Вьшод Rn, r, i и s на печать и дисплей
Вывод зависимостей
J2,-, (для7= 1,2, 3) на
дисплей и i рафопо-
строигель Величи-
Величины ins также
выводятся на дис-
дисплей и графопо-
графопостроитель
Z3=
+2
х
Переход к дру-
другому этапу
программы
Величину rmax можно
выбирать так,чтобы (Ли)тлх
было меньше некоторой
заданной нормы, но г не
т, о - г, должно быть больше N12.
Рис. 2,. Блок-схема программы расчета удобнее всеГда принимать
''max = N12.
Расчеты Rtj должны быть выполнены, конечно, до расчетов lt.
Блок-схема програмлхы расчетов Zx приведена на рис. 2.8.
и ls по формулам
Совершенно аналогично вычисляются L
A7.8) и A7.9).
5. Определение величин 8 и е^ по формулам разд. 2.10 очевид-
очевидно и специальных пояснений не требует.
2.18. Результаты некоторых расчетов и их анализ
Приведем в качестве примера результаты расчетов изотропной
турбулентности для рассмотренного случая очень больших чисел
(когда члены с вязкостью можно опустить). Для расчетов прини-
принимали прямоугольную сетку с Ах = Ay = Az = 1 и одинаковые
размеры рассчитываемой области по всем осям: Nx = Ny =
= Nz = N = 40. Шаг по времени А* принимался равным внача-
вначале 0,02 (см. разд. 2.16), а затем, через 50 шагов по времени, кор-
корректировался по A6.8) и увеличивался до 0,05. Начальное зна-
64
Запись 1 во вспомогательную ячейку памяти А
При г от 1 до ЛГ/2
1) определение (flj.i)rno A7.4);
2) определение 2 (Ri} )r и сложение этой
величины с числом в ячейке памяти А
Определение (R±l )r_ v/2 по A7 4) и сло-
сложение этой величины с числом в ячейке
памяти А
Умножение величины в ячейке памяти А
наДд: (т.е. определение/] по A7.7)
Вывод /] и s на печать и дисплей и запоминай
этих величин
D
Переход к следующему этапу программы
Рис. 2.8. Блок-схема программы
четов 1\
рас-
чеяие коэффициента А за-
задавалось равным 0,02, а за-
затем, через 50 шагов по вре-
временя, определялось по из-
изложенному в разд. 2.9 ме-
методу. Начальное поле ско-
скоростей задавалось случай-
случайным (см. разд. 2.5 и 2.12).
Величины ut при этом «ра-
«разыгрывались» в ячейках с п,
m,q = 8, 16, 24, 32, 40.
Скорости вдоль различ-
различных осей координат полу-
получились при «разыгрывании»
близкими друг к другу, как
и должны быть для изотроп-
изотропной турбулентности.
На рис. 2.9 показаны
рассчитанные по начальному
полю коэффициенты корре-
корреляции скоростей Rn, R12 и
R13 в различных точках в
зависимости от расстояния между ними г (см. разд. 2.17).
По этим корреляционным кривым были найдены интегральные
масштабы турбулентности (разд. 2.17); они получились равными:
1г = 0,65; 12 = 0,59; 13 = 0,61; (lx + l2 + Z3)/3 = 0,6. Таким об-
образом, для начала расчетов было задано близкое к изотропному
поле скоростей с м ж 1,33 и I ж 0,6. При расчетах статистиче-
статистические характеристики турбулентности (по методике разд. 2.10 и
2.17) определялись через каждые 25 шагов по времени (кроме ве-
величины А, которая вычислялась через 50 шагов; через 50 шагов
вычислялась также величина At).
Результаты расчетов показаны на рис. 2.10 (а также на
рис. 2.5 и 2.6). Зависимость от времени t1 величины ' *ц ~°-
(см. рис. 2.10, а) близка к линейной, что согласуется с опытными
данными и результатами полуэмпирических теорий [1, 2].
Оценки подтвердили, что при выбранной расчетной сетке и
начальных данных энергия подсеточной турбулентности состав-
составляет небольшую долю (<!3%) от энергии рассчитываемых круп-
крупномасштабных пульсаций.
На рис. 2.10, б построена зависимость от произведения tA
величины эксцесса распределения / =
ц >2
ц
Точнее, зависимость не от ?, а от произведения tA. Это сделано потому, что
при больших А процессы протекают быстрее, и для приведения расчетов
цри разных А к удобно сопоставимому виду можно воспользоваться аргу-
аргументом tA.
В. М. Иевлев
Рис. 2.9. Коэффициенты корреляции
скоростей i?ll7 R12 и i?13, рассчитан-
рассчитанные по начальному полю скоростей
Рис. 2.10. Расчетные зависимости
параметров турбулентности для раз-
личных значений А и различных
расчетных сеток
1 — А = 0,25, расчетная сетка 20 X 20 х
X 20; 2 — А = 0,02, расчетная сетка 40 х
X 40 X 40; 3 — А = 0,25, расчетная сет-
сетка 40 X 40 X 40
/
4
z
0
/
. '
' ¦
0/0 tA
—
/
J
/
г
2
- —'
/
/
J
.
0
0,0/ 0J/J 0,/0 0/f 0~C/ 0,00 0/0 tA
&f W 4ff &
66
величина получается близкой к
3, т. е. распределение вероятностей
различных значений скорости близ-
ко к гауссовскому, что согласуется
с опытными данными.
На рис. 2.10, в показано изме-
изменение интегрального масштаба тур-
турбулентности I = Aг + l2 -f ^з)/3 в
зависимости от произведения tA, a
на рис. 2.10, г —результаты расче-
расчетов 1и (где и =УКиг/и/> + <м*м*»/3).
Как видно, I возрастает с ростом
t, а величина 1и близка к постоян-
постоянной. Это также соответствует опыт-
опытным данным для больших чисел
Re [1, 2].
На рис. 2.10, д построена зави-
зависимость безразмерной диссипации
энергии е:
5 = el/u3. A8.1)
In/
?
/ / In г
Рис. 2.11. Зависимость In F =
= In [A - Ru) + A - i?21) +
+ A — #31)] от In г для раз-
различных моментов времени т
1 — «закон 2/з» А. Н. Колмогорова
В полуэмпирических теориях обычно принимается 8 = const
и задается как эмпирическая константа. Из рисунка видно, что
при t 2> 32 действительно получается 8 ^ const ^ 0,25. При
t << 32 переменность & связана с выработкой «равновесного» спек-
спектра турбулентности, который, конечно, отличается от заданного
при t = 0.
Таким образом, на основании результатов расчетов с уче-
учетом A8.1) можно записать
На рис. 2.10, ? в безразмерном виде показана скорость измене-
изменения масштаба Z; эта величина обозначена к:
dl
J
~п~ dt
A8.3)
Как видно, при t = 32—96 величина к мало изменяется.
Для изменения I справедливо уравнение
dl/dt
УЛ1
0,1м.
A8.4)
Система уравнений A8.2) и A8.4) описывает изменение и и
I во времени. Они могут являться основой полуэмпирической
теории, константы в которой найдены путем «численного экспери-
эксперимента». В то же время уравнения A8.2) и A8.4) являются соотно-
соотношениями, аппроксимирующими результаты численного модели-
моделирования. Уравнения такого вида обычно используются в полу-
67
эмпирических теориях, но величины констант в них определяют-
определяются из опыта.
Среднее значение квадрата разности скоростей в двух точках
пропорционально 1 — i?, где R — какой-либо из коэффициентов
корреляции скоростей. На рис. 2.11 в двойных логарифмических
координатах построена зависимость [A —Rn) + A—R21) -f
+ A — #3i)l 0T расстояния между точками г. Видно, что при
t = 0—2,4 четко выявляется инерционный интеграл спектра
турбулентности, где справедлив «закон 2/3» А. Н. Колмогорова.
Допустимые величины шагов по времени At, рассчитанные
по A6.8), были ранее показаны на рис. 2.6. Эти результаты имеют
методическое значение.
Из всех приведенных данных видно, что расчеты при различ-
различных значениях А и разных расчетных сетках дают близкие друг
к другу результаты (при выборе допустимых значений АО-
третья
МЕТОДИКА РАСЧЕТОВ
ОДНОРОДНОЙ МАГНИТОГИДРОДИНАМИЧЕСКОЙ \
ТУРБУЛЕНТНОСТИ
3.1. Характеристика решаемой задачи
и вводные замечания
В настоящей главе рассматривается эволюция во времени одно-
однородной турбулентности в электропроводной несжимаемой жид-
жидкости с постоянными свойствами, находящейся в постоянном маг-
магнитном поле, создаваемом внешними источниками. Постоянство
свойств жидкости и постоянство внешнего магнитного поля необ-
необходимы для обеспечения однородности турбулентности.
Естественно, кроме внешнего магнитного поля с напряженно-
напряженностью Н, в жидкости возникают магнитные поля, связанные с про-
протеканием в ней электрических токов. Напряженность такого соб-
собственного магнитного поля в жидкости обозначим h, так что сум-
суммарная напряженность магнитного поля равна Н + h.
Поле h связано с электрическими токами, источниками кото-
которых являются ЭДС, возникающие при турбулентном движении
жидкости в магнитном поле. Поэтому само поле h получается
«турбулентным».
Обозначим L — некоторый характерный размер крупных тур-
турбулентных вихрей; v — характерную величину скорости пульса-
ционного движения в этих вихрях; vM — так называемый коэф-
коэффициент магнитной вязкости; в гауссовой системе единиц изме-
измерения [11]:
vM = сЩло, A.1)
68
где с — скорость света в вакууме; а — удельная электропровод-
электропроводность среды.
Безразмерный параметр Lu/vM = ReM обычно называют маг-
магнитным числом Рейнольдса. Практически для всех технических
устройств ReM <^ 1 г. Это условие будет в дальнейшем считаться
выполненным.
Можно показать [11], что при ReM <^ 1 по порядку величины
. A.2)
В связи с этим в уравнениях удается провести ряд упрощений
(см.: [11]).
Граничные условия (периодичность) и начальные условия
в рассматриваемых в этой главе задачах совпадают с соответствую-
соответствующими условиями, сформулированными в гл. 2. Совпадает также
программа задания начальных скоростей. Поэтому указанные
вопросы не рассматриваются. Некоторых пояснений требует толь-
только определение начального поля h; это пояснение приводится
ниже.
3.2. Исходные уравнения
Полная система уравнений магнитной гидродинамики приведена,
например, в [11]. Если учесть постоянство свойств среды, несжи-
несжимаемость жидкости и если подставить в уравнения магнитное
поле в виде Н + h (где Н = const) и пренебречь членами, имею-
имеющими по отношению к другим членам порядок \h\/\H\<^.l
(см. разд. 3.1), то система уравнений магнитной гидродинамики
(ось хг направлена вдоль Н) 2 примет следующий вид:
диь , диьи* 1 Эр , v д\ ,
dt "г" дхк р 0*1 дхъдхк
Н @ht dhl\
^-i'2'3' BЛ)
дщ/дхк = 0; B.2)
dh. dut дЧ.
к = 0. B.4)
Показано [11], что если
<1, B.5)
Напомним, что речь идет о ReM, в котором использованы размеры и ско-
скорость турбулентных вихрей. Такое число ReM много меньше ReM для пото-
потока в целом, однако и для потока в целом в большинстве случаев (но не всег-
всегда) бывает ReM <^ 1.
В [И] подробно проделаны все преобразования, связанные с приводимыми
ниже уравнениями.
69
то членом dhjdt в B.3) можно пренебречь. При этом поле h це^
ликом определяется полем скоростей, а вместо B.3) получается
следующее уравнение для ht:
дЧ. ди.
В работе [11] подробно обсуждена физика явлений, связанных
€ возможностью пренебрежения членом dhjdt. Мы здесь на этом
останавливаться не будем, а при разработке методики расчетов
рассмотрим оба случая: П <^ 1 и П^1.
Приведенная система уравнений не включает в себя уравнение
энергии. Это связано с тем, что в рассматриваемой в настоящей
главе задаче мы считаем свойства среды (р, vM) заданными и для
их определения (т. е. для определения температуры) уравнение
энергии поэтому не нужно. Полная система уравнений (с уравне-
уравнением энергии, с переменными свойствами среды), как указывалось,
рассматривается в [11].
Для приведения уравнений к безразмерному виду отнесем все
скорости к некоторой характерной скорости и, все длины — к ха-
характерной длине Z, время — к величине IIv, величины ht к Н
(внешнее поле Н считается заданным), давление — к величине
Сохраним для безразмерных величин прежние обозначения:
И;, #м t, p, ht.
Уравнения B.1)—B.4) после приведения к безразмерному ви-
виду приобретают следующую форму:
dUi ¦ dUiUK dp 1 34 |
dt "•" дхк ~ дх. ~+~ Re дх^дх^ "~
дик/дхк = 0; B.8)
dh ди л дУь
i_ __ i | l i i = l 2 3' B.9)
dt dx\ ' ReM дх^дх^
dhJdxv. — 0 B 10)
Из B.6) получается
д%/дхкдхк = —ReM диг/дхг. B.11)
В B.7) обозначено
М - #2/4яру2; B.12)
величины Re и ReM определяются так:
Re = to/v, ReM - Zi;/vM. B.13)
Из формул B.5), B.12) и B.13) следует, что
М = П/Rei. B.14)
70
При расчетах должны быть заданы параметры ReM и П (от
реличины П зависит вид уравнения для h), а параметр М должен
определяться по B.14).
Перейти от дифференциальных уравнений к конечно-разност-
конечно-разностным обычным способом в рассматриваемом случае нельзя, так как
при больших Re размер мелких турбулентных вихрей будет зна-
значительно меньше ячеек расчетной сетки и величины скоростей
(и ДРУГИХ параметров) в пределах размеров ячеек (и даже в еще
меньших размерах) могут изменяться немонотонно. Поэтому для
получения сеточных уравнений, нужных для расчета крупномас-
крупномасштабной турбулентности, мы поступим так же, как в гл. 2: выбе-
выберем достаточно крупную расчетную сетку 2 и проинтегрируем
уравнения по объему ячеек этой сетки, т. е. перейдем от диффе-
дифференциальных уравнений к уравнениям баланса различных вели-
величин в конечных, объемах. Обозначим размеры ячейки сетки вдоль
осей х, у и z Ах, Ау и Az соответственно 3. Обозначим координаты
границ некоторой ячейки по оси х л2 и хи причем х2 ^> хх (так что
Ч = xi + &х); аналогично обозначим координаты границ ячей-
ячейки по оси у у2 и уг и по оси z z2 и zx (причем у2 = Ух + Ay, z2 =
= zx + Az). Обозначим символами </>Л2 или </>Х1 средние значе-
значения некоторой величины / по граням х = х2 и х = хх ячейки рас-
расчетной сетки; аналогичный смысл имеют величины </>У1, </>у„
</>Г1 и </>Г2 (т. е. средние значения / по граням ячейки у = уг,
у — у2, z — zx и z — z2. Обозначим (временно) /ср среднее значе-
значение величины / по объему ячейки.
Проинтегрируем уравнения B.7)—B.10) по объему какой-ли-
какой-либо ячейки расчетной сетки и разделим на AxAyAz. Опустим член
с I/Re (для Re ^> 1). Получается следующий результат:
д^- {<Щи3>2л — Фги3У21} = -^г {<Р>*г — <Р>х2) 6ц
f M Jj- {<htyX2 - {htyXt} + М ^ 1 12
М -^ {{h.X - ф^}
B.15)
М -±- {(h^ - <*!>„,} 82i + М -^ {{h.X - ф^} 68i,
д\
Ах ~^~ ReM\ Ах 1\ дхл /*% \ дхг /
2 Размер ячеек сетки должен быть в несколько раз (или на порядок) менып
размера крупных турбулентных вихрей, но может быть значительно боль"
ше наиболее мелких вихрей.
1 Как и в гл. 2, вместо координат яь х2, х2 иногда будут использоваться
обозначения координат х, у, z соответственно.
71
Ay
*, , <^>г/г~<^>У1 ,
Для случая П<^1 из уравнения B.11) получается
¦к-
; /Xl \ дх /
3.3. Аппроксимация отдельных членов уравнений,
преобразования сеточных уравнений
и порядок расчета
Применим систему уравнений B.15)—B.19) к некоторой ячейке
/г, т, q расчетной сетки. Используем такие же обозначения, как
в гл. 2: среднее по объему ячейки расчетной сетки значение лю-
любой величины / будем обозначать не /ср, как в B.15) и B.17), а
/n, m, q\ среднее значение / на грани ячейки х = хг будем обозна-
обозначать не </>Ж1, a </>n+Vi, m, q; среднее на грани х = хх — </>n-V2, m, q\
среднее значение на грани ячейки у = у2 — </n, w+y», g>; на грани
г/ = г/х — </>п, m-jA, g» среднее значение / на грани ячейки z = z2
обозначим <7>n, m, g+vi5 на грани z = zx — </>n, m, g-v2.
В уравнении B.14) члены с парными произведениями скоро-
скоростей можно представить следующим образом (как и в гл. 2):
l, m, q]
m, q = <
^^ V4 [(ut)n, m, q
n+V2, m, g»
и аналогичным образом для других м^7- и других граней ячейки
расчетной сетки.
В C.1) обозначено и/ = (щ)п+у2,т^— (щУп+ч* m,q, где
(^i)n+v2. m, g — величина скорости z^ в произвольном месте граня
ячейки х = х2. Отличие щ' от нуля определяется наличием тур-
турбулентных вихрей с размерами, меньшими размеров ячеек рас-
расчетной сетки.
Величины (ц{п]У определим так же, как в гл. 2.
Запишем уравнение B.14) в таком виде:
d(lt|)d7m'g = (M,)n, m, q + (Д()п, т, q, C-2)
72
где
с
(Ri)n, m, g = -д^~ [<P)n-V2. rn, g <P)n+»/2, rn, g] +
w, g = (^i)n-Vi. wi, g— (^i)n+Vt, m. g + (ОДп, in-*/,, g—
— (Фг)п, m+V«. « + (@i)n, rn, g-»/«— (^i)n, m, g+Vt + №)n-Vi. m, g
V*. m, g + №)п, m-V«. Я.— i^ih, m+*/«, g +
n, m, g-Vi— (A)n, m, g+V2 • C-4)'
В C.4) величины Z^-, Фг- и ^^ — те же, что и в гл. 2 [формулы
A3.1)—A3.24)].
m, g = "дТ" [<^1>п->/«. m, g&Ц — <^г>п->/в» rn, g], C.5)
, m, g = -д^" K^l>n+V2, rn, g S2i — <^i)n+V2, m, g ]» C#6)
Vf. a = "д^Г <^i>n' wi-v«. «S2i» C-7)
Vi, g ^ "Д^
, m, g-V2
)n, m, g+V2 = ~SF <^l)n, m, g+V^si- C.10)
Обозначим, как и в гл. 2:
(?i)n, m, g = Юп, m, д + (M^n, m, дА^- C'И)
При явной схеме интегрирования уравнения C.2) по времени
получается
'= B<)п, m, e + (ДО», т, д^- C.12)
Здесь (гг^)^^п, g —величина (^i)n, m,g в момент t + Д?; без верх-
верхнего индекса записаны величины, относящиеся к моменту време-
времени t.
Величина и^^ должна удовлетворять уравнению неразрыв-
неразрывности B.15) 2. Подставляя выражение C.11) для и?+М) в урав-
уравнение неразрывности и используя формулу C.3) для (Rt)nt m, g»
Как и в гл. 2 в качестве величины р будет фактически использоваться сум-
суммарное давление ps (сумма истинного давления и «турбулентного» давления
Рт, определяющегося «подсеточной» турбулентностью).
2 В этом уравнении <и1>Х2 = <u1>n+Vif т% q = V, [(ui)n> w, q + (щ)п+ь w> gJ,
<u*>yi = <i/2>n> m_1/8f fl = V2 [(iie)nt m> e + (^ m_lf g} и т. п.
73
получим для pn,m,q уравнение B.14.1). Величины pn,m,q
дятся, как было описано в разд. 2.14, методом итераций с исполь-
использованием формул A4.4) и A4.5).
Обозначим:
{^г)п+Ч2, m,q= (Р%)п+Чг, т, q + (^)„+1/2, т, qi C.13)
<Фг)п, m+q, «/,= (Фг)п, т+У2, q + (?*)„, „,+./„ g , C.14)
n, m, q+yt = (Qi)n, m, g+V2 + (A)«, m, g+V2 > C.15)
|)п, w, g =(F|)n_i/2, 77), q (^iJu+Va, «», q =
V2, ?)i, q J C.16)
C.17)
i)n, m, (q-l)+V2 —
Из C.4) следует, что
(Мг)П9 m, q = (Д^г)м, m, g + (ДФ|)п. m, q + (A^i)". ^> T (ЗЛ9)
Порядок расчета (wf)n, m, q (и блок-схема программы этого рас-
расчета) может быть сохранен полностью таким же, как описано
в разд. 2.13, но с заменой величин ^Ft)n+i/tt m,q, (Ф*)п, m+Vt.« и
F^n+V,, m,q> (Ф«)п, m+V,, g И (?«)n,m,q+V.
,qy2 (^V,, ,q («), V,, g (?),,qV.
соответственно 3.
После расчета (ггг-)п, m,g определяется поле давлений (в поряд-
порядке, указанном в разд. 2.14) и затем находятся u\t+At) (в порядке,
указанном в разд. 2.15).
Таким образом, дополнительных пояснений требует только
порядок определения поля h. Это поле рассчитывается после оп-
определения поля и (т. е., например, й(/+А/) определяется после рас-
расчета всех w(/+A<)). Порядок расчета поля h различен при П <^ 1
и при П ^ 1.
При П <^ 1 нужно пользоваться конечно-разностной аппрок-
аппроксимацией уравнения B.18), которая имеет следующий вид:
i)n, m, q = 0<i [(hi)n+l, m, q + (^i)n-l, m, g] + #2
n, m-1, g] + ^3 [(ki)n, m, g+1 + (^i)n, m, g-l] +
1, m, g - (Щ)п-Х, т, g]/BAx). C.20)
Здесь at определяется по B.14.2). Однако итерации проводятся
не по формуле C.20), а при применении метода верхней релакса-
релаксации по следующей формуле [30] [аналогичной B.14.4)]:
8 Для этого, конечно, в исходный момент времени t должны быть известны
поля и и h.
74
( q = (! — <°) (hi)n, m, g + «^ [(*i)n+l, m, g + (Ы)п-1, m q]
+ (oa2 [(/гг)п, ж+i, 9 + (
+ (hi)n, m, q-l] + CD ReM [(щ)п+1, m,q — (щ)п-1, ж,
C.21)
Здесь
со - 2/[l + sin (n/N)l C.22)
Итерации при расчете ht проводятся так: имеется некоторое
начальное поле ht (например, распределение в предшествующий
момент времени); затем последовательно для всех ячеек расчет-
ной сетки определяются новые значения /гг по C.21). Эти новые^
значения (&*)"? ™,<? сразу же (по мере определения) помещаются
в ячейки памяти ЭВМ на место (ht)ni m, g предыдущего приближе-
приближения. Так процесс повторяется много раз до достижения заданной
точности. Необходимую точность расчета ht Fh) можно оценить
исходя из вида уравнения B.14). Из этого уравнения видно, что<
влияние погрешности в ht на поле скоростей будет таким же, как
влияние погрешности в расчете давления бр, если
M6fc ж Ьр. C.23)
Используя оценку B.14.11) для 8р, получим с учетом C.23)
8h ж 10/М. C.24)
Построение программы расчетов ht аналогично описанному
в разд. 2.14 применительно к расчету давления 4.
При П 2> 1 расчет (ht)n, m, q проводится по уравнению, кото*
рое можно получить из B.16). Перепишем B.16) в следующем
виде:
d(frj)n, m, q ^ (hj)n, m;q — (hj)n, т, д __ (N v /q ос;ч
^ — д7 — \1}/г)п, т, q, (U.40)
(Ui)n+1, т, q — (ui)n-l, m, q] +
I ft^ I Ля2 i-( */n+1» m' Я. i (hi/n-l, in, q ^ (hi/n, m, q\ ~\~
[(k) + (^) m-1, q 2 (hi)n, m% q] +
+ -д^а" [{hi)n, m, q+1 + (hi)nt m, g_i—2 (^)П1 m, g]j . C.26)
Из C.25) получается
И m, g - (^г)п, m, e + (^)n, m, q M. C.27)
За исключением того, что при расчете давления ячейки расчетной сетки
разбивались на 8 групп, а здесь такая разбивка не производится.
75
Ввод исходных данных
Программа № 1: Определение
начального поля скоростей
-»»| Программа № 2: Определение поля h
,©
Г
I Программа № 3: Определение {щ)п mq C^y
Программа № 4: Определение давления р
SJ | Программа № 5: Определение новых (u,),,,m,J (б)
Увеличение номера шага по времени s на 1 | \j)
Программа № 6: расчет всех (uf>
Программа № 8: Опреде-
Определение <р2>,ей е,;
Проверка <р>
Программа № 7: Определе-
Определение Л; статистической
величины поля скоростей и h;
проверки
( Вывод <Р2>,е,е, ) Qj)
Вывод Л,
статистических величин
Рис. 3.1. Укрупненная блок-схема программы расчетов однородной МГД-
турбулентности при П<^1 (а)иП^1 (б)
Порядок расчета по этим формулам прост, и особых пояснений
не требует.
На рис. 3.1, а приведена общая укрупненная блок-схема про-
программы расчетов однородной МГД-турбулентности при П <^ 1,
на рис. 3.1,6 — аналогичная схема для П ^ 1. Необходимые по-
пояснения к этим схемам практически совпадают с пояснениями
в разд. 2.11 к укрупненной блок-схеме программы расчетов
однородной турбулентности (рис. 11.1). Более детальная расшиф-
расшифровка отдельных частей укрупненной блок-схемы также анало-
аналогична (или совпадает) с приведенной в. гл. 2; некоторые дополни-
76
Ввод исходных данных
Программа № 1: Определение начального
поля скоростей
Программа №2: Определение (или задание)
начального поля h
Программа №3: Определение (и,-),,, ,„ ч
0
Программа № 4: Определение давления р
Программа №5: Определение новых (w,-)H, m
Программа №6: Определение поля h
I
0
Увеличение номера шага по времени s на 1 \ ( SJ
Программа №7: Расчет всех < и,-2)
Программа №9: Определение
<Р2>, е и €/, проверка < р)
f
Программа №8: Оп-
Определение Л, ста-
статистических величин
поля скоростей и h ;
проверки
Вывод А
ческих в
., статисти- 1
величин I
(Заключительный ^j
вывод величин J
тельные вопросы были уже пояснены выше. Поэтому повторять
отоль же детальный разбор порядка расчетов, как это было сде-
сделано в гл. 2, нет необходимости. Отметим только, что при опреде-
определении статистических характеристик турбулентности представля-
представляет интерес вычислить, кроме величин, указанных в разд. 2.10 и
2.17, величины </#>, <й|>, </*з> и для контроля правильности рас-
расчетов, например, величину </ч/г2> (которая должна быть равна
нулю), а также величины типа (u^j} для различных i и /'. Можно
было бы определить двухточечные коэффициенты корреляции на-
напряженности магнитного поля h и соответствующие интегральные
77
масштабы турбулентности. Это легко включить в программу и:
поэтому специальных пояснений не требует.
В программе предусматривается также расчет величины
4ф
— отношения энергии пульсационного магнитного поля к кине-
кинетической энергии турбулентности.
Поясним также поз. 3 схемы на рис. 2.12,6. Начальное поле h
может задаваться, конечно, произвольно (при сохранении одно-
однородности турбулентности). Но целесообразно, по-видимому, ис-
использовать два следующих способа задания начальных h:
1) принятие h = 0 во всех ячейках;
2) определение h через поле скоростей по (8.14) (как для
П<1).
Рассмотрение МГД-турбулентности в настоящей книге ограни-
ограничивается, к сожалению, только изложенными методическими воп-
вопросами, так как в связи с большой трудоемкостью расчеты не вы-
выполнялись.
ГЛАВА ЧЕТВЕРТАЯ
МЕТОДИКА РАСЧЕТОВ
ОДНОРОДНОЙ ТУРБУЛЕНТНОСТИ
В СТРАТИФИЦИРОВАННОЙ СРЕДЕ
В ПОЛЕ СИЛЫ ТЯЖЕСТИ
4.1. Вводные замечания
Стратификация среды оказывает существенное влияние на турбу-
турбулентность в морях или океанах и в атмосфере. При этом в первом
случае изменение плотности среды (воды) по вертикали определя-
определяется главным образом изменением содержания соли, а во втором
случае — изменением температуры х. Изменения плотности мож-
можно считать относительно малыми 2, т. е. если плотность предста-
представить в виде суммы р + Ар, то можно принять
Ар<р, A.1)
и во всех членах уравнения, кроме членов с архимедовыми сила-
силами, считать плотность среды приблизительно постоянной и рав-
равной р.
* Мы не рассматриваем здесь вопрос о влиянии изменения плотности воздуха
с высотой из-за изменения давления.
2 Для плотности воды в океане это справедливо всегда, а для плотности воз-
воздуха — с несколько меньшей точностью (и если рассматривать слой возду-
воздуха не очень большой высоты).
78
Сформулировать строго задачу об однородной турбулентности
в стратифицированной среде невозможно, так как если рассмат-
рассматриваемая среда заполняет все пространство и если (что необходи-
необходимо для однородности) везде имеется постоянный градиент средней
плотности, то на больших расстояниях изменение плотности полу-
получится большим; условие A.1) не будет соблюдено, и из-за пере-
переменности плотности жидкости однородность нарушится. Тем не
менее, используя некоторую схематизацию реальной ситуации
для слоев не очень большой толщины, полезно рассмотреть одно-
однородную турбулентность в стратифицированной среде. При этом
(что, как указывалось, внутренне противоречиво) мы примем во
всем пространстве свойства среды (включая плотность) постоян-
постоянными 3, используем условие A.1), ускорение силы тяжести будем
считать постоянным по всему пространству. Будет рассматри-
рассматриваться эволюция во времени турбулентности, созданная в указан-
указанной среде, в начальный момент времени. Несмотря на схематич-
схематичность и внутреннюю противоречивость описанной постановки за-
задачи, результаты ее рассмотрения могут приближенно использо-
использоваться для расчетов, близких к однородному турбулентных движе-
движений в океане или в атмосфере (где условие A.1) соблюдено, разме-
размеры турбулизованной области конечны 4, но во много раз превы-
превышают размеры турбулентных вихрей).
В настоящей главе рассмотрена только методика расчетов.
В связи с трудоемкостью соответствующих вычислений результа-
результаты их пока отсутствуют. Это задача дальнейших исследований.
Однако в качестве иллюстрации эффективности метода прямого
численного моделирования при решении задачи об однородной
турбулентности в среде с пассивной примесью удается использо-
использовать некоторые имеющиеся литературные данные.
4.2. Исходные уравнения
Обозначим р = р + Др — плотность среды. Уравнения количе-
количества движения и неразрывности имеют вид h
д2и.
B.1)
B.2)
Здесь gt — i-я компонента ускорения силы тяжести.
Подставим в уравнения B.1) и B.2) р = р + Ар. Получится
(с учетом того, что р = const)
3 Во всех членах уравнений, кроме членов с архимедовыми силами.
4 Точнее, даже размеры области (т. е. толщина слоя), в которой можно счи-
считать приблизительно постоянным градиент плотности.
1 Обозначения скоростей, давления и осей координат такие же, как в гл. 2.
79
ди. ди. ди. . ди.
pv . » +Apv . * , B.3)
<2-4>
Сравнивая с учетом A.1) в уравнении B.3) попарно однотип-
однотипные члены, содержащие р и Др, можно убедиться, что всеми чле-
членами с Ар в левой части B.3) и в члене с вязкостью можно прене-
пренебречь. Иначе обстоит дело с членом Apgt. Этот член, конечно,
много меньше члена pgt, но член pgt нужно рассматривать совме-
совместно с членом —dp/dxt: дело в том, что действие силы тяжести
на среду со средней постоянной плотностью р может быть пол-
полностью скомпенсировано соответствующим изменением давления
с высотой. Нескомпенсированными останутся только силы Ар&,
так как Др — величина переменная и скомпенсировать член Apgt
во всем объеме соответствующим изменением давления невозмож-
невозможно. Поэтому член Др#г в B.3) опустить нельзя.
Производя в B.3) указанные допустимые упрощения, пере-
перепишем это уравнение в следующем виде 2:
ди. ди.
р ^
Здесь обозначено
"Ро = р + р#*2; BЛ>
х2 — координата по вертикали, направленная вверх (т. е. против
направления ускорения силы тяжести).
В уравнении неразрывности B.4) отдельные члены имеют сле-
следующие порядки величины: Др/т, pw/L, Дри/L, Apu/L. Здесь и —
характерная скорость; L — характерная длина; т — характерное
время. Если изменение Ар происходит вследствие движения сре-
среды, то т ~ L/u; при этом первый из указанных членов имеет по-
порядок Apu/L.
Как видно, отношение любого из членов в B.4) к члену, содер-
содержащему р, имеет порядок величины Ар/р <^ 1, поэтому всеми чле-
членами в B.4), кроме члена с р, можно пренебречь. Из B.4) полу-
получается
дик/дхъ « 0. B.7)
Замкнутая система уравнений должна содержать, кроме B.5)
и B.7), еще уравнение для Ар. Как указывалось, Ар изменяется
из-за изменения температуры среды Т или концентрации какой-
либо примеси (соли в воде, в океане) с. При малых Др зависимо-
При этом примем для определенности, что ускорение силы тяжести g на-
направлено вдоль оси х% в отрицательном направлении, т. е. gt = —g$2i.
80
сти между Др от Т или Ар от с являются линейными:
Ар = - *т (T - Гв), B.8)
Ар = хсс, B.9)
где хс может иметь любой знак (но в случае раствора соли в воде
хс^>0); То — температура, которой соответствует «невозмущен-
«невозмущенная» плотность р.
Изменение температуры Т описывается следующим уравне-
уравнением:
.? + «, *L)««cp ** B.10)
at к дх^ ] р дх1сдхтс
а / а а
Здесь cv и ср — удельные теплоемкости при v = const и при
р = const соответственно; а — коэффициент температуропровод-
температуропроводности среды (так что рсра — коэффициент теплопроводности).
В B.10) в правой части опущен член с тепловыделением из-за
трения, так как для рассматриваемой задачи (турбулентное дви-
движение) он пренебрежимо мал.
Изменение концентрации примеси с3 описывается следующим
уравнением:
дс , дс ъ д2с /О л л v
где D — коэффициент диффузии рассматриваемой примеси.
Умножая уравнение B.10) на х^ и принимая во внимание, что
То = const и хт = const, получим с учетом B.8):
Умножая уравнение B.11) на хс и учитывая, что хс = const,
получим
l^+Ub°*L=D-p?-. B.13)
dt » дх^ дхкдхк У /
Оба полученных уравнения — B.12) и B.13) — можно пере-
переписать в единой форме следующего вида:
" + и
"^г~ + ии ~1г^ = G "л—т— » B-14)
д? к д^ь дх.дх. ' v 7
а а а
гДе 6? равно ас, /сс в одном случае, и G = D в другом случае.
Таким образом, расчет должен производиться по системе урав-
уравнений B.5), B.7) и B.14).
Осредненное значение скорости <w^> в любой точке равно нулю
(так как оно было равно нулю в начальный момент и нет измене-
изменения количества движения, определяемого граничными условия-
Величина с безразмерная. Она определяется как отношение массы рассмат-
рассматриваемой примеси в каком-либо элементе объема к общей массе среды в этом
объеме.
8!
ми,— такова постановка рассматриваемой задачи). В то же время
осредненное значение <^Др]> отлично от нуля — в этом и состоит
стратификация среды.
Обозначим
<Ар> = Лр0 B.15)
и будем считать Ар0 заданной функцией только координаты хг
(«высоты»). Для обеспечения однородности должно быть
dApo/dx2 = Е = const. B.16)
Представим Ар в следующем виде:
Ар = Ар0 + Дрт, B.17)
где Дрт — пульсационная (турбулентная) составляющая Ар.
Подставляя B.17) в B.14) и учитывая B.16), получим
—
= G-щ^- . B.18)
Преобразуем также уравнение B.5), изменив при этом опреде-
определение B.6) величины р0. Для этого подставим в B.5) Ар в ви-
виде B.17). Сумма первых двух членов в правой части B.5) с учетом
B.6) после такой подстановки приобретает следующий вид:
? — Apo?S2i — ApTg82i. B.19)
Здесь в соответствии с B.16)
Аро = Ех% + F, B.20)
где
F = const = Ар0 (х2 = 0). B.21)
Если ввести для р0 вместо B.6) следующее определение:
Ро = Р + Р№ + Fgx* + Egx\l2, B.22)
то члены B.19) запишутся так:
-(dpo/dxt) - ДрЛ. B.23)
В уравнении B.5) нужно при этом заменить Ар на Дрг. Полу-
Получится,
Р at
ди{ диА /)Пл л . д%и,
к
Приведем уравнения к безразмерному виду. Для этого отне-
отнесем все скорости к некоторой характерной скорости ихар; все
длины — к характерной длине LXSiV; время — к характерному
времени LXap/^xap; давление (и величину р0) — к рг4ар; Арт и
Ар0 — к величине р (так, что Е должно быть отнесено к /г,хар)-
Обозначим безразмерные величины теми же символами, которыми
обозначались соответствующие размерные величины. После таких
S2
преобразований уравнения B.7), B.24) и B.18) приобретают сле-
следующий вид:
дщ/дхъ = 0, B.25)
где Fr = gLxap/uiap; B.27)
Re = uxapLxap/v; B.28)
МРт <?ДРт ! а»АРт
-5Г + и* -д^Г + "^ = Т5" ^цГ ' ( }
где
Ре = uxapLXap/G, B.30)
т. е.
ИЛИ
Ре - ИХар?хар/Я B-32>
в зависимости от определения величины G (см. выше).
Напомним еще раз, что в уравнениях B.25), B.26) и B.29)
все величины безразмерные. Дальнейший путь преобразований
следующий: необходимо, пользуясь уравнением неразрывности
B.25), преобразовать второй член слева уравнения B.26) к виду
дщщ/дхъ и второй член слева уравнения B.29) к виду дщАрт/дхк',
необходимо затем проинтегрировать все указанные уравнения па
объему Ах, Дг/, Az некоторой ячейки расчетной сетки с номе-
номерами по осям х, у и z соответственно п, т, q и разделить на этот
объем.
Обозначим среднее значение / по объему ячейки п, т, q (/),г, W} q.
Обозначим </>n-72. w,q среднее значение / по левой (по оси х)
грани ячейки тг, иг, q; </X+v2, w, q — среднее значение / по правой
грани; <f>n,m-y2,q и </>n, m+Vt. g ~~ то же> п0 левой и правой гра-
граням соответственно по оси у; </>n, m, g-v2 и </>n, m, q+v. — Т0 же,
do оси z. Если величина / — это парное произведение каких-либо
величин, в частности / = игщ, то, очевидно, что, например:
Чо, т, q — {^i)n+V25 m, q (икУп+Ч2, т, q + <
B.33)
гДе величины щ и ^к определяются мелкомасштабной («подсеточ-
ной») турбулентностью. После интегрирования по объему ячейки
й Деления на этот объем из уравнения количества движения B.26)
с Учетом B.33) получатся следующие соотношения для различных
°сей координат (аналогичные уравнениям гл. 2, но отличающиеся
от них дополнительным членом в правой части в одном из урав-
уравнений):
^r)-y2, m,g ^Ц^п-У2, m, g ~~ ч*Уп+У2, т,дя"^п+У2, т, д
>„, m_y2, g <w2>n, m_x/2, g — (и1>п, m+y2,
Ai
, <ц<ц9>п, w-Vf, q — <ц{ц8>л, m-J/,, q t
п, пг,
+
Az
/n+t/2, m, q
A*
г, m-Vit q ^Po^n, тп+*/2> q
Re ( A# L\ dx /n+y2, m,g \ dx /п-У2, m,q
f
Az L\ dz /n,m,g+4z \ dz q4\)
B.34)
Из уравнения неразрывности B.25) после интегрирования по
объему ячейки и деления на этот объем получается следующее
соотношение:
1 1
-дТ" КЦк>ти-*/«. w»» в — (ихУп-У21 m, q] + -д^" [<^2/>n, m+V«, q —
— (иу)п, »i-y,,q] И" "дТ"^^'7' т'^+1/г— (uz)n, m,q-y2] = 0-
B.35)
Из уравнения B.29) после таких же преобразований получа-
получается
g^дТ У2, ш, q \Ml/n-Vt, mt
— <ApT>n+y2, m, q (ЦхУп+Чг, т, д] +
S4
[<ЛР>п, т-Ч2, q O2>n, т-У2, q
— <Лрт>п, m+V2, q <^2>n, m+y2t q] +
+ ~д^~ LS^pT/n, m, g-»/2 \u3/n, m, g-72
— <ApT>n, m, q+Vi (^з)^, г», g+»/2] ~f~
+ -57- [<ApUl>n-V2, m, g — <Ap^l>iH-V., m, g] +
+
1 / ^ / /
[<Д> <АР>п, r»i, g+V«]
Pe \ As |_\ dx /n+*/«.m,g \ 0s /n-V2, rn, g
Az L\ 0z /n,m,g+V2 \ 02 /n, rn,g-V2
B.36)
Последние члены (с коэффициентами I/Re и 1/Ре) в B.34) и
B.36) далее учитываться не будут, так как будет рассматриваться
случай Re ^> 1 и Ре ^> 1. Выше эти члены были выписаны только
для того, чтобы представить уравнения в более общем виде (для
возможных будущих расчетов случая не очень больших чисел
Re и Ре).
4.3. Аппроксимация отдельных членов уравнений,
преобразования сеточных уравнений и порядок расчета
Определим приближенно средние значения (различных величин
на границах ячеек следующим образом:
xf/n-1/*, m,lq ~ /2 (/n-1, m, q ~Г /п, т, q)->
\//n+Ve» ™i g ~ /2 (fn+l, m, q ~h /n, m, g)>
M^n, тп-Va» g ~ /2 (/л, m-l, g + /n, m, g)?
\f/n, W+V2» g ^^ /2 (/n, rn+l, g ~b /n, m, g)»
\J/n, m, q-xj2 ~ /2 (/n, w, g-1 + fn, m, q)t
\J/n, m, g+V2 ^ /2 (/h, rn, g+1 "Г /n, m, g)*
Здесь / — любая величина (но не парное произведение величин).
Члены с мелкомасштабной турбулентностью (т. е. парное про-
произведение величин со штрихом в B.34)) определим так же, как это
было сделано в разд. 2.7 [формулы G.8)—G.16I. Члены типа
^A>n+i/2> m, q в B.36) определим по следующей приближенной
85
формуле:
— — С [(Арт)л+1, m, q — (Дрт)п, m, q] | Юдеф | г C.2)
п+1, m, q
01 н
п, rn, q
где С = const > 0, а последний сомножитель определяется так
(см. разд. 2.7):
| Юдеф | = | (Ид)п+1, m, g — (их)п, т, q \\- C.3)
п+1, т, q
оти
/г, m, q
Аналогичным образом определим члены <Api^>n, m+v2, q и
On, m, q+V2-
Величина С является константой, определяющей влияние мел-
мелкомасштабной турбулентности на перенос массы. Как и величи-
величина А (см. гл. 2), она может вычисляться в процессе расчетов.
Таким образом, примем в B.36):
>„+¦/„ m, q~ — C [(ApT)n+1, m, q — (Арх)„, m, <,] | (ttjn+l. п., « -
K)n,m,g], C-4)
• n, w+1/2, q '^ ^ L\ Рт)п, m+1, q (^Рт/п, m, qj J \^2/n> m+1, q
» w, q| ?
, q+i/2 Ж — С [(Лрт)п, m, q+1 — (Дрт)п, m, q] | (М8)п, m, q+1 —
(^з)п, m, q I •
Аналогичные величины, в которых в индексе записано п —
— 1/2, т, q; п, т — 1/2, q или п, т, q — 1/2, определяются по
формулам типа C.4) с уменьшением соответственно п, т или q
на 1.
Запишем уравнение B.34) в виде, аналогичном C.1) (гл. 2):
d (Ui)n, m, q/At = (Мг)п, т, q — Fl' (Арт)п, m, qS2i + (Ri)n, m, q- C-5)
оДеСЬ уШ. i)n, m, q :== (¦* i)n—V2, m, q — (-^ i/n+V2> w, q ~r \^i/n, r>i—1/2, q
\^*^i/n, m+ /2> q i" \xi/Ti, tn, q—J/2 V4:i/n, w, q+ /2' \ /
величины /^, Фо ^ определяются по формулам C.6)—C.11)
гл. 2 (или после подстановки членов с мелкомасштабной турбу-
турбулентностью — по формулам A3.1)—A3.18) гл. 2); обозначение
(Rt)n, m, q использовано для следующей величины:
+ 2Дг/ [(Po)n, rn-l, q (Po)n, m+1, q] +
+ ~9ЛТ~ [(Po)n, m-g, I (Po)n, m,q
86
где величина р0 включает в себя, кроме указанных в B.22) состав-
составляющих, также «турбулентное давление» р? (см. определение
\и\щУ в гл. 2).
Обозначим
(#,)n, m,q = (Щ)п, m,q + [(Mt)n, mt q ~ Fr (Дрт)п, m, gS2i] Af, C.8)
где A? — шаг по времени.
При прямом методе интегрирования из C.5) получается с уче-
учетом обозначения C.8):
(Щ)(п!т\ = (Щ)п, т, q + (Щи, т, qM, C.9)
где верхний индекс t + At отмечает величину в следующий мо~
мент времени (на следующем временном шаге).
Скорости (Mj)n,+m?g должны удовлетворять уравнению нераз-
неразрывности B.35). Подставляя (щ)%*т\ в виде C.9) в B.35), полу-
получим уравнение для р0У совпадающее по виду с уравнением A4.1)
гл. 2:
(Ро)п, т, q = а1 [(Ро)л+2, т, q + (Ро)п-2, m, q] + а2 [(ао)п, т+2, q +
+ (Ро)п, т-2, q] + аз [(Ро)п, т, q+2 + (Ро)п, т, q-2] + Fn> m, q-
C.10)
Здесь аи а2, а3 и Fnt m, q определяются по формулам A4.2) и A4.3)
гл. 2.
Обозначим Sn, m, q правую часть уравнения B.36) (без члена
с коэффициентом 1/Ре). Тогда из B.36) следует
= (Api)n, m, q + Sn, m, qAt. C.11)
Из B.36) с учетом C.1) и C.4) получается следующее выраже-
выражение дляЗ^, m, q:
&п, т, q = Tn^i/2i m> q Tn+yti ш> q +
+ •* n, m-xf2,q Yn, m+Vj.q + %п, m, g-Va ^n, m, q+V*e C.12)
Здесь
Tn+y2, m, q = Д^" [(Арт)п+1, m, q + (Apr)n, m, q] [(^i)n+l, m, q +
+ (^i)n, w, g] д-J" [(ApT)n+l, in, g — (ApT)n, m, g] | (^i)n+.i, m, g —
— K)n, m,g|, C 13)
Yn, m+V2, a = Д^~ [(ДРт)п, m+1, g + (ApT)rif m, g] X
X [(U2/n, m+1, q + (^2)«> m, g] д— [(ApT)n, ?n+l, g —
— (ApT)n, 77i, g] | (U2)n, m+i, q — (U2)nt m, q \ , C-14)
%n, m,g+V2 = ^д7-[(АрТ)п, t»i , g+1 + (Арт)л, m,q]X
[(из)п, m, g+1 + {иъ)п, m, q] д^~ [(ApT)n, m, g+1
(ApT),if m, q] | (as)n, m, q+l — (u3)nt m,q\. C.15)
87
Величины Tn-*/t1 m, g, 5^п, w-Vf. g и ^n, w, g-v2 определятся no
C.12)—C.15) с уменьшением и, w или q на 1, т. е.
^n-V2. ™, 9 = ^(n-lHVs» m, gi
Уп, m-Ve. Я. = Yn, (m-l)+V2, q» C .16)
%п, rn, д-»/г = ^п, m, (g-l)+Vt*
где величины в правых частях вычисляются по C.12)—C.15).
При расчетах однородной турбулентности в стратифицирован-
стратифицированной среде должны использоваться такие же начальные и гранич-
граничные условия, как и для других, рассмотренных ранее, случаев
однородной турбулентности: в качестве граничных условий необ-
необходимо использовать (и для щ и для Дрт) условия периодичности
с периодом, равным размерам рассчитываемой области течения
[условия 2.3.1]; начальное поле скоростей может быть задано слу-
случайным по изложенному в разд. 2.4 и 2.11 методу; начальное по-
поле Дрт также целесообразно задать случайным, используя анало-
аналогичный метод. Для этого, кроме «разыгрывания» Л|х) и А^ по
B.4.20), необходимо в тех же ячейках расчетной сетки х опреде-
определить еще две случайные величины g*1) и ?B> (равномерно распре-
распределенные в интервале 0 -г-1) и найти в этих ячейках случайные
значения Дрт по формулам [аналогичным B.4.20I:
Дрт = Дртх) + Дрт2\
где Др(т1} = fed) (?<!> — 0,5); Дрт2) = (&W/2) (?<2> — 0,5); C.17)
величину Ы1) можно приближенно определить заранее, задавая
значение У <ДртХ которое желательно получить:
Wl> « 4 /<Др2т>. C.18)
В промежуточных ячейках расчетной сетки, в которых Дрт5>
не «разыгрывается» (см. разд. 2.4 и 2.11), эта величина определя-
определяется с помощью интерполяции между «разыгранными» значения-
значениями по формуле, аналогичной B.11.15):
^ m, q = ар + 6Р (л — пг) + ср (т — т±) + gP(q — qx) +
+ гр(п — пг) (т — т±) + 5Р (п — пг) (q — q±) +
+f/p (m — т2) (q — qx) + h9 {n — n±) (m —[щ) (q — q±). C.19)
Напомним, что случайные величины А^ «разыгрываются» только в тех
ячейках, в которых пу т, q = 8, 16, 24, . . ., N; величины А& разыгры-
разыгрываются в каждой ячейке расчетной сетки. Можно разыгрывать Ар^ и не
в тех ячейках расчетной сетки, в которых разыгрываются А^\ а в более
редко или в более часто расположенных ячейках. Это повлияет на началь-
начальные значения интегрального масштаба турбулентных пульсаций плотности.
88
Здесь
Ср
gp
: ар = (А
= Ve[(Ap
= Ve[(Ap
= Ve[(Ap
/Л 1
т/п2, т1?
т)щ, т2,
h)nl mlt
i> l.
Qi
Qi
T2
-(Ap
чA)
'т/т- wi.
т)п!, fflj,
qiJy
Tl];
C.20)
C.21)
C-22)
C.23)
*. ».,.*]; C-24)
*p = Vm [(Дрт)(". n... e, + (Apr)!?. m, a, - (ApT)i,V. .»„ «. -
-(WnV.»...«,]; C.-25)
/p = V«4 [(ApT)nV, m,. g2 + ^ UV
C-26)
« ,„„ „ + (ApT)(nV, m,, 4l +
-(Apx)^, ,„„„]• C.27)
В этих формулах величины п^ mx, g^i и ^2» m2» ^2 определяют-
определяются по формулам A2.13) гл. 2:
тгх == 8 entier (w/8); 7тгх = 8 entier (щ/8); qx = 8 entier
гс2 = wi + 8; етг2 = га! + 8; q2 — Qi + 8. C.28)
Во всех ячейках, в которых индексы п, т, q составлены из
числа Пц т^ qt, n.2, m?, q2, величины Лр^ «разыгрываются по
C.17) 2.
Общий порядок расчетов в рассматриваемом случае сохраня-
сохраняется в основном таким же, как описано в гл. 2. Отличия состоят
только в следующем:
1. Задание начального поля не только ut, но и Арт.
2. Определение с помощью итераций не давления р, а величи-
величины р0. Эта величина, как указывалось, должна удовлетворять
Уравнению C.9). Итерации проводятся в том же порядке, как
и при расчете р в разд. 2.13, при этом используется соотношение
вида B.13.4):
(Po)n?m, q = A СО) (ро)п, т, q + (Оп± [(рО)п+2, т, q + (Ро)п-2, т, q] +
+ СОа2 [(ро)п, т+2, q + (Ро)п, т-2, q] + ^^3 [{Ро)п, т, q+2 +
+ (Ро)п, т, q-2] + ©/'п. т, д, C-29)
где (о — итерационный параметр, определяемый по A4.5) гл. 2#
Подробнее формулы типа C.19)—C.27) пояснены в разд. 2.11.
89
Ввод исходных данных
Программа № 1: Определение исходных
скоростей и исходных величин Арт
Программа № 2* Определение (%) „ m t
Программа № 3: Определение (р0 ) п т q
I
Программа № 4: Определение новых (щ)п.т q\
Увеличение номера s шага по времени ка 1
да
,0
0
0
Программа №5: Расчет всех <ы, 2 > и <Дрт2 >
Программа № 6: Определе-
Определение А, С; статистичес-
статистических величин поля скоростей
и Дрт; проверки
L
Программа №7:,
определение <Ро
е, е,- и d/dt (Ар*
проверка <р0)
Рис. 4.1. Укрупненная блок-схема программы расчетов турбулентности в
стратифицированной среде
Давление р может быть найдено при известном р0 по следую-
следующей формуле, получающейся из B.22):
р = Ро - Fr (I + F/p) x2 - (Е/2) Fr x\ - рт. C.30)
Здесь F определяется по B.21) (в отличие от B.22) формула C.30)
приведена к безразмерному виду); величину рт можно оценить
только приближенно.
Однако нет необходимости определять р на каждом временном
шаге. Для расчетов нужна только величина р0. Если требуется,
можно для некоторых моментов времени найти р по C.30).
90
3. Необходимость определения, кроме одной ранее использо-
использовавшейся константы А, характеризующей влияние мелкомасштаб-
мелкомасштабной турбулентности, второй константы С, входящей в C.4).
Методика расчета С рассматривается в следующем разделе.
4. Определение некоторых дополнительных статистических
характеристик турбулентности. Представляет интерес, в частнос-
частности, найти:
а) <Ap?>/?2Zy, где Е — величина, определяемая по B.16);
1У определяется по формуле A0.9), гл. 2;
б) зависимость <^|>/<^> и ljly или (u\yi(uly и ljly от Fr
и времени (при изотропном начальном состоянии турбулентности);
в) i^Uy)IEly Y<4>;
г) коэффициенты корреляции величин Арт в различных точ-
точках, удаленных друг от друга вдоль осей х, у и z, соответствую-
соответствующие интегральные масштабы турбулентности.
Расчеты интересно выполнить для положительных и отрица-
отрицательных значений Е.
Укрупненная блок-схема программы расчета приведена на
рис. 4.1. В основном она аналогична (за исключением перечислен-
перечисленных отличий) схеме на рис. 2.1, поэтому все пояснения, сделанные
к рис. 2.1, относятся также к схеме на рис. 4.1.
Заметим, что для решения задачи об однородной турбулент-
турбулентности в стратифицированной среде, требуется конечно несколько
больший объем памяти ЭВМ (и несколько большее время счета),
чем в случае отсутствия стратификации. Это связано с необхо-
необходимостью расчета и запоминания поля Арт.
4.4. Определение коэффициента С
(в членах, описывающих мелкомасштабную
турбулентность)
Формулы C.4), в которые входит коэффициент С, являются при-
приближенными; их точность может быть подтверждена только сопос-
сопоставлением результатов расчетов с опытными данными. Тем не ме-
менее можно попытаться оценить наиболее подходящее значение ве-
величины С. Для этого введем в рассмотрение, как и при определе-
определении А в гл. 2, более крупную расчетную сетку, отличающуюся
°т исходной тем, что в ней увеличен в 2 раза шаг по всем осям
координат. Отметим ячейки этой крупной сетки индексами а, |3,
V» являющимися порядковыми номерами этих ячеек вдоль осей
хт У и z соответственно. Каждая из целых величин а, |3, у изменя-
изменяйся в пределах от 1 до N12. В ячейку а, |3, у укрупненной сетки
входят 8 ячеек исходной сетки, в которых п = 2а — 1 и 2а, т =
^ 2р — 1 и 2|3, q = 2у — 1 и 2у (см. перечень этих ячеек в
РазД. 2.9). Введем следующие обозначения:
2а 2Р 2V
( 2Л /п. rn,q= S 2i ^J fn,m,q, D-1)
(аа, р, у) я=2а-1 m=2p-l q=2v—1
91
где /Л| m, q — любая величина в ячейке п, т, q исходной расчетной
сетки; (wf)a, p, v — средняя по объему ячейки а, |3, у скорость щ;
(Арт)а, р, v — средняя по объему ячейки а, |3, у величина Дрт;
(»*%, р, V = (ui)a, Р, V — (Й*)а, р, т» ГДв (И|)а, р, V ~ Мгновенная
скорость иг- в любой точке в ячейке а, р, у; (Др-г)а, p,v =
= (Арт)а, p,v — (ДРт)а, р, v» гДе (ДРт)а, р, v ~ ВвЛИЧИНа Дрт В ЛЮ-
бой точке в ячейке а, р, 7; (^/)п, m, g = Щ — (Ui)niYrijq, где uf ->
скорость в любой точке в ячейке тг, т, g, a (w,-)n, w, g, как и ранее,-^
средняя по объему ячейки п, т, q величина ut; (ApT)n, m, g ~ Дрт —
— (Дрт)п, w, g9 где Дрт относится к любой точке в ячейке п, т, qy
а (Дрт)п, т, д» как и ранее, средняя величина Др? в этой ячейке;
JV/2 N/2 N/2
S =222, D-2)
(a, p,v) a=ip=lv=l
JV iV JV
2 = 2 2 'S • D-3)
(n, «/, q) ??-— 1 m—1 q=l
Ясно, что
{Й,)а, Р> V = Vs S (^i)h, m, g, D.4).
<aa, P, V}
а, p, V = Vs 21 (Дрт)п, m,g. D.5>
Найдем среднее по объему всей рассчитываемой области зна-
значение величины Дртггг- для i = 1, 2, 3. Эту величину можно опре-
определить двумя способами, используя соответственно исходную или
укрупненную расчетные сетки (обозначим соответствующие сред-
средние значения <Дртг/^> и <Дртгг^> ).
Подставляя в произведения Дрт^г величину Дрт в виде
(Дрт)п, m, g -г (Дрт)п, щ, g (Для ячейки п, гп, q) и м? в виде
(И*)п,г>ьд + (мОп.тп.д» ПОЛуЧИМ
<ДртМ^> = -ууГ У^ {(Дрт)т7, m, g(M|)n, m, g + <Дрт^>п, m, g} , D-6)
/~ (n, m, g)
где <ДрТгг^>п, 77Ь q — среднее по объему ячейки п, т, q значение
произведения (Др;)п,?7ъд (и*)п,т,д.
Проведем далее преобразования для i = 1, а затем по аналогий
запишем формулы для i = 2 и ? = 3.
Обозначим <Дрт^1>х среднее значение Др^-ui по площади сече-
сечения ячейки /г, т, q плоскостью х = const. Ясно, что
m, q = Дд:ДуД2 ^ (Дрт)гг, m, g (^i)n, m, g dF =
D.7)
92
(Уп, т, g>
(*)л
гпе символ (Уп, m, q) под интегралом обозначает интегрирование
jjo объему ячейки п, т, q; (х^)п и (х2)п — значения координаты х
соответственно на левой и правой (по х) границе ячейки п, т, q.
Если аппроксимировать <Api'^i>x линейной зависимостью от
х то из D.7) получится
>п, т,
l)n_i/#> rn, g + (&pTUi>n+l/2, m, g}* D*8)
Здесь использованы ранее применявшиеся индексы п — 1/2, т, q
И Т1 Ч~ '21 ^' ?•
Это выражение для <Арт14>п,т, q нужно подставить в D.6) (для
i = l). Величины в фигурных скобках в D.8) определяются по
первой формуле C.4) [с уменьшением п на 1 для первого слагаемо-
слагаемого в D.8)].
Совершенно аналогично получаются формулы для i = 2 и i =¦
= 3.
Таким образом, можно записать:
у 1
(n,~m, q)
9
(n, тп, g)
^i>n+i/2, w, JJ ,
|(Арт)п, m, q (U2)n, m,q+
)
(
a, iiit q \из)п, т, q
(п, ??г, д)
+ 2
Здесь все величины в квадратных скобках определяются по C.4)
или по формулам такого же вида, в которых п, т или q уменьше-
уменьшены на 1.
При использовании для расчетов <ApTWi> укрупненной сетки
вместо D.9) получается:
/К ч 8 V4» Г/Т" ч /- ч
чАрт^з.> =-д^г 2^ [(АртК р, v(ul)a. P.V +
2 (а> Р» V)
1 ,,т-'-
— «Дрт»1>а-7.. Р. V + <ДртйЬа+»/1. Р. ?)]•
8__
(a,p,v)
>a, p_J/2, v + <АртЙ2>а, p+V«, v)]' D.10)»
2^
(а, 3,7)
-1-«ДртЙз>а, р, v-V. + <ЛртЙз>а. р, 7+V*)] •
Величины <Дрт&г> здесь должны определяться по формулам
типа C.4), отличающимся от C.4) только заменой везде ut на uiy
Дрт на Арт, п на a, га на |3, g на у, а также по аналогичным форму-
формулам с уменьшенными а, C или у на 1.
Обозначим fof = (ДртС/^) — <АртС/^>. D.11)
1 2
При подстановке в формулы D.9) и D.10) выражений типа
C.4) величины bt получаются линейно-зависящими от определяе-
определяемого нами коэффициента С:
bi = ai + C(V D.12)
После соответствующих (указанных выше) преобразований
для at и р^ получаются следующие выражения:
ai ~ ~дгГ ^У (Арт)п, т, q \Ui)n, m, q
(n, m, q)
(a, p,v)
(a, 3,7)
— (Ui)cc-l, p, V I + [(АРт)а+1, p, V — (Арт)а, p, vl I (^l
(n, m,q)
— (ApT)n_t, m, q] I (U^n, m,q — (^i)n-l, m,q\
— (ApT)n, w, g] I Юп+l, m, q — K)n, m, g | }, D'14)
(a, p,v)
— (Й2)а, p-1, V I + [(ApT)a, p+1, v — (ДРт)а, p, y\ \ {щ)а, p+1, v —
— (Й2)а, p,v|}— 2Д^ ^ {[(Арт)п, 7П, g — (Арт)п, m-i, q] X
(n, m, q)
X I (^2)™, rn, q (U2/n, m-l, q \ + [(Арт)п., m+1, q
— (Дрт)*!, m,q]\ (U2)n, w+1, 4 — (И2)п, m. 4 | }^ D-15)
= "Ж Щ ^(^PT)a' P V — (Дрт)а, p, 7-l] I (»8)a, 3,7 —
(a, p,7)
— (»3)a, 3, 7-1 I + [(ДРт)а, 3, 7+1 — (ДРт)а, 3, 7] I (йз)а, 3. V+l ~
— (пз)а,^у\}—^РР ^j ([(ДРт)п,т,4 —(ApT)n, m,q-l]X
(n, m,g)
X I (Ы3)п, m,q — (Щ)п, m, q-1 | + [(Арт)п, m, g+1 —
— (Арт)п, m, q] | (^3)n, m, q+1 — (щ)п, m, g | }• D-16)
При правильности формул C.4) величины <Дртг^> и
должны были бы быть равны друг другу. В связи с этим опреде-
определим С из условия минимума следующего параметра П:
П - Ь,^. D.17)
Подставляя сюда bt в виде D.12) и приравнивая дП/дС нулю,
найдем
С = —alb, D.18)
где
а = а?Г, Ъ = р,р|в D.19)
Вычисления величины С могут быть проведены на любом шаге
расчета по времени, когда известны поля иг и Дрт. Порядок вы-
вычислений прост.
1. Последовательно для каждой ячейки n, m, q определяется
h,m,q — величина, стоящая под знаком 2 D-13)—D.16) и эта
п, т, ф
величина складывается с суммой таких же величин для ранее уже
рассмотренных ячеек. После перебора таким образом всех ячеек
л, т, q общая сумма делится на N3 (для первого члена в D.13)) или
на 2N3 (для D.14)—D.16)).
2. Затем последовательно для каждой ячейки а, р, у находят-
находятся ut и Дрт по D.4) и D.5) и вычисляется фа, p,v» гДе фа, р, v —
величина, стоящая под знаком 2 в D-13)—D.16); эта вели-
(а, р, Y)
чина складывается с суммой таких же величин для ранее уже рас-
рассмотренных ячеек. После перебора таким образом всех ячеек а,
Р, у общая сумма умножается на коэффициент, стоящий перед ней
в D.13) или D.14)—D.16) (т. е. на 8/7V3 или 4/iV3).
3. Затем вычисляются все at и (Зг по D.13)—D.16), величины
ажЪио D.19) и С по D.18).
Расчет С не нужно делать, конечно, на каждом шаге по вре-
времени.
4.5. Краткое рассмотрение
некоторых результатов расчетов,
приведенных в работе [23]
В разд. 4.1 уже указывалось, что в настоящей главе излагается
только методика расчетов; результатов расчетов, достаточных для
анализа, пока нет. Однако для случая, составляющего часть рас-
рассмотренной задачи, имеются опубликованные данные [23]. Речь-
иДет о прямом численном моделировании крупномасштабного
Изотропного турбулентного движения при наличии пассивной
95
<(т. е. не влияющей на плотность среды) «примеси» в жидкости.
«Примесью» может быть, в частности, и температура среды, и кон-
концентрация какого-либо растворенного вещества. Если эта «при-
«примесь» мала, то влиянием ее на плотность можно пренебречь. В ра-
работе [23] в соответствии с этим не учитывается действие архимедо-
архимедовых сил, и турбулентность остается изотропной в течение всего
рассматриваемого при расчете промежутка времени. Поэтому
исследованная в [23] задача не совпадает с описанной в настоящей
главе. Однако общие черты у этих задач имеются: в [23] решается
-фактически та же система уравнений \ которая использовалась
нами в предыдущих параграфах, но без архимедовых сил в урав-
уравнении количества движения. При этом, конечно, может быть по-
получена только менее богатая информация, так как отсутствует
влияние стратификации и поля силы тяжести на динамику движе-
движения. В то же время хорошие результаты, полученные в [23], подт-
подтверждают возможность эффективного решения задачи с прямым
численным моделированием не только движения жидкости, но
и динамики изменения турбулентного поля пассивной «примеси».
Поэтому в настоящей главе представляет интерес дать краткое
описание некоторых результатов работы [23].
Члены, зависящие от «подсеточной» турбулентности, в работе
123] записываются в виде, близком к использованному нами (но
не совпадающем). Входящие в эти члены константы рассматрива-
рассматриваются как эмпирические; их значения подбираются так, чтобы по-
получилось наилучшее согласование расчетов и опытных данных.
Методика расчетов в [23] предусматривает определение трехмер-
трехмерного спектра пульсаций скорости и температуры. Начальные ус-
условия задавались в спектральной форме.
Для сравнения с расчетом использовались отфильтрованные
{т. е. сглаженные в пределах заданной длины) опытные данные
работы [31]. Как и в опытах, вместо зависимости от времени t
различных величин (которая рассчитывалась) представлена за-
зависимость этих величин от х/м, где х — продольная координата;
м — размер ячейки решетки, генерирующей турбулентность (при-
(принято, как и в опытах, м = 40 мм, продольная скорость потока
4,06 м/с). Начальные спектры скорости и температуры п (х/м) =
= 25 задавались совпадающими с экспериментальными. Ниже
на нескольких рисунках, заимствованных из [23], приведены ре-
результаты расчетов с подробными оптимальными значениями эмпи-
эмпирических констант 2 и их сравнение с опытными данными.
На рис. 4.2 приведены результаты расчетов кинетической энер-
энергии крупномасштабной турбулентности V2 (и]} и величины <92>*
тде 0—-пульсация температуры (также крупномасштабная). На
1 Но с сохранением членов с вязкостью и теплопроводностью.
"* Следует отметить, что результаты расчетов, как и следовало ожидать, не очень
чувствительны к некоторым (не слишком большим, конечно) изменениям
констант.
<0Z>-/0 Z
00
/0
fff
40
20
I i I i I i I i I i I i—
J0 40 60 S0 /0#z/*
/
40
00
Рис. 4.2. Зависимость от времени кинетической энергии турбулентности 4%
<и?> A) и среднего значения квадрата интенсивности пульсаций концентра»
ции пассивной примеси <02> B) по данным работы [23]
а — при 16*'узлах сетки; б — при 328 узлах сетки; отфильтрованные эксперименталь-
экспериментальные кривые; О — численный эксперимент
/f2
-г
S---
Pi
i 1
Ш
/
Рис. 4.З. Отфильтрованный экспериментальный спектр пульсаций скорости
(а) и температуры (б) при х/М = 46,5 и результаты расчетов по данным рабо-
работы [23J
- отфильтрованная экспериментальная кривая; О — результаты расчетов
этом же рисунке представлены отфильтрованные эксперименталь-
экспериментальные значения указанных величин.
На рис. 4.3, а показан отфильтрованный экспериментальный
спектр пульсаций скорости при х/м = 46,5 и соответствующие
Результаты расчетов.
На рис. 4.3, б представлены аналогичные данные для спектра
пУльсаций температуры.
В. м. Иевлев
97
Из приведенных данных видно, что прямое численное модели-
моделирование изотропной турбулентности с пассивной «примесью» дает
хорошо согласующиеся с опытом результаты. Нет сомнения, что
такими же удовлетворительными должны получиться расчеты при
учете архимедовых сил.
ГЛАВА ПЯТАЯ
МЕТОДИКА И НЕКОТОРЫЕ РЕЗУЛЬТАТЫ РАСЧЕТА
КРУПНОМАСШТАБНОЙ ТУРБУЛЕНТНОСТИ
В ПРИСТЕНОЧНЫХ ТЕЧЕНИЯХ
5.1# Вводные замечания
При построении методики расчетов пристеночных течений необхо-
необходимо учитывать следующие обстоятельства.
1. Размеры основных энергонесущих турбулентных вихрей
возрастают при удалении от стенки зоны потока, в которой про-
проводится расчет. Поэтому целесообразно выбирать переменный шаг
расчетной сетки по нормали к стенке. Переменный шаг также по-
полезен и в других направлениях (так как вихри увеличиваются
при удалении от стенки во всех направлениях), но особенно важно
принять переменность шага по нормали к стенке. В связи со ска-
сказанным в дальнейших расчетах принимали, что шаг по нормали
к стенке у непрерывно изменяется, а в двух других направлениях
(х и z) изменяется ступенчато (каждый раз вдвое), так что вся об-
область течения жидкости фактически разбивается на слои, в каж-
каждом из которых Ах и Az постоянны, а Ау изменяется.
2. Можно было бы (в простейших вариантах расчетов) прово-
проводить численное моделирование крупномасштабной турбулентно-
турбулентности только в «ядре потока», т. е. вне некоторого слоя у стенки («ло-
(«логарифмического»). При этом приближенные граничные условия
пришлось бы формулировать на верхней границе этого присте-
пристеночного слоя, считая, например, течение в нем квазистационар-
квазистационарным. Такой подход позволяет в принципе рассмотреть потоки
сложной геометрической формы х, но не позволяет, конечно, рас-
рассчитать собственно пристеночный слой. Первая работа по чис-
численному моделированию крупномасштабной турбулентности в ка-
канале [19] была так и построена. В работе [20] также использова-
использовались такие же граничные условия, в ней было выполнено преобра-
преобразование уравнения к случаю цилиндрической геометрии, впервые
введена модель для подсеточной турбулентности.
С такими же граничными условиями рассматриваются задачи
0 неоднородной турбулентности в обзорной статье [18], причем
1 Предполагается, что геометрическая форма потока должна в первую очередь
влиять на крупные вихри в «ядре потока», а течение в тонком пристеноч-
пристеночном слое может при этом оставаться универсальным.
,98
аяализ охватывает и тепловую задачу, и случай шероховатой
стенки, и-течение жидких металлов.
В другом, наиболее полном варианте построения методики рас-
расчетов рассчитываемая область охватывает все течение (от стенки
до Другой стенки при течении, например, в плоском канале).
Такие расчеты предъявляют очень высокие требования к быстро-
быстродействию и объему памяти используемых вычислительных майин,
поэтому они могут быть выполнены только как эталонные, для не-
немногих случаев. Детальный анализ течения в плоском канале
с таким полным подходом выполнен в [21] (см. также: [16] — [32]).
Приводимые ниже формулы и результаты расчетов отличают-
отличаются (как уже указывалось в разд. 1.1 и во Введении) от отмеченных
выше в двух отношениях:
а) делается попытка рассчитать отдельно пристеночный слой
и «ядро потока) и «сшить» эти зоны друг с другом. Первый шаг
в этом направлении — расчет пристеночного слоя без расчета «яд-
«ядра потока» (с некоторыми эффективными граничными условиями
на внешней границе этого слоя);
б) подсеточная турбулентность определяется без использова-
использования эмпирических констант, что пока еще не делалось ни в одной
из опубликованных работ по крупномасштабному моделированию
турбулентности (см., например, сравнение результатов расчетов
с разными моделями подсеточной турбулентности в [22]).
3. Различные пристеночные течения (течения в каналах с раз-
разной формой поперечного течения, пограничный слой на стенке
и др., в том числе и более сложные по своей геометрической форме
течения) имеют общие черты, относящиеся к тонкому слою тече-
течения жидкости у стенки. В связи с этим с методической точки зре-
зрения целесообразно рассматривать тонкий пристеночный слой
в первую очередь в наиболее простых типах течений, имея в ви-
виду, что принципы, отработанные при таких расчетах, должны
быть пригодны и для других, более сложных течений. В этой гла-
главе в качестве такого простого типа течения исследуется напорное
течение между двумя плоскими пластинами.
5.2. Рассматриваемые задачи и расчетная сетка3.
Рассмотрим несколько конкретных постановок задач. Хотя эти
задачи на первый взгляд кажутся частными примерами, они, как
уже было указано в разд. 5.1, в действительности составляют ос-
основу для исследования общего случая произвольного пристеноч-
пристеночного течения, так как движение жидкости в тонком слое у стенки
всегда в большой мере универсально.
Задача № 1. Напорное течение несжимаемой жидкости меж-
ДУ параллельными бесконечными плоскими пластинами. Выбе-
Выберем систему координат с осью х (х = хг) вдоль направления ос-
Редненной скорости (рис. 5.1), ось z (z = x3) направим параллель-
параллельно пластинке и перпендикулярно к направлению осредненной
скорости. Ось у при расчетах для нижней половины канала (т. е
4* 99
от нижней стенки до пунктирной линии отмечающей срединную
плоскость) принимается направленной от стенки вверх. При рас-
расчетах для верхней частц канала (от верхней стенки до срединной
плоскости) ось у направим вниз, перпендикулярно стенке. На
срединной плоскости скорости должны будут «сшиваться» с уче-
учетом изменения направления оси у (т. е. при этом и2 изменяет знак,
а их и и3 остаются неизменными).
Ячейки расчетной сетки примем прямоугольными. Вся об-
область течения разбивается на отдельные слои, перпендикулярные
оси у. Размеры ячеек расчетной сетки не изменяются вдоль осей
/////л
Рис. 5.1. Схема канала
'/////////////////////////////////////
х и z в пределах каждого слоя и изменяются вдоль оси у. Номер
ячейки далее отмечается тройкой чисел тг, т?г, д, где п — номер
вдоль оси х\ т — вдоль оси у; q — вдоль оси z. Размеры ячейки
п, /л, q: Ахт, Ауш, Azm. Индекс т при Ах и Az в ряде случаев бу-
будет опускаться (так как в пределах любого из слоев течения Ах
и Az не зависят от ттг). Величины Аут везде вне «ламинарного
подслоя» у стенки выбираются в 2,5-гЗ раза меньшими длины
пути смещения Прандтля. Величины Ахт в «ламинарном под-
подслое» и в «логарифмическом слое» принимаются в2-^3 раза боль-
большими, чем Ауш (так как продольный масштаб турбулентности
больше поперечного), а величины Azm — в 1,3-т-2 раза больши-
большими, чем Аут. В приосевой зоне разница размеров ячеек по раз-
различным осям уменьшается.
Далее все формулы будут записаны только для нижней поло-
половины канала. Ясно, что формулы для верхней половины канала со-
совершенно аналогичны.
Как уже указывалось, в каждом слое, на которые разбивает-
разбивается все течение, Ах, Az = const.
При переходе из слоя в слой величины Ах и Az изменяются
вдвое, поэтому на границе слоев каждая крупная ячейка верхнего
слоя граничит с четырьмя ячейками соседнего (нижнего) слоя
(с двумя вдоль оси х и с двумя вдоль z).
Разбивку течения на слои и выбор размеров ячеек удобно сде-
сделать, используя безразмерные координаты, так как в таких коор-
координатах известна толщина «ламинарного подслоя».
После перехода к безразмерному виду координата у будет (см.
ниже) заменена координатой г) = yvjv, где у отсчитывается от
стенки; и^ — «динамическая скорость»; соответственно вместо
&Ут будет использоваться Ar\m = Ayujv. Обозначим также
(Аг\х)т = Axmvjv И (AT)z)m = Azmvjv (пОЗЖв будут ИСПОЛЬЗО-
100
Таблица 5.1
т
ДЛт
(ДЫт
(Дг]г)т
г) на верхней
границе
ячейки
т
Д^т
(Дт1л;)т
(Af|z)m
1] на верхней
границе
ячейки
1 2
1 1
2 2
1,5 1,5
1 2
19
7
16
12
49
Слой
3
1
2
1,5
3
4
1
2
1,5
4
Слой
20
8
16
12
57
21
9
16
12
66
№ 1
5
1
2
1,5
5
№4
22
10
16
12
76
6
1
2
1,5
6
23
12
16
12
88
7 8
1,5 1,5
2 2
1,5 1,5
7,5 9
24
13
16
12
101
9
4
3
10,Е
25
15
32
24
116
Слой №
10
2
3
3
> 12,
26
17
32
24
133
11
2,5
4
3
5 15
27
19
32
24
152 '
2
12
2,5
4
3
17,5
Слой
28
21
32
24
173 1
13
3
4
3
20,5
29
23
32
24
96
Слой
14
3,5
8
6
24
5
30
25
32
24
221 :
15
4
8
6
28
31
26
32
24
247
№ 3
16 17 18
4 5 5
8 8 8
6 6 6
32 37 42
32 33-
26 27
32 32
24 24
273 300
ваны другие обозначения). Для случая, когда на оси г) = 300 (это
соответствует числу Рейнольдса течения в канале около 9000 *),
можно принять, например, величины Дг]т, (Дг]х)т и (АгJ)т, при-
приведенные в табл. 5.1.
При такой разбивке на ячейки (довольно крупные) на одну
ячейку в приосевой зоне приходится по всей ширине канала
(в обоих его половинах) 4962 ячейки.
Если выбрать для расчета зону длиной (по х) и шириной (по z)
по 10 ячеек в приосевой зоне (что очень мало), то получится во
всей области расчетов 496 200 ячеек.i Если для повышения точ-
точности число ячеек по х и по z удвоить (что тоже будет на пределе
допустимого разбиения), то получится около 2-106ячеек. Таким
образом, даже такой простой случай течения очень труден (мало
реален) для расчета; ниже расчеты для этой задачи проводиться
не будут. Можно попытаться путем увеличения размера ячеек
Уменьшить их количество в 1,5 ч- 2 раза (но это, конечно, умень-
уменьшит точность расчета).
Задача № 2. Расчет для тонкого пристенного слоя с эффек-
эффективными граничными условиями (применительно к такому же те-
тернию, как в задаче № 1).
Примем такие же, как указано выше, величины Дт]™, (Д*)*)™
й (Ать)™. Ограничим рассчитываемую зону величиной т = 18,
т- е. г) = 43 (слои № 1,2, 3). При этом на одну ячейку в слое № 3
При расчетах для большего числа Re необходимое число ячеек расчетной
сетки возрастает не сильно — несколько слабее, чем In Re. Однако для пер-
вых расчетов мы выбираем все же указанное небольшое число Re.
101
приходится 153 ячейки. Если взять по 10 ячеек в слое № 3 по х
и по z, то получится всего 15 300 ячеек. Результаты расчетов с эф-
эффективными граничными условиями можно считать правильными
до г\у несколько меньших 43.
Эффективные граничные условия будут сформулированы позже.
Задача № 3. Решение задачи № 1 для слоев № 4 и 5 в обоих
половинах канала (см. табл. 5.1) со «сшиванием» с пристеночны-
пристеночными слоями у обоих стенок (со слоями № 1—3) с помощью эффек-
эффективных граничных условий (с использованием результатов расче-
расчетов задачи № 2).
Если взять 20 X 20 ячеек (по х и z) в приосевой зоне, то по-
получится всего 26400 ячеек. Если взять 30 X 30 ячеек по х и z,
то получится 59400 ячеек. Если удастся (в будущем) решить за-
задачу № 1, интересно будет сопоставить результаты этого решения
с расчетами задач № 2 и 3.
Может быть интересно разбить всю область не на две, а на три
части, «сшиваемые» с помощью эффективных граничных условий:
сначала рассчитывать слои № 1 и 2, затем № 3 и 4 (со «сшива-
«сшиванием» со слоями 1, 2) и затем слои 5 (со «сшиванием» всего в ка-
канале) — это задача № 4.
5.3. ^Исходные уравнения
и приведение их к безразмерному виду
Цспользуем в качестве исходных уравнения количества движения
с неразрывностью для несжимаемой жидкости:
+ + ( ]
Осредненное напряжение силы трения на стенке в рассматри-
рассматриваемом напорном течении (задача № 1) равно
где Ар — осредненное значение перепада давления на длине L.
Обозначая v# = "jAtct/p, получим
Ар = 2Lpi?/S. C.2)
Это соотношение будет использоваться при формулировке гра-
граничных условий для давления по оси х: при длине рассчитываемо-
рассчитываемого участка L = NAx (где N — число ячеек вдоль х в приосевой
зоне; Ах — их длина) давление в каждой точке конечного сечения
и в каждый момент времени примем меньшим давления в соот-
соответствующей точке начального сечения на величину Ар, опреде-
определяемую по C.2), т. е. для колебаний р относительно осредненного
значения используются условия периодичности с периодом, рав-
равным длине рассчитываемого участка, а осредненное значение р
уменьшается по длине в соответствии с C.2), Такие же граничные
102
^л будут использоваться для задач № 2, 3, 4. Они соответст-
соответствуют определению напорного течения. Ниже эти условия будут
сформулированы более подробно.
Выберем для приведения к безразмерному виду в качестве ха-
характерной скорости z;^, характерной длины v/i;*, характерного
времени — vlv\ и в качестве характерного ^[давления pv\. Таким
образом:
(М|)безр — М,/у#< (Ж*)бе8р ^fcy*/v> /Q Qv
[6.6)
Выразим в уравнениях C.1) все величины через безразмерные
в соответствии с C.3).
Опуская затем индекс «безр», получим
Вместо безразмерных а^, х2, #3 иногда будут использоваться
обозначения х, z/, z, так что г/ соответствует координате т|, введен-
введенной в разд. 5.2.
Соотношение C.2) в безразмерном виде (опуская индекс «безр»)
приобретает вид
Ар = 2L/8, C.5)
где б — безразмерная ширина канала.
В разд. 5.1 было принято, что на оси канала т] = 300, так что
для этого примера в C.5) б = 600 и
Ар = L/300, C.6)
где L, конечно, безразмерное.
Если, в частности, принять, как в табл. 5.1, в приосевой зоне
кх = 32 (в таблице это обозначено (Дт)ж)т) и выбрать рассчитывае-
рассчитываемую зону длиной в 15 ячеек по х, то получим L = 15-32 = 480.
При этом по C.6) получим Ар = 1,6.
В задаче № 2 разд. 5.1 рассчитываемая зона ограничивалась
ш = 18. При этом Ах = 8 (см. табл. 5.1). Если взять по длине так-
также 15 ячеек, то получим L = 8-15 = 120, и по C.6) Ар = 0,4.
Для того чтобы различные зоны в задачах № 3, 4 (разд. 5.1)
«сшивались», во всех случаях нужно Ар определять по C.6).
Уравнения C.4) будут далее использоваться в виде, проинтег-
проинтегрированном по объему ячейки расчетной сетки. Обозначим fn,m,q —
среднее по объему ячейки п, т, q значение любой величины /,
так что
S C-7>
^ячейьи
п, vi, q
Обозначим </>n+v2» ™,,q — среднее значение / по поверхности
границы между ячейками п, т, q и п + 1, т, q, аналогично
</>n> m-v«. я. — среднее значение / по поверхности границы между
ячейками п, т — 1, q и п, т, q и т. п.
Из C.4) после интегрирования по объему ячейки п, т, q по-
получится:
&(и)
AxAymAz lfom'q = <utui>n-yt, m, qAymAz —
— <^i>n+V2, m, qAymAz + (Щи^п, m_i/2, qAxAz —
— <MjM2>n, W+Vl, g&zAz + <и,и8>п, m,
— <ЩЩ>п, m, q+t/2AxAym + 6
— 8nAymAz <p>n+i/if m, g +
— <P>n, m+V,, g] + б«3Д^Дг/т [<P>n, m, g-V2 ~ <P>n, m, g+t/J +
+ AymAz ^xx^7-^n+i/2j m> ^ — Vdr-/n-v,, m, J +
\ f 9U*\ / dU*\ 1
1 C.8)
Л»/ A? [/it \ ,. /?/ \ 1, Л _1_ А'гА'Г Г/7/ \ •«/
2 ».«-•/.,« * J/m U,n,m.g+./, »,n. «.,-/, Cg)
Здесь индекс тга при Дж и Az опущен. Это допустимо, если урав-
уравнения C.8) и C.9) используются только в пределах одного из вы-
выделенных в разд. 5.1 слоев течения жидкости, в пределах которого
Ах, Az = const. Ниже будут отдельно рассмотрены уравнения для
ячеек, расположенных на границах слоев.
5.4. Аппроксимация отдельных членов уравнений
C.8) и C.9)
Обозначим </>*, m,q — среднее значение какой-либо величины /
по площади сечения плоскостью х = const любой ячейки со вто-
вторым индексом т и третьим q. Аппроксимируем распределение
</>х, w, q в пределах ячеек п, т, q и п -\- 1, т, q линейной зави-
зависимостью:
</>*, m,q~A + Вх. D.1)
Примем на границе рассматриваемых ячеек х = 0, имеем:
oj
1 Г* Ах
J п, m>q — дх \ \//х, m, q u«^ ^^ Л ¦?> 2 »
—Ах
Лх
Jп+1, т, q дТ" \ \//х, m, q CuC ^^ Д + ij ~ -1
LAX J
О
104
отсюда
, In, m, q ~Г /n+1, m, q
Л — g '
/ -/ D-2)
п Jn+1, m, g /n, rn, g
"Kx *
С учетом D.1) и D.2) получается:
'п, т, q • 'п+1, ?п, g
КТ/п+Уг, m, q — \\//я,?т, qfx=0 ^
<df \ \ д ... I J n+l, m,
В частности, при / = ut из D.3) получается:
<Щ>п+У2, m, g Ж V2 [Ып, m, g + (^f)n+l, m, q], D.4)
n+V2» rn, q A^:
Совершенно аналогично (если аппроксимировать </>*, m, g ли-
линейной зависимостью в пределах ячеек п — 1, m, q и п, m, q}
получится:
<Щ>п-у2, m, g Ж V2 [Mn, m, g + (Mf)n-l, m, g]5 D.5)
_ (ц|) ntmtq—(ц|) n-l,m,q
g Аж
Также получится (при линейной аппроксимации величины
\//п, m, g ):
<И*>п, т, g+V2 = V2 [(ui)n, m, g + (^f)n, m, g+l],
<Щ>п. т, g-Vo = V2 [Ып, т, g + (Mf)n> m, g-l], D.6)
/ \ ^ (Ui'n, m, q \uj)n,m,q
\ui/n, m, g+Ve ~ д^ *
. m, д+*/г Аг
Величины D.4)—D.6) входят в C.8) и C.9).
Если в D.3) принять / = р, то получим
/ v ^^ Рп, т, q "Г ^п+1, гя, g
\Р/п+1/2у m, g :::^ 2 *
Аналогично этому:
Pn-l, m, g "г Pn, m, g
^ти формулы можно было бы написать сразу, если бы /n? m? g и fn+li w> g
2 были величинами / в центрах ячеек, а не средними по объему ячеек.
"Де </>n, m, z — среднее значение / по площади сечения плоскостью z — const
лЮбой ячейки с первым индексом п и вторым т.
105
• \ Рп, т, а ' Рп, т, д+1
<Р>п, т, q+'/t ~ *-~2 —
m, g-1 ' ^n, m, g
2
С помощью D.3) можно определить и парные произведения
скоростей, входящие в C.8). Рассмотрим, например, величину
<WjMi>n+72. т. q- Представим скорость в любой точке на границе
участков п, т, q и п -\- 1, т, q в следующем виде:
(щ)п+1/2, т, q = ФпУп+У» т, q + (щ)п+У2, т, q- D.9)
Очевидно, что <^>n+i/2, m, q = 0. Учитывая это и используя
D.9) и первое из соотношений D.3) (для / = ut и для / = ггх),
запишем
(UiUl)n+42, m, q = (и^)п+У2, т, q (,ui)v+i/9, m, q + (иги1)п+*/г, т, q ^
~ U l(ui)n, m, q + (Ui)n+1, m, g] [(^l)n, m, g + (^i)n+l, m, g] +
+ <HiMOn+V«, m, g. D.10)
Совершенно аналогично получится:
<MiMi>n-V2, m, g Ж V4 [Wn-1, m, g + Ып, m, g] [(^i)n-l, m, g +
^ DЛ1)
, m, g-V2
^3/n, m,
, m. g+V2
^3/n» w,
«1
+ <Ui\
,11 \(lj
' /4 LV^
+ (u'ii
,11 T/j,
+ <Uil
^l)n-72, m, q,
i)n, m, g-1 +
^з)п, m, g-V2»
i)n, m,q + (U
l3/n, m,g+V2#
m, g] [(^з)п, m, g-1 4"
. g] [(^з)п, m, g +
Рассмотрим теперь средние значения различных величин на
границах ячеек, перпендикулярных к оси у. Внутри любого из
слоев, выделенных в разд. 5.1 (см. табл. 5.1), величины Ах и Az
не изменяются, и нужно учесть только изменение Ауш.
Обозначим </>п, у> q — среднее значение любой величины / по
ялощади сечения плоскостью у = const какой-либо ячейки с пер-
первым индексом п и третьим индексом q. Аппроксимируем зависи-
зависимость </>п, у, q от у в пределах ячеек п, т, q и п, т + 1, q линей-
линейным выражением
фп,у,д^А + Ву. D.12)
Примем в этой формуле у = 0 на границе рассматриваемых
участков. Получается:
о .
1 С У
fn, m,q = -Г7.— \ СОть 2/>д ^У ~ ^ В о '
т Аи
Ут+1
J </>п.*,^4 + я-^. D.13)
106
Отсюда
a tv,m,q У т+1 i *п, rn+1, q Ущ // л /\
D ^ un, тп+1, g мг, m,gJ // л с\
Из D.12)—D.14) следует:
/ df \^ ^ -п ^, ^ ^п>w+1» g ^n> m'g^
\ ^У /n, m+i/t> g ~ ~ Дг/гг + Аг/ш+1
В частности, если / = ut, то из D.15) и D.16) получается:
(ц) n, m, дАУт+1 + (Цг) п, т+1, дАУт
i)n, пи-»/,, g =
D.1
Аналогично этому получается:
2 [(»i)n, m,
При f = р из D.15) получается
/A 4
DЛ
Аналогично этому
n, m-V2, g
Представим скорость щ в любой точке на границе между участ
ками п, т, q и п, т + 1, q в виде, аналогичном D.9):
(^jc)n, m+Vi. q = <^fc>n, w+V«,:g + (ик)п, ?n+V?, g» D-21)
где, согласно D.17):
С учетом D.21) и D.22) получается
1
iui)ntm+l,q&ym]X
107
Аналогично этому получается
/д., ,
-х] X
X
D.24)
Выписанные формулы аппроксимируют все члены уравнений
C.8) и C.9) (кроме «турбулентных членов» типа (щщ}) внутри лю-
любого из слоев, выделенных в разд. 5.1. Аппроксимация величин
на границах ячеек, перпендикулярных осям хж %, пригодна и для
крайних рядов ячеек в слоях.
Рассмотрим теперь вопрос об аппроксимации различных вели-
величин на границах ячеек, перпендикулярных к оси z/, для крайних
Рис. 5.2. Схема расположения
ячеек
рядов ячеек в слоях (ряд т в нижнем слое, ряд т + 1 — в верх-
верхнем). При этом в соприкасающихся друг с другом ячейках (по
оси у) величины Ах и Az изменяются вдвое (см. табл. 5.1), так что
ячейка п, т + 1, q соприкасается снизу с четырьмя ячейками
(рис. 5.2).
Номера ячеек в слое т, очевидно, следующие:
для ячейки I 2п — 1, т, 2q — 1;
для ячейки // 2д, т, 2q — 1;
для ячейки /// 2п — 1, т, 2q\
для ячейки IV 2п, иг, 2д.
Нужно определить различные величины на границах ячеек
/, //, ///, IV с соответствующими частями ячейки w, m + 1> #•
Для этого нужно определить средние по объему значения величин
отдельно в каждой четверти ячейки п, т + 1> #•
Проведем необходимые вычисления для части ячейки п, т +
+ 1, д, соприкасающейся с ячейкой /.
Обозначим </>™у — среднее значение какой-либо величины /
в ячейках ряда т + 1 вдоль линии, параллельной оси у, т. е.
где у = 0 на границе ячеек рядов т и т + 1. Аппроксимируем
распределение величины </>??-Jiy в пределах ячеек п, т + 1, ?;
108
# — 1, тп + 1, g и п, /га + 1, q — 1 линейной зависимостью
/ rv ЛИН У ^^ л i^ d __|_ Z^. • // 9^4
\//m+l ^^^ -Л ~т" ^^ г ^^ ... у±> *-о)
(ячейки п — 1, и1 + 1»?ий,/w + 1, g — 1 взяты потому, что они
прилегают к той части ячейки п, т + 1, q, которая граничит с
ячейкой / ряда т). Примем в D.25) х, z = 0 левом нижнем углу
ячейки пу m + 1, q (по рис. 4.1). Имеем:
Ах Az
О О
О Az
Лэс О
5 J
О —Az
Здесь Ля и Дя — это A#m+i и Am+i.
Из полученных соотношений следует:
/n-1,
/„,m+]
/ 'n, m+1
m+1, g ~r
2
, g ' n,
L
m+1
m+1, g-1
,g-i -
Обозначим /n, m+i, g — среднее значение / по объему четверти
ячейки /г, т + 1, д, соприкасающейся с ячейкой / в слое т (см.
рис. 5.2). С учетом D.25) и D.26) получается (с некоторой поправ-
поправкой S см. ниже):
Ах/2 Az/2
О О
~ V4 [2/п, m+1, q + /n-1, m+1, q + /n,|m+l, q-l] + S. D*27)
Совершенно аналогично можно получить выражение для сред-
средних величин / по объемам других частей ячейки я, т + 1, д, со-
соприкасающихся с ячейками //, ///, IV в ряде т. Получается:
/n, m+l,q~V4[2/7i, m+1, g + /n, m+l,g-l + /n+l,m+l,g] + б,. D.28)
/n, m+1, q ~ /4 [2/n, m+1, g + /n-1, m+1,g + /n, m+l,g+l] + 6, D«-29)
/n, m+1, g ^^ V4 [2/n/m+l, g + /n.Jm+l^g+i + /n+1, m+1, g] + 6. D.30)
Поправка б введена в формулы D.27)—D.30) в связи с тем, что,
очевидно, требуется, чтобы было
/n, m+1, g = /4 \Jn, m+1, g 4" fn, m+1, g ~h /n, m+1, g ~b /n, m+1,
109
bv Без поправки б это соотношение в общем случае не удовлетво-
удовлетворяется 3.
Подставляя D.27)—D.30) в D.31), можно найти б. После под-
подстановки этого б в D.27)—D.30) получается:
/п, т+1, q — fn, т+1, qT /8 \fn-l, т+1, q ~Г fn, m+l,|g-l
— fn+1, m+l, q fn,m+l,q+i)i
fn, m+l, q = fn, m+l, q + /& (/n,rm+l, q-l ~\~ fn+1, m+l,q
— /n,m+l, q+1 — fn-ltm+l.q)i D.J2)
fn, m+l, q == / n,|m+l, q ~T~ /8 \fn-l, m+Mq г fn, m+l, q+1
P fn+1, m+l,q fn, m+l,q-l)-)
fn, m+l,q ~ fn, m+l, q \ /s \fn+l, m+l, q ~T~ fn, vii+l, q+1
/n-1, m+l, q fn, m+l, q-l) •
Для ячейки / (т. е. для ячейки 2п — 1, т, 2q — 1) можно вос-
воспользоваться формулами D.15), подставив в них вместо. fn,n+i,q
величину /n, m+i, q, определяемую по D.32). Аналогично можно по-
поступить для ячеек //, ///, IV. Для записи этих соотношений
удобно определить номер ячейки в ряду т + 1, граничащей
с ячейкой п, т, q. Обозначим этот номер nv т + 1, qx. В соответст-
соответствии с указанным (для ячеек /, //, III, IV) величина п должна
быть равна 2пг или 2пг — 1, а величина q должна быть 2q1 или
2дх — 1. Отсюда следует, что •
q± =;entier
Из приведенных ранее номеров ячеек /, //, ///, IV и из формул
D.32) видно, что все выражения можно свести к одной формуле
(ДЛЯ /n, m+l,q):
An,m,q) S^r , д, г, , е
/(nlt m+l, gt) — /nlf m+l, qt ~Г /8 Lyni+(_i)a5 m+1> Ql "Г /nj, m+1> g1+(-i)b
/n-(-l)a, m+l, qx /щ, т+1, qt-i-l)bv D.34)
где fnt] m+i]qt — среднее значение / по объему той части ячейки
ггх, т + 1, #i, которая граничит с ячейкой тг, ттг, д; 7гх и дх опреде-
определяются по D.33); а —• четное число, если п четное и нечетное, если
п нечетное;, Ъ аналогичным образом связано с q. Можно принять,
3 Условием удовлетворения D.31) является справедливость соотношения
'п, m+l, q ~ /4 (/п-1, т+1, q ~Г /п+1, т+1, q "Г Аг, т+1, д-1 ~Ь /n, m+l, q+1^ таК
что поправка б определяется кривизной поля величины / вблизи ячейки гг»
m + I, g.
НО
например:
а = 2пх — п, D.35)
b = 2q1 — q.
С учетом сказанного запишем формулы типа D.15) и D.16)
в следующем виде:
</> •/ ( "'
я, о г/(п, т, д)
dy/ntm+4t9q кут + Ау
где /n^w+i?g определяется по D.34), пх и дх по D.33), а а и Ъ по
D.35).
Если, в частности, / = Uj, то из D.37) получим
dui
где
(иг)щ1 m+l, qx ~ (Щ)пи\т+1, qt + Vs [(Wi)n1+(-l)«, m+1, qx
D.39)
При том же / = ut из D.36) получим
Для величины (щщУп, ту» q имеем
m+V2, q == (ui)ri, m+V2. ^ (U2)n, m+V2> g 4"
D.41)
Здесь <tt;>n, m+v2, g и <^2>я, m+v«, g определяются no D.40), а
(щщУ будет определено ниже.
При составлении баланса количества движения или массы
в любой ячейке гг, т + 1, q необходимо учесть взаимодействие
этой ячейки со всеми четырьмя ячейками в слое тга, с которыми
граничит ячейка п, т + 1, q. Поэтому в уравнениях C.8) и C.9)
на нижней границе ячейки п, т + 1, q соответственно члены пе-
переноса должны быть представлены в виде сумм четырех членов
(напомним, что речь идет о ряде т + 1 ячеек, который является
крайним нижним в слое по разд. 5.2).
111
5.5. Уравнение неразрывности
С учетом приведенных в разд. 5.4 формул уравнение неразрывнос-
неразрывности C.9), записанное для ячейки п, т, q внутри какого-либо из
выделенных в разд. 5.2 слоев течения, имеет такой вид:
Ay Az АхАу
5" [("l)n+l, m, q — (^l)n-l, m, q] H ТГ^ [(из)п, in, q+1 —
)n, m-l, дАУт + (Ш)п, m,
Для ячейки п, т, q, граничащей сверху с более крупной (по
х и z) ячейкой следующего слоя течения жидкости (согласно
табл. 5.1), уравнение неразрывности C.9) приобретает такой вид:
Ay Az AxAy
2 [(Wl)w+1, т, q — \ul)n-l, m, q\ ~\ g L(^3/n, m, q+1 —
(u) 1 [ ^^У1 + Ы^^АУ
п, m,
Здесь (u2)n^lmi-i!q определяется по C.39).
nx = entier [—%—) > Qi = entier (~^-%—) >
a = 2^ — д, b = 2qx — q.
Для ячейки п, т, q, граничащей снизу с четырьмя ячейками
другого слоя течения (с вдвое меньшими Ах и Az), уравнение не-
неразрывности имеет такой вид:
AymAz AxAy
\ [(Ul)n+1, m,q — (^l)n-l, m, q] H
(u\ 14- Ar\7
- (^ m. q-i] + AxAz
Aym
^[(
4 (Ay ^-^y Г [(M2)an-1, m-l, 2g-l + (^2J/1, m-1, 2q-l +
, л. ч , /w ч 1 ^^(Ч.т.д) _ Q
+ \ЩJп-1, m-l, 2g "Г Vw2/2n, m-l,2gj д7—_i_ д/у У — U.
ym "г" и»т-1 J
E.3)
5.6. Определение «турбулентных членов»
типа (u'tUj}
Воспользуемся таким же методом, который был использован для
однородной турбулентности, т. е. примем для ячейки тг, иг, q внут-
внутри каждого слоя течения жидкости, выделенного в разд. 5.2:
112
<«;»;>„«„», ,=ы»«„ ... а<- -i пг I <тё%., „,, |х
%Х,„. J
= (Рт)п, m+V2, a82i —
I
I \ ^ / n, m+Vt,
, m, g+V2 = (Рт)п, m, q+vAi — A -g- | <(-^>n m> g+1/> | X
2 F.3)
Величины ]АжВ при больших числах Рейнольдса должны быть
постоянными. Для пристеночного течения А и В являются функ-
функциями Re. Этот вопрос будет рассмотрен ниже. Формулы для
-у2, m,
можно получить из F.1)—F.3) соответственно путем уменьшения
во всех индексах п, т или q на 1.
Подставляя в F.1) аппроксимационные формулы для различ-
различных производных, получим
V2, m,q — A\ {u^n+Xi m,q — (^i)n, m, q \ X
X [Wmi, m, g — (Mjn, w,g],( F.4)
<>п+7!, то, g = 2" | ("i)n+l, m, g — («i)n, m, a | |(«2)n+l, m, g —
(KlV m, дДУт+1 + (»l)n, tn-H, gA^m ,
, m, , - 2Дут |_
)n+l, то, дАУггч-1 + Ы„+1,
(Ч, то,
3ul/n+1/2, m, q 2~ I V^l/n+lj m, q \ul)n, m,q | *j(^3/n+l, m, q
V^3/n, m, q i /l\~7_ L(^l)rc> w. 9+1 "T" \Ц±)п+1, mtq+l
F.6)
Аналогичные формулы с индексом п — 1/2, т, q получаются
F.4)—F.6) путем уменьшения индекса п на 1.
113
Из F.2) получается:
* / _ 4 I/ v / Ч if/ Ч
\И±И2/Пу m+V2> g 9~ I \^2/П, m+1, g \^2/n, m, q \ j y^i)nt m+1, g
(^l)n, m, g г /д 1(^2/71+1, m, g \u2)n-l, ?n, gj "T~
m
Ay 1
4Дт-— L(^2/n+l, m+1, g — (^2/n-l, m+1, gj >¦ » \P* • )
m J
\(^г) /п, m+y2t q == (Рт)п, m+Va» 9 ^1 (^2)n, m+1, g
/^ \ I Г/ц \ (U ) m ] F.8)
\М-з^-2/п, m+y2» g :=:: o~" I \^2/n, m+1, g \^2/n, m, g | "j \^3/n, m+1, g
Д г/
/7. \ i m r/7. \ /7/ \ "i I
V 3/tt» m,g "T~ / д L\ 2/n, m, g+1 ч^г/п, г>г, g—1J "I
Ay л
' m r/ \ / \ i I /a n\
~T~ "Тд L\ 2/n, m+3, g+1 4 2/n* m+l,g-lj > • \ *v
m J
Аналогичные формулы с индексом п, т — V2, q получаются
из F.7)—F.9) путем уменьшения везде т на 1.
Формула F.3) для различных i преобразуется к такому виду:
\Цх^З/п, т, д+4/г =: о~ I \^3/п, т, g+1 ч^З/п, т, g j i \^l/n, m, g+1
Д2
/7I \ _i_ m r/7/ \ _i /7/ \
V^l/n, m, g "г /д^ LV^S/^+l» m, g "r V^s/n+l, m, g+1
m
(^3/n-l, ?n, g (^3/n-l, m, g+lj Г » (О. lUj
n, m, g+V2 == 2~ I (^3)n» m» 5+1 \U3/n, m, g | X
(, , , v Az...
XJ (л \ ы Лу \ _J_
S 4 2/n, m, g+] \ 2/n» m,g ~r
,
п, т>
> w,
n, т, g+V2 — (Рт)п, m, g+V2 — ^ I (Цз)п, m, g+1 —
— Wn, m, g | [(^з)п, m, g+1 — (^3)n, m, g]. F-12)
Аналогичные формулы с индексом п, т, q — V2 получаются
из F.10)—F.12) путем уменьшения q на 1.
114
Приведенные в настоящем разделе формулы относятся, как
указывалось, к случаю, когда ячейка тг, т, q находится не в край-
крайнем ряду какого-либо слоя течения жидкости (из числа выделен-
выделенных в разд. 5.2 слоев).
Рассмотрим теперь случай, когда ячейка тг, т, q находится
в крайнем верхнем ряду слоя течения жидкости, т. е. когда ячей-
ячейки в ряду 771 + 1 имеют вдвое большие Ах и Az, чем в ряду 7?г.
Величины (Uiii2)n, m-v2, q определяются при этом по таким же
формулам, которые были приведены выше (т. е. по формулам
типа F.7)—F.9) с уменьшением везде т на 1). Сохраняются также
формулы F.4), F.6), F.10) и F.12), так как в них не входят ско-
скорости со вторым индексом т + 1. Во всех этих формулах Ах
и Az относятся, конечно, к ряду ячеек 77г.
Формулы F.5), F.7)—F.9) и F.11) должны быть изменены.
В этих выражениях все величины типа (&г)п, ™+и q должны быть
заменены величинами (Mj)n?w+i?gi» которые определяются по D.39)
с учетом D.33) и D.35). Таким образом, везде в указанных форму-
формулах должны быть записаны вместо величин {ut)a, m+i, v величины
iui)ax\ m+l, Vi = (иг)аи m+l, Vi+ Vs l(ui) ^
)at т»г+1, Vi ^
m+l, Vi (M*'Oi, rn+1, v1-(-1)b-''
F.13)
где
a± = entier (a^ ) ; y± = entier Cy "^ ) ; F.14)
a = 2a1 — a; 61=27! — y. F.15)
Величины а в различных из приведенных формул для (щщУ
равны тг, п + 1 или п — 1; величины 7 равны q, q + 1 или q — 1.
Такими они и должны подставляться в F.13)—F.15) (для каждой
величины типа (иг)а> m+i, у свои).
Мы не будем здесь переписывать получающиеся из F.5), F.7)—
F.9) и F.11) указанным способом формулы. При программирова-
программировании необходимо предусмотреть в них два способа вычисления ве-
величин ТИПа (Щ)а,т+1,у-
1) так, как записано в указанных формулах для ячеек внутри
слоя течения жидкости;
2) по формулам F.13)—F.15) для крайнего верхнего (по у)
ряда ячеек в слое.
Рассматривать подробно формулы для (ц1и'2уп, т-у2, q для слу-
случая, когда ряд ячеек т является крайним нижним в слое течения
жидкости, нет необходимости, так как этот случай выражается
через только что рассмотренный (с учетом того, что действие
какой-либо ячейки М на соседнюю ячейку N равно действию
N на М). При этом нужно только учитывать, что если ряд т ячеек
является крайним нижним (по у) в слое течения жидкости, то
ячейка тг, 7гг, q граничит снизу с четырьмя ячейками с номерами
(см. разд. 5.3) 2тг — 1,.т — l,2q — 1; 2тг, m — l,2q — 1; 2тг — 1,
115
т — 1, 2q; 2n, m — 1, 2g. Поэтому
-Ve, Я.
>
+ <^г^2>2п, (m-l)+72, 2gb F.16)
Здесь все величины в правой части определяются по F.7)—F.9)
с учетом F.13)—E.15) и с заменой т на т — 1.
Особых пояснений требует также определение в рассматривае-
рассматриваемом нижнем (в слое) ряду ячеек величин типа (ик)а, w_i, v в фор-
формулах F.5) и F.11) и в аналогичных формулах для <14м{>п_1/2, mg
и (и&зУп, m,q-y2 (т. е. в формулах, получающихся из F.5) и F.11)
при уменьшении п или q на 1); здесь а = п, п — 1 или п + 1
и у = q, q — 1 или q + 1. Величины (щ)а, m-i, у нужно заменить
величинами, осредненными по четырем ячейкам в ряду т — 1,
прилегающим снизу к ячейке а, т, у, т. е. в записи формул F.5)
и F.11) (и в записи аналогичных формул, получаемых при умень-
уменьшении п или g на 1) нужно сделать замену:
)а, m-l, v ""* Хи {(икJа-1, m-1, 2V-1 + (ukJa, m-1, 2Y-1 +
+ (^fcW-l, m-1, 2V + (^к)га, т-1, 2у}# F*17)
В программе нужно предусмотреть два указанных варианта
расчета рассмотренных величин для различных случаев.
Коэффициент А в приведенных формулах должен, как отме-
отмечалось, зависеть от Re турбулентных пульсаций. Эти числа Re
различны для разных мест потока и для процессов переноса в раз-
разных направлениях. Обозначим Rn+*/t, m, q число Re, которое бу-
будет использоваться при расчетах (щщУп+*и, m, q\ Rn, m+v*, q — число
Re, которое будет использоваться при расчетах
, т, q+i/t1
Примем:
Rn+4um, q = | (^i)n+l, m,q — (ui)n, m,g | A#m + I (
— (^2)n+V2> rn-y2i q | Аг/т + | (из)п+*/2, m, g+*/i —
— (Изк+72, m, q-Чг I &Zm = | (M^n+x, m, q — (^i)n, m, q \
Л " _L_ fr/Л
г, т, qL
l, m,
1 Величины <^Mj>n_,/2> m? можно определить как <w^j>(n_1)+1/ ^ m> и
величины \щиг>п_у2>msg можно определить i
аналогично для других направлений переноса.
116
F.18)
4-l(u\
91 2
г, m, q+1
(^l)n+l, m, g "
l .
m, q-l
m+lt q
+
X
X
| (^з)п, m,:q+l — (^з)п,|г
F.20)
Эти формулы пригодны при расчетах для ячеек, расположен-
расположенных внутри какого-либо слоя течения жидкости (из числа выде-
выделенных в разд. 5.2). При расчетах для крайних рядов ячеек не-
необходимо внести изменения. Если ряд т является крайним верх-
верхним рядом ячеек слоя, то в формулы F.18)—F.20) вместо (щ)а, w+1, v
А\
Рис. 5.3. Характер зависи-
зависимости А от Re
(где а = п, п — 1 или п + 1; у = q, q — 1 или q + 1) необхо-
необходимо записывать величины (иг){?1%$У1, определяемые по F.13)—
F.15).
Если ряд т ячеек является крайним нижним рядом ячеек
слоя, то в формулы F.18)—F.20) вместо (щ)а,-п-1,у (где а = /г,
п — 1 или дг + 1; у = q, q — 1 или q + 1) необходимо записать
величину, определяемую по правой части F.17).
Зависимость коэффициента А от Пе должна иметь характер,
показанный на рис. 5.3. При больших Re A = const, при Re -> 0
117
величина А должна стремиться к нулю. Такой характер зави-
зависимости А от Re может быть хорошо аппроксимирован формулой
А=А0A —е-®**), F.21)
где AOl Q = const.
Число Re в каждом случае здесь должно быть использовано
свое, т. е. Ren+Vt, rn, g при расчетах <Z7i#i>n+v«, m, g5 Ren, m+v2, дЩ>и
расчетах <?/i#2>n, ™+v2, q и Ren, w, а+1/2при расчетах (Ui U3yn, m, g+v2«
На начальном (по времени) этапе любого расчета величины
Ао и Q должны задаваться, а затем они могут определяться по
излагаемому ниже методу. По-видимому, Ао и Q будут практи-
практически постоянными для различных задач, и поэтому после накоп-
накопления опыта их можно задавать достаточно точно. Кроме того,
некоторая неточность в определении Ао и Q не должна сильно
влиять на результаты расчетов.
5.7. Уравнение количества движения
С учетом приведенных формул уравнение количества движения
C.8) для ячейки, расположенной не в крайнем ряду слоя течения
жидкости (по разд. 5.2), имеет следующий вид:
bxnbym\zm d("^'m'9 = (M()n, m. q + (Д,)п. m, g, G.1)
где
Rl)n, m, q = —2~ [Pn-1, m,q — Pn+l, m, q] ^mAym +
Pn, m, д^Ут+1 + PWt m+1, дАУт 1
,
, 6f3AxmA^m r^ n i. JG 2\
H 2 LPn, m, q-1 — Pn, m, g+lj, ^^/.^
сумма давления и величины рТ;
> т, g + (АФ,)п, т, q + (&Qi)n, m, g5 G-3)
m>
m, g = (^i)(n-l)+V2» пг, g — (^t)n+yit m, q\ G.4)
(АФ|)п, m, g = (Ф|)п, (m-l)+V., Q — (Ф,')п, m+V,. ^ G'5)
n, m,q = (Qi)n, m, (g-l)+V2 — (Qi)n, m,
m, g
(Фг)п, «,+«/„ g = b*mbzm \ <М{М2>„, „+»/„ q — \-jf\ +/ e }
G.8)
118
, m, g+t/, = ^mAym {<И<И8>П, w, q+y2 — <^
G.9)
С учетом D.4), D.6), D.10), D.11), D.17) и D.23) из G.7)—G.9)
получается:
(Fi)n+y2, m, q = Az/mAzm|1/4 [(щ)п, m, q + (щ)п+Ь m, q] [Wn, m, q +
+ (^l)n+l, m, gj + <^i^l>n+V2, m, q ~\ 1TZ f »
m
G.10)
п, 777+1, дАг/m] [(И2)п, 7П, д
п, »7i+V«, g Н д.. | д.. > 1 К'ЛЧ
ут "Г" ^»m+l J
V4 [Nn, m, g + (^г)п, т, g+l] [Wn, m, q +
_i /,. \ i /7/7/\ _i_ (Цг'п, т, q ^г^п, т, g+l)
-f- ^зМ, т, q+lj — \ЩЩ)п, т, q+y2 Н д- У •
т J
G.12)
Величины <^z^i>n+v2, т, g для различных i в формуле G.10)
определяются по F.4)—F.6), где А определяется по F.21) с под-
подстановкой в качестве Re величины Rn+ytt m, q no F.18).
Величины (щи2уп, m+v8, я в G.11) для различных i определя-
определяются по F.7)—F.9), в которых А определяется по F.21) с под-
подстановкой в качестве Re величины Rn,m+yttq по F.19).
Величины <Wi&3>n, *w,g+v« B G*12) для различных i определяются
по F.10)—F.12), в которых А определяются по F.21) с под-
подстановкой в качестве Re величины Rn,m,q+yt по F.20).
Рассмотрим теперь случай, когда ячейка гг, т, q, для которой
записывается уравнение количества движения, расположена в край-
крайнем верхнем ряду в каком-либо из выделенных в разд. 5.2 слоев
течения жидкости, т. е. ячейка гг, т, q граничит сверху (по у)
с вдвое более крупной (по х и z) ячейкой. При этом уравнение
G.1) сохраняется. В формуле G.2) необходимо заменить вели-
величину рПу m+lt q величиной p^w+i?^» определяемой по D.34), т.е.
необходимо сделать замену:
(n, m, q) . 1 г
Рп, m+1, q —> Рщ, т+1, q — Рщ, т+1, q И g~ [Pn1+(-l)at m+1, qt +
~i Рщ, т+1, gi+(-l)b Pni-(-l)a, m+1, qt Рщ, т+1, qt-(-i)bb G.13)
где пх и qx определяются по D.33), а и Ъ — по D.35).
119
Формулы G.3)—G.6) сохраняются. Сохраняются и формулы
G.10) и G.12), но при i = 2 во входящих в них величинах
<MWl>n+y2t m, q И <^з>п, m, q+72, ОПрвДвЛЯвМЫХ ПО F.5) И F.11),
и в числах Rn+i/2tm,q и i?n, m, q_i/2, определяемых по F.18) и F.20),
ВелИЧИНЫ (^j)a, m+1, v (гДе a = п или ^ + 1, У = q ИЛИ g + 1)
должны быть заменены величинами (иг)а m+i v, определяемыми
по F.13): '
Wa, m+l, Y -> К)Й,' m^V G.14)
В формуле G.11) и в выражениях F.7)—F.9) для (щи'2уп, т+у2, q
и F.19) для числа Rn, m+v2, q также должна быть сделана замена
G.14), в которой a = п, п + 1 или п — 1, у = g, g + 1 или
5 — 1.
Каких-либо других изменений в приведенных формулах для
применения их к крайнему верхнему ряду ячеек в слое вводить
не нужно.
Если ячейка п, т, q находится в крайнем нижнем ряду ка-
какого-либо слоя течения жидкости из числа выделенных в разд. 5.2,
т. е. если она граничит снизу (по у) с четырьмя более мелкими
ячейками, то уравнение G.1) также сохраняется. В G.2) нужно
записать в правой части в величинах в квадратных скобках после
8i2AxmAzm вместо рп, m-i, q следующее выражение:
Pn, m-l, q ~~> /4 * Р2П-1, w-1, 2q-l + Р2п, тп-J, 2q-l + Р2п-1, rn-1, 2q +
+ hn, m-1, 2q)' G-15)
Формулы G.3), G.4) и G.6) сохраняются. В G.5) вместо
(Ф!)п,(т-1)+»/»,« нужно записать сумму Ф^ по четырем ячейкам,
граничащим снизу с ячейкой п, т, д, т. е. сделать в G.5) замену:
,(m-l)+V2,2qf G*16)
Все указанные здесь в правой части величины (Фг)а, (m-i)+v2> v
определяются по формуле типа G.11) с заменой в ней т на т — I1
и с учетом G.14) (с уменьшением в этом соотношении щ на 1),
так как ряд ячеек т — 1 — крайний верхний в слое.
Формулы G.10)—G.12) для рассматриваемого случая (когда
ячейка тг, т, q в крайнем нижнем ряду в слое) сохраняются, но
при вычислении членов типа (щщУ, входящих в G.10)—G.12),
и чисел Re (нужных для определения А и В) должна быть сде-
сделана замена величин (Wfc)a, ,m-i, v соответствующими величинами,
осредненными по четырем ячейкам, граничащим снизу с ячей-
ячейкой п, яг, q. Эта замена определяется формулой F.17).
1 В том числе, конечно, заменой величин Ля = Ахт и Az = Azm величинами
АжШв1 и А2т_х (вдвое меньшими).
120
5.8, Сводка формул окончательного вида
Так как многие формулы, обсуждавшиеся выше, имеют разный
вид для рядов ячеек, расположенных внутри выделенных в
разд. 5.2 слоев течения жидкости, и для ячеек в крайних рядах
в этих слоях и в предыдущих параграфах соответствующие фор-
формулы не переписывались, а только указывались изменения в них
для различных случаев, то полезно во избежание путаницы при-
привести сводку полученных формул для разных расположений слоев
ячеек расчетной сетки (конечно, только для тех формул, которые
зависят от расположения ячеек). При этом (как и в разд. 5.7)
индексами т, т + 1 или т — 1 будут помечаться не только
размеры ячеек Аг/, но также и Ах, и Az, так как на границах
слоев течения жидкости Ах и Az изменяются (в 2 раза).
Формулы типа E.1)—E.3), F.5), F.7)—F.9), F.11), F.18)—
F.20) запишем в следующем виде г:
Az/ Az
™2 т [(u)n+ltm,q — (^i)n-l, m,q] +
И о [\u3/n,m,q+l \u3)n,m,q-l\ ~Г
(8.1)
n+V2» w, q = g~ I (Wl)rc+1> wi,q — (ul)n, m,q \ X
^2)n+l,m,g—(Щ)п, m,q
(8.3)
1 Формулы F.4), F.6), F.10) и F.12) имеют одинаковый вид для всех рядов
ячеек.
121
п. m+V,, q = В [(W2)n, m+1> q - (U2)n, m,q]2 —
— (M2)n, m, g | [(W2)n, m+1, g — (М2)п, m, q],
(8.4)
. g = 2" I (^2)n,m+l,q — (и2)п,т,д I X
X \(W3)n,m+1,q - (u3)»,m,
X
X
(8.5)
t г д r
2u3/n,m,q+1/2== g~ I \^3/n,m,q+l (^3/n,m,g | j (^2/n, rn, q+1
Az
^х +
,
(Ws)n,m+l,q+l
J J *
(i\G)n+i/2, m, g === I (^i)n+l, m, q (^l)n, rn, g | ^%m \
(8.6)
nt m, q
_lt q
1, rn,
, m, g
(^3)n+l,m,g+l — (^з)п,т,д-1 — (из)п+1, туд-1\ —Т^~ ' (8-7)
Уm
, q
2 (Aw -L At/ Г
^ Уm ' "rn+1/
— (l^i)n
-f Aym+1
I l(Ml)w+l»w»^ (^l)n-l,m,
X
X I К^З/ть т,д+1 (^з)^> тп, g-lj ^Ут+1 ~Т
+ [(W3)n, m+1, g+l — (W8)n, m+1, g-l] Aym \,
(8.8)
Az
en, m, g+i/2 = ^- I (^i)n+l, m,
g+l +
, m, g
122
"/l)n-l,m,q+l V^l)n-1, m,q | "i <¦> ^
[Nn,m,?+ Mn,m,g+1] Дут+1+ [(И/2)п, W+l,<;
X
[№)n)rn4)q+^i,m4,q+l]A^+[Wrt)m,g+Nn)ffi,g+l]AVl ,
- ¦ —4—
Здесь введены обозначения:
1) Для рядов ячеек, расположенных не на границах любого
слоев течения жидкости, выделенных в разд. 5.2:
г/сс, т-1,у ==z
» (8.11)
где а может быть n, n — 1 или n + 1; у может быть q, q — 1
или q + 1.
2) Для ячеек расчетной сетки, расположенных в верхнем
ряду любого из слоев течения жидкости:
l,y = (ui)a,m_1,y, (8.12)
1, у = (Mi)ai,'m+l,Vi = (ai)a1? m+l,Vi + Ve [(wi)ai+(_i) ^
m+1,Yl+(-l)b - WM-l)e, m+l,vi ~ <"«)<*, m+l,Vi-(-
2/a, m+l, 7 = (^2/at, w+l, Vi+1 (^2)^, w +1, Vi-1 1
+ Vs [(u2)alH-i)a,m+l1y1+l~^U^alH-l)ayrn+ity
где
аг = entier (-2^-); Yi = entier (-Ц^-); (8.16)
a = 2o! — a; b=-2y1 — y; (8.17)
^ или у те же, что указано выше.
123
3) Для ячеек расчетной сетки, расположенных в нижнем
ряду любого из слоев течения жидкости:
at w+lf v = (Щ)а, w+i, v, (8-18)
a, m-l, v — V4 i(uiJa-l, rn-1,2V-1 + (uiJa, m-1,2Y-1 +
(uiJa-l,m-1,2y + (^г)га, m-l,2v}> (8.19)
,m+l,g» (8.20)
m+l,g-b (8.21)
где a = n, n — 1 или n + 1; Y = <z; Я. — 1 или g + 1.
Выше выписаны формулы для величин (щи2Уп> т+у2, q- Что
касается величин (u'iu2yn, m-v2, q» то они определяются так:
1) для рядов ячеек, расположенных внутри любого из слоев
течения жидкости, выделенных в разд. 5.2, и для ячеек в верх-
верхнем ряду любого слоя:
<^2>n,m-V,,q— <^i^2>n,(w-l)+72.q; (8.22)
2) для ячеек расчетной сетки, расположенных в нижнем ряду
любого слоя течения жидкости:
, Я = Хи K^iW-2>2n-l, (m-l)+72> 2q-l +
(m-l)+72. 2q-l + (ЦгЩ^Ъп-г, (т-1)+72, 2q +
(m-l)+72,2g}« (8.23)
Для величин <гг2^>п_72, т, q и <^2^з>п, т, д-«/« во всех случаях
справедливы следующие формулы:
n-l)+V2,m,q» (8.24)
п. т, (д-1)+7г*
где величины в правых частях определяются по (8.1) и (8.5) соот-
соответственно.
Различный вид для разных рядов ячеек имеют, как указы-
указывалось в разд. 5.6, также формулы G.2), G.5) и G.11). Запишем
формулу G.2) для общего случая в следующем виде:
, m, q =
^— [Рп-Ъ т> Я. — Рп+1, т. q]
Aym 1
J
+ ^Х"/Ут [Pn,tm,q-l — Pn.m. fffl]. (8-25)
124
Здесь для рядов ячеек, находящихся не на краю слоя тече-
течения жидкости:
?n,m-l,g = Pn,m-l,g, (g26)
gn, m+1, g — Рп, т+1, д»
Для ячейки расчетной сетки, находящейся в верхнем ряду
любого слоя течения жидкости:
gn, m-1, q = Pn, m-1, g> (8.27)
(n,m,g) . 2/ i _i
gn, m+1, g = Pnj, m+1,qx — Рщ, m+1, gt i /8 JPrjt+(-l)«, m+1, gt T"
+ Pnt.Tn+l.ft+K-lN ~ ^г(-1Лт+1.д1"~ РП1, m+i.g^-iN], (8.28)
где
t»! = entier ( п~^] \; (8.29)
(8.29)
a = 2n-. — n:
Для ячейки расчетной сетки, находящейся в нижнем ряду
любого слоя течения жидкости:
gn, m-1, g = V4 (Р2п-1, m-1,2g-l + Ргп, m-1,2g-l +
+ P2n-1, m-1,2g + jP2n,m-l,2g)? (8.31)
#n, m+1, g = Pn,m+l,g» (o.o2)
Формулу G.11) запишем в следующей форме:
(Д ¦ д Г2 [(Mi)n> m, gAl/m+l +
/,/,/\ . 2KWi)n,m,g'~(^/i)n,m+l,g 1
-Г <MiU>2>n,m+*/ttq H д , д f
уrn ' ym+] J
где (И^г)п, m+i, g определяется по (8.10), (8.13) или (8.18) в зави-
зависимости от расположения ячейки гг, т, q расчетной сетки.
Формулу G.5) запишем для общего случая так:
, m,q = (Щп, m-V,. Q ~ Фп, m+V,, fl- (8'34)
Здесь (Фг)п,гг+1/2,д определяется по (8.33), а (Ф^)п, m-yttq —
Различным образом в зависимости от расположения ячейки /г,
fa, q расчетной сетки.
При расположении ячейки не на краю слоя течения жидкости
или на верхней границе слоя
(Фг)п, m-V2, g = (Ф{)п, (m-l)+V«, 5»
ГДе правая часть определяется по (8.33).
125
При расположении ячейки в нижнем ряду ячеек слоя течения
жидкости
(Фг)п, m-V2, д = (Ф0гп-1, (m-l)+V2, 2q-l + (ФгЬп, (m-l)+V2, 2q-l +
+ (ФгJп-1, (?n-l)+V?, 2q + (ФгЬгс, (rr>-l)+72, 2q- (8.35)
Здесь все величины в правой части определяются по (8.37).
5.9. Порядок расчета поля скоростей.
Уравнение для определения поля давления
Ниже излагается порядок расчета скоростей и метод получения
уравнения для давления, основанный, как и в рассмотренных
ранее задачах об однородной турбулентности, на развитии идей,
изложенных в работах О. М. Белоцерковского [24—26].
Используя явную схему для расчетов шагов по времени, по-
лучим из G.1):
(,. \(*+Д*) /7/ \ _j_ ( Уп, т, д д. , (Куп, т, q д . /q ^
[Щ)п, га, д ~ (Щ)п, т, q + At + At, (9.1)
т ут т т ут т
Здесь А^—-шаг по времени; верхний индекс (t + Д?) отме-
отмечает величину, относящуюся к моменту t + At; без верхнего
индекса записаны величины, относящиеся к моменту t. Обозна-
Обозначим
{Щ)п, т, q = {Щ)п, т. 3+ Гх^у\1 М' (9-2)
Тогда (9.1) перепишется в таком виде:
(Щ)п*т, q = (Mi)n, m, q + Д^Ду' Д2 Д** (9*3)
Для вычисления нг не требуется знания поля давлений.
Величина (мг)п*т?д должна удовлетворять уравнению нераз-
неразрывности. Подставляя (iOn,+m?g в виде (9.3) в уравнение нераз-
неразрывности (8.1) и определяя в (9.3) величину (Ri)n,m,q по (8.25),
получим после преобразований соотношение для определения
давления.
Для более компактной записи этого соотношения введем сле-
следующие обозначения:
оо 4 А
(?п)
а (Ау
(тп) 1
126
(т) =_
1
J '
01 «(т)Аут+1 (Аут+ Aym+1) L Aj/m+1 + А»т+8 Д</т + Д^т
(9.11)
Дут 1
Д^.^ Д^ J'
п, т, q / 7П
, 2
(9.14)
Здесь величины (?P2)n, ?n-i, q и (l^2)n, m+i, g определяются раз-
различным образом для ячеек расчетной сетки, расположенных
внутри любого слоя течения жидкости (из числа выделенных
в разд. 5.2 слоев), и для ячеек, расположенных в крайних верх-
верхнем и нижнем рядах в слое. Для (W2)n,vi-i, q и (W2)n,m+i,q долж-
должны использоваться следующие выражения:
1) при расположении ячейки п, га, q в слое течения жидкости:
(W2)nt m+l,q = («г)п, m+l,g» (^г)п, т-1, q = (м2)п, т-З.д'» (9.15)
2) при расположении ячейки п, т, q в крайнем верхнем ряду
слоя:
•(^2)п,т-1,д = (и2)п,т-1,в, (9-16)
+ (M2)nt>m+l,gi + (—1)Ь—(^^.^^ ?n+1 ,gi—(M2)nj,m+1,gi—( —IM],
(9.17)
гДе %, ql4 а и b определяются по (8.29) и (8.30);
127
3) при расположении ячейки п, т, q в крайнем нижнем ряду
слоя
(^2)n, m+1, q = (S2)n, m+1, q> (9.18)
(^г)п, т-1, q = V4 [(^2Jn-l, m-1, 2q-l + (^2J71, т-1, 2q-l +
+ (^2J71-1, т-1, 2д + (мгJп, m-l,2q]* (9.19)
В уравнение для расчета давления, кроме (W2)n, m-i,q и
(W2)n, m+i, q» входит еще ряд величин, определяющихся по раз-
разным формулам в зависимости от расположения ячейки п, т, q
(внутри слоя течения жидкости или вблизи от его границ), в част-
частности входят величины qU} m_i, q и gn, m+i, g, определяемые по
(8.26)—(8.28), (8.31) и (8.32), а также величины, которые мы обо-
обозначим Qn, m, g, КП) m, q, Ln, w, q, #n, m, g и J?n, m> g и которые опре-
определяются так:
1) при расположении ячейки п, т, q внутри любого из слоев
течения жидкости (кроме двух крайних рядов ячеек этого слоя
с каждой стороны, т. е. вверху и внизу слоя):
Чгп, in, q == Pn, m, qy Kn, m, q == Pn, m+2, g» -^п, тп, q == Pn, m-2, qt
(9.20)
"n, m, g == Pn,Jm+l, q» -"n, m, q == Pn, m-1, g>
2) при расположении ячейки га, т, q в крайнем верхнем ряду
слоя течения жидкости:
Ч?п, т, q ~ /4 [Рп+а-1, т, д+Ь-1 Ч" Рп+а, т, q+b-1 ~\~ Рп+а-1, т, q+Ь ~Ь
+ Pn+а, т,
' ^п+а+2(-1)а, т, д+Ь-1 "г Рп+а+2(-1)°-1, т, q+b "г
~Г Рп+а+2(_1)а, т, g+ь Н~ Pn+a-if т, д+ь+2(-1)ь-1 ~"~
"¦ Рп+а, т, q+b+2(-l)b-l "• ^«+а-1, т, д+Ь+2(-1)Ь '
"• Рп+а, т, g+b+2(-l)b ^п+а-2(-1)а, т, q+b
а-2(-1)°, т, q+b-1 ^п+а-2(-1)а-1, т, g+b
п+а_2(-])а-1, m,g+b-l Рп+а-1, т, q+b-2(-l)
а, т, g+b-2(-l)b-l Рп+а-1, m,g+b-2(-l)b
т,
, т, q = Pri!, m+2, qx + Vs [Pni+(_i)a, m+2, qt + Рщ, m+2, qi+(-l)b
— Pni-(-l)a, m+2, fll — Рщ, m+2, qH-D^' (9#22)
m,q = Pn, m-2,Iq» (9.23)
, rn, q = Р74, m+1, gt + Vs [Pni+(_i)a, mflf Qi + Рщ m+lf q1+(-l)b
Pni-(-l)a, m+1, qx Р
m, q = Pn, m-1, q5 (9-25)
128
3) при расположении ячейки п, т, q в крайнем нижнем ряду
слоя течения жидкости:
Qn, т, g = Рп, m, g, (9-26)
Kn, m, q — Pn, m+2,g> (9.27)
-^n, m, q = /4 Lp2n-1, m-2, 2g-l T~ P2n, гд-2, 2g-l i Ргп-l, m-2, 2g ~T~
+ Р2П, m-2, 2g]> (9.28)
Hn, m, q z=z Pn, m+1, qi (9.^9)
Rn, m, q = Vu [P2n-1, m-:i, 2g-l + P2n, rn-1, 2q-l, + Р2П-1, m-1, 2g "h
+ P2n, m-1, 2g]; (9.30)
4) при расположении ячейки п, т, q во втором от верхнего
края слоя течения жидкости ряду (в «предкрайнем верхнем»
ряду ячеек слоя);
Qn, mtq — Pn, m, q> (9.31)
Кп, m,q= Рщ, m+2, qt + Vs [jPni+(_Dat w+2, 3l + Рщ, m+2, gi+(-l)b
— Pni-(-l)a, m+2, qx ~" Pnt, m+2, g4-(-l)^' (9#32^
^n, m, q == Pn, m-2, g» ¦" n, m, g r:= Pn, m+1, qi -t^n, m, q z== Pn, m-1, q»
(9.33)
5) при расположении ячейки гг, m, g во втором от нижнего
края слоя течения жидкости ряду (в «предкрайнем нижнем»
ряду ячеек в слое):
Vп, m, q == Pnt m, q\ **-n, m, q == Pn, m+2, q> (У.о4)
-^д, т, g = /4 [Р2п-1, т-2,2д-1 + Ргп, m-2, 2q-l + Р2п-1, m-2, 2g +
~\~ Ргп, т-2, 2д]> (9.35 )
Hn, m, q =Я! Pn, m+1, g> -"n, m, g == Pn, m-1, g- (9.36)
В этих формулах, как и ранее, величины w2, qx, а ж b опре-
определяются по (8.29) и (8.30).
С использованием указанных обозначений уравнение для опре-
определения давления (т.е. уравнение неразрывности для (w*)n*m?g)
приобретает следующий вид:
Рп, т, q = #0 (Рп, т, q Qп, m, q) ~Т~ &1 \Pn+2, m, g "T" Рп-2, m, q) ~f"
"Г Л3 VPn, m, g+2 ~T~ Pn, m, q-2/ ~T~ a2 An, m, q~T °2 ^n, m, q~T
+ 6i Яп, ш, q + d[gn, m_X, q +
^n,m,g. (9.37)
Это уравнение справедливо для любого места расположения
ячейки п, т, q расчетной сетки.
4 В. м. Иевлев 129
Расчеты поля давления по (9.37) должны проводиться мето-
методом итераций (подробнее см. ниже).
5.10. Граничные условия
По х движение будем считать приближенно периодическим с пе-
периодом, равным длине рассчитываемой области. Связанная с этим
погрешность будет тем меньше, чем больше длина рассчитывае-
рассчитываемой области. Во всяком случае, эта длина должна быть много
больше размера наиболее крупных вихрей (в соответствующем
направлении). Опыт «численных экспериментов» должен показать,
насколько большой реально должна приниматься зона расчета.
Из принимаемых нами условий периодичности следует:
(ui)Nx+K, w^q^ (Щ)к, m, q>
/X / ч A0-1)
(U>i)n, m, Nz+r = \Щ)п, т, г>
где Nx, Nz — общие числа ячеек по х и по z\ к и г равны лю-
любому из целых положительных или отрицательных чисел или
нулю (т. е. к, г могут быть —1, 0, 1, 2 — больше не требуется).
Расчеты по приведенным в предыдущих разделах формулам
проводятся для всех п от 1 до Nx и всех q от 1 до Nz, при этом
при расчетах для крайних ячеек (по х и по z) значения величины
скорости за пределами расчетной зоны берутся из A0.1).
Граничные условия для давления по z имеют вид, аналогичный
A0.1):
(Р)п, т, Nz+r = (Р)п, т, г (Ю.2)
для таких же г, как в A0.1).
Граничные условия по оси х для давления должны учитывать
напорный характер рассматриваемого течения, т. е. наличие про-
продольного перепада давления, определяемого по C.5).
Обозначим Nx и Ах число ячеек по оси х и величину Ах соот-
соответственно в приосевой зоне течения в канале для задачи № 1
(разд. 5.2) или в верхнем слое течения жидкости для других,
указанных в разд. 5.2 задач. Тогда в C.5) L = NXA%. Напомним
также, что в рассматриваемом примере принимается 6/2 = 300
[см.: C.6)], хотя расчеты могут выполняться, конечно, и для
других б.
Запишем граничные условия по х для давления следующим
образом:
где к такое же, как в A0.1). __
Заметим, что здесь Nx в индексе и Nx в последнем члене мо-
тут быть различными, ^гак как Nx изменяется от слоя к слою
течения жидкости, a Nx постоянно.
При Nx = 15, Ах = 32 и б = 600 (как в задаче № 1 из
130
разд. 5.2) из A0.3), в частности, получается
(P)NX+Tt, m, q = (P)k, m,q— 1,6. A0.4)
Граничные условия по #4 по z, сформулированные выше,
могут использоваться для всех задач разд. 5.2. При этом для
многозонных задач последний член в A0.3) должен быть одина-
одинаковым для всех зон.
Рассмотрим теперь граничные условия по оси у. Тут имеется
несколько типов условий: условия на стенке; условия на оси
канала (для задач № 1, 3, 4 в разд. 5.1); условия на внешней
границе (по у) рассчитываемых зон для задачи № 2 (названные
в разд. 5.2 эффективными граничными условиями); условия на
границах зон, т. е. условия «сшивания» зон для задач № 3 и 4.
Рассмотрим последовательно все указанные случаи.
1) Граничные условия на стенке и их следствия.
Эти условия сводятся к обращению на стенке в нуль всех
компонент скорости. Можно рассмотреть и случай вдува или
отсоса через стенку, причем под любым углом к стенке. При этом
скорости на стенке должны приобретать заданные ненулевые
значения. Для общности можно было бы принять
(щ)у=0 = Юст, (Ю.5)
где (щ)ст — заданная функция х, z и t (для всех индексов к).
Однако мы пока ограничимся случаем непроницаемой стенки,
т. е. примем
(ик)у=0 = 0. A0.6)
Индекс m = 1 относится к первому ряду ячеек у стенки, так
что стенка является нижней границей этих ячеек. С учетом этого
и с использованием ранее принятых обозначений можно запи-
записать на основе A0.6):
<ик>п,в«/,,й= °> <^J>»..«/,*H°-I (Ю.7)
С учетом A0.7) необходимо преобразовать уравнения коли-
количества движения и неразрывности для ячеек с m = 1. Удобно
воспользоваться уравнениями C.8) и C.9), принять в них пг = 1,
учесть A0.7) и преобразовать другие члены прежними (описай-
ными выше) способами с некоторыми изменениями (которые
указываются ниже).
Из уравнения неразрывности C.9) при m = 1 получится после
преобразований
J +
- <"•)"• »¦ «-•
Уравнение количества движения при m = 1 имеет обычный
вид G.1).
5* 131
Величина (Rt)n, 1, q> входящая в G.1), определяется так:
"-1» х» 9 — Pn+1, 1, g; ~Ь O
Здесь (/?Ст)?г, q—давление на стенке в ячейке п, 1, q.
Формулы G.3)—G.12), определяющие члены в уравнении
количества движения, сохраняются, но в отдельные составляю-
составляющие этих формул должны быть внесены изменения. В частности,
величина (Фг)п, <m-i)+Vi, q> входящая в G.5), при т = 1 с уче-
учетом G.8) и A0.7) приобретает такой вид:
dui
A0.10)
Должны быть внесены при т = 1 также изменения в форму-
формулы F.5) и F.11) (другие «турбулентные члены» определяются
по прежним формулам). Вместо F.5) необходимо принять:
' ' А Г
— | (^i)n+l, l,q— (^l)n, 1, g | j(U2)n+l,l,q—(U2)n,l, (? +
n, 2, q + (цД)т»+1, 2,
A0.11)
Вместо F.11):
' ' A f
n> x, g+i/2= 2~| ("з)п, 1, g+1 (^з)п, 1, qr ||(^2)n, 1, q+1 (^2)^, 1. Q+
A0.12)
Расчет (#j)n, 1, q в ячейках с т = l проводится по прежней,
формуле (9.2), также по-прежнему определяется (M*)n,+?*q по (9.3),
но с определением (Ri)n,i,q по A0.9).
Подставляя (9.3) для т = 1 в уравнение неразрывности A0.8),
получим после преобразований с учетом того, что при т = 1, 2, 3
величины Axm, Ai/m и Azm остаются постоянными, т. е. Дхх =
= Ах2 = Аа;з» A^/i = Д^/2 = д1/з» д% = Дг2 = д^з (см- РазД- 5-2):
7^(^Рл, 1, q Рп+2, 1, q Рп-2,1, q) Н ГТ(^П' 1» 9 ^п' 1» «+2 ^п' Х' ^-з)"'
+ -ri I2 (P«)n. в - P«. 2, g - Pn, 3, al-i- ^f"'.1'9. = 0, A0.13)
Ai/2 ^ * A^AjtjAj/jAzi
132
, 1, q — (^l)n-l, 1, q] H"
A0.14)
Изменяется также аналогичное уравнение [типа (9.37)] для
ячеек с т = 2 (действительно, в (9.37) входят величины со вто-
вторым индексом т — 2 (в Lnt m, g), т. е. 0 при т = 2, а таких ячеек
не существует). Для вывода соответствующего уравнения необ-
необходимо, как обычно, подставить в уравнение неразрывности E.1)
при т = 2 выражение (9.3) для (мг-)п?"?*д» но ПРИ дальнейших
преобразованиях учесть формулу A0.9) для (Ri)n, ъ q. Получа-
Получается с учетом того, что Ах± = Ахх, Аг/4 = Аух, Az4 = Azx (см,
разд. 5.2):
1 1
¦—^Bрп, 2, g Ргг+2, 2, q—Pn-2,2,q)~!" 'Т~2"(^Р^> 2, q Рп, 2, q+2 Pn, 2, q-2) +
A0.15)
где
¦Р п, 2, q ~ 2 1(^1/л+1, 2, q (^l)n-l, 2, qj И о 1(^3/и» 2, q+1
В уравнениях A0.13) и A0.14) появилось дополнительное
неизвестное—рст, и соответственно требуется дополнительное
соотношение. Для вывода его запишем уравнение количества
движения C.4) в проекции на ось у для точки, расположенной
на стенке (у = 0). С учетом A0.6) получим
др\ Г д2 (и>2)\
Подставляя сюда из уравнения неразрывности C.4)
ди,2 дщ дщ
ду дх dz 9
найдем
= —(р*\ —(р?-) . A0.17)
;=0 \дхду/у=о \dydz/y=o v
Это граничное условие на стенке для задачи об определении
ноля давлений. Для записи A0.17) в конечно-разностном виде
примем
? ^ 1,д(^ст)п,д] A0.19)
dyjci &y i ' \ ' /
133
Аппроксимируя затем производные по х и по z обычным об*,
разом, получим из A0.17) после простых преобразований
(Рст)п, q ~ Рп, 1, q + 2д^ [(ul)n+l, I, q — (^i)n-l, 1, q] +
[^n'x' *+1 "" (из)п, 1, g-l]- A0.20)
Это и есть искомое дополнительное соотношение для рст
Обозначим
A0.21)
ПодСТавЛЯЯ В A0.13) И A0.15) (рСт)п, g = Рп, ъд + /п,д (в С0°Т-
ветствии с A0.20) и A0.21)) получим после преобразований:
Рп, 1, д = а1 (Рп+2, 1, д + Рп-2, 1, д) + аЗ (Рп, 1, д+2 + Рп% 1, д-г) +
+ 4Х) (Рп, 2, д + Рп, з, д — 2/п, д) + ^п, 1, д, A0.22)
Рп, 2, д == #1 (Рп+2, 2, д 4~ Рп-2, 2, д) Н~ аЗ \Рп, 2, д+2 ~Ь Рп, 2, д-2) ~~Ь
+ 4!} (Рп, 4, д + Рп, 1, д + 2/п, q) + Fn, 2, q. A0.23)
Здесь aix), a^^, <2зХ), а[2\ а^ и аз3) определяются по (9.6),
(9.8) и (9.7) при т = 1 и т = 2 соответственно; /?n, 2, a определя-
определяется по (9.14); Fn,i,q определяется так:
2 г/_ .
2 2 ^ ]
A0.24)
Полученные соотношения исчерпывают все условия, которые
должны быть учтены на стенке и в прилегающих к стенке рядах
ячеек.
2) Условия на оси канала и их следствия.
Какие-либо граничные условия на оси канала формулиро-
формулировать нет необходимости, так как расчет одновременно должен
охватывать обе половины канала (в задачах № 1, 3, 4 разд. 5.2).
Однако некоторые особенности расчетов для рядов ячеек, при-
прилегающих к срединной плоскости канала, необходимо отметить.
Эти особенности связаны с тем, что (как указывалось в разд. 5.2)
для каждой половины канала (верхней и нижней) ось у счита-
считается направленной от стенки и нумерация рядов ячеек вдоль
оси у (т. е. по индексу т) производится от стенки (от своей стен-
стенки в каждой половине канала). Таким образом, оси у в двух
половинах канала направлены в противоположные стороны.
Обозначим т =¦*Ny номер последнего ряда ячеек по оси У
134
в одной (любой) половине канала (т. е. ряд ячеек с т = Ny при-
прилегает к срединной плоскости канала). Расчеты в задачах № 1,
3, 4 должны проводиться одновременно (т. е. на каждом вре-
временном шаге) во всей зоне расчета, охватывающей обе половины
канала. При этом при расчетах различных величин, зависящих
от скоростей щ, в ячейках с т = Ny в какой-либо (например,
нижней) половине канала соседнему ряду ячеек другой (верх-
(верхней) половины канала должен приписываться номер т = Ny + 1
(хотя в своей половине канала эти ячейки имеют по у номер Ny).
Во всех этих ячейках (с т = Ny + 1) должен изменяться знак
скорости и2. С учетом этого расчет должен проводиться по обыч-
обычным (приведенным выше) формулам. Аналогично нужно посту-
поступать для другой половины канала.
Таким образом, при расчетах для ячеек с т = Ny необхо-
необходимо принимать:
(^i)n, N +i, q = {(^i)n, Ny, q) Другой половины канала,
(и2)п, Ny+i, q = {— (u2)n, Ny, q} другой половины канала, A0.25)
(u3)n, N +i, q = {(u3)n,N ,q} другой половины канала.
Совершенно аналогичные формулы справедливы для (wx)n, n +i,g»
(#2)n, n +i,q и («з)п, n +i, q- Они необходимы для расчетов Fn, n ,q,
по (9.14).
При расчетах методом итераций поля давления (сразу в обеих
половинах канала) с использованием формулы (9.37) необходимо
в каждой половине канала принимать:
Рп, n, +i, q ~ (Рп, N , о) в другой половине канала,
V ч Д0.26)
Рп, N +2, q — (Рп, iv?-i, q) в другой половине канала.
С учетом этого могут использоваться прежние формулы
(т. е. (9.37)). Возможно, перебор ячеек при проведении каждой
итерации при расчете давления целесообразно проводить от
средней плоскости канала к стенке — сначала для одной поло-
половины канала, затем для другой.
Указанное исчерпывает особенности условий на оси канала.
3) Граничные условия на верхней границе (по у) зоны рас-
расчета для задачи № 2 (разд. 5.2) и их следствия.
Напомним, что граничные условия по х и по z для задачи
имеют вид A0.1)—A0.3). Эти условия справедливы для всех
Рядов ячеек по у (для всех т), в том числе и для верхнего ряда.
Если, как это было принято в задаче № 2, взять Ny = 18, то
По табл. 5.1 этому соответствует Ах18 = 8. Подставляя в A0.3)
Лх = Ах18 = 8 и полагая Nx = 15 и б = 600, получим
Для всех т.
135
Это условие обеспечивает напорный характер течения в за-
задаче № 2.
Обратимся теперь к предмету рассмотрения настоящего раз-
раздела — к граничным условиям по у. Эти условия могут быть
только приближенными, так как в задаче № 2 зона расчета ис-
искусственно ограничивается по у. Можно надеяться только на
то, что в глубине рассчитываемой зоны (т. е. ближе к стенке)
погрешность граничных условий на верхней границе зоны рас-
расчета будет не сильно сказываться, а особенности течения будут
определяться главным образом его напорным характером.
Будем считать (это соответствует табл. 5.1), что величины
Ах, Ау и Az в нескольких рядах ячеек (хотя бы в одном-двух),
прилегающих к верхнему ряду т = Ny, такие же, как и при
т = Ny. Введем в рассмотрение дополнительный ряд ячеек
cm = Ny + lnc такими же Ах, Ay, Az. Определим скорости
(щ)п, n +i, q в этом ряду следующим образом:
а) скорость (м2)п, n +i, q найдем из уравнения неразрывности
E.1), записанного для ячейки п, Nyy q. При Ay = const по-
получается
(U2)n, Ny+1, q = (U2)n, jv^-J, q + -д|" [(^i)n-l, Ny, q ~ (^l)n+l, tff, q] +
+ 4Г Wn, Ny. q-1 - Wn, Ny. «f J; (Ю-2»)
б) скорости (ujn, N +i,-g и (и3)п, n +i, q определим из прибли-
приближенного условия
(Щ)п, Ny+1, q + (Щ)п, Ny-U q ~ 2 (щ)п, Nyy q ДЛЯ j = lx 3. A0.29)
Отсюда
(ut)n, Ny+1, q~2 (Ui)n, N , q ~ (Щ)п, Ny, q ДЛЯ 1 = 1,3.
Расчеты всех величин, зависящих от скоростей, для ячеек
п, Ny, q должны проводиться по обычным (приведенным ранее)
формулам с использованием скоростей (щ)п, n +i, q, определяе-
определяемых по A0.28) и A0.29); так можно найти и величины (ui)n, n ,?•
Для определения Fn, n , q по (9.14) нужно знать (й2)П} у +ltq.
Определим эту величину по формуле, аналогичной A0.29):
(U2)n, JV+1, q ~ 2 (Й2)П| v q — (S2)n, N-1, q, A0.30)
V У У
и после этого можем найти по (9.14) Fn,N ,g.
Вычислим также по аналогичной формуле давление в ячейке
п, Ny + 1, q:
Рп, Ny+1, q ~ 2pn, Nyi q — рП} tf^l, q- A0.31)
Зная Рп, n +i, qi можно проводить расчеты давления по (9.37)
для т = Ny — 1 (и для меньших т, конечно). Для обеспечения
136
расчетов при т = Ny необходимо получить уравнение для дав-
давления в другом виде. Для этого обратим внимание на то, что
соотношение (9.3) (если в него подставить формулу G.2) для Rt)
является конечно-разностной аппроксимацией следующего вы-
выражения:
Дифференцируя это выражение по xt и учитывая, что для
поля u\t+At) справедливо уравнение неразрывности, получим
At д2р/(дхгдхг) = dut/dXi.
В конечно-разностной форме (при Ах, Аг/, Az = const) это
уравнение имеет такой вид:
{ Ах2 (Рп+1> т> Я. + Рп-1, m, q — 2pn, m, q) +
Н дТг" (Рп, т+1, q + Рп, т-1, q — 2/?n, w> g) +
п, m, q+1 +fPn, in, q-
, m, g — (gl)n-l, rn, q , (U*)n, m+l, q ~ (g«)n, m-1,
+ 2Дг/
n, m, q-1
Из A0.32) получается для случая т = Ny:
Рп, Ny, q = dl У (Pn+1, Nyt q + Pn-1, Ny, q)+ «2 У (Pnt Ny+1, q +
+ Pn, Ny-1, q) + ^3 ^ (pn, iVy, q+1 + Pn, Ny. q-l) + &n, N'yt qfe-
A0.33)
Это и есть искомое уравнение для pUj n >q. одесь ах у , a2 y %
a3 y и /"n, iv q вычисляются no (9.6)—(9.8) и (9.19) [причем в (9.19)
W2 определяются по (9.15)], a pn,N+i,q$ входящая в A0.33),—
по A0.31) г.
Приведенные соотношения полностью исчерпывают условия
на рассматриваемой верхней границе зоны расчета для задачи № 2.
4) Об условиях «сшивания» зон в задачах № 3 и 4 разд. 5.2.
1 Можно было бы получить другое, отличающееся от A0.33), уравнение для
давления в ячейках с т = Ny и при этом избежать необходимости исполь-
использования приближенного соотношения A0.30). Для этого продифференцируем
уравнение количества движения C.4) по xt; получим d2p/(dxidxi) =
= — d2 (uiU^^dxidx):). Аппроксимируя это уравнение конечно-разностными
выражениями (с учетом «турбулентных членов»), получим искомое уравне-
уравнение для давления. Из него можно выразить рп, Ny, q без использования wf.
Однако вряд ли общая точность при этом повысится.
137
Эти условия мы рассмотрим несколько менее подробно. После
накопления опыта расчетов задачи № 2 они должны быть уточ-
уточнены.
Будем для определенности говорить о задаче № 3 (присте-
(пристеночные слои и «ядро» потока), поскольку для задачи № 4 ничего
принципиально не изменяется. До расчетов «ядра» необходимо
рассчитать пристеночный слой (т. е. решить задачу № 2), при-
причем толщину его нужно взять большей (по-видимому, на 3—4 ряда
ячеек), чем будет затем приниматься при решении задачи № 3
(т. е. для «сшивания» с центральной зоной потока). Пристеноч-
Пристеночную зону рассчитывают при таком же продольном перепаде дав-
давления, какой будет затем использоваться для расчетов «ядра»
потока.
Обозначим, как и ранее, Nv число рядов ячеек по у в пред-
варительно решаемой задаче № 2, т — число рядов ячеек по г/,
которое будет затем использоваться в пристеночном слое при
решении задачи № 3.
Как указывалось, Ny — m ^ 3 ч- 4. Примем, что в зоне от
т = т до т = Ny Aym постоянно. Примем также при решении
задачи о «ядре потока» при т = 1, 2, 3 величину Аут постоян-
постоянной и равной Аут в задаче для пристеночного слоя при т = т
(это соответствует табл. 5.1).
При решении задачи для пристеночного слоя в каждый фик-
фиксированный момент времени (т. е. на каждом временном шаге)
необходимо определить (щУггп (цзут и <р>т*
б <Р>т = <Р>т — <Р>т+ъ (Ю.34)
— (u^mfym, A0.35)
(D3)m = У {(и3 - (изутJ>т, (Ю.36)
(D,)m = f<(p-<P>mJ>^ A0.37)
Здесь любая из величин типа </>т вычисляется путем осред-
осреднения /n, m, q по всем ячейкам ряда т = т в фиксированный
момент времени t.
Например:
Nx Nz
<{P — <P>mJ>m = дПГ ^ XI (РП' Й> ^ "" <P>^2 И Т* П*
x 2 n=lq=l
При расчете «ядра потока» (в задаче № 3) ряд ячеек сш = 1
граничит с рядом т пристеночного слоя, так что ряду т при-
пристеночного слоя в «ядре потока» соответствует ряд т = 0. В ка-
качестве граничных условий по у для расчета «ядра потока» необ-
необходимо определить скорости и давления в ячейках ряда т = 0»
138
Тогда можно будет проводить расчеты в «ядре» для всех яг, на-
начиная с т = I2.
Определим скорости (и^, 0, q в ряде ячеек с т = 0 для ядра
потока, вычисляя последовательно:
а) первое приближение для этих скоростей, обозначив его
(Ui)n, о, q по формуле, аналогичной A0.29):
К)п, 0, q\= 2 (Ujn, i, q — Юп, 2, q 5 A0.38)
(Ю.39)
A0.40)
~T~ l
г) (u^)ni 0, g по формуле
Здесь величины (ju^m и (D^m берутся из расчетов присте-
пристеночного слоя (задачи № 2) для того же момента времени t, для
которого производится расчет для «ядра потока» по A0.41) 3.
Таким образом, получающиеся по A0.41) скорости (ujn, 0, q
связаны со скоростями в «ядре потока» [так как в качестве ис-
исходных принимаются скорости (иг)п, 0, д, определяемые по A0.38)];
в то же время средняя величина иг при m = 0 и дисперсия от-
отклонений от этой средней величины принимаются по данным рас-
расчета для пристеночного слоя.
Аналогично определяют скорости (и3)п, 0, q, действуя в том
же порядке:
а) Ы'п, о,й = 2 (и3)п, 1} q — (и8)п, 2, q; A0.42)
б) <4>0 и (^H = /aw7 —<i4>o]a>o; A0^3)
^ Л'4 - Г/" Ч/, 0,9 — <^3>0] №)m/(^HT A0.44)
Здесь (D3)m берется из расчета пристеночного слоя для
Же момента времени ?, для которого проводится расчет по A0.44).
Скорости (и3)п, 0, д, полученные по A0.44), обеспечивают <и3>0=
^0.
2 При т = 1 расчет давления должен проводиться по формуле типа A0.33)
8 (только с иной нумерацией ячеек), а при других т — по (9.37).
Имеется в виду, что для задачи № 3 принимается некоторый начальный
профиль скоростей, охватывающий и «ядро потока», и пристеночный слой
и с этим профилем вначале решается задача № 2 (при этом запоминаются
зависимости <и{>т и фх)т от *), а затем рассчитывается «ядро потока».
139
Расчет давления при т = 0 проводится почти также, но с не-
небольшими изменениями. Определяют последовательно:
а) P1n>o,q = 2' (P)n, I, q — Рп, 2, q ] A0.45)
б) <р>0 и (Z$o = /<(pI-<pi>o)a>o; A0-46)
в) <P>i = ^y\Y\pn.i,q\ (Ю.47)
^4J
г) РП| 0, g по формуле
2) Рп, о, q = <Р\ + б <Р>т + (Рл, о, J- <P?>o)
A0.48)
Здесь б <р>т [см.: A0.34)] и фр)т берутся из расчетов при-
пристеночного слоя (задачи № 2) в соответствующий момент времени.
Порядок корректировок Pnt 0, q по A0.48) при выполнении
итераций в процессе расчета давления требует дополнительной
разработки (можно корректировать рПу 0, q после расчета каждого
рп, ъ q или рп, 2, q, а можно только после расчетов для всего ряда
ячеек — это проще, но менее точно).
Скорости (и2)п, Oj q определяются из уравнения неразрывности,
записываемого для ячеек п, 1, q. Получается
Юп, 0, q = Ып, 2, q + (Д»/Д^) [Ып+1, 1, q ~ Ып-1, 1, q] +
+ (Ду/Az) [(м8)п, 1, q+i — (и8)п. 1, «-J. A0.49)
Предложенные зависимости для скоростей и давления исчер-
исчерпывают граничные условия по у.
В заключение раздела о граничных условиях заметим, что
все изложенное пригодно и для решения задачи при изменяю-
изменяющемся по времени продольном перепаде давлений А^ (по задан-
заданному закону). В частности, можно рассмотреть периодически
изменяющуюся величину Ар. Для ненапорного течения (погра-
(пограничный слой при обтекании тела и др.) все расчетные формулы
сохраняются, но граничные условия должны быть частично из-
изменены. Здесь этот вопрос не рассматривается.
5.11. Определение констант Ао и Q,
входящих в формулы для «турбулентных членов»
уравнений
НаПОМНИМ, ЧТО веЛИЧИНЫ Jyt,q <2>,+V2,g <з>, m,g+V
определяются формулами F.4)—F.12) (для рядов ячеек расчет-
расчетной сетки, находящихся не на краю какого-либо слоя течения жиД'
кости,—по разд. 5.2). Для величин <адг{>п_1/2, w, q, <^2>n, m-v.. e»
<ЦЦс3уп, ™, q_i/2 справедливы аналогичные формулы с уменьшением
п, т или q на 1.
140
Коэффициент А в F.4)—F.12) равен [согласно F.21)J
n_V2, m, g;
А = Ао[1 —
где Re = Ren+i/2, ?n, q при определении
Re = Ren_V2,m,g при определении
Re = Ren, m+i/2fg при определении
Re = Ren, m-v2,g ПРИ определении (щи'2уп, m_i/1>fl;
Re = Ren, w, g+i/2 при определении <i44>n, m, g+v2;
Re = Ren, m, q-v2 ПРИ определении <^з>п, m, g-v«-
A1.1)
Величины Ren+v2, m, g, Rert,m+vl)g и Кеп,т,^/, должны вы-
вычисляться по (8.7)—(8.9), а величины Ren-v2, т, q, Ren, w_i/2, g,
Ren, m,q-42 —по аналогичным формулам, в которых ?г, т или
q уменьшены на 1.
Рассмотрим теперь наряду с принятой (исходной) расчетной
сеткой расчетную сетку с более крупными ячейками: каждая ее
ячейка объединяет по осям х, у и z по две ячейки исходной сетки.
Ограничимся рассмотрением только тех областей течения, где
ячейки крупной сетки не являются крайними в каком-либо слое
течения жидкости. Из табл. 5.1 видно, что в слое № 1 течения
Таблица 5.2
3
т
1
1,2
2
3,4
3
5,6
4
7,8
5
19,20
6
21,22
7
23,24
8
25,26
9
27,28
10
29,30
11
31,32
можно образовать 4 ряда ячеек укрупненной сетки, некрайними
являются второй и третий ряды. Только для них и будут справед-
справедливы приводимые ниже соотношения.
В слоях № 2 и 3 течения нельзя образовать ни одного некрай-
некрайнего ряда укрупненных ячеек.
В слое № 4 получаются три ряда укрупненных ячеек; из них
средний (охватывающий исходные ряды с т = 21 и т = 22)
не является крайним.
В слое № 5 можно образовать 4 ряда укрупненных ячеек.
Из них второй (охватывающий исходные ряды с т = 27 и т =
= 28) и третий (охватывающий т = 29 и т = 30) не являются
крайними.
Поскольку в формулы для различных величин в ячейках
некрайних рядов входят некоторые величины из соседних укруп-
укрупненных ячеек, расположенных в крайних рядах, полезно пере-
перечислить все ряды укрупненных ячеек по оси у. Обозначим р номер
ряда ячеек по оси г/, считая от стенки. В табл. 5.2 указаны номера
141
т рядов исходной сетки, которые входят в каждый ряд Р укруп-
укрупненной сетки. Подчеркнуты те номера р, которые относятся к не-
некрайним рядам в слоях течения жидкости, т. е. для которых бу-
будет выполняться дальнейший расчет. Укрупненные ячейки в
в слоях 2 и 3 течения не указаны (и соответственно не пронуме-
пронумерованы), так как в этих слоях нет некрайних рядов укрупненных
ячеек.
То, что ряды укрупненных ячеек не охватывают по оси у
сплошь всю область течения, не является существенным для на-
наших дальнейших целей.
Обозначим а и 7 номера укрупненных ячеек по осям х и z соот-
соответственно. В ячейку с номером а входят ячейки с п = 2а — 1
и п = 2а исходной сетки; в ячейку с номером 7 входят ячейки
с q = 2у — I и q = 2у исходной сетки.
Отметим скорость ut в крупной ячейке чертой сверху, т. е.
запишем ее для ячейки а, |3, 7 B виде (пг)а, р, у. Обозначим т\Р
и игр2) величины т для ячеек исходной сетки, входящих в ряд C
(в соответствии с табл. 5.2), причем т^ = т^ + 1. Ясно, что
для (^j)a, р, v справедливо следующее выражение:
А*/ A) 2а 2V
т V
1ьУ ) 2j Jl
p mp n=2a-l g=2v-l
) 2a 2V
Обозначим
(Щ)п, m, 9 = Щ + (^)n, m, qr A1.3)
(^i)a, p, v = ui — Ыа, Э. V С11-4)
Здесь w^ — скорость в произвольной точки в ячейке п, т, q —
для A1.3) или в ячейке а, р, 7 — Для (И-4)-
Обозначим (UiUj} — среднее значение величины utUj по обла-
области течения жидкости, которая по осям х и z охватывает всю зону
расчета, а по оси у — только ряды ячеек, для которых величина
р подчеркнута в табл. 5.2. Величины (jiiuf) можно найти, исполь-
используя исходную расчетную сетку (обозначим эти величины
() и <WjM/))*2* или укрупненную сетку (обозначим их
Примем:
2 =222, ("-б)
(bn, w, q) n^=l (™р) 9=1
N/2 N/2
2 = 2 22- (Ц.6)
(ba, р, у) а==1 (Р) V=l
142
Сумма по т$ в A1.5) охватывает 10 рядов ячеек, сумма, по
6 в A1.6) — 5 рядов (см. табл. 5.2).
Очевидно, что
(bn, m, q)
Здесь < >n, w, q — осредненная в ячейке п, т, q величи-
величина; < >a, p,v — величина, средняя по ячейке a, C, у.
Учтем A1.3):
<И,И/>П, m,q = (Щ)п, m, q (^^)n, т, <? + (ЩЩУп, т, q- (H.9)
Аналогично этому
<Й|Й;>а, р, v = (»|)а, р, V (^)а, р, V + <^j>a, p, v A1.10)
Примем приближенно:
, т, q ~ У2 {<"iwi>n+V«, m, q + <^i>n-V,, m, q}r A1.11)
, m, q Ж Х/г {<^2>п, m+V., 4 + <^2>n, m-V., «>* A1-12)
п, m, q«V2 (<^3>n, m, q+V2 + <^3>n, m, q-vJ- A1.13)
Здесь величины в правой части определяются по разд. 5.6.
Разности <MjMf>W—(UiUj)^ линейно зависят от Ао. Обозначим
<ц^>A) _ <и,ц,><2> = btJ = atJ + A?tJ. A1.14)
С учетом уже известных формул легко получить выражения
для а;; и Pjj. Так как они громоздки, мы их здесь приводить не
будем.
Обозначим
П= 2 ЬЬ- A1-15)
Определим Ао из условия минимума величины П. Используя
(ИЛ5) и A1.14), получим из условия дИ/дА0 = 0:
Л = -Е 2 ajjil 2 й- (U.16)
c=UVi=l г=1 ,^г=1
Расчет А 0 по этой формуле можно проводить через несколько
десятков временных шагов. Ао рассчитывается для нескольких
заранее заданных величин (?, а затем Q определяется из условия
получения nmin.
143
5.12.06 определении статистических характеристик
турбулентного потока
Мы не будем здесь выписывать соответствующие формулы (они
в большинстве случаев очевидны), а ограничимся перечислением
некоторых важных статистических характеристик. Большинство
из них определяется путем осреднения по п и q при заданном (или
заданных) т. После достижения статистически стационарного
режима можно осреднять по времени.
Представляет интерес найти, в частности: профиль средних
скоростей (т. е. (щУт для всех т)\ величины <w2>m B процессе
установления профиля; величины У <(иг — <г^>тJ>т = {Di)m
(без суммирования по i) для всех т и ц величины
— (РтУJУт = (Dp)m; профили третьих и четвертых одноточеч-
одноточечных моментов пульсационных скоростей, т. е. <(z/, — <Mj>mn>m
для п = 3 и 4, а также <(иг- — <цгутJ (и2 — <м2>т)>т; профили
— <ЦгУт)(Р — <рУт)Ут', ВвЛИЧИНЫ /<(Рст — <Рст»2> И
У(Тст — <тст»2» где тст — напряжение силы трения на стен-
стенке; турбулентный коэффициент вязкости vT; моменты типа
<(&i — (щУт) (uj — <^;>m)>m; различные двухточечные моменты
(их много) второго порядка, в том числе величины <j?CT (ut —
— <Wj>m)>m, <tCT {щ — <^i>m)>m; различные двухточечные коэф-
коэффициенты корреляции (их много) и масштабы турбулентности (по
всем осям), составляющие баланса энергии турбулентности и пр.
Все это можно найти, зная поле скоростей и давлений.
Необходимо сделать одно существенное замечание. Так как
при расчетах скоростей на каждом временном шаге поле давле-
давлений определяется на предыдущем временном шаге, моменты типа
((Щ — <Wj>m) (p — O>m>m И <рст (щ — <ЦьУш)Ут МОГУТ быть
найдены приближенно. Только при малом Ар за один временной
шаг погрешность в определении этих моментов будет невелика.
Точность их расчета можно повысить, если сохранять в памяти
ЭВМ поля давлений для двух моментов времени. При этом можно
вводить поправку в величину р, проводя экстраполяцию измене-
изменения р во времени.
Так как трудоемкость расчетов велика, большую часть из них
целесообразно делать один раз, только после достижения стати-
статистически стационарного режима. До достижения такого режима
можно ограничиться относительно малым числом характеристик
(которые определять тоже не на каждом временном шаге).
5.13.0 начальных условиях и о контроле достижения
статистически стационарного режима
Можно ожидать (это должен подтвердить опыт расчетов), что кон
кретный вид начальных условий не влияет в рассматриваемых
типах течений на характеристики статистически стационарног-
режима течения, который устанавливается по истечении некото-
144
рого промежутка времени. В этом случае конкретный вид началь-
начальных условий не очень существен. Однако очевидно, что чем ближе
будут начальные условия к условиям стационарного режима тече-
течения, тем меньше потребуется временных шагов для достижения
стационарного режима. В связи с этим в тех случаях, когда целью
расчетов является определение характеристик турбулентности и
осредненного течения на стационарном режиме, полезно для зада-
задания начальных условий воспользоваться известными эксперимен-
экспериментальными данными для течения в плоском канале.
Задать начальное поле пульсационных скоростей, удовлетво-
удовлетворяющее всем необходимым требованиям, очень сложно, поэтому
при расчетах начальная турбулизация потока будет задаваться
просто в виде близкой к однородной турбулентности, накладывае-
накладываемой на поле осредненной скорости. Метод задания этой однород-
однородной турбулентности можно использовать такой же, как и описан-
описанный в гл. 2; интегральный масштаб начальной турбулентности
в «ядре потока» ~0,18 (б — полуширина канала); у стенки мас-
масштаб изменяется пропорционально Аут г; энергия этой турбулент-
турбулентности может быть выбрана на уровне, соответствующем опытным
данным в приосевой зоне канала. Начальные осредненные ско-
скорости будут задаваться равными известным из опыта значениям на
стационарном режиме. Характерная для канала турбулентность
должна при этом формироваться в ходе расчетов.
При более удачном задании начальных условий можно попы-
попытаться сократить время расчетов.
Для контроля достижения статистически стационарного режи-
режима необходимо рассчитывать (на каждом временном шаге или через
несколько шагов) различные статистические характеристики
потока (из числа указанных в предыдущем разделе). Прекраще-
Прекращение их изменения с задаваемой заранее точностью (или, может
быть, установление регулярного режима их периодического из-
изменения) можно считать свидетельством достижения статистиче-
статистически стационарного состояния.
5.14. Общая структурная схема программы расчетов
Приведем укрупненную блок-схему программы расчетов для зада-
задачи № 2 разд. 5.2. Изменения в блок-схеме при решении других
задач этого раздела являются простыми и специально подробно
рассматриваться не будут.
Дадим краткие пояснения отдельных разделов программы
(рис. 5.4).
1) Исходные данные (поз. 1) включают в себя задание: всех
Л#т, Аут и Azm в зависимости от т, начальных значений At,
номера шага по времени s = 1,5, Av, {(МгУт^ая в зависимости
1 Напомним, что при задании случайного поля скоростей по описанному
в гл. 2 методу масштаб турбулентности изменяется пропорционально шагу
расчетной сетки.
145
Ввод исходных данных
Программа №1: Определение
начальных условий
х
J
Определение J,, q по A0.21)
I
Увеличение
номера
шага по време-
времени s на 1
Программа№2- Определение всех(щ)п, Ny + ,,<
и Pn.xy + l>q по A0.28), A0.29) и A0.31)
Программа №3. Определение всех
(Mi)и. »»,</> включая (и2)», л' + 1, д,по A0.30);
корректировка At
Программа №4: Определение Рп т q
\
Программа №5: Определение новых («,)„, ,„
1®
I©
Программа № 7:
Контроль достижения
стационарного режима
Вывод первой группы статистичес-
статистических величин
Увеличе-
Увеличение _
s на As
Программа№6: Определение первой
группы статистических характе-
характеристик турбулентности
Заключитель-
Заключительный вьюод
величин
Программа №8:
Определение второй
группы статисти-
статистических величин
Рис. 5.4. Укрупненная блок-схема программы расчета пристеночного тече*
ния
от т (т. е. начального поля осредненных скоростей), ((щJ для
i = 1, 2, 3 х, исходных Ао я Q, начального поля давления [р
принимается постоянным вдоль осей у и z и линейно падающим по
х в соответствии с A0.3)] и др.
2) Расчеты по другим разделам программы проводятся по уже
приведенным формулам. Методы расчетов во многих случаях были
указаны в предыдущих разделах, в других случаях они очевидны
1 Возможно задание различных <*ф по слоям течения жидкости.
146
0 иногда аналогичны детально изложенным в гл. 2. Поэтому
давать более подробные пояснения нет необходимости. Укажем
однако, что проверка условия s = 5 должна производиться не
только по поз. 8 рис. 5.4, но и в ходе расчетов йг по поз. 5. Если
5 = 5, то по мере определения (Mt)n, m, q для различных ячеек
расчетной сетки (что выполняется при расчете ut) должны прово-
проводиться вычисления, необходимые для определения шага по вре-
времени At. Методика этих вычислений излагается в разд. 5.15.
3) К первой группе статистических характеристик турбулент-
турбулентности (поз. 11) относится минимальное число параметров, которые
должны определяться на переходном режиме до достижения ста-
стационарного состояния. Все другие статистические характеристики
турбулентности находятся только для статистически стационар-
стационарного режима (поз. 14). Расчет Ао} Q и At на этом режиме прово-
ится только один раз.
5.15.0 выборе величины шага по времени At
Используя выражение (9.1) для {щ)п*т%, получим:
n, ffl, q (иэ)п, m9q\ (Щ)п, m,gi д д д Д* С X
д д
(и \ О. //,/ \ (Jlfj)n,m9q+(Rj)n9m,q ,
w, q (Uj)nt т, g + 1 (^ijn, m> q \х д„ \~ Г
)п, w, g]
Осредним это соотношение по всему объему течения жидкости:
Наличие последнего члена в этой формуле связано с погреш-
погрешностью конечно-разностной аппроксимации уравнений. Эта по-
погрешность тем больше, чем больше Д?. Для обеспечения точности
расчетов последний член в A5.2) должен быть мал по абсолютной
величине по сравнению со вторым членом в этой же формуле,
описывающим приращение величины ^иги^. Таким образом,
Должно быть
к-
ч
/ M, + R, Mt+Rt
/ \ ' AxAyAz + •> AxAyAz
A5.3)
147
Отсюда
AxAyAz h"> AxAyAz/l
A5.4)
Угловые скобки здесь означают осреднение по объему, поэтому
вместо A5.4) можно записать [вводя для At по A5.4) обозначение
Attjh
? if if к-
4»j ...__
m-— 1 n=l q=l
L Zj Ь \ ^AyiAzi / • A5-5)
771=1 >7-=l Q=l m *m m '
Здесь (Nx)m и (Nz)m — общие числа ячеек расчетной сетки вдоль
осей х и z соответственно в ряду т по оси у (величины (Nx)m и
(Nz)m различны для разных т, см. разд. 5.2). Таким образом,
в числителе и в знаменателе в A5.5) производится суммирование
по всем ячейкам расчетной сетки.
Чтобы значительно не увеличивать необходимый объем памяти
ЭВМ при расчете ttj по A5.5), можно действовать в следующем
порядке.
После вычисления Мг и Mj для какой-либо ячейки п, т, q
(в ходе расчетов, необходимых для определения ut и w7-, см. разд.
5.7, 5.8, 6.9) их не запоминать (для всего поля течения), а сразу
же определять приближенные значения Rt и Rj по G.2), исполь-
используя имеющиеся в памяти ЭВМ величины давлений на предыдущем
временном шаге. Затем для этой ячейки вычислить величины,
стоящие под знаками сумм в числителе и в знаменателе в A5.5).
Прибавить к соответствующим суммам по уже рассчитанным ячей-
ячейкам найденные величины для рассчитываемой ячейки п, т, q
и т. д. по всем ячейкам. При таком порядке вычисления в памяти
ЭВМ приходится постоянно сохранять только две величины —
частичные суммы в числителе и знаменателе в A5.5) по ячейкам,
для ^которых уже выполнен расчет.
Конечно, найденное описанным способом значение Attj являет-
является неточным, так как используется поле давления на предыдущем
временном шаге, однако вряд ли это очень существенно, по-
поскольку:
1) речь идет только об оценке допустимых значений At и
[в A5.5) параметр ? все равно произволен, ясно только, что долж-
должно быть 6<1];*
2) за один временной шаг поле давления не очень сильно из-
изменяется.
148
Допустимый шаг по времени можно затем (после расчетов всех
определить, например, так:
= 1/ SS
V г, j=l
/9- A5.6)
При расчетах для оценки допустимого At будет приниматься
I = 0,05.
Начальное значение At при решении любой задачи должно
задаваться, а затем через несколько десятков шагов по времени
нужно найти At по A5.6); его можно принимать далее постоянным
на протяжении некоторого количества временных шагов (напри-
(например ~ 40 -г- 50), после чего снова повторить расчет по A5.6) и
откорректировать At и т. д.
Опыт расчетов покажет, насколько часто нужно проводить
корректировку At.
5.16. Примеры расчетов и их анализ
Был проведен расчет задачи № 2 (разд. 5.2), т. е. течения в при-
пристеночном слое. Уже отмечалось, что с методической точки зре-
зрения эта задача является наиболее важной. Расчетную сетку
принимали такой, как указано в табл. 5.2 с Nx = Nz = 20 в верх-
верхнем ряду ячеек. В качестве начальных задавали Ао = 0,02;
Q = 25; At = 0,02. Далее эти величины определяли и коррек-
корректировали на 50-м шаге по времени и после достижения статисти-
статистически стационарного режима. Метод задания начальных усло-
условий принимался таким, как в разд. 5.13. После достижения ста-
статистически стационарного состояния были проведены расчеты
еще для ~100 временных шагов. Это позволило проводить вы-
вычисление различных осредненных величин как с осреднением
по х и по z по слою ячеек с заданным лтг, так и с осреднением
по времени в какой-либо одной ячейке в этом слое.
Полученные результаты расчетов различных величин сравни-
сравнивали, где это возможно, с опытными данными и с результатами
расчетов (методом прямого численного моделирования крупно-
крупномасштабной турбулентности), приведенными в работе [21] г. Все
эти материалы показаны на рис. 2.5 и частично в дальнейшем
тексте настоящего раздела.
На этом рисунке, во-первых, изображен полученный при рас-
расчетах профиль осредненной скорости (щУ = f (у), причем вели-
величина (игу определялась двумя методами: осреднением по х и z
по каждому слою ячеек с т = const (т. е. вычислением <u1>m)
и осреднением по времени после достижения стационарного
режима. На нем же нанесены данные из работы [21]. Как видно,
все результаты удовлетворительно согласуются друг с другом.
1 Напомним, что в этой работе (как и в других публикациях) константы в фор"
мулах для подсеточной турбулентности подбирались из условия наилучше-
наилучшего согласия с опытом.
149
Во-вторых на рисунке построены зависимости
* ((ut — (.ui}yJy + <(^гJ> от у (без суммирования по i) для
i = 1, 2, 3. (Здесь (щ}у — среднее значение щ при заданном у;
эта величина отлична от нуля только при i = 1.) На нем же
показаны опытные данные по пульсационным скоростям, заимст-
заимствованные из литературы 2.
Расчеты показали, что при выбранной расчетной сетке боль-
большая часть энергии турбулентности описывается путем прямого
численного моделирования и роль подсеточной турбулентности
невелика.
Данные рис. 2.5 показывают, что при прямом численном мо-
моделировании можно получить результаты, хорошо согласующие-
согласующиеся с экспериментальными. Путем статистической обработки «чис-
«численного эксперимента», кроме представленных, можно было бы
получить, конечно, еще много данных. В этом отношении эффек-
эффективность «численного эксперимента» значительно больше эффек-
эффективности реального физического эксперимента.
На основе расчетов тонкого пристеночного слоя можно строить,
как указывалось, методы расчета более сложных пристеночных
течений.
В заключение приведем расчетные значения еще нескольких
величин, представляющих интерес. При статистически стацио-
стационарном режиме для решавшейся задачи получается:
Л0=0,25; Q = 25; допустимое Д? ^ 0,05.
2 Данные работы [21] прямым образом использовать для сравнения нельзя,
так как там приведены только «отфильтрованные» величины пульсационных
скоростей.
150
ЧАСТЬ ВТОРАЯ
ИСПОЛЬЗОВАНИЕ ПРИНЦИПА
«ЛОКАЛЬНОГО ПОДОБИЯ»
В ТЕОРИИ ТУРБУЛЕНТНОГО ПЕРЕНОСА
ГЛАВА ШЕСТАЯ
ПОСТАНОВКА ЗАДАЧИ, ИСХОДНЫЕ УРАВНЕНИЯ
И ИХ ПРЕОБРАЗОВАНИЯ
6.1. Введение
Как уже указывалось во Введении к монографии, использование
методов прямого численного моделирования турбулентности (ко-
(которым посвящена часть I) для решения встречающихся в инже-
инженерной практике задач является пока слишком громоздким.
Поэтому те задачи, которые могут решаться с помощью более
простых, «полуэмпирических» теорий, следует так и решать.
Прямое численное моделирование при этом должно играть роль
«численного» эксперимента, который позволяет уточнить полу-
эмппрические теории. Во многих отношениях он может быть
шыре и богаче по информативности, чем реальный физический
эксперимент (который также должен быть основой полуэмпири-
полуэмпирических теорий). В этом и заключается роль прямых методов рас-
расчета турбулентности по отношению к излагаемым полуэмпири-
полуэмпирическим теориям.
С другой стороны, сами полуэмпирические теории могут
являться основой аппроксимации данных прямого численного
расчета и их обобщения. Более подробно это положение следует
пояснить так: прямое численное моделирование может произво-
производиться только для специально подобранного набора относительно
простых задач, позволяющих выявить влияние различных фак-
факторов на турбулентность (что и сделано в части I), а приближен-
приближенные («полуэмпирические») формулы, аппроксимирующие резуль-
результаты прямого численного моделирования, могут затем применять-
применяться для расчета практически важных сложных течений (сред с пе-
переменными свойствами, с объемными силами и пр.). Таким спо-
способом результаты прямого численного моделирования распростра-
распространяются на указанные сложные течения.
Следовательно, материал частей I и II настоящей книги со-
совместно образует некоторый единый метод расчета турбулентных
течений.
Существует много различных полуэмпирических теорий тур-
151
булентности, и некоторыми из них можно было бы воспользовать-
воспользоваться для аппроксимации результатов прямых численных расчетов.
Однако удобно использовать какой-либо единый и по возмож-
возможности простой подход к построению приближенных теорий при-
применительно к различным задачам. Именно такой единый подход
и используется ниже. Следует отметить, что он не является прин-
принципиально новым; речь идет только об изложении различных
идей, используемых в полуэмпирических теориях, с единой точ-
точки зрения.
6.2. Принцип «локального подобия»
в теории турбулентного переноса
В гидродинамике и в теории тепломассообмена (как и в других
областях науки) широко используются методы теории подобия.
В частности, опытные данные по теплообмену или массообмену,
как правило, представляются в безразмерной форме (в форме
связи между «критериями подобия»), допускающей распростра-
распространение полученных данных на другие случаи, подобные исследо-
исследованному. Такой подход играет и сейчас важную роль в технике,
однако для современных сложных технических устройств воз-
возможности достаточно точного моделирования часто очень огра-
ограничены. Это определяется неоднородностью свойств среды, во
многих случаях сложностью и разнообразием геометрических
характеристик потока, действием переменных по объему сил,
влиянием лучистого теплообмена при высоких температурах и пр.
Реальное физическое моделирование целесообразно дополнить
(или даже заменить) математическим моделированием, в котором
учитываются все указанные факторы. Для этого нужно уметь
определять характеристики турбулентного переноса (количества
движения, энергии, массы), так как движение сред в технических
устройствах, как правило, бывает турбулентным.
Фактически во всех полуэмпирических теориях турбулент-
турбулентности предполагается (явно или неявно) существование неко-
некоторого внутреннего равновесия в структуре турбулентности.
Действительно, использование наиболее простой формулы типа
формулы Прандтля для турбулентного трения равнозначно пред-
предположению о том, что характеристики турбулентности в каждой
точке потока целиком определяются только локальными харак-
характеристиками осредненного течения вблизи этой же точки. Во мно-
многих случаях такая гипотеза оказывается правильной.
В более сложных полуэмпирических теориях при применении
дифференциальных уравнений для компонент тензора напряже-
напряжений Рейнольдса и для «масштаба турбулентности» (или для ско-
скорости диссипации энергии турбулентности) записываются различ-
различные приближенные выражения для отдельных членов этих урав-
уравнений (содержащие эмпирические коэффициенты). Само сущест-
существование определенной формы этих выражений и часто делающееся
предположение о постоянстве указанных эмпирических коэф-
152
фициентов (т. е. о том, что это «эмпирические константы», как
часто пишут) возможно только при существовании некоторого,
«равновесного» при рассматриваемых условиях, спектра турбу-
турбулентности. Для другого спектра форма выражений и тем более
значения «констант» могут сильно измениться.
Успешность применения полуэмпирических теорий подтверж-
подтверждает правильность используемого в них подхода. Физической
причиной этого является то обстоятельство, что процессы обмена
энергией между турбулентностью и осредненным течением про-
протекают медленнее, чем обмен энергией между турбулентными
вихрями; для более мелких вихрей этот процесс протекает быст-
быстрее, чем для крупномасштабных пульсаций.
Гипотезу о существовании во многих случаях «локально рав-
равновесной» структуры турбулентности удобно принять в качестве
основы для некоторой приближенной теории «локального подо-
подобия» в турбулентном переносе. Такой подход к проблеме изла-
излагается в [11]; в настоящей монографии он дополнительно раз-
развивается. Эта теория локального подобия, как и теория подобия
вообще, предназначена прежде всего для определения формы,
в которой наиболее удобно обрабатывать опытные данные или
данные численного эксперимента. Ниже излагаются также не-
некоторые методы «теоретического» (очень приближенно) получе-
получения формул для локальных характеристик турбулентного пере-
переноса.
Вся теория развивается только применительно к двумерным
(по осредненным характеристикам) течениям типа пограничного
слоя (пристеночного или струйного). Это охватывает большое
число практически важных задач. Задачи с более сложной гео-
геометрией требуют развития новых полуэмпирических теорий или
непосредственного применения прямого численного моделирова-
моделирования.
Поясним изложенное более конкретно. В уравнения для ос-
редненного течения в пограничном слое входят величины (см.:
[11] <pV>, <mV>, <TV>, <cV> (последнее в случае неодноком-
понентной среды; с — концентрация одного из компонентов).
Здесь v' — пульсационная составляющая скорости v поперек
пограничного слоя (вдоль оси у, ось х всегда будет направлена
вдоль основного течения в пограничном слое). Все перечислен-
перечисленные величины не определяются из уравнений для осредненного
течения и требуют дополнительных соотношений. В данном слу-
случае <pV> описывает турбулентный перенос массы поперек по-
пограничного слоя; р (u'v'y представляет собой турбулентное на-
напряжение силы трения; с, р <T'i/> — турбулентный удельный
тепловой поток (в однокомпонентном случае); р <c'i/> — это плот-
плотность турбулентного переноса массы компонента смеси с кон-
концентрацией с («турбулентная диффузия»I;
1 В случае магнитодинамического течения в уравнения входят и другие ве-
величины, требующие приближенного определения (см. соответствующий раз-
раздел ниже).
153
Представим, как это часто делается, указанные величины
в следующем виде:
— <i*V> = v^du/dy, B.1)
—<rV> « атдТ/ду, B.2)
-<cV> = Didc/ду, B.3)
<pV> = -Бтдр/ду. B.4)
Здесь и, Г, с, р в правой части — осредненные значения соот-
соответствующих величин (продольной скорости, т. е. скорости вдоль
оси х в пограничном слое; температуры; концентрации компо-
компонента смеси и плотности среды); координата у для пристеночною
пограничного слоя направлена от стенки в поток; vT, aT, DT,
О? — турбулентные коэффициенты переноса (соответственно тур-
турбулентные коэффициенты трения, температуропроводности, диф-
диффузии и переноса массы).
Выражения B.1)—B.4) справедливы, конечно, не всегда.
Строго говоря, для этого необходимо, чтобы в каждой точке
турбулентность определялась равновесием между ее возникно-
возникновением из-за взаимодействия пульсаций с осредненным течением
и диссипацией энергии. Если в балансе энергии турбулентности
существенны члены с переносом энергии в пространстве (кон-
(конвективным или диффузионным), то формулы B.1)—B.4) стано-
становятся неточными. В частности, могут существовать места в по-
потоке, где ди/ду = 0, a <wV> Ф 0. Однако смещение друг отно-
относительно друга точек, где ди/ду = 0 и где (u'v'y = 0, получа-
получается незначительным, и использование формул B.1)—B.4) не
приводит к большим ошибкам при расчете общей картины тече-
течения. Это и позволяет нам использовать далее формулы B.1) —
B.4) для приближенных расчетов во всех случаях.
Таким образом, проблема замыкания уравнений для осреднен-
ного течения сводится к задаче определения турбулентных коэф-
коэффициентов переноса vT, <zT, DT и DT. Принимается следующая
гипотеза (которая и составляет основу «принципа локального
подобия»): величины vT, ат, DT и Вт в каждой точке погранич-
пограничного слоя зависят только от свойств среды в этой же точке, от
локального значения масштаба турбулентности, от энергии тур-
турбулентности Е = У2 (ji%Ui) и от некоторых характеристик поля
осредненного течения и объемных сил в этой точке.
Для равновесной турбулентности (когда производство энер-
энергии турбулентности равно ее диссипации в каждой точке) вели-
величина Е не должна входить в число аргументов, так как она сама
определяется теми же параметрами течения, что и vT, #т, От
и DT. Введение Е в число аргументов сделано с целью прибли-
приближенного учета «неравновесности».
Предполагается, что «масштаб турбулентности» I может быть
определен по чисто геометрической формуле вида
1 = 1(У, 6), B.5J
154
где у — координата поперек пограничного слоя; б — толщина
слоя. Это предположение (часто принимаемое) требует дополни-
дополнительных пояснений (см. также: [11]). Если баланс энергии тур-
турбулентности сводится к равновесию между ее производством и
диссипацией и если допустить, что в потоке существует возму-
возмущения различных масштабов, то легко прийти к выводу, что
максимальная энергия турбулентных пульсаций будет сосредо-
сосредоточена в наиболее крупных вихрях, размер которых может огра-
ограничиваться только расстоянием до стенки у или (для струйного
течения) шириной пограничного слоя б. Действительно, при ис-
использовании любых разумных выражений для скорости генера-
генерации турбулентности и для диссипации энергии и при варьиро-
варьировании I получается, что при возрастании I скорость производства
энергии турбулентности увеличивается, а скорость диссипации
энергии уменьшается. В связи со сказанным можно ожидать,
что для указанной «равновесной» турбулентности масштаб I
определяется формулой вида B.5), причем для пристеночного
пограничного слоя вблизи стенки I ~ г/, а для струйного погра-
пограничного слоя I < б, и не зависит (или слабо зависит) от у.
Если в балансе энергии турбулентности существенны и дру-
другие статьи (конвективный перенос, «диффузия»), то формула
вида B.5) не должна быть, вообще говоря, справедлива. Однако
универсальность и точность описанных в литературе дифферен-
дифференциальных уравнений для I еще далеко не подтверждена (см.
также замечание по поводу этих уравнений в разд. 5.16), а по-
поскольку имеется положительный опыт применения формулы B.5),
то для приближенных расчетов далее будет использована фор-
формула вида B.5) во всех случаях. Если она окажется неточной
для некоторых видов течений, то для них должна развиваться
новая приближенная теория или непосредственно использовать-
использоваться результаты прямого численного моделирования (где вели-
величина I определяется в ходе расчетов).
Выражения для vT, aT, DT и Z)T, представляемые в безраз-
безразмерном виде, и являются теми локальными универсальными
(т. е. пригодными для каждой точки, в том числе при переменных
свойствах среды и переменном поле объемных сил) соотношения-
соотношениями подобия, которые совместно с уравнениями для осредненного
течения, уравнением для Е и формулами B.1)—B.4) составляют
замкнутую систему уравнений для описания осредненного течения
в пограничном слое (решаемую численно). Формулы для vT, aTZ?T
и Z)T могут быть получены «теоретически» («полуэмпирическим»
способом) или чисто экспериментально (на основе реального физи-
физического или численного эксперимента). В последнем случае тео-
теоретически (на основе теории подобия) определяется только пере-
перечень безразмерных параметров, между которыми должна нахо-
находиться связь на основе опыта. _
Конкретный вид формул для vT, aT, DT и DT в различных слу-
случаях рассматривается в следующих главах. Здесь мы дадим только
некоторые пояснения.
155
В соответствии со сказанным выражение, например, для vT
должно в случае «равновесной» турбулентности иметь такой вид
(в размерной форме):
vT = vT (p, v, Z, ди/ду, /W), B.6)
где р, v — величины плотности и вязкости среды в рассматри-
рассматриваемой точке; величины I и ди/ду также относятся к этой же
точке; /(?с) (где может быть несколько значений к) — локальные
характеристики поля (или полей) объемных сил.
Если объемных сил нет, то аргументы /W в B.6), естественно,
отсутствуют. Вдали от стенки турбулентность слабо зависит от
вязкости среды, и величину v из числа аргументов можно исклю-
исключить. Тогда получается (при /W = 0):
vT = vT (p, Wu/ду). B.7)
Так как из оставшихся аргументов ни одной безразмерной
комбинации составить нельзя, то с точностью до постоянного
коэффициента получается
vT ~ Рди/ду. B.8)
С учетом B.1) отсюда следует
—<mV> ~ Z2 {ди/дуJ B.9)
— это формула Прандтля для турбулентного трения.
Вблизи стенки, где аргумент v опустить нельзя, получается
[при /<*> - 0 в B.6)]:
vT __,
v J
— это также хорошо известная зависимость.
Если объемные силы представляют собой только силы инер-
инерции, связанные с ускорением жидкости или газа в продольном
направлении, то в качестве /W в B.6) может быть включен аргу-
аргумент ди/дх. Тогда вместо B.9) получается
B.11)
v
du/ду j \ оу
а вместо B.10):
vT _ 11 Рди/ду ди/дх
~~Г[ v ' ои/ду
Для стратифицированной среды в поле силы тяжести, направ-
направленном поперек пограничного слоя, /^ = gdp/ду (g — ускоре-
ускорение силы тяжести). Тогда вдали от стенки, где можно пренебречь
влиянием вязкости, из B.6) и B.1) вместо B.9) получается:
)\ B.13)
оу J v
156
Вблизи стенки
др/ду Рди/ду 1
' v J '
Если ди/ду = О, а gdp/ду Ф О (слой свободной конвекции),
то турбулентность может генерироваться только действием архи-
архимедовых сил (при неустойчивой стратификации). Вдали от стен-
стенки, когда v в B.6) можно пренебречь, из остающихся аргументов
нельзя составить ни одной безразмерной комбинации и с точнос-
точностью до постоянного множителя получается
<2J5>
Вблизи стенки
—-гЧ- BЛ6)
9 ду I v '
При течении электропроводной среды в магнитном поле в ка-
качестве /<*> может быть принята следующая величина [11] (в гаус-
гауссовой системе единиц измерений):
/<*) == оН2/с\ B.17)
где а — удельная электропроводность среды; Н — напряжен-
напряженность магнитного поля; с — скорость света в вакууме. В этом
случае вместо B.10) получается
v^ _ / i4uidy от \
v ~~J\ v ' рсУи/ду )' \
Вдали от стенки, где действием вязкости можно пренебречь
имеем [вместо B.9)]
Конкретный вид функций / и i|) в B.18) и B.19) зависит, ко-
конечно, от ориентации магнитного поля относительно направле-
направления основного течения среды. Для случая продольного магнит-
магнитного поля эти функции приведены в [11JL
Общий вид выражений для ат, DT и Z>T (в размерной форме)
отличается от B.6) в случае «равновесной» турбулентности только
присутствием в качестве аргументов дополнительных свойств
среды: в выражение для аТ должны входить в качестве аргу-
аргументов (кроме перечисленных в B.6) величин) также коэффи-
коэффициент температуропроводности среды а и удельная теплоемкость
ср; в выражения типа B.6) _для DT аргумент D (коэффициент
диффузии); в выражение для D? могут входить все эти параметры.
Следовательно, в число безразмерных аргументов входят числа
Pr = v/a и Шмидта (т. е. диффузионное число Прандтля Ргд =
= v/D).
157
При отсутствии равновесия турбулентности с полем осреднен-
ного течения в B.6) (и в аналогичные выражения для ат, DT и Д^
в число аргументов должна входить также, как указывалось
энергия турбулентности Е; при этом в безразмерных выраже-
выражениях появляется один дополнительный аргумент, например
Е/12 (ди/дуJ. Общая система уравнений для описания течения
должна включать в себя в рассматриваемом случае уравнение
баланса энергии турбулентности (с учетом конвективных и «диф-
«диффузионных» членов).
6.3. Общая характеристика метода
приближенного теоретического получения формул
для vT, ат, &т и 1>т
Так как турбулентные пульсации обычно происходят с сущест
венно дозвуковой скоростью, для приближенного получения
формул локальных величин vT, aT, DT и DT среду можно считать
несжимаемой и имеющей постоянные физические свойства [11],
а действительную переменность свойств среды учесть затем только
в уравнениях для осредненного течения при расчете потока в це-
целом. Однако чтобы учесть влияние стратификации среды на тур-
турбулентность, мы будем вначале в приводимых выкладках счи-
считать плотность среды переменной, а затем сохраним в конечных
формулах только локальное значение плотности.
В качестве исходных при получении искомых формул исполь-
используются уравнения для компонент тензора напряжений Рейнольдса
<и*м?>, а также для вторых моментов вида (Т'щУ и (с'щУ. Для этого
используются уравнения количества движения, энергии, диффузии
и неразрывности. Однако, так как мы в уравнение количества
движения в правую часть введем дополнительные члены, харак-
характеризующие объемные силы /<ft\ и учтем стратификацию среды,
полезно повторить вывод указанных уравнений. Для ряда общих
выкладок обозначим вначале оси координат х^ х2, х3; скорости
щ, и2, и3 соответственно. В пограничном слое изменим затем обо-
обозначения: примем, что ось х (где х = х^) направлена вдоль основ-
основного течения в пограничном слое, ось у (где у = х2) — поперек
пограничного слоя в плоскости осредненного течения; и — осред-
ненная скорость вдоль оси х (т. е. обозначение и будет применено
вместо (и^У в первой из указанных систем координат); v — осред-
ненная скорость вдоль оси у (т. е. v = (и2У); и', i/ — соответствую-
соответствующие пульсационные скорости; w — пульсационная скорость вдоль
оси z (т. е. и' = u'i, v1 = u2, w' = и3; напомним, что (изУ = 0).
Запишем уравнение количества движения в следующем виде:
^L + U]s^L = Ft. C.1)
Здесь
158
где gi — i-я. компонента ускорения силы тяжести; ft — некоторая
объемная сила, действующая на среду (отнесенная к единице мас-
массы среды). Она может быть, например, электромагнитной силой,
силой, связанной с присутствием в среде полимерных добавок,
я т. д. Далее специально рассматриваются различные частные слу-
случаи. В связи с этим мы член с ft используем только в начале на-
настоящего раздела (для напоминания о существовании такого чле-
члена), а затем опустим его, имея в виду, что это не помешает общей
характеристике метода получения формул для vT, aT, DT и DT.
Конкретные выражения для ft будут приведены в следующих раз-
разделах.
Уравнение неразрывности имеет такой вид:
Ot
+ ин —— = — р —- . C.3)
Представим, как это обычно делается, все величины в виде
суммы их осредненных значений и пульсационных добавок:
Р = <Р> + р', Р = <Р> + р\ Щ = <щ> + щ, Ft = <Ft> + Fl
ft = </i> + /i. C.4)
Из C.1) получается
Вычтем C.5) из C.1). Умножая затем полученное уравнение
для щ на iij, умножая также аналогичное уравнение для и] на щ,
складывая эти уравнения и осредняя, получаем после преобразо-
преобразований
ot
C.6
Из C.2) получается
Отсюда и из C.2) и C.4) следует
F\ = /¦,-<*-,>= L IE- + /_L Jl>, + v_!^i_ + /;. C.8)
1 x l/ p бхг ' \ p Oxt/ ' dx]idx]i
С учетом C.4) имеем
P ox. <p>+p' 0x{ ~ <P>[1 + P7<P>] dxt
159
— р/<р>
дх
<р dxt
<р>2 дх€ <р>2
Отсюда следует
C.9)
^> ^ <р>2 \р *«
Используя C.9) и C.10), находим сумму двух членов в правой
части C.8):
_1_ др \ __ 1_ др' р' д <р>
р dx. / <р> (9х. "^ <р>2 dx. "^
С учетом этого выражения из C.8) получается
г ~~ <р> ~дх~ "*" <р>2 dx~t <p>2 дх.
Из C.2) с учетом (ЗЛО) получается
C.13)
Найдем отсюда -— .<р> , подставляя <^> из уравнения
<р> vx\
д <иЛ
количества движения C.5). Учтем при этом, что
ди. ди. ч у Du. v
~дГ + и*-щ > = <-зг> = а*' где а* -
ненная величина проекции ускорения среды на ось х^
Согласно C.5). </^> = аг и тогда из C.13) получается
1 д<Р> * \ 2
C.14)
Второй член в правой части C.12) можно записать в виде
Т7—7~Т тг^~ в Подставляя сюда —Ц ^- из C.14), перепи-
\Р> \Р/ ^Х\ P^
160
шем выражение C.12) для Ft в следующем виде:
дх. + <р>з \Р
Используем это выражение для F\ (и аналогичное выражение
для Fj) в уравнении C.6). При этом сумма членов C.6), содержащих
F'i и Fj, представится таким образом:
> дР'
_[_ v С -— uj у + v <
C.16)
Некоторыми членами в правой части этого выражения, можно
пренебречь. Это определяется следующими причинами:
1) члены типа < з \Р' "gf~/ малы, так как они пропорцио-
пропорциональны четвертой степени произведения пульсационных величин
и так как корреляция р' и dp'/dxt должна быть очень малой (она
определяется мелкомасштабной турбулентностью; при этом среду
можно считать несжимаемой);
2) члены типа v -т—=-* —^— малы, так как при больших числах
ox (JX-. \0У
[ д2 (и.> \
Re, характерных для турбулентного движения, первый v ——~—1
и второй I—т^—\ сомножители имеют существенное значение в раз-
разных частях пограничного слоя и так как член с вязкостью всегда
При этом мал;
3) члены типа —^ \Р*Щ "я^"^ содержат очень малые третьи
\ ^
6 В. М. Иевлев 161
моменты, определяющиеся к тому же мелкомасштабной турбу-
лентностью.
Часть из оставшихся членов уравнения C.16) можно преоб-
преобразовать обычно используемым способом:
,и-> ^ / dui dui\ о
J 2<-^-^->. C.18)
С учетом C.16)—C.18) уравнение C.6) приобретает такой вид г;
ди.
1 <p'iij> д <р'щ>
\ <р> [ дхг '
IX
дх.
VI
VIII
C.19)
Здесь в правой части в фигурных скобках записаны и прону-
пронумерованы члены, имеющие различный физический смысл, т. е.
разные статьи баланса, определяющего величину <щщ>:
I описывают возникновение турбулентности вследствие взаимо-
взаимодействия турбулентных пульсаций с неоднородным полем осред-
ненных скоростей;
// — это скорость диссипации энергии турбулентности (точ-
(точнее, изменения величины Ки%изУ вследствие диссипации);
/// описывают возникновение или подавление турбулентности
при движении стратифицированной среды в поле силы тяжести и
в поле инерционных сил, возникающих при неравномерном осред-
ненном движении среды;
IV связаны со взаимодействием турбулентности с полем объем-
объемных сил (они могут обеспечивать как рост энергии турбулентно-
1 В C.19) опущен также третий момент, записанный в качестве последнего
члена в C.6).
162
сти, так и ее уменьшение). В дальнейших выкладках в настоящем
разделе IV (и члены с ft в других уравнениях) будут опущены, по-
поскольку рассматриваются в последующих (об этом уже шла речь
в начале настоящего раздела);
V описывают обмен энергией между пульсациями по разным
осям координат; они подробно обсуждались в литературе;
наконец, члены VI—IX отражают влияние на (щщУ процессов,
связанных с различными механизмами переноса турбулентности
в пространстве: конвективного переноса со скоростью осредненного
течения {VI), турбулентной «диффузии» (VII), переноса вследствие
взаимодействия полей пульсационных скоростей и пульсационных
давлений (VIII), «диффузии» турбулентности под влиянием моле-
молекулярной вязкости (IX), т. е. вовлечение пульсирующей средой
в движение (вследствие наличия вязкости) соседних (до этого не
пульсировавших) слоев жидкости или газа.
Общая структура уравнения баланса энергии турбулентности
для (у\и$У, (viT'y, <(с'J> и подобных величин имеет вид:
ЪЛ ЬА
— + < v >
bt ^ к д
bt
обменные j
производство -h диссипация +
, 1
члены
Как указывалось в начале настоящего раздела, при расчетах
локальных характеристик турбулентности, изменения плотности
допустимо считать малыми по сравнению со средним значением.
В разд. 4.2 части I при таком же предположении об изменении р
проводилась оценка относительных величин членов в уравнении
неразрывности и было показано, что приближенно это уравнение
можно записать в таком же виде, как для несжимаемой жидкости
с р = const [см. уравнение B.7) в разд. 4.2, ч. I]. Не повторяя
этих оценок, мы далее вместо C.3) запишем следующее уравнение:
дщ/дхк ж 0. C.20)
В соответствии с этим для пульсационных скоростей получится
дщ1дхъж0. C.21)
Из уравнения C.19) можно получить уравнение баланса общей
энергии турбулентности Е = 1/2(щщУ, полагая для этого i = j
и суммируя по i. При таком суммировании обменные члены [чле-
[члены V в C.19)] выпадают в связи со справедливостью уравнения
неразрывности C.21). Получается (без членов с /,):
дЕ д <ui> , ' \ / dui du
дЕ О <Щ uiuil^> 1 д <Р и\
дх^ дхъ <р> дх.
6* 163
В общем случае «неравновесной» (по отношению к полю осред-
ненных скоростей и объемных сил) турбулентности нужно учиты-
учитывать все члены уравнений C.19) и C.22).
При приближенном определении локальных характеристик
турбулентности мы будем считать, как уже указывалось, что
в структуре турбулентности имеется некоторое внутреннее равно-
равновесие (хотя полного «равновесия» с полем осредненных скоростей
,и объемных сил может и не быть).
Опустим при этом в C.19) конвективные и диффузионные
-члены, а в C.22) эти члены сохраним 2.
Система уравнений C.19) (для всех i и /) и C.22) переразмере-
переразмерена — одно уравнение является лишним. В связи с этим опустим
одно из уравнений C.19), соответствующее i = ; = 3, точнее, за-
заменим его C.22). Перепишем получающуюся систему уравнений
применительно к случаю течения в стационарном и плоском (по
юсредненному течению) пограничных слоях. Для учета сжимаемо-
сжимаемости среды в правую часть C.22) введем дополнительно член
2 и2 да г? тлл1
_—__?? Где а — скорость звука 111J.
Из C.22) получается
+ (gv - av) -&p- + (gx - ax) ??± + Qg=0. C.23)
Здесь опущены знаки осреднения при осредненных значениях р
и введено обозначение Qg для суммы всех конвективных и диффу-
диффузионных членов. Чтобы учесть влияние быстрого ускорения или
замедления среды, сохранены члены д/дх и с турбулентным пе-
переносом вдоль оси х (что обычно в теории пограничного слоя не
делается).
В C.23) ускорения среды ах и ау равны:
ах ж иди/дх, C.24)
где R — радиус кривизны траектории осредненного движения
среды; знак«+»соответствует случаю, когда центр кривизны траек-
2 Уравнение C.22) является следствием C.19). Если опустить во всех уравне-
уравнениях C.19) (для всех i и /) конвективные и диффузионные члены, а для дрУ~
гих членов записать приближенные выражения типа обычно используемых
в полуэмпирических теориях турбулентности, то из получаемой при этом
системы уравнений можно найти все (и^иЛ, которые выражаются через ло-
локальные значения свойств среды производных от осредненной скорости»
g— а и масштаб турбулентности I (входящий в выражения для отдельных
членов уравнений). Энергия турбулентности Е и коэффициент переноса vT
также выражаются через эти же аргументы. Сохранение переносных членов
в C.22) и замена одного из уравнений C.19) уравнением C.22) позволяет
сохранить Е в качестве независимого аргумента в формулах для vT.
164
тории расположен дальше от стенки, чем рассматриваемая точка;
знак «—» — случаю, когда центр кривизны траектории располо-
расположен со стороны стенки. Часто вместо радиуса кривизны траектории
можно использовать радиус кривизны обтекаемой стенки (в плос-
плоскости течения).
Из C.19) при рассматриваемых условиях получаются (без кон-
конвективных и диффузионных членов и без уравнения для <^3J)):
а) уравнение для <(и'J>:
. , ,ч ди ,. ,ч9ч ди / ди' ди' \ ,
0; C.25)
б) уравнение для
в) уравнение для
C-27)
Уравнения C.19) для (ц'т'^} при j = 2, / = 3 и при i = 1,
7 = 3 для плоского осредненного течения дают тождественный нуль.
Используя опубликованные в литературе данные, примем
некоторые приближенные выражения для отдельных членов
в полученных уравнениях. Начнем с члена, описывающего обмен
энергией пульсаций вдоль различных осей координат [член V
в C.19)], развивая при этом описанный в 133] метод. Для этого
сначала необходимо получить выражение для р''. В качестве исход-
исходных используем уравнения количества движения и неразрывности.
Вычитая C.5) из C.1) и проводя преобразования с учетом того, что
ии — (иъУ + мк» получаем
—
ди- , д <иг> , ди.
Подставляя сюда FI из C.15) (без членов с </,> и /,), находим
диг , , ч ди\ , ' д <ui> , ' du'i / dui
165
~ <р> дхъдхь <Р>2 dxi <Р>2
C.28)
Это уравнение можно упростить, отбрасывая малые члены и
принимая (для определения локальных характеристик турбулент
ности) <р> = р = const и v = const; примем также gt — at =
= const, т. е. рассмотрим фактически однородную турбулентность
в стратифицированной среде с малоизменяющимися средними
свойствами среды.
С учетом сказанного запишем вместо C.28)
ди{ ди{ , д (и.> , ди\ / , ди\
C.29)
При оценке членов и отбрасывании малых членов в C.28)
[т. е. при переходе от C.28) к C.29)j принято, что р7<р> <^: 1.
Дифференцируя C.29) по xt и суммируя по i = 1, 2, 3, получа-
получаем 3
д <мр ди'{ ди^ ди\ \ dp' \ #2р'
C.30)
Из этого уравнения для безграничного пространства получается
следующая формула для давления р' в какой-либо точке М:
(у)
^ дх
ГММ
Здесь волнистой чертой снизу отмечены величины в некото-
некоторой точке М, по координатам которой проводится интегрирова-
интегрирование; гмм — расстояние между точками М иМ; (dx) = d^irl^2dx3 ==
— UZ' И — вся область (объем) интегрирования.
Поскольку рассматривается, как указывалось, однородная
турбулентность, то величины д (ик}/дхг ngt — at под знаком интег-
интеграла в C.31) следует считать постоянными и их можно вынести из-
под знака интеграла. В реальных условиях переменных д^иКу/дхг
и et — at речь идет о выносе из-под знака интеграла некоторых
3 При этом учтена принятая однородность турбулентности, т. е. положено
Р, v, gi—ui, iujtujdx^ = const и использованы уравнения C.20) и C.21).
166
средних значений соответствующих величин. Подынтегральная
функция круто возрастает (по модулю) при сближении точек М и М
(так как при этом гмм -> 0), поэтому средние значения d(ukyidxt
и gt — qt близки к значениям соответствующих величин в точке М.
С учетом этого получим из C.31)
р'(М) 1__5<V_ С dU'™ (dx) gm-um С _?_. (dx), I
Р 2jt **«i (J} dxU ГММ 4jtP (J} 5л:т 'ММ
+ -Л- \ -Н^-^11 -^- • C.32)
4Я ({) гп дхк ГММ V 7
Здесь индекс i заменен индексом т для удобства дальнейших
преобразований. Для определения члена V в C.19) умножим C.32)
на дщ/dxj и осредним. При преобразованиях учтем, что дщ/dxj
можно вносить под знаки интегралов, так как интегрирование про-
производится по координатам хк точки М.
Обозначим г = х — х. Для однородной турбулентности имеем
df (г)/дхк = df (r)/dr, df (г)/дхк = —df (r)/dr. C.33)
Ясно, что
у ди\ с ' ~~ . ' ' . ~« ' '
ди- Fit
С учетом этого получается
J_ / ' J^L\ ~ L ° <и*У С d2("'"m> (dr)
р V дх /~ 2л дхт ) дг.дг^ г
7 т (г) J К
(г)
(dr)
, 1_ Р /^ ^ie ^цт\ (dx) =
4Я Д4^ ^ ^^ "
C.34)
ММ
Здесь обозначено:
агт = i__ С д* <uium> (dr) „ ^
(г) j k
167
, г _ 1 ? д* <u'iP'> (dr)
°™* ~ "ЕГ ) dr дгт г •
(г) J m
В C.34) и C.35) (dr) = dr±dr2drs; (r) под знаком интеграла
обозначает интегрирование по всему пространству г.
Для однородной турбулентности величины а}1^ и Ъгт^ обладают
следующими свойствами:
гт im mi im r\ im о / ' ' \ /Q~O?»\
fljk =#fcj =«jfe» #ij = ^» а-кк =*\Щит), F.6b)
Knj = b}m» b?i = 0, &mw = — <^p'>. C.37)
Условия ац = 0 и feij = 0 следуют из уравнения неразрыв-
неразрывности. Действительно, например:
3 4я J dr.dr. r 4я ^ м,.*,. i/a,.
(r) J г (V) г J
ди,
так как-^— = 0.
дх.
/ ^j ^ Ч ((JX) _
\дх. 6х.> rMM -
Метод получения последних формул в C.36) и C.37) поясним
на примере формулы C.36) для а™. Обозначим
При заданном / (г) это уравнение типа Пуассона. Его решение
для г = 0 имеет вид
(г)
Подставляя сюда / (г) из C.38) и учитывая определение а)к1 по
C.35), находим
дгкдгк г
Отсюда следует последняя из формул C.36). Аналогично по-
получается последняя из формул C.37).
Размерность величины а)™ и вид последней из формул C.36)
наводят на мысль о том, что приближенное выражение для а^
целесообразно искать в виде линейной однородной функции от
величины типа (uiu'my. Члены этой функции должны содержать так-
также множители типа 67Jc. В наиболее общей форме рассматриваемая
линейная однородная функция имеет такой вид:
Ал*)- C-39)
Здесь а, |3, у, 8, \i = const.
168
Подставляя в C.36) выражение C.39) для а$, по лучаем у рав-
равнения, связывающие между собой коэффициенты а, C, у, е, \х.
Число этих уравнений на единицу меньше числа коэффициентов,
поэтому один из указанных коэффициентов остается произвольным
(это «эмпирическая константа»), а другие выражаются через него.
Получается:
р = -5/2 + п/4а, C.40)
Y = V2 - 3/4а, C.41)
е = и/10 - 5/4а, C.42)
|i = -8/6 + V2a. C.43)
В частном случае изотропной турбулентности [1]:
<щит> = Л (г) r,rm/r2 4- 5 (г) 6|т. C.44)
Функции А (г) и В (г) связаны между собой, так как C.44)
должно удовлетворять уравнению неразрывности: d^UiUmy/drt =
= d<UiUmyidrm = 0.
С учетом этого после преобразований C.44) приводится к сле-
следующему виду:
JL
C.45)
г
где обозначено / (г) = -^ \ В (г) г dr. C.46)
о
Выражение C.45) можно использовать для прямого вычисле-
вычисления а}™ по C.35). При этом получается результат, совпадающий
с C.39) 4, если C, у, е и |i определять по C.40)—C.43), причем при
любом значении а. Таким образом, рассмотрение изотропной тур-
турбулентности подтверждает формулу C.39), но ничего не может дать
для определения а.
Другой крайний случай, для которого также желательно, чтобы
формула C.39) была справедливой,— это случай турбулентности,
в которой пульсации вдоль одной из осей координат очень малы,
т. е. случай, близкий к «плоской» турбулентности. Анализ пока-
показывает, что при этом формула C.39) при а = const оказывается
неточной: для различных частных случаев «плоской» турбулент-
турбулентности правильность C.39) обеспечивается при разных а. Однако
все эти а близки между собой, поэтому для приближенных расче-
расчетов можно принять некоторое среднее между указанными значе-
значение а. При этом C.39) для «плоской» турбулентности будет давать
во всех случаях лишь малую погрешность. С учетом соответствую-
соответствующих вычислений примем а = 6/5 = 1,2; при таком а из C.40)—
4 В C.39) в рассматриваемом случае <и^ит> = u26im, где и2 — среднее зна-
значение квадрата пульсационной скорости по любой оси.
169
C.43) получается:
р = 0,8; у = -0,4; 8 = -0,4; (х = 0,2. C.47)
Ниже эти величины будут еще несколько уточнены.
Перейдем теперь к определению Ъгту Размерность этой величины
и вид последней из формул C.37) позволяют предложить для Ъгщ
линейное однородное выражение из величин типа (иф'У. В наи-
наиболее общей форме такое выражение имеет следующий вид:
blmj — а (щр'у 8mJ -f- P <^mp'> &ij + У (.Ujp'y 6im, C.48)
где а, C, у = const.
Подставляя выражение C.48) в C.37), можно найти уравне-
уравнения для a, P и у, которые позволяют полностью определить эти
коэффициенты. Получается:
a = —0,4; р =y = 0,1. C.49)
Нам осталось определить последний член в C.34). Для него
можно предложить только чисто «полуэмпирическое» выражение.
Целесообразно, однако, рассматривать не этот член [входящий
в выражение C.34) для — /р' -д-*-\ L а соответствующий член,
Р \ °Xj/\
входящий в выражение V в C.19), т. е. в выражение для
\ / / ди- ди• \\
— \Р' \ ~т^~ + ~а~^~ ) У • По аналогии с C.34) он имеет вид:
р х у ox. ax. j/
-^¦-Лу. C.50)
1
Следуя [5] (и многим другим работам), примем
где к — const — эмпирическая константа; т — период турбулент-
турбулентных пульсаций, т. е. отношение масштаба турбулентности (круп-
(крупных вихрей) вдоль какой-либо оси координат к среднеквадратич-
среднеквадратичному значению пульсационной скорости вдоль этой оси (величина т
будет приниматься одинаковой для всех осей координат).
Если, что далее будет предполагаться, в уравнениях исполь-
используется масштаб I по оси у (т. е. поперек пограничного слоя), то
т = liy <(v'>2> = l/Y <№)*>. C.52)
Учитывая все полученные результаты, запишем в окончатель-
окончательном виде формулу для обменного члена V в уравнении C.19):
п'
р \^ \dxj ] dxi]/~^K ' "гк/ дхт '
170
Диссипативный член в C.19) (член //) представим в следующем
виде (аналогичном использованному в [11]):
??-D+¦?¦)<¦«>¦ <**>
Здесь В, Q = const, I — масштаб турбулентности.
Формула C.54), как видно, учитывает прямое действие вязко-
вязкости на энергию турбулентности, т. е. должна быть пригодна и при
малых Re. Это сделано для того, чтобы расчеты для пристеночного
пограничного слоя можно было проводить по всему слою до стенки.
Подставляя C.53) в C.25)—C.27), получаем:
а) уравнение для <(м'J>:
, г /ч дц / / /\9\ ди (В Q
-<^>Ж-<(а)> —-bF + -2
+ (gx — ax) -1у- + аи-^- + «11^^
б) уравнение для <(г/J>:
В Qv \ //Т7/Ч9 , / \ <Р/у/> , 22 ди 21
Ы + )<^ + ^y-av)"V" + 21 "e + a
- ^ <<(^'J> - W*} = 0; C.56)
+ fe|2 + йЬ
в) уравнение для <uV>:
+ (gx - «*) ^y^ + % v <P « > + («л + flS) ^T +
71 т 2 \ &x — ax ^ / ' '\ n (^ 57\
Здесь обозначено
W = <u'(ui>/3, C-58)
так что
E = ШУ2. C-59)
Уравнение C.23) для полной энергии турбулентности Е при-
приобретает с учетом C.54) и C.59) такой вид:
, _ „„) i?|l + fe - «») ^ + ft = о. C.60)
171
В полученные уравнения входят величины <р'и'> и <CpV),
Чтобы их определить, необходимо использовать уравнение для
пульсаций температуры 7" и для пульсаций концентрации смеси
(двухкомпонентная среда) с'._Эти уравнения необходимы, кроме
того, чтобы найти ат, Dr и DT (из полученных выше уравнений
можно найти только vT).
Для среды, подчиняющейся уравнению состояния идеального
газа, при малых пульсациях р' получается следующее выражение
для р' при заданных Т' и с' (и при р = const):
Здесь Rt и R2 — газовые постоянные составляющих смеси газов;
концентрация в смеси газа с газовой постоянной Ri равна с, кон-
концентрация газа с газовой постоянной R2 равна 1 — с.
В более общем виде для произвольной двухкомпонентной среды
р'/р ^ -гГ + хс', C.62)
где, как видно из C.61), для идеальных газов % = 1/Г, х =
= (R2 — Ri)/[R2 — (R2 — Ri) с]. Величины % и к являются фи-
физическими свойствами среды, зависящими от Г и с, для неидеаль-
неидеальных сред, может быть, и от давления р.
Используя C.62), получаем:
; ()
Подставим в первое из уравнений C.63) выражения для вто-
вторых моментов из B.2)—B.4) и используем C.62):
DT = [Хат - кптдс/ду/дх/ду]/[х - кдс/ду/дт/ду]. C.64)
Таким ?бразом, нужно получить формулу только для ат и D?;
при этом Вт определяется по C.64).
В качестве исходного при получении уравнения для J" исполь-
используем уравнение энергии в следующем виде:
ЭТ 1рЛ_= 8*Т^ 65)
dt ' дхк дзскдхк
Подставляя сюда Т = <Г> + 7', щ = <ггк> + щ и осредняя,
находим
д<т> i д I/ \/т\ I / 'т'м д2<Т>
Вычтем это уравнение из C.64); получается
41 + 4т{<щУ Г+и*{ту+икГ - <и'*г>)=а -^ •
C.66)
172
Умножив C.65) на Т' и осреднив, получим после простых пре-
преобразований следующее уравнение для <(Г'J> (для стационарного
случая, когда d((T'Jy/dt = 0, и для «равновесной» турбулентности,
т. е. без конвективного и диффузионных членов):
д <7> / дГ дГ
^г=-а
Умножив (З.С6) на i^, сложив с уравнением C.29), умножен-
умноженным на Г', и осреднив, получим после преобразований следующее
уравнения для (и\Т'У (также для стационарного случая, без кон-
конвективного и диффузионных членов):
*? -?- = - (v +
Для пульсаций концентрации с' справедливо уравнение, ана-
аналогичное C.66):
дс' д / / \ г ' ' t ' t т\ ^2с'
! {\Мк/ с i ^к \С/ ~4~ UfcC — \U\C у) == U •
C.69)
Для <(с'J> и (u'ic'y получаются уравнения, аналогичные C.67)
и C.68):
д (и.у у ди. Ас' ч
^г=-(v+D) <^t^k
C-71)
Умножив C.69) на Т\ C.66) на с', сложив и осреднив, получим
следующее уравнение для (Т'с'У (без конвективного и диффузион-
диффузионных членов, для стационарного в среднем течения)
' ^ ^с> ' д <Т) /п , / дТ' дс' \ /о то\
"^Г = ~( + а) \^Г ^Г>' ( }
Используя C.62), находим
-1- <Г'р'> « - х <(П2> + х <Г V>, C.73)
J_ <с'р'> « _ х <Гс'> + х <(с/J>в C.74)
Таким образом, из системы уравнений C.67), C.68) и C.70)—
C.72) нужно определить величины <G1/J>, <гг;-Г'>, <(с'J>, <^с'> и
<ГУ>. Величины <G7/р')> и <с'р'> после этого вычисляются по
C.73) и C.74).
173
Рассмотрим приближенные выражения для отдельных членов:
в уравнениях C.67), C.68) и C.70)—C.72). Начнем с членов
— /рг —-—\ и — /р' -?—\ . При их вычислении будем считать тур-
турбулентность однородной. Величина р'/р определяется выражением
C.32). Обозначим в нем сумму первых двух членов (линейных по
пульсационным величинам) р'лип/р'<> третий член—^/
так что
р' Лпин . ^нелин
р р р
С учетом C.32), C.33) и C.75) получим:
*<»тТ'> (dr)
дх,
> (dr) _
т (г)
^ 4яр
(?)
C.76)
Здесь введены обозначения:
(г)
5- =— [ д2<Р'т'> (dr) C 78)
(г) m i
Величины qik ж Sim удовлетворяют следующим условиям:
1ТО 771 7J /~» W, с\ / ' rFf\ /Q 7Q\
5|m = Smi, Smm = -<р'Г>. C.80)
Второе из условий C.79) следует из уравнения неразрывности.
Последние условия в C.79) и C.80) получаются так же, как по-
последние условия в C.36) и C.37) (см. пояснения выше).
Представим q^ в виде линейной однородной функции от ве-
величин типа (щТ'У; наиболее общая форма этой функции такова-
С = <h <итГ> 8ik + рх (щТ'у 8mli + уг <и'кГ> 6im. C.81)
Подставив C.81) в услогия C.79), получим:
рз = Yl = _0,2; аг = 0,8. C.82)
Представим sim в виде линейной однородной функции от вели-
величин типа <71/р'>:
Sim = оа<Гр/> 6im. C.83)
174
С учетом C.80) получается
сс2 = —V8. C.84)
Таким образом, для — <^Рлин -*—\ в соответствии с C.76),
C.82)—C.84) получается следующее выражение:
- 0,2 ((щТ'у 6mk + <и'*Г> 6im)]
C.85)
Аналогичным образом получается выражение для — <^рЛ1Ш -^-
Р \ °xi
¦у <(р'пин -^У «[0,8 <umc'> 6iR —
C.86)
„ 1 / ' 07" 4 1 / ' 0C' \
ВеЛИЧИНЫ — <^Рнелин ~^"у И "р" <Г Рнелин ^F"J> МОЖНО аппроКСИ-
мировать только приближенным чисто «полуэмпирическим» спосо-
способом. Для этого учтем, что нами было принято «полуэмпирическое»
выражение C.51), которое с помощью C.75) и C.58) можно
переписать так:
Величина -^ \- -^-jL представляет собой компоненту тензора
ох • oxj
скоростей деформаций среды пульсационной скоростью и'. Примем
следующую гипотезу: величина Миелин коррелирует [указанным
дих ди-
в C.87) способом] с -^- + -^-> но не коррелирует с компонентами
ди\
ъ
rot u\ т. е. с величиной — т-^- . Так как
дх. дх.
и'х ди[- \ I ди\ ди\
дх, 2 \\ дх. ' дхг J ' \ дХ.
П , I "»i -j \i (з.88)
5 Физическая причина существования корреляции между р' и (dujdxj) +
+ (dy'j/dxj) хорошо пояснена в [5]. Какую-либо физическую причину воз-
возможного существования корреляции между р' и rot u' мы указать не можем.
175
то с учетом указанной гипотезы и C.87) получается
Предположим, что корреляция рнелин с производными от Т'
и с' определяется наличием статистической связи 7" и с1 с и'. Счи-
Считаем:
Г = 4тиж + Г', C.90)
с1 = Bmu'm + с". C.91)
Здесь Т" и с" — случайные величины, не коррелированные си'.
Умножая C.90) и C.91) на щ и осредняя, получаем:
i Ат(итщ\ C.92)
= Вт<итщ>. C.93)
Из этих систем уравнений (для всех тик) определяются коэф-
коэффициенты Ат ж Вт. В частности:
. = <Ти3>; <и3и2>; <(Цз)Ъ = <вТ>)<(рУ>-<1;Т/><цУ>
1 <КJ>;<^;>;<^;> ww-w • О3-94)
Здесь учтено, что для плоского пограничного слоя <Г/и3>= 0»
(ихи3у = 0, (щи3у = 0, а также обозначено (как и ранее) mx = м',
w2 = v\
Аналогичным образом получается:
а __ <(u')*Xv'T'> — <и'у'><и'Г> п псгч
^2 <(i*T><M1>-<»v>« ' ^°'у '
А3 = 0, C.96)
53 = 0. C.99)
С учетом полученных результатов и сделанных предположений
1 / ' агч
перейдем к определению ~у \. Рнелин "^р"у> • Имеем
— \Рнелин ~щ
гг/ Р
дх. /*
176
Первый член в правой части здесь может быть опущен, так как
при определении локальных характеристик турбулентного пере-
переноса пренебрегаем диффузией турбулентности (т. е. считаем тур-
турбулентность однородной). Тогда можно принять
1 /т, М
Подставляя сюда Т' из C.90) и учитывая, что Г" статистически
независимо от рНелин (так как Т" статистически независимо от и1,
а нами принято предположение о том, что корреляция рнелии с Т'
определяется наличием статистической связи Т с и'), получаем
1 / >
— \Рн
1 X , дР
нелин ^7/ ~
-—-_!- л <f л' Um\ п \м\
'—' гу ^т \/'нелин л^. /• lo.iui?
р \ ох{ /
Последний знак приближенного равенства здесь написан также
в связи с пренебрежением диффузионными членами в уравнениях.
Подставив C.89) в C.101) и учтя C.92), найдем
<>н
нелин -j?y ^ — Ат-^- {<ити\у — W28mi) =
JL {W*A. _ <zVi», C.102)
где Ai определяется по C.94)—C.96). Аналогично получается
ОС \ К ,ТТ7-О 7"» / t 'ч v
[с'щ>}% C.103)
где Bt определяется по C.97)—C.99).
Перейдем теперь к рассмотрению других членов уравнений
C.67)—C.72). По аналогии с C.54) примем:
'>, C.104)
где F и М = const.
Для определения члана (v -f- a) \--r- - -^—^>, входящего в
C.68),. примем
д*и- • , ,
v л * = Ьгтит + Qu C.106)
гДе vi — случайная величина, статистически независимая от и «
Va7 В. М. Иевлев 177
Умножая C.106) на Uj и осредняя, находим
\ \ ди\ ди]
<дих du;\Q ¦ г
1Гт?} =^<«««*i>- C.107)
?С It
С учетом C.54) отсюда получаем
^;>. C.108)
Из этой системы уравнений могут быть определены все Ъгт. По-
Получается:
в л Q ^2 ^
+
В Qv\ <MaMi> <(иТ> — <^i> <ц/^> C 110)
2т + 2Z2 У <(и')«> <(i/J> - <а^'>2 ' ;
Примем следующую гипотезу: случайная величина Qi, стати-
статистически независимая от и', не зависит также статистически от 7".
Обоснование (качественное) этой гипотезы состоит в том, что взаимо-
взаимодействие турбулентности с осредненным течением может привести
к корреляции Т' и и' только в крупномасштабных турбулентных
пульсациях, скорости мелкомасштабных пульсаций могут быть
связаны с 7" только вследствие наличия указанной корреляции
между и' и Т'. Поэтому величина Qi, статистически независимая
от и' и определяющаяся мелкомасштабной турбулентностью,
должна быть также независима от Т''.
С учетом указанной гипотезы из C.106) получается
= Ьт <ОГ">. C.112)
С такой же степенью качественного «обоснования» можно по-
лучить другую формулу, позволяющую найти \jr^~ -Q—/ • Для это-
го примем
а —bT'-\-R". C.113)
Здебь R" — случайная величина, статистически не зависящая от Т''
Из C.113) и C.104) получается в (пренебрежении диффузионным
6 Опущен диффузионный член.
17S
членом)
(f '^)>- C.114),
Отсюда следует
Будем считать, что R" не зависит статистически от и' (с «обосно-
«обоснованием», аналогичным приведенному для независимости Q" от Т').
Тогда из C.113) получается
С точностью до диффузионных членов и коэффициентов (v при а)
левые части C.112) и C.116) совпадают, однако правые части раз-
различны. Это является следствием приближенности всех проведен-
проведенных рассуждений. Лучшее, что можно сделать,— это принять при-
приближенную формулу, в которой суммируются C.112) и C.116).
С точностью до диффузионных членов имеем
ж Ьш (и'тТ'У 4- Ъ (щТ'у, C.117)
щеЬг1П определяются по C.109)—C.111) и Ъ—по C.115). Для раз-
различных m и i формулы C.109)—C.111) дают такой результат:
C.118)
С учетом этого формулы C.117) для плоского пограничного слоя
приобретают вид:
. Ма
+ —
W + ) <uT> = [Ь j ) <u T >'
ft я
C.119)
' + <QI*>*\<v,r>i (зл20)
179
Совершенно аналогичным образом получается:
с+°> аф
<3-122>
Аналогичные приведенным выкладки приводят к следующе-
следующе» входящего в C.72):
му выражению для члена (D -f- a) /^—
^—
Таким образом, получены приближенные выражения для всех
членов в уравнениях для вторых моментов (щщУ, <^7">, (щс'У
и <Г'с'>, а также выражения для величин (и'ф'у. Соответствующая
система уравнений применительно к двумерному (по осредненному
течению) пограничному слою включает в себя, как указывалось,
уравнения для <(гг'J>, <(v'J>, <(^>, <2V>, <Ги'>, <cV>, ^'м'),
^(Г7J), <(с'J>, ^Г'с'), в которых опущены члены с конвектив-
конвективным и «диффузионным» переносом турбулентности (т. е. при опре-
определении указанных величин турбулентность считается «равновес-
«равновесной», а также уравнение W2 = 2Е/3 (Е — полная энергия турбу-
турбулентности), в котором сохранены члены с переносом турбулентности
(чтобы учесть возможность неполного «равновесия» с осредненным
течением). Кроме того, система уравнений включает в себя выра-
выражения для <pV>, <p'iO и формулу для определения масштаба
турбулентности I. Все необходимые уравнения и выражения для
отдельных членов в них были приведены выше, для I был указан
только общий вид соответствующей зависимости, конкретные вы-
выражения для некоторых типов течений даются ниже. Так как эти
выражения распределены по всему тексту настоящего раздела,
полезно всю указанную систему уравнений еще раз переписать
в одном месте и ^ окончательном виде. При этом введем обозначения:
ди
дх
ди
ду
дТ
дх
дТ
дс
дс
C.126)
После всех подстановок и простых преобразований рассматри-
рассматриваемая система уравнений приобретает следующий вид:
а) уравнение для <(и'J>:
, г ,к ди ,. ,Ч9Ч ди ( В . Qv
ду ду
180
+ ('-!-)<»¦"'> ж+ [D «--В <w>+
+ {-W—Ta)W']i-W Г [«»')=>-И"] =0; C.127)
б) уравнение для <(у'J>:
-^] = 0: C.128)
в) уравнение для <гг'г/>:
- Ф'?> ¦%¦ - <»v> „ -g— D + -
+ 0,7 (Ь _ аж) J^L + 0,7 (gy -ay
+ [2 (а - 1) <(u'J> + D- + ^ «) <(П2> +
+ 3(-ш—i«)^]-5- + (-r«-r)<«v>nx
X-g—4<uV>==°5 C-129>
г) уравнение для W2:
, , /v 5w х/ ,Ч9Ч ди и2 Т179 ди 3 / В . Q
^ + (^ - aw) ^f- + Qg -= 0; C.130)
д) уравнение для <G"J>:
WT'y -|f + (Wry 9 °L. = - D + ^-) <G"J>; C.131)
е) уравнение для <(с'J> :
<,'с'> -*- + <«v> ^ ^ = - D +
ж) уравнение для <и'Т'}:
<ы v> f-+<(u'J9 -5f + °'2 <уТ'> -It + °'6 <uT'>ч ж
[
Qv
C.133)
181
з) уравнение для
w^^} Cл35)
к) уравнение для <у'с'>:
0,2 <г; с > т| -^ 0,2 <ц с > -_ + -j- (gy — av) -f- +
v>' <V ° У\; (ЗЛ36>
л) уравнение для <Г'с'>:
ГС>; C.137)
м) выражения для <м'р'>, <^'р'>» <^'р'> и <с'р'>:
<и'р'>/р - -х<и'Г> + х<и'с'>, C.138)
<У'р'>/р = -Х<^Г> + x<i/c'>f C.139)
<ГР'>/Р = -х <Г'J> + х<ГО, C.140)
<с'р'>/р = -х<^'^'> + *<(О2>. C.141)
В этих уравнениях величина а записана как неизвестный ко-
коэффициент [т. е. не использовано C.47)]. Это связано с тем, чтот
как уже указывалось, величина будет дополнительно уточнена.
Из приведенных уравнений находят все вторые моменты и W2.
При этом неизвестной остается величина Qg в C.130). Варьируя
ее при расчетах, можно получить зависимость вторых моментов
<(«Т>, <Ю2>, <«V>, <(ГJ>, <(с'J>, <и'Г>, <УГ>, (и'с'у, <р'с'У,
182
<TV>, <и'р'>, <Vp')> (Т'р'У, <е'р> от параметров осредненного
течения, от I и от W2 7.
После этого по B.1)—B.4) определяются коэффициенты турбу-
турбулентного переноса vT, aT, DT и по C.64) коэффициент DT.
Заметим, что после этого в общую систему уравнений для рас-
расчета течения должно быть включено уравнение для W2, в котором
величина Q записана в явном виде (см. следующий раздел).
Таким образом, мы завершили общее описание метода ^теоре-
^теоретического» (полуэмпирического) определения vT, ат, DT и Лт, что
и является задачей настоящего раздела. После расчетов можно
подобрать формулы для vT, ат, Z)T и DT, аппроксимирующие резуль-
результаты этих расчетов.
Для расчетов удобно заранее подставить во все уравнения вы-
выражения B.1)—B.4) для моментов и привести уравнения к без-
безразмерному виду (при этом величины vT, ат, DT и DT вблизи стенки
для приведения к безразмерному виду относить к v, а для расчетов
вдали от стенки — к Z2 ди/ду для сдвигового течения и к I Y^gl
для свободной конвекции). Аппроксимировать результаты рас-
расчетов целесообразно в безразмерном виде (см. о форме соответствую-
соответствующих выражений пояснения в разд. 6.2).
Заметим еще раз (хотя это и ясно из изложенного), что урав-
уравнения C.127)—C.191) представляют собой не дифференциальные
уравнения, а систему алгебраических уравнений для определения
различных моментов. Производные от и, Т и с являются в них за-
заданными параметрами, входящими в состав аргументов при опре-
определении локальных значений моментов.
Задача о расчете_(и удобной аппроксимации) безразмерных ве
личин vT, aT, DT и Dt является автономной и должна решаться
независимо от задач о расчете поля осредненного течения с исполь-
использованием указанных величин (и до решения таких задач, конечно).
Напомним, что предполагается возможность использования
полученных описанным методом коэффициентов турбулентного
переноса и при расчете течений сред с переменными свойствами.
Кроме описанного полуэмпирического метода получения вы-
выражений для vT, aT, DT и DT, для этого может использоваться,
конечно, прямая обработка и аппроксимация экспериментальных
данных или данных «численного» эксперимента 8. Возможен и
комбинированный подход: использование описанного полуэмпи-
полуэмпирического метода и проверка его (а также уточнение входящих
в уравнения эмпирических констант) при сравнении с опытными
данными или данными «численного» эксперимента.
Значения эмпирических констант будут указаны при рассмот-
рассмотрении отдельных задач. В различных частных случаях уравнения
могут упрощаться или усложняться (если, например, учитывают-
учитываются МГД-члены уравнений).
7 При этом т определяется по C.52).
8 В гл. 7 будут приведены такие примеры.
183
6.4. Система уравнений для расчетов
осредненных характеристик турбулентных течений
с использованием законов локального подобия
Для конкретности рассмотрим случай течения в двумерном по
осредненным характеристикам статистически стационарном по-
пограничном слое (пристеночном или струйном).
Необходимые уравнения получаются путем осреднения из-
известными (общепринятыми) методами уравнений количества дви-
движения, энергии, диффузии (т. е. переноса массы какого-либо ком-
компонента, входящего в состав среды), неразрывности и записи за-
затем в полученных уравнениях вторых моментов в форме B.1)—-
B.4).
Система уравнений включает также в себя формулы для vT,
ат, DT и Z>T, получаемые описанным в разд. 6.3 методом или пу-
путем аппроксимации опытных данных или результатов «численных»
экспериментов. Так как в число аргументов в формулах для vT,
ат, DT и Drj, входит W, то в состав системы уравнений включается
также уравнение C.130) для W2 с записанным в нем в явном виде
выражением для Q (т. е. для конвективных и диффузионных чле-
членов). В случае магнитогидродинамических течений в общую си-
систему уравнений входят также уравнения для определения на-
напряженности магнитного поля.
Как уже отмечалось, указанная система уравнений может
быть записана для среды с переменными свойствами, а коэффи-
коэффициенты vT, aT, DT и .DT в ней могут приближенно определяться
без учета переменности свойств среды (как это сделано в разд. 6.3).
Все перечисленные уравнения, описывающие рассматриваемую
задачу, приведены в [11] для общего случая течения среды с пере-
переменными свойствами. Чтобы не повторять здесь вывод указанных
уравнений, заимствуем их из этой работы. Запишем сначала
уравнения для однокомпонентной среды без учета архимедовых
сил при осесимметричном течении (для перехода к случаю плоско-
плоского течения нужно положить в них г = const). Система уравнений,
описывающих осредненное течение в пограничном слое, имеет сле-
следующий вид:
ди . ди dp , 1 д (гх) // л\
D.3)
~а hP^-д— = 7Г~-1 3-
дх ' г ду ах ' г ду
/0 = / + ««/2, D.4)
T = p(v + vm)-g-, D.5)
Qo = ? + их + Япуч,. D-6)
^- = pCp(a + av)-0j-. D.7)
184
Здесь т — напряжение силы трения; q — удельный тепловой по-
поток (без потока излучения дЛуч); для пристеночного течения по-
положительное направление q — к стенке, а ось у направлена от
стенки; / — удельная (отнесенная к единице массы) энтальпия
среды (так что d/ = Ср аТ).
В выражениях D.5) и D.7) присутствуют коэффициенты тур-
турбулентного переноса v— и а—. Уравнение для PF2, необходимое для
расчетов vm и ат и входящее поэтому в общую систему уравнений,
имеет в рассматриваемом случае следующий вид [11]:
2 и* ди
2 // /\2\ ди
- — <("J>^- ) | ^
D.8)
Для двухкомпонентной среды, состоящей из не взаимодейст-
взаимодействующих между собой идеальных газов (концентрация одного из
которых равна с), приведенные уравнения должны быть дополнены
уравнением диффузии г
дс , дс
где i » р (D + Z)-) 9с%. D.10)
Кроме того, изменяется выражение D.7) для q и смысл вели-
величины q. Вместо D.7) нужно принять
(также в пренебрежении термодиффузией).
Здесь Jx и /2 — удельные энтальпии компонентов 1 и 2 смеси
(с — концентрация компонента 1), начало отсчета которых уста-
устанавливается для невзаимодействующих компонентов произволь-
произвольно. В связи с этим в величине q смысл удельного теплового потока
имеет только первый член в правой части D.11).
Чтобы не загромождать изложение, уравнения для МГД-те-
чений и для течений с учетом архимедовых сил будут рассмотрены
в тех разделах, где о них будет идти речь.
Заметим также, что уравнения для потока энергии излучения
длуч, входящего в D.6), рассматриваются в [11]; обсуждается
там также вопрос о взаимодействии излучения и турбулентного
переноса тепла.
1 В пренебрежении термодиффузией, что в рассматриваемом случае почти
всегда можно сделать.
8 В. М. Иевлев 185
6.5. Получение сеточных уравнений
и порядок расчетов
Для определения осредненного в пограничном слое течения одно-
компонентной среды должна численно решаться двумерная за-
задача, описываемая системой уравнений D.1) — D.7), а также фор-
формулами для vT и ат, уравнением D.8) для W2 и выражениями для
свойств среды в зависимости от р и Т. Расчеты, необходимые для
получения формул для vT и ат, и расчеты свойств среды должны
выполняться по отдельным программам. Здесь мы будем считать
все эти величины известными.
Методы конечно-разностной аппроксимации уравнений погра-
пограничного слоя и порядок расчетов являлись предметом многих
опубликованных исследований (например, [34—39] и др.). Мы при
расчетах применяли методику работы [38], которая во всех слу-
случаях позволяла успешно проводить вычисления. В ней исполь-
используется расчетная сетка с переменным (в зависимости от расстоя-
расстояния от стенки) шагом по оси у. Метод расчета построен так, что
производится последовательный переход сечения пограничного
слоя с х = xt (i — номер узлов расчетной сетки по оси х) к сече-
сечению с х — xi+1 = xt + Ах и т. д. В каждом новом сечении опре-
определяются все величины. Форму конечно-разностной записи урав-
уравнения и указанный порядок расчета поясним на примере уравне-
уравнения количества движения D.1), которое с учетом D.5) и при г =
= const (плоский случай) записывается так:
ди , ди , dp , д Г . , ч ди 1 /г- л\
Отметим величины в узле г, / плоской расчетной сетки индек-
индексами i, / (/ — номера узлов по оси г/). Введем обозначения Аг/+ и
Аг/_ — для шагов сетки по г/, прилегающих к какому-либо рас-
рассматриваемому узлу i, ; (см. рис. 5.1).
Уравнение E.1) в конечно-разностной форме записывается
в [38] следующим образом:
л 7/ Ц*+1. i ~ "i-l, 5 , ui,j+l—ui,i-l Pi+l — Рг-1 ,
*'"*' Ш + Pi iy*i^I = Ш -г
2
Pi, j-l К j-l + (vT)i, j-l + Pi, j K, j + (vT)i, jl v
2 X
Д^/_ J
При расчете величин в слое х = Xi+i в памяти ЭВМ должны
сохраняться величины скоростей и температур в двух предшест-
предшествующих слоях: при х = xt-x и при х = xt. В E.2) единственная
186
неизвестная величина — это скорость щ+i, j. Она и вычисляется
последовательно для всех /, т. е. по всей толщине пограничного
слоя. Аналогичным образом из уравнения энергии D.2) [с уче-
учетом D.6)], записанного в конечных разностях подобно E.2), опре-
определяются (/0)г+х, j для всех /. После этого можно найти /i+i, j
до D.4), затем, зная /,— температуру 7\-+1, j и необходимые
свойства среды (р, v, а) в узлах г + 1» /• Подобно определяются
величины (W2)i+ir j no D.8).
Компонента скорости и находится из уравнения неразрывно-
неразрывности. Для двухкомпонентных сред таким же способом записывается
в конечно-разностном виде и решается уравнение D.9) [с учетом
D.10)].
Так рассчитывается пограничный слой по всей длине обтекае-
обтекаемого тела (или по длине струи для струйного пограничного слоя).
Мы широко использовали также другой, более простой метод
расчета, впервые описанный нами в [40] и затем подробно в [11].
Он удобен как из-за своей простоты и малых требований к ЭВМ
(что позволяет рекомендовать его для решения практически важ-
важных задач тем организациям, которые не имеют хорошей вычисли-
вычислительной техники), так и потому, что для уточнения этого метода
расчета легко использовать различные опытные данные, в том
числе и измерения теплообмена и трения, в которых нет подроб-
подробной информации о распределении параметров потока. Конечно,
такие преимущества достигаются за счет уменьшения точности и,
главное, универсальности метода расчета, поэтому обсуждаемый
упрощенный метод нельзя противопоставлять решению двумер-
двумерной задачи о течении в пограничном слое. Достигаемая точность
и степень универсальности, однако, в большинстве случаев впол-
вполне достаточны для практических целей.
Упрощенный метод расчета, о котором идет речь, основывается
на приближенной замене исходной системы двумерных уравнений
некоторой системой одномерных уравнений, которые решаются
с использованием быстро сходящихся последовательных прибли-
приближений (причем уже второе приближение дает точность, достаточ-
достаточную для расчетов трения и тепломассообмена во многих случаях).
Основное допущение, которое позволяет перейти к одномерной
задаче, состоит в следующем: предполагается, что формы безраз-
безразмерных профилей скорости и, удельной энтальпии торможения /0
и концентрации смеси с в пограничном слое достаточно медленно
изманяются по длине обтекаемого тела х.
Приведем, следуя [11], наиболее важные соотношения упро-
упрощенного метода расчета для случая однородной среды.
Профили скоростей и температур в этом методе вычисляются
путем интегрирования по у уравнений D.5) и D.7) с использова-
1 Это основное предположение является и основной причиной ограничения
универсальности метода: из рассмотрения исключаются задачи о течении
с произвольными профилями и, /0 и с в начальном сечении и о динамике
перестройки этих профилей. Фактически рассматриваются только некоторые
«равновесные» пограничные слои.
8* 187
нием приближенно задаваемых профилей величин т и q. Для опре-
определения профилей т и q = g0 — wt [при дЛуч = 0; см.: D.6)] из
системы уравнений D.1) — D.7) можно после простых преобразо-
преобразований получить следующие выражения:
У У
__ du . . (' дои2 , (' дои , /с Оч
т = тст — ри -^- г/ + РстУст^ + ^ ~^ di/ — w ^ -J^- dy, E.3)
о
Ч
= ?ст + Рст^ст (Л — /ст) + J -^-р- dp — /0 J -^r dy. E.4)
о о
Здесь индексом «ст» отмечены величины на стенке, чертой свер-
сверху — величины вне пограничного слоя (в «свободном» потоке).
Принято, что в общем случае может быть истф 0 (вдув или от-
отсос через стенки).
Обозначим т* и q* величины, описываемые соответственно сум-
суммами первых трех членов в правой части E.3) и первых двух чле-
членов в правой части E.4). На стенке величины т и т*, а также q0
и q0 и их первые и вторые производные совпадают 2. Поэтому если
в E.3) и E.4) интегралы определить очень приближенно, то за-
заметная ошибка втид0 будет допущена только вдали от стенки.
Это мало повлияет на профили и и /0, так как в турбулентном по-
пограничном слое вдали от стенки эти величины почти не изменяют-
изменяются (из-за больших значений vT и ат). Для приближенного вычисле-
вычисления интегралов в E.3) и E.4) принимается, что и/и и (/0 — JC1)/
(/0— /ст) зависят только от y/v и г//8 соответственно, где у и 0 —
толщины потери импульсов и энергии в пограничном слое. Это
позволяет приближенно выразить производные по х от различных
величин, входящих в интегралы в E.3) и E.4), через производные
по у. Например:
ди 1 dl ди 1 dv
дх и ах и ду v dx
о 1 dv I d9
Величины — -г- и -д- -т— находятся из так называемых интег-
интегральных соотношений импульсов и энергии для пограничного
слоя. Вынося, кроме того, из-под знаков интегралов некоторые
средние значения плотности (и сокращая их), принимая профили
скоростей и /0 подобными друг другу и выражающимися степен-
степенной формулой вида
Jo~ Jct / 4
ТТ.
и
J-h-t
2 Для величины (d2q0/dy2)CT это строго справедливо только при dTc,Jdx — 0,
но приближенно справедливо почти всегда.
188
где б — толщина пограничного слоя, а также проводя еще ряд
упрощений, можно получить из E.3) и E.4):
\2+1/п-
) J
E-5)
Г / ^0—7ст \2+1/'г1
gO~gcr I—f -j J +РстУст(/0— /«) X
<5-6>
При расчете первого приближения показатель степени п нуж-
нужно задать ориентировочно (например, для случая FCT = 0 п ж
ж 1/7 -г- 1/8). Затем по результатам вычисления профилей гг и /0
величина п может уточняться. В следующих приближениях можно
также определить профили т и q0 не по E.5) и E.6), а по E.3) и
E.4), вычисляя в них интегралы по найденным в предыдущем
приближении профилям.
Уравнения D.5) и D.7) при подстановке в них выражений для
профилей т и q [например, по E.5) и E.6)], а также формул для
vT и ат (общая форма которых указана в разд. 6.2, а конкретный
вид будет рассмотрен в гл. 7) образуют систему из двух обыкно-
обыкновенных дифференциальных уравнений первого порядка с двумя
неизвестными функциями от у: и и / (или Т). Эти уравнения чис-
численно легко решаются с учетом граничных условий и = 0 и / =
= /ст при у = 0. Проблема, однако, состоит еще в том, что в
уравнения входят неизвестные величины тст и дст. Нужно зада-
задавать различные значения этих величин и подобрать их такими,
чтобы приобрели заданное значение некоторые интегральные ха-
характеристики пограничного слоя — величины (ри) и (рЭ), опреде-
определяемые таким образом:
Эти выражения записаны для осесимметричного течения.
В них R = R (х) — радиус обтекаемого тела вращения (или ра-
радиус осесимметричного канала, в котором происходит течение);
г — текущий радиус точки в пограничном слое. Для плоского те-
течения нужно принять в E.7) rlR = 1.
Величины (pv) и (рб), к которым должны «подгоняться» интег-
интегралы в E.7) при варьировании тст и #ст, определяются заранее из
решения интегральных соотношений импульсов и энергии. В [11]
изложен простой метод решения указанных интегральных соот-
соотношений (допускающий также последовательные приближения).
Преимущества изложенного метода для обработки опытных
данных и сопоставления с этими данными можно проиллюстриро-
189
вать следующим примером. Предположим (это является довольно
типичной ситуацией), что при проведении экспериментальной ра-
работы подробно измерены профили различных величин только в од-
одном сечении пограничного слоя (при одном х). Сравнивать эти
данные с результатами двумерных расчетов трудно, так как не
известны условия в начальном сечении. В то же время можно по
опытным данным вычислить интегралы в E.7), т. е. найти (рг;) и
(р0), найти интегралы в формулах E.3) и E.4) для профилей т и д,
а затем провести «теоретический» (полуэмпирический, конечно)
расчет профилей и и / и подбор бст и дст путем интегрирования
уравнений D.5) и D.7) и подгонки расчетных величин интегралов
в E.7) к экспериментальным значениям (pv) и (рб). Форму профи-
профилей и величины тст и qCT (если они были измерены) можно срав-
сравнить с опытными данными; далее вводят при необходимости те или
иные коррективы в формулы для vT и ат, чтобы получить хорошее
согласие расчетов с опытными данными. Тем самым эксперимент
будет использоваться для уточнения теории.
«** Конечно, все это можно сделать (как и вообще применять упро-
упрощенный метод расчета) только для «равновесной» турбулентности,
когда W из числа аргументов, определяющих vT и ат, можно ис-
исключить. Для задач, где это сделать нельзя, должен использовать-
использоваться только двумерный метод расчета.
6.6. Граничные условия
Граничные условия для упрощенного метода расчета были указаны
в разд. 6.5. Поэтому здесь речь пойдет только об условиях, кото-
которые должны приниматься при двумерном расчете.
Должны быть заданы прежде всего условия на стенке и неко-
некоторые параметры «свободного» потока, вне пограничного слоя.
На стенке принимается и = О, W = 0 и задается vCT = vcr (x)
и Тст = ТСт (х). Условия вне пограничного слоя состоят в зада-
задании /0 = const и dp/dx в виде функции от х г. Скорость вне погра-
пограничного слоя п задается только в начальном сечении (х = 0), за-
затем она получается из расчетов. Это же относится к пульсацион-
ной скорости W.
Область расчетов должна быть несколько шире (по оси у) пред-
предполагаемой максимальной толщины пограничного слоя. Это поз-
позволяет не определять какую-либо конечную толщину погранич-
пограничного слоя, а рассматривать естественное развитие профилей ско-
скорости и температуры в потоке.
Условия в начальном сечении (при х = 0) должны включать
в себя данные по распределению скорости и, температуры Т и ве-
величины W2 по оси у (а для двухкомпонентных сред и зависимость
1 dp/dx определяется при расчете обтекания тела идеальной жидкостью или
газом. При этом во втором приближении контур тела может быть скорректи-
скорректирован путем «наращивания» на стенку слоя, равного «толщине вытеснения».
190
концентрации с от у). При этом часть (и значительная в начальном
сечении) профиля и и Т должна приходиться на зону «свободного»
потока вне пограничного слоя (т. е. там должно быть и = п =
= const, Т = Т = const, с = с = const, W = W = const). В эту
часть потока при х^> О может затем распространяться погранич-
пограничный слой.
Поскольку для расчетов нужны параметры в двух соседних се-
сечениях потока (xi-i и xt — Xi-i + Ах\ см. выше), при переходе от
начального сечения х — х0 = О и сечению х = хх приближенно
приходится принимать все параметры при х = —Ах равными зна-
значениям этих параметров при х = 0. Допускаемая при этом ошиб-
ошибка быстро «сглаживается» по длине х.
Методы определения всех профилей при х = 0 здесь не рас-
рассматриваются. Они могут иногда потребовать расчета начального
участка ламинарного пограничного слоя и зоны перехода к турбу-
турбулентному течению. Эти вопросы выходят за пределы задач настоя-
настоящей книги.
ГЛАВ Л СЕДЬМАЯ
ФОРМА ЗАКОНОВ ЛОКАЛЬНОГО ПОДОБИЯ
В НЕКОТОРЫХ ЧАСТНЫХ СЛУЧАЯХ.
РАСЧЕТЫ ТЕЧЕНИЙ, ИХ АНАЛИЗ
И СРАВНЕНИЕ С ОПЫТНЫМИ ДАННЫМИ
7.1. Течение несжимаемой жидкости
вдоль гладкой стенки
Для определения эмпирических констант в уравнениях разд.
6.3 и проверки согласования результатов расчетов с исполь-
использованием формул настоящего раздела с опытными данными рас-
рассмотрим два типа течения: слой постоянного трения у стенки и те-
течение в цилиндрической трубе (в том числе и с теплообменом).
В слое постоянного трения везде, кроме ближайшей окрестности
стенки, турбулентность является практически «равновесной»*,
т. е. в F.3.130) Qg zz 0. Целесообразно выполнить расчеты с Qg =
= 0 и у стенки, а затем уже вводить поправку на «диффузию»
турбулентности.
Для расчетов (и в слое постоянного трения, и в трубе) преобра-
преобразуем уравнения C.127) — C.137) так, как это указывалось в
разд. 6.3, т. е. подставим в них различные моменты в виде
F.2.1) — F.2.4) и учтем, что в слое постоянного трения
^тр/р = *4 = (v + vT) ди/ду = const, A-1)
1 Т. е. примерно уравновешены производство энергии турбулентности и ее
диссипация, а роль «диффузии» пренебрежимо мала [2, 4].
191
а в трубе
Ттр/р = v I (I - rlR) = (v + vT) ди/ду, A.2)
и выразим ди/ду из A.1) или A.2).
Приведем уравнения к безразмерному виду, относя все ско-
скорости к v*, а длины к ^
Аналогичные преобразования проведем в уравнении F.4.8)
для W2 (в котором в отличие от F.3.130) величина Qg выражена
в явном виде).
В уравнениях F.3.127)—F.3.137) примем р' = 0 и с' = 0
(так как рассматривается однокомпонентная жидкость с постоян-
постоянными свойствами).
Нет необходимости выписывать здесь все получающиеся соот-
соотношения; мы их будем использовать по мере необходимости.
Рассмотрим вначале течение в слое постоянного трения вдали
от стенки. При этом надо использовать из числа указанных толь-
только уравнения F.3.127)—F.3.130) с Qg = 0 в C.130) (так как
другие уравнения связаны с величинами Т' или С", которые в
этом случае не рассматриваются). В этих уравнениях х\ = 0 (так
как в слое постоянного трения ди/дх = 0); члены с v можно для
течения вдали от стенки опустить.
Примем, как это обычно делается для слоя постоянного трения
(и следует из соображений теории размерностей):
= *у, A.3)
где х = const ^r ОД»
Обозначим
R = -<uV>/f <(u'J>Y <И2>- A-4)
Варьируя величины эмпирических констант, можно найти из
получаемых указанным путем уравнений величины Y((v'Jy/v#,
Y<(u'J>/V<(v'J>, f<(WJ}/f<i(v'Jy, Wlv* и Я, которые можно
сравнить с опытными данными, имеющимися, например, в [2, 3, 4].
Наилучшие результаты получаются при следующих значениях
констант:
а = 1Д2; /с = 0,174; 5 = 0,25. A.5)
При таких константах значения перечисленных величин
равны:
Y<(WJ>/V<(v'Jy = 1,4243; Wlv+ = 1,443; R = 0,478.
Эти величины близки к соответствующим экспериментальным
данным.
Для определения константы Q в уравнениях F.3.127)—F.3.130)
применим их к течению в непосредственной близости от стенки
192
(в «вязком слое») при ттр = const. Примем* по-прежнему
I = ОЛу\
Величина vT, определяемая из F.3.127)—F.3.130) при Qg = 0,
получается равной нулю не на стенке (не при у = 0), а на неко-
некотором конечном расстоянии от стенки у = у0. Это объясняется
тем, что при Qg = 0 не учитывается «диффузия» турбулентности
к стенке (см. по этому поводу [11]). При у < у0 нужно принять
vm = 0 — получается тонкий слой ламинарного движения. Ес-
Естественно, при учете «диффузии» турбулентности, т. е. при ис-
использовании уравнения F.4.8) для W, этот слой частично турбу-
лизируется.
Для определения эмпирической константы Q воспользуемся
следующими соображениями.
Профиль скоростей в слое ттр = const определяется путем ин-
интегрирования уравнения
du/dy = ттр/[р (v + vT)] = v2j[v A + vT/v)], A.5)
т. е.
где т| = yVJv. A.7)
Если в выражение A.6) подставить в качестве vT/v значение,
определяемое по какой-либо хорошо совпадающей с опытом эм-
эмпирической формуле для этой величины (обозначим его (vT/veKCn),
то получится:
—) = i
у*/эксп J 1 + (v
vT/v)9KCn • К ' '
о
Здесь индексом «эксп» отмечена и величина w/y#, которая, оче-
очевидно, должна хорошо совпадать с опытными данными.
В качестве формулы для определения vT/v можно взять, на-
например, формулу Рейхардта [41], удачно аппроксимирующую
опытные данные:
vT/v = (vT/v)9KCn = 0,4 {Л - 7,15 [th (т|/7,15) +
+ 1/3 th3 (г)/7,15)]}. A.9)
Вычитая A.8) из A.6), получим
Л (JL) -С (УДксп-Ут^ d ,110)
»* UJ9Kcn J [l + vT/v][l + (vT/v)9KCn] Т|# V1#1U'
о
Проводя вычисления vT/v с использованием системы уравне-
уравнений F.3.127)—F.3.130) (и принимая vT/v = 0 при у < у0, т. е.
а При другом коэффициенте пропорциональности между I и у пришлось бы
соответствующим образом скорректировать величину Q.
193
при У] < г] = v^yjv) при различных значениях константы D [и при
значениях других констант по A.4)], можно найти такое D, при
котором будет близка к нулю величина интеграла в A.9) при боль-
больших значениях верхнего предела интегрирования (при которых
вязкость уже не играет роли, т. е. vT/v J^> 1). Получается
D ~ 1,6. A.11)
Такая величина D и будет принята.
На рис. 7.1, а построены кривые зависимости vT/v от г), рас-
рассчитанные по формуле Рейхардта A.9), по системе уравнений
F.3.127)—F.3.130) с принятыми значениями констант и по этой же
системе; но с Qg -/= 0 и с определением W по F.4.8). На этом же
рисунке показаны опытные данные, заимствованные из рабо-
работы [41], и результаты «численного» эксперимента по гл. 5 книги.
Как видно, приближенный расчет дает вполне удовлетворитель-
удовлетворительные результаты и хорошо согласуется с данными «численного»
эксперимента.
Перейдем теперь к рассмотрению переноса тепла в слое ттр =
=const [с целью определения дополнительных эмпирических кон-
констант FhI, входящих в C.131)—C.137)].
Вначале применим уравнения к течению вдали от стенки, где
членами с v и а можно пренебречь. Из уравнений F.3.127) —
F.3.137) и соотношений F.2.1), F.2.2) при Qg = 0, ц = 0, 0 = 0,
I = 0,4у можно найти, как указывалось, величины vT и ат и оп-
определить «турбулентное число Прандтля» вдали от стенки:
рГт = vT/aT. A.12)
На основании анализа экспериментальных данных (напри
мер, по так называемому коэффициенту восстановления темпера
туры в сверхзвуковом потоке — см.: [II]3) можно принять ве-
величину Ргт близкой к 0,85 -г- 0,9 (не с очень высокой степенью
точности). Примерно такое значение Pr-J получается из расчетов
при
F^2. A.13)
Для определения константы М в рассматриваемых уравнениях
выполним расчеты Prm = vT/aT в зависимости от Rev =
= Y({v'Yy-lh, используя уравнения F.3.127)—F.3.134), а так-
также соотношения F.2.1), F.2.2) при ф, = 0, т) = 0, 0 = 0. При
расчетах коэффициент температуропроводности а будем представ-
представлять в виде
а = v/Pr, A.14)
где Рг — число Прандтля.
3 Напомним, что хотя мы рассматриваем сейчас случай несжимаемой жид-
жидкости, но анализируемые локальные величины коэффициентов турбулент-
турбулентного переноса должны быть, по основному предположению, пригодны и для
среды с переменными свойствами.
194
0,6
Рис. 7.1. Распределение
турбулентного числа Пран-
дтля (а) при течении в тру-
трубе при Рг = 0,01 A), 1B)
и 10C) и пример расчета
профиля скоростей и тем-
температур в трубе при Рг =
= 0,01 и Re = 5-105 (б)
Рис. 7.2. Расчетные про-
профили осредненных и пульса-
ционных скоростей в при-
пристеночном слое трубы или
канала вдоль различных
осей координат
0,6 у/х
Можно ожидать, что если задать вдали от стенки, например,
Рг = 0,9, то Ргт будет мало изменяться поперек рассчитываемого
слоя, т. е. в зависимости от Rev. Примем это требование в качест-
качестве условия выбора константы М.
Была рассчитана зависимость Ргт от Rev при различных М.
Получилось, что можно принять
М^9. A.15)
По приведенным формулам можно найти также зависимость
vT/v от Rep.
Величина Ргт зависит от числа Прандтля Рг только у стенки,
где большую роль играют процессы молекулярного переноса,
так как турбулентный перенос, определяемый коэффициентом vT,
еще не очень велик по сравнению с молекулярным. В связи с этим
удобно представить Ргт в зависимости от vT/v (при различных
числах Рг). Ясно, что приРг<^ 1 (жидкие металлы) коэффициент
турбулентного переноса тепла ат меньше турбулентного коэффи-
коэффициента трения vT, так как турбулентные пульсации температуры
195
будут сглаживаться из-за влияния большой теплопроводности,
т. е. при Рг <^ 1 будет Prw ^> 1 вблизи стенки.
На рис. 7.1, б показаны результаты расчетов Ргт в зависимо-
зависимости от К A + vT/v) для различных чисел Рг. Эти «локальные»
свойства турбулентного переноса применимы, по нашему предло-
предложению, для различных типов течений. При приближенных рас-
расчетах пограничного слоя можно определять vT/v по уравнени-
уравнениям разд. 6.3 или любым другим способом (например, по эмпири-
эмпирической формуле Рейхардта), а величину Ргт находить затем по
рис. 7.1,а.
Обратимся теперь к случаю течения жидкости в трубе. Ис-
Используя указанные уравнения, найдем распределение величин
vT/v и Ргт 4. Профиль скоростей затем находится интегрированием
уравнения A.2), где г = R —г/.
При вычислениях масштаб турбулентности I определим по фор-
формуле
I « 0,4» {1 - {ylRf + Ч2(уШK}. A.16)
Обозначая
ф = ulv^i A.17)
находим из A.2)
где
Re* - Rujv. A.19)
Для средней величины ф по сечению трубы получится
A.20)
Число Рейнольдса Re = 2Rucv/v (где иСр — средняя по сече-
сечению скорость), очевидно, выразится так:
Re = 2Re*cpcp. A.21)
Легко показать, что коэффициент трения
I = 8/Ф2ср, A.22)
При вычислениях характеристик теплообмена жидкости со
стенкой трубы рассмотрим случай постоянного по длине трубы
удельного теплового потока на стенке qCi. Тогда удельный теп-
тепловой поток q на любом радиусе г будет пропорционален расходу
жидкости через часть поперечного сечения, ограничиваемую этим
4 При этих расчетах учитывается «диффузия» турбулентности, т. е. в F.3.130)
принимается Qg ф 0, a W2 определяется по F.4.8).
196
радиусом. При этом форма профиля разности температур Т —
— Гст будет сохраняться неизменной по длине трубы.
Распределение q/qCT по сечению трубы, соответствующее опи-
описанной ситуации, имеет такой вид:
У
Профиль температур определяется путем интегрирования урав-
уравнения
q = рСр(а + ат)дТ/ду, A.24)
где Cv — удельная теплоемкость среды.
Обозначая
ф = (Т — Гст) pCfd/iq^R), A.25)
запишем A.22) в следующем виде:
Pr vT v щ q
J (L26)
Ау. A.27)
Отсюда получается
Я/Яст
(Pr/PrT) (vT/v)
Профили скоростей и температур в трубе, рассчитанные по
указанным формулам, показаны на рис. 7.1, б.
Среднемассовое значение безразмерной температуры г^ в тру-
трубе равно
Фср
Из A.23) видно, что число Нуссельта Nu = qCT2R/[(Tcl) —
— ГСт) pCva] (где Гср среднемассовая температура) определяется
так:
Nu = 2/фСр. A.29)
Задавшись Re*, по приведенным формулам и ранее определен-
определенным значениям vT/v и Ргт можно найти профиль скорости ср, число
Рейнольдса Re, коэффициент сопротивления |; задавшись также
Рг, находят профиль температуры г|) и число Нуссельта Nu. Вы-
Выполняя эти расчеты при различных Re*, определяют ? = ? (Re)
и Nu = Nu (Re, Pr).
Для примера на рис. 7.2 показаны расчетные профили скоро-
скоростей и их сравнение с опытными данными из [42]; на рис. 7.3 —
зависимость Nu = / (Ре), которая хорошо согласуется с резуль-
результатами различных опытов; а рис. 7.4 иллюстрирует расчеты по
197
о
/ff* Pe
iff
ffl
/,2
Рис. 7.3. Расчетная зависимость
Nu = / (Ре) для жидких металлов и
сравнение ее с опытными данными
различных авторов
Рис. 7.4. Зависимость безразмерного
коэффициента теплообмена от скоро-
скорости подачи жидкости через пористую
пластину
Pjj^a = const; dp/йх = 0; w6**/v = 5,5-
• 108;*O — экспериментальные результаты
расчет
0,4 0S
Рис. 7.5. Сравнение расчетных и экспериментальных [43] профилей скоро-
скоростей (а) и температур (б) в пограничном слое на пластине
7 — нижняя шкала у; 2 — верхняя шкала у; О — экспериментальные данные; рас*
чет
198
Рис. 7.6. Коэффициент тре-
ния на теплоизолированной --
пластине в сверхзвуковом *
потоке
в сверхзвуковом
О, • — опытные данные [43];
теоретический расчет
Рис. 7.7. Теплообмен при
вдуве через пористую плас"
тину газа
а —^коэффициенты теплоотдачи
к .пластине при вдуве в погра-
пограничный ' слой газа; А =
= (pt?)em/(pvSC); б — профили
скоростей в пограничном слое
при разных интенсивностях вду"
ва: 1 — (pv)em/(iyu) = 2-Ю-8;
2 — (р*>)ет/(Р^) = 8-Ю"8
S Af
указанным формулам значений безразмерного коэффициента теп-
теплообмена на пористой пластине в зависимости от скорости по-
подачи жид кости через пластину.
7.2. Течение среды с переменными свойствами вдоль
гладкой стенки
Полученные в разд. 6.1 зависимости
1*ди/ду
— = /
B.1)
должны быть в соответствии с нашим предположением о справед-
справедливости принципа «локального подобия» в процессах турбулент-
турбулентного переноса пригодны и для сред с переменными свойствами.
Ниже приводятся некоторые иллюстрации подтверждения это-
этого положения. Формулы вида B.1) использовали для решения
рассмотренных в разд. 6.4 уравнений, при этом для большинства
случаев применяли упрощенный метод расчета разд. 6.5 (более
199
подробно вопрос рассмотрен в [11], откуда и заимствованы при-
приводимые примеры).
На рис. 7.5 (см. разд. 1.16) проведено сравнение расчетных и
экспериментальных профилей температур для пограничного слоя
в сверхзвуковом потоке (число Маха М = 6,83) при достаточно
высоком значении отношения температуры стенки Тст и темпера-
температуре газа вне пограничного слоя Т (ТС1/Т = 6,34). «Слишком
хорошее» согласование результатов расчета с опытом не должно
вызывать удивления, так как при расчете величины Гст, Т, а
(т. е. граничные условия) принимались, естественно, такими же,
как в опыте, и, кроме того, в соответствии с методикой разд. 5.6
расчетные интегральные характеристики пограничного слоя —
величины v и 6 — делались равными экспериментальным их зна-
значениям с помощью выбора соответствующих тст и q. Тем не менее
данные рис. 7.5, безусловно, демонстрируют применимость фор-
формул B.1) для среды с сильноизменяющимися свойствами.
Сравнение расчетных и экспериментальных данных по коэф-
коэффициенту трения на теплоизолированной пластине в сверхзвуко-
сверхзвуковом потоке (рис. 7.6) также подтверждают удовлетворительность
результатов, получаемых при применении универсальных формул
вида B.1).
При расчетах двухфазных течений использовались также урав-
уравнения разд. 4.1; при этом в связи с подобием уравнений, описы-
описывающих поле концентраций и поле температур, принималось
DT = ат, но при вычислении а? во второй формуле B.1) число
Прандтля Рг заменялось числом Шмидта * Sc = D/v.
На рис. 7.7 показано изменение коэффициентов теплоотдачи
к плоской пластине при вдуве в пограничный слой газа, как
совпадающего с текущим в основном потоке, так и отличающегося
от него. В последнем случае решалась, не только тепловая,
но и диффузионная задача. Эти данные также подтверждают при-
применимость формул вида B.1) для приближенных расчетов.
7.3. О влиянии шероховатости стенки
Вид уравнений, описывающих течение вдоль шероховатой стен-
стенки, не отличается от вида уравнений для течения вдоль гладкой
стенки включая вид формул типа B.1) для vT/v и Ргт, так как
в любых точках потока, удаленных от стенки дальше высоты
выступов шероховатости, прямое влияние шероховатости никак
не может сказаться. Отличаются только граничные условия.
Примем у = 0 в таком месте оси у, где осредненная скорость
(иУ равна 0. Ясно, что это место приходится не на «дно» впадин
между выступами шероховатости, а выше. В том месте, где
1 Для газов и Рг и Sc не очень отличаются от 1, поэтому влияние этих пара-
параметров на Ргт (или на ScT) невелико, значительное изменение его наблюдает-
наблюдается вблизи стенки только для жидких металлов и для сред с Рг ^> 1.
200
/с
Рис. 7.8. Общий вид функции
ф ip* hh)
=01, истинные скорости и (и дру-
другие компоненты скорости, т. е.
v и W) в каждом месте не равны
нулю, так как существуют вихри
между выступами шероховато-
шероховатости, обтекание этих выступов и
пр. Поэтому при у = О турбу-
турбулентный перенос не равен нулю.
Обозначим 10 — интегральный
масштаб турбулентных вихрей
при у = у0. Ясно, что 10 Ф 0.
Примем в качестве первой, са-
самой грубой гипотезы следую-
следующую формулу для распределе-
распределения I в пограничном слое:
I (у) ~ 1т (у) + h, C.1)
где 1ГЛ — использовавшаяся выше величина масштаба турбулент-
турбулентности при течении вдоль гладкой стенки.
Для определения vT, aT и DT сохраним прежние уравнения,
но будем в них подставлять I в виде C.1). Это единственное из-
изменение в методике расчета, к которому сводится учет влияния
шероховатости.
Естественно принять, что
IJh = Ф (vji/v), C.2)
где h — высота выступов шероховатости. Функция ф зависит,
конечно, от геометрической формы шероховатости, но общий ее
вид можно предвидеть. Он изображен на рис. 7.8. При vjilv -*0
должно быть ф -*0 (так как при этом влияние вязкости подав-
подавляет любые пульсации), при v^h/v ^> 1 должно быть
IJh = к = const, C.3)
так как при больших v*h/v величина IJh не должна зависеть от
вязкости.
Если имеются выступы шероховатости различной высоты и
/ (К) есть плотность вероятности того, что выступ имеет высоту /г,
то для 10 можно принять
г« =
C.4)
где интегрирование производится по всему возможному диапазо-
диапазону изменения h.
Применимость формулы C.4) требует экспериментального под-
подтверждения.
Детальные расчеты течения в трубе и трения при наличии
шероховатости стенки выполнены М. Д. Миллионщиковым [44].
Здесь <и> — средняя величина по участку стенки, много большему по раз-
размерам, чем расстояние между выступами шероховатости.
201
При этом использовалась формула C.1) и принималось Zo = kh
[по: C.3)], что справедливо, как указывалось, при vjnh ^> 1
(т. е. для сильного влияния шероховатости). Для коэффициента
трения в трубе получается формула следующего вида:
g = [A In (R/h) + B]~2, C.5)
где А, В = const.
Такой же вид имеет эмпирическая формула Никурадзе (см.:
[44]), полученная для труб с большой шероховатостью.
7.4. Турбулентная свободная конвекция
в горизонтальном слое
Уравнения разд. 6.3 и 6.4 позволяют рассчитать сложные случаи
течения среды с переменными свойствами, когда нужно учиты-
учитывать влияние на турбулентность и осредненного сдвигового тече-
течения, и архимедовых сил. Однако чтобы не делать изложение гро-
громоздким, мы ограничимся здесь в качестве примера рассмотре-
рассмотрением простейшего случая турбулентной свободной конвекции
в горизонтальном слое жидкости.
Задача ставится так. В слое шириной б, ограниченном двумя
параллельными плоскими стенками, имеется неподвижная в сред-
среднем жидкость. Ускорение силы тяжести g направлено сверху
вниз перпендикулярно к стенкам. Нижняя стенка имеет более
высокую температуру, чем верхняя, так что в слое из-за влияния
архимедовых сил развивается свободная конвекция. Числа Грас-
гофа будем считать настолько большими, что конвекция приоб-
приобретает турбулентный характер с развитым спектром турбулент-
турбулентности (т. е. с каскадным механизмом передачи энергии от крупных
вихрей к мелким г. Отклонения температуры от средней примем
настолько малыми, чтобы можно было пренебречь изменением
свойств среды р, v, а (везде, кроме членов с изменением р в выра-
выражениях для архимедовых сил,— см. разд. 6.3). Для определения
vm и аш (или Ргт) используем уравнения этого раздела с Qg Ф 0.
Для определения W2 (с учетом Qg Ф 0) применим уравнение
F.4.8). В этих уравнениях нужно принять и = 0, v = 0, gx =
= ?з = 0» аг = а2 = а3 = 0; gr = —g. Эмпирические константы
сохраняются такими, как было определено в разд. 6.1.
Из уравнения разд. 6.3 [без уравнения C.130)] получаются
после преобразований с учетом указанных исходных данных сле-
следующие четыре соотношения:
-+-^)И", D.1)
1 При «численном эксперименте», о котором шла речь в ч. I книги, можно
рассмотреть и меньшие числа Грасгофа, включая переходную область.
202
D.2)
D.3)
^ ^T). D.4)
Здесь, как и ранее:
т = i/YWfy; D.5)
PF2, как указывалось, определяется из F.4.8).
Обозначим:
Re, = Z2/vt - I /<(y'J>/v, D.7)
Примем поперек слоя тепловой поток q = const (стационар-
(стационарная передача тепла от нижней стенки к верхней), т. е.
q/Cpp = —(а + ат) dT/dy = const. D.9)
Обозначим:
/ = 1 + от/я, D.10)
Примем ^ = const.
Обозначим также:
Ф = П = <? (^бL. D-12)
ATdp/dT = —Ар, D.13)
где А Г—полная разность температур между стенками;
т = g63Ap/(pv2); D.14)
q = qb/(pCrJaAT). D.15)
Величина т — это число Грасгофа Gr; q — число Нуссельта
Nu.
Имеем:
Q = дт, D.16)
g = i^ * «-„j.^., D.17)
<p = qml\ D.18)
203
где
У = у/6; D.19)
i = 1/6; D.20)
Т = (Т — Тверхн)/АТ D.21)
(^всрхн — температура верхней стенки).
Из приведенных уравнений можно рассчитать
Ф = Ф (Ю- D.22)
После этого расчеты проводятся в таком порядке:
1) необходимо задать m и q (m, q = const);
2) разбить ось у на участки (для конечно-разностного реше-
решения одномерной задачи);
3) при известной зависимости Т_ от у 2 для каждой рассчиты-
рассчитываемой точки на оси у определить: I, ф по D.18), ? по заранее рас-
рассчитанной зависимости вида D.22) и dT/dy по D.17); _
4) проинтегрировать dT/dy по у от 0 до 1, принимая Тнижн =
= 1;
5) проверить условие Тве1)ХН = 0. Если оно не выполнено,
изменить заданное заранее q и повторить расчеты по п. 3, 4.
Выполнив указанные расчеты для разных задаваемых значе-
значений т, можно найти зависимость
Я=Я И, D.23)
т. е. Nu = / (Gr, Pr) 3.
Однако D.23) представляет собой итоговый результат полного
решения рассматриваемой задачи, а не «локальную» формулу для
аТ (или Ргт), которую можно было бы использовать при различ-
различных свойствах среды и разном распределении I = I (у). Из урав-
уравнений D.1)—D.4) и уравнения F.4.8) получается также (чис-
ленно) зависимость —, , = — от § и rr. dTO и есть «локаль-
«локальный» закон турбулентного переноса тепла.
На рис. 7.9 построена рассчитанная указанным способом за-
зависимость ат/а от |.
Для расчетов D.23) распределение I принималось по данным
работы [45]:
I = (х/я) sin Ki/, D.24)
где х = 0,4.
На рис. 7.10 построена зависимость D.23), т. е. Nu = / (Gr),
рассчитанная при Рг = 0,72. Заметим, что Nu = Яэ/Я, где %э —
эффективный коэффициент теплопроводности через слой жидкости
(с учетом конвекции), к — коэффициент теплопроводности.
2 См. пояснения по этому поводу далее по тексту.
3 Число Рг входит в уравнения D.1)—D.4), в которые нужно подставить а =
= v/Pr, поэтому от Рг, как от параметра, зависит D.22).
204
Nil
40
'Jt
Рис. 7.9. Турбулентный коэффициент температуропроводности при свобод-
нон конвекции в горизонтальной щели
Рис. 7.10. Расчетная зависимость D.23) для свободной конвекции в гори-
горизонтальной щели
Данные по конвекции в плоской щели обычно представляют
в виде Ко/к = f (Gr, Pr) [46].
Расчеты, проиллюстрированные рис. 7.10, удовлетворительно
согласуются с имеющимися экспериментальными результата-
результатами.
7.5. Замечания о влиянии градиента средней скорости
Мы не будем подробно рассматривать «локальные» законы турбу-
турбулентного переноса с учетом членов с ди/дх в уравнениях разд. 6.3
и 6.4 (хотя указанные уравнения позволяют это сделать), а огра-
ограничимся только некоторыми пояснениями качественного харак-
характера.
1. Учет членов с ди/дх в уравнениях разд. 6.3 и в уравне-
уравнении F.4.8) приводит при ди/дх >0 к снижению интенсивности
турбулентного переноса (и, наоборот, при ди/дх <0 к повыше-
повышению).
Если в F.3.130) принять Qg = 0 («равновесная» турбулент-
турбулентность), то для удаленной от стенки зоны из уравнений разд. 6.1
после расчетов получается
1 — 3,042т],
E.1)
ди/дх
где т) = , .
Формула E.1) может дать заметную поправку к обычной фор-
формуле Прандтля для турбулентного трения.
205
Если учитывать, что в действительности Qg Ф О и в качестве
предельного случая принимать при оценках конвективного члена
в F.4.8), что W ~ и, то вместо E.1) получается
I2 (ди/дуJ
; 1 — 14,34ti. E.2)
При более точном расчете W по F.4.8) получаются промежу-
промежуточные [между E.1) и E.2)] результаты.
2. При ди/дх ^> 0 снижение «локальной» интенсивности тур-
турбулентного переноса (при заданных ди/ду и I) является не единст-
единственной причиной влияния ускорения потока на турбулентность.
Есть еще две причины:
а) перестройка профиля скорости в пограничном слое. Он ста-
становится более «заполненным» х, так что зона с большими ди/ду
приближается к стенке, где меньше масштаб турбулентности I
и больше влияние вязкости (по крайней мере при не очень боль-
больших числах Re). Все это приводит к снижению интенсивности
турбулентности;
б) уменьшение при большом ускорении потока общей толщи-
толщины пограничного слоя и числа Re для течения в нем. Этот эффект
можно учесть, используя интегральное соотношение импульсов.
В сумме все указанные воздействия могут привести, как пока-
показывают и расчеты и опыт, к эффекту частичной (или почти пол-
полной) «ламинаризации» турбулентного пограничного слоя при боль-
большом отрицательном градиенте давления вдоль стенки (например,
течение в соплах) и не очень больших числах Re.
7.6. Магнитогидродинамическое течение в канале
в продольном магнитном поле
Для учета объемных МГД-сил мы не будем проводить допол-
дополнительные преобразования уравнений разд. 6.3, что подробно
проделано в [11], а просто приведем несколько заимствованных
из этой работы иллюстраций влияния магнитного поля на турбу-
турбулентный перенос. Во всех приводимых примерах фактически ис-
использовался принцип «локального подобия» турбулентного пере-
переноса, сформулированный в гл. 6, «локальные» законы переноса
определялись в следующем виде (см.: [11]):
vT _4( 1Чи\ду 6#2 \
~ т \ v » рс*ди/ду)»
ат „ f'Pdu/ду
— =Ф(——>
1 Это следует из характера изменения профиля т в пограничном слое — см*
соответствующую формулу в разд. 6.5.
206
На/Re
Рис. 7.11. Расчеты коэффициента сопротивления при течении жидкого
металла в трубе в продольном магнитном поле и сравнение их с опытными
данными работы [47]
На/Re = (ov/p)V2H/T>cp
где I — тот же масштаб турбулентности, что и в случае без маг-
магнитного поля (см. пояснения этого в [11]); а — удельная электро-
электропроводность среды; Н — напряженность магнитного поля; с —
скорость света в вакууме.
При больших числах Re (вдали от стенки в трубе, в струе)
вязкость среды и число Рг не должны влиять на vT и ат. При этом
из F.1) получается:
а#2
1*ди/ду TV рс2ди/ду
Pt.~Vv.~F' ""'
)•
рс*диЩГ)'
F.2)
F.3)
207
Все эти зависимости были в явном виде определены в [11] по
методу, аналогичному изложенному в разд. 6.3, и применены для
расчетов течений в трубах и в струях. Здесь мы приведем пример
результатов расчетов из [11] для течений в каналах (трубах).
На рис. 7.11 показаны результаты расчетов коэффициента со-
сопротивления для случая течения жидкого металла в трубе в про-
продольном магнитном поле и опытные данные работы [47]. При тео-
теоретических расчетах не использовалось ни одной новой эмпири-
эмпирической константы, кроме определенных выше. Введение одной
такой константы — поправочного коэффициента в приближенно
определенный МГД-член в уравнениях — могло бы сделать со-
согласие расчетов и опытов идеальным, но оно и так вполне удов-
удовлетворительно .
208
ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
В последней главе монографии приведены отдельные примеры ис-
использования принципа «локального подобия» в теории турбулент-
турбулентного переноса. Они не претендуют на то, чтобы охватить все слу-
случаи, важные для практических расчетов, но, по-видимому, доста-
достаточно поясняют возможности такого подхода к решению задач.
В [11] рассмотрены при примерно таком же подходе и другие
задачи: влияние химической неравновесности на теплообмен в дис-
диссоциированных газах, взаимодействие излучения и турбулентно-
турбулентного переноса тепла при высоких температурах, эволюция одно-
однородной турбулентности в электропроводных средах в магнитном
поле.
Мы специально, чтобы пояснить существо метода, не ослож-
осложняли изложение рассмотрением сложных течений. В действитель-
действительности принцип «локального подобия», основы которого были раз-
разработаны уже давно х, нашел широкое применение для решения
многих практически важных задач, в том числе и сложных (с пе-
переменными свойствами среды, с диссоциацией, ионизацией, с воз-
воздействием в ряде случаев объемных сил и с учетом влияния излу-
излучения).
Как уже отмечалось, существуют более точные и более уни-
универсальные (но и более сложные) полуэмпирические теории тур-
турбулентности, чем изложенные в ч. II теории. Однако, повторим
это еще раз, применимость этих теорий все же весьма ограничена,
а точность не всегда подтверждена. Поэтому нам представляется
более эффективным развивать теорию турбулентности по пути
прямого численного моделирования крупных вихрей и применять
получаемые результаты для уточнения простой полуэмпириче-
полуэмпирической теории, используемой для большинства прикладных расче-
расчетов. Принцип «локального подобия» нам представляется наиболее
подходящей основой для такой простой теории. Конечно, его
использование имеет смысл только в том случае, если коэффициен-
коэффициенты переноса vT, aT и DT не определять каждый раз из системы урав-
уравнений разд. 6.3, а получить для них апнроксимационные формулы
вида, указанного в разд. 6.2. Такие формулы могут быть получе-
получены как описанным в 6.3 методом, так и на основе аппроксимации
опытных данных или результатов «численного эксперимента».
Пример полученной на основе опыта формулы рассматриваемого
типа был приведен и использован выше — это эмпирическая фор-
1 Статьи [6, 7] были уже, по существу, построены на основе этого принципа
хотя многое в ном делалось еще не так, как было изложено выше.
209
мула Рейхардта [49] для vm/v. Принципиально важным является
то, что эта формула, полученная из опытов с несжимаемой жид-
жидкостью и при течении в слое т ^ const, может в соответствии с
с принципом «локального подобия» использоваться и для других
случаев (сред с переменными свойствами, многокомпонентных
сред, течений ст^ const).
В ч. II фактически не используются результаты расчетов ч. I
(кроме сравнения распределения vT/v в слое т = const, получен-
полученного полу эмпирическим методом и из «численного эксперимента»;
можно было бы построить на базе этого «численного эксперимен-
эксперимента» и аппроксимационную формулу для vT/v, но такие эмпириче-
эмпирические формулы уже есть, например уже упоминавшаяся формула
Рейхардта). Это объясняется тем, что расчетов с прямым числен-
численным моделированием сделано пока мало.
Все же следует отметить, что из «численного эксперимента»
уже получены некоторые результаты, полезные для развития
полуэмпирических теорий: определены коэффициенты а и C
в уравнениях
dWVdt = —aW3/l, dl/dt =
описывающих эволюцию изотропной турбулентности при боль-
больших числах Re; коэффициент у в формуле
(также для случая изотропной турбулентности); найдены коэф-
коэффициенты корреляции величин рст и тсг со скоростями на различ-
различных расстояниях от стенки для течения в пристеночном слое, что
важно для построения уравнения для интегрального масштаба
турбулентности; найдены многие другие характеристики течения
в пристеночном слое, позволяющие проверять полуэмпирические
теории. Расчеты других задач, рассмотренных в методическом
плане в ч. I книги (но пока не рассчитанных), позволят значи-
значительно расширить связь «численного эксперимента» с полуэмпи-
полуэмпирической теорией.
ЛИТЕРАТУРА
1. Бэтчелор Дж. Теория однородной турбулентности. М.: Изд-во иностр.
лит., 1955. 198 с.
2. Монин А. С, Я алом А. М. Статистическая гидромеханика М * Наука
1965. Ч. I. 640 с, 1967. Ч. II. 720 с. ' " У '
3. Хинце М. О. Турбулентность. М.: Физматгиз, 1963. 680 с.
4. Таупсенд А. А. Структура турбулентного потока с поперечным сдвигом.
М.: Изд-во иностр. лит., 1959. 400 с.
5. Rotta /. Statistische Theorie nichthomogener Turbulenz // Z. Phvs 1951
Bd. 129, N 6. S. 547-572; 1951. Bd. 131, N 1. S. 51-77.
6. Иевлев В. М. Некоторые вопросы гидродинамической теории теплооб-
теплообмена при течении несжимаемой жидкости// ДАН СССР. 1952. Т. 86 № 6.
С. 1077—1080.
7. Иевлев В. М. Некоторые вопросы гидродинамической теории теплообмена
при течении газа// ДАН СССР. 1952. Т. 87, № 1. С. 21—24.
8. Лущик В. Л, Павелъев А. А., Якубенко А. Е. Трехпараметрическая мо-
модель сдвиговой турбулентности // Изв. АН СССР. МЖГ. 1978. № 3. С. 13—
25.
9. Лущик В. Г., Павелъев А. А., Якубенко А. Е. Трехпараметрическая мо-
модель турбулентности: расчет теплообмена // Изв. АН СССР. МЖГ. 1986.
№ 2. С. 40—52.
10. Колмогоров А. И. Уравнения турбулентного движения несжимаемой
жидкости// Изв. АН СССР. Сер. физ. 1972. Т. 6, № 12. С. 56—58.
И. Иевлев В. М. Турбулентное движение высокотемпературных сплошных
сред. М.: Наука, 1975. 256 с.
12. Иевлев В. М. Уравнения для конечномерных распределений вероятно-
вероятностей пульсирующих величин в турбулентном потоке // ДАН СССР. 1973.
Т. 208, № 5. С. 1044—1047.
13. Онуфриев А. Т. Об уравнениях полуэмпирической теории турбулент-
турбулентности// Журн. прикл механики и техн. физики. 1970. № 2. С 66—71.
14. Zundgren Т. S. Distribution functions in the statistical theory of turbulen-
turbulence // Phys. Fluids. 1967. Vol. 10, N 5. P. 969—975.
15. Чепмен Д. Р. Вычислительная аэродинамика и перспективы ее развития:
Драйденовская лекция // Ракетная техника и космонавтика. 1980. Т. 18,
№ 2. С. 3-32.
16. Ferziger J. И. Large Eddy Numerical simulations of Turbulent Flows //
AIAA Journal. 1977. Vol. 15. P. 1261—1267.
17. Chapman D. R. Druden lecture: Computational Aerodynamic Developmen-
tand // AIAA Journal. 1979. Vol. 17, N 12. P. 1213—1313.
18. Schumann F., Grotzbach G., Kleiser L. Direct numerical simulation of tur-
turbulence // Prediction method for turbulent shear flow. 1980. P. 123—258.
19. Deardorff J. W. A numerical Study of three — dimensional turbulent
channel flow cet large Reynolds numbers// J. Fluid Mech. 1970. Vol. 41.
P. 453—480.
20. Schumann U. Subgrid Seale Model for Finite Difference Simulations of
Turbulent Flows in Plane Channels and Annuls. // J. Сотр. Phys. 1975.
Vol. 18. P. 376-404.
21. Moin P., Kim Y. Numerical investigation of turbulent channel flow//
J. Fluid Mech. 1982. Vol. 118, N 5. P. 341-377.
22. McMillan O. /., Ferziger J. H. Direct Testing of Sabgrid-Scale Models//
AIAA Journal. 1979. Vol. 17, N 12. P. 1340—1346.
23. Antonopoulos-Domis M. Large-eddy simulation of a passive scalar in iso-
tropic turbulence//J. Fluid. Mech. 1981. Vol.104. P. 55—79.
24. Белоцерковский О. МV Прямое численное моделирование «переходных»
течений газа и задач турбулентности // Механика турбулентных пото-
потоков. М.: Наука, 1980. С. 70—109.
211
25. Белоцерковский О. М. Прямое численное моделирование свободной раз-
развитой турбулентности // Журн. вычисл. математики и мат. физики. 1985.
Т. 25, №12. С. 1856-1882.
26. Белоцерковский О. М. Численное моделирование в механике сплошных
сред. М.: Наука, 1984. 519 с.
27. Leonard A. Energy cascade in large eddy simulations of turbulent fluid
flous // Adv. Geophys. 1974. A 18. P. 237—248.
28. Иевлев В. M. Приближенные уравнения турбулентного движения несжи-
несжимаемой жидкости// Изв. АН СССР. МЖГ. 1970. № 1. С. 91—103.
29. Лойцянский Л. Г. Механика жидкости и газа. М.: Наука, 1970. 904 с.
30. Самарский А. А., Николаев Е. С. Методы решения сеточных уравнений.
М.: Наука, 1978. 591 с.
31. Yeh Т. Т., Van-Atta С. W. Spectral trausfer of scalar and velocity fields
in treated-drid turbulence//J. Fluid, mech. 1973. Vol.58. P. 233—261.
32. Cante-Bellot G., Corrsin S. Simple Euleriantina cerrelation of full- and
narrow-band velocity signals in grid-generated isotropic turbulence // J.
Fluid. Mech. 1971. Vol. 48. P. 273-337.
33. Zundgren T. S. Model equation for nonhomogeneous turbulence // Phys.
Fluids. 1969. Vol. 12, N 3. P. 485-497.
34. Bradshaw P., Ferriss D. II., Atwell N. P. Calculation of boundary —
layer development using the turbulent energy equation // J. Fluid. Mech.
1967. Vol. 28. P. 593-616.
35. Computation of turbulent boundary layers // Stanford Conf. Stanford
Univ. 1968. Vol. 1. 590 p.; Vol. 2. 519 p.
36. Патанкар С, Сполдинг Д. Тепло- и массообмен в пограничных слоях.
М.: Энергия, 1971. 217 с.
37. Cebeci Т., Mesinshis G. J. Calculation of incompressible turbulent boundary
layers with mass transfer, including highly accelerating flows//J. Heat
Transfer. 1971. Vol. 93, N 3. P. 271-280.
38. Pletcher R. H, On a calculation method for compressible turbulent boun-
boundary layer flows with heat transfer. AIAA 9th Aerospace Sci. Meeting. N.-Y.,
AIAA Paper, N 71 — 165, 1971. 11 p.
39. Nee V. W., Kovasznag L. S. G. Simple phenomenological theory of turbu-
turbulent shear flows// Phys. Fluids. 1969. Vol. 12, N 3. P. 453—484.
40. Jevlev V. M. The methods of calculation of the turbulent boundary layer for
a high-temperature gaseous flow. AJAA 9th Aerospace Sci. Meeting. N.-Y.,
AJAA Paper, N 71-163, 1971. 15 p.
41. Schubauer G. B. Turbulent processes as observed in boundary layer and
pipe// J. Appl. Phys. 1954. Vol. 25, N 2. P. 188-196.
42. Конт-Белло Ж. Турбулентное течение в канале с параллельными стен-
стенками. М.: Мир, 1968. 176 с.
43. ЬоЪЬ R. К., WinklerE. М., PershJ. Experimental investigation of tur-
turbulent boundary layers in hypersonic flow//J AS. 1955. Vol. 22, X 1.
P. 1—9.
44. Миллионщиков М. Д. Турбулентные течения в пограничном слое и
в трубах. М.: Наука, 1969. 52 с.
45. Обухов А. М. О распределении масштаба турбулентности в трубах про-
произвольного сечения // Прикл. математика и механика, 1942. Т. 6, Л° 2—3.
С. 209-220.
46. Кутателадзе С. С. Основы теории теплообмена. Новосибирск: Наука,
1970. 660 с.
47. Левин В. В., ЧиненковИ.А. Экспериментальное исследование влияния
продольного магнитного поля на гидравлическое сопротивление при
турбулентном течении электропроводной жидкости в трубе // Магнит,
гидродинамика. 1970. № 3. С. 145—146.
48. Баушев Б. #., Красилъников Е. Ю., Лущик В. Г., ПаневинН.Г. Сме-
Смещение спутных струй в продольном магнитном поле // Изв. АН СССР.
МЖГ. 1972. № 5. С. 33—44.
49. Reichardt H. Warmeubertragungen in turbulenten Reibungsschrichten //
ZAMM. 1940. Bd. 20. S. 297-328.
ОГЛАВЛЕНИЕ
Введение 3
Часть первая
ПРЯМОЕ ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ КРУП-
НОМАСШТАБНОЙ ТУРБУЛЕНТНОСТИ 7
Глава первая
Постановка задачи. Некоторые принципиальные вопро-
вопросы, связанные с корректностью постановки и с возмож-
возможными методами ее решения 7
1.1. Постановка задачи прямого численного модели-
моделирования крупномасштабной турбулентности и ис-
используемые уравнения 7
1.2. Замечания о требованиях к точности описания
мелкомасштабной турбулентности 10
1.3. Роль и место прямого численного моделирования
в ряду других подходов к решению задач теории
турбулентности 12
1.4. О начальных и граничных условиях 12
Глава вторая
Методика и результаты расчета однородной турбулент-
турбулентности при больших числах Re 13
2.1. Вводные замечания 13
2.2. Исходные уравнения 14
2.3. Аппроксимация отдельных членов уравнений и
получение сеточных уравнений 16
2.4. Граничные условия 17
2.5. Начальные условия 18
2.6. Приведение уравнений к безразмерному виду ... 25
2.7. Определение членов уравнений, зависящих от
мелкомасштабной турбулентности 26
2.8. Порядок выполнения шагов по времени при рас-
расчете полей скоростей и давления 29
2.9. Определение коэффициента Л в формулах для мел-
мелкомасштабной турбулентности 30
2.10. Определение статистических" характеристик тур-
турбулентности 34
2.11. Укрупненная блок-схема программы расчетов 37
2.12. Порядок и блок-схема программы расчета началь-
начального поля скоростей (программа № 1 на рис. 2.1) 40
2.13. О программе определения ut (программа № 2 на
рис. 2.1) 44
2.14. О программе определения давления (программа
№ 3 на рис. 2.1) 52
2.15. О программе расчета (йг)п т> (программа № 4
на рис. 2.1) '. 58
213
2.16. Выбор шага по времени 58
2.17. О программах расчетов статистических характе-
характеристик турбулентности 62
2.18. Результаты некоторых расчетов и их анализ ... 64
Глава третья
Методика расчетов однородной магнитогидродинамиче-
ской турбулентности 68
3.1. Характеристика решаемой задачи и вводные за-
замечания 68
3.2. Исходные уравнения 69
3.3. Аппроксимация отдельных членов уравнений, пре-
преобразования сеточных уравнений и порядок рас-
расчета 72
Глава четвертая
Методика расчетов однородной турбулентности в стра-
стратифицированной среде в поле силы тяжести 78
4.1. Вводные замечания 78
4.2. Исходные уравнения * 79
4.3. Аппроксимация отдельных членов уравнений, пре-
преобразования сеточных уравнений и порядок рас-
расчета 85
4.4. Определение коэффициента С (в членах, описываю-
описывающих мелкомасштабную турбулентность) 91
4.5. Краткое рассмотрение некоторых результатов
расчетов, приведенных в работе [23] 95
Глава пятая
Методика и некоторые результаты расчета крупномас-
крупномасштабной турбулентности в пристеночных течениях ... 98
5.1. Вводные замечания 98
5.2. Рассматриваемые задачи и расчетная сетка ... 99
5.3. Исходные уравнения и приведение их к безразмер-
безразмерному виду 102
5.4. Аппроксимация отдельных членов уравнений C.8)
и C.9) 104
5.5. Уравнение неразрывности 112
5.6. Определение «турбулентных членов» типа <м^>. . 112
5.7. Уравнение количества движения 118
5.8. Сводка формул окончательного вида 121
5.9. Порядок расчета поля скоростей. Уравнение для
определения поля давления 126
5.10. Граничные условия , . . . » 130
5.11. Определение констант Ао и Q, входящих в фор-
формулы для «турбулентных членов» уравнений ... 140
5.12. Об определении статистических характеристик тур-
турбулентного потока 144
5.13. О начальных условиях и о контроле достижения
статистически стационарного режима 144
5.14. Общая структурная схема программы расчетов 145
5.15. О выборе величины шага по времени Д? 147
5.16. Примеры расчетов и их анализ 149
214
Часть вторая
ИСПОЛЬЗОВАНИЕ ПРИНЦИПА «ЛОКАЛЬНОГО
ПОДОБИЯ» В ТЕОРИИ ТУРБУЛЕНТНОГО ПЕРЕНОСА 151
Глава шестая
Постановка задачи, исходные уравнения и их преобра-
преобразования 151
6.1. Введение 151
6.2. Принцип «локального подобия» в теории турбу-
турбулентного переноса 152
6.3. Общая характеристика метода приближенного
теоретического получения формул для vT, aT,
DT, DT 158
6.4. Система уравнений для расчетов осредненных ха-
характеристик турбулентных течений с использова-
использованием законов локального подобия 184
6.5. Получение сеточных уравнений и порядок расче-
расчетов 186
6.6. Граничные условия 190
Глава седьмая
Форма законов локального подобия в некоторых част-
частных случаях. Расчеты течений, их анализ и сравнение
с опытными данными 191
7.1. Течение несжимаемой жидкости вдоль гладкой
стенки 191
7.2. Течение среды с переменными свойствами вдоль
гладкой стенки 199
7.3. О влиянии шероховатости стенки 200
7.4. Турбулентная свободная конвекция в горизон-
горизонтальном слое 202
7.5. Замечания о влиянии градиента средней скорости 205
7.6. Магнитогидродинамическое течение в канале
в продольном магнитном поле 206
ч
Заключительные замечания 209
Литература 211
Научное издание
Виталий Михайлович Иевлев
ЧИСЛЕННОЕ
МОДЕЛИРОВАНИЕ
ТУРБУЛЕНТНЫХ
ТЕЧЕНИЙ
Утверждено к печати
Отделением физико-технических проблем
энергетики АН СССР
Редактор издательства Н. В. Березникова
Художник Н. И. Казаков
Художественный редактор В. В. Алексеев
Технический редактор Л. В. Прохорцеза
Корректор А. Б. Васильев
ИБ № 37390
Сдано в набор 02.10.89
Подписано к печати 11.07.90
Т-00459. Формат 60 X 9O'/ie
Бумага типографская № 2
Гарнитура обыкновенная новая
Печать высокая
Усл. печ. л. 13,5. Усл. кр. отт. 13,63
Уч.-изд. л. 14,6. Тираж 1400 экз. Тип. зак. 4137
Цена 3 руб.
Ордена Трудового Красного Знамени
издательство «Наука»
117864, ГСП-7, Москва, В-485,
Профсоюзная ул., 90
2-я типография издательства «Наука»
121099, Москва, Г-99, Шубинский пер., 6