Альберт Мессиа
КВАНТОВАЯ
МЕХАНИКА
Том 2
Перевод с французского П. П. КУЛИША
под редакцией Л. Д. ФАДДЕЕВА
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ
ЛИТЕРАТУРЫ
1979

530.1
M 53
УДК 530.145
Квантовая механика (перевод с французского) под редакцией Л. Д. Фад-
деева. Альберт Мессиа. Монография. М.: Наука, Главная редакция физико-ма-
физико-математической литературы, 1979 г.
В книге рассматриваются общие вопросы квантовой механики и их много-
многочисленные приложения. Изложение теории симметрии н инвариантности начи-
начинается с квантования момента количества движения, спина, теории сложения
моментов и теоремы Вигнера — Эккарта. Для систем тождественных частиц
получены статистики Бозе — Эйнштейна и Ферми — Дирака. Часть, посвящен-
посвященная приближенным методам в квантовой механике, содержит стационарную и
нестационарную теорию возмущений. Из элементов релятивистской квантовой
механики подробно рассмотрены: уравнение Днрака, квантование скалярного
поля и основные понятия классической и квантовой теории излучения. В каж-
каждой главе имеются упражнения и задачи.
Книга рассчитана на широкий круг читателей — физиков и инженерно-тех-
инженерно-технических работников, а также может быть полезна студентам старших курсов
высших учебных заведений.
Илл. 33.
© Наука
Главная Редакция
20402—166 1р пплпопппп физико-математической
а 1*3-79. 1704020000 литературы
\) {Перевод на русский язык) 1979

ПЛАН КУРСА
Fluctuat пес mergitur *)
ТО.'Д 1
Часть I. Формализм и его интерпретация
Глава I. Истоки квантовой теории
Глава II. Волиы вещества и уравнение Шредингера
Глава III. Квантовые системы в одном измерении
Глава IV. Статистическая интерпретация корпускулярно-волнового дуа-
дуализма и соотношения неопределенности
Глава V. Формализм волновой механики и его истолкование
Глава VI. Классическое приближение и метод ВКБ
Глава VII. Общий формализм квантовой теории
А. Математический аппарат
Глава VIII. Общий формализм квантовой теории
Б. Описание физических явлений
Часть II. Простые системы
Глава IX. Решение уравнения Шредиигера методом разделения перемен-
переменных. Центрально-симметричный потенциал
Глава X. Проблема рассеяния. Центральный потенциал и метод фазовых
сдвигов
Глава XI. Кулоновское взаимодействие
Глава XII. Гармонический осциллятор
Дополнение А. Обобщенные функции, «функция» б и преобразование Фурье
Дополнение Б. Специальные функции и связанные с ними формулы
ТОМ 2
Часть III. Симметрия и инвариантность
Глава XIII. Момент импульса в квантовой механике
Глава XIV. Система тождественных частиц. Принцип запрета Паули
Глава XV. Инвариантность и законы сохранения. Обращение времени
Часть IV. Приближенные методы
Глава XVI. Стационарная теория возмущений
Глава XVII. Приближенные решения нестационарного уравнения Шре-
Шредингера
Глава XVIII. Вариационный метод и связанные с иим задачи
Глава XIX. Теория рассеяния
Часть V. Элементы релятивистской квантовой механики
Глава XX. Уравнение Дирака
Глава XXI. Квантовые поля. Теория излучения
Дополнение В. Коэффициенты векторного сложения и матрицы вращений
Дополнение Г. Элементы теории групп
*) «Качается, ио не тоиет» — девиз на гербе Парижа, где иа фоне волн
изображена каравелла. (Прим. перев.).

ОГЛАВЛЕНИЕ
ЧАСТЬ III. СИММЕТРИИ И ИНВАРИАНТНОСТЬ
Г ЛАВ А XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ. ..,,,« 13
§ I. Введение 13
Раздел I. Собственные значения и собственные функции момента им-
импульса 14
§ 2. Определение момента импульса 14
§ 3. Основные алгебраические соотношения 16
¦§ 4. Спектр операторов Р и /* 17
§ 5. Собственные векторы операторов Р и /г. Построение инвариантных
пространств &{1) 20
§ 6. Стандартное представление {/2/г} 21
§ 7. Заключение 23
Раздел II. Орбитальный момент импульса и сферические функции . . 24
§ 8. Спектр операторов Put 24
§ 9. Определение и построение сферических функций 26
Раздел 111. Момент импульса и вращения 28
§ 10. Определение вращений. Углы Эйлера 28
§ 11. Вращеняе физической системы. Оператор вращения 31
¦§ 12. Вращение наблюдаемых 33
§ 13. Момент импульса и инфинитезимальные вращения 34
§ 14. Построение оператора R(a.$y) 37
§ 15. Вращение на угол 2я и полуцелый момент импульса 38
§ 16. Неприводимые инвариантные подпространства. Матрицы вращений
/?<'> 40
§ 17. Инвариантность относительно вращений и сохранение момента им-
импульса 42
Раздел IV. Спин 44
¦§ 18. Гипотеза спина электрона 44
§ 19. Спин '/г и матрицы Паули 48
§ 20. Наблюдаемые и волновые функции частицы спина '/г- Спинорные
поля 50
§ 21. Векторные поля и частицы спина 1 52
§ 22. Зависящие от спнна взаимодействия в атомах ; . 54
§ 23. Зависящие от спина нуклои-иуклонные взаимодействия 55
Раздел V. Сложение моментов импульса .57
§ 24. Задача сложения 57
§ 25. Теорема сложения двух моментов импульса 58
§ 26. Приложения и примеры 60
§ 27. Собственные векторы полного момента импульса. Коэффициенты
Клебша — Гордана , , 61

ОГЛАВЛЕНИЕ 5
28. Приложение; система двух нуклонов . . , , , 64
29. Сложение трех и более моментов импульса. Коэффициенты Рака.
3/ . 67
Раздел VI. Неприводимые тензорные операторы 70
§ 30. Представление скалярных операторов 70
§ 31. Неприводимые тензорные операторы. Определение 71
§ 32. Представление неприводимых тензорных операторов. Теорема Виг-
нера — Эккарта 74
§ 33. Приложения 76
Задачи и упражнения 77
Г ЛАВ А XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ. ПРИНЦИП ЗАПРЕТА
ПАУЛИ 82
§ 1. Тождественные частицы в квантовой теории 82
Раздел I. Постулат симметризации 86
§ 2. Подобные частицы и симметрическое представление 86
<j 3. Операторы перестановки . 87
§ 4. Алгебра операторов перестановки. Симметризаторы и антисимметри-
заторы 89
§ 5. Тождественные частипы и постулат симметризации 93
§ 6. Бозоиы и статистика Бозе — Эйнштейна 96
§ 7. Фермионы и статистика Ферми — Дирака. Принцип запрета ... 98
| 8. Всегда ли необходимо симметризовать волновую функцию? . . . .100
Раздел II. Приложения 103
§ 9. Столкновение двух тождественных бесспиновых частиц 103
§ 10. Столкновение протонов 107
§ 11. Статистика атомных ядер 109
§ 12. Сложные атомы. Приближение центрального поля 112
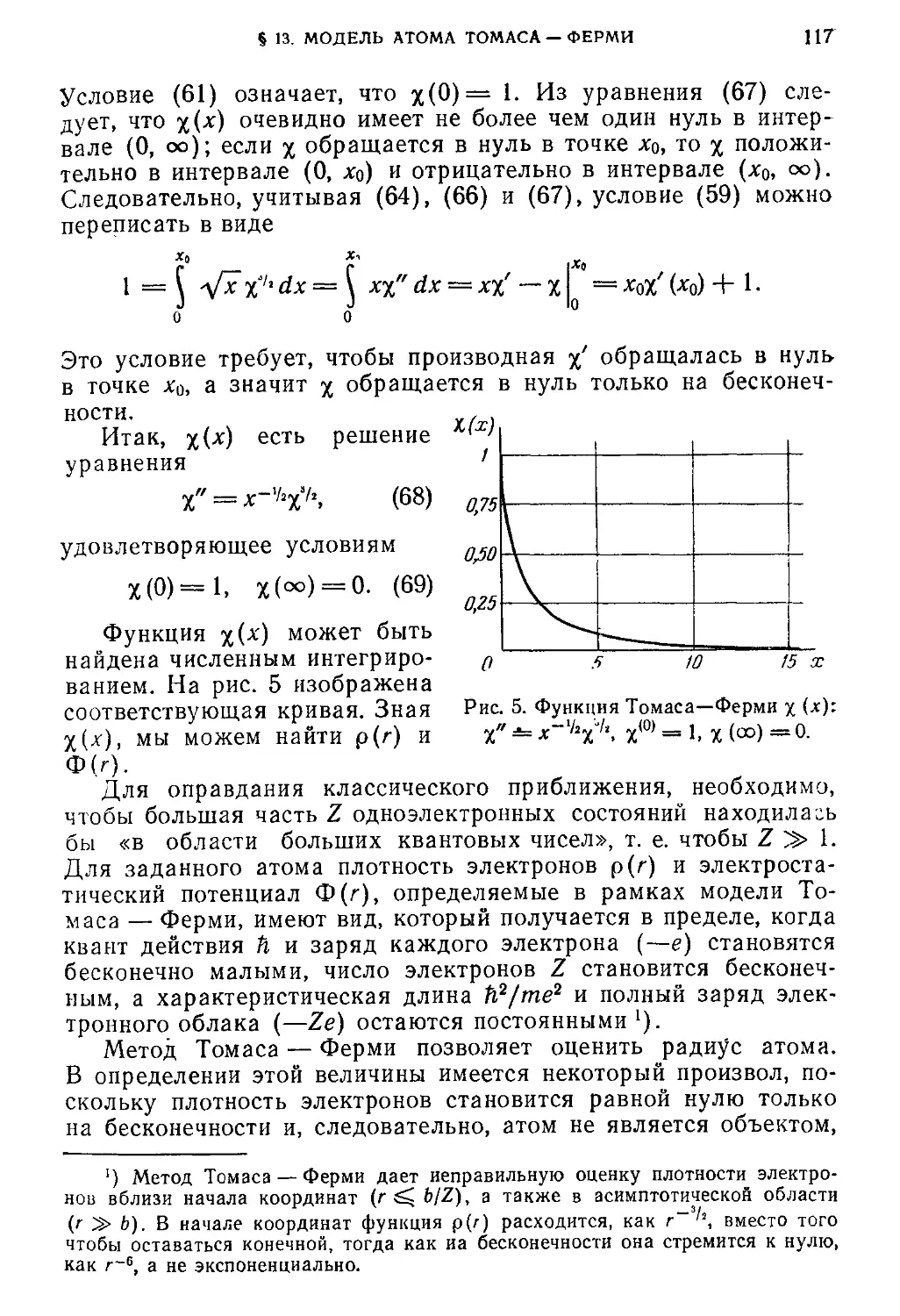
§ 13* Модель атома Томаса — Ферми 115
§ 14. Система нуклонов и изотопический спин 118
§ 15. Использование изотопического спина. Зарядовая независимость . . 124
Задачи и упражнения 128
ГЛАВА XV. ИНВАРИАНТНОСТЬ И ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕ-
ВРЕМЕНИ 130
§ 1. Введение 130
Раздел I. Дополнительные математические сведения. Антилииейные опе-
операторы 131
^ 2. Три полезные теоремы 131
| 3. Антилинейные операторы в гильбертовом пространстве 135
§ 4. Антиуннтарные преобразования 137
§ 5. Антилинейные операторы и представления 139
Раздел II. Преобразования и группы преобразований 140
§ 6. Преобразования динамических переменных и динамических состоя-
состояний системы 140
§ 7. Группы преобразований 144
§ 8. Группы операторов преобразований 145
§ 9. Непрерывные группы и инфинитезимальные преобразования. Тран-
Трансляции. Вращения 146
§ 10, Конечные группы. Отражения 150

6 ОГЛАВЛЕНИЕ
Раздел III. Инвариантность уравнений движения и законы сохранения 152
§ 11. Инвариантные наблюдаемые 152
§ 12. Свойства инвариантности гамильтониана и законы сохранения . . 154
§ 13. Свойства инвариантности н эволюция динамических состояний . . 156
§ 14. Симметрии эффектов Штарка и Зеемана 159
Раздел IV. Обращение времени и принцип микрообратимости .... 161
§ 15. Сдвиги во времени и сохранение энергии 161
§ 16. Обращение времени в классической и квантовой механиках . . . 162
§ 17. Обращение времени. Частица нулевого спина 164
§ 18. Общее определение обращения времени 166
§ 19. Обращение времени и комплексное сопряжение 167
§ 20. Принцип микрообратимости 169
§ 21. Следствие: вырождение Крамерса 172
§ 22. Вещественный гамильтониан, инвариантный относительно вращений 173
Задачи и упражнения 176
ЧАСТЬ IV. ПРИБЛИЖЕННЫЕ МЕТОДЫ
ГЛАВА XVI. СТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ 181
§ 1. Общее введение к четвертой части 181
Раздел I. Возмущение невырожденного уровня 182
§ 2. Разложение по степеням возмущения 182
§ 3. Возмущение первого порядка 184
§ 4. Основное состояние атома гелия 185
§ 5. Кулоновская энергия атомных ядер 187
§ 6. Поправки высших порядков 189
§ 7. Эффект Штарка для жесткого ротатора 191
Раздел II. Возмущение вырожденного уровня 193
§ 8. Элементарная теория 193
§ 9. Атомные уровни без учета спин-орбитального взаимодействия . . 195
§ 10. Спин-орбитальное взаимодействие. LS- и //-связь 198
§ 11. Атом с LS-связью. Расщепление за счет спин-орбитального взаимо-
взаимодействия 199
§ 12. Эффект Зеемана и эффект Пашена — Бака 201
§ 13. Симметрия Н и устранение вырождения 203
§ 14. Квазнвырождение 205
Раздел III. Явные выражения для разложений по теории возмущении
во всех порядках 206
§ 15. Гамильтониан Н и его резольвента G(z) 206
§ 16. Разложение G(z), P и HP в ряд по степеням XV 208
§ 17. Вычисление собственных значений и собственных функций . . . . 211
Задачи и упражнения 214
ГЛАВА XVII. ПРИБЛИЖЕННЫЕ РЕШЕНИЯ НЕСТАЦИОНАРНОГО УРАВНЕНИЯ
ШРЕДИНГЕРА 216
§ 1. Изменение «представления» и рассмотрение части гамильтониана по
теории возмущений 216
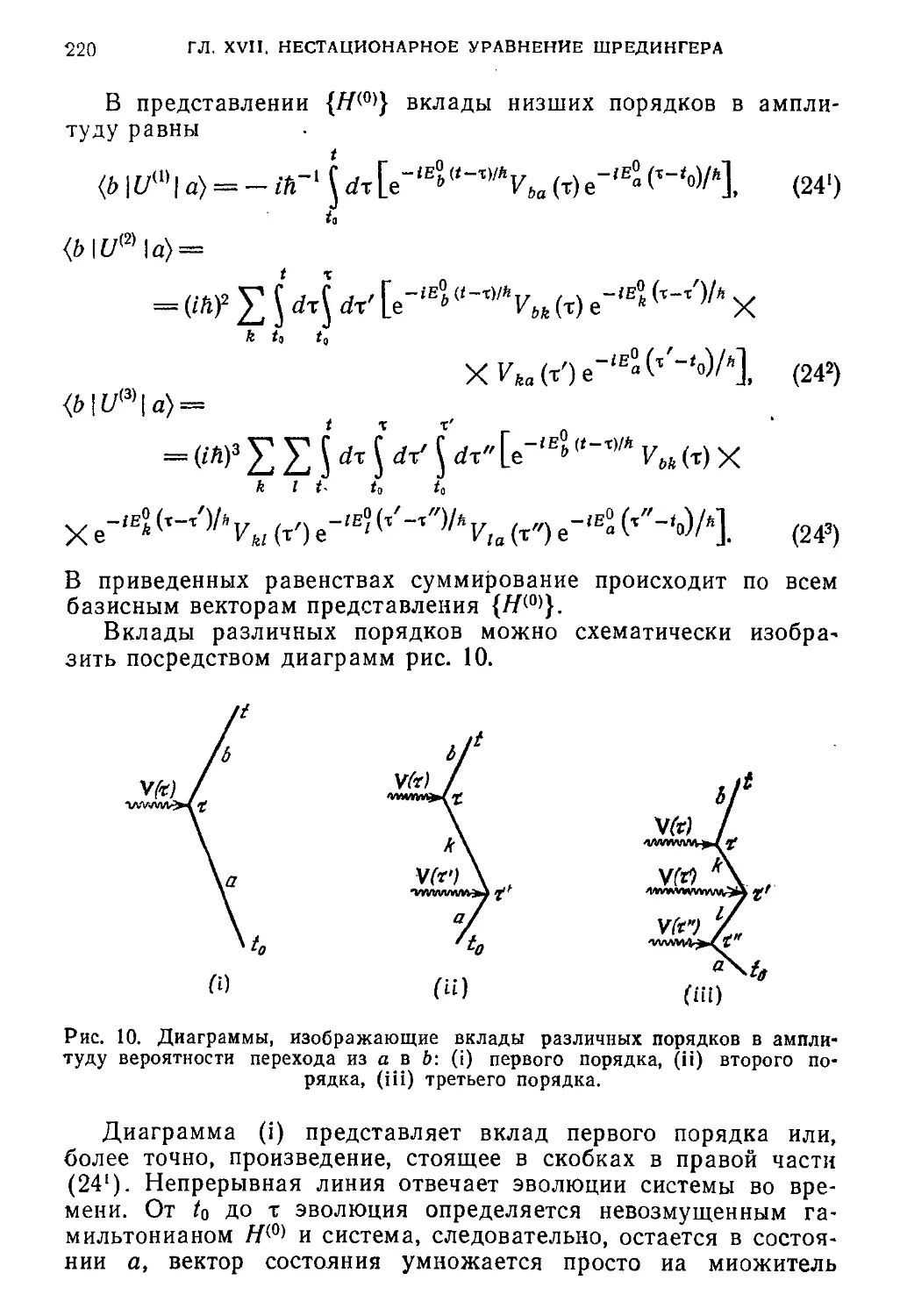
Раздел I. Нестационарная теория возмущений 219
§ 2. Определение и вычисление по теории возмущений вероятностей пе-
переходов 219
§ 3. Полуклассическая теория кулоновского возбуждения ядер .... 222

ОГЛАВЛЕНИЕ 7
§ 4. Случай, когда V не зависят от времени. Сохранение невозмущенной
энергии . . 226
§ 5. Приложение к вычислению сечений в борновском приближении . . 229
§ 6. Периодическое возмущение. Резоиаисы 231
Раздел II. Мгновенное и адиабатическое изменения гамильтониана . , 232
§ 7. Формулировка задачи и результаты 232
§ 8. Быстрый переход и мгновенное приближение 233
§ 9. Мгновенное обращение магнитного поля 235
§ 10. Адиабатический переход. Общие положения. Тривиальный случай . 236
§ 11. «Представление вращающихся осей» 238
§ 12. Доказательство адиабатической теоремы 240
§ 13. Адиабатическое приближение 243
§ 14. Адиабатическое обращение магнитного поля 247
Задачи и упражнения 251
ГЛАВА XVIII. ВАРИАЦИОННЫЙ МЕТОД И СВЯЗАННЫЕ С НИМ ЗАДАЧИ . .254
§ 1. Вариационный метод Ритца 254
Раздел I. Вариационный метод для связанных состояний ...... 255
§ 2. Вариационная форма задачи на собственные значения 255
§ 3. Вариационное вычисление дискретных уровней 258
§ 4. Простой пример: атом водорода 258
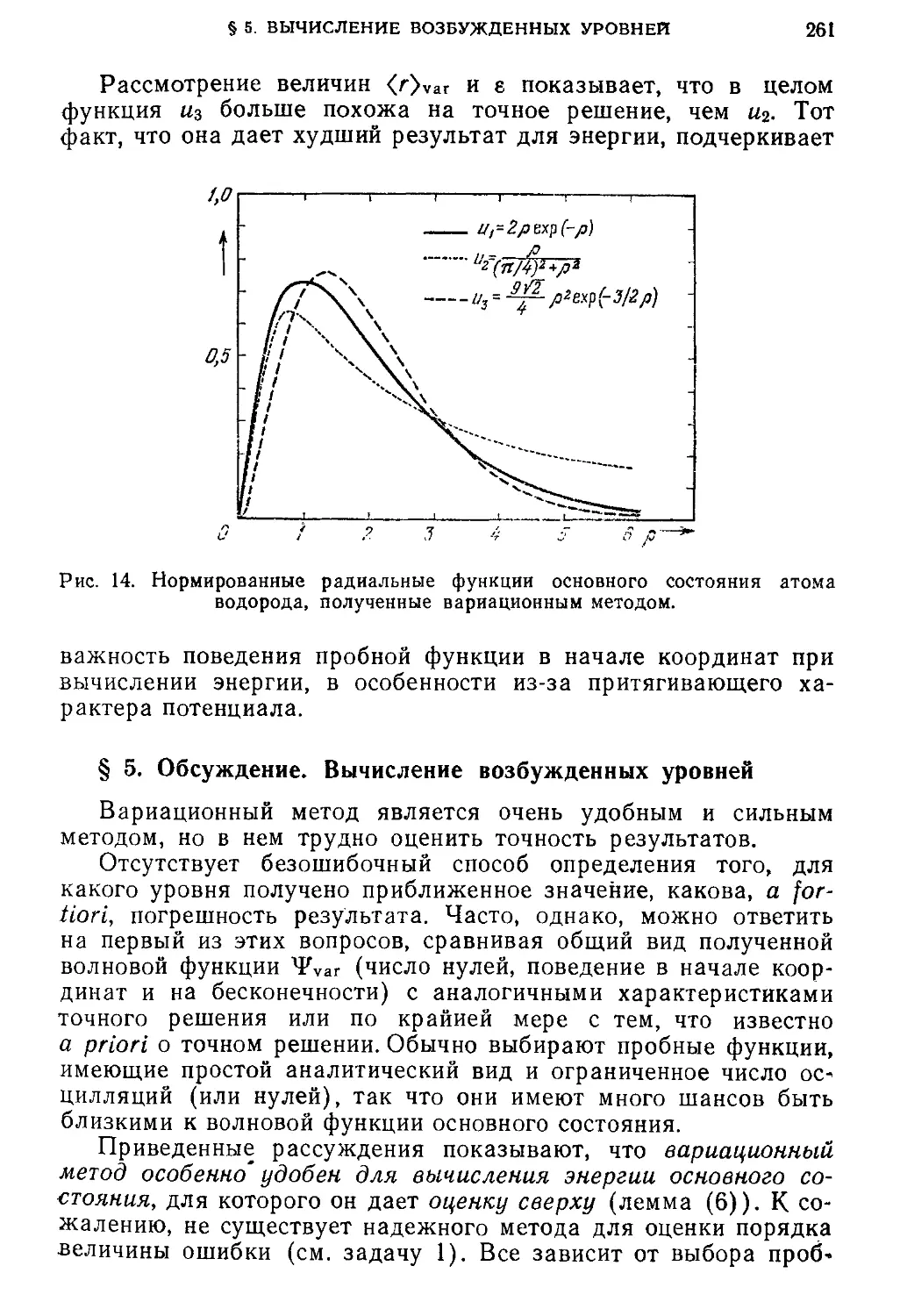
§ 5. Обсуждение. Вычисление возбужденных уровней 261
§ 6. Основное состояние атома гелия 262
Раздел II. Атомы Хартри и Фока — Дирака 265
§ 7. Метод самосогласованного поля 265
§ 8. Вычисление Е [Ф] 265
§ 9. Уравнения Фока — Дирака 267
§ 10. Обсуждение результатов 270
§ 11. Уравнения Хартри 272
Раздел III. Структура молекул 272
§ 12. Общие понятия. Разделение движения ядер и электронов .... 272
§ 13. Движение электронов в поле фиксированных ядер 275
§ 14. Адиабатическое приближение 277
§ 15. Гамильтониан ядер в адиабатическом приближении 280
§ 16. Метод Борна—Оппенгеймера 283
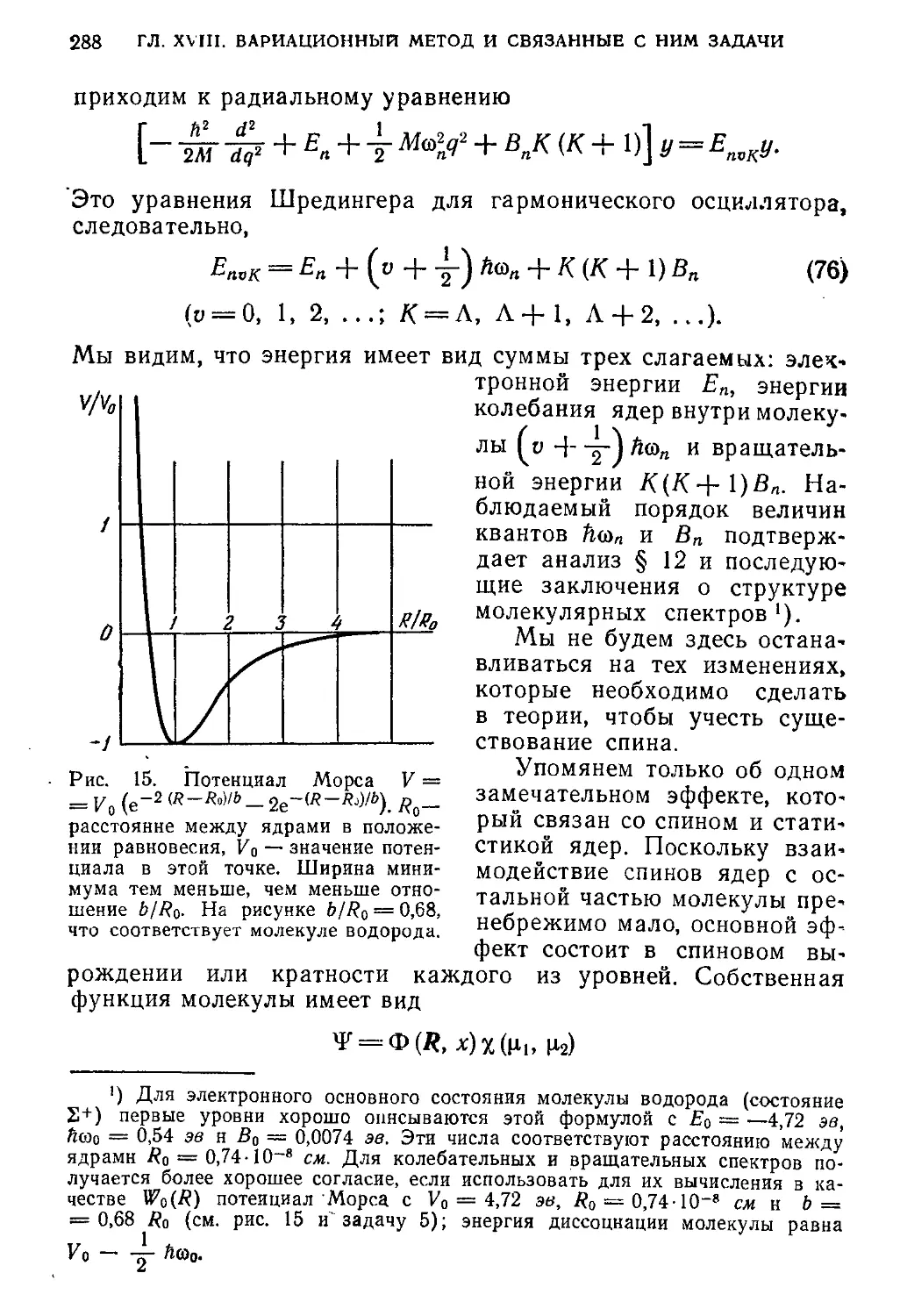
§ 17. Основные представления о двухатомных молекулах 284
Задачи и упражнения 290
ГЛАВА XIX. ТЕОРИЯ РАССЕЯНИЯ . , , 291
§ 1. Введение 291
Раздел I. Свободная функция Грина и приближение Бориа 292
§ 2. Интегральные представления амплитуды рассеяния 292
§ 3. Сечение рассеяния и Г-матрица. Микрообратимость 295
§ 4. Борновское приближение 297
§ 5. Интегральное уравнение теории рассеяния 299
§ 6. Борновское разложение 301
§ 7. Критерий применимости борновского приближения 302
§ 8. Упругое рассеяния электронов на атоме 304
§ 9. Центральный потенциал. Вычисление сдвигов фаз 307
§ 10. Функция Грина как оператор. Связь с резольвентой оператора Но . 308

8 ОГЛАВЛЕНИЕ
Раздел II. Обобщение иа искаженные волны 311
§ 11. Обобщенное борновское приближение 311
§ 12. Обобщение борцовского разложения 314
§ 13. Функция Грииа искаженных волн 315
§ 14. Приложения. Определение и формальные свойства Г-матрицы . . 318
§ 15. Замечания о потенциалах 1/г 320
Раздел III. Сложные столкновения и бориовское приближение .... 320
§ 16. Общие понятия. Сечения 320
§ 17. Каналы 322
§ 18. Вычисление сечений. Г-матрицы 323
§ 19. Интегральные представления амплитуды перехода 324
§ 20. Борновское приближение и его обобщения 327
§ 21. Рассеяние быстрых электронов атомом 329
§ 22. Кулоновское возбуждение ядер 331
§ 23. Функции Грииа и интегральные уравнения для стационарных реше-
решений рассеяния 334
§ 24. Рассеяние частицы иа двух центрах 335
§ 25. Простое рассеяние. Интерференция 338
§ 26. Многократное рассеяние 341
Раздел IV. Вычисление амплитуд перехода вариационным методом . . 343
§ 27. Стационарные выражения сдвигов фаз. Обсуждение 343
§ 28. Вариационные вычисления сдвига фаз. Обсуждение 347
§ 29. Распространение метода на сложные столкновения 348
Раздел V. Общие свойства матрицы перехода 350
§ 30. Сохранение потока. S-матрица 350
§ 31. Соотношение Бора — Пайерлса — Плачека (оптическая теорема) . . 353
§ 32. Микрообратимость 354
§ 33. Свойства инвариантности Г-матрицы 355
Задачи и упражнения 357
ЧАСТЬ V. ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ
КВАНТОВОЙ МЕХАНИКИ
Г Л А В А XX. УРАВНЕНИЕ ДИРАКА 361
Раздел I. Общее введение 361
§ 1. Релятивистская квантовая механика 361
§ 2. Обозначения и различные определения 362
§ 3. Группа Лоренца 366
§ 4. Классическая релятивистская динамика 368
Раздел П. Уравнения Клейна — Гордона и Дирака 370
§ 5. Уравнение Клейна — Гордона 370
§ 6. Уравнение Дирака 373
§ 7. Построение пространства Sw. Представление Днрака 375
§ 8. Ковариантная форма уравнения Дирака 377
§ 9. Сопряженное уравнение. Определение тока 378
Раздел III. Свойства инвариантности уравнения Дирака 380
§ 10. Свойства матриц Дирака 380
§ 11. Инвариантность уравнения Дирака при ортохронных преобразова-
преобразованиях системы координат 384
§ 12. Преобразования собственной группы 388
§ 13. Пространственное отражение и ортохронная группа 391
§ 14, Построение ковариантных величин 392

ОГЛАВЛЕНИЕ 9
§ 15. Другая формулировка свойств инвариантности: преобразование со-
состояний 393
§ 16. Условие инвариантности уравнения движения 394
§ 17. Операторы преобразования. Импульс, момент импульса, четность . . 395
§ 18. Законы сохранения и интегралы движения 397
§ 19. Обращение времени и зарядовое сопряжение 398
§ 20. Калибровочная инвариантность 401
Раздел IV. Интерпретация операторов и простые решения 401
§2!. Уравнение Дирака и принцип соответствия 401
§ 22. Динамические переменные частицы Дирака 402
§ 23. Свободный электрон. Плоские волны 405
5 24. Построение плоских волн посредством преобразования Лоренца . . 406
§ 25. Центральный потенциал 407
§ 26. Свободные сферические волны 410
§ 27. Атом водорода 412
Раздел V. Нерелятивистский предел уравнения Дирака 413
§ 28. Большие и малые компоненты . 415
§ 29. Теория Паули как иерелятивнстский предел теории Дирака .... 417
§ 30. Приложение: сверхтонкая структура и диполь-дипольная связь . . 420
§ 31. Поправки высших порядков и преобразование Фолди — Вотхойзена 421
§ 32. ФВ-преобразование для свободной частицы 423
§ 33. ФВ-преобразование для частицы во внешнем поле 425
§ 34. Электрон в центральном электростатическом потенциале 427
§ 35. Обсуждения и выводы 428
Раздел VI. Решения с отрицательной энергией и теория позитронов . . 429
§ 36. Свойства зарядово-сопряженных решений 429
§ 37. Особое поведение решений с отрицательной энергией 431
§ 38. Изменение интерпретации состояний с отрицательной энергией.
Теория дырок и позитронов 433
§ 39. Трудности теории дырок 435
Задачи и упражнения 436
Г Л АВ А XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ 439
§ 1. Введение 439
Раздел I. Квантование вещественного скалярного поля 440
§ 2. Классические свободные поля. Нормальные колебания 440
| 3. Квантование свободного поля 442
§ 4. Лагранжиан поля. Импульс, сопряженный к Ф(г) 445
§ 5. Комплексные базисные функции 449
§ 6. Плоские волны. Определение импульса 451
§ 7. Сферические волиы. Определение момента импульса 456
§ 8. Пространственное отражение и обращение времени 457
Раздел II. Взаимодействие с атомной системой 457
§ 9. Взаимодействие с системой частиц 457
§ 10. Слабая связь и рассмотрение по теории возмущений 461
§ 11. Сдвиги уровней 464
§ 12. Излучение квантов 468
§ 13. Квантовая теория распадающихся состояний. Ширина линии . . . 470
§ 14. Упругое рассеяние. Дисперсионная формула 477
§ 15. Резонансное рассеяние. Образование метастабильного состояния . 481
§ 16. Поглощение кванта (фотоэлектрический эффект). Радиационный за-
захват 48а

Ю ОГЛАВЛЕНИЕ
Раздел III. Классическая теория электромагнитного излучения .... 48S
§ 17. Уравнения классической теории Максвелла — Лоренца 485
§ 18. Инвариантность и законы сохранения классической теории .... 487
§ 19. Собственная энергия и классический радиус электрона ..... 489
§ 20. Электромагнитный потенциал. Выбор калибровки 490
| 21. Продольная и поперечная часть векторного поля 491
§ 22. Исключение продольного поля 494
§ 23. Энергия, импульс, момент импульса 49в
§ 24. Гамильтониан свободного электромагнитного поля 500
§ 25. Гамильтониан излучения, взаимодействующего с частицами .... 502
Раздел IV. Квантовая теория излучения 503
§ 26. Квантование свободного поля излучения. Фотоны 503
§ 27. Плоские волны. Импульс излучения 504
§ 28. Поляризация 505
§ 29. Разложение по мультиполям. Фотоны с определенным моментом им-
импульса и четностью 506
§ 30. Взаимодействие с атомной системой 509
§ 31. Излучение фотона атомом. Дипольное излучение 513
§ 32. Комптоновское рассеяние при низких энергиях. Формула Томсона . 516
Задачи и упражнения 520
Дополнение В. Коэффициенты векторного сложения и матрицы вра-
вращения 524
Раздел I. Коэффициенты Клебша — Гордаиа (К. — Г.) и «3/»-символы 524
Раздел II. Коэффициенты Рака и «6/»-символы 530
Раздел III. «9/»-символы 534
Раздел IV. Матрицы вращения 536
Раздел V. Неприводимые тензорные операторы 542
дополнение Г. Элементы теории групп 545
Раздел I. Основные понятия 545
Раздел II. Линейные представления группы 548
Раздел III. Конечные группы 559
Раздел IV. Перестановки (группа &п) 567
Предметный указатель 580

Ах, душенька! До какой степени
у твоего отца дух погряз в материи!
Ж- Б. Мольер. сСмешные жеманни-
жеманницы», VI
ЧАСТЬ Ш
СИММЕТРИИ
И
ИНВАРИАНТНОСТЬ

ГЛАВА XIII
МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
§ 1. Введение
Свойства симметрии уравнений движения в квантовой меха-
механике играют столь же большую роль, как и в классической ме-
механике. Систематическое изучение симметрии и ее следствий
будет проведено с общей точки зрения в главе XV. Настоящая
глава посвящена симметрии по отношению к вращениям — од-
одному из наиболее важных видов симметрии. В квантовой ме-
механике, так же как и в классической, вращение системы свя-
связано с ее моментом импульса, и из инвариантности уравнений
движения относительно вращений следует закон сохранения
момента импульса. Различия с классической механикой возни-
возникают из-за того, что момент импульса не является теперь обыч-
обычным вектором, а состоит из трех некоммутирующих операто-
операторов — компонент векторного оператора.
В разделе I мы определяем момент импульса правилами
коммутации его компонент Jx, Jy, Jz (соотношения C)) и ис-
исследуем задачу на собствейные значения операторов Р и JZt
пользуясь только этими правилами и утверждением, что все
три компоненты являются наблюдаемыми. Этот подход, пред-
предложенный Дираком, во многом аналогичен рассмотрению гар-
гармонического осциллятора в главе XII.
Раздел II посвящен специальному случаю — орбитальному
моменту импульса частицы и построению соответствующих соб-
собственных функций (сферических функций).
В разделе III устанавливается связь между вращениями и
оператором момента импульса. Вращение физической системы
описывается посредством некоторого оператора, который зави-
зависит от компонент полного момента, и его вид определяется
уравнением F0). Доказывается, что инвариантность уравнений
движения относительно вращений эквивалентна обращению
в нуль коммутаторов гамильтониана с тремя компонентами опе-
оператора момента, откуда следует закон сохранения момента им-
пульса.
Эксперимент показывает, что большинство частиц обладает
внутренним моментом импульса — спином. Понятие спина рас»
сматривается в разделе IV, ^

14 ГЛ. ХШ. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
Раздел V посвящен важному вопросу сложения моментов
импульса.
Различные операторы квантовой механики можно характер
ризовать в соответствии с законом их преобразования при вра-
вращениях. В частности, существуют скалярные операторы (ин-
вариантные относительно вращений), векторные операторы и,
вообще говоря, неприводимые тензорные операторы, трансфор-
мационные свойства которых особенно просты. Эти операторы
характеризуются также простыми коммутационными соотноше-
соотношениями с компонентами оператора момента, откуда следуют не-
некоторые важные свойства их представлений (теорема Вигне-
ра — Эккарта). Все это рассматривается вместе с основными
приложениями в разделе VI и последнем разделе этой главы.
Дополнение В к настоящей главе содержит наиболее важ-
важные формулы и основные свойства различных коэффициентов,
связанных с вращениями и сложением моментов импульса.
Раздел I. СОБСТВЕННЫЕ ЗНАЧЕНИЯ
И СОБСТВЕННЫЕ ФУНКЦИИ МОМЕНТА ИМПУЛЬСА
§ 2. Определение момента импульса
Мы уже встречались с оператором момента импульса при
рассмотрении квантовых систем одной частицы. По определе-
определению, момент импульса частицы равен
t^rXp, A)
где г и р — векторы координаты и импульса данной частицы.
В волновой механике I представляется векторным оператором ')
(—i)r~XV, три компоненты которого являются дифференциаль-
дифференциальными операторами, удовлетворяющими следующим правилам
коммутации:
[/*,/„] = //«, [.'„« = //*, [1г,1х] = Иу. B)
Каждая из компонент коммутирует с квадратом углового мо-
момента
т. е.
Эти свойства были получены в § V.18. Напомним, что послед-
последнее равенство является простым следствием соотношений B).
') В настоящей главе используется система единиц, в которой Л = I,

5 2. ОПРЕДЕЛЕНИЕ МОМЕНТА ИМПУЛЬСА 15
Операторы г, р и I — векторные. Векторный оператор В оп-
определяется своими компонентами Вх, Ву, Вг по трем ортогональ-
ортогональным осям, где Вх, Ву, Вг — операторы в обычном смысле этого
слова. При заданных трех компонентах мы можем определить
компоненту Ви оператора В в произвольном направлении «, за-
задаваемом единичным вектором и(их, иу, иг):
Ви s (иВ) = ихВх + иуВу + uzBz.
Таким образом, мы можем определить компоненты векторного
оператора В по ортогональным осям любой другой системы
координат. Различные операции векторной алгебры (сложение,
скалярное произведение, векторное произведение и т. д.) пере-
переносятся на векторные операторы без изменения.
Рассмотрим квантовую систему N частиц. Как и выше, мы
можем определить момент я-й частицы 1{п) = г<"> X Р(п). Пол-
Полный момент импульса системы является векторной суммой мо-
моментов N частиц
Так как каждый отдельный момент импульса удовлетворяет
коммутационным соотношениям B), а компоненты любого из
них коммутируют с компонентами всех других, то мы имеем
g-ZZ W, tr\- Z W, if]-/
n n' n
Аналогично получаются еще два соотношения, возникающие
после циклической перестановки индексов. Таким образом, ком-
компоненты полного момента импульса удовлетворяют тем же ком-
коммутационным соотношениям, Что и компоненты индивидуальных
моментов.
Тем самым мы пришли к следующему определению момента
импульса: векторный оператор J называется оператором мб-
мента импульса, если его компоненты являются наблюдаемыми
и удовлетворяют коммутационным соотношениям
[Jx,Jy] = iJz, Uy,Jz] = ux, [/„/*]-//,. C)
Из этих трех соотношений мы можем вывести аналогичные
соотношения для компонент / вдоль любой другой системы
осей. Пусть /и, /„, /а, компоненты / по трем ортогональным
осям, единичные векторы которых и, v, w ориентированы так,
что w = и X v. Тогда несложно доказать соотношение

16 ГЛ. XITI. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
[lu, Jv] = iJw и два других, получающихся циклической пере-
перестановкой индексов').
Если а и b — любые два вектора (или два векторных опе-
оператора, коммутирующие друг с другом и с /), то имеем более
общее соотношение
[а/, 6/] = /((аХ6)/). D)
§ 3. Основные алгебраические соотношения
Квадрат момента импульса
коммутирует с Jx, Jy и Jz. Это свойство является следствием
коммутационных соотношений C) и может быть выведено тем
же способом* что и аналогичное свойство для введенного в § 2
момента импульса /. Символически запишем
[/, Я] = 0. E)
Как следствие, Р коммутирует с произвольной функцией ком>
понент векторного оператора /.
Введем два эрмитово сопряженных друг другу оператора
J+=JX + iJy, J_=JX-iJy. F)
Три оператора /+, /_ и /г полностью определяют векторный опе-
оператор / и оказываются более удобными для алгебраических ма-
нипуляций, чем Jx, Jy и Jz. Их коммутационные соотношения
можно вывести из соотношений C)
[/„/+] = /+, Gа)
[/,,/_] = -/_, G6)
[/+, /_] = 2/г. Gв)
') Эти соотношения можно записать в компактной форме {i, /, k = и, v
или w\
[Jо }i] = ' Z eHkJk или Z zijkhIi = iJk>
k ii
где zi,k — полиостью антисимметричный теизор:
/¦ 0, если два индекса равны;
е//йв| "^" '' если '' '' * получаются четной перестановкой из «, о, w;
v — 1, если /, у, k получаются нечетной перестановкой из и, о, да.
Вторая форма эквивалентна соотношению между векторными операторами

§ 4. СПЕКТР ОПЕРАТОРОВ Я И 1г 17
Из равенства E) следует
[Я,/+] = [/»,/-] = [Л /г] = 0. (8)
Для /2 имеем
/* = у (/+/_ + /_/+) + &
откуда, используя Gс), получаем два тождества
/_/+ = /2-/2(/2 + 1), (9а)
/+/_==Я-/г(/г-1). (96)
§ 4. Спектр операторов /2 и /г
Так как /2 коммутирует с каждой компонентой векторного
оператора /, то можно построить полный набор собственных
функций /2 и одной из компонент, например, /2. Тот факт, что
Jx, Jy и /г — эрмитовы операторы, удовлетворяющие коммута-
коммутационным соотношениям C), накладывает жесткие ограничения
на спектр собственных значений.
Оператор /2 — положительно определен и эрмитов, так как
он является суммой положительно определенных эрмитовых
операторов1). Его собственные значения с необходимостью по-
положительны (или равны нулю). Следовательно, их можно пред-
представить в форме /(/+1) и параметризовать вещественным
квантовым числом / ^ 0.
Пусть |/т> — какой-либо собственный вектор операторов /2
и /г, отвечающий собственным значениям /(/+1) и m соот-
соответственно. Будем говорить, что \jm} онределяет состояние
с моментом импульса (//и). Если /2 и Jz не образуют полного
набора коммутирующих наблюдаемых, то могут существовать
несколько линейно-независимых состояний (//и). В этом случае
|/т> — один из кет-векторов, выбранный в подпространстве, со-
соответствующем моменту импульса (jm). Рассуждение, следую-
следующее ниже, справедливо для любого такого вектора. Единствен-
Единственные условия, которым должен удовлетворять вектор \jtn), сле-
следующие:
/*l/m> «=/(/+1)|/от),
Jz\jm) = m\jm).
') Это следствие эрмитовости операторов /«, /„ и /г. Для любого |«)',
(и \/2х\ и)^0 как норма вектора Jx\u). Операторы 12у и /| обладают тем же
свойством, поэтому («|/2|«) ^ 0 для любого |«),

18 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
Рассмотрим векторы /+1 jm) и /_ | jm). Из тождеств (9а)
и (96) имеем
/_/+1 jm) = [j (/ + 1) - т (т + 1)] I jm) = (/ - т) (} + т + 1) | jm),
(Юа)
/+/_ | jm) = [/(/+ 1) - т (т - 1)] | jm) = (/ + т) (/ - т + 1) I jm).
A06)
Тем самым нормы векторов /+1 jm) и /_ | jm) равны
(jm | /_/+1 jm) = (j-m)(j + m+l) (jm \ jm),
(jm | /+/_ | jm) = 0 + m) {j — m + 1) (jm | jm).
В силу одной из аксиом гильбертова пространства эти нормы
не могут быть отрицательны и, следовательно,
отсюда
Более того, так как равенство нулю нормы есть необходимое и
достаточное условие равенства нулю вектора, то имеем
/+|/ап> = 0 тогда и только тогда, когда (/ — т) (/ -f- т + 1)=0;
точно так же /_|/лэт> = 0 тогда и только тогда, когда
(j + m) (/ — т + 1) = 0. Поскольку т обязательно находится
в интервале (—/, +/), эти условия сводятся к т = / и т =
= — / соответственно.
Если m=?j, то (отличный от нуля) вектор /+|/т> является
вектором с моментом импульса (/, т -f- 1). Используя (8), по-
получаем
/2/+1 /от> = J+P\ jm) = / (/ + 1) /+1 /m>
и так как согласно Gа)
JzJ+ = J+{Jz+l), (lla)
то мы имеем
U+1 Jm) = J+ (Jz + 1) | /т> - (т + 1) /+1 /от>.
Используя тот факт, что /_ коммутирует с Я, и то, что со-
согласно G6)
V_ = /_(/,-l). A16)
получаем аналогичный результат для /_|/ал>.
В результате мы доказали важную теорему:
Если |/т> — вектор с моментом импульса (jm) и нормой N,
то
(i) -/" < т < U A2)

§ 4. СПЕКТР ОПЕРАТОРОВ Я И Гг 19
(ii) если т = i, то /+|//п>= 0;
если тф}, то J+\jm}—вектор с моментом импульса (/,
т+ 1) и нормой [/(/+ 1) —т(т+ 1)]#;
(Ш) если т = —/, то J-\jm) = 0;
если тф— /, то J-\jm} — вектор с моментом импульса
(j,m— 1) и нормой [/(/+ 1)— m(m— \)]N.
Рассмотрим теперь векторы, получаемые последовательным
действием оператора /+ на вектор |/т>:
/+l/m>, J\\jm) ПМт), ... A3)
Известно, что —/ <: m <; /. Если /п = /, то /+|/т> = 0. Если
т </, то /+|/т> — ненулевой вектор с моментом (/, т + 1).
Следовательно, он обладает всеми свойствами (i) — (iii), харак-
характерными для любого общего собственного вектора операторов
Р и /г, а значит, m + 1 <: /. Если m + 1 = /, то Р+\ jm) — 0.
Если же m + 1 < /, то J%\jm)— ненулевой вектор с момен-
моментом (/, m + 2) и также обладает свойствами (i), (ii) и (iii).
Таким образом, можно последовательно продолжать анализ
свойств векторов A3). Ясно, что эта последовательность должна
когда-то оборваться, в противном случае мы смогли бы по-
построить собственные векторы /г, отвечающие собственным зна-
значениям, превосходящим любое наперед заданное число, что
противоречит неравенствам A2), согласно которым значения m
не могут быть больше /. Следовательно, существует целое число
р ~^ 0 такое, что /+1 jm) — ненулевой вектор с моментом им-
импульса (/, т-\-р), действуя на который оператором /+ полу-
получаем нуль. Тем самым имеем т + Р = !¦ Итак, мы показали,
что (/ — т) — целое число (^3=0) и что р векторов
/+l/m>, Д|/т), .... /р+|/т> A4)
описывают состояния с определенным моментом импульса, от-
отвечающие собственному значению /(/+ 1) оператора Р и соб-
собственным значениям
m-fl» т + 2 m + p — j
оператора /г соответственно.
Подобное рассмотрение векторов, получаемых последова-
последовательным применением оператора /_ к вектору \jm}, показывает,
что j -f- m эн q также является целым числом (^0) и что q век-
векторов
/_|/m>, /2-|/m> Ji\jm) A5)
описывают состояния с определенным моментом импульса, от-
отвечающие собственному значению /(/+ 1) оператора Р и соб'
ственным значениям *
т — \, т — % ..., т — q — — i

20 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
оператора Jz соответственно. Так как р и q — неотрицательные
целые числа, то их сумма р + q = 2/ также является неотрица-
неотрицательным целым числом.
Объединяя эти утверждения, получаем следующую основную
теорему:
(A) Собственные значения оператора Р имеют вид /(/ +^ 1),
еде j — неотрицательное целое или полуцелое ' число
/ — 0, '/г, 1, 72> 2, ...
(B) Собственными значениями оператора Jz могут быть
только целые или полуцелые числа
±1, ±7г, ±2, ...
(С) Если /(/+1) и m— собственные значения операторов
Р и Jz, отвечающие общему собственному вектору этих двух
операторов, т. е. состоянию с моментом импульса (jm), то воз-
возможны следующие B/ + О значений пг:
-/, -/+1, .... +/•
§ 5. Собственные векторы операторов Р и /г.
Построение инвариантных пространств ?<^
Взяв вектор \jm} с определенным моментом импульса, мож-
можно построить все B/+ 1) собственных векторов операторов Р
и Jz последовательным применением операторов /+ и /_. Вообще
говоря, эти векторы не нормированы на единицу, однако легко
построить нормированные векторы, поступая следующим обра-
образом.
Допустим, что норма \jm} равна единице. Тогда, если m = /,
то вектор /+|/т> равен нулю; если пг < /, то J-[jmy—вектор
с моментом импульса (/, /п+1). Обозначим |/т-^1> норми-
нормированный вектор, определяемый равенством
J+\jm) = cm\jm+l).
Из приведенного выше выражения для нормы J+\jm} следует,
что
Фиксируем фазу вектора |//я + 1> так, чтобы ст было веще-
ственным и положительным числом. Тогда
/+1 jm) = У/(/+ \)-т{т+ 1)| jm +
') В этой книге под «полуцелыми» подразумеваются числа вида
13 5
2 ' 2 ' 2 ' ' * '

§ 6. СТАНДАРТНОЕ ПРЕДСТАВЛЕНИЕ {/! /г) 21
Действуя на обе части оператором У_ и используя A0а), полу^
чаем
С вектором \jm -\- 1> можно поступить точно так же. Доста-
Достаточно заменить всюду т на т -\- 1. Если т -\- 1=/, то J+\jtn -{-]
;+1> = 0. Если т -\- 1 ф '}, то мы получим вектор \jm-\-2}
с моментом импульса (/, т + 2) и единичной нормой, фаза ко-
торого фиксирована тем же способом. Этот процесс может быть
продолжен до тех пор, пока не получим вектор | //>.
Таким же образом, применяя последовательно оператор /_
к вектору |//п>, строим нормированные векторы \\т—1>, ...
•••> I/ — /) с моментами импульса (/, т—1), ..., (/, —/) со-
соответственно.
Итак, исходя из |//п>, мы построили B/+ 1) ортонормиро'
ванных векторов
l//">, I//-1), .... \!т), .... |/-/>, A6)
которые удовлетворяют уравнениям на собственные значения
/21/» = /(/+1)]/». A7>
¦ШИ> = Ц|/И> A8)
и фазы которых выбраны так, что эти векторы получаются один
из другого посредством соотношений
/+1/» = УНГ+1)-Mi*+DI/>+1), A9)
/-1 /H> = V/(/+D-Mn-l)I /> - 1 )• B0)
В частности,
/+1/7> = /-1/-/> = 0. B1)
Построенные B/+1) векторов образуют базис некоторого
подпространства Jf('>. Операторы /+, /_, Jz преобразуют эти век-
векторы в себя и, следовательно, любой вектор пространства S(i) —
в вектор из «?<'>. Другими словами, эти операторы оставляют
ё?(/> инвариантным. Произвольная функция F{J) операторов
J+, J-, Jz также оставляет <г?(/) инвариантным. В разделе III мы
увидим, что вращению квантовой системы как целого соответ-
соответствует применение к вектору состояния оператора типа F(J)y
следовательно, любые вращения всей системы оставляет <gw> ин-
инвариантным.
§ 6. Стандартное представление {Р Jz}
Если Р и Jz не образуют полного набора коммутирующих
наблюдаемых, то для этих двух операторов существует много
систем общих базисных векторов. Но даже в случае, когда они

22 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
образуют полный набор, фаза каждого базисного вектора мо-
может быть выбрана произвольной.
Среди представлений, в которых Р и Jz диагональны, суще-
существуют такие, где оператор момента импульса действует осо-
особенно просто. Мы назовем их стандартными представлениями
{PJZ}- В этих представлениях базисные векторы, отвечающие
определенному значению квантового числа /, могут быть сгруп-
сгруппированы в одну или несколько серий из B/ -|- 1) векторов, свя-
связанных соотношениями A9) — B0). Каждой серии отвечает под-
подпространство <gu\ а все гильбертово пространство является пря»
мой суммой этих подпространств.
Для построения стандартного представления можно посту-
поступать следующим образом. Среди собственных векторов Р, от-
отвечающих собственному значению /(/'+ 1), рассмотрим те, ко-
которые являются собственными для Jz с собственным значе-
значением /. Такие векторы, в зависимости от обстоятельств, обра-
образуют в гильбертовом пространстве некоторое подпространство
STU) размерности один, два, ... или бесконечномерное. В #"(/>
всегда можно выбрать полный набор ортонормированных век-
векторов |т//>. Индекс т служит для того, чтобы отличать векторы
с угловым моментом (//) один от другого и может, в зависимо-
зависимости от обстоятельств, принимать одно, два, ... или бесконечное
множество значений (дискретных или непрерывных; для опре-
определенности, будем предполагать их дискретными). По предпо-
предположению,
С каждым из этих векторов |т//> можно связать 2/ векторов,
которые получаются последовательным действием оператора /_
•согласно правилам предыдущего параграфа. Так строится
B/+ 1)-мерное подпространство «?(/); для того чтобы отличать
эти подпространства друг от друга, будем обозначать их &(j)
Базисными векторами в &{%')) служат
Они ортонормированы и удовлетворяют основным соотноше-
соотношениям
Я | т/ц> ==/(/+1)| т/ц>, B2)
ц|т/ц>, B3)
/+1 т/ц> = У/(/+1)-**дГТ1)| %1 ц + 1>, B4)
/-1 т/ц> = V/ (/Ч- 1) - Ц (Ц - 1) 11/ ц - 1>. B5)

S 7. ЗАКЛЮЧЕНИЕ 2Э
Из B4) и B5) легко получить следующие важные соотно-
соотношения (см. задачу 1):
/('^^"Ц|т/ ±>>¦ B6>
rt!/rU|т/ ±•*>¦ B7>
Легко показать, что подпространства ?Г(т/) с фиксирован-
фиксированным / и различными т взаимно ортогональны и их объединение
образует подпространство <S\, отвечающее собственному значе-
значению /(/ -+¦ 1) оператора Р.
Базисные векторы |т/ц> и |т'/ц'> подпространств <8'(т/) и
%> Wl) (т т^ т'). ортогональны, если ц =#= ц', так как они отвечают
различным собственным значениям Jz; то же справедливо и
если ц = [а', так как последовательное применение B4) дает
<т7|* |т/ц> = <т'/Ц + 1 |т/ц + 1) = ... = <т'/71 г//) = д„..
Чтобы показать, что любой собственный вектор Л, отвечаю-
отвечающий собственному значению /(/+ 1), является линейной комби-
комбинацией векторов |т/ц> (т и ц — переменные, / — фиксировано),
достаточно показать, что любой вектор |<о/|л> с моментом (/ц)
является линейной комбинацией базисных векторов |т/ц> с тем
же моментом импульса. Если \i = /, то это следует из первона-
первоначального предположения. Если же ц ф j, то задачу можно све-
свести к предыдущему случаю действия оператором J'~* на вектор
|ю/ц> и используя соотношения B6) и B7).
Итак, исходя из полного набора ортонормированных векто-
векторов с моментом импульса (/7), мы построили базисные векторы
стандартного представления {J2h} в подпространстве <§¦„ отве-
отвечающем собственному значению /(/+ 1) оператора Р. Повто-
Повторяя эту процедуру для всех допустимых собственных значе-
значений Р, получаем стандартный базис во всем гильбертовом про-
пространстве.
Отметим особенно простую форму матриц, задающих ком-
компоненты оператора / в таком представлении (см. задачу 2).
Из равенств B3), B4) и B5) имеем
<т/ц |/z| т'/V) = |*в«'в//Аи'»
<т/и I /* I t'/V> = V/(/+i)-wi' VW ± i • B8>
§ 7. Заключение
Приведенное выше исследование свойств оператора момент»
импульса основывалось исключительно на коммутационных со-
соотношениях и на том факте, что его компоненты являются

24 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
эрмитовыми операторами в гильбертовом пространстве. Мы пока-
показали, что квантовое число / может принимать только целые или
полуцелые значения и что каждому собственному значению
j(/+l) оператора отвечает одна или несколько серий из
B/+1) линейно независимых векторов. В каждой серии век-
векторы получаются один из другого применением операторов /_
или /+ и соответствуют B/+1) возможным значениям кван-
квантового числа т
-/, —/"+ 1, ¦•-, +/'.
Однако этих гипотез недостаточно для полного решения про-
проблемы собственных значений. Следует еще определить:
(i) какие целые и полуцелые значения действительно со-
составляют спектр /;
(и) сколько серий из B/+ 1) линейно независимых векто-
ров отвечают каждому из этих значений /.
Ответ на эти вопросы зависит от рассматриваемой задачи.
Только из коммутационных соотношений нельзя, например, за-
заранее исключить случай, когда / принимает одно значение (це-
(целое или полуцелое) и существует только один набор B/+ 1)
линейно независимых векторов, отвечающих этому значению;
пространство векторов состояний в этом случае B/+ 1)-мерно.
Такая ситуация встретится в разделе IV при рассмотрении
спина.
Другой важный частный случай связан с моментом им-
импульса I частицы, определяемым уравнением A). В разделе II,
где этот случай разбирается подробно, мы увидим, что спектр
значений / составляют все целые числа от 0 до ^ оо, а полу-
полуцелые значения отсутствуют').
Раздел II. ОРБИТАЛЬНЫЙ МОМЕНТ ИМПУЛЬСА
И СФЕРИЧЕСКИЕ ФУНКЦИИ
§ 8. Спектр операторов I2 и h
Вернемся к квантовой системе одной частицы, с которой мы
начали рассмотрение в § 2. Выбирая ось z в качестве полярного
направления, мы можем выразить оператор I2 и компоненты
') В задаче 15 рассматривается случай, в котором Р и /г образуют пол-
полный набор коммутирующих наблюдаемых (одна серия из B/ +1) векторов
для каждого значения /') я в котором / может принимать все целые и полу-
полуцелые значения. Из-за присутствия в спектре как целых, так и полуцелых
значений при рассмотрении / как оператора момента необходимо сделать не-
некоторые замечания о физическом смысле наблюдаемых этой системы (см,
$ 15).

S 8. СПЕКТР ОПЕРАТОРОВ Р И 1г 25
оператора I как функции полярных углов 8, ср и их производных
(см. уравнения (Б. 82) — (Б. 84)*)). В дальнейшем изложении
радиальную переменную можно опустить. Мы намереваемся
построить функции Ff (8, ср), удовлетворяющие двум уравнениям
на собственные значения:
l2Ff (8, q>) = /(/ + l)FT(e, ф), B9)
UFT(B, q>) = mF?(B, ср). C0)
Так как волновая функция является однозначной функцией г,
то Ff (8, ф) не должна меняться прн замене ф на ф + 2я').
Уравнение C0) уже исследовалось в § V. 12. Так как /2 =
= — id/дф, то Ff(Q, ф) имеет вид /Г(8)е'шф, где т— целое.
Коль скоро т — целое, должно быть целым и I, следовательно,
не существует полуцелого орбитального углового момента.
Для того чтобы среди целых чисел (^0) найти те, которые
являются собственными значениями I, и определить их вырож-
вырождение, построим собственные функции F\ (8, ф), отвечающие
угловому моменту (/,/). Такая функция определяется уравне-
уравнениями
W7{(8,q>) = /F{(8,q>), C1)
/+^(8,Ф) = 0. C2)
Они эквивалентны системе уравнений B9) — C0) при т = I, так
как в силу тождества (9а)
Из C2) вместе с C1) следует B9) и обратно. Система урав-
уравнений в частных производных первого порядка C1) — C2)
легко решается, коль скоро даны дифференциальные опера-
операторы 1г и /+ (ур. (Б. 82) — (Б. 83)). Из уравнения C1) имеем
Подставляя это выражение в уравнение C2), получаем диффе-
дифференциальное уравнение
решение которого с точностью до произвольного множителя есть
sin'8. Каждому целому числу / (^0) отвечает одна и только
*) Здесь и далее даны ссылки на формулы, приведенные в Дополнениях
А, Б, В, Г томов 1 и 2. (Прим. ред.)
') Кроме того, Ff @, ср) и Ff (я, ср) не зависят от <р, что автоматически
выполняется для полученных ниже решений,

26 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
одна собственная функция (определенная с точностью до мно-
множителя), соответствующая угловому моменту (/, /)
sin
Следовательно, спектр оператора Р состоит из последова-
последовательности чисел /(/+ 1), где / принимает все целые значения
от 0 до + оо. Каждому собственному значению /(/+1) со-
соответствует B/+1) собственных значений пг оператора
1г — B/+ 1) целых чисел в интервале (—/, +/). Каждой паре
(tm) соответствует одно и только одно собственное состояние
(если мы ограничимся только функциями от 9 и ф): спектр опе-
операторов Р и 1г в целом невырожден.
§ 9. Определение и построение сферических функций
Общая собственная функция Р и tz, отвечающая собствен-
собственным значениям (tm), определена с точностью до постоянного
множителя. Произвол исчезает, если нормировать ее на еди-
единицу и выбрать подходящее условие для фазы. Таким образом,
получаем сферическую функцию порядка (lm), которую будем
обозначать Yf (9, ф).
Функции Yf (9, ф) образуют ортонормированную систему
функций от 9 и ф с элементом объема du = sin В dB dtp в ин-
интеграле для скалярного произведения. Примем без доказатель-
доказательства утверждение о полноте этой системы.
Фиксируем фазы следующим образом1). Потребуем прежде
всего, чтобы Yf образовывали стандартный базис. Для этого
достаточно, чтобы они удовлетворяли уравнениям B4) — B5),
записанным в представлении {9ф} (ур. (Б. 89)). Тем самым оп-
определены относительные фазы B/+1) сферических функций,
отвечающих данному значению /, и остается только фиксиро-
фиксировать фазу одной из них, например У? (9, ф). Потребуем, чтобы
величина Y°i @, 0) была вещественным и положительным чис-
числом.
Если обозначить через |//п> векторы, которым в представ-
представлении {9ф} отвечают сферические функции Yf (9, ф), то они удо-
удовлетворяют уравнениям B4)—B5) и, следовательно, (ур. B6))
') Такая нормировка используется большинством авторов. Однако в об-
обсуждениях, использующих инвариантность относительно обращения времени,
при рассмотрении волновых функций в конфнгурационном пространстве пред-
предпочтительнее функции <W? (9, Ф) = ilYf (9, ф) (см. § XV. 22).

§ 9. ОПРЕДЕЛЕНИЕ И ПОСТРОЕНИЕ СФЕРИЧЕСКИХ ФУНКЦИЙ 27
Другими словами,
YT <в. Ф) =
(в. ф> - Vw.u+1).ll++mYrt (э-*>• C4>
или
Явные выражения для дифференциальных операторов /_ и /+
приведены в приложении (ур. (Б. 83)). Используя их, полу-
получаем
)/(в)-
При любой /(8) выражение в скобках следует рассматривать
как оператор, действующий на функцию /(9), стоящую справа
от него. Следовательно, последовательное применение /+ или /_
к функции е'^Дб) дает (ц и s целые)
. C5)
Из рассуждений, приведенных в § 8, нам известно, что
где Ci — константа, модуль которой определяется условием нор-
нормировки y\, откуда
Г^+'I C6)
а фазу следует определить согласно принятому выше условию.
Подставляя выражение Yi в уравнение C3) и принимая во
внимание тождество C5), получаем
^*'1- <37>
При т = — / отсюда имеем
YT1 (8, ф) = (-)' С/е-"ф sin' G. C8)
Подставляя это выражение в уравнение C4) и вновь используя
тождество C5), получаем новое эквивалентное предыдущему
выражение для Yf
C9)

28 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
При т = 0 эти выражения совпадают
С точностью до множителя получили полином Лежандра
P/(cos8) (yp. (Б. 71))
Y°t (9, ф) = (-
Условие вещественности и положительности У? (О, 0) определяет
выбор фазы
Тем самым полностью определены выражения C7) и C9) для
УГ(8, Ф).
Большинство свойств сферических функций, которые пере-
перечислены в Дополнении Б, можно легко получить из компактных
формул C7) и C9). Отметим, в частности, что
УГт(е, <p) = (-i)mJ7'(e, <р),
Yf является произведением е'тф sinlmi 8 и полинома по cos 9
степени / — \т\ и четности (—lLml, а четность Yf (задача 4)
равна (—\I, т. е.
Раздел III. МОМЕНТ ИМПУЛЬСА И ВРАЩЕНИЯ
§10. Определение вращений. Углы Эйлера
В этом параграфе мы напомним некоторые свойства враще-
вращений в обычном пространстве.
По определению, вращением вокруг точки О называется та-
такое перемещение точек пространства как целого, при котором
1-очка О остается неподвижной. При таком перемещении, каж-
каждая точка Р переходит в новое положение Р' и существует
взаимнооднозначное соответствие между Р и Р'. Можно было
бы определить вращение вокруг О как взаимнооднозначное со-
соответствие между точками пространства, при котором точке О
соответствует она сама и которое сохраняет как расстояния

S TO. ОПРЕДЕЛЕНИЕ ВРАЩЕНИЙ. УГЛЫ ЭЙЛЕРА 29
{а следовательно, и углы), так и ориентацию координатных
осей').
Единичный вектор и и угол ср определяют конкретное вра-
вращение 91а (ф) — поворот на угол ф вокруг оси, направленной по
и (положительное вращение вокруг этой оси определяется обыч-
обычным образом). Этот способ задания вращения не единственный.
Для выполнения &а (ф) = 52«, (ф), необходимо и достаточно,
чтобы
щ = и щ = — и
или
<Pi = Ф + 2пя Ф1 = — ф + 2nit
(п — произвольное целое число).
Будем называть вращение инфинитезимальным, если ф = е
бесконечно мало. Легко написать вектор V, в который при ин-
финитезимальном вращении $?«(е) пере-
переходит вектор V:
V'&V + s(uXV) (в<1). D0)
Другой способ задания вращения со-
состоит в фиксации углов Эйлера а, Р, "у-
Пусть Oxyz — правая система осей, а
OXYZ — система осей, получаемая из
предыдущей вращением, Ои — одна из
двух ориентированных осей, перпендику-
перпендикулярных плоскости OzZ (рис. 1). Углами
Эйлера будут 2) Рис. 1. Определение углов
а = (Оу, Ои), p = (Oz. OZ), y = (Ou, OY). Эйлера.
Полное вращение является результатом трех последовательных
вращений
Яг(а) — вращение на угол а вокруг Oz (Оу переходит в Ои);
&и (Р) ~~ вращение на угол Р вокруг Ou{Oz переходит в OZ)\
&z(v) ~~ вращение на угол у вокруг OZ(Ou переходит в OF).
Обозначим результирующее вращение через 52(аРу) и запишем
Я(аРу) = ЯгМЛЛР)ЯЛа). D1)
Углы а, р, у являются алгебраическими величинами. Они
положительны или отрицательны в зависимости от того, яв-
является ли вращение вокруг осей Oz, Ou, OZ положительным
!) В отличие от отражений, которые сохраняют расстояния, но меняют
ориентацию координатных осей.
2) Принятое здесь определение несколько отличается от используемого
обычно в теории гироскопа.

30 ГЛ. ХШ. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
или отрицательным. Для выбранной системы Oxyz одно и то же
вращение может быть задано несколькими наборами углов
Эйлера. Необходимыми и достаточными условиями равенства
52(P) 52(p) являются
а
ai — а + 2ппа щ = а + я -\- 2ша
р, == Р -|- 2лпр или Pi = — Р -)- 2лпр D2)
Yi = Y + 2ппу Yi = Y — я + 2япу
(«а, «р, «у произвольные целые числа).
С каждым вращением можно связать некоторую матрицу
3X3, определяемую следующим образом. Фиксируем правую
декартову систему координатных осей Oxyz с единичными век-
векторами аь а2, а3 в направлении осей Ox, Oy, Oz соответственно.
При вращении они преобразуются в три новых вектора Аь Л2,
Аз, образующих новую декартову систему OXYZ. Каждый из
векторов А,- является линейной комбинацией векторов аь а2, а3')
Коэффициенты Жц трех линейных комбинаций являются элемен-
элементами матрицы 3X3, которую мы обозначим той же буквой 52,
что и само вращение. Эта матрица полностью определяет вра-
вращение* Действительно, пусть V = a/V,- — некоторый вектор
в пространстве, определяемый его координатами (Vb V2, Уз)
в системе Oxyz. При вращении он преобразуется в вектор
V = М [V] = AtV, = а,ЛцУ,.
Компоненты V в системе координат Oxyz равны
V't^9iuVh D3)
Так как векторы Аг образуют декартову систему, то вец;;ст-
венная матрица 31 ортогональна и унимодулярна
Для фиксированной системы осей Oxyz матрица, связанная
с вращением, определена однозначно. Верно и обратное, каж-
каждой вещественной, ортогональной, унимодуляриой матрице со,-
ответствует одно и только одно вращение.
В Дополнении В (формула (В. 45)) дано выражение элемен-
элементов матрицы, соответствующей вращению 52(apv). через углы
Эйлера. В качестве примера приведем закон преобразования
') В этом разделе мы будем систематически пользоваться соглашением
о суммировании по повторяющимся индексам, так:

§ II. ОПЕРАТОР ВРАЩЕНИЯ 31
координат рассмотренного выше вектора V при вращении 52г(а)
на угол а вокруг Oz
V\ = Уi cosa—V2sin a,
D4)
Произведение двух вращений 9l\ и 522, т. е. преобразование
91 = 91ч91\, которое получается последовательным выполнением
вращений Я\, а затем Ыъ также является вращением. Соотно-
Соотношение D1) дает пример такого произведения. Углы Эйлера для
91 трудно выразить в виде функций от углов Эйлера 31\ и 912-
В то же время, матрица, соответствующая 91, легко получается
как произведение матриц Я\ и Я2
§11. Вращение физической системы. Оператор вращения
При обсуждении свойств физической системы, связанных
с вращениями, — все сказанное ниже справедливо для любого
преобразования пространства — можно принять одну из двух
точек зрения, которые следует четко различать. Согласно пер-
первой (иногда ее называют пассивной) производят вращение ко-
координатных осей, оставляя фиксированной каждую точку Р про-
пространства и связанные с ней физические величины. Согласно
второй (иногда ее называют активной) фиксированными
остаются оси координат, а вращают физическую систему. Обе
точки зрения эквивалентны. Поворот координатных осей или
поворот физической системы в противоположном направлении
приводят к одному и тому же результату. Далее, если не огово-
оговорено противное, мы будем придерживаться второй точки зрения
(будем вращать физическую систему).
Определение «вращения физической системы» в квантовой
механике требует большей осторожности, чем в классической,
так как связь между динамическими переменными и динамиче-
динамическими состояниями значительно сложнее. Рассмотрим для про-
простоты вначале случай одной частицы. Обозначим а — возмож-
возможное динамическое состояние частицы и ф(г) — соответствующую
волновую функцию. Состояние, получаемое после вращения 91,
обозначим а' и соответствующую а' волновую функцию — $'(r)
Когда мы говорим, что состояние а переходит при вращении Я
в состояние а', мы имеем в виду, что результаты любых наблю-
наблюдений над системой в состоянии а' могут быть получены по-
посредством вращения 91 из результатов, которые дали бы те же

32 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
наблюдения, выполненные над системой в состоянии а. Рас-
Рассмотрим, например, измерение координаты. Распределение веро-
вероятности для состояний а а а' равно |i|;(r)|2 и |ф'(г)|2 соот-
соответственно. Согласно приведенному выше утверждению послед-
последнее получается из первого при вращении Я, т. е. значение
второй функции в данной точке г равно значению первой функ-
функции в точке г\, которая переходит в г при вращении Я
W(r)t = \*(ry)t, г, = Я-'г. D5)
Аналогично, если ф(р) и ф'(р)—волновые функции в импульс-
импульсном пространстве, отвечающие ф и ф', то имеем
l<p'(p)f = l<P(Pi)f, Pi = ^~'p. D6)
Ясно, что для того чтобы выполнялись все эти условия, доста-
достаточно равенства значений функции ф' в точке г и функции о}).
в точке г и т. е.
] = ъ{Я.-1г). D7)
Можно показать, что это равенство является и необходимым
условием '). Следовательно, волновая функция определена од-
однозначно.
Соотношение D7) устанавливает взаимно однозначное соот-
соответствие между tp и tp'. Ясно, что это соответствие — линейное,
т. е. существует оператор R такой, что
Оператор R — унитарный, так как нормы tp и ф' равны,
(последний интеграл получается заменой переменной г{ = Я~1г
с учетом того факта, что при вращении сохраняется элемент
объема dr).
Все эти рассуждения без труда обобщаются на систему N
частиц; при вращении Я волновая функция ф(гA), fB)> • • •. f(JV))
переходит в
.... rw)- D8)
Как и выше, оператор вращения R — линейный и унитарный.
') Общее доказательство будет дано в § XV. 6. В действительности функ-
функция \|)' определяется этнмн условиями только с точностью до фазового мно-
множителя. Этот произвол исчезает, если потребовать, чтобы определенные далее
операторы R образовывали группу, изоморфную группе вращений; именно так
ыы и поступаем.

§ 12. ВРАЩЕНИЕ НАБЛЮДАЕМЫХ 33
В общем случае, с каждым вращением 91 физической си-
системы связан унитарный оператор R; действие R на вектор | а>,
представляющий динамическое состояние системы до вращения,
дает вектор \а"), представляющий ее динамическое состояние
после вращения,
##+ = #+Я=1, D9)
\aT> = R\a). E0)
Используя закон преобразования E0) и определение опера-
оператора плотности, легко получить закон его преобразования. Пусть
р — оператор плотности, представляющий некоторое (чистое
или смешанное) состояние системы, ар' — оператор плотности,
представляющий состояние, получившееся в результате враще-
вращения Я. Тогда имеем
E1)
§ 12. Вращение наблюдаемых
Кроме вращения исследуемой системы, можно вращать
также приборы, с помощью которых производятся наблюдения
над ней. Выше мы определили закон преобразования векторов
состояния, определим теперь закон преобразования наблюдае-
наблюдаемых, представляющих различные измерительные операции, ко-
которые можно выполнить над системой.
Пусть Q — наблюдаемая, a Q' = 52 [Q] —ее преобразование
при вращении Я.
По физическому смыслу с наблюдаемой Q связана некото-
некоторая операция измерения, и преобразование Q в Q' соответствует
вращению измеряющего прибора. Следовательно, среднее зна-
значение при измерении Q для системы в состоянии | а> равно
среднему значению при измерении Q' для системы в состоянии
|а'> = Я[|а>1,т. е.
(a\Q\a) = (a'lQ'\a').
Так как |а'> = 52|а>, предыдущее равенство можно переписать
в виде
Из того, что оно справедливо для любого I а), имеем (ср.
§ VII. 5)
или
q< = RqR\ E2)
2 A. Meocua

34 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
Другими словами, при вращении 91 наблюдаемые преобра-
преобразуются под действием того же унитарного оператора, что и век-
векторы состояний.
В частности, если наблюдаемая 5 является скалярной вели-
величиной, т.е. инвариантна относительно вращений1), то для лю-
любого R
S' ез RSRf = S.
Поскольку оператор R — унитарный, это равенство можно пере-
переписать так:
[R, S] = 0. E3)
Следовательно, инвариантная относительно вращений на-
наблюдаемая коммутирует со всеми операторами вращений.
Другой интересный случай представляют векторные опера-
операторы. Будем использовать обозначения § 10 и дополнительно
буквой К обозначим векторный оператор с компонентами Ki =
= (Kui). Если подействовать вращением 91 на оператор К\—
компоненту К по оси Ох, то получим оператор К[ — компо-
компоненту К по оси ОХ. В общем случае 91 \Ка] = Ка', где а' =
= 91 [а]; итак
Получили закон преобразования декартовых компонент вектор-
векторного оператора К
' * = 9iiiK,. E4)
Отметим, что в отличие от закона D3) здесь фигурирует мат-
матрица 91 — обратная матрице 91: компоненты К преобразуются
при вращении 91 так же, как компоненты вектора при враще-
вращении $Н.
§ 13. Момент импульса и инфинитезимальные вращения
Теперь мы можем установить фундаментальную связь между
моментом импульса системы и операторами бесконечно малых
(инфинитезимальных) вращений.
Как и в § 11, рассмотрим вначале случай одной частицы. Со-
Согласно D7) вращение 9tz{<x) на угол а вокруг оси Oz перево-
дит функцию 1|)(х, у, z) (см. ур. D4)) в
31г (а) [^ (*> У' z)\ — Ф (х cos а + г/ sin а, — х sin а + у cos а, г).
') Такое определение скаляра будет использовано в настоящей главе.
В дальнейшем величины, инвариантные относительно вращений, будут разде-
разделены на скаляры и псевдоскаляры. При отражениях первые не изменяются, а
вторые умножаются на —1,

§ 13. МОМЕНТ ИМПУЛЬСА И ИНФИНИТЕЗИМАЛЬНЫЕ ВРАЩЕНИЯ 35
В результате бесконечно малого вращения 52г(е), оставляя
в правой части только члены первого порядка по е тейлоров-
тейлоровского разложения в точке (х, у, z), получаем
х, у, z)] « ф (х + уе, — хе + у, z)
даA —Шг)$(х, у, г).
Последнее равенство следует из определения дифференциаль-
дифференциального оператора 1г (ft = 1). Следовательно, оператор инфините-
инфинитезимального вращения имеет вид
Rz (е) « 1 — Шг.
Для инфинитезимального вращения вокруг вектора и, исполь-
используя аналогичные рассуждения, имеем
Тот же результат получается для системы W частиц. Для этого
достаточно, исходя из D8), проделать те же преобразования,
что и в случае одной частицы D7)
или в более общем виде
/?«(e)«l-Ze (?•«),
где L — полный момент импульса системы.
Итак, справедливо утверждение.
Если J — полный момент импульса системы, то его компо-
компонента по произвольной оси и связана с оператором инфинитези-
инфинитезимального вращения вокруг этой оси соотношением
Ru (в) ж 1 — /в (/ • и). E5)
В случае, когда система не имеет классического аналога,
это фундаментальное соотношение служит определением мо-
момента импульса.
Для согласованности этого определения нужна уверенность
в том, что оператор (/-и) является компонентой некоторого век-
векторного оператора / по направлению и. Для этого достаточно '),
чтобы каждому инфинитезимальному вращению 52«(е) соответ-
соответствовал один и только один оператор инфинитезимального вра-
вращения /?и(е). Согласно закону преобразования векторов D0)
') Это равносильно предположению, что операторы вращений образуют
группу.
2*

36 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
операция 52и(е) эквивалентна, в первом порядке по е, произве-
произведению операций Я.х{гих)Я.у{ги,у)91г(&иг), что дает
Ru (e) ж Rx (eux) Ry (euy) Rz (еиг) » 1 — /е (uxJx + Uy]y + uzJz).
Из этого определения следует, что любой скалярный оператор S
коммутирует с компонентами / (ур. E3))
[(«•/), S] = 0. E6)
Из соотношения E5) получаются также правила коммута-
коммутации компонент J с компонентами произвольного векторного опе-
оператора К. Пусть Ка = Ка — компонента К по направлению век-
вектора а. По определению, ее преобразование при вращении
5?«(е) равно
Ка «- Ru (в) KaRt (В) да Ка - US [/«, Ка].
Кроме того, согласно закону преобразования вектора а (ур.
D0)), имеем
Приравнивая в этих выражениях члены первого порядка по е,
получаем
Uи, Ka] = iK(uXa),
или иначе
[(и/), (аК)] = Н(иХа)-К). E7)
Подставляя вместо R оператор J, снова получаем коммута-
коммутационные соотношения, характеризующие момент импульса (ур.
D)).
Следующее определение полного момента импульса эквива-
лентно данному ранее:
Если фундаментальными наблюдаемыми системы являются
скалярные операторы Si, S2, ... и компоненты векторных опе-
операторов Ki, Кг, • • •, то, по определению, полный момент им-
импульса системы — это векторный оператор /, компоненты ко-
которого коммутируют со всеми S и удовлетворяют коммутацион-
коммутационным соотношениям E7) с компонентами операторов К-
Если соотношения E7) выполняются не для всех векторных
операторов Ki, Ki то / не является полным моментом им-
импульса системы, даже если выполняются коммутационные со-
соотношения D). Так, для рассмотренного в § 11 случая W ча-
частиц любой векторный оператор, являющийся суммой некото-
некоторого числа моментов № отдельных частиц, будет удовлетворять
соотношениям D), ио только сумма L всех № равна полному
моменту импульса.

$ 14. ПОСТРОЕНИЕ ОПЕРАТОРА R(afiy) 37
§ 14. Построение оператора R (а$\)
Произвольное конечное вращение можно рассматривать как
последовательность инфинитезимальных вращений. Соответ-
Соответствующий оператор будет произведением операторов инфините-
инфинитезимальных вращений, и так как последние являются функциями
полного момента (ур. E5)), то и оператор произвольного ко-
конечного вращения тоже будет функцией полного момента им-
импульса.
Вращение 52«(ф) является последовательностью инфините-
инфинитезимальных вращений вокруг оси и. В частности,
#« (ф + <*ф) = &и (<*ф) Slu (Ф).
Полагая /„ = (/•«) и используя формулу E5), получаем
Ru (Ф + Лр) = R» (Лр) Ra (ф) = A - //„ Лр) Ru (Ф),
или иначе
-^Г/?„(Ф) = -//ИЛ»(Ф) (/?„@)=1).
Это дифференциальное уравнение легко интегрируется и дает
/?и(ф) = е-'ф/«. E8)
Рассмотрим теперь вращение 52(aPv). определяемое углами
Эйлера (а, р, у). Как показано в § 10, Й(аРу) можно рассмат-
рассматривать как последовательность вращений на углы а, Р, у во-
вокруг осей Oz, Ou, OZ соответственно (см. рис. 1). Следова-
Следовательно, имеем
Используя E8), три вращения в правой части можно выразить
через компоненты Jz, Ju и Jz момента импульса
#(apY) = e~'v/ze-w«e-'a/*. E9)
Обратим внимание на порядок экспонент в правой части.
Преобразуем выражение E9) к виду, в котором фигурируют
только компоненты момента импульса вдоль координатных осей.
Вращение Яг{а) переводит оператор ]у в оператор Ju, что
в силу закона преобразования операторов E2) дает
Ju = R* (a) JyRt (a) = е~ш'
Итак,
Подставляя это выражение в правую часть E9), получаем

38 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
Аналогично, Jz получается из Jz последовательными враще-
вращениями Яг(а), и 52U(P) и может быть устранено из окончатель-
окончательного ответа, так же как и Ju
R (opY) = e-|e/*e-'p/*e-'v/*. F0)
§ 15. Вращение на угол 2л и полуцелый момент импульса
Согласно уравнению E8)
Хотя вращение на 2я вокруг произвольной оси и возвращает нас
в исходную точку, соответствующий оператор вращения не обя-
обязательно равен 1. В представлении, в котором диагоналей опе-
оператор Ju, диагоналей и данный оператор, а его диагональные
элементы равны +1 или —1 в зависимости от того, является ли
соответствующее собственное значение 1и целым или полуце-
полуцелым.
Рассмотрим наблюдаемую D, которая есть функция /2, с соб-
собственным значением +1 при целом / и —1 при полуцелом.
Отметим, что
@ тО-г"^) — проектор на подпространство, соответствую-
соответствующее целым /;
(ii) y(l — D) — проектор на подпространство, соответствую-
соответствующее полуцелым /;
(iii) D2=l;
(iv) D коммутирует со всеми операторами вращений
[Д#] = 0.
Отсюда ясно, что
/?иBя) = ?>. F1)
Для того чтобы R,,Bn)—\, необходимо чтобы момент им-
импульса принимал только целые значения. С другой стороны,
всегда имеем
/?„Dя) = /J=1.
Существование взаимно однозначного соответствия между
инфинитезимальными вращениями и инфиннтезимальными опе-
операторами R (определение E5)) никоим образом не означает
существования аналогичного соответствия для конечных враще-
вращений. Имеется бесконечное число способов записать конечное
вращение в виде произведения инфинитезимальных вращений.
Каждый из рассмотренных выше операторов /?и(ф) и R(a$y)
соответствует одному из этих способов. A priori не существует
каких-либо причин полагать, что различные способы соответ-
соответствия будут давать один и тот же оператор.

§ 15. ВРАЩЕНИЕ НА УГОЛ 2Я И ПОЛУЦЕЛЫЙ МОМЕНТ ИМПУЛЬСА 39
Тем не менее можно показать (доказательство мы опускаем),
что каждому конечному вращению соответствует самое большее
два оператора R' и R", отличающиеся «вращением на 2я»,
R" = DR'. F2)
В рассматриваемых до сих пор физических системах момент
импульса мог принимать только целочисленные значения, в этом
случае D = 1 и R' = R", так что каждому вращению 91 соот-
соответствует один и только один оператор вращения. Если же си-
система имеет состояния с полуцелым угловым моментом, то опе-
операторы R' и R" не совпадают.
Обсудим факт существования двух различных операторов,
описывающих одно и то же вращение. То, что вращение на 2я
кет-вектора не дает в результате тот же вектор, не ведет к прин-
принципиальным трудностям, если только это не приводит к наблю-
наблюдаемому эффекту. Ясно, что результаты эксперимента не из-
изменятся, если заранее повернуть некоторые из приборов наблю-
наблюдения на угол 2л; два тождественных прибора, занимая одно и
то же положение, дадут один и тот же результат. Следовательно,
если наблюдаемая Q представляет измеримую величину, то она
должна быть инвариантна при вращении на 2я; говоря более
общим образом, если выполняется вращение 31 над Q, то полу-
полученная в результате наблюдаемая не должна зависеть от кон-
конкретного выбора способа вращения
Инвариантность относительно «вращения на 2л» гарантирует
выполнение этого более общего свойства. Формально ее можно
записать как
[D, Q] = 0. F3)
По определению, наблюдаемая является эрмитовым операто-
оператором, имеющим полный набор собственных векторов. Каждый
оператор, представляющий физическую величину, должен быть
наблюдаемой — необходимое условие самосогласованности
квантовой механики. Однако совсем не обязательно, чтобы было
верно обратное. Будем называть физической наблюдаемой на-
наблюдаемую, связанную с физически измеряемой величиной.
Предшествующий анализ показал, что любая физическая на-
наблюдаемая должна удовлетворять1) соотношению F3). При
') Все наблюдаемые физических систем, которые рассматриваются в этой
книге, удовлетворяют соотношению F3). Таким образом, между наблюдае-
наблюдаемыми и физическими наблюдаемыми имеется лишь чисто академическое раз-
различие. Однако можно представить себе физические системы, для которых не
все наблюдаемые удовлетворяют соотношению F3); пример такой системы
имеется в задаче 15.

40 ГЛ. XIII МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
изучении физической системы обычно неявно предполагают, что
все наблюдаемые системы являются физическими наблюдае-
наблюдаемыми; хотя такое предположение часто упрощает обсуждение,
оно несущественно и может быть заменено на более ограничи-
ограничительное, без серьезных модификаций в интерпретации теории.
Соотношение F3) представляет одно из таких ограничений;
с другими мы встретимся при о0суждении тождественных ча-
частиц ').
Таким образом, существование полуцелых моментов им-
импульса не противоречит никаким принципам квантовой меха-
механики. Действительно, полуцелые моменты существуют в при-
природе.
§ 16. Неприводимые инвариантные подпространства.
Матрицы вращений
Как установлено в конце § 5, выражение F0) показывает,
что любой оператор вращения есть функция компонент полного
момента импульса. Следовательно, векторы пространства ёA),
построенного в § 5, преобразуются при вращении в векторы §^\
т. е. пространство §^ инвариантно относительно вращений 2).
Точнее, если |и> — произвольно выбранный вектор этого
пространства, то множество векторов R\u~), получаемых из |н>
вращением, натягивают все пространство' ё^. Пространство,
обладающее этим свойством, называется неприводимым, по от-
отношению к вращениям. Если же, напротив, 'в SU) существовал
бы по крайней мере один вектор |о> такой, что множество век-
векторов R\v~) натягивало ё(^ лишь частично, то <g(I) было бы при-
приводимым по отношению к вращениям.
Неприводимость 8^> можно показать следующим образом.
Обозначим пространство, натянутое на векторы /?|и>, через
S^P- Тогда /+1 и) принадлежит $[1\ так как
/+1 и> s (Jx + Цу) | и) = j A - / + iR, (е) - Ru (в)) | и).
То же верно для /_|ы>. Более того, любой вектор, полученный
применением /+ или /_ к векторам 3?Y\ принадлежит ё^Р. Рас-
Рассмотрим разложение | «)= 2м11M) (JM \и) и обозначим m наи-
наименьшее значение М, для которого <ЛМ | «> Ф 0. Следуя мето-
методам § 5, получаем, что /+~от| и) — ненулевой вектор, пропорцио-
•) Общее обсуждение соотношений типа F3) и их следствий — правил су-
суперотбора — приведено в статье G. Wick, A. Wightman, E. Wigner. Phys. Rev.
»8, 101 A952). (При наличии русского перевода дается ссылка только на этот
перевод. Прим. перев.)
2) Далее будем использовать заглавные буквы J, М для обозначения
квантовых чисел полного момента импульса.

§ 16. НЕПРИВОДИМЫЕ ИНВАРИАНТНЫЕ ПОДПРОСТРАНСТВА 41
нальный |//>; отсюда |//> принадлежит <?(Р и поскольку по-
последовательным применением /_ к |//>, мы получаем все со-
состояния |/М>, они также принадлежат &['К Следовательно,
Ж[п содержит полный набор базисных векторов $w>, и, значит,
эти два пространства совпадают. ¦*).
Как указано в § 6, пространство кет-векторов физической си-
системы является прямой суммой некоторого числа B/+ ^-мер-
^-мерных подпространств с?Г(т/). Напомним, что т представляет
собой набор квантовых чисел, которые позволяют различать
полные наборы квантовых чисел, соответствующие одному соб-
собственному значению /2. Каждое из подпространств &(%)) яв-
является неприводимым и инвариантным по отношению к вра-
вращениям. В стандартном представлении {/2/z} компоненты /
в каждом из этих подпространств задаются простыми матри-
матрицами, не зависящими от т. Аналогично любой оператор враще-
вращения /?(аРу) выражается в каждом &(%J) некоторой B/-J-1)-
мерной матрицей RiJ)(a$y), зависящей от J, но не зависящей
от квантовых чисел т. По определению:
Rmm' (ору) = (rJM | R (ару) I xJM') = (JM | е-'^е^ЧГ1'7» I JMr).
F4)
Эти матрицы образуют особенно удобное представление опера-
операторов /?(aPv) и используются всякий раз, когда необходимо из-
изменить ориентацию векторов состояния или наблюдаемых. Их
называют матрицами вращений. Основные свойства этих матриц
и явный вид некоторых матриц приведены в Дополнении В (раз-
(раздел IV).
Непосредственно из определения матриц вращения следует,
что B/-J-1) базисных векторов подпространства ${%!) преоб-
преобразуются при вращении 52(aPv) п0 закону
R (apY) I т/М> = ? | xJM') R^'M (<#y). F5)
м'
Легко показать и обратное, а именно: если B/+1) векторов
\им} (М — — /, —/ -f- 1, •••» +/) преобразуются при вращении
согласно закону
R («PY) I Ил,) = Е I иМ') Rtt'M (opY); F6)
то они удовлетворяют уравнениям на собственные значения
и получаются один из другого действием операторов /+ и /_
в соответствии с соотношениями B4) —B5).
*) Знаком Щ отмечается конец доказательства. (Прим. ред.)

42 ГЛ. ХШ. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
§ 17. Инвариантность относительно вращений
и сохранение момента импульса
Инвариантность некоторой величины относительно вращений
всегда может быть выражена как ее специальное свойство по
отношению к моменту импульса. Действительно, любое враще-
вращение можно рассматривать как произведение бесконечно малых
вращений, а инвариантность данной величины .относительно
последних означает ее инвариантность и относительно всех вра-
вращений. В силу соотношений E5) момент импульса фигурирует
в условии инвариантности относительно бесконечно малых вра-
вращений.
Итак, для инвариантности волновой функции или кет-вектора
|> относительно вращений необходимо и достаточно, чтобы при-
применение к ним любой компоненты полного момента импульса
давало нуль
/!> = 0.
Фактически достаточно, чтобы выполнялось равенство
/2|) = 0. F7)
Этим свойством обладают, например, волновые функции частицы
в s-состоянии, которые зависят только от переменной г. Другой
пример — волновые функции нескольких частиц, зависящие
только от расстояний между частицами и от углов между ра-
радиусами-векторами частиц').
Для того чтобы наблюдаемая S была инвариантна относи-
относительно вращений (условие E3)), необходимо и достаточно,
чтобы она коммутировала с компонентами момента импульса
[/, S] = 0. F8)
Инвариантность гамильтониана относительно вращений за-
заслуживает особого рассмотрения. Если для любого R
[R, Н] = 0, F9)
то уравнения движения инвариантны относительно вращений:
два вектора состояний, из которых данное вращение преобра-
преобразует один в другой в момент времени t0, будут связаны тем же
соотношением во все остальные моменты. Это очевидно, по-
поскольку, если |ф(/)> удовлетворяет уравнению Шредингера, то
для любого R имеем
') Это свойство можно сравнить с равенством (I -\- f)P((cos a) =0, воз-
возникающим при доказательстве теоремы сложения (задача 5).

§ 17. ИНВАРИАНТНОСТЬ ОТНОСИТЕЛЬНО ВРАЩЕНИЙ 43
и, следовательно, /?|^(г)> также является решением уравнения
Шредингера.
Аналогично, если | > — собственный вектор Н, то все век-
векторы вида R\}, которые могут быть получены вращением дан-
данного, также являются собственными векторами Я, отвечающими
тому же собственному значению. Другими словами, подпро-
подпространство каждого собственного значения Я инвариантно отно-
относительно вращений.
Все следствия инвариантности уравнений движения относи-
относительно вращений можно получить из соотношений
[/, Я] = 0, G0)
выражающих инвариантность Я по отношению к бесконечно
малым вращениям.
При выполнении этих соотношений, операторы Р, Jz и Я по-
попарно коммутируют, и решение задачи на собственные значения
значительно упрощается: достаточно найти собственные функ-
функции Я среди общих собственных функций /2 и /г. Более того,
энергетические спектры, отвечающие данному значению / —
одни и те же, собственные функции, отвечающие B/ -f- 1) воз-
возможным значениям М, получаются одна из другой последова-
последовательным применением /+ или /_. Другими словами, собствен-
собственные значения энергии не зависят от М; каждому собственному
значению Ej, соответствующему данному значению /, отвечает
одна или несколько серий B/+ 1) собственных векторов; век-
вектора данной серии получаются друг из друга последовательным
применением /+ или /_ и натягивают неприводимое и инва-
инвариантное по отношению к вращениям подпространство. Такой
тип вырождения спектра энергии называется ротационным вы-
вырождением.
Случай частицы в центральном поле (гл. IX) служит хоро-
хорошей иллюстрацией приведенного обсуждения. Гамильтониан ча-
частицы в центральном поле, очевидно, должен быть инвариантен
относительно вращений; непосредственно проверяется, что он
коммутирует с тремя компонентами момента импульса I. Ме-
Метод, использованный в главе IX, и состоит в нахождении соб-
собственных функций Я среди общих собственных функций I2 и 1г,
отвечающих собственным значениям /(/+1) и m соответствен-
соответственно, т. е. среди функций вида
%,(/•) У™ (8, ф).
Задача сводится к решению обыкновенного дифференциального
уравнения второго порядка по г. Более того, поскольку m не
фигурирует в уравнении, то по каждой радиальной функции мы
можем построить B/+ 1) собственных функций Я, отвечающих
одному и тому же собственному значению.

44 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
Как отмечалось ранее, мы имеем здесь удивительную анало-
гию между классической и квантовой механикой. Инвариант-
Инвариантность уравнений движения классической системы относительно
вращений координатных осей приводит к сохранению полного
момента импульса системы. Это свойство позволяет получить
первые интегралы движения и значительно упростить решение
уравнений. Точно так же инвариантность относительно враще-
вращений уравнений движения в квантовой механике ведет к сохране-
сохранению полного момента; однако из-за некоммутативности компо-
компонент момента импульса законы сохранения в этом случае выра-
выражаются не столь просто.
Раздел IV. СПИН
§ 18. Гипотеза спина электрона
Теория Шредингера, вытекающая из простого применения
принципа соответствия, ие может объяснить свойств сложных
атомов, даже оставляя в стороне релятивистские поправки. Не-
Необходимы две важные модификации, причем ни одна из них не
имеет каких-либо аналогий в классической механике, которые
позволили бы предсказать их существование. Одна из этих мо-
модификаций заключается в выборе только тех решений уравне-
уравнения Шредингера, которые обладают определенными свойствами
симметрии относительно перестановки координат электронов.
Это требование известно как принцип Паули и будет рассма-
рассматриваться в главе XIV; при нижеследующем изложении оно мо-
может быть опущено. Другая модификация — гипотеза спина элек-
электрона.
Основное экспериментальное подтверждение этой гипотезы
следует из анализа поведения сложных атомов в магнитном
поле (эффект Зеемана, эксперимент Штерна — Герлаха).
Уравнение Шредингера для атома с Z бесспиновыми элек-
электронами уже было приведено выше (ур. A1.30)). Если считать
ядро бесконечно тяжелым, а его положение совпадающим с цен-
центром масс, то гамильтониан в системе центра масс имеет про-
простой вид
D)
1-Г ' ' К/
Для того чтобы получить гамильтониан того же атома, поме-
помещенного в статическое магнитное поле, которое описывается по-
потенциалом А(г), достаточно заменить в выражении G1) каждое
pt на pi — еА(г{Iс. В частности, для постоянного магнитногв

5 18. ГИПОТЕЗА СПИНА ЭЛЕКТРОНА 45
поля Ж А = y № X т) и
/ е \2 е е2
\Р с ) с кг!7 'т с!
где г2. — квадрат проекции г на плоскость, перпендикулярную
полю Ж. Тогда получаем
L—полный момент импульса Z электронов: i ^ T^( (r( X pt).
Для явлений, которые мы будем рассматривать, вклад третьего
члена в этом выражении для гамильтониана пренебрежимо
мал •). Итак, с очень хорошей точностью имеем
Мы получили такой ответ, как если бы каждый электрон, вра-
вращаясь по своей орбите, индуцировал магнитный момент
__?_/
~ 2тс *•
пропорциональный своему моменту импульса с константой про-
пропорциональности (гиромагнитное отношение), в точности рав-
равной величине е/2тс, которую дает классическая теория этого
эффекта. При такой интерпретации полный магнитный момент
атома равен сумме Z индивидуальных магнитных моментов, т. е.
и энергия атома в поле 5S? отличается от его энергии при отсут-
отсутствии поля на величину магнитной энергии — (ЛЖ).
Ряд замечательных свойств можно получить просто из рас-
рассмотрения выражения G2), если принять во внимание, что Яо,
будучи инвариантным по отношению к вращениям, коммутирует
с каждой из компонент оператора L.
') Этот член играет основную роль в атомном диамагнетизме. Зная, что
(г2) « 10-" см.1, можно оценить порядок его величины (Ze2/12mesM^2(r2).
Отношение этой величины к расстоянию между уровнями eh3^/2mc, которое
будет получено в дальнейшем, порядка 10~92ig (гаусс), что пренебрежимо
мало даже для очень сильных полей и очень тяжелых атомов. Поэтому отбра-
отбрасывание этого члена не может быть ответственным за приведенные далее рас*
хождения теории и эксперимента.

46 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
Направим вектор Ж по оси z. Операторы Яо, L2 и Lz имеют
общий набор собственных векторов \nLMy, а соответствующие
собственные значения Яо, E%L не зависят от М и BL -f- ^-крат-
^-кратно вырождены').
Согласно равенству G2) Я является функцией Яо и Lz и,
следовательно, имеет тот же набор собственных векторов, а соб-
собственное значение оператора Я, от-
отвечающее вектору \nLMy, равно
И =?0 -
где мы положили
eh
^=~2тс (магнетон Бора). G4)
Так как М может принимать все це-
Рис. 2. Эффект Зеемана для лые значения от —L ДО -\-L, то
/^-СОСТОЯНИЯ ([ —— О^* СЛ6ВЗ ~~~ пТ
уровень энергии при нулевом каждый уровень Ео под действием
поле, справа — уровни энергии магнитного поля Ж расщепляется
при 5^=5^=0. на BL+1) различных эквидистант-
эквидистантных уровней, распределенных по
закону G3). Итак, мы можем сделать следующие теоретиче-
теоретические предсказания (рис. 2):
(i) каждый уровень E%L атомного спектра в постоянном маг-
магнитном поле Ж расщепляется в «мультиплет» из BL + 1) экви-
эквидистантных уровней;
(и) уровни располагаются по обе стороны от E%L таким об-
образом, что их среднее расстояние от E%L равно нулю;
(iii) расстояние между двумя соседними уровнями равно
цё — величина, не зависящая от рассматриваемого атома и
пропорциональная Ш.
Эксперимент лишь частично подтверждает эти теоретические
предсказания. Имеется два важных отклонения:
а) в атомах с нечетным Z все мультиплеты четные и дело
обстоит так, как если бы L было полуцелым;
б) расстояние между соседними уровнями в одном мульти-
плете равно ц\хвЖ, где множитель g (множитель Ланде) ме-
меняется в зависимости от мультиплета в довольно широких пре-
пределах.
') Кратность вырождения больше, если несколько собственных значений
случайно совпадают, как в атоме водорода. Допустим, что Е% = ?" *¦', тогда
кратность равна BL + 1) + BL' + 1) н необходимо несколько изменить даль-
дальнейшие рассуждения. Однако выводы останутся справедливы, если всюду L
заменить наибольшей из двух величин L и L'. В частности, утверждение о
том, что каждый «мультнплет» Зеемана содержит нечетное число эквидистант-
эквидистантных уровнен, не меняется.

§ 18. ГИПОТЕЗА СПИНА ЭЛЕКТРОНА 47
Существование полуцелого момента импульса непосред-
непосредственно устанавливается в эксперименте Штерна — Г ёрлаха
(§ I. 10). Поскольку почти все атомы, составляющие пучок, на-
находятся в основном состоянии, число наблюдаемых на экране
пятен равно кратности вырождения основного состояния. Для
атомов серебра мы наблюдаем всего два пятна, следовательно,
основное состояние атома серебра двукратно вырождено, что
соответствует моменту импульса '/2- В более общем случае
атомы с нечетным Z всегда дают четное число пятен — резуль-
результат, характеризующий полуцелый момент импульса.
Свойства а) и б) встречаются вместе при изучении аномаль-
аномального эффекта Зеемана; спектральные данные позволяют в об-
общем случае одновременно определить кратность состояний, ме-
между которыми происходят оптические переходы, и соответствую-
соответствующие g — множители Ланде.
Чтобы устранить эти затруднения, необходимо ввести полу-
полуцелый момент импульса и гиромагнитные отношения, отличные
от е/2тс. Все это очень просто осуществляется, если принять
гипотезу спина электрона (Уленбек и Гоудсмит, 1925):
Каждый электрон обладает внутренним моментом импульса
или спином s, равным ll2h (спин '/2). с которым связан магнит-
магнитный момент
где gs — определенная константа. Согласие теории с экспери-
экспериментом достигается, если положить
gs*i2. G6)
Релятивистская теория электрона (гл. XX) позволяет вы-
вывести это значение gs.
Эксперименты показывают, что нуклоны (протоны и ней-
нейтроны) та-кже обладают спином '/г, который можно определить
непосредственным измерением связанного с ним магнитного мо-
момента *).
В оставшейся части этого раздела мы изложим нереляти-
нерелятивистскую теорию частиц спина 1/2 (теорию Паули).
') Если обозначить магнитный момент, спин и массу протона fip, sp и Мр
соответственно, то имеем (см. ур. G5))
rp-zp 2MpC op-
Аналогичная формула справедлива и для нейтрона. Эксперимент дает gp =••
= 5,59 и gn = —3,83.

48 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
§ 19. Спин >/г и матрицы Паули
Пусть s — оператор внутреннего момента импульса (или
вектор спина) частицы спина '/г- Согласно гипотезе собственное
значение s2 равно s(s+ l) = 3/4. Каждая из компонент, напри-
например sz, может принимать одно из двух значений -{-'/г или —'/г-
Будем предполагать эти собственные значения невырожден-
невырожденными. Следовательно, компоненты s будут операторами в про-
пространстве двух измерений, где в качестве базисных векторов
можно выбрать два собственных вектора операторов s2 и sz
Т ~~ Т/ •
В этом базисе легко выписать матрицы, соответствующие
операторам sx, sy, sz. Это будут конкретные матрицы Jx, Jy, Jz,
матричные элементы которых определяются уравнениями B8).
Кроме коммутационных соотношений для момента импульса,
компоненты s удовлетворяют следующим замечательным соот-
соотношениям:
С2 _ „2 — С2 — _L о2 — С2 — Г)
sx — sy — sz 4> 6+ — s_ и.
Поскольку
*2+ = («, + is,? - {si - si) + i (sxsy + sysx),
получаем
sxsy + sysx = 0.
Следовательно, операторы sx, sy, sz попарно антикоммути-
антикоммутируют ').
Удобно ввести матрицы Паули а 2= (ах, ау, аг)
G7)
явный вид которых следующий:
а* = {\ о)' av = {°i
Перечислим основные свойства этих матриц, которые следуют
из их определения и легко проверяются, если воспользоваться
Два оператора Л и В антикоммутируют, если АВ -J- В А = 0,

5 19. СПИН V» И МАТРИЦЫ ПАУЛИ 49
ИХ ЯВНЫМ ВИДОМ,
°1 = <>1 = о1 = 1, G8)
аха„ = — ауах = iaz, G9а)
ОуОг = - ozOj, = iax, G96)
<*г<*х = — охаг = iay, G9в)
= U (80)
= Traj, = Traz = 0, (81)
det ax = det <у„ = det az = -1. (82)
Справедливо важное тождество (задача 9)
(oA)(oB) = {AB) + io(AXB). (83)
где А и В — два произвольных вектора ').
Поскольку s есть момент импульса, то оператор Rj] (<p), пре-
преобразующий векторы данного пространства при вращении ^?и(ф),
равен, согласно формуле E8),
где ои==(аи). Раскладывая экспоненту в ряд и суммируя по
отдельности члены четные и нечетные по аи, а также используя
равенства (см. ур. (83))
получаем простое выражение
Я«Чф) —cosy*"ioa sin j<p. (84)
Отметим, что оператор вращения на 2я равен —1, в соответ-
соответствии с результатами § 15.
Оператор, отвечающий вращению 52(aPv), в силу формулы
F0) равен
^(аМ-е^е-^'е-*11*. (85)
Его явный вид можно вычислить тем же способом, что и для
Ми{у), ответ приведен в Дополнении В (формула (В. 74)).
Векторы рассматриваемого здесь пространства аналогичны
векторам обычного пространства. Последние представляют со-
') Они могут быть также векторными операторами, прн условии, что их
компоненты коммутируют с 0. В этом случае необходимо сохранить порядок
следования А я В в правой части тождества. Например,

50 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
бой геометрические объекты с тремя компонентами, которые
при вращениях преобразуются друг через друга по определен-
определенному закону. Такую же ситуацию мы имеем и для рассматри-
рассматриваемых здесь векторов (закон преобразования (85)), за исклю-
исключением того, что они имеют две компоненты вместо трех. Эти
двухкомпонентные объекты называют спинорами.
§ 20. Наблюдаемые и волновые функции частицы
спина 7г- Спинорные поля
Рассмотрим частицу спина 1/2. Основные наблюдаемые такой
частицы можно разбить на две категории: орбитальные пере-
переменные и внутренние, или спиновые, переменные. Первыми яв-
являются компоненты координаты г и импульса р; они удовлетво-
удовлетворяют коммутационным соотношениям (ft = 1)
[Гit /?/]=/б;/.
Вторыми являются компоненты спина, удовлетворяющие ком-
коммутационным соотношениям
и, кроме этого, дополнительному условию s2 = 3/4.
Поскольку орбитальные переменные коммутируют со спино-
спиновыми, пространство векторов состояний частицы <? является
тензорным произведением
орбитального пространства с?Г@> и спинового пространства c?f<s>
(ср. § VIII. 7). Здесь с?Г@> — пространство состояний бесспино-
бесспиновой частицы, a c?f(s)— двумерное пространство, построенное
в предыдущем параграфе.
Для описания векторов пространства & обычно выбирают
представление с диагональными г и sz. Вектор состояния |ф>
в таком представлении задается волновой функцией
(86)
которая является функцией непрерывной переменной г ==
= (х, у, z) и дискретной переменной ц,, представляющей соб-
собственные значения sz и равной ±1/2.
Полный момент импульса частицы равен
j^l + s. (8i)
Основные наблюдаемые системы — компоненты трех векторов г,
р, s. Ясно, что / удовлетворяет коммутационным соотношениям
E7), характеризующим полный момент импульса, так как I =

§ 20. ВОЛНОВЫЕ ФУНКЦИИ ЧАСТИЦЫ СПИНА Чг 51
ss г X Р удовлетворяет им и коммутирует с s, a s тоже удовле-
удовлетворяет этим соотношениям и коммутирует с г и р.
Теперь можно получить оператор вращения R(a$y) (yp.
F0)). Коль скоро I и s коммутируют, то он равен произведению
двух коммутирующих операторов
@)(a|}Y), (88)
где /?(s)(aPY) определено уравнением (85) и вращает спин,
а Ят(а$у) определено выражением
и вращает орбитальные переменные.
При вращении на 2я, R{0) — 1, а /?(s> = — 1 и, следовательно,
все кет-векторы при таком вращении меняют знак. Однако все
основные наблюдаемые при вращении на 2л не изменяются и,
как было показано в § 15, трудностей в их физической интер-
интерпретации не возникает.
Часто бывает удобно использовать обозначение
и записывать волновую функцию \|)(г, ц) в виде двухкомпонент-
ной волновой функции
Для каждого значения г функция г|> определяет кет-вектор
в пространстве «?(s>, а именно
{/¦|г|>>^г|>+(г)|+> + г|>_(г)|->. (89)
Другими словами, волновую функцию можно рассматривать как
спинорное поле ').
Рассмотрение системы Z частиц спина '/2 производится со-
совершенно аналогично. Пространством состояний системы яв-
является тензорное произведение пространств состояний отдель-
') При вращении Ж (ару) спинорное поле ф преобразуется в
что является непосредственным следствием (88); /Л2' — матрица вращений,
соответствующая I = Ч2. Можно сравнить этот закон преобразования с фор-
формулой D7) для скалярного поля. Существует аналогичная формула для век-
векторного поля с /?<" вместо R^2' (см. § 21).

62 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
ных частиц. Так, спиновое пространство есть тензорное произ-
произведение Z индивидуальных спиновых пространств и имеет раз-
размерность 2Z. Для каждого спина вводится система матриц Паули
о(''. Вращение всех спинов как целое можно выполнить, исполь-
используя полный спин
z
Вращение на 2я системы спинов задается оператором (—\)z.
§ 21. Векторные поля и частицы спина 1
Полезно подчеркнуть параллель между понятием спинорного поля в
более известным понятием векторного поля.
Пусть А(г) —векторное поле, связанное с физической системой. Им может
быть, например, магнитное или электряческое поле или, как мы увидим ниже,
волновая функция частицы спина 1.
Рассмотрим как преобразуется А (г) при вращениях. Пусть А'(г)—поле,
которое получилось из А(г) в результате вращения Я физической системы
А'вЯ [А].
Поле А' в точке г получается вращением Я вектора А{г{), задающего поле А
В точке Г| вз #J-'r, т. е. (см. ур. D3) и D7))
А\(г)-ЯцА,(Л-1г) (/ = *, у. г).
Так, для вращения иа угол а вокруг Ог находим (см. ур. D4))
Д' аэ <йг (а) [А], Г\ « (дс cos а + у sin а, — х sin а + у cos а, г),
А'х (г) = Ах (г,) cos а — Ау (г,) sin а,
А'и (г) = Ах (г,) sin а + Ау (г,) cos а,
В частности, ивфииятезималыюе вращение на угол е вокруг Ог дает
Лж (в) [А]-О-/« (/« + *«)) А, (91)
где U — определенный выше дифференциальный оператор, a s* — оператор,
определяемый равенством
-iAy(f)\
1Ая{г) .
/
/Ax(r)\ /-iAy
\ Лв (г) = 1Ая
\А,(г) J \ 0
Оператор S* преобразует каждую компоненту поля в данной точке в некото-
некоторую линейную комбинацию трех компонент поля в той же точке. Если поле А
определяется тремя декартовыми составляющими Ах, Ау и Az, то sz задается
матрицей
/О -/ 0\
',-( / 0 0.
\о о о/

/00 0\ / 0 0 / \
= 10 0 —f I, Sy = [ 0 0 0 I,
\o / o/ V-j о о/
$ 81. ВЕКТОРНЫЕ ПОЛЯ И ЧАСТИЦЫ СПИНА 1 5S
Аналогично определяются операторы s* и s,, их матрицы имеют вид
Легко показать, что s,, sy, s* удовлетворяют коммутационным соотношениям,
характеризующим компоненты момента импульса. Обозначим этот момент че*
рез s; вычисляя его квадрат, получаем
в2 = 2,
что соответствует моменту импульса s = 1. По определению, будем называть
s — внутренним моментом или спином векторного поля.
Поле Л (г) может описывать частицу спииа 1. Обозначим
А{ (г) е= А (г, «) (/ = х, у, г),
где A(r,i)—волновая функция, зависящая не только от координат частицы,
ио и от индекса i, который может принимать три значения и представляет
внутреннюю переменную, описывающую ориентацию частицы. Скалярное про-
произведение таких волновых функций равно
(В, А) = ? \ В* (г, /) А (г, 0 dr = \ (В* • A) dr. (92>
i
Оператор / действует только на пространственные координаты, в то же
время а действует только на внутренние переменные. Ясно, что операторы t
и s, действуя иа разные переменные, коммутируют. Оператор инфинитезималь-
иого вращения вокруг оси z определяется уравнением (91), аналогично полу-
получается оператор иифииитезимальиого вращения вокруг любой другой оси; ис-
используя определение E5), находим полный момент импульса частицы (см.
ур. (87)) ^
Верно и более общее утверждение: любое линейное преобразование век-
векторного поля можно представить как действие некоторого линейного опера-
оператора, который выражается в виде функции от трех основных операторов
г, р ш* - /V, а.
В частности, справедливо важное тождество
rot =э ар, (93)
которое легко проверить, пользуясь определением ротора и явным видом мат-
матриц sx, sy, s*.
Понятия скалярного произведения, вращения, линейного преобразования,
ие зависят от выбранного представлении. Волновая функция A(r, i) задает
динамическое состояние частицы в представлении, где базисные векторы вну-
внутренней перемеииой соответствуют единичным векторам вдоль каждой из трех
осей Ох, Оу, Oz; эти базисные векторы |дс), \у), \z) являются собственными
векторами операторов sx, sy, sz соответственно, с собственным значением 0 (см.
задачу 10). Часто удобнее использовать представление, где базисными векто-
векторами являются собственные векторы оператора sz, |+), |0), |—) с собствен-
собственными значениями +1,0, —1 соответственно; они получаются друг из друга со-
согласно закону, определенному в § 6. В этом представлении sx, sy и s* за-
задаются матрицами, которые удовлетворяют соотношениям B8) (с / = /' = 1),
а связанный с векторным полем Л кет-вектор \А) задается волновой функцией
А (г, ц.) es Лц (г) (ц = +, 0, —).

54 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
Согласно определению (ср. ур. (89))
<г | А) - А+ (г) |+> + Ло (г) | 0) + А- (г) | -)
имеем
A+ = --2f-(Ax-iAy), А0 = Аг, A- = ^-(Ax + iAy). (94)
§ 22. Зависящие от спина взаимодействия в атомах
Вследствие существования внутреннего магнитного момента
гамильтониан электрона в электромагнитном поле содержит
члены, зависящие от спина.
В частности, в присутствии магнитного поля Ж (г) в гамиль-
гамильтониане появляется слагаемое, которое описывает прямое взаи-
взаимодействие и получается из принципа соответствия,
— цЖ (г) = — цваЖ,
где ц — внутренний магнитный момент, определяемый уравне-
уравнениями G5) — G6).
Это не единственный дополнительный член. Даже в случае
чисто электростатического потенциала должны существовать
члены спин-орбитального взаимодействия, поскольку при дви-
движении в таком потенциале в системе, движущейся с электроном,
имеется магнитное поле, взаимодействующее с ц. Это класси-
классическое рассуждение может служить указанием для эмпириче-
эмпирического определения спин-орбитального взаимодействия. Однако
поскольку речь идет о релятивистском эффекте (стремящемся
к нулю в пределе о<Сс), предпочтительнее исходить из реляти-
релятивистского уравнения для электрона. Вид спин-орбитального
взаимодействия из этого уравнения можно получить, выполняя
разложение по параметру v/c и сохраняя ненулевые члены низ-
низшего порядка. Эта задача будет исследована в главе XX. Спин-
орбитальное взаимодействие для сферически-симметричного по-
потенциала, очевидно, инвариантно относительно вращений и,
следовательно, коммутирует с тремя компонентами полного мо-
момента импульса /. Релятивистская теория дает выражение
ft2 M I dV „„
По тем же причинам гамильтониан Но для Z электронов
сложного атома содержит спин-орбитальные члены в дополне-
дополнение к кулоновским, приведенным в ур. G1). Дополнительные
члены коммутируют с полным моментом импульса
но в отличие от остальных членов Но они не коммутируют с L
и S по отдельности. Более того, хотя вклад этих членов в пол-
полную энергию относительно мал (исключая самые тяжелые

5 23. ЗАВИСЯЩИЕ ОТ СПИНА НУКЛОН-НУКЛОННЫЕ ВЗАИМОДЕЙСТВИЯ 55
атомы), их присутствие качественно изменяет атомный спектр —
устраняет вырождение и, следовательно, ими никогда нельзя
пренебрегать').
Гамильтониан Н атома в постоянном магнитном поле Ж по-
получается из гамильтониана Яо без внешнего поля тем же спосо-
способом, что и в § 18, и добавлением членов прямого магнитного
взаимодействия — ]? ц'-'Ш. Если пренебречь, как и в уравнении
i
G2) для теории без спина, «диамагнитным членом» ~Ж2, то
получим
^ (96)
§ 23. Зависящие от спина нуклон-нуклонные
взаимодействия
В качестве второго примера зависящих от спина взаимодей-
взаимодействий рассмотрим взаимодействие двух нуклонов, нейтронов или
протонов. Пусть Мй — масса нуклонов, г = Г\—г2 — их отно-
относительная координата, p==V2(pi—Рг) —относительный им-
импульс, х1гО\ и '/202 — соответствующие спины. Движение центра
масс и относительное движение полностью разделяются. Рас-
Рассматриваемые ниже динамические переменные и динамические
состояния относятся исключительно к относительному движе-
движению. Орбитальный момент импульса равен
L = rXp,
полный спин
5=у((т, + (т2) (97)
и полный момент импульса
J = L + S. (98)
Гамильтониан имеет вид
Чаще всего используются четыре типа взаимодействий, которые
инвариантны, относительно вращений
Vi (r), (99а)
К8(г)(ог,о2), (996)
Vs(r)(LS), (99в)
(99г)
V, (г) [3
') Следовало бы также упомянуть об изменениях, вызванных существо-
существованием магнитного момента у ядер атомов (сверхтонкая структура).

56 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
В трех последних выражениях зависящие от спина операторы
записаны в их традиционном виде. Можно записать их и по-дру-
по-другому. Так, возводя обе части (97) в квадрат и используя тожде-
тождество
получаем
aia2 = 2S2 — 3, A00)
а возводя в квадрат обе части (98), получаем
JLS = y(/2-L2-S2). A01)
Наконец, из ур. (97) имеем
(Sr? = 1 [(а1Г) + (a2r)f = \ [@,if + (a2rf + 2 far) (a2r)] =
Отсюда
и, следовательно,
fi^bdA02)
2 [з-??--#]. A020
Оператор Si2 называется «тензорный оператор», а взаимодей-
взаимодействие (99г)—«тензорные силы».
Если V — линейная комбинация взаимодействий типа (99),
то гамильтониан будет инвариантен относительно как враще-
вращений, так и отражений (при отражении г и р переходят в —г и
—р, а операторы спина не меняются). Мы еще вернемся к свой-
свойству инвариантности относительно отражений. Отметим только,
что если обозначить Р — оператор, который, действуя на гр (г),
дает г|>(—г), то его собственные функции будут обладать опре-
определенной четностью. Инвариантность относительно отражений
означает, что [Н, Р] = 0. Если гамильтониан обладает указан-
указанным свойством, то его собственные функции можно искать среди
функций с определенной четностью.
Взаимодействия (99) расположены в порядке уменьшения их
симметрии.
Первое не зависит от спина. Второе коммутирует с L и S по
отдельности: оно инвариантно не только по отношению к общим
вращениям, но и к вращениям только орбитальных переменных
или только спинов. Если V содержит лишь члены вида (99а)
и (996), то собственные функции Н можно искать среди общих

§ 24. ЗАДАЧА СЛОЖЕНИЯ 57
собственных функций JL2, S2, Lz, Sz, и соответствующие собствен-
собственные значения будут BL + 1)BS+ 1)-кратно вырождены и не
будут зависеть от собственных значений Lz и Sz-
Если же V содержит также член вида (99в), то Я.будет все
еще коммутировать с L2 и S2, но перестанет быть инвариантным
относительно независимых вращений пространственных коорди-
координат и спинов. Собственные функции Я в этом случае можно
искать среди общих собственных функций L2, S2, /2 и Jz, а его
собственные значения будут иметь вращательное вырождение
только кратности BУ +1).
Взаимодействие (99г) имеет наименьшую симметрию. Опе-
Оператор 5i2 не коммутирует с L2. Однако он еще коммутирует с S2
(из выражения A02') для тензорного оператора видно, что
[S2, S12] =0). Если V содержит член вида (99г), то собствен-
собственные функции Я можно искать среди общих собственных функ-
функций операторов Р, S2, Р и Jz.
Раздел V. СЛОЖЕНИЕ МОМЕНТОВ ИМПУЛЬСА
§ 24. Задача сложения
Во многих задачах гамильтониан инвариантен относительно
вращений и, следовательно, коммутирует с компонентами пол-
полного момента импульса. В этом случае мы ищем собственные
функции Я среди общих собственных функций /2 и 1г. При этом
важно уметь перечислять и строить векторы с определенным
моментом (JM).
В простом случае бесспиновой частицы в центральном поле
(гл. IX) полный момент импульса совпадает с орбитальным мо-
моментом I и собственные функции полного момента имеют вид
%(Г)УТ(9, ф). В общем случае / есть сумма моментов отдельных
частиц
т. е. орбитальных моментов импульса и спинов частиц системы.
Метод построения собственных векторов индивидуальных
моментов известен. Так, для системы двух нуклонов, рассмо-
рассмотренной в § 13, имеем
a + <t A03)
а собственные функции индивидуальных моментов импульса
имеют вид г|> (г) Yf (8, q>) | щ) I На), где ^ и р,2 могут принимать
значения -f-'A или —'/г, в зависимости от направления спинов

58 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
первого и второго нуклонов вверх или вниз соответственно. За-
Задача сложения моментов импульса состоит в построении полной
системы собственных векторов оператора / из линейных ком-
комбинаций этих функций.
§ 25. Теорема сложения двух моментов импульса
Простейшей задачей является сложение двух моментов.
Предположим, что
/ = /.+/2,
где /i и /г — моменты импульса систем 1 и 2, которые вместе
образуют исследуемую систему, и предположим, что построена
полная система общих собственных векторов
I v.]\hmxnh) A04)
операторов \\, \\, /1г и /2г. Параметр а обозначает дополни-
дополнительные квантовые числа, которые необходимы для полного оп-
определения динамического состояния, или, если угодно, собствен-
собственные значения наблюдаемых А, образующих с pv /| /1г и \2г
полный набор коммутирующих наблюдаемых; Л коммутируют
также с компонентами \х и /V Предположим к тому же, что век-
векторы A04) образуют стандартный базис по отношению к мо-
моментам импульса 1 и 2. Каждому набору квантовых чисел
(a/i/г) соответствует столько векторов, сколько имеется раз-
различных пар (mim2); эти векторы получаются один из другого
последовательным применением операторов /1± и /2± по форму-
формулам § 6 и натягивают подпространство ^(a/i/2) размерности
( 1)B/1)
(/ + )(/)
Отметим, что А, ]\ и /| коммутируют с /. Поэтому будем
искать собственные векторы /2 и Jz среди общих собственных
векторов этих операторов, а значит каждое из подпространств
Ш'(a/i/г) можно рассматривать независимо. Возьмем произволь-
произвольное & и для упрощения записи обозначим векторы |a/i/2mim2>
этого подпространства \т\тг), а собственные векторы полного
момента импульса, находящиеся в этом подпространстве, \JM)
(предполагая, что задание / и М достаточно для определения
вектора \JM}, в дальнейшем покажем, что это так).
В этом параграфе мы определим возможные значения пар
(JM) и соответствующий им порядок вырождения. Построение
собственных векторов будет обсуждаться в § 27.
Решение нашей задачи основано на следующих двух замеча-
замечаниях:
(а) Каждый вектор \т\т,2) является собственным для Jz
с собственным значением
M = nti-\- пц.

§ 25. ТЕОРЕМА СЛОЖЕНИЯ ДВУХ МОМЕНТОВ ИМПУЛЬСА 59
Действительно, поскольку /z =/iz +/2z, имеем /2|mim2> =
= (mi -f- m2) | mim2>.
(б) Каждому значению J соответствует некоторое число
N (J) линейно независимых серий из BУ + 1) собственных век-
векторов полного момента импульса; векторы данной серии полу-
получаются один из другого последовательным применением J+ или
J- и соответствуют B/+1) возмож-
возможным значениям М:—/,—/+1, ..., +Л
Отсюда следует1), что если обозна-
обозначить п(М) кратность собственного зна-
значения М, то
ч ч ч ч
ч\\\
п{М)= ? NA)
ч\\ч
;\\\
\\\\
A05)
Рис. 3. Возможные значе-
значения М = nil + trii и их крат-
кратность п (М) (/, = 7/2, /2 = 2).
Тем самым для определения N(J) до-
достаточно найти п (М) для каждого воз-
возможного значения М. Согласно замечанию п(М) равно числу пар
() таких, что
М
ту + щ.
Для определения этого числа удобно использовать диаграмму
рис. 3, на которой каждая пара {т\ + гп2) представлена точкой
с абсциссой mi и ординатой т% Число п(М) равно числу точек,
расположенных на прямой х + у = М. Пусть для определен-
определенности /i > /2, тогда находим
{0, если | М | > /, + к,
/. + /2+1-1ЛН если /i + /2>|M|>|/,-/2|,
2/2+I, если |/, -/2|>|М|>0.
Подставляя эти значения в A05), получаем
N(J)=l для J = ji + j2, h + Za-l I/1-/2I.
Отсюда следует основная теорема сложения:
В B/i + 1) B/2 + I)-мерном пространстве, натянутом на
векторы |a/i/2mim2> (a, /i/2 фиксированы, mi, /Л2 меняются):
(i) возможные значения J равны2)
') Такие же рассуждения уже использовались в задаче о трехмерном гар-
гармоническом осцилляторе (§ XII. i5).
2) Другими словами, / принимает все значения, для которых /i -+-/2 + ^""
целое и /,, j2 и / могут рассматриваться как длины сторон треугольника.

60 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
(и) каждому из этих значений отвечает одна и только одна
серия из BJ -\- 1) собственных векторов \ JM} полного момента
импульса.
§ 26. Приложения и примеры
Вначале отметим очевидное следствие теоремы сложения.
Полный момент импульса, получающийся сложением произволь-
произвольного числа моментов, будет целым или полуцелым в зависимо-
зависимости от того, четно или нечетно число полуцелых моментов им-
импульса в сумме.
Мы увидим, что это свойство выполняется во всех нижесле-
нижеследующих примерах.
В качестве первого примера рассмотрим сложение двух
спинов '/а-
Пространство состояний имеет размерность 4. Полный спин
5 может принимать два значения: 0 и 1.
Спину S = 0 соответствует только один вектор |00>: гово-
говорят, что спин находится в синглетном состоянии.
Спину S = 1 соответствуют три вектора 11 1>, 11 0>, 11 —1>;
это векторы триплетного состояния.
Легко выписать проекторы Ро и Рх на синглетное и триплет-
ное состояния соответственно, как функции S2 или Оуа%. По-
Поскольку S2 = S{S + 1), S2 имеет собственное значение 0 в син-
синглетном состоянии и 2 — в триплетном, отсюда (ср. с A00))
Заметим, что
а1о2 = Р1-ЗР0. A06)
Второй пример — частица спина У2. Ее орбитальный
момент импульса и спин образуют полный момент /, который
может принимать два значения
за исключением случая / = 0 (s-состояние), когда / может при-
принимать только одно значение / = '/г- Итак, / может принимать
все полуцелые значения, от '/г до оо, и каждому из них соот-
соответствует два терма (две серии из B/+ 1) векторов) противо-
противоположной четности.
В качестве последнего примера рассмотрим двухнуклон-
ную систему из §23.
В этом случае необходимо связать три момента импульса —
орбитальный момент и два спина (ур. (98)). Сложим вначале

§ 27. СОБСТВЕННЫЕ ВЕКТОРЫ ПОЛНОГО МОМЕНТА ИМПУЛЬСА 61
спины, что дает полный спин S, который имеет два возможных
значения 0 и 1. Затем свяжем S с моментом импульса L для
относительной координаты, который может принимать все це-
целые неотрицательные значения. Каждой паре значений (LS)
отвечает BS + 1) BL + 1) векторов, подходящие линейные ком-
комбинации которых дают собственные векторы полного момента.
Согласно теореме сложения получаем следующие значения /:
синглетное состояние: S = О / = L;
¦¦ -' (;:Г"'
триплетное состояние: о = 1 s . , , п
F (. /= 1, если L=0.
Для обозначения полученных термов используем следующие
спектроскопические обозначения: заглавная буква отвечает зна-
значению L в соответствии с принятым в § IX. 6 соглашением; ин-
индекс слева вверху дает значение 2S + 1 (кратность полного
спина), а индекс справа внизу равен /. Например, 3D2 означает
терм с L = 2, триплетное состояние спина и полный момент
/ = 2. Каждому значению / соответствуют 4 терма (т. е. всего
4B/+ 1) векторов), исключение — значение /==0, которому
соответствует только два терма. Ниже приводятся различные
термы, соответствующие четырем первым значениям:
} п 3D 1С
J — и г о ^0
Те же обозначения часто используются и для рассмотрен-
рассмотренного выше случая частицы спина '/2- Орбитальный момент обо-
обозначается строчной буквой — заглавными будет обозначаться
полный орбитальный момент системы многих частиц — индекс
слепа просто опускается. Приведем термы, отвечающие первым
значениям /:
»— JL 1 1 L
]~ 2 2 2 2
sipi pidi dih hgr
22 22 22 22
§ 27. Собственные векторы полного момента импульса.
Коэффициенты Клебша — Гордана
Каждой паре (JM), которая удовлетворяет условиям тео-
теоремы сложения, соответствует собственный вектор \ajijiJMy
полного момента импульса. Для устранения произвола норми-
нормируем этот вектор на 1 и фиксируем его фазу подходящим уело*
вием, к обсуждению которого мы вернемся ниже. Векторы

62 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
\aj1j2JM), так же как и |a/i/2/ni/n2>, образуют ортонормирован-
ный базис в подпространстве ^(a/i/г). Переход от одного ба-
базиса к другому совершается посредством унитарного преобра-
преобразования
|a/1/2/VW>= ? \vhhmxm2) (a/i^i^l ay'^/Af). A07)
Коэффициенты этого преобразования обладают очень важ-
важным свойством: они не зависят от а, а зависят только от вели-
величин /ь /2, /, Ш\, m2, M. Действительно, в подпространстве
^ (а/1/2) векторы |a/i/2mim2> образуют базис стандартного
представления, в котором компоненты j{ и /2 задаются матри-
матрицами, не зависящими от а (см. ур. B8)); следовательно, мат-
матрицы, определяющие /2 и 1г, также не зависят от а и компо-
компоненты <a/i/2mim2|a/i/2/M> их общих собственных векторов об-
обладают тем же свойством. Тем самым, они имеют чисто геоме-
геометрическое происхождение и зависят только от рассматриваемого
момента импульса и его ориентации, тогда как физическая при-
природа динамических переменных 1 и 2, из которых строятся мо-
моменты, не существенна. Эти компоненты называют коэффициен-
коэффициентами Клебша — Гордана (К. — Г.) или коэффициентами век-
векторного сложения. Мы будем обозначать их символом
(jij2mim2\JM). Используя это обозначение, соотношение A07)
можно записать так:
I alihJM) = ? I 0/1/2^1^2} {!\kmxm2 \ JM). A08)
Ш\ТПу
Для полного определения коэффициентов К. — Г. остается
фиксировать фазы векторов |а/:/2.Ш>. Для относительных фаз
B/ + 1) векторов, отвечающих данному /, мы примем то же
соглашение, что и в § 6. Тогда эти векторы определены с точ-
точностью до фазы, зависящей от /. Мы устраним этот произвол
требованием, чтобы компонента |a/i/2J7> вдоль |a/i/2/i/ — /i>
была вещественной и положительной
O. A09)
Многие свойства коэффициентов К. — Г. следуют непосред-
непосредственно из их определения.
Согласно теореме сложения для отличия {1фт\т2\}МУ от
нуля необходимо, чтобы выполнялись одновременно условия
{правила отбора)
Ниже мы покажем, что все коэффициенты К. — Г., относя-
относящиеся к данному значению /, могут быть получены посредством
рекуррентных соотношений с вещественными коэффициентами
из коэффициента </i/2/V —/i|^>- Поскольку последний веще-

§ 27. СОБСТВЕННЫЕ ВЕКТОРЫ ПОЛНОГО МОМЕНТА ИМПУЛЬСА 63
ственный, то и все остальные коэффициенты К- — Г. вещест-
вещественны.
Более того, поскольку это коэффициенты унитарного преобра-
преобразования, то они удовлетворяют соотношениям ортогональности
S {к'кгпгпц | JM) {нк^пц |УМ') = Ь1ГЬММ', A10а)
S {hh., | JM) (j^ ,;г;
В простейших случаях линейные комбинации A08) можно
найти непосредственно. Отметим, что для / = /i + /2 и Л1 = /
имеем
I o/i/2/i + /a/i + /г> = I a/i/2/i/2>-
Последовательное применение /_ = /i_ + /2_ к обеим частям
этого уравнения дает все векторы |a/i/VAf>, отвечающие / —
= /i + /2- Затем можно построить векторы серии / = /j + /2 — 1,
используя оператор /_ и начиная с вектора, соответствующего
М = J, который однозначно определяется условием на фазу
A09) и свойством ортогональности к |a/i/2/i + /2/1 + /2 — !>•
Таким образом, можно построить все серии собственных век-
векторов.
При сложении двух спинов у2 собственные векторы полного
спина можно построить таким же способом из собственных век-
векторов |++). |Ч ). I Ь> и I ) операторов спинов от-
отдельных частиц
5=1 5=0
М=1 |Ц> = | + +>
М = 0 | 10) = ' + ~}+J| ~ +) [ 00) = ' + ~}~ ' ~ +)
М = -\ |1 -1> = [ ).
При сложении моментов импульса большей величины необ»
ходимо прибегнуть к более сложной технике. Можно устано-
установить различные рекуррентные соотношения (ур. (В. 18)—(В. 20)).
Например, применяя /+ или /_ к обеим частям уравнения A08),
получаем (см. ур. (В.19) и (В.18))
t/J(J+1)-M(M+ \){hhm,m., I JM + 1> =
= V/i (/i + 1) — mi (m, — lX/1/2^1 — lm2 \JM) +
+ V/2 (/2 + 1) - m2 (m2 - l)</i/2/ni/n2 - 1 I JM), A11)
t/J(J+1)-M(M- l)</i/>1ffi2 I JM - 1> =
= V/i (/'1 + 1) - mi (m, + l)<jii2mi + lm2\JM) +
+ V/2 (/2 + 1) - m2 (m2 + DiMmim* + 1 |/M>. A12)

64 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
Если М — J, то левая часть A11) исчезает и видно, что все
коэффициенты </iyVrcim2|//> пропорциональны одному из них,
скажем (/l/Vi/—/i|//>- Условие нормировки вектора \a]\j2JJ)
Bm,m! (iii2tnim2\JJJ=i) и соглашение о фазе A09) опреде-
определяет их полностью. Все другие коэффициенты К. — Г. можно
затем получить, последовательно используя рекуррентные соот-
соотношения A12). Такой метод вычисления коэффициентов К. — Г.
для записи их в компактной форме (В.21I) применялся Рака.
Кроме уже упомянутых свойств, коэффициенты К. — Г. об-
обладают важными свойствами симметрии, которые значительно
упрощают табулирование. Вместе с основными свойствами ко-
коэффициентов К- — Г. эти свойства симметрии приведены в До-
Дополнении В (раздел I), которое содержит также таблицу про-
простейших коэффициентов.
§ 28. Приложение: система двух нуклонов
Для того чтобы рассмотреть применения теоремы сложения
угловых моментов, вернемся к системе двух нуклонов из § 23.
Мы будем исследовать уравнение Шредингера с различной фор-
формой зависимости потенциала от спина. Ограничимся рассмотре-
рассмотрением потенциалов (99).
Допустим, что потенциал имеет вид
В этом случае гамильтониан коммутирует с L и S и собствен-
собственные функции являются произведениями спиновых функций |Sn>
и функций от г с определенным орбитальным моментом (/яг).
В силу тождества A06) потенциал имеет различный вид в за-
зависимости от того, равно ли S нулю или единице. Таким обра-
образом, решение уравнения Шредингера эквивалентно решению
двух уравнений Шредингера для бесспиновой частицы в цен-
центральных потенциалах, которые отвечают двум возможным зна-
значениям S. Если S = 0, то орбитальная часть собственной функ-
функции та же, что и для бесспиновой частицы в потенциале
V'i — 3V2; если же S = 1, то она та же, что и для частицы в по-
потенциале Vi -j- V2. Проблема определения собственных значе-
') Для того чтобы провести это вычисление до конца, необходимо вос-
воспользоваться полученным Рака тождеством
Z(a + s)\ (Ь — s)l (a + Ь + 1)! (а — с)! (b — d)\
(с + s)\ (d — s)\ e (с + d)\ (а + Ь — с — d + 1)!
S
(а, Ь, с, d — целые числа и a^c^O, b^sd^sO; s принимает все целые
значения от —с до -\-d).

§ 28. ПРИЛОЖЕНИЕ: СИСТЕМА ДВУХ НУКЛОНОВ 65
ний свелась к решению радиального уравнения для каждой
пары значений {LS).
Если потенциал имеет вид
V = V, (г) + V2 (r) (<,&) + V3 (r) (LS),
то гамильтониан не инвариантен относительно независимых
вращений пространства и спинов, но поскольку он все еще ком-
коммутирует с L2 и S2, можно искать общие собственные функции
L2, S2, Р и Jz. Каждому набору (LSJ) отвечают такие функции,
зависимость которых от углов 0, ср и от спиновых переменных
полностью определена и явно выражается с помощью коэффи-
коэффициентов К. — Г.
Щи - S Yl (в, Ф) | Sv) (LSmn | JM). {
Так, три функции состояния Р; имеют следующую «угловую за-
зависимость»: 0/^ =УрОО) (М — 0, ±1). Пять функций состоя-
состояния 3D2 имеют вид
mix
, ±1, ±2).
Действуя гамильтонианом на функции такого типа и используя
тождества A00) и A01), получаем
„шм Г ft2 I d2 , Л2 L(L + l) , t/ -|wjw
HWLsi = [- ж - -j-г г + -щ ? + VLSJ\ 4lsi,
где
Уlsj (г) =~ V, (г) + [2S (S + 1) - 3] V2 (г) +
+ ![/(/+1)-L(L + 1)-S(S-И)] М/0.
Таким образом, задача о решении уравнения Шредингера све-
свелась к решению радиального уравнения
Мы получили такую же задачу, как и в случае бесспиновой ча-
стицы в центральном потенциале с единственным отличием, что
«эффективный центральный потенциал» VLSj(r) зависит от три-
триплета (LSJ) ').
') Для S = 0 спин-орбитальные силы отсутствуют и при любых L и J
имеем
Аналогично, если S = 1 и L = /, то «эффективный потенциал» не зависит
от L
Ана
от L
8 А. Мессиа

66 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
В качестве последнего примера рассмотрим потенциал вида
V=Vc(r)+VT(r)Sl2.
Из-за присутствия «тензорных» сил гамильтониан не коммути-
коммутирует с L2, но продолжает коммутировать с S2 и оператором
«четности» Р, введенным в § 23. Следовательно, собственные
функции Н можно искать среди общих собственных функций Р,
S2, Р, Jz, т. е. среди функций с определенными значениями пол-'
ного момента (JM), четности и спина 5.
Если 5 = 0, то обязательно L = J (а значит Р = {—IO) и
собственная функция имеет вид F (г) °УУй,. Так как S|00> = 0,
то из A02') имеем
5,2^0/^^(9, Ф) I 00> = 0.
Следовательно, F(r) удовлетворяет радиальному уравнению
для частицы с моментом / в потенциале Vc{r).
Если 5=1 и Р = (—1);, то обязательно L = J и «угловая
зависимость» собственной функции, как и ранее, полностью оп-
определена
Можно показать (задача 11), что S12<yfu = 2Q/fu и функция
F(r) удовлетворяет радиальному уравнению для частицы с мо-
моментом импульса / в потенциале Vc(r) + 2VT(r).
Если S = l и Р=(—1)/+1, то возможными значениями L
будут только / + 1 и / — 1 (если же / = 0, то имеется только
одно значение L= 1) и собственная функция имеет вид
где для упрощения записи мы использовали обозначения
(?±=ayf+lu-Теперь Si2, действуя на °У+ или на О/-, дает ком-
комбинацию этих функций (задача 11), следовательно, выражение
(Н — E)W также будет линейной комбинацией этих функций с
коэффициентами, зависящими от г. Как следствие уравнения
(Н — E)W — 0, эти два коэффициента равны нулю, что приво-
приводит к системе двух обыкновенных дифференциальных уравнений
второго порядка для Fj-i (r) и FJ+1 (r).
Выпишем в качестве примера систему связных радиальных
уравнений для / = 1. Этот случай встречается при изучении
дейтрона. Волновая функция является смесью состояний 3Si и
ZD\ и может быть представлена в виде
\_

§ 29. СЛОЖЕНИЕ ТРЕХ И БОЛЕЕ МОМЕНТОВ ИМПУЛЬСА 67
Поскольку (задача 11)
л/8^, SnVm = У8 <Vou -
? ^211 = 6^211
уравнение (Я — ?) *Р = 0 эквивалентно системе уравнений:
\Ж~?* + Е - Yc (r)] Us = V8 W (r) uD,
§ 29. Сложение трех и более моментов импульса.
Коэффициенты Рака. «3s/» - символы
Двухнуклонная система, рассмотренная в § 28, представляет
собой пример системы, где полный момент импульса является
суммой трех индивидуальных моментов (ур. A03)). Мы смогли
разобрать этот простой пример без обращения к утонченным
методам. Исследуем теперь сложение трех моментов в общем
случае.
Предположим, что рассматриваемая система состоит из трех
различных систем, 1, 2 и 3 с моментами импульса ju j2 и /3 со-
соответственно. Полный момент импульса тогда равен
Проблема сложения заключается в построении собственных век-
векторов полного момента в подпространстве, натянутом на
B/i + 1) B/2 + 1) B/з + 1) собственных векторов
отдельных моментов импульса, отвечающих определенным зна-
значениям квантовых чисел а, /ь /2 и /3. Квантовое число а, опре-
определяемое здесь так же, как и в § 25, в последующем изложении
несущественно и будет опускаться.
Существует несколько способов построения векторов с мо-
моментом импульса (JM):
_(i) Можно связать /: и /2 (рис. 4, а), образуя момент Ji2 =
==/i +/г> а затем связать /i2 и /з, образуя /. Таким образом,
з*

68
ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
получаем собственные векторы
I (/i/г) /12, /з; 1Щ =
= S \Sikhmltn2m3){h'hmitn2\Jl2Ml2){!l2hMX2m3\JM), A16)
Мптз
общие для операторов j2, j\, /§, Pl2, I2 и /2.
(ii) Можно связать /2 и /3 (рис. 4, б), образуя момент /23 =
—/2 + /з. а затем связать /i и /2з, образуя /. Таким образом,
получаем собственные векторы
1/ь (/а/а) /яа; /М> =
== 2-i I /1/2/3^ 1^2^3/ (/2/3^2^31 ^23^23/ \/Н23'^1^'23 I ^"^/> A 17)
общие для операторов j\, /|, /^, /|3, /2 и /г.
(iii) Можно связать /i и /3> образуя /i3, а затем и /2, обра^
зуя 7.
Итак, у нас имеется выбор между тремя различными набо-
наборами базисных векторов полного момента. В большинстве задач
Рис. 4. Способы сложения трех моментов импульса.
важно уметь переходить от одного базиса к другому. Преобра-
Преобразование, которое осуществляет этот переход, является унитар-
унитарным. Например, имеем
= Z I (Ш /к, /а;
I /ь (Ш /2
(П8)
Очевидно, коэффициенты этого унитарного преобразования не
зависят от а по тем же самым причинам, что и коэффициенты
К- — Г. Действуя операторами /+ или /_ на обе части A18),
легко видеть, что они не зависят также от М, а зависят только
от шести моментов: /ь /2, /з, /i2, /гз и /.
Вместо непосредственного использования этих коэффициен-
коэффициентов более удобно использовать коэффициенты Рака W, или

§ 29. СЛОЖЕНИЕ ТРЕХ И БОЛЕЕ МОМЕНТОВ ИМПУЛЬСА 69
«6/»-символы Вигнера, которые пропорциональны им в соответ-
соответствии с определениями
= УB/12+1)B/23 + 1)
+1)B/23 +1) {}; ';
Из определения W ясно, что эти коэффициенты являются
суммами по индексам т четырех коэффициентов К- — Г. Исклю-
Исключая случай наиболее простых аргументов, непосредственное вы-
вычисление коэффициентов W чрезвычайно затруднительно; оно
заключается в вычислении большого числа коэффициентов
К. — Г., а затем в вычислении сложного выражения, построен-
построенного из этих коэффициентов. Рака удалось получить обозримое
и приемлемое для работы выражение для W (формула (В.36)).
Существуют таблицы коэффициентов W для наиболее часто
встречающихся аргументов.
«6/»-символы отличаются от W только знаком. Они инте-
интересны в основном благодаря их замечательным свойствам сим-
симметрии. Основные свойства коэффициентов W и «6/»-символов
приведены в Дополнении В (раздел II).
Рассмотренный выше способ сложения трех моментов им-
импульса может быть перенесен и на случай сложения большего
числа моментов
/ = /!+/2+ ... +/„• A19)
Складывая два любых момента: /,• -+¦ /*. = /,-*, мы сводим за-
задачу к сложению (п—1) момента, заменяя векторы /,- и /*
в правой части A19) их суммой /,> Повторяя эту операцию,
приходим к сложению (п — 2) моментов и т. д. Таким образом,
нам удается сложить п угловых моментов, вводя (п — 2) про*
межуточных момента. Так же строится и система базисных век-
векторов полного момента импульса.
Выбирая различные промежуточные моменты, можно по-
построить несколько различных наборов базисных векторов. Мы
видели, что при п = 3 существует три набора. Можно показать,
что в общем случае существует 1/2п\ наборов. Переход от од-
ного набора к другому осуществляется посредством унитарного
преобразования (с вещественными коэффициентами). Легко убе-
убедиться в том, что коэффициенты преобразования не зависят от
а и от М — собственного значения компоненты Jz оператора /,
а зависят только от квантовых чисел /, /ь /2, ..., /„ и двух на-
наборов из (п — 2) квантовых чисел, таких как Jiu, которые опре-
определяют длину промежуточных моментов, характеризующих каж-
каждый набор базисных векторов: всего 1 + п + 2 (я — 2)=3(я — 1)

70 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
квантовых чисел /. Коэффициенты преобразования можно пред/
ставить в форме «3(я—1)/»-символов, обобщающих «6/»-сим-
волы, введенные при сложении трех моментов, «3(я— 1)/»-сим-
волы являются суммами 2(п—1) коэффициентов К. — Г. по
индексам т. Основные свойства «9/»-символов (символы для
сложения четырех моментов) приведены в Дополнении В (раз-
(раздел III).
Раздел VI.НЕПРИВОДИМЫЕ ТЕНЗОРНЫЕ ОПЕРАТОРЫ ')
§ 30. Представление скалярных операторов
Если наблюдаемая инвариантна относительно вращений, то
и подпространство, соответствующее каждому из ее собствен-
собственных значений, инвариантно. Это важное, свойство уже упомина-
упоминалось в § 17. Там в качестве наблюдаемой рассматривался га-
гамильтониан, но это свойство справедливо и для любой другой
скалярной наблюдаемой.
В более общем случае, скалярная наблюдаемая, даже не
будучи диагональной, в данном стандартном представлении за-
задается, как мы увидим ниже, особенно простой матрицей.
Пусть \%JM) — базисные векторы стандартного представ-
представления {РJz} (обозначения § 6), a S — скалярный оператор (не
обязательно наблюдаемая). По предположению,
Отсюда следует, что вектор S\%'J'M'y, так же как \x'J'M"), яв-
является вектором с моментом импульса {I'M') и ортогонален
к любому вектору с другим моментом. Следовательно, матрич-
матричный элемент (xJM\S\x I'M') равен нулю, если J ф J' или М Ф
Ф М'. Более того, поскольку /+ коммутирует с S, то при J = J'
и М = М' имеем
<t/A1|S|t7A1>=
\_
\)-М {М- 1)] 2<-r/M|S/+|T7Af- 1> =
i_
1) — М(М— 1)] 2 (-vJM\J+S\t'JM- 1) =
— 1 \S\x'JM- 1>,
') Систематическое изложение алгебры неприводимых тензоров и ее при-
приложений в теории момента импульса в квантовой механике содержится в кни-
книге: U. Fano, G. Racah. Irreducible tensorial sets. N. Y., Academic Press Inc.
A959).

§ 31. НЕПРИВОДИМЫЕ ТЕНЗОРНЫЕ ОПЕРАТОРЫ 71
и, значит, матричный элемент не зависит от М. Полученные
свойства можно записать в виде равенства
(хШ | S | VJ'M') = 6jj>6MM>S[%, A20)
где Sxl' — величина, зависящая только от /, т и т'. В случае,
когда 5 — наблюдаемая, матрица S^ эрмитова и ее можно при-
привести к диагональному виду.
§ 31. Неприводимые тензорные операторы. Определение
В этом параграфе мы обобщим равенство A20) на класс
операторов, которые называются неприводимыми тензорными
операторами. Они не инвариантны относительно вращений, но
закон преобразования их при вращениях довольно простой.
Понятие тензорного оператора является обобщением понятия векторного
оператора.
Начнем с определения тензора. Допустим, что нам дано n-мерное про-
пространство Жп такое, что при вращении векторы нз Ж'„ линейно преобразуются
в векторы из Жп- с каждым вращением связан линейный оператор в Ж„- По
определению, векторы Жп являются n-компонентнымн тензорами. Например,
векторы в обычном пространстве и спиноры являются 3- и 2-компонентными
тензорами соответственно; векторы нз определенного в § 6 подпространства
Ж(т/) являются B/+ 1)-компонентными тензорами, а кет-векторы простран-
пространства состояний квантовой системы — тензорами с бесконечным числом компо-
компонент.
Если выбрать набор базисных векторов в Жп, то каждый из упомянутых
выше тензоров будет задаваться п компонентами, а вращение — действием
матрицы п X п на эти п компонент. Так, вращение вектора, заданного декар-
декартовыми координатами в обычном пространстве, осуществляется матрицей Я,
определенной в § 10. Аналогично, если мы возьмем стандартное представление
в &{xJ), то любой тензор \и) подпространства Ж(%1) определяется B/+1)
компонентами им = {xJM\u), а компоненты им его преобразования при вра-
вращении SZ(aPv) получаются применением к им матрицы вращения #(/)(аРу)
(§ 16)
»«=X>*?M'(aPY)«A!'. A21)
М'
В качестве другого примера рассмотрим девять величин ViW; (I, /=1,2,
3), получающихся перемножением различных компонент векторов V и W Они
представляют собой девять компонент тензора, который мы обозначим V® W.
Компоненты этого тензора после вращения Я получаются следующим обра-
образом:
[V ® W]'u ^ Vys = Л1кЯ11укУ1 = Я1кЯц [V ® W]k!.
Среди множества тензоров, которые можно построить, привилегированное
положение занимают неприводимые тензоры. По определению, тензор являет-
является неприводимым, если пространство Ж„, которому он принадлежит, неприво-
димо по отношению к вращениям.
Векторы обычного пространства, спиноры, векторы пространства <?Г(т/)
являются неприводимыми тензорами.
С другой стороны, тензор V ® W — приводимый. Девятимерное простран-
пространство, в котором он определен, является прямой суммой трех неприводимых ин-

72 ГЛ. ХШ. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
вариантных по отношению к вращениям подпространств, имеющих размерно-
размерности 1, 3 и 5 соответственно. Следовательно, проекции тензора V ® ИР на каж-
каждое нз этих подпространства дают неприводимые тензоры; с точностью до
константы они представляют собой: скалярное произведение V-W, векторное
произведение V X TF и неприводимый 5-компонентный тензор, компоненты ко-
которого преобразуются при вращениях как гармонические полиномы второго
порядка (см. § Б. 10) ').
Точно так же векторы Bji + 1) B/г + 1)-мерного пространства из § 25
являются приводимыми тензорами с Bji + 1) B/2 + 1) компонентами, н тео-
теорема сложения дает их разбиение иа неприводимые.
От понятия тензора переходят к понятию тензорного оператора точно
так же, как от понятия вектора к векторному оператору.
Если п операторов преобразуются прн вращениях линейно друг через
друга, как п линейно независимых векторов пространства Жп, то онн являют-
являются компонентами n-мерного тензорного оператора2). Линейное преобразова-
преобразование этих п компонент даст п новых операторов, которые можно рассматри-
рассматривать как компоненты того же тензорного оператора в другом представлении.
Если пространство Жп неприводимо, то и тензорный оператор называют не-
неприводимым. ,
Векторные операторы образуют специальный класс неприводимых тензор-
тензорных операторов.
Если V и W — два векторных оператора, то девять операторов ViWj яв-
являются компонентами приводимого тензорного оператора, который может быть
представлен в виде прямой суммы трех неприводимых тензорных операторов:
скаляра V-W, вектора V\W н тензорного оператора, который задается, на-
например, пятью компонентами, приведенными в предыдущем примечании.
Тензорный оператор в заданном представлении однозначно
определен законом преобразования его компонент при враще-
вращении.
По определению, BА + 1) операторов ГF) (<7 = — k,
—k + 1. • • •. -\-k) являются стандартными компонентами непри-
неприводимого тензорного оператора k-го порядка Г<*>, если они пре-
преобразуются при вращениях по закону
RTfR~l = ? TfR% A22)
ч'
Данный закон совпадает с законом преобразования базис-
базисных векторов \kq~y стандартного представления для B& + 1)'
') Матрицы вращения, конечно, зависят от выбранного для этого тензора
представления. В представлении, где его компоненты равны
~ {VWz + V2WA ~ (VtWs + V3W2), I (VtWi + V,W3),
они преобразуются друг через друга как линейно независимые полиномы ху,
уг, гх, *2—(Д 2г2 — *2 — /
2) Этот закон преобразования не совпадает с законом преобразования
векторов пространства Ж„, разложенных по п векторам базиса. Точно так же
закон преобразования E4) компонент векторного оператора К не совпадает
с законом D3) преобразования компонент вектора V в том же базнсе. Отме-
Отметим, в частности, различие в формулах A22) и A21),

§ 31. НЕПРИВОДИМЫЕ ТЕНЗОРНЫЕ ОПЕРАТОРЫ 73
мерного пространства, неприводимого по отношению к вращв'
ниям
Если равенство A22) выполнено для бесконечно малых вра-
вращений, то оно будет выполнено и для всех остальных враще-
вращений. Для бесконечно малых вращений оператор R определяется
формулой E5), матрицы /?<*> легко получаются из определения
F4), и закон A22) в этом случае эквивалентен следующим ком-
коммутационным соотношениям операторов 71**' с компонентами
полного момента импульса:
U-<7(<7±1) T%и A23а)
[/2( Tf\ = qTf. A236)
Соотношения A23), которые можно сравнить с B3) — B5),
позволяют дать другое определение неприводимого тензорного
оператора Г(*> (полностью эквивалентное приведенному выше).
Если операторы Г<6) соответствуют физическим величинам,
то они инвариантны относительно поворота на 2л (ср. § 15) и,
следовательно, k — целое число. В дальнейшем мы будем рас-
рассматривать только неприводимые тензорные операторы целого
порядка.
Легко показать, что Bk + 1) операторов
удовлетворяют соотношениям A23) (задача 16), и, следова-
следовательно, являются стандартными компонентами неприводимого
тензорного оператора S(*> порядка k. По определению, опера-
операторы S(*> и r<fc> эрмитово сопряжены друг другу
(поскольку k — целое, ясно, что операция эрмитова сопряже-
сопряжения обратима).
Скаляры являются неприводимыми тензорными операторами
нулевого порядка. Векторные операторы — неприводимыми тен-
тензорными операторами порядка 1: если Кх, Ку, Кг — декартовы
компоненты векторного оператора, то его стандартными компо-
компонентами будут
K? = (K + iK\ K? K K% ^(Kx-iKy). A24)
K? = (Kx + iKy\ K? = KZ, K%
(Отметим, что фигурирующие здесь коэффициенты отличны от
встречающихся в соотношениях (94).)

74 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
Сферические функции Yi(Q, <p) (q = —k -\-k), рассма»
триваемые как операторы, представляют собой стандартные
компоненты неприводимого тензорного оператора У(*> порядка k.
§ 32. Представление неприводимых тензорных
операторов. Теорема Вигнера — Эккарта
Наиболее важное свойство неприводимых тензорных опера*
торов отражено в теореме Вигнера — Эккарта:
В стандартном представлении {PJZ}, базисные векторы ко-
которого обозначим \xJM}, матричный элемент (xJM | T^ | x'J'M')
q-й стандартной компоненты данного неприводимого тензор-
тензорного оператора k-го порядка, Г<*> равен произведению коэффи-
коэффициента Клебша — Гордана
(J'kM'q \JM)
на величину, не зависящую от М, М' и q.
Таким образом, справедлива формула
(xJM 17f > | x'J'M') = ' <т/1| 7™ || %'У) (J'kM'q \JM), A25)
V2/ + 1
где величина <тЛ|Г<6)||т7'>, которая называется приведенным
матричным элементом, зависит от индексов т, / и т', /' и харак-
характеризует данный тензорный оператор (множитель 1/д/2/ + 1 вве-
введен для удобства).
Для доказательства теоремы рассмотрим Bk -\- 1) B/' + 1)
векторов Tf | VJ'AT) (q= — k + k; Af' = -/', .... + /').
Образуем следующие линейные комбинации этих векторов:
| <зУ'М") == Yu ТЩ x'J'M') {J'kM'q \J"M").
M'q q
Используя соотношения ортогональности для коэффициентов
К.— Г. (ур. A106)), получаем
Г<*> | х'ГМ') = ? | oJ"M") {J'kM'q \ J"M"). A26)
* Г'М"
Отметим, что векторы ГF> | x'J'M') могут и не быть линейно не-
независимыми, поэтому некоторые из векторов |a/"Af"> могут об-
обратиться в нуль.
Из формул A23а) и A24) вытекает, что
x'J'M') = [/+t Tf-]\x'J'M') + T«)J+1 x'J'M') =
= Vife {k + 1) - Я G+1) Tf+l | x'J'M') +
О - M' (M + 1) Tf\ x'J'M' +

§ 32. ТЕОРЕМА ВИГНЕРА — ЭККАРТА 75
и, следовательно,
J+\oJ"M") =
Е l)-q(q-l) < J'kM'q - 1 \J"M") +
M'q
+ y/'(/'+l)_Af'(M'-l) < J'kM' - \q\3"M")}.
В силу рекуррентных соотношений A11) для коэффициентов
К. — Г. выражение, стоящее в скобках, равно
s/j" {]" + 1) - М" {М" + 1) {J'kM'q \]"M" + 1>,
и мы получаем в правой части вектор \aJ"M" -\- 1> или, более
точно,
/+ | oJ"M") = a/J" (/" + 1) — М" {М" +1I oJ"M" + 1).
Тем же методом можно показать, что
/_ 1 а]"М") = л/J" (J" + О - М" (М" — 1) | ст/"М - 1)
]г | (j/"Af") = М" | oJ"M").
Из этих трех соотношений следует, что B7" + 1) векторов
\о]"М"У, соответствующих одному и тому же значению /":
(i) либо все равны нулю;
(И) либо являются (ненормированными) собственными век-
векторами с моментом импульса (J"M") и получаются один из
другого стандартным способом.
Следовательно, все скалярные произведения (xJM \ oJ"M"}
обращаются в нуль за исключением тех, для которых /" = / и
М" — М, т. е. B/+ 1) произведений (xJM | aJM), причем они
не зависят от М.
Отсюда следует приведенная выше теорема, поскольку мат*
ричный элемент (т/Л/1Т^ | x'J'M') с учетом A26) равен
(xJM | Tf | х'ГМ') = ? {xJM | aJ"M") (J'kM'q \ J"M"). Ш
Среди наиболее важных следствий теоремы Вигнера — Эк-
карта упомянем правила отбора для оператора Т^\
Для того, чтобы матричный элемент (xJM | Г(*' | x'J'M') был
отличен от нуля, необходимо одновременное выполнение соот-
соотношений:
q = M-M', A27)
|/-/'К?</ + /'• A28)
Эти соотношения непосредственно следуют из того факта,
что в правой части формулы A25) стоит коэффициент Клеб-

76 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
ша — Гордана. На практике чаще используется второе из этих
соотношений. Оно обычно формулируется в виде следствия ').
Матричный элемент компоненты Л(*> неприводимого тензор-
тензорного оператора порядка k между двумя векторами с моментами
J, J' обращается в нуль, если k не удовлетворяет неравенствам:
\1 — У\ <?</ + /'.
§ 33. Приложения
Теорема Вигнера — Эккарта имеет много приложений в атом-
атомной и ядерной физике, а именно: в теории р-распада, электро-
электромагнитного излучения и, вообще, в задачах об угловых корре-
корреляциях.
Рассмотрим, например, электромагнитное излучение атом-
ного ядра (у-излучение). Предположим, что при переходе из
возбужденного состояния JT* в основное JC ядро испустило
•у-квант
Пусть J я J' обозначают спины (т. е. полный момент им-
импульса) ядер JC и Jf* соответственно. В теории у-излучения из-
известно, что амплитуда вероятности излучения у-кванта поля-
поляризации v в направлении Q =(8, ф) пропорциональна матрич-
матричному элементу
(xJM\H(Q, у)
некоторого оператора #(Q, v) между векторами начального и
конечного состояний (см. § XXI. 31). Оператор H(Q, v) можно
разложить по сферическим функциям. Не вдаваясь в детали2)
заметим только, что тогда он принимает вид суммы неприводи-
неприводимых тензорных операторов двух типов (противоположной чет-
четности): электрических и магнитных мультипольных моментов.
Электрический 2'-польный момент Q('> является неприводимым
тензорным оператором порядка / и четности (—1)'; магнитный
2'-польный момент MSl) — неприводимым тензорным оператором
порядка / и четности (—1)'+1. Среди мультипольных моментов
наиболее известны следующие:
(i) магнитный момент (в обычном смысле этого слова), т. е.
дипольный магнитный момент МA);
(а) квадрупольный момент (в обычном смысле этого слова),
т. е. электрический квадрупольный момент QB).
¦) Компонента А<*> не обязательно стандартная; любые линейные комби-
комбинации стандартных компонент обладают этим свойством.
2) См. Дж. Блатт, В. Вайскопф. Теоретическая ядерная физика. М., ИЛ,
1954 (гл. XII н Дополнение Б).

ЗАДАЧИ И УПРАЖНЕНИЯ 77
В соответствии с правилами отбора для тензорных опера-
операторов, ненулевые вклады дают только моменты с мультиполь-
ностью /в пределах
\J-Г !</</ + /' A29)
(существует также правило отбора по четности, которое мы
здесь не рассматриваем). В силу теоремы Вигнера — Эккарта,
вклады компонент Qm моментов, удовлетворяющих неравен-
неравенствам A29), пропорциональны коэффициенту Клебша — Гор-
дана {J'lM'm\JM}; для их вычисления достаточно определить
коэффициент пропорциональности, т. е. приведенный матричный
элемент (tWMIt7'>.
Итак, вероятность перехода полностью известна, как только
определены приведенные матричные элементы мультипольных
моментов, удовлетворяющих правилам отбора. На практике,
разложение в ряд по мультиполям сходится быстро и основной
вклад дают один или два мультиполя низшего порядка.
Четные мультипольные моменты (МA), Q<2>, ...) появляются
также при вычислении сдвигов энергетических уровней атомов
или ядер в статическом электромагнитном поле. Так, взаимо-
взаимодействие ядра с постоянным магнитным полем позволяет изме-
измерить его магнитный момент, а взаимодействие с неоднородным
электрическим полем — его квадрупольный момент. Действи-
Действительно, при измерении получают среднее значение этих опера-
операторов в рассматриваемом состоянии ядра, т. е. матричные эле-
элементы
(xJM | М? | xJM'), (xJM | Q® | xJM')
или приведенные диагональные матричные элементы
Отметим, что магнитный момент обращается в нуль при /; = О,
а квадрупольный момент — при / = 0 или '/г- Вообще, 2;-поль-
ный момент ядра со спином / равен нулю при 2/ < /.
ЗАДАЧИ И УПРАЖНЕНИЯ
1. Исходя из соотношений B4) н B5) между векторами
|т/ц) (ц = -/, -/+1, ...,+/),
доказать соотношения B6) н B7).
2. Доказать, что в любом представлении, где Jx и /2 — вещественные (а
Эначнт н симметричные) матрицы, /у будет чисто мнимой (а значит н анти-
антисимметричной) матрицей.
[N. В. Стандартное представление попадает в эту категорию.]
3. Доказать, что для коммутативности оператора со всеми компонентами
момента импульса достаточно, чтобы он коммутировал с двумя его компонен-
компонентами.

78 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ МЕХАНИКЕ
4. Пусть I — орбитальный момент частицы, 8 и q> — полярные углы и Р —
«оператор четности>. Оператор Р соответствует отражению в начале коор-
координат, его действие на функцию F(&, ф) определено равенством: PF(Q, q>) =
= F(n — 8, ф + я). Показать, что [Р,1] — 0. Вывести огсюда, что сферические
функции обладают определенной зависящей от квантового числа / четностью,
и найти ее.
5. Пусть г, г' — два вектора в обычном пространстве, Q= (8, q>) и
Q' s= (8', q>') —их полярные углы, /, /' — соответствующие операторы момен-
моментов импульса; пусть а @ ^ а ^ я)—угол между векторами: t-f =
= /••/•'cos а. Полином Лежандра Pj(cosa) является функцией полярных углов
векторов г и г'. Показать, что он удовлетворяет уравнениям в частных про-
производных
l2Pt (cos a) = l'2Pl (cos a) = / (/ + 1) P, (cos a),
(i)l 0 (i = x,y,z).
Вывести отсюда теорему сложения:
-^Ь!р((со5а)^Г°(а)Г?@)= ? (-\)mYf (Q) 7fm (P/).
m=—I
6. Пусть и, v, w — трн единичных вектора, образующих правую декар-
тову систему. Показать, что бесконечно малое вращение
(обозначения раздела III) отличается от 5?ш(—е2) только членами порядка
выше е2. Используя формулу E8), вычислить оператор бесконечно малого
вращения 8 вплоть до членов порядка е2 и проверить соотношения коммута-
коммутации [/„, /„] = Uw.
7. Используя коммутационные соотношения E6), показать, что скалярное
произведение двух векторных операторов А и В, АВ = АХВХ + АУВУ + AZBZ
коммутирует с компонентами полного момента импульса.
8. Показать, что
ехр (— ф]у) = ехр (у Шх J ех? (— ф]г) ехр (— — Ш
Вывести отсюда, что матричные элементы {/М|ехр(—i$Jy)\JM') являются по-
полиномами степени 2/ по переменным sin -5- fi и cos — р.
9. Доказать тождество (стЛ) (аВ) == (АВ) + ia(A X В) (а = (ОхОуог) —
матрицы Паули, А а В — векторные операторы, коммутирующие с а, но не
обязательно друг с другом).
10. Пусть s — внутренний момент частицы спина 1 (s2=s(s+l) =2).
П) Показать, что для любой компоненты su = (su) имеем
4 = sw exP (— '<Psu) = 1 — ' sin <psu — A — cos <p) s2u,
и получить явное выражение для матрицы вращений R^ia^y).
(ii) Пусть \z) —нормированный вектор такой, что sz\z) = 0, а \х) н
| у) — векторы, получающиеся из него вращением иа + '/гя вокруг Оу и на
—'/гя вокруг Ох соответственно. Доказать следующие соотношения и соот-
соотношения, получающиеся из них циклической перестановкой х, у и z:
s2x\y)=\y),
sx\z)=-i\y),

ЗАДАЧИ И УПРАЖНЕНИЯ 79
Используя этн соотношения, показать, что |*), \у), |г) образуют ортонорми-
рованный базис, а матрицы, которые задают sx, sy н sz в этом базисе, совпа-
совпадают с приведенными в § 21.
(iii) Показать, что (i\R(a$y)\j) = Яц(а,$у) (i, \ = x, у или г) (обозна-
(обозначения § 10 и § 14).
11. Пусть S—полный спин системы двух нуклонов. Показать, что опера-
оператор Qs (S-rJ/r2—проектор. Показать, что «тензорный» оператор 5]2 =
«= 2 [2-Q — S2] удовлетворяет тождеству: S2l2 = 4S2 — 2S,2, и возможные его
собственные значения равны 0, 2 и —4. Определить действие операторов С?
ч Si2 на введенные в § 28 функции от угловых переменных и спинов ^
(Если прннять сокращенные обозначения
то подучим
Q^(o> = 0, B/ + 1)
Wo" = Vo". B/+D
12. Рассмотрим частицу спина Vs.. Показать, что в пространстве состоя-
состояний с данным орбитальным моментом / операторы
/+ \ + 1-о l — l-a
2/ + 1 Н 2/ + 1
являются проекторами на состояния с полным моментом импульса / = / + -»•
и / = / —;г- соответственно.
13. Сложим два равных момента /| = /2 = /. Не используя свойств сим-
симметрии коэффициентов К. — Г., показать, что при перестановке т\ и т2 соб-
собственные функции полного момента симметричны (инвариантны) или антисим-
антисимметричны (умножаются на —1), и характер симметрии зависит только от J.
Показать, что они симметричны илн антисимметричны в зависимости от того
(—1J'+/ равно +1 или —1.
14. Обозначим через /2{.Д} следующую функцию оператора А и компо-
компонент момента импульса:
Г {А} к [/„ []х, А]] + [Jу, Цу, А]] + [Jz, [Jz, A]).
Показать, что если T<ft) — неприводимый тензорный оператор й-го порядка, то
его компоненты удовлетворяют соотношению
15. Пусть ar, a$ (r = 1, 2)—операторы рождения и уничтожения дву-
двумерного изотропного гармонического осциллятора:
Обозначим
h = Y

80 ГЛ. XIII. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЯ МЕХАНИКЕ
Тогда Ju У2, ^а можно рассматривать как декартовы координаты некоторого
векторного оператора / [N. В. в обозначениях § XII. 14, L = 2/2].
(i) Показать, что компоненты / удовлетворяют соотношениям коммута-
коммутации / X I = U, характеризующим момент импульса, и справедливо равенстве!
Р = S (S + 1) (следовательно, [S, J] = 0).
(ii) Будем рассматривать / как оператор момента импульса системы и
обозначим /(/+ 1) и т — собственные значения J2 и /а соответственно. Пока-
Показать, что /2 н /а образуют полный набор коммутирующих наблюдаемых, а /
может принимать все целые и полуцелые значения ^ 0. т. е.
/ = 0, j, 1, |, 2,..., оо.
___
Показать, что векторы [(/ + т)\ (/ — m)!] 2 а^+тар~т\ 0) образуют базис
стандартного представления {/2/3}.
(iii) Показать, что а* и а\ являются соответственно +'/г н —'/г компонен-
компонентами неприводимого тензорного оператора порядка '/г н, как следствие, выра-
выражения Ra*R~l (r—l, 2), где /? означает оператор вращения
R = ехр (— iaJa) exp (— ifS/2) exp (— iyJ3),
являются линейными комбинациями d[ и а|. Определить коэффициенты в
этих выражениях.
(iv) Используя предыдущие результаты, доказать формулу Внгнера
(В. 72) и основные свойства матриц Ru\ приведенные в Дополнении В (за
исключением формул композиции и приведения).
16. Показать, что если Bfe+l) операторов 7^ (q = — k,..., -\-k) удо-
удовлетворяют коммутационным соотношениям A23), то и Bk + 1) операторов
S(9ft) = (— IL Т*?\ обладают тем же свойством.
17. Показать, что интеграл
% (9, Ф) Yf; (9, Ф) Y% (9, Ф) dQ.
пропорционален (—l)mi {likm^m^l^ — m3), а коэффициент пропорционально-
пропорциональности не зависит от Шь /я2 и тз. Определить этот коэффициент. (Использовать
теорему сложения, доказанную в задаче 5.)
18. Показать, что «тензорный» оператор
рассматриваемый как функция г, зависит только от углов 9 и q>, и эта зави-
зависимость выражается сферическими функциями порядка 2. (Получаем:
Vf CS- -

ЗАДАЧИ И УПРАЖНЕНИЯ 81
Оператор Si2 является скалярным произведением (в смысле определения
(В.87)) неприводимых тензорных операторов порядка 2, S<2) н У<2\ которые
зависят от спнна н угловых переменных соответственно).
19. Пусть Ки будет компонентой векторного оператора К в данном на-
направлении, 1и — компонентой полного углового момента / в том же направ-
направлении, а |т/а), \%Jb) —два кет-вектора, принадлежащие одному и тому же
подпространству & (т/) (определения § 16). Показать, что:
<т/а | Ки I т/6> - (т/а | /„ | т/6)
где (JK) означает среднее значение скалярного оператора /К в этом под-
подпространстве
(Другими словами, элементы матрицы К в S{xJ) совпадают с матричными
элементами ее «проекции» /(/К)//(/ + !)¦)

ГЛАВА XIV
СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ. ПРИНЦИП
ЗАПРЕТА ПАУЛИ
§ 1. Тождественные частицы в квантовой теории
Две частицы называются тождественными, если все
ческие свойства этих частиц в точности совпадают, что исклю-
исключает возможность экспериментально различать их. В классиче-
классической механике это свойство неразличимости тождественных ча-
частиц играет второстепенную роль, тогда как в квантовой меха-
механике с ним связаны серьезные проблемы.
Рассмотрим в качестве примера столкновение двух тожде-
тождественных частиц и выясним, в какой степени тождественность
этих частиц влияет на результаты теории.
Если система подчиняется законам классической механики,
то ее динамическое состояние определено в любой момент вре-
времени заданием величин: ?A) = (гA), рA>) — координата и им-
импульс частицы 1 и ?B) = (гB>, рB>) — координата и импульс ча-
частицы 2. Эволюция системы определяется функцией Гамиль-
Гамильтона, зависящей от 12 переменных
Я№«>, ?«)^Я(г<», рA>, г<2>,
Если задан потенциал V{r), зависящий только от расстояния
между двумя рассматриваемыми частицами, и если m — масса
этих частиц, то
#(?A>, iB)) = -Cr + ^r + F(lr<» —r<2> |). A)
Поскольку частицы тождественны, то их перестановка, т. е.
приписывание динамического состояния частицы 1 частице 2 и
vice versa, не должна влиять на динамические свойства си-
системы. В частности, функция Н инвариантна относительно та-
такой перестановки:
Н&', t") = H(t", Г). B)
С другой стороны, состояние системы в любой момент вре-
времени можно определить лишь с точностью до перестановки ин-
индексов 1 и 2. Наблюдение системы в заданный момент времени
показывает, что одна нз частиц находится в некотором состоя-

5 1. ТОЖДЕСТВЕННЫЕ ЧАСТИЦЫ В КВАНТОВОЙ ТЕОРИИ 83
нии ?', а другая — в состоянии %", однако при этом нельзя оп-
определить, в каком именно состоянии находится каждая из рас-
рассматриваемых частиц. На первый взгляд может показаться, что
это обстоятельство вызывает затруднение, однако, как мы уви-
увидим ниже, это затруднение — кажущееся. Предположим, что
в момент времени /0 одна из частиц находится в состоянии ^
а другая — в состоянии ?". Имеются две возможности: в состоя-
состоянии 1 находится либо частица 1, либо частица 2. Однако оба
варианта соответствуют одной и той же физической ситуации,
ибо поскольку Н обладает свойством симметрии B), законы
движения ?'(/) и ?"(/) частиц, находящихся в момент вре-
времени /о в состояниях |^ и ?d', одинаковы в обоих случаях, что
соответствует одной и той же ситуации. Нужно только прийти
к соглашению о том, следует ли частицу, которая в начальный
момент времени находится в состоянии |q, назвать частицей 1,
а частицу, находящуюся первоначально в состоянии go, — ча-
частицей 2, или же поменять нумерацию этих частиц.
Ситуация становится сложнее, если двухчастичная система
подчиняется законам квантовой механики. Начало предыдущего
анализа можно дословно повторить. В этом случае снова тож-
тождественность двух частиц выражается в инвариантности гамиль-
гамильтониана относительно перестановки динамических переменных
частиц (ур. B)) или, говоря точнее, в инвариантности относи-
относительно указанной перестановки всех физически наблюдаемых
величин. Как и в классической механике, это вызывает произ-
произвол в определении состояния системы, однако теперь этот про-
произвол более существен, а его следствия — более серьезны.
Предположим, что из наблюдения, осуществленного над си-
системой до столкновения, следует, что одна из частиц находится
в состоянии ty'0(r), а другая — в ¦vfoW)- На практике, эти функ-
функции представляют волновые пакеты, локализованные в различ-
различных областях пространства, так что функции
B)) C)
линейно независимы. Начальное наблюдение не позволяет ре-
решить вопрос о том, находится ли система в состоянии ф0 или
в -фо- Более точно, наблюдение состоит в одновременном изме-
измерении определенного набора совместных переменных, а обе
функции, -фо и фо. являются собственными функциями, отвечаю-
отвечающими одному и тому же набору собственных значений, полу-
полученных в результате измерения. Поскольку любая линейная
') Будем предполагать, что рассматриваемые частицы не обладают спи»
ном, подчеркивая тем самым параллель между классической и квантовой тео-
теориями.

84 ГЛ. XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
комбинация ktyo + ^о этих функций также обладает указан-
указанным свойством, то рассматриваемое наблюдение не позволяет
определить, какая из линейных комбинаций соответствует ис-
исходному состоянию системы. В такой ситуации говорят о нали-
наличии обменного вырождения.
Исследуем теперь развитие системы во времени. Пусть
¦ф(гA>, гB), /) и ф (гA), гB), /)—решения уравнения Шредингера,
отвечающие соответственно начальным условиям г|50 и $а. Из
свойства симметрии B) гамильтониана следует, что эти реше-
решения получаются одно из другого перестановкой аргументов гA)
и гB). Удобно ввести функции симметричные и антисимметрич-
антисимметричные относительно такой перестановки
Они являются решениями уравнения Шредингера, соответствую-
соответствующими начальным данным
Если система в начальный момент времени находится в состоя-
состоянии
то в момент времени / она будет находиться в состоянии
W (И1», г<2>, 0 = a*W + P^s>. D)
Плотность Р(г', г") вероятности обнаружить одну из частиц
в точке г', а другую — в г" определяется равенством ')
Р (г', г") = | ? (г', г") I2 +1 V (г", г') |2 = E)
= 2 [ | a P i|>W> (г', г") Р +1 р |21 ф№> (r'( r") P]. F)
Для того чтобы это выражение не зависело от а и р, следует
потребовать, чтобы выполнялось равенство
Это равенство справедливо при всех г' и г" до тех пор, пока ча-
частицы не взаимодействуют, а описывающие их волновые пакеты
г|/(г) и it>"(r) не перекрываются, и, вообще говоря, перестает
быть справедливым, когда одно из этих условий не выполняется.
В этом несложно убедиться, рассмотрев несколько конкретных
ситуаций. Предположим, например, что две рассматриваемые
частицы не взаимодействуют (Vdr*1'—г<2>|)=0) и свободно
') Во втором равенстве учтено свойство симметрии функций ¦ф*'4' и. ij)(lS'i
(г", г') = - а-ф(Л) (г', г") + HKS) (rr, г").

§ 1. ТОЖДЕСТВЕННЫЕ ЧАСТИЦЫ В КВАНТОВОЙ ТЕОРИИ 85
перемещаются навстречу друг другу. В этом случае \f> является
произведением двух свободных волновых пакетов ф =
= ^'(г*1*, /)г|/'(гB), t). В течение некоторого промежутка вре-
времени волновые пакеты будут перекрываться, т. е. существует
область пространства, в которой обе функции г|/(г) и ф"(г) от-
отличны от нуля. Если г — точка из этой области, то
\?S)(r, r)|
тогда как
|^> (г, г) | = 0 G)
при всех г. Другой интересный пример дает задача рассеяния
на центральном потенциале. Она будет рассмотрена в § 9, где
мы покажем, что амплитуда рассеяния для г|э(Л) является супер-
суперпозицией сферических парциальных волн нечетного порядка,
а для \f><s> — суперпозицией волн четного порядка. В общем
случае эти амплитуды различаются по абсолютной величине и,
следовательно, дифференциальное сечение рассеяния будет су-
существенно зависеть от отношения |а|2/|Р|2-
Итак, существование обменного вырождения служит источ-
источником серьезных затруднений ибо препятствует получению точ-
точных теоретических предсказаний о статистическом распределе-
распределении результатов измерений, осуществляемых над системой по-
после столкновения.
Эта трудность может быть преодолена введением следующего
постулата симметризации,, фиксирующего коэффициенты а и 6
в линейной комбинации ($) и, таким образом, легко допускаю-
допускающего экспериментальную проверку.
Динамические состояния системы двух тождественных ча-
частиц либо все симметричны (а = 0, р = 1), либо все антисим-
антисимметричны (а=1, р = 0) относительно перестановки двух ча-
частиц.
Какая из двух указанных возможностей реализуется в дей-
действительности, зависит от физических свойств рассматриваемых
частиц. Этот постулат несложно распространить на системы,
содержащие любое число тождественных частиц. В общем виде
он будет приведен в разделе I настоящей главы, где будут про-
проанализированы также основные следствия этого постулата. Раз-
Раздел II посвящен приложениям.
При изложении будут использоваться некоторые элементар-
элементарные свойства перестановок. Все они приведены в § 14 Дополне-
Дополнения Г1).
') Элементы теории групп, собранные в Дополнении Г, не являются не-
необходимыми для понимания материала настоящей главы. Содержание § 14
этого Дополнения не зависимо от его остальных частей. В § 14 используются
лишь несколько определений, относящихся к теории групп (группа, класс, ин-
инвариантная подгруппа и т. п.), которые приведены в § 2 Дополнения Г.

S6 ГЛ. XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
Раздел I. ПОСТУЛАТ СИММЕТРИЗАЦИИ
§ 2. Подобные частицы и симметрическое представление
Рассмотрим Af-частичную систему. Динамические перемен-
переменные, описывающие i-ю частицу, являются функциями от ее ко-
координаты г<'">, импульса р''> и спина s(l>. Эти три вектора в даль-
дальнейшем будем обозначать одним символом |<»>. Зная значение
спина /-и частицы, мы можем построить пространство &"№ ее
динамических состояний. Пространство <§ динамических состоя-
состояний всей системы является тензорным произведением
S = 9~т ® у и ® ... ®Я»>. (8)
По определению, две частицы называются подобными, если
они имеют один и тот же спин (подобные частицы не обязаны
быть тождественными). В этом случае наблюдаемые и векторы
состояния одной из частиц находятся во взаимно однозначном
соответствии с наблюдаемыми и векторами состояния другой
частицы и, следовательно, имеется возможность заменить ча-
частицу подобной ей. В общем случае, если имеется п подобных
частиц, то существует п\ перестановок этих частиц. Каждой
перестановке соответствует некоторый оператор в простран-
пространстве <§. Перейдем теперь к построению этих операторов пере-
перестановок. Для простоты будем считать, что п = N.
Рассмотрим одну из N подобных частиц. Пусть | — множе-
множество основных наблюдаемых этой частицы, а &~ — пространство
ее векторов состояния. Пусть q— полный набор коммутирую-
коммутирующих наблюдаемых в 8Г, а | qK}— базис собственных векторов
набора q, с собственными значениями qK (индекс или ряд ин-
индексов х служат для нумерации собственных значений этого на-
набора наблюдаемых). Тогда
<<7xl<7n> = V (9)
В качестве q можно, например, выбрать три компоненты х, у, z
вектора г и компоненту s» Спина по оси z. Каждая частица а
(а = 1, 2, ..., N) нашей системы имеет собственный набор qw
коммутирующих наблюдаемых. Ясно, что множество Q =
= (<7A)> <7B) ФЫ)) является полным набором коммутирую-
коммутирующих наблюдаемых в пространстве &'. Векторы
полученные как тензорные произведения базисных векторов
пространств ^"A>, ^"B), ..., ^"<w>, образуют базис некоторой реа-
реализации векторов и операторов в 8, т. е. {Q}-представление.
Мы будем называть представление такого типа симметриче-
симметрическим.

§ 3. ОПЕРАТОРЫ ПЕРЕСТАНОВКИ 87
§ 3. Операторы перестановки
Очевидно, что в состоянии, описываемом вектором A0), ча-
частица 1 находится в состоянии \qay, частица 2— в состоянии
|<7р>, ..., частица N — в состоянии |^v>. Перестановка частиц
изменяет их распределение по состояниям \qa}, |<7P>, ..., |^v>
и, следовательно, вектор A0) переходит в новый, вообще го-
говоря1), отличный от исходного, базисный вектор {(^-представ-
{(^-представления. Таким образом, операция перестановки устанавливает
взаимнооднозначное соответствие между векторами рассматри-
рассматриваемого ортонормированного базиса и, следовательно, опреде-
определяет некоторый линейный унитарный оператор в пространстве
векторов состояния. Указанная процедура сопоставляет каждой
перестановке N частиц оператор перестановки Р, удовлетворяю-
удовлетворяющий условию унитарности
рр+ = р+р=:1. (И)
Так, при транспозиции A2)—перестановке частиц 1 и 2 —
вектор A0) преобразуется в вектор, описывающий состояние,
в котором частица 1 находится в состоянии |<7р>, частица
2 — в \qay, тогда как каждая из остальных частиц находится
в исходном состоянии. Соответствующий оператор перестановки
P(i2) определяется соотношением
M12) I 4a. 4$ Чу • • ¦ Vv / \Ч$ЧаЧу • • • Чу )•
Для упрощения обозначений, мы продолжим изучение пере-
перестановок в случае N = 3. Устанавливаемые принципы будут,
конечно, справедливы и для любого значения N. В качестве
примера определим оператор P(i23>, соответствующий переста-
перестановке A 2 3), при которой 1 переходит в 3; 2 — в 1; 3 — в 2:
р I ama&)a&)
rA23) I vet Vp Чу
Если 1 ф) — вектор из <?, то
apv
Переобозначив индексы суммирования в последней строчке, по-
получаем
2)^3I *)¦
') В случае, когда среди N одночастичиых состояний \Ча)< •••> I QVY
имеются одинаковые, некоторые из перестановок оставляют вектор A0) не-
неизменным, если же все состояния совпадают, то ии одна из перестановок не
изменяет вектора A0).

88 ГЛ. XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
Если г|5(<7а9р9у) —волновая функция состояния |ф> в {Q}-пред-
{Q}-представлении (т.е. "^{ЯаЯ^Яу)—амплитуда вероятности обнару-
жить частицу 1 в состоянии |^а>, частицу 2 — в |<7в>, час-
частицу 3 — в |<7у>), то волновой функцией для P(i23)|it>> является
функция
а), A4)
которая получена действием на аргументы функции
перестановки обратной перестановке A 2 3).
Закон преобразования векторов при перестановке принимает
особенно простую форму на векторах вида
на которых он совпадает с законом преобразования базисных
векторов {Q}-представления. Действие Р на вектор такого вида
дает вектор, который получается при перестановке р частиц 1,
2,3, находящихся в одночастичных состояниях | и), | v}, | ш>,
т. е. (уравнение A2))
Доказательство несложно. Уравнение A3) в данном случае
имеет вид
М123) I W V W / == Zj ЯаЯлЯу) \Яа W) We ") \ЯУ v)>
где правая часть есть не что иное как разложение
по базисным векторам {QJ-представления.
Это свойство, доказанное только что для частного случая,
имеет общий характер (задача 1). Из него следует, что опера-
оператор Р, соответствующий заданной перестановке, не зависит от
конкретного симметрического представления, выбранного для
определения этого оператора.
Действие оператора Р на вектор порождает вектор, который
получается из исходного перестановкой р. Точно так же преоб-
преобразование оператора F(?A), ?B), . . ., ?(ЛГ)) в пространстве & под
действием унитарного оператора Р задает оператор, получаю-
получающийся из данного применением перестановки р к аргументам
оператора F. Если
2 ... Л
то
PF (?\ gB), .... tN)) Pf = F (!(«¦), §D .... |(eAf)). A5)

§ 4. АЛГЕБРА ОПЕРАТОРОВ ПЕРЕСТАНОВКИ 89
В частности
PiwF (f\ f\ f}) PU = F (f\ f\ |A)) A6)
(?<«> переходит в ?<•>; |(8) _ B gB>; ?<»> — в g<3)).
Для доказательства достаточно показать, что этот закон вы-
выполняется в случае, когда F — любая из основных наблюдае-
наблюдаемых системы. Рассмотрим одну из них. Всегда можно построить
симметрическое представление, в котором наблюдаемая диа-
гональна. Предположим для примера, что выбрана одна из рас-
рассмотренных выше наблюдаемых qM {Q}-представления. Для
того чтобы показать, что PqMP* = ^°'\ достаточно показать,
что выражения, стоящие в обеих частях этого равенства, оди-
одинаково действуют на любой из базисных векторов {Q}-пред-
{Q}-представления. Доказательство несложно, и мы ограничимся про-
проверкой этого утверждения в специальном случае N = 3, /= 1,
р=A23)
В применении к наблюдаемым приведенное определение пе-
перестановок согласуется с интуитивным: наблюдаемая РВР^,
полученная в результате применения перестановки р к наблю-
наблюдаемой В, имеет тот же спектр собственных значений, что и В,
а собственные векторы наблюдаемой РВР'^ получаются дей-
действием оператора перестановки Р на собственные векторы на-
наблюдаемой В, соответствующие тому же собственному значе-
значению.
В частности наблюдаемая В инвариантна относительно пере-
перестановки N частиц, если РВР^ = В для каждой из N\ переста-
перестановок этих частиц, т. е. если
[Р,В] = 0
для любого Р. В этом случае говорят, что наблюдаемая В сим-
симметрична относительно перестановки N частиц.
§ 4. Алгебра операторов перестановки. Симметризаторы
и антисимметризаторы
Последовательное действие двух перестановок р', р" экви-
эквивалентно действию одной перестановки р = р"р'. Из определе-
определения оператора перестановки очевидно, что то же соотношение
справедливо и для соответствующих операторов Р, Р', Р"
р = Р»р>. A7)

90 ГЛ. XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
Таким образом, операторы перестановок удовлетворяют тем же
алгебраическим соотношениям, что и определяющие их пере-
перестановки ').
В частности, любой оператор Р можно записать в виде про-
произведения транспозиций. В общем случае такая факторизация
не единственна. Однако все такие представления состоят либо
из четного, либо из нечетного числа транспозиций. Четность пе-
перестановки обозначается (—\)р и равна + или — в соответ-
ствии с четностью или нечетностью числа транспозиций, обра-
образующих перестановку. Если Р, Р' и Р" связаны соотношением
A7), то очевидно имеем: (—1)р= (—\)р'+р".
Некоторые перестановки, в частности транспозиции, совпа-
совпадают со своими обратными. В таких случаях (см. ур. A1)) со-
соответствующий оператор является наблюдаемой, возможные
собственные значения которой равны ±1.
В качестве примера рассмотрим транспозицию (ij):
Рщ)=\. A8)
Собственные векторы с собственным значением -f-1 инвариант-
инвариантны при транспозиции (ij). Они, по определению, являются сим-
симметричными по i и /. Проектор на подпространство векторов,
симметричных по i и /, есть оператор симметризации
SW] = ±(l + P{il)). A9)
Собственные векторы с собственным значением —1 изменяют
знак при транспозиции (//). Эти векторы, по определению, ан-
антисимметричны по i и /. Проектором на подпространство век-
векторов, антисимметричных по i и /, является оператор антисим-
антисимметризации
\ B0)
') В частности, Япгз) = -Р<12)-Р<23)- Проверим, что последовательное дей-
действие РB3) и Р(,2) на волновую функцию ^(<?a70<7Y) снова дает результат A4),
Обозначим
Тогда
*l (*a Vv) = *
Тот же результат будет получен и в том случае, когда на аргументы функции
•ф (q q q ) действует сперва перестановка A2), а затем перестановка B3).

§ 4. АЛГЕБРА ОПЕРАТОРОВ ПЕРЕСТАНОВКИ 91
Очевидно, справедливы соотношения
Sun + Mm = 1. P{H)siti) = 5ц/]Р(,-/) = Зц/],
S[il] — Аи] — рщ)> РтАцп = АцпРц1)= —^ил-
Каждый вектор является суммой вектора, антисимметричного
по i и /, и вектора, симметричного по i и /. Разложения такого
Типа использовались при обсуждении рассеяния двух тождест-
тождественных частиц в § 1.
Расширим понятия симметрии и антисимметрии динамиче-
динамических состояний, которое было определено выше лишь для пере-
перестановок Р(Ц), на общий случай N1 перестановок Р.
Выберем вектор | «> в & и обозначим &и — подпростран-
подпространство, натянутое на вектор | и) и на все векторы, которые могут
быть получены из него перестановками. Размерность подпро-
подпространства &и равна ЛП, если ЛП векторов Р|«> линейно незави-
независимы и меньше Л/!, если эти векторы линейно зависимы.
Экстремальным случаем будет ситуация, когда все Р\и}
представляют одно и то же состояние
Р\и) = ср\и) B2)
для любой перестановки р. Ниже будут приведены условия,
ограничивающие произвол в выборе постоянных ср. Если Р —
транспозиция, то, как мы знаем, ср может принимать только
значения ±1. Далее, поскольку любая транспозиция (ij) равна
произведению (It) B/) A 2) B/) (It), то
Л«7) = P(H)P{V)P(\z)Pezt)P{H)
или
С(«7) = C(li)CB/)CA2) = СA2)' B3)
Следовательно, постоянная с совпадает для всех транспозиций:
либо Си = + 1, либо Си = — 1, и так как всякая перестановка
является произведением транспозиций, то соответствующая по-
постоянная ср имеет вид степени си либо с четным, либо с нечет-
нечетным натуральным показателем в соответствии с четностью или
нечетностью перестановки р.
Таким образом, мы приходим к выводу, что уравнение B2)
справедливо только в двух следующих случаях:
(а) для любого р, ср=1, Р|ы) = |«); B4)
(б) для любого р, ср = (- 1)р, Р | и) = (- 1)р | и). B5)
Вектор |«> называется симметричным или антисимметричным
относительно перестановки N частиц в зависимости от того, ка-
какой случай (а) или (б) имеет место.
Симметричные векторы образуют подпространство <2f(S) в &\
а антисимметричные векторы образуют в & подпространство

92 ГЛ. XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
>, ортогональное к <2f(s>. Покажем, что проекторами на эти
подпространства являются соответственно операторы
1^ B6)
X распространяется на все N\ возможных перестановок).
Рассмотрим последовательность, полученную произвольным упо-
упорядочением всех перестановок. Если каждый элемент умножить
справа и слева на оператор Pi некоторой перестановки, то
в результате будет изменен только порядок расстановки эле-
элементов в рассматриваемой последовательности, так что
PlS = SP1 = S, Л<4 = ЛР, = (-1)Р'Л. B7)
Замена каждого элемента Р обратным Р+ также сказывается
лишь на порядке следования элементов, и так как перестановка
и обратная к ней имеют одну и ту же четность, то
S = S\ A = A\ B8)
Из равенств B7) и определений B6) легко получить соотно^
шения
S2=S, A2 = A B9)
и
SA==AS = 0. C0)
¦Соотношения B8) — C0) показывают, что S и А являются ор-
ортогональными проекторами. Далее, если \и) содержится в <2T(S>,
то из B4) имеем
и обратно, если |> — произвольный вектор, то согласно B7)
получаем
PS\)*-S\).
Следовательно, S действительно является проектором на
Аналогичным образом можно показать, что А является проек»
тором на <2Г(Л>.
В случае N = 3 для S я А легко вывести явные формулы
S — | A + РA2) + Яда + Р<8|) + Р<1И) + Рдао),
А = -q A — РA2) — РB3) — РC1) + РA23) + РC21)).

§ 5. ТОЖДЕСТВЕННЫЕ ЧАСТИЦЫ И ПОСТУЛАТ СИММЕТРИЗАЦИИ 93
К видно из этого примера, S -\- А Ф I при N > 2. Действие
тельно, S + А является проектором на пространство состояний,
инвариантных относительно четной перестановки N частиц, ко-
которое при Л/ > 2 является подпространством в &.
Вернемся к определенному выше пространству &и. Из соот-
соотношений B7) следует, что для любого Р справедливы равен-
равенства SP\ u) = S\ и), АР\и) = (-1)"А\и).
Таким образом, растягивающие 8и векторы Р\и} имеют одну
и ту же проекцию на c!T(S) и с точностью до знака одинаковую
проекцию на &"(АК Следовательно, в соответствии с тем, являют-
являются ли векторы S\u} отличными от нуля или нет, &и содержит
либо один и только один симметричный вектор, либо вовсе не
содержит таковых и аналогично, в зависимости от того равен
нулю или отличен от нуля вектор А | «>, <*?ы содержит один и
только один антисимметричный вектор либо не содержит ни од-
одного ').
§ 5. Тождественные частиды и постулат симметризации
Если все Л/ частиц рассмотренной выше системы будут не
только подобны, но и тождественны, то ни одно из динамиче-
динамических свойств системы не изменится в результате любой пере-
перестановки этих частиц. Из этого свойства инвариантности можно
вывести важные следствия относительно имеющихся законов
движения и наблюдаемых системы.
Если |г|?о> — состояние системы в начальный момент вре-
времени t0, то ее состояние в более поздний момент времени t
можно получить действием оператора эволюции U(t, t0): \tyt} =
— U(t, <о)|'Ф>- Если начальное состояние -Р11*Jpo>, то эволюция
системы отличается от исходной лишь перестановкой Р, и в мо-
момент времени t система будет находится в состоянии |
Следовательно,
U if, t0) Р\%) = Р\ Ъ) = PU (t, t0)
и так как эти равенства должны выполняться при любом вы-
выборе |г|зо>, то
[PU(to)) = O. C1)
Пусть Н — гамильтониан системы, тогда U(t, t0) является ре-
решением уравнения Шредингера
ih-^Uit, t0) = HU (t, t0),
удовлетворяющим начальному условию V{to, ^p)=l. Из C1) и
соотношения, получаемого из него дифференцированием по t,
') Если № векторов Р\и) линейно независимы, то конкретные линейные
комбинации S\u) и А\и) этих векторов, конечно, отличны от нуля. В этом
случае &и содержит один симметричный и один антисимметричный вектор.

94 ГЛ. XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
имеем
[Р,Н] = 0. C2)
Обратно, если Н и Р коммутируют, то оператор U(t, t0) и его
преобразование PUP^ при перестановке совпадают, так как
удовлетворяют одному и тому же уравнению Шредингера с од-
одним и тем же начальным условием. Следовательно, U и Р ком-
коммутируют. Итак, условие C2) коммутации гамильтониана Я
со всеми операторами перестановок Р является необходимым
и достаточным для инвариантности уравнений движения относи-
относительно перестановок.
Рассмотрим теперь физическую наблюдаемую1) В исследуе-
исследуемой системы и пусть ] «> собственный вектор В, соответствую-
соответствующий собственному значению Ь. Если хистема находится в со-
состоянии |«>, то при измерении В результатом всегда будет Ь,
а если система находится в состоянии Р\и}, полученным дей-
действием оператора перестановки Р на вектор |ы>, то измерение
В должно дать тот же результат
ВР\и)^ЬР\и)
для любой перестановки Р. Иными словами, каждый вектор из
пространства &и, порождаемого действием всевозможных пере-
перестановок N частиц на состояние | «>, в свою очередь должен
быть собственным вектором оператора В, соответствующим
тому же собственному значению Ь (обменное вырождение). Для
справедливости этого утверждения при всех собственных значе-
значениях наблюдаемой В необходимо и достаточно (ср. § VII. 15),
чтобы при всех Р выполнялось равенство
[В, Р] = 0. C3)
Таким образом, N частиц тождественны, если гамильтониан
Н и все физические наблюдаемые системы симметричны относи-
относительно перестановки этих частиц.
Следовательно, при определении состояния системы одно-
одновременным измерением переменных q каждой отдельной ча-
частицы состояние будет определено, в лучшем случае, лишь
с точностью до обменного вырождения2). Можно будет ут-
1) Выражению физическая наблюдаемая был придан смысл в § XIII. 15.
ПривЬдимый анализ инвариантности относительно перестановок можно срав-
сравнить с анализом инвариантности физической наблюдаемой относительно «вра-
«вращений на 2я», приведенным в указанном параграфе.
2) <7A), <7<2), ..., <7(ЛГ) образуют полный набор коммутирующих наблюдае-
наблюдаемых в пространстве S, но только симметричные функции этих величин могут
быть физическими наблюдаемыми, однако эти функции уже не образуют пол-
полного набора в &. Постулат симметризации, который будет введен далее,
состоит в ограничении пространства векторов состояния до некоторого под-
подпространства в S, в котором рассматриваемые физические наблюдаемые обра'-
зуют полный набор (и из которого, следовательно, полностью устранено об-
обменное вырождение),

§ 5. ТОЖДЕСТВЕННЫЕ ЧАСТИЦЫ И ПОСТУЛАТ СИММЕТРИЗАЦИИ 96
верждать, что щ частиц из полного числа частиц N находятся
в состоянии |<7i>;  — в состоянии |<7г>, ...; пк — в состоянии
| <7и>> ••• («1 +  + • • ¦ + «х + • • • = W); однако, наличность
частиц в каждом из этих состояний останется неопределенной.
В {Q}-представлении имеется (ЛП/я,! «21 ... пк\ ...) базисных
векторов, обладающих рассматриваемым свойством. Пусть
<$ {п\П1 ... пх ...) —пространство, образованное этими векто-
векторами (порождаемыми действием N\ перестановок на одно из
них, выбранное произвольно). Состояние системы описывается
одним из векторов этого пространства, но рассмотренное выше
измерение не позволяет определить, каким именно. Однако, как
мы видели в примере, приведенном в § 1, предсказания теории
существенно зависят от того, в каком состоянии находится си-
система, и эта неопределенность является источником действи-
действительного затруднения. Она может быть устранена введением
постулата симметризации: состояния системы, содер-
содержащей N тождественных частиц, будут все либо симметрич-
симметричными, либо антисимметричными относительно перестановок этих
N частиц.
Какое из этих предписаний следует применять, зависит от
природы рассматриваемых тождественных частиц. Частицы
с симметричными состояниями называются бозонами, а с анти-
антисимметричными— фермионами. (Мотивировка этих наименова-
наименований станет ясной из дальнейшего.) Эксперимент показывает,
что встречающиеся в природе элементарные частицы спина '/2
(электроны, протоны, нейтроны и т. д.) являются фермионами,
тогда как частицы с целым спином (фотоны, п-мезоны и т.д.) —
бозонами.
Определенное выше пространство <2f(«i«2 ¦•• пк ...) имеет
не более чем один симметричный и не более чем один антисим-
антисимметричный вектор. Таким образом, постулат симметризации пол-
полностью устраняет обменное вырождение. Остается только пока-
показать, что этот постулат не приводит к противоречиям с основ-
основными положениями квантовой механики, относящимися к эво-
эволюции физических систем и измерению физических величин.
Рассмотрим случай бозонов (фермионы можно рассмотреть
тем же способом). В предыдущем параграфе мы определили
проектор S на симметричные состояния. Он является комбина-
комбинацией операторов перестановки (ур. B6)) и, следовательно, ком-
коммутирует с оператором эволюции U(t, t0) системы
[S,U(t,to)]-=O C4)
и физическими наблюдаемыми
[S, В] = 0. C5)
Соотношение C4) показывает, что если система находилась
первоначально в симметричном состоянии, то она будет оста-

% ГЛ. XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
ваться в симметричном состоянии до тех пор, пока не будет
внешнего возмущения. Из соотношения C5) следует, что S и В
имеют по крайней мере один общий набор базисных векторов.
Если состояние системы симметрично, то разложение вектора
состояния по этому базису содержит только симметричные соб-
собственные векторы оператора В. Таким образом, очевидно, что
операция измерения наблюдаемой В оставит систему в сим-
симметричном состоянии.
§ 6. Бозоны и статистика Бозе —Эйнштейна
Рассмотрим систему N бозонов. Состояния системы обра-
образуют подпространство <2f<s> пространства &". Из векторов
{QJ-представления можно построить базис в пространстве <2f<s>.
В каждом подпространстве & {п\Щ .. . пк .. .) мы можем по-
построить один и только один нормированный симметричный век-
вектор (определенный с точностью до фазового множителя)
где q"'q™ • • • q"KK . • •) — базисный вектор {QJ-представления,
в котором первые щ частиц находятся в состоянии |^i>, следую-
следующие п2 частиц — в состоянии | q2}, ..., следующие пх частиц —¦
в состоянии |<7х>, ...; S — определенный выше (ур. B6)) опе-
оператор симметризации, а в квадратных скобках стоит нормирую-
нормирующий множитель @1 = 1). Доказать это можно следующим об-
образом.
Перестановка двух частиц, находящихся в одном и том же
состоянии, не изменяет вектор \q"lq12 .. ¦ q^x - • .)• тогда как
перестановка двух частиц, находящихся в разных состояниях,
порождает другой базисный вектор {Q}-представления. В об-
общем случае, рассматриваемый вектор инвариантен относительно
любой из Ц nj =^=щ\щ\ ... пк\ .. .перестановок, не изменяющих
распределение частиц по состояниям \q{), |<72>> ••• |<7х>, •••'»
любая из остальных перестановок переводит его в другой базис-
базисный вектор {Q} -представления. Применяя каждую из N1 пере-
перестановок к \q"lq • • • <7хк • • •)» мы получим [ЛП/Д nj] базисных
векторов пространства &"(п\п2 ... пх ...), каждый из которых
будет получен (Д nj) раз. Вектор C6) равен сумме этих базис-
базисных векторов, умноженной на [П^и'/^0'/г и> следовательно,
симметричен и нормирован на единицу.
Итак, каждой последовательности щ, п2, ... пк, ... неотри-
неотрицательных целых чисел такой, что

§ 6. БОЗОНЫ И СТАТИСТИКА БОЗЕ — ЭЙНШТЕЙНА 97
соответствует одно и только одно симметричное состояние си-
системы, которое описывается вектором C6). Множество таких
векторов образует ортонормированный базис в <2f(s).
Покажем теперь, что бозонный газ подчиняется статистике
Бозе — Эйнштейна. Бозонным газом называют систему, образо-
образованную очень большим числом N бозонов, взаимодействие ме-
между которыми достаточно слабое, так что в первом приближе-
приближении им можно пренебречь. Гамильтониан Н системы можно за-
записать в виде суммы N одночастичных гамильтонианов
Я = Л<1> + Л<2)+ ... +й»>+ ... +Л(Л0. C7)
Согласно теории Больцмана равновесное термодинамическое со-
состояние реализуется, когда система находится в наиболее веро-
вероятном «макроскопическом состоянии». Данное «макроскопиче-
«макроскопическое состояние» в действительности является набором квантовых
состояний (или «микроскопических состояний»), близких друг
другу, так что на макроскопическом уровне их невозможно раз-
различить. Согласно эргодической гипотезе микроскопические со-
состояния с одинаковой энергией равновероятны. Вероятность за-
заданного макроскопического состояния пропорциональна числу
образующих его различных микроскопических состояний. Опре-
Определение термодинамического равновесия системы существенно
зависит от этого числа. Будем предполагать, что h содержится
в множестве q динамических переменных, определяющих
{Q}-представление. Каждое распределение
П\, П%, . . ., Пк, . . .
N частиц по различным возможным одночастичным состояниям
I <7i>> I <72>, .... I <7х)> ...
определяет одно и только одно микроскопическое состояние си-
системы (описываемое вектором C6)). В этом как раз и состоит
основное предположение статистики Бозе — Эйнштейна, в кото-
которой частицы считаются неразличимыми. Следовательно, в ста-
статистике Бозе — Эйнштейна состояния системы, отличающиеся
друг от друга только различными расположениями тождествен-
тождественных частиц, заселяющих различные одночастичные состояния,
рассматриваются как одно и то же микроскопическое состояние.
С другой стороны, в статистике Максвелла — Больцмана, каж-
каждая частица предполагается различимой на микроскопическом
уровне и [iV!/Qnx!] состояний системы, соответствующих од-
одному и тому же распределению п\, «2. • • •. пк, ..., рассматри-
рассматриваются как различные микроскопические состояния.
Важное замечание. Оператор плотности, описывающий
состояние системы в термодинамическом равновесии, имеет вид
р^е-л/иуТге-"'*7". C8)
4 А. Мессиа

98 ГЛ. XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
Другие формы записи оператора р, полученные из этого выра-
выражения в § VIII. 25, сохраняют справедливость. Главное отличие,
вводимое в теорию постулатом симметризации, заключается
в том, что р ставится оператором в <2f<s), а не во всем простран-
пространстве &, и различные вычисления квантовой статистики, в част-
частности нахождение следов, следует проводить именно в этом су-
суженном пространстве. Итак, в случае, когда Н имеет вид C7),
оператор плотности р, рассматриваемый как оператор в про-
пространстве 8', является тензорным произведением операторов, оп-
определенных на одночастичных пространствах @~и\ &~B\ ...
Однако эта факторизация теряет смысл, если р является опе-
оператором в <2f(S), ибо каждый из N множителей, взятый в отдель-
отдельности, не является оператором в <2f(S>.
§ 7. Фермионы и статистика Ферми — Дирака.
Принцип запрета
Анализ, подобный приведенному выше, можно провести и
в случае системы N фермионов. Ее состояния образуют подпро-
подпространство <2Г<Л) в &.
В {Q}-представлении мы получаем полный набор ортонор-
мированных антисимметричных векторов, взяв по одному нор-
нормированному антисимметричному вектору (если таковые суще-
существуют) в каждом из подпространств 8{п\Пч ... пх ...). Для
существования такого вектора необходимо и достаточно, чтобы
вектор A l^^2 • • • Ях* • • •) был отличен от нуля. Предположим,
что среди целых чисел п\, Пъ, ..., пк, ... по крайней мере одно
превосходит 1. В этом случае в состоянии, описываемом векто-
вектором |<7"'<722 ••• <7ии •••)> п0 кРаиней мере две частицы, скажем
i-я и /-я, заселяют одно и то же одночастичное состояние, так
что рассматриваемый вектор симметричен относительно обмена
этих частиц, т. е.
•# ... <# ... > = 1 A + р(|Д) | ч№ ...#•..->.
Но из B7) следует
Л A+/>«/)) = О,
так что
|'<722...^...> = 0. C9)

§ 7 ФЕРМИОНЫ И СТАТИСТИКА ФЕРМИ — ДИРАКА
99
Другими словами, два фермиона не могут занимать одно и то
оюе одночастичное состояние одновременно. Это утверждение
известно как принцип запрета Паули ¦).
Предположим теперь, что каждое одночастичное состояние
занято не более чем одной частицей (пх = 0 или 1). Вектор
является суммой Л/*! взаимноортогональных векторов и, следо-
следовательно, отличен от нуля. Его норма равна A/Л/!). Если
I <7а>> 19р)> • • •. I <7v> есть N занятых одночастичных состояний,
то соответствующее антисимметричное состояние описывается
нормированным вектором ¦y/N\A\q<Uq'?> ... qW)\ Этот вектор
можно представить в виде определителя N X N-ro порядка (оп-
(определитель Слэтера)
п Ч*1* I п \B> I п \т
Улм
ч
Г
\"*У
B)
\(JV)
D0)
Тождество D0) можно проверить непосредственно, разложив
определитель, стоящий в правой части. Более того, соотноше-
соотношение D0) остается справедливым, когда некоторые из N одно-
частичных состояний тождественны, так как в этом случае две
или большее число строк матрицы совпадают и определитель
равен нулю, что соответствует принципу Паули.
Таким образом, каждому набору \qa~}, |<7p>> •••> |<7v> из N
различных состояний, выбранных из одночастичных состояний
|<7i>> |<72>, .... |<7и>. •••> соответствует одно и только одно ан-
антисимметричное состояние, описываемое вектором D0). Полу-
Полученное в результате множество векторов образует ортонорми-
рованный базис в <2Г(л>.
Фермионный газ подчиняется статистике Ферми — Дирака.
Доказательство подобно доказательству аналогичного утвержде-
утверждения в бозонном случае. Единственное различие состоит в ну-
нумерации микроскопических состояний. Каждый набор из N раз-
различных одночастичных состояний определяет одно и только одно
микроскопическое состояние системы фермионов, описываемое
') Принцип запрета был сформулирован Паули в 1925 г. как общее свой-
свойство электронов, позволяющее объяснить структуру спектров сложных ато-
атомов (ср. § 12).

100
ГЛ. XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
вектором D0). В этом и состоит основное положение статистики
Ферми — Дирака, которая означает, что эти частицы неразли-
неразличимы и что не более чем одна из них может находиться в каж-
каждом из одночастичных состояний.
Замечание, приведенное в конце предыдущего параграфа,
применимо также и к фермионам. Оператор плотности для си-
системы фермионов, находящихся в термодинамическом равнове-
равновесии, определяется равенством C8), однако в этом случае он
является оператором в й>(Л).
Итак, различия между тремя типами статистик для тожде-
тождественных частиц обусловлено различным определением про-
странства векторов состояния, как это указано в табл. I.
Таблица I
Статистика
Тип
частиц
Пространство
векторов
состояния
Максвелла —
Больцмана
Различимые
Ж
Бозе —
Эйнштейна
Неразличимые
Ферми —
Дирака
Неразличимые
+ принцип
запрета
§ 8. Всегда ли необходимо симметризовать
волновую функцию?
Рассмотрим систему п тождественных частиц. Если части-
частицами являются электроны, то состояние системы описывается
антисимметричной волновой функцией. Однако во вселенной
имеются не только эти электроны. Отказ от учета влияния дру-
других электронов и рассмотрение системы электронов в виде це-
целого, отделенного от всего остального, предполагает, что на" ди-
динамические свойства рассматриваемых п электронов не влияет
наличие других электронов. Возникает вопрос, является ли та-
такое предположение хорошо обоснованным или существуют оп-
определенные корреляции между п электронами исследуемой си-
системы и другими электронами, не входящими в нее, что означало
бы несправедливость рассматриваемого предположения.
В практических приложениях все электроны системы содер-
содержатся внутри некоторой области D пространства, а интересую-
интересующие нас динамические свойства соответствуют измерениям, ко-
которые следует проводить внутри этой области. Оказывается, что

§ 8. НЕОБХОДИМО ЛИ СИММЕТРИЗОВАТЬ ВОЛНОВУЮ ФУНКЦИЮ? Ю1
наличие других электронов можно попросту не учитывать до тех
пор, пока они остаются вне области D, и до тех пор, пока их
взаимодействие с электронами системы остается пренебрежимо
малым. Этот результат имеет общий характер и в одинаковой
степени применим как к фермионам, так и к бозонам. Докажем
его для специального случая системы, состоящей из двух фер-
м ионов.
Если пренебречь наличием всех остальных частиц, то дина-
динамическое состояние двух фермионов описывается нормирован-
нормированной антисимметричной волновой функцией фA,2), где 1 и 2
обозначают координаты и компоненты sz спина частиц 1 и 2
соответственно. В общем случае, заданное состояние системы,
скажем состояние х> описывается антисимметричной нормиро-
нормированной волновой функцией хA,2). Если в заданный момент
времени система находится в состоянии ф, то ее динамические
свойства в этот момент времени определяются набором вероят-
вероятностей
D1)
В реальной ситуации два рассматриваемых фермиона состав-
составляют часть системы из N фермионов. Рассмотрим вопрос о том,
совпадают ли полученные динамические свойства с теми, кото-
которые могут быть найдены при учете существования остальных
(JV — 2) фермионов. Пусть WC, 4, . . ., N)— нормированная ан-
антисимметричная волновая функция, описывающая динамическое
состояние остальных (N — 2) фермионов. Если фермионы 1 и 2
не тождественны с фермионами 3, 4, ... , N, то состояние всей
системы описывается волновой функцией
ФA, 2L43, 4 АО
и сохраняет это свойство факторизуемости до тех пор, пока
взаимодействие между двумя выделенными фермионами и
остальными фермионами системы остается пренебрежимо ма-
малым. В действительности же, вектор |Ф>, корректно описываю-
описывающий состояние всей системы, пропорционален антисимметрич-
антисимметричному вектору Alcp^P), где А — оператор антисимметризации /V
частиц (определение B6)).
По предположению, волновые пакеты ф и W не перекры-
перекрываются, иначе говоря, с достоверностью известно, что два фер-
фермиона находятся внутри указанной области D пространства,
тогда как остальные расположены вне D. Более того, нас инте-
интересуют только динамические свойства двух фермионов, находя-
находящихся внутри D.
Обозначим 8C, 4, ..,, N) нормированную антисимметрич-
антисимметричную волновую функцию, обращающуюся в нуль в случае, когда
какие-либо из (N — 2) координатных векторов гC>, ..., r((V> на^

102 ГЛ. XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
ходятся внутри D. Волновая функция W описывает состояние
системы из (N — 2) фермионов, находящихся вне D. По пред-
предположению, W является функцией такого типа. Если функции
вь вг, . .., в,-, .. . образуют полный ортонормированный базис
функций указанного вида, то
Обозначим хA. 2) произвольную нормированную антисимме-
антисимметричную волновую функцию частиц 1 и 2, обращающуюся в
нуль, когда хотя бы один из векторов, гО или г<2>, находится
вне D. Следовательно, % описывает два фермиона, находящихся
внутри D. По предположению функция ф имеет такой вид.
Перестановки N частиц можно разбить на два класса в со-
соответствии с их действием на вектор |хв>. Перестановки пер-
первого типа, обозначаемые F, изменяют только знак вектора |х©>-
Имеется всего 2! (N — 2)! перестановок, меняющих местами ча-
частицы 1 и 2 или переставляющих частицы 3, 4, .. ., N друг
с другом. Таким образом,
Все остальные перестановки G переставляют по крайней мере
одну из частиц 1, 2 с одной из остальных (N — 2) частиц. Сле-
Следовательно G|xB> описывает состояние, в котором по крайней
мере одна из частиц A, 2) находится вне D, так что этот век-
вектор ортогонален любому вектору |х®>
Далее, получаем следующее тождество:
А | хв> = 4
D2)
Заметим, что норма вектора Л|хВ> равна <ув IАI ув>, т. е.
2l(N — 2)\/N\.
Нам надо определить вероятность w того, что два фермиона,
расположенные внутри D, находятся в состоянии х- Если бы
(N — 2) оставшихся фермиона были отличны от этих двух, то
состояние системы описывалось бы вектором |фЧг>, а искомая
вероятность определялась бы по формуле
<хе, 1ф^> Р = I <xl ф)Р (ZI <е,| чо р)=| <Х| Ф> р. D3)

§ 9. СТОЛКНОВЕНИЕ ДВУХ ТОЖДЕСТВЕННЫХ ЧАСТИЦ 103
Поскольку все N фермионов тождественны, состояние системы
имеет вид
а искомая вероятность есть вероятность обнаружить систему
в одном из состояний, описываемых ортонормированными анти-
антисимметричными векторами
т. е.
w = ? (Xi |Ф> ?=(CnJ ? I (Хвг | Л
i i
Из D2) и D3) следует
что совпадает с D1).
Итак, результат, который получен в пренебрежении осталь-
остальными (N — 2) фермионами, является корректным.
РазделП. ПРИЛОЖЕНИЯ
§ 9. Столкновение двух тождественных бесспиновых
частиц
В этом параграфе мы подведем итоги обсуждению задачи
о столкновении, рассмотренной в § 1.
Пусть (/?, Р) и (г,р)—динамические переменные центра
масс и относительного движения двух частиц
# = ± (ru> + г®), г = г*1» - г<2>. D4)
Гамильтониан имеет вид
а динамическое состояние системы в любой заданный момент
времени описывается волновой функцией ^V{R, r), зависящей
от R и г.
При перестановке частиц R не меняется, а г переходит в —г.
Поскольку волновая функция обязана удовлетворять постулату

104 ГЛ. XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
симметризации, то ')
W(R, -r) = ±W(R,r), D6)
где верхний знак берется в случае, когда обе частицы — бозоны,
а нижний — фермионы.
Сперва рассмотрим эту задачу, предполагая, что частицы
различимы. Ее решение приведено в разделе I главы X. Напом-
Напомним кратко решение этой задачи, сохраняя обозначения § X. 4—7.
До столкновения (t <C 0) состояние системы, образованной
частицей мишени и налетающей частицей, характеризуется
относительной скоростью v = hk/l/2m и прицельным пара-
параметром Ь. Запишем волновую функцию в виде произведения
<b(R,t)q>t(r,t), где Ф и qp — два свободных нормированных
волнов'ых пакета2). В системе центра масс групповая скорость
волны Ф(/?, t) равна нулю, а волна <p(r, t) распространяется
со скоростью v. В приближениях, используемых при вычислении
поперечного сечения, расплыванием пакета ф(г, t) можно пре-
пренебречь, так что его форма фиксирована и может быть опреде-
определена соотношением (ур. A3))
Фб (Г, /) = е-'*»- iEtlh%(r — vt — b) eikr. D7)
После столкновения (t ^> 0) волновая функция Ч?ь (R, r, t),
удовлетворяющая этим начальным условиям, имеет вид
Ч'6 (R, г, 0 = Ф («, 0 [Ф. (г, 0 + <> (г, /)], D8)
где ф^' (г, t) — расплывающийся волновой пакет (ур. B0))
r, t)~e-ik-b-lEtl>l%[u(r — vt) + s — b]f(Q, q>)-—. D9)
Поскольку рассмотрение ведется в системе центра масс, волно-
волновой пакет Ф(/?, t) остается сконцентрированным в начале коор-
') Перестановка является операцией, отличной от пространственного от-
отражения, при котором оба аргумента Лиг изменяют знак. В приводимом
нами обсуждении, когда предполагается, что частицы бесспиновые, и когда,
как мы увидим ниже, центр масс не играет существенной роли, эти две опера-
операции можно легко спутать, поскольку они одинаково действуют на функцию
относительного движения.
2) Строго говоря, начальное состояние должно описываться произведением
вида C), поскольку до столкновения корреляции между частицами отсутст-
отсутствуют. Произведение Фф представимо в форме C) только в том случае, когда
волны Ф и ф имеют специальный вид. Например,
Фф ~ ехр [t (KR + kr)~a D (R - Я0J + (г - г»J)].
Однако вычисление сечений не зависит от конкретного вида начальных вол-
иовых пакетов, и можно пренебречь ошибкой, которая обусловлена тем, что
в качестве исходного берется волновой пакет вида Фф. Все это неявно пред-
предполагалось в обсуждении, приведенном в § 7,

§ 9. СТОЛКНОВЕНИЕ ДВУХ ТОЖДЕСТВЕННЫХ ЧАСТИЦ 105
динат и сечение рассеяния crA)(Q) первой частицы в направлен
нии Q = (в, ф) равно сечению рассеяния в относительной си-
стеме для того же направления, т. е. (§ X, 6)
oK»(Q) = |/(9, Ф)Р. E0)
Сечение рассеяния orB)(Q) второй частицы в направлении й
равно сечению рассеяния в относительной системе в противопо-
противоположном направлении, т. е.
а<2'(О) = |/(я-9, Ф + я)р. E1)
В случае, когда частицы тождественны, в приведенное рас-
рассмотрение необходимо ввести две важные модификации:
(а) детектор уже не может различить частицы 1 и 2, следо-
следовательно, сечение ог(Й) должно быть переопределено;
(б) функция ^?ь должна быть соответствующим образом сим-
метризована.
Модификация (а) характерна не только для квантово-меха-
нического рассмотрения. Определим ог(й) как число частиц
A и 2), испущенных в телесном угле (Q, Q + dQ) за единицу
времени в расчете на единичный падающий поток, т. е. (ср.
УР- E))
crB)(Q). E2)
Отметим, что в этом случае
4$@)<Ш, E3)
если мы сохраняем обычное определение полного сечения рас-
рассеяния a(tot) как числа частиц, отклоненных от падающего по-
потока за единицу времени в расчете на единичный падающий
поток.
С другой стороны, модификация (б) является специфическим
квантовым эффектом. Соответствующим образом симметризо-
ванный волновой пакет, воспроизводящий те же начальные ус-
условия, что и Чгб (/?, г, /), определяется, как мы сейчас покажем,
выражением
%(R, r, /) = -J=-pF»(*. r, f)±4b(R, -r, /)].
До столкновения, т. е. при / <С 0, эта функция Ч?ь имеет вид
Ф(#, /)ф»(г, /), где (ур. D7))
Ф»(г, /) = е-'»-'в<'*—5=-[x(r-u/-6)e'*r±x(-r — vt— b)e-{kr].
Таким образом, Фф является суммой двух волн. Первая описы-
описывает начальное состояние в системе центра масс при столкнове-

106 ГЛ. XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
нии, в котором частица 1 налетает на частицу 2 с относительной
скоростью v и прицельным параметром Ь, тогда как вторая
волна определяет состояние, в котором частицы 1 и 2 поменя-
поменялись местами. Поскольку эти волны не перекрываются (так как
<<0), а каждая из них имеет норму 1/2, то Фф является нор-
нормированной волновой функцией, описывающей, подобно Фф,
две частицы, налетающие друг на друга с относительной ско-
скоростью v и с прицельным параметром Ъ.
После столкновения W&, подобно Ч1», является суммой двух
членов (ср. ур. D8)). Первый член Фф описывает проходящую
волну и не дает вклада в сечение, второй член ф'ф*4' описывает
рассеянную волну и получается из Ф^а) применением к if(d)
операции симметризации того же типа, что и при переходе от
¦ф(<*> (г, t) = —=- \^ (Г, /) ± ¦tff* {— Г, 01-
Возвращаясь к асимптотическому выражению D9), видим, что
переход от Oij)<d> и фф<<*> состоит в замене амплитуды рассея-
рассеяния /(9, ф) на симметризованную амплитуду
f(9, ф) = -^[/(9, ф)±/(я-9,
Используя выражение для рассеянных волновых пакетов, по-
лучаем сечение рассеяния тем же способом, что и в случае раз-
различимых частиц
оК» (Q) = | f (в, ф)|2 = 1|/(9, ф)±/(я-в, ф + л)|2,
аи (Q) = 11 (Я - 9, ф + я) р = or"» (Q).
В соответствии с определением E2)
cr(Q) = 2|f(9, ф)|2 = |/(9, ф)±/(я-8, Ф + я)Р. E4)
Напомним, что амплитуда рассеяния является коэффициен-
коэффициентом при расходящейся волне в стационарном решении уравне-
уравнения Шредингера
имеющим асимптотический вид
Jkr
Симметризованная амплитуда рассеяния /(9, ф) получается
умножением над/ 2 либо четной части амплитуды /(9, ф), либо

§ 10. СТОЛКНОВЕНИЕ ПРОТОНОВ 107
ее нечетной части, в зависимости от того, являются ли рассма-
рассматриваемые частицы бозонами или фермионами. Если V—цен-
V—центральный потенциал, то четная часть /@) является суммой
вкладов от парциальных волн четного порядка, а нечетная
часть — суммой вкладов от парциальных волн нечетного по-
порядка. При энергиях, достаточно малых для того, чтобы основ-
основной вклад давала бы s-волна, два (бесспиновых) фермиона
практически не рассеиваются друг на друге, в то время как се-
сечение рассеяния двух бозонов в четыре раза больше чем в слу-
случае различимых частиц. (Амплитуда рассеяния умножается на
•\/2, а сечение равно удвоенному квадрату модуля симметризо-
ванной амплитуды, что и дает в результате множитель 4.) .
§ 10. Столкновение протонов
Проведенное в предыдущем параграфе исследование может
быть легко распространено на случай столкновения двух тожде-
тождественных частиц со спином. В качестве примера рассмотрим
столкновение двух протонов, предполагая, что потенциал взаи-
взаимодействия имеет центральную симметрию. Полный спин яв-
является постоянной движения, однако взаимодействие в синглет-
ном и триплетном состояниях может быть различным.
Пусть /s(9) и ft(Q) обозначают соответствующие несимме-
тризованные амплитуды рассеяния. Поскольку протоны являют-
являются фермионами, волновая функция должна быть антисимметрич-
антисимметричной относительно перестановки этих частиц. Если функция опи-
описывает триплетное состояние, то она симметрична относительно
обмена спинов и, следовательно, антисимметрична относительно
перестановки координат гA> и г<2), так что симметризованная
амплитуда рассеяния имеет вид
f, (в) = —1=- [f, (в) — f t (я _ в)].
Поперечное сечение рассеяния протонов в триплетном состоя-
состоянии
at (Q) = 2 | Мб) Р = | ft (9) -ft(n- 9) p.
Если же волновая функция описывает синглетное состояние, то
она является антисимметричной при обмене спинов и, следова-
следовательно, симметричной относительно обмена пространственных
координат, так что в этом случае симметризованная амплитуда
рассеяния имеет вид

108 ГЛ. XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
Таким образом, поперечное сечение рассеяния двух протонов
в синглетном состоянии
ae(Q) = 21 fa (в) р = | /в (в) + /в (я _ в) р.
Если мишень и налетающий поток состоят из неполяризован-
ных протонов, то в каждом столкновении имеется случайное
распределение спинов у налетающей частицы и частицы ми-
мишени. Поскольку пространство триплетных состояний трехмер-
трехмерно, а пространство синглетных состояний одномерно, то полный
спин в начальном состоянии с вероятностью 3/4 будет равен
единице и с вероятностью 1/4 равняется нулю, так что
a(Q) = -|cr<(Q) + -j-or.(Q) =
= || ЫЭ) - Ыя - 9) Р + \\ М9) + Ыя- в) Р. E5)
Если дополнительно предположить независимость потенциала
от спина, то
и мы получаем окончательно
а(й) = [/(Э)|2+|/(я-е)р-1[Г(Э)/(л-е) + /(е)Г(л-е)]. E6)
В частности, в области достаточно низких энергий, когда
можно пренебречь ядерными силами и рассматривать V(r) как
отталкивающий кулоновский потенциал е2/г, амплитуда рассея-
рассеяния Д9) определяется формулой (XI. 33), а сечение рассеяния —¦
формулой Мотта
E7)
где Е — энергия в системе центра масс, аи — относительная
скорость двух протонов. Полезно сравнить этот результат с фор-
формулой Резерфорда (ур. (XI. 36)).
Классическое рассмотрение дает только два первых члена
формулы Мотта
Третий член обусловлен чисто квантовым эффектом интер-
интерференции амплитуд рассеяния /(9) и /(я —9). Если e2/hv ».l,
то этот член осциллирует около нуля тем быстрее, чем больше
мы отклоняемся от угла 9 = '/гя (в любом направлении). В пре-
пределе h -*¦ 0 эти осцилляции, сохраняя амплитуду, становятся все

§ И. СТАТИСТИКА АТОМНЫХ ЯДЕР 109
более быстрыми, так что среднее значение сечения а(й), усред-
усредненное по малому, но не нулевому телесному углу р(й), стре-
стремится к классическому сечению aci(?2).
§11. Статистика атомных ядер
Во многих задачах ядра атомов можно рассматривать как
частицы, имеющие определенный спин /.
В атомной физике это приближение весьма эффективно.
Атомное ядро является ансамблем JC нуклонов: Z протонов и
JV нейтронов (Jf = Z-\-N). Динамические переменные атом-
атомного ядра описываются функциями фундаментальных перемен-
переменных образующих ядро JC частиц. Пусть R и Р — координата и
импульс центра масс (ср. § IX. 13). Обозначим р набор вну-
внутренних переменных: спинов, относительных координат и им-
импульсов нуклонов. Среди этих переменных особенно существен
полный момент импульса / внутренних переменных, так назы-
называемый спин ядра. Момент / представляет собой сумму спинов
JC отдельных нуклонов, и (JC— 1)-го относительного орбиталь-
орбитального момента импульса. Согласно правилу сложения моментов /
может принимать как целые, так и полуцелые значения, в зави-
зависимости от того является ли Л3 четным или нечетным.
В отсутствие внешнего поля движение центра масс отде-
отделяется, и гамильтониан системы представим в виде суммы двух
членов: кинетической энергии центра масс Р2/2М (здесь М —
полная масса ядра) и .внутренней энергии /t(p), включающей
как кинетическую энергию нуклонов, так и энергию их взаимо-
взаимодействий друг с другом. Гамильтониан h имеет определенное
число связанных состояний. Обозначим е0 собственное значение,
соответствующее основному состоянию. Поскольку силы между
нуклонами инвариантны относительно вращений, то /i(p) ком-
коммутирует с тремя компонентами векторного оператора / (см.
гл. VIII). Каждому собственному значению в дискретном
спектре гамильтониана соответствует определенное собственное
значение / спина, которое B/+ 1)-кратно вырождено. В даль-
дальнейшем / обозначает спин основного состояния, ц — возможные
значения }г{\ь = —/, —/+1> •••. +/). а Хм- ~ собственную
функцию основного состояния с моментом импульса (}\i)
h (р) Хц =
Эти B/ + 1) векторов %^ отличаются друг от друга только своей
ориентацией. Все они могут быть получены один из другого
действием операторов /+, ;'- и образуют базис представления
векторного оператора /. Радиус ядра имеет порядок от 10~13 до
Ю-'2 см и, следовательно, среднее межнуклонное расстояние для
ядра в состоянии Хц имеет тот же порядок.

ПО ГЛ. XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
До тех пор пока ядро остается в основном состоянии волно-
волновая функция системы имеет вид ?й ^ (R, I1) Хц. и ядро можно
рассматривать как частицу со спином / и волновой функцией
г|)(/?, \i) в представлении {/?, /г}, поскольку /i(p) в гамильто-
гамильтониане может быть заменено на постоянную е0, a ty(R, \i) разви-
развивается во времени так же, как и волновая функция свободной
частицы массы М (с точностью до не имеющего физического
значения постоянного фазового множителя).
Если ядро находится во внешнем поле, например, в электри-
электрическом поле с потенциалом V(r), то гамильтониан будет содер-
содержать, помимо уже упомянутых выше членов, члены, отвечаю-
отвечающие взаимодействию Z протонов с внешним полем. В этом слу-
случае ядро можно рассматривать как частицу со спином / только
приближенно, так как гамильтониан теперь не коммутирует
с h(p). Однако если поле незначительно изменяется на расстоя-
расстояниях, имеющих тот же порядок, что и радиус ядра, то это при-
приближение остается достаточно хорошим, ибо в этих условиях
значение поля в месте нахождения каждого из протонов можно
заменить его зналением в центре масс. В этом случае внешнее
взаимодействие равно ZeV(R) и собственные состояния гамиль-
гамильтониана имеют вид X ФС?> Ц)Хц>гДе ty(R> V-)— стационарное со-
II
стояние частицы массы М спина / и заряда Ze в электрическом
потенциале1) V(R).
Рассмотрим систему из п ядер, каждое из которых нахо-
находится в своем основном состоянии. Приближение, в котором
каждое из ядер рассматривается как частица с заданным спи-
спином будет оправдано до тех пор, пока эти ядра будут доста-
достаточно удалены друг от друга, что имеет место, например, в слу-
случае молекулы или твердого тела. Пусть /?A) координата t-ro
ядра, a |i<'> есть z-компонента его спина. Тогда волновая функ-
функция системы зависит от /?<•> и \i^\ а движение системы опреде-
определяется гамильтонианом, зависящим от переменных /?<'>, Р<'>
и /с».
Рассмотрим, как изменяется это упрощенное описание при
введении постулата симметризации. Можно ожидать, что сим-
симметризация будет существенна лишь в том случае, когда неко-
некоторые из ядер тождественны. Это можно доказать тем же мето-
методом, что и в § 8. Два разных ядра являются различными части-
частицами, несмотря на тождественность частиц, протонов и нейтро-
нейтронов, составляющих эти ядра.
') Первая поправка к этому приближению сохраняет используемое иа«
глядное представление о ядре и состоит в приписывании ядру квадрупольного
момента (если /5= 1), который может быть представлен в виде функции от
компонент / и приводит к взаимодействию между спином ядра и внешним
полем,

§ 11. СТАТИСТИКА АТОМНЫХ ЯДЕР Ш
Рассмотрим систему двух тождественных ядер спина /". Бу-
Будем описывать состояние системы волновой функцией
Перестановка двух ядер — операция Р, определяемая соотно-
шением
В действительности, система содержит 2Z протонов и 2N ней-
нейтронов, и ее динамическое состояние получается антисимметри-
антисимметризацией по протонам и нейтронам вектора
Операция Р состоит в замене координат и спинов протонов и
нейтронов первого из ядер на координаты и спины протонов и
нейтронов, второго — для всех Jf элементарных перестановок.
Поскольку каждая из последних приводит к изменению знака
у антисимметризованного вектора, то получаем
Так что
Сказанное легко может быть распространено на системы, содер-
содержащие более двух тождественных ядер. Волновая функция
должна быть симметрична или антисимметрична относительно
перестановок тождественных ядер в соответствии с четностью
или нечетностью числа нуклонов, образующих ядро.
Иными, словами, ядра атомов будут:
(а) бозонами, если они содержат четное число нуклонов;
(б) фермионами, если они содержат нечетное число нукло-
нуклонов.
Эти различия в статистике могут неожиданно проявиться во
многих явлениях, в которых на первый взгляд чисто ядерные
эффекты представляются несущественными. Именно такая си-
ситуация возникает при исследовании удивительных свойств жид-
жидкого гелия (Не4) при очень низких температурах. Не4 подчи-
подчиняется статистике Бозе — Эйнштейна, тогда как его изотоп Не3
подчиняется статистике Ферми — Дирака и ведет себя при низ-
низких температурах совершенно иначе.
В дальнейшем (§ XVIII.17) мы еще раз встретимся с необхо-
необходимостью учета статистики ядер при описании полосатых спек-
спектров гомонуклеарных диатомных молекул.

112 ГЛ. XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
§ 12. Сложные атомы. Приближение центрального поля
Принцип Паули существен при описании спектров сложных
атомов.
В отсутствие внешнего поля гамильтониан атома не зависит
от спинов его Z электронов и определяется формулой (XIII. 71).
Для большей точности следовало бы добавить члены, соответ-
соответствующие спин-орбитальному взаимодействию, но в рамках на-
настоящего обсуждения ими можно пренебречь. За исключением
специального случая атома водорода (Z=l) задача на соб-
собственные значения для такого гамильтониана не может быть
решена в явном виде.
Для определения стационарных состояний атома часто ис-
используется приближение независимых частиц или приближение
центрального поля, согласно которому каждый из электронов
движется независимо от других в центральном потенциале V(r),
описывающем притяжение со стороны ядра, и усредненный эф-
эффект отталкивания от других электронов. Ясно, что упомянутый
эффект зависит от динамического состояния электронов, и та-
таким образом один потенциал V{r) не может даже приближенно
объяснить особенности всего спектра атома. Однако если огра-
ограничиться изучением основного и первых возбужденных состоя-
состояний атома, то вид V(r) можно фиксировать, и чем разумнее бу-
дет выбор потенциала, тем лучше будет приближение. Суммар-
Суммарное действие электронов приводит к экранированию кулонов-
ского поля ядра, чтр становится все более заметным по мере
удаления от ядра: V(r), имеющий вид —Ze2/r вблизи начала ко-
координат, с ростом г все более значительно отклоняется от чисто
кулоновской формы и переходит в —е2/г в асимптотической об-
области. Эти полуколичественные рассмотрения достаточны для
наших целей. В дальнейшем мы обсудим два метода определе-
определения V(r): метод Томаса — Ферми (§ 13) и метод Хартри — Фока
(гл. XVIII).
В приближении центрального поля гамильтониан имеет вид
E8)
где
Собственными векторами гамильтониана Н являются опре-
определители Слэтера порядка Z У( Z, которые могут быть построены
из базисных векторов оператора п. Собственное значение опера-
оператора Н, соответствующее данному определителю Слэтера, равно
сумме энергий Z одночастичных состояний, которые участвуют

§ 12. СЛОЖНЫЕ АТОМЫ. ПРИБЛИЖЕНИЕ ЦЕНТРАЛЬНОГО ПОЛЯ ИЗ
в построении этого детерминанта. Таким образом, задачу на
собственные значения для Н легко решить, если известно ре-
решение задачи для одночастичного гамильтониана h.
Оператор h является гамильтонианом частицы со спином 1/2,
которая находится в не зависящем от спина центральном по-
потенциале. Решение соответствующей задачи на собственные зна-
значения в случае бесспиновых частиц было приведено в главе IX.
Наличие спина приводит лишь к двукратному вырождению каж-
каждого уровня. Операторы h, I2, 1г и sz образуют полный набор
коммутирующих наблюдаемых, базисные векторы |n//n//ns> ко-
которого нумеруются четырьмя квантовыми числами п, I, mi, ms.
Спиновое квантовое число ms может принимать значения ±'/2;
главное квантовое число п определяется так же, как и в задаче
об атоме водорода. (Число нулей радиальной волновой функ-
функции равно п — 1-Х.) Поскольку энергия каждого состояния е.к
зависит только от п и /, то каждый отдельный уровень 2B/ + 1)'
кратно вырожден.
Порядок следования уровней eni в спектре энергии слабо за-
зависит от формы потенциала V(r). При заданном / уровни рас-
расположены в порядке возрастания п. Если бы V(r) был чисто ку-
лоновским потенциалом, то все уровни, отвечающие данному
значению л(/=0, 1, ..., п — 1), совпадали бы (см. рис. 36, т. 1).
Экранирующий эффект остальных электронов приводит к тому,
что эти уровни поднимаются с увеличением среднего расстоя-
расстояния электрона от ядра, следовательно, уровни растут с ростом
п и /. Если ограничиться рассмотрением основных и возбужден-
возбужденных состояний атома, то порядок следования уровней для всех
атомов практически один и тот же:
Is 2s 2р 3s Зр [4s, 3d] Ар [5s, Ad] 5р [6s, Af, 5rf] 6p [7s, 5Д 6rf]
2 2 6 2 6 2+10 6 2+10 6 2+14+10 6 2+14+10
Уровни, заключенные в скобки, почти совпадают, и их порядок
может меняться при переходе от одного атома к другому. Число,
стоящее под каждым из термов, дает кратность вырождения
соответствующего уровня.
Каждому набору Z одночастичных состояний соответствует
определитель Слэтера и, следовательно, стационарное состоя-
состояние атома. Энергия этого состояния равна сумме энергий состав-
составляющих его одночастичных состояний и зависит только от числа
электронов, находящихся на каждом из уровней еы- Задание
чисел заполнения каждого одночастичного уровня определяет
конфигурацию. При таком определении состояния, отвечающие
одной и той же конфигурации, имеют одинаковые энергии.
Пусть v,- — число электронов, занимающих уровень е«, v* не
превосходит вырождения gi этого уровня. Если \i = gi, то элек-

114 ГЛ. XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
троны образуют замкнутую оболочку, если v/ < gi, то оболочка
не заполнена. Имеется
g|!/Vi!te< —v,)!
способов распределения V; электронов по gi одночастичным со-
состояниям уровня. Следовательно, почти все конфигурации вы-
вырождены за исключением тех, которые целиком состоят из за-
заполненных оболочек.
Для образования конфигурации основного состояния надо
разместить Z электронов на низших энергетических уровнях.
Эти электроны занимают h оболочек, из которых первые (h— 1)
заполнены, а последняя в общем случае не заполнена, за исклю-
исключением некоторых значений Z (Z = 2, 4, 10, 12, 18 и т. д.).
Рассмотрим для примера атом углерода (Z = 6). В основ-
основном состоянии оболочки Is и 2s заполнены, а два оставшихся
электрона находятся на 2р-оболочке. Поскольку имеется С%= 15
способов размещения этих электронов по б уровням этой обо-
оболочки, то основное состояние атома углерода (в приближении
независимых частиц) 15-кратно вырождено. В случае неона
(Z = 10) основное состояние состоит из трех заполненных обо-
оболочек: Is, 2s и 2р и, следовательно, невырождено.
Электроны, заполняющие низшие оболочки, находятся на
наиболее близком расстоянии от ядра. Химические свойства ато-
атомов практически не зависят от движения этих электронов. При
низких энергиях, которыми характеризуются химические реак-
реакции, взаимодействия между атомами зависят в основном, если
не исключительно, лишь от движения электронов на внешних
оболочках. Следовательно, два атома, внешние оболочки кото-
которых имеют сходную электронную структуру, имеют близкие хи-
химические свойства. Так, внешней оболочкой для всех инертных
газов (Ne, Аг, Кг, Хе) является заполненная р-оболочка. У га-
галогенов (F, C1, Вг, I) на внешней р-оболочке отсутствует один
электрон. Наконец, у щелочных элементов (Na, К, Rb, Cs) на
s-оболочке имеется всего один электрон, а р-оболочка, располо-
расположенная сразу под s-оболочкой полностью заполнена. В общем
случае положение каждого элемента в периодической таблице
легко может быть предсказано, если известен порядок заполне-
заполнения его электронных оболочек ').
') Дальнейшие детали кваитовомеханического объяснения химических
свойств атомов имеются в работах: М. Борн. Атомная физика. М., Мир, 1967;
L. Pauling, E. В. Wilson. Introduction to Quantum Mechanics, New-York,
McGraw-Hill, 1935. Общую теорию атомных спектров см. в кн.: Е. Кондон,
Т. Шортли. Теория атомных спектров. М., ИЛ., 1949; G. Racah. Phys. Rev. 62,
438 A942); 63, 367 A943).

§ 13. МОДЕЛЬ АТОМА ТОМАСА — ФЕРМИ 115
§ 13. Модель атома Томаса —Ферми
Потенциал основного состояния в случае Z ^> 1 можно оп-
определить, используя полуклассический метод, развитый Тома-
Томасом и Ферми.
Пусть р(г)—плотность вероятности обнаружить электрон
в элементе объема (г, г -f- dr) в случае, когда атом находится
в основном состоянии. Мы будем предполагать, что эта функ-
функция сферически симметрична. Она удовлетворяет условию нор-
нормировки
оо
4я J р (г) г2 dr = Z. E9)
о
Z электронов образует вокруг ядра облако с отрицательным
электрическим зарядом средней плотности —ер(г). Заряды
атома создают усредненный электрический потенциал Ф(г), ко-
который определяется:
(i) точечным зарядом Ze ядра, помещенного в начало коор-
координат;
(И) непрерывным распределением электрического заряда
с плотностью —ер (г).
Потенциал Ф является решением уравнения Пуассона
F0)
которое ведет себя в начале координат согласно условию
lirnr<D = Ze. F1)
В пределе Z\S?1 электрическое поле, порождаемое одним
электроном, мало по сравнению с полем остальных электронов,
и в приближении независимых частиц потенциал, действующий
на каждый электрон, имеет вид —еФ(г).
В основном состоянии атома Z электронов занимают Z низ-
низших квантовых состояний частицы с массой т в поле —еФ.
Плотность р(г) равна сумме плотностей |г|)|2 первых Z уровней.
Это означает наличие функциональной связи между р(г) и по-
потенциалом —еФ. Для определения этой зависимости мы обра-
обратимся к следующему «полуклассическому» приближению.
В классическом пределе число стационарных состояний в по-
полосе энергий (s, e -f- бе) пропорционально объему, занятому
этой полосой в фазовом пространстве соответствующей класси-
классической частицы. Коэффициент пропорциональности равен 2/ft3,
что в два раза больше, чем множитель, использованный
в § VI. 11, из-за того, что электрон имеет два состояния спина.
Когда заполнены Z низших квантовых состояний, распределение

116 ГЛ. XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧДСТИЦ
энергии электронов в атоме совпадает с распределением энер-
энергии статистической смеси Z классических электронов, имеющих
в фазовом пространстве плотность
Г 2 р2 Л
1 -7Т-, если в ss -? еФ < е0,
П(г,р) = \ h* 2т F2)
I 0, если е > е0,
где во — энергия высшего из заполненных уровней. Поскольку
начало отсчета энергии можно фиксировать произвольно, мы
положим 80 = 0.
Квазиклассическое приближение состоит в предположении,
что электроны в атоме имеют то же пространственное распреде-
распределение, что и классическая статистическая смесь
= -?¦ \ dp.
е<0
Заменив в его выражением через р и Ф, находим после неслож-
несложного интегрирования
если Ф > 0,
F3)
0, если Ф < 0.
Подставив F3) в правую часть равенства F0), получаем диф-
дифференциальное уравнение второго порядка для Ф. С учетом со-
соотношений E9) и F1) эта функция определена полностью. Ра-
Равенства F1), F3), E9) и F2) являются основными соотноше-
соотношениями модели Томаса ¦— Ферми.
Для определения Ф и р из полученных соотношений удобно
сделать следующую замену переменной и функции:
г = 1~ЧгЬх, ф = — х, F4)
где
V» л2 _ - ,.-8
—j fa 0,5 • 10 см.
Из F3) получаем р как функцию безразмерных величин % и х
р =
0, если % < 0.
Основное уравнение F0) эквивалентно уравнению
~'и%'\ если % > 0,
0, если % < 0.
-{

§ 13. МОДЕЛЬ АТОМА ТОМАСА — ФЕРМИ
117
Условие F1) означает, что %@)= 1. Из уравнения F7) сле-
следует, что %(х) очевидно имеет не более чем один нуль в интер-
интервале @, с»); если % обращается в нуль в точке хо, то % положи-
положительно в интервале @, хо) и отрицательно в интервале (х0, °о).
Следовательно, учитывая F4), F6) и F7), условие E9) можно
переписать в виде
х°
Это условие требует, чтобы производная %' обращалась в нуль
в точке Хо, а значит % обращается в нуль только на бесконеч-
бесконечности.
Итак, %(х) есть решение
уравнения
%" = х-Ч'%1*, F8)
удовлетворяющее условиям
Х@)=1, Х(°°) = О. F9)
Функция %(х) может быть
найдена численным интегриро-
интегрированием. На рис. 5 изображена
соответствующая кривая. Зная
%{х), мы можем найти р(г) и
Ф@-
Для оправдания классического приближения, необходимо,
чтобы большая часть Z одноэлектронных состояний находилась
бы «в области больших квантовых чисел», т. е. чтобы Z > 1.
Для заданного атома плотность электронов р(л) и электроста-
электростатический потенциал Ф(г), определяемые в рамках модели То-
Томаса — Ферми, имеют вид, который получается в пределе, когда
квант действия % и заряд каждого электрона (—е) становятся
бесконечно малыми, число электронов Z становится бесконеч-
бесконечным, а характеристическая длина Ь?/те2 и полный заряд элек-
электронного облака (—Ze) остаются постоянными1).
Метод Томаса — Ферми позволяет оценить радиус атома.
В определении этой величины имеется некоторый произвол, по-
поскольку плотность электронов становится равной нулю только
на бесконечности и, следовательно, атом не является объектом,
15 х
Рис. 5. Функция Томаса—Ферми х (х)г
V1. зс@) = 1. хМ=о.
') Метод Томаса — Ферми дает неправильную оценку плотности электро-
электронов вблизи начала координат (r^b/Z), а также в асимптотической области
(г > 6). В начале координат функция р(/-) расходится, как г~ '!, вместо того
чтобы оставаться конечной, тогда как иа бесконечности она стремится к нулю,
как г~е, а не экспоненциально.

118
ГЛ. XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
занимающим хорошо определенную область пространства. Ра-
Радиусом атома мы называем радиус R(a) сферы с центром в на-
начале координат, которая содержит заданную часть A —а) от Z
электронов атома. Согласно
этому определению
3
2 у/" Обозначим
, I R(a) = Z-'''bX(a).
Учитывая соотношения F4),
F6) и F8), получаем следую-
Рис. 6. Зависимость радиуса R от Z ^ee Уравнение для функции
25 50
75
100
ру
атома в теории Томаса — Ферми
X:
Это уравнение можно решить
численными методами.
При постоянном значении а для всех атомов X будет одно
и то же, а радиус атома будет пропорционален Z~'/s.
Если а = 1/Z, то соответствующий радиус
является радиусом сферы, содержащей все электроны, кроме
одного. На рис. 6 приведена зависимость R от Z. Заметим, что
R практически не зависит от Z (R ж B — 3) • 10~8 см).
§ 14. Система нуклонов и изотопический спин
Рассмотрим систему из Z протонов и N нейтронов. Эта си-
система описывается гамильтонианом Н. Нейтроны и протоны яв-
являются подобными частицами, и для того чтобы различать их,
мы припишем протонам номера от 1 до Z, а нейтронам номера
от Z + 1 до Z + N = J?. Обозначим Аг оператор антисимметри-
антисимметризации первых Z частиц, а Аы — оператор антисимметризации N
последних частиц. Мы будем придерживаться обозначений, вве-
введенных в §§ 2 — 4. Пусть
— волновая функция, описывающая возможное состояние си-
системы в симметрическом представлении {Q}. Функция <р

§ 14. СИСТЕМА НУКЛОНОВ И ИЗОТОПИЧЕСКИЙ СПИН ЦЭ
удовлетворяет условиям антисимметрии
= ф. G0)
Для описания системы Z протонов и N нейтронов имеется и
другой формализм, полностью эквивалентный предыдущему.
В новом формализме нейтрон и протон рассматриваются как
различные состояния одной и той же частицы — нуклона. Рас-
Рассматриваемая система описывается тогда как система JC нукло-
нуклонов, из которых Z находятся в протонном состоянии, а ^ — в
нейтронном. В этом случае JP нуклонов являются тождествен-
тождественными фермионами, и состояния системы антисимметричны отно-
относительно перестановки этих Jf тождественных фермионов. Цель
настоящего параграфа состоит в изложении этого формализма
и в доказательстве его эквивалентности обычному.
Для того чтобы отличать состояние протона от состояния
нейтрона, каждому нуклону следует приписать дополнительную
динамическую переменную — заряд, принимающий два значе-
значения. Мы будем обозначать соответствующие состояния © и v,
где © описывает протонное состояние, a v — нейтронное. Заря-
Зарядовое пространство нуклона, так же как и спиновое, двумерно.
Следовательно, мы можем определить в этом пространстве опе-
операторы, аналогичные операторам, введенным в случае спино-
спинового пространства, и имеющие те же математические свойства.
Рассмотрим, в частности, три матрицы Паули. В представлении,
в котором © и v являются базисными векторами, эти матрицы
описывают в зарядовом пространстве векторный оператор т =
= 0*1, х2, хз), аналогичный вектору а = (ах, ау, аг). Вектор
t^jr G1)
является аналогом спина s и называется изотопическим спи-
спином нуклона. Мы видим, что
,1 1,1 1
Проекторы По и nv на протонное и нейтронное состояния оп-
определяются формулами
Пш = -^A+т3), Пу = уA-т3), G2)
а оператор заряда нуклона равен
П 0 +)
Произведение JF одночастичных зарядовых пространств яв-
является зарядовым пространством <§с системы /С нуклонов.

120 ГЛ. XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
Полный заряд системы представляется оператором
N
С^?еП{» = е(±Ж + Т3), G3)
где Г3 — третья компонента полного изотопического спина
Т=1>>. G4)
Ортонормированный базис в &с можно получить, рассмо-
рассмотрев всевозможные произведения из Ж со- или v-векторов.
В частности, базисный вектор
. . . q(Z)v(Z+1) _ _ ^ VVT)
описывает состояние, в котором первые Z частиц — протоны,
а последние N — нейтроны. В дальнейшем будем рассматривать
только состояния с зарядом С = Ze, т. е. с
Можно построить (Jf\/Z\Nl) базисных векторов, соответствую-
соответствующих этому собственному значению. Типичный базисный вектор
имеет вид
.. V(V)
и описывает состояние, в котором Z частиц аь а2 аг яв-
являются протонами, а остальные — нейтронами.
Кет-векторы системы Ж нуклонов являются векторами про-
пространства, которое можно представить в виде тензорного про-
произведения пространства &с и пространства <gT0 остальных дина-
динамических переменных. При перестановке /С нуклонов осуще-
осуществляется одна и та же перестановка как зарядовых перемен-
переменных, так и остальных переменных. Если Рс описывает заданную
перестановку зарядов, а Ро — ту же перестановку остальных
переменных, то полная перестановка описывается оператором
Оператором антисимметризации системы JC нуклонов будет
оператор
Л = ЖЕ(-1)РР==ЖЕ(-1)РР<'РС- G5)
р
Состояния системы с полным зарядом Ze описываются векто-
векторами Ф пространства 8с®<§ъ, удовлетворяющими условию

8 М. СИСТЕМА НУКЛОНОВ И ИЗОТОПИЧЕСКИЙ СПИН 121
антисимметрии
ЛФ = Ф G6)
и уравнению
ф (Т) ___ / 7 \I\ iTl /77V
Покажем теперь, что имеется взаимно однозначное соответ-
соответствие между векторами Ф, для которых выполняются соотно-
соотношения G6) и G7), и векторами <р из ^Го, удовлетворяющими
условиям G0), а именно
1ф>=лАжЁгЛ|(рIс)' G8>
1ф>ял/1Йг<с|ф>' G9>
и что это соответствие сохраняет скалярное произведение.
Рассмотрим вектор |<р>, удовлетворяющий условиям G0).
Соответствующий ему вектор |Ф>, полученный по формуле G8),
очевидно, удовлетворяет G6), а также и G7), поскольку Т$
коммутирует с А и T3\Q = 1/2(Z — N) ID-
Покажем теперь, что Частичное скалярное произведение
в G9) определяет вектор |<р>. Используя G5) и G8), имеем
сЮ. (so)
Далее, Jf\ перестановок можно разбить на две группы. В пер-
первую группу входят те перестановки F, которые меняют порядок
первых Z частиц друг с другом и (или) переставляют послед-
последние N частиц между собой. Все (N\Z\) перестановок F не из-
изменяют вектор |?> и домножают вектор |<р> на (—1)'
Перестановки G из второй группы переводят вектор ? в другой
вектор ?а и
Следовательно, сумма в правой части равенства (80) имеет
(N\Z\) ненулевых слагаемых, каждое из которых равно |<р>,
что и дает доказываемое равенство G9).
Легко видеть, что соответствие G8) сохраняет скалярное
произведение, ибо если |Ф> и |Х> соответствуют |<р> и |х>, и

122 ГЛ. XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
поскольку
I Ф) удовлетворяет уравнениям G6) и G8), то имеем
Осталось показать, что соответствие взаимно однозначное.
Пусть |Ф> —вектор, удовлетворяющий условиям G6) и G7),
а |ф> — вектор, построенный по формуле G9). В силу G7) |Ф>
является линейной комбинацией векторов |?а> с векторами из
S'o в качестве коэффициентов
Вектор |ф> является коэффициентом при ? в сумме, стоящей
справа. Перестановка типа F, действуя на Ф, дает
а также
la)- (82)
Действие Fc на один из векторов |?a> переводит его в другой
вектор |?а> и, в частности, оставляет |?> инвариантным. Следо-
Следовательно, коэффициент при |?> в разложении F\O} равен ко-
коэффициенту при Fc\l) в правой части равенства (81). Прирав-
Приравняв его коэффициенту при |Е;> в соотношении (82), находим
Это показывает, что вектор |<р>, соответствующий |ф>, действи-
действительно обладает свойством антисимметрии G0). Н
Каждое состояние системы Z протонов и N нейтронов, опи-
описываемое вектором |ф> в обычном формализме, в новом фор-
формализме описывается вектором |Ф>. Поскольку между этими
векторами имеется сохраняющее скалярное произведение взаим-
взаимно однозначное соответствие, то амплитуды вероятности, вычис-
вычисленные по векторам нового формализма, совпадают с амплиту-
амплитудами, определенными векторами старого формализма. Это га-
гарантирует эквивалентность двух формализмов. Если динамиче-
динамическая переменная представляется в обычном формализме опе-
оператором Q, то в новом формализме ей соответствует оператор Q
в пространстве cfo<8>^V, оператор Q симметричен относительно

§ 14. СИСТЕМА НУКЛОНОВ И ИЗОТОПИЧЕСКИЙ СПИН 123
'Ж нуклонов, имеет тот же спектр собственных значений, что
и Q, и его собственные состояния можно получить из собствен-
собственных состояний оператора Q при помощи соотношения G8).
Q является симметричным оператором, матричные элементы ко-
которого удовлетворяют уравнению
<Х | Q | Ф> == <х | Q I ф>- (83)
В качестве примера построим оператор Я, предполагая, что
между нуклонами действуют только двухчастичные силы.
Гамильтониан имеет вид
Я = К + V, (84)
где К — полная кинетическая энергия. Если kp{%) и kn{%)—ки-
kn{%)—кинетическая энергия протона и нейтрона соответственно, то
где
¦*\р ' ,Z_j **р > 'V П ,Z_j **П *
Полная потенциальная энергия V состоит из }/2Jf(Jf— 1) чле-
членов, соответствующих взаимодействию двух частиц. Имеется
Y2Z(Z— 1) членов взаимодействия протон — протон
V рр = Z-i vpp »
где Vpp = VpP (|H), lu)) — потенциал взаимодействия между про-
протонами с номерами i и. /. Аналогично имеется ZN членов взаи-
взаимодействия протон — нейтрон
I/ V V ..('Л
У рп Zj Zj Vpn
и l/2N(N—1) членов взаимодействия нейтрон — нейтрон
v tin — Zj vnn •
Следовательно, полная потенциальная энергия есть
V = V 4-1/ 4-1/
' ' рр i ' рп I ' пп-
Оператор R, соответствующий К, имеет вид
N
А — Zj V«p Aio) -г «n iiv ;• (oo>
Он симметричен и коммутирует с А. Для того чтобы показать,
что R удовлетворяет равенству (83), учтем определение векто-
векторов |Ф> и \Х} и проекторов На и nv

124 ГЛ. XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
откуда
Поскольку К не действует на зарядовые переменные, частичное
скалярное произведение <?|/(|Ф> равно результату действия К
на <?|Ф>. Используя G9), находим
Точно так же оператор, соответствующий V, имеет вид
V = Vpp + Vpn+Vnn, (86)
где
Vpp= 2L Vpp iia Ii0 j (oba)
Vpn= Z ^[nil'ny + rfvWl (866)
Vnn= Z v'MuP. (86b)
Тем же методом, что и в случае Я, можно проверить, что 9 об-
обладает требуемыми свойствами.
Приведенная для случая протонов и нейтронов теория при-
применима и к системам, содержащим более двух типов фермио-
нов. Рассмотрим систему, содержащую г типов подобных, но
различимых фермионов: щ фермионов типа 1, п2 фермионов
типа 2, ..., пг фермионов типа г. Вместо того чтобы рассма-
рассматривать фермионы различных типов как разные частицы, эти г
типов фермионов можно рассматривать как г различных состоя-
состояний, 11>, |2> |г> одного и того же фермиона и рассмат-
рассматривать систему, состоящую из п\ -\- пч + ... + пт фермионов
одного типа, из которых п\ находится в состоянии \1},п2 — в со-
состоянии |2>, ..., пт — в состоянии |л>. Эквивалентность полу-
получаемого таким образом «изотопического» формализма стандарт-
стандартному можно показать, используя те же методы, что и в случае
системы нуклонов. Все эти замечания применимы и для бозон-
ных систем, если всюду операцию антисимметризации заменить
на операцию симметризации (задача 9).
§ 15. Использование изотопического спина. Зарядовая
независимость
Рассмотрим систему из Jf нуклонов. До тех пор пока рас-
рассматриваются системы с определенным числом Z протонов и .V
нейтронов, a priori проще рассматривать протоны и нейтроны
как различные частицы (обычный формализм), нежели описы-

§ 15. ИЗОТОПИЧЕСКИЙ СПИН 125
вать их как нуклоны, которые могут находиться в различных
зарядовых состояниях (формализм изотопического спина).
С другой стороны, когда рассматриваются явления, в кото-
которых заряд ядра не сохраняется, формализм изотопического
спина неизбежен. Классический пример дает р-распад. При рас-
распаде р--радиоактивных ядер число нуклонов остается постоян-
постоянным, но один из нейтронов преобразуется в протон. В теории
этого явления ядра рассматриваются как системы, состоящие
из Jf нуклонов, находящихся во взаимодействии с квантован-
квантованными полями электронов и нейтрино. Теория р-распада лежит
вне рамок этой книги, и мы упомянули ее лишь в качестве при-
примера.
Особо важное значение формализма изотопического спина
обусловлено тем, что ядерные реакции практически не зависят
от куклонного заряда.
Массы нейтрона и протона совпадают с погрешностью, мень-
меньшей чем 0,2% и, следовательно, кинетическая энергия нуклона
практически не зависит от его заряда
kp = kn^k. (87)
Нуклон-нуклонный потенциал также почти не зависит от
заряда, и до тех пор, пока допустимо пренебрежение электро-
электромагнитными взаимодействиями1), можно считать
vPP = vpn =!>„„ = и. (88)
Мы собираемся рассмотреть следствия зарядовой независи-
независимости в предположении, что между нуклонами действуют только
двухчастичные силы2).
В обычном формализме гипотеза зарядовой независимости
находит свое выражение в двух следующих свойствах гамиль-
гамильтониана Я:
(i) H не зависит ни от Z, ни от N, а зависит лишь от пол-
полного числа нуклонов Jf;
(И) Н симметричен относительно перестановок всех частиц,
а не только относительно перестановок друг с другом отдельно
протонов и (или) отдельно нейтронов.
') Электромагнитные эффекты становятся преобладающими только при
достаточно больших расстояниях между нуклонами (»10~13 см). На больших
расстояниях vpn и vn* практически равны нулю, a v,,p становится просто ку-
лоновским отталкиванием двух протонов. Обсуждение экспериментальных дан-
данных, подтверждающих гипотезу зарядовой независимости, имеется в моногра-
монография: Дж. Блатт, В. Вапскопф (см. сноску к § XIII. 33) и в работе D. H. Wil-
Wilkinson. Phil. Mag. 1, 1031 A956).
2) Для доказательства эквивалентности зарядовой независимости и свой-
свойства инвариантности (91) в этом ограничении нет необходимости. Эта эквива-
эквивалентность может быть доказана в общем случае применением теоремы из
§ 18 Дополнения Г.

126 ГЛ. XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
Эти свойства непосредственно следуют из (87) и (88), ибо
если эти соотношения выполняются, то гамильтониан (84) при-
принимает вид
И = ? № + ? v«l\ (89)
где ? означает, как и в соотношениях (86а, б, в), суммиро-
вание по всем -^ J? (Jf — 1) парам (ij) из множества JF частиц.
В формализме изотопического спина гипотеза зарядовой не-
независимости отражается в независимости гамильтониана Я от
зарядовых переменных, так что выполняется равенство
Н = Н, (90)
где Н в правой части следует рассматривать как оператор
в пространстве S'o ® <§с- Это можно показать, либо используя
определение (83) операторов в формализме изотопического спи-
спина, либо непосредственно вычисляя выражения (85) и (86) для
R и V, предполагая выполненными соотношения (87) и (88).
Последняя процедура дает для 9 выражение
и так как
то
Но, + Ilv
V= ? 0«л = у.
Поскольку Я не зависит от зарядовых переменных, то он
коммутирует с каждой из трех компонент полного изотопиче-
изотопического спина
[Я, Г] = 0. (91)
Покажем теперь, что справедливо и обратное утверждение,
т. е. что гамильтониан Я, удовлетворяющий соотношению (91),
можно записать в виде оператора, не зависящего от зарядовых
переменных.
С другой стороны, Я является некоторой функцией от обыч-
обычных переменных !• и зарядовых переменных т каждой из частиц.
В виду предположения о характере сил, действующих между
частицами, эта функция имеет вид
н= ??<»+ ? «<">,

§ 15. ИЗОТОПИЧЕСКИЙ СПИН 127
где ?A) зависит лишь от переменных с номером i, a v^!) — от пе-
переменных с номерами i и /. Однако изотопический спин обла-
обладает теми же математическими свойствами, что и обычный спин
и, в частности, компоненты векторов t(l) имеют те же свойства,
что и матрицы Паули. Это выражается в том (см. ур. G8, 79)),
что любая функция Й от tA), ..., г'-*"' может быть представлена
в виде линейной комбинации этих операторов. Поскольку Н
коммутирует с Т, то он инвариантен также и относительно вра-
вращений в &с, и, следовательно, является скалярной функцией
векторов т*1*, ..., x(Jf). Итак, #'> является линейной скалярной
функцией от t(l) и, следовательно, не зависит от t('\ тогда как
&i!\ будучи линейной скалярной функцией от t(I) и t(/), имеет
вид
где aW) и bW> — функции только от орбитальных и спиновых
переменных. Для завершения доказательства необходимо пока-
показать, что действие (т<''т(/)) на антисимметричные векторы про-
пространства &q®&c совпадает с действием на эти векторы опе-
оператора, затрагивающего только переменные из &й. Произведе-
Произведение (г(г)г(/)) связано с оператором Р{с\ описывающим транспо-
транспозицию (ij) в зарядовом пространстве, соотношением Дирака
Pg" = i-(l+T«Y'>). (92)
Для доказательства равенства (92) введем изотопический спин
пары (ij):
tt/ = fin -|_ fifl.
Любое состояние в зарядовом пространстве является суммой
состояния 11>, для которого tif = 1 и состояния |0>, для кото-
которого tij = 0. Каждое триплетное состояние симметрично, а каж-
каждое синглетное — антисимметрично по переменным i и ;'. Таким
образом,
й|1> = 2|1>, *?/1 0> — 0,
и, следовательно,
р8я-Й
Отсюда с учетом тождества
получаем (92). Итак, мы имеем

128 ГЛ. XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
Однако в пространстве антисимметричных векторов в
Тогда
Pg'> = _/><">,
и оператор t('V может быть заменен на выражение
действующее только на переменные обычного пространства. В
Эквивалентность зарядовой независимости и вращательной
инвариантности в зарядовом пространстве имеет общий харак-
характер1). Поскольку все математические результаты, относящиеся
к вращениям (сложение изотопических спинов, теорема Виг-
нера — Эккарта, правила отбора, и т. д.), справедливы и в част-
частном случае вращений в зарядовом пространстве, то указанная
эквивалентность обеспечивает удобный метод учета зарядовой
независимости ядерных сил.
ЗАДАЧИ И УПРАЖНЕНИЯ
1. Оператор Р, оисывающий перестановку р N подобных частиц, опреде-
определен в § 2 действием на базисные векторы заданного симметричного представ-
представления {Q). Показать, что это определение не зависит от выбранного представ-
представления.
2. Обозначим Sn, А„ операторы симметризации и антисимметрнзации для
частиц 1, 2, ..., л, a Sn_b An-\ — операторы симметризации н антисимметри-
антисимметризации частиц 1, 2, ..., п— 1. Показать, что
[га-1 -| Г п
»=i J L »
[ra-l -| г n-1 -i
3. Показать, что в множестве симметричных наблюдаемых системы ./V по-
подобных частиц имеется полный набор коммутирующих наблюдаемых только в
случае, когда N — 2.
4. Найти сечение протон — протонного рассеяния (в системе центра масс)
в случае, когда налетающий протон полностью поляризован в заданном на-
направлении Ои (компонента спина по оси Ои равна -Ь'/г). а протон мишени:
(i) полностью поляризован в том же направлении; (ii) полностью поляризо-
поляризован в противоположном направлении (компонента спина по оси Ои равна
') См. сноску 2 на стр. 125.

ЗАДАЧИ И УПРАЖНЕНИЯ 129
—'/г; ("') ие поляризован. Сравнить выражение E6) с теми, которые полу-
получатся в этих трех случаях.
5. Выражение E6) дает сечение рассеяния двух фермионов со спином V*
и взаимодействием, не зависящим от спииа. Как изменится это выражение в
случае, когда две сталкивающиеся тождественные частицы будут: (i) фермио-
нами со спином /; (ii) бозонами со спином /?
6. Вычислить среднее значение (г) расстояния от начала координат до ка-
каждого из электронов в модели атома Томаса — Ферми и сравнить с числовым
оо
значением {г) для атома водорода (использовать интеграл \хМ Лх « 1,8).
о
7. Атом с атомным числом Z ионизирован р раз. Используя модель То-
Томаса— Ферми, вычислить электронную плотность р(г). Показать, что выраже-
выражение F6) для р(г) справедливо при тех же определениях Ь и х, что и в § 13
(ур. F4—65)) и что функция %(х), встречающаяся в этом выражении, яв-
является решением уравнения F7), обращающимся в нуль в некоторой точке *о
интервала @, оо), и удовлетворяет условиям
X @) = 1, х' (*о) = -
Исследовать общий характер поведения кривой р(г) н электростатического
потенциала Ф(г).
8. Рассмотреть систему Z электронов с гамильтонианом, не зависящим от
спинов. Показать, что спектр энергии состояний, имеющих определенное зна-
значение М компоненты S* полного спина, совпадает (то же положение и то же
вырождение уровней) со спектром, который может быть получен, если элек-
электроны со спином Чг и со спином —'/г рассматривать как фермиоиы разных
типов и определять состояния в которых ('/г^ + Л!) первых электронов имеют
спин '/г, а остальные спин —'/г-
9. Построить «изотопический» формализм, определенный в § 14, для си-
системы, содержащей Jf фермионов г подобных, но различных типов, а именно:
ii фермионов типа 1, Пг фермионов типа 2, ..., п, фермионов типа г (n, -f-
+ п2+ ... +nr = yf). Как следует модифицировать этот формализм, если
частицы будут бозонами, а не фермионамн?
5 А, Мессиа

ГЛАВА XV ')
ИНВАРИАНТНОСТЬ И ЗАКОНЫ СОХРАНЕНИЯ.
ОБРАЩЕНИЕ ВРЕМЕНИ
§ 1. Введение
В данной главе систематически исследуются свойства инва^
риантности уравнений движения физической системы относи-
относительно некоторых преобразований. Изучаются выводы, которые
можно сделать о поведении физической системы на основании
этих свойств инвариантности.
Вспомогательные математические сведения приведены в раз-
разделе I.
В разделе II изучаются общие свойства преобразований и
групп преобразований. Каждому преобразованию 5Г перемен-
переменных и динамических состояний будет сопоставлен оператор Т,
действующий на кет-векторы, описывающие состояния. Опера-
Оператор Т — либо линейный унитарный, либо антилинейный унитар-
унитарный и определен с точностью до произвольного фазового мно-
множителя законами преобразования основных наблюдаемых си-
системы.
Как правило, в физических приложениях оператор Т линеен
за исключением оператора обращения времени. Различные пре-
преобразования, встречающиеся в физике, образуют определенные
группы преобразований. Каждой такой группе *3 сопоставляется
группа G операторов, реализующих эти преобразования2).
После краткого обзора наиболее важных из этих групп мы про-
продемонстрируем на простых примерах методы построения G
в случае, когда группа 'S конечная, и в случае, когда 'S — не-
непрерывная группа, конечные преобразования которой могут
быть определены как последовательность инфинитезимальных
преобразований.
Вопросы, специфически относящиеся к инвариантности, раз-
разбираются в разделе III. Преобразования этого раздела не за-
') Четвертая часть (гл. XVI—XIX), за исключением нескольких специаль-
специально отмеченных мест, которые могут быть опущены при первом чтении, не за-
зависит от настоящей главы, и последующие главы при желании можно изучать
в первую очередь.
2) Используемые в этой главе понятия, относящиеся к группам и их пред-
представлениям, приведены в разделах I и II Дополнения Г.

§ 2. ТРИ ПОЛЕЗНЫЕ ТЕОРЕМЫ 131
висят от времени и линейны, а полученные результаты являются
простыми обобщениями тех, которые были получены ранее
(гл. XIII) для вращений. Инвариантность уравнений движения
динамических состояний относительно преобразований некото-
некоторой группы 'З эквивалентна предположению о том, что гамиль-
гамильтониан Н коммутирует с операторами группы G. Таким обра-
образом, любая наблюдаемая, образованная из операторов группы G,
является интегралом движения, так что из G-инвариантности
следует существование законов сохранения. Учет свойств сим-
симметрии гамильтониана Н позволяет упростить процедуру его
диагонализации и сделать ряд предсказаний о наличии и ха-
характере вырождения его собственных значений.
Инвариантность относительно обращения времени выде-
выделяется как своим физическим значением, так и тем обстоятель-
обстоятельством, что соответствующий ей оператор антилинеен. Эта ин-
инвариантность обсуждается в разделе IV. Изложенный в этой
главе материал проясняет удивительную аналогию, имеющуюся
между классической и квантовой механиками в определении
преобразований, в связи свойств инвариантности уравнений дви-
движения, симметрии гамильтониана и в существовании законов
сохранения.
Раздел I. ДОПОЛНИТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СВЕДЕНИЯ.
АНТИЛИНЕИНЫЕ ОПЕРАТОРЫ
§ 2. Три полезные теоремы
Теорема I. Справедливость соотношения
{и | А | и) = (и | В | и) при всех | и)
является необходимым и достаточным условием равенства двух
линейных операторов А и В.
Теорема II. Необходимое и достаточное условие совпа-
совпадения с точностью до фазового множителя двух линейных опе-
операторов А и В
A = Beia A)
состоит в справедливости равенства
| <а | Д | v) | = | («| В | v) | для всех | и) и I v). B)
Теорема III. Если между векторами пространства Ж су-
существует взаимно однозначное соответствие 3~, определенное
с точностью до произвольного постоянного фазового множителя
и сохраняющее модуль скалярного произведения, то фазовые
множители всегда можно выбрать таким образом, чтобы Т
было либо линейным унитарным, либо антилинейным унитар-
унитарным.
5*

132 ГЛ. XV. ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕМЕНИ
Теорема 1 доказана в главе VII (§ 5). Она приведена здесь
только для полноты изложения.
В теореме II условие B) очевидно следует из A). Для до-
доказательства обратного утверждения выберем конкретное пред-
представление, в котором обозначим Ац и Вц матричные элементы
операторов А и В соответственно. Поскольку для базисных век-
векторов представления условие B) справедливо, то
| Ац | = | Вц | при всех i и /. C)
Считая, что |«> — t-й элемент базиса, a \v} — линейная ком-
комбинация /-го и k-то базисных векторов, мы получим аналогично
| AuXj + Aikxk | = | BuXj + Bikxk |
для всех значений комплексных коэффициентов х,- и Xk- Учиты-
Учитывая C), можно переписать последнее равенство в виде
Для справедливости этого равенства при всех XjX*k, необходимо
выполнение условия
Полученное соотношение с учетом C) дает
^--— (АЛ
При заданном i те же рассуждения можно применить к раз-
различным индексам столбцов / и k, что показывает независимость
отношения Aij/Btj от /. Переставив местами строки и столбцы,
мы можем повторить доказательство и показать, что отношение
не зависит также и от /. Поскольку C) означает равенство мат-
матричных элементов А и В по абсолютной величине, то модуль
рассматриваемого отношения должен быть равен единице и
—— = е'а при всех i и /.
Вц
Иными словами, операторы А и В совпадают с точностью до
фазы е'а. I
Рассмотрим теперь теорему III. По предположению каждому
вектору | м> из Ж отображение ?Г сопоставляет вектор |ы'>.
Этот вектор определен с точностью до фазового множителя.
Осуществим конкретный выбор значения фазы у каждого из
векторов |ы'>. Тогда отображение &~ устанавливает взаимно
однозначное соответствие между векторами из <§
)\, |«> = ^-1[1«/)]. (I)

§ 2. ТРИ ПОЛЕЗНЫЕ ТЕОРЕМЫ 183
сохраняющее модуль скалярного произведения
\(u'\v')\ = \(u\v)\. (ID
Пусть векторы
|1>, |2>, .... |л>, ... E)
образуют полное ортонормированное множество векторов в Ж.
Соответствующее ему множество
|1'), |2'), ..., In7). ••• E0
также является полным и ортонормированным. Его ортонорми-
рованность следует из того, что в силу (II) ?Г сохраняет норми-
нормировку и ортогональность. Полнота следует из того, что если су-
существует вектор | а'>, ортогональный всем векторам E'), то
вектор | а> = Э~~х [ | а'>] будет ортогонален всем векторам E),
что противоречит предположению о полноте системы E).
Обозначим
F)
Мы собираемся показать, что при соответствующем выборе фаз
для «штрихованных» кет-векторов справедливо одно из при-
приводимых ниже соотношений:
и'п = ип при всех | и) и п, Gа)
и'п = ы* при всех | и) и п. G6)
Заметим, что условие (II) означает
|ы'|==|« | при всех | и) и п.
Таким образом, нам следует изучить только фазовые соотноше-
соотношения между и'п и ип.
С этой целью зафиксируем фазу каждого из базисных кет-
векторов \п'}, требуя, чтобы вектору |1'>+|/г'> соответство-
соответствовал вектор |1> + \п}.
Докажем сперва соотношения G), предполагая, что |ы>—
«вещественный» кет-вектор, т. е. когда все ип вещественны. При-
Применив условие (II) к скалярному произведению векторов |
и 11> + \ti), имеем
Выбрав фазу вектора |ы'> так, чтобы и[ = и1, получим требуе-
требуемый результат, и'п=-ап. Приведенное рассуждение неприменимо
к случаю, когда щ = 0. Однако можно изменить аргументацию
так, чтобы включить в рассмотрение и этот случай. Поскольку
такое расширение очевидно, мы не будем приводить его.

134 ГЛ. XV. ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕМЕНИ
Рассмотрим теперь произвольный кет-вектор |и>. Применив
условие (II) к скалярному произведению |«> с «вещественным»
кет-вектором |/> + |/ + 1> + . . . + |/ + &>> получаем
(8)
что справедливо при любом выборе / и s. Для того чтобы этот
результат стал более наглядным, удобно использовать следую-
следующую геометрическую интерпретацию векторов |«> и |«'>. Сопо-
Сопоставим вектору |«> ломаную линию (Г), полученную путем со-
совмещения концов векторов комплексной плоскости, описываю-
описывающих последовательные компоненты «ь н2, . . . , ип, . . . . Анало-
Аналогично \и'} описывается ломаной линией (Г'), построенной из
векторов, представляющих и\, и'2 и'п, .... Соотношение (8).
означает тогда, что расстояние между двумя любыми верши-
вершинами ломаной (Г) совпадает с расстоянием между двумя соот-
соответствующими вершинами ломаной (Г")- Как следствие: а) либо
(Г) можно совместить с (Г') поворотом; б) либо (Г) можно
совместить с (Г') поворотом и отражением относительно веще-
вещественной оси.
В случае а) выберем фазу \и"), требуя и{ = иг При таком
выборе (Г) и (Г') совпадают, т. е.
и'п = ип при всех п.
В случае б) наш выбор фазы таков, что и\ = и\. В этом случае
(Г') является зеркальным отражением ломаной (Г) относи-
относительно вещественной оси, т. е.
и'п ¦= ы* при всех п.
Наконец, мы должны показать, что в действительности
имеются лишь эти две возможности: либо все кет-векторы со-
соответствуют случаю а), либо они все соответствуют случаю б).
Будем предполагать для конкретности, что заданный вектор
|/>+ eia\k}(a ф пп) соответствует случаю а). Тогда всякий
вектор |ы>, компоненты и/ и Uk которого не обращаются в нуль
и имеют относительную фазу, отличную от пп, также соответ-
соответствует случаю а), что легко получить применением условия (II)
к скалярному произведению |«> с |/>+е'а|&>. Эти рассужде-
рассуждения могут быть применены и к векторам, компоненты и,-, Uk ко-
которых обращаются в нуль, либо имеют относительную фазу,
равную пп. Те же аргументы переносятся и на случай б).
В результате получаем две возможности:
Случай а). При подходящем выборе фаз применимо со-
соотношение Gа). В этом случае соответствие ?Г очевидно

§ 3. АНТИЛИНЕЙНЫЕ ОПЕРАТОРЫ 135
является линейным. Более точно, справедливо равенство
<и/|о/> = <«|о>. (9а)
означающее, что ?Г— линейный унитарный оператор.
Случай б). При подходящем выборе фаз применимо соот-
соотношение G6). Отображение ?Г, очевидно, антилинейно.
В этом случае имеем
<и'И = <и1»>*- (96)
В соответствии с определением понятия унитарности для анти-
антилинейных операторов, которое приведено ниже, ?Г является уни-
унитарным антилинейным оператором. ¦
§ 3. Антилинейные операторы в гильбертовом
пространстве
Свойства антилинейных операторов в гильбертовом простран-
пространстве аналогичны свойствам линейных операторов. Мы кратко
опишем их в том же порядке, в котором в главе VII приведены
свойства линейных операторов.
Определение. Действие на кет-векторы. Если
каждому кет-вектору |«> в гильбертовом пространстве сопостав-
сопоставлен некоторый кет-вектор | t>> и если это соответствие антили-
антилинейно, то мы говорим, что |и> является результатом действия
на |«> некоторого антилинейного оператора А
|о> = Д|и>. A0)
Свойство антилинейности можно записать в виде
Д(Я,,| 1) + к2\2)) = к\(А\ 1» + ^(Д|2». A1)
Антилинейный оператор определяется своим действием на
каждый из векторов полного набора линейно независимых век-
векторов в Ж и, в частности, своим действием на элементы базиса
в &.
Алгебраические операции. Алгебраические опе-
операции определяются так же, как и в случае линейных опера-
операторов.
(i) Умножение на константу с. Если сфс*, то сле-
следует отметить, что Ас Ф сА; справедливо равенство
сА = Ас*. A2)
(п) Сумма двух антилинейных операторов определяется
точно так же, как и сумма линейных операторов.
(iii) Произведения: если Аи А2 — антилинейные one*
раторы, то произведение AtA2, определенное формулой

136 ГЛ. XV. ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕМЕНИ
является линейным оператором. Если А — антилинейный one-
ратор, а В— линейный, то их произведение АВ антилинейно.
В более общем случае, если набор А, В, ..., L содержит р + q
операторов, из которых р линейных, a q антилинейных, то про-
произведение (АВ . .. L) линейно или антилинейно в соответствии
с четностью или нечетностью q.
Описанные произведения все ассоциативны, но в общем слу-
случае не коммутативны. Определение коммутаторов совпадает
с их определением в случае линейных операторов, и справед-
справедливы все обычные алгебраические правила (V. 63) — (V. 66).
Обратный оператор. Если соответствие A0) между
векторами |ц> и |t>> взаимно однозначно, то оно определяет
также и оператор А~1, обратный оператору А
По определению, два антилинейных оператора А и В яв-
являются обратными друг к другу, если одновременно выпол-
выполняются соотношения
АВ=\, ВА=1. A3)
Если каждый из операторов А, В, С, . .., L является либо
линейным, либо антилинейным и если каждый из этих операто-
операторов имеет обратный, то оператор, обратный их произведению,
существует и определяется формулой
(ABC ... L)~' = L~l ...C~lB~lA~l. A4)
Действие на бра-векторы. Пусть А антилинейный
оператор, а <%| —бра-вектор. Величина, комплексно сопряжен-
сопряженная к скалярному произведению <%|(Л|ы>), будучи линейной
функцией от |«> определяет некоторый бра-вектор (ср. § VII. 3),
который мы обозначим (у\\. По определению,
(Ч\ = (%\А. A5)
Соответствие между (х | и (п | антилинейно
(Я, A | + \ B |) А = К\ «1 \А) + Г2 «2 | А). A6)
Из этого определения следует справедливость равенства
»Г. A7)
Полученное соотношение полезно сравнить с аналогичным соот-
соотношение^ (VII. 17) для линейных операторов. Следует учесть,
однако, что в антилинеином случае скобки опустить нельзя.
Для определения трех указанных выше алгебраических опе-
операций и действия обратного оператора на бра-векторы мы по-
поступим точно так же, как и в случае линейных операторов.

§ 4. АНТИУНИТАРНЫЕ ПРЕОБРАЗОВАНИЯ 137
Умножение на постоянную с имеет вид (ср. ур. A2)):
(%\(сА) = с*((%\А) = (х\(Ас*). A8)
Остальные определения переносятся без изменения.
Важное замечание. Соотношения A2) и A7) показы-
показывают различия в определении обычных линейных операций и
операций, содержащих антилинейные операторы:
(i) рассматриваемая как оператор, действующий в кет-про-
странстве или бра-пространстве, постоянная с не коммутирует
с антилинейными операторами, кроме случая, когда эта постоян-
постоянная вещественна;
(п) в скалярном произведении надо четко указывать, дей-
действует ли антилинейный оператор А на кет-вектор, стоящий
справа от него, или на бра-вектор, стоящий слева.
В практических расчетах скобки используются в той сте-
степени, в которой они необходимы для исключения каких-либо
сомнений, связанных со значением используемых символов. Рас-
Рассмотрим, например, произведение AtA2 двух антилинейных опе-
операторов. Символ <ыj Л1Л21f> является неопределенным, тогда
как символ
(и | (Л,Да) | v) = ({и | Л,Д2) | v) = [((и | Л,) (Л21 о»]* =
о» A9)
не вызывает никаких недоразумений. Аналогично при рассмо-
рассмотрении произведения (Л|ы><и|) линейного оператора |«><и| и
антилинейного оператора Л запись Л|ы><и|ш> и <ш|Л|ы><и|
непонятна, тогда как без каких-либо недоразумений можно ис-
использовать запись
(A\u)(v\)\w) = A(\u)(v\w)) = {A\u))(v\wy B0)
(w\(A \u)(v |) = ((w [ Л)I u)(v \ = [(w \(A \u))Y(v |. B1)
§ 4. Антиунитарные преобразования
Сопряжение (или эрмитово сопряжение) а н т и л и -
нейных операторов. Оператор Л+ является, по определе-
определению, сопряженным оператором к антилинейному оператору Л,
если Л+|«> является кет-вектором, сопряженным к <ы|Л при
любом | «>. Этот оператор антилинёен.
Из сказанного следует, что для любых кет-векторов |ы>
и |О
(*а>)^<а|(Л|/>). B2)
Это тождество следует сравнить с (VII. 20). Помимо этого ра-
равенства, все свойства, установленные в § VII. 7, могут быть пе-
перенесены на рассматриваемый случай без изменений.

138 ГЛ. XV. ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕМЕНИ
В частности, если каждый из операторов Л, В, С, ..., L яв-
является либо линейным, либо антилинейным, то (ср. ур. A4))
{ABC ... L)+ = L+ ... С+В+Л+. B3)
Антиунитарный оператор. Оператор А называется
антиунитарным, если он антилинеен и если А~1 — Л+
Если в наборе А, В, С, . .. , L (р + q) операторов имеется р
унитарных и q антиунитарных, то произведение ABC.. . L уни-
унитарно или антиунитарно в соответствии с четностью или нечет-
нечетностью q.
Антиунитарные преобразования линейных
операторов и векторов. Антиунитарный оператор К оп-
определяет антиунитарное преобразование векторов и линейных
операторов в S", при котором:
любой кет-вектор |ы> переходит в |й> = К\и};
любой линейный оператор В переходит в В = /СВ/С+;
любой бра-вектор <ц| переходит в <й| = (vlK^-
При таком преобразовании;
(i) сохраняется отношение сопряженности бра- и кет-век-
кет-векторов и отношение эрмитовой сопряженности операторов. Если
В является наблюдаемой, то В — также наблюдаемая с тем же
спектром собственных значений, а подпространство, соответ-
соответствующее каждому из собственных значений оператора В, пе-
переходит в подпространство, соответствующее тому же собствен-
собственному значению оператора В;
(и) скалярные произведения переходят в комплексно со-
сопряженные
<и|В|о> = (и|В|о>'; B4)
(Hi) любая постоянная с, рассматриваемая как оператор,
преобразуется в комплексно сопряженную величину
KcKf = с; B5)
(iv) любое соотношение между векторами и (или) опера-
операторами справедливо также и для преобразованных величин при
замене всех коэффициентов на комплексно сопряженные. Дру-
Другими словами, преобразование К сохраняет все равенства ме-
между векторами и (или) операторами, если условиться рассма-
рассматривать все постоянные, фигурирующие в равенстве, как опе-
операторы. Например, перестановочные соотношения
[q,p] = ih, [1х,1у] = 1Шг B6а)
переходят соответственно в
[q,p] = -ih, fjx,Jy}^-iHJz. B66)

§ 5. АНТИЛИНЕЙНЫЕ ОПЕРАТОРЫ И ПРЕДСТАВЛЕНИЯ 139
§ 5. Антилинейные операторы и представления
Оператор Kq комплексного сопряжения, свя-
связанный с представлением {Q}. По определению, Kq яв-
является оператором, переводящим волновые функции представ-
представления {Q} в комплексно сопряженные функции. Действие опе-
оператора Kq зависит от рассматриваемого представления и в осо-
особенности от выбора фаз базисных векторов.
Пусть 11>, |2>, ..., |п>, ... — базисные векторы представ*
ления {Q}. Тогда Kq — антилинейный оператор, оставляющий
эти векторы инвариантными,
KQ\n) = \n). B7)
Следовательно, Kq полностью определен. Очевидно, что выпол-
выполнены соотношения
. Kq — Kq, Kq = \, B8)
так что Kq — антиунитарен. Ясно, что для К выполняется упо-
упомянутое выше свойство, а именно: при антиунитарном преоб-
преобразовании Kq матрицы представления {Q} переходят в ком-
комплексно-сопряженные, таким образом, мы имеем
(п | (KQI и» = (п | и)\ ^ ((v \KQ)\n) = (v\ п)\
(in | (KqBKq) I n) = (m | В | n)* (В — линейный оператор).
Таким образом, в представлении {Q} действие оператора Kq
состоит исключительно в переходе к комплексно сопряженным
величинам. Действие любого другого антилинейного оператора /1
можно легко определить, заметив, что А является произведе-
произведением Kq и линейного оператора, т. е. А всегда можно предста-
представить в виде
Kq = Kq(KqA), B9)
где (AKq) и (KqA)—линейные операторы, переходящие друг
в друга при преобразовании Kq
KqA = Kq(AKq) Kq
(если А антиунитарен, то (KqA) и (AKq) унитарны).
Изменение представления. Рассмотрим другое пред-
представление {S}. Обозначим Kz оператор комплексного сопряже-
сопряжения, связанный с этим представлением, в остальном будем сле-
следовать обозначениям § VII. 21. В частности, матрицей преобра-
преобразования векторов и линейных операторов служит унитарная
матрица S(l; п) = <1|п>.
Если эта матрица вещественна, то векторы нового базиса
инвариантны относительно действия оператора Kq, иными сло-
словами,
если S = S\ то KS = KQ.

140 ГЛ. XV. ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕМЕНИ
В этом случае линейные операторы АКЕ и КЕА, соответствую-
соответствующие в представлении {Е} заданному антилинейному оператору,
те же, что и операторы, соответствующие А в представлении {Q}.
Если это не так, то оператор АК отличен от AKq- Полезно
найти способ построения матрицы (АКЕ)г, описывающей опе-
оператор АКВ в представлении {S} по матрице (AKq)q, оператора
AKq в представлении {Q}. Имеем
(| | (A Ks) 1Г> = (I I (AKQ) (KQKS) I Г> =
= ? (I I m) <m I (AKQ) \n)(n\ (KQKS) | Г> =
ttltl
= Z(l\m)(m\(AKQ)\n)(n\iy,
mn
(AKS)^S(AKQ)QS. C0)
Аналогично
GСаЛ)в = (AKs)l = S* (/CQ Л)р S+. C1)
Раздел II. ПРЕОБРАЗОВАНИЯ И ГРУППЫ ПРЕОБРАЗОВАНИИ
§ 6. Преобразования динамических переменных
и динамических состояний системы
Выше мы уже определили понятия «вращение физической си*
стемы» и «перестановка частиц физической системы».
В более общем случае, действие преобразования ?Г на си^
стему состоит в замене каждой из ее переменных на новую пе^
ременную, а каждого состояния — на новое состояние при со-
сохранении физических характеристик системы.
Таким образом, преобразование ?Г устанавливает взаимно-
взаимнооднозначное соответствие между динамическими переменными:
заданная переменная В преобразуется в новую переменную
По предположению образ В' имеет тот же спектр, что и В,
а собственные состояния для каждого собственного значения пе-
переменной В' являются образами собственных состояний, соот-
соответствующих тому же собственному значению переменной В.
Эти два условия выражают требование сохранения физических
свойств при преобразовании динамических переменных. Такое
условие можно сформулировать без ссылки на методы измере-
измерения, однако преобразование ЗГ особенно легко описать как пре-
преобразование, применяемое к измерительной аппаратуре, пред-
предназначенной для определения В: образ этой аппаратуры есть

§ 6. ПРЕОБРАЗОВАНИЯ ДИНАМИЧЕСКИХ ПЕРЕМЕННЫХ 141
аппаратура, предназначенная для измерения переменной В'.
Таким образом, определяются смещения динамических пере-
переменных (вращения, сдвиги), отражения динамических перемен-
переменных (отражение в точке, в плоскости) и т. д.
От преобразования переменных легко перейти к преобразо-
преобразованию состояний. Пусть | и} — вектор, описывающий возмож-
возможное динамическое состояние системы. Этот вектор можно рас-
рассматривать как общий собственный вектор полного набора ком-
коммутирующих наблюдаемых и считать, что он определен с точ-
точностью до фазы. Образ вектора |и> при преобразовании 3~.
является общим собственным вектором преобразованных на-
наблюдаемых. Таким образом, 0~ устанавливает взаимно-одно-
взаимно-однозначное соответствие между векторами состояния, определен-
определенными с точностью до фазы.
По определению, преобразование сохраняет физические свой-
свойства динамических состояний: для системы, находящейся в со-
состоянии \и'}, вероятность того, что при измерении будет полу-
получен результат, соответствующий состоянию )i/>, т.е. образу со-
состояния )и>, равна вероятности того, что для системы, находя-
находящейся в состоянии | и}, при том же измерении будет получен
результат, соответствующий состоянию \v). Иными словами,
|<u'|i/>|2= |<u|u>|2 для всех \и} и |и>. Таким образом, рас-
рассматриваемое взаимно-однозначное соответствие сохраняет мо-
модуль скалярного произведения. Согласно теореме III фазы пре-
преобразованных векторов всегда можно фиксировать так, чтобы
преобразование стало унитарным или антиунитарным. Это по-
позволяет записать
\иГ> = Т\и), C2)
где Т — унитарный или антиунитарный оператор, соответствую-
соответствующий преобразованию. В обоих случаях имеем
7Т+ = Г+Г=1. C3)
Из закона C2) преобразования векторов легко получить закон
преобразования оператора плотности
р' = ГрГ+. C4)
Рассмотрим еще одно преобразование наблюдаемых. По-
Поскольку физические свойства сохраняются при рассматривае-
рассматриваемых преобразованиях, то сохраняются и средние значения. Та-
Таким образом, для наблюдаемой В для всех |и> имеем
(и' \В'\ «')==<«\В\и)

142 ГЛ. XV. ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕМЕНИ
ИЛИ ')
Из теоремы I и соотношений C3) имеем
^ в = fcB'Tm C5)
Из равенств C5) следует важное свойство неизменности ал-
алгебраических соотношений между наблюдаемыми системы в слу-
случае, когда преобразование описывается линейным операто-
оператором Т. Если же Т антилинеен, то эти соотношения заменяются
на комплексно сопряженные соотношения.
Это приводит к весьма ограничительным условиям на за-
законы преобразования наблюдаемых. Всякая наблюдаемая В
является некоторой вещественной функцией F(g) фундамен-
фундаментальных наблюдаемых |i, |г, . . ., ?п, ... системы. Образ этой
наблюдаемой есть В' = F(|') Итак, преобразование 0~ пол-
полностью определяется, если известны законы преобразования ос-
основных наблюдаемых, т. е. если известны функции fi(?), ...
..., fn(l), ..., такие, что
г СУ «? = /„©•
Последнее определяет также перестановочные соотношения для
наблюдаемых ?'. Так как преобразования обязаны сохранять
алгебраические соотношения, то имеется всего две возможно-
возможности: либо преобразование сохраняет фундаментальные переста-
перестановочные соотношения, либо меняет их знак2). В первом случае
оператор Т, соответствующий преобразованию, линеен, во вто-
втором— антилинеен (см. ур. B6а — 266)).
Оператор Т должен удовлетворять равенствам
й = ПпТ\ ¦ C6)
содержащим все физические свойства Т. Однако этих равенств
недостаточно для полного определения Т. Пусть Т\ — другой
') В случае, когда оператор Т линеен, эти соотношения очевидны, они
справедливы также и при антилинейном Т, так как («|В|«) вещественны.
2) Преобразованиями классической механики являются преобразования,
сохраняющие скобки Пуассона
каждой пары (Ас1, Вс1) динамических переменных системы (канонические пре-
преобразования). Аналогично преобразованиями, сохраняющими физические свой-
свойства в квантовой механике, будут те преобразования, которые сохраняют со-
соответствующие выражения
7F[л' *!¦

§ 6. ПРЕОБРАЗОВАНИЯ ДИНАМИЧЕСКИХ ПЕРЕМЕННЫХ 143
унитарный (или антиунитарный) оператор, удовлетворяющий
тем же соотношениям. Тогда имеем (опуская индекс п для уп-
упрощения записи)
и, следовательно,
t\
или
\Т\Т, U = 0 для всех |. C7)
Если предполагать неприводимость пространства состояний &
по отношению к наблюдаемым |, т. е. что в & не содержится
подпространств, инвариантных относительно |, то равенства
C7) удовлетворяются тогда и только тогда, когда оператор
Т\Т пропорционален единичному.
Этот результат следует из леммы Шура (§ Г. 8). Ему можно
дать прямое доказательство следующим образом. Пусть |и> —
общий собственный вектор полного набора коммутирующих на-
наблюдаемых. Поскольку С = т\т коммутирует с каждой из этих
наблюдаемых, то |и> является собственным вектором С: С|и>=
= с\иу. Поскольку С коммутирует с каждой функцией F(?) на-
наблюдаемых системы, то имеем также и
CF®\u) = cF(l)\u) при всех F Ц).
Пространство, образованное векторами F(g)|u>, является
подпространством в %', инвариантным относительно |, а так как
<§, по предположению, неприводимо, то этим подпространством
может быть лишь само &. Следовательно С = с.
Если предполагать, как мы и делали до сих пор, что каждый
вектор пространства состояний можно рассматривать как соб-
собственный вектор некоторого полного набора коммутирующих
наблюдаемых, то свойство неприводимости выполняется авто-
автоматически (задача 1). Ясно, что приведенное выше обсуждение
имеет смысл только в том случае, когда используемые наблю-
наблюдаемые являются физическими наблюдаемыми. Мы всегда бу-
будем предполагать, что пространство & неприводимо по отноше-
отношению к физическим наблюдаемым1). В этом предположении по-
постоянная с равна единице по модулю, поскольку Т и Т\ унитар-
унитарны. Итак, имеем
Вывод: с каждым преобразованием 3~ связан унитарный или
антиунитарный оператор Т, определенный с точностью до фазы
законами преобразования фундаментальных переменных си-
') См. ссылку в § XIII. 14 на работу, в которой неприводимость не пред-
предполагается.

144 ГЛ. XV. ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕМЕНИ
стемы (ур. C6)). Оператор Т унитарен, если преобразование
сохраняет перестановочные соотношения, и антиунитарен, если
преобразование изменяет знак перестановочных соотношений.
Фаза оператора Т может быть выбрана произвольно и не
влияет ни на физические свойства преобразования, ни на за-
законы преобразования наблюдаемых и операторов плотности, ни
на различные алгебраические операции над операторами.
§ 7. Группы преобразований
Из различных имеющихся в нашем распоряжении преобра-
преобразований мы можем образовать некоторое число групп преобра-
преобразований, где термин группа используется в его математическом
понимании (ср. § Г. 2).
Произведение 3~ц = 3~т.3~\ преобразований Т\ и ?Г2
является преобразованием, которое состоит в применении 0~%
к результату действия *Э~\. Преобразующий оператор Г21 с точ-
точностью до фазового множителя равен произведению Т^Тх- Это
произведение ассоциативно, но не обязательно должно быть
коммутативным.
Тождественное преобразование & — преобразо-
преобразование, при котором каждая наблюдаемая переходит в себя.
Соответствующий этому преобразованию оператор является опе-
оператором умножения на произвольный фазовый множитель.
Обратное преобразование 3~~1 определяется соот-
соотношением Т~Х<Э~ = ТТ~Х = Э'. Поскольку Т определяет взаим-
взаимно однозначное соответствие, то обратное преобразование всегда
существует.
Итак, каждое из преобразований, описанных в § 6, можно
рассматривать как элемент некоторой группы 9.
Среди всевозможных групп группа пространственных преоб-
преобразований (трансляций, вращений и отражений) и ее разнооб-
разнообразные подгруппы являются группами, физическое значение ко-
которых очевидно. Среди подгрупп этой группы следует упомя-
упомянуть группу трансляций, группу вращений (вокруг точки), груп-
группу смещений (трансляций и вращений), группы отражений от-
относительно точки и относительно плоскости, группу вращений
и отражений (вращения вокруг точки и отражения относительно
той же точки), группы симметрии кристаллов.
В предыдущей главе мы встретились с группами другого
типа — группами перестановок подобных частиц. Мы также рас-
рассматривали перестановки, которые затрагивали только часть
переменных, описывающих частицы. В частности, там была вве-
введена группа преобразований в зарядовом пространстве, с кото-
которой в случае системы нуклонов связана группа изотопических
вращений, или группа вращений в зарядовом пространстве.

§ 8. ГРУППЫ ОПЕРАТОРОВ ПРЕОБРАЗОВАНИЯ 145
Преобразования, явно затрагивающие время, удобно рас-
рассмотреть отдельно. Среди них, в первую очередь, следует от-
отметить преобразования Галилея, которые мы упоминаем здесь
для полноты (задача 7). Они являются нерелятивистскими ана-
аналогами чисто лоренцевских преобразований. Последние вместе
с пространственными вращениями образуют собственную груп-
группу Лоренца, которая будет обсуждена в пятой части. Имеется
также группа временных сдвигов и, наконец, операция обра-
обращения времени. Временные трансляции и обращение времени
будут изучаться в разделе IV. В оставшейся части настоящего
раздела мы будем рассматривать только преобразования, не
затрагивающие время явно.
§ 8. Группы операторов преобразований
Пусть [?Г]— множество преобразований 3~\, 3~2, ¦ ¦ ¦ , У и
Каждому элементу 0~\ этого множества можно сопоставить опе-
оператор Tt, определяющий преобразование векторов и операторов
в пространстве состояний. Оператор Т задается своими физиче-
физическими свойствами только с точностью до фазового множителя,
который мы пока оставляем произвольным. Мы получим множе-
множество [Т] операторов преобразования, элементы которого находят-
находятся во взаимно однозначном соответствии с элементами из \3"\.
Предположим теперь, что [&~\ является некоторой группой
9. Отсюда еще не следует, что множество [Т] является группой.
Действительно, при указанном соответствии между \0~\ и [Т]
произведения сохраняются только с точностью до фазового мно-
множителя. Для каждого произведения
имеем
где а*у — некоторая фаза, зависящая от выбора фазы у Tr T\
и Tk- Для того чтобы [Т] было группой, надо чтобы все а/,- об-
обращались в нуль. Тогда группа [Т] изоморфна группе 9.
Если фазы операторов 7", могут быть выбраны так, чтобы
[Т] было группой, то такой выбор, очевидно, является наиболее
удобным. Такая возможность имеется для ряда групп, но не для
всех. В частности, это возможно для группы перестановок
(гл. XIV), но невозможно для группы вращений (§ XIII. 5), если
система содержит нечетное число частиц с полуцелым спином.
В последнем случае операторы вращений R(afiy), определяе-
определяемые соотношением (XIII. 60), образуют группу, однако каждому
вращению Я соответствуют два оператора R, отличающиеся
друг от друга знаком. Если мы выберем один из них в качестве

146 ГЛ. XV. ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕМЕНИ
элемента множества [R], то мы установим взаимно однознач-
однозначное соответствие между вращениями и операторами вращений,
однако произведение сохранится лишь с точностью до знака и
множество [R] не будет группой.
Для получения множества операторов преобразования мо-
может оказаться необходимым сопоставлять каждому преобразо-
преобразованию Ti не один оператор Г,-, а набор (Г,) операторов, отли-
отличающихся друг от друга фазовым множителем. Если набор (Г,)
выбран подходящим образом, то полученное множество {Т}
операторов преобразования образует группу G, гомоморфную
группе 'З. Пусть A)—множество операторов, каждый из кото-
которых соответствует тождественному преобразованию Э'. Элемен-
Элементами множества A) являются единичный оператор 1 и, воз-
возможно, другие операторы, получаемые из 1 умножением на фа-
фазовый множитель. Множество A) является инвариантной под-
подгруппой в группе G, а фактор-группа G/(l) изоморфна 'S (ср.
§Г.5).
Таким образом, можно построить много множеств {Т}, имею-
имеющих структуру группы1). Практически мы выбираем одно из
них. Очевидно, что следует выбирать множество {Т} по воз-
возможности более простым. В результате мы получим группу опе-
операторов G, гомоморфную группе &.
Во всех случаях, встретившихся к настоящему времени
в квантовой теории, всегда удается выбрать G так, чтобы каж-
каждому элементу группы § соответствовал либо один оператор из
G (изрморфизм), либо, если это не так, два оператора из G,
различающихся знаком. Первый вариант всегда осуществляется
в случае системы, содержащей четное число полуцелых спинов.
Выше мы уже имели пример реализации второго варианта при
рассмотрении вращений полуцелых спинов. Мы встретимся со
вторым вариантом также при рассмотрении обращения вре-
времени. Более того, второй вариант всегда реализуется, когда си-
система имеет нечетное число частиц с полуцелым спином.
§ 9. Непрерывные группы и инфинитезимальные
преобразования. Трансляции. Вращения
В качестве иллюстрации общей теории построим группы
операторов G для некоторых групп $. Сперва рассмотрим не-
непрерывные группы, которые имеют бесконечное число элемен-
>) Наиболее сложное из этих множеств получается при сопоставлении ка-
каждому преобразованию &~i всех операторов, удовлетворяющих C6): в этом
случае все элементы из G",) получаются домножением одного из них на фа-
фазовый множитель. Практически всегда можно наложить на 7"; условие вещест-
вещественности, фиксирующее фазовый множитель с точностью до знака без нару-
нарушения группового свойства. Множество G",) тогда состоит точно из двух эле-
элементов, отличающихся друг от друга знаком (см. сноску к § XV. 17).

§ 9 ИНФИНИТЕЗИМАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ 147
тов, зависящих от одного или нескольких непрерывно меняю-
меняющихся параметров, точнее, те группы, у которых все конечные
преобразования могут быть представлены рядами инфинитези-
мальных. Это справедливо для группы вращений и группы про-
пространственных трансляций. В этом случае для получения пре-
преобразования наблюдаемых под действием любого элемента
группы оказывается достаточным установить лишь преобразо-
преобразование наблюдаемых под действием инфинитезимальных опера-
операций. Каждому инфинитезимальному преобразованию группы
можно сопоставить инфинитезимальный оператор преобразова-
преобразования, т. е. унитарный оператор, бесконечно мало отличающийся
от 1 ').
Предположим для простоты, что элемент группы зависит
лишь от одного непрерывного параметра ос и что последний вы-
выбран так, что
Г (а) >&.
В первом порядке по бос оператор, соответствующий ?ГFос),
имеет вид
Т Fа) = 1 — гвба,
где в — эрмитов оператор (так как Т унитарен).
Если наблюдаемая ? преобразуется в § + б| при преобра-
преобразовании ^~Fос), то мы имеем (ур. (VII. 96))
т. е.
= ;¦§¦. C8)
При заданном преобразовании 3~'Fа) величины 6?/6ос из-
известны и соотношения C8) определяют в с точностью до по-
постоянной2).
') Этот оператор не может быть антиунитарным. Рассмотрим две неком-
мутирующие наблюдаемые. При инфинитезимальном преобразовании онн из-
изменятся только инфинитезимально, так что их коммутатор не может претер-
претерпеть конечного изменения и, в частности, ие может изменить знак.
2) В классической механике вариация Ьадуда каждой наблюдаемой ?
при инфинитезимальном смещении ?Г"Fа) определяется скобкой Пуассона
да [х' ёЬ
где т — сопряженный импульс, соответствующий а. Наблюдаемая fiG являет-
является квантовым аналогом т. (При бесконечно малом вращении вокруг и т —
компонента момента импульса вдоль и; при трансляции вдоль и т является
компонентой импульса вдоль и.)

148 ГЛ. XV. ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕМЕНИ
Рассмотрим, для примера, смещение частицы вдоль оси Ох.
Пусть r = (x, t/, z)—координата, рЕ=(рх, рУг рг) — импульс,
ass (sx, sy, sz)— спин частицы. При трансляции 0~х(а) на рас-
расстояние а вдоль оси Ох девять основных переменных инва-
инвариантны, за исключением х, которая переходит в х — а')
Т{а)хТ*{а) = х — а. C9)
В частности, при инфинитезимальном преобразовании
0~х{8а), Ьх = — 6а, а все остальные вариации 8у, ..., 8sz об-
обращаются в нуль. Соответствующий эрмитов оператор 9* удо-
удовлетворяет перестановочным соотношениям
[вх, x] = -t,
[е*, у] = ... = [&х, «2]=о,
что дает
©я — ~jj- + ^Oi
где ko — произвольная вещественная постоянная, которую мы
положим равной нулю. Это изложение легко распространяется
на случай трансляций N частиц и дает
е
N
где Pr=Ti Р1г) — компонента вдоль оси Ох полного импульса
i-l
системы. N частиц.
Инфинитезимальному сдвигу 3~х{8а), таким образом, соот-
соответствует инфинитезимальный унитарный оператор
Оператор конечного преобразования Тх(а) можно выбрать
в виде
') Образ х' прообраза х действительно есть х — а, а не х + а. Пусть
\Ь) —собственный вектор оператора х, соответствующий собственному значе-
значению Ь. Его образ \Ь') является собственным вектором оператора х, соответ-
соответствующим собственному значению Ъ + а
x\b)=b\b), х\Ь') = (Ь + а)\Ь').
Но из определения преобразоваиия иаблюдаемых имеем
х'\Ь')=Ъ\Ь'), '
откуда
х'' = х — а.
Эту аргументацию полезно сравнить с доказательством из § XIII. 12.

4 9. ИНФИНИТЕЗИМАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ 149
что легко проверяется подстановкой этого выражения в соот-
соотношение C9).
Полученные таким образом операторы образуют группу, изо-
морфную группе сдвигов вдоль оси Ох. В частности, мы имеем
Тх (а) Тх (Ь) = Тх (Ь) Тх (а) = Тх (а + Ь).
Группа сдвигов вдоль оси Ох является подгруппой группы
трансляций. Конкретный сдвиг 0~(а) определяется вектором а,
задающим смещение динамических состояний системы. Группа
трансляций, таким образом, зависит от трех непрерывных па-
параметров — компонент вектора а. Закон композиции в этой,
группе имеет вид
Т (а) Т (Ь) = Г (Ь) Т{а) = Т{а + Ъ).
Обобщая полученные выше результаты на случай произволь-
произвольных трансляций, сопоставим инфинитезимальному сдвигу 0~(&)
оператор
r(e)«l-JL(Pe), D1)
где Р — полный импульс системы Af частиц. Из сказанного ра-
ранее следует, что оператор, связанный с трансляцией Т(а), имеет
вид
Г(а) = е-гРв/й- D2>
Определенные таким образом операторы образуют группу, изо-
изоморфную группе трансляций, ибо
Т (а) Т (Ь) = Т (Ь) Т (а) = Т (а + Ь).
Группа вращений дает еще один пример непрерывной
группы с тремя параметрами. Операторы вращений уже были
найдены в главе XIII. Определяющую их формулу (XIII. 55)
следует сравнить с формулой D1). Полный момент импульса /
играет в группе вращений ту же роль, что и оператор полного
импульса Р в группе трансляций. Компонента (и/) полного мо-
момента импульса вдоль и определена с точностью до постоянной
перестановочными соотношениями (XIII. 56) и (XIII. 57), кото-
которые соответственно описывают инфинитезимальные вращения
скалярных и векторных наблюдаемых. Произвольная постоян-
постоянная может быть фиксирована требованием, чтобы моме'нт / был
векторным оператором ').
Операторы вращений R определяются как произведения ин-
финитезимальных вращений. Это приводит к формуле (XIII. 60),
') Это условие эквивалентно требованию, чтобы операторы Ra (в) были
иифинитезимальными операторами группы.

150 гл- XV. ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕМЕНИ
которую следует сравнить с формулой D2). Указанные опера-
операторы образуют группу, изоморфную группе вращений, если си-
стема содержит четное число полуцелых спинов, и только гомо-
гомоморфна ей, если система содержит нечетное число полуцелых
спинов. Этот вопрос уже обсуждался нами, и мы не будем его
рассматривать здесь снова.
Множество операторов Т и R, которые определены форму-
формулами D2) и F0), и всевозможные произведения этих операто-
операторов также образуют группу. Если система содержит четное
число полуцелых спинов, эта группа изоморфна группе смеще-
смещений, если это не так, то рассматриваемая группа только гомо-
гомоморфна группе смещений, и два оператора, отличающиеся зна-
знаком, соответствуют каждому из элементов последней.
§ 10. Конечные группы. Отражения
Среди всех групп простейшей, безусловно, является группа
отражений в точке. Она содержит всего два элемента, тожде-
тождественный элемент & и отражение^: 9'\ = У. При преобразо-
преобразовании 9>ъ полярные векторы г, р меняют знак, а аксиальные век-
векторы гХ р, s не меняются. Поскольку г и р одновременно изме-
изменяют знаки, это преобразование сохраняет перестановочные со-
соотношения орбитальных переменных, а также перестановочные
соотношения компонент спина. Следовательно, оператор So, оп-
определяющий отражение, линеен. Он является унитарным опера-
оператором, удовлетворяющим соотношениям
Vo *. D3)
которыми он определяется с точностью до фазы. Для того чтобы
операторы So и 1 образовывали группу, изоморфную группе
отражений, мы должны потребовать выполнения равенства
Sg=l (S0 = SJ), D4)
которое фиксирует фазу So с точностью до знака.
Оператор So полностью определяется своим действием- на ба-
базисные векторы представления, например, представления {г, sz}.
Мы примем следующее определение:
S0|rn> = |(-r)n>, D5)
которое согласовано с соотношениями D3) и D4) (задача 2).
Тогда отражение волновой функции описывается соотношением

§ 10. КОНЕЧНЫЕ ГРУППЫ. ОТРАЖЕНИЯ 151
Таким образом, оператор So совпадает с оператором четности,
введенным в § XIII. 23. Он является наблюдаемой с двумя соб-
собственными значениями, ±1. Приведенное рассмотрение без
труда можно распространить на случай систем, состоящих из
нескольких частиц.
Отражение коммутирует со всеми вращениями М. Произве-
Произведения операций группы отражений и группы вращений образуют
группу вращений и отражений. Отметим также, что So комму-
коммутирует с любым оператором вращений, поскольку последние яв-
являются функциями полного момента импульса /, a So коммути-
коммутирует с /, ибо согласно D3)
Итак, множество, образованное операторами So, R и их произ-
произведениями, также образует группу. В случае, когда группа [R]
изоморфна группе вращений (полный спин — целый), эта
группа изоморфна группе вращений и отражений. Если это не
так (полный спин полуцелый), то полученная группа только го-
гомоморфна группе вращений и отражений, и каждому элементу
последней сопоставляются два оператора, отличающиеся зна-
знаком. В частности, двумя операторами, соответствующими чи-
чистому отражению, являются -\-S0 и —So, а тождественному ото-
отображению соответствуют операторы +1 и —1.
Рассмотрим теперь другой тип отражения — отражение в
плоскости. Пусть 9*и—отражение в плоскости, перпендикуляр-
перпендикулярной единичному вектору и; Уи является преобразованием груп-
группы вращений и отражений, а именно, произведением д'о и вра-
вращения на угол л вокруг и (или —и)
?u = ?o®a(*)- D6)
Заметим, что
?1 = ЗГ. D7)
Следовательно, 9"'и и & образуют группу, и ее изучение можно
скопировать с приведенного исследования отражений в точке.
Помимо этого, используя соотношения D6), свойства одной из
этих групп можно получить из свойств другой.
Мы рассмотрим только случай одной частицы. Оператор Sa
является линейным унитарным оператором, удовлетворяющим
соотношениям
D8)
SasSl = - s + 2и (as)

152 ГЛ. XV. ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕМЕНИ
¦и его можно представить в виде
D9)
что дает
Sl = S2oe-2"iiJa) = (-\f. E0)
При таком выборе фазы имеем
С2 __ 1
я
в случае полуцелого спина. Для получения образующего группу
набора операторов преобразования отражению 9>а следует сопо-
сопоставить два оператора ') Su и —Su.
Еще одним примером конечной группы является группа пере-
перестановок п подобных частиц, которая изучалась в главе XIV.
Каждой перестановке был сопоставлен линейный унитарный опе-
оператор перестановки. Множество операторов, полученное таким
образом, образует группу, изоморфную группе перестановок2).
Мы не будем возвращаться к этим вопросам здесь. Добавим
лишь одно важное замечание. Перестановки коммутируют с про-
пространственными преобразованиями, и из самого способа опре-
определения операторов перестановок следует, что они обладают тем
же самым свойством по отношению к операторам пространствен-
пространственных преобразований.
Раздел III. ИНВАРИАНТНОСТЬ УРАВНЕНИИ ДВИЖЕНИЯ
И ЗАКОНЫ СОХРАНЕНИЯ
§11. Инвариантные наблюдаемые
Мы рассмотрим теперь вопрос об инвариантности сам по
себе. Пусть & — некоторая группа преобразований. Обозначим
G соответствующую группу операторов и пусть Г,- — фиксиро-
фиксированный элемент из G. Будем предполагать, что все Г,- линейны
(и унитарны). Обращение времени — единственное преобразо-
преобразование, приводящее к рассмотрению антиунитарных операторов,
будет исследовано в разделе IV.
') Если мы будем рассматривать только группу {Sa, 2/}, то предпочтитель-
предпочтительнее определить Sa = i2fS0Ra (я), что дает Sj= 1.При новом выборе фазы за-
закон умножения D6) сохраняется только с точностью до фазы.
2) Тот же результат может быть получен прн замене всех операторов, со-
соответствующих нечетным перестановкам, на противоположные им. Все рассу-
рассуждения, проведенные в главе XIV, могут быть повторены и при этом новом
соглашении о фазе с одним исключением — усложнением формул за счет до-
добавления знака (—) без каких-либо изменений полученных результатов.

§ It. ИНВАРИАНТНЫЕ НАБЛЮДАЕМЫЕ 153
Инвариантность наблюдаемой Q при преобразованиях груп-
группы выражается условием T{QTj = Q, т. е.
[Q, 7\] = 0 для всех 71,. E1>
Мы уже анализировали те следствия, которые можно из-
извлечь из этих коммутационных соотношений в случае группы
вращений (§ XIII. 17). Используя понятие группы и свойства
линейных представлений группы G (см. Дополнение Г и, в част-
частности, § Г. 9), эти следствия можно сформулировать весьма об-
общим образом. Обозначим |т/ц> базисные векторы стандартного
представления группы G. Эти векторы нумеруются тремя кван-
квантовыми числами (или тремя наборами квантовых чисел). Ин-
Индекс / обозначает неприводимое представление, которому при-
принадлежит вектор |т/ц>. Индекс ц различает базисные векторы
заданного неприводимого представления, а т — дополнительное
квантовое число, позволяющее, при необходимости, различать,
ортогональные эквивалентные неприводимые подпространства.
Мы намеренно будем использовать те же обозначения, что и
в § XIII. 6, очевидным обобщением материала которого яв-
является настоящее обсуждение. Важнейшим свойством Q яв-
является аналог соотношения (XIII. 120), а именно,
Полное доказательство этого соотношения приведено в Допол-
Дополнении Г (см. ур. (Г. 20)).
Во многих случаях это соотношение удается получить и без
ссылки на общую теорию представлений групп. Для этого не-
необходимо найти среди функций операторов 7\-:
(i) множество / наблюдаемых, которые инвариантны относи-
относительно всех операций группы и собственные значения которых
нумеруются квантовым числом / (или набором квантовых чисел);.
(И) множество М наблюдаемых, которые коммутируют друг
с другом, но не со всеми элементами из группы, и собственные
значения которых нумеруются квантовым числом ц.
Очевидно, что Q, / и М образуют множество коммутирующих
наблюдаемых и, следовательно, оператору Q соответствует осо-
особенно простая матрица в каждом из представлений, где наблю-
наблюдаемые / и М диагональны, а именно, матрица, определяемая
соотношением E2).
Этот метод успешно применялся нами к группе вращений
(см. ур. (XIII. 120)). В этом частном случае мы нашли одну на-
наблюдаемую категории (i), а именно, Р, и одну наблюдаемую
категории (и), а именно, /г. Этот метод также может быть при-
применен к группе вращений и отражений с Л и So, т. е. полным
моментом импульса и четностью, как элементами множества /

154 ГЛ XV. ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕМЕНИ
из категории (i) и наблюдаемой /2 в качестве множества М из
категории (ii). Отметим, что имеется определенный произвол
в выборе М. В случае группы вращений обычно используют /2,
однако с тем же успехом можно использовать 1Х или ]у,
а также любую другую компоненту векторного оператора /.
Собственные состояния наблюдаемой Q получаются диагона-
лизацией по отдельности матриц QTt" каждая из которых соот-
соответствует вполне определенному собственному значению опе-
оператора J. Итак, каждому значению / соответствует наборq{P соб-
собственных значений наблюдаемой Q, которые при необходимости
нумеруются квантовым числом (или числами) s. Пусть d,- есть
число возможных значений ц B/ + 1 в случае вращений). Каж^
дому из этих значений соответствует одна и та же матрица Qx\r-
Таким образом, каждое невырожденное собственное значение
этой матрицы является ф-кратно вырожденным собственным
значением наблюдаемой Q, а каждое р-кратно вырожденное
собственное значение этой матрицы является рф-кратно вырож-
вырожденным собственным значением Q. Если d\ ф 1, то все собствен-
собственные значения наблюдаемой Q, соответствующие квантовому
числу j, вырождены и степень их вырождения кратна d\. Это
вырождение является непосредственным следствием инвариант-
инвариантности Q относительно группы G и называется G-вырождением.
§ 12. Свойства инвариантности гамильтониана
и законы сохранения
Пусть гамильтониан Н инвариантен относительно преобра-
преобразований группы д. Тогда мы можем повторить для гамильто-
гамильтониана все то, что было сказано относительно инвариантных на-
наблюдаемых. Исходя из коммутационных соотношений
[Н, Г,-] = 0 для любого оператора Г,- из G, E3)
образуем наблюдаемые типа / и М. Эти операторы вместе с Н
образуют множество наблюдаемых, которые можно диагонали-
зовать одновременно. Более того, спектр оператора Н имеет
G-вырождение.
Как и в классической механике, инвариантность гамильто-
гамильтониана приводит к законам сохранения. Действительно, посколь-
поскольку всякая наблюдаемая (не зависящая явно от времени), кото-
которая перестановочна с Н, является интегралом движения, то мы
имеем очевидное свойство.
Если Н инвариантен относительно преобразований группы,
то всякая наблюдаемая, являющаяся функцией операторов
группы, представляет собой интеграл движения.
В частности, этим свойством обладают определенные выше
наблюдаемые (/, М) и поскольку они коммутируют друг с дру-

§ 12. СВОЙСТВА ИНВАРИАНТНОСТИ ГАМИЛЬТОНИАНА 155
гом, то их значения можно измерить одновременно и они
остаются фиксированными с течением времени.
Итак, с каждой группой связано некоторое число законов
сохранения. Всякий раз, когда сохраняющаяся наблюдаемая
имеет классический аналог, эти законы сохранения идентичны
соответствующим классическим законам1). Ниже указаны наи-
наиболее часто встречающиеся из них.
(i) Трансляционная инвариантность и сохранение полного
импульса. Необходимое и достаточное условие инвариантности
гамильтониана относительно трансляций состоит в инвариант-
инвариантности его относительно инфинитезимальных трансляций, т. е.
(УР- D1))
[Я,Р] = 0, E4)
где Р — полный импульс системы. Таким образом, три компо-
компоненты полного импульса являются интегралами движения и пол-
полный импульс сохраняется. Кроме того, поскольку Рх, Ру и Рг
коммутируют друг с другом, то их можно одновременно точно
определить и они сохраняют свои значения с течением времени.
(И) Инвариантность относительно вращений и сохранение
момента импульса. Эти вопросы уже изучались в главе XIII. На-
Напомним, что инвариантность гамильтониана относительно вра-
вращений выражается условием: [Я, J] — 0.
(iii) Инвариантность относительно отражений и сохранение
четности. Из инвариантности гамильтониана относительно от-
отражений в точке
[Я, So] = 0, E5)
следует, что четность So является интегралом движения.
(iv) Инвариантность относительно перестановок и сохране-
сохранение симметрии. В системе, состоящей из тождественных частиц,
гамильтониан Я инвариантности относительно любой переста-
перестановки Р этих частиц
[Я, Р] = 0 при всех Р.
Отсюда следует, что любая наблюдаемая, построенная из Р,
является интегралом движения. Таковыми являются проекторы
S и А на симметричные и антисимметричные состояния соответ-
соответственно
[Я, S] = 0, [Н,А] = 0.
Таким образом, S и А являются интегралами движения. Мы
видели в главе XIV, что эти свойства операторов S и А являются
') Это имеет место в случае, когда наблюдаемые связаны с инфнннтези-
мальными смещениями (см. 1-ю сноску к § XV. 9).

156 ГЛ. XV. ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕМЕНИ
необходимыми для внутренней согласованности постулата о сим-
симметризации.
(v) Зарядовая независимость и сохранение изотопического
спина. Пусть Т — полный изотопический спин системы нукло-
нуклонов. Если нуклон-нуклонные силы зарядово независимы, то га-
мильтониан системы инвариантен относительно вращений в про-
пространстве изотопического спина, т. е.
[И,Т] = 0. E6)
Следовательно, компоненты наблюдаемой Т, а также наблю-
наблюдаемые, являющиеся функциями этих трех компонент, являются
интегралами движения. В частности Т2 и Тг — интегралы дви-
движения. (N. В. Сохранение Тг есть не что иное как сохранение
заряда.)
§ 13. Свойства инвариантности и эволюция динамических
состояний
Покажем теперь, что из инвариантности Н относительно
группы & следует инвариантность оператора эволюции U{t,t0)
относительно той же группы. Этот оператор, по определению,
является решением интегрального уравнения
t
Домножив обе части этого равенства слева на Г,- и справа на
Г?» учитывая унитарность оператора 7\- и свойство E3), имеем
t
TiU (/, t0) Т\ = 1 + -L J НТ{и (/', /0) ft dt'.
h
Поскольку U и 7\ит\ удовлетворяют одному и тому же инте-
интегральному уравнению, то они совпадают. Таким образом,
[?/(/, t0), Tt] = 0 для всех Tt из О. E7)
Одним из следствий инвариантности U относительно преоб-
разований группы являются законы сохранения, приведенные
в предыдущем параграфе. Более того, если |г|з(О> — решение
уравнений движения, то так как U и Г,- коммутируют, преобра-
преобразованный вектор Ti\^(t)} также является решением. Динамиче-
Динамические состояния, описываемые этими векторами, в каждый мо-
момент времени связаны преобразованием 3~-t. Следовательно, за-
закон движения динамических состояний инвариантен относитель-
относительно преобразований группы 'S.

§ 13. ЭВОЛЮЦИЯ ДИНАМИЧЕСКИХ СОСТОЯНИЙ 157
Два динамических состояния, являющиеся образами друг
друга относительно некоторого преобразования ?Г,- группы Ъ',
сохраняют это свойство с течением времени.
Это свойство инвариантности можно эквивалентным обра~
зом сформулировать посредством операций измерения.
Предположим, что после того как в момент времени t0 си-
система приготовлена тем или иным способом, над системой в бо-,
лее поздний момент времени t осуществляется некоторая про-
процедура измерения. Результат такого измерения не изменится,
если осуществить преобразование ?Г,- группы как над началь-
начальным состоянием (т. е. над аппаратурой, используемой для при-
приготовления системы), так и над величиной (или величинами),
подлежащими измерению (т. е. над аппаратурой, используемой
для их наблюдения) при прочих равных условиях.
Предположим для примера, что система приготовлена в чи-
чистом состоянии, которое описывается вектором |ср> и измеряется
вероятность обнаружения системы в чистом состоянии, опреде-
определяемом вектором ]%>. Образы этих состояний при преобразова-
преобразовании описываются соответственно векторами Г,|ф> и 7\|%>. Из
коммутационных соотношений E7) получаем равенство вероят-
вероятностей
Кх!:г^(Мо)^ф>|2Ч<хИмо)к>|2- E8)
В более общей ситуации, пусть ро — оператор плотности, опи-
описывающий состояние системы в момент времени ее приготовле-
приготовления t0, а р описывает систему в момент времени ее измерения t.
Типичное измерение состоит в определении вероятности того,
что значения измеряемой величины (величин) будут находиться
в некоторой области D. Если PD — проектор на подпространство
собственных состояний, соответствующих этой области, то ука-
указанная вероятность определяется равенством
w = TrpPD = TrU (t, t0) Po Uf (t, t0) Po. E9)
Предположим теперь, что мы исходим из начального состоя-
состояния ро = 7^ро71]'и что измерение осуществляется над преобразо-
преобразованной величиной (величинами), рассматриваемой в первом
эксперименте. Собственным состояниям из области D соответ-
соответствует проектор Ро ^Т{РоТЬ Результатом нового измерения
будет
w=TrU(Ti9oTt)Uf(TiPDTt)- F0)
Принимая во внимание свойства следа, унитарность операто-
операторов Ti и соотношение E7), имеем
w' = w. F1)

158 ГЛ. XV. ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕМЕНИ
Действительно, если E8) справедливо при всех |ф> и |%>, то
имеем F1).
Выше мы, предполагая только инвариантность Н относи-
относительно преобразований заданной группы ^, получили помимо
прочего инвариантность «закона движения» динамических со-
состояний по отношению к группе д'. Обратно, можно постулиро-
постулировать инвариантность закона движения относительно группы $
и исследовать следствия этого постулата. Последний эквивален-
эквивалентен предположению о том, что для всякого преобразования 3~i
из группы, уравнение E8) выполняется при любых |ср> и |%>.
или (теорема II), что U и T\UTi совпадают с точностью до
фазы:
T\U{t,tQ)Tt = bla4J{},t^ F2)
На выбор фазовых множителей наложен ряд ограничений.
Для большинства групп, встречающихся в физических исследо-
исследованиях, эти фазовые множители равны 1 ').
Мы будем всегда предполагать, что это фазовое условие вы-
выполнено, даже когда оно и не следует из соображений внутрен-
внутренней согласованности. Постулат инвариантности тогда может
быть записан в виде
[Ti,U{t,to)] = 0.
В случае инфинитезимального оператора U, U(t-\-dt, t)~
= 1—(i/h)Hdt, из этого соотношения следует свойство сим-
симметрии гамильтониана
[Tt,H] = 0.
Итак, всякий постулат об инвариантности уравнения движе-
движения приводит к симметрии гамильтониана. В случае изолиро-
изолированной квантовой системы (нет внешнего поля) обычно посту-
постулируют инвариантность относительно группы смещений. Это оз-
означает, что пространство предполагается однородным (трансля-
') Это связано с тем обстоятельством, что множители е'а< образуют од-
одномерное представление группы & и являются непрерывными функциями i,
стремящимися к 1 при t-*-to. Если & — конечная группа или, по крайней мере,
если Э~; — элемент конечной группы, то существует целое число р, такое, что
0~р1=9. Отсюда следует, что eiai является одним из корней р-й степени из
единицы. Упомянутое выше условие требует, чтобы е'а» = 1. Отражения в
точке и отражения в плоскости дают примеры таких преобразований. Если
единственным одномерным представлением группы & является тождественное,
то мы, очевидно, имеем е'а< = 1 для всех операций группы. Группа вращений
и группа смещений являются группами такого типа. С другой стороны, если
группа инвариантности уравнения движения ограничивается до группы транс-
трансляций, то из сказанного не следует с необходимостью обращение в нуль
фаз щ.

§ 14. СИММЕТРИИ ЭФФЕКТОВ ШТАРКА И ЗЕЕМАНА 159
ционная инвариантность) и изотропным (инвариантность отно-
относительно вращений). До настоящего времени этот постулат ни-
никогда не вступал в конфликт с экспериментальными данными.
Долгое время считалось, что движение физических систем
инвариантно относительно отражений. Это экспериментально
подтверждается во всех явлениях, в которых участвуют только
электромагнитные и так называемые ядерные взаимодействия,
т. е. взаимодействия, ответственные за устойчивость атомных
ядер. Однако эксперимент показывает, что этот постулат нару-
нарушается рядом взаимодействий, и в частности теми, которые от-
отвечают за р-распад атомных ядер. Эти взаимодействия много
слабее тех, которые были упомянуты выше. Всякий раз, когда
этими взаимодействиями можно пренебречь, движение физиче-
физических систем инвариантно относительно отражений и четность
сохраняется. Такая ситуация имеет место в атомной физике,
когда рассматриваются только электромагнитные взаимодей-
взаимодействия.
При наличии внешнего поля свойства инвариантности урав-
уравнений движения зависят от симметрии внешнего поля. В каче-
качестве иллюстрации рассмотрим два примера, заимствованных из
атомной физики, — эффект Штарка и эффект Зеемана.
§ 14. Симметрии эффектов Штарка и Зеемана
Эффект Штарка. Рассмотрим атомную систему во
внешнем постоянном электрическом поле &, направленном по
оси г. Это поле инвариантно относительно трансляций, относи-
относительно вращений вокруг оси ги относительно отражений в пло-
плоскостях, параллельных оси z. Имеющаяся в этом случае группа
инвариантности является произведением группы трансляций на
группу отражений в плоскостях, содержащих ось Oz.
Будем предполагать, что движение центра масс уже отде-
отделено и рассмотрим только возможные состояния гамильтониана
относительно переменных Н, который инвариантен относительно
отражений в плоскостях, содержащих Oz. Приводимые ниже
рассмотрения базируются исключительно на этом свойстве ин-
инвариантности и не содержат ни детального описания, ни силы
взаимодействия системы с электрическим полем.
Пусть 9'и — отражение в произвольно выбранной плоскости,
содержащей Oz, a Su — соответствующий этому преобразова-
преобразованию оператор. Фазу Sa выберем так, чтобы выполнялось равен-
равенство 5^ = 1. Поскольку рассматриваемая группа порождается
отражением 9>а и инфинитезимальными вращениями вокруг
оси Oz, то оператор преобразования является функцией от Sa
и ]г. Итак, мы имеем два независимых интеграла движения,

160 ГЛ. XV. ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕМЕНИ
Sa и /2. Поскольку они не коммутируют
F3)
то некоторые из собственных значений Н вырождены.
Заметим, далее, что /| коммутирует как с /*, так и с Sa и,
следовательно, со всеми операторами группы. Оператор fz яв-
является наблюдаемой типа / для данной группы (см. определе-
определение в § 11). В качестве наблюдаемой типа М можно выбрать
либо /2, либо Sa. В первом случае стационарные состояния бу-
будут классифицироваться по собственным значениям оператора
/z, во втором — в соответствии с набором (j\, Sa)-
Предположим, что система содержит четное число полуце-
полуцелых спинов. Тогда возможными значениями /2 будут все целые
числа. Обозначим одно из них т. Если | > — стационарное со-
состояние, соответствующее этому значению, то Su|> является
стационарным состоянием с той же энергией, соответствующим
собственному значению — т оператора /2. Если т Ф О, то оба
эти состояния ортогональны. Итак, если состояния классифици-
классифицируются собственными значениями оператора /г, то два проти-
противоположных собственных значения т, —т порождают один и
тот же спектр энергий, причем каждый уровень спектра имеет
одну и ту же кратность вырождения. Иными словами, уровни
энергии зависят только от \т\, и все уровни, соответствующие
\т\ ф 0, имеют четную кратность вырождения.
Этот же результат можно получить и при классификации
состояний по собственным значениям пары (/|. Sa)- Для обо-
обозначения этих собственных значений будем использовать сим-
символы т+ и т~, где т — неотрицательное целое число, квадрат
которого равен собственному значению оператора J2Z, а верх-
верхний индекс положителен или отрицателен соответственно тому,
является ли +1 или —1 собственным значением оператора Sa,
Для примера рассмотрим состояние т+
]2г\т+)-=гп\т+) Sa\m+) = \m+)-
Если т Ф 0, то вектор /г|т+> не равен нулю и из F3) имеем
Итак, /г, действуя на состояние т+, дает состояние пг~. Если
первое из состояний стационарно, то стационарно и второе, со-
соответствующее тому же уровню энергии: энергетические уровни
зависят только от положительного целого числа т и все имеют
вырождение четного порядка. Случай т = 0 является исклю-

§ 15. СДВИГИ ВО ВРЕМЕНИ И СОХРАНЕНИЕ ЭНЕРГИИ 161
чением: спектры энергии в состояниях 0+ и 0~ могут быть раз-
различны.
Эффект Зеемана. Рассмотрим теперь атомную систему
в постоянном магнитном поле Ж, направленном по оси г. При
отражениях в плоскости, параллельной этой оси, Ж меняет
знак. С другой стороны, Ж инвариантно относительно отраже-
отражения 9"о в начале координат. Группой инвариантности внешнего
поля является группа, порождаемая трансляциями, вращениями
вокруг оси Oz и отражениями 9"о- Как и в случае эффекта
Штарка, будем рассматривать только симметрии гамильто-
гамильтониана Я относительных переменных. Этот оператор Н инвариан-
инвариантен относительно вращений вокруг оси Oz и отражений в на-
начале координат. Пусть So — оператор четности, фаза которого
фиксирована таким образом, что S^= 1. Все преобразования
группы описываются как функции наблюдаемых 1г и So, а эти
две наблюдаемые коммутируют
Следовательно, инвариантность Н при преобразованиях группы
не приводит к систематическому вырождению1).
Операторы Н, So и h можно одновременно диагонализовать,
и каждый общий собственный вектор этих трех наблюдаемых
является стационарным состоянием, инвариантным относитель-
относительно преобразований группы. Этот результат основывается исклю-
исключительно на свойствах симметрии Я и не зависит ни от деталей,
ни от силы взаимодействия системы с магнитным полем.
Раздел IV. ОБРАЩЕНИЕ ВРЕМЕНИ
И ПРИНЦИП МИКРООБРАТИМОСТИ
§ 15. Сдвиги во времени и сохранение энергии
Среди всех преобразований, затрагивающих время, простей-
простейшими являются временные сдвиги. В классической механике
инвариантность уравнений движения относительно временных
сдвигов приводит к хорошо известному закону сохранения энер-
энергии (это требует независимости от времени функции Гамиль-
Гамильтона). Мы получим аналогичное свойство в квантовой меха-
механике.
Пусть |^@> — возможное решение уравнений движения.
Инвариантность уравнений движения системы относительно вре-
временного сдвига т эквивалентна наличию другого решения
\ty'(t)y, описывающего в момент времени t то динамическое со-
>) Иными словами, все неприводимые представления группы обязательно
одномерны.

162 ГЛ. XV. ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕМЕНИ
стояние, которое в момент времени t -\- % описывалось исходным
решением, т. е.
Для того чтобы каждое решение уравнений движения обладало
таким свойством, необходимо, чтобы оператор U удовлетворял
равенству
U(i,0) = emt-%)U(t + r, т), F4)
где a(t, т) является фазой, которая может зависеть от t и т.
Для бесконечно малого t, положив f(т) = da/dt\t=0, имеем
-±H(x)dt),
Я(т) = Я@) + А/(т). F5)
Если закон движения инвариантен относительно произвольных
временных сдвигов, то F4) должно выполняться для всех т.
Иными словами, гамильтониан постоянен с точностью до добав-
добавления (вещественной) функции времени. В действительности,
эту функцию можно положить равной нулю без изменения ка-
каких-либо физических свойств системы. Замена гамильтониана
H(t) его значением в момент времени ^ = 0 сказывается лишь
в домножении U(t, t0) на фазовый множитель
¦
о
(задача 6).
Итак, мы можем предполагать независимость гамильтониана
от времени при инвариантности уравнений движения относи-
относительно временных сдвигов. Это предположение будет использо-
использоваться во всех приводимых ниже рассмотрениях. В этом случае
уравнение F4) сводится к инвариантности U(t,t0) при времен-
временных сдвигах
U(t + t,x) = U (t, 0). F6)
§ 16. Обращение времени в классической и квантовой
механиках
В оставшейся части этого раздела мы будем рассматривать
только консервативные системы. Законы движения таких систем
часто оказываются инвариантными не только относительно вре-
временных сдвигов, но и относительно обращения времени. Эта ин-
инвариантность встречается также и в классической механике.
Лагранжева функция Lci(q,q) классической механики яв-
является полиномом второго порядка по скоростям. Для многих

§ 16. ОБРАЩЕНИЕ ВРЕМЕНИ В КЛ. И КВ. МЕХАНИКАХ 163
систем функция Лагранжа не содержит членов первого порядка,
и мы имеем
Lei (q, q) = Lci (— q, q).
Системы, состоящие из изолированных частиц, всегда обладают
этим свойством симметрии. Введение статического внешнего
поля не всегда приводит к нарушению свойства симметрии. Оно
сохраняется, например, в чисто электрическом поле. С другой
стороны, в магнитном поле взаимодействие линейно по скоростям
и, следовательно, нарушает это свойство. Если же указанное
свойство симметрии имеется, то импульсы р являются линей-
линейными однородными функциями скоростей, а функция Гамиль-
тона инварианта относительно обращения времени.
Рис. 7. Изображение двух классических траекторий (а) и (б), связанных отра-
отражением времени ra (t) = r6 (— t), ra (t) = - гб (-1).
Для того чтобы обсуждение стало менее формальным, рас-
рассмотрим следствия такой симметрии на простом примере ча-
частицы в статическом потенциале. Тогда имеем
Я(р,г)=-|?- + 7(г) = Я(-р,г). F7)
Отсюда следует, что все решения r(t) уравнений движения об-
обратимы во времени: функция rrev@. которая определяется ра-
равенством
rrev (t) = r(—f) F8)
также является решением уравнений движения. Соответствие
между двумя решениями представлено на рис. 7.
Положение частицы в момент времени t в одном из решений
совпадает с положением частицы в момент времени —t в дру-
другом; ее скорость в момент / в одном из решений противоположна

164 ГЛ. XV. ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕМЕНИ
по направлению скорости в момент времени —t в другом реше-
решении. Соответствие между импульсами то же, что и между ско-
скоростями
Prev @ = -Р (~ /). F9)
Рассмотрим теперь аналогичную квантовую систему. Урав-
Уравнение Шредингера имеет вид
ih -| ф (г, t) = [- -^-Д + V (г)] ф (г, /). G0)
Гамильтониан является вещественным оператором. Если изме-
изменить t на —t и взять комплексное сопряжение от обеих частей
уравнения, то получим
[^ ](r, -t). G1)
Иными словами, если i|>(r, t)—решение уравнения Шредингера,
то функция
*w('. О «-*•(!¦,-0 G2)
также является его решением.
Соответствие между ф и iprev на удивление аналогично соот-
соответствию между двумя классическими решениями, рассмотрен-
рассмотренному выше (уравнения F8) — F9)). Обозначив P{r,t) и U(p,t)
плотности вероятности для координаты и импульса в момент
времени t, имеем
Ртеч(г,0 = Р(г, -0, F8')
Пге>,/) = П(-р, -/). F9')
§ 17. Обращение времени. Частица нулевого спина
Как видно из приведенного примера, обратимость во времени
решений уравнения Шредингера связана с инвариантностью га-
гамильтониана Н(р, г) при замене р на —р. Эта инвариантность
означает, что Н(р, г) описывается в волновой механике веще-
вещественным дифференциальным оператором. Мы приходим, таким
образом, к определению преобразования динамических перемен-
переменных и динамических состояний, которое будем называть обра-
обращением времени и при котором г и р переходят в г и —р соот-
соответственно. Обозначим К оператор, реализующий это преобра-
преобразование, а само преобразование обозначим Ж. По определению
КгК* = г, КрК? = -р. G3)
Это преобразование меняет знак коммутационных соотноше-
соотношений и, следовательно, К является антиунитарным оператором

§ 17. ОБРАЩЕНИЕ ВРЕМЕНИ. ЧАСТИЦА НУЛЕВОГО СПИНА 165
(см. § 6). Соотношения G3) определяют этот оператор с точ-
точностью до фазового множителя. Обозначим Ко оператор ком-
комплексного сопряжения в представлении волновой механики (ан-
(антиунитарный оператор такого типа определен в § 5). Поскольку
в рассматриваемом представлении матрицы, описывающие г и р,
являются вещественной и чисто мнимой соответственно, то Ко,
очевидно, удовлетворяет соотношениям G3). Следовательно, мы
можем взять Ко в качестве оператора обращения времени
К = К0.
При таком выборе фазы действие К на волновую функцию сво-
сводится к комплексному сопряжению
Предположение об инвариантности Н относительно замены —р
на р эквивалентно условию
[К,Щ = 0. . G4)
Применив (антиунитарный) оператор К к обеим частям уравне-
уравнения Шредингера, получаем
т.е.
Итак, если |^@) удовлетворяет уравнению Шредингера, то
ему удовлетворяет и вектор
I *$>„, = * 1Ф (-/)>• G5)
Динамическое состояние, описываемое вектором |^>rev в мо-
момент времени t, является при обращении времени образом со-
состояния, соответствующего вектору |if>> в момент времени —t.
Это и есть именно то свойство обратимости решений уравнения
Шредингера, которое было обнаружено в предыдущем параг-
параграфе.
Из определяющих соотношений G3) следует, что преобразо-
преобразование Ж коммутирует со всеми пространственными преобразо-
преобразованиями (трансляциями, вращениями и отражениями). Отме-
Отметим также, что К коммутирует с операторами пространственных
преобразований, определенными в разделе II1). В частности,
') Если преобразование Ж коммутирует с другим преобразованием У, то
мы имеем КТ = eia ТК, где фазовый множитель е зависит от выбора опе-
оператора Т. Легко видеть, что этот оператор определен с точностью до знака,
если выполнено равенство КТ = ТК.
Это позволяет получить определенные выводы о структуре группы onegg-'
торов G, сопоставляемой группе преобразований ^ в случае, когда последние

166 ГЛ. XV. ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕМЕНИ
К антикоммутирует с тремя компонентами импульса и, следо-
следовательно, коммутирует с инфинитезимальными операторами
трансляций. Аналогчно К антикоммутирует с тремя компонен-
компонентами момента импульса
К(гХр)К*=-(гХр) G6)
и, следовательно, коммутирует с инфинитезимальными опера-
операторами вращений.
§18. Общее определение обращения времени
Для того чтобы расширить понятие обращения времени на
самые общие системы частиц, мы должны определить обраще-
обращение времени для спиновых переменных. Поскольку спин яв-
является частным случаем момента импульса, то он должен пре-
преобразовываться подобно моменту импульса (ур. G6)), т. е.
KsKf = -s. G7)
Операция обращения времени обращает спин. Это опре-
определение сохраняет свойства коммутации Ж с пространствен-
пространственными преобразованиями и, в частности, с вращениями. Более
того, согласно G6) и G7) К антикоммутирует с компонентами
полного момента импульса /
KJKf = - / G8)
и, следовательно, коммутирует с операторами вращения (см.
задачу 8), т. е. так как К антилинеен, G8) приводит к соотно-
соотношению
Построим теперь оператор обращения времени для частицы
спина s. Этот оператор определяется соотношениями G3) и
G7). Обозначим Ко оператор комплексного сопряжения, ассо-
ассоциированный с представлением {г, s?}, в котором относитель-
относительные фазы базисных векторов фиксированы обычным соглаше-
соглашением и, в частности, используются базисные векторы в спино-
спиновом пространстве, взятые в «стандартном» виде, определенном
в гл. XIII. Таким образом, имеем
КогКо = г, КорКо = -р, G9)
q = sx, KoSyKo — — sy, KoSzKo = sz. (80)
коммутируют с Ж. Тогда мы можем взять за G\) (обозначения из § 8) пару
преобразующих операторов, коммутирующих с К- В частности, A) обозначает
пару (+1, —1). Множество {Т}, образованное этими парами операторов (один
из которых отличается от другого знаком), очевидно, образует группу и мо-
может быть взято в качестве группы G.

§ 19. ОБРАЩЕНИЕ ВРЕМЕНИ И КОМПЛЕКСНОЕ СОПРЯЖЕНИЕ 167
Положим
К = ТК0. (81)
Поскольку Т = ККо и Г+ = КоК^, то (линейное) унитарное пре-
преобразование Т действует по правилам
7>Г+ = г, TpTf = p, (82)
TsxTf = — sx, TsyT* = sy, 7ваГ* = — в2. (83)
Уравнения (82) и (83) порождают преобразование перемен-
переменных г, р, s, которое соответствует повороту спина на угол п во-
вокруг оси у. Пусть Y(s> — оператор, осуществляющий это враще-
вращение
Величины Т и У(8) различаются только фазовым множителем.
Поскольку фазовый множитель не имеет физического значения,
то мы можем положить его равным 1, что дает
(84)
Для специального случая частицы спина 1/2
К = - ioyKo. (85)
Все сказанное выше без затруднений можно распростра-
распространить на системы, состоящие из N частиц. Оператор К стано-
становится тензорным произведением операторов отражения вре-
времени отдельных частиц. Если Ко — оператор комплексного
сопряжения, ассоциированный со стандартным представлением
{гAMгО) ... rWSzm}t a Y{S) — оператор вращения спинов на
угол я вокруг оси Оу, то при указанном выше выборе фазы по-
получаем
К = Y{S)KQ = e~i7lSy/hK0. (86)
§ 19. Обращение времени и комплексное сопряжение
Операция обращения времени Ж имеет много общего с ком-
комплексным сопряжением. Расширяя эту связь, будем называть
комплексно сопряженными пару линейных операторов, являю-
являющихся образами друг друга при обращении времени. В частно-
частности, оператор Q называется:
(i) вещественным, если /CQ/C+ = Q;
(и) чисто мнимым, если KQK^ = — Q.
Всякая вещественная постоянная является вещественным
оператором, а постоянная i — чисто мнимым оператором. Про?
изведение i на вещественную постоянную дает чисто мнимый

168 ГЛ. XV. ЗАКОНЫ СОХРАНЕНИЯ- ОБРАЩЕНИЕ ВРЕМЕНИ
оператор; сумма и произведение двух вещественных операторов
являются вещественными операторами.
Не следует смешивать понятие вещественности с понятием
эрмитовости. В этой связи уместно сделать следующие два за-
замечания.
(а) В отличие от того, что имеется в случае эрмитова со-
сопряжения, комплексно сопряженные операторы не обязаны опи-
описываться в заданном представлении комплексно сопряженными
матрицами.
(б) Приведенное выше определение комплексного сопряже-
сопряжения не является единственно возможным. Всякое антиунитарное
преобразование, квадрат которого равен 3(, можно рассматри-
рассматривать как комплексное сопряжение.
При нашем определении комплексного сопряжения все на-
наблюдаемые, которые являются функциями координат, веще-
вещественны, все импульсы и все спины чисто мнимы, а операторы
пространственных преобразований, определенные так, как это
делалось в разделе II, все вещественны (задача 8).
Понятие комплексного сопряжения можно распространить
на случай векторов. Определим в качестве вектора, комплекс-
комплексно сопряженного вектору|>, вектор К\}. Повторное примене-
применение К может не давать исходный вектор кроме случая, когда
К2 = 1. Из равенства Ж2 = 3 не следует, что К2 = 1, а лишь
то, что К2 коммутирует со всеми динамическими переменными,
и, следовательно, является постоянной. Несложно показать (за-
(задача 9), что значение этой постоянной не зависит от выбора
фазы, используемой в определении К, и что возможными зна-
значениями ее являются числа ±1. Более того, это значение можно
вычислить из выражения (86) для К- Поскольку Ко коммути-
коммутирует с y(S) и /Сд = 1, то
к* = (уюу = е-п**в/н (87)
или, если обозначить п число частиц полуцелого спина в си-
системе, то
К2 = (-])". (88)
Если К2 = 1 (я четно), то комплексно сопряженные векторы
переходят друг в друга и можно определить вещественные век-
векторы. Вектор |г> называют вещественным, если
К\г) = \г).
По определению, вещественным представлением называют пред-
представление, все базисные векторы которого вещественны.
Для построения вещественного базиса можно поступать сле-
следующим образом. Выбирается произвольный вектор |а> и ли-

§ 20. ПРИНЦИП МИКРООБРАТИМОСТИ 169
нейной комбинацией векторов |а> и К\а} образуют веществен-
вещественный, нормированный на 1 вектор
\аг) = с\а) + с*(К\а)).
Вещественность вектора |аг> очевидна. Постоянная с выби-
выбирается так, чтобы норма вектора равнялась 1. Легко проверить,
что такой выбор всегда возможен. Затем выбирают вектор |6),
ортогональный к |ал>. и таким же образом конструируется ве-
щественный вектор
предположению, <аг
Ь1") нормы 1. Поскольку К\агУ=\агу и, по
by = 0, то
(аг | (К Ift» = ((аг | К*) (К | ft» - (аг | ft)' = О,
и, следовательно, |ЬГ> ортогонален к |аг>. Затем выбирается
произвольный вектор |с>, ортогональный к |аг> и |6Г>, и
строится вектор \сг). Эту процедуру повторяют до тех пор, пока
не будет образован полный набор базисных векторов.
Вещественные представления имеют ряд интересных свойств.
Оператором обычного комплексного сопряжения в этих пред-
представлениях является оператор /(. Всякий вещественный опера-
оператор описывается вещественной матрицей; дв-а комплексно со-
сопряженных оператора реализуются комплексно сопряженными
матрицами. Унитарные матрицы, связывающие два веществен-
вещественных представления, вещественны.
Если К2 = —1 (п нечетно), то вещественные векторы отсут-
отсутствуют. Однако так как К = —/С+, то для любого вектора |ы>
имеем
{и | (К\ и» Н" I (К* | и» = -{и | (К | и» = О,
так что мы получили интересное свойство:
Два комплексно сопряженных вектора | > и К \ > ортого-
ортогональны.
Кроме того, если вектор |Ь> ортогонален двум комплексно
сопряженным векторам |а> и К\а}, то это свойство справед-
справедливо и для комплексно сопряженного вектора К\Ь~). Из этого
легко проверяемого свойства можно получить, используя те же
рассуждения, что и в случае К2 = 1, что существует базис, це-
целиком построенный из комплексно сопряженных векторов.
§ 20. Принцип микрообратимости
Точно так же как ранее постулировалась инвариантность
уравнения движения заданной системы относительно некоторых
пространственных преобразований (§ 13), мы можем постули-
постулировать его обратимость по отношению ко времени, т. е. если

170 ГЛ. XV. ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕМЕНИ
\ = U(t, 0)|^> описывает возможное состояние системы,
то вектор
также представляет возможное состояние системы и, следова-
следовательно, с точностью до фазового множителя этот вектор совпа-
совпадает с U(t, 0)К\^}. Предполагая, что это свойство справедливо
для всех |i|5>, постулат обратимости по отношению к времени
можно записать в виде
U (t, 0) К = е'»Ю KU (— t, 0).
Этот постулат применим только к консервативным системам.
Если Н — гамильтониан системы, то
U (t, 0) = е-''™/*, U (-1, 0) = e+iHiih = [/+ (/, 0),
откуда имеем
U (t, 0) = е'° (KU* (t, 0) /С+). (89)
Домножив обе части этого равенства на К слева и на Kf справа
и учитывая, что К2 = Ю2 = (—1)", находим, что
Сравнив это соотношение с равенством, получаемым при эрми-
эрмитовом сопряжении соотношения (89),
получаем, что е'а может принимать только значения ±1, но
поскольку е'а — непрерывная функция t, равная 1 при t = 0, то
мы имеем е'а = 1. Применяя (89) к инфинитезимальному one-
ратору
U(dt, O)=\-~Hdt,
получаем
КНК* = Н. (90)
Итак, если уравнение движения консервативной системы об-
обратимо во времени, то гамильтониан веществен и наоборот
(обратное доказано в § 17).
Постулат обратимости под названием принцип микрообра-
микрообратимости обычно формулируется несколько отличным от выше
. приведенного способом. Эта формулировка такова.

§ 20. ПРИНЦИП МИКРООБРАТИМОСТИ 171
Пусть w — вероятность обнаружить консервативную систему
в некотором состоянии |х> в момент времени t, если она в мо-
момент времени t0 находилась в состоянии |ф>. Пусть шгеч — ве-
вероятность обнаружить систему в состоянии /С|ср> в момент вре-
времени t, если она в момент времени t0 находилась в состоянии
К\у). Тогда принцип микрообратимости утверждает, что
W (91)
для любых |ф>, |х>, U и t.
Условие (91) может быть записано в виде
| «ф | К*) (U (t, t0) K\ X)) Р = ] (XI U (t, t0) | ф) ]2.
Это соотношение можно сравнить с соотношением E8). По-
Поскольку
«Ф | К*) (UK | X» = (ф | (K*UK) I х>* = <Х I {К*и*К) I ф>.
то его можно переписать в виде
Так как последнее равенство выполняется при всех |ф> и \%У,
то U и K^U'^K совпадают с точностью до фазового множител?
(теорема II). Аргументация, подобная той, которая применялась
выше к множителю е'а, показывает, что и этот фазовый множи-
множитель равен единице. Таким образом, принцип микрообратимости
требует выполнения равенства
,to)K, (92)
которое в случае инфинитезимального оператора U как раз яв-
является условием инвариантности гамильтониана (90I).
Обычно предполагается, что любая квантовая система, не
взаимодействующая с внешними полями, удовлетворяет прин-
принципу микрообратимости. Вплоть до настоящего времени эта ги-
гипотеза не противоречит данным эксперимента. В присутствии
внешней) поля принцип микрообратимости выполняется или
нет в зависимости от того, является ли поле инвариантным или
нет по отношению к обращению времени. Электростатическое
поле обладает этим свойством инвариантности. Это легко по-
понять, так как источниками этого поля являются фиксированные
электрические заряды, а распределение статического заряда не
меняется при обращении времени. С другой стороны, источни-
источниками статического магнитного поля являются фиксированные
') Поскольку С* fa,ti) = U(tut2), то уравнение (92) можно записать
также в виде

172 ГЛ. XV. ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕМЕНИ
электрические токи: обращение времени обращает токи, а зна-
значит, и поля. Следовательно, принцип микрообратимости нару-
нарушается в присутствии магнитного поля даже в том случае, когда
оно не зависит от времени.
§ 21. Следствие: вырождение Крамерса
Вещественность гамильтониана Н, как и любая другая сим-
симметрия, отражается в наличии специальных свойств в задаче
на собственные значения.
Если |м> — собственный вектор оператора Н
Н\и) = Е\и),
то комплексно сопряженный вектор К\иУ также является соб-
собственным для Н и соответствует тому же собственному значе-
значению, т. е. по предположению
нк=кн,
и так как Е — вещественное число, то
Следовательно, подпространство <8Е, соответствующее соб-
собственному значению Е, инвариантно относительно действия ан-
антиунитарного преобразования К, и можно применить резуль-
результаты § 19. Следует рассмотреть два случая в соответствии
сК2 = ± 1.
1-й случай. /<С2 = + 1 (четное число спинов 1/2).
В каждом из подпространств <Se можно выбрать ортонорми-
рованный базис, все векторы которого вещественны. Таким об-
образом, Н имеет (по крайней мере) один базис, все векторы ко-
которого вещественны.
2-й случай. К2 = —1 (нечетное число спинов 1/2).
В каждом из подпространств <§ е можно выбрать ортонорми-
рованный базис, состоящий из пар комплексно сопряженных век-
векторов. Итак, каждое из подпространств Же имеет четную раз-
размерность: каждое собственное значение гамильтониана Н по
крайней мере двукратно вырождено и его вырождение обяза-
обязательно имеет четную кратность. Вырождение такого типа на-
называют вырождением Крамерса.
Некоторые системы не имеют симметрии, отличных от инва-
инвариантности относительно обращения времени. Пример этому
дает система атомов в асимметрической кристаллической ре-
1петке. Такой атом можно рассматривать как систему, находя-
находящуюся в чисто электростатическом внешнем поле. Гамильто-
ййан такого атома веществен. Если он содержит нечетное

§ 22. ВЕЩЕСТВЕННЫЙ ГАМИЛЬТОНИАН 173
число электронов, то все энергетические уровни двукратно вы*
рождены. Это вырождение можно устранить введением магнит-
магнитного поля.
§ 22. Вещественный гамильтониан, инвариантный
относительно вращений
Если гамильтониан Н обладает другими свойствами симме-
симметрии помимо обращения времени, то результаты предыдущего
пункта остаются справедливыми, хотя в значительной степени
теряют свой интерес. Вигнер х) систематически изучал свойства
Н в случае, когда:
(i) Н веществен: [К, Н] = 0;
(И) Н инвариантен относительно преобразований группы
линейных преобразований: [7\, Я] = 0;
(Hi) преобразования Г,- коммутируют с обращением вре-
времени: [К, Ti] = 0.
Мы рассмотрим здесь только случай, когда группой инва-
риантности является группа вращений2).
Пусть Y — оператор вращения на угол я вокруг оси у (не
следует смешивать этот оператор с введенным выше операто-
оператором y(S) вращения одних только спинов). Положим
(93)
Операторы У+ и К коммутируют с Л и антикоммутируют с Jz.
1) Е. P. Wigner, Gottinger Nachrichten 31, 546 A932) (см. Е. Вигнер.
Теория групп. М., ИЛ., 1961, гл. 26. Прим. перев.)
2) Для заданной группы G вещественность Н сказывается либо на удвое-
удвоении G-вырождения, либо в возможности диагонализацни оператора Н в пред-
представлении, базисные векторы которого удовлетворяют некоторому условию ве-
вещественности. Детальная формулировка результата состоит в следующем (см.
работу Вигнера, цитированную выше).
Пусть G<»— неприводимое представление G, a GU)* — сопряженное пред-
представление. Оператор К, действуя на вектор одного из этих представлений, дает
вектор из другого. Тогда G<'> и G<?>* либо эквивалентны, либо неэквивалент-
неэквивалентны. В первом случае матрица S, позволяющая перейти от одного представле-
представления к другому (G(^* = SG'AS1"), имеет следующее свойство: SS* = ±1. Обозна-
Обозначим G представление группы G в подпространстве, соответствующем задан-
заданному собственному значению гамильтониана Н. Следует рассмотреть три слу-
случая:
(а) если G<'>* ие эквивалентно G<», то оба представления одинаковое чис-
число раз встречаются в разложении иа неприводимые компоненты (двукратное
вырождение);
(б) если G»>* ж G»> и SS*K2 = —1, то G«> встречается четное число раз
в разложении G (двукратное вырождение);
(в) если G<'>*«G<'> и SS*K2 = + 1, то все базисные векторы каждой
компоненты G<" представления G можно выбрать удовлетворяющими усло-
условию «вещественности»: KS\u) = \и).
Все представления группы вращений соответствуют случаю (в),

174 ГЛ. XV. ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕМЕНИ
Следовательно, Ку коммутирует с Я и Jz. Этот оператор ком-
коммутирует также с J+ и /_
* ± Uу) = К+ (- Jx ± Uу) K = (JX± iJy)
Более того, поскольку [Y, К] = 0 и У2 = /С2 = (—1)" (ср. со»
отношение (88)), то
Ц = \. (94)
Антиунитарное преобразование Ку можно рассматривать как
комплексное сопряжение, точно так же как рассматривалось К
в § 19. Для того чтобы различать Ку и К, мы будем использо-
вать кавычки для нового типа сопряжения. Таким образом, «ве-
«вещественный» (линейный) оператор — оператор, коммутирующий
с Ку. Вектором, «комплексно сопряженным» к вектору |>, бу-
будет, по определению, вектор КУ\У- Поскольку К2 =1, то «ве-
«вещественные» векторы и «вещественные» представления суще-
существуют. Действие «вещественного» оператора на «вещественный»
вектор дает «вещественный» вектор. В «вещественном» пред-
представлении «вещественный» оператор описывается веществен-
вещественными матрицами.
Поскольку Р и Jz — «вещественные» операторы, мы можем
построить базис в пространстве момента импульса (//), все век-
векторы которого «вещественны». Поскольку J+ и /_ также «веще-
«вещественны», то и векторы стандартного базиса, который может
быть построен из этих векторов методом, развитым в § XIII. 6,
также все «вещественны».
Пусть |т/(л>—векторы «вещественного» стандартного ба-
базиса. Если Н инвариантен относительно вращений и отражения
времени, то он коммутирует с / и Ку и описывается в представ-
представлении {т/(л} вещественной матрицей вида E2), т. е.
с вещественными Щ%,. Отсюда следует наличие вращательного
вырождения и существование у Н по крайней мере одной орто-
нормированной системы собственных векторов, образующих
«вещественный» базис.
«Вещественный» базис в <8 можно построить, взяв тензор-
тензорные произведения базисных векторов в более простых простран-
пространствах. Предположим, что мы имеем
и что в каждом пространстве §',¦ определены операторы враще-
вращений и обращения времени. С каждым Si связан оператор «ком-
«комплексного сопряжения» /С^0 == К<*)+/С<г), а оператор Ку для всего

§ 22. ВЕЩЕСТВЕННЫЙ ГАМИЛЬТОНИАН 175
пространства является тензорным произведением этих опера-
операторов
К, = *«">*»....
Тензорное произведение «вещественных» векторов определяет
«вещественный» вектор. В частности, мы можем образовать
множество «вещественных» базисных векторов в <%, взяв тен-
тензорные произведения векторов, образующих «вещественный»
стандартный базис момента импульса в каждом из пространств
сомножителей. Исходя из этого базиса в &', мы можем образо-
образовать стандартный базис полного момента импульса в этом про-
пространстве путем сложения моментов импульса. Поскольку все
коэффициенты Клебша — Гордана вещественны, все векторы по-
построенного таким образом стандартного базиса также «веще-
«вещественны».
Мы закончим эту главу замечанием о «вещественности» сфе-
сферических функций.
Пусть со =F, ф) — угловые координаты вектора г частицы,
a Yf (со) — сферические функции, описывающие состояние мо-
момента импульса Aт). В этом частном случае (ft = 1)
так что (уравнения (Б.92) и (В.62))
Куу? (и) = е~шуУТ* (со) = е~шу (- \)m YJm (и) = (- \)lY? (со).
Итак, сферическая функция Yf «вещественна» при четном / и
«чисто мнима» при нечетном /. С другой стороны, функции
образуют «вещественный» стандартный базис для орбитального
момента импульса.
Пусть Юр = FР, фр) — угловые координаты импульса р,
a Yf (со ) — сферическая гармоника, описывающая состояние
момента импульса Aпг) в представлении {р}. Можно показать
(задача 10), что
где So — оператор четности (ур. D5)), а Кр — оператор ком-
комплексного сопряжения в представлении {р}. Тогда
к/г (%)==>? К)-
Следовательно, Yf (oap) образуют «вещественный» стандартный

176 ГЛ. XV. ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕМЕНИ
базис для орбитального момента импульса. Эти рассмотрения
«вещественности» без труда можно распространить на общий
случай неприводимых тензорных операторов (см. задачу 12).
ЗАДАЧИ И УПРАЖНЕНИЯ
1. Предположим, что пространство <$ векторов состояния системы пред-
представляет собой прямую сумму <$\ + Si + ... некоторого числа подпространств,
инвариантных по отношению к множеству физических наблюдаемых системы.
Показать, что проекторы Pi, Pz, ... иа этн подпространства коммутируют с
каждой физической наблюдаемой и что не все векторы из & являются одно-
одновременными собственными векторами полного набора коммутирующих физи-
физических наблюдаемых.
2. Показать, что оператор So, определенный равенством D5), удовлетво-
удовлетворяет соотношениям D3) и D4) и, в частности, соотношению SopS^ = — р.
3. Оператор отражения в плоскости, перпендикулярной вектору и, в слу-
случае частиц спина 7а является произведением оператора, действующего только
на орбитальные переменные, и оператора, действующего только на спиновые
переменные. Показать, что при специальном выборе фазового множителя по-
последний из упомянутых операторов равен (аи). Показать, что произведение
(ov)(au), которое описывает два последовательных отражения в плоскостях,
перпендикулярных векторам и и v, равно оператору, соответствующему вра-
вращению спина на угол 2(u, v) вокруг оси (u X v)/\u X v\.
4. Поток частиц спина s рассеивается на потенциале, зависящем от спина.
Пусть pi — начальный импульс. Частицы, рассеянные в заданном направлении,
выделяются диафрагмой. Пусть pf — импульс этих частиц, a D — плоскость
рассеяния, т. е. плоскость, в которой лежат векторы р< и pf. Мы предполагаем,
что налетающие частицы не поляризованы, так что их спиновое состояние опи-
описывается оператором плотности pi = \lBs + 1). Показать, что если потенциал
взаимодействия инвариантен относительно вращений и отражения в начале
координат, то оператор плотности рг, описывающий спиновое состояние рас-
рассеянных частиц, симметричен относительно отражения в плоскости D.
5. Показать, что оператор плотности, описывающий спиновое состояние
частицы спина '/г. может быть представлен в виде
где а =з (а*, оу, аг) — удвоенный вектор спииа частицы, а Р — вектор, длина
которого лежит между 0 и 1 и который полностью определяет состояние по-
поляризации частицы.
Возвращаясь к задаче 4 и предполагая, что s = Уэ, показать, что вектор
Pf, определяющий поляризацию рассеянных частиц, перпендикулярен плоско-
плоскости рассеяния.
в. Показать, что при добавлении к гамильтониану системы произвольной
вещественной функции времени оператор эволюции U(t, to) домножается толь-
только иа фазовый множитель,

ЗАДАЧИ И УПРАЖНЕНИЯ 177
7. При галилеевском преобразовании системы координат переменные г, р,
s частицы переходят в г — vt, р— mv, s соответственно. Показать, что такое
преобразование задается оператором
G (v, t) = exp [iv (mr — pt)/h].
Галилеевское преобразование системы N частиц описывается оператором
G{y,t) — exp[iv(MR — Pt)/H], где М, R и Р — масса, оператор координаты и
оператор импульса центра масс.
(N. В. Для заданного значения t галилеевские преобразования образуют
группу. При принятом соглашении о фазе операторы преобразований также
образуют группу.)
Уравнение движения инвариантно относительно этого преобразования,
если
G+ {v, t) U (t, t0) G (v, ta) = U (t, to) X фазовый множитель.
Показать, что это.условие эквивалентно «условию галилеевской инвариантно-
инвариантности уравнения Шредингера»
G+ (v, t) [ih -J- - я] G (v, t) = [ih -|- - Я] + f,
где f — произвольная вещественная функция времени, и что это условие дей-
действительно выполняется для шредингеровского гамильтониана (прн этом
/ = 0).
8. Показать, что операторы трансляций и вращений и оператор отраже-
отражений So (определение D5)) коммутируют с оператором обращения времени К
и что это свойство не зависит от выбора произвольной фазы, имеющейся в
определении К-
9. Показать, что если квадрат антиунитарного оператора равен постоян-
постоянной, то она равна либо +1, либо —1.
10. Пусть Кр — оператор комплексного сопряжения в представлении {р},
Ко — оператор комплексного сопряжения в представлении {г}, So — оператор
отражения (определение D5)). Показать, что Ко = S0KP. Вывести, что прн
обращении времени волновая функция Ф(р) переходит в
11. Пусть имеется система, инвариантная относительно обращения вре-
времени. Пусть В — чисто мнимая (см. § 19) наблюдаемая системы (импульс,
спин, орбитальный момент импульса и т. п.). Показать, что:
(i) если стационарное состояние ие вырождено, то среднее значение на-
наблюдаемой В в этом состоянии равно нулю;
(ii) след проекции наблюдаемой В на подпространство, соответствующее
любому собственному значению энергии, равен нулю.
12. Обозначим Т^ (q = —k, —k+\, ..., +ft) стандартные компоненты
неприводимого тензорного оператора Г<*>. По определению, комплексно сопря-
сопряженным к onepatopy Г(*> является тензорный оператор, компонента д = 0 ко-

178 ГЛ. XV. ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕМЕНИ
торого есть образ при обращении времени компоненты Г{,*' (при таком опре-
определении декартовы компоненты вещественных векторных операторов инвари-
инвариантны относительно обращения времени, а компоненты чисто мнимых векторных
операторов меняют знак). Показать, что стандартные компоненты оператора,
комплексно сопряженного к Г<*>, являются «комплексно сопряженными» (в
смысле § 22) соответствующим компонентам оператора (—1)*г<*> и что, в
частности, в «вещественном» стандартном представлении матричный элемент
(xj\>. | Т^ | т'/'ц/) веществен, если t*r<*> веществен, и чисто мнимый, если
1*Г<*> — таковой.
(N. В. Это свойство имеет непосредственное приложение в задачах об уг-
угловых корреляциях, ибо оно дает, с точностью до знака, относительные фазы
вкладов различных мультиполей.)

ЧАСТЬ IV
«Если блюда, которые я вам
предлагаю, плохо приготовлены, то
виноват в этом не столько мой по-
повар, сколько химия, еще не вышед-
вышедшая из детского возраста.»
А. Франс «Харчевня королевы
Педок»
ПРИБЛИЖЕННЫЕ
МЕТОДЫ

ГЛАВА XVI
СТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ
§ 1. Общее введение к четвертой части
Незначительное число задач в квантовой механике, которые
могут быть решены точно, относятся к очень простым и специ-
специальным системам. Практически ни одну из физических систем
нельзя изучать без использования подходящего приближенного
метода. Искусство физика в большой степени состоит в умении
определить относительную значимость различных факторов
в данной физической системе и в выборе подходящего прибли-
приближенного метода. Вообще говоря, для каждой задачи существует
свой приближенный метод, и рассмотреть все возможные ме-
методы мы не можем. В данной книге излагаются только доста-
достаточно общие методы, которые заслуживают систематического
изучения. Мы уже рассматривали классическое приближение и
метод ВКБ в главе VI и метод фазовых сдвигов для задач рас-
рассеяния в главе X. Другие методы будут предметом исследования
в этой, четвертой, части нашей книги.
Математическое описание квантовой системы состоит в оп-
определении ее оператора эволюции U(t, t0) или по крайней мере
в определении основных свойств этого оператора. Если гамиль-
гамильтониан Н не зависит от времени, то проблема сводится к реше-
решению задачи на собственные значения для оператора Н, так как
в этом случае
и свойства U(t, t0) непосредственно связаны со свойствами Я.
Ситуация становится более сложной, когда Н зависит от вре-
времени. Однако ясно, что и в этом случае важную роль в опре-
определении свойств U будут играть собственные значения и соб-
собственные функции Н, которые тоже будут зависеть от времени.
Как правило, задачи рассеяния, которые относятся к непре-
непрерывному спектру, значительно сложнее задач, относящихся
к связанным состояниям. Теория рассеяния будет рассматри-
рассматриваться в последней главе этой части (гл. XIX). В остальных
главах (гл. XVI — XVIII) в основном исследуются связанные

182 ГЛ. XVI. СТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ
состояния, хотя развитые в них методы могут использоваться
и для изучения состояний непрерывного спектра.
Задачи о связанных состояниях можно разделить на два
класса. Одни связаны с определением стационарных состояний,
иначе говоря, с решением задачи на собственные значения опе-
оператора Н. К другому классу относятся задачи о переходах ме-
между состояниями. Для решения задачи на собственные значе-
значения обычно используют один из трех методов. Метод В КБ ос-
основан на квазиклассическом приближении — приближении
больших квантовых чисел и малых длин волн. Стационарная
теория возмущений основана на точном решении задачи на
собственные значения для некоторого оператора Но, мало от-
отличающегося от Н, собственные значения и собственные функ-
функции Н выражаются в виде рядов по разности Н — Но. Если
упомянутые методы не применимы, то можно воспользоваться
вариационным методом при условии, что имеется хорошее ап-
априорное представление об общем виде искомых собственных
функций. В настоящей главе рассматривается стационарная
теория возмущений, а в главе XVIII — вариационный метод.
Основные методы исследования эволюции связанных состояний,
когда гамильтониан зависит от времени, и, в частности, вычис-
вычисление переходов между состояниями, изложены в главе XVII.
Раздел I. ВОЗМУЩЕНИЕ НЕВЫРОЖДЕННОГО УРОВНЯ
§ 2. Разложение по степеням возмущения
Предположим, что гамильтониан Н можно записать в виде
суммы «невозмущенного гамильтониана» Но и возмущения, ко-
которое принято записывать в форме XV, где X — вещественный
параметр, а V — так же как и Я не зависящий от времени
эрмитов оператор
H = H0 + W. A)
Предположим, что проблема собственных значений для опе-
оператора Но решена и
по по по
1' 2* • * '' V ' ' '
последовательность его собственных значений, а\Е°а,у — соот-
соответствующий набор собственных векторов; квантовое число а
различает собственные векторы, отвечающие вырожденному
собственному значению:
B)
Спектр Н непрерывно меняется с изменением % и совпадает
со спектром Но при X = 0. Рассмотрим данное собственное зна-

§ 2. РАЗЛОЖЕНИЕ ПО СТЕПЕНЯМ ВОЗМУЩЕНИЯ 183
чение Е°а оператора Яо. Мы хотим вычислить собственное зна*
чение (или значения) Я, которое стремится к Е°, когда Х-^0,
и определить соответствующие собственные состояния опера-
оператора Я. Для упрощения записи будем считать, что спектр Яо
чисто дискретный; в действительности нижеследующие рассуж-
рассуждения остаются справедливыми и в том случае, если часть
спектра Яо непрерывна, лишь бы Е°а принадлежало дискрет-
кому спектру.
Если собственное значение Е°а не вырождено, то метод вы-
вычисления особенно прост. В настоящем разделе мы будем рас-
рассматривать именно этот случай. Пусть Е — невырожденное соб-
собственное значение Я, которое стремится к ?°, когда Х->0. Со-
Соответствующий ему собственный вектор |^> определен с точ-
точностью до константы, которую можно фиксировать произволь-
произвольным условием. Мы примем следующее определение |tJ)>:
H\if) = E\if), C)
<0Ц>) = <0|0>=1, D)
где использовано обозначение |?^) = |0). Согласно этому оп-
определению |aj3> стремится к |0>, когда А,-»-0.
Если возмущение XV достаточно мало, то разумно предпо-
предположить, что Е и |а|)> можно разложить в быстро сходящиеся
степенные ряды по X, т. е. можно записать:
I Ф> = I 0) + X 11) + X212) + • • • + Хп \п) + .... F)
Сохраняя только первые члены этих рядов, получаем прибли-
приближенные выражения для Е и |i|3>, приближение будет тем лучше,
чем быстрее сходится ряд.
Метод теории возмущений заключается в определении ко-
коэффициентов разложений E) и F). Для этого мы подставим
выражения A), E) и F) в обе части уравнения C), которое
тем самым превращается в равенство между двумя степенными
рядами по X. Для того чтобы это равенство выполнялось, не-
необходимо, чтобы коэффициенты при каждой степени X были по
отдельности равны. В результате получаем уравнения
0, G°)
(Яо - El) | п) + (V - к,) |п- 1) ... - гп 0> = 0. G»)

Э84 ГЛ. XVI. СТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЯ
Переписав тем же способом условие D), получаем
<0|1> = <0|2>=...=<0|л>=...=0. (8)
Уравнение G°) определяет собственное значение и собствен-
собственный вектор в нулевом порядке. Вместе с условиями (8) урав-
ление G1) определяет поправки первого порядка к этим вели-
величинам, уравнение G2) — поправки второго порядка, . .., урав-
уравнение G") — поправки л-го порядка.
Покажем, что действительно уравнение Gп) определяет еп
и ]п> в терминах поправок низшего порядка. Для этого спроек-
спроектируем уравнение G") на базисные векторы На. Проектируя на
|0> и используя (8), получаем
en = @\V\n-l). (9)
Проектируя на другие базисные векторы Но, получаем соответ-
соответствующие компоненты вектора \п) вдоль этих векторов
- s2(E°a \n - 2} - ... - 8n_, (E°a | 1}] (
Поскольку <0|п> = 0, то вектор |п> полностью определен.
Удобно обозначить
Используя эти обозначения, можно записать
|„) = -^[(У_81)|п-1)-82|п-2)-...-8„_1|1)]. (И)
Уравнения (9) и A1) эквивалентны уравнению G"), что и за-
завершает доказательство.
§ 3. Возмущение первого порядка
Поправки первого порядка следуют из уравнения G1). Они
получаются, если записать уравнения (9) и A1) в частном слу-
случае п = \.
Уравнение (9) дает поправку первого порядка к уровню
энергии
«| =-= <0 | V 10>, A2)

§ 4. ОСНОВНОЕ СОСТОЯНИЕ АТОМА ГЕЛИЯ 185
откуда получаем выражение для энергии в первом порядке
т. е. среднее значение гамильтониана Н, вычисленное на соб-
собственном векторе невозмущенного гамильтониана Но.
Уравнение A1) дает поправку первого порядка к собствен-
собственному вектору
но поскольку Qo|O>= 0, это выражение сводится к
H)=-^V|0).
Вектор |i|)> в первом порядке дается выражением
^) A5)
а его норма |||ч|)>|| равна
Согласно A4) коэффициенты поправок первого порядка
к |0> вдоль других базисных векторов Но даются уравнением
M?oail)=j?^mo> (?Ol?t?S). A6>
Следовательно, коэффициент поправки, пропорциональной
Е°а), равен матричному элементу возмущения, связывающему
0) с \Е°а), деленному на разность энергий этих двух невозму-
невозмущенных состояний. Наименьшая из этих величин определяег
скорость сходимости ряда теории возмущений.
§ 4. Основное состояние атома гелия
В качестве первого примера ') применения метода теории
возмущений, вычислим энергию основного состояния атома ге-
гелия или, говоря более общим образом, энергию основного со-
состояния любого (Z — 2)-кратно ионизированного атома. Такой
атом состоит из ядра с зарядом Ze и двух электронов. Ядро
предполагается бесконечно тяжелым, так что получаем гамиль-
гамильтониан двух электронов в потенциале
~ - ,_ 1 _ »
') Мы используем пример из книги: I. Pauling, Е. В, Wilson, loc. cit.
(см. первую сноску к § XIV. 12).

186 ГЛ. XVI. СТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЯ
где Г\ и г2 — координаты первого и второго электронов, a г\2 =»¦
— \г\ — г2\ — расстояние между электронами.
Если пренебречь потенциалом взаимного отталкивания е2/г\2,
то гамильтониан системы сводится к гамильтониану двух неза-
висимых частиц в кулоновском поле —Ze2/r, для которого за-
задача на собственные значения может быть решена точно. Мы
возьмем этот гамильтониан в качестве «невозмущенного», а по-
потенциал е2/г[2 будем рассматривать как возмущение. В основ-
основном состоянии #о оба электрона находятся в состоянии Is.
Пусть Ен — энергия связи в основном состоянии атома во-
водорода. Тогда энергия основного состояния Но равна сумме
энергий двух электронов
Соответствующая собственная функция равна произведению
собственных функций каждого электрона (см. § Б. 3)
где
а = = ^ («?-'• 0,53-1(Г8 см).
Поправки к энергии от возмущения V = е2/г\2 в первом по-
порядке вычисляются по формуле A2) (к — 1)
е2
?l ^ ^ ФаУФа drx dr2 = ^r\ *] Г| __ гг, drx dr2. A7)
Это электростатическая энергия двух сферических распреде-
распределений электричества с плотностями —epi(n) и — ер2(/-2), где
3. A8)
Для вычисления интеграла
мы используем разложение (Б. 99). После интегрирования по
углам получаем
оо оо
о о
dr{ ^ dr2 р, (г{) р2 (r2) r\r\jr > =
\. A9)

§ 5. КУЛОНОВСКАЯ ЭНЕРГИЯ АТОМНЫХ ЯДЕР 187
Подставляя A8) и вычисляя /, находим, что поправка ъ\ = еЧ
равна
ei = 4-Z?H. B0)
Приближение тем лучше, чем меньше энергия взаимного от-
отталкивания электронов по сравнению с энергией притяжения
к ядру, т. е. чем больше Z. Это проиллюстрировано в табл. I,
Таблица I
Энергии связи атомов Не, Ы+, Ве++ в основном состоянии*)
Атом
Не
Ве++
1
Z
2
3
4
2
«°.
-108
-243,5
-433
3
ei
34
50,5
67,5
4
?pert = ?a + EI
-74
-193
-365,5
5
?var
—76,6
-195,6
—368,1
6
*exp
—78,6
— 197,1
—370,0
*) Энергии приведены в электрон-вольтах. Столбцы 2, 3, * дают невозмущен-
невозмущенную энергию, поправку первого порядка и их сумму соответственно. Столбец 5
содержит результат вычисления вариационным методом нз § XVIII. 6, последний
столбец—экспериментальное значение энергии основного состояния (по книге:
L. Pauling, Е. В. Wilson, loc. cit.)
где приведены экспериментально наблюдаемые энергии связи
для основных состояний Не, Li+ и Ве++ и результаты вычисле-
вычислений по теории возмущений. Разложение по теории возмущений
сходится быстрее, чем можно было бы ожидать, рассматривая
ситуацию a priori, и вычисление энергии связи в первом по-
порядке уже дает разумное согласие с наблюдаемой величиной
даже в случае гелия (Z = 2).
§ 5. Кулвнввская энергия атвмных ядер
В атомных ядрах, где расстояние между нуклонами порядка
Ю-13 см, силы, действующие между нуклонами и характеризую-
характеризующие ядерные взаимодействия, значительно превосходят силы
кулоновского отталкивания протонов. Таким образом, кулонов-
ское взаимодействие можно рассматривать как возмущение.
Обозначим Но сумму кинетической энергии нуклонов и потен-
потенциальной энергии чисто ядерного происхождения. Возмущение
V состоит из '/2-?(Z—1) членов кулоновского отталкивания Z
протонов ядра
~~ L, г„
B1)

188 ГЛ. XVI. СТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ
{гц — |Г( —г/| —расстояние между протонами / и /). Вычис-
Вычислим по теории возмущений сдвиг Ес уровня энергии стационар-
стационарного состояния, вызванный кулоновским взаимодействием.
Пусть / — спин невозмущенного состояния. Кратность выро-
вырождения такого состояния равна B/+1) и имеется B/+1)
ортонормированных невозмущенных векторов Ф^ соответствую-
соответствующих различным значениям (х компоненты /г полного момента
импульса.
Несмотря на это вырождение, мы можем использовать раз-
развитую выше теорию возмущений. Действительно, возмущение V,
как и #о, инвариантно относительно вращений, и можно рас-
рассматривать задачу на собственные значения независимо в каж-
каждом из подпространств c?(/fi) векторов состояния с заданным
моментом (/(х). Основное состояние в таком подпространстве не
вырождено, и поправка первого порядка к энергии вычисляется
по формуле A2)
Яв»(ф?|У|ф?>. B2)
Видно, что поправка не зависит от ц: возмущение не устраняет
вырождения. Это верно для всех порядков теории возмущений.
Поскольку Н, так же как и Но> инвариантен относительно вра-
вращений, то его собственные значения имеют ту же кратность
вырождения, что и собственные значения Но.
Волновая функция состояния ф? зависит от координат и
внутренних спинов Z протонов и N = Jf — Z нейтронов. Так
как она антисимметрична по переменным, которые описывают
протоны, то wZ{Z — 1) слагаемых в V дают одинаковый вклад
и ?, = 1Z(Z-I)e, где
суммирование происходит по спиновым переменным всех ну-
нуклонов. Обозначим p(ri, г2) плотность вероятности найти в дан-
данный момент протон 1 в точке ги а протон 2 — в точке г2:
Используя это обозначение, получаем
2/r,2) P (r,, r2) drx

§ 6. ПОПРАВКИ ВЫСШИХ ПОРЯДКОВ 189
Для оценки Ес возьмем очень грубую модель, в которой
пренебрегают корреляцией между протонами1), т. е.
P(fi, r2)«p(ri)p(r2) B3)
и в которой плотность р(г) постоянна внутри сферы радиуса R
B4)
при г > R.
Вычисления подобны проделанным в § 4. Подставляя плотно-
плотности в интеграл / (формула A9)), получаем
?e«|z(Z-l)-?. B5)
Хотя формула B5) дает относительно грубую оценку вели-
величины Ес, ее можно использовать для проверки гипотезы о неза-
независимости ядерных сил от заряда (см. § XIV. 15). При этом
удобно пользоваться формализмом изотопического спина. Со-
Согласно этой гипотезе невозмущенный гамильтониан инвариан-
инвариантен относительно вращений в зарядовом пространстве, и со-
состояния из данного изотопического мультиплета должны иметь
одну и ту же энергию связи. Наблюдаемая разность между
этими энергиями будет тогда равна разности их кулоновских
энергий. Если взять
\_
Я =1,45-Л53 • Ю~13см,
то, используя формулу B5), можно получить разумную оценку
для разности энергий основных состояний зеркальных ядер.
§ 6. Поправки высших порядков
Поправки второго порядка, которые следуют из уравнения
G2), мы получим, переписав уравнения (9) и A1) для случая
п = 2 и использовав выражения A2) и A4) для поправок пер-
первого порядка. Тогда имеем
^ B6)
\0). B7)
Выражения для поправок высших порядков получаются та-
таким же образом. Формулы слишком длинны для того, чтобы
выписывать их здесь, но они упрощаются в важном частном
') Таким образом, мы, конечно, завышаем Ес, поскольку принцип Паули
требует, чтобы р(г,, г2) было значительно меньше при гх = т%.

190 ГЛ. XVI. СТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЯ
случае, когда все поправки низких порядков к невозмущениой
энергии исчезают. Тогда, если
8i = e2= ... =е„_1 = 0, B8)
то рекуррентные формулы (9) и A1) дают
^O). B9)
(^y0), C0)
и условие B8) можно записать в виде
^)'1 = 0. B8')
В тех случаях, когда это условие не выполняется, редко
приходится продолжать вычисления до порядка п. Теория воз-
возмущений удобна, только если сходимость достаточно быстрая,
так что можно ограничиться вычислением поправок низших по-
порядков. Сложность вычислений быстро растет с увеличением
порядка, и вычисления становятся практически невыполни-
невыполнимыми.
Однако общий характер поведения поправок высших поряд-
порядков представляет интерес при исследовании сходимости разло-
разложений по теории возмущений. Так, переписав B6) в терминах
матричных элементов V в {| Е°а)}-представлении, для е2 полу-
получим выражение
Е|<0|У|?°а)Р
? ' ?о_?о • CD
Поправки зависят от отношений матричных элементов
%@\V\E°a} к разностям энергии \Е°а — Е°\. Более общим обра-
образом можно сказать, что сходимость ряда теории возмущений
тем лучше, чем меньше отношения матричных элементов
\(E°a\V\E°'a'y между двумя собственными состояниями На
с энергиями Е° и Е0' к разностям | Е°а — Е°\ и | Е°а — Е° | между
этими энергиями и невозмущенной энергией Е^.
Можно получить верхнюю оценку для ег, оценивая по абсо-
абсолютной величине каждое слагаемое в правой части равенства
C1). Заменяя каждый знаменатель на ЬЕты — расстояние от
Е°а до ближайшего уровня, получим
?<V?0 a

§ 7, ЭФФЕКТ ШТАРКА ДЛЯ ЖЕСТКОГО РОТАТОРА 191
ИЛИ
<0
0?min
Используя определение Qo, имеем
где (AVJ — среднее квадратичное отклонение потенциала в со-
состоянии |0>. Таким образом,
I e21 ^ тб • ¦ C2)
§ 7. Эффект Штарка для жесткого ротатора
Как правило, вычисление поправки второго порядка ег C1),
включающее суммирование бесконечного числа матричных эле-
элементов, значительно сложнее вычисления поправки первого по-
порядка, для которой нужно вычислить только один матричный
элемент потенциала V. Однако бывают случаи, когда большин-
большинство матричных элементов, фигурирующих в C1), равны нулю,
и сумма содержит только конечное число слагаемых.
В качестве примера рассмотрим сдвиг уровня энергии жест-
жесткого ротатора в эффекте Штарка. Задача такого типа встре-
встречается при исследовании поляризации двухатомных молекул
в электрическом поле. Жесткий ротатор описывает движение
ядер двухатомной молекулы в пределе, когда требуется беско-
бесконечно большая энергия для возбуждения колебательного дви-
движения. Единственные степени свободы ротатора это угловые
переменные (9, <р), фиксирующие пространственную ориента-
ориентацию. Обозначим L момент импульса ротатора, а / = тг\ — его
момент инерции (т — приведенная масса, г0 — расстояние ме-
между ядрами). Гамильтониан ротатора имеет вид
0'— ~27~'
а собственными функциями являются сферические функции
Г F, ф). Обозначим | /т> вектор, отвечающий Y?. Соответ-
Соответствующая энергия зависит только от /
Я0|/т) = ??|/т}> ?? = -?¦/(/+1).
Если ротатор находится в однородном электрическом поле
<?, направленном вдоль оси z, то к гамильтониану следует до-
бавить член
V = — d& cos Э,

192 ГЛ. XVI. СТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ
где d — электрический дипольный момент ротатора. Вычислим
влияние этого члена по теории возмущений.
В {\1т}}-представлении почти все матричные элементы V
равны нулю '). Для того чтобы
Aт\У\12т2)Ф О,
необходимо, чтобы
При выполнении этих условий матричный элемент можно вы-
вычислить по формуле (см. (Б. 90))
Aт | cos 9 | / - \т) = (I — \т | cos Э11т) = ( ^Г_Г* )Т • C3)
Все невозмущенные уровни энергии, за исключением уровня
/ = 0, вырождены. Однако поскольку Но и Н з= Но + V комму-
коммутируют с Ьг, то можно решать задачу на собственные значения
для Н независимо в каждом из подпространств gm, отвечаю-
отвечающих заданному собственному значению т оператора Lz. В каж-
каждом из этих подпространств спектр оператора Но не вырожден
и можно использовать развитую выше теорию возмущений.
Рассмотрим невозмущенное состояние 11т) в 8т. В силу
приведенных выше правил отбора
Aт | V11т) = 0,
и поправка первого порядка к энергии исчезает. Из тех же сооб-
соображений поправка второго порядка, "вычисляемая по фор-
формуле C1), содержит два члена, соответствующих /±1:
|(/m|cose|rm)P
21 (d&f f [(to |cos6| г+lm) |2 , I (lm | cos 6 11 - \m) 14
— ? ПТГ+Т) - (I + I) (I + 2) "Г l(l + \)-l{l-\) У
Выражение в скобках легко вычислить, используя формулы
C3). В результате получим
p lm —
2 ~ E\ 2 B/— 1) B/ +3)'
и спектр энергии с точностью до членов второго порядка равен
C4)
') Эти замечательные свойства связаны с тем, что V есть 0-компонеита
Неприводимого тензорного оператора порядка 1 н его четность равна (—1).

§ 8. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ 193
Вырождение снимается лишь частично, поскольку Eim за-
зависит от / и т2. Состояния, для которых т отличаются только
знаком, отвечают одному и тому же уровню. Это остаточное
вырождение сохраняется во всех порядках, так как является
следствием инвариантности Н по отношению к отражениям
в плоскостях, проходящих через ось Oz. Мы еще вернемся
к этому вопросу в § 13.
Раздел П. ВОЗМУЩЕНИЕ ВЫРОЖДЕННОГО УРОВНЯ
§ 8. Элементарная теория
Предположим, что собственное значение Е°а невозмущенного
гамильтониана ?а-кратно вырождено. Мы сохраним обозначе-
обозначения § 2 и обозначим $°а подпространство, отвечающее Е%, а
Ро — проектор на &°а.
Теперь к Е°а при Х-*-О может стремиться более одного соб-
собственного значения Н. Обозначим эти собственные значения
Е\, Е2, ..., Еп, кратности их вырождения gu g2, •••> gn и отве-
отвечающие им подпространства &\, &2, ..., $ п. Тогда имеем
gl+g2+ ••• +gn = ga,
и пространство &\ + <*Г2 + ... + 8п при К-^0 стремится к g\.
Если Р — проектор на 8\ + Si + ... + 8п, то он является не-
непрерывной функцией X и
Р—*Р
Определение собственных значений и собственных функций
по теории возмущений сложнее, чем в случае невырожденного
невозмущенного собственного значения. В разделе III будет
дано строгое решение этой задачи во всех порядках. Здесь же,
оставляя в стороне строгость изложения и ограничиваясь низ-
низшими порядками, рассмотрим, что дает метод § 2 в применении
к этой задаче.
Пусть Е — одно из собственных значений Е\, Е2, ..., Еп,
a |if>> — один из собственных векторов, отвечающих Е. В пре-
пределе, когда Х-*-0, |ф> стремится к некоторому вектору |0>,
о котором пока можно только сказать, что он принадлежит про-
пространству 8а- Предположим, что Е и |ф> можно представить
в виде разложений E) и F) с условием нормировки D). Их
коэффициенты связаны друг с другом уравнениями G) и (8) и
могут быть определены рекуррентно.
Уравнение G°) требует, чтобы вектор |0> принадлежал &а
РоЮ)НО). C5)
7 А, Мессиа

194 ГЛ. XVI. СТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИ,.
Проекция G1) на <8йа дает
/>o(V-e1)|O) = O, C6)
а проекция на дополнительное пространство
Q0|l)=^l/|0), C7)
где мы обозначили
Qo = 1 - Ро C8)
и определили Qo/a согласно формуле A0).
Уравнение C6) есть уравнение на собственные значения
в подпространстве &йа: ъ\ — собственное значение оператора
PoVPo в &°а> а 10> — соответствующий собственный вектор. За-
Запишем C6) в представлении \Е°а}
| V | Е°аа'> <?°ва' 10> = е,
откуда видно, что поправка первого порядка ei получается дна*
гонализацией ga X ga матрицы с матричными элементами
Возможные значения г\ — собственные значения этой матрицы.
Если имеется ga различных собственных значений, то все
они невырождены и возмущение полностью устранило вырож-
вырождение. Если же различных собственных значений меньше git
то некоторые из них будут вырожденными и вырождение устра-
устранено лишь частично.
Если поправка первого порядка ei — невырожденное соб-
собственное значение, то соответствующий собственный вектор |0>
полностью определен в нулевом порядке с точностью до кон-
константы уравнениями G°) и G1). Проекция Qo|l> поправки пер-
первого порядка к |ф> на дополнение к &°а дается равенством C7),
а проекция на &йа остается неопределенной, за исключением
условия D). Если же ei, gi-кратно вырождено, то уравнения
G°) и G1) показывают только, что вектор |0> принадлежит gr
мерному подпространству; для более точного определения |0>
нужно обратиться к высшим порядкам.
Выбрав одно из значений ei и проектируя G2) на подпро-
подпространство, отвечающее еь получаем поправку второго порядка
ег. Это подпространство,которое мы обозначим &аК содержится
в &\; обозначим соответствующий проектор РA), а проек»
тор на ортогональное дополнение в 8\ через Р'

§ 9. АТОМНЫЕ УРОВНИ 195
Тогда имеем
Р<»V = РA> V (РA> + Р' + Qo) =
Проекция уравнения G2) дает
PA)FQo|l>-e2PA)|O)-O,
следовательно, используя C7),
]) = O. C9)
Для поправок второго порядка уравнение C9) является
аналогом уравнения C6) для поправок первого порядка. Точно
так же, как ei было собственным значением PoVPo в &\, е2 яв-
является собственным значением PA)l/(Q0/a) VPA) в &"а\ а |0> со-
соответствующий собственный вектор.
Если ei — невырожденное собственное значение (gi = 1), то
|0> определено уравнениями низших порядков, и мы имеем
как и в случае невырожденного уровня. Если же g\ > 1, то
вычисление е2 требует нахождения собственных значений
gi X g\ матрицы. Если все они различны, то вырождение пол-
полностью устраняется во втором порядке; в противном случае,
если необходимо, переходят к высшим порядкам.
В ряде случаев вырождение сохраняется во всех порядках.
Мы встречались уже с такими примерами: кулоновская энергия
ядер (§ 5) и эффект Штарка для жесткого ротатора (§ 7).
Обычно, изучая симметрию Яо и Я, можно предсказать, на-
насколько вероятно устранение вырождения невозмущенного
уровня возмущением KV. Систематическое обсуждение этого во-
вопроса приведено в § 13, ниже мы проиллюстрируем метод вы-
вычисления поправок первого порядка на ряде примеров, взятых
из атомной физики.
§ 9. Атомные уровни без учета спин-орбитального
взаимодействия
В главе XIV мы изучали уровни энергии Z-электронных
атомов в приближении центрального поля (§ XIV. 12). В этом
приближении гамильтониан Я заменяется на

196 ГЛ: XVI. СТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ
Тем самым, учитывается только усредненное значение электро-
электростатического отталкивания электронов. Обозначим V\ разность
между точным кулоновским взаимодействием и потенциалом Не
Ts^rZ[] <40>
К1 I
Пренебрегая в Я членами, зависящими от спина электрона, за-
запишем его в виде
Hf*Hc+Vu D1)
и спектр Я можно получить из спектра Не, рассматривая V'i
как возмущение. Модификации, которые влечет включение за-
зависящих от спина сил, будут рассмотрены в § 10.
Как правило, все собственные значения Нс сильно вырож-
вырождены. Возмущение Vi, по крайней мере частично, снимает
вырождение. Уровни Я в окрестности данного собственного зна-
значения Не получаются диагонализацией V\ в подпространстве,
соответствующем этому собственному значению. В частности,
основное и первое возбужденное состояния Н получаются диа-
диагонализацией V\ в подпространстве ?fo, отвечающем низшему
собственному значению Ео оператора Яс.
Свойства симметрии Н значительно упрощают задачу диаго-
нализации. Поскольку оператор Я (так же как и Нс) не зави-
зависит от спинов, он инвариантен не только по отношению к об-
общим поворотам, но и к вращениям орбитальных переменных и
спиновых переменных по отдельности, т. е. Я коммутирует не
только с полным моментом импульса /, но и с полным орби-
орбитальным моментом L и полным спином S '). Поскольку свойства
симметрии Яс и Я одинаковы, оператор P0ViPo будет комму-
коммутировать с L и S. Его собственные значения в подпространстве
&о можно параметризовать собственными значениями опера-
операторов L2, S2, Lz и Sz, они будут зависеть только от L и S,
а кратность их вырождения будет равна BL + 1) B5 + 1).
Обозначим \yLSMLMsy векторы стандартного {L2, Lz, S2, Sz}-
базиса в &0, квантовое число у параметризует векторы, которые
имеют одинаковый орбитальный момент и спин. В таком пред-
представлении матрица оператора PoViPo имеет очень простой вид
(yLSMLMs | V, | y'L'S'M'LM's) = 6LL,6SS,6M , Ь 'W.
Li Li <_> О
Для полной диагонализации остается только диагонализовать
матрицы Ууу\ отвечающие каждой паре квантовых чисел (LS).
') Н инвариантен также относительно перестановок орбнтальных перемен-
переменных, но в силу теоремы § Г. 18 и принципа Паулн это эквивалентно инва-
инвариантности относительно вращений спинов.

§ 9. АТОМНЫЕ УРОВНИ
197
Рассмотрим, например, атом углерода. Конфигурация основ-
основного состояния равна Is22s22p2, т.е. — две замкнутых оболочки
Is и 2s, и незамкнутая оболочка 2р с двумя электронами. Эта
конфигурация имеет вырождение С|= 15. Для того, чтобы найти
возможные значения пар (LS) и их вырождение, т. е. число се-
серий из BL + 1) BS + 1) векторов, можно.рассматривать только
два 2р электрона, опуская замкнутые оболочки (задача 3).
Если не учитывать принцип Паули, то из двух 2р электронов
можно образовать следующие различные спектральные термы:
35 3Р 3D lS lP lD.
Поскольку триплетное и синглетное спиновые состояния при
перестановке спинов симметрично и антисимметрично соответ-
соответственно, а состояния 5 и D сим-
симметричны, а Р антисимметрично
при перестановке орбитальных
переменных, то из приведенных
спектральных термов принципу
Паули удовлетворяют
3Р '5 '?>,
всего 9 + 1 -f- 5 = 15 линейно не-
независимых антисимметричных со-
состояний, как и утверждалось
выше. В {LSMLMS}-базисе (в дан-
данном случае квантовое число у
излишне) возмущение V\ диаго-
диагонально и имеет три различных
собственных значения Т{ЪР),
T(lS) и T{lD), которые 9-, 1-
и 5-кратно вырождены, соответ-
соответственно. Эти значения не сложно
вычислить, если известны волновые функции отдельных состоя-
состояний. Вычисление показывает, что уровень 3Р расположен значи-
значительно ниже двух других (рис. 8I)-
Рис. 8. Энергетические уровни
основного состояния атома угле-
углерода: а) в приближении централь-
центрального поля (Vi = Уг = 0); б) в пре-
пренебрежении спин-орбитальной
связью (^2 = 0); в) прн учете
спин-орбитальной связи.
') Как правило, уровни данной конфигурации располагаются в порядке
убывания полного спина (правило Хунда). Поскольку второе слагаемое в
D0) дает один и тот же вклад во все уровни, порядок следования уровней
зависит только от величины энергии отталкивания J] е2/ \п — г/ |. Это сла-
слагаемое убывает с увеличением расстояния между электронами и, следова-
следовательно, с «возрастанием антисимметричности» орбитальной части волновой
функции. Спиновая часть волновой функции становится «симметричнее» с ро^
стом 5 (§ Г. 18) и, следовательно, орбитальная часть становится «более анти-.
симметричной» с ростом S.

198 ГЛ. XVI. СТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ
§ 10. Спин-орбитальное взаимодействие. LS- и //-связь
Выражение D1) равно Н только приближенно. Оператор Н
содержит члены, зависящие от спина, которые мы обозначим W
Н = Нс + V, + V2. D2)
В первом приближении каждый электрон движется незави-
независимо от других электронов в потенциале Vc(r), и его спии взаи-
взаимодействует с его орбитальным моментом по закону (XIII. 95).
Следовательно, с хорошим приближением имеем
У2«?(/| •**)?(/•,), D3)
где
Для того чтобы корректно учесть этот эффект, необходимо
в рассуждениях предыдущего параграфа заменить V на V\ + Кг.
Однако сумма V\ + V2 обладает меньшей симметрией, чем
V\: V\ + К2 коммутирует только с / и не коммутирует с L или
S. Задача диагонализации возмущения в подпространстве, от-
отвечающем невозмущенному собственному значению после учета
спин-орбитального взаимодействия становится значительно
сложнее. Эта задача несколько упрощается только в случае,
когда один из членов, V\ или V2, много меньше другого.
Если V\ ?§>! V2, то в первом приближении можно пренебречь
V2- Каждая конфигурация будет давать серию уровней, каждый
из которых отвечает определенной паре (LS) и имеет кратность
вырождения BL + 1) B5 + 1) (ср. § 9). Соответствующие соб-
собственные векторы являются линейными комбинациями опреде-
определителей Слетера, построенных из одночастичных состояний кон-
конфигурации. Это собственные векторы для L2, S2, Lz, Sz. Опера-
Оператор V2 рассматривается тогда как малое возмущение в подпро-
подпространстве, отвечающем каждому из этих уровней. Каждому
возможному значению J(J — L + S, L-\-S — 1, ..., \L — 5|)"
соответствует собственное значение У2 с кратностью вырожде-
вырождения B/+1). Соответствующие собственные векторы \yLSJM}
являются собственными для L2, S2, Р и /г. Такой метод по-
построения собственных векторов полного момента импульса из
определителей Слетера фиксированной конфигурации отвечает
связи Рассела — Саундерса или LS-связи.
Если lV>l?Vi, то в первом приближении можно пренебречь
V\. Тогда гамильтониан равен Нс + V%, что соответствует не-
независимым частицам, движущимся в потенциале Vc +{ls)g(r).
Обозначим / = I + s полный момент импульса каждой частицы.
Наличие спин-орбитального взаимодействия (Is)g(r) частично

§ 11. АТОМ С LS-СВЯЗЫО 199
устраняет вырождение одночастичных состояний с орбитальным
моментом, отличным от нуля, давая два уровня/=/±-^-. Со-
Соответствующие собственные векторы можно параметризовать
квантовыми числами (nljm). Во всем остальном рассмотрение
Нс+ V2 подобно рассмотрению Нс (§ XIV. 12); каждая конфи-
конфигурация Не приводит к нескольким конфигурациям Нс + V2.
Как только последние определены, V\ можно рассматривать
для -каждой из них как возмущение. Каждому собственному
значению / отвечает одно или несколько собственных значений
с кратностью вырождения B/ -\- 1). Соответствующие собствен-
собственные векторы являются собственными для fi, J2 и /г. Такой ме-
метод построения собственных векторов полного момента из оп-
определителей Слетера конфигурации основного состояния назы-
называется jj-связью.
Приведем схему этих методов
LS-связь //-связь
(V2)
(V2) it =
(Vx) / =
Относительное значение V2 быстро растет с числом Z1). Для
легких и промежуточных атомов Vi ^> V2 и LS-связь дает хоро-
хорошее приближение; для тяжелых атомов (начиная, скажем,
с Pb) Vi и У2 становятся величинами одного порядка и струк-
структура уровней конфигурации основного состояния является про-
промежуточной между структурами, которые получаются при LS-
и //-связях.
§ 11. Атом с LS-связью. Расщепление за счет
спин-орбитального взаимодействия
Рассмотрим влияние спин-орбитального взаимодействия в
случае LS-связи (Vii^\V2), когда V2 можно считать возмуще-
возмущением гамильтониана Не + У\-
Спектр невозмущенного гамильтониана был описан в § 9.
Каждый уровень отвечает определенному значению L и 5 и
') Vj представляет собой флуктуацнонный член, влияние которого иа
энергию каждого электрона растет приблизительно как •\[l. Энергия спин-
орбитального взаимодействия каждого электрона растет приблизительно как
Z2. Ее можно оценить, используя модель Томаса — Ферми; взаимодействие
пропорционально среднему значению A/r) (dVJdr), что приближенно равно
(обозначения § XIV. 13)
1 dVc ~ z*e2 d
dr ~ Ь3 dx

200 ГЛ. XVI. СТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ
кратность его вырождения равна BL + 1) B5 + 1); подпро-
подпространство соответствующих собственных векторов натянуто на
множество векторов с определенными значениями орбитального
момента и спина; обозначим их \aLSMLMs)- Квантовое число а
указывает конфигурацию Нс, к которой принадлежит данный
уровень, и служит для того, чтобы различать уровни одной и
той же конфигурации, имеющие одинаковые значения L и 5.
Энергия возмущения получится, если диагонализовать Vi
в подпространстве &(aLS), отвечающем каждому из невозму-
невозмущенных уровней. Покажем, что в каждом из подпространств
8(aLS) матричные элементы V% те же, что и у оператора
A(LS), где А— константа, характеризующая невозмущенный
уровень (aLS)
(aLSMLMs | У21 aLSM[M's) = A (aLSMLMs | (LS) \ aLSM'LM's). D5)
Доказательство. Поскольку базисные векторы антисимметричны,
вклады в матричный элемент Z членов в \7% (ур. D3)) равны, Следовательно,
достаточно рассмотреть только один из них, например, (l\S\)g(r{); индекс 1
не существен и далее мы его опускаем. Взяв произвольную компоненту 1п
оператора / и произвольную компоненту s оператора s, можно построить опе-
оператор g (г) I ms^, который является компонентой векторного оператора, непри-
неприводимого по отношению к вращениям орбитальных переменных, и компонен-
компонентой векторного оператора, неприводимого по отношению к вращениям спи-
спиновых переменных. Таким же свойством обладает н оператор LmS Исполь-
Используя теорему Вигнера — Эккарта, несложно получить (см. задачу XIII. 19)
(aLSMLMs | g/ms^ | aLSM'LM's) = a(aLSMLMs \ LOTS^ | aLSM'LM's)t
где a — не зависящая от магнитных квантовых чисел M^t M^t MSt MSt m, ц
константа. Следовательно,
_ (aLSMLMs | g (r) (Is) laLSM'LM's) = a(aLSMLMs | (LS) | aLSM'LM's)
и соотношение D5) получается, если каждый член умножить на Z и поло-
положить А = Za.
Оператор Vz в подпространстве & (aLS) не диагонален
в представлении {aLSMLMs}, но поскольку он инвариантен от-
относительно вращений, он диагонален в представлении {aLSJM},
базисные векторы которого являются собственными для опера-
операторов Р и /г. Соотношение D5) позволяет определить его соб-
собственные значения. Действительно, поскольку
имеем
(aLSJM | V21 aLSJM) = ±A (aLSJM | (P -L2- S2) | aLSJM) =
\ + 1)- L(L+ 1)- 5E+1)]. D6)

§ 12. ЭФФЕКТ ЗЕЕМАНА И ЭФФЕКТ ПАШЕНА — БАКА 201
Таким образом, невозмущенный уровень (aLS) расщепляет-
расщепляется на столько уровней, сколько имеется возможных значений
J(J = L-\-S \L — S\). Кратность их вырождения равна
B/ + 1), а энергия возмущения дается формулой D6).
На рис. 8 приведена схема уровней конфигурации основного
состояния атома углерода с LS-связью. Спин-орбитальное взаи-
взаимодействие влияет лишь на состояние гР; оно расщепляется на
три: 3Ро, 3Л и гР2. Так как в данном случае А > О, уровни рас-
расположены в порядке возрастания / и низшим является уро
вень 3Р0-
§ 12. Эффект Зеемана и эффект Пашена— Бака
В последних трех параграфах мы изучали структуру атом-
атомных уровней без внешних полей. Рассмотрим теперь атом, по-
помещенный в постоянное магнитное поле Ж. В этом случае га-
гамильтониан атома получается из гамильтониана Но без внеш-
внешнего поля прибавлением члена (ср. ур. (XIII. 96))
D7)
(а также «диамагнитного» члена, пропорционального Ж2, кото-
которым мы пренебрегаем).
Эффект Зеемана. Для достаточного малых Ж можно
рассматривать W как возмущение. Поскольку гамильтониан Но
инвариантен по отношению к вращениям, каждый уровень Но
отвечает определенному значению / полного момента импульса.
Будем предполагать, что 1Ф01), тогда кратность вырождения
уровня равна B7 + 1). Возмущение W снимает это вырожде-
вырождение.
Пусть Ео — один из невозмущенных уровней, / — его момент
импульса, a \E0JM}— собственные векторы Р и Jz, на которые
натянуто подпространство, отвечающее уровню Ец. Сдвиги дан-
данного уровня, вызванные магнитным полем, равны собственным
значениям матрицы
{E0JM\W\E0JM').
Если выбрать ось z параллельно Ж, то эта матрица будет
диагональна, поскольку W будет коммутировать с Jz-
Кроме того, в силу теоремы Вигнера — Эккарта матричные
элементы векторных операторов L + 2S и / в подпространстве
уровня Ео пропорциональны друг другу:
(E0JM | (L + 2S) | ЕОЗМГ) = g{E0JM \ J | E0JM'). D8)
') Если / = 0 (диамагнитный атом), то сдвиг уровня исчезает в первом
порядке по Ж. Вычисляя сдвиг во втором порядке по Ж, следует учесть вклад
«диамагнитного» члена.

202 ГЛ. XVT СТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ
Коэффициент пропорциональности g (множитель Ланде) ра-
равен отношению приведенных матричных элементов этих опера*
торов, он характеризует рассматриваемый уровень Ео. В част-
частности,
(E0JM | (Lz + 2S2) | Eo
Для выбранной ориентации осей
w = ?*L
w
(г 4 2S \
и, обозначая цв магнетон Бора (ур. (XIII. 74)), получаем
{E0JM | W \EoJM') = - MgpBmMM:
Таким образом, возмущение полностью устраняет вырож-
вырождение и B/ + 1) уровней определяются по формуле Зеемана
(Af = — /, — /-h I +/). D9)
Вычисление множителя Ланде в случае LS•
связи. Множитель Ланде g (фактор Ланде) определен урав-
уравнением D8). Предположим, что для рассматриваемого атома
верна схема LS-связи. Тогда, следуя обозначениям § 11, уровни
атома при нулевом внешнем поле будут характеризоваться
квантовыми числами aLSJ.
Для определения g вычислим двумя различными способами
среднее значение
(/ (L + 2S)> = (aLSJM | (/ (L + 2S)) | aLSJM).
(а) Используя тождество
J(L + 2S) = Р + S2+±(P-L2- S2),
имеем
(б) Непосредственно перемножая матрицы в {aLSJM}-
представлении и используя соотношение D8), получаем (ср. за-
задачу XIII. 19)
l-xyz M'
X {aLSJM' | (Lt + 2St) | aLSJM)
= g(aLSJM | P | aLSJM) = gJ (J + 1) tp.
Сравнивая эти два результата, находим
g—l-\

§ 13. СИММЕТРИЯ Я И УСТРАНЕНИЕ ВЫРОЖДЕНИЯ 203
Эффект Пашена — Бака. Приведенная теория эф-
эффекта Зеемана оправдана, только если расщепление уровней
возмущением W мало по сравнению с расстоянием между не-
невозмущенными уровнями. В случае LS-связи это предполагает,
что W мало по сравнению со спин-орбитальным взаимодей-
взаимодействием V2 или, более точно (см. ур. D6) и D9)), что
Предположим, что имеет место обратная ситуация и магнит-
магнитное поле так велико, что
АН2
В этом случае спин-орбитальное взаимодействие пренебрежимо
мало по сравнению с магнитным и последнее можно рассма-
рассматривать как возмущение уровней гамильтониана
Нс + Vx.
В обозначениях § 11 каждый из этих невозмущенных
уровней параметризуется квантовыми числами {aLS) и имеет
кратность вырождения BS + 1) BL + 1). Возмущение устра-
устраняет вырождение лишь частично. Этот эффект называется эф-
эффектом Пашена — Бака. Смещение относительно невозмущен-
ного уровня EaLS получают, диагонализуя W в соответствую-
соответствующем подпространстве. Поскольку W коммутирует с Lz и Sz,
матрица возмущения диагональна в {aLSMLMs}-представлении
(aLSMLMs | W | aLSM'LM's) = - рвЖ (ML + 2MS) 6MlM
Следовательно, сдвиги уровней определяются формулой
-L + L; Ms = -S, ..., + S)
Если L Ф 0 и S Ф 0, то некоторые из полученных уровней
остаются еще вырожденными. Введение малого спин-орбиталь-
спин-орбитального взаимодействия по крайней мере частично устраняет эти
остаточные вырождения.
§ 13. Симметрия Н и устранение вырождения')
Предыдущие примеры (§§ 5, 7, 9, 10, 11, 12) показывают, на-
насколько важно учитывать симметрию при вычислении сдвигов
вырожденных уровней по теории возмущений. Существование
вырожденных собственных значений можно почти всегда свя-
') Этот параграф, единственный в данной главе, в котором используются
результаты главы XV и ряд понятий из теории групп, может быть опущен при
Первом чтении.

204 ГЛ. XVI. СТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ
зать с симметрией гамильтониана. Если известны группы ин-
вариантности Но и Я, то можно предсказать изменение вырож-
дения уровня ?^ под действием возмущения и значительно уп-
упростить вычисление возмущенных уровней.
Во всех приведенных примерах невозмущенный гамильто-
гамильтониан Яо был инвариантен по отношению к некоторой группе Go,
а возмущение %V было инвариантно по отношению к некоторой
подгруппе G группы Go. Так, в случае эффекта Штарка для
жесткого ротатора (§ 7) Go была группой вращений и отраже-
отражений, a G — группой отражений по отношению к плоскостям,
проходящим через ось г (см. § XV. 14).
Воспользуемся обозначениями § XV. 11. Используя опера-
операторы G, можно построить наблюдаемые / и М с собственными
значениями / и ц соответственно. Каждому значению j отвечает
определенное неприводимое представление группы. Обозначим
dj размерность этого представления. Для данного / существует
df возможных значений ц, параметризующих d,- базисных век-
векторов данного представления. Каждой паре (/ц) отвечает неко-
некоторое подпространство &{}\и) пространства векторов состоя-
состояния <g. Так как Я и Но инвариантны по отношению к преобра-
преобразованиям из G и, следовательно, коммутируют с / и М, то за-
задачу на собственные значения можно решать отдельно в каж-
каждом из подпространств &"(j\i). Мы получим одинаковые спектры
и вырождение в dj подпространствах, отвечающих данному зна-
значению /.
Допустим, что Е°а есть собственное значение Яо в &"Цц)
с кратностью вырождения р\. Тогда имеем
ga = Y>Pid,. E1)
В подпространстве ё?(/ц) введение возмущения может с боль-
большей или меньшей полнотой устранить вырождение невозму-
невозмущенной энергии (считаем р,- > 1). Если Н инвариантен только
относительно преобразований из группы G, то рассматривае-
рассматриваемое вырождение, вообще говоря, устраняется полностью и мы
получаем ps различных уровней. Следовательно, во всем про-
пространстве <§ введение возмущения расщепляет невозмущенный
уровень самое большее на J] р/ различных уровней, каждый из
которых отвечает определенному значению j и имеет кратность
вырождения dj, если в <S (/ц) вырождение устранено полностью,
в противном случае вырождение уровня кратно dj.
Доказательство этих результатов использует только тот
факт, что группой симметрии гамильтониана Я является G, и
Я есть непрерывная функция X, стремящаяся к Яо при А,->0.
Эти результаты точны во всех порядках теории возмущений. .

§ 14. КВАЗИВЫРОЖДЕНИЕ 205
Если подпространство $"°а неприводимо по отношению к
группе G, то сумма E1) будет состоять только из одного сла-
слагаемого ') и вырождение уровня не может быть устранено ни
в каком порядке. Так происходит, когда Яо инвариантен отно-
относительно тех же преобразований, что и Н(Go = G). Мы встре-
встречались с такой ситуацией, когда вычисляли кулоновскую энер-
энергию ядер (§ 5).
В примере § 7 G представляет собой подгруппу Go- Размер-
Размерность подпространства <§\, отвечающего собственному значе-
значению ??, равна B/+ 1). Оно неприводимо по отношению к Go
и приводимо (если I фО) по отношению к G. В данном случае
(см. § XV. 14) оператором / является l\ с собственными зна-
значениями т2, которые можно характеризовать квантовым чис-
числом \т\ (\т\ = 0, 1, ...); размерность соответствующего не-
неприводимого подпространства раваа
B, если \т\фО
lml~ 1 1, если |т 1 = 0.
В этом случае соотношение E1) принимает вид
i
\ml-0
Таким образом, возмущение расщепляет уровень ?? на / -f- 1
различных уровней, один из которых не вырожден при \т\ =0,
а остальные двукратно вырождены. Именно это было установ-
установлено в § 7. Следует подчеркнуть, что такое использование сим-
симметрии позволяет только оценить сверху возможность снятия
вырождения. Происходит ли это в действительности, можно
сказать только после вычисления по теории возмущений до до-
достаточно больших порядков. Так, в примере из § 7 пришлось
вычислять до второго порядка включительно.
§ 14. Квазивырождение
Если два уровня ?° и Е°ь расположены настолько близко
друг к другу, что поправки к ним за счет возмущения V больше
чем \Еа — Щ|> то пользоваться развитыми ранее методами
нельзя. Однако и в этом «квазивырожденном» случае можно
') Подпространство <?а инвариантно по отношению к преобразованиям из
G и определяет некоторое представление размерности ga этой группы, кото-
которое мы обозначим^?,,. Его разложение на неприводимые части согласно E1)
имеет вид Ga с

206 ГЛ. XVI. СТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ
использовать теорию возмущений, если подходящим образом
изменить определение невозмущенного гамильтониана и возму-
возмущения.
Обозначим Р° проектор на подпространство, отвечающее
собственному значению Е] оператора Яо. Тогда имеем
„ ?
i
Модификация гамильтониана состоит в замене слагаемых
Е°аР°а и Е°ЬР° в этой сумме на Е°а(р°а +Р°ь), где Е°а - величина,
промежуточная между El и Е\. Так, получаем новый невоз-
невозмущенный гамильтониан, у которого собственное значение Е\
имеет кратность вырождения ga + ёь- Далее следует вычислить
поправки к E'i за счет возмущения
V + {Е°а- El) Pl + {El- El) Pi
Такой метод был использован при рассмотрении эффекта
Пашена— Бака (§ 12). Поле Ж было достаточно сильным, так
что сдвиги уровня данного LS-терма не были малыми по срав-
сравнению с расстоянием между уровнями. Тогда мы взяли в каче-
качестве невозмущенного гамильтониан Нс -+- V\ вместо Нс + V\ -j-
+ Уч, что привело к замене группы уровней ?az.s/ (/ =
= |L — S\, ..., L -f- S) на один уровень Еа . Далее, следо-
следовало бы вычислить поправки к ?„._, вызванные возмущением
Vz + W. Для чистого эффекта Пашена — Бака поле Ж на-
настолько сильное, что в первом приближении влиянием V2 можно
пренебречь (V2 < W), это и было сделано в § 12. Если V2 и
W — величины одного порядка, то такое приближение не при-
применимо и вычисления становятся значительно сложнее (за-
(задачи 7 и 8).
Раздел III. ЯВНЫЕ ВЫРАЖЕНИЯ ДЛЯ РАЗЛОЖЕНИИ
ПО ТЕОРИИ ВОЗМУЩЕНИЙ ВО ВСЕХ ПОРЯДКАХ')
§ 15. Гамильтониан Я и его резольвента2) G(z)
В этом разделе мы изложим кратко подход, дающий явный
вид членов любого порядка разложения по теории возмущений.
В подходе, предложенном Като3), используется разложение
') Этот раздел при первЛл чтении можно опустить.
2) Ряд автрров использует термин «функция Грина» вместо «резольвента».
s) Т. Kato. Prog. Theor. Phys. 4, 154 A949). Като интересовался в основ-
основном условиями сходимости теории возмущений, и его подход особенно удобен
при обсуждении этого вопроса. В большинстве встречающихся случаев раз-
разложение по теории возмущений является асимптотическим. Мы не будем »
данном разделе касаться математических аспектов работы Като,

§ IS. ГАМИЛЬТОНИАН Н И ЕГО РЕЗОЛЬВЕНТА 0(г) 207
резольвенты G(z) гамильтониана Н в ряд по степеням возму-
возмущения. В этом параграфе мы определим G(z) и опишем неко-
некоторые ее свойства.
По определению, если оператор Я— наблюдаемая, то его
резольвентой называется функция
°(г)-т=пг E2)
комплексной переменной г').
На рис. 9 изображена комплексная плоскость г и на веще-
вещественной оси отмечен спектр Я; спектр обычно состоит из
Г
Рис. 9. Комплексная плоскость г, определение контура Г. Спектр Н выделен
на вещественной оси жирными линией и точками.
дискретной части и непрерывной части, последняя распола-
располагается справа от дискретной части и тянется вплоть до беско-
бесконечности. Резольвента G(z) является аналитической функцией
г, а ее особенности образуют спектр Н.
Предположим для простоты, что спектр оператора Н чисто
дискретный. Собственные значения обозначим Ео, Еи ...
..., Ei, ..., а проектор на отвечающее ?, подпространство —
Pt
HPt = EtPt E3)
Соотношения ортогональности и полноты имеют вид
PtP, = bitPu E4)
5>?=1. E5)
') По определению, оператор Q в гильбертовом пространстве называется
ограниченным, если существует константа М такая, что для любого |ы)
Наименьшее значение М называется нормой оператора и обозначается ||Q||.
Строго говоря, различные операции алгебры и анализа, в частности, понятия
сходимости рядов, дифференцирования и т. д., могут быть перенесены без
ограничений только иа ограниченные операторы в гильбертовом пространстве
(см. М. Н. Stone Linear transformation in Hilbert space, № 4, Amer. Math.
Soc, 1932).
С математической точки зрения G(z) представляет большой интерес, по-
поскольку является ограниченным оператором на всей комплексной плоскости г,
за исключением собственных значений оператора Н, и аналитической функ-
функцией 2, особенности которой образуют спектр Н. Если обозначить Д(г) рас-
расстояние от точки г до ближайшего собственного значения Н, то ||G(z)|| =
1/Д()

208 ГЛ. XVI. СТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЯ
Из определения E2) имеем
и, следовательно,
Каждому дискретному собственному значению Ei оператора
Н отвечает простой полюс G(z), вычет в котором равен проек-
проектору Р(. Другими словами
где Г,- — замкнутый контур в комплексной плоскости, окружаю-
окружающий ?,-, а все остальные сингулярности G(z) лежат вне его.
В более общем случае, если Г — замкнутый контур, не прохо-
проходящий ни через одно из собственных значений Н (рис. 9),
а Рг — сумма проекторов Pt, соответствующих собственным зна-
значениям внутри этого контура, то
G (z) dz. E8)
f
Умножая уравнение E8) на Я и учитывая тождество
получаем важную формулу
НРГ = -^-г Ф zG (z) dz. E9)
г
§ 16. Разложение G(z), P и ЯР в ряд по степеням XV
Рассмотрим теперь собственно задачу теории возмущений.
Резольвенты операторов Н и Но обозначим соответственно
Заметим, что

§ 16. РАЗЛОЖЕНИЕ О(г), РИЯРВ РЯД ПО СТЕПЕНЯМ W 209
и, следовательно, G является решением интегрального уравне-
уравнения
F1)
Интегрируя это уравнение, получаем G в виде разложения
по степеням возмущения ')
п=0
F2)
Используя обозначения § 8, найдем разложение Р по сте-
степеням возмущения. Для достаточно малых % в комплексной
плоскости г существует замкнутый контур, содержащий внутри
себя невозмущенное собственное значение е\ и собственное
значение оператора Н, которое стремится к ?° при Х-+0, и не
содержащий каких-либо других собственных значений Н и Яо.
Обозначим такой контур Га. Согласно уравнению E8) имеем
Подставляя вместо G разложение F2) и меняя порядок сум-
суммирования и интегрирования, получаем разложение Р в виде
ряда по степеням X
оо
Р = Ро + S Ь"А{п), F3)
где
fe. F4)
Единственной особенностью функции Go(VGo)n внутри кон-
контура Го является полюс в точке Е°а порядка п + 1 и согласно
уравнению F4) Л<"> — вычет в этом полюсе.
Для вычисления вычета используем разложение Go в ряд
Лорана в окрестности точки Е°а- Коэффициенты разложения
легко вычисляются из выражения E6) для резольвенты. По-
Получаем
') Радиус сходимости для этого разложения равен ||Я VGa\\. Следователь-
Следовательно, ряд сходится абсолютно при ||ХК|| < Д0(г), где До(г)—расстояние от z
до ближайшего собственного значення Нй.

210 ГЛ. XVI. СТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ
Следуя Като, введем обозначение Sk(k ^ 0):
— Ро, если & = 0,
% если k>\. F5)
Тогда полученное разложение можно переписать в виде
"!S\ F6)
Коэффициент ири (z — E°a) в разложении GoCVGo)" в ряд
Лорана равен Л(">. Принимая во внимание разложение F6),
находим
(и)
' VSk>V ... VSkn+i, F7)
где X означает суммирование по всем наборам неотрицатель^
(о)
ных целых чисел k\, fe2 kn+i таких, что
fe,+fe2+...+fen+1=/7. F8)
Приведем несколько первых членов разложения Р:
h .... F9)
Исходя из уравнения E9) и действуя таким же образом,
получаем разложение HP. Находим
(Н-Е°а)Р=* f 1пВ(п\ G0)
где
Bw= ZSklVSk2V ... VSkn+K G1)
(я-1)
Итак,
(//-?°а)Р =
] + W(poVP0V^L + P0V-^VP0+ ^VP0VP0) + ....
G2)

§ 17. ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И ФУНКЦИИ 211
§ 17. Вычисление собственных значений
и собственных функций
Искомые собственные значения и собственные векторы Н
совпадают с собственными значениями и собственными векто-
векторами оператора HP в пространстве 8, для которого Р— проек-
проектор. Поскольку вид Р и HP известен, задача свелась к диагона-
лизации матрицы в пространстве размерности ga.
Невырожденный случай: ga = 1 • В этом случае
собственный вектор Н равен Р|0>. Разложение для квадрата
его нормы <0|Р|0> легко получается из разложения опера-
оператора Р. Собственные векторы Р|0> и построенный в разделе I
|г|)> пропорциональны друг другу; легко показать, что норма
последнего равна 1/<0|Р|0>.
Собственное значение Еа определяется из уравнения HP ~
= ЕаР. Поскольку ТгР = ТгРо = 1, имеем (ур. G0))
оо
Еа = Тг HP = Е°а + Z V (Тг В{п))
ИЛИ
в„ = Тг В[п)- G3)
Так как каждый член в В'п) содержит по крайней мере один
оператор Ро и так как, в силу известного свойства следа, спра-
справедливо тождество
Тг MP0N = Тг Р0ММ = @1 NM | 0),
то легко преобразовать е„ к виду среднего значения от некото-
некоторого оператора по невозмущенному состоянию |0>. Первые
члены разложения Еа равны
Еа = Е°а + Я@1 7| 0) + А,2<0 | V-%- V\ 0) +
) ..., G4)
что согласуется с результатами раздела I (ур. A2) и B6)).
Вырожденный случай: §аф\. Вместо того чтобы
решать задачу на собственные значения оператора HP в 8а, ее
можно заменить аналогичной задачей диагонализации в <$\.
Допустим, что любой вектор из подпространства <§а можно
рассматривать как проекцию в <§а некоторого вполне опреде-
определенного вектора из &\ (это предположение неявно использо-
использовалось в невырожденном случае). Поскольку <8а и &\ имеют
одинаковую размерность, проектор Р устанавливает взаимно
однозначное соответствие между векторами из <Sa н &\\ можно

212 ГЛ. XVI. СТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИИ-
также показать, что и проектор Ро устанавливает взаимно од-
однозначное соответствие между векторами <8а и <8\. Это условие
«неортогональности» двух подпространств, очевидно, выпол-
выполняется при достаточно малых X.
Таким образом, каждый собственный вектор Н в <8 а можно
представить в вндеР|?^а) и справедливо уравнение
HP | ?^а) = ЕаР | Е°аа).
Необходимым и достаточным условием такого равенства между
векторами <$'а является равенство их проекций в <8\
Р0НР | ?°а> = ЕаР0Р | Е°аа).
Обозначив
На = Р0НРР0, /Ca = P0PP0, G5)
перепишем предыдущее уравнение в виде
На\^аа) = ЕаКа\Е°аа). G6)
Операторы Ка и На можно рассматривать как эрмитовы
операторы в пространстве <$\. Уравнение G6) есть обобщенное
уравнение на собственные значения. Собственные значения
Еа — решения секулярного уравнения (см. § VII. 17)
det (На - хКа) = О,
они являются искомыми значениями энергии, а проекции соот-
соответствующих собственных векторов \Е°аа) в <Sa будут собствен-
собственными векторами Н.
Разложения На и Ка легко получаются из разложений HP
и Р соответственно (ур. F9) и G2))
-^VPQ+..., G7)
На = Е°аКа + ЯР0 VPQ + Я2Р01^ VP0 + . . .. G8)
Для того чтобы получить собственное значение Еа с точностью
до данного порядка, разложения На и Ка обрывают на том же
порядке.
Результаты данного порядка, полученные таким методом,
могут отличаться от результатов элементарной теории раз-
раздела II, но на величины высшего порядка. В первом порядке
результаты обоих методов в точности совпадают. Сравнивая
эти результаты, нужно также помнить, что вектор | Е°аа) отли-
отличается от вектора |0> элементарной теории, последний равен
пределу | ?^а) при Я -> 0.

§ 17. ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИИ И ФУНКЦИЙ 213
Метод, очень близкий к методу Като, но приводящий к бо-
более простым разложениям, был сформулирован Блохом '). В ос-
основе этого метода лежит тот факт, что оператор U, определяе-
определяемый равенствами
UPo^U G9)
имеет простое разложение
?/ = ? xnUln), (80)
ln) = Z'sklVSk2V VSk
Uln) = Z'sklVSk2V ... VSk"VP0, (81)
где 2 означает суммирование по всем наборам неотрицатель-
(л)
ных целых чисел k\, k<z, ..., kn, удовлетворяющих условиям
(Р=1,2, ...,П-\),
Отметим, что PQU = Ро, a PU = U. Действие U на вектор
пространства <S\ дает вектор из <$а, проекция которого в &1
есть исходный вектор.
Согласно определению V уравнение G5) эквивалентно сле-
следующему:
(РоНи-Еа)Ка\Еоаа) = 0, (83)
которое в методе Блоха играет ту же роль, что и уравнение
G5) в методе Като. Это обычное уравнение на собственные зна-
значения для неэрмитова оператора2) PqHU = НаКсГ{ в простран-
пространстве &\. Собственные значения и являются искомыми значе-
значениями энергии; соответствующие собственные векторы Ка\Е°аа}
есть проекции на &аа собственных векторов оператора Н, ко-
которые получаются действием оператора U. Разложение PqHU
легко следует из разложения U, если вспомнить, что
Несколько первых членов равны
= Е°аР0 + XPqVPo + X*PoV <%- VP0
Видно, что они проще членов разложений На и Ка (ур. G7) и
G8)).
') С. Block, Nuclear Physics 6, 329 A958).
2) Рассматриваемый как оператор в пространстве <§\ оператор Ка имеет
обратный, а как оператор во всем гильбертовом пространстве — не имеет.

5214 ГЛ. XVI. СТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЯ
В невырожденном случае энергия равна
откуда немедленно получаем коэффициенты ее разложения
в» == Е'<01 VSklVSk2V ... VSknV10>.
(л-1)
ЗАДАЧИ И УПРАЖНЕНИЯ
1. Взаимодействие V(q) добавлено к гамильтониану (/52+ЛУ)/2ш.
Вычислить в первом и втором порядках теории возмущений сдвиги энер-
энергетических уровней в следующих двух случаях:
(a) V-i-moV,
. (б) V-bq.
В обоих случаях сдвиги можно вычислить точно. Сравнить точные ответы с
результатами теории возмущений.
2. Рассмотрим атом водорода в теории Шредингера (глава XI). До какой
степени снимается вырождение каждого уровня постоянным электрическим по-
полем & (взаимодействие — еЩг)? Показать, что уровень п — 2 расщепляется
в первом порядке на три эквидистантных уровня (расстояние между уров-
уровнями равно 3ffh2/me), и определить кратность вырождения каждого.
3. Показать, что в приближении центрального поля полный момент, пол-
полный орбитальный момент и полный спин электронов замкнутой оболочки рав-
равны нулю. Используя этот результат, показать, что число линейно независимых
векторов (LSMLMs) для данной конфигурации определяется только электро-
электронами незамкнутой оболочки.
4. Определить спектральные термы конфигурации основного состояния
атома углерода при //-связи. Показать, что для полного момента У при /'/- и
LS-связях (§11) получается одно и то же значение с одинаковой кратностью.
Объяснить, почему.
5. Конфигурация основного состояния атома азота (Z=7) есть Is22s22p3.
Какие различные спектральные термы получатся при LS-связи?
6. Использовать метод § 13 для изучения сложных атомов из § 9, 10, 11,
Перечислить свойства симметрии операторов Нс, Vi и V?. и показать, в какой
степени снимает вырождение уровней Не последовательное включение возму»
щений Vt (i = 1, 2): (а) при LS-связи, (б) при //-связи.
7. Конфигурация основного состояния атома натрия (Z = 11) есть
Is»2s22p63s', а первая возбужденная конфигурация—Isi2s22p63pt. Следо-
Следовательно, основное состояние натрия есть Sy2, а два первых возбужденных
состояния — 2Р|д и 2Яз/1. Исследовать влияние на эти уровни постоянного маг-
магнитного поля 36. Вычислить соответствующие множители Ланде. При посте-
постепенном увеличении иитенсивиости X из области эффекта Зеемана переходят
в область эффекта Пашена — Бака. Получить выражение для уровней 2Я как
функцию параметра р = цв5^/ЛА2, где Ца — магнетон Бора, А — константа

ЗАДАЧИ И УПРАЖНЕНИЯ 215
спин-орбитальной связи, введенная в § 11 (Л > 0); нарисовать соответствую-
соответствующие кривые.
8. Исследовать тот же вопрос, что и в предыдущей задаче, для основного
состояния CЯ) атома углерода. (Уровни получаются как корни секулярных
уравнений, одно из которых третьей степени; основные характеристики кривых
можно получить, ие решая эти уравнения.)
9. Различные уровни ?i, ?2 Еп, полученные из go-кратно вырожден-
вырожденного уровня при введении возмущения Ц, можно охарактеризовать их «цент-
«центром тяжести» (?) и среднеквадратичным отклонением АЕ, определяемыми со-
соотношениями (обозначения § 8):
п п
Показать, что в первом порядке по V имеем
е=<?> - Е°а « -J- Tr P0V, (Д?J » -J- Тг Ри (V - е) Ро (V - е).
8а 8а
Использовать эти формулы для возмущения
из двух предыдущих задач. Показать, что в этих случаях е = 0; определить
зависимость и исследовать взиеиеиие Д? как функции параметра р из за-
задачи 7,

ГЛАВА XVII
ПРИБЛИЖЕННЫЕ РЕШЕНИЯ
НЕСТАЦИОНАРНОГО УРАВНЕНИЯ ШРЕДИНГЕРА
§ 1. Изменение «представления» и рассмотрение части
гамильтониана по теории возмущений
Данная глава содержит два раздела и посвящена методам
построения приближенных решений зависящего от времени
уравнения Шредингера. По известному динамическому состоя-
состоянию исследуемой квантовой системы в момент времени t0 тре-
требуется определить динамическое состояние этой системы в мо-
момент времени t. Следовательно, задача состоит в построении,
по возможности наиболее точном, оператора U(t, to), который
описывает эволюцию во времени динамических состояний си-
системы в представлении Шредингера.
Напомним вкратце основные свойства оператора U(t, t0).
Если гамильтониан системы H(t) известен, то этот оператор
однозначно определен и является решением интегрального урав-
уравнения
t
U (t, /0) = 1 - ifi~l J Н (т) U (т, /„) dx A)
и
или, что эквивалентно, решением уравнения Шредингера
^o)^H(t)U(t,t0) B)
с начальным условием
?/(*„,/о) =1. C)
Поскольку H(t)—эрмитов оператор, то U — унитарный
U(t,t')u4t,O = U*(t,t')U(t,t')=L D)
Более того, справедлив закон композиции ')
U{t,t') = U{t,t")U{t",tr), ' E)
') Для доказательства этого закона композиции, физический смысл кото-
которого очевиден, заметим, что, если V —унитарный оператор, ие зависящий от
/, то оператор U(t,t")V является решением уравнения Шредингера B). Для
того чтобы он был равен U(t, /') при всех /, достаточно, чтобы равенство вы-
выполнялось при некотором значении /, например, при t = t", это дает V =
U(t"t')

§ 1. ИЗМЕНЕНИЕ «ПРЕДСТАВЛЕНИЯ» 217
откуда следует
?/*(/, О=" (Л 0- <6>
Эквивалентное определение U можно получить, заменяя урав-
уравнение A) на эрмитово сопряженное. Принимая во внимание
F), получаем
t
U(t, Q=l- ih~l \ U(t, т) Я(т)dx. G)
и
Метод, описанный в настоящей главе, состоит в следующем.
Предположим, что гамильтониан Я представим в виде
H(t)^H^(t)+V(t), (8)
где Я@)(/) —гамильтониан уравнения Шредингера, решения ко-
которого известны. Пусть ?/@)(/, t0)—оператор эволюции, отве-
отвечающий Я<°>
/ft -^ Um (/, /0) - Я@) (/) Um (/, t0), Um (t0, t0) = 1. (9)
Поскольку оператор ?/@)(/, t0) известен, то для определения U
достаточно найти унитарный оператор
Физическое значение оператора Ui обсуждалось в § VIII. 14.
U] — оператор эволюции состояний в промежуточном «пред-
«представлении», получающемся из представления Шредингера уни-
унитарным преобразованием (/@)+ (t, to). Простое вычисление, детали
которого приведены в § VIII. 14, показывает, что зависимость
Ui от времени определяется гамильтонианом
V, (/) ^ ?/@»* (/,/о) V(/)l/m (/,/,,). A1)
Другими словами, Ut{t,to) есть решение уравнения
/Й jj- U, (t, /о) = Vj (/) U, (/, /о), U, (t0, t0) = 1 A2)
или, что эквивалентно,
t
V, (t, t0) = 1 - /И J Ку (т) ?/7 (т, /0) Л. A3)
to
Оператор Ui(t, to) обладает всеми свойствами оператора эво-
эволюции и, в частности, удовлетворяет уравнениям A) — G), в ко-
которых H(t) следует заменить на Vi(t).

218 ГЛ. XVII. НЕСТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
Интегральные уравнения A), G), A3) можно, по крайней
мере формально, решить методом итераций. Так, подставляя
в правую часть A3) вместо Ui{x, t0) выражение
т
1-Й-1 \vl{x')U1{x',tQ)dx',
и
получаем
t
и
t х
+ (/ft) \ dx\ dx' Vj (x) V, (tO V (x\ /0). A4)
J J
и и
Последовательные итерации дают разложение
где иУ есть интеграл
и\п) ^ (ifl)~n \ dxn dxn-\...
<>т„>т„_1>...>т,><0
... dx{ Vj(xn) Vjix^i) ... Vj(X[). A6)
Учитывая определения A0) и A1), получаем следующее раз-
разложение для U:
оо
1 [ dxn dxn_i ...
... dx{U{0) (t, xn) V (xn) Um} (xn, т„_,) V (т„_,) ...
...f/(OI(T2,T1)V(T1)?/ro(T1,/a). 08)
Разложения A5) и A7) представляют собой ряды по сте-
степеням V, которые сходятся тем лучше, чем ближе U^(t, ta)
к U(t, t0). Они служат отправной точкой для вычислений этой
главы. Оператор f/<0) суть приближение нулевого порядка,
а ?/(I), t/B) ?/'">, ... отвечают поправкам 1-го, 2-го, ...
..., /г-го, ... порядков к этому приближению. Сложность вы-
вычисления этих поправок быстро растет с увеличением их по-
порядка и обычно ограничиваются поправками низшего порядка.

§ 2. ТЕОРИЯ ВОЗМУЩЕНИЯ ДЛЯ ВЕРОЯТНОСТЕЙ ПЕРЕХОДОВ 219
Раздел I. НЕСТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ
§ 2. Определение и вычисление по теории возмущений
вероятностей переходов
Приведенные выше рассуждения можно использовать, в част-
частности, тогда, когда #<°> не зависит от времени. В этом случае
оператор эволюции Uw(t, t0) имеет простой вид
?/@) (/, t0) = ехр [- /Я@) (/ - /0)/й]. A9)
Предположим, что собственные значения #@) известны и, если
не оговорено противное, спектр #<°> будем считать для простоты
дискретным. Обозначим |а>, |6>, ..., \k} ... полный набор соб-
собственных векторов оператора #@>, а Е°а, Е°ь Е\, ...—от-
...—отвечающие им собственные значения. Будем использовать также
обозначения
B0)
B1)
где ш« — частота Бора, отвечающая переходу l-+k, a Vki(t) —
соответствующий матричный элемент V(t).
Предположим, что в момент времени t0 система находилась
в состоянии, собственном для #@>, например, в состоянии а. Мы
хотим вычислить вероятность того, что при измерении в момент
времени t система будет находиться в другом собственном со-
состоянии оператора #<°>, например, в состоянии Ъ. Эту величину,
которую, по определению, будем называть вероятностью пере-
перехода из а в Ь, обозначим через Wa-*b- Ясно, что
Wa+b = \{b\U{t,ta)\a)?. B2)
Если бы V равнялось нулю, то вектор, представляющий со-
состояние системы в момент времени t, отличался бы от вектора
начального состояния |а> только фазовым множителем
ехр [— iE°a (t — tQ)lh] и вероятность перехода Wa-+b была бы
равна нулю. Разложение амплитуды вероятности (b\U(t, tQ)\a}
в ряд по степеням V получается подстановкой вместо U(t,to)
разложения A7)
(b\U(t,to)\a)=t(b\U{n)\a), B3)
где ?/<"> определяется формулой A8).

220
ГЛ. XVII. НЕСТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
В представлении {#<0>} вклады низших порядков в ампли-
амплитуду равны
(Ь |U" | в> — ОТ1 \
~< [t-x)lh
Vba (т) е"'Е° ^
B4')
=(/fiJ z i
"'E° {%~хУн
B42)
T'
=(«)»E ? JdT S ^ S
J
x e-«2 (-
(т0
B43)
В приведенных равенствах суммирование происходит по всем
базисным векторам представления {#@>}.
Вклады различных порядков можно схематически изобра-
изобразить посредством диаграмм рис. 10.
Рис. 10. Диаграммы, изображающие вклады различных порядков в ампли-
амплитуду вероятности перехода из а в Ъ: (i) первого порядка, (ii) второго по-
порядка, (ш) третьего порядка.
Диаграмма (i) представляет вклад первого порядка или,
более точно, произведение, стоящее в скобках в правой части
B41). Непрерывная линия отвечает эволюции системы во вре-
времени. От U до х эволюция определяется невозмущенным га-
гамильтонианом #<0) и система, следовательно, остается в состоя-
состоянии а, вектор состояния умножается просто иа множитель

§ 2. ТЕОРИЯ ВОЗМУЩЕНИИ ДЛЯ ВЕРОЯТНОСТЕЙ ПЕРЕХОДОВ 221
ехр[—i?^(t — to)/h]. В момент времени т система под действием
возмущения переходит из а и ft, что выражается матричным
элементом перехода У&а(т). От т до / эволюция вновь опреде-
определяется #@), и система остается в состоянии Ь, а вектор состоя-
состояния умножается на ехр[—iE\ (t — x)/ti]. Следуя по диаграмме
снизу вверх, получаем три множителя, которые расположены
в скобках справа налево. Вклад первого порядка получается
после интегрирования этого произведения по т.
Точно так же диаграмма (и) представляет поправку вто*
рого порядка. Эволюция системы от t0 до %' определяется #@),
затем под влиянием У(т') система переходит из состояния а
в промежуточное состояние k, эволюция от х' до т определяется
Я@), в момент времени т под влиянием V{x) система переходит
из состояния k в конечное состояние Ь, после чего ее развитие
во времени от т до t вновь определяется оператором #@). Та-
Таким образом, мы получаем пять множителей, расположенных
в скобках правой части B42) справа налево. Вклад второго по-
порядка получается интегрированием по т' и x{to < т' < т < О
и суммированием по всем промежуточным состояниям. Имея
в виду такой способ описания развития во времени переходов
второго порядка, состояние k часто называют виртуальным со-
состоянием, в отличие от состояний а и ft, и говорят, что переход
второго порядка происходит через виртуальное состояние.
Таким же образом, переходы третьего порядка, представ-
представленные диаграммой (Hi), происходят через два виртуальных со-
состояния k и /. Возмущающий потенциал появляется последова-
последовательно три раза в моменты времени х", х1 и т, переводя систему
из состояния а в /, из / в k и из k в Ь. Аналогично переходы
n-го порядка происходят через (п— 1) виртуальных состояний.
Взяв п первых членов разложения B3), получаем искомую
амплитуду вероятности с точностью до порядка п. Квадрат мо-
модуля этой амплитуды дает, по определению, вероятность пере^
хода ') порядка п:
Wa+btt\(b\Um\a) + (b\Um\a)+ ... +(b\U"l)\a)\\
В частности, вероятность перехода в первом порядке дается
формулой
t
--2
B5)
') Полученное выражение представляет разложение Wa-*b по степеням V
по меньшей мере с точностью до (я + 1)-го порядка. Полученная точность
будет выше («+ 1)-го порядка, если (&|1/<'>|а) = 0.

222 ГЛ XVII. НЕСТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
Отметим, что в этом приближении
Wb + a.
Последнее соотношение, вообще говоря, перестает выполняться
в высших порядках. Его не следует смешивать со свойством
микрообратимости, т. е. с равенством №кь-*ка — Wa-+b, которое
выполняется только, когда гамильтониан инвариантен относи-
относительно обращения времени; в этом случае равенство выпол-
выполняется во всех порядках (§ XV. 20).
§ 3. Полуклассическая теория
кулоновского возбуждения ядер
В качестве приложения рассмотрим кулоновское возбужде-
ние ядра заряженной частицей, например, протоном1).
Предположим, что монохроматический пучок протонов стал-
сталкивается с ядерной мишенью. В результате столкновений ядра
мишени совершают переходы из основного состояния а в воз-
возбужденные состояния. Вычислим сечение перехода в данное
возбужденное состояние р.
Обозначим Ze заряд ядра, R— его радиус,/а и /р, Еа и ?р —
спины и энергии состояний аир соответственно. Имеется
B/а+1) линейно независимых состояний а, которые можно
отличать друг от друга по величине компоненты Ма спина по
направлению данной оси квантования; этим состояниям соот-
соответствуют векторы \aJaMa}- Если Hn — гамильтониан ядра, то
HN \а]аМа) = Еа |aJaMa) (Ma = -Ja Ja),
Обозначим Е = Mv2/2 энергию столкновения в системе
центра масс протона и ядра, Д? = ?g — Еа — энергию возбуж-
возбуждения ядра, Йа — направление налетающего протона, Qp — на-
направление неупруго рассеянного протона и 9 — угол между
этими направлениями. Нам нужно вычислить величину
da
rfQ
"• "• р р
т. е. сечение процесса, в котором протон неупруго рассеивается
в направлении Qp, а ядро переходит из состояния {aJaMa) в со-
состояние (р/рЛ1р).
Рассмотрим взаимодействие протона и ядра. Для больших
расстояний г между протоном и ядром (г ^ R) оно сводится
') О кулоновском возбуждении и его приложении к изучению структуры
ядра см.: Adler et al. Rev. Mod. Phys. 22, 432 A956); приведенное здесь полу-
класснческое рассмотрение следует работе К- А. 7ер-Мартиросяна. ЖЭТФ, 28
284 A952),

5 3. КУЛОНОВСКОЕ ВОЗБУЖДЕНИЕ ЯДЕР 223
к чисто кулоновскому взаимодействию Ze2/r. С уменьшением г
вид потенциала начинает отличаться от этой простой формы.
Пока г > R, отличие имеет чисто электромагнитное происхож-
происхождение и сводится в основном к разности между точным куло-
новским взаимодействием и членом Ze2/r
(v±*$ <26)
где г, — координата t-ro протона в ядре.
Как только протон «проникнет» в ядро (г < R), особо важ-
важную роль приобретут ядерные взаимодействия, которые будут
значительно превышать электромагнитные взаимодействия.
Если энергия Е достаточно мала, то кулоновское отталкива-
отталкивание Ze2/r не позволяет протону приблизиться к ядру и, следо-
следовательно, остается доминирующим взаимодействием в течение
всего процесса столкновения. Движение протона и ядра опре-
определяется тогда в первом приближении гамильтонианом
где р2/2М — кинетическая энергия протона. Движения протона
и ядра полностью разделяются. Последнее остается в своем ос-
основном состоянии, в то время как протон упруго рассеивается,
и дифференциальное сечение дается формулой Резерфорда
(VI. 29)
daRldQ = i a2 sin j-9,
где а — половина наименьшего расстояния между протоном и
ядром при классическом рассмотрении их движения
Данное приближение оправдано, если
а > R. B8)
Дополнительно будем предполагать, что
Щ-<1. B9)
Y > 1, C0)
где
v-i-TT <31>
Из-за отличия взаимодействия протона и ядра от Ze2/r мо-
могут произойти неупругие столкновения. Так как по условию B8)

224 ГЛ. XVII. НЕСТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
протон лишь незначительно «проникает» в ядро, отличие сво-
сводится в основном к члену V. В силу условия C0) кулоновское
рассеяние можно рассматривать классически (§ VI. 5). Движе-
Движение протона есть движение волнового пакета пренебрежимо ма-
малых размеров, центр r(t) которого удовлетворяет соответствую-
соответствующим классическим уравнениям движения. В данном неупругом
столкновении (QaMa->QpAfp) движение протона также можно
рассматривать классически. Если пренебречь членом V, то ре-
решение классических уравнений движения известно. При этом
требуется, чтобы можно было также пренебречь энергией АЕ,
переданной в течение столкновения от протона ядру. Такое при-
приближение оправдано, если выполнено условие B9). Так как
траектория протона r(t) определена, V становится зависящим
от времени возмущением, действующим на динамические пере-
переменные ядра
z
и может вызвать переход (a/aAfa)->(p/pAfp). Поскольку ве-
вероятность перехода Wa+$ мала (a posteriori можно оправдать,
что U^a-^p *C 1), то достаточно ограничиться приближением пер-
первого порядка. Формула B5) дает
А
—2
C2)
Искомое сечение равно произведению этой вероятности на се-
сечение Резерфорда
Остается вычислить Wa^.$. Мы ограничимся только тем, что
приведем схему вычислений. Обозначим (гг, Q*) и (г, Q) поляр-
полярные координаты векторов гг и r(t) соответственно; (г, Q) за-
зависят от t. Если разложить \r{t)—г^-1 по сферическим функ-
функциям (ур. (В. 99)), то получим
оо +1
У @ — L, L, \~ ч 4i Ti , C4)
l=\ m=-l
где
Qr=ZerliY?(Qi), C5)
4nZe Yf (Q)
-Ьтг- C6)

§ 3. КУЛОНОВСКОЕ ВОЗБУЖДЕНИЕ ЯДЕР 225
Разложение справедливо только при гг < г, что в нашем слу-
случае всегда выполняется, поскольку протон не «проникает»
в ядро. Подставляя разложение C4) в формулу C2), получаем
Wa+e = I Е (- 0т STm <р/эМр | Q? | aJaMa) 2, C7)
I lm
C8)
Коэффициенты S? зависят только от классической траекто-
траектории протона и могут быть найдены численным интегрирова-
интегрированием.
Операторы Qf (т = — /,...,+/) есть стандартные компо*
центы электрического 21-польного момента Q(t> (см. § XIII. 33).
Следовательно, в формуле C7) отличны от нуля только те мат-
матричные элементы, которые удовлетворяют правилам отбора по
моменту и четности
+ /р. л1 = М3-Л1а> C9)
(Па, Пр — четности состояний аир соответственно). Кроме
этого, согласно теореме Вигнера — Эккарта
„ \Q?\ aJaMa) = BJ& + 1)"</„Ш„т| W
В силу правил отбора C9) сумма в C7) ограничена конеч-
конечным числом значений / определенной четности и только одним
значением т. Грубая оценка показывает, что «/ + 2»-вклад со-
составляет порядка (R/aJ от «/»-вклада. Таким образом, можно
оставить только член, отвечающий наименьшему значению /,
допустимому правилами отбора: либо \Ja — /р|, либо
|/а — /р| + 1. Обозначив это значение /о, имеем
(Jal<>Mam | /рМэ>2 . |21 (W ,2
Wo--**** B/p + l) 'S/" I I <P M Q Ilo>l (m = Mp — Ma).
Подставляя это выражение в формулу C3), получаем теорети-
теоретическое значение для сечения, которое можно сравнить с экспе-
экспериментальными данными.
В эксперименте, где ядра мишени не ориентированы и не на-
наблюдается ориентация возбужденных ядер, измеряемое сече-
сечение получается усреднением определенного выше сечения по
2/а + 1 возможным значениям Ма и суммированием по 2/р + 1
возможным значениям М$. Принимая во внимание соотношения
8 А. Мессиа

226 ГЛ. XVII. НЕСТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
ортогональности коэффициентов Клебша — Гордана, получаем
Зависимость сечения от углов определяется выражением, стоя-
стоящим в скобках, и должна быть найдена численно. Отметим, что
начальное и конечное состояние ядра входит в эту формулу
только посредством таких характеристик, как спин, четность и
квадрат модуля матричного элемента электрического 2'о-поль-
ного момента <f$| IQ^o'l |a>, который фигурирует как множитель
пропорциональности. Следовательно, сравнение полученной фор-
формулы с экспериментом дает непосредственный способ определе-
определения этих характеристик структуры ядра.
§ 4. Случай, когда V не зависит от времени.
Сохранение невозмущенной энергии
Когда V не зависит явно от временч, интегрирование по вре-
времени в формулах B4) легко выполняется и полученные выра-
выражения обладают рядом интересных и простых свойств. Ограни-
Ограничимся обсуждением перехо-*
дов первого порядка.
Возьмем to = 0, тогда по
формуле B5) имеем
W
W
Ьа
'. ®*
D0)
-Sn/t-4rt,t-2njt ЯШЯПй Ш =2(l-cos«>0/«>2. D1)
Зависимость функции f(t, ©)
Рис. 11. Функцииf(<,a>) = 2A-cos юОМ от а изображена на рис. 11.
Отметим очень острый пик
в окрестности со = 0 ширины 2л//. Используя теорию вычетов, не^
сложно показать, что
и согласно (А. 156)
= 2л/
f {t, ©) ~ 2п б (о).
D2)
D3)

5 4. СОХРАНЕНИЕ НЕВОЗМУЩЕННОИ ЭНЕРГИИ 227
Для данного значения / величина Wa^-ь имеет простую зави-
зависимость от конечного состояния Ь. С точностью до константы
она равна квадрату модуля матричного элемента возмущения
<6| У|а>, умноженного на функцию /(/, а>&а), которая зависит от
частоты перехода а ->¦ Ъ. Поскольку этот множитель имеет ярко
выраженный пик ширины 2л// в точке <о&а = 0, переход будет
происходить в основном в состояния с энергией в интервале
шириной
6?0« 2nh/t,
центр которого совпадает с энергией начального состояния.
Другими словами, переходы сохраняют невозмущенную энер-
энергию с точностью до 2лН/{.
Этот результат в некотором смысле аналогичен соотношу
нию неопределенности для энергии — времени (§ IV. 10 и
VIII. 13). Однако следует отметить, что здесь фигурирует энер-
гия не всей системы, включая возмущение, а лишь #(°>, и время
t есть" время, после которого производят измерение #@), а не
время, характеризующее эволюцию системы.
Для данного состояния b зависимость Wa^-ь от t также оп-
определяется множителем f(t, ш&а). Если при переходе невозму-
невозмущенная энергия точно сохраняется (а>ьа = 0), то этот множи-
множитель растет как t2. В противном случае он осциллирует ме-
между 0 и 4/ю|а с периодом 2л/ю*а. Величина UV*-* осциллирует
с тем же периодом около среднего значения 2\Уьа\2/(Еъ — ЕаJ
и ведет себя как t2 только для значений t, малых по сравнению
с периодом.
Вместо того чтобы рассматривать переход в определенное
состояние, можно рассматривать переходы в группу состояний
с близкими энергиями. Именно так всегда поступают при ис-
исследовании переходов в состояния непрерывного спектра. Тогда,
сделав некоторые дополнительные ограничения, которые в даль-
дальнейшем будут уточнены, можно определить вероятность пере-
перехода в единицу времени.
Итак, рассмотрим некоторую последовательность собствен-
собственных векторов #<°>, принадлежащих непрерывному спектру. Век-
Вектор из этой последовательности будем обозначать |Ь>, а Е(Ь) —
соответствующее собственное значение #@).
При определении вероятностей перехода следует обратить
внимание на нормировку векторов |Ь>. Будем считать их нор-
нормированными так, что
где п(Ь)—некоторая вещественная положительная функция.
Проектор на состояния из области В переменной Ь есть (см.

228 ГЛ. XVII. НЕСТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
§ VIII. 13)
Рн=
Если выбрать Е(Ь) в качестве новой переменной и соответствую-
соответствующую область интегрирования обозначить В(Е), то получим
Рв= \ \Ь)9ь{Е)йЕ{Ь\, D4)
В(Е)
где
9b(E) = n(b)jt, D5)
эта величина известна как плотность уровней b при энергии Е.
Отметим, что рь{Е) зависит от нормировки |Ь>.
Вероятность перехода Wa-^-в в одно из состояний области В
равна
J E)dE. D6)
В (Б)
Формула D6) получена после подстановки вместо Рв выраже-
выражения D4) и использования равенства
Wa+b = \(b\U(t,0)\a)?. D7)
Здесь Wa-*b формально представляет вероятность перехода
a-f-b, определяемую уравнением B2). Все преобразования, от-
относящиеся к вычислению этой величины, полностью обоснованы
и в данном случае. В частности, подставляя D0) в правую
часть D6), получаем вероятность перехода Wa+в в первом по-
порядке по возмущению
\ D8)
где на зависимость от Е величины K&as=<b|V|a> указывает
параметр Ь.
В качестве конкретного примера рассмотрим переходы на
уровни Ь, лежащие внутри интервала (Е\ — 1/2в, Ei-\-1/2b),
предполагая е достаточно малым, чтобы Vba и р& были почти
постоянны на этом интервале и их можно было вынести за знак
интеграла. Предположим также, что / достаточно велико, так
что е много больше периода колебаний функции f
е>2пА//. D9)
В этих предположениях интеграл в правой части формулы D8)
легко вычисляется. Следует рассматривать два случая:
(i) Основной пик функции f лежит вне области интегриро-
интегрирования (переходы не сохраняют энергию). В этом случае можно

§ 5. ВЫЧИСЛЕНИЕ СЕЧЕНИЙ В БОРНОВСКОМ ПРИБЛИЖЕНИИ 229
заменить f ее значением, усредненным по нескольким колеба*
ниям, что дает не зависящее от времени выражение
(ii) Основной пик / лежит в области интегрирования (пере-
(переходы, сохраняющие энергию). Тогда пик дает главный вклад
в интеграл и расширение области интегрирования до всей оси
ведет лишь к незначительным погрешностям, после чего полу-
получаем (ур. D2))
Wa+B « 2ЯЙ-1 | Vba (Ea) P ?b (Ea) t.
В силу неравенства D9) эта вероятность превосходит сумму
всех остальных.
Определим вероятность перехода в единицу времени как
В соответствии с предыдущими результатами можно заключить,
что эта величина исчезает для переходов, не сохраняющих энер-
энергию, а для сохраняющих энергию переходов она дается важной
формулой
В этой формуле матричный элемент Vba = <b| V\a} и плотность
уровней рь относятся к состояниям Ь, энергия которых равна
энергии начального состояния.
Для справедливости формулы E0) величина t должна быть
достаточно велика для того, чтобы было выполнено условие
D9) и достаточно мала для того, чтобы было оправдано при-
приближение первого порядка (Wa+et "С 1).
Приведенное доказательство обладает тем преимуществом,
что демонстрирует значение формулы E0) и условия, при ко-
которых она справедлива. Эту формулу можно получить совсем
просто, заменив в правой части выражения D0) функцию f ее
асимптотикой D3), что дает
Wa+b~2nh-1\Vba?6(Eb-Ea)t, E1)
и подставив это в определение Wa-*e (ур. D6)).
§ 5. Приложение к вычислению сечений
в борновском приближении
Используя формулу E0), можно вывести выражение для
сечений рассеяния в так называемом борновском приближении,
т. е. в первом порядке по потенциалу взаимодействия частицы
и мишени. Рассуждения будут простыми, но не совсем строгими.
Строгое доказательство этой формулы будет дано в главе XIX.

230 ГЛ. XVII. НЕСТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
Рассмотрим простейший из возможных случаев — рассеяние
частицы на потенциале V(r). Последний рассматривается как
возмущение гамильтониана свободной частицы
Плоские волны е'кг являются собственными состояниями #<°>.
Такие волны представляют состояния частицы с импульсом
р = Ш и нормированной на единицу плотностью вероятности.
Будем обозначать соответствующие кет-векторы |й>, они удо-
удовлетворяют соотношениям ортогональности и полноты
В пространстве векторов k плотность нормированных таким об-
образом состояний постоянна и равна Bя)~3: число состояний
в интервале (k, k + dk) равно dk/BnK. Мы интересуемся со-
состояниями с импульсом в определенном направлении Q и обо-
обозначим, как и в предыдущем параграфе, их плотность р(Е) (ур.
D5)) (a priori эта функция могла бы зависеть от Q, однако
ниже мы увидим, что это не так): p(E)dQ dE— число состояний
с импульсами в телесном угле (Q, Q + dQ) и энергией Е =
= р2/2т в интервале (Е, Е + dE). Тогда имеем
Bя)'
используя равенство dp = p2 dQ dp, получаем
BяЛK •
и, следовательно,
.р, р2 dp тр
Р ' ' "~ BяАK ~~Ш ~ BяАK *
Перейдем к вычислению сечения рассеяния в заданное на-
направление Об монохроматического пучка энергии Е = mVa/2.
Пусть hka — импульс налетающих частиц, а Ькь — импульс, со-
соответствующий той же энергии, но в направлении Q&. Мы
знаем, что вероятность в единицу времени wa+BdQ системе пе-
перейти из начального состояния |fta> в одно из состояний Ь с им-
импульсом в телесном угле (Q&, Q<, + dQ) и энергией, близкой к Е,
дается в первом порядке формулой E0)
tdQ~2nh-l\(kb\V\ka)fp(E)dQ. E3)
Пусть d<Ja^.b/dQ будет дифференциальным сечением, тогда
оа-*ь равно числу частиц, рассеянных в телесный угол
(?2б, Q» +_ dQ) за единицу времени при единичном падающем

§ 6. ПЕРИОДИЧЕСКОЕ ВОЗМУЩЕНИЕ. РЕЗОНАНСЫ 231
потоке. Поскольку \ka} отвечает волне со скоростью потока va,
имеем
Подставляя вместо шя->-в приближенное выражение E3), полу-
получаем
^a)f9b(E), E4)
где рь(Е)—плотность конечных состояний (ур. E2)), а
есть матричный элемент потенциала, ответственного за переход
§ 6. Периодическое возмущение. Резонансы
Вероятность №<,->-!> в первом порядке по потенциалу (фор-
(формула B5)) пропорциональна квадрату модуля преобразования
Фурье частоты а>ьа функции Vba(t), гДе мы условились считать
Уьа = 0 вне интервала (to, t). Если V не зависит от t, то преоб-
преобразование Фурье вычисляется элементарно и в результате, как
мы видели, приходим к «сохранению невозмущенной энергии».
Несложно провести гармонический анализ и в том случае, когда
зависимость V от времени периодическая. Здесь возникает
очень важное явление — резонанс.
Предположим, что V зависит от t по гармоническому закону
с частотой о. Так как V — эрмитов оператор, то его можно
представить в виде
где А — некоторый оператор, не зависящий от времени. Вероят*
ность перехода Wa->-b в первом порядке равна (считаем to = 0)
t t
{Ъ\А\а)\ъ*<и*а+и)* dx + (b | А+ |а) \ е'("*«"•)х dx
о о
что можно сравнить с выражением D0).
Амплитуда перехода здесь состоит из двух членов. Для до-
достаточно больших t первый член мал, если только <дьа + ю не
близко к 0, т. е. если только энергия не лежит в интервале (ши-
(ширины 2nh/t) с центром в точке
Eb = Ea — ha, E5)
второй член мал вне интервала (той же ширины) с центром
в точке
Е„ = Еа + Ш. E50

232 ГЛ. XVII. НЕСТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
Практически всегда t достаточно велико (t 3> 2я/ю) и эти
интервалы не перекрываются. Значит Wa-*b мало для всех пе-
реходов кроме тех, при которых невозмущенная система излу-
излучает или поглощает энергию Йю, на что указывают уравнения
E5) и E5') соответственно.
В первом случае вклад в амплитуду перехода дает только
первый член и для вероятности перехода получаем выражение
Основное отличие этого выражения от D0) состоит в замене
(Оба на сойа + со. В полной аналогии с рассуждениями § 4 можно
рассмотреть переходы в группу уровней с энергией в интервале
Д? С^>2пН/() с центром в точке Еа—• На> и при подходящих
условиях определить вероятность перехода в единицу времени,
которая вновь дается формулой E0) с тем отличием, что теперь
Vba и р& относятся к состояниям Ь, энергия которых меньше
энергии начального состояния на /ш. Те же рассуждения при-
менимы к переходам, при которых система поглощает энергию
/гю (см. задачу 2).
Рассмотрим теперь более общий случай, когда V—произ-
вольная периодическая функция t с частотой ю. Сформулируем
кратко относящиеся к этому случаю результаты, доказательство
которых предоставим читателю. Имеем разложение Фурье
Если t ;> 2я/со, то в первом порядке вклады в вероятность пе-
перехода от различных членов этого ряда не интерферируют, по-
поскольку каждый из них вызывает переходы, отвечающие раз-
различному изменению энергии. При «Л.,-переходах» система те-
теряет с точностью до 2nh/t энергию sha>; при «Л^-переходах» си-
система поглощает с точностью до 2nh/t энергию sha>.
Раздел П. МГНОВЕННОЕ И АДИАБАТИЧЕСКОЕ ИЗМЕНЕНИЯ
ГАМИЛЬТОНИАНА
§ 7. Формулировка задачи и результаты
Часто возникает задача определения изменения состояния
системы при изменении внешнего поля. Классический пример
такой ситуации представляет атом, помещенный в магнитное
поле. Как правило, получаемые результаты существенно зависят
от времени Г, в течение которого происходило изменение га-
гамильтониана. В этом разделе мы исследуем предельные случаи,

§ 8. БЫСТРЫЙ ПЕРЕХОД И МГНОВЕННОЕ ПРИБЛИЖЕНИЕ 233
когда Т очень мало (мгновенное изменение) и очень велико
(адиабатическое изменение).
Будем предполагать, что гамильтониан изменяется непре-
непрерывным образом от некоторого начального Яо в момент вре-
времени to До конечного #i в t\. Обозначим
а Н (s) — значение гамильтониана в момент времени t = t0 +
'-f- sT. Гамильтониан H(s)— непрерывная функция s и
Я@) = Я0, ЯA) = Я,.
Эволюция системы от t0 до t\ зависит теперь только от пара-
параметра 7", который определяет скорость перехода от Но к Яь
Удобно ввести обозначение
Задача заключается в определении оператора U(t\, t0), т. е.
?/гA), и исследовании его зависимости от 7".
Особенно простые результаты получаются в упомянутых
выше предельных случаях.
В пределе, когда Т -> 0, т. е. в случае бесконечно быстрого
перехода, динамическое состояние системы остается неизмен-
неизменным
Ит?/ГA) = 1. E6)
В пределе, когда Т -> оо, т. е. в случае бесконечно медлен-
медленного или адиабатического перехода, если система первоначаль-
первоначально находилась в собственном состоянии гамильтониана Но, то
в момент времени t\ при выполнении некоторых сформулиро-
сформулированных ниже условий система перейдет в собственное состоя-
состояние Н\, которое получается из исходного состояния по непре-
непрерывности. Этот важный результат известен как адиабатическая
теорема :).
§ 8. Быстрый переход и мгновенное приближение
Первое из приведенных утверждений немедленно следует из
интегрального уравнения A), которому удовлетворяет опера-
оператор эволюции системы. Используя обозначения § 7, запишем
') Она также называется теоремой Эренфеста. Работа Эренфеста отно-
относится к классической механике н старой квантовой теории. Перенос этой тео-
теоремы в квантовую механику сделан в работе: М. Born and V. Fock. Zeit. f.
Phys. 51, 165 A928). См. также Т. Kato, Journ. Phys. Soc. Jup. 5, 435 A950);
K. 0. Friedrichs, On the Adiabatic Theorem in Quantum Theory, Report IMM.
NYU-218, New York, 1955.

234 ГЛ. XVII. НЕСТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
его в виде
UT (s) = 1 - ift-'r 5 Я (s) f/r (s) ds.
0
В пределе 7"-»- 0 второе слагаемое в правой части стремится
к нулю, и мы получаем нужный результат E6).
Для достаточно малых Т в первом приближении можно
предположить, что f/r(l)« 1. Это приближение называется
мгновенным.
Обозначим |0> вектор состояния системы в момент временя
to, и пусть Q — проектор на подпространство, ортогональное
к |0>. Считая норму |0> равной 1, имеем
Qo = 1 — 1 0><01-
Мгновенное приближение означает, что
U(thto)\0)&\0).
Величина ошибки при таком приближении дается вероятностью
& найти систему в состоянии, отличном от начального
E7)
Поправку к этому приближению можно вычислить, исполь-
используя описанную в § 1 теорию возмущений. В данном случае
(Я<°> = О, V = Я) приближение первого порядка равно еди-
единичному оператору 1, и разложение A7) имеет вид
1 1 S,
UT A) = 1 - ih~lT J Я (s) ds + (/A)"V J dsi J Я (s,) H (s2) ds2+ ....
0 0 0
E8)
В частности, подставляя это разложение в правую часть
E7), получаем разложение б по степеням 7". Поскольку
Qo|O> = O, член низшего порядка пропорционален Т2 и полу-
получается подстановкой двух первых членов разложения E8).
Введем обозначение
^j^ E9)
о и
Тогда имеем
И поскольку
<0 \HQ0H |0) =<0 |Я210> - @ |Я| ОJ = (Д ЯJ,

§ 9. МГНОВЕННОЕ ОБРАЩЕНИЕ МАГНИТНОГО ПОЛЯ 235
где АЯ— средне-квадратичное отклонение наблюдаемой Я в со-
состоянии |0>, получаем
ввЛ^ + 0(П. F0)
Итак, условие применимости мгновенного приближения & <С 1
требует, чтобы') _
F1)
Условие F1) является не чем иным как частной формой со-
соотношения неопределенности для энергии и времени. Согласно
определению E9) представляет собой гамильтониан системы,
усредненный по интервалу (t0, М- Грубо говоря, в этот интер-
интервал времени эволюцию системы определяет гамильтониан Я.
В силу соотношения неопределенности для энергии и времени
состояние системы, удовлетворяющей такому уравнению дви-
движения, не может заметно измениться за время, меньшее ft/ДЯ.
Следовательно, неравенство F1) действительно является усло-
условием того, что изменение состояния по прошествии промежутка
времени Т пренебрежимо мало.
§ 9. Мгновенное обращение магнитного поля
В качестве приложения рассмотрим, что произойдет с ато-
атомом в постоянном магнитном поле, если направление поля вне-
внезапно поменять на противоположное. Будем предполагать вы-
выполненными условия LS-связи и считать поле достаточно силь-
сильным для того, чтобы полностью отделить полный момент L от
полного спина S (эффект Пашена — Бака). Для простоты будем
считать, что магнитное, поле все время параллельно оси г и ме-
меняется от значения —5#0 до Жй по линейному закону
Ж (/) = Жй [2s - 1] = Жй [2 (t - to)/T - 1]. F2)
Согласно результатам главы XVI (§§ 9—12) гамильтониан
системы имеет вид
Я = Я<°> + A (LS) ---iL. (?a + 2SZ) Ж @, F3)
где Я<0) — невозмущенный гамильтониан в случае LS-связи. По-
Поскольку согласно F2) среднее по времени от магнитного поля
равно нулю, то среднее по времени от Я равно гамильтониану
атома в отсутствие внешнего поля
') Условие <5< 1 не требует, чтобы обязательно U(tx to)\O) « |0>, оно
требует только, чтобы эти векторы отличались лишь фазовым множителем.
Однако формула F0) предполагает быструю сходимость разложения E8), и
неравенство F1) является, вообще говоря, достаточным условием для такой
сходимости.

236 ГЛ. XVII. НЕСТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
Предположим теперь, что первоначально система находи-
лась в собственном для Я состоянии. Поскольку в этот момент
выполняются условия, при которых имеет место эффект Па-
шена — Бака, то вектор состояния почти равен одному из век-
торов \aLSMLMs}, определенных в § XVI. 11. Будем считать,
что |0> = \aLSMLMs}. Вычисление средне-квадратичного от-
отклонения ДЯ не представляет серьезных трудностей; так как
IolLSMlMs} есть собственный вектор Я@> + ALZSZ, то един-
единственный вклад дает только член 1/2A(L+S- -f- LS+). Проведя
вычисления, получаем
АЯ = 4 М*l2(L(L+l)-Ml)(S(S+l)-M2S) -
В скобках стоит числовой множитель порядка 1 (он равен нулю
в двух предельных случаях, Ml = ± L, Ms —±S). Следова-
Следовательно, отклонение АЯ равно по порядку величины Ah2, т. е. по-
порядку величины расщепления Z-5-уровней за счет спин-орби-
спин-орбитальной связи.
Как следствие, если
±
F4)
то выполняется условие быстрого перехода F1): вектор состоя-
состояния остается практически тем же при изменении направления
поля. Для того чтобы динамическое состояние атома оставалось
тем же, достаточно, чтобы изменение вектора состояния своди-
сводилось только к домножению на фазовый множитель. Таким об-
образом, неравенство F4) является достаточным, но не необхо-
необходимым условием неизменности состояния при обращении поля.
Мы вернемся к этому вопросу в конце § 14.
§ 10. Адиабатический переход. Общие положения.
Тривиальный случай
В оставшейся части этого раздела исследуется другой край-
крайний случай — очень медленное изменение гамильтониана. Мы
будем использовать обозначения § 7.
Прежде всего, сформулируем адиабатическую теорему. В ней
речь идет о свойствах состояний дискретного спектра гамильто-
гамильтониана H(s). Будем для простоты предполагать спектр Н ди-
дискретным, хотя это и несущественно 1).
Пусть ei, 62, ..., е/, ... — собственные значения Я, а проек-
проекторы на соответствующие им подпространства обозначим
•) Достаточно, чтобы дискретные собственные значения и отвечающие им
подпространства удовлетворяли сформулированным ниже условиям непрерыв-
непрерывности, дифференцируемости и «ие пересечения». См. Т. Kato. Ioc. cit.

§ ТО. АДИАБАТИЧЕСКИЙ ПЕРЕХОД 237
Ри Р2, .... Pj, ... . Все эти величины предполагаются непре-
непрерывными функциями s. Дополнительно будем считать, что:
(i) собственные значения отличаются друг от друга в тече-
течение всего перехода 0 ^ s ^ 1
Ej (s) ф гк (s), каковы бы ни были / и k; F5)
(ii) производные dPjIds, cPPjIds2 определены и кусочно-не-
кусочно-непрерывны на всем интервале.
Оператор эволюции UT(s) удовлетворяет уравнению Шре-
дингера
Ш~ UT (s) = TH (s) UT (s), F6)
а гамильтониан H(s) определяется выражением
Я (s)=S el(s)Pi(s). F7)
Адиабатическая теорема утверждает, что Ut(s) обладает асимп-
асимптотическим свойством ')
lim UT (s) Р, @) = Р, (s) lim UT (s) (/=1,2,...). F8)
Г-»оо Г-»оо
Предположим сначала, что подпространства, отвечающие
каждому собственному значению H(s), не меняются
P,(s)=*P,@)eaP, (/=1,2, ...)•
В этом случае гамильтониан H(s) имеет простой вид
и при любом s коммутирует с каждым из проекторов Pj. Сле-
Следовательно, каждый проектор есть интеграл движения
= Pr F9)
Соотношение F9) верно для любых Т и a fortiori для 7"->-оо.
') Это свойство эквивалентно приведенному в § 7. Действительно, если
|/) —собственный вектор Я@), отвечающий собственному значению е/@),
то Я/@)|/> = |/), н свойство F8) дает
lim UT(s)\j) = P,(s) lim UT(s)\j),
т. е. вектор Ut(s)\j) при Г->-оо стремится к вектору из подпространства, со-
соответствующего e/(s)

238 ГЛ. XVII. НЕСТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
Кроме этого, в данном частном случае уравнение F6) явно
интегрируется и дает
s
UT (8) = ехр (-/ Т J Я (a) da/h) =
о
Г ' " G0)
где нами использовано обозначение
s
Ф/ (s) = J ey (a) da. G1)
о
Итак, если в момент времени t0 вектор состояния системы был
собственным вектором для Но, отвечающим собственному зна-
значению е/@), то в момент времени ^ вектор состояния будет от-
личаться от собственного только фазовым множителем
§ 11. «Представление вращающихся осей»
Точно проинтегрировать уравнение Шредингера в общем
случае не удается, так как собственные векторы гамильтониана
Н(s) вращаются некоторым образом в гильбертовом простран-
пространстве. При рассмотрении общего случая первый этап заклю-
заключается в устранении, насколько это возможно, такого вращения
подходящим изменением «представления».
Введем для этого унитарный оператор A(s), обладающий
свойством
Р, (8) = A (s) P, @) Л* (s) (/=1,2....). G2)
Унитарное преобразование A(s) переводит любой базис из соб-
собственных векторов оператора Я@) в базис из собственных век-
векторов H(s), причем соответствующие векторы связаны друг
с другом непрерывным образом.
Преобразование A(s) однозначно определяется начальным
условием
Л@)=-1 G3)
и дифференциальным уравнением
G4)
где K(s) —подходящий эрмитов оператор. Для того чтобы вы-
выполнялись условия G2), необходимо и достаточно, чтобы one-

§ 11. «ПРЕДСТАВЛЕНИЕ ВРАЩАЮЩИХСЯ ОСЕИэ 239
ратор K(s) удовлетворял коммутационным соотношениям
[К {s), P, (s)] = ih dP,/ds (/=1,2... .)• G5)
Необходимость немедленно следует после дифференцировав
ния обеих частей G2) по s. Соотношения G5) достаточны, так
как если A(s) и P/(s) удовлетворяют уравнениям G4) и G5),
то выражение
A4s)P,(s)A(s)
не зависит от s (производная по s равна нулю) и равно своему
начальному значению Р/@).
Соотношения G5) не определяют K(s) однозначно, в част-
ности, можно добавить к K{s) оператор ZjPk(s)fk(s)Pk(s), где
fk{s)—произвольные операторы, зависящие от s. Другими сло-
словами, можно произвольно задавать проекции Pj(s)K(s)P,(s)
(j = 1, 2, ...). По причинам, которые станут понятны ниже, мы
устраняем произвол, накладывая дополнительные условия
Р, (s) К (s) P, (s) = 0 (/=1,2....). G6)
Это дает (задача 5)
Унитарное преобразование A^(s) переводит векторы и опе-
операторы шредингеровского «представления» в новое «представле-
«представление»— «представление вращающихся осей». Наблюдаемая H(s)
преобразуется в
и, используя равенства F7) и G2), имеем
Я(Л)E) = Е *!(s)Pi@). G7)
Точно так же K(s) преобразуется в
K(A)(s) = A*(s)K(s)A(s). G8)
Оператор эволюции в новом «представлении» равен
U(A)(s)^A*(s)UT(s). G9)
Он определяется (см. § 1, ур. A2), где следует взять V —
= ТН — К) уравнением и начальным условием
ih dU(A)/ds = \TH{A) (s) - К{Л) (s)] U(A) (s), (80)
{/(Л)@)=1. (81)

240 ГЛ. XVII. НЕСТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
§ 12. Доказательство адиабатической теоремы
Уравнение (80) легко бы интегрировалось, если бы можно
было пренебречь членом /С(Л) по сравнению с 7"#<л>. Тогда мы
имели бы тривиальный случай, рассмотренный в § 10. Обозна-
Обозначим <Dr(s) решение соответствующего уравнения Шредингера
/ft d(bT/ds = THiA) (s) Фт (s), (82)
Фг@)=1. (83)
Имеем (ур. G0))
Фг(*)=?е-'Тф'(8)/*/>/@)> (84)
где ф,- определены равенством G1).
Используя определения G7) и G8), мы видим, что #<A)(s)
и KiA)(s) не зависят от Т. Следовательно, можно ожидать, что
в пределе 7"->оо влияние /С(Л) в правой части уравнения (80)
будет полностью подавлено членом ТН^\ и оператор Uw(s)
будет стремиться к Фг($). Как мы увидим, это действительно
имеет место, и (см. ур. G9))
UT(s) ~ A(s)G)T(s). (85)
Для доказательства этого утверждения введем новое уни-
унитарное преобразование
?(Л) ?+/г (86)
Уравнение, которому удовлетворяет этот оператор, следует из
уравнений (80) и (82). В интегральной форме оно имеет вид
S
W(s)=l+-jr\~K(e)W(o)do, (87)
о
где _
K(s)^O>Us)K(A)(s)<J)t(s)= (88)
= Ф$А*КАФГ (89)
Мы собираемся показать, что ядро K(s) есть сумма осцил-
осциллирующих функций, частоты которых неограниченно растут
с ростом Т и, как следствие, интеграл в правой части уравнения
Вольтерра (87) стремится к нулю при 7"->оо.
Любой оператор Q допускает разложение ')
I2
') Выбранный нами метод состоит в том, что используется представление,
в котором оператор #@) диагоналей, и в то же время устраняются различные
трудности, связанные с вырождением собственных значений #@) и произво-
произволом в выборе фаз векторов базиса.

§42. ДОКАЗАТЕЛЬСТВО АДИАБАТИЧЕСКОЙ ТЕОРЕМЫ 241
В дальнейшем мы используем обозначение
Используя уравнения G2), (84) и (89), получаем
К$ = Л+ (s) Р, (s) К (s) Pk (s) A (s). (90)
В силу условия G6) все Kff (/=1,2, ...) исчезают и, следо-
следовательно, все диагональные части Кц разложения К равны
нулю
Ки = 0 (/=1,2, ...)• (91)
Недиагональные части К,к (/ Ф k) содержат осциллирующий
множитель
Частота осцилляции получается дифференцированием фазы экс*
поненты по s, что дает
T\e](s)-ek(s)\/h.
Согласно предположению F5) разность е/ — tk никогда в нуль
не обращается, и, следовательно, частота растет, как Т, при
Рассмотрим оператор
S
F(s) = J/C(or)d<r. (92)
о
Все его диагональные элементы в силу (91) равны нулю
Недиагональные элементы имеют вид
rf<r (/ ^ А). (93)
Операторы К$непрерывно зависят от s и не зависят от Т. По-
Показатель же экспоненты зависит от Т, и, следовательно, F/k
s
имеет вид \ elTa w f (a) da, где f(a)—непрерывная функция,
о
а а (от)—непрерывная монотонная функция. Как известно, та-

242 ГЛ. XVII. НЕСТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
кой интеграл стремится к нулю при Т-*~оо. Действительно, ин-
интегрируя по частям, имеем
± Ге"-(ф/-Ф*)/*_^!_ f_ [ е'Г(Ф/-Ф*)/А \j_ (_лш_) | da
}
(94)
Ясно, что выражение в скобках остается конечным, если /С$' и
производные по s от /С/а'» е/ и е* остаются конечными. Следо-
вательно, F/k стремится к нулю, как 1/7, т. е. при Г-»-оо
После интегрирования по частям интеграл в правой части
уравнения (87) можно переписать в виде
\
о
или, используя уравнение dW/do = iRW/%,
s
F(s)W(s)-ih-l^F{a)KW{a)da. (95)
о
Оба члена в (95) содержат множителем F(s) и, следовательно,
при Г-»- с» стремятся к нулю, как 1/Г, а значит '),
(96)
Подставляя (96) в формулу (86)—определение W, получаем
UT (s) - A (s) Фт (s) [l + O (-f)]. (97)
') Строго говоря, приведенные рассуждения справедливы только, если
оператор K(s) ограничен на всем интервале @,1) (см. примечание на
стр. 207). Тогда можно показать, что \\F (s)|| стремится к нулю, как 1/Г, рав-
равВ |I^C()ll н l|f|| б
р ) , ()|| р у, /, р
номерно по s. Верхние оценки дли |I^C(s)ll н l|f(s)|| обозначим у. и е соот-
соответственно. Поскольку операторы W, Ф и А унитарны, то нормы операторов
К, Kw, К и KW равны. Точно так же равны нормы F и FW. Следовательно,
IIFW || < е, У J Fjw da || < exs.
о
Используя для W — 1 формулу (95), получаем

5 13. АДИАБАТИЧЕСКОЕ ПРИБЛИЖЕНИЕ 243
Поскольку '(Dr(s) коммутирует с проекторами Р/@) (см.
ур. (84)), а унитарный оператор A(s) обладает свойством G2),
имеем
A (s) Фт (s) Р, @) = Р, (s) A (s) Фт (s).
Отсюда и из асимптотики (97) следуют соотношения F8). Ш
§ 13. Адиабатическое приближение
Если Т достаточно велико или, точнее, если образующие ба-
базис собственные векторы оператора H(t) вращаются достаточ-
достаточно медленно, то в первом приближении С/у A) можно заменить
его асимптотикой
U (/„ t0) я- UT A) « А A)ФГ A). (98)
Это и есть адиабатическое приближение.
Пусть |0> — нормированный вектор, представляющий со-
состояние системы в момент времени /0, a Qo — проектор на до-
дополнительное подпространство. Адиабатическое приближение
состоит в следующей замене:
Величина погрешности при таком приближении дается вероят-
вероятностью t| найти систему в момент времени U в состоянии, отлич-
отличном от АA)ФГA) |0>. Поскольку проектор на пространство, ор-
ортогональное этому вектору, равен
получаем
Поправки к адиабатическому приближению можно вычис-
вычислить методом теории возмущений из § 1. Оператор ЛA)ФГA)
играет роль ?/@>, a W(l) —роль U/. Метод заключается в со-
сохранении только начальных членов разложения W, которое по-
получается итерированием уравнения (87). Если ограничиться
только первым порядком, то получим
W (I) ж I + (tF/h), (99)
где F — оператор F(l), определенный равенством (92).
Это разложение можно использовать также и для вычисле-
вычисления t|. Аналогично вычислению S в случае мгновенного прибли-
приближения, имеем
П « ft @ \FQ0F 10> = (A F/hf, A00)

244 ГЛ XVII. НЕСТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
где AF — средне-квадратичное отклонение наблюдаемой F в со-
состоянии |0>. Условие применимости адиабатического прибли-
приближения ') г\ <С 1 дает
В приведенной здесь общей форме этот результат не так удо*
бен для использования, как соответствующий результат в слу-
случае мгновенного приближения (соотношение F1)). Фигурирую-
Фигурирующую здесь наблюдаемую F построить гораздо труднее, чем на-
наблюдаемую Я из предыдущего случая. В то время как Я полу-
получается просто интегрированием H(t), для вычисления F необ-
необходимо решить задачу на собственные значения #(/) для каж-
каждой точки из интервала (tQ, t\) и для каждой точки построить
оператор A (s).
Проверим условия применимости адиабатического прибли-
приближения в случае, когда система первоначально находилась в соб-
собственном для Я@) состоянии. В действительности, только этот
случай и представляет практический интерес.
В дальнейшем будем использовать непосредственно перемен-
переменную t, не переходя к s. Обозначим e/(f) собственные значения
гамильтониана в момент времени t, соответствующие проек-
проекторы— Pj{t), оператор «перехода к повернутым осям» — A(t) и
Ф(/)—оператор <br(s). Тогда определения F7) и (84) изме-
изменяются
Я@=1е,@М0, A01)
ф @ = ?ехр| _, J е/ (т) dx/fA P] (o). A02)
Определяющие А(() уравнения G3) и G4) примут вид
ih dA/dt = К' (t) А @, А @) = 1, A03)
где
К! (/) в К (s)/T = ih Z (dPjtdi) P, ((). A04)
Согласно определению (92) находим
и
F « F (/,) = J Ф+ @ Л+ @ К' (t) A @ Ф (() dt. A05)
и
Дополнительно, для простоты, предположим, что спектр
H(t) простой (не вырожден). Выберем множество базисных век-
') Здесь можно сделать те же замечания, что и в сноске к § XVII, 8, а
связи с критерием применимости мгновенного приближения,

§ 13. АДИАБАТИЧЕСКОЕ ПРИБЛИЖЕНИЕ 245
торов 11>0, |2>о, ..., |/>о, ••• гамильтониана #е и обозначим
|1>г, |2>( |/>f, ... множество базисных векторов H(t), ко-
которые получаются из предыдущих действием оператора A(t).
Для любого t
1/>* = 4@1/>о |
A=1,2,...). A06)
Пусть |/>0 — вектор состояния системы в момент /0. В адиа-
адиабатическом приближении ее вектор состояния в момент t\ с точ-
точностью до фазового множителя будет равен |/>i = A (U) |/>0:
U (tlt to) I0o« exp I - i \ e, (x) dx/h\ \ i>,. A07)
Вероятность /?;_>/ (/ Ф i) найти систему в другом собственном
состоянии оператора H(t\), по определению, равна
Вычисление по теории возмущений дает
(Ю8)
В согласии с формулой A00) имеем
Используя уравнения A02), A04), A05) и свойства A06)
вектора |/>г, находим
и г t
Ш \ ^н @ exp i \
Юо = Ш \ ^н @ exp i \ а>,{ (т) dx dt,
где
= t(j\(d\i)t/dt), A09)
в>Л = [в/@-в,@]/А. (ПО)
Отсюда и из формулы A08) следует
I
I г J ю/г (г) dx I
«у, @ ехр I г J ю/г (г) dx I d/
A11)
Физическая интерпретация величин ац и со;-г следует непо-
непосредственно из определений A09) и (ПО): ю/,@—«частота

246 ГЛ. XVII. НЕСТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
Бора» перехода i-*-j, an(t) характеризует скорость вращения
собственных векторов H(t), она равна компоненте вдоль |/>(
скорости вращения оси | *>*-
Подынтегральное выражение в правой части A11) равно
произведению функции а/* @ на осциллирующую с частотой
<i>ii(t) экспоненту. Если ац и <йц не зависят от времени, то по-
получаем
I 9,
2A —cos ©„Г).
Следовательно, величина р^/ имеет порядок |а/*/©/г[2. Если
же зависимость от времени ац и ©/* достаточно гладкая, то /?,->/
не превосходит по порядку величины максимального значения
отношения |а/г/©/{|2 иа интервале (to, М
^lf. (П2)
Точно так же r\i по порядку величины не больше значения,
получающегося суммированием правой части неравенства A12)
по всем /, отличным от L Обычно эта сумма не превосходит от-
отношения |а™а7©Г'п|2, где ©Г'° — наименьшее значение боров-
ской частоты перехода из состояния i в ближайшее по энергии
состояние, а™ах — максимальное значение положительной вели-
величины а*@, определяемой равенством
Возвращаясь к определению а/г A09) и замечая '), что
0, A13)
видим, что а; есть длина вектора d\Ot/dt, т. е. «угловая ско-
скорость» вектора | *>*. Следовательно, в большинстве случаев ус-
') Из соотношений A04) я A06) имеем
d d dP,
\f> A(t)\f)f
(/=1.2,...).
Сравнивая этот результат с тем, который получается при диффереицироваиии
тождества P,(t) |/>« = |/>,, получаем Pi \-jf\ /><) =°- Следовательно,
0 G=1.2,...). A13')
Условие того, что векторы \f) t являются собственными для оператора НA),
определяет их с точностью до фазового множителя. Условие A13') фиксирует
этот фазовый множитель.

§ 14. АДИАБАТИЧЕСКОЕ ОБРАЩЕНИЕ МАГНИТНОГО ПОЛЯ 247
ловие г\ -С 1 выполнено, если
максимальная угловая скорость | C)t
э™|п минимальная боровская частота для \i)t
«1.
Условие A14) можно рассматривать как критерий примени*
мости адиабатического приближения. В действительности оно
слишком ограничительно, хотя имеет то преимущество, что
с ним довольно просто обращаться. Следует отметить, в част-
частности, что для вычисления а,@ или |ау;(?)|> которые фигури-
руют в правой части A12), нет необходимости знать A(t), до-
достаточно только решить задачу на собственные значения H(t)
и определить с точностью до фазового множителя векторы \i}t,
('j)t\ кроме того, можно показать, что
«л @ = — *</1-^-1 О*/*»/* (О
(см. задачу 6).
§ 14. Адиабатическое обращение магнитного поля
Вернемся к задаче § 9 и будем использовать те же обозна-
обозначения. Начальные условия возьмем те же самые, но неравен-
неравенство F4) больше не выполняется.
Поскольку гамильтониан системы определяется выраже-
выражением F3), мы видим, что a, L, S и Mj н= ML + Ms — хорошие
квантовые числа (H(t) коммутирует с /г н= Lz + 5г для лю-
любых /). Следовательно, если \aLSMLMsy — начальный вектор
состояния, то с течением времени он будет меняться, оставаясь
в пространстве векторов, имеющих те же значения a, L, S и
ML + Ms.
Рассмотрим подробно случай, когда начальное состояние
есть 2Р. Имеется всего 6 различных состояний 2Р — это линей-
линейные комбинацииб-ти базисных векторов а 1 -g- MLMS\ (ML= I,
О, — 1; Ms = -?-, —g-J, которые мы будем обозначать \MLMs).
Поскольку все они являются собственными векторами
Я@), соответствующее собственное значение можно взять за ну-
нулевой уровень энергии. Легко определить отвечающие ему
уровни энергии Я (задача XVI. 7), которые являются функ-
функциями параметра р = цвЗ@1АН2 (цв = еН/2тс — магнетон Бора)
и изображены на рис. 12. Каждый уровень отвечает вполне оп-
определенному значению Мj = ML •+• Ms, а соответствующий соб-
собственный вектор, как показано на рисунке, стремится к неко-
некоторому вектору \MLMsy в каждом из пределов р-»-±оо. Мы
рассмотрим последовательно случаи Mj = 3/2 и Mi = '/г-

248
ГЛ. XVU. НЕСТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
Рассмотрим вначале случай Mi = 3/г- Существует только
одно состояние с таким значением 1г, и отвечающий ему вектор
есть |1'/2>. Это собственный вектор Н для любого t, и простое
вычисление дает
Если начальное состояние атома есть 11 '/2>, то мы имеем опи-
описанный в § 10 случай, когда уравнение Шредингера тривиально
Рис. 12. Положение уровней 2Р как функции напряженности магнитного
поля Ж (р = AВ5^/Лй2). Числа в скобках у каждой кривой — квантовые
числа (M^MS) собственных состояний в двух предельных случаях: р -> ± то.
интегрируется. Атом все время остается в этом состоянии,
а вектор состояния приобретает только фазовый множитель
[t
—
В случае линейного изменения магнитного поля (формула F2))
вектор состояния в момент времени Т равен
ехр(-МАГ)|17а>,
что верно для любого Т. В частности, в пределе, когда АНТ -С 1,
мы получаем результат мгновенного приближения, т. е. вектор
Рассмотрим теперь случай ЛЬ = 1/2, когда значению h от-
отвечает два собственных вектора Н — линейные комбинации век-

§ 14. АДИАБАТИЧЕСКОЕ ОБРАЩЕНИЕ МАГНИТНОГО ПОЛЯ 249
торов |0'/2> и |1—:/2>- Для решения задачи на собственные
значения H(t) в подпространстве, натянутом на эти два век-
вектора, выберем их в качестве базисных векторов, и тогда Н (t)
будет представлен матрицей
Если ввести матрицы Паули о = {ох, ау, аг), то эту матрицу
можно записать в особенно удобном виде
^ A15)
где вектор Ъ имеет следующие компоненты:
Ьх = 2 лД, Ьу = 0, bz=\— 2р.
Введем также единичный вектор и в направлении Ь:
-2рJ,
Заметим, что вектор Ь и векторный оператор а принадлежат
трехмерному векторному пространству, которое, однако, не
имеет ничего общего с обычным пространством. Мы использо-
использовали простой математический прием, позволивший нам вывести
некоторые свойства посредством геометрических соображений,
которые справедливы в обычном пространстве.
Из A15) и A16) получаем
H{t) = -j-Ah*[{-l-2Q) + b(ou)], A17)
т. е. H(t) есть функция оператора (аи). Задача на собственные
значения теперь легко решается, они равны— Ah2 (— 1 — 2р±6),
а проекторы Р± = -^-A ±аи).
Обозначим соответствующие собственные векторы |-f-> и
|—>. Они определены с точностью до фазы, которую можно
фиксировать первым из условий A06), но поскольку эта фаза
в дальнейшем несущественна, мы не будем на этом останавли-
останавливаться. Легко проследить за непрерывной эволюцией этих уров-
уровней и соответствующих им проекторов как функций параметра
p(t) (рис. 13). Когда р меняется от — оо до + °°> собственный
вектор |+> меняется (исключая фазовый множитель) от |0'/2>
до 11 — 'Д), а соответствующий уровень движется вдоль

250
ГЛ. XVII. НЕСТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
ней ветви гиперболы на рис. 13; в то же время собственный
вектор |—> меняется от |1 —'/2> До ] 01/г>, а соответствующий
уровень движется вдоль нижней ветви гиперболы.
Предположим, например, что начальное состояние системы
есть 10 х/2>- Если изменение направления поля происходит до-
достаточно медленно, то вектором состояния системы всегда бу-
будет вектор |+> (с точностью до фазового множителя), и, после
того как поле изменит свое направление на противоположное,
Рис. 13. Изменение двух уровней *Р, Mj= 1/2, при обращении магнитного
поля (обозначения те же, что и на рис. 3). Сплошная кривая соответствует
' адиабатическому обращению, пунктирная — мгновенному.
система будет находиться в состоянии 11 —'/2>. Используя ре-
результаты предыдущего параграфа, можно определить критерий
адиабатичности этого перехода. Используя те же обозначения,
находим (соотношение A12))
+ -* -
а (О
A18)
где a>(t) — боровская частота перехода + -»—.
со @ = ± Ahb = ± Ah У8 + A-2рJ
и a(t) —проекция скорости |+> на |—>. Отсюда следует, что
I о@ | = | (- \{dPJdt) |+) | = 4" К- \(odu/dt) | +) |.
Так как вектор du/dt перпендикулярен и, а |+> и |—> —соб-
—собственные векторы оператора (аи), то '
л/8~ _ф
8+A-2рJ d/

ЗАДАЧИ И УПРАЖНЕНИЯ 251
При изменении поля по линейному закону F2) максимум
]а/(о| достигается при р = + Х1г, т. е.
а_ _ 1 цв3®о 1
тах ю ~~ 2 АЬг AhT •
В этом случае условие A18) выполнено, если
Г шш Ш- Т » A/М), A19)
где V — время, необходимое для изменения магнитной энергии
связи \1в2@ от —2АН2 до 2АН2. Именно в течение этого периода
вектор |+> вращается от |0У2> к |1 — '/г). Условие A19) по-
показывает, что этот период должен быть велик по сравнению
с ЦАН— периодом, характеризующим переход -\—*¦—.
Интересно сравнить условие адиабатического перехода и ус-
условие быстрого перехода F4). Последнее, в действительности,
является излишне ограничительным. Это необходимое условие
для того, чтобы вектор состояния практически не менялся за
все время Т обращения поля. Однако за исключением опреде-
определенного выше интервала Т', собственные векторы гамильто-
гамильтониана остаются практически фиксированными в течение этого
времени, а вектор состояния системы просто умножается на
фазовый множитель. Для того чтобы динамическое состояние
системы осталось неизменным, т. е. чтобы вектор состояния за
время обращения поля изменился разве лишь на фазовый мно-
множитель, достаточно, чтобы условие быстрого перехода выполня-
выполнялось только в интервале времени Т', в течение которого проис-
происходит вращение собственных векторов Я, т. е.
Г < I/Ah. A20)
(см. задачу 8).
ЗАДАЧИ И УПРАЖНЕНИЯ
1. Пусть щ и иг — два ортогональных собственных состояния, отвечающих
двукратно вырожденному уровню гамильтониана Но системы. Введение по-
постоянного возмущения V устраняет вырождение и расщепляет уровень на два
с расстоянием е между ними. Предположим, что система первоначально нахо-
находится в состоянии щ, а возмущение V действует в интервале времени Т. Пусть-
Wi_>2 — вероятность иайти систему в состоянии Ыг, после того как возмущение
перестает действовать. Показать, что №i-*2 периодически зависит от Т с ча-
частотой е/Л и что в пределе, когда гТ ¦< Л, получается результат первого по-
порядка теории возмущений. Что необходимо для того, чтобы Wi-*2 исчезало,,
каково бы нн было Т?
2. Атом водорода находится в электрическом поле & = &ч cos со/, осцил-
осциллирующем с частотой со, которая больше частоты ионизации атома me*/2hK

252 ГЛ. XVII. НЕСТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА
Если первоначально атом находится в основном состоянии, то какова вероят-
вероятность в единицу времени перехода в ионизованное состояние (в предположе-
предположении, что можно использовать плоские волны для описания ионизированных
состояний)? Какого угловое распределение электронов, излучаемых в этом
процессе возбуждения атома? [N. В. Данный процесс является фотоэлектри-
фотоэлектрическим эффектом, для которого тем самым получено полуклассическое описа-
описание, при котором электрическое поле не квантуется... Результаты совпадают
¦с теми, которые получаются при корректном подходе с квантованным электро-
электромагнитным полем (см. задачу XXI. 12).]
3. При р-распаде атомное ядро испускает электрон со скоростью, которая
обычно близка к с, и заряд ядра меняется от Ze до (Z-\-l)e. Показать, что
влияние такого перехода на другие электроны можно рассматривать в мгно-
мгновенном приближении. Оправдать применение метода в случае перехода три-
тритона Н3 (з= 1 протон + 2 нейтрона) в Не* (= 1 нейтрон + 2 протона), где
средняя кинетическая энергия испущенного электрона только 16 кэв (тс2 =
= 500 кэв). Первоначально тритон находится в основном состоянии. Какова
вероятность найти после распада ион Не+ в ls-состоянин? В 25-состоянии,
в состоянии с / ф 0?
4. Пусть H(t)—гамильтониан неконсервативной системы. Предположим,
что существует не зависящий от времени вектор \и), удовлетворяющий урав-
уравнению H(t) \и) = е@ |«). Показать, что вектор
(-1 J е (т) rfr/fi J | ы>
exp|
удовлетворяет уравнению Шредингера для этой системы.
5. Пусть Р\, Я2, ..., Я/, ... — полный набор ортогональных проекторов.
Предположим, что каждый из них есть непрерывная и дифференцируемая
функция параметра s и что при изменении s сохраняются соотношения орто-
ортогональности и полноты
Показать, что оператор
К (s) - Л ? (dPj/ds) Р, = - ih 2 Р, (dP}/ds)
/ /
эрмитов и удовлетворяет коммутационным соотношениям G5). Показать, что
справедливы тождества
P,KPi = 0 (/=1, 2,...)
P,KPk = ihP, (dPklds) Pk = - ihP, (dP,/ds) Pk.
6. Пусть операторы P/(s) (/= 1, 2, ...) те же, что и в предыдущей за-
задаче. Показать, что производная от оператора
где E/(s) —дифференцируемая фуикция s, удовлетворяет уравнению
Pt (dHlds) Pk = (efc - 6/) Pj (dPk/ds) Pk + 6/ft (dBklds) Pk.

ЗАДАЧИ И УПРАЖНЕНИЯ 253
Вывести отсюда, что «угловая скорость» <*//(<), определяемая уравнением
A09), выражается также соотношением
hmn (t) dt
7. Однородное магнитное поле X заданной величины вращается с по-
постоянной угловой скоростью а вокруг оси, составляющей угол 9 с направле-
направлением магнитного поля В поле помещена бесконечно тяжелая частица со спи-
спином /. Положим h = 1, обозначим u(t) единичный вектор, параллельный маг-
магнитному полю, а у = \)Ж, где Ц — гиромагнитное отношение частицы. Тогда
движение спина / определяется гамильтонианом H(t) = —уAи). Пусть t = 0
есть начальный момент времени, /0—компонента / вдоль и@), /г — компо-
компонента по оси вращения поля.
Построить унитарный оператор «вращающихся осей», показать, что опера-
оператор эволюции в шредингеровском представлении дается формулой
U @ = ехр (- Ы2t) exp [i (yf0 + а/г) /].
Показать справедливость адиабатической теоремы для этого примера; устано-
установить непосредственным вычислением и методом § 13 критерий применимости
адиабатического приближения (asin9/vJ<C 1.
8. Для определенной в § 14 системы рассмотрим уравнение Шредингера
при М] = -^-. Пусть I I — компоненты решения в определенном там пред-
представлении. Возьмем ta = — Т н обозначим
B
Показать, что
и = у ехр (- ml2), v = / (dy/d%) exp (- /х|2),
где у как функция переменной | = AMlyi удовлетворяет уравнению
У
" \- / (V2 + 4х|) у' + у = 0.
Если ввести х = % + (V^V^x). то общее решение этого уравнения можно за-
записать в виде
Пусть начальное состояние есть |0-<>)- Показать, используя асимптотику ги-
гипергеометрических функций, что вероятность й того, что система останется в
том же состоянии в конце времени Т, дается формулой (справедливой, если
Т XT'/Ah)'1')
- ( 1 — V\2 х. я
V. 1 + у / 4х
Показать, что условия A19) и A20) действительно отвечают адиабатическому
и быстрому переходам соответствеино.

ГЛАВА XVIII
ВАРИАЦИОННЫЙ МЕТОД И СВЯЗАННЫЕ С НИМ
ЗАДАЧИ
§ 1. Вариационный метод Ритца
Кроме метода ВК.Б, который имеет очень узкую область
применения, существуют два основных метода приближенного
определения уровней энергии и волновых функций дискретного
спектра: теория возмущений (глава XVI) и вариационный ме-
метод. Настоящая глава посвящена второму из этих методов.
Вариационный метод является универсальным и может быть
использован во всех тех случаях, когда уравнения представимы
в вариационной форме. Основа метода состоит в следующем.
Искомые решения принадлежат некоторому функциональному
пространству #"; произвольную функцию из этого пространства
обозначим ЧЛ Предположим, что решения исследуемого урав-
уравнения есть функции из #", для которых стационарен некоторый
функционал Q[4T]. Тогда уравнение эквивалентно вариацион-
вариационному уравнению
6Q = 0. A)
Вариационный метод Ритца состоит в поиске решений уравне-
уравнения A) среди функций из пространства &"', которое уже, чем
пространство &~.
Предположим, например, что &" — множество всех волновых
функций системы. Выберем ряд конкретных волновых функций
ф(а, Ь, с), параметризованных некоторым числом непрерывных
индексов а, Ь, ... . Множество этих функций &"' представляет
собой только часть #". Величина Q, рассматриваемая как функ-
функционал от Ф, сводится к обычной функции от вариационных па-
параметров а, Ъ, ..., т. е.
q(a,b, ...)^Q[O(a, b, ...)].
Каждый набор значений ао, Ьо, ..., для которого эта функ-
функция стационарна, определяет приближенное решение Фо =
==Ф(а0, Ьо, Со, ...) уравнения A).
Успех метода существенно зависит от выбора пространства
пробных функций У. Пробная функция должна быть доста-
достаточно проста для проведения вычислений и в то же время

§ 2. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ 255
должна меняться в достаточно большой или достаточно подхо-
подходящей области, чтобы полученное решение было близко к точ-
точному.
На практике стационарные значения Q имеют вполне опре-
определенный физический смысл. Одно из основных достоинств ва-
вариационного метода заключается в непосредственной и точной
оценке этих значений. Ясно, что разность между Q[<Do] и Q^o]
тем меньше, чем ближе приближенное решение Фо к точному
Wo; более того, поскольку величина Ql^V] стационарна в точке
W = Ч'о, эта разность является бесконечно малой величиной бо-
более высокого порядка, чем разность между Фо и Wo. Таким об-
образом, вариационный метод особенно удобен для вычисления
таких величин, которые можно представить в виде стационар-
стационарных значений функционалов. Именно так обстоит дело в случае
уровней энергии связанных состояний. В главе XIX мы увидим
также, что метод может быть использован для вычисления ам-
амплитуд рассеяния.
Вычисление уровней дискретного спектра вариационным ме-
методом приведено в разделе I этой главы. В остальных двух раз-
разделах мы рассматриваем две важные задачи, используя методы,
более или менее связанные с вариационным методом: опреде-
определение волновых функций сложных атомов в приближении само-
самосогласованного поля методами Хартри и Фока — Дирака (раз-
(раздел II) и адиабатическое приближение Борна — Оппенгеймера
для молекул (раздел III).
Р а з д е л I. ВАРИАЦИОННЫЙ МЕТОД
ДЛЯ СВЯЗАННЫХ СОСТОЯНИЙ
§ 2. Вариационная форма задачи
на собственные значения
Для определения связанных состояний вариационным мето-
методом используется функционал — среднее значение энергии.
Справедлива следующая теорема 1):
Теорема. Пусть Н — гамильтониан квантовой системы и
Е \Ч] — среднее значение энергии системы
Любой собственный вектор, для которого среднее значение
энергии B) стационарно, есть собственный вектор дискретного
•) Это общий результат, относящийся к дискретному спектру эрмитовых
операторов в гильбертовом пространстве. При доказательстве используется
только эрмитовость оператора Н.

256 ГЛ. XVIII. ВАРИАЦИОННЫЙ МЕТОД И СВЯЗАННЫЕ С НИМ ЗАДАЧИ
спектра оператора Н, верно и обратное. Соответствующее соб-
собственное значение равно стационарному значению функционала
Е[Щ.
Следует отметить, что речь здесь идет о векторах с конечной
нормой: функциональное пространство 9" (определенное в § 1)
есть гильбертово пространство динамических состояний си-
системы. Следовательно, теорема утверждает, что собственные
функции Я, принадлежащие гильбертову пространству, яв-
являются решениями вариационного уравнения
6? = 0. C)
Заметим также, что функционал E[W] не зависит от нормы
и фазы вектора {^У}, а значит, теорема останется справедливой,
если на эти величины наложить любое дополнительное условие.
В частности, иногда удобно ограничить область изменения 1^)
векторами с единичной нормой, как это сделано в ряде приме-
примеров этой главы.
Доказательство теоремы. Вычислим вариацию
Я
= FW\ (Я - Е) | Ч>> + 0F| (Я -
Так как величина (Ч^Ч?) остается конечной и не равной нулю,
то уравнение C) эквивалентно следующему:
F?|(Я-?)|?) + (?|(Я-?)|6?) = 0. D)
Вектор 16ЧГ> есть вариация вектора l^), а <бЧ/|—вариация со-
сопряженного к \W} вектора. Следовательно, вариации 164х) и
(бЧ?! не независимы. Их можно, однако, считать таковыми. Дей-
Действительно, заменив |бЧ/> в уравнении D), которое справед-
справедливо для любых бесконечно малых ] б"Чг>, на 11 бЛ1г>
- iFW\(H -E)\4r) + iDf\(H- Е) |б?)== 0, D')
и образовав подходящие линейные комбинации уравнений D)
и D'), получим два эквивалентных уравнения:
Они эквивалентны уравнению D), если условиться рассматри-
рассматривать вариации \bW} и <бЧ/| как произвольные и независимые ').
') Это — общее правило, которое следует из того факта, что выражение
D) линейно относительно векторов 164*") и (бЧ^, а соотношение между со-
сопряженными друг другу векторами антилинейно.

S 2. ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ 257
Получили два уравнения:
или
(Я-?[44) |Ч0 = 0, Eа)
W) = 0. E6)
В силу эрмитовости Н (Н — Я+) уравнения Eа) и E6) тожде-
тождественны. Следовательно, уравнение C) эквивалентно уравне-
уравнению Eа): любой вектор J \fi>, для которого функционал Е ста-
стационарен, есть собственный вектор Я с собственным значением
]
Обратно, пусть l^i) — собственный вектор с конечной нор-
нормой и Е\ — соответствующее собственное значение
Умножая это уравнение слева на ОМ, получаем
Следовательно, вектор 14fi> удовлетворяет уравнению Eа),
а в силу эрмитовости Я и вещественности Е\ — и уравнению
E6). Отсюда заключаем, что функционал Е\*?\ стационарен
для ? = 4V ¦
Дополним полученную теорему следующей леммой.
Лемма. Каково бы ни было динамическое состояние си-
системы, среднее значение ее энергии больше или равно энергии
основного состояния
Е[Щ>Еа. F)
Для доказательства этого неравенства достаточно вычислить
разность между левой и правой частями в представлении, где
Я — диагоналей. Предположим для простоты, что спектр Я
чисто дискретный. Пусть ?0, ?i Е„, ... — уровни энергии,
расположенные в порядке их возрастания, а Ро, Р\,...,Рп,.. .—
проекторы на соответствующие подпространства. Используя
разложение единицы, находим
f (W | Рп | У)
Так как каждый член в этой сумме положителен или равен
нулю, то и сама сумма не меньше нуля, что и доказывает не-
неравенство F).
9 А, Мессиа

258 ГЛ. XVIII. ВАРИАЦИОННЫЙ МЕТОД И СВЯЗАННЫЕ С НИМ ЗАДАЧИ
§ 3. Вариационное вычисление дискретных уровней
Мы видели в § 1, что приближенное решение вариационного
уравнения C) можно получить, ограничивая область изменения
векторов I^F) только частью пространства состояний. При удач-
удачном выборе этой области &"' мы получаем некоторые собствен-
собственные векторы Н с хорошей точностью, а соответствующие им
собственные значения — с еще лучшей точностью.
Метод становится особенно простым в том случае, когда
пробная функция линейно зависит от вариационных параметров,
т. е. когда &~' также является векторным пространством. Тогда
8Г'— подпространство ЗГ в обычном смысле (§ VII. 2).
Введем обозначения: Р — проектор на ЗГ', Ф — произволь-
произвольный вектор ЗГ', а НР — сужение гамильтониана на У
НР в РНР. G)
функционал Е[Ф] (определение B)) равен среднему значению
НР. Эрмитов оператор НР линейно преобразует векторы из ЗГ'
в себя и может рассматриваться как эрмитов оператор в про-
пространстве У, для которого справедлива основная теорема § 2.
Следовательно, вариационное уравнение
6?[Ф] = 0 (8)
эквивалентно уравнению на собственные значения
НРФ = ЕФ. (9)
Таким образом, вариационное приближение состоит в замене
задачи на собственные значения оператора Н на аналогичную
Задачу, которая а priori легче для решения, поскольку она оп-
определена в более узком пространстве.
Отметим аналогию с теорией возмущений (§ XVI. 8). В част-
частности, если ЗГ' есть подпространство, отвечающее данному соб-
собственному значению невозмущенного гамильтониана, то вариа-
вариационный метод и вычисление в первом порядке по теории воз-
возмущений дадут одинаковые уровни.
§ 4. Простой пример: атом водорода
Прежде чем обсуждать подробно вариационный метод, его
достоинства и недостатки, полезно познакомиться с ним на кон-
конкретном примере вычисления основного состояния атома водо-
водорода и полученные результаты сравнить с точными ответами
главы XI.
Введем обозначения:
Ен =-$г (e2/hcJ тс2, р =

§ 4. ПРОСТОИ ПРИМЕР: АТОМ ВОДОРОДА 259
Так как мы ищем собственные состояния с фиксированным мо*
ментом импульса Aт), то пробные функции выберем в виде
Несложное вычисление дает
Ограничимся s-состояниями (/ = т = 0) и вычислим ста-
стационарные значения энергии для трех различных пробных
функций:
Каждая из этих функций зависит только от одного параметра Ь.
Следовательно, Е [Ф] в каждом случае сводится к функции от
Ь, и наша задача состоит в определении минимума этой функ-
функции. Несложные вычисления приводят к результатам, собран-
собранным в табл. I. Первым приводится аналитическое выражение
для нормы пробной функции Я2=<Ф|Ф> как функции от Ь,
затем среднее значение энергии, положение минимума bmin я
его значение EvaT. Интересно сравнить EvaT с энергией основного
состояния ?0 = — Ен и приближенное решение ^Fvar с точ-
точным — 4V Для этого в табл. I приведены нормированные ра«
диальные функции (u/N)vaT, а соответствующие кривые изобра-
изображены на рис. 14, их можно сравнить с точным решением 2ре~р.
Для каждого из трех приближенных решений Yvar в таблице
также приведены среднее значение <r>Var и величина е =
= 1—| <ЧГО|xFvar> |2 (предполагается, что *Fo и ?var нормиро-
нормированы на единицу); величина е служит хорошей мерой отклоне-
отклонения Yvar от основного состояния (она равна квадрату нормы
КОМПОНеНТЫ Yvar, ОрТОГОНЭЛЬНОЙ Wq) .
Все три пробные функции, как и волновая функция основ-
основного состояния, не имеют нулей (за исключением начала коор-
координат). Поэтому естественно ожидать, что они больше походят
на эту функцию, чем на волновые функции возбужденных со-
состояний, и величина Evar ближе к энергии основного состоя-
состояния — Ец, чем к какому-либо другому уровню (первый возбуж-
возбужденный уровень: Е[ = j- EHJ . Для того чтобы в этом убе^

260 ГЛ. XVIII. ВАРИАЦИОННЫЙ МЕТОД И СВЯЗАННЫЕ С НИМ ЗАДАЧИ
диться, мы приводим в таблице I под каждым значением Ечаг
соответствующее значение отношения (EvaT— E0)/(Ei — Ео),
которое хорошо отражает ошибку, возникающую при вычисле-
вычислении энергии основного состояния вариационным методом.
Таблица I
Вычисление вариационным методом основного состояния атома
водорода
и (Ь, р) =
Е (Ь)/ЕИ =
bmln =
?var =
F F
cvar c0
Ei-Eo
<«/A0var-
(r'vav ~
e-l-|<V0|Yvar)p-
1
1/468
62 —26
1
0
2pe~p
l,5a0
0
2
P
62 + P2
я/46
(n — 86)/2ji62
Jn
-0,81 EH
0,25
'[A")"+-Г
oo
9,21
3
p2e"^
3/465
ib2~b
3
2
—0,75?H
0,33
l,66a0
0,05
Лучший результат получается с пробной функцией щ, кото-
которая дает точную волновую функцию и точное собственное зна-
значение; отметим, что щ имеет то же поведение в начале коор-
координат (~р) и экспоненциальное убывание на бесконечности как
и собственные функции s-состояний (даже для притягивающего
потенциала, отличного от кулоновского, когда мы не получили
бы точной волновой функции, согласие результатов было бы
очень хорошим). Функция «2 имеет правильное поведение в на-
начале координат, но совершенно отличную от точного решения
асимптотику на бесконечности, однако она дает удовлетвори-
удовлетворительное значение Evar = — 0,81 Ен. Функция ы3, которая имеет
совершенно другое поведение в начале координат (~р2) и
правильное экспоненциальное убывание на бесконечности, дает
более скромный результат.

§ 5. ВЫЧИСЛЕНИЕ ВОЗБУЖДЕННЫХ УРОВНЕЙ
261
Рассмотрение величин <r>var и е показывает, что в целом
функция us больше похожа на точное решение, чем и2. Тот
факт, что она дает худший результат для энергии, подчеркивает
1,0
0,5
- /TV
- /7\
- //
//
" 1'
\
4 ^
N
\
"""
\
\
— u,
, p Ca p ^ Oft* P)
_
^^"
Рис. 14. Нормированные радиальные функции основного состояния атома
водорода, полученные вариационным методом.
важность поведения пробной функции в начале координат при
вычислении энергии, в особенности из-за притягивающего ха-
характера потенциала.
§ 5. Обсуждение. Вычисление возбужденных уровней
Вариационный метод является очень удобным и сильным
методом, но в нем трудно оценить точность результатов.
Отсутствует безошибочный способ определения того, для
какого уровня получено приближенное значение, какова, a for-
fortiori, погрешность результата. Часто, однако, можно ответить
на первый из этих вопросов, сравнивая общий вид полученной
волновой функции Tvar (число нулей, поведение в начале коор-
координат и на бесконечности) с аналогичными характеристиками
точного решения или по крайней мере с тем, что известно
a priori о точном решении. Обычно выбирают пробные функции,
имеющие простой аналитический вид и ограниченное число ос^
цилляций (или нулей), так что они имеют много шансов быть
близкими к волновой функции основного состояния.
Приведенные рассуждения показывают, что вариационный
метод особенно' удобен для вычисления энергии основного со-
состояния, для которого он дает оценку сверху (лемма F)). К со-
сожалению, не существует надежного метода для оценки порядка
величины ошибки (см. задачу 1). Все зависит от выбора проб-

262 ГЛ. XVIII. ВАРИАЦИОННЫЙ МЕТОД И СВЯЗАННЫЕ С НИМ ЗАДАЧИ
ной функции, т. е. от выбора и расположения функциональной
области SF'.
Необходимость выбора более сложных пробных функций,
трудности в интерпретации результатов, в определении порядка
и знака ошибок делают рискованным использование вариацион-
ного метода для вычисления возбужденных уровней. Суще»
ствуют, однако, две ситуации, в которых его использование воз-
возможно.
Прежде всего, если известна волновая функция основного
состояния То, то пробную функцию Ф следует выбирать среди
функций, ортогональных к Ч?о. В этом случае значение функ-
функционала Е[Ф] не меньше энергии первого возбужденного со-
состояния Е\
?[Ф]>?, A0)
и вариационный метод дает верхнюю оценку для Ех (см. за-
задачу 2). Может случиться, что вместо точной известна прибли-
приближенная волновая функция основного состояния Фо (определен-
(определенная, например, вариационным методом). В этом случае для
вариационного вычисления Ех используют пробные функции,
ортогональные к Фо, при условии, что разность между Фо и Yq
достаточно мала, т. е. если
(функции Wo и Фо имеют норму 1). Стационарная функция
Фь которая, как мы предполагаем, имеет норму 1, не ортого-
ортогональна больше То, и неравенство A0) может быть неверным,
но обязательно
|(Ф1|Т0)|2<е0, (Ц>
откуда следует, что
Е[Ф,}^Е1-г0(Е1-Е0). A2)
Вторая благоприятная ситуация возникает в случае, когда
оператор Я обладает симметрией. Предположим, например, что
Я инвариантен относительно вращений. Тогда собственные зна-
значения и собственные функции классифицируются посредством
квантовых чисел /, т. Пусть функции с моментом импульса
(jtn) образуют пространство &{}т). Выбирая пробную функ-
функцию из &, мы можем провести вариационное вычисление уров-
уровней (jtn), а точнее — низшего из них, и вариационный метод
автоматически дает оценку этого уровня сверху (задача 4).
§ 6. Основное состояние атома гелия
В этом параграфе вариационный метод применяется для
вычисления энергии основного состояния атома гелия Не или,
в более общем случае, (Z — 2)-кратно ионизированных атомов,

§ 6. ОСНОВНОЕ СОСТОЯНИЕ АТОМА ГЕЛИЯ 263
таких как Li+, Ве++ и т. д. Эта задача уже рассматривалась
методом теории возмущений в § XVI. 4, и в данном параграфе,
если не оговорено противное, мы будем использовать те же
обозначения.
В качестве пробной функции возьмем функцию, которую
даег нулевой порядок теории возмущений
где а будет рассматриваться как вариационный параметр, а не
как заданное значение ao/Z.
Поскольку пробная функция имеет норму 1, среднее значе-
ние энергии равно
Е (а) = <Фа | Я | Фа) = J J Ф; (ЯФа) drx drr
Гамильтониан системы можно представить в виде
где ki (г = 1,2) — оператор кинетической энергии i-ro элект-
рона, vi = Ze2/n — взаимодействие электрона с ядром, a Vn —
взаимодействие между электронами. Следовательно, Е(а) есть
сумма средних значений этих пяти операторов. Вычисление
этих величин значительно упрощается, поскольку волновую
ФУНКЦИЮ фа МОЖНО ПреДСТЭВИТЬ В ВИДе фа = /а (Л)/а (Г2) > гДе
fa (г)—собственная функция, отвечающая основному состоя-
нию электрона в кулоновском иоле заряда Z'e, Z' = ао/а. Пол-
Полная энергия такого электрона равна — Z' ?н> среднее значение
кинетической энергии + Z' Ен, а среднее значение потенциаль-
потенциальной энергии — 2Z' Ен (задача XI. 1). Следовательно,
<Ф«1^ \qa)
<Ф« I vi I Фа> = - 2Z'2?H (Z/Z0 = - 2ZZ'En-
Кроме того, согласно вычислениям § XVI. 4 (ур. (XVI. 17)—.
(XVI. 20))
откуда
= — Z'EH,
Е (а) = 2?н (Z/2 - 2 (Z - A) Z').
Это выражение, рассматриваемое как функция а или Z', имеет
минимум при

264 ГЛ. XVIII. ВАРИАЦИОННЫЙ МЕТОД И СВЯЗАННЫЕ С НИМ ЗАДАЧИ
и минимальное значение равно
Численные значения Еч&т, соответствующие атомам Не, Li+
и Ве++, приведены в таблице I в § XVI. 4. Интересно сравнить
их со значениями, полученными при вычислении в первом по-
порядке по теории возмущений. Заметим, что
?Var = — 2Z2Eh + ~ ZEn — -j^g- EH = ?pert —^ Eh,
и, следовательно, найденное значение меньше значения, кото-
которое получается по теории возмущений, на независящую от Z
величину
ПК.
-^-?н = 2,64 эв.
Как и следовало ожидать, Ечат дает лучшее приближение, ко-
которое, однако, больше экспериментального значения Еехр, в со-
согласии с неравенством F).
Полученная при этом вычислении функция имеет простой
физический смысл. Она отвечает двум независимым частицам,,
движущимся в кулоновском поле заряда Z'e, который опреде-
определяется формулой A2'), этот заряд меньше заряда ядра на
¦jg-e, и разница отражает эффект экранировки, которую испы-
испытывает каждый из электронов при движении в кулоновском
поле ядра из-за присутствия другого электрона.
Выбрав пробную функцию более сложной, можно получить
значение Еуат, которое еще ближе к точному собственному зна-
значению. В частности, можно взять вместо пробной функции q>e,
зависящей только от одного вариационного параметра а, про-
произведение фа на полином некоторой степени от переменных
г\, г2 и г]2, коэффициенты которого также рассматриваются
как вариационные параметры. С увеличением сложности по-
полинома получаемое значение ?Var будет уменьшаться и при-
приближаться к точному значению. Поступая таким образом, Хил-
лерас получил прекрасное согласие теоретического значения
с экспериментальным ').
') Hylleraas. Zeit. f. Phys. 65, 209 A930). Подробное изложение этого ме-
метода имеется в книге: Е. Кондон, Т. Шортли. Теория атомных спектров. М.,
ИЛ, 1949. Метод характеризуется очень быстрой сходимостью. При восьми
варьируемых параметрах вычисленное значение лежит несколько ниже экспе-
экспериментального, что на первый взгляд противоречит неравенству F). В дей-
действительности, Еехр несколько больше собственного значения ?0, соответствую-
соответствующего основному состоянию Н, за счет релятивистских эффектов, вклад кото-
которых можно оценить. Метод Хиллераса позволяет очень точно вычислять имен-
именно ?о, а не Eexv.

§ 8. ВЫЧИСЛЕНИЕ Е[Ф] 265
РазделП. АТОМЫ ХАРТРИ И ФОКА —ДИРАКА
§ 7. Метод самосогласованного поля
Мы уже проводили общее квантово-механическое рассмот-
рассмотрение сложных атомов. При этом использовалось приближение
независимых частиц, согласно которому каждый электрон дви-
движется независимо от других в потенциале, описывающем при-
притяжение к ядру и эффект усредненного отталкивания от других
электронов. В этом приближении волновая функция атома
записывается в виде определителя Слетера, который следует
выбирать как можно ближе к точному решению уравнения
Шредингера для атома. Наилучшая волновая функция полу-
получается, если использовать вариационный метод, а в качестве
пробной функции брать произвольный определитель Слетера Ф.
Этот важный частный случай вариационного метода носит на-
название метода самосогласованного поля. Не вдаваясь в детали
вычислений, мы рассмотрим в данном разделе основные этапы
этого метода ').
Метод используется не только в теории атомов. Важное
применение он находит при рассмотрении электронов в моле-
молекуле, в твердом теле и вообще систем тождественных частиц
в произвольном внешнем поле. Хотя в этом разделе речь будет
идти только об атомах, приводимые^ ниже рассуждения спра-
справедливы и для таких более общих случаев.
§ 8. Вычисление Е [Ф]
Гамильтониан системы из Z электронов можно записать
в виде
Н=Н1 + Н2, A3)
Я, = ? Л«>, № = y?~+V (г»>), A4)
A5)
Первое слагаемое Нх включает в себя кинетическую энергию
и потенциальную энергию электронов во внешнем поле (элек-
(электрическое поле ядра). Оно представляет собой сумму Z одина-
одинаковых одночастичных гамильтонианов. Второе слагаемое Н%
') Метод и его практическое приложение подробно разбирается в книгеа
Д- Хартри. Расчеты атомных структур. М., ИЛ, 1960. См. также цитированную
ранее книгу Кондона и Шортли.

266 ГЛ. XVIII. ВАРИАЦИОННЫЙ МЕТОД И СВЯЗАННЫЕ С НИМ ЗАДАЧИ
описывает энергию взаимодействия электронов, т. е. является
суммой x/iZ{Z— 1) одинаковых слагаемых, описывающих взаи-
взаимодействие каждой пары электронов; w<li)—потенциал между
электронами с номерами i и /. Если не учитывать силы, зави-
зависящие от спинов, то до('7) равен потенциалу электростатического
отталкивания
Дальнейшее рассмотрение не зависит от конкретного вида
мы будем предполагать только, что wW> есть функция динами-
динамических переменных электронов с номерами i и /, симметричная
относительно перестановки (//).
Поскольку Е[Ф] не зависит от нормировки пробной функ-
функции Ф, последнюю всегда можно считать нормированной на
единицу. Используя обозначения главы XIV, запишем ее в виде
У*А\ф), A7)
где А— определенный уравнением (XIV. 26) антисимметриза-
тор
а |Ф>—тензорное произведение Z произвольных, ортонормиро-
ванных одночастичных кет-векторов
|ф)=|а)<»|р)<2) ... |^)^|аA)рB) ...?<*)), A9)
<Я|Ц> = 6а|1 (К ц = а, р, .... Q. B0>
В этом случае условие нормировки выполняется автоматически
(Ф|Ф)=1. B1)
Величина Е[Ф] есть сумма средних значений операторов Hi
и Hi. Их вычисление упрощается в силу того факта, что Нх и
Н^ инвариантны относительно перестановок, коммутируют с Ау
а оператор А — проектор (А2 = А).
Для среднего значения Hi последовательно находим
Z Z
= Е И (- i)p <ф I л(«р | ф) = ? (ф |л(г) | ф).
i=i p г=1
Заменяя вектор |Ф> его определением A9), получаем
(Я = а, р, .... 0. B2)

§ 9. УРАВНЕНИЯ ФОКА —ДИРАКА 267
Таким образом, <#i> есть сумма средних значений одночастич-
ного гамильтониана Л по Z одночастичным квантовым состоя-
состояниям, занятым электронами.
Подобным образом <Я2> можно представить в виде суммы
матричных элементов оператора w между двухэлектронными
состояниями. Последовательно имеем
<Я2)=(Ф |Я21Ф) = Z! <Ф | Н2А | Ф) =
= Е Е (- 1)" <Ф I w^P I Ф> = Е <Ф I о>("> A - Pan) I Ф>.
Kl P i<!
т. е.
Е' B3)
где суммирование происходит по всем l/2Z(Z—1) парам одно-
частичных состояний %, ц, которые можно образовать из со-
состояний а, р, .... ?. Первое слагаемое в скобках представляет
собой среднее значение энергии взаимодействия в состоянии
|ХA>, цB)>, в котором электрон с номером 1 находится в состоя-
состоянии i, а второй электрон—в состоянии щ второе слагаемое
представляет собой обменный член, т. е. матричный элемент
оператора w между состояниями ^Оц'2') и |ц('>ДB>>. (Отме-
(Отметим, что это слагаемое вещественно и
Это свойство следует из эрмитовости оу<12) и его инвариантно-
инвариантности относительно перестановки A2).) Среднее <Я2> можно
также записать в виде
-(ЯО^ЧшО2)!^1)^2)» (Я,, |i = a, p С). B4)
Тем самым, для Е[Ф] имеем
?[Ф] = <#.> + <#2>, B5)
где <Я]> и <#2> даются формулами B2) и B4).
§ 9. Уравнения Фока — Дирака
При вариационном решении уравнения Шредингера в при-
приближении самосогласованного поля функционал Е[Ф] стацио-
стационарен по отношению к Z ортонормированным векторам \К)(к =
= а, р, ..., ?). Стационарность Е при вариации этих векторов,
которые удовлетворяют Z2 условиям B0), эквивалентна суще-
существованию Z2 постоянных eXfL (I, ц, = а, Р, .... I) (метод мно-

268 ГЛ. XVIII. ВАРИАЦИОННЫЙ МЕТОД И СВЯЗАННЫЕ С НИМ ЗАДАЧИ
жителей Лагранжа) таких, что выполнено вариационное урав-
уравнение
Е ? 0. B6)
Постоянные еХ|1 можно рассматривать как элементы неко-
некоторой Z X Z матрицы е. Эта матрица эрмитова, поскольку в
силу вещественности Е вариация 6Е также вещественна, и,
вычитая из уравнения B6) комплексно сопряженное уравне~
ние, получаем
откуда следует, что
Z векторов |а>, |Р>, ..., |?> образуют ортонормированный ба-
базис некоторого подпространства с?ф пространства одночастич-
ных состояний. Замена базиса в этом подпространстве приво-
приводит к умножению вектора |Ф> на фазовый множитель. Дей-
Действительно, пусть 5 — унитарная матрица Z X Z, определяю-
определяющая переход к новому базису |а'>, |Р'>, ..., |?'>, и
В силу хорошо известного свойства произведения детерминан-
детерминантов определитель Слетера Z новых векторов равен произведе-
произведению определителя Слетера Z старых векторов на det S. Следо-
Следовательно,
= (det5)|O),
а поскольку матрица 5 унитарна, то |detS|=l. Отсюда мы
заключаем, что функционал Е[Щ инвариантен относительно
изменения базиса, а вариационное уравнение B6) определяет
набор |а>, |Р>, ..., |D с точностью до такого изменения.
Используя уравнение B6), легко показать, что справедливо
аналогичное уравнение
где матрица е' связана с е преобразованием подобия
В частности, матрицу 5 можно выбрать таким образом, что-
чтобы матрица е' была диагональной. Так как вариационная
задача не зависит от выбора базиса, мы будем считать в даль-

5 9. УРАВНЕНИЯ ФОКА - ДИРАКА 269
нейшем матрицу диагональной. Тогда вариационное уравнение
B6) примет вид
? 0. B6')
Используя уравнения B2), B4) и B5), несложно сосчитать
&Е, после чего левая часть уравнения B6') становится одно-
однородной линейной комбинацией 2Z вариаций <6Я| и |6Я> (X =
= а, р, ..., ?). Потребовав, чтобы она обращалась в нуль при
любых вариациях, которые рассматриваются как независимые
(см. примечание на стр. 256), и учитывая эрмитовость гамиль-
гамильтониана Н, получаем (не приводя здесь детальных вычисле-
вычислений) Z уравнений для Z ортонормированных векторов |а>,
|Р>, ..., |D. a именно
> <ц | ш<12> | ц)<2> | я)<» -
и
(Я = а,
Отметим отсутствие множителя -«- перед суммами в левой
части. Умножив скалярно обе части на A><^| и просуммировав
по %, находим
1ея = <Я1) + 2(Я2) = ?[Ф] + <Я2). B7)
К обсуждению этого соотношения мы вернемся в дальнейшем.
Обычно используют представление кет-векторов их волно-
волновыми функциями
где q == (r, tns) обозначает пространственные и спиновые коор-
координаты.
Удобно ввести «электронную плотность»
р(q, q')^{q\p\q') = Z % (q) «й Ю- B8)
и
Это — матричное представление проектора на определенное,
выше пространство &ф
Диагональные элементы
I B9)
представляют собой плотность вероятности найти электрон з
точке q.

270 ГЛ. XVIII. ВАРИАЦИОННЫЙ МЕТОД И СВЯЗАННЫЕ С НИМ ЗАДАЧИ
Взаимодействие wV'"> является некоторой вещественной, сим»
метричной функцией переменных qW, q(i\ которую в дальней-
дальнейшем мы будем обозначать ш(<7@, <7(/)). Введем следующие обо-
обозначения:
Wexc (q, q') = р (q, q') w (q, q') C0)
C1)
s *«
где символ \ aq означает интегрирование по пространствен-
пространственным координатам и суммирование по спиновым переменным,
С учетом этих обозначений уравнения (I) принимают вид ин-
тегро-дифференциальных уравнений
Ш А + V W] "ь{q) + W ^ "* ^ ~ \ W™ fo' qf) % {q'] dq'=
(Я=а, р, ..., 0. (II)
Это интегро-дифференциальные уравнения Фока — Дирака.
Решать такие уравнения можно методом итераций. Исполь-
Используя приближенное значение ро для плотности и подставляя его
в уравнения C0) и C1), получаем приближенные значения
для величин W и Wexc. При известных величинах W и Wexs
уравнения (II) становятся уравнениями на собственные значе-
значения, первые Z решений которых —ы(^, ..., ы^} — дают новое
значение pi для плотности. Используя pi и повторяя предыду-
предыдущие операции, получаем новое значение — р2 и т. д. Если по-
последовательность ро, рь рг, ..., сходится, то она стремится к
точному решению. Однако обсуждать вопросы сходимости мы
здесь не будем. Отметим только, что скорость сходимости за-
зависит от выбора ро.
§ 10. Обсуждение результатов
Каждое из уравнений (II) напоминает уравнение Шредин-
гера, определяющее одно из Z одночастичных состояний, в ко-
которых находятся Z электронов атома. Однако эти уравненич
не являются в действительности настоящими уравнениями на
собственные значения, поскольку операторы W и №еХс зависят
от электронной плотности и, следовательно, собственные функ-
функции иа, ир, ..., «г входят в определение соответствующего га-
гамильтониана. Тем не менее, поучительно рассмотреть этот од-
ночастичный гамильтониан и попытаться придать физический
смысл различным слагаемым в этом гамильтониане.
С этой целью введем обозначение для плотности электро-
электронов в (Z— 1) состояниях, отличных от состояния Я:
I = Р - I Я) (Я |, р*> (<?, q') = p (q, q') - их (q) ul (q'),

§ 10. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ 271
а выражения, получающиеся заменой р на р(Я) в уравнениях
C0) и C1), обозначим wtxc и W<4 Введем также усредненный
потенциал Х^к\ создаваемый электроном в состоянии |А,>:
(?) = $ I % (<?') ? w (q, q') dq'. C2)
есть усредненный потенциал, создаваемый электронами,
находящимися в остальных (Z— 1) состояниях, а усредненный
потенциал W, создаваемый всеми электронами, равен
W (q) = W<M (<?) + ХМ (q).
Теперь можно записать уравнение системы (II), относящее-
относящееся к состоянию X, следующим образом:
—?А
- \ W& (q, q') uK {q') dq' = еЛ (<?) (X = а, р, ..., g), (HI)
поскольку 1^(Я)(<7)«х(<7) отличается от W(<7)«a,(<7) на слагаемое
«собственной энергии» X^(q)u^(q), a
Легко дать интерпретацию полученной форме (III) «уравне-
«уравнения Шредингера» для электрона в состоянии X. Гамильтониан
представляет собой энергию электрона в поле, состоящем из
поля ядра и усредненного поля остальных электронов. Гамиль-
Гамильтониан состоит из четырех слагаемых: кинетической энергии
1—Й2А/2т, потенциала ядра V(q), усредненного потенциала
(Z — 1) электронов Ww(q) и четвертого слагаемого, представ*
ляющего обменные эффекты между состоянием X и остальными
(Z—1) занятыми состояниями. Мы видим, что обменные эф-
эффекты ведут к нелокальному потенциалу, определяемому ядром
Данная интерпретация предполагает, что собственное зна-
значение ех есть энергия электрона в состоянии X. Уравнения
Фока — Дирака дают Z величин еа, е$, ..., е%, которые с хоро-
хорошей степенью точности равны энергиям ионизации Z электро-
электронов атома. Однако, складывая эти энергии, мы не получим пол-
полной энергии системы Z электронов. Складывая отдельные энер-
энергии, мы правильно учитываем кинетическую энергию каждого
электрона и энергию его взаимодействия с ядром, но дважды
учитываем энергию взаимодействия электронов друг с другом*

272 гл. xvm. вариационный метод и связанные с ним задачи
Следовательно, для получения полной энергии из результата
нужно вычесть усредненную величину межэлектронного взаи-
взаимодействия, т. е. <#2>. Это утверждение уже было получено
нами ранее (ур. B7)).
§ 11. Уравнения Хартри
Если в системе (III) пренебречь обменными слагаемыми,
то мы получим значительно более простую систему уравнений
(IV)
Эти уравнения были предложены Хартри на основе только ин-
интуитивных соображений. Они могут быть также получены ва-
вариационным методом, если в качестве пробной функции ис-
использовать простое произведение одночастичных состояний, та-
Ф> в формуле A9), а не антисимметризованное произ-
Ф>, формула A7I).
кое как
ведение
Систему уравнений Хартри, так же как и систему Фока
Дирака, можно решать методом итераций. Благодаря отсут-
отсутствию обменных членов, вычисления здесь значительно короче.
Однако эта система менее симметрична по сравнению с преды-
предыдущей, поскольку гамильтониан Хартри h + Ww не один и
тот же для различных одночастичных состояний. Как след-
следствие, собственные функции Z уравнений Хартри не ортого-
ортогональны друг другу, что ведет к ряду трудностей при использо-
использовании этого метода, на которых мы здесь не останавливаемся*
Раздел III. СТРУКТУРА МОЛЕКУЛ
§ 12. Общие понятия. Разделение движения ядер
и электронов
Молекула, представляя собой связанное состояние агомов,
состоит из нескольких атомных ядер и движущихся в поле
этих ядер электронов. Определение стационарных состояний
столь сложной системы является очень трудной задачей. Од-
Однако существует некоторое упрощающее обстоятельство: масса
электронов много меньше массы атомных ядер, в то время как
на них действуют силы одного порядка. Как следствие этого,
ядра движутся значительно медленнее электронов, и с хорошей
') Это, однако, не является последовательным выводом этих уравнений,
поскольку в отлнчне от векторов |Ф), векторы |Ф) ие принадлежат простран-
пространству состояний системы.

§ 12. РАЗДЕЛЕНИЕ ДВИЖЕНИЯ ЯДЕР И ЭЛЕКТРОНОВ 273
степенью точности движения электронов и ядер можно рас-
рассматривать независимо. Действительно, в первом приближении
ядра по отношению к электронам можно считать фиксирован-
фиксированными силовыми центрами, и динамическое состояние есть со-
состояние системы электронов в поле фиксированных ядер. По-
Поскольку последние движутся достаточно медленно, динамиче-
динамическое состояние электронов адиабатически меняется в соответ-
соответствии с изменением создаваемого ядрами потенциала (см. гла-
ву XVIII, раздел II). И наоборот, поскольку за время, необхо-
необходимое для заметных смещений ядер, электроны успевают со-
совершить много оборотов, ядра подвержены только некоторому
усредненному влиянию со стороны электронов. С хорошей сте-
степенью точности движения ядер можно описать, заменив их
взаимодействие с электронами его значением, усредненным по
нескольким электронным оборотам. Применение такого спо-
соба приводит к уравнению Шредингера, в котором полностью
отсутствуют переменные, описывающие электроны. Приближе-
Приближение, лежащее в основе этого метода разделения переменных,
называется адиабатическим приближением.
Цель данного раздела — дать общее представление о ме-
методе и обсудить границы его применимости. Прежде чем при-
приступить к изложению, мы закончим полуклассический
анализ движения ядер и оценим вклад различных эффектов.
Потенциал в уравнении Шредингера для ядер зависит толь-
только от расстояний между ядрами. Коль скоро молекула суще-
существует, этот потенциал должен иметь минимум для некоторых
вполне определенных конечных значений межядерных расстоя-
расстояний. Этот минимум соответствует точке устойчивого равновесия
системы, и относительно этой конфигурации ядра могут совер-
совершать малые колебания. На внутренние колебания ядер может
накладываться поступательное движение и вращение системы
как целого. Поступательное движение можно полностью отде-
отделить от других движений, вводя центр масс системы, который
движется, как свободная частица. В дальнейшем мы будем
предполагать, что такое разделение выполнено, и будем рассмат-
рассматривать только колебательное и вращательное движения ядер.
Вводя обозначение m для массы электрона, а М — для ве-
величины порядка ядерных масс, и обозначая среднее расстоя-
расстояние между ядрами в молекуле через а, имеем ')
а да 10~8 см, пг/М да 10~3 — 10~5. C3)
Молекула имеет линейные размеры порядка а, что дает
порядок величины амплитуды движения электронов. В силу со-
') Отношение масс имеет наибольшее значение для молекулы водорода
(m/Af)H2*0,5-10~3.

274 ГЛ. XVIII. ВАРИАЦИОННЫЙ МЕТОД И СВЯЗАННЫЕ С НИМ ЗАДАЧИ
отношения неопределенности импульс электронов имеет поря»
док h/a, что соответствует кинетической энергии порядка
h2/ma2. Эта кинетическая энергия равна по порядку величины
энергии связи основного состояния электронов и расстоянию
между энергетическими уровнями электронов
eei « h2/ma2 C4)
(ср. это с оценкой из § XI. 3).
Что касается движения ядер, то рассмотрим вначале их
вращение. Момент инерции системы имеет порядок Ма2. По-
Поскольку квадрат момента импульса изменяется на величину по*
рядка ft2, вращательная энергия будет меняться на величину
порядка
erot да Н'/МсР. C5)
В первом приближении колебания ядер можно рассматри-
рассматривать как гармонические с квантованной энергией eVib = ftcu.
Примем за нулевой уровень потенциальной энергии ее значе-
значение для устойчивой равновесной конфигурации ядер. Если з
этом случае одно из ядер отвести на расстояние а, то система
приобретет потенциальную энергию -х Ма>2а2. Поскольку это
приведет практически к полному отделению одного из атомоз
от молекулы и, следовательно, к увеличению энергии на вели-
величину порядка 8ei, то мы имеем
Мо>2а2 да Н2/та2,
откуда
\_
ewib & Н2/(тМJ а2. C6)
Сравнивая выражения C4) — C6), получаем
erot ^C evib <Ceei.
Если следовать более строгому подходу Борна и Оппенгей-
Оппенгеймера ') и ввести параметр
C7)
то получим
6rot да X2evib « И48е1. C8)
Расстояние между уровнями е связано с классической часто-
частотой е/Н. Следовательно, мы можем заключить, что движение
электронов значительно быстрее, чем колебательное движение
') М. Born, J. R. Oppenhelmer. Ann. der Phys. 84, 457 A927); о первона-
первоначальном методе Борна и Оппенгеймера см. § 16.

§ 13. ДВИЖЕНИЕ ЭЛЕКТРОНОВ В ПОЛЕ ФИКСИРОВАННЫХ ЯДЕР 275
•ядер, которое, в свою очередь, является более быстрым по
сравнению с вращательным движением всей системы, в согла-
согласии с замечаниями, которые были сделаны в начале параграфа.
Отношение частот этих движений имеет порядок х2, т. е. равно
приблизительно 0,01: за время одного оборота всей молекулы
ядра успевают совершить примерно 100 колебаний около ич
положения равновесия, а электроны — приблизительно 10000
оборотов.
§ 13. Движение электронов в поле фиксированных ядер
Основываясь на полуклассических рассуждениях предыду-
предыдущего параграфа, рассмотрим задачу определения стационар-
стационарных состояний молекулы. Поскольку наша цель — дать скорее
общее представление о методе, нежели его детальное изложе-
изложение, то мы без колебаний будем принимать упрощающие пред-
предположения, которые не влияют на сущность метода. В частно-
частности, электроны и ядра мы будем рассматривать как бесспино-
бесспиновые частицы.
Степени свободы электронов и ядер будем параметризовать
индексами i и / соответственно. Координаты электронов и ядер
обозначим xi и X/, а массу ядра с координатой Xs обозначим
Mj. Обозначим кинетическую энергию электронов Те, кинети-
кинетическую энергию ядер Тх, а потенциал взаимодействия различ-
различных частиц в молекуле V. Гамильтониан молекулы Н состоит
из трех слагаемых
H = Te + TN + V, C9)
где
а V = V(x, X)—некоторая функция, зависящая от координат
электронов и ядер, она равна сумме кулоновских потенциалов
каждой пары частиц системы.
Рассмотрим упрощенный гамильтониан
H® = T,+ V, D0)
который получается из выражения C9) отбрасыванием кинети-
кинетической энергии ядер. Он представляет собой гамильтониан си-
системы в пределе М/ -> оо, и его стационарные состояния есть
состояния системы электронов в поле фиксированных ядер.
Действительно, поскольку Я@) не содержит производных по А/,
то
[Х„НЩ=0,
и, следовательно, операторы #@) и X, можно диагонализовать

276 ГЛ. XVIII. ВАРИАЦИОННЫЙ МЕТОЛ И СВЯЗАННЫЕ С НИМ ЗАДАЧИ
одновременно. Другими словами, решая задачу на собственные
значения оператора Я<°>, можно считать координаты ядер опре-
определенными фиксированными величинами X,-. Заданный набор
величин X'j обозначим символом X'. Каждому набору X' отве-
отвечает набор собственных значений Wn(X') оператора Я@), ко
торые параметризуются квантовым числом п. При заданных п.
и X' существует один или несколько линейно независимых соб-
собственных векторов, которые в последнем случае следует пара-
параметризовать с помощью дополнительного индекса, например, s.
Таким образом, уравнение Шредингера для Я<°> имеет вид
Я<°> | nsX') = Wn (Xf) | nsX'). D1>
В {хХ}-представлении собственный вектор описывается вол-
волновой функцией
Ф„Л*, Г) 6 (X - Г), D2)
где функции ф есть решения уравнения Шредингера
[Те + V (х, X')] Фм (х, X') = Wa (Xf) q>ns (х, Г). D3>
В уравнении D3) X' играет роль параметра, т. е. мы имеем
уравнение Шредингера для электронов молекулы, когда поло-
положения ядер фиксированы в X'. Каждому решению этого урав-
уравнения соответствует собственная функция оператора Я'0' вида
D2), а все решения уравнения D3) при всех возможных зна-
значениях А" образуют полный набор собственных функций Я<°>.
Для дальнейшего важно условие нормировки, и мы всегда бу-
будем брать ортонормированные собственные функции, что будет
автоматически выполняться, если <p,-,s(;c, X'), рассматриваемые
как функции только переменных х, имеют норму 1.
Задача определения собственных значений D3) аналогична
задаче определения стационарных состояний атома и может
быть решена теми же методами, например, методом самосо-
самосогласованного поля. Однако в данном случае имеется несколько
силовых центров, что уменьшает свойства симметрии этой за-
задачи по сравнению с аналогичной задачей для атома.
Обсудим кратко вопросы, связанные с симметрией1). По-
Потенциал V{x, X) инвариантен относительно трансляций, вра-
вращений и отражений системы как целого, он инвариантен также
относительно обращения времени и перестановки тождествен-
тождественных частиц. Допустим теперь, что положения ядер фиксиро-
фиксированы в X'. Тогда свойствами симметрии потенциала V(x, X')t
рассматриваемого как функция только переменных к, будут те
') Общее изложение свойств симметрии электронных волновых функций
молекул содержится в книге: Л. Д. Ландау, Е. М. Лифшиц. Квантовая меха-
механика, М., Наука, 1963.

§ И. АДИАБАТИЧЕСКОЕ ПРИБЛИЖЕНИЕ 27?
из перечисленных выше свойств, которые оставляют неизмен-
неизменной конфигурацию ядер X'. Так, для двухатомной молекулы
С1Н потенциал V{x, X') инвариантен относительно вращении
вокруг оси, проходящей через ядра хлора и водорода, и отно-
относительно отражений в плоскостях, проходящих через эту ось^
Вместе с инвариантностью относительно обращения .времени
это все симметрии, которыми обладает в данном случае потен-
потенциал. Для достаточно сложных молекул потенциал инвариан-
инвариантен только относительно обращения времени. Как легко видеть,
свойства инвариантности оператора Я<°>, действующего только
на функции от х, те же, что и для потенциала V(x,X'). С этими
свойствами симметрии связано вырождение уровня Wn(X') (см..
главу XV).
Чтобы устранить сложности, связанные с вырождением, бу-
будем предполагать, что V(x, X') инвариантен только относитель-
относительно обращения времени. Тогда, поскольку речь идет о моле-
молекуле (а не о свободном радикале), число электронов четно п.
имеет место первый из случаев, обсуждавшихся в § XV. 21..
Предполагая дополнительно, что отсутствует случайное вырож-
вырождение, мы получаем невырожденное собственное значение
Wn(X') и при подходящем выборе фазы вещественную соб-
собственную функцию (f>n(x, X').
В заключение этого параграфа сделаем два замечания.
Рассматриваемый как оператор, действующий только на пе-
переменные х, Я<°> непрерывно зависит от X' как от параметра,,
так же как его собственные значения и собственные функции,
т. е. при заданном п, Wn(X') и арп(х,Х')—непрерывные функ-
функции от X'.
Рассматриваемый как оператор, который действует в про-
пространстве функций от всех переменных, Я<°> инвариантен по от-
отношению ко всем преобразованиям, которые были упомянуты
выше в связи с V(x, X). Следовательно, любой вектор, который
получается из \пХ'у при действии одного из таких преобразо-
преобразований, является собственным для Я<°» и соответствует тому же
собственному значению Wn(X). Другими словами, W.i{X') не
меняется при действии этих преобразований на X'. В частности,
Wn(X') зависит только от расстояний между ядрами, точнее,.'
от той геометрической фигуры, которую образуют ядра, и не
меняется при сдвигах (трансляциях и поворотах) или при за-
замене этой фигуры на зеркальную (отражение).
§ 14. Адиабатическое приближение
В предыдущем параграфе мы рассматривали стационарные
состояния электронов, когда положение ядер молекулы счита-
считалось фиксированным. Предположим теперь, что ядра медленно

278 ГЛ. XVIII. ВАРИАЦИОННЫЙ МЕТОД И СВЯЗАННЫЕ С НИМ ЗАДАЧИ
движутся согласно некоторому закону X'(t). Если эти движе-
движение достаточно медленное, то динамическое состояние элект-
электронов будет адиабатически меняться в соответствии с измене-
изменениями потенциала, в котором эти электроны находятся. Так,
если в момент времени to они находились в состоянии
{n,X'(to)), отвечающем уровню энергии Wn(X'(to)), т. е. со-
состояние описывалось волновой функцией q>n(x, X'(to)), то в мо-
момент времени t электроны будут находиться в состоянии
(п, X'(t)), которое получается из (п,X'(to)) по непрерывности
при фиксированном п.
Условия применимости этого приближения уже обсужда-
обсуждались нами в § XVII. 13 (см. критерий (XVII. 14)). Вероятность
найти электроны в состоянии, отличном от (п, X'), дается фор-
формулой
D4)
«п
тде ап — «угловая скорость» вектора q>n(x, X'), а со, — мини-
минимальная боровская частота, связанная с уровнем Wn(X').
Для оценки этой величины используем полуклассические
рассуждения из § 12. Расстояние между электронными уров-
уровнями дается формулой C4), откуда получаем
со„ r-J eeifh « h/ma2. D5)
Прежде чем вычислять ап, оценим норму dq>n/dX'j, считая функ-
функцию ср„ вещественной и нормированной на 1. Мы знаем, что
для отделения атома от молекулы необходимо соответствую-
соответствующее ядро переместить на расстояние порядка а от его положе-
положения равновесия, т. е. необходимо изменить координату X' на
АХ) ж а, чтобы функция tpn(x, X') перешла в функцию, ортого-
ортогональную исходной. Следовательно, дц>п/дХ/ приблизительно
равна этой новой функции, поделенной на а, и имеет норму
порядка 1/а2
По определению с? равна норме (вещественной) функции dyjdt.
Если vt = dxydt — скорость изменения Х'г то с? равна норме
функции 2 V/ {дфп/dXj) и имеет порядок
а2 « -V У v2,
п a2 L-i I'
i
Если кинетическую энергию ядра обозначить t^, то получим

§ 14. АДИАБАТИЧЕСКОЕ ПРИБЛИЖЕНИЕ 27&
Подставляя D5) и D7) в D4), находим
ть^х4-^-- D8)
8е1
Приведенный полуклассический анализ может служить ос-
основой при отыскании стационарных состояний молекулы. Рас-
Рассмотрим задачу на собственные значения гамильтониана Н.
В силу равенств C9) и D0) имеем
Н = Я<°> + TN. D9)
Если членом кинетической энергии ядер Тц можно было бы
пренебречь, то гамильтониан молекулы был бы равен Я@) и
каждое стационарное состояние \пХ'} соответствовало бы опре-
определенному электронному квантовому числу п и определенной
конфигурации ядер X'. Положения ядер X' оставались бы фик-
фиксированными, а движение электронов описывалось бы волновой
функцией ц>п(х, X'). Слагаемое Тц связывает собственные век-
векторы #@), отвечающие соседним конфигурациям X'.
В адиабатическом приближении связью между векторами с
различными электронными квантовыми числами пренебрегают
и считают п хорошим квантовым числом
п « const. E0)'
В этом случае собственные векторы Н являются линейными
комбинациями векторов \пХ'У с определенным значением п и,
следовательно, имеют вид
Х')Ъ(Х')йХ\ E1)
где ty(X') — произвольная функция X'. В {х, ^-представлении
таким векторам соответствуют волновые функции вида
E2>
Собственные функции гамильтониана Н в этом приближе-
приближении можно получить, используя вариационный метод и функ-
функции Ф„(х,Х) в качестве пробных функций. При этом пробная
функция варьируется в подпространстве пространства векто-
векторов состояния, а именно, в пространстве &п векторов вида E1).
Как известно (§ 3), в этом случае мы получаем уравнение на
собственные значения в этом подпространстве (ур. (9)), а в
данной ситуации — уравнение Шредингера для неизвестной
функции ty(X). Гамильтониан этого уравнения, который мы
обозначим Нп, равен проекции Н на Шп. Он действует только
на динамические переменные ядер. Собственные знзчения Нп
представляют собой уровни энергии молекулы относительно
электронного квантового числа п.

-280 гл. xvm. вариационный метод и связанные с ним задачи
Полученную при этом погрешность можно оценить, исполь-
используя рассуждения, которые были приведены в начале этого па-
параграфа. Пусть Ф„ — некоторое из приближенных решений, а
Wn — соответствующее точное решение. Оба решения предпола-
предполагаются нормированными на единицу. Разность № = Wn — Ф
описывает отклонение точного решения от адиабатического
предела. Этот вектор лежит в основном вне подпространства
<%п и имеет норму, которая равна определенной выше величина
цп. Учитывая приближенное равенство D8), получаем
п
.Другими словами, имеем
6Ч'«х3Ф'( E3)
где Ф' — функция, ортогональная подпространству <Sn, с нор-
нормой 1. Поскольку функционал
стационарен на решении 4V вычисление энергии с функцией
•Фп содержит ошибку второго порядка по отношению к откло-
отклонению 84*, т. е.
6? «F4? IН 1640 = х6 <Ф' I Н | Ф') at x6eel.
¦Сравнивая это с формулой C8), получаем оценку
6?/erot «х2 (« 10 < 1). E4)
Следовательно, адиабатическое приближение при определе-
определении молекулярной волновой функции приводит к ошибке по-
порядка к3 (ур. E3)) и к ошибке при определении энергии, ко-
которая в к2 раз меньше расстояния между вращательными уров-
уровнями (ур. E4)).
§ 15. Гамильтониан ядер в адиабатическим приближении
Пользуясь вариационным методом, найдем «уравнение
Шредингера» для функции ty(X).
Напомним, что q>n(x,X) есть решение уравнения D3), нор-
норма ц>п(х, X) при интегрировании по х равна 1
ц>п(х,Х) = ц>п(х, X), E5)
2(x, X)dx=l. E6)
•Функция фп непрерывно зависит от X и определена с точностью

§ 15. ГАМИЛЬТОНИАН ЯДЕР 281*
до знака. В дальнейшем окажутся полезными следующие ура в-
нения:
E6">
которые получаются дифференцированием равенства E6).
Функция $(Х) есть произвольная квадратично-интегрируемая
функция переменных X.
Определив таким образом область изменения пробной функ-
функции, выразим функционал ?[ФП] в виде функционала от ^(^).
Используя свойства срл, легко получить
<ф„ |ф„>» J J | ф„ ?dxdX = J | ф f dX. E7)
Можно также выписать следующее равенство:
<Ф« | Н \ Фп) = \ \ Ф; (НФп) dx dX = \ V (Я„г|)) dX, E8>
если ввести оператор
Я„ф = \ Фп (х, X) [ЯФ„ (х, Jf)« Ш] dx. E9)
Следовательно,
F0)
Определенный тождеством E9) оператор Нп в простран-
пространстве функций 1)з (X) является линейным и, как будет показано
ниже, эрмитовым. В адиабатическом приближении собствен-
собственными функциями уравнения Шредингера для молекулы яв-
являются такие функции, на которых функционал ?[Ф„] стацио-
стационарен по отношению к вариациям ф(Х). В силу соотношения
F0) ими будут решения уравнения на собственные значения
Это и есть «уравнение Шредингера».
Уровни энергии молекулы, соответствующие электронному
квантовому числу п, являются собственными значениями Нп.
Соответствующие собственные функции Ф„ получаются после
замены ф (X) в формуле E2) на решение (или решения) урав-
уравнения F1).

¦282 ГЛ. XVIII. ВАРИАЦИОННЫЙ МЕТОД И СВЯЗАННЫЕ С НИМ ЗАДАЧИ
Учитывая свойства функции ц>п, можно выполнить ряд И1Ь
тегрирований в формуле E9) и получить более удобное для
вычислений выражение Нп.
В силу уравнения D3)
Я«»фп (х, X) Ч> (X) = Wn (X) Ф„ (х, X) i|> (X),
откуда, используя нормировку E6), получаем
Ф» [Ж°)фпяЙ dx = Wn (X) ф (X). F2)
Согласно формуле C9') для кинетической энергии ядер
имеем
откуда можно вычислить
умножая обе части равенства на ф„(х, X) и интегрируя по х.
Рассмотрим отдельно вклады каждого из трех слагаемых в
квадратных скобках правой части равенства. В силу норми-
нормировки E6) вклад первого слагаемого равен
Вклад второго члена равен нулю в силу соотношения E6')\
Вклад третьего члена равен произведению некоторой функции
Wn{X) на ^ и, используя E6"), его можно записать в виде
?4$(w)^ F4)
Окончательно имеем
(TNq>nq)dx = (TN + W'n)q. F5)
Из определения E9) и уравнений D9), F2) и F5) полу-
получаем
Ha = Tn + W'a + Wn, F6)
Трем слагаемым в формуле F6) легко дать физическую ин-
интерпретацию.
Потенциальная энергия Wn(X) есть среднее от оператора
Я@), т. е. сумма энергии взаимодействия ядер и среднего зна-
значения энергии электронов в квантовом состоянии л, отвечаю-

§ 16. МЕТОД БОРНА — ОППЕНГЕЙМЕРА 283
щем определенной конфигурации ядер X. Согласно обсужде-
ниям § 12 величина Wn{X) имеет абсолютный минимум при
некотором значении Хо, которое представляет собой усгойчивую
равновесную конфигурацию ядер.
Остальные два члена связаны с кинетической энергией
ядер, усредненной по динамическому состоянию электронов.
Это дает, в дополнение к собственно кинетической энергии ядер
Tn, потенциальную энергию Wn(XI), которая представляет со
бой малую поправку к потенциалу Wn. Подставляя оценку D6)
в выражение F4), находим
Й2
Wn (Хо) «
Следовательно, потенциальная энергия W'n положительна и
равна по порядку величины вращательному кванту.
§ 16. Метод Борна — Оппенгеймера
При первоначальном рассмотрении молекул Борн и Оппен-
геймер2) использовали метод, отличный от описанного выше
вариационного метода. Их рассмотрение основывалось на раз-
разложении гамильтониана Н в ряд по степеням и и последующем
решении задачи на собственные значения методами обычной
теории возмущений.
В предыдущем параграфе мы обозначили положение мини-
минимума Wn{X) через Хо. В действительности это положение рав-
равновесия определено с точностью до вращений, поскольку вели-
величина Wn инвариантна по отношению к вращению системы ядер
как целого (отметим, что W'n таким свойством, вообще говоря,
не обладает). Пусть Х = (а>, ?), где со — три угловые перемен-
переменные (две — для двухатомной молекулы), которые фиксируют
ориентацию системы ядер, а ?-—радиальные переменные, опре-
определяющие относительное расположение ядер. Тогда \Уп зави-
зависит только от переменных |, и положению равновесия соответ^
ствует некоторый набор значений радиальных переменных.
Следуя Борну и Оппенгеймеру, введем новые радиальные
переменные и по формуле
Переменные и в* соответствующих единицах задают отклонение
ядер от их положений равновесия. Поскольку и приблизительно
равно отношению амплитуды колебания ядер к амплитуде дви-
') Появление этого члена аналогично появлению члена центробежной
энергии в уравнениях движения классической системы во вращающейся систе-
системе отсчета.
2) См. сноску к формуле C7).

84 ГЛ. XVIII. ВАРИАЦИОННЫЙ МЕТОД И СВЯЗАННЫЕ С НИМ ЗАДАЧИ
жения электронов, то область изменения переменны* и имеет
тот же порядок величины, что и область изменения х, т. е. а.
Сделав эту замену переменных и разложив потенциал в Н
по степеням и, получаем разложение оператора Н по степеням
х. Член TN имеет порядок у?. Чтобы получить вращательные
уровни, в разложении необходимо учесть члены порядка х*.
Если учесть члены порядка х5, то придем с точностью до по-
поправок высшего порядка к результату, который получается
при адиабатическом приближении. Отличия возникают только
в членах порядка х6 и выше, что согласуется с обсуждениями,
приведенными в § 12.
§ 17. Основные представления о двухатомных молекулах
Мы не будем продолжать далее общее исследование моле-
молекул в адиабатическом приближении. В частности, мы не будем
обсуждать проблемы разделения колебательного и враща-
вращательного движений. Чтобы осуществить такое разделениэ,
удобно несколько модифицировать вариационный метод, введя
три набора переменных вместо двух, а именно — угловые пере-
переменные, определяющие ориентацию молекулы, переменные от-
относительного расположения ядер и переменные, определяющие
положение электронов относительно ядер. Однако мы ограни-
ограничимся тем, что в заключение этого раздела приведем ряд ре-
результатов, относящихся к двухатомным молекулам.
После отделения движения центра масс динамические пе-
переменные двух ядер описывают их относительное движение.
В этом случае набор координат X сводится к компонентам век-
вектора /? = /?! — /?2, определяющего положение одного ядра от-
относительного второго. Для координат электронов в системе
центра масс ядер мы сохраним обозначение х. Пренебрегая
для простоты изложения спином частиц1), обозначим (орби-
(орбитальный) момент импульса электронов L, а момент импульса
ядер G(G = Ry^P). Тогда полный момент системы А' равен
/C = G + L. F7)
Введем единичный вектор вдоль оси молекулы и(и = R/R) и
будем обозначать индексом и компоненты векторов по этой
оси. Отметим справедливость операторного тождества
0, ' F8)
') Если спин-орбитальное взаимодействие мало по сравнению с расстоя-
расстоянием между вращательными уровнями, то присутствие спияоз несущественно
меняет результаты и приводит только к появлению тонкой структуры, так же
как в случае LS-связи в атомах. В противном случае общая форма спектра
довольно существенно меняется. См. Л. Д. Ландау, Е. М. Лифшиц, loc. cit.
{см. сноску к § 13).

§ 17. ПРЕДСТАВЛЕНИЯ О ДВУХАТОМНЫХ МОЛЕКУЛАХ 285
откуда следует, что Gu(= Gu) тождественно равна нулю и
Ки = Ьа.
В остальном мы будем придерживаться обозначений предыду-
предыдущего параграфа.
Рассмотрим вначале движение электронов. Свойства сим-
симметрии #<°> как оператора, действующего только на динамиче-
динамические переменные электронов, те же, что и в эффекте Штарка:
#<0) инвариантен относительно вращений вокруг оси и и отно-
относительно отражений в плоскостях, проходящих через и. Если
молекула состоит из одинаковых ядер, то #@) инвариантен
также относительно обычного отражения (х-*-—х); этот слу-
случай мы пока рассматривать не будем.
Чтобы классифицировать состояния, нам достаточно вспом-
вспомнить обсуждение эффекта Штарка из § XV. 14. Каждый уро-
уровень Я@) соответствует определенному собственному значению
оператора L2U, которое можно записать в виде №А2, где кван-
квантовое число Л принимает все неотрицательные целые значения.
Следуя спектроскопическим обозначениям, термы, которые со-
соответствуют первым трем значениям Л = 0, 1, 2, обозначим
греческими буквами 2, П, А. Если Л Ф 0, то уровень двукратно
вырожден и имеется два собственных вектора, отвечающих соб-
собственным значениям %А. и —НА. компоненты момента импульса
по оси молекулы. Уровни 2 (Л = 0) невырождены, их можно
разделить на две категории 2+ и 2~, в зависимости от гого ин-
инвариантен или меняет знак соответствующий им собственный
вектор при отражениях в плоскости, проходящей через ось мо-
молекулы. Для большинства двухатомных молекул основное со-
состояние есть 2+ состояние.
Рассмотрим теперь полный гамильтониан. Появление вы-
вырождения электронных уровней только на первый взгляд ус-
усложняет ситуацию. В действительности можно показать, что
вызванное TN взаимодействие между состояниями с *гЛ и —/гЛ
меньше расстояния между вращательными уровнями, и, сле-
следовательно, им можно пренебречь. Другими словами, в допол-
дополнение к приближению E0) мы будем считать, что и Lu =
= const.
С другой стороны, хотя использованный в §§ 14 и 15 вариа-
вариационный метод был удобен для обсуждения общей ситуации,
он не позволяет легко продемонстрировать разделение враща-
вращательных и колебательных возбуждений. Трудности связаны с
поправкой W'n(R), которая, вообще говоря, не инвариантна от-
относительно вращений. Предпочтительнее учесть инвариантность
Н и #<°> относительно вращений с самого начала, и искать
собственные векторы Н с заданным полным моментом. Соб-
Собственные векторы #<0) можно параметризовать:

286 ГЛ. XVIII. ВАРИАЦИОННЫЙ МЕТОД И СВЯЗАННЫЕ С НИМ ЗАДАЧИ
(i) квантовыми числами полного момента К и т.к.— компо-
компонентой К вдоль некоторой фиксированной оси (не смешивать
с К и);
(И) квантовыми числами, определяющими состояние элект-
ронов, п и, если Л ф 0, s (s = sign Lu);
(iii) расстоянием между ядрами R.
Уравнение Шредингера D1) тогда примет вид
Я<°> | KmKnsR) = Wn (R) | KmKnsR). F9)
Адиабатическое приближение состоит в том, что собственные
векторы оператора Н ищутся в подпространстве с вполне опре-
определенными значениями К, тц, п и s, т. е. среди векторов вида
со
\\KmKnsR)y(R)dR G0)
о
(см. формулу E1)). Так же как в §§ 14 и 15, вариационный
метод приводит к уравнению Шредингера для радиальной вол-
новой функции y{R), и собственные значения определяют уров-
уровни энергии молекулы, соответствующие квантовым числам К
и п (от гпц и s эти уровни не зависят).
Гамильтониан этого радиального уравнения h получается
таким же способом, как и в § 15. Вклад в него от Я<°> равен
Wn(R). Для вычисления вклада от кинетической энергии ядер
T.v удобно записать этот оператор в виде
T = + '
Tn = 2М
(где М — приведенная масса ядер, PR — радиальный импульс),
и каждое слагаемое рассматривать отдельно. Легко показать,
что первое слагаемое дает
+ ^М' <72>
где w'n(R) — малая поправка, не зависящая от К, тц и s.
Вклад второго слагаемого, которое представляет кинетическую
энергию вращения, требует более подробного анализа. Этог
вклад равен произведению h2/2MR2 на среднее значение опе-
оператора G2 в подпространстве векторов вида G0). Используя
равенство F7), находим
(G2) = ((К - LJ) = VK(K+l)-2 (KL) + <L2>.
Поскольку \KmKnsRy — собственный вектор оператора Lu, то
среднее значение компоненты L по оси, перпендикулярной и,
равно нулю. Отсюда, принимая во внимание соотношение F8),

§ 17. ПРЕДСТАВЛЕНИЯ О ДВУХАТОМНЫХ МОЛЕКУЛАХ 287
получаем
Среднее <L2> представляет собой некоторую положительную
величину, зависящую только от п. Если ввести функцию w"n{R) =
== (<L>2 — 2h2A2)/2MR2, то для вклада от кинетической энергии
вращения получим выражение
1} +wM- G3)
Малые поправки w'n{R) и w'n{R) можно включить в потен-
потенциал Wn(R). Тогда радиальный гамильтониан примет вид
т. е. это гамильтониан частицы массы М с моментом импуль-
импульса К в потенциале Wn(R).
Отметим, что возможные значения целого числа К зависят
от п. На самом деле, К~^\Ки\. Фиксируя п, мы фиксируем Л,
и, поскольку | Ки| = |Ьи| = Л, то
К> Л. G5)
Собственные значения h есть уровни энергии Е, и они нахо-
находятся из решений радиального уравнения
hy(R) = Ey(R).
При заданных Кип это уровни энергии частицы массы М с
моментом импульса К в потенциале Wn{R). Для их парамет-.
ризации мы будем использовать дополнительное квантовое чис-
число v. Таким образом, п — электронное квантовое число, v —
колебательное квантовое число, К — вращательное квантовое
число.
Основные характеристики получающегося спектра зависят
от поведения функции Wn(R), которая имеет четко выражен-
выраженный минимум при некотором значении расстояния между яд-
ядрами Ro, отвечающем положению устойчивого равновесия ядер
молекулы. Эксперимент показывает, что Wn(R) можно чаще
всего с хорошей степенью точности представлять как потенциал
Морса (см. рис. 15 и задачу 5). Для низших уровней волновая
функция y(R) сосредоточена в основном в малой области вок-
РУг Яо (с размером порядка %Ro) и описывает колебания ядер
около положения равновесия.
В первом (гармоническом) приближении можно заменить R
в члене вращательной энергии на Ro, а вместо Wn(R) подста-
подставить два первых неисчезающих члена разложения этой функ<
ции по степеням q = R — ^о. Вводя обозначения

288 ГЛ. XVIII. ВАРИАЦИОННЫЙ МЕТОД И СВЯЗАННЫЕ С НИМ ЗАДАЧИ
приходим к радиальному уравнению
Ш Ч? + Еп + Т
- EnvKy
"Это уравнения Шредингера для гармонического осциллятора,
следовательно,
(±)<un + K(K + l)Bn G6)
= 0, 1, 2, ...; К =
Л + 2, ...).
Мы видим, что энергия имеет вид суммы трех слагаемых: элек-
электронной энергии Еп, энергии
V/Vo
О
'I
Рис.
У
\
/
•
——
Фа
(
15. Потенциал Морса V —
2 «M/»«^/»)
-2 «-
расстояние между ядрами в положе-
положении равновесия, Ко — значение потен-
потенциала в этой точке. Ширина мини-
минимума тем меньше, чем меньше отно-
отношение b/Ro. На рисунке b/R0 = 0,68,
что соответствует молекуле водорода.
рождении или кратности
функция молекулы имеет вид
колебания ядер внутри молеку-
молекулы (v -}- -у) Ао„ и вращатель-
вращательной энергии К(К+ 1) В п. На-
Наблюдаемый порядок величин
квантов hton и Вп подтверж-
подтверждает анализ § 12 и последую-
последующие заключения о структуре
молекулярных спектров ').
Мы не будем здесь остана-
останавливаться на тех изменениях,
которые необходимо сделать
в теории, чтобы учесть суще-
существование спина.
Упомянем только об одном
замечательном эффекте, кото-
который связан со спином и стати-
статистикой ядер. Поскольку взаи-
взаимодействие спинов ядер с ос-
остальной частью молекулы пре-
пренебрежимо мало, основной эф-
эффект состоит в спиновом вы-
каждого из уровней. Собственная
') Для электронного основного состояния молекулы водорода (состояние
2+) первые уровни хорошо описываются этой формулой с Ео = —4,72 эв,
йшо = 0,54 эв я Во = 0,0074 эв. Эти числа соответствуют расстоянию между
ядрами Ro = 0,74-10~8 см. Для колебательных и вращательных спектров по-
получается более хорошее согласие, если использовать для их вычисления в ка-
качестве Wo(R) потенциал Морса с Уо == 4,72 эв, Ro — 0,74-10~8 см и Ь =
= 0,68 Ro (см. рис. 15 и" задачу 5); энергия диссоциации молекулы равна
Vo — -g- й»о.

§ 17. ПРЕДСТАВЛЕНИЯ О ДВУХАТОМНЫХ МОЛЕКУЛАХ 289
и кратность вырождения равна числу линейно независимых
функций %{щ, ц2), которые могут быть построены. Если спины
двух ядер равны /, и /2, то существует B/i + 1) B/2+ 1) таких
функций. Если ядра различны, то дополнительных ограничений
на функцию Т нет и кратность каждого уровня равна
B/i + 1) B/2+ !)• Если же мы имеем два тождественных ядра
со спином / (/1 = \ч = /), то волновая функция Т должна быть
симметричной или антисимметричной относительно замены
R *-+ — R, и-1 +-* Иг
в зависимости от того, являются ли ядра бозонами или фер-
мионами, т. е. целое или полуцелое число /. В B;+ 1 ^-мер-
^-мерном пространстве функций % можно построить (/+ 1)B/+ 1)
симметричных функций и /B/+ 1) антисимметричных функций
(задача XIII. 13). Следовательно, кратность g зависит от того,
симметрична или антисимметрична функция Чг(/?, х), другими
словами, она зависит от четности функции Ф при отражении
только координат ядер. Вводя для этой четности обозначение
й(й = ±1), мы имеем
(/ целое) (/ полуцелое)
(/+1)B/+1) /B/+1), если S = +1,
/ B/ + 1) (/ + 1) B/ + 1), если й = — 1.
Интересное следствие вытекает из того факта, что й зависит
от четности полного орбитального момента. Можно показать,
что й =(—l)KS>e, где йе(=±1), зависит от поведения элект-
электронной волновой функции, соответствующей Ф, относительно
отражения. Если Л Ф О, то каждому уровню отвечают две элек-
электронные волновые функции противоположной четности йе. Дл^
уровней 2 (Л = 0) существует только одна волновая функция
с вполне определенным значением четности йе ( + 1 или —1), и
кратность g меняется характерным образом при переходе от
одного вращательного уровня к другому ').
Эти характерные черты энергетического спектра 2 уровней
двухатомных молекул, состоящих из одинаковых ядер, легко
можно наблюдать при экспериментальном исследовании поло-
полосатых спектров таких молекул. Поскольку вероятности опти-
оптических переходов между состояниями с различными спиновыми
функциями очень малы, практически наблюдаются только пе-
переходы, сохраняющие четность К. Кроме того, при обычных
условиях наблюдения относительная интенсивность линий, со-
соответствующих четным значениям К, и линий, соответствующих
нечетным значениям К, непосредственно связана с отношением
') В частности, если / = 0, то отсутствуют уровни с 5 = —1 и К мо-
может принимать только значения вполне определенной четности.
10 А, Мессиа

290 ГЛ. XVIII. ВАРИАЦИОННЫЙ МЕТОД И СВЯЗАННЫЕ С НИМ ЗАДАЧИ
вычисленных выше кратностей, т. е. равна либо (/+ 1)//, либо
//(/ + 1) в зависимости от знака 5>е и того, являются ли ядра
бозонами или фермионами. Это позволяет непосредственно из-
измерять спины ядер.
ЗАДАЧИ И УПРАЖНЕНИЯ
1. Пусть Ец и Ч'о — энергия и волновая функция основного состояния дан-
данной квантовой системы. Вычисление вариационным методом дает энергию
?Var и волновую функцию Ч\аг- Будем считать Ч^о и 'Fvar нормированными на
единицу и введем обозначение 8=1— | (Ч^Ч^аг) |2. Величина е равна нор-
норме проекции функции Ч^,, на подпространство, ортогональное Ч'о, и характе-
характеризует отличие состояния 4rv«r от Ч'о. Доказать, что
(Ei — энергия первого возбужденного уровня). Показать, что результаты § 4
удовлетворяют этому неравенству, и провести обсуждение.
2. Предполагая известной волновую функцию основного состояния атома
водорода, вычислить первый возбужденный уровень, выбирая в качестве проб-
пробной функции ту часть функции и = ре~6р, которая ортогональна волновой
функции основного состояния (обозначения § 4). Сравнить с точным собствен-
собственным значением и волновой функцией.
3. Доказать неравенства A1) и A2).
4. Выбирая в качестве пробной функции и = р +1е~6р (обозначения § 4),
вычислить низший уровень атома водорода, соответствующий моменту импуль-
импульса /. Сравнить с точным ответом и прокомментировать.
5. Рассмотреть частицу с массой М на прямой в потенциале Морса
у((?) = у0[е-2'?/*-2е-*/ь].
Найти волновые функции и уровни энергии.
N. В. Волновое уравнение сводится к уравнению Лапласа следующей за-
заменой функции и аргумента:
где
Имеется конечное число дискретных собственных значений, зависимость кото-
которых от целого числа п определяется формулой

ГЛАВА XIX
ТЕОРИЯ РАССЕЯНИЯ
§ 1. Введение
До сих пор мы рассматривали лишь простейшие задачи тео-
теории столкновений: рассеяние элементарной частицы на цен-
центральном потенциале и столкновение двух частиц. Вторая за-
задача сводится к первой после разделения движения центра
масс и относительного движения. Решение задач такого типа
было приведено в главе X, в дальнейшем оно было дополнено
обсуждением кулоновского рассеяния (гл. XI, раздел II) и рас-
рассеяния двух тождественных частиц (§ XIV. 9—10). Кроме этого,
в § XVII. 5 мы получили простое выражение для сечения рас-
рассеяния частицы на потенциале V(r), считая потенциал V(r) воз-
возмущением и ограничиваясь только эффектами первого порядка
(ур. (XVII. 54)). Однако рассуждения в § XVII. 5 основывались
на нестрогом определении сечения, которое необходимо обос-
обосновать.
В этой глав.е мы, с одной стороны, построим формализм, по-
позволяющий рассматривать процессы столкновения сложных (со-
(составных) частиц, а с другой стороны, покажем как применять
для вычисления сечений рассения теорию возмущений и вариа-
вариационные методы, которые были развиты в предыдущих главах.
Существуют два различных способа изложения этих вопро-
вопросов. Первый — состоит в строгом обосновании определения се-
сечения из § XVII. 5 с использованием таких понятий как вероят-
вероятность в единицу времени и единичный падающий поток и связи
этих величин с матричными элементами оператора эволюции
U(t, f) в пределе, когда t-+-\-oo, f-»—оо. Второй способ
представляет собой простое обобщение рассуждений из раз-
раздела I главы X, согласно которым сечения рассеяния непосред'
ственно связаны с асимптотическим поведением стационарных
решений уравнения Шредингера. В данной главе мы будем сле-
следовать второму из этих эквивалентных подходов ').
') Изложение первого способа см. в работах: В. Lippmann, J. Schwinger.
Phys. Rev. 79, 469 A969); M. Gell-Mann, M. L. Goldberger. Phys. Rev. 91, 398
A953). Определение сечеиия, имеющееся в этих работах, в некоторых аспек-
аспектах дискуссионно. Обсуждение этих вопросов и возможные их решения приве-
приведены в статье S. Sunakawa. Prog. Theor. Phys. 14, 175 A955).
10*

292 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
Глава состоит из пяти разделов. В первых двух разделах
развивается формализм и описывается теория возмущений на
простом примере рассеяния частицы на потенциале V(r). Об-
Обобщение этих методов на случай сложных столкновений прове-
проведено в разделе III. В следующем разделе рассматриваются ва-
вариационные методы. Свойства амплитуд рассеяния, которые сле-
следуют из таких общих свойств гамильтониана как эрмитовость,
инвариантность относительно обращения времени, симметрия,
приведены в разделе V.
Раздел I. СВОБОДНАЯ ФУНКЦИЯ ГРИНА
И ПРИБЛИЖЕНИЕ БОРНА
§ 2. Интегральные представления амплитуды рассеяния
В этом и следующем разделах мы будем обсуждать рассея-
рассеяние частицы массы т на потенциале V(r). Обозначим оператор
кинетической энергии Но, а полный гамильтониан Н
Предположим, что потенциал V асимптотически стремится
к нулю быстрее, чем 1/г. Потенциалы типа 1/г будут кратко
исследованы в § 15.
В дальнейшем у нас появятся различные типы волн, кото-
которые мы будем обозначать соответствующими буквами. Так,
букву ф зарезервируем за плоскими волнами, ф — за стацио-
стационарными решениями гамильтониана Н. Для заданного волно-
волнового вектора k определим:
(i) плоскую волну фй==е'*г;
(п) стационарные волны i|)<+> и ф^-', которые характери-
характеризуются соответственно асимптотическим поведением: е'*г + рас-
расходящаяся волна и е'*г + сходящаяся волна.
В частности, если ka — волновой вектор падающих на потен-
потенциал частиц, а Е—их энергия (ka = k = BтЕ)'1*), то стацио-
стационарная волна рассеяния (определение § X. 3) есть ф^. Это ре»
шение и амплитуда рассеяния /ft* определяются условиями
Сечение рассеяния в направлении Q& обозначим doa-+b/dQ.
В главе X было показано, что

§ 2. ИНТЕГР. ПРЕДСТАВЛЕНИЯ АМПЛИТУДЫ РАССЕЯНИЯ 293
Пусть ka — вектор длины k в направлении пь. В этом раз-
разделе будут фигурировать только стационарные волны, опреде-
определяемые векторами ka и кь. Поэтому для упрощения записи мы
будем систематически заменять индексы ка, кь на а, Ь соответ-
соответственно.
Установим прежде всего наиболее общие свойства амплитуд
рассеяния. Рассмотрим два потенциала U(r) и 0(г) и обозна-
обозначим стационарные решения для соответствующих гамильтониа-
гамильтонианов соответственно g и §. Наибольший интерес для нас будут
представлять решения IjT* и |а+>:
)->=.??1->, E)
G)
Покажем, что
{IV \(U-U)\ ?а+)) - J 1Г (Г) (U (Г) - & (Г)) |<+) (Г) dr =
(посредством — Qa обозначаем направление, противополож-
противоположное па).
Доказательство проведем аналогично тому, которое исполь-
использовалось в § X. 17 при получении интегральных представлений
для фазовых сдвигов. В случае, когда это не будет приводить
к недоразумениям, мы будем опускать индексы Ь, а и сим-
символ ~ . Умножим уравнение F) на |<->* и вычтем из него ра-
равенство, полученное умножением выражения комплексно-сопря-
комплексно-сопряженного к уравнению E) на |1+). Так как U вещественно, по-
получаем
- -ш F(")Ф (д?(+)) - №*) ?(+)) + ^' & ~ °) ?(+)=о-
Интегрируя по объему сферы радиуса R с центром в начале
координат, имеем
(Г' I (U - О) 11<+)> = ?- Um \ (!<->• (А|(+>) - (Дб<->-) |<+>) dr.
•"-'<« A0)
Несмотря на эрмитовость оператора Л, интеграл в правой
части не обязан исчезать в пределе, так как функции | не яв-

294 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
ляются квадратично интегрируемыми. Используя теорему Гри-
Грина, преобразуем этот интеграл в поверхностный интеграл по
сфере радиуса R.
Пусть gi и |г — функции от г, будем обозначать интеграл по.
такой сфере от «радиального вронскиана»
следующим образом:
Ни h} = \w К,, |s] |г=я R2dQ=\w [г|„
В силу теоремы Грина имеем
<
Уравнение A0) можно теперь переписать так:
<|<-> | (U - U) ||<+>> - ? Дт {!<-»*, |<+>}. A2)
Поверхностный интеграл {|(~>*, ?(+)} стремится асимптотически
к константе, которую можно легко вычислить, подставляя вме-
вместо функций | и их производных первый член их асимптотиче-
асимптотического разложения по степеням \/г. Используя формулы G) я
(8), находим
lim few, g<+>}= lim {e-'V, e'V} + iim {e-f*»r, ;<^
i?-*-oo R-+°o R-+<x> l
+ lim {/<->* -^1, e' V] + lim If-*- J^L, f»J^
Асимптотика плоской волны имеет вид (задача 1):
&1кт7-Г«пЬ[б (Q' - пк) e'kr ~ б (Q' + Qft) е""Г] +
В правой части равенства Qr и ?2* обозначают направления век-
векторов г и k, б-функции определяются их свойством
справедливым для любой (гладкой) функции ф от угловых пе-
переменных Q. Если мы заменим плоские волны в правой части
формулы A3) их асимптотическими выражениями, то интегри-
интегрирование по углам легко выполняется. Поскольку векторы кь
и ka имеют одинаковую длину, то первый член равен нулю
(в согласии с результатом задачи 2). Во втором члене только
сходящаяся часть плоской волны дает ненулевой вклад, кото-

§ 3. СЕЧЕНИЕ РАССЕЯНИЯ И Г-МАТРИЦА 295
рый равен —4n/4+)(Q&). То же верно и для третьего слагаемого,
чей вклад равен 4я^->*(—Qa). Четвертое слагаемое равно нулю.
Таким образом, имеем
Ит (Г", |(+>} = - 4я (Г> (QJ - /<">«(- QJ).
Подставляя этот результат в уравнение A2), получаем соотно-
соотношение (9). ¦
Наиболее интересное свойство соотношения (9) — его неза-
независимость от конкретной формы потенциалов U и 0. Требуется
только, чтобы потенциалы были вещественными и убывали на
бесконечности быстрее, чем 1/г.
В качестве первого примера возьмем
U=V, 0 = 0.
Соотношение (9) тогда примет вид
h+)(Q)- A5)
Это интегральное представление амплитуды рассеяния будет
использовано в следующих двух параграфах в качестве исход-
лого для борновского приближения.
Положим теперь
u=u=v.
Левая часть соотношения (9) обращается в нуль и, следова-
следовательно, две амплитуды в правой части равны друг другу
К)(?ь) = П-)'(-па)- A6)
Наконец, пусть
U = 0, 0=V.
Тогда
Сравнивая соотношения A5), A6) и A7), получаем важное
равенство
§ 3. Сечение рассеяния и 7-матрица. Микрообратимость
Если подставить интегральное представление амплитуды
рассеяния A5) в формулу D), то получим следующее выраже-
выражение для сечения рассеяния:
m?

296 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
Для того чтобы преобразовать это выражение к виду, напоми-
напоминающему формулу (XVII.54), мы введем в согласии с опреде-
определением § XVII. 5 (ур. (XVII. 52)) плотность состояний с энер-
энергией
р (?) = BлН)~3 р2 (dpIdE) = mhklBnhf,
начальную скорость обозначим v — hk/m. Тогда формула для
сечения рассеяния принимает вид ')
Поскольку |\|з<,+)> и I Ф&> не являются базисными векторами
в одном и том же представлении, то, строго говоря , (a>b | Klifj+'V
не является матричным элементом оператора V. Удобно ввести
матрицу
B0>
Будем называть Т матрицей перехода, а элемент Та-*ь амплитуд
дой перехода а-^Ь. Следует отметить, что матричные элементы
берутся между плоскими волнами с одной и той же энергией.
Можно, очевидно, рассматривать Т как оператор в гильберто-
гильбертовом пространстве, удовлетворяющий условию B0). Однако эта
условие не определяет оператор полностью, оно фиксирует
лишь некоторые матричные элементы в представлении, базисом
которого являются плоские волны. Для полного определения Т
следует задать его матричные элементы между волнами, отве-
отвечающими различным значениям энергии. Это будет сделано
позже.
Формулу A9) теперь можно записать так:
da^ A9*)
Вспомним свойство микрообратимости. Обозначим индек-
индексами Ка и Kb различные волны, отвечающие импульсам —fea
и —kb. Для плоских волн имеем очевидное равенство
Кроме этого, в силу вещественности гамильтониана
') При другом изложении теории столкновений (см. предыдущую сноску)
эта формула получается естественным образом непосредственно из определе-
определения сечения рассеяния.

§ 4. БОРНОВСКОЕ ПРИБЛИЖЕНИЕ 297
В частности,
()>
и поскольку V вещественно «матричные элементы» (ф?~'I УI Фа)
и (ф^а|^|Фй.') равны. Следовательно, соотношение A8)
можно переписать так:
или, пользуясь определением B0),
Ткь+ка = Та+ь- B1)
A fortiori эти две амплитуды имеют одинаковые модули.
Возвращаясь к формуле A9'), мы получаем свойство микрооб-
микрообратимости упругого рассеяния')
B2)
§ 4. Борновское приближение
Формула A9)—точная. Подобно формуле (X. 2), из кото*
рой она была выведена, она связывает сечение рассеяния со
стационарным решением \р{+К В данном случае решение \|з*,+)
фигурирует не в асимптотической форме, а полностью как мно-
житель в интеграле. Если заменить его приближенным реше-
решением, то мы получим приближенное выражение для сечения.
В частности, для достаточно малых V(r) решение iJ)(a+) мало
отличается от падающей плоской волны фа и может быть заме-
заменено последней при вычислении амплитуды перехода. Это дает
борновское приближение
= <Ф»К|ф„>. B3)
В этом приближении равенство A5) сводится к формуле
(XVII. 54), оправдывая наше предположение о том, что оно
дает приближенное выражение для сечения в пределе, когда
V(r) можно рассматривать как возмущение.
Пусть
q = kb — ka,
%q — импульс, переданный частице в процессе столкновения
(рис. 16). Длина вектора q зависит от угла рассеяния 9 между
векторами ka и kb следующим образом:
q = 2ksin\b (k = ka = kb). B4)
') Для центрального потенциала это свойство можно вывести из инва-
инвариантности относительно вращений. Здесь мы убедились, что оно выполняется
и для нецентральных потенциалов.

298 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
Из формулы B3) имеем
Таким образом, в борновском приближении сечение рассея».
ния принимает особенно простой вид
Сечение пропорционально квадрату модуля преобразования
Фурье от V(r), соответствующего импульсу, переданному при
столкновении. Отметим, что зависимость сечения от энергии а
угла входит только посредством вектора q~
Для центрального потенциала ситуация
еще проще. После интегрирования по углам
правая часть B5) становится равной
r(q) = -^\ sin qrV (r) r dr. B7)
Рис. 16. q I
Дифференциальное сечение зависит в этом случае только от
величины hq переданного импульса. Используя в качестве пе-
переменной интегрирования q вместо 0, получим полное сече-
сечение (Jtot
2*
B8)
о
Из этих формул можно вывести ряд общих заключений от-
относительно поведения сечений при высоких энергиях. Обозна-
Обозначим радиус действия потенциала V(r) через о. Так как веще-
вещественная функция У (г) существенно отлична от нуля только
в области с линейными размерами порядка а, то ее преобразо-
преобразование Фурье сосредоточено в начале координат в области с ли-
линейными размерами порядка 1/а ').
Следовательно, сечение рассеяния отлично от нуля только
в области, где q с<С 1/а. Согласно формуле B4) эта область
соответствует углам рассеяния
1 1
Sln Т6 ^~2ka'
') В данном контексте в качестве а можно брать величину порядка сред-
не-квадратичного отклонения распределения
У2(г)
[ V2 (г') dr'

§ 5. ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ ТЕОРИИ РАССЕЯНИЯ 299
При высоких энергиях (ka ^> 1) происходит в основном рас-
рассеяние вперед в конусы с углом 0 меньше, чем Ilka. Эти вы-
выводы основаны на борновском приближении, их можно срав-
сравнить с результатами о высокоэнергетическом рассеянии на твер-
твердой сфере (§ X. 13).
Полное сечение стремится к нулю как 1/Е. Результат с оче-
очевидностью следует из формулы B8), откуда получаем следую-
следующую асимптотику:
B9)
Эти выводы легко обобщить и на случай нецентральных потен-
потенциалов.
§ 5. Интегральное уравнение теории рассеяния
До сих пор т|з(а+) определялось как решение уравнения Шре-
дингера, удовлетворяющее определенным асимптотическим ус-
условиям. Теперь мы покажем, что ¦ф[+) является также решением
некоторого интегрального уравнения. В результате мы сможем
разложить\|з(+) в ряд по степеням потенциала V и вычислить по-
поправки к борновскому приближению. Для этого мы восполь-
воспользуемся тождеством ')
Из него следует, что функция
m Jk\r-r'\
" \* > ' / — 2яА2 \r r'I \°v)
удовлетворяет уравнению
^-(A + fe2)^(r, r') = 6(r-rO. C1)
$ (r, r')—функция Грина свободной частицы с энергией Е =
= h2k2/2m. Комплексно-сопряженная функция обладает тем же
свойством.
') Это тождество следует понимать в смысле обобщенных функций,e'ftV-~
дифференцируемо произвольное число оаз. При вычислении лапласиана мы ио
пользуем тождество
ДA/г)=п-4яб(г)
и свойство
Д (/«) = (Aft g + 2 (Vft (V«) + / Aff-

300 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
Запишем уравнение Шредингера для г|)а<+)
¦^(A + ft8)*^*- C2)
Предположим, что нам известна функция F(r)z== У(г)г|з(г).
Тогда для ф(г) получим неоднородное дифференциальное урав»
нение в частных производных. Из C1) следует, что функция
1({r)^\${r,rf)F{r')dr'
является решением этого уравнения. Общее решение получится
добавлением к ф(г) общего решения однородного уравнения.
Другими словами, если ф удовлетворяет уравнению C2), то
ф — ф — плоская волна с той же энергией
¦|L(A+ **)(,!>.-$) «0 C3)
и наоборот.
Для полного определения этой плоской волны необходимо
найти ее асимптотическое поведение. Покажем вначале, что ф
стремится асимптотически к расходящейся волне. Подставляя
в C0) асимптотическое разложение
для г > г' имеем
V^f) <34>
отсюда
Ш\ C5)
Это выражение справедливо, когда г много больше радиуса
действия потенциала (г> а). Следовательно, если асимптотика
Ф определена формулой C), то ф — tj) будет также иметь асимп-
асимптотику (ег*вг + расходящаяся волна). Поскольку она также
удовлетворяет уравнению C3), то она должна быть плоской
волной. Поэтому
€' - е'V - -Ш? \ f^ V И Ф<+> И *г>. C6)
Уравнение C6) эквивалентно уравнению C). Оно называется
интегральным уравнением теории рассеяния.

§ 6. БОРНОВСКОЕ РАЗЛОЖЕНИЕ 301
Используя C4), асимптотическое поведение ^+] можно вы-
вывести непосредственно из правой части уравнения C6); свой-
свойство A5) можно доказать тем же способом.
Приведенные рассуждения можно повторить, заменив функ-
функцию &(г, г') на комплексно сопряженную &*{г, /), которая
также является функцией Грина свободной частицы, но соот-
соответствует асимптотическому условию со сходящейся (сфериче-
(сферической) волной. В результате получим интегральное уравнение
¦Г " e'V - Шг $ ПТ^Т-V И <~] И dr'. C7)
§ 6. Борновское разложение
Уравнения C6) и C7) можно решать итерациями. Метод
аналогичен тому, который использовался при решении уравне-
уравнения (XVII. 13) нестационарной теории возмущений.
Рассмотрим уравнение C6). Подставляя вместо ф**1 в ин-
интеграл в правой части равенства плоскую волну е'*°г, полу-
получаем
^+> = е' V + J 9 (г, г') V (г') е' *S dr'.
Подставляя Ц+) вместо i|>(e+), получим
(г, г')V(г')ф;+)(г')dr'.
Аналогично получаем a|^+) и так далее. При подходящих усло-
условиях возникающая в результате этой процедуры последователь-
последовательность сходится к точному решению o|j(aH Тем самым оно пред-
ставимо в виде разложения по степеням V
ф1+> = е' V + J] J Кп (г, г') е' V dr', C8>
Кп (Г, Г') = J К, (Г, Г") Кп-1 (Г", Г') dr", (Д > 1),
Это борновское разложение стационарной рассеянной волны.
Аналогичное разложение для Та-+ь можно получить, подстав-
подставляя разложение ф^' в интеграл (<р6 j V | ^+)). Это разложение

302 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
по степеням V сходится для достаточно малых Vм). Оставляя в
разложении только первый член, получаем борновское прибли-
приближение.
§ 7. Критерии применимости борновского приближения
Для того чтобы борновское приближение имело смысл, не-
необходимо, чтобы ошибка, сделанная при вычислении Та-уь, когда
¦ф^1"' заменяем на плоскую волну фа, была пренебрежимо малой.
Следовательно, в области, где потенциал V отличен от нуля,
точная стационарная волна должна мало отличаться от пло-
плоской. Полагая
получим условие
1*'(г)|<1 C9)
(во всех точках, где V{r) относительно велико).
Можно оценить i|/, оставляя первый член ее борновского
разложения. Выбирая ось z вдоль %а> после очевидной замены
переменных получим
/ (г) ва \ е'* (R+Z)V (Я + г) dR/R.
Так как в экспоненте присутствует k, |/| зависит от энер-
энергии. Однако можно получить независимую от энергии оценку
сверху для /@. заменяя выражение под знаком интеграла на
его модуль:
D0)
Обозначим через а радиус действия потенциала2), a Vo — его
среднее значение. В соответствующей области изменения пере-
переменной г верхняя оценка равна приблизительно 2nVoa2, и бор-
') Сходимость борновского приближения исследована в работах: R. lost,
A. Pais. Phys. Rev. 82, 840 A951); W. Kohn. Rev. Mod. Phys. 26, 292 A954).
Интегральное уравнение, полученное в нестационарной теории возмущений
(гл. XVII), является уравнением вольтерровского типа. Если бы ?/<0> и V были
функциями, а не операторами, то разложение для U, полученное итерационной
процедурой, всегда бы сходилось. Возможное отсутствие сходимости целиком
обусловленно операторной природой Um н V. (С/<0) и V — операторы в гиль-
гильбертовом пространстве.) С другой стороны, интегральное уравнение, рассма-
рассматриваемое нами здесь, имеет фредгольмов тип, и борновское разложение не
всегда сходится.
2) См. сноску к § 4,

§ 7 КРИТЕРИЙ ПРИМЕНИМОСТИ БОРНОВСКОГО ПРИБЛИЖЕНИЯ 303
новское приближение справедливо при всех энергиях, если
Vo < tflma2. D1)
Это условие, очевидно, слишком ограничительное. Интеграл
|/| достигает предела, определяемого D0), только при доста-
достаточно малых энергиях, когда множитель eik{R+Z) практически по-
постоянен в области изменения потенциала1), т. е. когда ka <C 1.
Если же ka > 1, то этот множитель быстро осциллирует в рас-
рассматриваемой области, и приведенная оценка излишне груба.
При fe->oo осцилляции становятся все быстрее, и интеграл /
стремится к нулю. Мы можем, следовательно, ожидать, что
борновское приближение будет справедливым при достаточно
больших энергиях.
Асимптотическое поведение / при больших энергиях можно
получить методом стационарной фазы. Основной вклад дает об-
область, окружающая точки, где осциллирующий фазовый мно-
множитель стационарен, эта область окружает полуось X = У = 0,
Z < 0. Опуская детали вычислений2), получаем
г
I~<Jf- \ V (х, у, z')dz' + O(k~2). D2)
— оо
Поэтому в таком пределе |/| имеет порядок 2nVoa/k в рассма-
рассматриваемой области изменения г. Критерий C9) будет выполнен,
если
ka>l, V0^.h2klma. D3)
Для того чтобы получить критерий применимости борнов-
ского приближения для промежуточных энергий, когда нера-
неравенство D1) не выполнено, необходимо оценивать интеграл /
в каждом конкретном случае. На практике его обычно оцени-
оценивают для одной специально выбранной точки в области изме-
изменения потенциала, например, г = 0. Для центрального потен-
потенциала после интегрирования по углам получим
оо
/ @) = ^L J A _ e2lfer) V (r)
dr.
') Если знак V постоянен. Более того, мы имеем
См., например, L. 1. Schiff. Phys. Rev. 103, 443 A956),

304 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
Это выражение хорошо согласуется с формулами D0) и D2).
Отсюда получаем критерий
(l-e2ifer) V(r)dr
о
h2klm. D4)
В теории столкновений величиной, характеризующей сече-
сечение, служит геометрическое сечение рассеяния 4яа2, соответ*
ствующее области взаимодействия частиц, размеры которой по-
порядка а. Когда применимо борновское приближение, полное се-
сечение мало по сравнению с этой величиной:
<rtot <C геометрическое сечение. D5)
Докажем это неравенство в двух предельных случаях: ka -С 1 и ka~>
>• 1. Воспользуемся выражением B8) для полного сечення. В соответствии
с определением (ур. B5)), функция V(q) имеет величину порядка Bя) V^a3
в области с радиусом 1/а и центром в начале координат. Во всех других точ-
точках она практически равна нулю. Подставляя эти значения функции в правую
часть равенства B8), получим
о[*\/4па « 2я G0та2/й2J, если ka < 1,
а^]/4яа2 ж -^ я (y0ma/h2kJ, если ka>\.
Условия применимости борновского приближения имеют вид неравенства
D1) в первом случае и неравенства D3)—во втором. В обоих случаях
?>/2
Для справедливости борновского приближения выполнение
неравенства D5) необходимо, но недостаточно. Бывает, чго
из-за резонансных эффектов, таких как эффект Рамзауера —
Таунсенда при рассеянии медленных электронов на атомах, се-
сечение рассеяния много меньше геометрического сечения и без
быстрой сходимости борновского разложения. На практике ре-
резонансные эффекты легко распознать по их большой чувстви-
чувствительности к изменениям энергии налетающих частиц. С учетом
этих фактов неравенство D5) является очень полезным Крите*
рием применимости борновского приближения.
§ 8. Упругое рассеяние электронов на атоме
В качестве приложения рассмотрим упругое рассеяние за-
заряженной частицы на атоме. В принятой нами упрощенной
трактовке атом рассматривается как распределение электриче-
электрических зарядов. Вычислим в борновском приближении сечение
рассеяния заряженной частицы на потенциале, создаваемом
этим распределением зарядов. Метод даст правильное сечение,
если мы будем работать в области, где борновское приближе-

§ 8. УПРУГОЕ РАССЕЯНИЕ ЭЛЕКТРОНОВ НА АТОМЕ 305
ние справедливо (см. § 21). Будем считать для определенности,
что налетающей частицей является электрон. Естественно было
бы учесть эффект обмена налетающего электрона с электро-
электронами атома. Однако для энергий, при которых справедливо бор-
новское приближение, такой эффект дает лишь малые поправки,
поэтому мы им пренебрегаем.
Атом, по предположению, будем считать нейтральным. Обо-
Обозначим атомный номер Z, а плотность электронов — р(г)
Электрический потенциал удовлетворяет уравнению Пуассона
ДФ=-4ш?[гб(г) — р(г)]. D6)
На электрон действует потенциал
который удовлетворяет аналогичному уравнению. Совершив
преобразование Фурье, получаем соотношение
D7)
которое связывает функцию T(q) (определение B5) или B7))
и функцию
оо
F (q) = ^ е-/?гр {г) dr = q~l ^ sin qr p (г) r dr. D8)
о
Используя D7), получим сечение в борновском приближении
(УР- B6))
da A[Z - Р {д)\* т*е*
Функция F(q) называется форм-фактором плотности элек-
электронов. Ее общую форму можно легко получить из р(г). В част-
частности, имеем F@)=Z. Пусть а — радиус атома, т. е. среднее
расстояние электронов от ядра. Тогда функция F в существен-
существенном отлична от нуля лишь в области q <z. I/a.
Например, если плотность электронов определена функцией
то форм-фактор равен
Когда qa ~Э> 1, т. е. для больших углов рассеяния,
sin 4-
2 ^ 2ka '

306 ГЛ. XIX ТЕОРИЯ РАССЕЯНИЯ
форм-фактор практически исчезает [F(q) <C Z] и формула D9)
сводится к формуле Резерфорда, дающей сечение рассеяния
только на ядре. Влияние электронов атома при этом пренебре-
пренебрежимо мало.
Их влияние становится существенным, если qar^. 1. Следо-
Следовательно, эффект экранировки значителен для малых углов
sin4e^w- <50>
Это согласуется с классической картиной, в которой малые углы
рассеяния соответствуют большим прицельным параметрам.
В заключение проверим справедливость борновского прибли-
приближения.
Радиус действия потенциала имеет порядок а. Оценка, ис-
использующая модель Томаса — Ферми, дает
те'
За среднее значение потенциала можно принять величину ку-
лоновского потенциала ядра при г = а
В дальнейшем мы используем привычные обозначения
_ Пк __ Ze2
т ' hv '
так что
2_
Критерий D1) требует, чтобы Z3 ^.1 и, следовательно, ни-
никогда не реализуется. Таким образом, борновское приближение
оправдано лишь для достаточно больших энергий. В этой обла-
сти (ka 3> 1), т. е. для y<g.Z3, критерий D3) требует у <С 1.
Итак, борновское приближение справедливо лишь при до-
достаточно высоких энергиях, для которых у <^ 1. В этом случае
эффект экранировки существен лишь при очень малых углах
и становится практически неощутимым вне области, определяе-
определяемой неравенством E0), т. е. вне области Q ^. у. Эксперимен-
Экспериментальное определение форм-фактора возможно посредством точ-
точных измерений углового распределения при малых углах и боль-
больших энергиях и последующего использования формулы D9).

§ 9. ВЫЧИСЛЕНИЕ СДВИГОВ ФАЗ 307
§ 9. Центральный потенциал. Вычисление сдвигов фаз
В случае центрального потенциала амплитуда Та-+ь зависит
только от угла рассеяния 6 (cos 8 = kakb/k2), и ее можно пред-
представить в виде разложения
= 16 Е W (h) Y? fa) = 4л S W + 1) TtP, (cos 9). E1)
I, m I
Коэффициенты Ti легко связать со сдвигами фаз, сравнивая это
разложение с (X. 31):
Г, =» — Й2ем' sin btl2mk. E2)
С другой стороны, разложение E1) можно получить непосред-
непосредственно из интеграла Лр61 V |^J,+)), если разложить волны cpft и
¦ф^+) по сферическим гармоникам. Учитывая соотношение ор-
тонормировки сферических гармоник, легко провести интегри-
интегрирование по углам и получить коэффициенты Ti в виде интегра-
интегралов по радиусу. Полагая
E3)
I, Ш
находим
оо
Г, = $/, (И К Wi|>, (г) г2 dr. E4)
о
Несложно показать (задача 4), что
sin {kr
Сравнивая соотношения E2) и E4), получим интегральное
представление sin б<, приведенное в § X. 17 (ур. (X. 73)). Оно
сводится к борновской формуле для сдвигов фаз (ур. (X. 75))
в пределе, когда /-волна достаточно близка к свободной волне.
Из интегрального уравнения теории рассеяния таким же об-
образом получаем интегральное уравнение для ofy. При этом удоб-
удобно использовать следующее разложение функции Грина (за-
(задача 4):
T! S h (*'<) h\+) (br>) Yf (?0 Yf (r), E5)
где г< и г> означают соответственно меньший и больший из двух
отрезков г и г'. Подставляя E3), E5) и разложение плоской

308 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
волны в интегральное уравнение C6), получаем интегральное
уравнение для расходящейся парциальной волны
ф, (г) = /, (кг) - Bm*/ft2) J /, (кГ<) Л<+> (йг>) V (г') ^ (rf) r'* dr'.
о
E6>
Итерирование этого уравнения дает ф; в виде разложения па
степеням V.
§ 10. Функция Грина как оператор. Связь с резольвентой
оператора Но
В предыдущих параграфах функция Грина фигурировала как.
ядро интегрального уравнения. Ее можно рассматривать также
как матричное представление некоторого оператора Go+>, опре-
определяемого формулой
S4r,r')-<r|G<+>|r'>. E7>
Возьмем вектор |ы> и обозначим соответствующую волновую
функцию u(r) = <r|u>. Вектор G?+)|u), который получается
после действия на |ы> оператора Go+>, задается функцией
(г | G<+> | и) - J S (г, г') ы (г') dr'. E8>
Аналогично определим оператор Go"'
В силу симметрии "Sir, г') по г и г' имеем
СИ"» — C3i+J*. F0)
Индекс 0 показывает, что эти операторы связаны с гамиль-
гамильтонианом свободной частицы Но. Значки (+) и (—) относятся
к асимптотическому поведению, которое с учетом асимптотиче-
асимптотической формы функции Грина (ур. C4)) имеет вид:
<г | G<±> | и)^ —^ ^- \ е*'*^ (г') dr' (k = kr/r). F1)
Результат справедлив для любого вектора |ы> с конечной нор-
нормой (последнее условие обеспечивает сходимость интеграла
в правой части).
Отметим сильную сингулярность этих операторов. Если не
все Фурье-компоненты и(г), отвечающие волновым векторам
длины k, обращаются в нуль, то (r\G<f)\u) на бесконечности

§ 10. ФУНКЦИЯ ГРИНА КАК ОПЕРАТОР 30&-
убывает недостаточно быстро для того, чтобы быть квадратично
интегрируемой функцией. Другими словами, действие Go+) или.
G{a~] на вектор гильбертова пространства дает функцию, не
принадлежащую этому пространству. Следовательно, Go+) и G^
не являются, вообще говоря, операторами в гильбертовом про-
пространстве.
Однако мы можем определить их как пределы операторов
в гильбертовом пространстве
0{о±]=ПтЕ_1Но±{е (е>0). F2>
В правой части формулы стоит резольвента (г — Но)-1 (см.
гл. XVI, раздел III). Это ограниченный оператор в гильберто-
гильбертовом пространстве при всех значениях комплексной переменной z,
за исключением собственных значений Но, т. е. точек положи-
положительной вещественной полуоси. Поведение резольвенты в ок-
окрестности этих точек определено формулой F2). Если z стре-
стремится к Е сверху от вещественной оси (Im г > 0), то (z — Но)-1
стремится к Go+); а если стремится к Е снизу от вещественной
оси (Im z < 0), то (z — Но)-1 стремится к Go~K
Докажем формулу F2). Рассмотрим диагональную матрицу
(г — Но)-1 в {р}-представлении и применим хорошо известное
унитарное преобразование для получения матрицы этого опе-
оператора в {/^-представлении
(г \(z- Но)-110 = -^ \ е- <''-> (г -
Это выражение легко проинтегрировать по углам. Вводя вели-
величину X» определяемую соотношением
г = ti%2/2m, Re ? > 0,
и обозначая
R = r-r',
находим
nh2R
'- Т k'eik'R dk'
Величина последнего интеграла не изменится, если замкнуть-
путь интегрирования дугой полуокружности, расположенной на
бесконечности в верхней полуплоскости. Получившийся контур-

310
ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
ный интеграл равен произведению 2ш на сумму вычетов в по-
полюсах, расположенных в верхней полуплоскости. В данном слу-
случае имеется только один полюс. Его положение зависит от знака
Im ?, а значит, от знака Im z (рис. 17):
(а) Imz>0. Полюс при k'—Z, с вычетом—2
(б) Imz<0. Полюс при k' = — ? с вычетом — ye~'
Следовательно,
т
> = — "V
( eW/R
\e~itR/R
, если Imz>0,
, если Im z < 0.
Эти выражения необходимо сравнить с выражениями для
3{г, г') (ур. C0)). Рассмотрим предел, когда z стремится к Е,
Рис. 17.
а ? стремится к k. При переходе к пределу, в зависимости от
знака (Im z > 0 или Im z < 0) мнимой части г, вычисленный
выше матричный элемент стремится к 'S(г, г') или ^*(г, г'). ¦
Часто легче производить алгебраические преобразования
с операторами, чем с задающими их матрицами. Поэтому зача-
зачастую предпочтительнее использовать операторы Gq+) и Gq"' вме-
вместо функций Грина. Тем не менее следует помнить, что это син-
сингулярные операторы и обращение с ними требует известной
осторожности1). Для полной строгости их следовало бы заме-
') В частности, необходимо помнить, что G действует только на векторы
о конечной нормой. Следующий пример иллюстрирует одну из ловушек, в ко-
которую можно попасть, забыв о сингулярности поведения эгих операторов. Из
соотношения C1) н симметричности функции Грина по г и г' имеем
Это означает, что при действии операторов, стоящих-в левой части этих урав-
уравнений, на вектор с конечной нормой, мы получим тот же вектор. Однако если
понимать эти соотношения буквально, то можно заключить, что оператор
Е — #о имеет обратный, что неверно, aOJ,+i н GJ,"" равны этому обратному
•оператору, а следовательно, равны друг другу, что также неверно.

§ П. ОБОБЩЕННОЕ БОРНОВСКОЕ ПРИБЛИЖЕНИЕ 311
нять регулярными операторами (Е — Но ± ie)~l и аккуратно со-
совершать предельный переход е -»- 0. Далее мы не будем придер-
придерживаться такого уровня строгости. Если хсе Go*' будут заме-
заменяться операторами (Е— Яо ± it)~l, то всегда будет подразу-
подразумеваться, что е — вещественное и положительное число. Фор-
Формулы необходимо рассматривать в пределе е -> 0+.
Интегральные уравнения C6) и C7) теперь можно записать
в виде
F3>
или
±)- <63'>
Итерируя эти уравнения, получаем борновское разложение
В этих выражениях символы я|з и ф означают либо стационар»
ные волны, либо представляющие их кет-векторы.
Сопряженные уравнения получаем из данных заменой кет-
векторов в обеих частях на соответствующие им сопряженные
бра-векторы. В силу эрмитовости Яо
&?. G<-* = G$». F5>
Тогда из формулы F3) получаем
а из формулы F4) получаем борновское разложение
Раздел П. ОБОБЩЕНИЕ НА ИСКАЖЕННЫЕ ВОЛНЫ
§ 11. Обобщенное борновское приближение
Может случиться, что потенциал V(r) слишком велик для
использования борновского приближения, но мы в состоянии
точно решить задачу рассеяния для потенциала, близкого к V.
Тогда удобно рассматривать разность между ними как возму-
возмущение, которое легко учесть, используя простое обобщение ме-
методов раздела I.

312 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
Пусть
V(r)«?/i(r) + BMr),
Hi = H0 + Ux (г). F8)
Тогда имеем
Н = Н, + Wu F9)
где #i — невозмущенный гамильтониан, W\ — возмущение. Бу-
Будем считать, что U\ и V стремятся к нулю быстрее, чем 1/г (об-
(обобщение на потенциалы 1/г будет сделано в § 15). Стационар-
Стационарные состояния Hi предполагаются известными. Будем обозна-
обозначать их буквой х. а соответствующие амплитуды — буквой g.
В дальнейшем мы следуем обозначениям § 2. Величины х|,+) и
?(+> определены соотношениями
Все результаты раздела I, относящиеся к гамильтониану Н,
справедливы также и для Hi. В частности, можно определить
матрицу перехода для столкновений при энергии Е, описывае-
описываемых гамильтонианом Hi. Обозначим ее 7W
(% | т{1) I %) - <ф* I ^ I xL+)> = <4-» I "х I фо>- G0)
Вспомним, что в § 2 мы получили
Интегральное представление для разности Та-*ь —
можно получить, используя (9). Пусть
u=*uu u=v.
Тогда получим
^ \wl
- gi+) (О,)] =
Аналогично, если U —V, U = и{,
D-)\Wl\W) = Ta_>b-T«lb. G2)
Из соотношений G1) и G2) следует
<*ГЧ^.|Х<+>> = <хП^.№+)>, G3)
что является обобщением соотношения A8).
Любое из этих двух интегральных представлений можно ис-
использовать для построения теории возмущений. Соотношение

§ И. ОБОБЩЕННОЕ БОРНОВСКОЕ ПРИБЛИЖЕНИЕ 313
G1) дает
Л*
а-*Ь
~ \**Ь 1^11 Та /•
Это — точное выражение для амплитуды перехода. Первый член
дает амплитуду перехода при отсутствии Wi. Второе слагаемое
дает поправку, обусловленную W\. Для достаточно малых W\
точная стационарная волна •ф(+> мало отличается от х[,+> и мо-
может быть заменена последней в поправочном члене. Таким об-
образом, получаем амплитуду перехода с точностью до первого
порядка по возмущению Wi
ГA) 4- М~> I W I y(+)\
Это обобщение борновского приближения (см. ур. B3)). Отме-
Отметим, что в интеграле возмущения
f (г) ^, (г) Х(о+) И dr G6)
одновременно присутствуют стационарные решения, соответ-
соответствующие уходящим и приходящим волнам.
Если взять U\ = 0, то получим обычное борновское прибли-
приближение. В общем случае, когда Ui ф 0, вычислить этот интеграл
гораздо труднее, чем интеграл из формулы Борна. Ситуация
становится отчасти проще, когда и И{ и V сферически симме-
симметричны. Тогда можно использовать разложения (задача 4)
XL±( =~ ? Л*^, (А; г) Yf (k) Y? (?), G7)
где F;!^; ^) означает регулярное решение радиального уравне-
уравнения
[?^^. + *]*-0 G8)
с асимптотическим поведением
Ft(k; r) ~ sin (kr - | /я + т,Л . G9)
Здесь т(/ — сдвиг фазы /-волны в потенциале U\. Подставляя
разложения Хд+> и х^"' в интеграл G6) и интегрируя по углам,
находим
оо
<ХГ I Wt |xl+)> = — J] B/ + 1) Рг (cos 9) ^ J ^ (ft; г) W, (г) rfr.
г о
Сходимость данного разложения тем лучше, чем меньше радиус
действия Wi.

314 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
§ 12. Обобщение борновского разложения
Для того, чтобы найти поправки высших порядков, необхо-
необходимо разложить т|)Н-> по степеням Wi. По аналогии с методом
раздела I найдем интегральное уравнение для ф@+)э итерируя
которое получим искомое разложение.
Обозначим Gj(+)(r, г') функцию Грина гамильтониана Ни
соответствующую энергии Е = h2k2/2m и имеющую асимпто-
асимптотику расходящейся волны. По определению, это симметричная
функция от г и г', удовлетворяющая дифференциальному урав-
уравнению в частных производных
(Е - #,)(?<+> = [? (Л + V) - U] G<+> (г, г') = 6 (г - г'), (80)
с асимптотикой eikr/r, когда г -> оо, а г' фиксировано. Согласно
определению
(
Эта матрица представляет некоторый оператор G\+\ В следую-
следующем параграфе будет показано, что существует одна и только
одна функция G[+)(r, rf), обладающая этими свойствами.
Мы получим интегральное уравнение, следуя методу § 5 и
используя эту функцию вместо свободной функции Грина. Урав-
Уравнение Шредингера для ¦ф<1+) запишем в виде
(Е - Я,)^+> ^ [-?- (А + А2) - U] Ч><+> = Wrf».
Заметим, что в силу ур. (80) функция
?а+) ~ \G[+> (г, г') Wx (г') я|4+> (г') dr'
удовлетворяет «однородному уравнению»
(?_Я,)Х = О.
Поскольку эта функция имеет ту же асимптотическую форму,
что и Ха+), она с необходимостью равна %<-+\ Следовательно, \|)^+
удовлетворяет интегральному уравнению
= Х(о+) (г) + \ G<+) (г, г') Wx (г') я|>Н"> И dr'. (81)
Разложение iJ)J,+) по степеням W\ легко получить из уравне-
уравнения (81). Подставляя это разложение в «матричный элемент»
правой части уравнения G4), получаем разложение Та-*ь по
степеням U^i. Если мы оставим только первые два члена этого
разложения, то получим приближенное выражение G5).

§ 13. ФУНКЦИЯ ГРИНА ИСКАЖЕННЫХ ВОЛН 315
Функция, комплексно сопряженная к G\+)(r,r'), также яв-
является функцией Грина Hi для энергии Е. Это функция
(/(-'(г, г), которая ведет себя асимптотически как сходящаяся
волна. Используя эти свойства, аналогичным методом можно
ввести интегральное уравнение
^ = Х<Г> + $ G(f' (r, rf) Wt (г') Ч>(,-> (г') йт'. (82)
Можно также получить разложение Та-*ь по степеням Wu если
в качестве исходного уравнения взять (82) и использовать свой'
ство G3). Очевидно, что от этого результат не изменится.
§ 13. Функция Грина искаженных волн
Остается еще доказать существование функций Грина (?<+' и
С?'"). Мы покажем, что при естественном обобщении уравне-
уравнения F2) их можно определить как пределы резольвенты опера-
оператора Н\
= ">-*¦*'•*• (83>
Аналогично для каждого значения Е можно связать с гамиль-
гамильтонианом Я функции
Рассмотрим вначале операторы G<+> и G<-> и покажем, что
(?-tf)G<±>=l, (?*>(?-Я) =1. (85)
Для произвольного вектора конечной нормы, очевидно, имеем
} \u) = \u)-E_i*+.e\u). (86)
Норма второго члена в правой части равна
N(e) = e>(u\{E_*J + e2\u)=s\ \ и (?0 J {Е _ ^ + е, dE'.
Последнее выражение получается, если использовать представ-
представление, в котором диагоналей гамильтониан Н; \u(E')\2dE' —
норма компоненты |и> с энергией Е'. При е^-Ов силу извест-
известного свойства б-функции (ур. (А. 15в)) интеграл стремится
к л|и(?)|2. Таким образом, норма N{&) в этом пределе исче-
исчезает. Следовательно, при е -»- 0 уравнение (86) дает
(Е — Н) G«+> | и) = | и).

316 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
Поскольку это верно для любого |и> (конечной нормы1)), то
имеем
Остальные соотношения (85) можно доказать таким же спосо-
способом. Аналогичным образом имеем
E-Hl) = \. (87)
Уравнения (85) и (87) показывают, что G(±) и G^*1 являются
¦соответствующими функциями Грина операторов Я и Hi при
энергии Е. В {/^-представлении они сводятся к дифференциаль-
дифференциальным уравнениям в частных производных, характеризующим
функции Грина; так, первое из уравнений (87) дает уравне-
уравнение (80).
В предыдущем доказательстве мы аккуратно проделали пре-
предельный переход е-»-0+, поскольку он играл решающую роль.
В дальнейшем мы не будем придерживаться такого уровня
строгости и, следуя соглашению со стр. 310, часто будем заме-
заменять G& на [Е — Hztit}-1, a G<*-—на [Е — Hi±ie]~l, где
е — вещественная положительная бесконечно малая величина.
Поступая так же как в начале § XVI. 16, получим фунда-
фундаментальные тождества
Е — Н ±ie Е — #о ± «е Е — Н ± re Е — #0 ± ге \°°а)
= E-H0±iBV E-H±ie- <88б>
Аналогичные тождества получаются и при замене #i и U\ на Я
и К соответственно, или при замене Я! и W\ на Яо и V.
Из тождеств (88) следуют соотношения2):
')-1, (89а)
)«=!. (896)
Теперь уравнение F3) можно записать в виде
Действуя оператором A + G(±)V) на обе части этого уравне-
уравнения и используя (89а) для упрощения левой части, получаем
важную формулу
¦?» = 0 + E-H±i* V ) Ф.. <90>
') Здесь полностью применимы замечания сноски на стр. 310.
2) Из этих тождеств нельзя сделать вывод, чтоA + G(±) V) и (l — G^** 7)
обратны друг к другу или, что каждый из них имеет обратный. См. сноску
к §10.

§ 13. ФУНКЦИЯ ГРИНА ИСКАЖЕННЫХ ВОЛН 317
Так как Я эрмитов, то, очевидно, имеем
Q(±>+ _ (jm, (91)
Следовательно, сопряженным уравнением к уравнению (90) бу-
будет
Теперь мы в состоянии получить асимптотическое поведение
и G<-) из асимптотического поведения G(o+) и G?~' соответ-
соответственно. Если вектор |и> достаточно быстро убывает на беско-
бесконечности, то из (886) имеем
где
Если вектор \ТУ также достаточно быстро убывает на беско-
бесконечности '), то можно использовать уравнение F1). Получим
(г | G<±> | и) - - -^ ly- <Ф±А | Г) (ft = *r/r). (93)
Оператор G(+>, действуя на вектор гильбертова пространства,
будет давать в общем случае вектор, который ведет себя асимп-
асимптотически, как чисто расходящаяся волна, а оператор G^ —
вектор, ведущий себя асимптотически, как чисто сходящаяся
волна. Заменяя \У"> в правой части (93) его определением и
используя тот факт (ур. (91)), что
<Ф±»ЮН
находим
(г | G(±> \и) ^г 4^ <+5? I и). (94)
Следует отметить, что в асимптотическом выражении для
появилась именно волна ty{?~K а в выражении для G^ — волна
Операторы G|+> и G~ обладают аналогичными свойствами,
а именно, их асимптотическое поведение таково:
^^l (95)
') Последующие рассуждения иесправедливы, если иа бесконечности V ве-
ведет себя как 1/г.

318 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
Если Ui сферически симметрично, то функции Грина Gi**
легко выразить в терминах решений радиального уравнения
G8). Находим (задача 4)
П '•» (96)
где г<и г>—соответственно меньшая и большая из двух длин г
и г', a r\i и Fi были определены в § 11. Функции и\±] представ-
представляют собой нерегулярные решения уравнения G8), которые
имеют асимптотическое поведение:
«Г* ~ е
Явные выражения (96), как легко видеть, имеют характерные
для G\+) и G\~ свойства.
§ 14. Приложения. Определение и формальные свойства
Т-матрицы
Используя формальные свойства функций Грина, приведен-
приведенные в § 13, можно получить большинство предыдущих резуль-
результатов посредством простых алгебраических преобразований.
Преимущество такой процедуры состоит в том, что с одной сто-
стороны, она формально очень проста, а с другой — легко под-
поддается обобщению.
В частности, так получаются интегральные уравнения (81)
и (82), которые можно записать в виде
Сравнивая асимптотическое поведение обеих частей уравнения
(97), получаем соотношение G4).
Можно также показать, что справедливы соотношения
„ (98)
\ (99)
доказательство которых предоставляем читателю.
Можно также привести формальное определение Т. Соотно-
Соотношение B0) дает его матричные элементы только между пло-
плоскими волнами одинаковой энергии Е. Принимая во внимание
уравнение (90), это соотношение можно, записать в виде
A00)

§ 14. ОПРЕДЕЛЕНИЕ И ФОРМАЛЬНЫЕ СВОЙСТВА Т-МАТРИЦЫ 319
Обобщим это соотношение:
TV+V V
В этом определении Е играет роль параметра, а Т равно зна-
значению операторнозначной функции комплексной переменной z
в пределе, когда г стремится к вещественному значению Е,
оставаясь в верхней полуплоскости (Im z >• 0).
Преобразуя правую часть уравнения A01) с помощью тож-
тождеств (88а) и (886), легко получить следующие интегральные
уравнения для оператора Т:
T=V + T E_l+.eV, A02a)
T=V+V E_}o + ieT. A026)
На практике обычно имеют дело с матричными элементами Т
между свободными волнами с энергией Е, в частности, между
плоскими волнами с энергией Е.
В качестве иллюстрации докажем соотношение микрообра-
микрообратимости B1), используя только формальные свойства Т. Обо-
Обозначим через К (антилинейный) оператор обращения времени.
Гамильтониан Я0) очевидно, инвариантен относительно обра-
обращения времени и, более того,
Ф*"а = Кфа. <$КЬ = #Ф&- (ЮЗ)
Предположим, что Н также обладает свойством инвариантно-
инвариантности
т. е.
Из определений (84) и A01) последовательно получаем
Т*. A04)
Приведенный закон преобразования оператора Т относительно
обращения времени позволяет заключить, что
Ткь+ка = (<Фа IЯ+) Т (К |Фб» = <Фа | (К*ТК) IФ*)* =
= <фд | (Л^ГЧ) I фа> = <ф6 IТ |фв> =
Это есть соотношение микрообратимости.

320 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
§ 15. Замечание о потенциалах 1/г
В предыдущих разделах всюду предполагалось, что потен-
потенциалы V(r), Ui(r) и W\(r) убывают на бесконечности быстрее,
чем 1/г. Это является необходимым условием того, чтобы раз-
различные волновые функции Грина, которые мы использовали,
имели нужное асимптотическое поведение. Однако те же ме-
методы, с незначительной модификацией, могут быть применены
в случае, когда оба потенциала, V(r) и V\\r), ведут себя, как
1/г в предположении, что их разность Wx(r) стремится к нулю
быстрее, чем 1/г. Асимптотики отличаются только присутствием
в показателе экспоненты дополнительного слагаемого, пропор-
пропорционального In 2kr. Асимптотики щ и Fi претерпевают те же из-
изменения. За исключением этих отличий, методы и результаты
остаются в существенном теми же. В частности, верны опреде-
определения (83) и (84) функций Грина, интегральное уравнение (97),
основное уравнение G4), а также формула G5) в пределе,
когда W\ можно рассматривать как малое возмущение.
Раздел III. СЛОЖНЫЕ СТОЛКНОВЕНИЯ
И БОРНОВСКОЕ ПРИБЛИЖЕНИЕ
§ 16. Общие понятия. Сечеиия
В данном разделе ') мы распространим исследования пре-
предыдущих разделов на случай столкновения любых двух частиц.
Здесь мы понимаем слово «частица» в его широком смысле,
считая, что частица может иметь сложную внутреннюю струк-
структуру. Для таких элементарных частиц как электроны, протоны,
нейтроны внутренние переменные сводились только к спиновым
переменным. Однако мы будем рассматривать также сложные
(составные) частицы — ионы, атомы, атомные ядра и т. д., ко-
которые состоят из нескольких элементарных частиц.
Пусть столкновение происходит между двумя частицами А
и X, элементарными или сложными. Тогда возможны три типа
процессов:
(а) упругое рассеяние — внутренние квантовые состояния
частиц не меняются после столкновения
А + Х->А + X;
(б) неупругое рассеяние — кроме отклонения, в результате
столкновения происходит изменение внутренних состояний ча-
') Более подробное объяснение используемой в данном разделе термино-
терминологии см. в книгах: С. Block. Cours sur la Theorie des reactions nucleaires,
Chap. I—III. Saclay A955—1956); Дж. Блатт, В. Вайскопф. Теоретическая
ядерная физика. М., ИЛ., 1954.

S 16. ОБШИБ ПОНЯТИЯ. СЕЧЕНИЯ
стиц1), например,
(в) столкновение с перераспределением (иначе говоря,реак-
говоря,реакция), когда частицы А и X в процессе столкновения обмени-
обмениваются некоторыми из составляющих их элементарных частиц.
Другими словами, система (А + X) переходит в две или боль-
большее число частиц, отличных от исходных. Например, в процессе
столкновения появляются частицы В и У, отличные от А и X,
A + X-+B + Y.
Химическая реакция представляет собой рассеяние молекул
с перераспределением, ядерная реакция есть столкновение с пе-
перераспределением между атомными ядрами. В дальнейшем бу-
будет приведено несколько таких примеров.
Столкновение двух частиц характеризуется такой величиной,
как сечение. Для упругого рассеяния определение этой вели-
величины уже было дано в главе X (§ 2). В общем случае сечение
рассеяния для процесса определенного типа в данном столкно-
столкновении равно числу событий этого типа в единицу времени от
одного центра мишени при единичном потоке падающих на ми-
мишень частиц.
Чтобы определить однозначно сечение для столкновения ча-
частиц А и X, необходимо точно задать начальные условия столк-
столкновения — квантовые состояния и относительные скорости этих
частиц. Обычно в эксперименте одна из скоростей равна нулю,
скажем, скорость частицы X. Мишень из частиц типа X практик
чески покоится, она бомбардируется моноэнергетическим пуч-
пучком частиц типа А. Однако движение центра масс можно пол-
полностью отделить от относительного движения. Простое кинема-
кинематическое рассмотрение позволяет установить связь сечений, ко-
которые соответствуют начальным условиям, отличающимся вы-
выбором разных систем отсчета. В частности, обобщая очевидным
образом метод § X. 7 (см. задачу X. 2), мы можем получить
связь сечений в лабораторной системе (скорость частицы X
равна нулю) с сечениями в системе центра масс (скорость
центра масс равна нулю). В дальнейшем рассматриваются
только сечения в системе центра масс.
Энергию в системе центра масс будем обозначать буквой Е,
гамильтониан относительного движения — Н (прибавляя энер-
энергию центра масс, получаем полный гамильтониан).
') Таковым может быть проетой переворот спипа. Принятое здесь опреде-
определение несколько отличается от обычного, согласно которому процесс рассея-
рассеяния считается неупругим или упругим в зависимости от того, изменилась ли~
внутренняя энергия частиц или иет.
11 А. Мессиа

322 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
§ 17. Каналы
Важную роль при изучении сложных столкновений играет
понятие канала реакции. Так называют каждую возможную
моду деления системы в результате столкновения. Одна из та-
таких мод — сами две сталкивающихся частицы — называется
входящим каналом. При упругом рассеянии две частицы
остаются во входящем канале. При двух других типах столкно-
столкновений выходящий канал отличен от входящего. Это будет не-
неупругое рассеяние или рассеяние с перераспределением в зави-
зависимости от того, имеем ли мы в выходящем канале реакции те
же частицы, что и во входящем, или другие. Каждый канал бу-
будем обозначать какой-либо греческой буквой.
С каналом можно связать некоторое число параметров. Для
простоты будем всегда предполагать, что каналы реакции со-
состоят только из двух частиц.
Рассмотрим канал у, который содержит частицы С и Z. Век-
Вектор rY определяет положение частицы С по отношению к Z, дру-
другими словами, ry = rc — rz, где гс и rz — координаты центров
масс С и Z. Так же определяется относительный импульс pY и
приведенная масса
_ MCMZ
Y Mc+Mz
Кинетическая энергия в канале у равна p2J2M .
Волновая функция cpY, которая нормирована на единицу и
описывает внутреннее квантовое состояние частиц канала,
равна произведению волновых функций <рс и фг частиц С и Z.
Если обозначить гамильтониан частиц hc и hz, то получим ра-
равенства
Фу == ФсФг> ei ~ ес + ez>
где eY—полная внутренняя энергия частиц канала у.
Пусть Vy — потенциал взаимодействия частиц С и Z, т. е.
сумма потенциалов взаимодействия между каждой элементар-
элементарной частицей, содержащейся в С, и каждой элементарной час-
частицей, содержащейся в Z. В пределе rY-»-oo значение VY стре-
стремится к нулю. Мы будем всегда считать, что VY убывает быст-
быстрее, чем l/rY. Как отмечалось в § 15, обобщение результатов
на потенциалы вида l/rY не представляет серьезных трудностей.
Гамильтониан системы равен
Я = Яу + Уу, A05)
где
A06)

§ 18. ВЫЧИСЛЕНИЕ СЕЧЕНИИ. Г-МАТРИЦЫ 323
§ 18. Вычисление сечений. Г-матрицы
В рассмотренном выше столкновении входящим является
канал (А -\- X), который мы обозначим буквой а. Чтобы фикси-
фиксировать начальные условия, нужно задать еще относительный
импульс tika частиц в начальном состоянии. Полные начальные
условия обозначим индексом а = (a, ka)- Имеем
Е = еа + ПЧЦ2Ма. A07)
Допустим, что возможна реакция Л + X-vB + У. В этом слу-
случае канал (В + У) или р называют открытым каналом. В силу
закона сохранения энергии частицы канала р имеют вполне оп-
определенную величину относительного импульса fikb
Е = е^+НЧЦ2Мг A08)
Для того чтобы канал р был открытым, очевидно, необходима
положительность Е — ер.
С каждым набором начальных условий а можно связать
плоскую волну
^Га A09)
и две стационарных волны, Ч^ и Ч^"'. Волна ч4+) есть ста-
стационарное решение Н, отвечающее энергии Е и имеющее во
входящем канале асимптотическое поведение (е'*аГа + расхо-
расходящаяся волна), а во всех других открытых каналах — поведе-
поведение чисто расходящейся волны. Чго~) определяется аналогичным
образом, но со сходящимися волнами. В соответствии с этими
определениями имеем равенства
(ПО)
, A11)
а для любого открытого канала у (мы предполагаем, что ни
один из них не содержит более двух частиц)
Не вдаваясь в обсуждения, мы считаем, что стационарные ре-
решения Чга+) и Чго~) существуют.
Сечения рассеяния непосредственно связаны с асимптотиче-
асимптотическим поведением Wo*'. Пусть doa^.b/d?lg — сечение испускания
И*

324 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
частицы В в направлении Q*,. Находим
где va = hka/Ma — скорость налетающей частицы, a Vb =
= HkbM.fi — скорость частицы В, появившейся в результате
столкновения. Вывод этой формулы аналогичен приведенному
в §§ 4—6 главы X ') и предоставляется читателю.
Обобщая рассуждения § 3, мы приходим к описанию про-
процесса с энергией Е посредством матрицы перехода Т:
b) A14)
Используя формулы A12) и A13), получаем
где ?>ь(Е) задает плотность конечных состояний в соответствии
с определением § XVII. 5. Полученная формула представляет
обобщение формулы A9'). Та-+ь есть амплитуда перехода
а ->Ь.
§ 19. Интегральные представления амплитуды перехода
Чтобы найти интегральные представления для Та-+ь, нужно
несколько модифицировать соотношение (9).
Пусть Я и Я — два возможных гамильтониана исследуемой
квантовой системы. Я и Я имеют одну и ту же кинетическую
энергию, но их потенциальные энергии могут быть различны.
Мы будем считать, что отличие сводится к членам, которые
убывают на бесконечности быстрее, чем 1/г. Стационарные ре-
решения для Я и Я с энергией Е обозначим ТиТ соответственно.
Отметим, что ряд каналов может быть открыт для столкнове-
столкновений, описываемых Я, и закрыт для столкновений, описываемых
Я, и наоборот. Пусть канал р открыт для столкновений, кото-
которые описываются гамильтонианом Я. Следовательно, сущест-
существует решение Фб"', отвечающее начальным условиям Ь = (р, кь).
Оноудовлетворяет уравнению
A16)
') Этот результат можно также получить, используя рассуждения § X. 2:
иие ра | jj* |2
патоку va.
р
сечеиие равно отношению потока частиц В, vb | fjjjj* (Qft) |2 к падающему

§ 19. ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ АМПЛИТУДЫ ПЕРЕХОДА 325
и для любого открытого канала б (напомним, что по предполо-
предположению любой канал имеет не более двух частиц) имеет асим*
птотики
Можно показать, что
<ФГ | (Я - Я) | Ч*»> == - ^1 f<J> (Q.) + *? f</ (- Qe). A18)
Метод доказательства тот же, что и в случае соотношения
(9). Умножая уравнение A11) на Ф'Г1*, а комплексно сопря-
сопряженное к уравнению A16)—на W^ и вычитая результаты друг
из друга, получаем
№Г>' {н?а+)) - (ЯФИ* Ч*.+>] + ЧУ* (Я - Я) ?<+) = 0.
К соотношению A18) приходим после суммирования по спино-
спиновым переменным и интегрирования по всему конфигурационному
пространству. Несмотря на то, что оператор Я эрмитов, вклад
от выражения в квадратных скобках может быть отличен от
нуля, поскольку ни одно из решений W, W не имеет конечной
нормы. Чтобы сосчитать этот вклад, вычислим вначале инте-
интеграл по конечному объему конфигурационного пространства,
а затем рассмотрим предел этого интеграла, когда объем стре-
стремится к бесконечности. Используя теорему Грина, интеграл по
объему можно преобразовать в интеграл по поверхности1). По-
Последний имеет вид суммы, слагаемые которой отвечают различ-
различным открытым каналам v, общим для Уи?,
I (я - я) | Ч+)> - ? ж
') Напомним, что существует много способов выделения центра масс, од-
однако величина
яе зависит от способа. Здесь г(, г2 Г/, ... — относительные координаты, от-
отвечающие выбранному способу, a Mi, Мг, ..., Af/, ... — соответствующие мас-
массы (см. § IX. 13). Упомянутый объем интегрирования можно определять усло-
условием х ^ X, где X — положительная константа, которая велика по сравнению
с радиусом взаимодействия. Используя теорему Грииа, можно преобразовать
интеграл по объему в интеграл по гиперповерхности х = X, который при
Jf-»-oo стремится к выражению, стоящему в правой части формулы A19).

326 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
Символ {. ..}v аналогичен обозначению, которое было исполь-
использовано в § 2. По определению
где символ (\ ••• dQv\ означает суммирование или интегри-
интегрирование по всем переменным кроме относительного расстоя-
расстояния гч. Различные слагаемые в правой части равенства A19)
можно вычислить, подставляя вместо W, W и их радиальных
производных соответствующие асимптотические выражения
A12) и A17). Для любого канала, отличного от а и р, Wo+>
представляет собой чисто расходящуюся волну, а Ч^"' — чисто
сходящуюся волну, следовательно, {. . .}v асимптотически стре-
стремится к нулю. Для каналов аир получаем отличный от нуля
вклад, поскольку в одном из двух асимптотических выражений
присутствует плоская волна. Вычисление аналогично выполнен-
выполненному в § 2 и приводит к двум членам, стоящим в правой части
соотношения A18).
Важное соотношение A18) можно преобразовать к более
удобному виду. Для этого выпишем A18) в частном случае,
когда fi — Н. Левая часть обращается в нуль, и мы имеем
Af
1 *<+) /О \ — _!_ f<->* /_
Сравнивая это равенство с определением Т (ур. A14)), полу»
чаем эквивалентное определение
-/(-Qa). (П4'>
Эти же определения справедливы и для матрицы перехода ?,
связанной с гамильтонианом Й. Таким образом, соотношение
A18) можно также записать так:
(b\T\a) = (b\f\a) + <${,-' \(Н-Н)\ Wa+)>. A20)
Именно в этом виде мы и будем его использовать.
Это соотношение выполняется и в случае, когда канал а за-
закрыт для волны Ф'Г1, если положить (b\T|a> = 0. Оно выпол-
выполняется также в случае, когда канал р закрыт для Wa+), если
положить 0\Т\аУ = 0.
В частности, если Й = Яр, то Фр~' сводится к плоской волне
ф/з и поскольку Н — Яр = Ур, соотношение A20) дает
(а+)). A21)

§ 20. БОРНОВСКОЕ ПРИБЛИЖЕНИЕ И ЕГО ОБОБЩЕНИЯ 327
Заменяя Я на На и Я на Я, получаем
{Ь\Т\ а) ^(^{Уа] Фа). A22)
Выведенные нами соотношения справедливы для любых ти-
типов столкновений: упругого рассеяния (а = р), неупругого рас-
рассеяния (а Ф р, Va = Vp) или рассеяния с перераспределением
§ 20. Борновское приближение и его обобщения
Подставляя в правую часть равенства A21) вместо Wa+) пло-
плоскую волну Фа, получаем амплитуду перехода а-+Ь в борнов-
ском приближении (см. ур. B3))
Га^б«Г^й = (Ф„|Ур|Фа>. A23)
То же приближение получается после подстановки в пра-
правую часть A22) плоской волны Фь вместо Ч^"'. Действительно,
если мы заменим Я на Яа и Я на Яр, то из соотношения A20)
получим
(Фй1^|Фа> = <Фб1^а|Фа>- A24)
Можно также записать
^ {Фь\Уа\Фа). A240
Переход от A21) к A23) оправдан, если WM мало отли-
отличается от Фа в области, где отличен от нуля потенциал Vp.
Точно так же для перехода от A22) к A24') достаточно, чтобы
Ч^"' мало отличалось от Фь в области, где сосредоточен потен-
потенциал Va- Эти два условия эквивалентны, хотя на первый взгляд
кажутся различными. Оба условия предполагают, что Wa+) и
Ч'гГ* можно заменить плоскими волнами Фя и Фй соответ-
ственно.
Более точные выражения получатся, если вместо плоских
волн использовать волновые функции, которые лучше аппрокси-
аппроксимируют стационарные решения W^ и Wlr\
Допустим, например, что Va можно представить в виде
и что известны стационарные решения для гамильтониана
На. + Uа, отвечающие энергии Е. Обозначим эти решения X,
а соответствующую матрицу перехода — Tw. В частности, Хо'+)
будет обозначать решение с расходящимися волнами, отвечаю-

328 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
щее начальным условиям а, и мы имеем
&<Ф6 I(На + Ua- Яр)|Х{а+)) = <Ф, I(Vp - Wa)|*L+)>. A25)
Если Wa достаточно мало, то Яа+) будет мало отличаться от
Точно так же предположим, что Ур можно представить
в виде
и известны стационарные решения для гамильтониана Яр + ?/р,
отвечающие энергии Е. Будем обозначать эти решения В, а со-
соответствующую матрицу перехода — Г(а). В частности, з?~' бу-
будет решение со сходящимися волнами, отвечающее начальным
условиям Ь, и мы имеем
TfU = (В»"' I (Ve - WJ I Ф„>. A26)
Если Wp достаточно мало, то Sfc"' будет мало отличаться от W'fK
В силу соотношения A20) имеем
Та-*ъ = Т{Ль + Ы'* I Wа | Ji+)> = A27)
A28)
Эти два выражения для Та-*ь являются точными. Заменяя
в первом из них Ч^ на З^1 или W^ на Хо+)— во втором, по-
получаем приближенные выражения
Та-* Ь « Г<Д6 + (Si"' | Гв I Х{а+)) « A29)
« Т(а%ь + (Si"» | l^p | Л-<+>). A30)
Хотя формально эти выражения различны при Wa Ф Wp, они
всегда равны друг другу, что легко увидеть, если воспользо-
воспользоваться соотношением A20) с Я« + Ua вместо Я и Яр + ?/р
вместо /?.
Данные формулы представляют собой обобщение борнов-
ского приближения (см. ур. G5)). Они точнее тех, которые по-
получаются, после простой замены Ч^+) в выражении A21) на
Ха+. Действительно, поскольку справедливо равенство (ур.
A25))
<Ф„ | V& | Xi+) > = Т{?ь + (Фь I Wa | *i+>>,
последнее приближение сводится к замене Ч^"' в выражении
A27) на Фб, а не на 3i~\ По этим же причинам формулы A29)
и A30) точнее тех, которые получаются после замены Wi"'на
3i-) в правой части равенства A22).

§ 21. РАССЕЯНИЕ БЫСТРЫХ ЭЛЕКТРОНОВ АТОМОМ 329
§ 21. Рассеяние быстрых электронов атомом
В качестве иллюстрации собственно борновского приближе-
приближения рассмотрим рассеяние быстрых электронов атомом.
Ядро атома будем считать бесконечно тяжелым и располо-
расположенным в начале координат. Гамильтониан системы имеет вид
Н = р¦- + h + V (г, А).
Первое слагаемое — кинетическая энергия налетающего элек-
электрона, второе — гамильтониан атома, третье слагаемое пред-
представляет собой энергию взаимодействия
V(r, A)--^l + f]T7^7T. A31)
где г — координаты налетающего электрона, а г\, r2, ...,rz —
координаты электронов атома. Пусть
Фо. <Pi Ф«> ... —
собственные функции гамильтониана h, a
во, в\, . . ., вп, ...
соответствующие собственные значения.
Рассмотрим процесс неупругого рассеяния, когда импульс
электрона меняется от hk0 до hkn, а атом переходит из основ-
основного состояния фо в возбужденное состояние фл. В силу закона
сохранения энергии имеем
Й2(^-^) = 2т(в„-ео).
Обозначим переда!:::ый импульс hq
q = K- К
Отметим, что соотношение B4) здесь не выполняется, вместо
него справедливо следующее равенство:
q* = (ko-knY + 4koknsm2±Q. A32)
В дополнение к прямому процессу, когда налетающий элек-
электрон, теряя часть кинетической энергии, просто рассеивается,
возможен и обмен налетающего электрона с одним из электро-
электронов атома. Обменный эффект может быть значителен в том слу-
случае, когда скорость рассеянного электрона равна по порядку
величины скорости электронов атома, т. е. kna « 1. При тех ус-
условиях, когда применимо борновское приближение, этот эффект
мал и им можно пренебречь. Мы будем рассматривать также
налетающий электрон как частицу, отличную от электронов

330 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
атома. Используя формулу A23) для амплитуды перехода
В борновском приближении, получаем
Га(А)У(г, A)%(A)drdA. A33)
Это есть борновское приближение для амплитуды перехода час-
частицы при переданном импульсе tiq в потенциале
*n(A)V(r, A)%(A)dA. A34)
Результат справедлив при любом п, в частности, при упру-
упругом рассеянии (п = 0).
Чтобы преобразовать ответ к виду, аналогичному тому, ко-
который был получен в § 8, введем «электронную плотность»
Р„ (г) = Z J ф* (г, г2 rz) ф0 (г, rv ..., rz) dr2... drz A35)
и соответствующий форм-фактор
В случае упругого рассеяния (п = 0) мы имеем просто элек-
электронную плотность основного состояния и соответствующий
форм-фактор (см. ур. D8))
Если подставить явное выражение для V(r, А) из уравнения
A31) в определение Fo(»"), то мы увидим, что Fo(»") представ-
представляет собой потенциал кулоновского взаимодействия электрона
и заряда с распределением
e[Zb(r)-p(r)).
Именно такой потенциал использовался в § 8. Таким образом,
мы получили обоснование использованной там модели.
Рассмотрим теперь неупругое рассеяние (пфО). Подставим
явное выражение для V(r, А) в определение A31). Поскольку
функции ф0 и фл ортогональны, вклад от члена Ze2/r исчезает.
Другие члены дают потенциал взаимодействия электрона
с плотностью заряда —ерп(г). Повторяя рассуждения § 8, на-
находим
и, следовательно, в борновском приближении сечение неупру»
гого рассеяния равно
do0_+n mV *„ | Fn (у) р
¦ = 4-ft4-"X T* • A36>
di

§ 22. КУЛОНОВСКОЕ ВОЗБУЖДЕНИЕ ЯДЕР 331
Отметим, что данная формула подобна формуле D9) для уп-
ругого рассеяния. Зависимость от углов определяется множите-
множителем |Fn{q) | 2/qi- Свойства функции Fn{q) легко вывести из
свойств р«(г). Так, Fn@)= 0. Если а — радиус атома, то функ-
функция Fn{q) в существенном отлична от нуля только в области
^а^: 1. В случае применимости борновского приближения
(у <С 1) имеем боа v?> 1, т. е. энергия столкновения значительно
больше расстояния между атомными уровнями, которое имеет
порядок h2/ma2. Следовательно, (&0 — kn)a имеет порядок l/koa.
Когда q меняется от ?0 — kn до kQ + kn, угол 8 меняется от нуля
до 2я, a qa меняется от l/koa до 2?0а (см. ур. A32)). Согласно
приведенным рассуждениям наибольшую вероятность имеет рас-
рассеяние электрона в интервал углов, для которых qa ^ 1, т.е.
в область малых углов
9^
В принципе неупругое рассеяние можно использовать для изме-
измерения координат электрона. Согласно предположению, попереч-
поперечные размеры падающего волнового пакета значительно больше
а и, следовательно, неопределенность величины поперечной
компоненты импульса значительно меньше ft/a. Сразу после не-
неупругого рассеяния, считая, что мы можем определить измене-
изменение квантового состояния атома, координаты электрона стано-
становятся известны с точностью порядка а. Однако направление им-
импульса электрона становится известным лишь с точностью l/koa,
неопределенность в поперечной компоненте упомянутого им-
импульса имеет порядок ft/a. Это полностью согласуется с тем,
что было сказано в главе IV 1 тома об измерениях координат
(см. в частности, обсуждение измерений с помощью камеры
Вильсона, сноска7) на стр. 144. 1 тома).
§ 22. Кулоновское возбуждение ядер
Для иллюстрации обобщенного борновского приближения
вернемся к задаче, которая уже рассматривалась в § XVII. 3, и
при ее решении откажемся от использованного там классиче-
классического приближения.
Если не оговорено противное, то используются обозначения
§ XVII. 3. Будем считать энергию столкновения достаточно ма-
малой, так что справедливо условие (XVII. 28). С другой стороны,
условия (XVII. 29) и (XVII. 30), т. е. условия применимости
классического приближения, могут не выполняться. Так как
энергия столкновения меньше высоты кулоновского барьера
Ze2/R, протон «проникает» в ядро в процессе столкновения
очень незначительно. Следовательно, эффекты, вызванные ядер-

832 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
ными взаимодействиями, малы и в данный момент мы их рас-
рассматривать не будем. Тогда столкновение описывается гамиль-
гамильтонианом Я@) + V.
Пусть а и Ь — набор данных, которые описывают начальные
и конечные условия столкновения, а Х^ и Хь-) — соответствую-
соответствующие собственные функции оператора #<°>. Поскольку в #<°> пе-
переменные, описывающие протон, и переменные ядра полностью
разделены, функция Х{а] есть произведение волновой функции
ядра в состоянии ос и кулоновской рассеянной волны ?а+)(г)>
описывающей стационарное состояние рассеяния протона с энер-
энергией Е и импульсом Tika на потенциале Ze2/r. Точно так жеХь~*
есть произведение волновой функции ядра в состоянии р и ку-
кулоновской волны ??"'(/•) сходящегося типа1), которая опись!'
вает состояние рассеяния протона с энергией (Е — АЕ) и им-
импульсом hh на потенциале Ze2/r. Так как Л1+) не дает вклада
в канал р, точная формула A27) принимает вид
Т и — /ш<-> I V I У{+)\
1а-*Ь — у?Ь \У\Ла /¦
Если V рассматривать как малое возмущение, то его вкладом
в Vft"* можно пренебречь и заменить Wj на Хь~\ получив,
в согласии с обобщенным борновским приближением A29), сле-
следующий ответ:
\ль | V \ Ла /•
Поскольку при г < R волны X практически равны нулю, мы
можем заменить потенциал V его разложением (XVII. 34), что
дает
('37)
Воспользовавшись формулой A15), получаем сечение кулонов-
ского возбуждения. Выражение для него аналогично выраже-
выражению для сечения в полуклассической теории. Последнее полу-
получается из первого заменой Rf на A (doR/dQJ S?, где положи-
положительная константа А определяется соотношением: А2 =
= 4n2h*va/M2Vb- Действительно, в пределе, когда выполнены
условия (XVII. 29) — (XVII. 30), основной вклад в интеграл RT
') Ее разложение по сферическим функциям дает уравнение G7), в ко-
котором в качестве Ft беруется регулярные кулоиовские решения. Отметим, что

§ 22. КУЛОНОВСКОЕ ВОЗБУЖДЕНИЕ ЯДЕР 333
дает окрестность классической траектории, и применение ме-
метода стационарной фазы приводит к полуклассическому ответу.
Обсуждение правил отбора, которое было проведено в конце
§ XVII. 3, может быть без изменений повторено и в данном слу-
случае. В частности, если в эксперименте ядра мишени не ориен-
ориентированы и не измеряется поляризация возбужденных ядер, то
имеем
dQ BJa + 1) B/0 + Г
В приведенные выше рассуждения можно включить также и
ядерные взаимодействия. Пусть Vpa — потенциал ядерного взаи-
взаимодействия протона с нуклонами ядра А. Потенциал Vpa очень
велик в области г < R и практически равен нулю при г > R.
Мы будем включать VpA в оператор #<°>. Удобно разбить потен-
потенциал V на внешнюю и внутреннюю части: V = Vmt + Vext со-
согласно определению
( V, если r>R,
Vext = l 0, если r<R,
и часть Vmt также включить в Я<0). После таких модификаций
использованное выше разделение переменных уже не имеет ме-
места, a .Xi+) и Хй-) не равны более чисто упруго рассеянным вол-
волнам. Согласно обобщенному борновскому приближению имеем
I Vext I Ла /•
Первое слагаемое ТаХь описывает ядерное возбуждение.
Оно равно амплитуде перехода, которая получается при замене
взаимодействия протона с ядром во внешней области (г > R)
чисто кулоновским взаимодействием. При этом возбуждение
а->-р возможно, только если протон проникает в ядро. Второе
слагаемое описывает собственно кулоновское возбуждение.
Из-за существования кулоновского барьера и характера
ядерных сил (короткодействующие и большие) волны Х^ и Хь^
при низких энергиях имеют узкие резонансы, подобные тем, ко-
которые исследовались в главе X (раздел IV). Зная характери-
характеризующие эти резонансы параметры — энергию, ширину резонанса
в различных открытых каналах — можно построить волны Х{^
и .Xif * во внешней области') и вычислить два члена ампли-
амплитуды рассеяния. Вне резонансов протон практически не прони-
проникает в ядро, амплитуда Т^Хь пренебрежимо мала, и ам-
') Детальное рассмотрение этого вопроса содержится в работе, упомя-
упомянутой в первой сноске к § 16.

334 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
плитуда кулоновского возбуждения с очень хорошей точностью
дается формулой A37), в которой волны X равны чисто куло-
новским рассеянным волнам. При переходе через резонанс вкла-
дом амплитуды Т^Хь нельзя пренебречь, а ее зависимость от
энергии имеет типично резонансный вид (см. ур. F4)). В то же
время амплитуда кулоновского возбуждения также несколько
модифицируется, на чем мы здесь не останавливаемся, и обе
амплитуды дают когерентный вклад в полное сечение.
§ 23. Функции Грина и интегральные уравнения
для стационарных решений рассеяния
Построение § 13 можно легко распространить на случай
столкновений сложных систем. С каждым из гамильтонианов
Н, На и т. д. можно связать соответствующую функцию Грина
[Е — Н ± ie]~\ [E — На± /ер1 и т. д. За исключением несколь-
нескольких изменений в обозначениях, результаты § 13 остаются спра-
справедливыми и в данном случае. Они могут быть получены ана-
логичным образом, в частности, свойства (85), тождества (88),
(89), асимптотические выражения для этих функций. Напри-
Например, для каждого открытого канала у имеем (см. ур. (94))
(kc = kcry/ry).
Используя упомянутые свойства функций Грина, можно вывести
интегральные уравнения
A38)
и т. д., а также формулы
)'а (И0)
Из приведенных интегральных уравнений легко получить
борновское разложение для амплитуд переходов. Подставляя
в формулу A21) выражение A40) и раскладывая функцию

§ 24. РАССЕЯНИЕ ЧАСТИЦЫ НА ДВУХ ЦЕНТРАХ 335
Грина, получаем
tB Va)\<l>a) = A42)
Фа>. A43)
В тех частных случаях, которые рассматривались в разде-
разделах I и II, амплитуды переходов можно было представить
в виде матричных элементов некоторого оператора Т, опреде-
определяемого формулой A01) или одним из интегральных уравне-
уравнений A02). В случае сложных столкновений нельзя определить
один такой оператор. Тем не менее, используя уравнение A42),
мы покажем, что любую амплитуду перехода из канала а в ка-
нал р при энергии Е можно рассматривать как матричный эле-
элемент некоторого оператора Т$а, определяемого формулой
Т"а==У,+ У,Е-Н + 1г У«- <144>
Отметим, что для столкновений с перераспределением
(У$ф Va) эти матричные элементы не согласуются с обычным
определением матричного представления операторов, поскольку
векторы |ФО> и <Фй|, встречающиеся в формуле
{Фь\Т&а\Фа), A45)
не ортогональны.
§ 24. Рассеяние частицы на двух центрах
Основное достоинство формальных построений предыдущего
параграфа состоит в том, что они годятся для любых сложных
столкновений. Для того чтобы ближе познакомиться с этим
формализмом, рассмотрим несложную задачу о рассеянии ча«
стицы на двух рассеивающих центрах и получим ряд известных
результатов.
Пусть, например, электрон сталкивается с двумя атомами.
В дальнейшем мы не будем учитывать обменных эффектов и не
станем делать каких-либо предположений о длине волны нале-
налетающей частицы.
Ядра атомов будем считать бесконечно тяжелыми, рассма-
рассматривая их как фиксированные центры. Ядро 1 выберем в каче-
качестве начала координат и обозначим R вектор, соединяющий
ядра 1 и 2 (см. рис. 18). Предполагается, что расстояние R ве-
велико по сравнению с атомными размерами а < R. Столкнове-

336 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
ние описывается гамильтонианом
Я = Я0+У, A46)
Яо = -^г + А1 + А2, A460
y = F1-fF2, A46")
где Л] и h2 — операторы энергии атомов 1 и 2, a Vi и Vi — по-
потенциалы взаимодействия атомов с нале-
налетающей частицей. Обозначим свободную
функцию Грина Go
Матрицу перехода Т, связанную с рас-
рассеянием частицы (упругим или неупру-
неупругим) на двух атомах, можно представить
в виде борновского разложения
Рис.18. T = V + VG0V+ VGQVG0V + .... A47)
Заменяя V на V\ + V2, получаем разложение Т по степеням V\
и V2
Гт/ I t/ I т/ /~> т/ I \7 f> ЛТ I I/ Л I/ I T 7 /~* Т/ I
= кт 4 V<i "г ViLinVt -Ь Vi&nVo Ч~ к оС/пк 1 Ч- к оС/л ко Ч-
+ T7 ^* T7 ^* T7 I 17 /~* \7 /~* I/ I
ViGoViGo! , + ViGQViGQV2 + ... .
Мы не будем делать каких-либо предположений о величине
потенциалов V\ и V2. По этой причине приведенное разложение
не обязано быстро сходиться, и в том виде, как оно записано,
его нельзя использовать в качестве отправной точки какого-
либо приближенного метода. Однако можно так перегруппиро-
перегруппировать члены этого разложения, что в результате получится
быстро сходящееся разложение.
Такая возможность основана на следующем замечании. Рас-
Рассмотрим матричный элемент члена второго порядка V\GqV2
в представлении, где диагоналей оператор г. Матричный эле-
элемент свободной функции Грина Go содержит множитель
eik I r~r' 1/1 г — г' \. Поскольку потенциал V\ сосредоточен в ма-
малой окрестности начала координат, a V2 — в малой окрестности
точки R, то упомянутый множитель имеет порядок 1/R. То же
справедливо и для члена V2GqV\. Грубо говоря, слагаемые
V1G0V2 и V2G0Vi в a/R раз меньше слагаемых ViGoVi и V2GqV2.
Это же замечание относится и к остальным слагаемым. Оно
позволяет нам классифицировать различные члены в соответ-
соответствии с тем, сколько раз Go стоит между Vi и V2. Мы будем на-
называть членами первого порядка такие, в которых Go ни разу
не появляется между Vi и V2, членами второго порядка, — если.

S 24. РАССЕЯНИЕ ЧАСТИЦЫ НА ДВУХ ЦЕНТРАХ 337
Go появляется между V\ и V2 один раз, ..., членами /г-го по-
порядка,— если Go появляется (п— 1) раз, и т. д. Согласно этой
терминологии V{G0V\ и V2G0V2 — члены первого порядка
a V\GqV2, V2G0V1 — второго порядка.
Введем индивидуальные матрицы перехода Т\ и Т2
Tt = Vt + VtGJ-t = V{ + VtG0Vt + VtGoViGoVi + ... A48)
(/=1.2)..
Матрица перехода Т\ отвечает рассеянию на атоме 1 в предпо-
предположении, что налетающая частица не взаимодействует со вто-
вторым атомом. Аналогичный смысл имеет матрица перехода Т2.
Используя операторы Ти Т2 и Go, просто записать вклады раз-
различных порядков. Искомые выражения определяются путем не-
несложного исследования структуры ряда. Первый порядок дает
7*1 + Т2, второй порядок TiG0T2 -f- T2G0T\ и т. д. В результате
получаем
Т = (Г, + Та) + (TfioT, + r2G0r,) +
+ Gда2ОоГ, + T2G0TxGQT2) + .... A49)
Разложение A49) является исходной точкой нашего под-
подхода к данной задаче. Легко дать интерпретацию различным
членам этого разложения. Члены первого порядка отвечают
рассеянию частицы либо на атоме 1 (Т\), либо на атоме 2 (Т2).
а) б)
Рис. 19. Графическое изображение членов разложения A49).
Члены второго порядка отвечают двойному рассеянию; так,
член TiGqT2 описывает рассеяние налетающей частицы на атоме
2 (оператор Т2), последующее распространение рассеянной ча-
частицы от атома 2 к атому 1 (оператор Go) и, наконец, рассея-
рассеяние на атоме 1 (оператор 7\). Точно так же каждый член
порядка п описывает п последовательных процессов рассеяния
на атомах 1 и 2.
В связи с такой интерпретацией каждый член можно схема-
схематически представить диаграммой того же типа, что и в неста-
нестационарной теории возмущений (рис. 10). На рис. 19 изображены
две такие диаграммы.

338 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
Разложение A49) связывает амплитуды переходов при рас-
рассеянии на двух центрах с амплитудами переходов при рассеянии
на отдельных центрах.
Предположим, для простоты, что атомы тождественны друг
другу, и обозначим t(e) матрицу перехода с энергией е при рас-
рассеянии на одном центре, т. е. при рассеянии частицы на одном
атоме, расположенном в начале координат.
Пусть \krnn) есть собственный вектор Яо, который равен
произведению волновой функции фот атома 1, волновой функции
фп атома 2 и плоской волны е'*г, описывающей налетающую ча-
частицу с импульсом fik,
#0| kmn) = {j^- +ет + еп) \ kmn).
Мы пользуемся нормировкой, при которой
{k'm'n' | kmn) = BяK 6(k- k') bmm.bnn,.
Точно так же вектор \km} равен произведению плоской волны
е'*г на волновую функцию фш атома из задачи с одним рассеи-
рассеивающим центром.
Из определения Т\ A48)легко получить, что
(k'm'n'\ Г] (?) | kmn) = 6„„< (k'm' \t (Е - еп) \km). A50)
Аналогичным образом можно найти связь матричных эле*
ментов Т2 с элементами матрицы перехода при рассеянии на
одном атоме, расположенном в точке R. Такая матрица пере-
перехода получается из t(e) общим сдвигом на R и, следовательно
(задача 5),
(k'm'n' | Т2 (Е) | kmn) = bmm<e (*-*!> * (k'n' \t(E-em)\ kn). A51)
Формулы A50) и A51) справедливы для любых переходов,
в частности, и в том случае, когда энергии состояний \krnn)
и \k'm'n") отличны от Е.
§ 25. Простое рассеяние. Интерференция
В качестве первого приложения разложения A49) вычислим
сечение упругого рассеяния частицы на двух атомах.
Допустим, что атомы находятся до и после рассеяния в ос-
основном состоянии ф0. Пусть k0 и k — волновые векторы падаю-
падающей и рассеянной волн. Таким образом, мы рассматриваем
переход (&000) -у (feOO) и имеем
Чтобы вычислить амплитуду перехода, сохраним в разло-
разложении A49) только члены первого порядка
T&Ti + T2. A52>

§ 25. ПРОСТОЕ РАССЕЯНИЕ. ИНТЕРФЕРЕНЦИЯ 339
Принимая во внимание соотношения A50) и A51) и вводя обо-
обозначения
q = k — k0,
находим
<ft00| T IftoOO) « [1 + e-'»«] <ft| П*о>. A53)
Мы увидим, что это соотношение дает амплитуду рассеяния
в рамках элементарной теории интерференции. Соотношение
A53) позволяет связать сечение упругого рассеяния на двух
атомах d2/dQ с сечением do/dQ, такого же упругого рассеяния
на одном атоме, т. е. с сечением процесса (k00) -+¦ (Щ. Первое
равно квадрату модуля элемента (k00\T\k000), умноженному на
соответствующий множитель, а второе сечение равно квадрату
модуля <&|^|&о>, умноженному на тот же множитель. Из соот-
соотношения A53) следует
2/ (Q) daldQ, A54)
A55)
Наличие в формуле A54) множителя /(Q) связано с явлением
интерференции волн, рассеянных каждым атомом. Не будь ин-
интерференции мы имели бы равенство /(Q) = 1 и сечение dH/dQ
было бы просто суммой сечений рассеяния на каждом из ато-
атомов 1 и 2.
Мы получим обычные результаты, характерные для интер-
интерференции, если исследуем поведение /(Q) как функции угла
рассеяния. Ограничимся обсуждением только двух предельных
случаев, когда длина волны К = 2n/k много больше или много
меньше R.
Если K^>R, то qR <#C 1 независимо от угла рассеяния и
/(Q) =2. Следовательно, сечение рассеяния на двух атомах
в четыре раза больше индивидуального сечения или в два раза
больше того ответа, который мы получили бы, если бы не было
явления интерференции.
В случае X <#С R функция /(Q) при изменении угла рассея-
рассеяния быстро колеблется между значениями 0 и 2. Пусть углы,
образованные векторами k0 и k с вектором R, равны ао и а со-
соответственно. Тогда
п 2nR (cos a0 — cos а)
qR==
Следовательно, /(Q) обращается в нуль всякий раз, когда
{cos a — cos ао) равно произведению K/R на полуцелое число,

340 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
и равно 2 всякий раз, когда (cos a—cos ао) кратно X/R. Соот-
Соответствующие значения а определяют направления минимумов
и максимумов интерференции. Ширина интерференционных по-
полос имеет порядок X/R. Возможность наблюдения этих эффек-
тов зависит от угловой разрешающей способности детектирую-,
щей аппаратуры. Последняя регистрирует частицы, рассеянные
в некоторый телесный угол с конечными размерами 6Я =FаJ.
Полное число регистрируемых частиц равно интегралу or
db/dQ по этой конечной области. Зависимость от углов dJl/dQ
в этой области в основном определяется множителем /(Q).
Если бос )$> X/R, то функция I(Q) сильно осциллирует в области
интегрирования и ее можно заменить средним значением, не
меняя результата, т. е. /(Q) = 1, и ответ получается такой, как
если бы рассеяние на двух атомах было некогерентным '). Если
же ба «С %/R, то /(Й) практически не меняется в области ин-
интегрирования и разрешающая способность детектора доста-
точна для наблюдения явления интерференции.
Рассмотрим теперь неупругое столкновение, при котором
один из атомов переходит из основного состояния в возбужден-
возбужденное. Пусть kn — волновой вектор рассеянной волны, тогда
h2k2
Сечение dl>n/du есть сумма сечений dI,no/dQ и dIiOn/dQ, кото-
которые соответствуют переходам (fe000)-v(fenn0) и (k00Q)-+(kn0n).
В приближении A52), когда мы сохраняем в разложении для Т
только члены, отвечающие простому рассеянию, эти сечения
легко вычисляются. При переходе (&оОО)->(&гаяО) атом 1 воз-
возбуждается, а атом 2 остается в основном состоянии. Вклад or
Т2 очевидно обращается в нуль (см. ур. A51)), а вклад от Т\
дает don/dQ — сечение процесса (&00)->-(&ля) — неупругого рас-
рассеяния частицы на одном атоме. Переход (k000)-*-(kn0n) отве-
отвечает противоположной ситуации: обращается в нуль вклад ог
Ти а вклад от Т2 равен dan/dQ. Окончательно,
d^ Л~? dl п da
dQ ~ dQ, ~*~ dil ~ dQ. '
i
В отличие от упругого рассеяния каждый атом действует так,,
как если бы он был одни в этом процессе: волны, неупруго рас-
рассеянные атомом 1 и атомом 2, отвечают различным каналам и
не могут интерферировать.
') Этот результат подтверждает и уточняет те условия из § X. 2, при вы-
выполнении которых можно считать, что мишень состоит нз независимых цент-
центров рассеяния.

§ 26. МНОГОКРАТНОЕ РАССЕЯНИЕ 34Г
§ 26. Многократное рассеяние
Рассмотрим процесс (k000)->-(kpq), при котором атомы 1 и 2
переходят из основного состояния в возбужденные состояния
р и q
Обозначим сечение этого процесса d'Lpq/du.
Поскольку при переходе меняются квантовые состояния
обоих атомов, вклад от членов простого рассеяния Т\ и Т2 об-
обращается в нуль и нам следует воспользоваться разложением
для Т вплоть до второго порядка. Это дает
{kpq \T\ feoOO) » Ai2 + Л2ь A56)
где
На рис. 20 изображены диаграммы для этих амплитуд дву-
двукратного рассеяния.
2 л . (кооо) г
(*"р°)Г^ /(к,0)
<кР9\Т1СоТг\коОО>
Рис. 20. Диаграммы амплитуд двойного рассеяния.
Вычислим вначале А2\. Чтобы воспользоваться условием
a^R, вычисления будем проводить в представлении {rmn}.
Используя коммутативность операторов Go, h\ и hi, находим
An = \ \ h ir") g (г", г') h (rf) dr" dr', A58)=
где
/. (г') ^ <г'рО I Г, | ЙООО) = -i±rr [ eib'r' (k'pO | Г, | ft000) dV, A59);
/2 (г") я (kpq | Т21 г"рО) = -^ \ е-*"'" (kpq \ Т21 ft"pO) dk",
A60)
(r», г')^{г"р ^*\УУ
В последнем выражении положительная величина Кр опреде-
определяется из уравнения

342 гл- Х1Х- ТЕОРИЯ РАССЕЯНИЯ
Мы будем использовать также вектор КР
Кр ^ KPRIR.
В силу свойств оператора Т\ функция fi(r') в существенном
отлична от нуля только в области с линейными размерами по-
порядка а и центром в начале координат. Аналогичным образом
функция f2(r") в существенном отлична от нуля в такой же об-
области, но с центром в точке R. Следовательно, в интеграле A58)
мы можем заменить g(r", r') первым членом его разложения
по степеням r'/R и (г" — R)/R- Возникающая при этом ошибка
в вычислении А21 имеет порядок a/R. Поскольку
\r"-r'\ttR + R{r"-R-r')IR+ ...,
:имеем
iK (r"-r')
Подставляя выражения A59), A60) и A62) в правую часть
A58) и выполняя интегрирования, находим
А2Х « - (m/2nh2R) (kpq | Т21 Крр0) (Крр0 | Г, | fe000). A63)
Точно так же, определяя вектор Кч следующим образом:
получаем для А{2 выражение (с ошибкой порядка a/R)
Al2« - (m/2nh2R) (kpq | Г, | Kq0q) (Kq0q | Т2 \ *ь00>. A64)
Отметим, что стоящие в выражениях A63) и A64) матричные
элементы Г] и Т2 соответствуют переходам, сохраняющим энер-
энергию. Воспользовавшись соотношениями A50) и A51), мы мо*
жем выразить Л21 и А\2 в терминах амплитуд перехода при не-
неупругом рассеянии на одном атоме. То же верно и для сечения
процесса tH,pc,/dQ, поскольку
2я
= -^ \А21 Р р (?) + -^ | АХ2 р р (?") + -g- {AnAl2 + A2lAU) p (?).
A65)
Произведя соответствующие вычисления, приходим к следую-
следующему результату:
= (dop (йо -* /Ср)/^2 du) (daq (KP -> *)/dQ) +
+ (da, (*ь -> Kp)/R2 du) (dap (Kq -> *)/ dQ) +
+ интерференционные члены. A66)

§ 27. СТАЦИОНАРНЫЕ ВЫРАЖЕНИЯ СДВИГОВ ФАЗ 34$
Вычисление интерференционных членов мы предоставляем чи-
читателю. Символ don(k — k')/dQ в этом выражении обозначает
сечение неупругого рассеяния частицы на атоме (kO)—*-(k'n).
Два первых члена в формуле A66) в точности совпадают
с теми, которые получаются при элементарном классическом
рассмотрении. Рассуждая классически, двукратное рассеяние
можно представлять себе двумя способами: либо частица вна-
вначале неупруго рассеивается на атоме 1 в направлении атома 2,
а затем неупруго рассеивается на атоме 2 в конечном направ-
направлении, либо вначале рассеивается на атоме 2 в направлении
атома 1, а затем — на атоме 1. Сечения этих двух процессов
участвуют в качестве первого и второго слагаемых в выраже-
выражении A66). К ним следует добавить члены, отвечающие интер-
интерференции двух типов рассеянных волн. Относительно этих чле-
членов можно сделать те же замечания, что и в § 25. Их наблю-
наблюдение возможно, если разрешающая способность детектора до-
достаточна для различия углов, разность которых имеет порядок
K/R.
Если К <С а, то амплитуды рассеяния при отклонениях, пре*
вышающих К/а, практически равны нулю и существенны
только сечения рассеяния вперед. Следовательно, как легко ви*
деть из уравнений A63)—A65), двукратное рассеяние воз-
возможно только в том случае, когда прямая, на которой располо-
расположены атомы, с точностью до К/а совпадает с направлением дви-
движения налетающей частицы, т. е. когда ko\\R или ko\\ (—R).
В первом случае величина Ai2 пренебрежимо мала, а вели-
величина А2\ отлична от нуля при малых отклонениях, т. е. при
k\\ko с точностью до К/а частица вначале рассеивается на
атоме 1, а затем — на атоме 2 в направлении, почти совпадаю-
совпадающим с первоначальным. Во втором случае порядок столкнове-
столкновений противоположный. На этих результатах основано наблюде-
наблюдение «траектории» ионизованных частиц в камере Вильсона (см.
сноску7) на стр. 144 тома 1).
Раздел IV. ВЫЧИСЛЕНИЕ АМПЛИТУД ПЕРЕХОДА
ВАРИАЦИОННЫМ МЕТОДОМ
§ 27. Стационарные выражения сдвигов фаз. Обсуждение
Вариационный метод уже использовался для определения
уровней энергии (гл. XVIII). В настоящем разделе мы кратко
рассмотрим его применение для вычисления сдвигов фаз и, в бо-
более общем случае, амплитуд перехода. Для этого надлежит вы-
выразить амплитуды как функционалы от волновых функций за-
задачи рассеяния, которые стационарны по отношению к вариа-

344 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
циям функций в окрестности их точного значения. Интеграль-
Интегральные выражения для амплитуд перехода, полученные в преды-
предыдущем разделе, для этой цели не годятся, поскольку они не
стационарны. Например, выражение E4) для Tt, рассматривае-
рассматриваемое как функционал от tf>;, не является стационарным, когда
г|Л( — точное решение радиального уравнения; аналогично вы-
выражение A27) для Тп-уь, рассматриваемое как функционал от
W[~\ не является стационарным, когда Ч'гГ1 меняется в окрест-
окрестности своего точного значения. Было предложено несколько
стационарных выражений для амплитуд перехода. Мы приве-
приведем здесь выражение, полученное Швингером '), которое ока-
оказалось наиболее удобным.
В этом параграфе мы рассмотрим случай частицы в цен-
центральном потенциале и получим стационарное выражение для
коэффициента Tt разложения амплитуды перехода по сфериче-
сферическим функциям (разложение E1)). За исключением нескольких
изменений, отмеченных ниже, мы следуем обозначениям § 9.
Если я^1 —полная стационарная рассеянная волна, то пар-
парциальная волна tf)( удовлетворяет интегральному уравнению
E6). Имея в виду дальнейшее обобщение, перепишем послед-
последнее в виде
A67)
где g\+)—интегральный оператор, ядром которого является
функция Грина
g(+) (Г) г/) s _ Bmk/h2) \l (kr<) A|+> (&•>); A68)
другими словами
5 g\+) (r, r') V (г') ф, (r') r'2 dr'.
Будем также использовать обозначение <q>i, q>2> для скалярного
произведения двух радиальных функций фЬ q>2
оо
<Ф,, Ф2)^5 q>;(r)q>2(r)r*rfr.
5 >;(r)q>2
о
Тогда интегральную форму E4^ для Ti можно переписать
в виде
Т, ~=<Jh Vq,). A69)
') См. цитированную в начале этой главы работу Липпмана и Швингера.
-Обсуждение относительных преимуществ различных выражений, предложен-
предложенных для вариационного вычисления сдвигов фаз, имеется в статье М. Мое,
D. S. Saxon. Phys. Rev. Ill, 950 A958).

§ 27. СТАЦИОНАРНЫЕ ВЫРАЖЕНИЯ СДВИГОВ ФАЗ 34&
Введем обозначения
00
A ft] ез\п, Щ) = <Ч»\ У/,) = J /, (кг) V (г) Ц> (г) г2 rfr, A7Q)
О
оо
в № в <*•, (К - Vgj+> v) -Ф> == 5 "*2 (r) v (
- S 5 (Ч> (г) К (г) gj+) (г, гО К (г7) ф (О) г2 rfr r'2 d/ A71)
о о
и рассмотрим функционал
^/N>] = ^-. A72)
зависящий от функции if. Область изменения ф ограничена
только условием локальной интегрируемости функции г2!^!2.
Как очевидное следствие соотношений A67) и A69) имеем
Отметим также, что функционал &~i не зависит ни от нор-
нормировки функции i(i (он не меняется при умножении \]р на про-
произвольную постоянную), ни от значений, которые принимает \|)
в области, где У(г)=О. Следовательно, 9~i принимает то же
самое значение Tt для любых функций -ф/, которые удовлетво-
ряют менее жесткому условию, чем уравнение A67).
¦%(r) = Cjt(kr) + gf>V% если У{г)ФО A67а)
(С — произвольная постоянная).
Вычислим вариацию b&~i как функцию от Ь$. Согласно оп-
определению A72)
Вариация дЛ равна
ОО
б А = J вф F (г) /, (Аг) г2 rfr = (б!),', VU),
и принимая во внимание, что V вещественно, a g{t+' (r, г') сим-
метрично по г и г', для вариации 6В получаем

346 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
Следовательно, мы можем записать
где
F (г) = В Ш V (г) jt (kr) -AWV (г) (t|> -
Для того чтобы SSTi — О при любых 8ty, необходимо и доста-
достаточно, чтобы F(r) — 0. Для этого необходимо, чтобы jt(kr) и
ч|з — gj+)Fi|) были пропорциональны друг другу в-области, где
V(г) отлично от нуля, т. е. чтобы ф была одной из функций,
удовлетворяющих уравнению A67а). Легко показать, что это
является также и достаточным условием. Итак, стационарное
значение 0~i равно искомой амплитуде
Tl = rl\si. A73)
Чтобы в вычислениях участвовали только вещественные
функции, мы выделили вещественную и мнимую части g\+)(r, r').
Вещественная часть будет фуикцией Грина
g@ (г, г') я - Bmk/h2) /, {kr<) nt (^r>),
и мы получим
g\+) (г, г') = g<» (г, г') - i Bmk№ )l (kr) }t (kr').
Подставляя это выражение в определение *3~i (т. е. в выраже-
выражение A71) для -В[г(>]), мы можем переписать A71) в эквива-
эквивалентной форме
2mk
—1
<//
<//
st
А2
и так как из уравнения E2) имеем
ТТ{ — i Bmk/h2) = — 2mk ctg д,/Й2,
то получаем следующее стационарное выражение для A ctg
оо оо
st
.0 J ^ ^
Я 0 0 0
J J (Ф (r) V (r) e'/> (r, r') V (rO « (rO) r2 drr'2 rf/
2m
st
A74)

§ 28. ВАРИАЦИОННЫЕ ВЫЧИСЛЕНИЯ СДВИГА ФАЗ 34Т
Можно показать, что функцию -ф/, для которой правая часть
уравнения A74) стационарна, можно брать вещественной и
что это условие вещественности пробных функций не меняет
полученного вариационного свойства.
§ 28. Вариационные вычисления сдвига фаз. Обсуждение
Отправной точкой при вычислении сдвигов фаз вариацион-
вариационным методом служит уравнение A74). Для вычисления функ-
функционала в правой части подставляют вместо г|з пробную функ-
функцию ф, зависящую от нескольких параметров, и определяют
значение получившейся функции, стационарное по отношению
к вариации этих параметров. Чем ближе будет пробная функ-
функция ф к точному решению г|), тем ближе будет приближенное
значение k ctg bt к точному значению. Как уже указывалось, и
в этом заключается основное достоинство вариационного ме-
метода Швингера, результат не зависит от нормировки ф и от
значений, которые принимает эта функция в областях, где по-
потенциал V обращается в нуль. Следовательно, для того чтобы
этим методом получить близкий к точному ответ, достаточно
взять такую пробную функцию, общий вид которой совпадает
с формой точного решения в области действия потенциала.
Оценка погрешности основана на этих полуколичественных
рассмотрениях и является, как и при вариационном вычислении
энергетических уровней, в значительной степени эмпирической.
Если мы ограничимся подстановкой в правую часть A74)
свободной волны ji(kr) вместо г|), то получим
075,
2m (lr Vi{) •
где
Л<^ </,.V/f) * A76>
Эта формула a priori точнее формулы борновского приближе-
приближения (ур. (X. 75)). В пределе, когда Д<<§;1, она эквивалентна
борновскому приближению второго порядка, в случае же, ко-
когда величина Дг не мала, эта формула, зачастую, значительно
точнее.
Для сравнения этих двух методов рассмотрим рассеяние
s-волны прямоугольной ямой в пределе низких энергий. Возь-
Возьмем
' ~Г° Wly A77)

348 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
Будем вычислять длину рассеяния
а = — lim (k ctg б),
используя упомянутые выше методы и сравнивая полученные
результаты с точным ответом. Вычисления не представляют
труда и, вводя обозначения b = BmV0ryti2y, результаты мо-
можно записать следующим образом:
точный ответ а = — Г-1 1J г0,
вариационное вычисление (A75)) avar = s—г0,
1-4 Ь2
О
борновское приближение ав = — j b2r0,
A 9 \
У ^2~^~nr^4) ro'
Критерий применимости борновского приближения выражается
неравенством D3), а именно:
(Ь является мерой глубины потенциала, т. е. числа связанных
s-состояний). В табл. I приведены численные результаты, со-
соответствующие четырем предыдущим формулам. Отметим, что
#var остается хорошим приближением для относительно боль-
больших значений Ь, включая интервал -jn< b <п, в котором,
конечно, борновское приближение ие сходится.
§ 29. Распространение метода на сложные столкновения
Предыдущие методы могут быть перенесены на более общие
задачи теории рассеяния. Не входя в детали всех возможных
расширений, мы ограничимся рассмотрением стационарного
выражения для матрицы перехода в случае упругого или не-
неупругого рассеяния двух составных частиц.
Если не оговорено противное, то будем придерживаться
обозначений раздела III. Амплитуда перехода a-vft дается
равенством
Та-* Ь = (Фь I Kp | W<,+)> = (?<„-> | Va

§ 29. СЛОЖНЫЕ СТОЛКНОВЕНИЯ
349
Таблица I
Сравнение вычисленной различными методами длины рассеяния
как функции параметра Ь = Bт1?0гЦ h2)'1*
(г0 выбрано в качестве единицы длины)
b
0
0,1я
0,2я
О.Зя
0,4я
n
2
0,6я
0,7я
0,8я
0,9я
n
Точное
вычисление
а
0
—0,034
—0,156
—0,460
—1,449
оо*)
2,63
1,63
1,29
1,11
1,00
Формула
стационарности
A75)
"var
0
—0,034
—0,156
—0,459
—1,428
—63,2 **)
2,81
1,72
1,38
1,21
1,12
*) a=»o соответствует существованию связанного
гиен.
•*) ovar обращается в бесконечность и меняет знак
Борновское
2-й порядок
0
-0,034
-0,152
—0,401
—0,859
-1,63
—2,9
чриближение
1-й порядок
0
—0,033
—0,132
—0,296
-0.296
состояния с нулевой энер-
прн 6=0,503я.
Эти выражения не стационарны по отношению к вариациям
'Ч/'а+) или Wft. Поскольку мы рассматриваем процесс рассея-
ния, то невозмущенные гамильтонианы равны, и можно исполь-
использовать обозначения
= G^ = [Е-Нй
Известно, что
Амплитуда Та-+ь дается также выражением
Та-+ь = ¦
A78)
Это выражение стационарно по отношению к независимым ва-
вариациям функций W^' и Wb'K Оно является обобщением ста-
стационарного выражения для Ti, приведенного в §27.,

350 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
Исключая простейшие случаи, такие как столкновение двух
элементарных частиц, при практическом использовании этого
выражения наибольшие трудности связаны с получением яв-
явной формы функции Грина Gq+>. Иногда оно может быть ис-
использовано в тех рассуждениях, где явная форма Go+) не тре-
буется. В любом случае это выражение имеет довольно огра-
ограниченную область применения.
Раздел V. ОБЩИЕ СВОЙСТВА МАТРИЦЫ ПЕРЕХОДА
Ряд свойств Г-матрицы непосредственно следует из харак-
характерных свойств гамильтониана, который описывает столкнове-
столкновение. Некоторые из них уже отмечались в предыдущих разде-
разделах, однако не подчеркивалась их большая общность. Система-
Систематическое исследование этого вопроса будет проведено в настоя-
настоящем разделе.
§ 30. Сохранение потока. S-матрица
Некоторые свойства Г-матрицы являются простым след-
следствием эрмитовости описывающего рассеяния гамильтониана Н.
Среди них полученные нами в § 19 интегральные представле-
представления A21) и A22). Используя тот же метод, мы получим два
новых соотношения, которые называются соотношениями со-
сохранения потока.
Используя обозначения § 19, рассмотрим две стационарных
волны Ч'а**, Wb+) отвечающие одной и той же энергии Е. Имеем
Следовательно, величина, которая получается в левой части
после суммирования по спинам и интегрирования по конечному
объему в конфигурационном пространстве, равна нулю. Приме-
Применяя теорему Грина, преобразуем эту величину в поверхностный
интеграл, который имеет вид суммы членов, относящихся к раз-
различным каналам, в пределе, когда поверхность стремится к бес-
бесконечности (см. сноску к § 19). Находим
lim {?ь+)\ ^{а+)}у = 0. A79)
Сравним левую часть этого уравнения с правой частью урав-
уравнения A19). Для вычисления заменим функции W1^, W^ их

§ 30. СОХРАНЕНИЕ ПОТОКА. S-МАТРИЦА 351
асимптотиками в каждом канале, тогда получим
2Af,
9Ла
2Mv
=o.
Вычисление вклада двух первых членов проводится тем же
способом, что и в § 2. Третий член представляет собой сумму
по всем каналам, включая аир, которую легко вычислить, ис-
используя определение символа {.. .}v; в отличие от вычислений
§ 19 вклад этого члена не равен нулю. Окончательно получаем
+ Е
П J W (Q) /Я? (Qv) ^v = 0.
Заменяя согласно определению A14) f(Q) матричными элемент
тами Г-матрицы, получаем
A80)
Здесь п обозначает плоскую волну в канале v, распространяю-
распространяющуюся вдоль Qv, и использовано определение плотности состоя-
состояний
С другой стороны, Т^ определяется обычным эрмитовым сопря-
сопряжением
Предыдущие преобразования можно проделать также, взяв
вместо 4f(+) волны ^н, Тогда получим соотношение
/j 9М.. _1ИП l^a ' ^* Jv — и> (И* )
которое связано с A79) заменой а на Ъ и Ч^ иа ?(->*. Для
вычисления левой части достаточно сделать необходимые под-
подстановки в предыдущих выкладках и использовать определение

352 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
матричных элементов Т A14') вместо A14). Тогда получим
b\T\n)dQv{n\T'r\a) = 0.
A800
Приведем другое, более формальное доказательство соотношений A80)
и A80'). Из соотношений
| Г1 д> = <Фй | Vp I Фа) +
<6 | Г+1 а) = (ФЬ \Va | Фа) + (Фь I Fp E_1H_le Va | Фа>,
вычитая их почленно и используя свойства A24) и (А.15в), получим
F | (Г - Г+) | а) = - 2ш (Фь | Fp6 (Е -H)Va\ Фа). A81)
Предположим, что множество стационарных волн YJfV отвечающих непре-
непрерывному спектру Н (и дополненное множеством подходящим образом норми-
нормированных собственных векторов дискретного спектра, если последний суще-
существует), образует полное ортонормированное множество собственных векто-L
ров Н н, следовательно, справедливо соотношение замкнутости
! A82)
(суммирование проводится по всему спектру Н, включая дискретный спектр).
Предположим также, что и f[j удовлетворяют соотношению замкнутости
1. A82')
Преобразуем скалярное произведение в правой части A81), используя A82),
к виду
BЯ)~3 J] <Ф6 | Fp | TJT'> б (Е - Еп) <ЧГ|Г> | Ve | Фв>
из которого следует соотношение A80). Таким же образом, используя A82'),
можно получить соотношение A80').
Матричные элементы F и Г+ между любыми состояниями
а и Ъ удовлетворяют уравнениям A80) и A80'). Их можно за»
писать короче
Т — Tf + 2шТ+Г = 0, A83)
Т — Tf + 2niTTf = 0, A83')
подразумевая суммирование по опущенным индексам в произ-;
ведениях матриц Т^Т и 7Т+, т. е. для каждого индекса v еле».

§ 31. ОПТИЧЕСКАЯ ТЕОРЕМА 353
дует учесть множитель pv(E), дающий плотность состояний
в канале v. Заметим, что все матричные элементы здесь берутся
между состояниями с энергией Е.
Введем матрицу 5
5 = 1—2я/Г. A84)
Эта матрица описывает столкновения при энергии Е, и так же,
как для Т, ее матричные элементы определяются между состоя-
состояниями с энергией Е. Выражая F и Г* в уравнениях A80) и
A80') через 5 и S+, находим
SfS = SSf=l. A85)
S-матрица унитарна.
Можно также показать, что если U(t,t') —оператор эволюции системы, то
S = lim U (t, t').
t-*+ оо
*'->— оо
Доказательство этого утверждения требует большой осторожности при пере-
переходе к пределам и здесь не приводится (см. 1-ю сноску к этой главе).
§ 31. Соотношение Бора — Пайерлса—Плачека
(оптическая теорема)
Рассмотрим соотношение A80) в частном сдучае, когда
a—b. (N.B. соотношения A80) и A80') совпадают при а=Ь.)
Тогда имеем
5]J A86)
С точностью до множителя 2n/hva интеграл в правой части ра-
равен сечению daa-*n/dQv и, следовательно,
где a^ot — полное сечение рассеяния, соответствующее состоя'
нию а. Возвращаясь к A86), имеем
0a ~~
hva
Для того чтобы преобразовать это выражение к более привыч
ному виду, выразим Таа в терминах амплитуды рассеяния
ред /^'(йд), которую мы обозначим fa@) (см. ур. A14))
12 А, Мессиа

354 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
Тогда
g0). A87)
Получили формулу Бора — Пайерлса — Плачека, связываю-
связывающую полное сечение с мнимой частью амплитуды рассеяния
вперед.
§ 32. Микрообратимость
Если Я инвариантен относительно обращения времени, го
матрица Т удовлетворяет соотношению микрообратимости (см.
§ XV. 20)
Т Ть- A88)
Это соотношение уже было доказано для случая рассеяния
частицы на вещественном потенциале (§§ 3 и 14). Формальное
доказательство § 14 можно также использовать и в общем слу-
случае с очень незначительными модификациями. Пусть, как и ра-
ранее, К — оператор обращения времени; начальное и конечное
состояния, которые получаются из а и b обращением времени
(изменение знаков импульсов и спинов), обозначим Ка и Kb
соответственно
Фкь = КФЬ, ФКа = КФа.
Для доказательства соотношения A88) используем выражение
A42), которое определяет амплитуду интересующего нас пе-
перехода:
Поскольку К—антиунитарный оператор, коммутирующий с Я,
Va и Ур, то получаем
= (Ф„ I [Va + V& E_!f + ie Va] I Фо> =
Вторая строчка следует из A24) и равна согласно A42) ампли-
амплитуде Та-+Ь-
Возводя обе части A88) в квадрат и переписывая результат
в терминах сечений doa->b/dQ$ и da/cb-^Ka/dQa, получаем соот-
соотношение микрообратимости для сечений
о» doKb+ Ka/9a (E) dQa = va doa^blPb (E) dQ&. A89)

$ 33 СВОЙСТВА ИНВАРИАНТНОСТИ Г-МАТРИЦЫ 35S
Здесь мы использовали тот факт, что vKb = Vb, Рка = ра- Из оп-
определения скорости и плотности состояний (ур. (XVII. 52)) для
каждого канала имеем равенства
Следовательно, соотношение A89) можно переписать, при
условии, что dQa = clQp = dQ, следующим образом:
=kldoa+b. A90)
§ 33. Свойства инвариантности Г-матрицы
Исследуем теперь следствия инвариантности Я по отноше-
отношению к вращениям, отражениям и вообще к преобразованиям,
которые представляются унитарными операторами.
Если Н, На, и Яр инвариантны относительно данного унитар-
унитарного преобразования X, то справедливо соотношение (ср.
§ XV. 13)
A91)
(N. В. Это соотношение отличается от соотношения микро-
микрообратимости по содержанию реакции, описываемой амплитудой
в левой части.)
Для доказательства A91) необходимо только заметить, что
согласно определению A44) оператор Т®а также инвариантен
относительно преобразования X
и, следовательно,
Тха+хъ = <Ф6 \Х^аХ\ Фа) = <Ф6 |7*а| Ф„> ^Та+ ь.
Из A91) легко получить следующее соотношение для сечений:
A92)
которое подобно соотношению A90).
Предположим теперь, что полный гамильтониан Н и различ-
различные «невозмущенные» гамильтонианы На, Яр, ..., инвариантны
относительно преобразований некоторой группы G. Как мы уви-
увидим, это приведет к некоторым свойствам Г-матрицы, аналогич-
аналогичным тем, которые были получены в § XV. 11 для матриц, задаю-
задающих наблюдаемые, инвариантные по отношению к G.
Будем использовать обозначения § XV. 11 и рассмотрим два
определенных там множества наблюдаемых / и М. Пусть v —
один из каналов, открытый для столкновений при энергии Е.
Операторы Hv, J и М образуют набор коммутирующих наблю-
12*

356 ГЛ. XIX. ТЕОРИЯ РАССЕЯНИЯ
даемых. Обозначим через |v?vtv/h> векторы общего базиса (мы
будем предполагать, что это стандартный базис, отвечающий
группе G, хотя такое ограничение несущественно). Индекс v со-
соответствует рассматриваемому каналу, Ev— собственное значе-
значение /7V, у и ц обозначают собственные значения / и М соответ-
соответственно, tv — дополнительное квантовое число, которое меняется
в области, зависящей от значений ?v> У и ц. Векторы \vEvxvj[iy
ортонормированы
<v?vV> |«/ У) = b(Ev- E>v) Ъч<Ъи,Ът,.
Будем для простоты считать индекс tv дискретным. Так обстоит
дело в случае 2-частичного канала, если G — группа вращений
или содержит ее как подгруппу. Тогда tv принимает конечное
число дискретных значений.
Рассмотрим столкновение при фиксированной энергии Е и
переход из некоторого канала v в другой канал v'; согласно
высказанной выше гипотезе соответствующий оператор 7vv/ (оп-
(определение A44)) инвариантен относительно преобразований из
группы G. Как очевидное обобщение свойства (XV. 52) имеем
|i |ГУ' | v'?twV> = в/л V <vtv |Г(»| v4v'>, A93)
где (vtv I T(i)! v'tV') зависит от квантовых чисел j, tv и tV' и не
зависит от ц. Все следствия, вытекающие из инвариантности по
отношению к группе G, содержатся в уравнении A93).
Следовательно, каждой паре (vv') открытых каналов соот-
соответствует некоторое число коэффициентов (vtv |Г(/)| v'tV'). Те
из коэффициентов, которые отвечают данному значению j (j и Е
фиксированы; v, tv, v' и tv- меняются), образуют квадратную
матрицу, которую мы обозначим Г(/). Она аналогична Г-маг-
рице, только ее размерность, как правило, значительно меньше.
В частности, если G содержит группу вращений, а во всех от-
открытых каналах имеется не более двух частиц, то Г</> — конеч-
конечная матрица; если же открыт только один канал и обе частицы
бесспиновые, то W> — одномерна, т. е. представляет собой
число, равное с точностью до легко определяемого множителя
коэффициенту Tj в разложении E1).
Легко разложить амплитуду перехода 7V.-6 в ряд из матриц
TV\ Для этого рассмотрим формулу A45), которую мы преоб-
преобразуем, используя соотношения полноты для стандартных бази-
базисов, отвечающих каналам а и р, и свойство A93). Коэффи-
Коэффициенты разложения зависят от проекций плоских волн Фа и Ф»
на базисные векторы. Обозначая Ф„ плоскую волну с энергией
Е в канале v, можно записать:
<ФЯ | v?vTv/|i> = б (Е - Еч) <Ф„ | vT?/|i>. A94)

ЗАДАЧИ И УПРАЖНЕНИЯ 357
Используя это обозначение, после небольших вычислений нахо«
ДИМ
= Z S <Ф61 РтэЛ1> <Ртр | Г") | ата) <ote/|i | Фа>. A95)
Полученное разложение обобщает E1). Как и последнее, оно
особенно полезно в случае быстрой сходимости; это верно для
ядерных столкновений, когда длина волны во входном и вы*
ходном каналах велика по сравнению с радиусом действия ядер-
ных сил, именно в такой ситуации разложение A95) исполь»
зуется чаще всего (см. 1-ю сноску к § 16).
ЗАДАЧИ И УПРАЖНЕНИЯ
I. Доказать асимптотическое свойство
г->оо '
(i) используя разложение плоской волны по сферическим функциям и со-
соотношение полноты для последних;
(ii) исследуя непосредственно асимптотику
exp (/?r) q>(Qr)dQr
(ф(Й) —непрерывная функция направления Я = (9 ф); Qr и Qq— направ -
ления, соответствующие векторам г к q).
2. Показать, что для двух плоских волн exp (iqir), exp ({до) с одинако-
одинаковой длиной волны (<7i = 92) справедливо точное равенство
{exp (iqtr), exp (iq2r)} = 0,
каково бы ни было R (определение {...} см. в § 2).
3. Вычислить сечение рассеяния в борновском приближении:
(i) для прямоугольной ямы глубины Vo и радиуса а;
(ii) для гауссова потенциала
V = Vo exp (- r2/a2);
(iii) для потенциала Юкавы
_ Vo exp (- Кг)
Кг
Оправдать для этих трех частных случаев утверждения § 4, относящиеся
к общему виду высокоэнергетического углового распределения; определить
асимптотический вид полного сечения.
4. Рассмотрим гамильтониан частицы массы т в поле короткодействую-
короткодействующего потенциала V (г), (rV —*¦ 0\
Я—- (ft2/2m) Д + К (г).

358 гл Х1Х- ТЕОРИЯ РАССЕЯНИЯ
При энергии Е = h2k2l2m и моменте I радиальное уравнение имеет вил
L dr2 r2 h2 \3l
Обозначим Fi(k\r) регулярное решение, и\+ (k; r) и и\~^ (k; r) — «уходящее»»
«приходящее» решения соответственно. Эти решения нормированы так, что-
(i) Показать, что стационарные волны W'^ (определения § 2) даются сле-
следующими формулами:
^ = 17 ? '1 ехр (* '*') Y"? {S) Y™ i?) Fi{k; r)'
Im
(ii) Показать, что функции G-{r, г'), определяемые формулами
,*Lош(р, /) = __j_ ^ ехр (± й/) у»- ('г) у- (;') F/ (fc r<)и(±, {k- r>>
1т
являются функциями Грина оператора Е — Н, т. е. симметричными по г и г*
функциями, удовлетворяющими уравнению
(? - Я) G(±) (г, г') = 6 (г - г'),
а их асимптотическое поведение имеет вид
(Формулы справедливы также и для потенциалов V с асимптотическим пове-
поведением 1/г, если подходящим образом определить Ft и й}±(; соответствующие
изменения произойдут и в асимптотике G(±).)
5. Доказать формулу A51).

«Я черна, но собою прекрасна ..>
(Песнь песней, 1. 5)
ЧАСТЬ V
ЭЛЕМЕНТЫ
РЕЛЯТИВИСТСКОЙ
КВАНТОВОЙ
МЕХАНИКИ

ГЛАВА XX
УРАВНЕНИЕ ДИРАКА
Раздел I. ОБЩЕЕ ВВЕДЕНИЕ
§ 1. Релятивистская квантовая механика')
В предыдущих главах в основе всех вычислений в квантовой
теории лежало уравнение Шредингера. Это уравнение, полу-
полученное из гамильтонова формализма нерелятивистской класси-
классической механики по принципу соответствия, обладает всеми
свойствами инвариантности функции Гамильтона, из которой
оно получено. В частности, для изолированной системы оно ин-
инвариантно относительно пространственных вращений и трансля-
трансляций. Можно также показать, что оно инвариантно относительно
преобразований Галилея (см. задачу XV. 7). Следовательно, фи-
физические свойства, которые предсказывает теория Шредингера,
инвариантны относительно галилеевских преобразований си-
системы координат, но не инвариантны относительно преобразо-
преобразований Лоренца, как того требует принцип относительности. По-
Поскольку преобразование Галилея получается-из преобразования
Лоренца при скоростях, малых по сравнению со скоростью
света, естественно ожидать, что упомянутая теория будет кор-
корректно описывать явления только при скоростях в<с (это под-
подтверждается экспериментально). В частности, все явления, ко-
которые включают взаимодействие света и вещества, такие как
излучение, поглощение или рассеяние фотонов, находятся вне
рамок нерелятивистской квантовой механики.
Одна из основных трудностей, которые возникают при по-
построении релятивистской квантовой механики, связана с тем,
что нарушается закон сохранения числа частиц. В силу эквива-
эквивалентности энергии и массы (одно из важнейших следствий прин-
принципа относительности) возможно рождение или поглощение ча-
частиц всякий раз, как только при взаимодействии происходит пе-
передача энергии, равной или превосходящей энергию покоя этих
частиц. Таким образом, полная релятивистская квантовая тео-
теория должна содержать в единой схеме динамические состояния,
') Для чтения этой главы рекомендуется ознакомиться с разделами I и И
Дополнения Г,

362 ГЛ. XX. УРАВНЕНИИ ДИРАКА
отличающиеся не только квантовым состоянием, но также видом
и числом элементарных частиц, которым эти состояния соответ-
соответствуют. Для этого необходимо обратиться к концепции кванто-
квантованного поля, в связи с чем релятивистскую квантовую теорию
часто называют теорией квантованных полей или квантовой
теорией поля. В том состоянии, в котором эта теория находится
в настоящее время, она не свободна ни от трудностей, ни даже
от противоречий, но способна объяснить множество эксперимен-
экспериментальных фактов.
Последняя, пятая часть этой книги служит введением в тео-
теорию квантованных полей и дает элементарные методы вычис-
вычисления ряда релятивистских эффектов, относящихся к динамике
электрона и взаимодействию электромагнитного поля с заря-
заряженными частицами.
Эта часть состоит из двух глав.
В настоящей главе рассматривается простейшая задача ре-
релятивистской квантовой механики: частица спина 1/2 в задан-
заданном внешнем поле. Наиболее важным примером такой ситуа-
ситуации является электрон в электромагнитном поле. Поле не кван-
квантуется, и эволюция системы должна описываться волновым
уравнением, которое обладает всеми свойствами инвариантно-
инвариантности, вытекающими из принципа относительности.' Уравнение
должно удовлетворять также принципу соответствия и в нере-
нерелятивистском приближении давать теорию Паули. Такое урав-
уравнение существует и называется уравнением Дирака. После крат-
краткого обзора группы Лоренца и релятивистской классической
динамики (раздел I) мы приводим уравнение Дирака (раздел II)
и подробно исследуем его свойства инвариантности (раздел III).
В оставшейся части этой главы мы обсуждаем физическое со-
содержание теории и, рассматривая основные приложения урав-
уравнения Дирака, исследуем его связь с классической динамикой
(раздел IV), нерелятивистской квантовой механикой (раздел V)
и квантовой теорией поля (раздел VI).
Вторая глава посвящена концепции квантованного поля, эле-
элементарной квантовой теории электромагнитного излучения и его
взаимодействию с атомными и ядерными системами.
§ 2. Обозначения и различные определения
Единицы. За редким исключением мы будем пользо-
пользоваться системой единиц, в которой
и, следовательно, время имеет размерность длины, энергия, им-
импульс и масса имеют размерность обратной длины, а электри-
электрический заряд является безразмерной величиной (е2 = e2/tic =

§ 2. ОБОЗНАЧЕНИЯ И РАЗЛИЧНЫЕ ОПРЕДЕЛЕНИЯ 363
•= 1/137). Общие выражения могут быть легко восстановлены
из соображений однородности.
Координаты. Задание момента времени / и точки г =
= (х, у, г) обычного пространства определяет точку простран-
пространства-времени. Обозначим координаты этой точки х°, х1, х2, х3;
х° = ct — координата времени, а х{, х2, х3 — три пространствен-
пространственных координаты: хх == х, х2 == у, хъ = г. Мы будем использо-
использовать индексы 0, 1, 2, 3 для обозначения компонент четырехмер-
четырехмерных векторов1) и тензоров по осям 0, 1, 2, 3 соответственно.
Пространственно-временные компоненты 4-векторов или тен-
тензоров будем обозначать греческими буквами. Эти индексы
могут принимать четыре значения: 0, 1, 2, 3; латинские буквы
будем использовать для обозначения компонент в обычном про-
пространстве, они могут принимать значения 1, 2, 3. Таким обра-
образом:
vU / уО vk\ /^0 v\ V2 V3\
Х^ \Л , X ) ¦ уХ , X , X , X ),
(ц = 0, 1, 2, 3), (k=l, 2, 3).
Метрический тензор, ковариантные и кон-
контравариантные индексы. Пространство-время имеет
псевдоевклидову метрику, которая задается метрическим тен-
тензором
п
0
0
0
0
j
0
0
0
0
j
0
0
0
0
I
или иначе
goo=l, gftfe = —I, guv = 0, если ц?=у- A)
Следует различать ковариантные векторы (которые преоб-
преобразуются как д/дх^) и контравариантные векторы (которые пре-
преобразуются как X»-), а также ковариантные и контравариантные
компоненты тензоров. Следуя общепринятому соглашению, ко-
ковариантные индексы пишут внизу, а контравариантные — на-
наверху. Так, а» означает контравариантный вектор. Соответствую-
Соответствующий ковариантный вектор получается применением метриче-
метрического тензора:
что дает
а0 = a0, ak = — ak.
') Для краткости также будем писать 4-вектор, 4-тензор.

364 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
Мы будем пользоваться соглашением о суммировании по по-
повторяющимся индексам. При этом предыдущее выражение при»
мет компактный вид
Операция поднятия индексов осуществляется применением
тензора gi*v
В данном случае мы имеем
Кроме того,
где бц — символ Кронекера
gPV = g" = 6V,
если (* —v»
если ц ф v.
Трехмерные векторы, четырехмерные век»
торы, скалярное произведение. Мы сохраним обозна-
обозначения, которыми пользовались ранее, для векторов обычного
пространства или 3-векторов, обозначая вектор буквой жирного
шрифта, а его длину — той же буквой обычного шрифта.
Три пространственных компоненты вектора а»- образуют
3-вектор. Используя принятые обозначения, имеем следующее;
а* = (а0, а\ а2, а3) = (а0, а), а = (ах, ау, аг),
Иногда мы будем обозначать 4-вектор а^ просто а, когда
это не приведет к путанице с длиной 3-вектора а.
Скалярное произведение двух 4-векторов а^ и Ь* получается
при свертке контравариантных компонент одного с ковариант-
ными компонентами другого, т. е. a^b* или а^Ь^
а^ = aabfl = a b — ab. B)
Норма вектора а» равна а^ == (а0J — а2.
Классификация 4-векторов. Четырехмерные век-
векторы можно разделить на три класса в соответствии со знаком
их нормы:
йрСР < 0 аР — пространственно-подобный вектор,
а^ = 0 аР — нуль-вектор,
а^а11 > 0 а" — времениподобный вектор.

S 2. ОБОЗНАЧЕНИЯ И РАЗЛИЧНЫЕ ОПРЕДЕЛЕНИЯ 365
Эта классификация соответствует положению вектора по от-
отношению к световому конусу x^xv- = 0. Два последних случая
можно классифицировать в зависимости от знака временной
компоненты:
а0 > 0 — вектор направлен в будущее,
а0 < 0 — вектор направлен в прошлое.
Градиент. Дифференциальные о п е р а т о р ы. Мы
сохраним обозначения V = (д/дх, д/ду, d/dz) и Д^ VV.
Четыре оператора частных производных dldxv- образуют ко-
вариантный вектор, который мы обозначим символом д»:
<?„ = д/дх» = (д/дх0, д/дхК д/дх1, д/дх?) = (d/dct, V). C)
Это оператор градиента.
Мы будем использовать также «контравариантныи градиент»
-V). D)
Определим оператор Даламбера ') (ср. § II. 12)
Тензор e^vp. Тензор e^lvP определяется как полностью ан-
антисимметричный тензор, компоненты которого равны 0, если
какие-либо два индекса совпадают, -fl, если (X|ivp) образуют
четную перестановку индексов @, 1, 2, 3), и —1, если (X^vp)
образуют нечетную перестановку.
Электромагнитное поле. Электромагнитный по-
потенциал состоит из векторной A(r, t) и скалярной q>(r,t) ча-
частей, которые образуют четырехмерный вектор Лц
Л* = (<р, А). F)
Электрическое & и магнитное Ж поля определяются по фор-
формулам
S = — Vcp — дА/дх°, Ж = rot A. G)
Компоненты векторов d? и Ж образуют антисимметричный
тензор F^v в пространстве-времени согласно определению
F^ = ~dx^~~dfi> (8)
что дает
/о Жх &у <%z \
I х п a» <v»l
(9)
') Ряд авторов использует обозначение D для оператора, отличающегося
от введенного нами знаком.

3 66 ГЛ XX. УРАВНЕНИЕ ДИРАКЛ
Мы будем использовать также векторный оператор
Од = ^ + ieA» = (^- + tap, V - ieA) . A0)
§ 3. Группа Лоренца
Преобразованием Лоренца системы координат называется
вещественное, линейное преобразование координат, сохраняю-
сохраняющее норму пространственно-временного интервала. Новые коор-
координаты x'v точки в пространстве-времени получаются из старых
лМ по формулам
Вещественный вектор а^ определяет трансляцию пространствен-
пространственно-временных осей. В дальнейшем преобразования трансляции
мы будем рассматривать отдельно, а преобразованиями Ло-
ренца назовем однородные преобразования (а^ = 0)')
A1)
Поднимая или опуская индексы у матрицы Q!J, можно по-
получить матрицы Оц, Q|1V, Qwv (например, Q^v = gvpQp]). Задание
одной из этих матриц определяет преобразование Лоренца.
Условия вещественности и инвариантности нормы имеют вид
Qlv = Qav, A2)
QnvQ1** = Qv»Qkn = 6v- A3)
Следовательно,
det|Q!j| = ±l A4)
и обратное преобразование можно записать в виде
х» = х'\1%. A5)
Такие преобразования образуют полную группу Лоренца:
группу вещественных линейных преобразований, сохраняющих
скалярное произведение четырехмерных векторов.
Если Q00 > 0, то преобразование сохраняет знак временной
компоненты времениподобных векторов. Такие преобразования
называются ортохронными, они образуют ортохронную группу
Лоренца.
Если дополнительно и det|Qv|=l, то преобразование со-
сохраняет ориентацию (правую или левую) осей координат
в обычном пространстве. Множество таких преобразований об-
]) Группа, обр;|.!пв?Н1:ня преобр.гюваничми Лоренца и трансляциями,
обычно называется неоднородней группой Лоренца или группой Пуанкаре.

i 3. ГРУППА ЛОРРНЦА 367
разует собственную группу Лоренца, которую мы будем обо-
обозначать j?o-
Преобразования собственной группы Лоренца можно рас-
рассматривать как последовательность бесконечно малых преобра-
преобразований. Матрица Q^v бесконечно малого преобразования имеет
вид
где величины co^v являются бесконечно малыми. Условия A2)
и A3) дают
Следовательно, м^ — вещественный антисимметричный тензор..
Положим
7<аЗ) — 7<Ва> = а а а а <\7)
Тензор Z'^?1 — антисимметричен и имеет две отличных от нуля
компоненты: ц = a, v = |3 и ц = |3, v = а, одна из которых
равна +1, а другая —1. Пусть е есть бесконечно малая вели-
величина, тогда
s „ ez«*3>
есть матрица бесконечно малого преобразования Лоренца, от-
отвечающего «вращению» на угол е в плоскости хах$.
Существует шесть бесконечно малых преобразований такого
вида. «Вращения» в плоскостях х1х2, х2хъ и хъхх есть вращения
на угол е в пространстве вокруг осей Oz, Ox, Оу соответственно.
«Вращения» в плоскостях х1х°, х2х°, х3х° представляют собой
специальные преобразования Лоренца (переход к движущейся
системе координат со скоростью е в направлении Ох, Оу, Oz со-
соответственно ').
Кроме бесконечно малых преобразований можно определить
преобразования различных отражений: пространственного от-
отражения s (х° = х°, xk = —xk) и отражения времени t
(х° = — х°, xk = xk). Ортохронная группа состоит из группы
') Если новые координаты получены из старых вращением на конечный
угол ф вокруг оси Oz, то имеем
х'Х = х1 cos ф + х2 sin ф, х'2 = х2 cos ф — х] sin ф, х'3 — х\ х'° — х^.
Если они получены из старых при специальном преобразовании Лоренца со
скоростью v = tg ф, направленной вдоль Ох, то имеем
хЛ = х} ch ф - ха sh ф, x'O=xochqp-x'sh?, л:'2 = х2, х'3 = х3.
Рассмотренные выше преобразования отвечают случаю, когда ф = ? — беско-
бесконечно малой величине.

368
ГЛ. XX. УРАВНЕНИЕ ДИРАКА
Таблица I
Det
+ 1
1
— 1
+ 1
a00
Л Л V V
о о о о
Обозначения группы
собственная
ортохронная
полная
j?o, отражения s и преобразований из произведения s3?0. Пол-
Полная группа образована преобразованиями из S'o, s3?o, tg§ и
stS'o- Свойства этих четырех подмножеств полной группы при-
приведены в табл. I.
§ 4. Классическая релятивистская динамика
Напомним динамические свойства классической релятивист-
релятивистской частицы с массой покоя тис зарядом е в электромагнит-
электромагнитном поле (ф, А).
Обозначим v скорость частицы
—?• с«
Определим релятивистскую массу М и механический им-
импульс ') я:
Набор (М, я) есть 4-вектор, норма которого равна
М2 - л2 = т2 B0)
и который налравлен в будущее (М > 0).
Если нет внешнего поля, то частица двигается равномерно
и прямолинейно: v есть величина постоянная.
Во внешнем электромагнитном поле траектория частицы
удовлетворяет уравнению
dt ¦
Это основное уравнение релятивистской динамики материаль-
материальной точки. Вектор F называется силой Лоренца.
') Не путать с импульсом, который в этой книге определяется как пере-
переменная, канонически сопряженная к координате (см. примечание на стр. 62
тома 1).

§ 4. КЛАССИЧЕСКАЯ РЕЛЯТИВИСТСКАЯ ДИНАМИКА 369
Из уравнения B1) следуют уравнения:
^- = (vF) = e(vS), B10
1(гХ") = гХЛ B2)
которые определяют зависимости от времени массы и момента
количества движения.
Если определить собственное время т частицы по формуле
_i_
dx = (dx» dx^Y = л/1 — v2 dt,
то приведенные соотношения можно записать в ковариантной
форме. Определим 4-скорость
dt
умножение которой на т дает механический 4-импульс
Уравнения B1) и BГ) эквивалентны формально ковариант-
ному уравнению
ИЛИ
dul e
dx =-^t "v.
где /^— тензор электромагнитного поля (ур. (8) — (9)).
Приведенные уравнения движения можно вывести в рамках
лагранжева или гамильтонова формализма (см. задачу 1.5).
Импульс р и энергия Е образуют 4-вектор р^, который связан
с яР соотношением
р^ == я -\- еА , B4)
т. е.
Е — М + еф, р = л + еА.
Функция Гамильтона равна
Н = еф + V(P — еАJ + т2, B5)
что согласуется с соотношениями B4) и B0). Используя это
равенство, получаем гамильтоновы канонические уравнения
df я dp

370 гл- XX. УРАВНЕНИЕ ДИРАКА
Первое уравнение есть определение скорости, а второе эквива~
лентно уравнению B1), что легко установить, используя опре-
определения й'и! (ур. G)) и равенство
dA f д \
dt V dt ° )
Раздел II. УРАВНЕНИЯ КЛЕЙНА — ГОРДОНА И ДИРАКА
§ 5. Уравнение Клейна—Гордона
Построение релятивистского волнового уравнения для элек-
электрона является сложной задачей из-за наличия у электрона
спина. Найдем вначале релятивистское волновое уравнение для
частицы спина 0, например, я-мезона. Такая частица не имеет
внутренних степеней свободы и ее волновая функция W может
зависеть только от г и t. Обозначим массу частицы т, заряд е
и предположим, что она находится во внешнем электромагнит-
электромагнитном поле Аи = (ф, А).
При выводе волнового уравнения будем действовать эмпири-
эмпирически, руководствуясь принципом соответствия. Это гарантирует
нам получение классических уравнений движения в случае,
когда справедливо квазиклассическое приближение.
Напомним правило соответствия Шредингера
?_>/JL> p^_/v. B6)
Вводя pu=s(E, p), получаем
рх -> 1б\ B6')
Из выражения B5) для гамильтониана имеем
Е = ец>+ д/(Р ~ eAf+n?, B7)
откуда, используя B6), следует волнозое уравнение
- *Ф) ч
= [(у v -
Данное уравнение обладает двумя серьезными недостатками.
Во-первых, асимметрия пространственных и временной коорди-
координат не позволяет увидеть явной релятивистской инвариантности.
Во-вторых, в правой части стоит квадратный корень, которому
трудно придать смысл оператора, за исключением случая
А = 0.
Оба недостатка исчезают, если в качестве исходной точки
выбрать соотношение B0), которое дает
(Е - ефJ - (р - eAf = т\ B8)

§ 5. УРАВНЕНИЕ КЛЕЙНА — ГОРДОНА 371
Это соотношение эквивалентно более общему соотношению,
чем B7)
Е = еф ± д/(Р — eAf + m2. BГ)
Классическим решениям отвечает знак «-}-»; знак «—» дает ре-
решения с отрицательной массой, что не имеет физического
смысла. Таким образом, выбирая в качестве исходного соотно-
соотношение B8), мы вводим лишние решения с отрицательной мас-
массой.
Применение правила соответствия к B8) дает уравнение
Клейна — Гордона
[(* -§;¦ - 6ФJ - (} V - еАJ] ? = ш2?, C0)
которое можно также записать в явно релятивистски инва-
инвариантном виде
2) У = [(<Э№ + 1еА„) (^ + «еЛ") + m2] W = 0. C0')
(D^ + m2
Рассмотрим кратко интерпретацию этого уравнения '). Огра-
Ограничимся для простоты случаем, когда внешнее поле равно
нулю. Уравнение приобретает простой вид (см. § II. 12)
(?+т2)Ч' = 0. C1)
Это дифференциальное уравнение второго порядка по вре-
времени и для определения Ч; при всех временах необходимо знагь
в начальный момент как W, так и dx?/dt. Возникшую трудность
легко обойти, если постулировать, что динамическое состояние
системы в данный момент определяется не одной функцией VF,
а двумя — W и dx?/dt или их линейными комбинациями
W~* ^ m dt ' Х ~ Т m dt ¦
Иначе говоря, состояние системы определяется волновой функ-
функцией с двумя компонентами Ф и %. Такая волновая функция
удовлетворяет дифференциальному уравнению первого порядка
по времени, которое легко получить из уравнения Клейна — Гор-
Гордона. В нерелятивистском пределе энергия частицы приблизи-
приблизительно равна ее массе покоя m. a
следовательно, % <§С Ф. Одна из компонент становится прене-
пренебрежимо малой по отношению к другой, и мы получаем нереля-
') Более потное изложение содержится в статье Н, Feshbach, F. Villars.
Rev. Mod. Phys. 30, 24 A958).

372 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
тивистскую теорию Шредингера, в которой динамическое со»
стояние частицы со спином 0 определяется однокомпонентной
волновой функцией.
Для интерпретации волновой функции необходимо опреде-
определить плотность вероятности положения частицы Р и плотность
вероятности потока /, которые удовлетворяют уравнению непра-
рывности (см. § IV. 4)
4f + V/ = O, C2)
или, вводя обозначение fsssfP, /), получим
<V* = 0. C3>
Функции V и Ч?* удовлетворяют уравнению C1), следова-
следовательно,
^(?40 —(?ЧГ*)ЧГ = О
и, используя определение оператора Даламбера, имеем
д» [V (д^чО - (сРЧГ) ?] = 0.
Уравнение непрерывности будет выполнено, если выбрать ]\
пропорциональным выражению, стоящему в квадратных скоб-
скобках. Коэффициент пропорциональности выбирается так, чтобы
в нерелятивистско:л пределе получилось обычное определение
f = J- [4f' (cf4f) - {d^W* )V],
Р(г л- i ГЧг» ЭУ av»lri
Исследуя выражение C4) получаем, что плотность Р(г, ()
нз является положительно определенной. В этом заключается
основная трудность, связанная с уравнением Клейна — Гордона.
Другая трудность, связанная с предыдущей, относится к «ре-
«решениям с отрицательной энергией». Если, например, рассматри-
рассматривать плосковолновые решения уравнения без внешнего поля
то, подставляя это выражение в C1), получим
Следовательно, существуют решения с отрицательной энергией
— Vp2 + ni2 • Их появление, очевидно, вызвано упоминавшимся

§ 6. УРАВНЕНИЕ ДИРАКА 373
выше введением в теорию отрицательных масс (было бы более
корректным называть их решениями с отрицательной массой;
однако при нулевом внешнем поле различие между массой и
энергией иллюзорно). Для преодоления этих трудностей мы,
следуя Паули и Вайскопфу1), изменим интерпретацию 4-век-
тора р и определение средних значений. При новой интерпре-
интерпретации теории величина е/м- отвечает 4-вектору плотности тока,^
в частности, eP(r, t) есть плотность электрического заряда. Сле-
Следовательно, уравнение C3) выражает закон сохранения заряда.
С другой стороны, число частиц не сохраняется, что вызвано
возможностью аннигиляции или рождения пар частиц с проти-
противоположными зарядами. Последовательное рассмотрение таких
явлений возможно только в теории поля. При выбранной интер-
интерпретации мы получаем теорию одного заряда, а не одной ча-
частицы. В теории Дирака нам удастся построить положительно
определенную плотность Р, однако мы увидим, что трудность,
связанная с отрицательными энергиями, остается, и теорию Ди-
Дирака также нельзя считать удовлетворительной одночастичной
теорией (раздел VI).
§ 6. Уравнение Дирака
Перейдем к построению релятивистского волнового уравне-
уравнения для электронов. Следуя Дираку, будем поступать по анало-
аналогии с нерелятивистской квантовой механикой.
В нерелятивистской теории электрон описывается двухком-
понентным спинором, который при вращениях преобразуется,
как момент импульса, равный '/2- Поэтому в релятивистской
теории электрон должен описываться волновой функцией, кото-
которая состоит из нескольких компонент и изменяется определен-
определенным образом при преобразованиях Лоренца, Обозначим ips(r,/)
компоненту с номером s волновой функции Y. Тогда W можно
записать в виде матрицы, состоящей из одного столбца:
¦ф2
Как и в нерелятивистском случае, волновую функцию W
в данный момент времени можно рассматривать как функцию
пространственных координат г и внутренних, или спиновых, пе-
переменных s (s = 1, 2, ..., N). Такая волновая функция задает
>) W. Pauli, V. Weisskopf. Helv. Phys. Acta 7, 709 A934); см. также ци-
цитированную в предыдущей сноске статью Н. Feshbach, F. Villars.

374 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
некоторый вектор состояния |яр(О>. а пространство Ж таких
состояний есть тензорное произведение
8 =
пространства <??@) орбитальных переменных и пространства
спиновых переменных; волновая функция W отвечает этому век-
вектору в подходящем представлении
Ч(г, s; l) = $a{r, t) = {rs\W(t)).
Продолжая аналогию, мы определим плотность вероятности по-
ложения частицы формулой
/>(/-, 0= II ^Р. C5)
В соответствии с такими гипотезами волновое уравнение
должно иметь вид
i 4г = Н^> C6)
где Hd — эрмитов оператор в пространстве векторов состояния.
Действительно, поскольку W полностью определяет динамиче-
ское состояние электрона в данный момент времени, волновое
уравнение должно быть первого порядка по времени, а для того,
чтобы гарантировать самосогласованность нашего определения
P(r, t), оператор HD должен быть эрмитовым (см. § IV. 3).
Поскольку мы ищем релятивистское волновое уравнение,
естественно потребовать, чтобы оно обладало формальной сим-
симметрией между пространственными координатами и временем,
т. е. было уравнением первого порядка и по отношению к про-
пространственным переменным.
Рассмотрим вначале электрон в случае, когда внешнее поле
равно нулю. Гамильтониан должен быть инвариантным отно-
относительно трансляций и, следовательно, не зависит от г. Учиты-
Учитывая все вышесказанное, его можно записать в виде
HD = ар + |3m, C7)
где оператор р получается по правилу соответствия B6), т. е.
р = — /V, а а з= (ах, ау, аг) и р означают 4 эрмитовых оперч-
тора, действующих только на спиновые переменные. Если ис-
использовать обозначение Е = id/dt, то волновое уравнение можно
записать в виде
[Е-ар- рт] V = 0. C8)
Для определения аир мы воспользуемся принципом соответ-
соответствия и потребуем, чтобы решение этого уравнения удовлетво-
удовлетворяло уравнению Клейна — Гордона
[Е2 - р1 - т2[ У = 0. C9)

§ 7. ПРЕДСТАВЛЕНИЕ ДИРАКА 375-
Умножая уравнение C8) слева на оператор [Е -f- «Р + $т], по-
получаем уравнение второго порядка
\Е2 - ? (a*J (pkf - p2m2 - ? (aV + аV) рУ -
А *l ^ = 0.
Полученное уравнение и уравнение C9) тождественны, если
4 оператора аир антикоммутируют, а их квадраты равны 1
(afcJ == 1, aV + «'a* = 0 (k ф I),
Уравнение C8), в котором матрицы аир эрмитовы и удовле-
удовлетворяют соотношениям D0), называется уравнением Дирака.
Для того чтобы получить уравнение Дирака, описывающее
электрон во внешнем электромагнитном поле (ср, А), нужно сде-
сделать подстановку
Е->Е — еф, р->р — еА D1)
(е — заряд электрона: е < 0). Тогда получим
[(? - еф) - а (р - еА) - Рт] ^ = 0, D2)
т. е.
г = 0. D3)
Сравнивая полученное уравнение с уравнением C6), находим
выражение для гамильтониана Дирака при наличии внешнего
поля
Яд = еф + <х (р — еА) + Рт. D4)
§ 7. Построение пространства &м
Представление Дирака
Нам осталось сконструировать пространство <S(S). Операто-
Операторами в этом пространстве являются четыре основных оператора:
р, а.х, ау, аг и различные функции от этих операторов. Простран-
Пространство <o{s) должно быть неприводимым по отношению к этому
набору операторов.
Для построения <g{s) мы используем свойство эрмитовости
четырех основных операторов и соотношения D0), которые оп-
определяют их алгебраические свойства.
Эги свойства аналогичны свойствам трех операторов аи аг,
а3 нерелятивистской теории спина 1/2. В этом случае размер-
размерность пространства <??<а> спиновых переменных равна двум. Оно
строилось следующим образом. Так как а3 — эрмитов оператор

376 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
и о\= 1,то его собственными значениями могут быть только ±Ь
Более того, с каждым собственным вектором ст3 можно связать
другой собственный вектор, отвечающий собственному значению
противоположного знака. Рассмотрим, например, вектор |+>,
такой, что сг3|+> = |+>. Тогда в силу антикоммутативности аз
и (Ti для вектора |—>^<у1|+> получим ст3|—> = (—1I—>•
В результате имеем cti | ±> = 1+) и а3|±> =(±1) |±>. Следо-
Следовательно, пространство, натянутое на векторы |+> и I—>. ин-
инвариантно по отношению к действию операторов сг3 и (Т[ и по
отношению к функциям от этих операторов (а именно сг2 =
= iaia3). Из способа построения пространства видно, что оно
неприводимо, следовательно, нами построено искомое простран-
пространство <%(а). В представлении, где базисными векторами являются
|+> и |—>, операторы <ть а2 и сг3 задаются матрицами Паули
(см. § XIII. 19 или формулу (VII. 65)).
Сведем задачу построения <2?(s) к предыдущей. Рассмотрим
операторы ах, ау, az и рь р2, р3, определяемые равенствами
ог = — io.xay, ax = — iaya2, ау = — тгах, D5)
Рз = Р, Pi = ozaz = — iaxayaz, p2 = tp,p3 = — Рахауаг. D6)
Четыре основных оператора выражаются через р и ст по фор-
формулам
ft ft D7)
Таким образом, построение 0>^ свелось к построению про-
пространства, неприводимого по отношению к операторам р и а.
Легко показать, что:
(i) каждый оператор р коммутирует с каждым а;
(ii) a — три антикоммутирующих эрмитовых оператора,
квадраты которых равны единице;
(Ш) р — три антикоммутирующих эрмитовых оператора,
квадраты которых равны единице.
Следовательно (см. § VIII. 7):
(i) e?(s) есть тензорное произведение
пространства S(e), неприводимого по отношению к р, и про-
пространства Ж(°\ неприводимого по отношению к ст;
(ii) размерность Ж^ равна двум и оно может быть по-
построено приведенным выше способом;
(ш) размерность &<•& также равна двум и оно может быть
построено тем же способом.
Таким образом, размерность пространства ^<s) равна четы-
рем.
В следующих разделах мы покажем, что операторы а свя-
связаны со спином, ар — со знаком энергии, поскольку уравнение

§ 8. КОВАРИАНТНАЯ ФОРМА УРАВНЕНИЯ ДИРАКА 377
Дирака, так же как и уравнение Клейна — Гордона, имеет ре-
решения с отрицательной энергией. В частности, мы увидим, что
а есть полярный векторный оператор, а о = {ох, оу, аг) — ак-
аксиальный векторный оператор. Кроме того, формально имеем
а X а = 2ia. D8)
Оператор спина электрона есть !/г о, а знак энергии опреде-
определяется собственным значением оператора р = р3.
Динамическое состояние электрона определяется волновой
функцией W, имеющей 4 компоненты, что в два раза больше,
чем в нерелятивистской теории частицы со спином '/г- Пред-
Представление, в котором р и а задаются матрицами Паули (см.
ур. (VII. 65) — (VII. 66)), называется представлением Дирака.
В этом представлении каждая компонента отвечает определен-
определенной ориентации спина по оси Oz и определенному знаку энер-
энергии.
§ 8. Ковариантиая форма уравнения Дирака
Дирак первоначально получил свое уравнение в форме D3).
Такая запись удобна для физической интерпретации и пере-
перехода к нерелятивистскому пределу. Получим форму уравнения
Дирака, которая симметрична относительно временной и про-
пространственных координат и более предпочтительна в тех слу-
случаях, когда основную роль играют вопросы релятивистской ко-
ковариантности.
Умножим уравнение D3) слева на р, тогда, вводя обозна^
чения
V^(y°, y1, Y2, Y3) = (V\ Y),
Y° = p, Y^P«, D9)
получим
-m]W = [y»{t^ -еЛц) — m]? = 0. E0)
Свойства Vм" легко получить, используя определения D9) и
свойства аир. Десять соотношений D0) переходят в десять
соотношений
ytlyV _|_ yVyU. = 2gM.V, E1)
Условия эрмитовости а и р эквивалентны условиям
Yo+ = Yot Yft+ = _ ykt E2)
которые можно записать в компактной форме
-ум-+ = y°yuy°. E3)

378 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
Удобно распространить на операторы у правила подъема и
опускания индексов
Y^ = g,xvYv. E4)
Отметим, что
Yo = Y°, Y* = -Yft, E5)
r===Yt = Y-i. E6)
§ 9. Сопряженное уравнение. Определение тока
Выше мы построили положительно определенную плотность
вероятности (ур. C5)). Как отмечалось, эрмитовость гамильто-
Биана Дирака гарантирует самосогласованность этого опреде-
определения. Определим плотность тока и покажем, что для решений
уравнения Дирака плотность тока удовлетворяет уравнению
непрерывности. Вначале рассмотрим этот вопрос, используя
¦форму Дирака, а затем повторим рассуждения с ковариантной
формой.
Допустим, что выбрано некоторое представление для р и а,
тогда волновая функция W есть матрица-столбец
Обозначим эрмитово-сопряженную к ней
Операторы в спиновом пространстве являются матрицами 4X4.
Можно определить скалярное произведение, в котором сумми-
суммирование происходит только по спиновым переменным. Обозна-
Обозначим такое скалярное произведение простыми скобками. Тогда
плотность Р можно записать в виде
P(r, /) = 0F+40. E7)
В качестве другого примера рассмотрим матричный элемент р**
матрицы р, стоящий в строке s и столбце / (s, / = 1, 2, 3, 4),
тогда имеем
Пусть W — решение уравнения Дирака
/ 4^ = HDW = U + ? а*(- i -^ - еА>) + рт] ?, E8)

§ 9. СОПРЯЖЕННОЕ УРАВНЕНИЕ. ОПРЕДЕЛЕНИЕ ТОКА 3791
тогда W* есть решение эрмитово-сопряженного уравнения, ко-
которое получается комплексным сопряжением уравнения E8) и
заменой каждой матрицы в нем на транспонированную:
l
^ - еАкЛ ? V - mW^. E9)
Умножая скалярно уравнение E8) слева на Ч?^, а уравнение
E9) справа на W и складывая, получим
^0fW). F0)
Слева стоит производная по времени от плотности вероятности
Р, а справа—дивергенция некоторого вектора /(г, t)
/(/-, /) s (чг+аЧО- F1)
Полученная величина /(г, /) и представляет собой искомую
плотность тока, а уравнение F0) есть уравнение непрерывно-
непрерывности
~Р + Ъ = 0.
Можно повторить приведенные выше рассуждения, исполь-
используя ковариантную форму уравнения Дирака (ур. E0)). Эрми-
тово-сопряженным к уравнению E0) будет
(-/аA-еЛA)?+уи+-т?+ = 0, F2>
(где символ d^+Y^ обозначает матрицу-строку из четырех эле-
элементов (д^^/дх^у^). Удобно ввести обозначение
F3>
Умножая уравнение F2) справа на у° и учитывая соотноше-
соотношения E3), получим уравнение
(-id]1-eAil)Wya-mV = 0, F4>
которое эквивалентно E9). Величина W называется сопряжен-
сопряженной к Т, а уравнение F4) — сопряженным уравнением.
Умножая скалярно уравнения E0) слева на У, а F4) —
справа на Ч^ и вычитая их, имеем
Р = 0.
Определим четырехмерный вектор плотности тока
F5)

380
ГЛ. XX. УРАВНЕНИЕ ДИРАКА
Тогда предыдущее уравнение эквивалентно уравнению непре-
непрерывности
Легко показать, что jv- == (Р, /); таким образом, мы записали
уравнение непрерывности в ковариантной форме. В следующем
разделе мы покажем, что четыре компоненты /i* действительно
образуют 4-вектор.
Раздел III. СВОЙСТВА ИНВАРИАНТНОСТИ
УРАВНЕНИЯ ДИРАКА
§ 10. Свойства матриц Дирака
Прежде чем рассматривать свойства инвариантности уравне-
уравнения Дирака, изучим свойства 4X4 матриц у»-=в(у°, Y1. Y2> Y3)>
которые удовлетворяют соотношениям
, F6)
где / — единичная матрица. Матричные соотношения F6) яв-
являются аналогами соотношений E1) между операторами, од-
однако рассматриваемые здесь матрицы не обязаны удовлетворять
условиям унитарности E3). Все свойства, которые мы получим,
будут следовать только из соотношений F6).
Матрицы уА. Поскольку матрицы у& антикоммутируют,
а квадрат любой из них равен +/ или —/, то любое произве-
произведение нескольких матриц у& равно, с точностью до знака, одной
из 16-ти матриц уА, приведенных в табл. II. Матрицы уА сгруп-
сгруппированы в пять классов (S), (V), (Т), (Л) и (Р), каждый из
которых содержит 1, 4, 6, 4 и 1 элементов соответственно (при-
(причины такой классификации станут ясны в конце этого раздела
(см. §14)).
Таблица II
Матрицы \А
Обозначения
(S) 1 =
(V) У1 = (y°. Yfc} =
(A) y^v' ^ {y°Y5> YftY5} ^
Явный вид
<Y*)*-/
Y°
Y^Y^ y^Y^ Y^Y^
y'yV
(yaJ=-/
Y1 Y2 Y3
YY yV yY
Y^y^V^ y^Y^Y* y^Y^Y^
y°y'yV

§ 10. СВОЙСТВА МАТРИЦ ДИРАКА 381
Ясно, что квадраты этих матриц (уАJ равны +/ или —/;
шесть матриц, квадраты которых равны +/, расположены в ле-
левом столбце, десять матриц, квадраты которых равны —/, рас-
расположены в правом столбце.
Из всех этих матриц только единичная матрица / коммути-
коммутирует со всеми остальными. Если уА ф I, то она антикоммутируег
с 8 из 16 матриц и коммутирует с 8 оставшимися.
В частности, матрица у5, которая определяется следующим
образом •):
75 = УУу?, F7)
антикоммутирует с у11:
V5YM' + VV = 0, F8)
а ее квадрат равен
(Y5J = -/. F9)
Обратные матрицы (уА). Определим матрицы у^ соот-
соотношением
^ = ?^. G0)
Очевидно, что
Как следствие, мы получим обратную к матрице уА, если в ее
выражении через матрицы у& изменим порядок их следствия на
обратный и каждую матрицу у& заменим на у^. Обозначим по-
получившееся выражение уА
^л = ^л = /. G1)
Действуя таким образом, находим обратную матрицу к у5
Y5 = Y3Y2Y1Y0.
След и определитель. Справедливо равенство
4, если уА = /,
0, если V**/.
Для доказательства предположим, что уА Ф I и пусть ув одна
из 8 матриц, антикоммутирующих с уА
уЛ = _ уВуАуд.
Тогда имеем
Тг уА = — Tr y^Yb = — Тг увувуА = — Тг уА == 0.
Отметим также, что (задача 3)
') Индекс 4 обычно используется для обозначения временной компоненты,
которая определяется равенством х* = ixf> = let.

382 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
Лемма о перестройке. Следующее свойство устанав-
устанавливается простой проверкой. Если умножить 'каждую из 16 мат-
матриц уА справа (или слева) на одну из них, то с точностью до
знака и порядка получим те же 16 матриц.
Линейная независимость и неприводимость.
Используя лемму о перестройке и свойства следа, можно легко
показать, что
1°. Матрицы уА линейно независимы.
2°. Любая 4X4 матрица М однозначно представляется
в виде линейной комбинации матриц уА
А
3°. Всякая матрица, коммутирующая с каждой из матриц у^
и, следовательно, с каждой из матриц уА, пропорциональна еди-
единичной матрице
если [М, уц] = 0 для любого ц, то М — const X/•
Фундаментальная теорема. Пусть yi* и у'* — два
набора матриц 4X4, которые удовлетворяют соотношениям
F6). Тогда существует несингулярная (deiS=?=0) матрица S,
определенная с точностью до множителя и такая, что
y|1 = Sy'uS-1 (|* — 0, 1,2, 3). G3)
Доказательство теоремы проведем следующим образом.
С каждым набором ум. и у'^ связаны 16 матриц уЛ и у'А, опре-
определение и свойства которых были приведены выше, так что
каждой матрице у* соответствует некоторая матрица у'А, ин-
индекс А принимает 16 различных значений. Возьмем некоторую
матрицу F и обозначим S следующую матрицу:
где суммирование ведется по всем возможным значениям ин-
индекса А.
Выберем конкретную матрицу ув, обратная к ней матрица ув,
а соответствующая матрица из другого набора у'в. В силу
леммы о перестройке, имеем
y's5Yb =э Z У'вУАРУлУв = 2 Y aFVa ^ 5,
А А
следовательно
y'BS = SyB. G4)

§ 10. СВОЙСТВА МАТРИЦ ДИРАКА 383
Для доказательства соотношений G3) остается показать,
что матрица S имеет обратную. Построим матрицу Т
T^Z \AGy'A,
где G — произвольная матрица. Рассуждая как и ранее, полу-
получаем
Следовательно,
увт5 = Ту-в8 = Т5у-в
для любой матрицы ув. Поскольку матрица TS коммутирует со
всеми ув, она пропорциональна единичной матрице: TS = сХ I-
Постоянная с вычисляется по формуле
с = 1 Тг 7-S =4 ? ? Тг yAGy'Ay'BFyB =
А В
Матрицу F всегда можно выбрать так, чтобы по крайней
мере один из матричных элементов 5 был отличен от нуля.
В противном случае легко показать, что матрицы уА не были бы
линейно независимы. После этого можно выбрать G так, чтобы
Тг GS ^ У У GstSte=|.
следовательно с = 1 и TS = I. Таким образом, матрица 5 имеет
обратную и, умножая равенство G4) на S~l справа, получаем
соотношения G3).
Если существует другая матрица S', для которой выполнены
те же соотношения, то S^S' коммутирует со всеми матрицами
7м и, следовательно, S~lS' = с X I- Верно и обратное: если для
5 выполнены соотношения G3), то они выполнены и для любой
матрицы, пропорциональной S. Тем самым мы доказали, что
несингулярная матрица S существует и определена с точностью
до множителя. В
Если матрицы у*, удовлетворяющие соотношениям F6), уни-
унитарны
Уц = yVy° = Yut. G5)
то унитарны все матрицы уА и, следовательно, они эрмитовы
или антиэрмитовы в зависимости от того, равен ли квадрат
(у4J единичной матрице +/ или —/.

384 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
Следующее утверждение, доказательство которого предо-
предоставляем читателю, дополняет фундаментальную теорему:
Если v*1 и y'v* — два набора унитарных матриц 4X4, удовле-
удовлетворяющих соотношениям F6), то существует определенная
с точностью до фазового множителя унитарная матрица U, та-
такая, что у'» = UyvU* (ц = 0, 1, 2, 3).
Комплексное сопряжение, матрица В. В част-
частности, если матрицы у^ удовлетворяют соотношениям F6) и
унитарны, то 4 комплексно сопряженных матрицы у&* тоже уни-
унитарны и удовлетворяют тем же соотношениям. В силу преды-
предыдущего утверждения матрицы у^ и у&* связаны унитарным пре-
преобразованием. Обозначим В матрицу этого преобразования
(В определена с точностью до фазового множителя)
G6)
Можно показать, что В антисимметрична
В = -В,
или, что то же самое, справедливы равенства
ВВ* = В*В = — I. G7)
Если для матриц у выбрано представление Дирака, то
В = BD = -yV = - ip3Oy.
В этом случае легко проверить справедливость равенств G7).
§ 11. Инвариантность уравнения Дирака
при ортохронных преобразованиях системы координат
Принцип относительности требует, чтобы уравнение Дирака
и уравнение непрерывности сохраняли одну и ту же форму
в различных системах координат, связанных преобразованием
Лоренца. В действительности, строго говоря, требуется инва-
инвариантность только по отношению к собственным преобразова-
преобразованиям Лоренца '), однако теория инвариантна по отношению
к полной группе. Рассмотрим вначале подробно инвариантность
по отношению к ортохронной группе. Обращение времени,
а также другие свойства инвариантности уравнения Дирака, не
') А также по отношению к пространственным и временным трансляциям.
Эту инвариантность легко установить, используя рассуждения, которые анало-
аналогичны приводимым ниже. Если начало координат сдвигается на 4-вектор о**,
т. е. л:/>*л:=л(*+о|1)то А'^ (*') = А^ (х) н закон преобразования волновых функ-
функций (аналог закона (85)) имеет простой вид
?' (*') = W (х).

S 11. ИНВАРИАНТНОСТЬ УРАВНЕНИЯ ДИРАКА 385
связанные непосредственно с преобразованиями Лоренца, будут
рассмотрены в конце этого раздела.
Будем считать, что динамическое состояние электрона в си-
системе координат (R) задается четырехкомпонентной волновой
функцией, удовлетворяющей уравнению Дирака
= O. G8)
Фиксируем некоторое представление для операторов в про-
пространстве <§f(s); символы yv означают тогда вполне определен-
определенные матрицы, и соотношение G8) сводится к системе из четы-
четырех уравнений (s = 1, 2, 3, 4)
/-1, 2, 3, 4 а
— т-ф, (А1*2*3) = О
для четырех компонент tys(x) волновой функции.
Рассмотрим ту же физическую систему в новой системе ко-
координат (/?')> связанной с исходной ортохронным преобразова-
преобразованием Лоренца 3?
Преобразование & характеризуется некоторой матрицей Qv,
удовлетворяющей соотношениям A2), A3) и определяющей
линейное соответствие между координатами х& данной точки
в системе (R) и координатами л> той же точки в системе (/?').
т. е. закон преобразования контравариантных векторов (ур.
A1) и A5)). Символически можно записать
x = S~Kx'. G9)
Операторы частных производных преобразуются, как ковариант-
ные векторы
6^ = 6^. (80)
Если обозначить А^.(хг) ковариантные компоненты электромаг-
электромагнитного потенциала в новой системе координат, то они связаны
с Аи(х) по закону преобразования ковариантных векторов
А* (х) s А* BГ Y) = Л; (/) QJ. (81)
Как функция новых координат ^(а:) удовлетворяет уравне-
уравнению, которое получается из G8) после подстановки (80) и (81)
if 04 - вМ (/)) - m] v (ar1/)=о, (82)
где
ф—фр. (83)
13 А, Мессиа

386 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
Матрицы у» унитарны и удовлетворяют соотношениям F6).
Четыре матрицы у»- не обязательно унитарны, но в силу ортого-
ортогональности Qv (соотношения A3)), они также удовлетворяют
соотношениям F6), т. е.
В силу фундаментальной теоремы § 10 существует несингуляр-
несингулярная матрица Л, которая преобразует матрицы у в у
YM'^QoYp = A~1ym'A (ц = 0, 1, 2, 3). (84)
Подставляя это соотношение в уравнение (82), вводя обозна-
обозначение
ЧГ (*') = AW (*) ез AW (&~ хх'), (85)
и умножая слева на Л, получаем
[yv (id'n — еА'ц (л/)) — tn\ гР' ОО = 0.
Это волновое уравнение описывает эволюцию системы в новой
системе координат, оно формально тождественно с G8). Таким
образом, уравнение Дирака формально инвариантно относи-
относительно ортохронных преобразований системы координат, и за-
закон преобразования волновой функции определяется уравне-
уравнением (85).
В общем случае матрицу Л, которая определена с точностью
до постоянного множителя, нельзя выбрать унитарной. Однако
мы покажем, что множитель всегда можно выбрать таким об-
образом, чтобы
A+ = y°A~1y°. (86)
и произвол остается только в фазе.
Поскольку Qp вещественны, а у& унитарны и удовлетворяют
соотношениям G5), то, сравнивая (83) и эрмитово-сопряжен-
эрмитово-сопряженное соотношение, находим
Переходя от соотношения (84) к эрмитово-сопряженному и под-
подставляя предыдущую формулу, получаем
Сравнивая эту формулу с (84), видим, что матрица
коммутирует с четырьмя матрицами yv- и, следовательно, про-
пропорциональна единичной
(87)

§ 11. ИНВАРИАНТНОСТЬ УРАВНЕНИЯ ДИРАКА 387
Покажем, что постоянная с обязательно вещественна и положи-
положительна. Используя формулы (87) и (84), имеем
Л+Л = с/ (Л"УЛ) = с (Q? + ? Q2W) ,
откуда, принимая во внимание G2), получаем: Тг Л+Л == 4cQq«
Поскольку след эрмитовой матрицы Л+Л вещественный и поло-
положительный и число Qo также вещественно и положительно, то
приходим к искомому утверждению о постоянной с. Если мат-
матрицу Л разделить на Vе > то новая матрица также будет Л-мат-
рицей и будет удовлетворять уравнению (86). В
Закон преобразования волновых функций (85) определяет
закон преобразования сопряженных функций
w' ^ w'V=^+лУ = Ф А V.
откуда, с учетом (86), получаем
W(x)A~l. (88)
Используя этот закон преобразования, читатель без труда
проверит, что сопряженное уравнение F4) также формально
инвариантно относительно ортохронных преобразований си-
системы координат.
Остается показать инвариантность уравнения непрерывности
или что ток /i* (определение F5)) преобразуется как контра-
вариантный 4-вектор ').
Последнее легко установить, используя (85), (88) и (84)
/) 'V О ) == ОДР (х).
Условия (84) и (86) для каждого преобразования Лоренца
определяют Л с точностью до фазового множителя. В данном
случае эта фаза не имеет физического смысла.
Удобно устранить, насколько это возможно, произвол в фазе,
потребовав, чтобы Л образовывали группу, гомоморфную орто-
хронной группе Лоренца (см. обсуждение в § XV. 8).
Условие (84), с учетом вещественности Q!J, дает
откуда, вводя унитарную матрицу В (определение G6)), полу-
получаем
•) В противном случае нормировка волновой функции зависела бы от си-
системы координат и нельзя было бы интерпретировать /° как плотность вероят-
вероятности положения.
13*

388 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
Сравнивая это уравнение и уравнение (84), видим, что
ВА*В*А~1 коммутирует с четырьмя матрицами у^ и, следова-
тельно, пропорциональна единичной матрице. Легко показать,
вычисляя, например, det ВЛ*В+Л-', что модуль коэффициента
пропорциональности равен единице; другими словами
Так как Л определена с точностью до фазового множителя, его
всегда можно выбрать так, что в полученной формуле будет
еа = 1. В дальнейшем будем считать, что сделан именно такой
выбор, тогда Л определена с точностью до знака.
Таким образом, каждому ортохронному преобразованию Ло-
ренца отвечают две матрицы Л, отличающиеся знаком и опре-
определяемые тремя условиями:
(89а)
Л+ = у°Л~У, (896)
Л* = В*АВ. (89в)
Набор матриц Л, удовлетворяющих этим условиям, образует
группу, которая гомоморфна ортохронной группе Лоренца.
В следующем параграфе мы увидим, что произвол в знаке Л
нельзя устранить, не нарушив при этом групповой структуры ').
§ 12. Преобразования собственной группы
Найдем явные выражения для матриц Л, которые удовле-
творяют условиям (89). В этом параграфе мы будем рассма-
рассматривать только преобразования собственной группы.
Вначале рассмотрим инфинитезимальные преобразования,
Каждому из шести инфинитезимальных «вращений» guv — zZffi
соответствует матрица Л^Р^е), которая отличается от единич-
') Вместо условия (89в) можно использовать более общее условия: Л* =;
= г\В*АВ, где постоянная Т) зависит от рассматриваемого преобразования Ло-
ренца. Множество матриц Л будет иметь структуру группы, если величины г\
образуют абелево представление группы Лоренца. Следовательно, для преоб-
преобразований из собственной группы Лоренца З'п обязательно имеем т| = I, что
«нова дает условие (89в). Для преобразований, включающих отражение, т.е.
принадлежащих sS'o. имеются две возможности выбора тр
(а) т] == I для любого 55*0, что дает (89в);
(б) т| = — 1 для любого s3?a, т. е. Л* = — В+ЛВ.
Физическое содержание теории, очевидно, не зависит от этого выбора. Обе
группы G<"> и G<*>, которые соответствуют возможностям (а) и (б), гомо-
гомоморфны ортохронной группе Лоренца, но не изоморфны друг другу. В частно-
частности квадрат матриц, соответствующих отражению s, равен +/ в G<*> и —/ в
G((S) (см. следующую сноску).

§ 12. ПРЕОБРАЗОВАНИЯ СОБСТВЕННОЙ ГРУППЫ 389
ной матрицы на бесконечно малую величину и может быть за*
писана в виде
Л'арЧе) » / + /eSe(J, (90)
где Sap — конечная матрица, подлежащая определению. Имеем
Из условия (89а) получаем
или, используя A7),
Матрица Sap удовлетворяет тем же коммутационным соот-
соотношениям с у1*, что и матрица y/YaYp- Их разность коммутирует
с матрицами у^ и, следовательно, пропорциональна единичной
матрице. Легко показать, что условия (896) и (89в) будут вы*
полнены тогда и только тогда, когда коэффициент пропорцио-
нальности равен нулю. Удобно ввести обозначение
<V> — Y'fv Yvl = «YnYv (fi=^v). (91)
Окончательно имеем
Sag == ~% аар (92)
Обозначения Sap и <тар будут также использоваться для опе-
операторов, которые задаются матрицами Sap и aap соответствен-
соответственно. В дальнейшем мы увидим, что Sap есть антисимметричный
тензорный оператор F компонент), который отвечает внутрен-
внутреннему моменту импульса или спину частицы. Точнее говоря,
спин — это пространственная часть C компоненты) оператора
Sap, который связан с операторами <тиаиз§6и§7 соотно-
соотношениями
Sio=2~faje, S2o = "г" faj,, •5зо = у'аг> (93а)
5гз = y ax> 53i = ~2 0у> 5i2 = -? ог. (936)
Любое конечное преобразование собственной группы Ло-
Лоренца можно представить в виде произведения последователь-
последовательных инфинитезимальных преобразований. Следовательно, мы
можем построить матрицы Л, отвечающие конечному измене-
изменению системы координат, беря произведения определенных выше

390 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
матриц, отвечающих инфинитезимальным преобразованиям.
В этом случае условия (896) и (89в) выполняются автомати-
автоматически и мы получаем одну из двух возможных матриц Л.
В частности, «вращение» на угол ф в плоскости хах& есть-
произведение матриц инфинитезимальных вращений в этой пло-
плоскости, и матрица Л(ар)(ф)> задающая преобразование, имеет
вид
Л'а3)(ф) = е'ф5«е. (94>
Таким образом (см. сноску на стр. 367), если задано чисто-
лоренцево преобразование со скоростью v = th ф, направленной
вдоль оси х, то, принимая во внимание соотношения (93а) и
свойства ах, находим
Л<"> (ф) = е~* а*Ф = сЦ- Ф - ах sh 1Ф. (95)
В более общем случае, если Asp(v) —матрица, отвечающая
чисто лоренцеву (специальному) преобразованию со скоростью
v, то имеем
Asp (v) = ch т Ф — (аи) sh -к ф,
(96)
где ussv/v, ф
Введем обозначение
Предыдущее выражение после элементарных вычислений можно
привести к виду
Asp (v) - /-1—- [ 1+ b - (av) b]. (97)
Рассмотрим теперь вращения в обычном смысле этого слова.
Для вращений вокруг оси Oz выражение (94) дает
Л(ед) (Ф) = е'5'* = е^ ^ = cos 1Ф + /<т2 sin ± Ф. (98)
В более общем случае, если Л« (ф) — матрица, отвечающая
вращению на угол ф вокруг оси, направленной вдоль единич-
единичного вектора и, то имеем
Л„ (ф) = cos у ф + iau sin -j ф, (99)
где оа = (ои).
Теперь мы можем обсудить вопрос о спине частицы, которая
описывается уравнением Дирака. Спин определяется трансфер-

§ 13. ПРОСТРАНСТВЕННОЕ ОТРАЖЕНИЕ 391
мационными свойствами внутренних переменных по отношению
к пространственным вращениям. Формула (99) дает общее вы-
выражение для матриц преобразования внутренних переменных
при вращении. Это выражение отличается от выражения
(XIII. 84) только знаком перед аи, и одно переходит в другое
при замене ср на —ср. Следовательно, эти матрицы обратны
одна к другой. Различие вызвано тем, что в главе XIII мы рас-
рассматривали изменение переменных и состояний при вращениях,
оставляя оси фиксированными, а здесь мы придерживаемся
противоположной точки зрения. Итак, мы видим, что волновая
функция, удовлетворяющая уравнению Дирака, преобразуется
при вращениях как волновая функция частицы со спином 1/2.
Отметим, в частности, что повороту на угол 2jt вокруг лю-
любой оси не соответствует единичная матрица. Действительно,
имеем
(-1)п/; A00)
такое свойство матрицы преобразования характеризует полу-
полуцелый спин. Ясно, что произвол в знаке матриц Л нельзя устра-
устранить без того, чтобы не нарушить их групповой структуры.
В дальнейшем будем называть волновые функции теории
Дирака спинорами.
§ 13. Пространственное отражение и ортохронная
группа
Коль скоро мы знаем, как меняются спиноры при собствен-
собственных преобразованиях системы координат, то для определения
закона изменения при ортохронных преобразованиях достаточ-
достаточно найти закон их преобразования при отражении s.
Матрицу, соответствующую отражению s, обозначим Л5. Со-
Соотношение (85) в этом случае принимает вид
-r). A01)
Условие (89а) дает
лгУл, = y°. лгУл, = - yk,
откуда As = csy°. Постоянная cs определяется из условий (896)
и (89в): cs = ± 1. Следовательно,
AS=±Y° A02)
и в согласии со сказанным выше') Л« определена с точностью
до знака.
') Выражение A02) соответствует выбору (а) (см. предыдущую сноску).
Выбор (б) ведет к As di"

392
ГЛ. XX. УРАВНЕНИЕ ДИРЛКА
§ 14. Построение ковариантных величин
Из компонент спинора Ч?(х) и сопряженного спинора ?(*)}
можно построить 16 линейно независимых функций, билиней-
ных по W и ? и зависящих от х°, х1, х2, х3. Эти функции можно
разбить на пять классов в соответствии с их тензорными свой'
ствами: скаляр S, вектор V*, антисимметричный тензор с двумя
индексами Т^>\ антисимметричный тензор с тремя индексами
^[*М и антисимметричный тензор с четырьмя индексами или
псевдоскаляр Р. Выражения для перечисленных функций при-
приведены в табл. III.
_ Таблица III
Тензоры, билинейные iro V и V
Обозначения
S (X) вэ (??)
Vй (х) в (?/?)
jlnv] ^ в (^y^yvT) (h=?v)
А1*"*1 (х) в (f yVvv^) (Л =И= Ц, ц ^= v, v ^ Л)
Р (^) в (Уу*ЧГ)
Число
компо-
компонент
1
4
6
4
1
Тип
скаляр
вектор
тензор 2-значковый
псевдовектор
псевдоскаляр
Указанные тензорные свойства можно легко доказать, ис-
используя закон преобразования спиноров ? и f (yp. (85) и
(86)) и соотношение (89а) между матрицами Л и коэффициен-
коэффициентами Qy соответствующего преобразования Лоренца.
Напомним, что закон преобразования псевдоскаляров отли-
отличается от закона преобразования скалярных величин только
дополнительным множителем det | Qv I
Таким образом, при собственных лоренцевых преобразованиях
псевдоскалярные и скалярные величины преобразуются одина-
одинаково, а при отражении s псевдоскаляры меняют знак. Точно
так же закон преобразования псевдовекторов отличается от за-
закона преобразования векторов дополнительным множителем
det|Qg|.
Вектор Vv(x) уже интерпретировался нами как четырехмер-
четырехмерный вектор плотности тока

§ 15. ПРЕОБРАЗОВАНИЕ СОСТОЯНИИ
393
Можно дать соответствующую интерпретацию и остальным ве-
величинам. Так, тензор Г^у' равен, с точностью до постоянного
множителя, тензору S^v, который можно интерпретировать как
плотность спина
I
/
§ 15. Другая формулировка свойств инвариантности:
преобразование состояний
В предыдущих параграфах мы рассматривали преобразова-
преобразование как операцию, которая выполняется над системой коорди-
координат, оставляя физическую систему неизменной. Можно изменить
точку зрения и преобразовать физическую систему, оставляя
неизменной систему координат. Именно так мы поступали
в третьей части (см., в частности, замечания § XIII. 11). Хотя
вытекающие результаты формулируются
различным образом, обе точки зрения
эквивалентны.
Поясним указанную эквивалентность.
Пусть (S) — состояние физической си-
системы, которое в системе координат (R)
задается спинором ^(х). Пусть (S')
есть состояние, которое получается из
(S) при преобразовании &, a (R) есть
система координат, которая переходит ~^ 
в (R) при том же преобразовании (см. ~^\
рис. 21) "^"^
Рис. 21. Два сцособа рас-
рассмотрения преобразова-
преобразования Лоренца: изменение
системы отсчета (х -> ?)
и преобразование систе-
системы (S->S0.
/
/
Рассмотрим три следующих спинора:
W (х), представляющий (S) в системе (R),
f(i), » (S) » (R),
У'(х), » (Я » (/?).
Ясно, что W и W равны при совпадающих значениях аргу-
аргументов
?'(*) = *(*). A03)
Соответствие между Фи? было установлено в § 11. Поскольку
преобразование 5? переводит систему ($) в (R), то, исполь-
используя (85) и вводя связанную с S матрицу Л, имеем
Следовательно,
A04)

394 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
Сравнивая с уравнением (85), видим, что в преобразовании со-
стояний участвует оператор, обратный к оператору, отвечаю-
отвечающему изменению системы координат.
Эти замечания относятся также и к электромагнитному полю,
в котором движется дираковская частица. Обозначим поле (Л)
и пусть (Л') — поле, которое получается при преобразовании SS:
Рассмотрим следующие три (ковариантные) 4-вектора:
Лй (х), представляющий (А) в системе (/?),
АЛ*), * (А) » (R),
К{х), » {А') » (/?).
Мы можем повторить приведенные выше рассуждения для
спиноров, тогда получим
А'а (х) ¦¦= Лц (х). A05)
Согласно уравнению (81) имеем
AVi(^-1x) = Av(x)Ql
следовательно,
К ? A06)
Допустим теперь, что 'Ф(х) удовлетворяет уравнению Ди-
Дирака с потенциалом А^х):
[у* {id» - еЛц) - т] У = 0. A07)
Принимая во внимание равенства A03) и A05), из инвариант-
инвариантности уравнения Дирака при изменении системы координат
(/?)(?) получаем
еА1) — т]ЧГ = 0. A08)
Таким образом, свойство инвариантности формы уравнения
можно сформулировать так:
Если ?(х) удовлетворяет уравнению Дирака с потенциалом
А»,(х), то состояние W{x), которое получается при преобразо-
преобразовании 3?, также удовлетворяет уравнению Дирака с преобразо-
преобразованным потенциалом Ли (х).
§ 16. Условие инвариантности уравнения движения
Уравнения A07) и A08) в общем случае различны. Они
совпадают, только если внешний потенциал (А) инвариантен
относительно преобразования 3?, т. е. если

§ 17. ОПЕРАТОРЫ ПРЕОБРАЗОВАНИЯ 395
В этом случае спиноры W и W удовлетворяют одному и тому
же волновому уравнению. Следовательно, уравнение для дина-
динамических состояний инвариантно относительно любых преобра-
преобразований 5?, которые не меняют внешний потенциал.
До сих пор в качестве 3? мы рассматривали ортохронные
преобразования Лоренца. Однако все сказанное выше можно
повторить для пространственно-временных трансляций (см.
сноску на стр. 384). Установленные свойства инвариантности
сохраняются и в этом случае.
§ 17. Операторы преобразования.
Импульс, момент импульса, четность
Для того чтобы продолжить этот анализ в соответствии
с общей схемой, которая была развита в главе XV, мы запишем
закон преобразования A04) в виде
W' = rP, A09)
где Т — соответствующий линейный оператор. Инвариантность
уравнения Дирака при преобразованиях можно тогда выразить
как соотношение между операторами
A10)
где 2>(А) и @ (А') — операторы Дирака с потенциалами Л и Л'
3>{A)^-^(idVL — eAVL). (Ill)
Условие того, что уравнение движения не меняется при преоб-
преобразовании 3?, можно записать как соотношение коммутации
[Т,3>(А)]*=0. A12)
Оператор Т легко построить. Он является произведением
операторов ГE>, действующего только на спиновые переменные,
и Г@>, действующего только на орбитальные переменные,
Т =
Сравнивая формулы A09) и A04), видим, что
r(s) = A-', A13)
где Л обозначает оператор, который представляется определен-
определенной в § 11 матрицей Л.
Найдем явный вид Т для инфинитезимальных трансляций
и лоренцевых «поворотов» и для отражения s.
В случае трансляций Г<*> = 1. Введем дифференциальный
оператор
Рц^Юц, A14)

ГЛ. XX. УРАВНЕНИЕ ДИРАКА
который представляет собой четырехмерный вектор энергии-им-
энергии-импульса (более точно — ковариантные компоненты этого 4-век-
тора). Для бесконечно малого сдвига на е вдоль оси х° нахо-
дим
Рассмотрим «инфинитезимальный поворот» на угол е в пло-
скости хах&. В этом случае имеем
(ад1 «=*¦*- ez™ v=*¦* - е («*э - фа).
Если tys(x) — некоторая компонента спинора \Р(я), то в первом
порядке по е
Введя дифференциальный оператор
Azp = *аРр — ДГрРа, A15)
перепишем предыдущее соотношение в виде
Ч>, (^де) » A — /eZ,ep) Ч». (лг).
С другой стороны, на основании формул (90) и A13) имеем
где 5ар — оператор, определяемый равенством (92). Оконча-
Окончательно формула A09), которая выражает закон преобразова-
преобразования спиноров, для случая «инфинитезимального поворота» при-
принимает вид
W (х) «A - /eSep) A - /eLep) У (х) « A - 1в/вA) ^F (Д
где
+ у Ofap. A16)
Три пространственных компоненты /гз, /з1 и /i2 оператора
/ар связаны с инфннитезимальными вращениями вокруг осей
Ох, Оу и Oz соответственно. Они являются компонентами пол-
полного момента импульса / и справедливы равенства
/ = L + S, L = rXp, S = ja. A17)
Компоненты L действуют только на орбитальные перемен-
переменные: L — оператор орбитального момента импульса. Компо-
Компоненты S действуют только на внутренние переменные: S — опе-
оператор спина частицы.

5 18. ЗАКОНЫ СОХРАНЕНИЯ И ИНТЕГРАЛЫ ДВИЖЕНИЯ 397
Легко показать, что /, L и S удовлетворяют коммутацион-
коммутационным соотношениям, характеризующим момент импульса, и
S2 = 3/4, откуда следует, что спии частицы равен 1/2.
Оператор, связанный с пространственным отражением, на-
называется оператором четности и обозначается Р. Пусть Р0)
обозначает оператор «орбитальной четности»:
В силу равенства A13) и результатов § 13 (см. равенство
A02)), мы можем выбрать для Р два выражения, отличаю-
отличающиеся знаком. Выберем наиболее часто употребляемое
Отметим, что оператор Р эрмитов и Р2 = 1.
§ 18. Законы сохранения и интегралы движения
Если преобразование зависит от времени, то связанный
с ним оператор Т изменяет зависимость W от времени. Так про-
происходит в случае временных трансляций и специальных преоб-
преобразований Лоренца.
С другой стороны, если преобразование не зависит от вре-
времени, то действие Т определяется независимо от уравнения дви-
движения состояний, на которые он действует. Тогда оператор Т
можно определить как оператор преобразования векторов со-
состояния и наблюдаемых системы, как это было сделано в главе
XV (раздел II). Свойства инвариантности уравнения, которое
определяет зависимость состояний от времени, можно сформу-
сформулировать при этом в виде законов сохранения.
Например, если 3? есть преобразование только простран-
пространственных переменных, то оператор Т является некоторой функ-
функцией операторов инфинитезимальных трансляций, инфинитези-
мальных вращений и отражения, т. е. функцией р, J и Р. Сле-
Следовательно, Т коммутирует с у° и, поскольку
коммутационное соотношение A12) в этом случае эквивалентно
[Т, Яо] = 0.
Мы получили то же условие, что и в § XV. 12 и все сказанное
там о связи между свойствами инвариантности гамильтониана
и законами сохранения справедливо и в этом случае.
Так, если потенциал А^(х) инвариантен относительно транс-
трансляций, то справедливы коммутационные соотношения

398 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
и сохраняется импульс. Если потенциал А11(х) сферически-сим-
сферически-симметричен, то
и сохраняется полный момент импульса. Если Ау.(х) инвариан-
инвариантен относительно отражения в начале координат, то
и сохраняется четность.
§ 19. Обращение времени и зарядовое сопряжение
В этом параграфе мы покажем, что уравнение Дирака ин-
вариантно относительно двух антилинейных операций: обраще-
обращения времени и зарядового сопряжения. Для этого в простран-
пространстве векторов состояния удобно ввести антиунитарный опера-
оператор К '), который имеет очень простые свойства.
Антиунитарный оператор К- Определим антиуни-
антиунитарный оператор К, который переводит р в —р и не изменяет г
и у*1:
KrK*=--r, КрК* = -р, A19)
/CyV = Y* (ц = 0, 1, 2, 3). A20)
Мы покажем, что такой оператор существует, определен с точ-
точностью до фазового множителя и
К* = -1. A21)
То, что оператор К, если он существует, определен с точ-
точностью до фазового множителя, следует из соотношений A19),
A20) и неприводимости пространства векторов состояния по
отношению к базисным операторам г, р и у». Выберем какое-
либо представление, например, представление Дирака. Тогда
каждый оператор у» задается некоторой матрицей у?. Обозна-
Обозначим BD оператор, который задается «матрицей В», преобразую-
преобразующей y? в их комплексно сопряженные. Мы будем рассматри-
рассматривать Bd как (унитарный) оператор, действующий во всем про-
пространстве, а не только в спиновом. Это унитарный оператор,
который коммутирует с г я р. Пусть Kd — оператор комплекс-
комплексного сопряжения, связанный с данным представлением (опре-
(определение § XV. 5). Соотношения G6) дают
') Следует предостеречь, что этот оператор не есть оператор обращения
времени, последний ниже будет обозначаться Кт-

§ 19. ОБРАЩЕНИЕ ВРЕМЕНИ И ЗАРЯДОВОЕ СОПРЯЖЕНИЕ 399
Следовательно, антиунитарный оператор
К = BdKd
удовлетворяет соотношениям A20). Поскольку Во коммути-
коммутирует с г и р, а из определения Kd имеем
то К удовлетворяет также соотношениям A19). Наконец, так
как Kd = Ко. равенство G7) дает
т. е. соотношение A21). Очевидно, что при умножении К на
фазовый множитель эти свойства сохраняются.
Зарядовое сопряжение. Умножая обе части урав-
уравнения A07) слева на К и используя тот факт, что оператор К
антилинеен и коммутирует с у&, д» и А^(х), получаем
[у* (_ (д№ - еА„ (*)) - т] KW (х) = 0. A22)
Следовательно, КЧ? удовлетворяет волновому уравнению, ко-
которое отличается от уравнения Дирака заменой —i на L Умно-
Умножим получившееся уравнение на у5. Так как у5 антикоммути-
рует с/ и коммутирует с остальными операторами, стоящими
в скобках, имеем
[Y^ К + еА» (х)) - т] Y W (*) = 0. A23)
Положим
КС^У5К. A24)
Тс (*) в КсУ (х). A25)
Уравнение A23) примет вид
[у» (id» + еА„ (х)) - т] Ч?с (х) = 0. A26)
Уравнения, которым удовлетворяют функции ~ФС (х) и ^?(х), от-
отличаются знаком заряда. Таким образом, если ^(х) описывает
движение дираковской частицы массы m и заряда е в потен-
потенциале А11(х), то хИс(х) описывает движение дираковской ча-
частицы той же массы m и противоположного заряда (—е) в том
же потенциале А^(х).
Спиноры W и Фс называются зарядово-сопряженными друг
к другу, а преобразование Кс — зарядовым сопряжением.
Из свойств /Сиу5 следует, что
Кс = 1. A27)
Тем самым, соответствие между Ч? и ^Fc взаимно обратное.
Легко показать, что зарядовое сопряжение коммутирует с транс-
трансляциями и ортохронными преобразованиями Лоренца. Точнее,

400 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
если спинор Ч? при одном из этих преобразований переходит
в L4t, то зарядово-сопряженным к последнему будет спинор
ЬЧ?С в случае трансляций и собственных преобразований Ло-
Лоренца и —LWC — в случае отражения (см. задачу 5).
Обращение времени. Инвариантность уравнения Ди-
Дирака по отношению к обращению времени можно доказать не-
непосредственно, но в данном случае мы используем результаты
о зарядовом сопряжении.
Вектор-потенциал Ац(^, г) создается некоторым числом дви-
движущихся зарядов. Соответствующий ему при обращении вре-
времени потенциал А[>. (/, r) получается при обращении движения
этих зарядов. Токи и, следовательно, магнитное поле меняют
знак, а электрические заряды и, следовательно, электрическое
поле остаются неизменными
Ш' (/, г) = - Ж (- /, г), Г (t, г) = & (-1, r).
Отсюда следует, что А^ «преобразуется как псевдовектор»
Л' (/, г) = - Л (- /, г), А'о (t, г) = Ло (- /, г).
Если в уравнении A26) сделать замену t на —t, то получим
[- y° (id0 - еА'о (/, г)) + S Ук Иди - eA'k (t, r)) - m] ^Fc (- /, г) = 0.
Умножим полученное уравнение на y5y°- Поскольку этот опе-
оператор антикоммутирует с у0 и коммутирует с yk, имеем
[V1 №* - еА\ (/, г)) - т] V (t, г) = 0, A28)
где
Ч" (/, г) = Y5YOii"c (~ /, г) = YW ( -1, r). A29)
Введем (антиунитарный) оператор обращения времени
КТ = У°К. A30)
Спинор W(t,r) является, по определению, преобразованием
Ч?(—/, г) при обращении времени. Он удовлетворяет уравне-
уравнению A28). Следовательно, если W удовлетворяет уравнению
Дирака с потенциалом А^, то спинор Ч*', получающийся при об-
обращении времени, удовлетворяет уравнению Дирака с потен-
потенциалом All, который при обращении времени получается из А^.
В частности, если потенциал Лц инвариантен по отношению
к обращению времени (например, если частица находится в ста-
статическом электрическом поле: А = 0, dA0/dt = 0), то Ч? и Ч/*
удовлетворяют одному и тому же уравнению Дирака.
Из свойств y° и К следует, что
К2т = -1. A31)

§ 21. УРАВНЕНИЕ ДИРАКА И ПРИНЦИП СООТВЕТСТВИЯ 401
Это результат, характеризующий системы с полуцелым мо-
моментом импульса, уже был получен в нерелятивистском случае
(ур. (XV. 88)). Все следствия, которые из него вытекают, на*
пример, вырождение Крамерса, справедливы и в данной ситуа-
ситуации.
Выразив оператор BD в терминах р и а (см. конец § 10),
из определений A24) и A30) легко получить равенства
Кс = iP
которые используются при работе с операторами Кс и Кт
в представлении Дирака.
§ 20. Калибровочная инвариантность
Упомянем здесь для полноты свойство калибровочной инва-
инвариантности (см. § XXI. 20).
Изменение калибровки электромагнитного потенциала озна-
чает переход от компонент А11(х) к
A'll(x)^Ail(x)-daG(x), A32)
где G(x)—произвольная функция пространственно-временных
координат. Это дает
Электрическое и магнитное поля при таком преобразовании ин-
инвариантны.
Если ^?(x) —решение уравнения Дирака с потенциалом А^,
то спинор
f'(jc) = eieOw?W A33)
есть решение уравнения Дирака с потенциалом А^. Данное
свойство и называется калибровочной инвариантностью урав-
уравнения Дирака.
Раздел IV. ИНТЕРПРЕТАЦИЯ ОПЕРАТОРОВ
И ПРОСТЫЕ РЕШЕНИЯ
§ 21. Уравнение Дирака и принцип соответствия
В случае отличного от нуля электромагнитного поля реше-
решения уравнения Дирака удовлетворяют дифференциальному
уравнению второго порядка, которое отлично от уравнения
Клейна — Гордона, однако и для него выполняется принцип со-
соответствия.

402 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
Чтобы получить это уравнение, подействуем оператором
(—iyxD% — т) на левую часть уравнения Дирака, записанного
в ковариантной форме E0),
+ т2] "? = 0. A34)
Используя алгебраические свойства операторов у&, получаем
Y*y*e=gMi + i-[Y\ уи]. A35)
Замена немых индексов суммирования дает
[Y\ Г] ОД ^ - [у*-, Yi ОД = j [Y\ у»] [D%, Z)J A36)
и в силу определения операторов D^ (yp. A0))
дJ ^
Уравнения A35), A36) и A37) приводят к равенству
Y УОД ^ Z?^ + eS**^, A38)
где Sx* описывает спин частицы (определение (92)). Таким об'
разом, уравнение A34) можно записать в виде
[D^lf + eS^F^ + ml W = 0. A39)
Сравнивая с уравнением Клейна — Гордона C0), мы видим,
что отличие состоит в наличии дополнительного слагаемого
, (НО)
которое описывает взаимодействие спина частицы с электромаг-
электромагнитным полем. Это слагаемое не имеет классического аналога
и его вклад становится пренебрежимо малым в условиях, когда
справедливо классическое приближение. В этих условиях дви-
движения волновых пакетов, подчиняющихся уравнениям Дирака
и Клейна — Гордона соответственно, одинаковы.
§ 22. Динамические переменные частицы Дирака
Мы уже приводили физическую интерпретацию некоторых
динамических переменных теории Дирака. Теперь мы рассмо-
рассмотрим этот вопрос более подробно и укажем те переменные кван-
квантовой теории, которые соответствуют приведенным в § 4 раз-
различным классическим величинам.

§ 22. ДИНАМИЧЕСКИЕ ПЕРЕМЕННЫЕ ЧАСТИЦЫ ДИРАКА 403
В этом обсуждении релятивистская инвариантность не иг-
играет существенной роли. Поэтому мы будем следовать той же
схеме изложения, что и в нерелятивистской квантовой механике:
система описывается определенным числом динамических пе-
переменных, удовлетворяющих заданной алгебре перестановоч-
перестановочных соотношений, а уравнение Дирака — в форме Дирака (ур.
C6), D4)) —описывает эволюцию динамических состояний си-
системы в «представлении» Шредингера.
Таким образом, далее мы будем рассматривать время в ка-
качестве параметра, а пространственные координаты — в качестве
динамических переменных. Фундаментальными переменными
будут г, р н а, р. В данном случае можно использовать весь
формализм теории представлений без изменения. В частности,
в представлении Дирака векторы состояния \Ч?}, |Ф>, ... опи-
описываются четырехкомпонентными волновыми функциями Ч?(г),
Ф{г), ..., зависящими от координат х, у, z. Скалярное произ-
произведение <Ф|ХР> в этом представлении определяется следующей
формулой:
Такое определение скалярного произведения согласуется с оп-
определением плотности вероятности положения частицы в про-
пространстве, приведенном в § б (формула C5)). Более того, мы
можем использовать здесь без изменений статистическую интер-
интерпретацию, которая была развита в первой части этого курса.
В частности, среднее значение оператора Q в данном состоянии
равно
где |ы> — нормированный кет-вектор, представляющий данное
состояние.
Те наблюдаемые, которые не действуют на внутренние сте-
степени свободы, имеют очевидную интерпретацию. Например,
г — вектор положения (координата);
р — импульс;
я S3 р — eA(r, t) — количество движения.
Среди функций от г отметим б (г — г0) —проектор на под-
подпространство, отвечающее собственному значению го.

404 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
Среди наблюдаемых, зависящих от внутренних степеней сво-
свободы, отметим '):
энергию: Я ез еср + ая + P«; A41)
релятивистскую массу: Мг=Я — еф^ал + рт; A42)
плотность потока: / (г0) = аб (г — г0); A43)
полный момент импульса: / з= (г X р) + •% а> A44)
спин: S^ya; A45)
четность: Р = $Р®К A46)
Определения величин Я и М основаны на соответствии
с классической механикой. Что касается определения /(г0), та
оно следует из уравнения непрерывности, а определения /, S а
Р связаны с законами преобразования состояний прн враще-
вращениях и отражении соответственно.
Наконец, принцип соответствия приводит к интерпретации
переменной а как скорости частицы. К. этой интерпретации при-
приводит также выражение для плотности потока. Действительно,,
сравним уравнения A8), A9) и B1) классической теории с со-
соответствующими уравнениями квантовой теории. Для этого нам
нужно перейти к «представлению» Гейзенберга, где уравнения
движения для г и я имеют вид
dnldt = — / [я, Я] + дя/д(.
Заменяя Я и я в правой части этих уравнений их явными вы-
выражениями и используя перестановочные соотношения для г, р>
аир, получаем (задача 6)
A47)
X^. A48)
Из определения A42) и свойств оператора а имеем тождество
я = j (Ма + аМ). A49)
Уравнения A47) — A49) для динамических переменных
в «представлении» Гейзенберга совпадают по виду с уравне-
уравнениями A8), A9) и B1) классической теории, если считать, что
а совпадает со скоростью v.
") Отметим, что импульс р зависит от выбора калибровки; только полный
импульс системы (частица + электромагнитное поле) не зависит от этого вы-
выбора. Такое же замечание можно сделать об энергии Н и моменте импульса JP
(см. § XXI. 23).

§ 23. СВОБОДНЫЙ ЭЛЕКТРОН. ПЛОСКИЕ ВОЛНЫ 40S
Здесь следует отметить, что компоненты скорости а не ком-
коммутируют друг с другом, а кроме того, каждая компонента
имеет только два собственных значения +с и —с (-J-1 и —1
в используемых нами единицах измерения). Это еще раз пока-
показывает, что развитую классическую интерпретацию нельзя по-
понимать слишком буквально. Мы вернемся к этому вопросу
в §37.
§ 23. Свободный электрон. Плоские волны
В оставшейся части этого раздела мы рассмотрим решения-
уравнения Дирака при отсутствии внешнего поля и в статиче-
статическом центральном потенциале. Чтобы решить уравнение Ди-
Дирака, достаточно найти собственные функции гамильтониана
HD. Далее, если не оговорено противное, мы будем использо-
использовать представление Дирака, а также введенные в § 7 опера-
операторы рь р2, рз и ох, оу, ог.
Пусть внешнее поле равно нулю. Тогда гамильтониан Но
коммутирует с тремя компонентами импульса, и, следовательно,
мы можем искать собственные функции Но, отвечающие вполне
определенному значению импульса р. Такими решениями будут
плоские волны — функции вида
где и(р) —не зависящий от г четырехкомпонентныи спинор. Он
определяется из уравнения на собственные значения
Ни(р) = Еи(р), A50)
где Н — оператор в пространстве
Н = ар + рт н= Pl (ар) + р3т. A51)
Несложное вычисление дает
Следовательно, собственными значениями Н могут быть
только два значения ± Vp2 + «2:
Е = еЕр (е = ±1)
+S A52)
Легко показать, используя, например, антикоммутативность р2
и Н, что эти собственные значения двукратно вырождены.
Как видно из формулы A51), компонента спина ар/2р в
направлении р коммутирует с Н. (Другие компоненты спина с И
не коммутируют.) Таким образом, мы можем искать собствен-

406
ГЛ. XX. УРАВНЕНИЕ ДИРАКА
ные векторы, общие для Н и ар/2р. Имеем четыре пары соб-
собственных значений:
• ~Y)' V Ер' ~^~Т)' V ?р> ~Т
Каждой паре отвечает одно собственное состояние. СоотвеТ'
ствующий спинор несложно найти из двух уравнений на соб*
ственные значения. Другой метод построения этого спинора мы
приведем в следующем параграфе.
В табл. IV содержатся компоненты собственных спиноров
(нормированных на единицу) в случае, когда импульс р на-
направлен по оси z. Напомним, что в представлении Дирака C
и Ог — диагональные матрицы.
Таблица IV
Компоненты спиноров, соответствующих волне с импульсом
р = @, 0, р) в представлении Дирака \Ер = ут2 + р2 )
Энергия Е-
Положительная
+ер
Отрицательная
Спин
Ор/2р = -г- аг
+ ¦
X
«2 =
и3 =
Ер + га
о
р
Спиноры нормированы иа единицу: u+u=l
§ 24. Построение плоских волн посредством
преобразования Лоренца
Если Л|Х = 0, то преобразование Лоренца переводит решение уравнения
Дирака в решение того же уравнения. В частности, плоскую волну с импуль-
импульсом р можно получить преобразованием Лореица из плоской волны с нуле-
нулевым импульсом. На этом замечании основан метод, который позволит нам
построить спиноры «(р), приведенные в предыдущем параграфе.
Для нулевого импульса уравнение A50) принимает вид
Рт и @) = Ей @).

§ 25. ЦЕНТРАЛЬНЫЙ ПОТЕНЦИАЛ 40Г
Два возможных собственных значения равны +т н —т. Собственному зна-
значению em (е =±1) отвечает спинор t/e) @)—собственный вектор оператора fi.
Будем предполагать, что этот спинор нормирован на единицу, направление
спина фиксируем произвольным образом. Тогда и'8'@) определен с точностью
до фазы.
Плоская волна
есть решение уравнения Дирака, соответствующее нулевому импульсу и энер-
энергии гт или 4-вектору энергии-импульса (ет, 0).
Рассмотрим то же решение в новой системе отсчета, движущейся по от-
отношению к исходной со скоростью v = — р/е ¦ут2 + р2 = — р/вЕр. В новой
системе отсчета 4-вектор энергии-импульса равен
р»^(вЕр,р). A53)
Решением будет плоская волна
Т« = Asp (v) «(Е> @) ехр (- г>%) = [Asp (v) и(Е> @)] ехр [- i(tEpt - Рг)].
Таким образом, выражение в скобках пропорционально искомому спинору и(р),
который далее мы будем обозначать и<8>(р)- Его норма равна временной ком-
компоненте соответствующего 4-вектора потока, который можно получить посред-
посредством преобразования Лоренца из 4-вектора потока, связанного с u(f'@). Эта.
норма в результате равна
Ь зз Vl — tJ = Ер/т.
Таким образом, мы определяем
а(Е> (р) в Ъ 2 Asp (о) а(Е) (о).
Подставляя в это определение выражение (97) и приведенные выше зна-
значения v и Ь, находим
_\_
а<е) (р) = [2Ер (т + Ер)] 2 [т + Ер + еар] «<Е) @). A54)
В частности, если и<8)@)—собственный вектор для {ар), то и г/е)(р)— соб-
собственный вектор, который совпадает с одним из спиноров предыдущего пара-
параграфа. Если импульс р направлен по оси г, то получаем результаты, приве-
приведенные в табл. IV.
Выражение A54) можно записать также в виде
а<Е) (р) = [ЧЕР (т. + Ер)] 2 [т + /pj a<e) @), A55)
где />„ — определенный формулой A53) 4-вектор энергии-импульса.
§ 25. Центральный потенциал
Исследуем состояния дираковской частицы, находящейся
в статическом центральном потенциале V(r). Гамильтониан Ди-
Дирака в этом случае имеет вид
tfD^ap + pm+V(r). A56>

408 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
Он инвариантен относительно вращений и отражений
[HD, /] = 0, [HD, Р] = 0.
Таким образом, мы можем искать решения, соответствующие
определенному моменту импульса и четности.
Удобно записать решение в виде
где
Проектируя V на подпространства, отвечающие |3 = -f-~ 1 и [3 =
= — 1, находим
(J) i (J) A59)
Функции Ф и х зависят от г и компоненты спина ц по оси г.
Их можно рассматривать как функции радиальной перемен-
переменной г и «угловых переменных» (9, ср, ц) в полной аналогии
с волновыми функциями теории Паули.
Будем считать, что V есть собственная функция операторов
J2, 1г и Р. Квантовые числа момента импульса обозначим (JM).
Четность будем указывать посредством квантового числа со
такого, что
/+-
+1 для состояний с четностью (—1) 2.
;_± A60)
— 1 для состояний с четностью (—1) 2.
Итак, согласно предположению,
Пусть су и (9, Ф, Н*) — функция с полным моментом (JM), об-
образованная композицией собственных векторов для спина 1/2
со сферическими функциями порядка L. Четность этой функции
равна (—1)L. В силу теоремы о сложении моментов импульса L
может принимать только два значения
L = /h=/ + yco, L = /' = /-ja>, A62)
а функции <У'и и Щп имеют противоположную четность:
(—1) 2 и (—1) 2 соответственно. Из уравнений A61) за-

5 25. ЦЕНТРАЛЬНЫЙ ПОТЕНЦИАЛ Ш
ключаем, что функция Ф, зависящая от (г, 0, <р, ц), отвечает
L
/-I—La)
моменту импульса (JM) и четности (—1) 2 . Следовательно,
эта функция равна произведению функции от г на <yfj. Анало-
гично, функция х равна произведению функции от г на <Уп.
Итак, если Ч^у описывает состояние с моментом импульса
(JM) и четностью (—1) 2 , то эта функция может быть пред-
представлена в виде
F У
где / и V определяются равенствами A62), a F a G — произ-
произвольные функции от г.
Рассмотрим теперь уравнение на собственные значения
HDW^ = EW^j. A64)
Следуя методу, использованному в главе IX, проведем в опера-
операторе Но разделение «угловых» и радиальных переменных.
Введем радиальный импульс рг и «радиальную скорость» со-
Pr^-ij-^r, A65)
ar = ar = pi (or)lr. A66)
Воспользовавшись тождеством (XIII. 83), получаем
(аг) (ар) = (or) (op) = rp + ioL = rpr + i(\ + oL).
Отсюда, после умножения слева на ar/r и использования ра-
равенства аг = 1, следует тождество
ap^ar(pr + f A-bcrL)). A67)
Исследуем оператор 1 -j- aL. Легко показать, что
Далее, из формулы A61) ясно, что действие L2 на W& сводится
к умножению на
Следовательно,
% ±%. A68)

410 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
Подставляя соотношения A67) и A68) в уравнение A64),
получаем
( К/ + 1) "l 1 м
Воспользуемся в этом уравнении выражением A63) для соб-
ственной функции, определениями A65) н A66) операторов рг
и аг и равенствами (задача 8)
~ ' A69)
(or) О/Р/ = — Щи-
Тогда уравнение перейдет в систему из двух дифференциальных
уравнений для радиальных функций F(r) и G(r)
'^(E-m-V)F, A70a)
A706)
Эти уравнения аналогичны уравнению (IX. 20) нерелятивист-
нерелятивистской теории.
После интегрирования по углам для нормы функции W&
получаем выражение
оо
A71)
которое естественно сравнить с формулой (IX. 21).
Обсуждение свойств регулярности функций F и G можно
провести в полной аналогии с тем, что было сделано для функ-
функции fi(r) в нерелятивистской теории. На деталях мы здесь не
останавливаемся.
§ 26. Свободные сферические волны
Если потенциал V равен нулю, то полученные в предыдущем
параграфе стационарные решения уравнения Дирака для сво-
свободного электрона соответствуют определенным моменту им-
импульса и четности и представляют собой свободные сферические
волны.
В этом случае, из уравнения A706) находим
A72)

§ 26. СВОБОДНЫЕ СФЕРИЧЕСКИЕ ВОЛНЫ 411
Подставляя это выражение в ур. A70а), получаем
(E2-m2)F = \--jF +
Легко показать, что
где I — целое число (см. ур. A62)). Таким образом, полученное
уравнение совпадает с радиальным уравнением для свободной
частицы в нерелятивистской теории, если к тому же заменить
Е2 — т2 на произведение 1т и нерелятивистской энергии. Это
уравнение имеет одно и только одно регулярное решение для
любой положительной величины Е2 — т2. Введя обозначение
k = -y/E2 — tr?{\ Е\^т), перепишем уравнение в виде
L dr2 л2 ^
Регулярное решение (с точностью до постоянного множи-
множителя) равно
Соответствующая функция G легко получается по формуле
A72). Используя рекуррентные соотношения (Б. 42) и (Б. 43J
(первое — при ю=1, второе — при со = —1; в обоих соотно-
соотношениях положили у = 0), находим
Итак, для любого значения энергии Е вне интервала
(—т, +т) существует свободная сферическая волна с момен»
том импульса (JM) и четностью (—1) 2 , которая (см. ур,
A63)) может быть записана в виде
1
const-| , " '¦ "' |. A73)
йое | Е — т |
где е = El\ E |.

412 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
§ 27. Атом водорода
В качестве второго примера исследуем связанные состояния
электрона в кулоновском поле атомного ядра. Последнее будем
считать точечным зарядом, равным заряду электрона, умно-
умноженному на (—Z), и покоящимся в начале координат1). Мы
будем интересоваться связанными состояниями релятивистской
частицы спина 1/2 в центральном потенциале
Эта задача на собственные значения может быть решена точно.
Здесь мы опишем только основные моменты метода решения,
который представляет собой простое расширение метода, ис-
использованного в § XI. 4.
Из анализа асимптотического поведения решений системы
радиальных уравнений A70) ясно, что энергия Е должна ле-
лежать в интервале (—т, +т). Искомое собственное значение
характеризуется тем, что соответствующее решение должно
быть регулярно в начале координат и на бесконечности вести
себя, как ехр (— д/т2 — Рг).
Введем обозначения
'т~Е A74)
( ^) A75)
и новую переменную
р^хг. A76)
Тогда система уравнений A70) примет вид
j)- <177б>
Будем искать решения в виде рядов
(ao#O), A78а)
(bo?=O). A786)
Подставляя эти разложения в систему A77) и приравнивая
члены соответствующих порядков, получаем набор уравнений,
первое из которых определяет s, а последующие представ-
') Тем самым, ядро считается бесконечно тяжелым. Возникающей при
этом ошибкой пренебречь нельзя, поскольку она по порядку величины срав-
сравнима с релятивистскими поправками. Эта ошибка существенно уменьшается,
если во всех формулах массу электрона от заменить приведенной массой.

§ 27. АТОМ ВОДОРОДА ' 413
¦ляют собой рекуррентные соотношения для коэффициентов
ао, Ьр, а\, ..., ап, Ьп, ... Уравнение для s имеет два корня
± д/т2 — ?2- Для регулярности решений F и G и выполнения
условия ^(О) = G@) ==0 необходимо и достаточно, чтобы
s > 0. Так выбирается положительный корень1)
Следовательно, для любого значения Е существует одно ре-
решение, регулярное в начале координат. В общем случае, это
решение на бесконечности ведет себя, как psep, если только раз-
разложения A78) не обрываются. Последнее возможно только для
специальных значений Е — искомых уровней энергии. Вычис-
Вычисление показывает, что эти значения равны
Т
где п —радиальное квантовое число — равно степени полино-
полиномов, фигурирующих в разложениях A78). Для каждого поло-
положительного п' существует регулярное решение при любом из
двух значений со; для п' = 0 регулярное решение существует
только при со = — 1.
Введем главное квантовое число
Тогда предыдущие результаты можно сформулировать следую-
следующим образом. Уровни дискретного спектра зависят от двух
квантовых чисел пи/и определяются формулой
/ = / +1 - л/(/ + IJ - ZV, A790
где п может принимать все целые положительные значения,
а / — все полуцелые значения из интервала @, п)
») Мы предполагаем, что С < |т|, т. е. Ze2 < Г/ + -jrj. Это условие вы-
выполнено, если Z < 137, что практически почти всегда имеет место. В против-
противном случае обсуждение условий регулярности в начале координат стало бы
вначительио более деликатным вопросом.

414 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
Каждому значению J соответствуют два набора из B/ -f 1)
решений противоположной четности, за исключением значения
J — n — y> которому соответствует один набор из B/+ 1) ре-
решений четности (—I)"-1. Вместо того, чтобы фиксировать чет-
четность, можно фиксировать величину / — значение орбитального
момента двух первых компонент спинора. Напомним, что чет-
четность спинора равна (—1)'.
Для энергетических уровней и состояний обычно используют
спектроскопические обозначения nlj. Ниже приведены несколько
первых уровней и соответствующие спектроскопические термы
(вырождение каждого терма равно 2/ + 1):
j
п— —т s^ п —
J-j 3<
/ з
/=|
2 2
Зрз
2
2
3d5
2
(и ' =
(я' =
(«'=
2)
1)
0)
Если выражение A79) разложить в ряд по степеням Z2e*,
то получим
*/—"Ч " 2«2 2«< г , 1 4
Первое слагаемое — масса электрона. Второе —Z2ei/2n2, в точ-
точности совпадает с результатом нерелятивистской теории. Сле-
Следующие слагаемые определяют релятивистские поправки, ко-
которые частично устраняют «случайное вырождение» уровней
нерелятивистской теории: при фиксированном п энергия связи
т — Е каждого терма зависит только от / и тем больше, чем
меньше /.
Экспериментальные результаты о тонкой структуре спектра
атома водорода или водородоподобных атомов (а именно, Hef)
находятся в хорошем согласии с этими предсказаниями.
Однако совпадение результатов не является полным. Наи-
Наибольшее расхождение наблюдается в тонкой структуре уровней

§ 28. БОЛЬШИЕ И МАЛЫЕ КОМПОНЕНТЫ 415
с п = 2 атома водорода1). В нерелятивистском приближении
три уровня 2si , 1p\_ и 2р3, совпадают. В теории Дирака уровни
2 Т ~2
2s i и 2/71 остаются равными, а уровень 2рз расположен ниже
~2 ~2 *2
(расстояние между ними порядка 10~4 эв). Расстояние 2рз —

— 2pi согласуется с предсказаниями теории, в то же время уро-
У
вень 2s 1 расположен ниже уровня 2р\ и величина 2s i —2/л
"г" 7 Т 7
равна приблизительно одной десятой расстояния 2рз—2р|.
7 7
Этот эффект называют лэмбовским сдвигом. Для его объясне-
объяснения необходимо строгое рассмотрение полного взаимодействия
между электроном, протоном и квантованным электромагнит-
электромагнитным полем. В теории Дирака учитывается только основная
часть этого взаимодействия — кулоновский потенциал. Лэмбов-
ский сдвиг связан с «радиационными поправками» к этому при-
приближению2).
Раздел V. НЕРЕЛЯТИВИСТСКИИ ПРЕДЕЛ
УРАВНЕНИЯ ДИРАКА
§ 28. Большие и малые компоненты
Рассмотрим плоские волны с положительной энергией. Ком-
Компоненты этих волн приведены в табл. IV. Будем считать, что
энергия Ер мало отличается от энергии покоя
W = Ер — т < т.
Тогда можно воспользоваться нерелятивистским приближением,
поскольку кинетическая энергия W почти равна mv2/2 и спра-
справедливо неравенство
Мы увидим, что в этом случае отличная от нуля компонента
соответствует |3 = + 1 и по величине она значительно больше
') W.E. Lamb, R. С. Retherford. Phys. Rev. 72, 241 A947).
2) Экспериментальное значение величины 2s l — 2р, равно 1057, 77 ±
7 ?
±0,10 Мц/сек (мегацнклов в секунду); теоретическое значение, полученное
при учете «радиационных поправок», существование которых предсказывается
квантовой электродинамикой, равно 1057,99 ± 0,2 Мц/сек (С. М. Sommerfield.
Phys. Rev. 107, 328 A957)),

413 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
компоненты, которая соответствует р = —1,
Аналогичное утверждение справедливо для сферических волн
(см. выражение A73)) и для собственных функций атома во-
водорода (см., например, собственные функции, определенные
в задаче 10). Все это позволяет предположить, что в нереляти-
нерелятивистском приближении две компоненты Ч'з и W* спинора W, от-
отвечающие собственному значению —1 оператора [J, очень малы
по абсолютной величине. Следовательно, ими можно пренебречь
и теория Дирака становится при этом эквивалентной двухком*
понентной теории.
Чтобы продемонстрировать эту эквивалентность явно, за-
запишем дираковский спинор W в виде A57), где Ф и % опреде-
определяются уравнениями A58), A59). Как мы уже отмечали в § 25,
величины Фи/ можно рассматривать как векторы простран-
пространства состояний двухкомпонентнои нерелятивистской теории.
В этих обозначениях уравнение Дирака для стационарного
состояния с энергией Е в представлении Дирака принимает вид
(а (р - еА)) % + (е<р + т) Ф = ?Ф, A80а)
(а (р - еА)) Ф + (еФ - т) % = Е%. A806)
Введем обозначения:
я = р — еА, М — Е — еср,
, , 081)
Определив из уравнения A806) спинор % и подставив его
в уравнение A80а), получим
[{on) 2^7 (an) + еу] Ф = ГФ. A83)
Уравнения A82)—A83) полностью эквивалентны уравнению
Дирака.
В нерелятивистском пределе справедливы соотношения
W, щ, р, eA<.m, M'тат, A84)
и из уравнения A82) ясно, что % < Ф, а отношение этих двух
величин порядка р/т, т. е. v/c. Спиноры % и Ф называются ма-
малыми и большими компонентами соответственно.

§ 29. НЕРЕЛЯТИВИСТСКИП ПРЕДЕЛ ТЕОРИИ ДИРАКА 417
Далее в этом разделе мы будем использовать понятие «чет-
«четных» и «нечетных» операторов. По определению:
(i) оператор 9* называется «четным», если все его матрич-
матричные элементы между малыми и большими компонентами равны
нулю (например, р, г, L, a, J, P(r0), P);
(и) оператор $Г называется «нечетным», если у него не
равны нулю только матричные элементы между малыми и боль-
большими компонентами (например, а, fia, у5, /(Го))-
Это определение эквивалентно тому условию, что опера-
оператор ^ коммутирует с [J, а оператор Э~ антикоммутирует с [J
A85)
Любой оператор Q можно однозначно представить в виде суммы
«четного» и «нечетного» операторов
Произведение двух «четных» или двух «нечетных» операторов
есть «четный» оператор; произведение «четного» оператора на
«нечетный» есть «нечетный» оператор.
§ 29. Теория Паули как нерелятивистский предел
теории Дирака
Вернемсяк системе уравнений A82) — A83). Если пренебречь
малыми компонентами, то в нормировке волновой функции мы
получим ошибку порядка v2/c2. Ошибка того же порядка воз-
возникает, если в уравнении A83) оператор М' заменить массой т.
В этом приближении уравнение A83) принимает вид уравне-
уравнения на собственные значения ')
Яп. Г.Ф = ГФ A86)
для гамильтониана
Нп.г.^^(ап)(ап)+еср, A87)
который действует на двухкомпонентную волновую функцию
ф. Уравнение A86) определяет энергию W с точностью до о2/с2.
Чтобы привести оператор Яп.г к более привычному виду,
воспользуемся тождеством (XIII. 83) и учтем некоммутатиз-
ность компонент векторного оператора я:
я X я = ie rot A = ie
') Исходное уравнение A83) не является уравнением на собственные зна-
значения, поскольку стоящий в левой части оператор зависит от собственного зна-
значения W, которое участвует в определении М'.
14 А. Мессиа

418 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
Отсюда следует, что
Яп. г. в-1 (р - еА? -Л-{оЖ) + еу. A88)
Мы получили гамильтониан теории Паули для частицы с мас-
массой ш, зарядом е и внутренним магнитным моментом ц = цвсг,
где цв = е/2пг — магнетон Бора.
Таким образом, теория Дирака не только предсказывает су-
существование внутреннего магнитного момента, но и дает его
правильное численное значение (§ XIII. 18). Это одно из наи-
наибольших достижений теории ').
Для доказательства эквивалентности теории Дирака в рас-
рассматриваемом здесь приближении двухкомпонентной теории
Паули мы должны указать операторы, соответствующие опера-
операторам теории Дирака, но действующие только в подпростран-
подпространстве больших компонент.
Это можно сделать, если в вычислениях с интересующими
нас операторами участвуют только их матричные элементы ме-
между состояниями W, W с положительной энергией, близкой
к массе покоя. Последнее условие необходимо для обоснования
нерелятивистского приближения.
В случае четного оператора & матричный элемент
<Чг//|^>|Чг/> представим в виде суммы
(Ф" \& \Ф') + {х" \& Ю-
Второе слагаемое имеет порядок (v/cJ по сравнению с первым
и в рассматриваемом здесь приближении им можно прене-
пренебречь. Тем самым оператор $Р можно заменить его проекцией
на подпространство больших компонент. Эта проекция в нере-
нерелятивистской теории Паули описывает физическую величину,
которая в теории Дирака задается оператором !Р.
') В действительности, экспериментальное значение це*р несколько отли-
отличается от теоретического значения магнитного момента электрона (P. Kusch,
Н. М. Foley. Phys. Rev. 72, 1256 A947)). Согласно последним данным
«Радиационные поправки» квантовой электродинамики приводят к существова-
существованию аномального магнитного момента, что дает (Sommerfield, loc. cit.)
1,163- 10~3 цв.
Отметим еще, что добавление к оператору Дирака члена xnBcrtlv.Fuv при-
приводит к уравнению, которое обладает теми же свойствами инвариантности, что
и уравнение Дирака, при любой константе х. В результате такое уравнение
описывает частицу с массой т, зарядом е и внутренним магнитным моментом
О+)

§ 29. НЕРЕЛЯТИВИСТСКИЙ ПРЕДЕЛ ТЕОРИИ ДИРАКА 419
Для нечетного оператора ST имеем
(V IГI V) = <Ф"| Т Iх'> + <х" \Т\Ф').
Малые компоненты входят в каждое слагаемое этой суммы. Од-
нако в силу уравнения A82) и нерелятивистского приближения
справедливы равенства
"' \Т \У) = 2^- <Ф [<Tpi (<ие) + (сие) p,iT]
Следовательно, оператор 9~ можно заменить проекцией на под-
подпространство больших компонент оператора
Так, «скорость» а = pia можно заменить действующим в про-
пространстве больших компонент оператором
л а (ал) + (ал) а
m 2m
Аналогично плотность потока в точке г0
/ (Л>) = Piord (г — г0)
можно заменить оператором
U (го))п. г. - в (г - го) а О + (?) аб (г - г0)
или, используя тождество (XIII. 83),
(/(го))п., = /A) + /(П>, A89)
у(» _ 6 (г - гр) л + яб (г - го) ^ A90а)
•tin _.г- 6 (>" — га) (р X ") — (р X <г) 6 (г - г0) A906V
Мы видим, что электрический ток е] теории Дирака в этом при-
приближении представляется суммой из двух слагаемых. Первое,
е/(|), совпадает с током теории Шредингера (см. задачу IV. 1).
Чтобы найти интерпретацию второго слагаемого, рассмотрим его
матричный элемент между Ф' и Ф"
Ф') = ^rot <Ф" |6 (Г - Г0)ОГ| Ф'>-
Это ток, связанный с магнитным моментом, и величину
^- <Ф"| б (г - г0) о\ Ф'> ^ (Ф" |6 (г - г0) ц |Ф'>
14*

420 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
можно интерпретировать как плотность магнитного момента.
Мы увидим, что дивергенция этого тока обращается в нуль и он
не дает вклада в уравнение непрерывности.
§ 30. Приложение: сверхтонкая структура
и диполь-дипольная связь
Рассмотрим электрон в электрическом поле атома, которое
описывается некоторым электростатическим потенциалом q>(r),
и исследуем эффект, к которому приводит дополнительное поле,
создаваемое магнитным моментом М ядра. Магнитный диполь
М, расположенный в начале координат, порождает поле, кото-
рое можно представить векторным потенциалом,
^- A91)
щ* rot (М/г). A91')
Такое поле ведет к дополнительному слагаемому —еаА в га-
гамильтониане Дирака.
Для определения влияния этого поля в нерелятивистском
приближении можно вычислить нерелятивистский предел опе-
оператора —еаА, используя метод предыдущего параграфа. Можно
также рассмотреть те изменения в гамильтониане Паули A88),
к которым приводит наличие М. Оба подхода эквивалентны и
мы воспользуемся вторым.
Если мы учтем только линейные по М члены, то гамильто-
гамильтониан Паули будет содержать два дополнительных слагаемых
h = - о^г (рА + Ар),
где Ж — поле, порожденное диполем М.
Слагаемое 1а представляет собой спин-орбитальное взаимо-
взаимодействие (спин ядра и орбита электрона). Поскольку divA = 0
(см. ур. A91)), то
Подставляя в правую часть выражение A91) и вспоминая оп*
ределение орбитального момента электрона L =з г X Р, полу-
получаем
?? 092)

§ 31. ПРЕОБРАЗОВАНИЕ ФОЛДИ — ВОТХОЙЗЕНА 421
Слагаемое /& представляет собой спин-спиновое или ди-
поль-дипольное взаимодействие. Вычислим это слагаемое, ис-
используя формулу A91),
= №) А (у) - [(jiV) (Л*V)] A) . A93)
Если г Ф О, то дифференцирование легко выполнить и полу-
получить
з (Mr) (цг) - (М») г2
Выражение A93), как функция г, имеет в начале координат
особенность порядка 1/г3. Чтобы определить действие опера-
оператора /б, применим его к регулярной функции f(r) и проинтегри-
проинтегрируем это произведение по малой окрестности точки г = 0. Для
этого запишем h в виде
1Ь = | ОШ) Л A) - [0*V) (Ш) - | (»Ш) Л] A) . A93')
Второй член в этом выражении является тензорным оператором
второго порядка в пространстве функций от г. Если функцию
f(r) разложить по сферическим функциям, то после интегриро-
интегрирования по углам останутся только коэффициенты при сфериче-
сферических функциях второго порядка. Эти коэффициенты обращаются
в нуль в начале координат не медленнее, чем г2 и, следова-
следовательно, вклад второго члена в выражение A93), несмотря на
сингулярность 1/г3, также обращается в нуль в начале коорди-
координат. Используя тождество (А. 12), первый член можно записать
в виде —(8я/3) (цЖ)б(г). Таким образом, для любого г, вклю-
включая и начало координат, справедливо равенство
/6 = - -у-(Mti) 6(r)-|[3(jlff) (ц f) - (Mfi)]. A94)
Равенства A92) и A94) получены в нерелятивистском пре-
пределе и позволяют определить сверхтонкую структуру атомных
уровней с точностью до v2/c2. В частности, вклад «-электро-
«-электронов в сверхтонкую структуру дается контактным членом
— (8я/3)(цЛ!N(г).
§ 31. Поправки высших порядков и преобразование
Фолди — Вотхойзена
В низшем порядке по v/c теория Дирака эквивалентна двух-
компонентной теории Паули. Используя, как и ранее, уравнения
A82) — A83), можно получить релятивистские поправки вые-

422 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
ших порядков. Для этого следует заменить величину 1/ЛГ ее
разложением по степеням [(W — ец>)/2т]:
1 ¦¦_ 1 Г. W-eq> (W-eq>y "I
М' ml 2m "¦" V 2т ) "'У
Поскольку
то это по существу ряд по степеням v2/c2. Если в этом разло-
разложении ограничиться первым членом, как это было сделано*
в § 29, то получим теорию Паули. Учитывая последующие члены
разложения, найдем релятивистские поправки высших поряд-
порядков, однако как только мы учтем поправки порядка v2/c2, мы-
потеряем эквивалентность теории Дирака в форме A82) — A83)
двухкомпонентной теории. Это происходит потому, что:
(i) нельзя более пренебрегать вкладом малых компоненг
в нормировку и в матричные элементы четных операторов;
(ii) уравнение A83) не является более уравнением на соб-
собственные значения (см. первую сноску к § 29).
Хотя возникающий при этом метод не является совершенно-
непригодным, его применение и интерпретация результатов ста-
становится довольно деликатной проблемой. Фолди и Вотхойзеш
предложили иной метод, позволяющий находить двухкомпоненг-
ную теорию, которая является приближением к теории Дирак*
в данном порядке по v/c. Основу этого метода составляет под-
представление), гамильтониан Дирака является четным опера-
операторов теории Дирака. В новом «представлении», которое мы '
будем называть представлением Фолди — Вотхойзена, (ФВ-
представление), гамильтониан Дирака является четным опера-
оператором в данном порядке по v/c, так что в этом приближении-
малые и большие компоненты полностью разделены в волновом,
уравнении. Следовательно, малые компоненты можно просто:
отбросить и получить искомую двухкомпонентную теорию. Опе-
Операторы этой двухкомпонентной теории получаются из четных
операторов ФВ-представления, а не из операторов исходного
представления. Таким образом, приходят к новой интерпрета-
интерпретации операторов нерелятивистской механики, в частности, более
удовлетворительную интерпретацию получает оператор коор-
координаты.
В оставшейся части этого раздела мы будем заниматься.
ФВ-представлением и его применением к нерелятивистскому/
пределу уравнения Дирака.

§ 32. ФВ-ПРЕОБРАЗОВАНИЕ ДЛЯ СВОБОДНОЙ ЧАСТИЦЫ 423
§ 32. ФВ-преобразование для свободной частицы
В случае свободной частицы малые и большие компоненты
¦можно полностью разделить во всех порядках v/c.
Рассмотрим гамильтониан Дирака
#0 = ар
Пусть Г+ и Г. — проекторы на решения с положительной и от-
отрицательной энергией соответственно
Пусть В+ и В-—проекторы на подпространства больших и
малых компонент:
По определению, оператор U, который переводит величины
в ФВ-представление, преобразует Г+ в В+, а Г_ в ?_. Обозначая
штрихом векторы и операторы в ФВ-представлении, можно, сле-
следовательно, записать, что
Г'± в 6Т±?/+ = В±.
Потребуем также, чтобы оператор U был инвариантен отно-
относительно трансляций, вращений и отражения. Предоставим чи-
читателю доказательство того, что в этом случае U определен
¦с точностью до фазового множителя. Фиксируя эту фазу, полу-
получаем
«-лАтгИ1+»¦?]- <196>
ар
¦Легко проверить, что данное выражение удовлетворяет всем
упомянутым требованиям.
Поскольку оператор U не зависит от времени, гамильтониан
Ир, который определяет зависимость от времени векторов со-
состояния в ФВ-представлении, дается равенством
Нр = UHDU\
Используя выражение A96), получаем
Я^ = р?р^р(т2 + р2Й. A97)

424 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
В силу четности оператора HF, большие Ф' и малые %' ком-
компоненты расцепились в уравнении движения
/ = ЯрФ', A98а>
t = -Ep%'. A986)
Если мы ограничимся решениями с положительной энергией
(a fortiori нерелятивистскими энергиями), то теория Дирака
будет эквивалентна во всех порядках v/c двухкомпонентной
теории, которая описывается уравнением A98а).
Оператор U коммутирует с р, / и оператором четности Р, но
не коммутирует с оператором г. В представлении, где оператор
г диагоналей, U задается интегральным оператором с матрич-
матричными элементами
(r\U\r')=\\{r\p)dp{p\U\p')dp'{p'\r').
Откуда, используя формулу A96'), находим
{r\U\r') = BяГ3 \ \лРЩ^- + Р
J L V 2Ер
Л/2Ер (т + Ер)
Матричный элемент <г|?/|г'> является функцией (г — г'), кото-
которая практически исчезает при \г—r'\ S> \jm и сосредоточена
в области, где \г — г'| меньше или порядка \jm. Следовательно,
ФВ-представление является нелокальным преобразованием, при
котором спинор W(г) —преобразование спинора Чг(г) —полу-
—получается некоторым усреднением значений спинора W по окрест-
окрестности точки г, и линейные размеры этой окрестности имеют по-
порядок 1/т — длины комптоновской волны частицы.
Оператор координаты частицы определяется в ФВ-предста-
влении равенством
Этот оператор отличен от г. Следуя Фолди и Вотхойзену, мы
будем называть величину, которая задается оператором г
в ФВ-представлении, усредненной координатой. В исходном
представлении она задается некоторым оператором /?, и, по~.
скольку /?' == г, имеем
В представлении Дирака R является нелокальным оператором.
Действие этого оператора на спинор Чг(г) состоит, грубо го-
говоря, в умножении на г и замене значения в каждой точке на
некоторое усредненное значение спинора по области порядка
1/т с центром в этой точке. Это объясняет приведенное выше
название усредненной координаты.

§ 33. ФВ-ПРЕОБРАЗОВАНИЕ ДЛЯ ЧАСТИЦЫ ВО ВНЕШНЕМ ПОЛБ 425
Если Q' — четный оператор в ФВ-представлении, то в двух-
компонентной теории ему соответствует наблюдаемая Qn. г., ко-
которая получается, если в Q' оставить только матричные эле-
элементы между векторами из подпространства больших компо-
компонент: Qn.r. = B+Q'B+. В частности, наблюдаемая г, соответ-
соответствующая координате в двухкомпонентной теории, отвечает
«средней координате» /?, а не оператору координаты собственно
теории Дирака').
§ 33. ФВ-преобразование для частицы во внешнем поле
В присутствии внешнего поля гамильтониан Дирака имеет
вид
Вообще говоря, не существует «представления», в котором га-
гамильтониан был бы в точности «четным» оператором. Однако
применяя последовательно унитарные преобразования, можно
получить «представления», в которых «нечетная» часть соответ-
соответствующего гамильтониана имеет все более высокий порядок
по v/c. Для доказательства рассмотрим унитарный оператор
U = ехр (fiT/2m).
Гамильтониан Н\, который определяет зависимость от времени
в новом представлении, дается равенством
Н{ = UHU* - Ш dUf/dt.
Используя тот факт, что $Т антикоммутирует с ($т-\-Т),
a f/+ = ехр(—$Т/2т), получаем
U фт + T)U* = U2 (pm + Г) =
= рт [cos {Tim) + (Т/т) sin (Т/т)] +
+ т {(Т/т) cos (Т/т) — sin (Tim)}.
Члены U&W и —il)dW/dt можно представить в виде рядов
по степеням Т/т, используя следующее операторное тожде-
•) В соответствии с даииой здесь интерпретацией орбитальный момент
г X Р и спин а двухкомпоиеитиои теории соответствуют ие орбитальному мо-
моменту и спииу теории Дирака, а «усредненному моменту импульса» R X Р
и усредненному спииу S. Здесь 2 — оператор, которому в ФВ-представлеиии
отвечает оператор а; 2' = а. Читатель может убедиться в том, что каждая
из компонент среднего спииа и среднего момента импульса коммутирует с га-
гамильтонианом свободной частицы, собственно спин и орбитальный момент
этим свойством ие обладают. Отметим также, что

426 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
ство, которое справедливо для любых двух операторов А и В?
(см. задачу VIII. 4):
QABe~A = В + И, В] +
п скобок
+ ±[А. [А, В]]+ ... +-^[А, [А, ... [А, [А, В)] ...]]+ ...
Мы приведем только результат вычисления Н' в случае,,
когда ?Г не зависит от времени. В первом приближении спра-
справедливо равенство Н' = Н\. Находим
—(да. fK
Эти разложения для «четной» и «нечетной» частей оператора Ну
определяют ёР\ с точностью до (&~/тN или (Р/т) {Т/тУ «¦
0~\ — с точностью до (9~1т)ъ или (Р/т) {0~/тK, в зависимости,
от того какая из этих величин больше. Следовательно, «нечет-
«нечетная» часть гамильтониана Hi меньше «нечетной» части Н на
множитель порядка (Р/т или (!Г/тJ. В нерелятивистском пре-
пределе величины SPIm и &~/т имеют порядок (v/cJ и v/c соот-
соответственно. Таким образом, ST\ имеет порядок (v/cK.
Для оператора Hi повторим ту же операцию, что была сде-
сделана для Н, т. е. совершим унитарное преобразование с опера-
оператором
?/, = ех
и новый гамильтониан обозначим Н2. «Нечетная» часть этого
гамильтониана меньше ?Г[ на множитель порядка SPi/m или
(JTi/mJ. В нерелятивистском пределе &*i/m имеет порядок
(v/cJ, а (Т\/тУ — порядок (v/cN, следовательно, Т^ имеег
порядок (v/cM. Если пренебречь членами такого порядка, та
гамильтониан Н2 будет «четным» оператором, который имеет
вид
Я2« Pm + &i + О (v5) «
+ «р + г^Г Р ("">' - Ш К""*' |(<П1)' ФИ - » Р (""i'' +
Аналогично, если пренебречь членами .порядка (v/cK, to
также является «четным» оператором и имеет вид
Hi « pm + e<f + —¦ р (аяJ + О (у3).

§ 34. ЭЛЕКТРОН В ЦЕНТРАЛЬНОМ ПОТЕНЦИАЛЕ 427
После этих преобразований мы можем перейти к двухком-
чюнентной теории, так же как и в случае свободной частицы.
? точностью до (v/cM решения с положительной энергией за-
задаются волновыми функциями Ф' из пространства больших ком-
компонент, которые удовлетворяют уравнению
i дФ'/dl = (т + Н'п. г.) Ф'.
Здесь (т + Н'а. г.) — проекция приведенного выше приближен-
¦ного выражения для Я2 на пространство больших компонент,
1. е.
Н'а. , = е<р + ^ (onf - -?р [(an), [(on), <p]] - -^ (ап)\ A99)
Два первых слагаемых представляют собой гамильтониан тео-
теории Паули, следующие два слагаемых — релятивистские по-
поправки порядка (v/cJ к нерелятивистской энергии Н„л..
Несложные вычисления приводят нас к равенствам
(аяL = (л2-е(аЖ)J, B00)
[(<тя), [(on), <р]] = div S + 2а (& X я), B01)
«которые позволяют записать Н'п г. в более привычной форме.
Производя последовательно такие унитарные преобразова-
преобразования достаточное число раз, можно построить двухкомпонентную
теорию, которая определяет состояния с положительной энер-
энергией с точностью до любого заданного порядка по v/c. Каждое
.новое преобразование увеличивает точность на множитель
(v/cJ. Исследование сходимости получившихся рядов является
довольно деликатным вопросом. Весьма вероятно, что в боль-
большинстве случаев мы имеем лишь асимптотическое разложение.
Это разложение по степеням операторов р/т, т. е. (h/tnc) grad,
и d/mdt, т. е. (h/mc2) d/dt. А следовательно, скорость сходимо-
сходимости этого ряда зависит от характера изменения потенциала
(А, ф) на расстояниях порядка h/tnc (и за время порядка
ti/mc2 — отношение комптоновской длины волны к скорости
света).
§ 34. Электрон в центральном электростатистическом
потенциале
В качестве приложения описанной в предыдущем параграфе
техники рассмотрим электрон в центральном электростатиче-
электростатическом потенциале V(r)=eq>(r). В этом случае А(г) =0 и га-
гамильтониан Паули совпадает с гамильтонианом теории Шре-
дингера

428 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
Если учесть поправки порядка v2/c2, то к гамильтониану
Яп.г. добавятся два последних слагаемых выражения A99).
В данном случае
ediv<o = — ДУ,
и принимая во внимание соотношения B00) и B01), получаем
Первое дополнительное слагаемое, — р4/8т3с2, представляет
собой релятивистскую поправку к кинетической энергии р2/2пк
следующее — спин-орбитальное взаимодействие (см. формулу
(XIII. 95)). Третье слагаемое, h2AV/8m2c2, определяет поправку
к центральному потенциалу, которая называется поправкой
Дарвина; в случае чисто кулоновского потенциала V(r) =
= — Ze2/r. Эта поправка имеет вид
(nZe2h2/2m2c*N{r)
и влияет только на «-состояния.
§ 35. Обсуждения и выводы
Независимо от того, имеется ли внешнее поле или оно равно
нулю, операторы двухкомпонентной нерелятивистской теории
представляют собой проекции операторов представления Фол-
ди — Вотхойзена на пространство больших компонент. В част-
ности, оператор нерелятивистской теории г следует отождест-
отождествить с оператором /?, который мы назвали «усредненной коор-
координатой». В теории Дирака взаимодействие частицы с электро-
электромагнитным потенциалом локально, другими словами, частицы
взаимодействуют с электромагнитным потенциалом в точке г.
При переходе к ФВ-представлению, где г представляет усред-
усредненную координату, взаимодействие становится нелокальным и
оно зависит от значений электромагнитного потенциала в обла-
области с линейными размерами порядка h/tnc, содержащий точку г.
Если изменение потенциала в этой области незначительное, го
это взаимодействие можно представить посредством ряда Тей-
Тейлора, включающим в себя значения потенциала и его производ-
производных в точке г. Так, гамильтониан #„. г. (ур. A99) или B02))
содержит первые члены этого разложения.
Следовательно, в нерелятивистском пределе электрон пред-
представляет собой не точечный заряд, а распределение заряда и
тока в области с линейными размерами h/mc. Это объясняет по-
появление членов взаимодействия, которые связаны с магнитным

§'36. СВОЙСТВА ЗАРЯДОВО-СОПРЯЖЕННЫХ РЕШЕНИЙ 429
моментом (взаимодействие — цЖ, спин-орбитальное взаимодей-
взаимодействие) и распределенной плотностью заряда (дарвиновское сла-
слагаемое).
Наконец, следует отметить, что использование нерелятивист-
нерелятивистского приближения для потенциалов, которые сингулярны в на-
начале координат, таких как А — MX, г/г3 или ф = —Ze/r, не
обосновано, поскольку в окрестности точки г = О изменение ве-
величин еА/т и еф/т не мало. Если воспользоваться описанным
выше методом последовательных приближений достаточное
число раз, то в нерелятивистском гамильтониане появятся сла-
слагаемые, которые будут иметь достаточно сильную сингулярность
в начале координат и будут давать бесконечный вклад в энер-
энергию. Пути преодоления этой трудности уже были предложены
в предыдущих обсуждениях. В нерелятивистском гамильтониане
величины А и ф заменяются их средними значениями по обла-
области с линейными размерами порядка h/mc. Если нерелятивист-
нерелятивистское приближение является обоснованным, то это ведет к эф-
эффективному обрезанию сингулярностей на расстоянии h/mc от
начала координат во всех сингулярных выражениях, которые
возникают при вычислениях. Для того чтобы нерелятивистское
приближение было обоснованным в упомянутых выше двух слу-
случаях, достаточно чтобы в точке г = h/mc выполнялись неравен-
неравенства ')
е | А | <С тс2, e<f <C тс2.
Раздел VI. РЕШЕНИЯ С ОТРИЦАТЕЛЬНОЙ ЭНЕРГИЕЙ
И ТЕОРИЯ ПОЗИТРОНОВ
6aXaaaa\QaXaaaa\ *)
(Анабасис, IV. 8)
§ 36. Свойства зарядово-сопряженных решений
В дальнейшем мы будем использовать понятие зарядового
сопряжения, которое было введено в § 19. Зарядовое сопряже-
сопряжение представляет собой антилинейное взаимнооднозначное соот-
соответствие между волновыми функциями, которые описывают по-
поведение двух различных частиц с одной и той же массой т, но
с противоположными зарядами +е и —е в заданном электро-
электромагнитном поле (А, ф).
Если физическая величина, связанная с первой частицей,
представлена наблюдаемой Q(e), то для второй частицы та же
') Если Шц — масса атомного ядра, то \М\ « Zehlntnc; величина
еА/тс2 в точке г — h/mc имеет порядок (e2/hc)(ZmJmN), т. е. 10~5—10-°.
Таким образом, наши вычисления сверхтонкой структуры полиостью обосно-
обоснованы. Что касается примера из § 34, то величина еф/mc2 имеет порядок ^ZJh
и вычисления являются обоснованными, если 2 <Ц 137.
*) Море\ Море\ (греч., прим. перед.).

430 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
самая величина представляется наблюдаемой Q(—е). Так,
в обоих случаях для импульса имеем р = — /V, а для опера-
оператора энергии в первом случае имеем
Н(е) = а (р - еЛ) + рт + е<р,
а во втором случае
Я (— е) зз а (р -f еЛ) -f 0m — еф.
Рассмотрим решение Ч^г, /) и зарядово-сопряженное ре*
шение 4го(г, t). Мы хотим сравнить физические характеристики
состояний, которые описываются этими решениями. Если Кс —
антилинейный оператор, определенный равенством A24), то
^с = Кс^- B03)
Пусть <Q> обозначает среднее значение Q в состоянии lF,
а (Q}c—среднее значение того же оператора в состоянии W0.
Предполагая, что состояния W и Wc нормированы на единицу,
имеем
Из соотношения B03) получаем
= <^ I (KcQKc) I 40* = (V IШ Qf/Cc) I 40,
откуда следует соотношение для средних значений
B04)
Используя это соотношение и свойства антиунитарного пре-
преобразования Кс, находим следующие соотношения для средних
значений в состоянии W и в зарядово-сопряженном состоянии:
B05)
Мы видим, что зарядово-сопряженные решения имеют совпа-
совпадающие плотности вероятности и плотности потока, — таким об-
образом, противоположные плотности зарядов и электрических то-
токов — но противоположные по знаку энергии: зарядовое сопря-
сопряжение меняет знак энергии.

§ 37. РЕШЕНИЯ С ОТРИЦАТЕЛЬНОЙ ЭНЕРГИЕЙ 43»
§ 37. Особое поведение решений с отрицательной энергией
После этих предварительных замечаний мы можем перейти
к более подробному обсуждению вопроса о состояниях с отри-
отрицательной энергией.
Вначале рассмотрим случай свободной частицы. Решения-
уравнения Дирака в этом случае были получены в § 23. Спектр
энергии состоит из двух полупрямых (— оо, —тс2) и (тс2, + °°),.
разделенных интервалом длиной 2тс2 (см. рис. 22, а). Первая
часть спектра отвечает состояниям с отрицательной энергией:
Е=—?Р—— ¦у/т2-\-р2, а вторая часть — состояниям с поло-
положительной энергией.
Исследуем движение свободного волнового пакета. Мы по-
покажем, что, вообще говоря, центр волнового пакета только
в среднем движется по классической траектории. Для этого про-
проинтегрируем уравнения движения в представлении Геизенберга^
которые в данном случае имеют вид
i[H,r] = a, B06)
da/dt = i [Я, а] = i (На + аЯ) — 2гаЯ = 2ip — 2/аЯ. B07>
Поскольку р и Я не зависят от времени, уравнение B07) легко
интегрируется
Таким образом, получена явная зависимость dr/dt от времени /,.
и уравнение B06) тоже легко интегрируется
±w-. B08>
Формула B08) определяет оператор г в представлении Гейзен-
берга в момент времени t как функцию от значений, которые
принимают операторы г и а в начальный момент времени t=0.
Отсюда мы можем получить закон движения центра <г> любого
волнового пакета, который поучительно сравнить с классиче-
классическим законом
U
В отличие от классического равномерного прямолинейного дви-
движения свободный волновой пакет испытывает сложное движе-
движение— результат сложения равномерного прямолинейного дви-
движения со скоростью (р/Ну и быстрых осцилляции

432 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
Амплитуда и период этих осцилляции («Zitterbewegung» — дро-
дрожание) имеют порядок Н/2тс и h/2mc2 соответственно.
Таких осцилляции ие возникает, если пакет представляет со-
собой суперпозицию волн только с положительной энергией или
только с отрицательной. Чтобы убедиться в этом, достаточно
показать, что
, р \ е
Г± 1а ~ ~ТГ ) чн Г± = 0>
где Г+ и Г_— проекторы на состояния с положительной и отри-
отрицательной энергией соответственно (определение A95)). После-
Последовательно находим
[Я, а] = 2р - 2аЯ,
И, поскольку ЯГ± = ±?РГ±, то получаем
Откуда мы получаем упомянутое выше свойство, используя до-
дополнительно коммутативность Я и Г+, Г_. Следовательно, быст-
быстрые осцилляции связаны с интерференцией компонент волнового
пакета с положительной и отрицательной энергией.
Собственно «дрожание», являясь любопытным эффектом, не
представляет какой-либо трудности для теории. Трудность воз-
возникает, когда исследуется движение волнового пакета, построен-
построенного только из состояний с отрицательной энергией. В этом слу-
случае «дрожание» исчезает и центр пакета движется равномерно
и прямолинейно со скоростью
-(¦*)—<*)¦
которая противоположна по направлению импульсу пакета
<р>. В частности, в нерелятивистском пределе (Яда — тс2) по-
получаем соотношение* v = — (р)/т, т. е. частица ведет себя так,
как если бы она имела отрицательную массу.
Трудность такого рода становится еще более очевидной при
исследовании движения волнового пакета в статическом поле.
Рассмотрим, например, электрон в кулоновском потенциале
притяжения —Ze2/r. Спектр состоит из непрерывной части по-
положительных энергий от тс2 до сю, серии дискретных уровней
положительных энергий, меньших тс2, и непрерывной части
отрицательных энергий от —тс2 до —сю (см. рис. 22,6). На-
Напомним, что состояния с отрицательной энергией соответствуют
при зарядовом сопряжении состояниям частицы с той же мае-

§ 38. ИЗМЕНЕНИЕ ИНТЕРПРЕТАЦИИ РЕШЕНИЙ
433
сой, но с противоположным зарядом (т. е. состоянием пози-
позитрона), которая находится в том же потенциале. Можно сказать
и иначе, что состояния с отрицательной энергией соответствуют
состояниям электрона в потенциале Ze2/r. При этом соответ-
соответствии меняет знак энергия и переставляются большие и малые
компоненты, а плотность потока и плотность остаются теми же
(см. ур. B05)). Спектр электрона в потенциале отталкивания
Рис. 22. Спектр энергий электрона Дирака: а) свободного; б) в потенциале
притяжения — Ze2/r; в) в потенциале отталкивания Ze2jr.
Ze2/r изображен на рис. 22, в. Непрерывная часть положитель-
положительных энергий в потенциале отталкивания соответствует непре-
непрерывной части отрицательных энергий в потенциале притяже-
притяжения.
Рассмотрим движение волнового пакета из состояний с от-
отрицательной энергией в потенциале —Ze2/r, предполагая, что
справедливо нерелятивистское приближение (Ze2 <C 1, энергии
порядка —тс2). Движение будет тем же, что и для пакета волн
с положительной энергией, получающегося зарядовым сопряже-
сопряжением. В пределе очень малых скоростей можно использовать
классическое приближение (см. § VI. 5), и движение центра
пакета будет почти совпадать с движением классического элек-
электрона, т. е. с движением частицы отрицательной массы —т
в потенциале —Ze2/r. Направление скорости противоположно
импульсу, а направление ускорения противоположно направле-
направлению силы. Такие явления никогда не наблюдались в экспери-
экспериментах.
§ 38. Изменение интерпретации состояний
с отрицательной энергией. Теория дырок и позитронов
В приведенной выше формулировке состояния с отрицатель-
отрицательной энергией не имеют никакого физического смысла. Если бы
было возможно полностью устранить взаимодействие между со*

434 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
стояниями с положительной и отрицательной энергией, то по-
последние можно было совсем не учитывать. Однако поступить
так не удается.
Рассмотрим, например, свободный электрон в состоянии
с положительной энергией Е+ и подвергнем его в течение вре-
времени от 0 до t действию электромагнитного излучения ча-
частоты со. Если интервал времени достаточно велик, а напряжен-
напряженность поля не слишком большая, то вычислить результирующий:
эффект можно, используя методы § XVII. 6. Таким образом, мы
получим отличную от нуля вероятность перехода электрона
в состояния с энергией Е+ -f- Йсо и Е+ — Йсо. В частности, если
Йсо > (?+ + тс2), то второй переход совершается в состояния
с отрицательной энергией.
В качестве другого примера рассмотрим полный спектр атома
водорода (рис. 22,6). В .результате взаимодействия электрона
с электромагнитным полем всегда существует вероятность ра-
радиационного перехода из данного состояния атома в состояние
с более низкой энергией. Следовательно, электрон, который на-
находится в одном из связанных состояний атома водорода, даже
в случае изолированной системы, может совершить квантовый
переход в состояния с отрицательной энергией, излучив один
или несколько фотонов. Более того, поскольку спектр энергий
не ограничен снизу, атом водорода не имеет устойчивых состоя-
состояний ').
Чтобы обойти эти трудности, Дирак сделал следующее пред-
предположение. В состоянии, которое мы называем «вакуумом», все
состояния отрицательной энергии заняты электронами. Если
к такому «вакууму» добавить один электрон, то, поскольку все
состояния отрицательной энергии заняты, а электроны подчи-
подчиняются статистике Ферми — Дирака, этот электрон может на-
находиться только в состояниях с положительной энергией.
Таким образом, «вакуум» представляет собой полностью вы-
вырожденный ферми-газ бесконечной плотности. Кроме этого,
предполагается, что этот газ совершенно ненаблюдаем и не
приводит к каким-либо гравитационным или электромагнитным
эффектам. Наблюдаемые физические характеристики данного
состояния будут определяться отклонениями этого состояния от
такого «вакуума». Так, наблюдаемый заряд системы (элек-
(электрон -f- «вакуум») равен разности полных зарядов системы и
«вакуума», т. е. заряду электрона. Точно так же наблюдаемая
энергия системы равна разности полных энергий системы и
«вакуума» и, следовательно, — энергии добавленного электрона.
') О. Клейн сформулировал знаменитый парадокс, нз которого также вид-
видно, что вероятность перехода в состояния с отрицательной энергией не равна
нулю. Парадокс Клейна излагается во многих книгах, см., например, М. Борн,
loc. tit. (прим. 2, гл. I).

§ 39. ТРУДНОСТИ ТЕОРИИ ДЫРОК 435
Тем самым, переопределение наблюдаемых величин до сих пор
сводилось к тому, что оказались запрещенными переходы в со-
состояния с отрицательными энергиями ').
Рассмотрим теперь, что будет наблюдаться, если из «моря»
отрицательных энергий удалить электрон. Согласно сформули-
сформулированным выше правилам можно заключить, что возникшая
«дырка» будет иметь заряд, противоположный заряду элек-
электрона. Кроме этого, ее энергия будет иметь противоположный
знак, т. е. будет положительной, а импульс — противоположное
направление. Эти утверждения справедливы независимо от того,
находится или нет удаленный электрон в собственном состоя-
состоянии гамильтониана. В частности, если этот электрон описывается
волновым пакетом, движущимся со скоростью v, то дырка дви-
движется с той же скоростью, но с противоположным импульсом:
дырка ведет себя, как частица положительной массы -\-т и за-
заряда —е. Такие частицы наблюдаются в природе, их называют
позитронами.
Под действием электромагнитного поля или других подхо-
подходящих возмущений электрон из «моря» отрицательных энергий
может совершить квантовый переход в состояние с положитель-
положительной энергией. Дырка в «море» отрицательных энергий будет
вести себя, как позитрон. Таким образом, появляется пара ча-
частиц с противоположными зарядами. Рождение электрон-пози-
тронных пар наблюдается экспериментально.
Точно так же, если в море отрицательных энергий имеется
дырка, то электрон с положительной энергией может совершить
переход в незанятое состояние с отрицательной энергией с ис-
испусканием фотонов. Такое явление аннигиляции электрон-по-
зитронных пар с излучением фотонов также наблюдается экс-
экспериментально.
§ 39. Трудности теории дырок
Теория дырок, которая была кратко сформулирована выше,
позволяет примирить теорию Дирака с такими эксперименталь-
экспериментальными фактами, как отсутствие состояний с отрицательными
энергиями, существование позитронов, рождение и аннигиляция
пар. В этом отношении она представляет собой значительный
шаг вперед, однако в ней встречаются серьезные трудности и
ограничения.
Прежде всего, теория не является цолной. Постулируя заня-
занятость всех состояний с отрицательной энергией, мы уже не
имеем одночастичной теории даже при описании одного элек-
электрона. Построенный в этой главе формализм теории Дирака
') В частности, автоматически исчезает осцнлляторное движение («Zitter-
bewegung»).

436 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
для одной частицы недостаточен для описания такой ситуации,
и можно надеяться получить самосогласованное описание только
в рамках теории поля.
Теория дырок представляет собой лишь первый шаг в по-
построении корректной теории квантового электронного поля. Ее
преимущество состоит в том, что она рисует нам простые кар-
картины физических явлений и служит, таким образом, подспорьем
при разработке последовательной теории. Однако как только
мы пожелаем извлечь из нее нечто большее, нас встречают ло-
ловушки и противоречия.
Например, непоследовательно считать, что «вакуум» содер-
содержит бесконечное число электронов, и предполагать, что эти
электроны не взаимодействуют между собой.
Другим слабым местом теории является явная несимметрия
между электронами и позитронами. Можно сформулировать за-
рядово-сопряженную теорию, в которой позитроны будут играть
роль частиц, а электроны — роль дырок, все физические след-
следствия при этом не изменятся. Устранить все эти трудности
можно в формализме теории поля, который использует уравне-
уравнения, инвариантные относительно зарядового сопряжения.
Отметим, наконец, что даже определение состояний отрица-
отрицательной энергии зависит от приложенного электромагнитного-
потенциала. В двух случаях, рассмотренных в § 37, свободной
частицы и частицы в кулоновском поле, пространства состояний
отрицательной энергии не совпадают. Если, например, волновую
функцию основного состояния атома водорода разложить nq
плоским волнам, то плоские волны с отрицательной энергией
дадут в это разложение хотя и малый, но не исчезающий вклад.
В приведенном выше определении «вакуума», под состояниями
с отрицательной энергией понимались состояния свободной ча-
частицы (действительно, вакуум естественно определять в отсут-
отсутствие внешнего поля). Введение электромагнитного поля моди-
модифицирует вакуумное состояние за счет рождения пар. В ре-
результате возникает нечто вроде поляризуемой среды и величина
электрического заряда в «вакууме» кажется меньше своего на-
настоящего значения. Такие же эффекты возникают и в теории
поля. Теория дырок позволяет предсказать эти эффекты, од-
однако не в состоянии дать надежного и самосогласованного ме-
метода вычисления этих эффектов.
ЗАДАЧИ И УПРАЖНЕНИЯ
1. Показать, что если V удовлетворяет уравнению Клейна— Гордона с по-
потенциалом №, то уравнению непрерывности удовлетворяет следующий 4-ток:
у* = _1_ [V* (дир) _ у (№)•] = J- |V (д»у) -
(см. задачу IV. 1).

ЗАДАЧИ И УПРАЖНЕНИЯ 437
2. Рассмотрим атом водорода, в котором электрон заменен частицей с те-
теми же массой и зарядом, но волновая функция которой удовлетворяет урав-
уравнению Клейна — Гордона. Тогда уровни дискретного спектра определяются
уравнением на собственные значения
(е2 \2
Показать, что это уравнение можно решить точно, разделяя угловые н ра-
радиальную переменные, и что зависимость уровней дискретного спектра от кван-
квантовых чисел ли/ дается формулой
1 1
(п= 1, 2, ..., оо; / = 0, 1, ..., п — 1).
Сравнить этот спектр с тем, который получается в нерелятивистской теории
Шредингера.
3. Показать, что все приведенные в табл. II (§ 10) матрицы уА (не обя-
обязательно унитарные) имеют определитель, равный 1.
4. Пусть В — определенная в конце § 10 матрица. Доказать, что ВВ* =
= В*В = —/. (Показать сначала, что
(i) матрица ВВ* кратна единичной и, следовательно, ВВ* = В*В = ±/;
(ii) матрица ВВ* не зависит от выбора 4 унитарных матриц У1, которые
участвуют в определении В.)
б. Вывести следующие свойства (антиуннтарного) оператора зарядового
сопряжения Кс, введенного в § 19:
i\ /">Г i\ /"¦ ™— """"" Гч л\ Г1 i\ Т*\ О "™" ^~ *\ Г«
Показать, что, если выбрать фазы операторов преобразования так, как
это сделано в § 17, то Кс коммутирует с операторами трансляций и собствен-
собственных преобразований Лоренца и антикоммутнрует с пространственным отраже-
отражением и обращением времени. Как следует изменить выбор фаз, чтобы Кс ком-
коммутировал со всеми операторами этих преобразований?
6. Используя гамильтониан Дирака, получить уравнения движения для
операторов г и я в гейзенберговском представлении. Аналогичным образом
вывести уравнения
где Р — «сила Лоренца»: F = е (8 + а X Щ- Сравнить эти уравнения с урав-
уравнениями B2) н BГ) классической динамики.
7. В случае свободного уравнения Дирака любое его решение удовлетво-
удовлетворяет уравнению Клейна—Гордона. Показать, что обратное не верно (приве-
(привести контрпример).
8. Доказать тождества A69).

438 ГЛ. XX. УРАВНЕНИЕ ДИРАКА
9. Разложить плосковолновое решение уравнения Дирака с импульсом р,
направленным по оси г, по сферическим волнам.
10. Провести систематическое нсследование таких волновых функций ато-
атома водорода, для которых радиальные функции F и G пропорциональны друг
другу. Показать, что соответствующие уровни отвечают л'= 0 Г следова-
следовательно, / = л —— J и/ = л — 1. Ответ (обозначения § 27):
F = const • pse~p, G = — vF,
s = V — e\ x — тег/п, p = w, \ = y./(E + m) я* ег/2п.
11. Используя предложенный в § 27 метод, вычислить уровни атома во-
водорода в теории Дирака.
12. Сравнить тонкую структуру уровней атома водорода, которая полу-
получается в теории Дирака и в теории Клейна— Гордона для частицы с одной и
той же массой н зарядом в заданном кулоновском поле (см. задачу 2).
13. Исходя из выражения B02), вычислить релятивистские поправки по-
порядка ч2/е2 к уровням 2sx, 2р1 и 2р3 атома водорода. Показать, что в этом
Т ~2 Т
приближении уровни 2Siya и 2р^% не меняются и сравнить это с точным резуль-
результатом из § 27.

ГЛАВА XXI
КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
Se поп ё vero, ё bene trovato *)
§ 1. Введение
Настоящая глава преследует две цели, с одной стороны, —
являясь введением в квантовую теорию полей, познакомить чи-
читателя с понятием квантового поля, физическим смыслом, до-
достижениями и трудностями теории; с другой стороны, — дать
элементарное изложение квантовой теории электромагнитного
излучения и его взаимодействия с атомными и ядерными систе-
системами.
При построении квантовой теории поля мы будем использо-
использовать тот же метод, что и для нерелятивистской квантовой тео-
теории частиц. В основе метода лежит принцип соответствия и
канонический гамильтонов формализм классического поля.
Единственным отличием является то, что в данном случае ме-
метод применяется к системе с бесконечным числом степеней сво-
свободы. Получившийся формализм называют гамильтоновым или
каноническим квантованием.
Основной недостаток гамильтонова формализма заключается
в отсутствии явной ковариантности1). Теорию можно строить
и в явно ковариантной форме, используя ковариантные уравне-
уравнения классического поля и метод квантования, сохраняющий ко-
ковариантность. Такая формулировка обладает неоспоримыми-
преимуществами как техническими, так и концептуальными.
Многие вычисления упрощаются в силу того, что возникающие
выражения должны сохранять компактную и симметричную
форму. С другой стороны, ковариантный формализм использует
сложный математический аппарат. Математические понятия
гамильтонова формализма более привычны, и поэтому ои лучше
подходит для первого знакомства с предметом.
Глава состоит из четырех разделов. В первых двух разделах
исследуется простейшее из полей — вещественное скалярное
поле. Случай свободного поля рассматривается в разделе 1У
*) Если и не верно, то хорошо сработано (итал. поел., прим. перев.).
') Конечно, отсюда не следует, что нарушается принцип относительности.
Однако релятивистская инвариантность теории не очевидна a priori и должна
быть доказана. Такого доказательства мы приводить здесь не будем.

-440 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
где излагается метод квантования классического поля, опреде-
определяется пространство квантовых состояний и их физическая ин-
интерпретация. В разделе II мы изучаем взаимодействие поля
с частицами, и на примере простой модели выясняем характер-
характерные свойства поля, взаимодействующего с атомными или ядер'
ными системами. Приведенные в этом разделе приложения ил-
люстрируют методы, физическое содержание и трудности кван-
товой теории полей. В двух последних разделах рассматри-
рассматривается электромагнитное поле. В разделе III напоминается
классическая теория, а квантовая теория и ее приложения
кратко рассмотрены в разделе IV. Большинство утверждений
и выкладок, относящихся к скалярному полю, без труда пере-
переносятся на случай электромагнитного поля. Мы кратко повто-
повторяем их, особо отмечая те отличия, которые вызваны вектор-
ным характером электромагнитного потенциала и нулевой мас-
массой фотона ').
Раздел I. КВАНТОВАНИЕ ВЕЩЕСТВЕННОГО
СКАЛЯРНОГО ПОЛЯ
§ 2. Классические свободные поля. Нормальные колебания
Классическое вещественное скалярное поле определяется
в каждый момент времени / заданием его амплитуды Ф(г, t)
в каждой точке пространства г.
Поле можно рассматривать как динамическую систему с бес-
бесконечным числом степеней свободы. Каждой точке простран-
пространства отвечает некоторая координата системы — значение поля
в этой точке.
Динамика такой системы не существенно отличается от ди-
динамики системы с конечным числом степеней свободы. Однако
') Существует много монографий по квантовой электродинамике. Назовем
в частности: В. Гайтлер. Квантовая теория излучения. М., ИЛ, 1956;
А. И. Ахиезер, В. Б. Берестецкий. Квантовая электродинамика М., «Наука»,
1969; Н. Н. Боголюбов, Д. В. Ширков. Введение в теорию квантованных по-
полей, М., «Наука», 1976; В. Тирринг. Принципы квантовой электродинамики. М.,
«Высшая школа», 1964; С. Швебер. Введение в релятивистскую квантовую
теорию поля. М., ИЛ, 1963; J, M. Jauch, F. Rohrlich. The Theory of Photons
and Electrons. Addison Wesley, 1956.
Гайтлер пользуется гамильтоновым формализмом н рассматривает основ-
основные приложения теории к атомной физике. Ахиезер и Берестецкий, Яух и Рор-
лих дают полное изложение коварнантного формализма и подробный обзор
приложений. Боголюбов и Ширков, а также Швебер дают последовательное
изложение квантовой теории поля в ковариантном формализме, включая под-
подробное обсуждение проблемы перенормировки и вопросов причинности в тео-
рнн поля. В книге Тнррннга содержится общий обзор коварнантного форма-
формализма, обсуждение его физического смысла н трудностей теории. Обсуждение
вопросов измерения величин и операторов, характеризующих поле, можно най-
найти в классических работах: N. Bohr, L. Rosenfeld, Det. kid. Danske Viddenskab,
Selskab. 12, № 8 A933); Phys. Rev. 78, 794 A950).

§ 2. КЛАССИЧЕСКИЕ СВОБОДНЫЕ ПОЛЯ 441
поскольку координаты в данном случае нумеруются непрерыв-
непрерывными параметрами, например, тремя компонентами х, у, z pa»
диус-вектора г, дифференцирование по времени заменяется на
частную производную и эволюция системы определяется урав-
уравнением движения вида
ф(г, $в=д*Ф/дР = Р[Ф(г, t), Ф(г, t)\.
Правая часть этого уравнения F есть функционал амплитуды
ф (г, t) и ее частной производной Ф = дФ/dt, которые берутся
в один и тот же момент времени t. Динамическое состояние си-
системы в данный момент времени определяется, если известны
ее положение и скорость в начальный момент времени to, т. е.
значения поля Ф (г, /0) и их производные по времени
дФ (г, t)
Ф (г, /о);
dt
Из всех уравнений движения, которые инвариантны относи-
относительно неоднородной группы Лоренца, простейшим является
уравнение Клейна — Гордона
где \к — некоторая постоянная. Это линейное и однородное по
ф уравнение определяет эволюцию свободного поля. В даль-
дальнейшем мы увидим, что \i есть масса связанных с квантовым
полем частиц (§ 6).
Если бы в левой части уравнения A) отсутствовал член АФ,
то движения различных координат системы были бы независи-
независимыми и каждое представляло бы собой гармоническое колеба-
колебание с частотой [1, а амплитуда и фаза определялись бы на-
начальными условиями. Слагаемое АФ связывает эти гармоничен
ские колебания.
Сейчас мы покажем, что введя нормальные координаты, та-
такое множество связанных осцилляторов можно преобрязовать
в множество независимых осцилляторов.
Обозначим /ь /2, ..., /г, ... полный ортонормированный на^
бор вещественных собственных функций эрмитова оператора
(—А). Спектр собственных значений расположен от 0 до + сю.
Собственное значение, отвечающее функции /,-, обозначим k\.
Таким образом, имеем
(А + /ф/, = 0, B)
\f1(r)f,(r)dr = 6u, C)
r'). D)

442 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
Из соотношений ортогональности и замкнутости C), D) полу-
получаем разложения
Ф(г, 0 = W)Mr), E)
F)
Величины <7ь q%, •••» <7<> ••• представляют собой нормальные
координаты. Из уравнений F) и A) получаем
$, + ©& = (), G)
а>| = (*» + ця)'*. (8)
Таким образом, каждое <7< определяет движение независимого
гармонического осциллятора с частотой со,. В силу уравнения E)
амплитуда поля равна линейной суперпозиции этих независи-
независимых осцилляторов.
В предыдущих рассуждениях мы предполагали, что базисные
функции нумеруются дискретным индексом. В действительности
спектр оператора (—А) непрерывный, заполняющий полуось
(О, -f- со), и функции нумеруются набором индексов, из которых
по крайней мере один непрерывный. Несложно повторить при-
приведенные выше рассуждения в случае непрерывных индексов.
С учетом незначительных модификаций, на которых мы здесь
не останавливаемся, результаты останутся теми же. Однако
наличие непрерывных индексов осложняет изложение кванто-
квантовой теории. Чтобы избежать этого, мы будем предполагать, что
поле находится в конечном объеме пространства и на поверхно-
поверхности этого объема удовлетворяет подходящим граничным усло-
условиям. Физические величины, которые мы хотим сосчитать, по-
получаются из величин, вычисляемых в формализме с конечным
объемом, при неограниченном увеличении этого объема. Искус-
Искусственный прием такого типа уже был описан в § V. 11. Этот
прием, очевидно, не является строгим, следует отметить также,
что он частично нарушает свойства инвариантности теории.
§ 3. Квантование свободного поля
Переход к нормальным координатам дает возможность про-
квантовать вещественное скалярное поле наиболее простым
способом. Он заключается в сопоставлении каждой моде нор-
нормальных колебаний классического поля квантового осциллятора
с той же частотой (см. главу XII).
Запишем классический гамильтониан в нормальных коор-
координатах. Пусть pi — импульс, сопряженный qi. Тогда уравне-

§ 3. КВАНТОВАНИЕ СВОБОДНОГО ПОЛЯ 443
ние G) эквивалентно гамильтоновым уравнениям
которые получаются, если для i-ой степени свободы взять га-
гамильтониан
А| = Т(Р?+ "?«?)¦ (9>
Следовательно, полный гамильтониан имеет вид
Я = 2,й,. A0)
Соответствующее квантовое поле получается заменой веще-
вещественных динамических переменных qt и pt на наблюдаемые,
которые удовлетворяют коммутационным соотношениям (й=1),
\Чь Pt] = ibtt. A1)
Каждой моде отвечает набор дискретных эквидистантных
энергетических уровней
Ent = (л, + |) со,- (щ = 0, 1, 2, ... оо). A2)
Для дальнейшего удобно ввести операторы рождения н уни-
уничтожения, которые мы обозначим через b\ и 6, соответственно,
A3)
Коммутационные соотношения A1) для наблюдаемых эквива-
эквивалентны коммутационным соотношениям для операторов рожде-
рождения и уничтожения
[Ь,,ЬП = Ь,, A4)
а собственные векторы Ы получаются последовательным дей-
действием оператора b\ на вектор основного состояния (см. ур.
(XII. 20)).
Взяв тензорное произведение собственных состояний гамиль-
гамильтонианов hi, /12, • • •, hi, ..., получим полный набор собственных
состояний Н. Такие состояния нумеруются квантовыми чис-
числами ль л2, ..., nh ..., энергия состояния равна сумме энергий
отдельных мод, входящих в это состояние;
...в,... = J] (re,
i
-f g-)ю,. 'A5)
Нормированный собственный вектор, отвечающий такому со-
состоянию, получается из вектора |0>, представляющего основное

444 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
состояние, по формуле
(• tV* i
I /i!«a ... я* •••> = Пт^7Г|0>-
i \nr)
Поле в точке г представляется эрмитовым оператором Ф(г),
который определяется равенством
полученным по принципу соответствия из классической фор-
формулы E). Удобно переписать формулу A7) в терминах опера*
торов bi и bt
Ф (г) = Z Bсог)"? 0< + bi) /,. A8)
До сих пор поле рассматривалось как множество квантовых
осцилляторов. В рассмотренных выше стационарных состояниях
каждое квантовое число п определяло число квантов, относя*
щихся к определенной моде нормальных колебаний. Собствен-
Собственным состояниям Н и операторам системы можно также дать
корпускулярную интерпретацию, которая уже обсуждалась
в § XII. 6. Тогда tii представляет собой число частиц в состоя-
состоянии /,¦ с энергией со,-, онЪ является собственным значением неко-
некоторого оператора Ni — оператора «числа частиц в состоянии /,»,
который определяется равенством
A9)
где bi — оператор уничтожения частицы в состоянии /,-, a b\ —
оператор рождения частицы в том же состоянии.
Интерпретация является самосогласованной, только если
полная энергия данного динамического состояния равна сумме
энергий частиц, образующих это состояние. Как уже отмечалось
в § XII. 6, для этого достаточно из каждого гамильтониана hi
в правой части формулы A0) вычесть константу —сог. Это из-
изменение полного гамильтониана никак не влияет на уравнения
движения, зато новый гамильтониан обладает желаемым свой-
свойством
Jtt B0)
В частности, вакуум является состоянием с нулевой энергией,
представляемым кет-вектором |0>. Вектор Ь*\0) представляет
состояние с одной частицей, и энергия этого состояния равна
энергии этой частицы со*.

§ 4. ЛАГРАНЖИАН ПОЛЯ . 445
Рассматриваемые здесь частицы неразличимы и динамиче-
динамическое состояние всей системы полностью определяется числом
частиц п\, /12, ..., tii, ... в каждом из индивидуальных состоя-
состояний, f\, ft ft в которых могут находиться частицы. Эти
«числа заполнения» могут принимать целые неотрицательные
значения от 0 до + °°- Следовательно, рассматриваемые ча-
частицы подчиняются статистике Бозе — Эйнштейна (см.
§ XIV. 6), и квантовое поле представляет собой систему с не-
неопределенным числом бозонов.
В заключение этого параграфа сделаем замечание об основ-
основном состоянии системы. Вакуум квантового поля сильно отли-
отличается от классического вакуума. Последний является состоя-
состоянием с минимальной энергией, в котором поле всюду равно
нулю. В квантовом случае поле является оператором, который
не коммутирует с гамильтонианом. Вакуумное ожидание поля
равно нулю, что легко показать, используя свойства операто-
операторов bi и bt, но среднеквадратичное отклонение отлично от
нуля. Действительно, используя выражение A8) для поля, на-
находим
<Ф2 <г)>о -Z Z T fa^/)"* <° I ^ + Ь^ (Ь* + 6') I °> ^ W fi <r>'
i I
и так как
<0 | (bt + bt) (bt + ЬЦ) | 0) = <0 |btb]\ 0) = fii/,
получаем
4
В правой части стоит ряд из положительных членов, следова-
следовательно, мы получили отличное от нуля положительное значение.
В действительности можно показать, что полученный ряд рас-
расходится1). Появление расходящихся величин характерно для
систем с бесконечным числом степеней свободы и является
источником серьезных трудностей в квантовой теории поля. Мы
еще вернемся к этому вопросу в разделе II.
§ 4. Лагранжиан поля. Импульс, сопряженный к Ф(г)
Прежде чем продолжать рассмотрение квантовой теории,
вернемся к классической и опишем кратко обобщения лагран-
жева и гамильтонова формализмов для систем с бесконечным
') С другой стороны, интеграл от поля по конечному объему нмеет конеч-
конечные флуктуации. Эти флуктуации возрастают с уменьшением области инте-
интегрирования и в пределе, когда объем стремится к нулю, стремятся к беско-
бесконечности (см. задачу 1).

446 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
числом степеней свободы. Если координаты нумеруются дис-
дискретным индексом, то обобщение очевидно. Такое обобщение
было использовано в случае с нормальными координатами. Си-
Ситуация становится сложнее, если координаты зависят от непре-
непрерывного индекса, например, координаты поля определяются его-
амплитудой в каждой точке пространства. Именно такой выбор,
координат интересует нас здесь.
Функция Лагранжа L зависит от координат системы и ско-
скоростей; в данном случае L — функционал от Ф и Ф. Предполо-
Предположим, что она имеет вид
B1)
Плотность лангражиана & зависит от г и / через Ф, гра-
градиент ФиФ
S = S (Ф, дФ!дхк, Ф).
Зная L, можно определить действие
и и
I=\Ldt = \dt \drS, B2)
которое также является некоторым функционалом от Ф(г, /).
Уравнения движения получаются из принципа наименьшего
действия (ур. A.12))
б/ = 0 (предполагая, что 6Ф (/,) = 6Ф (t2) = 0). B3)
Из равенства B2) следует, что уравнения движения удовле-
удовлетворяют принципу относительности, если плотность лагранжиа-
лагранжиана & ведет себя при преобразованиях из группы Лоренца как
скаляр. Это условие на 3? упрощает нахождение функции Ла-
Лагранжа.
В данном случае уравнения Лагранжа являются дифферен-
дифференциальными уравнениями в частных производных для Ф(г, t),
которые получаются из принципа наименьшего действия
)• B4)
L+ Y
dt дФ i-i dxk д (дФ/дхк) дФ
k
k
Это есть уравнение движения для поля Ф.
Для более строгого определения координат поля делим мыс-
мысленно все пространство на бесконечно малые области. Каждой
такой области (г, г + dr) отвечает координата системы — вели-
величина Ф(г, t)dr. Уравнения движения определяют зависимость
координат от времени. В соответствии с обычным определением

§ 4. ЛАГРАНЖИАН ПОЛЯ 447
импульс П(г, t), сопряженный координате Ф (г, t)dr, равен функ-
функциональной производной L по скорости Ф(г, t)
Щг.О—— —^- B5)
v ' 6Ф (г, 0 dr (ЭФ v '
Использованное здесь понятие функциональной производной
является естественным обобщением понятия частной производ-
производной, и 8L есть вариация L при условии, что Ф меняется на
бесконечно малую величину 6Ф в малой области dr в окрест-
окрестности точки г и не меняется в остальной части пространства.
После того как мы определили для каждой координаты со-
сопряженный импульс, можно сосчитать, в соответствии со стан-
стандартным определением (ур. (I. 13)), функцию Гамильтона, ко-
которая является функционалом от Ф и П
B6)
Ж е= Ж (Ф, дФ/дхк, П) = ПФ - 2,
где Ж — плотность гамильтониана. Канонические гамильтоновы
уравнения имеют вид (см. ур. (I. 14))
дП '
д дЖ B7)
дФ ?-? дхк д (дФ/дхк) '
В случае свободного скалярного поля в качестве плотности
лагранжиана можно взять функцию
2 = тг [(^Ф) (аиФ) - ,xW] = 1 [ф2 - (УФJ - ц2Ф2], B8)
поскольку уравнение B4) тогда совпадает с уравнением A).
Сопряженный к Ф импульс равен
П=Ф, B9)
а функция Гамильтона имеет вид
И = -i- J (П2 + (gra d ФJ + ]х2Ф2) dr. C0)
Функция Н совпадает с полученной ранее функцией A0),
которая записана в терминах нормальных координат. Для того
чтобы это показать, достаточно заменить Ф и П их разложе-
разложениями по qi и pi и воспользоваться свойствами функций /. Раз*

448 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
ложение для ф мы знаем (ур. E)). Для П из уравнения B5)
получаем
П(г, f)dr = —. =У г-^—.
v ' 6Ф (г, t) ^ dqt 6Ф (г, t)
По определению рг=д1/д<^ в силу уравнения F)
откуда
f
6Ф (г, t) li
следовательно, мы имеем
Щг, 0=Zp//i(r). C1)
Подставляя полученные разложения в Н, имеем
Я = {ЕЕ [PtPl \ ftfi dr + g,q, J (V/.V/,) dr + ji2?,^ J /,/, dr ].
C2)
Интегрируя по частям и применяя уравнение B), получаем ра-
равенство
J (v/да dr = - J /, д/; dr = k\\ fit, dr.
Подставляя полученное выражение в правую часть C2), ис-
используя соотношения ортонормированности функций /C) и оп-
определение со,- (8), получаем упомянутое совпадение
(Напомним, что в квантовом случае данное выражение отли-
отличается от выражения B0) на бесконечную константу.)
При квантовании поля в качестве основных переменных
можно брать как qt и р, нли bi и b\, так и Ф(г) и П(г). Ком-
Коммутационные соотношения для Ф и П можно получить из ком-
коммутационных соотношений для b и fe+. Из уравнений A3) и
разложения C1) находим
П (О = У \l V2^ (bt - bt) ft (r). C3)

S 5. КОМПЛЕКСНЫЕ БАЗИСНЫЕ ФУНКЦИИ 449
Используя разложения A8) и C3), коммутационные соотно-
соотношения для Ь и bf и соотношение замкнутости D), получаем
[Ф (г), Ф (г')] = [П (г), П (г')] = О,
/б(г-г') ( '
§ 5. Комплексные базисные функции
В предыдущем параграфе мы видели, как можно прокванто-
вать поле, не прибегая к нормальным координатам. Однако ис-
использование нормальных координат обычно упрощает вычисле-
вычисления, а также интерпретацию квантового поля. В силу вырож-
вырожденности собственных значений оператора (—А) имеется боль-
большой произвол в выборе базисных функций и нормальных коор-
координат. В частности, можно проквантовать поле с помощью ком-
комплексных базисных функций. В этом параграфе мы рассмотрим
такой метод квантования и покажем, что полученное квантовое
поле не зависит от выбора базисных функций.
Пусть и\, щ, ..., Us, ... — полный ортонормированный ба-
базис, a (os — соответствующие энергии, так что (см. ур. B) —
D), (8))
*")«НО = 3(г-г'), C5)
(Д+ **)«. = О, C6)
<os = (kt + tff. C7)
С каждой модой us связаны два эрмитово-сопряженных опера-
оператора, as и
ношениям
тора, as и at, которые удовлетворяют коммутационным соот
[а., а,] = [а+, aj] = 0, [а., а+] = 6st. C8)
Используя эти операторы, можно построить пространство дина-
динамических состояний системы. Таким образом, каждой моде us
отвечает квантовый гармонический осциллятор, а операторы as
и aj интерпретируются как операторы уничтожения и рождения
частицы в состоянии us- Наблюдаемые системы выражаются
через операторы рождения и уничтожения. Например, наблю-
наблюдаемая Ns^a^as соответствует числу частиц, находящихся
в состоянии Us- Для поля Ф(г) справедливо разложение (см.
ур. A8))
Ф (г) = Z (ЧР (*.«. (г) + аХ (г)), C9)
15 А. Мессиа

450 гл- XX1- КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
для сопряженного импульса П(г) —разложение (см. ур. C3))'
T
П <г> = I Tl Bа*? (°К (') - вЛ-И). D0)
S
для гамильтониана Я, определяющего эволюцию системы (ур,
B0)),
tf=Ea+ae<V D1)
Найдем теперь связь между а, а+ и операторами fe, fe+ из
§ 3 и покажем, что построенная здесь система совпадает с кван-
квантовой системой, определенной в § 3.
Мы обозначали индексом s множество квантовых чисел, ну-
нумерующих функции и. По условию в этом множестве имеется
квантовое число, определяющее энергию, и дополнительные
квантовые числа а, которые параметризуют функции, отвечаю-
отвечающие одному значению энергии. Будем параметризовать энергию
волновым числом k
co = (fe2+jiV. D2)
Таким образом s = (k, a).
Аналогичным образом индекс i, нумерующий функции f,
представляет собой множество квантовых чисел, которое со-
состоит из волнового числа k, определяющего энергию, и допол-
нительного множества квантовых чисел р: i == (k, р).
Функции fkp, отвечающие данному значению k, связаны
с функциями Uka посредством унитарного преобразования (Т —
унитарная матрица)
ика = ? Tapfkp, fkp = ? (Г+)ра uka. D3)
P о
Все величины, которые появляются ниже, отвечают фиксиро-
фиксированному значению k, поэтому в дальнейшем индекс k мы будем
опускать.
Для того чтобы разложения A8) и C9) задавали один и
тот же оператор Ф(г), а разложения C3) и D0)—оператор
П(г),'необходимо и достаточно, чтобы для любого значения k
выполнялось равенство
Y, ааиа = ? bjр.
о р
Принимая во внимание второе из соотношений D3), видим, что
это эквивалентно равенствам
Oo==ZOp D4)
р
или
а1=^ТаЛ- D4+)

§ 6. ПЛОСКИЕ ВОЛНЫ. ОПРЕДЕЛЕНИЕ ИМПУЛЬСА 451
Таким образом, мы установили линейное соответствие между
операторами а, а+ и Ь, &+. Более точно, линейное соотношение
между операторами рождения &+ и а+ D4+) тождественно ли-
нейному соотношению между функциями / и и D3).
Из равенств D4) и D4+) следует, что разложения A8) и
C9) определяют одно и то же поле Ф(г). Для эквивалентности
двух методов квантования данного поля необходимо, чтобы так
определенные операторы а и а+ удовлетворяли коммутацион-
ным соотношениям C8), а определяемый уравнением B0) га*
мильтониан Н, будучи записан в терминах операторов а, а+,
имел вид D1). Это легко доказать, используя унитарность мат*
рицы Т. Действительно, для каждого значения k имеем
[й<т. Ост'] = 2j ТарТа'р> [b0, &J'] = J] ТорТз'о'&ро' = 6<т<т',
рр' рр'
откуда следует
Точно так же для каждого значения k получаем
2] aJa<T= Л 2j TacTw'btbp' = ? 6PP'&p6P' = 2 blb0,
а рр7 а рр' р
откуда следует требуемое выражение для Н.
§ 6. Плоские волны. Определение импульса
Среди различных наборов комплексных базисных функций
имеется выделенный набор — плоские волны. Как мы увидим
ниже, они соответствуют состояниям отдельных частиц с опре-
определенным импульсом.
Для того чтобы иметь дело с дискретными индексами, мы
будем предполагать, что поле заключено в кубе со стороной L,
и потребуем для функций us выполнения соотношения
2L> У' z)~us{—-zL> У'
и аналогичных соотношений для аргументов у я г. Данные усло-
условия являются простыми обобщениями условия периодичности,
описанного в § V. 11.
В качестве базисных функций мы можем выбрать плоские
волны
uk = L V*', D5)
для которых компоненты волнового вектора кратны 2n/L
kx = 2nnJL, ky = 2nny/L, kz — 2nnJL.
15*

452 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
Мы получаем полную ортонормированную систему базисны
функций, придавая числам пх, nv, пг все возможные целые зна»
чения
пх, пу, яг = 0, ±1, ±2, ...
Каждой из этих плоских волн соответствует оператор уничто-
уничтожения ak и оператор рождения а\. Поле Ф(г) задается разло-
разложением (см. ур. C9))
_\_
Ф И = ? B©AL3) 2 (akeiltr + aje"'*'), D6)
сопряженный полю импульс (см. ур. D0))
П (г) = ? i D>J2L3y (aje-'*' - аьёк<), D7)
а гамильтониан (см.ур. D1))
D)>*. D8)
где суммирование происходит по всем возможным значениям k,
т. е. по всем возможным значениям пх, пу, пг.
Как уже объяснялось в § V. 11, ответы для случая неогра-
неограниченного пространства получаются при стремлении L к беско-
бесконечности. В этом пределе суммирование заменяется интегриро-
интегрированием. В каждом малом интервале (k, k -f Щ имеется
(L/2nK8k возможных значений трех чисел пх, пу, пг. Если до-
допустить, что суммируемые члены можно рассматривать как не-
непрерывные функции параметра k (это естественно, имея в виду
цредельный переход L->-oo), то каждый символ ? можно за-
заменить на символ интегрирования
Величина (L/2nK есть плотность индивидуальных состояний
в пространстве волновых векторов. Название плотность уровней
используют, как правило, для числа состояний в единице телес-
телесного угла и в единичном интервале энергии, так что плот-
плотность уровней есть функция энергии pz.(co). Число состояний
da>, волновой вектор которых находится в телесном угле
2, Q -f- dQ), а энергия расположена в интервале (со, со -f- day),
равно
р? dQ, da = (L/2nK k2 (dkfda>) d® dQ = (L/2nf &k da> dQ.

§ 6. ПЛОСКИЕ ВОЛНЫ. ОПРЕДЕЛЕНИЕ ИМПУЛЬСА 453
Следовательно,
D9)
(см. ур. (XVII. 52)).
В действительности, можно полностью устранить искусственное введение
куба и использовать плоские волны, заданные во всем пространстве. Тогда вол-
волновой вектор ft может принимать без ограничений все возможные зиачения, и
плоские волны зависят от 3 непрерывных индексов kx, ky, кг, а нормировка
с символами Кронекера заменится на нормировку с б-функциями.
В качестве базисных выбирают функции
и (ft) = и (ft; г) = е'*7Bя)'/г
и с каждой из них связывают эрмитово-сопряженные операторы а (к) и а+ (к).
Все формулы получаются из предыдущих заменой uk на BnjL)^ и (к),
ak на Bn/LK/ia(k), символа Л на \ (L/2jtK dk. Так, основные свойства
базисных функций (см. ур. C5), C6) C7)) примут вид
\ и* (к; г) и (ft'; r) dr = 6 (ft - ft'), \ и (ft; г) и* (ft; г') dk = 6 (г - г'),
(A + ?2)«(ft;r)=0,
Коммутационные соотношения операторов a (ft) и а+ (ft) равны (см. ур. C8))
[a (ft), а (ft')] - [а+ (ft), a+(ft')] = 0,
[а (ft), а+ (ft')] = б (ft - ft').
Поля Ф (г) и П (г) запишутся в виде интегралов (см. ур. C9) и D0))
Ф (г) = BП)-'/' [ -^Lr (a (ft) elkr + a+ (ft) е"'*'),
П (г) = {2пГь/Ч J /y^ dk (а+ (ft) e-ikr - a (k) e'*').
а гамильтониан (см. ур. D1))
Н = [ а+ (ft) a (ft) to (k) dk.
Остается установить связь между импульсом поля W и
ложением на плоские волны.
По определению векторный оператор W связан с бесконечно
малыми преобразованиями по формуле (XV. 41). При конечном
преобразовании 0~(а) (обозначения § XV. 9) оператор Ф(г0),
дающий амплитуду поля в точке г0, переходит в оператор
Ф(г0 + а), дающий амплитуду поля в точке, которая получается
из г0 сдвигом '). Точно так же П(г0) преобразуется в П(г0 + а).
') Подчеркнем отличие от закона преобразования наблюдаемой х из
§ XV. 9 (см. предыдущую сноску). Здесь г0 — параметр, фиксирующий точку
в пространстве, где измеряется амплитуда поля.

454 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
Используя этот закон преобразования наблюдаемых в случае,,
когда а равно бесконечно малому вектору е, получаем
E0>
Поскольку эти коммутационные соотношения должны быть вы»
полнены для любого Го, они определяют W с точностью до по-
постоянного (векторного) слагаемого. Так, компонента Wx ш>
оси х является оператором, который с точностью до константы
определяется коммутационными соотношениями
[Wx, Ф(го)] = * —
ОХ
[Wx, n(ro)] = i4r . E2)
Предыдущие соотношения выполнены, если ;
Wx = — ^ П -^- dr + const. E3)
Интегрируя по частям, получаем эквивалентное выражение
Wx — \ 42- ф dr + const. E4)
Подставляя выражение E3) в левую часть уравнения E1) и
используя коммутационные соотношения C4), находим
- \ П (г) i^U- dr, Ф (г0)] = - $ [П (г), Ф (r0)]
[(г) ;-_,дФ
' дх " дх
Аналогичным образом можно показать, что соотношение E2J
выполнено, если воспользоваться для Wx выражением E4).
Такие же формулы справедливы для Wy и Wz. Следователь-
Следовательно, мы получили три компоненты W с точностью до постоян-
постоянных слагаемых, которые определяются из требования, чтобы W
был векторным оператором. Таким образом, импульс поля
можно записать в виде двух эквивалентных выражений
E5)
E6)
[N. В. В классической теории для импульса получаются выра-
выражения, которые формально тождественны приведенным.]

§ 6. ПЛОСКИЕ ВОЛНЫ. ОПРЕДЕЛЕНИЕ ИМПУЛЬСА 455
Выразим теперь W в терминах операторов ак и а\. Для
этого подставим в правую часть равенства E5) вместо Ф и П
их разложения D6) и D7) соответственно и воспользуемся со-
соотношениями ортогональности для плоских волн. Получим
Y
к
или, используя коммутационные соотношения для операторов а
и а+,
т Е * о -а-а - а-*а*
Суммирование в полученных формулах происходит по всем воз-
возможным значениям k. Выражение в скобках под знаком послед-
последней суммы не меняется при замене k на —k. Следовательно, два
слагаемых, отвечающие k и —k, отличаются только знаком и
эта сумма равна нулю. Таким образом,
W=Z(a$ak)k. E7)
к
Отсюда легко получить коммутационные соотношения W
с операторами а и а+
[W, ak] = - kak, E8)
[W, at~] = + kat E9)
Формулы E7), E8) и E9) просто интерпретировать, если
считать, что частица в состоянии иц имеет импульс Л. Поскольку
{atak) определяет число частиц в состоянии Uk, формула E7)
означает просто, что полный импульс поля W равен сумме им-
импульсов частиц, образующих поле. Точно так же, формулы E8)
и E9) согласуются с интерпретацией операторов ak и а? как
операторов уничтожения и рождения частицы с импульсом k.
Действительно, если \w} — собственный вектор оператора пол-
полного импульса, отвечающий собственному значению w, то век-
вектор ak\ w) (в случае, если этот вектор отличен от нуля, т. е. со-
состояние поля содержит хоть одну частицу с импульсом k) удо-
удовлетворяет уравнению
и») = аи (W — k)| w) = ak {w — k)\ w) = (w — k)пкI w).
Точно так же, используя формулу E9), получаем

456 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
Отметим, что связанные с полем частицы с импульсом к
имеют энергию со = (&2 + р2)'1'. Следовательно, масса этих частиц
равна ц.
§ 7. Сферические волны. Определение момента импульса
В качестве базисных функций часто используются плоские
волны. Столь же часто, вероятно, используются и сферические
волны. В последнем случае базисные функции равны
«WB, = consU,(*r)l7(8, ф) F0)
и зависят от непрерывного индекса k и двух дискретных ин-
индексов I и т. Для того чтобы иметь дело только с дискретными
индексами, можно предположить, что поле содержится внутри
сферы радиуса R, и потребовать обращения базисных функций
в нуль на поверхности сферы. Формулы для случая неограни-
неограниченного пространства получаются предельным переходом
R-+0O.
Используя новые базисные функции, можно повторить все
рассуждения предыдущего параграфа. Таким образом, вводятся
операторы уничтожения аыт и рождения atim частицы в со-
состоянии, описываемом сферической волной иыт-
Можно показать, что сферические волны отвечают одноча-
стичным состояниям с определенным моментом импульса, точно
так же как плоские волны отвечают одночастичным состояниям
с определенным импульсом. Для полного момента импульса
поля / получаем выражение
\r, F1)
где / есть оператор —i'(rXV), действующий на функцию Ф
/ф = — ir х (УФ).
Можно использовать также эквивалентное выражение
Операторы аыт и a\im интерпретируются соответственно как
операторы уничтожения и рождения частицы с энергией со =
=(&2+ц2I''2 и моментом импульса Aт). Кроме этого, B1 + 1) опе-
операторов а\1т, отвечающие данному значению / и k, образуют
стандартные компоненты неприводимого тензорного оператора
порядка I, а B/+ 1) операторов аыт образуют с точностью до
порядка и знака стандартные компоненты эрмитово-сопряжен*
ного тензорного оператора (определение § XIII. 30).

§ 9. ВЗАИМОДЕЙСТВИЕ С СИСТЕМОЙ ЧАСТИЦ 457
§ 8. Пространственное отражение и обращение времени
К преобразованиям, оставляющим инвариантными уравнения движения,
относятся отражение пространства и обращение времени. Эти преобразования
полностью определяются их действием на поле Ф(г) и сопряженный ему им-
импульс П(г), соответствующие (унитарный или антиунитарный) операторы пре-
преобразований определяются с точностью до фазового множителя.
При отражении пространства имеем
Ф (г) -> Ф (- г), П (г) -> П (- г). (I)
Это закон преобразования скалярного поля, соответствующий оператор пре-
преобразования So — унитарный и, следовательно, коммутационные соотношения
полей при этом преобразовании не меняются. Поскольку все операторы тео-
теории являются функциями Ф и П, то из соотношений (I) легко получить закон
ях преобразования прн пространственном отражении. В частности, для опера-
операторов а и а+, связанных с разложением по плоским волнам, получаем
V*so = а-к>
В случае обращения времени поле Ф не меняется, а скорость меняет свое
направление на противоположное, следовательно,
Ф (г) -> Ф (г), П (г) -> - П (г). (Г)
Соответствующий этому преобразованию оператор К — антиунитарный и ком-
коммутационные соотношения полей при преобразовании меняют знак. Закон пре-
преобразования операторов а и аУ легко следует из определения этих операторов
и закона (Г)
Таким образом, операторы рождения и уничтожения преобразуются одина-
одинаково при пространственном отражении н обращении времени. Не следует, од-
однако, путать эти преобразования, поскольку одно является унитарным, а Дру-
Другое — антиунитарным.
Преобразования (I) илн (II) и (I') или (II') определяют операторы So и
К с точностью до фазового множителя. Мы устраним произвол в фазе, потре-
потребовав чтобы вектор |0) был инвариантен относительно этих преобразований
s01 о> = | о>, /с | о> = f о>.
Раздел II. ВЗАИМОДЕЙСТВИЕ С АТОМНОЙ СИСТЕМОЙ
§ 9. Взаимодействие с системой частиц
Рассмотрим взаимодействие поля и частицы. Нижеследую-
Нижеследующие рассуждения в существенном не изменятся, если частицу
заменить системой нескольких частиц.
Динамические переменные системы частица + поле являются
функциями основных переменных подсистем. В качестве основ-
основных переменных частицы, которую мы будем считать для про*
стоты бесспиновой, возьмем вектор R, описывающий ее поло-

458 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
жение, и ее импульс Р. В качестве основных переменных поля
мы можем взять ф(г) и П(г) или определенные в предыдущем
параграфе операторы рождения и уничтожения. В дальнейшем
мы будем часто использовать операторы ak и а\, связанные
с разложением по плоским волнам.
Состояния всей системы образуют пространство, которое яв-
ляется произведением пространства состояний частицы <?ГчаСт и
пространства состояний свободного поля &п-
со со jfx SP
0=0П® © част-
Гамильтониан всей системы равен сумме трех слагаемых
Яп + Я'. F2)
Первые два слагаемых отвечают свободным подсистемам, по-
последнее представляет собой энергию взаимодействия.
Выше мы получили несколько эквивалентных выражений
для гамильтониана свободного поля Яп, отметим, в частности,,
выражение D8). Гамильтониан Ячаст описывает эволюцию ча-
частицы без поля Ф. Предположим для определенности, что ча-
частица находится во внешнем потенциальном поле и ее масса М
удовлетворяет неравенству М 3> ц. Будем считать, что движе-
движение частицы можно рассматривать в нерелятивистском прибли-
приближении, т. е.
+V(R) F3)
Остается определить Я'. Простейшее из возможных выра-
выражений для Н' получится, если предположить, что взаимодей-
взаимодействие пропорционально величине амплитуды поля в точке Ry
где находится частица
F4)
+ а+е-'**). F4')
Безразмерная постоянная g называется константой связи. Вто-
Вторая формула для Я' получается из первой и разложения D6).
Такая форма взаимодействия почти однозначно определяется
из требования релятивистской инвариантности. Однако в иссле-
исследуемой здесь теории с самого начала используется нерелятн-
вистское приближение. Это следует не только из того факта,
что Ячаст не обладает ковариантными свойствами, вытекаю-
вытекающими из принципа относительности, но и потому, что сама кон-
концепция материальной системы, состоящей из одной или опреде-
определенного числа частиц, не может быть оправдана в релятивист-
релятивистской квантовой механике. Эти два ограничения, имеющиеся

§ 9. ВЗАИМОДЕЙСТВИЕ С СИСТЕМОЙ ЧАСТИЦ
459
в теории, следует иметь в виду при выборе Н'. Выбору может
помочь исследование из главы XX о нерелятивистском прибли-
приближении для уравнения Дирака. Оно подсказывает нам, что взаи-
взаимодействие поля и нерелятивистской частицы массы М не яв-
является локальным, как записано в формуле F4), а зависит от
значений поля в области размером 1/М с центром в точке, где
находится частица. Поэтому выражение F4) для W мы заме-
заменим на выражение
r — R\)dr, F5)
где р(г)=р(г)—вещественная, сферически-симметричная
функция, удовлетворяющая условию нормировки
оо
р (г) dr = 4л\ р (г) г2 dr — 1
о
и сосредоточенная в области радиуса 1/М с центром в начале
координат (см. рис. 23,а). Подставляя в правую часть фор-
формулы F5) вместо этой функции б (г — R), мы получим фор-
формулу F4).
1
fi/Mc r Не/ft 'Н
а) 6У
Рис. 23. Общий вид функций р (л) и С (k).
Мы назовем обрезающей функцию C(k), которая опреде*
ляется равенством
Это вещественная, сферически-симметричная функция, удовле-
удовлетворяющая условию С@)= 1 ив силу хорошо известного свой-
свойства преобразования Фурье сосредоточенная в окрестности
точки ^ = 0 размером порядка М (см. рис. 23,6). Подставляя
в правую часть формулы F5) разложение D6) для Ф(г), после
несложных вычислений получаем
F6)

460 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
Отличие от формулы F4') заключается только в присутствии
множителя C(k) в каждом слагаемом. Этот множитель обрезает
вклад во взаимодействие высокочастотных членов, для которых
Покажем, что пренебрежение вкладом высоких частот со-
согласуется с нерелятивистским приближением. Каждое слагае-
слагаемое в сумме F6) соответствует передаче определенного им-
импульса и энергии от частицы полю и обратно. Так, член akzlklt
соответствует поглощению кванта поля с импульсом k и энер-
энергией ю^ и передаче этого импульса и энергии частице, член
a+e-ift« соответствует рождению кванта поля с импульсом k и
энергией юй и уменьшению на эти величины импульса и энергии
частицы. Если k ^>, M, то изменение энергии достаточно велико,
так что может нарушиться закон сохранения частиц и поле мо-
может поглотить частицу или испустить вторую частицу массы М.
Таким образом, нерелятивистское приближение оправдано толь-
только, если вклад высокочастотных слагаемых пренебрежимо мал,
и результаты, которые дает это приближение, если они справед-
справедливы, не должны меняться при введении функции C(k). A for-
fortiori, они должны быть нечувствительны к форме этой функции.
В дальнейшем мы считаем, что
{1 для O^.k^.K,
л *,^ «г F7>
О для k > К,
а параметр К имеет значение порядка М.
Исследуем свойства инвариантности Н. Из уравнения F5)
видно, что Н' инвариантен относительно сдвигов и вращений
всей системы (поле + частица), поскольку легко показать, что-
Н' коммутирует с операторами полного импульса Р -\- W и пол-
полного момента импульса (/? X Р) + ' системы. Оператор Н' ин-
инвариантен также относительно пространственного отражения,
при котором Ф(г) переходит в Ф(—г) (скалярное поле). Этими
же свойствами инвариантности обладают гамильтонианы Нп и
(при условии, что V(/?)=0) Ячаст, а следовательно, и полный
гамильтониан системы Н. Если У(Я)фО, то #чаСт инвариантен
только по отношению к вращениям и отражению и, следова-
следовательно, Н инвариантен относительно вращений и отражений, на
не инвариантен относительно трансляций.
Рассматриваемая квантовая система интересна в силу того,
что она в простейшей форме демонстрирует основные свойства
атома, взаимодействующего с электромагнитным излучением.
Частица является аналогом атома, а скалярное поле — анало-
аналогом электромагнитного излучения. Основное отличие заклю-
заключается в том, что кванты электромагнитного поля — фотоны —>

§ 10. СЛАБАЯ СВЯЗЬ 461
имеют нулевую массу и спин 1, в то время как кванты исследуе-
исследуемого скалярного поля имеют нулевой спин и отличную от нуля
массу. В оставшейся части этого раздела мы воспользуемся
этой упрощенной моделью для изучения характерных свойств
атома, находящегося в электромагнитном поле.
§ 10. Слабая связь и рассмотрение по теории возмущений
При достаточно малых g оператор Н' можно считать ма-
малым возмущением и использовать методы, развитые в главах
XVI и XVII.
Невозмущенный гамильтониан имеет вид
Н0==Нп-\- Ячаст.
В теории возмущений используют представление, в котором диа-
диагоналей оператор Но. Мы будем пользоваться представлением,
базисные векторы которого получаются следующим образом.
Обозначим |а>, |р>, ..., |Я>, ... полный ортонормированный
набор собственных векторов Ячаст, рассматриваемого как опе-
оператор в пространстве ё?Част, и Еа, ?р, ..., Е%, ...— соответст-
соответствующие собственные значения (расположенные в порядке воз-
возрастания). Умножая данный вектор |Я> этого множества на ва-
вакуумный вектор |0> пространства &а, получаем вектор про-
пространства <1Г, который для упрощения записи будем также обо-
обозначать \К}. Ясно, что
НО\Х) = ЕК\К).
Полный ортонормированный набор собственных векторов опе-
оператора #п в пространстве &а можно получить, последовательно
действуя операторами рождения а\ на вакуумный вектор |0>
(см. ур. A6)). Точно так же полный ортонормированный набор
собственных векторов Но в пространстве & можно получить по-
последовательным применением операторов рождения а\ к каж-
каждому из определенных выше векторов |а>, |р>, ..., |Я>, ... .
Так будет получен требуемый базис. Пусть |л>— один из вех-
Торов этого базиса и Еп — соответствующая энергия
В динамическом состоянии |«> частица находится в определен-
определенном собственном состоянии оператора Ячаст, а поле содержит
определенное число квантов с заданными импульсами.
В дальнейшем мы будем пользоваться только векторами
с небольшим числом квантов и параметризовать эти век-
векторы будем греческой буквой, соответствующей динамическому
состоянию частицы, и волновыми векторами каждого из кван-
квантов поля. Так, |Яй> представляет состояние, которое получается

462
ГЛ. ХХГ. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
добавлением кванта с импульсом ft к частице в состоянии Л,
\Xkk'y — состояние, получающееся добавлением двух квантов
с импульсами ft и ft' к частице в состоянии Я и т. д. Отметим,
что
Но |
F8)
Имеем также |A,ft) —а+|Я) и, если ft ф ft', | Xftft') = а\а\, \ X).
Характерная спектроскопическая диаграмма нижних уров-
ней энергии гамильтониана Но изображена на рис. 24. В соот-
соответствии с обычными соглашениями о таких диаграммах (см.
о -
УроВни с
Z квантами
кСантов
Рис, 24. Типичная схема расположения первых энергетических уровней опе-
оператора Но.
том 1, рис. 36 и 37) высота уровней над основным состоянием
равна разности их энергий и энергии основного состояния; как
следствие, уровни с одинаковой энергией расположены на одной
высоте. Уровни на рисунке расположены в соответствии со
структурой собственных состояний. В левом столбце находятся
уровни состояний без квантов. Затем идут несколько столбцов,
отвечающих состояниям с одним квантом, каждый столбец со-
соответствует определенному квантовому состоянию частицы.
Первый отвечает уровням |aft>; когда частица находится в ос-
основном состоянии, уровни заполняют непрерывную зону (в пре-
пределе L->-oo), нижняя граница которой соответствует одному
кванту с нулевым импульсом и, следовательно, удалена от^
уровня основного состояния |а> на расстояние ц. Второй стол-
столбец отвечает состояниям |pft>, где частица находится в первом
возбужденном состоянии, и так далее. После уровней с одним
квантом следуют уровни с двумя квантами, расположенные
в виде столбцов, каждый из которых соответствует определен-
определенному квантовому состоянию частицы, и так далее.
Возмущение Н' связывает различные уровни. В определен-
определенном выше представлении Н' задается особенно простой матри-
матрицей. Из формулы F6) видно, что оператор Н' имеет отличные

§ 10. СЛАБАЯ СВЯЗЬ
463
от нуля матричные элементы только между базисными векто-
векторами, для которых число квантов отличается на единицу. Легко
вычислить эти матричные элементы, пользуясь свойствами one*
раторов рождения и уничтожения. Находим
Я' | v*> =
)* = Bn/LK'> g
(Я IU (k)
F9a)
= Bn/Lf g
(X IU+ (k') | v), (k Ф k'). F96)
(Если к = k', то в последнем выражении нужно добавить мно
житель л/2.) Мы использовали обозначение
= е'**/Bя)\
U
G0)
1
U>
Независимо от того, насколько слабой является связь уров-
уровней, она ведет к качественному изменению спектра, поскольку
большинство связанных состояний стано-
становятся неустойчивыми и частица может со-
совершить переходы в состояния с меньшей
энергией, излучая один или несколько
квантов поля. Рассмотрим, например, изо-
изображенное на рис. 24 состояние |Я>; оно
расположено на том же уровне, что и не-
некоторые состояния непрерывного спектра,
а именно: состояния с одним квантом |ft>
|>
или |pft> и состояния с двумя квантами рис. 25. Радиационные
\akk'}. Введение малого возмущения Н' переходы с уровня |%}.
связывает дискретные собственные состоя- Двойная стрелка спра-
ния и состояния с одним квантом, состоя- идуОиаВосноВвУнвТйПу?о-
НИЯ С ОДНИМ КВаНТОМ И СОСТОЯНИЯ С ДВуМЯ вень с испусканием
квантами и т. д. Следовательно, появляет- двух квантов. Это
ся возможность «радиационных» переходов переход более высо-
из состояния |Я> в состояния непрерывного кого п°РяДка-
спектра, расположенные на том же уров-
уровне. Возможные переходы из состояния |Я,> схематически изо-
изображены на рис. 25. Остаются устойчивыми только те свя-
связанные состояния, энергия которых в сравнении с энергией ос-
основного состояния достаточно мала и излучение кванта массы ц
энергетически запрещено, т. е. состояния, энергия которых
меньше Еа + ц. В примере на рис. 24 устойчивым является
только основное состояние.
Появление в гамильтониане члена Н' ведет также к сдвигу
уровней связанных состояний. Как мы увидим, это эффект вто-
второго порядка. Тем не менее, он может влиять на устойчивость

464 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
различных состояний частицы, и моды «радиационных» пере-
переходов, поскольку даже малый сдвиг уровня может оказаться
достаточным, чтобы сделать энергетически возможными неко-
некоторые «радиационные» переходы, которые были запрещены, или
привести к обратной ситуации.
§ 11. Сдвиги уровней
В качестве первого приложения вычислим упоминавшиеся
в конце предыдущего параграфа сдвиги уровней. Эти несложные
вычисления по теории возмущений познакомят нас с основными
трудностями теории поля, позволят понять физический смысл
и границы применимости теории.
Рассмотрим устойчивый уровень, например, основное состоя-
состояние, и вычислим порожденный членом Н' сдвиг, пользуясь ста-
ционарной теорией возмущений. Для простоты будем считать
уровень невырожденным. Поскольку свойства инвариантности
Н' и ЯЧаст совпадают, то рассмотрение вырожденного уровня не
имеет принципиальных различий. В первом порядке сдвиг оп-
определяется формулой (XVI. 12). Из свойств Н' следует, что
<<х|Я'|а> = 0,
и вычисления необходимо проводить во втором порядке. Пусть
ЬЕа— поправка к энергии второго порядка, тогда имеем (см.
§ XVI. 6)
6Еа = (а\Н'-Ё-^7ГоН'\а). G1)
Вычислим это выражение, используя определенное выше
представление. Из промежуточных состояний вклад будут да-
давать только состояния, содержащие один квант. Принимая во
внимание соотношения F8), F9а) и G0), последовательно по-
получаем
|<а | Н' | vft
V *
= g2 Bn/LK ? ? [(С2 (k)/2<ok)\ (a\Uk\ v> Р/(?а - ?v - «*)].
V ft
Заменяя суммирование по k интегрированием согласно прави-
правилам, описанным в § 6, и используя обрезающую функцию F7),
имеем
0ta— g

$ 11. СДВИГИ УРОВНЕЙ 465
Отметим, что
ЬЕа < 0.
Действительно, все слагаемые в правой части формулы G2) не-
неотрицательны, так как речь идет об основном состоянии и
(о -\- Ev — Еа) > 0 для любого v.
Чтобы получить оценку сверху для |6?а|, можно заменить
величину Еч — Еа в знаменателе ее минимальным значением,
т. е. нулем. Тогда суммирование по v легко выполнить, исполь-
используя соотношение полноты ]Cl\>)(v|=l. Поскольку (/(/+ =
V
= Bл), сумма равна Bя)-3/2еэ2 и после интегрирования по
углам имеем
к
G3)
Интеграл в неравенстве G3) можно легко вычислить, и так как
К ^> \х, он лишь незначительно меньше К- Следовательно,
\6Е*\< g2Wn\ G4)
Более точную оценку правой части формулы G2) можно получить сле-
следующим образом. Если воспользоваться соотношением полноты и заменить
U{k) согласно формуле G0), то получим
W \ (^^(ю + Я-ЯГ'е-^а)-^-. G5)
Унитарный оператор exp(ikR) коммутирует с R и преобразует оператор Р в
(Р — ^.Следовательно,
V(R) = Ячаст + ? -?
е<*« ((о + Ячаст - Еа)~х в""* - (а> + -^- + Ячаст - Еа -
Подставляя это выражение в правую часть формулы G5), находим
*Е — Ш
Членом Pk/M в правой части можно пренебречь, поскольку среднее значенне
скорости частицы Р/М в состоянии |<х) много меньше 1 (нерелятивистское
приближение). В этом приближении после иитегрирования по углам получаем
6Еа « - -ид- \ Л. A + (fc»/2AI«))~' dk G6)

466 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
выражение, которое отличается от правой части неравенства G3) только мно«5
жителем A + (^/2Ми))~' под знаком интеграла. Поскольку ц < К « М, зна»
чение этого множителя меняется от 1 до 2/3 на промежутке интегрирования,
и мы можем написать
1). Щ
Фигурирующая в этой формуле константа s имеет значение между 2/3 и 1<;
Для оценки этого эффекта вычислим порядок его величины
в случае, когда различные параметры модели имеют численные
значения того же порядка, что и встречающиеся в атомах').
Так, М равна массе электрона, g2 — постоянная тонкой струк»
туры
/«КГ1. G8)
Пусть D/M — расстояние от рассматриваемого уровня до бля*
жайшего соседнего уровня
G9)
С данными числами
| ЬЕа/D |« g2M/4n2D да 100.
Таким образом, это очень сильный эффект, значительно превос-
ходящий сдвиги, наблюдаемые экспериментально. Естественно,
возникает вопрос о справедливости рассмотрения по теории воз-
возмущений и физическом смысле результата.
Однако разумное сравнение теории и эксперимента должно
учитывать следующее. Масса М, которая фигурирует в вычис-
вычислениях невозмущенных уровней, не есть экспериментально на-
наблюдаемая масса. Последняя получается на основании измере-
ний энергии и импульса «свободной» частицы, т. е. частицы вне
потенциала V(R). Такая «свободная» частица, тем не менее»
взаимодействует с полем и, следовательно, измерение дает:
Мэкса = М + 6М, где 6М представляет собой вклад в энергию
покоя «свободной» частицы, порожденной наличием поля. В дан-
данном случае несложные вычисления дают 8М « — <д2/(/4я2. Точ-
Точнее, вычисление 8М во втором порядке по теории возмущений
приводит к правой части формулы G6) (задача 2). Следова-
') В силу того, что вид взаимодействия в данном случае отличается ог
случая атома и электромагнитного поля, численные результаты скалярной тео-
теории не могут точно согласовываться с результатами квантовой теории излу-
излучения. Для того чтобы сравнивать соответствующие величины, константу g*
фиксируют так, что значение вероятности дипольного перехода получается ве-
величиной того же порядка, что и вероятность дипольных переходов в атомах
(см. (81) и B45)), т. е. ?2/4я ta 1/137.

§ II. СДВИГИ УРОВНЕЙ 467
тельно, сдвиг 8Еа почти полностью вызван «перенормировкой»
массы ').
В вычислениях уровней атома водорода в теории Шредин-
гера или Дирака фигурирует экспериментальная масса элек-
электрона. Таким образом, учитывается основная часть взаимодей-
взаимодействия электрона с полем излучения, что объясняет замечатель-
замечательное согласие вычисленного спектра с наблюдаемым.
«Экспериментально наблюдаемый сдвиг» ЬЕ'а равен разно-
разности между вычисленным сдвигом &Еа и сдвигом, порожденным
заменой теоретического значения массы на экспериментальное
(«перенормированная» масса) в гамильтониане частицы. Для
нашей модели подстановка «перенормированной» массы ведет
к замене #Част на
и к сдвигу всех уровней на величину 6М. Тем самым, имеем
Если ограничиться вторым порядком теории возмущений, то
вычисление 6Е'а = ЬЕа — 6В® не представляет серьезных затруд-
затруднений, и для \&E'JD\ получается значение порядка 10~3, что яв-
является разумным по порядку величины.
Тем не менее, к полученному значению ЬЕ'а следует отно-
относиться с осторожностью, поскольку оно очень чувствительно
к выбору обрезающей функции. Реалистические вычисления
должны основываться на полностью релятивистской теории.
В действительности мы встречаемся здесь с трудной проблемой
квантовой теории поля, которая в настоящее время не имеет
удовлетворительного решения. Взаимодействие в релятивист-
релятивистской теории является локальным, и для ЬМ получается выра-
выражение вида: 6М = ZM, где Z представляется расходящимся ин-
интегралом (см. предыдущую сноску). Точно так же 6Еа и ЬЕ(®>
представляются расходящимися интегралами, так что выраже-
выражение для ЬЕ'а является неопределенностью типа оо — <х>.
Несмотря на упомянутые ограничения, мы продолжим ис-
исследование нашей упрощенной модели, которая корректно опи-
описывает большое количество экспериментальных фактов. Такие
эффекты как «перенормировка» массы, удовлетворительное рас-
рассмотрение которых возможно только в рамках ковариантного
формализма, мы оставляем в стороне.
') Считая К « М, получаем 8М/М « 10~3. Следовательно, относительное
изменение массы мало, что оправдывает a posteriori использование теории воз-
возмущений. Однако если не вводить обрезающей функции, то 8М выражается
расходящимся интегралом. К этому вопросу мы еще вернемся.

468 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
§ 12. Излучение квантов
Вернемся к рассмотрению состояний частицы, которые яв-
являются нестабильными в силу взаимодействия Н'.
В этом параграфе мы вычислим вероятности перехода в едц'-
ницу времени для различных «радиационных переходов», поль-
пользуясь нестационарной теорией возмущений (§ XVII. 4).
Предположим для определенности, что спектр оператора Ht$
совпадает со спектром, изображенным на рис. 24, и рассмеь
трим состояние |Я>. Из этого состояния энергетически возможна
только переходы в основное состояние с излучением одного
или двух квантов C(х > Е^ — Еа > 2ц) и переходы в пер-
первое возбужденное состояние с излучением одного кванта
Bц > Ех — ?р > ц). Ниже мы будем рассматривать только
переходы с излучением одного кванта. Испускание двух кван-
квантов представляет собой процесс высшего порядка и при прочих
равных условиях происходит в g2 раз реже, чем испускание-
одного кванта. Поэтому, интересуясь только первым порядком
теории возмущений, мы такие процессы рассматривать не бу-
дем.
Пусть частица первоначально находится в состоянии |Я>^
Тогда вероятность в единицу времени перехода частицы в со*
стояние | а> с излучением кванта в телесный угол (Q, Q + rffi)^
т. е. вероятность в единицу времени перехода X->-ak, где ft—f
вектор в данном телесном угле, в первом порядке дается выра-
жением (см. ур. (XVII. 50))
'\ ak) p pL (а>) dQ, (80>
в котором энергия кванта со вычисляется из закона сохранения
Принимая во внимание соотношения D9), F9а) и G0), из фор-
формулы (80) получаем
Интегрируя по углам, получаем вероятность перехода в еди-
единицу времени из состояния Ява, которую мы обозначим Г
Аналогичные выражения можно получить для переходов в со-
состояние р. Полная вероятность перехода в единицу времени Г* :
равна
(83)

§ 12. ИЗЛУЧЕНИЕ КВАНТОВ 469"
Величина Гя, обратна времени жизни состояния (Я>, что
можно увидеть из следующих полуклассических рассуждений.
Рассмотрим статистический ансамбль частиц и обозначим Nx(t)
число частиц в состоянии |Я> в момент времени t. Число ча«
стиц, участвующих в радиационном переходе в интервале вре-
времени (t, t + dt), равно Y%N%{t)dt. Следовательно,
или
4^
dt
Это хорошо известный экспоненциальный закон распада, и
Бремя жизни равно 1/Гл,. В рассмотренном нами случае имеется
две моды распада, Я->-аиЯ->-р, и отношение первой ко второй
равно IV»o/I\-p.
Ясно, что приведенные полуклассические рассуждения
не могут считаться доказательством экспоненциального закона,
поскольку вычисление вероятностей перехода по теории возму-
возмущений оправдано только для IV <С 1 (см. обсуждение в конце
§ XVII. 4), т. е. для достаточно малых t, пока вектор состояния
мало отличается от начального. Для больших времен требуется
более глубокий анализ, который будет проделан в § 13.
Чтобы определить Г по порядку величины, вернемся к обозначениям и
численным данным § 11. Для не слишком больших энергий возбуждения
имеем k та D. и, поскольку размеры (R) области, где сосредоточена волновая
функция, порядка BMD) ''8, получаем
k (R) да (D/2M)'1' да 5 • 10~3 < 1.
Величину (А. | е'** | а) можно оценить, заменив экспоненту первым членом
ряда Тейлора, который дает отличный от нуля вклад (длинноволновое при-
приближение); порядок этого члена определяется в основном правилами отбора
по моменту импульса. В наиболее благоприятной ситуации (дипольные пере-
переходы) имеем
откуда
Если взять это же значение для величины Г^ то получим время жизин 1/Г^.
значительно превосходящее (в 106 раз) характерный период \jD движения ча-
частицы во внешнем потенциале. Следовательно, разумно рассматривать, что и
было сделано выше, взаимодействие Н', которое ответственно за излучение
кванта, как малое возмущение.
Можно получить формально очень простое и общее выра-
выражение для Гя,, исходя непосредственно из формулы (80) и ио

470 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
пользуя определение плотности уровней, закон сохранения энер.
гии и соотношение полноты. Последовательно имеем ')
k {% | Н'Ь {Ех - Нч) | v*> (vft | Я' | Я) =
= 2л (Я | Я'6 {ЕК - Яо) Я' | X). $
Полученное выражение будет использоваться в дальнейшем.
§ 13. Квантовая теория распадающихся состояний.
Ширина линии
В этом параграфе мы используем квантовую теорию для
анализа точной зависимости от времени распадающихся квази-
квазистационарных состояний. Мы покажем, что результаты, кото-
рые были получены в § 12 с помощью упрощенных рассужде*
ний, в существенном не меняются, и, в частности, распаД
с очень хорошим приближением имеет экспоненциальный xa*i
рактер. Будут введены также такие важные понятия, как сдвиР
уровня и ширина линии.
Предположим, что в начальный момент времени / = 0 си*
стема находилась в связанном состоянии, отвечающем собствен-
собственному значению Е\ гамильтониана Яо, и рассмотрим изменение?
этого состояния с течением времени. •
Др сих пор мы считали собственное значение Е>, невырож-
невырожденным. Это упрощение потребуется нам при обсуждении ре-
результатов, однако приводимые ниже рассуждения применимы
также и к случаю вырожденного собственного значения. Обо-
Обозначим S\ подпространство, натянутое на векторы, которые опи-
описывают связанные состояния, отвечающие собственному зна-
значению Ex. Пусть Р\ и Q% — проекторы на <8\ и его ортогональ-
ортогональное дополнение соответственно
Оператор эволюции, как обычно, имеет вид
=Q-im) (86)
') Выражение (85) возникает во многих задачах. Оно представляет собой
общее выражение для вероятности перехода в единицу времени в первом по-
порядке теории возмущений и его можно вывести сбгласно общей теореме
§ XVII. 4 из формулы (XVII. 40), используя для фигурирующей в этой фор-
формуле функции / асимптотический вид (XVII. 43).

§ ТЗ. КВАНТОВАЯ ТЕОРИЯ РАСПАДАЮЩИХСЯ СОСТОЯНИЙ 471
и наша задача состоит в вычислении для t >¦ О величины
UV)P*
Введем резольвенту оператора Я
(87)
сингулярности которой как функции комплексной переменной г
совпадают со спектром Я (дискретному спектру соответствуют
полюса, а непрерывному спектру — разрез). Справедливо ра-
равенство ')
Uif) = --~ \ e-ixi[G(x+)-G(x-)]dx, (x±=x±iz). (88)
—оо
Операторы Щ и Э, определенные в пространстве <&%, соотноше-
соотношениями
<U(t) = PKU(t)Pb, 3{г) = Р?(г)Р%, (90>
связаны по формуле
). (91)
Чтобы получить удобное для работы выражение для
воспользуемся соотношениями:
Я, es PKHPK + QKHQK = H
!) Соотношение (88) непосредственно следует из формулы *)
которая справедлива для бесконечно малого положительного е (см. ур.
(А.15д)). Отметим, что при t > 0 вклад G(x~) в интеграл в правой части со-
соотношения (88) равен нулю. Более общие формулы, связывающие U{t) и
G(z), имеют вид
Т)оо
G(z) = -i^ eiztU (/) Л, У @ = -L J е-'г'0 (г) dz,
о с
где т] — знак Imz, С — контур в комплексной плоскости г, идущей из оо -f- is
в оо — ('е, по отношению к которому спектр Н лежит слева. Этн формулы лег-
легко вывести в представлении, где оператор Н диагоналей.
*) Символ v. Р. означает, что интеграл с этим ядром понимается в смысле
главного значения. (Прим. перев.)

472 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
Заметим, что
НХРХ = Р%Н, = ад, [Qk, #1] = О,
РХН" = H"Qh Q^tf " = Н"РХ.
Из этих соотношений и операторного тождества
(Л -
следуют равенства
(Л - В) в Л + А~ХВ (А - В)'1
„
__ , „
z-H ~ z-Я, "*" г-Н, z-H
г-Я,Т2-Я, z-Н, г -
*¦ г — Н А 2 — Ех г — Ех \ *¦ г — Н, *•) *• г — Н
Формула (94) представляет собой соотношение между опер'«|
торами, действующими в пространстве 8\, а именно
я"р* - ^'^ тз^яог о^'Рх. Щ
Из уравнения (95) получаем ¦;
= , _ р. _ w i,\ • $ч
Выражения (96), (97) и (91) представляют собой точны!
соотношения, которые могут служить основой для вычисления
{) \
Формулы (96) и (97) определяют Ж (г) и 9-(г) как функци«|
комплексной переменной г в плоскости с разрезом вдоль Henpte
рывного спектра Н. Нас будет интересовать поведение эти|
-функций в окрестности разреза. Используя соотношение (89Д
выпишем отдельно эрмитову и антиэрмитову части Ж (я*), т. ей
д(х)ч=/г(х),
Д (х) - P,H'v. P. тгг^яоГ Н'Р»
r(x) = 2nPbH'b(x-QbHQJH'Px. A00
Отметим, что Г(д:) —положительно определенный эрмитов one
ратор.

§ 13. КВАНТОВАЯ ТЕОРИЯ РАСПАДАЮЩИХСЯ СОСТОЯНИЙ 47S
В дальнейшем будем предполагать, что собственное значе-
значение Е\ оператора Но невырождено ')•
По предположению система в начальный момент времени
/ = 0 находилась в состоянии |Я>. Требуется определить состоя-
состояние системы в момент времени t
\W(i)) = U(t)\X) A01)
и, в частности, проекцию этого состояния на вектор |Я>.
Всюду ниже операторы iKt"), &(z), W(z), А(х) и Т(х) можно
заменить их средними значениями по состоянию |Я> и рассма-
рассматривать как числовые функции своих аргументов. Определения
(90), (99) и A00) перейдут в
4l{t)^{%\U{f)\X), $(z)^(l\G(z)\X), A02)
А (х)«<Я 1 H'v. P.(x_ Q^ ) И' | Я), A03)
Г (х) ^ 2я {% | Н'Ь {х - QKHQK) W | Я), A04)
а из уравнений (97) и (91) получаем
9(х±)*=[х-Ек-Ь(х)±±1Г(х)\ , A05)
(U(t)==— \ e-ixtF(x)dx, A06)
где
P (*) = I (9 (x+) - $ (лГ)) = ^^ i . A07)
') В большинстве случаев вырождение Е\ связано с симметрией Но, кото-
которая не нарушается при добавлении взаимодействия #'. Например, при радио-
радиоактивном распаде ядра со спином / вырождение кратности 2/+ 1 связано с
инвариантностью относительно вращений, которая сохраняется при включении
взаимодействия, ответственного за распад. Поскольку в этом случаев, — не-
неприводимое подпространство, а операторы Ж (г), $ (г) и 1t(t) инвариантны,
то эти операторы в пространстве <В^ пропорциональны единичному оператору
и их вычисление проводится точно так же, как и в невырожденном случае.
Все состояния из $^ описывают один и тот же закон радиоактивного распада
с определенным временем жизни и сдвигом уровня.
С другой стороны, если эти условия симметрии не выполняются, то могут
возникнуть несколько времен жизни и несколько сдвигов. Эта ситуация имеет
место для первого возбужденного уровня атома водорода (см. обсуждение
лэмбовского сдвига в конце § XX. 27). В качестве другого примера укажем
Я°-мезои. Рассмотреиие общего случая по существу можно провести аналогич-
аналогично. Воспользовавшись тем же приближением для *?/(/), получаем
что является обобщением выражения A09). Вещественная и мнимая части
собственных значений иеэрмитова оператора Ж (¦?>!") определяют сдвиги и со-
соответствующие времена жизни.

474
ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
im
До сих пор мы не пользовались какими-либо приближениями.
Для вычисления F(x) и Щ{г) будем предполагать взаимодей-
взаимодействие слабым и в выражениях A03) и A04) оставим только
члены младшего порядка по Н'. Это сводится к замене Q%,HQ^
на Но, после чего величины Л (я) tfv
Г (я) легко вычисляются. Форма,
Г (л:) приведена на рис. 26. При до*
статочно малых Д(л:) и Г (л:) функр
ция F(x) имеет четко выраженный
максимум около точки х = Е^, Ъ
наибольший вклад в интеграл (lOijfl
дает окрестность этой точки. Сле«
довательно, можно оценить этот ин|
теграл, подставляя вместо медленна!)
меняющихся функций А(х) и Т(х) их значения в точке х = Е\
А(?,)^б?„ Г^аГ,, A08)
что сводится к замене функции F{x) (см. рис. 27) на функцию
Л (х) = ^ г— . v.
f lt
Рис. 26. Общий вид функции
Г (х). Заметим, что Г (х) = О
при х < Еа + ц.
На рис. 27 для функций А и Г использовалась зависимость
от х, типичная для дипольных переходов
и следующие значения 8Е\/% = 0,2, Г>,Д := 0,1.
Ошибка при вычислении °U(t) не превосходит величины
2я
\[F{x)-Fx{x)\dx.
При 1\ и б?я достаточно малых по сравнению с Е\ — Еа — ц и
Еь — ?|j — \i вне области больших времен (t ^> 1/Гя) эта вели-
величина пренебрежимо мала относительно °U{t).
После упомянутой выше замены интегрирование проводится
несложно и дает в результате
41 @ » ехр [
Следовательно,
+
- ^ IV].
A09)
(ПО)
и мы получили экспоненциальный закон распада ').
') Более строгое рассмотрение приводит к наличию дополнительных не-
экспоненциальных членов в законе распада. Из работы: Н, С. Крылов,
В. А. Фок. ЖЭТФ 17, 93 A947) — следует, что амплитуда распада полиостью
определяется энергетическим спектром начального состояния. (Прим. перев.)

§ ТЗ. КВАНТОВАЯ ТЕОРИЯ РАСПАДАЮЩИХСЯ СОСТОЯНИЙ
475
Величина 1/1\ — время жизни — была сосчитана нами в § 12
(см. ур. (84), (85), A04) и A08)).
Как видно из формулы A09), взаимодействие Н' привело
к изменению временной зависимости для уровня К, а именно,
1,00.
0,75
0,50
0,25
-
-
F(xl
Ш N
-У
1
\
Рис. 27. Характерный вид функций F (х) и f i (х). Функции Д и Г имеют
энергетическую зависимость, типичную для диполышх переходов:
На рисунке
в показателе экспоненты к ?\ добавилась комплексная энергия
Вещественная часть 8Е\ представляет собственно сдвиг уровня,
и формула для нее аналогична формуле для сдвига уровня
стационарного состояния (см. ур. G1), A03) и A08)). Харак-
Характеризующая квазистационарное состояние мнимая часть равна,
с точностью до знака, полуширине уровня и отвечает за экспо-
экспоненциальный характер закона распада.
Вычислим другие компоненты состояния I^F^)) в прибли-
приближении слабой связи, когда отличны от нуля только проекции на
состояния, содержащие один и только один квант
E*v*(')|v*>, (HI)
A12)
Учитывая уравнения (92), имеем
— Hi)~{ H"| Я)9 (г).

476 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
Это точное уравнение. Приближение слабой связи состоит в за-
замене Н\ на Но в знаменателе, что дает
<vft \Q B)| %) = <vft \H'\ %) (z - (о - Ey)~l9(z).
Зная приближенное значение матричного элемента G(z), полу*
чаем приближенное значение соответствующего матричного элф
мента U(t). Для этого используется формула (88), интеграш
в которой можно взять по вычетам. Для достаточно больших j
главный вклад дает полюс на вещественной оси, и мы имеем
@ «<vft|#'!
1)
х-а+В„
Квадрат модуля этого выражения равен вероятности обнаруй
жить систему в состоянии (vk) при больших по сравнении!
с временем жизни значениях времен /.Квадрат модуля можащ
записать в виде
'| Я) ?ЩтШ'
где функция F(x) определена формулой A07). Квадрат модул|
|ftvA(oo)|2, в силу указанных выше свойств функции F(x) (ся|
рис. 27), близок к нулю вне окрестности точки ш + Еч » ?»|
т. е. наблюдаемые переходы в основном сохраняют невозмущен*!
ную энергию. Для таких переходов — в рассматриваемом здес§
примере это переходы с v = а и v = $ — мы можем заменит*!
F(x) на F\{x). Таким образом, для переходов X-+ak мы полу!
чаем формулу .¦
\h (nn\P- \(ak\H'\X)\* I
I Пац @0) р = . ...А
Следовательно, распределение энергии квантов, испущенныж
в этом переходе, подчиняется закону Лоренца с шириной 1\ Щ
центром в точке Е%, -\- б?л — Еа, т. е. положение максимума рас-,
пределения совпадает с боровской частотой перехода при учете
сдвига 8Ек-
Таким образом, ширина линии испущенных в радиационном
переходе квантов равна величине, обратной к времени
жизни (в системе единиц, где Й = 1), в соответствии с соотно*
шением неопределенности энергия — время.
Необходимо сделать несколько замечаний о применимости
полученных результатов.
Прежде всего при сравнении закона распределения A14)
с данными опыта необходимо указать, как можно эксперимен-

§ 14. УПРУГОЕ РАССЕЯНИЕ 477
тально приготовить состояние \Х}. Мы вернемся к этому во-
вопросу в § 15.
Кроме этого, приведенное рассмотрение имеет довольно су-
существенные ограничения. Если воспользоваться численными ре-
результатами § 11, то мы увидим, что 6?\ является величиной
того же порядка, что и 8Еа, и, следовательно, значительно пре-
превосходит расстояние между уровнями. Однако если обозначить
dEf] вклад, связанный с перенормировкой массы, то можно по-
показать, что разность
является малой поправкой по сравнению с расстоянием между
уровнями. Это затруднение в точности совпадает с тем, которое
обсуждалось в § 11, и приведенные там рассуждения можно
дословно повторить здесь.
Наконец, и это, очевидно, связано с приближением слабого
взаимодействия при вычислении амплитуд hvk, мы не учитывали
сдвиги уровней, на которые происходит переход, и a fortiori тот
факт, что некоторые из этих уровней из-за взаимодействия Н'
сами могут стать квазистационарными.
Для переходов на стационарные уровни или на уровни,
время жизни которых больше времени жизни начального со-
состояния, формула |П4) корректна при учете упомянутых выше
эффектов. Если обозначить В®, ..., ?|0), ... уровни, которые
получаются при замене в гамильтониане НЧЛСт параметра М на
экспериментально наблюдаемое значение массы, то корректная
формула запишется в виде
Результаты, вычисленные по этой формуле, находятся в отлич-
отличном согласии с экспериментальными данными.
§ 14. Упругое рассеяние. Дисперсионная формула
В заключение этого раздела рассмотрим несколько простых
задач о столкновении.
Первой задачей будет вычисление сечения упругого рассея-
рассеяния кванта поля на частице, находящейся в основном состоя-
состоянии. Пусть ki — волновой вектор налетающего кванта, a kf —¦
вектор той же длины, указывающий направление, в котором
квант наблюдается после столкновения. Таким образом, нас ин-
интересует процесс
/->/-(а*,)->(€*,).

478 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
Положим
и обозначим Е начальную энергию системы
Е = а + Еа. A15)
Общая формула для сечения имеет вид
dQ = падающий поток \Ti->f\ Pf^1 A16)
где 11+} — амплитуда перехода
Tt-*f = (f\T\i) = (a,kf\T\a,kt), A17)
Т = Н' + Н'Т—±-—Н'. A18)
Падающий поток равен произведению начальной скорости k/<a
на плотность квантов в состоянии |afe/>, что с учетом принятой?
нормировки дает L~3k/<u. Величина р/(?) есть плотность конеч»;
ных состояний с энергией Е (см. ур. D9)). Таким образом, по»
лучаем
2npf (Е) _ L6©2
падающий поток 4я2 '
dQ 4я* 1"-»П«
При этом мы неявно предполагали, что в рассматриваемом
случае применимы все основные формулы теории рассеяния.
Так, уравнения A16) и A18) совпадают с уравнениями
(XIX. 115) и (XIX. 144) соответственно. Незначительные отли*
чия связаны с выбором обозначений, системы единиц и условий
нормировки волновых функций, участвующих в определения
амплитуды перехода.
Однако использование этих формул в интересующем нас случае не сов-
совсем корректно. При выводе формул предполагалось, что эволюция системы до
и после столкновения почти точно описывается гамильтонианом Но, а операто-
оператором взаимодействия можно преиебречь. Такое предположеиие было оправдан-
оправданным в главах X и XIX, ио оно не выполняется здесь.
Рассмотрим, например, состояние системы до столкновения. Частица на-
находится в основном состоянии, а кваит описывается волновым пакетом, кото-
который движется по направлению к частице. Волновой пакет еще не достиг об-
области в окрестности начала координат, где находится частица. Следовательно,
на первый взгляд представляется, что ситуация не отличается от имеющейся
в обычной теории рассеяния: взаимодействие кваита с частицей пренебрежимо
мало, и движение кваита свободно. Однако оператором Н' пренебречь нельзя,
поскольку частица, даже находясь достаточно далеко от налетающего кванта,
взаимодействует с полем. Поэтому ее начальное состояние не совпадает с соб-
собственным состоянием |<х) гамильтониана Нй, отвечающим энергии Еа, а яв-
является собственным состоянием | а) гамильтониана Н, Соответствующая со-

§ 14. УПРУГОЕ РАССЕЯНИЕ 479
стоянию la) энергия Еа + 6Еа была вычислена в § 11, и состояние |<х) сов-
совпадает с |<х) только в пределе g ->0.
Точная теория должна учитывать отличие «физического состояния» |й),
от невозмущенного состояния |<х). Если взаимодействие достаточно мало, то
это отличие в основном сводится к эффекту перенормировки массы, не влияя
на процесс рассеяния ').
В этом случае применимы обычные формулы теории рассеяния, но с заме-
заменой массы М в определении невозмущенного гамильтониана на эксперимен-
экспериментально измеряемую массу М + ЬМ.
Для вычисления сечения рассеяния будем рассматривать Н'
как возмущение, и заменим оператор Т борновским разложе-
разложением (см. ур. (XIX. 143)). Так как амплитуда в первом по-
порядке равна нулю, то имеем
и необходимо учитывать второй порядок по Н'. Амплитуду во
втором порядке обозначим
A20')
Суммирование во второй строке происходит по всем базис-
базисным векторам гамильтониана Но- Благодаря специфике опера-
оператора Н' большинство слагаемых в сумме исчезает. Виртуальные
состояния, вклад которых отличен от нуля, можно разделить на
две категории:
(i) состояния без квантов |v>;
(ii) состояния \vktkf}, содержащие два кванта с импуль-
импульсами ki и kf соответственно.
Первые состояния отвечают переходам
(akt)-+(v)-+(akf),
в которых частица поглощает налетающий квант прежде, чем
испустит квант конечного состояния; вторые отвечают перехо-
переходам
(aki)->(vklkf)-+(akf),
в которых квант конечного состояния излучается прежде, чем
произойдет поглощение налетающего кванта.
Введя частоты Бора
A21)
') В высших порядках необходимо учитывать модификацию взаимодей-
взаимодействия между налетающим квантом н частицей, что связано с наличием окру-
окружающих частицу виртуальных квантов. Эта модификация в существенном сво-t
дится к изменению константы взаимодействия («перенормировка заряда»).

480 рЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
получаем
<> =У Г-
'¦*f l—i L © — fi>va
v
Воспользовавшись равенствами F9) и G0), в которых мы счи-
считаем C(k) = 1 (что является обоснованным, если ft<M), на-
находим
' 2ю
где
ZjLfi>-
П23>
Х'ч = <а |е'*'*| v) <v |e~"f*| а). A24')
Подстановка полученного выражения в правую часть формулы
A19) дает сечение рассеяния во втором порядке борновского
приближения
do?L ,
dQ ~ 16я2
L-I \ Ю — @
@va СО + @V
A25)
Каждое слагаемое в этой сумме отвечает вкладу одного нз
упомянутых выше переходов. Этот вклад возрастает с умень-
уменьшением разности энергии системы и энергии виртуального со-
состояния, которое соответствует этому переходу. При совпадении
этих энергий вклад становится бесконечно большим. Для каж-
каждого перехода первой категории существует одно значение ш,
когда промежуточное состояние может распасться на частицу
в основном состоянии и излученный квант.
При переходе энергии ю через одно из таких критических
значений, например, -ЕйДюяа > ц), знаменатель ю — o)ta обра-
обращается в нуль и меняет знак, слагаемое Хх/(в> — о)д,а) неогра-
неограниченно растет и выражение для сечения расходится. Борнов-
ское приближение в этой области становится неприменимым ')
') В длинноволновом пределе (k{R)<L\) имеем | Х\ i « (k (R)J. Обозна-
Обозначив Дю = | Е — Е\ | и сохранив только вклад главного члена, из выражения
A25) получаем
do .. g4 f feW У
dQ, ~ 16л2 V Дю
Согласно известному критерию (§ XIX. 7) борновское приближение не приме-
применимо, когда полное сечение является величиной одного порядка с геометриче-

§ 15. РЕЗОНАНСНОЕ РАССЕЯНИЕ 481
независимо от малости значения константы связи. В действи-
действительности, сечение остается конечным, но имеет в этой точке
четкий максимум. Как мы увидим ниже, здесь имеет место ре-
резонансное явление, аналогичное тому, которое исследовалось
нами в главе X (§ 14—16).
§ 15. Резонансное рассеяние.
Образование метастабильного состояния
Для вычисления сечения упругого рассеяния в окрестности
одной из критических энергий, например Е\, вернемся к точ*
ному выражению для амплитуды перехода. Согласно определен
ниям (П7) и A18)
<Л Л0 = ? {t\H'\n){n\E_lH+.6\n'){n'\H'\i). A26)
п, п'
Борновское приближение состоит в замене в каждом члене
этого разложения точной функции Грина (Е— Я-j-ie) на
функцию Грина (Е — #o + ie)-' невозмущенного оператора
(см. ур. A20) и A20')). Если константа связи достаточно мала,
то такое приближение оправдано для всех слагаемых, за исклю-
исключением члена с п = к и п' — X, для которого множитель
<А,| (Е — Яо + ге)-1!^) неограниченно возрастает при стремле-
стремлении энергии к Ex. Обозначим слагаемое, характеризующее ре-
резонанс
Л<рез> ^(f\H'\l) <Я 1?_^+.е|А) (к \H'\i), A27)
а остаток, связанный с потенциалом рассеяния, Л(пот), т. е.
(/|Г|/> = Л(рез) + Л(П0Т). A28)
Для вычисления Л<пот> будем использовать борновское прибли-
приближение. Полученное в результате выражение отличается от фор-
формулы A23) только отсутствием в сумме по состояниям v сла-
слагаемого Х\/(& — (Оя,а). Остается вычислить величину Л<рез>.
ским сечением 4я (RJ. Именно это имеет место в рассматриваемом случае,
поскольку
Используя численные значения, приведенные в § 11, мы видим, что это про-
происходит в очень узкой области порядка 10—* D, которая, тем не менее, много
больше ширины Гд,.

482 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
Заменяя в выражении A27) матричные элементы опера»
тора Н' их точными значениями (см. ур. F9) и A24)), полуй
чаем ;i
где &(Е+) — введенное в § 13 среднее значение функции Грина
?(Е+)^(Я|?_/;+.е|Я). A30)
Подставляя выражение для этой функции, вычисленное в § 13
(см. ур. A05)), в уравнение A29), находим
E-Ek-b(E) + jiT (E)
Это точный ответ для Л(рез). Он отличается от борновского при-
приближения только наличием в знаменателе устраняющей сингу-
сингулярность комплексной добавки Д(?)— -^1Г(Е), свойства кото-
которой обсуждались в § 13. Заменяя Е на Е^. (см. ур. A03), A04)'
и A08)), что, конечно, оправдано в приближении слабой связи,
поскольку зависимость этой добавки от энергии в интересую-
интересующем нас интервале несущественна, имеем
Л(ре3) = _^ ХХ
Полученное выражение характеризует амплитуду рассеяния
ширины Гя,, сосредоточенную в окрестности точки ?*, -f- 6Ex-
Здесь можно повторить рассуждения главы X о рассеянии
резонансов и их связи с распадающимися состояниями. Кон-
Конкретизируя модель, легко получить выражения для амплитуды
рассеяния, дифференциального и полного сечений и времени
задержки прохождения рассеянной волны, которые практически
совпадают с приведенными в § X. 15 (при условии, что Л(пог>
можно опустить {см. задачу 4)). Упомянутый резонанс связан
с распадающимся состоянием |Х>, свойства которого мы уже
обсуждали в §§ 12 и 13.
Для достаточно точного измерения сечения и, в частности,
для определения его характеристической зависимости от энер-
энергии необходимо, чтобы неопределенность в энергии падающего
волнового пакета Дю была достаточно мала, а амплитуда рас-
рассеяния оставалась практически постоянной в интервале энер-
энергий Дш. В области резонанса это требование можно записать
так:
. Дсо < Гя. A33)

§ 16. РАДИАЦИОННЫЙ ЗАХВАТ 483
Тем самым, время столкновения 1/Аш должно быть значительно
больше времени жизни 1/Г*,, а последнее и не наблюдается
в данном процессе.
Если же выполняется условие дополнительное к предыду-
предыдущему
Лю » 1\, A34)
то можно изучить временную зависимость явления и обнару-
обнаружить экспоненциальный закон распада, характерный для не-
нестабильного состояния \ку. Все это возможно в силу специаль-
специальной формы амплитуды рассеяния в резонансной области (ур.
A32)) и может быть легко обосновано, если повторить вычис-
вычисления § X. 16.
Полученный результат является общим, он справедлив не
только для процесса рассеяния, но и для всех остальных столк-
столкновений. Любой резонанс, возникающий при столкновении и
характеризуемый энергией Е и шириной Г, соответствует ме-
тастабильному состоянию с той же энергией и с временем
жизни Й/Г, которое можно наблюдать при условиях экспери-
эксперимента дополнительных к тем, при которых обычно наблюдают
резонанс').
§ 16. Поглощение кванта (фотоэлектрический эффект).
Радиационный захват
До сих пор мы рассматривали задачи, в которых речь шла
о частице, находящейся только в связанных состояниях. В этом
параграфе мы исследуем процессы поглощения кванта и ра-
радиационного захвата, в которых появляются состояния непре-
непрерывного спектра.
Будем предполагать, что HmF(/?)=0 при /?->оо и, сле-
следовательно, спектр подсистемы, содержащей частицу, состоит
из дискретного множества отрицательных энергий Еа, Е§, ...
..., ?*, ..., которым отвечают связанные состояния, и располо-
расположенного от 0 до оо непрерывного спектра, которому отвечает
') Здесь мы встречаемся с дополнительными проявлениями одного и тога
же свойства системы, поскольку они связаны с одной и той же характеристи-
характеристикой резольвенты G(z). Последняя определяется равенством G(z) = (z—H)~l
иа комплексной плоскости г с разрезом вдоль непрерывного спектра опера-
оператора Н. Единственно допустимые сингулярности резольвенты на этой пло-
плоскости могут лежать на вещественной оси, они отвечают собственным значе-
значениям дискретного спектра оператора Я. Однако аналитическое продолжение
резольвенты на другой лист римановой поверхности может иметь дополии-
нительиые сингулярности. Резонанс и квазистациоиарное состояние связаны
с такой характеристикой G(z), как полюс в точке z = E — -^-'Т вблизи веще-
вещественной оси на втором листе римановой поверхности в нижней полуплоско-
полуплоскости.
16*

484 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
континуум несвязанных ненормируемых состояний. Пусть ф
и ф^-) — стационарные волны, соответствующие согласно опре
делению § XIX. 2 волновому вектору q. Это собственные состоя
ния оператора Нчаст, отвечающие собственному значению
—Ш-
038)
Их можно рассматривать и как собственные состояния гамиль-
гамильтониана Но, задающие стационарные состояния рассеяния всей
системы в случае, когда не учитывается оператор взаимодей-
взаимодействия. Мы будем обозначать соответствующие стационарные
состояния рассеяния при учете взаимодействия символами ?|+1
и WI-)
ч '
Предположим теперь, что частица, находясь в основном со-
состоянии, облучается потоком моноэнергетических квантов, дви-
двигающихся со скоростью fe/co. Если энергия падающих квантов
достаточно велика для того, чтобы «ионизировать атом», т. е.
если ш > (—Еа), то может произойти поглощение кванта ча-
частицей и она приобретет кинетическую энергию Е, равную раз-
разности полученной энергии <в и энергии связи (—Еа)
Е = ш + Еа.
В этом процессе мы узнаем фотоэлектрический эффект (§ 1.4).
Вычислим сечение поглощения кванта с импульсом k и ис-
испускания частицы в заданном направлении. Пусть вектор q за-
задает направление, а его длина связана с энергией Е соотноше-
соотношением A35). Таким образом, нас интересует процесс
'•-/^ (aft)->(?)•
Так же, как и в случае упругого рассеяния, будем пользоваться
формулами теории столкновений (здесь справедливы те же за-
замечания, что и в § 14). Следовательно, сечение рассеяния оп-
определяется формулой A16) с тем же выражением для падаю-
падающего потока, но р;(Е) = Mq/BлK, а амплитуда перехода равна
(см. ур. (XIX. 122))
Если ограничиться низшим порядком по Н', то в этом мат»
ричном элементе состояние Ч*^-' можно заменить на ф?-> (см.
ур. (XIX. 129, 130)). В результате получим
Ti+f» Wf* | Я' 1 ok) = (L~V/2co)l/2 (ф?-* I e'** | a>
и, следовательно,
> P. / A36)

§ 17. УРАВНЕНИЯ ТЕОРИИ МАКСВЕЛЛА — ЛОРЕНЦА 485
Таким же образом можно вычислить сечение обратного про-
процесса, когда частица, движущаяся с импульсом q, излучает
квант с импульсом k и оказывается захваченной потенциалом
V(R)b состояние а:
q—>ak.
В первом порядке по Н' находим
—1й—~w~Ka|e "*14+>>г- A37)
Это выражение можно вычислить непосредственно или получить
из предыдущего, воспользовавшись соотношением микрообра-
микрообратимости (XIX. 190) для двух реакций q-*-ak и (Да) (—k) ->-
->¦ (—q), переходящих друг в друга при обращении времени.
Действительно,
<а | е-'** I Ч+)) = (Фи I e-'*« (К I а».
Раздел III. КЛАССИЧЕСКАЯ ТЕОРИЯ
ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ
§ 17. Уравнения классической теории Максвелла — Лоренца
В основе классической теории излучения лежат уравнения
Максвелла ')
A8 + dX/dt Q A38а)
A386)
rot Ж — dSldt = Ans, A39а)
A396)
Эти уравнения определяют электрическое и магнитное поля
<§ и Ж при наличии распределенной плотности заряда s° и
плотности тока s. Последние удовлетворяют уравнению непре-
непрерывности
di
которое следует из уравнений A39) и выражает закон сохра*
нения заряда.
Уравнения Максвелла должны быть дополнены уравнением
Лоренца, определяющим движение электрических зарядов в
электромагнитном поле. Согласно этому уравнению, плотность
инерциальных сил равна плотности электромагнитных сил
A40)
') В отличие от случая скалярного поля мы не пользуемся здесь рацио-
рационализованной системой единиц, как следствие этого в правых частях уравне-
уравнений A39) появляются множители 4я.

486 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
Согласно классической теории электрона Лоренца матери*;
состоит исключительно из частиц с определенной массой и за*
рядом. Уравнение движения частицы получится, если в уравне»'
нии Лоренца перейти к пределу, когда заряд сосредоточен':
в бесконечно малом объеме. Рассмотрим, например, частицу,
массы т и заряда е. Обозначим через R, V и П координату, ско»
рость и механический импульс частицы (П = MV, где М есть.':
релятивистская масса, определение (XX. 20)). Плотности s° и s, ,
точнее, вклад данной частицы в эти плотности, даются равен-,;
ствами
so = e6(r-R), s = eV6(r-R).
Действующая на частицу электромагнитная сила F равна ин-
интегралу от / по малой окрестности точки R. Из уравнения Ло-
Лоренца следует (см. ур. (XX. 21)):
dUjdt = F*se{ff + VXX). A42>
Величины & и Ж в этом уравнении равны значениям электри-
электрического и магнитного поля в точке R. Напомним, что
V = dR/dt = П/Af = П/Vm2 + П2. A43>
Уравнения A42) и A43) описывают движение частицы в при-
присутствии электромагнитного поля.
Все предыдущие уравнения и определения можно записать-
в ковариантной форме. Величины & и Ж образуют в соответ-
соответствии с определением (XX. 9) антисимметричный тензор F^v*
a s° и s образуют 4-вектор s» == (s°, s). Уравнения Максвелла —-
Лоренца принимают вид1)
A39>
а уравнение непрерывности dvsv = 0. Плотность силы / есть про-
пространственная часть 4-вектора
?*^Г%. A40')
Аналогично F dt есть пространственная часть 4-вектора eF^v dxVr
а П — пространственная часть определенного в § XX. 4 4-век-
') Вводя теизор, дуальный к электромагнитному: ?**•=— е4^^^, урав-
уравнению A38') можно придать более простой вид

§ 18. ИНВАРИАНТНОСТЬ И ЗАКОНЫ СОХРАНЕНИЯ 487
тора № = (М, П). Вводя собственное время частицы и ее
4-скорость, уравнение A42) и аналогичное уравнение для М
также можно записать в ковариантном виде.
§ 18. Инвариантность и законы сохранения
классической теории
Релятивистская инвариантность классической теории ведет
к ряду законов сохранения. В этом параграфе мы подробно рас-
рассмотрим законы сохранения энергии и импульса и кратко упо-
упомянем закон сохранения момента импульса и свойства симме-
симметрии относительно пространственного отражения и обращения
времени. Будем считать для простоты, что исследуемая система
состоит только из одной частицы (электрона); обобщение на
случай нескольких частиц очевидно.
Для того чтобы получить законы сохранения энергии и им-
импульса, покажем вначале, что определенный формулой A40)
4-вектор /i* равен дивергенции некоторого тензора при условии,
что F^v удовлетворяет уравнениям Максвелла — Лоренца.
Используя уравнение A39'), получаем
f ^F-Sv = 1Lf^ (^pv) = ^r[a0(^V/;-pv)-FpvEPfv)]. A44)
Принимая во внимание антисимметрию тензора F и уравнение
A38'), имеем
-1 Fpv (d°F»v +
Подставляя это выражение в правую часть формулы A44) и
вводя обозначение
fS <й. ;• A45)
¦приходим к нужному равенству
fo^dfj**. A46)
Величина Tw называется тензором энергии — импульса. Выпи*
тем явно его компоненты
Т00 = — ~ («* + Ж2),
l

488 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
Энергия W0 и импульс W поля определяются как интегралы по
всему пространству
A47а)
A476)
леи ij
т. е.
A48)
A priori не очевидно, что W^ есть 4-вектор. Однако, используя
законы сохранения энергии и импульса, это можно доказать.
Для доказательства законов сохранения энергии и импульса
запишем уравнение движения частицы в виде
Это уравнение удовлетворяется независимо от области инте-
грирования V, в предположении, что эта область содержит
точку, в которой находится частица. Используя для /^ выраже-
ние A46), получаем
Второй интеграл можно преобразовать в интеграл по граничной
поверхности объема V. Будем теперь неограниченно увеличи-
увеличивать объем V так, чтобы в пределе получилось все простран-
ство. Считая, а это в данном случае вполне оправдано, что
электромагнитное поле достаточно быстро убывает на бесконеч-
бесконечности, заключаем, что интеграл по граничной поверхности стре-
стремится к нулю и, учитывая определение A48), находим
Это обосновывает принятое выше определение энергии и им-
импульса поля и представляет собой закон сохранения энергии и
импульса всей системы как целого (частица + поле)
M-\-W° = const во времени, A49а)
П -|~ W = const во времени. A496)
Аналогичные рассуждения приводят к следующему закону
сохранения полного момента импульса:
(Ц X Щ +1 = const во времени, A50)

§ 19. КЛАССИЧЕСКИЙ РАДИУС ЭЛЕКТРОНА 489
если для момента импульса поля использовать определение
Если система состоит из нескольких частиц, то П и М нужно
заменить на суммы импульсов и релятивистских масс, а
(/? X П) — на сумму моментов импульса. После такой замены
три закона сохранения— A49а), A496) и A50) остаются вы-
выполненными.
Рассмотрим отражения пространства и времени.
Уравнения движения инвариантны относительно пространственного отра-
отражения (t-*t, r->—г), если заряд е является истинным скаляром, а напря-
напряженность поля f*v — истинным тензором. В этом случае s° преобразуется как
скалярная функция, заданная в трехмерном пространстве, s и Ш — как поляр-
ио-векторные поля, а X — как аксиально-векторное поле; в частности, имеем
g (t, r) -> - g (t, - г), %(t, r) -> + Ж (t, - г). A52)
Уравнения движения инвариантны при обращении времени (t-*-—t,r-*-r),
если заряд е считать скаляром, a F^ — «псевдотензором». В этом случае ве-
величины s° и g не меняются, a s и Ж меняют знак
g {t, r) -> + g (- t, г), К (t, r) -> - Ж (- t, г). A53)
§ 19. Собственная энергия и классический радиус электрона
На данной стадии нам следует напомнить о серьезной труд-
трудности классической теории излучения. Во всех предыдущих рас-
рассуждениях предполагалось, что заряд каждой частицы сосредо-
сосредоточен в очень малом объеме, например, в сфере, радиус а кото-
которой стремится к нулю. В действительности, гипотеза о чисто
точечном заряде не является самосогласованной. Рассмотрим
изолированный электрон, расположенный в начале координат,
и вычислим энергию Ьт создаваемого электроном поля. Эту
энергию обычно называют электростатической собственной
энергией. В соответствии с рассуждениями § 11, которые можно
повторить здесь без изменений, величина Ьт является перенор-
перенормировкой массы, и экспериментально наблюдаемая масса равна
Поскольку электрическое поле в области (г > а) равно ег/г3,
то из формулы A47а) получаем
dr
и так как б/п < /пЭКсп. то а > e^\2mbWXL. Величина
го = -=?-(«2,82-103 см)

490 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
называется классическим радиусом электрона. Таким образом,
классический электрон имеет конечные размеры порядка гд.
Однако теория не в состоянии объяснить его устойчивость и
a fortiori детали его внутренней структуры, т. е. распределение
зарядов и токов в области г < г0. Это связано с тем, что элек-
электромагнитные силы между отдельными составляющими элек-
электрона являются в основном силами отталкивания, которые стре-
стремятся развалить электрон. Для устойчивости их необходима
скомпенсировать связующими силами неэлектромагнитного про-
происхождения. Введение таких сил в релятивистской теории стал-
сталкивается с серьезными трудностями. В действительности до-
довольствуются какими-либо гипотезами ad hoc о внутренней
структуре электрона. Следовательно, естественно ожидать, чго
мы будем в состоянии правильно описывать только явления, за-
зависимость которых от деталей внутренней структуры несуще-
несущественна, т. е. явления, характерная длина которых достаточна
велика (X.3> г0) ').
§ 20. Электромагнитный потенциал. Выбор калибровки
Можно получить уравнения, которые эквивалентны, но
проще уравнений A38), если ввести векторный А и скалярный q>
потенциалы следующим образом (см. ур. (XX. 17)):
Ж = rot А, ё= — дА/dt — gradcp. A54>
Уравнения A38) тогда выполняются автоматически, а уравне-
уравнения A39) эквивалентны следующим:
А — АЛ + grad (ф + div A) = 4ns, A55а)
ф —Дф — ^-(ф + div A) = 4ns°. A556)
Уравнения A54) определяют А и ф только с точностью до-
произвольной функции G(t,r). Эти уравнения не изменятся,
если сделать подстановку
А-*А — gradG, ф->ф + аО/а/. A56)
Такая замена называется калибровочным, преобразованием, (см.
§ XX. 20).
Приведенные соотношения можно записать в ковариантном-
виде. Потенциалы А и ф образуют 4-вектор (см. ур (XX. 6));
в соответствии с уравнениями A54) ротор вектора А* равен F**
') В квантовой теории существует «ультрафиолетовая катастрофа» тог»
же происхождения. Тем ие менее не следует проводить аналогию между клас-
классической и квантовой теориями слишком далеко. Такие эффекты как рождение
пар заставляют считать радиус «квантового электрона» порядка h/mc, т. е.
в 137 раз больше г а.

§ 21. ПРОДОЛЬНАЯ И ПОПЕРЕЧНАЯ ЧАСТЬ ВЕКТОРНОГО ПОЛЯ 491
¦(см. ур. (XX. 8)), последняя величина определяет А^ с точ-
точностью до градиента произвольной функции. Калибровочное
преобразование A56) и состоит в добавлении к потенциалу та-
такого градиента
Ли -> Ли + b*G (G - произвольна). A57)
Уравнения A55) принимают вид
П/-а" (dvAv) = W\ A58)
Не нарушая явной ковариантности теории, можно частично
устранить произвол в калибровке, потребовав, чтобы выполня-
выполнялось дополнительное условие Лоренца
dv,4v = 0. A59)
В этом случае уравнение движения для потенциала примет бо-
более простой вид
ПА» = 4л5». A60)
Условие Лоренца фиксирует калибровку потенциала с точно-
точностью до функции % — произвольного решения уравнения П%=0.
Другими словами, уравнения A59), A60) и определение поля
JF^V инвариантны относительно лоренцевых калибровочных пре-
преобразований, которые называют иногда специальными:
А»-+А» + д\ (ПХ = О). A61)
Простые уравнения движения можно также получить, если
потребовать выполнения условия
div4 = 0. A62)
В отличие от условия Лоренца оно нарушает явную кова-
ковариантность теории. Тем не менее, его преимущество состоит
в том, что полностью устраняется произвол в калибровке. Вве-
Введенная калибровка обычно называется радиационной калибров-
калибровкой. Ее мы и будем использовать в дальнейшем. Прежде чем
начать изложение теории излучения в этой калибровке, полезно
напомнить важное свойство разложения векторных полей.
§ 21. Продольная и поперечная часть векторного поля
Любое вещественное или комплексное векторное поле В (г)
можно рассматривать как суперпозицию двух полей
B(r) = BB(r) + Bx(r), A63)
одно из которых Вц — безвихревое, а другое В± — поле с нуле-
нулевой дивергенцией. Получаем
rot В,, = 0, div Вц = div В, A64)
A65)

492 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
Если ограничиться рассмотрением квадратично-интегрируемых
векторных полей, то такое разложение единственно '). По опре-
делению поля -Вц и Вх представляют соответственно продоль-
продольную часть и поперечную часть поля В. Справедливы соотноше-
соотношения
^\ yf^dr', A66)
Bx-rotF, V(r) = -^\^i^-dr'. A67)
Такое разложение легко произвести, используя преобразова-
ние Фурье. Обозначим преобразования Фурье полей В, Вх и В$
соответственно Ь, Ъх и 6ц:
Ь (ft) = Bя)~ J В (г) е-»' dr,
6|l (ft) = ... etc.
Уравнения A64) и A65) эквивалентны следующим уравнениям:
(ft&x) = 0, ftX6x
Проекция Ь вдоль вектора k равна 5ц, отсюда название для
в и — продольная часть2). Проекция Ь, перпендикулярная век~
тору k, равна Ъх, отсюда название для Вх — поперечная часть.
Уравнения A66) и A67) эквивалентны соответственно уравне-
уравнениям
A69)
Преобразование Фурье функции U (определение A66)) равно
и (ft) = - i (bk)/k2.
[N. В. Преобразование Фурье 1/г равно f\
Говоря более общим образом, пространство квадратично»
интегрируемых векторных полей — пространство волновых функ-
ций частицы спина 1 — представимо в виде прямой суммы двух
ортогональных подпространств: пространства продольных полей
и пространства поперечных полей. Рассмотренное нами разло-
разложение сводится к тому, что поле В можно записать в виде
суммы его проекций на эти дополнительные друг к другу под-
пространства.
') Следует также считать квадратично интегрируемыми поля Вц и Bj_,
г) Не следует путать Вц с радиальной составляющей вектора В — проек-
проекцией В идоль вектора г: Вгал = г (В, г)\тг. Отметим, что радиальная состав-
составляющая чисто поперечного поля в общем случае отлична от нуля.

§ 21. ПРОДОЛЬНАЯ И ПОПЕРЕЧНАЯ ЧАСТЬ ВЕКТОРНОГО ПОЛЯ 493
Проекции можно получить автоматически, выбирая подхо-
подходящий базис. Пусть
полный ортонормированный набор продольных полей, а
ГA), Г<2), .... Г(т)
полный ортонормированный набор поперечных полей:
rot /,<*> = 0, J (#W*?(V)) rfr = 6U'. A70a)
div ГЮ = 0, J (ГО7М) rfr = б„-, A706)
? Lf> (r) Lf>' (rO + ? 7f > (r) Tf' (/¦') = б/уб (г - r'). A70b)
A, T
(i, / = дс, i/, 2)
Введем обозначения
pw = J (L»)'B) dr, $? = J (rW'B) dr. A71)
Тогда имеем
Д, = Z P{i^(A). Bx = Z P'P^. A72)
Использование преобразования Фурье позволяет выбрать
подходящий базнс, состоящий из продольных н поперечных
плоских волн. Каждому волновому вектору отвечает продоль^
ное поле
Lw = Bnr3hkeikr (k = k/k) A73a)
и два ортогональных друг другу поперечных поля
Т(Ш) = BяГ'W*r (© = 1, 2), A736)
где 8A) и еB) — два произвольных единичных вектора1), орто-
ортогональных вектору k и друг другу:
(ft8(i)) = (ft8B))==0) A74а)
(8<1>*е»>) = (8<2>*е<2>) = 1, (8<i)#8<2)) = 0. A746)
') Эти векторы не обязательно вещественные. По определению вектор на-
называется вещественным, если вещественны его декартовы компоненты. Так,
вектор k — вещественный вектор. Скалярное произведение двух комплексных
векторов А и В определяется формулой
(А'В) ^ А*ХВХ+ AlBy + А*гВг.

494 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
Компоненты вектора В в этом базисе (определение A71)).
связаны с векторами 6ц и Ьх. равенствами
6„ = р<*4, 6Х = Е Рх(*и)8'ш>. A75);
Плоские волны здесь зависят от непрерывного индекса k .и]
нормированы на б(k — k'). Для того чтобы иметь дело только,
с дискретными индексами, применяют обычный прием. Систему;
помещают в куб со стороной L, тогда множитель Bя)~'А в опре*1
делении A73а, б) нужно заменить на L~l%. :
Часто в качестве базиса выбираются также сферические/
волны. К этому вопросу мы еще вернемся в § 29. «
§ 22. Исключение продольного поля
Среди уравнений Максвелла уравнения A386) и A396),
строго говоря, не являются уравнениями движения, они пред-»
ставляют собой накладываемые на поля & и Ж связи, которые
фиксируют продольные составляющие этих полей.
Из уравнения A386) следует, что <#?ц —О, а нз уравнения^
A396) следует, что &ц (/, г) есть электростатическое поле, со-
созданное распределением заряда So(t, r). Следовательно, для оп-
определения динамического состояния системы достаточно задать
распределения зарядов и токов (т. е. координаты и скорости:;
частиц) и поперечные поля Ж и &. Таким образом, можно?
сформулировать теорию, полностью устранив продольную часть*
электромагнитного поля. Я
Вместо того, чтобы проводить такое исключение непосред-»;!
ственно, удобно ввести потенциал (ф, А) в радиационной ка-|
либровке (см. ур. A62)). Речь идет о простой замене перемен-f
ных. По определению поле А — чисто поперечное 1
Л,1 = 0, А = Ах. A76)
Старые переменные выражаются через новые по формулам1
A54) или
iSt = — gradq>, A77)|
Ж = rot A, &s. = — dA/dt. A7Щ
Потенциал можно найти из уравнения A56), которое в данному
случае принимает вид !
Дф = -4я5°. A79|
Получаем | Ь

§ 22. ИСКЛЮЧЕНИЕ ПРОДОЛЬНОГО ПОЛЯ
откуда следует упоминавшееся выше выражение для <ац в тер-
терминах s°. Для исключения потенциала ф из уравнения A55а)
достаточно переписать это уравнение отдельно для продольной
и поперечной составляющих. Первое из этих уравнении,
A81)-
выполняется тождественно, если потенциал определяется фор-
формулой A80I).
Второе уравнение не зависит от ф и является уравнением
движения
А —ДА = 4явх. A82>
Остается исключить продольное поле из уравнений движе-
ния частиц (ур. A42), A43)), т. е. из выражения для силы Ло-
Лоренца, которая действует на каждую из частиц. Различные ве-
величины, связанные с частицами, будут обозначаться теми же
символами, что и в § 17, и нумероваться индексами 1, 2, ...
..., п, ... . Так, вклад в плотность заряда частицы с номером
п равен5^ = еяб(г — Rn), и уравнение A79) принимает вид
ДФ = - 4я ? е„б (г - *„). A83)
п
Решением этого уравнения является кулоновский потенциал
<P=?e«/k-JU. A84).
п
Пусть Fi — сила Лоренца, действующая на частицу с номе-
ром L Ее можно представить следующим образом
Fi = F? + F\ons,
Pf = е, (8L (i) + VtXM@) = et (- ЦР- + V X rot A (i)) .
A85)-
i?iong = ept (/) = ei gra d Ф (/),
где &±.(i), №(i), ...—значения полей @±, Ж, ... в точке Ri.
Подставляя выражение A84) в формулу для F\onsy мы оконча-
окончательно исключаем продольное поле.
Однако такую подстановку нельзя произвести непосред-
непосредственно, поскольку потенциал ф расходится в точке Ri. Труд-
Трудность возникла оттого, что мы считаем заряды точечными. Be-
') Для справедливости этого равенства достаточно, чтобы были равны ди-
дивергенции каждой из его частей: A(p = 4ndivs. Это уравнение следует и*
уравнения A79), если последнее продифференцировать по / и воспользоваться
уравнением непрерывности.

496 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
личина .Ftong есть действующая на частицу i электростатическая
сила, порожденная всеми имеющимися зарядами. Обозначим
F'i вклад в F°ne со стороны заряда частицы i, a FJOU| — вклад
со стороны всех остальных зарядов. Если частицы находятся
достаточно далеко друг от друга, то, вычисляя Ficoui, можно
считать заряды точечными, и мы получим
РГ'= ? eten(Rc-Rn)/\Rt-Rnf. A86)
ф I
I
При вычислении F'i гипотеза точечности заряда, очевидно,
неприменима. В действительности, при любом распределении
заряда внутри частицы i получим
Таким образом, на каждую частицу действуют сила Ло-
ренца, порожденная поперечным полем, и электростатическая
сила со стороны всех других частиц (ур. A86))
Fi = Fir + Pful. A87)
§ 23. Энергия, импульс, момент импульса
Исключив продольное поле из уравнений движения, есте-
ственно исключить его и из законов сохранения энергии, им-
пульса и момента импульса.
Заменяя в выражении для энергии поля (ур. A47а)) <% на
&±, мы получаем новое выражение, зависящее только от по-
поперечных составляющих. Будем называть эту величину энер-
энергией излучения U
U e-gL J {&\ + Ж2) dr. A88)
Аналогичным образом определим импульс излучения X (см.
ур. A476)) и момент импульса излучения G (см. ур. A51))
A89)
r. A90)
Величины U, X и G равны соответственно энергии, импульсу
и моменту импульса системы, когда отсутствуют заряды.
Эти величины можно представить в форме, аналогичной при-
приведенной в разделе I для энергии, испульса и момента импульса
скалярного поля (см. § 4, 6 и 7). Заменяя в выражениях
A88) — A90) Ж на rot Л, интегрируя несколько раз по частям

§ 23. ЭНЕРГИЯ, ИМПУЛЬС, МОМЕНТ ИМПУЛЬСА 497
и исггользуя тот факт, что &х и А — поперечные поля, исче-
исчезающие на бесконечности, получаем
) dr>
G = G^ +C«, A90')
где
xX^dr. A916)
При получении этих выражений удобно использовать методы и обозначе-
обозначения тензорного исчисления, в частности, полностью антисимметричный тензор
трехмерного эвклидова пространства ец* (определение даио в сноске на
стр. 16) и тождество
EUkeklm = 6il6Im-6im(>W
Тогда
дАт (
дх1
т
dxt
keklm
д
дх,
дА,
и
\ т
дАт
дА„
дхх
|-Г т
г дАт
d*At
дхт дХ[ '
дА[ дАт
9хт дх1
и поскольку А — поперечное поле, исчезающее на бесконечности, имеем
откуда следует уравнение A88')- Пользуясь аналогичным приемом, находим
откуда следует уравнение A89'). Подобным образом,
(г X («j. X X))t = SLm {гтх] ^ - -А- (гтхриА%) + гтвXjAk,
откуда следует уравнение A90') при условии, что G<°> и O(s> определяются
формулами A91а, б).
Поучительно сравнить полученные выражения с соответ-
соответствующими формулами для скалярного поля. Рассмотрим, на-
например, формулы A30) н A88') для энергии. Различия возни-
возникают в силу того, что: (i) поле А — векторное; (и) его масса
равна нулю; (ш) использованные здесь единицы отличаются от

498 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
принятых в разделе I множителем д/Чя. В остальном выраже-
выражение A88') является простым обобщением выражения C0),
если считать — tax, как это подсказывает нам второе из урав-
уравнений A78) и что будет подтверждено в дальнейшем, канони-
канонически сопряженным к полю А импульсом. То же можно сказать
о формулах E5) и A89') для импульса и для момента импульса
(ур. F1) и A90')). Векторный характер поля отчетливо про-
проявляется в выражении для момента импульса, где кроме члена
G<0), который является простым обобщением выражения для
момента импульса скалярного поля, появляется дополнительное
слагаемое G(s). Величина G@) представляет собой «орбитальный
момент импульса», a G(s) — «спин» поля ').
' Теперь мы можем исключить продольное поле из получен-
полученных в § 18 выражений для полной энергии, полного импульса
и полного момента импульса системы, состоящей из электро*
магнитного поля и взаимодействующих с ним заряженных ча-
частиц.
Рассмотрим вначале полный импульс системы.
В соответствии с определением § 18 имеем
Р4о,= ЕП„+^=ЕП„+Х + Г( A92>
п п
где
Заменяя &^ и Э€ по формулам A77), A78), получаем
= — (gr a d ф X Щ = Ф rot Ж — rot (фЛ?) =
= — ф (Л Л) — rot
Интегрируя по частям и учитывая, что ф и А исчезают на
бесконечности, получаем
*'= ~ i$ф (Д Л) dr = - iH л (Лф) rfr-
В силу уравнения A83) Аф равно сумме б-функций, интегриро*
вание легко выполняется, в результате имеем
') В данном случае ситуация усложняется из-за условия поперечности.
Среди других следствий из него вытекает, что амплитуды поля А в каждой
точке пространства не являются независимыми динамическими переменными.
По этой же причине в задаче 5 получается специфическая форма коммута-
коммутационных соотношений, а векторные операторы О@> и О(в> по отдельности не
удовлетворяют коммутационным соотношениям, характеризующим момент им-
импульса.

§ 23. ЭНЕРГИЯ, ИМПУЛЬС. МОМЕНТ ИМПУЛЬСА 49»
где, как и ранее, А (п) s= A (Rn)- Подставляя найденное выра-
выражение в формулу A92), приходим к определению импульса Рп
частицы с номером п ')
Рп = Пп + <?„Д(/г). A93)
Выражение для полного импульса принимает вид суммы им-
импульсов частиц и импульса излучения
Ptot =?Р„ + Х. A94)
л
Эта сумма является интегралом движения.
Поступая аналогичным образом с моментом импульса, при-
приходим к определению момента импульса Ln частицы п
Ln^RnXPn, A95)
где Рп — определенный выше импульс. Вычисления приводят
к следующему выражению для полного момента импульса си-
системы:
/tot =?*•«+<?. A96)
л
Наконец, рассмотрим полную энергию системы. Согласно
определению § 17 ее можно представить в виде
где
Используя формулу A77) и интегрируя по частям, получаем
и' = ж\ terad <рJ dr = - -ш $ф (Дф) dr'
где ф — порожденный зарядом электростатический потенциал.
Если считать заряды точечными, как это мы делали до настоя-
настоящего момента, то находим
ту... 1
и ~ 2
2 Z-. Z-. | Rn - RP
л р
') Напомним, что мы используем радиационную калибровку, в которой
поле А чисто поперечно. Мы получим определение, независящее от калибров'
ки, если положим

500 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
В полученной двойной сумме «перекрестные члены» (п Ф р}
отвечают кулоновской энергии взаимодействующих зарядов
tW^st- A97>
(символ 2j означает суммирование по всем парам частицД
п<р /
Все члены с совпадающими индексами обращаются в беско-
бесконечность. Эта трудность имеет то же происхождение, что и
встретившаяся в конце § 22 прн вычислении F[°"s. Слагаемое
с двумя индексами i представляет собой электростатическую-
энергию частицы I в собственном электрическом поле. Эта энер-
энергия существенно зависит от распределения заряда внутри ча-
частицы и становится бесконечной в пределе, когда размеры ча-
частицы стремятся к нулю (см. § 19). Чтобы получить разумную
величину собственной энергии, следовало бы добавить в нее
вклад упоминавшихся в § 19 сил сцепления, что не было сде-
сделано в данных вычислениях. Не имея последовательной теории
внутренней структуры частиц, мы будем считать, что при под-
подходящей модификации массы покоя /и,- эти члены «собственной
энергии» можно опустить. Тогда для полной энергии системы
получим следующее выражение:
= ? „ Мп + Ясйи1 + U. A98>
Перед нами сумма энергий масс частиц, кулоновской энергии
частиц и энергии излучения.
§ 24. Гамильтониан свободного электромагнитного поля
Полученные в § 22 уравнения движения можно представить
в каноническом виде. Рассмотрим вначале случай свободного
излучения, т. е. электромагнитное поле без зарядов.
Динамическое состояние поля в каждый момент времени оп-
определяется заданием поперечного векторного потенциала А и
его скорости dA/dt. Электрическое и магнитное поля связаны
с этими векторными полями формулами A78). Зависимость
от времени определяется уравнением A82), которое в случае
отсутствия зарядов принимает вид
ПА^А — ДЛ = 0 (div4 = 0). A99>
Получили то же уравнение, что и для свободного скалярного
поля (см. ур. A)). Единственное отличие состоит в том, что
в данном случае мы имеем поперечное векторное поле и отсут-
отсутствует член с массой. В остальном канонический формализм

§ 24. ГАМИЛЬТОНИАН ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 50t
можно строить тем же способом, что и в разделе I для случая
скалярного поля. Пусть Г*1', Т<2> Т<т>, ... — полный набор
ортонормированных поперечных полей (см. ур. A706)), анало-
аналогичный определенному в § 21. Предположим далее, что этот на-
набор является базисом вещественных нормальных координат
(А + й2т) Т{х) = 0. B00>
Соответствующие нормальные координаты qx определяются со-
соотношением (см. ур. F))
^ BШ)
Величины qx — вещественные функции времени, удовлетворяю-
удовлетворяющие уравнению для гармонического осциллятора с частотой k%
qx + kxqx = 0. B02)-
Такое движение порождается гамильтонианом Ат
где pi — импульс, канонически сопряженный qx. Импульс рх
равен q% и получается из «скорости» поля А по формуле
Складывая гамильтонианы, отвечающие различным собствен-
собственным частотам, получаем полный гамильтониан свободного из-
излучения
Ягау=ЕаЛт- B05)
Множитель 1/д/4зх в определениях B01) и B04) возник как
следствие выбора единиц измерения электромагнитного поля ').
Гамильтониан Ягау представляет собой энергию излучения,
выраженную в канонических переменных. Действительно, имеем
.(см. ур. A78I
У ? B06)-
B07).
') См. первую сноску к § 17.

S02 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
Из вещественности и ортонормированности множества Г<т> сле-
следует
$3\rfr = 4,ijyT. B08)
•t
Кроме этого, поскольку Л*> — поперечные векторные поля, удо-
удовлетворяющие уравнению B00), то, интегрируя по частям,
имеем
J I wdr=- \ I Ai (ААдdr=4я Е *&• »
Подставляя соотношения B08) и B09) в выражение для энер-
энергии U (ур. A88)), находим
§ 25. Гамильтониан излучения,
взаимодействующего с частицами
В общем случае можно взять в качестве канонических пере-
переменных, с одной стороны, введенные в предыдущем параграфе
q-c, px, которые описывают динамическое состояние излучения,
а с другой стороны, координаты Rn и импульсы Р„ частиц. Им-
Импульс Рп связан с механическим импульсом частицы соотноше-
иием A93).
Используя результаты § 22 (уравнение движения A82) и
уравнения для силы Лоренца A85)—A87)), легко получить
уравнения движения в новых переменных. В частности, урав-
уравнение B02) для свободного осциллятора перейдет в уравнение
qx + kxqx = 4л ? еп <УЯТ™ (л)). B10)
п
Полученным уравнениям можно придать канонический гамиль-
тонов вид с гамильтонианом
Н^Н (дх, pt; *„, Ря) = Ягау + //cOuI + ? #„, B11)
Л
где Ягау — гамильтониан свободного электромагнитного поля
B05), //coui — кулоновский потенциал A97), Нп — энергия ча-
частицы с номером п, выраженная з канонических переменных
А (л) = л/4л Z Q-J™ («)• B13)
т
Доказательство этого утверждения не составляет труда и
предоставляется читателю.

5 26. КВАНТОВАНИЕ СВОБОДНОГО ПОЛЯ ИЗЛУЧЕНИЯ 503
Раздел IV. КВАНТОВАЯ ТЕОРИЯ ИЗЛУЧЕНИЯ
§ 26. Квантование свободного поля излучения. Фотоны
И сказал Бог: «Да будет свет!» И был свет.
И увидел Бог, что свет хорош... Был день первый-
Квантовую теорию электромагнитного излучения можно по-
построить, исходя из классической теории и используя принцип
соответствия, так же как это было сделано в случае скалярного
поля.
В качестве исходного пункта мы выберем гамильтонов фор-
формализм, который был развит в §§24 и 25.
Рассмотрим вначале свободное излучение. Вещественным ди-
динамическим переменным классической теории qx, pT соответ-
соответствуют квантовые наблюдаемые, которые удовлетворяют кому-
тационным соотношениям (см. ур. A1))
[<7т> Qi') = (Рт. РА = 0, [<7х, рТ'] = гбтт-.
Уравнения B03) и B05) определяют оператор Н,ау — гамиль-
гамильтониан, который описывает развитие системы с течением вре-
времени. Видно, что излучение, в согласии с законом Планка, пред-
представляет собой суперпозицию квантовых осцилляторов.
Обсуждение, которое было проведено в § 3, можно повторить
и в данном случае, в частности, ту часть, которая касается кор-
корпускулярной интерпретации. Кванты излучения называются фо-
фотонами. С каждой модой т связан фотон, который характери-
характеризуется «волновой функцией» Г(т> и энергией kx. Фотоны подчи-
подчиняются статистике Бозе — Эйнштейна, что находится в пре-
прекрасном согласии с экспериментальными результатами, относя-
относящимися к термодинамическим свойствам излучения (излучение
абсолютно черного тела и т. д.). Замечания в конце § 3 об энер-
энергии вакуума и вакуумных флуктуациях поля можно повторить
без изменения и в этом случае.
Использованный метод не зависит от набора базисных век-
векторных полей Т^\ однако эти поля предполагались веществен-
вещественными. Можно привести такую формулировку метода, чтобы он
годился для комплексных полей Г(х) и дословно повторить рас-
рассуждения § 5 о квантовании с использованием комплексных по-
полей. Легко написать общие формулы, но мы здесь этого делать
не будем. Мы кратко обсудим разложение по сферическим вол-
волнам и более детально — разложение по плоским волнам. Среди
возможных разложений последнее применяется чаще всего. Раз-
Разложение по сферическим волнам удобно использовать в задачах
об излучении и поглощении квантов.

504 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
§ 27. Плоские волны. Импульс излучения
Квантование электромагнитного поля, использующее разло-
разложение по плоским волнам, аналогично приведенному в § б кван-
квантованию скалярного поля. В данном параграфе мы ограничимся
только наиболее важными формулами, отмечая в процессе из-
изложения отличие от случая скалярного поля.
Рассмотрим полный набор поперечных плосковолновых по-
полей. Для того чтобы иметь дело с дискретными индексами, бу-
будем рассматривать эти поля в кубе со стороной L и потребуем
выполнения обычных условий периодичности. Принадлежащее
этому набору поле и1Ш определяется волновым вектором к
и квантовым числом со — параметризующим поляризацию
(© = 1,2)
и<ы) = L-3V<V*r_ B14)
"Выражение для T(ka>) из § 21 (ур. A736)) отличается от дан-
данного только нормировкой. Векторы еA) и еB> удовлетворяют
уравнениям A74), которые определяют эти векторы с точ-
точностью до унитарного преобразования.
Сопоставим каждой плоской волне {J(kai) оператор уничтоже-
уничтожения п(к(й) и оператор рождения а^шу Поле А зададим разложе-
разложением (см. ур. D6) и B06))
A=Z? B«/*)*(W/<" + aU^'). <215)
ft a
а поле &± (см. ур. D7) и B07)) — разложением
#х = Z Е / (W (W^ - aUUim'). B16)
ft a>
Операторы а и a+ удовлетворяют коммутационным соотноше-
соотношениям, характеризующим операторы рождения и уничтожения:
[W V<o0] [>(*«» (*<o)] !>(*«) ato>] *A«
Оператор числа фотонов, находящихся в состоянии U(ka>\ есть
Гамильтониан электромагнитного поля, выбранный таким
образом, чтобы энергия вакуума была равна нулю, опреде-
определяется равенством
//гаУ = Е2>(,Ы,*. B19)
k a
Оператор импульса X выражается через операторы &± и А по
формуле A89). Подставляя в эту формулу разложения B16)
и B15), получаем (задача 6)
X = Z Z N{ka)k. B20)
ft а

§ 28. ПОЛЯРИЗАЦИЯ 505
Из приведенных выражений B19) и B20) видно, что фотон
в состоянии V{ka>) представляет собой частицу с импульсом k и
энергией k, т. е. частицу нулевой массы покоя с импульсом k.
Число состояний фотонов с импульсами, лежащими в интер-
интервале (k, fc + 5fc), равно 2(L/2nLk. Множитель 2 возник всилу
линейной независимости состояний с различной поляризацией
при данном импульсе (ш = 1 или 2). Плотность рх.(й) уровней
энергии k при заданных направлениях импульса Q и поляриза-
ции а» (определение § 6) равна (см. ур. D9))
pL{k) = L3k2/BnK. B21)
§ 28. Поляризация
Фотоны с одинаковым импульсом k могут иметь различную
поляризацию. В классической теории поляризация определяет
направление осцилляции поперечного электрического поля и
фиксируется (с точностью до фазы) вещественным или ком-
комплексным единичным вектором, перпендикулярным направле-
направлению распространения k. Такое определение поляризации без
труда переносится и на случай квантовой теории. Каждому зна-
значению импульса отвечают две линейно независимые поляриза-
поляризации еA) и еB) и любая другая возможная поляризация фотона
задается линейной комбинацией таких поляризаций1).
В качестве базиса можно выбрать две ортогональных линей-
линейных поляризации, т. е. два вещественных вектора еA) и еB). Эти
векторы можно выбрать таким образом, чтобы тройка еA), в<2)
и k образовывала орты правоориентированной декартовой си-
системы координат, что фиксирует еA) и еB) с точностью до вра-
вращений вокруг оси распространения
е<°» == е<°»•, е«> X ?B) = k/k.
Используют также в качестве базиса круговые поляриза-
поляризации е<+> и е<-) _ _
^ & B22)
Отметим, что е<+> = — е<->*. Символом Л будем обозначать ве-
величины, выраженные в этом базисе. Так можно определить опе-
операторы рождения $+ и уничтожения a,k , фотонов с круговой
поляризацией; соответствующая плоская волна равна
#<*Ч> = L-VV*r (л = + или -).
') Мы рассматриваем только чистые состояния, которые называют также
полностью поляризованными. Состояние частично поляризованное является
статистической смесью, оно определяется оператором плотности, действующим
в (двумерном) пространстве состояний поляризации.

506 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
Интерес к круговой поляризации вызван следующим свой-
свойством.
Фотон с круговой поляризацией имеет определенное значе-
значение момента импульса вдоль направления распространения, со-
соответствующая компонента момента импульса равна + 1 или
— 1 в зависимости от поляризации (правой х\ = + или левой
п = -)-
Для доказательства предположим, что излучение находится
в одном из состояний |fc±>, определяемых равенством
Такое состояние представляет фотон с импульсом k и правой
( + ) или левой (—) круговой поляризацией. Можно показать
{задача 8), что
(k,Gm)\k±) = 0, B23)
(k, Gis))\k±) = (±k)\k±), B24)
где векторные операторы G(°> и G(s) определены равенствами
A91а) и A916). Согласно уравнению A90) полный момент
импульса G равен сумме этих операторов. Обозначая компо-
компоненту G вдоль вектора k через G/,
Gk = (kG)/k
и используя предыдущие уравнения, получаем требуемый ре-
результат
G
Это свойство характеризует частицу спина 1. Точнее, если
частица спина 1 имеет определенное значение импульса k, то
компонента орбитального момента импульса вдоль k исчезает,
а соответствующая компонента спина может принимать три
значения: 1, 0, —1. Однако в случае фотона продольные пло~
ские волны, отвечающие нулевому значению компоненты спина,
отсутствуют.
§ 29. Разложение по мультиполям.
Фотоны с определенным моментом импульса и четностью
Кроме разложения по плоским волнам можно использовать
разложение по сферическим волнам, каждая из которых отве-
отвечает вполне определенному значению момента импульса и чет-
четности. Мы ограничимся тем, что приведем здесь основные фор-
формулы, опуская несложные доказательства.
Векторное поле В (г) можно рассматривать как трехкомпо^-
нентную волновую функцию, определяющую динамическое со-

5 29. РАЗЛОЖЕНИЕ ПО МУЛЬТИПОЛЯМ 507"
стояние частицы спииа 1. В представлении поля В посредством
компонент существует некоторый произвол. Например, можно
было бы задавать Вх, Ву, Вг, однако для нас предпочтительнее
использовать стандартные компоненты
Волновая функция зависит от координаты г и индекса ц„
который параметризует рассматриваемые компоненты (ц= +.
О,-)
Здесь можно отметить'явную параллель между частицами спи-
спина 1 и частицами спина 1/2 (см. §§ XIII. 20—21).
Наблюдаемые для частицы спина 1 являются функциями ее
координаты г, импульса р и спина s. В используемом нами
представлении р = — i'V матрицы компонент спина s+, sz, s_
определены уравнениями (ХШ.28), в которых следует считать-
/ = /' = 1. Легко показать, что s2 = 2 — число, соответствую-
соответствующее моменту, равному 1.
Орбитальный момент импульса I частицы определяется фор-
формулой
1 = гХр,
а полный момент / равен
Компоненты оператора / связаны с инфииитезимальиыми вра-
вращениями векторного поля в соответствии с обычным определе-
определением оператора момента импульса.
Аналогичным образом определим оператор четности Р, дей-
действие которого на поле В (г) соответствует преобразованию от-
отражения относительно начала координат1)
РВи(г) = -В (-г).
Построим полный набор векторных полей с заданным мо-
моментом импульса (jtn), которые удовлетворяют волновому урав-
уравнению
Это эквивалентно отысканию набора общих собственных функ-
функций операторов р2, /2 и /2. Соответствующие собственные значе-
1) Мы предполагаем, что значениями поля В (г) являются полярные век-
векторы. В результате появляется знак минус при пространственном отражении..
С точностью до знака четности все приводимые ниже свойства справедливы я
для аксиальных векторных нли псевдовекторных полей (см.сноску в § XX. 11)^

508 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
ния обозначим k2, /(/+ 1) и т; k может быть любым веще-
вещественным числом от 0 до со (спектр k можно сделать дискрет-
дискретным, рассматривая поле внутри сферы конечного радиуса R),
/ может принимать любое целое значение от 0 до со, щ — целые
значения от —/ до +/•
Используя свойства сложения моментов импульса, можно
показать, что операторы р2, I2, /2, \г образуют полный набор ком-
коммутирующих наблюдаемых и каждой тройке (kjm) отвечают:
(i) если / =^= 0, три линейно независимых состояния:
* = /+!. /, /— 1;
(ii) если / = 0, то одно и только одно состояние с / = 1. Эти
состояния имеют определенную четность Р = (—1)'+'.
Вместо классификации состояний (kjm) по возможным зна-
значениям I, можно классифицировать их по свойствам попереч-
ности или продольности и четности. Поперечный или продоль-
продольный характер поля связан с оператором (sp).
В используемом представлении имеем (ур. (XIII. 93))
(sp) = rot,
(spJ — р2 = grad div (= rot rot + A).
Для продольного поля (spJ = 0, для поперечного поля
(spJ — р2 = 0. Можно показать, что операторы р2, (spJ, P, /2
и /г образуют полный набор коммутирующих наблюдаемых, и
каждой тройке (kjm) отвечают:
(i) если / Ф 0, три линейно независимых состояния
(spJ = 0, k\ k2,
Р = (-{)', (-1)', (~1)ж;
(ii) если / = 0, то одно и только одно состояние — четное и
продольное
(spJ = 0, P = +I
(т. е. уже упоминавшееся р-состояние).
Для построения базисных функций будем использовать
функции Ukjm, которые были введены в § 7 при рассмотрении
скалярного поля. Константу в определении F0) будем считать
такой функцией k, что множество ы*/т образует полный орто-
нормированный набор скалярных функций. Каждому набору
(kjm) отвечает одно и только одно продольное состояние. Соот-
Соответствующая базисная функция равна
Kim = grad ukljk
(векторное поле четности (—1)'). Каждому набору (kjm),
исключая случай j = m = 0, отвечают два поперечных состоя*

§ 30. ВЗАИМОДЕЙСТВИЕ С АТОМНОЙ СИСТЕМОЙ 509
иия противоположной четности. Соответствующие базисные
функции равны ')
l) (Р = (-1)Ж), B25а)
eiU = V X lukimlk V/(/+D (P = (-1H- B256)
Отметим, что
Множество полей в/$т (й меняется от 0 до со; /= 1, 2, ...
,.., со; т = — /,..., +/'> «) = +1 —) образует полный ортонор-
мированный набор поперечных полей, которые можно исполь*
зовать для разложений операторов А и &х'-
А= Z (гя/^'Ча^вЙ^ + аЩ-вМ, B26)
k, i, m, a
х Z (I]Ц}(№1 B27)
k, j,m,a
Согласно принятой терминологии слагаемые в^ в этих разло-
разложениях отвечают электрическому 2'-польному вкладу, а сла-
слагаемые 6*7т — магнитному 2'-польному вкладу. Все рас-
рассуждения § 27, где рассматривалось разложение по плоским
волнам, можно повторить здесь для разложения по мультипо-
лям. Операторы а$т и afjm можно интерпретировать как опе-
операторы уничтожения и рождения фотонов с энергией k, момен-
моментом импульса (jm) и четностью (—l)Jo). Спектры значений k,
}, т и и уже приводились ранее, следует отметить только, что
не существует фотонов с нулевым моментом импульса.
§ 30. Взаимодействие с атомной системой
И сказал Бог: «Да будут светила иа
тверди небесной для отделения дня от
ночи...»
И увидел Бог, что это хорошо... Был
день четвертый.
Рассмотрим взаимодействие излучения с системой частиц.
Рассуждения будут подобны тем, которые проводились в случае
скалярного поля, и мы выделим здесь только наиболее суще-
ственные пункты.
') Четности этих функций отличаются знаком от тех, которые встречаются
в большинстве монографий (см., в частности Блатт и Вайскопф, loc. cit.). Это
связано с тем, что мы используем полярные векторные поля, в то время как
другие авторы используют аксиальные.

510 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
Гамильтониан системы, с точностью до очевидных модифи-
модификаций, совпадает ч: гамильтонианом классической теории (см.
ур. B11)). Упомянутые изменения связаны с динамическими
свойствами и спином рассматриваемых частиц. Мы ограни-
ограничимся случаем атомной системы, состоящей из Z электронов и
ядра с зарядом — Ze, где е — заряд электрона.
Предположим, что ядро отсутствует, и напишем гамильто-
гамильтониан системы из Z электронов + излучение. Такой гамильто-
гамильтониан дается формулой B11), где Нтау соответствует свободному
излучению, ЯСои1 — кулоновскому взаимодействию электронов
и Нп — гамильтониан Дирака для /г-го электрона в поле А, т. е.
$пт, B28)
матрицы Дирака ап и р„ относятся к я-му электрону.
В нерелятивистском приближении, вычитая массу покоя из
Нп, получаем
<"¦>«« = " 2т - ш <««* <«»• <229>
Отметим, что слагаемое в #„ (ур. B28)), описывающее взаи-
взаимодействие электрона с излучением, имеет вид
K = -e\(]n(r)A(r))dr, B30>
где jn(r) —дираковская плотность потока электронов в точке г,
т.е. (см. ур. (XX. 143))
/п(г) = а„6(*п-г). B31)
Величина ejn(r) есть плотность электрического тока для я-го
электрона. Подставляя в формулу B30) нерелятивистское при-
приближение для /„ (ур. A89), A90)), получаем оператор взаимо-
взаимодействия {Hn)NK в нерелятивистском приближении
(Н'п)т «е Н™ + Я<,И) + Я:, B32)
Я™ = - -^ ((РпА (л)) + (А (п) Рп)), B33а)
B336)
^ B33в)
Таким образом, мы пришли к выражению для взаимодей-
взаимодействия электрона с излучением, которое фигурирует в фор-
формуле B29).

§ 30. ВЗАИМОДЕЙСТВИЕ С АТОМНОЙ СИСТЕМОЙ 511
Наличие атомного ядра заставляет нас добавить к гамиль-
гамильтониану оператор кулоновского взаимодействия ядра и Z элек-
электронов и гамильтониан, описывающий ядро в электромагнитном
поле. Последний гамильтониан состоит из двух слагаемых, со-
соответствующих кинетической энергии ядра и взаимодействию
с излучением1). В нерелятивистском приближении, когда ядро
предполагается бесконечно тяжелым, эти два слагаемых прене-
пренебрежимо малы, и расположенное в начале координат ядро тре-
требует добавления к гамильтониану только Z кулоновских чле-
членов — Ze2/Rn- В этом случае атом рассматривается как си-
система, состоящая из Z электронов во внешнем кулоновском
потенциале — Ze2/R, которые взаимодействуют с электромаг-
электромагнитным полем. Соответствующий гамильтониан имеет вид
Я = Ягау + Яа, + Я', B34)
где Ягау — оператор энергии свободного излучения, #at — га-
гамильтониан электронов во внешнем кулоновском поле ядра
с кулоновским взаимодействием между электронами и Я'—
оператор взаимодействия электронов атома с излучением. Опе-
Оператор Я' равен сумме Z членов взаимодействия Я„ (см. ур.
B30)). В дальнейшем мы будем использовать нерелятивистское
приближение, и, следовательно, н'п определяется формулами
B32) и B33), т. е.
Н' = Нв) + Н01) + Н", B35)
ЯA)=Е^, Я"»=?Я<">, H"=ZH'n. B35')
п п п
При исследовании такой системы обычно пользуются одним
из двух приближенных методов.
В первом методе электромагнитное поле считают классиче-
классическим. Это предположение оправдано в тех случаях, когда обмен
энергией между атомом и полем столь велик по сравнению
с энергией каждого испущенного или поглощенного фотона, что
можно не учитывать дискретного характера этого обмена. Сле-
Следовательно, таким приближением можно пользоваться при боль-
больших интенсивностях и малых частотах, когда присутствует
много фотонов. В частности, метод годится для исследования
атома в статическом электромагнитном поле или в поле радио-
радиоволнового диапазона. В этом случае электромагнитное поле
рассматривается как заданное, возможно, зависящее от времени
внешнее поле, и задача сводится к исследованию атома во
внешнем поле.
') Предполагается, что ядро может рассматриваться как точечный заряд.
Такое рассмотрение оправдано до тех пор, пока участвующие в анализе ча-
частоты малы по сравнению с энергией возбуждений ядра.

512 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
При втором методе оператор взаимодействия Н' рассматри-
рассматривают как малое возмущение. Мы уже пользовались этим мето-
методом в случае скалярного поля.
Рассуждения § 10 здесь можно повторить почти дословно.
Невозмущенный гамильтониан имеет вид
Но = Ягау + //at.
Для применения теории возмущений нужно использовать пред-
представление, в котором оператор #0 диагоналей. Воспользовав-
шись определенным в § 27 представлением плоских волн для
электромагнитного поля, мы определим базисные векторы Но
как одновременные собственные векторы оператора #at и опе-
операторов числа фотонов с заданным импульсом и поляриза-
поляризацией N{ke>).
Матричные элементы Н' в этом представлении легко вычис-
вычислить, если использовать выражение этого оператора через опе-
операторы а(йи) и at^y Подставляя разложение для А B15) в вы-
выражение B33), находим
'
{а*{Р&) еШ?+эрм- ^"р-)' B36а)
Я»П) = - Ш ? {-шТ {Ш* {ak X e) е'** + эрм. сопр.), B366)
S
я« = ? ? ?
+ (flJaS' (eV) ег(&'-ft)* + эрм. сопр.)). B37)
(Чтобы упростить запись, мы ввели обозначения s = (ftco),
s' =а (fe'co'). а векторы Rn, Р„, а„, eto>, е<ш') записали как /?, Р, а,
е, е'.) Полученные формулы и формулы B35), B35') дают тре-
требуемое выражение для Н'.
Добавление к гамильтониану Но оператора взаимодействия
И' приводит к сдвигу всех атомных уровней и делает все
уровни, за исключением основного состояния, нестабильными
(напомним, что масса фотона равна нулю). Эти эффекты можно
изучать в рамках теории возмущений. Однако несмотря на ма-
малость константы связи е (е2 « 1/137) здесь встречаются те же
трудности, что и в случае скалярного поля. В частности, как
следствие локальности взаимодействия Н' (см. ур. B30) и
B31)) возникает «ультрафиолетовая катастрофа». Эта труд-
трудность устраняется из вычислений введением подходящего обре-
обрезающего параметра. По тем же причинам, что и выше, в каче-
качестве такого параметра выбирают частоту порядка т. Мы уже
обсуждали вопросы, относящиеся к введению обрезающего па-

§ 31. ИЗЛУЧЕНИЕ ФОТОНА АТОМОМ. ДИПОЛЬНОЕ ИЗЛУЧЕНИЕ 513
раметра и к трудностям, которые связаны с необходимостью
перенормировки массы и заряда частиц. Весь материал раз-
раздела II о сдвиге уровней и свойствах квазистационарных со-
состояний (время жизни, ширина линии, моды распада...) можно
без больших изменений перенести на случай взаимодействия
с электромагнитным полем1). Рассмотренные в разделе II за-
задачи о столкновении можно исследовать в случае излучения
теми же методами. Заканчивая эту главу, мы приведем два про-
простых примера применения квантовой теории излучения: вычис-
вычисление вероятности испускания фотона атомом и вычисление се-
сечения комптоновского рассеяния в пределе низких частот.
§ 31. Излучение фотона атомом. Дипольное излучение
Рассмотрим атом, находящийся в одном из возбужденных
состояний \Х} с энергией ?\. Такой атом может перейти в любое
из состояний |а>, |Р>, ... с энергиями ?<х, ?р, ..., меньшими чем
Ei, и испустить при этом фотон, энергия которого равна разно-
разности энергий начального и конечного состояний.
Будем исследовать переход
Я -> fifte,
где (х — конечное состояние атома, k, e — импульс и поляриза-
поляризация испущенного фотона и
k = EK-Ell. B38)
Вероятность перехода в единицу времени wK^ ft8 в первом по-
порядке теории возмущений дается формулой (см. § 12)
«W. = 2я | <Я, | /П !**»> Р (ВДBяK). B39)
Как видно из уравнения B35), Н' является суммой трех сла-
слагаемых. Вклад третьего члена Н" в интересующий нас матрич-
матричный элемент исчезает2). Вклады первого и второго членов легко
>) Изменения связаны с тем, что фотоны представляют собой частицы
нулевой массы и спина 1. Тот факт, что масса фотона равна нулю, приводит
к дополнительным трудностям. Кроме «ультрафиолетовой» возникает «инфра-
«инфракрасная катастрофа» — расходимость в области инзких частот некоторых ин-
интегралов теории возмущений по заряду. Эти расходимости связаны непосред-
непосредственно с используемым методом и нх можно избежать, если модифицировать
теорию возмущений. «Ультрафиолетовая катастрофа» представляет действи-
действительную трудность собственно теории, полностью удовлетворительного реше-
решения которой в настоящее время ие существует.
2) Действуя на состояния, Н" либо сохраняет число фотонов, либо уве-
увеличивает или уменьшает это число на две единицы. Отметим, что Н" содер-
содержит множителем е2, и, следовательно, при вычислении по теории возмущений
в первом порядке по е этот оператор можно не учитывать. При вычислении
сдвига уровней, который является эффектом второго порядка (см. § 11), вкла-
вкладом Н" нельзя пренебрегать. Его необходимо учитывать также при вычисле-
вычислении рассеяния фотонов (см. § 32).
1/„17 А. Мессна

514 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
вычислить, используя выражения B36). В результате имеем
_?(-*-)VV B40а)
?($) ">. B406)
где
^"(^ЕСРЛ^Ч) B41а)
n
Подставляя полученные выражения в формулу B39), оконча-
окончательно находим
„, _ e2k I р*1) /рA1) I2. /9491
Для атомов вероятность перехода по порядку величины су-
существенно зависит от моментов импульса Д, /„ и от четностей
Щ, Пц состояний |Х>, |(х> соответственно.
Если ]\ = /ц = 0, то вероятность перехода исчезает, по-
поскольку матричные элементы Л1) и Я11' тождественно равны
нулю (задача 10). Это — известное правило отбора 0-*-0. Оно
связано с тем, что не существует фотона с нулевым моментом
импульса (см. § 29).
Если Д или /ц отличны от нуля, то вероятность перехода
можно оценить, используя приближение больших длин волн.
Пусть R — длина порядка атомных размеров для обычных атом-
атомных переходов
k
так что
Следовательно, величины B41) можно оценить, если заменить'
экспоненты первым, дающим неисчезающий вклад членом их'
ряда Тейлора. Порядок величины этого вклада в основном оп-
определяется правилами отбора по моменту импульса и четности,
но вникать в эти детали мы здесь не будем [). При прочих рав-;
') Более естественным образом эти результаты получаются при использо-
использовании разложения по мультиполям, а не по плоским волнам. В этом случае из
правил отбора следует, что большинство вкладов обращается в нуль, а остав-,
шиеся вклады легко оценить, заменяя мультипольные поля в первым членом
их разложения по степеням кг. Отметим (см. ур. B25)), что при кг •< 1
Подробное изложение этого метода с приложением к радиационным перехо-
переходам в ядрах можно найти в книге: Д. Блатт, В. Вайскопф. Теоретическая
ядерная физнка. М., ИЛ, 1954 (гл. XII).

§ 31. ИЗЛУЧЕНИЕ ФОТОНА АТОМОМ. ДИПОЛЬНОЕ ИЗЛУЧЕНИЕ 51S
ных условиях наибольшая вероятность перехода получается,
для так называемых электрических дипольных переходов, когда
A/-l/x-/,J<l. АП = ПхПц = -1 B43)
(исключая /\ -f- /ц = 0)-
Далее следуют магнитные дипольные (А/ ^ 1, ДП = 1, /\ -f-
+ /и Ф 0) и электрические квадрупольные (А/^ 2, ДП = 1,.
Д + /ц Ф 0 или 1) переходы, порядок величины которых »
(&i?)~2 раз меньше электрических дипольных переходов.
Если выполнены условия для электрического дипольного из-
излучения B43), то мы можем записать
Грубая оценка этих матричных элементов
показывает, что слагаемое ЯП) значительно меньше Я1' и им
можно пренебречь. Для вычисления Я"> удобно ввести электри-
электрический дипольный момент электронов
D = eY.Rn. B44>
(Это векторный оператор, который мы в §§ XIII. 33 и XVII. 3-
обозначали Q<'> см. ур. (XVII. 35).)
Оператор D удовлетворяет уравнению
[D, #at] = le Z PJm.
n
Следовательно,
(ie/m) (X | E Pn | ц> = <A-1 (DHai - H«D) | ц> =
откуда F<1) == /m/fe (Я, | (D e) | p)/e и
»!*,*—S" I <*•!(*) I |i> P. B45>
Здесь удобно взять определенные магнитные квантовые
числа т*. и /Пц начального и конечного состояний и ввести в со-
соответствии с определением (XIII. 125) приведенный матричный
элемент <Я||/)||ц>. Если Dq есть q-я стандартная компонента
векторного оператора D, то согласно теореме Вигнера — Эк-
карта имеем
Чг 17*

•516 гл- XXI- КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
Поскольку (е/>) = ? е„Ц,, где е„ (<? = +, 0, —) есть стандарт-
ч
ные компоненты вектора поляризации (определение (XIII. 94)),
то окончательно получаем
B46)
'Если атом в начальном состоянии неполяризован и в конечном
состоянии поляризация не измеряется, то нам следует просум-
просуммировать по т„ и усреднить по т%, т. е.
Вычисления легко проделать, используя свойства симметрии и
«ортогональности коэффициентов Клебша — Гор дана (см. ур.
(В. 13в) и (В. 14а)), в результате получим
6яB/ц.+ 1) *
Как и следовало ожидать, это выражение не зависит ни от*а-
правления излучения, ни от поляризации испущенного фотона.
"Полная вероятность перехода 1-»-у в единицу времени полу-
¦чается после суммирования по двум состояниям поляризации и
.интегрирования по направлениям излучения, т. е. после умно-
-жения этого выражения на 8л
f<247>
§ 32. Комптоновское рассеяние при низких энергиях.
Формула Томсона
В качестве примера задачи рассеяния, отличной от приве-
приведенных в разделе II, но которая может быть решена теми же
¦методами, рассмотрим комптоновское рассеяние (рассеяние фо-
фотонов свободными электронами) [).
В начальном состоянии системы имеются электрон с импуль'
•сом Pi и фотон с импульсом ki и поляризацией е«. Такое состоя-
состояние представляется кет-вектором |г> е= [P,ft(E(>. Нас интересует
сечение рассеяния из начального состояния в конечное, которое;
содержит электрон и фотон с импульсами и поляризацией Pf,
k соответственно. Конечное состояние обозначим |/> *¦•
>. Энергия и импульс при рассеянии сохраняются.
') Для скалярного поля сечение рассеяния кванта поля на свободной ча-
•стице исчезает.

§32. КОМПТОНОВСКОЕ РАССЕЯНИЕ ПРИ НИЗКИХ ЭНЕРГИЯХ 517
Для вычисления сечения рассеяния при всех энергиях элек-
электрон следует рассматривать как частицу, удовлетворяющую
уравнению Дирака и взаимодействующую с излучением па за-
закону— eaA(R). В этом параграфе мы ограничимся рассмотре-
рассмотрением рассеяния в области малых частот ').
Пусть в начальном состоянии электрон покоится (Р,- = 0)
и энергия налетающего фотона достаточно мала, чтобы пере-
переданная электрону в результате рассеяния энергия была мала
по сравнению с его массой
(следовательно, kf « kt, Pf « kf). В этом случае можно ис-
использовать нерелятивистское приближение для электрона и
в качестве гамильтониана системы взять оператор
Н = Hq-\- Н ,
где
р
Согласно формуле B35) Н' есть сумма трех слагаемых #(|),
#(Н) и Я", которые определяются уравнениями B36а), B366)
и B37) соответственно.
Для вычисления сечения рассеяния воспользуемся форму-
формулами теории рассеяния (глава XIX). Ясно, что все оговорки,
сделанные в аналогичной задаче из § 14, остаются в силе и
в данном случае. Мы не будем повторять их здесь, а предполо-
предположим, как и в § 14, что формулы теории рассеяния применимы
при условии замены в этих формулах массы электрона т на
экспериментально измеряемую величину.
Непосредственное применение формализма теории рассеяния
сталкивается с дополнительной трудностью, которая связана
с невозможностью определить и отделить переменные центра
масс. Однако трудность эта только кажущаяся. Отделение дви-
движения центра масс играет в нерелятивистской теории столкно-
столкновений вспомогательную роль: в силу сохранения при столкнове-
столкновении полного импульса системы формулы становятся проще.
Можно сформулировать теорию рассеяния, не прибегая к отде-
отделению движения центра масс, тогда закон сохранения импульса
будет фигурировать в формулах явно.
Мы воспользуемся здесь такой формулировкой. Единствен-
Единственное изменение связано с определением амплитуды перехода
') В общем случае задачу можно решить таким же методом (см. Гейт-
лер, loc. cit.) и получить формулу Клейна — Нишины. Вычисления будут не-
несложными, но длинными. Их можно значительно сократить, если воспользо-
воспользоваться ковариантиои формулировкой квантовой теории излучения (см. Яух и
Рорлих, loc. cit.).
17 А, Мессиа

518 ГЛ. ХХГ. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
Ti-+f. Примем для Т формальное определение
Поскольку оператор Т инвариантен относительно трансляций,
то матричный элемент </|Г|г>.пропорционален б-функции, обес-
обеспечивающей закон сохранения полного импульса. Амплитуда
перехода 77+f определяется равенством
(f\T\i) = BяKб (Pf + kf-P{- kt) T,+r B48)
Множитель BлK учитывает принятую нормировку плоских
волн
(Р[Р') = BяKб(Р — Р').
При таких определениях сечение рассеяния дается общей фор-
формулой (XIX. 116).
Будем вычислять амплитуду перехода (f\T\iy, раскладывая
Т в ряд по степеням е и ограничиваясь только низшим нетри-
нетривиальным порядком, т. е. е2:
(f\T\i)=(f\H"U) +
+ (f | (ЯA> + Я<">) E_XHu + is (ЯA> + Я*1") | /> + О И. B49)
Из выражений B36а, б) и B37) видно, что каждое слагаемое
в правой части содержит множитель
prkf) *dR== Bя)з 6 (Pf + kf_p._ k.y
Это и есть упоминавшийся выше множитель, выражающий за-
закон сохранения импульса. Используя выражение B37), полу-
получаем
(f I H" \i) = Srr M \ e' (p*+*<-pf-*f>««, B50)
где k — {kikff2-Поскольку мы интересуемся только областью ма-
малых частот, то членами порядка k/tn по сравнению с единицей
пренебрегаем и можем считать
1цж kftt k.
Легко показать, что вклад второго слагаемого в правой ча-
части уравнения B49) порядка k/m по сравнению с вкладом пер-
первого слагаемого. Таким образом, в данном приближении
(в2 <С 1, k < m) имеем

§ 32. КОМПТОНОВСКОЕ РАССЕЯНИЕ ПРИ НИЗКИХ ЭНЕРГИЯХ 519
Следовательно, сечение рассеяния (см. ур. A16)) равно
^g± = 2я?з17^f|W/W) = ^ |(tyt) |\ B52).
Чтобы получить сечение рассеяния неполяризованных фото-
нов, следует усреднить по двум возможным начальным поляри-
поляризациям и просуммировать по двум конечным поляризациям.
Вводя обозначение 0 для угла рассеяния фотона (cos 0 =
= (kikf)/k2), получаем
неполяр
Интегрируя по всем направлениям излучения, приходим к фор-
формуле для полного сечения рассеяния фотонов
8я е4 ,OK.V
о т
Эти результаты хорошо согласуются с экспериментальными на-
наблюдениями.
Выражения B52) — B54) совпадают с теми, которые полу-
получаются в классической теории излучения1). В частности, для
полного сечения мы получили классическую формулу Томсона.
Такое совпадение результатов двух теорий убеждает нас в спра-
справедливости сказанного в § I. 5 о значении и пределах примени-
применимости классической теории эффекта Комптона. Очевидно, что
классическая теория не может учесть корпускулярный характер
излучения и тот факт, что обмен импульсом и энергией между
излучением и электроном осуществляется посредством квантов.
Но эта теория правильно предсказывает целый ряд характе-
характеристик, таких как среднее значение за единицу времени и на
единичный падающий поток переданного электрону импульса
(ур. B54)), угловое распределение и поляризацию рассеянного
излучения (ур. B52)), а также, при учете эффекта Допплера,
изменение длины волны рассеянного излучения (ур. A.5) и
A.6)).
Полное совпадение результатов двух теорий происходит
только в пределе малых частот, когда длина волны электромаг-
электромагнитного излучения l/k настолько велика, что процесс рассеяния
практически не зависит от внутренней структуры электрона.
Поскольку электрон является квантовым объектом, то его раз-
') В эти формулы не входит постоянная Планка Й. Каждая из формул
содержит множителем квадрат классического радиуса электрона г0 = ег/тс*.
Например, выражение B52) можно записать как г$со$,2а, где а — угол ме-
между направлениями начальной н конечной поляризаций (предполагается их
линейность).
17*

520 ГЛ. ХХГ. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
меры порядка 1/т, и эффекты, обусловленные его структурой '),
по порядку величины равны k/m. В нерелятивистском пределе
они определяются вторым слагаемым в выражении B49). С ро-
ростом энергии налетающего фотона квантовая природа элек-
электрона проявляется все отчетливее, становится все более суще-
существенной для описания процесса рассеяния и наблюдаются рас-
растущие и ярко выраженные отклонения от предсказаний класси-
классической теории.
ЗАДАЧИ И УПРАЖНЕНИЯ
1. Пусть Ф(г)—веществеииое скалярное поле, которое было введено в
разделе I, и мы хотим измерить интеграл от этой наблюдаемой по конечной
области. Точнее, рассмотрим интеграл
ф ss [ ф (г) Р (Г) dr,
где Р(г)—вещественная неотрицательная функция, интеграл от которой по
всему пространству равен 1. Положим
X (к) - J exp (fter) P (r) dr (х @) = 1).
Показать, что статистическое распределение Ф по вакуумному состоянию яв-
является гауссовым и что
¦dx.
16я3 (ц2 +:
В частности, если весовая функция Р(г) сосредоточена в области с лн-
нейными размерами а н ца < 1, то ДФ « 1/а.
Рассмотреть эту же задачу для электромагнитного поля и показать, что
2. Показать, что определенная в § 11 поправка к массе 6М с точностью до
второго порядка дается выражением, стоящим в правой части уравнения G6).
3. Рассмотрим задачу упругого рассеяния из § 14. Будем считать мишень
неполяризованной, и угол рассеяния обозначим 9: cos 9 = ktkflk2. Показать,
что во втором порядке бориовского приближения и в длинноволновом пре-
пределе (k(R) ^ 1) угловое распределение квантов при упругом рассеянии
пропорционально cos2 G и сечение рассеяния стремится к нулю в пределе
/е-»-0 (это свойство характеризует скалярную связь).
4. Рассмотрим резонансное рассеяние из § 15, используя введенные там
обозначения. Предположим, что момент импульса атомной системы в началь-
начальном состоянии |а) равен нулю, а момент импульса резонансного состояния
|Я) равен I. Показать, что если пренебречь вкладом А(аот), то амплитуда пере-
') Такие эффекты в классической теории по порядку величины равны
кеЦт — отношению классического радиуса электрона к длине электромагнит-
электромагнитных волн.

ЗАДАЧИ И УПРАЖНЕНИЯ 521
хода Т для процесса упругого рассеяния ki-*-kf дается формулой
где 9 — угол рассеяния, а ГЛ>а —вероятности радиационного перехода Х-»-а
(см. ур. (82)). В качестве следствия получить формулу упругого рассеяния
Показать, что эти выражения являются простым обобщением тех, которые
были получены для резонансного рассеяния частицы на центральном потен-
потенциале (ур. (X. 64) и (X. 65)), и что приведенные в § X. 15 н X. 16 обсуждения
понятий резонанса и метастабильного состояния применимы и в этом случае.
5. Пусть Aj(r) и Si{f) обозначают соответственно / и i компоненты по-
потенциала А (в радиационной калибровке) и поперечного электрического поля
Ж .. Доказать, что выполняются коммутационные соотношения
\$1 {г), А, (г')] = 4яг% (г - г'),
где
Ъц (г - г') = 6г/6 (г - г') —г( !
' ' дХ1дх\ \ы\г-г'
(9,, {г — г')—проектор на подпространство поперечных векторных полей).
6. Вывести для полного импульса свободного электромагнитного поля
формулу B20).
7. Показать, что для внутреннего момента импульса излучения G(I) спра-
справедлива формула
fcoxo'
(обозначения § 27). В частности, если Nk+ н Nk_ — обозначают число право-
и левополяризованиых фотонов с импульсом k (см. ур. B22)), то имеем
8. Доказать равенства B23) и B24).
9. 1° Пусть иш(г) —скалярное поле, которое преобразуется при враше-
ннях как сферическая функция К?* (9, ф), a V(r,p) — (полярный или аксналь-
иый) вектор, построенный из векторов г и р. Показать, что векторное поле
ULM(r), определяемое равенством
ULM <r)^V(r,- /V) иш (г),
где V — действующий на функцию uLM оператор, задает состояние с моментом
импульса (LM).

522 ГЛ. XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
(В силу этого утверждения определенные в § 29 векторные поляАА/т в
задают состояния с моментом импульса (/«))'.
2° Точно так же, как 3-компонентная волновая функция частицы спина 1
образует векторное поле, Bs + 1)-компонентная волновая функция частиц»
целого спина s образует неприводимое тензорное поле порядка Bs + 1). Пусть
Ху? (r> P) есть Ц-компочента неприводимого тензора порядка s, построенного-
из векторов г и р. Показать, что тензорное поле ULM(r), ц-компонента кото-
которого определена равенством
U™ (г) = *{•> (г, - /V) иш (г) (ц = - s, ..., + s),
задает состояние частицы спнна s с моментом импульса (LM).
10. Используя явные формулы для матричных элементов уравнений
B41а, б), показать, что вероятность излучения фотона обращается в нуль, если
спины начального н конечного состояний равны нулю @->-0 правила отбора).
(N. В. Это свойство становится очевидным, если вместо разложения по-
плоским волнам использовать разложение по мультиполям).
11. Вычислить вероятность за единицу времени радиационного перехода
2р->- Is в атоме водорода (ответ: и>2р-ч» = 6,25-10е сек~1).
12. Показать, что в длинноволновом приближении вероятность магнитно-
днпольного радиационного перехода А,—>- (Afce (обозначения § 30) дается фор-
формулой (см. ур. B45))
где М— полный магнитный момент атомной системы
(N. В. Эта формула дает правильный ответ для вероятности радиацион-
радиационного перехода, если ДП = +1 и /\ + /„^1; еслн же •'я.'^'ц^^1 то вкЛад
электрического квадрупольного момента отличен от нуля, и, вообще говоря,
нм нельзя пренебречь).
Вывести отсюда, что вероятность полного магнитного днпольного пере-
перехода дается формулой (см. ур. B47))
Показать, что для перехода 2s-»- Is в атоме водорода эта величина в нере-
лятивнстском приближении исчезает (т. е., еслн использовать волновую функ-
функцию теории Шредингера).
13. Вычислить сечение фотоэлектрического эффекта на основном состоя-
состоянии атома водорода. Предположим, что те* ¦< k < т. {т — масса электрона,
k — импульс налетающего фотона, ft = с = 1). Следовательно, переданная фо-
фотоэлектрону энергия достаточно велика для того, чтобы его конечное состоя^

ЗАДАЧИ И УПРАЖНЕНИЯ 623
яне можно было считать плоской волной, а его скорость достаточно мала для
того, чтобы можно было рассматривать его как нерелятивнстскую частицу.
Поскольку магнитное взаимодействие (член #<">) дает пренебрежимо малый
вклад, то находим
\'/z e4 cos2 ф
dQ v ^ k ) тг A-bcosG)*'
где ф, G обозначают соответственно углы между направлением излучения и
направлениями поляризации (линейной) н импульса налетающего фотона. Счи-
Считая в этой формуле v = 0, получаем результат полуклассической теории (см.
задачу XVII. 2).

ДОПОЛНЕНИЕ В1)
КОЭФФИЦИЕНТЫ ВЕКТОРНОГО СЛОЖЕНИЯ
И МАТРИЦЫ ВРАЩЕНИЯ
§ 1. Момент импульса. Основные обозначения
и принятые соглашения
В данном приложении приняты следующие условные обозначения, отно-
относящиеся к моменту импульса.
Постоянная Планка: Й = 1.
Составляющие момента импульса:/ — оператор момента им-
импульса, имеющий декартовы компоненты lx, Jy, lz
Коммутационные соотношения:
[/* /»1 = //* Ну. /«] = //* [/» 1х\ = Uу, B)
Базисные векторы в стандартном {J2h} -представлении
\xJM)
J2\tJM)=J(J + \)\tJM), D)
Jz | iJM) = M |
/± | tJM) = л/1(]+\)~М(М±\) | xl M ± 1), F).
(J — целое или полуцелое число ^0, М = —/, —7+1, ..., +/). Буквой т
обозначены квантовые числа, которые следует добавить к / и М для того^
чтобы получить полный набор; далее, там где это не ведет к недоразумению,
индекс т будет опущеи.
Раздел I. КОЭФФИЦИЕНТЫ КЛЕБША — ГОР ДАНА (К. — Г.)
И «3/Ч-СИМВОЛЫ
§ 2. Определение и основные обозначения
Пусть /i и /г — моменты импульсов квантовых систем 1 и 2 соответствен-
соответственно, а / — момент импульса полной системы, составленный из систем 1 и 2,
/-/, + /,. (8)
') Это Дополнение подготовлено в сотрудничестве с Дж. Горовицем. Для
более полного ознакомления с этими вопросами см. в первую очередь работу
А. Е. Эдмонс. Угловые моменты в квантовой механике (в сб.: «Деформация
атомных ядер», М., ИЛ, 1958), где приведены ссылки иа основные работы. Ре-
Рекомендуется также U. Fano, О. Racah. Irreducible tensorial sets, N. Y., Acade-
Academic Press, 1959

ВЕКТОРНОЕ СЛОЖЕНИЕ И МАТРИЦЫ ВРАЩЕНИЙ 525
Тензорное произведение B/i + 1) векторов системы 1
l/i«i> (/1 фиксировано, nti = — ji +/,)
с Х2/2+ 1) векторами системы 2
I /»/»я> (/г фиксировано, тг = — }г +/г)
дает B/j + 1) Bj2 + 1) собственных векторов операторов }\, j\, /1г, /^
I /imi) I /2»n*>, (9)
из которых мы можем получить посредством унитарного преобразования
\ )\ 2
{2/i + 1) B/2 + 1) собственных векторов операторов j\, )\, /2, /г:
р
\ )\ /2 /г:
(Ю)
G = l/i-/2l /1 + /1; M = -I, .... +1).
Определение. Коэффициенты Клебша — Гордаиа ') или коэффициен-
коэффициенты векторного сложения
являются коэффициентами унитарного преобразования
? I/1/2"» 1»»»)(Jijimlm2\JM).
Выбор фазового множителя2). Мы закончим определение век-
векторов в (9) н A0), фиксируя их относительные фазовые множители следую-
следующим образом:
(i) векторы \'!\Ш\), \j2m2) и \jij*JM) удовлетворяют соотношениям F);
(ii) (/'/2/1 (/1 — 1)\Н) —вещественная величина (>0);
«3/»-с нмволы Внгиера3):
~"'~2 A2)
i т% —г '
') Для коэффициентов Клебша — Гордана в литературе используются
различные обозначения. Приведем основные:
| I1J2JM) (Е. Кондон, Т. Шорт/.и. Теория атомных спектров.
М., ИЛ, 1949).
; mlm,2) (Дж. Блатт, В. Вайскопф. Теоретическая ядерная фн-
зика. М., ИЛ, 1954).
, (^- П" Виенер. Теория групп н ее применение в квантовой меха-
механике. М., ИЛ, 1961).
2) Такой выбор используется большинством автором, в частности, Вигне-
ром, Кондоном и Шортлн, Блаттом и Ванскопфом, loc. cit. и G. Racah. Phys.
Rev. 62, 437 A942).
3) Рака (см. предыдущую ссылку) использует обозначение ,
V (аЬс, ару) - (-1)а-й (а Ь с

526 ДОПОЛНЕНИЕ В
§ 3. Основные свойства коэффициентов К. — Г.
Вещественность:
(y,/2mim21 Ш)* = A\]гтхтг \ JM).
Правила отбора:
(П /л, + т2 = М;
(ii) | /i — /2 К ^ < /i + 1% («неравенство треугольника»).
Если эта два соотношения не выполняются, то QiJ2mim2 \ JM) = 0.
Симметрия: Символ
/7l /2 /3 \
\т.\ т2 ms/
(i) инвариантен при циклической перестановке столбцов;
(ii) умножается на (—l)i'+'»+'' при перестановке двух столбцов;
(iii) умножается на (—1)^+/!+/> прн одновременном изменении знака
Следствия:
A3a>
- ma | /,»»,>- A3б>
"»'« I /^> = A3в>
= (-l)'1+'2-J(iU2 - m, - m, | / - M). A3г>
Соотношения ортогональности:
+А
Z (/l/2mlm2|/A1>(/l'2'nl'n2|/'A1'> = 6//'eMM', A4a>
(l/i —/2l</</i + /2; — / < М < /)
(XI) A4б>
/ < < + /i; — /a
"
h \ (h h h
Щ ) \ Щ m2 m3
hy\ Ё (з/з+оГ1 h h)(h' h
2
Соотношение для сферических функций:
rB/, + l)Bfa+l)B*3+l)-lT (h h h\ (h h h \
L 4ji J lO 0 OJU m2 mj

ВЕКТОРНОЕ СЛОЖЕНИЕ И МАТРИЦЫ ВРАЩЕНИИ 527
отсюда следует
4jxBZ. )
L = \h-U\ M—L
X <V200 I LO) {lll2mim2 | LM) Y? (Q) = A7a)
V ( 1)мГBг, + 1)B/2+1)B^ + 1)|Т
. x(o о
§ 4. Методы вычисления
Рекуррентные соотношения. Приведем соотношения между ко-
коэффициентами К. — Г., аргументы которых отличаются на величины)
(i) Л/ = 0, ЛМ = + 1
V/ {/ + 1) — Af (A1 + 1) {jxhmxm2 I /Л1> =
1 V/i (/i + 1) — m, (mi + 1) (/,/2 m, + 1 m21 / л/ + l)
+ V/2 (/» + 1) - m2 (m2 + 1) </i/, m.ma+U/M+l). A8)
(ii) Д/ = 0, ДМ= —1,
V/ (/ + 1) - M (M - 1) </i/2m,m21
= V/i (/i + 1) - mi (wi - IH/1/2 Mi - 1 m2 I / M - 1} +
+ V/2 (/2 + 1) -m» (m2 - 1) {/i/V»i «2 - 1 I / M - 1). A9)
(iii) Д/=±1, ДЛ/ = 0,
Ao {jij2mim21 /Л1) = A+ Ци^пцтг \ J + 1 M) + A- (jij2mxm2 \ J — Ш), B0)
где
A = mm+M h Ut "'"/V' + («"« +«)
f,rv _ Л/Х2 _ M2Г [(/¦ + /2 + IJ - *2] W - (/i - /гJ] IT
Формула Рака:
a b
\ a p Y /
X V(a + a)! (a — aI (b + P)! F — P)l (c + YI (c — Y)l X
X 2 (~1)' I" (c ~ b + f + a)! (c — a + f — fi)! (a + 6 — с — t)\ X
где

528 ДОПОЛНЕНИЕ В
Суммирование пронсходит по всем целым значениям t, для которых фак-
факториалы имеют смысл, т. е. для которых аргументы факториалов положи-
положительны илн равны нулю @1 = 1). Число членов в этой сумме равно v+ 1, где
v — наименьшее из девяти чисел:
adz a, ft±P, c±Y>
a + b — c, b + с — а, с + a — b.
§ 5. Специальные значения и таблицы
Специальные значения
(i) Если J ц М принимают наибольшее значение, то
Oi/Wi/s I /1 + /2 /i + /2) = 1.
(ii) Если одно из / равно нулю, то
/ / ; q\ (—\)*~т
(JOmO | jm) = 1 или { ' ' . = .
V. tn — tn 0 / V 2/ 4" 1
если h + /2 + /j нечетно, то
(о о о) = 0' B3а>
если 2р ^ /i + h + 'а четно, то
(J о o)"(-|)i>vrro5(p-/,)»(p-/J.(p-/,). B3б>
(А. 'г. 'а — целые числа ^0, удовлетворяющие неравенствам треугольника).
Специальные случаи формулы Рака. Следующие формулы,
а также те, которые получаются при использовании соотношений симметрии,
дают коэффициенты К. — Г. в специальных случаях:
(i) mi = ± /ь нлн otj •= ± /г. или М = ± /:
, _ / B/ -
'¦ ' V Ц|+/1+/+1
(ii) одно из / есть сумма двух других:
если / = /i + it, то
(Л - m,)I (/2 + т2)! (/г -
B6)

ВЕКТОРНОЕ СЛОЖЕНИЕ И МАТРИЦЫ ВРАЩЕНИЙ
529
Та б л и ц ы «3/» -символов. Таблицы I—IV дают выражения для
символа
(] s U + e)
\ т ц (— т — ц)
1 3
как функции /йот для значений s = О, -^-, 1, —, 2;
Таблица I
Таблица Ф^ и <Dj t
77
лО ,
фоо— 1
1
?7
Таблица II
Таблица
s=l
ц = 0
е = 0
-2/п
- V2 (/ -
т)
-V2
е =
(/-
1
= 1
т-
М)
Таблица III
Таблица
3
S==-2
3
j — Зт
- уз 0 - /п)
3
е = Т
-V3(/-/n+ 1)
1
Таблица IV
s = 2
ц = 0
ц = 1
ц = 2
е = 0
2 [3/л2-/(/+1)]
Bm+l)V6(/-«)
V6 0 —«) (/— т — 1)
е=1
2ш л/&а—т + 1)
2 (/ - 2т)
— 2 V0' — т)
е = 2
V6(/-m + 2)(/-m+l)
- 2 V/ - т + 1
1

630 ДОПОЛНЕНИЕ В
Используя эти выражения, а также соотношения симметрии, мы можем
просто вычислить любые из коэффициентов К. — Г., для которых одно из /
1 3
равно 0,-~-, 1, -=- или 2.
Z 2,
В таблицах приведены значения функций Ф*е (]т), которые определяют-
определяются посредством соотношений
K
s (;' + e) \ , t\i+m I B/ 4- e — s)l (I "b m ~b t1 + e)l ^s
B7)
Раздел II. КОЭФФИЦИЕНТЫ РАКА И «6/»-СИМВОЛЫ
§ 6. Определение и основные обозначения
Сложение трех моментов импульса. Пусть / — полный мо-
момент импульса системы, которая состоит из трех отдельных частей, обладаю-
обладающих моментами /, /', /" соответственно:
В B/+ 1) B/'+1) B/" + 1)-мерном пространстве, натянутом на векторы
\тт'т") = \}т) \j'tn')\j"m") (/, /', /" — заданы; т, т', «" — переменные),
подпространство момента (JM) обычно имеет размерность, большую единицы
B/ и 2М — целые числа, четные или нечетные в зависимости от числа 2{j ¦'
гЬ/' + /"); min|/±/'±/"| ^^^/+
J
:——*
V
«) J'*J = g\g '+J"-J S)j >j"=g"J'ig"- J
Рис. 28. / = /' + /' + /''. Различные схемы сложения.
Следующие две схемы сложения дают конструкцию двух, вообще говоря,
различных систем базисных векторов нз этого подпространства1):
а) /' + / == g\ g' + /" = / (рис. 28, а) - векторы | (/'/) g\ \"; JM)
2 I тт'пП (Пт'т | в'ц'> <g'/"n'm" \JM).
mtn'm"
б) / + /" = Я". У' + в'-/ (рис. 28, б)-векторы 1/', (jj")g"; JM)
I /', 07") g"\ JM) -= ^ I mm'm")<jj"mm" | g"n"> </Y'm V
mm'»"
1*"
Можно перейти от одной системы к другой с помощью некоторого уни-
унитарного преобразования.
Определение «6/»-символов Вягнера | >.
Ui '! JsJ
') Здесь важен порядок, в котором складываются различные векторы.
При изменении порядка, например, векторов / и /" при сложении по схеме (а}
изменяется знак результирующего вектора.

ВЕКТОРНОЕ СЛОЖЕНИЕ И МАТРИЦЫ ВРАЩЕНИЙ
531
Эти символы связаны с коэффициентами упомянутого унитарного преоб-
преобразования посредством соотношений
</'. 07") g"; ш I (/'/) в'. Г; гм') =
B8"
'
B8)
= ? I г
g"
х
X VBg' + 1) B8" + 1) (-
Г'
i" J urf J
B9)
^-коэффициенты Рака1). Рака использовал коэффициенты
которые совпадают с «6/»-еимволами с точностью до знака:
/2
/i
C0)
Присоединенные коэффициенты. В выражениях для угловых
распределений иногда встречаются коэффициенты Z(LJL'J'\ jk) и Fx (LL'JxJi),
для которых имеются подробные таблицы и которые определяются соотноше-
соотношениями:
Z(LJL'J'\ /Я) = (-1) 2 "¦""' X
X VBL + 1) BL' + 1) B/ + 1) BГ + 1) BЯ + 1) ( J ^ J ) { {", ^' *}.
C1а)
i) (f _f
C16)
Коэффициенты F\ (LL'JiJ2) используются главным образом в тех случаях,
когда в результате реакции появляются частицы со спином 1 н не регистри-
регистрируется поляризация.
Присоединенный тетраэдр для
«6/» -символов. Чтобы избежать путаницы
при обращении с ^-коэффициентами и «6р-сим-
волами, удобно связать с каждым символом
\
, у
некоторый тетраэдр, каждое ребро
которого представляет один из шести моментов
импульса, входящих в этот символ (рис. 29).
В этом представлении каждая пара противолежа-
противолежащих ребер ассоциируется с двумя моментами
данного столбца, а три момента первой строки
соответствуют ребрам одной из граней тетраэдра.
Кроме того, каждая грань соответствует трем моментам импульса, один из
которых получен с помощью векторного сложения двух других, как это
следует нз определения «6/»-символов.
Рис. 29. Тетраэдр, ассо-
ассоциированный с символом
V '¦ 8'\
Xi" 1 8" У
') Racah, loc. cit. Знаковый множитель исчезает из двух предыдущих со-
соотношений при подстановке W вместо «6/»-символов. Однако *6/»-символы
имеют более простые соотношения симметрии (см. § 7).

532 ДОПОЛНЕНИЕ В
§ 7. Основные свойства «6/»-символов
Вещественность. Все «6/»-символы вещественны.
Правила отбора. Для того чтобы
f /1 h h \
\h h hi
три момента импульса, составляющие каждую грань тетраэдра, должны быть
таковы, чтобы каждой из них был векторной суммой двух других. Иными
словами, необходимо, чтобы элементы каждой тройки
(Ш»), UihJ3), (ЛШ.
(i) удовлетворяли неравенствам треугольника;
(ii) имели целочисленную сумму
(N. В. Отметим, что каждое нз шести / — целое, или три / одной и той же
грани — целые, или же два /, соответствующие противоположным ребрам,—
целые числа.)
Соотношение симметрии. «6/»-снмволы инвариантны:
(i) относительно перестановки столбцов, т. е.
f /i h h \ _ Г h h h \.
\h h hi l/j /i hi'
(ii) относительно перестановки двух элементов первой строки с двумя со-
соответствующими элементами второй строки, т. е.
f/i /i h\ ГА h h\
\h h hi l/i /i hi'
Иначе говоря, для задания «6/»-символа достаточно задать шесть момен-
моментов импульса и их относительное расположение иа" присоединенном тетра-
тетраэдре.
Основные соотношения между «6/» -символами и ко-
коэффициентами К.—Г. Следующие соотношения связывают символ
I / 1 I \ с коэФФиииентами К. — Г., которые составлены из троек
(/i/s/s). ihhh), (hJ2h), (Jihh)> соответствующих четырем граням присоеди-
присоединенного тетраэдра:
м,м,м,
h h\(h h h\(h Ji h\(>i h
-M2 mJ\M2 -Af3 тг)\М3 — Af, m2 J
C2)
(N. В. Фактически суммирование сводится к суммированию по двум ин-
индексам, поскольку Мат связаны.)
/»^ (h h h
h /i (A (ii /t lz\(h h h\ C3)
Мг -Af, m2) \тг m2 mt)\jl h hi'

ВЕКТОРНОЕ СЛОЖЕНИЕ И МАТРИЦЫ ВРАЩЕНИЯ 533
(N.B. Здесь индекс суммирования только один.)
U, * -М3)\М3 тг ~M
U
V Bi 4- П ( /[ h h\( h '* U Л ( h h h \ (Si)
(Л^.В. Суммы по М3 и m3 имеют всего лишь одно слагаемое.)
Соотношения Рака—Эллиота и соотношение ортого-
ортогональности:
\
\ я-1- (з5а)
}f,+l)B6+l) , C56)
a b x\ (с d хЛ , 1 ,„с.
С rf /На Ъ ffJ-VS/TT' C5B)
\ = { ПИ
b a li \e a di\f b с
H« *
§ 8. Формула Рака, таблицы
Формула Рака:
X
(-!)<(<+ 1I
/« /Ь /2. /3, /l> /j, /з) '
t
где
Л {t, /i, • • •. /з) = С - /i - /2 - /зI (< - /i - /2 - /з)! X
X(t-Ji-h-h)\ V-Jy-h-W (/,+/, + /,+/,-О! X
X (/i + /з + /2 + /з - 01 (/» + /1 + /з + /1 - О,
Определение Д(абс) и соглашеиие о суммироваиии то же самое, что и
в формуле B2). Число слагаемых в ^ равно 1 + а, где а—иаимеиьшее из
t
двенадцати чисел:
Л+ /»-/», h + h-h, Ji + U-h, Л + /2-/3.
/» + /» — /ь /2 + ^3-/1, h + 1% — Ji, Jt + h — Ju
/a + /1 — /a» /»+ /i — /2. /3 + /1 — /2, /з + /i — /2-

534 дополнение в
Специальные случаи-
(i) одно из / равно нулю
(ii) одно из / равио-^-
LB/+l)B/ + 2)B/+l)B/ + 2)
C8>
Л;
C9)
Раздел III. «9/»-СИМВОЛЫ
§ 9. Определение и основные свойства
Сложеняе четырех моментов импульса и определе-
определение «9/» - с и м в о л а. Пусть полный момент импульса J относится к систе-
системе, составленной из четырех отдельных систем, моменты которых соответст-
соответственно равны /ь /2) Is, /4:
Й
4
В JJ B/j 4- 1)-мерном пространстве, натянутом на векторы
4
5 Ц I hml) (h ~ const, mi меняются),
г=1
следующие две схемы сложения ведут к двум различным системам базисных
векторов подпространства с моментом импульса (JM):
а) /i 4" /г = /12> /з ~Ь jt= ^з4> /i2 4" /34 = J*
векторы | (/i/2) /12, (/3/4) /34; JM);
б) h 4- /з = /13» /г4-/4 = /24. /13 + J24 = h
векторы | (/i/з) /i3, (/2/4) /24; 1М).

ВЕКТОРНОЕ СЛОЖЕНИЕ И МАТРИЦЫ ВРАЩЕНИИ 535
«9/»-символы Вигнера при этом определяются как коэффициенты унитар-
унитарного преобразования от одного базиса к другому:
«Ш'м. (Ш/.4! /ЛЦ(ШЛ„ (Ш/м; /'М') —
Г /I /2 /|2 ")
Ah и 1»Л.
Ul» /24 /J
X
D0а)
Можно также определить «9/»-символы следующим образом:
<[(Ш /12, /з] /,м/4; /Af | [(/«/,) /42> /,] Imh\ J'M')*=
. f /* /12 /l
< /42 /з /423
I /« /ш /
X VB/i2+ 1) B/.23 + 1) B/42 + 1) B/423 + 1) \ /42 /3 /423 \ . D06)
Используется также обозначение
-I
Связь «9/» -символов с «3/» -символами:
(h /2 /12 \ f/i /2 /12 "I
/3 /4 /34 )=»< h /4 /34 >.
/ll /24 // Ull /24 /J
//13 /24 /\{A (
V Af,3 Af24 М J 1 ^3 '
/
^ 4 La Кгщ т2
/13 /24 J ) m,mtm3m,
( h h /34 \ ( h h h* \ ( h /4 /24 \ ( In hi / \ D0b)
\m3 пц MuJKnti m% M]3 / \ m2 m4 Af24 / V M12 M34 Afj'
Соотношения симметрии. Символ
{h /2 /з)
< /4 /б /. >
I/? /8 h)
(i) при перестановке двух строк или двух столбцов умножается
9
на (-1)*, где R=Y, 7<;
<-1
(ii) инвариантен при зеркальных отражениях относительно диагоналей.
Соотношение ортогональности:
B/I3+1) B/.+1) к / / /з ;• 4 -B/1д;;Bз;3;4+1).
Ul3 /24 /J 1/.3 /24 /J
Выражение «9/» -символов через «6/» -символы:
D„

536
ДОПОЛНЕНИЕ В
Случай, кеда одно из / равно нулю:
I a a' 0 I VB/ + 1) Bg + 1) l/« /3 g
Раздел IV. МАТРИЦЫ ВРАЩЕНИЯ
§ 10. Вращения. Операторы вращения, /^-матрицы
а (ф) — вращение иа угол ф вокруг оси и,
& (<*Р\) — вращение на углы Эйлера (а, р, \),
Я (apY) = &z (Y) ^а (Р) ^г (а).
D2>
D3>
Операцяи, иаписаниые в правой части равенства, выполняются в порядке-
справа налево (см. рис. 30).
Рис. 30. Углы Эйлера a = (Оу, Ои), р = (Oz, OZ), у = (Ои, OY).
Присоединенная матрица: матрица преобразования координат-
векторов (обозначена той же буквой Ш, что и само вращение).
Если V(Vu V2> Vi)—некоторый вектор, а V' (у[, V2, F3) — его преобра-
преобразование при вращении 91, то имеем:
Vf=9liiVj, 91ц — элементы присоединенной матрицы.
(Следствие. Если А/ есть преобразование единичного вектора а^
вдоль /'-й оси (/' = 1, 2, 3), то получим:
. 91ц = (аи
D4>
/
I
\
cos v cos p cos a — sin у sin a
cos у cos p sin a + sin y cos a
— cos y sin P
— sin \ cos p cos a — cos \ sin a sin P cos a\
— sin у cos p sin a + cos у cos a sin P sin a I.
sin у sin p cos p /
D5)
Оператор вращения. Унитарный оператор R, примененный к век-
вектору |), задает его преобразование при вращении 91

ВЕКТОРНОЕ СЛОЖЕНИЕ И МАТРИЦЫ ВРАЩЕНИИ 53Г
Если Q — наблюдаемая квантовой системы, то
. D7).
Если В &ш (В*, Ву, Bz) есть векторный оператор, то (В< гш Bat)
x )=^,/В/. D8)
(Л/. В. Здесь фигурирует преобразование, обратное к 5?, а ие само #.)
Применение D8) к преобразованию компонент момента импульса / при-
вращении 5?(сфу) Дает
RJ±R~l = е*" [±±pL **t*I± _ ±=™± e±<% - sin p/J, D9a).
Я/./Г1 = -i- sin P (e-ia/+ + e'a/_) + cos р/г. D96)
Выражение через составляющие полного момента
импульса /. Бесконечно малое вращение:
Яв (е) - 1 - ie (/ «) (е<1). E0)
Конечные вращения:
<(/), E1).
'P'ffe-W*. E2)
Соответствие между вращениями и операторами вра-
вращения. Взаимнооднозначное соответствие, существующее между бесконечно
малыми вращениями и операторами R, близкими к 1, может не иметь места
в случае конечных вращений.
В общем случае любому конечному вращению Я, соответствуют два опе-
оператора R' и R", удовлетворяющие уравнению
R" = DR'.
где оператор D определяется так:
+ 1, если / — целое,
— 1, если / — полуцелое.
Для равенства R' = R" необходимо, чтобы пространство векторов состоя-
состояния было образовано векторами, отвечающими только целым значениям I.
Пусть (aPv) и (otiPiYi) — два набора углов Эйлера, определяющих одно
и то же вращеине (уравиение (XIII. 42)). Тогда
R (а,Рт) = Z>"a+'l3+nY# (apv). E3)
Матрицы вращевий /?(/)(aPv). Это матрицы порядка BУ + 1) с
элементами
Ялш< =*(JM\R (aft) IW) = (JM| е-ш* е~{^и e~W*| /Af'). E4)
Векторы |Ш) (/ фиксировано, Af = —/, ..., +/) есть собственные век-
векторы операторов Р и /*, которые связаны друг с другом соотношениями F).

.538 ДОПОЛНЕНИЕ В
Матрица /¦</>(Р):
г(/) (Р) = RW (О, р\ 0),
г{мм' (Р) s </M I e"'3/" I 'М'>, E5)
«$*' («PY) = е"'ал1 rg>M, (Р) е-'^ . E6)
§ 11. Основные свойства матриц R{J)
Обратная матрица:
[/?<'> (aPv)]"' = R{t) (-Y. -P. -«)¦ E7)
Определитель:
det #<y> == 1. E8)
Вращение на 2я:
/?'a/)Bn) = (-lJ/. E9)
Каждому набору углов Эйлера соответствует единственная матрица /?(/).
Каждому вращению 91 соответствует единственная матрица /?(/>, если
.1 — целое, и две матрицы, отличающиеся знаком, если / — полуцелое.
Вещественность: г(/)(р) — вещественная матрица.
Вращения на угол я вокруг координатных осей. Обо-
Обозначения: X, Y, Z — операторы вращения на угол +я вокруг осей Ох, Оу, Ог
соответственно:
*(—l J/. F0)
= е~ш\1-М), Х$м,=*е~ш6м_м,. F1)
) = (-\)}-M\J-M), Y$M,=*(-1I+M6M_M,. F2)
Z\JM) = e-^\JM), г$м,=*е-'"мЬмм,. F3)
Преобразование оператора момента при вращении Y:
¦Следовательно,
K/W = /?">*. F4)
Соотношения симметрии, следующие из F2) и F4):
$ (-ПМ-М'г%_м,. F5)
^)М-М'^м-М'- F6)
Унитарность и соотношения ортогональности: RV>~1
~= /?(/)+, отсюда получаем соотношения унитарности
F7)

ВЕКТОРНОЕ СЛОЖЕНИЕ И МАТРИЦЫ ВРАЩЕНИЙ 539
Используя соотношения симметрии, получаем соотношения ортогональности
S, tsJ+M р(П г>(/) _/ П/+М'л
(—1) КмМ'К-М-М" — (—1> °М'М">
М F8)
У 1> 1<М'МК-М" -М —- ( ' I °М'М"-
м
Формулы композицяи и ред.укции. В следующих формулах
матрицы R^l\ /?"г>, /?(/> относятся к одним и тем же углам Эйлера.
Разложение тензорного произведения
^m'L *»»'™ ^ Z
mlml m2m2 l = \U-h\M,M'=-l
Формула композиции:
<V Z Z {/.^«.^ I ^) ^\mf{^m'2 {hiA«h I ^')- G0)
В частности, если / = /i + /»> то
§ 12. Вычисление матричных элементов Rmm'
Основные методы вычисления. Если матрица г(/)(Р) известна,
то матрицу /?(/)(аР\) легко получить нз соотношения E6). Матрица г(/) ве-
вещественная, унитарная, обладает свойством симметрии F5)
Поэтому нужно только знать матричные элементы, соответствующие М Гз= О
и М Г2= М', чтобы получить все остальные. Для этого мы можем:
а) вычислить их непосредственно с помощью приводимой ниже формулы
Вигнера;
б) получить их с помощью формулы G0) для композиции г '' г ' с
меньшими значениями момента импульса; в частности, все матрицы ги) могут
быть получены одна из другой, начиная с г(|/2);
в) получить нх друг из друга, используя рекуррентные соотношения, вы-
вытекающие нз уравнений D9).
Формула Вигнера. Введем обозначения
1 = cos — Р, г] = sin — р.
Получаем
<) у п
ММ' /-л ( ' (J + M — t)\(J — M' — t)\t\(t—M
-M'-2t 2t~M+M'
В даииом случае при суммировании используется то же соглашение, что и в-
формуле B1). Число членов в ? равно 1 + т, где т — наименьшее из четы-

540
ДОПОЛНЕНИЕ В
рех чисел / ± Af, / ± М'. По отношению к переменным 1 и т) выражение г$и
есть однородный полином степени 2J.
Частные случаи формулы Вигнера:
г(/) =(— \I~мг^1 =/!' =(—I)/-A1'
r-M -J ¦
¦v
(/ + M)! (/ — M)!
-M
G3)
r(/)
Случай /= 1/2:
2
()
rI-I
1 -f'
Pe 2
e sin-ре 2
G4)
(в этом выражении верхняя и нижняя строки соответствуют Af = — и —т-,
этим же значениям соответствуют левый и правый столбцы).
§ 13. Целые значения / (/ =/) и преобразование
сферических функций при вращениях
Случай / = 1
.A)
(Р)-
COS?
-j V2
i(l-cosp)
G5)
(В этом выражении расположенные сверху вниз строки соответствуют
.М = +1, 0, —1; расположенные слева направо столбцы соответствуют тем
же значениям М.)
Преобразование сферических функций при враще-
вращении. Пусть <в е= (8, ф)—сферические координаты единичного вектора v от-
относительно координатной системы Оку г
(Oi = sin 9 cos ф, i>2 = sin 9 sin ф, Vz = cos 9).
Q ss (8, Ф)—сферические координаты того же вектора о относительно
системы OXYZ.
(afry) — углы Эйлера вращения, переводящего систему Охуг в систему
OXYZ1).
1) Для устранения произвола в выборе углов Эйлера мы потребуем вы-
выполнения дополнительных соотношений
0<а<2я, 0<р<я, — я <-у < + я.
(При таком выборе система OuzZ является правой.) Тогда:
(i) сферические координаты оси OZ в системе Охуг есть (р\ а);
(ii) сферические координаты оси Ог в системе OXYZ— (Р, я — \).

ВЕКТОРНОЕ СЛОЖЕНИЕ И МАТРИЦЫ ВРАЩЕНИЙ 54Г
6 и ф — однозначные функции от 9 и ф, в которые а, р, у входят в ка-
качестве параметров.
о)! s (9i, (pi) —сферические углы в системе Охуг вектора x>i = Я~*х>, ко-
который при вращении Я(а$\) преобразуется в вектор v. Справедливо равен-
равенство @i = Q.
Сферическая функция У{"(со) соответствует кет-вектору \1т) в пред-
ставленви {со}:
уу»(и)«<(в| 1т).
Вращение Я(а$у) преобразует этот вектор в вектор R(a§y) \lm), состав-
составляющие которого в направлении вектора v равны составляющим \1т) по на-
направлению V\,
Y? (Q) = <co1|/7n) = (co|i?|/ffi>;
отсюда следует формула преобразования сферических функций при вращении
!?(?)= ? KJ1'<»)*?„ (еру). G6)
т'*—1
Скалярное произведение и теорема сложения. Пусть v
и v' — два единичных вектора, со и со' — соответствующие им сферические ко-
координаты относительно системы Охуг, Q, Q' — сферические координаты тех же
иекторов относительно системы OXYZ. Соотношение G6) и унитарность дают
? Y? (О) КГ (Q0 = Z Y? (M) YT (ш')- G7)
т т
В частности, если х>' направлен вдоль оси OZ, то получаем теорему сло-
сложения
1-±± У? (Q) - 2±± Pt (созв) = % Y? <в- ») УГ (P. «)• G8)
m-n—l
Выражение г^т, через cos ft и sin ft. Для / целых:
(i) если (—\)m+m =+1, то r^m, — полином по cos P степени I,
(ii) если (— \)m+m =— 1, то r^'m/= sin ft X (полином по cos p степени
В частности,
Выражения для #^т, при /и или т' = 0:
TT У™(Р> а)' (80а)
(-Dm <\/-2ПГГ Y™(р- Y)- (80б)
(cosp). (80в>

S42 ДОПОЛНЕНИЕ.
Раздел V. НЕПРИВОДИМЫЕ ТЕНЗОРНЫЕ ОПЕРАТОРЫ
§ 14. Определение и основные свойства
Определение. Тензорный оператор — совокупность операторов, лиией-
яо преобразующихся друг через друга при вращении.
Неприводимый тензорный оператор — набор нз BЙ+1) операторов
Тц (ч = —k, ..., + k) представляет собой, по определению, стандартные ком-
компоненты неприводимого тензорного оператора Г*** порядка k, если при враще-
вращении они преобразуются по формуле
Векторный оператор — неприводимый тензорный оператор порядка 1. Если
Vx, Vy, Vz — его компоненты относительно осей Охуг, то стандартными компо-
компонентами являются
Скалярный оператор — неприводимый тензорный оператор порядка 0.
Коммутационные соотношения с/
Г] т(к)~\ л/и (и i i\ п (n _i_ i"\"Т&) ГЯОяЧ
[/2, Г^'] = ^Г^'. (826)
Эрмитово сопряжение1)
g(fc)__y(fc)+ если $№)__/ j\<7 y(ft)t /gq\
Основное свойство (Вигнер — Эккарт)
{XIМ | r<f> | tVm'> = (/~1), (т/|| T(ft) II т'/> (/йЛ!^ | /ЛО =
-м J L'-} (84)
По определению (т/||Г(*)||т//') —редуцированный матричный элемент2).
Сопряженное соотношение (k — целое)
'). (85)
') Мы принимаем здесь определение Рака (loc. cit.). При таком определе-
определении сферические функции Y™ образуют эрмитов тензорный оператор порядка /.
Отметим, что тензорное произведение (определенное ниже) коммутирующих
неприводимых эрмитовых тензорных операторов в общем случае нёэрмитово.
Для того, чтобы оно стало эрмитовым, мы должны модифицировать опреде-
определение эрмитова сопряжения и заменить (—1)' на (—1) *+'. При новом опре-
определении сферические функции нечетного порядка антиэрмитовы.
(N. В. Наше определение эрмитова сопряжения применимо также к тен-
тензорному оператору полуцелого порядка, если множитель (—1)' записывать
«ак е'"я<0
г) Определение принято такое же, как у Рака (loc. cit.).

ВЕКТОРНОЕ СЛОЖЕНИЕ И МАТРИЦЫ ВРАЩЕНИЙ 543
Специальные тензорные операторы.
Единичный оператор
(а!\\ а'У) = 6аа,6/у, УгТТТ.
Оператор полного момента импульса
§ 15. Тензорное произведение неприводимых
тензорных операторов')
Определения. Пусть У'¦ , V — неприводимые тензорные операто*
ры порядка ku ki соответственно. По определению T(ft'' <8> U^*1 — набор Bkt +
+ 1) Bйг + 1) операторов T^U^ (не обязательно линейно независимых).
Это (приводимый) тензорный оператор.
у(Ю gj, Jy(fti) g) {/<*')]^ г тензорное произведение порядка К, есть непри-
неприводимый тензорный оператор порядка К с компонентами
VQ ' = Z (*lMl<72 | Щ T^UM (86)
(обязательно должны выполняться неравенства |й, — Й2|^ К ^ ^ж +
Если Й1 = А2 = k, то определено скалярное произведение2)
S ^(T^V{k)) = 2 (-D* rf^'i^- (87)
(N. В. )
Выражение для редуцированных матричных элемен-
элементов. Допустим, что мы имеем квантовую систему, состоящую из двух систем 1
и 2 с моментами импульса 1\ и /2 соответственно (J = Ji + Jt).
|ti/[AJi) —базисные векторы системы 1,
|тг/г-Мг) —базисные векторы системы 2.
Г'6'\ ?/'*"'—неприводимые тензорные операторы, действующие только на
переменные систем 1 и 2 соответственно.
у (К)—тензорное произведение порядка К в соответствии с определе-
определением (86).
В стандартном представлений {т^/]/^/2/.,) редуцированные матричные
элементы V"" даются формулой композиции
') Во всех следующих формулах мы ограничиваемся тензорными операто-
операторами целого порядка.
^ При таком определении скалярное произведение двух векторных опе-
операторов (VW) дается в соответствии с обычным определением выражением
VxWx + VyWy + V*WZ.

544 ДОПОЛНЕНИЕ В
Частные случаи, когда «9/>-символ сводится к «б/»-символу:
2T2 ''2 2
X (_!)/'+/.+/.+* VB/ + 1) B7' + 1) ( /] k }Л, Щ
4| *
j}, (90)
t;t^/^> - ь„,ьмм, (_i
; f
•'г ' y2
Случай Г((() =
(J1J2J + ' II¦/1IIJ
27+ 1
¦ у [/i (Л + l) + / (/ + l) - h (h + 1I V777T1T'
y (/, + /,). d-y
12d К / < 2S.

ДОПОЛНЕНИЕ Г
ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП
§ 1. Введение
Уравнения движения исследуемых в квантовой механике систем часто ока-
оказываются инвариантными относительно некоторых групп преобразований или,
иначе говоря, рассматриваемые наблюдаемые имеют особенно простые транс-
трансформационные свойства по отноЕгению к этим группам. Методы теории групп
позволяют получить все следствия, которые вытекают из существования этих
свойств симметрии.
В действительности, при наличии достаточно богатой интуиции и опреде-
определенного навыка в обращении с операторами, часто удается использовать свой-
свойства симметрии без явного обращения к теории групп. Многие физики пред-
предпочитают поступать именно так, несмотря на то, что это означает необходи-
необходимость время от времени переоткрывать в каждой конкретной задаче «хорошо
известные» результаты теории групп, которые необходимы для соответствую-
соответствующих выводов. Однако в ряде разделов физики требуемая доза интуиции и на-
навыков столь велика, что честное и добросовестное использование теории групп
неизбежно. Даже в тех случаях, когда имеющиеся симметрии не столь слож-
сложны, ссылка на теорию групп, хотя и не является неизбежнрй, позволяет проще
сформулировать задачу и предсказать ряд свойств ее решения.
Данное приложение знакомит читателя с элементами теории групп и мо-
может рассматриваться как введение к более подробным работам на эту тему1).
В приложениях обсуждаются основные понятия и результаты теории
групп, которые наиболее часто используются в квантовой механике. Практи-
Практически все доказательства опущены, хотя большинство из них, особенно в раз-
разделах I н II, весьма просты.
Раздел I. ОСНОВНЫЕ ПОНЯТИЯ
§ 2. Определения
Группа. Множество ?? элементов а, Ь, с, ... образует группу, если вы-
выполняются следующие условия:
') Мы отсылаем читателя, в частности, к монографиям: Е. Вигнер. loc. cit.
стр. 525; Б. Л. Ван дер Варден. Методы теории групп в квантовой механике,
Харьков, 1938. О непрерывных группах см. G. Racah. Group Theory and Spec-
troscopy, Princeton, 1951 (см. перепечатку в препринте ОИЯИ, R-1869, Дубна,
1964). В настоящее время на русском языке имеется большое число книг, как
по теории групп так и по ее приложениям. Помимо ссылок, указанных авто-
автором, можно рекомендовать для более подробного ознакомления следующие
книги, посвященные изложению методов теории групп и их физических при-
приложений: М. И. Петрашень, Е. Д. Трифонов. Применение теории групп в кван-
квантовой механике. М., Наука, 1967; Г. Любарский. Теория групп и ее применение
в физике. М., Наука, 1958; М. Хамермеш. Теория групп и ее применение к фи-
физическим проблемам. М., Мир, 1966; Сб.: Теория групп и элементарные части-
частицы. М., Мир, 1967. (Прим. переводчика.)

546 ДОПОЛНЕНИЕ Г
(i) произведение любых двух элементов также принадлежит множеству &
если ') а е= 9 и Ь <= 9, то 2) sis?:
(ii) среди элементов множества 9 имеется единичный элемент I
I е 9 такой, что для всех as?, la = al = а;
(iii) каждый из элементов имеет обратный, е-1, принадлежащий множе-
множеству 9
если а е!? существует а~' е^ такой, что a-'a = aa-' = /;
(iv) произведение элементов ассоциативно
(аЬ) с== a (be).
Конечная группа. Группа, имеющая конечное число элементов N,
называется конечной. Число N называется порядком группы.
Примеры. Группа пространственных отражений есть конечная группа
порядка 2. Двумя ее элементами являются тождественный элемент / и отра-
отражение относительно начала координат s; s2 = /. Группа перестановок п объ-
объектов 5Рп есть конечная группа порядка л!.
Непрерывная группа. Группа, имеющая бесконечное число эле-
элементов, которые зависят от одного или нескольких параметров, называется не-
непрерывной группой.
Примеры. Группа вращений в пространстве 91ъ\ группа пространствен-
пространственных трансляций.
Абелева группа. Если все элементы группы коммутируют
ab = Ьа для любых аи te^,
то группа называется абелевой, или коммутативной группой.
Примеры. Пространственные отражения, пространственные трансляции,
вращения вокруг оси Ог.
§ 3. Классы сопряженных элементов
Сопряженные элементы. Два элемента а и Ь группы & назы-
называются сопряженными друг другу, если существует элемент хе? такой, что
Ь ~=хах~1.
(N. В. Элемент х не единственный.)
Если Ь сопряжено а, то и а сопряжено Ь, так что сопряжение — рефлек-
рефлексивное соответствие. Более того, если два элемента а и с сопряжены элемен-
элементу Ь, то два элемента а и с порознь сопряжены между собой.
Класс сопряженных элементов. Множество элементов груп-
группы 9, сопряженных данному элементу а, называют классом сопряженных эле-
элементов, или просто классом группы 9. Элемент а принадлежит определяе-
определяемому им классу.
Класс элементов, сопряженных 6, и класс элементов, сопряженных а, сов-
совпадают, если Ь сопряжено а, в противном случае эти классы не имеют общих
элементов. Каждый элемент группы 9 принадлежит вполне определенному
классу, а вся группа может быть разбита на классы сопряженных элементов.
') Запись a s 9 означает: элемент а принадлежит множеству 9.
2) Преобразование, обозначаемое ab, состоит в последовательном приме-
применении преобразования а к результату действия преобразования Ь. Преобразо-.
вания ab н Ьа в общем случае различны.

ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП 547
Если данный элемент группы 9 коммутирует со всеми элементами группы,
то он образует класс сам по себе. В частности, единичный элемент / образует
класс сам по себе.
Пример. Множество вращений 52(<р) на один и тот же угол ф, которые
различаются только направлением оси вращения, образует класс группы Sl3.
Каждому значению угла ф@ ^ ф < it) соответствует свой класс этой группы.
§ 4. Подгруппы
Определение. Множество Ж называется подгруппой группы 9, если
оно является группой, все элементы которой содержатся в 'S.
Примеры. Вращения вокруг осн Ог образуют подгруппу группы 5Е3;
сдвиги, параллельные оси Ог, образуют подгруппу группы пространственных
трансляций.
Класс смежности. Если х — элемент группы 9, то, используя про-
произвольный элемент h подгруппы Ж, мы можем образовать новый элемент xh.
Обозначим множество всех элементов, построенных таким образом, хЖ.
Имеется взаимнооднозначное соответствие между элементами из Ж и элемен-
элементами из хЖ.
Следует различать два случая:
(а) если х е Ж, то хЭв совпадает с Ж;
(б) если хфЖ, то множество хЖ не образует группу, оно называется
левым классом смежности подгруппы Ж.
Правые классы смежности Жх определяются аналогично. В дальнейшем
мы будем рассматривать только левые классы смежности. Очевидно, что пра-
правые классы смежности имеют те же свойства, что и левые.
Два класса смежности Х\Ж и х?$ё либо совпадают, либо не содержат об-
общих элементов вовсе, в зависимости от того, принадлежит или не принадле-
принадлежит элемент x^ixi подгруппе Ж.
Каждый элемент из 9 принадлежит либо подгруппе Ж, либо одному из
классов смежности Ж. Подгруппа Ж и ее различные классы смежности со-
составляют всю группу 9.
Подгруппы, сопряженные подгруппе Ж. Если Ж — подгруп-
подгруппа группы 9, а х — элемент 9, не принадлежащий Ж, то множество хЖх~1
также является подгруппой в 9 и называется подгруппой, сопряженной с Ж
(N. В. Если х s Ж, то хЖх~1 совпадает с подгруппой Ж.)
Сопряженные с Ж подгруппы не обязаны различаться между собой или
быть отличными от Ж.
Инвариантная подгруппа, фактор-группа. Подгруппа Ж
называется инвариантной подгруппой группы W, если Ж совпадает со всеми
сопряженными с Ж подгруппами
х при всех х<^9.
Эквивалентное определение. Подгруппа группы 9 является ин-
инвариантной, если ее элементы полностью исчерпывают элементы одного или
нескольких классов сопряженных элементов.
(N. В. Второе определение особенно полезно прн описании всех инвариант-
инвариантных подгрупп данной группы.)
Если Ж — инвариантная подгруппа, а хЖ и уЖ — два ее левых класса
смежности, то произведение элемента из хЖ на элемент из уЖ принадлежит
классу смежности ухЖ
(хЖ) = (ухЩ.
(N. В. Если Ж — инвариантная подгруппа, то хЖ = Жх.\

548 ДОПОЛНЕНИЕ Г
Множество, образованное инвариантной подгруппой и всеми ее классами
смежности, образует группу, в которой 36 является единичным элементом.
Эта новая группа называется фактор-группой '3136 группы 3 по 36.
Пример. Группа ?Фп четных перестановок п объектов является инва-
инвариантной подгруппой в Уп. Она имеет одни и только одни класс смежности —
множество нечетных перестановок, так что фактор-группа состоит из двух
элементов.
Простая и полупростая группы. Группа называется простой,
если единичный элемент является единственной инвариантной подгруппой в
ней.
Пример. Группа пространственных вращений.
Группа называется полупростой, если единичный элемент является един-
единственной абелевой инвариантной подгруппой.
Пример. Группа ^„.
§ 5. Изоморфизм, гомоморфизм
Изоморфизм. Две группы, 'S и §, называются изоморфными, если су-
существует взаимнооднозначное соответствие между их элементами, сохраняю-
сохраняющее закон умножения, т. е.:
(i) каждому элементу gi группы & соответствует один н только один эле-
элемент gi из §, и наоборот;
(И) если g,g, = gk, то gigj = gk.
Примеры. Преобразования симметрии равностороннего треугольника
образуют группу, изоморфную ^"з-
Гомоморфизм. Если соответствие между элементами групп $ и § не
взаимнооднозначно, то эти группы гомоморфны.
Точнее, группа 'S гомоморфна 9, если:
(i) каждому элементу gt группы 9 соответствует один и только один эле-
элемент gi группы §, а каждому элементу группы § соответствует по крайней
мере один (а возможно, и большее число) элемент группы 9;
(И) нз gtgj = gk следует, что gig, = gk.
Если 9 имеет инвариантную подгруппу 36, то $ гомоморфна фактор-груп-
фактор-группе 3/Ж
Если 3 гомоморфна §, то множество 36 элементов из 9, гомоморфных
единичному элементу В группы §, образует инвариантную подгруппу в $, а
множество элементов из 9, гомоморфных заданному элементу из %, отлич-
отличному от В, образует класс смежности в группе $; фактор-группа S/3SS изо-
изоморфна §.
Раздел II. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ
§ 6. Определения
Группы линейных подстановок. Произведение квадратных
матриц ассоциативно. Если множество п X п матриц удовлетворяет аксиомам
(i), (ii) и (ш), определяющим группу, то эти матрицы образуют некоторую
группу G.
Каждая матрица представляет некоторый линейный оператор G и-мер-
ного векторного пространства &п и, следовательно, определяет линейное пре-
преобразование векторов этого пространства. Если |1), |2) \п) — п базис-
базисных векторов в &п (этот базис не предполагается ортонормированным), то
преобразование каждого из них задается уравнением

ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП 649
Группы указанного типа, которые мы будем обозначать буквами жирного
шрифта латинского алфавита, называются группами (га-мерных) линейных
подстановок.
Представление группы. По определению линейным представле
нием группы 9 называют ее гомоморфизм в группу линейных подстановок.
Пусть G— группа линейных подстановок, а $ — векторное пространство,
в котором действуют матрицы, являющиеся элементами этой группы. Ж назы-
называется пространством представления, а число п его измерений называется раз-
размерностью (или степенью) представления.
Если 'S изоморфна G, то представление называется точным. Если же это
не так, то элементы из 9, гомоморфные единичной матрице 1, образуют инва-
инвариантную подгруппу %иС является точным представлением фактор-группы
Одномерные представления. Каждая группа имеет по крайней
мере одно одномерное представление — тривиальное, или единичное, представ-
ление, в котором каждый элемент группы представляется числом 1.
Для того чтобы существовали одномерные представления, отличные от
тривиального, группа должна иметь инвариантные подгруппы, соответствую-
соответствующие которым фактор-группы абелевы. Все нетривиальные одномерные пред-
представления являются представлениями этих абелевых фактор-групп (см. обсу-
обсуждение группы Я'п в § 17).
Унитарное представление. Представление G называется уни-
унитарным, если все матрицы, принадлежащие G, унитарны.
Эквивалентные представления. Два представления G и G' на-
называются эквивалентными, если они имеют одинаковую размерность и если
каждая матрица G'(g) одного из представлений получается при помощи фик-
фиксированного линейного преобразования Т из матрицы G(g) другого представ-
представления, соответствующей тому же элементу g группы 9:
G' (g) = TG (g) Г для всех gel,
или
Если G и G' — эквивалентные представления, то используется символиче-
символическая запись
Если отождествить пространства представления & и !$', то переход от
представления G к эквивалентному представлению G' соответствует выбору
нового набора базисных векторов в пространстве представления.
Сопряженные представления. Два представления G и G*, ма-
матрицы G(g) и G*{g) которых комплексно сопряжены друг другу, называются
сопряженными представлениями.
Представление G называется самосопряженным, если оно эквивалентно
своему сопряженному G tv G*.
Характеры. След матрицы G(g), которая соответствует элементу g
в представлении G группы 9, называют характером % элемента g в этом пред-
представлении
Из свойств следа вытекает, что два элемента из одного и того же класса
сопряженных элементов имеют один и тот же характер: характер является
функцией от класса.
По тем же причинам: два эквивалентных представления имеют один и
тот же набор характеров:
если о' (g) = TG (g) T~l, то %' (g) = % (g).

550 ДОПОЛНЕНИЕ Г
Символически это можно записать так:
если G' « G, то V = %.
(N. В. Если представление G самосопряжено, то его характеры веще-
вещественны.)
§ 7. Операции над пространствами представлений.
Приводимость')
Прямая сумма. Пусть G", С — два представления одной и той же
группы размерности па и пь соответственно, и пусть &а, <%ъ — соответствую-
соответствующие пространства представления.
Если \а\), |а2), .... \апа) — базисные векторы в <$а, а |61), |62); ...
..., \Ьпь) —в &ь, то линейные подстановки, описывающие преобразование g
в этих двух представлениях, определяются законами преобразования базис-
базисных векторов
8 11 a*>J = ? I "Я) Оы (8), ?[l^>] = i;i*v>G^(g). A)
Прямой суммой <Ва~\~%ь пространств 8 а и Шь называется пространство,
растянутое па-\-пь векторами
|о1>, |а2>, .... \апа), |*1) \Ьпь).
Матрицы в этом новом пространстве могут быть представлены в виде
аа Mab
где Маа — По Xя" матрица, переводящая векторы пространства &'а в векторы
из &а, а Мьь — Пь X пь матрица, переводящая векторы из &ь в Жь, Маь —
— пау<.пь — матрица, переводящая векторы пространства <%ъ в векторы нз <$а.
В частности, если А — матрица, оставляющая инвариантным пространство <Sa,
а В — пространство Шь, то их прямой суммой А-\-В будет матрица, имеющая
блочно-диагональный вид:
! 1\
Отметим, что
Тг(Л+В)=ТгЛ + ТгВ, det(/l + B) = deM-detB. B)
Операция взятия прямой суммы матриц сохраняет единицу и закон мат-
матричного умножения
Ua+b) = »(«, + W (Al + Bl) (Л2+ Ч = W + В1В2-
Из сказанного выше следует, что множество Ga+b матриц Ga(g)-\-G (g)
образует представление группы ^. Элементу g соответствует линейная под-
подстановка, которая определяется законами преобразования A) базисных векто-
векторов пространства IS* ~Ь %ь- Характеры этого представления имеют вид:
Хо+*(«г) = 1"(S) +Xr(g), иными словами
a+b a b О)
') Рассматриваемые в этом параграфе свойства являются общими для
множеств матриц. Они сохраняются и в том случае, когда эти множества мат-
матриц не образуют группу.

ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП 551
Тензорное произведение (кронекерово нлн прямое произведе-
произведение). Операция взятия тензорного произведения пространств нли матриц
была определена нами ранее (гл. VII).
При образовании тензорного произведения пространств 8 а и 8ь мы полу-
получаем геаи*-мерное пространство 8а®8ь, базисными векторами которого слу-
служат векторы |а6и|х) = \а%) |6|х) (х = 1, 2, ..., па; ц = 1, 2 пь). Мат-
Матрицы Ga(g) ® Gb(g), полученные тензорным умножением матриц, которые со-
соответствуют элементу g в G" и G6, образуют представление Gab за Ga ® G*
размерности папь для группы &. В этом представлении заданное преобразо-
преобразование группы действует по правилу
g [ | abxy.)) = ? \аЬЩ Оаы (g) О»ц (g). D)
Характеры этого представления определяются соотношением
Xa"(g) = Xa(g)xb(g). E)
Приводимость. Инвариантным подпространством пространства 8
представления G называется подпространство в 8, каждый вектор которого
прн действии матриц из G линейно преобразуется в другой вектор из этого же
подпространства.
Представление G называется:
(!) неприводимым, если 8 не содержит инвариантных подпространств, от-
отличных от самого пространства S, н нулевого подпространства;
(ii) приводимым, если оно не является неприводимым
<? = #i Ч~ ^2 (&u ^2?=0), <S\ — инвариантное подпространство.
Во втором случае, если &г также инвариантно, то говорят, что G разло'
жимо. При этом можно, используя подходящее линейное преобразование, пе-
перевести базисные векторы пространства 8 в векторы, целиком лежащие либо
в &\, либо в 8г- В реультате получается эквивалентное представление, являю-
являющееся прямой суммой представления G\ в 8\ и представления G2 в 8t
Представления G\ и G2 называются компонентами представления О.
Представление G является вполне приводимым, если оно может быть
представлено в виде прямой суммы неприводимых компонент
G я* GA) + G<2) + ... (G'1», GB), ... - неприводимы).
Каждое унитарное представление либо неприводимо, либо вполне приво-
приводимо.
Матрицы вращений Ra) (Дополнение В, раздел IV) при заданном значе-
значении \ образуют неприводимое унитарное представление Z)(/> группы вращений.
Строго говоря, Д</> является представлением группы вращений 91% только прн
целом /.
Для любого / Д(/) является неприводимым представлением группы %¦
инфинитезимальные преобразования которой те же, что и у Я3 («накрываю-
(«накрывающая группа» группы 5?з).
Группа <иг состоит из двумерных унимодулярных унитарных линейных
подстановок, и Яз является фактор-группой группы <Ui- В случае, когда /
полуцелое, /)</' является точным представлением группы <Ui, и каждому эле-
элементу из 5?3 соответствуют в DM две матрицы противоположного знака.
Все неприводимые представления абелевой группы одномерны (первой
степени).
Гомоморфное отображение одного пространства пред-
представления на другое. Линейным отображением пространства 8а в 8ь

552 ДОПОЛНЕНИЕ Г
называется линейное соответствие, при котором каждому вектору \а) нз &а
соответствует один и только один вектор |6) нз 8Ъ. Соответствие называется
гомоморфным, если оно сохраняет трансформационные свойства векторов под
действием всех преобразований группы, т. е. если нз соответствий
|а>->|6>
следует, что
8 11 а» -> 8 [ I 6» при любом gel.
Отображение &а в &ъ, полиостью определено, если задана Пь~Х.па мат-
матрица, которая определяет вектор нз Шь, соответствующий каждому базисному
вектору в 8а-
| ах> -»- 52 | Ь|г) 5№Ж. F)
и
Если отображение гомоморфно, то выполняется матричное равенство
S Qa (g) = G* (g) S для любого fe?,
т. е.
SOa = ObS. G)
Если множество векторов |6), соответствующих векторам из 8а, растя-
растягивает все пространство 8ь (это предполагает, что па ^ гс»), то мы имеем
отображение Шл на 8ь (надо понимать как на все 8ь). В этом случае все
определители матриц я» X nj, содержащихся в матрице S, отличны от нуля.
Если соответствие взаимнооднозначно (па = пь), то матрица S несингу-
несингулярна: det S Ф 0. При этом гомоморфное отображение 8а на 8ь называется
изоморфным соответствием, и мы имеем
§ 8. Основные теоремы
Применение теории групп в квантовой механике в основном базируется
иа следующих теоремах.
Лемма Шура. Если G" и Gb — два неприводимых представления од-
одной и той же группы и если существует гомоморфное отображение простран-
пространства одного из представлений на пространство другого представления, то мат-
матрица S, определяющая это отображение (S удовлетворяет уравнениям F) и
G)), имеет следующие свойства:
а) если G" и С неэквивалентны, то S = 0;
б) если Ga « Gb, то либо S = 0, либо det S ф 0;
в) если G" з= Gb, то S кратна единичной матрице: S — с\ (с — постоян-
постоянная).
Следствие. Если квадратная матрица S коммутирует со всеми матри-
матрицами неприводимого представления G некоторой группы, то она кратна еди-
единичной матрице:
если [S, G] = 0, то обязательно S — с\.
Вполне приводимые представления. Теоремы един-
единственности. Пусть заданы два разложения на неприводимые компоненты
вполне приводимого представления G:
Можно показать, что в этом случае р = р', н существует взаимнооднозначное
соответствие между каждым членом первого разложения и эквивалентным

ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП 553
ему членом второго разложения. Иными словами, справедлива следующая
теорема.
Теорема единственности I. Если представление G вполне приво-
приводимо, то его разложение на неприводимые компоненты единственно с точ-
точностью до эквивалентности.
Начиная с этого места, если не отмечено особо, мы не будем делать раз-
различия между эквивалентными представлениями. Одно и то же неприводимое
представление может тогда фигурировать несколько раз в разложении G. Обо-
Обозначим
GA), GB> G<»,...
последовательность неприводимых представлений группы &. Согласно теореме
единственности каждое вполне приводимое представление G подчиняется со-
соотношению эквивалентности
G « ? n,Gif), (8)
в котором последовательность неотрицательных целых чисел пи п% ..., щ, ...
определена единственным образом. Аналогично множество характеров пред-
представления G удовлетворяет соотношению
Х = ?л/Х<Л. (9)
/
Теорема единственности дополняется следующими двумя теоремами.
Теорема II. Если G вполне приводимо, то и любая компонента G\ пред-
представления G также вполне приводима, а разложение этой компоненты на не-
неприводимые есть сумма определенного числа неприводимых компонент пред-
представления G.
Итак, если G « Gj + G2 и если G может быть разложено согласно соот-
соотношению (8), то
61 « ЕЛ/6<Л' где п)<п1 (/=1.2,...).
Теорема III. Если G вполне приводимо и если существует гомоморф-
гомоморфное отображение пространства 8 представления G на пространство 8\ другого
представления Gx той же группы, то Gx является компонентой G.
Теорема III применима, в частности, и тогда, когда каждому базисному
вектору \х) в пространстве 8 можно сопоставить вектор |х:) из пространства
8\. В такой ситуации векторы | ft), растягивающие 8и не обязаны быть ли-
линейно независимыми, но линейно преобразуются друг в друга по тем же мат-
матричным формулам, что и векторы \х), т. е.
В этом случае очевидно, что соответствие |х) -*• |й) устанавливает гомоморф-
гомоморфное отображение 8 на 8\.
В частности справедливо следующее следствие.
Следствие. Если пространства, натянутые на векторы \ак) (с перемен-
переменным х) и на векторы |6|х) (с переменным |х), связаны с представлениями Ga
и Gb и если тензорное произведение Gab этих представлений вполне приво-
приводимо, то представление G', определенное в пространстве, натянутом на про-
произведение векторов \ак) |6|х), является компонентой Gab.
(N. В. Векторы \ах) |6ц) не обязаны быть линейно независимыми, если
же это так, то С ж Gab.)
18 А, Мессиа

554 ДОПОЛНЕНИЕ Г
§ 9. Приложения к квантовой механике
Группы, встречающиеся в квантовой механике, являются группами преоб-
преобразований в пространстве векторов состояния. Этн преобразования почти всег-
всегда линейны и унитарны, и мы ограничимся в дальнейшем обсуждении именно
такими преобразованиями.
Обозначим 8 пространство векторов состояний, а Э — множество унитар-
«ых операторов G\, G% ..., образующих группу.
Пусть \и) —вектор из &. Вектор \и) и векторы Gi|«), G2|u), ..., полу-
полученные действием операторов группы на \и), растягивают в общем случае не
все пространство &, а лишь подпространство &и в нем. &и является инва-
инвариантным подпространством относительно преобразований группы и связано с
некоторым унитарным и, следовательно, вполне приводимым представлением
G" группы а. Мы будем говорить что вектор \и) преобразуется по представ-
представлению G".
Аналогичным образом, если Q — линейный оператор в &, то Q и множе-
множество операторов GjQGj, G2QG^1,..., полученных действием на Q преобразо-
преобразований группы 2?, растягивают векторное пространство 8q (векторами этого
пространства служат операторы), элементы которого линейно преобразуются
друг в друга под действием операторов группы. Пространство Sq связано с
представлением GQ группы $, которое во всех рассматриваемых ниже случаях
будет либо вполне приводимым, либо даже неприводимым. Мы будем гово-
говорить, что Q преобразуется по представлению GQ.
По определению оператор Q называется инвариантным относительно груп-
группы $, если он преобразуется по единичному представлению. В этом случае Q
коммутирует со всеми операторами из группы. В более общем случае
оператор Q является компонентой неприводимого тензорного оператора
группы. S, если он преобразуется по неприводимому представлению G<<>
этой группы.
Неприводимые подпространства &(т/). Стандартное
представление группы з. Пространство S является прямой суммой
неприводимых инвариантных подпространств 8{х'\). Каждое из них связано
с некоторым неприводимым представлением G"' группы &. Индекс т пара-
параметризует пространства, связанные с одним и тем же неприводимым представ-
представлением.
Обозначим dj размерность представления GUK Пусть |т/ц) (изменяется
только ц.) —dj векторов, образующих базис в пространстве &(%'}). Поскольку
С(/) определяется только с точностью до эквивалентности, то конкретный вы-
выбор базиса произволен. Удобно раз и навсегда фиксировать эти векторы, опре-
определив стандартный базис в S(xj), в котором каждому элементу группы соот-
соответствует вполне определенная матрица Gy^:
d,
Й A0)
В дальнейшем изложении мы будем всегда предполагать, что выбран
именно этот стандартный базис.
Множество векторов |т/|х) (изменяются т, /, |х) образует систему базис-
базисных векторов пространства 8. Мы будем называть представление {т/ц} груп-
группы & стандартным. Термин представление здесь используется в привычном
квантовомеханнческом смысле. Трансформационные свойства компонент кет-
векторов и операторов под действием преобразований из группы & имеют осо-
особенно простой вид в этом представлении. Эти свойства суммируются двумя
приводимыми ниже теоремами.

ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП 555
Компоненты кет-векторов и операторов в представ-
представлении {т/ц}.
Теорема А. Если векторы \и\), ..., \и\), ... линейно преобразуются
друг в друга, подобно базисным векторам унитарного представления G", т. е.
если
G|uv>=?|«p>G?v>
р
то их компоненты (t/|i|uv) имеют следующие свойства:
1°. Если G(/) не встречается в разложении
Ga«5>*G<ft) A1)
k
представления Ga на неприводимые компоненты, то
<т/|х | uv> = 0.
2°. Если G</> встречается в разложении A1) и если (av|a/n) — матрица,
реализующая это разложение, то
п!
(T/|i|av>=?«4,<ev|o/|ir. A2)
a=l
где Лу постоянных и}%а не зависят от ц и v.
Теорема В. Если операторы Qb Q2, ..., Qv. • • • линейно преобразуются
друг в друга, подобно базисным векторам унитарного представления G", т. е.
если
GQvG~'~lQp<&.
р
то матричные элементы (xi/ijxi | Qv (тг^гМ^г) имеют следующие свойства:
1°. Если G*'1' не встречается в разложении
Ga ® вш « ? nakhG(k) A3)
h
тензорного произведения Ga ® G(^' на неприводимые компоненты, то
<t,/>1|Qv|t2/#2) = 0.
2°. Если G^1' имеется в разложении Ga ® G^ и если (a/2VH21 ok%) —
матрица, реализующая это разложение, то
где (tj/j II Q || т2/2^ есть riff* постоянных, не зависящих от \i{, ц2 и V.
Важное замечание. Матричные элементы (av | ak%>, (a;2vn21 ok%) \
унитарных матриц, которые фигурируют в формулировке теорем, удовлетво-
удовлетворяют уравнениям
? (av | akxf G^W \ o'k'%) = 6aa,6kk,G<»,, A5а)
vv'
(a/vix | ok%)* 0^,0Щ, (a/v'n' | o'k'%') = 6CT0,6Aft,G$,. A56)
18*

566 ДОПОЛНЕНИЕ Г
Эти матричные элементы полностью определяются по заданным представле-
представлениям Ga, Ga® G"> и зависят только от того, как преобразуются векторы
|uv) или операторы Qv под действием группы S'.
Доказательство теоремы А. Подействуем унитарным преобразо-
преобразованием (av|o"fcx) на базисные векторы |«1), |u2>, .... |uv) В резуль-
результате получим новый набор базисных векторов
E A6)
V
Из условия унитарности получаем
A7)
ak%
Из определения этого унитарного преобразования следует, что d« векторов
\uak%) (здесь а, к фиксированы, а меняется %) растягивают подпространство
<?u(ok) и образуют стандартный базис для представления G'*> в этом под-
подпространстве. Разлагая эти векторы по базисным векторам представления {т/ц},
имеем
I uak%) = ? | т/ц) (т/ц. | uak%).
т/ц
Матрица (т/|л|иа?/) (где ц. и % — переменные, а остальные индексы фиксиро-
фиксированы), содержащая d/ строк и d«. столбцов, осуществляет гомоморфное ото-
отображение пространства Su(ok) в !?(%}). Поскольку представления в этих про-
пространствах либо неэквивалентны, либо совпадают, то из леммы Шура сле-
следует:
(т/ц. | uak%) = Ь!кЬ^%и{а, A8)
где u'ta— не зависящая от Ц постоянная. С учетом этого результата, проектируя
обе части равенства A7) на |т/ц,), получаем
(т/ц | uv)= У 6/ft6_ (У и' (av I
Оба утверждения теоремы А содержатся в этом равенстве. Щ
Доказательство теоремы В. Рассмотрим векторы QJ
(здесь v и ц2 меняются, а tj и /2 фиксированы). Эти векторы линейно преобра-
преобразуются друг в друга подобно базисным векторам представления G°®C .
Отсюда в общем случае не следует, что пространство, растягиваемое этими
векторами, связано с этим представлением, так как эти векторы не обязаны
быть линейно независимыми. Однако если это представление не совпадает
с представлением Ga ® G(/>), то, согласно следствию, соответствующее пред-
представление является одной из компонент представления Ga ® G . Несмотря
на то, что рассматриваемые векторы могут и не быть линейно независимыми,
мы будем оперировать с ними точно так же, как с векторами \и\), ...
..., | их), ... в теореме А.
Определим векторы
Из соотношения унитарности для матрицы (a/2v[i.2| ok%} следует:

ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП 557
- dk векторов \qx2i2aky) (где % меняется, а остальные индексы фиксиро-
фиксированы) либо все нулевые, либо образуют стандартный базис представления
G<*>. В последнем случае можно применить теорему А. Итак, в любом случае
имеем
(т/|х | gx2j2ak%) = б,^ (т/ || Q |[ r2i2)g,
где (xj || Q || т2/2) — постоянные, не зависящие от |х. Следовательно, проекти-
проектируя обе части равенства A7') иа |ti/i(Ai), получаем равенство
(Tl/>1 I Qv IW2) = ? б/,А
ftX
из которого следуют оба утверждения теоремы В.
Правила отбора. Если \и), Q, \v) преобразуются по представле-
представлениям G", GQ, Gv соответственно, и если ни одна из неприводимых компонент
представления G" не встречается в разложении GQ ® Gu, то
Это правило широко используется. В случае, когда Gu н G" иеприводнмы,
оно следует непосредственно из утверждения 1° теоремы В. Однако оно спра-
справедливо и в том случае, когда ни одно из представлений Gu, GQ, G" не яв-
является неприводимым. Для доказательства достаточно заметить, что Q\u)
преобразуется (следствие) по представлению G®<&GU илн по одной из его
компонент, и применить теорему А к вектору Q\u).
Пример: группа вращений. Теоремы А и В применимы, в част-
частности, к группе вращений.
Задача сложения двух моментов импульса есть не что иное как конкрет-
конкретное воплощение теоремы А. Введенные в § XIII. 25 B/i + 1) B/2+ 1) векторов
la/i/Vni/nj) преобразуются как базисные векторы представления i)'® D',
образованного тензорным перемножением неприводимых представлений
Д', D"'' группы вращений '). Согласно результатам раздела V главы XIII
разложение этого представления на неприводимые имеет вид
D(/l) ® О(/г) ж X' D(/), A9)
/H/.-W
а элементами унитарной матрицы, осуществляющей это разложение, являются
коэффициенты Клебша — Гордана (j\itmimz\IM) . Поскольку каждое неприво-
неприводимое представление встречается в разложении A9) не более чем один раз,
т. е. Иу''! = 1 при J = /i + /2, /1 + /2 — 1 |/i — /г|, то сумма в правой ча-
части равенства A2) содержит в рассматриваемом случае только один член.
Таким образом, компоненты вектора Ioc/i/Vh^) в каждом из подпространств
^Р(тУ) известны с точностью-до постоянной (не зависящей от М).
Аналогично теорема Вигнера — Эккарта (§ XIII. 32) следует из примене-
применения теоремы В к компонентам Т^' тензорного оператора, неприводимого по
отношению к вращениям, т. е. к Bk + 1) операторам, преобразующимся как
базисные векторы представления Д(*>.
Матричный элемент (r^m^ | T^ | ¦x2j2m2^ определяется выражением A4).
Поскольку каждая компонента D<7> представления fl(ft) ® D^ встречается
') Термин «группа вращений 5?з» используется для упрощения. Фактиче-
Фактически имеется в виду «накрывающая группа» Ч/г группы Из.

658 ДОПОЛНЕНИЕ Г
только один раз в разложении этого представления на неприводимые (п)*' = I
при / = к + jt, k + /2—1, ..., \k — /2|), то сумма в правой части равенства
A4) содержит в рассматриваемом случае только один член.
(N. В. Определение приведенных матричных элементов (Ti/il|T<*>i]T2/2> ^
используемое в главе XIII, отличается от принятого здесь только множителем
V2/l + 1 •>
Инвариантные наблюдаемые, ^-вырождение. Наблюдав*
мая Q называется инвариантной относительно группы &, если
[Q, G] = 0 при всех ge?.
d) векторов Q\xjn) (т/ фиксированы, ц переменно) преобразуются как ба-
базисные векторы представления G(/). Теорема В (или, что эквивалентно, тео-
теорема А, или лемма Шура) означает в рассматриваемом случае, что
<г/|г I Q I т'/У> = в/Лн-вй* B0>
Таким образом, Q описывается матрицей особенно простого вида в стандарт-
стандартном представлении группы Э.
В таком представлении задача на собственные значения наблюдаемой Q
сводится к диагоналнзации эрмитовых матриц Q</>, элементы Q<?, которых за-
зависят только от двух индексов т н %'. Каждому значению ;, таким образом*
соответствует некоторое число собственных значений наблюдаемой Q, а имен-
именно,— собственные значения q\ , q% q*p, ... матрицы Q(/). Каждое невЫ'
рожденное собственное значение этой матрицы является df-кратно вырожден'
ным собственным значением наблюдаемой Q. Каждое р-кратно вырожденное
собственное значение матрицы Q(/) является pdj-кратпо вырожденнным соб-
собственным значением для Q.
Укажем, в частности, следующие два свойства:
1°. если Q инвариантна относительно &, то подпространства, соответствую-
соответствующие каждому из собственных значений наблюдаемой Q, также инвариантны'
относительно 9;
2°. если наблюдаемая Q, иивариаитиая относительно группы &, опреде-
определена на конечномерном пространстве, векторы которого преобразуются друг
в друга согласно представлению G и если разложение этого представления на
неприводимые имеет вид
то число различных собственных значений наблюдаемой Q не превышает
?"*•
ft
Неприводимые тензорные операторы. Если оператор Q
преобразуется по представлению GQ, то всегда можно представить Q в виде
суммы операторов, каждый член которой нреобразуется по одной из неярн-
водимых компонент представления GQ. Поэтому неприводимые тензорные #пе-
раторы заслуживают особого рассмотрения.
По определению компоненты неприводимого тензорного оператора Т<*>
порядка k линейно преобразуются друг в друга в соответствии с неприводи-
неприводимым представлением G(*>. Таким образом, этот оператор определяет й*-мерное
пространство представления G(*>. В частности, этот оператор имеет dk стан-
стандартных компонент 1*® (k фиксировано, % переменно), образующих стан-
стандартный базис в указанном пространстве представления. По определению

ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП 559
{см. соотношение A0))
O^G-'-ET^Gg. B1)
р
Пусть разложение на неприводимые тензорного произведения неприво-
неприводимых представлений Glg) и G(/1) имеет вид
в« ® G<h) я* ? nf "G(Z) B2)
и пусть {gh\r\ | а(Я) (а = 1 nf ) — элементы унитарной матрицы, реали-
реализующей это разложение. В стандратном представлении компоненты Т^ имеют,
согласно теореме В, следующие свойства:
0, если л?/г = 0
если
\ * * (I JL Н Ли +*4 /TV" 4t"' At I "I" 1/
0=1
B3)
Заключение. Из изложенного выше следует, что мы можем исполь-
использовать во всей полноте свойства кет-векторов и операторов квантовой меха-
механики относительно преобразований данной группы, если известны:
(i) все неприводимые представления (с точностью до эквивалентности)
данной группы и в каждом из этих представлений определены матрицы, отве-
отвечающие выбору стандартного базиса;
(ii) разложения тензорных произведений таких представлений на непри-
неприводимые компоненты, н построены матрицы, задающие разложения каждого
«з таких произведений (т. е. определены коэффициенты nfh в уравнении B2)
я «коэффициенты Клебша — Гордана» (ghyy\jolK) ),
Раздел III. КОНЕЧНЫЕ ГРУППЫ
Обозначения:
9~ — рассматриваемая группа;
N — порядок группы;
L — число классов (L ^ N);
'в — класс сопряженных элементов;
1а — число элементов в классе 9S'„;
F — представление группы ^";
F — матрица, соответствующая элементу f в F;
F — регулярное представление;
f — элемент группы;
/ — единичный элемент;
fa — элемент класса 92а;
ka= ^ /? — сумма элементов класса ^j
*=1
X — множество характеров представления F-t

560 ДОПОЛНЕНИЕ Г
1
'о
f(/) —у.ое неприводимое представление (с точностью до эквивалентности);
d, — размерность представления F">: d/ = %(пA);
FU) — унитарная матрица, соответствующая элементу / в представлении
F(/> в фиксированном стандартном базисе;
Fak = (/ I /°Р) ~~ элемент матрицы Fa\ находящийся на пересечении a-ft
строки и р-го столбца;
X(/)(a) = (а\П—характер класса Ч?а в представлении F(/).
§ 10. Основные понятия
Лемма о перенумерации. Если /ь /2, . •., /л — элементы группы,,
записанные в определенном порядке, то каждый элемент группы появляется
один и только одни раз в последовательности f\f, fj fnf, которая полу-
получается умножением каждого из элементов группы на одни и тот же элемент f.
Эта последовательность состоит из всех элементов группы, расставленных в
другом порядке.
(Все свойства данного параграфа следуют из этой леммы.)
Подгруппа группы <?". Если Ж — подгруппа группы &~ порядка Nh,
то N кратно Nh
N = hNh (h — целое и > 0).
Целое число h называется индексом подгруппы.
Если Ж—инвариантная подгруппа, то ее индекс h равен порядку фактор-
факторгруппы 0"/Ж
Классы сопряженных элементов. Порядок N кратен 1а — чис-
числу элементов в любом из классов сопряженных элементов
N = pJa (Pa ~ положительное целое > 0).
Элементы нз 9Г, коммутирующие с данным элементом [а класса Фа, об-
образуют подгруппу индекса U.
Групповая алгебра. Сумма ka элементов класса. Линей-
N
ные комбинации элементов группы 2_, xsfs> где *'> х2 х" — произвольные
5=1
комплексные числа, образуют алгебру, которую мы будем называть групповой
алгеброй.
L элементов групповой алгебры, которые получаются сложением элемен-
элементов каждого класса, называются суммами элементов класса
(a=1- 2
Эти L элементов коммутируют со всеми элементами групповой алгебры, и лю-
любой другой элемент, обладающий этим свойством, является линейной комби-
комбинацией сумм элементов класса.
Алгебра сумм элементов класса. Групповая алгебра является
коммутативной только в том случае, когда ST—абелева группа. Однако ли-
линейные комбинации L операторов ka образуют коммутативную алгебру, назы-
называемую алгеброй сумм элементов класса или центром групповой алгебры. (Ее-

ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП 561
ли группа &" абелева, то алгебра сумм идентична групповой алгебре.) Имеем
L
Zabc B5)
с-1
где коэффициенты g?6 — целые неотрицательные числа.
Будучи линейно независимыми, L сумм элементов класса связаны соотно-
соотношением B5) и могут быть представлены как функции от меньшего чем L чис-
числа сумм.
Каждая сумма ka удовлетворяет алгебраическому уравнению, порядок ко-
которого не превосходит L.
§11. Представления
Регулярное представление F'. Регулярным называют ЛГ-мерное
представление, которое получается, если за элементы базиса в пространстве
представления взять N элементов группы. Векторами пространства регуляр-
регулярного представления служат элементы групповой алгебры.
Все элементы каждой строки и каждого столбца N*X.N матрицы, отве-
отвечающей элементу f в представлении F', равны нулю, кроме одного, равного 1.
Почти все основные свойства представлений группы являются простыми
следствиями леммы о перенумерации, леммы Шура и свойств регулярного
представления.
Общие свойства представлений. Всякое представление конеч-
конечной группы эквивалентно унитарному представлению этой группы.
Если два представления имеют один и тот же набор характеров, то они
эквивалентны ') (обратное очевидно).
Если F\, F2, ..., F» — набор линейных операторов, образующих конечную
группу У, и если \и) —заданный вектор в пространстве кет-векторов, то
представление F", по которому \и) преобразуется под действием элементов
группы, является компонентой регулярного представления Fr (если F" имеет
размерность N, то F" « Fr).
В заданном представлении F суммы k\, k2, ..., kb описываются матри-
матрицами К\, Кг, ¦ • •, Kl, которые можно одновременно привести к диагональному
виду и которые коммутируют с каждой матрицей, представляющей элемент
группы:
B6)
Неприводимые представления.
а) Число неэквивалентных неприводимых представлений равно числу клас-
¦сов L.
б) Размерность. Если rf,- — размерность /-й неприводимой компоненты F(",
</= 1,2,...,!), то
Sid,- целое, B7)
?d* = tf. B8)
•) Это следует из единственности разложения на неприводимые компо-
компоненты и из свойства ортогональности характеров неприводимых представлений
(см. ниже). Это свойство сохраняетси и в случае бесконечных групп, если два
рассматриваемых представления вполне приводимы.

562 ДОПОЛНЕНИЕ Г
в) Соотношения ортогональности. Если унитарные неприводимые пред-
представления F">, F<*> либо не эквивалентны, либо равны1), то
B9)
Из B9) следует соотношенне ортогональности для характеров
L
]Г ¦!§-(a\j)(a\k)' = 6lk. C0)
Каждое представление вполне определиется стандартным выбором его ба-
базисных векторов. N2 величин
1,2,..., TV; / = 1,2 L; a, 0=1,2 d,)
являются элементами унитарной N X N матрицы. Аналогично I? величн»
¦y/TjN %{h (a) ^ л/TjW (а | /) являются элементами унитарной LY.L мат-
матрицы. Из двух соотношений унитарности B9) и C0) получаем соответственно
L d, d
/¦-1 a, 0-1
C2>
г) Специальные случаи. Если F<*> — единичное представление (й = 1), то
из B9) и C0) следует
N L
(J | /ар) = ЛГ6/ ,, 2 /а (а | /) = ЛЮд. C3а>
2
a=l
Если ^ — единичный элемент (g = /), то C1) и C2) дают
d, (f\ /op) = iV6f/, Л d/ (a 1 /) = Ndal. C36>
/
') Доказательство. Если 5 есть dj X с?*-матрица, то матрица
N
Т = ^ р(П$р(к)-1 удовлетворяет соотношению ft'T = 7F<*> для всех / (лем-
f-i
ма о перенумерации). Следовательно (лемма Шура), матрица Т либо тожде-
тождественно равна нулю, если F(" и F<*> неэквивалентны, либо кратна единичной,
если представления совпадают. Фиксируя S подходящим образом, получаем
соотношения B9).

ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП 563
д) Соотношения между характерами и суммами элементов класса. Мат-
Матрицы К*?, представляющие ka, кратны единичной матрице (лемма Шура)
K$ = k^\ C4)
^^ C5)
Из B5) и C5) следует равенство
L
IJb (« 1 /) (*> I /) = <*/ Z Sab'c (С I Л- C6)
из которого в силу соотношения ортогональности C2) имеем
L
rf7(a|/)F|/)(c|/)*- C7)
§ 12. Неприводимые компоненты представления
Общий метод. Для получения коэффициентов nt разложения пред-
представления F на неприводимые компоненты
L
1=1
достаточно знать множество его характеров %(а) и мнвжество характеров L
неприводимых представлений группы. Согласно уравнению (9) и соотноше-
соотношениям C0) имеем
L
U (а I /)* X («)• C9)
[
(N. В. Справедливо соотношение
L L
Таким образом, равенство р = 1 является критерием неприводимости пред-
представления F.)
Регулярное представление {%r(a) = NbaI). Регулярное пред-
представление содержит каждое неприводимое представление группы столько раз,
какова размерность этого цредставления
L
{Отсюда следует соотношение B8).)
Тензорное произведение неприводимых предс»авле-
н и й.
D1)

564 ДОПОЛНЕНИЕ Г
Уравнение (9) в рассматриваемом случае имеет вид
L
nf(a\j), D2)
а соотношение C9) означает, что
L
/. <«!*)(« I А) (в | Л*.
а-1
Эти два соотношения следует сравнить с C6) и C7).
Лемма. Представление F<" столько раз содержится в разложении
F(e)®/?t*> на неприводимые, сколько раз содержится F(g> в разложении
f(/) (g) F<*>*.
(Л'. В. Если все неприводимые представления самосопряжены, ronf сим-
симметрично по всем трем индексам.)
Одномерные компоненты. Тензорное произведение F<g> ® Fт
двух неприводимых представлений содержит одномерную компоненту не бо-
более одного раза. Необходимое и достаточное условие наличия одномерного
-представления Ft в разложении этого произведения состоит в эквивалентности
F(8) « Fj ® F(;t)*. D4>
В частности, пространство представления <§?8® 8h рассматриваемого про-
произведения содержит не более одного вектора, инвариантного относительно
преобразований группы. Такой вектор существует в том н только в том слу-
случае, если
jrfe) « FW\ D5>
§ 13. Построение неприводимых
инвариантных подпространств
Начиная с этого места, мы будем предполагать, что для каждого непри-
неприводимого представления F<" выбран стандартный базнс. Мы будем говорить,
что вектор имеет тип (/ц), если он преобразуется как fi-я компонента вектора
стандартного базнса представления F<". В этих предположениях унитарные
матрицы F('> определены однозначно. Таким образом, наша задача состоит в
построении стандартного базнса, отвечающего группе &~, в пространстве <§
представления F, определенного в начале § 12. Мы ограничимся случаем, когда
8 порождено действием операторов Flt F2, ..., Fn группы на заданный век-
вектор |) пространства кет-векторов (я/ ^ d,). В квантово-механических прило-
жевиях теории групп общий случай всегда можно свести к этому специаль-
специальному.
Базисные операторы В^ регулярного представления.
Введем .V операторов
(/=1,2 L; ц, v=l,2 dj).

ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП 565
Из соотношений ортогональности C1) следует, что все N операторов
группы являются линейными комбинациями этих операторов
L dj
f=HE tfl/l»v)Bjfl. D7)
/—1 и. v—1
Из унитарности F, леммы о перенумерации и соотношений B9) получаем
основные свойства операторов
% D8)
D9)
W»v!2 E0>
Согласно D9) N элементов групповой алгебры, описываемые матрицами
Вц^, образуют стандартный базис регулярного представления.
Построение стандартного базнса при помощи опера-
операторов В^. Если известно как построить операторы В^, т. е. если известны
N2 матричных элементов (fl/Hv), T0 задача построения стандартного базиса
в & практически решена.
Действительно:
а) если вектор В^ | \ отличен от нуля, то он имеет тип (/ц) (ур. D9));
б) N векторов В^| ^ растягивают все пространство 8 (ур. D7));
в) d2j векторов В^ | V соответствующих одному и тому же значению ин-
индекса /, имеют перечисленные ниже свойства:
(i) dj векторов, соответствующих одному н тому же значению v (ц = 1,
2, ..., dj), имеют одну и ту же норму и образуют стандартный базис пред-
представления F(";
(ii) dj векторов, соответствующих одному н тому же значению ц (v = 1,
2, ..., dj), растягивают я,-мерное пространство &t векторов типа (/ц). Они
связаны друг с другом (dj — я,) линейными соотношениями, коэффициенты ко-
которых не зависят от ц (в частности, если п/ = 1, то эти dj векторов пропор-
пропорциональны друг другу и коэффициенты пропорциональности не зависят от ц).
Таким образом, для построения стандартного базиса в &, соответствую-
соответствующего заданной группе, нам необходимо только выбрать для каждого значе-
значения / определенное значение Д индекса ц и, используя, например, метод орто-
гоналнзацин Шмндта, построить я, базисных векторов в пространстве 8^.
Z
v=l
Тогда векторы
v-1
(/=1.2 L; ц=1, 2 d,\ т=1,2 n,)
образуют искомый стандартный базис; dj векторов |т/ц) (т и / фиксированы,
I* = 1. 2, .... dj) образуют стандартный базис для представления F<«.

566 ДОПОЛНЕНИЕ Г
Другие свойства операторов В^. Проекторы на под-
подпространства 8 ^ и переход от одного из них к другому.
Введем обозначения
d N
П"» - В# --jf ? (Л/МО'Л E1)
f-l
Операторы П*/* (/= 1, 2 L; ц = 1, 2,..., dj) образуют множество орто-
ортогональных проекторов, сумма которых равна 1 '):
E2)
E3)
E4)
Оператор П[/' есть проектор на пространство 8 ^ векторов типа (/ц) (ур.
D9)). Разложение единицы E4) позволяет записать каждый вектор из 8 в
виде суммы векторов, каждый нз которых принадлежит соответствующему
подпространству 8^;
i«)=Enu/)i">-
При \х ф v оператор B''.J является оператором, перехода из подпростран-
подпространства <?"yv в пространство S^. Смысл такого термина очевиден: из уравнений
E0) н D8) следует
{u4v i E6)
Таким образом, оператор BJ^, действуя на произвольный вектор, ортогональ-
ортогональный подпространству <S'/v, обращает этот вектор в нуль, а при действии на
вектор из S"jv переводит его в вектор из 8'^. Тем самым В^ устанавливает
биоднозначное соответствие между подпространствами <%^ и &, , сохраняю-
сохраняющее скалярное произведение.
Если | ff/v) — вектор типа (/v), то d/ векторов
B(Jl |a/v> (ц= 1,2 d,)
образуют стандартный базис представления Z7'".
Использование сумм элементов класса К.а. Проектор
Р<-1>. Если мы можем ограничиться определением неприводимых инвариантных
подпространств в пространстве 8, то нет необходимости в определении №
матричных элементов t^L s= (f | /^v) в стандартном базисе.
') Это верно для любого представления F даже в том случае, когда оно
не является компонентой Fr.

ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП 567
Суммы элементов класса
имеют по крайней мере один общий набор базисных векторов. Каждому век-
вектору этого набора соответствует некоторая последовательность k s= {k\, k^, ..,
..., ki) собственных значений операторов Ка- Всего имеется L наборов воз-
возможных собственных значений &<¦>, ?<2>, ..., ?<L>, определяемых соотношением
C5), каждый нз которых соответствует определенному неприводимому пред-
представлению группы. Следовательно, если нам удастся одновременно диагонали-
зовать К\, К.2 Kl, to каждая последовательность собственных значений
&«> будет я,й;-кратно вырождена и соответствующее подпространство &'/
определяет компоненту «//"'> представления F. Если все л,- равны единице, то
разложение $ на неприводимые достигнуто. Если же это не так, то такое же
разложение следует провести в каждом из подпространств %/, для кото-
которого я, > 1.
Напомним, что L операторов К являются функциями от меньшего числа
этих операторов, и задача днагоиалнзациин будет решена, если мы диагонали-
зуем эти последние операторы.
Задача диагоналнзацни операторов К практически сводится к определе-
определению характеров всех неприводимых представлений группы. (Таблицы харак-
характеров имеются для большинства групп, используемых в физике. Соответст-
Соответствующая литература указана в первой сноске этого Дополнения.) Действи-
Действительно, проектор />"> на подпространство &s имеет вид
/><'¦> я ? п</> = -/ Yj %{1)' (/) f=if E <a i л *** <57>
|i=l f=l a=l
Раздел IV. ПЕРЕСТАНОВКИ (ГРУППА 9>пУ)
§ 14. Основные понятия. Циклы. Классы
Определение. Предположим, что нам даны я объектов, распределен-
распределенных в я «ящиках» например, п частиц в п квантовых состояниях. Перестанов-
Перестановкой этих я объектов называется изменение их распределения по этим я «ящи-
«ящикам». Мы можем обозначить объекты целыми числами от 1 до я и определить
данную перестановку символом
1 <*2 ... ап'
где ось 0&2 а.п — целые числа от 1 до п, записанные в произвольном по-
порядке, а рь Р2, ¦ • •, Рл — те же целые числа, записанные в таком порядке, что
объект Рг занимает прн новом распределении место объекта с номером а,- в
исходном распределении. Так, при перестановке 5 объектов
_/ 1 2 3 4 5\
Ра~\5 3 2 1 А)
объект 5 занимает место объекта 1, 3 — место 2 и т. д. Как видно, значе-
значение символа перестановки не меняется при изменении в нем расположения
столбцов.
') Простое и подробное изложение теории таблиц Юнга и их приложения
к группе перестановок приведены в книге: D. E. Rutherford. Substitutional Ana-
Analysis, Edinburgh, University Press, 1948. Основы теории группы SPn содержатся
в книге: Б. Л. Ван-дер-Варден. Алгебра. М., Наука, 1976.

568 ДОПОЛНЕНИЕ Г
Последовательное применение двух перестановок ра, Рь эквивалентно од-
одной перестановке рс as рьра- Последнюю легко выписать, если верхняя строка
символа рь совпадает с нижней строкой символа ра. Например, если ра —
определенная выше перестановка, а рь имеет вид
_/ 1 2 3 4 5\_/5 3 2 1 4\
РЬ~\А 3 5 1 2) \2 5 3 4 l)'
/12 3 4 5
ТО рс = PbPa= I о к о л i
г. \25341
В частности, обратной к р будет перестановка, символ которой получается
из символа р заменой строк
р-1 _f Pi Рг ••• Рл'
/Pi Р2 ... РлЛ
\ О] Ог ... ап )
Перестановки п объектов образуют группу порядка п\
Циклические перестановки. Обозначение. Перестановка
/а, а2 ... ak_x ак ak+i ... а„ \
\а2 аз ... ak а, ak+l ... ап)'
в которой а2 занимает место oti, аз — место аг, ..., а* — место а*_ь ai—
место а*, а остальные (я — k) объектов остаются на своих местах, по опреде-
определению называется циклической перестановкой нли циклом k объектов ось
аг, ..., a*; k называется длиной цикла. Такую перестановку можно предста-
представить символом
р = (aia2 ... at). E8)
Условимся, что первый объект в этой строке ai занимает место последнего а*,
а каждый последующий at — место предыдущего аг_г. При таком обозначении
порядок k элементов определен только с точностью до циклической переста-
перестановки.
Два цикла, не имеющие общих элементов, коммутируют.
Произвольная перестановка п объектов равна произведению коммутирую-
коммутирующих циклов (эти циклы не имеют общих элементов) и такое разбиение на
циклы единственно.
Так, определенная выше перестановка ра равна произведению двух циклов
A54) и B3) и ее можно записать в виде
ра =A54) B3) = B3) A54).
Аналогично
р6 = A4) B35), рс=A25) C) D).
Цикл единичной длины эквивалентен тождественному преобразованию и его
можно опустить, записав просто рс = A25). Если такие циклы не опускать,
то сумма длин всех циклов перестановки равна п.
Каждая перестановка полностью определяется:
(i) ее структурой циклов, т. е. числом циклов h (h ^ n) а длинами цик-
циклов %i, %г %н Ы + А,2 + ... + %н = п);
(ii) набором чисел в каждом цикле и порядком этих чисел с точностью до
циклической перестановки.
Если обратить порядок следования чисел в каждом цикле, то получится
обрати аи перестановка. Так,
р~' = D51) C2).

ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП
Классы. Две перестановки с одинаковой структурой циклов принадле-
принадлежат к одному классу. Обратное утверждение также справедливо.
Циклическое обозначение для сопряженного к р элемента р' = хрх~1 по-
получается применением перестановки х к последовательности п чисел, фигури-
фигурирующих в циклическом обозначении р. Например,
12345\/54 132\ _, /2534 14
.2413 5J~\5 3 2 1 \)' X ~\l 542 3/'
Транспозиции. Транспозицией называется перестановка двух объек-
объектов (цикл длины 2). Транспозиции образуют класс в Э'п.
Произвольный пикл данной длины k равен произведению (k—1) транс-
транспозиций
(«1а2 •••М = (а1а2) (а2аз) ¦¦¦(ak-iak)-
Вообще, любая перестановка р может быть записана как произведение
транспозиций. Такое разбиение не является единственным, но число транспо-
транспозиций в нем имеет определенную четность, оно либо четное, либо нечетное,
что мы будем обозначать как (—1)р. По определению, перестановка называется
четной или нечетной в соответствии со знаком (—1)" = +1 или — 1.
Подгруппы группы Э'п. Группа $tn. Группа У„ имеет только
одну инвариантную подгруппу — группу четных перестановок $1п. Индекс бФп
равен 2, дополнением к ней является множество нечетных перестановок, а
фактор-группа ^Jst-n— абелева.
Среди других подгрупп в Э'п отметим группы перестановок из m объектов
Ут, где т < я, группы $tm (m < я) и т. д. Индекс Э'т равен (я!/т!), а ин-
индекс si-m равен 2 (я!/т!).
Снмметризаторы и антисимметризаторы группы 9>п.
Особую роль играют две линейные комбинации всех перестановок группы Уп—
снмметризатор « и антисимметризатор а:
(суммирование происходит по всем элементам 9s,,). Они коммутируют со все-
всеми элементами группы и обладают следующими свойствами:
qs = sq = s, qa — aq = (— l)qa, F0)
(q — произвольная перестановка)
s2 = s, a* = a. F1)
§ 15. Разбиения
Определение. Разбиением X зэ [Х^... Xh] целого числа п называется
упорядоченная последовательность положительных целых чисел Xi ^ Хг ^ ...
... &%н, сумма которых равна я:
Поскольку структура циклов перестановки определяется некоторым раз-
разбиением числа я, то каждое разбиение п определяет класс в У*.

570
ДОПОЛНЕНИЕ Г
i •.. Р-ь] — Два разбиения я.
Неравенства. Пусть X = [Я1... Хн\, (i
По определению
X = ц, если h = k и Я] = Ць Яг = Цг, •.., Хн = Ц*;
Я > ц, если первый отличный
от нуля член в последовательно-
последовательности Х\ — Hi, Я2 — Цг, ... положи-
положителен;
Я < ц, если первый отличный
от нуля член в последовательности
Я] — A,1, Я2 — Цг, ... отрицателен.
Пример: для я = 5 [5] >
>[41]>[32]>[312] и т. д. (Мы
использовали условное обозначе-
обозначение [312] для [311].)
Диаграммы Юнга УА>
[J 2] Данное разбиение [Я^ ... Я;,] мо-
можно представить диаграммой Юн-
Юнга Yfo которая построена из п кле-
клеток н состоит из h строк, располо-
^^_^ I | жеиных одна под другой. Первая
I I | | ?j /г] _ строка содержит Ai клеток, вто-
М Hj рая — Х2 клеток ..., строка h co-
Ц держит Хн клеток (см. рис. 31).
Таблица Юнга 8?. Пер-
Первые п целых чисел можно распо-
расположить в я клетках я1 способами,
получая всякий раз некоторую
таблицу Юнга.
Будем обозначать символом в^ и называть нормальной таблицей такую,
в которой числа 1, 2, ..., я расположены в обычном порядке: последователь-
последовательность 1, 2 Xi в первой
строке, Х\+ 1; Х\-\- 2, ..., Я,+
+Яг — во второй строке и т. д.
Применяя перестановку р к п . I' \г\з I |.2|5| 3 \4
числам, таблицы в^, мы полу-
получим новую таблицу в? = P®v
Отметим, что о@? = в?р, и
для каждой диаграммы Юнга
Рис. 31. Разбиения 5-ти элементов и
соответствующие диаграммы Юнга.
1
4
2
5
3
z\S
А
/ [г
таб-
таб„С«Я
в
существует я! различных
лиц (см. рис. 32).
Ассоциированные
разбиения. Два разбиения
называются ассоциированными
друг другу, если диаграмма
Юнга одного получается из
диаграммы Юнга другого заме-
заменой строк на столбцы (отраже-
(отражение относительно главной диа-
диагонали). В дальнейшем будем
обозначать такое преобразова-
преобразование символом ~. Так, А = [А,!... Aft] обозначает разбиение, ассоциированное в
Я = [Я1... Я/t]. Отметим, что k = Ai, a h = Ai и что As равно числу элементов
разбиения Я, равных или больших s, и наоборот.
И г]
Рис. 32. Несколько таблиц, соответствую-
соответствующих разбиениям X = [32] и X = [221] 5-ти эле-
элементов

ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП 571
Аналогичным образом определим диаграмму Юнга У^ ва Y%, ассоцииро-
ассоциированную с Кх, и таблицу Юнга ё?, ассоциированную с в?. Отметим
(см. рис. 32), что
Ч
но, вообще говоря,
§ 16. «Симметризаторы» Юнга.
Построение неприводимых представлений
«Симметризаторы» sx, ax, sk, ax строк и столбцов 6^. Опре-
Определим операторы s^ — симметризатор строк в^, и а^ — антиснмметризатор
строк в^, следующим образом:
,' 5ГТ У К' F2)
\ ... Ад! /_( А v '
ft
ft
суммирование происходит по всем Л|! Л,21 ... Лй! перестановкам h, которые
оставляют инвариантными строки вЛ, т. е. в любой цикл которых входят эле-
элементы из одной строки в^. Это множество перестановок А^ образует под-
подгруппу 9"уц группы SPn. Если обозначить группу перестановок Я(- объектов,
стоящих в (-й строке таблицы в^, $Р^; то ^11] есть пРоизведение следующих
подгрупп группы 5* :
Операторы s^ и а^ равны соответственно произведению симметризаторов и
аитисимметризаторов этих А подгрупп.
Аналогичным образом определяются симметризатор s^ и антисимметри-
затор а^ столбцов 6^ (т. е. строк вх). Приведем соответствующие формулы
V v.,
F4)
тт Z(-1H^ F5>
где суммирование происходит по всем Ль'Лг!.. .Я,&1 перестановкам о,, которые
оставляют инвариантными столбцы таблицы в.
Основные свойства.
а) Введенные операторы s^ и а^ равны произведениям симметризаторов
или антисимметризаторов, следовательно,
4 = 8л- 4 = av *x= •-.. F6)

672 ДОПОЛНЕНИЕ Г
б) Если <о аз ? х^р _ произвольная линейная комбинация элементов 9'п
р
(элемент групповой алгебры) и если ')
Л>ц или А<Д, F8}
тогда
«^^ = ^@^=0. F9>
В частности, при выполнении любого из условий F8) справедливы равенства
Vn-^-Vx-Vi»-0- G0>
«Неприводимые симметризаторы» i^ и ]^.
'л - *A - Е (-1 Wi (Ь + о).
2 (
А»
Будем называть /^ «неприводимым симметризатором», /^ — «неприводимым
антиенмметризатором» таблицы 8^. Аналогично определяются неприводимые-
симметризатор и антисимметризатор 8,:
Пусть и — определеннаи выше линейная комбинация, тогда можно пока-
показать, что
const iv Hjfus^ => const /^ G2>
Из соотношений F9) и G2) легко вывести соотношения
'Vn = V4 = constVv 4/(i = V\=const/A(i- <73>
Основная теорема.
(i) В пространстве регулярного представления группы 9>п векторы ai.
(со — произвольный элемент групповой алгебры 9*п) натягивают неприводи-
неприводимое инвариантное подпространство <8* и, следовательно, порождают некото-
некоторое неприводимое представление Р^ группы Уп.
(п) Векторы со/, натягивают то же инвариантное подпространство &.
(iii) Если К ф р., то неприводимые представления Р^ и Р^ неэкви-
неэквивалентны.
Поскольку число неприводимых представлений 9"„ равно числу классов
этой группы и, следовательно, числу разбиений п, то теорема позволяет по-
построить все представления. Как следствие, каждое неприводимое представле-
представление группы Фп можно характеризовать определенной диаграммой Юнга.
Симметризаторы ассоциированных таблиц и ассоции-
ассоциированные представления. Сопоставим каждому элементу и = ? Хрр
р
') Из справедливости одного из условий F8) не следует справедливость
другого. Например, если Л = [4 I*] н ц = [3 3], то А > ц; однако А = [3 I3],
Д = [23] и, следовательно, А > Д.

ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП 573
групповой алгебры элемент со <= ? (—\)р хрр. Это соответствие — линейное,
р
взаимно однозначное и обладает следующими свойствами:
а) если Ti = рсо, то п' = (—1)"рсо';
б) если ?= <от|, то ? =(o't)' (сохраняет произведение).
Отметим, что таким образом возникает взаимно однозначное соответствие ме-
между «симметризаторами» ассоциированных таблиц 8^ и 8^:
откуда
\-«А =¦'»,' k — aJ\==ik- G4)
Пусть и,^, со2/л — множество базисных векторов, которые согласна
основной теореме определяют представление Р . В силу G4) им соответст-
соответствуют векторы Ш[/^, ш2/^,.... которые определяют представление PW. Ясно, что
при таком выборе базисов матрицы Р^ и Р^\ отвечающие в каждом из пред-
представлений данной перестановке р, связаны соотношением
р(*) = (_1)Рр<«_ G5)
«Симметризаторы таблиц» в?. Точно так же, как мы действо-
действовали, используя таблицы 8^, мы можем определить перестановки А?, v^ и
симметризаторы s?, ..., (?, ..., используя таблицы 8^. Отметим, что
откуда
sl = pskp~\ аРк= ... и т. д. G6)
Свойства «снмметризаторов», связанных с 8^, можно вывести, используя свой-
свойства «симметризаторов», связанных с 8,, и соотношения G6).
§ 17. Основные свойства неприводимых представлений
группы д>„
Большинство свойств неприводимых представлений Э'п следуют из свойств
«симметризаторов», которые были приведены в предыдущем параграфе.
Каждое неприводимое представление Р^ группы ff'n характеризуется оп-
определенной диаграммой Юнга и может быть построено с помощью неприводи-
неприводимого симметризатора /^ (или /^) Неприводимые представления являются само-
самосопряженными
pW'»p(M. G7)
Представления размерности 1. Существует только два пред-
представления размерности 1:
(i) тождественное (или симметрическое) представление S;
(и) антисимметрнческое представление А, в котором каждой перестановке
р отвечает (—1)".
Эти представления порождаются s и а соответственно (ур. E9)).
Диаграмма Юига для S имеет одну строку и отвечает разбиению [л], а-
для представления А — одни столбец и отвечает разбиению [Iя].

S74
ДОПОЛНЕНИЕ Г
Ассоциированные неприводимые представления. Два
неприводимых представления Р(Л) и р*' называются ассоциированными, если
их диаграммы Юнга являются ассоциированными друг к другу. Из уравнения
G5) следует соотношение
я» А ® Р(К).
G8)
Компоненты размерности 1 тензорного произведения
J>(K) 0 Р(и). Тензорное произведение двух представлений Р(М ® Р(и) имеет одну
(и только одну) компоненту размерности 1 в том и только в том случае, если
выполнено одно из следующих условий:
(П X = |i, то компонентой будет S;
(п) Л, = р., то компонентой будет А.
Неприводимые представления Уп-ъ содержащиеся в
Р' . Любое неприводимое представление группы SPn есть представление (воз-
(возможно приводимое) ее подгруппы Э'п-ь
Обозначим символом Р^ неприводимое представление 9>и отвечающее
разбиению X целого числа t. Можно показать, что разложение Р^ на пред-
представления, неприводимые по отношению к группе SPn-\, дается формулой
рМ « V Р^Ч[, G9)
и
тде суммирование происходит по всем разбиениям ц. числа (п—1), отвечаю-
отвечающим диаграммам Юнга, которые получаются из диаграммы Юнга разбиения X
числа п отбрасыванием одной из возможных клеток.
Пример:
Используя формулу G9) можно связать некоторые характеры !Уп-1 с ха-
характерами 9"п- В частности, иа основании этой формулы можио вычислить раз-
размерность представлений Э'п, зная размерность неприводимых представлений
¦9>„-х.
Построение неприводимых инвариантных подпро-
подпространств представления Р. Различные «симметризаторы» в предста-
представлении Р задаются линейными эрмитовыми операторами, которые мы будем
обозначать соответствующими прописными буквами.
Метод построения неприводимых компонент представления Р следует из
основной теоремы § 16. Пусть |а> — произвольный вектор пространства S
представления Р; тогда вектор /, | и) в случае, если он отличен от нуля, пре-
преобразуется по представлению Р , и в соответствующем пространстве пред-
представления Ш^ содержится ненулевой вектор
I и). Множество векторов
получающихся действием оператора /, на векторы базиса пространства &,
натягнвают подпространство 3^, размерность которого равна п^ — числу ком-
компонент Р , содержащихся в Р. Пусть |а) —один из векторов ортонормиро-
ванного базиса в 3^, тогда пространство &' ^, образованное действием опера-
операторов группы на вектор [0), есть пространство представления Р"'. Поступая
таким образом со всеми п^ базисными векторами Э'^, получим п^ ортого-
лальных друг другу пространств представления Р' .

ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП 575
Оператор Q в &, инвариантный относительно Я'п, переводит векторы ка-
ждого из подпространств^ в векторы того же подпространства. Таким обра-
образом, задача диагонализации Q в пространстве & сводится к задаче диагона-
лизации этого оператора в каждом из подпространств 21..
Свойства симметрии векторов представления Р( \ В об-
общем случае кет-векторы не обладают определенными свойствами симметрии
нли антисимметрии. Будем приписывать вектору |) симметрию S, в том слу-
случае, если он принадлежит подпространству проектора S^. Такой вектор сим-
симметричен относительно перестановки элементов из одной строки в в.. Точно
так же будем считать вектор А^ антисимметричным, если он принадлежит
подпространству проектора А^.
Аналогичным образом, используя таблицы Юнга вх, в?, определяют сим-
симметрии типа Sfo S? и антисимметрии А^, А%').
Из двух векторов с определенной симметрией S?, S^ более симметричным,
по определению, считается тот, который соответствует большему из разбие-
разбиений Л, |х. Из двух векторов с определенной антисимметрией Л?, А^ более ан-
антисимметричным считается тот, который соответствует большему из разбие-
разбиений X, ц.
На основании равенств F9) и основной теоремы мы можем сделать вы-
вывод, что пространство неприводимого представления Р'*1) содержит один
и только один S^-симметричный вектор (и, следовательно, один и только один
^^-симметричный вектор, где р — произвольная перестановка) и не содержит
векторов с большей симметрией2). Это пространство содержит один и только
один А^ — антисимметричный вектор и не содержит векторов с большей анти-
антисимметрией.
Оператор суммы элементов класса транспозиций Кт.
Каждому разбиению ц соответствует некоторый класс н оператор суммы эле-
элементов класса К^- Различные возможные собственные значения^' этого опе-
оператора соответствуют различным неприводимым представлениям Р^ группы
Р'я. Эти собственные значения являются функциями целых чисел Хь %2, ..., %h,
участвующих в разбиении %. {N. В. Для двух различных разбиений соответ-
соответствующие собственные значения некоторого /Сц не обязательно различны: из
Л ф %' не следует, что *<*¦> ф kfi'K)
Рассмотрим оператор суммы элементов класса транспозиций Кт:
') Перестановка Р преобразует любой S^-симметричный вектор в 5^-сим-
метричный и любой Л^-антисимметричный вектор в Л^-аитисимметричный
(см. соотношения G6)).
Такого соответствия не существует между симметриями типа 5,, А, и
S , А . Последние эквивалентны симметриям типа 5?, А\ соответственно, где
перестановка q определяется равенством в^ = ^в^.
2) Точнее, не существует S -симметричного вектора, отвечающего любому
из разбиений ц. которые удовлетворяют одному из неравенств: \i > X, jl < Kw

576 ДОПОЛНЕНИЕ Г
Оператор К.т коммутирует со всеми перестановками и, следовательно,
Используя это соотношение и уравнения F7), легко показать, что kj^ равно
разности числа транспозиций типа h^ (симметричиых пар) и числа транспози-
транспозиций типа о^ (антисимметричных пар):
(80)
§ 18. Система я фермионов спина 1/2
Симметрия состояний п тождественных спинов—.
Теорема. Пространство векторов состояний п тождественных спинов -у
с полным спином (SM) отвечает неприводимому представлению группы 9>ы
Диаграмма Юнга этого представления соответствует разбиению I — п + S,
— п — 5 (т. е. имеет не более двух строк).
Следствие I. Если п = 2, то существует одно антисимметричное со-
состояние со спином 5 = 0 и три линейно независимых симметричных состоя-
состояния со спином 5=1.
Следствие II. Если п > 2, то антисимметричных состояний нет; су-
существует п + 1 линейно независимых полностью симметричных состояний, а
именно, 25 + 1 =» п + 1 состояний, для которых полный спин имеет макси-
(*-¦*•)¦
Доказательство. Размерность пространства c?(s), которое образовано
векторами состояния п спинов -=¦, равна 2". Динамические состояния индиви-
дуального спина с номером i, отвечающие собственным значениям +— н —
оператора sz, обозначим щ и vi соответственно. Взяв все возможные произве-
произведения из п таких векторов и и v, получим ортонормированный базис в c?(s).
Приведем пример базисного вектора
мальное значение
м . . . Vn.
Это собственный вектор компоненты 5г оператора полного спина
соответствующее собственное значение равно М = \—г-л. Действуя на
лсеми перестановками, мы получаем

ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП
677
различных векторов, которые натягивают подпространство, отвечающее собст-
собственному значению М. Каждый из этих векторов содержит -<г п + М векторов
типа л и -л-Л векторов типа о.
Подпространство с заданным значением М можно разложить на ортого-
ортогональные подпространства, отвечающие различным возможным собственным
значениям оператора S2. Соответствующее квантовое число 5 может прини-
принимать •=- п — | М | + 1 значений: \М\, \ М | + 1 — п. Подпространство, об-
разованное векторами с полным спином (SM), обозначим IT<S)EAI). Посколь-
Поскольку операторы S2 и 52 коммутируют со всеми перестановками, каждое нз этих
подпространств определяет некоторое представление группы SPn. Более того,
поскольку 5+ и 5- также коммутируют со всеми перестановками, то пред-
представления, которые определяются двумя подпространствами с одним и тем
же значением S, эквивалентны.
Докажем теперь следствие II (следствие I очевидно). Для доказательства
достаточно рассмотреть проекции векторов ортонормированного базиса в ^P(s)
на пространство симметричных состояний и на пространство антисимметрич-
антисимметричных состояний. Это легко сделать для определенных выше базисных векторов.
Коль скоро п > 2, то любой вектор базнса Z, содержит не меньше двух от-
отдельных спинов в одинаковом состоянии и или V. Допустим, что в С имеется
множитель тщ\ тогда в силу равенств А = А — A — ((/)) и -^ A—(//)) и{и .=0,
имеем At, = 0. С другой стороны, существует одна и только одна пол-
полностью симметричная линейная комбинация базисных векторов подпростран-
подпространства, отвечающего собственному значению М, а именно, сумма всех Cj[ ба-
базисных векторов. Поскольку это верно для любого возможного значения М,
то такой полиостью симметричный вектор обязательно соответствует макси-
максимальному значению полного спнна 5 = — п. Это завершает доказательство
следствия II.
Приведенное выше рассуждение с А можно повторить, используя анти-
симметризатор А^, и получить, что А^ = 0, если диаграмма Юига содержит
больше двух строк. Осюда следует, что диаграммы Юнга для неприводимых
компонент представления группы Р'п, которое порождено пространством ^P(s),
имеют, самое большее, две строки.
Пусть к = [Х1Я2] — разбиение числа п, удовлетворяющее этому условию.
Число неприводимых компонент Р' ' равно числу линейно независимых векто-
векторов типа /. I \ = Sj/4, | ). Для перечисления последних достаточно рассмо-
рассмотреть табл. I.
Таблица 1
Таблица вх
1
л1 + л,
Мы можем разделить п спинов-г- на два множества: (\i — Хг) элементов
: X] первой строки, для которых нет соответствующих эле-

578 ДОПОЛНЕНИЕ Г
ментов во второй, и Лг пар элементов, расположенных в соответствующих
столбцах. Обозначим полные спины этих множеств Si и S2
Пусть S^1"^ — проектор на состояния, симметричные относительно (Я,1
перестановок спинов первого множества. Ясно, что
Однако по определению оператор А^ — проектор на сннглетное состояние каж-
каждой из пар спииов второго множества. Существует только один вектор, обла-
обладающий таким свойством (следствие I), этот вектор соответствует спину
5г = 0. Оператор 5 ' проектирует векторы состояний первого множества
на подпространство размерности B5j + 1), отвечающее наибольшему возмож-
возможному значению 5, (следствие II), а именно, -г- (Ях — Я2). Таким образом,
5* '~ А. — проектор на подпространство размерности BS+1), отвечающее
1
значению полного спина 5 = — (Я,1 — Ki). В силу того, что проектор 5, ком-
коммутирует с S, действуя на векторы этого подпространства, он либо аннулирует
их всех, либо преобразует их в векторы с тем же полным спином. Первая
возможность исключается, в противном случае в c?(s) не существовало бы век-
векторов с полным спином — (Ki — Лг), а из второй возможности следует при-
приведенная выше теорема.
Построение полностью антисимметричных векторов.
Динамнческие состояния п фермноиов спина '/г принадлежат тензорному про-
произведению с?'0)® c?'s) определенного выше пространство c?(s> и пространства
орбитальных переменных с?@). Последнее можно разложить на взаимно орто-
ортогональные, неприводимые подпространства с?(О)@|л), инвариантные по отно-
отношению к группе 5Рп- В подпространстве ^><О)@|х) определено'некоторое непри-
неприводимое представление Р^\ индекс 0 нумерует подпространства, в которых
задано одно и то же неприводимое представление. Для того чтобы построить
полный набор ортогональных антисимметричных векторов, достаточно по-
построить их в каждом из подпространств #(о)@|л)® S'is). В этом подпростран-
подпространстве имеется столько линейно независимых антисимметричных векторов, сколь-
сколько раз компонента А встречается в разложении представления, заданного в
этом подпространстве. Следовательно (§ 17), число таких векторов равно чис-
числу неприводимых представлений Р^\ участвующих в разложении представле-
представления, заданного в c?(s). Если диаграмма Y содержит более двух столбцов, то
таких векторов нет. Если диаграмма Y содержит не более двух столбцов и
если мы в согласии с приведенной выше теоремой положим
(81)
тогда имеется B5-J-1) неприводимых представлений, и антисимметричные
векторы, которые можно образовать в этом случае, являются собственными
векторами оператора S2, соответствующими полному спину (SM) (М = —S,
-S+1 5).
Не зависящие от спина скалярные наблюдаемые. LS-
связь. Независимую от спина скалярную наблюдаемую Q можно рассма-

ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП 57Ф
тривать как наблюдаемую пространства с?<0), инвариантную относительно вра-
вращений и перестановки только орбитальных переменных
[Q,?]=0, [Q, Я@)] = 0.
Пространство Sw есть прямая сумма подпространств с?@) (%L\i) размерности
BL + 1) rfp,, которые неприводимы по отношению к группам вращений и пере-
перестановок1). L — квантовое число момента импульса, ц — разбиение, отвечаю-
отвечающее представлению P(ii\ т — дополнительное квантовое число, нумерующее эк-
эквивалентные подпространства. В частности, подпространства S^ (tZ-ц) можно
выбрать так, чтобы наблюдаемая Q в каждом из них была равна некоторой
константе f^11 (см. § 9).
Собственные векторы Q, отвечающие собственному значению*^ , являют-
являются антисимметричными векторами подпространства &"i0) (xL\i) (&&<-s\ Исходя
из предыдущих рассуждений, такие векторы можно построить, только если
Кц содержит ие более двух столбцов. В этом случае разбиение |х однозначно
определяется квантовым числом S (ур. (81)). Подпространство антисимме-
антисимметричных векторов в с?@)(т?ц.) ® #"(s) отвечает определенному значению 5 пол-
полного спина системы частиц. Это подпространство &{t;LS) имеет размерность
BL + 1) B5 + 1) ив нем можно иайти собственные векторы полного момента
импульса и полного спина
\%LSMLMS)
которые образуют стандартный базис
') Подпространство с?@)(т/.ц) прнводимо относительно группы вращений
и является суммой du эквивалентных неприводимых подпространств (здесь
du — степень представления Р^). Оно также прнводимо относительно группы
ffn н является суммой BL + 11 эквивалентных неприводимых подпространств.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Адиабатическая теорема 233, 237, 240—243
Адиабатический переход 232, 236—239
Адиабатическое приближение 243—247, 273,
277-284
Алгебра групповая 560
Амплитуда перехода 296
. бориоаское приближение 327
— —, вычисление вариационным методом
343-350
, интегральное представление 324
— рассеяния 107, 292
вперед 353
. интегральное представление 293—295
Антиснмметризатор 89-93, 120, 128, 266, 569
— группы перестановок 569
— Юнга 571
Атом водорода 214, 251, 412-415
, основное состояние 258 — 261
— гелия 185—187
, основное состояние 261 —262
— сложный 112
— углерода 197
— Фока—Дирака 265—272
— Хартри 265-272
Атомные уровни 195—197
Бозон Е5-Э8, 103, 290
Бозониый газ 97
0-распад 125, 159
Вакуум 443-444, 461
Вектор антисимметричный относительно
перестановок 91
— ковариантный 363
— контраварнантный 363
— нулевой 364
— пространственно-подобный 364
— симметричный относительно перестано-
перестановок 91
4-вектор, времеииподобный 364
— эиергии-импульса 395—396
Векторное поле 52—54
, поперечная часть 491
, продольная часть 491, 494
Вероятность перехода 219, 221
Вещественные нормальные координаты 501
Взаимодействие, зависящее от спина 54—57
— излучения с частицей 509
— иуклон-иуклоиное 55—57
— поля и частицы 457
— спии-орбитальное 54, 198-19S, 420
Возбуждение ядер, кулоиовское 222—226, 331
Возмущение вырожденного уровня 193—206
— невырожденного уровня 182—193
— первого порядка 184 — 185
— периодическое 231—232
Волна искаженная 311—320
— плоская 405-407, 451, 504
— свободная сферическая 4Ю—411
Волновая функция частицы спииа '/2 50
двухкомпоиеитиая 51
Вращение 13, 28—36, 536
— иифииитезимальное 29, 34—36
— наблюдаемых 33—34
— на угол 2л 38—40
Вращения матрица 30, 41, 536—537
— оператор 31—33, 536
Время жизии состояния 469, 475
— собственное 368
Вырождение 473
— Крамерса 172-173
— обменное 84—85, 94
— ротационное 43
— уровней 113
G-вырождение 154, 173
Газ бозонный 97
— фермиониый 99 . _. .
Гамильтониан атома в постоянном магнит-
магнитном поле 55
— Дирака 374, 405
частицы в центральном потенциале 407
во внешнем поле 375
— свободного электромагнитного поля 500
Y-излученйе атома 76
Y-матрица 377, 380-384
Гипотеза эргодическая 97
Гиромагнитное отношение 45
Гомоморфизм группы 548
Градиент ковариантный 365
—контравариантный 365
Группа 545
— абелева 546
— Галилея 145, 177
— изотопических вращений 144
— коммутативная 546
— конечная 546, 559
— линейных подстановок 548
— Лоренца 366
— —, неоднородная 365
, полная 366
, ортохроииая 366, 384-388, 391
, собственная 367, 388—ЗП
— непрерывная 146, 546
— операторов преобразования 145—146
— перестановок 144, 567
— полупростая 548
— преобразований 140—145
— простая 548
— пространственных преобразований 144
— Пуанкаре 366
Диаграмма Юнга 570, 576
Диамагнитный член 55
Длина рассеяния 348
Дырка 435

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
581
Задача на собственные значения 255—257
Закон Лоренца 476
— распада, экспоненциальный 469
— сохранения 154-156
изотопического спина 156
импульса 398
— — момента импульса 155
— — полного импульса 155
— момента импульса 398, 488
— — симметрии относительно перестано-
перестановок 155
четности 155, 398
——энергии 161
энергнн-нмпульса 488
Зарядовая незавнсимнсть 124—128, 156
Зарядовое сопряжение 399—401, 429
Захват радиационный 483
Излучение кванта 468
Y-излучеиие атома 76
Изоморфизм групп 548
Изотропность пространства 159
Импульс излучения 496, 504
— механический 368
— ПОЛЯ 451-456, 488
— сопряженный, классического поля 445
Инвариантное подпространство представле-
представления 551
Инвариантность относительно перестано-
перестановок 155
— по отношению к вращениям 40—44.
155, 159
Индекс коварнантный 363
— контраварнантный 363
— подгруппы 560
Интеграл движения 154, 397—398
Интерференция 340
Искаженная волна 311—320
Калибровка радиационная 491
Калибровочная инвариантность 401
Калибровочное преобразование 490
Лоренца 491
Канал реакции 322
— — входящий 322
открытый 323
Катастрофа ультрафиолетовая 512
Квазивырождейне 295
Квантовое поле 362, 439
Класс смежности 544
— сопряженных элементов группы 546, 560
Ковариантная компонента тензора 313
Ковариантный вектор 363
— градиент 365
— индекс 363
Константа связи 458
Контраварнантная компонента тензора 363
Коитравариантиый вектор 363
— градиент 365
— индекс 363
Конус световой 365
Координата нормальная 44о, 442, 501
Коэффициенты векторного сложения 61—67
— Клебша — Гордана 61—67, 74—76, 175,
524—528, 532
, свойства симметрии 64, 526
— . соотношение ортогональности 63, 526
— Рака 67-70, 530, 531
Кулоиовская энергия атомных ядер 187—189
Кулоиовское возбуждение ядер 222—226, 331
Лагранжиан поля 445
Лемма Шура 143, 552
Магнетон Бора 46
Магнитный момент атома 45
внутренний 54
Масса отрицательная 371
— релятивистская 368, 404
Матрица перехода 296, 312, 350—357
S-матрнца 353
Г-матрнца 295, 318, 323
—, свойства инвариантности 355
Матрицы вращения 30, 41
— Днрака 377, 380-384
— Паули 48
Y-матрнцы 377, 380-384
Метод Блоха 213
— Борна —Оппенгеймера 274, 283-284
— вариационный 254—290
Ритца 254-255
для связанных состояний 255—257
— Като 206-213
— Томаса —Ферми 112, 115, 118
Метрика псевдоевклидова 363
Метрический тензор 363
Микрообратнмость 354
— упругого рассеяния 297
Множитель Лайде 46, 47, 202, 214
Модель атома Томаса —Ферми 115-118, 199
Молекула двухатомная 284—290
Момент импульса 13-81, 524
излучения 496
,инвариантное подпространство 20, 21
, коммутационные соотношения 14, 15
орбитальный 24—26
, собственные состояния 26
, спектр 24-26
полный 404, 537
, собственные векторы 61
полуцелый 38—40
——поля 489
орбитальный 498
, собственные значения 17—20, 23—24
, Функции 20, 21
, сохранение 42
, спектр 17—20, 24
, стандартное представление 21—23
— магнитный 75, 420
Момент мультнпольцый 75—77
— спина 404
— электрический 76
Море Дирака 435
Наблюдаемые инвариантные 558
— частиц спнна Va 50
Неприводимость по отношению к вращениям
40-41
Нормальные координаты 440, 442, 501
Нуклон 119
Нуль-вектор 364
Обращение времени 161-178, 307, 398—401,
457
— магнитного поля адиабатическое 247—251
мгновенное 235—236
Однородность пространства 158
Оператор антилниейный 131, 135—137,
139-140
— антнснмметрнзацнн 89—93, 120, 155
— антнунитарный 138, 141, 166
— векторный 14, 15
— Даламбера 365
— зарядового сопряжения 398
— комплексного сопряжения 139, 167—169,
398
— перестановок 86—98
— преобразования 145-146, 395

582
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Оператор рождения 443, 449, 504—505
— симметризации 89—93, 96, 120, 155
— скалярный 70—71
— спнна 369
— тензорный неприводимый 70—77, 542—544
— уничтожения 443, 449, 504—505
— четности 397
— числа частиц 444, 449
— эволюции 93, 95, 181, 217, 219, 470
Орбитальные переменные 50
Основное состояние 461, 463, 443—444
Отиошенне гиромагнитное 45
Отражение координат 161, 367, 391, 457
Приближение борновское 229, 297, 299, 327
, критерий применимости 302
обобщенное 311, 327-328
— независимых частиц 112
— слабой связи 476
— центрального поля 112—114, 195
Принцип микрообратимости 161, 169—172
— наименьшего действия 446
— соответствия 401
Произведение скалярное 3-векторов 364
——4-векторов 364
Пространство—время 363
Прямая сумма представлений 550
Переменные орбитальные 58
— спиновые 50
Перенормировка массы 467, 489
Перестановка 567
— циклическая 558
Переход адиабатический 232, 236—239
— мгновенный 232—236
— радиационный 463—469
Плотность тока 404
— 4-тока 379.
Поглощение кванта 483
Подгруппа 547, 560
— инвариантная 547
—, индекс 560
—, сопряженная 547
Подобные частицы 86—93
Подпространство инвариантное 205, 551
Позитрон 435
Поле векторное 52—54
, поперечная часть 491
, продольная часть 491, 494
— квантовое 362, 43Э, 442
свободное 442
— скалярное классическое 440
— спинорное 50, 51
Поляризация круговая и линейная 505
Поправка второго порядка 464
— высшего порядка 189—191, 421
Порядок группы 546
Постоянная тонкой структуры 466
Постулат симметризации «5—96. 98, 110
Потенциал Гаусса 357
— Морса 288, 291
— центральный 307, 407—410
— электромагнитный 365, 490
— Юкавы 367
Правило отбора 62, 75
— Хунда 197
Представление вещественное 168
— вполне приводимое 551
— вращвющнхея осей 238—239
— Днрана Э75—377
— единичное 549
— линейное 548
— неприводимое 551, 561
— приводимое 551
— регулярное 561, 563, 564
— симметрическое 86, 86
— сопряженное 549
— стандартное 554
— тривиальное 549
— унитарное 549
Представления эквивалентные 549
Преобразование 140
— антилниейиое 137
— антнунитарное 138—141
— калибровочное 490
лоренцево 491
— Фолдн—Вотхойзена 421—427
Приближение адиабатическое 243—247, 273,
277-284
Радиационный захват 483
Радиус электрона классический 489
Разбиение целого числа 569
Разложение борновское 301—304, 311
обобщенное 314
Размерность представления 549
Рассеяние быстрых электронов на атомах
329
— двукратное, амплитуда 341
—, интегральное представление решения 334
— многократное 341
— иеупругое 320
— простое 338
— резонансное 481
— упругое 304, 320
— частицы на двух центрах 335—336
Резольвента 207-210, 471, 483
Резонанс 231-232
Решение с отрицательной энергией 431—435
Ротатор жесткий 191 — 193
Сверхтонкая структура 55
Связь днполь-дипольная 420
— Рассела —Саундерса 198—202, 214, 235
— слабая 461
//-связь 214
LS-связь 198-202, 214, 235
Сдвиг во времени 161
— лэмбовскнй 415
— уровня 464
— фаз, стационарное выражение 343
— —, вариационное вычисление 347
Сечение рассеяния 107, 108, 295, 321
геометрическое 304
——дифференциальное 298
_—_ неупругого в борновском приближе-
приближении 330
полное 105, 298
——Резерфорда 224
Сила Лоренца 368, 495
— тензорная 56, 66
Символы Вигнера 69, 530
— «3/» 524
— «6/> 69, 530, 532, 535
— «9/» 69, 534
— *3п1» 67
Снмметрнзатор 89-93, 98, 120, 128, 569
— группы перестановок 569
— Юнга 571
Симметрия 13
Система тождественных частиц 82—129
Скобки Пуассона 147
4-скорость 369
Сложение моментов импульса 57—70,
524-544
— спинов V» 60
Собственная энергия электрона электроста-
электростатическая 489
Соотношение Бора—Пайерлса—Плачека
353-354

предметный указатель
583
Соотношение Дирака 127
— микрообратимостн для Г-матрнцы 354
— ортогональности 562
Сопряженная подгруппа 547
Сопряженные элементы группы 546
Состояние виртуальное 221
— динамическое 256—259
— микроскопическое 97
— метастабильное 481
— микроскопическое 97
— основное 443-444, 461, 463
— собственное вырожденное 470
невырожденное 470, 473
— с отрицательной энергией 431—435
Спектр полосатый 111
Спнн 13, 44
— изотопический 118—128
полный 120
— поля 498
~ядра 109
— i/j 48-55
— 1 50
Спиновые переменные 50
Спинор 50, 391
Спинорное поле 50, 51
Статистика атомных ядер 109—111
— Бозе —Эйнштейна 96—98, 503
— Ферми —Дирака 98-100
Столкновение двух тождественных частиц
103-109
— протонов 107
— сложное 348
— с перераспределением 321
Структура молекул 272-290
— сверхтонкая 420
Сферические функции 26—28
, условия иа фазу 26
Таблица Юнга 570
Тензор 71
— метрический 363
— неприводимый 71—72
— приводимый 71 — 72
— электромагнитного поля 365, 369
— энергии-импульса 487
HVA.0
— р. 365
Тензорное произведение представлений
551, 563
Теорема адиабатическая 233, 237, 240—243
— Вигиера —Эккарта 74-75, 77, 200, 201, 225
— оптическая 353
— сложения моментов импульса 58—61
, основная 59—60
— Эреифеста 233, 237, 240-243
Теория возмущений нестационарная 219—232
стационарная 181—215
— излучения 43Р, 503-520
— Максвелла — Лоренца 485
— Паули 48, 417
— рассеяния 291—358
, интегральное уравнение 299—301
Трансляционная инвариантность 155, 158
Транспозиция 569
Тритон 252
Угловой момент 14
Углы .Эйлера 28-31, 37, 536
Уравнение Днрака 361, 438
в ковариаитиой форме 377
, инвариантность 384—388
, нерелятивистский предел 415, 417
сопряженное 379
— Клейна —Гордоиа 370-373, 401, 436, 438,
441
Уравнение Лагранжа 446
— Лоренца 485
— Пуассона 115
— Фока—Дирака 267—270
— Хартрн 272
— Шредннгера 93, 106, 240
нестационарное 202—253
Уравнения гамильтоновы классической
релятивистской частицы 369
— Максвелла 488
Условие Лоренца 491
Фазовый множитель, выбор 525
Фактор-группа 547
Фермиоииый газ 99
Фермиоиы 95, 98-104, 290
Физическая наблюдаемая 39—40
Формула Вигнера 80, 539-540
— Мотта 108
— Рака 528, 533
— Резерфорда 306
Форм-фактор плотности электронов 305
Фотон 460, 503, 506
Фотоэлектрический эффект 252, 483, 522
Функция антисимметричная относительно
перестановок 84
— базисная комплексная 499
— Гамильтона классической релятивистской
частицы 369
— Грина 292, 307, 308, 315, 334, 344, 481
искаженных волн 315—318
как оператор 308
— Грина, разложение 307
свободная 292-311
— Лагранжа 446
— обрезающая 459
— симметричная относительно перестановки
аргументов 84
— сферическая 26-28, 74, 540
, условие на фазу 26
— Томаса — Ферми 117
Характер 549, 561
Частица в статическом потенциале 163—164
— спина >/г 50-52
— спина 1 52—54
Частицы тождественные 82
Частота Бора 219, 246, 476
Четность 155, 404
— перестановки 90
Ширина линии 470
Эквивалентные представления 549
Эксперимент Штерна — Герлаха 47
Электрон в кулоновском поле 412—415
центральном электростатическом потен-
потенциале 427
электромагнитном поле 54, 420
— свободный 405
Энергия 404
— излучения 496
— отрицательная 431
— поля 488
Эргодическая гипотеза 97
Эффект Зеемана 46, 201, 214, 159, 161
аномальный 47
— Пашеиа —Бака 203, 235
— Рамзауэра — Таунсенда 304
— фотоэлектрический 252, 483, 522
— Штарка 159-285
для жесткого ротатора 304