МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ
УКРАЇНИ
“Київський політехнічний інститут”
Інститут моніторингу якості освіти
Фізико-технічний інститут
Серія “На допомогу студенту”
Теоретична фізика
О. В. Кравцов
Задачі з класичної механіки
Навчальний посібник
Київ 2006

Кравцов О.В. Задачі з класичної механіки. Навчальний
посібник - К.: НТУУ “КПІ”, 2006.- 87 с. - (Серія “На допомогу студенту”.
Теоретична фізика)
Затверджено до друку
Радою ФТІ НТУУ иКПГ
Протокол N 7 від 29 серпня 2006 р.
Навчальне видання
КРАВЦОВ Олег Васильович
Задачі з класичної механіки
Навчальний посібник
За редакцією
завідувача кафедрою загальної і теоретичної фізики
академіка НАН України В. М. Локтева
Комп’ютерна верстка
у вид. системі LaTeX-2e
© ФТІ НТУУ “КПІ” 2006

Згідно сучасним тенденціям розвитку освіти, в
навчальному процесі суттєво збільшується питома вага
самостійної роботи студентів. В цих умовах, підвищення
якості освіти вимагає особливої уваги до всебічного
забезпечення навчального процесу з усіх дисциплін. З цією
метою інститут моніторингу якості освіти разом з
фізикотехнічним інститутом започатковують видання серії
навчальних посібників “На допомогу студенту”. Дану
збірку задач з базового розділу теоретичної фізики -
класичної механіки, яка є основою і багатьох курсів
інженерного профілю, можна розглядати як перший крок у цьому
напрямку.

Зміст
Задачі 6
А Ньютонова механіка 6
1. Закони та рівняння руху 6
2. Динаміка 8
3. Рух у центральному полі 12
4. Елементи теорії подібності та розмірності 17
5. Теорема про віріал 19
6. Рух при наявності в’язей 20
В Лагранжева механіка 22
1. Принцип Гамільтона. Рівняння Лагранжа 22
2. Електромеханічні системи 28
3. Вступ до теорії коливань 31
4. Динаміка твердого тіла 35
С Механіка суцільного середовища 38
1. Кінематика суцільного середовища 38
2. Динаміка і інтеграли руху суцільного середовища . 39
D Механіка Гамільтона 42
1. Рівняння Гамільтона. Канонічні перетворення.
Дужки Пуассона 42
2. Рівняння Гамільтона-Якобі. “Змінні дія-кут” 46
Е Релятивістська динаміка частки 51
1. Кінематика спеціальної теорії відносності 51
2. Динаміка спеціальної теорії відносності 54
Відповіді 57
Додатки 68
1 Криволінійні системи координат 68
А Загальні співвідношення для довільних
координатних систем 68
В Сферична система координат 74
С Циліндрична система координат 76
D Еліптичні циліндричні координати 77
4

2 Деякі формули векторного та тензорного аналізу 79
3 Дельта-функція (5-функція Дірака) 85
5

Задачі
А Ньютонова механіка
В бесконечном разнообразии явлений,
непреривно сменяющих друг друга, в
небесах и на Земле, ми распознали небольшое
число основних законов, которим в своих
движениях следует материя. Все
подчиняется им в природе, все витекает из них
с такой же необходимостью, как смена
времен года.
Пьер Симон Лаплас
1. 	Закони та рівняння руху
1. Знайти вирази для швидкості і прискорення частки в циліндричній
системі координат (орти: ер, еф, ez).
2. Знайти вирази для швидкості і прискорення частки в сферичній
системі координат (орти: ег, еф).
3. Закон руху в циліндричній системі координат має такий вид: р =
At + B,(f) = Ct + D,z = Et + F, де А, В, С, D, Е, F - сталі. Знайти
траєкторію, швидкість, прискорення і секторіальну швидкість в
трьох випадках: а) А=0, б) С=0, с) В = D = Е = F=0.
4. Нехай закон руху частки задається в криволінійних
ортогональних координатах ¢1, ¢2, Яз співвідношеннями qi = qi(t) (і = 1,3),
а зв’язок між ними і декартовими координатами визначається
залежностями: х = </>і(<?ь¢2,<?з), У = </>2(91,92,93), Z = </>з(9і,92,9з)·
Покажіть, що проекції прискорення частки на дотичні до
координатних ліній криволінійної системи координат визначаються
виразами
d д
^ д {/дфі \
2 / dqj \ 2 /_ .=1 \dqj )
21 - V2
dt dqj
6

тут
(Координатною лінією називається крива в просторі (xyz), вздовж
якої змінюється тільки одна з координат qi, і = 1,3).
5. Використовуючи розв’язання задачі N4 знайдіть величину
швидкості частки та проекції її прискорення на дотичні до координатних
ліній наступних криволінійних ортогональних координат:
a) циліндричні координати р, ф, z: х = pcos</>, у = psin</>, 2 = z\
b) сферичні координати г, 0, ф\ х = rsin0cos</>, у = rsin0sin</>,
2: = r cos0;
c) координати еліптичного циліндра и, 17 z: х = b cosh и cos 17
у = 6 sinh u sin і/, 2 = 2, тут т = ±Ь - фокуси еліпса, який
утворений перетином кофокусних циліндрів ПЛОЩИНОЮ 2 =
const (див. додаток 1, стор.ТТ).
6. У полі відштовхуючого силового центра частка рухається в
площині (ху) за законом х = a cosh ωί + β sinh ωί, у = 7 cosh ωί + δ sinh ωί,
де α, /3, 7, Φ ω - сталі величини, знайдіть радіальну ар і
трансверсальну αψ компоненти прискорення частки.
7. Частка рухається в площині так, що кут між векторами швидкості
ν і радіус-вектором г дорівнює a = const. Знайти рівняння
траєкторії частки в полярній системі координат, якщо в початковий
момент часу г(0) = тд, ф(0) = </>о·
8. Знайдіть закон руху частки, якщо відомо, що вона рухається по
еліпсу, а її секторіальна швидкість σ відносно центра еліпса -
стала.
9. Знайти прискорення частки, що рухається по еліпсу зі сталою
відносно центра еліпса секторіальною швидкістю σ = const. Півосі
еліпса а, Ь.
10. Знайти прискорення частки, що рухається по еліпсу зі сталою
відносно фокуса еліпса секторіальною швидкістю σ = const. Півосі
еліпса а, Ь, рівняння еліпса р = р(1 + ecosф)~1.
11. Бусинка масою т вільно ковзає по дротяному колу радіуса і?, яке
обертається з кутовою швидкістю Ω = const навколо осі, що
проходить через одну з точок кола перпендикулярно до площини кола.
Знайдіть швидкість бусинки відносно лабораторної системи
відліку. Силами тяжіння і тертя знехтувати.
12. Точка М обода колеса обертається навколо осі колеса за законом
s = At2 + Bt + С. Центр колеса рухається зі швидкістю, проекції
якої на осі т, у відомі: vx = Dcosut, vy = Dsincji, де D,cj - сталі.
7

Визначте закон руху точки М відносно системи координат ту, якщо
радіус колеса і?, а площина колеса співпадає із площиною z = 0.
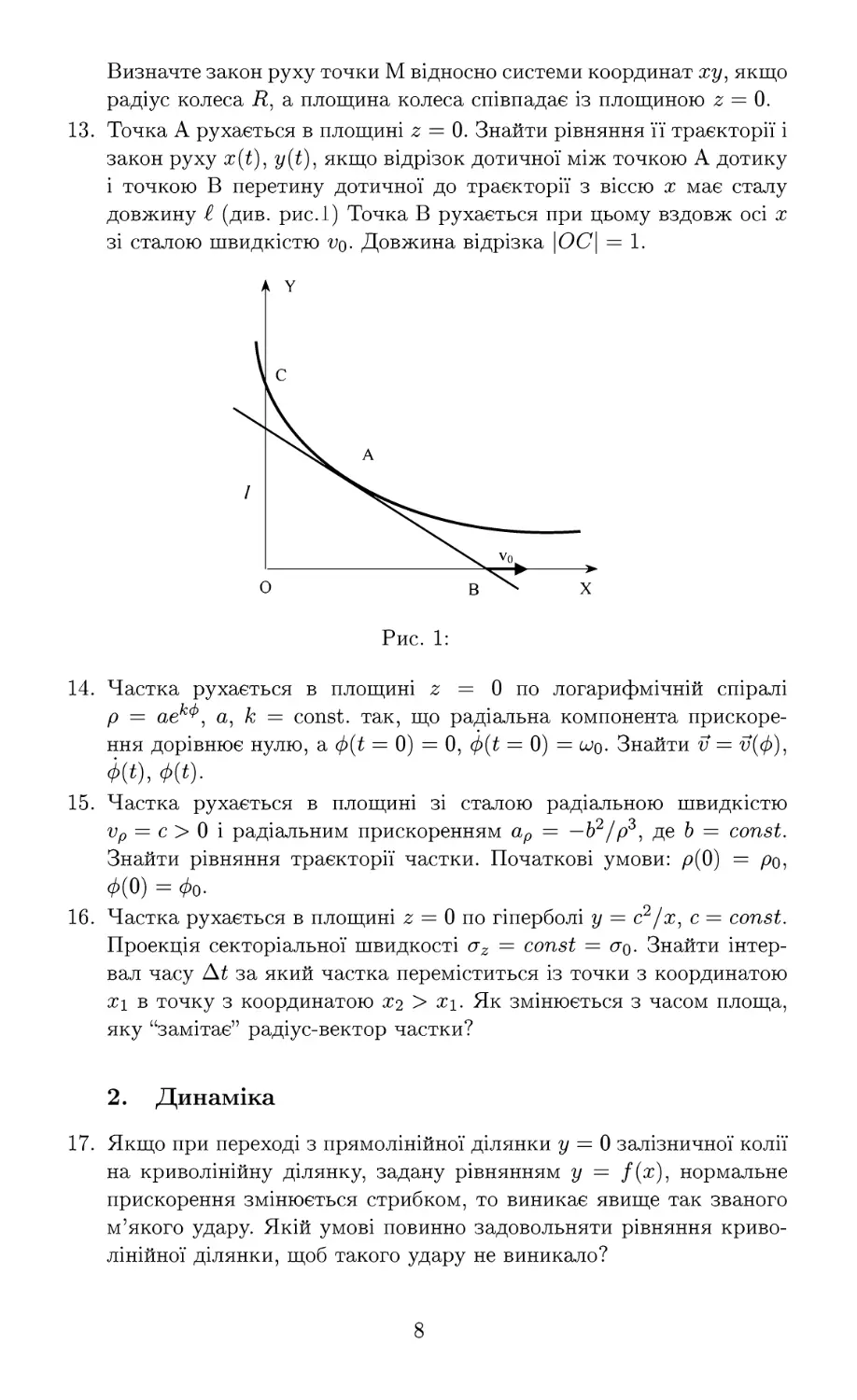
13. 	Точка А рухається в площині z = 0. Знайти рівняння її траєкторії і
закон руху x(t), y(t), якщо відрізок дотичної між точкою А дотику
і точкою В перетину дотичної до траєкторії з віссю х має сталу
довжину £ (див. рис.1) Точка В рухається при цьому вздовж осі х
зі сталою швидкістю vq. Довжина відрізка \ОС\ = 1.
Рис. 1:
14. Частка рухається в площині 2 = 0 по логарифмічній спіралі
р = аекФ, а, к = const, так, що радіальна компонента
прискорення дорівнює нулю, а φ(ί = 0) = 0, φ(ί = 0) = cjo· Знайти v = ν(φ),
<j>(t), ф(і).
15. Частка рухається в площині зі сталою радіальною швидкістю
Vp = с > 0 і радіальним прискоренням ар = — 52/р3, де b = const.
Знайти рівняння траєкторії частки. Початкові умови: р(0) = ро,
Ф{ 0) = 0о.
16. Частка рухається в площині z = 0 по гіперболі у = с2/т, с = const.
Проекція секторіальної швидкості σζ = const = σο· Знайти
інтервал часу At за який частка переміститься із точки з координатою
х\ в точку з координатою х^ > х\- Як змінюється з часом площа,
яку “замітає” радіус-вектор частки?
2. 	Динаміка
17. Якщо при переході з прямолінійної ділянки у = 0 залізничної колії
на криволінійну ділянку, задану рівнянням у = /(#), нормальне
прискорення змінюється стрибком, то виникає явище так званого
м’якого удару. Якій умові повинно задовольняти рівняння
криволінійної ділянки, щоб такого удару не виникало?
8

18. Частка маси т рухається під дією сили F = F(t)ex вздовж осі х.
Знайти закон руху. Початкові умови: а?о, vo-
19. Частка маси т рухається під дією сили F = F(x)ex вздовж осі х.
Знайти закон руху за умов x(to) = то, і (to) = F(x) > 0.
20. Частка маси т рухається вздовж осі х під дією сили F = F(v)ex,
де v = dx/dt. Знайти закон руху. Початкові умови: то, то-
21. На частку маси т діє сила F = —/сг, к = const. Знайти рівняння
траєкторії частки, f(t), v(t), якщо при t = 0, г(0) = тд, т(0) = щ.
22. Заряд е, маса якого ш, рухається в однорідних сталих полях
тяжіння і магнітному полі: g = (0, 0, —g), В = (0,5,0). Початкові
умови: г(0) = (0,0,/і), т(0) = (0,0, то). Знайдіть межі області руху
по координаті 2 і закон руху.
23. Частка маси т рухається за законом т = a sineut, у = acoscut,
z = bt (гвинтова лінія). Покажіть, що такий рух може відбуватися
під дією сили F = mv х cj, де ω = cje2, v - швидкість, a, Ь, cj -
сталі.
24. Бусинка може ковзати по шорсткому (коефіцієнт тертя дорівнює
к) нерухомому кільцю радіуса і?, розташованому в горизонтальній
площині.В початковий момент бусинці надали швидкість то-
Знайти таке значення то, при якому б бусинка повернулася в початкове
положення з нульовою швидкістю.
25. Парашутист маси т стрибає з літака, який летить горизонтально
на висоті Н зі швидкістю то- По якій траєкторії рухається
парашутист під час затягнутого стрибка (до моменту розкриття
парашута), якщо сила опору повітря F = —/Зт, де т - швидкість
парашутиста, β = const. Прискорення вільного падіння g вважати сталим.
Із знайденого рівняння шляхом граничного переходу /3—^0 знайти
рівняння траєкторії за відсутності сили опору.
26. На висоті Н над Землею частці маси т надали швидкість г>о,
напрямлену вертикально вниз. Знайти швидкість частки на висоті
h, якщо на неї діє сила опору повітря F = — /Зг>2, а сила тяжіння
змінюється з висотою за законом
= mgR2
~ (Д + г)2’
де R - радіус Землі, а г - відстань до її поверхні, g = cosnt.
27. Тіло рухається в струмені повітря, що піднімається вгору. Сила
опору повітря, яка діє на тіло, пропорційна квадрату відносної
швидкості тіла і повітря. Знайти залежність швидкості тіла
(відносно поверхні землі) від часу. Маса тіла ш, коефіцієнт
пропорційності в виразі сили опору fc, прискорення земного тяжіння g,
початкова швидкість тіла v(0) = (0,0,г^о), швидкість повітря и = (0,0,їх).
Дослідити можливі випадки: г>о > гх, Уо < Щ при и > у/mg/k та
и < у/mg/k.
9

28. Поблизу поверхні Землі діє однорідне магнітне поле, вектор
напруженості якого Н напрямлений горизонтально. В початковий
момент часу зарядженій частці (маса т ,заряд е) на висоті h надають
швидкість г>о, напрямлену вертикально вниз. При яких значеннях
h частка не впаде на Землю? Поле тяжіння вважати однорідним.
29. Електрон рухається в однорідному сталому магнітному полі,
індукція якого В = (0,5,0), і електричному полі квадрупольного
конденсатора, потенціал якого Ф = /Уо/2а2(т2 — у2) (a, Uo = const).
Знайдіть закон руху r = f(t) за умови В > {с/a)y/mUo/е, де с -
швидкість світла.
30. Парадокс супутника. Доведіть, що для траєкторій близьких до
кола, із рівняння руху
” тМ
тг = —7—
Κ(ν)
випливає рівняння mv = Κ{ν)ν. Оцініть приріст Аг та періоду AT
за один оберт, якщо К{у) ос pSv, де густина повітря р змінюється
з висотою за законом
р(г) = ро ехр
r — R
а
Для оцінок взяти а=7170 м, ро = 1,225 кг/м3, r = (R + 160) км,
т = 100 кг, 5—1 м2, v = 7, 9 км/с.
31. 	1. Вивести рівняння руху тіла зі змінною масою (рівняння
Мещерського) і формулу для потужності внутрішніх сил
Р =
dm
dt
Тут и - швидкість Am відносно тіла.
2. Знайти, як змінюються з часом маса ракети при
вертикальному підйомі в однорідному полі тяжіння у випадках:
а) стала швидкість підйому; швидкість витікання газів стала;
б) стале прискорення підйому; швидкість витікання газів стала;
в) стала потужність в струмені газів.
32. Покажіть, що імпульс ракети, яка рухається прямолінійно за
відсутності зовнішніх сил, досягає максимального значення в момент,
коли швидкість ракети стає рівною швидкості витікання газів и
(■и = const).
33. Ракета рухається прямолінійно під дією реактивної сили. Дія
зовнішніх сил нехтовно мала. В початковий момент ракета знаходилась
10

в стані спокою і мала масу то; відносна швидкість витікання
газів и = const. При якому значенні маси т слід вимкнути двигун,
щоб імпульс Р, отриманий ракетою, був максимальним? Чому він
дорівнює?
34. Розв’язати задачу N33 за умови, що початкова швидкість ракети
vo ф 0 і менша за и.
35. Знайдіть значення маси, при якій кінетична енергія ракети із
задачі N33 буде мати максимальне значення.
36. Частка рухається в сталому силовому полі F = const. Знайти
потенціальну енергію частки.
37. Заряд е рухається в однорідному електричному полі, напруженість
якого Е = Eq coscot, де Eq, ω - сталі. Знайти потенціальну енергію
38. Частка маси m рухається із півпростору, де її потенціальна
енергія дорівнює U\ = const у півпростір, де її потенціальна енергія
U2 = const фП\. Площина поділу півпросторів перпендикулярна
осі х. Знайти швидкість частки після того, як вона перейде
площину поділу цих півпросторів. Початкова швидкість г>о- При якій
умові на кут між вектором швидкості і віссю х частка буде
відбиватися від потенціального бар’єру?
39. Частка маси т рухається в потенціальному полі
U(x) = — Щ ехр(т/а), а, Щ - сталі. Знайти x(t). Початкові
умови т(0) = 0, і(0) = vo > л/21Іо/т. Дослідити випадки а) Е > 0,
b) Е = 0.
40. Частка маси т рухається в потенціальному
полі U(x) = — ZTocosh-2 /ст, початкові умови х(0) =—£,
г>(0) = г>о, к£ = const 1. Повна енергія частки дорівнює 1¾.
Знайти час руху частки від точки х = — £ до точки х = £.
Дослідити випадки a) 2¾ > 0, b) 2¾ < 0.
41. Частка маси т рухається в потенціальному полі
U(x) =—Е cos(x/£), де £- стала, Е - повна енергія.
Початкові умови т(0) = 0, і(0) = vo = у/АЕ/т. Знайти x(t).
42. Частка маси т рухається в потенціалі U{x) від точки х = 0 у
напрямку до точки повороту од, 0 < х\ < а. Нехай потенціал на
відрізку має форму:
Тут Uo > 0. Енергія частки Е трохи менша від Uo’· Е = С7о(1 — 52).
Скільки часу необхідно, щоб з положення х = 0 досягти точку
х = χ\Ί Розгляньте у випадку Ь) границю 5 —0.
заряду.
11

43. 	Покажіть, що перетворення координат: г/ = т + а, де d2a/dt2 = 0,
не змінює форми рівняння моментів
Ш
dt
= N
(М - момент імпульсу, N - момент сили).
3. 	Рух у центральному полі
44. Протягом всього часу руху частки вектор її прискорення
напрямлений до нерухомого силового центру О. Покажіть, що траєкторія
точки лежить в площині, що проходить через центр О.
45. Частка маси ш рухається в полі з потенціальною енергією U =
U(\r\). Знайти перші інтеграли руху, показати, що рух частки
відбувається в площині і отримати рівняння цієї площини. Початкові
умови: г(0) = го, г?(0) = щ.
46. Зведіть вирази div F, rot F для центральної сили F{f) = [f(r)/r]f
до якомога найпростішого вигляду; покажіть, що
f(r) = -
dU(r)
dr
де U(r) - потенціальна енергія.
47. Покажіть, що при русі частки в полі U(r) = — α/r (а > 0), існує
інтеграл руху Л = v х М + ar/r = const, де a = const, М - момент
імпульсу. Інтеграл руху Л інколи називають вектором Лапласа, а
інколи - вектором Рунге-Ленца.
48. На частку маси m діє сила F = —/сг, к = const. Знайти
потенціальну енергію частки, межі руху, інтеграли руху і v{r).
49. а) Покажіть, що величина вектора Лапласа Λ (див. задачу
47) може дорівнювати |Л| = ае, де ексцентриситет еліпса
е = у/і + 2EM2/(та2), Е - енергія та ш- маса частки.
б) Покажіть, що в полярних координатах вектор Лапласа має
вигляд
Λ = (гфМ — а)ег — гМеф.
50. Частка маси m рухається в потенціальному полі
и0
U(r) = -
[1 + (г/с)2]2’
де Uq, с - сталі. Знайти рівняння траєкторії (в полярних
координатах, границі руху і період руху, якщо повна енергія Е = 0.
Початкові умови: г(0) = г*о, г(0) = 0, υ(0) = щ, момент імпульсу
М{ 0) = М0.
12

51. Розгляньте рух частки маси т в потенціалі U(г) = — α/r (а > 0) за
умови, що момент імпульсу М = 0. Скільки часу необхідно частці,
щоб досягнути силового центру?
52. Визначьте траєкторію руху частки в потенціалі притягання 1/г2.
Що відбувається при г 0?
53. Опишіть рух у потенціалі
Щг)
—к(3 — г2)/2, г < 1,
—/с/г, г > 1,
де к = const.
54. Для потенціалу притяганння 1 /г запишіть у декартових
координатах інтеграли руху в площині, перпендикулярній до моменту
імпульсу М, і визначте за їх допомогою рівняння траєкторії.
55. Тривимірне рівняння руху зарядженої частки (маса ш, заряд е) в
сталому магнітному полі з індукцією В відносно центра кола має
вигляд
сІг _ _ ^ еВ
—— = CJ X Г, UJ — —,
at тс
(с - швидкість світла), г = (х, у, z). Покажіть, що вказане рівняння
можна записати у вигляді
- = ;(£■ S)f,
де три компоненти вектора S складаються з матриць, а саме
/ 0 0 0 \ /00 і \ /0 —і о \
5і = 0 0 і І , 52 = 0 00 , 53= г 0 0
у о —і о / \ -і о о; V000/
Розв’язок рівняння руху тепер запишеться просто
f(t) = foexp(icj · St).
Зауваження! Експоненційна функція від матриці А означається
через степеневий ряд
ехр А = і + А + ^А2 + —
Компоненти вектора S мають такі властивості (доведіть*.):
SkSj — SjSk = iekjiSi, S2 = 2/,
тут €kji - символ Леві-Чівіти (сума по повторним індексам).
Використайте ці властивості, щоб в явній формі записати розв’язок
рівнянь руху.
13

56. Планета рухається по еліпсу, рівняння якого в полярних
координатах r = р/( 1 + е cos ф). Знайти залежність радіальної аг і
трансверсальної αψ компоненти прискорення планети від г, використовуючи
закон площин г2ф — σ — const.
57. Рух частки в площині задається в полярній системі координат
компонентами швидкості vr = 1/г2, νφ = 1 /(5г), де b = const. Знайти
траєкторію руху частки r = г(0), а також радіальну аг і
трансверсальну аф компоненти її прискорення. Початкові умови: г(0) = го,
Ф{ 0) = 0о.
58. Частка маси т рухається по колу радіуса тд в полі ценральної сили
з потенціалом U(r) = —кт/гп. Доведіть, що якщо п < 2, то орбіта
буде стійкою відносно малих коливань.
59. Дві частки рухаються одна відносно другої по коловим орбітам з
періодом т під впливом гравітаційних сил. В деякий момент часу
рух раптом припиняється і частки починають падати одна на одну.
Доведіть, що зіткнення часток відбудеться через час t = т/4\/2
після моменту припинення руху по колу.
60. Гравітаційна система двох тіл складається із однорідної кулі
маси М радіуса R і точкової частки маси т. Знайти першу і другу
космічні швидкості маси т відносно кулі М.
61. Планета рухається навколо Сонця по еліпсу.
a) показати, що величина великої напівосі еліпса залежить
тільки від енергії: а = а/2\Е\;
b) показати, що при заданій Е, якщо момент імпульсу М =
Л^тах, еліпс вироджується в коло, радіус якого дорівнює
великій напівосі еліпса;
c) показати, що при заданому М, якщо Е = E’min, еліпс
вироджується в коло;
d) отримати 3-й закон Кеплера
Т = 2тг βα3/2.
V а
62. а) В задачі Кеплера отримати для кута відхилення при інфіні-
тному русі
Φ = π + 2Μί:(>η(^^Ζ
Ь) 	Покажіть, що при русі в полі F = —kr (к = const > 0)
Ф = 2
fT max
^rmin
М dr/r2
7 У(2/μ^Ε-Щ
= 2π.
14

с) 	Знайти часовий період руху в полі F = — kr (к = const > 0).
63. В деякому наближенні орбіту Меркурія можна описати плоскою
розеткою, рівняння якої в полярних координатах має вигляд
r = р(1 + ecos(</>cj))-1, де to = const ф 1. Використовуючи закон
площин г2ф = σ = const, знайти залежність величини
прискорення а планети від г.
64. Орбіти більшості планет є майже коловими. Тому їхня енергія
Е тільки трохи більша від енергії 2¾ = £4ff(ro) = U^m.
Внаслідок цього в околі значення г = го рух визначається потенціалом
Ueft = М2/(2μν2) — α/r. Розвиньте Ues(r) в околі г = го в ряд до
квадратичних членів включно і розв’яжіть в цьому наближенні
радіальне рівняння руху. Порівняйте колову частоту коливання
(частоту “лібрації·”) у змінних г з частотою обертання ф по коловій
орбіті радіуса т*о. Який вигляд має траєкторія?
65. Покажіть, що в полі будь-якої центральної сили притягання за
рахунок належного вибору початкових умов можна реалізувати
колову орбіту довільного радіуса R. Покажіть, що швидкість на такій
орбіті буде сталою.
66. Знайти рівняння траєкторії частки маси т в полі центральної сили
з потенціалом U = kr2/2, к = const.
67. Знайти рівняння траєкторії частки маси т з моментом імпульса Мо
в полі центральної сили з потенціалом U = —α/τ + β/r2, (α,β > 0).
68. Частка маси т рухається під дією сили
Ρ=-ί{τ)--β?,
г
де г = у/х2 + у2 + ζ2, β = const. Знайти залежність від часу
кутового моменту (моменту імпульсу) M(t).
69. 	В якому центральному полі траєкторія частки визначається
рівнянням
(і
dr2
де ио — const?
70. 	Диференціальне рівняння траєкторії частки маси т у
центральному полі має вигляд:
ί (;)+ Ψ(Γ) = 0і
де ф(г) - задана функція. Знайти залежність сили від г.
71. 	При дослідженні проблеми N тіл розглядають так званий момент
т -> -> -> · ...
інерції системи J = 2^і=ітігігі, де Ті - радіус-вектор г-тої
частки. Якщо величина J обмежена, то система здійснює фінітний
15

рух, якщо ж при t —ї оо величина J необмежено збільшується, то
система здійснює інфінітний рух. Знайти вираз для d 2 J/dt2 і
використовуючи його, показати, що в задачі N тіл рух буде інфінітним,
якщо початкове значення повної енергії 2¾ буде додатним.
72. 	Задача двох тіл (позначення звичайні):
а) 	Отримати умову падіння на центр
r2C/(r)Uo<
М2
2μ
b) 	Показати, що
М = тйс х Vc + μτ х ν,
_ mVc2 μν2
2 2
73. В полі сили F = аг (a > 0, f = (x,y,z)) рухаються дві частки з
масами ті і m2. Частки між собою не взаємодіють. Знайти закон
руху центра мас системи. Початкові умови відомі.
74. До двох точкових мас т\ і m2, що взаємодіють, прикладені
залежні тільки від часу сили F\(t) і F2(£), відповідно. Покажіть, що
така задача двох тіл може бути зведена до задачі про рух у
центральному полі точкової маси, на яку діє сила
Φ(ί) = μ
А
ті
Ελ
т2
де μ — зведена маса.
75. При недружній взаємодії частки з ядром атома повна енергія ядра
змінюється. Знайти найбільшу величину енергії, яку частка може
передати ядру. Дослідити випадки: m « М, m » М, m = М. До
зіткнення ядро нерухоме.
76. В задачі про розсіяння часток отримати співвідношення
a) для прицільного параметру р = р tan(%/2), де р - параметр
гіперболи, х - кут розсіяння в системі відліку центра мас;
b) для кута розсіяння θ\ в лабораторній системі відліку на
нерухомій “мішені” 777-2
tan θι =
7772 Sin χ
777ι + т2 COS χ ’
с)
Ρί = Ρι\ 1
P2 = Pl
2 m2
sm ■
X
m
Тут Pi - імпульс частки mi до розсіяння, P[, P'2 - імпульс
часток після розсіяння, т = ті + m2, μ - зведена маса.
16

77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
Комета маси т рухається в полі тяжіння зірки S маси М (М » га),
маючи на нескінченості швидкість і прицільний параметр р,
Знайти рівняння траєкторії комети і визначити кут #, на який
відхилиться траєкторія, коли комета знову віддалиться на
нескінченість. Чи може статися захоплення комети зіркою?
Енергія взаємодії часток U(r) = — α/r, a = const > 0.
Використовуючи рівняння траєкторії в системі “центр мас”, знайти
залежність прицільного параметра р від кута розсіяння χ. Зведена маса
μ, швидкість на нескінченості дорівнює Vqq.
Пучок часток, що рухається вздовж напряму осі Z, розсіюється на
поверхні обертання Z = r2/2а, r = у/х2 + у2, a = const. Знайти
залежність прицільного параметру р від кута розсіювання.
Знайти повний (інтегральний) переріз падіння часток з
енергією Е на кульку радіуса і?, яка знаходиться у центрі поля U(r):
U = —а/гп, п > 2.
а) 	В задачі розсіяння отримати кут відхилення
Ф = 2
Щг)
Е
-1/2
-Р
г
де р — прицільний параметр.
б) Знайти Ф у полі U{r) = α/r, a = const > 0..
Знайти ефективний диференціальний переріз розсіяння у полі
U = —α/r2, (a=const>0).
а) Визначити інтегральний переріз для падіння частки на центр
поля U = —α/r2, (a=const>0).
б) Як залежить ефективний диференціальний переріз від
швидкості часток Vqq на нескінченості при розсіянні в полі U ос г-п?
Знайти співвідношення між диференціальними перерізами
розсіяння в лабораторній системі відліку і в системі центра мас.
Розглянути випадок, коли атоми мішені розподілені хаотично (не
утворюють кристалічної структури), і густина речовини мішені настільки
мала, що можна знехтувати багаторазовим розсіюванням.
4. 	Елементи теорії подібності та розмірності
Газовий пузир, що утворився як наслідок підводного вибуху,
коливається з періодом Т ос РарьЕс, де Р - тиск, р - густина води, Е -
повна енергія вибуху. Знайти а, Ь і с.
Виведіть закон Стокса, виходячи з міркувань розмірностей, за
умови що сила не залежить від густини рідини. Який вид буде мати
цей закон, якщо таке припущення невірне?
17

87. Нехай £ - енергія, Т - температура, S - ентропія, m - маса, Q -
заряд, V - швидкість, h - стала Планка, а = Μ/m - момент імпульсу
на одиницю маси, t - час, £ - довжина. Тоді, якщо ввести величини
(вони часто використовуються при дослідженнях в рамках
загальної теорії відносності) £g = (G?/c4)£, Tg = (0/с^/с4)Т, ag = а/с,
rrig = (G?/c2)m, Qg = (y/G/c2)Q, Sg = S/кв, hg = (G/c3)/i, tg = ct,
Vg = v/c, £g = £ (тут c- швидкість світла, G - гравітаційна стала,
кв - стала Больцмана) і покласти с = G = кв = 1(як безрозмірні),
то всі вказані величини будуть вимірюватися в одиницях довжини
[£]п (кажуть, в геометричних одиницях). Яким набором вказаних
сталих повинні бути звя’зані Hg і Н - напруженість магнітного
поля, Eg і Е - напруженість електричного поля, Mg і М - момент
імпульсу, Ig і І - момент інерції, Qg і Ω - кутова швидкість, Jg і
J - сила електричного струму, щоб і вони могли вимірюватися в
одиницях довжини?
88. Покажіть, що нижче вказані величини -£*, £*, т* (так звані
“планковські одиниці”) мають розмірність: см, с, г, відповідно, і
обчисліть їх величину £* = (Gft/c3)1/2, t* = (Gft/c5)1/2, m* = (M/G)1/2]
тут c - швидкість світла, G- гравітаційна стала, h = h/(2n) -
стала Планка. Також визначте розмірність і обчисліть величину
р* = с5/(G2h).
89. Покажіть, що якщо вибрати в якості основних одиниць
універсальні сталі с - швидкість світла, h= h/ (2π) - стала Планка, і покласти
с = h = 1 (як безрозмірні), то всі фізичні величини (за винятком
тих, в означення яких входить стала Больцмана) будуть мати
розмірність [£]п, де £ - одиниця довжини. Наприклад, частота буде
мати розмірність £~1, заряд - £°, гравітаційна стала - ^2, маса -
£~1. Визначте відповідні співвідношення (як у задачі N87) в цьому
випадку для всіх величин із задачі N87.
90. Якщо покласти с = h = кв = 1 (як безрозмірні, див. задачі NN87,
89), то єдиною розмірною величиною у такій системі одиниць буде
величина розмірності маси [т\. Всі інші величини t - час, £ -
довжина, М - момент імпульсу, Е - напруженість електричного поля,
і т.п., будуть мати розмірність [т]п. Визначте відповідні
співвідношення (як у задачі N87) в цьому випадку для всіх величин із
задачі N87.
91. Як залежить висота стрибка тварини, а також швидкість її бігу
по рівній місцевості і в гору, і час бігу по рівній місцевості без
вживання води від розміру L тварини?
92. Виходячи із міркувань подібності, покажіть, що
а) період коливань гармонічного осцилятора не залежить від
амплітуди;
18

b) квадрати інтервалів часу падіння частки в полі тяжіння
відносяться як початкові висоти;
c) при русі в гравітаційному (чи кулоновому) полі квадрати
інтервалів часу обертання по орбітам пропорційні кубам їх
розмірів.
93. Вважаючи, що радіус планети в а раз менше радіуса Землі, а маса
в β раз менше, знайдіть, виходячи із умов подібності, у скільки
разів прискорення сили тяжіння, а також перша і друга космічні
швидкості на такій планеті менше, ніж на Землі?
94. Заряд д, т рухається в потенціальному полі U(r) і
магнітному полі з напруженістю Н(г), які є однорідними функціями
U(af) = akU(f), H(af) = апН(г). Знайдіть для даної системи
принцип подібності і уточніть, при якому п він має місце.
95. Знайти інтеграли руху для частки, що рухається в полі /7(г), де
U - однорідна функція U(af) = anZ7(r), уточніть, при якому п,
перетворення подібності не змінює вид рівняння руху.
96. Знайти інтеграли руху для частки, що рухається у магнітному полі
з векторним потенціалом Л(г), який є однорідною функцією
координат. Чому повинен дорівнювати ступінь однорідності Л(г), щоб
перетворення подібності не змінювали вида рівняння руху?
5. 	Теорема про віріал
97. За допомогою теореми про віріал знайти середнє значення
кінетичної енергії одновимірного руху частки маси ш, на яку діє
гармонічна сила F = Acosut, якщо в початковий момнет часу швидкість
частки дорівнювала нулю.
98. Безпосереднім обчисленням показати, що у відповідності із
теоремою про віріал середні за період значення кінетичної і
потенціальної енергії математичного маятника, що здійснює малі коливання,
рівні. Чи буде вірним це твердження для маятника при довільних
коливаннях?
99. Використовуючи теорему про віріал покажіть, що при фінітному
русі частки маси т у полі всесвітнього тяжіння повна енергія
частки завжди від’ємна.
100. За допомогою теореми про віріал знайти середній тиск газу на
стінки посудини, нехтуючи міжмолекулярною взаємодією і
приймаючи, що середня кінетична енергія однієї молекули дорівнює £,
концентрація молекул п.
101. Знайдіть рівняння стану неідеального газу, виходячи з теореми про
віріал. Вважайте, що сили молекулярної взаємодії є
потенціальними.
19

102. Нехай частки, загальна маса яких М і які взаємодіють за
законом тяжіння Ньютона, рухаються в області, що є сферою
радіуса R. Нехай густина маси системи є однорідною.
Використовуючи теорему про віріал знайдіть середню кінетичну енергію
системи. Використайте свої розрахунки для оцінки власної гравітаційної
енергії нашої Галактики, маючи на увазі, що вона складається із
N ж 1,6· 1011 зірок, приблизно однакової маси Мі « ΜΘ · 1033 г і
з приблизно однаковими середніми відстанями між ними г 1023
CM.
103. Припустимо, що газова туманність складається із часток, які
взаємодіють за законом тяжіння і які мають суттєву кінетичну енергію.
Нехай цю систему можна умовно вважати ізольованою
консервативною системою з енергією Е = const. За допомогою теореми про
віріал доведіть, що при Е < 0 туманність буде стискатися і (при
виникненні дисипативних сил) може конденсуватися, утворивши
зірку. Як буде поводити себе туманність, якщо із самого початку
вона мала енергію Е > 0?
104. Узагальніть теорему про віріал для системи зарядів в
однорідному магнітному полі Н. Потенціальна енергія системи є однорідною
функцією U(агі,..., afs) = akU(агд,..., аг^), а рух системи
відбувається в обмеженій області.
6. 	Рух при наявності в’язей
105. Частка маси т ковзає без тертя по похилому жолобу (кут нахилу
а) в полі тяжіння g = const. В’язі задаються рівнянням жолоба
/(#,у) = хtana — у = 0. Використовуючи рівняння Лагранжа 1-го
роду знайти силу реакції в’язі Р і множник Лагранжа Λ.
106. Покажіть, що якщо виконуються співвідношення
dfi dfk f
охк + дхпТг
dfk
дХі
+
dfi
dXn
fki І 1)
к = 1, п — 1,
то лінійна диференціальна в’язь виду
η—1
Жг + У fk(Xl,X2, · · · , Хп)Хк = 0.
к=1
Є ГОЛОНОМНОЮ.
107. 	Частка маси m рухається по поверхні циліндра радіуса R. Активні
сили, що діють на частку, врівноважені. Знайти траєкторію частки
і силу реакції поверхні, якщо при t = 0 частка знаходилась у точці
А(і?, 0, 0) і мала початкову швидкість щ = voyey + гще2.
20

108. Частка масою т рухається по поверхні сфери радіуса R в полі
тяжіння. Знайдіть силу реакції як функцію координат та швидкості,
і координати точки, в якій сила реакції дорівнює нулю, а також
положення рівноваги за початкових умов;
а) tf(0) = 0, г(0) = (0,0, і?);
б) #(0) = (0,0, >/gR), r(0) = (0,0, і?).
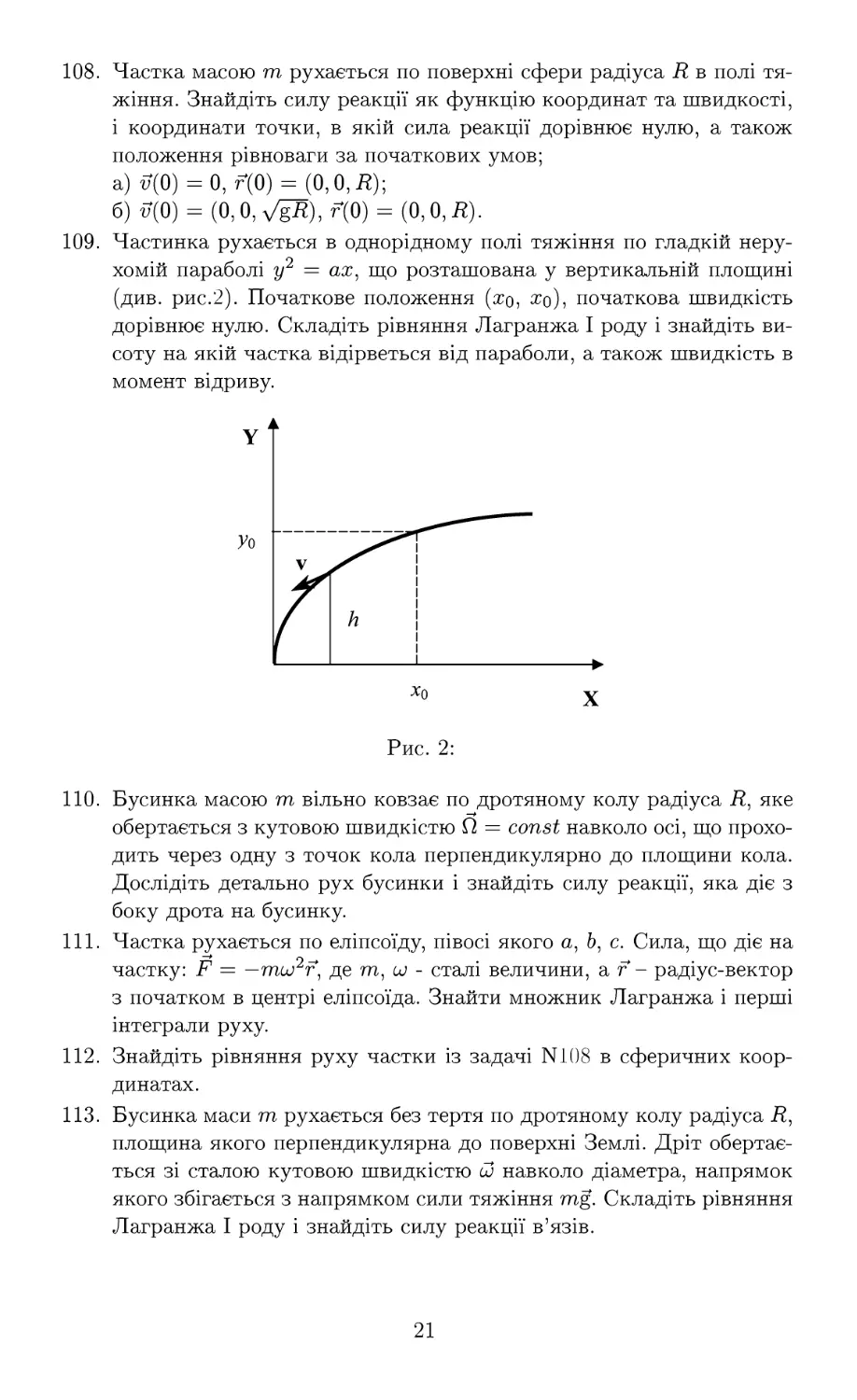
109. Частинка рухається в однорідному полі тяжіння по гладкій
нерухомій параболі у2 = ат, що розташована у вертикальній площині
(див. рис.2). Початкове положення (то, #о), початкова швидкість
дорівнює нулю. Складіть рівняння Лагранжа І роду і знайдіть
висоту на якій частка відірветься від параболи, а також швидкість в
момент відриву.
Рис. 2:
110. Бусинка масою т вільно ковзає по дротяному колу радіуса і?, яке
обертається з кутовою швидкістю Ω = const навколо осі, що
проходить через одну з точок кола перпендикулярно до площини кола.
Дослідіть детально рух бусинки і знайдіть силу реакції, яка діє з
боку дрота на бусинку.
111. Частка рухається по еліпсоїду, півосі якого а, 6, с. Сила, що діє на
частку: F = —mcj2r, де ш, ω - сталі величини, аг- радіус-вектор
з початком в центрі еліпсоїда. Знайти множник Лагранжа і перші
інтеграли руху.
112. Знайдіть рівняння руху частки із задачі N108 в сферичних
координатах.
113. Бусинка маси т рухається без тертя по дротяному колу радіуса і?,
площина якого перпендикулярна до поверхні Землі. Дріт
обертається зі сталою кутовою швидкістю ω навколо діаметра, напрямок
якого збігається з напрямком сили тяжіння rag. Складіть рівняння
Лагранжа І роду і знайдіть силу реакції в’язів.
21

В Лагранжева механіка
По Лейбницу наш мир являєшся лучшим
из всех возможних миров, и позтому
закони природи можно описать
жстремальними принципами.
Карл Людвиг Зигель
1. 	Принцип Гамільтона. Рівняння Лагранжа
114. Обчислити значення дії у випадках: 1) частка маси т рухається
в однорідному полі тяжіння g; 2) частка рухається за відсутності
силових полів і проходить через точки r\(t) та Г2(£); 3) частка
здійснює гармонічні коливання вздовж осі Ох під дією пружної сили.
115. Знайдіть закон перетворення дії S при переході від однієї
інерціальної системи відліку до іншої.
116. Камінь маси т кинули під кутом до горизонту. Поле тяжіння
g = const. Запишіть функцію Лагранжа і відповідні рівняння
Лагранжа: а) у векторній формі; б) в декартових координатах (х, у, z);
в) 	в циліндричних координатах (ρ,φ,ζ)] г) у сферичних
координатах (г, #, ф).
117. Запишіть функцію Лагранжа, рівняння Лагранжа і узагальнену
енергію для бусинки із задачі N11 у системі відліку, що обертається
з дротом.
ti
118. Дія S = f fdt. Покажіть, що якщо / = f(t,q,q,q), то рівняння
*2
Ейлера-Лагранжа будуть мати вид:
(&U.\ _ , я/ = п
dt2 \ dq2 ) dt dq dq
Зауваження: до звичайних граничних умов додаємо Sqj = Sqjj = 0.
119. Покажіть, що якщо прискорення & входять в функцію Лагранжа
лінійно з коефіцієнтами, які залежать тільки від координат (але
не швидкостей), то рівняння Лагранжа залишаються рівняннями
другого порядку.
120. Узагальнені координати пов’язані із декартовими перетворенням,
що не залежить від часу: qj = fj(rk)· Покажіть, що при такому
перетворенні кінетична енергія залишається додатно визначеною
квадратичною формою виду (сума по повторним індексам)
Т — — CLjkiQj і Qk)QjQki ajk ^ 0.
22

121. Заряджена частка(маса га, заряд е) рухається в електричному полі
з напруженістю Е = const. Запишіть функцію Лагранжа і
відповідні рівняння Лагранжа: а) у векторній формі; б) в декартових
координатах (x,y,z); в) в циліндричних координатах (ρ,φ,ζ); г) у
сферичних координатах (г, #,</>).
122. Покажіть, що рівняння Лагранжа інваріантні відносно точкових
перетворень узагальнених координат: qj = fj(Qk,t).
123. Покажіть, що рівняння Лагранжа інваріантні відносно
перетворень узагальнених координат і часу: Qj = fj{qk,t),T — Φ{ΐ)·
124. Знайти рівняння плоскої кривої, по якій треба вигнути жолоб, щоб
період коливань (ковзання) кульки маси т між точками А і В цього
жолобу в однорідному полі тяжіння g = const був мінімальним?
Тертям знехтувати, ул — Ув (див. рис. 3).
125. Знайти рівняння геодезичної лінії (лінії найкоротшої довжини)
між двома точками А(і?, 0,0) і В(—і?, Ο,π) на поверхні циліндра
х2 + у2 — R2 = 0. Знайти довжину цієї лінії.
126. Частка маси т рухається в силовому полі F = const. Записати
функцію Лагранжа і рівняння Лагранжа у векторній формі.
Проінтегрувати їх і знайти закон руху. Початкові умови г(0) = го,
tf(0) = v0.
127. Бусинка маси т рухається без тертя по дротяному колу радіуса і?,
площина якого перпендикулярна до поверхні Землі. Дріт
обертається зі сталою кутовою швидкістю ω навколо діаметра, напрямок
якого збігається з напрямком сили тяжіння rag. Знайти функцію
Лагранжа для миттєвого положення θ(ί) бусинки на колі (початок
координат в центрі кола), узагальнену енергію і записати рівняння
Лагранжа.
128. Запишіть функцію Лагранжа, знайдіть узагальнені імпульси та
узагальнену енергію при русі частки маси т в полі нерухомого
23

силового центру: а) в декартових координатах; б) в полярних
координатах. в) Застосуйте ці формули для часткового випадку поля
сил F = —/сг, де к = const, r = (т,у, z). Запишіть також для цих
випадків рівняння Лагранжа.
129. Знайдіть функцію Лагранжа, рівняння руху та перші інтеграли
руху для задачи Кеплера у системі відліку, що обертається зі сталою
кутовою швидкістю Ω.
130. Точка підвісу математичного маятника маси т та довжини і
рухається у вертикальному напрямку (поле тяжіння g = const) за
відомим законом S = S(t). Знайдіть функцію Лагранжа та
рівняння руху частки.
131. Покажіть, що похідні за часом від узагальненої енергії та функції
Лагранжа зв’язані співвідношенням
т _ _дс
dt dt
132. Покажіть, що для системи часток, які взаємодіють між собою і
знаходяться в зовнішньому потенціальному полі виконується
співвідношення
Ш _ dUex
dt dt ’
де Η - узагальнена енергія системи, Uex - потенціальна енергія
системи у зовнішньому полі.
133. Заряджена частка (маса ш, заряд е) рухається в магнітному полі
з індукцією В = const. Запишіть функцію Лагранжа, узагальнену
енергію та рівняння Лагранжа в векторній формі і покажіть, що
вони зводяться до звичайного рівняння руху (в системі СГС):
dv е ^ -*
т— — -V х В.
dt с
134.
Частка т рухається у площині і притягується до нерухомого
центру з силою
F
а
~2
де г - відстань до центра, а - стала, г- радіальна швидкість,
г = dr/dt. Знайдіть узагальнений потенціал, функцію Лагранжа
системи, узагальнену енергію (наведена сила є силою взаємодії
двох зарядів в електродинамиці Вебера). Як змінюється з часом
узагальнена енергія?
135. 	Покажіть, що у випадку, коли узагальнений потенціал лінійно
залежить від швидкостей, тобто, /7* = Uo(q, t) + Ui(q, ί)φ,
узагальненопотенціальні сили Qi мають вид (сума по повторним індексам):
^ _ dUo , dUi , . _ dUi duk
Qi — Ь -ДГГ + 7ikQk: Де 7ik — я x—·
dcfo dt dqk dqi
24

Визначте ^ік для сили Коріоліса F = 2πιΰ х ω, та магнітної сили
F = (e/c)v х В, де ω = const, В = const (позначення звичайні).
136. Покажіть, що рівняння Лагранжа
/з£\ _ ас _
Jt (dHj ~W~'
для заряда (m, е) в електромагнітному полі зводяться до
звичайного виду
dp -> е ^ -+
— = е£ 4—v х В.
dt с
Знайдіть узагальнену енергію заряду.
137. Електричний заряд е, маса якого т, рухається у магнітному полі
В = gr/r3, g = const. Запишіть рівняння Лагранжа і знайдіть
перші інтеграли.
138. Нехай узагальнені сили визначаються через узагальнений
потенціал /7* = U*(qj,qj), так що
^ d ди* ди* . _
Qi = ТХ7- - , г = 1 ,П.
dt осц oqi
Покажіть, що сили (¾¾ не зміняться, якщо замість потенціала /7*
ввести узагальнений потенціал (сума по індексам, що
повторюються)
д^Ь дф
П = U*(qj,qj) + + -7^, /г = Т7п,
Ф — ФІЧіт - - - довільна диференційована функція.
139. Частка маси т рухається під дією сили F = (a/r3)7 х f, a = const.
Покажіть, що ця сила має узагальнений потенціал і знайдіть його.
140. Покажіть, що компоненти сили F пов’язані із компонентами
узагальненої сили Qi співвідношеннями:
a) в циліндричній системі координат (р, ф, z): Qp = Fp, Q<p = ρΒφ,
Qz =
b) у сферичній системі координат (ν,θ,φ): Qr = Fr, Qq = ri7#,
= гРф sin (9.
141. Знайдіть, як і в задачі N140, зв’язок між F{ та Qi у параболічних
координатах и, v, ф, де х = л/ййсоБ ф, у = yjuvsm ф, z = (u—v)/2.
Вказівка: в параболічних координатах r = Hudueu + Hvduev + Ηφάφβφ,
де TTu, ІЇі,, Нф - коефіцієнти Ламе (див. додаток 1 або задачу N143).
142. Нехай рух системи визначається функцією Лагранжа, що наведена
нижче. Запишіть рівняння руху системи (рівняння Лагранжа) для
25

всіх випадків (нижче - сума по всім індексам, що повторюються,
£і, Л< const.).
a) £= -{dig? + 2ді<іі sint) - -(с* - k cos t)qf, і = 1,п.
b) С = \atqf - Лі
Яг + Qit . -л—
о т> і = 1,п.
cosz qit
т
С) с = '-^(х2+ у2 + Z2)-mg
і X у
z + Ь [ - + -
X У J J
ш, g, b = const.
143. 	Частка маси т рухається в потенціальному силовому полі U =
U(x,y,z,t). Декартові координати частки пов’язані з
ортогональними криволінійними координатами ¢1, ¢2, Яз рівностями х =
x(QuQ2, Яз), У = УІЯі, 92,9з), * = %і,32,4з)· Знайти функцію
Лагранжа частки в координатах ¢^, використовуючи коефіцієнти
Ламе
Нк
оЯк) \ОЯк) \ОЯк)
144. Для плоского руху частки маси т в полі з потенціалом U(т, у)
знайти функцію Лагранжа в координатах ¢1, ¢2, якщо х = (qi — ¢2)/2,
У — у/ЯЇЯ2- знайти також зв’язок між компонентами сили F{ і
комопонентами узагальненої сили (як в задачі N140).
145. Знайти закон руху системи з функцією Лагранжа
С = £(ф, ¢2, · · ·, Яп) тобто такої, яка залежить тільки від
узагальнених швидкостей і не залежить від координат і часу.
146. Знайдіть закони перетворення енергії і узагальнених імпульсів,
спряжених полярним і декартовим координатам, при переході до
системи відліку, що обертається навколо осі Z з кутовою
швидкістю Ω:
а) φ = φί + Ωί, р = pt
б) у = xt sin Qt + yf cos Qt; x = xt cos Qt — yf sin Qt.
147. Нехай неконсервативна система має кінетичну енергію
Т = Т(ф,^Д), (і = 1 , п) і знаходиться під дією узагальнених
сил Qi. Отримайте рівняння Лагранжа такої системи із
варіаційного принципу δψ = 0, де функціонал ψ = (Т + A)dt, тут А -
робота узагальнених сил.
148. Покажіть, що для сил, які залежать від швидкостей лінійно,
дисипативна узагальнена сила
Qi
аd
Wi'
де D - дисипативна функція Релея.
26

149. 	Покажіть, що за наявності дисипації, яка описується функцією
Релея D має місце співвідношення
Ш
dt
-“-І-
Тут Ή - узагальнена енергія системи.
150. Кінетична енергія системи Т = а^ф^/2, потенціальна енергія
U = cikqiqk/2, функція Релея D = bikqiqk/2 {і,к = 1 , п), тобто,
всі вони є додатно визначеними квадратичними формами зі
сталими коефіцієнтами. Покажіть, що середні за часом значення (Т) і
(U) дорівнюють нулю.
151. Покажіть, що рівняння руху осцилятора під дією сили
пружності Felas = —кх та СИЛИ в’язкого тертя (сили опору) Ffric = —/Зі,
β = const, можна записати як рівняння Лагранжа виду
d ίдС\ дС
dt І дх ) дх
якщо ввести відповідним чином функцію Лагранжа £(т, і, t).
Знайдіть узагальнену силу та функцію Релея.
152. Частка маси гп рухається в сталому силовому полі F = const.
Використовуючи головне співвідношення теореми Ньотер
/ „ дС \ с дС dfi λ
st + W,dKXs = const w
знайти інтеграли руху частки. Тут
j··
= q'S') - 4i(t) = S = 1, n -1, 5t = t' -t
n - число параметрів групи перетворень.
153. а) Знайдіть інтеграл руху частки в силовому полі, яке має гвинтову
симетрію, користуючись співвідношенням (*), (див. задачу N152).
б) Покажіть, що перетворення повороту навколо осі Х%
задовольняє всім умовам теореми Ньотер для системи з функцією Лагранжа
С = f(x\ + ±2+ ±1) + Ω(ί)(χι±2 — £2Іі)· Знайдіть відповідні перші
інтеграли руху.
154. Покажіть, що для вільної частки маси m існує 5 (а не 7!)
незалежних інтегралів руху.
155. Нехай нескінченно мале перетворення координат і часу має вид
Qi = Я.г + εψί (Q) £) ? t' = t + єХ(q,t), є —> 0
і нехай при цьому перетворенні дія S змінюється за законом
t2
S = J £(q,q,t)dt = J j £ (</, q', i') +
¢1 t[
27

Доведіть, що величина
дТ- ІЯіХ - фг) - £Х - / = const,
OQi
тобто є інтегралом руху.
156. Покажіть, що інтеграл руху М&с — Pt = const відповідає
перетворенню Галілея. Тут М -повна маса системи часток, Rq -
радіусвектор центра мас системи, Р - імпульс системи. Чи є цей інтеграл
руху восьмим незалежним інтегралом замкненої системи?
Вказівка: використайте результат задачі N155.
157. Знайти закон перетворення інтегралів руху системи часток: Е -
енергії, М - моменту імпульсу, Р - імпульсу, а також функції
Лагранжа С для випадків: а) просторового зсуву системи відліку; б)
просторового обертання системи відліку; в) перетворення, що
відповідає однорідній групі Галілея.
158. Перевірте групові властивості неоднорідної групи перетворень
Галілея (а і б): а) Р = Sr + vt + b; б) tr = t + т, де S - матриця
повороту, dS/dt = 0, S'-1 = 5Т, v = const, b = const, т = const.
2. 	Електромеханічні системи
Формалізм Лагранжа є зручним при розрахунках електричних
кіл, які мають конденсатори, індуктивності, резистори та сторонні
ЕРС. Узагальненими координатами qn є параметри, що
характеризують просторову конфігурацію системи та кількість заряду Qn,
що тече по ділянці кола між двома вузлами. Узагальнена
швидкість Qn є електричним струмом. Функція Лагранжа системи є
сумою функцій Лагранжа електромагнітного поля конденсаторів,
індуктивностей, механічної системи і функцій Лагранжа взаємодії
струмів і зарядів з зовнішніми електричними і магнітними полями:
Р — Рмех Н” 2 -LikiQityQiQk ~ ~2^%k QiQk Η” W30BH,
де Lik і Cik - коефіцієнти індуктивності та ємності. Енергія
взаємодії струмів з зовнішнім магнітним полем
W30BH = J A jdV = Qk ^ Л ’ dlk = Qk^ki
Ф = £ A-dS,
де Φ& - потік магнітної індукції через контур струму Q&, А -
векторний потенціал магнітного поля. Джоулеві втрати і сторонні
28

ЕРС враховуються введенням узагальнених сил:
d дС _ дС_
dt dQk dQk
—RkQk — £k(t)·
Таким чином, функція Лагранжа є С = £мех + £ем, де
£мех = Т-и, Сем = Weл — WMar, тобто, аналогом кінетичної
енергії є магнітна енергія системи, а аналогом потенціальної енергії - її
електрична енергія. Приклад: математичний маятник з провідною
ниткою підвісу є елементом електромагнітного контура, площина
якого перпендикулярна зовнішньому магнітному полю з індукцією
В = const (див. рис 4).
С
мех
£
ЄМ
т£2ф2
2
_ LQ2
2
+ ЗФ
2mg£ sin2
Q2
2С
Ф
2’
Узагальненими координатами є: кут відхилення ф і заряд Q,
узагальненими швидкостями - кутова швидкість коливання маятника
ф і сила струму Q = dQ/dt = J, тут LQ2/2 = LJ2/2- власна
магнітна енергія, ζ)Φ = JФ = J В ■ ndS = JBS(t)~ магнітна енергія
у зовнішньому магнітному полі (магнітний потік зовнішнього поля
змінюється за рахунок зміни величини площини внаслідок
коливань маятника). Рівняння Лагранжа
а)
d / дС
dt \дф
дС
дф
0 b)
d_ idC
dt VdQ
дС
dQ
ε-RQ.
Підкреслимо, що в обидва рівняння а) і Ь) входить повна функція
Лагранжа £ = £Мех + В&и-
29

159. 	Знайти функцію Лагранжа і рівняння Лагранжа
конденсаторного мікрофону (див. рис.5); задані ш, fc, Zo, 5, і?, £, F(t). Нижня
пластина фіксована, а верхня пластина маси т може рухатися під
дією сил.
F(t)
Рис. 5:
160. 	В умовах задачі N159 відсутня сила повітряного тиску F(t), але
є зовнішнє однорідне електричне поле = (Eo(t), 0, 0). а)
Знайдіть функцію Лагранжа і запишіть рівняння Лагранжа; б)
покажіть, що із виразу для узагальненої енергії
дС . „
R = - С
дсц
маємо в цьому випадку Ή, = тх2/2 + /7мех + Weл і
т
dt
дС
dt
+ Q£— Q2R
-QX
дЕр
dt
+ Q£ — Q2R.
161. Електричне коло є двохпроводовою ідеально провідною лінією, що
розташована в горизонтальній площині і підключена до джерела
ЕРС Вздовж лінії може рухатися провідна перемичка масою
т. Вся система знаходиться у зовнішньому однорідному
магнітному полі з індукцією В, яке перпендикулярне до площини кола.
Електричний опір системи і?, довжина перемички £, початкова
швидкість vo. Знайдіть розв’язок рівнянь Лагранжа за умови, коли
магнітний потік зовнішнього поля значно більший за потік власного
поля струму. Як буде поводитися перемичка, якщо зовнішнє поле
відсутнє (В = 0)? Чи можливий при цьому рух зі сталим
прискоренням? Врахувати індуктивність лінії.
162. Дві паралельні металеві шини розташовані в площині (zx) на
відстані £ одна від одної і на кінцях ОС з’єднані перетинкою, опір якої
R (див. рис. 7). По шинам може рухатись без тертя провідник АВ
масою ш, який паралельний осі z, Вся система знаходиться в
магнітному полі, що створюється нескінченим провідником зі сталим
струмом /, який знаходиться в площині (yz) на відстані а від осі
ЗО

в
t В
Рис. 6:
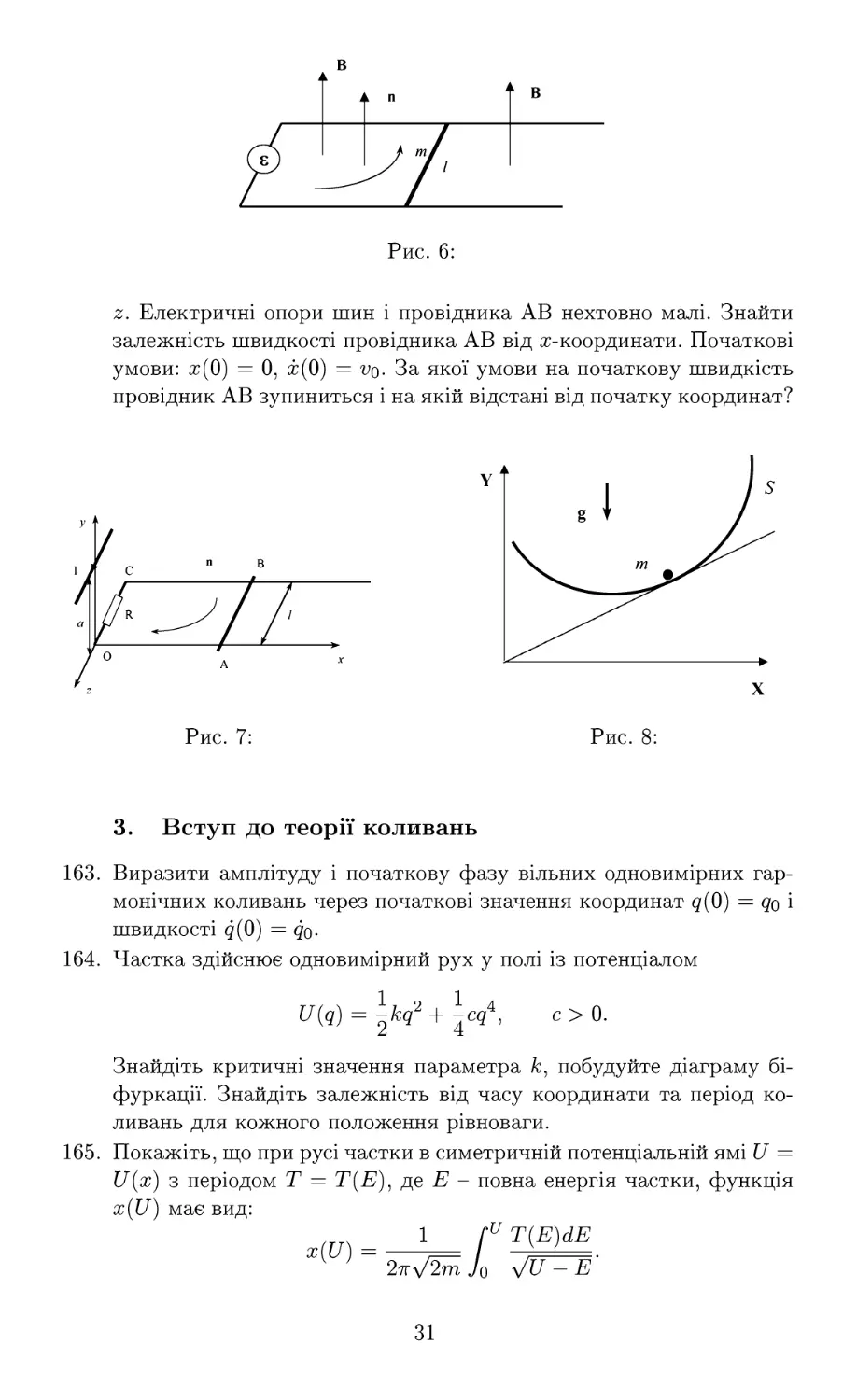
2:. Електричні опори шин і провідника АВ нехтовно малі. Знайти
залежність швидкості провідника АВ від т-координати. Початкові
умови: т(0) = 0, х(0) = г>о- За якої умови на початкову швидкість
провідник АВ зупиниться і на якій відстані від початку координат?
3. 	Вступ до теорії коливань
163. Виразити амплітуду і початкову фазу вільних одновимірних
гармонічних коливань через початкові значення координат ¢(0) = до і
швидкості ¢(0) = ¢0-
164. Частка здійснює одновимірний рух у полі із потенціалом
Знайдіть критичні значення параметра к, побудуйте діаграму
біфуркації. Знайдіть залежність від часу координати та період
коливань для кожного положення рівноваги.
165. 	Покажіть, що при русі частки в симетричній потенціальній ямі U =
U(x) з періодом Т = Т(Е'), де Е - повна енергія частки, функція
x(U) має вид:
X
Рис. 7:
Рис. 8:
U(q) = 1%2 + leg3  4, с>0.
31

166. Виведіть диференціальне рівняння утримуючої поверхні, на якій
частка маси т осцилює в поля тяжіння з періодом Т, не залежним
від амплітуди (див. рис. 8).
167. Знайти форму кривої (див. задачу N166) при коливанні вздовж
якої в полі тяжіння частота коливань не залежить від амплітуди.
168. Знайти закон вимушених коливань частки маси т під дією сили
F(t), якщо в початковий момент t = 0 частка знаходилась в
положенні рівноваги (¢(0) = 0,(7(0) = 0), для випадків
a) F = Fq = const.
b) F = at, a = const.
c) F = Fq exp (—at), a, Fq = const.
Власна частота коливань частки дорівнює ω. Згасанням
знехтувати.
169. 	Визначити кінцеву амплітуду коливань частки маси т під дією
сили
0
т = (
Fot/r
Fo
t < 0
0 < t < τ
t > т.
Власна частота коливань частки ω. До момента t = 0 система
знаходилась в стані рівноваги.
170. Кінець пружини закріпили на відстані £ + г від центру кільця
радіуса г. По кільцю без тертя може ковзати тіло маси ш, прикріплене
до пружини. В стані, коли пружина має довжину £, вона
натягнута з силою F. Знайти положення рівноваги та частоту лінійних
коливань. Кільце і пружина розташовані у вертикальній площині.
171. Знайти закон вимушених коливань частки маси ш під дією
сили F{t) = Fq exp(at) coscji, a,cj,Fo = const, якщо в початковий
момент t = 0 частка знаходилась в положенні рівноваги (¢(0) =
0,9(0) = 0). Власна частота коливань частки с^о, коефіцієнт
згасання 7.
172. Математичний маятник здійснює довільний рух у вертикальній
площині з параметром є = E/(m£g) = 2. Знайти залежність ф{Ь) -
кута відхилення маятника від вертикалі. За який час маятник
досягне положення ф = π? Чому буде дорівнювати період коливань в
межах фо = ±7г/4? Початкові умови ф{0) = 0, ф(0) = 2eg/£.
173. Гармонічний осцилятор описується рівнянням х + ω2χ = 0 з
початковими умовами т(0) = 0,і(0) = vq. Покажіть, що величина
_ 1 . / сjx(t) ]
Т* = — arcsm - t,
ω \^2E/m j
32

є інтегралом руху, тобто dT*/dt = 0. Тут т - маса осцилятора, Е
- його енергія.
174. 	а) Визначте у квадратурах період τ руху частки в потенціалі із
задачі N164 (розв’язок зводиться до еліптичного інтегралу), б)
Вважаючи в цьому потенціалі с малим параметром розвиньте
загальний вираз для періоду
в степеневий ряд до першого порядку по с і визначте період. Тут
а(#о) - масовий коефіцієнт.
175. Кінець пружини закріпили на відстані h від горизонтальної рейки.
По рейці без тертя може ковзати шайба маси ш, що прив’язана до
пружини. Пружина має жорсткість к та довжину £о в
ненавантаженому стані. Знайти частоту коливань в околі положення стійкої
рівноваги. Вважаючи h параметром, який можна змінювати,
побудувати діаграму біфуркації.
176. Частка маси m здійснює коливання під дією сили F = — fcr, де
т = (ж,у), к = const > 0 (так званий ізотропний двовимірний
гармонічний осцилятор). Покажіть, що величина І = ху + си2ху
є інтегралом руху такого осцилятора.
177. Запишіть рівняння Лагранжа для осцилятора із задачі N176 в
полярних координатах (г, ф) і знайдіть їх розв’язки. Початкові умови
го, Фо, Чц Фо - відомі.
178. Частка рухається в полі з потенціалом
Знайдіть стаціонарні точки (точки рівноваги). Які з них є
стійкими?
179. Масу ті прикріплено до вільного кінця вертикально підвішеної
пружини жорсткості к\. До маси т\ прикріплено пружиною
жорсткістю /¾ іншу масу ттт-2 (див. рис. 9) Положенню рівноваги
відповідають значення х\ = £и Х2 = £і + £2- Система знаходиться в полі
тяжіння g = const. Запишіть функцію Лагранжа для відхилень,
паралельних до сили тяжіння і відповідні рівняння руху.
Визначте стійкі положення рівноваги і відповідні частоти сколивань
системи. Дослідіть ці результати для випадку = 7772, к\ = к^.
180. Модель амортизатора: дві частки з’єднані пружиною з жорсткістю
к так, що можуть рухатися вздовж вертикально гладкої прямої.
Одна з часток масою т коливається за законом S(t) = Socosut.
Знайти умови, за яких амплітуда вимушених коливань однієї
частки відносно другої менше So· Пружина має довжину £о в
ненапруженому стані, S - відстань між частками, ω = const.
U(x,y) = ^(χ2 + у2) + X2y - ^y3■
33

X
Рис. 9: Рис. 10:
181. Точки підвісу двох однакових математичних маятників, з’єднаних
горизонтально розташованою пружиною жорсткості fc,
знаходяться на одному рівні. Знайти розв’язок рівнянь руху в околі
положення стійкої рівноваги. Дослідити ефект биття.
182. Визначити закон коливань x(t), y(t) і частоти коливань системи
з двома ступенями вільності, функція Лагранжа якої має вид:
С = (і2 + у2)/2 — cjq(t2 + у2)/2 — аху, a = const (два однакових
одновимірних осцилятора з власною частотою cjo, пов’язані
взаємодією —аху). Знайти нормальні координати системи і записати
функцію Лагранжа в цих координатах.
183. Математичний маятник є частиною електричного кола
(конденсатор з ємністю С, котушка індуктивності L, див. рис.11). Система
знаходиться в сталому однорідному магнітному полі з індукцією
В. Поле ортогональне до площини рисунка. Знайдіть нормальні
частоти коливань в системі. Амплітуду коливань вважати малою.
184. 	Точка підвісу математичного маятника коливається вздовж
горизонтальної прямої за законом s(t) = socosQt, де Ω » \J~gfi ξ cjq,
34

5o ί. Знайти ефективну потенціальну енергію, положення
стійкої рівноваги маятника і відповідні частоти коливань.
185. Точка підвісу математичного маятника (ш, і) рухається вздовж
горизонтальної прямої Ох за законом x(t) = at2/2 + ^βίηΩί, де α,
Д cj=const. Запишіть функцію Лагранжа і рівняння руху
маятника (через кут ф відхилення від вертикалі) в системі відліку, що
рухається поступально вздовж осі Ох за законом at2/2.
186. Точка підвісу математичного маятника рухається вздовж
вертикального напрямку за законом s(t) = 5о соsQt, де Ω » \fgj~t = cjo,
5о L Знайти ефективну потенціальну енергію, положення стійкої
рівноваги маятника і відповідні частоти коливань.
4. 	Динаміка твердого тіла
187. Розгляньте обертання твердого тіла навколо закріпленої точки О.
Нехай ф - кут повороту лінії вузлів Οξ в площині (т, у) навколо
осі 2. Нехай βξ - одиничний вектор вздовж лінії вузлів. Покажіть,
що = Дпеп (еп - орти системи координат (x,y,z): п = 1,2,3).
Матриця
(cos ф sin ф 0 \
— sin ф cos 0 0.
о 0 1 J
188. 	Покажіть, що для довільного вектора В ф 0 виконується співвід¬
ношення ΩΒ = —CJ х В, де Ω - тензор кутової швидкості твердого
тіла, ω - кутова швидкість.
189. 	Покажіть, що із формул для кінетичної енергії обертання твердого
тіла
со - М
-L обер = 2
випливає, що
= Ν·ω.
dt
Тут М -момент імпульсу, а N - момент сил.
190. 	Обчислити тензори інерції для наступних тіл маси т з однорідним
розподілом маси в системі координат, початок якої розташовано в
геометричному центрі тіла (розміри тіла відомі): а) кулі; б) куба;
в) 	прямокутного паралелепіпеда; г) прямого круглого циліндра.
191. 	Знайдіть тензор інерції половинки тонкого диску маси т і радіуса
R в системі координат з початком у центрі мас, осі якої направлені
вздовж головних осей інерції.
35

192. 	Доведіть, що для будь-якої плоскої фігури в системі Oxyz, осі якої
Ох і Оу лежать в площині фігури, тензор інерції має вид
193. Головні центральні моменти інерції тіла в деякій системі одиниць
дорівнюють 3, 4, 5, а маса дорівнює 2. В системі координат Cxyz
з початком в центрі мас С деяка точка А тіла має координати
(1, 2, 0). Знайти тензор інерції тіла відносно системи координат з
початком в точці А, осі якої паралельні осям системи Cxyz.
194. Прямий однорідний циліндр маси ш, радіуса R і висоти h
обертається з кутовою швидкістю ω = const навколо осі, яка
перпендикулярна осі циліндра, знаходиться на відстані R від неї і дотикається
до основи циліндра. Знайти момент імпульса М циліндра відносно
точки дотику осі обертання до циліндра.
195. Покажіть, що при обертанні твердого тіла відносно нерухомої
точки О, кінетична енергія тіла зберігається в тому і тільки в тому
випадку, коли під час руху вектор момента імпульсу Мо тіла і
вектор кутового прискорення β є ортогональними.
196. Упевніться, що кути повороту рамок і тіла, що знаходиться в
кардановому підвісі, відповідають кутам Ейлера.
197. а) Фізичний маятник маси т коливається відносно точки А, що
лежить на одній із головних осей інерції на відстані £ від центра
інерції С. Покажіть, що функція Лагранжа для цієї системи має
вигляд (позначення звичайні)
тут Іо - головний момент інерції відносно точки С.
б) Визначте функцію Лагранжа фізичного маятника і частоту його
малих коливань навколо горизонтальної осі в полі тяжіння, якщо
вісь обертання складає кути а, /3, 7 з напрямками центральних
головних осей, а моменти інерції маятника відносно цих осей
дорівнюють /і, /2, 7з, відповідно, Відстань від осі обертання до центра
маси т дорівнює £.
198. Запишіть рівняння Ейлера твердого тіла в тензорній формі.
199. Кінець невагомої нитки, що намотана на обруч маси т і радіуса і?,
закріплений у деякій точці (див. рис. 12). Знайдіть функцію
Лагранжа, яка описує рух обруча у вертикальній площині і запишіть
рівняння Лагранжа. Знайдіть також прискорення s видовження
нитки.
І
36

Рис. 12:
200. Тонкий стержень, маса якого ш, момент інерції /, ковзає по гладкій
вертикальній нерухомій нитці, що проходить через отвір в
середині стержня. Поле тяжіння g = const. Як узагальнені координати
візьміть кути Ейлера Θ, ф та координату центра мас 2. Початкові
дані: ¥>(0) = cjo; 0(0) = 0; 2д, іц. Запишіть функцію Лагранжа і
знайдіть розв’язок рівнянь руху: z(t), 0(ί), φ(ί).
201. Кінці тонкого стержня довжиною £ ковзають по гладкій параболі
у = х2/2а з вертикально розташованою віссю. Поле тяжіння g =
const. Знайти частоти коливань стержня.
202. Знайти функцію Лагранжа, яка описує вільне падіння однорідного
стержня маси т з головними центральними моментами інерції її =
І2j Із поблизу поверхні Землі. Знайти перші інтеграли руху.
203. Покажіть, що для узагальнених імпульсів твердого тіла, яке
описується функцією Лагранжа С виконується співвідношення
дС
досі
М-еи г = 1,3,
204.
де щ - кути Ейлера, а Є{- відповідна трійка одиничних ортів (ез,
е/з), М - момент імпульсу.
За умов і позначень задачі N203 покажіть, що виконується
співвідношення
дС
досі
N-eu
де N — момент сили.
205. 	За умов задачі N202 знайдіть узагальнену енергію Н стержня,
виражену через параметр центра мас і кути Ейлера.
37

С Механіка суцільного середовища
Трагедия науки - в умервщлении
прекрасной теории мерзким фактом.
Томас Гексли
1. Кінематика суцільного середовища
206. 	Довести, що матеріальні похідні за часом (похідні по Лагранжу)
зв’язані з просторовими похідними (похідними по Ейлеру)
співвідношеннями
<*(···)
dt
д(···)
dt
+ v-V(...)
207. 	Довести, що похідна за часом від об’єму V
середовища дорівнює
f dV суцільного
V(t)
dV
dt
/ div v dV,
v(t)
де v - поле швидкостей.
208. Довести формулу Ейлера (загальний випадок)
-j- = Jdivu,
dt
де й = {и\, U2j... un) N-мірна швидкість, і якобіан перетворення
j _ д(хі,... ,тдг)
д(хю,..., тдго)
209. Показати, що якщо тензор швидкості деформації суцільного
середовища D = 0 (рух твердотільний), тобто
dvj dvk
—- Η = 0,
дх k dxj
то, як наслідок, маємо
де
V= х ^
ξ = rot v = 2cj,
тут ω - локальна кутова швидкість.
38

210. 	Покажіть, що (див. задачу N209)
r.D = v(\D),
де D = т · D · г, тобто D = DikX%Xk.
211. Доведіть, що
г-Ω = X f),
де Ω - тензор локальної швидкості обертання середовища.
212. Нехай dr - векторний елемент дуги, що складається протягом
всього руху із одних і тих же самих малих часток “рідинного”
середовища. Доведіть, що
jt{dr) = (dr-V)v
213. Покажіть, що TrD = div v
214. Покажіть, що якщо тензор локальної швидкості обертання Ω = 0
(рух безвихровий), тобто,
dvj dvk _
dxk dxj
то течія середовища є потенціальною: v = VV>, де ψ - потенціал
швидкості.
2. Динаміка і інтеграли руху суцільного середовища
215. Отримати рівняння неперервності маси у формі Лагранжа:
po(R,t) = Jp(f,t), де R - лагранжеві змінні, а т - змінні Ейлера.
216. Із лагранжевої форми закону збереження маси (рівняння
неперервності, див. задачу N215) отримати це рівняння у формі Ейлера:
dp л
—- + pdiv v = 0,
dt
або
-X + div (pv) = 0,
де pv - вектор густини потоку маси.
217. Виведіть рівняння неперервності виходячи із постулату
збереження маси.
218. Нехай ψ = ψ(ν,ί) - одна із фізичних характеристик суцільного
середовища. Доведіть, що
άφ д{рф)
(,Λ=-όΓ + ά"
39

219. 	Використовуючи рівняння Коші
доведіть, ЩО тензор напруг Т Є симетричним тензором, тобто Fki —
Fik, що є наслідком закону збереження моменту імпульсу.
220. 	Нехай ψ = ψ(ν,ί) - одна із фізичних характеристик суцільного
середовища. Доведіть, що
[ ρφάν = [ p^j-dV.
dt Jv(t) Jv(t) dt
221. 	Доведіть, що
d_
dt
ί φάν= [
Jv{t) Jv{t)
άψ
dt
+ V’div v ] dV.
222. 	Доведіть, що потужність результуючої сили, що виконує роботу
над суцільним середовищем, дорівнює:
dA
dt
ί ν · fdV + (f
Jv(t) Js
v · fdV + Φ v · T · ndS.
Sit)
Тут / - об’ємна густина сили.
223. 	Нехай
Т
-S
JV{t)
p^-dV
кінетична енергія суцільного середовища в об’ємі V(t). Доведіть,
що
ν ■ Т ■ ndS + ί ν · fdV — f P-.DdV,
dt Js(t) Jv(t) Jv(t)
за звичайними позначеннями.
224. 	Із узагальненого 1-го принципу термодинаміки в формі
Т+Е=Q+А
і рівняння Коші отримати:
de
Р
dt
Т : D — div q.
Тут Т - кінетична енергія, Е - внутрішня енергія, є - внутрішня
енергія на одиницю маси, q - вектор потоку тепла.
40

225. 	Для випадку, коли об’ємні сили мають потенціал, незалежний явно
від часу, тобто, дф/ді = 0, із рівняння
,_=dlv (,*·_?)
отримати диференціальну форму закону збереження енергії для
суцільного середовища
Г\
^(ρε*)+άϊνΫ = 0.
тут ε* = {v2/2) + ф + є, Y - вектор Умова.
226. 	Показати, що для ідеальної рідини
d (v2 \ д
μ{υ + φ+η)-&{φ+,ι)'
де h - ентальпія на одиницю маси.
227. 	Показати, що для адіабатичного руху ідеальної рідини:
±(і
dt 1 р
ξ ΞΞ rot V.
228. Показати, що для ідеальної рідини справедливе рівняння баланси
ентропії
§^(pS) +div 0s) = о,
js = pSv - вектор густини потоку ентропії, a S - ентропія на
одиницю маси. Яка гранична умова звідси випливає?
229. Показати, що при адіабатичному русі ідеальної рідини із умови на
границі [π·η] = 0, де π = Ρ + ρνν- тензор густини потоку імпульсу,
як наслідок, маємо
[Р + pvl\ = о, [ρνηντ\ = 0.
230. Для адіабатичного руху ідеальної рідини отримати граничну умову
ξ£ = ηχ [vr\,
Де ζί = ζ/£ ~ лінійна густина “завихреності”.
231. Доведіть, що швидкість руху поверхні розриву в суцільному
середовищі (в даній точці поверхні) визначається формулою
^ п 8F
VS = ~Wf\'^'
де F(x, у, z, t) = 0 задає рівняння поверхні розриву.
41

232. Покажіть, що якщо розглядати адіабатичний рух ідеального газу
з рівнянням стану Р/Ро = (р/ро)7, де 7 = cp/cv - показник
адіабати, то хвильові рівняння для тиску і густини газу будуть тотожно
задовольнятися, якщо швидкість звуку дорівнює С = у/Ро'у/РО-
233. Покажіть, що об’єднаний закон термодинаміки (І+ІІ принципи)
для в’язкої течії рідини має вигляд
prf = f : W+ V· (kVT),
де S — ентропія на одиницю маси, Т -абсолютна температура, т -
тензор в’язких напруг, к - коефіцієнт теплопровідності.
D Механіка Гамільтона
Математики, как французи: все что ви
им говорите, они переводят на свой на
язик, и ото тотчас же становится
чемто совершенно иним.
Поган Вольфанг Гете
1. Рівняння Гамільтона. Канонічні перетворення.
Дужки Пуассона
234. Камінь маси т кинули вертикально вгору з імпульсом ро в
полі тяжіння g = const. Нехтуючи опором повітря, знайти функцію
Гамільтона, записати рівняння Гамільтона, знайти і зобразити
графічно фазову траєкторію і траєкторію каменя в конфігураційному
просторі.
235. Каменю маси т надали вектор імпульсу ро під кутом до горизонту
в полі тяжіння g = const. Нехтуючи опором повітря, знайти фазову
траєкторію каменя, і зобразити проекцію цієї фазової траєкторії на
конфігураційний простір.
236. Частка рухаєтсья вздовж осі Ох під дією сили F = F(x), яка
залежить від положення частки. Довести, що фазові траєкторії частки
в площині (р,х) можуть бути тільки трьох типів (див. рис. 13, 14,
15): а) імпульс частки не змінює свого напрямку під час руху; б)
напрямок імпульсу змінюється один раз; в) рух частки є
періодичним. Проаналізуйте, який з рис. 13, 14, 15 відповідає випадкам а),
б), в).
237. Рух зарядженої частки (ш, е), що відбувається в силовому полі,
описується функцією Гамільтона
,2 д2
-Ххг + уг),
Н = + U(V^+?) + βΖβ1
2т
8тс2
42

де Б, с - сталі. Запишіть рівняння Гамільтона і проаналізуйте
розв’язки для випадку U{y/x2 + у2) = Ι/λ/χ2 + у2.
238. Доведіть, що
<т_&н
dt dt ’
де Н - функція Гамільтона системи.
239. Доведіть, що при наявності дисипативних сил
dt
дН
dt
+ Фі118®’
де Н - узагальнена енергія, Q^1S - узагальнені дисипативні сили.
240. 	Доведіть, що із умови 6S = 0, де дія
5
РкЧк - ЩРк,Як,і)
dt,
випливають рівняння Гамільтона.
241. Складіть канонічні рівняння руху для фізичного маятника в полі
тяжіння g = const і покажіть, що з них випливає відоме рівняння
коливань маятника Ιζζφ = — mgasin^ (позначення звичайні).
242. Знайти функцію Гамільтона і скласти канонічні рівняння руху
осцилятора з в’язким тертям, функція Лагранжа якого є
С =
1 pPt/m
2
тх2 + βχχ
к
2т
х
2
де к - коефіцієнт пружності, а β - коефіцієнт опору.
243. 	Знайти функцію Гамільтона і скласти канонічні рівняння руху
осцилятора з в’язким тертям, функція Лагранжа якого є £* =
е^/т(ші:2 — кх2)/2. Покажіть, що £* і С із задачі N242
пов’язані співвідношенням
£*(<?, <М) = £(q,q,t) + dF<f' ^ ·
43

244. Складіть рівняння Гамільтона для заряду, який рухається в
сталому однорідному магнітному полі з індукцією В = const і
електричному полі з потенціалом φ.
245. Система складається з частки масою М і п часток з однаковими
масами т. Виключити рух центра мас і звести задачу до задачі
про рух п часток. Знайти функцію Гамільтона.
246. Дві частки з масами т\ і Ш2 взаємодіють з потенціальною енергією
/7(г), де г - відстань між частками. Вкажіть циклічні координати
у цьому русі, запишіть відповідні їм інтеграли руху і складіть
канонічні рівняння.
247. Знайдіть функцію Гамільтона та отримайте рівняння руху частки
маси т в потенціальному полі в системі відліку, що рівномірно
обертається із кутовою швидкістю Ω.
248. Функція Лагранжа важкої симетричної дзиги має вид:
С = sin2 θ + Θ2) + ~^(Ф cos# + ψ)2 — mg^cos#,
ί - відстань до центру мас від точки закріплення, φ і Θ - кути
Ейлера; Д, Ιζ - головні моменти інерції в системі координат “дзига”.
Знайдіть узагальнені імпульси, запишить рівняння Гамільтона і перші
інтеграли руху. Виведіть рівняння з розподіленими змінними
І£в2 = П0-^-иев(в).
Тут Рфо і По - узагальнені імпульс і функція Гамільтона при t = 0.
249. Частка маси т рухається (без тертя) по лінії перерізу нерухомої
гладенької сфери радіуса R і гладенької горизонтальної площини,
що перпендикулярна осі 2 і рухається у вертикальному напрямку
(поле тяжіння g = const.) за законом 2 = R sin cut, де ω = const.,
0 < t < π/2ω.
a) Знайдіть фазову траєкторію частки (початкові дані відомі).
b) Розгляньте ансамбль часток з умови задачі (уявну сукупність
часток, які розрізняються тільки початковими умовами, у
всьому іншому однакові, сили і в’язі тотожні). Нехай Го -
фазовий об’єм цієї системи в початковий момент. Покажіть, що
він зберігається. Дослідіть, як деформується цей об’єм.
250. Покажіть, що якщо для системи другого порядку q = Q(^,p,i),
р = P(q,p,t) зберігається фазовий об’єм, то ця система є
гамільтоновою, тобто, існує така функція 7Ї(^,рД), що
п< л τ>( +\
Q(q,P,t) = φ-, P(q,p,t) = - — .
44

251. 	У канонічній системі, що описується функцією Гамільтона l~L(q,р, t)
визначений перехід до нових координат і часу: q[ = /*(#,£), tf =
φ(ς,ί). Перетворення імпульсів р\ = hi(q,p,t) визначається у
відповідності з рівністю
P%dq% - l~L(q,p,t)dt = p-dg- - H'(q\p\ t')dt', і = Ι,η,
що гарантує гамільтоновість рівнянь у нових змінних. Довести, що
змінні g,p, £, qr,pr,tr і функції l~L(q,p,t) T~Lr(q',pf,t') зв’язані
співвідношеннями
^АР'_^±П' = Р, ?lip>_<!±H, = H ік = т-
dqPl dqkH Pk’ 8tPl dt* H’ ’ ’
252. Для нижченаведених одновимірних систем використовуючи
результати задачі N251, обчисліть функцію Гамільтона у нових
змінних, якщо міняються ролями час і координата qr = t,tr = q : a) pyx
частки по вертикалі в однорідному полі тяжіння Землі; б) лінійний
осцилятор; в) осцилятор з в’язким тертям (див. задачу N242).
253. Розгляньте функцію Гамільтона для одновимірного осцилятора
р2 mu2q2
= 2т+ 2
У рівняннях перетворення Q = \{р + imujq), Р = \{р — imujq),
і = \/—Т, визначте сталу Λ так, щоб перетворення (q,p) (Q,P)
було канонічним. Знайдіть T~L{Q, Р) і канонічні рівняння для Q і Р.
254. Твірна функція фі(g, Q) для осцилятора із задачі N253 має вигляд
■tpi{q,Q) = 7^mujq2 cot Q.
Знайдіть за допомогою канонічних перетворень нову функцію
Гамільтона і розв’язок канонічних рівнянь.
255. Знайти твірну функцію фї(д,Р) для перетворення з твірною
функцією фі(g, Q) із задачі N254.
256. Знайти розв’язок канонічних рівнянь для осцилятора із задачі
N253 методом канонічних перетворень з твірною функцією ^2(^, Р)
із задачі N255.
257. Неізотропний гармонічний осцилятор. Нехай на частку маси т діє
сила, проекції якої на декартові осі дорівнюють Рх = —к\х, Ру =
—/С2У, Fz = —де &і, &2, &з - сталі. Знайти загальний розв’язок
рівнянь руху частки методом канонічних перетворень.
258. Доведіть, що канонічні перетворення залишають незмінними
дужки Пуассона будь-яких динамічних змінних / і д\ [/, g\pq = [/, g\pQ.
259. Перевірити канонічність перетворень з твірними функціями
фі(д,Я) і ф2(д,Р) із задач N254, N255, відповідно.
45

260. Обчислити дужки Пуассона [Mj,pk\ складені із декартових
компонент імпульсу р і моменту імпульсу М частки.
261. Обчислити дужки Пуассона а також [М2,Мз], складені
із декартових компонент моменту імпульсу М частки.
262. Обчисліть дужки Пуассона для функцій
a) ф = q2 + р2, ψ = arctan(p/g);.
b) ф = q cos ωί + (ρ/ω) sin ωί, ψ = ρ cos ωί — qu sin ωί, ω = const]
c)
П П
φ = cos ^ (p? + qf), i) = sin^2 ІРЇ + ЯЇ)·
ί=1 ι=1
263. Покажіть що, якщо гамільтоніан системи не залежить від часу
явно (тобто, dB/dt ξξ 0) і якщо існує перший інтеграл f(t,q,p) = а,
явно залежний від часу, то похідні df/dt, d2f/dt2, ... також є
першими інтегралами руху.
264. Покажіть, що функції фі = (р? + <?22), ф2 = (р2 + Яі), Фз = [Фі,ф2І
є незалежними першими інтегралами руху механічної системи з
гамільтоніаном Н = р\Р2 + ЧіЧ2-
265. Покажіть, що дужки Пуассона [Μζ,φ\ = Оде ф = 0(г2,р2,г-р) -
будь-яка скалярна функція координат і імпульсу частки.
266. Покажіть, що дужки Пуассона [/, Мз] = / х ез, де / - будь-яка
векторна функція координат і імпульсу частки, а ез - одиничний
вектор в напрямку осі 2.
2. Рівняння Гамільтона-Якобі. “Змінні дія-кут”
267. Скласти рівняння Гамільтона-Якобі, знайти його повний інтеграл
і знайти закон руху вільної частки маси т (за відсутності сил)
при наступних початкових умовах т(0) = а?о, #(0) = хо, у(0) = уо,
2:(0) = 20, рж(0) = ШУ()Х, ру(0) = mv0y, pz{0) = m%.
268. Скласти рівняння Гамільтона-Якобі, знайти його повний інтеграл
і знайти закон руху частки маси т у полі тяжіння g = const: а) в
декартових; б) в циліндричних координатах.
269. Методом Гамільтона-Якобі знайти розв’язок рівнянь Гамільтона
для осцилятора
9 2 2
п, _ Р х πιω q
270. Складіть рівняння Гамільтона-Якобі для заряда (е,га), що
рухається в електромагнітному полі з напруженістю Е і індукцією В.
46

271. 	Методом Гамільтона-Якобі знайти розв’язок рівнянь Гамільтона
для трьохвимірного осцилятора
272. Складіть рівняння Гамільтона-Якобі для фізичного маятника в
полі тяжіння g = const (див. задачу N241), знайдіть його повний
інтеграл і, використовуючи його, знайдіть розв’язок канонічних
рівнянь.
273. Зайдіть повний інтеграл рівняння Гамільтона-Якобі для заряду е
масою ш, який рухається в однорідному сталому електричному
полі Е. Знайдіть закон руху заряду. Початкові дані: го ро- Розгляньте
два випадки: а) ф ф 0, А = 0; б) ф = 0, А ф 0 де ф і А - електричний
і векторний магнітний потенціали.
274. Складіть рівняння Гамільтона-Якобі для математичного маятника,
розв’яжіть його і, записавши повний інтеграл канонічної системи,
знайдіть закон малих коливань і зміну укороченої дії за один період
коливань.
275. Частка маси т рухається в однорідному полі тяжіння g = const
по гладенькому твердому стержню, який обертається зі сталою
кутовою швидкістю ω навколо вертикальної осі, що проходить через
кінець стержня. Кут між стержнем і вертикальною віссю дорівнює
#0· Знайти закон руху частки (у квадратурах) методом
ГамільтонаЯкобі.
276. Двовимірний ізотропний гармонічний осцилятор описується
функцією Гамільтона
П =
РІ+РІ
2т
Складіть рівняння Гамільтона-Якобі, знайдіть його повний
інтеграл і знайдіть рівняння траєкторії осцилятора. Вказівка:
розділити змінні в рівнянні Гамільтона-Якобі у вигляді: So = Sox(x) +
Soy{y)·
277. Частка маси т здійснює плоский рух під дією центральної сили
з потенціалом U(r). Скласти рівняння Гамільтона-Якобі і знайти
його розв’язок в полярній системі координат. Визначити довільні
сталі розв’язку.
278. Складіть рівняння Гамільтона-Якобі, знайдіть його повний
інтеграл і знайдіть закон руху системи, функція Лагранжа якої у
сферичних координатах має вид:
£ = ^(г2 + г2в2 + г2ф2 sin20) - сфі{в)ф - bf2{9) - ^h{9) - /4(7).
c, β, b - сталі.
47

279. 	Частка маси т рухається у центральному полі з потенціальною
енергією
U(r)
μι μ2
2 ’
де Ці, Ц2 - сталі. Складіть рівняння Гамільтона-Якобі у сферичній
системі координат, знайдіть його повний інтеграл і отримайте з
нього траєкторію частки. Початкова швидкість частки лежить в
площині ф = const.
280. 	Частка маси т рухається в потенціальному полі
U{г, Θ) = /(r) +
де г, ф - сферичні координати. Скласти рівняння
ГамільтонаЯкобі і знайти його перші та другі інтеграли.
281. 	Для руху частки маси т в полі із потенціалом [7(г, 0) =
и(г) + Ь(в)/г2, де г, θ,φ - сферичні координати, знайти
(r(t), 0(f), 0(f)}, {Ρτ(ί),Ρβ(ί),Ρφ(ί)} у квадратурах, користуючись
функцією Гамільтона-Якобі
5
Ρώ
X - 2тЬ(в) %-άθ
sin θ
+ J \j2m(E - u(r)) - ^dr.
282. 	Частка маси m рухається відносно сферичної системи координат в
силовому полі з потенціалом и(г,в,ф) Знайти частковий інтеграл
(у квадратурах) рівняння Гамільтона-Якобі у випадку, якщо
U(r,e) = F(r) +
Ф(М)
г2 ’
де F(r), Ф(θ,φ), - задані функції.
283. Знайти змінні дія-кут J — ω для осцилятора із задачі N271.
284. Ізотропний двовимірний осцилятор у полярних координатах
описується функцією Гамільтона
П
1+
2 2
тсor
Знайти змінні дії
285. 	Частка маси т здійснює вільні гармонічні коливання під дією
пружної сили із коефіцієнтом пружності к. Визначити частоту
коливань за допомогою змінної “дія”.
48

286.
287.
288.
289.
290.
291.
292.
293.
294.
295.
296.
297.
Нехай одна із узагальнених координат є циклічною. Покажіть,
що в цьому випадку дія визначається за формулою = 2πΡ&.
Довести, що період Т руху по замкненій кривій Ή, = Е на фазовій
площині (р, ¢), дорівнює похідній від площини (обмеженою цією
кривою) по Е\ Т = dH(E)/dE. Знайдіть за цією формулою період
коливань осцилятора із задачі N269.
За допомогою змінних “дія-кут” знайдіть частоти коливань
неізотропного осцилятора із задачі N271.
Знайти змінні “дія-кут” для випадку фінітного руху двох тіл зі
зведеною масою μ і енергією взаємодії U(r) = —α/r, a = const > 0.
Знайти функцію Гамільтона задачі Кеплера (потенціальна енергія
U(r) = —α/r, a = const > 0) у змінних “дія-кут” для випадку
фінітного руху частка маси ш.
Функція Лагранжа £(q, ¢, t) є строго опуклою функцією
узагальнених швидкостей. Функція S(q, t) є розв’язком рівняння
ГамільтонаЯкобі. Покажіть, що вектор-функція q%{t), (і = 1 , п) буде рухом
системи, якщо при всіх t виконується співвідношення
dS(q(t),t)
dt
C(q,q,t).
Частка вільно рухається всередині сфери з пружними стінками,
радіус якої повільно змінюється. Як змінюється енергія частки і
кут, під яким вона налітає на стінку?
Частка маси m рухається в одновимірній прямокутній
потенціальній ямі, ширина якої £. Знайти, як змінюється енергія частки при
повільній зміні £, розглядаючи зіткнення частки зі “стінкою” ями.
Частка здійснює коливання в потенціальній ямі. Визначте закон
зміни з часом повної енергії частки під дією сили тертя і7]^ = — ах
з малим коефіцієнтом a = const (х - декартова координата).
На нитці, що пропущена через невеличке горизонтально
розташоване кільце А (див. рис. 16), підвішена частка маси ш. Визначити
середню силу, що діє на кільце А з боку нитки при малих
коливаннях частки. Знайти зміну енергії частки при повільному
вертикальному переміщенні кільця.
Показати, що при адіабатичній зміні довжини і
математичного маятника амплітуда відхилення від положення рівноваги
фо = con5i[^(i)]-3/4.
Повний інтеграл рівняння Гамільтона-Якобі S(q,р, t) = Et+So(q,p)
припускає таку геометричну інтепретацію: рівняння S = const
можна розглядати як рівняння поверхні фронту хвилі, що
розповсюджується з певною швидкістю и. Виведіть формулу зв’язку між
швидкістю и хвилі і швидкістю v частки маси ш, рух якої
описується відповідним рівнянням Гамільтона-Якобі у декартовій системі
координат.
49

Рис. 16:
298. Нехай частка рухається в площині (х,у) в потенціальному полі
U = U(у). Знайдіть співвідношення, яке є аналогом закону Снелла
заломлення світла.
299. Розглянемо рівняння ейконалу L: (VL)2 = п2, де п - показник
заломлення середовища. Введемо вектор п такий, що \п\ = п, тоді
VL = п і L = J n-dr = f ndt (де dl -елемент траєкторії). Як відомо,
рівняння траєкторій світлових променів є наслідком варіаційного
принципу 6L = 0, тобто,
5
0,
η
цей принцип називається принципом Ферма: промінь світла
розповсюджується в неоднорідному середовищі так, що виконується
(*), де п = n(x,y,z). Знайдіть потенціал U = U(x,y,z) силового
поля, в якому траєкторії часток будуть співпадати з траєкторіями
світлового променя.
300. 	Як відомо, аналогом рівнянь Гамільтона
dT~L(f,p,t) ^_ dT~L(f,p,t)
дг др
в оптиці є рівняння променевої оптики:
дио
д?'
г
дио
дГ
тобто, аналогом р є хвильовий вектор fc, аналогом функції
Гамільтона Ή, є колова частота ω. Покажіть, що аналога функції
Лагранжа в оптиці не існує, тобто, С = р · v — T~L не переходить у
співвідношення (к · г — ω).
50

E
Релятивістська динаміка частки
- У нас, - сказала Алиса, - когда долго
бежигиь со всех йог, непременно попадешь в
другое место.
- Какая отсталая страна! - сказала
Королева. - Ну, а здесь, знаешь ли, приходится
бежать со всех йог, чтоби только
остаться на том же месте.
Льюис Кзррол
“Алиса в стране чудес”
1. Кінематика спеціальної теорії відносності
ЗОЇ. Перевірте групові властивості однорідної групи перетворень
Лоренца:
, Х\ — vt . t — VX\ , , 1/-,4
Xl = 1 = y/T^j2’ = = ^3’ C = L ^
302. 	Нехай v = tanh^, тоді перетворення Лоренца можна записати у
вигляді:
х[ = Х\ cosh^ — t sinh^
tf = t cosh^ — x\ sinh^, (2)
де c = 1. Отримайте формули (2) із виразів (1) задачі N301 і
перевірте їх групові властивості. Перевірте, чи є перетворення Лоренца
комутативними в загальному випадку.
303. Використовуючи формули (1) задачі N301 показати, що і =
ів\/і — г?, Аг = Aty/l — v2,
/ ~ v / uy,z / &х
Ux ~ 1 — vux ’ Uy’z ~ r(l-vuxy Λχ ~ Г3(1 - vux)z ’
тут Г = (1 — v2)~1^2.
304. У двовимірному просторі-часі (£, х) системи координат К і К’ з
точки зору спостерігача в системі К мають вигляд, зображений на
рис. 17. Чому дорівнює кут нахилу осі t' відносно t? Зробіть
градуювання осей.цих систем кооординат за допомогою інваріантності
інтервалу s2 = t2 — х2 = s'2 = tf2 — х/2 = inv.. Зобразіть ці
координатні системи з точки зору спостерігача в системі К\
305. Користуючись рисунками (у градуйованому вигляді) задачі N304
зробіть висновки щодо релятивістського скорочення часу і
довжини.
51

t
X
Рис. 17:
306. Нехай задано метричний тензор (gap) в ортогональній тривимірній
системі координат. Покажіть, що коефіцієнти Ламе (див. задачу
N143, або додаток 1) і компоненти тензора ga^ пов’язані
співвідношеннями: На = x/g^, #і#2#з = д/g, де g = det gap, α,β = 1, 3.
307. Нехай маємо локальний базис {еД в Сп так, що значення
метричного тензора на векторах бази є gij = §2 [є*, ej\ Є 5Ї, і нехай маємо
базис ковекторів в спряженому С* просторі, тобто дуальний базис
{е*}, так що g2 = gije1 ® б?. Нехай вектор С = ¢72¾. Доведіть, що
для компонент векторів виконуються співвідношення Aj = gjiA1,
Ак = g кгАі, А* В = А/Б·7 = АБ^ (скалярний добуток).
308. За умов задачі N307 для випадку п = 2 доведіть, що
309. 	а) Нехай ej · е& = gjk (скалярний добуток) і detgjk ф 0, нехай
е? = g^e*, тоді (доведіть): е5 · = е5 · = g7fc і В = Бде
Б- довільний вектор.
б) Нехай для векторів бази справедливо е? · е) = |е^ | · |ej|cosa
(скалярний добуток), тобто, е не є одиничними векторами.
Покажіть, що можна ввести такі одиничні вектори kj, що для будь-якого
вектора маємо A = A^kj = A(f)jkJ, де Д^·, так звані фізичні
контра- і ко-варіантні компоненти вектора, що мають розмірність
самого вектора, а
П = §22 12
§12
§
11 = gn
§
g = detgQ/3 = gllg22 -g?2·
52

Покажіть, що Аф = А^ ^fgjj і в ортогональній криволінійній системі
координат kj = /еф Af^j = Аф.
З’ясуйте, чи є в загальному випадку “фізичні компоненти”
дійсно компонентами вектора, тобто чи перетворюються вони
відповідним чином при переході від однієї системи координат до іншої.
Відповідь обґрунтуйте математично.
310. В ортогональному базисі eb = (1,0,0,0), е\ = (0,1,0,0), Є2 =
(0,0,1,0), е3 = (0,0,0,1) маємо псевдоевклідову метрику ds2 =
{gμν}άχμάχν {<> 0), {μ, ту = 0,1,2,3,я0 = t,c= 1), де
1 	0 о о \
0-100
0 0-10
0 0 0 -1 /
Знайдіть базис е^, тензор {g^} і співвідношення між
компонентами goo І І g00, gа І І gn, де і = 1,2,3.
311. Покажіть, що в умовах задачі N310 по відношенню до чисто
просторових поворотів системи координат, які не зачіпають часу £,
три просторові компоненти 4-вектора Αμ складають звичайний 3-
вектор А: а часова компонента А0 по відношенню до цих
перетворень є скаляром, тобто, (Αμ) = (Л°, А) і при цьому для
коваріантних компонент маємо (Αμ) = (Л°,— А). Покажіть також, що для
вказаних компонент 3-вектора А= — Ак, к = 1, 2, 3.
312. Покажіть, що метричний тензор {g^} (див. задачу 310) є
інваріантним відносно перетворень Лоренца.
313. Показати, що при перетвореннях Лоренца властивості симетрії та
антисиметрії тензора зберігаються.
314. Показати, що W0 = Г4їИ, W = Г2а + W°v, де W» = (W°,W),
- 4-вектор прискорення, а і v - звичайні 3-вектори прискорення і
швидкості, відповідно (див. задачу 311). Тут Г = (1 — г»2)-1/2.
315. Записати закон перетворення 4-векторів
Α'° = Γ*(Α0-υ*Α1), Άι =Τ*{Αι -ν*Α°)
в звичайних одиницях, коли с ф 1.
316. Показати, що два ортогональні ізотропні 4-вектори паралельні,
тобто, що із а2 = Ь2 = 0 та (αμ5μ) = 0 випливає αμ = Α5μ, де Λ
- скаляр.
317. Показати, що для 4-швидкості і 4-прискорення виконується
співвідношення ημ\νμ = 0, тобто, вони ортогональні.
{§μ^} —
53

2. Динаміка спеціальної теорії відносності
318. Показати, що із припущення для потенціальної енергії взаємодії,
що вона залежить тільки від координат, U = С7(г), випливає
наявність нескінченої швидкості передачі взаємодії.
319. Показати, що рівняння руху для 3-векторів
приводиться до вигляду
Гта = F — v(Fv),
де Г = (1 — г»2)-1/2.
320. Показати, що найбільш загальний вираз для сили, який існує в
природі, згідно із СТВ, єР = Ф + іїхО, де и - швидкість частки,
a G- релятивістський вектор, тобто, G 0 при v <С с; вектор Ф
існує і в релятивістських, і в нерелятивістських випадках.
Вказівка: знайдіть зв’язок між векторами 3-сили F в системах відліку К
і К'.
321. Функція Лагранжа релятивістської частки з масою спокою т в
заданому полі тяжіння з потенціалом U = — α/r (г = \/ х\ + х\ + х%)
в декартових координатах має вигляд
С =
-т
1 - (х\ + х\ + ±1) +
а
χ/xf + ^2+^35
с = 1.
Знайти функцію Лагранжа в сферичній системі координат.
322. Функція Лагранжа вільної релятивістської частки з масою спокою
т має вигляд С = —тп^/\ — (і2 + х\ + х%). Скласти рівняння руху
частки і знайти їх розв’язок.
323. Покажіть, що для частки із задачі N322 функція Гамільтона % =
у/т2 + Pi + v\ + v\ і? ПРИ v — 0, % = т. Складіть канонічні
рівняння і знайдіть закон руху частки.
324. У сферичних координатах знайти функцію Гамільтона для частки
із задачі N321.
325. Функція Гамільтона релятивістської зарядженої частки (маса ш,
заряд е) у заданому зовнішньому електромагнітному полі (ЕМП)
має вигляд Т~і = \Jт? + (р — еА)2 + еф, де А - 3-векторний
потенціал, ф - скалярний потенціал ЕМП, р- 3-імпульс. Знайти функцію
Лагранжа частки.
326. Покажіть, що 4-сила Τμ Мінковського завжди ортогональна
прискоренню \¥μ частки.
54

327. 	Використовуючи співвідношення, отримані в задачі N231, для
релятивістської частки в зовнішньому (заданому) полі тяжіння, яка
описується функцією Гамільтона
Н = ^т2 + р\ + РІ + РІ
а
\/х\ + х\ + х\ ’
328.
329.
знайти її функцію Гамільтона в сферичній системі координат.
Знайти для випадків вільної частки і частки у зовнішньому
електромагнітному полі зв’язок між 3-функцією Лагранжа та 4-
функцією Лагранжа.
І3 2
S = J £ί(ιιμ,χμ,τ)άτ, 5S = 0,
330.
отримати
άΡμ _ дСА
dr 8χμ’
де νμ - коваріантний 4-імпульс, £4 - 4-скаляр функції Лагранжа.
Із рівняння Лагранжа
άΤμ дС4
dr 8χμ
отримати для 3-векторів імпульсу, швидкості і сили рівняння
dP__P de
dt ’ dt
Fv,
в тому числі і для заряду в зовнішньому електромагнітному полі.
Тут б - релятивістська енергія частки.
331. Із рівняння Мінковського отримати для 4-сили Τμ = (Г(vF),TF).
332. Із коваріантної форми рівняння Гамільтона-Якобі
g
μν
dS dS
8χμ dxv
= m
2
отримати
333. Із релятивістського рівняння Гамільтона-Якобі для вільної частки
отримати рівняння для нерелятивістського випадку.
334. Записати коваріантні рівняння Лагранжа для релятивістської
частки у зовнішньому заданому гравітаційному полі із потенціалом
ф{х1, т2, т3) (записати часові та просторові компоненти такого
рівняння).
55

335. 4-функція Лагранжа зарядженої частки (маса ш, заряд е) у
заданому зовнішньому електромагнітному полі (ЕМП) має вигляд
£4 = —т ημΐίμ — βΑμημ,
де ημ - 4- швидкість, Αμ = (φ,Α)- 4-потенціал ЕМП. Знайдіть
компоненти 4-імпульса Ρμ, а саме Vk (к = 1, 2, 3).
336. Для частки із задачі N335, використовуючи інваріант νμνμ = ш2,
складіть рівняння Гамільтона-Якобі у 3-вимірному вигляді і у
коваріантній формі.
337. 4-хвильовий вектор електромагнітної хвилі має вигляд Α5μ = (ω, /с),
або в звичайних одиницях Α5μ = (ω/c, к), де к - 3-хвильовий вектор.
Використовуючи закон перетворення 4-векторів при переході від
однієї системи відліку до іншої, знайдіть закон перетворення
частоти ω хвилі (ефект Допплера) і хвильового вектора к.
56

Відповіді
Відповіді наведені не до всіх задач.
Sapere aude! - май сміливість
користуватись власним розумом.
Іммануїл Кант
і) V = а/ р2 + р2ф2 + і2, ар = р — рф2,
αψ =
1 d_
р dt
(Λ).
az = z.
ii) v = \J f2 + r202 + г2ф2 sin2 #, ar = r — ν(θ2 + ф2 sin2 0),
a<9 =
r dt
(ν2θ\ — гф2 sin 0 COS 0, GU = —- -f- fr20 sin2
V / r sin Θ dt V /
iii) V = ^Jb2p(f + i2), au = —
VP
— (up) — f sinh u cosh u
Од/ —
VP
d_
dt
(Op) — f sin I/COS I/
a2 = 2:,
ДЄ p ΞΞ sinh^ U + sin^ I/, / Ξ UZ + Z> ·
6. ap = cj2p, αψ = 0.
7. r = ro exp [(0 — 0o) cot O'].
9. a = -(4a2/c‘2b2)r.
10. ap = -4(σ2/ρ)ρ~2, αφ = 0.
11. v = Ω x R + Ω x г/ + 17/, де г/ - радіус вектор частки відносно осі
обертання ( в площині кола), 17/ = г/.
57

13. Відповідна крива називається трактрисою, або “собачою кривою”:
х = vot — ^tanh ( ^ J , у =
cosh(vot/i) ’
або
х = Ппі+^£2 y2-^/P^f.
У
14. v = аиое^/к(кер + βψ),
■ ωο , k , ,ч ч к2 — 1
Ф=ГГ,' ^ = ^31^(1 + 7). Ί = к
15.
1G.
1 =
Р Ро Ь
At = — In —.
σ0 Хі
17. 	В точці переходу х = а повинні виконуватися умови /(а) = 0,
//(а) = 0, ///(а) = 0.
is. t t
x(t) = J ~~dr) dt + + °2·
19.
rx / 2 fx \_1/2
20. Закон руху x(i) знаходиться із співвідношення
22.
X ^
f vdv
t
ί dv
h Сі = І
F(vy
l· C2 =
1 F(v)’
т J
m j
2 = /ι+ά(
-g± >
/g2 + ν0ω2] >
Be
ω = —
m
24.
vo = у/g і? sinh(47r£;n) ,
де п - число обертів.
25.
У=^1п(1
β2
βχ
mvo
при β —t 0, у —t Η — gx2/(2г>о).
+
mgx
+ Я,
58

2G.
v2 = vle~^H~h) + 2gR2elh
L
H л-
Є 72бк
ft (д+^’
27
тут 7 ξ 2β/πι.
Для випадку г>о > и
vo - c(tan(gi/c)) с υ0-ίχ
υ(ί) = и + с -— , для t <t\ = - arctan ,
г>о tan (gt c) + c g c
υ(ί) = u- ctanh^—для t>h\ c=\H^·
c V k
28.
h>
c - швидкість світла.
g+ л/g2 + VqU2
eH
ω =
me
29. x(t) = Ai cos(u;ii + од) + y(f) = A2 cos(u^i + од),
ζ(ί) = —Ai sin(iJif + Од) - Cf f —") +20,
ωι \ω1/
ω = eB/(mc), ω\ = eUo/(ma2), ω\ = ω2 — ω\> Ο, А, С, а - сталі.
30. Аг яв —2krot/m=-5,37 км, AT яв —3kTot/m=-6,4 с.
31. a) m(t) = m(0) ехр(—gt/u), б) m(t) = m(0) ехр[— (a + g)t/u], в)
rt ті
m(t) = m( 0)
1 +
m
2P
f dt(z + g)2
20 J
33.
34.
33.
3G.
37.
38.
τη = шо/e, Ργηαχ — mu-i e _ основа натуральних логарифмів.
Ш = 777-0 exp (φο/τχ- 1), Pmaa: = 77l0U exp (v0/u - 1).
m = шо/е2, e - основа натуральних логарифмів.
/7 = —F · r + const.
U = —eEo · rcosut + const.
v = voJl + -F(Ui-U2), cos2a<F-(U2-U1).
mvn
mvz
59

39.
a) x(t) = a In
^sinh-1 (T-i)-J —
t/o α V m
rp _ I m , \/E~+Uo + \/E
“12£
6) z(i) = -2aln(l-|^i) .
40.
r =
2£q (2£+ кІП Eq + Uo) 5
«0
π
771
k у 22¾
41. sin (#/2^) = t&nh.(v()t/2£).
42. a) T= (a/Uo) \fmE]2.
45. (mii2/2) + C/(|r|) = E, M = M0 = mfo x г?о, Mo · r = 0.
50. r2 = c2 — (cr/k)V 1 — 4A:2 cos(</> — фт),
fc =
M0
c\/2mUo
г(Фт) —
T = π
m2c4[/o
M03
5G. ar = —a2/(pr2), αψ = 0.
57. r = г0 + Ь(ф- фо), аф = 0,
ar
γ-2>
2 1
7*2 62
GO.
Vi = \j&R{1+ ’ υπ =
63. a = — σ2[ων +(1- ω2)ρ\/(ν3ρ).
67. r = p(l + ecos(0cj + 7))_1, e,p,7 = const, cj2 = 1 + 2βτη/Μ$, Mo
mfo x +ο·
68. M(t) = Moexp[—/3(t — to)/m\.
69. Сила притягання
F = -
ma2(l+u2) f
• -, Де
r
σ = г2ф.
60

70.
_. . та2 /,., 1 \ о ;
F(r) = І ^(Г) - “ ) > Де СГ = гф.
71. d2J/dt2 = 2(Eq + Т), Т - кінетична енергія системи.
73.
хМ) = αμ (+ Φ^)\ ф _ λ . cosh(fc-i + фЛ
V mi m2 /
Тут μ - зведена маса, Щ = a/rrij, j = 1,2. Аналогічно для yc{t),
zc{t).
73. ДЕтах = (μ/πι)Τ, Т - кінетична енергія частки до зіткнення.
78. р = (α/μνΖο) cot(*/2).
79. р = а · cot(x/2).
80. rmin = r0 = (η - 2)ιΙη(2Ε/α)~1/η, при R < r0, σ = προ, де
прицільний параметр Рф = n(n — 2)(α/2Ε)2Ιη\ при R > tq, σ =
irR2[l + a/{ERn)\.
83. a) σ = 2?ra/(m»^); б) ос ν^^άΩ.
83. α = -5/6, 6= 1/2, с = 1/3.
91. L°, L°, L-1, L1.
93. S' = /За-2, (3 = \[β~[α.
94. При r —»· аг, ί —>■ al~k/2t, і якщо n = (/:/2) — 1, то L —>■ akL.
93. р ■ Е — 2Et = const.
9G. p-r1 — 2Et = const, де p = mv + eA, якщо A(ar) = a~1A(r).
97. (T) = Α2/(4πιω2).
100. (p) = (2/3)n£.
102. (T) =-(17)/2 = 0,3Gm2/R,
U = -(1/2)G(N - 1 )NMl = -4 · 1051 Дж.
104.
2(T) + (У2 —Ma) · H = k(U).
a ™a
Тут Ma - момент імпульсу частки ma.
107. x = Rcosut, у = i?sincj£, 2: = vozt, N = —πιω2 R(cosutex +smut ey)^
іoR = voy
61

108. a) N = 0, 2 = 2І?/3; 6) N = 0, 2 = і?;
iV == (-у2 + gr) f = (2-Е + 3mgr).
109. h знаходиться з рівняння 4/ι3 + 3a2h — 2a2yo = 0.
111. Якщо / = 0 рівняння поверхні еліпсоїда, то
Л =
т
d
,«yV/- 2ω2
(V/)2 V dt
E =
• 9 9 9
mr πιω r
+
' = 2ω2
112.
ImE2
Тут Mg = M · g/g.
2 COS0
sin3 Θ
I sine
124. Циклоїда.
125. Гвинтова лінія: x = coscj£, у = sincji, z = t, S = πχ/i?2 + 1, £ -
параметр.
129.
(+ =
m
E + ΛΓ^Ω
Mq2 a
2mr2 2
130. φ + ί x(g + S) sine/) = 0.
134.
m
С = ^(т2 + т2ф2)
1 +
n =
p2r2ci
2m
mrc-
- 2a2)'
+
РІ '
m2r2
+
9 9 9
pfr c
[mrc
- 2а2У
137. I = M — (eg/c)f/r = const., кінетична енергія =const.
143. £ = (m/2)Hlq2k -U(x(qi,q2,qz),y(qi,q2,qz),z(qi,q2,qz)), k = 1,2,3.
144.
£ = + q2^q^q2 + - u (41 2 42 ’ \/^2^ ·
145. qi — ait + /3/,г = 1, n, a/, /3/ = const.
146. Ef = E — ΩΡφ, P'r = mr' = Pr, Ρφ = тгР(ф' + Ω) = P^.
62

147.
±(дт\_дт_ .
dt\dqi) dqi u
151.
r — \Ρβί/πι
L~ 2Є
mxz + βχχ — [k — -— I XX
2m
153. a) Ρφ/2π + M3 = const, h- крок гвинтової лінії, б) Р\Х2 ~ Ρί^\ —
const.
ιοί. v(t) = {ε/вг) (і - е-(/т) + уоє~1/т\ i{t) = {£/Κ){ε - у0в£)е~г/т·
т = MR/(B£)2.
162. v(x) = Vo — βχ/{α + x), де β = [μοΙ£/2π)2 / {amR), μο~ магнітна
стала.
163. А = VQo + <?оД2> tana = -Qo/i^qo).
166. dy/dS = oj2S/g, ω = 2π/Τ.
167. Циклоїда:
X =
168. a) x
(Fo/mcj2)(l — coscut); 6) x
F0
x =
m( ω2 + a2)
(e_
at
= — {a/muft)(u)t — sineut)] в)
a ·
— cosuot H— smut),
ω
169. A = (2Fo/mtou3) sm(uto/2).
170. ω = y/F(r + t)/{mrt).
172. = —π + 4arctanei.
175. cj2 = (k/m)( 1 — ίο/h), h > ίο] = (fc/m)(l — /i2/^q), h < ίο.
180. k > 2mu2.
183.
2 = + + , If+ ω\ + ω2Η
1>2 2 v V 2
де ω? = g/t, = 1/(LC), ωΗ = Η£/{2ΧΧί).
185. ίφ + gsm(f) + a cos φ — ΑΩ2 sin Qt cos φ = 0.
2
— / ,2, ,2
CJiCJ2,
63

186.
Ues = -mge
cos φ — ( - sin φ
, b =
soQ
2£cjq
Φι = ο, Φ2 = 7г; cos03,4 = -2/62;
2 2
Wi = 4)
1 +
2 2
, ω2 = Ч)
b2
- 1
191.
/11 =
та
I22 =
та
64 \ та
1 ~ 9л+ ’ /зз = ~
2 ' 32
9π2
194.
197.
198.
199.
200.
201.
202.
М = т(15і?2 + 4h2)Co/12.
о2 =
mg£
mi2 + Д cos а + /2 cos ,6 + /3 cos 7'
+ ¢(787+8^7 /q//77., Ma + 6q,LOβΜΊ €αβ^Χβΐ^,у.
S = g/2.
z = 2:0 + io — gi^2, cos 9(t) = cos^o cos(cjo sino ί), φ(ί)
arctan[tan(u;o sino £) / sin #0] ·
3g 4a2 - /2
1 “ "a 12a2 + /2 ’
2 o6 ™ — <, 2 6g / — 2a
— , і < 2a; ω1 = -
an =
2a ’
> 2a.
C = 1^£- + ^-(92 + φ2 sin2 9) + ^(</cos <9 + φ)2 - mgz,
h
2 ' 2 4' ' 1 2
тут Vc - швидкість центра мас, φ, 9, φ - кути Ейлера.
242.
245.
Η = —
2m
p2e-0t/m _ βρχ + Jit/m ^km _ 0pj χ2
5Ζ*)' + υ■
_ . 1 v—> 9 Ad + 7ΎΙΤΙ
«=2йЕл’ +
2M2
247. Ή = p2/(2m) — Ω · (r x p) + £7.
64

248.
249.
дС „ дС „
—т = Рф = Рф0 = const., —г = Рф = Рф0 = const.,
дф οψ
Ή = Ρψφ + ΡθΘ + Ρψψ — С = Hq.
Рфоtan ωί
Ф — E>2 ^ 0°’
πιΚΑω
Рф = Рфо, фазова траєкторія ф(Рф) - пряма лінія.
252.
а) Ή! = -\J-2m{mgt' + р');
б) Ή! = —m(kt'2 + 2р'), к - коефіцієнт пружності;
в) Ή7 = —yj—m (/ceW/m£/2 + 2j/e№/ш).
255.
257.
260.
261.
267.
268.
. , _ч muq / 2Р 0 q
ψ2 (¢, Р) = —— у q + Р arcsm ■
2 V πιω
VzpJ
πιω
Qi{t) = Рг0 cos(cOit + Qio), i = 1,3, uf = —.
mcjj m
= -eyfcPfc
= [M2,M3] = 0.
5 = тщг- mvQt/2, f = vot + fo, p = po = тщ, де r = (x,y,z),
ro = (xo,yo,zo)·
a) Xi = βι + ait/m, і = 1,2,3, r = (жі,ж2,жз), «і, A=const.;
Οίφ
s 2 2
б) cos (φ-βφ) =
m
2mar
ryj2mar
Z = — - |(Дг + ί)2, ατ,βτ,αφ,βφ,αζ,βζ = const,
mg 2
272.
273.
t-t0 = (dS/dE), рф = (dS/дф) = y/2Izz(E + pa cos ф),
S = I ^2hjE + pa cos φ)άφ.
f=fo+ Pot/m + eEt2 / (2m).
65

275.
S = ± J \J2mT~Lo 2m2gr cos #o + '
тсо2г2 sin θοdr,
dS
Pr = —, t + β = , β = const,
or
dS
dW
276. Рівняння траєкторії
1
/¾ = — arcsin
^2a2/{mul)
arcsin
P^Jk
moot
тут a\ + a2 = E, /¾ = dSo/dE, β2 = dSo/da2.
277.
5 = α0 + χ/^ / —J2(U + E)ri-—;
J r V m
Рф = ск, Pr = -ТГ- = const
as
5r
1
P = -m(?Q + г$ф ) + Щ a = тг^фо = const, t — to =
as
dP‘
278.
S = -Et
+ афф + J 2m(E - f4(r)) - dr
+ f J2m (a, - ft/3(0)) - K + - bh(9) άθ
J V sin Θ
279.
(S — —Pi + Οίχφ + f \fOt2 ;—o'—
J V sir 0
/
2ш/іі 2ш/і2 + »2
+ / a / 2mE +
(ІГ,
умова на початкову швидкість дає дф/dt = 0, ця умова разом із
рівністю <95/<9αι = /Зі, має наслідком оц = 0. За цих умов маємо
рівняння траєкторії r = p/[l + ecos(cj$ — 7)], дер = 1/Ь, е = у^І + с/Ь2,
7 = 2ω/32λ/θ2,
Ь =
τημΐ
2 mu2 2т Е
1 -|- , с = — .
α2 а2 + 2шц2
282.
5г(г) = J dr\j2mF(r)
+ 2т,Е ■
от
’
a = const.
66

283. v = (dE/dJ) = (1/2-7Γ)\Jk/m.
289.
290.
7, 	= / \j—2μ\Ε\ + dr> h = W = M.
П =
2π2α2πι
(Ιν + Ιθ + Ιφ)*Λ
292. ER2 = const, якщо M - момент імпульсу, то
Μ
tana =
R\pErnE
293. Εί2 = const.
294. Адіабатичний інваріант I = І((Е)) = I(Eo)e~at/m, отже (і?) =
(E(t)).
295. Ε2ί = const.
298. v(y) sma(y) = const, де a - кут між віссю Oy і дотичною до
траєкторії частки; знайдена формула аналогічна закону Снелла для
плоскошарових середовищ: п(у) sina(y) = const.
299. U = const — п(х,у, z)/2.
321.
£ = —m\J 1 — (r2 + r2#2 + г2ф2 sin2 Θ) + —.
322. a;* = ait + βι, і = 1, 2, 3, a*, /¾ = const.
324.
Ή = \lm2 + p2 + Ц + βΦ 2 ■
323. 	£ = —m\/l — n2 + e(v · A) — еф.
327.
Ή = \ m2 +РЇ + Щ +
r* r2 sin2 Θ
333. Τμ = (£ + еф,р + eA), тут Є, р- енергія і 3-імпульс частки.
336.
(ж + Є^) -(VS-eA)2 = m2,
Уμν
dS
дХ»
+ еА,
dS
дХи
+ eAv І = т2.
67

Додатки
1 Криволінійні системи координат
А Загальні співвідношення для довільних координатних
систем
Для спрощення будемо розглядати тривимірний простір (п= 3, хоча це і
не обов’язково). Введемо в декартових координатах (х\ Х2 хз) однозначні
і неперервно диференційовні функції
Ча = ЗаОь Я2, яз), а = 1, 3 , (1)
ЯК НОВІ криволінійні координати (¢1 Q2 #3), причому
det(so #0·
Тоді за теоремою про неявні функції існує обернене до (1) відображення
Хі = Xi(qi, 92, 9з), і = 1, 3 . (2)
Взагалі кажучи, qa можуть бути будь-якими фізичними величинами,
що параметризують так звані „координатні” лінії, вздовж яких
змінюється параметр qa (див. рис. 1 для п= 2).
Рис. 1: Криволінійні координати
68

Візьмемо ЛІНІЮ ¢1, яка є кривою перетину поверхонь ¢2 = const і
¢3 = const, а також відповідно означені лінії ¢2 та ¢3. Тоді похідні
радіусвектора (2) утворюють локальні вектори бази (або просто: локальну
базу), тобто трійку векторів еа, дотичних до вказаних ліній:
Єї =
(3)
dr dr д т
oqi dq2 dq3
Оскільки матриці Якобі (dxi/dqa) і (dqa/dxi) є взаємнозворотними,
то база еа криволінійних координат і декартова база /¾ пов’язані
співвідношеннями:
д<1а~ ,л,
еа · (4)
дхі ї
С(х о і
9qa
kj~ дх^а
! Тут і надалі будемо використовувати умову сумування по
індексах, що повторюються.
На противагу до декартової бази, напрямок (і величина) векторів
бази еа залежать від вибору точки (¢1, ¢2, ¢3), що розглядається, тому
така база і називається локальною.
Введемо тепер симетричну матрицю gяка визначає квадрат
відстані між двома нескінченно близькими точками простору (інакше кажучи,
„метрику простору”):
ds2 = dr ■ dr = ——
dqi
dr
—dqidqk = e* · ekdqidqk = glkdqldqk (5)
dqk
(крапкою позначено скалярний добуток векторів). Тобто, gik = сі ' Ск]
ясно, що gik = gki- Матриця коефіцієнтів gik називається
фундаментальною матрицею або метричним тензором (точніше — елементи цієї
матриці є компонентами геометричного об’єкта — метричного тензора другого
рангу g2).
При заміні одних криволінійних координат на інші q\ —> q'x їх
диференціали перетворюються за правилом
-¾=§|<%· («і
Будь-який об’єкт Бг, що перетворюється за законом (6)
В*
(7)
називається контраваріантним вектором. Інший тип векторів
утворюється величинами (d(p/dqi), де (p(q) — скалярна функція точки простору.
Згідно правилам диференціювання маємо
9φ _ 8φ_ dqk
dq[ dqk cjq''
69

Будь-який об’єкт, що перетворюється за законом
w _
Щ
(8)
називається коваріантним вектором.
Метричний тензор gік є коваріантним тензором. Оскільки detg^ ф 0,
то існує контраваріантний тензор glk = (g~1)ik, зворотний до gтобто
gikgkj = 5\, (9)
Де $ — елементи одиничної матриці (одиничного тензора) — „дельта
Кронекера”. Неважко показати, що елементи контраваріантного тензора
мають вигляд
ік = 1 dg
g dgik ’
де g = detg^. Згідно (6) диференціали координат є контраваріантними
векторами. Тому, строго кажучи, ми повинні на всіх координатах
ставити індекс вгорі.
Будь-який вектор в базі (3) має вигляд
А = АкЄк, (10)
де Ак є контраваріантними компонентами вектора, в чому легко
впевнитися, використовуючи співвідношення (4) і (7). Тим же способом із (4) і
(8) для коваріантних компонент вектора отримуємо
Ак = А - ек. (11)
Тоді з (9) — (11) маємо
Aj = g jiA1 (операція „опускання індекса”),
Ак = g кгАі (операція „підняття індекса”). (12)
Добуток коваріантної і контраваріантної компонент вектора АкАк =
А2 визначає скалярну величину — квадрат довжини вектора.
Використовуючи введений апарат, нескладно записати функцію
Лагранжа і рівняння Лагранжа в будь-якій криволінійній системі
координат. Наприклад, для частки маси т в потенціальному полі U = U(r):
L _ mv?_ _u(r) -, -*>(*), (13)
де <p(q) = U(xj(qi))\
d_ id.L\ _ dL
dt \dv J dr
m
j _ chp_
2 dqa dqa
70

Розглянемо трійку векторів е>, отриману з бази (3) таким чином:
&=fgjaSa·
(14)
Із (14) маємо:
є» · е* = δί е> · е* = s>k. (15)
Вочевидь:
141 = %/gкк- Отже, вектор е1, наприклад,
є ортогональним до векторів Є2 і ез, а його скалярний добуток з
вектором Єї дорівнює одиниці. Введену систему векторів е1, е*2, е6
називають базою, що взаємна (або спряжена, або дуальна) з базою еі, Є2, ез
(математичною мовою: маємо локальну базу ковекторів в спряженому
лінійному просторі).
Для будь-якого вектора із (12) і (14) маємо:
A = Alei = Ajgjiei = Αό&.
(16)
Таким чином, будь-який вектор А можна розкласти як за векторами
бази еа (тоді його компоненти будуть контраваріантними), так і за
векторами бази ек (з коваріантними компонентами):
Л=Аієі = Аієі. (17)
При цьому коваріантні і контраваріантні компоненти вектора А
визначаються через скалярний добуток вектора з векторами бази ек і е к
відповідно:
Ак = А-ек, Ак = А-ек. (18)
Наочна різниця між контраваріантними і коваріантними
компонентами вектора легко вбачається в найпростішому випадку лінійної
косокутної системи координат (рис. 2): контраваріантні компоненти Аг —
паралельні проекції, коваріантні компоненти А{ — ортогональні проекції
(точніше, Аі/\єі\).
42
Рис. 2: Контраваріантні і коваріантні компоненти вектора
Підкреслимо суттєву різницю між базою ек і базою ек. Якщо вектори
ек пов’язані безпосередньо з системою координат (вони є дотичними до
71

координатних ліній), то вектори ек вводяться формально за формулою
(14) і, взагалі кажучи, не є дотичними векторами ні до яких
координатних ліній (так звана „неголономна база”).
В загальному випадку фізичні розмірності контра- і коваріантних
компонент одного і того ж вектора є різними - вони визначаються
розмірностями базових векторів і співвідношенням
ek · е к = |е^||е к\ cos а = 1.
При визначенні операцій вектори розглядаються геометрично як
напрямлені відрізки з довжиною, пропорційною величині вектора, і
фізична їх розмірність не береться до уваги (за винятком основного правила:
додаються величини однакової розмірності). Всі обчислення проводять
зі звичайними ко- і контра- компонентами і тільки наприкінці
переходять до відповідних розмірностей. У зв’язку з цим вводять так звані
„фізичні” компоненти векторів. Для довільного вектора маємо
В = Ваеа = Ва\еа\ϋ В$ка,
\еа І Ψ
де одиничний безрозмірний вектор
а фізичні контраваріантні компоненти вектора є
В% = Ва\еа\ = £αν& (20)
Аналогічним чином вводяться „фізичні” коваріантні компоненти вектора
Ваф = ва |е“| = ВаУ/.ка=щ = -|=. (21)
Підкреслимо, що „фізичні” компоненти векторів в загальному випадку
не є компонентами „справжнього” вектора, оскільки вони не
перетворюються за законом (7) або (8).
Розглянемо далі ортогональні криволінійні системи координат.
Якщо в кожній точці простору лінії перетину кожної пари поверхонь
qi = const, ¢2 = const, = const взаємно перпендикулярні, то коорди¬
нати називають ортогональними криволінійними координатами. В цьому
випадку вектори локальної бази (3) є ортогональними, і для метричного
тензора gap = еа - ер маємо співвідношення
ga/З = 0 при а ф β.
Отже, незалежних компонент тензора gар, що не дорівнюють нулю,
є тільки три. Як правило, їх позначають так:
\/Έββ = Ηβ , )6 = 173, (22)
72

де величини Ηβ називають параметрами Ламе.
Для компонент контраваріантного фундаментального тензора
знаходимо
£ДО = —
т
Визначник матриці gik буде
1
ч
(23)
g = detgifc = (#!#2#3)2. (24)
При перетвореннях (1) змінюється залежність елемента об’єму dV =
dx\dx2dxз від диференціалів координат, і виникає якобіан. В
ортогональній системі координат він визначається коефіцієнтами Ламе і пов’язаний
з визначником метричного тензора співвідношенням
^='=<*(ІІ)=яія>я*·
тому елемент об’єму набуває вигляду
dV = ^/gdqidq2dqz. (25)
В ортогональній системі координат доцільно користуватися
нормованою базою (одиничних безрозмірних) векторів (19). Зауважимо, що у
цьому випадку зникає різниця між ко- і контраваріантними „фізичними”
компонентами як бази, так і векторів:
%β = Ρ, Вкф = вкф.
Для вектора переміщення dr маємо
dr = eadqa = Hakadqa = Hidqiki + H2dq2k2 + Hzdqzkz, (26)
де у відповідності з (22)
Нк
\/gкк = л/^к ■ Є>с
дг дг
dqk dqk
(, (
\dqk) V dqk
2
+
дхЛ2
dqk) ’
(27)
ТОДІ як
ds2 = dr ■ dr = gn{dqi)2 + g22(dq2)2 + gzz(dqz)2 =
= (Яц%)2 + (H2dq2)2 + (Hzdqz)2. (28)
73

Зауважимо, що формула (26) необхідна для обчислення узагальнених
сил
д т -> -> ->
Qa = F = Нака · F = HaFa (29)
dqa
(! Якщо ліворуч у компоненти фізичної величини залишається індекс,
то це означає, що праворуч немає суми по цьому індексу).
Розглянемо далі найбільш вживані ортогональні криволінійні
системи координат.
В Сферична ортогональна система координат (г, θ, φ)
Зв’язок між декартовими і сферичними координатами визначається
формулами:
х\ = r sin Θ cos φ,
Х2 — r sin Θ sin φ,
Xs = r COS0,
причому 0 < r < oo, 0 < θ < π, 0 < φ < 2π (див. рис. 3). Тут
qi = r, ¢/2 = θ, ¢3 = локальна нормована база: k\ = er, fc2 ξ
e#, /сз ξ (права трійка векторів: ег, є#, е<Д.
Рис. 3: Сферичні координати
Координатні лінії утворюються попарним перетином відповідних
координатних поверхонь. Для сферичної системи координат це:
• поверхні г = \/х\ + х\ + х\ = const — сфери з центром у початку
координат — т. О;  •• поверхні Θ = arccos(T3/г) = const — прямі кругові конуси з
вершиною в т. О;
74

• поверхні р = arctan^/^i) = const — напівплощини,
перпендикулярні до площини (а?і, #2).
У кожній точці ці поверхні є ортогональними (вісь Х3 лежить в площині
р = const).
За формулами (26) — (28) маємо:
сIs2 = (dr)2 + (νάθ)2 + (r smOdp)2; (30)
Hi = Hr = x/gn = 1, H2 = He = \/g22 = Λ
я3 = Ηφ = x/g^ = rsin#;
dr = drer + rdOeg + r sin θάρβφ. (31)
Матриця коефіцієнтів метричного тензора:
(1 о о \
gik = о г2 0 , det gifc = g = r4 sin2 Θ.
\ 0 Or2 sin2 # J
Елемент об’єму у сферичній системі координат:
dV = y/gdrd9dp.
І оскільки ga = Єі · Єі, дістаємо компоненти векторів локальної
(ненормованої!) бази в проекціях на декартові осі:
Єї = (1, 0, 0), е2 = (0, г, 0), е3 = (0, 0, rsin#). (32)
Компоненти векторів нормованої бази в проекціях на декартові осі
мають вигляд
βγ
(sin# cos(/9, sin#sinp, cos#),
Ce =
(cos# COS (/9, COS# sin (/9, —sin#),
Οφ —
(—sin (/9, COS (/9, 0),
(33)
спосіб їх обчислення покажемо на прикладі βφ:
г = _ е3 _ е3 _ 1 дг
3 6ψ \/g33 r sin Θ r sin # dp
_ 1 дх ду dz\ _
r sin # у* dp Єу dp Cz dp )
= —- (ex(—r sin # sin p) + ev (r sin # cos p) + 0).
rsin# y
Тобто
75

e(φ = — sin φβχ + cos ipey. (34)
Тут тимчасово використані позначення декартової системи: орти
ех, Єу, ez І Х\ = Я, Х2 = У, Х3 = Z.
Аналогічним чином дістаємо інші компоненти (33). Зауважимо, що
за законом (ЗЗ)знаходять і компоненти довільного вектора, наприклад,
Aq = Ах cos Θ cos φ + Ау cos# sin p + Az(— sin#),
так само і Ar, Аф.
Нескінченно малий елемент поверхні r = const у сферичній
системі координат визначається як площа прямокутника зі сторонами τάθ і
rsm6d(p, тобто
da = r2 sin θάθάφ = #2 #3^92^93· (35)
С Циліндрична ортогональна система координат (р, <р, z)
Зв’язок з декартовими координатами такий (див. рис. 4):
х = р cosp, у = р sinp, 2: = 2:,
0 < р < оо, 0 < <р < 2π, —оо < 2: < оо.
Локальна нормована база (права трійка векторів: ер, е<р, ez): к\ =
z
Рис. 4: Циліндричні координати
Єр, &2 = е^, ^3 ΞΞ е2 (орт ОСІ 2:).
Координатні лінії є перетином поверхонь:
76

• ρ = yjx2 + у2 = const — нескінченно довгих циліндрів,
коаксіальних ДО ОСІ Z]
• φ = arctan(у/х) = const - напівплощин, що проходять через вісь Z]
• z = const — площин, паралельних площині (т, у).
Так само, як і для сферичної системи координат, знаходимо:
ds2 = (dp)2 + (ράφ)2 + (dz)2; (36)
Яі = Яр = x/gH = 1, H2 = Ηφ = = p, Яз = Я2 = v/g33 = 1;
<ir = dpep + ράφβφ + (37)
Елемент об’єму = ΗιΗ2Η^άράφάζ = ράράφάζ, елемент циліндричної
поверхні 6?σ = Η2Η^άφάζ = ράφάζ. Для векторів бази дістаємо
Єр = (cos (/9, sin (/9, 0),
е<р = (—sin (/9, COS (/9, 0),
βζ = (0, ο, 1), (38)
в той же час для векторів локальної ненормованої бази маємо
Єї = (1, о, 0), е2 = (0, р, 0), ез = (0, 0, 1).
D Еліптичні циліндричні координати (и, и, ζ)
Координатні поверхні утворюються (див. рис. 5):
• співфокусними еліптичними циліндрами: и = const, 0 < и < сю;
• гіперболічними циліндрами: v = const, 0 < і/ < 2π;
• площинами, паралельними площині (т, у): z = const, —сю < 2 <
сю.
Рис. 5: Еліптичні циліндричні координати (переріз площиною 2 = const)
77

Зв’язок з декартовими координатами:
х = b cosh и cos і/, у = b sinh и sin і/, 2 = 2.
Тут b — це координата фокуса еліпса на осі х (нагадаємо: всі
еліптичні циліндри софокусні).
Коефіцієнти Ламе
Hi = Ни = by/sinh2 и + sin2 і/, Н2 = Hv = by/sinh2 и + sin2 1/,
H3 = HZ = 1.
·
Далі звернемо увагу на те, що у криволінійних координатах при
обчисленні швидкості і прискорень, на відміну від декартової бази,
виникають вирази dea/dt ф 0; відповідні співвідношення легко знайти із
формул для компонент векторів бази, типу (33) або (38).
Наприклад, для циліндричної бази маємо dep = — sin φάφβχ +
cos φάφ£ν і, порівнюючи цей результат з виразом для е^, дістаємо dep =
βφάφ, тобто
dep ^ άφ
dt φ dt
і τ. д.
Із формули для dr у сферичній системі маємо
dr - · - λ - . л . ^
—- = V = rer + TuCq + r Sin Όψβφ
dt
і, знаходячи далі dv = (dr)er + fder + ..., за вказаним методом дістаємо
для прискорення
а = ^ = (г — гв2 — гф2 sin2 в)ег + (2гθ + гв — гф2 sin Θ cos в)ео
+ (2гф$тв + 2гвфсо$в + гф sin θ)βφ.
Аналогічним чином в циліндричній базі маємо:
а = — = {р- рф2)ер + (2рф + ρφ)βφ + zez.
Залежність напрямків базових векторів криволінійних координат від
точки у просторі необхідно враховувати як при обчисленні похідних
за напрямком, так і при застосуванні оператора набла V ξ -β* =
(^, Наприклад, для визначення grad^ = у криволіній¬
них координатах необхідно виходити з означення: Уф · dr = άφ. Тоді,
враховуючи (26), дістаємо
(^Ф)а
1 дф
На dqa ’
78

Так, в циліндричних і сферичних координатах маємо відповідно
дф
1 дф
V'p-ipd^ + g'’~pd^+il~·
дф
dz
-> _ дф _ 1 дф 1 дф
^ф = ег——l· β,-— + βφ—:—.
or г ов r sin θ οφ
І наостанок зауважимо, що у криволінійній ортогональній системі
координат скалярний і векторний добутки векторів, записаних через свої
„фізичні” компоненти, обчислюють за тими ж правилами, що і у
декартовій системі координат.
Наприклад, нехай для сферичної системи координат
А — Агег + Αβββ + Αφβφ, В — Brer + Ββββ + Βφβφ,
тоді Α'Β = ArBr + ΑβΒβ + ΑφΒφ, а А χ В = ΑνΒβ — ΑβΒν і τ. д. Підкре-
ψ
слимо, що тут використовуються саме „фізичні” компоненти векторів.
2 	Деякі формули векторного та тензорного
аналізу
! Формули наводяться в ортогональних системах
координат (в тому числі і в криволінійних).
! Використовується правило сумування по повторних
індексах.
! Всі індекси пробігають значення 1, 2, 3.
! єі — декартова база; зд, зд, — декартові координати.
1. Диференціальний оператор набла:
V =
2. Оператор Лапласа (лапласіан):
Δ = V2
_д__д_
дхі дхі'
3. 	Градієнт скалярної функції φ(τ) = ψ(χ\, Х2, жз):
grad φ = V<p =
79

4. 	Похідні від скалярної, векторної або тензорної функції (...) за
напрямком деякого вектора а дорівнюють
(£a-V)(... ) =
Де
5. Дивергенція вектора А:
- - - дА д
div A = V · A = ViAi = де ξξ -—;
στ* шд
div (φΑ) = V · (<ρΑ) = ipV · Л + Vip - А, де = φ(τ).
6. Важлива властивість мішаного добутку векторів А, В, С:
А-(ВхС) = (АхВ)-С.
7. 	Векторний добуток:
А х В = ЄіЄікіАкВі.
Тут Єікі — компоненти тензора Леві-Чівіти („символ” Леві-Чівіти)
з властивостями:
£■123 = £-312 = £231 = +1, £321 = £132 = £213 = —1, £ijk = 0 ПРИ
співпадінні будь - яких двох індексів із трьох, Eijk^ijk = 6. Часто
використовується зв’язок компонент тензора Леві-Чівіти і тензора
Кронекера („дельта Кронекера”):
£α/?7£μΐ'7 = $αμ$βν ~ $αν$βμι
£(χβη£\βη — 25q:A·
8. 	Ротор вектора
А:
rot A = v х А =
Єї Є2 ез
Vi V2 V3
Αχ А2 As
— ^i^ijkS' jAk\
rot (φΑ) = V x (φΑ) = φ\7 x Α + \7φ хі, де φ — φ(ν).
80

9. 	Нагадаємо, що дивергенція тензора понижує ранг тензора на
одиницю, а градієнт, навпаки, підвищує на одиницю. Наприклад, для
тензора другого рангу Т2
div Т2 = V · Т2 = ej
ОХі
— вектор,
grad ή=(S)"(Cm)=6з·
тензор третього рангу, або для вектора швидкості
grad v = (ViVj) = = D2
— тензор другого рангу.
10. 	При використанні тензорних величин часто вживають символічні
позначення. Наприклад, у виразі
А · Т2 · В = AiTijBj = TijAiBj
кожна крапка (·) означає згортку (суму) по одному з індексів
тензора; одержаний результат є скаляром. Ще приклад — для двох
тензорів другого рангу і D^'.
Т2 : І) 2 = TijDij = TijAiBj,
таке позначення було вже використано в п. 9.
11. Ротор градієнта скалярної функції:
rot grad φ — V х Vφ — 0.
12. Дивергенція ротора вектора:
div rot A = V · (V х А) = 0.
13. Дивергенція векторного добутку:
div {А X В) = V · {А X В) = В · V X А - А · V X В.
14. 	Ротор від ротора:
rot rot 4 = Vx(Vx4) = V(V*4)- V2 A = grad div A — A A.
81

15. Ротор векторного добутку:
rot (Ах В) = Vx(AxB) = (B-V)A~(A-V)B-B(V-A) + A(V-B).
16. Градієнт скалярного добутку векторів:
grad (А-В) = V(A-B) = (A-V)B+(B-V)A+Ax(VxB)+Bx(VxA)
17. Деякі похідні з оператором “набла”:
Тут скрізь φ = ψ{τ) = φ(χι, Х2, #з)· Ці співвідношення можна
застосовувати і в криволінійних (ортогональних) системах
координат, але використовуючи „фізичні” компоненти векторів (див.
додаток 1).
18. 	Диференціальні операції в циліндричній системі координат
р, ψ, хг (див. додаток 1):
- г
Vr = де
г
(С · V)r = С
-, dF ->
VFM =
^ = ¾ ^
~ т». . -z> дА
V X Α(φ) = νφχ —;
вв
{Α·ν)Β{φ) = —{Α·νφ).
Єр ρβφ Є3
J- Я Я я
До ρΑφ Аз
d)
82

19. 	Диференціальні операції у сферичній системі координат г, φ
(див. додаток 1):
ч Ί . дф 1 дф ^ 1 дф _
a) grad ф = — ег + + —— ^-е^;
от г οΘ r sin θοφ
1 Г)
b) div A = V · A = r2Ar) +
rz or
1
c) rot A = S7 x A =
d . . <94^
(A# sin 0) H
1
r2 sin#
rsin# \<9#
er ree r sin #e<^
A A A
dr δθ δφ
Ar τΑβ r sin θ Αφ
dip
тут
<*>
2 1 5 / . <? \ 1 <92
θψ sin θ дв \1П дв) sin2 0 θψ2
20. 	Узагальнена формула Гаусса:
£ ^{n)dS = J Φ{ν)άν,
s V
де η — одиничний вектор зовнішньої нормалі до замкненої поверхні
5, який в інтегралі по поверхні треба замінити на вектор V
(„набла”) в інтегралі по об’єму.
Часткові випадки узагальненої формули Гаусса:
a) / ηφdS = J VpdV = J gradipdV\
S V V
b) формула Гаусса - Остроградського:
c)
£ η ■ AdS = J V · AdV = J div AdV]
S V V
η X AdS = J V X TdF = J rot AdV]
V V
7^,
d) £n-V<pdS = J Vz<pdV]
S V
ή j) n- (A x B)dS = J V - (Ax B)dV = J div (A x B)dV.
S V V
83

21. 	Теорема Стокса:
/
A-dl
/ V х А · = / rot Л · dS,
Js Js
де S — поверхня, що „спирається” (або „натягнута”) на замкнений
контур L. Напрямок вектора п нормалі до цієї поверхні пов’язаний
з напрямком обходу контура L правилом правого гвинта.
22. 	Формула для градієнта скалярної функції, що аналогічна п. 21:
п х VtpdS,
де S — поверхня, що „спирається” на контур L, а напрямок обходу
контура задає напрямок п, як в п. 21.
23. 	Формули Гріна:
a) j) φ4ψ · ndS = / (φν2ψ + νφ · Vip)dV·
S V
b) j) (φνψ - ψ4φ) ■ ndS = J {φν2φ - φ42φ)άν.
S V
24. 	Наостанок наведемо теорему Гаусса - Остроградського для
тензорних функцій, наприклад, для тензора третього рангу Т3:
f TijkdSk = J ^-dV.
S V
! Зауваження: часто для позначення оператора V використовується
символ
д
~д?
тобто
«ь life
III
тоді, наприклад,
div A = ■ A, rotT =
or
d r
8fXA
і т. д.
84

З Дельта-функція (^-функція Дірака)
δ - функцією називається така функція δ{χ — то), яка дорівнює нулеві
скрізь, крім особливої точки т = то, в якій вона перетворюється на
нескінченність так, що інтеграл від цієї функції по довільному проміжку,
який містить всередині себе точку То, дорівнює одиниці. Таким чином,
за означенням
Ж0) = j
0
при
Т ^ То,
оо
при
х = яо;
- то) dx -
= 1
при
а < то < Ь.
(39)
а
Графік функції δ(χ — то) намалювати, строго кажучи, неможливо,
оскільки довелося б зображувати нескінченно високий та нескінченно
вузький пік, „площа” під яким скінчена і дорівнює одиниці.
Найважливіші властивості 5-функції виражаються рівностями
(нижче f(x) — довільна неперервна функція):
//(,)«(*-*>*={ '<*> прл:<“Л°с
(40)
f(x) δ(χ - хо) = /(жо) δ(χ - х0у,
ь
J δ(χ — Х\) δ(χ — Х2)dx = δ(χχ — Жг) при а < χχ < b;
а
δ(—χ) = 5(ж);
ж^(ж) = 0;
(41)
(42)
(43)
(44)
δ (ах) = т—j- <5(ж);
δ(χ2 — а2) = ——-[5(ж — а) + δ(χ + а)];
\Qj\
(45)
(46)
S(f)df = δ(χ)άχ,
Κ№)
δ(χ-
dL
dx
X=Xq
(47)
де то визначено умовою /(то) = 0 і /(т) — однозначна диференційовна
функція.
Співвідношення (39) — (47) слід розуміти як інтегральні рівності, з
яких випливає, що
85

зокрема
ь
df(x)\
dx )x=xo
άδ(χ)
Ж dx
δ(χ).
δ - функція не може входити ні в які остаточні вирази. Завжди, коли
пишеться δ - функція, мається на увазі подальше інтегрування по тих
змінних, від яких вона залежить. Тому вказані рівності означають
наступне: якщо ліву і праву частини кожної з цих рівностей домножити на
неперервну функцію f(x)і проінтегрувати по х, то одержані результати
будуть однакові. Наприклад, для формули (44) маємо:
J/(χ)χδ(χ)άχ = f(x) · x\x=q = 0.
δ - функцію можна розглядати як границю послідовності функцій.
Зокрема, такі властивості має вираз
F(a, х)
sin ах
πχ ’
який при а сю поводить себе як δ(χ), тобто
.. sin аж
inn
а—>оо 7ТХ
+оо
i(i); J -
sin αχ
dx = 1.
πχ
Інші аналітичні зображення 5-функцїї:
1
2π
+оо
J eikxdk·,
—oo
фгг)
1
π
lim ;
a^-0 xz + az
i(i) = -L
у/π
• lim ae
Тривимірна 5-функція визначається співвідношенням
δ{τ- го) = δ(χ - χο)δ{ν - Уо)δ{ζ - ζ0).
Основна властивість функції S(r — vq) виражається рівністю
(48)
86

(49)
J f{r)d(r- fo)dV = /(ro),
де точка з радіусом-вектором г"о знаходиться всередині об’єму
інтегрування У, в якому задана неперервна функція f(r). Якщо вказана точка
знаходиться поза У, то інтеграл (49) дорівнює нулю.
Тривимірну 5-функцію зручно подати у вигляді потрійного інтеграла
в необмеженому к—просторі:
В фізичних задачах (наприклад, при описі ефекту
ВавіловаЧеренкова) часто використовується формула
S(f — vt) = — [ el^'r~ut^ δ{ω — к · v)dk άω.
2π J
Тривимірна 5-функція з’являється, наприклад, в результаті
наступного диференціювання по компонентах г:
Рівняння Пуассона для потенціала точкового заряду е, який
знаходиться у точці го, запишеться таким чином:
а густина струму, утворюваного таким зарядом, що рухається зі
швидкістю v, має вигляд
7* — Г‘
VV=_rf(r-r5)
j(r) = evS(r- fe).
87