-	ЗАДАЧ <
ЗБІРНИК
МАТЕМАТИКИ
ЗБІРНИК ЗАДАЧ З ВИЩОЇ МАТЕМАТИКИ
Ф. С. ГУДИМЕНКО, Д. М. БОРИСЕНКО,
В. 0. ВОЛХОВА, Г. М. ЗРАЖЕВСЬКА,
0. А. ЮЩЕНКО
ЗБІРНИК З вищої
" МАТЕМАТИКИ
ЗА РЕДАКЦІЄЮ Ф. С. ГУДИМЕНКА
Допущено Міністерством вищої
і середньої спеціальної освіти
УРСР як учбовий посібник для
студентів природничих факульте-
тів університетів
ВИДАВНИЦТВО
КИЇВСЬКОГО УНІВЕРСИТЕТУ-1967
517
3-41
Збірник складається з 17 розділів і містить задачі з аналітичної
геометрії (на площині та в просторі), векторної алгебри й векторного
аналізу, лінійної алгебри, диференціального й інтегрального числення
функцій однієї та багатьох змінних, диференціальних рівнянь, дифе-
ренціальної геометрії та рядів Фур’є.
У кожному розділі є вправи та задачі різноманітного характеру,
з різною трудністю та складністю, включаючи й задачі на доведення.
Дібрано чимало задач з механіки, фізики, хімії тощо. До багатьох
задач у відповідях подано короткі вказівки до розв’язання.
Розрахований на студентів природничих (фізичних, радіофізич-
них, хімічних, біологічних, геологічних, географічних) факультетів
державних університетів. Може бути також корисним для студентів
механіко-математичного факультету.
2-2-3
12-67
Гудименко Федор Исидорович,
Борисенко Даниил Михайлович,
Волкова Валентина Александровна,
Зражевская Галина Мефодиевна,
Ющенко Алексей Андронович
Сборник задач по вьісшей математике
(на украинском язьіке)
Редактор Костенко Ю. І.
Художник Самойлов М. С,
Художній редактор Конопляна О. К-
Технічний редактор Дюк Л. Ш.
Коректор Іващенко Е. С.
Здано до набору 15/ХІ 1966 р. БФ 13684. Зам. № 2193. Тираж 13000. Формат паперу 60 X 84і/і в •
Фіз. друк, аркушів 22,0. Умови, друк, аркушів 21,84. Обл.-видави, аркушів 18,4. Паперових
аркушів 11,0. Підписано до друку 13/УІІ 1967 р. Папір друкарський № 3. Ціна 67 коп.
Видавництво Київського університету, Київ, Героїв революції, 4.
Зведен. Т. П. видави. Київ., Львів., Харк., унів-тів. — 1967. поз. 12
Київська фабрика набору Комітету по пресі при Раді Міністрів УРСР, вул. Довженка 5.
ЗМІСТ
Передмова .......................................................... 7
Розділ І. Аналітична геометрія на площині .......................... 9
§ 1.	Прямокутні та полярні координати точки на площи-
ні. Віддаль між двома точками. Площа трикутника 9
§ 2.	Поділ відрізка в даному відношенні. Центр ваги
системи матеріальних точок ...................... 11
§ 3.	Перетворення координат ...................... 12
§ 4.	Геометричне тлумачення рівнянь .............. 13
§ 5.	Рівняння прямої на площині .................. 14
§ 6.	Найпростіші рівняння кривих другого порядку та
їх властивості .................................. 17
§ 7.	Загальна теорія кривих другого порядку....... 21
Розділ II. Векторна алгебра ....................................... 25
§ 1.	Лінійні операції над векторами. Лінійна залежність
векторів ........................................ 25
§ 2.	Координати вектора.	Проекції вектора ........ 26
§ 3.	Скалярний добуток	векторів .................. 27
§ 4.	Векторний добуток	................. ЗО
§ 5.	Мішаний добуток трьох векторів. Подвійний век-
торний добуток .................................. 32
Розділ III. Аналітична геометрія в просторі........................ 34
§ 1.	Координати точки. Перетворення координат ...	34
§ 2.	Площина ..................................... 36
§ 3.	Пряма у просторі ............................ 38
§ 4.	Пряма й площина ............................. 39
§ 5.	Геометричний зміст рівнянь з трьома невідомими.
Сфера ........................................ 42
§ 6.	Циліндри та конуси .......................... 43
§ 7.	Поверхні другого порядку..................... 44
§ 8.	Загальна теорія поверхонь другого порядку ...	48
1*	З
Розділ IV. Лінійна алгебра ........................................... 51
§ 1.	Визначники другого і третього порядку ....	51
§ 2.	Означення, основні властивості та обчислення ви-
значників довільного порядку ....................... 54
§ 3.	Правило Крамера. Гауссів метод................. 58
§ 4.	Загальна система лінійних рівнянь.............. 60
§ 5.	Матриці та дії над ними........................ 63
§ 6.	Афінні векторні простори ...................... 66
§ 7.	Лінійні перетворення векторних просторів ....	69
§ 8.	Евклідові простори ............................ 72
§ 9.	Квадратичні форми ............................. 73
Розділ V. Диференціальне числення функції від однієї змінної 75
§ 1.	Функціональна залежність....................... 75
§ 2.	Графіки функцій ............................... 79
§ 3.	Границя й неперервність / (х) ................. 81
§ 4.	Границя функції неперервного аргументу ...	84
§ 5.	Неперервність функції ......................... 90
§ 6.	Рівномірна неперервність функції .............. 93
§ 7.	Похідні та диференціали; їх застосування ....	94
§ 8.	Геометричні застосування похідної.............. 99
§ 9.	Механічні, фізичні та хімічні застосування похідної 101
§ 10.	Похідні вищих порядків .......................102
§ 11.	Диференціали першого та вищих порядків . . . 103
§ 12.	Застосування основних теорем диференціального
числення (теореми Ролля і Лагранжа).................104
§ 13.	Застосування формули Коші та формули Тейлора 106
§ 14.	Зростання й спадання функції. Екстремуми . . . 106
§ 15.	Задачі на відшукання найбільших та найменших
вартостей змінних величин ...........................109
§ 16.	Відшукання граничних вартостей функцій. Асимп-
тоти.................................................112
§ 17.	Опуклість, угнутість, точки перегину ..........113
§ 18.	Наближене розв’язання рівнянь .................114
§ 19.	Побудова графіків функцій .....................114
Розділ VI. Комплексні числа та алгебра многочленів....................116
§ 1.	Комплексні числа ..............................116
§ 2.	Розклад многочлена на незвідні множники ... 119
Розділ	VII.	Невизначений інтеграл .............................121
§ 1.	Основні методи інтегрування.....................121
§ 2.	Інтегрування раціональних функцій ..............125
§ 3.	Інтегрування ірраціональних функцій ............126
§ 4.	Інтегрування трансцендентних функцій............128
§ 5.	Різні приклади на інтегрування функцій .... 130
§ 6.	Застосування невизначених інтегралів ...........131
Розділ	VIII.	Визначений інтеграл ...............................134
§ 1.	Обчислене визначених інтегралів ...............136
§ 2.	Наближене обчислення визначених інтегралів . . 141
4
§ 3.	Невластиві інтеграли ..............................................141
§ 4.	Застосування визначеного інтеграла ................................144
Розділ IX. Функції багатьох змінних ......................................................155
§ 1.	Означення. Область існування. Границя та непе-
рервність ...............................................................155
§ 2.	Диференціювання функцій багатьох змінних . . 157
§ 3.	Диференціювання зложених функцій .................................159
§ 4.	Похідні та диференціали вищих порядків .... 161
§ 5.	Заміна змінних ...................................................163
§ 6.	Геометричні застосування. Дотична площина.
Нормаль .................................................................166
§	7.	Тейлорова формула і Тейлорів ряд..................................167
§	8.	Екстремуми функцій багатьох змінних...............................167
§ 9.	Умовний екстремум ................................................169
§ 10.	Особливі точки. Обвідна ..........................................169
Розділ	X.	Криволінійні інтеграли ................................................171
§	1.	Криволінійні інтеграли першого типу..............................171
§	2.	Криволінійні інтеграли другого типу..............................172
§	3.	Застосування криволінійних інтегралів .... 173
Розділ	XI.	Інтеграли, залежні від параметра ......................................175
Р і з д і л	XII.	Кратні інтеграли ......................................................179
§ 1.	Подвійний інтеграл ...............................................179
§ 2.	Застосування подвійних інтегралів до обчислення
координат центра ваги та моменту інерції .... 181
§ 3.	Обчислення об’ємів тіл та площ кривих поверхонь 181
§ 4.	Потрійні інтеграли ...............................................183
§ 5.	Невластиві кратні інтеграли.......................................185
§ 6.	Многократні (багатократні) інтеграли .............................186
Розділ XIII. Поверхневі інтеграли. Елементи теорії поля...................................187
§ 1.	Поверхневі інтеграли першого типу.................................187
§	2.	Поверхневі інтеграли другого типу.188
§ 3.	Елементи теорії поля (векторний аналіз) .... 189
Розділ XIV. Ряди	..................................................................196
§	1.	Числові ряди...........................................196
§	2.	Функціональні	ряди ...................................202
§	3.	Степеневі ряди	...................................205
Ро з д і л XV. Диференціальні рівняння ...................................................209
§ 1.	Утворення диференціальних рівнянь. Поле напря-
мів .....................................................................209
§ 2.	Диференціальні рівняння першого порядку з відо-
кремлюваними змінними................................210
§ 3.	Однорідні рівняння та звідні до них...............................212
§ 4.	Лінійні рівняння. Рівняння Бернуллі...............................212
§ 5.	Рівняння в повних диференціалах. Інтегрувальний
множник..................................................................214
5
§ 6.	Рівняння першого порядку, не розв’язані відносно
похідної. Рівняння Лагранжа та Клеро . . . 215
§ 7.	Задачі на траєкторії.........................216
§ 8.	Диференціальні рівняння вищих порядків . . . 216
§ 9.	Лінійні рівняння	вищих	порядків..............217
§ 10.	Системи звичайних	диференціальних рівнянь 219
§ 11.	Диференціальні рівняння	з	частинними похідними 220
Розділ	XVI.	Диференціальна	геометрія ..........................221
§ 1.	Лінії на площині	..........................221
§ 2.	Лінії в просторі .............................226
§ 3.	Поверхні	...............................231
Розділ	XVII.	Ряди	Фур’є ........................................239
Відповіді ...........................................................244
Додатки .............................................................349
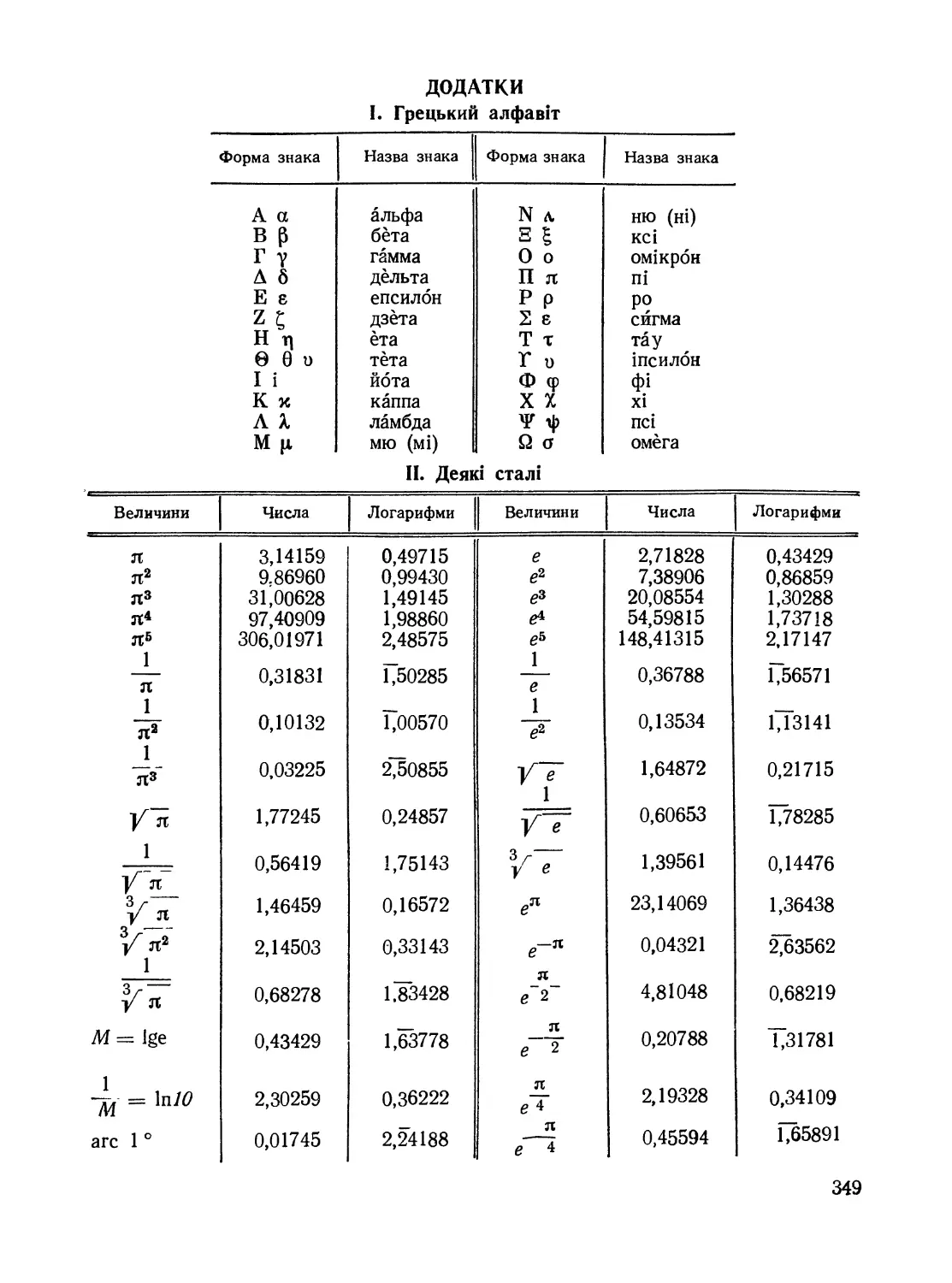
І.	Грецький алфавіт .............................................349
II.	Деякі сталі .................................................349
III.	Тригонометричні функції ....................................350
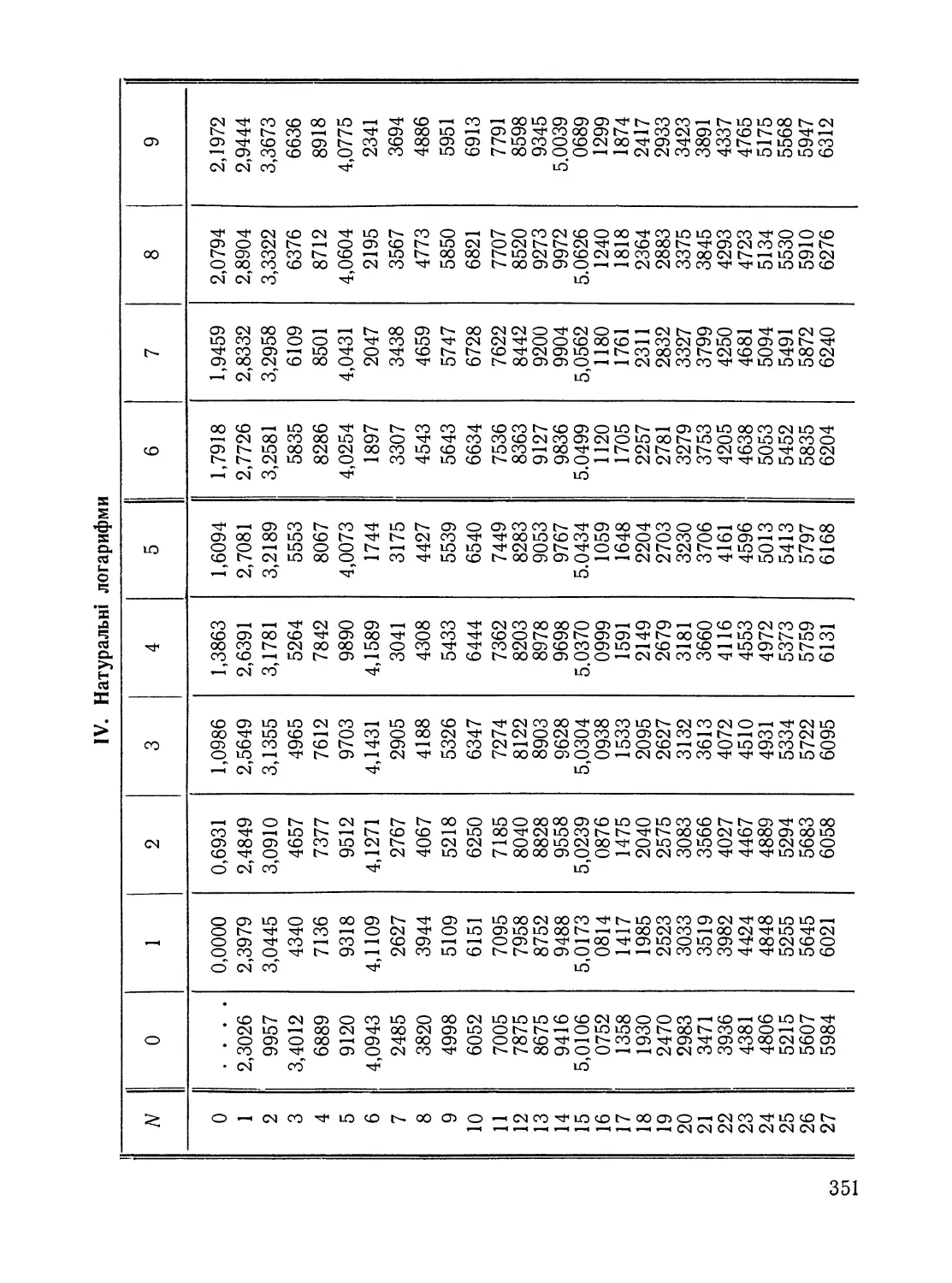
IV.	Натуральні логарифми .......................................351
ПЕРЕДМОВА
Збірник укладено відповідно до програми з курсу вищої математики для фі-
зичних та радіофізичних факультетів державних університетів. На цих факуль-
тетах для вищої математики (аналітична геометрія, векторна та лінійна алгебра,
математичний аналіз, диференціальні рівняння та диференціальна геометрія)
в навчальному плані відведено понад 700 год. На біологічному, геологічному,
географічному та хімічному факультетах кількість годин коливається від 160
до 470, і, звичайно, тут деяким розділам (лінійна алгебра, диференціальна гео-
метрія, ряди Фур’є тощо) у програмах відводиться дуже мало місця або вони
зовсім відсутні.
Автори поставили собі завдання скласти посібник, який задовольнив би
потреби студентів усіх згаданих факультетів.
У кожному розділі є задачі різноманітного характеру, з різною трудністю
і складністю, включаючи й задачі на доведення. Дібрано чимало задач з механіки,
фізики, хімії тощо.
Майже у всіх збірниках з вищої математики, що вийшли в світ у післяво-
єнні роки (переважно для вищих технічних учбових закладів, бо для універси-
тетів видано тільки «Сборник задач и упражнений по математическому анализу»
В*. П. Демидовича), подано і короткі відомості з теорії. Ми відмовилися від
цієї «традиції», виходячи з того, що студент, вдовольняючись тією мізерією
з теорії, що є в збірнику, розв’язує задачі і не вивчає за підручником теоретич-
ного матеріалу. Замість цього у відповідях скрізь, де тільки автори вважали
за потрібне, подано короткі вказівки до розв’язання задач і вправ.
Крім оригінальних задач та вправ, збірник містить також загальновідомі,
запозичені з різних посібників, підручників та журнальних статей.
Збірник є результатом багаторічної праці авторів на різних факультетах
Київського ордена Леніна державного університету ім. Т. Г. Шевченка.
Написання матеріалу між авторами розподіляється так: розділи І, III та
XVI — Г. М. Зражевська; розділ IV — О. А. Ющенко; розділи VIII та XV —
7
В. О. Волкова; розділи VI та XIV —Д. М. Борисенко; розділ II —Д. М. Бо-
рисенко разом з Г. М. Зражевською; розділи V, VII, IX — XIII та XVII —
Ф. С. Гудименко.
Автори «Збірника» складають щиру подяку акад. АН УРСР О. С. Парасюку,
працівникам Львівського університету доц. В. О. Гукевич, канд. фіз.-мат. наук
С. В. Дениску, канд. фіз.-мат наук Б. В. Ковальчуку, працівникам Харківського
університету доц. О. С. Лейбіну (зав. кафедрою загальної математики), асист.
Л. В. Дмитрієвій, асист. П. К. Шпильовому за грунтовний критичний розгляд
рукопису та цінні вказівки і зауваження, а також ст. лаборанту кафедри за-
гальної математики Київського університету В. І. Шматок за допомогу у підго-
товці рукопису.
АВТОРИ
РОЗДІЛ І
АНАЛІТИЧНА ГЕОМЕТРІЯ
НА ПЛОЩИНІ
§ 1. Прямокутні та полярні координати
точки на площині. Віддаль між двома точ-
ками. Площа трикутника
1.	Визначити розміщення тих точок площини, координати яких
задовольняють умову
2.	Де знаходяться ті точки площини, для яких виконується одне
з таких співвідношень:
а) |х| = а\ Ь) |х| = |у\?
3.	Де знаходяться точки площини, координати яких справджу-
ють одну з нерівностей:
а) > 0; Ь) ^ + у| < 0?
7 х2 — 4	7 8 2х — З
4.	Знайти координати точки, симетричної до точки Р (хх, у±) від-
носно а) осі ОХ; Ь) осі ОУ; с) початку координат; й) бісектриси
першого координатного кута.
5.	Як зміняться координати точки Р(хь г/х), якщо за вісь ОХ
взяти вісь ОУ, а за вісь ОУ взяти вісь ОХ?
6.	Побудувати відносно прямокутної системи координат кожну
з точок
Л(0, 2), В(-1, 0), С(—2, 1), 0(3, —4).
7. Знайти координати вершин квадрата із стороною а, беручи за
осі координат а) його сторони; Ь) діагоналі.
8. Побудувати точки, задані полярними координатами Рг [ 2,	),
І о І
9
9. Знайти координати точок, симетричних точкам
л(1> 1"), Рг (2, у), Р3^, у), л(з, -у)
щодо полярної осі.
(4 \
З, -дЛ
і В (б, паралелограма АВСИ, точка перетину діагоналей якого
збігається з полюсом. Знайти дві інші вершини цього паралело-
грама.
11.	Як розміщені точки, полярні координати яких справджують
одне з таких рівнянь:
а) р = 1; Ь) р = а\ с) ф =	; й) ф =	; е) ф = ф0?
12.	Полюс полярної системи координат збігається з початком
декартових прямокутних координат, а полярна вісь — з додатною
піввіссю абсцис. Знайти полярні координати точок, якщо відомі їх
декартові координати Л4х(0, 5), Лї2(—3, 0), Л43С|/3, 1), Лї4(1, — ]/3).
13.	На осі ОХ знайти точку, рівновіддалену від точок 4(1, — 1)
і В (4, 2).
14.	Знайти центр кола, описаного навколо трикутника АВС з вер-
шинами А (0, а), В 0), С (0, 0).
15.	Дано координати двох суміжних вершин квадрата: А (0, 1) і
5	-у-)’ Знайти інші його вершини.
16.	Яку умову повинні задовольняти координати вершин три-
кутника АВС для того, щоб кут С був прямим?
17.	Чи можна описати коло навколо чотирикутника ЛВСО з вер-
шинами 4(0,0), В (2,0), С(1, 3), £>(—1, 2)?
18.	Довести, що при довільних дійсних числах ах, а2, а3, Ьу Ь2,
Ь3, справедлива нерівність
V (а2 — ах)2 + (Ь2 — 6Х)2 + V (аз — ах)2 + (Ь3 — £>х)2 >
> V («2 — «з)2 + (62 — &з)2-
19.	Точка, рухаючись прямолінійно, перемістилась з точки А (2,—7)
у точку В (—3,5). Який шлях вона пройшла і під яким кутом до
осі ОХ нахилена траєкторія руху?
20.	Переконатися, що чотирикутник АВСИ з вершинами 4(1, 3),
В (4, 7), С(2, 8) і £>(—1,4) є паралелограм, та знайти його площу.
ю
21.	Знайти площу трикутника з вершинами А (2, 1), В(—3, 2) і
С(2, —2).
22.	Обчислити площу п’ятикутника з вершинами Л(—2, 0),
В(0, -1), С(2, 0), 0(3, 2) і В(—1, 3).
23.	У полярній системі координат дано дві вершини правильного
(я \	/	7	\
4,-----і В 8, я . Визначити його площу.
24.	Одна з вершин трикутника ОАВ лежить у полюсі, дві інші
точки Л(рх, фі) і В(р2, ф2). Визначити площу цього трикутника.
§ 2. Поділ відрізка в даному відношенні.
Центр ваги системи матеріальних точок
25.	Точки Л(—2, —1), В(— 1, 3) і С (2, — 1) — послідовні вер-
шини паралелограма АВСЬ. Знайти його площу.
26.	Визначити відношення /г, в якому кожна з точок А (2, — 1),
В (3, 1) і С(4, 3) поділяє відрізок, обмежений двома іншими.
27.	Знайти, які з трьох точок лежать на одній прямій (колі-
неарні):
а)	(5,	1),	(2, 3),	(1	4);
Ь)	(1,	1),	(-2, 3),	(2,	3);
с)	(0,	4),	(1, —2),	(3,	1).
28.	Показати, що координати довільної точки прямої, яка спо-
лучає точки Л(%і, уА і В(%2, г/2), можна зобразити у вигляді
х = іх1 + (1 — і) х2, у = Іуг + (1 — 0 У2‘ Які вартості параметра і
відповідають внутрішнім точкам відрізка АВ прямої?
29.	На прямій, що проходить через точки Л(—З, 1) і В (2, 2),
знайти точку перетину її з віссю 0¥.
ЗО.	Довести, що точки А (0, 0), В(—3, —3) і С(1, 1) лежать
на одній прямій, та знайти просте відношення (ЛВС).
31.	Знайти координати точок, що поділяють відрізок, обмежений
точками Л(—1, 3) і В (2, 4), у відношенні а) /г = 2; Ь) /і = —^-.
32.	Знайти точку перетину діагоналей чотирикутника АВСО
з вершинами А (0, 0), В (2, 0), С(1, 2) і О (—2, 3).
33.	Знайти довжину бісектриси внутрішнього кута А трикутни-
ка ЛВС, заданого вершинами Л(3, —5), В(—З, 3) і С(— 1, — 2).
34.	Дано Л(—1, —1), В (3, 5) і С(—4, 1) —вершини трикут-
ника. Знайти точку перетину бісектриси зовнішнього кута при вер-
шині А з продовженням сторони ВС.
11
35.	Точка Л4 перетину медіан трикутника лежить на осі ОХ;
точки Л(2, —3) і В (—5, 1) —дві його вершини, а третя вершина
С лежить на осі ординат. Визначити координати точок М і С.
36.	Знайти центр ваги суцільної однорідної трикутної платівки
з вершинами А (хх, ух), В (х2, у2) і С (х3, у3).
37.	У точках Л4Х (%х, г/х), М2 (х2, г/2), ..., Мп(хпі уп) зосереджені
відповідно маси тх, т2, ..., тп. Довести, що центр ваги такої си-
стеми визначається формулами
_ ГП-^Хх 4~ ^2*2 + • • • + тП^П .	_ Ч~ ^2#2 + • - - Ч~ тґіУп
с Ші Ц- пі2 + ... + тп ' с	. + тп
38.	Знайти центр ваги трикутника з однорідного дроту з вер-
шинами Л(%х, і/х), В (%2, у2) і С (х3, у3).
39.	Однорідний дріт зігнутий у вигляді прямого кута зі сторо-
нами т і п. Знайти центр ваги такої системи.
40.	Дано послідовні вершини суцільної однорідної чотирикутної
платівки Л(—2, 0), В(1, 4), С(4, 5) і О (4, —2). Знайти коорди-
нати її центра ваги.
§ 3. Перетворення координат
41.	Знайти формули перетворення координат, якщо початок ко-
ординат перенесено в одну з точок (без зміни напряму): а) А ( — 1, 2);
Ь) В (З, 4); с) С(2, -3).
42.	Відносно деякої системи координат точка А має координати
х = 7, у = —5. Знайти її координати за умови, що початок координат
перенесено в одну з таких точок: Ох(2, 3), О2(—3, —1), О3(4, —2).
43.	Точка Р відносно двох різних систем з однаково напрям-
леними осями має координати (2, 5) і (—3, 6). Визначити коорди-
нати початку кожної з цих систем відносно іншої.
44.	Знайти координати точки Р(—3, 1) у новій системі, якщо
осі координат повернуто на кут: а) —45°, Ь) 90°, с) 180°.
45.	Знайти кут, на який повернуто координатні осі, якщо фор-
мули перетворення координат мають вигляд
у=^-х + ^-у.
46.	Дві сторони прямокутника АВСВ спочатку збігалися з ося-
ми координат (ЛВ = 5, АО = 2). Потім прямокутник був пересуну-
тий так, що вершина Л, яка раніш знаходилася у початку коорди-
нат, опинилася в точці Лх(4, —1), а сторона ЛВ, що лежала на
12
осі ОХ, повернулася на кут а ^30°. Визначити нове положення
інших вершин.
47.	В яку точку потрібно перенести початок координат, щоб
рівняння лінії 8х2 — 4ху + 5г/2 + 4х — 10г/ + 3 = 0 не містило чле-
нів з х та у в першому степені?
§ 4. Геометричне тлумачення рівнянь
48.	Знайти рівняння геометричного місця точок, рівновіддалених
від точок А (2, —1) і В(—1, 3).
49.	Сила Р = 10 кГ розкладена на дві сили, відношення яких
2: 3. Визначити геометричне місце вершин силових трикутників.
50.	Точка М рухається так, що відношення віддалей її від то-
чок Лі (%х, г/х) і А2 (х2, у2) є стале й дорівнює Я. Яка буде траєкто-
рія руху?
51.	Знайти рівняння в декартових прямокутних координатах та-
ких кривих:
( х = Р соз і + а,	х = а соз /,	х = а сЬ /,
(£/ = /? 8ІП / + Ь\	у = Ь 8ІП /;	у = Ь 8І1 і.
52.	Скласти рівняння кривої, яку описує точка відрізка з дов-
жиною /, що поділяє його у відношенні К: ц, коли кінці відрізка
ковзають по координатних осях. Якою буде крива при 1?
53.	Скласти рівняння траєкторії руху тіла, кинутого під кутом
а до обрію з початковою швидкістю &0.
54.	Написати параметричні рівняння кривих:
а) рф = а; Ь) р = 27? 8іп ф.
55.	Відрізок довжиною 2/ ковзає по сторонах прямого кута.
Знайти рівняння геометричного місця точок М — основ перпенди-
кулярів, опущених з початку координат на відрізок.
56.	Довести, що рівняння х2 + у2 + 2х — 4у = 20 є рівнянням
кола, та знайти його центр і радіус.
57.	Через початок координат проведені всі можливі хорди кола
(х — 8)2 у2 = 64. Скласти рівняння геометричного місця середин
цих хорд.
58.	На лінії, що визначається рівнянням х2А~у2—2х—2г/+1=0,
знайти точки з ординатою 1. Побудувати цю лінію.
59.	Знайти точки перетину ліній:
а)	х + у — 2 = 0 та х + ,2г/ + 3 = 0;
Ь)	х2 + у2 + 2х + 2у — 2 = 0 та х — у + 2 = 0;
13
с)	Зх2 + 4г/2 — 12х + 8у + 13 = 0 та х — 1 = 0;
й) + У2 = 3 та у2 = 2х.
60.	Знайти точки перетину кривої Зх2 + 2ху — у2 4- 8х + 10г/ —
— 2 = 0 з прямими а) х — у + 2 = 0; Ь) 2х + Зу — 1 = 0; с) 2х +
4- 2у — 1 = 0; сі) х + у = 0.
61.	Знайти точки перетину кривої х2 — 4ху + 4г/2 — 2х — 2у —
— 8	0 з віссю ОХ.
62.	При яких а, Ь та с коло х2 + 2ах + У2 + 2Ьу + с = 0
а)	не перетинає вісь ОХ\
Ь)	перетинає її в двох точках;
с)	дотикається до неї?
§ 5. Рівняння прямої на площині
63.	Визначити, які з точок Лх(1, —2), Л2(1, 1) чи Л3(3, —4)
лежать на прямій х + 2у — 3 = 0.
64.	Знайти відрізки, що відтинає пряма х — Зу + 6 = 0 на осях
координат.
65.	Довести, що рівняння т2х2 + 2тпху + п2у2 — 4/2 = 0 визна-
чає пару прямих. Знайти рівняння кожної з цих прямих.
66.	Довести, що рівняння всякої прямої можна подати в пара-
метричній формі х = х0 + //, у = у0 + /и/.
67.	Знайти рівняння геометричного місця точок, різниця квадра-
тів віддалей яких від точок Л(—2, 1) та В(1, 3) дорівнює 5.
68.	Сторони ЛВ, ВС і АС трикутника АВС дано відповідно рів-
няннями 2х — Зу — 1 = 0, Зх — 4у — 1 = 0 та х — у — 1 = 0. Ви-
значити координати його вершин.
69.	Скласти рівняння медіан трикутника з вершинами А (—4
-2), В (2. 0) та С(2, -4).
70.	Дано дві вершини трикутника АВС Л(2, 1) і В(—1, —1).
Довжина його сторони АС = ]/2*, а центр ваги лежить на прямій
5х — 1у — 2 = 0. Знайти його третю вершину С.
71.	Скласти рівняння прямої, що проходить під кутом ф=150°
до осі ОХ і відтинає на осі О¥ відрізок Ь = 3.
72.	Під яким кутом до осі ОХ нахилена пряма, що проходить
через точки Л(—1, 3) та В (4, —2)?
73.	Сила прикладена в початку координат і складові її на коор-
динатних осях відповідно дорівнюють 5 і —2. Знайти рівняння пря-
мої, вздовж якої напрямлена сила.
74.	Точка, що вийшла з початку координат, рухається одночас-
14
но в напрямі осі ОХ з постійною швидкістю і в напрямі осі
ОУ з постійною швидкістю У2. Знайти рівняння траєкторії руху.
75.	Знайти кут між прямими
( X = Хо + //,	. ( X = хг +
І У = Уо + ті 1 І У = У1 + ту,
76.	Знайти внутрішні кути трикутника АВС з вершинами
Л(0, 0), В(2, -1) і с(4-, -5-У
77.	Довести, що чотирикутник з вершинами 4(1, 1), В(0, 3),
С(2, 4) та О (3, 2) є квадрат.
78.	Довести, що чотирикутник, обмежений прямими х-у^у +
+ 3 = 0, х — 2г/ + 3 = 0, х А-^У — 3 = 0 та % — 2г/ — 3 = 0, є ромб.
79.	За якої умови вісь ОХ для прямих Ігх + т^у = 0, /2% +
+ т2у = 0 є бісектрисою утворених ними кутів.
80.	Довести, що прямі, які відтинають на осях координат від-
різки однакової довжини, або паралельні, або перпендикулярні.
81.	Через точку Р(—1, 3) провести пряму, паралельну до пря-
мої 4х — 2у + 3 = 0.
82.	Через точку Р(1, 2) провести пряму, перпендикулярну до
прямої 5х + 2у — 11 = 0.
83.	Скласти рівняння висот трикутника з вершинами 4(1, 0),
В (4, 5) та С(7, 3).
84.	Через точки перетину прямої х — 2г/ + 6 = 0 з осями коор-
динат провести прямі, до неї перпендикулярні.
85.	Знайти проекцію точки Р(1, —2) на пряму 3% —г/ —9 = 0.
86.	Знайти точку, симетричну точці Р(8, —9) відносно прямої,
що проходить через точки 4(3, —4) і В(—1, —2).
87.	Скласти	рівняння	сторін	трикутника,	знаючи	вершину
4(3, —4) та рівняння двох висот їх— 2у—1=0 і 2х—7у—6=0.
88.	Скласти	рівняння	сторін	трикутника,	знаючи	вершину
4 (2, —4) та рівняння бісектрис двох його кутів х + у — 2 = 0,
х — Зу — 6 = 0.
89.	Скласти рівняння сторін трикутника, знаючи вершину
4 (—4, 2) та рівняння двох медіан Зх — 2у + 2 = 0 і Зх + Зу —
-12 = 0.
90.	Через точку Л4(5, —1) під кутом 45° до прямої 5х + 2г/—
— 11=0 проведена пряма. Знайти її рівняння.
91.	Скласти рівняння катетів прямокутного рівнобедреного три-
кутника, якщо С(5, —1) — вершина прямого кута, а 2х—Зу+5 =
= 0 — рівняння гіпотенузи.
15
92.	Нехай /4(3,4) — вершина кута а = 30° прямокутного три-
кутника, а х — г/ + 2 = 0 — рівняння протилежного катета. Скласти
рівняння двох інших сторін трикутника.
93.	Промінь світла, що має напрям прямої х + Зу = 0, падає на
дзеркало, визначуване рівнянням 2х — Зу + 5 = 0. Написати рівнян-
ня відбитого променя.
94.	Точка Р(1, —1) є центром квадрата, одна із сторін якого
лежить на прямій х — 2у + 12 = 0. Знайти рівняння інших сторін
квадрата.
95.	При якій вартості параметра а три прямі 2х — у + 1 =0,
х + у — 4 = 0 і Зх + ау — 2 = 0 проходять через одну точку?
96.	Через точку перетину прямих х -\-2у — 1=0 і 2х + у —
— 4 = 0 провести пряму:
а)	що проходить через точку М (—1, 3);
Ь)	паралельну до осі О¥',
с)	перпендикулярну до прямої х — 2у + 11 =0.
97.	Через точку перетину прямих х — 2у — 5 = 0 і х у —
— 8 = 0 провести дотичні до кола х2 + у2 = 25.
98.	Знайти ту пряму в’язки х + 2у — 1 + К (2х + у — 4) = 0,
яка утворює з прямою Зх — у + 17 = 0 кут .
99.	З’ясувати, які з поданих нижче рівнянь прямих написані в
нормальному вигляді
а) -|-х —	— 3 = 0;	1 = 0:
£	19
с) 4-х - ^у + 2 = 0; О) х + у - 2 = 0; е) у - 2 = 0.
1 О	1 о
100.	Звести до нормального вигляду такі рівняння:
а) 4х + Зу + 11 =0, Ь) х + 2у — 1 =0, с) х + 2 = 0.
101.	Обчислити віддаль точки від прямої:
а)	Р(-2, 1); 4х - Зу - 2 = 0;
Ь)	Р (3, -2); 12х + Зу - 3 = 0;
с)	Р(0, 1); х — 2у + 1 =0.
102.	Нехай Зх — 2у — 5 = 0, 2х + Зу + 7 = 0 — рівняння двох
сторін прямокутника, а Л(—2, 1) —його вершина. Обчислити пло-
щу прямокутника.
103.	Дві сторони квадрата лежать на прямих х — 2у + 2 = 0,
х — 2у — 5 = 0. Обчислити його площу.
16
104.	Знайти віддаль між прямими 5х —12г/—65 = 0 і
5х — \2у + 26 = 0.
105.	Дано 4х — Зу + 3 = 0, 4х — Зу — 17 = 0 — рівняння двох
сторін квадрата; А (2, —3) — його вершина. Скласти рівняння ін-
ших сторін квадрата.
106.	З’ясувати, чи перетинає пряма 2% + Зг/ — 5 = 0 відрізок,
обмежений точками Л41(—1, 3) і Л42(2, —5)?
107.	Чи лежить точка М(—3, 2) всередині, чи зовні трикутни-
ка, обмеженого прямими х у — 4 = 0, Зх — 7 г/ + 8 = 0, 4х — у —
— 31=0?
108.	Нехай Л(—3, 5), В(—1, —4), С(7, —1) та 0(2,9) —
послідовні вершини чотирикутника. Встановити, чи буде чотирикут-
ник опуклий.
109.	Скласти рівняння бісектриси того кута між прямими
7х + у — 3 = 0, Зх — 3 у — 6 = 0, що містить початок координат.
ПО. Скласти рівняння бісектриси тупого кута, утвореного пря-
мими х — Зу + 5 = 0, Зх — у + 15 = 0.
§ 6, Найпростіші рівняння кривих другого
порядку та їх властивості
111.	Скласти рівняння еліпса, фокуси якого лежать на осі абс-
цис, симетрично відносно початку координат, якщо: а) мала вісь до-
рівнює 8, а віддаль між фокусами 2С = 6; Ь) віддаль між дирек-
* 1
трисами дорівнює 16, а ексцентриситет = —.
112.	Дано рівняння еліпса 25х2 + 9г/2 = 225. Знайти його осі,
фокуси, рівняння директрис.
113.	Прямі х = ±8 є директрисами еліпса, його мала вісь до-
рівннє 8. Скласти рівняння цього еліпса.
114.	Меридіан земної кулі має форму еліпса, відношення осей
299
якого дорівнює  зоо Визначити ексцентриситет земного мери-
діана.
115.	Еліпс проходить через точки Л4()/3, —2) і N (—2]/3, 1).
Скласти рівняння еліпса, якщо його осі лежать на осях координат.
116.	Скласти рівняння гіперболи, фокуси якої розміщені на осі
абсцис симетрично відносно початку координат, якщо:
а)	її осі 2а = 10 і 2Ь = 8;
Ь)	віддаль між фокусами 2с = 10 і вісь 2Ь = 8;
5
с)	вісь 2а = 16 і ексцентриситет
2 2193
17
4
й) рівняння асимптот у = ± —х і віддаль між фокусами
2с = 20;
е) рівняння асимптот у — ± -у х і віддаль між директрисами
дорівнює 12-у.
117.	Скласти рівняння гіперболи, фокуси якої розміщені на осі
ординат симетрично відносно початку координат, якщо віддаль між
18 .	5
директрисами дорівнює -у і ексцентриситет е = -у .
118.	Довести, що добуток віддалей точки гіперболи до її асимп-
тот є сталий щодо точки.
119.	Скласти рівняння двох спряжених гіпербол, якщо віддаль
між директрисами першої з них дорівнює 7,2 і віддаль між дирек-
трисами другої дорівнює 12,8.
120.	Скласти рівняння параболи, якщо:
а)	фокус має координати (5, 0), а вісь ординат є директрисою;
Ь)	парабола симетрична відносно осі ОХ, проходить через поча-
ток координат і через точку Л4(1, —4);
с)	парабола симетрична відносно осі ОУ, фокус знаходиться в
точці (0, 2), а вершина збігається з початком координат;
сі) парабола симетрична відносно осі ОУ, проходить через по-
чаток координат і через точку Л4(6, —2).
121.	Через точку М(—1, 3) провести прямі, паралельні до
асимптот гіперболи х2 —~ = 1.
122.	Визначити довжину хорди параболи у2 = 2рх, що прохо-
дить через її фокус, перпендикулярно до осі.
123.	Визначити фокальний радіус точки М параболи у2 = 20%,
якщо її абсциса дорівнює 7.
124.	Скласти рівняння кривих другого порядку з фокусом
Р (хо» Уо) 1 відповідною директрисою ах + Ьу + с = 0.
125.	Скласти рівняння еліпса, якщо його ексцентриситет е —
= -у, фокус знаходиться в точці /'(І, —2), а відповідна дирек-
триса визначається рівнянням х — у + 1 = 0.
126.	Точка М (8, 0) лежить на гіперболі, фокус якої знаходить-
ся в точці /'(І, 1), а х — Зу + 2 = 0 — рівняння відповідної дирек-
триси. Знайти рівняння цієї гіперболи.
(5
-у, 1) лежить на гіперболі 4х2 — 5у2 = 20.
Знайти її фокальні радіуси.
18
ці
128.	На еліпсі —	= 1 знайти точку з фокальним радіу-
10
сом г =
О
129.	Скласти рівняння еліпса, якщо його лівий фокус знахо-
диться в полюсі системи координат, фокальна вісь лежить на поляр-
ній осі, а точки Л41(р1, 0) і Л42(р2, лежать на еліпсі.
130.	Відносно полярної системи координат скласти рівняння ко-
ла з радіусом Я та з центром а) у полюсі; Ь) у точці (рх, фх).
131.	Відносно прямокутної системи координат написати рівнян-
ня кривої:
ч	9	1	ч	1
а) р = -е—л-------; Ь) р =-------—----; с) р =	.
7 г 5 — 4 соз ф 71	2 —]/5соз(р	2 —2 соз ф
132.	На кривій
2
Р =" ---7=-----
1 — ]/ 2 соз ф
знайти точку з найменшим фокальним радіусом.
133.	Довести, що довільна пряма може перетинати конічний пе-
реріз не більше як у двох точках.
^2 о2
134.	Знайти точку перетину еліпса	= 1 з прямою
х — 2у + 2 = 0.
135.	В еліпс	24“^ 1 вписано прямокутник, дві проти-
лежні сторони якого проходять через фокуси. Обчислити площу
цього прямокутника.
136.	Знайти точки перетину гіперболи -----= 1 з прямою
УС) <50
х — у + 5 = 0.
137.	Скласти рівняння спільної хорди параболи у2 = 18% і кола
(%+6)2 + г/2= 100.
138.	Визначити рівняння діаметрів еліпса х2 + 6г/2 = 2, довжина
яких дорівнює 2.
139.	Скласти рівняння прямої, яка сполучає середини паралель-
них хорд Зх — 4у — 6 = 0, Зх — 4у + 12 = 0 гіперболи х2 — у2 = 1.
140.	Через точку Л40(х0, г/0) провести таку хорду еліпса
£.2
— ф- = 1, що ділиться в цій точці навпіл.
141.	Знайти кутовий коефіцієнт тієї хорди гіперболи--1~ = 1.
О т:
яка проходить через точку А (3, — 1) та поділяється в ній навпіл.
2*
19
Хг І?
142.	Скласти рівняння діаметра гіперболи ---у- = 1, який
ділить навпіл її хорду, що лежить на прямій Зх + 2г/ — 1 = 0.
і/2
143.	Скласти рівняння діаметра еліпса —який про-
ходить через середину хорди, що лежить на прямій х + 2у— 1=0.
144.	Скласти рівняння двох спряжених діаметрів еліпса 4%2 +
+ у2 = 1, один з яких нахилений під кутом а = 60° до осі ОХ.
145.	Скласти рівняння двох спряжених діаметрів еліпса
ї/2
-д- +~у = І, один з яких паралельний до прямої х-\-2у — 17=0.
146.	Скласти рівняння двох спряжених діаметрів гіперболи
х2 — 2у2 = 4, один з яких перпендикулярний до прямої х + 4# —
- 23 = 0.
147.	Скласти рівняння хорди параболи у2 = 8х, що проходить
через точку Л4(2, 3) і ділиться в ній навпіл.
148.	Скласти рівняння діаметра параболи х2 = 2ру, спряженого
з хордами, кутовий коефіцієнт яких к.
149.	Знайти площу паралелограма з вершинами на кінцях спря-
X2 у2 .
жених діаметрів еліпса	= 1.
150.	Серед чотирикутників, вписаних в еліпс, знайти той, що
має найбільшу площу.
х2 и2
151.	Знайти рівняння дотичної до еліпса — + ф- = 1 у точці
М) (*0> У о)-	2	2
152.	Знайти рівняння дотичної до гіперболи ----1 у точ-
ці Л40(х0, у0).
153.	Знайти рівняння дотичної до параболи у2 = 2рх у точці
Мо (*о, Уо)-
X2 І}2
154.	Скласти рівняння дотичних до еліпса + -^-=1 в його
вершинах.
155.	Скласти рівняння кола, яке має центр на прямій 2х-|-і/=0
і дотикається до прямих 4х — Зу + 10 = 0 і 4х — Зу — ЗО = 0.
156.	Скласти рівняння нормалі до параболи у2 = 8% у точці, аб-
сциса якої дорівнює 2.
157.	Через точку Л4(2, 4) провести дотичні до еліпса
у2	«»2
— = 1
4'9
158.	Скласти рівняння дотичних, проведених через точку
Л4 /ї),	до гіперболи 9х2 — 2у2 = 1.
20
159.	Знайти дотичні до гіперболи х2 — у2 = 16, паралельні до
прямої 5х — Зу — 17 = 0.
160.	Знайти дотичну до параболи у2 = 2%, перпендикулярну до
прямої 4х + у — 23 = 0.
161.	На параболі у2 = Зх знайти найближчу точку до прямої
х — 2у 4- 10 = 0.
162.	Осі еліпса збігаються з осями координат. Еліпс дотикаєть-
ся до прямих х + у = 5 і 4х -(-£/= 10. Скласти його рівняння.
163.	Довести, що дотична до конічного перерізу має з ним лише
одну спільну точку — точку дотику.
164.	Довести, що дотична до гіперболи разом з асимптотами
утворює трикутник з постійною площею.
165.	За якої умови пряма Ах + Ву ф- С = 0 дотикається до кри-
•• %2 і У2 14
^2	^>2
166.	З правого фокуса еліпса	= 1 під кутом а до
осі ОХ напрямлено промінь світла. Дійшовши до еліптичного дзер-
кала, промінь відбивається. Написати рівняння відбитого променя,
якщо = —2.
167.	З фокуса параболічного дзеркала у2 = 12х під кутом а на-
прямлено промінь світла. Дійшовши до параболи, промінь відби-
з
вається. Написати рівняння відбитого променя, якщо а = — .
168.	Довести, що дотичні до еліпса і гіперболи утворюють рівні
кути з фокальними радіусами, проведеними в точку дотику (оптична
властивість).
169.	Довести, що дотична до параболи утворює рівні кути з фо-
кальним радіусом і діаметром, проведеним через точку дотику (оп-
тична властивість параболи).
§ 7. Загальна теорія кривих другого
порядку
170.	Написати рівняння кривої другого порядку, що прохо-
дить через точки А41(0, —3), Л42(1, 0), М5 3^, Л44(2, —1) та
М5(-1, —2).
171.	Дві криві другого порядку мають п’ять спільних точок.
Довести, що вони збігаються (однакові).
172.	Дано рівняння лінії х2 + ху + 6% + Зу + 9 = 0. Встанови-
ти, при яких вартостях к пряма у = кх:
а)	перетинає цю лінію;
21
Ь)	дотикається до неї;
с)	має відносно неї асимптотичний напрям;
(1) не має з нею спільних точок.
173.	Знайти координати центра кривих:
1)	х2 — 2ху + 4г/2 + 5% — 1у + 12 = 0;
2)	х2 4- 2ху — у2 + 8х 4- 4г/ — 8 = 0;
3)	х2 — 2ху + у2 — 10а: — 6г/ 4“ 25 — 0;
4)	4х2 4- 4хг/ 4- у2 — 8% — 4г/ — 21 = 0;
5)	За2 4- 4ху 4- у2 — 2х — 1 = 0;
6)	х2 4- у2 4- 2хг/ — 2х — 2у 4- 4 = 0.
174.	Скласти рівняння діаметра параболи х2 — &ху 4- 9г/2 — 12% 4-
4- 14г/— 7 = 0, спряженого з хордами, що паралельні до осі ОХ.
175.	Знайти два спряжені діаметри кривої х2 4-2хг/— 4г/2 4-
4- 2х — 2 = 0, що утворюють між собою кут у 45°.
176.	Через точку Л4(5, 5) провести таку хорду кривої х2 — 2хг/4-
4- 2г/2 — 4% — 6г/ 4- 3 = 0, яка б у цій точці ділилася навпіл.
177.	Знайти середину тієї хорди кривої 5х2 — 2хг/4-#2 — Зх 4~
4- 2г/ — 5 = 0, яка лежить на прямій х — 2г/ — 1 = 0.
178.	Знайти асимптоти гіпербол:
1)	13х2 - 12ху - у2 4- 8х 4- 6г/ - 1 = 0;
2)	х2 — 4хг/ 4- 3% — 2г/ — 3 = 0;
3)	Зх2 4- 2ху — у2 4- 8% 4- 2г/ — 2 = 0;
4)	4хг/ 4- 2г/2 4- 4% — 6г/ 4- 1 = 0.
179.	Крива другого порядку проходить через точку Л4(1, —1),
а її асимптоти визначаються рівняннями 2х 4- Зг/ — 5 == 0, 5х 4~
4- Зу — 8 = 0. Скласти рівняння цієї кривої.
180.	Знайти осі симетрії кривих:
1)	х2 - г/2 4- 8х 4- 4г/ - 8 - 0;
2)	5х2 4- 8хг/ 4- 5г/2 - 18х - 18г/ 4- 9 = 0;
3)	5х2 4- 4хг/ 4- 8г/2 — 32х — 56г/ 4- 80 = 0.
181.	Знайти вісь та вершину кожної з парабол:
1)	х2 — 2ху 4- у2 - 10х — 2г/ — 1 = 0;
2)	х2 4- 2ху 4- г/2 4- 4х + 8г/ 4- 7 = 0;
3)	х2 4- 4хг/ 4- 4г/2 — 6х — 2г/ 4- 1 == 0.
22
182.	Звесги до канонічного вигляду рівняння кривої х2 — хг/ +
+ г/2 — 2х — 2г/ — 2 = 0 за допомогою ізометричних перетворень.
Відшукати формули перетворення координат.
183.	Віднести до головних осей рівняння ліній:
1)	5х2 + 4ху + 8г/2 - 32х - 56г/ + 80 = 0;
2)	5х2 + 12хг/— 22х — 12г/ — 19 = 0;
3)	х2 + 2ху + у2 — 8х + 4 = 0;
4)	5х2 + 8ху + 5г/2 — 18х — 18г/ + 9 = 0;
5)	4х2 — 4ху + у2 — 2х — 14г/ + 7 = 0.
184.	Визначити форму, розміри та розміщення ліній другого по-
рядку, заданих рівняннями:
1)	х2 - 8ху + 7г/2 + 6х - 6у + 9 = 0;
2)	Зх2 + ІОхг/ + Зг/2 - 12х - 12г/ - 23 = 0;
3)	4ху + 4х + 1 = 0;
4)	х2 - 2ху + у2 - 12х - 16г/ + 25 = 0.
185.	Які лінії зображають рівняння:
1)	2ху — 4х — 2г/ + 3 = 0;
2)	х2 — 2ху + у2 — 4х + 4у + 3 = 0;
3)	х2 — 2ху — Зу2 + 6х + 10г/ — 7 = 0;
4)	х2 + 2хг/ + г/2 + 2х + 2г/ + 1 = 0.
186.	З’ясувати особливості в розміщенні осей координат, якщо
параболи мають такі рівняння:
а)	х2 — 2ху + г/2 + 2х — 6г/ = 0;
Ь)	2х2 + 6х — у — 1 = 0;
с)	х2 — 5г/ = 0.
187.	Додати до лівої частини рівняння х2 + бхг/ + у2 + 6х +
+ 2г/ — 1 = 0 таке число, щоб після цього рівняння зображало па-
ру прямих.
188.	Які лінії зображаються рівнянням х2 — 2ху + Хг/2 — 4х—6г/+
+ 3 = 0 при різних вартостях параметра X?
189.	Методом вилучення квадратів встановити тип кривої:
1)	х2 + 2ху + 4У2 + 6х — 12г/ + 1 = 0;
2)	х2 + 4ху + 6г/2 — 2х + 4г/ + 18 = 0;
23
3)	х2 — 2ху + 4г/2 — 2х — 4г/ 4- 4 = 0;
4)	х2 — 2ху — Зу2 — 6х — 18г/ 4-1 = 0;
5)	ху 4- 4х — 2у 4- 3 = 0;
6)	х2 4- 4ху 4- 4г/2 4- Зх — 2у — 7 = 0;
7)	х2 — 2ху 4-г/24-6х4-у — 5 = 0;
8)	4х2 4- 4ху 4- г/2 — 8х — 4у 3 = 0;
9)	4х2 4- 8хг/ 4- 4г/2 — 12х — 12г/ 4- 9 = 0.
190.	Довести, що кожне з рівнянь
1)	х2 — вху 4- Зу2 — 4у — 4 = 0;
2)	5х2 — бху 4- 2г/2 — 2х 4- 2 = 0;
3)	4х2 4* 4хі/ 4-г/2 — 12х — 6г/ 4- 5 = 0;
4)	х2 4- 2ху 4- 2г/2 4- 6у 4- 9 = 0
зображує пару прямих.
РОЗДІЛ II	.———--------------
ВЕКТОРНА АЛГЕБРА
§ 1. Лінійні операції над векторами. Лінійна
залежність векторів
191.	За даними векторами а і Ь побудувати кожний з векторів:
1)	а +	2) а-Ь-, 3) 6-а; 4) -а-6; 5)	6) 2Ь 2 За-
192.	За яких умов вектори а-\-Ь і а — Ь будуть колінеарні?
193.	Яку особливість повинні мати вектори а і Ь, щоб справед-
ливі були рівності:
а) |а + &| = |а —&|; Ь) |а + &| = |а| + |&|;
с) а + Ь = К (а — 6); (і) | а + Ь | = | а | — | Ь |;
е) І а — & І = ] а ] + |6|?
194.	Яку умову повинні задовольняти вектори а і Ь, щоб век-
тор а + Ь ділив кут між ними навпіл. (Припускаємо, що всі три
вектори зведені до спільного початку).
195.	Довести, що сума векторів, які сполучають центр пра-
вильного многокутника з його вершинами, дорівнює нулеві.
196.	У трикутнику знайти таку точку, щоб сума векторів, що
виходять з цієї точки до вершин трикутника, дорівнювала нулеві.
197.	У трикутнику АВС вектор АВ = а, а вектор ВС = Ь. Знай-
ти вектори, що збігаються з медіанами цього трикутника.
198.	Довести, що з медіан трикутника можна побудувати три-
кутник.
25
199.	Визначити будь-який вектор, що ділить навпіл кут між век-
торами а \ Ь.
200.	Нехай гх, г2 і г3 — радіуси-вектори трьох послідовних вер-
шин паралелограма АВСО, Знайти радіус-вектор вершини О.
201.	Знайти рівнодійну п’яти компланарних сил однакової вели-
чини, прикладених до однієї і тієї ж точки, якщо кути між кожними
двома послідовними силами дорівнюють 72°.
202.	Визначити, при яких вартостях х і у вектори а та &, зв’я-
зані співвідношенням (3% — у + 2) а + (х + 2у + 3) Ь = 0, неколі-
неарні?
203.	При яких вартостях х, у та г вектори а, Ь і с, зв’язані
співвідношенням (х + у — г — 2) а+(2х — 2у + г — 1) Ь + (х — 1)с=
== 0, некомпланарні?
§ 2. Координати вектора. Проекції вектора
204.	Накресліть довільний базис ех, е2, е3. Побудуйте вектори
а= {1,2,0}, Ь — {-1, 3, 0}, с = {1, 2, 1}, 2 = {1, 2, -3}.
205.	Дано вектори а = { — 1, 3, 2}, &={0, 1, 4}. Обчислити ко-
. 7	7 а + 26 а — 2Ь сҐ ,
ординати векторів а + Ь, а — Ь, ——, 2а + оЬ.
о	£
206.	Чи можна з векторів	2, —3}, Ь = {2, —1, 1} та
с = {—3, —1, 2} скласти трикутник?
207.	Дано вектори а = {2. 1} і Ь — {3, 4}. Розкласти вектор т ~
= { —1, 2} за базисом а і Ь.
208.	Дано вектори а = {2, 1, —3}, Ь = {3, —2, 1} і с = { —1,
0, —2}. Розкласти вектор т = {—2, 2, 1} за базисом а, Ь і с.
209.	Дано точки А (2, —3, 4) і В (5, 6, —1). Обчислити коор-
динати векторів АВ і В А.
210.	Початок вектора а = {3, 1, — 5} збігається з точкою
Л1(—2, 7, 1). Знайти точку, з якою збігається його кінець.
26
211.	На матеріальну точку діють дві сили Рг = 2а і Рг = 36, де
а= {5, —2, 3}, &= {1, 0, —4}. Знайти їх рівнодійну.
212.	Дано чотири вектори а = {1,5,3}, Ь = {6, —4, —2},
с = {0, —5, 7} і (1 = {—20, 27, —35}. Дібрати числа а, р і у
так, щоб з векторів аа, р£ та ус можна було утворити замкнену
ламану лінію.
213.	Перевірити, що чотири точки Л(—1, 5, —10), В(5,—7,8),
С(2, 2, —7) і 0(5, —4, 2) є вершинами трапеції.
214.	Дано модуль вектора |а| = 5 і кути, які він утворює з
осями координат а = 120°, р = 4о° та у = 60°. Знайти його проек-
ції на координатні осі.
215.	Вантаж вагою з Р, підвішений на нитці до нерухомої точки,
затримується горизонтальною силою у положенні, при якому
нитка утворює з вертикаллю кут 45°. Знайти величину горизон-
тальної сили (2 і натягу Т нитки.
216.	Дано вектори а = {1, 3, 2} та Ь = {2 1, —1}. Визначити про-
екції на базисні вектори таких векторів:
1)а + &; 2)а-&; 3) 2а + ЗЬ та 4)^4.
217.	Знайти компоненту вектора а = 4пг-[-Зп — р на вісь орди-
нат, якщо т = 3і 2/ — 3£, п = і + 21г, р = — / 4- к.
§ 3. Скалярний добуток векторів
218.	Показати, що (а Ь)2 < | а |21Ь |2.
219.	Знайти кут між векторами а і Ь, знаючи, що | а |2 = 2,
\ї> |2 = 32, (а 6) = 4.
220.	Довести, що вектор с = Ь — а ^а~----перпендикулярний до
«2
вектора а.
27
221.	Подати синусі тангенс кута між векторами а та Ь через їх
квадрати та скалярний добуток.
222.	Яку умову повинні задовольняти вектори а і Ь, щоб
а + Ь І а — &?
223.	До вершини куба прикладені сили з величиною 1, 2, 3 та
направлені по діагоналях граней куба, що проходять через цю
вершину. Знайти величину рівнодійної цих сил.
224.	Знайти кут між бісектрисами двох координатних кутів
площин ХОУ та Х02.
225.	Знайти модуль вектора а = {5, —7, 6} та його напрямні
косинуси.
226.	Знайти орт вектора а= {3, —4, —5 ]/3].
227.	Визначити вектор а, знаючи дві його координати х = — З,
у — 4 та модуль | а | = 13.
228.	Знайти орт трьох векторів, які, виходячи з початку коор-
динат, ділять навпіл кути між ортами осей координат.
229.	Знайти модуль вектора а = — Зт + п, якщо \т \ = 1,
| п | = 3, (т, п) =	.
230.	Знайти кут між векторами а = 2т + п і Ь = — Зт + 2п,
якщо (т | = І п І = 2, а (т, п) = -у .
231.	Визначити внутрішні кути трикутника з вершинами
Л(0, 0,5), В(1, 1, 1) і С(—1, 2, 3).
232.	Вектори а, Ь і с утворюють трикут ник. Обчислити (а Ь) +
4- (Ь с) + {а с).
233.	Знайти вектор х, колінеарний до вектора а = {1, —1, 2}
-> ________________ ,
знаючи, що |хі = 31/6 та утворює він з віссю ОХ тупий кут.
234.	Знайти вектор, перпендикулярний до осі ОУ та до вектора
а = {1, 2, —3} з модулем ЗУ10.
235.	Знайти вектор х, який перпендикулярний до векторів
а={1, 1,2} і Ь = {3, 1,2} та задовольняє умову (х, Зі4-2/+&) = —6.
28
236.	Обчислити проекцію вектора а = 5/ + 2/ + 5к на вісь, ви-
значувану вектором Ь = 2і — ] 4- 2к.
237.	Дано три вектори а = {3, —6, 21}, &={1, 4, —5} і
с ~ {3, —4, 12}. Обчислити прс(а + &).
238.	Чи може вектор утворювати з координатними осями кути
1)а = 45°, 0 = 30°, у =120°;
2) а = 150°, р = 90\ у = 60°?
239.	Вектор утворює з осями ОХ, ОУ кути а = 30°, 0 = 90°.
Який кут він утворює з віссю 07?
240.	Вектор а утворює з осями координат ОХ, ОУ рівні кути,
а з віссю 02— кут у два рази більший, ніж з кожною з осей ОХ
і ОУ. Знайти а, 0 і у.
241.	Чи може вектор утворювати з віссю ОХ кут у 30°, а з
віссю 02 кут у 45°?
242.	Задано дві точки Л(— 1, 3, 2) і В(1, —2, 1). Знайти про-
екцію вектора АВ на вісь, яка утворює з координатними осями
рівні тупі кути.
243.	Задано вектори, що збігаються зі сторонами трикутника
АВС, АВ = 5і + 2/ і ВС = — 2і + 4/. Знайти довжину висоти
цього трикутника, опущеної з точки А.
244.	Перевірити тотожність
245.	Обчислити роботу, що її виконує сила / = {4, 5, 2}, коли
точка, до якої вона прикладена, рухаючись прямолінійно, перемісти-
лась з положення А (3, —7, 1) у положення В (6, —1, —2).
246.	Дано три сили Д = {3, —4, 2}, /2 = {2, 3, —5}, /3 =
== {—3, — 2, 4}, прикладені до однієї точки. Обчислити роботу, яку
виконує рівнодійна цих сил, коли точка, до якої вона прикладена,
рухаючись прямолінійно, перемістилась з точки Д(5, 3, —7) у точ-
ку В (4, —1, —4).
247.	Маса т, зосереджена в точці А(х, у, г), притягується,
згідно з законом Ньютона, до маси М., що зосереджена в початку
координат. Знайти силу притягання.
248.	У початку координат розміщений заряд д. Визначити в до-
вільній точці М (х, у, г) простору напругу Е електростатичного по-
ля, утвореного цим зарядом.
29
249.	До однієї і тієї ж точки прикладені дві сили Д та /2 і ді-
ють під кутом а. Знайти величину рівнодійної.
250.	Дано вектор а = {3, —4, 12}. Знайти координати одинич-
ного вектора, напрямленого однаково з вектором а.
251.	Дано точки Д(—2, 3, —4), В (3, 2, 5), С(1, —1, 2) та
£)(3, 2, —4). Обчислити пр^ДВ.
§ 4. Векторний добуток
252.	Вектори а і Ь утворюють кут ф =	| а | = ]/3, | Ь | = 4.
О
Обчислити |[а&]|.
253.	Позначивши через а кут між векторами а і &, виразити
через векторний і скалярний добуток цих векторів.
254.	При якій вартості а вектори р — аа — 4Ь і д = 2а Д- 5Ь
колінеарні?
255.	Вектори а, Ь та с задовольняють умову а Д- Ь Д- с = 0.
Довести, що [аЬ] = [Гс] = [са].
256.	Дано [ас] = [&, с], с=£0. Чи можна зробити висновок, що
а = к?
257.	Довести, якщо [а&] = [ссІ] і [ас] то вектори а—(і
та Ь — с є колінеарні.
258.	Обчислити площу паралелограма, побудованого на векторах
а = {8, 4, 1}, Ь = {2, —2, 1}.
259.	Дано точки А (3, 1, 2), В (4, 0, 1) і С (5, 4, 7). Обчислити
площу трикутника АВС.
260.	Знайти орт вектора, перпендикулярного до векторів
а = 2і Д- 2/ Д- к та Ь = 4і Д- 5/ Д- Зк.
261.	Знайти площу паралелограма, побудованого на векторах
-	-	-	->	->	->	->л-> я
а = т Д- п та Ь — Зт Д- 2п, де т і п — орти та (т, п) = -у .
262.	За якої умови момент сили відносно точки дорівнює ну-
леві?
зо
263.	До однієї точки А прикладено кілька сил /х, /2,...,
Довести, що момент рівнодійної / цих сил, обчислений відносно
деякої точки, дорівнює сумі моментів складових сил /х, /2, • • • , іп
відносно тієї ж точки.
264.	Сила / = {2, —4, 3} прикладена до точки Д(1, 5, —2).
Знайти момент цієї сили відносно точки В (5, —3, 4).
265.	Знайти момент сили відносно точки Д(3, —2, 1), якщо
ця сила прикладена до точки В (2, —1, 3), причому |/| = 5 і
7 II а, де а-= {2, 1, —2}.
266.	Сила ! = {2, 2, 9} прикладена до точки А (4, 2, —3). Ви-
значити величину та напрямні косинуси момента цієї сили відносно
точки В (2, 4, 0).
267.	По нескінченному прямолінійному провіднику тече струм з
силою І. Знайти в будь-якій точці простору напруженість Н маг-
нітного поля, утвореного цим струмом, використовуючи при визна-
ченні напряму вектора напруженості Н правило свердлика.
Використовуючи розв’язок задачі 267, розв’язати такі задачі:
268.	Обчислити в будь-якій точці простору напруженість Я маг-
нітного поля, утвореного струмом, що тече по прямолінійному про-
віднику, якщо напрям провідника збігається з напрямом а) осі ОХ\
Ь) осі О¥\ с) осі 02.
269.	Обчислити в точці Л4(—3, 4, 2) напруженість Н магніт-
ного поля, утвореного струмом з силою І — —Зк, який тече по пря-
молінійному провіднику.
270.	Обчислити в точці Л4(4, —3, 1) напруженість Н магнітно-
го поля, утвореного струмом з силою І — 5і, який тече по прямо-
лінійному провіднику. Знайти орт вектора Н.
271.	Обчислити в точці М(2, 5, 0) напруженість Н магнітного
поля, утвореного струмом з силою І = — 2/, який тече по прямо-
лінійному провіднику та знайти напрямні косинуси вектора Н.
272.	Обчислити в точці Л4(—1, 3, —2) напруженість Н маг-
нітного поля, утвореного струмом з силою І = 2к, який тече по пря-
31
молінійному провіднику. Знайти кут, утворений вектором з бісек-
трисою координатного кута а:) ХО¥', Ь) Х07; с) ¥07.
§ 5. Мішаний добуток трьох векторів.
Подвійний векторний добуток
273.	Обчислити мішані добутки векторів:
1)	(7, 1); 2) (1, /, 7); 3) (7, І, /); 4) (7, [7, 7+7+їв.
274.	Довести, що при будь-яких векторах а, Ь і с вектори Ь — с,
а — Ь та с — а компланарні.
275.	Довести, що а [Ь г] == а [Ь, с + Ха + ц&], де Я та р — будь-
які числа.
276.	Довести, що кінці радіусів-векторів і\ = {4, —2, —2},
г2 — {3, 1, 1}, г3 = {4, 2, 0} і г4= (7, —1, —6} лежать в одній
площині.
277.	Довести, що
І аЬ 6 + с с + а ]	1 Ґ Т "Т
2~ ’ ~2~’	— Ь’СУ
278.	Точки Л(— 1, 2, —3), В(—2, 5, 1), С(—1, 6, 0),
О (2, 5, —6) є вершинами чотирикутника. Довести, що цей чоти-
рикутник плоский, та знайти його площу.
279.	У тетраедрі ОАВС з вершини О проведені медіани боко-
вих граней. Беручи їх за ребра нового тетраедра, довести, що об’єм
його становить об’єму тетраедра ОАВС.
280.	Встановити, чи компланарні вектори:
1)	а = {2,	1, 3}, Ь = {1,	-3,	2),	= {4,	-5, 7};
2)	7 - (1,	-1, 2}, Ь =	(5 1,	3},	"с = (0,	1, -1}.
281.	Довести,	що вектори а	= [3,	2,	—1}, Ь={1, —	1,	3}	і
с ~ {9,	1,	7} лінійно залежні, та	знайти	будь-яку	лінійну	залеж-
ність між ними.
282.	З’ясувати, чи лежать точки Л(2, 3, 1), В (6, 1, 4),
С(0, —1, 1) та 0(2, —1, 3) в одній площині.
32
283.	З’ясувати, праву чи ліву трійку утворюють вектори:
а)	а = }2, 1, 2}, Ь = (3, -2, 1}, с= {З, -1, -2};
Ь)	а — {2, —2, -3}, Г=}2,0,3}, с*={1,1,1}.
284.	Знайти об’єм тетраедра за вершинами А(—5, —4, 8),
В (2, 3, 1), С(4, 1, —2) та 0(6, 3, 7).
285.	Знайти довжину висоти тетраедра з вершинами А(1, 0, 6),
В (4, 5, —2), С(7, 3, 4) та О(—1, 2, 1), опущеної з вершини О.
286.	Об’єм тетраедра V = 5, три його вершини знаходяться в
точках А (2, 1, —1), В (З, 0, 1), С(2, —1, 3). Знайти координати
четвертої вершини, коли відомо, що вона лежить на осі 0¥.
287.	Обчислити [[а ~Ь\ с], якщо:
1)	а= {1, 2, -1}, £={2, 1,-2}, с={3, 1, — 1};
2)	а = (3, 2,1},	£={0, 1, -1},	с={—1, 1, 1}.
288.	Обчислити [[а&]с] —	якщо а={1, —1,3},
6= }-2, 2, 1} і с = {3, -2, 5).
289.	Довести тотожності:
а)	[а |Ьс]] + іИсаЦ +	=0;
Ь)	\а Ь\ |і>с] [са] = (а Ьс)2.
290.	За якої умови [[а &] с} = 0.
З 2193
РОЗДІЛ III
АНАЛІТИЧНА ГЕОМЕТРІЯ
В ПРОСТОРІ
§ 1. Координати точки. Перетворення
координат
291.	Побудувати точки Л(3, 2, 1), В (4, —1, —2), С(—5, 3, 4)
та 0(0, 5, —2).
292.	Ребро куба дорівнює а. Знайти координати його вершин, бе-
ручи за початок координат одну з його вершин, а за осі — прямі,
на яких лежать ребра.
293.	На осі 02 знайти точку, рівновіддалену від точок
Л(3, 5, —2) і В (—4, 1, 7).
294.	Знайти центр сфери, описаної навколо тетраедра з вершина-
ми (0, 0, 0), (а, 0, 0), (0, 6, 0) та (0, 0, с).
295.	Довести, що трикутник з вершинами Л(3, 1, —2)
В (6, 2, —2) і С(0, 2, 1) рівнобедрений.
296.	Довести, що трикутник з вершинами Л(3, 1, —2), В(6, 2,
—2) і С(0, 2, 1) прямокутний.
297.	Дано Л4Х(3, 2, -5), Л42(1, —4, 3) і Л43(-3, 0, 1)-сере-
дини сторін трикутника. Знайти його вершини.
298.	Нехай Л(3, -1, 2), В(1, 2, -4) і С(-1, 1, 2) - три
вершини паралелограма. Знайти його четверту вершину.
299.	На вершинах тетраедра Ах (х^	г4), В (х2, у2, г2),
С(х2, Уз, гз) і О(х4, у4, г4) зосереджені відповідно маси /пь т2, т3
та т4. Знайти центр ваги цієї системи.
300.	Нехай Л(1, 2, -1), В(2, -1, 3) і С(-4, 7, 5) - верши-
ни трикутника. Знайти довжину бісектриси його внутрішнього кута
при вершині В.
ЗОЇ.	На прямій, що проходить через точки Л(—1, 2, 1) та
В (2, 3, —2), знайти точку з абсцисою х = 5.
302.	Знайти відношення, в яких кожна з координатних площин
поділяє віддаль між точками А (2, —1, 7) та В (4, 5, —2).
34
303< З’ясувати, чи лежать точки Л(1, —5, 3), В (5, —1, 7) {
С(6, 0, 8) на одній прямій.
304.	Координатні вектори базисів и, V, ію та и!, V', їо)' зв’язані
співвідношеннями и' = и —	V' = и — гю та = 2и — V —
Вектор а відносно базису и', V', їо)' має координати {1, 1, 1}. Знайти
координати а в базисі иу V, до
305.	Дано координатний базис иу V, ію і відносно його вектори
а — (2, 2, 0}, Ь = (— 1, 3, 1} та с— {1, 0, 2}. Новий базис а', V',
ю)' пов’язаний з даним так: и = и' — 2г/, V = и' V' — ге/, ш =
= 2и'— V' + ге/. Знайти координати векторів а, Ь та с відносно ба-
зису и!, г/, їо)' .
306.	Нові координати довільної точки визначаються через старі
х' = 2х + Зу — 1, у' = 2х — 2у + 2 + 1, г' — х + у — 2. Визначити
а) старі координати через нові; Ь) залежність між векторами обох
базисів.
307.	Вершини тетраедра спочатку збігалися з точками А (— 7,
З, __2), В(0, 2, 1), С(4, — 1, 0) і £>(—1, 0, —3). Внаслідок по-
ступового руху центр ваги тетраедра перемістився в точку
Л4(6, —2, 1). Які будуть координати його вершин після перемі-
щення?
308.	Координати деяких точок справджують рівняння Зх2 + У2—
— 2x2 + 2х — 6у + 4г — 5 = 0. Яке рівняння будут справджувати
нові координати тих же точок, якщо перенести початок координат
у точку О\—1, 1, 2)?
309.	Якого вигляду набере рівняння 2 = ху, якщо, не змінюючи
осі 02, бісектриси кутів ХОУ взяти за нові осі ОХ і ОУ?
310.	Переконатися, що перетворення координат
2х' + Зу' + 6г' . су	6х' + 2у' — Зг' «
х —----------------2, у =----------7-------о,
___ Зх' — Зу' -|- 2г' і
г— 7	і
ортогональне. Знайти формули, які виражають нові координати че-
рез старі і пересвідчитися, що і це перетворення є також орто-
гональне.
З”
35
311.	Знайти такі а, 0 і у, щоб матриця
а	0	у
1	4	8
9	9	9
8	4	1
9	9	9
була ортогональною та щоб її визничник дорівнював +1.
312.	Положення нових осей прямокутних координат відносно
старих визначається Ейлеровими кутами 0 = 30°, яр = 60°, ер = 45°.
Початок координат спільний. Визначити старі координати довільної
точки через її нові координати.
§ 2. Площина
313.	Перевірити, які з точок Л(—1, 2, 3), В(1, —2, 1),
С(0, 1, 2), І) (3, 0, 3) і а Е(5, —7, 11) лежать на площині 2х —
— Зу + г — 9 = 0.
314.	Знайти об’єм тетраедра, який відтинає від координатного
кута кожна з площин:
а)	Зх — 2у + 2 — 12 = 0;	с) х — у + Зг — 3 = 0;
Ь)	х + 2у — 5г + 10—0;	сі) 2х + §у — 4г — 20 = 0.
315.	Визначити координати нормального вектора площини, яка
проходить через точки А (2, —1, 1), В (3, 1, 0) і С(1, 5, —2).
316.	Скласти рівняння площини, якщо точки Л(1, —2, 0) і
В (3, 2, 6) симетричні відносно неї.
317.	Скласти рівняння площини, якщо точка Д(—1, 2, 3) є ос-
новою перпендикуляра, опущеного з початку координат на площину.
318.	Скласти рівняння кожної площини, що проходить через
точку Р{—3, 2,5) і паралельна до координатної.
319.	Скласти рівняння кожної площини, що проходить через
точку Р{—1, 3, 7) та координатну вісь.
320.	Площина проходить через точки А (1, 2, 1) та В (0, 3, — 1),
паралельно до осі 02. Написати її рівняння.
321.	Скласти рівняння площини, що проходить через точку
Р(—1, 2, 3) і відтинає від осей ОХ та О¥ відрізки а=2, Ь — — 1.
322.	Через точку Р(1, 2, —1) провести площину, що відтинає
від осей координат рівні відрізки.
323.	Знайти точку перетину площин х + у — г 2 = 0, 2х +
4- у — 5 = 0 та 4х — Зу — 2г + 5 = 0.
36
324.	При яких вартостях І і т площини 2х — у 4- Зг — 1 =0,
х-[-2у — г + т = 0 та х + Іу — 6г -|- 10 = 0 перетинаються а) в од-
ній точці; Ь) по прямій; с) по паралельних прямих?
325.	Через точку Р(1, —1, 3) провести площину, перпендику-
лярну до площин х — 2у — 23 = 0, Зх 4- 2у — г — 1 = 0.
326.	Через лінію перетину площин х + у — г -}- 5 = 0 та 2х 4-
У + г~ 3 = 0 провести площину:
а)	що проходить через точку М(—1, 3, 4);
Ь)	паралельну до осі О¥\
с)	перпендикулярну до площини Зх — у + 2г — 11 =0;
й) що утворює з площиною х — 2г/+ 2г—17 = 0 кут
1
а = агссоз —— .
3/3
327.	Написати рівняння площини, яка перпендикулярна до пло-
щини Зх — у + Зг — 2 = 0 та перетинає її по прямій, шо лежить у
площині ХО¥.
328.	Довести, що площини х — 2г/ + Зг — 13=0, 5х 4- — г —
— 11 = 0 та Зх 4- 5г/ — 7г 4- 15 = 0 проходять через одну й ту ж
пряму.
329.	Через точку перетину площин 5х 4- Зу — г — 7 = 0, х 4-
4- 2у 4- Зг — 1 = 0 та 2х — Зу 4- 2г — 9 = 0 провести площину, яка
проходила б:
а)	через точки Рх(1, 2, 4) і Р2(—1, 3, 1);
Ь)	через вісь ОУ;
с)	через пряму і/4-2 = 0, х 4- 2г 4- 1 = 0;
через ту ж точку провести площину, яка
ії) була б паралельна до площини Зх — Зу 4- 8г — 19 = 0;
е) була б перпендикулярна до площин у = 0, 2х 4- Зг — 11 = 0.
330.	На осі О¥ знайти точку, рівновіддалену від двох площин
х — 2у -|- Зг — 6 = 0 і 2х 4~ Зу 4- г — 1 = 0.
331.	На віддалі 5 одиниць від площини х — 2у 4- 2г — 14 = 0
провести площину, паралельну до неї.
332.	Знайти віддаль між площинами 2х-|-2і/ —г—15 = 0
і 4х 4- 4і/ — 2г 4- 11=0.
333.	Дві грані куба лежать на площинах 2х — 2у 4- г — 1 = 0 і
2х — 2у -|- г -|- 5 = 0. Знайти його об’єм.
334.	Скласти рівняння геометричного місця точок, рівновіддале-
них від двох площин х 4- 5і/ — 2г — 3 = 0 та х 4- Зу — 2г 4- 1 = 0.
335.	Довести, що точки простору, координати яких задовольня-
ють умову | Ах 4- В у -|- Сг 4- О | < й2, розміщені між паралельними
площинами Ах + Ву 4- Сг 4- О ± с?2 = 0.
37
336.	Скласти рівняння площини, що поділяє навпіл двогранний
кут між площинами:
а)	х — 2у + 5г — 11 = 0 та 2х + у + 5г — 5 = 0;
Ь)	Зх + у — г— 1=0 та х — Зг/ + г — 3 = 0.
337.	Скласти рівняння площини, що поділяє навпіл той двогранний
кут між площинами 2х — у + 2г — 3 = 0 і Зх + 2у — 6г — 1 = 0, в
якому знаходиться точка М(1, 2, —3).
338.	З’ясувати, чи перетинає площина х — 2г/ + Зг — 2 = 0 від-
різок ЛВ, якщо Л(—3, 1, 2), В(—1, 0, 2).
§ 3. Пряма у просторі
339.	Скласти рівняння прямої, що проходить через точки
Р1( — 1, 2, 1) і Р2(1, 2, 4), та знайти координати її напрямного
вектора.
340.	Дано рівняння руху точки М (х, у, г): х = 3 — 4/, у = 5 +
+ Зі та г = — 2 + 12/. Визначити її швидкість.
341.	Нехай х = 5 — 2/, у = — 3 + 2/, г = 5 — і — рівняння руху
точки Л4(х, у, г). Визначити шлях 5, пройдений точкою за промі-
жок часу від і = 0 до і = 7.
342.	Знайти точки перетину прямої х — 2у + Зг — 6 = 0, х-\-у—
— 2г + 4 = 0 з координатними площинами.
343.	Знайти канонічні рівняння прямих:
|х — Зу + 2г — 5 = 0,	(2х — у + 5г — 1 = 0,
а) [Зх - 2у - г + 6 = 0;	|3х - 2у + 6г - 1 = 0;
С \х + У + 2 — 1 = 0.
344.	Через точку Р(—1, 2, 3) провести пряму, паралельну до
прямої
| 2х — Зу + г — 11=0,
( х — у + 2г + 9 = 0.
345.	Скласти рівняння прямої, яка проходить через початок ко-
ординат і точку (а, &, с).
346.	Знайти рівняння ребер тетраедра з вершинами Л(0, 0, 2),
В (4, 0, 5), С(5, 3, 0) і В(—1, 4, —2).
347.	Знайти кути, які утворює пряма	= ---^1- з
осями координат.
38
348.	Визначити плоскі кути при вершині А тетраедра з верши-
нами А(3, —1, 0), В(0, —7, 3), С(—2, 1, —1) і Р(3, 2, 6).
349.	Довести, що прямі
І 2х	2у	г 10 = 0 х + 7 у — 5	2 — 9
2 —22 = 0 Та З-	= —~
паралельні.
350.	Скласти рівняння бісектриси кута А трикутника з верши-
нами Д(—1, 0, 2), В(3, 3, —10), С(11, —4, —1).
351.	Довести, що прямі
х — \ у — 7 _ г — 5 х — 6 у + 1 __ г
~~2~ ~ "Т“ ” “ПГ“ т з “ ~~2~~ - 1
перетинаються.
352.	З точки Р(—1, 3, 1) опустити перпендикуляр на пряму
X + 1 у — 1	2 — 2
"У” ~ “У ~ У"'
353.	Скласти рівняння прямої, яка проходить через точку
М(—4, —5, +3) і перетинає прямі
х4-1__# + 3_г—2 . х — 2 __ у \ __2 — 1
"У “ УГ“ УГ 1 “У ~"У “ “У ‘
354.	Скласти рівняння прямої, яка проходить через точку
М(—1, 2, — 3) перпендикулярно до вектора {6, —2, —3}
і пе-
X — 1 у + 1	2 — З
ретинає пряму —= —=-
О	--□
355. Довести, що прямі
х = 3/ — 7,
у = — 2/ + 4, та
2 = 3/ 4“ 4
х = і 4- 1,
у = 2/ — 8,
г= —і— 12
мимобіжні, та знайти рівняння їх спільного перпендикуляра.
§ 4.	Пряма й площина
356.	Через точку Л40(х0, г/0, г0) провести пряму, паралельну до
площин Атх 4- ВіУ 4- Сг2 + Ї)1 = 0 та А2х 4- В2у 4- С2г + О2 = 0.
357.	Через точку Л40(1, —3, 5) провести пряму, перпендикуляр-
но до площини х4- 6г/ — 5г — 17 = 0.
358.	Знайти проекцію точки Ро(—1, 3, 2) на площину х —2г/4-
+ 5г 4- 27 - 0.
359.	Положення дзеркала визначається рівнянням Зх 4- У — 2г =
= 0. Визначити положення дзеркального відбиття точки А (1, 3, —4).
39
360.	На площині 2х — */4-Зг — 9 = 0 знайти точку, сума від-
далей якої від точок Л(—1, 0, 1) та В (3, 1, 1) була б найменшою.
361.	Довести, що прямі
х — 1  у — 7 г — 5	х — 6	г/ —1   г
~2“ “ ~Т“ “ ~Т~ та Т “	“ Т
перетинаються, та скласти рівняння площини, на якій вони лежать.
362. Довести, що прямі х = 2/ 4- 5, у — — /4-2, г = / — 7 і
| х 4~ Зі/ 4- г 4- 2 = 0,
І х — у — Зг — 2 = 0
паралельні, та знайти рівняння площини, на якій вони лежать.
363.	Скласти рівняння площини, що проходить через точку
г(5, 7, —1) та перпендикулярна до прямої —~	-
364.	Знайти проекцію точки Р(1, 2, у) на пряму	=
= г+1
2	‘
365.	Знайти точку, симетричну точці Р(1, —2, —6) відносно
прямої
їх — у 2г — 1=0,
(х — г + 2 = 0.
366.	Знайти віддаль точки Р(—1, 3, 3) від прямої
х—1 у _ г+2
—2 — 1	1	’
367.	Знайти віддаль між прямими
( 2х -|- 2у г Ю = 0, х 7 у — д г — д
(х — у — г — 22 = 0	1 — = “=Г = ~Т~ ‘
368.	Точка М(х,у,г) рухається прямолінійно й рівномірно з по-
чаткового положення Мо(11, —21, 20) у напрямі вектора
5= ( — 1, 2, —2} з швидкістю V = 12. За який час вона пройде
відрізок траєкторії між двома паралельними площинами 2х 4~ Зг/ 4-
4- 5г 4- 31 = 0 та 2х 4- Зу 4- 5г — 41 = 0?
369.	Довести, що геометричне місце точок, рівновіддалених від
вершин трикутника, є пряма. Скласти її рівняння, якщо А (хг, уу гг),
В (х2, у2, г2) та С3 (х3, у3, г3) є вершини трикутника.
370.	Скласти рівняння площини, що проходить через пряму
х 4- 2/ 4- 1, у = —Зі 4-2, г = 2/ — 3 і точку М (2, —2, 1).
40
371.	Знайти проекцію кожної з прямих
1 _ у — 2_ г + і. м /х ~ У + ? — 2 = 0,
' 2 ~ 1 “ -1 ’	\2х + у-г+ 1 = 0
на координатні площини.
372.	Знайти проекцію прямої
х — 2 у 4- 1	2 4~ З
= Т" = ~2~
на площину х + 4у — 2г — 11 = 0.
373.	Скласти рівняння площини, яка проходить через пряму
х = Зі 4- 1, у = 2/ 4- 3, г = — і — 2 та паралельна до прямої
( 2х — у + г— 3 = 0,
І х 4- 2# — г — 5 = 0.
374.	Скласти рівняння прямої, що проходить через точку Л40 (З,
—2, —4), паралельна до площин Зх — 2у — Зг — 4 = 0 та перети-
нає пряму
х — 2	#4-2 г — 1
“3~ “ ^=6" “ 19 ‘
375. На прямій
1 х 4- 2у + г — 1 = 0,
| Зх — у + 4г — 29 = 0
визначити точку, рівновіддалену від точок Л(3, 11, 4) та
В (-5, -13, —2).
376.	При яких вартостях параметрів А і И пряма
х —З у—1 ____ г + З
~Т~ = "=4 І
лежить на площині Ах 4- 2у — 4г 4- В = 0?
377.	Знайти рівняння спільного перпендикуляра двох мимобіж-
них прямих:
м *-~9 — У + 2 _ 2	х _ У + 1 — 2 —2
4 “ —3 “ 1	—2 ~ 9 “ 2 •
378.	Знайти найкоротшу віддаль між прямими:
ч х 4- 3 у — 6 г — 3 х —4	#4-1	г4-7
а) — =^з-=-г-та
41
Мх + 4 —^“~4— г+1 та * + 5 у —5	2 — 5 .
~2~ “	“ “=Т" Т3 ~4~ ~ -3 - "=Г~ ’
с) £+$ =	= г~^- та х = 6/ + 9, у = — 2/; г = — і 4- 2.
§ 5.	Геометричний зміст рівнянь з трьома
невідомими. Сфера
379.	Знайти рівняння геометричного місця точок простору, су-
ма віддалей яких від двох даних точок /\(—с, 0, 0) та Рг(с, 0, 0)
є стала й дорівнює 2а.
380.	Знайти рівняння геометричного місця точок, рівновіддале-
них від данної точки і даної площини.
381.	Скласти рівняння поверхні, яку описує стержень, що ков-
зає по трьох ребрах куба, з яких жодні два не лежагь в одній
площині. Ребро куба дорівнює а.
382.	Скласти рівняння поверхні, що утворює пряма, ковзаючи
по трьох прямих
х у — 1 г х — 2 у г п п х у 4-1 г
~б- — Т~— Т та	~о~ ~ Т’
кожні дві з яких є мимобіжні.
383.	Скласти рівняння поверхні, утвореної прямою, яка ковзає
по прямих
х — 6_ У _ 2-1 X	у — 8 _ г 4- 4
З	2	13	2	- — 2 ’
залишаючись паралельною до площини 2х 4- Зу — 5 = 0.
384.	Знайти геометричне місце гочок, однаково віддалених від
(у = г,
осі 02 та від прямої {	1
385.	Скласти рівняння сфери з центром С (а, Ь, с) та радіусом г.
386.	Скласти рівняння сфери, центр якої знаходиться в точці
С(5, —3, 7), а радіус дорівнює 9.
387.	Сфера проходить через точку А (2, —1, —3) і має центр у
точці С (3, —2, 1). Скласти рівняння цієї сфери.
388.	Визначити центри і радіуси сфер:
а)	х2 4- у2 + г2 — 6х 4- 2у — 2г 4- 7 = 0;
6)	х2 4- у2 + г2 — 4х 4- Зу — 8г 4- 22 = 0;
с)	х2 4- #2 4- г2 — х 4~ З# — 2г — 3 = 0.
42
389.	Скласти рівняння сфери з радіусом г = 3, яка дотикаєте ся
до площини х + 2у + 2г + 3 = 0 у точці М (1, 1, —3).
390.	Скласти рівняння діаметра сфери х2 4- у2 + г2 — 4х — 2у +
4- 2г — 19=0, паралельного до прямої х = 21 — 1, у = — З/ + 5,
г = 4/ -р 7.
391.	Знайти найкоротшу віддаль від точки А до даної сфери в
таких випадках:
а)	А (—2, 6, -3), х2 4- У2 + г2 = 4;
Ь)	Л(1, -1, 3), х* + у2 + г2-6х + 4у- 10г — 62 = 0.
392.	На сфері (х — І)2 4- (у + 2)2 4- (г — З)2 = 25 знайти точку,
найближчу до площини Зх — 4г 4- 19 = 0.
§ 6. Циліндри та конуси
393.	Скласти рівняння циліндра з напрямною
{у2	»/2
— 4- —= 1
а2 Ь2	’
г = 0
й твірною, паралельною до осі 02.
394.	Скласти рівняння циліндра з напрямною
І у2 = 2рх,
і г =0
й твірною, паралельною до осі 02.
395.	Скласти рівняння циліндра з напрямною
і х2 4- 4#2 = 8,
І г = 0
й напрямним вектором твірної и = {—3, 2, 1}.
396.	Напрямна ціліндра визначається рівнянням х = у2 4- ?2,
х = 2г, а твірна перпендикулярна до площини напрямної. Скласти
рівняння циліндра.
397.	Скласти рівняння циліндра, описаного навколо сфери х2 4-
4- у2 4- г2 = 4, якщо його твірні перпендикулярні до площини
х — у 4- 2г — 11 =0.
398.	Скласти рівняння циліндра, описаного навколо двох сфер
(х - 2)2 4- (у - І)2 4- г2 - 25, х2 4- у2 4- г2 = 25.
43
399.	Визначити рівняння конуса, який проектує еліпс
( у2 + 2г2 = 10,
І х = 0
з точки 5(—1, 3, 2).
400.	Скласти рівняння конуса з вершиною в точці 5 (0, 0, с) та
напрямною
х2 ,	_ і
. а2 б2 “ ’
.2 = 0.
401.	Напрямна конуса визначається рівнянням
| Зх2 + б#2 — г = 0,
| х + у + г= 1,
а вершина його знаходиться в точці 5 (—3, 0, 0). Скласти рівняння
конуса.
402.	Скласти рівняння круглого конуса, якщо координатні осі
є його твірними.
403.	Скласти рівняння конуса з вершиною 5 (—4, 3, 6), дотич-
ного до сфери х2 + у2 + г2 = 1.
404.	Скласти рівняння конуса з вершиною в точці 5(3, 0, — 1),
якщо його твірні дотикаються до еліпсоїда х2 + Зу2 + 22а = 6.
§ 7. Поверхні другого порядку
405.	Пряма у — а, задана в площині ХОУ, обертається навколо
осі ОХ. Скласти рівняння описаного нею циліндра.
406.	Знайти рівняння поверхні, утвореної обертанням прямої
х — 2 у г	.
-у- =	— навколо осі ОХ.
407.	Пряма х — 1 = у + 1 = 2 обертається навколо осі 02. Знай-
ти рівняння поверхні обертання.
408.	Скласти рівняння поверхні, утвореної обертанням еліпса
%2	22
— —а- = 1, у = 0 навколо осі 02.
409.	Скласти рівняння поверхні, утвореної обертанням гіперболи
^2	2^2
—-------Г = 1, у — 0 а) навколо осі ОХ; Ь) навколо осі 02.
( х2 = 2рг,
410.	Парабола | у —0 обертається навколо своєї осі симет-
рії. Знайти рівняння утвореної поверхні.
44
411.	Коефіцієнт рівномірного стиску простору до площини ¥02
дорівнює Скласти рівняння поверхні, в яку перетвориться
о2 ^2
еліпсоїд обертання — + -у- 4- — = 1 при цьому стисканні.
412.	Визначити коефіцієнти кг і к2 двох послідовних рівномір-
них стискань простору до координатних площин Х0¥ і Х02, які
.	х2 * у2 г2 1	х2 , у2 .
перетворюють сферу ~2Г + -^- + -25“ = 1 в еліпсоїд -25" +	+
^2	£<2
413.	Визначити відрізки, які відтинає еліпсоїд— +г2 = 1
на осях координат.
л і л тт •	•	х2 , у2 г2
414.	Де розміщені ТОЧКИ Простору, ДЛЯ ЯКИХ	“
- 1 <0?
415.	Довести, що площини г — 2 = 0 і г + 2 = 0 перетинають
і/2
гіперболічний параболоїд х2 —^- = 2г по спряжених гіперболах; ви-
значити їх осі та ексцентриситет.
416.	Довести, що площина # — 4 = 0 перетинає еліптичний па-
раболоїд -~- + ~- = 4г по параболі; визначити її параметр і вер-
шину.
417.	Визначити лінію перетину однополого гіперболоїда х2+
+ у2 — г2 = 1 з площиною х — г + 1 = 0, проектуючи її на коорди-
натні площини.
418.	Визначити рівняння проекції на площину ХО¥ лінії
| х2 — у2 = г,
| 2х — г — 1 = 0.
419.	Визначити тип лінії, що її дістаємо внаслідок перетину
^2	£<2
еліпсоїда "[є + 4 + г2 = 1 з площиною х + 4г — 4 = 0, та обчис-
лити координати її центра.
420.	Встановити, які лінії визначаються рівняннями:
а)
2 + 6 ~2г’	Ь) 4 З
Зх — у + 6г — 14 = 0;	| х — 2# 4- 2 = 0;
с)
( 6х24-г/2 —г2 = 1,
I 6х + 2# — Зг — 1 = 0.
45
421.	Встановити, при яких вартостях І площина х + іг — 1 =0
перетинає двополий гіперболоїд х2 4- у2 — г2 = — 1 а) по еліпсу;
Ь) по гіперболі.
х2 г2
422.	Довести, що еліптичний параболоїд —	— = 2у має од-
ну спільну точку з площиною 2х — 2у — г — 10 = 0, та знайти її
координати.
£/2	2»2
423.	Довести, що двополий гіперболоїд -у + —---= — 1 має
лише одну спільну точку з площиною 5х + 2г + 5 = 0, та знайти
її координати.
424.	Знайти точки перетину поверхні:
. х2 , у2 . г2 .	х — 4 у + 6	? 4- 2
й) -де- +	-т~ -4- — 1 3 Прямою -у— — —у — —— ;
<х х2 . у2 9	<	х — 4 у -(-З г — 1
+ —2- = 1 3 ПРЯМОЮ —Г==-Т- = —
с) х2 — Ьу2 = 4г з прямою = ~Т =	’
425.	Знайти геометричне місце прямих, що проходять через центр
поверхні другого порядку й дотикаються до неї у нескінченності.
426.	Через точку Р(—1, 2, 1) провести прямі так, щоб кожна
з них перетинала поверхню -§- + -4----х~ =\ лише в одній точці.
427.	Скласти рівняння дотичних площин до поверхонь:
х2 у	у2 .	г2 . м х2 , у2 о	х2 у2 г2	А
і)	±	= і; е) х2 = 2ру у точці	М(| (х0, у0,	г0).
428.	Скласти рівняння нормалі до поверхні 10х24- Ібу2 — г2 = 1
у точці Р(1, —1,5).
429.	Написати рівняння дотичної площини до поверхні х2 4-
4- 4у2 — 2г у точці Р(—2, 1, 4).
430.	Знайти дотичну площину до еліптичного параболоїда
І!2
х2 +	= 2г, паралельну до площини 2х — у 2г — 17 = 0.
431.	Скласти рівняння дотичної площини до однополого гіпер-
«2 г2
болоїда х2 + ---------4~~1’	перпендикулярної до вектора
п = {6, 1, 3}.
46
432.	Дано гіперболічний параболоїд у2-— = х. Скласти рів-
няння дотичної площини до нього в точці М (21, 5, 4) та визначи-
ти лінію перетину її з поверхнею.
433.	Скласти рівняння дотичного конуса до еліпсоїда	+
г2
+ -5- = 1 з вершиною в точці 5(3, 0, —1).
ІІ/-0.
434.	Через пряму ] г । провести площини, дотичні до дво-
х2 и2 г2
полого гіперболоїда -у + у-------їб’“ — та визначити точки їх
дотику.
435.	Рівняння ІОх — 2у — г — 21 = 0 визначає одну з дотичних
ї/2
площин гіперболічного параболоїда х2 —у — г. Знайти рівняння
кожної з тих двох прямих, по яких вони перетинаються.
436.	Довести, що площина 4х — 5у — 10г — 20 = 0 перетинає
х2 и2 з2
ОДНОПОЛИЙ гіперболоїд 25" + -у0---4“— 1 по прямолінійних твір-
них. Скласти рівняння цих твірних.
437.	Впевнившись, що точка Л4(1, 3, —1) лежить на гіпербо-
лічному параболоїді 4х2 — г2 = у, скласти рівняння його прямолі-
нійних твірних, що проходять через точку М. і визначити гострий
кут між ними.
438.	Скласти рівняння прямолінійних твірних однополого гіпер-
X2 І!2
болоїда -у + -------= 1, паралельних площині 6х + 4у -{- Зг —
-11-0.
439.	Знайти прямолінійні твірні гіперболічного параболоїда
г — аху.
440.	Довести, що точки А (12, 4, 12) і В (6, 8, —12) лежать
.	. х2 у2
на одній твірній поверхні -------- = г.
441.	Під яким кутом до осі конуса х2 — 4у2 — 9г2 — 0 нахилені
площини його колових перерізів?
442.	Визначити геометричне місце центрів і радіуси колових
перерізів циліндра х2 + 5г2 — 1. Скласти рівняння їх площин.
443.	Визначити точки заокруглення еліпсоїда х2 + 2у2 + 6г2—15.
444.	Визначити колові перерізи, які проходять через точку
X2 її2
М(—2, 0, 1) еліптичного параболоїда -у + -у--=г, і обчислити
кут між їх площинами.
47
445.	Скласти рівняння сфери, яка проходить через точку
М (2, 2, 2) та перетинає двополий гіперболоїд Зх2 — у2 — 5г2 = 4
по колу.
446.	Знайти точки заокруглення еліптичного параболоїда
4'2
447.	Визначити радіуси кіл, які лежать на однополому гіпербо-
у2 £^2
лоїді -§ - + ~4-г2 = 1 і дотикаються до горлового еліпса.
§ 8. Загальна теорія поверхонь другого
порядку
448.	Скласти рівняння поверхні, яка проходить через дев’ять
точок
Мх(0, 0, 0), М2(1, 0, -1), Л43(-1, 0, -1), М4(0, 1, 1),
М>(0, -1, 1), Мб(1, 1,0), М7(1, -1,0), М8(2, 1,-3), М9(1, -2,3).
449.	Визначити точки перетину поверхні х2 — у2 — г2 — 2ху +
уг + хг — 5х — 5у г6 = 0 з координатними осями.
450.	Визначити точки перетину прямої з поверхнею в таких
випадках:
а)	х 7~— =	з х2 + Зхг — Зуг — ху = 0;
Ь)	~	з 9х2 + 5г/2 + 9г2 — 12хг/ — &уг + 12г/ — 36г = 0
с)	= т = Т 3 х2 + У2 — 2^2 — 2x2 — У2 + 4хУ + Зх — 5у =0.
451.	Скласти рівняння дотичної площини й нормалі до поверх-
ні х2 — 5у2 — г2 — 4хг/ — &уг — 4х — 2у — 6г + 8 = 0 у точці
Мо(-4, 0, 4).
452.	Знайти дотичні площини поверхні 6х2 + 4г/2	4г2 + 4уг —
— 8х — 1 =0, паралельні площині 2х + Зг/ + 8 = 0.
453.	На поверхні Зу2 + 5г2 + 2ху — бхг — 12г/г + 2х + 10г —
— 3 — 0 визначити точки, в яких нормалі паралельні до осі 07.
454.	Скласти рівняння конуса, описаного навколо поверхні
х2 + 2у2 + 2г2 + 2ху — 2х — 4г/ — 4г + 2 = 0, вершина якого знахо-
диться в точці О (0, 0, 0).
455.	Знайти прямі, що проходять через початок координат і
цілком лежать на поверхні у2 + Зху + 2уг — хг + Зх + 2у = 0.
48
456.	Скласти рівняння асимптотичних конусів поверхонь:
а)	6х2 — 2г/2 + 6г2 + 4хг + 8х — 4у — 8г 4- 1 = 0;
Ь)	х2 + у2 4- г2 — бху + 2хг — 2уг — 4х 8у — 12г + 14 = 0.
457.	Визначити конус асимптотичних напрямів поверхні х2 4-
4-і/2 — г2 4- 2ху — Зх 4- 2 г/ — 1 = 0 з вершиною в точці М (—9, 0, 0).
458.	Визначити центри поверхонь:
а)	х2 4* 2г/2 — Зг2 4- 2хг — 2уг 4- 4х = 0;
Ь)	х2 4- 4г/2 4- 9г2 4- 4ху — 6х — 12г/ = 0;
с)	х2 4- 4г/2	9г2 — 12уг — бхг 4- 4хг/ 4- х 4- 2г/ — Зг — 12 = 0;
сі) 4х2 4- Зг/2 4* г2 — 4хг 4- г/ — Зг — 2 = 0.
459.	Знайти діаметр поверхні х2 4- 9г/2 4- 2г2 — 4ху — бхг 4-
2уг 4- 8х — 16г/ 4- 1 = 0> Щ° проходить через початок координат
та скласти рівняння спряженої з ним діаметральної площини.
460.	Скласти рівняння тієї діаметральної площини поверхні
6х2 4~ 9г/2 4- 22 — 4хг 4- бхг/ — 2г/ — 3 = 0, яка паралельна до площи-
ни х 4- Зг/ — г 4- 5 = 0, та знайти спряжений з нею діаметр.
461.	Визначити орти головних напрямів поверхонь:
а) 2х2 4- 2у2 — 5г2 4- 2хг/ — 2х — 4у — 4г 4- 2 = 0;
&)	х2 4- У2 4- 5г2 — бхг/ — 2хг 4- 2г/г — 6х 4- 6г/ — 6г 4- 9 = 0.
462.	Знайти головні осі й головні діаметральні площини по-
верхонь:
а)	х2 4* У2 + 5г2 — бхг/ — 2хг 4- 2г/г — 6х 4- 6г/ — 6г 4- 9 = 0;
Ь)	х2 4- У2 — Зг2 — бг/г — бхг — 2ху 4- 2х 4- 2у 4- 4г = 0.
463.	Спростити рівняння поверхонь:
а)	їх2 4- 6г/2 4- 5г2 — 4уг — 4ху — 6х — 24г/ 4- 18г 4- 30 = 0;
Ь)	5х2 4- 8г/2 4- 5г2 4- 4ху — 8хг 4- 4уг — 27 = 0 віднесенням до
головних осей.
464.	Спростити рівняння поверхонь:
1)	6х2 — 2г/2 4- 6г2 4- 4хг 4- 8х — 4у — 8г 4- 1 =0;
2)	х2 — 2у2 4- г2 4- 4ху — 8хг — 4уг — 14х — 4г/ 4- 14г 4- 16 = 0;
3)	х2 4- у2 4- 5г2 — бхг/ 4- 2хг — 2уг — 4х 4- 8г/ — 12г 4- 14 = 0;
4)	4х2 4- 5г/2 4- 6г2 — 4ху 4- 4уг 4- 4х 4- 6г/ 4- 4г — 27 = 0;
5)	х2 4* 2г/2 4- 2г2 — 2хг — 2ху 4- 2х 4- у 4- * = 0;
6)	2х2 4- 5г/2 4* 2г2 — 2ху — 4хг 4- 2г/г 4- 2х — 10г/ — 2г — 1 = 0.
465.	Спростити рівняння параболічного циліндра
4х2 4* У2 4- 9г2 4- 4ху — 12хг — бг/г 4- 6х — 2г/ — 6г 4- 2 = 0.
4 2193
49
466.	Вилучаючи квадрати, визначити тип поверхонь:
1)	х2 4- 2у2 + Зг2 + 2х — 4у — 12г -[-8 = 0;
2)	2х2	-[- 10г/2 — 2г2 4- 12хг/ + 8уг 4- 12х -[- 4у 4- 8г —	1=0;
3)	6х2	— 2г/2 4- 6г2 4- 4хг 4~ 8х — 4г/ — 8г 4- 1 =0;
4)	Зх2	4- 5у2 -|- Зг2 — 2хг/ -(- 2хг — 2уг 4- 2х — 6у — 2г	4-	3 = 0;
5)	4х2	4- 2г/2 4- г2 — 4ху — 2уг — 2у 4- 2г — 4 = 0;
6)	г/2 4- 2хг/ 4хг 4- 2уг — 4х — 2г/ = 0;
7)	х2 4- 4г/2 4- 9г2 — 4ху 4- бхг — 12г/г — х 4- 2у — Зг — 6 = 0;
8)	5х2 4- 4г/2 4- Зг2 4- 9хг/ 4- 8хг 4- Іуг 4- 7х 4- 6г/ 4- 5г 4- 2 = 0;
9)	х2 4- 2г/2 4- 2г2 — 2ху — 2уг — 9 = 0;
10)	у2 — 2уг 4- г2 -)- х — 1 = 0:
11)	ху 4- 2хг —1=0.
РОЗДІЛ IV ——==———————
ЛІНІЙНА АЛГЕБРА
§ 1. Визначники другого і третього порядку
Обчислити визначники другого порядку:
467.
472.
476.
4 -1
З 2
470.
а + Ь
Ь
474.
468.
зіп а
соз а
—2 (а + Ь)
а — Ь
-1
2 -1
З -4
—соз а
зіп а
473.
469.
471. І 1
1
475.
.2
а 4- Ь
а — Ь
478.
СО82 ф — ЗІП2 ф
—2 соз ф зіп ф
соз а
зіп а
-1
соз а
СО3 0
ЗІП Р
477.
2 соз ф зіп ф
СОЗ2 ф — ЗІП2 ф
х
V _1_ у2
1
1
а — Ь
а + &
479. Показати, що система лінійних рівнянь
а11х + а12у = &1,
а2]х + а22у = Ь2
має єдиний розв’язок, якщо £> =
інтерпретацію.
аи #12
#21 #22
0. Дати геометричну
4*
51
480. Показати, що при
£> =
#11 #12
#21 #22
= 0
система лінійних рівнянь
#11* + #12*/ = ^1>
#21* + а22у = Ь2
або несумісна, або невизначена. Дати геометричну інтерпретацію.
За допомогою формул Крамера розв’язати системи лінійних
рівнянь:
481 .ґ2х + Зу = 0,	482. (5х + У = 8,	483. Ґ5х— 1у = 1,
ібх- 12г/--7.	І— 15х	4- 2г/ = 11. їх —2# = 0.
484. ґх соз ос — у зіп ос	—	соз р,	485. (х ос 4~ У — зіп (ос 4~ Р),
(хзіпа 4- у созос	=	зіпр.	\х — уї&а = соз (а 4- Р),
п	486. (х зіп а 4- у соз а = а,
де а “к- 4- кл (к — ціле число). і	.	,
2 1 к	7	(хсозос — у$іпа = Ь.
Дослідити, при яких умовах, накладених на коефіцієнти, систе-
ма лінійних рівнянь визначена (має єдиний розв’язок), невизначена
(має нескінченно багато розв’язків) або несумісна (не має розв’язків):
487.|ах 4- 4г/ = 2, 488. (ах 4- Ьу = ай, 489.ґях — 9у = 6,
19x4- ау = 3. [Ьх 4- су = Ьй. 110*— &//=10.
Дослідити, при яких вартостях параметра К система лінійних
рівнянь буде визначеною, невизначеною, несумісною, і розв’язати ці
системи при тих значеннях К, при яких система визначена:
490. | (2 — Х)х4-6і/= 1, 491. (5х 4- Зу = 4 4- Ях,
Ібх 4- (2 — Я) у = 1. І7х 4- Зу = 1 4- \у.
492. ҐЯх 4- (Я 4- 1)У = 5,
ІЗх 4- 4у = 5.
493. ґЯх + (Я 4- Ю) і/ = — 1,
І(Я - 10) х 4- (Я 4- 1) У - 2.
494. Дослідити, при яких
ненулеві розв’язки:
вартостях к однорідна система має
а)( кх 4- у = 0,
1 х 4- ку = 0;
&)р-1)х4-2г/^0,
( 2х 4- (к— \)у = 0.
52
Обчислити визначники:
495.	1	2 —2		496.	6	3		0	497.		0 1 2
	2 1 -1		.		4	1		-3			1 0 3
	3 1	4					—2 -3	2			2 3 0
498.		4 1 2		499.		1 3 0	500.		1	1 1
		-12 3		.		2 0 1	.		4	5 9
		—2 з :	1			0 2 1			16	25 81
Користуючись властивостями визначника
числити такі визначники:
третього порядку, об-
501.	а	Ь	с
	с	а	Ь
	Ь	с	а
503. а х сі
а а + х
а а
502.	СІ X а а	а а а + х а а а	•
а	504.	1 а а2	
а	.	1 Ь 1	>2
а + х		1 С 1	>2
505.
2
1
1
со82а	зіп2а	506.	1		і§2а
СО82 Р	8ІП2 Р		1		
СО82 у	8ІП2 V		1		іЄ2у
507. зіп2а 1 соз2а
8іп2 р 1 СО82 Р
8ІП2 у 1 СО82 у
Користуючись лише властивостями визначника (не розгортаючи
його), розв’язати рівняння:
508.		1 —7	1		509.		5 2	3		
		2	8	2		= 0.		4 3	1	= 0.	
		3	5 х + 5				3 2 х + 1		
510.	1	1 1		511.	X	-3	1	0	
	2	5-х 2	—	0.		0 х+ 1	0	= 0.
	8-	х 3	3				0	0 Л	' + з	
512. Довести тотожність
1 + Хх + рх2 X X2		1 X X2
1 +	+ НУ2 У У2 1 + %г -|- рг2 г г2	=	1	У	У2 1	г	г2
53
Розв’язати за правилом Крамера системи лінійних рівнянь:
513.
2хх — х2 + х3 = 2,
хі — Х2 ~ %хз —З,
к 5хх + х2 — 4х3 = 2.
515. (ЗХ]^ + 8%2 — хз — 7 = 0,
* X} 4~ 2х2 4~ Зх3 — 1 = 0,
. 2хх — Зх2 + 2%3 —9 = 0.
514. (4хх + 3%2 — 8х3 = 1,
- х± — 6х2 + 6х3 = О,
2хх + 9х2 — 4х3 = 3.
516. 3%х 4~ 4%2	7%з	1=0,
* — 2%х ~5%2 Зх3 1 — О,
,5хх — 6х2 + 11%3 + 3 = 0.
517. 2бїл:х — 3/?%2 4~ ^-^3 —
< За*! — 6&%2 + 5сх3 = 2аЬс,
,5ах1 — 4&%2 + 2с%3 — ЗаЬс.
Дослідити, які з поданих систем
ні або несумісні:
518. 3%х + х2 + 2х3 = 6,
рівнянь визначені, невизначе-
2%х — х2 — х3 = 2,
4%х — 2х2 — 2%3 = 6.
520. (х£ —
521.
< Х1 + х2 — хз = 2,
к5%і + х2 — хз = 7.
522. ах± + 4%2 + х3 = 0,
2х2 4~ Зх3 — 1,
,3%х — £>х3 = —2.
— 2х3 = З,
< Хі + 2х2 -}- х3 = 4,
^Х1 + %х2 — Х3 = 7.
2ах± — 23%2 + 29,г3 = 4,
7%х 4- ах2 + 4%3 = 7,
к5%х -р 2х2 4“ о>х3 = 5.
523. Зхх — 2х2 4- х3 = Ь,
< 5хх — 8х2 4- 9%3 = З,
^2.гх 4" х2 4- ах3 — — 1
519.+ х2
§ 2. Означення, основні властивості
та обчислення визначників довільного
порядку
524.	Обчислити число інверсій в перестановках:
а)	8, 1, 5, 9, 7, 4, 3, 6, 2;
Ь)	10, 5, 3, 8, 4, 7, 2, 6, 1, 9;
с)	2, 4, 6,...,2п, 1, 3, 5, ...,2п-1;
й) 1, 3, 5, ...,2п-1, 2, 4, 6, ...,2п.
54
525.	З’ясувати, які з наступних добутків є членами визначника
відповідного порядку; вказати порядок визначника і знак члена:
й) ^43^61^52^13^25^34»
Ь) ^27^63^14^56^35^41^72 \
С) ^27^'36^51^'74^25^'43^'62 >
б/) ^43^21^35^12^54 •
Користуючись лише означенням, обчислити визначники:
526.
аи
а21
азі
а22
а32
0
0
азз
0>п\	0>п2 0>пЗ • • @>пп
Розв’язати рівняння:
528.
527.
0	... 0	0	& 1п
0	• • • 0	а<2, п—і	0>2п
0	••• йЗ, п-2Лз,п-1	Я3п
0>п1	• • • &п, п—2 ап, п—ї	®>пп
1	X	2 X . .	. хп
1	а\	а, ..	. аі
1		аі ..	.. 0,2
1	0>п	2	3 3
= 0,
0
0
0
о
де ах, а,..., ап — різні числа.
529.
1
1
1
1	1	...
1-х 1	...
1	2-х...
1
1
1
= 0.
1	1	1 ... п -1
530.	Як зміниться визначник п-го порядку, коли перший стов-
пець переставити на останнє місце, а всі останні стовпці зсунути
вліво, зберігаючи їх порядок?
531.	Як зміниться визначник п-го порядку, коли його рядки
написати в зворотньому порядку?
532.	Як зміниться визначник, коли кожний його елемент замі-
нити елементом, симетричним з даним відносно «центра» виз-
начника?
533.	Як зміниться визначник, коли кожний його елемент за-
мінити елементом, симетричним з даним відносно побічної діагоналі?
55
534.	Як зміниться визначник п-го порядку, коли змінити знаки
всіх його елементів на супротивні?
535.	Як зміниться визначник, коли кожний його елемент по-
множити на с1—\ де с Ф 0?
536.	Що станеться з визначником п-го порядку, коли від його
першого рядка відняти другий, від другого третій, від третього ряд-
ка перший рядок, залишивши всі інші рядки без змін?
537.	Обчислити визначник, розкладаючи його по елементах
третього рядка,
2-341
4-232
а Ь с сі
3-143
538.	Обчислити визначник, розкладаючи його
2-го стовпця,
по елементах
З	а	1	З
5	6	8	1
1 с -1 -1
2	сі	7	2
Обчислити визначники:
539.	2	-1	1	0	540.	1	1	1	1
	0	1	2	-1		1	-1	1	1
	3	-1	2	3		1	1	-1	1
	3	1	6	1		1	1	1	-1
541.	0	1	1	1	542.	1	2	3	4
	1	0	1	1		2	3	4	1
	1	1	0	1		3	4	1	2
	1	1	1	0		4	1	2	3
543.	1	1	0	0	544.	6	1	1	1	1
	1	1	1	0		1	5	1	1	1
	0	1	1	1	•	1	1	4	1	1
	0	0	1	1		1	1	1	3	1
						1	1	1	1	2
56
545.	1 2 3 4 5	546.	1	2	3 4
	5 12 3 4		-2	15 6
	4 5 12 3		-3-5	17
	3 4 5 1 2		-4 -6 —7 1
	2 3 4 5 1		
Обчислити визначники п-го порядку, зводячи їх до трикутно-
го вигляду:
547.	1	1	1 ..	. 1	548.	1	2	3 ..	,. п
	1	0	1 ..	.. 1		-1	0	3 ..	.. п
	1	1	0 ..	.. 1		-1	—2	0 ..	,. п
1 1 1 ... 0
549.	3	2	2 .,	.. 2
	2	3	2 ..	.. 2
	2	2	3 .,	.. 2
	2	2	2 ..	.. 3
551.	X	X . <	, . X	X	1
	X	X . ,	.. X	2	X
	X	X .,	.. 3	X	X
X п ... X X X
X X ... X X X
Обчислити визначник Вандермонда
552.
1 а{ а\ ...
1 а2 аі ... а”-1
1 л д? дп—1
1 ип ип ’ •’ ип
Обчислити наступні визначники, зводячи їх до визначника Ван-
дермонда:
553.		хї ..	.. X"	554.	ЗІП”-1	ЗІП'г-2ф1 .	.. ЗІПфц 1
	Х2	4 ••	' ‘ л2	.	ЗІП"-1 <р2	ЗІП"-2 Ф2 ...	ЗІПф2 1
	Хп	х2п-	Хп п		ЗІГр-1 ф т п	ЗІП"-2 фп .	. . ЗІПфга 1
57
555.
1 С08 ф1 СО82 ф1 ... СОЗ"-1 ф1
1 СО8 ф2 СО82 ф2 • .. СО8П-1 ф2
1 СО8 фп СО82 фп . . . СО8П-1 фп
§ 3. Правило Крамера. Гауссів метод
Користуючись правилом Крамера розв’язати системи лінійних
рівнянь:
556» / х± — %2 4“ -^з 4~ ^4 ==
І X} 4~ х2 — Зх3 4~ 2х4 = 1
| -^1 4“ 2Х2 - Хд 4~ х4 = З,
\	— Х2 + х3 — х4 = 1.
557./х± — х2 — х3 4- х4 = 0,
Х^ 4“ Х2 4“ Х3 4“ -^4 “ 0,
Х1 4" 2%2 4" *3 4" = — 1 ’
х4%і 4~ х2 4~	4“ Зх4==
558./ 2х4 4- -^2 + -^з + -^4 + %5 —	559. /	4~ х2 4~ -^з 4~ -^4 4~ 5х5 — 5,
%і 4- 2х2 4- *з 4- *4 4- -Ч = З»
Х1 4“ Х2 + 2%з 4" *4 + ХЬ ~
Х1 4" Х2 4" Х3 4" 2%4 4~ Хь — — 1,
*1 4" х2 4“ Х3 4~ Х4 4“ %Х5 — 2*
хі 4- х2 4- хз 4- 4х4 4- х5 = З,
хі 4~ х2 4~ Зх3 4~ х4 4~ х5 = 15,
хі 4~ 2%2 4~ хз 4~ х4 4~ х5 — 15,
хі 4~ х2 4" хз 4~ х4 4~ х5 = 9*
560./ х^ 4~ Х2 4~ хз 4~ Х4 4~ х§ — Ю,
4- 2х2 4- Зх3 — %4 — х5 = 2,
<	4~ 5%2 4- 2%3 4~ 3%4 — х§ = 1,
Х1 4- Х2 — Х3 — х4 = °»
\ х4 — 2%2 — Зх3 — 4х4 — 5х5 = —8.
Користуючись Гауссовим методом, розв’язати системи лінійних
рівнянь:
561 2х± 4- х2 4~ х3 4~ х^ = 1,	562./ 2х^ — х2 4~ ^хз 4~ 2х4 = 1,
І 3%4 4~ 4%2 х3 %4 = 0,	13%4 4- 3%2 4~ 5%з 4~ ^%4 == 1,
І 4- 3%2 — х3 4- %4 = 2,	І Зхг — х2 — х3 + 2%4 = — 1,
^5%х — Зх2 4- 6%3 4- 3%4 = 3.	І3%! — х2 4- Зх3 — х4 = —1.
563.^ Зх^ 4~ 4%2 4~ 5%з 4~ 7%4 = 1,
І 2х^ 4~ 6%2 — 5%з 4~ 4%4 = 2.
І ^хі 4- ^Х2 4- ІЗхз 4- Ю-^4 ==
\ 5хі 4*~	21х3 4“ 13х4 = 3.
564./4~ 2%2 4~ 5%з 4~ х4 — 0,
І 2%і 4~ 5х2 4~ хз — 2%4	1,
І х± — 2х2 — Зх3 4- х4 = 2,
\Зхі 4- х2 — §хз — х4 = 0.
58
Обчислити ранг матриць методом облямування мінорів:
565.	2 —4 3	—3 5	566.	1	3	5 —1
1-21	53.	2-1-34
1 —2 4 -34 0	5	1 -1	7
7	7	9	1
567. 2	3	1 -1
3	14	2
1	2	3-1 ‘
1-4-7	5
568. Довести, що будь-яку матрицю з рангом г, елементарними
перетвореннями можна привести до вигляду, де елементи ап=а22;=:
= ... = агг = 1, а останні елементи дорівнюють нулеві.
569. Довести, що елементарними перетвореннями тільки рядків
або тільки стовпців квадратну матрицю можна звести до трикут-
ного вигляду, де всі елементи по одну сторону від головної діаго-
налі дорівнюватимуть нулеві.
За допомогою елементарних перетворень обчислити ранг матриць:
570.	25 31 17	43	571.	24	19	36	72	-38
	75 94 53	132		49	40	73	147	—80
	75 94 54	134		73	59	98	219 -118
	25 32 20	48		47	36	71	141	-72
572. ЗО-		-1	5	573.		17	51 1	П 31
	1 1 -	-1 -	-2		93	25 :	14 121
	2 3	0	4		94	27 15 120	
	6 3-	-4 -	-1		18	53 1	>8	30
	574.	3	-2	4 -	-1	-1		2
	-5	3	2	0	—4		3
	8	-5	3	4	1		3 •
	7	-5	19	1	-10		9
	11	12	— 15	8	17	-20	
	575.	23	8 -8		55 -	-22	
		31	25	35		80 -	-32	
		-13	3	17	—	10	4	
		5	14	26		35 -	-14	
59
§ 4. Загальна система лінійних рівнянь
Дослідити сумісність (згідність) системи рівнянь та знайти їх
загальний розв’язок:
576.
Х^ “Т" Х2 — ^-^3 ~Н -^4
Зхх 4~ Х2 — 5%3 4~ 3%4 — 5 = 0,
хі + х2 ~ 5хз ~ 2а:4 4-2 = 0,
хх 4- §х2 ~ 17*з + 2х4 —10 = 0,
к — х2 4- х3 — 4х4 4-8 = 0.
578. рхх — 9х2 — х3 4- -^4 = 8,
І хх 4- 2х2	— х4 = 4,
| 7хх — 20х2 — 2х3 4- Зх4 = 12,
\3хх — 11х2 — хз + 2*4 = 4.
580.
577.
579. Зхх — 5х2 4- 2х3 4- 4х4 = 2,
* 7хх — 4х2 4~ хз 4- Зх4 = 5,
к 5хх + 7х2 — 4х3 — 6х4 = 3.
2хх — х2 4~ х3 4” 2х4 4~ 3-^5 — 2,
6хх — Зх2 4- 2х3 4~ 4х4 4~ 5х5 = З,
6хх — Зх2 4- 4х3 4- 8х4 4- 13х5 = 9,
4хх — 2х2 4- х3 4- х4 4- 2х5 = 1.
581. Зхх 4~ 4х2 — х3 4~ Х4 = 1,
%і — х2 4- 2х3 — Зх4 = 5,
к 4хх 4~ Зх2 4- Хз — 2^4 = 3.
582.
Дослідити розв’язки систем
раметра:
583.ґ Ххх 4- х2 4- хз = 1,
' Х1 4” ^2 4~ Х3 ~ 1’
к хі 4" х2 4~ ^хз — 1 •
585. (1 4- X/) хх 4-
У
1 2хх 4~ х2 4~ х4 = 2,
Зхх — х2 — 2х3 + Зх4 = 1,
4хх 4- Зх2 4- хз ~ 2х4 = —1,
9хх 4- Зх2 — х3 4- 2х4 = 2,
хх 4- Зх2 4- 2х3 — х4 = 3.
вартостей па-
залежності від
х3 — 1,
х3 = X,
584.ґ Ххх 4— х2 4~
1 Х1 + ^Х2 4~
к х4 4— х2 4— ^х3 ==
Х1 + (1 +	+	Х3 —
*1 + Х2 + (1 + Х3 ~ А2.
60
586. Лхі 4~ *2 -Н *з “І- *4 — 1,
*1 4” ^*2 4“ *3 4” *4 — 1’
*1 4~ *2 4” ^*з 4~ *4 = 1,
* %} —}— *2 4“ *3 ~Р ^*4 — 1 •
Користуючись теорією лінійних рівнянь, розв’язати подані ниж-
че задачі (розглядаючи лише прямокутні декартові системи коор-
динат):
587.	Знайти умови, необхідні й достатні того, щоб п площин
СЦХ + ЬіУ + Сі2 + (Іі = 0 (і = 1, 2, ..., п) проходили через одну пря-
му, але не зливалися в одну площину.
588.	Яка система лінійних рівнянь визначає три різні прямі на
площині, що проходять через одну точку?
589.	Яка система лінійних рівнянь визначає гри прямі на пло-
щині, що утворюють трикутник?
590.	Яка система лінійних рівнянь визначає три площини про-
стору, що не мають спільної точки, але перетинаються попарно?
591.	Яка система лінійних рівнянь визначає чотири площини
простору, що утворюють тетраедр?
Знайти нормальну фундаментальну систему розв’язків систем
лінійних рівнянь та записати їх загальний розв’язок:
592.	/2*х + 3*2 — 7*3 4- 3*4 = 0, 593.<2*х4- х2— 3*5 — *4 = 0,
І 2*х —	3*2 —	З*3	+	5*4 — 0,	і *х	+	2х2 — З*3 4- *4	= 0,
| 2*х 4-	9*2 —	11*3	+	*4 = 0,	] 5х±	+	4х2 — 9*3 — *4	=	0,
\ 4*х +	6*2 —	14*3	4-	6*4 = 0.	\ 4х±	4-	3*2 — 9*з + *і	—	0-
594. /2*х 4- 2х2 — З*3 — х4 = 0,
І 2*х — 2х2 4- *3 — 3*4 = 0,
| 8*і 4~ 4*2 — 8*3 — 6*4 = 0,
І 2х2 — 2*3 4- *4 — 0.
595.	*х 4-	*2 4- 2*3 —	6*4	—	*5 = 0,
х± —	2х2 4- 6*3 —	6*4	4-	10*5 = 0,
5 3*х —	4*2 4- 4%3 —	х4	4-	17*5 = 0,
хх 4-	*2 — 4,г3 4-	3*4	—	4*5 = 0.
596. /2*! — 5*2 4- З*3 — 4*4 = 0,
3*х — 4*2 4- 5*з 4- *4 = 0,
5*х — 9*2 4- 4*з — *4 = 0,
к4*і — 6*2 4- З*3 4- *4= 0.
61
597./ х4 4- *2 — З*3 4“ *4 “4“ *5 = О,
І — *2 + хз + 3*4 — 3*5 = О,
/ *х — 2х2 + З*3 + 4*4 — 5*5 = О,
І хх — *3 + 2*4 — х5 = О,
\ х4 3*2 — 7*3 — х4 4~ 5*^ = 0.
За допомогою нормальної фундаментальної системи розв’язків
відповідної їм однорідної системи та частинного розв’язку неодно-
рідної системи знайти загальний розв’язок систем лінійних неодно-
рідних рівнянь:
598./Хі -}- х2 — 2*3	= 0, 599./ х4 + *2 — *3 4~ 3*4 = 2,
І *х — *3 + х4 = 1, *х — х2 — З*3 + х4 = 4,
І *х — *2	+ 2*4 = 2,	12*х — *2 — 5*3 + 3*4 = 7,
\	*2 — х3 — х4 = — 1.	І, *х — 2%3 + 2*4 = 3.
600.
3*х + 4*2 — З*3 — х4 — — З,
6*х 4~ 2*2 — З*3 —х4 == 0,
3%-£ — 4%2 4~ хз + 8%4 :=:: 5,
—	4х2	—	х3	+	5х4 =	7.
601. / х4	х2	—	2%з	—	х4 4*	2х&	=	1,
І 2%х	+	х2	—	Злг3	+	%5	=	З,
І Х1	—	х3+	х4—	х5	=	2,
х4 — 2х2	+ х3 4-	5х4 — 7%5	=	4.
' 2х4 4- 3%2	+ 2лг3 —	4%4 — 2х5	=	2,
2х4 4- 3%2	— 2х3 —	2%4 4- 2х5	=	—4,
4х4 + 3%2	+ 2%з —	5%4 — х5	=	З,
\2х4 4- 6%2	4- 2х3 —	6х4 — 3%5	=	0.
6х4	4- 2%б = 2,
4х4 — 4%5 + 4%б = 0,
7*4 4- 2*5 4- *б = З,
602.
603./ 2*х + 3*2 + 4*3 —
2*х — 3*2 + 4*3 —
12*х + 6*2 + 4*3 —
4*х + 3*2 4~ 8*3 — 11*4 — 2*^ -|~ ^х& — З,
4*3 — 3*4 — х5 + 2*б = 2.
62
§ 5. Матриці та дії над ними
Додати матриці:
604.
13 5 7
2 4 6 8
4 2 0
5 З 1
605.
1	0	2
2	1	0
З	2	1
0	1	-1
2
З
1
0
606.
1 0
4 1
2 З
1 —2
0
0 .
6
Помножити матрицю на число:
607.	1 2 З
3-456
7 8 9
608.	12 1 З
2- „
3 12
Перемножити квадратні матриці:
611.
—2
З
2
4.
1
-З
З
—2
1
1
З
5
1
З
5
—зіп р
СОЗ Р
1
З .
5
63
614. II 4
I 7
615.
1
2
З
4
З
5
4
З
2
1
II ~28
II 38
1 З
2 4
4 1
З 2
93 II 7 3 II
—126 І 2 1 Г
12 3 4
0 12 3
0 0 12'
0 0 0 1
Обчислити степені квадратних матриць:	
619. | 1 2 3 620.	1	1 -1Ц3 621- II Лх 0||"
II 2 3 ‘	3 -1	2 .	||о Л2 Г
	2-1 о|
622. Ц соз а —зіп а ||	і" 623. X X ||П	624. Ц X 1 |"
| зіп а соз а |	II 0 X І	II о 2 І ’
625.	Хх 0 0 ... 0 п
	0 Хг 0 ... 0
	0 0 Я8 ... 0 '
0 0 0 ... А*
Перемножити прямокутні матриці:
626. || 1
2 3 4 5 ||	5	627.	1	| 5 4 3 2
	4		2	
	3		3	
	2		4	
	1		5	
Ц
64
631.	Довести, що матриці А і В квадратні та одного порядку,
якщо їх добутки АВ і ВА визначені, а АВ й В А — матриці одного
порядку.
632.	Як зміниться добуток АВ матриць А та В, якщо:
а)	переставити Лй та /-й рядки матриці Л;
Ь)	переставити Лй та /-й рядки матриці В?
633.	Показати, що множення матриці А зліва на діагональну
матрицю В = (Хх, Х2,..%Л) зводиться до множення рядків матриці
А відповідно на Я2,. • А,Л, а множення справа — на аналогічну
зміну стовпців.
Знайти обернені матриці для матриць:
634. 11 3 1 ||		635.	І1 2	5 Ц 636. Ц	соза -		-зіпа ||
	||4 2|Г		ІЗ	8ІГ 1	зіпа		соз а |
637.	1 0	2	638.		1 -1	3	639.		-12	4
	—1 і 2			0	1 -1			2 1 -6
	0 1 -1			2	2-2			3 5—7
	640.		1	1 1	1		
1 1-1-1
1-1 1-1
1-1-1 1
Розв’язати матричні рівняння:
641. ||3 5 11 ЦІ 3 11
І 1 2 ІГ = II 2 4 ||
5 2193
65
642.
1 О
-1 1
О 1
2
2 Х =
З
2
4
643.	II 4	З Ц	Ц 3 5
I 5 4 її II 1	2
644.	Ц З —1 Ц Ц 5 6 Ц
I 5 -2|Х|7 8 І
-1 5
2 З
1 2
1	3 І
2	4 І'
14 16
9 10
§ 6. Афінні векторні простори
Чи буде лінійним простором кожна з поданих сукупностей
векторів:
645.	Усі вектори п-вимірного простору, координати яких — ці-
лі числа?
646.	Усі вектори площини, кожний з яких лежить на одній з
осей координат?
647.	Усі вектори площини, кінці яких лежать на даній прямій,
(за початок будь-якого вектора, якщо не застережено протилежне,
береться початок координат)?
648.	Усі вектори площин, початки і кінці яких лежать на да-
ній прямій?
649.	Усі вектори тривимірного простору, кінці яких не лежать
на даній прямій?
650.	Усі вектори площини, кінці яких лежать у першій чверті
системи координат?
651.	Усі вектори з координати яких справджують рівняння
Хі + х2 4- • • 4~ хп = 0?
652.	Усі вектори з Кп, координати яких справджують рівняння
Хі 4~ х2 4~ • • • + хп = 1 ?
653.	Усі многочлени Рп(х) степеня п, якщо за операції просто-
ру взяти звичайне додавання многочленів і множення многочлена
на число?
654.	Усі многочлени степеня -<п?
655.	Усі вектори, що утворюються лінійними комбінаціями век-
торів ХІУ Х2, . . ., Хп з 7?п?
656.	Знайти лінійну комбінацію:
а)	2ах — За2 + 5а3 системи векторів = (1; 0; 2), а2 = (3; 0; 1),
І = (1; 2; 3);
66
Ь)	Заг — а2 + 2а3 — системи векторів — (1; —1; 0; 2),
І = (2; 1; -1; 3), а3 = (4, 3; 1; -1), а4 = (9; 2; 3; 1).
657.	Розв’язати рівняння:
а)	2ах + 3а2 — 2а3— 5% = а4, де аг = (—1; 0; —3; 4), а2 =
= (1; 2; 4; 0), а3 = (0; 1; 2; —1), а4 = (2; 3; 1; 2);
Ь)	х + у — г = Лі, х — у + -г = а2, 2% + у + Зг = а3, де аг =
= (0; 5; 2; 1), а2 = (2; -3; 0; 1), а3-(13; -10; 3; —2).
З’ясувати, які системи векторів (подані нижче) лінійно залежні,
а які лінійно незалежні:
658.	І = (1; 2; 4; 3), а2 = (4; 1; 3; 2), а3 = (5; 3; 7; 5).
659.	ах=(1; —2; 1; -3), а2 = (1; 4; 1; 2), а3 = (1; -3; 1; 4).
660.	І = (1; 0; 2; 0; 6), ~а2 = (0; 1; 0; 3; 5), а3 = (0; 0; 1; 2; 7),
а4 = (3; 5; 7; 9; 11).
661.	І! = (1; 2; 3; 4), а. = (4; 3; 2; 1), а3 = (4, 3; 1; 2), а4 =
= (3; 4; 2; 1).
662.	Довести, що система векторів, яка має два рівних векто-
ри, лінійно залежна.
663.	Довести, що система векторів, два вектори якої відрізня-
ються скалярним множником, лінійно залежна.
664.	Довести, що система векторів, яка містить нульовий век-
тор, лінійно залежна.
665.	Довести, що коли частина системи векторів лінійно залеж-
на, то і вся система лінійно залежна.
Вектори е2,еп та х задані координатами в деякому бази-
сі. Показати, що вектори е19 е2,...,еп самі утворюють базис та
знайти координати вектора х у цьому базисі:
666.	Єі = (-1; 2; 1), е2 = (2;1; — 1), ^=(1; 2; —1), х =
= (7; 9; -4).
667.	^ = (2; 3; 4), 7, = (3; —2; 1), 73 = (-1; 2; 1), х =
= (4; 3; 6).
668.	7Х = (1; -1; 1), е2 = (2; 1; 1), 73 = (1; 3; 1); х = (3; -4; 2)
5*
67
669.	<?! = (!; 1; 1; 2), еч = (1; 1; 2; 3), е3 = (3; 2; 1; 1), е4 =
= (1; 3; 2; 1), х = (-2; -3; 0; 3).
670.	7і = (-1; 1; 1; 1), е3 = (1; -1; 1; 1), е3 = (1; 1; -1; 1),
е4 = (1; 1; 1; -1), х = (2; 4; 2; 4).
Довести, що кожна з систем векторів утворює базис простору
та знайти зв’язок між координатами довільного вектора в цих двох
базисах:
671.	71 = (1; 1; 1), ^ = (1; 2; 1), 73 = (1; 1; 3);
;; = (1; 2; 1), ^=(2; 1; 3),	= (3; 2; 1).
672.	І = (1; 1; 1), ^ = (1; -1; 2), ^ = (1; 3; -1);
еі=(1; -1; 1), ^ = (1; 2; -1), ^ = (2; 2; -1).
673.	^ = (1; 2; 1), е2 = (2; 3; 3), е3 = (3; 7; 1);
ї = (3; 1; 4)Д = (5; 2; 1), ^ = (1; 1; -6).
674.	Знайти координати многочлена /(%) = а0 = агх + а2х2 4- —+
+ апхп:
а)	у базисі 1, х, х2, ..., хп;
Ь)	у базисі 1, (х — а)> (х — а)2, ..., (х — а)п.
675.	Як зміниться матриця переходу від одного базису до
другого, коли:
а)	поміняти місцями два вектори першого базису;
Ь)	поміняти місцями два вектори другого базису;
с)	записати вектори обох базисів у зворотньому порядку.
Знайти базис і розмірність системи векторів, що утворюють
підпростори:
676.	Усі п-вимірні вектори, у яких перша і остання координати
рівні між собою.
677.	Усі п-вимірні вектори вигляду (а, р, а, р, а, р,...), де а і
Р — довільні числа.
678.	Сукупність всіх многочленів степеня від одного неві-
домого.
679.	Довести, що всі квадратні матриці порядку п утворюють
векторний простір, якщо за операції в ньому взяти додавання мат-
риць і множення матриць на число. Знайти базис і розмірність
цього простору.
68
680.	Довести, що симетричні матриці утворюють лінійний під-
простір простору всіх квадратних матриць порядку п\ знайти базис
і розмірність цього простору.
Знайти розмірність і базис лінійних підпросторів, що утворюють
системи векторів:
681.	І = (1; 0; —1; 0), а2 = (2; 0; 1; 1), а3=(1; —1; 0; 1), а =
= (1;1;1;0).
682.	І = (1; 1; 1; 1), а2 = (1; 2; 1; 0), а3 = (1; 1; 3; 1),	=
= (1; 2; -Г, 1).
683.	а1 = (—1; -1; —1; 0; 0), а2 = (0; 1; 1; 1; 1), а3 =
= (— 1; 0; 0; 1; 1), а4 = (—1; -2; -2; -1; -1),а5 = (-1; 1; 1; 2; 2).
§ 7. Лінійні перетворення векторних
просторів
684.	З’ясувати, які з перетворень ф у просторі и3 будуть лі-
нійними:
а) фх = х + а (а — фіксований ненульовий вектор); Ь) фх = а;
с) фх = | х | а; й) фх = (а, х)а; е) срх = (а, х)х; /) фх = (8Іпхх,
соз х2, 0), де х = (хх, х2).
685.	Довести, що поворот площини на кут а навколо початку
координат є лінійним перетворенням, і знайти матрицю цього пере-
творення в ортонормованому базисі.
686.	Довести, що проектування тривимірного простору на коор-
динатну вісь вектора еь паралельно координатній площині векторів
е2 і е3, є лінійним перетворенням, та знайти його матрицю в бази-
сі е2, е3.
687.	Довести, що проектування тривимірного простору на коор-
динатну площину векторів е19 е2і паралельно осі координат вектора
е3, є лінійним перетворенням, і знайти його матрицю в базисі
Єї, е2, е3.
688.	Довести, що ортогональне проектування тривимірного про-
стору на вісь, яка утворює рівні кути з осями прямокутної системи
69
координат, є лінійним перетворенням, та знайти його матрицю в
базисі одиничних векторів координатних осей.
З’ясувати, які з перетворень ер є лінійними, і для лінійних знай-
ти їх матриці в тому базисі, в якому задано координати векторів
х і фх:
689.	фх = (хх + х2, х2 + х3, хх + х2 — х3).
690.	фх = (хх, х2 + Зхх, х3).
691.	фх = (хх + 1, х2, х3).
692.	фх = (хх, х3, х2 — 2х3).
693.	фх = (х, х|, х± + %2).
694.	фх = (х3, х2, хх + Зх2 — х3).
695.	фх = (х4 + х3, х2 + х4, х3 + хх, 2хх + х4).
Показати, що існує єдине лінійне перетворення тривимірного
простору, яке переводить вектори ах, а2, а3 відповідно у вектори
Ь19	Ь3. Знайти матрицю цього перетворення в базисі, у якому
задано координати усіх векторів:
696. а, = (1, 0, 3),	Ь = (2, 2, 1),
а. = (2, 1, 0),	І = (2, 1, 0),
І = (0, 0, 1);	І = (1, 2, 3).
697. ак = (1, 2, 3),	Ьх = (—2, 4, 9),
І = (1, 1, 2),	1 = (—1,2, 6),
І = (3, 1, 1);	63 = (2, -1, 6).
698. І = (1, 0, 0),	І = (1, 2, 0),
І = (0, 1, 0),	І = (4, 1, 1),
а8 = (0, 0, 2);	І = (1, 2, 3).
699. а1==(—1, 2, 3),	= (6, 9, 8),
а2 = (1, —2, -1),	Ь2 = (-4, -3, -6),
а3 = (2, 1, 1);	= (5, 8, 6).
70
700.	Нехай лінійне перетворення ф простору Кп переводить ліній-
но незалежні вектори а2, а2,.. .,ап відповідно у вектори Ь2,..
Ьп. Показати, що матрицю Лф цього перетворення в деякому бази-
сі ех, е2, еп можна знайти за формулою Лф = ВЛ-1, де стовпці
матриць А та В складаються з координат векторів ак, а2, а3,..., ап
та відповідно Ь19 Ь2,..Ьп у базисі еі9 е2,. .,еп.
701.	Показати, що диференціювання є лінійним перетворенням
простору усіх многочленів степеня п від одного невідомого.
Знайти матрицю цього перетворення в базисі:
а)	1, х, х2,..., хп;
і	(х — а)2 (х — а)п
Ь)	1, х — а, -—2^“» • • • >1» Де а ~ Д1исне число.
702.	Як зміниться матриця лінійного перетворення, коли в ба-
зисі е19 е2,...,еп поміняти місцями два вектори Єі І Єр
703.	Лінійне перетворення ф у базисі еІ9 е2, е3 має матрицю
1 2 З
2 12.
З 3 1
Знайти матрицю цього перетворення в базисі:
а)	ех, <?3
Ь)	7і = еі, /2 = ех 4- е2, /3 = ех + е2+ е3.
704.	Лінійне перетворення ф в базисі
І = (8, -6, 7), а2 = (—16, 7, —13), а3 -(9, -3, 7)
має матрицю
1 -18 15
-1 -22 15 .
1 —25 22
Знайти його матрицю в базисі
&1 = (1, —2, 1), 62 = (3, —1, 2), &3 = (2, 1, 2).
Знайти власні значення і власні вектори лінійних перетворень,
заданих у деякому базисі матрицями:
71
705.		0 1	1	706.		0		1	4		707.		7	-12	6
		0 1	0	.		0		1	0	.			10	-19 10
		1 1	0			1		1	0				12	-24 13
708.	4 —5		2		709.		1	0	с	1	0	710.		1 -3 4
	5 —7		3		.		0	0	с	1	0			4-7 8
	6 -9		4				0	0	с		0			6-7 7
							1	0	0		1			
З’ясувати, які з наступних матриць лінійних перетворень можна
звести до діагонального вигляду. Знайти діагональну матрицю, від-
повідний		до неї базис та матрицю переходу до							базису з власних			
векторів:												
711.		0 1	4	712.		1—341	713.		0 1 0			
		0 1	0	.		4—7 8	.		-4 4 0		•	
		1 1	0			6 —7 71			—2 1 2			
714.	0	1 0		715.		2-1	2		716.		7 —12	6	
	1	0 1	.			5—3	3		.		10 -19	10	
	0	8 0			—	1	0 -2				12 -24	13	І
§ 8. Євклідові простори
717. Чи буде простір тривимірних рядків евклідовим, якщо за
скалярний добуток взяти вираз (%, у) = х1у1 — х2у2 + х^у3?
Переконатися, що вектори наступних систем попарно ортого-
нальні й доповнити їх до ортогональних базисів:
718. (1, -2, 2, —3),	719. (1, 1, 1,	2),
(2, -3, 2,	4).	(1, 2, З, —3).
Застосовуючи процес ортогоналізації, побудувати ортогональний
базис підпростору,	напнутого на дану систему векторів:
720. (1, 2,	2, -1),	721. (1, 1, -1, -2),
(1, 1,	—5,	3),	(5, 8, —2, —3),
(3, 2,	. 8, -7).	(3, 9,	3,	8). 722. (2,	1,	3,	-1), (7,	4,	3,	-3), (1,	1,	-6,	0), (5,	7,	7,	8).
72
Лінійне перетворення задано в деякому ортонормованому базисі
матрицею А; знайти ортонормований базис з власних векторів, діа-
гональну матрицю В і ортогональну матрицю Т, для якої В =
= Т-ЧТ:
723. -1 —2 2
-2 1 0
2 0 1
725.
727.
724.
£
З
2
З
2
з
2
З
з
2
З
2
з
2
з
2_
з
728.
726.
0
1
1
-1
—2
6
-2
11
2
-8
1
0
-1
0
-2 .
5
2 —8
2	10
10	5
1	-1
-1	1
0	1
1	0
§ 9. Квадратичні форми
Методом вилучення повних
квадратів звести квадратичні форми
до нормального вигляду:
729.	А (х, х) — х2 + х2 + Зх| + 4х, х2 + 2х, х3 2х2 х3.
730.	А (х, х) = х? — 2х2 + х? 4- 2х, х„ -4- 4х, х, + 2х, х,.
х /	1	2’0’	12’	10*	О
731.	А (х, х) = х? — Зх? — 2х. хо + 2х,	— 6хох~.
х 7	1	О	12’10	20
Звести подані квадратичні форми до нормального вигляду (знай-
ти також невироджене перетворення, яке зводить до цього вигляду):
732.	А (х, х) = х2 4- 5х2 — 4х| + 2х1 х2 — 4х, х3.
733.	А (х, х) = 4х2 А- х2-\- х3 — 4х, х2 + 4х1 х3 — Зх2 х3.
734.	А (х, х) = х1 х2 + х, х3 + х2 х3.
735.	А(х, х) = 2x1 +	— ^х^+ЗХіХд—27х2Х3.
73
736.	А (%, х) = х±х2 + х2 х3 + х3 %4 + х± Хі .
У наступних прикладах знайти ортогональне перетворення, яке
зводить квадратичні форми до канонічного вигляду, та написати
цей канонічний вигляд:
737.	А (х, х) = — х? + х| + хі — 4х1 х9 + 4^ х3.
738.	А (х, х) = 1х\ 4- 6х? — 5%2 — 4х. х9 — 4х9 хч.
739.	А (х, х) = хі — 2x2 + х| + 4х, х2 — 8Х[ х3 — 4х2х3.
740.	А (х, х) = 6х^ + 5x2 + 7х^ — 4х1 х2 + 4х, х3.
741.	А (х, х) = 11x2	5х2	2х| -|- 16х, х2 + 4х1 х3 — 20х2 х3.
742.	А (х, х) = х\ А- х^ +	— 6х, х2 — 2Х; х3 + 2х2 х3.
743.	А (х, х) = х^ + х2 + х| + 4х1 х2 + 4х1 х3 4х2 х3.
744.	А (х, х) = 2х, х2 — 6х; х3 — 6х2 х4 + 2х3 х4.
745.	А (х, х) = х? 4- 2х. х, + х^ — 2х% — 4х, х. — 2х%.
746.	А (х, х) = 2х; х2 2х, х3 — 2х, х4 — 2х2 х3 + 2х2 х4 + 2х3 х4.
РОЗДІЛ V	-
ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ
ФУНКЦІЇ ВІД ОДНІЄЇ ЗМІННОЇ
§ 1. Функціональна залежність
747.	Нехай /(х)— лінійна функція. Знайти її, якщо /(0) = —5
і/(2)=1.
748.	Дано /(х) = х2 — 7х 4- 10. Показати, що /(2) = /(5) = 0.
749.	Знайти цілу раціональну функцію (многочлен) /(х) другого
степеня, якщо /(0) = 2, /(1) = 0, /(2) = 4.
750.	Дана функція
Знайти /(-1); /(0);
751.	/(х) = 2х2— 7х+3. Знайти корені рівнянь:
а)/(х) = Л0); &)/(х) = /(2).
752.	Дана функція /(х) = х3 — 2х2 — ІЗх — 10. Знайти всі коре-
ні рівнянь:
а)Цх) = /(5); Ь) /(х) = /(-3).
753.	Визначити функцію третього степеня
/ (х) = ох3 + Ьх2 + сх -|- сі,
якщо: /(—1) = _8; /(0) = -1; /(1) = 2; /(2) = 7.
754.	Дано /(х) =	. Знайти та /(х — 1).
755.	Нехай ф(/) = И /2 + /+ 1. Знайти ф(/2); [ф(/)]2.
756.	Дано /(%) = х2 — х + 1. Знайти /(%—1), /(х-4- 2).
757.	/(%) = %3, ф(%) = 3\ Знайти Дф(%)] та ф [/(%)].
758.	Функція у = Е (х) означає найбільше ціле число, що не
перевищує х (ціла частина числа х). Знайти £(—2л), Е (—1,2),
£(0), В(1), е ]^, £ ()/ТГ), В(л).
75
759.	Відомо, що /(х 4-2) = х2 — 4, знайти /(х), /(х— 1).
760.	Дано / (х) = х2 + 2. Знайти / (х-
761.	Дана функція /(х) = зіпх— соз2х. Знайти /(0), /('З')»
/(т)>	ї(¥)‘
762.	Знайти /(х), якщо /	= х — ]/1 4-х2, х> 0.
763.	Дано / (х ф- -у) = х2 4-	. Знайти / (х).
764.	<р (х) = 2х5 — бх3 4- х. Показати, що <р (—х) = — <р (х).
765.	Р (х) = Xі — Зх2 4- 1. Показати, що Р (—х) = Р (х).
766.	Показати, що функція / (х) = (ах 4- а~х) є парна, а
<р (х) = -±-(ах — а~х) — непарна.
767.	Дана функція / (х) = агсзіп (Зх — 1). Знайти /(0); /(Ц-)’
/(4);
768.	Дано ф (х) = У х2 4- 9. Знайти ф (Зх); 2ф (х).
769.	Визначити, які з функцій, що подані нижче, є парні, які
непарні та які не належать ні до тих ні до других:
1) /(х) = 2х2 - Зх3 4-	2) /(х) = х2 --£^- 4- 1; 3)/(х) = х2зіпх;
4) /(Х) = х1п}=^; 5) /(х) = 1-44-^-; 6) /(х) = -^г;
7) Цх) =	; 8) /(х) =	; 9) ^(х) =
10) / (х) = 2—2; 11) ї(х) = еХ~Є~_Хх і 12) / (х) = 4 (ех - Є~х);
13) /(х) = ^ (х 4-І)2 — V (х—І)2; 14) / (х) = х3 — 2х 4-зіп х;
15) / (х) = 1п (х 4- / х2 + 1).
770. З’ясувати, які з поданих нижче функцій є періодичні, та
визначити найменший їх період:
1) /(х) = соз (х2); 2) / (х) = 2; 3) / ('х) =
76
4) / (*) = соз 2х + 3 зіп 2х — 1; 5) / (х) = соз х — соз 2х + соз Зх;
6) І(х) = соз4; 7) /(х) =	; 8) /(х) = соз2х;
9) / (х) = зіп х + зіп (х ]/2); 10) /(х) = £(х); 11) /(х) = х —£(х);
12) /(х) = соз лх; 13) /(х) = агсзіп(8іп х); 14) /(х) = соз(х + 1).
(х -1 1\
*
772. Дано у = ц3, и = 2х + 1. Зобразити у як функцію від х.
773. Визначити обернену функцію х = у(у) та її область існу-
вання, якщо:
1) г/= Зх; 2) у = х—1; 3) у = 5х + 2; 4) у = х*—1;
5) у = (х т<= 1); 6) у = 2х — х2; 7) у = У 1 — х2;
8) у = 10*+‘; 9) г/ = 1§4-; 10) у=3соз2х;
О
11) у =	12)
774.	Дано у = У 1 + г2, г = сі§х. Подати у як функцію від х.
775.	/ (х) = ах. Показати, що / (а) • / (0) = / (а + 0).
776.	<р (х) = 1§{^ • Довести, що ф (а) + ф (0) = Ф
777.	Подати зложені функції в наступних прикладах за допо-
могою основних елементарних функцій:
1)г/ = соз3х; 2) у = (х3 + І)2; 3) у = зіп2 (5х — 1);
4)	у = 1п ]/ х2-і- 1; 5) у = 2С‘8 х; 6) у = 108Іп2 4х.
778.	Подати ці функції в явному вигляді:
1)х2~у2 = а2; 2)-^-4-^=1; 3)ху = 2; 4)х3-^=1;
5)	2*+» = 3; 6) 1§(у — 2)4-1§х= 1; 7) 2х —(х2 + 1)зіпі/= 0.
Визначити область існування таких функцій:
779.	у = х2 — 5х + 6.
780.	у = Ух+7.
781.	у = /9 - х2.
782.	у = /х2 — 5х + 6
77
784.	у = ]/х2 — 1.
785.	у = ^х2 — 1.
786.	^ = х2 + 1§(х + 2).
787.	у = агсзіп (2х — 1).
788.	у — агсзіп 5х~3 4- У 4х2 — 1
789.	у = агссоз (Зх — 5).
790.	у — агссоз	(Зх 4- 6).
791.	у - Іпсозх.
792.	ї/ = /зіп 2х + / 4 — х2.
793.	у = агсзіп (х2 + 1).
794.	у = ~=2=- + 1§(х-1).
У І — х2
795.	у = /3 — 2х+ уЧ-х + /4-х2.
796.	у — зіп І§ (Зх — 1).
797.	у = 1Є(/Г=^3 + /8^)+у^=.
798.	у = —... * + 1	- з--.
/х2-7х+12 У^+З~х
799.	у = У 7х~*2 + VЗ’п 2х — агссоз 2х~5.
800-	У =  2 х71, с •
х2 — 4х + 5
801.	у =	.
Ух
802.	і/ = / х2 - 6х 4- Ю.
803.	у = /|х| — х.
804.	у = -   1 —.
]/х2 — X 4-1
805.	Чи тотожні функції / (х) = зіп2 х 4~ соз2 х та <р(х) = 1?
806.	Чи тотожні функції /(х) = 1§х2 та <р(х) = 21§х?
807.	Чи тотожні функції / (х) = х та <р (х) = 4- /х2?
808.	Чи тотожні функції /(х) = х та д>(х) = (/х)2?
78
1	X
809.	Чи тотожні функції /(х) = — та ф(х) =
810.	У кулю з радіусом 7? вписано ціліндр. Визначити об’єм V
цілійдра як функцію його висоти И.
811.	У кулю вписано конус. Визначити об’єм конуса як функцію
його висоти. Радіус кулі 7?.
812.	У коло з радіусом 7? вписано прямокутний трикутник.
Визначити його площу як функцію И (висота трикутника).
813.	Дано циліндр з радісом 7? і висотою Н. Навколо нього
описано конус (площі основ циліндра і конуса збігаються). Визна-
чити об’єм описаного конуса як функцію його радіуса г.
814.	Периметр трикутника 10 см. Визначити його площу як
функцію сторони х.
815.	Зобразити площу рівностороннього трикутника а) як функ-
цію його сторони а\ Ь) як функцію висоти Н.
816.	Зобразити площу 5 трикутника, вписаного в коло з радіу-
сом 7?, як функцію однієї з його сторін х.
817.	Подати площу 5 круга як функцію його радіуса х.
818.	Нехай АВ = х деяка хорда в колі з радіусом 7?. Зобрази-
ти віддаль хорди від центра як функцію довжини хорди.
819.	Зобразити площу поверхні кулі як функцію радіуса кулі г.
§ 2. Графіки функцій
Побудувати графіки (по точках) таких функцій:
820.	а) у = Зх + 2; Ь) у = — 2х + 1; с) у — 4х — 3.
821.	а) у = -^-х2; Ь) у =-^-х2; с) у = х2 + 1; (і) у = х2*—2;
е) у = 3-х^ /) у = |х2— 11.
9	11	1
822.	а)у = т; Ь) У = ~1; с) У=^, О) У =	=
	X	при —4 С х <	со,
823. у = -	X2	при 0 < х <	С 1,
	—2х + 3	при 1 х <	£2.
	[ —х при	—2<х<0,	
824. 0 = |	[ ]/х при	0<х<2.	
79
— 1	при х < 0.
825. у — \	, і	а
а І х2 4- 1 при х >• 0.
826.	а) у = |х| + 1; 6)і/ = х|х| —1; с)у=\х\ — х.
827.	а) у = х2 — 4х + 3; Ь) у = х2 + х + 2; с) у = х2 — 2х — 3.
828.	а) у = х- + Зх; Ь) у = 2х — х2; с) у = | х — х2
829.	а) у = Ь) У=^, с) У = 2{=±-
830.	а) у = -^-х3; Ь) у = —^-х3; с) у = 0,1х3 — 0,9х.
831.	Побудувати криву у — х3 на міліметровому папері та ско-
ристуватися нею для графічного розв’язання рівнянь:
а) _ 9Х _ 5 = 0; Ь) х3 + Зх - 5 = 0; с) х3 - 6х + 2 = 0;
й) х3 + х — 3 = 0; е) х3 — 4х — 1=0.
Побудувати графіки функцій:
832.	а) у = ±]ґх — 1; Ь) у = ± "Кх-(- 2; с) у = х]/х;
2	З
ії) у = х 3 ; е) у = ± х 4 .
833.	у = 1о§2 х; у = 1о§5 х; у = І£ х.
834.	а) у = зіпх; Ь) у = зіп 2х; с) у = зіп ; й) у = | зіп х |.
835.	у = соз х; у = соз (х + 1); у = 2 соз Зх;
836.	а) у = 2Л; Ь) у = З*; с) у = — 3х; О) у = 3х — 2.
837. а) у = ( ~	' "Р"
Ь) у =
2х при 0 < х < 3;
х, якщо 0 <х < 1,
х2, якщо 1 < х < 4,
2х, якщо 4 < х < оо.
838.	Побудувати на міліметровому папері графік функції у = 2х
та використати його для графічного розв’язання рівнянь:
а) 2х — Зх = 0; Ь) 2х + х — 4,3 = 0; с) 2х — х — 5 = 0;
й) 2х — 5х 4~ 6 = 0; е) 2х — 4х = 0.
839.	Накреслити на міліметровому папері графік функції у = х2
і користуючись ним розв’язати графічно рівняння:
а) х2 — 5х + 3 = 0; Ь) Зх2 — 2х — 1 = 0; с) х2 — 0,6х — 2 = 0;
сі) х2 + х — 2 = 0.
80
840.	Побудувати графіки таких функцій:
2)^=1§И; 3) у = Iх + М; 4)у=1§х—1;
5) у = 1+ І£(Х + 1); 6)г/ = агс(§—Ц; 7)і/ = агсі§—
ЛІ	Л
1 - —
8) у = агсі§ ; 9) у = 2х ; 10) у = 2х-1 •
841. Розв’язати графічно рівняння:
а) Зх — соз х — 1 = 0; Ь) (4”)* — х =
сі) 10І§х —х = 0; е) зіп 2% — х = 0;
§) зіп х + х — 1 = 0; і) х — х = 0,
с) 2х — 1§ х — 7 = 0;
/) соз х — х = 0;
—2л <х <2л.
842. Побудувати графіки функцій,
формі:
[ х = І 4- 1,	( х = 4 соз і, і
1) і о 2)	• .	3)
7	[ У = 1	—	7	І у = зіп /;	7	(
( х = 2 соз і — соз 2/,	( х == сЬ /,
г\ І	/?\ І
' І у == 2 зіп і — зіп 2/;	7 | у = зЬ і.
поданих у параметричній
X = /2,	( х — 1 — зіп /,
4)
х = /3;	( у = 1 — соз і\
Те ж саме для функцій, заданих у полярній системі координат;
1
7) р = 1; 8) р == — ф (Архімедова спіраль)', 9) р = е2л (ло-
гарифмічна спіраль)', 10) р
=----- (гіперболічна спіраль)', 11) р =
= 1 4-созф (кардіоїда); 12) р = 4созф; 13) р = ІОзіпЗф (трипе-
люсткова троянда)', 14) р = 5зіп2ф (чотирипелюсткова троянда).
§ 3.	Границя й неперервність / (х)
843.	Послідовність (функція натурального аргументу) набуває
вартостей ик = 2, и2 = -|-, и3 =	, и^— -|- і т. д. Знайти ип, вста-
новити чому дорівнює 1іш&п. Якщо є = 0,01, є = 0,0001, знайти
відповідне 7\7, тобто таке, що коли п> М, \ип — а | < є.
844.	Функція ип = ? (п) набуває вартостей и± = 0,7, и2 = 0,77,
и3 ~ 0,777 і т. д. Знайти ип та його границю. Яке повинно бути п,
0,0001.
І 7
щоб було \ип ——
6 2193
81
845.	Функція ип, набуває вартостей = 0,4, и2 = 0,46, и3 =
= 0,466, и4 — 0,4666 і т. д. Знайти границю ип, коли п -> оо.
846.	Функція ип набуває вартостей = 1, и2 =------р	,
и4 =----і т. д. Знайти ип та його границю. Яке повино бути /г,
щоб різниця між ип та її границею була меншою від додатного
числа є?
847.
з якого
Показати, що змінна ип
І 2
п, \ип ~ Т
є, зокрема
|рр! прямує до Починаючи
2 І
ип — 4 <0,0001?
□
848.	Довести, що Ііт	= 1. Починаючи з якого п,
11 — ип | < е, зокрема 11 — ип | < 0,0001 (при є = 0,0001)?
Зи2 І 2
849.	Показати, що послідовність ип =	1 є спадною і має
З	і З І
границю -р. Починаючи з якого п, \ип--------— | < є, зокрема, для
8 = 0,001?
. З
81П — Л
тт	•	•	• Л	81П Л	2
850.	Дана послідовність = зіп — , и2 = 9 —, и3 = --------5—,
2	2	о
2
..., ип —--------,... Знайти 1ітип. Починаючи з якого п, абсо-
П	п-+ж>
лютна вартість різниці між ип та її границею стане меншою за
0,0001? Для яких п ип дорівнює своїй границі?
2д__і
851.	Показати, що змінна ип = -рру має границю 2. Почина-
ючи з якого п, \ип — 21 <є, зокрема менше за 0,001?
4	9
852.	Функція ип набуває вартостей иг = 1, и2 = у, и3 = -р-,
,... Знайти ип та його границю. Починаючи з якого п, бу-
демо мати \ип — а | <є. Обчислити для є = 0,01; є = 0,00001.
Знайти границі послідовностей (функцій натурального аргументу):
853. 1іт^4~
2п
854.
855.
Ііт_______________
. ™ (л+1)3-(п + 3)з
82
856.
Ііш
/г->сс
З —2п3
4 + Зп3 •
857.
858.
Ііт-^+^Т”4.
,~оо п* + З
|іш'»+.,<„+2, Й.-Ц
„« 4"3 + 1
859.	1іт1 + г + 3 + 4 + -- + " .
' + 1
860.	Дт(1 + 4 + V + • + ж)-
о е 1	і • 1 — 2 + 3 — 4 + ... — 2/2
861.	Ііт-----!—.
П-юо	/22 + 1
862.	1іт1- + 2Ч-33+4Ч-... + „3
»-» “3
..	1 Г/	1 ' 2	/	9 \2	/	п— 1\21
863.	Ііт — (о + — І +(а + "7'| + ---4~(аН——) •
П-юо а [\	" /	\	" /	\	71	/ ]
1.2+2.3+ . + »(,+ !>
п3
П->оо
865‘ Д™ +	+ • • • + (Зп-2) (Зп+ 1) ] •
866. ІітІагсі§ + агсі^-^ + агс1£ 2І + • • • + агсі§
868.
869. Ііт 1 и^-оо	'1 - зМ’ 5и ) •
870. Ііт । П-^оо	/ 2п \п \2п + 1у •
871. Ііт П->оо	ґі + -Мп+5.
872. Ііт п [1п (2п 4-3) — 1п 2п].
П-^<хз
873.	Пт^а—1)п, а>0.
п^-оо
6*
83
874.	Ііт п2 а — п+у/~а), а > 0.
П->оо
875.	Ііт п (у^а — у^б), а > 0, Ь > 0.
876.	Ііт (Ц+Ц) ( а > о, ь > 0.
/г->	\	2	/
877.	Іітп2 Іпсоз —.
П->оо
§ 4. Границя функції неперервного
аргументу
878.
зокрема
повинно
/ (х) = Зх + 1 • Довести, що Ііт / (х) = 4. Яке повинно бути
х->1
б, щоб з нерівності | х — 11 < б випливало | / (х) — 4| < є,
при є = 0,003?
879.	/ (х) = х2 4- Зх. Довести, що 1іт/(х)=10. Яке
х-*2
бути б при заданому є, зокрема при є = 0,0001?
880.	/(х) = х2. Коли х-^3, то /(х)-^9. Яке повинно
щоб з нерівності | х — 3 | < б випливало | / (х) — 91 <8,
при 8 = 0,0001?
881.	Дано /(х) = 4х— 3. Довести, що 1іш/(х) = 9. Яке новин-
х—>3
но бути б, щоб з нерівності | х — 31 < б, випливала нерівність
|/(х) —9/ <8?
882.	Довести, що
Ііт
бути б,
зокрема
Яке слід вибрати б при
випливала нерівність
х2 — Зх + 2 __	1
х2 — 1	~	2 ’
заданому є, щоб з нерівності | х — 11 < б
2
883.	Довести, що
Ііт х-ух + 6	1
х—з + х — 6	5
Яке повинно бути б, щоб для | х 31 < б виконувалась нерівність
є?
84
884 Довести, що Ііш (2х2 — Зх + 1) = 3. Яке треба взяти б, щоб
при | х — 21 < б / (х) = 2х2 — Зх + 1 відрізнялася від 3 менш ніж
на 0,007?
885. Довести, що
1іт/(х) = Ііту^у = 2.
<<->3	х-3 X -г 1
Яке повинно бути б, щоб при | х — 3 | < б виконувалася нерівність
|/(х) - 2| <є?
886. Довести, що
Знайти залежність між є
887. Довести, що
г х2 — З З
Йх*+1- 5 •
та б.
і. 2х + 5	9
™ ЗГГ2 - Т •
та б.
Знайти залежність між є
888. # = Зх ^~2  Довести, що 1іш^-^=3. Яке треба взяти N.
%	1	Х->ОО % І~ 1
щоб з нерівності | х | > N випливала нерівність | у — 3 | < є?
2х2 І З
889. у =...2 Т г -* 2 ПРИ *-^оо. Яке повинно бути М, щоб з
Х“ -р 4
| х | > N випливало | у — 21 < є?
890. Знайти границю функції
Зх при —3 <С х < 0,
/ (%) =	1 при х = 0,
х 1 при 0 < х <: 3
у точках х =	, х = 0, х = 0,01. О
891. Знайти границю функції
	' х при —2 <х	<1,
/(*) = • у точках х = 0,99, х = 1	0 при х = 1, х2 при 1 < X < та х = 1,01.	;2
892. Знайти границю /(*) = ' у точках х = — 0,1, х =	функції х3 + 1 при —3 0,5	при	х = х2 + 1 при 0 < 0, х = 0,1.	< х < 0, 0, х <3
85
х<2,
оо
893.	Знайти границю функції
( х2 — 2 при -
'(х)==( 2х_! при 2
у точках х = — 1, х == 2 та х = 3.
Знайти границі функцій неперервного аргументу:
894.	Ііт/Зх---
х-М х-4/
895.	Ііт -1.
х-і 1-х
у2 ____ Л
896.	Ііт—4,	....
х-2 х + Зх — Ю
оп? і- х2 — 3x4-2
897. Ііт -5—т.--^ - .
х-> і %2 — 6х 4- 5
898.	Ііт
899.	Ііт Зх2~4*+1 .
ХН-1	X3 — X
ппп і •	X3 — 8
900.	Ііт -»—г—г-д-.
^2 X2 — 6x4-8
ЛЛі і- х3 — Зх2
901.	Ііт—о—х-.
хм.3 X2 —9
х5 — 4х
х2 — 2
902. Ііт
У3 _ 1
903. Пт^—і.
904. 1іт-х-^44-.
х-2 х ~4
пл_ .. 5х3 4-Зх2— 5х — З
905. Ііт—.Т- ----і—
плс і- х4— 5х2 + 4
906. Ііщ---т—г1—
х->2 х3 —4х
907. Ііт / "
т \
Х__хп----1 __	> п Та —шлі числа.
X
908. Ііт
х->0
ЛАП 1* X 4~ 3 — 2
909. Ііт -—5.—
1
86
910. Ііт
х~>0
911. Ііт
х-»0
/9 — ха — З
V ха+25 — 5
3/х +1 — 1
X
912. Ііт	.
х—>1 ух — 1
913. Ііт
V-! X— 1
з<-----
914. Ііт	.
915. Ііт
Х-*оо
Зх2 — 2х + 7
4х2 — х + 2 *
916. Ііт
Х-*оо
5х2 + 4х + з
х3 + 2х2 + х *
917. Ііт СКх2 + 5х + 4
х-*оо
х).
918. 1іт(х — V х2 + 2).
Х->оо
.. зіп Зх
919. Ііт----------
х~>0 х
лпл 1- 5Іп5х
920. Ііт—;—.
х-0 4х
921. Ііт
2х
922. Ііт
х~>0
8ІП 4х
8Іп7х
923. Ііт
х-*-0
Зх
і§5х
924. Ііт
х-»0
925. Ііт
х->0
926. Ііт
х->0
927. Ііт
у-*о
1 — СОЗ X
X
X2
1 — соз 2х *
х зіп 2х
1 — СО82 X *
1 — 2 соз (і/+
\ о /
зіп ї/
87
928. Ііт
зіп 4а
соз2 2а
929.	Ііт -------------------7=-----.
л (соз а — зіп а) (1 — у 2 соз а)
лпл 1-	1 —У^СОЗХ
930.	Ііт ---т-4-----ї—.
„ СІ§2Х— 1
Х'*~4
931.	Ііт Зх + агсіех,
х_>о + агсзіп х
932.	Ііт 3" зіп .
П->ОО
X2
933.	Ііт	.
х»о у соз х — 1
з <----------------
СОЗ ф — у СОЗ ф
934.	Ііт зіп2 ф
935.	1іт(х- 1)і§
г->1	*
936.	Ііт -2^
Г 2 /
ЗІП (х—
937.	Ііт—7=----—
я У2
ХЧ-- — — СО8Х
938.	Ііт 52^х-зіп7х
г_П	ЗІП X
939.	Ііт (х------2х.
Х 4
940.	Ііт -^-5Іпх-.
х^О 81П3 X
941 Ііт 5Іп + х) + зіп (д — х) — 2 зіп а
’ х-0	х2
942.	Ііт .П+^А-/±±Л*£
х->0	х3
88
943.	Ііт .созх-У 1 + хзіпх
х->0	зіП2
944.	Ііт
я
ї->з
І§3Х — ЗІ£Х
1 — І£3 X
2 — X — І£3 X
945. Ііт
946. Ііт
X	X
зіп-у — соз-у
СО8 X
947.	Ііт (2+_?Ґ
Х-оД х І
948.	Ііт -4-0 •
х-оо \х+2)
плп і* /Зх -р
949.	Ііт ——
V-.™ І Зх /
951. Ііт 1------------
%->оо \	Х
953. Ііт	1
954. 1іт(1 + 5і§2х)с‘е2\
955. ііт /
х_а 1 8іпа
957. Ііт-—1
х->0 х
пх________кх *
958. Ііт —----а>0, Ь>0.
х->0 х
89
959. Ііт
х->10
1&Х— 1
х — 10
960.	Ііт
х-*е
961.	Ііт
х->0
ІП X — 1
X — е
еах__еЬх
X
962.	Ііт---------—
х->0 х
963.	Ііт
х->0
е*2 — СОЗ X
Т2
964.	1ітх[1п(1 х)— !пх].
Х->оо
965.	Ііт .	.Т.
х-о 1п(1 Н-х)
«зіп Зх__лЗІП X
966.	Ііт ---------------
х->0	х
967.	Знайти однобічні границі:
1)	Ііт —2) Ііт	3) ііте*  4) цт-------------Ц_
Х 1	Г-4.—П Х	П	—
5) Ііт----—г—	; 6) Ііт агсі§	—Ц- ;	7) Ііт агсі§	—Ц-	;
х->-0	1 . о—	х->1+0	х~~ 1	х->1—0	х~"1
1 + 2*
і	і
8) 1ітех""2; 9) 1ітгх“2; 10) 1іт£(х); 11) Ііт £(х);
х->2—0	х->2+0	х->3—0	х~>—2+0
12) Ііт ——£; 13) Ііт
Х-+2+0 X 2	- -
15)Дг^; 16)1іга
|х-2|.
•2+о х —2 ’
х3 — 8	1 і- 1
^2-; 14)х!™1-Зс‘е*;
17) 1іт^|!; 18) Ііт
х->2—0 Х 2	х->+0 У | ЗІП X І
§ 5.	Неперервність функції
Виходячи з означення неперервності, довести неперервність на
проміжку (—оо, +©о) таких функцій:
968.	/ (х) = ах + Ь у будь-якій точці. Якщо користуватися мір-
куванням «є — 6», то яка між є і б буде залежність?
90
969.	/ (х) = х2 у довільній точці х0. Яка буде залежність між
є та б?
970.	/ (х) = зіп (2х 4- 1) у довільній точці х0.
971.	/ (х) = | х | у довільній точці х0. Вказівка:
972.
973.
974.
975.
/ (х) = СОЗ X у довільній точці.
( Зх при —2-<х<1,
/ (х) — I 2 + х при І < х < 2.
Дослідити на неперервність функцію
і 2х ф- 1 при
/(х) = { , . .
4 І х2 + 1 при
Дослідити на неперервність
і х3 + 1 при
/ (х) =	2
' І х2 при
0<х< 1.
<0,
3.
976. Те ж
/(*) =
х2 — 1
при х=/=—1,
при х = — 1.
Ь
Який розрив має /(х)? Яку треба взяти вартість для функції в
точці х = — 1, щоб вона стала в ній неперервною?
977.	Нехай
Цх) =
х2 + х — 2
х+2
ь
При X —2,
при х = —2.
Який розрив має / (х) при х = —2?
Дослідити на неперервність функції:
978.	/(х) = | 2Т> ~00 <х < 0;
( X2,	0 X < ОО.
979.	/(х) = агсі§
980.	/(х) = ^±4-
' ' ’ X— 1
1
981.	/(х) = /-1.
91
982.	/(Х) = М.
(х^°>
983.	Цх) =	1*1
І 1 при х — 0.
984.	/ (х) = х — Е (х).
985.	/(х) = хзіп-у-.
986.	/(х) = -*££-~1іп*. .
987.	/(х) = 2х
[	1 при х = 0.
988.	Довести, що будь-який многочлен Р(х) непарного степеня
має принаймні один дійсний корінь.
989.	Використовуючи властивість неперервних функцій, показа-
ти, що рівняння х3 — 2х — 2 = 0 має на проміжку (1; 2) один дійсний
корінь. Обчислити його (наближено).
990.	Довести, що рівняння х = а $іпх + &, де 0 < а < 1, Ь > 0,
має єдиний (додатний) корінь, який не перевищує а + Ь.
991.	Використовуючи властивість неперервних функцій, показа-
ти, що рівняння х3 — 6х + 2 = 0 має дійсні корені на проміжках
(—3; —2), (0; 1), (2; 3). Обчислити їх (наближено).
992.	Дослідити на неперервність функцію / (х) = в околі
точки х = 0.
993.	Дослідити на неперервність функцію /(х)=-----—у— та по-
1 + ет
будувати схематичний ЇЇ графік.
Дослідити на неперервність функції:
о* ___ 1
994.	/(х) = ^—1.
2х + 1
/____і_
995.	/(х) = -| Х ПРИ Х¥=0,
( 0 при х = 0.
92
996.	/(х) =соз-ї-.
3/~
997.	/(х) = /х.
998.	Показати, що рівняння х3— Зх2 + 3 = 0 має дійсні корені
на проміжках (—1; 0), (1; 2), (2; 3).
§ 6. Рівномірна неперервність функції
999.	Дано /(х) = -|-. Показати, що на проміжку [0; 1] вона не-
перервна, але необмежена. Чи буде вона рівномірно неперервна на
цьому проміжку?
1000.	Показати, що /(х) = х2 рівномірно неперервна на проміж-
ку [1; 2]. Яке слід взяти 6 при даному є, що годитиметься для
точок всього проміжку?
1001.	Показати, що /(х) = х2 рівномірно неперервна на будь-
якому скінченному інтервалі (— 7?, 7?). Яке треба взяти 6 при
8>0?
1002.	Показати, що функція /(х) = созх рівномірно неперервна
на будь-якому проміжку.
1003.	Дослідити на рівномірну неперервність функцію /(х) =
X2
= -2 --2 на проміжку [—1; 1].
1004.	Дослідити на рівномірну неперервність функцію
на проміжку ^0;	.
1005.	Дослідити функцію / (х) = агсі§ х на рівномірну непе-
рервність.
1006.	Дослідити на рівномірну неперервність / (х) = ]Лх на про-
міжку [1; 4] та [0; 2]. Яке треба взяти 6 при є> 0?
1007.	Дослідити на рівномірну неперервність функцію /(х) =
= Зх+2 на проміжку (—оо, +°о). Яке треба взяти б при є>0?
1008.	Дослідити на рівномірну неперервність /(х) = у на про-
міжку [0,01; 1]. Яке треба взяти б при є>0?
1009.	Дослідити на рівномірну неперервність функцію /(х) =
— 1п х на проміжку (0; 1). Розглянути також проміжок [а0, 1] і
визначити б при заданому є > 0.
93
§ 7. Похідні та диференціали;
їх застосування
Виходячи з означення похідної, безпосередньо знайти похідні від
таких функцій:
1010.	/(х) = х2 —х4-1 та обчислити /'(0), /'(1) і /'(2).
1011.	/(х) =-1-х3 4-х—1 та обчислити Л(~1) і /'(2).
1012.	/(х) =	* та обчислити /'(—3) і /' (0).
1013.	/(х) = -|- та обчислити (2).
1014.	/(х) = та обчислити /'(—2).
1015.	/(х) = 2Х4 та обчислити (-у) .
1016.	/(х) = та обчислити /'(—1) і
1017.	/(х) = Ух 4- 1 та обчислити Г (0) і
1018.	/ (х) = ]/ х2 4- 1 та обчислити Г(УЗ) і Л(—1)-
1019.	/(х) = ух та обчислити /'(—1) і /'(]/8).
1020.	/(х) = 4= та обчислити ['(—і /'(—І).
У х	\	^ /
1021.	/(х) = зіп-^- та обчислити /'(0) і /'	•
1022.	/(х) = созЗх та обчислити }'(—і
1023.	/(х) = іех та обчислити	і
1024.	/(х) = сі§х та обчислити /'(—у-),	і
1025.	/(х) = -уу-| та обчислити /'(0) і /'(1).
1026.	/(х) = у х2 та обчислити /'(—1) і Гіу).
1027.	/ (х) ~ХХ^ у та обчислити /'(0) і /' (2).
94
1028.	/ (х) = Зх + 2 та обчислити /' (1) і /' (—2).
1029.	/(х) = агс1§х та обчислити /'(—1) і /' (0).
Використовуючи формули і правила, знайти похідні від таких
функцій:
1030.	і/ = х4 —Зх3 + 4х2—1.
1031.	у =— 2х2 + Зх + 2.
1032.	у = 4- + 4-х3-Зх2 + х — 7.
□ о
1033.	у = х3зіпх.
Ю34. , =
1035.	у =
1 — х2
1036.	у = х4(х2 —2).
1037.	у = х2 с!§ х — 5х.
1038.	г/ = і§х— х4-2.
1039.	у = -^- + х2— 1.
V .п
81П -=-
□
1040. у = -^-х31пх-----^-х®+1.
1041.	у = 2созх + 2хзіпх — х2созх.
1042.	о = 4-1п—г4------з-агсіех.
1043.	у = (х3 — І)2.
1044.	ї/ = зіпЗх.
1045.	у = і§25х.
1046.	у = 1пзіп4х.
1047.	у = соз4х.
1048.	у = 4- соз3 х — соз х Ч- соз •
3	'7
1050. у=---І-сі£2х—Іпзіпх.
1051. і/ = 4-і§3х4-і§х— 1.
О
95
1052.	у
1053.	у
1054.	у
1055.	у
1056.	у
1057.	у
1058.	у
1059.	у
1060.	у
1061.	у
1062.	у
1063.	у
1064.	у
1065.	у
1066.	у
1067.	у
1068.	.
1069.	у
1070.	у
1071.	у
1072.	у
1073.	у
__ 1 | , X СОЗ X
Г П ~2	•
=	---^-1§3х+ Ї&Х — X.
= х3-3~х.
= №.
__ 2СО82 х.
— хп е~х.
___ ^8ІП4
_ 4х —З
X4
1 + х3
~ 1 — х3 ’
= 4-х5(1 — Xі).
_ 2 і
2х2 3 х
-(1-х2) (2-х3).
_ 1
— X4 + Г
_ х
= (х2—І)2 •
1 і 1 + х 1	,
— — іп-г-^------т-агсІ£ х-
4	1 —х 2	&
1 ! X — 1	,	1	. 2х + 1
< = -г- 1п—== 4- —агсі& —~.
3	/ х2 + х + 1 /З	/З
у = X + X-------1- СІ§3 X.
_ 1
— і§х+ 1
=
у 1 — X2 ,
= -— ------1- агсзіп х.
= 1п ]Лх2 4- 2х + 2 + агсі§ (х + 1).
= агсзіп 2 Ух.
96
1074
1075
1076
1077
1078
1079
1080
1081
1082
1083
1084
1085
1086
1087
1088
1089
1090
1091
1092
1093
1094
1095
1096
1097
у=4-(х3 + 2)Г 1-х3.
у - агсзіп-—-----і- К 2 — х2.
у =	(х2 — 2) У 4 — х2 + 2 агсзіп -у .
2	, 2х — 1
У = —у=~ агсі£ ——- .
* /з 5 /з
1	2х — 1
у = —— агссоз —.
/2	/З
у = х агссоз х —	1 — х2.
у — агссоз —.
у = агссоз х + агсзіп х.
1 — X
у = агссоз—— .
/2
У =
у = агссі£ (1 — х).
у = агссі§ 2 Ух.
у = агсі§ х + агссІ£ х.
У = 1о& (х3 + 1).
У = Іо§3 По& (2х + 1)].
у = 10-*2Л
у = ІП ЗІП	.
2
г 1 — х
у = а агсзіп + ]/х2 — а2.
у = ]/3 — 2х.
у = е~ 5х+2.
зіп3 х
у = ЗІП х------х—.
О
7 2193
97
1098.	113 у = 22" зіп 4х	зіп 2х + -у
1099.	у = ІП СОЗ X + -І- X.
1100.	У — £ агсі§х— 2 .
1101. 1102.	у = Ух —	1 —х агсзіп Ух. у = х 1п2 х — 2х 1п х + 2х.
ПОЗ.	у = х2 У1 +х2--^-У(1 + х2)’
1104.	у = (агсзіп х)2.
1105.	у=іп^±!-'. Гх+1+1 1	о	/
1106.	1п(.
1107.	у = х агсі§ х	і- 1п (1 + х2).
1108. 1109.	у = 1п (х зіп х У 1 — X2). у = е~хг (Xі ф- 2х2 + 2).
1110.	^=4-^+^).
1111.	* * 1 1 1 + п» п» II
1112. 1113.	у = хсо&х. И'-Н-
1114. у = х^х. Знайти похідні від функцій, заданих 1115. Зх —5ї/+2 = 0. 1116.	у2 — 6х = 0. 1117.	х2 + у2 —6х + 2у + 1 = 0. 1118.	х2 — у2 = а2.	
1119.	%2 1 у2 _ 1 а2 -Г Ь2 — Ь
1120.	Ух + ]/’у = 4 та, зокрема, в г
|3
неявно:
точці Л4(9; 1).
98
1121.	х2 — Ьху + у2 — 7 = 0 та, зокрема, в точці (1; —1).
1122.	х2 +	= Зхї/.
1123.	ху = 1.
1124.	— 1пу = 2.
1125.	агсі§-^- = 1п]/х2 4- у2.
1126.	(х + у)е« — ех = 0.
1127.	х — у = ї&у.
1128.	ху = агсі§ .
2	2
1129.	х3 4- У3 = 1.
1130.	(х - а}2 4- (У - Ь)2 = г2.
Знайти похідні у' функцій у (х), заданих у параметричній формі.
1131.	х = 2/, у = 2і — Iі.
1132.	х = г‘34- 1, у=~Ія — і.
1133.	х = е2', у = 2е~і.
1134.	х = а соз ф, у=а зіп ер.
1135.	х = а(ф— зіпер), у~ а(1 — созер).
1136.	Х=аСО32ф, £/ = Л8ІП2ф.
1137.	х = а соз3 /, у = а зіп3 і.
.. ОО	За/	За/2
1138.	х — 1 + /3 , у - 1 _^_/3 .
1139.	Х = Є*81П/, у^е^озі.
1140.	х = а (созі + і зіп/), у = а(зіп/ — /соз/).
§ 8. Геометричні застосування похідної
1141.	Скласти рівняння дотичної до кривої у = х2—1 у точці
М(1, 0).
1142.	Знайти кут нахилу дотичної до кривої / (х) = х2 — х + З
л	1	1
у точках х = 0, х = та х = 1.
7*
99
1143.	Через дві точки кривої і/=—-х24-1, що мають абсциси
х = 0 та х = 4, проведена січна. Знайти точку на цій кривій, в якій
дотична паралельна до цієї січної.
з
1144.	Скласти рівняння дотичної та нормалі до кривої У = —
у точці Л4(1; 3).
1145.	Скласти рівняння дотичної до кривої у = х3, паралельної
прямій Зх — у + 5 == 0.
1146.	Під яким кутом крива у= 1 —х2 перетинає вісь ОХ?
1147.	Під яким кутом тангенсоїда перетинає вісь ОХ?
1148.	Знайти точку, в якій дотична до параболи у — х2 — Зх — 1
паралельна до прямої у = —5х + 2.
1149.	Під яким кутом крива £/=1п(х+1) перетинає вісь
абсцис?
1150.	Скласти рівняння дотичної до параболи у = ^-х2 — Зх —
— 6, перпендикулярної до прямої х + 5у — 10 = 0.
1151.	В яких точках кривої у =	----11 дотична
паралельна до прямої у = — 2х + 7?
1152.	Скласти рівняння дотичної у точці Л4(2; 1) до кривої
у = х3 — 2х2 + 1.
1153.	Знайти точки, в яких дотичні до кривих Зу = х3 — 18х2 + З
та у = — 4х2 + Зх — 1 паралельні прямі.
1154.	Скласти рівняння дотичної до цисоїди У2 = ^а — х У точці
Л4(а; а).
1155.	Скласти рівняння дотичної до кола х2 + у2 = г2 у точці
(хо, ^/о)«
1156.	Скласти рівняння дотичної до параболи у2=^(1рх у точці
ЛІ (х0> Уо)-
^2 У2
1157.	Скласти рівняння дотичної до гіперболи -------рг = 1 У
точці М(х0> у0).
1158.	Скласти рівняння дотичних до еліпса +-|^-= 1, па-
ралельних прямій у = 2х — 3.
^2	£/2
1159.	Скласти рівняння дотичних до гіперболи -------у- = 1, пеР'
пендикулярних до прямої у =------X + 1 •
1160.	Під яким кутом перетинаються криві х2 + у2 = 2 та
£/2 = х.
100
1161.	Визначити кути, під якими перетинаються лінії х2 + у2 4-
+ 2х — 4г/ — 20 = 0 та х — у — 4 = 0.
1162.	Скласти рівняння дотичної та нормалі до кривої у = х3—
— 2х2 + Зх — 3 у точці М (2; 3).
1163.	Скласти рівняння дотичних та нормалей до кривої у2 = х3
у точках Л4(1; 1) та Р(4; 8).
1164.	Визначити кутовий коефіцієнт дотичної до кривої х3 + у3 —
— 5(хг/ + 1) = 0 у точках М (2; 3) та Р (3; 2).
1165.	В яких точках кривої у =  2 * дотичні до неї па-
ралельні до осі ОХ?
§ 9. Механічні, фізичні та хімічні
застосування похідної
1166.	Два пароплави одночасно виходять з гавані. Один іде на
північ з швидкістю 20 км/год, а другий — на захід з швидкістю
24 км/год. З якою швидкістю змінюється віддаль між пароплавами?
1167.	Куля, випущена з швидкістю 250 м/сек під кутом 30° до
обрію, пройшла за і сек у горизонтальному напрямі віддаль х ==
= 125]/3/, а у вертикальному — у= 125/ — 4,9/2 (опором повітря
нехтуємо). Знайти швидкість кулі наприкінці 5-ї сек.
1168.	Тіло рухається по прямій так, що його віддаль 5 від по-
чаткового пункту через і сек визначається за формулою
5 = 4-/4-4/3+ 16/2.
4	'
Знайти швидкість руху. Коли тіло рухається в зворотному напрямі?
1169.	Тіло, кинуте вертикально вверх з швидкістю уо=ЗО м/сек,
знаходиться на висоті /і = ЗО/ — 4,9/2. Визначити час підіймання,
момент знаходження в найвищій точці, час падіння та найбільшу
висоту.
1170.	Тіло рухається прямолінійно за законом 5 = 1 Зі + і2.
Визначити його швидкість у момент часу і = 4.
1171.	Закон руху точки по прямій є 8 = 9і — і3. Знайти швид-
кість руху для і = 1 та і = 2 (5 дано в метрах, а і — в секундах).
1172.	Відомо, що при мономолекулярній реакції за час і утво-
рюється молекул (продукту реакції) х = А (1 — е~кі). Якому законові
підлягає швидкість утворення нової речовини при названій реакції?
1173.	За законом відбиття променів, кути падання та заломлення
зв’язані залежністю зіп а = п зіп р, де п — показник заломлення
середовища. Знайти .
101
1174.	Кількість молів, що перетворилася за час під час три-
молекулярної реакції (початкові кількості всіх трьох речовин одна-
кові і дорівнюють а) визначається формулою
а
х = а-----г	,
/ <2а*кі + 1
де к — константа. Якому законові підлягає швидкість реакції?
§ 10.	Похідні вищих порядків
У наступних прикладах знайти похідні зазначеного порядку:
1175. у — --- х4 — 5х3 + 2х — 1; знайти у™.
1176.	у = х3 — Зх + 2; знайти у".
1177.	у = х5 + Зх4 — 7х2 + 1; знайти у4.
1178.	у = (х3 + 1)(3х2 — 7х); знайти ущ.
1179.	у — 23х; знайти у4.
1180.	£/ = 8Іп2х; знайти уш.
1181.	у = соз2 х\ знайти у™.
1182.	у = Іпзіпх; знайти у".
1183.	у = -гХ- знайти
1 — X
1184.	у = зіп 2х; знайти
1185.	у = соз ах; знайти у&\
1186.	г/ = 1п(1 4- ах); знайти у^.
1187.	у = агсі§х; знайти у" (—1).
1188.	у = агсзіп х; знайти г/"	•
1189.	у = зіп4 х + соз4х; знайти у™.
1190.	у = знайти і/111 (2).
1191.	г/ = х2ех; знайти у<п>.
1192.	у — х2 Іпх; знайти г/ш .
1193.	£/ = х31пх; знайти у^п\
1194.	у = аохп + йіХ'1-1 + ... 4- ап\ знайти у<п\
1195.	х = асо8/, у = Ьз\пі\ знайти -44-
102
1196. х = асо8і, у = азіп/; знайти -А- та

зт
1197.	х=а(і — зіп/), у=а(1—соз/); знайти при
1198.	х = а соз3 /, у = а зіп3 /; знайти при і = 4-.
1199.	х = агсі§Л у = 1п(1 4- і2); знайти .
1200.	х = е~^ у = і* \ знайти 44-
у	йх3
СІ3ІІ
1201.	х = соз/4-/зіп/, = зіп/—/соз/; знайти -^4.
1202.	х = зес/, у = !§/; знайти 4"4-
’ ь ’	йх3
1203.	х=1п/, і/ = /3; знайти 4"4-
д,х3
1204.	х = е~аі, у = еаі' знайти -44 •
луЗ
1205.	Показати, що коли у = а соз Ях + Ь зіп Хх, то існує спів-
відношення у" + №у — 0.
1206.	Довести, що функція у = Скеах + С2е~ах справджує спів-
відношення у" — а2у = 0.
1207.	Показати, що у = зіп (ті агсзіп х) задовольняє співвідношен-
ня (1 — х2) у" — ху' + п2у = 0.
§ 11. Диференціали першого та вищих
порядків
1208.	Користуючись наближеною рівністю ку^сіу.
а)	обчислити приріст функції у = х2 — Зх, що відповідає зміні
аргументу від х0 = 2 до хг = 2,02. Знайти потім точну вартість Дг/
та обчислити абсолютну й відносну похибки.
Ь)	Те ж саме при зміні х від х0 = 3 до х± = 3,01.
с)	Те ж саме при зміні х від х0 = 10 до хг = 10,1.
1	2
1209.	Дана функція / (х) = х3 4- х2 4- х + -5-. Обчислити на-
«5	«5
ближено Ау при зміні аргументу від х = 1 до х= 1,03 та вартість
функції у точці х = 1,03.
103
1210.	Дана функція у = ух + 1. Знайти (наближено) Дг/ при
зміні х від х0 = З до хх = 3,02 та у (3,02).
1211.	Знайти наближену вартість приросту функції у = з\пх
при зміні х від 30° до 29°30'. Чому дорівнює зіп 29°30'? Порівняти
здобутий результат з табличним і з’ясувати, чому табличний мен-
ший за нього?
1212.	Знайти наближену вартість приросту функції г/ = созхпри
зміні х від 45° до 45°20'. Чому дорівнює соз45о20'?
1213.	Знайти наближену вартість приросту функції у — 1&х при
зміні аргументу х від 45° до 45°30\ Чому дорівнює 45°30'? Чому
табличний більший за здобутий результат?
1214.	Знаючи, що сі§ 30° = 1,73205, наближено обчислити
сі§ 29°45'.
1215.	Знаючи, що 2 = 0,30103 і 1§3 = 0,47712, обчислити
І£ 12,2. Порівняти знайдений результат з табличним і з’ясувати, чо-
му він більший за табличний.
1216.	Обчислити наближено 1§ 89, знаючи, що 3 = 0,47712.
1217.	Обчислити наближено агсі§ 0,98.
1218.	Обчислити наближено агсзіп 0,49.
1219.	Обчислити диференціал функції у = }/ х при х = 8 і Дх=
= 0,03.
1220.	Обчислити диференціал функції у — сї^х при х = ~ і
1221.	Знайти приріст Ау та диференціал йу функції у = х2 +
+ 4х — 1 при х = 5 і Ах = 0,01.
1222.	Обчислити наближено агсі§1,03.
§ 12. Застосування основних теорем
диференціального числення
(теореми Ролля й Лагранжа)
1223.	Показати, що між коренями функції /(х) = х2 — їх + 12
міститься корінь її похідної.
1224.	Перевірити справедливість Ролльової теореми для функції
у = у х2 — 5х + 6 на проміжку [2; 3].
1225.	Перевірити справедливість Ролльової теореми для функції
/ (х) = х3 — 6х2 + 1 їх — 6 на проміжку [1; 3].
1226.	Чи застосовна Ролльова теорема до функції /(х)=1—-
з >—
— ух2 на проміжку [—1; 1]?
104
1227.	Показати, що рівняння х3 + ЗхЦ-с=0 при будь-якому с
не може мати більше одного дійсного кореня.
1228.	Показати справедливість Ролльової теореми для функції
/(х) = 2х2~х на проміжку [0; 1].
1229.	Застосовуючи Лагранжову формулу до функції /(х) =
= х3 — Зх2 + х + 1 на проміжку [1; 3], визначити точку х = £, що
фігурує в цій формулі.
1230.	Застосовуючи Лагранжову формулу, довести нерівність
| зіп |3 — зіп а |	| р — а |.
1231.	Скласти Лагранжову формулу для функції у=2х на про-
міжку [0; 1]. Обчислити х = |.
1232.	Скласти Лагранжову формулу для функції г/==агсі§х на
проміжку [ 1; ]/3] та визначити точку х = |.
1233.	Дана функція /(х) = х2 + х + 2. Скласти для неї Лагран-
жову формулу на \а, Ь] і визначити х =
1234.	Скласти Лагранжову формулу для / (х) = Ух на проміжку
[х0, х0 + Дх]. Поклавши Дх = 1, переконатися (за таблицями), що
квадратні корені з двох натуральних чисел, які перевищують 100,
відрізняються між собою менше ніж на 0,05.
1235.	Скласти Лагранжову формулу для /(х) = х3 на проміжку
[а, &], 0 < а < Ь, та визначити х = £.
1236.	Дана функція ї{х) = 1п(1 +х). На проміжку [а,Ь] скла-
сти для неї Лагранжову формулу.
Застосовуючи Лагранжову формулу, довести нерівності:
1237.	— і£а <	0<а<р<-2--
соз2 а & г ь соз2 р	г 2
1238.	4^-<1п(1 + й)-1п(1 +й)<4=|, 0<а<Ь,
Користуючись наближеною рівністю
/ (X + Дх) « / (Хо) + Дх/' (х0 + -у-) ,
обчислити вирази:
1239.	82, знаючи 1§2 = 0,30103.
1240.	агсзіп 0,46, знаючи, що агсзіп 4- =	.
2	6
1241.	Застосовуючи Лагранжову формулу, довести нерівності
< 1п (1 + х) < х, якщо х > 0.
1242.	Застосовуючи Лагранжову формулу, довести нерівність
6х > 1 + х, х 0.
105
§13. Застосування формули Коші
та формули Тейлора
1243.	Скласти формулу Коші для функції /(х) = х4 та ф(х) = х2
на проміжку [а, Ь], де 0 < а < Ь, та знайти х = £, що фігурує в
формулі.
1244.	Скласти формулу Коші для функцій /(х) = зіпх та ф(х) =
= соз х на проміжку	та знайти х = |.
1245.	Скласти формулу Коші для функцій /(х) = созх та
Ф (х) = 1п (1 + х) на [а, Ь], —1 < а < Ь.
1246.	Скласти формулу Коші для функцій /(х) = х та ф(х) =
= }/х на проміжку [а, Ь], 0 < а < &.
1247.	Розкласти многочлен / (х) = х5 — Зх4 — 2Х3 + 4х2 — х + 2
по степенях двочлена х— 1.
1248.	Розкласти многочлен /(х) = х3 -{- 2х2 — Зх+1 по степенях
двочлена х+ 1.
1249.	Розкласти многочлен / (х) = х4 — 2х + 3 по степенях дво-
члена х— 1.
1250.	Розвинути по степенях х функцію / (х) = зіп х до чле-
на з х5.
1251.	Розвинути по степенях х функцію / (х) = соз х, до чле-
на з х2.
1252.	Розвинути по степенях х функцію /(х) = ех до члена зх4.
1253.	Розвинути по степенях х— 1 функцію Іпх до члена
з (х— І)3.
1254.	Розвинути по степенях х— 1 функцію /(х) = ]/х до
члена з (х— І)2.
1255.	Розвинути по степенях х функцію /(х) = і§х до чле-
на з х3.
1256.	Розвинути по степенях х функцію / (х) = У 1 + х до чле-
на з х4.
1257.	Розвинути по степенях х функцію /(х) = 1п(1 -]-х) до
члена з х3, та хп.
§ 14. Зростання й спадання функції.
Екстремуми
1258.	Показати, що функція / (х) = х3 — Зх2 + 6х — 5 скрізь
зростає.
1259.	Показати, що функція у = х2 — 4х3 спадає на проміж-
ку (— ос, 2) і зростає на проміжку (2, оо).
106
1260. Визначити проміжки зростання та спадання функції у =
]/4х —х2.		
1261. Довести, що	81П р . 81П а	А . —з-1- <	, якщо 0 < а < р	а	/\ л
1262.	Довести, що 1263.	Довести, що 1264.	Довести, що 1265.	Довести, що 1266.	Довести, що 1267.	Довести, що	—, якщо 0 < а < а	р 2 (х — 1)	.	, 	 ,  ;	< ІП X, X > 1. х+ 1 1п (1 + х2) < 2хагсі§х. <1п(1 +д х>0. х3 X	< 81П X при X > 0. . X3 . .	~	я х + ^-<і§х 0<х<^-.	, п	Я
1268. Довести, що 1269. Довести, що	Х^ х	2" < ІП (1 + х) < х, X > у2 1	— < СОЗ X, X =/= 0.	0.
1270. Довести, що 1271. Довести, що	2х < зіп х + х, 0 < х <-у созх < 1 —	, х =£ 0.	
2 1272. Довести нерівність — х<зіпх, 0<х<		. я т*
1273. Довести нерівність х	5- < агсі§ х, 0 < О		X < 1.
1274.	Довести нерівність	<агсзіпх, 0<х<1.
Визначити проміжки монотонності функцій:
1275.	у = — х2+ 6х+ 1.
1276.	/ (х) = 4--^ - 2х2 + Зх + 2.
О
1277.	Цх) = -^х4 — 2х2 + 1.
1278.	/(х) = зіпх.
1279.	/ (х) = х3 + 6х2 + 9х — 4.
1280.	/(х) = Іпх —х3.
1281.	/(х) = у< (2х— а)(а — х)2, а>0.
107
1282.	/(х) = х3е~\
1283.	/ (х) = агсі§ х — 1п х.
1284.	/(х) = х1§х.
1285.	=
1286.	/(х) = х-К2 8іпх, —
1287.	/(х) = 4-(е" + е-х)-
Знайти максимуми та мінімуми таких функцій:
1288. /(х) = 3х —х2.
1289.	/(х) = х2 — 12х+ 1.
1290.	/ (х) = 12х —х3.
1291.	/(х) = -^- —х24-2.
1292.	/(х) = х34-3х24-6х —4.
1293.	/=(х) = -1х3+ * %2_ 2x4-3.
1294.	у= 2х2 —
1295.	у= -І-х44-2х2 — 5.
1296.	у = х4-^-.
1297.	у = х?~ 4--
я	4
1298.	у = х5 4- бх4 4- 5х3 — 2.
1299.	ї/ = х2(2 —х).
1300.	/(х)=х24-4-
1301.	/(х) = хе-Л
1302.	/ (х) = агсІ§ х —і- 1п (1 4-х2).
1303.	у =	— х4 + х3+ 1.
1304.	І(х) — ехсо8х.
1305.	/ (х) = х — х.
1306.	/(х) = (х — І)4 (х 4- 2)2.
108
1307.	/ (х) = (х - 5)2 (х + І)2.
1308.	ї(х) = ——.
1309.	/ (х) = х (х + а)2 (а — х)3, а > 0.
1310.	/ (х) = (х~а^“—- , а > 0, Ь > 0.
1311.	/(х) = 8ІПХ + 3§іп.
о
Відшукати найбільші М та найменші т вартості функцій на
зазначених проміжках. (Якщо проміжок не дано, то слід визначити
найбільші та найменші вартості /(х) в усій області існування):
1312.	у = х2 на [—2; 2].
1313.	у = 2зіпх + соз2х на [0, л].
1314.	у = х> на [—2; 3].
1315.	у — 1п(1 +х) на (—1; 1].
1316.	у = V 9 —х2 на [—3; 3].
1317.	у=-^-х4 — х3 на [0; 4].
1318.	у = 2х3 — 15х2 + 36х— 18 на [1; 3].
1319.	/(х) = зіп4 х + соз4х на —у,	.
1320.	у= 2х® —х24-3х—2 на [0; 2).
1321.	у = сі§2х — 2сі§х на ^0;	.
1322.	у = х — агсі§х на [0; 1).
1323.	у = х— !п(1 4-х) на	1 .
1324.	у = 2х на [—3; 3].
§ 15. Задачі на відшукання найбільших та
найменших вартостей змінних величин
1325.	Число а розбити на дві частини так, щоб сума їх квад-
ратів була найменша.
1326.	Знайти додатне число, яке, будучи складене з оберненим
до нього, дає найменшу суму.
1327.	З квадратного бляшаного листа, сторона якого дорівнює а,
треба зробити відкриту зверху скриньку з найбільшою місткістю,
109
вирізаючи рівні квадрати по кутах і відкидаючи їх, а потім згинаючи
бляху так, щоб утворити боки скриньки. Яка повинна бути сторона
вирізуваного квадрата?
1328.	Відомо, що міцність балки з прямокутним поперечним
перерізом пропорційна ширині та квадратові висоти. Вирізати з круг-
лої колоди, діаметр якої б/, балку з прямокутним перерізом так, щоб
вона в горизонтальному стані чинила найбільший опір згинові.
1329.	З усіх прямокутників, що мають дану площу 5, знайти
той, периметр якого найбільший.
1330.	Знайти висоту циліндра найбільшого об’єму, який можна
вписати в сферу з радіусом 7?.
1331.	Тиск води по твірній на конічну посудину при витіканні
визначають за формулою р = ах (Н — х), де И — висота посудини,
х — віддаль до рівня води, а — стала. На якій глибині тиск най-
більший?
1332.	Периметр трикутника 2р, а одна з сторін дорівнює
а (а < р). При яких розмірах двох інших сторін площа трикутника
буде найбільшою?
1333.	Теплоємність води при температурі /° С визначається за
формулою
Сі = 1 — 0,0006684/ + 0,00001092/2.
При якій температурі теплоємність води найменша?
1334.	Беручи об’єм деякої кількості води при 0° С за одиницю,
визначають об’єм тієї ж кількості води при /° С за формулою, що
її встановив Копп
V = 1 — 0,000061045/ + 0,0000077183/2 - 0,00000003734/3.
При якій температурі об’єм води стає найменшим, а отже, густина
її найбільшою?
1335.	З бляшаного круга з радіусом 7? вирізають сектор з цен-
тральним кутом а і з нього скручують конічну лійку. При якій
вартості кута а об’єм лійки буде найбільшим?
1336.	Важіль другого роду має точку опори на одному кінці і
зрівноважується силою /(х) на другому кінці. На віддалі а від точки
опори підвішено вантаж р. Вага одиниці довжини важеля т. Яка
повинна бути довжина важеля, щоб вантаж р зрівноважувався най-
меншою силою?
1337.	Додатне число а розкласти на два доданки так, щоб їх
добуток був найбільшим.
1338.	Число 60 розкласти на дві частини так, щоб сума по-
двоєної однієї частини та квадрата другої була найменшою.
110
1339.	У сферу з радіусом 7? вписано конус. Знайти той, що
матиме найбільший об’єм.
1340.	У конус з висотою Н і радіусом основи 7? вписано ци-
ліндр. Знайти той, що має найбільший об’єм.
1341.	Треба повісити над центром круглого майданчика з радіу-
сом а електричний ліхтар. На якій висоті /г ліхтаря найкраще буде
освітлена доріжка, що оточує (проходить по краю) майданчик?
(освітленість прямо пропорційна косинусу кута падіння та обернено
пропорційна квадратові віддалі від джерела світла).
1342.	Навколо кулі з радіусом 7? описано конус. Знайти конус,
що має найменший об’єм.
1343.	Треба виготовити бляшану посудину циліндричної форми
місткістю 3 л, відкриту зверху. Які повинні бути розміри посудини,
щоб на ії виготовлення пішла найменша кількість матеріалу?
1344.	На пароплаві витрати на паливо пропорційні кубові його
швидкості; при швидкості в 10 км/год витрати на паливо станов-
лять 5 крб. на годину, інші витрати (не залежні від швидкості)
становлять 80 крб. При якій швидкості пароплава загальна сума
витрат на кілометр шляху буде найменшою та яка буде при цьому
загальна сума витрат на годину?
1345.	Прямокутний трикутник, обертаючись навколо одного з його
катетів, утворює прямий конус. Знайти об’єм найбільшого з них, як-
що гіпотенуза дорівнює 3 см.
1346.	Переріз тунеля має форму прямокутника з насадженим пів-
кругом. Периметр перерізу а м. При яких розмірах його сторін
площа перерізу буде найбільшою?
1347.	З пункту Л, розташованого на схід від пункту В на від-
стані 300 км, вирушає автомобіль в напрямі на захід (на В)
з швидкістю 60 км/год. Одночасно з пункту В вирушає вантажна
машина в напрямі на південь з швидкістю 45 км/год. В який
момент часу (від початку руху) віддаль між ними буде най-
менша?
1348.	З кругових секторів (різних радіусів), що мають даний
периметр /, визначити той, який має найбільшу площу.
1349.	Сума довжини та обхвату поштового пакунка не повинна
перевищувати 150 см. Визначити розміри найбільшого пакунка ци-
ліндричної форми, який можна відправити поштою.
1350.	З прямокутного листа бляхи завширшки а см треба зро-
бити (зігнувши лист) відкритий жолоб циліндричної форми (пере-
різ жолоба має форму кругового сегмента). Який повинен бути
центральний кут <р, що спирається на дугу цього сегмента, щоб
місткість жолоба була найбільша?
Ш
§16, Відшукання граничних вартостей
функцій. Асимптоти
1351.	Ііт	соз 5х	1352. Ііт	...4..
	л	соз Зх	Х-1	х2~1
			
1353.	Ііт	хт—1	1354. Ііт --~7х,+ 2-.
	х-1	X — 1	х—2	*2 - 4
1355.	Ііт х->'8	^-2 х — 8	1356. 1іт?^1. х->0 81ПХ
1357.	Ііт	ех — е~~х — 2х	у2 1п(1+х)-х + 4-
	Х-4-0	1 — СОЗ X	1358. Ііт	5	і.
			п	X3 х->0	л
1359.	Ііт	1п зіп Зх	1360. Ііт -?Х~1~Х .
	х->0	1п зіп 2х	Х->0	1 — СО8 X
1361.	Ііт	агсі£ х — х	1362. Ііт—.
	х—>0	Xа	Х-4-ОО Х
1363.	Ііт	хп ах	1364. Ііт	.
	х->оо		5Ш2 Зх
1365.	Ііт х->0	1п X	1366. ІітхзіпД-. Х-4-ОО	Х
1367.	Ііт х->1	[_1		1368. Ііт /Ц-— сі£2хк х-0 \ х	)
		\ 1п X	1п X ) *	
1369.	Ііт агсзіп (1 —х) х		1370. Ііт (агсзіп х)іе х.
	х—> 1	X СІ§(1 — х).	х->0
		2 •	1 Xі ЗІП 		1
1371.	Ііт		X	1372. Ііт (е3^ + х)х.
	х~>0	ЗІП X	х->0
1373.	Ііт	еах — е$х	1374. Ііт	.
	х->0	зіп ах — зіп Ьх *	х~>оо 81П Х Х
1375.	Ііт х->1	, ЛХ (3 - 2х)	ах3— 1 1376. Ііт а. * . ^0 8ЩЗ 2х
1377.	Ііт х->0	1 + х__ 1 * □ X2	1 1378. Ііт (созЗх)*'. х—>0
112
1379. Ііт (я — 2х) і§ х.
л
х~>'~
__1
1381. Ііт (сіє х) іпх.
х->0
1383. Ііт !_
х->0	• 1 X
1
<пл,-	1- Є----(1Ч-Х)*
1385. Ііт------	д.„ #
Х-.0	Х
1380. Ііт (а2 —х2)іє
х-*а
1382. Ііт (і§ }ІВ 2
ж-1 \	4 /
2
1384. 1ітх‘ + Іпх,
х->0
1387. Ііт
х->0
X СОЗ X — ЗІП X
X2 ЗІП X
,386.111^+^+;.
„-і 2х4 — х — З
X3
ЗІП X — X + -д-
1388. Ііт----г--ї-
*-о х
1389. Ііт
сі§ 2х
1390. Ііт
х->0
г 1
8ІП2Х
_1_\
X2
Знайти асимптоти кривих:
1391. у = -±т>
& х+ 2
1392. у = х + 4- •
у2	о2
|393- -5Г-Т-1-
|395. ц = ^.
1394.
, _	1 х*
У~ 2	(х 4- 1)2 •
1397. у= е~х\
і
1399. у = хех.
1401. у — і§х.
1396. у = 2х + агсІ£ у-.
1!
1398. у = ех.
1400.	 2	.
х2 — 2х + З
1402. у2 = 2х.
1405.	= 1 - х3.
§ 17. Опуклість, угнутість, точки перегину
Знайти проміжки опуклості, угнутості й точки перегину кривих:
1406. у = х3 + 1.	1407. х = х4 — 6х2 + 2.
1408. у = х3 — 6х2 -р 2х + 10. 1409. у = х4.
8 2193
113
1410. # = 2-Зх-х2. 1412. у = х 36х2 — 2%3—х4.	3/-	 1411. у —а—ух—Ь. 1413. у = егх2.
1414. у = 8Іпх.	1415. у = ^А-у.
1416. у — агсі§х.	1417. у — х2 Іпх.
§ 18. Наближене розв’язання рівнянь
Користуючись методом дотичних (Ньютонів метод), обчислити
дійсні корені рівнянь:
1418. х8-}-2х—11 =0. 1420. х3 + Зх2 — 3 = 0. 1422. Зх — соз х — 1=0 1424. х3 + 3х2 —4х— 1 =0. 1426. х4 —х — 1 =0. 1428. х3 — 6х2 + Зх + 5 = 0. 1430. созх — х = 0. 1432. х — х = 0. 1434. х4 — Зх3 + 8х2 — 5 = 0. 1436. х3 — Зх + 1 = 0. 1438. х3 — 4х— 1 = 0. 1440. х3 — Зх + 5 = 0. 1442. е* — і§х = 0. 1444. х4 + 4х — 2 = 0.	1419. х3 — 4х2 + 2 = 0. 1421. х3 —Зх2 —3 = 0. 1423. 2х— І£Х — 7 = 0. 1425. х3 — 6х + 2 = 0. 1427. 6х + х = 0. 1429. зіп 2х — х = 0. 1431. созх — х2 = 0. 1433. х3 + 6х- 8 = 0. 1435. х4 — Зх2 + 4х — 1 = 0. 1437. х4 + Юх— 100 = 0. 1439. х5 —х —0,2 = 0. 1441. 2зіпх — х = 0. 1443. є? — зіпх = 0. 1445. 2Х3 —х2-7х + 5 = 0. § 19. Побудова графіків функцій
1446. у = ^х? — 4х. О	1447. у = х4 — 2х2 -}- 2.
1448. у2 = х3+ 1.	1449. £ = —8. у	1 + X2
1450. у= 1452. г/=-|-х3 —2х2Зх—1.	1451. У = 1453. У = ^^.
114
уЗ 1 ДКД п	Л	1455 ц	 *2	*
1154. у— зіх—ху	1455. у — 4 (д,2 +	.
1456. ^ = -і4-|.	1457 и —	*
	
1458. у2 = х (х — а)2, а > 0.	1459. у = х2е~х2.
	 х2	
1460. у ~ хе 2.	1461. у = х*е~3х.
1462. У = *-^. І	1463. (/ = 4^. X2 — 1 1ДСК 1г 	 	!	
1464. у=еі{х2-3х+2\	1465' У X2 —Зх+ 2 •
1466. у = зіп х + Іп зіп х.	1467. у = е~а‘х2 (а >0).
1468. у = 2 зіп х + соз 2х.	1469. у2 = 2х2 — х4.
1470. у^х2-—.	1471. у = х — 1п(14-*)-
1472. у= —.	1473. г/ = х21пх.
1474. у = х!пх. 1476. у = 3х — х3.	1475. у = — агсі§х. 1477 и	х3
	У — 2(д._|_ 1)2 •
1478. у = х+ зіпх. 1480. у=(1 + ±)х.	1479. у = х2 — 3|х|4-2. з	з 	
	1481. у = у(х -}-1)2— V х2 4-1
1482. у = х3 — Зх+ І.	1483. у = ^±-1. X2
1484. у = х — 4-.
X4
8*
РОЗДІЛ VI
КОМПЛЕКСНІ ЧИСЛА ТА АЛГЕБРА
МНОГОЧЛЕНІВ
§ 1.	Комплексні числа
1485.	Знайти х і у, вважаючи їх за дійсні, якщо:
а)	(3 — і) х + (2 + 51) у = 1 — 2/;
Ь)	(6 + 8/) х — (4 + 30 у = 5 + 2/.
1486.	Розв’язати системи:
а) (2 + 30 х + (4 — 0 у 4- (—1 — 20 и 4- (5 4- 0 V = 8 + 6/,
(—2 + 0 х + (2 + 40 у + (6 — 50 и + (1 — 0 V = —7 4- 5/;
&) (1 4~ 0 х 4~ (1 4~ 20 у + (1	30 и + (1 4~ 40 V = 1 4~ 5/,
(З — І)х 4- (4 — 20 у 4- (1 + 0 и 4- 4ш = 2 —/,
вважаючи х, у, и, V за дійсні.
1487.	За яких умов модуль суми двох комплексних чисел дорів-
нює різниці модулів доданків?
1488.	За яких умов модуль суми двох комплексних чисел дорів-
нює сумі модулів доданків?
У наступних прикладах комплексні числа зобразити в тригоно-
метричній формі:
1489.	а) 1; Ь) с) —і\ (і) 1 +У3і.
1490.	а)УЗ — і\ Ь) —1 4- 0 с) — 1— і\	й) — 1 — УЗі.
1491.	(2 — ]/3) — і.
1492.	а) соз ф — /зіпф; Ь) —созф4-/зіпф; с) —созф — /зіпф.
1493.	а) 1 4-соза 4-/зіпа; Ь) 1—соза 4-/зіпа
1494.	Перевірити тотожність:
х4 4~ 4 = (х —- 1 — /) (х — 1 4~ 0 4~ 1 4~ 0 4- 1 — 0*
116
Обчислити вирази.
1495.	а) (1 + 2і)в; Ь) (~	+ 2і- 5.
1496.	(і^у-2 («>2 —Ціле).
1497 (2-02~(3 + 2іУ 8 (1-У-1
(_ 1+2І)2	•	(1+05+1 ’
Користуючись теоремами про модуль та аргумент, обчислити:
1499. а) 2(1—0(/3 + і)(—1—/Зі); Ь) (-ЦУ^-)М
1590	(-! + /3016 , (-1-і/3)Ц
ІЬШ). (1—4)18	+	(1+018
1501. а) (1 + І)п\ Ь) (]/3 — ї)п (п — ціле число).
1502 П +
!502.	(1 + 08л	’
Знайти всі вартості коренів:
1503. а) уП; Ь) ^7; с) ^=8.
і5м- Ой  і5°5- Ой; б) ’/її+*;
с) /ТО; (і) ^—2 + 2і.
1506.	]/ 1 +
Розв’язати рівняння:
1507.	х2 — (3 — 2і) х + (5 — 5і) = 0.
1508.	х2 — (3 + 7і) х — (10 — 11і) = 0.
1509.	(З + і)х2 + (1 — і)х— 6і = 0.
1510.	х4 + бх3 + 9х2 + 100 = 0.
1511.	х4 + 2х2 —24х + 72 =0.
1512.	х4—Зх2 + 4 = 0.
Виразити через созср і зіпер функції:
1513.	зіпЗф. 1514. соз4<р. 1515. зіпбф. 1516. зіп6фсоз6ф.
Виразити через тригонометричні функції кратних дуг такі функції:
1517. соз3ф. 1518. зіп3ф. 1519. соз4ф. 1520. зіп4ф.
1521. соз*ф. 1522. соз7 ф 4-зіп7 ф.
117
1523. Виразити 6ф через <р.
Довести рівності:
1524.

сп ф— ф ф—сп ф+-
1 — С2пі^ ф + С*п і§4Ф — С£ (§6ф + ...
„„ гк п(п— 1)(п — 2)...(п — £4-1)
ДЄ	.
т—1
1525. 22тСО32тф = 2^ (Хс03 2(/П—Л)ф +<Х
/г=0
1526 . 22”1 со82т+1 Ф = 2 ^+і со8 (2т — 2к + 1) Ф-
/г=0
/п—1
1527.	2й”зіп2"1 ф = 2 2 (—1Г+"С2тсоз2(т—А:)ф + СГт.
6=0
1528.	22т зіп2,п+І ф = 2 (—1 )т+к С2т+1 зіп (2т — 2/г + 1) ф.
к=0
Знайти суми:
1529.	1 + 2 соз ер + 2 соз 2ср 4~ ... + 2 соз Пф.
1530.	зіпф + зіпЗф + зіп5ф + ... + зіп(2п — 1)ф.
Довести рівності:
1531.	1 + С* + С® + С\2 + ... = -і- (2П-1 + 2Гсоз •
1532.	С'п 4-С^ + С® + ...= 4~(2"-1+ 2Тзіп-^).
1533.	С2п + С6п + Сп + ... = -і- (2"“’ — 2Тсоз-^) •
1534.	С3п + С7 + С'1 + ... = 4 (з"-1 - 2Т зіп-^-) •
1535.	1 +С^ + С®+С9„ + ... =4- (2" + 2 соз
1536.	С‘+С4+С7„ + ... =4- 2п + 2созЦ^л).
О \	О ]
118
§ 2. Розклад многочлена на незвідні
множники
1537.	Число 1 4- г є коренем многочлена х4 — 5х3 + 4х2 4- 2х‘-’8.
Знайти всі інші корені та розкласти многочлен на множники.
1538.	Знайти дійсні корені многочлена х1—х& — 2х54-14х4—
— 15х3 —25х2 + 48х— 20, визначити їх кратність, знайти інші коре-
ні та розкласти многочлен па множники.
1539.	Число 2 + і]/3 є двократний корінь многочлена х6—
— 8х5 4- 29х4 — 48г3 4- 19х2 4- 56х — 49. Знайти всі інші корені та
розкласти многочлен на множники.
1540.	Знайти кратність кореня х=— 2 многочлена х5 4-7Х4 4-
4- 16х3-|-8х2— 16х— 16.
1541.	Знайти кратність кореня х=2 многочлена х5 — 5х4 4-
4- їх3 — 2х2 4- 4х — 8.
1542.	Чи є число 1 коренем з кратністю 4 многочлена х2п —
— п2 хп+1 4- 2 (п2 — 1) хп — п2 хп~1 4- 1?
1543.	Довести, що для многочленів:
а)	х2п — пхп+{ 4- пх"-1 — 1;
Ь)	х2п+1 — (2п 4- 1) хп+1 4- (2п 4- 1) хп — 1
число 1 є коренем з кратністю 3.
Розкласти на множники многочлени:
1544. х5 —6х44-12х3—12х24-Их—6. 1545. х8— 16. 1546.
х6 4- 27. 1547. х7 —2х5—х44-х34-2х2— 1. 1548. х5-х44-2х3 —
— 2х2+х*—1.
Довести тотожності:
п— 1
1549. х2п — 1 = (х2 — 1) П (х2 — 2хсоз — + 1).
б=і \	п 1
п
1550. х2"+‘ —1 = (х2 —1)П (х2 — 2хсоз <4^-+ її
к=1 \	л +	/
п
1551. х2п+‘ + 1 = (х + 1) П (х2 + 2хсоз 2^4 + 1).
п.—1
1552.	х2« + 1 = П (х2 — 2хсоз?4^л + її
6=0 '	П	/
Користуючись алгоритмом Евкліда, знайти найбільший спільний
дільник многочленів:
119
1553.	х4 + х3 + 2х2 + х + 1 і х3— 2х2 + х — 2.
1554.	х3 + х4 + Зх3 4- 4х2 + 4х + 2 і х3 4- 2Х4 4- Зх34-6х24-6х4-2.
1555.	х64-6х3 4-2х3 + Зх2 4-6х + 1 і х3 4- 6х4 4- 4х2 4* 4х 4- 6.
1556.	х3 4-х4— х3 —2х — 1 і Зх4 4-2Х3 4-х2 4-2х — 2.
1557.	х6 —7х44-8х3 —7x4-7 і Зх5 — 7х3 4-Зх2 — 7.
1558.	х64-2х4—4х3 —Зх24-8х —5 і х34-х2 —х4-1-
1559.	х5 4-Зх4—12Х3 —52х2 —52х —12 і х4 4-Зх3 — 6х2—
— 22х—12.
1560.	х6 4-4х3 4-4х*—х2 — 4х—4 і х3— х4 — х 4~ 1-
1561.	х34-х4 — х3 — Зх2 — Зх—1 і х4 — 2Х3 — х2 — 2x4-1.
1562.	х4— 1 Ох2 4-1 і х4 —4рг2х34-6х24-4]<2х4-1.
У наступних прикладах розкласти на елементарні такі дроби:
1563.	х2 4~ і X (х2 — 1) ’	1564.	4 (Xа — 1)а •
1565.		2		1566.	Xі	X3	Xа
	(х —1)(х —2)(х —3) •		X2	 1
1567.	х8 4- 1	1568.	х*+ і
	(х2 + X + І)2 ’		Xа (Xа 4- 1) •
1569.		2		1570.	1
	х« + 2x3 + 2х2 4-2х 4-1 •		х2Л + 1 •
1571.	8	1572.	1
	х*4- 4’		Х2п+14-1 
1573.	2x4	1574.	х3 + 5х 4- 2
	х* + х2 + 1 ‘		х*-|-хз-|-Зха4-2х4-2-
РОЗДІЛ VII
НЕВИЗНАЧЕНИЙ ІНТЕГРАЛ
§ 1.	Основні методи інтегрування
Користуючись таблицею елементарних інтегралів
1)	рах=-^ + С, и=#-1;
2)	у-^. = 1п|х| + С;
3)	У ах йх =	+ С, зокрема, У ех сіх = е* + С;
4)	У зіп хсіх — — соз х + С;
5)	Усозхгіх = зіпх 4~С;
6)	Ут^7=У8ес2хйх = і§х4-С;
7)	У^Г = Усозес2х</х = — сі§х + С;
8)	Г -Д—= — агсі§ — + С;
'	Л х2 4- а2 а ® а 1 ’
9)	С   --- = агсзіп — + С
ЗУсР — х*	а
та властивостями первісних, знайти інтеграли:
1575. У Зх3 ах.	1576. У (х2 —	+ 3)
121
1577.		1578.	2*сіх.
1579.		1580.	Р 4х
			3 3/ї
1581.	С	1582.	(*	Лх
	3 2х2 + 8		3 ]/ 2 — 2х2
1583.	Г 5б/х	1584.	ґ (х — І)2 4х
	3 х2+ 3		3 /х
1585.	ґ х2сіх 3 х2+ 4	1586.	У 1§2х йх.
1587.	[ (х —3)24х 3 х(х2 + 9)	1588.	ґ	йх
			І ЗІП2 X СОЗ2 X ’
1589.	С 2і§2х-_5_^ Л	ЗШ2 X	1590.	Г 3<2+І-^ Зх2(х2+1)
1591.	У 2х ех сіх.	1592.	Г	сіх
			3 соз 2х 4- зіп2 х
1593.	У 5ІП2 СІХ.	1594.	Г сіх
			3 уз—х2 
1595.	С х^ + х2-!.^ 3 X2 + 2	1596.	С2+ сс&х^ ] 1 + соз2х
1597.	Г	1598.	(•/»+2
	3 1 — соз 2х		-/4 —х4
1599.	У СІ§2 X іх.	1600.	Г хМх
			р+1-
1601.	р	&х	1602.	Р 4біх
	] У 4 — Зх2		] 5х2 + 4 ’
1603.	С 8ІП 2х Лх 3 СОЗ X	1604.	С-4^-^. 3 /х-1
1605.	3 1+/х	1606.	іг-уу
1607.	У<і§х — сі§х)Мх.	1608.	Р сіх
			\ 1 + СОЗ X •
1609.	С х ,) зіп 2х	1610.	р соз 2х сіх
			1 СОЗ2 X ЗІП2 X ’
122
Користуючись заміною змінної або підведенням під знак дифе-
ренціала (роблячи заміну мислено, в умі, інтегруючи, як кажуть,
безпосередньо), знайти інтеграли:
1611.	(х + 2)Мх =	(х + 2)4 й (х + 2).		
1612.	\ зіп х соз2 х сіх =	— (* соз2	ХСІ (соз х).	
1613.	(• ах	і_ г 4 (Зх + 2)			
	рх+2 33	Зх + 2 ’		
1614.	(*	СІХ		1615.	(X2— 1)5ХС?Х.
	3 (х-1)3			
1616.	§хУ Зх2 + 4 сіх.		1617.	1 зіп 5х сіх.
1618.	Р сіх		1619.	Р сіх
	СОЗ2 Зх			) 1— 4х ’
1620.	У 2е~2л сіх.		1621.	С е~х2 хйх.
1622.			1623. 1	? (ІХ
				) 1 + 4х2 •
1624.	Р хйх		1625. 1	Р	(ІХ
	X4 + 4 •			) Зх2 + 25 •
1626.	Р хйх		1627. 1	Р	(ІХ
	3 У 4-х4			) К1 — бх» 
1628.	р ах		1629.	і і§хгіх.
	] у 2 — 9х2			
1630.	У СІ§ X СІХ.		1631.	зіп4 X СОЗ X (їх.
1632.	У 1§(5х — 1) йх.		1633.	ґ ЗІП X (ІХ
				і Зл	 ’ ) у СОЗ X
1634.	Р СОЗ X СІХ | Ззіпх— 1 ’ РЗ г			1635.	уіпхб/х
1636.	1 /3 — 2хгіх.		1637.	х2‘|Лх3 + Згії.
1638.	Р	сіх		1639.	Р (ІХ
	3 (агсзіп х)2 /1 — >	<2		) ех — 1 '
123
1640.	Р йх І ХІПХ *	1641.	Р 3х йх ] е2Х + 9 *
1642.	\^йх.	1643.	Р 8ІП X СІХ І СО84 X
			
1644.	Р хйх	1645.	С	СІХ 1 р— агссоз х
	] 3 — 2х2 ‘		]	/1 —Xа 
1646.	^’хМх.	1647.	Г 1п х — 1 < 1 ——ах.
			ху Іпх
1648.		1649.	У 8ІП2 X СІХ.
1650.		1651.	С сіх
			3 ЗІП X *
Застосовуючи формулу § ийо —		от — І	знайти інтеграли:	
1652.	У X3 Іпхйх.	1653.	У X созхЛх.
1654.	У х2х йх.	1655.	У х2е* (ІХ.
1656.	§хп1пхйх, п=/=—1.	1657.	У х агсі£ х сіх.
1658.	У х агсзіп х гіх.	1659.	У х2 зіп х йх.
1660.	У хе? йх	1661.	У е°х соз Ьхйх.
1662.	У е“х зіп Ьхйх.	1663.	Р хд,х
			1 СО82 X
1664.	У х (агсі§х)2 йх.		
		1665.	1п (х 4- У1 + Xа) йх.
1666.	С 1п3 х і		
	I 	2~ <ІХ.	1667.	і ]/х2 4- а2йх.
1668.	Р	(ІХ	1669.	§ агссоз хйх.
	](х4-1)2 		
			
1670.	С агсзіп 'Ух , \		(їх.	1671.	]1п(/14-х4-
	Л У 1-х		4- V1 —х)йх.
1672.	Р х зіп х 4х 1 СО83 X	1673.	У 1п(х2 4- 1)с?х.
124
1674. С (агсзіп х)2 йх.	1675.
Л	Л Iх т 4
1676. У Рп (х) еах(Іх = фп (х) еах + С, де Рп (х) та Сіп (х) — много-
члени одного й того ж степеня. Довести цю рівність.
1677. ^хС^сіх.	1678. У(х3 — Зх-\-2)ехйх.
1679. у1—(1ПХ> дх.
। лпл Р сіх ___________________х_____________2м — З Р сіх
З (*2 + а2)п ~ 2а2 (п — 1) (х2 + а2)""1 + 2а2(п—1) ] (х2 + ^-1’
Вказівка. Щоб довести цю формулу зведення, зробіть спочат-
ку перетворення
Р (іх _______ 1 Р х2 + а2 — х2 і
(х2 + а2)*1 “ "а? ]	(х2 + а2)п йХ'
§ 2. Інтегрування раціональних функцій
Розкладаючи на елементарні дроби підінтегральну функцію (там,
де потрібно, вилучивши спочатку цілу частину), знайти інтеграли:
1681.	С 2*+3 йх У х(х+1) ах-	1682.	Р	X2 + 1	. ] х(х + !)(%—!) ах‘
1683.	Р х3сіх	1684.	Р х4 + 2х + 6 і 1 Ч ,	2	 \ х3 + х2 — 2х
			
1685.	Р (х — 2) (іх	1686.	Р	СІХ
	У х2 — 7х+ 12 •		] X2 (х — 1) •
1687.	С йх	1688.	Р (х2 — 1) (ІХ
	1	Л	Л	•		У (х + 2)3 •
	X4 — X2		
1689.	РхЗ —2х2 + 4 , ] х3(х — 2)2 ах’	1690.	Р Зх2 + 1	, ] (Х2_1)3 ах-
1691.	Р Зх2 + 2х + 1	. У (х+ 1)2(х2 + 1) ЛХ-	1692.	р ах
			
1693.	Р Лх	1694.	Р х5б/х
	]х3+ 1-		] X3 — 1 •
1695.	Р Лх	1696.	Р	2хс1х
	Р+Г		\ (X + 1) (X2 + І)2 •
125
1697.
1699.
1701.
1703.
йх
X4 (х3 4- І)2 •
сіх
Х2(х24- 1)2 •
хМх
(X4 — І)2 •
(х2 + \)(іх
х4+ 1 •
1698.
1700.
1702.
1704.
Р (х + 2) йх
] (х2 +2х+2)3‘
(* СІХ
(Х3 — І)2 •
Рх2— 1 1
І х* + 1 ^Х‘
§ 3. Інтегрування ірраціональних функцій
Застосовуючи потрібну заміну нижче інтеграли та знайти їх:		змінної,	раціоналізувати подані
1705.		1706.	Г Vх ^х
			] Зх-3/+
1707.	Р сіх	1708.	г	ах
1709. 1711.	Л 1 + У^  Г		(/х+г'-*2)* С +£!+* а*. 3 1/іч-х—і р	ах	
	4<- • ух2 — у х С	1710.	
	Л 1 +^х+ 1 Г	ах	1712.	
1713.			] )/2х— 1 —3/2х— 1
	1 з<—	 •	1714.	Р	СІХ
	л у (х + І)2 (х— І)4 С 1 / 1 — X СІХ 3 V 1 + х Г— Лх		.		3 у (х-2)(х— 1)3
1715.		1716.	Г У2х-3
1717.			І 3 г	 л »/2х-з+і С -.V і — х ах 3 V г+і~
	Л / (*+ І)2 — Ух+ 1	1718 •	
Знайти ностей:	інтеграли від найпростіших квадратичних ірраціональ-		
1719.	ґ	хсіх		1720.	Г	сіх
	] У 1-х—Х2		] X /х2 + 2х — 1 
1721.	г ах	1722.	Р	сіх
	] х — Ух2~ ґ		] / 4 + 2х —х2 ‘
126
1723.	р ах	1724.	р	ах
	Л У х2 + а2		] У Х2+ 2х —3
1725.	р	ах	1726.	р	ах	
	] У 9х2 — 6х + 2		3 У 12х— 9х2—2 р	
1727.	У У а2 — х2 ах. р 		1728.	1 у 2х — х2 йх. с 	
1729.	У Xі — 4х + 5 йх.	1730.	і У 1 — 4х — х2 йх.
1731.	У У Xі — 2х + 2 йх.	1732.	ґ х2д.х } У 4 — х2
1733.	С]/1-х2 , і -—5— йх.	1734.	У*’+.2-^х.
1735.	Р (2х — 5) ах	1736	р	ах
	3 У X2-7х + 1 '	І / ОІ).	З (х— І)2 Ух2— 1
1737.	Г	Лх	1738.	р	ах
	] х2 -у X2 + 9		] у (х2 + а2)3 '
1739.	Г	Ох		1740.	р	ах
	3 + У %2 + %+ і		3 х2 У х2 — а2
1741.	р ах	1742.	р ах
	Л У (х2— 1)3		3 У X — X2
	С /х2+ 1	1744	р
Знайти інтеграли від диференціальних біномів:
1745. 1747.	]"х !(1 С(4±^х. Л / X	1746. 1748.	У X3 (1 4-Х2)~2ЙХ. р ах
			Ь(і+3/-хГ
1749.	С ]/ 1 + у" X 1 \ 	7=Г— йх. Л Ух	1750.	У X5 У (1 +Х®)2ЙХ.
1751.	У X7 У Xі 4- 1 йх.	1752.	
1753.	С	1754.	р ах
	3 у(2х2 + І)3 '		Л	1
127
1755.	С ——*—.	1756. С	. Л х/х3 + 1	Ух» + 1
1757.	«) Xі у'х2+ 1	3 /1 — X2
1759.	С йх	Р з.	 3/__.	1760.	/х(1-х2)Л. V у X3	1	V
1761.	1 х У Xі 1 йх.
§ 4. Інтегрування трансцендентних функцій
Знайти подані нижче інтеграли, вдаючись до того чи іншого спо-
собу раціоналізації та використовуючи залежності між тригономет-
ричними функціями:
1762.	соз3 х зіп х йх.	1763.	СО83 хйх.
1764.	У зіп5 х йх.	1765.	Р 5ІП х йх
			] СО52 X
1766.	Р соз хйх	1767.	Р йх
	\ ЗІП4 X ’		] СОЗ X ’
1768.	У зіп2 х соз3 х йх.	1769.	Р йх
			5ІП3 X •
1770.	У зіп3 х соз4 хйх.	1771.	Р 5ІП3 X йх І СО54 X
1772.	р соз3 х йх	1773.	Р	йх
	| 5ІП4Х		\ СО5 X 5ІП3 X
1774.	У зїп^хйх.	1775.	У соз4 хйх.
1776.	У СО82 X 8ІП4 х йх.	1777.	У зіп6 х йх.
1778.	Р йх	1779.	Г йх
	СО84 X *		5ІП6 X *
1780.	Р СО55 х йх	1781.	Р	йх
	І 5ІП3 X		] 5ІП2 X СО54 X
128
1782.	г ах	1783.	Р СОЗ2 X ах
	3 1 + 8ІП2 X *		3 зіп6 X
1784.	С ах	1785.	Р ЗІП4 X , \ —т— ах. 3 соз6 X
	3 У1 — ЗІП4 X '		
1786.	р	ах	1787.	р
	2 4-3 СОЗ2 х *		] СОЗ4 X ЗІП4 X •
1788.	г	ах	1789.	У 1§3ХС?Х.
	] а2 зіп2 х 4~ & соз2 х *		
1790.	У с(§8хс?х.	1791.	уі§4хс?х.
1792.	У СО5^ X ЗІП5 X (ІХ.	1793.	У ]/зіпх СО83 хйх.
1794.	Г1/2і^х 4 V СОЗ7 X	1795.	р ах
			] 1§ X + 1 р 	
	Г (зіп х 4- соз х) ах 3	У8ІП 2%		
1796.		1797.	1	1 + 8ІПХ (ІХ.
1798.	р	ах	1799.	С
	І 5 — 4 зіп х 4- 3 соз х ‘		3 5 — 3 соз х
1800.	с ах	1801.	р	ах
	3 зіп X 4- соз X		3 3 4- 2 зіп х 4- соз х
1802.	г ах	1803.	Г А*
	3 5 4- 4 зіп х '		3 У 1 — соз X
1804.	У 8ІП 4х СО3 2х/ЇХ.	1805.	У соз Зх соз 4х(іх.
1806.	У ЗІП 4х ЗІП Зхгіх.	1807.	У зіп х зіп 2х зіп Зх (їх.
1808.	У СОЗ X соз Зх СОЗ Зх (ІХ.	1809.	С х 4-1 л 1	• Т	<ІХ- 3	зіп 2х
1810.	г	ах	1811.	Р зіп X СОЗ X ах
	3 ЗІП4 X 4- СО34Х •		1 4" ЗІП4 X ’
1812.	У У"і§х (іх.	1813.	У	X (ІХ.
1814.	ґ ЗІП X ах	1815.	р	ах
	3 У соз 2х		] соз х соз (х, — а) ’
9 2193
129
1816.	Р йх ] (е-г+1)2 •	1817.	Р е2Х йх ) ех + 1 
1818.	Р йх	1819.	У сЬ2х йх.
	] У ех + 1 '		
1820.	У Ні2 х йх.	1821.	У 8Й3ХС?Х.
1822.	Р йх	1823.	г ах
	] сії х '		СІЇ4 X '
1824.	Р	йх	1825.	У X2 2х СОЗ х йх.
	зЬ2 х + сЬ2 х		
1826.	Р	йх	1827.	ЦУУУ-
	егх + ех _ 2 		
1828.	Г е*(1 Ч-зіпх) . 1 + СОЗ X	'	1829.	Р е2Х йх
			а Уех+ і
§ 5. Різні приклади на інтегрування
функцій
Знайти	інтеграли:	
1830.	Р йх	1831.
	З х(х2 + 2)	
		
1832.	г ах	1833.
	] х(х®+ 1)2-	
1834.	Г *2 +1 н ] х4 + X2 + 1 ах‘	1835.
1836.	Р	(х2 — 1) йх	1837.
	]	(х2+1)/^+і- Р зіп 2х йх	
1838.		1839.
	зіп4 х + соз4х ‘	
1840.	р рХ і/ рХ	 1 \ е	1 йх.	1841.
	Єх+ з	
1842.	У хі§2хйх.	1843.
1844.	Р хйх і чл4		О "	1845.
Р сіх
} х(х3 + 4) •
Р ХЬйх
х8 — 1 '
Р Х2йх
] х4+ Г
У У1 4- С08ЄСХ СІХ.
Р соз х йх
) зіп3х — соз3 х‘
Р	^х
1 5 зіп2 х — 3 соз2 х + 4
У У1 — 8ІП X йх.
130
1846.
1848.
1850.
1852.
1854.
1856.
1858.
йх_______
х4 — 2х2 — 1
соз 2х йх
соз4х+ зіп4х‘
х2йх
V (і + х2)5 ‘
(х2 4~ 1) йх
(X2 — 1) /хП
х агсзіп х
(1-х2)/1 —х2
ех (зіп X — СОЗ х) Дх
зіп2 X
сіх.
1847.	Р агсзіп х йх 3 уі+х
1849.	С	х	х 1 СОЗ ЗІП -у СІХ.
1851.	У "|/ 1 + х йх.
1853.	Г х 4~ зіп х і ] 1 + соз X йх-
1855.	
1857.	(*	X 1п X	1 \	-=- ах. 3 (х2 — 1) у х2 — 1
1859.	Р зіп X СІХ
	) зіп (х — а)
§ 6. Застосування невизначених інтегралів
1860.	Знайти таку функцію, похідна якої є х24-4х+ 1, а вар-
тість її при х— — 1 дорівнює 1.
1861.	Знайти криву, яка проходить через точку Л1(1; і в
кожній точці якої кутовий коефіцієнт дотичної дорівнює абсцисі
цієї точки.
1862.	Сповільнююча дія тертя на диск, що обертається в рідині,
пропорційна кутовій швидкості со. Знайти залежність со від часу і.
При і = 0, о) = ю0.
1863.	Тіло рухається прямолінійно з швидкістю V = З/2 + 2Л Ви-
значити довжину шляху пройденого тілом від моменту /0 = З до
/і = 6.
1864.	Знайти функцію, перша похідна якої дорівнює 24-х—4х2,
знаючи, що при х = 2 функція дорівнює 8.
1865.	Знайти функцію, перша похідна якої дорівнює 8Іпх4-со8х,
знаючи, що при х — ~ / (х) дорівнює 2.
1866.	Знайти криву, яка проходить через точку Лї(1; 0), а ку-
товий коефіцієнт дотичної в кожній точці дорівнює
9*
131
1867.	Тростинний цукор розпадається на складові речовини
(глюкозу та фруктозу) при наявності кислот. Швидкість процесу
розпаду пропорційна масі х нерозкладеного цукру. Показати, що
х = Се~кі. Який фізичний зміст сталої С?
1868.	Якщо бактерії розмножуються в середовищі, де є необме-
жена кількість поживи, то швидкість їх розмножування пропорцій-
на наявні кількості бактерій. Визначити залежність кількості бакте-
рій від часу і.
1869.	Знайти рівняння кривої, яка проходить через точку
Л4(0; 1), а кутовий коефіцієнт її дотичної у кожній точці дорівнює
ординаті цієї точки.
1870.	Кутовий коефіцієнт кривої у(х) дорівнює 2х —6. Знайти
найнижчу точку на цій кривій, коли відомо, що крива проходить
через точку Л4(1; —2).
1871.	Кулька вільно падає на землю (з початковою швидкістю
г>0 = 0) з височини 100 м. Через який час кулька досягне землі?
(Опір повітря нехтуємо).
1872.	Бомба, кинута з літака, досягла землі з швидкістю
100 м/сек. З якої височини кинуто бомбу? (Опором повітря
нехтуємо).
1873.	Знайти криву, яка проходить через точку Л4(1; 0) і під-
нормаль якої дорівнює абсцисі точки дотику.
1874.	У культурі пивних дріжджів швидкість приросту чинного
ферменту пропорційна наявній його кількості х. Коли протягом го-
дини кількість ферменту подвоюється, то в скільки разів вона
збільшиться через 3 год від початку реакції. Кількість ферменту на
початку реакції дорівнює а.
1875.	Знайти віддаль, яку пройде за і сек тіло, вертикально
вниз з початковою швидкістю щ — ЗО см/сек.
1876.	Атмосферний тиск р є очевидно функцією висоти К над
рівнем моря. Уявімо собі циліндричний стовп повітря, що спирається
на площу в 1 см2 на рівні моря. Утворимо горизонтальні перерізи
А та В цього стовпа на висотах И та К + ДЛ. При переході від А
до В тиск зміниться (коли ДЛ > 0) на величину Др < 0 (вага від-
повідної частини стовпа). Якщо ДЛ достатньо мале, то можна вва-
жати (наближено), що густина р повітря в цій частині стовпа стала,
і тому
Др — рД/г.
За законом Бойля — Маріотта, густина р пропорційна тискові
р = кр, тому
Др — кр№і,
132
і ця наближена рівність тим точніша, чим менше ДЛ. Отже, пере-
ходячи до границі,
йр = — крсіїї, або = — кр.
Показати, що р = рье~кі, де рц — тиск на рівні моря. Обчислити
к, знаючи, що р0 = 1,033 кг/см2, а на височині 500 м р =
= 0,925 кг/см2.
1877.	Знайти криву, що проходить через точку Л4(І; 1), піддо-
тична якої скрізь дорівнює подвійній абсцисі точки дотику.
1878.	Тіло рухається так, що швидкості його в напрямах коор-
динатних осей відповідно дорівнюють кх та — ку. Показати, що
рух тіла відбувається по рівнобічній гіперболі ху = с.
1879.	Визначити траєкторію руху артилерійського набою, кину-
того з початковою швидкістю Уо під кутом а до горизонту (опором
повітря нехтуємо).
РОЗДІЛ VIII -----
ВИЗНАЧЕНИЙ ІНТЕГРАЛ
Виходячи з означення визначеного інтеграла як границі інте-
гральної суми, обчислити такі інтеграли:
4
1880.	У хйх.
і
Вказівка. Ділити проміжок на рівні частини,
з
1881.	У хЧх.
0
ь
— , 0 <а<Ь.
X ’
Вказівка. Розбити проміжок так: х0 = а, х± = ад, х2 = ад2,...
..., хп-і = адп~1, хп = адп — Ь.
ь
1883.	{ Ух ах.
а
Вказівка. Див. 1882.
ь
1884.	^хЧх, 0<а<Ь.
а
Ь
1885.	| ехсІх, 0 <_а < Ь.
а
Вказівка. Ділити проміжок на рівні частини.
134
1886.	У 2х сіх.
о
ь
1887.	Іпхйх, 0<а<&.
а
я
1888.	У$іпахйх.
б;
Вказівка. Скористатись формулою
пх . п + 1
зіп -у- зіп —х
5ІП х + 8ІП 2х + ... + 5ІП пх = --------------•
5111 ~2
ь
Ґ889. Усозхйх.
а
Вказівка. Скористатись формулою
соз {а + х) + соз {а + 2х) +
зіп І а
+ ... + соз (а + пх) =
Оцінити такі інтеграли:
1890. 5 (іх.
2
4
1892. £ (х + 2]/х) (іх.
о
Я
4~
1894. ехсо5Х(іх.
о
Я
2
1896. | ^-йх.
0
П + ~2/ х] “ 8ІП V + "2"х)
п • х
2з>пт
4
1891. (^=4гіх.
з %+1
о 1
2
1893. [ і-^-гіх.
Л 1п х
1,5
я
т
1895. хЇ£Х(іх.
б
і
1897.	]Л1 +х4йх.
135
Не обчислюючи,	встановити, який
2	2
1898. [ — (їх	Г йх л ЧИ \ —г~?
і х	3 х2 1
3	3
1900. ] 5х2 ах 1	чи § 5х’ сіх? і
я	я
-	
4	4
1902. ^зіпаЯх	чи § соз хгіх?
0	0
5	5
1904. § 1п хсіх	чи У 1п3хб/х?
3	3
з інтегралів більший:
і	і
1899. $ 3х* ах чи { 3х' ах?
О	о
я	я
4	4
1901. У зїпхйх чи У 5іп2хйх?
о	о
2	2
1903. [ Іпхйх чи 1п2хйх?
І	1
Знайти середню вартість функцій:
1905. у = 2х + 5 на проміжку (2; 3).
1906. г/= 2х2 4-3% + 3 на проміжку (1; 4).
1907. у = 6х на проміжку (0; 2).
1908. і/— соз 2х на проміжку ^0;	.
1909. у = Іпх на проміжку (1; 2).
§ 1. Обчислення визначених інтегралів
Користуючись формулою Ньютона — Лейбніца, обчислити такі ін-
теграли:
3	1
1910. ^ах.	19П. \е3хах.
—1	0
6	2
1912.	1913. ( 2х ах.
Л х + 4	.) і 1	0
3	1
1914. |(1 + 2х + 3х2)йх.	1915. (’ &х — ]/Т)йх.
2	6
Я

4	а
1916. С зіп 2хах.	1917. [	.
3	0? + **
136
1918.	0 с ах	1919.	е2 с ах 3 X е л У СОЗ2 хйх. 0 л 2 У соз5 х зіп 2хйх. л т л Л у зіп X Г л
	4х2 — 9 ’ 1 р				
1920. 1922. 1924. 1926. 1928. 1930.	] У х + 1 йх. 0 3	х 1 3 — 2 л2 ( ах. і	V* 2 г	ах	1921. 1923. 1925. 1927.	
	] Х2 + 6х + 10 ’ л ~8 Г йх	1929.	У соз(2х + йх. 0	х	7 і 4
	З 1 + 4х2 • п	1	1931. 1933. 1935. 1937. 1939.	с	ах
1932. 1934. 1936.	л т ] сі^Зхгіх. л 1Г С 	йх.		уі — 16х2 л Т зіп3 х соз2 хйх. 0 5 г ах
	3 х12 + 1 и 0 3 г ах 3 ск2х 2 л 2 Г	• /	зт\		3 X2 + 2х + 10 ’ 2 л зЬ2 хйх. 0 а Г хб/х
1938.	СОЗ X ЗІП І2х—’^ІаХ. л	Х 2		3 а 4- Ьх ’ 0	*
137
1940. [ 7-Ґа \г-
.) (а + М2
Користуючись правилом заміни змінної у визначеному інтегралі,
обчислити	такі інтеграли:		
1941.	і С хйх	1942.	3 с х2ах
	4 /2-х		і /* + і
	$ У*+ 2		1
1943.		1944.	У XіУ 1 4-х2 (іх. 0
1945.	0 с ах		2а /2 Г йх
	іі^/	її —1 1 + у х + 1	1946.	
			2д х У х3 — а3
1947.	1 е	ах		У~з 1
	3 х2 У х2 + а2	1948.	У х2 1 — х2 йх.
			0
1949.	1 г ах	1950.	2 Г х2^х
	3 (X2 + 1)3/2 •		Л 1 + х2 + х4 • 0,5	~	1
1951.	1 г ах	1952.	їй 8 с е2хах
	3 ех+е-х •		і;!з	і
	1п 2		4	1
1953.	У У"ех — 1 (ІХ.	1954.	У х 2 е^х йх.
	0		1
1955.	е3 Г Лх	1956.	2 г ах
	Л х (1п х + І)2 е		1 (9-х2)2 ’
1957.	1 С Ах	1958.	Є У (хіпх)2 (ІХ. 1
	(4 — х2)3/2’		
1959.	л 2 ґ соз хах	1960.	0 С зіп 2хах
	я у/ ЗІП3 X ~б~		3 зіп2 х + 2 ’ ___л_ 2
138
1961. Г-(^)3/? йх.
Л СОЗ2 X
О
2	____
1963. і агсзіп 1/
V	' X -у- £
2
1965. [,/** ,-.
V х (а + о 1п х)
я
4
1967. ]* ]Л§хгіх.
О
я
Т
1969- I 1 + 2^/'
О
я
Т
1962. У сі£ х 1п зіп хйх.
Я
1Г
я
1964. У(хсозх)2гіх.
о
я
Т
1966. У зіп3 х зіп 2хйх.
о
Я
1968. Уі§2-^-гіх.
О
ь ь
1970. Показати, що У /(х) йх = / (а Ь— х)йх.
а	а
Обчислити інтеграли:
х зіп хйх
1 + СОЗ2 X ’
Я
т
ілчо г х с°з2 2%б/х
1У7Д Л 1 + зіп2 2х ’
з	______
1973. І агсзіп іЛйх.
я
Т
1974. У Іпзіпх-созхгіх.
Я
~6~
1975. Нехай функція /(х) задовольняє умову /(а — х)=/(х) на
а	а
сегменті [0; а]. Довести, що [ х/ (х) йх = У / (х) йх.
о	2 о
Спираючись на рівність, доведену в попередньому прикладі, об-
числити такі інтеграли:
139
я	я 1П-7С	Г Х 5ІП хйх	1077	С Х СО82 хЛх 1976’ Л 1 + СО82 X •	1У/Л 3 1 + ЗІП2 х • 0	0 Користуючись формулою інтегрування частинами, обчислити такі інтеграли: і	і 1978. хе~х йх.	1979. У хе3х йх. —1	0 е2	е 1980. ^х21пхгіх.	1981. У —”2Х- йх. е	1			
я 1982. У х8Іп-|-б/х. 0 1984.	агссоз хйх. —і я Т 1986. Ух2со8хі/х. 0 /3 1988. у агсі§хйх. і		1983. 1985. 1987. 1989.	1 У х агсі£ хйх. 0 я 2 У Є2хСО8Х(ІХ. 0 я т У Х25ІПХЙХ. 0 1 У х агсзіп хйх. 0 і
1 т і пил Г х агс5Іп Х(^Х Ї990.	(1__х2)2	• 1992. Позначаючи Іп = довести, ЩО Іп =  "'п ~ІП-	Я у ЗІЕРхб/х 0 -2 •	1991. У Xа-1 Іпхгіх, а> 0. 0 Я т = ] созпхйх, п — ціле та> 1, 0	
1993. Позначаючи Іп = » 2п — 3 , Іп ~2п-21п~1-	оо С йх	Г> 	 ТІ І ПО ТСІ	1	ПППОГТП ТТТ/Л	
	3 (х* + 1)«’	,	11, 	 А	Лі а і/їй	X}	1 хх^ іл_цч/
140
§ 2. Наближене обчислення визначених
інтегралів
Користуючись формулами прямокутників, трапецій та парабол
(Симпсона), обчислити подані нижче інтеграли. Порівняти здобуті
результати з точними. Обчислення вести з точністю до четвертого
знака:
і	і
1994. (’т-Йу-, п = 6.	1995. (7^-5, п = 10.
Л 1 + 2х	Л 1 4- х2
0	1	0 і
я	1
У	1997. {ул — х2 сіх, п = 4.
1996. хсозхЛс, п = 6.	о
о
і
1998. \ех(1х, п = 10.
б
Користуючись формулою	Симпсона, обчислити такі інтеграли
з точністю до 0,0001: і 1999. §е-х2сіх, п = 5.	0,5 2000. І -йх .
0 л ~2~ 2001.	я =10. 0	о' Л+х4 1 2002. ]У1+х4с!х. 0 л
3 2003. ( 0 1п х 2	2004. ] У 1 — 0,1 зіп2 <рс?<р. 0
2005.
л
б”
Г
(У У1 — 0,5 8іп2ф
§ 3. Невластиві інтеграли
Обчислити інтеграли з нескінченними межами або встановити їх
розбіжність:
оо	оо
2»»6- ]-$-•	20»7- ЇмТТї)'
141
	со С х2йх	9ПП0	оо	8аМх
£ V 1/О«	3 %з + 1 ‘ 0	1		0	х2 + 4а2
	со		оо	
	С	йх	2011.		а > 0,
£у) І V*	3 х2 4- 2х + 2 ‘ —оо		б	а2 + 62х2 ’ £ > 0.
оо
2012.	Г	йх		 Д2 '*•	> 0.
	3 а + Ьх + ех2 ’ —оо	“еге/	и	
оо
2013.	Г	йх		/7	> 0, Ь > 0,	т > 0, п > 0. оо
	3 (а + М (т + пх) ’ оо			
2014.	Г	хйх		2015.	Г 1/4 + *' Лх 3 хб
	3 (а + Ьх + ех2)2 —оо			
2016.	ОО С у хйх		2017.	со Г йх
	.) (1 +х)2 •			І х)Ах2 — 1
2018.	оо [ е~ах (іх, а > 0.		2019.	хе~ах йх, а > 0.
	6			6
	0			оо
2020.	У х^аїсіх. —оо		2021.	У е~ах соз Ьх йх. 0
2022.	оо У е~ах зіп Ьхйх. 0		2023.	оо С е2х—1 . 3 ех —оо
2024.	Се^х , Лх-		2025.	оо У х зіп хйх. і
2026.	оо с і	. і	, —й- зіп — йх. Л х2	х 2		2027.	оо 3 1 + х2 І
Я
Обчислити подані нижче інтеграли від розривних функцій (або
встановити їх розбіжність):
2а г—
2028. Г сіх.
6і
2029. І" —
X а V „2
142
5	1
2030.	Г 5б/х	2031.	Г йх
	$ У 25 — х2		Д у і — х2
	і		3
2032.		2033.	С_£±А_^Х.
	0 /х		у х2 — 4
	1		ь
2034.	(іх	2035.	Ґ	сіх
	3	, з,- 1 о У х + у х		2 У (х — а)(Ь — х)
	1		а < Ь.
2036.	С хсіх		2
	] У 1 — X2	2037.	У 1п ХСІХ.
	Т		0
	5		1
2038.	С (іх		2 С сіх
	3 х Іпх 1	2039.	
			3 %1п2х ‘
2040.	1 Г (іх	2041.	0 1 У 1п2 хсіх.
	{ /е* — 1		
			0
	я		
	т		1	(	Зг-\
2042.	Г х(іх	2043.	Г 1.(2 +_✓»>.
	3 зіп X2 0		
			-1	X
Користуючись ознаками збіжності, дослідити на збіжність пода-
ні нижче інтеграли:
2044.	оо	ХСІХ	2045.	оо	Х^СІХ
	Є	х3 + ґ		0	(%3 + 2х + І)3
2046.	оо	Х2СІХ	2047.	оо	2х2с1х
	6^	%3 + 2% + 1		0	х4 + 2% + 1
2048.	оо [	(ІХ	2049.	оо	ХСІХ
	3 2	1 + У7 ’		0	1
2050.	оо /	V	2051.	оо	5ІП Хп (ІХ, П > 0.
		Л		0	
	оо			5	
2052.		зіп ахйх.	2053.		(Іх 1п X
143
2054.	і С	-^=-ах. /1-х*	2055.	1 Г йх
	3 0			с) е^-1
2056.	1	СІХ	2057.	я Г Іп зіп хйх
	0	ех — СОЗ X		л і/х ‘ 0	Vх
2058.	©о я ~2		2059.	2 + агсзіп — (	-^-ах. Ґ 1 + /х Я
2060.	?	йх	2061.	т С зіп хйх
	е	У X ІП X + 1		3	у3/2 0	х
2062.	3	соз хйх	2063.	2 к	Х+3 о у (х2 — х— 2)2
		х — 2		
2064.	Пр	и яких вартостях к будуть збігатися інтеграли:		
оо	оо
«) 1^7-- І-Аг-
2 Xй ІП X	% X (ІП Х)к
Знайти головну вартість (V. р.) таких інтегралів:
2065.	1 Г йх Л х	2066.	оо У 5ІПХЙХ. —оо
2067.	оо С йх	2068.	2 С йх
	3 х2 — Зх + 2 0	1		Л х Іп х *
2
§ 4. Застосування визначеного інтеграла
Обчислити довжини дуг таких кривих:
2069. у =-%- (параболи) між точками Д(1; 1) та В(2; 4).
Х^
2070.	у- = -^-, що відтинається прямою х = 1.
2071.	у = У~х від точки х — 0 до точки х = 1.
2072.	у — 1п(х -|- 1) від точки х - 0 до х — 1.
144
2073.	у = а 1п зіп -у між точками х = та х = 2а.
2074.	Однієї арки у = агсзіп (зіп х).
2075.	у = агсі£(і£х) від точки х — — -у до точки х — у.
2076.	у = аск-^- від х = 0 до х = 1.
2077.	у = 1 — 1п соз х, яка відтинається прямою х = -у.
2078.	у = Ух — х2 + агсзіп х.
(X	X \
еа е а] (ланцюгова лінія) від точки х = 0 до
точки (х, у).
2080.	х2 4- у2 = г2 (коло).
2	2	2
2081.	х3 4-у3 = а3 (астроїда).
\— \—
2082.	(-у)3 4- І-|-)3 = 1, яка знаходиться в першому квад-
ранті.
2083.	(у — агсзіп х)2 = 1 — х2.
2084.	еу = ееХ^_ * від х = а до х = Ь.
2085. 9а/ = х(х — За)2.
2086.
еа
X
соз —
а
(лінія
рівного опору) між точками х =
ла
та
па
~ *
= 1
х
2087.	у2 = ? (еволюта параболи) від точки (р, 0) до точ-
ки перетину з параболою у2 — 2рх.
2 4~ і2	і
2088.	х =	, У = і — 1	> Щ° відповідає зміні параметра
від /0 до 4.
2089.	х = (7? + т/?) соз ті — т% соз (і + ті), у = (/? + тЦ) х
X зіп ті — тЯ зіп (і + ті) (епіциклоїда) від точки, що відповідає вар-
тості параметра і = 0 до точки, в якій параметр і = 2л.
ю2193
145
і	21	і	21
2090.	х = 2г соз -х- 4- г соз -х-, у = 2г зіп -=-г зіп (крива
О	о	о	о
Штейнера).
2091.	х = К соз3 , у = 7? зіп3 у (астроїда).
2092. х = а 1п Д- а соз і, у = а зіп / (трактриса) від А (0; 0)
до В (х; у).
2093. Однієї арки х = г(і — зіп/), у — г(1 —соз/) (циклоїда).
2094. х = Я соз і + Кі зіп І, у = Р зіп / — /?/ соз / (евольвента
кола).
2095. х = 3а( "°Ґ —соз/), г/ = азіп3/ (крива Рібокура) від
/ = 0 до / = /х.
2096. х = 8а/3, у = За (2/2 — /4), яка лежить над віссю ОХ.
/з
2097. Петлі кривої х = /2, у = і-------у .
2098. х = За/2, у = аі (3 — /2) (замкненої частини).
2099. х= 6аіь, у = 5а/(1 —/8) між точками Д(0; 0) та В (6а; 0).
2100. х = 2азЬ3/, г/ = ЗасЬ/ між точками (0; За) та (х\ у).
2101. р = 2г (1 + созср) (кардіоїда).
2102. р = а<р (спіраль Архімеда) між точками Лї(рх; фх) та
М2(р2; Ф2).
2103. р = -у- (гіперболічна спіраль) між точками (рх; фх) та (р2;ф2).
2104.
(р2; Фа)-
2105.
р = аф (логарифмічна спіраль) між точками (рх; фх) та
г = а зіп3 -у.
2106.	г = азіп4-^-.
4
Обчислити площі фігур, обмежених:
^2_Зх
2107.	Кривою у = —, віссю абсцис та прямою х = 5.
2108.	Кривою у = —о— та віссю абсцис.
О
2109.	Лініями у = хге~х, у = 0 при х>0.
2110.	Кривою у= -ту та прямою у = Юх.
146
2111.	Кривою у2 = х — 2 та прямою х = 4.
2112.	Кривою у — зіп3 х 4~соз3х та віссю абсцис між двома по-
слідовними точками перетину кривої з віссю.
2113.	Петлею лінії у2 = х2 (2 — х).
2114.	Кривою у2 — х4 + х® = 0, яка лежить у першому
квадранті.
2115.	Кривою у = х®е 8 та її асимптотою у = 0.
2116.	Кривою г/2 = х3— 2х2-|-х та віссю ОХ.
2117.	Лініями х2 + г/2 = а2 та у2 = а(а—х).
2118.	Лініями х2 -|- у2 = 16 та х2 = 12 (у— 1).
2119.	Лініями у=0 та х4 = а(х3— у3).
2120.	Кривою у = ах , прямими х = 1, х = 2 та віссю ОХ.
2121.	Кривими + X- = 1 та	= 1.
г	а2 о2	а2 1 о
(X _______х\
е3 +Є 3 /, х = 3, у = 0, х = 0.
2123.	Кривими х2 + у2 = 2ах та х2 + у2 = 2ау.
2124.	Кривими у2 + 2ах = а2 та г/2— Ьх — Ь2 при а > 0, Ь > 0.
2125.	Кривими г/2 = 4ах та х2 = -^-ау.
2126.	Кривими х2 + у2 = 2а2, у2 = ах та віссю абсцис.
2127.	Замкненою кривою (у — х)2 = а2— х2.
2128.	Кривою у = агссоз х, що міститься в першому квадранті.
2129.	Кривою у = зіпх -^-зіп2х 4- 4-зіпЗх та віссю абсцис.
2130.	Петлею астроїди у2 =	•
2131.	Петлею кривої у2 (а2 + х2) = х2 (а2 — х2).
1	X2
2132.	Лініями у = у—;—« та у =
17	14-х2 а 2
2133.	Лініями у = ех, у = е~х та х= 1.
2134.	Лініями г/= Іпх, у= Іпа, у= Іпй та віссю ординат.
2135.	Віссю абсцис та кривими у = агсзіп х, у = агссоз х.
гт	За/	Заі2
2136.	Петлею декартового листка х = 1	, у = 1 <3 •
10*
147
2137.	Кардіоїдою х = а (2 соз/—соз 2/), г/ = а(2зіп/—зіп 2/).
2138.	Трактрисою х = аіп -у + асозі, у = азті та її асимп-
тотою у = 0.
2139.	Петлею кривої х = З/2, у = Зі — і3.
2140.	Петлею кривої х = /2— 1, у-—I і— і-
2141.	Петлею кривої х = —г—т—, у =	. (трактриса Мак-
81П Г	СОо І
лорена).
2142.	Кривою р = 2гсозф І > 2г (равлик Паскаля).
2143.	Кардіоїдою р = 2г (1 —соз ер).
2144.	Кривою р2 = а2 соз2 ф + Ь2 зіп2 ф (лемніската Бути).
2145.	Кривою р2 = а2соз2ф (лемніската Бернуллї) між її віссю
та радіусом-вектором, що відповідає кутові ф.
2146.	Дугою гіперболічної спіралі р = ~~ та двома радіусами
векторами, що відповідають кутам фт та ф2.
2147.	Лемніскатою р2 = а2 соз 2ф і колом р =
2148.	Кривою р = 2а (2 соз ф) та прямою ф = ~ .
2149.	Кривою р = 2 + созф.
2150.	Лініями р = 3 + соз4ф та р = 2 — соз 4ф.
2151.	Однією петлею кривої р2 соз ф = а2 зіп Зф.
2152.	Одним витком спіралі Архімеда р = аср та полярною віссю
2153.	Трипелюстковою трояндою р = асозЗф.
2154.	Однією петлею кривої р = асоз2ф.
2155.	Петлею кривої р2 = а2зіп4ф.
2156.	Кривою р = асі§ф та прямою ф =
X3
2157.	Показати, що площа, обмежена кривою у2 = та її
асимптотою х = 2а, дорівнює потроєній площі кола, яке проходить
через початок координат і має своїм центром точку А (а; 0).
2158.	Показати, що площа, обмежена кривою У = х2.1^2 та її
асимптотою у = 0, у чотири рази більша за площу круга з радіусом а.
148
2159.	Показати, що площа фігури, обмеженої цисоїдою Діоклеса
х = 2а зіп /, у = --2а-5Іп3і  та її асимптотою х = 2а, втроє більша за
СОЗ і	г
площу круга з радіусом а.
2160.	Показати, що площа трипелюсткової троянди р = а зіпЗср
дорівнює чверті площі описаного навколо неї круга.
Обчислити об’єми тіл, що утворені від обертання:
^2 _
2161.	Фігури, обмеженої кривою у= —2— та віссю абсцис, на-
вколо осі абсцис.
X4
2162.	Криволінійної трапеції, обмеженої кривою у= уу та пря-
мою х = 2, навколо осі абсцис.
__%2
2163.	Фігури, обмеженої кривою у = —5— та прямою у =
О
=	, навколо осі абсцис.
О
2164.	Фігури, обмеженої кривою у =Д/~х — 2 та прямою у = 2, нав-
коло осі абсцис.
2165.	Еліпса +-тг = 1 навколо осі абсцис.
2о 1о
|
2166.	Фігури, обмеженої кривою у— у та прямою х=3
навколо осі абсцис.
2167.	Фігури, обмеженої кривою у = х3/4 та прямою у = х, нав-
коло осі абсцис.
2168.	Параболи у = 10 — х2 навколо осі абсцис.
2169.	Фігури, обмеженої петлею кривої у2 = х2(2—х), навко-
ло осі абсцис.
2170.	Фігури, обмеженої замкненою кривою х4 + у^ = а2х2, нав-
коло осі абсцис.
2171.	Фігури, обмеженої замкненою кривою х4 + у^ = ах3, нав-
коло осі абсцис.
2172.	Фігури, утвореної аркою циклоїди х = а (і — зіп і), у =
= а(1—соз/), навколо осі абсцис.
2173.	Фігури, обмеженої кардіоїдою х = 2асоз/— а соз 2і, у =
= 2а зіп і — а зіп 2і, навколо осі абсцис.
2174.	Фігури, обмеженої астроїдою х = а соз3-|-, у = а зіп3 ,
навколо осі абсцис.
149
2175.	Фігури, обмеженої кривою х = 2а8Іп2/, у = 2а соз/, нав-
коло осі ординат.
2176.	Фігури, обмеженої кривою х = 2азіп/, у = а зіп/соз/, нав-
коло осі абсцис.
а3
2177.	Фігури, обмеженої дугою кривої х = і, у = та пря-
мими х =-----, х = —, навколо осі абсцис.
/з Уз
2178.	Фігури, обмеженої параболою у = 2х— х2 та віссю абсцис,
навколо осі ординат.
2179.	Криволінійної трапеції, обмеженої дугою синусоїди у =
= зіп х, що відповідає півперіоду, навколо осі ординат.
2180.	Фігури, обмеженої кривою х4 + г/4 = 2аху2, навколо осі
ординат.
2181.	Фігури, обмеженої кривою х = а (і — зіп і) у = а (1 —соз /),
навколо осі ординат.
2182.	Фігури, обмеженої кривою х = а(і -}- зіп/), у = а (1 4-соз/),
навколо осі ординат.
2183.	Фігури, обмеженої цисоїдою х = 2азіп2/, у =
на її асимптотою х = 2а, навколо осі ординат.
2184.	Фігури, обмеженої кривою у = е~х2 та її асимптотою, нав-
коло осі абсцис.
2185.	Знайти об’єм тіла, обмеженого поверхнею, що утворена
обертанням кривої х2 + і/2/з = 1 навколо осі ординат.
2186.	Крива у2 = 2ехе~2х обертається навколо своєї асимптоти.
Знайти об’єм тіла, обмеженого утвореною поверхнею.
2187.	Знайти об’єм тіла, обмеженого нескінченною поверхнею, що
. .. 1
утворена обертанням кривої у = навколо 11 асимптоти.
Користуючись формулою для обчислення об’ємів, коли відома
площа поперечного перерізу, обчислити об’єми тіл, обмежених таки-
ми поверхнями:
2188.	у2	/»2	^2 Л-+4г + Лг = і- а2	о2	с2
2189.	у2	«і2	у2	^2 —-к—=1 — 4-— = 1 а2 ' Ь2	’ а2 ' Ь2
2190. 2191.	г2 + у2 = 1, х2 г2 = 1. г2 = 2рх, у — 0, у = х, х = а, г = 0.
150
у2 //2
2192.	г = ^+ 2~’ г= 1.
2193.	г2 = 2рх, г2 = 2ду, х = 0, у = 0, г = а.
2194.	+	— г2 = 1, г = — 2, г= 1.
2195.	г2 = 2рх, у2 = 2ц(а — х).
2196.	х2 4- 4г/2 = 8г, х2 + 4г/2 = 1, г = 0.
2197.	г2 = 2рх, х2 + г/2 = 2Р.х.
2198.	г = х2 + 2г/2, х2 + 2г/2 + г2 = 6.
2199.	х2 4- г2 = 2ах, у = 0, у = ах, г = а.
у2	«2
2200. (г — 2)2 = -^-+2’ 2==°
2201.	х2 + г/2 = 2ах, 2 = ахх, 2 = а2х, ах > а2.
2202.	х2 + у2 = ах, х — 2 = 0, х -}- г = 0.
2203.	х2 + у2 + г2 = За2, х2 + у2 = 2аг.
2204.	х2 + г/2 + г2 = а2, х2 + у2 = а(а — 2г).
2205.	4 + ^ + ЛЇ=1,2г = С.
^«2	ї/3
2206.	Еліптичний циліндр	= 1 перетинається пло-
щиною, яка проходить через малу вісь так, що висота тіла, утворе-
ного при цьому, дорівнює 5. Знайти об’єм цього тіла.
2207.	Прямий круговий конус перетинає площина, яка проходить
через центр основи паралельно твірній. Знайти об’єм частини ко-
нуса, що при цьому утворюється. Перерізи конуса площинами, па-
ралельними твірній, є параболічні сегменти.
Знайти площі поверхонь, утворених обертанням:
X3
2208.	Параболи У = — навколо осі абсцис від вершини до точ-
ки з абсцисою х = 2.
2209.	Кола х2 + у2 = г2 навколо діаметра.
2210. Кола х2 4- (у—&)2 = г2 навколо осі абсцис (тор).
(X	X \
еа + е а ) навколо осі абсцис
від хг = 0 до х2 = а (катеноїд).
2212.	Петлі кривої ?>а2у2 = а2х2 — 4х4 навколо осі абсцис.
2213.	Кривої % = а8іп3/, у = асо§3? навколо осі абсцис.
151
2214.	Кривої х = 2азіп/, у = азіп/соз/ навколо осі абсцис.
2215.	Кривої х = а/2, у = -у(3 — /2) між точками Л(0; 0) та
В (За; 0): а) навколо осі абсцис; Ь) навколо осі ординат.
2216.	Однієї арки циклоїди х = а(/— зіп/), у = а(\—соз/):
а) навколо осі абсцис; Ь) навколо осі ординат.
2217.	Кривої х =	а/4, у =	(5/3 — З/5) між точками А (0; 0)
та В (5а; 0): а) навколо осі абсцис; Ь) навколо осі ординат.
2218.	Кривої %=2а/3, г/ = -^-(2/2—/4) між точками Д(0; 0)
та В(4а]/2; 0): а) навколо осі абсцис; Ь) навколо осі ординат.
Знайти статичні моменти:
2219.	Відрізка прямої у = 5, що лежить між точками %х = 0
х2 = 2, відносно осі абсцис.
2220.	Дуги параболи у2 = 2х, що лежить між точками %х == 0
та х2 — 2, відносно осі абсцис.
2221.	Дуги кривої у = соз% від точки хх = 0 до точки х2 = ~
відносно осі обсцис.
2222.	Дуги кривої х=3а/2, у = аї(3—/2), що лежить між точ-
ками ,ух = 0 та х2 = 9а, відносно осі абсцис.
2223.	Дуги кривої х = 6а^5, у = 5а (і — /9) між точками %х = 0
та х2 = 6а відносно осі абсцис.
2224.	Трикутника, утвореного прямою х + у = 2 та осями ко-
ординат, відносно осі абсцис.
2225.	Фігури, обмеженої кривою у = Ух — 2, віссю абсцис, та
прямою х = 3, відносно осі абсцис.
2226.	Фігури, обмеженої чвертю еліпса у—-^~У25 — х2, що
лежить у першому квадранті, та осями координат: а) відносно осі
абсцис; Ь) відносно осі ординат.
2227.	Фігури, обмеженої кривою у =	, віссю абсцис та
прямою х = 2, відносно осі абсцис.
2228.	Фігури, обмеженої кривою у=і^х, прямими г/ = 0 та
х =	, відносно осі абсцис.
152
2229.	Фігури, обмеженої кривою у = —* ~ та прямими х =
=---------та х =	, відносно осі абсцис.
2230.	Фігури, обмеженої кривою г/ = 1пх, віссю абсцис та пря-
мою х = 2, відносно осі ординат.
2231.	Фігури, обмеженої кривими у = х2У х + 1 та +	+
+ у2 = -і-, відносно осі абсцис.
2232.	Фігури, обмеженої кривими ау = хУ х (а — х) та х2 —
— ах 4- У2 = 0, відносно осі абсцис.
2233.	Фігури, обмеженої лініями у — —у— та у = ~, відносно
осі ординат.
2234.	Чверті еліпса х = ]/2 зіп /, г/ = соз/, що лежить у першо-
му квадранті: а) відносно осі абсцис; Ь) відносно осі ординат.
Знайти координати центра ваги:
2235.	Дуги півкола х2 + у2 = а2, що лежить у верхній півпло-
щині.
2236.	Дуги астроїди х2/з + у*/* = а2/з, що лежить в першому
квадранті.
(X	X \
2	2 І
Є + е /, що лежить
між точками = — а та х.2 = а.
2238.	Першої арки циклоїди х = а(і — зіп/), у=а(\—соз/).
2239.	Трикутника, обмеженого прямими х у = а, х — 0, у = 0.
2240.	Фігури, обмеженої параболою Ух + У у = У а та осями
координат.
2241.	Фігури, обмеженої замкнутою лінією у2 = ах3—х4.
2242.	Фігури, обмеженої кривою у2 = х — 2 та прямою х = 4.
2243.	Фігури, обмеженої кривою у2 = х2(2 — х) та віссю абсцис.
РІЗНІ ЗАДАЧІ
2244.	Обчислити силу тиску води на прямокутні ворота шлюзу
шириною 20 м і глибиною 16 м, якщо їх верхня грань лежить на
поверхні води.
153
2245.	Гребля має форму рівнобічної трапеції з горизонтальними
сторонами 200 м і 50 ж, а висоту — 10 м. Обчислити силу тиску
на греблю, якщо довша основа лежить на рівні вільної поверхні
води.
2246.	Прямокутна пластинка, сторони якої а та Ь (а > &), зану-
рена у воду під кутом а до поверхні води. Обчислити величину
тиску на кожну сторону пластинки, якщо більша сторона її пара-
лельна поверхні і лежить на глибині И.
Вказівка. У задачах 2244— 2246 вагу 1 м3 води вважати за
1000 кг.
2247.	Обчислити роботу, яку необхідно виконати, щоб викачати
воду з циліндричної цистерни, що має радіус 2 ж, а глибину — 5 м.
2248.	Яку роботу потрібно виконати, щоб насипати купу піску
конічної форми з радіусом г та висотою Л, коли питома вага піску
дорівнює 2?
2249.	Яку роботу потрібно виконати, щоб тіло масою т відда-
лити у нескінченність з поверхні Землі, вважаючи, що силу притя-
гання тіла Землею можна визначити за формулою / = т§ , де
т — маса тіла, Я — радіус Землі, г — віддаль тіла до центра Землі?
2250.	Казан має форму півсфери з радіусом г. Яку роботу необ-
хідно виконати, щоб викачати з нього воду?
2251.	Знайти масу квадратної пластинки із стороною 2я, якщо
густина матеріалу пластинки пропорційна квадратові віддалі від точ-
ки перетину діагоналей, а на вершинах квадрата вона дорівнює
одиниці.
2252.	На фігурі, обмеженій еліпсом з піввісями а та Ь, маса
розподілена так, що густина її пропорційна віддалі від великої пів-
вісі, а на віддалі 1 від цієї осі вона дорівнює у. Знайти всю
масу.
2253.	Знайти масу кулі з радіусом 7?, якщо її густина пропор-
ційна кубові віддалі від центра, а на віддалі 1 вона дорівнює у.
2254.	Неоднорідна суцільна куля х2 + у2 + г2 7?2 має густину
що змінюється за законом у = Кг2. Обчислити силу, з якою вона
притягує матеріальну точку з масою т, що лежить на осі г на від-
далі 27? від центра кулі.
2255.	Однорідне тіло обмежене двома концентричними сферами.
Довести, що сила притягання цим тілом точки, яка знаходиться
всередині тіла, дорівнює нулеві.
РОЗДІЛ IX ————
ФУНКЦІЇ БАГАТЬОХ ЗМІННИХ
§ 1. Означення. Область існування.
Границя та неперервність
2256.	Зобразити площу 5 паралелограма як функцію сторони й
висоти.
2257.	Зобразити об’єм V циліндра як функцію радіуса 7? основи
та висоти Н.
2258.	Зобразити площу 5 трикутника як функцію його сторін
х, у та г.
2259.	Зобразити об’єм V прямого колового конуса як функцію
радіуса 7? основи та твірної /.
2260.	Зобразити об’єм V певної кількості газу залежно від тиску
р та абсолютної температури Т.
2261.	Обчислити вартість функції г = Ух2— Зу2 при х=7,
у=-Г8.
/2	\	/ 1	\
2262.	/(х, у) = соз і — пх + у\. Знайти вартість /І-уї 0 ,
/(т- Я таф т)-
2263.	/(х, у) =	. Знайти вартість /(2; —2), /(1; —3) та
/(4; -2).
2264.	І (х, у) = агсі§ . Знайти вартість /(0; 1) та
і ху
і (— —V
'[2 ' 3]
2265.	/(х, у) = агсзіп . Знайти /(2; 1), /(—2; р^З) та/(1; 1).
155
Визначити та зобразити область існування таких функцій:
9266 7		2207	~ _ *+у
			.
	_ 1		х~у
22оо. г	X2 — у2 '	2269.	2 = У 4 — X2 — у2.
2270 7		1			
	1/1 X2 у2	2271.	2 = /х2 -|- уг — 1.
	У	а2 Ь2		
2272. г	= у% — у.	2273.	г = У х-\- у — У х—у.
2274. 2	= У 4х — у*.	2275.	2 — кЦг/2 — х + 2).
2276. 2		2277.	2 = ІП ху.
2278. 2	= агсзіп-^- + У1 — у2-	2279.	• у— 1 г = агсзіп 		. X
2280. 2	= У зіп я (х2 + у2).	2281.	2 = У х 4- 1 -|- агссоз у.
2282. 2	= ]/(х24-у2 — 1)(9 —х2-	— у*)-	
2283. и	= 1/4 —х2 —у2 —г2.		
2284 у	_	і і ।	1		
	Ух	Уу	/г '		
2285. и	= Іпхуг.		
2286. 2	= агсзіп [2г/ (1	х2) — 1].		
2287. 2		 Іп (1 — X2 — у2)		
Знайти границі функцій:
2288.	Ііпі^М. х->3 У 1/->О
2289.	Ит X- х->0	х + У ї/->0
2290.	у2	 <»2 ііт --2--£ 		—— х-> 1 х + 2х — ху — 2у і/->1
2291. Показати, що
не існує.
Ііт
х->0
у-+0
х2 — у2
х2 + у2
156
2292. Показати, що
У->0
не існує.
2293. Показати, що
2294. Показати, що
Ііт	Х(/ 4-У2		
у2 х->0 х			
г/->0			
не існує. Знайти точки розриву функцій: 2295. г = =^-.	2296.	2 =	1п (1 —X2— у2),
2х — у 2297. г = 1п]/х2 4-г/2.	2298.	2 =	у2 4-х у2 — х'
9 9900	7 	-		2300.	2 =	. 1 81П	.
			
4 — х2 — у2 2301. 2= ..2....=.	2302.	2 =	Хї/ X —г/
у х2 + 2у2 Дослідити на неперервність функції: 	 -и2 	 у/2	О*ІПЛ		2 —	х3 — У3 ‘ х2у2
«с — л	£7 *	—V * .		х24-і/2 '
2305.
X2!/2
2306.
х3у3
7 — ---------—
X2 + Г/2 •
§ 2. Диференціювання функцій багатьох
змінних
Знайти частинні похідні від функцій:
2307.	г-х2 — у+ 1.
2308.	/ (х, у) = Xі у — ху3 + х 4- у + 3.
2309.	2= 4^4-	2310. г = —.
2311. х = Ух2 — у\	2312. /(х, г/) = 5Іп(Зх —2г/).
157
2313.	Ж у) = (Зх2у2—І)4.	2314. г = соз (ах—Ьу-\-\).
2315.	2 = 2х3у*.	2316. г = ет-ху\
2317.	г = 1п (х3 — соз у).	2318. г = агсзіп х ]/у.
2319.	2 =2 аГССО8 2 Уху.	2320. г = агсі§
2321.	У 2 = агсзіп —. X	2322. г = агсіеі^.. & 1 — ху
2323.	2 = Xу. Xі	2324. г=1пі£-^-.
2325.	2=3 У .	2326. 2 = е~х со5 у.
2327.	и = х2у3гі.	2328. и = х^2. х У
2329.	и = ]Лх2 + Зу2 + 5г2.	— х<Ле— 2330. и = е	2 .
2331.	и = 1п (х2 + 2у 4- 2г).	
2332.	Показати, що х	+ у-	дг	г	п /— . у -Ч— = -Ч- , ЯКЩО 2 = V X 81П —. ду	2 ’	г	х
2333.	гр	дг	дг Те ж саме	• -з— = г, дх ду	якщо 2 = (х 4- а) (у 4- Ь).
2334.	Показати, що 2х-~- 4- у= 0, коли г = еуг.
’	дх 1 а ду ’
2335.	Показати, що 4-	= 1, коли г = їй (е* + еу).
2336.	Показати, що х 4- у — = 2, коли г = 1п(х2 4- ху+у2).
Знайти повні диференціали функцій:
2337.	г=-^-.	2338. г = х3 4- г/3 — Заху.
2339. 2 = агсі£ — + агс!§ —.	2340. г = соз (ху).
х	у
2341. г = е~Т.	2342. г = агсзіп-і-•
2343.	Знайти вартість повного диференціала функції г = х2—у2
при х = 3, у = 2, Дх = 0,02, Дг/ = — 0,01.
2344.	Знайти вартість повного диференціала функції г =
= У х2 + у — 1 при х = 3, у = 1, Дх = 0,03, ку = 0,02.
158
2345.	Обчислити наближено приріст функції г = у2 — х при
змінюванні х від х0 = 1 до х1 = 0,98, а у від у0 = 3 до у± = 3,04.
2346.	Використовуючи те, що Лг»с?г, обчислити (наближено)
вираз V (6,02)2 + (7,97)2.
2347.	Період коливання маятника визначається за формулою
Т = 2л . Знайти похибку у визначенні Т, обумовлену незнач-
ними похибками при вимірюванні довжини /, та прискорення сили
ваги
2348.	З якою абсолютною Д та відносною 6 похибками обчисле-
но об’єм циліндра, якщо радіус основи /? = 2,4 ± 0,02 м, а висота
Н = 4,0 м ± 0,03 м.
§ 3. Диференціювання зложених функцій
2349.	2 = х2 — ху + у2, х = у = соз 2/; знайти .
2350.	г = х = 1/7, у = зіп 2/; знайти .
г	аі
2351.	г = агсі§-у , х = і2, у ~і + 1, знайти .
2352.	2 = агсзіп (х — у), х = і3 — 1, у = і2\ знайти	.
2353.	2 = х31пу, х = — , у=и2щ знайти 4^ і
и	ди ди
2354.	и = агссоз —, 2 =	1 — х2; знайти .
' І1	СІХ
2355.	г = 1п (х2 — у2 1), у = е~х2\ знайти ~ та .
2356.	2 =	(2х + Зу), х =	, у = 2и — у; знайти та
2357.	Знайти та , якщо г = / (і), де і = х2 — у2.
2358.	Знайти ~ та	, якщо г = уц> (х2 — у2).
2359.	Знайти та	, якщо г = /(и, V), де и = х—Зу,
V =
159
2360. Знайти та , якщо и = ер (£, г]),	% = х2 4- у2,
Г] = ху.
2361. Показати, що функція г — ху + лхр справджує рів-
няння
дг , дг
х~дї+У1ії=хУ + г-
2362. Показати, що функція г = <р (х2 + №), Де ф — диференці-
йовна функція, справджує рівняння
дг дг	п
У~а----х-а~ =	0.
дх ду
2363. Показати, що функція г = / («, ц), де и = х аі, V = у +
+ ЬІ, справджує рівняння
дг	дг , .дг
“чт — СІ ~ч— 4- О ~ч— .
ді	дх 1 ду
2364. Поклавши х = р соз 0, у = р зіп 0, довести, що
дх	дх	
ф-’	~д§~	= Р-
ду	ду	
др ’	00	
2365. Довести, що
дх	дх	дх	
др ’	дф ’	“д(Г	
ду	ду	ду	9	. А
др ’	дф ’	00	= р2 ЗІП 0,
дг	дг	дг	
~др~'	дф ’	"00"	
ЯКЩО X = Р СОЗ ф зіп 0, у = р ЗІП ф ЗІП 0, 2 = р соз 0.
о2
2366. Показати, що функція г = 4- + ф(-Ч/) справджує рівняння
о дг	дг
дх у ду
2367. Якщо 2 = еуе$\уеу /, то вона справджує рівняння
/9 ох дг . дг
(X- -У )~^+ху-^= хуг.
160
2368.	Показати, що функція г=хп[^-^, де /— довільна ди-
ференціиовна функція, справджує рівняння х + 2у = пг.
2369.	Знайти повний диференціал функції г = / (и, ц), де и =
X
= ху, V = ---.
У
2370.	Знайти повний диференціал функції и = { (£, г), С), де £ =
= х2 + у2, Г] = х2 — у2, £ = 2ху.
§ 4. Похідні та диференціали вищих
порядків
2371.	г = х3 + х2у — Зху2 + г/*. Показати, що
2372.	Те ж саме для функції г — агсзіп х~
2373.	Знайти сРг функції г = агсі§ .
і ху
2374.	Знайти й2г, якщо г = еЛсоз£/.
2375.	и = зіп (х2 + у2). Знайти й2и.
2376.	Показати, що функція и = ер (х — аі) + ф (х + а/), де ф та
ф— двічі диференційовні функції, справджує рівняння
д2и 2 д2и
ді2 а дх2 ’
2377.	г = е~хуг. Знайти й2г.
2378.	г = Іп (х2 4- у2). Знайти й2г.
2379.	«==зіп(2х — Зу). Знайти та
2380.	Переконатися, що функція
и = Іп— 1
/ X2 + у2
справджує рівняння
д2и &2и _ „
дх2 ‘ ду2
2381.	Знайти (і2г, якщо г =/(/)> де і = х2 — у2.
2382.	Знайти й2г, якщо г = /(«, о), де и = хгу і V = уех.
11 2193
161
2383-	« = /	• Переконатися, що 4-	4-
4-	= 0
+ Зг2 и’
І/	д22	д22
2384.	г = агсі§ -2-. Переконатися, що	= 0.
2385.	и = хуг. Знайти сРи.
X2
2386.	и =	4аЧ • Переконатися, що
ди 9 д2и
ді и дх2 *
2387.	и = е“"ахф(х—у). Показати, що
д2и	д2и	о ди	2
-4-й----ч-й-	— 2а -4—	= а2и.
дх2	ду2	ду
2388.	Показати, що и = -^-(Ае~аг + Веаг), г = ]/х2 у2 + г2,
справджує рівняння
д2и	.	д2и	.	д2и	2
+ тт +	= а и.
дх2	‘	ду2	1	дг2
2389.	х2 — 2х + у2 — 5=0. Знайти та •
ах ах
2390.	х3 4- у3 — Зху = 0. Знайти .
2391.	-^2 +	— 1=0. Знайти зокрема, при х=0, у=Ь.
2392.	1п ]/>2 + У2 = агсі§ . Знайти 
2393.	Знайти та зокрема, при х = 1, у=1, г=1
ах	ах
якщо функції задані рівняннями х2 — у2 4- г2 = 1 та у2 — 2х 4- г = 0.
2	2	2
2394.	х3 4~у3 = а3  Знайти -4^--
' а	д.х
2395.	Довести, що з рівності х2^2 4- х2 4- У2— 1=0 випливає
Лх , Лу _ 0
/ 1-х4 ’Г /1-у4
2396.	Дано 4- -та —"Г = !• Знайти та 44-.
а* ' &	дх ду
162
2397. (х2 + у2)2 — 2а2 (х2 — у2) = 0. Знайти у'.
2398.	ух3 = еЧ Знайти у'.
2399.	х2у2 — 1п у = 1. Знайти у'.
2400.	Дано х2 + у2 — г2 = 0, х2 + 2у2 + Зг2 = 4. Знайти та
зокрема, при х = 1, у = 0, г = 1.
2401.	Показати, що функція г, визначувана рівнянням Р (х— аг,
у — Ьг) = 0, справджує співвідношення
дг , , дг <
а -ч—Ь о -ч- = 1.
дх 1 ду
2402.	Переконатися, що функція г, задана рівнянням г =
==хф0-^, задовольняє співвідношення
дг ,	дг
х -ч—[- у — = г.
дх 1	ду
2403.
. Показати, що
9 д2и о д2и 2 д2и (
х2 -з-т + 2хг/-ч-ч—Ь у2 -ч-ч- = п (п — 1) и.
Ох2 1 дхду ду2 '	7
2404. г = хзіп2г/. Знайти с12г.
2405.	— 2	= 0, якщо и = х<р (х+у)	(х+у).
§ 5. Заміна змінних
2406.	Перетворити рівняння
дх2 ' дх ’
взявши за аргумент у, а за функцію х.
2407.	Перетворити рівняння
х45+2г3-й-+^=0’
1
поклавши х=—.
2408.	Перетворити рівняння
поклавши х == соз /.
н*	163
2409.	Перетворити рівняння
*2-&+3*~й-+^=0’
зробивши заміну незалежної змінної х = е*.
2410.	Перетворити рівняння
йу .	о / &У \2 = Л
(ІХ СІХ3 у (ІХ3 у ’
взявши за аргумент у, а за функцію х.
_ і
2411.	Зробивши заміну шуканої функції у = х 2 г, перетвори-
ти рівняння
*25-+х-й- + (х2-т)^ = °-
2412. Перетворити рівняння
взявши за нову незалежну змінну /= Т%2‘
2413. Поклавши х = перетворити рівняння
2414.	Перетворити рівняння
(X + І)3 5+ з (х + 1)2-^ + (х + 1)	+ <2у = 0,
поклавши х + 1 = е*.
2415.	Перетворити рівняння
(1 +х2)4ї—У = 0>
поклавши	(і — нова незалежна змінна) та у=и&есі,
и = и (і).
2416.	Перетворити рівняння
запровадивши нові незалежні змінні и та V за формулами и = х, а
V = X2 4- у2.
164
2417.	Перетворити до нових незалежних змінних и та V рівняння
дг , дг
г ~Х~дх + У~ду'
поклавши х = и, а у = ух.
2418.	Поклавши и = у + ах, V = у — ах, перетворити до цих
нових незалежних змінних рівняння
д2г __ 2 д2г
дх2 а ду2 '
2419.	Лапласове рівняння
д2и д2и __ ~
~дх^ ' ~д^~~^
перетворити до полярних координат, поклавши % = рСО5 0, Г/ = р8ІП0.
2420.	Перетворити рівняння
д^г Д- 9 д22 І д2* = п
дх2 дхду ду2
поклавши и = х у, V = х — у, гю = ху — г, розглядаючи и й V як
нові незалежні змінні, а ш — нову функцію ш = ср(и, V).
2421.	Перетворити рівняння
дг_ _1_ д2г _ 1
ду ”1" 2 У ду2 ~~ ху
поклавши а =	, V = х, & = хг — у, розглядаючи а й V як нові
незалежні змінні, а ш — нову функцію.
2422.	Якого вигляду набуває рівняння
д2и д2и	п
дх2 + ду2 + и ~
якщо и = <р (г), де г = ]/х2 + у2.
2423.	Перетворити рівняння
д2г д2г ________________________ 1 дг
дх2 У ду2 ~ 2 ду ’
якщо и = х — 2 у та V = х + 2 У~у — нові незалежні змінні
(У>0)-
2424.	Перетворити рівняння
о д2г 2 д2г п
Х“ ~ді^ У ~д^ ~
X	о	.	...
поклавши и = ху, V = —, розглядаючи и и V як нові незалежні змінні.
165
§ 6. Геометричні застосування. Дотична
площина. Нормаль
Скласти рівняння дотичної площини та рівняння нормалі до
поверхні:
2425.	г = х2 + г/2 у точці Д4 (3; —1, 10).
2426.	2 = ху у точці Л4(—2; 2; —4).
2427.	х2 + у2 + г2 = а2 у точці М (х0, #0, г0).
у 2	</2
2428.	-г +4- + тг = 1 У точці М (х0, у0, г0).
2429.	------------= 1 У точці М(а, Ь, с).
2430.	г=агсі§-^- у точці М^І; 1;
2431.	х3 + у3 + г3 + хуг — 6 = 0 у точці М(1; 2; —1).
іА 2^
2432.	В якій точці еліпсоїда	= 1 нормаль до
нього утворює однакові кути з осями координат?
2433.	До поверхні х2 — у2 — Зг = 0 провести дотичну площину,
яка проходить через точку А (0; 0; —1) паралельно до прямої
х __ у _ г
2	1	2 *
2434.	Скласти рівняння дотичної площини до поверхні 2 = ху
перпендикулярної до прямої
% + 2_у + 2 г— 1
2	1	— 1 •
2435.	Провести дотичну площину до еліпсоїда х2 2у2 + г2 = 1,
паралельну до площини х — у + 2г = 0.
2436.	Провести дотичну площину до еліпсоїда 4-	+
2*2
4-	— = 1, яка відтинає на координатних осях однакові відрізки.
2437.	Показати, що дотичні площини до поверхні Ух -\~УУ
+ У2 = У~а відтинають на координатних осях відрізки, сума яких
стала.
2438.	До поверхні х2 + 2у2 + Зг2 = 21 провести дотичну площи-
ну, паралельну до площини х + 4у + 6г = 0.
166
2439.	Показати, що поверхні г2 = ху та х2 + у2 + г2 = 1 ортого-
нальні.
2440.	Показати, що дотичні площини до поверхні хуг = а3
{а > 0), утворюють з координатними площинами тетраедр сталого
об’єму. Знайти його.
2441.	На поверхні х2 + у2 + г2—6г/ + 4г—12 = 0 знайти точ-
ки, в яких дотичні площини паралельні до координатних площин.
§ 7. Тейлорова формула й Тейлорів ряд
2442.	Функцію /(х, у) = х2 — Зху + У2 розвинути по степенях
х — 1 та у 1.
2443.	Розвинути функцію г = х3 ху2 за формулою Тейлора в
околі точки Л4(1; 1).
2444.	Розвинути функцію г = е* зіп у по степенях х та у, обме-
жившись членами третього порядку.
2445.	Функцію / (х, у) = агсі§ — розвинути по степенях х — 1
та у, знайшовши члени другого порядку включно.
2446.	Знайти декілька перших членів розвинення в Тейлорів ряд
функції г = соз х • соз у в околі точки (0, 0).
2447.	Функцію г = агсі§ РОЗВИНУТИ в Тейлорів ряд по
степенях х та у,
2448.	Розвинути в Тейлорів ряд функцію г = е* 1п(1-}-і/) по
степенях х та у.
2449.	Розвинути в Тейлорів ряд функцію г = зіп(х2 + У2) в око-
лі точки (0, 0).
2450.	Функцію г = розвинути в ряд по степенях х та у.
2451.	Розвинути в ряд в околі точки (0, 0) функцію г=ехсозг/.
2452.	Функцію г — ху розвинути по степенях х— 1 та у — 1 до
третього порядку включно. Обчислити наближено 1,1і*02.
2453.	Розвинути в Тейлорів ряд функцію г = 1п(1-рх-р#) в
околі точки (0, 0).
§ 8. Екстремуми функцій багатьох змінних
Знайти максимуми та мінімуми таких функцій:
2454.	г = х2 + у2 + ху — 2х — у.
2455.	г — х2 — ху + у2 + 9х — &у -р 20.
2456.	2 == 2ху — Зх2 — 2у2 + 10.
167
2457.	2 = 4 (х — у) — х2 — у2.
2458.	г = Xі + уі — 2х2 + 4ху — 2у2.
2459.	2 = х3 + у3 — Заху.
2460.	2 = х3 + Зу3 — бху + 1.
2461.	г = х?у2(6— х — у).
X
2462.	2 = Л (х + у2).
2463.	г = е~хг~уг (ах2 4- Ьу2), а > 0, Ь > 0.
2464. 2 <= (2х — х2) (2у — у2).
2465.	г = х2 + ху + У2 + -^- + -у, х>0, у>0.
2466.	Знайти найбільшу М та найменшу т вартості функції
г = ху у крузі ? + /<!.
2467.	Знайти найбільшу М та найменшу т вартості функції
2 = X2 + у2 — ху 4- X + у у трикутнику, обмеженому ЛІНІЯМИ X = 0,
у = 0 та х 4~ # 4- 3 = 0.
2468.	Знайти найбільшу М та найменшу т вартості функції
2 — зіп х + зіп у 4- зіп (х 4- у) у прямокутнику 0 < х < -у-, 0 <
2469.	Знайти найбільшу М та найменшу т вартості функції
г = х2 — у2 у крузі х2 + у2 4.
2470.	Знайти найбільшу М та найменшу т вартості функції
г = х2у (4 — х — у) у трикутнику, обмеженому лініями х = 0, у = 0
та х + у — 6 = 0.
2471.	Визначити найбільшу М та найменшу т вартості функції
2 = х3 + у3 — Зху у прямокутнику 0 < х •< 2, —1 •< у С 2.
2472.	Визначити найбільшу М та найменшу т вартості функції
г = агсі§ (х2 — ху + у) у прямокутнику, обмеженому лініями х = —2,
х = 2, у = —3, у = 3.
2473.	Знайти найбільшу М та найменшу т вартості функції
2 = є~х2--у2 (2х2 + З#2) у крузі х2 + у2 < 4.
2474.	З усіх трикутників, які мають периметр 2р, знайти той,
що має найбільшу площу.
2475.	У коло з радіусом 7? вписати трикутник, сума квадратів
сторін якого є найбільша.
2476.	Визначити розміри прямокутного відкритого водоймища,
яке має найменшу поверхню при умові, що його об’єм V = 32 дм3.
168
2477.	На полі трикутника з вершинами Л(хх, #х), В(х2, у%) та
С (х3, у3) знайти точку, сума квадратів віддалей якої до вершин три-
кутника найменша.
2478.	Знайти найкоротшу віддаль від точки Л(1; 0) до кривої
4х2 + 9у2 = 36.
2479.	Знайти прямокутний паралелепіпед з даною поверхнею 5,
який має найбільший об’єм.
§	9. Умовний екстремум
2480. Знайти екстремум функції г = х2 + у2 при умові
2481.	Знайти максимуми й мінімуми функції г = ху при умові
х2 + у2 = 1.
2482.	Знайти екстремуми функції г = хт 4- ут при умові
х + у = 2а (а > 0, т > 1).
2483.	Знайти екстремуми функції и = хуг при умовах х + у +
+ г = 5, ху + хг + ух 8.
2484.	Знайти максимуми та мінімуми функції г	ПРИ
умові х + у — 2.
2485.	Знайти екстремуми функції г = соз2 х 4- соз2 у при умові
я
У — х = "7" •
4
2486.	Знайти екстремуми функції и = х2 4- 2 2 + Зг2 при умовах
х2 + У2, + з2 — 1, х + %у + Зг == 0.
2487.	Знайти максимуми й мінімуми функції а = х — 2у 4- 2г
при умові х2 + у2 4- г2 = 9.
2488.	Знайти екстремуми функції и = х2г/3г4 при умові 2х +
4“ Зг/ 4~ 4г = а.
§10	. Особливі точки. Обвідна
Визначити особливі точки алгебраїчних кривих:
2489. у2 = х2 4- х3.	2490.	у2 =	;
2491. х34~^3 — Заху — 0.	2492.	у2 =	.
2493. (у — х2)2 — х* = 0.	2494.	у2 =	.
2490. у2 = х3.
2492. у2 = х3 — х2.
2494. у2 = х4 — х6.
169
2495.	х4 4- г/4 = х2 4- у2.	2406	9	X3 	 	
2497. 2499.	о II > । 1 о II 1 сч |со ' + + 1 сч Ісо *	2498.	V 2а — х* (х2 + У2)2 = о2
Дослідити особливі точки трансцендентних кривих:			
2500. 2502.	у = X Іпх. , 1 у = хагсі§ —.	2501. 2503.	X У~	2_ • 1 + ех у — хх.
2504. 2506.	_ 1 V 1п х у2 = 1 —е-*2.	2505.	У2 = 8ІП (X2).
Знайти обвідні таких сімей:
2507. (х— а)2 + у2 = 1 (сім’я кіл).
2508. (х — а)2 + у2 — — (сім’я кіл).
2509. у = 2ах + а4 (сім’я прямих).
2510. у = а?(х — а)2 (сім’я парабол).
2511.	+ -р- = 1 (сім'я еліпсів) при умові а2 + Р2 = 1.
2512. -^2“ +	= 1 (сім'я еліпсів) при умові а + р = 8.
2513.	Коло котиться по прямій без ковзання. Знайти обвідну
різних положень його діаметра.
2514.	Знайти обвідну кіл, що мають центр на параболі у2 = 2рх
і проходять через її вершину.
2515.	Пряма рухається так, що добуток відрізків, які вона від-
тинає на координатних осях, дорівнює сталій а. Знайти обвідну цих
прямих.
2516.	На хордах кола х2 + у2 = а2, паралельних до осі ординат,
будуємо, як на діаметрах, кола. Знайти їх обвідну.
2517.	Знайти обвідну сім’ї у2 = (х— а)3.
2518.	Знайти обвідну сім’ї півкубічних парабол (у—-а)2 = (х— а)3.
РОЗДІЛ X ...  -.......-....-...—- 
КРИВОЛІНІЙНІ ІНТЕГРАЛИ
§ 1. Криволінійні інтеграли першого типу
Обчислити такі криволінійні інтеграли:
2519.	У хсіз по параболі у = х2 від точки Л(2;4) до точки
В(1, 1).
2520.	У у2(І8, де Ь — перша арка циклоїди х = а (і — зіп /), у =
ь
= а(1 — соз/).
2521.	У (х — у) (із, де А — коло ^х--+ у2 =
С	х2 и2
2522.	хуіїз, Ь — чверть еліпса —що міститься
в першому квадранті.
Г СІЗ
2523.	І -	... .... , де Л —відрізок прямої, що сполучає
£ У х2 + у2 + 4
точки 0(0, 0) та Л(2; 4).
2524.	У (х2 + і/2)4 б/з, де Ь — коло х2 + у2 — а2,
ь
2525.	У х2сі8, де Ь — верхня половина кола х2 + У2 = сі2 між
ь
точками А(а\ 0) та В (—а; 0).
2526.	[ (х2 + у2 + ?2) ^5, де Ь — дуга кривої х = а соз /, у =
ь
= а зіп /, г = Ьі, 0 СІС 2л.
2527.	2г/2 + г2 (із, де А — коло х2 + у2 + г2 = а2, х = у.
ь
171
2528.	[ (2г — Ух2 + у2) йв, де Ь — дуга кривої х = І соз /, у =
І
= і зіп /, г = /, 0 •< і С 2л (конічна гвинтова лінія).
2529.	У хуйз, де Ь — контур прямокутника з вершинами 0 (0, 0),
4(4; 0), В (4; 2), С (0; 2).
С	З/2
2530.	] (х + у) йз, де £ — дуга кривої х = і, у =	, г = /3,
£	У 2
[0</< 1].
§ 2. Криволінійні інтеграли другого типу
Обчислити такі криволінійні інтеграли:
2531.	( (х2 — 2ху) йх + (у2 — 2ху) йу, де Ь — дуга параболи
ь
у = х2 між точками 4(—1; 1) та В(1; 1).
2532.	У хуйх, де £ — синусоїда, взята між А (я; 0) та В (0,0).
ь
2533.	^хйу — усіх по кривій у = х3 від 0(0, 0) до 4(2; 8).
ь
Р	^2	£»2
2534.	у2йх + х2йу, де Ь — верхня половина еліпса —2 +	=
= 1, яка пробігається за годинниковою стрілкою.
2535.	У	, де £ — дуга астроїди х3 + у3 = а3 від
в А- у$
точки А (а\ 0) до точки В(0; а).
(і.і)
2536.	У 2хуйх + х2йу вздовж лінії: а) у = х; Ь) у = х2;
(0,0)
с) у = х4; (1) у2 = х.
2537.	У (х2 + у2) йх + (х2 — у2) йу, де Ь — контур трикутника з
ь
вершинами в точках 4(0; 0), В(1; 0), С(0; 1).
25	38., ( +	।	—УІ^У, де £ — коло х2 + у2 = а2, яке про-
І х -ту
бігається в напрямі проти годинникової стрілки.
172
(4, 4, 4)
('	хйх 4- уйу + гйг
2539.	*  	. вздовж прямої.
(1, 1. і)/х2 + і/2 + г2-х-(/+2г
2540.	угсіхгУа2—у2 йу + хуйг, це Ь — дуга гвинтової
ь
. . Ьі .	. ...
ЛІНИ Х=ЯСО8/, £/ = 0 8111/, 2 = -^- від точки перетину ЛІНИ з
ПЛОЩИНОЮ 2 = 0 до точки її перетину З ПЛОЩИНОЮ 2 = Ь.
§ 3. Застосування криволінійних інтегралів
Обчислити площі фігур, обмежених такими кривими:
X2 . у2, _ <
2541.	Еліпсом-^? ~г~^2 — Е
2	2	2
2542.	Астроїдою х3 + у3 —а3 .
2543.	Петлею декартового листка х3 + у3 — Зху = 0.
2544.	Петлею кривої (х + і/)4 = ах2у.
2545.	Кривою у2 = х2 — х4.
2546.	Знайти роботу сили Р = хуі + (х + у) ] при переміщенні точ-
ки з масою т з початку координат по кривій у = х2 в точку А (1; 1).
2547.	Знайти силу, з якою струм І у нескінченному прямоліній-
ному провіднику діє на точкову магнітну масу т, яка знаходиться
на віддалі а від провідника.
2548.	По контуру, що має квадратну форму, йде струм І. З якою
силою цей струм діє на точкову магнітну масу т, що знаходиться
в центрі квадрата? Сторона квадрата дорівнює а.
2549.	З якою силою струм /, що йде по контуру еліпса
а2
діє на точкову магнітну масу т, яка знаходиться у фокусі еліпса?
2550.	Знайти масу куска ланцюгової лінії у = а сії між точ-
ками х = 0 та х = а, якщо густина кривої у кожній її точці обер-
нено пропорційна ординаті точки.
2551.	Обчислити притягання, що справляє однорідне півколо
(густина р= 1) на одиницю маси, вміщену в його центрі.
2552.	Знайти площу фігури, обмеженої кривою х3 + у3— х2 —
— у2 = 0 та осями координат.
РОЗДІЛ XI ----- —
ІНТЕГРАЛИ,
ЗАЛЕЖНІ ВІД ПАРАМЕТРА
Я
2 .
2553.	Дано Р(а) = йх. Знайти Р'(а).
о
а
2554.	Дано І (а) = (	Знайти І' (а).
6
2
і* (&Х,
2555.	Дано І (а) = ] йх. Знайти Г (а).
і	і
2556.	Знаючи, що |	= 2- 1п(Ц- а), обчислити
диференціюючи по а.
і
2557.	Знайти похідну функції І (а) = Іп (х2 + а2) йх, 1 <а <2.
о
і	і
2558.	Відомо, що С —-2	9 = — агсі£ —, обчислити »ч2.
м ’ Л х2 + а2 а & а ’	(х2 + а2)2
Дослідити на збіжність інтеграли:
оо
2559.	ае~ах йх, 0 -< а < 1.
о
сю
2560.	Ч^^йх.
.) 1+x^
174
2561.	0<а<оо
0Л* — а)2+1’	"
2562. §хае~~хсІх,
і
оо
2563.	[ е~ах зїпхсіх, 0<а0<Са<оо.
о
оо
2564.	У Xа""1 е~х йх.
і
і
2565.	У Xа-1 е~~х йх.
о
і
2566.	Довести, що У^-ЦІ—х)?-1 йх збігається рівномірно від-
0
носно р й д, якщо тільки р > р0 > 0 та ? > ?о > 0-
оо
2567.	Довести, що Уе-ахб/х рівномірно збіжний на [1; 2].
о
оо
2568.	Показати, що | -1ПОІ* йх рівномірно збіжний для <х >
о х
> «О > 0.
2569.	Довести рівномірну збіжність інтеграла І —гт-г	Для
о 'х
а > а0 > 0.
2570.	Довести рівномірну збіжність для всіх а інтеграла
е~хсозахйх.
о
Обчислити такі інтеграли:
2571.	] —сіх (а > 0), інтегруючи по параметру а.
о х У 1 х2
р х&___ха
2572.	] —— (а та Ь > — к > — 1), інтегруючи по параметру.
175
Диференціюючи по параметру, обчислити інтеграли:
2573. Г|п (‘~к2*2)-(аа < 1).	2574. ї -~е~^ах (а>~1).
2575.	[ агс^* .
З х (1 + х2)
2576.	С _!ПП+асозх) Лх (а8<і)
Л	СОЗ X
о
я
т
2577.	у 1п (а2 соз2 х + зіп2 х) йх.
о
1
2578.	Дослідити на збіжність «Xа-1 йх, 0<а< 1.
о
Обчислити інтеграли:
2579. ? 5Іпо“ 5Іп рх ах (р > а > 0).
V	ХЛ
0
оо
(* а аХ _ р
2580. ]  ------—ах (а і &>0).
о
©о
ОСО1 Г —ах 8ІП Ьх — 8ІП СХ і /
2581. е --------------------йх (а>0).
о	х
л
2582. у ігсі^а^х)	2583. ^п^х^
0	о
1
2584.	У ха(\пх)гпйх, де т—ціле додатне число а>—1.
о
ОО	°С	_
2585.	С е-а*2 ах, а > 0, користуючись рівністю С е~х2 ах =	.
о	о
ОО	7
Р — ---Г
2586.	] е х ах, а>0.
0
176
2587.	оо У зіп (х2) йх (Френелів інтеграл). 0
2588.	сю У соз (х2) сіх (Френелів інтеграл). 0 сю	&	о© „ — ах2			р
2589.	) е	х йх.	2590. ] е~~х2 соз 2ахйх. 6	0 я
2591.	Іп (1 — 2а соз х + а2) йх. 0
2592.	оо С соз ахйх Т , х . Л ] 1+х2 -Л«). «>0- 0	1 оо
2593.	С х зіп ах і —гп— Л 14-х2 0	1 я
2594.	р і	1 4~ а зіп х (іх	/ Іп -і—-—.	— (а > 0). 3	1—азіпх	зіп х	к	7 0
2595.	Г 1. (І-.-,.) х2 У 1 — х2
Дослідити на рівномірну збіжність інтеграли:
	оо
2596.	У	(*—«)2йх, а < а < 6, —сс < а < оо. оо
2597.	У е~ахг йх, 0 < а0 < а < со. 0
Обчислити інтеграли:
2598.	Г Іп (1 + «х) , 3	14- X2 ах' 0 оо
2599.	У е_“х2 соз рх йх = І (Р), а = сопзі > 0. 0
2600.	оо [ -агс*£ ах ~ агс1£--- йх (інтеграл Фрулланї). V	X 0
12 2193
177
оо .
С р—Ьх_р—ах
2601. ]------—йх.
о
2602. У со5б*-£оза*.^.
0
оо
2603. У5іп6х-5іпах-^.
о х
Застосовуючи Ейлерові інтеграли Г (р) та В (р, д), обчислити та-
кі інтеграли:
і
2604. Уху^Г^Т
0
°°	4/-
2606- [' •
’ (1+х)2
2605.
2607.
(ах
^1 / (1 + X)2 (1 - х)
х2п д.х
2608. ( ; ах - .
$ /1-х4
я
Т І _5_
2610. | соз2 хзіп2 хйх.
о
я
т
2611. у зіпр—1 х соз’-1 хйх,
о
2609.
о х (1 — х2)
ОО
Г х2а~~1 йх
о
Р>0, <7>0.
я
2
2612. у зігЛсгіх, т>—1
о
РОЗДІЛ хн —
КРАТНІ ІНТЕГРАЛИ
§ 1. Подвійні інтеграли
Обчислити такі повторні інтеграли:
2613. 2615. 2617.	4	1 У йх ] (х + Зї/2) йу. 0 б 4 Уз 1	1 2	1 У йу У х^уе** йх. 0	0	2614. 2616. 2618.	3	2 РИ (х + # • 2	0 3	1 \йу\^=. 2	Уїх ^йх у хуйу. 1	X
	а	Уа2—у2		2	2
2619.	У йу у йх. 0	а—у я 2	а соз 0	2620.	$ йу § (х2 + у2) йх. о	у а	2 Уах
2621.	У М у р 8ІП 0 б/р. 0	0	2622.	йх \ ~(х2 + у2)йу. 0	— 2Уах
Поставити межі інтеграції (в одному й другому порядку) в по-
двійному інтегралі
] У І(х, у) йхйу
І)
для таких областей:
2623.	О — трикутник з боками х = 0, у = 0, х 4- у = 5.
2624.	О — фігура, обмежена лініями у = х, у = х — 4, у = 0,
12*
179
2625.	О — поле круга х2 + у2 — 2ах = 0.
2626.	И — область, яка міститься в першому квадранті та обме-
жена кривими у = х, х2 + у2 = 2 і прямою у = 0.
2627.	О — область, яка міститься в першому квадранті та обме-
| _______________________^2
жена лініями х = 0, у = —— » х2 + г/2 = 1.
2628.	О — область, обмежена кубічною параболою у = х3, пара-
болою у = 2 — х2 та віссю О¥.
2629.	Знайти середню вартість функції г = х2 + у в області, обме-
женій кривими х = у2 та у = х2.
2630.	Знайти середню вартість функції г = У а2 — х2 — у2 в об-
ласті, обмеженій кривою х2 4- У2 — ах = 0.
2631.	Знайти середню вартість функції г = х2 + у2 в області, об-
меженій лініями у = 0, у = х та х = 1.
І
2632.	Знайти середню вартість функції г = — в області, об-
меженій кривою х2 + у2 = ах.
2633.	Знайти середню вартість функції г = зіп2 х • зіп2 у в квад-
раті 7? = [0, я; 0, я].
Обчислити площі фігур, обмежених лініями:
2634.	Параболою у2 = 4ах та прямими у = 0, у — За — х.
2635.	Параболою у2 = 2х і прямою у = х.
2636.	Параболами у = х2 та у = 2х — х2.
2637.	Прямими х = 0, у = х та кривою у = 2 — х2 (х>0).
2638.	(х2 + у2)2 = х2 — у2 та кривою х2 + у2 — 2х = 0.
2639.	(х2 + у2)2 = ху.
2640.	(х2 + у2)2 = Зх2 — у2.
2641.	Xі + у4 = 2а2ху.
2642.	х + у = 2, х + у = 5, у = х, у = Зх.
2643.	ху = Ь2, ху = а2, у2 = рх, у2 = дх (Ь2 > а2, р~> у).
2644.	у2 = х, у2 = 8х, х2 = у, х2 = 8у.
2645.	х3 + у3 = 2ху (петля).
2646.	(х + у)5 = х2^ (петля).
2647.	(х2 + у2)2 = х3.
2648-	=4^-
180
2649.	(х2 + г/2)3 = а2 (х4 + /).
2650.	= х2 +у* (х > 0, у > 0).
2651. ('Її' + Т')3 = ^_ (петля).
§ 2. Застосування подвійного інтеграла
до обчислення координат центра ваги
та моменту інерції
Визначити центр ваги плоскої однорідної фігури, обмеженої лі-
ніями (густина ц(х, у) = 1):
2652.	у2 = Зх та у = х.
2653.	х2 + у2 = г2\ х>0, у>0.
2654.	х = а (і — зіп/), у=а(\— соз/) та у = 0; (0<7<2л).
2655.	р = а(1 4-СО3 0).
2656.	х = асоз30, г/ = азіп30 та у = 0 (х>0, г/>0).
2657.	Знайти центр ваги кругового сектора з радіусом а та ку-
том при вершині 2а.
2658.	Обчислити момент інерції відносно осі ОХ площі трикут-
ника, обмеженого прямими у = а, у = та х = а.
2659.	Обчислити момент інерції сегмента, відрізуваного від пара-
боли у2 — х прямою х = 1, відносно прямої х = — 1.
2660.	Обчислити момент інерції площі лемніскати р2 = 2а2 соз 20
відносно осі, перпендикулярної до її площини в полюсі.
2661.	Обчислити момент інерції площі кардіоїди відносно полюса.
2662.	Визначити полярний момент інерції площі, обмеженої лі-
ніями — 4-	= 1, х = 0, у = 0.
а 1 Ь
§ 3. Обчислення об’ємів тіл та площ кривих
поверхонь
Обчислити об’єми тіл, обмежених поверхнями:
2663.	х	у 2 = 4, х 2, у = З, х = 0, у = 0 та 2 — 0.
2664.	х + у + 2 = а, Зх + У = а, Зх + 2у = 2а, у = 0, г = 0.
2665.	2 = х2 + у2, х + у = 4 та координатними площинами.
181
2666.	2г = х2 + У2, %2 + у2 — ах = 0 та г = 0.
2667.	г = ху, х2 + у2 = 2х, г = О (у >0).
2668.	х2 + У2 = 2ах, г = х, г = Зх.
2669.	2г = х2 — у2, г = 0, х = 2.
у2	«2
2670.	Л- + 4- + 4- = 1-
0“ 0і сй
2671.	Сферою х2 + у2 + г2 = За2 та параболоїдом 2аг = х2 + у2.
2672.	Конусом г2 = 4 (х2 + у2) та сферою х2 + у2 + (г — 2г)2 = г*
(розглянути внутрішність конуса).
2673.	Сферою х2 + у2 + г2 = г2 та параболоїдом 2гг = г2 — х2 —
-У2 (г>0).
2674.	Еліптичним циліндром х2 + 4у2 = 4 та площинами г = 1,
г -= 12 — Зх— 4г/.
2675.	Сферою х2 + у2 + г2 = г2 та циліндром х2 + у2 — гх = 0
(задача Вівіані).
2676.	Знайти площу частини площини + -у +	= 1, роз-
ташованої між координатними площинами.
2677.	Знайти частину поверхні х2 + у2 + г2 = 100, розташованої
між площинами х = — 8, х = 6.
2678.	Обчислити частину поверхні сфери х2 + у2 + г2 = а2, що
міститься всередині циліндра х2 4- у2 — ах = 0.
2679.	Обчислити частину поверхні конуса х2 = у2 + ?2, розташо-
ваної в першому октанті та обмеженої площиною у + г = а.
2680.	Обчислити частину поверхні х2 + у2 — 2ах = 0, що міс-
титься між площиною ХОУ та конусом г2 = х2 + у2.
2681.	Обчислити частину поверхні аг = ху, розташовану всере-
дині циліндра (V2 + у2)2 = 2а2ху
2682.	Обчислити частину поверхні 2г = х2 + у2, вирізаної цилінд-
ром х2 + у2 = 1.
2683.	Обчислити частину поверхні г2 = х2 + у2, вирізаної цилін-
дром г2 = 4у,
2684.	Обчислити частину поверхні г2 = 2ху, що знаходиться над
площиною ХОУ та розташована між площинами х = 2 та у = 1.
2685.	Обчислити частину поверхні 2г --------у, яка розташо-
вана всередині циліндра	= 1, г>0.
182
§ 4. Потрійні інтеграли
Обчислити інтеграли:
268в- ф(,+1+а-'[<у<г'‘<г<2-
2«87- ПІ х2у2гйх(1у(1г, 0<Сх<1, 0	0<г<х//.
2688-	Ш ,-.+і.Х’-а-  * У-кул. ^ + / + ^«1.
2689.	+ Де область V — еліпсоїд -^-+
2690.	^Ух2 + у2 + г2сІУ, де V — область, обмежена поверх-
нею х2 + у2 + г2 — 2 = 0.
2691.	+ у2) <ІУ, де V — область, обмежена поверхнями
2г = х2 + у2 та г - 2.
2692.	Обчислити об’єм тіла, обмеженого поверхнями ах — х2 + у2
та 2аг = а2 — х2 — у2.
2693.	Визначити об’єм тіла, обмеженого сферою х2 4- у2 4- г2 = а2
та конусом г2 = х2 4- у2 (всередині конуса).
2694.	Обчислити об’єм тіла, обмеженого поверхнями х2 4- у2 4-
4~ г2 = 2а2 та аг = х2 4- у2.
2695.	Обчислити об’єм тіла, обмеженого поверхнями г2 = х2 4- у2
та г = 6 — х2 — у2.
Визначити об’єми тіл, обмежених поверхнями:
2696.	(х2 + у2 + г2)2 = х.
2697.	(х2 + у2 + г2)2 = ах (х2 4- у2}.
2698^ (х2 4- У2 4- г2)2 = ахуг.
2699.	(х2 + у2 + г2)2 = а2(х24-у2 — г2).
2700.	(х2 4- У2)2 4- 2і = а2 (х — у).
2701.	(х2 4- у2)2 4- 2і = а3г.
183
/ 1*2	//2	$»2 З
2703.	(|+4 + у| = ^.
(у2 /»2 \ 2
-^г + Я +тг=г-
2705. (^-+ -т- + -гї = 2 (*>°> У>°’ 2>°>-
\ а о ь /
2706. (х2 + у2 + г2)3 = а2у2г2.
2707. (-г + ^- + т)2 = х— у (х>°’ у>()’ 2>°)-
2708.	(-у +-т)2 + -%т=х — У (х>0, у>0, г>0).
Знайти координати центра ваги однорідних тіл, обмежених по-
верхнями:
2709.	х2 + у2 + г2 = а2 (х> 0, у> 0, г> 0).
2710.	х + у + г = 0, 2 = х2 + у2.
2711.	г = х2 + у2, х + у = 1, х = 0, у = 0, г = 0.
у2	о2	е»2
2712.	А- + ^ + -^-= 1, х = 0, у = 0, г = 0.
2713.	(х2 4- у2 + г2)2 = ахуг, х > 0, у > 0, г > 0.
2714.	х2 = 2рг, у2 = 2рх, х =	, 2 = 0.
2715.	г = ]/а2—х2 —у2, 2 = 0.
Визначити моменти інерції відносно осі 02 однорідних тіл, об-
межених поверхнями (р = 1):
2716.	х2 + у2 — ах = 0, г2 = 2ах, 2 = 0.
2717.	х + у + 2 = а, х = 0, у,= 0, 2 = 0.
2718.	х2 + #2 + г2 = 2, х2 + і/2 = г2 (г>0).
у2	«»2
2719.	4- + 4г + Л- = 1.
а2	Ь2	с2
2720.	Знайти момент інерції однорідної кулі з радіусом г від-
носно її дотичної.
2721.	Визначити момент інерції циліндра з радіусом 7? та висо-
тою Н ВІДНОСНО ЙОГО осі.
2722.	Визначити момент однорідної кулі з радіусом г відносно
її діаметра.
2723.	Визначити масу сферичного шару між поверхнями х2 4-
+ г/2 + г2 = г2 та х2 у2 + г2 = 4г2, якщо густина р в кожній його
точці обернено пропорційна віддалі точки від початку координат.
184
2724.	Визначити масу циліндра з радіусом К та висотою Н, як-
що густина пропорційна висоті та дорівнює 1 на нижній основі.
2725.	Густина кулі х2 + у2 + £2 — %г2 = 0 у будь-якій її точці
дорівнює квадратові віддалі цієї точки від початку координат. Знай-
ти координати центра ваги кулі.
2726.	Обчислити притягання, яке чинить однорідний конус на
матеріальну точку, що має одиницю маси та міститься в його вер-
шині (Н — висота конуса, 7? — радіус його основи).
2727.	Визначити силу, з якою одиниця маси, що знаходиться в
центрі основи циліндра, притягується масою цього циліндра. Висота
циліндра Н, радіус основи 7?.
§ 5. Невластиві кратні інтеграли
Обчислити невластиві інтеграли:
2728.	де Р.= [0, 1; 0, 1].
ух
2729.
2730.
2731.
2732.
Исіхсіу	.
, (х2 + У2)р ’ Р> *
х2+у*> 1	1 57 '
У у----ОхОу— > де р — вся ПЛОіцИна-
Р (х2 + г/2+ір
Исіхсіу
х4+(/2 •
С Г (іхіїу
V Л . V 1  X2   О2
х2-Н/2<1 г 1	х	У
З”»- И е~(х2+^2) йхбй/, де Р — вся площина.
2734.	У зіп (х2	у2) йхйу, де Р — вся площина,
р
2735.	У У еак^чЬху-\-су^-\-2(іх-\-2еу^ йхйу, де Р — вся площина, а < 0,
р
6 = ас — &2>0.
2736.	У У Іп зіп (х — у)йх(1у, де Р — область, обмежена прямими
р
у = 0, у — х, х = я.
185
2737.	] ]
х*+у2<х
2738, У У хуегх‘-Уг <іхЛу.
о о
Дослідити на збіжність такі інтеграли:
2739.	( (----, де Р — вся площина.
•У (х2 + у2 + 1)а
2740.	УУ 1п (х2 + у2) (іхіїу, де Р — круг х2 + у2 < 1.
Г Г в сіхсіи
2741.	( )----2т-'-2- , де Р — круг з радіусом г та з центром
на початку координат.
2742.	СС	, дЄ р — квадрат |х| < 1, | у\ С 1.
Р / (X — у)2
2743. Обчислити об’єм тіла, обмеженого поверхнею г=х2£/2е“(х2+г/2)
та площиною 2 ~ 0.
2744. Обчислити об’єм тіла, обмеженого площиною г = 0 та час-
тиною поверхні 2 = Х£“х2“^2, розташованою над цією площиною.
§ 6. Многократні (багатократні) інтеграли
Обчислити такі інтеграли:
2745.
2... йхп, де всі Хі
71 <Д.
1 1
2746.
0 0 о
2747.
... + Хп-1 Хп) ^ХГ(ІХ2 ... (ІХп.
2748.
0 0 о
1 XI
Х-^Х2 ... Хп (ІХп.
0
о о
2749.
хп (ІХіСІХг... йхп, де всі хі 0 та
186
РОЗДІЛ XIII	....--.-.-. .
ПОВЕРХНЕВІ ІНТЕГРАЛИ.
ЕЛЕМЕНТИ ТЕОРІЇ ПОЛЯ
§ 1. Поверхневі інтеграли першого типу
Обчислити поверхневі інтеграли:
2750.	У У (х + у + г) 48, де 8 — поверхня куба 0<х< 1, 0 <
8
<[/< 1, 0<2<1.
2751.	УУ (6х + 4г/ + Зг) 48, де 8 — частина площини х + 2у +
4-	Зг — 6 = 0, що міститься в першому октанті.
2752.	У У	> Де 5 — частина площини х-\-у-\-г=1,
що міститься в першому октанті.
2753.	У У (/48, де 8 — півсфера г = У Р2— х2—у2.
8
2754.	У У х2(/248, де 8 — півсфера г = У Р2 — х2 — у2.
2755.	У [ (х2 + у2) (18, де 8 — сфера х2 + у2 + г2 = Р2.
8
2756.	У У	, де 8 — циліндр х2 + у2 = а2, обмежений площи-
5
нами г = 0 та г = Л, а г — віддаль від точки поверхні до початку
координат.
2757.	УУ (х соз а+ (/соз Р + г соз у) 48, де а, р, у — кути зов-
8
нішньої нормалі до 8 (8 — замкнена поверхня, що обмежує тіло з
об’ємом V).
187
§ 2. Поверхневі інтеграли другого типу
Обчислити такі поверхневі інтеграли другого типу:
27	.58. У У угйуйг + хгйхйг + хуйхйу, де 5 — зовнішня сторона
поверхні тетраедра, обмеженого площинами х + у + г = 1, х = 0,
у = 0, 2 = 0.
2759.	У [ х2у22йхйуі де 5 — нижня сторона нижньої половини
сфери X2 + у2 + 22 = Я2.
2760.	У У х2йуйх + у2йхй2 + 22йхйу, де 5 — зовнішня сторона
8
поверхні півсфери х2 + у2 + г2 = /?2 (г > 0).
2761.	УУ (х2 + у2)йхйу, де 5—нижня сторона круга х2-\-у2=а2.
8
У У х^йуйх, де 5 — верхня сторона верхньої половини
5
х2 . у2	г2	.
У гйхйу, де 5 — зовнішня сторона еліпсоїда
5
«»2	2>2
л_ 4. — = 1
' №	с2
2764.	У^гМхйг/, де 5 — зовнішня сторона поверхні
8
»/2	?2
2765.	У У у2хйх(іу + хгйуйх і- х2уйх(І2, де 5 — зовнішня
8
поверхні, що міститься в першому октанті та складена з параболоїда
обертання г = х2 + У2, циліндра х2 + у2 = 1 та координатних
площин.
2766.	У У 2йх(1у 4- хсІхсІ2 + уіїусІ2, де 5 — зовнішня сторона пі-
8
раміди, обмеженої поверхнями х = 0, у = 0, 2= 0, х у 2 = а.
188
2762.
еліпсоїда
х2
О2
2763.
х2
а2
сторона
2767.	У У (х2 соз а + г/2 соз Р + г2 соз у) й8, де 5 — зовнішня пов-
8
2%
на поверхня конуса	(0
2768.	У У х^йуйг + у^йгйх г^йхйу, де 5 — зовнішня сторона
8
сфери х2 + у2 + г2 = /?2.
Г Г &Ч& , «іггіх . ЛхЛц	о
2769.	\ і —----1--------1---—, де 5 — зовнішня сторона
X	у	2
X2 .	. З2 і
еліпсоїда — +	= 1.
Користуючись Стоксовою формулою:
2770.	Обчислити інтеграл (х2 — гу) йх + (у2 — хг) йу + (г2 —
с	— ху) йг.
2771.	Перетворити (у2 + г2) йх + (х2 + г2) йу + (х2 + у2) йг в
І
інтеграл по поверхні, «напнутій» на цей замкнений контур Ь.
2772.	Обчислити (£ (у — г) йх + (г — х) йу + (х — у) йг, де £ —
ь
крива х2 + у2 = 1, х + г = 1.
2773.	Обчислити х3у*йх + йу + гйг, де Ь — коло х2 4- у2 = а2,
г = 0, а поверхня — півсфера г = + У а2 — х2 — у2.
2774.	Обчислити (£ хйх + (х + у) йу + (х + у + г) йг, де Ь —
ь
крива х — а зіп і, у = а соз і, г = а (зіп І + соз і), 0 < І < 2л.
2775.	Довести рівність У У соз (п, х)й8 = 0, де 5 — замкнена по-
5
верхня, п — зовнішня нормаль до неї.
§ 3. Елементи теорії поля (векторний
аналіз)
Накреслити лінії рівня скалярного поля:
2776.	г = х2 — у.	2777. г = х2 + у2.
2778. г = х2 — у2.	2779. г = ху.
189
2780. г= (х— у)2.
2782.
2781. 2 = ]ґху.
2783. г = у-^>

Визначити поверхні рівня скалярного поля:
2784. а = агсзіп —— г-.		2785.	и — х + у — 2.
	У х2 + У2		
2786.	и = х2 + у2 + г2.	2787.	и = х2 — у2 + 22.
2788.	х2 + У2 — 2г		х2 — у2
	и ~ X2 + У2 •	1 О «7.	и~ г •
2790. Знайти похідну функції (скалярного поля и (Л4)) и = х2 +
4-г/2 — Зх + 2у у точці М.± (0, 0, 0) у напрямі, що йде від цієї точ-
ки до точки 7И(3; 4; 0).
2791.	Знайти швидкість зміни функції (скалярного поля) и^хух
у точці Л4(5; 1; —8) в напрямі, що йде від цієї точки до точки
Р(9; 4; 4).
2792.	Знайти величину й напрям градієнта функції (скалярного
поля) и = х2 + у2 + г2—2хуг у точці Л4 (1; —1; 2). В яких точках
§гас1 и = 0?
2793.	Знайти кут ф між градієнтами функцій (скалярних полів)
и = х2 + у2 + х2 та V = агсзіп у точці М (1; 1; ]/7).
2794.	Знайти найбільшу швидкість зростання функції (скаляр-
ного поля) и = Іп (х2 + 4г/2).
2795.	Знайти величину і напрям градієнта поля и = х3 + у3 +
+ г3 — Зхух у точці Л4(2; 1; 1). Визначити в яких точках він пер-
пендикулярний до осі 07 та в яких дорівнює нулеві.
2796.	Знайти похідну функції г = х2 + у2 у точці М (3; 2) в на-
прямі, що утворює з віссю ОХ кут ф — 45°.
2797.	Знайти похідну функції 2 = х2— ху + у2 у точці Л4 (2;—1),
в напрямі, що утворює з віссю ОХ кут 120°.
2798.	Знайти похідну функції 2 = х2 — Зху— у2 у точці Л4(3;1)
в напрямі від цієї точки до точки Р (6; 5).
2799.	Знайти похідну функції 2 = агсі§ ху у точці М (2; 2) в
напрямі бісектриси першого координатного кута.
2800.	Знайти вартість похідної від функції 2 = х2 — у2 у точці
Л4(1; 1) в напрямі, що утворює кут ф = 30° з віссю ОХ.
2801.	Обчислити вартість похідної функції 2 = х2у2 — ху3 — 3у у
точці Л4(2; 1) в напрямі від цієї точки до початку координат.
190
2802.	Обчислити похідну від функції и = х2 + у2 + г2 — х +
+ у + ? + 1 У точці Л4(1; —2; 3) в напрямі, що утворює однакові
кути з координатними осями.
2803.	Знайти вартість похідної від функції г — 4х2 — у2 у точці
ТИ 1), що міститься на кривій у2 = 2% в напрямі цієї кривої.
2804.	Знайти похідну функції г = агсі§-у у точці 714^1;-^,
що міститься на кривій Зу — х3 в напрямі цієї кривої.
2805.	Показати, що похідна функції г =	, обчислена в будь-
якій точці кривої 2х2 4- у2 = 6 вздовж нормалі до неї, дорівнює
нулеві
2806.	Знайти похідну и = х2 + у2 + г2 у точці Л4(1; 3; 2) в на-
прямі, який утворює з координатними осями кути 60°, 60°, 45°.
2807.	Знайти похідну від функції и = хуг у будь-якій точці в
напрямі, що утворює однакові кути з осями координат.
2808.	и = х2 + у2 — Зх + 2у + 1. Знайти §гас1 и в довільній точці.
2809.	и = х3 + у3 — бху. Знайти §гас1 и та | §гас1 а | у точці
Л4(1; 2).
2810.	и = Ух2 + у2. Знайти §гас1 и та його модуль у точці
Л4(3; 4).
2811.	Знайти найбільшу стрімкість підйому поверхні г = х2 + Зу2
у точці М (2;	4-^.
2812.	Знайти найбільшу стрімкість підйому поверхні г =—
у точці Лї (3; 1; 4).
2813.	г = агсзіп -. Знайти кут між градієнтами цієї функції
в точках Л4(1; 1) та Р(3; 4).
2814.	Дано функції 2 = ]/х2 + у2 та 2 = х — Зу + УЗху. Знай-
ти кут між градієнтами цих функцій у точці М (3; 4).
2815.	Знайти кут між градієнтами функції г = у точках
-Ь) та Р(1; 1).
2816.	Довести рівності:
а} §гас1 (и + V) = §гас1 и + §гас1 у;
191
Ь)	§гад (ші) — и §га<і V + V §га<1 и;
с)	§гад (и2) = 2и §га<1 и;
, [ и \ V ега<1 и — и §га<1 V
V §гас1	.
2817.	Знайти градієнт поля -2 . * г-т у точці М (1; 2; 2).
х т У тг
2818.	Обчислити §га<1и, якщо и = г2\ и = де
г = У X2 + у2 + г2.
2819.	Знайти похідну скалярного поля и = у-, де
г = У х2 + у2 + г2,
у напрямі 7 {соз а, соз0, соз у}. При якій умові -|^-=0?
2820.	Обчислити потік вектора А = (х — 2г) і + (Зг — 4х)} +
+ (5* + у) к через зовнішню сторону поверхні тетраедра, утвореного
площинами х = 0, у = 0, г = 0, х + у + г = 1.
2821.	Обчислити потік вектора г через повну поверхню циліндра
х2 + £/2-/?2, 0<г<#.
2822.	Обчислити потік вектора А = х2 і + х ] + хгк через зов-
нішню сторону поверхні у = х2 + г2, яка міститься в першому ок-
танті та обмежена площиною у = 1.
2823.	Обчислити потік вектора А — х2 і + У3 ] + через бічну
поверхню конуса х2 + у2-^-г2, 0<2<Я.
2824.	Визначити потік електростатичного поля точкового заряду
д, вміщеного в точці Л4, через поверхню сфери з радіусом а з цен-
тром у точці М.
2825.	Знайти потік вектора А = х і 4~ 2г/ / — гк через поверхню
х2 + у2 + г2 == 4.
2826.	Обчислити потік вектора А = х і — ] + г2к через цилінд-
ричну поверхню х2 + у2 = 16, обмежену поверхнями г = 0, х + у +
+ г = 4.
2827.	Визначити потік вектора А = х і + (у + г) / + (г — у) к
через пластину поверхні х2 + у2 + г2 = 9, розташовану в першому
октанті.
192
2828.	Довести справедливість формул:
а)	сНуДіЛі + с2Л2) = схдіу Лх + с2сііу А2, де сх та с2—довільні
сталі;
Ь)	діу (иЛ) = и діу А + (Л, §га4 и);
с)	4 іу / (г) г = 3/ (г) + гГ (г).
2829.	Обчислити сііу (у-)’
2830.	Показати, що сііу §гасі (х2 ~Ь г/2 + г2) = 6.
2831.	Показати, що сііу І -^-) = 0.
\ г3 /
2832.	Знайти потік вектора А = ху2і + уг2 ] + гх2~к через зов-
нішню сторону поверхні х2 + у2 + г2 = К2.
2833.	Показати справедливість формул:
а)	гоі (СіЛі + с2А2) = с± гоі Д. + с2 гоі Л2, де с± та с.2 — довільні
сталі;
Ь)	гоі (иА) = [§гас1 а, Л] + и гоі А.
2834.	Показати, що сііу гоі А = 0 і гоі §гас1 и = 0. Пояснити зміст
цих рівностей.
2835.	Обчислити циркуляцію векторного поля А — х2у3 і + / + гк
вздовж кола х2 + у2 = а2, г = 0.
2836.	Обчислити роботу силового поля Р =*= і а соз і + / Ь зіп і
вздовж дуги еліпса	= 1, г = 0 від точки А(а\ 0; 0) до
точки В(0; Ь\ 0).
2837.	Обчислити роботу силового поля Р = (2а — у)і + (у — а) ]'
вздовж першої арки (від початку координат) циклоїди х = а (і —
— зіп /), у = а (1 — соз /), г = 0.
2838.	Обчислити циркуляцію вектора А = у і — х ] + гк вздовж
замкненого контура х2 + у2 + г2 = 4, х2 + у2 = г2 (г > 0).
2839.	Обчислити лінійний інтеграл векторного поля А == (х2 +
+ у2 — 2ах) і + а (х у) ] вздовж дуги кола (х — а)2 + у2 = а2,
г = 0 від точки О (0, 0, 0) до В (а\ а\ 0).
13 2193
193
2840.	Знайти вихровий вектор у будь-якій точці векторного поля
А = х і — г2 ] + у2 к.
2841.	Знайти потік вектора А = х і — у2 ] + (х2 + г2 — 1) к через
и2 22
поверхню -^2- +	+ 7Г = 1 3 її середини.
2842.	Обчислити дивергенцію напруженості поля точкового за-
ряду у, тобто вектора Е = г.
2843.	Обчислити потік електричного поля точкового заряду у,
вміщеного на початку координат, через поверхню сфери, яка не мі-
стить в собі початку координат.
2844.	Показати, що електричне поле точкового заряду є поле
потенціальне, тобто гоі Е = 0.
2845.	Електричне поле має осьову симетрію, його вектор напру-
женності	, оІ Обчислити (ІіуЕ та гоіЕ.
І У х2 + У2 У х2 + у2 )
2846.	Обчислити циркуляцію вектора А = у і по колу х2 + (у—
— Ь)2 = Ь2.
ля, о	у і + г і 4- х к
2847.	Знайти ротор векторного поля А = 	'.... ......
Г Г Г	Ух2 + у2 + 22
2848.	Показати, що векторне поле А = (у + г) і + (х + г) / +
+ (х + £/) й потенціальне.
2849.	Довести, що векторне поле ~А = / (г) г трубчасте (солено-
їдне) тільки тоді, коли / (г) =	, де к — довільна стала.
2850.	Показати, що сила Р центральна, тобто напрямлена до не-
рухомої точки О, і залежить тільки від віддалі г до цієї точки
— Р = [ (г) г, де / (г) — однозначна й неперервна функція, — то поле
потенціальне.
2851.	Знайти вихровий вектор векторного поля А = хугі + (х +
+ у + ^І~х2у2к.
2852.	Показати, що електромагнітне поле Н =	(— у і + х /)
трубчасте (соленоїдне).
194
2853.	Показати, що векторне поле А = потенціальне й труб-
часте, а його потенціал справджує рівняння Лапласа
А д2и . д2и . д2а А
/\и = -4-2 + тт +	= 0.
дх2 1 ду2 дг2
2854.	Показати, що гоі Н = 0, де Н — поле магнітної напруже-
ності лінійного струму
2855.	Середовище обертається, як тверде тіло навколо осі ОЬ з
кутовою швидкістю со. Вектор швидкості V має проекції на осях
“Ох = — (ду, І'у = СОХ, VI = 0. Знайти ГОІ V.
2856.	Користуючись формулою Остроградського, довести, що
И = Ш ^ахаусіг, де +-^ + -& •
5	V	у
13*
РОЗДІЛ XIV
РЯДИ
§ 1. Числові ряди
У наступних прикладах дано частинні суми рядів; написати ці
ряди і знайти їх суми:
2857. 5„	-44-	2858.	= 2ІЇТГ
2850	_____и (и 3)	2860 2 _(
2859.	— 4 +	+ 2).	2850.	+ 1 .
У поданих нижче прикладах, користуючись означенням збіжності
числового ряду, встановити, які ряди збігаються, і знайти їх суми:
2861. "з" + 27 +'24ЇГ + *72<Г + ‘ ‘'
2862. + +
2863. 1 +4—+	+	...
28б4. 3-4+4-4+4—4+...
28Ю- -пг + тйг + тй- + тг+-
2886‘	1-4 + 4.7 + 7-Ю + 10-13 +   •
2867 ГТЗ + 4-3-6	5407 + 6-7-8 +   
2868. 4 + -1_ + А+А+...
196
2869.	5	.	13	35	,	3« +	2« , 6	“Г	36	+" 216	+ • • • "і” 6« +	• • •
2870.	і 1	। і	2-4	. ,	3-7	, ,	4.10 , ІП 4 + Іп 1 7 + Іп 2 10 І Іп 3.13 + •
2871.	1О§о 2 + І0£а + І0§д 4 +	+ • • • &	О	*і
2872.	2 , 3	4	п+1	, 9 * 64 1 225 1 ‘ ‘ ‘ 1 п2 (п + І)2	‘ ’
2873.	/2-1.	/3-/2	уп+і-/п /2	/6	Уп(п+1)
2874.		!	і_	!	і_	_і_ 1-2 ...(&+1) 1 2-3... (£+2) ' п (п + 1). .. (п + к)
2875.	агсі§ 1 + агсі§ 3 + • • • + агсі§ п2 _й+ 1 + • • •
Використовуючи теорему порівняння, дослідити на збіжність та-
кі ряди:
2876.	1-2 1 2-22 1 3-23 ~ 4-24 “ *'•
2877.	10	10	.	10	10 3	1 1 + 22 1 1 + 23 1 1 + 24 1  • * _і_	_2_	_з_	_4_
2878.	Є2	.	Є3	Є4	Є5 , 2	+	22	+ 23	+ 2*	-г-"
2879.	ЗІП-^ + 5ІП-4+ ЗІП4г+ •••
2880.	1 н—!—|—-—|—ї—|-... /2 1 /3	/4
2881.	1 + “22" + “з? + “42" +  • •
2882.	агсзіп 1 + агсзіп 4 + агсзіп 4 + агсзіп 4	... 2»	о	4
2883.	1 	!—і—!—і	!	1- .. Ь2 1 1-2-3 1 Ь2.3.4^
197
2884. зіп я 4- зіп -5- -}- зіп 4- зіп + ...
2885.
. пя
*§ 4ІЇ+7
2886. У -54-т.
И3 + 1
п=1
оо
2887. У ( 1 — соз —V
п—І '	'
2888.
п=1	П
оо
2889- 5-----------тт»— •
оо
28’»- 2»
гг=1
оо
2891. Нехай ряд 2 (ап > 0) збігається, довести, що ряд
п=1
оо
2 ап, Де а> 1, також збігається.
п=1
оо
2892.	Припустивши, що ряд а" збігається, довести, що ряд
п=1
оо
2 (ап > 0) також збігається.
п=1
оо
2893.	Нехай ряд ап (ап > 0) збігається, довести, що ряд
п—1
2Г-а.п також збігається.
, 1 + ап
п—ї
У наступних прикладах дослідити ряди на збіжність, використо-
вуючи ознаки Даламбера, Коші та інтегральну ознаку Коші:
а . а2 . а3 . а4 ,	м
2894.	— + — + — 4-..., а>0.
198
2895.	1 + 2_ + _^ + _1г+...
1	Ч2 42	52
2896. -у + 1 “Ь"2з+“24‘ + “25'“Ь-**
2897.	2 + 2 + ^-+... + в-+...
2898.	1 + 1 + 4++
2899.	2- + 4.+-±- + ... + -^ + ...
2900.	4-+4-+і+... + ^-+...
2901.	зіп —(- 2 зіп -д—3 зіп —(- ...
2902.	Л + (^ + (^+(4)‘+...
2903.	1 + ^ + -^+... + ^- + ...
1	/ 9 \4	/ Ч \9	/ 4 16
2904.	- + (1) +(4) +(тг) +
2905.	-І + Ц2-+ ... + 3“Ш".
2906.	агсзіп 4 + агсзіп2 + • • • + (агсзіп —т-їУ + • • •
&	&	І	Л "р 1 /
1	/ 4 \2	І 2п \ п
2«<”- 4-+(—) +--+(зї+=) + -
2908. 1 + -Г+ Х+ ... + і + .... «>1.
О
2909, 2ІЇГ2 + "ЗТпТ + "ЇТпТ + • ’'
2<)10.	-2“ +-[Г +-82" + •••+ і _|_пі+ •••
2911. 2+^ + ^ + ^-+...
199
2912.	е +	/г/5 +	—!	1—!—1_ 2е2
2913.	1	-1	Цг	 н	Цг + • • •
	2(1п2)а	3(1п3)“	4 (1п 4)“
9014		1		і	 > 	!	,
1 Ч.	21п2-1п1п2 1 ЗІпЗ-ІпІпЗ 1 41п4-1п1п4 ”		
2915.
2916.
2917.
1	4	9 		і	і	і	і	»2	1
4	11 ' ЗО *	+	пз _|_ з п- • • •
1п2 + 2 1п 4 + 3 1п4 + £	0	...
оо	оо		
у 2п+1 ^(Я« + п+ 1)3-	2918. У	Ч ^2
со
2919. 2(агсі§7Г^Г.
п=1 '	‘
2920.
2922.
оо
"V п!
оо	______
2923. 2 ]/(ЧтУ •	2924.
Дослідити на збіжність такі ряди:
_____1____
У 4^ — ^+^ +
2925.
2927.
2929.
2930.
2931.
1
(2п + 3)(3п—1)
оо
Довести, що
п=0
2926.
пз[/2+ (-!)"]”
З"
ОО
Довести, що 2г^<4- + ^Г-
п=1
200
У наступних задачах встановити, які ряди збігаються абсолютно, умовно чи розбігаються:
2932. -1 +4-	4 + •••С-4г-+ •••
Л	1	2	3	4
2933. Ю2	104 | 106	Ю8 + • •.
2934. 1	+ 2'?	Д+...
Л _	1	2	3	4
902е»			 і		 і	
/2	/5 /їб 1 /17	”
2936. —	-=!	н 		+... /2—1	/2+1	/3 — 1	/3+1
2937. -4=	7^+^=-	^=+«.. /2	/6	/12	/20
2938. 100—50 +	^-+... О	4
1п2	ІпЗ . Іп 4	1п5 .
2939.	2	+ 4	5 +•••
2940. 1-4-+... + (-1)^4 + ...
2941- 4—4 + 1—!-+•••
2942.	зіп а 1	. зіп 2а 1	4	+	зіп За ! 9 "Н
2943.	1п4	Л 2 \2 + (!п-з-)	/ з \з + (!п-г) + •••
2944.	_1	 2	+р(-	6 \8	/ 8 \4 10 )	13 ) +
2945.	_3		4.5	--6-+
	2	6 1	12	20 1 * ‘ ’
2946.	
2947. 2(-1)"-'(-5^пу
201
«М». 2^Г-	2949.
п=2	п=1	І ' 7 З
оо
2950. Нехай ряд ап збігається абсолютно, довести, що ряд
П=1
оо
2 —— сіп також збігається абсолютно.
п=1
§ 2. Функціональні ряди
Визначити область збіжності поданих нижче рядів:
2951. Ц-х2 + х4 + х6 + ...
2953. х + 2х2 + Зх3 + 4х4	...
2954‘	1 4-х2 + 4 4-х2 + 9 4-х2 + 16 4-х2 + • • •
1	г2	г2п“2
2935‘ -і+7 + г+^+- + -ЇТ^=г + -
29о6‘ Т+х + 2 (1 4- х)2 + 3(1 4-х)з + 4(1 4-х)4 "*•••
2957.	— + Л + “У + А- + ...
X 1 X2 1 X3 1 X4 1
2958.	-4 + -4-Ч—4 + -4- +...
&Л 1	і	і
2959.	4- ...
2960.	^4-^ + ^+...
гав'	+
ОПЛО	С08 Х І С08 І С08 ^Х І
29Ь2.	+	+ —9- + •••
2963. 1п х 4- їй2 х 4- 1п3 х 4- ...
2964. З* 4- З2* 4- З3* 4- З4* 4- ...
202
1
2965. У -/ІПГіГ-
"(п +!)
2966. 2Дх + п—1)(х + п)
2967. У
/я
2968.
2969. У £1
п=1
2970.
хп
хп
2971- 2 (1 + х) (1 4-х3)... (1 +х«) •
П=1
2972.
п
Довести рівномірну збіжність у зазначених проміжках таких
функціональних рядів:
2973.	+ —4—+ —-1—+ ..	(—оо, +оо).
1 + х2 1 4 (1 + х2) ‘ 9 (1 + х2) 1	'	’	7
2974	1_____І_____!_____-4_______________!_________і_
/1 + х 4 V1 + Зх	4"-1/1 + (2тг — 1) х
+ • • •; [0, +°°).
2975.	8ІП X . 5ІП 2Х . 8ІП ЗХ ,	,	, ч 3 +-9—Н^4-..-; ( 00,4-00).
2976.	1 + СО82 X ' 4 + СО82 X ' 9 + СО82 X	‘	°°’ ""Г °°)‘
2977.	. . соз х . соз 2х . соз Зх .	,	, х 1+ 1! + 2!		3!“+---: (-00,4-00).
2978*	(х+1)(х + 3) + (х4-3)(х4-5) + (х + 5) (х + 7) +"';
[О, 4-оо).
у 2	у 2	у 2	у 2
2979. Лг + ~4г+^5х+Чг + ---; [0, 4-0°).
рл * р&'Ь 1 рЗ*™ 1 р***™ 1	7 Ь 7 1	/
2980.	у-^-5 4- , Лаз 4- Лї-т 4- т-т4еа-2 4- • • •; [0, 4-о=).
1 + х2 1 1 + 16х2 1 1 + 81х2 1 1 + 256х2 1	/
оо
2981.	У ...г . г, 4-, л---аіг—; [—0,99; 3,99].
п2 + [Іп (4 + Зх — х2]2	1	7
П=1
203
/__1)л%2
2982.	Довести, що ряд Л \ збігається рівномірно на всій
п=1 * Х
числовій осі, а ряд, складений з абсолютних величин його членів,
збігається нерівномірно.
оо
2983.	Довести, що ряд 2 п збігається рівномірно на всій
п=1
числовій осі, але не є абсолютно збіжним,
оо	оо
2984.	Нехай ряд ап збігається. Довести, що ряд
п=Л	п=1
збігається рівномірно в області [0, 4-°°)-
Знайти суми поданих нижче рядів:
2985.	1 + х3 + х6 + х9 + ...
2986.	1 —4х+16х2 —64х3 + ...
2987.	Зх2 + 6х5 + ... + Зпх3"-1 + ...
2988.	х + 2х2 + Зх3 + 4х4 + ...
2989.	х + ДІ _і_ ДІ _і_	_і_	_і_
5 + 9	4п — 3‘ •••
уЗ	у5	у7
2990.	±-+^ + ^+_.
у2	уЗ	у4	у5
299Е + +
оо
2992.	Інтегруванням прогресії 2 хП~1 знайти суму ряду
П=1
1-3 *" 2-Зг "* 3-3® + • • •
2993.	Знайти суму ряду
А_______1_ + _!_______!_ +
2	4-24 ' 7-27	10.21оТ'”
2994.	Знайти суму ряду
Ч-------1-------Ь
4 “ 3-43 ' 5-46 ।	•
204
§ 3. Степеневі ряди
Знайти радіус та область збіжності поданих нижче степене-
вих рядів:
2995.	Зх + 9х2 + 27х3 + ...
у2 уЗ у4
2996.	х +	+
у2	уЗ	у4
2997.	х + 15- + ^ + ^-+...
2998.	1 + 2х2 + 4Х4 + 8х6 + ...
2999. (х- 2) + 2І(Х~2)2 +	+ ...
3000. 1 +х + 2х2 + 6х3 + 24х4+120х5 + ---
3001.	Зх+-^+^ +	81х4 24	, 243x5 1	120 +	‘	
3002.	у (х + 1)" 2П—1 п(«+1)’		3003.	І П=1
3004.	у (2х + 1)" Зп - 2 ’ п=1		3005.	оо 2«" хп. п=1
3006.	оо V п2 „ 2л 4« Х • п=1 *		3007.	у	Хп п ІП (п + 1) П=1
3008.	у Упхп п\ • П=1		3009.	оо п=1 2
ЗОЮ.	У <п!>2 хп (2п)!	‘ п=1		ЗОН.	оо П=1
3012.	у		3013.	У <2ге)!! ХП
	№+1 			(2гг + 1)1! п=1
3014.	у (-1)" (п\пх* п\ \е П=1	\	'		3015.	©о /. 1 \«2 2 1 + V л П=1 \	/
Розвинути в ряд Тейлора за степенями (х — 1) функцію
3016.
у = ]Лх3.
205
3017.	Розвинути в ряд Тейлора за степенями (х + 2) функцію
1
У = —•
3018.	Розвинути в ряд Тейлора за степенями (х — функцію
у = соз х.
3019.	Розвинути в ряд Тейлора за степенями (х—1) функцію
У = Ух.
3020.	Розвинути в ряд Тейлора за степенями (х + 1) функцію
1
У = і— •
1-х
Розвинути в ряд Маклорена функції:
3021.	У	— сЬх.	3022.	у = х зЬ х.
3023.	У		 X 4 + х ‘	3024.	у = е* зіп X.
			3026.	у ~ зіп2х
3025.	У	= сЬ2 х.		
3027.	У	= х2 агсі§ х.	3028.	X9 У = і—• 1 — X
3029.	У	X - (1+х)3 •	3030.	
3031.	У		3032.	у = 1п (х2 — Зх + 2).
3033.				X2	3034.	у = 1п (х + ’Кі + X2).
	У	]/ 1 — X2 '		
			3036.	у ••= У1 + х2.
3035.	У	= агсзіп х.		
3037.	У	= Є-*2.	3038.	У = ЗІП-у .
3039.	У	_ 1 _ (1-Х)2 •	3040.	у = Xі СОЗ X.
3041.	У	= (х — X) СОЗ X.	3042.	у = агсі§ -у-.
Розвинувши функції в ряд Маклорена, знайти границі таких виразів:
3043. Ііт
3044. Ііт (-4- — сі§2 х'і.
3045. 1іт(-4—3046. Ііт їх—х21пД +— V
Я-МД*2 Х )	Х-.0І	\ Х)
206
Користуючись Тейлоровим рядом, обчислити з точністю до 0,0001:
3047.	150. 3050.	1027.		3048. 3051. 3054.	І/Т5. 4*250. 1 5^-- * V е	3049. ^5Ї6. 3052. у' 1,015- 3055. зіп 1°.
3053.	1 е *			
3056.	соз 10°.	3057.	зіп 0,5.	3058. агсір • □
3059.	2 СОЗ-д-.	3060.	Іп 1,2.	3061. 1Є5.
Обчислити з точністю до 0,001:				
3062.	Уе.	3063.У500.		3064. агсзіп 4- □
Обчислити з точністю до 0,00001:				
3065.	зіп 10°.	3066.	1п2.	3067. зіп 18°.
У наступних прикладах подати первісні у				вигляді ряду:
3068.	\^йх. 0		3069.	
	X			X
3070.	0 х		3071.	] є*2 йх. 0
3072.	У-І^х. б х		3073.	X Г йх
				І -X4 ‘
	X			X С йх 3 1 — X*' 0
3074.	у 1 4- х3 йх. 0		3075.	
Обчислити з точністю до 0,001:				
3076.	1 3		3077.	і У зіп х2 йх.
	1 V і + **			0 і
3078.	0,1 у Іп (1 + х) йх о	Х		3079.	4 У е~**йх. 0
207
2	1 .
3080. | а-^^сІх.	3081.
о	о
х
3082. Показати, що в інтервалі (—0,1; 0,1) функція Уе~х2б/хвід-
о
^5
різняється від агсі§х-----не більше ніж на 0,0000001.
Знайти розвинення в степеневий ряд по степенях х (до вказано-
го степеня х) розв’язків таких рівнянь:
3083. (1 + х2)у" + х/ -у = 0, у (0) = 1, у' (0) = 1 (до х3).
3084. у' = х + х2 ф- у-, у (0) = 1 (до х3)
3085.	= уу' —Xі, у(0) = 1, у' (0) = 1 (до х3)
3086. #" = хзіп/, у(1) = 0, /(1) = -у (дох5).
РОЗДІЛ XV -.... —=——---------———=
ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ
§ 1. Утворення диференціальних рівнянь.
Поле напрямів
Знайти диференціальні рівняння таких сімей кривих:
3087. у = Сх2.
3089. х2 + #2—Сх = 0.
3091. у = зіп (х + С).
3093. агсзіп— 4- х = С.
х '
3088. у2 = 2Сх.
3090. х — у — Сх-г/ = 0.
3092. х + г/ + С(1-хг/)=0.
3094.	Знайти диференціальне рівняння всіх прямих на площині.
3095.	Знайти диференціальне рівняння всіх кіл на площині.
3096.	Знайти диференціальне рівняння всіх парабол, осі яких
паралельні до ОУ.
Побудувати поле напрямів та накреслити схематично хід інте-
гральних кривих таких диференціальних рівнянь:
3097.	-^-= — —.	3098. -^-=у + х2.
ах	у	ах
3099. -%-=х(у-1)	3100. А- = ^(х-1).
3101. -%-=у — х.
3102.	= х2 + У2- Побудувати ізокліни у' = 0, у' =
3103.	— х2 — у2. Побудувати ізокліни у' = 0, у' = ± 1.
14 2193
209
	§ 2. Диференціальні рівняння першого порядку з відокремлюваними змінними
Зінтегрувати диференціальні рівняння 1-го порядку з відокрем-
люваними змінними та вилучити ту інтегральну криву, яка прохо-
дить через указану точку.
3104. х (1 + у2) (іх — у (І + х2) (іу = 0.
3105. (14-х2) уМх — х3 (1 4- у2) йу = 0.
3106.	^ + т/р^ = о. сіх 1 г 1 —X2
3107. 3108. 3109.	ху' = у 1п у. ху(\ 4-х3)/ =14-/. 5ЄС2 X • усіх 4- 5ЄС2 у • Х(1у = 0.
3110.	уУі+у.іх + хУ~у. іи = 0 /Г+З:	1	У
3111.	
3112.	у2 (іх 4- е*+у (іу = 0.
3113.	у	4-]/1 4-созг/^-О. У 3 СО5 X + 51П х е2х^ + 1пх
3114.	„ , , (іх	сіу = 0. з 4- У3	у 2 4- 2у2
3115. 3116.	х(1 +у*)іх + е-х (1 4-х)2(1 4-/)^ = 0. / = 8ІП(Х — у).
3117.	у' = ех+у, М. (0; 0).
3118.	(1 4-/)йх-(1 +х2)3/2(у 4-К1 +у2)(іу = 0, Л4(1; 0).
3119.	+	=	Л1(0; 0).
3120.	0у_=£У^±У2 М(1. п сіх	х2у — х2 1	1;-
Скласти диференціальні рівняння та знайти їх розв’язки:
3121. Довжина І еластичного шнура під дією сили натягу /
210
зростає на величину &//, де к — стала. На скільки збільшиться дов-
жина шнура, почепленого за один кінець, під дією тільки його
власної ваги р?
3122.	У залі з кубатурою 10800 м? після зборів повітря містило
0,12% СО2. Скільки кубічних метрів повітря, що містить 0,04% СО2,
треба щохвилини подавати в залу, щоб через 10 хе у ній було
0,06% СО2?
3123.	У чан налито 100 л ропи, що містить 10 кг розчиненої
солі. З швидкістю 3 л за хвилину в чан вливається вода, і суміш
з такою ж швидкістю витікає з чана. Перемішуючи воду, у чані
підтримують рівномірну концентрацію. Скільки солі залишиться у
чані через годину?
3124.	Посудину, що має форму півкулі з радіусом 2 лі, напов-
нено водою. За який час витече вода крізь круглу відтулину з ра-
діусом 0,1 лі, вирізану в дні посудини?
3125.	Деяка кількість нерозчиненої речовини містить у своїх по-
рах 10 кг солі. Піддаючи її дії 90 л води, довідалися, що протягом
години розчиняється половина наявної кількості солі. Скільки солі
розчинилося б протягом того самого часу, коли б кількість води
подвоїти? Швидкість розчинювання пропорційна кількості нерозчи-
неної солі та різниці між концентрацією розчину в даний мо-
мент і концентрацією насиченого розчину (1 кг на 3 л). Концентра-
цією С даної речовини звуть кількість її, що міститься в одиниці
об’єму.
3126.	Парашутист спускається на парашуті. Сила ваги парашу-
тиста	а сила опору повітря	к = солеї. Знайти
швидкість V парашута через /0 сек після початку спуску і шлях 5,
пройдений за той же час.
3127.	Швидкість розмноження деяких бактерій пропорційна в
кожний момент часу кількості бактерій у розглядуваний момент.
Кількість бактерій подвоюється протягом 3 год. Знайти: а) залеж-
ність кількості бактерій від часу; б) у скільки разів збільшиться
кількість бактерій протягом 9 год.
3128.	Швидкість охолодження тіла в повітрі пропорційна різниці
між температурою тіла і температурою повітря. Температура повітря
20°С, тіло протягом 20 хв охолоджується від 100 до 60° С. Знайти
залежність температури від часу та через який час температура тіла
знизиться до 30° С.
3129.	У культурі пивних дріжджів швидкість приросту діючого
ферменту пропорційна наявній його кількості. Якщо ця кількість
подвоюється протягом години, то в скільки разів вона збільшиться
протягом 2,5 год?
14*	211
§ 3. Однорідні рівняння та звідні до них
Зінтегрувати рівняння:
3130.	х-^г = у\п^.
3131.	хйу— (у + Ух2 + у2) йх = 0.
3132.	(хуеу + у2) йх — х2е у йу = 0.
3133.	(х—у соз -^йх + х соз	йу = 0.
3134.	(6х + г/ — 1)йх + (4х + # — 2)йу = 0.
3135.	(5х—7у-\-І) йу(х + у — 1)йх = 0.
3136.	(х + 2у+ї)йх — (2х + 4у + 3)йу = 0.
3137.	(2Х3 + Зхг/2) йх + у*йу = 0.
3138.	ху' = хе х + У + х.
3139.
Xі — у2
3140.	(4х2 + ху — Зу2) сіх + (у2 + <2ху — 5х2) йу = 0.
3141.	(2х3 + х2у + у*)йх + (2#3 + ху2 + х2)йу = 0.
3142.	Визначити криву, всі дотичні до якої проходять через по-
чаток координат.
3143.	Знайти криву, у якої піднормаль дорівнює різниці між ра-
діусом-вектором та абсцисою точки дотику.
3144.	Знайти форму дзеркала, що відбиває всі промені, які ви-
ходять з одної точки О, рівнобіжно з даним напрямом.
3145.	Визначити криву, у якої відношення відрізка, утворюва-
ного нормаллю на осі ОХ, до радіуса-вектора, є величина стала і
дорівнює к.
§ 4. Лінійні рівняння. Рівняння Бернуллі
3146.	+ 2х» = 2хе-^2.
3147.	+ ху = х3, М (0; —2).
212
3148.	йи + У СО8 X = 81П X СОЗ X. йх
3149.	хіпх+ у = 2Іпх, М(е-, 0).
3150.	Лу ,	у _ * + /1 — X2 йх ‘ (і	х2)3/2	(І —%2)2
3151.	х-^- + # = хг/21пх.
3152.	£ УЇ£Х= г/2созх.
3153.	йу ,	, . созу	+ &ту = Х + 1.
3154.	—V- • 4г~ + х У = х- СО52 у йх	ь
3155.	у	+ 1 = X2 + 1. Уу2+ і
3156.	+ ху = у* (8Іпх + хсозх), Л4(0; 1).
3157.	у' + у соз х = г5'" х, М (0; —1).
3158.	у' + зіп г/ + хсозу + х = 0.
3159.	+ г/ = ^2!пх.
3160.	
3161.	йу _ у йх х + у3'
3162.	и' _і_ 2У - 2^У .
3163.	8ІПХ~ЗГ — У 2зіп2_Г> М[т'' °)-
3164. Знайти криву, дотична до якої утворює на осі ОХ відрізок,
1
що становить — частину суми координат точки дотику.
213
3165.	Знайти закон зміни струму в колі з опором та самоін-
дукцією Ц якщо початкова сила струму /0, а електрорушійна сила
змінюється за законом V = V^ зіп соА
3166.	Знайти криву, в якої площа трапеції, що утворена дотич-
ною, осями координат і ординатою точки дотику, є стала величина.
3167.	Знайти криву, в кожній точці якої піднормаль є середнє
арифметичне квадратів координат цієї точки.
§ 5. Рівняння в повних диференціалах.
Інтегрувальний множник
Знайти загальні інтеграли рівнянь:
3168.	(х3 — Зхг/2) сіх + (у3 — Зх2//) йу = 0.
3169.	(х2 — 4х// — 2г/2) йх + (у2 — 4ху — 2х2) йу = 0.
3170.	(бху + х2 + 3) у' + З#2 + <2ху + 2х = 0.
зі7і.	^^ах + + хау = о.
X2 -\-у2	1 X2 + у2
Г 1	/72 1	Г X*	11
3172.-----------,-у в &-М, хз---------4^ = 0.
[ X	(X — у)2\	[(х— у)2	у ] а
3173.	+ ^ах—2^ау = 0.
3174.	(1 +еу)ах + е~^1 — -у)ау = 0.
3175.	(2х — у)йх — хйу = 0.
Розв’язати рівняння методом інтегрувального множника, коли
відомо, що дані рівняння мають інтегрувальні множники вигляду
|А = /(х) або н = /(«/):
3176.	(2у + ху3) ах + (х + XV) а у = 0.
3177.	(1 + х2у) ах 4- х2 (х + у) <іу = 0.
3178.	(х2 + у2 + 2х) йх + 2уау = 0.
3179.	2хуйх + (г/2 — Зх2) ау = 0.
3180.	у' + ау = Опх.
3181.	еу~х ах + іхеу~х-ау = 0.
Зінтегрувати диференціальні рівняння, коли відомо, що вони ма-
214
ють інтегрувальні множники вигляду р = / (ху), або р = / (х2 + у2),
або р = / (х2 — у2).
3182.	у2йх + (ху — \)йу = 0.
3183. (2х3у2 — у) йх + (2хV — х) йу = 0.
3184. (х2у3 + у) ах + (х3у2 — х) ау = 0.
3185. (2х3у — \)уах + х(2ху3 — 1)гіу = 0.
3186. (х34-ху2 — у)ах + (у3+ х2у+х)йу = 0.
3187.	(х2 + у) ау + х (1—у)ах = 0.
3188.	(х + х2 + у2)у'-у = 0.
3189.	(х2 + у2 + у)ах— хау = 0.
§ 6. Рівняння першого порядку,
не розв’язані відносно похідної. Рівняння
Лагранжа та Клеро
Знайти загальні та особливі, якщо вони є, інтеграли рівнянь:
3190. у'2 — (Зх — 2у) у' + (2х2 — ху — Зу2) = 0.
3191. у'2 — (2х + у)у'+ х2 + ху = 0.
3192. у'3 — (х2 + ху + у2)у'+ху(х + у) = 0.
3193. ху'" — 2у' — у = 0.
3194. у = |(у' + А).
3195. у = ху' 4~ зіп у'.
3196. (Зх + 1) у'2 - 3 (у + 2) у' + 9 = 0.
3197. хКі+у'2—у' = 0.
3198. у'2—х5 = 0.
3199. х3 + у'3 — Зху' = 0.
3200. у'3 — 1 = 0.
3201. у,г 4-у'— 2 = 0.
215
3202.
3203.
3204.
3205.
3206.
г/2(/-1) = (2-/)2.
ху'2 — 2уу' + 4х = 0.
4/(х-2)= 1.
ху'2 — 2уу' + 4х = 0.
=0.
§ 7. Задачі на траєкторії
Знайти ортогональні траєкторії сімей кривих:
3207.	г/2 —Сх3 = 0.
3208.	у = ах“.
3209.	у ~ ах2.
3210.	х2 + у2 = 2ах.
3211.	г = а(1 + соз <р).
3212.	(х2 + г/2)2 = а2ху.
3213.	Знайти лінії, що перетинають криві сім’ї ху = а під ку-
том 45°.
3214.	Знайти лінії, що перетинають криві сім’ї х2 4- у2 = 2ах
під кутом 45°.
3215.	Знайти лінії, що перетинають криві сім’ї х2 у2 = а2 під
кутом а.
§ 8. Диференціальні рівняння вищих
порядків
3216. -^- = х1пх, х0=1, у0 = 0, Ув = 0, Уо = — 4
3217. у'" = 0, х0 = 0, у6 =1, % = 0, у0 = 2.
3218. г/ІУ = зіп2х.
3219. г/'" = х + соз х.
3220. у'^^созх, х0 = 0, уи = 0, уа— -|“'
3221. /" = зіп3х.
216
3222.	у" = -Т"’ хо=1> г/0=1, г/;=1.
3223.	II Т 1—4 * о? II о II II 1—4 II II 1—1
3224.	У'3 — 2у" — х= 0.
3225.	У'-/'* = 0.
3226.	у"'^+у,2)-3у'у"г = 0.
3227.	у"-а(1 +/Г/2 = 0.
3228.	/'= 4 У У
3229. 3230. 3231.	УУ" = 1- /У=1. г/"(х2+1)-2х/ = 0, х = 0, г/(0) = 1, г/'(0) = 3.
3232. 3233.	УУ"~У'г + У'3 = 0, х=1, г/(1)=1, /(1) = -1. /У +1 = 0, х=1, г/(1)=1, /(1) = 1.
§ 9. Лінійні рівняння вищих порядків
Знайти загальні розв’язки лінійних рівнянь із сталими коефіць
єнтами:
3234. 3235. 3236. 3237. 3238. 3239. 3240. 3241. 3242. 3243. 3244. 3245.	у" -Іу' + 10г/= 0. у" + Зу' = 0. у"—О2г/ = 0. У" + 2у" — 5у' — 6у = 0. у'" + 6у" + 12/ + 8у = 0. г/"'-2г/" = 0. /"-4/ = 0. + 27у = 0. У^ — &У = 0. —Зу"' = 0. У" — У^= х2+ 1. у" — Зу' + 2у = х3.
217
3246.	у" — 4/ + 4у = хе*.
3247.	у" + 4у = соз х.
3248.	у™ + у" = х2 + х.
3249. у'" — 4у' = х2.
3250.	у'" — Зу" = х3 + х2 — х + 1.
3251.	у" + у = сї%х.
3252.	У"~У = Т^.
3253.	у" + 4у = —V.
3254.	/ + г/ = І£Х.
Розв’язати лінійні рівняння зі змінними коефіцієнтами (частин-
ний розв’язок дається):
3255.	х2 1п х • у" + у = 0, г/і (х) = 1п х.
3256.	(1 + х2) у" — 2ху' + 2у = 0, уг (х)	= х.
3257. (2х — х2) г/" + (х2 — 2) у' + 2(1 — х) у = 0, у1(х) = ех.
3258.	у" + (і§ х — 2 сі§ х) у' + 2у с!§2 х	=	0, у і (х) = зіп х.
3259.	(1 + х2) у" + ху' — у = 0, уг (х)	=	х.
3260. ху" + 2у' + ху = 0, ^(х) = ^і.
3261. ху" — (х+ \)у' + у = 0, г/1(х)=е*.
3262. у" + ±у' + Ії-ЛДу = 0. ^(х) = ^.
х \ чх /	ух
3263. х2(1пх—І) у"— ху' + у = 0, у1(х)=х.
Розв’язати Ейлерові рівняння:
3264. х3у"'+ ху'— у = 0.
3265. х2г/да — 2у' = 0.
3266. х3^" — ху' — Зу = х2.
3267. х*у™ + 10ї/ = 0.
3268. х2у" + Зху' + 2у = х3.
3269. х3у"' — Зх2у" + бху' — 6г/ = 0.
3270. х2у" — ху' — Зу = 5х4.
218
§10. Системи звичайних диференціальних
рівнянь
Розв’язати системи лінійних рівнянь:
3271.	(ІХ	(Іи ~тг =	“я7“	= —	*• аі	аі
3272.	т-* + * тг = 4* + 3»-
3273.	-^=Х~У’^ = Х + 3У-
3274.	(ІХ	о	СІу	1	7 л — =	— Зх — у,	-^	= Х~У< Х~У~ 1	при /	= 0.
3275.	(іх	.	,	(іу	.	(іг	. — =-Х^у + г, —=Х-у^г, —=х + у^г.
3276.	~аГ = У + г’ ~аГ = г + х’ -йГ = х + У’ Х=~^У=^
= 0 при	/ = 0.
3277.	(їх	.	<іу	.	<іг -аГ=У + г’ ~аГ=х + г’ Чі=х + у-
3278.	-^ + Зх + 4г/ = 0,	+ 2х + 5у = 0.
Зінтегрувати системи:	
3279.	сіх   сіу   (іг х	у	г
3280.	(іх 	 (іу 	 (1г х	у * + у'
(іх ____ (іу ______ (іг
х — у ~ х + у ~~ г *
3282.	сіх = (х3 + Зх//2) йі, Лу —	йх = 2уг		
3283.	(ІХ 	 СІу 	 ~ ~~~	(іг	
		г —	х2-\-у2-\-г2	
3284	СІХ			(іу 	 (іг	
	х2 — у2 — г2	2ху	2хг	
3285.	сіх 	 (іу	_ (іг	
	у + г х+ г	х + у'	
3286.	(ІХ	 V 1(Л І сг2\	Лу		 	її /1 сг2\	<	(іг і /л<2	1	і,2\	•
219
§11. Диференціальні рівняння
з частинними похідними
Знайти загальний інтеграл рівнянь:
3287.	х + У = 0- Визначити поверхню, що проходить че-
о2
рез криву ----= 1 в площині х = а.
3288.	у — х -^ = 0. Визначити поверхню, що проходить че-
рез криву у2 = 2рг в площині х — 0.
3289.	соз ц 4- соз х = соз х соз ц.
дх 1 ду	&
3290.	а^-+Ь^- = \.
дх 1 ду
3291.	у>^- + ху^=гх.
3292.
3293.	хг + уг -ч- = х,
дх 1 ду
3294.	х + у	= 2ху Уа^ — г2.
дх 1 ду г
3295.	х^—у-^=г. Визначити поверхню, що проходить че-
рез криву г ~ х3, у = х.
опле	дх І дг
3296‘ дх + ду ~ аг-
3297.	(х-а)£ + (у-Ь)^- = г-с.
3298.	2хг + 2уг-^ = г2 — х2 — у2. Знайти поверхню, що про-
ходить через криву г2 — у2 = а2 у площині х = а.
РОЗДІЛ XVІ	.   ..   ,-:=
ДИФЕРЕНЦІАЛЬНА ГЕОМЕТРІЯ
§ 1. Лінії на площині
3299.	Знайти похідну від таких функцій: г2, г'2, [г', г"], (г', г",
г"'), г2 (г = г (/), штрихом позначено диференціювання по і).
3300.	На інтервалі (/х, /2) І г | = сопзі. Довести, що г' І г. Чи
справедливе обернене твердження?
3301.	Довести: якщо |г'| =0 при всіх /2), то на Цьому
інтервалі г = сопзі. Чи справедливе обернене твердження?
3302.	Чи можна твердити, що | г' | = | г |'?
3303.	З початку координат до кіл з радіусами г та з центрами
на ОХ проведені дотичні. Знайти рівняння геометричного місця то-
чок дотику.
3304.	Знайти криву, коли відомо, що довжина відрізка дотичної
між точкою дотику й точкою перетину дотичної з віссю ОХ є стала
й дорівнює а (трактриса).
3305.	Довести, що астроїда |х|2/з+ |г/|2/з = а2/з є аналітичною
кривою.
3306.	Знайти параметричні рівняння кардіоїди р = а(1 + созф).
3307.	Скласти рівняння дотичної та нормалі до таких ліній:
а)	г = {а соз/, Ь 8Іп/};
Ь)	\хр + \ур = а2^
с)	р = «ф;
гі) х2 (х + у) — а2 (х — у) = 0 у точці (0, 0);
е) 2х2 —х2у2 —Зх + у -\-7 =^0 у точці (1, —2).
221
3308.	Скласти рівняння нормалі до лінії х2у— х2 + Зх— 6 = 0 у
точці, де х = 3.
3309.	Довести, що нормалі до кривої х = а (соз і + і зіп /), у =
= а (зіп і — / соз /) однаково віддалені від початку координат.
3310.	Знайти суму відрізків, які відтинає на координатних осях
дотична до кривої х + угу = ']/г а.
3311.	Знайти дотичну до кривої х3—у3 = Зх2, паралельну пря-
мій у = х.
ОСОБЛИВІ ТОЧКИ КРИВИХ. АСИМПТОТИ
Дослідити особливі точки та знайти рівняння дотичних у цих
точках таких алгебраїчних кривих:
3312.	г/2= Ьх3-\-ах2.
3313.	х3 + у3 = ху.
3314.	х4 — 2ах2у + 2ау3 + а2у2 = 0; а =£ 0.
3315.	х6 — 2а2х3у — Ь3у3 = 0.
3316.	2у3х—у* = х(у— х)2.
3317.	(х2 + у2)3 = 12х2у2.
3318.	При якому співвідношенні між а і Ь крива г/2=х34-ах+&
має подвійну точку.
Визначити асимптоти кривих:
3319.	у = а ^соз/ + Іп , х = Л8Іп/ (трактриса).
-*	( /2	і )
3320.	г = (га> Т^ї}-
3322. Дослідити і побудувати такі лінії:
а)	г = {4/2 + 8/ + 6, /);
Ь)	х = а соз3 і, у = а зіп3 /;
с)	х = /2, у = Iі + /5;
Х = 1 + Іг ’	=	+ 1 /З
. і2 — 3	, іг — З
е> х — /2 _|_ і > у — ^2 _|_ і;
222
Знайти асимптоти таких алгебраїчних ліній:
3323.	_ 1 У ~ (х — З)2 •	3324.	о х3 — а2 У“- х + Ь •
3325.	х3 4- у3 = а3.	3326.	х3 4- У3 — X 4- 2у = 0.
3327.	х3 у3 = Заху.	3328.	у2 (х2 4- 1) = х2 (х2 — 1).
3329.	ху2 4- х2у = а3.	3330.	х (х2 4- у2) = ау2.
3331. (х2 — г/2)2 — 2а2 (х + у)2 — 2Ь2 (х — у)2 = 0.
3332.	2х4 — х3у + х2у2 — ху3 — у^ — 8х3 + 2х2у — 8ху2 +
+ 2у3 + 8х2 + 8у2 — 4-0.
3333.	Знайти асимптоти ліній, поданих рівняннями в полярних
координатах:
а) р2ср = а2; Ь) р = а зес 2<р; с) рср = а.
СТИКАННЯ ЛІНІЙ. ОБВІДНА ОДНОПАРАМЕТРИЧНОї СІМ’Ї КРИВИХ
3334.	Знайти рівняння параболи типу у — х2 + ах + Ь, що до-
тикається до кола х2 + у2 — 2 у точці (1, 1).
3335.	Скласти рівняння кола, що має з параболою х —4(у—І)2
в її вершині стикання другого порядку.
3336.	Довести, що лінії у — зіпх і у — х4-^-х3 + х мають у по-
чатку координат стикання третього порядку.
3337.	Знайти лінію типу у — а0 + ахх + а2х2 + ... -4- апхп, яка
має з лінією у = !(х) у точці (0, /(0)) стикання п-го порядку.
3338.	Скласти рівняння параболи з віссю, паралельною до осі
ОХ, яка з колом х2 + у2 — 5 має в точці (1,2) стикання другого
порядку.
3339.	Знайти гіперболу, яка дотикається до лінії у = 1—созл
в початку координат і має найвищий порядок дотику.
3340.	Скласти рівняння параболи, яка дотикається вершиною
до косинусоїди в точці (0, 1) і має найвищий порядок стикання. Ви-
значити порядок стикання.
3341.	Знайти обвідну сім’ї прямих, на яких координатні осі від
тинають відрізок зі сталою довжиною /.
3342.	З початку координат під різними кутами до горизонту з
початковою швидкістю Уо кидається матеріальна точка. Знайти об-
відну траєкторій руху (парабола безпеки).
3343.	На хордах кола х2 + у2 — а2, паралельних до осі ОУ, як
на діаметрах, будуються кола. Знайти їх обвідну.
3344.	Скласти рівняння обвідної сім’ї нормалей до кривої у — / (х).
223
3345.	Знайти обвідну світлових променів, що виходять з початку
координат, після їх відбиття від кола х2 + у2 = 2ах.
3346.	Знайти обвідну сім’ї ліній г = {і2 + С, /34-С}, де і — па-
раметр точки на лінії сім’ї; С — параметр лінії у сім’ї.
3347.	Знайти обвідну сім’ї ліній г = [і2 + С, /3}.
КРИВИНА КРИВОЇ. ЕВОЛЮТА. НАТУРАЛЬНЕ РІВНЯННЯ
3348.	Знайти кривину кола.
3349.	Обчислити кривину таких ліній:
а)	г = {асо$і, &зіп/} (еліпс);
Ь)	х = а сЬ /, у = Ь зЬ і (гіпербола);
с)	у=з\пх у вершині;
сі) у = ас\\-^- (ланцюгова лінія);
е)	у = — 1п соз х;
/) (х — У)2 = %5 У точці (0, 0).
3350.	Знайти радіус кривини гіперболи ху = 4 у точці (2, 2).
3351.	Знайти радіус кривини параболи у2 = 8% у точці з).
3352.	Довести, що кривина кривої р2 = а2 соз 2ф пропорційна р.
3353.	Вершиною лінії зветься точка, в якій кривина має екстре-
мальну вартість. Знайти вершини ліній:
а) Ух + У у = У а; Ь) у = ех; с) р = а зіп3
О
3354.	Скласти рівняння геометричного місця центрів кривини
кривої х = х (і), у = у (і) (еволюта кривої).
Скласти рівняння еволют таких кривих:
3355.	г={асоз/, &зіп/} (еліпс).
3356.	у2 = 2рх (парабола).
3357.	г = {асЬ/, &зЬ/} (гіпербола).
3358.	у = ас\\^~ (ланцюгова лінія).
3359.	Довести, що еволюта циклоїди є циклоїда.
3360.	Знайти рівняння еволюти кривої у = $ (х).
3361.	Довести, що обвідна множини нормалей плоскої кривої
є її еволюта.
224
3362.	Другою еволютою кривої зветься еволюта її еволюти.
Знайти рівняння другої еволюти кривої г — г(з).
3363.	Скласти рівняння кола кривини для лінії (х2 + у2)х—2ау2 =
= 0 у точці (а, а).
3364.	Знайти центр кривини кардіоїди р = а (1 + соз ер) для
/ Я \
точки а, -у І.
3365.	Скласти рівняння еволюти для кривої
-> і
% = Г-----У | г' | й/, де г = г (/).
ІИ о
3366.	Скласти рівняння евольвент кола.
Знайти натуральні рівняння кривих:
3367.	« = асИ—.
а
3368.	р = а (1 + соз <р).
3369.	г =г {а(/— зіп/), а(1—соз/)}.
3370.	г = |(2 соз і + соз 2/),	(2 зіп І зіп 2/)| •
\ о	о	)
3371.	г = |а(1псі§-|- —соз^, азіп/|.
3372.	Знайти всі плоскі криві з натуральним рівнянням к = к (5).
Скласти параметричні рівняння ліній, заданих натуральними рів-
няннями:
3373.	к = 0.	3374. к = с. 3375. к = —.
аз
3376. 4- + -ікї- = 1-	3377. з = а2к.
а2 1 к2о2
3378. £ = . °	3379. 2азк2 = 1.
а2 + з2
3380. На нормалях кривої Г з рівнянням г = г (5) по один бік
від неї відкладається відрізок зі сталою довжиною а. Геометричне
місце кінців таких відрізків є крива Г*, яка зветься паралельною
щодо Г. Довести, що для кривих Г і Г* у відповідних точках:
а)	дотичні і нормалі паралельні;
Ь)	Я* = % ± я;
152193
225
С) б/$*=(1±	де /?, 5 І /?*, 5*—радіуси кривини та
дуги кривих ГіГ*.
3381.	На дотичних до кривої г = г (5) відкладається відрізок
з довжиною /. Знайти кривину кривої, яку описує кінець відрізка.
§ 2. Лінії у просторі
ТРИГРАННИК ФРЕНЕ
3382.	Точка М одночасно обертається рівномірно навколо осі
02 і рівномірним рухом переноситься паралельно осі 02. Знайти
рівняння її траєкторії (гвинтова лінія).
3383.	Знайти проекції гвинтової лінії на координаті площини.
3384.	Сфера перетинається поверхнею кругового циліндра, діа-
метр якого дорівнює радіусові сфери, а одна з твірних проходить
через центр сфери (крива Вівіані). Скласти параметричні рівняння
лінії перетину.
3385.	Знайти проекції гіперболічної гвинтової лінії г = {асИ/,
азЬ/, аі] на координатні площини.
3386.	Довести, що лінія г= {асоз3/, а зіп3/, асоз 2/} лежить на
циліндричній поверхні з напрямною-астроїдою і твірними, паралель-
ними до осі 02.
3387.	Знайти радіус сфери з центром у точці С (0, 4",	, на
якій лежить лінія
/	/2	~	/З
Х ~ 1 + /2 + У ~	1 + /2	/4 > г —	1 4- /2 + /4 •
3388.	Скласти рівняння кривої г = {/, /2, в1} у декартових ко-
ординатах.
3389.	Знайти параметричні рівняння лінії у2 = х, х2 = г.
ґ /	і	і
3390.	Довести, що крива г = (е 1/2соз /, в 2 зіп/, в лежить на
конусі х2 + у2 = г2. Знайти кут, під яким вона перетинає його пря-
молінійні твірні.
3391.	Довести, що дотична до гвинтової лінії х=асоз/, у —
= а зіп /, г = Ні утворює з віссю 02 сталий кут.
”*	( /4	£3	£2 ]
3392.	Знайти рівняння дотичної до лінії г =	> -у- > -^-г у
довільній точці.
226
3393.	Скласти рівняння дотичної до лінії х = асо8/, у~Ь$їпі,
2 — е1 у точці і = 0.
3394.	Скласти рівняння дотичної до лінії х2 + у2 = 10, у2 + г2=
= 25 у точці (1,3, 4).
3395.	Скласти рівняння головної нормалі та бінормалі лінії
( У2 = х,
| X2 = 2
у точці (1, 1, 1).
3396.	Скласти рівняння нормальної площини в довільній точці
кривої
| X2 + у2— 22 ~ 1,
( X2 — у2 — 22 = 1.
Скласти рівняння ребер і граней тригранника Френе для таких
кривих:
3397.	х~а(і — зіп/), у = а(\—соз/), г = 4#8Іп-^- у точці,
що відповідає / =
3398.	г — {/, /3, /2 + 4} у точці, що відповідає / = 1.
3399.	г = {/2, 1—/, /3}.
3400.	г = {зіп/, соз/, і§/} у точці, що відповідає / = -^--
3401.	х2 + г2 = а2, у2 + г2 = Ь2.
( 2х2 + Зг/2 + г2 - 47,
3402	<
{ х2 + 2у2 — 2	у точці (—2, 1, 6).
Знайти орти дотичної, головної нормалі та бінормалі кривих:
3403. г = {/, /2, /3}.
3404. г = |а(/ — зіп/), а(1—соз/), 4асоз-^-|-
( х2 + у2 + 22 = З,
( х2 + у2 = 2 у точці (1, 1, 1).
( X2 + у2 + 22 = 9,
34®®* | х2 у2 _ 5 у точці (і, 2, 2).
3407.	Довести, що головна нормаль гвинтової лінії г= {асоз/,
азіп/, Ні] перетинає її вісь під прямим кутом.
15*
227
3408.	Довести, що всі нормальні площини кривої г~{аз\п2і,
азіп/соз/, а соз/} проходять через початок координат.
3409.	Довести, що нормальні площини кривої х = а соз /, у =
= а зіп а зіп/, г = асозазіп/ проходять через пряму
( х = 0,
| г + у а = 0.
3410.	Показати, що лінія х = а^2 + Ьгі + у = а2і2 + &2/ + с2,
2 == а3/2 + &3/ + с3 плоска, та знайти рівняння площини, в якій вона
лежить.
3411.	На бінормалях гвинтової лінії відкладається відрізок зі
сталою довжиною /. Написати рівняння геометричного місця кінців
відрізків.
3412.	На головних нормалях кривої г = {а(/— зіп /), а (1 —соз/),
4а зіп 1 відкладаються відрізки довжини а 1 + зіп2 . Склас-
ти рівняння геометричного місця кінців відрізків.
ДОВЖИНА ДУГИ КРИВОЇ. КРИВИНА. СКРУТ. НАТУРАЛЬНЕ РІВНЯННЯ КРИВОЇ
3413.	Знайти довжину дуги гвинтової лінії г = {Засоз/, Зазіп/,
4а/} від точки перетину з площиною г = 0 до довільної точки М (/).
3414.	Визначити довжину дуги одного витка між двома точка-
ми перетину з площиною у = 0 лінії х — а (/ — зіп /), у = а (1 —
— соз/), х = 4асоз-^-.
3415.	Довести, що замкнена лінія г= {соз3/, зіп3/, соз2/} має
довжину 5= 10.
3416.	Знайти довжину гіперболічної гвинтової лінії г = {асЬ/,
азЬ/, а/} між точками / = 0 і і =
3417.	Визначити довжину дуги кривої х — сі, у = с]Л21п/,
2 = — між точками, що відповідають / = 1 та / = 10.
3418.	Знайти кривину кривої г = |/ — зіп/, 1—соз/, 4зіп-^-|-
3419.	Визначити кривину і скрут кривої
( х2 — у2 + 22 = 1,
| у2 — 2х + 2 = 0
у точці (1, 1, 1).
228
3420.	Визначити кривизну кривої
І х + зЬ х = зіп у + у,
( 2 + Є2 = X + 1п (1 + х) + 1
у точці (0, 0, 0).
3421.	Довести, що кривина й скрут гвинтової лінії сталі.
3422.	Довести, що лінія г — {3/—/3, З/2, 3/+/3} має рівні
кривину і скрут.
3423.	Довести, що скрут плоскої кривої дорівнює нулеві.
3424.	Довести, що лінія
( х2 == 2аг,
I у2 = 2Ьг
лежить в одній площині.
Визначити кривину і скрут таких ліній:
3425.	г {^,	іУ%}.
3426.	{2/, 1п/, і2}.
3427.	г = {е1 зіп /, еґсоз/, е*}.
3428.	г = (З/ — /3, З/2, З/ + /3}.
3429.	г= {соз3/, зіп3/, соз2/}.
3430.	При якому значенні Н скрут гвинтової лінії х = а соз /,
у = а зіп /, г = Кі має найбільшу вартість.
3431.	Написати натуральне рівняння гвинтової лінії.
3432.	Довести: якщо кривина та скрут кривої є сталі й відмін-
ні від нуля, то ця крива — проста гвинтова лінія.
3433.	Скласти натуральне рівняння гіперболічної гвинтової лінії.
3434.	Показати, що скрут кривої г = а \Ь (/), Ь' (/)] сІЇ, де
Ь(і) — вектор-функція, яка задовольняє умову |&(/)|= 1, Ь (/) 7=0,
сталий.
ФОРМУЛА ФРЕНЕ - СЕРРЕ
3435.	Знайти розклад векторів г, г, г у базисі з векторів три-
гранника Френе.
3436.	Довести, що формули Френе — Серре і— кп, п = —кі +
229
+	Ь = — ип можна подати у вигляді І = [со, /], п = [со, и], Ь =
= [со Ь]. Знайти вектор со (вектор Дарбу) та з’ясувати його кі-
нематичний зміст.
3437.	Знайти (6, Ь, Ь).
3438.	Довести, що (/, /, і) = £5	•
3439.	Довести, що коли крива має одну з таких чотирьох вла-
стивостей: 1) існує напрям, з яким дотичні до кривої утворюють
сталий кут; 2) бінормалі кривої утворюють сталий кут з деяким
напрямом; 3) головні нормалі кривої паралельні до деякої площи-
ни; 4) відношення кривини до скруту стале, то вона має й інші
три властивості (лінія укосу).
3440.	Показати, що лінія х = а зіп а (і) (11, у = а соз а (і) йі,
г = Ні є лінією укосу.
3441.	Довести, що лінія х2 = Зу, 2ху = 9г—лінія укосу. Знай-
ти вектор, з яким її дотичні утворюють сталий кут.
3442.	Криві Гх і Г2 звуться кривими Бертрана, якщо між їх
точками можна встановити таку взаємооднозначну відповідність, за
якої головні нормалі збігаються у відповідних точках. Довести такі
властивості кривих Гх і Г2:
1)	віддаль між відповідними точками кривих Гх і Г2 — стала;
2)	дотичні до кривих Гх і Г2 у відповідних точках утворюють
сталий кут;
3)	кривина і скрут кожної з кривих зв’язані співвідношенням
ак + Ьи = 1, де а і Ь — сталі.
3443.	Довести: що коли кривина та скрут кривої зв’язані ліній-
ною залежністю ак + Ьи = 1, то ця крива є кривою Бертрана.
3444.	Усі нормальні площини деякої лінії містять сталий век-
тор е. Довести, що лінія плоска.
3445.	Усі стичні площини кривої Г містять один і той же век-
тор. Довести, що лінія Г плоска.
3446.	Довести, що головні нормалі в двох суміжних точках не-
плоскої кривої не перетинаються.
3447.	Довести, що бінормалі в двох суміжних точках неплоскої
кривої не перетинаються.
3448.	Знайти найкоротшу віддаль між двома суміжними голов-
ними нормалями гвинтової лінії.
230
3449.	Знайти найкоротшу віддаль між двома близькими а) го-
ловними нормалями; Ь) бінормалями кривої г =-- г (5).
3450.	На кожній дотичній до кривої г = г (5) відкладається від
точки дотику сталий відрізок а = 1. Знайти кривину кривої —гео-
метричного місця кінців цих відрізків.
3451.	Подати кривину лінії р = г(з) + \Ь (5) (% = сопзі) через
кривину та скрут кривої г = г (5).
3452.	На бінормалях плоскої лінії г = г ($) в одному напрямі
відкладаються відрізки МР, пропорційні дузі МСМ. Скласти рівнян-
ня лінії, описаної точкою Р, знайти її дугу, кривину і скрут. До-
вести, що вона перетинає прямолінійні твірні циліндра, утвореного
бінормалями першої кривої під сталим кутом. Знайти цей кут.
3453.	Розглянемо однопараметричну множину нормалей кривої
Г — Г (5): Р (5) = Г (5) + % {Ь (5) СОЗ ф (5) + п (5) ЗІП ф ($)}.
Визначити функцію ф($) так, щоб ця множина мала обгортку
(еволюту).
3454.	Знайти кривину та скрут еволюти р = г + Рп + Р сі£ ф&
лінії, що відповідає г = г (5).
3455.	Визначити радіус стичної сфери лінії г = {/, /2, /3} у
точці і = 0.
3456.	Знайти радіус стичної сфери лінії г= {е* зіп/, еґсоз/, е*}.
3457.	Визначити всі лінії, кривина яких дорівнює нулеві.
3458.	Визначити всі лінії, скрут яких дорівнює нулеві.
§ 3. Поверхні
ДОТИЧНА ПЛОЩИНА. НОРМАЛЬ
3459.	Скласти рівняння поверхні, утвореної обертанням кривої
х = ф (и), у = 0, 2 = ф (и) навколо осі 02.
3460.	Скласти рівняння поверхні, утвореної обертанням трактри-
-* І і , І я і \	)
си г = 1пг§	І — а зіп/, а соз/, 0| навколо її асимптоти.
Ця поверхня зветься псевдосферою.
3461.	Скласти параметричні рівняння сфери.
3462.	Коло (х— а)2 + г2 = г2, у = 0 (а >г) обертається навколо
осі 02. Скласти параметричні рівняння поверхні обертання.
231
3463.	Скласти рівняння циліндра з напрямною р = р (и) та твір-
ними, паралельними векторові е.
3464.	Скласти рівняння конуса з вершиною в початку коорди-
нат і напрямною р = р(и).
3465.	Знайти рівняння поверхні, утвореної дотичними до кри-
вої р = р (5).
3466.	Знайти рівняння поверхні, утвореної головними нормаля-
ми кривої р == р ($).
3467.	Визначити поверхню, утворену дотичними до гвинтової
лінії.
3468.	Прямим коноїдом називається геометричне місце прямих,
які перетинають під прямим кутом деяку фіксовану пряму — вісь
коноїда. Знайти рівнянйя коноїда.
3469.	Знайти параметричні рівняння поверхні х2г2 = а\х2 + у2)
та довести, що це є прямий коноїд.
3470.	Поверхнею перенесення називається поверхня, утворена
паралельним, переміщенням однієї кривої вздовж другої. Показати,
що поверхню перенесення можна задати рівнянням г = гг (и) + г2(р).
3471.	Показати, що еліптичний і гіперболічний параболоїд и є по-
верхнями перенесення.
3472.	Показати, що геометричне місце середин відрізків, кінці
яких належать двом даним кривим, є поверхня перенесення.
3473.	Знайти рівняння дотичної площини до поверхні
Р (X, у, 2) = 0.
3474.	Рівняння дотичної площини до поверхні х = х(иу г>),
у = у (и, о), 2 = 2 (и, V) можна записати у вигляді
X — х У — у 2 — 2
Хи Уи %и — 0.
Ху Уу 2у
Довести це.
3475.	Скласти рівняння дотичної площини до сфери х =
= асоз Vзіпи, у = асоз Vсоз и, 2 = азіпо у точці (0, 0, а).
3476.	Скласти рівняння нормалі псевдосфери х = а зіп г/соз V,
у = а зіп г/ зіп у, 2 — а 1п + а соз и.
3477.	Визначити орт нормалі гелікоїда х = и соз у, у = и зіп у,
2 = ІТО.
232
3478.	Написати рівняння дотичної площини до поверхні ху2 +
+ г2 — 12 у точці (1, 2, 2). Визначити орт нормалі.
3479.	Довести, що поверхні х2 + у2 + г2 = ах, х2 + у2 + г2=Ьу,
х2 у2 х2 = ух попарно ортогональні.
3480.	Довести, що нормаль до поверхні обертання перетинає
вісь обертання.
3481.	Показати, що всі дотичні площини поверхні г = х<р^-у-^
проходять через початок координат.
3482.	Скласти рівняння дотичної до площини та нормалі до по-
верхні, утвореної бінормалями кривої р = р (5).
3483.	Довести, що дотична площина до поверхні, утвореної до-
тичними до кривої вздовж прямолінійної твірної, стаціонарна.
ОБГОРТКА ОДНОПАРАМЕТРИЧНОЇ СІМ’Ї ПОВЕРХОНЬ
3484.	Знайти обгортку сім’ї сфер (х — с)2 + у2 + г2 = 1 (—сю <
< с < оо).
3485.	Знайти обгортку сім’ї сфер радіуса г, центри яких знахо-
дяться на колі
( х2 + у2 = /?2,
| х = 0, де 7?>г (тор).
3486.	Знайти обгортку сім’ї сфер із сталим радіусом г, центри
яких розміщені на кривій р = р (5) (каналова поверхня).
3487.	Скласти рівняння сім’ї сфер, для яких обгорткою є конус
х2 + у2 — х2 — 0.
3488.	Довести, що розгортну поверхню можна розглядати як
обгортку однопараметричної сім’ї площин.
3489.	Знайти обгортку, характеристики та ребро звороту сім’ї
стичних площин лінії р = р (5).
3490.	Знайти обгортку, характеристики і ребро звороту сім’ї нор-
мальних площин лінії р = р (5).
3491.	Знайти характеристики, обгортку і ребро звороту сім’ї
спрямних площин лінії р = р (5).
3492.	Довести, що поверхня, паралельна розгортній, теж роз-
гортна поверхня.
3493.	Знайти площу сферичного відображення розгортної по-
верхні.
233
3494.	Скісна лінійчата поверхня, всі твірні якої паралельні де-
якій площині, зветься поверхнею Каталана. Довести: щоб лінійча-
та поверхня г = р (и) + оі (и) була поверхнею Каталана, необхідно
й досить, щоб (/, ґ, Г) = 0, Г =£ 0.
ПЕРША КВАДРАТНА ФОРМА ПОВЕРХНІ
3495.	Знайти першу квадратичну форму поверхні обертання
(див. 3459).
3496.	Довести: поверхню обертання можна параметризувати так,
що її перша квадратична форма набуває вигляду
гіз2 = сій2 + С (и) (№.
Обчислити першу квадратичну форму поверхонь:
3497.	г = {г соз г/соз у, г зіп и соз V, гзіпу} (сфера).
3498.	г = {а соз г/соз у, Ь зіп и соз у, сзіпу} (еліпсоїд).
3499.	г =	) соз и, 4г (& + —) зіп и, 4г (у---(одно-
Г (2 \	1 V /	’ 2 \	1 V /	2 \ V /)	4
полий гіперболоїд).
3500.	г = і4г(у--)сози, 4г (я-----Цзіп^, +	(^в0‘
полий гіперболоїд).
3501.	г'= р (з) + Хе, е = сопзі (циліндр).
3502.	г = ор (в) (конус).
3503.	г = {(/? + гсози)созо, (Я + гсози)зіпг;, гзіпг/} (тор).
3504.	г= {усозг/, узіпг/, ки\ (мінімальний гелікоїд).
3505.	Написати першу квадратичну форму поверхні г = [ (х, у).
3506.	Обчислити першу квадратичну форму поверхні, утвореної
дотичними до кривої г = г (з).
3507.	Знайти довжину дуги кривої, заданої рівнянням 2и = V
на поверхні з першою квадратичною формою сІ82= сій2 + з№шіо2.
3508.	Довести, що на поверхні х = и (з^2 — и2 —	, у =
=	— о2---г 2ио координатні лінії ортогональні.
3509.	Знайти кут між координатними лініями х = х0, у = у0 на
поверхні г = аху.
234
3510.	Знайти на параболоїді г = аху криві, які перетинають
під прямим кутом його прямолінійні твірні.
3511.	Знайти криві на сфері, які перетинають її меридіани під
сталим кутом (/іоксодроми).
3512.	Знайти площу чотирикутника на гелікоїді х = аисо$о,
у = аи зіп V, 2 == Но, обмеженого кривими и = 0, и — — , V = 0,
V = 1.
3513.	Показати, що площі областей на параболоїдах г~
= а (х2 + у2} і 2 = їаху, які проектуються на одну й ту ж область
площини ХОУ, рівні.
3514.	Поверхні Рг і Р2 звуться ізометричними, якщо існує од-
нозначне відображення поверхні Рг на Р2, при якому відповідні
криві на цих поверхнях мають однакові довжини. Довести: щоб
дві поверхні були ізометричні, необхідно й досить, щоб вони дозво-
ляли таку параметризацію, за якої їх перші квадратичні форми
будуть однакові.
3515.	Довести: поверхня, яка дозволяє параметризацію, за якої
перша квадратична форма має вигляд йз2 = Е(и)йи2 + О(у)(1о2, є
локально ізометрична площині.
3516.	Довести, що існує ізометричне відображення гелікоїда
х — и соз V, у = и зіп у, г = то на катеноїд х = а соз р, у = а зіп р,
і а
2 — т сп —.
т
3517.	Довести: існує таке конформне відображення поверхні
обертання на площину, за якого меридіани поверхні переходять в
прямі, що проходять через початок координат, а паралелі — у кола
з центрами в початку координат.
ДРУГА КВАДРАТНА ФОРМА ПОВЕРХНІ.
ТЕОРЕМА МЕНЬЄ. КРИВИНА ПОВЕРХНІ
3518.	Обчислити коефіцієнти другої квадратичної форми поверх-
Ні г = / (х, у).
3519.	Знайти другу квадратичну форму поверхонь, у задачах
3497 — 3504.
3520.	Знайти нормальну кривину параболоїда 2 = ах2 — Ьу2 у
точці (0, 0) у напрямі = -і-.
3521.	Довести, що за всякої параметризації площини її друга
квадратична форма тотожньо дорівнює нулеві; за всякої парамет-
ризації сфери друга квадратична форма пропорційна першій.
235
3522.	Довести, що сферу навіть локально неможливо ізометрич-
но відобразити на площину.
3523.	Знайти середню та Гауссову кривину гіперболоїда г=аху
у точці х = у — 0.
3524.	Визначити головні кривини параболоїда г = а (х2 + У*) У
точці (0, 0, 0).	______
3525.	Визначити середню кривину катеноїда г = а сЬ|/—
3526.	Довести, що середня кривина гелікоїда дорівнює нулеві.
3527.	Дослідити характер точок: а) на еліпсоїді, Ь) на гіпербо-
лоїдах, с) на параболоїдах, ІЇ) на циліндрах, е) на конусі.
3528.	Знайти еліптичні, гіперболічні та параболічні точки тора.
3529.	Дослідити характер точок поверхні, утвореної обертанням
х = (1 —е 22)
у = 0 навколо осі г.
кривої
3530.	Дослідити характер точок поверхонь: а) г = а2х4 + Ь2у\
Ь) г = х4 + #4 + *2#2; с) у ~ х4.
3531.	Обчислити повну кривину поверхні, утвореної дотичними
ДО кривої Г = Г (5).
3532.	Довести, що поверхня, усі точки якої параболічні, є роз-
гортною поверхнею.
3533.	Довести, що повна кривина лінійчатої поверхні недо-
датна.
3534.	Знайти повну кривину поверхні, утвореної головними нор-
малями кривої Г = Г (5).
3535.	Довести, що при проективному, зокрема афінному, пере-
творенні зберігається властивість точки бути еліптичною, гіпербо-
лічною чи точкою сплощення.
3536.	Довести, що замкнена поверхня обов’язково має еліптичні
точки.
3537.	Якщо край поверхні належить одній площині і поверхня
не є областю на цій площині, то вона має еліптичні точки. До-
вести це.
3538.	Довести, що єдиною поверхнею, усі точки якої — точки
сплощення, є площина (або кусок площини).
3539.	Поверхня, усі точки якої — точки заокруглення, є сфера
(або область на сфері). Довести це.
3540.	Знайти точки заокруглення на еліптичному параболоїді.
3541.	Подати кривини координатних ліній через коефіцієнти
першої та другої квадратичних форм поверхні.
236
3542.	На нормалях поверхні Р відкладаються відрізки з сталою
довжиною. Геометричне місце кінців відрізків є поверхня У7*, пара-
лельна даній. Довести, що:
1)	властивість паралельності взаємна;
2)	дотичні площини до Р і У7* у відповідних точках паралельні;
3)	лініям кривини поверхні Р відповідають лінії кривини по-
верхні У7*;
4)	повна та середня кривини їх зв’язані співвідношенням
Н2 — 4К __ Я*2 —4/С*
№	—	/<*2
3543.	Виходячи з того, що еліпс можна спроектувати в коло,
знайти радіуси кривини еліпса в його вершинах, користуючись тео-
ремою Менье.
3544.	Показати, що поверхня з лінійним елементом
. 2 _ ^2 + ^2
~ (а2 + о2 + с)2
має сталу Гауссову кривину.
3545.	Знайти Гауссову кривину поверхні з лінійним елементом
йз2 = сій2 + 2 соз асіисії + (IV2.
ЛІНИ НА ПОВЕРХНІ
3546.	Знайти асимптотичні лінії гіперболічного параболоїда
г = аху.
3547.	Визначити асимптотичні лінії поверхонь:
х । У
7 у х
2)	х = ей и соз V, у = ски зіп V, г = и\
3)	г =	+ V, и3 + и4 +	‘
3548.	Дослідити асимптотичні лінії тора.
3549.	Поверхня зветься мінімальною, якщо її середня кривина
тотожньо дорівнює нулеві. Довести, що на мінімальній поверхні
асимптотична сітка ортогональна.
3550.	Який вигляд будуть мати коефіцієнти другої квадратич-
ної форми, якщо за координатні лінії взяти асимптотичні лінії?
3551.	Знайти асимптотичні лінії довільної лінійчатої поверхні
г = р (а) + Я («).
3552.	Довести, що при проективних перетвореннях поверхні
асимптотична лінія переходить в асимптотичну лінію.
237
3553.	Поверхня Г утворена головними нормалями кривої Ь. До-
вести, що лінія Ь на цій поверхні є асимптотичною лінією.
3554.	Довести, що на поверхнях перенесення г =	(и) + г2 (V)
ЛІНІЇ и = СОП8І, V = СОП8І утворюють спряжену сітку.
3555.	На поверхні ах2 + Ьу2 + сг2 = 1 знайти лінії, спряжені з
сім’єю ЛІНІЙ у = СОП8І.
3556.	Сітка кривих на поверхні зветься сіткою Чебишова, якщо
будь-який чотирикутник, утворений лініями сітки, має рівні проти-
лежні сторони. Довести, що на поверхнях перенесення г = (й) +
+ г2 (у) координатні лінії утворюють сітку Чебишова.
3557.	Визначити лінії кривини поверхонь:
а)	аг = ху;
Ь)	еліптичного параболоїда — +	= 2г;
с)	х = и соз V, у = и зіп V, г = /го (гелікоїда).
3558.	Знайти лінії кривини поверхні обертання.
3559.	Знайти лінії кривини розгортної поверхні.
3560.	Визначити геодезичні лінії круглого конуса х2 + у2 = г2.
3561.	Знайти геодезичні лінії гелікоїда г= {исозо, изіпу, Но}.
3562.	Довести: якщо геодезична лінія є одночасно й асимпто-
тичною, то вона пряма.
3563.	Довести: якщо геодезична лінія є одночасно й лінією
кривини, то вона лежить в одній площині.
3564.	Згинанням поверхні зветься така її деформація, за якої
зберігаються довжини лінії на поверхні. Довести, що при згинанні
поверхні геодезичні лінії переходять у геодезичні.
РОЗДІЛ XVII____________________________
РЯДЦЛ ФУР’Є
а+л	я
3565.	Довести рівність / (х) йх =	/ (х) йх, якщо / (х) — ін-
а	— л
тегрована періодична функція з періодом 2л, де а — будь-яка стала.
а	а
3566.	Довести рівності § /(х)йх = 2 \/(х)йх, якщо /(х)—пар-
—а	0
а
на, та / (х) йх = 0, якщо / (х) — непарна функція.
—а
3567.	Довести формулу
1	зіп (« + у) *
-7	7- 4- соз х 4- соз 2х 4-... 4- соз пх =----—.
2	1	11	„ . х
25,пт
Розвинути в ряд Фур’е такі функції:
3568.	/ (х) = на проміжку (—я; я). Знайти суму ряду 1 —
3^5	7 1 “•
3569.	ї (%) = х2 на проміжку [0; л] по косинусах. Користуючись
здобутим рядом, обчислити суму рядів 1 + -^2 +	+ • • •+
і	1 । 1	1 ।
та 1	22 з2	42	* • •
3570.	ї(х) =—1 на проміжку (—л; 0) та /(%) = ! на про-
міжку (0, л).
239
3571. / (х) =
— ~~ на проміжку (—я; 0),
на проміжку (0; я).
3572. / (х) = — -у на проміжку (0; я) по косинусах.
3573. / (х) = х на проміжку (0; я) по косинусах.
3574. /(х) = | х [ на проміжку [—я, я]. Користуючись здобутим
результатом, знайти суму ряду
1 +	+ -р- + "7? + • • •
3575. / (х) = х2 на проміжку (0; 2я).
3576. / (х) = х на проміжку (0, 2я).
д;2	д-2
3577.	/ (х) = -уу-на проміжку [—я; я].
3578.	/ (х) = | зіп х | на проміжку [—я; я].
3579.	/ (х) = я 9 * на проміжку (0; 2я). Використовуючи задачу
3575, дістати рівність
соз пх _____Зх2 — блх 4- 2л2
3580. /(х) = я2 — х2 на проміжку [—я; я].
3581. ?(х) = со$ах на проміжку [—я; я], де а—не ціле число.
3582. / (х) = є* на проміжку (—/, /).
3583. /(х) = х3 на проміжку (—я, я).
3584.	/(х) = |созх| на проміжку [—я; я].
3585.	/(х) = -^-х(я— х) на проміжку [0; я] по синусах. Корис-
туючись розвиненням, знайти суму ряду
33+53	73 + • • •
3586.	/(х) = Іпсоз на проміжку (—я; я).
3587. / (х) — (я2—х2)2 на проміжку (—я; я). Обчислити ряд
24 ‘ З4 44 ' ' * *
Зообразити за допомогою інтеграла Фур’є такі функції:
240
3588. /(х) =
1 при І X | < 1,
0,5 при ] х | = 1,
0 при | х| > 1.
3589. /(х) = І 1	2 ПРИ 0<х<2’
І 0 при х > 2,
продовживши її як парну для
3590. /(х) =
е~х, якщо
0, якщо
— е\ якщо
від’ємних вартостей х.
х>0,
х = 0,
х< 0.
х>0, продовживши її як парну на
при
0<х<1,
х> 1, продовживши її як непарну на
при
при
при
0<х<1,
х — 0 та х = 1,
х < 0 та х > 1.
я,
3591. ї(х) = е~ах, а>0,
від’ємну піввісь.
( х — 1 при
3592. /(х) = |	0
від’ємну піввісь.
1
3593. /(х)= 0,5
0
( ЗІПХ ПрИ ।
3594. /(х)=	„ ті
(	0 зовні [0; я].
3595. Перетворити многочлени Чебишова Тп (х) = соз (п агссоз х),
п = 0, 1, 2, 3, ..., до вигляду
Т„(х) =
1)" .
3596. Довести, що система функцій
^(^^зіпип+Дагссозх]^ = 0>
V і —%2
ортогональна на проміжку (—1; 1) з вагою р (х) =	1 —х2.
3597.	Довести ортогональність Лежандрових многочленів
^М=-2Лг--^(^-1)'г> « = 0’ 2> 3>--
на проміжку [—1; 1]. Знайти Р0(х), Рі(х), Р2(х) та Р3(х).
16 2193
241
3598.	Довести, що Лягеррові многочлени
Ьп = еХ е~Х^ « = 0. 1. 2, 3,. ..
ортогональні на проміжку [0; оо) з вагою р (х) = е~х
”	і 0, к =/= т,
\Ц(х)Ьт(х)е-хах = \
о	((&!)2, к = т.
3599.	Ермітові многочлени визначаються рівністю
Нп(х) = (-!)«-^г(Гхг), П = 0, 1, 2, 3,...
Довести їх ортогональність з вагою р = е~х2 на проміжку (—оо,
4-оо). Знайти Н0(х), Н1(х), Н2(х) та Н3(х).
3600.	Користуючись розвиненням
оо
х = 2 'У --------зіп пх, —я < х < я.
п=1 '
Знайти, інтегруючи почленно, ряди для х2 та х3 у цьому ж проміжку.
3601.	Довести ортогональність системи функцій
8ІПХ, зіп Зх, зіпбх, ..., зіп(2&—1)х,...
на проміжку |\);
3602.	Рівняння і§х—х = 0 має безліч коренів (додатних і від’-
ємних). Позначивши додатні корені через ах, а2, а3,..., ап,... довес-
ти, що система функцій зіп ахх, зіп а2х,..., зіп апх,... ортогональна
на проміжку [0; 1].
Поліпшити збіжність таких тригонометричних рядів:
оо
3603.	/ (х) = 2	5*п пх-
п=2
оо
3604.	/ (х) = 2 ^пі — і З'п пх-
п=2 П
ОО
3605.	/(х) = У  УУ'Уп1 зіппх.
п (д3 + о
оо
3606.	/ (х) = У -;-п, . зіп пх.
' ' '	п5+ 1
п=1
242
3607.	/ (х) = У мЛГТ 5ІП пх-
оо
3608.	/ (х) = У -^-г Зіп пх.
І V '	П3 1
П=\
оо
3609.
п=1
оо
3610. /(х) = 2 (-іГЙ^зіппх.
п=2
3611. /(х) = 2^> «>0-
16*
ВІДПОВІДІ
РОЗДІЛ І
АНАЛІТИЧНА ГЕОМЕТРІЯ НА ПЛОЩИНІ
1.	— 1 < х < 2. Точки розміщені у смузі між прямими, паралельними осі
ОУ, що проходять через точки на осі ОХ, для яких х — —1 і х = 2.
2.	а) На прямих х — а та х — — а; в) на бісектрисах координатних кутів.
3.	а) Точки розміщені в таких чотирьох областях площини: 1) над віссю ОХ
праворуч від прямої х = 2, 2) під віссю ОХ ліворуч від прямої х — —2, 3) над
віссю ОХ між прямою х — —2 та віссю ОУ, 4) під віссю ОХ між віссю ОУ та пря-
3
мою х = 2; в) ліворуч від прямої х — -у.
4.	а) (хр — і/і); Ь) (—хь у^, с) (—хь —у^); Л) (уь х^.
/' а 1Л2	\
5.	Р(У1, %і). 7. а) (0, 0), (а, 0), (а, а), (0, а); Ь) І-, ОЬ
(5	\	ч	’
З,-л І15,-—	л
9/1	4
11.	а) На колі з центром у полюсі та радіусом 1; в) на колі з центром у полюсі
та радіусом а; с) на промені, що виходить з полюса під кутом ф0 до полярної осі.
12.	мМ, -2-\, ЛМЗ, я), М3І2,	М^2, АЯА
13.	(З, 0). 14. (4, 4К 15	-2~^ (1 + Х3 3-^ і
\ 2	2 /	\ 2 ’	2	/’ І 2	’	2 /
(	1	2 + /3\ //3—1 3+/3\
\	2 ’	2	/’ \	2	’	2 /
16. Якщо А(Хі, уг), В(х3, у2),	С(х3,у3), то (х3 — Х])(х3 — х2) +
+ (Уз-Уі)(Уз~У2) = 0- 17. НІ. 19. 5=13,	=	20. 11. 21.
О	2
244
25	1
22. -у. 23. 28 /3. 24. 5 = -±- РіР2 ] зіп (<р2 — фО |. 25. 16.
26. —-і- 1, —2. 27. а). 28. 0 < і < 1. 29. (б, ЗО. —
31. а) (1, 	; Ь) (—4, 2). 32. О	Вказівка. Позначи-
мо точку перетину через О (х, у). Точка О лежить на відрізку АС, тому х =
1	2
= •=—г-т- » У = і—г-1- • 3 умови, що точка О лежить на відрізку ВИ, одержує-
1 Т 4	1 Т 4
зл2
І +Л2‘
2 — 2Л2
Х~ 1+62
невідомими.
14 г-
33. -у /2.
МО
ма
У —
Розв’язуємо систему чотирьох рівнянь з чотир-
34. (—11, —3). 35. М(—1, 0), С(0, 2).
36.	/	+ *2 + *з Уі + Уг + Уз.
ІЗ	З І
_ а (х2 + *з) + Ь (%і + х3) + с (хх + Хг)
б' с~	2(а + Ь + с)	;
а {у2 4~ ^/з)	ІУі 4~ Уз) 4~ £ (уі 4- у%) і.
Ус = 	 у 9 / ь д_ \—, де а, Ь, с — довжини сторін.
Г" с/ р" СІ
39. Вершину кута візьмемо за початок координат, а осі координат спрямує-
те2	п2
мо по сторонах кута, тоді х = ——:, у =	:—у .
г '	2 (те + п) 2 (т + п)
(31	23 \
~Ї7 / Р°3^иваємо чотирикутник на два трикутники і шука-
ємо центр ваги кожного з них. Потім вважаємо, що вага трикутника зосеред-
жена в його центрі і шукаємо центр ваги двох матеріальних точок.
41. а) х* — х 4- 1, у' — У — 2; Ь) х' = х — 3, у' — у — 4; с) х' = х — 2,
/ = (/4- 3. 42. (5, —8), (10, —4), (3 —3). 43. О'(5, —1), О (—5, 1).
44.	а) (—2/2, —У2); Ь) (1, 3); с) (3, —1). 45. а = 4“ + 360п.
О
46.	Вх(4 + Ц1, с/з+ЦА /3+-|-). Ох(3, /3-1). Нове
накладання сторін прямокутника, що лежали на осях координат, візьмемо за но-
ві осі координат. Перетворення координат при цьому буде складатися з пара-
лельного перенесення в точку А (4 ,— 1), і повороту осей на кут а = 30°. Фор-
,/З 1 , , . .
мули перетворення координат матимуть вигляд х .= х	-----—у 4~ 4 і у =
1 , . /з , , и
= —х 4—2~У —1- Координати вершин прямокутника після переміщення
відносно нової системи координат будуть Лі(0, 0), Ві(5, 0), Сі(5, 2), І>і(0, 2). Зали-
шається обчислити за формулами перетворення координат координати цих же
точок відносно старої системи координат.
245
47.	(О, 1). 48. 6% — Зу + 5 = 0. В к а з і в к а. Нехай М(х, у) — довільна
точка заданого геометричного місця точок. Співвідношення між х та у і буде
шуканим рівнянням.
49.	(х + 8)2 + У2 = 144. Вказівка. Візьмемо таку систему координат,
щоб початок сили Р знаходився в початку координат і сила Р лежала на
осі ОХ.
у2 г/2	у2 о2
50.	Коло. 51. а) (х-а)2 + (у-Ь)* = Я2; 5) — +	1; с) --у- = 1.
52.	X =	-СОЗ І, у = г-у"— зіп і, де і — гострий кут, утворений відріз-
л 4~ М»	а ~г р»
ком, що ковзає, і віссю ОХ.
оі2
53.	х = соз а, у = зіп а-----------.
54.	а) х = соз ф, у = зіп ф; Ь) х = Р зіп 2ф, у = 2% зіп2 ф.
55.	р = І зіп 2ф. 56. С (—1, 2), г = 5. 57. (х — 4)2 + у2 = 16.
58.	(0, 1), (4-2, 1); коло з центром у точці С (1,1) та радіусом г = 1.
59.	а) (7, —5); Ь) (—1, 1), (—3, —1); с) (1, — 1) — точка дотику ліній;
(7	3 \
---— ,----£-1; Ь) дотикається в точ-
ці (—1, 1); с) дотикається в нескінченності; б/) (—1, 1), друга точка перетину — в
нескінченності. 61. (4, 0), (—2,0). 62. а) а2 — с< 0, Ь — довільне; в) а2>с,
Ь — довільне; с) а2 = с, Ь — довільне. 63. А2. 64. а = — 6, Ь — 2.
65.	тх 4- пу — 21 = 0, тх 4- пу 4- 2/ = 0. 67. 6х 4~ ^У — Ю — 0» 6х 4~ ^У “ 0.
68.	(2, 1), (—1, —1), (3, 2). 69. у 4- 2 = 0, х — у — 2 = 0, х + у 4-2=0.
/ 27	14 \	1
70.	(З, 2), — , -А- . 71. у =-----7=-х4-3. 72. ф = 135д.
\ 37	37 у	у з
73.	2х 4- Зу = 0. 74. у = „2- х. 75,	0 =
76.	А = 90°,	В = агсі£ С = агсі£ 3. 79.	4- тг12 = 0.
О
81.	2х — у -|- 5 — 0. 82. 2х — 5у + 8 = 0.
83.	Зх — 2(/ — 3 = 0,	2х + у — 13 = 0, Зх + 5у	—	36 =	0.
84.	2х+</+ 12 = 0,	2х + у —3 = 0. 85.	,-.	86.	(10,	—5).
у □	□ І
87.	2х 4- Іу 4- 22 = 0, їх 4- 2у — 13 = 0, х — у	4-	2 = 0.
88.	х 4- Іу — 6 = 0,	х — у — 6 = 0, їх 4- у—10	= 0.	Вказівка.	При
розв’язанні цієї задачі можна використати те, що сторони кута лежать симет-
рично відносно його бісектриси. Тому точки, симетричні з точкою А відносно
бісектриси кутів В і С, лежать на прямій ВС. Знайшовши рівняння прямої
ВС, легко знайти координати вершин В і С трикутника як точок перетину ВС з
бісектрисами кутів.
89.	2х 4- У — 8 = 0; х — Зу 4- 10 = 0; хА-4у — 4 = 0. Вказівка. По-
значимо координати невідомих вершин трикутника: В (хх, уг), С (х2, Уг)- Ко-
ординати точки В (хх, у±) задовольняють рівняння медіани, проведеної через
246
о	Мг — 4 ї/і 4~ 2\	. .
вершину В, а точка і—-—, -—-—і лежить на медіані, що проходить через
вершину С. Одержуємо систему двох рівнянь відносно хь у±. Аналогічно зна-
ходимо координати точки С.
90.	Зх + 7у — 8 = 0, 7х — Зг/ — 38 = 0. Вказівка. Кутовий коефіцієнт
шуканої прямої знаходимо за формулою	± ~	, знаючи кут 9
1 + «1«2
і кутовий коефіцієнт даної прямої.
91.	5х — у — 26 = 0, х 4- Зу = 0. Вказівка. Див. 90.
92.	х + у — 7 = 0, (2 +/3) х + г/— 10 — З/3 = 0 і (2 —/3)х+г/ —
— 10+3/3 = 0. 93. 5х — у — 26 = 0. 94. 2х + у — 16 = 0, 2х + у + 14 = 0,
х — 2у— 18 = 0. 95.----96. а) 11х+ 10г/ — 19 = 0; Ь) Зх — 7 = 0; с) 2х +
+ у — 4 = 0. 97. 4х — Зу — 25 = 0, Зх + 4г/ —25 = 0. 98. Зх — 6у — 11 = 0,
2х+(/ — 4 = 0. 99- «); е). 100. а) —4-х--%-у----У-= 0; Ь) 4-
5	5	5	/5
4-	+-У-------Уг- = 0; с) —х —2 = 0. 101. а) + ; Ь) ; с) Ю2. 6.
]/5	15	13	у5
49
103.	-=-. 104. 7. 105. Зх 4- 4у 4- 6 = 0, Зх 4- 4у — 14 = 0 або Зх 4- 4у+
□
+ 6 = 0, Зх + 4у + 26 = 0.
106.	Так. Вказівка. Найбільш доцільно використати геометричне тлу-
мачення лінійних нерівностей. Позначимо ліву частину рівняння заданої прямої
через /(х, у). Якщо для точок М± (хь уі) і Л42(х2, у 2) /(хі» Уі) і /(х2> У2) ма-
ють однакові знаки, то точки і М2 лежать по одну сторону від прямої, в
противному разі — по різні.
107.	Зовні. Вказівка. Знаходимо вершини трикутника. Легко можна
з’ясувати, чи лежить точка М і вершина трикутника по одну сторону протилеж-
ної їй сторони, чи по різні сторони. 108. Опуклий.
109.	2х + 6у + 3 = 0. Вказівка. Бісектриса є геометричне місце то-
чок, рівновіддалених від сторін кута, тому рівняння бісектрис кутів, утворених
. АіХ —І— Ві,у + Сі А2х В2г/ С2
прямими можна зобразити у вигляді ---- — = ±--------------- _	—.
±/ А1+В{ ±Уа*+ІР
Знак плюс буде в тому випадку, коли в даному кутові міститься початок коор-
динат, знаки мінус — у протилежному випадку. ПО. х + у + 5 = 0.
25
112.	а = З, Ь = 5, Р (0, ± 4); директриси у = ± —— .
у 2	і/2	у2	«»2
113.	— 4-_^-=1. 114.	0,08. 115•+ + + = 1.
□210	155
116.
у2 £/2	х2 £/2
X2	у2 _ .
64	36
247
а) 36	64 Ь Є) 64	36	‘ 9	16
120.	а) у2 = 10% — 25; Ь) у2 = 16%; с) х2 — 8у, сі) х2 = — 18#.
121.	4х —#+7 = 0 і 4%+ #+1=0. 122.2р. 123.12.
124.	(х — х0)2 + (у — #0)2 + к (ах + Ьу + с)2 = 0. Вказівка. Нехай
М (х> У) — довільна точка кривої. Доцільно використати фокальну власти-
г
вість кривої другого порядку = е, де г — віддаль точки М(х, у) до фоку-
са, сі — віддаль її до відповідної директриси, е — ексцентриситет кривої.
125.	7х2 + 7у2 + 2ху — 18х + 34# + 39 = 0.
126. 23х2 + 23(/2 — 50х(/ + 104х — 96 г/ + 98 =0. 127. гх =Ц^- > г2 = 3^-.
129.	р =-----------— 12 .----------. 130. а) р = К; Ь) а* = р2 + р2 — 2ррх X
Рі — (Рх — Рг) соз <р	г	11	,Г1
X соз (<р — фх). 131. а) -^- + Х = 1; Ь) -І-----------------------і/2 = 1; с) у2 = х.
У	т:
132.	{--134. (—2, 0) і + , + . 135.-^-.
\ 1 + /2	)	\ 5	5 /	7
136.	Дійсних точок перетину немає. 137. х — 2 = 0. 138. у — ±-і-х.
4
139.	у — х. Вказівка. Це буде діаметр кривої, спряженої з напря-
О
мом хорд.
140.	Ь2х0х + а2у$у — (а2 #2 + Ь2 х2) = 0. Вказівка. Діаметр еліпса, що
пройде через точку /Ио, буде спряжений з шуканою хордою. Користуючись цим,
легко знайти кутовий коефіцієнт шуканої хорди.
141.	—4. 142. # =----1- х. 143. у = х. 144. у = "/Зх, # =----------х.
V з
1	2
145. у =------х, у = — х. 146. х — 8# = 0, 4х — у = 0.
Л	о
147. 4х — З# + 1 =0. 148. х = рк. 149. 2аЬ.
150. Паралелограм, що має вершини в кінцях спряжених діаметрів.
151
а2 + Ь2 ~ Ь 152
%хо УУо і	,
~^2	^2~ —	153. ##о — р (х + хо).
154. х = ±4, # = ±3. 155. (х—1)2 + (#+2)2=16.
156. х + у — 6 = 0, х — у — 6 = 0. 157. х —2 = 0, 7х — 16# + 50 = 0
Вказівка. Рівняння дотичної в даному випадку має вигляд
хх0
УУо
9
248
Дотична проходить через точку (2, 4), а тому -у- + -ур- = 1. Крім того, коор-
динати точки дотику (х0, у$) задовольняють рівняння кривої.
158. 9х — 4(/— 1 = 0, 9х + 4у + 1 = 0. 159. 5х — Зу — 48 = 0, 5х — Зу +
+ 48 = 0. 160.x — 4# + 8 = 0. 161. (6, 6). Це точка, в якій дотична до кри-
у2
вої паралельна заданій прямій. 162. -у + -|^-= 1. 165. А2а2 ± В2Ь2—С2 = 0.
166. х — 2у + 5 = 0. 167. (/—18 = 0. 170. 2ху + Зх — у — 3 = 0.
172. а) При к > 0 і к < — 1; Ь) к = 0 їк — —1; с) при к = — 1 пряма доти-
(13	1 \
---ТІ’
о	о /
2) (—3; —1); 3) центра немає; 4) лінія центрів 2х + у — 2 = 0; 5) (—1, 2);
6) лінія центрів х+ у— 1=0. 174. х — Зу — 6 = 0.	175. х+у+1=0
Зу + 1 = 0; Юх — 25(/ + 3 = 0 і 7х — З#+ 5 = 0. Вказівка. Кутові кое-
фіцієнти таких діаметрів задовольняють рівнянням ап + а12 (к + к') + а22/?&' =
_________________&
~ і і ьь' • Рівняння діаметра, спряженого з напрямом к, шукаємо
1 "р КК
178. 1) 14х-14(/+
0,91x4-7^ — 35 = 0; 2) 2х —8г/4-5 = 0, 2x4-1=0;
179.
1)	У — 2 = 0, х 4-4 = 0; 2)
2х — у— 1=0.	181. 1)
у вигляді Рх + кру — 0. 176. х = у.
3) 6х —2г/ +
10х2 + 21хг/ +
х + у — 2 = О,
х — у — 2 = 0,
182’_~ПГ 1
+ У’ -ХД + 2.
4) — 4-у2=	-|/5 Л	“9
вої, х — 2у + 1 = 0, 2х-\- у — 3 = 0 — головної осі
+ 6 = 0 — асимптоти; 2) —-------V— = 1, С /,
4	16 у 4
— 3 = 0, х + Зу — 3 = 0, Зх + у — 3 = 0; 3) 2х'2 —
2=2/2х':
X .
+ 14
+ 7 = 0, 2х + 2у + 3 = 0; 4) у + 1 = 0, 2х + у — 4 = 0.
+ 9(/2 — 41х — 39(/ + 4 = 0. 180.
х — у = 0;	3) х + 2у — 8 = 0,
/ 7	17 \
("Ї2’“'Ї2‘); 2) х + ^+3=-0’ (~3> П; 3) *+2(/-1 =
*'2 . у'2 _ . „ _ х' /2 у' /2 , о _ X' ]/2 ,
' 4	’	2	—У~~Г~
Vі 2	у,,2‘	і/2
183.	1) —4- + = 1; 2) А--------= 1; 3) у'
6	х'2
1; 5) і/'2 = ——184. 1) —-------у'і== 1, С (1, 1)—центр кри-
, х — у = 0 і х — 7^4-
х — (/=0, 2х4-2(/—
2/2 = 1, С(0, —1), х +
4- у 4~ 1 = 0, х — у — 1=0, у 4- 1 — 0, х = 0; 4) у'2 = 7]/^2х', х — у 4- 1 = 0—
(5	19
-у-у-, -уу-|— вершина. 185. 1) Гіпербола; 2) пара паралельних
прямих; 3) дві прямі, що перетинаються; 4) дві прямі, що збігаються.
186. а) Парабола проходить через початок координат; Ь) вісь ординат пара-
лельна осі параболи; с) вісь ординат збігається з віссю параболи, вершина па-
раболи — у початку координат. 187. 2. 188. При X = —24 — пара дійсних
прямих, що перетинаються; при X > 1 — еліпс; X < 1, X + —24 — гіпербола;
X = 1 — парабола. 189. 1) Еліпс; 2) уявний еліпс; 3) дві уявні прямі, що пе-
249
ретинаються в дійсній точці; 4) гіпербола; 5) гіпербола; 6) парабола; 7) парабо-
ла; 8) дві паралельні прямі; 9) дві прямі, що збігаються.
190. 1) х— 4у — 2 = 0, х — 2# 4-2 = 0; 2) уявні прямі, що перетинаються
в точці (2, 3); 3) 2х 4~ У — 5=0, 2х 4- У — 1=0; 4) уявні прямі, що перетина-
ються в точці (3, —3).
РОЗДІЛ II
Векторна алгебра
192. а Ц Ь. 193. а) а ± Ь; с) а || 6; сі) е) 194. | а | = | Ь |.
196.	Точка перетину медіан.
197.	АЬ = а+~, ВЕ = ^^-, СР=-------------— Ь.
199.	І -4" + 4— І 200. го = а — гг + г3.
\|«|	1*1/
201. 0. В к а з і в к а. Вектори, що зображають дані сили, утворюють пра-
вильний п’ятикутник. 202. х = —1, у = — 1. 203. х = 1, у = 0, г = — 1.
206. Так, тому що а 4- Ь 4- с = 0. 207. т = — 2а 4- 6- Вказівка. Зоб-
разимо т = ах-]-Ьу. Така ж сама лінійна комбінація буде між координатами
векторів: — 1 = 2х 4- Зг/, 2 = х 4~ 4у\ звідси знаходимо х і у.
208. т = —Г—с. 209. АВ = {3, 9, —5}, ВА = {— 3, —9, 5}.
210. #(1, 8, —4). 211. ^4-^2= {13, —4, —6}. 212. а = 2, р = 3, у = 5.
214. а = {--Ці, -І}- 215. 101 = ^ ІГ1-У2Р.
216. 1) (1, 4, 1); 2) (-3, 2, 3); 3) (4, 9, 1); 4) (-, 0, у).
217.9/. 219. <р —	+	221.8Іп<р= _» 4  Ф5=1	,де а =
________________ І а 116|	(а, Ь)
= 1/< |а|2|&|2 — (аЬ)2.
222. Вказівка. Розглянемо скалярний добуток векторів а-\- Ь і а — Ь.
я
Дістанемо, що | а | = | Ь |. 223. | Р | = 5. 224. ер = -у. Вказівка. Одинич-
ні вектори бісектрис розкласти по координатному базису і знайти їх скалярний
* г-------------------	5	7	6
добуток. 225.	І а І	= 1/ 110, соз а = —т=*,	соз р	= — 7^-,	соз у = —__
*	1 1	/по н /по г /по
226. 4 = —— =4-4-> — 4-> —	227. а= {—3, 4, ± 12}.
, *	( 10 о 2 1	1
|а|
250
228.	—(і + /), — (: + к), — (/ + й).
229.	| а | = 3. Вказівка. Використати те, що | а і = V (а, а).
9
230.	ер = — я 4- 2лп. 231.	А =	В = 459. С = 90°.
232.	Розв' озування. а + Ь + с = 0, тому (а + &4-с, а4-&4-с)==0 і
2 (аЬ) + 2 (7с) + 2 (Ге) = — а2 — Г2 — с2. 233. х = {— З, 3, — 6}.
234.	{±9, 0, ±3}. 235. х = {0, —4, 2}. 236. 6. 237. —4. 238. 1) Ні;
2) да. 239. соз у «=» ±	. 240. а = Р = 45°, у — 90а та а = р = 90°, у =
4	12
180а. 241. Ні. 242. —. 243. —— . 245. 36. 246. 13.
}/3	V 5
вектора /: в/~— ег~-------------—і де ет—орт радіуса вектора точки
М (у, х, г,), / = |Д
г
248.	Е — ± д ———. Вказівка. Розглянути два випадки: 1) д > 0,
тоді Е = І Е і = | Е І є? —	— г; 2) д < 0, тоді Е =
іГр
249.	V ^+2^0080+^. 250. а0=-^- =
Іа|
13 ’ 13
251.	— 6-І- 252- 6- 253. 1§а =
ІЙ1-. 254. а
(« Ь)
255. Вказівка. Помножити обидві частини рівності векторно спочат-
ку на а, а потім на Ь. 256. Ні. 257. Вказівка. Розглянути векторний добу-
ток з векторів а — сі та Ь — с.
258. 18/2. 259. 5 = -1 |Л78. 260. ±	2Т+ 2й).
2/	о
261.	262. г||£, тобто пряма, вздовж якої діє сила, проходить через точ-
ку, відносно якої знаходимо момент.
251
263. / = 2 Ік- М = [г, /] = г, 2 Ік = 2 к. Ік]- 264. 0.
к—ї	[ к=\ 3	к=1
->	5	->	З
265.	М == ± -у (— 4 і + 2 ] — 3 й). 266. | М. І = 28, соз а = — ~ ,
□
6	2
СО8(3^=-соз у = —. 267. Н =	[/, г]. Вказівка. Відомо,
що
Н = к — , де к— коефіцієнт пропорціональності. При розв’язанні задачі тре-
ба силу струму і напруженість магнітного поля розглядати як вектори / та Н.
2В8 Н - к1^~гУ>. м » -- кІ(~хк + ^  С}Н= /к(хІ~У^
268. а) п — у2 + г2 • °> н х2 + г2	’ х2 + у2
269.	Н = -Ц-(47+3“/). 270. Я = --|"(/ + ЗЛ),^=-1С1?(/+ЗІ).
-	->	- к - -	2
271.	Н = к-кг, Н0={0, 0, 1}. 272. Н = — -у(3 і + і). а)со8а1 = —
6) 008 0!= — -Д= : с) €08?! = -—^. 273. 1) 1; 2) —1; 3) —1; 4) 1.
у	у £х)
278.	/74. 280. 1) Так; 2) ні. 281. 2ка + Зк Ь — к с — 0. 282. Ні.
283.	а) Праву; Ь) ліву. 287. 1) {3, —12, —3}; 2) 0. 288. {2, —3, 10}.
290.	Або а Ц Ь, або а і Ь перпендикулярні до с, або один з векторів є
нуль-вектор.
РОЗДІЛ III
Аналітична геометрія в просторі
292.	(0, 0, 0), (а, 0, 0), (а, а, 0), (0, а, 0), (0, а, а), (0, 0, а), (а, 0, а),
/	14 \	/ а \2	Ь \2	/ с 2
(а, а, а). 293. /0, 0,	294.	+12~Т) =
а2 І ^2 І С2
= —Х-4—-- • 297. (—1, 6, —7), (7, —2, —3), (—5, —6, 9).
г,
298.	Можливі три розв’язки: Рх(—3, 4, —4), Д» (1, —2» 8) і £>3 (5, 0, —4).
29д х = /71!%! + т2Х2 + т3Х3 + /714*4 .	^1 + ^2 + 77?3//3 +/774//4 .
С т1 4“ т2 + ~Ь ^4 С	4“	4"	4~ ^4
= т-іХі + ш2х2 + т3х3 -4- т4х4
Л71 4- /772 4- ^3 4- т4
9	__
. 300. -5- У74. ЗОЇ. (5, 4, —5).
<5
252
7	1	1
302.	=-=, Х2 =, Х3 = — — . 303. Так. 304. {4, —3, —1).
305.	а = {4, —2, —2}, 6 = {4, 4, —2}, с = {5, —4, 2}.
306.	а) х = — х' + Зг' + 5, у =* х* — 2г' — 3, г = 4х' + у' — 10г' — 17;
Ь) и — 2иг + 2а' 4-а/', а = За' — 2а' 4-а/', ш — V*.
307.	(0, 0, 0), (7, —1, 3), (11, —4, 2) і (6, —3, —1). Вказівка. Почат-
кове положення центра ваги С(—1, 1, 1). Задача зводиться до такого пара-
лельного перенесення осей, при якому точка, що має координати (—1, 1, 1),
матиме нові координати (6, —2, 1).
308.	Зх'2 4- /2 — 2х'г' — 8х' — 4/ 4- 6г' 4- 3 = 0.
1^2
309.	х'2—у'2 = 2г'. Формули перетворення мають вигляд х= ——х' —
У2 ,	/2 , , /2 ,	,	4О7	4
- —	У=—х +—У.г = 2.ЗП. а = т, р = _,ї=__.
-У2/-5/2/+ 2/Зг' . З/6х'— ]/б/— 2г' .
312. х =------------§---------- , у----------£-------,
/2х' + /2/ + 2/3/	5° .	9 .
г = -------------------. Зів. і и. 014. а) 48; о) —— ; с) — ,
4	3'6
315.	п = {0, К 2Х}. 316. х+2(/ + Зг— 11 = 0. 317. х — 2у —
— Зг+14 = 0.	318. г —5 = 0, у — 2 = 0, х + 3 = 0.	319.	7у	— Зг = 0,
7х + г = 0, Зх + (/= 0. 320. х + у — 3 = 0. 321. Зх — 6у + 7г — 6 = 0.
322.	х-\- у г — 2 = 0, х — у 4- г 4~ 2 = 0, х-\- у — г — 4 = 0.
323.	(2, 1, 5). 324. а) 1^=7\ Ь) І = 7, т = 3\ с) 1^7, т^З.
325.	2х 4~ У 4“ З2 — 25 = 0. Вказівка. Позначимо вектори, перпенди-
кулярні до заданих площин через ггг і гг2. Тоді [ггігг2] буде нормальним векто-
ром шуканої площини.
326.	а) 4х 4-ї/4" 5г—19 = 0; Ь) х4~2г — 8 = 0; с)х-\-у — г4-5 = 0;.
(і) 13x4- 7у 4- 5г— 13 = 0, 7х 4-5г/— г 4 9 =0. 327. 15х — Зу — 26г — 6 =0.
Вказівка. Рівняння шуканої площини можна зобразити у вигляді
5х — у 4- Зг — 2 4-	= 0.
329.	а) ІЗх 4- 14г/ — 4г — 25 = 0; Ь) г = 0; с) х — 4у 4- 2г — 7 = 0; й) Зх—
— Зу 4- 8г— 14 = 0; е) Зх —2г —9 = 0. 330. (0, —1, 0), (0, 7, 0).
331.	х — 2у 4- 2г 4- 1 = 0, х — 2#4~2г — 29 = 0. Вказівка. Шукані
площини будуть геометричним місцем точок, віддалених від заданої площини
на віддалі 5 одиниць, тому їх рівняння можна зобразити у вигляді
х —2г/4- 2г— 14 = ± 5
З
41
332.	д, = —— . Вказівка. Можна взяти конкретну точку однієї пло-
о
щини та знайти її віддаль до другої площини. 333. 8. 334. х 4~ 5у — 2г — 1 =0.
253
336. а) х-|-Зі/ + 6 = 0, Зх — у + 10г•—16 = 0; Ь) х-\-Чу-—г+1=0«
2х — у — 2 = 0. 337. 23х — у — 4г — 24 = 0. 338. Так.
339. 44 = 44 = 44: «={2,0,3}. 340.о=13. 341.21.
2	0 о
Ь)
342. (0, 0, 2), / 1, —о). 343. а)	= Ц--А = Дг-І ;
\ О	О І	11	1
X—1 у— 1	2	. X у — 2	2 4- 1 пл. х+1 у — 2
— = Ч- = —; С)-2- = ^Г=Ч-- 344-^- = —=’
= ^4. 345. ^-=4 = ^. 346.4=4=^4; 4^ = 4=
—1	а Ь с	4	0	3’1 З
г — 5 х __ у __ г — 2 х _ у __ 2 — 2	х+1__ї/ — 4 __ г 4 2
=5"; "5" Т —2 ;	ПГ ~ “=Г ~ “2“*
347. —ф * = -—_і= ДхА	348. Усі кути прямі. 350. --7^ * = —^т- =»
5	—4	7	1о	—1
= —гр-. В к а з і в к а. За напрямний вектор бісектриси можна взять вектор
—10
и — АВц + ЛС0, де АВ0 і АС0 — орти відповідно векторів АВ і АС.
о-л Х + 1	У~%	2—1	. тт
352. —і— = —=— =-----5— . Вказівка. Напрямний вектор перпен-
1 □ ------------£
дикуляра шукаємо з умови перпендикулярності та умови перетину перпен-
о-о х + 4 у + §	2 — 3	х+1 у — 2
дикуляра з прямою. 353. —— ==	. 354. —5— = -—у- =»
о	— 1	Л	•—о
г + 3 оее х + 5 У—1	2 г» • тт „х—х0
= —т— . 355. —4— = -—х- =-----— . Вказівка. Нехай —:—- =»
о	2	—3	—4	І
У — Уо	2 — г0 .	.	л
«=  т =—--------рівняння спільного перпендикуляра, його напрямний век-
тор знаходимо з умови перпендикулярності до двох прямих, а точку — з умови
перетину з даними прямими.
ЧЧК Х~Хй - У~У° - г~г» ЧЧ7 *—1 = У+3 = г~5
ІВ^І ~ іСіЛхі “ (ЛхВхІ ’	1	6	—5 '
I В2 ^2 I I ^2 ^2 І | ^2 І
/4	19 \
358.	(—2, 5, —3). 359. (—5, 1, 0). 360. ІЗ, -=- . Вказівка. Точ-
І о о /
ки А і В лежать по один бік від площини. Шукаємо точку Л*, симетричну точ-
ці А відносно даної площини. Її координати (3, —2, 5). Точка перетину площини
з прямою Л*В буде шуканою.
361.	9%+101/ —7г —44 = 0. 362. 2х + 9у + 5г + 7 = 0. 363. 2х — у —
— 2г — 5 = 0. 364. (0, —2, 1). 365. (—5, —4, 6). 366. Л = /14. В к а з і в -
к а. Через точку Р перпендикулярно до прямої проводимо площину 2х — у —
— ?4 8= 0. Точка перетину проведеної площини і даної прямої: (—3, 2, 0).
Віддаль РРі і буде шуканою. 367. 25. Вказівка. Беремо точку на одній
254
прямій і шукаємо її віддаль до іншої (див. 366). 368. і = 3. Вказівка.
Траєкторією руху буде пряма х — 11—/, у = — 21 + 2/, г = 20 — 2/. Точки
перетину її з площинами: Рг(—4, 9, —10) та Р2(®» —15, 14). Відрізок траєк-
торії РЛ = 36; і =	.
2х (хг — хз) + 2(/	— і/2) + 2г (гх —	+ х* + у* + г| — х* — у* —
369.	-г? = 0’
2х (хї — х3) + 2у (у± — у3) + 2г (г2 — г3) + х| + у% + г| — х[ — у[ —
— гі = °-
370.	4х + 6у + 5г — 1 = 0.
( у + 2 — 1 = 0,	( х + 2г + 1 = 0,	( х — 2у + 3 = 0,
371‘	“+ X = 0,	І у = 0,	I г = 0;
| Зі/ — Зг + 5 = 0, | Зх — 1 = 0, Ґ Зх — 1 = 0,
І х = 0,	І. у = 0, (г = 0.
( 2х + г— 1=0
372.	і .. п „ Л Вказівка. Рівняння даної прямої запи-
( х + 4у — 2г — 11 = 0.	н
( х + у — 1=0,
шемо у вигляді у 2у г 1 — 0 ^еРез не1 проводимо площину перпендику-
лярно до площини, на яку проектується пряма х-\- у — 1 + X (2у — г — 1) = 0,
X =-----• Проекція прямої буде лінією перетину даної площини і проведеної.
373.	13х—14і/+11г + 51 =0. 374.	= -г + 4 .
□	—о 9
375. (2, —3, 5). 376. А = З, И = — 23.
( х — 2г/ + г + 2 = 0,
377.	я) І _______г_^2 — 0 В к а 3 і в к а* Напрямний вектор спільно-
го перпендикуляра и = [ні, и2], де і ц2—напрямні вектори даних прямих.
У нашому випадку и={1, 1, 1). Через кожну з даних прямих паралельно
вектору и проведемо площини
х у — 1	г		X	У	г —2	
1	0	—1	= 0 та	0	1	—1	= 0.
1 1	1		1	1	1	
Лінія перетину цих площин і буде шуканим перпендикуляром;
ґ 16х + 27г/+ 17г —90 = 0,
І 58х + 6і/ + 31г — 20 = 0.
378.	а) (і = 13. В к а з і в к а. Через кожну з даних прямих проведемо пло-
щину, паралельну іншій; дістанемо дві паралельні площини. Віддаль між
цими площинами дорівнює довжині спільного перпендикуляра даних прямих.
Отже, через першу пряму проводимо площину, паралельно другій; у нашому
255
випадку вона зображується рівнянням Зх — 4у—12г+ 69 = 0. Шукаємо від-
даль цієї площини від точки (4, —1, —7) на другій прямій; в) 3; с) 7.
х^ у2 г2
379.	= 1, де Ь2 = а2 — с2. Вказівка. Спрямуємо вісь
ОХ по прямій РіР2» початок координат візьмемо посередині відрізка РіР2- Цю
х2 у2
поверхню можна дістати обертанням еліпса “^"4“ -^- = 1 навколо фокальної осі.
х2	у2
380.----Ь = 2г. Вказівка. Позначимо віддаль даної точки від
Р	Я
даної площини через р. За вісь ОХ візьмемо перпендикуляр, опущений з точки
на площину. Площину ХОУ проведемо через середину цього перпендикуляра.
Здобуту поверхню можна утворити обертанням параболи х2 = 2рг навколо
своєї осі.
381.	у(х + г — а) = 0. Вказівка. Нехай М (х, уу г) — довільна точ-
ка шуканої поверхні. Точка М. лежить на одній прямій з трьома точками, що
належать трьом ребрам куба, наприклад А (а, уь 0), В (х2, а, а) та С (0, 0, г3).
З колініарності векторів МА, МВ та /ИС одержуємо (х — а) : (у— Уі)-г~
= (х — х2): (у — а) :(г — а) = х : у: (г — г3) = а : [3: у. Звідси візьмемо лише
• •	.	.	.	& У — а
ті відношення, в яких немає проміжних параметрів х2, уі і г3: — = ——— ;
V г а х _	...	о
— = ——— та -р- = —. Перемноживши ці рівності, виключимо параметри а, р
та у, і дістанемо рівняння поверхні.
X2
382.	— + У2 — г2 = 1. Вказівка. Довільне положення прямої зо-
х	•	X—х ¥— У	%—2	і \
бразимо рівнянням —— = - —  =--------, де (х, уу г) — біжуча точка
шуканої поверхні. Запишемо умови перетину твірної з даними прямими:
X у — 1		г		х —2 у г			X у 4- 1 г	
2	0	—1	= 0,	0	1 1	= 0,	2	0	1	= 0.
1	т	п		1	т п		1 т п	
Одержана система лінійних рівнянь відносно /, т і п однорідна і має нетри-
віальний розв’язок. Прирівнюючи визначник цієї системи до нуля, одержимо
рівняння шуканої поверхні.
383.	Гіперболічний параболоїд -= 2г (див. 382).
18	8
384.	Гіперболічний параболоїд у2 4- 2уг — г2 + 4х — 2 = 0.
385.	(х — а)2 + (у — б)2 + (г — с)2 = г2.
386.	(х - 5)2 + (у + З)2 + (г - 7)2 = 81.
387.	(х - З)2 + (у + 2)2 + (г - І)2 = 18.
388.	а) С(3, —1, 1), г = 2; Ь) С (2, —3, 4), г = /7; с) с(-у, — -1. 1),
г=]/-^-. 389. (х — 2)2 + (у — З)2 + (гІ)2 = 9 і х2 4" (у 4- І)2 + (? +
+ 5)2 = 9. 391. а) 5; Ь) 7. 392. (—2, —2, 7). Вказівка. У шуканій точці
дотична площина до сфери паралельна даній.
256
393.	±	= 1. 394. у* = 2рх. 395. (х + Зг)* + 4 (у - 2г)* = 8. В к а-
зівка. Нехай 7И0 (х0, Уо, ?о) — точка напрямної. Рівняння довільної твір-
.. л	X *0 У уо 2	_
ноі зобразиться так:   ~|—• 1очка Мо лежить на напрям-
ній, тому х2 + 4ї/2 = 8, г0 = 0. Виключивши із знайдених чотирьох рівнянь
параметри х0, у0 та г0, дістанемо рівняння шуканого циліндра.
396.	(2х + г)2 — 10 (2х + г) + 25г/2 = 0.
397.	(5х + г/ —2г)2 + (х+5г/ + 2г)2 + (—2х+2г/ —Зг)2= 144. В каз і в-
к а. Напрямною циліндра може бути коло, здобуте від перетину сфери пло-
щиною, що проходить через центр сфери, паралельно даній площині. Напрям-
ну можна зобразити рівняннями х2 + у2 + г2 == 4, х — у + 2г = 0.
398.	х2 + 4у2 + 5г2 — 4ху — 125 = 0. Вказівка. Твірна буде паралель-
сфер площиною, що проходить через її центр перпендикулярно до твірної.
399.	0/+ Зх)2 + 2 (г + 2х)2 — 10 (х + І)2 = 0. Е_1____ ..........
довільну точку напрямної через Мо (х0, #0, г0).
твірної як рівняння прямої, що проходить
у —З _ г-2
*/о — з г0 2
дених чотирьох рівнянь параметри
400 ^- + ^—(г~с)2 =0.
а2 ф б2 с2
+ 50уг + 18х — 54у — 66г + 27 = 0.
напрямну можна взяти коло, яке
у площині, що утворює з координатними осями рівні кути. Таке коло можна
зобразити рівнянням: (х — а)2 + (у — а)2 + (г — а)2 = 6а2, х + у + г =За.
403. 45 (х + 4)2 + 52 (у — З)2 + 25 (г — б)2 + 24 (х + 4) (у—3) + 48(х + 4)X
X (г — 6) + 36 (у — 3) (г — 6) = 0. Вказівка. Запишемо рівняння довіль-
ної прямої, що проходить через точку 5: х = — 4 + Іі, у = 3 + ті, г = 6 +
+ пі. Шукаємо точки її перетину з сферою і вимагаємо, щоб пряма дотикалась до
сфери. 404. 4х2 — 15#2 — 6г2 — 12хг — 36х + 24г + 66 = 0. 405. у2 + г2 = а2.
Вказівка.
Тоді х0 — 1 ==
ну можна зобразити рівняннями х2 + у2 + *2 == 4, х — у + 2г = 0.
398. х2 + 4у2 + 5?2 — 4ху — 125 = 0. Вказівка. Твірна буде паралель-
на векторові, що сполучає центри сфер; напрямна — лінія перетину однієї з
Вказівка. Позначимо
Запишемо рівняння довільної
д . . о X -4- 1
через точки Мо і 5: —- =
Крім того, у2 + 2г2 = 10,
х0, #о» го* матимемо рівняння конуса.
401. Зх2 + 123г/2 + 23г2 — 18хг/ — 22хг +
402. ху + хг + уг = 0. Вказівка. За
перетинає всі три координатні осі і лежить
х0 = 0. Виключивши із знай-
г2 и2
406. 40 (х — 2)2 — 9#2 — 9г2 = 0. 407. — +	— г2 = 1.
Нехай Мо (х0, Уо, г0) — довільна точка на прямій обертання.
= у0 1 == г0. Крім того, нехай М (х, у, г) — точка поверхні, одержана обер-
танням точки Мо. У такому разі г = г0 і х2 + #2 = х2 + у2. Виключаючи із
знайдених чотирьох рівнянь три параметри, здобудемо рівняння поверхні.
408. ^+4=1- 4О9.а)4-^ = 1;	=
_—ь-4= 1- 409-“) X—= і; Ь)—=
а2 с2	а2 с2	а2
х2 а2 22
410. х* + у* = 2рг. 411. —+-£-+_-=1.
Ч	а
2	4
412.	=	413. а=±2, 6= + 3, с=±1.
□	" о
х2	у2	г2
414.	Всередині еліпсоїда —5- +	Н—5- = 1.
а2	о2	с2
17 2193
257
415.	1) 4, 12, е = /10; 2) 12, 4, е =	• 416. р=10, А (0, 4, 1).
О
417.	Парабола. Вказівка. Виключаючи з рівняння поверхні і площи-
ни, наприклад, г, знайдемо рівняння циліндра, що проектує лінію перетину
( у2 = 2 (х + 1),
на площину ХОУ: у2 ~ 2 (х + 1); рівняння проекції |
( х — у — 1 = 0,	( х + у — 1=0,
418.	Дві прямі, що перетинаються: | д	1 1	0
419.	(х — 2)2 + 2у2 — 4 = 0, г = 0, С (2, 0, А). 420. а) Еліпс з центром
С(—1, 1, 3); Ь) парабола, немає центра; с) дві прямі, що перетинаються.
421.	а) 1 < І < У 2; Ь) 111 < 1. 422. (9, 5, —2). 423. (З, 0, —10).
424.	а) М1(2І —3, 0) і М2(0, 0, 2); Ь) пряма лежить на поверхні;
с) Мх (4, 1, 3), друга точка перетину — у нескінченності; пряма паралельна
одній з асимптот поверхні.
х2 у2
425.	Асимптотичний конус поверхні; для центральної поверхні:	+
22	X2 І/2	22	X2 У2
+	= 1, -д- +	= 0; для параболоїдів: — ± — = 0.
(х + І)2 (и___2)2
426.	Геометричне місце таких прямих є конус: -—-— -------------------
— (г—1)2 = 0. 427. а) ^-+^1 + ^ = 1; Ь)	=г + го;
/Я ±5	р у
С) -^ + -^ + -^=0; гі)-^±-^ = 1; е) хх^ріу + Уо).
428.	=	=	429. 2х-4(/ + г + 4 = 0.
430. 2х — #4-2г 4-2 = 0. Вказівка. Рівняння дотичної площини до
даної поверхні зображено у вигляді хх0 4-	= г 4" ?о- 3 умови паралельно-
сті дотичної і даної площини одержуємо 2х0 = —у0 = —2, звідси х0 — —1,
Ув = 2. г0 знаходимо з умови того, що координати точки дотику Л40 (х0, у0, г0)
задовольняють рівняння поверхні. 431. 6х 4- У + Зг — 3 = 0 та 6х 4- У 4~ Зг 4-
_________________________________________ О 1	£> _ 2 ______ Л
4- 3 = 0. 432. х— 10г/4- 2г 4-21 = 0;	6	= -у~ = —у— та х = 21 4- 4
4- 14/, г/ = 54-Л г = 4 —2/.
433. 4 (х — З)2 — 15#2 — 6 (г 4- І)2 — 12 (х — 3) (г 4~ 1) = 0. Вказівка.
Сукупність прямих, що проходять через точку 5 визначається рівнянням х =
= 3 4- У —	? = —1 4- пі. Шукаємо точки перетину прямих цієї су-
купності з еліпсоїдом і вимагаємо, щоб вони дотикались до поверхні. Знайдемо
залежність між /, т, п.
434. УЇ5у — 2г+2 = 0 та /Ї5р + 2г — 2 = 0; (0, 2/15, 16) та
(0, —2/15, 16). 435. 2х+у— 14 = 0, Юх — 2у — г — 21 = 0 та 2х — у—6 =
= 0, ІОх — 2у — г — 21=0. Вказівка. Виключаємо з рівнянь поверхні і
площини, наприклад, г. Здобуте рівняння зображує дві площини 2х+ у —
— 14 = 0, 2х — у — 6 = 0, що проектують лінію перетину на площину ХОУ.
Перетинаючи їх даною площиною, дістанемо шукані прямі.
258
436.
у + 2г = 0,	( 2х — 5г = 0,	лоя? х	_ у +	1 _ г — 1	х
х — 5 = 0;	[(/4-4 = 0.	1	4	—2	1
у + 9 г 4“ 3	45
 +   = —5— ; <р = агссоз
12	2	/149-/21 ’
х _ у — 3 __ г	х — 2 __ у _ г
438.	~ї~ — о — 3^2 * о	"з~ “ ^4 • Вказівка. Рівняння пря-
молінійних твірних даної поверхні можна зобразити у вигляді
Параметри и і V знаходимо з умови, що шукані прямі паралельні даній площині.
ах — аг, ах ----- V,
439.	1
її ------•
1
у — — г,
V
де — оо < и < оо, — ОО < V < оо.
441.	45°. Вказівка. Зображуємо рівняння конуса у вигляді Л (х2 +
4- у2, 4- ?2) 4~ °Ф + V = 0» Де а, р і у — лінійні вирази відносно х, у і г.
Площини а = сопзі, [3 = сопзі будуть перетинати конус по колах.
442.	х = 0, г = 0; г = 1; 2г — у = сь 2г 4- У = с2-
443.	Мг (3, 0, 1), М2 (—3, 0, 1), М3 (3, 0, —1), М4 (—3, 0, —1). В к а з і в -
к а. Задача зводиться до знаходження точок параболоїда, в яких дотичні пло-
щини паралельні площинам колових перерізів.
444.	4" + -у- = г> У — г+1=0 та і- + у = г. !/ + ?- 1=0; <р =
= 4* • 445- - 2)2 + У2 + <г - 2)2 = 4- 446‘ Мі <°> — Ь х/з)» Л«в(О. 1. 1/2)-
6|/І0	„	.	„
447.	г = —+— • Вказівка. Площини колових перерізів визначають-
5
ся рівняннями у ± Зг = С. Вони паралельні осі ОХ. Коловий переріз може
дотикатися до горлового еліпса лише в тому випадку, коли він проходить через
одну з його вершин, що лежать на осі ОУ, тобто через точку (0, 2, 0) або (0, —2, 0)
449.	Лі (2, 0, 0),	Л2(3, 0, 0),	(0, —6, 0), В2 (0, 1, 0), Сх(0, 0, 3),.
С2(0, 0, —2). 450. а) Мі (3, 2, 1) і М2(—4, —1, 2); Ь) пряма лежить на по-
верхні; с) дотикається до поверхні в точці М (—3, 0, 0).
451. 6%4-5(/+ 7г — 4 = 0, ^Цр= 4-=	452. 2х+3г/ —5 = 0 і
о □ і
6х + 9у + 7 = 0. 453. Мг (3, —1, 0); М2 (0, 2, 1). 454. х2 — 4хг — 8уг = 0.
455. Вісь 02 і пряма —= 4г =	 451 * * * * 456- а) 6 (х + І)2 — 2 (у + І)2 +
+ 6 (г — І)2 + 4 (х + 1) (г—1) = 0; Ь) (х+1)2 + (у-2)2+(г-9)2-6(х +
+ 1) (у — 2) + 2 (х + 1) (г — 9) — 2 (у — 2) (г—9) = 0. 457. (х + у + 9)2 = г2;
розпадається на пару площин. 458. а) (—14/9, —2/9, —4/9); Ь) х + ^У— 3 = 0,
г = 0; с) 2х + 4у — 6г + 1 = 0; сі) немає центра. 459. х = у = г; х — 2у + 1 = 0.
1	2	2
3~	V 9~	2 З
460. х + Зу — г — 1 = 0; ---— =--------;— =----=— .
17*
259
-	*	( 1	1	1 -»	( 1 її
461.	а) «х={0, 0,	1), “2=(у-.	О},	«з=(у=-. ~^=.	0);
->	ґ_1_	1	|	_ (_________2_	1	_41	- _	ґ_1__1_	_1Д
иі ~ 1/2 ’ )/ 2 ’ °Г	и2 ~ |	5	’ 5 ’	5 /	’	~	|-|Лз ’ -|Лз ’ ]Лз] ’
Вказівка. Розв’язки характеристичного рівняння: а) Хх = — 5, Х2 = З*
Хд = 1; Ь) Х^ = — 2, Х2 = 6, Хз = 3.
. X— 1 V 4- 1	?— 1 х— 1	//+ 1	2 — 1 X— 1	#+1
462.	а) —=1^ = —=^г=_ —=^ =
111 111
1 х------ У----Е~ 2-5" х-----У----2------Т"
2 — 1	, О	6	3	6	*	6 _ З
“ ~2~ ; Щ “=4	ї - б ’	1	"	1	~ —1 ’
1	1	1
а	а	з
--і— = —|	= —2	; х — у = 0, х +у — г = 0, X + г/ + 22 — 1=0.
х'2--------------Зг'2
463.	а) А_ + /2+-ї|- = 1; Ь) х'2 + /2 = 3.
464.	1) 4х'2 + 8/2 — 2г'2 — 5 = 0; 1) х'2 +/2 — 2г'2 = 0; 3) Зх'2 + б/2 —
— 2г'2 4-6 — 0; 4) 2х'2 + 5/2 4- 8г'2 — 32 = 0; 5) 2х'2 4- Зу'2 = /бг'; 6) х'2 4-
+ 2у'2 — 2 = 0. Вказівка. Рівняння еліптичного та гіперболічного цилінд-
рів зводимо до канонічного вигляду так. Серед розв’язків характеристичного
рівняння два розв’язки будуть відмінні від нуля і коефіцієнтами в канонічному
рівнянні при квадратах. Для знаходження вільного члена «а» беремо одну
з точок лінії центра циліндра Мо (х0, у0, г0), і тоді а = 2Р (х0, у& г0).
т/5
465.	у'2 =	—х'. 466. 1) Еліпсоїд; 2) параболоїд; 3) однополий гіпербо-
лоїд; 4) уявний конус; 5) еліптичний циліндр; 6) дві площини: 2х + у = 0, у 4-
+ 2г — 2 = 0; 7) дві паралельні площини: х — 2у + Зг + 2 = 0, х — 2у + Зг —
— 3 = 0; 8) дві площини, що перетинаються; 9) еліпсоїд; 10) параболічний ци-
ліндр; 11) гіперболічний циліндр.
РОЗДІЛ IV
Лінійна алгебра
467.	11. 468. —5. 469. зіп (Р — а). 470. 1. 471. 2 соз2472. (а+&)2.
473. 1. 474. зес2 а. 475. 4аА. 476. —1. 477. 1. 478. 1. 481. х =-і-;
11	2	1
у = -у • 482. х = — ; у = 7. 483. х = у-; у =	484. х = соз ф — а),
у = зіп ф — а). 485. х = соз а соз [3, у = соз а зіп р. 486. х = а зіп а + Ь соз а,
г/ = асоза — Ьзіпа. 487. При а 4 ±6 система визначена, при а —6 —
невизначена, а при а = — 6 — несумісна. 488. При ас — Ь2 0 система ви-
значена, при ас — Ь2 = 0—невизначена.
260
489. При аЬ 4= 90 система визначена, при аЬ = 90 і а = 6 — невиз-
начена (несумісна). 490. Система визначена при X 4= —4, X 4= 8;
=— у — —	* -. При X =—4 — система невизначена, а при
X —8	X — о
= 8— несумісна. 491. Система визначена при X #= —2, X =£ 10;
7 — 4Х	—X —23
(X + 2) (X — 10) ’ У (Х + 2)(Х—10) •
X =
X =
X =
При X = —2 і при X = 10 — система несумісна. 492. Система визначена
X 4= 3; х = —5, у = 5. При X = 3 — система невизначена.
л	З (А,+ 7) ЗХ —10
визначена при X —100; х = - х цо = У= х+100
система несумісна.	_
497. 12. 498. —31. 499. —8. 500. 20. 501. (а + Ь + с) (а2 + Ь2 4-е2 — аЬ — Ьс — ас).
Вказівка. До першого стовпця додати другий та третій. 502. ах2. Вка-
зівка. Відняти останній стовпець від перших двох. 503. х2 (За 4- х). Вка-
зівка. Відняти від першого стовпця другий, а від другого третій.
504. (а—Ь) (Ь—с) (с—а). Вказівка. Відняти від першого рядка дру-
гий, від другого третій. 505. соз2 [3 — соз2 у. Вказівка. До третього стовп-
81П (а — Р) 8ІП (Р — V) 8ІП (ї — а) ГА. Л ГЛО
ця додати другий. 506. -------—-----тгп--й--------• 507. 0- 5®®* х в
г}	соз2 а соз2 (З соз2 у
= —2. 509. х = 0. 510. хг= 3, х2 = 5. 511. хг = 3, х2 = — 1, х3 = — 3.
хх=1, х2=1, х3=1. 514.	—, х2 = -у, х3 = —•
З 1	З
516. %!= —, х2 = —, х3 = —— •
513.
при
493. Система
Х + 100 ’ * - X + 100  При х = —10°
494. а) к = ± 1; Ь) к = — 1; 3. 495. —15. 496.-48.
Хі = З, Х2 — — 1» х3 — 0.
так:
х2.
а3 —
515.
517.	Хі = 6с, х2 = ос, хз —	518. Система несумісна.
519.	Система невизначена, х± і х2 виражаються через х3, наприклад,
= 5х3 + 2, х2 — 1 — Зх3; надаючи х3 довільні значення, дістанемо х± і
520.	Система несумісна. 521. При а3 4= 27 система визначена, при
= 27 — несумісна. 522. При аЬ 4= 15 система визначена, при а — З, Ь = 5 —
невизначена, при аЬ = 15, але Ь З, Ь 5 — несумісна. 523. При а 4= — З
— система визначена; при а = —3 — несумісна, якщо Ь 4= 1 .
524. а) 23. Ь) 27. с)	, а) п(п~ .
525. а) не є членом визначника; Ь) член визначника сьомого порядку має
знак мінус; с) не є членом визначника; (і) член визначника п’ятого порядку і
п(п— 1)
має знак плюс. 526. апа22а33... апп. 527. (—1) 2 а1п а2 п_1.. .ап1.
528. Хі = аь х2 = а2,..., хп^= ап. 529.	== 0, х2 — 1, х3 = 2,..., хп =
= п— 1. 530. Визначник змінить знак на (—1)п—1. 531. Визначник змінить
п(п—ї)
знак на (—1) 2 . 532. Визначник не зміниться. 533. Визначник не змі-
ниться. 534. Визначник змінить знак на (—1)л. 535. Визначник не зміниться.
Вказівка. Розглянути загальний член визначника. 536. Визначник дорів-
нюватиме нулеві. 537. 8а + 156 4- 12с — 19с?. 538. —2а 4- 386 — 76с — 54с/.
539. 0. 540. —8. 541. —3. 542. 160. 543. —1. 544. 394. 545. —8204.
546. 396. 547. (—1)п—1. 548. а!. 549. 2п 4- 1- Вказівка. Відняти пер-
ший рядок від усіх останніх, а потім у здобутому визначнику до першого стовп-
ця додати всі останні.
261
п(п—1)
550. 2ге-1 (Зп + 2). 551. (—1) 2 х(х — 1)... (х — п).
552. (^2 — аі) (“з — аі) (“і — «і) • • • (ал — “і) X
X (а3 — а2) (а4 — а2)... (ап — X
X (а4 — а3)... (ап — а3) X
X (ап — а^) = П (аі — а]).
в к а. Відняти перший рядок від усіх наступних, розкласти по першо-
Вказівка. Відняти перший рядок від усіх наступних, розкласти по першо-
му стовпцю; потім з кожного стовпця відняти попередній, помножений на
Винести спільні множники з кожного рядка, визначник зведеться до початково-
го вигляду, далі процес продовжити аналогічно.
553. хіх2х3... хЛ П (хі — ху).
п(п—1) и
554.
‘<1	2	2
п(п—1) _
555	П зіп Фг + зіп фі’ ”
1<1	2	2
556. Хі = х2 = х3 — х4 = 1. 557. хг = х2 — — 1, х3 = х4 — 1.
558.	‘	‘	'	~
559.
560.
561.
562.
хх =1, х2 = 2, х3 = — 1, х4 = — 2, х5 -= 1.
хх = 5, х2 = 4, х3 = 3, х4 = — 2, х5 = — 1.
91
^і=“їу-» х2
21
Х1 — '5' ’ х2 — — Х3 —-----
1	1	З
Х1 = -Т, х2=т. х3 = т, х4=т
х4 = 2, х2 = — 2, х3 = 1, х4 = — 1. 565. 2. 566. 3. 567.3. 570.3.
3. 572. 3. 573. 3. 574. 4. 575. 2.
50
11 ’
Х3- п
33
25	_ 16	_ 28
, х4- п , х5- п .
16
х4 - 5 .
— і-. 563. Система несумісна.
5 ’
564.
571.
576.	Наприклад, загальний розв’язок х4 = х3 — 2х4 +1, х2 = 2х3 + х4 + 2.
577.	Наприклад, загальний розв’язок х± — 2х3 + Зх4 — 5, х2 = Зх3 —х4 + 3.
578.	Наприклад, загальний розв’язок х3 — 5хі — 7х2 — 12, х4 = х± + 2х2 —
— 4. 579. Система несумісна. 580. Наприклад, загальний розв’язок х3 = — 8хх +
+ 4х2 — 1, х4 = 0, х5 = 2хх — х2 + 1. 581. Система несумісна.
582.	Наприклад, загальний розв’язок х± = 6х4 — 11, х2 = —13х4 + 24, х3 =
«= 17х4 — 29. 583. При (1 — X) (2 + X) =^= 0 х4 = х2 = х3 = а—г-х • При X = 1
/\а	।
розв’язок, залежний від двох параметрів, наприклад, х± — 1 — х2—х3. При X =
= —2 — система несумісна. 584. При (X — 1) (X + 2) =/= 0 х4 = — х2 —
1
“Х + 2’
рів. При
585.
X3 + 2Х2 — X — 1
Х + 2’
(Х + 1)2
х3 — —л—пі— • При X — 1 розв язок, залежний від двох парамет-
Л -ь 2
X = — 2 — система несумісна.
ГГ \	А	2 — X2	2Х — 1
При X (X + 3) #= 0 хх - х + 3) , х2 - х, (X + 3) ’ Хз~
X (X _[_ 3)---’ ПРИ = 0 і при = — 3 — система несумісна.
262
586. При (X — 1) (А, + 3) =# 0	= х2 = хз = *4 = т~т“5-
Л о
При Х=1 загаль-
ний розв’язок
сумісна.
587. Ранг
має вигляд = 1 — х2 — хз — х4- При X = 3 — система не-
матриці
аі &і Сі с?і
<22 ^2 ^2 ^2
дорівнює двом і не змінюється при ви-
ап^псп^п,
кресленні останнього стовпця.
588.	Система трьох лінійних рівнянь з двома невідомими, для якої розши-
рена матриця та три матриці з коефіцієнтів при невідомих для будь-якої пари
рівнянь мають ранг 2.
589.	Система трьох лінійних рівнянь з двома невідомими, в якій ранги мат-
риць з коефіцієнтів при невідомих у будь-якій парі рівнянь дорівнює двом, а
ранг розширеної матриці дорівнює трьом.
590.	Система трьох рівнянь з трьома невідомими, в якій ранги усіх мат-
риць з коефіцієнтів при невідомих довільних двох, а також усіх трьох рівнянь
дорівнює двом, а ранг розширеної матриці дорівнює трьом.
591.	Система чотирьох лінійних рівнянь з трьома невідомими, в якій ран-
ги матриць з коефіцієнтів при невідомих будь-яких трьох рівнянь дорівнюють
трьом, а ранг розширеної матриці дорівнює чотирьом.
592.	=
А. і. о.
, 0, 1 ). Загальний розв’язок
х = Сі х(1) + с2х<2\ де Сі і с2 — довільні сталі.
593.	х^ = (1, 1, 1, 0), х<2) = (1, —1, 0, 1). Загальний розв’язок х =
->(1)	-> (2)
= СіХ + с2х.
594.	= Н,------------------------------» 0, 1). Загальний розв’язок
уу(і) _і с у(2)
595.	х^ := (1, 2,	1, 0^ ,	—1, 3,---^-, 0, 1^ • Загальний
РОЗВ’ЯЗОК X = СіХ^ = с2 х<2\
596.	Система має єдиний нульовий розв’язок. Фундаментальної системи
розв’язків не існує.
597.	х(1) = (1, 2, 1, 0, 0), х(2) = (—2, 1, 0, 1, 0), х(3) = (1, —2, 0, 0, 1).
Загальний розв’язок х = сх х^ + с2 х<2) + с3 х<3).
598.	х(0) = (1, —1, 0, 0), х(1) = (1, 1, 1, 0), х(2) = (—1, 1, 0, 1). Загаль-
ний розв’язок X = Х^ + Сі Х<*> + с2 х<2>.
599.	х(0) = (3, —1, 0, 0), х(1) = (2, —1, 1, 0), х(2) = (—2, —1, 0, 1). За-
гальний розв’язок X = Х<°> + СіХ^) + с2 х<2\
263
600. х(о)=(4- ’ — ь °- °) ’ «(1)=(4 • 4 - !> °) ’ *(2)=(— 4 ’
\ О	/	\ О	/	\ м
2
2
, 0, 1). Загальний розв'язок х =	+ с2
601. х(0) = (2, —1, 0, 0, 0), х(1) = (1. 1, 1, 0, 0), х(2) = (—1, 2, 0, 1, 0),
х<3) = (1, —3, 0, 0, 1). Загальний розв’язок х =	+ с2 х^ + с3 х^3).
602. > = (±,-2., -1,0, о). >) = (-!. -1’ 4’ 1’0)’ *(2)=
= ----2~» “з”» 1» Д Загальний розв’язок х — х^ +	+ с2х^-
боз. х(о)=[—і, -і- 4’ °’ °’	4’ 4’ !> °> °)<
\	£ о Л	]	\ о 4	/
> = (1,-2 , 1 0, 1, о), >> = (--1, 4.-4- 0- 0,1). За-
\ & О	\	& О	&	1
гальний розв’язок х =	+ с±х^ + с2 х^ + сз *<3)’
5 0 0
0 7 0
0 0 9
604.
608.
605.
609.
4 2 3 3
2 4 4 4
3 3 3 3
110 0
—2 —4 —5
33	1	—10
23	6	З
606.
. 607.
3 6 9
12 15 18
21 24 27
соз (а + Р) — зіп (а + (3)
зіп (а + Р) соз (а + (3)
9 7 7 7
9 9 9 9
4 2 6
6 2 4
611.	5 16 2	5 16 2	5 16 2	. 612.	—15 —7 1	—4 —3 0	—1 6 19	9 11 25	613.	1 0 0 0 2 0 0 0 5
					—19	—8	—1	1		
II 2 0 II		
614.	Поз'	615.
1 6 12 21		1 0 0
2 7 14 25	616.	0 2 0
3 8 17 27		0 0 3
4 9 17 27		
617. Ноль-матриця.
	«1Р1	0	0	0		19 31 |		7 0 0
	0	а2?2	0	0	І 619.	34 55 1	. 620.	0 7 0
ОІО.	0	0	азРз	0				0 0 7
	0	0	0	«4^4				
622.	Ц соз па	—зіп па
	11 зіп па	соз па
623. V
1 п
0 1
624. А,"-1
X П II
о Г
264
625.
X?	0	0 ..	. 0	626. 35.
0	X"	0 ..	. 0	
0	0	X" ..	. 0	•
627.	5	4	3	2	1
	10	8	6	4	2
	15	12	9	6	3
	20	16	12	8	4
	25	20	15	10	5
628.
0 0 0 ... X"
—1	629.	—2	2
5	.	10	— 10
13		8	—8
		13	— 13
		5	—5
632. а) і-и і
630.
10 0 16
4 0 5
/’-й рядок добутку АВ поміняються
пець добутку АВ поміняються місцями.
місцями; Ь) і-и і /’-й стов-
634.
1
—2
637.
639.
641.
_____1_
2
З
2
2
З
5 “ 5
1
5
1
5
__23
З
4
З
____7_
З
В к а з і
2_
5
£
"5
1
5
1
5	]
1
5 ~ <
34
З
5
З
__Н_
З
635.
16
З
__2_
З
5
З
8
—5
2
сова зіпа
—зіпа соза
638.
0
—1
1
2
1
2
640.
£
4.
2
1
1
1
1
1
1
2
____1_
4
____1_
4
1
1
—1
—1
1
—1
1
—1
1
—1
—1
1
в к а. Помножити
матрицю, обернену до матриці А
обидві частини рівняння з лівого боку на
З 5 II	_і Ц 2 —5 11
, тобто на А =	, тоді
12	—1	З
11-8 -14
5	9
644. X =
1
З
642. X = у
2
4
13
21
1
—5
5
0
13
16
6
—4 10
5 —12
. 645. Не буде.
646. Не буде.
647. Буде, якщо пряма проходить через початок координат, не буде в ін-
ших випадках. 648. Буде. 649. Не буде. 650. Не буде. 651. Буде. 652. Не
буде. 653. Не буде. 654. Буде. 655. Буде. 656. а) (—2, 10, 16); Ь) (0, 0, 0, 0).
265
657. а) х = (-4". 4’ 4-’ 4-): &) * = <Ь Ь Ь !)- У =
\ о О О о /
== (2, 0, 1, —1), г = (3, —4, 0, —1). 658. Лінійно залежні. 659. Лінійно неза-
лежні. 660. Лінійно незалежні. 661. Лінійно незележні. 666. Вказівка. Пер-
ший спосіб. Визначник, складений з координат векторів ві, е2, е3, дорівнює 4;
тому вектори ві, е2, ез лінійно незалежні і утворюють базис. Базис, в якому
задані вектори, позначимо через /і, /2, /3, тоді е± == — /і + 2/2 + /3, е2 = 2/4 4~
+ /з — /з»	== /і + % — /з»
х = 7/4 + 9/4 — 4/3. Матрицею переходу від ба-
—1	2	1
зису {/} до базису {е} є матриця Т =
2	1	2
1 —1 —1
а обернена
до
неї
рівність у базисі,
коефіцієнти лінійної комбінації х = х е± + х2 е2 + х3 е3. Ця
в якому задано координати усіх векторів, має вигляд:
—1	2	1
2	1	2
1 —1 —1
X
хі
Х2
хз
II 7
9
II	—4
Звідси х*=1, х* = 3, х' = 2. 667. (1, 1, 1).
668. (2, 1, —1). 669. (1, 1, —1, —1). 670. (2, 1, 2, 1).
671. Доведення. Хай вектори задано в деякому базисі { / }. Обчислюючи
визначники, складені з координат системи векторів, бачимо, що вони не дорів-
нюють нулеві. Тому системи векторів лінійно незалежні і утворюють бази. По-
значимо координати довільного вектора х у базисі {е} через хі, х2, х3, а в базисі
(є'} через X . х', х'- ТОДІ X = Х1 ех + Х2 Єг + х3е3 = х’ е + х е + X е . Ця рів-
к а О	X X	£	£	о О
	1 1 1	Х1		1 2 3	Х1	
ність у базисі {/} набуває вигляду:	12 1	• х2	=	2 1 2	4	Помно-
	1 1 3 |	Хз		1 3 1	хз	
266
живши останню рівність з лівого боку на матрицю А
1 1 1
1 2 1
1 1 З
5 —2 —1 II
—2	2	0 ,
—1 о 1 II
2
2
обернену до матриці А —
5	' і с '
дістаємо *і = —х2-і~ 5хз
х2 ==
х3 =
672. х =	+ Зх2 + х3,
х'2 = 6хх + 4х2 + 4х3,
х — — 4х1 — Зх2 — 2х3.
673. Хі ~—27х—71х —41х
х	12	3
%2 =	9х' + 20/ + 9х'з
*з =	4х[ + 12х'+ 8х'
674. а) а0, аь а2, ..., ап\ Ь) £ (а), ?' (а),
пУ.
675.	а) Поміняються місцями два рядки; Ь) поміняються місцями два стов-
пці; с) матриця симетрично відобразиться відносно її центра.
676.	Базис утворюють, наприклад, вектори (1, 0, 0,..., 0, 1), (0, 1, 0,...
..., 0, 0), (0, 0, 1,..., 0, 0),...»(0, 0, 0,..., 1, 0). Розмірність дорівнює п—1.
677.	Базис утворюють, наприклад, вектори (1, 0, 1, 0, 1, 0,...) і (0, 1, 0, 1,
0, 1,...). Розмірність дорівнює 2.
678.	Базис утворюють, наприклад, 1, х, х2,..., хп. Розмірність дорівнює
п + 1. 679. Базис утворюють, наприклад, матриці Ец (ї, / = 1, 2, 3,..., п), де
Ец — матриця, елемент якої в і-му рядку і /-му стовпці дорівнює одиниці, а
всі останні елементи дорівнюють нулеві. Розмірність дорівнює п2.
680.	Базис утворюють, наприклад, матриці рц (і < /; ї, / = 1, 2,..., п),
де Ру — матриця, у якої елементи [у = /< = 1, а всі інші елементи — нулі.
Розмірність дорівнює П	. 681. Розмірність дорівнює 3. Базис утворю-
ють, наприклад, вектори аІУ а2у а3. 682. Розмірність дорівнює 3. Базис
утворюють будь-які три вектори. 683. Розмірність дорівнює 2. Базис утворю-
ють, наприклад, вектори аІУ а2. 684. а) Не є лінійним перетворенням; Ь) не є
лінійним перетворенням; с) не є лінійним перетворенням; сі) є лінійним перетво-
ренням; е) не є лінійним перетворенням; /) не є лінійним перетворенням.
685. |	1 сова	—	зіп а |	
	| зіпа		соз а І	
688.	1	1	1	
	-			
	3	3	3	
	1	1	1	
			— —	
	3	3	3	
	1	1	1	
	-		— .		
	3	3	3	
686.
687.
689. ер — лінійне перетворення. Вказівка. Ба-
1 0 0
0 0 0
0 0 0
1 0 о
0 1 о
0 0 0
267
зис, в якому задано координати векторів х і (рх, позначимо через еІУ е2, е3, тоді
координати базисних векторів {е} у цьому самому базисі: ві = (1, 0, 0), е2 ==
= (0, 1, 0), е3 = (0> 0» 1) і фЄі = (1, 0, 1), ер е2 = (1, 1, 1), ф е3 = (1, 1, —1),
а матриця перетворення ф буде: Лф =
1 1	0
0 1	1
1 1 —1
690. ф — лінійне перетво-
1 0 0
З 1 0
0 0 1
рення, а його матриця Лф =
. 691. Вказівка, фх — (хх + 1,
х2, х3), <ру = (У1 + 1, у2, у3), <р (X + у) = (хХ + Уі + Ь х2 + у2, Хз + Уз), <рх +
+ <РУ = (хх + У! + 2, х2 + у2, х3 + Уз). Отже, <р (х + у) ± <рх + <р«л і перство-
рення ф не є лінійним. 692. ф — лінійне перетворення, його матриця
1 0 0
0 0 1
0 1 —2
693. ф — не є лінійним перетворенням. 694. ф — лінійне
перетворення, його матриця Лф =
0 0 1
0 1 0
1 3 —1
695. ф — лінійне перетворен-
ня, його матриця Лф —
0 0 11
0 10 1
10 10
2 0 0 1
696. Доведення. Щоб переконатися в
існуванні єдиного лінійного перетворення, досить показати, що вектори аІ9
а2у а3 лінійно незалежні. Позначимо базис, в якому задані всі вектори через
Єї, е2у е3, а матрицю шуканого перетворення в цьому базисі через Л, тоді Аа±==
Роз-
268
701. а)
0	1	0	0 ...	0	0
0	0	2	0 ...	0	0
0	0	0	3 ...	0	0
ь)
О	1	о	о	...	о	о
О	0	1	о	...	о	о
О	0	0	1	...	о	о
0 0 0 0 ... п О
О 0 0 0 ... О О
О 0 0 0 ... 1 о
о о о о ... о о
702. У матриці поміняються місцями і-й і /-й рядок та і-й і /-й стовпець.
1 3 2
З 1 З
2 2 1
703. а)
; Ь) Разе'язання. Матриця переходу від базису {е} до ба-
зису {/} є Т =
а обернена до неї Т~1 =
1 —1	0
0	1	—1
0	0	1
Тоді за
1 1 1
0 11 =
0 0 1
формулою А^~Т~1АеТ дістанемо Л/ =
1 —1	0
0	1	—1
0	0	1
1 2 З
2 1 2
З 3 1
	—1	0	1	704.	1	2	2	
5=	—1 —3 _2		3 —1 —2	. 705. Розв язання. Складаємо харак-
	3	6	7		2 —3	1	
теристичне рівняння перетворення: | А — ХЕ | =
1-Х 0
1	— А
1 1 1
0 1 1
0 0 1
0
1
Корені його = Х2 = 1, Х3 = —1 є власними значеннями. Позначимо через
ві, е2, е3 базис, в якому задане лінійне перетворення матрицею Л, а через
х2, хз — координати власного вектора. Складаємо систему однорідних рівнянь
0
0
0
(Л — ХЕ)
, фундаментальні
розв’язки якої і будуть власними век-
торами. Для кореня X = 1 дана система набуває вигляду
— хі + х2 + х3 = 0,
+ х2 — х3 = 0,
х2 = 0.
Ранг матриці системи дорівнює двом, тому фундаментальна система має (п — г)
розв’язків, наприклад, (1, 0, 1). Власні вектори для X = 1: с (1, 0, 1), де с =/= 0.
Для кореня X — —1 система однорідних рівнянь набуває вигляду
хі 4“ х2 4~ хз — 0>
 Х2 =0,
Хі + х2 + х3 = 0.
Фундаментальна система має один розв’язок, наприклад, (1, 0, —1), а власні
вектори для X = —1 будуть: с(1, 0, —1), де с 0.
269
706.	1Х = 1, 12 = 2, 13 = —2. Власні вектори: С (5, —3, 2) для 1 = 1;
С (2, 0, 1) для 1 = 2; С (2, 0, —1) для 1 = — 2, де С =£ 0.
707.	1і = 12 = 1, 13 = —1. Власні вектори: Сі (2, 1, 0) + С2(1, 0, —1) для
1=1, С (З, 5, 6) для 1 = — 1, де Сх і С2 не дорівнюють нулеві одноразово
і С=# о.
708.	її = 1, 12 = 13 = 0. Власні вектори С (1, 1, 1) для 1=1; С (1, 2, 3)
для 1 = 0, де С 0.
709.	її = 12= 1, 13 = 14 = 0. Власні вектори: С (0, 0, 0, 1) для 1 = 1;
Сі (0, 1, 0, 0) + С2 (0, 0, 1, 0) для 1 = 0, де Сі і С2 не дорівнюють нулеві од-
норазово і С 0.
710.	її = 3, 12 = 13 = — 1. Власні вектори: С (1, 2, 2) для 1 = 3; С(1, 2, 1)
для 1 = — 1, де С 0.
711.	Характеристичне рівняння | А — 1Е | = І2 (1—1) — 4(1—1) =
= (1—1) (І2 — 4) = 0 має три різні корені 1Х = 1, 12 = 2, 13 =— 2. Отже,
10	0
В =
матриця А подібна до діагональної матриці
0 2 0
0 0—2
Ця матриця є
матрицею лінійного перетворення у базисі {/}, який складають власні векто-
ри. Власні вектори, що відповідають власним значенням 1, 2, —2, відповідно
запишемо у вигляді Ц = (5, —3, 2), /2 = (2, 0, 1), /3=(2, 0, —1). Координати
цих векторів записані в базисі {е}, в якому перетворення має матрицю А. За-
писуючи
власних
5
= —З
2
координати власних векторів {(.} стовпцями відповідно до порядку
значень матриці В, дістаємо перетворну матрицю Т =
2 2
0 0
1 —1
712.	Вказівка. Характеристичне рівняння | А — 1Е |=
= І3 — І2 — 51 — 3 = 0 має корені 11=12 = — 1, 13 = 3. Власні вектори, що
відповідають власному значенню 1 = —1, знаходимо з системи рівнянь
2%і — Зх2 —р 4х3 = 0,
4хі — 0х2 -р 8х3 = 0,
бхі — 7х2 + 8х3 = 0.
Фундаментальна система складається з одного розв’язку, наприклад, (1,2, 1);
власні вектори С (1, 2, 1), де С 0. Тому що двократному кореневі 1х =12=—1
відповідає лише один лінійно незалежний власний вектор, матрицю А лінійного
перетворення не можна звести до діагонального вигляду. Власні вектори, що від-
повідають 13 = 3, мають вигляд с (1, 2, 2), де с 0. Зауваження. Якщо,
хоча б для одного кореня 1х з кратністю /ті, фундаментальна система розв’язків
містить менше ніж т розв’язків, то матриця А не може бути зведена до діаго-
нальної; перетворної матриці Т не існує.
713.	Матриця до діагонального вигляду не зводиться, і перетворної матри-
ці не існує.
714.	7і=(1, 0,-1),	0 0	0
7 = (1, 3, 8), В= 0 3 0
->	І 0 0 —З
/3 = (—1, 3, —8);
II 1	1	—1	І|
;	Т = 0	3	З
II —1	8	—8	II
270
715.	Матриця до діагонального вигляду не зводиться, і перетворної матри-
ці не існує.
716.	£=(2,	1,0),	||1	0	0	112	1	З II
= (1,0.-і), В= 0 1	0 ; Т = 1	0 5.
-	|| 0	0	—1	II 0	—1	6 II
їз = (3, 5, 6);
717.	Не буде, бо для вектора а = (0, 1,0) (а, а) = — 1 < 0.
718.	Вказівка. Вектори аІУ а2 — ортогональні, бо (аІУ а2) — 0. Решту
векторів базису знаходимо з умови попарної ортогональності. Шуканий вектор
позначимо через х = (хі, х2, *з» *4). Дістанемо
(х, ах) = х4 — 2х2 + 2х3 — Зх4 = 0,
(х, д2) — 2х4 — Зх2 —р 2х3 —р 4х4 — 0.
Розв’язки (2х3— 17х4, 2х3— 10х4, х3, х4) цієї системи утворюють двовимірний
підпростір, ортогональний до векторів а± і а2, а тому будь-які два взаємно
ортогональні вектори цього підпростору задовольняють поставлені вимоги. Візь-
мемо довільний частинний розв’язок а3 = (2, 2, 1, 0). Другий розв’язок знахо-
димо з умови ортогональності до а3: 2 (2х3 — 17х4) -|- 2 (2х3 — 10х4) + х3 = 0,
звідси х3 = 6х4. Покладаючи х4 == 1, дістаємо шуканний розв’язок а4 =
= (—5, 2, 6, 1).
719.	Можна добавити вектори а3 — (1, —2, 1, 0); а4 = (25, 4, —17, —6).
720.	Візьмемо Ь± = «і = (1, 2, 2, —1). Вектор Ь2 шукаємо у вигляді Ь2 —
= а2 + аЬх; а — знаходимо з умови ортогональності векторів і Ь2, тобто
(62, Ь±) = 0. Звідси а — —	; а= 1, тоді Ь2 = (2, 3, —3, 2). Вектор Ь3
(Ьь £)
шукаємо у вигляді Ь3 = а3 4-	+ а2Ь2; а4 і а2 знаходимо з умови ортого-
нальності вектора Ь3 до векторів і Ь2, тобто (Ь3, Ь4) = 0, (Ь3, Ь2) = 0. Звідси
«і = — 3, а2 = 1, тоді Ь3 = {2, —1, —1, —2}. 721. (1, 1, —1, —2), (2, 5, 1, 3).
722. (2, 1, 3, —1), (3, 2, —3, —1), (1, 5, 1, 10).
723. Розв'язання. З характеристичного рівняння
-1-Х —2	2 II
—2	1-Х	0	=0,
2	0	1-М
І А — КЕ | =
визначаємо власні числа матриці А:	= 1, К2 — З, К3 = —3. Відповідні їм
власні вектори будуть: — (0, 1, 1), е2 = (1, —1, 1), е3 = (2, 1, —1). Матриця
271
А симетрична, а власні числа різні, тому власні вектори взаємно ортогональ-
1
ні. Матриця В = 0
0
0 0
З 0
0 —З
Нормуючи власні вектори та записуючи їх
координати стовпцями,
дістанемо ортогональну матрицю
/з	у б
т_ і__________і_	і
~	/2	/3	/6
1	1 1
/2	УЗ	/6
~,пл -*	І і 2	2 \	-	( 2	1	2 \ -*	(	2	2	1 \
724‘ Є1	\ 3 ’ 3 ’ 3 /	\ 3	’ 3	’	З/’*3	\	3’3’	Зр
в =
3 0 0
0 6 0
0 0 9
1	2	__2
3	3	3
2	1	2
З	~3~	З
2	2_____1^
3	3	3
- І 1	1	1 \	( 1	1 \
/25. Єї = | —х=-, —-хх, —хг , е2 = —-хг-, 0,-— ),
\ /З	/З	/З У	\ /2	/2 у
•*	/2
726. ех=
1	1	1
УЗ	/2	/6
7=	0 -4- .
уз	Уб
1______1	1
уз	/2	/6
2 М	_ і
З’ З/’	\ 3 ’ — з ’ з/
* __ М 2	2 \
Єз	\ 3 *	3 ’ з) ’

9 0 0
0 18	0
0 0—9
2	2	1
3	3	3
2	1	2
З	—	3 “ З
1	__2_	2_
З	~	З	З
272
727. Єі =
4-- -4-’° -
]К2	/2	/
* / 1
^2 — І /— >
\ ^18
1	4 \
]/ 18 ’	/Ї8 /’
9 0 0
7ОЯ -* _	( 1 і і м -* _ ( 1
728‘ Є1	\ 2	’ 2	’ 2	’ 2 /	’	\ 2	’
7	( і 1	1 И 7 / 1
Єз	І 2	’	2	’ 2	’	2	' *4	4 2	’
1	1	2
/2	/18	3
1_______1 __2_
/2	/Ї8 ~~ 3
4	1
°	“ УТ8	3
1	__1_ _ _1_\
2	’	2 ’	2 /
1	1_ __£\ .
2	’	2 ’ 2 /’
в =		10 0 0 0 10	0 0 0 1	0 0 0 0 —3		; т =
1	1	1	1
2	2	2	2
1	1	1	1
2	2	“ 2	“	2
1	1 1
2	2	2	—	2
1	__1_ __1_ 1
2	2	2	2
729. уі + у^-уі.
730. уї-уі-уг 731. у{~	732. у^уі-у*- Х1 = У1 -	+
+ -|-»з> х2 = ~у2 — А-і/з, х3 = -^-у3. 733. у[ + у2г — уІ; х1 = -^-у1 + у2,
4 = Уз + Уз, Хз=—Уг + Уз- 734. у[ — у2 —	; хх = у2 — Уз — Уз, х2 = ух +
+ Уз — Уз> хз = Уз- 735. у2 + УІ — У%, х2 = Ц- У2у±-1- /Зу2 + УЗу3,
1 г- Уз	У 3	т/з
х2 =-з~/Зу2Н-%—Уз, х3 = —— у2 + —д— у3. 736. у{ —у2', х2 =
= Уг—Уг — Уз, *з = Уі + Уз~ У і, *3 = Уз, ^4 = У і- 737. у* + Зу2 — Зу2 ; хх =
1	2	1	1	1	1	1	1
= У=3У2 + У=^ Хі = у2У1-^ + у-бУз’ Хз = ^У1+уІУ*~у=6Уз-
738. Зу2 + 6(/2 + 9і/2; хх = ух + -|- у2 —	у3, х2 = -|- у2 + у2 +
+ -^Уз- *з = -у ^і~Т Уі~^У3- 739- —3^ —3^ + 6у«; хх = ^_ +
,	4	, 2	2,2,1	5
+ ~у^ Уз + 'з~У3' Х2 - “ у, + узГ Уі + ‘з’Уз' Хз ~ ТЇГ Уг ~
18 2193	273
2	2	1	2	2	2
---у Уз- 740. Зу* + вуї + 9УІ1 Х1=-^-у1 — -3У2+-3 Уз- Х2 “у Уі+ у Уз —
— у Уз. х3 =-у Уі + у Уз + у Уз- 741. 9у£+18^ — 9^; хх = уух+
21	122	212
+ у*/-2-з~^3’ х2 — у Уі + у Уі + у Уз> хз—~у*/і-з“^2“І—3~ У3*
742. 3^ + 6^-2у*; х1 = -р=-у1+у=-у2+^у8> х2 = -^=(/1-
11	12
"ТГ’г+ТГ’- '-"7ГЙ"ТГ!'- 743-
~-уїУ1+УЇУз+УТУз’ Х2 = -ґїУ1 + уТУз~^їУз’ Хз =
=—^уУі---Тг~У*' 744. 2^ + 4(/| — 2і/| — 4і/2 ; х2 = у (і/1 + (/2+</3+їм)
у о	у О
х2 = у (—У1 + Уі + Уз — У і)’ х3 = у .( У1 — Уї + Уз + У і)- *4 = у (У1—УзЧ-
+ Уз — Ул)- 745. 2і/2 — 4у2 ; хх = -у=- (ух + Уз), х2 = (уг — у3), х3 =
= -^(у2 + У4). х4= -р^-(у2— Уі)- 746. у* + у| + у* — Зу*; хх =
= у (Уі + Уг + Уз + У& х2 = у (Уі + У^ — Уз — У^)у *з — у (Уі — Уі + Уз —
— у& Х4 = ~ (Уі — У2 — У3+ У4)-
РОЗДІЛ V
Диференціальне числення функції від однієї змінної
747. /(х) = 3х —5. 749. Цх) = Зх2 — 5х + 2.
750.	—у:—Т’~Т:—Пі’ ^2) неіснУє-
7	З
751.	сі) = 0, х2 = ~2~ ; Ь) х^ = 2, х2 =	.
752.	«) хх = — 1, х2 = — 2, х3 — 5; * Ь) хх = — 3, х2 —	» ^з —
274
= 5 У17- 753. / (х) = х3 — 2х2 4-4х — 1. 754. / М-) = ТХТ ’ Н*-’)=
£	\ X ] X £
X— 1	_________
= 2х-Г • 755. Ф № = V ** + (2 + !’ [ф (О]2 = і2 + і + 1- 756. І(Х— 1) =
= х2 —Зх + З, /(х4-2) = х24-3х-|-3. 757. / [<р (х)] = Ззх, <р [/ (х)] = 3х’.
758.	£(—2я) = —7, £(— 1, 2) = — 2, Е (0) = О, Е (1) = 1, £^ = 1.
£(/П) = 3, £ (я) = 3. 759. / (х) = х2 — 4х, / (х — 1) = х2 — 6х 4-5.
760.	х2-|-~2— 761. / (0) = — 1, /(^-) = 0,	И1) =
= 8іп1-со32, /(^) = 2. 762. /(-!)= 1	^2+1-
763.	/ (х) = х2 — 2. Вказівка. Додати й відняти в правій частині 2.
існує. 768. 3)/гх2 + 9, 2]Лх2 + 9. 772. у = (2х + І)3. 774. у = созесх.
777.	1) у = и3, и = соз х; 2) у = и2, и = х3 + 1; 3) у = и2, и = зіп у, V =
= 5х — 1; ’4) у ~ І£ и, и = у, V = У до, до = х2 + 1; 5) у = і1и\ и — сі£ х;
6) у = 10й, и = у2, V = зіп до, до — 4х. 778. 1) у — ± ]/" х2 — а2 ; 2) у == і
±А|/^2—3)У = ^-, 4)у = ^^Т; 5) У=-^-~х<	6) ? =
10	2х
=------Р 2; 7) у = агсзіп -х—;—г. 779. — оо < х < оо.
X	' V	X2 + 1
780. — 1 < х < оо. 781. — 3 < х < 3. 782. (—оо; 2] та [3; оо).
783. (— оо; 1); (1; 4) та (4; оо). 784. (— оо; — 1] та [1; оо).
785. (—оо, 4-оо). 786. (—2; -|- оо). 787. [0; 1]. 788. |^-і-; 1}.
789. [4-;2і. 790. (—2; 8]. 791. {(2к — 1)	, (2к 4- 1)	, к =
І о І	І	Л	Л І
Г*	_ - -
== 0, 2, 4,... 792. 0;	. Вказівка. У 4 — х2 визначений на [— 2; 2], а
У зіп 2х — на
[-4я: -я]> [0; -т]' [я;
_3
2
і Т. д.
793. Визначена тільки в х = 0. 794. Не має змісту.
Г 3 1	/1	\
795. —2; — . 796.	; оо . 797. [3; 8). 798. (—оо; 0), (0; 3), (4; оо).
І	\ І
л
799. [2; 4]. 800. (— оо, + оо). 801. (0; оо). 802. (— оо, + оо).
803. (— оо; оо). 804. (— оо,	оо). 805. Так.
18*
275
806.	Ні, бо визначені на різних інтервалах. На (0; оо) — тотожні.
807.	Ні: для х < 0 / (х) < 0, а ер (х) > 0; на [0; оо) — тотожні.
808.	Ні: /(х) визначена на (—оо, + оо), а <р(х) —тільки на [0; оо).
809.	Так. 810. о =-І-(4^2 — Д2) й. 811. V =	(27? — й) й2.
812.	$=/?й. 813. V =	---55Г-. 814. 5 = х (5 — х).
З (г — 7?)	'
815.	а) 5 = У8 а2. 6) 5 =	816. 5 = х К47?2 _ х2. 817. 5 = лх2.
4	у З
818. (/=-і-]Л47?2— х2. 819. а=4лг2.
831. а) —2,67, —0,58, 3,25; 6)1,15, два інших корені — комплексні;
с) —2,6, 0,34, 2,26; <7) 1,21, два інших корені — комплексні; е) — 1,86, — 0,25,
2,11. 838. а) 0,46, 3,3; 6) 1,5; с) 3, —4,97; сі) 2, 3,56; е) 4, 0,3. 839. а) 0,7,
4,3; 6) 0,3, 1; с) 1,74, —1,14; О) —2, 1. 841. а) 0,61; 6) 0,64; с) 3,79; О) 10;
е) 0,948; /) 0,739; §) 0,51; 0 0, ±4,49. 843. 1; 7У = 100; IV = 10 000.
7	7	(—1)"+1	1
844. -тг ; п > 4. 845.	. 846. ип =----------; 0; п >	
9	15	" п2
1 / 7	\	2
847. п >	----Ь 5 ; п > 2800. 848. п > , .	; п > 142.
25 е у	|/ег 2е
849. п > 1/ -4е,~^ 11 ; п > 27. 850. п > 10 000; Ііт ип = 0; п = 2й.
г Іоє
З	п2	1
851. п>-----1; п > 3000. 852. ип = -ггу—;; 1іти„= —;
в	"	2п2 — 1	2
п>-^-1/2 + —;п>6; п. > 159. 853. 1,5. 854.1. 855. — 4~-
2 г є	6
2	11	1
856. — -Т. 857. 0. 858. —. 859. —	860. 1,5. 861. — 1. 862. А-.
о	2	2	о
863. а2 + а + 4-. 864.	. 865.	. 866.	867- ЯКІ«0 І«І>1;
3	3	3	4
1	2
-х-, якщо [ а | < 1; — , якщо а = 1; не існує, якщо а = — 1. 868. е2.
2»	о
_ 1
869.	е 5. 870. е 2 . 871. е5. 872. 1,5. 873. Іпа. Вказівка. По-
класти у а — 1-а. 874. 1па. 875. 1па — 1пЬ. 876. у аЬ.
5^2
877.	Вказівка. Додати й відняти 1 під знаком логарифма.
878.	б <4-; 6 = 0,001. 879.	6 < 0,000012.
З	о
276
880. 6 < 4-; б < 0,00001. 881. б < 4“ • 882- 6 = о ЛгГ
7	4	о + 2е
883. б < ч 25бс . 884. б < 4- ! б < 0,001. 885. б < -4г"
4 + 5є	7	1+і
886. 6	887.	888. д^-Е + 1.
і /~ 5	4	4
889.	N > І/---4, якщо & <	; N = 0 при є >
т	Є	□	□
890.	—1; не існує; 1,01. 891. 0,99; 1; 1,0201. 892. —0,999; 1; 1,01.
4	1
893.	—1; 2; 4. 894. 8. 895. —2. 896.	897. ~г  898. —2. 899. 1.
7	4
900.	—6. 901. 1,5. 902. 4/2. 903. -4 904. 0. 905. 8. 906. 1,5.
907.	П 2^ * Вказівка. Покласти х = 1 + у і скористатися Ньютоно-
5	12
вим біномом. 908. 0,5. 909. 0,25. 910.-911. —. 912.	913. 0,25.
о	о	□
9	5
914.	4 - 915. 0,75. 916. 0. 917. 2,5. 918. 0. 919. 3. 920. -т-.
<5	*
4	—
921.	1,5. 922. —. 923. 0,6. 924. 0. 925. 0,5. 926. 2. 927- /3.
5	12
928.	- 929.-2/2. 930.--------т-. 931.^-. 932. 0. 933. —4.
4	4	3
1	2
934, — -о-* 935.--------. Вк а з і в к а. Покласти х — 1 == а. 936. 0,5.
З	л
937.	/2. 938. —2. 939. —0,5. 940. 0,5. 941. — зіпа. 942. 0,25.
1	іЛ2	—2
943.	—4. 944.----945.	0,75. 946.--/—• 947.	е3.	948.	е .
24	2
949.	Уе. 950.	е~\	951. е~\ 952. е“Р.	953. е2. 954.	е5.	955.	ес1е“.
Вказівка. У дужках додати й відняти 1. 956. еах. 957. Іпа.
958.	іпа — 1п&.	959.	960. е~‘.	961. а — Ь.	962.	2. 963.1,5.
96	4.1. 965.1.	966.2.	968.	б < —. 969. б < - ,	•
а	2 І х01 + 1
973.	Неперервна на [—2; 2]. 974. Неперервна на [—1; 1]. 975. Неперер-
вна, за винятком точки х = 0. Стрибок дорівнює 1. 976. Розрив усувний;
Ь — —2. 978. Неперервна скрізь. 979. Розрив першого роду при х = 1.
980.	При х = 1 розрив другого роду. 981. Розрив другого роду при
х = 1; (і (1 — 0) = 0, / (1 + 0) = оо. 982. Розрив першого роду при х = 0.
983.	Розрив першого роду при х = 0;	—0) = — 1; / (+0) = 1.
277
984.	х — п (ціле число) — точки розриву першого роду.
985.	х — 0 — усувний розрив. 986. Усувний розрив при х = 0.
987.	Розрив другого роду при х == 0.
988.	Записати Р (х) у вигляді хп	1 розглянути
достатньо великі вартості х. 989. ^ 1,7693. 991. —2,602; 0,340; 2,262.
992. Розрив другого роду. 993. При х = 0 розрив першого роду.
994. Розрив першого роду при х = 0. 995. Скрізь неперервна.
996. Розрив другого роду при х = 0, / (—0) та / (+ 0) не існують.
997. Неперервна скрізь. 998. —0,8794; 1,3473; 2,5321. 999. Ні.
1000. д < -р. 1001. 6 < ЮОЗ. Рівномірно неперервна.
1004. Рівномірно неперервна. 1005. Рівномірно неперервна на (—оо, 4-оо).
1006. 6 < є; 6 < є2. 1007. 6 <	1008‘ 6 < 0,0001є.
о
1009.	Нерівномірно неперервна; д < аоє.
1010.	/' (х) = 2х — 1; Г (0) = — 1; І' (1) = 1; Г (2) = 3.
1011.	/' (х) = ха + 1;	(-1) = 2; Г (2) = 5.
1012.	г (х) = з -; Г (-3) = 4-; Г (0) = 2-
Н ~г Ч	*
2	1	2	1
1013.	=	Г(2)=-т. 1014. Г(х) = —±-;П_2) = 2-.
1018.	_і-=-  1019. -Д—.	1022. — ЗзіпЗх. 1025.	.
/х2+1	Зу^'х2	(ха+1)а
2	1
1026.	—----• 1029. ——х. 1030. 4x3 —9х2 + 8х. 1031. х2 — 4х 4- 3.
З3/х	*+х
1032.	х4 + 4х2 — 6х + 1. 1033. Зх2 зіп х + х3 соз х.
1034.	1Д^72Х5122Х. 1035. 4х . 1036. 6x5 — 8x3.
(х2 + І)2 соз2 х	(1 — X2)2
1037.	2х сі£ х — х2 созес2 х — 5. 1038. І£2 х. 1039. созес зес2 х 4- 2х.
□
1040.	х21пх. 1041. х2 зіп х. 1042. - 1 , . 1043. 6х2 (х3 — 1).
х4 — 1	у 7
1044.	З соз Зх. 1045. 10 5х зес2 5х. 1046. 4 сі£ 4х. 1047. —4 соз3 х зіп х.
1048.	зіп3х. 1049. сІ£3х созес х. 1050. сі£3х. 1051. зес4 х. 1052. созес3 х.
1053.	І£6 х. 1054. 3“* (Зх2 — х31п 3). 1055. х зес2 х.
1056.	—2СО52 х зіп 2х-1п 2. 1057. е~х (п — х) х^1.
1058.	20а5Ш4 5х зіп3 5х-соз 5х-1п а. 1059. 12(1 —х) х-5.
278
6х2	х4	о
1060. -п _ 3<2- . 1061. -ф-(5 —9х4). 1062. (х — 1)х“3.
(1 Xа)	о
Зу2 1 1
1063. 5х« — Зх2 — 4х. 1064. —4х»(х4+І)-2. 1065.	—2^.
у2	У	-----1
1066. Т——д. 1067. -у---------7. 1068. сі£4х. 1069.
1 — х4	х3 — 1	(зіп X + соз х)2
1070.
1071.
1074.
—х5
У 1 — х3
X2
X2
1075. —=
уТ
1072. ~.4> X» " 1073 	1
Xі + 2х + 2	/х — 4х2
1076. х2/4 —х2.
— х2
1077. (х2 — х + 1)—1. 1078. — (1 + 2х —2х2) 2. 1079. агссозх.
1080.
а
хУ х2 — а2
1081. 0. 1082.	........• 1083. —=.
у 1 + 2х — х2	Ух2 4-а2
1084. зесх. 1085. іп (х 4-У *2 4-а2). 1086. (х2 — 2х 4-2) .
1087.	——----------. 1088. 0. 1089.	. ,3*"	. .
/х(14~4х)	(х»4-1)1п2
Ю90. і—, 2„ . о .о ,	. 1091. — 10~а2*2-2а2х.1п 10.
1о£2(2х 4- 1)-1п З-Іп 2-(2х 4- 1)
їх	1	1/" х2 — оь2	1
1092.-4-4-. 1093.	4;. 1094.	. 1095. — ,	.
2	6 2	1 —х2	х	/3 —2х
1096. — 5е~5*+2. 1097. соз3 х. 1098. зіп4 х. 1099. 1§3х. 1100. хагсі§х.
ип» агсзіп/х 1102. 1п2х. 1103. -Х=. 1104.
2/1—х	/14-х2	/1-х2
1І05' хЛ+ї  /ктз- "°7-
1108. —---, *	4- х. 1109. 2х^е~хг. 1110. Д- (ех — е~х).
х 1 —х2	2	'
1111. 4(ех + е~	-х)—2.	1112. хС05х ^созх —зіпх-хСО5Х-Іпх.	
1113. /і+і? /	'і х 4~ 1 1п	1		1 ’	V 1114. —х/^. 1115.0,6.
к х / \	X	х 4-1	1	2х У х
з	3 — х		х	Ь2х
1116. —. 111	7- —	. 1118.	— . 1119.	Л.
У	у+ і		У	а2У
1120. — "У 4"	1 ’	3 *	1121. -	5у — 2х	у—Xі 2у — 5х *	у3— У

1123.------
X
1124. —
ху — X2
1125.
Х — У
1126.
1127.
1130.
СО82 у
1 Н- СОЗ2 у *
х — а
~ У — Ь'
1128.
У (х2 + У2 + В
х (1 — х2 — у2)
ех~у — 1
+ 1 ‘
1129.
1131.1—2/5. Ц32.	1 .	1133. —є-
Зг
1134. —сіє<р.	1135. сі§-?-. 1136. —1. 1137. — і§/. 1138. 2^~/4_
2	6	1—2/5
1139. СО5^~~5Шг. 1140. і§/. 1141. у = 2х — 2. 1142. 135°; 0°; 45°.
соз / + зіп /	г
1143. М (2; 3). 1144. Зх + у — 6 = 0. 1145. Зх — у — 2 = 0.
1146. І£а = 2, І£а = —2. 1147.-^-, 1148. М (— 1; 3). 1149. 45ч.
1150. Точка дотику М. (8; 2) ; дх— у — 38 = 0.
1151. Л4Х/1; З.') та Л12(2; —2). 1152. 4х — у — 7 = 0.
1153.
1156.
х1 = 1; х2 = 3. 1154. у = 2х — а. 1155. ххо + ууо = г2.
уу0 = р(х + ха). 1157.-^---^-= 1. 1158. 2х-у+12 = 0;
2х — у — 12 = 0. 1159. 2х — у + 1 = 0; 2х —у — 1 = 0. 1160. агсі§3.
1161. агсі§3-. 1162. 7х — у — 11 = 0; х + 7у — 23 = 0.
1163. Зх — 2у — 1=0; 2х + Зу — 5 = 0; Зх — у — 4 = 0; х + Зу — 28 = 0.
1164.	П65. М І2; та У /10; А-Г
1 / О	\	£ І	І 10 у
1166. ~ 31,2 км/год. Вказівка. Позначаючи через х та у віддалі па-
роплавів від гавані, а через 5 — віддаль між ними, будемо мати 5 = Ух2 + у2,
у = 20/, х = 24/. 1167. ~ 229,4 м/сек. 1168. о = /3— 12/2 4-32/; рух у зво-
ротному напрямі від і — 4 до / = 8. 1169. « 3,06 сек', 45,9 м. 1170. 11.
1171. 6 м/сек\ —3 м/сек. 1172.	= Аке~~кі = к (А — х) (швидкість ут-
ворення молекул нової речовини пропорційна наявній кількості перетворюва-
••	\	1 ПО СОЗ ОС 1	&Х . ,	\2 /
ноі речовини). 1173. со5 р •	1174.	= к (а — х)3 (швидкість при тримо-
лекулярній реакції пропорційна добуткові з наявних кількостей усіх трьох ре-
човин). 1175.31. 1176. 6х. 1177.51. 1178.0. 1179. 2ЗХ (3 Іп 2)5.
ПІ
1180. —4зіп2х. 1181. 23соз2х. 1182. —созес2 х. 1183. ------—г-г-.
(1—х)л+1
і"-1 ап (1 + ах)~п. 1187. 0,5.
1184. 2Л зіп ^2х + п
280
4
1188.—— .	1189. 43 соз 4х. 1190. —12.
3]/3
1192. 4. 1193. 6(—1)«(п —4)! х~л+3, п > 4.
1191. ех (х2 + 2их 4-й2 — и).
1194. «о-п!. И95.---------
а2 зіп3 /
Ь
Я	4	49
1196.— — .	Ц97.------. Ц98.	Ц99. 2(/2+1).
а	а	27а	к ‘ 7
1200. — 6 (/2 + Зі + 1) ез/. 1201. ЗІ / ~ С°8 1 .
'	1	'	/о Ґ'ЛСЗ +
1202. З сі£4 Лсозес і. 1203. 27/3. 1204. — 6е4Ч
1208. а) Ду=0,02, Ду = 0,0204, | Аг/— сії/ ] = 0а0004, 6 = 0,019;
Ь) Ду = 0,03, Ду = 0,0301, ІДу — гіу | = 0,0001, 6 = 0,003;
с) Дуда 1,7; Ду = 1,71, | Ду — йу | = 0,01, 6 = 0,0058.
1209. Ду = 0,12; /(1,03) да 3,12. 1210. Ду = 0,005; у (3,02) = 2,005.
1211.	Ду = —0,0076; зіп 29°30' « 0,4924.
1212.	Ду = —0,004; соз 45°20'да 0,703.
1213.	Дуда 0,01746; 1§45°30' « 1,01746.
1214.	Дуда 0,01744; сі§ 29°45' да 1,7495. 1215. 1,0864.
1216.	1,9494. В к а з і в к а. х„ = 90, Дх = — 1. 1217. 0,7754. 1218. 0,5120.
1219.0,0025. 1220.0,01745. 1221. Ду = 0,1401; йу = 0,14. 1222. 0,8004.
1226. Ні. 1231. —	~ 0,5289. 1232. агсі§ /3 — агсі§ 1 =	;
ІП 2	1 4“ ь
В « 1,34. 1233. (62 + & + 2)-(а2 + а + 2) = (6-а)(2£+1); В =
1234. 1'х0+1 —/х0 =--------- . __ . 1235. &3 — а3 = 3(Ь — а) В2;
2 У «о + 0
а_1Л2 + ^+£. 1236.	Ь~“--------.
ь — у з	14-а	1 4- а 4- 0 (& —а)
1239. 1,9138.	1240. 0,478.	1241. Вказівка. Розглянути різницю
1п (1 4- х) — 1н 1- 1242. Вказівка. Розглянути різницю ех е°.
т /~Ь2 -4— а2
1243. а2 4- Ь2 = 2^2; £= І/ ----- (£ — від’ємне не придатне).
л	созЬ — соз а	/і ( 9-х • 9.
1244. І - -4- • 1245. 1п ц +	_ ]п ц _|_ а) - — (1 + 5)ЗІП Ь
1246.	у^2	+	+ |/а2	=
1247.	/ (х)	= 1 — 6 (х — 1) —	10 (х — І)2	— 4 (х —	І)3 +	2 (х — І)4 + (х — І)6.
1248.	/ (х)	= 5 —	4 (х + 1) —	(х + І)2 +	(х + І)3.
1249.	/ (х)	= 2 +	2 (х — 1) +	6 (х — І)2 + 4 (х — І)3	+ (х — І)4.
281
^3	^5	^7	^3
1250.	зіп х = х---зг + “Еї-----V соз Ох або зіп х = х------5Г + Ті---------х
□І	□!	і	□!	01 О!
^2	^3	х^
ХзіпОр:. 1251. созх=1------------2Г + "зГ8ІП0а: аб° С05 х = 1-------------2Г + "4Г х
у2 уЗ іг4 у5 а
Хсоз ЄіХ. 1252.	= 1+ х +-^-+ ЗГ + 4Г + -5Г е ’
1253.	Іп х = х - 1 -	, де І = 1 + Є (х - 1),
2	О	ЧгС,
0<в< 1 1254. /5=1 + 4-(х— 1)— 4-(*— 1)2+ —3--(--^?^,
'	2	8	23-3!/^
5.	1 І О/ їх Іпс- *	। •** , зіп 0х (24 — 8 соз2 0х) X4
|=1 + 0(х— 1). 1255. х = х +-5-Н------------------------1-------------“ •-7Г •
ь	'	'	6	1 3	соз5 Ох	41
, 1	2х2	, 2-5-х3	2-5-вх4 , 2-5.8-11-х5
1256.	/1 4-х	1 4- 3 х 2! З2 + З®.З!	34-4!	И
З5-5! (Ж*)3
1257.	1п(14-х) = х 2" + "з 4(14- 0Х)4-
1260.	(0, 2) — проміжок зростання; (2; 4) — спадання,
зіп X
1261.	Вказівка. Розглянути функцію /(х) =	— та ЇЇ похідну.
2 (х__1)
1263.	В к а з і в к а. Розглянути функцію у — Іп х----та її похідну*
х т 1
взявши до уваги, що у (1) = 0.
1266.	Доведення. Розглянемо. / (х) = зіп х — х + — . Тоді / (0) = 0, /' (х) =
о
х^ ,
•= соз х— 1 4* “2”» Г (0) = 0» а який знак має /' (х) при х > 0 сказати не мо-
жемо. Шукаємо другу похідну /" (х) = — зіп х + х > 0, бо х > зіп х при х>0.
Отже, /' (х) — функція зростаюча, але /' (0) = 0, тому при х > 0 /' (х) > 0.
Звідси / (х) — функція зростаюча, але / (0) = 0, отже, при х > 0 £ (х) > 0, що
й треба було довести.
1275.	(— оо; 3) — проміжок зростання; (3; оо) — спадання.
1276.	/(х) зростає на (—оо; 1); на (1; 3)—спадає; на (3; оо) — зростає.
1277.	(—оо; —2), (—2; 0), (0; 2), (2; оо).
.	/ я я \ / я 3 \	/	З
1278.	(	-^-1,	«) , І — п.
і т. д.
1279.	(—оо; —3), (—3; —1), (—1; оо).
1280.	(о; —4^1,	оо).
\	/2 /	\ /2	/
тої ( а \ І а 2а \	/ 2а \	.	.
1281^-оо;—^	(«<»)•
282
1282. (—оо; 0), (0; 3), (3; оо). 1283. (0; оо), /(х) спадає.
1284. ^0;	; оо^. 1285. (— оо; 0), (0; 2), (2; оо).
І9ЙЙ ( п  я \	( я я \	/ я я \
1286.	,-------у — —у	, —у
9	З
1287.	(— оо; 0), (0; оо). 1288. г/тах = — при х = — .
1289.	#тіп = — 35 при х = 6.
1290.	утах = 16 при х = 2; #тіп = — 16 при х = — 2.
2
1291.	#тах = 2 при х = 0; #тіп = — при х — 2. 1292. Екстремумів нема.
11	1	19
1293.	0тіп = -у- при х = 1; утах = -у- при х = — 2.
1294.	г/тіп = 0 при х = 0; г/тах = 4 при х = ± 2.
1295.	#тіп = — 5 при х = 0.
1296.	(/тіп = 2 при х = 1; г/тах = — 2 при х = — 1.
27
1297.	#тах = -у при х = 3; при х = 0 екстремуму нема.
1298.	ї/тах = 25 при х => — 3; утіп = — 3 при х = — 1.
32	4
1299.	(/тіп = 0 при х = 0; (/тах = при х = -у .
1300.	і/тіп = 2 при х = ± 1.
1-у	/2	1 - у	/2
1301.	ушах = -у=- е 2 при х = ^-;г/тіп = —— е 2 прих=—
1302.	(/шах= у-----1п 2 при х = 1.
6	22
1303.	г/тах=у при х=1; утіп =----------д— прих = 3.
л
1304.	х — у + кп — точки екстремумів.
З з _____ З
1305.	#тах= у у<0»25 при х = —; при х—1	екстремуму	нема.
1306.	#тіп = 0 при х = — 2; #тах = 16 при х =	— 1;	£/тіп =	0	при х = 1.
1307.	Максимум при х = у ; мінімум при х — —	1 та	х = 5.
1308.	Максимум при х— 1; мінімум при х —	.
тпп	а	а	. .
1309.	х — — а та х —	— точки максимуму; х ------------мінімум,
о	2
283
1310.
1311
2аЬ
х =	— точка максимуму.
З	З
х = ± —л + Зкл — максимуми; х — ± “ я + §&л — мінімуми.
З
1312.	М = 4; т = 0. 1313. М = — ; т = 1. 1314. М = 27; т = — 8.
1315.	Л4 = 1п2; т—не існує. 1316. М — 3; т = 0.
27	1
1317.	М = 0; т =------ . 1318. М 10; т = 5. 1319. М = 1; т=^ —
4
1320.	М не існує; т — — 2. 1321. М. не існує; т — — 1.
1322.	М не існує; т == 0. 1323. М = 1 — 1п 2; т = 0.
1324. М = 8; т = 4-. 1325.	• 1326. 1. 1327.	
о	2	О
1328. х = —; висота у — сі 1/	. Вказівка. Найбільша міцність
/З	'	З
буде тоді, коли ху2 матиме максимум. 1329. Квадрат із стороною а = уГ5.
27? 1/~3	К	сі
1330. Н——у—• 1331. — •	1332. х — р---(трикутник рівнобедре-
О	Л	1
ний).	Вказівка.	5 = У р (р — а) (р — х) (а +	х — р).	1333.	30,6°.
1334.	4,075°. 1335.	а = 2л	або	293°56'.	Вказівка. V =
ла27?2	1Лг»9	а27?2 тол і /~ 2ар _	.	.
« . Л—-2- •	|/ 7?2---—2	• 1336. х =	І/	—.	Вказівка,	х{ (х) = ар	+
12Л	•	4Л	г	ҐП
+ тх-4-	І337-	-н- та	4 • ї338- 1	та	59-	І339- 4^- І340-	ііїЯІІ2Н-
<5	Лі
. а г»	г-	г /псоза
1341. Н — —. Вказівка. Сила світла т ~----------з— , де т — стала
/2	' г2
(сила джерела). Отже, НН)=——.......... 1342. -^-лТ?3.
/ (а2 + Л2)»	3
1343. її = И =	• 1344. V = 20 км/год-, витрати 120 крб. В к а з і в -
7?	80
к а. — 0,005а2 -|----— , де 7? — витрати, 5 — шлях, і — час.
1345. а = 2]ЛЗл. 1346. Радіус півкруга дорівнює висоті прямокутника.
1347. З год 12 хв. 1348. г —	. 1349. Обхват повинен дорівнювати по-
двійній довжині пакунка. Вказівка, а — л7?2Я, 2л7? Н — 150.
284
1350. ф = я, тобто поперечний переріз жолоба є півкруг. В к а з і в к а.
Дослідити на екстремум площу сегмента, а саме:
1	г2
5 = — г2ф-----— зіп ер, гф = а.
1351.-----|-. 1352. 4- 1353. т. 1354.----------Ц-. 1355. -4.
3	2	4	12
1356. 1п 2. 1357. 0. 1358. -і-. 1359. 1. 1360. 1. 1361.--------1362. 0.
о	<5
1	2
1363. 0. 1364. -о-. 1365. —оо 1366. 3. 1367. —1. 1368.
У	о
4
1369. 1. 1370. 1. 1371. 0. 1372. е«. 1373.	 1374. —1. 1375. еп.
а — Ь
__9_
1376. 4- 1п а. 1377.---------і-. 1378. е 2 . 1379. 2. 1380. —.
8	9	я
1381. е-1. 1382. е-1. 1383. —	. 1384. е2. 1385. | е.
1386. — 4 . 1387.-------у. 1388.	. 1389. —2. 1390- 4-.
У	о	120	«З
9
1391. х = — 2; у = 2. 1392. х = 0; у — х. 1393. у — ± -р- х.
□
1394. х = —1; у = -^-х — 1. 1395. х=±/3; у = — х.
1396. у = 2х ± 4" • 1397. у = 0. 1398. х = 0; у = 1. 1399. у = — х + 1; х = 0.
2к 4- 1
1400. у — 0. 1401. х =—& = 0; ±1... 1402. Асимптот нема.
1403. х = 2а. 1404. х — 2а\ у — ± (х + а). 1405. у — — х.
1406.	(—оо; 0), (0; оо); М (0; 1) — точка перегину.
1407.	(—оо; —1), (—1; 1), (1; оо). Точки перегину /И1(—1; —3) та М2(1; —3)
1408.	(—оо; 2), (2; оо); М (2; —2) — точка перегину.
1409.	Угнута скрізь. 1410. Опукла скрізь. 1411. (—оо; Ь), (Ь; оо);
М (Ь; а) — точка перегину. 1412. (—оо; —3), (—3; 2), (2; оо) при х = — 3 та
О	1Л19 /	1	\	/	1	1 \	/ 1	\
х = 2 — точки перегину. 1413. —оо;----------— І-----------— ; —-1	—; оо •
\	/2 Г \	К2	/2/	1^2	)
1 1
у точках х =-------та х =	—------перегин кривої.
1414. [2£я; (2к + 1) я] — проміжки опуклості; [(2к— 1) я; 2кя] — проміж-
ки угнутості; х = кл — точки перегину (к = 0, ±1, ±2,...).
285
1415. (—оо; —/3), (—/3; 0), (0; /3), (/З, оо); х = — /З, х = 0 та
х=]/г3 — точки перегину. 1416. (—оо; 0), (0; оо); точка перегину х = 0.
_2_	_з_	__з_
1417. (0; е 2 ), (е 2 ; оо); х «= е 2 — точка перегину. 1418. 1,92627.
1419. —2,214; 1,675; 2,539. 1420. —2,532; —1,347; 0,879. 1421. 3,27902.
1422. 0,6071. 1423. 3,78928. 1424. —3,9488; —0,2172; 1,1660.
1425. —2,602; 0,340; 2,262. 1426. —0,724; 1,22074. 1427. —0,5672.
1428. —0,67; 1,42; 5,25. 1429. 0,947; 0; —0,947. 1430. 0,739.
1431. —0,824; 0,824. 1432. —4,4935; 0; 4,4935. 1433. 1,0755. 1434. 0,90506.
1435. —2,234; 0,327. 1436. —1,8794; 0,3473; 1,5320. 1437. —3,40; 2,9.
1438. —1,8608; —0,2541; 2,1149. 1439. —0,9421; —0,20032; 1,0447.
1440. —2,2868. 1441. 0; 1,895; —1,895. 1442. 1,306 — найменший додатній
корінь, а взагалі є безліч коренів. 1443. —3,183; є безліч коренів. 1444. 0,48;
—1,72. 1445. —1,9509; 0,756; 1,694. 1446. Визначена на (— оо; + оо). При
16
х — — 2 #тах ==—— ; (—оо; 0) — проміжок опуклості; (0; оо) — проміжок уг-
О
1447. Визначена на (— оо,
1 . 1
-----—- 1 х = ——— точ-
уз уз
нутості; х = 0 — точка перегину. Асимптот нема.
4-оо); при х = 0 утах = 2; х = ± 1 утіп = 1; х =
І 1 \ . І 1	\	.	. /	1
ки перегину; —оо;--------1	’ °°/ — проміжки угнутості; ---------.
— проміжок опуклості. Асимптот нема. 1448. Визначена на [—1; оо);
двозначна; 7И(0; —1) N (0; 1)—точки перегину; екстремумів нема, асимптот—
теж. 1449. Визначена на (—оо; +©о); при х=1 #тах = х =—1 г/тіп =
= і-; х = — /З, х = 0, х = /З — точки перегину; (—оо; — |ЛЗ) і (0;
/3)— проміжки опуклості; (—УЗ; 0) і (У'З; оо) — проміжки угнутості; у =
=0 — асимптота. 1450. Визначена на (—оо; +©о); прих = 0 #тах=1; х =
= ± 1 —точки перегину; (—оо; —1) та (1; оо) — проміжки угнутості; (—1; 1)
— проміжок опуклості; у = 0 — асимптота. 1451. Визначена на (—оо; —1),
(—1; 1), (1; оо). При х = 0 утах — — 1; (—оо; —1) та (1; оо) — проміжки
угнутості; (—1; 1) — проміжок опуклості; х— ± 1, у — 0—асимптоти.
1452. Визначена на (—оо; +©о); при х = 1 #тах = ~ ; х = 3 г/тіп =— 1;
х = 2 — точка перегину; (—оо; 2) — проміжок опуклості; (2; оо) — проміжок
угнутості. Асимптот нема. 1453. Визначена на проміжках (—оо; —2), (—2; 2)
та (2, оо); при х — — 2 ]/3 #тах « — З ]/3; х = 2У 3 #тіП = З )АЗ; х = 0 — точка
перегину; (—оо; 0) — проміжок опуклості; (0; оо) — проміжок угнутості; х==—2
та х — 2 — вертикальні асимптоти; у = х — похила асимптота. 1454. Визна-
9
чекана (—оо; 1) і (1; оо). При х = 3 ї/тіп = -^-» х ~ 0 — точка перегину;
286
(— оо; 0) — проміжок опуклості; (0; оо) — проміжок угнутості; х = 1 — верти-
кальна асимптота; у = -і- х + 2 — похила асимптота. 1455. Визначена на
(—оо; —|—оо). При х = 0 Утіп =-------х = — 1 та х = 1 — точки перегину кри-
вої; (—оо; —1) і (1; оо) — проміжки опуклості; (—1; 1) — проміжок угнутості;
у = —-----асимптота. 1456. Визначена скрізь, за винятком х = — 1. При х = 0
З —	4 ^/4	3 у—
#тіп = 0; ПРИ х = — у/4 #тах= —; х==	—точка перегину; х =— 1 —
вертикальна асимптота; у = х —похила асимптота. 1457. Визначена на (—оо;
— 1), (—1; 1) та (1; оо). При х —- 0 #тах =-; х = 2 — )/5 та х = 2 + Iа5
— точки перегину; х = 1, х = — 1 та у — ----асимптоти. 1458. Визначена для
л	т-г	а л,	і/— <	\	• •	2а у а
х > 0,- двозначна. При х = -у функція у = у х (х — а) має мінімум — —, а
.	•	,/•-/ ч	2а Vа	о
функція у=—у х (х — а)—максимум ---------асимптот нема. 1459. Визначена
х — 1 Утах. — х —
перегину; у = 0 — асим-
на (— оо; 4-оо). При х = 0 #тіП = 0; при х = — 1 та
, т / 10+ /68	, !	10-/68
= ± У —т8	та х— ± |/ ------------точи
птота. 1460. Визначена на (—оо; +©о). При х = — 1 Утіп -------— ; при
У е
1	г-	г~
х = 1 і/тах = —ггг- » ПРИ х = 0, х = — у 3 та х—у 3 — точки перегину;
У е	_
У ==і 0 —асимптота. 1461. Визначена скрізь; при х = 1 #тах = е 3; х = 0
1ЛЗ	1/3
х = 1 — -у— та х = 1 4—-------------точки перегину; у — 0 — асимптота.
1462. Визначена скрізь, за винятком х = 0. При х = 2 утіП = 3; -точок
перегину нема: # = х та х = 0 — асимптоти. 1463. Визначена скрізь, за винят-
ком точок х = —1 та х = 1. При х = "\ґ2 1/5 ~ 2,С 5 */тіП = 3,4; при х =
= — "\ґ2 + 1/5 г/тах ~ — 3,4; вертикальні асимптоти х = — 1 та х = 1; у =
— х — похила асимптота; х = 0 — точка перегину. 1464. Визначена скрізь,
З	1
за винятком точок х = 1, х = 2. При х = у #тах — у і х = 1 та х — 2 —
вертикальні асимптоти; у = 1 — теж асимптота. Точок перегину нема.
1465. Визначена скрізь, за винятком х = 1, х = 2. При х = 1,5 г/тах = — 4.
Точок перегину нема, х = 1, х = 2 та у — 0 — асимптоти. 1466. Визначена
зі
на проміжках (2/гтт, (26 + 1) я), к = 0, ±1, ±2,... ; при х = — -\-2кл утах=
= 1. Точок перегину нема; х = кл (к — 0, ± 1,...) — вертикальні асимптоти.
287
1467. Визначена на (—оо, 4-оо). При х — 0 #тах=1; х=±—=------точ-
У 2а
ки перегину; # = 0—асимптота. 1468. Визначена на (—оо; 4-00), періодична
•Гї	5«П/	З
з періодом 2л. При х==-^-+2кл та х——^—[- 2кл утах = -^~; при х =
= ± -у- + 2кп утіП = 1; х « 1,001 + 2£л та 3,775 + 2кл — точки переги-
ну. 1469. Визначена на [— ]/^2; У2], двозначна. При х = — Іта ху =
= У2х2 — х4 має максимум (+1); а у = — У 2х2 — х4 — мінімум — 1. Крива зам-
кнена; х = 0 —точка перегину кривої. 1470. Визначена на проміжках (—оо;0)
З	п /	2*
та [-/2; оо). При х — — 1 функція у ~ у х2 — — має мінімум УЗ, а функ-
ція у — — у х2 — —-----максимум — У3; точок перегину нема; у — х, у —
=—х та х = 0—асимптоти. 1471. Визначена для х> —1. При х = 0
*/тіп = 0- Крива скрізь угнута; х = — 1 — асимптота. 1472. Визначена скрізь,
за винятком х = 0. При х — 1, #тіП = е; х = 0 та у — 0 — асимптоти; (—оо; 0) —
проміжок опуклості; (0; оо) — угнутості. 1473. Визначена на (0; оо). При
х = "у- #тіп =-----; х —	---точка перегину. 1474. Визначена на
(0; оо). При х== -— Утіп =---крива скрізь угнута. 1475. Визначена на
/	І \ гт	1	ЛІ	1	ІЛ
(—оо, +оо). При X = — 1 #тах = -^-----—; при х = 1 утіп= -у-----4" ; У =
= ------та у — -у- + --------асимптоти; х = 0 — точка перегину; (—оо; 0)—
проміжок опуклості; (0; оо) — угнутості. 1476. Визначена на (—оо; -|-оо).
При х == — 1 #тіП = — 2; при х = 1 ї/тах = 2; х = 0 — точка перегину;
(—оо; 0)—проміжок угнутості; (0; оо) — проміжок опуклості. 1478. Визна-
чена на (—оо; 4-оо). Екстремумів нема; х — кп, к = 0, ±1, ±2,..., — точки
перегину. 1479. Визначена скрізь. Крива симетрична відносно ОУ\ при х —
З	1
= ± -у- #шіп = —-4-; точок перегину та асимптот нема. 1480. Визначена на
(—оо; —1) та (0; оо). На проміжку (—оо; —1) зростає від е до оо; на про-
міжку (0; оо) зростає від 1 до е; у — е та х — — 1 — асимптоти. 1481. Визна-
чена скрізь. При х = 0 (/шах = 2; при х = — 1 #тіП = 0; х = — ~-точка ле-
те ги ну; у = 1 —асимптота. 1482. Визначена на (—оо; +©о). При х — — 1
#тах = 3; при х = 1 г/тіп = — 1; х = 0 — точка перегину; (—оо; 0) — промі-
жок опуклості; (0; оо) — проміжок угнутості. 1483. Визначена на (—оо; 0) і
(0; оо). При х — ± 1 #тіП = 2; х = 0 — асимптота. 1484. Визначена на
(—оо; 0), (0; оо). При х = — 2 утах = — 2,5. Точок перегину нема; х = 0 та
у — х — асимптоти.
288
РОЗДІЛ VI
Комплексні числа та алгебра многочленів
моє ч	9	5	1
1485. а) х = -уу- , у =-------ру- ; Ь) х = —
з
у --0, и = — 1, V = 1; Ь) х = — 2, у = и = 2;
різниця аргументів цих чисел дорівнює я -\-2кл, де
< леїгх ~ч__Л і • гч. Х.ч_____і -•
1-ХМ..	V, -Т- ,	™ -І- * —
у = — 2. 1486. а)
х — 1,
о=--^-.	1487.
к — ціле число.
1489. а) соз 0 4- і зіп 0; Ь) соз 4- і зіп -у ; с) соз -у^ 4- §іп (
(і) 2 і соз 4- і зіп . 1490. а) 2 | соз |-
'о	о /	І І О /
. . Зя \	. ч/гї І 5я . . 5л
4- і зш — • с) 1/ 2 (соз ----к 1 зіп —т
1	4 у	\	4
1491. 2	2 _ / з /Соз у 4- і зіп -у 1.
Ь) У 2 /соз
7 г 4
, . . 4л \
4- ізш-у-1.
Якщо
я’
~2
, . . / я \]
4" 4 Зіп-----•
\. & ] І
ї \	.. „ І	4л
- ; 4) 2 | соз—5-4
І \	о
Вказівка.
2
+ і зіп (-Ф);
а) соз (—ф) +
1	Я
1 — соз —г-	_
о	я оя .
-----2------=51П ПГ = со3 ТГ  1492-
Ь) соз (я — ер) 4- і зіп (я — ф); с) соз (я + ф) + і зіп (я 4- ф)«
0/6	0 \	0
1493. а) 2 соз-у/соз у + / зіп-у) при 0 < 0 < я, — 2 соз-у X
/	0 4-2я , . . 0 4-2я\	л л гчгч. 0 / я —0,
X І соз— -----Н151П'—----- —	‘	*
, . . я — 0\ „
4- і зіп —-— І. В к а з і в
0 /
2— . при я < 0 < 2я; Ь) 2 зіп у / соз —
1495. а) 117 4-44/; Ь)
к а. Покласти а = 0 4- 2я&, 0 <
2,
—2,
2/,
—2/,
—5 — 62і. 1496. 2»«—1 =
о	___і __ 'іп/
1497. 4(7 + 4/).	1498.
О	20
коли
коли
коли
коли
1499. а) 8/2/соз-у
п = 46 4- 1,
п = 4к 4- З,
п = 4к 4- 2,
п = 4к.
п
<В,Л< ч п~9~ І	ПІЇ . . . ПЯ \
1501. а) 2 2 соз -----------Н 1 зіп—— •
І	4	і 4 / ’
+ і зіп ; Ь) 2» (1 - /Зі). 1500. 0.
Ь) 2п ^соз + і зіп • 1502. При
1 У^З	1 Уз
дорівнює----------і —у—; при п = Зк 4- 2 дорівнює---------у 4- і —у-
п — Зк дорівнює 1; при п = Зк 4- 1
19 2193
289
1503. а) 1,	1 ± і’КЗ); &) соз я + і §іп	де
2	о	о
1, 2, 3; с) 2^- (± /3 ± і), ± /2І.	1504.	(соз--4** 19 л +
+ і зіп	де к — 0, 1, 2, 3, 4, 5. 1505. а) —!— (соз	5 я +
72 І	і® п І У о
/	у 2 \
+ і зіп	» Де = 0> 1» 2, 3, 4, 5, 6, 7; Ь) 2 + і, — 2 — і;
. 4 -- І	7я	... 7я ]	4/-- І
с) у 2 соз —з—|- і зіп —5— , у 2 соз
\	о	о /	\
б/) ]/2 /"соз я + і зіп —ї^-~ я І, к = 0, 1, 2.
...	15я
+ і зіп —8~
'	94& — 1	24& — 1 \
с°5 —84—я + і зіп —£4— я), де к — 0, 1, 2, 3, 4, 5, 6.
Вказівка.
/З
2
2
я
~СО8Т2”
1507. х± = 2 + і, х2 — 1 — Зі. 1508. х± = 2 + Зі, х2 = 1 + 4і.
1509. х± — 1 + і, х2 — —=-(6 + Зі). 1510. х± = 1 + 2і, х2 — 1 — 2і, х3 =—4 +
□
+ 2і. Х4 =— 4 — 2і. Вказівка. Розкласти на множники. 1511. х1 = 2 + і 1^2,
х2 = 2 — і /2, х3 = — 2 + 2і /2, Хі = — 2 — 2і /2- 1512. хх =	>
1Л 7 — і — 1Л 7 + і — 1Л7 — і
х2 = —-—2----» хз = —~2—~ ’ %4 = — 2--------’ 1513. З соз2 ф зіп ф — зіп3 ф.
1514. соз4 ф — 6 соз2 ф зіп2 ф + зіп4 ф. 1515. 5 зіп ф соз4 ф — 10 зіп3 ф соз2 ф+
+ зіп5 ф. 1516. соз6 Ф + 6 соз5 ф зіп ф — 15 соз4 ф зіп2 ф — 20 соз3 ф зіп3 ф +
+ 15 соз2 ф зіп4 ф + 6 соз ф зіп5 ф — зіп6 ф. 1517.	(3 соз ф + соз Зф).
1518. -^-(Ззіпф — зіпЗф). 1519.	(3 + 4 соз 2ф + соз 4ф).
1520. -І-(3 — 4 соз 2ф + соз 4ф).	1521.	(10 + 15 соз 2ф + 6 соз 4ф +
о	о2
+ соз 6ф).	1522. -^-[(соз7ф —зіп7ф) + 7(соз5ф +зіпбф)+ 21 (созЗф —
зіп Зф + 35 (соз Ф + зіп Ф)]. 1523.	•
т к т 1	1 — 15 І£2 ф + 15 І£4 ф—І£6 ф
290
1529.
5Іп(п+-^-) <р
• ф
5ШІ
1530. 5іп2 П-ф- . 1537. 1 -і; —1; 4; (х2—2x4-2) х
X (х 4- 1) (х — 4). 1538. 1 — корінь з кратністю 3; — 2 — корінь з кратністю
2; 1 4- 2і, 1 — 21 — прості корені; (х — І)3 (х 4- 2)2 (х2 — 2х 4- 5). Вказівка.
Дійсні корені знаходимо, перевіряючи дільники вільного члена. 1539. 2 — її/3.
1, — 1; (х4-1)(х— 1)(х2 — 4х 4-7)2. 1540.4. 1541.3. 1542. Так.
1544. (х — 1) (х — 2) (х - 3) (х2 4- 1). 1545. (х2 4- 2) (х2 4- 2х 4- 2) (х2 — 2x4-
4- 2) (х 4- /2) (х — V2). 1546. (х2 4- 3) (х2 4- Зх 4- 3) (х2 — Зх 4- 3).
1547. (х- 1)3(х4- І)2 (х2 4-х 4- 1). 1548. (х - 1) (х2 4-І)2. 1553. х2 4-1.
1554. х3 4-2х 4- 2. 1555.1. 1556. х2 4- 1. 1557. х3 4- 1. 1558. х3—х+ 1.
1559. х 4-3. 1560.x4 — !. 1561. х2 4-х 4- 1. 1562. х2 — 2 ]/2х — 1.
1563.	4-—Ц-+—ГГ- 1564. /—? пг + —7~г + / -Ц-
X х— 1	х+1	(х + І)2 X + 1 (х — І)2 х— 1
1565. —Ц---2-4- -А—. 1566. х3- 1 4--- . 1	-—1—
х— 1 х — 2 х — 3	2(х—1)	2(х+1)
1	х	11 2х
1567. 2 , -., , - , 2 ,	, -па . 1568.	.
Х2+ X + 1	(х2 + X + 1 )2	X3 X X2 + 1
1569.
1570.
1
(14-х)2
.	2*4-1
1	— х соз —-— я
2и
~ й 2^+ 1
2	— 2х СОЗ ——!— я
2и
п
X
1571	х+2	х~2
’ х24-2x4-2	х2—2x4-2’
1572' їтї
1
1573. 2--------<
Xі
2к 1
2и4- 1 Я
26	'
х2 + 2х соз -—-—г я + 1
2п 1	->
1574. ~^Х,+,4
1
Зх — 1
РОЗДІЛ VII
Невизначений інтеграл
1575. х4 4- С. 1576. -у- 4-	4- Зх 4- С. 1577. -|- /х3 — 1п х 4- С.
1578. і|^- + С. 1579. 1п х -А. 4- С- 1580. А3/^ -)- С.
1581. 4 агсі§ -4- 4- С- 1582. —4 агсзіп х -)- С. 1583. —|т. агс(§4- С.
4	5 2 х	уз	УЗ УЗ
19*
291
Є) ___ А .	_ у
1584.	/х3 + 2/х+С. 1585. х — 2агсі£~ + С. Вка-
О	О	£
зівка. Додати й відняти в чисельнику 4. 1586. х — х + С. 1587. Іп х —
— 2 агсІ£ -і- + С. 1588. Ї£х — сІ£ х + С. Вказівка. Замінити в чисель-
□
нику 1 тригонометричною 1 = зіп2 х + соз2 х. 1589. 5 сі£ х + 2 х + С.
1590. 2 аг сіє х-- + С. 1591. , ^7-,-4-С. 1592. ї£х-]-С.
ь х	Іп 2 + 1 1
1593. х---------зіп х + С.
1
агсі£
/2
1598.
1601.
1603.
х	х$
1594. агсзіп -^=- + С. 1595.	— х +
/З	з
X	1	1
-^ + С. 1596. х + — х + С. 1597. -—с^х+ С.
У 2
х	х3
агсзіп —— 4- С. 1599. — сі£ х — х 4- С. 1600. -х 4- агсі£ хС.
У 2	6
—агсзіп Х - 4- С. 1602. —агсі& -Х 4- С-
у 3	2	У 5	2
-2созх4-С. 1604. 4/х® 4-х 4-С. 1605. 4 — 4/х®4-х4-С.
о	2 о
1606. ~ - 9^/х4 + 9^/Р + -2— + с. 1607. і£х — сі£х — 4х 4- С.
1608. 4—І-С. Вказівка. 1 4-созх = 2 соз2 . 1609. ~І£х-}-С.
1610. — 1§х — сі§х+ С. 1611. -^І-^-4-С. 1612. - С°|3% 4-С.
О	<5
1613. 4 іп (Зх + 2) + С. 1614. - -2-^4-ї7 + С- 1615- (%2 й 1)6 + С-
1616. у + 4)3 + с. 1617. — 4 с°5 5х 4- С. 1618. 4 Зх 4- С.
1619. — 41п(! — 4х)4-С. 1620. — е-2х4-С. 1621.------------е~х‘+ С.
1	1	X2
1622. — еСО8Х4-С 1623. — агс^2%4-С. 1624. -А-агсІ£4-С.
1	х	1	х2
1625. ---=- агсі& —|--1- С. 1626. — агсзіп — 4- С.
5 У 3	5	2	2
1	-	1 Зх
1627. —— агсзіп ]^5х 4- С. 1628. — агсзіп—— 4- С.
/5	3/2
1629. — 1псозх4-С. 1630. Іп зіп х 4- С. 1631. -і-зіп5 х 4-С.
5
292
і	з з _______
1632. - -=- 1п соз (5х — 1) + С. 1633. — 4 /соз2 х + С.
О	2
і	9	______
1634. 1п (3 зіп х — 1) + С. 1635.	/(1п х)3 + С.
0	0
1636. — -|-|Л(3 —2х)4 4-С. 1637.	/(х3 + 8)3 + С.
1638.--------І------1- С. 1639. 1п (1 — е~х) 4-С. Вказівка. Помножити
агсзіп х
_	1 ех
чисельник і знаменник на е х- 1640. 1п1пх-|-Є. 1641. -у- агсі£ -у- 4~ С.
о о
1642. _|_^(Х-І)ь+С. 1643. ^-І5-+С. 1644. —і- 1п (3-2х2)+С.
О*3	о _________ _________
1645. е~агсс03 х + С. 1646. -А 4-С. 1647. -^-/(Іпх)3 —2/1пх4-С.
0 1П 0	0
1648.	У(агсі&х)3 4- С. 1649. х — 5Ш 2* с. Вказівка. Скорис-
о	2	4
татися формулою зіп2 х = --2х. 1650. х 4-	4- С.
X
1651. 1п — 4- С. Вказівка.
п . X X	X ’
2 зіп — соз —	2	—
1652. -І- 1п х---4- Є. 1653. х зіп х 4- соз х 4- Є. 1654.	---
4	16	1п2
2х	.Л-1-1	хл+1
ТГо+С. 1655. (х2-2x4-2)	4-С. 1656. Іпх-——4-С.
1п2 2	у । /	।	«4-1	(«4-1)
х2 4- 1	х	1
1657. —-— агсі£ х------- 4- С. 1658. — агсзіп х-------- агсзіп х4-
4- У 1 — х2 4- С. 1659. — х2 соз х 4- 2х зіп х4-2 соз х 4- С. 1660. хех—ех-[-С.
еах / А , А . І п	еах (я зіп Ьх — Ь соз Ьх) . п
1661‘ ~& + Ь2 С08 Ьх + ь 5111 Ьх) + а 1662‘ -а2~+Ь2---- + с’
1663. х х 4- 1п соз х 4- С. 1664. —(агсі£ х)2 — х агсЇ£ х 4-
+ 41п(1 +х2) + С. 1665. х 1п (х + /1 + х2) — /1 + х2 + С.
1666. —	(1п2 х + 31п2 х + 6 1п х + 6) + С.
293
1667.	+	+ 4 !п (х +/х2 + а2) + с. 1668.	-------------|-С.Вка-
2	2	1 —г" X
зівка. У чисельнику додати та відняти 1, а потім інтегрувати частинами.
1669. х агссоз х — У1 — х2 + С. 1670. 2У х — 2	1 — х агсзіп Ух + С.
_____ 1 х
1671. х 1п (У 1 + х + У1 — х) + -у (агсзіп х — х) + С. 1672. ---
---і- х + С. 1673. х 1п (х2 + 1) — 2х + 2 агсі£ х + С. 1674. х (агсзіп х)2 +
_________________
2 агсзіп х-У1 — х2 — 2х + С. 1675. ех — —— + С. Вказівка. У чи-
сельнику додати й відняти 2. 1677. (х4 — 4х3 + 12х2 — 24х + 24) ех + С.
1678. (х3 — Зх2 + Зх — 1) ех + С. Вказівка. Див; 1676. 1679. 1п х X
уЗ	у2 — 1	у2
X [Іпіпх-11 + С. 1681. Іп^рї + С. 1682. 1п—---ЬС. 1683. ^- +
1	у2 _1_ у _ О
+ 2 1п (х — 2) + 2 1п (х + 2) + С. 1684. — х2 - х + 1п ----------— + С.
1685. 2 1п (х — 4) — 1п (х — 3) + С. 1686.	+ 1п (х — 1) — 1п х + С.
1687. ± + 2. ,п 1^! + с. 1688. 2^2, + >„(., + 2) + с.
1x111	V
1689- — 1я73^2 ~~х	2Х2” — 2 (х — 2) + С' 1690,	(х2 — І)2 + с’
1691. Іп К.Х1±...У--* +агсІ8х + С. 1692. -і-1п^4 - 4" х
х +1 X +1	4х+1	2
X агсіе х + С. 1693. А- 1п  /_+агсІ§ + С.
1694.	х3 4—5- 1п (х3 — 1) 4- С- Вказівка. Зробити заміну х3 — \=и.
о	о
1695. —4^ 1п х х 4- 1'4------агсі§ / ^2 +С- Вказівка. х*+1 =
4/2	х2- х/2 +1	2/2	1 - х2
= (Х2 + 1)2 _ 2х2. 1696.	- 4 1п (Х +	+ “Г 1П (*2 + 0 + С
— а , 1 . ч 4~ Вказівка. Зробити спо-
Зх3 3(х34-1) 1	г
ч іапо 15х5 4~ 40х3 4~ ЗЗх ,5	,	. п
чатку заміну г = х3 1698.--1)3----------Ь агсІ£ х 4- С.
16"- ~ 2хТх2+21)---У^х + С.
1697. 4"
З х3
294
X
*700' 4 (№ + 2х + 2)2 + 8 (х2 + І + 2) + 8 аГСІ§ + С’
2хв _ 3.%^	3 х2_____ 1
1701. -т-г-л-гг + “77" Іп -т-—г 4- С. Вказівка. Спочатку зробити за-
4 (х4 — 1) ' 8 х2 + 1
міну г = х2. 1702. Х  —Іп .	----= + агсі§ _|_С.
’	3(1-х3)	9	/ х2 4-х 4-1	9	/З
х — 1
1	х2 _ 1
1703. —— агсія----+ С. Вказівка. Скоротити на х2 і застосувати
/2	х/2
1	1	у2 _ у тЛо 4- 1
потім заміну г == х — —. 1704. ---— Іп-----------------|- С. В к а з і в -
*	2/2 х2 + х /2 + 1
к а. Покласти г = х 4---
х
1705. 2 /х — 2 /2 агсі§ /^Г + С.
9 / — й
1706. 4 /* + /х +
□ \
1
/З
агсі§ 8|/ 27х І + С.
1707.	2 /х — 2 Іп (]/х + 1) + С.
1708.	іп -----+ -!°________________^+-*^______________
(1+р<х) Ух Ух З1^3 2Ух*
1709.	4" і?/*5 + 2 У& + 2 Іп (УXі — 1)] + С.
□
с.
1710.	х 4- 4 /Г+х + 4 Іп (уТ+х — 1) + С.
1711.	А^(7+і)2_з3/7+1 + 31п(^Т+1+1) + С.
1712.	/2х — 1 4—|- 3/2х— 1 4- 3 у/ 2х — 1 4- 3 Іп (в/2х — 1 — 1) 4- С.
1713.	-|~1/~-т4~ Х + С. Вказівка. Покласти г3 = Х ! •
2 у 1 — х	х + 1
1714.	2 1/4- С. 1715. Іп +	_ Vі -у2. + с
г х-1	/1-х-/14-х х
1716. 4 ®/(2х - З)7- -|- ’/(2х-3)34- /2х-3 - 3 ^2х- 3 4-
і	о
4- 3 агс<§ >Л2х — 3 4- С. 1717. З Ух+ 1 4- 6 ’/х+Т 4- 6 іп	— 1) + С.
1718.	уз агсі§ — + 1 4- іп — “2~ 1	4-С, де и = /.
УЗ [ иі 4-й2 4-1	V 14- х
1719.	— /1 — х — х2-агс5іп	—Ь	Вказівка. Утворити в
чисельнику (—1 — 2х) — похідну від підкореневого виразу.
295
X   1	І
1720.	агсзіп-— + С. Вказівка. Заміна г = —.
х/2	х
у 2	у і/" у 2   1	1	-
1721.	— -|---------------— 1п (х + /х2 — 1) + С. Вказівка. Чи-
сельник і знаменник помножити на х+ )/х2 — 1.
х — 1
1722.	агсзіп -|- С. Вказівка. Підкореневий вираз перетворити на
алгебричну суму квадратів.
1723.	1п (х	Ух2 ± а2) С. Вказівка. Застосувати Ейлерову під-
становку |<х2 ± а2 = і — х.
1724.	1п (х + 1 + /х2 + 2х — 3) + С.
1725.	± 1п (Зх - 1 + У9х2 — 6х + 2) + С.
О
1726.	агсзіп — — + С. 1727. 4~х У а2 ~ х2 + агсзіп — + С.
З т/2	2 г	1 2 а
Вказівка. Заміна х = а зіп і.
1728.	(х — І) У2х — х2 + агсзіп (х — 1) + С. Вказівка. Пере-
творити до вигляду 1727.
1729.	-|-(х — 2) /х2 — 4х + 5 + -±- 1п(х — 2 + / х2 — 4х + 5) + С.
1730.	і (х + О V1 -4х —х2 + 4- агсзіп + С.
2	2	У 5
1731.	4- (х - 1) /х2 - 2х + 2 + ~ 1п (х - 1 + /х2 - 2х + 2) + С. В к а-
зівка. Див. 1667.
1732.	2 агсзіп----1- У 4 — х2 + С. В к а з і в к а. Див. 1727.
1733.	~Т х2 — агсзіп х + С. 1734. Ух2 + 2х + 1п (х + 1 +
х
+ Ух2 + 2х) + С. Вказівка. Помножити чисельник і знаменник на
Ух2 + 2х та розглянути два інтеграли.
1735. 2 /х2 - 7х + 1 +2 іп (х -+/х2 — 7х + 1) + С. Вказівка.
Див. 1719. 1736.	1/^4 + С’ Вказівка. Заміна г = _1 .
3(х — 1) г х — 1	х — 1
296
т/х2 4- 9
1737.---—----|-С. Вказівка. Покласти х = Зер.
у	ЗІ/4
1738. -т== + С. 1739.	+ — 1п , 1ЧЧ + С, де і = х +
а2/х24-а2	4/4-2 ~ 2	(2/4-1)3^
+ Ух2 + х + 1. 1740. ^Ха2х а - + С. Вказівка. х = а$есі.
1741.--~~Х 	+ С. 1742. — 2агсі& 1/ --- 4-С. Вказівка.
ух2— 1	* х
-----------------/(1+х2)з	3 2	. 2х — а
у х — х2 = іх. 1743.	- -- -тго— -Н С. 1744. — а2 агсзіп-
Зх3 1	8	а
--+ $а у ах — х2 4- С. Вказівка. Див. 1742.
1745. З агсі§ Ух-----3^х  + С. 1746. .%2 + 2 + С.
Ух 4- 1	У 1 + х2
1747. ^Ух2
1748. З 1п —&----------Н 6^+9 + С.
уі + 1	2 У х + І)2
з - л	7~1
1749.	(4 Ух 4- У - 3) V 1 4-	4- С.
1750. -^-3/<*3+ І)8- г 1)* + С. 1751.	1>5
-1®рі + с. 17Е. ' 1П ГЇ^±2 _ ' /17?
6	4	х2	4 х4
1753.
х2 + 1
2 /2х2 + 1
С. 1754. 4- 1п
(V х6 + 1 - І)2
3/(*5 + і)2 + 3/ІЧГГ+1
, Уз .
+ ^агсій х
X 2/х6+_1	+ 1 + С. 1755. Ц-	1п 1-------!	+ -|- агсі§ УXі + 1	+ С.
УЗ	3	177+1	+ 1	3
4/---А--
1 V х—-4- 1 -І- 1	1	4/-----
1756. -у- 1п	"Н——-----— агсі£ у х~~4 4-1+С. Вказівка.
Л л	1 т 4- 1 . А
т — У), п = 4, р =----------1- р = 0, третій випадок.
1757. 2*з” 1 Ух2 + 1 + С. 1758. -	(2х3 + Зх) /1-х2 +
297
+ 4" агсзіп х+С. 1759. 1п г ~ агс*Є + С’ де
г 1. г +1	1	. 2г - 1 , _
2 (г3 4- 1)	6 П у г2 — г + 1	2 /З аГС 8 /З
1761. -1- х2 /х*+ 1 + -1- 1п (х2 + /х4+ 1) + С.
С05^ X
Вказівка. Можна застосувати заміну г == х2. 1762.--------------------------1- С.
• 1760.
х
3/і~^
де г —  ------
х2
г
зіп2 х	2	1
1763. зіп х-г— 4- С.	1764. — соз х + -у- соз3 х-=~ соз6 х + С.
о	О	О
1765. —-Н С. 1766. — 5-Д-Н С. 1767. 1п (і§ х + зес х) + С.
соз х 1	З зіп3 х	ь	‘
зіп3х ЗІП6 X , ~	„„„	1 . , X созх ,
”«•—--------“+ с' ™--'"18ТГ-2Ж + с-
+ І771. ї_±_г^_1_ + с.
‘772-4~зяк + с- |773'~2їк + с-
3	1	1
1774. -о- х-— зіп 2х -|—зіп 4х + С. Вказівка. Див. 1649.
о	4
-__е	3	) 1 : о ! зін 4х . Г	х зіп 2х зіп 4х .
1775. -гх + -зш2х + -^ + С. 1776.	----------—+
+ лУг+С‘ 1777'	---у ЗІП 2* + + ЗІП 4х + + зіп2 2х + С.
1778.	І£3 х + х + С. В к а з і в к а. Взяти до уваги, що 1 + І£2 х = зес2 х.
□
2	1
1779. — сі£ х — сі£3 х---------5~с^5 Х + С- Вказівка. Взяти до ува-
ги, що 1 + сі£2 х = созес2 х. 1780. —---------------2 1п зіп х + С.
Л	ОІГ1 х
ІсгЗ у	1	__
1781. і§х + Лі---2сі$х + С. 1782. —— агсі§ (/2 х) + С.
6	У 2
сі§3£ _ сі§^х с 1784. -2_ 1п (/21§х + /1 + 2 і§2 х) + С.
—кг агсі§ (	+ С. 1787. - 8 сі§ 2х -
У 10	\ /То}
в к а. Взяти до уваги, що зіп 2х — 2 зіп хсозх і
1783.
З
5
1785.+ с.
О
1786.
о
-4сі^2х + С. В
о
к а з і
298
созес2 2х = 1 + сІ§2 2х. 1788. Ц- агсі§	+ С. 1789. -і-і§2х +
ио \ о і
+ Іп соз х + С. Вказівка. Див. 1778.
1790. х--сі£7 х + -Д- сі£5 *--5" с*£3 * + сі£ х + С.
І	О	О
1791. Ц- х —	х + х + С. 1792.---|-улс088 х + -А усоз18 х —
---А_ ®/СО828х + С. 1793. А-/зїпЗх----А Vзіп7X + С.
28	о	і
2	___
1794.	1£2 х У х + С. Вказівка. Покласти г = х.
□
1795. ~ х + —- іп (зіп х + соз х) + С. 1796. агсзіп (зіп х — соз х) 4- С.
X	X
Вказівка. Покласти г = зіп х — соз х. 1797. 2 зіп —-2 соз — + С.
В к а з і в к а. зіп2 -Д- 4- соз2 = 1. 1798. ---1- С. Вказівка.
2	2	Л . х
2-<§Т
X	1	/ X \
Покласти г =	. 1799. — агсі& 12	— І + С.
1	і§-^--1+/2
1800. г_ Іп--------------Н С. 1801. агсі§ + 1 + С.
/2	к 2	)
2	5^4-+4
1802. т агсі§ -х---Ь С. 1803. /2 Іп -у- + С.
о	о	4
1803.--!- соз 2х-Д- соз 6% 4- С. Вказівка, зіп тх соз пх =
4	12
= ~ [зіп (т + п) х + зіп (т — п) х]. 1805. —^-зіп9х-|—і-зіпх + С.
2	18	2
1806. ± зіп х--Д-	зіп 7х 4-	С. 1807. -Дг	соз 6х-Д-	соз 4х —
2	14	1	24	16
---Д соз 2х + С. 1808. -Д зіп х 4- -Д- зіп Зх + -Д- зіп 7х + -Д- зіп 9х 4- С.
о	4	12	28	оо
1	1	1	(Ї0 2х \
1809. -- х + — Іп х + С. 1810. —— агсі£ | І + С. В к а з
2	2	]Л2	\/2/
к а. Зробити заміну г = Ї£х. 1811. агсі£ (зіп2 х) + С.
299
1812.	[1п (зіи х + соз х — Узіп 2х) + агсзіп (зіп х — соз х)] + С. Вка-
зівка. Розглянути суму /х + /2 та різницю /2 — /р де /х =
= С У *£ * сіх, а /2 = І У сі£хсїх, і брати до уваги 1796.
1814.
4~ С. В к
-----=7- 1п (У2 соз х Ч- Усоз 2х) + С. 1815. --
т/2	‘	8ІП а
а з і в к а. Винести за дужки в знаменнику соз2 х.
1п (І£ х + сі& а)+
1816. —1—. _ 1п (ех + 1) + х + С. 1817. ех - 1п (6х + 1) + С. Вка-
зівка. Поділити чисельник на знаменник. 1818. 1п—, ------к С.
У ех + 1 + 1
Вказівка. Покласти У ех + 1 = г. 1819. — (зіі х сії х + х) + С.
сЬ3 4 * * х
1820. х - їй х + С. 1821. 	- - сй х + С. 1822. агсІ£ (зіі х) + С.
О
|ИЗ у
1823. йіх----+ С. 1824. агсі§ (їй х) + С.
1825.	[х2 (зіп х + соз х) — 2х зіп х + зіп х — соз х] + С.
х	1	1
1826. -4-+-^-1п(ех-1)+—1п(^ + 2) + С. Вказівка.
2	о	О
и — ех. 1827. 1п	2 агсі£ 1/"Є- х	* 4-С. В к а з і в -
У^+ 1 ~Уех~ 1	V ех+\
з у ех — 1
к а. Покласти г = І/	—г.
Г ех + 1
на два доданки і другий доданок інтегрувати частинами.
X
1828. ех 4- С. Вказівка.
Розбити
4 4/_____4 4 ________
1829. — У (ех + І)7-—У (ех + І)3 4-С. Вказівка. Покласти и =
І	<5
4 >---- 1 х^	1
/6х + 1. 1830. —1п-4—+С. 1831.	- 1п 4- С.
4 х2 4" 2	12 х3 4- 4
1 х’	1	1
+ « 1П^Л+С- 1833- -о-(х2~ 1)--о-1П(*2+1) +
о л 1	о	о
1	X2 — 1
1834. -— агсі&
Е_з
х2-х/2 4- 1
183!- м?Ті>
+4 агсі8	+с-
Xе
1835. —і— ід _------------
4/2	х2+х/2 + 1
Див. 1704 та 1703. 1836. —кг- агссоз
/2
--7=7-4-С. Вказівка.
х/З
1	х2 — 1
У^агсіе^—У 4-С. В к
У2 хУ2
х У 2
—г 4-С. Вказівка.
ил ____ 1	1
Див. 1703.
а з і в к а.
Див. 1704.
300
1837.
-1) + С.
агсзіп р^зіп х + С. Вказівка-. Див.
1839. -і" Іп 	~ 1......  1_
3	+	+ 1 /З
1797. 1838. агсі£ (2 зіп2 х —
, 2 X + 1 . п
а"‘г у?“ + с-
1840. 2 У ех - 1 - 4 агсі§	—- + С. 1841. агс1§ (3 х) + С.
2	о
1842. х х + Іп соз х------у- + С. 1843. ± 2 ^зіп + соз + С.
1844. 2- Іп ? + С. 1845. /х2 + 1 агсі§ х - Іп (х + /х2 + 1) + С.
———	—————	1	у2 І 1
1847. 2	+ х агсзіп х + 4)Л1—х + С. 1846. агссоз —^-=- + С.
2 х2 |/ 2
1849. З соз 4- — 4—
о о
х + у 2 X + 1 с
1§2х-/2і§х+1 +
1848.
1849.
х агсзіп у %	। агсі& Ух — Ух-{-С.
З соз----соз х + С. 1850. —1-=- Іп
6	5	6 і	2)^2
12	18	36
Вказівка. Заміна г = зіп 2х.	1851. —гг- и13-=— а10-— и7 —
1о	о	І
6/ л _	1	X3
— За4 4- С, и = V 14- Ух 1852. —-—:------+ С. Вказівка. По-
?	3	|Л(1+х2)3
X	1	1/х4 4- 1 _ тЛо X
класти х = і&0. 1853. хі£—-}-С. 1854. —— Іп—----------------Ь с-
2 ‘	т/2	х2 — 1
Вказівка. Після елементарного перетворення покласти х-і- = г.
1	1	У^+ 1 -У2х ,	1	хУ2 , _ „
1855. --— Іп—---------------------— агссоз -х-п—г + С. В к а з і в -
2 уі	х2— 1	2 У2 -г-1-і'
х4 + 1	1 /х2 4
к а. Скористуватися тотожністю	'—ї = — 1-^—1.
1856. 4^-+ 4-Іпі^
/1-х2	2	1 +х
1
г — агсзіп--1- С. 1858.
х
+ зіп а - Іп зіп (х — а) + С. Вказівка.
х3	1
1860. г/ = — + 2х2 + х +	. 1861.
о	о
П	•	О	б/й)	,
Вказівка. За умовою = — к(а.
х2, — 1\
:—г	та взяти до
уваги 1836 і 1854.
1857.
Іп х
—;----р С. 1859. х соз а 4-
зш х 1
Покласти и — х — а.
1
2
1862. й) =
у2
1863. 216. 1864. у = 2х +	—
4 з. 38
— х3 4——
3^3
301
1865. у — зіпх — созх + 1.	1866. 5 = 1п (2/— /2). 1867. С — наявна
(ІХ
кількість цукру в початковий момент. Вказівка. — — кх. бо
х (/) — спадна функція і її похідна повинна бути від’ємною. 1868. х = Секі,
С — кількість бактерій при і — 0. 1869. у = ех. 1870. Л (3; — 6).
г,	•
Вказівка, т — т@, х —
зівка. Вважаємо = 0, к — 0
1871. / = |/ — = у —^4,4 сек.
=	. 1872. к = 5д-в--	510 м. В к а
при і = 0. З рівності V — знайдемо і —   - & . 1873. х2 — у2 — 1. Вка-
зівка. Піднормаль дорівнює уу'9 отже, за умовою уу' = х. 1874. х = 8а.
В к а з і в к а. ^ = кх, х = аекі, к = 1п2. 1875. З =	+ ЗО/.	Вка-
зівка.	1876. к<=г 0,0002. 1877. у2 = х. Вказівка. Піддо-
І!	0Х%
тична дорівнює . 1879. у —- х І£ а — СО52 а (парабола). Вказівка.
йУх п <*У	V йх	„ йу
— = “& зв.дси Ух=-^- = С1 = Уосоза, 7у=^- =
= — §і + С2 = — §і + Уо зіп а.
РОЗДІЛ VIII
Визначений інтеграл
1880. 7,5. 1881.9. 1882. 1п— . 1883. Д (/б5 —/а5)- 1884. & ~а\
а	о	о
1885. є" — еа. 1886.-Д-. 1887. Ь 1п Ь — а 1п а + а — Ь. 1888. ~ С05 аЯ,
1п 2	1	а
12
1889. зіп Ь — зіп а. 1890. З < / < 7,5. 1891. — 4 < І <
□
я
1892. 0 < І < 32. 1893. -Д- < І < ДД . 1894. ^<7<	.
1п 2 1п 1,5	4	8
1895. 0 <І<~. 1896. 1 <7<Д. 1897. 1 <І<Ґ2.
1о	2
1898. Перший. 1899. Перший. 1900. Другий. 1901. Другий.
1902. Другий. 1903. Перший. 1904. Другий. 1905. 10. 1906. 24,5.
302
е*_ 1	9	Р3 _ 1
1907. —— . 1908. -. 1909. 2 1п 2—1. 1910.20. 1911.  3 - .
2	л	З
1912. 1п 2. 1913. -Д. 1914.25. 1915. Д. 1916. Д. 1917. Д- .
ш 2	12	2	4а
іп 5	7	4 іДо_о	З
1918. —1919. 4-. 1920.	1921. 1. 1922. -Д-.
12	4	3	2
1923. Д • 1924. /е — Д. 1925. ДД. 1926. 2. 1927. ДД - 12).
Л	ОО	оЛ
1	9__ 1/~9	1	п
1928. агсі§ кт-. 1929. -. 1930. Д. 1931. -3--
21	4	2	о
1932. Д 1п-1Д-. 1933. -Д. 1934. -Д. 1935. Дагс^Д-
о Л	10	24	О	о
1936. 1113 —1112. 1937. Д«112л — 4-. 1938.-4Д
4	2	З
1939. ® р + 1п(1+ед. 1940. ДПпД-Д-ДД 1941. 2/3-Д
о	с/ і	и С& "т* С/1	о
1942.	. 1943.41114—1. 1944. 4^-+4^-/2.
1945. З 1п 2 — А . 1946. Д—. 1947. Д [/ 1 + 4а2 - /1 + а2].
2	12а	а
1948. -Д. 1949. ДД 1950. -Д- агсі§ -ІД-. 1951. агсі§ а - Д.
1952. -Д. 1953. 2-Д-. 1954. 2е(е- 1). 1955. Д.
З	2	4
1	1	*1/”Ч	Ч	9
,956--45" + -І0Г1п5- 1957*Л2-- 1958-4є3-^Г'
1959. 4— 21960. 1п Д. 1961. Д 1962. — Д1п22.
о	О	2
1963. Д Я —/3+1. 1964 Д — Д- 1965. 4 Щ Д + & 1П 2  1966. Д
6 г 1	6	4	Ь а	5
1967. —Д [Я+ 2 їй (/2— 1)]. 1968. 3/3 —я. 1969. —Д--
2/2	3/3
1971. Д. 1972. я2<2~Д2) . 1973. Д_ _ /3. і974. 1п2 ~ 1 .
4	8/2	3	2
л2	9	9?з 4-1	рЗ
1976. -Д-. 1977.0. 1978.——. 1979. ІД-- . 1980. -Д-(5е* - 2).
4	е	9	9у'
303
о	зт 1	рН____2
1981. 1 ——. 1982. 4.	1983. 4------—. 1984. я. 1985. -------=----
е	4	2	5
1986.-5^ — 2. 1987. я — 2. 1988. -5-( ^4--------------41 + 4-1112-
т:	Л \ О	Л ] Л
1989.-?-. 1990.-5-----------1"1- -Д-- 1994.0,5493.
8	9	2 Г 3	«2
1995. 0,7853. 1996. 0,5796. 1997 . 0,7853. 1998. 1,7182. 1999. 0,7468.
2000. 0,4969. 2001. 1,371. 2002. 1,09. 2003. 1,118. 2004. 1,53.
2005. 0,5356. 2006. 4. 2007. 1п 2. 2008. Розбіжний. 2009. 2яа2.
О
2010 л 2011	- 2012. — .  Я . 2013. ---------т—
зх. ^и. 2аЬ	У 4ас — Ь2	ап — Ьт Ьт
2014.	-. 2015. -1—(1 + 15/3). 2016.-4+4-
/(4ас —б2)3	120 ' 1	2'4
2017. -5-. 2018. —. 2019. -4- 2020. -Д— 2021. -.......
2	а	а2	1п3 а	а2 + Ь2
Ь
2022. —	. 2023. Розбіжний. 2024. 2е. 2025. Розбіжний.
а2 + Ь2
2026. 1. 2027.-^-- 2028.4а. 2029. 2/108. 2030. 4-я. 2031. Я.
2032.-4- 2033. /5 + ЗІп2034. 5 — 6 1п 2. 2035. я.
2036.-44-. 2037. 2 (1п 2 — 1). 2038. Розбіжний. 2039.-Д—•
2	'	1п 2
2040. 2агсі§ /е — 1. 2041.2. 2042. Розбіжний. 2043. 6 — 1п 3.
2044. Збіжний. 2045. Збіжний. 2046. Розбіжний. 2047. Збіжний.
2048. Розбіжний. 2049. Збіжний. 2050. Розбіжний. 2051. Збіжний при
п > 1. 2052. Розбіжний. 2053. Розбіжний. 2054. Збіжний. 2055. Збіжний.
2056. Розбіжний. 2057. Збіжний. 2058. Збіжний. 2059. Розбіжний.
2060. Розбіжний. 2061. Збіжний. 2062. Розбіжний. 2063. Збіжний.
2064. а) при к > 1; Ь) при к > 1. 2065. 0. 2066. 0. 2067. 1п-у.
2068. 0. 2069. -4 І (2 /5 — /2 + 1п . 2070. 44 •
2 \	1 + /2/	54
2071. 1п (2 + /5) + -4^- . 2072. /5 — /2 +
304
+ 4-1" т~=----?	+ . 2073. а Іп Ш 1. 2074. 2л /2. 2075. я /2.
2	(|/5+1) (/2-1)
(X _ X \
еа — е ° І.
/
/?2 _1_ /уА _!_ А2	о2>Ь — 1
2080. 2лг. 2081. 6а. 2082.	. 2083. 8. 2084. Іп ------г +
а + Ь	е2а — 1
. Зл
+ а — Ь. 2085. 4а У3. 2086. а Іп------— . 2087. р (З УЗ — 1).
, л
-з
2088. Уї ( —!------------!---\ . 2089. 87?т(1 -4-т). 2090. 16л 2091. 67?.
\1 +	1 + у
2092. — а Іп зіп і. 2093. 8л 2094. 2я27?. 2095. За — ?1п2М.
\ 2	4 у
2096. 48а. 2097. 4/3. 2098. 12а/3. 2099. 10а.
2Ю0. а- у + ~^  2101.16л 2102.	[<р /ТТф2 + Іп (Ф +
+ /1 + Ф2)]
Ф2
2103. а Іп (<р + У1 + ф2) — Х1+-2І
Ф1
Ф2
Ф1
2104.	1, + 1П2а (р2-Рі).	2105. -£-ла. 2106. а. 2107.
Іп а у ”	2	3	6
2108. -^-.2109. 2. 2110.250.2111.	• 2112. -%~У2- 2113. 32
9	3	3	1о
2Н4. -І-. 2115.	-. 2116. -	4 ІГ 2,17	. а2^- 2	4 3 /
2118.	(8я — 2/3).	9 2119.	а2. 2120. -	Я 1	(а — 0- Іпа '	'	
2121. 2аб(-%- — -|Д. 14	3 /	9 2122.	1	1 \ 	. \ е /	2123. а2 (-	М-
2124. УаЬ (а + 6). О	9 2125. а О	2. 2126. а21	—+—V < 6 4	2127. яа2.
2128. 1. 2129.	2130. 2а2-	ЛС^	гної	а2 / -	2 • 213Е 2 (Я-		-2).
2132.-5----2133.4. 2134. Ь — а. 2135. р 2—1. 2136.-^-.
о	Л
20 2193
305
2137. бла2. 2138.	. 2139.	/3. 2140.	2141. 3а2/3.
2	О	10
тґ	/?2
2142. 2я(2г2 + /2). 2143. 6лЯ2. 2144.	(а2 + б2).	2145. -^-8Іп2<р.
2,48.
2149.-^-. 2150. -^--5/3.	2151. -у (-у - 1п 2^.
2152.л3а2. 2153.-^-. 2154.	2155.	.
З	4	о	о
2156. ~ (і-^-У 2161.	2162. 2Ц-Л. 2163.
2164.8л. 2165. -^-л. 2166. 2л (1 — 1п2). 2167.-^--
З	10
2168. 3202169.-^-. 2170. па3. 2171. -і- л2а3.
З	о	о	10
2172. 5л2а3. 2173. па3. 2174. -^йла3. 2175. 4л2а3. 2176.-Д-ла3.
З	105	15
2177. па3 (4- + -К1). 2178.-^-. 2179.2л2. 2180. -І^-л2а3.
\ 6	4 )	3	4
2181. 6л3а3.
4
2185. -=- л.
0
2182.
2186.
-^-(Зл2------^-)а3. 2183. 2л2а3. 2184. я 1/
2 \	о у	г 2
лв	л2	4	16
2187.	2188. 4- лаЬс. 2189. 44 ад2.
£	£	О	О
16	9	——	___ /у5
2190. —2191.	а2 V‘іра. 2192. л/2. 2193.	. 2194.72л.
З	5	20р?
2195. па2 Vрд.	2196.	. 2197.	П2 VрП-
о2	10
2198. Ух = я/2(2 /6 -	, У2 = л /2 (2 /6 + ДА2).
\	/	\	з І
2199. а(-|----^")а3-	2200- —	• 2201. я (с^ — а2) а3.
2202.	2203. ^2/3---їй ла3. 2204. -^-ла3. 2205. -^-лаЬс—
4	І	3 у	12	24
2	1	І 4 \
менша частина. 2206. —аЬН— 133—. 2207. —— л---------—).
З	3	о І 3 /
2208.^(10/10— 1). 2209. 4лг2. 2210. 4л2аг. 2211.~ (е2 — е~2 + 4).
306
2212.	2213. -^-ла2. 2214.	[2/5 + 1п (2 + / 5)].
2215. а) Зла2; Ь) -28У?- ла2- 2216. а)	яа2. 6) 1бя2а2.
2217. а) 4^- ла2; 6) 1240 ла2. 2218. а) бла2; 6) —^2 па2.
З	63 /3	35
2219.10. 2220. Мх = 4- (5*/2 — 1). 2221. 4~ [/2 + а2 1п (1 + /2)].
<5
27	4	15	125
2222. -5-а2. 2223. 20а2. 2224. -5-. 2225. —2226. Мх = —=^--
б	о	4	12
Му = ~гг~- 2227. 4 (1 + 1п 4-1 • 2228. 4- (1 —	 2229. 1-
2230. 1п 2-----1~. 2231. 2. 2232. -^-а2	2233. 4-.
о	120	4
2234. а) -4^-; Ь)  2235. £ = 0; я = —• 2236. £ = т) = -|-а.
о	О	Л	□
2237. 5 = 0; і) =*т ' 24^Ь2 • 22381 ь = яа- П = 4- а.
4 8П 1	<5
2239. £ = Я“4г- 2240. £ = я = 4г • 2241. £ =-|-а, т] = 0.
о	□	о
2242. = 4г- • 0 = -4^- • 2243. £ = 4£- . П = —. 2244. 2560т.
5	4/2	7	4/2
2245. 5000т. 2246. аЬ (к +	. 2247. 50 000л кгм.
1	4
2248. — 103лг2/г2 кгм. 2249.	2250. 250ЛГ4 кгм. 2251. ~а\
6	о
4	2	17 кМ
2252. -у уаЬ2. 2253. -у лу^. 2254.	, к — гравітаційна стала.
РОЗДІЛ їх
Функції багатьох змінних
2256. 5 = а!іа. 2257. V = л№Н.
2258. 5 =	/(х + у + г)(у + г — х)(х — у + г)(х + у — г).
2259. И = 4-лі?2/І2 — 7?2. 2260. И=—. 2261. г = 5.
З	Р
20*
307
2262. 4~;	2263-	-4-; «є існує. 2264.	4--
2	2	□	4	4
2265.	---2- ;	. 2266. Уся площина,
о о 2
2267.	Уся площина, за винятком точок прямої у = х.
2268.	Уся площина, за винятком точок прямих у — х та у = — х.
2269.	Круг з радіусом 2 разом з його контуром.
^2	£»2
2270.	Усі точки всередині еліпса +	~ Контур вилучено.
2271.	Зовнішність круга х2 + у2, = 1 з долученням точок його контура.
2272.	Півплощина під прямою у = х з долученням точок цієї прямої.
2273.	Поле кута між променями у — х та у — — х, х > 0.
2274.	Внутрішність параболи у2 — 4х з долученням точок параболи.
2275.	Точки площини зовні параболи у2 — х — 2 (тобто у2 > х — 2).
2276.	Півплощина над віссю абсцис (у > 0).
2277.	Частина площини всередині першого й третього квадрантів, за ви-
нятком меж.
2278. Прямокутна область — 2 < х < 2; —1 < у < 1.
2279.	Поле кута між півпрямими і/ = х + 1 та у — х, х > 0.
2280.	Круг х2 + у2 — 1 та кільця 2и < х2 + у2 < 2и + 1 (п — натураль-
не число) з долученням контурів.
2281.	Півсмуга між прямими у = — 1, у — 1 та х— —1 з долученням меж.
2282.	Поле кільця 1 < х2 + у2, < 9.
2283.	Куля з радіусом 2 з долученням точок її поверхні (сфери).
2284.	Перший октант, за винятком точок площин, що його обмежують
(х > 0, у > 0, 2 > 0).
2285.	І, III, VI та VIII —октанти, за винятком площин, що їх обмежують.
2286. Частина площини між кривою у
— і—;—з та її асимптотою у = 0
1 + X2	*
з долученням меж.
2287. Частина площини між параболою у2 = х та колом х2 + У2 = 1 все-
редині параболи, за винятком межі.
1	2
2288. 3. 2289.----2290. —.	2295. Точки прямої у = 2х.
2	о
2296. Точки кола х2 + у2 = 1. 2297. О (0; 0). 2298. Точки параболи у2 =» х.
2299. Точки кола х2 + у2 = 4. 2300. Точки прямих х = 0 та у = 0.
2301. 0(0; 0). 2302. 0(0; 0). Точки прямої у = х—усувний розрив.
2303. Неперервна скрізь. 2304. Неперервна скрізь і, зокрема, в О (0; 0).
2305. Розривна в (0; 0). 2306. Неперервна скрізь і, зокрема, в О (0; 0).
2307.	= 2х,	= — 1.
дх	ду
2308. ^- = 3х2(/-уз+1, 21 = X» - Зу2х + 1.
дх	і	&	і/ ।
308
оо0« дг _ у2 + 2ху — х2 дг	у2—ху — х2
дх ~	(х2 + у2)2	’ ду (х2 + у2)2 •
2310.-^- = -*-, -^-=-4- 2311.	=	*
дх у ду у2	дх	ух2 _ у2 ду
2312. ^_3«»(3,-ЗД,
2313.	= 24 (Зх2у2 - І)3 ху2, = 24 (Зх2/ — І)3 х2у.
2314.	= —а зіп (ах — Ьу + 1),	= Ь зіп (ах — Ьу + 1).
2315. -^- = 2*3ї'‘-Зх2/1п2, -~==2х2у'-4х2у2Лп2.
2316.	= — у2е ху2,	= — 2хуе ху2-
дх	ду
2317 92 =	3%2 дг = ЗІпу
дх	х3 — соз у ’ ду	х3 — соз у ‘
2318. 4-=-^=, -^=_—і—.
дх	у\-х2у	ду	2/1 - х2у-Уу
2319. — = —	^~У	, — = — —
дг Ух — 4х2у ду у у _ 4x^2
л _л дг	2у дг 2х
2320. -х— =-----2	2-	, -д—	= -2- , . 2	.
дх	х2	+ 4г/2 ду х2 + 4ї/2
2321.-$— =-------7^=, *
дх х)/ х2 — у2 ду х2 — у2
2322.
дг 1	дг
дх ~ 1 + х2 ’	ду
1
1 +г/2‘
2323. ~ = ух^1, -^ = ху 1п х.
дх	ду у
2324. 4- =
дх
2у	дг __	2
9 . 2у ' ду , 2у "
х2 зіп —у х зіп —2—
2325.	= -З у — 1п 3,	= З у 1п 3.
дх	у	ду	у2
2326.	-^- = -Є-ХСОЗУС08У> -^- = Є-ХСОЗ»Х8ІП(/.
2327.	-^- = 2ху3г4,	= Зх2у2г*, -^- = 4х2у2г2.
2328.	= угхуг~і, = гху21п х, = ухуг 1п х.
дх	ду	дг
309
2329	________х________ ди	3У	ди
дх	у хг + Зуг + 5г2 ’ ду	у Х2 + зу2. + 5г2 ’ дг
у
=	.	2330.	= —е сі§-^-,
Ух2 + Зу2 + 5г2	<**	г
ди х сгг г	г ди	х СІ8 г ху
____ — £ ___________________ ________ —  £ _____________
ду	г ’ дг	2 . 2 у *
*	г2 зіп2 —
г
ди	2х	ди	2У Іп 2 ди
2331‘ ~дх “ х2 + 2^ + 2г ’ ~ду~ ~ х2 + 2? + 2г ’ ~дГ ~
2 чес2 2г	и	1
= 9 ,	п . 2337.	= - Л- дх Ч--------ду. 2338. дг = (Зх2 — Зау)дх +
х2 + 2У +	2г	х2	х	’
+ (З#2 — Зах) ду. 2339. 0. Вказівка. агсі£ ~~ + агсі§ — —	•
X
2340. дг = —8Іп (ху) (усіх + хсіу). 2341. дг = е у (•-----у •
2342. дг = уйх ~ Х(Іу . 2343. 0,1& 2344. -4г . 2345. да 0,0216.
х V у2 — X2	30
2346. 9,988. 2347. АТда я • ^Аг~/А^ . 2348. Д = 1,76 м2, д « 2,4%.
2349. —6е“ а + Зе~3‘ сов 21 + 2е-3/ 8Іп 21 — 2 8іп 4А
2350. е2^ зіп2ґ/_1 _
І / і
2со8 2^. 2351. /4 + /2^2/+1.
2352.
З/2 — 21
V і — (/» —/2 — і)2
V2
и3
Зг/2 іп и2у
и3
ОЛГ-« д?	Зу3 . _ , 2ц3
2353. -з— =------т- Іп и2у Ч--— ;
ди	и*	и*
2354. --------- 1	---------.
а+*)1/
дг
дV
дг	2х дг 2 (х Ч~ 2хе 2х2)
дх 38 х2 —і/2 Ч- 1 ’	~ х2 _ е-2^2 і *
2356. 2 8ес2 + би - зЧ /Д- + з), зес2 (Д- + би - ЗіА (— з'
І У2	) \ V2 І	І Іг	/ І г/3
2357. -^--2/'(0*- -^- = -2Г(ОУ- 2358.	2у^’(х2 - у2)х.
= д> (х2 — у2) — 2у2У (х2 — у2).	2359.	------- е~ху у,
ду	і/ / і/ V \ у і	дх ди ду *
310
дг	3	д/
ду	ди
п ди	,	ди
= 2“^-^+ “Т“
д;	1
—хп «ппл	о	. ди
— е ху х. 2360. —д— = 2 -3— х +	— у\
ду	дх д^ дх\
1 дг \	, І дг
	ч- \дх + х -т^—
У ду у
ди . ди \	( ди
х дг] +у )ах +2 (у
,. Х йх2 4- т. У „ „ гіу2]
(1 + х2)2	(1 + у2)2 * ]
— 2 зіп удхду — соз уду2). 2375. д2г = [2 соз (х2 + у2) — 4х2 зіп (х2 + у2)] дх2 —
— 8ху зіп (х2 + у2) дхду + [2 соз (х2 + У2) — 4у2 зіп (х2 + у2)] ду2.
2377. д2г — [у^дх2 + 4 (ху3 — у) дхду + (4х2#2 — 2х) ду2] е~~ху2>
2278. й2г =	~ Х^ ~ 4хУахе1У +	~ У2) аУ2
2370. 2 їх
2373. б(2г = — 2
2369. йг
ди
~ду~
________х дг \
ди у2 ду у
ди , ди \ ,
2374. <ї2г = 6х (соз уйх2—
(х2 + у2)2
л д3и	д3и
2379.	= 12 с°8 (2Х “ Зу)> ~дуї = 27 008 (2Х “ Зу)'
2381. а2г = /" (/) (2хйх — 2уйу)2 + /' (0 (йх2 — йу2).
' , д} ।
Уе ~
у ду 1
+^4і+2!,г+»-®-+/^	+<,^+
ди2	диду 1 у ду2)	ди 1 ду 1
-й- +еХ+у <1+йхйу+(хеУ -іт+
+ х2е2у + 2хех+у -^0- + Є2* йу2. 2385. й2и = 2 (хйуйг + уйхйг -)-
+ гй'хйу). 2389. у' = 1	, «/"=—	+ (1 ~. 2390. /=	.
' а'	У	У3	у — X
2391. / = -	, о. 2392. у' = ^-±-£. 2393.	,
у а2у	* х — у	йх у (1 + 2г)
= -21(\~7Х) > У' = 1. г' = 0. 2394. у' = 1У-У-. 2396.	,
дх 1 + 2г у	V х	дх а2г
. С2Х 9347	»' _ *(а2~ *2~ У2)	2398 і/ -	3*2у
ду ь2г '	' У ' у (х2 + у2 + а2) '	'	зез»_д.3'
2399. у' = 2ху2 (у + х/). 2400.	; не існує; ±
д2х / дх \2
2404. д2г = 2 зіп 2удхду + 2х соз 2уду2. 2406. х — у ~ &
2407. -^-+У = °.	2408. ^-+п2у^0. 2409.	+ 2	+ у = 0.
. 2396.
311
24'°.^=°. 24П. 5- + г = °. 2412. ^+у = 0.
2413. -^- + у = 0. 2414. §- + 2^ = 0. 2415. -§- = 0. 2416.-£=0.
2417.
дг л
и -з----г = 0.
ди
х+ = 0. 2420. 4^.
др	ди2
д^г
‘	диди
д2г
+4- = 0. 2419.
диди
2421.	= 0.
ди2
0. 2424. ——= —________________.
диди 2и ди
2418.
д2и 1 д2и 1
ф5’+'р2' І02’ +V Х
д2и 1 ди
дг2	~ дг
2422.
дг
2425. 6х — 2г/ — г +
1
2 ’
— 10 = 0;= ^1 = 5—р. 2426. 2х - 2і/— г + 4 = 0;
х — 2	?+4 пло„ .	,	9 х— х(} у — Уо г —г0
—9~=—4-- 2427. хх0 4- ууй + гг0 = а2; ——5	—2.
£	1	ло	У о	4о
2428 х*° +	+ 220 = 1- а2 & ~ *о) _ 62 (У ~ Уо) _ с2 (г — г0)
а2 Ь2 с2 ’ х0	у0	г0
2429.	+ з-----2~ = 1; а (х — а) = Ь (у — Ь) = с (г — с). 2430. х - у +
Я
— 1	— 1 г----Г
+ 2г-+ = 0; +— = +ї- =—------------• 2431. х + Ну + 5г - 18 = 0;
х-1 =	У-2 = г+	1	2432і	а2	Ь2
1	И 5	'	±У а2+ Ь2	+ с2 ' ±Уа2 + Ь2+с2	'
----	—	2433. 4х —2у —Зг —3 = 0. 2434. 2х + у — г — 2 = 0.
±/ а24-У2 + с2
2435. х — У + 2г = ]/+ , х — у + 2г = — У^- 2436. х + у + г —
— 13 = 0, х + у + г + 13 = 0. 2438. х + 4у + 6г — 21 = 0 та х + 4у + 6г +
9
+ 21 =0. 2440. у= -|-аз. 2441.	(0; 3; 3); М2 (0; 3; —7).
2442. 5 + 5(х-1)-5(у+1)+А-[2(х-1)2-6(х-1)(у+1) +
+ 2(у + 1)2]. 2443. 2 + 4 (х - 1) + 2 (у - 1) + ^-[6 (х - І)2 + 4 (х - 1) X
Х(у-1) + 2(у-1)2]++[6(х-1)з+6(х-1)(у-1)2]. 2444. у + ху +
+ -1- (Зх2у - у2) + ... 2445. у - (х - 1) у + ... 2446. 1 -	+
312
, Xі 4- 6х2(/2 4- г/4	,	1 , , , ,ч , 1 , . , еч
4-------4і---------• • • 2447. х 4- У — -3- (*3 + і/3) 4- -5- (*5 + У6) — • • •
2«8- » + 4г<2Ч-«’> +4г <^,»-3»»г + 2Я + ---
жо. 1 + х + „+^_+
+ «/ + < + ••. 2451. 1 +х+^Х2 + ^Ц^- + ... 2452.г=14-
4-(х- 1)4- (X- 1) (у- 1) + ±-(х - і)2(У- 1)4-.. •; 1,1021.
2453. х + у - (£±^+	_ ±±^_+ ...	2454. Мінімум у
Л	о	4
(1; 0). 2455. Мінімум у (—4; 1). 2456. Максимум у (0; 0). 2457. Максимум
у (2; —2). 2458. Мінімум у ()Л2; —]Л2) та (— ]/2, У2); у точці (0, 0)
екстремуму нема. 2459. У точці (а\ а) — мінімум, якщо а > 0, і максимум,
якщо а < 0; у точці (0; 0) екстремуму нема. 2460. Мінімум у ^1;-
2461. Максимум у (3; 2). 2462. Мінімум у (—2; 0). 2463. Максимум у
точках (1; 0) та (—1; 0), якщо а > Ь\ максимум у точках (0; 1) та (0; —1),
якщо а < Ь\ при а = Ь — максимум у точках кола х2 + у2 = 1. 2464. Макси-
мум у (1; 1). 2465. Мінімум у [ а_ ; ——-V 2466. гНайб = 1 ?найм =
\ Уз Уз )
3УЗ
= —1-	2467. 2найб ~ ?найм ~	1*	2468. ?найб =--%--* 2найм = 0*
2469. 2Найб = ?найм = —4.	2470. ?Найб = 4, ?найм = —64.
2471. 2найб =13, ?Найм = —2.	2472. £цайб ~ агСІ£ 7, ?найм = ИГСІ£ ( 5).
З
2473. Л4=—, /п = 0.	2474. Рівносторонній трикутник. 2475. Рів-
носторонній трикутник. 2476. 4-4-2. 2477. %1 Х% ——- , —.
З	З
4	36
2478. "у==“- 2479. Куб. 2480. гтіп =	. 2481. Максимуму точках
/ 1 1 \	/ 1 1	\	. . / 1	1 \
----— , —,-----------— ,------—- , мінімум у точках —	т=- ,
\ У 2	У2 )	\	У2	У2	]	\ У2	У2 )
(---’ ""І/2")	2482. Мінімум у точці (а, а).
313
2483. гтах — 27— ’ гтіп —	24®^* 2тіп — 2. 2485. гтах —	-	*
_ 2-/2 . 2486.	_12 + /Ї8	12 —/І8
«іп/п—	2	мтах—	у ’ итіп	у
2487. итах = 9, ггтіп = - 9. 2488. итах = (-^ . 2489 .(0; 0) - вузол. 2490.
(0; 0) — точка звороту першого роду. 2491. (0; 0) —вузол. 2492. (0; 0) — особ-
лива ізольована точка. 2493. (0; 0) — точка звороту другого роду. 2494. (0; 0) —
точка самодотику. 2495. (0; 0) — особлива ізольована точка. 2496. (0; 0) —
точка звороту першого роду. 2497. (0; 0) — особлива ізольована точка.
2498. (0; 0) — вузол. 2499. (а\ 0), (0; а), (—а; 0), (0; —а) — точки зво-
роту першого роду. Вказівка. Перетворити рівняння до вигляду (х2 +
4-ї/2 — а2)34- 27а2х2ї/2 = 0. 2500. (0; 0) — точка припинення. 2501. (0; 0) —
кутова точка кривої. 2502. (0; 0) — кутова точка. 2503. (0; 1) — точка
припинення., 2504. (0; 0) —точка припинення. 2505. (0; 0) —вузол.
2506. (0; 0) — вузол. 2507. у= ± 1. 2508. у = х та у = — х.
2509. 16ї/3 + 27х4 = 0. 2510. у = 0 та у =	. 2511. | х | + | у | = 1.
2512. х/з + у/з = 4. 2513. Циклоїда. 2514. х3 + ху2 + ру2 = 0.
2515. 4ху — а. 2516. -~—г + -т- — 1. 2517.	« = 0 —обвідна сім’ї й
2а2 а2
одночасно геометричне місце точок звороту першого роду. 2518. у = х—
4
---2у” » У ~ * — геометричне місце точок звороту першого роду.
РОЗДІЛ X
Криволінійні інтеграли
2519. -4(17/17-5/5). 2520.	а3. 2521.	. В к а з і в к а.
12	10	2
Покласти х = р соз 0, у = р зіп 0. 2522.	• Вказівка. Зро-
□ 4~
бити заміну х = а соз Л у = Ь зіп і. 2523. 1п (3 4- /5) — 1п 2. Вказівка.
Шлях у = 2х, сіз =У5сІх. 2524. 2ла9. Вказівка. Покласти х = а соз 0,
(/ = азіпЄ. 2525. 4 па3. 2526.	/ а2 + &2 (За2 + 4л2&2). 2527. 2ла2.
2	о
2528. -2^2 [/(1 + 2л2)8 — 1}. Вказівка. *=/’«+2й.
<5
314
2529. 24. 2530.-і-(56/7 — 1). 2531.-І-. 2532. —я. 2533.8.
54	'	15
4
2534.	-у аЬ2. Вказівка. Зробити заміну х — а соз іу у = Ь зіп і.
з Зг-
2535.	-уу на у а. Вказівка. Зробити заміну х = а соз3 Л у=а зіп3/.
2536.	Скрізь 1. 2537. 0. 2538. — 2л. Вказівка. Покласти х ==
==асоз/, у = азіпЛ 2539. 3]АЗ. 2540. 0 (0 < і < 2л). 2541. лаЬ. В ка-
? і в к а. Покласти х = а соз іу и — Ь зіп і. 2542. -4- ла2. Вказівка. Пе-
*	8
рейти до параметричних рівнянь х = а соз3 іу у — а зіп3 і. 2543. 1,5. В к а з і в-
к а. Покласти у = іх і знайти параметричні рівняння кривої.
4
2544. 'о*ї*а • Вказівка. Див. 2543. 2545. —. Вказівка. Пара-
^10	о
метризувати криву, поклавши х=зіп і. 2546.	. 2547.	. Вка-
зівка. Скористуватись законом Біо — Савара. 2548. --------—
2549.
ефіцієнт
2лт/а _еел , о	п	к
—— . 2550. т — к. Вказівка. Густина р —	, де
пропорційності, сіз сЬ сіх = йх. 2551. /?у=-^-,
к — ко-
^ = 0.
Вказівка. Застосувати Ньютонів закон тяжіння та взяги до уваги фор-
„ Срсозф, г Г р зіп ф	1 / 4л \
мули	---2 т сіз. 25о2. -у ^1 +	• Вка-
зівка. Покласти у = іх.
РОЗДІЛ XI
Інтеграли, залежні від параметра
ал зіп — 2553.	— . а	2554.	+ 3 (1 + ах) (І-)-*2)	14- а2
2555. І' (а) =	2а _ а	,	! 	— . 2556. -г 1п (1 4- а)	—-• а	а2 у 1 7 а (14-а)
2557. /' (а) = 2 агсід — . 2558. агсі§ — + 4=- (1 + а2).
у '	а	2а3 ь а ‘ 2а2	1	’
315
2559» Збіжність нерівномірна на [0; 1]. Вказівка. Зробити заміну
и ах.
2560. Збігається рівномірно щодо а на (0, оо). Вказівка. Взяти до
уваги, що	=
о
оо
. (* СІХ
теграЛІ ] (х-аГ+1
А
. 2561. Збігається рівномірно. Вказівка. В ін-
0 < а < оо, покласти и = х — а та взяти А — а> Ао.
2562. Збіжність рівномірна відносно а на [а, 6]. Вказівка.
оо
хае~х <^хь е~х для х > 1, а У хь е~х(іх — збіжний, у чому не важко пере-
о
конатися. 2563. Збіжність рівномірна. Вказівка, зіп х < ^х
X | зіп х | < е“аоХ. 2564. Збіжність рівномірна в будь-якому скінченному
проміжку [а0, В], а0 > 0. Вказівка. Xа""1 е~'х < х5"”1 е~х.
2565. Збіжність рівномірна на [а0, 1], а0 > 0. Вказівка. Xа-1 е~х <
Xа0”1 е~х < Xа0-"1 при 0 < х < 1. 2566. Збігається рівномірно відносно р
й ц, якщо тільки р > р0 > 0 та Я > до > 0- Вказівка. хр—1 (1 — х)р“1 <
< хр0—1 (1 — х)'70-1 при 0 < х < 1.
е~™(іх
—А.
2567. Вказівка.
2568. Вказівка.
А
\ зіп ахНх < —9 у чому не важко переконатися.
X	ао
2569. Вказівка. Див. 2568.
2570. Вказівка.
1 а
2571. -у- Іп (а + ]/*1 + а2). Вказівка. І (а) = у (іх У X
о о
1 ь
X -------------. 2572. Іп . Вказівка. І (а) = С (іх С ха сіа.
/1 -х2(1 + а2х2)	1+а	7 З З
2573. І (а) = я Іп '-І-ЦІ------------------------2574. -А-1п(1+а). 2575. І-1п(1+а).
якщо а > 0,------Іп (1 — а), якщо а < 0. 2576. я агсзіп а. 2577. я Іп
2
2578. На [а0, 1], ав > 0, збіжність рівномірна.
316
оо
«Гї г*	•	г/ / \	5Ш ах , «Гї	Л
2579. -у а. Вказівка. ї (а) = —, бо \---------б/х = — при а > 0.
л	х	£
о
оо Ь
2580. 1п-^-. Вказівка. /= ^ сіх § сіа. 2581. агсі£-^- —
о а
оо Ь
— агсі£ . Вказівка. І = § сіх § е~ах соз ахгіа та скористуватися рів-
0 а
оо
ністю Г е~ах соз Ьхсіх =—. 2582. -^-1п(14-а).	2583. пі. В к а-
.)	а2 4- Ь2	2	1 '
о
оо
зівка. Диференціювати п раз тотожність е~ахйх = — по а.
о
2584. (—1)т — ——‘т.р'1' • Вказівка. Диференціювати по а т разів.
2585. -і-	- . Вказівка. Заміна і = У ах. 2586.	У ле““2^
п •	І г і	• У \	•
Вказівка. —— =--------— І (після заміни ~--- = г). Стала інтегру-
йа У а	х
вання С =  при а = 0. 2587.	"|/*Вказівка. Зробивши
зіп ійі
9	,	1 г зіп ійі	р зіп і
заміну х2 = і, дістанемо — \	, і розглядаємо і ---—
2 З У і	З Уі
 е~кі <іі. Далі,
б ‘
о
беручи до уваги, що —— = —=- е іи2 (іи (див. 2585), знайдемо / =
У і Ул $
= С зіп ійі С е~іи2 д,и = - -1 С (Іи С е~~ зіп ійі =
І	і	0] е’
__	1 С йи	п и а Т 1 С	1 1/"^
= /й .) 1 + (£ + и2)2- При к^О. /-	] 1 +ц4- 2 |/ 2 •
2588. -4-1/-?-. Вказівка. Див. 2587. 2589. 4- 1/ —0-2 УаЬ-
і сі	£ г а
Вказівка. Поклавши і = У ах, з точністю до множника -7=- дістанемо
У а
Ул
інтеграл, обчислений у задачі 2586. 2590.	— е”"а2. Вказівка, /'(а) =
317
оо
—2 £ хе~~х2 зіп 2ахйх, а після інтегрування частинами Г (а) = —2аІ (а),
0
/ (а) = Се~а2‘ Але при а = 0 / (0) = 	, отже, С = —2591. І (а) = 0,
якщо ] а | < 1, та я Іп а2, якщо | а ] > 1. Вказівка. Взяти похідну по а,
потім використати підстановку г = Ї& 2592. -у- е~а- Вказівка.
оо	00
г , ч ГхЗІПаХбІХ „	.	. Г ЗІПОХ . Я .	,
/'(0)= — І ————. Додавши рівність \ ----------------ах = —, дістанемо/ (а)+
Л 1 “і- Х&	Л	х	/
о	о
оо
+ Д- = Г ^4,-  а звідси (а) = 1 (“) Отже, І (а) = Сгеа + С2е~“. Але
2 Л X (1 “і- X )
оо
/(а) — величина обмежена | / (а) | <	0 у» і тому	Таким чи-
о
ном, / (а) = с^~а. При а -> 0 /(0)=у - С2. 2593. - -у- е~а.
2594.	я агсзіп а. Вказівка. Можна вдатися до інтегрування по па-
1	.	1 + а зіп х п Г Жх
раметру, поклавши -----Іп	;--- = 2а | —=----9 9 . 9—
н	зіп х 1 — а зіп х ЛІ — а2а2 зіп2 х •
о
2595.	я 1 — а2 — 1). 2596. 1) Збігається рівномірно;
2)	збігається нерівномірно. 2597. Збіжність рівномірна. Вказівка.
е— аох2, । далі за ознакою Коші. 2598. агсі£ а.іп (1 + а2).
___________ З2
2599. -і- 1/ е 4а. Вказівка. Див. 2590. 2600. Іп -2-.
2га	2 Ь
оо
Вказівка. Застосувати рівність £ Ках) дх =	(0)] х
о
X Іп— . 2601. 1п~у • 2602. 1п-2-. Вказівка. Застосувати рівність
Г ------Но*) = _ ^0) 1п А 260Х 0 2604>	Вказівка.
З х	а	9|/з
2я
Покласти г = х3. 2605. —. Вказівка. Покласти 2и = 1 4- х.
Уз
я 2	(* х^ 1 (іх
2606. —-—. Вказівка. Застосувати формулу В (д, д) =
318
Маємо р =
5 . З ОСЛ, 1-4-7-10.. . (Зп — 2)
2607- - 376—12... 3«
л
/з 
2608.
4]/ 2л
Вказівка. Покласти і = х4. 2609.
у—. В к а-
2 зіп ал
зівка. Покласти и = х2 та взяти до уваги формулу для В (р, д) із зада-
чі 2606. 2610.	. Вказівка. Покласти г — зіп2 х.
1о
2611. ---;----. Вказівка. г = зіп2 х. 2612.
2Г(Ц-’)
РОЗДІЛ XII
Кратні інтеграли
2613. 12. 2614. 1п 2615.	2616.	• 2617. 2. 2618. 3,75.
□	о	2
/ ят	1 \	1	п2	344
2619. а2 ---------- . 2620. 5 -у-. 2621.-4-. 2622. а\
\ 4	2 )	3	6	105
5	5—х	5	5—у	2 х
2623. У (іх / (х, у) (іу\ У (іу У / (х, у) (іх. 2624. (іх § [ (х, у) сіу +.
об	0	0	0	0
4	2	6	2	2	у-\-4
+ У	У Г(х,	у) ау + У	ах у / (х,	у) ау, У Ж/	У	/ (х, у) ах.
2	0	4 х—4	0	у
2а	У 2ах— х2	а	а-{- V а2—у2
2625.	У ах	/ (х, у) йу, йу	/ (х, у) (іх.
0	—У 2ах—х2	~~а	а— У а2—у2
1 УІ^у2	1 Ух	/2	/2-х2
2626.	У (іу	У	/ (х, у) йх*, У ах	У	/ (х, у) ау 4- У	(іх У	/ (х, у) (іу.
0	У2	0	0	1	0
і	і/2	—у2	і
2627.	ах [ /(х, у)ау\ ^ау У / (х, у) <іх + У (іу /(х, у) ах.
о і-*2	о	72 о
319
	з_ 1	2-х2	1 У"у	2 У2—у
2628.	У йх У / (х, у) Лу; \ йу [ (х, у) йх + йу у / (х, у) 0х. 0	хз	0	0	10 99	4	2	За2	1
2629.	2630. 4-а. 2631.	2632.	2633. — 140	3	3	16	4 10 о	2	1	7 Л	я—1
2634.	-4-а2. 2635. 4-. 2636. -у. 2637.	2638. —5. 3	3	о	О	2
2639.	4г- 2640. /3+4-я. 2641.-4-ла2. 2642. 2	3	2	о
2643.	4-(Ь2 — а2) 1п —. 2644. -±-. 3	я	3	2 2645. -тг О	 1»
2647.	4± . 2648. 2а2Ь2. 2649. ~ а2л- 4	2650. -	^-(а2 + &2).
2651.	аЗЬЗ 6 _ 3 60с* • 2652' Хс~ 5 ’ Ус ~ 2 •	2653. хс	4г ' ~ Ус ~ "зГ •
2654. хс — яа, ус = 256а ~~ 315л ’ “657‘ Хс "	5	5 а. 2655. Хс = о	о		 Ус — 0* 2656. хс — ус — 17а4 2658.	. 2659. 1,6. Уо
	2а зіп а За	. </с = 0.	
2660. ~ ла*. 2661.	44- ла4. 2662.	. 2663. 9. 2664.-і а2. ІО	12	1о		
2 2665. 42-^-. 2666. О	Зяа4 64 *	2 2667. гг- О	2668. 2ла«. 2669. О
4 2670. гг лаЬс. 2671 <5	яа3 ’	3	(6 /3-5);	-^(6/3 + 5). 2672. ^-лг». 3	/□
5 2673.яА 2674.	22я.	4	/ 2675. -у-г3	-у-4)-2676-
2677. 280л. 2678. 2а2 (я —		2). 2679. -	1^2 ——. Вказівка. Проекту-
вати на площину У ОХ. 2680. 8а2. Вказівка. Проектувати на площину
Х02.. 2681. 4-(20 —Зл). 2682. -4-(2/2—1). 2683. 8 /2я. 2684. 4.
У	З
2685. ±(2/2- 1)а6агсІ§1/4-- З686-	2687‘ "Ип-
О	г О	А 1/0	11м
2я
2688. Вказівка. Перейти до циліндричних координат.
О
А	/п*	1Л
2689. лаЬс. 2690. -77г-. 2691. —— я. Вказівка. Перейти до
□	10	о
циліндричних координат.
320
2692.	• 2693. -2па3 (2 — V2). 2694.	(8 /2 - 7).
1Л	о	О
2695. -4|- я. 2696. -Ї-. 2697.	2698.	. 2699.
З	3	60	360	4 у 2
2
2700.	па3. Вказівка. Перейти до циліндричних координат.
З
2701.	—. Вказівка. Перейти до циліндричних координат.
2702.	Вказівка. Перейти до узагальнених сферичних коор-
3
а2Ь2с2 п	л2аЬс2	о	аЬс^ _ Л 32
динат. 2703. —. 2704. —~—. о	о 27О7._^£_. 2708.-^ 60 (л —І- Щ	64 —І- 1 1	2705. -^г-. 2706. 60	Зіо з . 2709. хс = ус =	~ 5	„	2	7
2710. хс —	~, ус —	, 2С	~-8-. 2711. хс-ус- -у, гс-
3	3 2712. хс = я, ус — —&• Ь, 2С =	3	_	9ал & с. 2713. хс — ус — 2С —	.
7	7	3 2714. хс= 18 р, рс = 0, гс= 176 р. 2715. хс = ус = 0, гс = 8 а.	
2716. ЦІД а\ 2717.	. 2718.	(4 /2 - 5).
1 ЗО	Зі)	10
2719. 4я(а2 + &2) в—. 2720. -^-яіА 2721.	• 2722. ~ лЛ
15	1о	2	1о
2723. бклг2 (к — коефіцієнт пропорційності). 2724. (Н -|- 2).
5	/ Н \
2725. хс = 0,	= 0, 2С = — г. 2726. 2л£р# 1______________ . , де к — ко-
4	\	уя2 + /?2/
ефіцієнт пропорційності, р — густина. Вказівка. Вершину конуса взяти
за початок, а його вісь — за вісь 07 і запровадити сферичні координати.
2727. 2я (7? + Н — У Я2 4-Я2). 2728. 1. 2729. ? ї • 2730- 2я-
2731. я Уї(У2- 1). 2732. 2я.
А	а, Ь, (і
2735. —^=- е6 , А = Ь, с, е
V 6	а, е, /
л
2733. я. 2734. —.
Вказівка. Зробити спочатку за-
міну х — и соз а — V зіп а, у = и зіп а 4- V соз а, а потім и = р соз О, V = р зіп 0.
21 2193
321
2736.---— Іп 2. Вказівка. Зробити заміну и = х — у, V = х.
2737. 2. 2738. -і- . 2739. Інтеграл збігається при а > 1. 2740. Збігається.
2741. Розбігається. 2742. Збігається. 2743.	. 2744.
2745. -1.. 2746. А 2747.	. 2748.	.
2749> (п-1)!(2п+1) •
Р034/Л ХНІ
Поверхневі інтеграли. Елементи теорії поля
2750. 9. 2751. 54 /14. 2752.
2755. -|-ЛЯ4. 2756. 2лагс1§ —.
О	(X
2760.	. 2761. -у а4. В к
(21п 2 - 1). 2753. 0. 2754.
1 о
2757. ЗУ. 2758. 0. 2759.	.
Юо
а з і в к а. 5 збігається з своєю про-
екцією (Р) на ХОУу і тому І — — У (х2 + у2) сіхсіу.
о
2762. яа3Ьс. 2763. ~ паЬс. 2764. 0. 2765.	. Вказівка.
О	З	о
Застосувати формулу Остроградського. 2766.	. Вказівка. Застосу-
<5
вати формулу Остроградського. 2767.
2768. —=— я/?5. Вказівка.
□
Застосувати формулу Остроградського.
зівка. Вдатися до параметричних
2769. 4л	+ Вка-
с а Ь І
рівнянь поверхні х — а соз ер зіп 0,
у = Ь зіп ф зіп 0, г ~ с соз 0. 2770. 0. 2771. 2 £ У (х — у) сіхсіу + (у — г) йуйг +
5
4-(2 — х)ЛхЛг. 2772. 4л. 2773.----------------2774. — па3. 2776.
О
Сім’я пара-
бол у = х2 + С. 2777. Сім’я концентричних кіл. 2778. Сім’я рівнобічних
гіпербол з асимптотами у — х та у — —х. 2779. Сім’я гіпербол ху ~ С.
322
2780. Паралельні прямі. 2781. Сім’я рівнобічних гіпербол, розташова-
них у І та III квадрантах. 2782. Сім’я кіл х2 + у2 = 2Сх. 2783. Параболи
у = ах2. 2784. г — х2 + у2 зіп С, | С | <	, тобто конуси з вершиною на
початку координат. 2785. Паралельні площини. 2786. Концентричні сфери
з центром на початку координат. 2787. Сім’я однополих гіперболоїдів при
и > 0; при и — 0 — конус, сім’я двополих гіперболоїдів при и < 0. 2788. Сім’я
параболоїдів обертання. 2789. Сім’я гіперболічний параболоїдів.
1	92
2790.--=—. 2791.--------2792. £га(і и (М) = 6 і — 5 / + 6/г,
□	ІЗ
| Єга«і и (Лї) | = /Ї08, Л4Х(1; 1; 1), М2 (-1; -1; 1), М3 (1;-1; -1),	(-1; 1; — 1).
Мі (0; 0; 0). 2793.	. 2794. ]С3 . 2795. £га<і и (М) = 9?- З /*- 3 к;
| £гас1 и (М) | = ]Л99. У точках конуса г2 — ху — перепендикулярний до 07;
при х — у = г — дорівнює нулеві. 2796. 5)^2. 2797.---------- (5 + 4)^3).
2798.	2799. 2	. 2800. /3- 1. 2801. /5. 2802. —|=-
5	17	/З
2803. /2. 2804. - $	. 2806. 2 (2 + /2). 2807. ^£±^±2^
2808. §га<1 и = (2х — 3)"і + (2</+ 2)}. 2809. —97+б7;/117.
2810. -|-7+-|-7; 1- 2811. 1§<р = 5, <рда78°40'. 2812. 13<р=-1^_,
<рда69°37'. 2813. соз а да 0,990, ада8°4'. 2814. соз а да—0,199, адаЮГЗО'.
2815. соз ф —-	3 , <рда 18°25'. 2817. 7г~ 1/~4А:. 2818. 2^ —4-
/10	81	г3
2819. хсоза + УсозР + гсозу	Г = 2	1	1 _
г3	с З	3	3	6
— 1 = Вказівка. Поверхня складається з чотирьох трикутників.
Одиничний вектор нормалі V до х-(-1/ + г- 1 = 0 є V = *	+ до пло-
У З
щини х — 0, V = — ї; до у = 0, V ~ — /; до г ~ 0, V = — к. Можна також ско-
ристатися формулою Остроградського. 2821. Зл/?2#. Вказівка, гх =>
«=пр-*г відповідно дорівнює 7? (на бічній поверхні), 0 (на нижній основі),
Н (на верхній основі).
21*
323
2822.	—. В к а з і в к а. Рівняння поверхні х2 + г2 — у — 0,
1 □
* 2х і — і 4- 26 г а	1
/4х2 + 1 + 4г2	/4х2 4-1 + 4г2
2823.	0,1л/?2# (З/?2 + 2#2). 2824. 4лд. В к а з і в к а. Вектор напруги
поля Е — -Ц,-, V = гх. 2825* я. 2826. 80л. 2827. Я. В к а з і в-
г3	3	2
->->	2	1	* "*
к а. А V = 3. 2829. — . Вказівка. Покласти и = — та А == г і скори-
г	г	г
4
статися формулою із задачі 2828. 2832. -у я/?5. Вказівка. Скористати-
ся формулою Остроградського. 2834. Вихрове поле не має джерел і стоків,
поле £гас! и не має вихрів. 2835.-. Вказівка. Застосувати фор-
о
мулу Стокса. За «напнуту» поверхню взяти півсферу г = |/а2 — х2 — у2,
2836. —-— . Вказівка. Скористатися параметричними рівняннями
6 — л
х~асозі, у = Ь зіп і. 2837. яа2. 2838. — 2я. 2839. -----а3.
*	4
->	4
2840. 2 (у + г) і. 2841. -~-лаЬс. Вказівка. Скористатися формулою
Остроградського, сііу А = 1 — 2у + 2г. 2842. сііу Е = 0. Отже, у будь-якій
точці поля, де визначений вектор Е, нема ні джерел, ні стоків. У точці, де
вміщений заряд, це несправедливо, бо там г = 0 і Е невизначена.
2843. 0. 2844. Вказівка. Ех = Я~^»	Я а за-
ряд я вміщено на початку координат. 2845. сііу Е — ~, гоі# = 0.
2846. — лЬ2. Вказівка. Покласти х = Ь соз у = Ь + Ь зіп і.
2847. гоі Л = — -і- [(х2 + у2 + ху) і + (у2 + г2 + гу) ] + (х2 + г2 + хг) й].
2849. Вказівка. ШV А = 3/ (г) + г/' (/•) = 0 для турубчатого поля.
2851. — (2х2у + 1) і 4- (ху + 2ху2) / — (хг — 1) к = гоі А.
2853. гоМ = 0; (ііу А = 0. 2855. гоі V = 2соГ.
324
РОЗДІЛ XIV
Ряди
2857.	’ $ = "4"- Вказівка. Знаходимо загальний член ряду,
п=1
користуючись рівністю ап = 8п —
оо	оо
«“• 2 (2п—І) (2п+1)  5“Т' 2“ 2 „ („+')(„+ 2) ' 3"
п—\	Л=1
оо
=4-. 2860. У(—1)" <~і1й ,5 = 0. 2861. Збігається, 5 = -|-.
4	к 7 п (п + 1)	8
п=1
2862. Збігається, 5 = 4г- 2863. Збігається, 5= 1 4~. Вказівка,
о	о
Записавши ряд у вигляді 1 + ( —-------т~ І +1----5“ 4—їт") + -.•> обчислити
12	4 / І	о	]
різниці в дужках. 2864. Збігається, 5=5-|-. 2865. Збігається, 5 = 1.
о	•	ІЛ	•	•	1	1	1
Вказівка. Користуючись рівністю —1)' = "и-----------------п _|_ 1 * зобразити
кожний член ряду у вигляді різниці. 2866. Збігається, 5 — -4“- 2867. Збігається,
о
13	3
5 =	. 2868. Збігається, 5 = —. 2869. Збігається, 3 = ——
24	4	2
2870. Збігається, 5 = 1п-^-. 2871. Розбігається, 5 = оо. 2872. Збігаєть-
О
5	1
ся, 5 = —г—. 2873. Збігається, 5 = 1. 2874. Збігається, 5 = ,	. В ка-
16	к.(к\)
зівка. Використати рівність
________1________= 1 Г______________1_________________________1____________1
п (п + 1)... (и + к) к п (п + 1)... (п-\-к—1)	(п + 1) (п + 2). .. (п + к)
я
2875. Збігається, 5 =	. Вказівка. Для знаходження частинної
суми 5Д ряду використати метод повної математичної індукції. 2876. Збі-
гається. 2877. Збігається. 2878. Збігається. 2879. Збігається. 2880. Роз-
бігається. 2881. Збігається. 2882. Розбігається. 2883. Збігається. 2884. Збі-
гається. 2885. Збігається. 2886. Збігається. 2887. Збігається. 2888. Збі-
гається. Вказівка. У кожному члені ряду перевести ірраціональність з
чисельника в знаменник. 2889. Збігається. Вказівка. Використати рів-
ність -----!----- =----!---. 2890. Збігається. Вказівка. (2п)!! = 2-4Х
(1п£)1п*	£1п Ід я
Хб .. . 2п = 2л.д!. 2894. Збігається. 2895. Збігається 2896. Збігається.
325
2897. Збігається 2898. Розбігається. 2899. Збігається. 2900. Збігається.
2901. Збігається. 2902. Збігається. 2903. Збігається. 2904. Збігається.
2905. Розбігається. 2906. Розбігається. 2907. Збігається. 2908. Збігається.
2909. Розбігається. 2910. Збігається. 2911. Збігається. 2912. Збігається.
2913. Збігається. 2914. Розбігається 2915. Розбігається. 2916. Розбігається.
2917. Збігається. 2918. Збігається. 2919. Збігається. 2920. Збігається.
2921. Збігається. 2922. Розбігається. 2923. Розбігається. 2924. Збігається.
2925. Збігається. 2926. Збігається. 2927. Розбігається. 2928. Збігається.
2929. Розбігається. 2930. Вказівка. Використати інтегральну ознаку
збіжності. 2932. Збігається умовно. 2933. Розбігається. 2934. Збігається
абсолютно. 2935. Розбігається. 2936. Розбігається. Вказівка. Ознаку
Лейбніца тут використати не можна: члени ряду спадають немонотонно.
2937. Збігається умовно. 2938. Збігається умовно. 2939. Збігається умовно.
2940. Збігається абсолютно. 2941. Збігається абсолютно. 2942. Збігається
абсолютно. 2943. Збігається абсолютно. 2944. Збігається абсолютно.
2945. Збігається умовно. 2946. Збігається абсолютно. Вказівка. (2га +
+ 1)1! — умовне позначення добутку всіх непарних чисел від 1 до2п4~1.
2947. Розбігається. Вказівка. Використати рівність (2гг4~2)!! = 2П-*"1 X
X (п + 1)!. 2948. Збігається умовно. 2949. Збігається абсолютно.
2951. (—1; 1). 2952. (—2; 2). 2953. (—1; 1). 2954. ( —оо, оо).
2955. (—1; 1). 2956. (—оо; —2]. 2957. (—оо, —1), (1, оо). 2958. (0, оо).
2959. (0, 4). 2960. (0, оо). 2961. [0, оо). 2962. (—оо, +<*>). 2963. і—, е)
І Є І
2964. (—оо, 0). 2965. (—оо, оо). 2966. Збігається при будь-якій варто-
сті х, що не дорівнює нулю або цілому від’ємному числу. 2967. [—1, 1).
2968. (—2, 2). 2969. [—1, 1). 2970. [—1, 1). 2971. (—оо, —1), (—1, оо).
2972. (—со, 0). 2985.	. 2986.	. 2987. тг-3** ,ч,. Вказівка.
1 — х*	1 + 4х	(1 —х3)2
Цей ряд можна дістати з ряду (задача 2985) почленно здиференціювавши остан-
ній. 2988. - х ... 2989. 4агс{§* + 4 |п4^- 2990. 4 Іп — х.
(1-х)2	2	4	1 -х	2	1-х
Ч	00	і
2991. (х+1)1п(х+1) —х. 2992. ІПу. В к а з і в к а. ^х	.
2	п=1	1 “х
1
З
Г (іх
Ряд рівномірно збігається на проміжку [—7, 7], 0 < д < 1, тому І -------=
± ^-х
оо З
= У Г хп~1ах. 2993. 4 (1п 3 + —7=г ). 2994. 4 1п“4
~і 5	6 V /3 /	2	3 
2995. £ = -4; (—4> 4-У 2996- К=1; [—1» 1). 2997. £=10;
[-10, 10). 2998. £= X2-:	XI). 2999. £ =е; [2-е, 2 + е).
326
3000. /? = 0; збігається тільки при х == 0. 3001. /? = -}- 00> (—00» + °°)
3002. Я = 2; [—3, 1]. 3003. Я = 1; [3, 5]. 3004.	[—1>0).
3005.	Я =	0;	збігається тільки при х = 0. 3006. Я	= 4; (—4,	4).
3007.	Я=	1;	[—1,	1).	3008. Я = + со; (—оо, 4-00).	3009. Я =	1;	[—1,	1].
ЗОЮ.	Я =	4;	(—4;	4).	ЗОН. Я = тах (а; Ьу, (—Я, Я).	3012. Я=	1;	(—1,	1).
3013.	Я =	1;	[—1.	1).	3014. Я = 1; (—1, 1). 3015.	Я=-^-;
чпік і 4. 3 Гґг п. 1	(* — О2 1	(*-1)3 ,	пЛу
3016. 1 + —	- 1) + т-------—-------------------зі-+. .. + (-1)« X
Г3-- @П-------(х — 1)" + ... 1. 3017.
2П—1 п!	І
+ <д; + г)^' + ...1.зов. XI
2"	2
4
1"1  х + 2 < (*+2)2
2	2 ”ґ 22
З!
4!
X —------— (х — 1)"+1. 3020.
г^Сп+і)!
Х2Л
(2Л - 1)! •
п=1
п=1
3019. 1 4
2п
,П—1 Хп
4" ’
х— 1
2
п=1
х2п-2
)/2л зіп хп
3024. У ----------- *-------
п\

22Л-1 х2п
(2пу.
3026.
22п-1 х2п
(2п)!
3027.	(—!)"'
я2"*1
2п— 1 '
3028.	х«.
и=9
3029.	(~ї)'
П=1
! П(Л+ 1)
2 Х *
со
3031. Ц-У [(-1)п+І-2«+1]-^-.
о	П
п=1
оо	оо
3032. 1п2 — У (1 + 2-п) —. 3033. х2 + У	х2п+2.
п	(2и)!!
п=\	п=1
3034. і + 2<-1)"^=й5Г[
П=1
х$ З
. 3035. * + -£- + Xі + ...
327
3036. 1 + 2 (-І)п+І %П)||)І! *2П- 3037. 2 (-!)п+1 (7Т7ПГ•
п=1	п=1
00	„2п—1	00
3038. V (—1)п+1 -5-4- . 3039. V пх"-1.
22п-’(2п-1)!
п=1	4	'	П=1
«»• І (^г-
п=1	п=1
1	я2"-1	1	2
3042. > (—І)""1——. 3043. —. 3044.	. 3045.
22п-1(2п— 1)	4	3
П=1	'	’
3046. -і-. Вказівка. Здійснити заміну х = —. 3047. 5,0658.
2	у
3048. 1,7188.	3049.	2,1831,	3050.	2,0006.	3051.	3,0173.	3052.	1,005.
3053. 0,3679.	3054.	0,8187.	3055.	0,0175.	3056.	0,9848.	3057.	0,4794.
3058. 0,1972.	3059.	0,9754.	3060.	0,1823.	3061.	0,6990.	3062.	1,649.
3063. 7,937. 3064. 0,339. 3065. 0,17365. 3066. 0,69315. 3067. 0,30902.
хл	х2"+'	х«
3«,8..+(-о- (2я+1).<г„+І),  ’«»с+>” ।«।+2
п=1	п=1
00	00	1
(— 1)” о *	• 3071. х + У ------4-7-----—- .
2п-(2п)!	Лші (2п—1)-(п—1)!
п=1	п=2
1	я2"-1
3072. V (-І)—1
3073. 2
п=1
1-3...(2п —З)х4ге~3
2П—1 • (4п — 3)-(п— 1)!
3074. х + 2 (—О"-’
п=2
1-3... (2п — 5) х3п~2
2ге~І.(Зп —2).(п—1)!
^.9/2—8
9п — 8 ’
3076. 0,333. 3077. 0,310. 3078. 0,098. 3079. 0,245. 3080. 0,487.
«2 і	із	1.35
3081. 1,057. 3083. 1 + х +	х> + х* —х' +...
3084.	у=1+х + -^-х2 +	+ • • •
3085.	ї/ = х+4г + ^- + ...
3086 «- Я <х П4- (Х-ІР . (Х-1)8	6(Х-1)»
3086.	0 = —(х-1) + —27—+ —з,-----------5і--------------+ •••
328
РОЗДІЛ XV
Диференціальні рівняння
3087. ху' — 2у = 0. 3088. 2ху' — у = О. 3089. х2 — у2 + 2хуу' = 0.
3090. х — 2у + уу' = 0. 3091. у'2 + у2 — 1 = 0. 3092. (1 + х2) у' + 1 +
+ У2 = 0.	3093. ху' — у + X ]/х2 —у2 = 0. 3094. у" = 0. 3095. у"'(1 +</'2) -
— Зу'у"2 = 0. 3096. у"' = 0. 3104. 1 + х2 = С (1 + у2). 3105. Д--------V 4-
У2 X2
+ 2 1п-^- = С. 3106. агсзіп х + агсзіп у — С. $\$1.у = еСх- 3108. (1 + х2) X
X (1 + у2) = Сх2. 3109. і£хі£(/ = С. 3110. Іп ДД+ Х~У^~Х 4-
/1+х + /1-х
+ 2 агсі§ 1Д Д + Іп ——1 = + /З агсі§ 1 ДД = С, и
' 1 +х V и* + и2 + 1	]/3
ЗШ- /П^агсі§х-1п(х + ]/Г+^) + 2(1/у-]/ї^ X
X агсзіп }/(/) = С. 3112. еУ (у2 — Зу2 + Зу— 6) — е~х (2 + 2х + х2) = С.
3113. 4-1пі§(Д- + Д-')+}/21пІ§ Д- = С. 3114. Де2*-
2 І 2 о /	4	4
- -^У^(у+УТ+^) + ~(у2-2)УТ+72 ] = С. 3115.	+
е~у = С,
+ агсі§^—- = С. 3116. х + С=сі§/'Ц-^+-4
у2(/	\ 2	4
^+е-» = 2. 3118.	---і-1п(1+(/2)-1п(У + |/Пь7) = С,
1/ 1 4-
х
4- У 2
У = 0-
3122.
Д Іп (1 + У2) - Іп (у + ]/1 + у2)--Д-. 3119. еУ - 1 = Се~\
£	у 2
+ с = Іп Л_+2	3121. 5=^-.
ху у	2
йх -= а 10,0004--пХопа і Де х—кількість
\	10 оОУ /
3120. 4ЕЕ = іп —
ху у
а ^ 1497. Рівняння
величина. 3123. а = 1,653 кг. Вказівка.
3124. 32,5. В ка-
СО2 в момент і, а — шукана
йх = — 0,03х^Л якщо х — кількість солі в чані через і хв.
зівка. п = 0,б/2ІЛ, де К — глибина. 3125. 5,2 ка. Вказівка. Якщо
х — маса нерозчиненої солі, і — час, к — коефіцієнт пропорційності,
„	1 4х /10 —х 1 \	, тЛТ е2/^—1
С — 3 ’ Т° йі ~ кх ( 90	3 ) ’ 3126, 0 ~
(Хга'. + !
329
1	І е—
8 — — 1п -------—---------. Вказівка. Диференціальне рівняння
т = т§ — £а2,	-— § — ац°, а = — 3127. х = хоекі = х0А*, А — ек,
сії	М	пі
і
А = |/"2. Шукана залежність х —- х023 . Через 9 год кількість бактерій збіль-
.	80
п х___20
шиться у 8 раз. 3128. і — 20----, і = 60 хв. 3129. Диференціальне
рівняння = кх дає х = х$екі з урахуванням початкових умов к = 1п2,
5
а тому після 2,5 год х = 22 х0 — 5,65х0. 3130. у = хеСх+1- 3131. Сх2 = у +
+ )/х2 + г/2. 3132. еу +1пх = С. 3133. х = Се х. 3134. (2х-}-у—3)2=
= С (6х + 2г/— 5). 3135. (х — у)(х + 7у — 4)з = С. 3136. 1п (4х -1- 8у + 5) +
у
+ &у — 4х = С. 3137. 2х2 + у2 =С ]/х2 + у2. 3138. ех (1—Сх) = Сх.
3139. х2 + у2 = Су, 3140. (у — х)8 (у — 2х)9 = С (у + 2х)5. 3141. (х + У)Х
хУх3 + у3 = С. 3142. у = Сх. 3143. )/х2 + у2 = х (Сх + 1). 3144. у2=С—
— 2Сх. 3145. Р —і-------соз ф (конічні перерізи).
3146. у = (С 4- х2) е~х2.
X2
3147. у — х2 — 2 + Се 2 , у = х2 — 2. 3148. у — зіп х — 1 + Се~5Ш
х
3149. у — 1п х 4-	, у = 1п х — *	. 3150. у — Се	+
1п х	1п х
4-	і-.,-..г . 3151. ху (1п2 х 4~ С) 4- 2 = 0. 3152. у (х 4~ С) = зес х.
У 1 — х2
X2
3153. зіпу = х 4- Се~х. 3154. Ї^у=1 + Се 2. 3155. }/у2 4- 1 =
= х2 — 2х 4- 3 4- Се~~х. 3156. у~1 = Се 2 4- с08	у~1 = соз х. 3157. у =*
= (х 4~ С) е—51пх, у = (х— 1)е“51пх. 3158. =Се~х — х4-1.
3159. у (1 + 1п х + Сх) = 1. 3160. У у = С 1 —х*-і- (1 — х2).
О
3161. х = Су +	. 3162. х2у = (С + 1п соз х + х і§ х)2.
3163. 0 = хі§Х 4- + Сі8* г/ = хі§4--4 і§4-.
£ £ £ £
330
3164. у = Схп. Вказівка. Диференціальне рівняння ху' — у =
І	\ Я ,	„
--'4^- зю.
—	т?2 соз аі.	3166. у = Сх2 + -^-.
21/
Вказівка. Диференціальне рівняння у'----------
2а2
х2
а2—площа трапеції. 3167. уу' = *	, у2 = Сех— х2 — 2х— 2, С > 0.
3168.	_ бхV + г/4 •= С. 3169. (х + у) (х 2— Іху + у2) = С.
3170. х2 + у2 + 2 агсзіп-у = С. 3171. 1п (х2 + у2) — агсі§-^-=С.
3172. 	4- 1п — = С. 3173. х2 — у2 = Сх. 3174. х -4-уе* = С.
х—у у
3175. х2 — ху = С. 3176. Зх2у + х3у3 = С. 3177. ху2 + 2х2у — 2 = Сх.
етх
3178. ех (х2 + у2) = С. 3179. х2 — у2 = Су3. 3180. у = Се~ах +
3181. х2 + у2 = Сх3. 3182. у — СехУ. 3183. х3у + ху3 + 1 = Сху.
Си2	1
3184. х2у2 = 1п —. 3185. х2 + у2-{--------= С. 3186. х2 + у2 +
х	ху
+ 2 агсі§ = С. 3187. С (у — І)2 = х2 + у2. 3188. у + агсі§ -4- = С.
3189. х + агсі£— = С. 3190. у = Сех - х — 1, у = Се~3х + -|- (Зх - 1);
У	У
х	,	.	.
У = -^ — не розв язок, а геометричне місце точок дотику інтегральних кривих.
X2
3191. у —	+ С, у = Сех— х — 1; у = 0 — не розв’язок. 3192. (2у — х2 —
— С) (у — Се*) (у + х + 1 — Се—Ж) = 0. 3193. х — 2<~^22Пір+С ’ У = хії~
— 2і, у = 0. 3194. у = Сх2 +	, у2 = 4х2. 3195. у = Сх + зіп С,
у = х(л — агссоз х) + ]/1 — х2. 3196. ЗСу — ЗС?х + (С — З)2, у2 + 4у — 12х.
3197. х2 + (у-С)2 = 1. 3198. 49 (у — С)2 = 4х7. 3199. х =	У =
= 2 її +С 32°°-	----1г-=°- 3201.(у-х-С)(г/ + 2х-С) =
= 0. 3202. у = х — С------Ц^г. 3203. х2 = 2С (у — 2С); у = ± 2 — особливий.
X — с,
3204. (у + С)2 = х — 2; х = 2 — особливий розв’язок.
331
3205. х2 + Су 4- С2 — 0; у2 = 4х2 — особливий розв’язок.
3206. у — зіп (х + С); у2 = 1 — особливий розв’язок. 3207. 2х2 + З#2 = С.
X2
3208. х2 + ау2 = С. 3209. у2 + -у = С. 3210. х2 + у2 = Су. 3211. г —
= С (1 — соз <р). 3212. (х2 + у2)2 = С (х2 — у2). 3213. у2 + 2ху — х2=С.
3214. х2 + у2 = С (у — х). 3215. р = Се~к\ к = а. 3216. у =	~
13х4 г х2 п ~ п _______________х4 Іп х 13х4 , 5х З
— 288 + С1 2 + С2*+ Сз’ У ~ 24	288 + 36	32 ’
3217. у = СіХ2 + С2х + С3, у = х2 + 1. 3218. у = 3“^Х + Схх3 +
+ С2х2 + С3х + С4. 3219. у •— -----------зіп х + С4х2 + С2х +	3220. у
ех зіп X . „	, „	ех ЗІП X ,	СОЗ3 X , 7 СОЗ X
=—2-------+ сі* + с* у =----------2------І-х- 3221. у =-------27“4------у-
+ СуХ2 + С2х + С3. 3222. £/ = х1пх — % + Сгх + С2, у = х Іп х + 1.
3223. (/ = ^--^-+С1х3 + С2х2+С8х + С4,	=	+
9	9	/2	\
3224, ^ = -28 р7~Т0’р5+(Т + С1)р8-2С1Р + С2’ Х = Р3 —2р.
3225. Зу = (Сх - 2х)3/2+ С2х + С3. 3226. х2 + у2 + Схх + С^у + С3 = 0.
3227.	-,?4 --г-х + Сь 3228. Зх + С2 = 4	- 2СХ) /Сх +
3229. х + С2 = С	. 3230. (х+С3)2 — С1(/2+С2=0. 3231. у=х»+
уСі + Іпі/2
+ 3x 4- 1. 3232. у—х=21пі/. 3233. у2=2х— 1, у2=3— 2х. 3234. (/=С1е5Х+
+ С#2Х. 3235. у = Сх + С2е~зх. 3236. у = Сгеах + С2е-ах. 3237. у = С^е—х +
+ Сге2х + С3е~2Х. 3238. у = Сге~2х + С2хе~2х + С3х2е~2Х. 3239. у = Сх +
+ С2х + С^. 3240. у = Сх + С2е2лг + С3е~2х. 3241. у = Схе-зх +
+ е~ Х Сг соз х + С3 зіп —х^. 3242. у = СіЄах + С2е~ах +
+ С3 соз ах + С4 зіп ах. 3243. у = Сх + С2х + С3х2 + С^х. 3244. у =	+
+ -С2е~х - х2 - 3. 3245. у = С1Є2Х +	+	+ -у- •
3246. у = С1Є2Х + С2хе2х + ех (х + 2). 3247. у = Сх соз 2х + С2 зіп 2%+^Л
3248. у = С! + С2х + С3 соз х + С4 зіп х -|—-----х2.
332
3249. у = Сі + С2е2* + С3е~2х -	----. 3250. у = Сх + С^х + С^х-
уЬ	уЗ 5х^
---60-----18" “ 'Й------27- 3251- У = С1созх+С2зіпх +
. ЗІП X , соз х — 1	„ х , п г , хех
+ — 1п созх + 'ґ • 3252- У = Сіе +	+ -2--------
_ ех1п0 + <) _ 2- + е~х1п0 +е~Г) . 3253. у = Сі соз 2х + С2 зіп 2х +
4-2сО8 2х 1п соз 2x4- -^-зіп %х- 3254. у=Сі соз х-}-С2 зіп х+соз х 1п -.
(* йх
3255. у = Сх 1п х + С2 їй х І -у-2 *-♦ 3256. у = С1х-{-С2(х2—1).
3257. у = СіЄх + С2х2. 3258. у = Сх зіп х + С2 зіп2 х. 3259. у == Сгх
+ С2 ]/1 + х2. 3260. у = Сгех + С2х + С3е~х + х3. 3261. у =-• С1ЄХ + С2(1 + х).
3262. у = Сі £15±4-С2	3263. у = Сіх+ С21пх. 3264. у = Схх +
ух ух
-|- С2х 1п х -{ С3х 1п2 х. 3265. у — С± -|- С21п х -|- С3х3.	3266. у =* С4х3 -|-
х2
С2 соз 1п х + С3 зіп Іпх-3267. р = Сх соз 1п х + С2 зіп 1п х+
□
. « о ,	1^0.1 олло	п СОЗ 1п х . „ ЗІП 1п X , X3
4- С3х3 соз 1п х + С4х3 зіп 1п х. 3268. у = Сх —--1- С2 —------р -уу- •
г
3269. у = Сіх + С2х2 + С3х3.	3270. у = -у- + С2х3 + х4. 3271. х =
«= Сі со8 і 4- С2 зіп і, у = —Сі зіп і 4- С2 соз і. 3272. х = С^1 4' С2е~і, у =
= 2СіЄ^( — С2е-{. 3273. х = (Сх 4- С2і)у = — (Сх 4- С2 4- С2і) е2і.
3274. х = е~2і(1—2і), у = е~2І(\ 4-2/). 3275. х = Сів14- С2е~2і, у =
= Сів1 4- С^~2І, 2 = СіЄ( — (С2 4- С3) е~2і. 3276. х = —е—/, у = е~2 = 0.
3277.	х = — (С2 4- С3) е~{ 4- Сів2і, у = С2е~14- СіЄ2і, г = С3е-' 4- Сі&2і.
3278.	х = 2СІЄ-* 4- С2е~7/, у = — С^14- С2е~2І. 3279. у = С2х, г = С2х.
3280.	у = Сіх, г = С2 -4- х 4- у. 3281. Іпг — агсі§-^-=Сх, 2 — С2г, г2 =
= х2 4~ У2- 3282. 2 = Сіу, (х2 4- У2) У = С2х. 3283. у = СуХ, г-\-Ух? 4- 4- г2 =
«= С2. 3284. х2 4- У2 4- г2 — СіУ’ 2 =	3285. (г — х) = Сх (у — х), (х—у)2 X
X (х 4- У 4- 2) = С2. 3286. X2 4- У2 + г2 = Сі> уг = С2х. 3287. г = Р ,
х2 Н---. 3288. г —- / (х2 + у2), х2 + у2 = 2рг. 3289. г ~ зіп у +
+ Р (зіп х — зіп у). 3290. Ф (х — аг, у — Ьх} = 0. 3291. г — ур (х2 — у2).
333
3292. г = ху + Р (х2 + у2). 3293. г2 = 2х + Р
3294. г а зіп ^ху + Р . 3295. г = хР (ху), г = х2у.
3296. г = е°У Р(х — у). 3297. Ф {* ~ °	= °-
3298. ФІ-^, -^^-г2)2 ) = °' х(х2^-у2+г2)=---2а(х2+у2).
РОЗДІЛ XVI
Диференціальна геометрія
3299. 2 (г', г), 2 (г' г"), \г' /•"'], (г', г", гІУ), . 3300. Вказівка.
V 72
(гг) = сопзі, (г г)' = 0, (г, г') = 0. Обернене твердження: (г, г') = 0» тоді
(г г)' = 0, | г | = сопзі. 3301. г (і) = х (0 і + у (0 і + 2 (/) к, г' (і) = х' (і) і +
+ У' (0 І + г> (0 звідси х* (/) = у' (і) = г' (£) — 0, х (/) — сопзі, у (і) = сопзі,
2 (/) = сопзі. Обернене твердження справедливе. 3302. Ні. Наприклад, для
Г = {соз Л зіп і} | г' І = 1, І г І' = 0. 3303. (х2 + у2) у2 = г2х2.	3304. В к а-
звідси
зівка. Точка перетину дотичної з віссю
у 1 +	~ а- Нехай ер— кут, утворений дотичною з віссю ОХ, тоді
—Замінюючи-^- на сі£ф, дістанемо, що ї/ = азіпф, звідси
(іу — а соз фб/ф. Але (іх = сі£ ф гй/ — а [ —Д— —зіп ф) <їф тому
= а(1п і§_ї._|-со8 ф)Н-
С. 3305. Вона дозволяє параметризацію х = а соз3 /,
у = а зіп3 і. 3306. х~а (1+соз ф) соз ф, у=а (14-соз ф) зіп ф. 3307. а) Ьх соз і +
+ ау зіп і — аЬ = 0 — дотична, ах зіп і — Ьу соз і + (&2 — а2) зіп і соз і == 0 —
нормаль; Ь) 2х зіп і + 2у соз і — а зіп 2^ = 0 — дотична, х соз і — узїпі —
— а соз 2і — 0 — нормаль. Вказівка, (див. 3305); с) (зіп ф + ф соз ф)х —
— (соз ф — ф зіп ф) у — аф2 = 0 — дотична, (соз ф — ф зіп ф) х + у (зіп ф +
4- фсозф) — аф = 0—нормаль. Вказівка. Див. 3306; (і) х — у = 0 —
дотична, х + у = 0—нормаль; е) 7х — 5у — 17 = 0 — дотична, 5х + Іу +
+ 9 = 0 — нормаль. 3308. 27х — Зу — 79 = 0. 3310. а. 3311. х — у — 4 = С«
334
3312. (О, 0) — подвійна точка; при а > 0 — точка самоперетину; при
а < 0 — ізольована; при а = 0, Ь =/= 0 — точка звороту; у = ± }/ ах — дотич-
ні. 3313. (0, 0) — точка самоперетину, х = 0, у = 0 — дотичні. 3314. (0, 0) —
точка звороту; у = 0 — дотична. 3315. (0, 0) — потрійна точка, у = 0 — до-
тична. 3316. (0, 0) — потрійна точка з дотичними х ~ 0, у — х. 3317. (0, 0) —
особлива точка, чотирикратна. 3318. 4а3 + 21 & — 0. 3319. х = 0.
3320. ї/= 0, 2х + 1 = 0, 2х — 4у~ 3 = 0. 3321. 2у + 9 = 0, 2х — 9 = 0,
х — у — 6 = 0. 3322. а) Парабола з вершиною в точці (2, —1) й парамет-
ром р= &) астроїда; (0, 1), (0, —1), (1, 0), (—1, 0) — особливі точки кри-
о
вої — точки звороту першого роду; с) г' = 0 лише при і = 0. Цьому відпо-
$
відає точка (0, 0), яка є точкою звороту другого роду. При і =-----маємо
точку перегину. Дана лінія перетинає вісь ОХ у точках (0, 0) і (1, 0);
І 8
1ІШХ=4-оо, 1ІШЇ/= + °о, 1ІШ X = + ОО, Ііш у = — оо; 4) ТОЧКИ
точки
перетину
0 і
. У точці при і = 0 дотична
паралельна осі ОУ.
Для
лінія увігнута
«вверх», а
— опукла «вверх». Для і < —
лінія увігнута «вправо», а при

«вліво».
в бік осі ОХ, а для
лінія увігнута
— опукла в бік осі ОХ. Для
— лінія увігнута в бік осі ОУ. Для і <
> І/ —-----опукла в бік осі ОУ; х = 1 —асимптота (1ішх=1. 1ішх = 1,
V О	/->-{-ОО	—оо
Ііш у = + оо, Ііш у = — оо). Область існування 1 < х < 2; е) Точка (0, 0)
{—со	—СЮ
— точка самоперетину лінії, точок перегину нема. При і > 0 лінія ввігнута
«вверх», при і < 0 — «вниз». При і = 0 дотична паралельна до осі ОУ, а при
і = ± 1^2/3-З — до осі ОХ. Пряма х = 1 є асимптотою кривої: Іітх = 1,
/-*±оо
1іті/= ± оо. Область існування: — 3 < х < 1; /) Рівняння лінії у неявному
335
ВИГЛЯДІ X (х2 + у2) — ху + у2 — О,
у параметричному
__1— і2	_і2 — Р
х~ 14^2’ У- ! +^2 •
Точка (0, 0) — точка самоперетину лінії. При і = — 1—|Л2— 4 — точка
перегину. При і = — 1 ±1^2 дотична паралельна до осі ОУ, а при і = 0 —
— збігається з віссю ОХ. Лінія увігнута «вверх» при і < — 1 3>/2 — і
— )/2 — 1 < і < |/2 — 1, опукла «вверх» при — 1 — 7Л2 — уП <і < — )/2—1
і і > ]/2 — 1. 3323. х = 3, у = 0. 3324. 2у = ± (2х — 6), х + Ь = 0.
3325. х + у = 0. 3326. х + у = 0. 3327. х + у + а = 0. 3328. х ± у = 0.
3329. х == 0, у = 0, х + у = 0. 3330. х = а. 3331. х — г/ ± а }/2 = 0, х4-
+’# ±	= 0. 3332. х — у — 2 = 0, 2х у — 4 = 0. 3333. а) Полярна вісь.
Вказівка. Написати рівняння кривої у параметричному вигляді (див.
3306); Ь) (х — у) ]/2 ± а = 0, х + у У 2 ± а = 0; с) у ~ а. 3334. у = х2 —
/	1 \2	1
-Зх + 3 = 0. 3335. х--у +(^-1)2=—. 3337. (/ = /(0) + Г (0)х +
\	о /	04
+ Г(0)^- + ... + /('г)(0)4г- 3338. х = -А^4-8у-5. Вказівка.
Рівняння параболи, вісь якої паралельна осі ОХ, можна зобразити у вигляді
х — ау2 + Ьу 4-е, або х = аі2 4- Ьі + с, у = і. 3339.	-І- = 1. Стик
У	о
п’ятого порядку. 3340. у = 1-у-. Стик третього порядку. 3341. х2/з +
4- у/з = ег/з. 3342. у = -£-
----парабола з вершиною ^0, у.
Вказівка. Параметричне рівняння сім’ї кривих можна записати у вигля-
ді х = У0/соза, # = У(/8Іпа, де а—параметр лінії у сім’ї. Виключаючи
/,
знайдемо рівняння сім’ї у декартових координатах. 3343. х2 + 2у2 = 2а2<
1 + Г2
3344. Параметричне рівняння обвідної X = х — /' —, У = #4-
1 + Г2
Н--рт—. Вказівка. Рівняння сім’ї нормалей має вигляд У — £(%) =
---(X — х); параметром нормалі в сім’ї є х. 3345. Улитка Паскаля (х2 +
4л2 /	16лх \
-\~у2—2ах)2-)-у- | х2 4- у2-й— = 0. 3346. Дискримінантна крива роз-
□ І	У І
4
надається на дві прямі х = у, х — у-~=- = 0. Пряма х = у є геометричним
місцем особливих точок кривих сім’ї і не є обвідною. 3347. Вісь ОХ є обвід-
ною і геометричним місцем особливих точок кривих сім’ї. 3345. —.
336
3349. а) ---------—-------— ; Ь) -------—------гг- ; с) 1;
(а2 8Іп2 / + Ьг соз2 і) !г (а2 8І12 і + б2 сЬ2 і)
сі)---!---; е) | соз х НО. 3350. 2/2. 3351.-^-. 3353. а) ,
ич х	І 4
а сЬ2 —	\
а
а \ іл І 1 і 1 \ ч [ Зл \ _О1Ї_	, х'2 + /2
"ЗГ ;	---Г- 1п 2, —7=- ; с) -77—, а . 3354. X = х — у - , „	,
4/	\	2	|/2 )	\ 2	/	х'у" — у'х? ’
І * и'*	с?	г*
У = у х' ...„ •. 3355. х =--------соз3 Л у =------— зіп3 і. 3356. 27ру2 =»
* х у" — ух"	а	Ь
= 8 (х — р)3 (півкубічна парабола). 3357. (ах)2^ — (ру)*^ = (а2 + д2)2^3.
зет. ,_а1п «±кгЕ® ЖІ. х-х-г-ш1’'
2а	4а	'	/"
1 4- Г2
У = у 4—-у/— (див. 3354). 3361. Вказівка. Див. 3344 і 3360.
3362. р = г 4- 7? п — ЯЯ іу де К — радіус кривини кривої. В к а з і -
в ка. Задача зводиться до еволюти кривої = г + Яп. Диференціюємо по $:
1	б/г і г> і	а -і.	-х і гі і г» /
~ЗГ = ~ІГ + *п + *-аГ’ аб° = і + Кп +
п	х	ттт	(кі Лп •
к=—7—, іі = п. Ще раз диференціюємо по з: —г-^—т£-=”з—> звідси
аз	азі аз аз
Г ^51	1.4.	у. ^51	»	"Г . Л	/ а ,
^іоі —г2- = — кіу отже, к± —7і- = ку пл= — і. Але Я ~ Т0МУ М =
аз	аз	аз
а Яі = ЯЯ. Підставивши знайдені вирази для п± і 7?і у рівняння р = Гі+/?іПв
одержимо рівняння другої еволюти. 3363. З (х2 + у2) + 14ах— Івау — 4а2 = 0.
ззи- т)
3365. г — г (і). 3366. х = Я [соз ф + (<р — с) зіп ф],
у = Я [зіп ф — (ф — с) соз ф]. 3367. к = а
к =-------!-----
1—9 Х
а сЬ2 —
а
> х = 0. Розв’язування. Кривина
, X . .X з К . 9 х . . , 2 X . . з2
у з ~ а 8П —, звідси зЬ — =—. Але сп2— = 14-зп2 — = 14-5"
а	а а	а ‘а 1 а2 *
1
значить, к ==
а	9
V,...V 3368‘ 52+	16а2, х = 0. 3369. б2-—--------2І
а2 + з2	к2	16а2—з2
2з
х = 0. 3370. 82 + 9К2 =	, х = 0. 3371. 7?2 + а2 = а2е ° , х = 0.
3372. Нехай х = х (з), у = у (з) — шукане рівняння кривої, а — кут, який
22 2193
337
утворює її дотична з віссю ОХ. Тоді вектор дотичної / = {соза, зіпа},
звідси х = у соз а (з) б/з, у = зіп а (з) б/з, причому = к (з).
3373. Пряма лінія. 3374. х = с соз /, г/ = сзіп/ (коло). 3375. Розв'язу-
вання. ~к = —, з — еаа, б/з = аеааб/а; х = Г соз аб/з = а Ссоз аеааб/сс =
б&	аз	]
б^оа
——т- (а соз а + зіп а), у = 2 --у (а зіп а — соз а). Покладемо
ч>.
і після ряду перетворень знайдемо р = Сеф — логарифмічна спіраль.
3376. Покладемо з = а зіп /, 7? = Ь соз і, тоді а = С ксіз ~ Г ,	--а соз /х
і о соз/
..	аі ,	~ Р аі ...	(*	зіпа/	...
х сіі =	—.—к	Сп	х = І	соз -г-	соз іаі,	у — | Е— соз	іаі.
Ь 1 1	\ Ь	Ь
р З2
3377. х = І соз  -г- (із,
е)	2а2
о
р з2
у = зіп б/з. (клотоїда). 3378. з = аі£/й
о
_	9 . Г соз2 і-а . і а соз/
7? = а зес2 і у а = | -------------------аі =---- і у х = | аі = а
і а • соз2 /	] соз2 /
0 а зіп і	а ,	...	_ ___	?	......
у = І соз2Т ™ =	соз7 (ланЦюгова	ЛІНІЯ)-	3379.	х = а (соз і + і зіп і),	у =
«7
= а (зіп і — і соз /) — евольвента кола. 3380. Розв'язування. Рівняння утво-
реної кривої г* = г-]*• ап. Диференціюємо по з:	—— = і (1 — ак\ тобто
б/?*	->	->	Л-*	/	\
/* —т— = і (1 — ак), звідси і* = /, а —— = 1 — ак, тобто б/з* = 1-------— 1б/з.
аз	аз	\ К ]
Диференціюємо /* == і по з: —— • —-— = кПі або к*п* — = кп, звідси
из аз	(іо
еквівалентне співвідношенню 7?* = 7? ± а.
де к — кривина кривої г = г (з). Вказівка.
п* = п, а. к* = т——т, що
1 ± ак
3381. 41_‘-±А+^,
(1 +#72)/2
Рівняння утвореної кривої = Г + ІЇ. Довжина дуги кривої г ~ г(з)
не буде натуральним параметром для гх, тому користуємося формулою
Г Г	->	( у2 1 {,2 —
, 1 ,?-*1 . 3382. г = {а соз/, а зіп/, Ні}. 3383. 7	‘ у ’
*' 3	І 0-
338
. г
у ь
х = 0;
2
х = а соз -г- ,
Ь
У = 0-
3384. Розв'язування. Рівняння лінії в декар-
ґ х2 Ц- + г2 = г2, и -	• 2 /	•	• ,
тових координатах ]	Нехай х = г зіп2 тоді у = г зіп і X
І х2 + у2 = гх.
, 2	(	,2
і „2	„2 у = а зп —» х = а сЬ — »
х у — а ,	а	<	а
X соз 2 = г соз і. 3385. 1 Л	Л	А
(2 = 0;	х = 0;	( у = 0.
3387. 4- • 3388. І У = *2’ 3389. х = /2, у - /, 2 = і*. 3390. Ф = 4" -
2	І 7 = Рх	у	т 4
/4
Х 4
3392. ——
У~^
і
3394. ——ї^- = —3 — —_£ Вказівка. Нехай х = х (/), у = у (/).
2 = 2 (/) — параметричні рівняння даної кривої. Якщо в даних рівняннях кри-
вої х, у і 2 замінити на х (/), у (/), 2 (/), то вони перетворяться в тотожності.
Диференціюємо ЦІ ТОТОЖНОСТІ ПО і І одержуємо XX' + уу' = 0, уу' + 22Г = 0.
У даній точці З/ + 4г' =0, х' + З/ = 0, звідси г' [] де = {0, 3, 4},
и2 = {1, 3, 0}. 3395. Головна нормаль —  ? = ^~~оЬ ~~	’ бінормаль
Х-ГІ = У-2І = 1^1.. 3396. г(Х-х) + х(2-г) = 0.
->	(	1	О/	9/2	->
3403. / = І	- 	-	=,	,-=- -, п||{9^+2/,
11/9^4-4^4-1	/9/« 4- 4/2 + 1	/9^ + 4/2 + 1
9/4—і. —б^з-ж),	3<2	~ЗІ -----, —	1------V
(У9^ + 9<2 + 1	У 9^ + 9/2 4- 1	/9<3 + 9/2 + 1]
3404. і = {——зіп— , —— соз —,------—}, п = (соз-^, —зіп-^-, 0
|}/2	2	|/2	2	У^2 І (2	2
Ь= {-----У^- зіп 4-,--к- соз-У .---7^!  3405. і = 1 —У-,
(	/2	2	|/ 2	2	/2 /	1/2
1	1	( 1	1	1	*	(	2
-----0 , п= —, 0 , Ь= {0, 0, 1). 3406. і= І-------------—.
У 2	І	[ У 2	/2	]	[	/З
1	1	( 1	2	1
—^-,0 , п=	, Ь={0, 0, — 1}.
/з	]	[ /з	/з	|
3410.
х — Сі у —с2 2— С3
^1	^2	^3
^1	^2	а3
л оли	± । МЗІП/
= 0.	3411. х = а соз і -4—	-----,
У а2 + Н2
> 22*
339
. . /Лсоз^	, > . аі	->	(	і ї
і' = а81П'“У^Г^’	+7^ТР- 3412. г = |а/, а, За зіп-^-|.
3413. 5а/. 3414. 8а/2. 3416. а/2з1і/. 3417.9,9с.
1/ 1 + 8ІП2	і
3418. к = —______-______— • 3419. к —----=- , х = 1.	Розв'язування.
хх' — уу' + 22' — 0, 2уу' — 2х' + г' =0, х'2 + хх" — у'2 — уу" г'2 4- гг" = 0,
2у'2 + 2уу" — 2х” + г" — 0. У точці х' — у' + г' = 0,	2г/' — 2х' + г' = 0«
-	- - тЛб
г' 0 {1, —1, 0}. Аналогічно знаходимо г" і г'", 3420.	.
3425. к =	, х = ~	  3426. к =	4>	, х =
(е* + е~*)2	(е1+е~()2	(14-2/2)2
*=.. Го/212 • 3427. к = -^-ї-, х =------. 3428. ^ = х= _	1Ч„.
(1+2/2)2	зеі	&	3(/2 + 1)2
3429. к= п. . З----- х =  _ . *-------3430. /і = а. 3431. к = сх>
25 зіп і соз і	25 зіп і соз і
и = с2. 3433. к = 9 Л г-, X = в 2 . 3435. г = і, г = к п, г =
2а2 + 52	2а2 + 52
= — к2і 4- кп + киЬ. 3436. Вказівка. Вектор со шукати у вигляді со =
— аі-\-Ьп-\-сЬ\ а = пі к Ь — вектор миттєвої кутової швидкості репера
V
— *
к	к
3440. Знайти відношення . 3441.	= 1; шуканий вектор е=*
-> к	*	->	->
= і + — Ь — і 4- Ь — {1, 0, 1}. 3442. Вказівка. Нехай г — г (з) — рів-
няння лінії Гі, тоді рівняння лінії Г2 запишемо у вигляді р = г 4-Хи. Пере-
множимо скалярно обидві частини на п і, ураховуючи, що р' ± и, знайдемо
І — 0, тобто 1 = сопзі. Таким чином, р' = і (1—,кк)-\-'КкЬі ар" — кп(\ —
— кк) 4- (1 — кк)* — кк2п. Вектори р', р", п лежать у стичній площи-
ні, тому[Др', р", и) — 0. Потім знаходимо, що х4-М^х — &х) = 0, звідси
(1	/ ь \*	і ь
-----1 4- 11 —1=0,------1- X — = с, ак 4- Ьи — 1.
X / 1 X /	Xі X
340
3444. (е, /) = О, к (е п) = 0, к = 0 — пряма; (е и) = 0, (е, — к і + х Ь) = 0,
звідси х (е, Ь) = 0. х = 0 — лінія лежить у площині.
3445. (е, Ь) = 0, х (е, и) = 0, х = 0; (е, и) = 0, —к (/, е) + х (Ь, е) = 0,
(е, 0	0, значить, к = 0 — пряма лінія. 3446. Вказівка. Нехай у двох
точках М (г) і М' (г + сі г) кривої головні нормалі є п і п + сі п. Для їх пе-
ретину необхідно, щоб вектори б/г, п і и + б/и були компланарні. 3448. Якщо
х~ а соз/, у = а зіп /, г = М, то б = —====. 3449. а) Дві близькі голов-
на2 + /г2
ні нормалі кривої п і п + б/п. Напрям їх спільного перпендикуляра е =«
[п, и + б/и] [иб/и] кі-\-кЬ	.	-
=	—!------ — —--. Наикоротша віддаль о = пр»б/ г =
|[и, п + б/и]|	|[иб/и]|	е
=	; Ь) е~і, (еіїг) = і2сі8 = б/з. 3450. Розв'язування. Рівняння
лінії Сх має вигляд р = г (з) + і (з), р' = і + к и, р" = — к? і + (к к) п
, ь И? рчі _ V к^ + к^ + (к + к + ^у а р л,
-4- кКО, Кі = ------= -------------------. о401. —;---------------з— =
(;Чз	а+^) /2	6/5
» і — Ххи, /х —і — Ххи, = |/ 1 + А,2х2, а і1~ —* .Л.ХП - . Ди-
б/з	б/з	г	у і + ^х2
ференціюємо по з і після нескладних перетворень одержимо
__ Х2х4 (1 + Х2х2) + (к - кк + Х2^х2)2
~	(1 + Х2х2)3
3452. Рівняння лінії р = г + к Ьз;
51 = з/1 4-А2, кг=
X	г
і	* 3453е	] Х6І5-
«0
к	кк
Г+Т*’ Х1~(1 4-Х2) ;
СО80 = ^П
ІР'І
г І & зіп3 (р І	к соз ф зіп2®
3454. к± = ----------------------- , хх = -----------------. 3455.
І зіп ф — Рк соз ф Г 7? зіп ф — Рк соз ф
3456. 31/2еґ. 3457. | г | — 0, звідси г = Сз + Со— рівняння прямої.
3458. Плоскі лінії. 3459. х — ф (и) соз у, у = ф (м) зіп у, г = ф (м).
(л	і \
4- -тг — а зіп /, у — а соз і соз и, г = а соз і зіп и.
4	2/
341
3461. х = г соз и соз у, у ~ г зіп и соз у, г = гзіпу. 3462. Параметричне
рівняння кола х — а + г соз у, 2 = г зіп V. Рівняння тора х = (а + г соз у) соз и*
у = (а-\-гиж V) зіп и, г = г зіп V.
3463. г = р + V е. 3464. г = ур. 3465. г = р + V ~і. 3466. г = р + V -у-*
л	, а зіп і	. , . а соз і	.
3467. х = а соз і---г .V, у = а зіп і +    —.у, г = Ні +
У а2 + /і2	У а2 + Н2
і	- V. 3468. х = и соз V, у = и зіп у, г = /(о). 3469. х — и соз у, у =
У а2 + /г2
= изіпо, г=^7- 3473. ^(х-хо) + Г“({/-уо)+Г»(г-го)=О.
3475. г —а = 0.
3476.	=
созусі^а зіпусі^а —1	І зіп а
зіп V сі§ и —1 І 3477	[ й зіп у —Н соз у и
зіпм ’ зіпи Г '	)уй2 + и2 ’ У /г2 + и2 ’ /й2 + и2
3478. х + у + г = 5, т= | —^=- , —4 ,	1. 3482. г = р (з) +
І /З уз /3 /
4-у Ь (з), г8 = і — ух и, гк — Ь\ [Гу г^] = — п — ух Л Дотична площина (7? —
— р — у Ь, п 4- ик і) = 0, або (7? — р) (и + ух і) = 0. Нормаль Р = р 4-	+
4- £ (п 4- ™ 0- 3484. у2 4- ?2 = 1. 3485. г2 - г2 = (7? ± У х2 4- У2)2-
3486. Розв'язування. (Р — р)2 = г2. Диференціюємо по з: (7? — р, і) == 0,
значить, (Р — р) лежить у нормальній площині, тому 7? — р = ад4~Ри> а24~
4- Р2 = г2; можна вважати, що а — г соз ер, р = г зіп ер, і рівняння обгортки
->	с2
запишемо у вигляді Р = р 4- г (соз ер Ь 4- зіп ер п). 3487. х2 4- У2 + — с)2— —.
3488. Вказівка. Рівняння однопараметричної сім’ї площин можна
записати у вигляді А (с) х 4- (с) У + (с) ? 4~ (с) = 0- 3489. Розв'язування.
Рівняння стичної площини (Р — г (5), Ь (5)) = 0; 5 — параметр сім’ї. Знайдемо
дискримінантну поверхню — (г' Ь') 4- (Р — г, Ь') — 0, або (Р — гу її) — 0. Та-
ким чином, вектор Р — г перпендикулярний до п і до Ь. Дискримінантна по-
верхня складається з характеристик — прямих, що при кожному з збігають-
ся з відповідною дотичною до кривої. Для знаходження ребра звороту
потрібно приєднати ще третє рівняння, знайдене диференціюванням по з:
342
(7? — г, и) = 0. Ребром звороту є сама крива. 3490. (7? — г, і) — 0. Після ди-
ференціювання по 5 знайдемо — 1 + (# — г, п) к — 0. 7? лежить на прямій,
и-	-	-	1	,
яка паралельна Ь і проходить через центр кривини р = г = п, тобто харак-
теристика при кожному значенні 5 збігається з віссю кривини. Ребро звороту
збігається з геометричним місцем центрів стичних сфер. 3491. (7? — г, п) = 0.
Характеристики збігаються з миттєвими осями обертання. 3493. 0. Вказівка.
Викорйстати залежність між Гауссовою кривиною поверхні і площею сферич-
ного відображення. 3494. Розв'язування. Необхідність. Нехай п — нормаль-
ний вектор спрямної площини. Тоді (п, /) = 0, звідси (и, /') = 0 і (и, /") ~ 0,
тому (/,	/") — 0. Достатність. Нехай (/,	/") — 0, Г =£= 0. Вектор с =
=	----сталий, тому що с' =0. І±с, тобто паралельний сталій площині.
ІИ
3495. (<р'2 + Ч'2) ^“2 + <Р2^2- 3496. (<р'2 + Ч'2) <іи2 = Л)2, V =	<р'2+Ч'2 Ли.
3497. г2 соз2 осій2 + г2б/а2.	3498. (а2 зіп2 и + Ь2 соз2 и) соз2 осій2 + 2 (а2 —	х
X зіп а соз и зіп V соз оіїиіїо + {(а2 соз2 а + Ь2 зіп2 и) зіп2 о + с2 соз2 у} сіо2.
і /	1 \2	і
3499. — / V + —) (а2 зіп2 а + Ь2 соз2 а) сій2 + — (Ь2 — а2) зіп а соз а X
/	1 \	( 1 /	1 \2	с2 /	1 \2Ч
X І V---ті \ ~Г І 1--------------ТІ (а2 СО82 и + ^2 ЗІП2 и) Ч----Т І 1 Ч-т І І ^2*
І у3/	141 а2 /	41а2 / І
1 /	1 \2	1
3500. — (V-----— 1 (а2 зіп2 а + Ь2 соз2 и) <іи2-\- — (Ь2 — а2) зіп а соз а X
/	1 \	ґ 1 І	1 \2	Г2 /	1 \2Ї
Х и-----т І б/ггб/а 4~ < ~г 11 Ч-т І (я2 соз2 а Ч~ Ь2 зіп2 а) -|-— [ 1-- ] І б/а2.
І	а3 /	І 4 і	о2 /	4 \	о2 І і
3501. (із2 Ч-- 2 (77) (І8(і% Ч- ^2- 3502. оЧз2 + 2а (7, р) б/зб/а + рМа2.
3503. (Р 4- г соз а)2 (іо2 + г2(іи2. 3504. (а2 + к2) сій2 + (іа2.
3505. (1 4- /2) йх2 + [Х[усіх(іу 4- (1 4- [у) йу2- Вказівка. Параметризу-
вати поверхню х = и, у~о, 2 — [ (іг, а). 3506. Рівняння поверхні Р = г(з) 4-
4- а і (з). Перша квадратична форма (1 4- ^к2} сіз2 4- 2б/зб/а 4- б/а2. 3507. з =
+ І зЬ «2 ~ 811 “і І- 3508. Р = 0. 3509. соз <р =.   д2д:оУо_
У1+а2Х2У1+а2у2
3510. (1 + а2х2) у = сопе!. 3511. осі§ а = 7? Іп	; і§ (4" +
343
— еауу де а — довільне стале. 3512. о =	[]Л2 + 1п (1 + 1^2)].
3513. Вказівка. Досить довести, що Е6 — Р2 =	— Р2 .
їху  м їуу
, М =  --------, N =
V і +П + РУ
3518. Ь =
2
3520. -у (4а— Ь). 3521. Вказівка. Розглянути формулу нормальної
. Ьди2 + 2М(1шіи + №о2	.
кривини поверхні кн =	+	+	' 3522' в к а 3 і в к а. Га-
уссова кривина поверхні є інваріантом ізометричного відображення.
3523. Н = 0. К — — а2. 3524. 2а, 2а. 3525. 0. 3527. а) Еліптичні; Ь) на
однополому—гіперболічні, на двополому — еліптичні; с) на еліптичному —
еліптичні, на гіперболічному — гіперболічні; д) параболічні; е) параболічні.
3528. Сама верхня і сама нижня паралелі тора — параболічні лінії, що
відокремлюють зовнішню частину тора з еліптичними точками від внут-
рішньої частини, точки якої — гіперболічні. 3531. 0. 3533. Вказівка.
лінійчатої поверхні можна зобразити у вигляді г = р (а) + о І (а).
іг__	X2	.	.
д ~~ ~~ Т(Г -	+ я2*2]2' ’ к 1 кРивина 1 скрут кривої Г = Г (5).
Рівняння
3534.
3539.
Доведення. У точці заокруглення для всякого напряму дт~— кдг.
Звідси (тиди + т^сіо) =---(гисІи + г^до). Це справедливо для довільного
напряму, тому ти =------^ги- ту~-------Продиференціюємо перше
А
1 - -
співвідношення по о, а друге — по и: тиі) =-------т,уи =
— ~Е-гт+ Гг, , звідси ги-------------Гу = 0,	= 0. Інтегруємо
сфери.
(О, ±
В к а-
дг = — Рдт : г — — Ет + с, г — с~ — Дт, | г — с |2 = 7?2 — рівняння
X2 І]2
3540. У параболоїда — -\-^— = <2г —дві точки заокруглення
±/^7, ^27^)- 3541. *і=4->	=	3543- V * ~Т-
Е	и	а о
зівка. Розглядаємо на круговому циліндрі коло і еліпс, що дотикається
до кола вершиною. Одержимо на циліндрі два перерізи із спільною дотич-
ною: нормальний — коло, похилий — еліпс. Використовуємо теорему Меньє.
3544. Вказівка. Використати формулу Гаусса, яка виражає Гауссову
кривину через коефіцієнти першої квадратичної форми та їх похідні.
344
3545.	~	’ 3546. Прямолінійні твірні поверхні.
3547. 1) х = с1У,
-----% = с2; 2) и + V — СОП8І, и — у = сопзі; 3) дифе-
ренційне рівняння асимптотичних ліній 5(гг2 а+ с2) сій2 — 2іМисії = 0.
Звідси а) и — сопзі — прямолінійні твірні; Ь) + с2) сій — 2и3сії = 0
— диференційне рівняння Бернулі. Його інтеграл визначає другу сім’ю асимп-
тотичних и (V + и2)2 — с2и2 — 0. 3548. Диференційне рівняння асимптотичних
соз V (Е + г соз с) д,и2 + г2сіи2 —0 (див. 3503.). Рівняння має загальний роз-
,	зх Зл
В ЯЗОК при — < V < —-----------
и + с= ± \	..
Л У —СОЗ V (Е + ГСОЗ V)
ГГ' •••	Ззх	у	,	• о	.	.
Ліни V = -у , V ~ -“2----теж Р03в язки Диференціиного рівняння (особливі
розв’язки). Тому вони є обвідними обох сімей асимптотичних ліній, розмі-
щених на внутрішній частині тора. 3549. За координатні лінії поверхні візь-
МР
мемо її асимптотичні лінії, тоді Ь ~ N — 0 і Н =---------—г-, звідси Р = 0
ЕС — Р2
при Н — 0. 3550. Ь ~ N — 0. 3551. и ~ сопзі; друга сім’я асимптотичних
ліній визначається рівнянням {(/",/', І) V2 + (р",	/) + (/", р', /)] V +
+ (р" р' І)} сій + 2 (/' р' /) б/ц = 0. 3552. Вказівка. Асимптотична лінія
поверхні характеризується тим, що дотична площина до поверхні в кожній
точці є її стичною площиною. Таке визначення проективно-інваріантне.
3555. 1 — Ьу2 = сх2. 3557. а) (х 4- /а2 4-х2) (у 4- /а2 4~ У2) = &
і х 4- У а2 4* У2 = С2 (у 4~	4~ </2)- 3558. Паралелі і меридіани.
3559. Прямолінійні твірні та їх ортогональні траєкторії. 3560. Вка-
зівка. Параметричне рівняння конуса х = и соз с, у = и зіп с, г = а. Візь-
мемо рівняння геодезичних у вигляді 2 —(Ри + 6у) — Еу и2 + 2руш)
-|- Су V2. Звідси знайдемо 2 (іг2ц)* = 0,	— з; сіз2 — 2сіи2 + и2^2, тому м4б/о2=
е= с2 (2<іи2 + и2^2). Після інтегрування одержимо
с соз V
-------
зіпМ^
/2
С ЗІП V
. Сі ± V
ЗІП —---=-
1/2
зіп
Сі ±
У2
Р	сйи____________
З / (и2 4- Н2) (и2 4- Л2 — с2) ’

345
РОЗДІЛ XVII
Ряди Фур’є
х . зіп 2х , зіп Зх зіп 4х . зт
3568. т = зіпх--------ї- + —------------— + > -4
соз 2х , соз Зх соз 4х ,
С08Х------22“+ —32----------42— 4
тґ2
3569. х2 = -й-
О
л2 л2
“б”’ 12 •
3570. і (х) =
/г=0
к=0
зіп (2к + 1) х
2ГЙН
ГМ- 2 V С03 (2Й + П Х 3573 ІМ-Я 4 уі со5(2*+1)х
3572. Ш ~ — 2, (2Л+ І)* ' 3573’ ' (%)	“ ТІЛ ~(2Й+1)2
6 = 0	А-П '	'	'
л	4	/
3574. |х| =	-----—	СО8% +
2	Л	\
соз Зх , соз Зх
б2”
З2
к=0
л2
іг •
3575. х2 =
соз кх
3576. х = л — 2
к=ї
зіп 2х
2~
к=1
зіп Зх
~1~
зіп кх
~~к~
Л2 X2
3577.	— = соз х
соз 2х
соз Зх соз 4х
“З2	ї2-
2
3578. | зіп х | = —
1	зт
4 /соз 2х ! соз 4х , соз 6х , соз 8х
л~ ~	1	Ї5“+ 35 + “63“
°°	.	со
Я = У 5Ш ^ ... 3580. я2 _ Х2 = 2 П2 + 4 У (—.1)	соз^х
2	к	3	к2
к=1	к=1
2зіпзта
3581. соз ах =--------
а соз х
1 —а2
л
3582. ех = зЬ І
,	. клх
кл зіп ——
І2 + к2л2
. клх
І соз —~
3583. х3 =	(—І)6 —2 ^2д2 8іп кх.
к=1
3584. | соз х | = — + — У (~-.^ї?- С03 2кх..
1	1 я 1 л	4к2 — 1
346
лх (л ~ х) Vі 8іп — 1) х я3
3585.	£	~	(2^—1)3 ’’ 32 ’
оо
3586. 1п соз ^ = - 1п 2 +	(—1)*	•
к=1
оо
2 С 8ІП и
3588. — | ---------соз ихсіи =
я З и
о
3587. (л2 - х2)2 = -А. - 48	(-1)*	! ^|о“
к=1
1, ЯКЩО І х І < 1,
, якщо | х | = 1, Вказівка. /(х) —
0, якщо | х | > 1.
парна функція.
2 (* зіп2 ц
3589. ї(х) = — І —^2— С08 их(іи.
о
оо
г / ч 2 Г и зіп их ,
3590. Ш =	-1+^^
0
Вказівка. / (х) — непарна функція.
оо	оо
е/ ч 2а Г созо , Ог-л_ ...	2 е и + зіпи .
3591. / (х) =--------- |	—х-б/и.	3592. / (х) = — \ ——$-----------зш ихйи.
1 ' ' л ,) а2 + а2	' 4 ' я З и2
о	о
р . и и ,л
зш-^- соз “2" (1 — 2х)
3593.	і (х) = —	-	сій.
0
г» ли (я — 2х) а
2	С08 ~ С08----2-
3594.	/ (х) = — І -1 _ -------йи. 3595. Вказівка. Ско-
0
ристатися формулами Ейлера. 3600. Вказівка. Див. 3569 та 3573.
1
3602.	Вказівка. С зіп ах зіп Ьхйх -= соз а соз Ь	, а 4= Ь.
З	а2 — Ь2
о
3603.	Вказівка. г = — (1 + Д- + Д- + • • 3 = — + 4г +
п2 — 1 п п2 п4 ) п 1 дз г
.	1 оеп. о .	И3 п3 1.11.
+ о~7~ 9—г? • 3604. Вказівка. --г = —-?-------------=-4
1 п3(п2—1)	п4—1 п4 — 1 п г п п
1
п5 — п
3605. В к а з і в к а.
п3 + п + 1	1	1
п (п3 + 1) ~ п п3 + 1 *
347
п*	1	1 1	1
ооі/о» о к а з і в к з. еі"7 и5 + 1 п	п — п	п (п& + 1) *
п3	1	1	Й V Я Ч і п іг а
И4+ 1	п	п (п* + 1) ’	оммо* о к сі □ і в к а
П4 — П2 4- 1 __	1
и2 (и4 +1) ~ п2
1		_ гс-1 |	1	ЯВ11	К V О
И4+ Г	П2 + 1	п (п2 + 1) 1	п	оо 1 і •	ока
а2 а3 І __ 1 а а2 а3
п2 п2 (п + а)]	я п2 ' п3 п3 (и + а) *
ДОДАТКИ
І. Грецький алфавіт
Форма знака	Назва знака	Форма знака	Назва знака
А а	альфа	N х	НЮ (ні)
в р	бета	и	КСІ
Г у	гамма	0 0	омікрбн
А 6	дельта	П я	пі
Е 8	епсилбн	Р р	ро
2 С	дзета	2 8	сигма
Н п	ета	Т т	тау
0 0 і)	тета	Г ”	іпсилон
І і	йота	Ф ф	фі
К %	каппа	X X	хі
А X	ламбда	¥ ф	псі
М	мю (мі)	І й о	омега
II. Деякі сталі
Величини	Числа	Логарифми	Величини	Числа	Логарифми
я	3,14159	0,49715	е	2,71828	0,43429
я2	9.86960	0,99430	е*	7,38906	0,86859
я3	31,00628	1,49145	е3	20,08554	1,30288
я4	97,40909	1,98860	е4	54,59815	1,73718
я6	306,01971	2,48575	6?5	148,41315	2,17147
1 я	0,31831	Г50285	1 е	0,36788	Г56571
1 я2	0,10132	ї?00570	1 е2	0,13534	1713141
я3	0,03225	2^50855	У~	1,64872	0,21715
/я	1,77245	0,24857	гг	0,60653	Ї78285
1	0,56419	1,75143	3/-	 у Є	1,39561	0,14476
У я 3/-	 у я	1,46459	0,16572	ел	23,14069	1,36438
3/^ 1	2,14503	0,33143	е~п	0,04321	2^63562
1 37= у я	0,68278	1.83428	л Є~2~	4,81048	0,68219
М = І£е	0,43429	1,63778	л Є~~2	0,20788	7731781
	2,30259	0,36222	я Є 4	2,19328	0,34109
агс 1 °	0,01745	2,24188	л Є 4	0,45594	П65891
349
ПІ. Тригонометричні функції
а 0	зіп а	а	а	соз а	
0	0,0000	0,0000		1,0000	90
1	0,0175	0,0175	57,2899	0,9998	89
2	0,0349	0,0349	28,6363	0,9994	88
3	0,0523	0,0524	19,0811	0,9986	87
4	0,0698	0,0699	14,3007	0,9976	86
5	0,0872	0,0875	11,4301	0,9962	85
6	0,1045	0,1051	9,5144	0,9945	84
7	0,1219	0,1228	8,1443	0.9925	83
8	0,1392	0,1405	7,1153	0,9903	82
9	0,1564	0,1584	6,3138	0,9877	81
10	0,1736	0,1763	5,6713	0,9848	80
11	0,1908	0,1944	5,1446	0,9816	79
12	0,2079	0,2126	4,7046	0,9781	78
13	0,2250	0,2309	4,3315	0,9744	77
14	0,2419	0,2493	4,0108	0,9703	76
15	0,2588	0,2679	3,7321	0,9659	75
16	0,2756	0,2867	3,4874	0,9613	74
17	0,2924	0,3057	3.2709	0,9563	73
18	0.3090	0,3249	3,0777	0,9511	72
19	0,3256	0,3443	2,9042	0,9455	71
20	0,3420	0,3640	2,7475	0,9397	70
21	0,3584	0,3839	2,6051	0,9336	69
22	0,3746	0,4040	2,4751	0,9272	68
23	0,3907	0,4245	2,3559	0.9205	67
24	0,4067	0,4452	2,2460	0,9135	66
25	0,4226	0,4663	2.1445	0,9063	65
26	0,4384	0,4877	2,0503	0,8988	64
27	0,4540	0,5095	1,9626	0,8910	63
28	0,4695	0,5317	1,8807	0,8829	62
29	0,4848	0,5543	1,8040	0,8746	61
ЗО	0,5000	0,5774	1,7321	0,8660	60
31	0,5150	0,6009	1,6643	0,8572	59
32	0,5299	0,6249	1,6003	0,8480	58
33	0,5446	0,6494	1,5399	0,8387	57
34	0,5592	0,6745	1,4826	0,8290	56
35	0,5736	0,7002	1,4281	0,8192	55
36	0,5878	0,7265	1,3764	0,8090	54
37	0,6018	0,7536	1,3270	0.7986	53
38	0,6157	0,7813	1,2799	0,7880	52
39	0,6293	0,8098	1,2349	0,7771	51
40	0,6428	0,8391	1,1918	0,7660	50
41	0,6561	0,8693	1.1504	0,7547	49
42	0,6691	0,9004	1,1106	0,7431	48
43	0,6820	0,9325	1,0724	0,7314	47
44	0,6947	0,9657	1,0355	0,7193	46
45	0,7071	1,0000	1,0000	0,7071	45
	| соз а	І сі§ а |	і§ а	| зіп а	|	а °
350
IV. Натуральні логарифми
N	0	1	2	3	4	5	6	7	8	9
0		0,0000	0,6931	1,0986	1,3863	1,6094	1,7918	1,9459	2,0794	2,1972
1	2,3026	2,3979	2,4849	2,5649	2,6391	2,7081	2,7726	2,8332	2,8904	2,9444
2	9957	3,0445	3,0910	3,1355	3,1781	3,2189	3,2581	3,2958	3,3322	3,3673
3	3,4012	4340	4657	4965	5264	5553	5835	6109	6376	6636
4	6889	7136	7377	7612	7842	8067	8286	8501	8712	8918
5	9120	9318	9512	9703	9890	4,0073	4,0254	4,0431	4,0604	4,0775
6	4,0943	4,1109	4,1271	4,1431	4,1589	1744	1897	2047	2195	2341
7	2485	2627	2767	2905	3041	3175	3307	3438	3567	3694
8	3820	3944	4067	4188	4308	4427	4543	4659	4773	4886
9	4998	5109	5218	5326	5433	5539	5643	5747	5850	5951
10	6052	6151	6250	6347	6444	6540	6634	6728	6821	6913
11	7005	7095	7185	7274	7362	7449	7536	7622	7707	7791
12	7875	7958	8040	8122	8203	8283	8363	8442	8520	8598
13	8675	8752	8828	8903	8978	9053	9127	9200	9273	9345
14	9416	9488	9558	9628	9698	9767	9836	9904	9972	5.0039
15	5,0106	5.0173	5,0239	5,0304	5.0370	5.0434	5.0499	5,0562	5.0626	0689
16	0752	0814	0876	0938	0999	1059	1120	1180	1240	1299
17	1358	1417	1475	1533	1591	1648	1705	1761	1818	1874
18	1930	1985	2040	2095	2149	2204	2257	2311	2364	2417
19	2470	2523	2575	2627	2679	2703	2781	2832	2883	2933
20	2983	3033	3083	3132	3181	3230	3279	3327	3375	3423
21	3471	3519	3566	3613	3660	3706	3753	3799	3845	3891
22	3936	3982	4027	4072	4116	4161	4205	4250	4293	4337
23	4381	4424	4467	4510	4553	4596	4638	4681	4723	4765
24	4806	4848	4889	4931	4972	5013	5053	5094	5134	5175
25	5215	5255	5294	5334	5373	5413	5452	5491	5530	5568
26	5607	5645	5683	5722	5759	5797	5835	5872	5910	5947
27	5984	6021	6058	6095	6131	6168	6204	6240	6276	6312
Продовження
м	0	1	2	3	4	5	6	7	8	9
28	6348	6384	6419	6454	6490	6525	6560	6595	6630	6664
29	6699	6733	6768	6802	6836	6870	6904	6937	6971	7004
ЗО	7038	7071	7104	7137	7170	7203	7236	7268	7301	7333
31	7366	7398	7430	7462	7494	7526	7557	7589	7621	7652
32	7683	7714	7746	7777	7807	7838	7869	7900	7930	7961
33	7991	8021	8051	8081	8111	8141	8171	8201	8230	8260
34	8289	8319	8348	8377	8406	8435	8464	8493	8522	8551
35	8579	8608	8636	8665	8693	8721	8749	8777	8805	8833
36	8861	8889	8916	8944	8972	8999	9026	9054	9081	9108
37	9135	9162	9189	9216	9243	9269	9296	9322	9349	9375
38	9402	9428	9454	9480	9506	9532	9558	9584	9610	9636
39	9661	9687	9713	9738	9764	9789	9814	9839	9865	9890
40	9915	9940	9965	9989	6.0014	6.0039	6.0064	6.0088	6.0113	6.0137
41	6.0162	6.0186	6.0210	6.0234	0259	0283	0307	0331	0355	0379
42	0403	0426	0450	0474	0497	0521	0544	0568	0591	0615
43	0638	0661	0684	0707	0730	0753	0776	0799	0822	0845
44	0868	0890	0913	0936	0958	0981	1003	1026	1048	1070
45	1092	1115	1137	1159	1181	1203	1225	1247	1269	1291
46	1312	1334	1356	1377	1399	1420	1442	1463	1485	1506
47	1527	1549	1570	1591	1612	1633	1654	1675	1696	1717
48	1738	1759	1779	1800	1821	1841	1862	1883	1903	1924
49	1944	1964	1985	2005	2025	2046	2066	2086	2106	2126
50	2146	2166	2186	2206	2226	2246	2265	2285	2305	2324
N	0	1	2	3	4	5	6	7	8	9
6? коп.
ХИІЗСЬКА -ФАБРИКА НАБОРУ