Міністерство освіти і науки України
Житомирський інженерно-технологічний інститут
В.Б. Струтинський
МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ
ПРОЦЕСІВ ТА СИСТЕМ МЕХАНІКИ
Підручник
Рекомендовано Міністерством
освіти і науки України
як підручник для студентів
напряму “Інженерно, механіка"
2001
УДК 510:621.9
С 87
С 87 Струтинський В.Б. Математичне моделювання процесів та систем
механіки: Підручник. - Житомир: ЖГП, 2001. - 612 с.
І8ВМ 966-7570-94-0
Сформульована методологія побудови математичних моделей проце-
сів та систем механіки. Розглянуті в основному математичні моделі у
вигляді символьних залежностей і дискретні математичні моделі. Стис-
ло викладений сучасний математичний апарат, який використовується
при побудові математичних моделей. Значну увагу приділено конкрет-
ним чисельним розрахункам за допомогою сучасних математичних па-
кетів, зокрема пакетів МаДіСАГ) та МАТЬАВ останніх версій.
Методологія математичного моделювання процесів та систем меха-
ніки реалізована в багатьох прикладах розроблених автором математи-
чних моделей реальних технічних систем і процесів. Приклади охоп-
люють системи різного рівня складності В основному це моделі елеме-
нтів механічних систем, математичні моделі системи приводів, розгляд
задач гідравліки, гідродинаміки та теплофізики механічних систем. На-
ведені математичні моделі технологічних машин і систем різного при-
значення.
Для студентів механічних спеціальностей вузів, які навчаються за
програмами бакалавра, інженера-спеціаліста та магістра, а також аспі-
рантів. науковців, спеціалістів промисловості, викладачів вищих нав-
чальних закладів.
Іл.: 392. Табл.: 3. Бібліогр. 122 назв.
Рецензенти:
Петраков Ю.В., д.т.н.. професор, завідувач кафедри “Технологія
машинобудування” Механіко-мапіинобудівного
інституту Національного технічного університету
“Київський політехнічний інститут”;
Грабар І.Г., д.т.н., професор, завідувач кафедри “Автомобілі і
механіка технічних систем”, перший проректор
Житомирського інженерно-технологічного інституту
І8ВК' 966-7570-94-0
УДК. 510 621 9
© Струтинський В Б , 2001
ВСТУП
Даний підручник є узагальненням матеріалів лекційного курсу і практич-
них занять з дисципліни «Математичне моделювання процесів та систем», які
читаються в Національному технічному університеті України «Київський по-
літехнічний інститут» для студентів-магістрантів факультетів та інститутів
механічного напрямку.
Підручник охоплює близько половини матеріалів лекційного курсу,
основні теми практичних занять та багато прикладів, які рекомендуються
студенту для подальшого розвитку і використання у магістерській роботі.
Матеріали, викладені в підручнику, згруповані за трьома напрямками.
Перший напрямок відповідає стислому викладу сучасного математичного
апарату, який застосовується інженерами-дослідниками при математичному
моделюванні процесів та систем.
Другий напрямок включає засоби виконання чисельних розрахунків, яки-
ми звичайно завершуються інженерні дослідження. Ці засоби зосереджені в
сучасних математичних пакетах. В підручнику розглянуті основні процедури,
реалізовані в програмних середовищах МаіЬСАВ і МАТЬАВ останніх версій.
Третій напрямок об’єднує приклади математичних моделей конкретних
технічних систем та їх робочих процесів. Розглянуті математичні моделі різ-
них ступенів складності. В основному викладені математичні моделі процесів
оригінальних технічних систем, розроблених за участю автора.
Всі вказані напрямки взаємно пов’язані та орієнтовані на математичне
моделювання процесів і систем механіки. Розглянуті чисто механічні системи
та їх робочі процеси, системи, що включають рідкі робочі середовища та від-
повідні їм гідромеханічні процеси та інші системи. Значну увагу приділено
розробці математичних моделей реальних технічних об’єктів, зокрема, мета-
лорізальних верстатів, технологічних машин іншого призначення та їх окре-
мих вузлів.
Головна мета підручника - подати в зручній та доступній формі набір за-
собів, необхідних для розробки математичних моделей середнього рівня
складності та виконання математичного моделювання процесів та систем.
Випускник технічного університету повинен володіти глибокими знаннями
в галузі математики, вміти застосовувати їх для розробки і використання ма-
3
Струтипський В.Б.
тематичних моделей процесів та систем, подати у взаємозв’язку абстрактні
математичні поняття та їх застосування для математичного моделювання кон-
кретних технічних систем є головним призначенням підручника.
Матеріали підручника дають потужний теоретико-практичний інструмент
майбутньому спеціалісту (інженеру, науковцю, педагогу) - фахівцю в галузі
інженерної механіки.
Підручник орієнтований на практичне застосування наведених в ньому
методів і методик математичного моделювання процесів та систем. Зокрема,
матеріали підручника покликані надати допомогу студенту при виконанні до-
сліджень в рамках магістерської атестаційної роботи.
Підручник включає частину запланованого загального циклу видань. В
даному підручнику знайшли висвітлення методи побудови і використання
найбільш поширених і ефективних математичних моделей, а саме: моделей у
вигляді символьних функцій та функціональних рядів, дискретних матема-
тичних моделей, сучасних інформаційних технологій, які базуються на вико-
ристанні графоаналітичних (візуальних) математичних моделей процесів та
систем.
В подальшому планується продовження циклу видань, які будуть включа-
ти підручники, присвячені:
-	векторним, матричним, тензорним математичним моделям процесів та
систем;
моделям процесів та систем у зосереджених і розподілених парамет-
рах, які базуються на
-	розв’язку систем нелінійних звичайних диференціальних рівнянь та
диференціальних рівнянь в частинних похідних;
-	стохастичним математичним моделям, зокрема реалізації методів іміта-
ційного математичного моделювання процесів та систем інженерної механіки.
Запланований цикл видань охопить всі розділи дисципліни «Математичне
моделювання процесів та систем», що читається для студентів-магістрантів
Національного технічного університету України «Київський політехнічний
інститут».
Підручник призначено для бакалаврів, спеціалістів та магістрів механіч-
ного напрямку, а також аспірантів, науковців, спеціалістів промисловості, які
займаються дослідженням складних процесів та систем механіки.
4
Розділ 1 Основні поняття та визначення
РОЗДІЛ 1
Основні поняття та визначення
1.1. Технічні системи та їх робочі процеси
У природі та техніці існують різноманітні системи, наприклад, механічна си-
стема, термодинамічна система. Системи є об’єктом дослідження. При дослі-
дженні технічних систем здійснюється їх аналіз. За результатами аналізу вико-
нується цілеспрямована зміна системи з метою поліпшення її характеристик.
Аналіз системи базується на особливостях її функціонального призначен-
ня. Розрізняють технічні системи, призначені для реалізації прогресивних
технологій, для автоматичного керування об’єктами, для приведення в рух
робочих органів машин тощо [6, 8, 40, 98].
Деякі характерні технічні системи та виконувані ними функції наведені
на рис. 1.1.
частоти	частоти
е?)	?)
рухомих	параметрів
д)	об’єктів	е)
Рис. 1.1. Характерні технічні системи та виконувані ними функції:
а - механіко-машинобудівна; б - зварювальна; в — інженерно-фізична;
г - електромеханічна; д - інженерно-хімічна; е - вимірювальна
5
Струтинський В. Б.
Кожна система має зовнішні зв’язки, по яких здійснюється обмін інфор-
мацією з іншими системами. Ці зв’язки є різноманітними і не завжди визна-
ченими. З метою аналізу системи виділяють деякі характерні причинно-
наслідкові зв’язки між системою та іншими системами. Вони формуються як
входи і виходи системи. Ступінь деталізації входів і виходів визначається за-
дачами аналізу системи. Для вищеназваних систем (див. рис. 1.1) входами і
виходами є як окремі параметри, так і їх комплекси.
Кожна технічна система містить підсистеми (елементи системи). Кількість
підсистем може бути різною. В системі можна виділити дві та більше підсис-
тем. Складні системи розбиваються на десятки і сотні підсистем. В середині
кожної підсистеми відбувається перетворення енергії, обмін і поширення ін-
формації між елементами підсистеми. Між підсистемами також наявні зв’язки
по яких передаються потоки енергії та розповсюджується інформація.
В загальному вигляді під технічною системою розуміють органічно єди-
ну сукупність підсистем (елементів), яка виконує певну функцію.
Довільну технічну систему зручно зобразити графічно у вигляді блок
схем (рис. 1.2).
а)
в)
Рис. 1.2. Графічне зображення технічних систем у вигляді блок-схем:
а — система, яка складається з одного елемента; б — система, яка включає
послідовно з’єднані елементи; в - система з кількома входами і виходами,
яка. складається із багатьох елементів і має розгалужену структуру
Виділення підсистем, входів і виходів здійснюється виходячи із суті задачі,
поставленої мети досліджень та наявного досвіду аналізу аналогічних систем.
В деяких випадках розділення системи на складові підсистеми є очевидним
(рис. 1.3).
6
Розділ 1. Основні поняття та визначення
Рис. 1.3. Приклад механічної коливальної динамічної системи, її основних
підсистем, входів і виходів: Рі, Р?, Р3 ~ входи у вигляді сил, що діють
на маси; ¥/, У? ~ виходи у вигляді переміщення мас
Для технічної системи гідроприводу (рис. 1.4) входом є навантаження на
робочому органі Р(і), а виходом - швидкість переміщення поршня V [91).
Рис. 1.4. Приклад технічної системи гідроприводу
Система гідроприводу має додаткові входи у вигляді взаємозв’язаних між
собою параметрів- подачі рідини на вході О,,, пульсацій тиску на вході Рн(і)
та витрат рідини через дросель (Д
В загальному випадку виділення підсистем, а також формування входів і
виходів викликає певні труднощі. Це пов’язано як із складністю задачі, так і
з вибраним напрямком моделювання.
В системах мають місце різноманітні робочі процеси. Більшість процесів
відзначається різноманітністю фізичних явищ та складністю. Наприклад, ко-
7
Струтинський В. Б
ливальні процеси, гідродинамічні процеси, процеси на границях (поверхнях
поділу), такі як: емісія, теплообмін, поверхневий натяг, процеси переносу те-
пла і речовини в середовищі тощо.
В загальному вигляді під процесом розуміють семантичну категорію,
яка відображає послідовність зміни стану системи.
При дослідженнях шляхом математичного моделювання розглядаються
процеси у вигляді послідовної зміни предметів та явищ, які виникають зако-
номірним чином у відповідності з відомими фізичними законами.
Для математичного моделювання системи чи процесу, який в ній відбуваєть-
ся, вводяться математичні об’єкти, які кількісно описують систему чи процес.
Математичні об’єкти мають різну природу. Зокрема для опису систем і
процесів використовують числа (скаляри), взаємозв’язані множини чисел
(вектори, матриці, тензори)
Математичні об’єкти звичайно групуються між собою, утворюючи спів-
відношення, залежності, умови тощо.
Загалом математичні об’єкти, які служать для опису технічної системи чи
процесу, утворюють цілісну множину (комплекс) параметрів системи.
З метою зручності опису системи параметри поділяються на групи
(рис. 1.5).
Вектор проміжних
параметрів (станів)
в підсистемі	підсистемі
Рис. 1.5. Параметри системи, які використовуються для її кількісного
аналізу при математичному моделюванні
Вхідні та вихідні параметри дають кількісні характеристики входів і ви-
ходів. Вони звичайно представляють собою векторні функції, які задаються
або символьними виразами, або умовами чи обмеженнями.
8
Розділ 1. Основні поняття та визначення
Вхідні параметри, як правило, е незалежними функціями часу, а вихід-
ні - залежать від вхідних параметрів і від характеристик системи. В більшос-
ті випадків вхідні параметри не можуть бути описані точно, складно дати на-
віть якісний опис деяких вхідних параметрів.
Вхідні та вихідні параметри можуть бути детермінованими або стохастич-
ними. Вибір такого опису входів чи виходів визначається специфікою задачі
та поставленою метою дослідження.
Внутрішні параметри системи служать для опису процесів, які в ній про-
тікають. Ці параметри подаються у вигляді векторів проміжних параметрів
(станів), що характеризують зв’язки між підсистемами або у вигляді внутрі-
шніх параметрів підсистем (див. рис. 1.5).
Підсистеми також описуються набором операторів, які в умовному симво-
лічному вигляді описують процеси в підсистемі.
Внутрішні параметри підсистем можуть бути функціями часу або постій-
ними величинами, зокрема випадковими величинами або випадковими
процесами, логічними умовами чи деякими співвідношеннями.
Параметри у вигляді операторів представляють собою, наприклад, лінійні
диференціальні оператори, інтегральні перетворення, алгоритми, реалізовані
в чисельній формі, формалізованому вигляді чи у вигляді графоаналітичних
комплексів.
1.2. Математичні моделі процесів та систем
Моделювання є одним з основних методів одержання науково-технічних
результатів при проведенні прикладних досліджень технічних систем і проце-
сів, що в них протікають.
Під моделлю розуміють об’єкт, що знаходиться у відношенні подібності
до системи або процесу, які моделюються.
Процедура моделювання включає дослідження об’єкта шляхом створення
його моделі, визначення закономірностей її роботи та перенос отриманих ре-
зультатів на об’єкт, що моделюється.
Розрізняють фізичне і математичне моделювання систем і процесів При
фізичному моделюванні створюється фізична модель об’єкта, а при математи-
чному - модель у вигляді математичних об’єктів.
Математична модель охоплює клас иевизначених (абстрактних, символі-
чних, формальних) математичних об’єктів, таких як числа, вектори, тензори
і відношення між цими об’єктами.
Математична модель наближено відображає властивості системи або
процесу, які моделюються.
Математичні моделі використовуються для визначення властивостей процесів
9
Струтинський В. Б.
чи систем. Зокрема, за допомогою математичного моделювання здійснюється:
-	розрахунок системи з метою вибору раціональних або оптимальних зна-
чень параметрів;
-	прогнозування надійності роботи системи, зміни стану системи в часі;
-	аналіз критичних режимів роботи систем.
В залежності від мети і задач, використовують різні класи математичних
моделей.
За способом використання експериментальних даних моделі поділяються
на апріорні (розроблені теоретично) і апостеріорні (отримані в результаті
обробки експериментальних даних).
За підходом до опису характерних властивостей об’єкта моделювання
розрізняють моделі систем в розподілених параметрах і моделі систем в зо-
середжених параметрах.
Ряд параметрів технічних систем, зокрема маса, при математичному моде-
люванні може зосереджуватись в характерних точках системи. Одержана в
результаті зосередження параметрів математична модель є значно простіша,
ніж модель, що враховує розподіл параметра у просторі. Наприклад, для ме-
ханічної коливальної системи зосередження параметрів призводить до мате-
матичної моделі у вигляді системи звичайних диференціальних рівнянь. В
той же час врахування розподілу параметрів потребує використання рівнянь
в частинних похідних, розв’язок яких є набагато складніший за розв’язок
звичайних диференціальних рівнянь.
За характером врахування особливостей характеристик систем розрізня-
ють лінійні та нелінійні математичні моделі.
Лінійні математичні моделі базуються на припущенні про лінійність мате-
матичних залежностей, що описують характеристики системи та її елементів.
Нелінійні моделі враховують характерні особливості характеристик, такі як
розриви, обмеження (суттєві нелінійності) або кривизну, ступінь збільшення
(гладкі нелінійності). Нелінійні моделі, як правило, точніші лінійних і більш
адекватно відображають властивості систем і процесів. Лінійні моделі значно
простіші за нелінійні, допускають більш широкі узагальнення. їх використання
знижує трудомісткість моделювання, дозволяє використовувати апробовані часом
формалізовані методи математичного опису різноманітних процесів та систем.
За особливостями врахування зміни параметрів системи в часі розрізня-
ють математичні моделі для опису стаціонарних та нестаціонарних процесів.
Моделі стаціонарних процесів описують усталені процеси з усередненими в
часі закономірностями. Моделі нестаціонарних систем враховують зміни па-
раметрів у часі.
За підходом до опису параметрів та характеристик процесів і систем роз-
різняють детерміновані та стохастичні математичні моделі. Детерміновані
10
Розділ 1. Основні поняття та визначення
математичні моделі включають лише визначені параметри і характеристики
процесів. Стохастичні математичні моделі включають випадкові величини,
функції та умови і служать для імітації процесів, які реально мають місце в
технічних системах.
Імітація реальних процесів та систем випадковими величинами і випадко-
вими функціями значно спрощує процес опису реальних властивостей систе-
ми, підвищує достовірність одержаних результатів, дозволяє виконати про-
гнозні оцінки властивостей системи. Застосування сучасних засобів обчислю-
вальної техніки дозволяє автоматизувати процес імітаційного математичного
моделювання, одержати вагомі науково-технічні результати в мінімальні
строки з помірними трудовитратами.
За видом математичного опису процесів розрізняють неперервні та диск-
ретні математичні моделі. Неперервні моделі оперують залежностями, які ви-
значені в певних проміжках часу чи простору. Дискретні моделі описують
процес в окремих точках. Дискретні моделі особливо ефективні для опису
складних фізичних процесів, що мають місце в реальних технічних системах.
Дискретні моделі відзначаються надійністю роботи, високою точністю та
достовірністю аналізу результатів. Вони дозволяють використати прогресивні
сучасні інформаційні технології для аналізу технічних систем і процесів.
За особливостями математичного апарату, що використаний при розробці
математичних моделей, розрізняють моделі у вигляді функціональних залеж-
ностей (функцій, рядів, скалярних, векторних полів) та моделі у вигляді
співвідношень (систем рівнянь, диференціальних рівнянь, інтегральних рів-
нянь). Звичайно моделі у вигляді співвідношень в кінцевому підсумку транс-
формуються у відповідні функціональні залежності, таблиці чи графіки.
В процесі розробки та використання математичних моделей виконуються різ-
норідні роботи, які є послідовними етапами розробки і використання моделі.
Спочатку здійснюється постановка задачі моделювання, окреслюється ме-
та і результати досліджень, прогнозується вихід моделі.
Постановка задачі моделювання проводиться в кожному випадку відпові-
дно до загального плану досліджень (розрахунок параметрів, аналіз режимів,
оцінка показників системи). За вихід моделі приймається комплекс парамет-
рів, що спостерігаються і що вимірюються. На основі аналізу може бути
отриманий новий науково-технічний результат.
Вихід моделі звичайно відповідає параметрам виходу системи, що моде-
люється. Вихід моделі є основою для подальшої обробки результатів моделю-
вання та формування наукових результатів і практичних висновків дослі-
джень.
Постановка задачі моделювання здійснюється на основі інформаційних
досліджень, обробки та аналізу інформації.
11
Струтинський В.Б.
Аналіз наявної інформації виконується на основі літературних джерел,
досвіду розробки і використання моделей аналогів.
Після постановки задачі та визначення мети моделювання здійснюється без-
посередня розробка загального плану моделі технічної системи. Система та її ро-
бочі процеси формалізуються шляхом введення та обґрунтування припущень.
Припущення служать для одержання максимально простої математичної
моделі. Кожне з припущень обґрунтовується.
Обґрунтування припущень проводиться шляхом оцінки порядку величин,
дослідним шляхом або в результаті спеціальних досліджень. Використовуєть-
ся досвід розробки аналогічних моделей, які описані в літературних джере-
лах, а також дослідна апробація висунутих положень шляхом спеціальних
експериментальних досліджень.
Для введення припущень проводять ранжування факторів з метою вста-
новлення ступеня впливу кожного із них на результати моделювання.
Ранжування факторів полягає у дослідженні впливу комплексу парамет-
рів (факторів) на вихід моделі. Фактори, які незначним чином впливають на
вихід, виключаються з розгляду, за допомогою чого досягається спрощення
загального плану моделі та одержання розрахункової схеми.
Розрахункова схема є результатом ідеалізації реальної технічної системи.
Вона відображає всі основні параметри системи, її логіку роботи і функціо-
нальне призначення. Розрахункова схема представляє собою графоаналітичне
зображення системи або процесу в рамках прийнятих припущень.
Розрахункова схема є основою вибору методів і стратегії моделювання.
Вибір стратегії моделювання виконується з метою раціоналізації процесу
розробки моделі. Він полягає у визначенні необхідної послідовності виконан-
ня робіт, одержанні та використанні проміжних результатів, зниженні ймові-
рності появи помилок, використанні готових блоків моделей, методів і мето-
дик.
Згідно вибраної стратегії на основі розрахункової схеми здійснюється
розробка базової математичної моделі.
Базова математична модель - це система рівнянь, складена на основі ви-
користання фундаментальних законів фізики відповідно до прийнятої розра-
хункової схеми системи або процесу. Базова модель представляє собою за-
мкнену систему співвідношень, що описує технічну систему або процес.
З метою раціоналізації процесу розробки моделі базова математична мо-
дель приводиться до стандартного вигляду.
Стандартний (нормалізований) вигляд рівнянь утворюється з базової ма-
тематичної моделі шляхом її перетворення.
Стандартний вигляд рівнянь має великий ступінь загальності. Наприклад,
запис системи диференціальних рівнянь в матрично-векторному вигляді дає
12
Розділ 1. Основні поняття та визначення
можливість розробити універсальну методику розв’язку цих рівнянь.
Для розв’язку рівнянь формується алгоритм і створюється відповідне
програмне забезпечення.
Алгоритм представляє собою схему розв’язання рівнянь, записаних у ста-
ндартному вигляді.
Алгоритм вказує на послідовність дій, які в подальшому реалізуються в
обчислювальн їй процедурі.
Обчислення виконуються необхідним програмним забезпеченням. Найдо-
цільніше як програмне забезпечення використати сучасні математичні пакети,
зокрема МаІСАІЗ і МАТЬАВ відповідних версій.
В результаті проходження вищевказаних етапів математичного моделю-
вання буде одержана закінчена математична модель, придатна для розраху-
нків.
При розробці моделі звичайно допускаються помилки - як грубі, так і не-
суттєві. Тому одержана математична модель підлягає аналізу з метою підтве-
рдження її достовірності. Проводиться комплекс пробних розрахунків (“пер-
ший розрахунок”). При цьому одержується початковий масив інформації за
результатами математичного моделювання. Одержаний масив піддається ана-
лізу з метою перевірки адекватності (достовірності) математичної моделі.
Термін “адекватний” означає рівний, відповідний, тотожний (лат.
асІаерцаЬ.із - прирівняний).
Перевірка адекватності необхідна для підтвердження правильності ре-
зультатів моделювання.
Перевірка адекватності виконується шляхом порівняння результатів мо-
делювання з еталоном (експеримент, модельний (достовірний) розрахунок,
явище тощо).
При наявності еталона умовою адекватності є відповідність виходів моделі
та еталона при тотожних входах. Відповідність встановлюється досягненням
необхідної точності розрахунків (рис. 1.6).
Якщо точні експериментальні дані відсутні, то перевірка адекватності
проводиться шляхом статистичного аналізу наближених експериментальних
даних або іншими методами.
Якщо адекватність моделі не підтверджується, то здійснюється уточнення
напрямку і стратегії моделювання та проводиться доопрацювання моделі від-
повідно до вищевказаних етапів.
У випадку, коли модель задовольняє умовам адекватності, процес розроб-
ки моделі вважається завершеним, і тоді переходять до безпосереднього ви-
користання моделі для математичного моделювання процесу чи системи.
Розроблена математична модель повинна задовольняти певним вимогам і
критеріям. Основними параметрами оцінки якості математичної моделі є точ-
13
Струтинський В.Б.
ність, економічність, універсальність, інформативність. Головним із цих па-
раметрів є точність.
Еталон
Процесе
моделювання
[X]
[Хс]
Експеримен-
тальні
дослідження
Чисельний
експеримент
ї
Математична
модель
|ХМ\]
[¥]-[¥е] < [А]
____І____
(Еталон)
Рис. 1.6. Схема перевірки адекватності моделі
шляхом порівняння її з еталоном
Достовірний
розрахунок
[ Явище ]
І[¥]
І [¥Л
Точність моделювання оцінюється похибками розрахунку виходу моделі.
Похибки розрахунків оцінюються абсолютними або відносними похибка-
ми. Аналіз похибок розрахунків є важливим етапом розробки математичної
моделі.
Економічність визначається витратами або часом реалізації процесу мате-
матичного моделювання. Витрати розділяються на різні групи. Зокрема це -
розробка моделі, витрати на експлуатацію обладнання та обчислювальної
техніки, витрати на матеріали тощо. Витрати на розробку моделі можуть бути
знижені шляхом розширення класу об’єктів, що моделюються, підвищення
універсальності моделі.
Універсальність оцінюється широтою охоплення процесів і систем, які
моделюються. Звичайно намагаються розробляти універсальні моделі. Уні-
версальність моделі підвищується при використанні блоково-модульної схеми
побудови моделей, використання ефективного математичного апарату, гнучкої
системи введення-виведення інформації.
Інформативність математичної моделі визначається обсягом одержуваної
інформації і залежить від ступеня ідеалізації об’єкта моделювання. Інформа-
тивність моделі підвищується з використанням сучасних інформаційних тех-
нологій, шляхом впорядкування та узагальнення вихідної інформації.
Всі характеристики математичних моделей взаємозалежні. Як правило, більш
точна модель є менш економічною, а універсальна модель є менш точною.
Основним критерієм оцінки математичної моделі є точність. Необхідна точ-
ність визначається умовою адекватності і залежить від помилок моделювання.
Помилки, які виникають при математичному моделюванні, мають різний
14
Розділ 1. Основні поняття та визначення
характер і величину. Для їх визначення та врахування здійснюється аналіз
причин і місця виникнення помилок (рис. 1.7).
Похибки моделі
Масив
Похибки Похибки задання Похибки
входу параметрів моделі обчислень
Похибки Похибки
виводу	аналізу
результату
Рис. 1.7. Причини виникнення сумарних похибок
математичного моделювання процесу чи системи
Похибки введення вхідних та проміжних параметрів поділяються на грубі
(10 % і більше), які виникають від недостатньої інформації про дійсні вхідні
параметри моделі, а також на несуттєві похибки, пов’язані із особливостями
математичного аналізу вхідних параметрів.
Похибки моделі спричинені, як правило, неточностями, допущеними при
виборі стратегії моделювання, а також особливостями алгоритму і обчислю-
вальної процедури. Деякі з цих помилок є прогнозованими. Наприклад, ви-
користання методу Рунге-Кутта ІУ-го порядку при чисельному інтегруванні
диференціальних рівнянь вводить похибку обчислень, що відповідає кроку
інтегрування в 4-й степені.
Похибки обчислень виникають при виконанні арифметичних операцій,
зокрема, це - похибки обмеження та похибки округлення. В сучасних ЕОМ
ці похибки, як правило, дуже малі (порядку 1О-360).
Похибки виведення та аналізу результатів моделювання можуть бути до-
сить грубими і привести до помилкових висновків при аналізі результатів мо-
делювання. Серед похибок виведення можна виділити похибку інтерполяції
значень вихідного параметра, похибки, які виникають при екстраполяції про-
цесів, похибки апроксимації та згладжування, похибки, що викликаються ви-
сокочастотними осциляціями вихідних параметрів, та інші.
Похибки інтерполяції часто виникають при формуванні виходу моделі у
вигляді розрахункового масиву значень вихідного параметра. При інтерполя-
ції елементів масиву втрачається інформація про поведінку вихідного параме-
тра між двома елементами масиву
15
Струтинський В.Б.
Розрахунок виходу моделі виконується звичайно в певних межах зміни па-
раметрів. Наприклад, для нескінченного діапазону зміни параметра вибирається
обмежений, досить великий діапазон розрахунку. В подальшому для одержання
наукових результатів здійснюється оцінка характеру зміни виходу моделі за ме-
жами розрахункового діапазону. При цьому виникають як грубі, так і несуттєві
похибки екстраполяції результатів математичного моделювання.
Виведення результатів моделювання потребує обмеження числового мате-
ріалу до вигляду, який включає 4.. 10 значущих цифр. При цьому виникають
похибки апроксимації та згладжування досить грубих значень модельованого
процесу.
Похибки внаслідок високочастотних осциляцій виходу можуть суттєвим
чином вплинути на результати моделювання. їх врахування часто призводить
до необхідності зміни стратегії моделювання, використання спеціальних алго-
ритмів і програмного забезпечення.
Це має місце, наприклад, при чисельному інтегруванні “жорстких” дифе-
ренціальних рівнянь.
Таким чином, при розробці та використанні моделі обов’язково є похиб-
ки - як грубі, так і малосуттєві. Оцінки похибок проводяться при перевірці
адекватності моделі.
Як міру точності математичного моделювання використовують вектор по-
хибок розрахунку.
Вектор своїми компонентами має або абсолютні похибки-у вигляді:
[Д] = [¥-¥е],
або відносні похибки визначені як
де ¥ - розраховане значення деякого параметра системи;
¥е - достовірне значення параметра.
Достовірні значення параметрів звичайно знаходять в результаті експери-
ментальних вимірювань.
Чим менші похибки [8], тим точніша модель. Абсолютна точність моде-
лювання досягається при [8] -> [0].
Математична модель вважається точною, якщо абсолютні або відносні по-
хибки не перевищують встановлених граничних значень, тобто
[Д] <[¥_], [8]<[8гаах].
Результати експериментальних вимірювань та розрахунків, як правило, є
випадковими величинами. У цьому випадку мірою точності математичного
моделювання є моменти розподілу значень похибок: математичні сподівання,
дисперсії тощо.
16
Розділ 1. Основні поняття та визначення
При математичному моделюванні випадкових процесів мірою оцінки точ-
ності вибирають характерні значення кореляційної функції чи спектральної
щільності процесу. Порівняння розрахункових та експериментальних спект-
ральних щільностей часто здійснюють по частотних діапазонах або по вели-
чині резонансних піків.
Результати моделювання та експериментальні дані часто представляють
собою функції з нескінченною областю визначення.
Наприклад, перехідні процеси в системах автоматичного керування мають
вигляд нескінченного процесу (рис. 1.8).
Функції з нескінченною областю визначення можуть порівнюватись між
собою шляхом визначення та порівняння їх характерних значень.
Рис. 1.8. Приклад оцінки точності математичного моделювання процесу
з нескінченною областю визначення: 1 - залежність, одержана в результа-
ті математичного моделювання; 2 - експериментально визначений процес
Наприклад, для процесу, зображеного на рис. 1.8, можна використати
порівняння значень процесів при і = 0.1 або 1 = 0.2:
Можна дати оцінку точності розрахунку за якимось середнім параметром,
наприклад, за часом перехідного процесу:
11 - і; І
5 =	. юо % .
Для оцінки точності допускається використовувати відносну похибку роз-
рахунку є = 5/¥е . При цьому похибка є функціональною залежністю:
¥ - У
є(О = у е • 100 % .
Ця величина змінюється в широких межах і незручна для аналізу. Більш
доцільно оцінювати точність введенням таких параметрів, як нормована абсо-
17
Струтинський В. Б.
лютна похибка:
де ¥еусг - усталене значення процесу.
Для оцінки точності можна використати максимальне значення нормова-
ної похибки
Єнтах =тах[єн(О].
Для оцінки точності можуть бути використані характерні параметри про-
цесу, наприклад, період коливань, частоту коливань або коливальність систе-
ми, логарифмічний декремент або максимальне перегулювання процесу.
При математичному моделюванні використовують інтегральні оцінки точ-
ності, які мають вигляд деяких функціоналів, тобто залежностей, визначених
на певній множині функцій.
Інтегральна нормована похибка для процесу, наведеного на рис. 1.8, ви-
значається функціоналом:
І,
= рн(Оск= —-------------
0	0	1 уст
СІ і .
Дана залежність не зовсім зручна в користуванні з причини наявності мо-
дуля під знаком інтеграла.
Більш зручна інтегральна оцінка у вигляді квадрата відхилення розраху-
нкових і експериментальних даних:
_М¥(О-¥Д)]2
1 •) — І	СІ ь .
I №уст1
Іноді застосовують більш складні формули для оцінки точності моделю-
вання, які враховують характер зміни кривої, наприклад, функціонал абсо-
лютної похибки у вигляді:
І3 = |[а(¥ - ¥с)2 + р(¥ - ¥с)2 + у (¥ - ¥е)2]с1і,
0
де а, Р, у - вагові коефіцієнти, які враховують значущість параметрів про-
цесу, швидкості його зміни ¥ та прискорення ¥ .
Вибір необхідної функціональної залежності здійснюється з врахуванням
особливостей системи і поставленої мети моделювання.
18
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
РОЗДІЛ 2
Математичні моделі процесів
на основі символьних функціональних залежностей
2.1. Обчислення та перетворення
символьних функціональних залежностей
2.1.1. Обчислення залежностей засобами пакету МаіЬСАО
При аналізі технічних систем і процесів широко використовуються функ-
ціональні залежності. Вони можуть бути задані рівняннями, графіками, су-
купністю точок тощо. Рівняння представляє собою символьну (аналітичну)
функціональну залежність. Графік або таблицю, що визначає сукупність
дискретних значень процесу можна привести до символьної залежності шля-
хом застосування методів інтерполяції та апроксимації функцій.
При розробці математичних моделей процесів використовують функції
однієї змінної, задані аналітичною (символьною) залежністю. Ця залежність
звичайно задана в явному вигляді:
у = Кх).
Функції однієї змінної класифікуються за видом аналітичних залежнос-
тей, з яких утворена функція [15, 41, 53, 114]. Якщо аналітичні залежності
складені з алгебраїчних виразів (поліномів, дробів тощо), маємо алгебраїчні
функції однієї змінної. Поширеною в практиці математичного моделювання є
поліноміальна функція:
І(х) = ао + а(Х +... + апхп (п - ціле додатне число).
Широко вживана дробово-раціональна алгебраїчна функція має вигляд:
£(х) = в() + Ь;х + ••• + ЬтХт
а0 + а,х + ... + апхп
Ірраціональні функції містять корені різного порядку. Прикладом ірра-
ціональної алгебраїчної функції є функція:
Кх) = ^(1 + х)2 .
Трансцендентні функції включають ех, Іпх тощо.
Тригонометричні функції включають яіпх, созх, і§х, сі§х, а також обер-
нені їм функції: агсзіпх, агссозх, агсідх, агссх^х.
Показникові функції мають аргумент в показнику степеня. Наприклад,
ех, ах.
Логарифмічні функції включають аргумент під знаком логарифма, на-
19
Струтинський В. Б.
приклад, Іпх.
Існує також численний клас спеціальних функцій, які визначаються як
розв’язки диференціальних рівнянь певного виду (функції Бесселя та інші).
Крім явного способу визначення функції у вигляді у = і(х), також має
місце неявний спосіб задання функції <р(х, у) = 0 або параметричний спосіб
задання функції:
Гх = х(0
ІУ = у(0 ’
де І -- деякий параметр, від якого залежать аргумент х і функція у.
Наприклад, параметрично задане рівняння кола має вигляд:
у = К*8Іп(і), х = К'созСі), К = Сопяі.
Параметр і змінюється в межах від 0 до 2л. Якщо виключити параметр і,
то одержимо неявне визначення цієї функції у вигляді:
<р(х, у) = у2 + х2 - Е2 = 0
або явний вигляд даної функції:
у = Кх) =	.
При математичному моделюванні широко використовуються векторні та
матричні функції. Наприклад, векторна функція у(х), компоненти вектора
якої є тригонометричними функціями, визначається наступним чином:
У(х) -
8ІПХ
СО8Х
І^Х
Матрична функція одної змінної х чи багатьох змінних визначається матри-
цею певного виду, компоненти якої залежать від вказаних змінних. Наприклад,
матрична функція однієї змінної може бути:
1 х2 х3
і(х)= ух ух ух .
8ІПХ СО8 X І£Х
Разом з елементарними функціями широко застосовуються різноманітні
спеціальні функції, зокрема функції Бесселя, гамма-функція, функція похи
бок, інтегральні функції та інші, які розглянуті нижче.
При математичному моделюванні використовуються не тільки дійсні, а й
комплексні (комплекснозначні) функції. При цьому комплекснозначна функ-
ція у = і(х) є комплексною величиною, а х може бути як дійсною, так і
комплексною величиною. Прикладом комплекснозначної функції є амплітуд-
но-фазова частотна характеристика динамічної системи [63]:
\¥(>) = \ф) • егч'(и),
де (о - дійсний аргумент (частота);
20
Розділ 2, Математичні моделі процесів на основі символьних функціональних залежностей
\У(<о), \р(и9 - дійсні функції, що відповідають амплітудно-частотній та
фазочастотній характеристикам динамічної системи;
І - 7-Л - уявна одиниця.
Функція \У(]ш) є комплексною величиною. Вона має також алгебраїчну
форму запису:
’Л'Чісо) = СТ(<о) + у-У(со).
Дійсна частина Щй) відповідає дійсній амплітудно-частотній характерис-
тиці, а уявна частина У(®) - уявній амплітудно-частотній характеристиці [6].
Для обчислення функцій та побудови їх графіків у математичному пакеті
МаіЬСЛВ 2000 (МаНіСАО 7 Рго, МаДіСА1) 8) наявний цілий ряд засобів
[22, 56, 62]. Воші зосереджені в основному в панелі інструментів МаіЬ
РаїїеЬе:
Дана панель включає вісім кнопок-піктограм, кожна з яких відкриває додат-
кову панель.
Кнопка	активізує панель АгііЬтеїіс Раїїеіе (калькулятор)
(рис. 2.1), яка включає в себе цифри від 0 до 9, знаки алгебраїчних опера-
цій, деякі елементарні функції та загальновживані константи.
Рис. 2.1. Панель АгіНітеііс Раїїеіе (калькулятор)
Активізація кнопок панелі виводить на екран символи з позиціями для
введення інформації. Позиції для введення позначені затушованими прямоку-
тниками. При введенні в позицію необхідного виразу затушований прямокут-
ник зникає. Наприклад, активізувавши кнопку
21
Струтинський В. Б.
одержимо на екрані заготовку
"Й 
Якщо в позицію введення, відзначену затушованим прямокутником, ввес-
ти, наприклад, х, то одержимо
•
В панелі АгіИішеііс РаіІеЬе наявні заготовки деяких практично важливих
загальновживаних функціональних залежностей.
Кнопка призначена для обчислення абсолютної величини змінної,
константи чи виразу, що записується між вертикальними лініями замість за-
тушованого прямокутника.
Па панелі наявні кнопки, яким відповідають знаки арифметичних операцій:
та два знаки рівності.
Кнопка відповідає оператору присвоєння і виконує функції присво-
єння значення величини, що знаходиться справа від цього знака, змінній або
функції, що знаходиться зліва від знака. Наприклад, запис
у := 72
означає, що змінній у буде присвоєно значення 1.41...
Кнопка па панелі калькулятора використовується для виведення на
екран значення змінної, вектора, матриці або функції. Приклади застосуван-
ня цього знака наведені нижче. Зокрема, обчислення тригонометричної функ-
ції зіпх при х = 0 з використанням цієї кнопки:
8Іп(0) = 0.
Якщо є вектор, заданий своїми трьома компонентами 1, 2, 1, то застосу-
вання знака “=” призведе до виведення значення вектора у вигляді:
т
V = 2 .
Кнопка
1
панелі калькулятора означає присвоєння змінній зліва від
знака ряду послідовних значень. Наприклад, і:= 0..3 означає, що змінна і є чо-
тиривимірним масивом цілих чисел, елементи якого мають значення 0, 1,2, 3.
Кнопка відповідає виразу, взятому в дужки.
22
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
На панелі є кнопки визначення загальновживаних констант е, л та кнопка
для визначення уявної одиниці і(л/-~ї).
Кнопка забезпечує визначення елемента індексованої змінної: ком-
поненти вектора, матриці або елементу масиву. За її допомогою вводиться ін-
дексація масивів необхідної розмірності.
Показникові функції та вирази набираються за допомогою кнопок
Наприклад, для введення виразу х5 необхідно використати останню кнопку,
або змінити в першій чи другій заготовці числа відповідно -1 чи 2 на 5. Для вве-
дення квадратного кореня використовується розглянута раніше кнопка
а для введеній; кореня довільного порядку — кнопка
На панелі калькулятора розташовані кнопки, що дозволяють набрати де-
які практично важливі елементарні функції, зокрема логарифмічні, тригоно-
метричні, експоненціальні та факторіал. Для цього служать наступні кнопки
заготовки:
Обчислення функцій у символьному вигляді здійснюється за допомогою
панелі символьних операцій ЗутЬоІіс КеуЬоагсІ (ключові слова символьних
операцій) (рис. 2.2). Ця панель відкривається за допомогою кнопки
і ’
що наявна на панелі інструментів (див. с. 21).
Рис. 2.2. Панель символьних операцій ЗутЬоІіс КеуЬоагсІ
23
Струтинський В. Б.
Панель символьних операцій включає в себе кнопки символьних перетворень
та ряд кнопоі. і к г мміі’Ми ' чи. ь'чречл
(розв’язати, ряд, спростити) та інші.
Використання кнопки і відповідної заготовки
| (розкласти на множники)
виконує розклад на множники виразу, наприклад:
х2 — 2х + Зх — 2 (асіог, х - 1 -> (х + 2)(х — 1).
Результат одержано в символьному вигляді і його наведено справа від
стрілки.
Спрощення виразу виконується аналогічно, наприклад:
х2 2
~-------------- яітрііґу -> х - у .
X + у
Обчислення похідних довільного порядку, визначених та иевизначених
інтегралів, сум, добутків, границь здійснюється за допомогою панелі матема-
тичних операцій Саіспіиз РаїїеЬ?. Панель відкривається кнопкою
панелі математичних інструментів (Магії Раїїеіе).
Панель математичних операцій Саісиїпз Раїіеіе (рис. 2.3) включає різний
інструментарій здійснення різноманітних розрахунків.
Рис. 2.3. Панель математичних операцій
Похідні .|н і-'.чіь обчислюються з використанням кнопок
для обчислення відповідно першої похідної та похідної довільного порядку.
На панелі є кнопки
ІІІІІІ та ІіІІІІ
для організації обчислення визначених та иевизначених інтегралів відповідно.
24
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
Приклади обчислення визначених та невизначених інтегралів у чисельному
та символьному вигляді наведено нижче:
|е28ІП (х/2х)Нх -> 1.304098
о
Г---	—__ (1Х	Іп(соз(х))+ 1п(1 + с
’ СО8(хДІ + соцх))
Обчислення сум та добутків здійснюють кнопками:
Приклад обчислення суми числової послідовності у символьному вигляді:
ЛІ	1 ,
п-1 П	”
На панелі математичних операцій є кнопки для обчислення границь функцій:
Активізація даних кнопок призводить до появи иа екрані заготовок
Ііт ї]
І
ііт
8
1ІЙІ
і в
Приклад знаходження границі функції £(х) = |х2 - 4[ в точці х:= 2 з ви-
користанням даних засобів має вигляд:
|(х + Ах ¥ - 41 - іх2 - 4|
1іт 12-----'----О-------і _> 4 .
АХ-ХГ	Дх
Панель математичних операцій включає кнопку
яка служить для введення числа, що відповідає нескінченності.
Застосування символьних диференціальних операцій розглянуто більш
детально в розділі 2.2.
Формування знаків відношень еквівалентності та функцій здійснюється за
допомогою панелі рівностеіі та відношень (Еуаіиаііоп апсі Воо'еп Раїїеіе).
Вона відкривається за допомогою кнопки
панелі математичних інструментів (Маій РаїеіХе).
Панель рівностеіі та відношень (рис. 2.4) включає спеціальні знаки рів-
ності, нерівності та тотожності:
25
Струтижький В.Б.
Рис. 2.4. Панель рівностей та відношень
На панелі є кнопки для формування строгих і нестрогих нерівностей
та операцій з функціями.
2.1.2. Побудова та аналіз плоских графіків
Аналіз функцій однієї змінної доцільно проводити при графічному супро-
воді у вигляді побудованих графіків функції або допоміжних функцій (на-
приклад, похідних необхідного порядку).
В математичному пакеті МаіЬ.САО є ряд засобів для побудови графіків
функцій
Побудова графіків різного виду здійснюється за допомогою панелі графі-
ків (рис. 2.5).
Рис. 2.5. Панель графіків
Панель включає ряд кнопок, за допомогою яких формуються заготовки
двовимірних і просторових графіків.
Для побудови плоского графіка функції однієї змінної, заданої символь-
ним (аналітичним) виразом у декартовій прямокутній системі координат, слу-
жить кнопка-пікто грама на панелі графіків:
При ініціалізації цієї піктограми на екрані з’являється заготовка графіка
у вигляді прямокутника з полем графіка (рис. 2.6).
26
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
Рис. 2.6. Заготовка графіка
У виділеному нижньому затушованому квадратику заготовки графіка не-
обхідно помістити значення аргументу (наприклад, х), а у лівому затушова-
ному квадратику - функцію, яка повинна бути зображена.
Функція може бути задана аналітичним виразом, наприклад,
8Іп(х) + 2*СО8(х),
або у загальному вигляді, як
с <ії(х)
Г(х) чи —.
(ЇХ
При цьому загальний вигляд функції конкретизується перед графіком,
наприклад
Г(х):=5Іп(х) + 2*со$(х).
Приклади побудови графіків функцій та їх похідних наведено на рис. 2.7.
Засоби математичного пакету дозволяють задавати область зміни аргумен-
ту х. Також визначаються верхня та нижня межа значень графіка. Побудова
графіків здійснюється автоматично. При наявності розривів функції побудова
графіка здійснюється як звичайно, а точки розриву з’єднуються умовними
лініями. Для рис. 2.7, а точки розриву похідної при х = 2 та х = 3 показані
вертикальними асимптотами функції в точках розриву.
Для побудови графіка в полярній системі координат служить кнопка
на панелі графіків. При ініціалізації цієї кнопки піктограми на екран виводиться
.заготовка графіка у вигляді прямокутника з колом, на якому знаходиться два
затушованих прямокутника' один - внизу; другий - зліва від кола
Також, як вказано раніше, в заготовку графіка заносяться аргумент
(нижній затушований квадрат) та функція (лівий затушований квадрат).
Приклад побудови графіка в полярній системі координат наведено нижче
(рис. 2.8).
27
Струтинський В. Б.
б)
Рис. 2.7. Приклад побудови графів функції та її похідних: а - графік
функції ((х) та її похідної; б - графік функції д(х) та її похідної.
Похідні показані пунктирними лініями
Ділянки плоских графіків можуть бути збільшені до потрібного розміру.
Для цього служить кнопка (див. рис. 2.5)
(7оош),
28
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
яка знаходиться на панелі графіків. Ініціалізація цієї кнопки здійснюється
після виділення на графіку деякої ділянки (виділена ділянка показана пунк-
тиром) (рис. 2.9, а).
Рис. 2.8. Приклад побудови графіка в полярній системі координат
Рис. 2.9. Збільшення виділеної прямокутної ділянки графіка: а — графік
з виділеною прямокутною ділянкою; б - меню, яке визначає параметри
збільшеної ділянки; в - збільшена прямокутна ділянка графіка
29
Струтинський В.Б.
В результаті на екран виводиться меню (рис. 2.9, б). В його діалоговому
вікні вказуються координати х та у виділеної ділянки. Після ініціалізації
кнопки 2оош з меню ця ділянка буде збільшена до розмірів початкового гра-
фіка. «Збільшена у декілька разів частина графіка наведена на рис. 2.9, в.
Повернення назад здійснюється кнопкою ІЗпгоот. Після цього графік на-
буває вигляду, який він мав до збільшення.
Для визначення координат точок графіка (трасування) служить кнопка
(Тгасе)
мямі
на панелі графіків. Визначення координат називається грасуванням (визна-
ченням точок) кривої. При ініціалізації кнопки Тгасе на екран виводиться
меню, показане на рис. 2.10, а.
а)
X
б)
Рис. 2.10. Визначення координат характерних точок графіка
шляхом трасування кривої графіка
зо
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
Трасування графіка здійснюється двома лініями, координати перетину
яких показуються у вікні X—У Тгасе (див. рис. 2.10, а). Ці координати мож-
на скопіювати Сору X, Сору V в буфер обміну, а потім перенести в потрібне
м і сце Ма і Ь С АО-д оку менту.
Приклад трасування графіка наведено на рис. 2.10, 6. Шляхом трасуван-
ня визначено координати максимуму кривої, показаної суцільною лінією.
2.1.3. Побудова об’ємних графіків поверхонь та діаграм
Для побудови поверхні в панелі графіків (див. рис. 2.5) є кнопка
(Зигґасе РІоі).
швои®
При ініціалізації цієї кнопки на екран виводиться заготовка об’ємного
графіка поверхні, що має вигляд прямокутника, в лівому нижньому куті яко-
го знаходиться чорний квадратик. На його місце треба помістити ім’я матриці
чи вектора, які потім будуть зображені у вигляді об’ємного графіка
Для побудови графіка функції двох змінних перед його заготовкою за-
дається додаткова інформація:
-	визначається функція, наприклад:
Г(х,у):= 1 + (со§(х)-10 * 8Іп(у)2)*е 2	(2.1)
-	вводиться індексація вузлів сітки
і:	= 0..10 Ф = 0..7
-	формуються вектори значень аргументів, що відповідають вузлам сітки
хр — і*0.2 - 1	у,: = .1*0.1
-	обчислюється матриця значень функції (2.1), аргументи якої відпові-
дають вузлам сітки:
Цд := Р(Хі, ур.	(2.2)
Ця інформація, як вказано раніше, розміщується перед полем графіка.
Побудований відповідно до заданої матриці (2.2) графік функції двох
змінних має вигляд просторової сітки (рис. 2.11).
Графічне зображення матриці можна подати у вигляді точкової діаграми.
Координати точок відповідають значенням матриці (2.2) у вузлах сітки
(рис. 2 12).
Засоби математичного пакету дозволяють в широкому діапазоні змінювати
вигляд і формат графіка - здійснювати нахил графіка, поворот його на необ-
хідний кут, нумерувати осі, задавати вигляд сітки тощо.
На полі графіка вказуються необхідні параметри координат, зображують-
ся координатні осі, координатні площини та граничні лінії, змінюються коор-
динати вузлів сітки та відповідна їм кількість ліній на графіку поверхні.
31
Струтинський В.Б.
Рис. 2.11. Тривимірний графік поверхні, що відповідає функції (2.1),
побудованій на сітці 11x8
Рис. 2.12. Зображення матриці (2і^(2.2) у вигляді точкової діаграми
Елементи вектора чи матриці також можна зобразити у вигляді стовпчас-
тої діаграми. Для цього на панелі графіків (див. рис. 2.5) є кнопка:
(ЗВ Ваг СЬагі).
Висота стовпчиків діаграми відповідає значенню вектора чи матриці у вузлі
сітки. Зображення матриці чи вектора у вигляді стовпчастої діаграми подається в
аксонометрії (рис. 2.13).
Для побудови графіка у вигляді стовпчастої діаграми задається раніше
вказана додаткова інформація про сітку, на якій визначена функція двох
змінних або значення матриці.
Стовпчаста діаграма дає зручну візуальну інтерпретацію функції двох
змінних або елементів вектора чи матриці.
Засоби математичного пакету МаїЬСАІ) дають можливість дослідження
багатьох властивостей функції кількох змінних, заданих аналітичним вира-
32
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
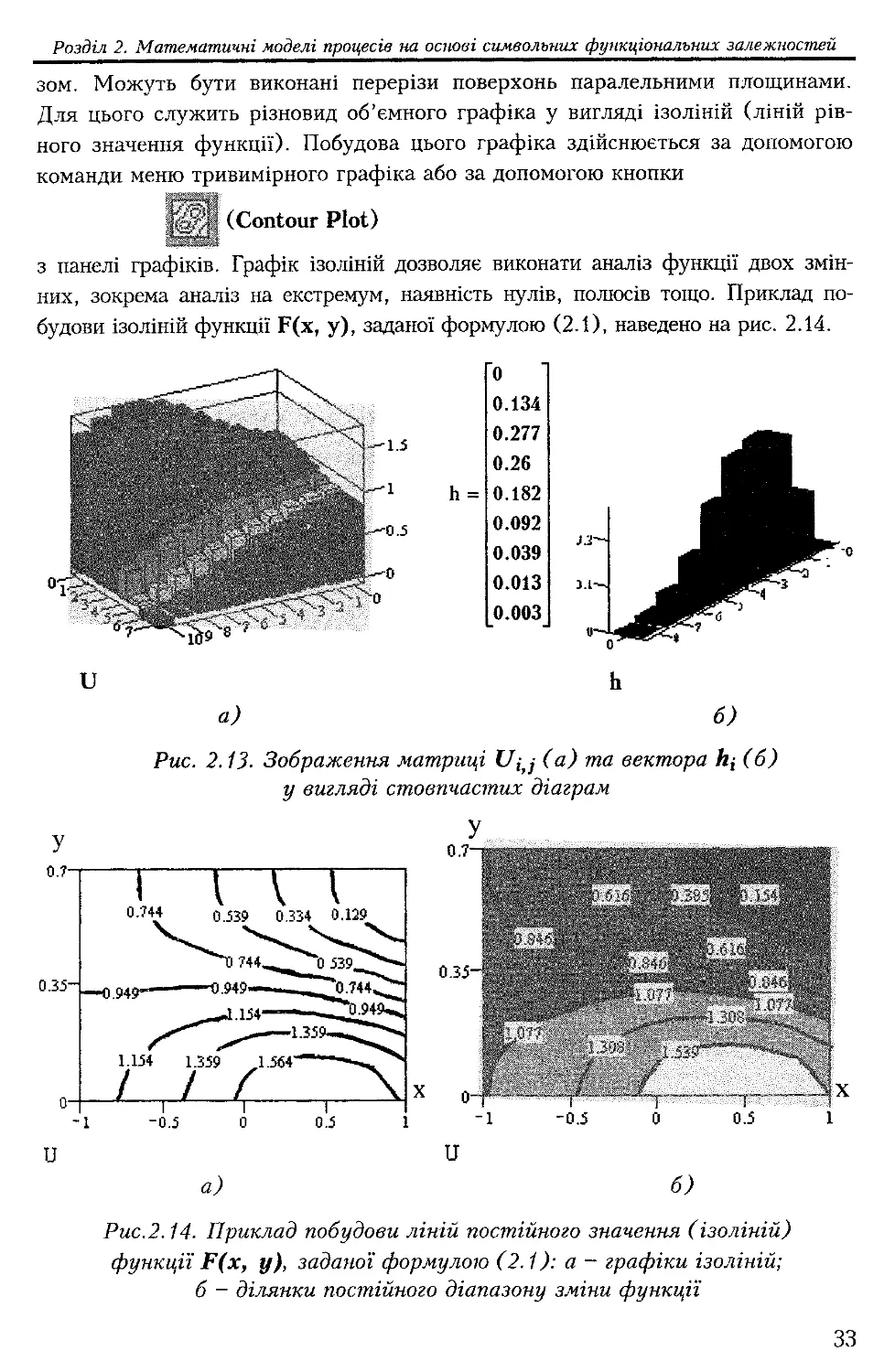
зом. Можуть бути виконані перерізи поверхонь паралельними площинами.
Для цього служить різновид об’ємного графіка у вигляді ізоліній (ліній рів-
ного значення функції). Побудова цього графіка здійснюється за допомогою
команди меню тривимірного графіка або за допомогою кнопки
(Сопіоиг Ріоі)
з панелі графіків. Графік ізоліній дозволяє виконати аналіз функції двох змін-
них, зокрема аналіз на екстремум, наявність нулів, полюсів тощо. Приклад по-
будови ізоліній функції Р(х, у), заданої формулою (2.1), наведено на рис. 2.14.
0.134
0.277
Ь = 0.182
0.092
0.039
0.013
0.003
Ь
б)
Рис. 2.13. Зображення матриці (а) та вектора /?, (б)
у вигляді стовпчастих діаграм
а)	б)
Рис. 2.14. Приклад побудови ліній постійного значення (ізоліній)
функції Р(х, у), заданої формулою (2.1): а - графіки ізоліній;
б - ділянки постійного діапазону зміни функції
33
Струтинський В. Б.
Засобами математичних пакетів можна побудувати векторне поле функції
двох змінних. Для цього на панелі графіків (див. рис. 2.5) є кнопка
(Уесіог Гікі РІоО.
Векторне поле визначається спеціальною векторною функцією, яка повин-
на бути задана перед графіком.
Наприклад, розглянемо функцію двох змінних (потенціал):
г := 0 ф(х, у) := 1п(і + х + у + г) + (х2 + у2 + г2)2.
Дана функція утворює скалярне поле, яке характеризується вектором-
градієнтом. Вектор-градієнт визначається наступною векторною функцією:
(1 + х + у + г)‘ + 4 * (х2 + у2 + х2)х
(1 + х + у + г)"1 + 4 * (х2 + у2 + г2)у
Проекції вектора градієнта даного скалярного поля:
П(х, у) := §га<1(х, у)0
£2(х,у):= §га<1(х,у)1.
Виконаємо індексацію вузлів сітки та формування векторів значень аргу-
ментів:
і:=0...20	] := 0...20
Хі := 0.05 * і у; := 0.05 * ]
обчислення матриць-компонент вектора-градієнта:
М.,5 := П(хі,Уі);
Зображення векторного поля розглянутої функції двох змінних §гасі (х,у)
має вигляд сукупності стрілок, напрямок і довжина яких визначаються ком-
понентами векторів (1 та £2 (рис. 2.15).
§га<1(х, у) :=
1 $уі / у! / у!
1 уі уі 7
і	у	уі	ф	уі	/	/
і	у	/	/і	/	/	$
(	У	У	ф.	$	-а
'У у у 7	1
<	у	у	і	и	$	ї
(	/	у	/	/	у	/
1	У	/	X	/	X	/
«//////
/777
/ 7 л х
7	X	/	/	у?	/	/
7	/	у)	у?	/	у?	/	/
7	7	7	7	7	X	X	X
/ / ///XXX
/	/	5?	X	/	7	X	X
7/7/77ХХ
/ХХХХХХ'.Т'
х/хххххл
X /7/7777
М, N
Рис. 2.15. Приклад зображення векторного поля
34
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
В математичному пакеті МаНіСАО є засоби для побудови тривимірного
точкового графіка. Для цього служить кнопка
(ЗВ Зсаііег Ріоі).
Для побудови цього графіка також задається додаткова інформація, яка
визначає кількість точок і координати кожної точки в просторі трьох вимірів.
Наступний приклад ілюструє побудову точкового графіка. При побудові
графіка задано масив з 81 точки.
і: = 0..80 ар = 0.3*і.
Для визначення координат точок введено параметр, який характеризує
точку і та має вигляд масиву а. Визначено параметри масивів значень коор-
динат кожної точки:
хр = а|8Іп(аі) ур = аісоз(аі) гр = 0.2е'/аі .
Побудований графік визначає криву в параметричній формі та зображу-
ється у вигляді точок (рис. 2.16).
Рис. 2.16. Тривимірний точковий графік
Точки тривимірного точкового графіка можуть мати різні форму та розмі-
ри. Ланцюжок точок є зручним і наочним засобом аналізу функції трьох
змінних, заданої в параметричному вигляді.
Повертаючи графік, визначають проекції одержаної просторової кривої на
площини координатних осей.
35
Струтинський В. Б.
2.2. Символьні залежності із диференціальними операціями
2.2.1. Символьне диференціювання та інтегрування
Символьні методи диференціювання та інтегрування широко реалізовані в
сучасних математичних пакетах. Зокрема, програмне середовище МаіЬСАВ
має різноманітні засоби для знаходження похідних та інтегралів функцій, за-
даних в символьному вигляді. Якщо функція задана таблично, то вона при-
водиться до символьного вигляду шляхом застосування процедури інтерполя-
ції чи апроксимації. Знаходження похідних функцій та інтегралів у матема-
тичному пакеті МаЯїСАО 7 Рто (МаіІтСАВ 8, МаіЬСАО 2000) здійснюється
за допомогою кнопок панелей операцій математичного аналізу (рис. 2.17).
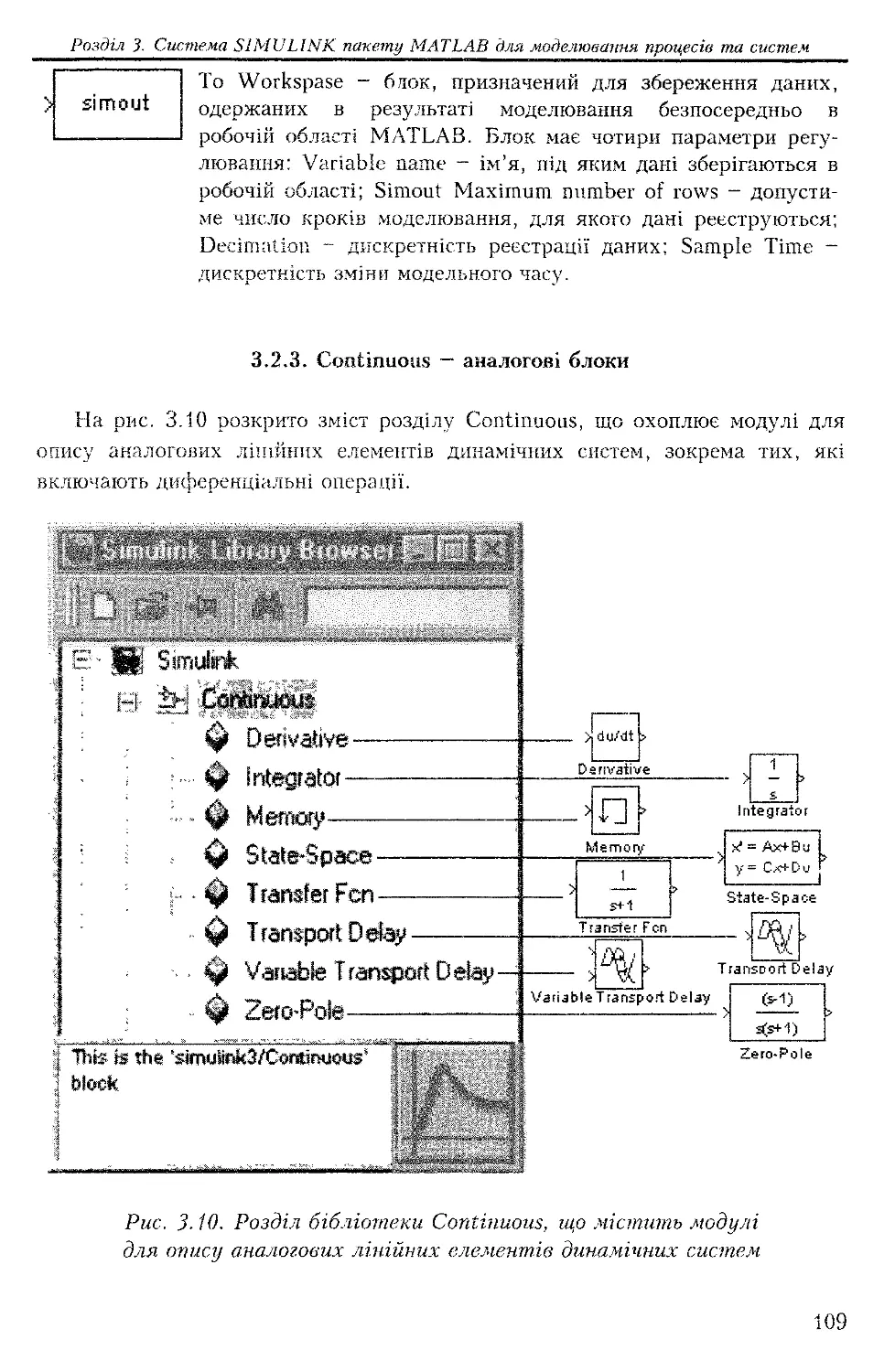
а)	б)	в)
Рис. 2.17. Панель інструментів МаІІїСАИ Раїїеіе (а), панель операцій
математичного аналізу Саісиїиз Раїїеіе (б) та панель символьних операцій
ЗутЬоІіс КеуЬоагй (в)
Активізуючи кнопку
панелі інструментів МаіЬСАВ Раїїеіе (рис. 2.17, а), виведемо на екран па-
нель операції математичного аналізу (рис. 2.17, б). Для обчислення першої
похідної функції ініціалізується кнопка
цієї панелі. В результаті на екрані з’явиться заготовка
а
— 
сії '
У правий чорний прямокутник цієї заготовки треба помістити символьний
вираз або ім’я функції, а у нижній - ім’я змінної, за якою знаходиться похід-
36
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
на. Для знаходження похідної необхідно використати кнопку
із панелі символьних операцій ЗутЬоІіс КеуЬоагсІ (рис. 2.17, в). Натиснув-
ши клавішу Егйег, справа від стрілки одержимо результат символьного дифе-
ренціювання. Наприклад:
— хпаіап(х) -> х" — аіап(х) +	.
сіх	х	(1 + х )
Процедура обчислення похідної в символьному вигляді відзначається на-
дійністю роботи, але одержаний результат часто має досить громіздкий ви-
гляд, наприклад:
Символьне диференціювання може здіснюватись для функцій різного ви-
ду, зокрема трансцендентних функцій, наприклад:
~1п(х)8Іп(х)*	— 8Іп(х)Х + 1п(х)8Іп(х)Х 1п(8Іп(х)) + X С°8(Х)1 .
ах	х	8Іп(х))
Вираз під знаком похідної може включати довільні величини і функції.
Диференціювання здійснюється за змінною, вказаною у заготовці похідної.
Фактично здійснюється знаходження частинної похідної функції. Інші змінні
у виразі функції не враховуються. Таким чином, диференціювання за змін-
ною у деякої функції від х буде відповідати похідній константи, наприклад:
-^-асо8Іі(х) -> 0 .
<іу
Обчислення похідної довільного порядку здійснюється кнопкою
панелі операцій математичного аналізу Саісиїиз Раїїеіе (рис. 2.17, б). Після
ініціалізації даної кнопки на екрані з’явиться заготовка
сі*
--- і
сі і1
У правий чорний прямокутник цієї заготовки, як і раніше, треба помісти-
ти символьний вираз або ім’я функції, а у нижній лівий - ім’я змінної, за
якою знаходиться похідна. Порядок похідної у вигляді цілого числа, більшо-
37
Струтинський В. Б.
го за 1, заноситься у верхній чорний прямокутник.
Нижче наведені приклади обчислення похідних дев’ятого та сьомого по-
рядків:
^9
—у ех • 8Іп(х) -> 16 ехр(х)зіп(х) +16 ехр(х)соз(х)
ах
а7 г---у 10395	7	19845	5	11025	3	1575
^! + х	-ррух
Обчислення похідної порядку вище першого здійснюється за змінною,
вказаною в заготовці. Нижче наведено приклади знаходження похідних дру-
гого порядку функції двох змінних по кожному із двох аргументів:
іап(х + Ту ) -> 2іап(х + Ту )• (1 + іап(х + Ту )}
За допомогою засобів математичного пакета МаїЬСАН здійснюється обчи-
слення частинних похідних та диференціалів функцій кількох змінних. Час-
тинна похідна може бути знайдена за означенням похідної як границя:
аКх,, х2, ..., хР ..., хп) _ Кхр х2, ..., Xі + 5Хр ..., хп) - Кхр х2,..., Хр ..., хп)
дхі	^і-»0	8х;
Знаходження частинної похідної в математичному пакеті МаійСАВ здійс-
нюється так само, як і знаходження звичайної похідної. Нижче наведено
фрагмент документа МаійСАО, в якому знаходяться частинні похідні функції
по аргументах у та х:
£(х,у) := хе^см(у)х2+8іп(х)у2)
-^-£(х,у)-> х^іп(у)х2 - 2 8Іп(х)у)ехр(- сов(у)х2 -8Іп(х)у2)
~ і'(х, у) -> ехр(со8^)х2 - 28Іп(х)у2)+х(- 2 со$(у)х - со>(х)у2)ехр(- со4у)х2 - зіг(х)у2)
Можливе обчислення частинних похідних порядку вище першого, а також
змішаних частинних похідних другого і вищого порядків. Наприклад, знахо-
дження змішаної частинної похідної другого порядку здійснюється у
наступному фрагменті документа МаїЬСАГ):
£(х, у) := (1 - у2)* соз(х * у)
£(х, у) -> -(1 + у2)* 8Іп(х * у) * у
ах
5£х(х, у):= -(1 + у2)* 8Іп(х * у)* у
(і
^У
8£х(х, у) -> -2 * у2 §іп(х * у) - (1 + у2)* со»(х * у)* х
(1 + у2)*8Іп(х *у)
38
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
Використовуючи частинні похідні, обчислюється приріст (диференціал)
функції багатьох змінних. Якщо задана функція кількох змінних
((х^ х2, .... хп),
то приріст цієї функції:
_	дї .
ог = — ох, +-----ох, + ... +----- охп.
1	«	і.	п
£/Х і	оХ 2	(7Х п
Приклад обчислення приросту функції за допомогою засобів пакета
МаїЬСАО:
“£(х,у)* 5х +-^-£(х,у)* 5у- у2 * ехр|
ах	<1у	(І
- 2 ♦ х * у ♦ ехр
8у
— х
~¥
Наведені вище способи знаходження похідних не завжди доцільно вико-
ристовувати. Зокрема, для розривних функцій, а також нескінченно малих чи
нескінченно великих функцій використовуються інші методи. Один із методів
використовує знаходження границь. Похідна в точці хд може бути обчислена
за формулою визначення похідної з використанням операцій знаходження
границі функції, тобто
№,) = Ііт + 5х) ~ [(х«),
ах-»о	5х
де 5х - нескінченно малий приріст функції в точці X = Х().
В математичному пакеті границя обчислюється з використанням кнопки
панелі операцій математичного аналізу Саісиїиз Раїїеіе (рис. 2.17, б) та від-
повідної заготовки
ІШі і
І І
Як приклад визначимо похідну функції Дх) =	—созЗх	Т0Чщ х = о
х
Ця функція при х = 0 має невизначеність типу . Для знаходження значен-
ня функції в точці х = 0 використаємо правило Лопіталя:
созх - созЗх 5ІПХ - 3 8ІпЗх
г(0) = ііш----------= 1іпі--------------= 0 .
х->0	х	х->0	|
Враховуючи, що хо = 0, £(х0) = 0, одержимо £(хо + 5х) - Цхд) = ДЗх).
Обчислення значень похідної здійснюється наступним фрагментом документа
МаНіСАО:
39
Струтинський В. Б.
;= СО8(х)-СО8(3*х)	1іт Ц8х)	4
х	8Х~>0 8х
В результаті даних обчислень встановлено, що похідна функції в точці
х = 0 існує і її значення дорівнює 4.
Знаходження похідних в точках розриву функції здійснюється з викорис-
танням односторонніх границь. В загальному вигляді одностороння похідна
зліва визначається за формулою:
,,, ч Г(х0 + 8х)-Кх0)
г_(хп) = 1іш--*----——х < х0, 8х < 0 ,
8х->-0	§х
а одностороння похідна справа:
( ) _ 1ІШ «хо+5х)-Кх„>	5х>0
5х	0
Обчислення односторонніх похідних в пакеті МаіЬСАВ здійснюється за
допомогою односторонніх границь. Знаходження односторонніх границь здій-
снюється з використанням кнопок
панелі операцій математичного аналізу Саісиїиз Раїїеіе (рис. 2.17, б) і відпо-
відних заготовок
Ііт і Ній і
і Іі"^ і'
Нижче наведено фрагмент документа МаіЬСАВ, в якому обчислені одно-
сторонні похідні функції £(х) = І х2-4і в точці х = 2.
1(2 + 8х/ - 4І -122 -4І
Ііш  ----------1—1------- -> ипйеНпей
бх->о
|(2 + 5хУ-4|-|22-4|
Ііт ]---------1—------і —> 4
6х->0+	5х
1(2 + ЗхУ - 4І -І22 - 4І
Ііт 12------------------І _> -4.
бх-»о~	8х
В результаті обчислень встановлено, що в точці х = 2 похідна функції
£(х) не існує. Похідна справа існує та дорівнює 4. Похідна зліва теж існує,
але її значення (-4) не дорівнює значенню похідної справа.
Обчислення невизначеного інтеграла здійснюється за допомогою кнопки
панелі операцій математичного аналізу Саісиїиз Раїїеіе (рис. 2.17, б). Після
ініціалізації кнопки на екрані з’явиться заготовка
і сії .
40
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
У правий чорний прямокутник цієї заготовки треба помістити змінну інте-
грування, а у лівий прямокутник - символьний вираз або ім’я функції, неви-
значений інтеграл якої треба знайти, наприклад:
Г------8Іп(х)-------(}х	-1п(соз(х)) + 1п(1 + соз(х)).
» СО8(х) * (1 + СО8(х))
Кратні невизначені інтеграли обчислюються повторним застосуванням
вищевказаної кнопки в потрібній кількості. Для знаходження потрійного ін-
тегралу кнопка ініціалізується 3 рази:
Відповідна заготовка для обчислення потрійного інтеграла має вигляд:
р І* І*
і сії ііісІі .
Нижче наведено приклад обчислення в символьному вигляді потрійного
інтегралу:
Ще а/хДхгіхсіх -> 8ехр(-	- 72ехр(-л/х^3/2^ - 312ехр(- 7х-
-720ехр(- 7х^/х - 720ехр(- л/х).
Для обчислення визначеного інтеграла використовується кнопка
панелі операцій математичного аналізу Саісиїиз Раїїеіе (рис. 2.17, б) і відпо-
відна заготовка
І СІІ
В нижній та верхній ліві затушовані прямокутники заготовки вставляють-
ся межі інтегрування у вигляді констант, змінних чи функціональних вира-
зів. Результатом обчислення визначеного інтеграла буде число, символьна
константа чи функція. Приклади обчислення визначених інтегралів у число-
вому та в символьному вигляді наведені нижче.
. ҐС.	1г- ’г х л п *Ф
ІП — <1Х -> — * ул	І------у-у---у—сиХ -> у\ .
<х;	2	'1 + СО8(ф)*8Іп(х) 8Іп(ф)
Процедура символьного інтегрування в пакеті МаїЬСАВ здійснюється на-
багато складніше, ніж диференціювання. Часто інтеграл не обчислюється або
обчислення дають невірний результат.
Обчислення інтегралів може бути здійснене і тоді, коли відрізок інтегру-
вання необмежений, тобто інтеграл є невласним. Нижче наведено фрагмент
документу МаійСАІ), в якому обчислено невласні інтеграли.
41
Струтинський В. Б.
ш := 2 а := 0.5
]еа’х * 8іп(л/т * <х)йх -> 1.30409866434658436.
0
Даний інтеграл є табличним і його точне значення дорівнює [19]:
^5“еї»О04.
2а
Обчислення невласних інтегралів у символьному вигляді часто викорис-
товується у задачах математичного моделювання. Нижче наведено приклад
знаходження перетворення Лапласа функції £(і) шляхом обчислення невлас-
ного інтеграла у символьному вигляді:
;= 8Іп(2*Укї)
7л*к
с/ \	1- -1»	/ «,ч. 8Іп(2*Ткї) 1 8Іп(2*7кї)
Е(з) := Іе £(1)<1і -> 11Ш — * ехр(-8 * і) * —-^==—+ - •----...... '.
4->со	§	ул*к 8 V Я * к
Результатом обчислення інтеграла може бути символьна функціональна
залежність, реалізована в пакеті МаійСАО.
Наведені нижче функції призначені для безпосереднього обчислення ча-
сових характеристик системи автоматичного керування з використанням про-
цедури знаходження визначеного інтеграла у символьному вигляді.
2*| И(<д) 8*П——— Нсо	2 * |іі((о) * со8(ю * і)<1со
Н(1) :=----—------------------ уг(і) :=-------------------------------.
я	я
2.2.2. Дослідження процесів з використанням диференціальних операцій
Математичні моделі процесів, визначені символьними функціональними
залежностями, досліджують з використанням апарату математичного аналізу.
Встановлюється область визначення та область зміни функції, яка описує
процес. Для складних процесів бажано проводити аналіз графіка процесу.
Труднощі із знаходженням області визначення пов’язані зі встановленням
особливостей процесу в областях ±<ю, в точках розриву другого роду та неод-
нозначностях. Область визначення та область зміни функцій уточнюється
масштабуванням графіків процесу.
При математичному моделюванні визначають характерні особливості про-
цесів, пов’язаних з їх внутрішньою структурою [3, 15, 17, 36, 42, 53, 54, 70,
114]. Головні з них це - тенденції зміни функцій та кількісні показники цих
тенденцій. Процес описується зростаючою функціональною залежністю, коли
його значення збільшується при зростанні аргументу. Спадна функція змен-
42
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
шує свої значення при збільшенні аргументу. Інформацію про вид залежності
одержують аналізуючи похідну функції. Якщо похідна є додатною, то функ-
ція зростаюча. Спадна функція має від’ємну похідну.
Похідна функції визначає швидкість її зміни. Геометрично похідна характе-
ризує дотичну до кривої (рис. 2.18).
Рис. 2.18. Дотична та нормаль плоскої кривої
Для знаходження рівняння дотичної використовують обчислене значення
похідної. Рівняння дотичної до кривої, заданої виразом у = у(х), має наступ-
ний вигляд:
- у(а) =
сіх х = а
де х = а - точка, в якій знаходиться дотична;
у(а) - значення функції в даній точці.
Аналогічно визначається рівняння нормалі до кривої в точці х = а
(рис. 2.18). Воно має вигляд:
Уп - у(а) = “з— -----(х - а).
<1у
сіх х = а
Друга похідна визначає кривизну кривої. Кривизна кривої к є величи-
ною, оберненою до радіуса кривизни рк, і визначається виразом:
к= —
Рк
<і2У
сіх2
—-|3
2
Радіус кривизни к визначає дотичне до даної кривої коло (рис. 2.19),
центр якого (точка Ок) лежить на нормалі до кривої в точці А.
Центр кола називають центром кривизни.
Координати центра кривизни визначаються за формулами:
43
Струтинський В. Б.
Рис. 2.19. Кривизна кривої та центр кривизни
Похідні необхідного порядку дозволяють знайти геометричні характерис-
тики гладких кривих, зокрема точки перегину кривої, екстремуми, цикли.
Локальні екстремуми функції знаходяться з використанням першої та
другої похідних. Якщо в деякому інтервалі [а; Ь] є мінімум функції у = у(х)
(рис. 2.20, а), то в середині цього інтервалу знаходиться стаціонарна точка
функції, в якій
І.о.
<1х
і в цій точці виконується умова
Рис. 2.20. Екстремуми функції: а - мінімум; б - максимум
44
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
У випадку наявності максимуму функції в інтервалі [а; Ь] (рис. 2.20, б) в
даному інтервалі є стаціонарна точка, в якій
*=0,
ах
а друга похідна функції у стаціонарній точці від’ємна:
^<0.
Для практичного знаходження локального екстремуму визначають коор-
динати стаціонарних точок шляхом розв’язку рівняння:
ау(х). 0
СІХ
У знайдених стаціонарних точках знаходять другу похідну функції, ви-
значають її знак і роблять висновок про характер екстремуму (максимум чи
мінімум).
Вищесказане відноситься до гладких неперервних функцій. Знаходження
екстремумів в більш складних випадках розривних функцій буде розглянуто
нижче.
Похідні функції різних порядків дають ефективний інструмент їх аналізу,
зокрема, визначаються особливі точки функції, неоднозначності, цикли тощо.
Функція з неоднозначністю відповідає складному процесу, поточне зна-
чення якого залежить від передісторії процесу. Гладкі неоднозначні процеси
не мають розривів і зламів (рис. 2.21).
Рис. 2.21. Процеси з неоднозначностями, які описуються гладкими
неперервними функціями: а - монотонно зростаюча функція;
б - петлеподібний процес із неоднозначністю
Неоднозначні процеси характеризуються множиною значень та деякою
додатковою інформацією. Наприклад, для процесу, зображеного на
рис. 2.21, а, символьна функція, що описує процес, записується у вигляді ло-
45
Струтинський В. Б.
гічної конструкції:
Уі(х) при х < х2> у < ув
У(х) = У2(х) при х, < х < х2я ув < у < уА
Уз(х) при X > х1( у > уА
Дана схема опису неоднозначного процесу є досить складною.
Радикальним способом спрощення символьного опису процесу з неодно-
значностями є перехід до параметричного визначення функції у вигляді
у = у(0, х = х(і). Значення параметра І вказують на графіку процесу (див.
рис. 2.21, б). Прикладом використання параметричного опису складної неод-
нозначної функції [16] є амплітудно-фазова частотна характеристика дина-
мічної системи [6, 18]:
Мію) = Ш) + ]У(<в),
яка має петлеподібні неоднозначності (рис. 2.22).
Параметром, прийнятим для опису цієї функції, є частота. Відповідно ар-
гумент П(со) і функція \'(и) задаються в параметричному вигляді. Параметр
о) (частота) вказується на полі графіка.
Процеси в технічних системах і відповідні їх символьні залежності часто
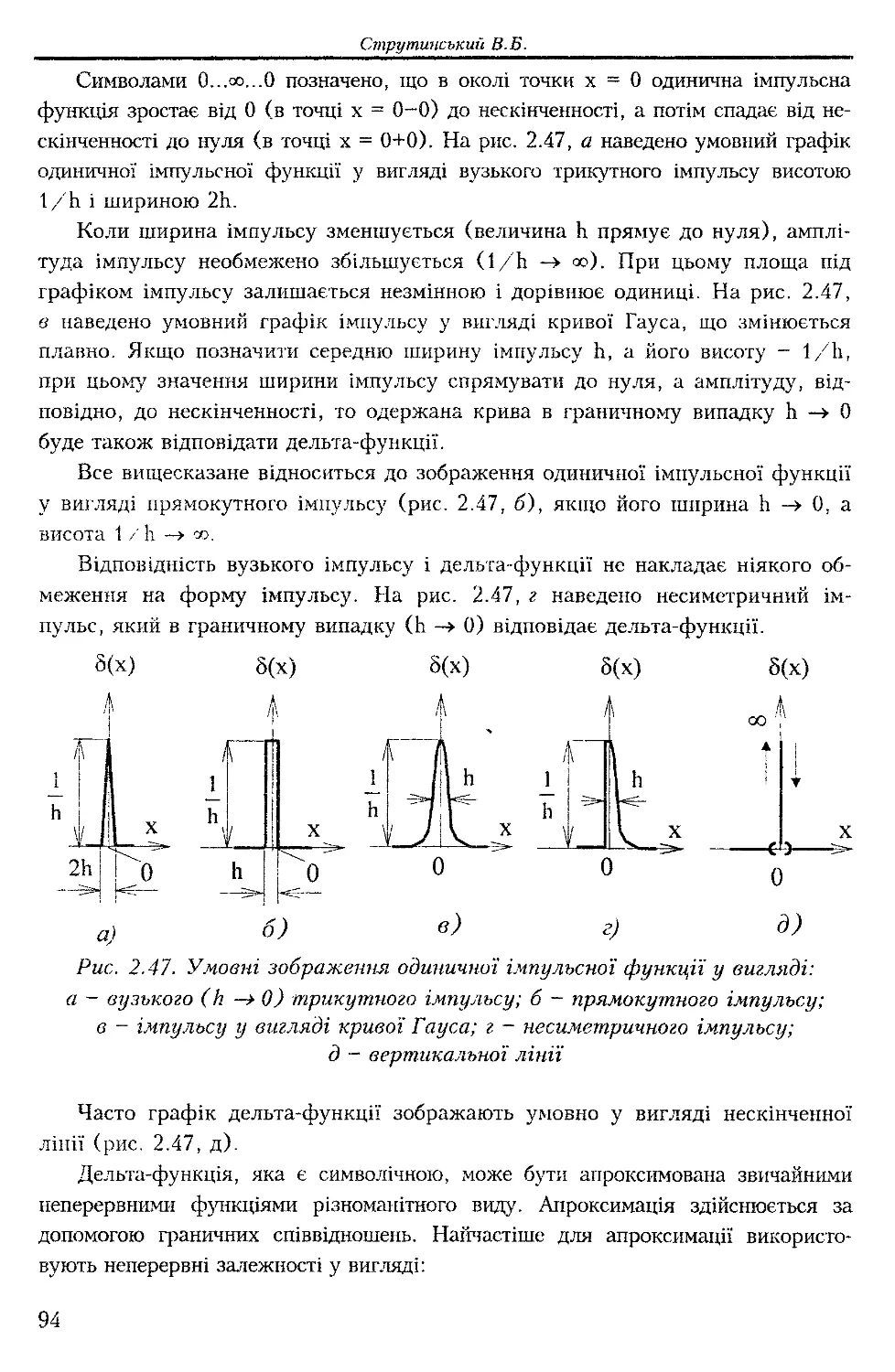
мають злами і точки розриву (рис. 2.23).
Дослідження процесів із зламами і точками розриву здійснюється за до-
помогою односторонніх границь функції або її похідної. Наприклад умовою
зламу функції в точці хз( (рис. 2.23) є нерівність значень похідних зліва та
справа від точки зламу:
.. сіу.(х)	(ІуДх)
х-»хЗ, сіх	СІХ
Наявність розриву першого роду визначається співвідношенням
Ііш у2(х) ф Ііт у2(х)
х->х;,	х-+х;,
за умови існування границь функції зліва і справа від точки розриву. Це
співвідношення виконується для точок х = хрі та х = хр2 (рис. 2.23).
Наявність розриву другого роду визначається в залежності від поведінки
функції в точці розриву. Наприклад, для точки хп1 (див. рис. 2.23)
Ііт у3(х) = оо , Ііт у3(х) = оо .
х->х;,	х->х;.
Для точки хп2 відповідно маємо:
Ііт у3(х) = -оо , Ііт у3(х) = +а>.
х->х;2	х->х;2
Аналогічним чином досліджуються неоднозначні процеси із точками зла-
му. На рис. 2.24 наведено ряд характерних випадків процесів, які відповіда-
ють залежностям з гістерезисом, що є неоднозначними процесами із зламами.
Рис. 2.24, а відповідає функціональній залежності, яка змінюється відпо-
відно до знака аргументу. При зміні х від 0 до точки А залежність відповідає
46
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
кривій 1. При зменшенні аргументу, починаючи з точки А, залежність набу-
ває вигляду кривої 2. При черговому збільшенні аргументу х (в точці В) зно-
ву має місце крива 1. В залежності від розташування точки А змінюється
крива 2. Так, для точки А' відповідна крива 3 не співпадає з кривою 2.
Рис. 2.22. Амплітудно-фазова частотна характеристика динамічної
системи як приклад неоднозначної функції, заданої параметрично
Рис. 2.24, б відповідає більш складній залежності, коли крива 1 не є фіксо-
ваною, а змінюється відповідно до передісторії процесу. При зміні аргументу х
від 0 до точки А маємо залежність, яка відповідає кривій 1. При зменшенні ар-
гументу х, починаючи із точки А, маємо залежність 2, при збільшенні аргументу,
починаючи з точки В, процес відповідає кривій 3. Подальше зменшення аргуме-
нту х, починаючи з точки А, визначає процес у вигляді кривої 4. Аналіз проце-
сів із розривами і зламами, включаючи неоднозначні процеси, виконується із за-
стосуванням граничних співвідношень (границь функцій).
47
Струтинський В. Б.
Рис. 2.23. Процеси, які описуються функціональними залежностями,
зі зламами та розривами різного виду: уі(х) - процес із зламами
(розривами похідної); уфх) - процес із розривами 1-го роду;
и-/х) - процес із розривами 2-го роду
Рис. 2.24. Приклади неоднозначних гістерезисних процесів із зламами,
які змінюються в залежності від передісторії процесу
Обчислення границь засобами математичного пакету МаїЬСАІЗ є ефектив-
ним інструментом аналізу процесів. Воно може бути здійснене як в чисельно-
му, так і в символьному вигляді. Для знаходження конкретного значення
границі функції достатньо використати відповідні заготовки з панелі матема-
тичних операцій та з панелі калькулятора.
Наприклад, обчислення границі функції здійснюється наступним
х
оператором пакету МаїйСАО:
48
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
8ІПХ
Ііт—— = 1.
х->0 X
Обчислення границь в символьному вигляді ілюструється наступним до-
кументом МаіЬСАІ):
Х(п) := 2 * аіап(п4) Ііт Х(п) -» я	Ііт—----> шкіе£іпе<1
п->со	х-М X — 1
Останній приклад означає, що границя функції
£(х) = (х - 1)и при х —> 1 не існує.
При обчисленні границь складних функцій використовують правила опе-
рацій з границями. Вони полягають в основному у наступному:
•	границя алгебраїчної суми функцій дорівнює сумі границь:
1іш[Кх) + §(х)] - Ііт £(х) + Ііт §(х) ;
•	постійну величину С можна виносити за знак границі:
1іт[с • £(х)] = С • Ііт £(х), С = Сопзі ;
х —х —
• границя добутку функцій дорівнює добутку границь:
1іт[Кх)  §(х)] = Ііт £(х) • Ііт §(х) ;
х-»а‘г	х->а	х->а
• границя відношення функцій дорівнює відношенню границь:
ІітЦх)
Ііт - 	-	при Ііт §(х) * 0 .
х-^дСх^ 1іт§(х) х-»а
Ці правила діють як при обчисленні односторонніх, так і при обчисленні
двосторонніх границь.
В практиці розробки і використання математичних моделей часто виникає
необхідність в обчисленні границь, які включають невизначеності. Напри-
клад, коли обчислюються границі виду:
,. іДх)
Ьт——— ,
У(х)
де 1ітЦ(х) = 0, 1ітУ(х) = 0,
х->а	х->а
о
то наявна невизначеність типу — .
При обчисленні границь функцій, які включають відношення функцій,
добутки, різниці, степені виду:
Ц(х)-У(х), Ц(х) - У(х), [и(х)]у(х)
можливі невизначеності наступних типів:
2	—	0-00, 0°, 0“ , 00°, Г, 00 - 00.
0 оо
Для обчислення вищенаведених невизначених границь здійснюють «роз-
криття» невизначеностей.
49
Струтинський В. Б.
Невизначеності типу
0	00
— і —
0	00
«розкриваються» згідно з правилом Лопіталя:
11(Х)	..	1Г(Х)	„	,,,, V „Ч
Ііт—— = Ііт——— ( У(х) 0 при х = а, V (х) * 0 ).
хУ(х) У'(х)
Правило Лопіталя можна застосувати послідовно до границь похідних ко-
0	00
ли ці границі похідних також мають невизначеність типу — чи —.
0	00
Невизначеності типу
0 • оо , 0®, оо°, 1“ , 00 — 00
звичайно можна привести до невизначеності типу
0	оо
— чи —
0	00
за допомогою співвідношень:
чи
іДх)У(х) =
И(х) У(х)
1/У(х) 1/И(х)
[іі(х)Р'(х) н е«<х)
8 Х 1/У(х) " 1/1пН(х)]’
або
1_____1_
И(х) - У(х) уу ж 1п к(х)],	§(х) ж УЇЇ
йбО’ У(х)
Нижче наведені деякі практично важливі границі, які часто зустрічаються
при аналізі та обчисленні функцій і широко використовуються при розробці
математичних моделей:
1ітГ1 + У =е» 2.718281828;
п-»"ф п
сх -1	-
Ііш-------= іпс, с > 0;	1іш(1 + х)х = е ;
х->0 х	х->0
8ІП X , ІЙХ .. зЬх П1Х
1ші-------= Ііт——— = ііш—— = Ііт-----------= 1 ;
х->0 х х—>0 х х—>0 х х—>0 х
Ііт ха 1п х = Ііт х‘а 1п х = Ііш хае“х =0, а > 0 ;
Х->0+	х-»со	X—>+®
Ііт -—= >/2л ; Ііт Xх = 1.
п->=оПпе“л/П
«Розкриття невизначеностей» представляє собою порівняння нескінченно
великих і нескінченно малих функцій.
50
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
Функція 0(х) вважається нескінченно малою при
х = а, якщо Ііт П(х) = 0 .
х-»а
Нескінченно великою в точці х = а функція вважається у випадку, коли
Іітіі(х) = оо.
х->а
Нескінченно великі та нескінченно малі функції порівнюються шляхом
граничних співвідношень.
Порівняння нескінченно малих функцій здійснюється шляхом визначення
порядку їх малості. Визначимо особливості порівняння функцій.
Розглянемо дві нескінченно малі в точці х = а функції
1)(х) та У(х).
Якщо І5(х) та У(х) - нескінченно малі функції в деякій області точки
х = а, то, як визначено раніше,
1ітП(х) = 0 і 1ітУ(х) = 0.
х-»а	х—>а
Але ці функції можуть зовсім по-різному поводитись поблизу ТОЧКИ X = а.
Якщо в цій точці
то вважається, що 1)(х) є більш високого порядку малості, ніж У(х), тобто
И(х) = 0[У(х)] в точці х = а.
Якщо границя відношення двох нескінченно малих функцій існує і є кі-
нечною (не дорівнює нулю або нескінченності), то функції вважаються
асимптотично еквівалентними. Прикладом асимптотичних еквівалентних фу-
нкцій в околі точки х - 0 є функції ІІ(х) = зіпх та У(х) = х.
Якщо границя відношення двох нескінченно малих функцій не існує, то
ці функції вважаються непорівняними.
При аналізі процесів часто використовують асимптотичні лінійні залежності
(асимптоти). Знаходження асимптот функції представляє собою самостійну ва-
жливу задачу аналізу процесу. Асимптоти звичайно знаходяться як граничні
прямі лінії, до яких прямує досліджувана функція в певній області.
Розглянемо практичне знаходження асимптоти функції для границі облас-
ті визначення (х -р оо) (рис. 2.25).
Під знаходженням асимптоти розуміють визначення коефіцієнтів лінійної
залежності £а(х).
Рівняння асимптоти має вигляд:
£а(х) = а0 + аіх.	(2.5)
Асимптота є лінією, до якої прямує функція £(х) при х -> оо. При X -> оо
функція та її асимптота приблизно співпадають.
51
Струтинський В. Б.
Рис. 2.25. Графічна інтерпретація визначення асимптоти
функціональної залежності
(2.6)
Коефіцієнти асимптот визначаються із двох умов:
1іт[(а(х)-Кх)] = 0;
1іт7ГТ = к
х->«° ЦХ)
Підставивши в другу умову (2.6) рівняння асимптоти (2.5), визначимо:
а0+а(х
Ііт 11 , ' = 1.
Кх)
Оскільки ао « а^х при х -» °о , то
1-	аіх Л
Ііт—— - 1.
г(х)
Звідси знаходимо коефіцієнт:
,. Кх)
— 1ІШ----,
Х
Підставивши рівняння асимптоти (2.5) в першу умову (2.6), одержимо:
1іт[а() +а,х - Кх)] = 0 ,
(2.7)
звідки знаходимо:
а0 = 1іт[Кх) - а,х].	(2.8)
х->®
Знаходження асимптотичних залежностей часто використовується з метою
аналізу процесів.
Розглянемо практично важливий приклад знаходження асимптот логариф-
мічної амплітудно-частотної характеристики лінійної динамічної системи, яка
має вигляд аперіодичної ланки 1-го порядку [6]. Характеристика відповідає
нелінійній функції частоти:
Ь(<о) = 20......К .	(2.9)
л/1 + Т2и2
Характеристика (2.9) має дві асимптоти: першу - при <в -> оо, а другу -
при со —> 0 .
Знайдемо коефіцієнти першої асимптоти, прийнявши аргумент у формулі
(2.9) х = 1§о). Враховуючи, що при ш —> оо Т2и2 » 1, одержимо, використо-
52
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
вуючи формулу (2.7):
, .	201Є-
а, =1,т^= Ііт -------;
Х-»х х |8<о^х.	1ош
20И§|-2]§Ю
аі = ——г-----:
1§ш
І8и
1 -к
18 —
де враховано, що —-1- ® 0 при 1§со -> оо .
18®
Для знаходження коефіцієнта а0 використаємо залежність (2.8):
а„ = Ііт 201§ —.—+ 20со .
Враховуючи, що Т2со2 » 1, одержимо значення коефіцієнта:
а„ = Ііт
X—>30
201§ — - 20о + 201е и
чЛ	чЛ
= 20І8-|.
Таким чином, рівняння першої асимптоти, яка відповідає функції (2.9),
при со —> СО (1§ со -> оо) буде мати ВИГЛЯД'
£,(х) = 20- 20ш = 20р Д - хК 201§^ .	(2.10)
Т	( 2.	) Ти
Аналогічно знаходиться рівняння другої асимптоти (описує характеристи-
ку (2.9) при и -> 0). Воно відповідає прямій, паралельній осі со:
Ьа(®) = 201§К .	(2.11)
Графіки асимптот (2.10) і (2.11) та значення характеристики (2 9) є бли-
1
зькими скрізь, за виключенням околу точки (о =— (рис. 2.26).
Рис. 2.26. Приклад використання асимптот для опису нелінійної
функції Ф(а>), яка визначає логарифмічну амплітудно-частотну
характеристику динамічної системи, що відповідає
аперіодичній ланці першого порядку
53
Струтинський В. Б.
2.2.3.	Диференціальні оператори поля
В багатьох задачах математичного моделювання виникає необхідність
аналізу скалярних чи векторних полів, визначених в лінійному просторі двох
чи трьох вимірів [1, 31, 37, 38, 42, 46. 58, 62, 77, 80, 103].
Розглянемо практично важливий випадок скалярної Ф чи векторної Е
функції трьох змінних х, у, х. Якщо наявна скалярна чи векторна функція
трьох змінних, то кажуть, що в просторі задане скалярне чи векторне поле.
При дослідженні процесів та систем механіки розглядають скалярні поля
густини середовища, розподілу температури чи концентрації речовини. Век-
торне поле утворюють швидкості частинок рухомої рідини, потоки тепла або
переносу речовини. Неперервні скалярні та векторні поля досліджуються з
використанням диференціальних операцій над скалярними та векторними
функціями, які називаються диференціальними операторами поля.
Для характеристики поля використовують, зокрема, наступні диференціа-
льні оператори'
•	градієнт §га<і Ф - векторна функція, аргументом якої є скалярна функ-
ція точки Ф(х, у, х);
•	дивергенція сііу Е - скалярна функція, аргументом якої є векторна
функція точки Е(х, у, х) з проекціями Ех, Еу, Е2;
•	ротор тої Е - векторна функція, аргументом якої є векторна функція
точки Г(х, у, х);
•	лапласіан (оператор Лапласа) - скалярна функція ДФ, аргументом
якої є скалярна функція точки Ф(х, у, х), або векторна функція ДЕ, аргуме-
нтом якої є векторна функція точки Г(х, у, х).
Диференціальні оператори звичайно виражають через оператор V (наб-
ла). Він же має назву оператор Гамільтона. В прямокутних декартових коор-
динатах цей оператор визначається формулою
д - д - д
V = — і +—] +—к ,
Зх Зу Зх
де і, у к - орти декартової прямокутної системи координат.
Відповідно градієнт скалярної функції Ф(х, у, х) в декартовій прямокут-
ній системі координат визначається як вектор
„.	6Ф ~ ЗФ - ЗФ .-
\?Ф = ягасіФ = -— і +-і -<--к.
Зх Зу Зх
Для поширеної в технічних системах циліндричної системи координат р, <р, х
з ортами ір, і„, градієнт скалярної функції Ф(р, ер, х) визначається залежністю:
ЗФ т	1 ЗФ т ЗФ -
§га(1Ф = — і + - • — іф + —12 .
Зр	р Зір 02
54
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
Вектор-градієнт дає можливість визначити похідну скалярної функції по
певному напрямку, визначеному в просторі.
Розглянемо тривимірний лінійний простір, де визначена скалярна функ-
ція Ф(х, у, 2) та її вектор-градієнт §гас1Ф. В цьому просторі задано одинич-
ний вектор
1 = (созир соза2, соза3),
де соя а,, сояа2, сояа3 - напрямні косинуси одиничного вектора.
Даний вектор має одиничну довжину, тобто
|1| = д/соя2оц + сох2 а2 + соз2 а3 = 1.
Зміна скалярної функції Ф в напрямку вектора 1 характеризується похід-
ною функції по напрямку:
5Ф
— = егайФ • 1.
51
Скалярний добуток векторів у правій частині цієї формули можна вира-
зити через модулі векторів. При цьому одержимо:
5Ф ।	,	і,,
= |£гааФ| * |1| * сояср,
де ср - кут між векторами §га<ІФ та 1.
Звідси випливає, що вектор-градієнт визначає напрямок найшвидшого
зростання функції Ф.
Обчислення вектора-градієнта та похідної по напрямку здійснюється за
допомогою засобів математичних пакетів. Нижче наведено фрагмент докумен-
та МаЙіСАВ, де подано приклад знаходження вектора-градієнта скалярної
функції трьох змінних ї(х, у, г), заданої аналітичним виразом, визначено ча-
стинні похідні функції шляхом символьного диференціювання та компоненти
вектора-градієнта.
£(х,у,г) := (0.5 + х2) *зіп(у) *(£)*+й+Л
2
Н£х(х,у,2) := — Г(х,у,г) <1іу(х,у,2) := -^-£(х,у,г) <1£г(х,у,2) := -^-£(х,у,г)
ох	оу	аг
<і£х(х,у,2) -> х * у * ехр(х + у + г) + х*у*2* ехр(х + у + г);
/ ^(х+у’+Л)
сКу(х,у,г) -> (0.5 + х2) * соз(у) * — І +
/ мх+уЧЛ) /е\
+ 2 * (0.5 + х2) * 8іп(у) * І —	*у*1п —
\г)
/ -цх+й+а/ї) г ,	! X , . 2 , Г\
,с . ч	2\	• / \ І е і	1	, ( е 1 (х + у + уг)
шг(х,у,г) -> (0.5 + х ) * 8іп(у) * —	* -і---* ІпІ — - --------------- .
\г)	Д2*д/г)	\г) і
55
Струтинський В. Б.
Обчислені символьні значення неможливо використати в подальших роз-
рахунках. Тому далі здійснено присвоєння одержаних символьних значень
змінним компонентам вектора-градієнта:
гі£х(х,у,з) := х * у * ехр(х + у + г) + х * у * 2 * ехр(х + у + г)
/ \(х+у2+^г)
гі£у(х,у,г) := (0.5 + х2) * со»(у) * —	+
к2 )
/ \(х+у’+7г)	(еА
+ 2*(0.5 + х2)*8Іп(у)* —	*у*1п—
к2У	<2)
/• -\(х+у2+Л) Г .	/ X /	2 Г
- їх . , . е\	1	, (еі (х + у +уг)
сі£г(х,у,г) := (0.5 + х2) *5іп(у)* —	* -[---ї=л*1п — ------------------
к27	Ц2*У2)	г
Вектор-градієнт скалярної функції:
Одержаний вектор-градієнт може бути використаний при виконанні
обчислень. Можлива графічна інтерпретація вектора-градієнта скалярної
функції. Графічна інтерпретація ілюструється наступним фрагментом
документа МаіЬСАО, призначеним для знаходження вектора-градієнта
скалярної функції трьох змінних £(х, у, г,), заданої аналітичним виразом:
£(х,у,г) := (х2 + у2 + г2)
гі£х(х,у,г) := -^-£(х,у,г) гі£у(х,у,г) := -^-£(х,у,г) <і£г(х,у,2) := -^-£(х,у,г)
ах	гіу	гіг
гі£х(х,у,г)-» 2 * х гі£х(х,у,г) := 2 * х гі£у(х,у,г)-> 2 * у
гі£у(х,у,г) := 2 * у гі£г(х,у,г) —» 2 * г гі£г(х,у,г) := 2 * г
Визначення вектора-градієнта та вектора, по напрямку якого буде взята
похідна:
	гі£х(х, у, г)		0.Ґ
§гагі£(х,у,2) :=	й£у(х, у, 2)	§(х, У, 2) :=	0.4
	<1£х(х,у,г)		0.2
Визначення похідної скалярної функції £(х, у, /,) в напрямку вектора §:
§гагі£(х, у, г)  §(х, у, г) -> 0.6 * х + 0.8 * у.
Графічне зображення вектора-градієнта функції трьох змінних проведено для
перерізу г = 1. Результати розрахунків подані в графічному вигляді на рис. 2.27.
2 := 0 £1(х,у) := §гагі£(х,у,г)0 £2(х,у) := 8га<1£(х, у, з),
і:=О...2О	]:=0...20	х;=0.05*і у. =0.05*^
:=:^(хі.Уі) Мі5 :=£2(хі,у]) Ам ^ІйгагіЦХі.Ург)!
56
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
М,^'
а)
б)
Рис. 2.27. Графічна інтерпретація знаходження вектора-градієнта
скалярної функції для перерізу г ~ Сопзі: а — у вигляді векторного поля;
6-у вигляді просторової поверхні; в - зображення рівних значень модуля
градієнта; г — стовпчаста діаграма значень модуля градієнта
Для графічного зображення вектора-градієнта використано двовимірні
графіки. Якісний аналіз поля вектора-градієнта доцільно здійснити за допо-
могою графіка у вигляді векторного поля (рис. 2.27, а), а також використо-
вуючи зображення градієнта у вигляді стовпчастої діаграми (рис. 2.27, в).
Для знаходження кількісних параметрів векторного поля використовуються
графіки у вигляді просторової поверхні (рис. 2.27, б) та ізолінії модуля-
градієнта (рис. 2.27, в).
Дивергенція векторної функції Р(х, у, г) часто використовується в зада-
чах математичного моделювання. Дивергенція представляє собою скаляр. Він
визначається через оператор Гамільтона (набла) або через частинні похідні
проекцій векторної функції.
В декартовій прямокутній системі координат дивергенція:
57
Струтинський В. Б.
ар	зр„	ар
сііуГ = V  Г = -^ + —і + —
Зх	ду	дт.
де Рх, ру, Р2 - відповідно проекції вектора Р на осі х, у, г.
Для циліндричної системи координат р, <р, 2 дивергенція векторної функ-
ції Е(р,<р,г) :
,. _ 1 з(р?р) 1 5РФ ЗР2
р Зр р Зср дг
Значення дивергенції обчислюється через частинні похідні. РІижче наве-
дено приклад знаходження дивергенції вектора засобами пакету МаіЬСАГ).
Фрагмент документа МаіЬСАВ задає вектор Р, проекції якого є функціями
трьох змінних. Вектор подано у символьній формі запису. Визначено частин-
ні похідні проекцій вектора.
Р(х,у,г) :=
Х*у*2*ЄХ+У+2
е»+У+г ф 8іп(у) + 2
ех+у+г * со»(г) + у
(1£хх(х,у,г) :=-^-Р(х,у,г)0
ах
<	іїуу(х, у, г) := — Р(х, у, г)і <ІЇ2х(х, у, г) := — Р(х, у, г)2
ау	аг
Знайдені символьні значення частинних похідних:
<	Ихх(х, у, г) -> у * г ♦ ехр(х + у + г) + х*у*г* ехр(х + у + г)
сИхх(х, у, г) := у * г * ехр(х + у + г) + х*у*г* ехр(х + у + г)
сІ£уу(х, у, г) -> ехр(х + у + г) * зіп(у) + ехр(х + у + г) * соз(у)
с1£уу(х, у, г) := ехр(х + у + г) * 8Іп(у) + ехр(х + у + г) * соз(у)
й£гг(х, у, г) -> ехр(х + у + г) * со§(г) - ехр(х + у + г) * 8іп(г)
сИгг(х, у, г) := ехр(х + у + г) * со8(г) - ехр(х + у + г) * 8Іп(г)
Обчислено дивергенцію вектора:
<	1іуР(х, у, г) := <1£хх(х, у, г) + <1£уу(х, у, г) + й£гг(х, у, г) .
Знайдено символьне значення дивергенції:
4іуР(х, у, г) —> у * 2 * ехр(х + у + г) + х*у*г* ехр(х + у + г) +
+ ехр(х + у + г) * 8іп(у) + ехр(х + у + г) * соз(у) + ехр(х + у + г) * СО8(г) -
- ехр(х + у + г) * 8Іп(г).
Обчислено значення дивергенції в конкретних точках простору:
ФуР(1,1,1) = 61.876
<1іур(0,2,3) = 795.797 .
Результати розрахунків дивергенції подані у графічному вигляді на
рис. 2.28.
г := 1	£1(х,у) := Р(х,у,2)0	£2(х,у) := Р(х,у,2Х
і:=0..10	]:=().. 10	хі:=0.1*і у. =0.1*]
58
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
МІ1} := ГЦхрУ;) МІЛ := £2(хітуі) Аі4 := (ІіуЩх^у^г)
Рис. 2.28. Графічна інтерпретація знаходження дивергенції
векторної функції для перерізу г - Сопзі: а - зображення вектора Р
у вигляді векторного поля; б - стовпчаста діаграма обчислених
значень дивергенції
Ротор деякої векторної функції
векторного добутку оператора набла
Е є вектором, одержаним як результат
на вектор Г. В декартовій прямокутній
системі координат:
гоіЕ = V х Г =
А ЗР
—- і + —-
дг ) у дг
ЗР2У рРу ЗРХ\-
----- л + —- - —- к .
Зх ) І дх Зу І
Для циліндричної системи координат р, <р, гз ортами ір, і^, і, ротор даної
векторної функції визначається залежністю:
- ґізр2	агД	ргр	аг V	ір(Ргф)	агр
ГОІР =----------- г + —-------- +--------2------
р Зф	дг ) р дг	др )	р [_ Зр	Зф
Ротор обчислюється з використання частинних похідних від проекції вектор-
ної функції. Приклад знаходження вектора-ротора векторної функції наведено в
наступному фрагменті документі МаЙіСАВ. Функція задана символьним векто-
ром, за компоненти якого залежать від трьох просторових координат:
х2 *еу 4-у2 4-х2
Е(х, у,г) :=
X2 +у2 *ег +22
х2 4-у2 4-х2 *ех
Обчислення частинних похідних символьного вектора Р(х,у,х) здійснене з
використанням засобів пакету МаЙіСАВ. Введені нові функції, що визна-
чають частинні похідні.
59
Струтинський В. Б.
с1£гу(х, у, г) := СІ р(х, у, г)2 «У	сКуг(х, у, г) := Р(х, у, г\ аг
а£хг(х,у,2) := -^-Р(х,у,г)0 аг	с!£гх(х, у,г) := -^-Р(х,у,г)2 ах
<1£ух(х,у,г) := Ар(х,у,г)1 ах	<Й’ху(х, у, г) := Р(х, у, г)0 <іу
Знаходження символьних значень частинних похідних:	
<1£гу (х, у, х) -» 4£уг(х,у,г) -+ й£хг(х, у, г) -> <1£гх(х, у, г) —)	2*у	й£гу(х, у, г) := 2 ♦ у у2 * ехр(г) + 2*г й£уг(х, у, г) := у2 * ехр(г) + 2 * г 2*г	4£хг(х, у, г) := 2 * г 2 * х + г2 * ехр(х) сИ/х(х, у, г) := 2 * х + г2 * ехр(х)
й£ух(х,у,г) -	► 2 * х	<і£ух(х, у, г) := 2 * х
сИху (х, у,г)	► х2 * ехр(у) + 2 * у <1£ху(х, у, г) := х2 * ехр(у) + 2 * у
Визначення вектора-рс	пора векторної функції Р : б£гу(х, у, г) - с1£уг(.х, у, г)
го££(х, у, г) :=	й£хг(х, у, г) - Н£гх(х, у, г) <і£ух(х, у, г) - Н£ху(х, у, г)
Виведення символьних	значень компонент вектора-ротора: 2 * у - у2 * хр(г) - 2 * г
гоі£(х, у, г) ->	2*г-2*х-г2 *ехр(х) • 2 * х - х2 о ехр(у) - 2 * у
Результати розрахунків вектора-ротора функції Р(х,у,г) наведені в гра-
фічному вигляді різних модифікацій на рис. 2.29. Здійснена графічна інтер-
претація результатів розрахунків вектора-ротора у вигляді векторного поля
(рис. 2.29, а). Даний вид графічної інтерпретації в даному випадку є най-
більш доцільним. Він дає уявлення про зміну вектора-ротора.
Для аналізу одержаних результатів корисно дати графічне зображення
модуля вектора-ротора. Його можна представити у вигляді стовпчастої діаг-
рами (рис. 2.29, г) або просторової поверхні (рис. 2.29, е). Для більш якіс-
ного кількісного аналізу використовують графік у вигляді ліній рівного зна-
чення модуля градієнта (рис. 2.29, б).
Диференціальні оператори дивергенція та ротор визначають фундаментальні
властивості векторного поля. Поле вважається безвихровим, якщо ротор скрізь
дорівнює нулю. Поле вважається соленоїдальним, коли дивергенція дорівнює
нулю. Наявність безвихрового чи соленоїдального поля встановлюється за ре-
зультатами обчислення відповідних диференціальних операторів.
60
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
г := 1	£1(х, у) := гоі£(х, у, г)0	£2(х, у) := гоі£(х, у, г),
і:=О..1О	]:=О..1О	Х;:=0.1*і	у}=0.1*]
:=£1(хі,уі) ^^(Хі.ур Ац :=|гоі£(Хі,у?г)|.
в)
г)
Рис. 2.29. Графічна інтерпретація результатів розрахунків ротора
векторної функції для плоского перерізу г - 1: а - зображення ротора
у вигляді векторного поля; б — лінії рівного значення модуля вектора-
ротора |гоіЕ| = Сопзі; в - зображення модуля вектора-ротора у вигляді
просторової поверхні; г - стовпчаста діаграма, що відповідає значенням
модуля вектора -ротора
Нижче наведено фрагмент документа МаїЬСАО, що включає приклад
встановлення наявності безвихрового векторного поля. Задана векторна
функція, для якої визначено ротор:
61
Струтинський В. Б.
Р(х,у,х) := <і£ху(х,у,х)	X + у + X X + у + X X + у + X 11 к/ :=¥р<х	у,х)2	<1£ух(х, у,х)	= ^Р(Х’ У’2>і
<1£хх(х, у, г)	:=Аг(х, ах	у,х)0	<1£хх(х,у,х) :	= ^-Р(х,у,г)2 ах
гі£ух(х,у,х)	а Р(х ах	,у,г\	(1£ху(х,у,х)	:=-^-Р(х,у,г)в «У
<і£ху(х,у,х) -> 1	<1£ху(х, у, г) := 1 сіїух(х, у, х) -> 1		<і£ух(х,у,х) := і
<1£хх(х, у,х) -> 1	<і£хх(х, у, х) := 1 й£хх(х, у, х) -> 1		<1£хх(х, у, х) := 1
<1£ух(х, у,х) —> 1 сі£ух(х, у, іі£ху(х, у, г) -		х) := 1 б£ху(х, у, х) —> 1 - <Иух(х, у, х)	<1£ху(х, у, х) := 1 0
го££(х, у, г) := <1£хх(х, у, х) - сІ£ух(х, у, х)		- й£хх(х, у, х)	го££(х, у, х) -» 0 . -й£ху(х,у,х)	0	
Всі компоненти ротора векторної функції дорівнюють нулю. Тому вектор-
не поле, яке визначено функцією Г (х, у, х), є безвихровим.
Аналогічним чином встановлюється наявність соленоїдального поля. Роз-
раховується значення дивергенції у всіх точках поля. Якщо розраховане зна-
чення дорівнює нулю, то поле є соленоїдальним.
В багатьох задачах математичного моделювання використовується
диференціальний оператор поля - оператор Лапласа або лапласіан скалярної
чи векторної функції. Лапласіан скалярної функції Ф(х, у, х) визначається у
символічному вигляді через квадрат оператора Гамільтона (набла) або через
частинні похідні другого порядку від скалярної функції:
а2Ф а2Ф з2ф
ДФ = V Ф = —г +----------=- .
Зх2 Зу2 Зх2
Лапласіан скалярної функції є скалярною функцією. Лапласіан векторної
функції Е(х, у, х) представляє собою вектор, що визначається залежністю:
_„2„ Ґ32РХ	32РХ	32РХ>	р2Ру	32РУ	32РД	Гз2Рг	32Р2	32рД
АР — V Р — ----г- 4--у- 4--т- 1 4- -у- 4----- 4-у- І 4- -— 4---у- 4--т- к .
Зх2	Зу	Зх2 у Зх2	Зу	Зх2 Зх2	Зу2	Зх2
Знаходження лапласіана скалярної та векторної функцій здійснюється з
використанням частинних похідних 2-го порядку від скалярної функції або
від проекцій векторної функції. Нижче наведено фрагмент документа
МаіЬСАВ, що включає приклад знаходження лапласіана скалярної функції,
заданої аналітичним виразом. Приклад включає визначення частинних похід-
них другого порядку.
62
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
£(х, у, г) := х ♦ у * г * ех+у+г
а£уу(х, у, г) := —у £(х, у, г)
<іу
<1£хх(х, у, г) :=	£(х, у, г)
а2
(Игх(х,у,2) :=—2Д(х,у,х)
Знаходження символьних значень частинних похідних:
<і£хх(х, у,г)->2*у*2* ехр(х + у + г) + х*у*г* ехр(х + у + г)
(1£уу(х, у, г) -> 2*х*у ♦ ехр(х + у + г) + х*у*г* ехр(х + у + 2)
а£гг(х, у,г)->2*х*у* ехр(х + у + г) + х*у*г* ехр(х + у + 2)
Визначення лапласіана скалярної функції:
Ьар(х, у, г) := (Ихх(х, у, г) + <1Гуу(х, у, г) + а£гг(х, у, г) .
Знаходження символьного значення лапласіана:
Ьар(х, у,г) -> 2 * у ♦ 2 * ехр(х + у + г) + 3*х*у*г* ехр(х + у + г) +
+ 2 ♦ х * 2 * ехр(х + у + г) + 2*х*у* ехр(х + у + 2).
Для циліндричної системи координат р, ер, г лапласіан скалярної функції
Ф(р, ер, 2) визначається залежністю:
_ і з ( зфЛ	і а2Ф а2Ф
АФ = — ’-- р---- Ч--у ‘--у +---у •
р бр^ <3р у р 5<р2	дтг
Знаходження диференціальних операторів в циліндричній системі коор-
динат за допомогою пакета МаіЬСАВ виконується так, як і в декартовій сис-
темі координат.
Диференціальні оператори дозволяють використовувати для аналізу про-
цесів фундаментальні інтегральні співвідношення (інтегральні теореми):
•	теорему Остроградського-Гауса:
Л|діуГ(х,у,г)сіУ = ||(І8 • Е(х,у,х) .
V	8
З неї видно, що потік вектора Г через замкнуту поверхню 8 дорівнює інтег-
ралу від дивергенції вектора Г по об’єму V, який обмежений поверхнею 8;
•	теорему про ротор:
|ДгоіГ(х,у,/)(1У = Д(І8 х Е(х,у/) ;
V	8
•	теорему про градієнт:
|Д§га(1Ф(х,у,2)с1У = |рІ8 • Ф(х,у,х).
V	8
Дана теорема застосовується для скалярної функції Ф(х, у, х), визначеної
в об’ємі V;
•	теорему Стокса:
|рІ8 • го<Р(х,у,х) = ^<ІГ • Е(х,у, х) .
8	С
Вона зв’язує потік ротора із циркуляцією вектора по замкненому контуру
С, який обмежує поверхню 8.
63
Струтинський В. Б.
2.3. Символьні моделі процесів у вигляді спеціальних функцій
2.3.1.	Елементарні трансцендентні та спеціальні функції
Елементарні трансцендентні та спеціальні функції широко застосовуються
при математичному моделюванні. Характеристики технічних систем та зако-
номірності робочих процесів часто визначаються певними співвідношеннями,
що формулюються в компактній математичній формі. Наприклад, це визна-
чені інтеграли, диференціальні рівняння певного вигляду, умови ортогональ-
ності функцій тощо. Хоча вищевказані співвідношення мають зовні простий
вигляд, але їх практична реалізація викликає певні труднощі і не зводиться
до обчислення елементарних функцій.
При розробці математичних моделей у даному випадку застосовуються
так звані спеціальні функції. Існує широкий клас різноманітних спеціальних
функцій. їх використання при розробці та аналізі математичних моделей є
надзвичайно ефективним. В даному підручнику розглянуті деякі із спеціаль-
них функцій.
Згідно [42], до спеціальних функцій віднесено ряд елементарних трансцен-
дентних функцій, таких як гармонічні, гіперболічні та експоненціальні функції:
8ІПХ, СО8Х, 8ІЇХ, СІЇх, Єх.
Синусоїдальні (гармонічні) функції (зіп х, сов х,...) визначають проекції
вектора, що рівномірно обертається. Такі задачі надзвичайно розповсюджені
в технічних системах. Це, наприклад, вектор відцентрових сил, які виника-
ють при дисбалансі ротора, або вектор довільних навантажень на вал, якщо
його розглядати в системі координат, що обертається разом з валом. Синусої-
дальними функціями описуються різноманітні коливальні процеси.
Гармонічна (синусоїдальна) функція є частковим розв’язком диференціа-
льного рівняння другого порядку виду:
^ї + у = 0.
сіх2 У
Зв’язок між різними гармонічними функціями встановлюється за форму-
лами тригонометрії, основними з яких є:
 2	2 Л	. 8ІП X
81П X + СО8 х = 1;	1§х =---- .
СО8 X
Гармонічні функції є періодичними з періодом 2тг.
Гіперболічні функції (зЬх, сіїх,...) широко використовуються при матема-
тичному моделюванні процесів і систем. Гіперболічні функції є окремими
розв’язками рівняння:
сРу п
-Н-~у = 0-
ах
(2.12)
(2.13)
64
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
Зв’язок між різними гіперболічними функціями встановлюються залеж-
ностями, основними з яких є:
,2	і_2 і ч 5Ьх
х - сЬ х = 1; ііїх =---.
сЬх
Гіперболічні функції є періодичними з комплексним періодом 2лі = 7~ї).
Гармонічні та гіперболічні функції в загальному випадку представляють
собою комплекснозначні функції комплексного аргументу.
Узагальненням множин гармонічних та гіперболічних функцій є експоне-
нціальна функція:
У = ех.	(2.14)
Для комплексного аргументу х = хк +]хі із формули Ейлера одержимо:
у = ех = еХк(со5Х| + )8ІПХ() .	(2.15)
Змінюючи комплексний аргумент х на X] = х + 2кл] (к = 1, 2,...), одер-
жимо
еХ| - ех • е2хМ = ех.
Таким чином, експоненціальна функція комплексного аргументу також є
періодичною функцією з комплексним періодом 2л].
Для комплексного аргументу ]х також має місце формула Ейлера:
е^ = СО8Х + ]8ІІ1Х .
Відзначимо співвідношення, аналогічне формулі Ейлера:
ех = сЬх + 8ПХ .
Гармонічні (синусоїдальні) функції виражаються через експоненціальну
функцію згідно формул:
е!Х - е ІХ	е-х + е іх
81ПХ=---------;	СО8Х=——--------.	(2.16)
21	2
Аналогічними формулами визначаються гіперболічні функції:
зііх - ЄХ ~е Х ;	сЬх=-^Ц^.	(2.17)
Між гармонічними та гіперболічними функціями існують наступні спів-
відношення визначені в полі комплексних чисел:
кіп х = і * 8Іі0х);	соз х = сЬ(]х);
зк(х) = -] • 8іп(]х); сЬх = соз()х).
Елементарні трансцендентні функції мають обернені функції:
агсзіпх, агссозх, агзйх, агскх, Іпх.
Деякі практично важливі співвідношення між оберненими елементарними
трансцендентними функціями наведено нижче:
агсзіп х -	• агзЬ()х);	агзйх = -Д • агсзіп(]х);
агссоз х = ] • агсйх ;	агсЬх = ] • агссоз х ;
агсзіпх = -Д  Іпух + 71 - х2	);	агзЬх = Іпіх + 7х2 + 1І;
65
______________________________Струтинський В. Б._____________________________
агссоз х = -і • іЦх + р -\/1 - х2 ; агсЬх = Іп^х + х'х2 - 1).
Логарифмічна функція 1п(х) є оберненою до експоненціальної функції,
тобто
(2.18)
(2.19)
(2.20)
(2.21)
(2.22)
Для комплексного аргументу
х = хк + І' хі = V/ • е-ІЧ',
де хк _ дійсна частина аргументу; X] - комплексна частина аргументу,
одержимо значення логарифмічної функції у вигляді:
X,
+ гагсС§ —Ч
хк
або, використовуючи модуль та аргумент у/ комплексного числа:
1п х = 1п + і • (у/ + 2кл).
Відзначимо залежності, справедливі для комплексних значень х:
хз _ еіІп* _ со5(іп х) + і • 5іп(1п х);
•	X ХІПІ	7ГХ . . ЛХ ,	ч
=	е ' = соб —+ і"8іп— (головне значення).
З цієї формули зокрема випливає:
=	еЛпІ _ е 2 (головне значення).
Елементарні трансцендентні функції мають асимптотичні співвідношення, які
корисні для їх аналізу в процесі математичного моделювання. Асимптотичні
співвідношення в околі малих значень аргументів мають вигляд:
, (п я) . 2х ( л лД
І 2)	л < 2	2)
8ІП X ,	/	х
соз х <----<1 (- л < х < л);
X
ех > 1 + х; ех < —-—;	е ’"х < 1 - х < е~х (х < 1);
1-х	у 7
—< 1п(1 + х) < х (~1<х); х <-Іп(1-х)<-—- (х<1);
1 + х	1-х
|1п(1-х)|<у (0 < х < 0,5828).	(2.23)
Ці асимптотичні співвідношення (обмеження) перетворюються в асимпто-
тичній рівності при X = 0.
Відзначимо розклади в ряди елементарних трансцендентних функцій.
Обмежуючись першими (лінійними) складовими, одержимо при х —> 0:
, X2 х ,
8іпх « х; созх » 1------; е » 1 + х ;
2
х2
8Йх я» х; сЬх «1-і----;	1п(1 + х) ~ х ;
66
Розділ 2 Математичні моделі процесів на основі символьних функціональних залежностей
агсзіп х ® х; агзЬх » х; агіЬх » х .
Для великих значень аргументу (х -> оо) справедливе співвідношення:
,	, ех
8ПХ ® СПХ ®.
2
Для обчислення елементарних трансцендентних та спеціальних функцій
в математичних пакетах наявний широкий набір засобів. Зокрема, в пакеті
МаДіСЛВ є вбудовані функції для обчислення різноманітних гіперболічних,
тригонометричних екпоненціальних та логарифмічних функцій. їх синтаксис
співпадає із загально прийнятими позначеннями [42].
На рис. 2.30 наведено діалогове вікно МаДіСАО 2000 для вибору вбудо-
ваних функцій. Зокрема, на даному рисунку відзначено гіперболічні функції
показано вибір гіперболічного косинуса.
Рис. 2.30. Меню Іпзегі Рипсііоп математичного пакету МаІігСАВ 2000,
в якому відмічено вбудовану функцію косинус гіперболічний
Після ініціалізації кнопки Іпзегі на екрані з’явиться заготовка сЬ(И). В
затушований квадратик вноситься ім'я аргументу, вираз або константа. В ре-
зультаті буде визначено косинус гіперболічний, наприклад:
х: = 1 сЬ(х) = 1.543.
Елементарні трансцендентні функції є найбільш важливими представни-
ками спеціальних функцій.
Спеціальні функції, що найчастіше використовуються, наведені нижче.
Розглянуто важливий клас спеціальних функцій, заданих визначеними ін-
тегралами. Це - інтегральний синус 8і(х), інтегральний косинус Сі(х), інтег-
ральний логарифм 1і(х) та інтегральна показникова функція Еі(х).
67
Струтинський В. Б.
Багато задач математичного моделювання технічних систем вирішуються з
використанням гамма-функції Г(х) та пов’язаних з нею функціями, зокрема, це
функція похибок егі’(х), інтеграл ймовірності Ф(х).
На рис. 2.31 наведено фрагмент діалогового вікна пакету МаШСАВ 2000, в
якому показані відповідні вбудовані функції. Там же знаходяться засоби знахо-
дження ортогональних поліномів, зокрема поліномів Лежандра, Лагерра, Чеби-
шева та інших.
ВМИІВИІІВІИІО
ІІІііІІіИ
Рис. 2.31. Діалогове вікно, за допомогою якого
використовуються спеціальні функції
В підручнику розглянуто деякі приклади застосування ортогональних по-
ліномів, зокрема поліномів Чебишева, Ерміта, Якобі та інших.
Значну увагу приділено розгляду спеціальних функцій, заданих як
розв’язок диференціальних рівнянь, зокрема функції Бесселя.
Обчислення спеціальних функцій, які наведені в математичних пакетах,
здійснюється із застосуванням певних методів. Використовуються різні мето-
ди обчислення спеціальних функцій. Найбільш простим є зведення обчислень
до вбудованих функцій математичних пакетів.
Багато спеціальних функцій допускають розклад в ряд або нескінченний
добуток. В таких випадках обчислення здійснюється підсумовуванням кінеч-
ної кількості членів ряду чи обмеженого числа співмножників. Іноді для цієї
мети використовуються ланцюгові дроби.
Деякі спеціальні функції можуть бути обчислені шляхом чисельного
розв’язку базового диференціального рівняння чи чисельного інтегрування
і нтегра л-фу нкції.
В деяких випадках для знаходження сукупності спеціальних функцій не-
обхідно застосовувати рекурентні співвідношення між ними. При цьому вся
сукупність функцій знаходиться за декількома (найпростішими) функціями
сукупності. Ряд спеціальних функцій може бути обчислено за допомогою
граничного переходу.
Можливе знаходження функції як границі деякого параметра або зведен-
ня спеціальної функції до асимптотичної функціональної залежності.
68
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
2.3.2. Інтегральні функції, гамма-функція та зв’язані з нею функції
Інтегральні функції задаються інтегральними залежностями. Вони широко
застосовуються при розробці та аналізі математичних моделей [1, 7, 15, ЗО,
42, 110, 122].
Інтегральний синус відноситься до групи інтегральних функцій і задаєть-
ся визначеним інтегралом:
8і(х)=ї— (іг.	(2.24)
*	7
0
Функція інтегрального косинуса відповідає залежності:
Сі(х) = -р^2> х>0.	(2.25)
х 2
Інтегральна показникова функція є невласним інтегралом виду:
х е2
Еі(х) = |—сіг, х < 0.	(2.26)
Інтегральна логарифмічна функція має вигляд:
1і(х)= РЧ	х>0.	(2.27)
о1пг
Між інтегральними функціями існують наступні співвідношення:
Еі(х) = 1і(ех) (х < 0);
Еі(±]х) = Сі(х)± ] • 8і(х) + ~ (х > 0, ] = V-"?).
Значення інтегральних функцій розраховуються за допомогою вбудованих функ-
цій математичних пакетів. В пакеті МАТЬАВ 5.3 наявні вбудовані функції для
обчислення інтегрального синуса та косинуса, синтаксис яких:
У = 8ІПІПІ(х), у = СО8ІПІ(х).
Дані вбудовані функції обчислюють значення відповідних інтегральних
функцій від символьних або числових матриць х, які можуть бути і комп-
лексними.
В пакеті МаіЬСАВ знаходження інтегральних функцій здійснюється об-
численням інтегралів (2.24)-(2.27).
Графіки деяких інтегральних функцій, розрахованих за допомогою пакету
МаїЬСАВ наведені на рис. 2.32.
В процесі математичного моделювання часто виникає необхідність в якіс-
ному аналізі інтегральних функцій. Для аналізу інтегральних синуса та ко-
синуса використовуються наступні ряди:
„З	5	„2п+1
8і(х) = —-----1—- + -А-- ... +(-1)" ---- ------ +...;
4 ’ 1-1! 3 -3! 5-5! к ’ (2п + 1>2п +1)
69
Струтинський В. Б.
. .	1	х2	х4	.	. х2п
к 7	2	2!	4-4!	'	7	(2п)-(2п)!
де С = 0,577216... - константа Ейлера-Маскероні, яка визначається за фор-
мулою:
С = Ііт] У у-— Іп(п) | = - [є4 • 1п(і)*с1і.	(2.28)
к ) о
Рис.2.32. Графіки інтегрального синуса (а) та інтегрального косинуса (б),
обчислені в пакеті МаіЬСАО
б)
Для великих значень аргументу інтегральні синус і косинус розкладають-
ся в асимптотичні ряди наступного вигляду:
5і(х). 2 .=£(. 0-	1)"
Я X ~о х X	х2п+1
Сі(х) , ЇЇЇА£(- 0-	1)" (Зи + О.
х п=0 X	X п=0	X
Застосування інтегральних функцій при математичному моделюванні досить
різноманітне. Вони застосовуються в задачах аналізу випадкових величин та ви-
падкових процесів, при здійсненні багатьох службових операцій. Інтегральні
функції застосовуються також при аналізі розривних функцій. Наприклад, до-
слідження явища Гібса, що має місце при описі розривних функцій рядом Фур’є
(див. розд. 3.3), здійснене за допомогою інтегральних функцій.
Важливими спеціальними функціями, визначеними за допомогою інтегра-
лів, є гамма-функція Г(х) та пов’язані з нею функції [1, 70]. Гамма-функція
звичайно визначається інтегралом Ейлера другого роду:
Г(х) = |е 7хх Мх , Ке(х) > 0 .	(2.29)
о
Гамма-функція, графік якої наведено на рис. 2.33, має ряд полюсів (при
х = 0, -1, -2, -3,...) та локальних екстремумів.
70
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
Характерні значення гамма-функції складають:
Г(о,5) = лАГ;	г(1) = 1;	Г(1,462) = 0,886 ;
Г(- 0,5040) = -3,545 ;	Г(-1,573) = 2,302 ;	Г(- 2,611) = -0,888 ,
Гамма-функція є узагальненням факторіала. Необхідно відзначити залеж-
ність, справедливу для цілих додатних аргументів:
Г(п + 1)=п! (п = 0, 1, 2,...).	(2.30)
Значення гамма-функції в математичному пакеті МаіЬСАО розраховуєть-
ся за допомогою вбудованої функції Г(х). Для цього використовується меню
вбудованих функцій (див. рис. 2.30). Результати розрахунків гамма-функції
з використанням вбудованої функції пакету МаіЬСАВ наведено на рис. 2.33.
Рис. 2.33. Графік гамма-функції, побудований за допомогою
математичного пакету МаііїСАГ)
Для обчислення гамма-функції іноді використовуються співвідношення:
( ) п-*” х(х + 1)(х + 2).. .(х + п)
(2.31)
де С = 0,57... - як і раніше, константа Ейлера-Маскероні (2.28).
Для аналізу гамма-функції використовуються також функціональні
співвідношення:
Г(х +1) = х-Г(х);	Г(х) • Г(1 - х) = ——— .
8ІП 7ТХ
При великих значеннях аргументу маємо розклад гамма-функції в асимп-
тотичний ряд (ряд Стірлінга):
Г(х)- е”х • хх• л/2л • 1 + —+ —-у--——-	|аг§х| < л.	(2 32)
у ’	[_	12х 288х2 51840х3 І 8 І
З гамма-функцією пов’язаний ряд важливих спеціальних функцій. Одна з
них - бета-функція:
71
Струтинський В. Б.
В(р,ч)=	(2.33)
Г(р + ч)
Застосування гамма-функції надзвичайно широке, зокрема, це ряд прак-
тично важливих задач теорії ймовірностей. Деякі обчислювальні процедури,
зокрема обчислення інтегралів, знаходження факторіалу, часто здійснюється
за допомогою гамма-функції [76, 122].
До класу важливих спеціальних функцій, визначених інтегралами, відно-
ситься функція похибок ег£(х) та інтеграл ймовірностей Ф(х).
Функція похибок задається інтегральним співвідношенням:
егї(х) =|е г ск .	(2.34)
Разом з функцією похибок застосовують додаткову функцію:
ег(с(х) = 1 - ег((х).
Функція похибок є частковим розв’язком диференціального рівняння
другого порядку:
-^-у + 2х~ = 0.	(2.35)
сіх сіх
Рис. 2.34. Графік функції похибок, побудований за допомогою
математичного пакету МаїіїСАГ)
Для обчислення функції похибок в математичному пакеті МаДСАО наяв-
на вбудована функція ег£(х) (див. рис. 2.31).
Для аналізу функцій похибок часто використовується розклад у нескін-
ченний ряд:
еД(х) = х —-— + —----------... + (- 1)" • —--г... .
3-1! 5-2!	’ п!(2п + 1)
Функція похибок зв’язана зі спеціальною функцією - інтегралом ймовір-
ності Ф(х) - наступним співвідношенням:
ф(х) = —т==-• [е 2 сІ2 = — ег£|І.	(2.36)
Ф2х *	2 У2)
72
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
Залежність функції похибок від гамма-функції встановлюється нескінчен-
ним рядом:
(2.37)
Застосування функції похибок досить різноманітне. Це, зокрема, аналіз ре-
зультатів експериментальних вимірювань параметрів, вирішення задач механіки,
гідравліки, гідродинаміки, теплофізики та інших. В розділі 9 наведено ряд при-
кладів застосування математичних моделей на основі функції похибок.
2.3.3. Функції Бесселя
Функції Бесселя (циліндричні функції) надзвичайно широко використо-
вуються при моделюванні процесів та систем. За допомогою функцій Бесселя
вирішується ряд важливих задач теорії коливань, зокрема, це коливання сис-
тем у розподілених параметрах, які розглядаються в циліндричній системі
координат. Тому функції Бесселя і називаються циліндричними (круговими
циліндричними функціями) [1, 42, 50, 122].
Вперше бесселева функція )о(х) була знайдена відомим вченим Д.Бернуллі у
1732 році при вивченні коливань маятника у вигляді однорідної важкої нитки.
Детальне вивчення властивостей всього широкого класу даних функцій було
здійснене Бесселем у 1824 році при дослідженні збурень руху планет.
Функції Бесселя використовуються для опису коливань різноманітних
технічних систем, які описуються хвильовим рівнянням. Зокрема, це - меха-
нічні коливальні системи типу масивної нитки, круглої або циліндричної
мембрани. За допомогою функцій' Бесселя описується нестаціонарний рух рі-
дини в циліндричній трубі із врахуванням розподілу параметрів.
Ряд прикладів використання функцій Бесселя наведено нижче.
Розглянемо фізичне обґрунтування введення функцій Бесселя [1]. Коли-
вальні процеси в системі із врахуванням розподілу її параметрів описуються
хвильовим рівнянням:
Л1і=^-----у,	(2.38)
с2 ді2
де і - час; с - швидкість розповсюдження збурень в даній системі; II - деяка
функція просторових координат і часу.
В лівій частині рівняння знаходиться оператор Лапласа Д, вигляд якого
залежить від вибраної системи координат. Так, для декартової системи коор-
динат хуг оператор Лапласа (лапласіан):
г2ьт з2і)	а2и
д2х	ду2	5/2
(2.39)
73
Струтинський В. Б.
В даній системі координат
д2У
Л-2
(2.40)
Ряд технічних систем в силу їх конструктивних особливостей природно
розглядати в циліндричній системі координат рф"
хвильове рівняння має вигляд:
а2Ц 1 С [ сій 1 52ц _ 1
дг р др др) р Зф с
де функція 11, що підлягає знаходженню, залежить від просторових коорди-
нат (радіуса р, полярного кута ф та осьової відстані г) і часу і.
Розв’язок хвильового рівняння знаходиться у вигляді розкладу у нескін-
ченний ряд за експоненціальними функціями виду:
е.ікс1, І = V— 1 , к = -со, ..., +оо.
Коефіцієнти розкладу є функціями лише просторових координат. Відпо-
відно розв’язок хвильового рівняння має вигляд:
Ц(р, ф, 2, 0 = £е*" • У(р, ф, г),
(2.41)
де У(р, ф, г) - деяка функція лише просторових координат, яка не залежить
від часу.
Підставивши значення розв’язку (2.41) у хвильове рівняння (2.40), оде-
ржимо рівняння Гельмгольця для знаходження невідомої функції V:
ДУ+к2-У = 0,	(2.42)
або в розгорнутому вигляді:
а2У 1 ЗУ 1
-------------__ 4- — •-1--
Зр2 р др р2
<?2У Р2У >
^4+^-4 + к2 • V = 0.
6ф2 дг2
Будемо шукати розв’язок рівняння Гельмгольця (2.42), (2.43) у вигляді
добутку трьох функцій (так званого добутку Лапласа), які забезпечують
розділення змінних по просторових координатах:
У(р, ф, 2) = К(р)-Ф(ф)-2(г).	(2.44)
Після підстановки розв’язку (2.44) в рівняння Гельмгольця (2.43) та ді-
лення на КФ7 знайдемо:
і га2к 2.сЖ
К <1р2 р сір
і	і	а2Ф	і	а2г	., „
— • -V-----г +------г + к = 0 .
Ф	р	сіф2	2	сіг
(2.43)
(2.45)
(2.46)
Перші два доданки в лівій частині (2.45) не залежать від просторової коор-
динати 2, тому і третій доданок не повинен залежати від 2. Отже, одержимо:
1	а7?	4- 2
— •---т- = ±0 = СОП5І .
2 сі/2 1
Це рівняння відповідає рівнянням (2.12) та (2.13) з відповідними
розв’язками у вигляді тригонометричних та гіперболічних функцій.
Знаку мінус в правій частині (2.46) відповідає розв’язок даного рівняння
у вигляді суми тригонометричних функцій:
2 = с1’СО8(дг) + С2'8іп(д2),
(2.47)
74
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
де Сі, С2 - постійні інтегрування.
Знаку плюс відповідає розв’язок у вигляді суми гіперболічних функцій:
7 = сі-сЬСцг) + С2'8Й(дг).	(2.48)
Враховуючи вищенаведене, рівняння (2.45) набуде вигляду:
р2[а2к і ак] і а2Ф 2\ „
-------- +------+---------=- + р!к ±о =0
К |_сІр‘ р Ф сіср2 '
(2.49)
Перший та останній доданки цього рівняння не залежать від <р, тому і
другий доданок не залежить від (р. Отже
— • —-—=- = ±У = Сота.	(2.50)
Ф сіф
Дане рівняння також має два типи розв’язків. Для знака мінус в правій
частині рівняння (2.50) маємо суму тригонометричних функцій:
Ф = с1*соз(уф) + С2’8Іп(у<р).	(2.51)
Для знака плюс в рівнянні (2.50) одержимо розв’язок:
Ф = срсЬ(уф) + С2,8Іі(уф).	(2.52)
Розв’язок (2.52) не відповідає умові періодичності функції Ф(ф). Для то-
го щоб функція Ф(ф) була періодичною з періодом 2л, потрібно брати
перший розв’язок (2.51). Тому треба прийняти:
Ф(ф) = СрСО8(уф) + С2’8ІГ1(уф),
де з умови періодичності розв’язку (2.51) випливає, ЩО V - ціле число.
Підставивши значення (2.51) у диференціальне рівняння (2.49), одержи-
мо для визначення К звичайне диференціальне рівняння другого порядку:
й2К 1 ак
---2—І-------
бр р (Ір
+ і к2 ± я2 -	= 0 .
І Р )
(2.53)
Це рівняння шляхом заміни
7(к2 +я2 )р = х , К = у
(2.54)
приводиться до диференціального рівняння спеціального виду, яке називаєть-
ся диференціальним рівнянням Бесселя:
<12у
йх2
(2.55)
Рівняння Бесселя є нелінійним диференціальним рівнянням другого по-
рядку. Воно не має точного розв’язку в елементарних функціях.
Розв’язок рівняння Бесселя виражається через спеціальні циліндричні
функції (функції Бесселя).
Таким чином, розв’язок хвильового рівняння в циліндричній системі ко-
ординат неодмінно потребує розв’язку рівняння Бесселя, а отже, і викорис-
тання функцій Бесселя.
Функції Бесселя утворюють широкий клас спеціальних функцій. Основ-
ними з них є функції Бесселя першого
75
Струтинський В. Б.
1У(х) та другого ¥у(х) роду порядку V (у = 0, 1, 2,...).
Функції Бесселя першого та другого роду є частковими розв’язками дифере-
нціального рівняння Бесселя (2.55).
Якщо ф(х) та ¥у(х) - два незалежних окремих розв’язки рівняння Бесселя,
то загальний розв’язок рівняння має вигляд:
у = Ху(х) = срЛ-Сх) + с2'¥у(х),	(2.56)
де С] і с2 ~ константи інтегрування.
Значення параметра х може бути цілим числом або довільним дійсним чи
(2.57)
комплексним числом.
До диференціального рівняння Бесселя зводиться багато диференціальних
рівнянь. Зокрема, рівняння
З/у 1 СІу 4 2 V2
—ч— • — 4* к —у — 0 ,
ас2 с ас с)
де к - постійна величина,
приводиться до рівняння Бесселя (2.55) шляхом заміни кС = х.
Нелінійне рівняння 2-го порядку
£1і1.±1 + |'ьсЧ-—\ = 0
і?  ? лД4 Д/1
де ш, а, Ь, с — постійні величини,
приводиться до рівняння Бесселя (2.55) шляхом заміни функції та аргумен-
ту. При цьому загальний розв’язок рівняння буде мати вигляд:
(2.58)
х-1? г? ґ 2л/ь”
п =Д2 -2у----С  ;
ш + 2
V = —-----
ш + 2
де значення постійної т задовольняє умові: т + 2 0.
Разом з функціями Бесселя першого Ду (х) та другого ¥у(х) роду вико-
ристовуються модифіковані функції Бесселя першого
Іу (х) та другого Ку (х)
роду порядку V. Модифіковані бесселеві функції є дійсними величинами, але
виражаються через функції Бесселя першого роду з комплексним аргументом
згідно залежностей:
ІУ(х) = г'ДДгх); з = 4-ї;
Ку(х) = - • тг •	~	.
2 8Іп(лу)
Модифіковані функції Бесселя є частковими розв’язками рівняння:
<12у	1 (іу С V2)
--і. +---^_-1+ у = 0.
сіх2 X Зх х2)
Це рівняння відповідає рівнянню Бесселя (2.55), в якому замість змінної
х взято значення ]х. Тому модифіковані функції Бесселя відповідають функ-
(2.59)
(2.60)
76
Розділ 2. Математичні моделі процесів па основі символьних функціональних залежностей
ціям Бесселя з комплексним аргументом.
З функціями Бесселя зв’язані функції
Ьегу(х), Ьеіу(х), кегу(х), кеіу(х),
які мають назву функцій Кельвіна. Вони зв’язані з функціями Бесселя на-
ступними формулами:
кегу(х) +.) • кеіу(х).
(2.61)
Функції Бесселя виражаються через елементарні функції за допомогою ря-
дів. Так, для знаходження функції Бесселя першого роду цілого порядку
(у = п > 0) маємо ряд:
/ \п
2г
Для функції 1()(х) при великих х маємо наближену рівність:
іДг)нік“Т^'
Після підстановки косинуса різниці двох кутів (2.62) набуде вигляду:
я	. я
СО8 X - СО8 — + 81П X • 81П — .
4	4
(2.62)
1о
Враховуючи числові значення тригонометричних функцій, одержимо
асимптотичне значення функції при великих значеннях аргументу:
І0(х) = -4=(со8х + 8іпх).	(2.63)
л/ях
Функції Бесселя обчислюються за допомогою математичних пакетів.
Для знаходження функцій Бесселя в математичному пакеті МаіЬСАІ) є
набір вбудованих функцій. На рис. 2.35 наведено фрагмент меню пакету
МаФСАВ 2000, в якому показано наявні вбудовані функції пакету, що слу-
жать для розрахунку функцій Бесселя.
Засоби математичного пакету дозволяють обчислити різноманітні бесселе-
ві (циліндричні) функції. Нижче наведено синтаксис деяких вбудованих фу-
нкцій пакету МаіЬСАВ:
Д0(х) - функція Бесселя першого роду нульового порядку;
Д1(х) - функція Бесселя першого роду першого порядку;
Дп(т, х) - функція Бесселя першого роду т-го порядку;
¥0(х) - функція Бесселя другого роду нульового порядку;
¥1(х) - функція Бесселя другого роду першого порядку;
¥п(т, х) - функція Бесселя другого роду т-го порядку;
І0(х) - модифікована функція Бесселя першого роду нульового порядку;
І1(х) - модифікована функція Бесселя першого роду першого порядку;
Іп(т, х) - модифікована функція Бесселя першого роду порядку т;
77
Струтинський В.Б.
КО(х) - модифікована функція Бесселя другого роду нульового порядку;
К1(х) - модифікована функція Бесселя другого роду першого порядку;
Кп(ш, х) - модифікована функція Бесселя другого роду т-го порядку.
"і'-'	,	- 4л у®
ИМІіМйМіЕМіІИіЯЙ^
Ояіив^
Рис. 2.35. Фрагмент меню пакету МаІ.ИСАІ) 2000,
в якому наведені функції Бесселя
Аргумент даних вбудованих функцій - х - дійсне додатне число, т - по-
рядок функцій Бесселя, т - 0..100.
В пакеті МАТЬАВ функції Бесселя розраховуються за допомогою наступ-
них вбудованих функцій:
1 = Ье88е1(а1рЬа, х) - функція Бесселя першого роду порядку аІрЬа;
Ье88е1у(а1рЬа, х) - функція Бесселя другого роду порядку аірЬа;
Ье88еІі(а1рЬа, х) - модифікована функція Бесселя першого роду порядку
аірЬа;
Ье88еік(а1рЬа, х) - модифікована функція Бесселя другого роду порядку
аірЬа.
На рис. 2.36 наведені графіки деяких бесселевих функцій, побудовані з
використанням математичного пакету МаНіСАО.
Застосування функцій Бесселя при математичному моделюванні процесів
та систем надзвичайно широке і різноманітне. Крім раніше вказаного застосу-
вання деяких функцій при аналізі коливальних процесів, функції Бесселя
знаходять використання при вирішенні задач гідромеханіки, теплопровіднос-
ті, дифузії та інших. Деякі конкретні приклади математичних моделей, що
використовують функції Бесселя наведено нижче.
Функції Бесселя використовуються при математичному моделюванні най-
різноманітніших технічних систем. В [1] наведено ряд характерних прикладів
застосування бесселевих функцій. Зокрема, розрахунок параметрів розпов-
сюдження електромагнітних хвиль в середині циліндра, пояснення СКІН-
ефекту, що виникає при проходженні змінного струму в провіднику круглого
перерізу тощо.
78
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
Рис. 2.36. Графіки деяких функцій Бесселя, побудовані за допомогою
вбудованих функцій математичного пакету МаііїСАГ)
Своєрідним застосуванням функцій Бесселя є спектральний аналіз проце-
сів. За допомогою цих спеціальних функцій знайдено спектр процесу, який
відповідає гармонічній функції, модульованій по частоті [1].
Наявний ряд інших практично важливих задач, де використовуються
функції Бесселя.
79
Струтинський В,Б.
2.3.4. Ортогональні поліноми
Ортогональні поліноми Чебишева, Лежандра, Якобі, Лаггера і Ерміта е
спеціальними функціями у вигляді поліномів з певними властивостями [1, 23,
33, 35, 42, 50, 53, 122]. Ці поліноми задовольняють умовам ортогональності,
тому вони називаються ортогональними поліномами.
Поширеним класом ортогональних поліномів є поліноми Чебишева (першого
роду). Перші кілька поліномів Чебишева мають досить простий вигляд:
Т0(х) = 1;
ТДх) = х;
Т2(х) = 2х2 - 1;
Тз(х) - 4х3 -- Зх;
Т4(х) = 8х4 - 8х2 + 1;
Т5(х) = 16х5 - 20х3 + 5х.
Поліноми Чебишева є розв’язками нелінійного диференціального рівнян-
(2.64)
ня другого порядку виду:
/. 2 і 6 у СІ V 2 л
(1 - X і--V - X — + П у = 0 .
к 'ах2 ах у
(2.65)
Це рівняння нагадує рівняння Бесселя (2.55), яке було розглянуто раніше.
Поліноми Чебишева мають ряд особливих властивостей. Зокрема, вони
задовольняють умовам ортогональності. Ці умови зв’язують поліноми різного
порядку інтегральним співвідношенням:
+гТп(х)-Тт(х>іх
0 при т п
71	• л
— при т - п ?= 0 .
п при т = п = 0
(2.66)
Для обчислення поліномів Чебишева (першого роду) використовують аналі-
тичні залежності:
Тп(х) = со8(п,агссоз(х)), 'х| < 1; Тп(х) = сЬ(п,агсЬ(х)), |х| > 1 . (2.67)
Для поліномів Чебишева другого роду:
1)п(х) = 8іп(п-агссо8(х)), |х| < 1;	11п(х) = 8Ь(п-агс1і(х)), |х| > 1.	(2.68)
Зручно розраховувати поліноми Чебишева за допомогою простого реку-
рентного співвідношення:
Тп+1(х) = 2х-Тп(х) - Тп.Дх).	(2.69)
Поліноми Чебишева мають важливий фізичний зміст. Якщо розглянемо
циліндр (рис. 2.37) радіусом г = 1, довжиною 2г, на поверхні якого нанесена
синусоїда з періодом —, т - 1, 2, ..., то графік полінома Чебишева з поме-
лі
80
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
ром щ буде проекцією на площину ХО¥ синусоїди, нанесеної на поверхню
циліндра. На рисунку показано напрям проекції по стрілці А.
А
Рис. 2.37. Фізична інтерпретація поліномів Чебишева як проекції
синусоїди, нанесеної на поверхню циліндра (гвинтової лінії) на площину
В основному поліноми Чебишева використовуються для апроксимації
функцій. Поліноми Чебишева забезпечують найкращу апроксимацію функції
в заданому інтервалі, тобто при апроксимації функціональної залежності по-
ліномом найкраще брати цей поліном у вигляді полінома Чебишева. При
цьому похибка апроксимації буде найменшою.
При математичному моделюванні застосовують також ортогональні
поліноми Лежандра, Лагерра, Ерміта та інші. Основне застосування поліно-
мів - це апроксимація функцій, розробка лінійних і нелінійних математичних
моделей дискретно заданих процесів.
Розглянемо деякі властивості поліномів Лежандра. Перші три поліноми
Лежандра мають вигляд:
Р1(х) = х; Р2(х) = 1(3х2-1); Р3 = | (бх3 - Зх).	(2.70)
Поліноми Лежандра є частковими розв’язками рівняння:
(1 - х2)4~у~ 2х-~- + п(п + 1)у = 0 , п = 1,2, ...	(2.71)
’ сіх2 сіх '
Умови ортогональності поліномів Лежандра:
+1	Г0 при т^п
ІРп(х)-Рт(хМх= 2	•	(2.72)
,	------ при т = п
-1	І2п + 1
81
Струтинський В. Б.
Між поліномами Лежандра існують наступні рекурентні співвідношення:
Рп+1(х) = ^~-х-Рп(х)—5-Рп_,(х);	(2.73)
п + 1	п + 1
Рпи(х) = х • Рп(х) +	.	(2.74)
п +1 ах
Аналогічні властивості мають поліноми Лагерра. Ортогональні поліноми
Лагерра є частковими розв’язками диференціального рівняння:
х-^-у + (1 - х)—+ пу = 0 , п = 1, 2, ...	(2.75)
дх2 У 'дх
Перші три поліноми Лагерра мають вигляд:
Ь1(х) = -х + 1; Ь2(х) = х2-4х + 2 ;
, \	’	(2.76)
Ь3(х)--х3 +9х2 -18х + 6.
Умови ортогональності поліномів Лагерра:
. .	(0 при т * п
К •Ьп(х)-Ьт(х)ах = Г	.	(2.77)
І	|(п:) при т = п
Поліноми Лагерра довільного порядку визначаються через експонен-
ціальну функцію диференціальною залежністю:
Ь (х) = ех •-^-•(хпе-х).	(2.78)
ах
Аналогічною залежністю визначаються ортогональні поліноми Ерміта:
Нп(х) = (-1)"-ехг-^(е-х2).	(2.79)
ах
Поліноми Ерміта є частковими розв’язками рівняння:
^у-2х —+ 2пу = 0 .	(2.80)
Зх ах
Перші три поліноми Ерміта мають наступний вигляд:
Н1(х) = 2х; Н2(х) = 4х2 - 2; Н3(х) = 8х3 - 12х .	(2.81)
Умови ортогональності поліномів Ерміта:
_ ,	. .	.	[0 при п * ш
]е“х •Нп(х)-Н„л(х)ах = і	.	(2.82)
|2 • пі• Vл при п = ш
Нижче наведено застосування поліномів Ерміта для розробки математич-
ної моделі безвихрового руху рідини в осесиметричному каналі.
Узагальненням ортогональних поліномів є поліноми Якобі. Вони визна-
чаються диференціальною залежністю:
аа^р)(х) = Ь_0_. х-“ • (1 - х)р • — [х“+п • (1 - хУ+п 1,	(2.83)
пі	ах	*
де а, Р - константи; п - порядок полінома.
82
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
Поліноми Якобі задовольняють наступній умові ортогональності:
|х“(1 - х)0Іа^ар)(х)- 5а^,р)(х)сіх = 0 при п * 0.	(2.84)
о
Поліноми Якобі при а = р = 0 є поліномами Лежандра, при а = р = -0,5 -
Чебишева першого роду, а при а = р = 0,5 - Чебишева другого роду.
Окремим важливим випадком застосування поліномів Якобі є знаходжен-
ня оберненого перетворення Лапласа.
д)
Рис. 2.38. Приклади розрахунків значень ортогональних поліномів
за допомогою засобів математичного пакету Маі/гСАВ 2000.
Графіки поліномів: а - Чебишева 1-го роду; б - Чебишева 2-го роду;
в - Лежандра; г - Лагерра; д - Ерміта; е - Якобі
В математичних пакетах наявні вбудовані функції для обчислення ортого-
нальних поліномів (див. рис. 2.31).
На рис. 2.38 наведено приклад розрахунків типових представників орто-
гональних поліномів за допомогою математичного пакета МаНіСАП.
83
Струтинський В. Б.
2.3.5. Типові розривні функції
При математичному моделюванні процесів у технічних системах виникає
необхідність аналізу розривних функцій або функцій з розривами похідних
[1, 2, 7, 9-11, 21, 33, 42, 45, 48, 50, 63, 73, 74, 96, 101, 102]. Нижче наведе-
но приклади розривних функціональних залежностей, які мають місце при
математичному моделюванні технічних систем. Зокрема, контур поверхні де-
талі, на поверхні якої є поздовжня канавка, описується розривною функцією
полярного кута (рис. 2.39, а).
в)
Рис. 2.39. Приклади технічних систем, процеси в яких описуються
розривними функціями: а - контур деталі з канавкою; б - зміна припуску
при точінні деталі ступінчастої форми; в - гідропривод, переключення
розподільника якого здійснюється дискретно, з нелінійною залежністю
сили тертя та обмеженням руху штока на упорі
84
Розділ 2. Математичні моделі на основі функцій, заданих у символьному вигляді
Розривними функціями описується процес зміни припуску при точінні
ступінчастої деталі (рис. 2.39, б).
Розриви функції обумовлені геометричними факторами або специфікою
роботи системи. Для системи, зображеної на рис. 2.39, в, переключення гід-
ророзподільника здійснюється дискретно, іцо відповідає ступінчастій зміні
тиску в трубопроводах і описується розривними функціями. Розривною фун-
кцією визначається сила тертя в гідроциліндрі в залежності від швидкості
поршня. Закон переміщення поршня при його взаємодії з упором також опи-
сується функцією з розривом похідної.
Розривними функціями описуються імпульсні ударні процеси в механіч-
них системах. Всі логічні пристрої технічних систем, як правило, описуються
розривними функціями.
Функція Кх? є неперервною в точці х = а, якщо в цій точці існує границя
функції і вона дорівнює самому значенню функції, тобто
Ііт £(х) = На) .
Інше визначення неперервності включає границі функції справа і зліва.
Функція є неперервною в точці, коли її границя зліва існує і дорівнює гра-
ниці справа, а також дорівнює значенню функції в точці. Відповідна аналіти-
чна умова неперервності при х = а:
Ііт і(х) = Ііт £(х) = £(а).
х->ін()	х-»а-0
Це співвідношення використовують для перевірки наявності точки розри-
ву функції.
Розрізняють розриви першого роду, коли границі функції зліва і справа
існують, але не дорівнюють одна одній або не дорівнюють значенню функції
в точці. Графік функції £(х), яка має розриви першого роду при х =	Х2,
хз, має характерний вигляд, показаний на рис. 2.40.
При збільшені масштабу графіка в напрямку осі х функція в точці розри-
ву набуває вигляду кусково-постійної залежності зі сходинкою (рис. 2.40, б).
Тому всі процеси з розривами першого роду в точках розриву описуються
лише однією розривною функцією у вигляді сходинки. Звичайно значення
сходинки ур приймаються за одиницю, а початок сходинки (точку А) беруть
за початок системи координат. Сформований таким чином розривний процес
має назву одиничної ступінчастої функції (або функції Хевісайда). Її сим-
вольний запис включає логічну конструкцію:
0 при - сс < х < 0
1уЦ при х = 0, 0 < 1у0 < 1у,
(2.85)
1у при 0 < х < +оо
де 1у - кінцеве значення ступінчастої функції; 1у0 - значення ступінчастої
функції при х = 0.
85
Струтинський В.Б.
нГ(х)
а)	б)
Рис. 2.40. Приклад графіка процесу, який описується функцією
з розривами першого роду в точках х = х/, хр, Х3, (а) та зображення
функції в точці розриву х-> при збільшені масштабу в напрямку осі х (б)
Кінцеве значення одиничної ступінчастої функції відповідає величині
сходинки 1у = ур. Звичайно кінцеве значення позначають 1у = 1, маючи на
увазі, що одиниця може мати довільну величину та знак, наприклад, сходин-
ка сили 1у = 1 Н або 1у = ІОН, або 1У = -50 Н тощо. Значення одиничної
ступінчастої функції при х = 0 10у = 1(0), взагалі кажучи, може бути дові-
льним в діапазоні 1уо = 0..1у.
В залежності від прийнятого значення при х = 0 розрізняють якісно різні
ступінчасті функції. Загалом можна визначити безліч одиничних ступінчастих
функцій, які будуть відрізнятись своїми значеннями при х = 0 (рис. 2.41).
Для якісного аналізу розривних функцій і, зокрема, одиничної ступінчас-
тої функції використовують умовне зображення графіка функції у вигляді
ламаної лінії чи гладкої кривої (див. рис. 2.41, в, г). При зображенні
враховують, що А; та А2 є нескінченно малими (нульовими) величинами.
Значення одиничної ступінчастої функції при х = 0 не обов’язково пови-
нно бути фіксованим. Використовуються ступінчасті функції, в яких
1у0 = Дт), де т - деякий параметр. Функція Кт) може бути як детермінова-
ною, так і випадковою. При моделюванні складних процесів тертя, контакт-
ного деформування та різання автор використовував одиничні ступінчасті
функції, значення яких при х = 0 є випадковими величинами з певним зако-
ном розподілу (рівномірним, нормальним). Використовувались одиничні сту-
пінчасті функції, величина яких при х = 0 є неоднозначною. Зокрема, неод-
нозначність, яка залежить від напрямку зміни аргументу, відповідає матема-
тичному опису деяких задач взаємодії рухомого елемента механічного приво-
ду з упором. Окремим випадком є ступінчасті функції, величина яких при
86
Розділ 2. Математичні моделі на основі функцій, заданих у символьному вигляді
х = 0 є багатозначною (має нескінченну кількість значень).
11(Х)
А
Ь(х)
А
а)
б)
в)	г)
Рис. 2.41. Можливі варіанти визначення одиничної ступінчастої
функції (а, б), які відрізняються своїми значеннями при х = 0,
та умовне зображення одиничної ступінчастої функції
неперервною лінією (в, г)
Найбільш широко в практиці математичного моделювання використо-
вуються одиничні ступінчасті функції, значення яких при х = 0 дорівнюють
значенням функції до чи після точки розриву або середньому значенню.
Одинична ступінчаста функція, в якій 1у0 = 1у/2, називається симетричною,
а функції з 1уо = 0, Іуо = 1у називаються асиметричними одиничними ступін-
частими функціями (рис. 2.42).
Симетрична одинична ступінчаста функція (рис. 2.42, б, д) описується
залежністю:
[0 при х < 0
10(х) = <! 1/2 при х = 0 .
[1 при х > 0
(2.86)
87
Струтинський В. Б.
1	* Цх)
1 ’	
	
	
	0	х
і 1	> 1о(х) >	 4 1 2
	0	х
і	і 1+(х)
1	>	
	0	X
а)	б)	в)
і Цх)
Рис. 2.42. Симетрична (б) та асиметричні одиничні ступінчасті функції
(а, в) і їх умовні зображення (г, д, е)
Асиметричні одиничні ступінчасті функції відповідають рівнянням:
. ч (0 при х < 0
ІДх)=-<
[1 при х > 0
та
[0 при х<0
1_(х) = (
[1 при х > 0
(2.87)
(2.88)
Остання функція застосовується найбільш широко і звичайно позначаєть-
ся як
, , [0 при х < 0
ІхНі,	(2.89)
[1 при х > 0
Графік цієї функції наведено на рис. 2.42, а, г.
В математичному пакеті МаЙіСАО для обчислення даної залежності ви-
користовується вбудована функція
Ф(х) (функція Хевісайда).
Значення цієї функції рівне 1, коли х > 0 , а при х < 0 значення функції
рівне 0.
Значення симетричної та асиметричних одиничних ступінчастих функцій
88
Розділ 2. Математичні моделі на основі функцій, заданих у символьному вигляді
у пакеті МаїЬСАВ зручно розрахувати використовуючи панель програмуван-
ня. Наприклад, симетрична одинична ступінчаста функція розраховується за
допомогою наступного оператора МаІІїСАВ:
Е0(х)
0 і£х < 0
- і£х = 0
2
1 оіЬепсізе
Для обчислення ступінчастих функцій використовуються різні методи.
Один із них полягає в апроксимації ступінчастих функцій неперервними
функціями відповідного виду. Симетрична одинична ступінчаста функція
(2.86) може бути апроксимована наступними виразами:
	10(х)= Ііт ^ + —агсід(ах) ;	(2.90) ^->ж[_2 тс 10(х) = 1іт — Г——— сіС;	(2.91) а ->«> 71	1 -ОС 10(х) = 1іт2-е °х ;	(2.92) а-* оо 10(х) = 1іт-^[ег£(ах) + 1].	(2.93) а->» 2
Ступінчаста функція може бути виражена через інтеграл Фур’є. При цьому
	* / \	1 Г 5ІИ С0І- ]	1	. 1п(0=„ ї	СІСО+	(2.94) 2л •' <в	2 —X
За допомогою одиничної ступінчастої функції можна описати довільну
ступінчасту (розривну) функцію. Наприклад, функцію, що визначає знак чи-
сла (рис. 2.43).
Рис. 2.43. Ступінчаста функція, яка визначає знак аргументу
Функцію
1
-1
при х > 0
при х < 0
(2.95)
89
Струтинський В. Б.
виражають за допомогою одиничної ступінчастої функції згідно виразу:
8§п(х) = 2 • 10(х) -1.	(2.96)
Такі залежності зустрічаються при описі сил сухого та змішаного тертя в
механічних системах. Характеристика турбулентного дроселя також опи-
сується залежністю, що включає функцію 8<(п.
При математичному моделюванні технічних систем використовується ряд
кусково-постійних функцій, зокрема, це функції Радемахера [28], які визна-
чаються залежністю:
га<і(т, 0) = 8§п[8іп(2т7г0)], т = 0, 1, 2,..., 0 < 0 < 1.	(2.97)
Кусково-постійні функції Радемахера є ортогональними.
Графіки деяких функцій Радемахера наведені на рис. 2.44.
«3(2,0)
гаск>,0) :=
1 і? яп(2?“ Я-й)>0
0 її вйі^я^вО
-1 яп^Я-б) <0
гаЦІ.в)
5іп(2 л в)
ЯП(4-7Г0 )
«3(3,8)
5Й(8"Л-8)
Рис. 2.44. Графіки кусково-постійних ортогональних функцій
(функцій Радемахера)
Застосовуються також ортогональні функції Уолша [28]. Графіки функ-
цій Уолша і відповідні їм тригонометричні функції наведено на рис. 2.45. За-
стосування функцій Уолша дозволяє здійснити розклад довільних сигналів у
ряд Уолша-Фур’є.
Функції Уолта споріднені з тригонометричними функціями.
У зв’язку з подібністю функцій Уолша до тригонометричних функцій ви-
користовують позначення, аналогічні соз та зіп:
са!(н, 0) та заКп, 0) (п = 1, 2, З,...).
90
Розділ 2. Математичні моделі на основі функцій, заданих у символьному вигляді
са!(пл0)	1	соз((2-Яп-Й)) >0	:=	1	8Ій(2 я п-0)>О
	0 і£ со5((2 я-п-Й))=0		0 іґ 5Їп(2 л п-6)=0
	-1 і£ со5((2 я п-Й)) <0		-1 і£ зіп(2 я-п.-0)<О
5<1,Є)
5іи(2лЄ)
іяЦЗ.Є)
5іп(4л-8)
сїКІ.З)
сім(2 л 6)
саК2.8)
С05(4я-9)
е<3,8)
$іп(6лЄ)
1^3,8)
С05(6л-8)
Рис. 2.45. Графіки кусково-постійних ортогональних функцій Уолша,
які відповідають знаку синусоїд чаКп. 0) та косинусоїд саІ(п, 0)
О	0.5	1
8
Із рис. 2.45 випливає, що функції Уолша визначають знаки відповідних
тригонометричних функцій соя та яіп.
Застосування функцій Уолша доцільне при моделюванні механічних сис-
тем, в яких є циркуляційні навантаження. Зокрема, ці функції використо-
вуються для опису дії відцентрової сили, що виникає при обертанні вала, на
опори підшипника. Знак проекції відцентрової сили, що діє на вал, описуєть-
ся функцією Уолша
яа1(1, 0) або саІ(1, 0).
За допомогою функцій Уолша описуються нелінійні процеси в підшипни-
ках кочення. Ці функції описують логічну умову наявності несучого силового
контакту між кільцем підшипника і тілом кочення.
Підключення плунжерів аксіально-поршневого насоса до гідромагістралі
також можна описати функціями Уолша.
91
Струтинський В. Б.
В деяких випадках використовуються своєрідні ортогональні кусково-
постійні функції Хаара [28]:
йаг(1, п, 0).
Оператор залежності, за якими вони визначаються в пакеті МаїйСАО, і
графіки деяких функцій Хаара наведені на рис. 2.46.
Рис. 2.46. Залежності, за якими визначаються функції Хаара,
та графіки деяких функцій
Кусково-постійні ортогональні функції широко застосовуються при роз-
кладі аналогових і дискретних процесів. Функції Уолша застосовуються
більш широко. Але в деяких випадках більш раціональним є застосування
функцій Хаара [28].
92
Розділ 2. Математичні моделі на основі функцій, заданих у символьному вигляді
2.3.6. Символічні імпульсні функції
В практиці математичного моделювання різноманітних процесів та технічних
систем широко застосовуються символічні імпульсні функції [1, 11, 42, 122].
Зокрема, символічні імпульсні функції використовуються при розробці
моделей процесів з розривами та особливостями типу ізольованих імпульсів.
Стосовно механічних систем символічні імпульсні функції описують:
-	контактні процеси у люфтових з’єднаннях;
-	стохастичні ударні процеси в складних механічних системах;
-	трибологічні процеси (сухе тертя);
-	процеси крихкого руйнування на мікро- і макрорівні;
-	кавітаційні процеси на поверхнях розділу «рідина - тверде тіло» (ку-
мулятивні струмені);
-	нелінійні гідродинамічні процеси з особливостями (облітерація, виник-
нення турбулентності);
-	динамічні процеси в системах автоматичного керування;
-	випадкові процеси, що мають місце при роботі динамічних систем.
Під символічними імпульсними функціями розуміють імпульсні залежнос-
ті різного виду. Симетрична символічна імпульсна функція 5(х), яку ще на-
зивають дельта-функцією або функцією Дірака, визначається залежністю:
0 при х < а
=‘|^(х) при
х = а
(2.98)
1(х) при а < х < Ь
де Цх) - довільна функція, неперервна в точках а і Ь.
Дельта-функція 8(х) не є функцією в загальному значенні. Вона відно-
ситься до класу символічних (узагальнених) функцій. Дана функція не має
точної відповідності з існуючими в природі процесами. її можна розглядати
як границю широкого класу процесів, що відповідають залежностям у вигляді
коротких ізольованих імпульсів. Звичайно в інтегральному співвідношенні
(2.98) приймають:
((?) = 1, х = 0, а = - оо, Ь = +да.
Тоді інтегральна умова (2.98) набуває вигляду:
рШ = 1.
(2.99)
Ця умова є інтегральною нормою одиничної імпульсної функції, яка ви-
значається символічною залежністю:
(О при х * 0
[0...оо...0 при х = 0
(2.100)
93
Струтинський В.Б.
Символами 0...ОО...0 позначено, що в околі точки х = 0 одинична імпульсна
функція зростає від 0 (в точці х = 0-0) до нескінченності, а потім спадає від не-
скінченності до нуля (в точці х = 0+0). На рис. 2.47, а наведено умовний графік
одиничної імпульсної функції у вигляді вузького трикутного імпульсу висотою
1/Ь і шириною 2Ь.
Коли ширина імпульсу зменшується (величина її прямує до нуля), амплі-
туда імпульсу необмежено збільшується (1/Ь -> оо). При цьому площа під
графіком імпульсу залишається незмінною і дорівнює одиниці. На рис. 2.47,
в наведено умовний графік імпульсу у вигляді кривої Гауса, що змінюється
плавно. Якщо позначити середню ширину імпульсу Ь, а його висоту - 1/Ь,
при цьому значення ширини імпульсу спрямувати до нуля, а амплітуду, від-
повідно, до нескінченності, то одержана крива в граничному випадку Ь —> 0
буде також відповідати дельта-функції.
Все вищесказане відноситься до зображення одиничної імпульсної функції
у вигляді прямокутного імпульсу (рис. 2.47, б), якщо його ширина Ь -> 0, а
висота 1/Ь —> оо.
Відповідність вузького імпульсу і дельта-функції не накладає ніякого об-
меження на форму імпульсу. На рис. 2.47, г наведено несиметричний ім-
пульс, який в граничному випадку (Ь —> 0) відповідає дельта-функції.
8(х)	5(х)	8(х)	§(х)	б(х)
Рис. 2.47. Умовні зображення одиничної імпульсної функції у вигляді:
а — вузького (її —> 0) трикутного імпульсу; б - прямокутного імпульсу;
в - імпульсу у вигляді кривої Гауса; г ~ несиметричного імпульсу;
д - вертикальної лінії
Часто графік дельта-функції зображають умовно у вигляді нескінченної
лінії (рис. 2.47, д).
Дельта-функція, яка є символічною, може бути апроксимована звичайними
неперервними функціями різноманітного виду. Апроксимація здійснюється за
допомогою граничних співвідношень. Найчастіше для апроксимації використо-
вують неперервні залежності у вигляді:
94
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
8(х, а) = -7-----г при а —> <х>;
тЦа х_ -т і )
д(х. а) -- е " ’ при а —> »
У Я
Залежність (2 102) відповідає кривій Гауса’
„/ ч а зшах
о(х, а) ---------при а —> со.
я ах
Для всіх виразів (2.101)-(2.103) виконуються умови’
]іт8(х,а) = 0 при х ф 0 та Ііт [§(х,а)сіх = 1.
(2.101)
(2.102)
(2.103)
Неперервні апроксимуючі залежності (2.101)—(2.103) допускають операції
диференціювання та інтегрування і є звичайними, а не символічними функ-
ціями Ними можна описати реальний фізичний процес
Наприклад, сила, що виникає при ударі пружних тіл. описується імпуль-
сом криволінійної форми Для удару абсолютно жорстких тіл імпульс сили
наближається до залежності, що відповідає дельта-функції.
Одиничну імпульсну функцію також апроксимують розривними функція-
ми, наприклад, одиничною ступінчастою функцією. При використанні симет-
ричної ступінчатої функції (2.86) маємо граничне співвідношення:
!,,(х + Ь) - І0(х - Ь)
й(х,її)  -------—--------1 при Ь -> 0.	(2 104)
21і
Використання символічних імпульсних функцій завжди повинно строго
обгрунтовуватись як фізичними, так і математичними методами.
Для символічної одиничної імпульсної функції вводяться формальні спів-
відношення, які випливають з її властивостей [42]:
5(ах) = —5(х) (а > 0); 5(-х) = 5(х);
а
і'(х)- 5(х - а) = -|[і(а -0)+ Ца + 0)]- §(х - а); х-5(х) = 0:
й(х2 - а2) = — [§(х - а) + 8(х + а)], а > 0;
2 з.
(2 105)
|з(а - х)  §(х - Ь)сіх = §(а - Ь).
На практиці використовуються також асиметричні імпульсні функції різ-
ного виду (рис. 2 48).
Між узагальненими функціями мають місце символічні співвідношення
для диференціальних операцій, зокрема символічна рівність:
5(х) = -^-[10(х)].	(2.106)
ах
Вона визначає дельта-функцію як символічну похідну одиничної ступін-
95
Струтинський В.Б.
чатої функції.
а)
5+(х)
Рис. 2.48. Умовні графіки симетричної (б) та асиметричних (а, в)
одиничних імпульсних функцій
Символічна рівність (2.106) є, безумовно, точною для неперервних функ-
цій (2.90)-~(2.93) та (2.101)-(2.103), які відповідно апроксимують ступінчас-
ту та одиничну імпульсну функції.
Символічні операції знаходження похідних дельта-функцій довільного
порядку здійснюються згідно з формулами:
8(г,(х) = (-1)гт!^, г = 0,1,2,.;	8'(х)=-^	(2.107)
X	X
Похідні дельта-функцій є також символічними функціями і також допус-
кають апроксимацію неперервними або розривними функціями.
Наприклад:
/ А 2 а3х
о (х,а) =-т———при а -> оо.
я (а2х2 +1)2
(2.108)
На рис. 2.49 наведені криві, які апроксимують симетричну одиничну сту-
пінчасту функцію (рис. 2.49, а), її символічну похідну у вигляді дельта-
функції (рис. 2.49, б) та символічну похідну дельта-функції (рис. 2.49, в),
яка є символічною другою похідною ступінчастої функції.
При цьому маємо символічні диференціальні залежності:
\ сіб(х) сР1,,(х)	,,Л	, .
5'(х) =-2-2 - —.	(2.109)
сіх СІХ
Похідні асиметричних одиничних ступінчастих функцій виражаються че-
рез асиметричні одиничні імпульсні функції (рис. 2.50).
При зображенні асиметричних одиничних імпульсних функцій на
рис. 2.50 використані імпульси різної форми. Для апроксимації дельта-
функції використано трикутний імпульс (Ь -» ос), а для апроксимації похід-
ної дельта-функції - прямокутні імпульси.
96
Розділ 2. Математичні моделі процесів на основі символьних функціональних залежностей
Д 1о(х)
Символічна похідна
Символічне
диференціювання
о
0
Рис. 2.49. Графічне зображення симетричної одиничної ступінчатої
функції (а), її похідної - одиничної імпульсної функції (б),
та другої похідної (в)
97
Струтинський В. Б.
Рис. 2.50. Графічне зображення асиметричних одиничних ступінчастих
функцій (а), їх похідних у вигляді несиметричних одиничних імпульсних
функцій (б) та других похідних (в)
98
Розділ 3. Система 8ІМПпакету МАТІ.АР для моделювання процесів та систем
РОЗДІЛ з
Система 8ІМІЛЛІЧК пакету МАТЬАВ
для моделювання процесів та систем
3.1. Загальна характеристика системи
3.1.1. Принципи побудови системи, приклади 8-моделей
Система візуального математичного моделювання 8ІМІЛЛ\ТК входить до
програмного середовища МАТЬАВ (МАТЬАВ 5.3, МАТЬАВ 6.0). Вона при-
значена для математичного моделювання лінійних та нелінійних динамічних
процесів та систем [14, 24]. Об’єкт моделювання описується у вигляді струк-
тури, яка включає різноманітні блоки (елементи, модулі) та зв’язки між ни-
ми. Структура чи блок-схема об’єкта утворює математичну модель в графо-
аналітичному вигляді. Структура об’єкта моделювання доповнюється блока-
ми, що визначають входи і виходи моделі. При цьому входи задаються набо-
ром конкретних функцій, а виходи невідомі і розраховуються в процесі мате-
матичного моделювання.
Математична модель включає набір блоків, які утворюють замкнену стру-
ктуру з вхідними та вихідними блоками. Ця структура становить так звану
8-модель процесу чи системи.
На рис 3.1 наведена найпростіша 8-модель, яка включає лише два вхідні
та один вихідний блоки.
.-'Пе Vі 2 Н.
ІИжІІ
йсоре
-	ВХІДНИЙ блок, ЩО
формує синусої-
дальну функцію;
-	вхідний блок,
що визначає ліній-
ну функцію - час;
-	вихідний блок
реєстрації резуль-
татів моделювання.
Рис. 31. Приклад найпростішої 8-моделі в системі 81МІЛЛПК
99
Струтинський В. Б.
Процес моделювання розпочинається за допомогою кнопки
(М.ІІІ Р.лін'1,
яка знаходиться на пане ті інструментів:
Після > пти \ моделі на кнопку Зіагі/Раизе виводиться символ
 ’'..уза),
якому відповідає команда Ранзе (призупинити моделювання). Закінчити про-
цес моделювання можна в довільний момент часу. Для цього служить кнопка
• '•> ор)
на панелі інструментів.
Після завершення пронесу моделювання у вихідному блоці
зберігається відповідна інформація про вихід системи, який змінювався в ча-
сі Активізація вихідного блока 5соре виводить на екран оглядове вікно блока
з графіками вихідних параметрів.
Оглядове вікно (рис. 3.2) за виглядом нагадує екран електронного осци-
лографа До початку моделювання вікно включає лише шкали, після обчис-
лень з’являються графіки відповідних величин.
Рис. 3.2. Оглядове вікно блока Зсоре, що відповідає моделі,
зображеній на рис. 8.1
Вікно має панель, кнопки якої дозволяють регулювати параметри графі-
ків та здійснювати виведення графіків на принтер.
100
Розділ 3. Система ЗІМЬ'ШМК пакету МАТСАГІ для моделювання процесів та систем
Система візуального математичного моделювання 8ІМІЛЛМК. дозволяє
виконувати математичне моделювання технічних систем і процесів різними
методами, зокрема, моделювання в часовому просторі, моделювання на основі
спектральних перетворень Фур’є, моделювання стохастичних процесів з ви-
користанням методів Монте-Карло та інших.
Розроблювані 8-моделі можуть мати різний рівень складності. На рис. 3.3
наведено приклад 8-моделі середнього рівня складності.
Блоки, які включені в дану 8-модель (див. рис. 3.3), зв’язані один з од-
ним як за інформацією, так і за керуванням. Тип зв’язку залежить від типу
блока і логіки роботи моделі. Модель включає різні вхідні та вихідні блоки.
Вхідними блоками є:
1 “► (СопзіапО,
ІіГ (Вапсі-Ьітіїесі \УЬі(е Коізе),
(Спйогт Капсіот МигпЬег)
а вихідними:
(8соре)
Фізріау).
Структура моделі включає нелінійні елементи:
(!)еа<1 Ходе),
(Миііірогі 8\\’іі.сЬ),
-и (МаІ.Гі Рипсііоп).
8-модель включає зворотні зв’язки, блоки одержання суми сигналів
, інтегруючі
ланки.
Дана 8-модель здійснює математичне моделювання динамічної системи, на
яку діють випадкові збурення у вигляді “білого” шуму. При цьому структура
технічної системи, а отже, і математична модель системи, змінюється випад-
ковим чином. В процесі обчислень модель набуває форми диференціального
рівняння третього або другого порядку. Запуск моделі здійснюється так, як
це показано раніше. Після виконання моделювання кнопкою Зіагі/Раизе
інформація виводиться по кожному із чотирьох блоків 8соре.
На рис. 3.4 наведене оглядове вікно блока 8соре без номера, який реєструє
вихід моделі.
Блоки 8соре 1 ... 8соре 3, а також всі блоки Нізріау служать для контролю
проміжних параметрів системи в процесі моделювання.
Зв’язки між блоками служать для обміну інформацією між ними. Напрямки
розповсюдження інформації показані стрілками. Дані, якими обмінюються блоки,
можуть бути скалярними чи векторними величинами довільної розмірності (в цій
моделі вони скалярні).
101
Струтинський В. Б,
Рис. 3-3- Приклад 8-моделі технічної системи з нелінійними
характеристиками, на яку діють випадкові збурення,
а структура системи змінюється випадковим чином
102
Розділ 3. Система .ЗІМС'СІМК пакету МАТЬАВ для моделювання процесів та систем
Рис. 3-4. Оглядове вікно блока 8соре,
в якому показані результати моделювання
Кожна 8-модель .може мати ієрархічну структуру, тобто включати матема-
тичні моделі більш низького рівня. Число рівнів ієрархії не обмежене. На
рис 3.5 наведено приклад нескладної 8-моделі технічної системи, яка вклю-
чає в себе 8-модель більш низького рівня.
Рис. 3-5. Приклад 8-моделі ієрархічної структури
8-модель нижчого рівня названа ЗиЬЗузіет 1. Вона має вхідний Іп 1 та
вихідний О ні 1 порти, які служать для обміну інформацією між 8-моделями
основної системи ЗшоЗіг та її підсистеми 8иЬ8узіет 1 Підсистема в основній
моделі зображена у вигляді блока з назвою ЗиЬЗузіеш 1, на якому позначені
вхід Іп1 та вихід Оції.
103
Струтинський В. Б.
3.1.2. Бібліотека модулів (блоків) 8ІМІЛДМК
Необхідна візуальна математична модель в системі 8ІМІЛДМК формується з
використанням технології Нга^-апсі-Огор (Перетягти і Залишити). Як елементи
моделі використовуються блоки із бібліотеки Зітиііпк ЬіЬгагу Вгохузєг
(рис. 3.6).
Версії МАТБАВ 5.3 та МАТЬАВ 6.0 мають близьку структуру розділів біб-
ліотеки.
Р] Ш		
й 0-	й- Е- в й- в а- й а •й Я	Сопііпиои$ 5| 0І5СГЄІЄ Рипсііопї & Т аЬІе® 5-І МаіЬ 5| Мопііпеаі Щ ЗідпаІ® & 5у$іет$ ЗД 5іпк$ Зоигсе$ СопігоІ 5у«іет Т ооІЬох ЗіаіеЛоил Зітиііпк Ехігає
ТЬії із іНе 'гітиІіпкЗ' ІіЬгагу
Рис. 3.6. Розділи бібліотеки:
СопНпиоиз - лінійні елементи системи;
ВІ8СГЄІЄ - дискретні елементи системи;
ГипсНонз & ТаЬІек - функції та таблиці;
МаіЬ - математичні функції;
Мопііпеаг - нелінійні елементи системи;
8і§паІз & Зузіетз - зв’язки між системами;
Зіпкз - вихідні параметри (отримувачі);
Боигзез - вхідні параметри (джерела);
Сопітої Зузкет ТооІЬох - засоби аналізу;
8іаіе(1о\у - зміна стану системи;
8іпш1іпк Ехігая - додаткові блоки
Бібліотека модулів є набором графічних елементів, використовуючи які мож-
на скласти довільну структуру моделі. Бібліотека модулів (блоків) має ряд роз-
ділів. Деякі із них є базовими, інші можуть змінюватись в залежності від потреб.
Розділи, які можуть змінюватись, включають компоненти МАТЬАВ, що
додатково включені до бібліотеки модулів.
Кожен модуль (блок), який входить в бібліотеку, має, як правило, один і
більше параметрів, які задаються з метою корекції характеристики блока.
Параметри блока задаються у діалоговому вікні. Вікна всіх блоків мають
ідентичну структуру і включають коротку характеристику блока, поля вве-
дення (або вибору значень параметрів) і 4 кнопки: Арріу ~ застосувати;
Кєуєгі - повернути попередні значення; Неір - виклик файлу допомоги;
Сіозе - закрити діалогове вікно.
Розглянемо окремо всі розділи бібліотеки модулів 8ІМІЛЛМК.
104
Розділ 3. Система 81МСРІ.\'К пакету МАТЬАВ для моделювання процесів та систем
3.2. Основні розділи бібліотеки, характеристика модулів
3.2.1. Зопгсез — вхідні модулі (джерела)
На рис. 3.7 розкрито зміст розділу бібліотеки Зоигсез (джерела, вхідні
блоки).
-З Зітіик	;<
- а шВЯ
' ф ВапсНітЙегіМЛйеМоіве-і;
- ф СНгр Зідпа!------------
ф Сіоск-------------------
 •	ф	Сотіапі-------------
:	ф	ОідііаІСЬск---------й
	ф	0І8СІЄІЄ Рсйе бепенйог —і
• 	ф	РготМ/огкерзсе------?
5	:	ф	ЕготЕіе--------------:
ф Риїїебепемк»------------
ф	Ватр-----------------?
’	;	ф	АагЛт ІЧитЬег---------
Ф Нереайпд Бедиепсе------
ф	Зідпаїбепеггйої------г
-	ф	ЗіпєШує--------------Л
ф	51ер-----------------І
:	'	ф	Ііпііат РізпботМигпЬег—-
ТЬії ге Ле 'їітиіпкЗ/Зоигсм' Ьк-ск І 2 \
1^’
ВапсШтіисі
ШЬііе Моіге
12:34	>
ОідііаІ Сіоск
іт.и] Ь
Егот МУоікграсе
РиІ§е Оепеїаіог
Ж
Кзпбот ИитЬег
0000
00 ?
Зіер
СЬігр ЗідпаІ
----------!
1 к
Сопгіапі
Ж
Оігсгеіе РиІ5Є
Оепагаіог
ипШІей ггіаі
Егот Еііе
Ратр
Керезїіпд
Зедиепсе
Зідпаі Сепегзіог
ЗіпеМУаие
ІІпгїогт Раліст
ИигтїЬег
?
Рис. 3.7. 8оиг8Є8 — розділ вхідних параметрів
8оиг8Є5 - розділ вхідних параметрів - модулі, що входять до даного роз-
ділу, призначені для формування сигналів, що забезпечують роботу 8-моделі
в цілому або окремих її частин. Кожній назві відповідає окремий блок з від-
повідним графічним зображенням. Модулі даного розділу мають по одному
виходу і не мають входів.
Основними джерелами вхідних параметрів є:
105
ії.и] і?
ипШІеітаі >
□ □□□
□о >
Струтинський В. Б.
Вапсі-Ьітіїесі ХАІіііс Моізе - генератор “білого шуму” в
обмеженому діапазоні частот.
СЬігр 8і§па1 - генератор гармонічних коливань змінної
частоти.
Сопй.апі: - блок, який формує постійну' величину (скаляр чи
вектор), значення величини (в даному випадку 1 - показано
в середині блока).
□ізсгеїе Риїзе ОепегаГог - генератор дискретних імпульсних
сигналів.
Ггот АЛ’огкзразе - блок, який забезпечує введення даних в
8-модель безпосередньо із робочої області МАТЬАВ.
Ггот Ріїе - блок, призначений для введення в 8-модель да-
них із файла ипііііесі.таї. Структура даних в цьому файлі є
масивом із змінною кількістю рядків. Елементи першого ряд-
ка включають послідовні значення модельного часу, елементи
інших рядків - відповідні значення змінних.
Кагор - блок, який формує лінійно зростаючий (або лінійно
спадний) сигнал.
Капсіот МитЬег - блок, який формує дискретний сигнал,
амплітуда якого розподілена за нормальним законом. Блок
мас чотири параметри регулювання: Меан і Уагіапсе - за-
дають математичне сподівання та дисперсію нормального за-
кону; Іпіііаі 8еесі - задає початкове значення для генератора
випадкових чисел. При фіксованому значенні цього
параметра генерується завжди одна і та ж послідовність
випадкових чисел. Четвертий параметр 8агор1е іігое є кроком
зміни модельного часу. Його можна задати у формі констан-
ти або виразу. Якщо результат обчислення виразу є дробом,
він округляється до найближчого цілого значення.
8і§па1 Оепегаіюг - блок, який формує вхідний сигнал різної
форми: синусоїдальний; послідовність прямокутних імпуль-
сів: послідовність трикутних імпульсів та випадковий вхідний
сигнал.
106
Розділ 3. Система 8ІМСИ\К пакету МАТІ. АР для моделювання процесів та систем
8іпе \¥ауе - блок, який генерує гармонічний (синусоїдаль-
ний) вхідний сигнал системи, який є скалярною або вектор-
ною функцією часу.
8іер - блок, який задає дискретний вхідний сигнал, що від-
повідає ступінчастій функції. Блок має три регульованих
параметри: час зміни сигналу, початкове та кінцеве значення.
Ііпіїогт Капсіоп МитЬег - блок, що формує сигнал, ампліту-
да якого є рівномірно розподіленою випадковою величиною.
Блок має чотири параметри регулювання. Два з них, Іпіііаі
8ессі і ЗатЬІе Тіте, мають ті ж значення, що і в блоці
Капйот МитЬег, два інших параметри, Міпітит і Махіпшт,
задають діапазон розподілу випадкової величини.
3.2.2. Розділ Зінкз - вихідні модулі (отримувачі)
На рис. 3.8 розкрито зміст розділу Біпкк, що охоплює модулі для виве-
дення інформації.
ЗІпкй
*
Сйріау-------
5соре--------
5іор Зйшіайоп
ТоЕІІе-------
ТоЧ'огклрасе-
• ф ХУЄгарИ--------
моск
Оіерізу
Язїорі
5іор 8ітиіаііоп
5ІГП0ЦІ
соре
Т о Рііе

То ЇЛ(оН<5расе1
Х¥ ОгарЬ
Рис. 3.8. Розділ бібліотеки б'іпкз (блоки виведення інформації,
одержаної при математичному моделюванні)
8іпкз - розділ бібліотеки, який включає модулі реєстрації вихідних па-
раметрів (отримувачі). Блоки, шо входять до даного розділу, дозволяють
здійснити виведення або передачу інформації, одержаної в результаті матема-
тичного моделювання конкретної системи.
107
Струтинський В. Б.
Виведення інформації здійснюється наступними блоками.
о] Візріау - блок, призначений для виведення на екран число-
„з
 вих значень величин, одержаних при моделюванні. Блок має
чотири параметри регулювання, а саме: Рогшаї - задає фор-
мат виведення; Оесішаїіоп - визначає періодичність виведен-
ня; Р1оаІіп§ сіізріау - визначає спосіб використання блока
Візріау; 8атр1е Тіте - задає величину кроку модельного ча-
су, тобто дискретність виведення даних у вікно Візріау.
Блок Візріау може використовуватись для виведення як скалярних, так і
векторних чи матричних величин. Робота блока в цих випадках ілюструється
рис. 3.9. На рис. 3.9, а показано, як здійснюється виведення скалярної вели-
чини, а на рис. 3.9, б - як здійснюється виведення вектора, компонентами якого
є і, 2 і 3.
Сопзіапі Бізріау
а)
б)
Рис. 3.9. Приклади 5-моделей, що ілюструють роботу блока Пізріау
при виведенні скалярних (а) та векторних (б) величин
8соре - блок, який здійснює графічне виведення результатів
моделювання в функції часу. Він включає ряд регульованих
параметрів, що дозволяють змінювати масштаб графіків.
Одночасно в блоці 8соре можна вивести до ЗО графіків вели-
чин в функції модельного часу. Блок дозволяє роздруковува-
ти одержану графічну інформацію.
Приклад застосування блока 8соре наведено раніше (див. рис. 3.1 та 3.2).
І
>ипіііІесі.таі
8іор Зітиіаііоп - блок керування моделюванням, який до-
зволяє зупинити процес моделювання при виконанні певних
умов. Блок зупиняє моделювання, коли на його вході
з’являється ненульовий сигнал.
То Ріїе - блок, який забезпечує запис в МАТ-файл шйіііесі.таї
результатів математичного моделювання. Блок використо-
вується в парі з раніше розглянутим блоком Ргош Ріїе.
108
Розділ З Система 81МІЛЛМК пакету МЛТЬАВ для моделювання процесів та систем
> гігпоиі
То ХУогкзразе - блок, призначений для збереження даних,
одержаних в результаті моделювання безпосередньо в
робочій області М.АТЬАВ. Блок має чотири параметри регу-
лювання: УагіаЬІе пате - ім’я, під яким дані зберігаються в
робочій області; Зітоиі Махітшп піітЬег о£ го\уз - допусти-
ме число кроків моделювання, для якого дані реєструються;
Оесітаїіоп - дискретність реєстрації даних; Запіріе Тіте -
дискретність зміни модельного часу.
3.2.3. Сопііпионз — аналогові блоки
На рис. 3.10 розкрито зміст розділу Сопііпиопз, що охоплює модулі для
опису аналогових лінійних елементів динамічних систем, зокрема тих, які
включають диференціальні операції.
ф ОєиуМіує-----
•у-ф НедгШи------
- ф Мето?-------
. ф 5іайН»расе—
у-ф ТгагйІегРсп—
ф ТгапфотіОейу
Оєпузііує
Метопу
І піедгаіо г
х1 = Ах*-Ви
у = Сх+ 0 и
ф УагіаЬІе Тгапзрогі Оеіау
ф 2е(О’РоІе----------------
Х/агізЬІе Т гапгрогі Оеїзу
Зіаіе-Зрасє
ТЬІг й» їМ ’гітиііпкЗ.Сотюиоиз
ЬІоек
Тгапїоогї Оеіау
І I
2его-РоІе
Зтиіігй
Рис. З.і‘0. Розділ бібліотеки Сопііпиоиз, що містить модулі
для опису аналогових лінійних елементів динамічних систем
109
Струтинський В.Б.
Оегіуаііуе — блок обчислення похідної вхідного сигнала
(.диференціююча ланка системи автоматичного керування).
Іпіе§гаІог - блок-суматор неперервного часу (інтегруюча
ланка системи автоматичного керування).
Метогу - блок, що здійснює затримку сигналу на один крок
модельного часу.
Бґаіе-Зразе - блок формування змінних стану систем.
ТгапзГег Геп - блок, який відповідає лінійній ланці системи
автоматичного керування із трансформуючою функцією,
показаною в середині блока. Коефіцієнти трансформуючої
функції визначаються параметрами регулювання блока.
Останній блок призначений для розв’язку диференціальних рівнянь, за-
даних в операторній формі.
В початковому стані блока трансформуюча (передавальна) функція від-
повідає аперіодичній ланці першого порядку з постійною часу та коефіцієн-
том передачі, що дорівнюють 1.
Робота блока Тгапзіег Рсп ілюструється наступним прикладом. В ньому
виконується розрахунок перехідного процесу системи, яка відповідає аперіо-
дичній ланці першого порядку. Блок-схема моделі та результати розрахунків
наведені на рис. 3.11.
ТгапїїегРсп Зсоре
а)	б)
Рис. 3.11. Блок-схема 5-моделі (а) та результати розрахунків (б)
Регулювання блока 8іер, який задає ступінчасту зміну вхідного сигналу,
ПО
Розділ 3. Система ЗІМІЗЬІМК пакету МАТЬАВ для моделювання процесів та систем
здійснено таким чином, що сигнал на вході системи змінюється від 0 до 1 в мо-
мент часу 1 = 0.
Блок Тгапзгег Ген, як і інші блоки 8-моделей, можуть з’єднуватись до-
вільним чином, зокрема паралельно чи послідовно.
Наступний приклад (рис. 3.12) ілюструє розрахунок виходу моделі, яка
включає 4 послідовно з’єднані аперіодичні ланки першого порядку при пода-
чі на вхід системи одиничної ступінчастої функції.
ТгапзїегЕсп2 ТгапзгегРспЗ Зсоре
Рис. 3-12. Математична модель системи
з послідовним з’єднанням елементів
Трансформуючі функції, які задаються блоком ТгапзГег Геп, відповідають
довільній дробово-раціональній функції. Єдине обмеження полягає в тому,
що степінь чисельника трансформуючої функції не повинен бути більшим за
степінь знаменника функції. На рис. 3.13 наведено характерні приклади бло-
ків Тгапзіег Геп.
1
г^+з+І
Тгапі^ег Геп
5+1
> ------- >
2*1
Тгапгїег ЕспЗ
252+3*1
®2+55+7
Тгапзїег Есп1
5
зЗ+з2*5+ 4
ТгапДег Есп4
Рис. 3.13. Приклади трансформуючих функцій,
які реалізуються блоками Тгапз/ег Рсп
За допомогою блока Тгапзіег Геп здійснюється розв'язок диференціаль-
них рівнянь з постійними коефіцієнтами. Як приклад розглянемо диферен-
ціальне рівняння:
а3у ! а2у . ву
аі3 аі2 а і
сіх
<11
де х = 8іп(і) - синусоїдальна функція часу.
Початкові умови для даного рівняння є нульовими, тобто
111
Струтинський В. Б.
<ІУ еРу
при 1 = 0 х = 0, у = 0, -7- = 0 ,	= 0 .
*	~ Л <к2
Перетворимо диференціальне рівняння по Лапласу і одержимо:
¥(з) • [з3 + 82 + 8 + 1] = Х(з) • [з + 1].
Знайдемо трансформуючу функцію системи:
\¥(з) =	= з У"'-------•
Х(§)	83 + 82 + 8 + 1
Для розв’язку рівняння необхідно використати правий крайній блок, зо-
бражений на рис. 3.13. Подавши на вхід даного блока синусоїдальну функ-
цію з розділу Зоигзе (див. рис. 3.7), на виході одержимо розв’язок рівняння
у вигляді у(і).
Ттапзрогі Веіау - блок, що забезпечує затримку сигналу на за-
дану кількість (не обов’язково цілих) кроків модельного часу.
Регулювання блока здійснюється за допомогою трьох парамет-
рів: Тіте йеіау - кількість кроків модельного часу, на який
здійснюється затримка сигналу; Іпійаі іприї - значення амплі-
туди вхідного сигналу, при якому відбувається активація блока
(встановлено нуль); Іпійаі ЬиНег зіге - об’єм пам’яті в байтах,
що виділяється в робочій області МАТЬАВ для зберігання па-
раметрів затриманого сигналу (встановлено 1024 байт).
УагіаЬІе Тгапзрогі; Оеіау - блок, який дозволяє задавати ке-
ровану ззовні величину затримки сигналу. Для цього блок
має додатковий вхід. Регулювання блока здійснюється трьо-
ма параметрами: Махіпппп сієїау встановлює найбільшу до-
пустиму величину затримки сигналу; два інших параметри -
ІпіНаї іприі. і ВиНег Зіге - мають ті ж самі значення, що і в
блоці Тгапзрогі Веіау який розглянуто вище.
Хего-Роіе - модуль формування трансформуючої функції
нульового поля. Блок має три параметри регулювання (Хегоз,
Роїез, Оаіп), які призначені для формування змісту блока.
На рис. 3.14 наведено характерні приклади трансформуючих функцій,
реалізованих за допомогою блоку Хего-Роіе.
Зего-Роіе
7»3)
2его-РоІе1
2его-РоІе2
3 > 		/ >	(Я) 52	> >	з з2
2его-Ро!еЗ		ІЄГ0-Р0ІЄ4		Зего-Роіеб

Рис. 3.14. Приклади трансформуючих функцій,
які реалізуються блоками Него-Роіе
112
Розділ 3. Система ММОІ.ІМК пакету МАТЬАВ для моделювання процесів та систем
3.2.4.	Пізсгеіе та Рипсііоп & ТаЬІез — дискретні модулі, функції та таблиці
На рис. 3.15 наведено зміст розділів Візсгеїе та Еипсііоп & ТаЬІез.
і ; Є ® Відане	[і
З ' ф Оіїсійє Тіагайк Есп—2
ч : І- ф ОгесгеЛе 2еїо-РоІе----
іі  = ф Оіксгв’е Еіег
|і . ф 5Ше-5р«се---------------1
;5	,	ф Ойае»е-Тіп® ігЧеднйх—
ї	І	ф Ягй-ОкЬНйИ----------г
: і ифіМОеІ^-----------—-----
Іі ;	' • <• ф НоИ------------!
:	в 'ЙМ ГигхйогаЗЛаЬЬ»
{ . ' гФ?®----------------------=
н > ф І0ок*Цр ТаЬ’е-------------
	 ф Іоок-Ор ТаЬЬ(2-О)---
] ’ і ф МАТШ Есті---------------
ф 5-РжсШі
- ТІ® « Йж ШЙ*ЗЯ)вяШ'
} г«-0.5	|
Оігсіеїе Тгап5Іег геп
І
бі$сгеіе ГіИег
ОІ5СГЄІЄ 8іаів-8расе
,РІ£ссеіе:Тіте ІпіеягаЬг
ІІпії &еіау
(г-1)
ОІ5СІЄІЄ 2еі»-РоІе
у(п>=С5<п)*С>и(г>)
><п+1 )= А)<п> 0 и(г>)
Рігй-Оісіег Моїй
2его-ОМег
НоН
ч МАТІАВ
Еипсііоп
МАТЬАВ Геп
-&?. а)
Рис. 3.15. Розділи бібліотеки Візсгеіе та Рипсііоп & ТаЬІез,
які мають модулі для опису дискретних елементів та функцій
Візсгеіе - розділ бібліотеки модулів, призначених для опису дискретних
систем. Основні модулі розділу наведені нижче.
1	Візсгеїе ТтапзГег Епс - матричний вираз дискретної трансфор-
> —	? муючої функції. Векторний вираз для знаменника тієї ж
2*0.5	функції. Розмірність вектора дорівнює числу колонок матриці.
> ±12_	Візсгеїе Хего-Роіе - матричний вираз для . нульового поля. у Векторний вираз для поля та коефіцієнтів підсилення. Роз-
2(2-0.5)	мірність вектора дорівнює числу колонок матриці нульового
	поля або одиниці, коли нульове поле є вектором.
113
Струтинський В. Б.
" Оізсгеіе Гіііег - блоки, які забезпечують /-перетворення
 вхідного сигналу.
1+0.5е^
х(п+1)=А}(п>Ви!;п)
Візсгеїе 8іаІе-8разе - блок формування змінних
стану системи.
і)і«:геіе Тіпіе Іпіедгаіог - блок, що дозволяє одержати суму
інтервалів часу між значеннями, при яких на вхід блока
подається сигнал. Регульовані параметри блока визначають
метод інтегрування (параметр Іпіедгаіог шеіНосі), підключен-
ня додаткового керуючого сигналу (параметр Ехїегпа! гезеї) і
використання зовнішнього встановлення початкового значен-
ня вхідного сигналу (параметр Іпіііаі сопсііНоп яоигке).
Рігзі-Огсіег Ноісі - екстраполятор першого порядку.
П'пії сіеіау - блок затримки сигналу. Він забезпечує затримку
вхідного сигналу на задане число кроків модельного часу.
Блок має два параметри регулювання. Параметр Іпііаі
сошііііоп задає значення амплітуди вхідного сигналу, при
якому блок активізується. Цей параметр задається як конс-
танта або вираз, що обчислюється в процесі моделювання.
Другий параметр - Заіпріе (ігое - визначає число кроків мо-
дельного часу, протягом якого зберігається значення сигналу,
що поданий на вхід блока. Параметр є додатним і може бути
заданий як константою, так і обчислюваним виразом.
7его-Ог<іег НокІ - блок-екстраполятор нульового порядку.
Рипсііоп & ТаЬІез - розділ бібліотеки модулів, призначених для опису до-
вільних функцій. Основні модулі розділу наведені нижче.
Геп - універсальний обчислювальний блок. При його регу-
)	> люванні може бути введений довільний аналітичний вираз,
аргументом якого є вхідний сигнал и. Вхідний сигнал може
мати векторну форму. Результатом обчислення є скаляр.
Прикладом функцій, які реалізуються даним блоком, є довільні ірраціональні
114
Розділ 3- Система 8ІМІЗ1ЛКК пакету МАТЬАВ для моделювання процесів та систем
функції.
Для реалізації ірраціональної функції виду
у = £(и) -
необхідно використовувати наступний блок:
> (1-(1-и)Л2)Л1/2 >
За допомогою даного блока можна задати дробово-раціональну або полі-
номіальну функцію з відповідними значеннями коефіцієнтів.
МАТІАВ
Еипсііоп
Ьоок - ІІр ТаЬІе ~ блок, який виконує лінійну інтерполяцію
вхідного сигналу у відповідності із таблично заданою функцією.
Ьоок - ІІр ТаЬІе (2В) - блок, який здійснює лінійну
інтерполяцію двовимірного вхідного сигналу.
МАТЬАВ Геп - блок, який містить програму із середовища
МАТЬАВ. Дозволяє застосувати до вхідного сигналу довільну
програму, реалізовану у вигляді М-файла. Це може бути як
бібліотечна функція пакета МАТЬАВ. так і власна розробка.
Якщо використовується бібліотечна функція МАТЬАВ, то у вік-
ні регулювання параметрів блока вказується ім’я функції (мож-
на без аргументу и). Інший параметр регулювання блока
ОиХриї. у'./ісЦ.Ь (ширина вихідного сигналу) вказує, що виходом
блока є вектор, розмірність якого дорівнює Оигриі ілйсІШ.
Блок, який визначається при моделюванні. Він може бути
написаний з використанням мови програмування С або
РОКТКАМ, відповідає 8-функції стандартного вигляду і ав-
томатично транслюється в 8-функцію ЗІМІТЬІМК.
Останній блок має важливе значення і дає можливість об’єднати тради-
ційні засоби програмування з можливостями системи візуального математич-
ного моделювання ЗІМІІЬІМК.
Застосування даного блока дозволяє використовувати наявний пакет при-
кладних програм написання на мові С чи РОКТКАЦ.
115
Струтинський В.Б.
3.2.5.	МаіЬ — модулі для реалізації математичних операцій
На рис. 3.16 наведено зміст розділу МаїЬ.
			АЬ5	Я«г) 3оІ*е г >	
< -	ЯіусЯХаіС чДХШГ’ЗІгк			—	' 'Чг)=О	
		>	[иі]		
ткДЗиЖл» ІСКУг«^3» •	їй Сопюіех іо Млітйисівт^поі#-		СотЬіг	іаіогіа	1 Ьодіс	_ГІи|>
<	'	^.^1 Г*"ЛІ*ГМҐ»ІіЙ^	йО.ЛМГґкійїГї		>	Це(и) ЇЇп(и) ЇХІО й	1	Со	^-їи > тріех іо
< >	'	^ииірісїл- ш о^сягі-Нияу <	*	ї**1 айЛ	«лі		СотрІ		>	Мадп еаі-ітад	>	ИисІе-АпдІе
		>	с>	> к>	В< >	і Ргрііисі АМО > елі Орегаіот еи >
,	.	изіп			Оаіп		
?	;	у>-	м^іБаирегжої і	'	І- ф Мадлйий^^іоСвтріеи- і. й Ма£Ь ГипсЬог»		> 	> Мадп іо	II Л_ 1-г ііисіе-> Сотр	> Ьод і^пдіе ех	>	
-	,.	Л Ма^їшП&Іа.		>	к	>	Ма	Ь Гипсііоп
		М<	ігіх 0	аіп	?	
?	- V ЇТіЯЇ’п®-		>	X		ІіпМах Вед_
;. <Х-Л *ЗДГ * І'М’ММИоА :	'	А.			>1	>годис	>	
псет’Шнзу ш 	; г-ф ЯеЙюмІОрдааія '	А Аі ШґІйГїА Рі ®ГИ“4й!ІГї		> > Реіаіі	>паІ 0	> >	Ке регаіог	Іт-^ * аі-ітад іо Зотріех
і	А е^.			—	> *	Еоип	їіоог > «ііпд Еипсііоп
ж і	;	ф 5МегІЗ«п			Зідп		
'	.	С і ІІЕЧ&			> л+	У	5	і<іег Оаіг< 2ІП >
	”	-• Тшзопоіпв&іс ЕипсНоп			42_	ьит		
.	_.	х	Яьга«КіЛЛІ «»* « \ЛТ	і					
Тйй й *й данйггкл'МИЬ’ ійеек і	і 1				Тп	Зопотепіс -ипсііоп
Рис. 3.16. Розділ бібліотеки Маііі, який містить функції
та операції математичного аналізу
116
Розділ 3. Система 8ІМСЬІ\'К пакету МАТЬАВ для моделювання процесів та систем
Модулі розділу МаіЬ містять функції та операції математичного аналізу.
5е(ц)|>
АДО
АЬх - блок, який формує на виході абсолютне значення
вхідного сигналу. Цей блок не має параметрів регулювання.
АІ^еЬгаіс СопзЬгаіпі - блок, що забезпечує знаходження
параметра г, при якому Кг) = 0. При цьому здійснюється
розв’язок рівняння.
СотЬіпаіогіаІ Ьодіс - блок, який забезпечує перетворення
вхідного сигналу у відповідності із заданою таблицею. Блок є
узагальненою моделлю дискретного детермінованого автома-
та. На вхід блока може подаватись як скалярна, так і век-
торна величина.
Сотріех то Ма§піІи<і-Ап§1е - блок, який для вхідного сигна-
лу обчислює амплітуду і/або фазовий кут в радіанах.
Сотріех іо Кеаі Іта§ - блок, що обчислює дійсну і/або
уявну складові вхідного сигналу.
Ооґ-Ргосіисї - блок обчислення скалярного добутку двох
вхідних сигналів.
Саіп - лінійний підсилювач. Даний блок здійснює множення
вхідного сигналу блока на величину, вказану в трикутнику.
Ьофсаі Орегаїог - блок, який включає набір основних логіч-
них операцій: ЛШ), ОК, І\ЮТ тощо. Необхідна операція ви-
бирається при регулюванні блока. Блок може мати довільну
кількість вхідних параметрів (портів).
Ма§піПі(іе-Ап§1е Іо Сотріех - блок, який утворює комплек-
сне число із вхідних сигналів у вигляді амплітуди і/або фа-
зового кута.
МаіЬ Рипсііоп - блок, який використовує для перетворення
вхідного параметра деякі елементарні функції, зокрема екс-
поненту, логарифм, корені, степені та інші. Потрібна функ-
ція вибирається в меню блока.
Маігіх Оаіп - матричний підсилювач вхідного сигналу.
Мін Мах - блок, який забезпечує знаходження мінімального
чи максимального значень елементів вхідного вектора.
117
Струтинський В.Б.
Ргосіпсі - блок, який виконує множення чи ділення кількох
вхідних сигналів. Регульованими параметрами є число входів
блока та вид функції, що виконується.
Кеаі - Іпіа§ іо Сотріех - блок, який утворює комплексне
число із дійсного і/або уявного вхідних сигналів.
Кеіаііопаї Орсгаіог — блок, який реалізує операції відношен-
ня над двома вхідними сигналами. Зокрема, реалізуються
відношення <, >, >, <, == (тотожність), != (не дорівнює).
Вибір операції здійснюється при регулюванні блока. Знак
операції показується на зображенні блока.
Коппс1іп§ Епсііоп -- блок, що включає різноманітні функції
округлення значень амплітуди вхідного сигналу блока.
8і§п - блок, який формує ідеальну релейну характеристику
(сигнатуру).
81ісіег Оаіп - блок-підсилювач зі змінним коефіцієнтом під-
силення.
Тгідопотеігіс Рппсііоп - блок, що забезпечує перетворення
вхідного сигналу за допомогою однієї з тригонометричних
функцій, яка вибирається при регулюванні параметрів із ме-
ню блока.
8пт - блок-суматор вхідних сигналів (у даному випадку
трьох та двох). Іконка блока може мати різну форму.
Даний модуль може використовуватись у двох режимах роботи: перший -
додавання (із врахуванням знаків) вхідних сигналів; другий режим відповідає
підсумовуванню компонент вектора, що подається на вхід блока. Для керування
роботою блока використовується лише один параметр Ьізі оі 8іп§5 (список зна-
ків). Цей параметр може бути заданий у вигляді послідовності знаків “+” і
Наприклад, (+ + -). При цьому число знаків визначає число входів блока, а сам
знак - полярність вхідного сигналу. Якщо параметр задається у вигляді цілої
додатної константи (більше 1), то ця константа визначає число входів, які всі
вважаються додатними. Коли значення константи дорівнює 1, то блок працює у
другому режимі і, отже, визначає на виході суму компонент вхідного вектора.
Число входів і знаки відображаються на виході блока.
Еквівалентом позначення блока на структурних схемах систем автоматич-
ного керування є суматор
118
Розділ 3. Система ЗІМІЗШМК пакету МАТРАВ для моделювання процесів та систем
3.2.6.	Мопііпеаг - модулі, що реалізують нелінійні функції
На рис. 3.17 наведено основні модулі розділу Мопііпеаг.
: ф ВаскІа$И---------------г
: - ф Соиіопіз & Шгаш Рпс&жН
ф Оеадгопе--------------
у ф Мегш!5йиЛ--------------
• ф МиМрогі ЗйГсЬ--------і
\ 9
ВаскІагЬ
Реасі 2опе1
СоиІотЬ &
т/ігсоиї Ггісііоп
биапйда__
ВМе Ійійе»
ВеІ^-----
$акіайоп-
5«івЬ----
>н
йаіе Цтііеґі
5аіигаііоп1
Миііірогі ЗучіісЬ
Мапиаі ЗілііісЬ
ЗілііісЬ 1
№ і$ їм *§гпу«<3№гійпеаг* Ьк ск

Рис. 3.17. Розділ бібліотеки Мопііпеаг, який включає модулі
для опису нелінійних елементів систем, що моделюються
Мопііпеаг - розділ бібліотеки, що включає модулі для опису нелінійних
елементів системи.
Блоки, що входять до розділу, дозволяють виконати математичне моде-
лювання всіх основних суттєвих не лінійностей, які зустрічаються при моде-
люванні процесів та систем. Суттєві нелінійності відповідають розривним
функціям довільного виду, петлеподібним неоднозначним характеристикам та
логічним умовам.
Розділи блоку є потужним засобом математичного моделювання реальних
технічних систем і процесів, що в них протікають.
Блоки розділу Мопііпеаг дають можливість формувати дискретні матема-
119
Струтинський В. Б.
тичні моделі процесів з неперервних функціональних залежностей, які опи-
сують процес.
Основні модулі розділу Копііпеаг:
ВаскІазЬ - блок призначення для формування петлеподібної
лінійної характеристики (гістерезис у системі).
СоиІотЬ & Уізсоиз Ггісілоп - характеристика модуля відпо-
відає сумі кулонівського і рідинного тертя.
Веасі 2опе - блок, який заміняє значення вхідного сигналу,
що лежить в даному діапазоні, нульовим значенням.
МапиаІ 8\уіісй - блок, який переключається “вручну” і ви-
конує функцію перемикача на блок-схемі.
Використання даного блока дає можливість реалізувати зміну структури
моделі.
МиИірогІ ЗшіїсЬ - модуль, що забезпечує підключення до
виходу одного із інформаційних каналів.
Робота модуля ілюструється блок-діаграмою, показаною на рис. 3.18.
ЗууіісЬ
Рис. З-18. Схема, яка ілюструє роботу блока Миііірогі Зтіісії
Підключення здійснюється в залежності від значення амплітуди керуючо-
го сигналу, що подається на вхід К. Сигнал на вході К округлюється до ціло-
го числа, яке визначає номер входу. Якщо керуючий сигнал менший 1, то
підключається 1-й канал. Коли керуючий сигнал більший 3, то підключається
3-й канал. Параметром регулювання блока є число інформаційних каналів
МшпЬег о( іприіз. Для даного випадку цей параметр дорівнює трьом.
Цей блок призначений для формування математичних моделей змінної
структури. Зміна структури 8-моделей здійснюється автоматично при вико-
120
Розділ 3. Система 8ІМІЗ[.ІХГК пакету МАТРАВ для моделювання процесів та систем
нанні певних умов.
Опапіігег - блок, який формує дискретний вихідний сигнал із
заданою дискретністю.
Цей блок призначений для формування Кусково-постійних дискретних
моделей процесів. Нижче наведено приклади застосування даного блоку (див.
розділ 6.3.2).
Каїе Іітіїед - блок, що обмежує величину відношення сигна-
лів.
Кеіау - блок, який забезпечує формування релейної характе-
ристики з петлею гістерезису. Блок має чотири параметри
регулювання: 8\чіІсЬ оп роіпі - точка включення; §\уіісЬ о£
роіпі - точка виключення; Опірні \сйеп о£ - вихід при
виключеному стані; Опірні хчЬеп оп - вихід при включеному
стані.
Заінгаїіоп - блок, який формує лінійну характеристику з на-
сиченням.
ЗиіїсЬ - модуль (перемикач), який служить для перемикання
входів 1:3 на вихід. Якщо значення амплітуди сигналу 2-го
входу більше або дорівнює заданому пороговому значенню
ТйгезЬоІсі, то на вихід подається сигнал з 1-го входу, а якщо
менше - з третього.
На рис. 3.19 наведено приклад використання блока 8'Л'іссЬ (параметр
ТЬгезІюІБ = 7).
СопзіагЧ 2
Рис. 3.19. Схема, яка ілюструє роботу блока 5тісИ
Періодичність переключення блока БхсіІсЬ визначається кроком модельно-
го часу (параметр Зашріе Ііте) блока, підключеного до його 2-го (керівного)
входу. Блок ЗшіїсЬ має один параметр регулювання ТЬгеНіоІсІ (поріг). Він
може задаватись як константа або обчислюваний вираз.
121
Струтинський В. Б.
3.2.7.	8і§па1 & Зувіет - модулі для формування структури системи
На рис. 3.20 наведено основні модулі розділу 8і£па1 & Зузіет.
$ оді*	
	
'		ф 8іЛ8у5іет—	к	
г	і	& іпі	ЗиЬЗузіет	(_ і
	
І . і	ф ЕгаЬІе		СпП |п1
	ГТІ
,	,. V * "99^	;	Я	1-і'
Р«*<?> С		 -Г-	< ,—
 чф ви* □еіссим	" '	
ї :	'	Г>дейлі наКІА іЬ:^о^«Е*т		р5<і
!		,  ф Оаіа Зіоіе Мелгкху		СоМіділаЬІе 	 А	ЗиЬгугіет
!	;	..... А Оаіа £іоіе Яеагі	Оаіа Зіоге Метену	А >
І ‘	і . А ГївІА ^»ІМйХл/|ЙА	4.	^”7“!	Оаіа Зіоге
	1„._.ІЦ. 1
<;	1- ф 0а*аТуре Сопуег5іоп—к	Раь виТГшпіе 1 І>иЬІе) [> И	Оаіа Туре
ф Оетих		ї*	С0П¥ЄГ5І0П
' Еїош	|> !		 1 (А1 >>
	1	1	1	/
& ЕипсІюггСаІІ Бепеї’аіог—1	) Ю р	Егот
	Еипсііоп-СаІІ	Г/11
Й	: А (ЇГЙП		1	Оепегаіог	л, 1-І
	
| * ! ;--ф ОоІоТадУШЙу	[	_____ !А! ‘3’1°
	«оіо Іад УІ5 ЬіІІІу	| г~|.
♦,	- «аг игоипи	।	
і,	і	А	_ ІУ'	ОгоипсІ
у	:	. • - ф Нй Сктіпд		
	Ні( сгозгігід	>——— >
* - Ф їй		
;	— ф Меіде	ь	іс 	 Мегде >
і] -	ф МогіеІІгЙо	1	Мегде 		  • 		 МоаеІ Іп^о
тил	1	1	1	
„	. ф РгоЬе						ЯШ:0. Т5:(0 О). С:0 Ь
' ф Зеїесіог			>о"*1	Р,°Ье
" ;	ф Твттйа	г			Зеїесіог	
;	; .ф щйь	ї-	.	Теипіпаіог 	х 	- >
	: А ПиН	*	игілк	/ 1 1
•	иід і	
	□иі1
ТЬії із ГКе ’5ігпи8пІ<І/8іопаІ5	~	;	
 & Зум®тй‘ Моск|	
Рис. 3.20. Розділ бібліотеки Зідпаї & Зузіет
122
Розділ 3- Система 8ІМІТТІМК пакету МАТБАВ для моделювання процесів та систем
8і§па1 & Зузіеіп - розділ бібліотеки, що включає модулі формування
підсистем та зв’язків між ними. Більшість блоків розділу 8і§па1 & Зукіет
призначено для розробки 8-моделей підсистем. Основні модулі розділу:
-------- ЗиЬзухіега - блок, який є заготовкою підсистеми, що входить в
~основну систему моделі. Підсистема — це самостійна 8-модель
більш низького рівня, ніж основна система. Підсистема може
включати підсистеми ще більш низького рівня. Блок використо-
вується для створення нової підсистеми.
Підсистеми, що входять в 8-модель, можуть бути приведені до вигляду
бібліотечних блоків системи 8ІМШІМК. Ця операція називається маскуван-
ням підсистеми.
Маскована підсистема (Мазкесі ЗнЬЗузіет) - це підсистема, структуру
якої не можна побачити безпосередньо з блок-діаграми. Ця підсистема має
власне діалогове вікно вибору параметрів і, як правило, власну іконку.
Засоби системи 8ІМІЛЛМК. дозволяють створити власну бібліотеку бло-
ків, використовуючи масковані підсистеми. Бібліотеки можуть включати бло-
ки, розроблені самостійно, або блоки з наявних розділів бібліотеки.
Іп 1 — блок (вхідний порт), який забезпечує вхід в підсистему в
точці Іп 1. Він має три параметри регулювання: Роті пишЬег - ви-
значає порядковий номер вхідного порта; Рогї тсісІЙі - змінює роз-
мірність вхідного сигналу; 8атр1е гіте - визначає дискретність ча-
су, з якого блок Іп буде реагувати на зміну вхідного сигналу.
------- ЕпаЬІе - блок, який здійснює керування роботою підсистеми.
Підсистема, яка має хоча б один блок ЕпаЬІе, є керованою і має
-І 1— назву Е-підсистеми.
При включенні даного блока в підсистему їй автоматично добавляється
керуючий вхідний порт. Підсистема включається в роботу, коли сигнал, що
додається на керуючий вхідний порт, є додатним. Якщо керуючий сигнал змі-
нює знак, то підсистема включається на тому кроці модельного часу, коли
величина сигналу переходить нульове значення. Блок ЕпаЬІе має два пара-
метри регулювання: 8іаіе хгЬеп епаЬІіпд - стан при запуску; 8Ьо\у опірні
роті - показати значення вихідного порта.
" Тгі§£ег - модуль, який здійснює керування роботою підсис-
>>	теми шляхом блокування. Підсистема, яка має хоча б один
— блок Тгі§§ег, має назву Т-підсистеми.
Т-підсистема працює лише на тому кроці моделювання, на якому була
зміна полярності вхідного сигналу, що подається на блок Тгі§§ег.
123
Струтинський В. Б.
Т-підсистема не повертається у вихідний стан, її поточний стан зберігається
до чергового запуску.
Якщо підсистема має хоча б один блок ЕпаЬІе і хоча б один блок Тгі§§ег,
то вона має назву ЕТ-підсистеми. Дана підсистема має два вхідні керуючих
порти. Підсистема працює наступним чином. Коли на певному кроці моделю-
вання має місце зміна полярності керуючого сигналу, який подається на блок
Тгі§§ег, то перевіряється значення сигналу, що подається на блок ЕпаЬІе.
Якщо це значення більше нуля, то підсистема включається і працює протягом
даного кроку моделювання.
------ Ваіа 81оге Метогу - блок, призначений для збереження да-
Д них. Він має два параметри регулювання: Вага 8іоге пате -
------- імена даних, що зберігаються; ІпіХіаІ єаіие - початкове зна-
чення. Останній параметр визначає також і формат даних,
що зберігаються.
Наприклад, якщо початкове значення встановлене як [[2 4] [3 7]], змінна
є масивом розмірністю 2x2. Область доступності змінної, яка зберігається,
визначається тим, де розміщено блок Оаїа 8іоге Метоге. Коли він розміще-
ний в блок-діаграмі самого верхнього рівня, то дані, які зберігаються, досту-
пні у кожній підсистемі 8-моделі. Якщо ж цей блок знаходиться в деякій під-
системі, то область доступності даних розповсюджується на цю підсистему і в
неї включені підсистеми (при їх наявності). Разом з блоком Ііаіа 8іоге
Метогу використовуються блоки введення-виведення даних.
Блоки мають два параметри регулювання.
□аіа 8іоге Кеасі Параметр Оаіа 8іоге Мате (ім’я) повинен
співпадати з параметром блока Ваі.а 8соге
Метогу. Інший параметр 8атріе Ііте ви-
Е)аіа 81оге \¥гй.е значає крок зміни модельного часу.
Оетнх - модуль, який виконує операцію розділення вхід-
ного вектора на вектори меншої розмірності або скаляри.
Його функція протилежна функції блока Мих, який буде
розглянуто нижче.
Параметром регулювання блока є величина МишЬег о( оиіриіз - число ви-
ходів. Число виходів може відрізнятись від розмірності вхідного вектора
(може бути меншим). Якщо число виходів дорівнює розмірності вхідного век-
тора, то на кожному виході блока формуються скалярні величини. Блок-
схема моделі, що відповідає даному випадку, наведена на рис. 3.21, а.
Якщо розмірність вхідного вектора М більша за число виходів блока N.
124
Розділ 3. Система 8ІМІ/ИМК пакету МАТЬАВ для моделювання процесів та систем
то на перших (п — 1) виходах блока формуються вектори, розмірність яких
М
дорівнює цілій частині відношення —. Розмірність вектора на останньому
N
виході дорівнює остачі від ділення. Блок-схема моделі, що відповідає даному
випадку, наведена на рис. 3.21, б.
Ргош - блок, який забезпечує прийом даних А з підсистеми.
Блок Ргош може бути зв’язаний лише з одним блоком СоСо.
Соіо - блок, призначений для передачі даних із підсистеми в
систему. Він має два параметри регулювання. Та§ (ознака)
означає ім’я даних - А. Інший параметр Та.Ц чізіЬіІііу має
три пункти: Іосаі - змінна, що передається, є локальною,
тобто вона визначена тільки в тій підсистемі, де знаходиться
блок Ооіх>; 8соре - змінна, визначена у всіх підсистемах
більш низького рівня, що пов’язані з даною підсистемою;
ОІоЬаІ - змінна є глобальною, тобто вона доступна у всіх
підсистемах і в основній системі 8-моделі. Для локальної
змінної на позначенні блока застосовуються квадратні дужки
(як у даному випадку), для параметра 8соре - фігурні, для
глобальної змінної - без дужок.
а)
Рис. 3.21. Приклади застосування блока Петих
Приклад застосування блоків Соі.о та Ргош наведено на рис. 3.22.
125
Струтинський В. Б.
> Іп 1
> !П2
ЗиЬзузіет
а)
б)
Рис. 3.22. Застосування блоків Ргот та Соіо
для зв’язку основної системи (а) з підсистемою (б)
Огоиші - блок, який використовується для блокування вхід-
ного порта.
НІГ СгО88ІП§ - блок, який виявляє момент часу, при якому
вхідний сигнал приймає певне значення. В даній ситуації на
вході блока формується одиничний сигнал. Блок має три па-
раметри регулювання: Ніг сгоз8іп§ оіНег - задає певне зна-
чення вхідного сигналу; Ніі сго88іп§ сіігесііоп - вказує на-
прямок переходу вхідного сигналу через задане значення;
8Ьо\у опірні, рогі - вказує формат використання блока.
ІС - блок, який дозволяє встановлювати довільне початкове
значення сигналу. Тривалість перебування системи в даному
стані відповідає кроку моделювання.
Мег§е - блок, який виконує об’єднання сигналів, що по-
даються на його входи, в один сигнал. Всі вхідні сигнали по-
винні мати одну розмірність.
Мих - модуль, який виконує об’єднання вхідних параметрів
в один лінійний вектор. При цьому вхідні параметри можуть
бути як скалярними, так і векторними. Блок Мих має один
параметр регулювання - МшпЬег о£ іприіз (число входів).
Призначення блока Мих протилежне функції розглянутого
блока ІЗетих.
Шляхом трансформації іконки блока він приводиться до
більш простого вигляду. При цьому назва блока, як правило,
не вказується. Така форма іконки використовується з метою
спрощення блок-схеми моделі.
Наприклад, якщо на перший вхід блока подається матриця розміром 2><2,
а саме: [[1 2] [3 4]], на другий вхід блока подається константа 5, на третій
126
Розділ 3- Система	пакету МЛТЬАВ для моделювання процесів та систем
вхід - константа 6, то вихідний вектор буде мати вигляд: [1 2 3 4 5 6]. Блок-
схема моделі, що реалізує дану процедуру, показана на рис. 3.23.
Зеїесіог - модуль, який здійснює вибір відповідних компо-
нент вхідного вектора і формування із них нового вихідного
вектора. Блок має два параметри регулювання: ЕІетепіз -
список номерів компонент вхідного вектора, які потрібно ві-
дібрати; Іприі роті и’їсігії - розмірність вхідного вектора.
Розмірність вихідного вектора менша або дорівнює розмірності вхідного
вектора.
Якщо на вхід блока Зеїесіог подається матриця, то використовується на-
скрізна нумерація її компонент по рядках. Приклад роботи блока ілюструєть-
ся схемою, зображеною на рис. 3.24.
Рис. 3-23. Використання блока Мих для об’єднання одного матричного
та двох скалярних входів в один векторний вихід
Зеіесіог
Рис. 3.24. Формування двомірного вихідного вектора із входу у вигляді масиву
На вхід блока Зеїесіог подається масив, у першому рядку якого три елементи
127
Струтинський В. Б.
[1 2 3], а у другому - два елементи [4 5]. На виході одержано двомірний вектор.
Теппіпаіог - модуль, який виключає вихідний порт.
^Уісіііі - блок, призначений для знаходження розмірності
сигналу. Знайдена розмірність виводиться на зображенні
блока.
Оні 1 - модуль (вихідний порт), призначений для виходу із
підсистеми. Даний модуль має три параметри регулювання:
Рогі нитЬег - встановлює порядковий номер вихідного
порта; Опірні 'Л'Ьеп сІізаЬІесі (значення на виході при
забороненому стані) - використовується тоді, коли блок
входить до підсистеми, що керується. Даний параметр
відповідає двом пунктам: Неісі - на вихід подається сигнал,
сформований при останньому спрацюванні підсистеми;
Кезеі - на вихід подається сигнал, що відповідає
початковому стану підсистеми. Третій параметр Іпіііаі Опірні
встановлює початкове значення вихідного сигналу.
Приклад застосування модулів Іп та Оні наведено на рис. 3.25.
Рис. 3.25. Застосування модулів для зв’язку блока основної системи (а)
із 5-моделлю підсистеми (б)
Вхідні та вихідні блоки (порти) дозволяють зміну назви та коментарі.
У випадку навності в 8-моделі кілька вхідних (вихідних) блоків з однією
назвою, вони нумеруються цифрами: 1, 2,... При цьому блок, який введено
першочергово, немає номера.
128
Розділ 3. Система 8ІМЇЛ.ШК пакету МАТІ.АВ для моделювання процесів та систем
3.2.8. Сопігої Зузіега ТооІЬох, ЗіаіеНоми та Зітиііпк Ехігаз —
модулі зв’язку між системами, візуалізація процедури моделювання
та модулі обробки сигналів
На рис. 3.26 наведено основні модулі розділів Сопігої Ьукіст ТооІЬох,
8ЬаіеНо\у та Зітнііпк Ехігаз.
		-							
В І	4И Сопігої Зузіеп) ТооЬох	’ і	Ігммй РгагЛ	• - .. .....								
	чф- нфШГцим.	Іприі Роіпі			іШ1 1П				
	* чф иі і	В5->							
	П і 4л. £5лі»лі	’:					ЬТІ Зугіе			
	 ф иікриггсіпс И зійеіісж	!; "	Р|лм»і ______- - --- .	.				Оиіриі Роіпі							
в							&		
	•И 5п*ЛпкЕЛа®	іі дд АскйопаІ Оі«с«йе Й Асіс£Цопаі Ціпе®	' Із  ІЙ АЖЙопаІ 5іпк$	;;						43		
і-3		>1					СИагі		
	'	7 '	А-МДи иСНГскзил • 1	?'	Аиіо Соггеїаіог				>	В		
		>	Е		Ауєг 5ре		адіпд с±гаі 0	5 оіліег ЄП2ІІУ	
	А¥ЄГауіПС| зреСиІІіП АПоіу2.ЄІ	"т	> АуегадіпдЗ	іесіги	ті Апаїугег		>	ї<£|		
	клоа-ї иляїстокм						.. .. Ть-ьі 1			? С гозз		Согге	аіог	
	*	’ 'і|г ГлЖ<?( ОрЄ?Си£Я МСЛ^Ну'"		;	Роілієг ЗресігзІ Оепзііу				>	рхЗ		
	а ЕірПор« ЯЗ-І1І Цпеегіг^огі	;• Ш-йУ Тгап5Іогт<йіопз	І					£ А	ресіги паїугє	ТІ {	
к Ше *5ітиШ*3‘ Нижу									
Рис. 3.26. Основні модулі розділів Сопігої Зузіет ТооІЬох, 81а1е{1огю
та Зітиііпк Ехігаз
129
Струтинський В.Б.
Розділи включають набір додаткових модулів, що дозволяють здійснити ана-
ліз результатів моделювання. Найбільш характерні модулі наведені нижче.
Іприі Роіпі - блок, призначений для формування входу сис-
теми.
Оиірні Роіпі - блок формування виходу системи.
ЬТІ Зузіет - системний блок, який може описувати як непе-
рервні, так і дискретні процеси. В даному блоці може бути за-
дано довільну трансформуючу функцію.
СЬагІ - блок формування заготовки діаграми 8іаІе£1о\у.
Аніо Соггеїаіог - автокорелятор, що використовує графічне
вікно. Потребує засобів для обробки сигналу.
Ауега§іп§ Ро’лег Зресігаї Оепзіїу - аналізатор спектра, що ви-
користовує графічне вікно.
Сго88 Соггеїаіот - блок визначення кореляції сигналів. Для
своєї роботи потребує бібліотеку 8і§па1 Ргосе88іп§ ТооІЬох.
Рохчег Зресігаі Пепзіїу - аналізатор спектра, який визначає
спектральну щільність сигналів. Використовує графічне вікно.
Зресігит Апаїугег - аналізатор спектра, що використовує гра-
фічне вікно. Має два входи, які підключаються відповідно до
входу і виходу системи.
В математичному пакеті МАТЬАВ версії 6.0 додаткові розділи бібліотеки
8ІМІЛАМК. значно розширені, в них наявний широкий набір засобів обробки
сигналів, значну увагу приділено роботі з матрицями, реалізовані всі основні
операції з ними.
130
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
РОЗДІЛ 4
Математичні моделі процесів у вигляді функціональних рядів
4.1. Числові послідовності, функціональні ряди
4.1.1. Визначення числових послідовностей та функціональних рядів
Числові послідовності, числові та функціональні ряди є ефективним засо-
бом аналізу процесів та систем. Вирішення багатьох задач математичного мо-
делювання процесів зводиться до обчислення сум функцій з досить великим
(нескінченно великим) числом доданків [1]. Звичайно функції, які утво-
рюють суму, записуються в загальному вигляді, який залежить від порядко-
вого номера доданка.
Найбільш простим випадком таких сум функцій є числові послідовності.
Послідовність, яка позначається як {ап}, - це функція, задана на множині на-
туральних чисел п = {1, 2,...}. Зокрема, числовими послідовностями є ариф-
метична та геометрична прогресії.
Арифметична прогресія - це числова послідовність, формула обчислення
кожного члена якої має вигляд:
аи = а0 + п-д,	(4.1)
де а0 - перший член арифметичної прогресії; сі - різниця прогресії; п - індекс,
значення якого охоплює всю множину натуральних чисел, п = 0, 1, 2,...
Для обчислення суми перших п-членів арифметичної прогресії використо-
вують формулу:
Еа.	+пс!)	(4.2)
іл> 2
Геометрична прогресія - це числова послідовність, члени якої обчислю-
ються за формулою:
ан = аогп (п = 0, 1, 2,...),	(4.3)
де а0 - перший член прогресії; г - знаменник геометричної прогресії.
Формула для обчислення суми п перших членів геометричної прогресії
має вигляд:
п	1 - гп+1
5п=£а,=ай——-.	(4.4)
ІЛ)	1 — 1
При математичному моделюванні часто виникає необхідність знаходження
сум, які складені з великого числа доданків. При цьому корисно використо-
вувати більш прості суми, які представляють собою типові ЧИСЛОВІ ПОСЛІДОВ-
ОЇ
Струтинський В. Б.
кості. Нижче наведено деякі практично важливі числові послідовності та фо-
рмули для обчислення їх часткових сум:
п(п + 1) .	V- <4	2

5>2

2
п(п +1) (2п + 1)
6
п2(п + І)2
у (2і - О2 = ЛИвіїІІ
&	з
V (2і - І)3 = п2(2п2 -1);
(4.5)
4
1
= 1--1
і(і + 1)
1
1
І=1 і(і + 1)(і + 2)
Обчислення часткових
2 1______________
2 _2 (п + 1)(п + 2)
сум числових послідовностей довільного виду
здійснюється за допомогою математичних пакетів. Нижче подано фрагмент
документа МаСЬСАВ для обчислення часткових сум числових послідовностей:
і» 1
У—= 2.718 .
іГоп!
з нескінченно великою кількістю складових утво-
У—= 2.717
п!
Числові послідовності
рюють числові ряди.
Нескінченний ряд ао, а); аг,..., а,Л)... чисел (членів) збігається, якщо по-
слідовність його часткових сум
має границю. В цьому випадку сума ряду визначається за формулою:
8 = Ііт У а..
Використання числових рядів дозволяє в деяких випадках значно спрос-
тити алгоритми математичних моделей. Числові ряди корисні для оцінки па-
раметрів систем і процесів. Для цього можна використати набір деяких ха-
рактерних числових рядів. Нижче наведено суми деяких практично важливих
числових рядів:
1 _ я2
1 + І71г = сЬ1; 1 + уЬ12і = со8І;	=	(4 6)
“ї (2і)!	(2і)!	£ 2і — 1	4 К 7
У_1_=1; У-------------1------ = . 1
і(і + 1)	Ти Кі + 1).. .(і + т) т • т!
Для знаходження суми числових рядів застосовують засоби математичних
пакетів.
132
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
Нижче наведено фрагмент документа МаїЬСАІ), який ілюструє знахо-
дження суми числових рядів:
Ііт %/2 -> 1	1іт(-1)” він —	0
п->оо	п—>0С	Л
Ііт 7 * 1п(10 * п +1) —> оо	. ч
’	(4./)
Якщо результатом розрахунку є нескінченність, це означає, що ряд не
збігається. В останньому випадку формул (4.7) сума ряду символьно не роз-
раховується, про що свідчить відсутність результату розрахунків, тобто
повтор умови. Якщо сума ряду не обчислюється, то результатом розрахунку
буде повідомлення про відсутність збігу ряду.
Узагальненням числових послідовностей та числових рядів є функціо-
нальні послідовності та функціональні ряди.
Функціональний ряд представляє собою ряд функцій незалежної змінної
х, а саме:
<Ро(х), Фі(х), ф2(х),...
Функціональний ряд збігається до функції (суми) 5(х) при кожному зна-
ченні х, при якому існує границя:
8(х) = ііт У <р; (х).
Нижче наведені деякі приклади функціональних рядів. Практично важ-
ливий функціональний ряд складений із степеневих функцій. Його сума до-
рівнює:
а0 +аох + аох2 +...= а0]Гх' =(|х| < 1).	(4.8)
м 1-х
Цей ряд іноді називають нескінченною геометричною прогресією.
Нижче наведено приклади практично важливих рядів, складених зі спе-
ціальних функцій, зокрема із функцій Бесселя першого роду та тригономет-
ричних функцій [ 1 ]:
10(х) + 2^ (-!)'• 52і(2) • соя(2і0) = соя(г • соя 0) ;
к І=1	(4.9)
- 2]Г (-1)1 • 5 2і (и) • [соя((2і -1)0)] = яіп(г • соя 9).
І = 1
Узагальненням даних залежностей є ряд з комплекснозначними функція-
ми, який визначає експоненціальну функцію уявного аргументу:
Л<2) +	+(-!)’ •е 8п,й]=е^5,г‘й, і = лГї. (4.10)
І = 1
Використання функціональних рядів забезпечує спрощення багатьох опе-
133
Струтинський В. Б.
рацій математичного моделювання та дає можливість надати певного фізично-
го чи математичного змісту математичній моделі процесу чи системи.
Для спрощення обчислювальних операцій часто використовуються степе-
неві ряди виду:
^аі(х-х0)і =((х),	(4.11)
де Хо - деяке значення х (може бути х0 = 0).
Багато функцій, в тому числі і спеціальних, порівняно просто виражають-
ся через степеневі ряди такого виду. Нижче наведено приклади розкладу в
степеневі ряди деяких широко використовуваних функцій:
ег = 1 + х + —— + —— + ... (Іг| < оо) ; 8іп г = г - — + — + ...;
2! З! "	3! 5!
7.2	7' _	23	25
соя 2 = 1----------+ — + ...;	8Йг -? + — + — + ..,;
2!	4’	3!	5!
’2	7і	72	73	7і
сйг = 1 + — + — +... ;	1п(1 + г) - г----------+ -----------± ...
2!	4!	2	3	4
(4.12)
(4.13)
Розклад деяких спеціальних функцій у степеневі ряди наведено нижче.
При математичному моделюванні використовуються різноманітні функ-
ціональні ряди. Такі ряди функцій (функціональні ряди) називаються в за-
лежності від виду їх складових.
Найбільш поширеним при математичному моделюванні є використання
степеневих рядів, рядів, складові яких є тригонометричними, гіперболічними
чи показниковими функціями, а також рядів, складові яких є спеціальними
функціями. Деякі практично важливі функціональні ряди мають спеціальні
назви, наприклад, це степеневі ряди - ряди Тейлора чи Маклорена, ряди,
складені із тригонометричних функцій - ряди Фур’є, ряди складовими яких
є циліндричні функції, ~ ряди Фур’є-Бесселя, тощо.
В даному підручнику розглянуто найбільш важливі для практики матема-
тичного моделювання технічних систем механіки функціональні ряди. В пер-
шу чергу, це - ряди Фур’є, складовими яких є тригонометричні функції.
Розгляду таких рядів присвячено спеціальні розділи підручника. Окремим
пунктом розглянуто степеневі ряди Тейлора і Маклорена та їх застосування з
використанням засобів математичних пакетів. Певну увагу приділено рядам
на основі спеціальних функцій. Це, зокрема, ряди Фур’є-Бесселя, що вклю-
чають циліндричні функції.
Розглянуто також ряди на базі розривних функцій. В даний час вони не-
достатньо широко застосовуються в практиці математичного моделювання
технічних систем механіки, хоча їх використання є перспективним і забезпе-
чує нові можливості аналізу процесів та систем, в тому числі стохастичних
процесів у технічних системах.
134
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
4.1.2.	Ряди Тейлора та Маклорена
Такі ряди застосовуються в багатьох випадках аналізу процесів та систем,
зокрема для опису довільних гладких функціональних залежностей викорис-
товують їх розклад в ряд Тейлора.
Нехай функція Кх) має в точці Хд похідні всіх порядків до п-го включно.
Тоді для функції Кх) справедлива формула Тейлора, яка дає розклад даної
функції в степеневий ряд наступного виду:
Кх) = Кх0) + “р- (х - х0) + (х - х„)2 +
+ ... +-—^-(х-х0)п + Кп(х),	(4.14)
п!
де всі похідні обчислені в точці х = хо і є константами.
Останній доданок у формулі Тейлора
Кп(х) = О[(х - х0)п]
називається остаточним членом ряду Тейлора. При всіх х -» хд Кп(х) є вели-
чиною нескінченно малою у порівнянні 3 (х - Хд)п.
Ряд Тейлора, в якому розклад здійснено відносно нульової точки
(хо = 0), називається рядом Маклорена. Ряд Тейлора (4.14) без остаточного
члена називається поліномом Тейлора.
Інструментарій математичного пакету МаійіСАП дозволяє безпосередньо
знайти поліном Тейлора необхідного степеня довільної функції. Для цього в
панелі символьних операцій пакету МаНіСАП (див. рис. 2.3) є кнопка
якій відповідає заготовка:
 8ЄГІЄ8,  ->
В лівий затушований квадрат цієї заготовки треба внести функцію, що
розкладається в ряд, а в правий затушований квадрат - змінну і точку, в якій
здійснюється розклад, наприклад, х = хд.
Приклади розкладу деяких елементарних функцій в ряд Тейлора за до-
помогою пакета МаіЬСАВ наведено нижче.
8Іп(х)8ЄГІЄ8, X = її —> ~Х + її + —  (х - їїУ-(х - її
' ’	6 '	’	120 '	•
V	а	1	2	1 3	1	4 І5
Є 8ЄПЄ8.Х = 0 -> 1 + Х+ — X + —X +---X +-----X
2	6	24	120
1п(х)їЄПЄ8, X
= 7->1п(7)+|
х -1 - — -(х - 7Ї +
98 4	7
(4.15)
+ —-(х-7)1-
1029 у 1	9604
.(х-7/
—-(х-7)5.
84035 '	7
135
Струтинський В. Б.
Можливості математичних пакетів дозволяють здійснювати розклад в ряд рі-
зноманітних, в тому числі спеціальних, функцій. Розклад гіперболічних функцій
в ряд Тейлора (ряд Маклорена) за допомогою пакету МаіЬСАО має вигляд:
1 1
(сО8Ь(х))8ЄГІЄ8, х = 0 -> 1 + — х2 + — х“;
(іапЬ(х))8егіе8, х = 0 —> х - — х3 + — х5.
'	' "	’	3	15
(4.16)
Розклад спеціальних функцій в ряд Тейлора часто дає змогу значно
спростити математичну модель. Нижче наведено розклад в ряд Маклорена
функції Бесселя першого роду нульового порядку:
(11 <- 0), (12 <- 0), (ІЗ <- 0Ц14 <- 0), (*5 <- 0)
мо)+ 1’ х+х2 +
(Д0(х))8ЄГІЄ8,Х = 0 -»
• х4
х5
(4.17)
Розклад в ряд Тейлора дає наближення функції степеневим рядом з необ-
хідною точністю. Абсолютно точно розклад в ряд відповідає функції, якщо
вона представляє собою поліном, а кількість членів ряду взята не менша за
кількість складових поліному. Це ілюструється наступним прикладом:
1 + 2х2 + Зх3 + 4х4 + 5х5 8егіе8, х = 0 -> 1 + 2х2 + Зх3 + 4х4 + 5х5.
Розклад функції в ряд дозволяє здійснити її кількісний та якісний аналіз
в точці розкладу. Наприклад, за розкладом функції
8іп(х)8егіе8, х = 0.2 -» 0.00265601522681288924 + 0.98006657784124163112х -
- 0.099334665397530607730(х - 0.2)2 - 0.163344429640206938(х - 0.2)3
можна зробити висновки, що в точці х = 0.2 функція зіпх має значення
0.00265... (перший доданок поліному Тейлора). В цій точці функція є зрос-
таючою, оскільки коефіцієнт при (х - 0.2) більший 0, причому швидкість
зростання зменшується, бо коефіцієнт при (х - 0.2)2 є від’ємним.
Аналіз розкладу функції в ряд Тейлора дає можливість знайти екстрему-
ми функції і, навіть, точки розриву функції та її похідних.
Ряд Тейлора використовується і для аналізу функцій кількох змінних.
Якщо визначена функція £(хі, Х2, ..., хп) п змінних, то її розклад в точці з
координатами х] = а^, Х2 = а2, ..., хп = ап має наступний вигляд:
4 П П
1=1 І=1
~аіХхі -аі)+°[(хі ~аі)(х, - аЛ
дх^х,	\
(аРа2,...,ап)
(4.18)
136
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
Зокрема, для функції двох змінних £(х, у) її розклад в ряд Тейлора в то-
чці (хо, у0) має вигляд:
+ (У“Уо)2
(4.19)
Розклад функції двох змінних в ряд Тейлора при х = у = 0, як і раніше,
називається рядом Маклорена. Для функції двох змінних ряд Маклорена має
вигляд:
(4.20)
При розкладі функцій кількох змінних в ряд Тейлора обчислення частин-
них похідних може бути здійснене аналітичним способом або з використан-
ням інструментарію пакету Магії САП у символьному чи чисельному вигляді.
Нижче наведено фрагмент документа МаіЬСАВ, що містить приклади
розкладу в ряд Тейлора функції двох змінних:
(8Іп(х • у)) • е ^ +У )8егіе8, х = 0; у - 0, —> х • у - х3 • у - х • у3
(віп(х • у))’ е'^^зегіев, х = 1; у = 0,4 -> у • ехр(-1)-
— у *ехр(—1)* (х — 1) —(х — і)2 "У •ехр(-1)-^"у3 -ехр(-1)
о
(соз(х • у))* Є 2^8ЄГІЄ8, X = 0; у = 0, -» 1 - х2 - у2 + — • х4 + — • х2
2	1	4
У +2*У
(сО8(х • у))’ е ^2+У ^8ЄГІЄ8, X = 0; у = 0,8 -> 1 - х2 - у2 + — • х4 + - • х2 • у2 +
1	4
+ — • у
2
6
6
+ —«у
6 ?
6
137
Струтинський В. Б.
4.1.3.	Ряди, складені з функцій Бесселя
Такі ряди широко застосовуються при розробці та використанні математи-
чних моделей різноманітних процесів та систем. При достатньо загальних
умовах довільну функцію і'(х), визначену в інтервалі [0, 1] можна розкласти
в ряд Фур’є—Бесселя [42] виду:
1(х) = ^ак/(хкх),	(4.22)
де аК - коефіцієнт ряду; хк - послідовні корені функції Бесселя першого ро-
ду Т.(х) відповідного порядку V, розташовані в порядку їх зростання.
Коефіцієнти ряду (4.22) визначаються за наступними залежностями:
і
(123)
’ [з:м
Розклад в ряд має місце для довільного дійсного значення V > -1/2, якщо
£(х) - кусково-неперервна та має обмежену варіацію в інтервалі [0, 1], а та-
кож існує інтеграл:
|ТхІ£(х)|сіх.
о
В точках розриву функції х = ха значення розкладу в ряд (4.22) функції
£(х) відповідає величині:
-0) + £(ха +0)].
Звичайно застосовують розклад в ряд для бесселевої функції першого ро-
ду нульового порядку (V = 0). Тоді
£(х) = ЕакЛ(хкх),	(4.24)
к=0
де коефіцієнти знаходяться за формулами:
ак =	* Iх ’ £(х)’ Л(хкх)йх .
ІЛ(хк)г о
Визначимо похідну функції Бесселя першого роду нульового порядку.
Використаємо співвідношення між похідною функції Бесселя та функцією
Бесселя іншого порядку, яке має вигляд [1]:
л(х)=|к-і(х)-л+і(х)].
Із властивостей функцій Бесселя випливає залежність:
З.ц(х) = (-1ЮДх).
Об’єднуючи дані залежності для випадку, коли V = 0, ц = 1, одержимо:
138
Розділ -І Математичні моделі процесів у вигляді функціональних рядів
Л'і(х) = -л(х).
При цьому коефіцієнти ряду визначаться за залежностями:
2-	Гх  £(х)- }р(хкх)сІх
*	(4.25)
ак = [Л(хк)Г
Ряди Фур’є-Бесселя доцільно застосовувати для функцій, визначених у
полярній системі координат. При цьому в околі осі симетрії не спостерігаєть-
ся розривів функцій. Нижче наведено приклад застосовування рядів для опи-
су мікро- і макрогеометрії торцевих поверхонь деталей типу тіл обертання
(див. розділ 9).
Ряди, що включають функції Бесселя, досить широко застосовуються при
розробці математичних моделей. Нижче наведено приклад застосування таких
рядів для аналізу коливань круглої мембрани (див. розділ 8).
В задачах знаходження оберненого перетворення Лапласа [23] використо-
вуються ряди типу Неймана, складені з функцій Бесселя. Такі ряди визна-
чаються залежністю’
Цх)= ЕаіЛЛх)> ^>0.	(4.26)
к=<)
Відмітимо розклад в ряд по функціях Бесселя деяких практично важли-
вих функцій.
Наприклад, степенева функція розкладається в ряд по функціях Бесселя:
хп -ОПУ (П +21іХП +к-1)’	/ \
х -2 А----------П------^2^п(хЛ	(4.27)
к=0
Суми деяких характерних рядів, що включають функції Бесселя наведено
нижче. Зокрема:
Л(х) + 2£з2к(х)=^(х)+2£^(к)=1.	(4.28)
к=1	к=1
Експоненціальна функція комплексного аргументу допускає розклад в
ряди по функціях Бесселя:
+0С	ЗО
е±.іх5ті = £зт(х>чп'1 = ;Дх) + £[;2к(х)со8(2кь)±г }2к_,(х) яіп(2к - 1)с].
т - -х	к -1
(4.29)
Зокрема, для випадку коли параметр (; має конкретне значення 8іпС = 1, і
, л
відповідно І = — ,
одержимо:
е±іх = Л)(х)+ Е Лк(х)- соз(кл)± і • }2к_,(х)- 8ІП^—л
к = 1 І
(4.30)
Приклади застосування рядів на базі функцій Бесселя при розробці мате-
матичних моделей технічних систем наведені нижче.
139
Струтинський В. Б.
4.2.	Характерні властивості рядів Фур’є
4.2.1.	Ряди Фур’є. Загальні положення
Ряди Фур’є надзвичайно широко використовуються при математичному
моделюванні технічних систем [1, 28, 42]. Це, зокрема, гармонічний аналіз
детермінованих та стохастичних процесів, спектральний аналіз процесів
різного виду. Ряди Фур’є використовуються при аналізі технічних систем, що
описуються звичайними диференціальними рівняннями та рівняннями в
частинних похідних. Теорія випадкових процесів, багато задач теорії
ймовірності також базуються на використанні рядів Фур’є [і, 47, 60, 72, 94].
Ряди Фур’є є функціональними рядами, складеними із гармонічних
функцій. Синусоїдальні (гармонічні) функції є найпростішими періодичними
функціями, що задовольняють умовам неперервності. Більш складні
періодичні функції можна виразити через синусоїдальні. Засновником теорії
періодичних функцій вважається Фур’є. Працюючи над математичною
теорією теплопередачі у 1807 році, він довів теорему, згідно з якою всяка
періодична функція, за деяких умов, може бути виражена через суму
синусоїд, періоди яких відносяться як ряди цілих чисел. Дана сума синусоїд
носить назву ряду Фур’є.
Ряди Фур’є представляють собою суму достатньо великого числа доданків
складених із лінійної комбінації пар тригонометричних функцій
зіп(кх) та соз(кх),
де к - ціле число (к = 0, 1, 2,...).
Ряди Фур’є застосовуються звичайно для опису періодичних функцій
дійсного аргументу, які задовольняють так званим умовам Діріхле. Ці умови
полягають в наступному:
1	Функція повинна бути однозначна, обмежена і кусково-неперервна.
2	. Функція має певне обмежене число максимумів і мінімумів
Приклади періодичних процесів з періодом 2л, які задовольняють умовам
Діріхле, наведено на рис. 4.1.
Для періодичних функцій £(х) з періодом 2п нескінченний ряд Фур’є має
вигляд:
Кх)== лл + ЕК ’ С08(кх)+Ьк • зіп(кх)].	(4.31)
і-.=і
Ряд Фур’є в кожній точці інтервалу 0 < х < 2 л збігається до значень
функції Кх) в усіх точках неперервності. В точках розриву функції (х = а)
ряд збігається до значень:
((а) = № + °) +	- °)) 
140
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
Рис. 4.1  Приклади періодичних процесів з періодом 2 л. а - процес
у вигляді гладкої неперервної залежності; б - процес з розривом
першого роду; в - процес, який містить високочастотні осциляції
Постійні коефіцієнти ряду а^, (к = 1, 2, .... =с) не залежать від х і
зв’язані із функціональною залежністю Кх) наступними інтегральними
співвідношеннями (інтеграли Коші):
1 2ж
ак - — р(х)соз(кх)сіх ;
11 о
Ьк = — р(х)зіп(кх)сІх .
71 (і
(4.32)
Ряд Фур’є виду (4.31) точно описує функцію Кх) при нескінченній кількості
складових ряду. Практичне застосування ряду вимагає обмеження числа його
членів. Звичайно, для практичних потреб, розглядаються складові ряду’ (прості
141
Струтинський В. Б.
гармоніки) з номером до ктах = 10, .... 200. При кінечному числі членів ряду ряд
Фур’є найкращим чином (найбільш точно) описує функцію в порівнянні з будь-
яким іншим тригонометричним рядом з такою ж кількістю членів.
Ряди Фур’є є результатом розкладу періодичної функції ((х) на суму
системи функцій, яка є ортогональною. Вид даної ортогональної системи
функцій:
ф/х) = 1;	ф2(х) = соз х;	Фз(х) = кіп х;
<р4(х) = соз (2х), ф5(х) = зіп (2х);	Фб(х) = соз (Зх).
Ця система функцій ортогональна в інтервалі [0, 2л]. Відповідно для неї
виконуються умови ортогональності виду:
( = 0
кп(х>Рт(х>1Х<
Л	V
при II * 111
при п = т
(4.33)
В залежності від вигляду функції )(х)
ряд Фур’є може набувати різних
форм. Практично важливими випадками є ряди для симетричних і
кососиметричних функцій (рис. 4.2).
б)
Рис. 4.2. Приклади процесів, що мають вигляд симетричних (а)
та кососиметричних (6) функцій
142
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
Для функцій, симетричних ВІДНОСНО ТОЧКИ X = 71, ряд Фур’є має вигляд
(Ьк = 0):
Л	а?
і: (х) = ~7 + £ ак • соа(кх).	(4.34)
**	к = 1
Для функцій, кососимегричних ВІДНОСНО ТОЧКИ X = 7Ї, розклад в ряд
Фур’є (ак = 0) буде:
1(х) = Ьк  зіп(кх).	(4.35)
6-	к - і
Коефіцієнти ряду Фур’є для заданої функції £(х) знаходяться звичайно
шляхом обчислення інтегралів. В математичному пакеті МаїЬСАО запис
процедури обчислення визначеного інтеграла співпадає із загальновживаним
записом (4.32). Засоби пакету дозволяють знайти коефіцієнти ряду як у
числовому, так і в символьному вигляді. Наступний приклад ілюструє
обчислення коефіцієнтів ряду Фур’є у символьному вигляді для функції,
заданою залежністю:
0 при - тс < х < 0
4
Фрагмент документа Магії САГ), який здійснює обчислення коефіцієнтів а^
та 6^ у символьному вигляді, наведено нижче. Знаходження а^:
— ♦ [х2 ♦ -*-----♦ СОя(кх)сІХ ->
71 о	4
1
—> — ф
я
-1	12 5іп(кл) + 6к со§(кл)л: + к2 8Їп(кл)л2) З
Т*	к5~	“к7
Обчислення коефіцієнтів Ьк у символьному вигляді:
1	г 2 (х-л)2	. А у.
и о	4
1*1 ^ (-12 со§(кл) + 6к 8Іп(кл)гс + к2 соя(кл)тг2) 1 (-12 + к2л2 )"|
"1?	~2* к5
Ряд Фур’є виду (4.31) часто записується в більш компактному вигляді:
і(х) = 4^ + ХАк ,Мкх +Уко)>	(4.36)
к-1
де Ак =	- амплітуда к-ї гармоніки;
\|7к() = агсЦ— - початкова фаза к-ї гармоніки.
Ьк
Запис ряду Фур’є у вигляді (4.36) набагато зручніший для аналізу ніж
формула (4.31).
143
Струтинський В.Б.
Ряди Фур’є широко використовуються при аналізі періодичних функцій,
період яких відрізняється від 2л (рис. 4.3).
Рис. 4.3. Приклад періодичної функції з періодом Т 2л
Затушована частина графіка відповідає періоду Т 2л.
Для періодичної функції
Г(і) = £Д + Т)	(4.37)
відповідно завжди повинна виконуватись умова:
£(0) = £(Т).	(4.38)
Якщо функція £(0 має період Т, то виконавши заміну аргументу функції
2лі	.	.	. ґ. ..	,	,
на х -	, одержимо функцію з періодом 2л. При цьому ряд Фур є для
функції ((і) має вигляд:
^) = -лг + Хак • совківД)+Ьк •5іп(ко0і),	(4.39)
2	к=і
2 ті
де ш0 = — - параметр (базове значення кругової частоти), який враховує
відмінність періоду функції £(і) від 2л. Цей параметр характеризує періодичність
функції.
Якщо розглядають процес - функцію часу ((і), то параметр со(| називається
базовою частотою процесу і вимірюється в 1/с (радіанах на секунду).
Коефіцієнти ряду Фур’є для функції з періодом Т, відмінним від 2л,
обчислюються за формулами:
т
4 Т	1 2
а0 = - р(т)Ф = - р(т> ;	(4.40)
1 о	1 т
її
т
ак = — |((т) • со8(кю0т)с1т = Д |1(т)  со8(ки()т)с1т ;
Ч	3 т
2
144
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
т
2 т	2 2
ьк = — р(т)- 8іп(кй0т)сіт = — р(т)- 8іп(к®0т)с1т,
1	О	_Т
2
к = 1,2,...
При математичному моделюванні також використовують ряди Фур’є,
складені для неперіодичних функцій. В неперіодичній функції не
виконуються умови (4.37) та (4.38). Приклад неперіодичної функції наведено
на рис. 4.4.
Рис. 4.4. Приклад неперіодичного процесу, який відповідає
неперіодичній функції з розривом першого роду

Розглянемо розклад в ряд Фур’є неперіодичної функції. Як вказано
раніше, ряди Фур’є використовуються для періодичних функцій довільного
періоду. Неперіодичну функцію можна вважати функцією з перідом Т —> оо.
2	ті
При цьому базове значення частоти ®0 = ——> 0. Розклад в ряд Фур’є (4.39)
функції нескінченного періоду набуде вигляду:
+ —Х“о[акс08(юО+Ьк8іпИ)]>	(4.41)
“о
де о - к®о “ величина, яка змінюється неперервно, і різниця між нескінченно
близькими значеннями <о складає оу). Тому можна розглядати (Оо ~ А® як
нескінченно малий приріст величини ®.
Підставивши значення коефіцієнтів із (4.40) у формулу (4.41), одержимо:
т	т
~2	+~2
£(і) = — |((т)сіт + —•— ^А®-	[соз(®т)-С08(®і) + 8іп(®т)* 5іп(®і)]с1т .
Т т	що Т и=Ио _т
2	2
Будемо вважати, що границя інтегралу існує і є кінечною, тобто
145
Струтинський В. Б.
т
2
Ііт |£(т)сіт Ф оо .
Т—>00 З,
“”2
Виконавши перетворення тригонометричних функцій, одержимо:
т	+І
4 2	4 е0	“
ї(0=™ р(т)сіт + -р(т)‘ [с08[и(і — т)Цсіт .	(4.42)
1	_Т	77 ш=ш0	_т
2	2
В цій формулі виконаємо граничний перехід при Т -> <ю.
При цьому А® -» <1®, а сума трансформується в інтеграл:
Тоді формула (4.42) набуде вигляду:
. «О -НС
1(0 = - |с!со р(т)- со8[(й(і - т)]<іт .	(4.43)
71 0 -оо
Ця залежність представляє собою запис деякої неперіодичної функції ДО
у вигляді інтегралу Фур’є.
Перетворимо запис функції у вигляді інтегралу Фур’є (4.43) до наступної
форми:
і’(і) = — |[Ьт(ю)• соз((оі) + У(га)• зіп(соі)]с!со ,	(4.44)
71 о
де значення функцій Ц(ш) та У(®) задані інтегралами:
Ц(со)= р(т)-соз(®т)йт ; У(®) = 8іп(®т)сіт .	(4.45)
— 00	- х>
Запишемо формулу інтегралу Фур’є (4.44) у більш компактному вигляді,
що відповідає:
£((;) = — |Д¥(®)- со8[«й - ц/(о>)]ско .	(4.46)
71 о
У формулі (4.46) введені позначення величин, що відповідають амплітуді
гармонічної функції \У(ш) та початковій фазі \|/(и). Вони виражаються через
функції Що) та У((в) згідно співвідношень:
\У(ю) =	+[У(<°)Г > у(®) = агсі:§^^.	(4.47)
сіро)
Із формули (4.46) випливає, що довільну дійсну неперіодичну функцію
Цх), визначену в інтервалі (-оо, +со), можна розглядати як нескінченну суму
синусоїдальних (косинусоїдальних) функцій з амплітудами \У(о) і
початковими фазами \р(со).
Для аналізу технічних систем застосовуються ряди Фур’є в так званій
комплексній формі. Для одержання комплексної форми у формулі (4.31),
146
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
яка визначає ряд Фур’є, виконаємо заміну тригонометричних функцій на
експоненціальні відповідно до залежностей:
. . еЛ“+е-Ікх	,	--
соз(кх) =----------; 8ін(кх) =------—-----, і = /Л .
2	2]
При цьому одержимо ряд Фур’є в комплексній формі для функції з
періодом 2л:
і(х) = Еск  еДх >	(4.48)
к=-»
де коефіцієнти ряду є комплексними величинами, зв’язаними з дійсними
коефіцієнтами ряду Фур’є і Ьк, знайденими за формулами (4.32).
Відповідно значення коефіцієнтів для додатних, від’ємних і нульового
індексів будуть:
С-к =Ц(ак +)Ьк); са = ск =4(ак -)Ьк).	(4.49)
2	2.	4.
Формула (4.48) здійснює розклад дійсної періодичної функції ї(х) з
періодом 2л в ряд по системі комплекснозначних експоненціальних функцій
<рк(х) = е^кх,
де к - ціле число, - к < к < + ос.
Враховуючи, що коефіцієнти ряду Фур’є визначаються інтегральними
залежностями, із (4.49), враховуючи (4.32), одержимо формул}' для
знаходження комплексних коефіцієнтів ряду:
сі< = - р(х)е •	(4.50)
71 о
Формули (4.48)~(4.50) можуть бути використані для функцій г(О
довільного періоду Т, якщо покласти
2п ,
х = —і або х = соді.
В результаті одержимо ряд Фур’є в комплексній формі для функції з
довільним періодом Т:
£(0= Еске]кш”* >	(4.51)
к=-оо
де значення коефіцієнтів ряду визначаються інтегралами:
т
Ск = | р(т)- е <іт = | Р(т)- е^сіт .	(4.52)
1 о	1 Т
2
Позначимо, як і раніше, кшу = и, До = (Оо і введемо позначення сК = ш-О()ю).
Комплекснозначна функція О()со) визначається інтегралом:
т
1 Л
С(]®) = У- р(т)-е-^с1т.	(4.53)
~~2
147
Струтинський В.Б,
Тоді розклад функції К0 в ряд Фур’є у комплексній формі:
£(о=Т°0‘в)-еіоі-А(в-
(0 = -ос
Перейдемо до значення Т -> со або Дш = ®0 -> 0. В цьому граничному
випадку сума буде трансформована в інтеграл і одержимо розклад в ряд
функції нескінченного періоду. Цей розклад є інтегралом Фур’є:
Ч-Хі
£(і)= рб^-е^а®.	(4.54)
Відповідно значення функції:
О(ю) = А р(т)-е~^дт.
(4.55)
Ця функція має назву спектральної функції або комплексного спектра
процесу, який відповідає функції Ці).
Підставивши значення спектральної функції (і()и) в (4.54), одержимо:
.	4-Х	+О>
г(0 = -А. р® • р(т) • е-іо(і-т)ат .	(4.56)
2тс *
— *	- X
Цей вираз являє собою комплексну форму інтеграла Фур’є.
Запишемо комплексну величину під знаком інтеграла (4.56) в
тригонометричній формі:
еИі й _ соф)^ - т)] + і •	- г)].
Тоді одержимо значення функції £(с) у вигляді:
4	+»	4 х	.	+'» +х
(р) = р® р(т)- сохрр - т)] + рш р(т)- 8іп[со(і - т)]сіт . (4.57)
Функція 8іп[ю(с - т)] - непарна функція аргументу со, тому другий
інтеграл в правій частині дорівнює нулю. З іншого боку, со8[и(ї - т)] -
парна функція. Обмежуючись розглядом половини інтервалу інтегрування по
(о, знайдемо:
Г(і) = — _|ско р(т)- сох[ш(ї - т)]сіт.	(4.58)
71 о
Це співпадає із знайденою раніше формулою (4.43) запису інтеграла Фур’є.
Враховуючи (4.46), знайдемо:
О(і®) = —\¥(ш)-еНч,(в).
2л
Звідси одержимо комплексну форму інтеграла Фур’є (4.54) у вигляді:
((і) = у- р¥(а>)* е^’1'^*!® = — созрі - \р(со)]с!со = рфі®)- е]ИМ® .
(4.59)
Формула (4.59) відповідає залежності (4.46).
148
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
4.2.2. Ряди Фур’є розривних функцій. Явище Гібса
Ряди Фур’є є ефективним засобом для опису нелінійних функцій. Зокрема
для опису залежностей, які мають розриви функції або її похідних,
використовуються ряди з кінечним або нескінченно великим числом складових.
Використання рядів Фур’є дозволяє замінити суттєво нелінійні залежності
сумою неперервних гладких функцій. Знаходження коефіцієнтів ряду Фур’є
нелінійних функцій здійснюється звичайними методами, шляхом обчислення
інтегралів Коші (4.32). В літературі наведено багато прикладів обчислення
коефіцієнтів ряду [11, 15, 42, 47, 72].
В табл. 4.1 наведені графіки деяких практично важливих нелінійних
періодичних функцій та коефіцієнти їх розкладу в ряд Фур’є.
В таблиці використана спеціальна функція
. / х зіп(лг)
зіпцг) = —.
Прямокутні імпульси, наведені в поз. 1 таблиці як парна функція, мають
лише косинусні складові (Ь^ = 0).
Знакозмінні імпульси (поз. 2) є непарною функцією. Тому їх розклад в
ряд включає лише синусні складові (а^ - 0).
Застосування ряду Фур’є потребує врахування деяких його особливостей,
зокрема наявність характерних похибок ряду при описі розривних функцій
(явище Гібса) та виникнення похибок при розкладі в ряд Фур’є функцій, що
визначені неточно. Задача опису нескінченним рядом Фур’є функцій, заданих
неточно, відноситься до класу некоректно поставлених задач і буде
розглянута нижче в розділі 4.2 3.
Розглянемо особливості ряду Фур’є, що мають місце при описі розривних
функцій. Математичний опис розривних функцій рядами Фур’є вимагає
врахування характерної властивості часткових сум ряду в точці розриву. Ця
властивість має назву явища Гібса (по імені американського фізика, який у
1899 році виявив цю характерну особливість ряду Фур’є).
Явище Гібса полягає в тому, що ряд Фур’є розривної функції £(х) в точці
розриву х - а, хоча і співпадає зі значенням Ца), але в безпосередній
близькості від точки розриву не зовсім точно описує вид функції. При цьому
відхилення значень часткових сум ряду від значення функції є суттєвими, а
їх врахування є досить складною задачею.
Наведені в таблиці розривні функції та функції з розривами похідних
(ламані лінії) широко використовуються при математичному моделюванні
процесів у механічних системах. За їх допомогою описуються закони зміни
положення робочих органів механізмів періодичної дії, зміни навантаження в
люфтових контактах, нелінійно періодично діючі зусилля тощо.
149
Струтинський В. Б.
Таблиця 4.1
Практично важливі нелінійні функції
150
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
(4.60)
Для виявлення особливостей ряду в околі точки розриву розглянемо
типову розривну функцію у вигляді знакозмінних прямокутних імпульсів [ 1 ]:
- 1 при - л<х<0
£(х) = -< 0 при х = 0, -л, +л .
+1 при 0< х<л
Ряд Фур’є для цієї функції в силу її кососиметричності включає тільки
синусні складові і має вигляд:
\	4 Г8ІПХ 8Іп(Зх)
Цх) =  ----------*—-
я
8Іп[(2п - 1)х]
2п-1
(4.61)
1
З
151
Струтинський В. Б.
Для точного опису функції (4.60) необхідно, щоб п було достатньо
великим ЦІЛИМ ЧИСЛОМ (п -> со).
Розглянемо часткову суму ряду (4.61), яка залежить від числа складових п:
Чя(х) =
4]Г8ІПХ . 5Іп(Зх)
лі З
5Іп[(2н- 1)х]
2п -1
(4.62)
Дослідимо поведінку цієї функції в точці X = 0, яка є точкою розриву
функції Кх). Функція Цп(х) є неперервною та однозначною. її значення в
точці х = 0 дорівнює 0, тобто вона співпадає з Кх) в точці розриву, а саме:
цп(х) = Кх) при х = 0.
Визначимо похідну функції цп(х) шляхом диференціювання залежності
(4.62):
= — [созх +- соз(Зх) + ... + соз[(2п - 1)хД.
ах п
Якщо число складових п достатньо велике (п -> ос), то значення похідної
в точці х = 0 дорівнює
Ііт
<ад„(х)
(ІХ
І
х = 0_|
Похідна
сіх
є сумою тригонометричних функцій, аргументи яких
складають арифметичну прогресію. Відомо, що [1]:
скг(х) 4Г	_	/„	2 8іп2пх
—= —ІС05 X + СО8ОХ + ... + СО8(2і1—1 )х] = — "----
СІХ Л	я 8ІПХ
(4.63)
Враховуючи співвідношення між похідною та функцією, одержимо:
Чп(х)= р^Міх + (х)|
' ах	|х=0
Враховуючи, що дп(х)
= 0 і рівність (4.63), знайдемо:
Чп(х) = - І^^х.	(4.64)
Застосуємо інтегральні функції для аналізу поведінки функції цп(х).
Залежність (4.64) виражається через спеціальну функцію - інтегральний
синус (див. розділ 2.2). Функція інтегрального синуса визначається залежністю:
Поклавши в формулі (4.64) 2пх = 2, одержимо часткову суму ряду у
вигляді:
8ІП2
* . г
0 81П--
2п
сіх
2п
152
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
Враховуючи, що при великій кількості членів ряду (п -ч ос)
г
81П---- ®
2п
2
2п ’
одержимо:
о 2
Запишемо даний інтеграл у вигляді:
Для великих п маємо г - х = 2пх - х « 2пх ® г і відповідно інтервал
інтегрування для другого інтеграла дорівнює нулю. Тому
/ ч 2 р8іп(2)сіг 2 ,< ч
Чп^) = -|---------= -Ьі(г).	(4.65)
2 7Г
Підставивши г = 2пх, одержимо:
Чп(х) = -5і(2пх).	(4.66)
я
Дана залежність визначає часткову суму ряду Фур’є, записаного для
розривної функції £(х) визначену формулою (4.60). На рис. 4.5, а наведені
графіки функцій дп(х) та £(х) в околі точки х - 0.
а)	б)
Рис. 4.5. Часткова сума ряду Фур’є дп(х), складеного
для розривної функції (їх), (а) та опис рядом Фур’є
спіралі Архімеда в точці розриву (б)
Із аналізу поведінки функції інтегрального синуса (див. розд. 2.3.2) при
великих значеннях аргументу випливає, що коливання затухають при
значеннях аргументу:
153
Струтинський В. Б.
= 2пх « 100.
Відповідно, значення аргументу х, при якому затухають коливання:
100
х? = —— при п —•> оо.	—> 0.
Безпосередньо біля точки розриву функції £(х) функція я„(х) досягає
максимального значення шах [д(х)]=1,179... (Атах ~ 0,179). Там же має місце
(1.4247^
і локальний мінімум функції Атах = 1 - І-----— .
У 71/2 )
Таким чином, похибки опису розривної функції £(х), обумовлені явищем
Гібса, полягають в наявності високочастотної осциляції часткової суми ряду
Фур’є в області, що безпосередньо межує з точкою розриву. Період осциляції
відповідає періоду коливань функції інтегрального синуса. При збільшенні числа
складових ряду (п -» оо) період осциляції асимптотично зменшується до нуля.
Виявимо, як впливають зміни самої функції на ряд Фур’є в околі точки
розриву. Для цього розглянемо періодичну розривну функцію, яка монотонно
змінюється за межами точки розриву:
ОМ = И1-2/) "РИ 05 Х-2’
0 при х = 0
(4.67)
Ця функція відповідає спіралі Архімеда скрізь, за винятком точки
розриву при х = 0.
Графік цієї функції в околі точки розриву наведено на рис. 4.5, б. На
ньому ж показано графік часткової суми ряду Фур’є, що описує функцію
£1 (х) в околі точки розриву.
В околі точки розриву функція у вигляді спіралі Архімеда з уступом веде
себе аналогічно розглянутій раніше кусково-постійній розривній функції
(4.60). Нахил спіралі Архімеда в околі точки розриву є несуттєвим (див.
рис. 4.5, б). Із порівняння рис. 4.5, а та рис. 4.5, б випливає, що зміни
розривної функції поза межами точки розриву не є суттєвими і не впливають
на високочастотну осциляцію часткових сум ряду Фур’є.
Значення максимального (Атах) і мінімального відхилень та періоду
осциляцій Тп чисткової суми ряду Фур’є залежать від числа складових ряду.
Ці параметри змінюються складним чином і при збільшенні числа складових
ряду наближаються до залежності інтегрального синуса (4.66).
Характер зміни часткових сум ілюструється розрахунками, наведеними на
рис. 4.6. Спочатку графік часткової суми ряду є плавним із низькочастотними
коливаннями.
При збільшенні числа складових ряду (гармонік) період осциляції
зменшується, а частота зростає. Має місце збільшення максимальної
амплітуди осциляцій та скорочення протяжності ділянки графіка, на якій
154
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
мають місце коливання.
Рис. 4.6. Зміна часткових сум ряду Фур’є в силу явища Гібса
для плоского контура у вигляді спіралі Архімеда з уступом:
а - число гармонік в частковій сумі 25; б - 50; в - 100; г - 200
Врахування явища Гібса при математичному моделюванні потребує
аналізу застосування ряду Фур’є для опису конкретної функції з розривами.
В деяких випадках явище Гібса не є суттєвим фактором. Наприклад, якщо на
вхід динамічної системи подається функція часу у вигляді відрізка ряду Фур’є і
при цьому частота осциляції часткової суми є високою і перевищує смугу
пропускання частот динамічної системи, то явище Гібса не внесе суттєвих похибок
в розрахунок вихідного динамічного процесу системи. В інших практично
важливих випадках необхідно компенсувати негативні наслідки явища Гібса. Для
цього рекомендується кілька методів.
155
Струтинський В. Б.
Один з них полягає у використанні асимптотичного значення часткової суми
ряду Фур’є для повної чи часткової компенсації явища Гібса. Наприклад, для
розглянутої раніше функції Кх), визначеної формулою (4.60), її розклад в рад
Фур’є має вигляд:
со Кх) = У Ь к-1	к8Іп(кх),	(4.68)
де коефіцієнти ряду		
Ьк =.	4	і 		- для непарних к тгк 0	- для парних значень к	(4.69)
Даний ряд, як і раніше (формула (4.62)), запишемо у формі: \ ’хУ 45іп[(2п - 1)х] л(2п-1)	'		(4.70)
Для великих значень N (X -» <х>) часткова сума ряду г / \	48іп(2п - 1)х Х	л(2п-1)		
асимптотично відповідає функції інтегрального синуса:		
цч1(х) = - Я	8і(2Хх).	
Враховуючи, що при N -» <ю с^Сх) = 1, одержимо:
Чь,(х) 8і(2Их)	(2п-1)		(471)
Це відношення можна застосовувати при всіх х > 0 або х < 0 для
достатньо великих N. При цьому похибки, пов’язані з явищем Гібса, будуть
скомпенсовані. Звичайно треба врахувати, що формула (4.71) складена для
асимптотичних залежностей. Тому необхідно перевірити якість компенсації
явища Гібса для конкретних значень N. При незадовільній компенсації
формула (4.71) підлягає уточненню.
З метою покращення асимптотичного опису функції (4.71) доцільно
виконувати в цій формулі граничний перехід:
Кх)- Ііш___-___V 5^П.И^-. ~
Ц '“І™ 8і(2Мх)^ (2п-1) '
Іншим методом усунення негативних наслідків явища Гібса є обмеження
значень часткової суми ряду Фур’є в безпосередній близькості від точки
розриву. Одержана наближена залежність немає високочастотних осциляцій.
Враховуючи складність явища Гібса при розробці математичних моделей
рекомендується виконувати детальний аналіз поведінки процесу в околі точки
розриву.
156
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
4.2.3. Некоректно поставлені задачі
щодо нескінченного ряду Фур’є та їх регуляризація
Некоректність постановки задачі про розклад у нескінченний ряд Фур’є
функції, що задана неточно, е характерною особливістю ряду [33, 111].
Якщо коефіцієнти ряду ак і знайдені абсолютно точно (наприклад,
задані аналітичним виразом), то нескінченна сума ряду буде відповідати даній
функції. Але коли коефіцієнти визначені з деякими, навіть невеликими,
похибками, то похибки нескінченної суми зростають до значних величин і
результат стає невірним.
Розглянемо ряд Фур’є виду:
00
£(х) = Еаксо5(кх)-	(4.72)
к=і
Змінимо коефіцієнти ряду (4.72) на деякі малі величини:
8.1к=єсо5кф є-» 0 ,	(4.73)
де -- довільне число з інтервалу 0 < ^ < 2л.
Згідно з [33], зміна суми ряду Фур’є визначається як:
є со8(к^)со§(кх) = єЗ[к(х-^)],	(4.74)
к-1
де 5(г|) - дельта-функція Дірака (див. розділ 2.3.6).
Із аналізу цієї залежності випливає, що при х = £, зміна суми ряду Фур’є
є нескінченно великою.
Таким чином, підсумовування нескінченного ряду Фур’є є задачею
некоректно поставленою і для її вирішення необхідно виконати операцію
регуляризації підсумовування ряду.
Розглянемо деяку неперервну функцію £(х), яка задана неточно.
Неточності зокрема пов’язані із обчисленням функції, а також з іншими
причинами, в тому числі причинами випадкового характеру. Це означає, що
між точними значеннями функції бДх) і реальним значенням £(х) наявна
похибка Д|(х, а-,, «2> •••)> яка залежить від значного числа факторів, в тому
числі і випадкових оц, 02,...
Визначимо похибки функції при двох сусідніх значеннях аргументу х та х':
ДДх], «і, аг,...) та Д[(х',а],,...).
Значення цих похибок будуть суттєво різні, оскільки значення факторів
ОС-1, 02,... будуть суттєво різними при цих двох обчисленнях. Спрямуємо
х - х' —> 0 і обчислимо похідну залежності А( по аргументу х:
дДДх.ОрОг,...) _ і Д((х,Ора2г..)--Д{(х + Дх,а'ра.2,...)
СІХ	Ах -»•>	Дх
Похідна цієї функції в загальному випадку не існує, оскільки величини в
157
Струтинський В.Б.
чисельнику і знаменнику мають різні порядки малості. Знаходження похідної
виконаємо використовуючи символічні функції - одиничну ступінчасту
функцію та одиничну імпульсну функцію (див. розділи 2.3.5, 2.3.6).
Запишемо похибку у вигляді суми:
ь
Д?(х, ар а2,...) = У ф,(х, а,, а2,...) • 1(х - х,),	(4.75)
і=і
де 1(х - X]) - одинична ступінчаста функція; ф|(х,	сс2,--) неперервна
функція аргументу х.
Відповідно похідна похибки визначається символічною залежністю:
(4.76)
= У Кх - X,) + <р( - 8<х - х,).
СІХ	сіх	1
Знайдемо коефіцієнти ряду Фур’є враховуючи, що функція Цх) задана з
похибкою, тобто функція задана сумою:
Кх) = Мх) + А((х):
1
ак = — [[іт(х) + АДх, ос.)]-созкхсіх.
7Г
Я 0
Враховуючи лінійність операції інтегрування, одержимо:
ак ~ акт + Дак,
де акт - точне значення коефіцієнта; 5ак - похибка обчислення коефіцієнта,
обумовлена похибками визначення функції Кх).
Ці величини знаходяться як інтеграли:
акт = — |7т(х) • соз(кх)сіх ; Д.1к = — ГдДхд,)• соз кхсіх .	(4 77)
Д 0	я 0
Для знаходження Дак застосуємо формулу інтегрування по частинах, а
саме формулу:
2я	2тс
|псіу = ігу]^ - |гс'и.
о	о
При цьому покладемо
І
и = Д£, сіу = соз(кх)с1х) V = — зіп(кх).
к
Відповідно
.	1 2г. (	\	/, х, дДх,а )зіп(кх)
Дак = — ДДх, а^соз^кхдх = —ц
я '	як
2’_1!ф5іп(кх)4Ші)]ах
0 я к	сіх
Після перетворень, скорочень та підстановки
залежності (4.76) одержимо:
значення похідної із

і 2Ц і- Ят	27гГ ц	“|
— І У’Т’1' ^х ~ хі) 8ІП кхсіх ~ т / У, ФГ Мх - хі) • 8іп(кх)сіх
(4.78)
Перший із інтегралів в правій частині (4.78) визначимо наступним чином.
158
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
Розглянемо величину
Єг(х)=
1=1 ах
Ця величина є кусково-неперервною функцією, тому її інтеграл існує при всіх
значеннях к, включаючи (к -> »). Апроксимуємо цю величину поліномом:
Єі/х) ЯВ Є0(1 + Є1Х + Є2Х2 + • ••)•
Обчислимо інтеграл:
|еь(х)8іп(кх)сі(кх) = є0 |8іп(кх)сі(кх) +-— |кх8іп(кх)сі(кх) +
0	0	X о
~ |(кх)2 зіп(кх)сі(кх)
к о
= є0
2к £
соз(кх)^ + |5іп(кх) - (кх)со§ кх
2л
0
е2
к2
[2(кх)зіп х
- [(кх)2 - 2]соз(кх)^1'
4- ...
Звідси випливає, що значення інтеграла при к -> со дорівнює нулю.
Знайдемо значення другого інтеграла формули (4.78). Враховуючи
властивість дельта-функції, одержимо значення другого інтеграла у вигляді:
£ч>і(х)-5(х-х1)-8іп(кх)ах = ^((хЗ-зіп^),	(4.79)
0 1=1	1=1
тобто значення другого інтеграла не дорівнює нулю при довільних значеннях
к (також і при к -» »). Враховуючи вищенаведене, похибку обчислення
коефіцієнта знайдемо у вигляді:
1 Е
=--^Х(Рі(хі)‘5Іп(кХі).	(4.80)
Ця похибка певним чином прямує до нуля при збільшенні к -> оо. Знайдемо
точне значення коефіцієнтів ак для випадку, коли к -> оо. Точне значення функції
£г(х) відповідає неперервній, гладкій функції однієї змінної.
Визначимо характер зміни інтеграла при к -> оо. Розіб’ємо проміжок
2ті
х = [0, 2л] на елементарні ділянки Ах = — (к -> оо, Ах -> 0). Тоді значення
к
коефіцієнта
1 к-1 Г
акт=— У Ит(х)со8(кх)с1х .
2У
Для елементарної ділянки точне значення функції запишеться у вигляді
розкладу в ряд Тейлора. Обмежуючись лінійною складовою розкладу,
знайдемо:
£г(х) - (рої
ді
ох
(х - х;),
і
159
Струтинський В. Б.
де X; = 2тг-^-, £ТОІ - значення функції ї-рої ~ £т(хі)-
к
Запишемо це значення у вигляді:
£т(х) = с0 + с^х,
ді _ ді
Зх і ’ ’ Зх і
Визначимо інтеграл:
2 71-
к
| (с0 + с1х)соя(кх)(і
ч
Інтеграли в правій частині
знайдемо значення коефіцієнта:
де с0 - (ТОІ
,х = ^-
2^-
|хк соз кхсі(кх).
табличними. Після їх обчислення [19]
Є
к
2л.
1 к~’ с
аКТ =—У—-зіпкх +
лк к
(соз кх + кх яіп кх
2л——
к
2л —
1 к-1
—У
лк 6;
~ І + 1
2л-----
к
(4.81)
2л —
к
Тригонометричні функції під знаком суми при підстановці границь у
формулі (4.81) дадуть нульові значення. Тому можна вважати, що при к-> оо
акт - —У • 0 . Визначимо відношення при великих значеннях к:
лк	акт
1 ь
л --гЕфіМкх!)
= -Лк ! »----------> оо >	(4.82)
акт _________1_о
лк2
тобто при великих к (к -> оо) Дак = оо(а«т) або акт ~ О(Дак).
Таким чином, хоча похибка Дак і прямує до нуля, але в порівнянні із
величиною обчисленого коефіцієнта ряду Фур’є вона є нескінченно великою,
тобто величина коефіцієнта набагато менша за похибку його обчислення.
Враховуючи наявність великих відносних похибок обчислення
коефіцієнтів гармонік високих порядків, ряд Фур’є при наявності похибок
може бути записаний у вигляді:
Кх) = £(акт + Аак)соз(кх)+ У ДаК соз(кх).	(4.83)
к=1	к-кт
Перша сума у формулі (4.83), яка включає гармоніки від 1 до кт,
відповідає коефіцієнтам акт. які більші чи порівняні із похибкою ДаК
160
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
обчислення коефіцієнта. Друга сума включає високочастотні гармоніки. В них
похибка обчислення коефіцієнтів Дак більша від значень коефіцієнтів акг.
Друга сума дає невизначену відносну похибку ряду Фур’є, яка може мати
довільне (в тому числі нескінченно велике) значення.
З метою запобігання виникнення суттєвих похибок обчислення здійснюється
регуляризація некоректно поставленої задачі обчислення нескінченного ряду
Фур’є. Найпростішим способом регуляції є використання обмеженого числа
гармонік ряду Фур’є. При цьому у формулі (4.83) залишається лише перша
сума, а друга сума, яка дає невизначену похибку ряду, ігнорується. В цьому
випадку задача підсумовування ряду стає коректною. Для регуляції задачі
необхідно відкинути гармоніки, в яких похибки обчислення коефіцієнтів Аа;.
більші за значення самих коефіцієнтів ак.
Другим поширеним способом регуляризації є введення так званого
формфактора. Суть даного способу регуляризації полягає у діленні
коефіцієнтів ряду Фур’є на відповідно підібрану величину, яка дорівнює
одиниці для гармонік з невисоким номером і прямує до нескінченності для
високочастотних гармонік. При цьому ряд Фур’є стає скоригованим і набуває
вигляду:
£(х) = Е (ГГр^ С05^кх) ’	(4.84)
де Рк - формфактор, рк ® 0 при малих значеннях к і -> оо при великих
значеннях к.
Якщо вибрати значення формфактора у вигляді:
[0 при к < кт
Рк = 1	її’
(<ю при к < кт
(4.85)
то маємо розглянуту раніше регуляризацію шляхом обмеження числа
складових ряду.
За формфактор рк можна вибрати довільні функції числового параметра к.
Автором використаний формфактор Рк - еак -1, де а, V - додатні
константи. Зокрема, як формфактор вибрано функцію:
Рк = е0'00,к2 - 1 .	(4.86)
Залежність (4.86) використана при регуляризації задачі опису просторових
поверхонь типу тіл обертання за допомогою рядів Фур’є [94].
Чисельні дослідження та практична апробація підтвердили ефективність
використання формфактора даного виду.
Ступінь росту залежності формфактора (4.86) від параметра к перевищує
ступінь росту експоненціальної функції. В деяких випадках ця обставина є
суттєвою.
161
Струтинський В. Б.
4.3. Застосування рядів Фур’є для аналізу процесів
у технічних системах
4.3.1. Гармонічний аналіз процесів
Гармонічний аналіз процесів механічних систем дозволяє вирішити ряд
практично важливих задач математичного моделювання. Під гармонічним
аналізом динамічного процесу мають на увазі знаходження складових ряду
Фур’є, який описує цей процес. Це відповідає розкладу процесу на суму
гармонічних складових.
Гармонічний аналіз шляхом розкладу в ряди Фур’є надзвичайно широко
використовується при математичному моделюванні різноманітних технічних
систем. Аналіз базується на виявленні характерних особливостей окремих
складових ряду та їх сукупності.
Розглянемо фізичну інтерпретацію складових ряду стосовно аналізу
процесів та систем механіки. Механічні системи включають обертові вали. Всі
силові та геометричні параметри, які діють на обертові вали, мають циклічну
дію з періодом 2л. Прикладом циклічної зміни геометричного параметра
обертового вала є кулачковий механізм. Циклічними є навантаження на опори
підшипників, зусилля в зубчастих передачах тощо.
Математичний опис даних циклічно змінюваних параметрів процесів є
ідентичним. Графічна інтерпретація зміни параметра відповідає круговій
діаграмі. Діаграму можна подати у вигляді замкненого контуру Ь, який в
полярній системі координат описується радіусом-вектором К, що залежить від
полярного кута <р. Контур Ь відповідає формі плоского кулачкового
механізму. В даному випадку аргументом є х = (р, а функцією - К(ср) = Кх).
Ряд Фур’є, використаний для математичного опису контуру Ь, має вигляд:
^(<р) = Дг + £Ак8Іп(к<р + ц/0к),	(4.87)
2
де а0 - деяке постійне значення радіуса-вектора;
к - номер гармоніки;
Ак - амплітуда к-ї гармоніки;
ц/Ок - початкова фаза гармоніки.
Розглянемо фізичну інтерпретацію окремих складових ряду Фур’є
стосовно кулачкового механізму.
Поклавши амплітуди гармонік Ак = 0, одержимо нульову гармоніку
розкладу, яка є постійною складовою ряду:
К(ф) = -^ = Кв=-^ = Соп8І.
162
Розділ 4. Математичні моделі процесія у вигляді функціональних рядів
Звідси випливає, що постійний коефіцієнт ряду а0 являє собою діаметр
базового кола сіо, відносно якого відбуваються відхилення поточного радіуса-
вектора К(ф) контуру Ь. Коли амплітуди всіх гармонік Ак = 0, контур Ь
представляє собою коло (рис. 4.7).
Рис.4./. Контур Ь, що описується рядом Фур’є, всі гармоніки якого
мають нульові амплітуди, а наявна лише постійна складова ау = сіу
Контур Ь у вигляді кола зручно взяти за рівень відліку значень поточного
радіуса. 'Годі замість радіуса-вектора К(<р) розглядається його відхилення 5(ф)
від базового кола:
3(ф) = К(ф) - Ко .
Розглянемо відхилення контуру Г від базового кола:
5(ф) = К(ф)- Ко = £ Ак • 8іп(кф + фок).	(4.88)
к=1
Для першої гармоніки розкладу (к = 1) відхилення контуру Ь від
базового кола відповідає залежності.
ЗДф) = А|8іп(ф + фоі)-	(4.89)
Графічна інтерпретація даної залежності для різних значень амплітуди А|
та нульової початкової фази ц/оі = 0 наведена на рис. 4.8.
Виконаємо аналіз параметрів, які визначають першу гармоніку розкладу.
Відхилення контуру від базового кола має нульові значення в точках В і С
(рис. 4.9). Із формули (4.89) випливає, що в даних точках:
ф + Фоі = 0; я.
Відповідно кутові координати, при яких функція ф(ф), визначена
формулою (4.89), приймає нульові значення:
Ф = Фо = -фоі: я - фок
Із аналізу рис. 4.9 випливає, що початкова фаза гармоніки відповідає
повороту контуру Ь на кут (я - фоД у від’ємному напрямку (в напрямку
повороту годинникової стрілки). Якщо розглядати опис контуру у новій
системі координат х'у'(рис. 4.10, а), то початкова фаза буде дорівнювати
163
Струтинський В. Б.
нулю, а залежність відхилення контуру Ь від базового кола буде визначатися
формулою:
бфср') = А^іпф’,
де нове значення аргументу:
Рис. 4.8. Контури Ь, що описуються рядом Фур’є, всі гармоніки якого,
крім першої, мають нульові амплітуди та нульові початкові фази:
позиції а, б, в відповідають послідовному збільшенню амплітуди А/
Рис. 4.9. Контур Ь, що описується рядом Фур’є, всі гармоніки якого,
крім першої, мають нульові амплітуди, а початкова фаза
першої гармоніки у/()1 відмінна від нуля
Покажемо, що для амплітуди гармоніки А5 « Ко форма контуру Ь
відповідає базовому колу з радіусом Ко, причому контур Е зміщений відносно
центра координат на величину е = А] [113].
164
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
Рис. 4.10. Графічна інтерпретація першої гармоніки ряду Фур’є з нульовою
початковою фазою при малих значеннях амплітуди (а) та контур
у вигляді кола, зміщений на величину е відносно базового кола (б)
Для доведення розглянемо два кола однакового радіуса Ко, центри яких
зміщені на величину е, причому е « Ко (рис. 4.10, б).
165
Струтинський В. Б.
Визначимо відхилення радіуса кругового контуру від радіуса базового
кола 3„ в функції кута <р. Із розгляду трикутника ОМИ (рис. 4.10, б),
одержимо довжину радіуса-вектора:
ОМ = ТММ2 +О№ .	(4.90)
Із трикутника О^МК знайдемо катет МК = К08ІПфі. Відповідно
МЦ = МК + е = е + Козіпфр
Враховуючи, що ОМ = К0со8фі, із формули (4.90) знайдемо значення
радіуса-вектора у вигляді'
ОМ - д/(е + Ко 8Іп <Р] )2 + (Ко соз ф, )2 .
Після елементарних перетворень цієї залежності одержимо:
ОМ = Л/К(2) + е2 + 2еК(, зіпф( .
Визначимо відхилення 8И як функцію кута ф:
5(ф) = ОМ - К(| = д/к(2 + е2 + 2еК0 8ІПф( - Ко.
Ця залежність є нелінійною. Розкладемо її в ряд Маклорена по змінній
£ = 8ІПф]. Обмежуючись лінійною складовою ряду Маклорена, одержимо:
З(^) = 5(У|^Й + -^	• с .
(4.91)
Визначимо коефіцієнти розкладу в ряд Маклорена:
5,Д)Ц = >2-еГ-К0;
2еК„	еК0 _
5„0 27ЇЇГ+ е2 + 2еКЕ,	г2 '
Враховуючи, що е « К.д, одержимо значення коефіцієнтів:
5,Д)|	=0:	=е
^()
Відповідно із формули (4.91) знайдемо:
З,, (ф, ) = Є-8ІПф( .
Для значень ексцентриситету е « Кд можна вважати, що ф^ « ф. Тоді
5„(ф,) = 8„(ф) = е • зіпф.	(4.92)
Це відповідає першій гармоніці розкладу функції в ряд Фур’є (4.89).
якщо покласти е = А}, фоі = 0-
Розглянемо другу гармоніку розкладу контуру Ь в ряд Фур’є (рис. 4.11).
Покажемо, що друга гармоніка розкладу контуру І. в ряд Фур’є при
малих амплітудах відповідає еліптичному контуру Для доведення розглянемо
еліпс (див. рис. 4.11, в).
166
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
Рис. 4.11. Контури Ь, які відповідають другій гармоніці розкладу
в ряд Фур’є при нульовій початковій фазі: а, б - послідовне зменшення
амплітуди А2; в - схема розміщення еліптичного контуру
відносно базового кола
Еліптичний контур характеризується своїми півосями а і Ь. Рівняння
еліпса в полярній системі координат має вигляд:
Ь
р_-------(4 93)
у! - Є  СО8 Ц/
де р - радіус-вектор; у/ - полярний кут; є - ексцентриситет еліпса, який
визначається через півосі згідно з формулою:
І і?
є = ЛИ-^.	(4.94)
її а‘
Визначимо відхилення форми поверхні еліптичного контуру від базового
167
Струтинський В.Б.
кола:
52(ф) = р - Ко = '	- Ко.
^/1 - Є~ СОЗ ЦІ
Виразимо квадрат косинуса через косинус подвійного кута та введемо
нову змінну £ = сох 2ці .
Відповідно одержимо
52(£) = _±—- Кй.
^1-Є-(1 + Ю
Розкладемо дану функцію в ряд Маклорена по змінній Е, і, обмежуючись
першими двома складовими розкладу, визначимо:
Виберемо значення радіуса базового кола Ко таким, щоб
При такому значенні радіуса формула (4.95) спроститься і для є « 1
набуде вигляду:
„ / \ Ьє „
сох 2\/.
Підставивши значення ексцентриситету є, із формули (4.94) визначимо:
626у) = ----(а2 -Ь2)со8 2у .
4а"
.	Ь
Врахуємо, що для еліпса, який мало відрізняється від кола, — ® 1,
а
а + Ь ® 2а . Отже, одержимо:
526и) =	2і|і.	(4.96)
а - Ь
Позначимо величину —-— = А2. Вона буде відповідати амплітуді другої
гармошки. Використовуючи співвідношення
соз(2ц/) = 8ІП
„	я
перейдемо до нового значення полярного кута <р = ці .
4
В результаті одержимо рівняння контуру еліптичної форми:
+ 2 І ’
168
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
82(<р) = А2 8ІП 2<р.
Це відповідає другій гармоніці розкладу (4.88) довільного контура Ь в
ряд Фур’є.
Таким чином, для малих амплітуд гармонік перша гармоніка розкладу
відповідає колу, зміщеному відносно початку координат, а друга гармоніка
відповідає еліпсу, центр якого знаходиться в центрі координат.
Третя гармоніка відповідає фігурі з трьома виступами і трьома
впадинами, розташованими рівномірно по колу (рис. 4.12).
Рис. 4.12. Контури І., які відповідають третій гармоніці розкладу
в ряд Фур’є при нульовій початковій фазі: а, б - послідовне зменшення
амплітуди А?
При зменшенні амплітуди гармонік форма контуру наближається до
базового кола, а відхилення проявляються в огранці контуру по кількості
169
Струтиіилкий В. Б.
граней, що відповідає номеру гармоніки (рис. 4 13, а).
Рис. 4.13. Форми контуру з охранкою, що відповідають третій (а),
четвертій (б) і п’ятій (в) гармонікам розкладу періодичної функції
з періодом 2л в ряд Фур’є при нупьових початкових фазах
і малих амплітудах
Гармоніки більш високих порядків відповідають хвилястості або огранці
контуру по числу граней, рівному номеру гармоніки.
При невеликому числі граней (до 10) огранка контуру простежується
візуально (рис. 4.13, б, в). При великому числі граней огранка проявляється
у хвилястості контуру (рис 4.14).
Рис. 4.14. Форми контуру з охранкою чи хвилястістю, що відповідають
гармонікам високого порядку: а - огранка контуру по семи гранях,
що відповідає сьомій гармоніці; б - хвилястість контурі),
яка відповідає шістнадцятій гармоніці
170
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
Таким чином, кожна гармоніка має конкретний фізичний зміст. Перша
гармоніка визначає ексцентричність контуру, друга - його овальність.
Наступні гармоніки визначають хвилястість чи огранку контуру по числу
граней, яке дорівнює номеру гармоніки.
Гармонічний аналіз процесів полягає у визначенні набору гармонічних
функцій, сума яких відповідає вихідному процесу. При цьому необов’язково
знати обернений процес - синтезу або знаходження суми синусоїд. Однак з
метою аналізу процесу корисно вивчити результати, одержані при складанні
різних гармонічних функцій [47].
Порівняно простими є процеси, складені із довільного числа гармонічних
функцій одного періоду. Ці процеси мають період, який відповідає періоду
кожної складової гармонічної функції. В загальному вигляді сума кількох
синусоїд одного періоду являє собою одну синусоїду:
У А, • 8Іп(іОХ +	) = А * 5Іп((ВХ + ф'() ) ,
де А; - амплітуда і-тої гармоніки;
крої початкова фаза і-тої гармоніки;
А -амплітуда результуючої гармоніки;
Уо — початкова фаза результуючої гармоніки.
В залежності від значень масиву початкових фаз ц/Оі одержаний процес
зміщується відносно вихідних синусоїд. Зокрема, у випадку суми двох
гармонічних функцій результуючий процес зміщується відносно обох
вихідних синусоїд (рис. 4.15).
10	-5	0	5	Ю - |()	-5	о	5	И,
а)	б)
Рис. 4.15. Приклад процесу ф(х) = ф(х) + ф/х), складеного із двох
гармонічних функцій: одного періоду ффх) = 1.4зіп(х), ф/х) = 0.8зіп(х + 1) (а),
та окремий випадок суми двох гармонічних функцій одного періоду
з однаковими початковими фазами (б)
Для окремого випадку суми двох гармонічних функцій одного періоду з
однаковими початковими фазами результуючий процес не зміщується
відносно складових синусоїд (рис. 4.15, б).
Більш складні процеси відповідають сумі гармонічних функцій різних
171
Струтинський В Б.
періодів. Сума двох синусоїд різних періодів дає складний циклічний процес
(рис. 4 16).
Рис. 4.16 Приклад процесу /(х) = ^(х) + (/х), складеного із двох
гармонічних функцій різного періоду: /фх) = $іп(х), ^х) = 0.6зіп(Зх + І)
Процеси у вигляді суми двох синусоїд можуть мати особливі властивості.
Сума двох гармонічних функцій, відношення частот яких близьке до одиниці,
визначає процес із биттям. Биття проявляється в наявності характерної
циклічної зміни обвідної лінії процесу (рис 4.17).
Рис. 4.17. Приклад процесу із биттям {(х), складеного із двох гармонічних
функцій близьких періодів: /(х) ;= 0.2 * соз(50х) + 0.3 * соз(бОх)
Процеси з биттям, утворені при складанні двох синусоїд (компонент
процесу), відношення частот яких близьке до одиниці, мають наступні
властивості:
-	амплітуда процесу періодично змінюється (биття);
-	фази верхньої та нижньої обвідних протилежні;
-	частота обвідної дорівнює різниці частот компонент;
-	найбільша ширина смуги між обвідними дорівнює сумі подвійних
амплітуд компонент;
172
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
-	амплітуда обвідної дорівнює амплітуді другорядної гармонічної
компоненти;
-	на довільному відрізку число піків процесу дорівнює числу піків
головної компоненти.
Останнє положення має винятки в окремих випадках, які розглянуті нижче.
В залежності від співвідношення амплітуд і частот складових гармонічних
функцій мають місце окремі випадки биття (рис. 4.18).
,|--1----(----,----,-----,----!----т-----,----,----[----
Г(х):= 02*соз(50х) + 0.3*со8(60х)
4-----1-----1----1-----1----і----- І...4---і-------и
1	1!	12 ІЗ 14	15	16	17	18 І
в)
Рис. 4.18. Різні варіанти процесу із биттям [(х), що відповідає сумі
двох гармонічних функцій близьких періодів: а - процес при наявності
биття загального виду; б - биття із широкою впадиною ((ф);
в - биття із точкою перегину (Р)
173
Струтинський В.Б.
Процес биття з широкою западиною (рис. 4.18, б) характеризується
наявністю плавної (широкої) западини. Другим особливим випадком биття є
перегин кривої (рис. 4.18, в).
Гармонічний аналіз процесів, складених із трьох і більше синусоїд, є
набагато складнішим процесу, що має дві гармонічні складові. Процеси
описуються складними циклічними залежностями (рис. 4.19).
0	2	4 -е 8	10	12	14	16	18	20
а)
0	2 д 6	8	10	12	14	16	18	20
б)
Рис. 4.19- Типові циклічні процеси складені із суми трьох синусоїд (а)
та семи синусоїд (б)
Процеси мають багато особливостей. В залежності від співвідношення
параметрів синусоїд можливі особливі випадки биття, появи сідлових точок
високочастотних флуктуацій процесу та інші.
Гармонічний аналіз складних полігармонічних процесів здійснюється
шляхом розкладу в ряди Фур’є.
При математичному моделюванні також виникає потреба в синтезі
складних циклічних процесів. Обчислення значень процесу здійснюється
звичайно з використанням часткової суми ряду Фур’є або із застосуванням
довільного полігармонічного процесу. В деяких випадках використовуються
візуальні математичні моделі процесів. На рис. 4.20 наведено приклади
візуальних математичних моделей процесів, виконані в системі 8ІМІЛЛМК
пакету МАТЬАВ.
Вхідний блок 8іпе Х\'ауе (рис. 4.20, а) формує вектор синусоїдальних
174
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
складових процесу. Амплітуди, частоти і початкові фази синусоїдальних
складових процесу задаються в меню вхідного блока (рис. 4.20, б).
ІНШІ

б)
а)
в)
Рис. 4.20. Візуальні математичні моделі, призначені для синтезу
полігармонічних процесів (а), меню для визначення параметрів гармонік (б)
та результату розрахунків (в, г)
В меню вказуються вектори даних амплітуд, частот і початкових фаз
окремих гармонік, з яких складається полі гармонічний процес. Сума
гармонічних функцій знаходиться суматором. Можливе окреме визначення
складових полі гармонічного процесу. Параметри гармонік можна задавати у
вигляді довільних функцій, в тому числі і випадкових (див. рис. 4.20, а).
175
Струтинський В. Б.
4.3.2. Спектральний аналіз процесів
Спектральний аналіз процесів є ефективним засобом аналізу процесів при
математичному моделюванні. Спектральний аналіз дає графічну
інтерпретацію розкладу функції довільного періоду в ряд Фур’є.
Спектральний аналіз здійснюється для періодичних і неперіодичних функцій.
Для періодичних функцій спектр процесу є лінійчатим, а для неперіодичних
(функцій нескінченного періоду) - неперервним.
Розглянемо спектри періодичних функцій. Для періодичної функції з
періодом 2л її розклад в ряд Фур’є має вигляд:
^(х)--у + Еак -с08(кх) + Ьк •8іп(кх) = -^-- + ХАк '8іп(кх + ук), (4.97)
к=І	к=!
де амплітуди і початкові фази % зв’язані з відповідними коефіцієнтами
ряду Фур’є ак і Ьк:
Ак = 7аї + Ь2к ; крк = агсІ§-|^.	(4.98)
ок
Ряд Фур’є графічно зображується у вигляді нескінченної сукупності
ліній, довжина яких в певному масштабі відповідає коефіцієнтам ряду.
Одержані графіки дають сукупність (спектр) коефіцієнтів ряду (рис. 4.21).
4'Ьк
б)
Рис. 4.21. Графічне зображення коефіцієнтів (спектр) ряду Фур’є
для функції з періодом 2/г. а - спектр коефіцієнтів ряду а^;
б - спектр коефіцієнтів ряду Ьк
176
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
Цей спектр називається лінійчастим або дискретним, тому що він
складається із нескінченної кількості ліній, кожна з яких відповідає
коефіцієнту ряду з номером к.
Графічна інтерпретація ряду Фур’є є ефективним засобом аналізу
процесів. За значеннями коефіцієнтів (спектра) можна зробити висновок про
те, із яких гармонічних функцій складається процес. Спектр дозволяє
виявити головні (превалюючі) гармоніки, які присутні в розкладі.
Наприклад, розглянемо спектр процесу, який має ізольований викид при
к = 5. Значення амплітуди при к = 5 набагато перевищує сусідні значення
коефіцієнтів (рис. 4.22). Аналіз спектра показує, що процес має головну
(превалюючу) косинусну гармоніку з номером к = 5. Відповідно можна
зробити висновок, що процес включає основну гармонічну складову виду
Кх) = а5‘соз5х.
ЛЬк
X—1__1-і__і__।_і—і
0 1 2 3 4 5 6 7
б)
Рис. 4-22. Лінійчатий спектр коефіцієнтів ряду Фур’є, який виявляє
головну (превалюючу) косинусну гармоніку процесу а^созбх з номером к = 5:
а - спектр коефіцієнтів аі:; б - спектр коефіцієнтів ф.
Лінійчасті спектри, наведені на рис. 4.21 і 4.22, часто бувають незручні в
користуванні. Більш ефективними для аналізу є зображення амплітуд і
початкових фаз окремих гармонік, визначених формулами (4.98). Спектр
такого вигляду для періодичної функції з періодом 2л наведено на рис. 4.23.
Лінійчасті спектри також використовуються для рядів Фур’є, складених
для функцій довільного періоду. Для функції з періодом Т з базовим
значенням частоти ®0
= — розклад в ряд Фур’є подано у формі:
Г(х) =	+ X ак • со8(к®0х) + Ьк • 8іп(кю0х) = — + £ Ак • 5Іп(кш0х + ук)•
2 км	2	к==1
(4.99)
Графічна інтерпретація даного ряду здійснюється зображенням
коефіцієнтів ак, Ьк в функції частоти о = кшо- Зображення коефіцієнтів
представляє собою лінійчастий спектр. На рис. 4.24 наведено приклад
зображення коефіцієнтів ряду (спектр) в залежності від частоти и = кюо-
177
Струтинський В.Б.
Рис. 4.23. Спектр амплітуд (а) і початкових фаз (б) розкладу
в ряд Фур’є періодичної функції з періодом 2л
ак 1'
юо 2соо к®о
Ьк А
і
Ьк
ІЬ'ІЬ2І І І І ш
0	„	1
соо 2(оо	к(оо
б)
Рис. 4.24. Графічне зображення коефіцієнтів (спектр) ряду Фур’є
для функції довільного періоду Т = —: а - спектр коефіцієнтів ас
®0
б - спектр коефіцієнтів
Лінійчасті графіки визначають значення коефіцієнтів в залежності від
номера гармоніки (для функції періоду 2л) або в залежності від частоти (для
функції довільного періоду).
Наявність двох графіків для опису спектра функції довільного періоду
має певну незручність. Тому найчастіше використовується графічне
зображення (спектр) амплітуд і початкових фаз гармонік. Для функції
довільного періоду так, як і для функції з періодом 2л, одержимо лінійчасті
спектри амплітуд і початкових фаз гармонік (рис. 4.25).
Значення початкових фаз (рис. 4.25, б) визначене з точністю до
постійного доданка 2л. Часто значення початкових фаз не є суттєвими. Більш
178
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
важливим є значення амплітуд. Тому на практиці більше використовується
графік (рис. 4.25, а), який зображує сукупність амплітуд (спектр амплітуд)
гармонік ряду Фур’є.
Рис. 4.25. Лінійчасті спектри амплітуд (а) і початкових фаз (б)
періодичної функції довільного періоду Т = 2л/<в0
Спектр амплітуд або просто спектр функції г(0 дає зручний засіб аналізу
функції по розкладу цієї функції в ряд Фур’є. Він застосовується в різних
видах. Разом зі спектром амплітуд використовують спектр квадратів
амплітуд. Даний спектр більш зручний в користуванні, тому що графіки ліній
завжди знаходяться в додатній напівплощині системи координат. Вибір виду
спектра здійснюється із умов зручності аналізу процесу.
Використовують також зображення амплітуд (спектр) для ряду Фур’є в
комплексній формі.
Розглянемо ряд Фур’є в комплексній формі для функції довільного
~ 2л
періоду 1 =---.
®0
г(х)= Уске*'!‘ .	(4.100)
Для цього ряду графічне зображення амплітуд с^ особливо зручне.
Враховуючи, що коефіцієнти ряду з додатними та від’ємними номерами є
комплексно спряженими величинами, а саме:
с к =4(ак + фк): с0 с+к =4(ак -]Ьк); с к = с . ,
одержимо співвідношення:
Ке ск = Ке с_к , Іт ск = - Іт с_к ,
тобто дійсні частини коефіцієнтів є\ не змінюються при зміні знаку частоти, а
уявні частини при цьому змінюють знак. Відповідно, при графічному
зображенні складових коефіцієнтів с^ одержимо симетричне зображення
дійсних частин коефіцієнтів і кососиметричне зображення уявних частин
коефіцієнтів (рис. 4.26).
Враховуючи симетрію графіків, звичайно розглядають лише їх праві
частини, що охоплюють додатну смугу частот 0 < <о < оо.
179
Струтинський В.Б.
а Яеск
Рис. 4.26. Спектри дійсних (а) та уявних (б) частин коефіцієнтів су,
ряду Фур’є в комплексній формі
Користування двома графіками часто буває незручним, тому їх
об’єднують, зображаючи модулі коефіцієнтів
|ск| = |ї® +Ьк =
З метою спрощення обчислень звичайно застосовують зображення значень
квадратів модулів комплексних коефіцієнтів ряду
І І2 -	1,2 1 Ак
Ск ~ ‘7 \ак + Ьк ) ~ ~ •
1 '	4 ' к	4
Зображення значень модулів коефіцієнтів ряду Фур’є в комплексній формі
утворює лінійчасту діаграму, яка інтерпретує спектр модулів (квадратів
модулів) комплексних чисел ск. Спектр (рис. 4.27) охоплює всю область
частот о = ко>о від -оо до +<ю.
Спектр є симетричним відносно нульового значення частоти. Даний
лінійчастий спектр відповідає періодичній функції з періодом Т.
Зазначимо, що середній квадрат функції ((х) дорівнює сумі квадратів
модулів коефіцієнтів:
------ і ТР	«о „ і 4 » ,
-Т/2	к-1
(4.101)
180
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
ш —> - оо	-2(00 -®о 0 оо 2ио к(оо (о —> оо
Рис. 4.27. Графічне зображення квадратів модулів коефіцієнтів ск
ряду Фур’є в комплексній формі, яке є спектром періодичної
функції з періодом Т
Графічне зображення розкладу функції в ряд Фур’є (спектр)
використовується для функцій довільного періоду, в тому числі нескінченно
великого періоду. Розглянемо функцію з нескінченним періодом Т -> се. При
цьому базове значення частоти ©о -> 0. Це означає, що лінії спектра
розташовані нескінченно близько одна від одної та зливаються в одну фігуру,
яка утворює неперервний спектр. Непевний спектр процесу є узагальненням
дискретного спектру.
Введення неперервного спектра здійснюється шляхом граничного переходу
для розкладу Фур’є в комплексній формі (формула (4.54)). Згідно з цією
формулою, довільна неперіодична функція НО записується у вигляді:
£(х)=	.	(4.102)
Під знак інтеграла входить комплекснозначна функція:
С(їю) = ~ р(т)-е^шМт.	(4.103)
^.1
Ця функція є комплексним спектром функції 1(0. Функцію О(]ю)
називають ще спектральною функцією розкладу функціональної залежності
К0 в ряд Фур’є. Спектральна функція зображується в функції частоти і
утворюється неперервний спектр функціональної залежності 1(0.
Спектральна функція О(](о) з точністю до множника відповідає
перетворенню Фур’є С(](о) (прямому) функції К0 [42]:
С(]со) = -Д=г Г((і)-е 3“Мг .
42п ф
(4.104)
Відповідно зворотне перетворення Фур’є визначає функцію ((і) через її
перетворення Фур’є:
=	(сО(о)'е^’М(о .
(4.105)
Знаходження прямого і зворотного перетворення Фур’є здійснюється
різними методами [1, б, 28, 62]. Зокрема, перетворення знаходяться
181
Струтинський В. Б.
безпосереднім обчисленням інтегралів за формулами (4.104), (4.105) або з
використанням таблиць [50, 72, 1 10].
В табл. 4.2 наведено ряд функцій, що відповідають практично важливим
процесам, та перетворення Фур’є даних функцій.
Таблиця 4.2
Перетворення Фур’є деяких практично важливих функцій
№ з/п	ко		С()й>)
1	8ІП	/ л\ —— (а > 0)		рГ । । лк при |со| < а 0 при {©І > а
2	е-ЖРі (а>0,і>0) 0 (і < о)		І
			л/2я(р - є» + ]а)
3	е“'л2 (Ке р > 0)		(2р)''/2е-“г/4”
4	с 12/2		е~“'2
5	сов аі.2 (а > 0)		Л, V1/2	Ґ<1Г к (2а) сох— (_ 4а 4)
6	ІГ		І 1~‘‘/2 |®|
7	-арі Чт (а > ж		\/Уа2 +оз2 + а Уа2 + о2
8	(а2-і2)'" при |1| < а 0 при |1| > а		рг т ( \ ^-Д(Да®)
9	кіп ьУа2 + і2 Уа2 + І2		ст і А ст
10	сок(ьУа2 -12 Уа2 - і:2 0 при |і|	при |іІ < а > а	ЛДУш2 + ь2)
11	сЬ^ьУа2 -12 Уа2 -Є 0 при |і|	при |і| < а > а	^ЇДУ®2 -ь2)
Пряме і зворотне перетворення Фур’є можна здійснити засобами
математичних пакетів. В пакеті МаПіСАВ дані процедури здійснюються за
допомогою кнопок
182
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
панелі символьних операцій (див. рис. 2.17). Активізувавши дані кнопки,
одержимо па екрані відповідні заготовки. Для прямого перетворення Фур’є:
Й^оигїела~>|
В лівий затушований прямокутник записується функція £(0, а в правий -
змінна (в даному випадку І), за якою здійснюється перетворення.
Натиснувши кнопку Епіег, справа від стрілки одержимо символьний вираз,
який відповідає перетворенню Фур’є С(]со) функції Ці).
Зворотне перетворення Фур’є здійснюється аналогічним чином. Для цього
використовується заготовка:
£ іпуіоигіег.и->
В лівий прямокутник записується функція С(ш), а в правий - ®.
Результатом дії даної процедури буде функція £(£).
Знайдене таким чином перетворення Фур’є є спектром неперіодичної
функції. Одержаний неперервний спектр функцій нескінченного періоду
використовується для їх аналізу. Ця операція має назву спектрального
аналізу неперіодичної функції (процесу). Спектральний аналіз виконується
як для неперервних, так і для розривних процесів.
Спектральний аналіз періодичних та неперіодичних процесів здійснюється, як
правило, в порівнянні зі спектрами відомих функцій. Нижче наведені спектри
деяких практично важливих періодичних і неперіодичних процесів.
Розглянемо знаходження спектра процесу КО, який має вигляд серії
прямокутних імпульсів висотою її і шириною 2є, що повторюються з частотою
V імпульсів за секунду. Даний процес є періодичним з періодом Т
(рис. 4.28, а).
Період Т цієї функції зв’язаний зі значеннями циклічної V та кругової ®о
частот згідно зі співвідношеннями:
...	1	гр. 2л	2л ,,
Т = —; Т = —; ®0 = — = 2т .
V	т
Розклад в ряд Фур’є даної періодичної функції має вигляд [1]:
ф) = - У ,------------еЛ 0 	(4.106)
я	к(ос
Спектр цього процесу складається із окремих ліній, які знаходяться на
відстані ®о = 2лу одна від однієї (див. рис. 4.28, б). Пунктиром показано
обвідну лінію спектра. Вона є неперервною функцією частоти о = к®(! і
визначається залежністю:
( \ Ь®„ 8Іп((0є)
§>) --- .
л га
183
Струтинський В.Б.
Рис. 4.28. Періодична функція у вигляді серії прямокутних імпульсів (а)
та її лінійчатий спектр (б)
Розглянемо функцію нескінченного періоду у вигляді одного ізольованого
одиничного прямокутного імпульсу (рис. 4.29, а).
Рис. 4.29. Одиничний прямокутний імпульс (а) та його спектр (б)
у вигляді неперервної кривої
Функцію у вигляді одиничного імпульсу можна вважати окремим
випадком серії імпульсів, коли Т —> оо. Тому маємо функцію нескінченного
періоду. Значення базової частоти ото —> 0 і розклад у ряд Фур’є даної
функції має вигляд:
(4.107)
1 -і-со .	4-00
і(і) = —	(о(ф)-е^асо.
Я (0	4
-ОО	-00
Спектральна функція С(со), що входить в (4.107), відповідає процесу
нескінченного періоду у вигляді одиничного прямокутного імпульсу. Вона є
дійсною функцією частоти (рис. 4.29, б):
\ Ь 8ІП (ВЄ
Сдш) = — •----------------------
Л (0
(4.108)
184
Розділ -І. Математичні моделі процесів у вигляді функціональних рядів
Таким чином, серія прямокутних імпульсів (див. рис. 4.28, а) як
періодична функція має лінійчастий спектр, а один ізольований імпульс (див.
рис. 4.29, а) як функція нескінченного періоду має неперервний спектр.
Збільшимо амплітуду одиничного імпульсу її —> оо, одночасно зменшивши
його ширину 2к -> 0 за умови, що площа імпульсу Ь2є = 1. Імпульс при цьому
буде відповідати одиничній імпульсній функції 5(0 (див. розділ 2.3.6). Спектр
цього імпульсу знайдемо шляхом граничного переходу в формулі (4.108):
\	.. Ь 8ІІКВЄ 1 8ІПЮЄ 1
О(й)) = Ііт------------= Ііт-------------= — = сопзі .
11 л о) ,- ’п 2л соє 2л
Е—>0
(4.109)
Одиничний імпульс у ВИГЛЯДІ
5-функції та його спектральна функція
наведені на рис. 4.30.
АС(®)
-------Т—
1
2л
-і-----> (0
0

б)
Рис. 4.30. Одинична імпульсна функція (а)
та її спектральна функція (спектр) (б)
Таким чином, спектральна функція процесу у вигляді одиничної імпульсної
функції є дійсною постійною величиною С(со) = —. що не залежить від частоти.
2л
Спектр розповсюджується на всю область частот від -оо до +оо.
Розглянемо пакет нескінченно близьких імпульсів нескінченно малої
ширини, але нескінченно великої амплітуди, тобто пакет одиничних
імпульсних функцій (рис. 4.31, й).
Для даного пакету імпульсів період між імпульсами Т —> 0,
відповідно <в0 -> оо. Із формули (4.106) з врахуванням того, що 2йє
випливає, що максимальне значення амплітуди гармоніки
2Ьє шп
---------------£0 А _   _ 00 ,
тому
= 1,
тобто спектр представляє собою одну лінію нескінченної висоти.
відповідає 5-функції, тобто О(со) = 5(и) (рис. 4.31, б).
Розглянемо функцію нескінченного періоду, яка визначається залежністю:
, , ҐО при і < 0
Ь „р„ ^>0
Вона
(4.110)
185
Струтинський В. Б.
0(ю)
5(ю)
б)
Рис. 4-31. Процес у вигляді пакету нескінченно близьких одиничних
імпульсних функцій (а) та його спектр у вигляді одиничної імпульсної
функції( б)
Графік даної функції наведено на рис. 4.32, а.
Рис. 4.32. Неперіодична функція (а) та
її комплексний спектр (б)
Дана функція має нескінченний період і тому її спектр є неперервним.
Спектр даної функції є комплексною величиною і має вигляд
комплекснозначної функції дійсного аргументу частоти й:
СО) = |	~	-	(4.111)
2 ф	2л уЗ + ю )
Спектральна функція (4.111) включає дійсну та уявну складові, які
відповідають залежностям:
186
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
Ке[б(>)] = ^--2-^-2-;	=	(4.112)
2л р + ©	2л р + со
Дійсна та уявна складові спектра (4.112) наведені на рис. 4.32, б.
Для спектрального аналізу даної функції можна використати також
спектр у вигляді квадрату модуля спектральної функції О()и), а саме:
залежності |С(з©)|2 від частоти. Ця залежність має вигляд:
|ОИ2	=^тр-ф-рт-	(4.113)
Цей спектр відрізняється від спектра дійсної частини Ке[о(ісо)] лише
масштабом по осі ординат.
Спектральна функція СИдіо) має певні недоліки і тому при спектральному
аналізі процесів часто використовується дещо інша спектральна
характеристика процесу.
Візьмемо квадрат модуля |(3(ій))2 спектральної функції С(]®) і
проіитегруємо по всіх частотах ш від ~<ю до +=с. Враховуючи, що квадрат
модуля |С(і®]2 = О(і©) • б(- і©), одержимо:
б(- і©)<ісо .	(4.114)
— ОС	—X)
В цю формулу підставимо значення С(]ш) згідно з (4.103). Відповідно
знайдемо:
||б(,і(0р(й	/<3(-	р(т>-^с!ї .	(4.115)
Змінимо в правій частині цієї залежності порядок інтегрування:
|[С{і<о)(2сісо =	]Ї(т)сіі: |с(- і®)е^“тс1(В .	(4.116)
—сс	—ос	—ос
Враховуючи формулу (4.102) із (4.116). одержимо:
=	р[(т)]Лт.	(4.117)
З цієї залежності одержимо формулу Релея [6], яка відповідає
енергетичній формі інтеграла Фур’є:
2л ||О(і©)|2сіш = |[1(т)рс1т.	(4.118)
— со	—ос
Права частина формули (4.118) представляє собою величину,
пропорційну енергії процесу £(О.
Для більшості фізичних процесів енергія за нескінченний інтервал часу
дорівнює нескінченності. Тому замість енергії використовують середню
потужність процесу £(О, а саме:
1	(4 110)
іітА Ііол.мчад.
187
Струтинський В.Б.
де [ї(і)]2 являє собою середній квадрат значення процесу.
Взявши середні значення в часі для обох частин формули (4.118),
знайдемо:
4	4 +Х>	.	-»*т
Ііт —— [|2лСг(>)Ґс1<й = N = Ііт — Ді’(г)]2 гіт.	(4.120)
Т 2Г 2л	і —>» 21 у
Введемо позначення:
8(со)= 1іт-^-І2лО(ісо)|2.	(4.121)
т->» 21
Одержана дійсна функція 8(ю) параметра ® має назву спектральної
щільності потужності процесу, визначеного залежністю Ні) [10, 60, 119].
Спектральна щільність потужності зв’язана із середнім квадратом процесу
згідно з інтегральною залежністю:
= [£(і)р .	(4.122)
2л 4
— X
Спектральна щільність потужності дає кількісну характеристику розподілу
потужності процесу по частотах гармонік у всьому частотному діапазоні.
Формули (4.122) є узагальненням залежності (4.101) на випадок функції
нескінченного періоду.
Застосування спектральної щільності потужності є дуже зручним і широко
вживаним методом спектрального аналізу процесів, зокрема, вона
використовується для спектрального аналізу випадкових процесів [6, 10, 42,
47, 48, 60, 63, 117, 119].
Розглянемо застосування спектральної щільності потужності для
спектрального аналізу стаціонарного випадкового процесу. Такі випадкові
процеси в часі протікають приблизно однорідно. Вони мають вигляд
неперервних випадкових коливань відносно деякого середнього значення,
причому ні зовнішній вигляд коливань, ні їх амплітуда не виявляють суттєвих
змін з часом (рис. 4.33, а).
Кожний стаціонарний випадковий процес можна розглядати як нескінченно
довгий. Початок відліку часу для такого процесу не має значення.
Для стаціонарного випадкового процесу всі статистичні характеристики не
залежать від часу, зокрема, математичне сподівання та дисперсія
тДО = соп8І; сГф(ь) = сопзі.
Випадковий процес <р’(і) (рис. 4.33, а) характеризується кореляційною
функцією К(т), яка є математичним сподівання добутку значень процесу:
К(т)= М[ф*(і;)-<р‘(і + т)].
Кореляційна функція є дійсною парною затухаючою функцією аргументу
т (рис. 4.33, б).
188
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
в)
Рис. 4.33. Стаціонарний випадковий процес (а), його кореляційна функція
(б) та спектральна густина потужності процесу (в)
189
Струтинський В.Б.	
Кореляційна функція дає можливість визначити основні	статистичні
параметри випадкового процесу:	
— середнє значення процесу (момент першого порядку):	
[ф* ОО] = л/к(°°)	(4.123)
Для процесу, що відповідає рис. 4.33, середнє значення процесу дорівнює	
нулю (процес є центрованим);	
- середньоквадратичне значення (статистичний момент другого	порядку):
[ф’2(0] = К(0);	(4.124)
- дисперсію випадкового процесу:	
=К(0)-К(оо);	(4.125)
- середньоквадратичне відхилення випадкового процесу:	
= 7К(°)-К(°°)-	(4.126)
Для центрованого випадкового процесу дисперсія середньоквадратичному значенню і кореляційній функції при т = 0:	дорівнює
= ИО]-	(4.127)
Введемо спектральну щільність потужності 80(<в) випадкового процесу	
Ф*(і). Враховуючи (4.127), із залежності (4.122) одержимо:	
-!-75о(й))с1® =ИФ о •	(4.128)
Спектральну щільність' потужності 8с(со) ще називають	спектром
випадкового процесу або спектральною щільністю дисперсій. Вона	зв’язана із
кореляційною функцією інтегральним перетворенням, згідно з залежностями [6]:	
К(т) = — Г8(оі)еітта®; 2л 3(й)= |к(т)е^втсіт	(4.129) (4.130)
Ці формули з точністю до постійного множника відповідають формулам
(4.102) та (4.103), а також з точністю до постійного множника вони
відповідають зворотному та прямому перетворенню Фур’є (4.105), (4.104).
Для опису стаціонарних випадкових процесів загального виду
використовуються базові кореляційні функції [97]:
К,(т) = о2-е"а|т|;	(4.131)
К2(т) = о2 •	• соз(рт)	(4.132)
де о, , о2, ст3 - середньоквадратичні відхилення процесів; а, 0 - деякі
параметри, що характеризують резонансні властивості процесів.
190
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів
(4.134)
Кореляційним функціям виду (4.131)—(4.133) відповідають базові вирази
спектральних щільностей. Кореляційній функції (4.131) відповідає
спектральна щільність:
с і А 2о2а ст2  2Т,
5,	(й ) = —--г- =-1--5— ,
л ' а2 + а2 1 + ю2Т2
1
де = — •
а
Кореляційній функції (4.132) відповідає спектральна щільність:
2аст2(а2 + р2 + <в2)	_	а2(1 + Т2ю2)
[со4 +2(а2 -р2)в2 +а2 + р2] (і _ т2и2 + 4^2Т>2 ’
(4.135)
$з(С0) - °3
Кореляційній функції (4.133) відповідає спектральна щільність:
а 2р - со 2р + ю
Р оґ + (р - <в)2	а2 + (р + <вУ
(і-Т^У+І^о2 ’
(4.136)
Спектральна щільність довільного стаціонарного випадкового процесу
може бути одержана у вигляді лінійної математичної моделі, базисні ф_, нкції
якої відповідають набору спектральних щільностей виду (4.134)—(4.136) [60].
Ця властивість використовується для побудови математичних моделей
випадкових процесів, що мають місце у складних динамічних системах [97].
В розділі (12.5) наведена методика розробки і використання математичної
моделі спектральної щільності віброакустичного процесу складної динамічної
системи побудована з використанням базових залежностей (4.134)-(4.136).
Спектральний аналіз випадкових процесів реалізується в сучасних
математичних пакетах. Застосування засобів математичних пакетів, зокрема,
системи 8ІМІЛЛМК для проведення спектрального аналізу, показано у
розділі 12.4.
При математичному моделюванні випадкових процесів спектральний
аналіз застосовується в різних формах, як неперервних, так і дискретних.
Зокрема, елементи спектрального аналізу дискретних математичних моделей
розглянуті у розділі 6.2.
191
Струтинський В. Б
РОЗДІЛ 5
Операторні математичні моделі,
визначені в лінійному просторі
5.1.	Елементи теорії лінійних операторів
5.1.1.	Відношення еквівалентності, лінійний простір, базис
При розробці математичних моделей технічних систем та процесів
застосовуються відношення між математичними об’єктами, які називаються
відношеннями еквівалентності. Вважається, що між математичними об’єктами
а, Ь, с,... існує відношення еквівалентності, коли це відношення має наступні
властивості:
•	а = а (рефлексивність);
•	із а = Ь випливає, що Ь - а (симетрія);
•	із а ~ Ь та Ь = с випливає, що а = с (транзитивність).
Прикладами реалізації відношень еквівалентності є рівності, тотожність
функцій, рівність та подібність геометричних фігур.
Якщо є класи (множини) математичних об’єктів Сі С', то набір правил,
що ставить у відповідність кожному об’єкту х із класу С об’єкт у із класу С',
називається перетворенням (відображенням) класу С в клас С'. Наприклад,
аргумент х із класу С відображається в значення функції у із класу С'. В
символах це записується як у = Кх). Його можна розглядати як операцію над
операндом х, яка дає результат у.
Якщо в класах (множинах) С і С' задані визначення рівностей, що
задовольняють вищевказаним умовам еквівалентності, то операція
перетворення визначена коректно. При цьому із умови х = г (в класі С)
випливає Кх) = Кг) (в класі С')-
Розглянемо клас математичних об'єктів, які утворюють лінійний простір.
Нехай М - множина елементів (векторів) х, у, 2, ... довільної природи, для
яких визначені операції додавання та множення на дійсне число:
•	парі елементів х є М та у є М відповідає елемент х + у є М
(сума елементів х і у);
•	парі х є М та а (а - довільне дійсне число) відповідає елемент
ах є М (добуток числа а на елемент х).
Множина М називається лінійним простором, якщо для елементів
множини виконуються аксіоми лінійного простору, а саме:
192
Розділ 5. Операторнг математичні моделі, визначені у лінійному просторі
•	х+у=у+х (додавання комутативне);
•	х + (у + г) = (х + у) + г (додавання асоціативне);
•	існує нульовий елемент 0 є М такий, іцох + 0 = х;
•	для елемента х є обернений елемент -х такий, що х + (-х) = 0;
•	множення на число асоціативне, тобто а(рх) = (сф)х;
•	існує одиничний елемент 1 є М такий, що 1 х х = х;
•	а(х + у) = ах + ау (множення на число дистрибутивно);
•	(а + р)х - ах + Рх (множення суми чисел на елемент простору х
дистрибутивно відносно суми чисел).	(5.1)
Лінійний простір включає множину елементів (векторів), для яких
виконуються вищевказані аксіоми.
На рис. 5.1 наведена графічна інтерпретація класу математичних об’єктів,
що утворюють лінійний простір.
Ь - багатовимірний лінійний простір
елемен ги (вектори) х, у, г,
нульовий елемент Хо^О
’ ОДИНИЧНИЙ елемент Х| = 1
обернений елемент X 1 =
Умови, що висуваються до
елементів простору:
АКСІОМИ . афх) -- («р)х
а(х + у) = ах + ау
(а + р)х = ах + рх
^лементи множини М. що
; утворюють простір:
х + (у + г) = (х + у) + г
МЄ
а)	б)
Рис. 5. /. Схематичне зображення множини елементів х є М,
які утворюють лінійний простір, (а) та умови, що накладаються
на властивості елементів — аксіоми лінійного простору (б)
Лінійний простір характеризується розмірністю п.
Багатовимірний лінійний простір Ь часто називають векторним
простором, а його елементи х - векторами. Для позначення векторів
застосовують фігурні чи квадратні дужки або виділення жирним шрифтом, як
це зроблено в тексті даного підручника. В лінійному просторі Ь елемент
(вектор) х лінійно визначається через деякі базисні елементи (вектори):
е2> •”»
Елемент (вектор) х можна записати у вигляді лінійної комбінації базисних
векторів, тобто
193
Струтинський В. Б.
х = аіЄ] + а2е2 + ... + апеп.	(5.2)
Якщо хоча б один з векторів системи
Єї, е2, .... еп
лінійного простору Ь лінійно визначається через останні вектори системи, то
дана система векторів є лінійно залежною.
Система векторів еі, е2,..., еп лінійного простору Ь лінійно незалежна
тоді і тільки тоді, коли із рівняння
а^еі + а2е2 + ••• + апЄц = 0	(5.3)
випливає, що всі коефіцієнти ссі, а2, ..., ап дорівнюють нулю.
Лінійний простір характеризується розмірністю ті. Якщо в просторі існує
лінійно незалежна система із п векторів, а довільна система векторів, що
складається із (п + 1) вектора, лінійно залежна, то число п називається
розмірністю лінійного простору Е і позначається:
п = сііпт(Е).
В цьому випадку простір Ь = Ьп називається п-мірним лінійним
простором або п-мірним векторним простором.
Розрізняють одновимірний лінійний простір (п = 1), двовимірний простір
(п = 2), тривимірний лінійний простір (п = 3) та простори більш високих
вимірів (п = 4, 5,...).
Довільна впорядкована лінійно незалежна система п векторів
еь е2, ..., еп
п-мірного простору Е утворює базис простору, а довільний вектор х є Е
однозначно визначається через вектори базису
х = Х]Єі + х2е2 + ... + хпеп,	(5.4)
де X], х2, ..., хп ~ координати вектора х в базисі е^, е2, .... еп.
Вектор х, який належить лінійному простору Е, визначається своїми
координатами. їх запис у вигляді вектора-рядка має вигляд:
х = [х); х2, ..., х„].
На рис. 5.2, а схематично показано лінійний простір Еп розмірності п.
Його елементи (вектори) х визначаються через систему векторів - базис-
простору та набір чисел координат вектора х. Координати елемента (вектора)
па рисунку зображені у вигляді матриці-стовпця.
Для двох довільних векторів п-мірного лінійного простору
X = [хь х2, .... хп]
та
х' = [хі, х', ..., х' ]
сума векторів визначається за формулою:
х + х' = [х', +х;,х, +х',...,х„ 4-х;],
а множення вектора на довільне число а визначається як:
ах - [ах(, ах2, ..., ахп].
194
Розділ 5. Операторні математичні моделі, визначені у лінійному просторі
Всі елементи лінійного простору характеризуються координатами у
вигляді векторів-стовпців. Кількість компонент у стовпцях однакова для всіх
елементів і дорівнює розмірності простору. Компоненти векторів-стовпців є
довільними дійсними числами. Для двох чи більше лінійних просторів
однакової розмірності координати елементів у вигляді векторів-стовпців
мають однакове число компонент. Вектори-стовпці розрізняються лише
значеннями компонент.
Ьп - лінійний простір розмірності п = сііт(О
Простір векторів-стовпців п дійсних чисел К'
Рис. 5.2. Схематичне зображення п-мірного лінійного простору (а)
та ізоморфного йому лінійного простору Кп (б), складені
із векторів-стовпців дійсних чисел
Це означає, що всі п-мірні лінійні простори мають однакову структуру,
таку як простір Кп векторів-стовпців із п дійсних чисел.
Розглянемо два лінійні простори X та ¥. Вони називаються ізоморфними,
коли між їхніми елементами встановлена така взаємно однозначна
відповідність, що коли вектори х і х' із простору X відповідають векторам у і
у' із простору V, то вектору х + х' відповідає вектор у + у' , а вектору ах є X
відповідає вектор ау є ¥.
Відповідно всі п-мірні лінійні простори ізоморфні простору К", який
складений із елементів - векторів-стовпців п дійсних чисел. На рис. 5.2, б
показано лінійний простір, складений із векторів-стовпців п дійсних чисел.
Даний простір є ізоморфним для довільного п-мірного лінійного простору.
Ізоморфізм п-мірних лінійних просторів простору Кп означає, що відношення
між елементами довільного п-мірного лінійного простору і операції з ними можна
вивчати як відношення між векторами із В” і операції з ними. Відповідно, всяке
195
Струтинський В. Б.
твердження відносно векторів із Кп справедливе для відповідних елементів
довільного п-мірного лінійного простору. Одне з таких тверджень, що має строге
доведення, наступне. Якщо система векторів-стовпців
еі> е2> •••> еп
із Кп утворює базис, то це має місце тоді і лише тоді, коли визначник
матриці, складеної із стовпців - координат векторів базису - не дорівнює
нулю. Єї =	Відповідно для векторів базису е<, е2, ...,						еп з координатами				
	Єн е21	; е2 =	Є12 е22		Єц> Є2„	: сієї А =	еи е2.	е)2 . ^22	• е1п • Є2о	ф 0.	(5.5)
			_Є„2.				<4.1	Єр2 •	• епп		
ІЗ ЦЬОГО твердження випливає, ЩО вектори Єї, Є2, еп із довільного
лінійного простору Ьп утворюють в даному просторі базис тоді і тільки тоді,
є
базису Єї, Є'2, .
еп утворюють
коли визначник матриці, стовпцями якої є компоненти даних векторів
відмінний від нуля.
Розглянемо ДВІ системи векторів: Є], е2, ..., еп
утворюють два базиси в деякому лінійному просторі
другого базису £,, Ь, ..., £п через вектори першого
Координати векторів £,, £2,	('п У базисі е(, е2, ....
стовпці, компоненти яких виражають вектори другого базису через
першого базису:
і £1, £2, ..., £п, Щ°
Ьп. Виразимо вектори
еп.
вектори-
вектори
+ £21е2 +	+ (піеп;
Ь = (]2е1 + (22е2 + ••• + (п2епі
(5.6)
~ (іпЄ1 + (2пЄ2 + ... + £п11еп.
Матрицею переходу від базису
Є], е2, ..., еп до базису £1, £2, •••>
називається матриця С, стовпцями якої є координати векторів
£1, £2, ..., £п в базисі Є], е2, ..., еп.
Матриця переходу від першого базису
е1; е2, ..., еп до другого базису £(, £2, ..., £п має вигляд:
£	£	£
*п	Й2	Чп
£	£	£
С _ '21	‘22	••• х2п
£	£	£
‘пі	ап2	*пп
(5 7)
196
Розділ 5. Операторні математичні моделі, визначені у лінійному просторі
Оскільки вектори £), £2,	утворюють базис, то визначник матриці
переходу С завжди відмінний від 0, тобто ЗсТС * 0.
На рис. 5.3 схематично показано процес переходу від першого до другого
базису в деякому п-мірному лінійному просторі.
п-вимірний лінійний простір Ьп
Базис 1
е1? е2, ..., е„
Елемент простору
X = Х]Є1 + Х2Є2 + ... +
хпеп
Хс = [X), Х2, .... Х„]т
Взаємозв’язок векторів
координат
X,. = С X х;
Матриця переходу
від базису 1 до базису 2
*!! ^2	•  ’ї.
іг	... *
їк2 - і;
Базис 2
...Л„
Елемент простору
х = ХА + &£>+
+ Х./п
Х| = ІХі, Х2...Хч1Т
Взаємозв’язок векторів
координат
Х( = С ! х хс
Рис. 5.3. Перехід від одного базису лінійного простору до іншого
В деякому лінійному просторі довільний вектор х лінійно виражається
через вектори обох базисів. Таким чином,
X = Х]Єі + Х2Є2 + ... + х„еп
або
х = Хі<"і + Х2*2 + ... + хЛ-
Координати
Х|, х2, ..., хп вектора в базисі Є], е2, ..., еп
та його координати
Хі, Х2. •••> Хп в базисі <
зв'язані матрично-векторною залежністю:
(5.8)
X Х(,
або
хе = С
де вектор и-стовиці
Хе = [х1; Х2> .... ХП]Т
та
Хт = [%1, Х2. Хп1Т
є результатом транспонування відповідних векторів-рядків координат.
Звідси випливає
197
Струтинський В.Б.
хг = С1 х хе,
де С'! - матриця, обернена С.
Вона існує тому, що визначник матриці С відмінний від нуля.
Вказані матрично векторні співвідношення також наведені на рис. 5.3.
В п-мірному лінійному просторі існує довільна кількість базисів. Вибір
певного базису обумовлюється задачами математичного моделювання.
При математичному моделюванні звичайно використовуються окремі види
практично важливих лінійних просторів. Вид лінійного простору залежить від
властивостей додаткових операцій, які здійснюються над елементами
простору.
Найчастіше використовується евклідовий лінійний простір. Лінійний
простір Е називається евклідовим, якщо кожній парі векторів х, у із цього
простору поставлено у відповідність дійсне число, яке називається скалярним
добутком і позначається х-у. Шоб розрізнити скалярний добуток від інших
операцій, між співмножниками ставиться крапка.
Скалярний добуток характеризується наступними властивостями. Для
довільних векторів х, у, 2 що належать Е, і довільного дійсного числа а
справедливі наступні рівності:
х-у = у-х; (ах)-у = а(х-у);
(х + у)-г = х-2 + у-/;	(5.9)
х-х > 0 при х 0;	0-х = 0 - нульовий вектор.
На рис. 5.4 наведено схему евклідового лінійного простору із введеним
скалярним добутком.
п
З /------
| Елемент
! простору
!(вектор)X
г<
Евклідовий п-мірний лінійний простір Е,
Визначення скалярного добутку
:	"	Л	'
векторів х-у = £х,у,
І=1
Довжини (модулі) векторів
Кут між двома векторами ,
 ср = агссо5Іх-у/(|х||у|)1
Елемент
простору
(вектор)у
Рис. 5.4. Евклідовий лінійний простір, в якому визначено скалярний
добуток векторів, довжину вектора | х | та кут ер між векторами х і у
198
Розділ 5 Операторнг математичні моделі, визначені у лінійному просторі
Введення скалярного добутку обумовлює появу нових характеристик
елементів лінійного простору. Зокрема, дійсне додатне число
|х| = л/х-х	(5.10)
називається довжиною (модулем) вектора х;
число, одержане як
|х - УІ = л/(х’-У) • (х - У)	(5.11)
називається відстанню між вершинами векторів х і у;
кут, визначений за залежністю
X у
а) = агссозт-тг-7- 0..Л
НІ?!
є кутом між векторами х і у (при цьому х 0, у * 0).
Вектори х і у із евклідового простору Е називаються ортогональними,
якщо їх скалярний добуток дорівнює нулю, а саме:
х-у = 0.
Система векторів евклідового простору називається ортонормованою,
якщо вектори системи попарно ортогональні і мають одиничну довжину.
Базис евклідового простору називається ортонормованим базисом, коли
вектори базису попарно ортогональні і мають одиничну довжину. Доведено,
що в кожному евклідовому просторі існує ортонормований базис
Найпростішим прикладом евклідового простору є Еп - простір стовпців із
дійсних чисел. В даному просторі скалярний добуток векторів заданий
формулою:
х ' У = £хіУі 
і=1
Для довільних векторів х та у із цього простору справедливі формули:
Уі
Скалярний добуток х-у, довжини векторів |х[ та |у|, а також кут між
векторами ф не залежать від вибраного ортонормованого базису, тобто є
інваріантними відносно зміни системи координат.
Якщо е,, е-2, еп і Б>, :	~ ортонормовані базиси в п-мірному
евклідовому просторі, то матриця переходу від одного з цих базисів до іншого
є ортогональною. Визначник ортогональної матриці дорівнює одиниці.
199
Струтинський В.Б.
5.1.2.	Лінійні оператори та їх характеристики
Важливе значення при математичному моделюванні має операція
перетворення лінійних просторів. Перетворення одного простору в інший
здійснюється за певним законом (правилом), який має назву оператора.
Лінійні закони (оператори) використовуються найбільш широко.
Оператори можуть мати різноманітний вигляд і включати математичні
операції різного виду. Алгебраїчні оператори використовуються в аналітичній
геометрії, при розв’язку систем рівнянь. Оператори, які використовують
диференціальні та інтегральні операції, застосовуються при розв’язку
диференціальних рівнянь різного виду. Існує багато інший видів операторів,
зокрема, оператори перетворення дискретних значень процесів та неперервних
інтегральних перетворень.
Розглянемо відношення перетворення двох лінійних просторів X, V.
Правило, за яким кожному вектору (елементу) х є X ставиться у
відповідність єдиний елемент у є ¥, називається оператором. Результат дії
оператора А на елемент х позначають наступним чином:
у = Ах або у = А(х).	(5.13)
Елемент у називають образом (зображенням) елемента х, а елемент х
прообразом елемента у.
На рис. 5.4 показана схема перетворення елементів двох лінійних
просторів.
Лінійний простір X	Лінійний простір V
В(А) - область дії оператора	Іт(А) - образ оператора
Рис. 5-5. Схема дії лінійного оператора А, що здійснює перетворення
елементів х із лінійного простору X в елементи у лінійного простору ¥
Множину елементів лінійного простору X, для яких визначена дія
оператора А, називають областю визначення оператора А і позначають В(А).
Множину елементів лінійного простору ¥, які є образами елементів із О(А),
називають образом оператора А і позначають Іт(А).
Якщо перетворення просторів визначене у вигляді:
200
Розділ 5. Операторні математичні моделі, визначені у лінійному просторі
У = Ах,
ТО X Є Е)(А), у є Іт(А).
Оператор А, який діє в лінійних просторах х і у, називається лінійним
оператором, коли виконуються умови
А(х + х') = А(х)+А(х') і А(ах) = аА(х)	(5.14)
для довільних елементів х і х’ та довільного числа а.
Якщо простори X і ¥ співпадають, то вважають, що оператор А діє в
просторі X.
Розглянемо лінійний оператор А, який діє в лінійному просторі X
розмірності п = <1іт(Х).
В цьому лінійному просторі X визначено базис е1; е2, ..., еп. Позначимо
Ае( = (ап, а21, ..., ап]);
Ае2 = (а]2, а22>	ап2);
Аеп — (аіп, а2п, ..., апп).
Ці залежності представляють собою образи базисних векторів Є(, е2..... еп.
Матриця
'ан а|2 ...а1п "	(515)
.	а21 а22 •" а2п
_ап, ап2 апп_
стовпці якої є образами базисних векторів, називається матрицею
лінійного оператора А в заданому базисі.
На рис. 5.6 схематично показано дію оператора в одному лінійному
просторі, наведено матрицю оператора та його характеристику.
Лінійний простір X
а)
Рис. 5-6. Схема дії лінійного оператора А в одному лінійному просторі (а)
та параметри оператора (б)
ИІІ
б)

201
Струтинський В. Б.
Кожному лінійному оператору, що діє в п-мірному просторі X. відповідає
єдина квадратна матриця порядку п.
Навпаки, кожна квадратна матриця порядку п задає єдиний лінійний
оператор, що діє в п-мірному просторі. При цьому результат дії оператора,
визначений у вигляді у = Ах, зв’язує координати вектора образа у з
координатами прообразу х матрично-векторною залежністю:
	’Уі' У2	—	’а.і а21	а12 ... а22	ач/ а2п	X	’хф х2		(5.16)
При змії	У». Іі б	азі	Зої ісу	аг,2 лінійного	апп. пр<	зет	_Хп. °РУ	матриця	оператора змінюється.
Нехай здійснено перехід від базису
Є = {Єї, е2, еп}
до базису
е' = {є') , е2, е'п}.
Зв'язок між матрицею Ае оператора А в базисі е і матрицею Ае' цього
оператора в базисі е' задається формулою:
ас. = р;Дє.аєр_„	і
де Р(,^е, - матриця переходу від базису е до базису е',
Р;Де. - матриця, обернена до неї.
Розглянемо лінійний оператор А, який діє в лінійному просторі.
Розмірність образа лінійного оператора називається рангом оператора і
позначається:
г = К(А) = 8іт(Іт(А)).
Ранг оператора дорівнює рангу його матриці.
Ядром лінійного оператора називається множина елементів із простору X,
образом яких є нульовий елемент. Ядро оператора позначають:
Кег(А) = {х є X при яких Ах = 0}.
Ядром лінійного оператора є лінійний простір. Розмірність ядра лінійного
оператора називається дефектом оператора:
сі = ИеКА) = 6іт(Кег(А)).
Ядро оператора співпадає з множиною розв’язків лінійної однорідної
системи рівнянь, матрицею якої є матриця оператора.
Лінійні оператори характеризуються певними числовими параметрами. Ці
параметри мають назву власних значень та власних векторів. Власні
значення операторів і власні вектори мають широке практичне застосування.
Нехай А - лінійний оператор, що діє в лінійному просторі.
Число "к називається власним значенням, а вектор х - відповідним
власним вектором лінійного оператора А, якщо вони зв’язані між собою
202
Розділ 5. Операторні математичні моделі, визначені у лінійному просторі
відношенням:
Ах - Хх.	(5.17)
В лівій частині цієї формули стоїть образ вектора х, одержаний як
результат дії оператора А на цей вектор. В правій чистині формули
знаходиться вектор х, помножений на число (власне значення оператора).
Таким чином, з формули (5.17) випливає, що образи власних векторів
пропорційні самим власним векторам. Коефіцієнти пропорційності
представляють собою власні значення оператора. Для кожного оператора
існує певний набір власних значень.
Сукупність власних значень називається спектром-оператором.
Розглянемо матрицю оператора А в деякому базисі. Власні значення
оператора і відповідні їм власні вектори зв’язані співвідношенням:
(А - ХЕ)х = 0,
де Є - одинична матриця.
Дане співвідношення випливає з рівності (5.17).
Це означає, що кожний власний вектор оператора є ненульовим
розв’язком лінійної однорідної системи рівнянь (х *- 0). Цей розв’язок існує
Тоді і тільки тоді, коли визначник матриці (А - ХЕ) рівний нулю, тобто
йеЦА - ХЕ) = 0.	(5.18)
Відповідно, власні значення лінійного оператора можуть бути знайдені як
корені рівняння (5.18), а власні вектори - як розв’язки відповідних однорідних
систем. Рівняння (5.18) називається характеристичним рівнянням оператора А.
Поліном, одержаний при розкритті визначника в лівій частині рівняння (5.18)
називається характеристичним поліномом оператора А.
Для власних значень та власних векторів лінійного оператора справедливі
наступні твердження:
•	характеристичний поліном с1еі(А - ХЕ) = 0 оператора А, що діє в п-
мірпому просторі, є поліномом п-го ступеня відносно власних значень X;
•	лінійний оператор, що діє в п-мірному просторі, має не більше ніж п
різних власних значень;
•	власні вектори, що відповідають різним власним значенням оператора,
лінійно незалежні;
»	якщо лінійний оііератор4 що діє в п-мірному лінійному просторі X, має
п різних власних значень, то в просторі X існує базис із власних векторів
оператора, який називається власним базисом оператора;
•	матриця оператора в базисі із його власних векторів має діагональну
форму із власними значеннями на головній діагоналі.
Знаходження власних значень та власних векторів операторів надзвичайно
широко використовується при математичному моделюванні процесів та
систем. Методи знаходження цих параметрів розглянуто нижче.
203
Струтинський В.Б.
5.2. Операції з векторами і матрицями в пакеті МаіЬСАО
5.2.1.	Алгебраїчні операції з векторами і матрицями
При математичному моделюванні використовуються різноманітні векторні та
матрігчні математичні об’єкти Вони утворюють математичні моделі, пов'язані з
обробкою елементів лінійного простору. Математичні моделі реалізуються
використовуючи апарат лінійної алгебри та засоби математичних пакетів.
Векторні та матричні математичні об’єкти мають свою специфіку визначення.
Матриця розміру шхп - це прямокутна таблиця, яка складена з дійсних
або комплексних функцій (дійсних або комплексних чисел), що є
компонентами матриці. Прямокутна матриця має ш рядків та п стовпців.
Якщо кількість рядків дорівнює кількості стовпців, то матрицю називають
квадратною матрицею порядку п. Компоненти (складові) матриці позначають
аіг де індекс і - визначає номер рядка, і - номер стовпця.
Коли матриця має лише один рядок, її називають матрицею-рядком або
вектором-рядком. Матрицю, що має лише один стовпець, називають
матрицею-стовпцсм або вектором (вектором-стовпцем).
Матриці та вектори записують звичайно у табличному вигляді, як це
показано нижче для прямокутної матриці А, вектора-рядка її та вектора-
стовпця V:
аі1 аі2
а21	а22
ат1 йт2
тп
При математичному моделюванні використовуються окремі випадки матриць,
частина елементів яких є нульовими.
Діагональною матрицею називається квадратна матриця, в якій відмінні від
нуля лише елементи головної діагоналі. Для діагональної матриці:
а,, = 0 при і ф ], а,! 0 при і = у
Окремим випадком діагональної матриці є одинична матриця, всі елементи
якої, що знаходяться на головній діагоналі, дорівнюють одиниці: аі( = 1.
Верхньою трикутною матрицею називають квадратну матрицю з нульовими
компонентами знизу від головної діагоналі.
Нижньою трикутною матрицею називають квадратну матрицю з нульовими
компонентами, розташованими вище від головної діагоналі.
Стрічкова матриця - це квадратна матриця, в якій ненульовими
компонентами є компоненти головної діагоналі та сусідні з ними. Стрічкові
матриці розрізняють в залежності від кількості ненульових компонент,
розміщених біля головної діагоналі. Тридіагональна матриця має три ненульових
204
Розділ 5- Операторні математичні моделі, визначені у лінійному просторі
компоненти в кожному рядку.
Нижче наведені таблиці діагональної В, одиничної Е, верхньої трикутної Т та
стрічкової тридіатональної С матриць:				
О = Т =	’сі,,	0	0	...	0	' 0	ф,	0	...	0 0	0	0	...	дпп ^11 (-12 ^13 ’ ' *Пп 0 ^22 ^23 • ' Фі	; Е = ; с =	'10	0	...	0' 0 1	0	...	0 0 0	0	...	1 ’с(1 с,2	0	... С2І С22 С23 ••	> (5.20) 0
Квадраті	_о 0 о ... V пі матриці, компонег	гги яких	.0	0	0 ... сп„_ розташовані симетрично відносно	
головної діагоналі, називаються симетричними. Відповідно діагональна та
одинична матриця є симетричними.
Математичний пакет МаЙіСАВ різних версій включає ефективні засоби
обробки математичних об’єктів у вигляді векторів і матриць. За допомогою них
можна формувати матриці, виконувати алгебраїчні операції над векторами і
матрицями, здійснювати графічну інтерпретацію векторних і матричних
математичних об’єктів. Операції з векторами і матрицями здійснюються двома
способами. По-перше, операції з матрицями виконуються аналогічно операціям із
звичайними скалярними величинами, по-друге, наявні спеціальні засоби
(вбудовані функції) здійснення операцій над векторами і матрицями.
В математичному пакеті МаЙіСАВ наявний широкий набір функцій та
операцій для роботи з векторами і матрицями. В панелі математичних
інструментів МаїпСасІ РаїїеЬе (рис. 5.7, а) наявна панель операцій з матрицями і
векторами іМаїгіх ог уєсіог (рис. 5.7, б).
а)
Рис. 5.7. Панель інструментів МаПгСАО Раїїеіе (а), панель роботи з
матрицями та векторами Маігіх ог оесіог (б) та панель символьних
операцій ЗутЬоІіс КеуЬоагсі (в)
205
Струтинський В.Б.
Формування матриці або вектора необхідної конфігурації та розмірності
здійснюється шляхом ініціалізації кнопки
н
на панелі роботи з матрицями (рис. 5.7, б). При цьому відкривається
діалогове вікно (рис. 5.8, а).
В діалоговому вікні (рис. 5.8, а) задається число рядків матриці (Коик)
та число стовпців (Соїитпя). Після визначення цих параметрів на екрані
з’являється заготовка матриці (рис. 5.8, б). Задаючи відповідну кількість
рядків та стовпців формують прямокутні матриці довільної розмірності, в
тому числі вектор-рядок, заготовка якого наведена на рис. 5.8, в, або вектор-
стовпець (рис. 5.8, г). Коли заготовка виведена на екран, наприклад,
рис. 5.8, д, тоді на місце чорних квадратиків вводяться числові дані або
символьні вирази (рис. 5.8, <?). Це один із способів формування векторів і
матриць. Існує ряд інших способів, які будуть розглянуті нижче.
І І >
І І І
д)
е)
Рис. 5.8. Формування векторів та матриць необхідної конфігурації
та розмірності: а - діалогове вікно; б - заготовка квадратної матриці;
в, г ~ заготовки вектора-рядка та вектора-стовпця; д - заготовка
прямокутної матриці; е ~ приклад формування символьної
прямокутної матриці
Панель операцій з векторами і матрицями (див. рис. 5.7, б) дозволяє
виконувати різноманітні операції лінійної алгебри. Визначник матриці або
довжину вектора обчислюють за допомогою кнопки
II
При цьому/ довжина вектора з компонентами х, (і = 0, 1, 2, .... п)
Гп—
розраховується за формулою |х№ По-елементні операції з матрицями
ї і=0
здійснюються шляхом ініціалізації кнопки
206
Розділ 5- Операторні математичні моделі, визначені у лінійному просторі
Якщо задано дві матриці А = {а^} та В = {Б,,}, то АВ = ^а^Ь^ф Кнопка
служить для . іб'їнслення скалярного добутку двох векторів X і У , а кнопка
для обчислення векторного добутку векторів. Обчислення суми компонент вектора
V здійснюється пі іяхом ініціалізації кнопки
Нижче наведено фрагмент документа МаїЬСАВ, який ілюструє виконання
вищевказаних операцій, а саме: формування двох числових векторів и і V,
обчислення довжини кожного вектора, знаходження суми компонент векторів,
визначення скалярного
операції з векторами:
та векторного добутків векторів, а також поелементні
1
З
5
у • х = 19
5,916	|и| = 4,583 £и = 7
(5.21)
Формування окремого вектора із стовпця матриці здійснюється за
допомогою кнопки
Вона служить для виділення із матриці стовпця з номером ), що
вказується в трикутних дужках. Кнопка
ИІ
йОЙ
призначена для виконання операції транспонування матриці. Транспонування
матриці полягає в заміні місцями рядків і стовпців при збережені
послідовності елементів в середині кожного рядка чи стовпця. Симетрична
матриця співпадає з транспонованою.
Нижче наведений фрагмент документа МаіЬСАО, який ілюструє
виконання вищевказаних операцій, зокрема формування квадратної матриці
та її транспонування, а також формування векторів із окремих стовпців
матриці. Нумерація стовпців здійснюється починаючи з першого стовпця,
який має нульовий індекс.
207
Струтипськигі В.Б.
В математичному пакеті є можливість візуалізації інформації, що
відповідає компонентам вектора чи матриці. Для цього служить кнопка
ІИІ1
на панелі роботи з матрицями (рис. 5.7, б). Ініціалізація даної кнопки
призводить до появи на екрані графічної заготовки (рис. 5.9, а).
В чорний прямокутник заготовки необхідно помістити ім’я матриці чи
вектора. При візуалізації матриця зображується у вигляді прямокутника.
Затушована частина прямокутника відповідає компонентам матриЦІ, які
дорівнюють або перевищують значення -0,5.
Даний спосіб візуалізації не завжди є раціональним, оскільки числова
інформація подається у спрощеному вигляді.
Рис. 5.9. Візуалізація матриці за допомогою засобів математичного
пакету МаіНСАО: а - графічна заготовка; б - матриця, візуалізація
якої здійснюється; в - результат візуалізації матриці
за допомогою кнопки
Засоби пакету дозволяють здійснити більш ефективну візуалізацію
числової інформації, наведеної в матриці. Це здійснюється за допомогою
просторових графіків. На рис. 5.10 наведена візуалізація матриці С
(рис. 5.9, б) за допомогою стовпчастих просторових діаграм.
Компоненти матриці зображуються у вигляді стовпців, висота яких
визначає значення компоненти. Враховується знак компонентів матриці. За
допомогою меню просторового графіка можна змінювати величину перерізу
елементів діаграми, а також просторове розташування графіка і масштаби.
208
Розділ 5- Операторні математичні моделі, визначені у лінійному просторі
Можливе зображення матриці по окремих стовпцях (рис. 5.10, в).
Візуалізація за допомогою просторових графіків дає геометричну
інтерпретацію інформації, наведеної в матриці.
а)
б)
в)
Рис. 5.10. Графічна інтерпретація числових даних із прямокутної матриці
за допомогою тривимірної стовпчастої діаграми (ЗО Ваг 8/іагі):
а - матрична стовпчаста діаграма; б - варіант оформлення кольорової
гами; в - зображення матриці по стовпцях
При математичному моделюванні використовуються різноманітні операції
з матрицями. Це, зокрема, порівняння матриць.
Дві матриці
А = [аі5] і В = [Ь^]
однакового виду і розмірності вважаються рівними, коли рівні їх відповідні
компоненти а^ = Ь^.
Сумою двох чи більше матриць
А = [ам] і В = [Ьч],	(5.23)
які мають однакову структуру (однакове число рядків і стовпців), вважається
матриця
с = [сц],
компоненти якої сц є сумами відповідних компонент матриць-доданків, тобто
209
Струтинський ІЗ. Б.
СЦ - аі; + 1>і].
Множення матриці
А= [а^]
на число а означає множення кожної компоненти матриці на це число.
Операція множення двох матриць є більш складною.
Якщо матриця
А = [а; і]
множиться на матрицю
В = [Ь,]],
то компоненти одержаної матриці
С (С = АВ)	(5.24)
визначаються наступним чином:
сіі ЇХЧ.
к-1
Дане правило допускає геометричну інтерпретацію, наведену на рис. 5.11.
Лініями (рис. 5 11) показано добутки яких елементів складають суму, що
відповідає компоненті сц результуючої матриці, яка знаходиться в і-тому
рядку та і-стовпці.
Рис. 5.11. Геометрична інтерпретація знаходження компоненти
результуючої матриці С при множенні двох прямокутних матриць:
А (розміром тхр) та В (розміром рхп)
Добуток матриць визначено в загальному випадку для матриць різної
розмірності. Єдиною умовою є те, що число стовпців р матриці А повинно
дорівнювати числу рядків р матриці В. Тому допустимі операції множення
210
Розділ 5. Операторні математичні моделі, визначені у лінійному просторі
матриці на вектор та множення вектора-рядка на вектор-стовпець. На рис. 5.12
наведена схема множення квадратної матриці М на вектор-стовпець V та
множення вектора-рядка V/ на вектор-стовпець О.
За допомогою засобів математичного пакету МаІІїСАО виконуються всі
операції з матрицями, які потрібні при моделюванні процесів та систем.
Рис. 5-12. Геометрична інтерпретація множення квадратної матриці М
на вектор V (а) та множення вектора-рядка ЇУ на вектор-стовпець ф (6)
В математичному пакеті МаНіСАВ можна виконувати різноманітні
алгебраїчні операції з матрицями і векторами. Операції додавання, віднімання
А і В та множення матриці
та множення здійснюються як операції зі звичайними скалярними величинами
чи функціями. Результати множення двох матриць
А на вектор V наведені нижче:
А :=
5
-1
0
0
-1
5
0
0
А*В =
’ 26
-10
0
0
Використовуючи множення
матриць, можна здійснювати
деякі додаткові
операції обробки матриць, наприклад, знаходження суми елементів матриці
по стовпцях або рядках. Для цього вводяться допоміжні вектори:
[Тк
СІ: = (1 1 1) та С2 = 1
1
211
Струтинський В.Б.
1
2 З
5 6
8 9
Тоді для матриці
А := 4
суми по стовпцях знаходяться як
компоненти вектора:
С1*А = [12 15 18],
а суми елементів по рядках - як компоненти вектора:
А*С2
6
15
24
Виділення одного стовпця матриці здійснюється допоміжним вектором СЗ.
Він має всі нульові компоненти, крім компоненти, яка відповідає номеру
виділеного стовпця. Відповідно для виділення третього стовпця допоміжний
вектор буде визначатися як:
0
СЗ := 0
а третій стовпець буде виділений множенням матриці А на вектор СЗ:
А * СЗ =
З
6
9
Виділення одного рядка матриці здійснюється допоміжним вектором:
С4: = (100)- для першого рядка;
С5: = (010) - для другого рядка;
С6: = (0 0 1) - для третього рядка.
Відповідно перший рядок матриці буде результатом добутку С4 на
матрицю А, тобто
С4*А =[12 3].
Використовуючи допоміжні матриці, можна переставляти рядки і стовпці,
наприклад, перестановка першого та другого рядків матриці А здійснюється
наступною процедурою МаїйСАО:
	1 2 3‘		0 1 0’			
А :=	4 5 6		1 0 0	* А =	1 2 3	
	7 8 9		0 0 1		7 8 9	
Перестановка	другого та третього рядків матриці					А здійснюється
наступним чином:
212
Розділ 5- Операгпорнг математичні моделі, визначені у лінійному просторі
Аналогічно можна переставити стовпці матриці. Перестановка першого та
другого стовпців матриці А виконується наступним чином:
	'0 1 0’		2 1 3’
А ♦	1 0 0	=	5 4 6
	0 0 1		8 7 9
Перестановка другого та третього стовпців матриці А. має вигляд:
	1 0 0~		і 3 2
А *	0 0 1		4 6 5
	0 1 0		7 9 8
Всі вищеназвані операції лінійної алгебри можна виконувати з матрицями,
які мають як дійсні, так і комплексні числові компоненти. Матриця із
комплексними складовими включає уявну одиницю і — V— 1 - Нижче наведено
приклад реалізації в пакеті МаіЬСАІ) визначення числової матриці з
комплексними складовими, транспонування цієї матриці, виділення першого
стовпця з матриці та знаходження визначника комплексної числової матриці,
який відповідно є комплексним числом.
	"5	+ і -	І 0 0		"5 +і 1 0 0
		1	5	2і 0		-1	5 і 0
А :=				Ат =	
		0 і	4 0		0 2і 4 0
		0	0	0 6		0	0 0 6
					
		5 + 1І			
д<0>	—	1	ІА|	= 684 + 132І.	
		0			
		0			
Всі наявні операції з комплексними матрицями не відрізняються від
операцій з дійсними числовими матрицями.
Засоби математичних пакетів також дозволяють здійснювати операції з
матрицями, компоненти яких задані у символьному вигляді, тобто є
функціями. Матриці, компоненти якої залежать від одного аргументу х або
кількох аргументів, є функціями відповідно одного або декількох аргументів.
Операції з символьними матрицями виконуються з використанням панелі
символьних операцій ЗутЬоІіс КеуЬоагсІ (рис. 5.7, «)- Панель символьних
операцій включає процедури для роботи з символьними матрицями.
Процедура транспонування (Тгапзрозе) здійснюється за допомогою кнопки
обчислення визначника (ОеіегтіпапО символьної матриці - з використанням
кнопки
213
Струтинський В. Б.
Дані процедури можуть бути застосовані як для символьних, так і для
числових матриць з дійсними або комплексними компонентами.
Нижче наведено приклад реалізації в пакеті МаЙіСАИ визначення символьної
матриці, компоненти якої залежать від одного аргументу х, знаходження
транспонованої символьної матриці, визначення стовпців символьної матриці та
1
X
1
1
А(х)‘
А(х)‘

1
З
З
1
Якщо визначник квадратної матриці
називається сингулярною (виродженою),
сингулярними.
Для несингулярної матриці А існує
задовольняє матричним рівностям:
А* А-1 = А1 *А = Е ,
де Е - одинична матриця.
Обернена матриця добутку дорівнює
записаних у зворотному порядку, наприклад:
(А*В*С)=СИ *В 1 *А’1 .
дорівнює нулю, то матриця
Всі прямокутні матриці є
обернена матриця А1, яка
(5.25)
добутку обернених матриць,
(5.26)
В пакеті МаЙіСАВ знаходження оберненої матриці (ІпчегО здійснюється
за допомогою кнопки
Нижче наведено фрагмент документа МаіЬСай, де виконано знаходження
символьної оберненої матриці. Обернена матриця існує, оскільки визначник
матриці А не дорівнює нулю (с!еї(А(х)) 0):
214
Розділ 5. Операторні математичні моделі, визначені у лінійному просторі
X X 1 1
12 11
	"1	(-7 + 5-х)	2	(х-2)	1	(х2 - 5  х + 6)	-1 (3-х2-4-х-1)'
	3 (-2-х + х2+1) -2	1	3	(-2 • х + х2 + 1) — 2	1	я?	(-2 • х + х2 +1) 1 (х-3)	3	(—2-х + х2+1) 1 (З-х-1)
А(х)": ->	3 (-1 + х) 2	1	1	3 (-1 + х) (З-х-1)	-2	3 (-14-х) X	3 (-1 + х) -1	(3-х —1)
	3 (-2-х + х2+1) -1 1	3	(~2 - X 4- X" 4-І) -1 1	3	(-2-х + х2 +1) 1	X	3 (-2-х + х2+1) 1 1
Всі с	3 (-1 + х)	3 (-1 + х) іперації з символьними матрицями			3 (-1 + х)	3 (—14-х) виконуються також для комплексних		
складових компонент матриці. Наведений нижче фрагмент документа МаНіСАГ)
ілюструє операції з комплексними символьними матрицями, зокрема визначення
символьної матриці з комплексними складовими,
операції транспонування
матриці, знаходження визначника та оберненої матриці:
	4 + і	х-і 7‘		4 4- І 1	2 + х"
А(х):=	1	х 1	А(х)т -+	і • X X	3
	2 + х	3 5		7	1	5
।А(х) —> бх + 9 + 2іх - Зі + іх2 - 7х2
(5х - 3)	_____-(5іх-21)______ х(- 7 + і)
+ 9 + 2іх - Зі + іх2 -^Тх2)	(бх + 9 + 2іх - Зі + іх2	- 7х2)	(їх +9 + 2іх - Зі + Ііх2	- 7х2)
А(ху 7__________________(і' 3) ч	у.____________________________(Ь'О__________________________________ч
(бх+9 + 2іх - Зі + іх2 - 7х2)	(бх + 9 + 2іх - Зі + іх2	- 7х2)	(бх + 9 + 2іх - Зі + ііх2	- 7х2)
- (2х - 3 + х2)_ (-12 - Зі + 2іх + іх2)	4х
+ 9 + 2ІХ-ЗІ + іх2 - 7х2) (бх + 9 + 2іх - Зі + іх2 - 7Х2) (>х + 9 + 2іх - Зі 1- Ііх2 - 7х2)
Для символьних матриць з комплексними складовими також
застосовується візуалізація. Звичайно символьна матриця перед візуалізацією
трансформується в числову матрицю шляхом підстановки значення
аргументу. При візуалізації затушовані прямокутники відповідають елементам
матриці, дійсні частини яких більші -0,5. Нижче наведено фрагмент
документа МаіЬСАО, що здійснює візуалізацію символьної матриці А(х) з
комплексними складовими
Для матриці з комплексними складовими може бути окремо виконана
візуалізація дійсних та уявних складових компонент матриці. При цьому
215
Струтинський В. 15.
формуються допоміжні матриці дійсних та уявних складових компонент. Далі
здійснюється візуалізація одержаних допоміжних матриць. Нижче (рис. 5.14)
наведено фрагмент документа МагІїСАО, що здійснює дані операції стосовно
матриці А(х), наведеної на рис. 5.13 (при х = -3).
х*1 -7
X	- і
3-2і 5
А(х)
х := -З
Рис. 5.13. Візуалізація символьної матриці з комплексними складовими
для значення аргументу х = -З
С(х) := Ке(А(х))
В(х) := Іт(А(х))
Рис. 5.14. Візуалізація матриць дійсних С(х) та уявних В(х)
складових компонент матриці А(х) з комплексними складовими:
а - візуалізація матриці дійсних складових: б - візуалізація матриці
уявних складових
Із порівняння рис. 5.13 і рис. 5.14, а випливає, що результати візуалізації
матриці з комплексними складовими співпадають з візуалізацією дійсних
складових компонент матриці.
Разом з плоскою візуалізацією використовується також об’ємна візуалізація
дійсних чи уявних складових компонент матриці за допомогою просторових
стовпчастих діаграм. Вона здійснюється так, як показано раніше (див. рис. 5 10).
Практично важливим випадком квадратної матриці є ортогональна
матриця:
О = |1
Для неї транспонована матриця співпадає із оберненою, при цьому.
216
Розділ 5. Операторні математичні моделі, визначені у лінійному просторі
от = д-’.	(5.27)
Для ортогональної матриці:
О * От = 0т * р = О1 * 0 - 0 * О1 = Е,
де Е - одинична матриця.
Ортогональна матриця має ряд особливих властивостей.
Визначник ортогональної матриці дорівнює одиниці:
Сума квадратів елементів стовпця або рядка дорівнює одиниці, тобто
ЇХ =їх = <-
І=1	3=1
Сума добутків елементів двох стовпців і та к:
ЇХЖ=°-	(5.28)
І=1
Теж саме маємо для суми добутків елементів двох рядків і та т:
ІЛіДп^0-	.	(5.29)
і=і
Прикладом символьної ортогональної матриці є наступна матриця А:
СО8Х 8ІПХ
- 8ІП X СО8 X
Визначник цієї матриці дорівнює одиниці, а її транспонована матриця
співпадає з оберненою. Це підтверджується наступними символьними
обчисленнями в пакеті МаїЬСАО:
СО8Х -8ІПХ
8ІП X СО8 X
СО8 X - 8ІП X
8ІПХ СО8Х
Символьними ортогональними матрицями є наступні:
А(х):=
ІЛ(х 1	1 А(х)т
А(хУ ->
	СО8 ф	- 8ІП ф	0'		1	0	0
А1 =	8ІПф	СО8 ф	0	; А2 =	0	СО8ф	-8ІПф
	0	0	1		0	8ІП ф	СО8 ф
	СО8 ф	0 8ІП ф					
АЗ-	0	1	0					
	-8ІП ф	0 СО8 ф					
Дані ортогональні матриці використовуються в операціях перетворення
систем координат шляхом повороту осей [ 1 ].
217
Струтинський В. Б.
5.2.2. Вбудовані функції пакету МаіЬСАВ
для роботи з матрицями та векторами
Вбудовані функції пакету Маі:ЬСА13 для роботи з матрицями та вектора-
ми дозволяють здійснювати різноманітні операції над векторами і матрицями.
Вбудовані функції МаіЬСАВ виводяться за допомогою меню (рис. 5.15).

іВ’Оз»-
(ЖШЙИ
Й®ИЙ
ідаяііс
1 и* С.	‘
ВИИЖіЯИИііІІ
а)
Рис. 5.15- Меню вбудованих функцій, в яких розташовані функції
для здійснення операцій з векторами та матрицями: а - група вбудованих
функцій сортування; б - основні вбудовані функції для роботи
з матрицями пакету МаіІїСАГ) 8
218
Розділ 5. Операторні математичні моделі, визначені у лінійному просторі
Вбудовані функції поділяються на три групи:
• функції формування матриць та операцій з блоками матриць;
» функції обчислення різних числових характеристик матриць;
• функції, що реалізують різноманітні чисельні та символьні алгоритми
рішення задач лінійної алгебри.
Розглянемо функції формування матриць та операцій з блоками матриць
і функції обчислення різних числових характеристик матриць. Дані групи
функцій включають, зокрема наступні функції:
таігіх(іп, п, £) - формує та заповнює матрицю розміром щхп, причому
елемент, розташований в і-му рядку, фму стовпці дорівнює значенню £(і, р
функції Г(х, у). Дана функція особливо ефективна, коли матриця має велику
розмірність. Нижче наведено фрагмент документа МаІІїСАІ), що здійснює
формування матриці розмірності 7x20:
ї(х, у): = 1 + х2 + у
	0	1	2	3	4	5	6	7	8	9	10	11
0	1	2	3	4	5	6	7	8	9	10	11	12
1	2	3	4	5	6	7	8	9	10	11	12	13
2	5	6	7	8	9	10	11	12	13	14	15	16
3	10	11	12	13	14	15	16	17	18	19	20	21
4	17	18	19	20	21	22	23	24	25	26	27	28
5	26	27	28	29	ЗО	31	32	33	34	35	36	37
6	37	38	39	40	41	42	43	44	45	46	47	48
<1іа§(у) - формує діагональну матрицю, елементи головної діагоналі якої
знаходяться у векторі V. Фрагмент документа МаЬїСАВ, який ілюструє за-
стосування даної функції, має вигляд:			V] = і + 2	
ОВЮІі\: = і	і: = 1..4			
		3 0	0 0'	
		0 4	0 0	
В: = Йіа§(у)	В =	0 0	5 0	
		0 0	0 6.	
і<1епгіі:у(п) - створює одиничну матрицю порядку п;
аи§тепі(А,В) - формує матрицю, в перших стовпчиках якої записується
матриця А, а в останніх - матриця В (матриці А і В повинні мати однакове
число рядків);
8Іаск(А,В) - формує матрицю, в перших рядках якої записується матри-
ця А, а в останніх - матриця В (матриці А і В повинні мати однакове число
стовпців);
8иЬшаІгіх(А, іг, ]г, іс, ]с) - формує матрицю, яка є блоком матриці А,
розташованим у рядках з іг по іг і в стовпцях з іс по іс (іг < )г, іс < )с).
Приклади застосування вбудованих функцій і<1еп±іку(п), аи§тепі(А,В),
зіаск(А,В) та 8иЬтаігіх(А, іг, ф, іс, ]с) для формування матриць наведено в
219
Струтинський В. Б.
наступному фрагменті документа МаіліСЛО:
С =
1
2
З
1
З
2
З
4
1
2
-5
1
і<1епІІІу(3) =
5
1
2
1
1
З
8ііЬтаігіх(С, 2,5,0,1) =
З
1
З
2
1
2
-5
1
операції з вектором у:
5
7
9
Вищенаведені вбудовані функції дозволяють проводити операції як з
матрицями, так і з векторами, наприклад,
5
7
9
5
7
9
числових характеристик матриць
Г7
8иЬтаігіх(у, 1,2,0,0) =
9
Функції обчислення різноманітних
включають, зокрема, наступні функції:
1а8І(у) - обчислює номер останньої компоненти вектора у;
1єп§іЬ(у) - обчислює кількість компонент вектора у;
го\У8(А) - знаходить число рядків матриці А;
соІ8(А) - знаходить число стовпців матриці А;
тах(А) - знаходить найбільший елемент в матриці А;
іг(А) - обчислює слід (суму діагональних елементів) матриці А;
гапк(А) - обчислює ранг матриці А.
Приклади застосування даних вбудованих функцій наведено нижче:
Гзі
4
у :=
5
7
1а8І(у) = 3 1еп§Ьі(у) = 4
220
Розділ Операторні математичні моделі, визначені у лінійному просторі
	5	-1	0	0
	-і	5	0	0
А :=	0	0	4	0
	0	0	0	6
го\ув(А) = 4 тах(А) = 6
сок(А) = 4 іг(А) = 20 гапк(А) = 4.
В пакеті наявні вбудовані функції для обчислення узагальнених характе-
ристик матриці так званих норм:
поппІ(А), попп2(А), погшс(А), погті(А) - функції обчислення норм
квадратної матриці А. Дані функції обчислюють наступні норми для векто-
рів-стовпців чи рядків х, що утворюють матрицю:
= Еіхіі ; Н =	; 114 = тНХіІ -
і=і	V і=і
де X = (хь х2, хп).
(5.31)
Важливою властивістю всіх цих норм є те, що коли послідовність векто-
рів по одній з цих .норм наближається до нуля, то і по інших нормах вона та-
кож прямує до нуля. Якщо для векторів
X = (х1; х2, Хп)
введена деяка норма ||х)|, то узгодженою з нею нормою матриць називають
величину (зир означає найбільше із значень):
п п ІІМ
IIАІІ = 5иР1ДГ 
х*° М
Так, для норми ЦхЦ, узгоджена з нею норма матриці дорівнює:
ІІАІІі =тахЕІа4
а для норми ||х||, :
п
||а||. = тах]Г аи .
Для норми ||х|і2 узгоджена з нею норма матриці має вигляд:
Иаіі2 =	,
Де ’>чпах(ААІ) - максимальне власне значення матриці ААТ.
Використовують також так звану евклідову норму матриці
І П П , л
Н. = ,£Ж 
V і=! І=1
При цьому справедлива нерівність І|А||2 < ||А||с .
(5.32)
(5.33)
(5.34)
(5.35)
(5.36)
Обчислення норм матриці здійснюється вбудованими функціями
поппІ(А), погт2(А), погті(А), погте(А).
221
Струтинський В. Б.
Приклади застосування даних вбудованих функцій наведено нижче:
	' 5 -1	-1 5	0 0	0' 0	
А :=					
	0	0	4	0	
	0	0	0	6	
погт2(А)		= 6			погтІ(А) = 6
поппе(А) = 10.2 погші(А) = 6.
Норми використовуються, зокрема, для контролю збіжності ітераційного
процесу розв’язку системи лінійних рівнянь, як це показано нижче.
В пакеті наявні функції для різноманітного перетворення матриць.
Вбудовані функції пакету МаВіСАВ реалізують чисельні алгоритми рішення
задач лінійної алгебри, зокрема:
гге£(А) — функція, яка здійснює приведення матриці до ступінчастого вигля-
ду з одиничним базисним мінором. Наприклад, для матриці
1 0 0 0'
0 0 10
0 0 0 1
0 0 0 0
На рис. 5.16 наведено результати візуалізації даних матриць.
а)
Рис. 5.16. Графічна інтерпретація матриці А(а)
та результат дії функції ггер(А) (б)
ггеГ(А)
б)
Дана вбудована функція здійснює перетворення матриці згідно алгоритму
прямого та зворотного ходу методу Гауса. При цьому матриця зводиться до
трикутного вигляду (прямий хід Гауса), а потім трикутна матриця приво-
диться до одиничної (зворотній хід метода Гауса). Розглянемо схему роботи
цієї функції на прикладі розв’язку системи лінійних рівнянь.
В загальному вигляді система лінійних рівнянь записується у формі:
апХ| + а.2х2 + ... + а^х,, = Ь,;
^х, +а22х2 + ... +а2„х„ =Ь2;
апІХ1 +ап2Х2 + ••• +ап„Х„ = Ьп
222
Розділ 5. Операторні математичні моделі, визначені у лінійному просторі
або
Ах = Ь,
де матриця коефіцієнтів А, вектор невідомих х та вектор правих частин Ь да-
ні у вигляді:
	аи	а12 .	.. а,/		’х1'		V	
А =	а21	а22 .	а2п	; х =	х2	; ь =	Ь2	(5.37)
	?»1	а„2		 ап„.		Л>.		_Ь„_	
системи Є сукупність значень X), х2, ..., хп, які обер-
Розв’язком даної
тають рівняння системи в тотожності.
Прямий хід методу Гауса здійснює приведення розширеної матриці систе-
ми К до трикутного вигляду Т, а зворотній хід метода Гауса здійснює
творення матриці Т в матрицю Р, як це схематично показано нижче:
пере-
а21
а)2
а22
а,„
ь;
ь.,
с12
1
ап2
’пп
2
матриці Р буде являти
розв’язку системи рівнянь. Фрагмент документа іМаіЬСЛВ,
приклад розв’язку лінійної системи рівнянь
х, + 2х2 + Зх3 = 7
• х( - Зх2 -т 2х3 = 5
В результаті
останній стовпець
сооою вектор
який включає
(5.38)
К =
а
а
ь
0
о
о
за допомогою функції гге£(А), наведено нижче:
1
ггєГ(Аг)= 0
0
0
1
0
0
0
1
1
0
2
Таким чином, розв’язок системи рівнянь (5.38):
Ах = Ь
одержано як останній стовпець матриці гге((Аг), а саме:
т
о
2
х2 = 0, х3 = 2.
хі = 1,
X =
Ряд вбудованих функцій математичного пакету призначений для обчис-
223
Струтинський В. Б.
лення власних векторів та власних значень матриці, зокрема:
еі§епуа!$(А) - здійснює обчислення вектора власних значень І числової
чи символьної квадратної матриці А;
єі§єпуєс(А, 10 - обчислює власний вектор матриці А, що відповідає вла-
сному значенню 1^;
еі§епуес.ч(А) - знаходить набір власних векторів квадратної матриці А,
причому порядок розташування власних векторів відповідає порядку власних
значень, обчислених функцією еі§епуаІ8(А).
Функція єі§єпуєс8(А) обчислює модальну матрицю [ц] для матриці А.
Модальна матриця переводить матрицю А в діагональну форму шляхом пере-
творення:
^'А[р]=Л,	(5.39)
де Л - діагональна матриця, яка включає власні значення матриці А як ком-
поненти головної діагоналі.
Модальна матриця дозволяє знайти матрицю А за власними значеннями
згідно з формулою:
[р]л[цр‘ = А .	(5.40)
Модальна матриця визначена з точністю до множника. Цей множник має
вигляд довільної діагональної матриці.
Фрагмент документа МаіЬСАЦ, що включає приклади застосування ви-
щеназваних вбудованих функцій, наведено нижче:
	1	3	5'	Г 8.312'
в =	7	4	3	еі§епуаІ8(в) = -2.12
	1	1	0	[-1.192
				0.467 -0.643 -0.492'
єі§єпуєс§(в)				= 0.87	0.764	0.825
				0.161 -0.057 -0.279
еі§епуес(в, 8.312) =
-0.467
-0.87
єі§єпуєс(В, -2.12) =
-0.161
0.643
0.764
0.057
0.492'
єі§єпуєс(В, -1.192) = -0.825
0.279
На рис. 5.17 показана графічна інтерпретація знайдених власних векторів
матриці В та обчисленої модальної матриці. Модальна матриця з точністю до
знаків відповідає власним векторам.
224
Розділ 5. Операторні математичні моделі, визначені у лінійному просторі
ЄІ§ЄПУЄС8(В)
б)
г)	д)
Рис. 5-17. Візуалізація процедури знаходження власних векторів матриці В
за допомогою вбудованих функцій пакету МаНіСАО. а - якісне зображення
матриці В; б - матриця, складена із власних векторів; в, г, д - графічна
інтерпретація власних векторів матриці В
Одним із важливих алгоритмів рішення задач лінійної алгебри є
розв’язок системи лінійних алгебраїчних рівнянь. Існує багато методів
розв’язку системи рівнянь. Один із них, що використовує метод виключення
Гауса, розглянуто вище.
В загальному випадку для розв’язку системи, ранг матриці якої дорівнює
числу невідомих, в пакеті МаіЬСасІ наявна спеціальна вбудована функція
І8о1ує(А, Ь), яка здійснює розв’язок системи лінійних алгебраїчних рів-
нянь, поданої в матрично-векторному записі:
225
Струтинський В. Б.
Ах = Ь,
де А - матриця коефіцієнтів; Ь - вектор правих частин рівнянь; х - вектор
значень розв’язків.
Приклад застосування даної функції для знаходження коренів системи
рівнянь
На рис. 5.18 наведена графічна інтерпретація матрично-векторної форми
запису даної системи трьох лінійних алгебраїчних рівнянь та її розв’язку.
Рис. 5-18. Графічна інтерпретація матрично-векторної форми запису
системи лінійних рівнянь та знайденого розв’язку системи
Корені рівняння одержані у вигляді вектора X = (-0.145 1.727 0.382)т.
Б пакеті МаїЬСАБ наявний ряд спеціальних вбудованих функцій, які здійс-
нюють розклад матриці на матриці спеціального вигляду (трикутного тощо):
226
Розділ 5. Операторні математичні моделі, визначені у лінійному просторі
8усі(А) - здійснює сингулярний розклад матриці А розміром пхт:
А = У8УТ,
де 0 і V ~ ортогональні матриці розміром тхт і пхп відповідно;
8 - діагональна матриця, на діагоналі якої знаходяться сингулярні числа ма-
триці А;
8У(к(А) - вектор, який включає сингулярні числа прямокутної матриці А,
яка має розмірність пхт, де п > т.
Приклад сингулярного розкладу та знаходження сингулярних чисел мат-
риці наведено в наступному фрагменті документа МаіІїСАО:
	1 3 0'		
			7.131
А :=	12 4 2 5 0	8УЙ8(а) =	3.686
			0.748
	0 2 1		и.
-0.442 -0.26	0.083
-0.467	0.853	0.227
8У(1(а) =
0.719
0.294
0.326
-0.441	-0.28
0.099	0.929
-0.079 -0.942
-0.895 -0.294	0.335
-0.303	0.953	0.026
Графічна інтерпретація сингулярного розкладу прямокутної матриці А на-
ведена на рис. 5.19;
1и(М) - здійснює трикутний розклад матриці М, який задовольняє мат-
ричній рівності:
РМ - Ш,
де Ь і 11 - нижня та верхня трикутні матриці. Всі чотири матриці квадратні,
одного порядку.
Схема знаходження трикутного розкладу конкретної числової матриці М
ілюструється наступним фрагментом документа МаіЬСАО:
	0	2	0'			0	0 1	1	0 0 1	2 Г
М :=	-1 -2	5	її	>(М) =	1	0 0	0	І 0 0	2 0
	1 2	1			0	1 0 -1	0 1 0	0 6 —
Складові розкладу матриці знаходяться як						блоки матриці 1и(М):		
	0 0 і			1 0	о'		1 2 і	
Р :=	і 0 0			0 1	0		0 2 0	
	0 1 0			-1 0	1			1 «5 О о)	
227
Струтинський В. Б.
Рис. 5-19. Результати візуалізації прямокутної матриці А(а),
графічні зображення сингулярних чисел даної матриці (б)
та її сингулярний розклад (в)
Для перевірки правильності розкладу знайдемо праву та ліву частини
рівності.
Обидві частини рівності РМ		= ЬІД однакові:	
	1	2 1		1	2 1
Р*М =	0	2 0	1*0 =	0	2 0
	-1 -2 5		-1 -2 5
Графічна інтерпретація одержаного трикутного розкладу матриці наведена
на рис. 5.20;
ЬоІезку(М) - здійснює трикутний розклад матриці М методом Холецько-
го. Матриця М повинна бути симетричною та додатно визначеною. її розклад
має вигляд:
М = ЬЬТ,
де Ь - трикутна матриця.
228
Розділ 5. Операторні математичні моделі, визначені у лінійному просторі
Рис. 5-20. Графічне зображення одержаного трикутного розкладу Іи(М)
квадратної матриці М та складові трикутного розкладу
у вигляді квадратних матриць Р, Г, 12, де £ і І/ - нижня та верхня
трикутні матриці
В результаті розрахунків повертається матриця Ь.
Реалізація розкладу матриці методом Холецького та перевірка розкладу
засобами пакету МаїЬСАО наведені нижче:
М?
14 -4
-4 10
7	2
7
2
12
3.742
сЬо1езку(м) = -1.069
1.871
0	0
2.976	0
1.344 2.587
Ь := сЬо1езку(м)

14
-4
7
-4
10
2
1
2
12
Графічна інтерпретація розкладу симетричної матриці М методом Холе-
цького наведена на рис. 5.21.
229
Струтинський В. Б.
Рис. 5.21. Результати візуалізації симетричної матриці М
та її трикутного розкладу методом Холецького
дг(А) - здійснює розклад матриці у вигляді добутку ортогональної та
трикутної матриці:
X = ОН,
де О - ортогональна матриця;
0.996
-9.001
0
0
о
з
фк =
9.994 • 10“4
2
1
Одержаний добуток ОК дає матрицю, що відповідає вихідній матриці А.
Матриця 0 є ортогональною, тобто її детермінант дорівнює одиниці, а транс-
понована матриця дорівнює оберненій,
що і підтверджується наведеним ниж-
че фрагментом документу МаїЬСАО:
|Р| -> 1.0
<У->
о
0.11
0.994
о Г
-0.994 0
0.11 0
0
<Г‘->
0.11
0.994
0 1
-0.994 0
0.11 0
230
Розділ 5- Операторпі математичні моделі, визначені у лінійному просторі
На рис. 5.22 наведена графічна інтерпретація даного розкладу.
Рис. 5.22. Графічне зображення розкладу дг(А) квадратної матриці А
та складові розкладу у вигляді квадратних матриць (ф Е,
де О - ортогональна матриця; Е — верхня трикутна матриця
Засоби математичного пакету МаійСАВ дозволяють виконати практично
всі операції з векторними і матричними математичними об’єктами.
Математичний пакет МАТЬАВ включає широкий набір засобів для роботи
з векторами і матрицями.
Перспективним є використання візуальних математичних моделей на
основі матричного числення, реалізованих в системі 8ІМІЛЯМК пакету
МАТЬАВ 6.0.
231
Струтинський В. Б.
РОЗДІЛ 6
Дискретні математичні моделі процесів
6.1. Формування дискретних математичних моделей
6.1.1. Знаходження дискретних множин значень неперервного процесу
При розробці математичних моделей процесів та систем часто
використовують дискретні множини значень параметрів. При розгляді
взаємозв'язаних параметрів ці множини є взаємозалежними. Залежність
встановлюється зазвичай за номером дискретного значення параметра.
Наприклад, виконані вимірювання параметра V в моменти часу
ІО, Ц, Є2, Й, ••• Іп-
В результаті цього одержано дискретну множину значень параметра:
^0> V], У2, ..., VI, ..., Уп.
Таким чином, кожен елемент множини дискретних значень часу І,
відповідає елементу множини значень параметра
V, (і = 0, 1, 2, .... п).
Множини значень параметрів процесів звичайно записуються у вигляді
векторів. Наприклад, вектор послідовних значень часу:
І — [1-0> 1-1 > 12>  • • > 1-пі>
де (п + 1) - число елементів вектора, який відповідає множині значень часу.
Число (п + 1) називається розмірністю вектора. Вектор значень параметра,
що відповідає вектору значень часу:
V = [уо, V,, У2, уп].
Номер компоненти вектора
і (і = 0, 1, 2, ..., п)
визначає зв’язок між елементами множин значень часу та параметра у,.
Розглянемо дві взаємозалежні множини значень двох параметрів ех та уу.
Ці параметри задані векторами однакової розмірності (п + 1). Нехай
параметр ух є аргументом, а уу - функцією, тобто між величинами уу та ух є
функціональна залежність, задана дискретною множиною значень величин ух
та уу. Аргумент ух, як і аргумент звичайної функції, характеризується
областю визначення. Крім того, суттєвим є те, яким чином розміщені
дискретні значення аргументу
УХо, УХ|, УХ2, ..., УХП
в області визначення. Значення аргументу ух утворюють числову
послідовність Аналогічно числову послідовність утворюють і значення функції
232
Розділ 6. Дискретні математичні моделі процесів
УУО, Уу1; уу2, .... ууп.
Дані числові послідовності кількісно можуть мати різний вигляд. При їх
аналізі користуються графічним зображенням числових послідовностей у
вигляді стовпчастих або точкових діаграм. На рис. 6.1 наведено точкові
діаграми двох взаємозв’язаних числових послідовностей.
Рис. 6.1. Графічне зображення двох числових послідовностей у вигляді:
а - залежності від номера і; б -функціональної залежності Vуі від VXі
Графічне зображення послідовностей аргументу та функції подається у
двох якісно відмінних формах. Перша полягає у зображенні окремо кожної
послідовності в залежності від номера (рис. 6.1, а), а друга відповідає
звичайному графіку функціональної залежності, де по осі абсцис відкладено
значення аргументу ух,, а по осі ординат - функції ууі (рис. 6.1, б). Якщо
різниця між сусідніми значеннями аргументу постійна, то обидва графіки
дають подібні форми залежності числової послідовності уу від аргументу ух.
Множини значень уу деякого неперервного процесу можуть знаходитись
різними методами, зокрема в результаті експериментальних вимірів або за
допомогою розрахунків.
Між процесом (функцією), заданим аналітично, і відповідним процесом
(функцією), заданим таблично (дискретною множиною значень), існує
своєрідний взаємозв’язок. Якщо множина дискретних значень процесу
розраховується за аналітичним виразом, що описує процес, то ця операція є
однозначною і має назву дискретизації (квантування) аналітичної залежності.
Обернена операція, а саме: знаходження аналітичної залежності по множині
значень параметра, не є однозначною. Вона має назву інтерполяції або
апроксимації табличних даних певного функціональною залежністю.
233
Струтинський В. Б.
Розглянемо процедуру знаходження множини дискретних значень
деякого процесу, який описується аналітично за допомогою функції у = Кх).
Будемо вважати, що дискретні значення аргументу х змінюються за
законом:
X; = Дх • і (Дх=Соп8і).	(6.1)
При цьому дискретні значення функції, що відповідають дискретним
значенням аргументу, визначаються як:
У; = КАх • і) = £[і].	(6.2)
Дискретні значення функції і’!і] називають решітчастою функцією [6].
Вона має широке застосування, зокрема при аналізі дискретних систем
автоматичного керування.
Якщо функція у = Кх) є гладкою та неперервною, то одержаний за
допомогою формули (6.2) масив у; дискретних значень кількісно і якісно
відповідає функції і'(х) так, як це показано на рис 6.2, а.
а)	б)
Рис. 6.2 Знаходження множини дискретних значень у і функції, заданої
аналітичним виразом у = /(х): за допомогою решітчастої функції
чи зміщеної решітчастої функції (а) та ілюстрація неоднозначності
процесу встановлення виду неперервної функції за заданою
решітчастою функцією
Кількісна та якісна відповідність масиву дискретних значень у, самій функції
полягає в тому, що при необмеженому збільшені числа точок (Дх —> 0) масив
дискретних значень буде точно відповідати функції £(х). Розбіжність між масивом
дискретних значень та функцією зменшується із збільшенням числа точок.
Існує багато способів формування дискретного масиву значень
234
Розділ 6. Дискретні математичні моделі процесів
неперервного процесу. Один із них - це використання розглянутої раніше
решітчастої функції. Застосовується також зміщена решітчаста функція.
Вона визначає ряд дискретних значень вихідного процесу Кх) у вигляді:
уЬ। = {(хі + ДЬ) = ([і, є],	(6.3)
., х	.	Дії
де Дп - абсолютне значення зміщення; є = — - відносне зміщення
Дх
решітчастої функції.
На рис. 6.2, а дано геометричну інтерпретацію впливу зміщення на
формування дискретного масиву значень функції.
Дискретний масив, що описує деякий процес, може формуватись у вигляді
комбінації решітчастих функцій. Наприклад, масив
У: = |(Ф]+ Ф-0.5]),	(6.4)
відповідає середньому арифметичному значенню функції у вузлі з номером і
та значенню функції посередині інтервалу між вузлами і та (і ч- 1).
Встановлення зв’язку між решітчастою функцією та базовим неперервним
процесом має певні особливості. Одна решітчаста функція відповідає
нескінченній кількості базових неперервних процесів. Ці процеси називаються
обвідними. Всі вони співпадають із решітчастою функцією. На рис. 6.2, б
показано ряд обвідних, що відповідають одній і тій же решітчастій функції.
Серед нескінченної кількості обвідних є основна (0(х) (показана на рис. 6.2, б
суцільною лінією). Основна обвідна може бути одержана як результат
розв’язку диференціального рівняння, порядок якого найменший в порівнянні
з рівняннями, що описують всі інші можливі обвідні. Для періодичних
решітчастих функцій для основної обвідної додатково виконується умова
мінімальності значень частот гармонік, з яких вона складена.
Так, наприклад, решітчастій функції
ї[і]=е^Дх	(6.5)
відповідають обвідні:
та
£,(х) = С' ;' • (сО8(®0х)+ с • 8Іп(шох)) ,	(6.6)
2лк .
де ю0 =-----; к - ціле число; с - довільна константа.
Лх
Обвідна і()(х) є основною, оскільки вона може бути одержана як розв’язок
диференціального рівняння 1-го порядку. Інша обвідна (Дх) (6.6) не є основною
тому, що може бути одержана як розв’язок рівняння другого порядку.
Для дискретизації неперервного процесу використовують не тільки абсолютні
значення аргументів, а й їх прирости (кінцеві різниці). На рис. 6.3 показані
можливі схеми формування масивів кінцевих різниць із неперервних процесів.
235
Струтинський В.Б,
а)
б)
Рис. 6.3. Схеми формування масивів кінцевих різниць із неперервного
процесу: а - масив Ауі змінних кінцевих різниць функції при постійних
кінцевих різницях аргументу Дх = Сопзі: б - масив змінних кінцевих
різниць аргументу Дгу при постійних кінцевих різницях функції Ау = Сопзі
Для рівновіддалених значень аргументу х (Дх = СопзО формується масив
змінних кінцевих різниць функції Дуі (рис. 6.3, а). Цей масив наближено
відповідає значенням похідних вихідного процесу £(х), тобто
АУ,
сИ(х)
СІХ
(6.7)
Якщо кількість дискретних значень аргументу х, збільшується, то точність
формули (6.7) зростає.
Для рівновіддалених значень функції £(х) (Ау = Сонзі) формується
масив змінних кінцевих різниць Дх, (рис. 6.3, б). Значення масиву Дх[
обернено пропорційні похідній базового процесу:
(6.8)
ЛХі~ жя
сіх
Для формування дискретного масиву використовуються також інтегральні
характеристики процесу. Зокрема, на основі залежності
У і =
Дх
(6.9)
236
Розділ 6. Дискретні математичні моделі процесів
формується масив дискретних значень інтегралу, значення якого буде
відповідати величинам площ між сусідніми вузлами.
Даний масив утворює дискретну множину значень, яка наведена у
графічному вигляді на рис. 6.4, а.
Рис. 6.4. Формування дискретного масиву значень інтегральної
характеристики процесу: а - масив у і змінних значень інтегралів
по постійних інтервалах інтегрування; б - масив постійних (ір = Сопзі)
значень інтегралів по змінних інтервалах інтегрування Дх,- = ваг
Масив значень інтегралів по елементарних ділянках аргументу процесу
дозволяє розраховувати всі інші інтегральні характеристики процесу. Зокрема
обчислювати інтеграл процесу в довільному інтервалі [хо, хп]. Останнє
здійснюється простим підсумовуванням значень елементів масиву у;. При
цьому значення інтегралу процесу в довільному інтервалі:
|т(х>іх = £у,Дх .	(6.Ю)
х„	:=і
З метою спрощення обчислень по формулі (6.10) доцільно прийняти
змінні значення інтервалів між вузлами. Поклавши
у і Ах і = Ау = Сопзі ,
одержимо дискретну множину значень інтегральної характеристики процесу у
вигляді сукупності точок рівних значень інтегралів (рис. 6.4, б).
Використання точок рівних значень інтегралів дозволяє спростити
формули для обчислення інтегральних характеристик процесу. Враховуючи,
237
Струтинський В, Б.
що Ду = Сопзі, одержимо формулу для обчислення визначеного інтеграла в
інтервалі [хр, хп]:
М.	п
р(х>Іх = Ду^і = Ауп.	(6.Ц)
Таким чином, обчислення інтеграла зводиться до простого підрахунку
числа точок, які попадають в інтервал інтегрування.
Дана методика особливо ефективна при обчисленні подвійного інтеграла
функції двох змінних [76].
Розглянемо особливості обчислення інтеграла. Для обчислення подвійного
інтеграла попередньо формується масив відносних дискретних значень
функції двох змінних по елементарних ділянках:
г. =~р(х,у)бо,	(б12)
де Аз - елементарна ділянка, по якій проводиться інтегрування функції двох
змінних Кх, у).
На рис. 6.5, а наведена графічна інтерпретація масиву 2Ь який відповідає
дискретним значенням функції по однакових ділянках Дз.
Рис. 6.5- Графічна інтерпретація масиву дискретних відносних значень
функції по елементарних ділянках області визначення: а - масив г,-
змінних значень інтегралів функції по постійних елементарних ділянках
Дз = Сопзі; б - масив точок, що відповідають однаковим ( г,Д8 = Сопзі )
значенням інтегралів елементарних ділянок змінної площі
238
Розділ 6. Дискретні математичні моделі процесів
Масив 2і дискретних значень подвійних інтегралів по елементарних
ділянках області визначення дозволяє знайти подвійний інтеграл по довільній
ділянці. Обчислення подвійного інтеграла зводиться до обчислення суми:
ДГ(х,у)сІСТ = £2іД8.	(6.13)
5	І=1
Якщо при дискретизації виконати умову Аг = гіА8 = Соп.чі, то одержимо
дискретну множину значень інтегральної характеристики у вигляді точок
однакових значень інтегралів по елементарних ділянках, площа яких є різною.
Точки, що відповідають однаковим значенням інтегралів, показані на рис. 6.5, б.
Таким чином, в області 8 існування функції Кх, у) знайдено точки, які
відповідають однаковим значенням інтеграла функції по елементарних ділянках.
Розміри і форми елементарних ділянок можуть бути різними.
З використанням точок однакового значення інтеграла по елементарних
ділянках обчислення інтеграла по довільній області інтегрування 8; зводиться
до простого підрахунку числа точок Пі, які попадають в область інтегрування.
Для обчислення подвійного інтеграла по деякій області .у здійснюється
підрахунок кількості всіх точок п, які попадають в область інтегрування:
|р(х,у> = Дг-п.	(б 14)
ч
Звичайно обчислення інтегралів по довільних ділянках є наближеним.
Точність обчислення збільшується при зменшенні розмірів елементарних
ділянок або значення Дх.
6.1.2. Дискретизація процесів з розривами
або особливостями типу дельта-функції
Для гладких неперервних процесів можна одержати масив дискретних
значень будь-якої щільності (рис. 6.6, а). Як вказано раніше, цей масив при
нескінченному збільшенні числа точок дискретизації (Дх -> 0) буде
наближатись до вихідного процесу. Зовсім інша ситуація виникає при
дискретизації процесів, які мають розриви похідної (рис. 6.6, б). Одержаний
масив значень у; кількісно та якісно відповідає базовому процесу скрізь, за
виключенням околу точки зламу.
В околі точки зламу множина дискретних значень процесу кількісно
відповідає базовому процесу, але якісно відрізняється від нього. Відмінність
полягає у тому, що відтворити точно процес Кх) за масивом його дискретних
значень Уі неможливо. Якщо з’єднати одержані при дискретизації точки
деякою плавною кривою Кх), то вона ніколи не набуде вигляду кривої, що
відповідає базовому процесу Кх), тобто інформація про точку зламу М
втрачається при дискретизації процесу.
239
Струтинський В.Б.
Рис. 6.6. Особливості знаходжений множини дискретних значень процесу у і,
заданого аналітичним виразом у ~ [(х): а - дискретизація гладкої
неперервної залежності ; б - виникнення якісних відмінностей залежності
та її дискретних значень при дискретизації процесів з розривом похідної
При дискретизації процесів з розривами похідних результат залежить від
способу визначення значень аргументу. На рис. 6.7 наведено ряд варіантів
дискретизації процесів з розривом похідної.
Рис. 6.7. Варіанти дискретизації процесу з розривом похідної:
а, б - симетричні відносно точки зламу масиви дискретних значень;
в, г — несиметричні масиви дискретних значень процесу
г)
240
Розділ 6. Дискретні математичні моделі процесів
В залежності від вибраних дискретних значень аргументу можуть мати
місце втрати деяких якісних особливостей базового процесу. Для варіантів,
показаних на рис. 6.7, а та рис. 6.7, б, якісна особливість базового процесу у
вигляді симетрії відносно точки х = 0 зберігається, а для варіантів,
зображених на рис. 6.7, в та рис. 6.7, г, одержаний дискретний масив значень
процесу не є симетричним, тобто якісна особливість базового процесу
(симетрія) втрачається.
Щоб зберегти якісні особливості базової (вихідної) залежності при
дискретизації процесів з розривами похідних, доцільно використовувати
наступний метод. Для дискретизації використовують не сам процес, а його
інтеграл. При цьому інтеграл є гладкою неперервною функцією, яка не має
розривів та зламів (розривів похідної). При дискретизації одержаного
інтегралу не виникає проблем втрати якісних особливостей базового процесу.
Як приклад розглянемо процес з розривом похідної, визначений
залежністю:
[0 при х < 0, х > 2
Кх) = (х при 0<х<1 .	(6.15)
[2-х при 1 < х < 2
Графіки, які відповідають даному процесу та його інтегралу, наведені на
рис. 6.8.
Рис. 6.8. Дискретизація процесу з розривом похідної та його інтегралу
Функція ї(х), що описує базовий процес, має розриви похідної в трьох
точках х = 0; 1; 2. Для дискретизації цієї функції використаємо дискретні
значення аргументу у вигляді: х, = (1/п)ч (п - ціле число). При цьому
будуть обчислені значення функції безпосередньо в точках розривів похідної,
тобто при х = 0, 1, 2.
Якщо з’єднати одержані точки плавною кривою £а(х), то вона буде мати
якісні відмінності від базового процесу £(х). При зменшенні інтервалів між
точками дискретизації плавна крива (а(х) буде наближатись до базової
241
Струтинський В. Б.
залежності. Але вона ніколи не набуде якісної особливості базового процесу у
вигляді зламів при х = 0; 1; 2.
Виконавши операцію інтегрування базового процесу (6.15), визначимо
його інтеграл у вигляді:
	0	при	X < 0
	х2	при	0 < х < 1
Р(х) = |Кх)с1х = 	2 х2		(6.16)
-оо	2х - 1 - — 2	при	1 < х < 2
	1	при	х > 2
Одержана залежність Кх) не має розривів похідної (рис. 6.8). Вона може
бути дискретизована довільним чином як гладка неперервна функція. При
цьому дискретизована залежність не буде мати якісних відмінностей від
вихідної інтегральної залежності.
Якісні відмінності процесу та його дискретних значень особливо
проявляються при дискретизації процесів з розривами та особливостями типу
8-функції. Це ілюструється наступним прикладом (рис. 6.9). Наведений на
рисунку графік процесу Кх) має точки розриву першого роду хрі, хрз, точку
розриву другого роду (хрз) та особливість тину 5-фупкції в точці Хр4.
Рис. 6.9. Дискретизація процесу з розривами першого і другого роду
та особливостями типу дельта-функції
При дискретизації даного процесу знайдена сукупність точок з
координатами (х,, уЦ. Вона кількісно та якісно суттєво відрізняється від
242
Розділ 6, Дискретні математичні моделі процесів
базового процесу. Дійсно, з’єднавши одержану сукупність точок плавною
кривою, одержимо криву (а(х), яка як кількісно, так і якісно, зовсім не
відповідає вихідній залежності Кх). В даному випадку при дискретизації
втрачена інформація про процес справа від точки розриву першого роду хрі,
повністю втрачена інформація про процес в околі точки розриву другого роду
хр2 та про наявність особливості типу 5-функції в точці хр4. При
дискретизації процесу в точці розриву хрз виникає невизначеність обчислення
дискретного значення у, = £(хрз) в точці розриву. Дискретне значення може
бути прийняте рівним середньому від значень процесу справа і зліва від точки
розриву так, як це показано на рисунку. При цьому
(6.17)
Можливі й інші варіанти вибору дискретного значення процесу в точці
розриву, зокрема це вибір значень зліва чи справа від точки розриву:
УрЗ = КхрЗ - 0) чи ур3 = £(хрз + 0).	(6.18)
Обчислені за формулами (6.17) та (6.18) значення є суттєво різними і їх
застосування призведе до різних результатів дискретизації базового процесу.
Одержаний масив дискретних значень, іцо відповідає процесу з
розривами, суттєво залежить від способу визначення дискретних значень
аргументу. Незначні зміни чи похибки у визначенні значень аргументу
призведуть до суттєвих змін одержаного масиву дискретних значень процесу.
Одержана залежність може суттєво відрізнятись як від вихідної Дх), так і від
залежності £а(х), яка знайдена раніше.
При дискретизації процесів з розривами і/або особливостями типу
8-функції доцільно застосовувати метод, аналогічний розглянутому раніше.
Він полягає в дискретизації не самого процесу, а його інтеграла відповідної
кратності. Як вказано раніше, для процесів з розривами похідної достатньо
використовувати інтеграл процесу. Для процесів з розривами першого роду
використовують подвійний інтеграл. Подвійний інтеграл розривної функції
(якщо він існує) є гладкою неперервною функцією. Як приклад розглянемо
процес з розривами першого роду визначений функціональною залежністю:
І'О
Кх) = И
при
при
- 1 при
х < 0, х = 1, х > 2
0 < х < 1
1 < х < 2
(6.19)
Графік цієї залежності, її інтеграла та подвійного інтеграла наведено на
рис. 6.10.
Процес, визначений функцією Кх) (рис. 6.10, а), має розриви першого
роду в точках х = 0, х = 1, х = 2. Дискретизація цієї залежності не дозволяє
зберегти якісні особливості процесу в точках розриву. Якщо з’єднати
одержані при дискретизації точки плавною кривою (а(х), то одержана крива
243
Струтинський В.Б.
не буде відповідати базовому процесу. При зменшенні інтервалу між точками
дискретизації вигляд кривої іа(х) змінюється, але якісно вона залишається
відмінною від вихідної залежності. Виконавши інтегрування функції Кх) в
межах від -ос до х, одержимо неперервну ламану лінію з розривами похідної
в точках х = 0; 1; 2 (рис. 6.10, б):
Р(х) = |Кх)ах.	(6.20)
в)
Рис. 6.10. Графік, що відповідає процесу з розривом першого роду (а),
інтеграл цього процесу (б) та його подвійний інтеграл (в)
244
Розділ 6. Дискретні математичні моделі процесіє
Дана залежність може бути дискретизована так, як це показано на
рис. 6.10, б. Дискретизація функції Р(х) також не дозволяє зберегти якісні
особливості даної функції в точках розриву похідної. Одержана з’єднанням
точок плавна крива Ра(х) якісно відрізняється від вихідної залежності Р(х).
Вигляд кривої Ра(х) залежить від кількості та місця розташування точок
дискретизації.
Виконавши подвійне інтегрування базового процесу Кх) з розривами
першого роду, одержимо плавну неперервну криву
Ф(х) = ) }кх)(<іх)2.
Дана залежність може бути дискретизована довільним чином рис. 6.10, в.
При цьому одержана дискретна сукупність значень не буде мати якісних
відмінностей від залежності Ф(х). З’єднавши точки гладкою неперервною
кривою, одержимо залежність Фа(х), яка якісно відповідає Ф(х) і співпадає з
нею при необмеженому зменшенні інтервалу між точками дискретизації.
Аналогічним способом здійснюють дискретизацію процесів з
особливостями типу 5-функції. При цьому треба використати не подвійний, а
потрійний інтеграл базового процесу. Інтеграл базового процесу не має
особливостей типу 5-функції, а потрійний інтеграл базового процесу
представляє собою гладку неперервну функцію.
Як приклад розглянемо базовий процес з особливостями типу 5-функції:
£(х) = 8(х - 1) - 3(х - 2).	(6.21)
Ця залежність показана у графічному вигляді на рис. 6.11, а. Вона має
особливості типу 5-функції в точках х - 1 та х = 2.
Дискретизація цієї залежності не дозволяє зберегти її кількісні та якісні
особливості. Якщо з’єднати одержані точки плавною кривою £а(х), то вона
буде мати складний вигляд, який зовсім не відповідає базовому процесу. На
відміну від базового процесу, одержана крива відрізняєтьсь від нуля і має
точки розриву другого роду при х = 1, 2, тобто дискретизована залежність, як
кількісно, так і якісно, не відповідає базовому процесу. При зменшенні
інтервалу між точками дискретизації вигляд кривої £а(х) змінюється. При
цьому вона набуває високочастотних осциляція, які повністю відсутні у
базовому процесі.
Виконаємо інтегрування вихідної залежності (6.21) з особливостями типу 5-
функції. Враховуючи символічну диференціальну залежність між імпульсною та
одиничною ступінчастою функціями (див формулу (2.106)), одержимо:
Р(х) = |[5(х -1) - 5(х - 2)]сіх = 1(х - 1) - 1(х - 2).	(6.22)
- X
В правій частині (6.22) знаходяться одиничні ступінчасті функції. Вони
визначають розривний характер одержаного процесу Р(х).
245
Струтинський В, Б,
Рис. 6.11. Графічне зображення процесу, що має особливості типу
дельта-функції (а), інтеграл процесу (б), подвійний інтеграл (в)
та потрійний інтеграл (г) процесу
246
Розділ 6. Дискретні математичні моделі процесів
Графік залежності (6.22) наведено на рис. 6.11, б. Вона відповідає
функції з розривами першого роду в точках х = 1 та х = 2. Дискретизація цієї
функції здійснюється за схемою, наведеною вище (див. рис. 6.10). Спочатку
знаходиться інтеграл від розривної функції (6.22):
Ф(х) — /НхИх = ) р(х)(сіх)2.	(6.23)
-X	-00-30
Графік даної залежності представляє собою ламану лінію, що має розриви
похідної в точках х = 1 та х = 2 (рис. 6.11, в). Інтеграл від функції Ф(х),
який є подвійним інтегралом від функції Г(х), а саме:
Т(х) = ]ф(хИх = | |Г(х)(<1х)2 = | | р(х)(6х)3	(6.24)
-оо	-зо-х	-х-ос-х
представляє собою потрійний інтеграл від базового процесу Кх).
Одержана функція Т(х) визначає гладкий чи неперервний процес.
Дискретизована множина значень процесу Т/х) кількісно та якісно
відповідає залежності ЧДх).
Аналогічним чином здійснюється дискретизація процесів, які включають
імпульси у вигляді похідної 5-функції (див. рис. 2.49, є). При цьому
знаходиться не потрійний інтеграл, а чотирикратний інтеграл базового
процесу. Він представляє собою гладку неперервну функцію.
Дискретизація процесів з розривами другого роду можлива, коли існує
інтеграл процесу. Процес з розривами другого роду приводиться до процесу з
особливостями типу 5-функції або її похідної. При наявності в базовому
процесі особливостей типу похідної 5-функції спочатку виконується
послідовне інтегрування з метою одержання гладкої неперервної функції, а
вже потім виконується дискретизація одержаної залежності.
Даний метод корисний не лише при розробці дискретних моделей
процесів. Послідовне інтегрування функцій, які описують процеси з
особливостями, дозволяє провести кількісний та якісний аналіз процесу.
Даний метод був використаний автором для аналізу випадкових циклічних
ударних навантажень у складних динамічних механічних системах [101, 102].
247
Струтинський В.Б.
6.2.	Аналіз дискретних моделей шляхом інтегральних перетворень
6.2.1.	Дискретне перетворення Фур’є
При дискретизації процесу часто використовують не саму функцію Дх), а
її інтегральне перетворення відповідного виду.
При математичному моделюванні процесів, заданих дискретною
множиною значень, використовують різноманітні перетворення дискретних
значень процесу. Зокрема, це перетворення Фур’є, швидке перетворення
Фур’є, перетворення Уолша, Хаара, хвилькове (\уауе1еі) перетворення та
інші.
Для періодичних з періодом 2л функцій має місце обернене перетворення
Фур’є наступного вигляду [28, 72, 110]:
§[п] = ~ р(х)-е*пФс.	(6.25)
2л і
-ті
Даному оберненому перетворенню Фур’є відповідає пряме перетворення
Фур’є у вигляді:
+ао
£(х)= Ей[п]-е^х" .	(6.26)
П = -х>
Пара залежностей (6.25) і (6.26) встановлює взаємозв’язок між функцією
Дх) та масивом значень д(п), який в дискретній формі описує залежність Дх).
Формула (6.26) відповідає дискретному ряду Фур’є, коефіцієнтами якого
є числова послідовність §[п].
Звичайно дискретний ряд Фур’є використовується не для неперервної
функції Дх), а для її дискретних значень, що відповідають решітчастій
функції £[к].
При цьому пряме та обернене дискретні перетворення Фур’є для функції
довільного періоду мають вигляд:
Тї	_ .2д
0<к<И-1, ХУ^е^';	(6.27)
п-0
< М-1
0<п<К-1.	(6.28)
N
В формулах (6.27), (6.28) вважається, що послідовність
§[п] є періодичною з періодом N. тобто §[п + гМ] - §[п], (г = 0, 1,2, ...).
Складові (компоненти) послідовностей Дк] та §[п] можуть бути як
дійсними, так і комплексними.
Нижче наведено фрагмент документа МаНіСАО, який реалізує приклад
обчислення дискретного перетворення Фур’є згідно з (6.27) та (6.28).
248
Розділ 6. Дискретні математичні моделі процесів
Числова послідовність задана
у вигляді:
е-в.005п! і£ 12 > п > 0
8(п):=	.,	.
0 оспенте
пп 64 Д¥п е пп
Пряме перетворення Фур’є
послідовності:
пп-1
£(к);= ]Г§(п)*\уппк .
п = 0
Обернене перетворення Фур’є:
к:=0..63;
укк := £(к);
ук := §(к).
ук =
[10.387
[8.514-4.761 і
[І282-6.765І
1-0^53-2.91 і
[0.12-к229і
[1.102-1.188І
1.079-1.79і
0.359-1.811і
ГМ34-1.118
І0.305-0.501І
[0.828-0.541 і
10.863-0.95 і
0.439-1.058І
[о.145-О.676і
Пряме перетворення Фур’є Як) представляє собою комплексну числову
послідовність. В таблиці справа наведені обчислені скк перших 15 складових
даної комплексної числової послідовності.
На рис. 6.12 наведено у графічному вигляді числову послідовність §[п] та
дійсну і уявну частини її дискретного перетворення Фур’є - Як).
Рис. 6.12. Значення числової послідовності д\п\ = ехр[- 0.005 * л2], п = 0..12
та дійсна Яе і уявна Іт частини її дискретного перетворення Фур’є
249
Струтинський В. Б.
Обчислення перетворення Фур’є має певні труднощі, пов’язані з великим
об’ємом обчислювальних операцій. Тому використовуються спеціальні
алгоритми, що дозволяють оптимізувати обчислювальні процедури.
Найбільш широко використовуються алгоритми швидкого перетворення
Фур’є в різних модифікаціях. Одним із них є алгоритм швидкого
перетворення Фур’є з проріджуванням в часі. При цьому вхідна числова
послідовність розбивається на послідовності меншої довжини, іншим
алгоритмом обчислення швидкого перетворення Фур’є є обчислення з
проріджуванням по частоті. При цьому результуюча (вихідна) послідовність
розбивається на послідовності меншої довжини. Використовуються й інші
форми алгоритмів швидкого перетворення Фур’є
Обчислення дискретного перетворення Фур’є звичайно здійснюється з
використанням засобів математичних пакетів. В математичному пакеті
МаїЬСАО для обчислення прямого і оберненого швидкого перетворення
Фур’є наявний ряд вбудованих функцій.
Вбудована функція І = «м здійснює швидке перетворення Фур’є
дійсних чисел, які задані у вигляді векіора V. Розмірність цього вектора 2"1
(т - ціле додатне число). При обчисленні повертається вектор и, розмірність
якого (1 + 2'п~1).
Вбудована функція РРТ(у) здійснює аналогічну операцію швидкого
перетворення Фур’є, використовуючи інші норму і знак ніж функція ££і(у).
Для обчислення прямого швидкого перетворення Фур’є масиву
комплексних чисел використовуються наступні функції. Вбудована функція,
синтаксис якої В := с££і(а), обчислює масив комплексних чисел В, що
відповідає комплексному масиву аргументу А. Функція СРРТ(А) здійснює
аналогічні обчислення, використовуючи інші норму і знак. Розмірності
масивів комплексних чисел А і В є однаковими. Звичайно ці функції можна
застосувати і для масиву дійсних чисел.
Для обчислення оберненого перетворення Фур’є наявні кілька вбудованих
функцій. Функція V := і££ї(н) здійснює обернене перетворення Фур’є дійсних
чисел у відповідності до функції ££і(у). Вектор и має розмірність (1 + 2П1 ’)
де ш - ціле число. Після обчислень повертається дійсний вектор V,
розмірність якого 2т. Аналогічним чином визначаються аргументи вбудованої
функції ІРРТ(и), що відповідає РРТ(у). Для знаходження оберненого
перетворення Фур’є масиву комплексних чисел використовуються вбудовані
функції іс££і(В) та ІСРРТ(В). Функції повертають комплексні масиви того ж
розміру, що і аргументи.
Нижче наведено фрагмент документа МаіЬСАВ, який здійснює обчислення
швидкого перетворення Фур’є числової послідовності, розглянутої раніше (у).
250
Розділ 6. Дискретні математичні моделі процесів
[(п).= Ґ'“5П’іГ 12>п>0
|0 оіЬепуіге
п :=0..63
у„ := £(п)
їй = РРТ(у)
и := сіїі(у)
Такий же результат и=
дає застосування функцій
СРРТ(у) та т(у).
Одержані результати
обчислення швидкого
перетворення Фур’є
наведені в графічному
вигляді на рис. 6.13.
1.064+0.595і
0.535+0.846і
4
1.298
ІІЗЗ-О.О74І
0.074+0.69і
-0.082+0.364І
Ф.015+0.154І
0.138+0.149і
0.135+0.224І
0.045+0.226І
-З
4.276.10 Л+0.14і
І0 0.038+0.063І
Г.
0.103 0.068І
и1 =

1.108+0.119і
10.067-0.1 Обі________
9.247-10~3-0.086і __
-0.01-0.045І_________
1.867.10~3-0.019і____
0.017-0.019І_________
0.017-0.028І________
5.606-10~3-0.028і
-4
* ' 344.10 -0.017і
 4.761-і0~3-7.831-10'3і
’* 9:1!3А44610'2
III 0.013-0.015І
1.055+0.132І
а)
Рис. 6.13- Числова послідовність топ, дійсна та уявна частини її швидкого
перетворення Фур’є, здійснених за допомогою: а - вбудованої функції
и сйі(у); б - функції иіРРТ(у)
251
Струтинський В. Б.
Із співставлений результатів розрахунків, наведених на рис. 6.12 та 6.13,
випливає, що результати обчислення швидкого перетворення Фур’є за
різними алгоритмами і результат знаходження дискретного перетворення
Фур’є є аналогічними, відмінність полягає лише в масштабах і знаках
величини.
6.2.2.	Дискретне перетворення Лапласа, /-перетворення,
хвилькове (\уауе!е£) перетворення
Для побудови моделей неперервних процесів або перетворення одержаних
дискретних значень використовуються різноманітні дискретні перетворення,
зокрема дискретне перетворення Лапласа. Для решітчастої функції ї|к|
дискретне двостороннє перетворення Лапласа [42] визначено у вигляді:
ь[з]= £ф]-е-$и\	(6.29)
де 8 - оператор Лапласа (комплексна величина); Ах - крок, з яким
визначається решітчаста функція.
Дискретне перетворення Лапласа шляхом заміни / = е*4* приводиться до
так званого /-перетворення.
Двостороннє /-перетворення визначено формулою:
2(/)= £і[к]-2“к ,	(6.30)
к = -оо
де 2 - комплексна величина.
Дискретні масиви значень неперервних функцій можуть бути одержані з
використанням перетворення Уолша чи перетворення Хаара [13].
Для неперервної функції Кх) з періодом Т масив дискретних значень у
вигляді спектра Уолша визначається як:
8Іп] = у р(х)’ ^аі(п,у^1х,	(6.31)
де \уа!(п, 0) - функція Уолша порядку п (див. розділ 2.3.5);
А х
0 = — - відносне значення аргументу.
Значення самої функції визначається через спектр Уолша за наступною
залежністю:
£(х)=	(6.32)
п-0	V * )
Аналогічним чином визначається дискретний ряд Уолша:
252
Розділ 6. Дискретні математичні моделі процесів
£[к1= Е зЬ] 	’	(в.зз)
п-0	\
1 _ао.	А	V Л
й[п] = 77 £	• М п. 771	(6.34)
N п=О	к Л )
де N - період числової послідовності §[п].
Звичайно значення періоду приймається N = 2'” (т - ціле число).
Одержання та перетворення дискретних масивів значень процесів
здійснюється з використанням перспективної інформаційної технології -
хвилькового перетворення (хуауеіеі Ьгапзіогт) [27]. Неперервне хвилькове
перетворення в цілому подібне до неперервного перетворення Фур’є і
визначається залежністю:
С[х(і); а,Ь] = |х(і)- ч\ь(і)сЙ ,	(6.35)
де х(0 - функція параметра І;
ц/ад,(ї) ~ базова функція, визначена у вигляді:
Уа,іЛЧ = ~7гї V ---- 
VIа! 1 а >
(6.36)
Функція в правій частині цієї залежності \р*(с) = ц/,0(і) називається
материнською хвилькою (тоїЬег шауеІеО.
Базова функція (6.36) характеризується масштабом а та зсувом у часі Ь.
Звичайно приймають хвилькову функцію типу МНАТ (“Мехісап йаі”),
аналітичний вираз якої:
\у(і) = (1 - і2)-е 2 .	(6.37)
При цьому базова функція перетворення має вигляд:
1 ґ^-ЬЇі
Жа.і>(ч = -/п 1- ------ -є 2" •	(6.38)
І < а л
Обернене неперервне хвилькове перетворення визначається залежністю:
х(0 = + . ,.-1 .2 .. І ]с[х(£>а,ЬНа.ь(0- °а 2гіЬ .
* УМ ,	а	(6.39)
Г~М-- (1а
-а? ґ
де V - циклічна частота.
Крім неперервного перетворення, визначене також і дискретне хвилькове
перетворення.
Для його обчислення в пакеті МаЙіСАВ наявна вбудована функція
и:= \уяує(у). Вона здійснює дискретне хвилькове перетворення масиву
дійсних чисел з використанням 4-коефіцієнтного хвилькового фільтра. Вектор
253
Струтинський В. Б.
V повинен включати 2'” дійсних компонента (т - ціле число).
Обернене хвилькове перетворення здійснюється вбудованою функцією
у: = і\уауе(и).
Нижче наведено фрагмент документа МаїЬСАВ, який реалізує обчислення
прямого та оберненого дискретних хвилькових перетворень. Масив значень
вектора у задано як синусоїдальну числову послідовність:
і := 0..63 :	ух;:=і*—: уі:=8ІпГ2—
64	' І 64 >
уу := \уяує(у) ; \гг := і\уауе(уу);
£(х) := 1іпіегр(ух, уу, х):	§(х) := Ііпіегр(ух, ух, х) .
На рис. б 14 наведено в графічному вигляді дану числову послідовність та
її хвилькове перетворення. Для виведення графіків одержані масиви
згладжено за допомогою функції Ііпіегр.
Рис. 6.14. Синусоїдальна числова послідовність та її дискретне хвилькове
перетворення, одержане за допомогою математичного пакету МаікСАП
В результаті здійснення прямого, а потім оберненого хвилькового
перетворення одержана вихідна синусоїдальна числова послідовність.
Дискретні перетворення є ефективним засобом аналізу і широко
використовуються при математичному моделюванні.
В розділі 9.2 наведено конкретну математичну модель, в якій використано
дискретне перетворення масивів числових параметрів.
254
Розділ 6. Дискретні математичні моделі процесів
6.3. Аналіз і синтез дискретних модельних процесів
6.3.1. Процеси у вигляді числових послідовностей
Дискретні множини значень параметрів процесів аналізуються за своїми
кількісними та якісними властивостями. Незалежно від способу отримання
масиву дискретних значень процесу, ці значення утворюють числову
послідовність. Числові послідовності мають різний вигляд і розрізняються за
своїми параметрами. Розглянемо дійсні числові послідовності, які в
дискретизованій формі описують деякий базовий процес. Серед дійсних
числових послідовностей існує кілька особливих (типових) видів. Характерні
типові числові послідовності наведені на рис. 6.15.
Рис. 6.15. Графічне зображення типових числових послідовностей
у вигляді точкових діаграм: а - послідовність з нульовими складовими
(нульова послідовність); б - одиничний імпульс; в - послідовність
з постійним значенням складових; г — одинична знакозмінна
числова послідовність; д - одинична ступінчата послідовність;
е - додатна рівномірна послідовність
Нульова послідовність, зображена на рис. 6.15, а, має нульові складові
V; = 0 у всьому діапазоні свого існування -<» < і < +оо.
Послідовність у вигляді одиничного імпульсу (рис. 6.15, 6) визначається
залежністю:
255
Струтинський В. Б.
|1 при і = О
уі=іл • п-	(6.40)
[О при і О
Довільну числову послідовність можна подати у формі лінійної комбінації
одиничних імпульсів, зміщених за номером імпульсу.
Послідовність, що відповідає постійному значенню параметра процесу,
наведена на рис. 6.15, в. Величина постійного значення параметра в даному
випадку прийнята за одиницю.
Зміни параметра процесу в часі описуються рядом типових числових
послідовностей. Зокрема, це одинична ступінчата послідовність, що
визначається залежністю:
0 при і < 0
V; = (
[1 при і > 0
Вона наведена в графічному вигляді на рис. 6.15, д.
Важливе значення має одинична знакозмінна числова
(6.41)
послідовність
(рис. 6.15, г). Вона відповідає символьній залежності:
V і= (-І)І
При аналізі дискретних математичних моделей часто застосовується
лінійна рівномірна числова послідовність:
V; = а + Ь*і,
де а і Ь - довільні константи, які не залежать від індексу і.
Окремим випадком лінійної рівномірної послідовності є додатна
рівномірна послідовність (рис. 6.15, е):
= а • і, а > 0 .	(6.42)
В дискретних математичних моделях, що відповідають функціональній
залежності між двома числовими послідовностями ух, та ууь аргумент ух,, як
правило, визначається з однаковим інтервалом. Тоді послідовність уХі є
додатньо рівномірною. Різниця між сусідніми значеннями даної послідовності
однакова для всіх значень номера і. Для характеристики цієї послідовності
достатньо одного параметра:
Дух = ухі+1 - ух і = Сопзй
Значення елементів цієї послідовності визначаються залежністю:
УХ; = Дух • і.	(6.43)
Дискретні математичні моделі процесів, як правило, є складними
числовими послідовностями. При їх аналізі застосовують розклад числових
послідовностей на більш прості з відомими властивостями.
Ці послідовності звичайно називаються за назвою функцій, за допомогою
яких вони одержані. Кожній елементарній або спеціальній функції
відповідають певні числові послідовності. На рис. 6.16 наведені дійсні
експоненціальна та синусоїдальна числові послідовності.
Довільна дискретна математична модель, яка має дійсні складові, може
256
Розділ 6. Дискретні математичні моделі процесів
бути подана як сума деяких елементарних базових числових послідовностей.
а)
Рис. 6.16. Експоненціальна (а) та синусоїдальна (б) числові послідовності
В деяких випадках доцільно використовувати дискретні математичні
моделі із комплексними складовими. Числові послідовності, які входять до
складу таких моделей, мають комплексні складові. В цьому випадку кожному
порядковому номеру і відповідає два значення послідовності — дійсне та
уявне. Дискретні масиви значень процесу із комплексними складовими
формуються так, як і дійсні масиви.
Як приклад розглянемо практично важливий процес, що відповідає
частотному сигналу у вигляді:
КО = еім1 = СО8ШІ + І8ІПОІ .
Послідовності, які відповідають дійсним та уявним складовим цього
процесу одержані як решітчасті функції, що мають дійсну і уявну частину. їх
значення наведені на рис. 6.17,
Рис. 6.17. Зображення комплексної числової послідовності
у вигляді дійсної та уявної синусоїдальних послідовностей
Важливим окремим випадком даного процесу є процес зі значенням:
юі; = ктг,
де к - довільне ціле число.
Для такого процесу уявна частина послідовності відсутня. Якщо к = 1, то
одержана числова послідовність відповідає одиничній знакозмінній
послідовності, наведеній на рис. 6.15, г.
257
Струтинський В. Б.
З одержаними дискретними масивами значень процесу можна здійснювати
довільні алгебраїчні та диференціальні операції. Особливо просто
здійснюється операція інтегрування послідовностей. Обчислення інтегралу
трансформується в суму елементів послідовності.
6.3.2. Ступінчасті та імпульсні дискретні процеси
Аналіз дискретної математичної моделі процесу включає визначення
відповідності дискретної моделі та неперервного процесу. Відповідність між
дискретною моделлю та базовим процесом встановлюється різними способами.
Розглянемо деякий базовий процес і його дискретну модель у вигляді
масиву значень цього процесу. За масивом дискретних значень базового
процесу сформуємо дискретний модельний процес, пов’язаний із базовим.
На рис. 6.18 наведено ряд схем формування модельного процесу із масиву
дискретних значень базового процесу.
Рис. 6.18. Різні способи формування дискретного модельного процесу Р(х)
із масиву дискретних значень (решітчастої функції), базового процесу {(х):
а - екстраполяція значень решітчастої функції на крок вперед;
б - визначення процесу відповідно до значень решітчастої функції,
зміщеної на крок назад; в - формування дискретного прогресу
із середньоарифметичних значень решітчастої функції;
г - дискретний процес у вигляді ламаної лінії
258
Розділ 6. Дискретні математичні моделі процесів
Дискретний модельний процес може бути кусково-постійним
(рис. 6.18, а-в) або у вигляді ламаної лінії (рис. 6.18, г). Кусково-постійні
модельні процеси знайшли широке застосування при математичному
моделюванні. Вони формуються із значень решітчастої функції базового
процесу. Модельний процес часто визначається екстраполяцією значень
решітчастої функції на крок вперед (рис. 6.18, а). Аналогічним чином
формуються процеси, значення яких відповідає решітчастій функції, зміщеній
на крок назад (рис. 6.18, б). З метою підвищення точності використовують
ступінчасті функції, значення яких в середині інтервалу зміни аргументу
дорівнює середньоарифметичному значенню решітчастих функцій на межах
інтервалу (процес показаний на рис. 6.18, в). При цьому значення кусково-
постійного модельного процесу в для інтервалу [хі-і, Х|]:
Г(х) = |(£[і-1]+£[і]).	(6.44)
Всі кусково-постійні дискретні процеси кількісно відповідають базовому
процесу і наближаються до нього при зменшенні інтервалу дискретизації.
Недоліком кусково-постійного модельного процесу є наявність у ньому точок
розриву функції першого роду.
Цього недоліку можна позбутися, сформувавши дискретний модельний
процес у вигляді ламаної лінії (рис. 6.18, г).
Модельний дискретний процес, побудований на базі решітчастої функції, що
визначена із базового процесу, не завжди точно відповідає базовому. Більш
точними є модельні дискретні процеси, параметри яких вибрані за умови
найкращого наближення модельного процесу до базового. Такою умовою, як
правило, є рівність визначених інтегралів базового і модельного процесів в
середині інтервалу, в якому модельний процес є постійним:
хі х;
р(х)ах = |р(х)сіх .	(6.45)
Враховуючи, що значення кусково-постійного процесу в середині інтервалу
[Хрі, х;] є постійним (Т(х) = СоїМ), із залежності (6.45) одержимо:
=--------Р(х)с1х .	(6.46)
хі -X, , /
Якщо визначити значення процесу таким чином, він буде мати вигляд,
близький до процесу, показаному на рис. 6.18, в.
Дискретний процес у вигляді ступінчастої лінії можна формувати
використовуючи засоби математичних пакетів. На рис. 6.19 наведена
структурна математична модель, побудована засобами системи візуального
математичного моделювання 8ІМНШНК математичного пакету МАТЬАВ.
Наведена на рисунку модель ілюструє дискретизацію (квантування)
259
Струтинський В. Б.
символьних залежностей, реалізованих засобами системи ЗІМІІЬІМК. В
даному випадку символьні залежності 1п(0,6*х) та е°’2*х перетворені в
модельні дискретні кусково-постійні процеси за допомогою блоків Риапілхег
системи зімньшк.
Дані блоки здійснюють дискретизацію символьних залежностей по точках з
постійним приростом функції.
Рис. 6.19. Структурна
математична модель в системі
5ІМС/ШМК, яка здійснює
формування дискретних кусково-
постійних модельних процесів
із символьних залежностей
Рис. 6.20. Графіки базових
неперервних і відповідних їм
модельних дискретних процесів,
сформованих структурною
математичною моделлю
Значення постійного приросту функції задається в меню блока. Вибір
дискретних інтервалів зміни аргументу здійснюється за умови найкращого
наближення дискретного модельного процесу до неперервного базового.
Кусково-постійні дискретні процеси є одним із видів модельних
дискретних процесів. При розробці математичних моделей застосовуються
також інші види дискретних модельних процесів. Поширеними є дискретні
процеси у вигляді ізольованих імпульсів різної форми. На рис. 6.21 наведені
дискретні модельні імпульсні процеси у вигляді прямокутних імпульсів.
Коли амплітуда імпульсів пропорційна значенням елементів дискретного
масиву, що утворений з базового неперервного процесу Кх), то говорять про
амплітудноімпульсну модуляцію (рис. 6.21, а). При цьому ширину імпульсів
260
Розділ 6. Дискретні математичні моделі процесів
Літ звичайно приймають постійною, а амплітуду імпульсів - пропорційною чи
рівною значенню решітчастої функції.
Рис. 6.21. Дискретні модельні детерміновані процеси у вигляді пакету
ізольованих прямокутних імпульсів: а - амплітудноімпульсна модуляція
базового неперервного процесу; б - широтно-імпульсна модуляція;
в - частотно-імпульсна модуляція; г - фазо-імпульсна модуляція
базового процесу
У випадку, коли змінюється ширина імпульсів при постійній амплітуді
(рис. 6.21, б), говорять про широтно-імпульсну модуляцію базового процесу
Кх). При цьому ширина імпульсу ДЬ, пропорційна значенню решітчастої
функції ДЬ - £[і].
Якщо і амплітуда, і ширина імпульсів є постійними, а змінюється тільки
частота дії імпульсів, тобто змінюється відстань між сусідніми імпульсами, то
говорять про частотно-імпульсну модуляцію. При частотно-імпульсній
модуляції кількість імпульсів Пі, які попадають в інтервал дискретизації
аргументу [хи, Х(], пропорційна значенню базового процесу Г/х), тобто
частота п, ~ Г;[і].
Іноді частоту імпульсів приймають пропорційною інтегралу від базового
процесу в межах інтервалу дискретизації. При цьому
261
Струтинський В. Б.
Пі - |1(х)с1х .	(6.47)
Процес у вигляді однакових прямокутних імпульсів, які мають різні
значення зміщення імпульсу відносно точки визначення решітчастої функції,
наведено на рис. 6.21, г. Цей випадок відповідає фазо-імпульсній модуляції
базового процесу. Величина зміщення (фази) прямокутних імпульсів, як
правило, приймається пропорційною значенню решітчастої функції Дх, ~ Ці].
Крім прямокутних імпульсів, можна використовувати імпульси іншої
форми, зокрема трикутні, трапецієвидні, імпульси у вигляді ламаної лінії,
синусоїд тощо.
Як модельні дискретні процеси широко застосовуються процеси із
плавними формами імпульсів. На рис. 6.22 наведені ряд характерних форм
імпульсів, які використовуються при математичному моделюванні.
Рис. 6.22. Типові імпульсні дискретні процеси, які використовуються
при математичному моделюванні: а - імпульси у вигляді кривої Гауса;
б — частини синусоїди; в - трапецієвидні заокруглені;
г — несиметричні імпульси
При формуванні модельних дискретних процесів застосовують засоби
математичних пакетів. На рис. 6.23 наведена структурна математична модель,
262
Розділ 6. Дискретні математичні моделі процесів
яка формує дискретні модельні процеси засобами системи візуального
математичного моделювання ЗІМБЕШК математичного пакету МАТЬАВ.
І;
Зідпаі

Рис. 6.23. Формування дискретних модельних процесів засобами системи
5ІМІЗІЛМК: а - структурна математична модель; б - дискретні
модельні процеси, сформовані структурною моделлю
Дискретні модельні процеси формуються у вигляді періодичних імпульсів
різноманітної форми (рис. 6.23, б). Кожен з блоків структурної моделі
(рис. 6.23, а) має відповідні засоби для встановлення потрібних параметрів
імпульсів. Зміна амплітуди, частоти та інших параметрів при необхідності
здійснюється використанням додаткових структурних моделей.
Математичні пакети дозволяють сформувати різноманітні дискретні
процеси. Окремим випадком таких процесів є випадкові дискретні процеси
різного виду. Застосування випадкових дискретних процесів при
математичному моделюванні розглянуто у розділі 12.4.
263
Струтинський В. Б.
РОЗДІЛ 7
Знаходження символьних математичних моделей
за дискретними множинами значень процесів
7.1. Інтерполяція та екстраполяція засобами пакету МаіЬСАО
7.1.1. Лінійна та поліноміальна інтерполяція
Необхідність знаходження значень функції між двома заданими точками
часто виникає при ' розробці різноманітних математичних моделей. Ця
процедура має назву інтерполяції функції, тобто знаходження проміжних
значень функції між двома заданими точками. В більш загальному вигляді
процедура інтерполяції полягає в знаходженні аналітичної функції Р(х), що
точно (в межах необхідної точності) відповідає значенням функції у заданих
точках (вузлах інтерполяції) [17, 20, 32, 33, 35, 42].
Застосування інтерполяції при математичному моделюванні є досить
поширеним. Як правило, це службові процедури та операції, пов’язані з
побудовою графіків залежностей (одномірнії інтерполяція) або дво- чи
багатовимірних поверхонь. Широке застосування інтерполяції має місце при
виконанні диференціальних операцій, зокрема при чисельному
диференціюванні та інтегруванні. Інтерполяція різноманітного виду
застосовується при розв’язку рівнянь та систем рівнянь. Чисельне
інтегрування звичайних диференціальних рівнянь та рівнянь у частинних
похідних також базується на методах інтерполяції функцій. Інтерполяція
функцій є необхідним елементом вирішення оптимізаційних задач та задач,
пов’язаних з аналізом робочих процесів і характеристик технічних систем.
Обробка і аналіз експериментальних даних також включає процедуру
інтерполяції.
Використання інтерполяції функцій дозволяє вирішити ряд питань
формування математичних моделей. Це стосується визначення граничних
умов, опису залежностей з розривами функцій та їх похідних. Інтерполяція
функцій дає можливість правильно організувати введення та виведення даних
при математичному моделюванні, виконати аналіз одержаних результатів.
При порівнянні результатів розрахунків з експериментальними даними, як
правило, теж використовуються методи інтерполяції функцій. Існує ще досить
значний клас випадків застосування процедури інтерполяції. Зокрема, це її
застосування при аналізі випадкових величин, апроксимації функцій
довільного виду та інші.
264
Розділ 7. Знаходження символьних математичних моделей
Розглянемо практично важливі випадки та особливості процедури
інтерполяції.
Нехай деяка функція, що описує процес в технічній системі, задана у
дискретній множині точок, які називаються вузлами інтерполяції:
Ао, А<, ..., Ап
Ці точки відповідають значенням аргументу
х; (і = 0, 1, 2, ..., п)
і в них задані значення функції
Уі (і = 1, 2, .... п).
Задача інтерполяції полягає у знаходженні функції Р(х), графік якої
з’єднує задані точки Ао, А„.
Задача інтерполяції може бути вирішена нескінченним числом способів.
На рис. 7.1 показано геометричну інтерпретацію характерних варіантів
процедури інтерполяції процесів, заданих дискретними множинами значень.
Рис. 7. /. Геометрична інтерпретація різних способів інтерполяції:
а - лінійна; б - поліномгальна (параболічна);
в - інтерполяція експонентою; г - інтерполяція синусоїдою
Коли точки Ао, А-1, Ап з’єднуються найкоротшими кривими, а вони, як
відомо, є прямими лініями, то одержимо функцію Р(х) у вигляді полігона
маємо лінійну інтерполяцію функції (рис. 7.1, а).
Для інтерполяції можна використати залежності різного виду. Найбільш
поширеним є використання поліноміальних залежностей (рис. 7.1, б).
Окремими випадками поліноміальної інтерполяції є розглянута раніше
лінійна інтерполяція. Вона використовує поліноми першого степеня.
Параболічнії (квадратична) інтерполяція використовує поліном другого
степеня. Інтерполяція кубічною параболою використовує поліном третього
степеня. На практиці застосовуються поліноми не вище 5... 10 степеня.
265
Струтинський В Б.
В ряді спеціальних випадків для інтерполяції використовують залежності
іншого виду, наприклад, експоненціальну (рис. 7.1, в) або тригонометричну
(рис. 7.1, г). Звичайно у цих випадках повинна виконуватись умова
належності вузлів інтерполяції вибраній залежності або виконання необхідних
асимптотичних співвідношень.
Найбільш простим і поширеним способом інтерполяції є лінійна
інтерполяція. Процедура інтерполяції за даним методом полягає у
знаходженні ламаної лінії, яка проходить через всі задані точки. Для
знаходження параметрів прямої, яка проходить через дві точки, необхідна
інформація про функцію лише в цих двох точках, тому що через дві точки
можна провести лише одну пряму. Задача лінійної інтерполяції є
однозначною і вона полягає у знаходженні сукупності лінійних аналітичних
залежностей, кількість яких на одиницю менша кількості вузлів інтерполяції.
Геометрична інтерпретація процедури лінійної інтерполяції наведена на
рис. 7.2.
Рис. 7.2. Геометрична інтерпретація процедури лінійної інтерполяції
процесу, заданого у вигляді масиву точок Ац, ..., Ап
Рівняння прямої, що з’єднує вузли інтерполяції А, та Аі+1, має вигляд:
Г;(х) = а, + фх,	(7.1)
де аІ7 Б, - постійні коефіцієнти, визначені для інтервалу [хі; хі+Д.
Застосувавши формулу (7.1) для всіх вузлів інтерполяції, одержимо
систему рівнянь:
(а. + Ь ,х : = У;
( '	1	, і = 0,..., п -1.	(7.2)
Iа, +ЬіХ,и =уі+1
Розв’язок системи (7.2) знайдемо за правилом Крамера. Відповідно
—•	Ь =	і = о,...,п-і.
хі+і ~ хі	хі+і _ хі
(7.3)
Формули (7.3) визначають в загальному вигляді коефіцієнти лінійних
залежностей для кожного інтервалу між вузлами інтерполяції. В результаті
для кожного проміжку між вузлами інтерполяції А;, Аі+1, що відповідає
266
Розділ 7. Знаходження символьних математичних моделей
інтервалу зміни аргументу [хі, хі+;], визначена пряма, коефіцієнти якої
залежать від координат вузлів інтерполяції, а саме:
а, = а/хі, хі+1, Уі, уі+1); Б, = Ь/х,, хі+1, уІЛ уі+1).	(7.4)
Враховуючи, що відрізків, які з’єднують всі вузли інтерполяції, на
одиницю менше, ніж вузлів, одержимо (п - 1) пар коефіцієнтів
аі( Б,, і = 0, 1, ..., п-1.
Наведена вище процедура знаходження аналітичних залежностей при
лінійній інтерполяції функцій має одну особливість, до речі, типову для
багатьох чисельних методів. Формули (7.3) для обчислення коефіцієнтів є
порівняно простими, але велика кількість формул і особливості їх
застосування є досить громіздкими і незручними при розрахунках.
Використання ЕОМ суттєвим чином спрощує розрахунки і зводить
процедуру лінійної інтерполяції до найпростішого виду.
В математичному пакеті МаГІїСАО процедуру лінійної інтерполяції
здійснює вбудована функція
ііпіегр (уХ,Уу,х).
Вона розраховує значення полігонального (лінійного) наближення
функції у = у(х) на всьому інтервалі зміни аргументу хц < х < хп.
Вхідними параметрами вбудованої функції Ііпіегр є вектори ух та уу, які
задають координати вузлів інтерполяції. При цьому ухо = х0, ухп = хп.
Розглянемо застосування вбудованої функції 1іпіегр(ух,уу,х) для
інтерполяції функції, заданої своїми значеннями в деяких точках. Як приклад
ілюстрації процедури взята дискретна математична модель, одержана із
аналітичної залежності
§(х) = 8іп(х)-агсІ§(х).
Обчислені значення цієї залежності в 11 точках наведені нижче:
і := 0...10 ух; і §(х) := 8Іп(х)*аіап(х) ууі := 8іп(ухі)*(аіап(ухі) УХ = Е(х) := 1іп1егр(ух,уу,х)		0	Уу =		0
	0	0		0	0
	1	1		1	0,661
	2	2		2	1,007
	3	3		3	0,176
	4	4		4	-1,003
	5	5		5	-1,317
	6	6		6	-0,393
	7	7		7	0,939
	8	8		8	1,431
	9	9		9	0,602
	10	10		10	-0,8
Введена нова функція Г(х) відповідає лінійній інтерполяції залежності,
267
Струтинський В. Б.
заданої в 11 точках.
На рис. 7.3 побудовано залежність §(х), яка визначає 11 вузлів
інтерполяції Ао, А(, .... Аю, а також полігональна функція Р(х), яка
здійснює лінійну інтерполяцію дискретної моделі між вузлами.
Рис. 7.3. Приклад лінійної інтерполяції дискретної моделі,
що відповідає масиву з 11 точок, за допомогою вбудованої функції
Ііпіегр пакету МаИгСАИ
Вбудована функція Ііпіегр відзначається зручністю в користуванні та
надійністю роботи. Майже не зустрічаються випадки збою програми при
застосуванні процедури лінійної інтерполяції.
В математичному пакеті МАТЬАВ лінійна інтерполяція здійснюється
вбудованою функцією, синтаксис якої:
уі = іпіегр1(х, у, хі),
де х, у - масиви значень функції в точках Ао, А-|, ..., Ап, які визначають
задану дискретну математичну модель;
хі = хо, X], ..., хп; уі = уо, уі, ..., уп ~ вектори (масиви значень), що
відповідають лінійній інтерполяції функції в масиві точок хі.
При цьому масив хі може відповідати більш дрібній градації сітки, ніж х,
а масив уі включає інтерпольовані методом лінійної інтерполяції значення
функції.
Лінійна інтерполяція функцій є найбільш простою і найбільш грубою
інтерполяційною процедурою. Основними недоліками лінійної інтерполяції є
низька точність та наявність неоднозначності (розриву значень) похідних
одержаної кусково-лінійної аналітичної функції у вузлах інтерполяції. Тому
для інтерполяції застосовуються більш точні методи, зокрема, це інтерполяція
функцій поліномінальними залежностями довільного виду. В цьому випадку
аналітична функція, що використовується при інтерполяції, має вигляд:
268
Розділ 7. Знаходження символьних математичних моделей
Р(х) = ао + а^х + ... + атхп1,	(7.5)
де ао, а], ..., ап - коефіцієнти полінома;
ш - степінь полінома (ціле додатне число).
Найпростішим випадком полінома є лінійна функція (т = 1), що
відповідає розглянутій раніше лінійній інтерполяції функції.
При інтерполяції функцій поліномами необхідно враховувати наступне.
Через два вузли інтерполяції можна провести лише одну лінію, яка відповідає
поліному першого степеня, через три вузли можна провести єдину
квадратичну параболу (відповідає поліному другого степеня), через чотири
вузли - лише одну кубічну параболу (відповідає поліному третього степеня).
В загальному випадку через (п + 1) вузлів інтерполяції може бути проведена
крива, яка відповідає поліному п-ого степеня. Цей поліном буде єдиний для
даних вузлів інтерполяції.
Відповідно до цього можна послідовно об’єднати вузли інтерполяції по
парах, по трійках, по чотири п’ять, шість та більше вузлів і виконати
інтерполяцію відповідно поліномами першого степеня (розглянуту раніше
лінійну інтерполяцію), другого степеня (квадратичну інтерполяцію), третього
степеня і вище.
Розглянемо практично важливий випадок інтерполяції функції поліномом
другого степеня - квадратичну інтерполяцію. Поліном другого степеня
відповідає квадратичній параболі.
На рис. 7.4 показана геометрична інтерпретація квадратичної інтерполяції
функції, заданої в трьох вузлах.
Рис. 7.4 Графічна інтерпретація квадратичної інтерполяції функції,
заданої в трьох вузлах
269
Струтинський В. Б.
Аналітична функція (поліном другого степеня), що використовується для
квадратичної інтерполяції, має вигляд:
Ь'2(х) = а0 + а^ + а2Х2.	(7.6)
Визначимо коефіцієнти полінома. Для спрощення викладок приймемо, що
різниця аргументів сусідніх вузлів інтерполяції є постійною:
х2 - х1 = Хі - Хо = А,
а центр координат розташуємо в точці 0. Тоді
хі =0; хо = -А; Х2 = + А.
Для визначення коефіцієнтів прирівняємо значення функцій у вузлах
інтерполяції. Одержимо систему рівнянь для визначення невідомих
коефіцієнтів:
а0 - а,А + а2Д2 = у0
 ао = у,
а0 + а,А + а2Д2 = у2
Розв’язком даної системи рівнянь є значення коефіцієнтів полінома:
п . я _(У2-Уо). я _У2-Уо-2у(
ао “ Уі, аі - —гт-------------. а2  --------------•
2А	2А
(7.7)
Якщо вузлів інтерполяції більше трьох, квадратична інтерполяція може
здійснюватись послідовно для кожної трійки вузлів. Для вузлів Ао, Аі, А2
маємо криву Е] (рис. 7.5), для вузлів А,.!, А,, Аі+1 - криві Г,, і = 1, 2, ..., 6.
Рис. 7.5. Квадратична інтерполяція, здійснена послідовно
для кожної трійки вузлів
Геометрична інтерпретація, наведена на рис. 7.5, ілюструє характерний
недолік квадратичної інтерполяції. Він полягає в тому, що сусідні криві
спряжуються таким чином, що виникає неоднозначність (наприклад, між
точками Аі та А2) та порушення неперервності похідної результуючої кривої.
Наприклад, в точці А2 похідні кривих Рд і Г3 є суттєво різними.
270
Розділ 7. Знаходження символьних математичних моделей
Цих недоліків можна позбутися, якщо для інтерполяції використати
поліном відповідного, більш високого степеня. Для випадку, наведеному на
рис. 7.6, поліном 7-го степеня буде відповідати кривій, що проходить через
всі вісім вузлів інтерполяції.
Рис. 7.6. Інтерполяція функції, заданої у восьми точках поліномом
сьомого степеня
При інтерполяції дискретної моделі процесу, зображеного на рис. 7.6,
знайдено поліном виду:
Рп(х) = 100 + Юх - х2 - 0.5х3 + 0.004х4 - 0.007х5 + 0.00052х6+ 0.00038х7.
В загальному випадку для довільної дискретної моделі процесу, заданого
в (п + 1) точках, знаходять поліном степеня п.
Цей поліном часто записують у вигляді інтерполяційного полінома
Лагранжа [32, 42] (інтерполяційна формула Лагранжа):
Р„(х) = <>у0 + Ц'")(х)у, + ... + Ц(”)(х)уп,	(7.8)
де Ц^(х) - функції форми, які залежать від значення змінної х.
Інтерполяційна формула Лагранжа (7.8) може бути записана у матрично-
векторному вигляді:
Еп(х) = [цМ(х)]- к]«	<7 9>
де М^(х)] - матриця-стрічка, компонентами якої є функції форми;
у;] - вектор-стовпець значень функції у вузлах інтерполяції.
Функції форми мають властивість:
1^п)(х) = 	1 При X = X, , (і = 0, 1, 2, ..., п).	(7.10) 0 ПРИ X = Х} X;
Функції форми виражаються через поточне значення аргументу х та через
масив точкових значень аргументу х, у вузлах інтерполяції за наступними
залежностями:
271
Струтинський В. Б.
(7.11)
м(п) =	(х-ХрХх-х^-.-^х-х^) .
(х„ -х0Хх„ -х,)- ...-(хп -хп_1)‘
Крім інтерполяційної формули Лагранжа, відомі та використовуються й
інші форми інтерполяційних поліномів [42], зокрема, це інтерполяційні
формули Ньютона, Стірлінга, Бесселя, Ерміта, Еверета, Стефенсона та інші.
Деякі з цих формул, крім значень функції, використовують також
значення її похідних або значення кінцевих різниць.
Існують методи оцінки точності інтерполяції, збіжності методів тощо [42].
Інтерполяція дискретних значень функції поліномом реалізована в пакеті
МаДіСАО. Для цього служить вбудована функція роїуГіі. Застосування цієї
функції буде розглянуте нижче у розділі 7.2.2.
Загалом треба визначити, що при значній кількості вузлів інтерполяції, як
це звичайно має місце, інтерполяція поліномами не завжди доцільна. На
практиці інтерполяція поліномами годиться лише для точно заданих функцій,
якщо їх значення не спотворюються збуреннями та шумами.
Крім того, використання інтерполяційних поліномів високого степеня при
значній кількості вузлів інтерполяції призводить до громіздких формул та
складності обчислення коефіцієнтів і часто буває недоцільним.
7.1.2. Інтерполяція сплайнами
Одним із поширених методів обробки дискретних математичних моделей є
інтерполяція функцій кубічними сплайнами (сплайн-інтерполяція).
Для ілюстрації процедури сплайн-інтерполяції розглянемо процес, який
включає ряд вузлів інтерполяції Ао, А^, Аз....Ап (рис. 7.7).
Вузли інтерполяції зображені у вигляді точок на координатній площині.
Для проведення через ці точки гладкої неперервної кривої використано
гнучку пружку лінійку (зрііпе - стрижень, балка, рейка). Якщо лінійку
встановити так, щоб вона проходила через всі вузли інтерполяції, то пружна
вісь лінійки буде відповідати кривій, що інтерполює значення дискретно
визначеної функції. Форма пружної осі буде описуватись законами
деформації пружних тіл.
Для лінійки без зовнішніх навантажень, її ділянки між вузлами
відповідають графіку полінома третього степеня (кубічної параболи). Тому
даний вид сплайн-інтерполяції і має назву інтерполяції кубічними сплайнами.
272
Розділ 7. Знаходження символьних математичних моделей
Рис. 7.7. Графічна інтерпретація інтерполяції дискретних математичних
моделей кубічними сплатами
Покажемо, що форма кривої дійсно відповідає поліному третього степеня.
З курсу опору матеріалів відомо, що диференціальне рівняння осі зігнутої
пружної балки при відсутності зовнішніх навантажень має вигляд [109]:
^) = 0.	(7.12)
дх
Це рівняння має місце для кожної ділянки пружної балки між вузлами
інтерполяції, зокрема для ділянок
АоАі, А]А2, ..., АІ_1АІ, ..., Ап^Ар.
Розглянемо довільну ділянку між вузлами Аі-і Аі; інтервал зміни
аргументу якої [х^, х,].
Розв’язком диференціального рівняння (7.12) є поліномом третього
степеня. Для розглянутого інтервалу зміни аргументу х поліном (сплайн-
функцію) запишемо у вигляді:
рфх) = а( + ф(х - хг1)+с^х - х^,)2 +ді(х--хі1)3,	(7.13)
де а,, Ь|, Є;, ф - коефіцієнти, що відповідають інтервалу зміни аргументу в
межах X).] < х < х;.
Значення коефіцієнтів для кожного інтервалу повинні бути знайдені.
Задача сплайн-інтерполяції має два етапи:
-	перший - це знаходження в результаті розрахунків сукупності коефіцієнтів
для всіх ділянок між послідовними сусідніми вузлами інтерполяції;
-	другий етап - це, власне, інтерполяція, яка полягає у знаходженні
проміжних значень функції в усьому діапазоні зміни аргументу хо х < хп.
Коефіцієнти поліномів визначають виходячи із умов відповідності
аналітичної залежності заданим значенням у вузлах інтерполяції та виконання
умови неперервності похідних сплайн-функцій у вузлах інтерполяції.
На межах і-го інтервалу інтерполяцій будемо мати рівності:
Рі(хі) = уі; Рі(хі.1) = уи.
273
Струтинський В, Б.
Це відповідає проходженню графіка аналітичної залежності Е(х) через
вузли інтерполяції А, та Аг |.
У вузлах інтерполяції похідні аналітичної залежності є неперервними.
Тому, для кожного вузла похідна зліва Е'(х - 0) дорівнює похідній справа
Е'(х + 0). Звідси випливає співвідношення:
Еі'(хі - 0) = Еі+1'(х; + 0).	(7.14)
Це ж стосується і другої похідної. Тому маємо рівняння:
Еі"(Хі - 0) = Еі+1"(Хі + 0).	(7.15)
Ці рівняння мають місце лише для внутрішніх вузлів інтерполяції. Для
крайнього лівого вузла Ао та для крайнього правого Ап необхідно ввести
додаткові умови. Звичайно вони задаються у вигляді умови відсутності
крутного моменту в перерізі пружної лінійки. При цьому:
Е"(х0) = Е"(хп) = 0.	(7.16)
ЕІульове значення відповідає нескінченному радіусу кривизни кривої (осі
пружної лінійки) на границях інтервалу інтерполяції.
Визначення всієї сукупності коефіцієнтів сплайн-функцій може
здійснюватись різними методами. Розглянемо метод, наведений у [32]. У кожному
вузлі інтерполяції сплайн-функція відповідає заданому табличному значенню.
Підставивши значення величин відповідно для точки А,^, одержимо:
Е/х;^) = уі-! = а, + Ь;0 + сД2 + сЦО3 = а;.	(7.17)
Таким чином, для всіх і = 1, 2, ..., п ~ 1 будемо мати а, = у^.
Підставивши значення величин відповідно для точки А(, одержимо:
Еі(хі_1) = уі = а, + Ьі(хі - Хі.]) + сі(хі-хі.1)2+ б/х, - хи)3.	(7.18)
Введемо позначення Ь, = х, - хи. Підставляючи це значення та значення
коефіцієнтів а;, одержимо:
Уі = Ум + ЬіЬ, + еф;2 + бфі3..	(7.19)
Знайдемо першу і другу похідні сплайн-функції для хн< х < хр
Е)'(х) = Б, + 2с,(х - Хрі) + Зф(х - Х).])2;
ЕДх) = 2с, + 6сЦ(х - Хі-Ц.
Похідні сплайн-функції неперервні в усіх точках, включаючи вузли
інтерполяції А,.! та А;. Прирівнюючи границі похідних зліва і справа у
кожному вузлі інтерполяції, одержимо:
Еі'(хі - 0) = Еі+1'(хі + 0).
Підставивши значення похідних зліва і справа у кожному вузлі
інтерполяції, одержимо рівняння:
Б, + 2с,(х - хм) + Зф(х - хи)2 = Ьі+1 + 2сі+1(х - хи) + Зф+Цх - хм)2.
Звідси знаходимо значення коефіцієнтів:
Ьі+1 = Ь| + 2с;(х - хи) + Зф(х - хи)2.
Вводячи, як і раніше, приріст аргументу ф = х, - х^, одержимо:
Ьж = Ф + 2сіЬі + Зфф2.	(7.20)
274
Розділ 7. Знаходження символьних математичних моделей
Прирівняємо в кожному вузлі інтерполяції А, значення других похідних
зліва і справа:
Р^Хі _0) = Р'+1(хі +0).	(7.21)
Звідси знайдемо:
сі+і = С( + ЗсЦЬі; Ф = (сі+1 - Сі)/ЗЬі.	(7.22)
Як вказано раніше на кінцях загального інтервалу інтерполяції в точках
Ао, Ап кривизна кривої дорівнює нулю. Це дає необхідні умови для
замикання системи рівнянь. Значення другої похідної сплайн-функцій в
крайніх вузлах інтерполяції будуть дорівнювати нулю. Відповідно
Р/Чхо) = рп"(хп) = 0.	(7.23)
Звідси одержимо:
2сі + 6ф(хо - хо) = 0; С] = 0;
2сп + 6с1п(хп - хп.]) = 0;
й =____£д_
п (зь„У
(7.24)
Дані рівняння (7.17)-(7.24) утворюють лінійну систему рівнянь для
визначення Зп невідомих коефіцієнтів Ь,, с,, ф. Розв’язок даної системи
дозволяє знайти коефіцієнти і визначити таким чином сукупність сплайн-
функцій.
Процедури інтерполяції сплайнами широко реалізовані в сучасних
математичних пакетах. В пакеті МаНіСАИ є ряд вбудованих функцій для
інтерполяції сплайнами з різними граничними умовами [22, 56, 62].
Коефіцієнти сплайн-функцій (сплайнів) розраховуються за допомогою
наступних вбудованих функцій.
Коефіцієнти кубічного сплайна розраховує вбудована функція
С8р1ІПЄ(УХ, Уу).
Вона використовує вектори ух, що містить значення х0, х(, Х2, ..., хп, та
уу, що містить значення уо, у і, У2, • ••, уп-
Результатом розрахунків є вектор уз, що містить шукані коефіцієнти
кубічного сплайна.
Для розрахунку коефіцієнтів сплайнів з іншими граничними умовами
служать вбудовані функції:
рзрііпе (ух, уу) та Ізрііпе (ух, уу).
Власне, процедура інтерполяції функції однієї змінної реалізується
вбудованою функцією
іпіегр (УЗ, УХ, уу, х),
яка повертає значення сплайна в точці х по заданих векторах ух, уу та по
коефіцієнтах сплайна уз.
Розглянемо приклад застосування процедури інтерполяції функції однієї
змінної, заданої своїми значеннями в 5 точках. Використаємо сплайни різного
виду, які реалізовані в пакеті МаїЬСАБ.
275
Струтинський В. Б.
Для рівномірно розташованих значень ух задамо значення функції у
вузлах інтерполяції уу:
ухт = [0 1 2 3 4]	уут=[12 134].
Визначення вектора коефіцієнтів кубічного сплайна виконується
функцією:
У	8 := С8р1ІПЄ(УХ, уу).
Знаходження функції §(х), яка обчислює значення кубічного сплайна в
точці х, здійснюється оператором:
§(х) := іпіегр(у8, ух, уу, х),
визначення коефіцієнтів сплайна із зглаженими (параболічними) граничними
умовами:
У	8 := р8рііпе(ух, уу),
обчислення функції к(х), яка розраховує значення даного сплайна:
к(х) := іпіегр(у8, ух, уу, х),
визначення коефіцієнтів сплайна із спеціальними (лінійними) граничними
умовами:
У	8 := І8р1іпе(ух, уу),
обчислення функції Кх), яка визначає значення даного сплайна:
1(х):=іпіегр(У8, ух, уу, х).
Результати виконаних різних видів сплайн-інтерполяції показані у
графічному вигляді на рис. 7.8.
Рис. 7.8. Інтерполяція дискретної математичної моделі, визначеної
в п’яти точках за допомогою: крива 1 - кубічного сплайна д(х);
крива 2 - “параболічного” сплайна к(х); крива 3 - “лінійного” сплайна Кх);
ламана лінія 4 - лінійна інтерполяція /(х)
276
Розділ 7. Знаходження символьних математичних моделей
Для порівняння на рисунку наведена лінійна інтерполяція заданої в
точках Ао, А4 залежності за допомогою вбудованої функції Ііпіегр.
Обчислення реалізується процедурою:
£(х) := 1іпіегр(ух, уу, х).
Графіки залежностей, одержаних при інтерполяції таблично заданої
функції сплайнами різного виду (див. рис. 7.8), мають вигляд плавних
кривих, ЩО проходять через вузли інтерполяції. Між точками Ао“Ад вони
якісно та кількісно відповідають заданому значенню функції у.
Із порівняння графіків випливає, що сплайн-інтерполяція суттєво
згладжує залежність, задану в дискретних точках. При сплайн-інтерполяції
відсутні злами кривої у вузлах, як це має місце при лінійній інтерполяції.
В математичному пакеті МАТЬАВ для інтерполяції функції однієї змінної
використовується вбудована функція [24, 64]:
Уі := іпіегрі (х, у, хі; «метод»).
Ця функція є узагальненням розглянутої раніше процедури лінійної
інтерполяції і співпадає з нею, коли вказано лінійний метод інтерполяції,
тобто «метод» —> «Ііпеаг».
Коли вказано метод інтерполяції «метод» -> «сиЬіс», то реалізується
поліноміальна кубічна інтерполяція. Інтерполяції кубічними сплайнами
відповідає параметр «метод» -> «зрііпе». Прийнято, що аргумент х
змінюється монотонно, а у випадку кубічної інтерполяції проміжки між
значеннями х вважаються однаковими.
Інтерполяція застосовується також для обчислення проміжних значень
функцій двох і більше змінних. Практично важливим випадком є
інтерполяція функції ДВОХ ЗМІННИХ X і у.
В математичному пакеті МаПіСАЦ наявний ряд вбудованих функцій, які
інтерполюють функцію двох змінних, задану своїми значеннями у вузлах
інтерполяції за допомогою сплайнів різного виду.
Інтерполяція здійснюється вбудованою функцією:
2 := іпіегр(У5, Мху, Мг, п),
яка повертає інтерпольоване значення г, що відповідає точкам х = По і у = П].
Вектор аргументів функції двох змінних
п:=К
їм
являє собою двовимірний вектор, компоненти якого відповідають значенням
аргументів х і у в точці, в якій обчислюється інтерпольоване значення
функції ДВОХ ЗМІННИХ 2.
При інтерполяції задається прямокутна матриця Мху, перший стовпець
якої включає значення першої змінної: хд, х^, ..., хп, а другий стовпець -
значення другої змінної уо, уі, ..., уп у всіх вузлах інтерполяції.
277
Струтинський В. Б.
Задані дискретні значення функції х у всіх вузлах інтерполяції
визначаються матрицею Мх. Вектор уз включає розраховані коефіцієнти
кубічного, параболічного чи лінійного сплайна. Значення коефіцієнтів
розраховуються наступними вбудованими функціями:
с8рііпе(Мху, Мх) рврІіпе(Мху, Мх) І8р1іпе(Мху, Мх).
Розглянемо приклад сплайн-інтерполяції за допомогою пакету МаіЬСАО
функції двох змінних, заданої в 9-ти точках.
Матрицю значень аргументів у вузлах інтерполяції Мху та матрицю
значень функції Мх задамо у вигляді:						
	0	0'		0	50	60
Мху :=	1	1	Мх :=	0	40	20
	2	2		0	10	ЗО
Одержані результати обчислення вектора коефіцієнтів кубічного сплайна
мають вигляд:
(С8р1іпе(мху, Мх))т = [ 0 3 2 » 0 0 -40 -20 0 100 50 0 ].
Для знаходження інтерпольованих значень функції двох змінних введена
допоміжна функція §(п) з векторним аргументом п. Обчислення значень цієї
функції здійснюється наступним чином:
§(п) := іпіегр(У8, Мху, Мх, п).
Перевірка роботи допоміжної функції §(п) виконана шляхом обчислення її
значень у вузлах інтерполяції:
= 50
= 60
Звідси
випливає, що значення допоміжної функції §(п) у вузлах
інтерполяції відповідає компонентам матриці Мх.
Побудову графіка інтерпольованих значень здійснено на сітці розміром
10x10:
і := 0...10
І := 0...10
х, := і*0,2	Ур=.і*0,2
X;
Одержаний
інтерпольованим
графік
значенням
поверхні,
функції, наведено па рис. 7.9.
що відповідає розрахованим
м,,
= §
Аналогічно здійснюється процедура інтерполяції функції двох змінних
сплайнами з параболічними та лінійними крайовими умовами.
Якщо клітинки сітки при побудові графіка взяті достатньо малими,
наприклад, використана сітка розмірами 100x100, то побудована поверхня
буде гладкою та неперервною.
278
Розділ 7. Знаходження символьних математичних моделей
Рис. 7.9. Графічна інтерпретація інтерполяції функції двох змінних д(п)
за допомогою кубічних сплайнів
В математичному пакеті МАТЬАВ для інтерполяції функції двох змінних
використовуються дві вбудовані функції:
гі = іпіегр2(х, у, хі, уі);
гі = іпіегр2(х, у, хі, уі, «метод»).
Перша функція здійснює лінійну інтерполяцію дискретних значень,
заданих в точках з координатами:
X = х0, X;, .... хп; у = Уо, У1, уп.
Вихідний масив значень функції гі може бути визначений на більш
дрібній сітці, координати якої:
хі = х!0, хіі, ..., х!пі; у! = у!0, уіь у!т.
Друга вбудована функція пакету МАТЬАВ
іпіегр2(х, у, хі, уі, «метод»)
дозволяє задати метод інтерполяції. Зокрема, при значенні «метод» -> «Ііпеаг»
здійснюється лінійна інтерполяція, а при значенні «метод» -> «сиЬіс» - кубічна
інтерполяція функції двох змінних.
В пакеті МАТЬАВ є також вбудовані функції, що дозволяють виконати
інтерполяцію функції двох змінних, заданої на нерівномірний сітці значень
змінних. Синтаксис цих функцій:
2І = §гі(1<1аіа(х, у, 2, хі, уі)
[хі, уі, гі] = §гіск1а<;а(х, у, 2, хі, уі).
Перша функція розраховує масив інтерпольованих значень, який
визначений на новій сітці з координатами:
ХІ = ХІО, ХІ1,	ХІт
уі = у10, уіі,	уіт.
Друга функція
[хі, уі, 7І] = §гі(1<1аіа(х, у, 2, хі, уі),
крім масиву /1, повертає впорядковані масиви хі та уі.
279
Струтинський В. Б.
7.1.3. Прогнозування параметрів процесів методом екстраполяції
В практичних задачах математичного моделювання часто виникає
необхідність обчислення значень параметра процесу за межами інтервалу
[х0, хп], в якому деякий параметр процесу у є заданим. Знаходження значень
функції за межами інтервалу відомих значень складає задачу екстраполяції.
Вона поляїає в продовженні (прогнозуванні) відомих значень функції
параметра процесу в більш широку область визначення. Це відповідає
прогнозуванню поведінки процесу в майбутньому.
Застосування екстраполяції при математичному моделюванні досить
широке. Як службова операція вона використовується при чисельному
інтегруванні диференціальних рівнянь різного виду. Екстраполяція дає
можливість прогнозувати параметри робочих процесів і характеристик
технічних систем. Важливе значення екстраполяція залежностей має при
обробці експериментальних даних, при розробці оптимального плану
наукових досліджень тощо.
Екстраполяція дає можливість правильно організувати введення та
виведення даних при математичному моделюванні. Власне методи
математичного моделювання екстраполюють відомі якісні характеристики
технічної системи на нову область параметрів системи.
Задачу екстраполяції формулюють двома дещо відмінними способами.
Перший стосується екстраполяції функції, заданої в символьному вигляді
скрізь між двома заданими гачками Ао, Ап в межах інтервалу [х0, хп]. Другий
спосіб полягає в екстраполяції функції, яка задана в інтервалі [хд, хп] лише в
деяких окремих точках - вузлах. Процедура екстраполяції, згідно цих
способів, ілюструється графіками, наведеними на рис. 7.10.
Для реалізації другого способу звичайно здійснюють інтерполяцію або
апроксимацію таблично заданої залежності в межах відомого інтервалу
[х(), хп] з одержанням символьної залежності Ц(х) (див. рис. 7.10, б). Після
цього виконують екстраполяцію, використовуючи вищевказану символьну
залежність. Іноді більш доцільно при екстраполяції використовувати лише
залежність у табличному вигляді.
Процедура екстраполяції може бути здійснена з необхідною точністю для
довільного інтервалу в одному практично важливому окремому випадку. Цей
випадок стосується екстраполяції періодичних процесів. Періодична функція
значення якої відоме протягом всього періоду, екстраполюється на
необмежений інтервал шляхом періодичного повторення її значень.
Символьне значення функції в інтервалі [х0, хп] може бути задане
аналітичним виразом або деякою процедурою чи алгоритмом. Якщо цей вираз
допускає продовження за межі відомого інтервалу, то екстраполяція може бути
280
Розділ 7. Знаходження символьних математичних моделей
здійснена простим обчисленням символьного виразу за межами інтервалу. Більш
складним є випадок, коли обчислення неможливі або недоцільні. Наприклад,
коли екстрапольовані значення за межі інтервалу треба подати в більш простому
вигляді, ніж символьно задана функція в середині відомого інтервалу.
відомих значень прогнозованих значень
б)
Рис. 7.10. Різні способи формулювання задачі екстраполяції функції {(х)
за межі відомого інтервалу заданих значень цієї функції: а - функція,
відома у символьному вигляді в кожній точці інтервалу [х(), хп]
і яка екстраполюється в кожну точку області прогнозованих значень:
б - функція в заданому інтервалі, визначена дискретною множиною
значень у0, у у ... уп і яка екстраполюється на ряд точок області
прогнозованих значень
281
Струтинський В. Б.
Розглянемо методику і особливості екстраполяції функції, яка задана в
символьному вигляді в деякому інтервалі [хо, хп]. Екстраполяція даної
залежності не є однозначною процедурою. Можливі різні варіанти здійснення
процедури екстраполяції. На рис. 7.11 показано графічну інтерпретацію
багатозначності процедури екстраполяції функції.
Рис. 7.11. Графічна інтерпретація можливих варіантів екстраполяції
функціональної залежності ф(х) за межами інтервалу [х^, хп]:
ф(х) ~ екстраполяція лінійною залежністю; ф(х) - екстраполяція
параболічною залежністю; фГх) - екстраполяція кубічною параболою
Екстраполяція здійснюється за умови, що властивості функції, які вона
має в заданому інтервалі [хц, хп], зберігаються і за межами інтервалу. Треба
зазначити, що для здійснення екстраполяції недостатньо одного лише
значення функції в точці хп. Властивості функції визначаються похідними
різних порядків. Якщо функція гладка і неперервна, то масив значень її
похідних на межі інтервалу (в точці хп) в принципі дозволяє виконати
екстраполяцію на довільний проміжок х(. Точність екстраполяції
підвищується із збільшенням числа похідних, які використовуються для
розрахунку екстрапольованих значень. Похідна нульового порядку, тобто
саме значення функції, самостійно не дає можливості виконати
екстраполяцію, але її застосування є необхідним в комплексі з похідними
першого і більш високих порядків.
Найбільш простим випадком екстраполяції є екстраполяція лінійною
функцією. Аналітична залежність для розрахунку екстрапольованих значень
включає значення функції та похідної на межі інтервалу і має вигляд:
<і(х)= Цхп) + у-
ах
(7.25)
282
Розділ 7. Знаходження символьних математичних моделей
Цей вид екстраполяції має невисоку точність і застосовується лише для
малих значень інтервалу екстраполяції [хп; х,]. Лінійна функція дає
можливість врахувати лише першу похідну відомої залежності (див.
рис. 7.11).
Для врахування похідних другого і вищих порядків екстраполяція
здійснюється за допомогою полінома Тейлора. На рис 7.11 показано характер
підвищення точності екстраполяції при врахуванні другої (крива Ц(х)) та
третьої похідних (крива із(х)).
В загальному випадку екстрапольоване за допомогою полінома Тейлора
значення функції визначається формулою:
/ ч  ч 1 <Л(х)	/	1 й2ї(х) , у
4(х) = Цхг,)+---^^ .(Х-ХЗ+-.-ДЛ	•(х-х„У + ..+
•(х-хг)т +о[(х-х)т].	<7.26)
ш! сіх'”	1	1
х=х„
Як приклад нижче розглянуто екстраполяцію засобами пакету МаіЬСАО
символьної залежності виду:
£(х) := е * 8Іп(х) .
Екстраполяція здійснюється починаючи з точки х = 0. Для цього
залежність розкладається в ряд Тейлора з використанням панелі символьних
операцій пакету МаіІтСАО:
( _х . . А . п 7 з 27	3
'	''	6	40
Г(х) := е х * 8Іп(х)
, ч 7 з 27	5
е(х) := х--* х + — * х .
6	40
Ряд обмежено значеннями складових, що включають похідні до п’ятого
порядку включно. Результати розрахунку екстрапольованих значень показані
на рис. 7.12, а пунктирною лінією.
Рис. 7.12. Результати екстраполяції (пунктирні криві) функції
ї(х) = ех *зіп(х) на проміжку х > 0 за допомогою полінома Тейлора
5-го (а) і 11-го степеня (6) та графік функції ї(х) (суцільна крива)
283
Струтинський В. Б.
На рисунку показано також точні значення функції (суцільна крива) Із
порівняння кривих випливає, що розрахунок екстрапольованих значень із
врахуванням похідних 5-го порядку відповідає точній залежності для значень
х < 0,5. Врахування похідних до 11-го порядку включно збільшує відрізок
достовірних значень екстраполяції до х < 1,1 (див. рис. 7.12, б).
Обчислення похідних високого порядку звичайно вносить похибку в
розрахунки Це особливо суттєво у випадку, коли функція змінюється мало, а
значення похідних є великими. Ця ситуація є типовою при прогнозуванні
значень процесів, які мають високочастотні осциляції. На рис. 7.13
схематично показано залежність, яка має високочастотну осциляцію.
Якщо виконати екстраполяцію залежності, наведеної на рис. 7.13, за межі
відомого інтервалу [хо, хп] використовуючи похідні навіть дуже високого
порядку, то одержаний результат прогнозу уе(х) буде суттєво відрізнятись від
фактичного значення процесу. Високочастотні осциляції суттєво знизили
точність екстраполяції.
Для підвищення точності екстраполяції в даному випадку рекомендується
проводити екстраполяцію не самого процесу, а його обвідних уа(х) та у/х)
або середнього значення у(х), яке визначається згідно умови:
У|у<х) — у(х)|<1х = 0 .	(7.27)
У(х)
/\ Задані
Екстрапольовані
значення уе(х)
Уотіп
Рис. 1.13 Особливості екстраполяції процесу,
в якому наявні високочастотні осциляції
Високочастотні осциляції процесу, при необхідності, враховуються як
додаткова періодична чи квазіперіодична складова процесу.
Екстраполяція функцій, заданих дискретною множиною точок, може
здійснюватись різними методами, зокрема з використанням процедури
інтерполяції функції. Як вказано вище, процедура інтерполяції має свої
особливості, тому при екстраполяції функцій необхідно враховувати можливість
284
Розділ 7. Знаходження символьних математичних моделей
виникнення суттєвих похибок пов’язаних з використанням певного методу
інтерполяції. Дана обставина ілюструється графіками, наведеними раніше на
рис. 7.8. Продовження аналітичних залежностей, що інтерполюють значення
функції в інтервалі х = [0, 4] за межі цього інтервалу (ділянка 4 < х < 5), дає
суттєво різні екстрапольовані значення. Так, при х = 4,5 діапазон одержаних
значень функції складає у = 2, ..., 4,5. Це означає, що екстраполяція функції
здійснена дуже грубо. Підвищення точності екстраполяції звичайно здійснюється
за рахунок збільшення кількості розглянутих точок та використання спеціальних
методів екстраполяції.
Екстраполяція процесів, заданих у вигляді дискретних моделей, може
бути виконана засобами математичних пакетів. В математичному пакеті
МаНіСАЦ процедуру екстраполяції реалізує спеціальна вбудована функція:
р := ргеНісі (у, ш, п).
Вона обчислює вектор р, який включає рівновіддалені прогнозовані п
значень функції, розрахованих по ш останніх заданих в масиві V даних.
Розглянемо реалізацію процедури екстраполяції функції за допомогою
вбудованої функції ргесіісі. Як приклад екстраполяції функції використаємо
аналітичну залежність, що фізично відповідає руху маси на пружній опорі з
лінійним демпфуванням. Закон руху маси визначено у вигляді:
у(х) := е о о1х(8Іп(О.1*х) + 0,5со8(0.1*х)).
Обчислимо вектор сі, який включає сукупність із 100 значень функції:
к = 0..99	ак:=у(к).
Задамо ш останніх значень (1к (ш = 7). Використаємо вбудовану функцію
ргефсі для обчислення масиву р,, і = 0..99, який включає прогнозовані
значення функції в інтервалі:
і := 100, 101..199
т := 7
р = ргес!іс1:(с1, т, 100).
Результати екстраполяції наведені в графічному вигляді на рис. 7.14.
Функція у(х) визначена в інтервалі х = [0; 200]. Розраховані значення
даної функції у вигляді 100 значень йк розташовані в інтервалі х = [0; 99]. За
даними 7-ми (ш = 7) останніх значень масиву сік вбудована функція
ргесіісі (4, ш, п) розрахувала 100 (п = 100) нових значень, які розташовані в
інтервалі х = [100; 199]. Вони показані на рисунку пунктирною лінією
(і > 100). Таким чином, суцільна крива - це точне значення функції, а
пунктирна крива - екстрапольоване (прогнозоване) значення. Одержані
прогнозовані значення несуттєво відрізняються від точної залежності в межах
інтервалу екстраполяції ( =	100... 125. При розширенні інтервалу
екстраполяції похибки збільшуються і загалом прогнозовані значення суттєво
відрізняються від точних при і = 150... 199.
285
Струтинський В Б.
Рис. 7.14. Результати екстраполяції залежності
у(х): = е~0 01х (хіп(0.1*х) + 0,5соя(0.1*х))
за допомогою вбудованої функції ргесіісі
Екстраполяція точкових значень функції за межі відомого інтервалу
здійснюється як для функції однієї змінної, так і для функції двох чи більше
змінних.
Один із можливих варіантів застосування функції ргесіісі полягає у
пошаровій екстраполяції значень процесу, заданого точковими значеннями.
Розглянемо дискретну модель процесу у вигляді прямокутної матриці.
Застосування функції ргесіісі дозволяє продовжити рядки або стовпці
матриці, тобто екстраполювати значення функції двох змінних на нову
область.
Нижче наведено фрагмент документа МаїйСАВ, який здійснює цю
операцію.
Нехай задано матрицю М розмірністю пІхпД.
Визначимо окремий вектор б - стовпець матриці
І := О..пД - 1
і := 0..ПІ - 1
ф := Мц т := 7 п := 5
Обчислимо п екстрапольованих значень для стовпця матриці:
Р := ргесіісі (сі, т, п).
Елементи подовженого стовпця матриці:
ір := пі..пі + п
^ір,І Рір - пі
Таким чином, обчислена матриця розмірністю (пі + п)хп5, рядки якої з
номерами пі. пі + п, є результатом екстраполяції матриці М на нову область.
286
Розділ 7. Знаходження символьних математичних моделей
7.2. Апроксимація дискретних множин значень процесу
7.2.1. Принципи і критерії апроксимації. Метод найменших квадратів
Знаходження аналітичних залежностей, які в детермінованій постановці
точно чи наближено відповідають табличним значенням функції, часто має
місце при математичному моделюванні технічних систем та процесів. Якщо
аналітична залежність точно відповідає табличним даним, маємо розглянуту
раніше задачу інтерполяції функцій. У випадку наближеної рівності
табличних даних і аналітичної залежності маємо задачу апроксимації функції.
Апроксимація функцій широко застосовується при математичному
моделюванні. Як службова процедура апроксимація функцій зустрічається
при побудові графіків експериментальних залежностей. Апроксимація
функцій дає можливість визначити кількісні та якісні характеристики трендів
різних факторів-оцінок характеристик конкретної технічної системи.
Порівняння результатів математичного моделювання з експериментальними
даними також здійснюється за допомогою методів апроксимації функцій.
Апроксимація функції, заданої таблично, завжди здійснюється з певною
похибкою. Ця похибка залежить як від заданих табличних значень функції,
так і від виду вибраної для апроксимації аналітичної залежності.
Процедура апроксимації може бути реалізована нескінченним числом
способів, які визначаються можливими видами аналітичних залежностей. Із
суті задачі випливає, що вибір аналітичної залежності повинен здійснюватись
за умови найкращого наближення аналітичної залежності до наявних
табличних даних. Вибір аналітичної залежності здійснюється з метою
досягнення кількісної та якісної відповідності апроксимованих значень
базовим табличним даним.
Для забезпечення якісної подібності використовують попередню оцінку
табличної залежності, а також враховують фізичні особливості процесу, який
відповідає табличній залежності.
Для виявлення характерних особливостей процесу апроксимації
розглянемо декілька характерних прикладів.
На рис. 7.15, а наведено в графічному вигляді таблично визначену
залежність, що відповідає перехідному процесу технічної системи, на вхід
якої подана ступінчаста функція.
Дискретна математична модель, як«. відповідає перехідному процесу, має
характерні особливості. Табличні дані розташовані в межах смуги між
кривими 1 та 2. Ця смуга визначає якісні особливості табличної залежності і
використовується для встановлення якісних особливостей функції, яка
287
Струтинський В. Б.
повинна бути знайдена по дискретній моделі. В даному випадку залежність
характеризується монотонним ростом з наближенням до горизонтальної лінії
(асимптоти) при збільшенні значення аргументу функції. Для перехідного
процесу має місце тенденція зменшення розсіяння табличних даних, тобто
звуження смуги. Для узагальненої характеристики цих табличних даних іноді
достатньо розглянути криву середніх значень в смузі (крива 3). Для більш
детального аналізу смуга повинна бути звужена (крива 4). При цьому
аналізуються такі властивості табличних даних, як періодичність, зміна
періоду, а також ступінь затухання коливань (пульсацій) табличних даних.
Визначаються також локальні максимуми і мінімуми, точки зміни знака
кривизни та інші особливості похідних. При аналізі треба враховувати
область суттєвих значень табличної залежності. Для перехідного процесу
системи, який показаний на рис. 7.15, а, область суттєвих значень включає
окіл точки х = 0, а також табличні дані в кінці перехідного процесу. Область
суттєвих значень при апроксимації повинна враховуватись набагато більше,
ніж область несуттєвих значень.
Рис. 7. /5. Дискретно-математична модель, яка відповідає
перехідному процесу технічної системи, (а) та дискретний масив,
який має властивість періодичності (б)
Властивість періодичності. На рис. 7.15, б наведена дискретна модель
процесу, який має властивість періодичності з періодом хпер. Періодичність
табличних даних оцінюється за достатньо вузькою смугою (криві 1 та 2), в
яку попадають значення процесу.
Дана періодичність відповідає низькочастотним змінам процесу і не
залежить від хаотичних змін положення сусідніх точок таблиці. Для
встановлення періодичності, що відповідає високочастотним змінам процесу,
необхідно розглянути достатньо велику кількість точок, що визначають
дискретну модель процесу.
Важливими якісними особливостями дискретних математичних моделей
288
Розділ 7, Знаходження символьних математичних моделей
процесів є парність або непарність. Ці властивості звичайно випливають із
аналізу фізики процесів і повинні враховуватись при апроксимації.
Як приклад на рис. 7.16, а наведено дискретну математичну модель, яка
наближено відповідає символьній залежності у вигляді кривої Гауса.
Г(х), у,
0
а)
б)
Рис. 7.16. Вибір апроксимуючих аналітичних залежностей, які враховують
властивість парності (а) та непарності (б) вихідного дискретного масиву
значень процесу
Дана дискретна математична модель має похибки. Тому одержана з
таблиці смуга значень функції не є симетричною. При виборі апроксимуючої
залежності необхідно враховувати необхідність забезпечення симетрії
£(х) = {(- х).
Із фізичних міркувань, даний процес, який описується таблично заданою
функцією, що має властивість парності, повинен бути описаний кривою Гауса
£(х) = е 'х7(2,3'),
яка також має цю властивість. Для підвищення точності апроксимації може
бути скориговане положення центра координат (див. рис. 7.16, а). Для цього
лінія симетрії кривої зміщена відносно нуля на величину хц. В результаті
аналітична залежність, яка використовується для апроксимації, набуває
вигляду: ї(х) = еА*--х»)7(2,п' ).
Аналогічно враховується властивість непарності дискретної математичної
моделі процесу. На рис. 7.16, б наведено приклад таблично заданої непарної
функції. Вибрана для апроксимації залежність повинна відповідати умові
£.(х) = Ч(~х)-
Введене нове положення початку координат. В даному випадку воно
289
Струтинський В. Б.
відповідає зміщенню апроксимуючої кривої на величину хд.
При виборі аналітичної залежності для апроксимації таблично заданої
функції часто використовують набір типових елементарних функцій, з якими
порівнюють наявні табличні дані. За типові елементарні функції вибирають
лінійну, обернену, поліноміальну, показникову, експоненціальну,
логарифмічну або інші функції.
Для апроксимації періодичних дискретних математичних моделей
використовують синусоїдальну або суму синусоїдальних функцій.
Для апроксимації плавно змінних зростаючих або спадних табличних
залежностей використовують степеневі функції або їх суму (лінійні або
поліномінальні залежності).
Для апроксимації дискретних математичних моделей, які мають
прогресивний ступінь росту похідної, використовується показникова функція.
Практичне значення має окремий випадок показникової функції
експоненціальна функція з додатнім чи від’ємним показником степеня.
В деяких випадках використовують обернені та дробово-раціональні
функції або ірраціональні функції різного виду.
Коли треба встановити порядок значень параметра процесу та тенденції
його росту, то застосовують лінійну функцію:
р(х) = а + Ьх.	(7.28)
При використанні логарифмічного масштабу тінійна функція дозволяє
описати дискретну математичну модель, яка відповідає степеневому закону.
Розглянемо одержання лінійної функції із степеневої табличної залежності
виду:
у । =£(хі) = с-ах',	(7.29)
де с і а - постійні величини.
Виконавши логарифмування в формулі (7.29), одержимо:
їй Уі = 1§ с + X; • Ія а .
Позначивши 1§у; = гі, 1§с = а, 1§а = р одержимо лінійну функцію
відносно аргументу х:
г. =1§с + хі1§а = а + р-хі.	(7.30)
Якщо аналітична залежність для апроксимації вибрана в загальному
вигляді, постає задача перетворення її таким чином, щоб вона найбільш точно
відповідала табличним даним. Вибрана аналітична залежність має ряд
параметрів (постійних коефіцієнтів). Задача апроксимації полягає у виборі
найкращих (оптимальних) значень цих параметрів. Ця задача вирішується
багатьма способами.
На рис. 7.17 наведена геометрична інтерпретація процедури апроксимації
функції однієї змінної. Задані табличні значення функції у = у(х) показані у
290
Розділ 7. Знаходження символьних математичних моделей
вигляді сукупності точок Ао, А-і, Аз, Ап. Апроксимуюча аналітична
залежність Р(х) вибрана таким чином, що її графік проходить найближче до
даних точок. За міру похибки апроксимації, як правило, вибирають
відхилення заданих табличних значень функції від вибраної аналітичної
(апроксимуючої) залежності.
Рис. 7.17. Геометрична інтерпретація апроксимації таблично заданої
функції аналітичною залежністю
Відхилення Лі утворюють вектор, компоненти якого мають різні величини
і знаки. За критерій точності апроксимації можуть бути вибрані різні
параметри вектора відхилень.
Один із методів апроксимації має назву рівномірного наближення. Згідно
методу рівномірного наближення, при апроксимації мінімізують найбільше
абсолютне значення компоненти вектора відхилення у всій області визначення
функції або в деякому інтервалі.
В даному випадку критерієм точності апроксимації служить умова
мінімуму найбільшого абсолютного відхилення. Використовуючи даний
критерій, знаходять параметри апроксимуючої залежності. Недоліком методу
рівномірного наближення є складність розрахунків коефіцієнтів
апроксимуючої залежності.
За критерій апроксимації іноді вибирають не умову мінімуму, а строгу
рівність деякого комплексу, складеного із компонент вектора відхилень [ 171.
Наприклад, візьмемо окремо всі додатні значення та всі від’ємні значення
відхилень. Для випадку, наведеного на рис 7.17, сума додатних відхилень:
— До З- Д2 + Д| ,
а сума від’ємних відхилень:
2. =А, +Д;., +ЛП .	(7.31)
Порівнявши суми додатних і від’ємних відхилень, одержимо умову, яку
можна взяти за критерій точності апроксимації При цьому будемо вважати,
що апроксимуюча крива відповідає заданим табличним даним тоді, коли сума
291
Струтинський В.Б.
додатних відхилень дорівнює сумі від’ємних відхилень. Такий критерій
доцільний у випадках, коли відхилення мало відрізняються між собою за
абсолютною величиною.
Розглянемо застосування даного критерію для апроксимації прямою
лінією функції, заданої в дискретній сукупності точок [17].
Нехай задано (п + 1) точок (рис. 7.18):
(Ао, ..., А,, ..., Ап1, ..., Ак, .... Ап).
Апроксимуємо задані значення лінійною залежністю виду:
Р(х) = а + Ь • х.	(7.32)
Рис. 7.18. Апроксимація табличних даних лінійною функцією згідно
критерію рівності додатних та від’ємних відхилень
Дана задача апроксимації полягає у знаходженні коефіцієнтів а і Ь
лінійної залежності за умови, що сума додатних відхилень дорівнює сумі
від’ємних відхилень. Знаходження двох параметрів а і Ь потребує виконання
двох умов, наприклад, запису двох рівнянь, що включають дані коефіцієнти.
Для одержання двох рівнянь з двома невідомими розіб’ємо число заданих
точок на дві приблизно рівні групи, а саме:
Ао, А-1, А2, ..., А,, ..., Ат-і та Ат, Ат+(, ..., Ак, ..., Ап.(, Ап.
При цьому приймемо т » у .
Для кожної групи точок визначимо алгебраїчні суми відхилень. Згідно з
вибраними умовами апроксимації, алгебраїчні суми відхилень для кожної
групи точок повинні дорівнювати нулю. Це дає два рівняння:
П1-1	II
Ер(хі)~Уі=0; £н(хк)-ук =0.
і=0	Єя
Підставивши значення лінійної залежності (7.32) в дані рівняння замість
Р(х) та змінивши позначення індексу в другому рівнянні, одержимо систему
двох лінійних рівнянь з двома невідомими а і Ь:
292
Розділ 7. Знаходження символьних математичних моделей
Е(а + Ьх> -Уі) = О; £(а + Ьх;-у.) = 0.
і=0	і=т
(7.33)
Дану систему рівнянь запишемо у вигляді:
[а • с, + Ь • ф = е(
[а * с2 + Ь * сІ2 — ^2
Постійні величини, які входять у рівняння (7.33), визначаються нескладними,
але досить громіздкими залежностями, що включають табличні значення функції:
т-1	п
С] = т ; с2 = п - т + 1; б, = ^хі ; б2 = ^хі;
і=0	і = т
т-1	п
єі = Хуі ; є2 = Іуі-
і=0	і = т
Розв’язок системи рівнянь (7.33) знаходимо за правилом Крамера:
, с,е,-с,е,	фе, -Фе.
Ь = ——і----і-і- ; а = ——--------—-.
с,<і2 - СзСІ,	с,с12 - с2сІ,
(7.34)
Наведена вище процедура апроксимації, яка полягає в обчисленні
коефіцієнтів а та Ь за формулами (7.34), ілюструє характерні особливості
цього процесу. Зокрема, це наявність громіздких обчислень коефіцієнтів та
складність оцінки точності апроксимації.
За критерій (міри) оцінки точності апроксимації іноді вибирають середнє
значення модуля (абсолютної величини) відхилень. Тоді загальна похибка
апроксимації оцінюється значенням величини:
1 п
Асер=—тЕИ	(7-35)
п + 1 і=0
Наявність в даній формулі абсолютних величин під знаком суми
призводить до незручностей у розрахунках. Тому замість середнього значення
модуля для оцінки точності апроксимації функції приймають середнє
значення квадрата модуля
Мер =~	<7.36)
п + 1
Критерій оцінки точності по квадратах модулів відхилень записується
звичайно не для середнього значення, а для всієї суми квадратів відхилень.
При цьому маємо так званий метод найменших квадратів при апроксимації
функції. Згідно з методом найменших квадратів, функція Р(х) найкращим
чином апроксимує задані табличні значення у0, ..., уп, якщо сума квадратів
відхилень апроксимуючої залежності від табличних значень є мінімальною:
8 = ЕЕНх^-Уі]2 = тіп-	(7.37)
і=0
Апроксимацію (наближення) функції за методом найменших квадратів
іноді називають квадратичними наближеннями.
При визначені суми квадратів відхилень часто вводять ваговий коефіцієнт
293
Струтинський В. Б.
Уі, який враховує значимість відхилення в кожній точці. Тоді критерій
апроксимації за методом найменших квадратів набуває вигляду:
5 = Еу,[р(хі)-У,]2 = тіп-	(7.38)
і=0
Знаходження мінімуму суми квадратів відхилень здійснюється різними
методами. Вибір методу залежить від виду аналітичної залежності Р(х), яка
вибрана для апроксимації табличних значень функції. В деяких випадках
достатньо знайти умови мінімуму наближено. Наприклад, якщо аналітична
залежність задана у вигляді функції, яка включає деякий параметр:
Р(х) = Р(х, а),
де а - параметр, який потрібно вибрати із умови найкращого наближення
табличних даних.
У цьому випадку для знаходження залежності Р(х) здійснюється ряд
розрахунків величини:
8к=Е[Р(Хі,ак)-УіГ	(7.39)
і=0
де к = 0, 1, 2, ..., К (К - достатньо велике число).
Найменше із значень 8к = 8кт вважається мінімальним, а відповідна
величина параметра акт приймається як найкраща для апроксимації функції.
Знаходження мінімуму суми квадратів відхилень звичайно здійснюється
точними методами оптимізації, як це буде розглянуто нижче.
Метод найменших квадратів є найбільш поширеним при апроксимації
функцій. Проте, він також не позбавлений недоліків. Один із них - це та
обставина, що більші за модулем відхилення (грубі) будуть враховуватись
більше, ніж менші відхилення (точні значення).
Метод найменших квадратів допускає корекцію з метою підвищення
точності. Розглянемо випадок, коли табличні дані мають обмежену кількість
відхилень, які суттєво відрізняються від середніх значень. Ці відхилення
доцільно виключити із розгляду. Для цього знаходиться перше наближення
апроксимуючої залежності Ро(х), яке мінімізує суму квадратів всіх відхилень:
Зо = Е[р«(хі)-УіГ=тіп-
і=0
Потім знаходяться відносні квадрати відхилень у всіх точках:
ЗШІ-уі	(7 40)
§0
Визначаються відхилення, які значно перевищують середній рівень і в
яких а? »—!— Великими вважаються ті т відхилень (т = 2..4), в яких
п +1
2	2...7 „ „	.
о. =-----. Знайдені т великих відхилень виключаються із розгляду.
п + 1
294
Розділ 7. Знаходження символьних математичних моделей
Потім знаходиться друге наближення апроксимуючої залежності Ефх).
Воно визначається із умови мінімуму суми квадратів:
п-т
8, = Еірі(х)-УіГ =тіп.	(7.41)
і=0
Якщо в результаті другого наближення виявляються кілька відхилень,
значення яких набагато перевищують середнє значення, вони також
виключаються із розгляду. Таким чином, грубі відхилення табличних даних
від загального середнього рівня ігноруються і виключаються із розгляду.
7.2.2. Розробка лінійних математичних моделей
Задачу апроксимації дискретної математичної моделі символьною
залежністю можна значно спростити, якщо за апроксимуючу залежність взяти
лінійну комбінацію деяких, в загальному випадку нелінійних функцій.
Аналітична залежність при цьому має вигляд суми відомих (базисних)
функцій, помножених на деякі коефіцієнти, що визначаються із умови
найкращої апроксимації дискретної математичної моделі.
Таким чином, при апроксимації функцій використовуються аналітичні
залежності Е(х) двох видів. Перший вид відповідає лінійним відносно
невідомих коефіцієнтів залежностям, а другий - нелінійним залежностям
(відносно коефіцієнтів). В першому випадку маємо лінійну математичну
модель для апроксимації табличних даних, а в другому - нелінійну.
Лінійна математична модель записується у вигляді:
Е(х) = ао-фо(х) + аі-ф^х) + ... + ат’фт(х),	(7.42)
де а<), аі, .... ат - коефіцієнти, які вибираються з метою забезпечення
найкращого наближення даної залежності до табличних даних;
ффх), і = 0, 1, ..., т - деякі заздалегідь відомі (задані) функції, які
називаються базисними;
т - ціле число, яке визначає загальну кількість базисних функцій та
коефіцієнтів математичної моделі.
Базисні функції можуть мати різноманітний вигляд. Поширеною формою
лінійної математичної моделі є поліном. При цьому базисні функції
математичної моделі є степеневими функціями:
ф0(х)=1; фі(х) = х; ф2(х) = х2; ...; фт(х) = хт. (7.43)
При розробці лінійних математичних моделей також використовуються
базисні функції виду:
ч’і (х) = 7—’ ‘рі (х) = ^ х);
(“і + х/	(7.44)
фДх)=е“іХ («і = СопзО,
а також інші елементарні та спеціальні функції.
295
Струтинський В. Б.
Задача апроксимації таблично заданої функції у, = у((х) лінійною
математичною моделлю полягає в знаходженні коефіцієнтів ао, а^, ат, які
забезпечують мінімум суми квадратів відхилень апроксимуючої функції від
табличних даних. Існує ряд методів і методик знаходження коефіцієнтів лінійної
математичної моделі Розглянемо один із способів знаходження коефіцієнтів
моделі. Сума квадратів відхилень табличних даних і апроксимуючої залежності
визначається згідно з методом найменших квадратів:
5 = ЕІУі “ао -Фо(х)-аі -<Рі(х)- ••• -ат •фт(хі)]2 .	(7.45)
і=0
Сума квадратів відхилень залежить від заздалегідь невідомих коефіцієнтів
ао, а^ ..., ат. тобто є функцією багатьох змінних від вказаних коефіцієнтів.
Мінімум цієї функції буде в стаціонарній точці, де:
58	„	08	„	08	п	у
— -0; ч- = о;	=	(7.46)
5а0	5а,	5ат
Знайдемо частинні похідні шляхом диференціювання залежності (7.45) і,
прирівнявши їх до нуля згідно з (7.46), одержимо систему рівнянь:
у^ = -2£[у, -а0 -фДхЗ-а, -фДх,)-... -ат • Фт(х,)]-<р0(Хі) = 0 ;
оа()
“ = -2ЕІУі -ао %(хі)-аі *Фі(хі)- -ат •фт(хі)]’Фі(х,) = ° :
і=0
(7.47)
= ~22ЕУі ~ао ’ФоСхЗ-аі -фД)- ... -ат •фт(х,)]-фт(хі) = О.
5ат і=0
Після перетворення співвідношень, які входять у (7.47), одержимо
систему, яка називається нормальною системою рівнянь і має вигляд:
а<> -ЕМ^)]2 +аі •Е(Ро(хі)’ф,(хі)+ ... +ат •^ф0(хі)-фт(хі) = ^ф0(хі)-уі ;
і-0	і=о	і=0	І = 0
а0 •Ефі(хі)-фо(хі)+а-1 ХіфХХі)]2 + +ат ' ^Ф1(Хі)' Фт(Хі) = ^Фі(Хі)‘ Уі ;
і=0	і=()	і=()	і=0
 22<р(1(х,) + а,  22фт(х,)-(р1(х,)+ ... +ат • 2[фт(Хі)]2 = 2<Рт(хі)-Уі •
І^О	і=()	і=()	і = 0
(7.48)
Нормальну систему рівнянь, розгорнутий вигляд якої відповідає (7.48),
запишемо у матрично-векторному вигляді:
[В] • а = с ,
де матриця коефіцієнтів [В] та вектори а і с визначаються залежностями:
296
Розділ 7. Знаходження символьних математичних моделей
ЕкД)?
і=0
п
^ф1(хі)-ф0(хі)
£<Ро(х,)-фі(хі) ... £ф0(хі)-фт(хі)
і=0	і=0
Е[фі(хі)Г	£фі(хі)-фт(хі)
І=0	і=0
(7.49)
Іфт(хі)-Фо(х,) ІФт(хі)-фі(хі) Екк)]2
,і = 0	і=0	і=0
Е Фо(хі)- Уі
і=0
ЕФі(хі)-Уі
і=0
Ефт(хі)-Уі
,і=0
Розв’язок нормальної системи рівнянь (7.48) дає значення коефіцієнтів,
які забезпечують мінімум суми квадратів відхилень.
Процедуру розв’язку нормальної системи рівнянь можна значно
спростити, зробити більш зручною та раціональною, якщо вибрати певним
чином базисні функції <ро(х),	ф(х). Виберемо за базисні функції:
Т0(х) = ф0(х>; Т/х) = фі(к); ...; Тт(х) = фт(х),	(7.50)
які задовольняють наступним умовам ортогональності:
£тк(Хі)-Т](х;) = 0 ,	1*к;
і=п°	(7.51)
І[Тк(Хі)Г^О к = 1,2, ...,т.
і=()
Функції То(х), Т|(х), ..., Тт(х), які задовольняють умовам (7.51),
називаються ортогональними. Вони можуть мати різний вигляд. Зокрема,
існує багато наборів ортогональних функцій у вигляді поліномів. Найбільш
поширені з них - ортогональні поліноми Чебишева, Лежандра, Лагерра,
Ерміта та інші.
Ортогональні поліноми є практично важливими спеціальними функціями.
Iх основні властивості та застосування розглянуті в розділі 2.
Для апроксимації таблично заданих функцій широко застосовуються
ортогональні поліноми Чебишева першого та другого роду. Поліноми
Чебишева мають характерну властивість. Якщо використати їх для
апроксимації функції на деякому інтеовалі, то в цьому інтервалі максимум
відхилення табличних даних від аналітичної залежності буде найменшим в
порівнянні з будь-яким іншим поліномом. Ця властивість відповідає
апроксимації табличних даних згідно з критерієм рівномірного наближення.
297
Струтинський В.Б.
При рівномірному наближенні функцій мінімізується найбільше значення
абсолютної похибки апроксимації. На практиці використання поліномів
Чебишева забезпечує як рівномірне наближення, так і мінімум суми
квадратів відхилень (метод найменших квадратів).
Використання ортогональних базисних функцій (наприклад, поліномів
Чебишева) приводить матрицю (7.49) нормальної системи рівнянь (7.48) до
діагонального вигляду:
’±Ето(Хі)Г
і=0
0
о
±[т,(Хі)Г
і=0
0
о
о
(7.52)
Відповідно, нормальна система рівнянь (7.48) спрощується. Її розв’язок у
загальному вигляді визначається у формі:
^Уі -Т^Хі)
ак=^------------ (к = 0, 1, 2, ..., ш).	(7.53)
2Лтк(х5)Г
і-О
Такий вид розв’язку є зручним і раціональним. Зручність обчислень
забезпечується нескладними формулами, а раціональність полягає в тому, що
можна послідовно підвищувати степені апроксимаційних поліномів ш
(підвищувати точність апроксимації). При цьому знайдені раніше достатньо
розрахувати значення коефіцієнтів поліномів більш високого порядку, не
повторюючи обчислень, для коефіцієнтів раніше обчислених (вони
зберігаються).
Наприклад, розрахувавши три коефіцієнти а0, а^ а2, виявилось, що
точність апроксимації недостатня. Для підвищення точності розраховується
коефіцієнт аз, а у випадку необхідності - а4 та вище. При цьому значення
коефіцієнтів ао, а(, а? залишаються незмінними.
Процедура апроксимації дискретних математичних моделей символьними
залежностями різноманітного виду широко реалізована в математичних пакетах.
В програмному середовищі Маі.КСАП для визначення коефіцієнтів
лінійних математичних моделей, що служать для апроксимації табличних
даних використовується вбудована функція ІіпНі. Дана вбудована функція
розраховує коефіцієнти лінійної математичної моделі ао, а^, ..., ат за методом
найменших квадратів. Синтаксис даної функції:
1іп£іі(ух, у, £),
де ух, у - вектори координат точок, що підлягають апроксимації:
УХ = [х01 хь ..., хп1, у = [уо, У1, ... , уп];
298
Розділ 7. Знаходження символьних математичних моделей
І - символьний вектор розмірності т, компоненти якого визначають
вибрані базисні функції.
Базисні функції, як раніше вказано, можуть мати різноманітний вигляд.
Визначимо типові лінійні математичні моделі з використанням функції
ІіпНі. Вони показані у фрагменті документа МаіЬСАО, який наведено нижче.
Обчислення коефіцієнтів лінійної математичної моделі поліноміального
виду здійснюється наступним фрагмента документа МаіЬСАО:
і := 0..7		УХ := і Уо 0 ух := 1	У2 := 2	Уз == 4
У4 == 8	1	У5 := 4 Уб = 2 у7 := 0	- 0,303'	
£(х) :=	X х2	а := ІіпНЦух, у, £) а =	1,151 0,376	
	х3		-0,078	
8(х) = £(х)*а
Результати апроксимації дискретної множини значень процесу наведені в
графічному вигляді на рис. 7.19.
Рис. 7.19. Апроксимація дискретного процесу лінійною математичною
моделлю поліноміального виду
Із аналізу рис. 7.19 випливає, що поліноміальна лінійна математична
модель належним чином апроксимує табличні значення. Вбудована функція
1іп£іі забезпечує також відповідність табличних значень та математичної
моделі на межах інтервалу апроксимації (точки Ао і Ау). Найбільше
відхилення табличних даних від апроксимуючої залежності має місце для
точки А4 і приблизно складає 50 % від розрахованого значення.
Розглянутий приклад апроксимації відповідає апроксимації даних
поліномом степеня ш (на рис. 7.19 т = 3). Степінь полінома може
299
Струтинський В. Б.
змінюватись в межах ш = 0, п ((п + 1) - число точок дискретної моделі).
При т = п маємо розглянутий раніше випадок інтерполяції функції, заданої в
(п + 1) точках поліномом степеня п.
Апроксимація табличних значень поліномом досить зручна і тому
поширена. Для вибору коефіцієнтів полінома існують спеціальні процедури.
В математичному пакеті МаікСАО для цього наявна окрема спеціальна
вбудована функція:
а: = роїуНЦх, у, т).
Дана вбудована функція знаходить коефіцієнти полінома
а = [ао, а1; .. , ат]
сіепеня т, що апроксимує функцію, задану таблично
X = [х0, х1( .... хп]; у = [у0, Уь ... , уп],
за методом найменших квадратів.
В окремому випадку, коли ш = п, вбудована функція роїуНі знаходить
коефіцієнти інтерполяційного полінома.
Крім поліномів, як лінійні математичні моделі використовуються
залежності, базисні функції яких є дробово-раціональними,
експоненціальними, логарифмічними та іншими.
В залежності від вибраних базисних функцій одержимо відповідну
апроксимуючу криву. При цьому вид одержаної апроксимуючої залежності
може якісно не відповідати заданим табличним даним.
Нижче наведено фрагмент документа МаїЬСАІЗ, який апроксимує дані із
розглянутого раніше (див. рис. 7.19) прикладу з використанням дробово-
раціональних базисних функцій.
£(х) :=	г (1 + 0.1*х)‘ (1 + 0.2*х2) 1	а := ііпНЦух, у, £)	а =	27,025 43,017 - 25,099
	(1 +0.003 *х3)-1			8,99
§(х) = £(х)*а
Результати апроксимації дискретної множини значень процесу з
використанням дробово-раціональних базисних функцій наведені в
графічному вигляді на рис. 7.20.
Одержана апроксимуюча крива кількісно відповідає табличним даним, але
якісний характер залежності табличних даних і апроксимуючої функції різко
відмінні. Це означає, що апроксимація табличних даних дробово-
раціональними функціями в даному випадку не є доцільною.
З рис. 7.20 випливає, що одержана лінійна математична модель здійснює
також екстраполяцію (прогноз) значень табличної залежності за межі
заданого інтервалу. Екстраполяція здійснюється для значень х = 7...10.
300
Розділ 7. Знаходження символьних математичних моделей
Рис. 7.20. Апроксимація дискретного процесу лінійною математичною
моделлю з дробово-раціональними базисними функціями
Наведені вище табличні дані ух, у також аироксимовано лінійною
математичною моделлю з базисними функціями експоненціального виду.
Фрагмент документа МаіЬСАП, що реалізує дану процедуру, має наступний
вигляд:
£(х):=
а := 1іп£іі(ух, у, £);
5,662
-5,574*10 3
-19,176
13,573
8(х) := £(х)*а.
Результати апроксимації дискретної множини значень процесу з
використанням експоненціальних базисних функцій наведені у графічному
вигляді на рис. 7.21.
Одержана апроксимуюча крива (див. рис. 7.21) кількісно та якісно (за
виключенням інтервалу між точками А0Аі) відповідає табличним даним.
Найбільше відхилення має місце в точці А4 і приблизно складає 40 % від
розрахованого значення.
Апроксимація функцій за допомогою лінійних математичних моделей є
порівняно простою та надійною процедурою. Разом з тим, вона має ряд
особливостей, які треба враховувати при математичному моделюванні.
Одна із специфічних особливостей процедури полягає в невизначеності
301
Струтинський В. Б.
вибору базисних функцій. Висока точність апроксимації табличних даних
лінійною математичною моделлю забезпечується при значній кількості точок та
правильному виборі базисних функцій. Якщо базисні функції вибрані невірно, то
можливе значне зниження точності апроксимації, одержання результату, який
кількісно та якісно не відповідає вихідним табличним даним.
Рис. 7.21. Апроксимація дискретного процесу лінійною математичною
моделлю з експоненціальними базисними функціями
Цей недолік лінійних математичних моделей ілюструється фрагментом
документа МаїЬСАВ, наведеним нижче. Вибраний в цьому документі вектор
експоненціальних базисних функцій має нераціонально задані параметри
експонент.
0,083
- 2,672 * 10 4
1,744 *10 ’
- 0,068
§(х) := £(х)*а.
Одержані результати апроксимації дискретної множини значень процесу з
використанням експоненціальних базисних функцій з неправильно вибраними
коефіцієнтами наведені в графічному вигляді на рис. 7.22.
Одержана апроксимуюча крива (рис. 7.22) набагато гірше, ніж крива,
наведена на рис. 7.21, відповідає табличним даним. Найбільше відхилення
має місце в інтервалі між точками А^, Ау і сягає 16, що більше ніж у 5 разів
перевищує відхилення кривої, наведеної на рис. 7.21. Таким чином,
нераціонально вибрані параметри експонент суттєво знизили точність
апроксимації функції.
Розробка лінійних математичних моделей конкретного виду має певні
особливості. Це, зокрема, стосується математичних моделей у вигляді
тригонометричних рядів.
302
Розділ 7. Знаходження символьних математичних моделей
Рис. 7.22. Апроксимація дискретного процесу лінійною математичною
моделлю з нераціонально вибраними параметрами експоненціальних
базисних функцій
Методика знаходження коефіцієнтів тригонометричного ряду згідно з [42]
включає обчислення сум числових послідовностей.
Нехай дано т значень періодичної функції з періодом Т:
у(хі) = уі при хі = ——- (і = 0,1, 2,т - 1).
Виконаємо апроксимацію функції в інтервалі [0, Т] тригонометричним
поліномом, який відповідає відрізку ряду Фур’є:
, \ ап А (. 271x^1 ,	. ґ.2лхУ т
р(х) = 4- + ^аз	+ьз зт’ П<Т- (7.54)
Сума квадратів відхилень табличної та апроксимуючої залежностей
пі —1
8 = Е[Г(Хі)-Уі]2 =8тіп
і=0
буде мінімальною, якщо коефіцієнти тригонометричного полінома а^ і
обчислюються за формулами [42]:
2	ґ. 2лі)
а,	= —ЛУі • соз ]— ;
’ тй	Іт)
,	2	. ( 2лі) .. . т
ь,	= — 2,Уі'5іпи—Ь
т	у т )	2
Обчислені коефіцієнти а, і Ь, дають можливість визначити
тригонометричний поліном (тригонометричний ряд), який апроксимує
табличні дані згідно з методом найменших квадратів. Кількість складових
ряду вибирається від 1 до т/2 .
(7.55)
В окремому випадку, коли п = т/2 , маємо тригонометричну інтерполяцію.
При цьому для визначення коефіцієнтів використовуються додаткові умови:
•4 т--1
а„ =ат/2 =-Е(-1)’Уі 	(7.56)
т
Значення коефіцієнта Ьп може бути довільним.
303
Струтинський В. Б.
Наведені вище формули застосовуються при розрахунках за допомогою
математичних пакетів. Нижче наведено фрагмент документа МаФСЛГ), що
реалізує процедуру знаходження коефіцієнтів тригонометричного ряду за
формулами (7.54) та (7.55) за заданими масивами ух та уу, які визначають
координати точок періодичної функції з періодом 2л. В даному прикладі
масиви координат точок мають вигляд:
ухт=(-3.142 -2.749 -2.356 -1.963 -1.571 -1.178 -0.785
-0.393 0 0.393 0.785 1.178 1.571 1.963 2.356 2.749)
уут = (0 -0.117 -0.487 -1.211 -1.588 -1.445 -1.031
-0.935 -3.398 0.224 2.454 3.082 2.131 0.747 -0.024 -0.012)
Обчислення коефіцієнтів тригонометричного ряду здійснюється
наступними операторами:
к := 0..7
ак :=	*СО8(к*ух)); Ьк	*8Іп(к*уХі).
Виведення результатів розрахунків коефіцієнтів тригонометричного ряду:
ат=(-0.13 -0.277 -0.621 -0.907 -0.44 -0.34 -0.306 -0.289)
Ьт=(0 1.612 0.719 -0.307 -0.16 -0.075 -0.037 -0.016).
Обчислення тригонометричного ряду, що відповідає апроксимуючій
залежності:
7
* соз(к * х) + Ьк * 8Іп(к * х)).
к = 0
Таблично задана функція та тригонометричний ряд, який апроксимує
табличну залежність, наведені у графічному вигляді на рис. 7.23.
Із аналізу графіків випливає, що апроксимація дискретних даних
відрізком ряду Фур’є забезпечує необхідну точність, кількісну та якісну
відповідність залежностей.
Однак розрахунки коефіцієнтів за формулами (7.55) дуже часто
призводять до невірних результатів, тобто даний метод апроксимації
дискретних даних відрізком ряду Фур’є має низьку надійність. В практиці
автора зустрічались випадки, коли обчислені значення коефіцієнтів
перевищували 1О360.
Причини ненадійності методики полягають у некоректності формулювання
задачі знаходження коефіцієнтів ряду Фур’є функції, заданої неточно (див.
розділ 4.2.3). В даному випадку неточними є не значення самої функції, а сам
метод обчислення коефіцієнтів, що базується на наближеному обчисленні
визначених інтегралів.
Апроксимація табличних даних тригонометричним рядом в багатьох
випадках є суттєво неточною. Іноді апроксимовані значення зовсім не
відповідають табличним даним.
304
Розділ 7. Знаходження символьних математичних моделей
Рис. 7.23- Графічне зображення табличної залежності суг
та тригонометричний ряд {(х), який апроксимує табличну залежність
Як приклад нижче наведено фрагмент документа МаїЬСАВ, який
визначає математичні моделі у вигляді тригонометричних рядів.
і := 0..11 ух= := і * 2 —
1	12
ак :=
и
2]Г уу, * соз(к * ух.)
і-0
Ьк :=
12
н
2^ууі * 8іп(к * ух;)
і=а
5
£5(х):= £(ак
8
га(х):= Е(ак
_к=і
12
*	со$(к * х) + Ьк * 8Іп(к * х))
*	соз(к * х) + Ьк * 5Іп(к * х))
0
4
5
З
7
0
5
-2
7
-З
-4
З
Функція £5(х) визначає тригонометричний ряд, що має 5 складових, а
функція £8(х) - ряд, що має 8 складових.
Тригонометричний ряд £5(х) досить грубо відповідає табличним даним
(рис. 7.24, а), а функція £8(х) має ще більші кількісні та якісні відмінності від
табличних даних. Це означає, що механічне збільшення кількості складових ряду7
305
Струтинський В. Б.
Рис. 7.24. Апроксимація табличних даних (ламана лінія)
тригонометричними рядами (а) та кубічними сплайнами (б): (5(х) -
тригонометричний ряд, що має 5 складових; (8(х) — ряд із 8 складових;
/с(х) — апроксимація табличних даних кубічним сплайном; (с1(х) -
апроксимація сплайном табличної функції, продовженої на період вперед та
назад; ф7(х) - графік відрізку ряду Фур’є, що співпадає з кривою (с1(х)
306
Розділ 7. Знаходження символьних математичних моделей
Для підвищення точності апроксимації гармонічним рядом
рекомендується наступна методика. Табличні дані інтерполюються
сплайнами. Одержана в результаті інтерполяції символьна залежність
використовується для знаходження коефіцієнтів ряду Фур’є.
У випадку апроксимації періодичних функцій сплайн-інтерполяція може
дати суттєві похибки на межах області визначення функції. Запобігти цьому
можна продовживши табличні дані на період вперед і назад. Інтерполяція
сплайнами продовжених табличних даних буде періодичною функцією, що
відповідає табличній залежності в межах періоду.
Нижче наведено документ МаНіСАВ, який здійснює апроксимацію
табличних даних, що відповідають рис. 7.24, а, відрізком ряду Фур’є.
Попередньо здійснюється інтерполяція табличних даних кубічним сплайном:
У8 := С8р1ІПе(уХ, уу)	£с(х) := ІПІЄГр(у8, УХ, уу, х).
Одержана залежність £с(х) дає суттєві похибки апроксимації на межі
визначення таблично заданої функції (див. рис. 7.24, б).
Продовження табличних даних на період вперед і назад здійснюється
наступним чином.
Утворено вектори уу2 та ух2 із трьох періодів табличних даних:
ууі := 5Їаск(уу, уу)	уу2 := 8Іаск(уу1, уу)
ухі := 8Іаск(ух, ух + 2л) ух2 := 8Іаск(ух1, ух + 4л).
Інтерполяція одержаних трьох періодів таблиці кубічним сплайном
здійснена наступним чином:
У8І := С8р1іпе(ух2, уу2) Сс1(х) := іпіегр(у8І, ух2, уу2, х).
Одержана залежність ІсЦх) в точності відповідає табличним даним
скрізь, включаючи межі інтервалу періодичності (див. рис 7.24, б).
Використовуючи залежність (сі(х), виконано знаходження коефіцієнтів
ряду та обчислення відрізку ряда Фур’є:
рс1(х + 2л)* сов(к * х)йх
к := 0..7 а!к := -5------------------------
л
|£с1(х + 2л) * 8Іп(к * х)(1х
Ь1к := —----------------------
£7(х):=^ +
7
X (а!к * сов(к * х) + Ь1к8Іп(к * х))
кі
Одержані результати апроксимації табличних даних відрізком ряду Фур’є
наведені на рис. 7.24, б. Із рисунка видно, що апроксимація сплайном (крива
£с(х)) дає суттєві похибки на межах області визначення (0...360”).
Апроксимація трьох періодів таблиці точно відповідає вихідним даним (крива
і'сі(х)). З цією кривою точно співпадає відрізок ряду Фур’є (крива £7(х)).
307
Струтинський В.Б.
7.2.3. Нелінійні математичні моделі дискретних процесів
Апроксимація дискретних множин значень процесів за допомогою
лінійних математичних моделей дещо звужує можливості аналізу процесів. Як
правило, більш ефективним є застосування нелінійних математичних моделей.
Для апроксимації функції можна використати будь-яку нелінійну
математичну модель. Звичайно вид моделі задають виходячи із фізичної суті
задачі або із досвіду досліджень аналогічних систем і процесів. Вид
математичної моделі повинен якісно відповідати табличним даним. При цьому
враховуються такі властивості, як симетрія, монотонність, періодичність
таблично заданої функції. При виборі моделі доцільно виконати початкову
грубу апроксимацію табличних даних, наприклад, методом лінійної
інтерполяції. Одержане перше наближення використовується для
обгрунтування вибору нелінійної математичної моделі.
В загальному вигляді нелінійна математична модель записується у формі:
Р = Р(х, а0, а1; ..., ат),
де а; - заздалегідь невідомі параметри моделей.
Задача апроксимації процесу у, = Уі(хі), заданого у вигляді таблиці
дискретних значень, полягає у виборі набору значень параметрів ао, а\, ...,
апі, які забезпечують найкраще наближення аналітичної залежності до
табличних даних. Згідно з методом найменших квадратів, умовою найкращого
наближення є мінімум величини:
8 = Е[Р,(хі,аі,а1,..., ат)-Уі]2 = тіп .	(7.57)
і=0
Знаходження мінімуму суми квадратів відхилень для нелінійної моделі
ускладнюється з причини нелінійності аналітичної залежності. Тому розробка
нелінійних математичних моделей процесів, заданих дискретною множиною
значень, є набагато складнішою, ніж розробка лінійних моделей.
Звичайно нелінійні математичні моделі розробляються з використанням
програмних засобів. Процедура знаходження параметрів нелінійної
математичної моделі реалізована в математичних пакетах.
В програмному середовищі МаіЬСАВ останніх версій для цього служить
спеціальна вбудована функція §епйі, яка розраховує вектор параметрів
нелінійної моделі а = [а0, а(, ..., ат] і має синтаксис:
а := депПЦух, уу, у§, £).
Задані табличні значення функції визначаються векторами:
УХ = [х0, х1? х2, .... хп] та уу = [у0, У1, у2, ..., уп],
де п - число заданих в таблиці точок.
Вектор у§ розмірності (т + 1) задає початкові наближення параметрів
308
Розділ 1. Знаходження символьних математичних моделей
нелінійної математичної моделі ад, а,, ат. Символьний вектор
’ 1В
£(х,а0,а,,...,ат)
як свою першу компоненту
£0 = Р(х, а0, аь ..., ат)
має, власне, нелінійну математичну модель у вигляді функції від х та (ш + 1)
параметрів а0, а^, ат. Друга і наступні компоненти символьного вектора {
включають символьні значення частинних похідних нелінійної моделі по
окремих параметрах, а саме:
аг аг £ аг
’ =<К; 2 = сіа, ;	т+1 = Пат-
Розглянемо приклад апроксимації значень дискретного процесу, заданого
у вигляді таблиці значень Хі та у, нелінійною математичною моделлю у
вигляді степеневої функції з використанням вбудованої функції депГіі.
Фрагмент документа МаЙіСАВ, який здійснює знаходження нелінійної
математичної моделі має вигляд:
і := 0...7	хі := і Ус	:=0
У4 := 16	у5:=30	у6:=71	
	а0 * ха’	
£(х,а) =	Xа'	
а0 * Xа' * 1п(х)
У1 == 4 У7 := 8'	У2 ••= 4 Уз := 15 )
- Я [2]	:= £епїїе(х, у, у§, £) _аі.
ао1ГО,731
а ~ [2,442
р(х) := а0 * ха' .
Графічна інтерпретація одержаної нелінійної математичної моделі та
дискретного масиву значень вихідного процесу наведена на рис. 7.25.
Із аналізу графіків випливає, що одержана нелінійна математична модель
кількісно та якісно відповідає табличним даним.
Задача апроксимації табличних значень процесу нелінійною математичною
моделлю не є однозначною. Наступний приклад ілюструє той факт, що
наведена вище апроксимація таблично заданого дискретного процесу
степеневою функцією Р(х) = а()ха' , може бути замінена апроксимацією даних
таблиці показниковою (експоненціальною) функцією виду
Р(х) = аоеа,х .
Знаходження коефіцієнтів нелінійної експоненціальної математичної
моделі та її графічна інтерпретація наведені нижче.
309
Струтинський В.Б.
Рис. 7.25. Результати апроксимації табличних даних нелінійною
математичною моделлю р(х) = аоха'
Фрагмент документа МаійСАО визначення
нелінійної експоненціальної
математичної моделі має вигляд:
£(х, а) :=
ап
1
0,7
ао
аі
§еп£іі(х, у, ап, і")
а0 3,687
_а1]”|_0,45
Р(х):= а0*е^.
Графічна інтерпретація одержаної нелінійної математичної моделі та
дискретного масиву значень вихідного процесу наведені на рис. 7.26.
Рис. 7.26. Апроксимація табличних даних нелінійною математичною
моделлю у вигляді експоненціальної функції
310
Розділ 7. Знаходження символьних математичних моделей
Із аналізу графіка випливає, що математична модель у вигляді
експоненціальної функції також дає добре кількісне та якісне наближення до
табличних даних.
Використання функції §епПп потребує визначення початкових наближень
параметрів нелінійної математичної моделі. Звичайно ці наближення повинні
досить грубо відповідати точним значенням коефіцієнтів. В наведеному вище
прикладі початкові наближення відрізняються від точних значень параметрів
в 2...4 рази. При цьому одержано позитивний результат.
При неправильно заданих початкових значеннях параметрів результати
можуть бути абсолютно невірними. Це ілюструється наведеними нижче
обчисленнями в пакеті МаНіСАВ, який відповідає попередньому прикладу з
іншими початковими значеннями параметрів:
ап
10
7
а := §епНі(х, у, ап, £)
6,519 * 10 14
4,854
Одержані коефіцієнти і сама нелінійна модель
Рв(х):= а0*е’-
не відповідає табличним даним (крива Рн(х) на рис. 7.26).
Нелінійні математичні моделі не враховують ряду особливостей
дискретних процесів, зокрема, наявності різких змін сусідніх значень
процесу. На рис. 7.27 показана в графічному вигляді нелінійна математична
модель
Р(х) = аоеа-,
використана для апроксимації дискретного процесу із різкими змінами
сусідніх значень.
Рис. 1.21. Застосування експоненціальної математичної моделі для
апроксимації дискретного процесу із різкими змінами сусідніх значень
311
Струтинський В. Б.
Із аналізу графіків випливає, що одержана математична модель досить
грубо кількісно та якісно описує наявні табличні дані.
Для підвищення точності апроксимації необхідно змінити вид нелінійної
моделі. Наприклад, взяти її у формі:
р(х,аи,а1,а2,а3) = аиеа,х + а2 8іп(а3х).
Вбудована функція §епНі математичного пакету МаіЬСАО дозволяє
розробити довільну нелінійну математичну модель процесу, заданого у
вигляді таблиці. Разом з тим, в пакеті є додаткові вбудовані функції для
створення окремих практично важливих нелінійних математичних моделей.
На рис. 7.28 наведена частина меню вбудованих функцій, що служить для
вибору коефіцієнтів конкретних нелінійних математичних моделей.
ІЯійіійІИв
Рис. 7.28. Вбудовані функції математичного пакету МаііїСАІ) 2000,
призначені для розрахунку коефіцієнтів окремих практично важливих
нелінійних математичних моделей
В математичному пакеті також наявні функції, які здійснюють
статистичне усереднення табличних даних за певними законами, наприклад,
функція шесИіі.
Наведені в меню вбудовані функції дають можливість визначити
коефіцієнти а, Ь, с математичних моделей за значеннями таблично заданого
процесу. Процес задається у вигляді вектора значень аргументу ух та вектора
значень функції уу. Вбудовані функції потребують визначення початкових
значень коефіцієнтів математичних моделей а, Ь, с. Ці початкові значення
задаються у вигляді вектора у§. Нелінійні математичні моделі та відповідні
вбудовані функції пакету МаїЬСАВ 2000 наведені в табл. 7.1.
312
Розділ 7. Знаходження символьних математичних моделей
Таблиця 7.1
Вбудовані функції математичного пакету МаійіСАІ) 2000
та відповідні їм нелінійні математичні моделі
з/п	Синтаксис вбудованої функції	Нелінійна математична модель	Коефіцієнти моделі, які розраховуються
1	ехрНЦух, уу, у§)	а*еь*х +с	а, Ь, с
2	1§8£іі(ух, уу, У§)	а/(1 + Ье-с*х)	а, Ь, с
3	1іпє(ух, уу, УЦ)	а * х + Ь	а, Ь
4	1о§£іі(ух, уу, У§)	а * 1п(х + Ь) + с	а, Ь, с
5	те<1£іі(ух, уу, у&)	а + Ь * х	а, Ь
6	р\УҐІІ(УХ, уу, У§)	а*хь +с	а, Ь, с
7	8Іп£і£(ух, уу, у§)	а * кіп(х + Ь) + с	а, Ь, с
Вбудовані функції пакету дозволяють значно спростити процедуру
знаходження нелінійних математичних моделей. Використання вбудованих
функцій корисне як перше наближення при розробці більш складних
математичних моделей.
Вбудовані функції пакету, призначені для розробки нелінійних моделей,
відзначаються надійністю роботи.
Нижче наведено фрагмент документа МаїЬСАО, який визначає
коефіцієнти нелінійної синусоїдальної математичної моделі:
уУо := 0	уу1 := 0.38	уу2 := 0.71
уу3 := 0.92	УУ/, := 1	уу5 :=0.2
уу6 := 0.71	уу7 := 0	уУ8 :=0
уу9 := 0.38	уу10 := 0.31	уу1( := —0.92
УУ12 := -1	уУіз := “0-92	уу14 := -0.71
уу15 := -0.38 т	і := 0..15	
у§ := 0 г 0.902'	2л Л. ух, := — * і 1	16	а := 8Іп£іі(ух, уу, у§)
а =	0.088 с 0.069,	£(х) := а0 * 8Іп(х + а,	+ а2.
Вектори уу задано	значеннями їх складових. Початкові значення	
коефіцієнтів, які задані	вектором у§, визначені	шляхом підбору. Замість
окремих змінних а, Ь, с, які вказані у сьомому рядку табл. 7.1 використано
вектор коефіцієнтів моделі а, який має три компоненти.
Графічна інтерпретація нелінійної синусоїдальної математичної моделі та
дискретного масиву значень вихідного процесу наведена на рис. 7.29.
313
Струтинський В. Б.
Одержані в результаті розрахунків по нелінійній моделі зіпіті значення
процесу, наведені на рисунку, відповідають табличним даним. Нелінійна модель
згладжує табличні дані. Значні відхилення (викиди) при цьому ігноруються.
90
270
X
Рис. 7.29. Нелінійна математична модель дискретного процесу, заданого
векторами юх та VI/, визначена за допомогою вбудованої функції зіп/И
Дана вбудована функція може бути використана для гармонічних процесів
довільного періоду.
Використання вбудованої функції 8Іп£іі дозволяє значно спростити
виконання розглянутого в розділі 4.3.1 гармонічного аналізу процесів.
Нелінійні математичні моделі, реалізовані за допомогою вбудованих
функцій пакету МаіЬСАІ) 2000, можуть бути використані для опису складних
процесів та систем.
Для складних процесів, які описуються сумою різних нелінійних
функціональних залежностей автор використовував наступну методику.
Спочатку здійснюється визначення головної нелінійної математичної моделі.
Потім знаходиться дискретний масив значень різниць базового дискретного
процесу і розрахункових значень згідно з базовою моделлю. Одержаний
масив різниць використовується для розробки уточнюючої нелінійної моделі.
При необхідності здійснюється наступне уточнення і одержують уточнюючу
модель другого, третього чи вищих ступенів.
Рекомендується проводити розробку при графічному супроводі і
послідовному аналізі дискретних масивів значень різниць. Методика дозволяє
поступово підвищувати точність створюваної нелінійної моделі. Одержана
нелінійна математична модель сама є ефективним інструментом аналізу
процесу. У розділі 12.5 розглянуто приклад побудови нелінійної моделі
складного процесу згідно з даною методикою.
314
Розділ 8. Математичні моделі простих механічних коливальних систем
РОЗДІЛ 8
Математичні моделі простих механічних коливальних систем
8.1. Визначення прогинів та критичної частоти обертання
пружних протяжних деталей з розподіленою масою
Визначення прогинів та критичної частоти обертання пружних протяжних
деталей зводиться до обчислення лінійної комбінації тригонометричних та
гіперболічних функцій. Визначення критичної частоти обертання виконується
для довговимірних деталей при різних видах розміщення та закріплення
деталей [2, 108]. Прогин довговимірної деталі при її обертанні визначається
відцентровими навантаженнями. Математичну модель складемо із
врахуванням розподіленості параметрів деталі (рис. 8.1).
Рис. 8.1. Схематичне зображення прогину деталі під дією
відцентрових сил (а) та розрахункова схема зігнутої осі деталі (б)
Розподіленим параметром є маса деталі, яка приймається рівномірно
розподіленою по довжині. Тому можна вважати, що деталь навантажена
нерівномірно розподіленою по довжині поперечною силою, інтенсивність якої
на одиницю довжини деталі складає:
315
Струтинський В.Б.
Ч = тои2у,
де то - погонна маса деталі;
ш - кутова швидкість її обертання;
у - прогин деталі.
Диференціальне рівняння прогинів осі деталі в системі координат, що
обертається разом із деталлю, має вигляд [108]:
Ю-у-у = Я = т0о2у ,	(8.1)
ах
де Е.І - жорсткість при згині перерізу деталі;
х - поздовжня координата.
Характеристичне рівняння, що відповідає диференціальному рівнянню
(8.1), знаходиться із (8.1) і має вигляд:
Xі - к4 =а2 - к2Х + к2) = 0,
,4 гпоа>2
де постійний коефіцієнт визначено через параметри системи: к =----—.
Е.1
Характеристичне рівняння має і дійсні, і комплексні корені. Тому
розв’язок диференціального рівняння (8.1) визначається залежністю:
у = с,  зіп(кх)+ с2 • со5(кх) + с3 • зЬ(кх) + с4 • сЬ(кх),	(8.2)
де С(, ..., Сд - постійні інтегрування, які визначаються умовами опирання та
закріплення деталі по торцях.
Розглянемо схему закріплення, яка відповідає обробці деталі в центрах.
Установка деталі в центрах з деякими припущеннями відповідає схемі
балки на шарнірних опорах. В цьому випадку маємо наступні граничні умови
для диференціального рівняння (8.1):
при х = 0 та х = Ь у = у" = 0.
Відповідно для визначення постійних інтегрування одержимо однорідну
систему чотирьох лінійних алгебраїчних рівнянь:
с2 + с4 = 0
- к2с2 +	к2с4 = 0
с18іп(кЬ)+ с2соз(кЕ) + с3зЬ(кЕ)+ с4сй(кЬ)=0 (8.3)
- с,к2 8іп(кЬ)- с2к2 соз(кЕ) + с3к28к(кЬ) + с4к2сЬ(кЬ) = 0
Однорідна система рівнянь (8.3) має розв’язок лише тоді, коли її
визначник дорівнює нулю, тобто
	0	1	0	1		
	0	- к2	0	к2		
сієї	8іп(кЬ)	соз(кЕ)	8Й(кЬ)	ск(кЬ)	= 0.	(8.4)
	- к2 8іп(кЬ)	- к2 со8(кЬ)	к28Ь(кЬ)	к2ск(кЬ)		
Розкриття визначника (8.4) приводить до рівняння:
316
Розділ 8. Математичні моделі простих механічних коливальних систеч
5Іп(кЬ)-8Іі(кЬ)=0.	(8.5)
Трансцедентне рівняння (8.5) має найменший відмінний від нуля корінь
кЬ = я, який визначає критичну кутову швидкість обертання деталі у вигляді:
®р
(8.6)
Трансцендентне рівняння (8.5), крім (8.6), має нескінченну кількість коренів:
кЕ = іті, і = 1, 2,...
Цим кореням відповідають резонансні частоти обертання деталі:
(8.7)
Таким чином, розв’язок (8.2) диференціального рівняння (8.1), який
виражається через гіперболічні та тригонометричні функції, встановлює
значення критичної кутової швидкості обертання деталі та резонансних частот
динамічної системи обертової деталі.
Для запобігання резонансу в системі привода верстата необхідно
виключати коливання із вказаними частотами. Звичайно для надійного
забезпечення вібростійкості застосовують конструктивні заходи.
Па рис. 8.2 наведено як приклад довговимірну деталь, для забезпечення
вібростійкості якої використано люнет.
Рис. 8.2. Загальний вигляд обробки довговимірної деталі
на. токарному верстаті з використанням люнету
317
Струтинський В Б.
Аналіз вібростійкості деталей при обертанні здійснено за різних умов
закріплення деталей. Зокрема, розглянута деталь із консоллю (рис. 8.3).
Рис. 8.3. Схема прогину консольної деталі, що обертається:
а ~ конструктивна схема; б - зігнута вісь деталі
Граничні умови для диференціального рівняння (8.1), що описує прогини
консольної жорстко защемленої деталі, мають вигляд:
при х = 0 у = у" = 0;
при х = 1	у" = у'" = 0.
Використовуючи дані граничні умови, знаходиться однорідна система
рівнянь, аналогічна (8.3).
Із умови рівності нулю визначника даної системи знаходиться рівняння:
со3(к1)'сЬ(к1) --1.	(8.8)
Корені трансцендентного рівняння (8.8) наближено відповідають
залежності:
ла л К .	, .	(8.9)
(кЦ ® (і - — )л , 1 = 1,2,...
Перший корінь кі = 1,57 . Йому відповідає критична швидкість обертання
консольно защемленої деталі:
~ 2,46 ГеГ	(8Л0)
% ~ і2 ^т(1 '
Ряд резонансних частот для консольно закріпленої деталі відповідає
нескінченному числу коренів трансцендентного рівняння (8.8). Резонансні частоти
визначаються формулою:
318
Розділ 8. Математичні моделі простих механічних коливальних систем

1\2 2
2)Л
(8.11)
Цих частот коливань необхідно уникати в динамічній системі верстата з
метою запобігання виникненню резонансних явищ.
Окремим випадком є знаходження критичних частот обертання заготовки
із консоллю значної довжини. Верстати, які використовують пруткові
заготовки, завжди мають обертові консолі значної довжини. На рис. 8.4
показано кінець пруткової заготовки токарного автомата. При обертанні
заготовки часто має місце втрата її стійкості з причини резонансних явищ.
Рис. 8.4. Заготовка, яка встановлена в одношпиндельному токарному
автоматі і має консоль значної довжини
Для запобігання втраті стійкості кінець консольної заготовки
підтримується спеціальним пристроєм.
Розглянемо схему обробки деталі із консоллю, кінець якої підтримується
протяжною трубчастою опорою (рис. 8.5). Ця схема є характерною для
верстатів, які виготовляють деталі із довгих пруткових заготовок та мають
напрямні труби.
Прогин заготовки, як і раніше, відповідає розв’язку (8.2)
диференціального рівняння (8.1).
Рис. 8.5. Схема обертання довгої пруткової заготовки,
кінець якої підтримується напрямними трубами
319
Струтинський В. Б.
Граничні умови для даної схеми закріплення заготовки наступні:
при х = 0 у = у' =0;
при х = 1 у = у' = 0.
З цих граничних умов випливає система рівнянь аналогічна системі (8.3).
Визначник одержаної із граничних умов системи рівнянь дорівнює нулю
за умови, що
со5(к1) - сЬ(к1) = 1.	(8.12)
Трансцендентне рівняння (8.12) має нескінченну кількість коренів, які
розраховуються за формулою:
(к1)і = ^і +	• я , і = 1, 2,...
Значення критичної швидкості обертання заготовки визначається першим
коренем і складає:
24 [ЕІ
“Р 12\ш0'
Із порівняння формул (8.10) та (8.14) випливає, що наявність трубчастої
опори заготовки підвищує значення критичної частоти обертання в 10 разів.
Ряд
будуть:
(8.13)
(8.14)
резонансних частот, які відповідають кореням рівняння (8.12),
(і+-„)л2
ИРІ = —[ї—
(8.15)
При розробці та експлуатації верстата необхідно уникати частот обертання
шпинделя, які відповідають розрахованим за формулою (8.15) резонансним
частотам та кратним частотам.
Наведені математичні моделі для визначення критичної частоти обертання
пружної протяжної заготовки є наближеними. Похибки моделей обумовлені в
основному недостатньо точним визначенням умов затискання заготовки в
патроні. Уточнення математичних моделей доцільно здійснити з
використанням експериментальних даних про умови опирання заготовки.
Практичне застосування вищенаведених математичних моделей для
визначення критичних частот обертання пружних протяжних деталей вимагає
всебічного обґрунтування відповідної розрахункової схеми. Загалом дані
моделі використовуються лише для попередніх досліджень процесів.
Підвищення точності та достовірності моделей досягається їх корекцією за
результатами комплексних експериментальних досліджень динамічної системи
верстата [101, 102].
320
Розділ 8. Математичні моделі простих механічних коливальних систем
8.2. Розрахунок параметрів високочастотних коливань гільзи
шпинделя координатно-розточувального верстата
Розрахунок параметрів високочастотних коливань гільзи шпинделя є
прикладом використання спеціальних функцій (функцій Бесселя) для
моделювання процесів у реальних технічних системах механіки. Застосування
функцій Бесселя дає можливість врахувати якісну особливість динамічної
системи, що полягає у наявності обертового барабана. Звичайно ця система
характерна для аналізу динаміки рухомої маси, що піднімається за допомогою
барабана. Координатно-розточувальний верстат (наприклад, 2Д450АМФ2)
має рух вертикальної подачі шляхом переміщення гільзи шпинделя. Привод
гільзи шпинделя має врівноважуючий механізм у вигляді барабана, на якому
знаходиться гнучка стрічка, зв’язана із гільзою шпинделя. Схеми механізмів
наведені на рис. 8.6, а загальний вигляд приводи показано на рис. 8.7.
Рис. 8.6. Схема механізму вертикальної подачі токарно-розточувального
верстата (а) та розрахункова схема приводи переміщення гільзи (б):
1 - гільза шпинделя; 2 - барабан врівноважуючого механізму; 3 ~ гнучка
металева стрічка; 4 - пружина; 3 - привод переміщення гільзи
Гільза 1 (див. рис. 8.6) має механізм врівноваження, виконаний у вигляді
барабана 2, на якому розміщена металева стрічка 3, один кінець якої
закріплений на гільзі шпинделя, а другий кінець утримується пружиною 4,
321
Струтинський В.Б.
що врівноважує гільзу.
Рис. 8.7. Загальний вигляд гільзи шпинделя
вертикально-розточувального верстата
Гільза переміщається за допомогою привода 5 із зубчасто-рейковою
передачею. Передача має зазори і переспряження зубців, які виникають за
рахунок неточностей виготовлення деталей, а також за рахунок відносного
зміщення шестерні та зубчастої рейки. Наявність зазорів призводить до
виникнення імпульсних навантажень в динамічній системі верстата.
Розрахункова схема переміщення гільзи шпинделя показана на рис. 8.6, б.
Умовно зазори зубчастої передачі шестерня-рейка показані збільшеними. Гільза
шпинделя 1, яка має масу пі, рухається вниз зі швидкістю V під дією зусилля з
боку шестерні 5. Зусилля передається в точці контакту зубців А. Точка А може
бути в різних місцях між контактуючими зубцями шестерні та рейки. Нехай
контакт зубців буде в точці А, показаній на рисунку. Можна вважати, що в даний
момент гільза шпинделя 1 рухається вниз рівномірно. При цьому барабан 2
обертається з кутовою швидкістю ®, яку можна вважати постійною. При
подальшому повороті шестерні 5 зачеплення зубців у точці А припиняється. Під
дією крутного моменту Мд шестерня 5 швидко повертається у напрямку кутової
швидкості о)! вибираючи зазор між зубцями. При цьому утворюється нова точка
контакту зубців, наприклад, між точками В| та В^. Має місце інтенсивне
імпульсне навантаження між шестернею 5 і зубчастою рейкою.
Під дією імпульсного навантаження гільза шпинделя 1 починає
коливатись у вертикальному напрямку. Амплітуда цих коливань незначна, а
частота висока (103 Гц і вище). Барабан 2 має значну масу і встановлений в
підшипниках. Тому він не встигає реагувати на швидкі зміни зусилля і
322
Розділ 8. Математичні моделі простих механічних коливальних систем
продовжує обертатись рівномірно. Відповідно основним чинником, що
визначає характер коливань, є пружність стрічки 3 механізму врівноваження.
В першому наближенні будемо вважати, що при мікропереміщеннях сили
опору в напрямних гільзи набагато менші сил пружності стрічки. При цьому
розрахункова схема для аналізу високочастотних вертикальних коливань
гільзи шпинделя під дією імпульсного навантаження буде мати вигляд,
показаний на рис. 8.8, а.
а)	б)
Рис. 8.8. Спрощена розрахункова схема визначення параметрів
високочастотних коливань гільзи у вертикальному (а)
та в горизонтальному (б) напрямках
Барабан обертається з постійною кутовою швидкістю о. Радіус барабана
позначимо г, а еквівалентну масу гільзи шпинделя - т. В момент часу Іо під
час дії імпульсного навантаження центр маси гільзи знаходиться на відстані 1о
від осі барабана. Відстань від центра барабана до центра маси гільзи складає
10 = гой(). Стрічка вважається невагомою, але пружною. Площа стрічки - Р,
модуль пружності матеріалу - Е.
Розглянемо випадок наявності коливань гільзи у вертикальному напрямку
під дією імпульсного навантаження. В момент часу і = 10 швидкість гільзи
раптово змінюється під дією імпульсу на величину (ДУ)о- При цьому
абсолютна швидкість гільзи складає:
V = ом + (ДУ)0.
323
Струтинський В.Б.
Диференціальне рівняння, що описує малі високочастотні коливання
гільзи у вертикальному напрямку, має вигляд [108]:
т£Ні + II = о ,	(8.16)
аі2 і ог
де Ах - відносні вертикальні переміщення гільзи шпинделя.
Розв’язок рівняння (8.16) знаходимо за наступних початкових умов:
при і = Со Ах = 0,	= (АУ)0 .
ас
Розв’язок диференціального рівняння (8.16) включає функції Бесселя
першого До, .її та другого ¥0, ¥і роду:
, , т»г . [Л(т„)-У,(ї)-Т,(».)•>,(.)]	<8.17)
(8.18)
(8.19)
ЕР
де т = 2.1----• і - безрозмірна змінна, яка відповідає часу І.
V тсог
Для тривіального випадку, коли імпульсне навантаження має місце при
х = 0, розв’язок рівняння записується в більш простій формі:
(АУ)ош<вг _
2ЕР
Під дією імпульсу мають місце коливання гільзи в різних напрямках.
Зокрема наявні високочастотні горизонтальні коливання гільзи малої
амплітуди (порядку 1 мкм), які проходять в межах зазорів.
Розглянемо коливання гільзи в горизонтальному напрямку. Збуренням руху
гільзи є початкове ступінчасте відхилення її від вертикалі (див. рис. 8.8, б).
Відхилення від вертикалі характеризується кутовим положенням гільзи ф.
Рівняння зміни кутового положення гільзи при її русі вниз має вигляд:
32ф 2 сі<р	§
--І- +-----	 + -2-Ф - 0 ,
сії2	І сії-соті
де § - прискорення вільного падіння.
Розв’язок цього рівняння знаходиться за наступних початкових умов:
при 1 = Іо Ф ~ Фо-
Розв’язок рівняння (8.19) виражається через функції Бесселя:
.... - тю .	У2(тї0)~ V
П -Шо)’ ^2(т10)-1
де ті, Т2 “ безрозмірні величини:
т - 2	 т - 2
ті - А > тіо ~ А
V о • г	V (в • г
Рівняння зміни кутового положення при русі гільзи вгору має вигляд:
д2ф	2 дф §	Л
<Д|	1] <11,	огі,
(8.20)
(8.21)
де її = і0 ~ 1 ~ нове відносне значення часу.
324
Розділ 8. Математичні моделі простих механічних коливальних систем
Розв’язок рівняння (8.21) знаходиться за вищевказаних початкових умов і
має вигляд:
На рис. 8.9 наведені результати розрахунків коливань гільзи шпинделя у
вертикальному та горизонтальному напрямках, які відповідають розв’язкам
(8.17) та (8.20).
Рис. 8.9. Результати розрахунків параметрів високочастотних коливань
гільзи шпинделя токарно-розточувального верстата у напрямку:
а - вертикальному; б - горизонтальному
Наведена вище математична модель коливань гільзи є досить грубою.
Наявність сил опору та напрямних призводить до суттєвих відхилень
розрахункових параметрів руху гільзи від фактичних. Але дана модель дає
можливість встановити суттєві якісні закономірності високочастотних
мікропереміщень шпиндельного вузла верстата. Крім того, модель корисна як
ілюстрація застосування функцій Бесселя при математичному моделюванні
реальної технічної системи. Дана математична модель буде більш ефективною
для аналізу механічних коливальних систем, вантажопідйомних машин, в
яких наявні вантажі, що піднімаються.
325
Струтинський В. Б.
8.3. Розрахунок параметрів коливань гнучких масивних
протяжних тіл із розподіленою масою
В багатьох технічних пристроях застосовуються гнучкі масивні протяжні
тіла. Як правило, вони зібрані із багатьох однотипних деталей (ланцюги) або
складені із тонких стрижнів (канати). В літературі масивні протяжні тіла
звичайно називаються масивними нитками чи струнами. Під масивною
ниткою розуміють протяжне тіло, яке майже не опирається згину і має
незначні розтягувальні зусилля в своєму перерізі. Струною умовно називають
гнучке масивне протяжне тіло, яке розтягнуте значною поздовжньою силою.
На рис. 8.10 наведено деякі приклади застосування масивних ниток і
струн в технічних системах механіки.
Рис. 8.10. Приклади технічних систем механіки, в яких використовуються
масивні нитки і струни: а - система демпфування поперечних коливань
платформи; б - абразивна стрічка шліфувального верстата
Окремі, практично важливі задачі розрахунку параметрів коливань
масивних ниток і струн вирішуються з використанням спеціальних функцій.
Вони відповідають елементам технічних систем, які наведені на рис. 8.10.
Перша задача відповідає розрахунку коливання маятника у вигляді масивної
нитки, підвішеної за один кінець. Параметри коливань такого маятника
виражаються через функції Бесселя. Друга задача відповідає коливанням
струни, розташованій на пружній опорі.
Перший приклад є характерним, оскільки бесселева функція До(х) була
знайдена Д. Берну лі в 1732 році при вивченні коливань однорідної важкої
нитки. Звичайно, сучасну назву і класифікацію широкого класу бесселевих
326
Розділ 8. Математичні моделі простих механічних коливальних систем
функцій було зроблено значно пізніше. В 1824 році Бессель, досліджуючи
питання, пов’язані зі збуреннями руху планет, детально вивчив властивості
цих функцій [1].
На рис. 8.11 наведена схема коливань масивної нитки довжиною Ь,
підвішеної за один кінець в точці А.
Рис. 8.11. Схема поперечних коливань масивної нитки,
підвішеної за один кінець
Поперечні переміщення точок нитки в динаміці описуються
диференціальним рівнянням в частинних похідних, яке має вигляд [1]:
1 . ^У _ 'А , „ д2У
§ д‘С дх дх2
де у - переміщення нитки в точці з координатою х;
§ - прискорення вільного падіння;
і - час;
ц - маса одиниці довжини нитки.
Частинний розв’язок рівняння (8.23) знаходиться у вигляді:
у = фСхБеі'ф
де ф(х) - деяка невідома функція координати х;
<в - постійна величина (частота);
І - >/-ї ~ уявна одиниця.
Для знаходження функції ф(х) підставимо (8.24) у (8.23) і
звичайне нелінійне диференціальне рівняння другого порядку:
| 1 _ бф ! ю2  ф _ 0
Зх2 х сіх 8 х
(8.24)
одержимо
(8.25)
327
Струтинський В. Б.
Це диференціальне рівняння шляхом перетворень приводиться до
рівняння Бесселя і, відповідно, має розв’язок у вигляді лінійної комбінації
функцій Бесселя. Остаточно розв’язок рівняння (8.25) має вигляд:
<р(х)
с2
¥”Н)
(8.26)
де С| та С2 - довільні константи інтегрування.
Враховуючи, що розв’язок (8.26) повинен мати кінечне значення при х =
0, одержимо значення константи С2 = 0. При цьому переміщення кожної точки
нитки буде визначено нескінченною сумою розв’язків виду:
X Я
• Л 2со І.
Уш = сі ’ е>е
В точці закріплення х = Е маємо у = 0. Тому величина
(8.27)
повинна бути коренем функції Бесселя першого роду нульового порядку,
тобто коренем рівняння
Іо(а) = 0.
Функція Бесселя має нескінченне число коренів. Відповідно маємо
нескінченний ряд частот юг.
Нехай ар - один із коренів рівняння Ло(а) = 0. Тоді частота <ог дорівнює:
Оскільки коренів нескінченна кількість, то дана залежності визначає
нескінченне число частот і відповідно форм коливань нитки.
Перші (основні) форми коливань нитки наведені на рис. 8.12. Вони
нормовані відносно загальної довжини нитки.
-0,2 о '°>2	0	0	-0,2 о
Рис. 8.12. Перші форми коливань важкої нитки, підвішеної за один кінець
328
Розділ 8. Математичні моделі простих механічних коливальних систем
Перша форма (Ф1) характеризується плавним викривленням осі нитки,
яке нагадує прогин балки. Друга форма (Ф2) включає вузлову точку,
розташовану на відстані 0,19 довжини нитки від її нижнього краю. Друга
форма має дві, а третя - три вузлові точки. Із підвищенням номера форми
інтенсифікуються рухи перерізів нитки в околі її нижнього краю. Фактично
коливання по всіх високочастотних формах зосереджуються в безпосередній
близькості від нижнього краю нитки. Із результатів математичного
моделювання можна зробити висновок про характер коливального процесу в
нитці- Зокрема, високочастотна зміна форми нитки має місце в околі її
нижнього кінця.
Таким чином, використання функцій Бесселя дає можливість описати
параметри коливань важкої нитки, підвішеної за один кінець. Використовуючи
одержаний розв’язок, можна знайти необхідні динамічні характеристики технічної
системи, яка включає масивні протяжні тіла типу важкої нитки.
Другий приклад розрахунку параметрів коливань за допомогою функції
Бесселя стосується струни, що лежить на пружній основі [23].
Па рис. 8.13 наведена розрахункова схема динамічної системи у вигляді
нескінченної струни, що лежить на пружній основі.
Рис. 8.13. Розрахункова схема струни, що лежить на пружній основі,
до якої в точці А прикладене ударне навантаження, що відповідає
одиничній імпульсній функції
Розглянемо поперечні коливання нескінченної струни, яка має погонну
масу ш, розтягнена із зусиллям Т і розташована на пружній основі з
коефіцієнтом деформації к.
В момент часу і = 0 в точці А струни діє імпульсне навантаження
(ідеальний удар), яке моделюється нескінченно коротким імпульсом:
Р = Ра-5(О,
що відповідає дельта-функції Дірака 3(1).
Поперечні переміщення точок струни II = И(х, і) залежать від
поздовжньої координати х і змінюються в часі І.
Для визначення поперечних переміщень струни И маємо диференціальне
рівняння в частинних похідних у вигляді:
•л2тт	-^2т т
ш--^-Т-~ + к-П = 0.	(8.30)
Зі	бх
329
Струтинський В. Б,
Розв’язок рівняння (8.30) виражається через функцію Бесселя першого
роду нульового порядку згідно залежності:
Розрахунок переміщення струни, що відповідає залежності (8.31),
наведено на рис. 8.14.
б)
Рис. 8.14. Розрахунок параметрів коливального процесу, що виникає
в струні, яка лежить на пружній основі, при дії удару на початку
координат (х - 0): а - форма струни в деякий момент часу; б - закон
коливання перерізу струни, розташованого на деякій відстані
від початку координат
Із аналізу форми струни та її залежності від часу випливає, що після дії
на струну ударного навантаження виникає місцеве викривлення струни, яке
розповсюджується по струні у вигляді вузького ізольованого імпульсу (див.
рис. 8.14, а). З часом коливання струни в перерізі затухають (див.
рис. 8.14, б). Розрахунок дає кількісні та якісні характеристики хвильових
явищ, що мають місце у струні.
330
Розділ 8 Математичні моделі простих механічних коливальних систем
8.4.	Поперечні коливання стрижнів із розподіленою масою
без врахування втрат енергії
Поперечні коливання стрижнів із розподіленою масою без врахування
втрат енергії визначаються за допомогою функціональних рядів, що
включають тригонометричні функції [2, 109].
На рис. 8.15 показані розрахункові схеми стрижнів з розподіленою по
довжині масою, що здійснюють поперечні коливання.
г)
Рис. 8.15. Схеми поперечних коливань стрижнів з розподіленою масою
при різних умовах опирання: а - опирання стрижня на дві шарнірні опори;
б - консольно-закріплений стрижень; в - консольно-закріплений стрижень
із шарнірною опорою на кінці консолі; в - незакріплений стрижень
Під дією зовнішніх збурень, які можуть мати різноманітний вигляд,
кожна точка стрижня здійснює поперечні переміщення у(х, і), які
331
Струтинський В. Б.
визначаються координатою х та часом Е Параметри поперечних коливань
перерізів стрижня залежать від трьох груп факторів:
•	геометричних, масових та жорсткісних характеристик стрижня;
•	умов закріплення стрижня (граничних умов);
•	виду і характеру збурення, що визначає початкові умови коливань.
Коливання стрижня визначаються умовами опирання. Схема, зображена
на рис. 8.15, а, відповідає шарнірно опертому стрижню, схема, зображена на
рис. 8.15, б, - стрижню, один кінець якого жорстко защемлений, схема,
зображена на рис. 8.15, в, - стрижню, один кінець якого защемлений, а
другий вільно опертий, схема, зображена на рис. 8.15, г, відповідає стрижню
з вільними кінцями.
Закон коливання стрижня буде різним для кожної схеми опирання, але
диференціальне рівняння, яке описує закон коливання, буде однаковим.
Диференціальне рівняння поперечних коливань стрижня з розподіленою
масою розміщеного на двох опорах або незакріиленого взагалі, без
врахування втрат енергії має вигляд [109]:
5‘у	2 34у
~- + а-----V = 0,
а2 ах4
де у - поперечне переміщення перерізу стрижня, що знаходиться на відстані
х від початку системи координат;
і час;
а - постійна величина, яка залежить від масових та жорсткісних
параметрів стрижня і визначається через його параметри:
а2 _ ЕІ
рр
де Е - модуль пружності матеріалу стрижня;
] - момент інерції перерізу стрижня;
р - густина матеріалу стрижня;
Р - площа поперечного перерізу.
Розв’язок рівняння поперечних коливань стрижня (8.32) знаходиться у
вигляді тригонометричного ряду [109]:
(8.32)
(8.33)
у(хА) = ^у.(х)’[А> • с°8(РіО + В8 • 8іп(РіО],	(8.34)
де ¥/х) - нормальна функція, яка визначає і-ту нормальну форму коливань;
Рі - і-та частота коливань;
А, і В, — постійні інтегрування, які залежать від умов опирання стрижня та
виду збурення, яке на нього діє.
Підставляючи розв’язок (8.34) у диференціальне рівняння в частинних
похідних (8.32), після скорочення одержимо звичайне диференціальне
рівняння для знаходження нормальної функції ¥;(х):
332
Розділ 8. Математичні моделі простих механічних коливальних систем
^^-А.І¥і(х) = О,	(8.35)
сіх
де нова постійна величина л, залежить від частоти коливань:
^=-4.	(8.36)
а
Частинний розв’язок звичайного диференціального рівняння (8.35)
знаходиться у вигляді експоненціальної функції:
¥і(х)=епх,	(8.37)
де п - постійна величина, яка може мати дійсне чи комплексне значення.
Після диференціювання розв’язку (8.37) і підстановки його в рівняння
(8.35) одержимо трансцендентне рівняння, яке зв’язує постійні величини:
ета(п4 -Х4) = 0.	(8.38)
Враховуючи, що епх Ф 0, одержимо умову, якій повинна відповідати
постійна п. Ця умова відповідає алгебраїчному рівнянню:
(п4-А.;)=0.	(8.39)
Алгебраїчне рівняння (8.39) має два дійсні та два комплексні корені:
Пі = А.,; п2 = — Л.,; п3 = Ц,; п4 =^ = 7-1).	(8.40)
Відповідно загальний розв’язок диференціального рівняння (8.35) буде
включати складові, що відповідають всім чотирьом кореням (8.40) і
представляє собою залежність:
¥й(х) = М, • еЛ,х + ЬІ2 • е *•* + N3 • е,К|Х +	• е'|Лх ,	(8.41)
де N5, ..., N2 - постійні інтегрування.
Використовуючи співвідношення між тригонометричними, гіперболічними
та експоненціальними функціями, одержимо розв’язок рівняння (8.35) у
вигляді лінійної комбінації тригонометричних і гіперболічних функцій:
¥|(х) = сн • (соз(Хіх)+ сЬ(Хіх))+ с2і  (соз^х)- сй(Хіх)) +
+ сЗІ • (біп^х) + бЬ^х)) + с4і • (біп^х) - біг^х)),	(8.42)
де сц, с2і, сзі, с4і - константи, які визначаються із умов закріплення стрижня
(граничних умов).
Розв’язок (8.42) має місце для довільного стрижня на двох опорах або
вільного стрижня. Конкретизація розв’язку здійснюється із врахуванням умов
опирання стрижня.
Розглянемо окремі випадки опирання стрижня, які наведені на рис. 8.15.
Для шарнірно опертого стрижня (схема рис. 8.15, «) нормальна функція
¥;(х) повинна задовольняти наступним іраничним умовам:
при х-0 ¥(0) = ¥"(0);
,,	(8.43)
при X = Ь ¥І(Ь)= ¥; (Ь) = 0.
Врахування граничних умов дає співвідношення між константами:
333
Струтинський В.Б.
<?1 = С2 ~ О І С‘з = Сд.
Підстановка розв’язку (8.42) із врахуванням цих значень в граничні
умови дає рівняння для визначення частоти коливань стрижня (частотне
рівняння) у вигляді:
з1і(А.,Е).8іп(Л.іЕ) = 0.	(8.44)
Це частотне рівняння є трансцендентним і має нескінченну кількість
розв’язків виду:
К=~, і = 1,2....	(8.45)
Відповідно маємо нескінченну кількість власних частот коливань стрижня
на двох шарнірних опорах:
.2 _ і2л2 іеГ
рі а • Л: — --5~~ЛІ— 
І? \'рГ
(8.46)
Власним частотам (8 46) відповідають форми коливань у вигляді набору
синусоїдальних функцій різного періоду.
Остаточно закон поперечних коливань шарнірно опертого стрижня
описується залежністю:
у(х,і) = У В; • зіп(
£ І М
•81п(Ріі)-
(8.47)
Залежність включає ряд констант І), (ІЗ, = 2с3і), які визначаються із
початкових умов задачі. Початкові умови залежать від навантаження, яке діє
на стрижень. Навантаження бувають зосередженими або розподіленими.
Закон зміни навантаження в часі може бути найрізноманітнішим.
Практично важливим випадком є дія на стрижень зосередженого ударного
навантаження, прикладеного на відстані х( від опори стрижня (рис. 8.16).
Навантаження відповідає 8-функції
Рис. 8.16. Схема стрижня, на який діє ударне (імпульсне) навантаження
у вигляді одиничної імпульсної функції
При дії удару на короткій ділянці стрижня Дх на відстані X! від опори всі
334
Розділ 8 Математичні моделі простих механічних коливальних систем
точки стрижня в даному перерізі раптово набувають швидкості V. Згідно
[109] для цього випадку значення величин, які входять у загальний розв’язок
(8.47), визначаються залежністю:
27 • Дх . ГілхЛ
Г>,=—т------5іп —.	(8.48)
ЙРі І Ь >
Динамічне зміщення поточного перерізу стрижня, розташованого на
відстані х від опори, знаходиться об’єднанням (8.48) та (8.47) і
розраховується за формулою:
і \ 2У • Дх-7- 1	. (ілх. . (іпх) . /
у(х, і;) = —--У — • ви —- • віл — •	(8.49)
ь Рі ( Ь )	( Ь )
Одержаний тригонометричний ряд швидко сходиться. Він легко
обчислюється засобами макету МаСЬСАІЗ.
Аналогічні залежності одержані для динамічного навантаження стрижня у
вигляді раптової зміни навантаження (рис. 8.17)
б)
Рис. 8.17. Схема стрижня, до якого прикладене динамічне навантаження
у вигляді одиничної ступінчастої функції (а) та розподілене
навантаження, інтенсивність якого змінюється
за ступінчастим законом (б)
На рис. 8.17, а. показано стрижень, навантажений зосередженою силою
335
Струтиш.ькгій В.Б.
Ро. В момент часу і = 0 ця сила була раптово знята. Закон зміни
навантаження відповідає одиничній ступінчастій функції.
В даному випадку власні коливання стрижня визначаться функціональним
рядом 1109], який в цілому аналогічний формулі (8.49):
і 2РП1? ЛІ . (ілх) . (ІЯХ,''|	/ , і	.
у(х,0 = —грт V-- • 51П — ; • 81П -—4- • соДр Д.	(8.50)
л ЕЗ і \ ц )	< В )
Одержаний тригонометричний ряд дає можливість обчислити динамічні
переміщення стрижня.
Розглянемо коливання стрижня у випадку, коли до нього було прикладене
рівномірно розподілене навантаження інтенсивністю ц, а в момент часу 1 = 0
це навантаження було раптово зняте (рис 8.18).
Динамічні переміщення стрижня при цьому складають [109]:
у(х.і) = ~^ У	СО5(Рі1)-	(8.52)
х В.) '-1,3 5. 1	< В .)
Розрахунок параметрів незатухаючих коливань стрижнів здійснено і для
інших схем опирання, зокрема для консольного стрижня та вільного стрижня.
Розглянемо консольно закріплений стрижень (рис. 8.15, б). Для цього
стрижня нормальна функція повинна задовольняти наступним граничним
умовам:
при х = 0	УДо)-- У('(о)~ 0 ;
при х = Ь	У'(Ь) = У"'(ь) - 0 .	(8’52)
Із перших двох умов (8.52) випливає, що константи = с2 в рівнянні
(8.42) повинні дорівнювати нулю. Відповідно одержане частотне рівняння:
со^лф)- сІі(ДЕ) = -1 .	(8.53)
Дане частотне рівняння має нескінченну кількість розв’язків, які
наближено визначаються формулою:
(8 54)
Відповідні значення власних частот коливань консольного стрижня будуть
складати числову послідовність:
Iі 2,1 Я [її . . „	(8.55)
р, = а • к. = --V----‘	, і=1,2,...
Ь-
Для консольного стрижня, вільний кінець якого шарнірно опирається
(рис. 8.15, б), частотне рівняння набуває вигляду:
Ій(УіЬ)=іЬ(ХіЬ).	(8.56)
Приблизні значення коренів даного частотного рівняння дорівнюють:
336
Розділ 8 Математичні моделі простих механічних коливальних систем
.	1 ) Я	,	.
<8.57)
к	47 ь
Відповідні власні частоти коливань консольного стрижня з шарнірною
опорою на кінці складають:
ґ. 1? 2
1 + —	71	;--
12 <	4; ЕІ	(8.58)
р — ад- —------г---• І— .
И'	’ І?	УрР
Аналогічні викладки зроблені для стрижня з вільними кінцями
(рис. 8.15, г). В цьому випадку частотне рівняння має вигляд:
со®(\х) • сЬ^х) = 1	(8.59)
Наближені значення коренів цього рівняння складають:
Відповідно власні частоти коливань стрижня з вільними кінцями:
ґ. 1 У 2
к 2) ЕЗ	(8.61)
Рі ~ ь2 ’^РР'
Наведені математичні моделі у вигляді функціональних рядів дозволяють
виконати оцінку незатухаючпх поперечних коливань стрижнів на двох
опорах. В реальних технічних системах, які включають металеві стрижні з
розподіленою масою, затухання коливань, як правило, незначне. Тому
вигценаведені математичні моделі у вигляді функціональних рядів мають
практично важливе значення і широко застосовуються.
Розрахунок частот і форм коливань стрижнів з розподіленою масою дає
можливість оцінити наявність високочастотних резонансних областей
динамічних систем. Використовуючи ці моделі можна виконати наближений
аналіз коливальних процесів у системах з дисипацією енергії. Один із методів
побудови таких моделей розглянуто в [16].
Метод полягає у перетворенні по Лапласу залежностей, що описують
поперечні коливання стрижня (формули (8.49)-(8.51)). Одержані
зображення по Лапласу поперечних переміщень стрижня розкладаються на
суму елементарних динамічних ланок. Враховуючи відсутність затухання,
розклад на елементарні ланки включає лише консервативні ланки. Для
врахування затухання консервативні ланки замінюються коливальними. Для
одержаної сукупності коливальних ланок здійснюється обернене перетворення
Лапласа. Одержані ряди описують коливання стрижнів із врахуванням
дисипації енергії.
337
Струтинський В. Б.
8.5. Коливання круглої мембрани
Мембраною називають плоске тіло, яке не опирається згину.
Коливання круглої мембрани описуються функціональними рядами, до
складу яких входять функції Бесселя [ 1 ].
Розглянемо малі поперечні коливання мембрани з постійним натягом
о = Сотій, маса одиниці площі якої складає ц. Втрати енергії при коливаннях
мембрани не враховуються (затухання коливань немає) Поперечні коливання
мембрани загального виду описуються диференціальним рівнянням в
частинних похідних, яке називається хвильовим рівнянням:
=	(8.62)
С/
де С = — - постійна величина, яка характеризує швидкість розповсюдження
Ц
збурень по площі мембрани; О - переміщення точки мембрани в напрямку
перпендикулярному площині мембрани; Д - оператор Лапласа (лапласіан).
Розглянемо круглу мембрану, закріплену по периметру (рис. 8.18).
Рис. 8.18. Схема поперечних коливань круглої мембрани
338
Розділ 8. Математичні моделі простих механічних коливальних систем
В циліндричній системі координат р, ер, г хвильове рівняння (8.62), яке
описує коливання мембрани, має вигляд:
о2ц к і . аи і . а2и _ і . а2ц
ар2 р ар р2 а<р^ с2 зі2
(8.63)
(8.64)
Розв’язком даного рівняння є невідома функція І), яка залежить від
полярних координат р, ф і часу І. Розв’язок рівняння (8.63) знайдений у
вигляді функціонального ряду, який включає експоненціальні,
тригонометричні та спеціальні функції і має вигляд:
+'» /
и(р,<м) = Е еішс • СО5(»ф)• ЛІ тг
В залежність (8.64) входять параметри п і <о - взаємопов’язані константи,
які визначаються граничними умовами задачі і будуть знайдені нижче.
Враховуючи осьову симетрію мембрани, можна зробити висновок про
періодичність функції ІД по кутовій координаті ф, причому за фізичним
змістом задачі період цієї функції - 2л. Це означає, що в формулі (8.64)
константа п - ціле число, або нуль.
Для кожного значення п експонента, що входить у (8.64), дає залежність
переміщення точки мембрани від часу, а добуток
Ут(р,ф)= со8(шр)-
(8.65)
визначає відповідну форму коливань, частота яких відповідає деякому
заздалегідь невідомому параметру и.
Форма коливань мембрани є просторовою. Вона включає діаметральні та
кругові вузлові лінії, в яких значення переміщення точок мембрани дорівнює
нулю, і відповідно ІІт = (р, <р) = 0. Із (8.65) випливає, що діаметральні
вузлові лінії відповідають рівнянню:
соз(пф) = 0 .	(8.66)
Діаметральні вузлові лінії є діаметрами, які ділять круг на кілька однакових
секторів з кутами при вершині, рівними — . На рис. 8.19 умовно показані форми
п
коливань, що мають діаметральні вузлові лінії.
Кругові вузлові лінії є концентричними колами, радіуси яких рь
задовольняють рівнянню:
Лр7тЧ = 0’ тобто тВк = “г.Р>	(8.67)
де о:пр - один з коренів функції Бесселя Іп(х) = 0 (корінь з номером р).
Периметр мембрани, за фізичною суттю задачі, є нерухомим і повинен
відповідати круговій вузловій лінії. Тому К - радіус мембрани - задовольняє
наступному співвідношенню:
ипрКС“‘ = а„р .	(8.68)
339
Струтинський В. Б.
Рис. 8.19- Форми коливань круглої мембрани,
які мають діаметральні вузлові лінії
Значення частот коливань мембрани, що знаходяться з коренів функцій
Бесселя, утворюють нескінченний ряд:
И = 5е£.
пр К
На рис. 8.20 наведені
коливань, іцо описуються
порядку ;0(х).
кругові вузлові лінії, які визначають форми
функціями Бесселя першого роду нульового
Р = 3
Рис. 8.20. Форми коливань мембрани, які відповідають функції Бесселя
першого роду нульового порядку і мають концентричні колові вузлові лінії
340
Розділ 8. Математичні моделі простих механічних коливальних систем
Як видно із рис. 8.20, функції Бесселя Зо описують форми коливань
мембрани з опуклостями на осі симетрії.
Для функцій Бесселя, що входять у (8.65) і мають порядок п, відмінний
від 0, тобто (х), 3?(х), ..., на осі симетрії знаходиться вузлова точка, в якій
поперечне переміщення мембрани дорівнює нулю.
Як приклад на рис. 8.21 наведені вузлові лінії та форма коливань
мембрани для п = 3, р = 3. Коливання відповідають формі, яка описується
функцією Бесселя першого роду третього порядку для третього кореня
функції Бесселя.
00,746
Рис. 8.21. Форма коливань мембрани, що відповідає трьом діаметральним
та трьом коловим вузловим лініям
Розглянута математична модель коливань мембрани дозволяє виконати
оцінку динамічних процесів мембрани, які застосовуються в багатьох
технічних системах.
Математична модель, що описує форму коливань мембрани, може мати
широке застосування в інженерній практиці. Зокрема, нею можна описати
форму поверхні точної плоскої круглої деталі. Ця модель придатна для опису
макро- і мікрогеометрії поверхні. При описі мікрогеометрії коефіцієнти
функціональних рядів беруться у вигляді сукупності випадкових величин з
певними законами розподілу. Параметри моделі знаходяться як в результаті
теоретичних розрахунків, так і за даними експериментів.
341
Струтинський В.Б.
8.6. Математичне моделювання позиційних приводів
металорізальних верстатів з використанням
символьної математичної моделі
В технологічних машинах різного призначення використовуються
позиційні механічні приводи. В таких приводах між положеннями вхідного і
вихідного елементів є взаємно однозначний зв’язок (позиційний зв'язок).
Характеристики точності позиційних приводів визначаються численними
факторами як детермінованого, так і випадкового характеру. Врахування цих
факторів доцільно здійснити методами математичного моделювання.
Розглянемо ряд практично важливих конструкцій позиційних приводів.
На рис 8 22 наведена схема привода з механічною передачею у вигляді
кулісно-важільного механізму і основні параметри привода.
Рис. 8.22. Схема позиційного привода з кулісним механізмом переміщення:
у(і) - переміщення стола (вихідна координата); Рх(і) - корисне
навантаження; тс, т$ - маси стола і деталі відповідно; 1Р - момент
інерції важеля; Ср - еквівалентна жорсткість важеля; Ьн, Ьп, Ьо, ЬР -
коефіцієнти опору відповідно напрямних стола, кулісного механізму,
опори важеля та вузла переміщення важеля; х( і) - вхідна координата
342
Розділ 8. Математичні моделі простих механічних коливальних: систем
Основними нелінійностями характеристик привода є люфти і зазори в
передачах, нелінійні залежності сил опору від швидкості, а також
нелінійність, яка обумовлена поворотом важеля.
Механізм позиційного привода стола може мати різний вигляд. На рис.
8.23 показано позиційний привід, в якому переміщення стола здійснюється
передачею із зубчасто-рейковим механізмом і редуктором.
Рис. 8.23. Схема позиційного привода із зубчасто-рейковим механізмом
На схемі, показаній на рис. 8.23, позначено, зокрема, коефіцієнти опору в
елементах передачі: Ь„ - коефіцієнт опору напрямних; Ьи - коефіцієнт опору
зубчасто-рейкової передачі; Ьв - коефіцієнт опору в з’єднанні вал-втулка;
Ьо - коефіцієнт опору в підшипниках вала; Ьр - коефіцієнт опору редуктора.
Основними нелінійностями даного привода є люфти і зазори в зубчастих
передачах та нелінійні пульсацій ні залежності сил опору від переміщення та
швидкості.
Позиційні приводи призначені як для здійснення зворотно-поступального
прямолінійного руху, так і поворотного руху.
На рис. 8.24 наведені схеми приводів із поворотним столом.
Такі конструкції приводів, як правило, мають зубчасту або черв’ячну
приводну передачу і кінематичний ланцюг (редуктор).
Основними нелінійностями привода є люфти і зазори в передачах,
нелінійні сили опору. В черв’ячній передачі мають місце гістерезисні явища, а
в редукторі - імпульсні навантаження.
Приводи з поворотним столом характеризуються своїми інерційними
дисипативними та жорсткісними параметрами. Як інерційний параметр
використовується приведений до осі обертання стола момент інерції привода та
момент інерції деталі Між кутом повороту приводного вала привода фо(і) та
кутом повороту стола <ру є взаємно однозначний зв’язок. Приводи з поворотним
343
Струтинський В.Б.
столом характеризуються дисипативними коефіцієнтами, які визначають втрати
енергії в напрямних стола, підшипниках і передачах привода.
Рис. 8.24. Схеми позиційних приводів із поворотним столом:
а — із зубчастою конічною передачею; б - із черв’ячною передачею;
Ьн - коефіцієнт опору в напрямних стола; Ьп - коефіцієнт опору
в конічній чи черв'ячній передачі; Ьо - коефіцієнт опару підшипників;
Ср - еквівалентна жорсткість кінематичного ланцюга привода
Позиційні приводи часто мають гідравлічні чи пневматичні механізми
переміщення. На рис. 8.25 наведена схема позиційного привода з пневматичним
механізмом руху столам у вигляді мембранного пневмоциліндра.
На схемі показано вхідний сигнал привода у вигляді тиску р0 = х.
Основними нелінійностями привода є нелінійні залежності сил опору. Для
пневматичного мембранного привода нелінійності сил опору не є суттєвими.
Але при використанні поршневого пневмоциліндра сили опору мають суттєву
344
Розділ 8. Математичні моделі простих механічних коливальних систем
нелінійність, що відповідає силі змішаного тертя в парі поршень-гільза.

Рис. 8.25. Схема стола із одностороннім пневматичним приводом
ло
На рис. 8.26 наведено схему поширеного в технологічному обладнанні
прецизійного позиційного привода з передачею гвинт-гайка [86~89, 93, 95].
Рис. 8.26. Принципова схема (а) позиційного механічного привода
з передачею гвинт-гайка та його динамічна модель (б): у - переміщення
стола; Рх - корисне навантаження; під, тс - маси деталі та стола
відповідно; Іа - момент інерції гвинта; ІР- момент інерції редуктора;
Ьн, Ьп, Ьо, Ьр — коефіцієнти опору відповідно напрямних стола,
пари гвинт-гайка, підшипників гвинта та редуктора; ср - еквівалентна
крутильна жорсткість редуктора; Рр - зусилля, яке діє з боку гвинта
па стіл; МК)) - крутний момент в перерізі гвинта; <р - кут повороту
гвинта; Н - крок гвинта: х - кут повороту приводного вала
В даному позиційному приводі мають місце складні робочі процеси. Вони
проявляються в наявності суттєвих нелінійностей характеристик окремих
вузлів привода Основними нелініїшостями є сили сухохого та змішаного
тертя, люфти і зазори в кінематичних парах. Це, зокрема, люфт в передачі
гвинт-гайка, зазори між зубцями шестерень в редукторі, зазори в
підшипниках. В прецизійних приводах ці люфти і зазори зведені до мінімуму
345
Струтинський В. Б.
або ліквідовані зовсім.
Всі сили опору мають нелінійні складові з гістерезисом. Це стосується
напрямних стола, тертя в передачі гвинт-гайка та у підшипниках. В
прецизійних приводах сили тертя мають характеристики, близькі до лінійних.
Цього досягнуто використанням спеціальної системи змащування,
застосуванням передачі гвинт-гайка кочення.
Всі вищенаведені позиційні приводи відповідають механічній динамічній
системі із одним ступенем вільності. Для розробки математичних моделей
таких систем застосовують різні методи.
Звичайно складають рівняння рівноваги сил в динаміці, використовуючи
загальне рівняння динаміки або із застосуванням принципу Даламбера.
Більш загальним методом є використання рівняння Лагранжа 2-го роду.
Розглянемо застосування рівняння Лагранжа 2-го роду для розробки
спрощеної математичної моделі практично важливого прецизійного
механічного позиційного привода з передачею гвинт-гайка (рис. 8.26).
При розробці математичної моделі характеристики всіх окремих елементів
привода приймаються лінійними. Вважається, що всі залежності є
однозначними, люфти і зазори в кінематичних парах відсутні.
Диференціальне рівняння руху стола знайдемо використовуючи рівняння
Лагранжа другого роду, яке має вигляд [109]:
де Т - кінетична енергія механічної системи позиційного привода;
П - потенціальна енергія системи, яка визначає консервативну складову
узагальненої сили;
К - дисипативна функція Релея, яка враховує дисипативну складову
узагальненої сили;
О - узагальнена сила, що діє на привод ззовні.
Кінетична енергія системи має складові, що відповідають кінетичній
енергії стола і кінетичній енергії кінематичного ланцюга привода:
Т = |(га< +тг)’У2 +|(ів + ір)'Ф2 •
(8.70)
В передачі гвинт-гайка наявні кінематичні співвідношення між
поступальним переміщенням стола і поворотом гвинта. Вони мають вигляд:
ФУ.	1	сіф _ 1 Ну
2л Ь	2л сИ Ь сій
(8.71)
Враховуючи кінематичні співвідношення (8.71), із (8.70) знайдемо
загальну кінетичну енергію динамічної системи привода:
346
Розділ 8. Математичні моделі простих механічних коливальних систем
Кінетична енергія не залежить від переміщення у. Тому п частинна
похідна:
*І = 0.
Зу
Знайдемо частинну похідну кінетичної енергії по швидкості стола:
ат
Зу
(	\ 4л2
піс + та +(Тв +Ір/"р“
Похідна по часу частинної похідної кінетичної енергії визначається
шляхом диференціювання і відповідає залежності:
а (ат"і
ацзу;
т \ 4л2
тс +т5 +(ІВ +Ірф-р-
у = т-у,
(8.72)
де вираз в квадратних дужках є приведеною масою привода:
/	\4л2
т = тс + т5 + (Ів + ІрГ^Г 
(8.73)
Потенціальна енергія привода залежить від пружності кінематичного
ланцюга (редуктора) і складає:
П = |ср  (х - <р)2.
де Ср - еквівалентна крутильна жорсткість редуктора.
Використовуючи кінематичні співвідношення (8.71), знайдемо:
гт 1 ґ 271 У
П = 2‘4	
Частинна похідна від потенціальної енергії по переміщенню стола:
5П	(	2л 'і (	2л	2л	Ґ2лУ
-^~ = СР ’ Х~ТУ Г V Г ~ТГ‘ср ’х + V ’ср ‘у-
Зу	(.	п ; (	п 7	п	кЬ,/
Дисипативна функція Релея для динамічної системи привода:
(8.74)
*	2 й*7	2 ' н о р/т
Використовуючи кінематичне співвідношення (8.71), одержимо:
/о_\2
Ьн +
К =-
2
•у2-
Знайдемо частинну похідну дисипативної функції:
+
5К
З У
де постійна величина в квадратних дужках рівна:
ь = ьн+ґМ-(ьп+ьо+ьр)
= Ь-у,
(8.75)
347
Струтинський В. Б.
представляє собою еквівалентний коефіцієнт опору позиційного привода.
Узагальнена сила О, що діє на привод ззовні, з точністю до знака
співпадає із корисним навантаженням на деталь. Відповідно
<2 = -Рх •	(8.76)
Підставимо значення величин із (8.72), (8.74), (8.75), (8.76) в рівняння
Лагранжа другого роду (8.69) і одержимо звичайне диференціальне рівняння:
щ.у + Ь-у + ср-С^І  У ='V”'ср  х — Р .	(8.77)
и < п ) п
Таке ж рівняння можна одержати і для інших конструкцій приводів,
наведених на рис. 8.22-8.25. Відмінність рівнянь, складених для інших
приводів, полягає лише в значеннях коефіцієнтів.
Виконаємо аналіз математичної моделі привода у вигляді рівняння (8.77).
Розглянемо рух стола в окремому випадку, що відповідає усталеному
рівномірному обертанню гвинта. При цьому:
X = <о06 ,	(8.78)
де и0 - постійна кутова швидкість обертання гвинта.
Введемо нову змінну у вигляді відносного зміщення стола:
Уд=У-уо-і>	(8.79)
де у0 - постійне значення швидкості стола.
Ця змінна визначає відхилення положення стола від його номінального
(8.80)
значення.
Знайдемо похідні змінної у д :
уд=у-уо; уд=у-
Із залежностей (8.79) та (8.80) знайдемо:
У = Уд + уо ’ ; У = УД+VО.	(8.81)
Підставимо величини із (8.80) та (8.81) у диференціальне рівняння (8.77)
і одержимо
(8.83)
(8.84)
(2яУ	(2л	2л
тУд + Ьуд + Ьу0 + сР уд + ср уоі = "т~Ср 	- Рх.	(8.82)
( п )	у П )	п
Із кінематичного співвідношення (8.71) випливає:
2л
= -^0 
п
Враховуючи дану залежність із (8.82) одержимо рівняння руху стола у
відхиленнях відносно номінального значення положення стола:
,. Ґ2лУ к п
туд + Ьуд + сР —- уд = -Ьу0 - Рх.
( п )
В правій частині рівняння з’явилася постійна складова, яка і
постійній (квазістатичній) силі опору, що має місце при русі <
складова не впливає на динамічну точність позиціювання привода.
Перейдемо до нової змінної в диференціальному рівнянні (8.84):
відповідає
стола. Ця
348
Розділ 8. Математичні моделі простих механічних коливальних систем
Т =
(8.85)
(8.86)
(8.87)
поданій у
(8.88)
(8.89)
Ьу0 ( ь У
V = УД + — • — •
С р у 27Г у
Введемо нові коефіцієнти, які зв’язані з параметрами привода:
ь . ь . к _ ь2
4л ^тср	4л сР
При цьому диференціальне рівняння (8.84) набуде вигляду:
л2у	НУ
Т2^4- + 2£Т—— + ¥ = КРХ.
аі2	аі
Це рівняння є математичною моделлю привода,
нормалізованому (стандартному) вигляді.
Для аналізу динамічних процесів у приводі використаємо динамічну
характеристику системи у вигляді перехідної функції. Перехідна функція
привода визначає відхилення положення стола від номінального значення при
ступінчастій зміні нормованого корисного навантаження на стіл у вигляді:
(1 при
х [0 при
Рівняння (8.87), в якому сила визначена одиничною ступінчастою
функцією (8.88), описує динаміку процесу позиціювання привода.
Дане рівняння є звичайним диференціальним рівнянням другого порядку
з постійними коефіцієнтами і ненульовими початковими умовами:
я2у	я у
Т2 44 + 2^т4— + ¥ = К  1(0.
сШ	<11
Початкові умови для цього рівняння визначаються положенням і
швидкістю стола в деякий (нульовий) момент часу:
б¥
при і = 0	¥ = ¥0, 4- = Уо .
аг
Для розв’язку диференціального рівняння (8.89) складемо відповідне
йому характеристичне рівняння:
Т2 • г2 + 2фГ • г + 1 = 0 ,
де г - деяка змінна, визначена в полі комплексних чисел.
Корені характеристичного рівняння є комплексними спряженими:
2
Г1,2 ~ у ± у
Розв’язок диференціального рівняння, який відповідає парі комплексних
спряжених коренів характеристичного рівняння, має вигляд:
¥ = К + С.е т  зів
(8.90)
’2
Т
де перший доданок в правій частині (8.90) відповідає окремому розв’язку
неоднорідного рівняння (8.89), а другий доданок - загальному розв’язку
349
Струтинський В. Б.
однорідного рівняння. Постійні інтегрування С] та С2 визначаються із
початкових умов.
Для визначення постійних знайдемо похідну розв’язку:
—  Є т • 81П
Т
ау „
— = Сл
аі 1
--------------і: + С
Т
-----СО8
Т
'2
£
т
(8.91)
Для знаходження постійних інтегрування з початкових умов та залежності
(8.90) випливає система рівнянь (при 1 = 0):
'¥(і^=0=У0=К + С1-8ІпС2
ау
ас
1=0" Уо - С,<
-£ 2
у----СО8 С2
(8.92)
Е
- — • 8іп С, >
т 2
З першого рівняння системи (8.92)
постійними інтегрування:
С, • зіп(С2) = ¥0 - К .
Використавши дане співвідношення виразимо константу С] через С^.
Підставимо значення величини Сі в друге рівняння системи (8.92),
одержимо трансцендентне рівняння для знаходження невідомого €3:
1___
Т і£С2 Т ‘'
Звідси знайдемо значення постійної Сз в функції початкових умов і всіх
параметрів привода:
знайдемо співвідношення між
Уо=(¥о-К)
С2 = агсід-
Т-Уо
і
Враховуючи зв’язок між тригонометричними функціями, знайдемо:
зкі(С,) = -/8(сд)
Відповідно одержимо співвідношення між постійними інтегрування:
С (Уо-к)-7і + і§2(с2)
№
Підставивши значення постійної С2, знайдемо постійну Сі в функції
початкових умов і параметрів привода:
с,=(^Ьу4+25.^+1
1	'	ІІІ V Т7 І	—- К.
о
350
Розділ 8. Математичні моделі простих механічних коливальних систем
Таким чином, розв'язок рівняння (8.89) для ненульових початкових умов'
у(И - к + АХ + АгУ,,(У, - К)-І-(У„ - К)7 -А .
71-Є
X 5ІП
ТГч2 4
....... 1 + агс1§
Для нульових початкових умов ¥0
1%
¥0 - К
= У() - 0 розв’язок рівняння (8.89):
(8.94)
1
¥(е) = К • (1 -
 е т • 8ІП
------£ + агс1§
1
(8.95)
Розв’язок (8.94) визначає відхилення положення стола від номінального
значення Це відхилення являє собою основну складову динамічної похибки
позиніювання привода. Динамічна похибка залежить від випадкових параметрів
привода, які враховуються в значеннях постійних величин К, Т та
випадкових початкових умов ¥о, Уд.
Функціональна залежність (8.94) являє собою символьну математичну
модель, яка визначає динаміку позиційного привода верстата.
Для визначення впливу випадкових параметрів на динамічну похибку
привода виконані розрахунки перехідних процесів. Розрахунки проведені в
програмному середовищі МаФСАО 8. Нижче наведено приклад аналізу
процесу позиціювання конкретного привода металорізального верстата. На
рис. 8.27 наведено розрахований ансамбль реалізацій випадкового процесу зміни
положення стола при ступінчастій зміні сили різання.
351
Струтинський В. Б.
Залежності одержані розрахунком за формулою (8.94). Початкові
значення положення стола ¥0 та його швидкості Уо були задані як випадкові
числа з рівномірним законом розподілу, параметри і Т прийняті
постійними. Значення коефіцієнта К задавалось генератором випадкових
чисел з нормальним законом розподілу.
Із аналізу результатів розрахунків випливає, що динамічна похибка
змінюється за затухаючим гармонічним законом з періодом 6...8 мс.
Амплітуда динамічної похибки досягає 80 % від статичного значення похибки,
що має місце після затухання перехідного процесу.
На рис. 8.28 показано вплив випадкової зміни коефіцієнтів опору привода
на динамічну похибку позиціювання.
Рис. 8.28. Вплив випадкового значення сил опору, що задається
коефіцієнтом £, на динамічну похибку процесу позиціювання стола
Зміна сил опору мало впливає на період коливань стола при його виході в
позицію. Зміна періоду коливань не перевищує 10 % від середнього значення.
В той же час випадкові зміни сил опору суттєво впливають на амплітуду
коливань та швидкість затухання перехідного процесу. Зменшення сил опору
на 20 % в 2 рази зменшує максимальну похибку привода та скорочує час
перехідного процесу в 5 і більше разів.
На рис. 8.29 наведено ансамбль реалізацій перехідного процесу в приводі
при випадкових змінах постійної часу привода (параметра Т).
Зміни параметра Т майже не впливають на значення максимальної
динамічної похибки, але суттєво впливають на період (частоту) коливань.
Зміни періоду визначаються в основному жорсткісними параметрами привода.
Звичайно випадкові параметри привода змінюються в обмеженому діапазоні
(±5 %) При цьому суттєвих змін перехідного процесу не спостерігається.
Ансамбль реалізацій перехідного процесу займає обмежену вузьку смугу.
352
Розділ 8 Математичні моделі простих механічних коливальних систем
¥(1, 2, Т)
¥(1,3 Ті)
¥(1. 4. Т2)
¥(1. 5, ТЗ)
¥(1, 6, Т4)
Рис. 8.29. Вплив випадкового значення параметра Т на динамічну похибку
процесу позиціювання стола
На рис. 8.30 наведено ансамбль реалізацій перехідного процесу привода
при випадкових змінах як параметрів привода, так і початкових умов
перехідного процесу. Загалом значення перехідних функцій, що відповідають
різним реалізаціям, розрізняються на 1...3 %.
Рис. 8.30. Масив реалізацій перехідного процесу при випадкових змінах
всіх параметрів привода та початкових умов
353
Струтинський В. Б.
Для знаходження статистичних характеристик перехідного процесу виконана
статистична обробка ансамблю реалізацій і знайдені математичне сподівання та
розсіяння перехідної функції. Для цього використані формули усереднення.
Перехідна функція е суттєво нестаціонарним випадковим процесом. Математичне
сподівання перехідної функції залежить від часу і знаходиться за формулою:
¥(О = ІУ¥І(О,
N
де ¥;(!) - і-та реалізація перехідної функції, яка визначається залежністю (8.94)
для деякого набору випадкових параметрів привода і випадкових початкових
умов.
Середнє значення відносної швидкості переміщення привода знаходиться як
7(0 =	,
а дисперсія перехідної функції обчислюється за формулою:
ЇМ ~ 1
Розрахункові значення математичного сподівання перехідної функції та
середнього значення швидкості наведені рис. 8.31.
Рис. 8.31. Математичні сподівання переміщення стола (крива 1)
та його швидкості (крива 2) при ступінчастій зміні зусилля різання
В результаті проведених досліджень виконано теоретичне узагальнення
впливу різноманітних параметрів, які змінюються випадковим чином, на
показники динамічної якості привода. Результати досліджень послужили
основою для вдосконалення гами прецизійних позиційних приводів
металорізальних верстатів [75, 82, 83, 86-88, 90, 93, 95, 98]. Розроблена
математична модель є простим і ефективним засобом дослідження
стохастичних процесів позиціювання привода металорізального верстата.
354
Розділ 9. Математичні моделі прогресивних технологічних процесів
РОЗДІЛ 9
Математичні моделі прогресивних технологічних процесів
механічної та фізико-технічної обробки деталей
9.1. Математичний опис мікро- і макрогеометрії
деталей типу тіл обертання
Математичний опис мікро- і макрогеометрії, деталей типу тіл обертання
здійснено з використанням функціональних рядів на базі спеціальних
функцій [94]. Розроблені методи математичного опису мікро- і макрогеометрії
деталей типу тіл обертання використовують різні функціональні ряди. Для
циліндричних поверхонь використовують ряди Фур’є та ряди, складені із
гіперболічних функцій, а для торцевих поверхонь - ряди Фур’є-Бесселя.
Опис мікрогеометрії поверхні деталей дано у вигляді канонічного
розкладу випадкового процесу [10, 60, 63], координатні функції якого
відповідають складовим вищеназваних рядів.
Оцінка точності обробки деталей типу тіл обертання звичайно
здійснюється за допомогою системи допусків на лінійні та діаметральні
розміри, а також допусків форми і взаємного розташування поверхонь. При
цьому вводяться деякі інтегральні показники відхилень розмірів, форми і
розташування поверхонь. Для підвищення якості оцінки точності обробки
деталей доцільно застосовувати більш досконалі детальні методи оцінки
точності. Введення деталізації в методику оцінки потребує застосування
відповідного математичного апарату і значного обсягу обчислень, але для
наявних засобів обчислювальної техніки ці фактори не є суттєвими.
Розроблені методи оцінки точності придатні для деталей різного виду.
Найбільш ефективно ці методи застосовуються для плоских деталей та
деталей типу тіл обертання складної форми.
Розглянемо типову деталь з класу тіл обертання (рис. 9.1).
Вісь деталі 7 приймається за базу відліку координат реальної поверхні.
Всі поверхні деталі розділено на дві різнорідні групи в залежності від їх
розташування відносно осі. До першої групи віднесено поверхні, твірні лінії
яких паралельні осі або нахилені до осі під деяким кутом а « 90°. На
рисунку це циліндричні поверхні 2, 5, 7, 10 та криволінійна поверхня 8.
До другої групи віднесено поверхні, перпендикулярні осі, а також
поверхні, твірні лінії яких нахилені до осі під кутом Р « 90°. На рис. 9.1 це
торцеві поверхні 1, 3, 6, 9 та конічна поверхня 4.
355
Струтинський В. Б,
Рис. 9-1. Характерні поверхні типової деталі з класу тіл обертання
Номінальна форма деталі задана кресленням, в якому визначено контур
Ь, обертання якого навколо осі утворює номінальну просторову форму деталі.
Контур Ь може бути заданий аналітично у вигляді різних залежностей для
різних груп поверхонь. Для поверхонь першої групи (циліндричних) контур
задано у вигляді залежності від осьової координати г по ділянках і:
Ц = £;(/), і = 2, 5, 7, 8, 10, Рі = сопзі.	(9.1)
Для поверхонь другої групи (торцевих) контур задано у вигляді
залежності від радіальної координати р по ділянках у а саме:
Ьі = Ц(р), ) = 1, 3, 4, 6, 9, 11,	2, = соизЬ.	(9.2)
Оцінка точності обробки деталей здійснюється введенням функції
відхилень 11, що залежить від трьох просторових координат: осьової відстані
2, радіуса р та полярного кута ф. Функція відхилень визначає відстань по
нормалі від точки номінального контуру до точки реальної поверхні деталі.
Фактично функція відхилень для першої групи поверхонь (циліндричні
ділянки контуру Ь, (г)) залежить лише від координат г, ф і не залежить від
радіуса р, тобто функція відхилень:
Ц = І)/?, ф).	(9.3)
Для другої групи поверхонь (торцеві ділянки контуру Ь|(р)) функція
відхилень залежить лише від координат р, <р. В цьому випадку:
Ц = Ц(р, ф).	(9.4)
Функцію відхилень для всього класу деталей типу тіл обертання
запропоновано подати у вигляді добутку функціональних рядів, складених із
універсальних базисних функцій однієї змінної:
2к(2), Фт(ф), Кп(р).
Дані функції залежать від відповідних просторових координат. Число
базисних функцій вибирається в залежності від необхідної точності
математичного опису поверхонь. Таким чином, функція відхилень для
356
Розділ 9. Математичні моделі прогресивних технологічних процесів
циліндричних поверхонь визначена у вигляді добутку:
Пі(г,ф) = 2(г)’ф(ф) = £Ф„,(ф)’ Е2к(р),	(9.5)
т=0	к=0
де М - число складових функціонального ряду, складеного із базисних
функцій Фт(ф), які залежать від полярного кута ф;
К - число членів ряду, складеного із базисних функцій 2к(г).
Для торцевих поверхонь функція відхилень має вигляд:
Ц(р,ф) = К(р)-Ф(ф) = Ефп>(ф)'ЕКп(р),	(9.6)
т-0	п-0
де N ~ число членів ряду, складеного із базисних функцій Кп(р).
Така форма математичного опису реалізує розділення змінних по
просторових координатах р, ф, г.
Базисні функції під знак сум (9.5) та (9.6) включають в себе довільні
константи, тому вони можуть бути домножені на величини, що не залежить
від аргументів. Відповідно обидві формули (9.5), (9.6) можна об’єднати і
записати у загальному вигляді:
и(р,ф,2)= Ф(ф)-2(х)-Н(р)= £фт(ф)-£2к(г)- £к„(р).	(9.7)
т=0	к=0	п=0
Дана залежність буде мати місце для поверхонь деталі як першої
(циліндричних), так і другої (торцевих) групи, і відповідає кожній
конкретній ділянці контуру деталі Б.
Функція відхилень визначена для полярного кута ф = О...2л. Значення
функції для кутів ф = 0 та ф = 2л співпадають, тому функція відхилень 15 є
періодичною з періодом 2л по змінній ф. Відповідно базисні функції Фт(ф) є
періодичними з періодом 2л. Для опису таких залежностей найбільш доцільно
взяти складові ряду Фур’є, і базисну функцію визначити як
Фт(ф) = С1т’С08(п)ф) + С2т-8іп(тф),	(9.8)
де С1т і С2т - постійні коефіцієнти базисної функції (в загальному вигляді
можуть залежати від координат гір).
Коефіцієнти ряду Фур’є зв’язані зі значенням функції залежностями:
1 2,1
С1т = — |ф(ф)- соз(тф)сіф ;
" І	(9.9)
С2т = — |ф(ф)- 8іп(тф)сІф , т = 0, 1, 2,...
71 о
Визначення коефіцієнтів ряду С1т та С2т для реальних поверхонь
проведено за спеціальною методикою, тка враховує некоректність постановки
задачі знаходження коефіцієнтів ряду Фур’є функції, визначеної неточно, та
здійснює регуляризацію некоректно поставленої задачі знаходження
коефіцієнтів (див. розділи 4.2.3 та 7.2.2).
Базисні функції 2к(г) в загальному вигляді не є періодичними. Вони
357
Струтинський В.Б.
визначають залежність функції відхилень від осьової координати в перерізі
деталі поздовжньою площиною, що проходить через вісь деталі. На рис. 9.2
показані можливі форми перерізу поздовжнього контура деталі для поверхонь
першої групи.
2к(г)
0	1	2
Рис. 3.2. Характерні форми контуру деталі, які мають місце
для поздовжнього перерізу циліндричних поверхонь: 1 - контур близький
до періодичної кривої, який відповідає тригонометричній базисній функції;
2 - контур у вигляді неперіодичної кривої з особливостями на межах
(похідна залежності прямує до ж), який доцільно описувати
гіперболічною базисною функцією
Можливі два якісно відмінні випадки. Перший відповідає приблизній
рівності функції опису контуру відхилень на початку і в кінці ділянки (крива
1 на рис. 9.2). При цьому:
Д2К = 2К(1) - 2к(0); 2к(0) ® 2К(1),	(9.10)
де І - довжина ділянки.
Враховуючи приблизну рівність значень функції на початку і в кінці
ділянки її можна вважати періодичною з періодом 1. Для математичного опису
даної залежності використано тригонометричний ряд, базисні функції якого
мають вигляд:
2к1(г) = С)к • соз^2лк-|^ + С2к • зіп^лк ,	(9.11)
де СІК і С2к - постійні коефіцієнти, які в загальному вигляді залежать від ф.
Другий випадок відповідає контуру у вигляді неперіодичної функції з
особливостями на межах інтервалу (крива 2 на рис. 9.2). Для опису такої
функції можна використовувати залежність (9.11), в якій період функції
прийнятий рівним 21, а базисна функція включає тільки косинусну складову.
В деяких випадках такий опис контуру неможливий в силу особливостей
твірної лінії контуру на межах ділянки. Наприклад, це має місце у випадку,
коли похідна контуру на межі ділянки набуває достатньо великих значень.
Для опису контуру при наявності таких випадків доцільно використовувати
ряд, складові якого є сумою гіперболічних функцій.
358
Розділ 9. Математичні моделі прогресивних технологічних процесів
Базисні функції при цьому мають вигляд:
2^2(2) = Сзк’сЬ(кдг) + С4к-8Ь(1щг),
де ц - параметр, що залежить від форми твірної лінії даної ділянки.
Для поверхонь деталі, віднесених до другої групи (торцевих)
математичний опис повинен враховувати особливість функції при р = 0 (на
осі деталі). Складову К(р) функції відхилень для даних поверхонь
запропоновано описувати рядом Фур’є-Бесселя (див. розділ 4.13).
Базисні функції при цьому визначаються залежністю:
Кп(р) = ап-І0(рп-р),	(9.12)
де ап - постійні коефіцієнти ряду (в загальному випадку коефіцієнти
залежать від полярного кута ср);
рп - послідовні корені функції Бесселя пертого роду нульового порядку:
•ІО (х) = 0.
Коефіцієнти ряду Фур’є-Бесселя для відносних значень радіуса в
інтервалі р = [0; 1] зв’язані із значенням функції наступними залежностями:
9	1
а„ = тттЧр (р ‘ К(р)’ Л(р„рИр ,
Мі\Рп)1 0
(9.13)
де 51 - функція Бесселя першого роду першого порядку.
В загальному вигляді функція відхилень форми поверхні деталі
визначається залежністю (9.7). Підставивши в неї значення базисних функцій
(9.8), (9.11), (9.12), одержимо формулу, яка описує реальну форму поверхні
деталі по всіх ділянках контуру:
Г м
и(р,Ф,2) = £с,т • соз(кф) + С2т • 8іп(кф)
_т=0
К	/
£С1к • соз 2лк— І +
_к7о	І	У
(	2 |
2к - 8іп1 2лкуІ + Сзк
• сЬ(кдх) + С4к • 8й(кЧг) • £а„ • }0(р„,р) . <9.14)
В формулі (9.14) перша сума в правій частині описує зміну форми
перерізу деталі в залежності від полярного кута ф. Зміна функції відхилень в
залежності від полярного кута ф визначає форму циліндричних поверхонь,
зокрема їх ексцентричність, овальність, огранку.
Па рис. 9.3 наведені типові форми деталі в перерізі циліндричної
поверхні, які відповідають базисним функціям виду (9.8).
В залежності від номера базисної функції вона описує відповідну
особливість реального контуру деталі (див. розділ 4.3.1).
Базисна функція з номером ш — 0 відповідає колу з центром на осі деталі.
Функція з номером т = 1 при значеннях констант С4т, С2т, набагато менших
за діаметр деталі, відповідає колу, центр якого зміщено відносно осі деталі.
Базисна функція при ш = 2 (рис. 9.3, а) описує овальність перерізу, а базисні
функції з т = 3, 4, 5, б,... описують огранку поверхні деталі відповідно по З,
4, 5 та більше гранях (рис. 9.3, б, в).
359
Струтинський В. Б.
Рис. 9-3- Форми перерізу циліндричної ділянки деталі, що відповідають
базисним функціям виду: Фт(ср) = Сітсоз(т<р) + С^іпбтср)
Загалом сума базисних функцій дозволяє описати довільний контур
деталі. Як приклад на рис. 9.4, а наведено контур деталі у вигляді гладкої
замкненої лінії. Вона описана за допомогою базисних функцій виду (9.8).
Рис. 9-4. Довільний контур циліндричної поверхні деталі,
який відповідає обмеженій сумі базисних функцій виду (9.8)
Наведені на рис. 9.3 та 9.4 форми контуру деталі, якщо їх розглянути не
в полярній, а в декартовій системі координат, відповідають математичному
опису перерізу деталі поздовжньою площиною за допомогою базисних
функцій, що відповідають формулі (9.11). Такими функціями можна описати
зміщення контура (к = 0), поздовжню синусоїду на поверхні деталі (к = 1), а
також хвилястість поверхні із різним числом хвиль к = 2, З,...
За допомогою базисних функцій гіперболічного виду, описуються
поздовжні перерізи деталі спеціального виду.
Торцеві поверхні деталі описуються базисними функціями, вигляд яких
відповідає формулі (9.12). На рис. 9.5 наведено розрахункові перерізи
опукло-ввігнутих і хвилястих торцевих поверхонь деталей, які описані за
допомогою ряду Фур’є-Бесселя.
360
Розділ 9. Математичні моделі прогресивних технологічних процесів
Рис. 9.5. Форма опукло-ввігнутих (1) і хвилястих (2)
торцевих поверхонь деталей, описаних рядом Фур’є-Бесселя
На межах інтервалу зміни радіуса (точка р = 1 кривої 2 на рис. 9.5)
можливі характерні короткоперіодичні осциляції розрахункового контура, які
аналогічні явищу Гібса для ряду Фур’є (див. розділ 4.2.2).
Застосування базисних функцій, що відповідають формулі (9.12),
дозволяє описати функцію відхилень торцевих поверхонь різного виду. На
рис. 9.6 наведені розрахункові перерізи тороіюдібних торцевих поверхонь,
зокрема на рис. 9.6, а - переріз, близький до синусоїди, а на рис. 9.6, б -
переріз, в якому наявні зміни кривизни значення функції відхилень.
Рис. 9.6. Тороподібні перерізи торцевих поверхонь, описані базисними
функціями виду Рп(р) = ап /цбрп, р): а — поверхня, близька до синусоїди;
б - поверхні зі зміною кривизни по радіусу (поверхня з осциляцією
функції відхилень)
Запропонована методика допускає узагальнення математичного опису на
випадок врахування мікрогеометрії поверхні деталі. При цьому
функціональні ряди продовжуються у високочастотну область, де вони
361
Струтинський В. Б.
трансформуються в канонічний розклад випадкового процесу, що описує
закономірності мікрогеометрії поверхні деталі.
Як приклад розглянемо функціональний ряд, який описує функцію
відхилень в тангенціальному напрямку при наявності випадкового процесу,
що відповідає мікрогеометрії поверхні деталі. В загальному вигляді
функціональний ряд записується в формі:
м	мг
Ф(<р)= £фт(ф)+ Хф’т(ф),	(9.15)
т=0	т-М1
де перша сума в правій частині відповідає детермінованим відхиленням
контуру, а друга сума представляє собою канонічний розклад
високочастотного випадкового процесу, що відповідає мікрогеометрії поверхні
деталі.
Координатні функції канонічного розкладу (9.15) вибрані у вигляді
синусної та косинусної функцій, тому базисна функція для опису випадкового
мікрорельєфу поверхні має вигляд:
Фп, («>) = < СО8(піф) + \’*т 8Іп(гЛф) ,	(9.16)
ДЄ ит >	~ випадкові величини з певним законом розподілу ймовірності.
Дані випадкові величини при розрахунках контуру деталі визначаються за
результатами вимірів або задаються генераторами випадкових чисел з
рівномірним чи нормальним законами розподілу. Канонічний розклад
застосовується для високочастотних процесів (М) » М у формулі (9.15)).
Звичайно число складових канонічного розкладу приймається достатнім для
опису всього спектра випадкових відхилень (Мз - Мі » М).
Запропонований математичний опис функції відхилень реальної форми
деталі від її номінальних значень дозволяє визначити детерміновані та
випадкові похибки обробки. Цей метод доцільно використати для аналізу
мікро- і макрогеометрії оброблених поверхонь, зокрема для визначення
показників опуклості, ввігнутості, бочкоподібності, конусності,
неплощинності, а також взаємного розташування поверхонь (биття,
неперпендикулярності тощо). Застосування запропонованого методу дозволяє
підвищити якість оцінки точності деталі.
Математичний опис мікро- та макрогеометрії деталей типу тіл обертання
можна легко узагальнити на опис будь-якого параметра деталі, який
визначено на її поверхні. Такими параметрами можуть бути твердість,
залишкові напруження, параметри шорсткості поверхні, наприклад,
середньоарифметична величина мікро нерівностей (Ка) та інші.
362
Розділ 9- Математичні моделі прогресивних технологічних процесів
9.2.	Спектральний аналіз форми поверхні, одержаної
в результаті обробки на токарному верстаті
Металорізальний верстат являє собою складну динамічну систему, що
містить сотні окремих масивних жорстких деталей, з’єднання яких між собою
потребує створення прецизійних спряжень. Динамічні процеси, що
супроводжують роботу металорізального верстата, відзначаються значною
складністю. Це обумовлено нелінійними характеристиками основних
елементів динамічної системи, зокрема контактних деформацій в прецизійних
з’єднаннях деталей верстата. Динамічні процеси, які супроводжують роботу
верстата, є стохастичними. Динамічна якість верстата визначає сталість руху
інструмента і деталі, що обробляється, а також переміщення ланок системи
при зовнішніх впливах, що змінюються у часі. Ці параметри залежать від
характеристик пружної системи, власних частот коливань, динамічної
деформативності ланок і схем їх навантаження.
Основні показники динамічної якості верстата наступні:
-	найбільш продуктивний режим роботи верстата, що допускається
сталістю різання при можливих відхиленнях його параметрів, зокрема
найбільша ширина зрізу, що визначає, продуктивність обробки;
-	амплітуда відносних коливань інструмента і деталі по нормалі до
поверхні, що обробляється при різанні та на холостому ході;
-	швидкодія виконання допоміжних рухів елементів протягом всього
циклу обробки деталі;
-	надійність безперервної автоматичної роботи верстата протягом досить
тривалого часу;
-	шум і коливання основи, на якій встановлений верстат.
Запропонована методика визначення показників динамічної якості
базується на спектральному аналізі форми обробленої поверхні, одержаної
при обробці заготовок спеціального виду. Заготовки мають зовнішні поверхні,
сформовані у вигляді випадкових процесів з наперед визначеними
статистичними характеристиками [92, 106].
Здійснена обробка базової заготовки із спеціальним профілем, що має
прямокутні виступи, висота яких є випадковою величиною (рис. 9.7).
Базова заготовка була розроблена і виготовлена з метою забезпечення
необхідних статистичних характеристик випадкового контуру її зовнішньої
поверхні. Ескіз розробленої базової заготовки наведений на рис. 9.8.
Контур заготовки представляє собою випадковий процес у вигляді
прямокутних виступів однакової ширини, висота яких змінюється як
випадкова величина з нормальним законом розподілу. Визначимо статистичні
характеристики даного випадкового процесу, а саме: кореляційну функцію та
спектральну щільність.
363
Струтинський В.Б
Рис. 9- 7. Обробка базової заготовки з прямокутними виступами
однакової ширини, розташованими рівномірно по периферії,
причому висота виступів є випадковою величиною
Рис. 9.8. Ескіз базової заготовки з прямокутними виступами,
висота яких є випадковою величиною
Протяжність імпульсу позначимо як уТ, середнє значення амплітуди
імпульсів визначено як середнє арифметичне висоти:
х=Т7Ех>-	(9.17)
і'і і=і
Середньоквадратичне значення амплітуди імпульсів:
364
Розділ 9. Математичні моделі прогресивних технологічних процесів
Хск=ДЕХі-	(9.18)
Розглянемо випадковий процес у вигляді прямокутних періодичних
імпульсів, які діють з кроком Т (рис. 9.9, а).
а)	б)	в)
Рис. 9.9. Випадковий процес, що відповідає заготовці з періодичними
імпульсами однакової ширини і випадкової амплітуди, (а) та складові
процесу у вигляді однакових імпульсів (б) та випадкових імпульсів,
математичне сподівання яких дорівнює нулю (в)
Розкладемо загальний випадковий процес у вигляді прямокутних
періодичних імпульсів на дві окремі складові:
х(і) = Х((0 + х2(0 .
Першу складову х/0 виберемо у вигляді постійних прямокутних
імпульсів, амплітуда яких дорівнює середньому значенню вихідного процесу
х (рис. 9.9, б). Другу складову одержимо як центрований випадковий процес
у вигляді знакозмінних імпульсів випадкової амплітуди (рис. 9.9, в).
Складову у вигляді постійних прямокутних імпульсів х,(і) розкладемо в
нескінченний ряд Фур’є в комплексній формі (див. розділ 4.2):
юо	. 2пкІ
х1(0= £ск-е' т , і =	,
к=-оо
де ск - комплексні коефіцієнти ряду;
Т - період дії прямокутних імпульсів.
Згідно [6], модулі комплексних коефіцієнтів дорівнюють:
N = Л-8іп(ктгу) ,
кя
(9.19)
(9.20)
де у - коефіцієнт ширини імпульсу (див. рис. 9.9, а).
Враховуючи, що спектральна щільність гармонічної функції відповідає
дельта-функції, одержимо для окремої гармоніки розкладу (9.19), а саме для:
.2 які
хк(0 = ске'т -	(9-21)
відповідну їй складову спектральної щільності:
365
Струтинський В. Б.
/ \ тг і із сч 2лк ]	_л
8к(®) = 2 Іск! 5І ® —	0-22)
Загалом спектральна щільність складової х/0 буде одержана у вигляді
нескінченної суми, що включає дельта-функції і має вигляд лінійчастого
спектра (визначається за формулою):
/ х Vі х28іп2(клу) ( 2тткЛ	.
5/и) = 2,----772—5 “ —7~ Ґ	(9 23)
кХ 2як < Т )
Спектральні характеристики, що визначають випадкові зміни контуру
базової заготовки розраховані за формулою (9.23) для конкретних
геометричних параметрів контуру заготовки, наведено на рис. 9.10.
Рис. 9.10. Спектральна щільність періодичної складової
випадкового процесу, що описує контур базової заготовки
На рисунку висота лінії відповідає множнику при дельта-функції.
Спектральна щільність випадкової х2(і) складової центрованого процесу
у вигляді імпульсів випадкової амплітуди згідно [6] визначається залежністю:
де ст = 7х?к -х~ задано у відповідності з формулами (9.17) та (9.18).
Спектральні характеристики, що визначають випадкові зміни контуру
базової заготовки і розраховані за формулою (9.24) для конкретних
геометричних параметрів контуру, наведені на рис. 9.11.
Враховуючи, що функція спектральної щільності парна, тобто
8(<о) = 8(-о) ,	(9.25)
розглянуто спектральну щільність лише в інтервалі со є [0, +оо[.
366
Розділ 9. Математичні моделі прогресивних технологічних процесів
Рис. 9.11. Спектральна щільність центрованої випадкової складової
процесу, що описує контур базової заготовки
Разом з базовою заготовкою, розроблені та використані заготовки з
випадковими профілями іншого виду. Заготовка з прямокутними виступами
різної ширини (рис. 9.12) має виступи однакової висоти, канавки між
виступами мають постійну ширину, а ширина виступів є змінною випадковою
величиною з нормальним законом розподілу.
Особливістю заготовки є деяка відмінність форми виступу від
прямокутної форми. Це обумовлено особливостями технологічного процесу
виготовлення заготовки. Канавки між виступами обробляються дисковою
фрезою постійної товщини за один прохід, тому виступи мають невелике
розширення у напрямку збільшення радіуса заготовки.
На рис. 9.13 дано ескіз третього варіанта заготовки. Заготовка має
однакові прямокутні виступи, ширина канавок між якими є випадковою
величиною з нормальним законом розподілу.
Всі розглянуті заготовки виконані з одного матеріалу і мають однакові
поверхні для закріплення в патроні верстата. При виготовленні заготовок
використана спеціальна технологія, і похибка виконання розмірів ширини
виступів і пазів не перевищувала ±0,01..±0,05 мм. Номінальні усереднені
значення ширини виступів та пазів складали 6 мм, а висоти виступів - 10 мм.
Тому максимальні відносні відхилення дійсного контуру заготовки від
розрахованого випадкового процесу не перевищували 8 %. Середні значення
відхилень були значно менші та складали 1..3 % від номінальних розмірів.
Обробка заготовок виконувалась на новому токарно-гвинторізному
верстаті мод. КА280 виробництва АТ “Веркон”.
В процесі обробки здійснювалися виміри параметрів вібрацій різця та
корпуса шпиндельної бабки. Оброблена поверхня вимірювалася з метою
визначення параметрів точності її виготовлення (рис. 9.14).
367
Струтинський В.Б.
а)
Рис. 9-12. Креслення заготовки з радіальними виступами,
ширина яких є випадковою величиною, (а)
та обробка даної заготовки на токарному верстаті (б)
368
Розділ 9. Математичні моделі прогресивних технологічних процесів
Рис. 9-13- Креслення заготовки з однаковими радіальними виступами,
відстань між якими є випадковою величиною
Рис. 9.14. Вимірювання обвідної обробленої поверхні заготовки з
однаковими виступами, відстань між якими є випадковою величиною
Вимірювання геометрії обробленої поверхні проведені кількома методами.
Безпосередньо на верстаті після обробки зроблені вимірювання обвідної в
різних перерізах заготовки. Вимірювання ординат обвідної здійснені
індикатором з ціною поділки 0,001 мм. При цьому шпиндель верстата
повертався вручну з дискретністю по куту повороту шпинделя 3°.
Додатково вимірювання форми перерізу обробленої поверхні
виконувалися на кругломірі. На рис. 9.15 наведено одержані типові
круглограми оброблених поверхонь для розглянутих заготовок різного виду.
369
Струтинський В.Б.
Рис. 9-15. Круглограми поверхонь, одержаних при обробці заготовок
спеціального виду на верстаті КА280: а, б, в - круглограми поверхні,
одержаної при обробці заготовки з прямокутними виступами, ширина
яких є випадковою величиною з нормальним законом розподілу; г, д, е -
круглограми поверхні, одержаної при обробці базової заготовки
з прямокутними виступами, висота яких є випадковою величиною
з нормальним законом розподілу; ж, з, і - круглограми поверхні, одержаної
при обробці заготовки з однаковими прямокутними виступами, ширина
пазів між. якими є випадковою величиною з нормальним законом розподілу
370
Розділ 9. Математичні моделі прогресивних технологічних процесів
В результаті аналізу круглограм встановлено, що форма циліндричної
обробленої поверхні в різних перерізах по довжині поверхні є ідентичною.
Геометричні параметри перерізів відрізняються на величину випадкових
флуктуацій. Порівняння різних перерізів (див. рис. 9 15, а~в) дало
можливість встановити смугу розташування контурів випадкових перерізів
обробленої поверхні. Це явище має місце при обробці всіх видів заготовок.
Виключенням є круглограма, наведена на рис. 9.15, з. На цій круглограмі
наявні зміни контуру поверхні у вигляді імпульсних викидів значної
амплітуди. Ця круглограма відповідає перерізу, в якому було здійснено
зупинку супорта верстата з подальшим продовженням процесу обробки. В
цьому перерізі наявний суттєво нестаціонарний випадковий перехідний процес
при нестаціонарному стохастичному вході.
Разом із наведеними раніше заготовками, використовувалася заготовка
ступінчастої форми, профіль якої було сформовано як комбінацію двох
випадкових процесів. Довжина кожної сходинки формувалась як випадкова
величина, розподілена за законом Пуассона, а висота сходинки визначалась
як випадкова величина, сформована генератором випадкових чисел з
нормальним законом розподілу (рис. 9.16).
Для заготовки з контуром у вигляді процесу Пуассона визначені
статистичні характеристики. Зокрема, кореляційна функція даного процесу,
згідно з [6], має вигляд експоненціальної залежності:
К(т) = Ц • е т" ,	(9-26)
де В - дисперсія амплітудних значень радіальної координати профілю;
Т„ - середня довжина сходинки на поверхні заготовки.
Спектральна щільність випадкового процесу, що відповідає перерізу даної
заготовки згідно з [6] визначена у вигляді:
ї 2Тп°
8(®) = --	(9 77)
V )	1 + Ю2Т2
Циліндрична поверхня, одержана в результаті обробки даної заготовки,
також мала характерну хвилястість. Параметри поверхні в невеликих межах
змінювались випадковим чином по довжині деталі.
В результаті обробки експериментальних круглограм одержані статистичні
характеристики зміни форми перерізу по довжині деталі. На рис 9 17
наведена смуга розташування виміряних десяти різних перерізів обробленої
поверхні, по довжині деталі. Знайдені їх математичне сподівання та
автокореляційні (коваріаційні) функції. Автокореляційні функції визначені
як зміни радіальних координат в залежності від полярного кута
371
Струтинський В. Б,
а)
б)
Рис. 9.16. Креслення заготовки, контур якої відповідає
випадковому процесу Пуассона (а, б) та загальний вигляд
даної заготовки під час обробки на верстаті(в)
ЗТ1
Розділ 9. Математичні моделі прогресивних технологічних процесів
Рис. 9.17. Смуга зміни радіальної координати контурів обробленої поверхні
в різних перерізах та коваріаційні функції випадкового процесу при різних
значеннях полярних кутів
Значення коваріаційних функцій розраховані за формулою [6]:
К(т) = ТгХ(хкЮ - н(0)(хк(ї + т)-м(і + т)),	(9.28)
к=1
де Хк(і), хк(і + т) - радіальні координати контуру обробленої поверхні в
к-му перерізі відповідно в моменти часу і та (і. + т);
ц(і + т) - математичне сподівання радіальної координати контуру
обробленої поверхні в моменти часу Ь та (і + т);
N - кількість точок, в яких проводились виміри радіальної координати
обробленої поверхні.
Для уточнення кореляційних властивостей радіальних координат контурів
в тангенціальному напрямку визначені потокові діаграми кореляційних
функцій (рис. 9.18). Зміни кореляційної функції мають груповий характер по
полярному куту.
Як правило, кореляційні функції є затухаючими знакозмінними із
короткоперіодичною та довгоперіодичними складовими.
Контур перерізу обробленої поверхні представляє собою циклічний
373
Струтинський В.Б.
випадковий процес. Для дослідження параметрів цього процесу виконано його
спектральний аналіз.
Ф, град
Рис. 9 18. Потокова діаграма автокореляційних функцій параметрів
випадкового процесу зміни радіальної координати контуру обробленої поверхні
в залежності від тангенціальної координати для різних полярних кутів (р
Контур обробленої поверхні є складною полігармонічною функцією. Цю
функцію можна вважати періодичною з періодом 2л. Тому спектр контуру є
лінійчастим. Його одержано з використанням процедури швидкого
перетворення Фур’є за допомогою вбудованої функції іїі пакету МагЬСАІ)
(див. розділ 6.2.1). Результати розрахунку спектра показані на рис. 9.19.
З аналізу лінійчастого спектра випливає, що контур поверхні заготовки має
превалюючі гармоніки з номерами 2 і 3. Це означає наявність овальності та
огранки його по трьох гранях. Модулі амплітуд цих гармонік в 4-5 разів
перевищують середні значення амплітуд гармонік до 25-ї. Основні гармоніки
мають періоди по куту 120° і 36°, що відповідає частотам коливань 31,5 і 105 Гц.
Контур обробленої поверхні має складові гармоніки з номерами 13, 18 та
25, амплітуди яких дещо більші середнього значення. Загалом суттєві
374
Розділ 9. Математичні моделі прогресивних технологічних процесів
гармоніки, що утворюють контур, обмежуються номерами до 28-ї включно.
Деякі з гармонік з даного діапазону мають незначні амплітуди (11, 16, 17, 26
та 29-33 гармоніки). Вклад цих гармонік у формування контуру обробленої
поверхні не є суттєвим.
Ь8Ї:=	8іаск(Ьз,8иЬтаІгі>(Ь8,1,3,			1.0)			
с := ҐЙ(Ь8І)		А := 1аяі(с)					
І :=	..А	V/ '= 1 .. 8					
	180		48			21	
	120		32			31.5	
	36		9.5			105	
ф =	27.6	град т =	7.3	мс	£=	136.5	Гц
	25.7		6.8			147	
	20		5.3			189	
	17.1		4.5			220.5	
	14 4		3.8			262 5 _	
1Т :=	1 ІКе <	2 т	2 +- Іт с.					
							
зо
20
10
0
0
Рис. 9.19. Фрагмент документа пакету МаІЇїСАП та результати
розрахунків спектра випадкового контуру перерізу обробленої поверхні:
//і - модуль амплітуди і-ї гармоніки дискретного розкладу за схемою
швидкого перетворення Фур’є; (р - вектор полярних кутів, що відповідає
кутовим періодам восьми суттєвих гармонік розкладу; Т - вектор періодів
коливань контуру; / - вектор циклічних частот суттєвих гармонік '
Спектральний аналіз форми контура дає можливість порівняти показники
динамічної якості двох різних токарних верстатів.
Для цього виконані обробка одніс" заготовки на двох різних верстатах
(рис. 9.20) та порівняння спектрів оброблених поверхонь.
На рис. 9.21 наведені круглограми двох типових перерізів обробленої
поверхні. Поверхні одержані обробкою однієї й тієї ж заготовки з випадковим
профілем у вигляді процесу Пуасона на двох різних верстатах.
375
Струтинський В.Б.
а)
ШМІ
б)
Рис. 9.20. Обробка однієї заготовки на двох різних верстатах з
проведенням вимірювань параметрів обробленої поверхні:
а - на верстаті КА280 з використанням трикомпонентного
динамометра для вимірювань сили різання; б - на верстаті 1К62
По круглограмах визначені розбіжності форми контурів обробленої
поверхні на різних інтервалах зміни полярних кутів. В цілому розбіжність
376
Розділ 9. Математичні моделі прогресивних технологічних процесів
двох круглограм по амплітуді знаходиться в межах 6..8 мкм. На ділянках
підвищеної коливальності процесів розбіжність досягає 8.. 12 мкм. Фазове
зміщення основних максимумів та мінімумів обох круглограм становить не
більше 10°..20°. Для аналізу точності обробки на круглограмах визначене
базове коло, діаметр якого відповідає середньому значенню радіальної
координати поверхні обробленої на верстаті 1К62. Відхилення радіальних
координат поверхні обробленої на верстаті КА280 має постійну від’ємну
складову близько 2..З мкм. Розмахи коливань круглограм складають 17 мкм
для верстата 1К62 та 7 мкм для верстата КА280.
в)
Рис. 9.21. Порівняння експериментально визначених круглограм поверхонь,
одержаних в результаті обробки однієї заготовки на верстатах 1К62 та КА280
при імітаційному навантаженні у вигляді процесу Пуассона: а — круглограма
поверхні, обробленої на верстаті 1К62; б - круглограма поверхні, обробленої
на верстаті КА280; в - порівняння контурів поверхонь шляхом приведення
до єдиної системи відліку (крива 1 - верстат 1К62, крива 2 - верстат КА280)
Для аналізу частотного складу експериментально визначених круглограм
розраховані їх лінійчасті спектри амплітуд (рис. 9.22).
Спектри амплітуд знайдені шляхом застосування процедури швидкого
дискретного перетворення Фур’є до масиву значень радіальної координати
кожної круглограми. При формуванні дискретної математичної моделі
прийнято об’єм масиву дискретних значень в кількості 4096 (212). Для
одержання даного масиву використана сплайн-інтерполяція експериментально
визначених круглограм, що відповідають рис. 9.21 з подальшим розрахунком
необхідної кількості точок (ординат круїлограм).
З аналізу спектрів, наведених на рис. 9.22, випливає, що обидві
круглограми мають дві різнорідні за порядком значень амплітуд групи
гармонік - низькочастотну групу, яка включає гармоніки до 25-ї (до частоти
близько 150 Гц), та високочастотну з гармоніками №№ 25-100.
377
Струтинський В. Б.
а)
б)
Рис. 9-22. Лінійчасті спектри амплітуд, розраховані за одержаними
експериментально круглограмами поверхонь, оброблених на верстатах
КА280 (а) та 1К62 (б)
Середні значення амплітуд гармонік низькочастотної частини спектра
приблизно в 5.. 10 разів більші, ніж середні значення амплітуд високочастотних
гармонік. Це співвідношення має місце для поверхонь, оброблених на обох
верстатах. Порівнюючи амплітуди гармонік одного номера, для двох круглограм
можна зробити висновок, що амплітуди гармонічних складових контуру поверхні
при обробці на верстаті 1К62 в 2..4 рази більші, ніж відповідні амплітуди
поверхні, обробленої на верстаті КА280. Не пояснюється суттєво вищим рівнем
вібрацій елементів динамічної системи відремонтованого верстата 1К62 в
порівнянні з новим верстатом КА280.
З аналізу спектра круглограми поверхні обробленої на верстаті КА280
випливає наявність превалюючої гармоніки з номером 24. Це вказує на наявність
резонансної області в динамічній системі верстата, частота якої відповідає 24
гармоніці і складає 144 Гц.
378
Розділ 9, Математичні моделі прогресивних технологічних процесів
9.3.	Дискретизована математична модель
для визначення ефективності процесу обробки поверхонь
інструментом інтегральної дії
При обробці поверхонь часто використовується технологічне обладнання з
інструментом інтегральної дії. В інструментах інтегральної дії продуктивність
обробки залежить від часу дії інструмента на конкретну ділянку
оброблюваної поверхні. Такими інструментами є щітки різноманітної
конструкції, голкофрези, полірувальні круги, гідроструменеві інструменти.
Продуктивність обробки інструментом інтегральної дії загалом визначається
деякою інтегральною функцією часу. Наприклад, якість полірування можна
оцінити коефіцієнтом, оберненим до параметру шорсткості (На)
оброблювальної поверхні. Цей коефіцієнт залежить від часу взаємодії
полірувального круга з оброблюваною поверхнею. Інтенсивність
полірувальної обробки в часі змінюється. Вона залежить від якості поверхні
полірувального круга, наявності зносу круга, забруднень тощо.
Якщо позначити інтенсивність обробки р(0, то коефіцієнт, що визначає
якість обробки поверхні, буде визначатися інтегралом:
Прогресивними інструментами інтегральної дії є пристрої для
гідроструменевої обробки [99]. Вони можуть мати різноманітну конструкцію.
На рис. 9.23 наведена конструктивна схема поворотної гідроструменевої
головки для обробки зовнішніх плоских, внутрішніх циліндричних та
внутрішніх торцевих поверхонь високонапірними струменями води.
Рис. 9-23- Гідроструменева головка для обробки зовнішніх плоских,
внутрішніх циліндричних та торцевих поверхонь
379
Струтинський В. Б.
Головка має нерухомий корпус 1 та рухомий ротор 2, в якому встановлені
поворотні соплові пристрої 3 із струменеформуючими насадками 4.
Обертання ротора здійснюється реактивними силами, що виникають при
витіканні струменів із насадок. Для цього насадки 4 встановлюються під
певними кутом відносно осі головки. Даний пристрій дозволяє також
виконувати обробку різноманітних внутрішніх поверхонь, зокрема
циліндричних. Для цього поворотні соплові пристрої 3 встановлюються таким
чином, що їх осі утворюють з віссю головки кут 75...90 .
Пристрої для гідроструменевої обробки виконуються в різних
модифікаціях. На рис. 9.24 наведене фото загального вигляд}7 ручного
гідроструменевого інструменту.
Рис. 9.24. Загальний вигляд ручного інструменту
для гідроструменової обробки зовнішніх та внутрішніх поверхонь
Пристрій для гідроструменевої обробки призначений для очищення
зовнішніх і внутрішніх поверхонь струменями середнього тиску. Тиск робочої
рідини (води, миючого розчину чи абразивної суспензії) для даного пристрою
складає 5,0..50 МПа. Обробці підлягають поверхні із залишками фарби,
консистентного мастила, промислового бруду тощо. Пристрій
використовується при ремонтних роботах машин різного призначення, у
будівництві, сільскому господарстві.
Ручний гідроструменевий пристрій включає корпус із системою керування
та гідроструменеву головку. Загальний вигляд корпусу наведено на рис. 9.25.
Рис. 9.25. Корпус ручного гідроструменевого інструменту,
в якому розміщена система керування
380
Розділ 9. Математичні моделі прогресивних технологічних процесів
В корпусі розташовані елементи системи керування, які приводяться в дію
важелями, розміщеними на рукоятках.
Гідроструменева головка має ротор із встановленими в ньому сопловими
насадками. Загальний вигляд головки наведено на рис. 9.26.
Рис. 9.26. Загальний вигляд гідроструменевої головки
Головка має змінні соплові пристрої Зокрема, соплові пристрої, наведені
на рис. 9.26, дозволяють регулювати форму і розміри отвору для витікання
рідини. Може бути всиновлена довільна по площі полігональна (шестигранна)
форма отвору.
Розроблено ряд конструкцій головок для обробки внутрішніх поверхонь
різної форми. На рис. 9.27 наведена конструктивна схема головки із
напівсферичною робочою зоною дії струменів.
Головка із напівсферичною робочою зоною призначена для обробки
внутрішніх поверхонь резервуарів. Головка має шпиндель 1, виконаний з
можливістю обертання навколо осі, корпус 2 із встановленою в ньому
турбіною 3. В тілі турбіни виконані соплові отвори, через які витікають
струмені рідини. Струмені рідини витікають під кутом до осі турбіни і
утворюють конічну просторову поверхню. При обертанні шпинделя конічна
поверхня рухається забезпечуючи обробку напівсфери. З метою захисту
соплових отворів на турбіні встановлена захисна кришка 4.
Аналогічну конструкцію має гідроструменева головка із сферичною
робочою зоною (рис. 9.28).
Головка включає нерухомий корпус 1, шпиндель 3, що обертається за
допомогою турбіни 2, поворотний корпус 4, встановлений на шпинделі, і
розміщену в ньому турбіну 5 із соплами для формування високонапірних
струменів рідини.
381
Струтинський В.Б.
Рис. 9.27. Конструктивна схема гідроструменевої головки
із напівсферичною робочою зоною
Струмені рідини витікають симетрично під кутом до осі турбіни. При
цьому утворюється дві конічні просторові поверхні, які обертаються. При
обертанні шпинделя конічні поверхні охоплюють сферичну область.
Характерні деталі виготовлених дослідних зразків вищевказаних
струменевих головок, зокрема турбіни, показані на рис. 9.29.
Застосування пристроїв гідроструменевої обробки потребує оцінки їх
ефективності. Оцінка ефективності обробки здійснена методами
математичного моделювання з використанням дискретних масивів
характерних параметрів процесів обробки.
Ефективність гідроструменевої обробки поверхні визначається часом дії
струменя на оброблювану поверхню. Струмінь зміщується відносно поверхні
по складній траєкторії. Створення точної математичної моделі дії струменя на
поверхню є складною задачею і недоцільною з причини громіздкості
382
Розділ 9. Математичні моделі прогресивних технологічних процесів
одержаних рівнянь. Тому для оцінки ефективності гідроструменевої обробки
використано спрощену дискретну математичну модель, побудовану на базі
дискретизації параметрів процесу.
Рис. 9.28. Гідроструменева головка із сферичною робочою зоною
Розглянемо основні принципи та методику побудови такої моделі для
гідроструменевої головки, наведеної на рис. 9.23. При відсутності руху подачі
одиночний струмінь рідини рухається по колу послідовно і неперервно,
здійснюючи обробку поверхні в різних точках (рис. 9.30).
Розіб’ємо колову траєкторію руху струменя по оброблюваній поверхні на
окремі ділянки довжиною Ь приблизно рівною ширині струменя. Таким
383
Струтинський В.Б.
чином, одержимо ш ділянок (дискретних значень процесу):
т = лЦ/Ь,
де т - ціле число.
Рис. 9-29- Характерні деталі гідростпруменевих головок: 1 - кришка;
2 ~ турбіна головки з напівсферичною робочою зоною; 3 - корпус;
4 - турбіна головки із сферичною робочою зоною
Рис. 9.30. Схема обробки поверхні високо напірним струменем,
що рухається по колу
384
Розділ 9. Математичні моделі прогресивних технологічних процесів
Кожній ділянці поставимо у відповідність точку з індексом і (і = 1..т),
якій відповідає одне дискретне значення параметра процесу. При
проходженні струменя через ділянку на неї попадає певний об’єм рідини:
ц = О * Ді ,
де ф - об’ємна витрата рідини в сопловому пристрої;
Лі: - проміжок часу, за який сопло проходить відстань по колу довжиною Ь.
Якщо струменева головка рівномірно обертається з кутовою швидкістю V
обертів за секунду, то час проходження струменя
Лі = 7сВ/(упі) .
Відповідно об’єм рідини, що відповідає одній точці:
ц = О • 7гВ/(ут).
При повороті струменевої головки на кут 360° на оброблювану поверхню
попаде об’єм рідини, що відповідає всім т точкам:
= п і • я .
Визначимо ефективність гідроструменевої обробки кількістю точок, що
попадають на одиницю площі поверхні. За один оберт струменевої головки з
одним соплом буде досягнута ефективність:
ЕП1 = т/(лПЬ).
Ефективність за час І дорівнює (у - число обертів за секунду):
Е = і т/(лПЬу).
Якщо струменева головка має два соплових пристрої, то відповідно
ефективність обробки збільшується вдвічі.
При обробці поверхні струменева головка зміщується в напрямку руху
подачі зі швидкістю V . Ефективність обробки визначається загальною
траєкторією струменя. Траєкторія є складною петлеподібною періодичною
кривою. Її рівняння визначається як рівняння кола, центр якого рівномірно
переміщується. Визначимо траєкторію струменя в параметричному вигляді,
враховуючи, що обертальний рух головки є рівномірним. Рівняння траєкторії
одного соплового пристрою в параметричній формі матиме вигляд:
X = Ухґ+-уСО8(шІ + \|/0); у = Ууі + -у8Іп(йї + у0),	(9.29)
де - проекції швидкості руху подачі на осі координат х і у;
а> - кутова швидкість струменевої головки;
\|/0 - кут, що визначає початкове положення соплового пристрою.
Траєкторія руху струменя залежить від багатьох факторів. Деякі з них є
несуттєвими і мало впливають на ефективність струменевої обробки. Це
стосується, зокрема, початкового положення струменя та наявності двох
складових \'х та єу швидкості подачі.
Виберемо осі координат таким чином, щоб вісь х співпадала з напрямком
385
Струтинський В. Б.
X = ух( + соз(<вІ + л)
у = — 8іп(со1 + я)
Ьи ,	В	(	,	\
X =	— І	+ — СОЗІЮГ +	я І
2я	2	'	’
у =	— 8іп(соі; +	я)
швидкості подачі, а початкове положення струменя відповідало деякій точці
А, яка знаходиться на осі х. При цьому рівняння траєкторії в
параметричному вигляді:
(9.30)
Для забезпечення рівномірної обробки необхідно вибрати значення
швидкості подачі таким, щоб при повороті головки на кут 2л зміщення
соплового пристрою з точки А в нове положення А' дорівнювало ширині
струменя. Ця раціональна швидкість подачі досягається у випадку:
|йіо6 = 2я
1^06 = ь ’
Виключаючи час одного повороту головки і.об, із даної системи рівнянь
знайдемо раціональну швидкість подачі головки:
Ух = Ьо/(2л).
Відповідно рівняння траєкторії струменя (9.30) набуде вигляду:
(9.31)
Не дивлячись на порівняно простий вигляд залежності (9.31), її важко
використати для практичних розрахунків ефективності струменевої обробки.
Одержані аналітичні вирази стають дуже громіздкими, а головне -
ускладнюється інтерпретація фізичної суті процесу, необхідна при
інженерному аналізі ефективності гідроструменевої обробки.
Тому, для аналізу ефективності рухомої струменевої головки використана
математична модель у вигляді дискретної множини значень характерного
параметра процесу. Так, як і для випадку відсутності руху подачі розіб’ємо
траєкторію руху соплового пристрою на ділянки довжиною Ь, кожній ділянці
поставимо у відповідність точку у Одержана сукупність точок утворює
складний спіралеподібний ланцюжок (рис. 9.31).
Розташування точок, що відповідають ділянкам оброблюваної поверхні є
незручним для аналізу. З метою спрощення виконаємо дискретизацію процесу
переміщення струменевої головки.
Положення центра рухомої головки описується лінійною функцією:
х0 = іЬю/(2я) = ухі .
Будемо вважати, що головка зміщується дискретно по кроках.
Виконаємо дискретизацію (квантування) положення головки Хд для
інтервалу часу, рівному одному оберту головки. При цьому масив дискретних
386
Розділ 9. Математичні моделі прогресивних технологічних процесів
значень аргументу і має вигляд числової послідовності:
ч = ^-об" і — і * 2л/<о .
V
|Ь
А-
А
„ . . «ґ X X X X X х X ’• ®. •
¥ і	> у у ї у V > # і»
, Х-4---< А--ААМуАхМІ* ~ У~У~У~У~4
X і» *»	« хй Ай. А* л *' * *'
О
Рис. 9.31. Масив точок, що відповідають ділянкам оброблюваної поверхні
при поступальному русі струменевої головки
Відповідно положення центра рухомої головки буде визначене числовою
послідовністю виду:
х; = Ь • і.
Для кожного значення індексу і будемо мати один оберт головки і
відповідно т точок. На рис. 9.32 наведено одержаний розрахунковий масив
точок. Одержаний масив точок зручно обробити використовуючи
графоаналітичні методи.
Рис. 9.32. Масив точок, що відповідають ділянкам оброблюваної поверхні
при дискретному покроковому зміщенні струменевої головки
Переміщення головки призводить до послідовного попадання точок на
387
Струтинський В. Б.
оброблювану поверхню. Кількість точок на одиницю площі суттєво різниться
на периферійних і центральних ділянках оброблюваної поверхні.
Розіб’ємо всю оброблювану площу на ділянки таким чином, щоб виділити
ділянки інтенсивної обробки площею 5;, ділянки обробки середньої
інтенсивності площею 85 і ділянки низької інтенсивності обробки площею 8т.
Підрахувавши кількість точок на одиницю площі по кожній ділянці
визначимо інтенсивність обробки по ділянках. Відповідно для трьох видів
ділянок ступінь інтенсивності обробки:
іі=пі/5і; і5=п8/85; Іт=Пт/8т.
де П], п3, нт - кількість точок, які попадають на відповідні ділянки
оброблюваної поверхні.
Нормуємо інтенсивності обробки по ділянкам. Максимальну інтенсивність
ф приймаємо за норму інтенсивності. Тоді відносні інтенсивності обробки по
всіх ділянках будуть складати:
е, = 1; е3 = п^/пд ; ет = п^/п, зт .
Величини площ ділянок можуть бути змінені в певних межах. Доцільно
вибирати їх таким чином, щоб відносні інтенсивності по ділянках визначалися
простими дробами. Для ділянок, показаних на рис. 9.32, площі зі, 8т,
підібрані так, що виконуються прості співвідношення:
Єї = 1; е5 = 1/2 ; ет = 1/4 .
При цьому розподіл відносних інтенсивностей по різних ділянках області
обробки має вигляд наведений на рис. 9.33.
Ь+ 1,5А
Рис. 9.33 Розподіл відносних інтенсивностей обробки
по окремій смузі оброблюваної поверхні
На основі встановленого розподілу інтенсивностей різних ділянок
формується раціональна траєкторія руху головки по оброблювальній
поверхні. На рис. 9.34 наведено варіанти руху головки по оброблюваній
поверхні.
388
Розділ 9- Математичні моделі прогресивних технологічних процесів
Варіант послідовного дострокового сканування оброблювальної поверхні
(рис. 9.34, а) є найбільш очевидним. Головка рухається по зигзагоподібній
траєкторії. З аналізу рисунка випливає, що цей варіант руху головки не є
раціональним. В цьому випадку обробка здійснюється смугами, інтенсивність
яких відрізняється в 2 рази. Крім того ліва та права смуги обробленої
поверхні мають ділянку низької ефективності обробки.
Більш рівномірну обробку забезпечує петлеподібний рух головки
(рис. 9.34, б). При петлеподібному русі головки інтенсивність обробки по
смугах складає 1,5; 1,0. Даний спосіб переміщення головки рекомендується
при ручній обробці. Рух головки при ручній обробці має певну
нерівномірність, тому межі смуг різної інтенсивності розмиваються і
нерівномірність інтенсивності обробки зменшується до значень 10.. 15 %.
Рис. 9.34. Варіанти траєкторій руху струменевої головки,
що забезпечують різні ступені рівномірності обробки поверхні:
а - послідовно-построкове сканування; б - петлеподібне сканування;
в - перехрестно-построкове сканування з подальшим обходом по контуру
389
Струпшпський В. Б.
Для забезпечення рівномірної обробки ділянок з правого і лівого країв
деталі рекомендується додаткова обробка по контуру.
Найбільш рівномірну обробку забезпечує перехрестно-построкове
сканування головки по оброблюваній поверхні (рис. 9.34, в). Перехрестно-
построкове сканування забезпечує постійну інтенсивність обробки в
центральній частині оброблюваної поверхні. Деяке зниження інтенсивності по
краях оброблюваної поверхні не є суттєвим. Воно звичайно компенсується
контурною обробкою по периферії оброблюваної поверхні.
Таким чином, використання дискретної математичної моделі дало
можливість оцінити ефективність та показники рівномірності обробки
поверхні. На основі розробленої математичної моделі сформульовані
пропозиції по забезпеченню раціонального технологічного процесу обробки.
Дискретна математична модель гідроструменевої обробки допускає
узагальнення на обробку поверхонь різної форми. При обробці сферичних
поверхонь розглядається розташування точок дискретної моделі на сфері. Для
внутрішніх поверхонь у вигляді циліндра точки розташовуються на
циліндричній поверхні.
Дискретна модель гідроструменевої обробки може враховувати зміну
інтенсивності обробки в залежності від відстані соплового пристрою від
оброблюваної поверхні. Врахування зміни інтенсивності здійснюється
зменшенням числа точок в залежності від соплового пристрою. Уточнення
дискретної моделі може бути здійснене із врахуванням розподілу швидкості
по перерізу струменя або зміни форми струменя. Дискретні моделі струменів
із врахуванням їх структури розглянуті в розділах 11.1 та 11.3.
Розглянуті дискретні моделі гідроструменевої обробки поверхонь
узагальнюються на процеси обробки іншими інструментами інтегральної дії.
Таким чином можна отримати продуктивність обробки поверхонь при
поліруванні, нанесенні покриттів, фарби, осадженні шару матеріалу на деяку
поверхню (гальванопластика).
Використання даних моделей є ефективним засобом підвищення
ефективності процесу обробки.
Дискретні математичні моделі такого типу порівняно просто обробляються
засобами сучасних математичних пакетів.
390
Розділ 9. Математичні моделі прогресивних технологічних процесів
9.4. Дискретна математична модель
процесу вібраційної обробки деталей
Вібраційна обробка деталей здійснюється у вібробункері [121], що
встановлений на пружних опорах (рис. 9.35).
Рис. 9.35. Загальний вигляд вібробункера,
що призначений для вібраційної обробки деталей
Вібрації бункера виникають під дією спеціального інерційного
навантажувача з електроприводом. Вібробункер має порожнину, в якій
розміщується робоче середовище, що включає оброблювані деталі, гранули
абразиву та спеціальний розчин. Під дією вібрації відбувається відносне
зміщення деталей та гранул абразиву і відповідно здійснюється обробка
поверхні деталі. Деталі можуть мати різну форму і розміри (рис. 9.36).
При віброобробці використовуються різноманітні гранули абразиву
(рис. 9.37), а також шматочки дерева, войлока, пластмас, металеві кульки.
391
Струтинський В.Б.
Рис. 9-36. Типові деталі, оброблені у вібробункері
(показано зовнішній вигляд деталей до обробки та після неї)
Рис. 9.37. Зовнішній вигляд типових гранул абразиву,
які використовуються при вібраційній обробці
392
Розділ 9. Математичні моделі прогресивних технологічних процесів
Розміри та форма деталей і гранул абразиву змінюються в широких
межах, але у порожнині вібробункера вони утворюють квазіоднорідне робоче
середовище. Робоче середовище заповнене спеціальним лужним або
кислотним розчином. Воно може розглядатися як своєрідна рідина із дуже
складними реологічними властивостями та суттєво нелінійними параметрами
розподілу маси. Тому математичне моделювання процесу вібраційної обробки
викликає значні труднощі.
Для виконання теоретичних досліджень процесу розроблена та
використана математична модель процесу вібраційної обробки деталей,
побудована на основі дискретизації всього робочого простору вібробункера з
приведенням його до кінцевого числа ділянок, в яких здійснюється
віброобробка окремих деталей. Виконано аналіз загальних вібраційних
параметрів вібробункера, повільного відносного руху деталей та гранул
абразиву у всьому об’ємі робочого середовища, а також здійснене визначення
базових технологічних параметрів процесу віброобробки (середньої швидкості
взаємодії деталей з гранулами абразиву) [121].
Загальні вібраційні параметри вібробункера визначені шляхом
математичного моделювання бункера як динамічної коливальної системи.
Вібробункєр представляє собою слабодемпфовану механічну динамічну
коливальну систему, яка приводиться в рух вібраційним механізмом, що
включає обертову ексцентричну масу (рис. 9.38).
З метою спрощення теоретичних розрахунків динамічна модель бункера
прийнята умовно у вигляді масивного твердого тіла, яке здійснює плоский
коливальний рух (рис. 9.39).
При плоскому русі вібробункера, його положення як твердого гіла
характеризується трьома ступенями вільності. В даному випадку це -
положення центра мас в напрямку осей х та у і поперечно-кутові коливання
вібробункера відносно центра мас. Коливання відбуваються під дією
неврівноважених сил, що діють у вібраційному механізмі. Ці сили
змінюються за гармонічним законом і залежать від частоти обертання вала
вібраційного механізму. Проекції на осі х і у навантаження на вібробункєр з
боку вібраційного механізму визначаються залежностями:
Кх = тьє©2 • со8(юі); Ку = тьєсо2 • 8Іп(ю1),	(9.32)
де іпь - ексцентрична маса вібраційного механізму;
є - ексцентриситет маси відносно осі обертання;
<в - кутова швидкість обертання вала вібраційного механізму;
І - час.
Крутний момент, який діє на вібробункєр з боку вібраційного механізму,
визначається наближеною залежністю:
М = Кхув,
де ув - плече дії горизонтальної проекції сили на вібробункєр.
393
Струтинський В. Б.
Рис. 9.38. Схема вібробункера з вібраційним приводом: 1 - корпус;
2 - робоче середовище; 3 - вібраційний механізм; 4 - пружна опора бункера;
5 - центр мас системи бункера та робочого середовища

Рис. 9.39. Динамічна модель вібробункера у вигляді твердого тіла,
яке здійснює плоский коливальний рух
394
Розділ 9- Математичні моделі прогресивних технологічних процесів
(9.33)
Розглянуто окремо рівняння вимушених коливань вібробункера для
кожного з трьох ступенів вільності.
Коливання вібробункера в напрямку осі х описується диференціальним
рівнянням:
<12х , сіх	„
т—г + іК — + с,х = К
сії2 х аі х
де т - маса бункера;
ігх - еквівалентний коефіцієнт опору при горизонтальному переміщенні
вібробункера;
сх - еквівалентна жорсткість пружин в горизонтальному напрямку.
Розв’язок даного рівняння із врахуванням (9.32) описує вимушені
коливання вібробункера в напрямку осі х і відповідає залежності:
зіп сої - агсій
тЬ	с
X = є — --ь======
т й „	>
(9.34)
і2 ь2
+ ”5'
1	© т
Аналогічно одержано залежність вимушеного переміщення вібробункера у
вертикальному напрямку (у) та
вібробункера відносно центра мас (ф):
( пко2
зіп ©і - агсіи
закон поперечно-кутових коливань
- с_,
11 (О
+ . пу .
то/ І и2т2
кіп - агсід
Ф = є-Ув—~
т
™м2 ~ сф
Ьф®
(9.35)
-З—-і] + .Ьі5..
2	2	2
тог ) ш т
ть
т
Знайдені залежності дозволяють визначити векторне поле прискорень в
робочому середовищі вібробункера, яке має місце при його усталеному
вібраційному русі. Векторне поле прискорень в кожній точці робочого
середовища характеризується проекціями віброприскорень (Ах, Ау) на осі
координат х і у. Проекції віброприскорень визначаються залежностями:
. <і2х . .	.
А, = —- - Ат зш а - А„ сох а ;
х й(2
4	А	А
А„ = —V - А, сов а - А„ ат а ,
-	(Й2	п
(9.36)
395
Струтинський В.Б.
. СІ2ф	.
де Ат = г •	- тангенціальне віброприскорення, що виникає при поперечно-
кутових коливаннях вібробункера відносно центра мас;
л	{гіф У	,л
А( - г • —і.	- нормальна складова віброприскорення поперечно-кутових
угії/
коливань вібробункера;
г ~ відстань від центра мас до точки робочого середовища (радіус-вектор);
а - кут між радіусом-вектором г та горизонтальною віссю х.
Значення інших складових векторного поля віброприскорень знаходяться
шляхом подвійного диференціювання законів руху вібробункера відповідно
по всіх трьох ступенях вільності (формули (9.34) та (9.35)).
При коливаннях вібробункера деталі та гранули абразиву підлягають дії
знакозмінних прискорень, величина і напрямок яких визначаються
залежностями (9.36). Прискорення призводять до виникнення інерційних
навантажень на деталі та гранули. Інерційні навантаження спричиняють
високочастотний коливальний рух деталей та гранул наповнювача. У процесі
коливань деталі та гранули стикаються між собою. В залежності від
швидкості зіткнення змінюється енергія ударної взаємодії деталей і гранул, а
отже, і енергетичні параметри процесу віброобробки.
Розглянемо процес зіткнення деталі та гранули абразиву (рис. 9.40).
Рис. 9-40. Розрахункова схема для визначення швидкості зіткнення
деталі та гранули наповнювача внаслідок вібрації вібробункера:
1 — деталь; 2 - гранула наповнювача
396
Розділ 9- Математичні моделі прогресивних технологічних процесів
Інерційна сила, яка діє на деталь, у проекціях на осі координат
визначається залежностями:
(9.37)
(9.38)
де Гах, Рау - проекції на осі координат інерційних навантажень, що діють на
деталь;
Ра - щільність матеріалу деталі;
рр - щільність робочого розчину, в якому знаходиться деталь;
\У5 — об’єм деталі;
А5х і Аау - проекції на осі координат прискорень у центрі деталі,
координати якої ха і уа.
Аналогічно інерційна сила, що діє на гранулу наповнювача, в проекціях
на осі координат визначається залежностями:
Рих=(рн-рР)-ХУн-А11х(Хн,¥н);
Рну = (рн - Рр)' ' Ану(Хн,У„) ,
де Рих, Р1іу - проекції на осі координат інерційних навантажень, що діють на
гранулу наповнювача;
рн - щільність матеріалу гранули;
\¥н - об’єм гранули;
х„, уи - координати гранули у системі координат із початком у центрі мас
вібробункера;
Аих, Аку - проекції прискорення гранули на осі координат.
Інерційна сила призводить до переміщення деталі в робочому середовищі з
подоланням сили опору. Сила опору, що діє на деталь з боку робочого
середовища, в
залежностями:
р
1 ссх
гсЗу
ДЄ Р сЗх > сЗу ~
проекціях на осі координат може бути визначена наступними
= СЙХ-80Х-Уд[;
= ^•8^-4^,
проекції сили опору;
С3х, Сау “ коефіцієнти еквівалентного гідродинамічного опору;
8ах, 8г.у - площі міделевого перерізу деталі при її русі в напрямку осей
координат х та у відповідно;
У3х, У^, - проекції швидкості деталі на відповідні осі.
Аналогічно сили опору при переміщенні гранули наповнювача:
^снх “ Снх Знх Унх ,
17	— о V	'
•‘•сну ““ '~,ну *^ну * ну ’
де Снх, Сну - коефіцієнти гідродинамічного опору гранули наповнювача;
8НХ, Зцу ~ площі міделевого поперечного перерізу гранули;
Унх, У ну “ проекції швидкості гранули.
(9.39)
(9.40)
397
Струтинський В.Б.
Складемо рівняння динамічної рівноваги у вигляді рівностей проекцій
інерційних сил і сил опору, що діють на деталі та гранули наповнювача:
~	=	> ^нх = х ;	“ Е„у •	(9.41)
Підставляючи значення сил, визначимо проекції швидкостей деталі та
гранули наповнювача на осі координат:
= (рг-Рр^дА^ДС^З^);
= (рв - Рр - (с,ф. Д	(9’42)
Чх = (р„ -РрНанх/(Снх8нх);
Уну =(рн-Рр)\УнАну/(Сну8ну).	(9 43}
Визначимо модуль різниці швидкостей деталі та гранули наповнювача,
який у випадку зустрічного руху деталі та гранули являє собою осереднену
швидкість зіткнення деталі та гранули наповнювача в функції проекцій
векторного поля прискорень:
V = $Ут~У^+(Уку~У^ 	<9-44)
Підставляючи значення швидкостей деталі та гранули із формул (9.42) та
(9.43), знайдемо осереднену швидкість зіткнення деталі та гранули
наповнювача:
С„„8
СА,3
(9.45)
Цей вираз дає можливість визначити швидкість зіткнення деталі та
гранули наповнювача в процесі віброобробки для всього робочого середовища.
Процес віброобробки характеризується наявністю мікрорізання та
пластичного деформування поверхні деталі. Кінематичні режими різання та
пластичного деформування вирізняються відсутністю певних швидкостей різання.
Швидкості різання в процесі віброобробки є змінними. Вони змінюються в
залежності від місця розташування оброблюваної деталі у вібробункері. Крім
того, швидкість різання змінюється протягом періоду коливань.
Кінематичні режими різання можуть бути охарактеризовані значеннями
швидкостей співудару деталі та гранули наповнювача, що визначені в процесі
аналізу кінематичних параметрів робочого середовища. В загальному вигляді
швидкість співудару гранул наповнювача і деталі отримана у вигляді складної
аналітичної залежності і є функцією багатьох змінних. Тому для визначення
швидкостей співудару і відповідно до кінематичних режимів різання
використана спеціально розроблена дискретна математична модель.
Модель базується на розрахунку параметрів випадкових швидкостей
різання в окремих точках робочого середовища. Розроблено спеціальний
алгоритм і програма розрахунку на ЕОМ стохастичних параметрів взаємодії
398
Розділ 9. Математичні моделі прогресивних технологічних процесів
деталі та гранул у всьому об’ємі робочого середовища.
Еквівалентний плоский простір робочого середовища розбито на дискретне
число вузлів (точок) рівномірною прямокутною сіткою в декартовій системі
координат (рис. 9.41).
Рис. 9.41. Дискретизація простору робочого середовища ортогональною
сіткою для моделювання на ЕОМ дискретної множини швидкостей
співудару деталей та гранул наповнювача
Сітка охоплює близько 95 % площі простору робочого середовища, а у своїх
нижніх кутах має декілька зайвих вузлів, вплив яких на результати розрахунків
неістотний. Вузли мають індексацію І = 1, 2, 3,... та 5 = 1, 2, 3,... в напрямку
осей координат X і У. Прийнято, що в центрі кожного вузла, стохастично
осереднено в часі, знаходиться деталь. Оскільки процес віброобробки тривалий, а
в робочому середовищі має місце інтенсивний циркуляційний рух деталей, це
припущення є обгрунтованим. Середньостатистична деталь, що знаходиться у
вузлі, має координати Хо і Ур, які вимірюються від центру мас вібробункера. В
дискретній математичній моделі координати кожної статистично середньої деталі
(вузла) задаються у вигляді числових послідовностей:
Хц = -0,2 + Ох-І; Уо = -0,2 + Пуф	(9.46)
де І)\ і Су ~ постійні коефіцієнти, рівні крокам сітки.
На статистично середню деталь, що знаходиться у вузлі сітки, діють
гранули наповнювача. Прийнято середньо статистичну схему взаємодії деталі
і гранул. Згідно даної схеми, гранули наповнювача мають вигляд куль,
399
Струтинський В.Б.
причому взаємодіють із поверхнею деталі 8 гранул з номерами к = 1, ..., 8
у восьми взаємно перпендикулярних напрямках (рис. 9.42).
Деталь одночасно взаємодіє з декількома гранулами наповнювача. Тому
можна вважати, що відносне зміщення деталі під дією ударів є незначним.
Робоче середовище розміщується в порожнині контейнера компактно. У
зв’язку з цим можна вважати, що зазори між поверхнею деталі та поверхнею
гранул наповнювача значно менші характерних розмірів деталі та гранули
наповнювача. Тому прийнято, що середня статистична відстань між центром
деталі та центром гранули дорівнює (до + <іїчт)/2, де сїц і д^т - характерні розміри
деталі та гранули наповнювача. В цьому випадку координати к-й (к = 1. .8)
середньо статистичної гранули наповнювача визначаються залежностями:
Хи = Хп + [(до + д0/2]-со8[7г/4-(к - 1)];
= ¥р + [(до + дм)/2]-8Іп[л/4-(к - 1)].	'
Хх
Рис. 9.42. Середньостатистична схема взаємодії деталі та гранул
наповнювача, прийнята при розробці дискретної математичної моделі
процесу віброобробки деталі
Формула яка визначає швидкість взаємодії деталі та гранули
наповнювача, не враховує знаки швидкості, тобто той факт, що деталь та
гранула наближаються чи розходяться. Тому, строго кажучи, швидкостями
співудару є тільки швидкості тих гранул, які рухаються в напрямку до
деталі. Проте, з огляду на те, що гранула, яка віддаляється від деталі, буде
взаємодіяти з іншою деталлю, знак швидкості гранули можна не враховувати
і відповідно знаходити для однієї деталі повне число (к = 8) значень
швидкості співудару.
Швидкість співудару залежить від різниці щільностей деталі та робочого
400
Розділ 9. Математичні моделі прогресивних технологічних процесів
розчину, а також від коефіцієнтів гідродинамічного опору і форми деталі.
Швидкості співудару деталі та гранули наповнювача (формула (9.45))
визначаються за раніше знайденими значеннями проекцій прискорень в
точках робочого середовища (9.36), координати яких відповідають
координатам центрів середньостатистичної деталі та гранули наповнювача.
Прискорення залежать від амплітуди, частоти коливань вібробункера і часу.
В процесі чисельних досліджень знайдені швидкості співудару для
різноманітних моментів часу при частоті коливань вібробункера 40 Гц, яка є
характерною для процесу віброобробки. Для визначення кінематичних
режимів різання у вигляді стохастичних швидкостей ударів розроблений
алгоритм, блок-схема якого наведена на рис. 9.43.
Згідно алгоритму (див. рис. 9.43) математичне моделювання починається
з визначення параметрів задачі та вихідних даних. При цьому задаються
значення параметрів коливань вібробункера, розміри деталей і гранул
наповнювача, усереднені коефіцієнти опорів деталей та гранул наповнювача.
Наступний блок алгоритму служить для організації циклу обчислень при
фіксованому значенні часу в одній з восьми точок періоду коливань
вібробункера. При цьому знаходиться значення часу та обчислюються
тригонометричні функції, які визначають параметри задачі.
Потім організовується цикл для обчислення масиву швидкостей у всіх 800
точках робочого середовища. Обчислюються координати кожної статистично
середньої деталі та відповідних гранул наповнювача. Координати деталі та
гранул є вихідною інформацією для розрахунку проекцій прискорень, який
здійснюється у відповідному блоці моделі. Блок здійснює розрахунки
проекцій прискорень деталі та гранули наповнювача. За значеннями
прискорень знаходяться значення проекцій швидкостей деталі та гранули
наповнювача, а потім визначається модуль швидкості співудару деталі та
гранули наповнювача.
В результаті для фіксованого моменту часу знаходиться масив значень
модулів швидкостей співудару у всіх виділених точках робочого середовища.
В алгоритмі передбачений блок для визначення мінімального та
максимального значень швидкостей з масиву. Результати розрахунків
піддаються статистичній обробці. При цьому діапазон швидкостей співудару
розбивається на розряди (всього 5 розрядів) і знаходиться число дискретних
значень швидкостей удару, що попадають у кожний розряд.
Отримані дані, разом із значенням часу, мінімальним і максимальним
значеннями швидкостей, є виходом математичної моделі. Розрахунки масивів
швидкостей виконуються для конкретних (всього 8) моментів часу протягом
одного періоду коливань вібробункера.
Результати математичного моделювання наведені в табл. 9.1.
401
Струтинський В. Б.
Рис. 9-43- Блок-схема алгоритму дискретної математичної моделі
для визначення стохастичних кінематичних режимів віброобробки деталі
402
Розділ 9. Математичні моделі прогресивних технологічних процесів
Таблиця 9.1
Результати розрахунків швидкостей співудару деталі та гранули наповнювача
Значення часу 8 точок протягом одного періоду коливань, при якому визначається масив швидкостей, с	Макси- мальне значення швидкості співудару м/с	Мінімальне значення швидкості співудару, м/с	Частота попадання значення швидкості у відповідний розряд діапазону швидкостей				
			ЇМ"л(г‘о- о)	«3 гч ©	5 °? о	(0,6.. 0,8)4,,^	а Я— 00 •3
0	5.872	0	3	14	25	33	41
0.0031	3.935	0	3	15	23	40	35
0.0062	1.298	0.21	0	40	50	12	13
0.0093	4.564	0	3	6	32	34	40
0.0125	5.877	0.12	3	14	25	33	41
0.0156	3.812	0	3	14	23	36	39
0.0187	1.382	0	8	21	13	48	26
0.0219	4.742	0.172	'З	8	26	32	46
Результати розрахунків наведені на рис. 9.44 у вигляді гістограм
розподілу частості появи певних значень швидкості співудару для
різноманітних моментів часу протягом періоду коливань контейнера. З
аналізу гістограм випливає, що протягом періоду коливань контейнера
розподіл кількості співударів за значеннями швидкостей є змінним і не
описується типовою однозначною залежністю. Значення максимальної
швидкості змінюється в широких межах. Для даної розрахункової задачі
протягом періоду коливань максимальна швидкість співудару деталей та
гранул наповнювача змінювалася від 1,29 до 5,87 м/с.
Для знаходження статистичних закономірностей розподілу швидкостей
проведене їх усереднення протягом періоду коливань вібробункера. При
цьому гістограми апроксимовані відповідними гладкими функціями (див.
рис. 9.44) з використанням нелінійних математичних моделей і стандартних
процедур апроксимації (див. розділ 7.2). Знайдені розподіли ймовірності
виникнення відповідної швидкості співудару у всьому об’ємі робочого
середовища у фіксований момент часу.
Потім виконана композиція законів розподілу ймовірностей для всіх
восьми фіксованих моментів часу протягом періоду коливань вібробункера,
для яких були розраховані масиви швидкостей. В результаті отримано
усереднений в часі розподіл ймовірностей швидкостей співудару деталей та
гранул наповнювача в процесі віброобробки рис. 9.45.
403
Струтинський В. Б.
Рис. 9.44. Гістограми розподілу частості появи певних швидкостей
співудару деталей та гранул наповнювача у всьому об’ємі робочого
середовища в різні моменти часу протягом періоду коливань вібробункера
404
Розділ 9. Математичні моделі прогресивних технологічних процесів
Рис. 9.45- Розподіл ймовірностей значень швидкостей співудару
у всьому об’ємі робочого середовища: криві 1~8 ~ розподіл для різних
моментів часу впродовж періоду коливань; крива 9 - середній за період
коливань розподіл швидкостей співудару; пунктирна крива 10
відповідає нормальному закону розподілу Гаусса
З аналізу закону розподілу швидкостей випливає, що цей закон є
мультимодальним (багатовершинним) і асиметричним.
Розподіл швидкостей співудару деталей та гранул наповнювача залежить
від великої кількості факторів. Всі ці фактори не можуть бути враховані в
процесі чисельних досліджень математичного моделювання. Тому положення
вершин розподілу і значення ймовірностей у них визначаються наближено і
можуть змінюватися в залежності від конкретних умов процесу віброобробки.
З урахуванням цього в загальному вигляді можна вважати, що асиметрія та
мультимодальність розрахункового закону не є суттєвими, і прийняти, що
розподіл швидкостей співудару відповідає одновершинному стандартному
закону нормального розподілу Гауса.
На рис. 9.45 подана апроксимація розподілу швидкостей кривою
нормального розподілу Гауса, що відповідає залежності:
, 1
ф(у) = —7=-е2	,	(9.48)
СУ у "V 2л
де Ф - ймовірність наявності швидкості співудару значенням V;
- середньоквадратичне відхилення швидкостей ударів;
Уто - математичне сподівання розподілу швидкостей співудару.
405
Струтинський В.Б.
Значення параметрів розподілу визначені за результатами апроксимації
розрахункових значень кривою Гауса. Для конкретної розрахованої задачі
математичне сподівання швидкості Уто = 3,5 м/с, стандарт су = 1,5 м/с.
Апроксимація розподілу швидкостей залежністю, що відповідає
нормальному закону, як видно з рис. 9.45, дає суттєві похибки в області
малих швидкостей співудару. Проте, з огляду на те, що процес віброобробки
визначається кінетичною енергією гранули наповнювача, яка пропорційна
квадрату швидкості співудару, можна припустити, що вплив малих
швидкостей співудару на процес віброобробки не є істотним.
Вібраційні швидкості елементів робочого середовища пропорційні частоті
коливань вібробункера. Тому можна вважати, іцо математичне сподівання
швидкості співудару деталі та гранули наповнювача лінійно залежить від
частоти коливань вібробункера, і визначити залежність математичного
сподівання швидкості від частоти:
Уто = 3.5-СГ/40) = 3,5-(со/25О),	(9.49)
де £ - циклічна частота коливань вібробункера, Гц;
<в - кругова частота коливань вібробункера.
Кінематичні режими різання при віброобробці характеризуються частотою
співудару деталі з гранулами наповнювача. Для наближеного аналізу
прийнято вважати, що протягом періоду коливань вібробункера кожна
гранула наповнювача, що стикається з поверхнею деталі, співударяється з
нею один раз. Кількість гранул наповнювача, що безпосередньо стикаються з
поверхнею деталі, залежить від форми і розмірів деталі та гранул
наповнювача. Кількість гранул, що безпосередньо стикаються з поверхнею
деталі, визначена із геометричних міркувань. Якщо кількість гранул, що
безпосередньо стикаються з поверхнею деталі, дорівнює пн, то частота ударів,
які наносяться гранулами наповнювача на поверхню деталі, складе:
£1 = ппш/(2тг),	(9.50)
де О - кількість ударів у секунду, які наносяться на поверхню деталі;
пн - число гранул, що контактують з поверхнею деталі.
Проведене математичне моделювання процесу віброобробки дало
можливість встановити усереднені параметри взаємодії деталі з гранулами
наповнювача. Ці параметри визначають статистично середню швидкість
різання на поверхні деталі. Від цього залежить інтенсивність обробки
конкретної ділянки поверхні деталі. Іншим важливим параметром
технологічного процесу є рівномірність обробки. Вона визначається взаємним
зміщенням деталі та гранул. Це зміщення забезпечується відносним рухом
деталі та гранул, що має місце при коливаннях вібробункера.
В процесі віброобробки робоче середовище перемішується. Конкретні
деталі та гранули наповнювача, які знаходяться в ньому, здійснюють
повільний циркуляційний рух. Оскільки щільність деталей і гранул
406
Розділ 9. Математичні моделі прогресивних технологічних процесів
наповнювача різна, то під дією гравітаційних сил відбувається додаткове
переміщення деталей відносно наповнювача (рис. 9.46).
Це впливає на технологічний процес обробки поверхні деталі. Для
з’ясування основних закономірностей відносного переміщення деталей та
гранул наповнювача розглянемо спрощену схему руху деталей у робочому
середовищі. На статистично середній елемент робочого середовища (деталі
або гранули наповнювача), щільність якого відрізняється від усередненої
щільності робочого середовища, діє Архімедова сила. Якщо елемент рухається
вниз і Архімедова сила позитивна, то це призводить до його уповільнення
відносно робочого середовища. Це має місце для зони робочого середовища з
вертикальним рухом вниз (ділянка АВ на рис. 9.46).
Рис. 9.46. Траєкторії переміщення деталей та гранул наповнювача
при повільному циркуляційному русі робочого середовища: 1 - траєкторія
деталі, щільність якої менша щільності наповнювача; 2 - траєкторія
циркуляційного руху гранули наповнювача, щільність
якої більша щільності деталі
Розглянемо рівновагу сил, які діють на статистично середній елемент
робочого середовища (деталь) на ділянці АВ. Під дією Архімедової сили
елемент (деталь) зміщується відносно робочого середовища, зазнаючи
гідродинамічного опору (рис. 9.47, а). В першому наближенні можна
вважати, що опір середовища пропорційний (з коефіцієнтом С[) відносній
швидкості зміщення елемента відноси > середовища і прямо пропорційний
міделевій площі перерізу елемента. З урахуванням цього, спрощене рівняння
рівноваги сил, що діють на елемент, має вигляд:
6 = СД(УЖ-Уе),	(9.51)
де О - Архімедова піднімальна сила;
407
Струтинський В. Б.
С,- - коефіцієнт опору елемента;
5(. - площа міделевого поперечного перерізу елемента;
Уж - середня швидкість робочого середовища в області в даний момент, де
розташований елемент робочого середовища;
Уе - швидкість переміщення елемента.
Рис. 9.47. Схеми відносного повільного переміщення статистично
середнього елемента (деталі) в робочому середовищі: а - на ділянці руху
елемента вниз; 6-е околі дна вібробункера; в - поблизу поверхні
робочого середовища; г - при повільному повороті елемента з причини
його гальмування на стінці вібробункера
Архімедова піднімальна сила не залежить від переміщення елемента і
визначається через його об’єм і різницю щільностей матеріалу елемента та
середньої щільності робочого середовища:
6 = рЖ ,	(9.52)
де р’ - різниця щільностей елемента і робочого середовища;
408
Розділ 9. Математичні моделі прогресивних технологічних процесів
§ - прискорення вільного падіння;
\УЄ - об’єм елемента.
Підставимо значення сили (9.52) в рівняння (9.51). З огляду на те, що
об’єм елемента пропорційний кубу його характерного розміру сІе, а площа
. .	аь
пропорційна квадрату розміру і враховуючи V = — одержимо:
аі
§р;ксае=уж-^,	(9.53)
аі
XV
де Кс =—- с - - постійна величина, що залежить від форми елемента;
сдае
Ь - координата, що характеризує положення елемента.
Інтегрування одержаного рівняння (9.53) дає можливість знайти рівняння
траєкторії переміщення елемента робочого середовища на ділянці АВ:
Ь = (Уж - Кср’§ас)і .	(9.54)
Підставимо в формулу (9.54) значення часу
= ^Лв/^ж >
де ЬАВ - відстань від точки А до точки В див. рис. 9.46). який відповідає
проходженню середовища з точки А в точку В.
Із формули (9.54) визначимо зміщення елемента відносно робочого
середовища при його переміщенні від точки А до точки В:
АЬдв =Ьав(1-КсрХ/Уж).
У першому наближенні можна прийняти, що швидкість робочого
середовища біля бокової стінки контейнера близька до швидкості на вільній
поверхні робочого середовища. Встановлено, що ця швидкість залежить від
параметрів вібрації, зокрема, від частоти коливань вібраційного механізму.
Швидкість на поверхні робочого середовища визначено згідно зі [121]:
у КХуррдр/у,
Гч 7?	’	<9-55)
2	2 2
^(тьа) ть) тью
де КА - емпіричний коефіцієнт, що враховує втрати енергії в робочому
середовищі;
¥с - відстань від осі вібраційного механізму до центра мас вібробункера;
Ьк - ширина вібробункера (характерний розмір);
є - ексцентриситет дебалансної маси вібраційного механізму;
рр - середня щільність робочого середовища;
ор - еквівалентний усереднений по об’єму вібробункера коефіцієнт
кінематичної в’язкості робочого середовища;
Сф - крутильна жорсткість пружної опори вібробункера;
409
Струтинський В.Б.
шь - маса дебалансного вантажу вібраційного механізму;
т - загальна маса вібробункера з робочим середовищем;
Ьф - коефіцієнт опору при поперечно-кутових коливаннях вібробункера.
Відповідно одержимо максимальне зміщення елемента (деталі) відносно
робочого середовища у вигляді:
АВ
~ ^АВ
2
(9.56)
При русі елемента робочого середовища вгору (ділянка ОЕ на рис. 9.46)
Архімедова сила буде прискорювати його рух. Для випадку, коли густина
елемента (деталі) менша густини гранул наповнювача, елемент (деталь) буде
зміщуватись вгору відносно гранул наповнювача (рис. 9.47, б). Зміщення
елемента відносно робочого середовища буде визначатися залежністю:
АЕ^р

КА¥^'Ькррєш7©
(9.57)
Із наведеного вище розрахунку випливає, що протягом одного оберту
рідинно-деформованого тіла робочого середовища кожний його елемент
спочатку сповільнюється при русі вниз, а потім прискорюється при русі
нагору. Це забезпечує необхідні умови рівномірної обробки всієї поверхні
деталі. Додаткове зміщення елемента досягається при його взаємодії із
стінками вібробункера.
Розглянемо переміщення елемента робочого середовища при русі його в
околі дна вібробункера (ділянка ВСЦ на рис. 9.46). В першому наближенні
можна вважати, що робоче середовище рівномірно обертається відносно
центра мас О. Тому можна визначити рух елемента в полярній системі
координат К і а (рис. 9.47, в). При цьому Архімедова піднімальна сила О діє
під кутом до швидкості переміщення елемента (деталі), і елемент буде
зміщуватися в двох напрямках - радіальному К і тангенціальному т
(рис. 9.47, в). У першому наближенні можна вважати, що опір робочого
середовища пропорційний відносній швидкості. Покладемо, що коефіцієнт
опору при зміщенні деталі в радіальному напрямку дорівнює Сф, а площа
міделевого перерізу §£. Відповідно коефіцієнт опору і площа при зміщенні
деталі в тангенціальному напрямку складжають Ст та 8г.
Рівняння рівноваги елемента, показаного на рис. 9.47, в, в проекціях на
410
Розділ 9. Математичні моделі прогресивних технологічних процесів
радіальну і тангенціальну осі координат мають вигляд:
-бзіпа = СГ8ГУК ; Осоза = СХ8Т(УЖ - Уг),
де Сг і Ст - коефіцієнти опору елемента в радіальному і тангенціальному
напрямках відповідно;
8Г і 8Т - площі міделевого поперечного перерізу елемента;
Уг і \\ - відповідно радіальна і тангенціальна складові швидкості
елемента;
Уж - швидкість робочого середовища.
У полярній системі координат швидкості елементів частинок робочого
середовища визначаються диференціальними залежностями:
6К .
Ут =К—.
1 аі
Беручи до уваги, що Архімедова сила пропорційна кубу характерного
розміру елемента, а площі перерізу пропорційні його квадрату, рівняння
рівноваги запишемо у вигляді:
6К V * я 
--уг = Кгре§ае8іпа і
аі
уж -К^ = Ктр*е§сІесо8а,
аг
V/
—— - постійні, що залежать від форми конкретного
Ун
(9.59)
(9.60)
де Кг =
(9.61)
XV
-----------, І
згсгае
елемента (деталі);
ф - характерний розмір елемента;
\¥е - об’єм елемента (деталі).
У першому наближенні можна вважати, що швидкості елементів робочого
середовища, яке обертається, лінійно залежать від радіуса, тобто
Уж = <всК,
де шс - еквівалентна кутова швидкість робочого середовища.
Тоді друге рівняння системи (9.60) набуде вигляду:
сіа К.р’есі соза
ф------= —- е°----------
с аі я
У лівій частині цього рівняння стоїть різниця кутових швидкостей
елемента і середовища. Величина цієї різниці дуже мала. Тому можна
знехтувати виразом у правій частині рівняння (9.61) і вважати, що
сіа
—	= со..
сії
Враховуючи дану рівність, з першого рівняння системи (9.60) одержимо
диференціальне рівняння, що визначає траєкторію руху елемента в околі дна
вібробункера на ділянці ВСВ (див. рис. 9.46):
411
Струтинський В.Б.
(9.62)
СІК	Кгр*§<іе .
--- -----Щ££_е.81п а .
сіа а)с
Інтегрування залежності (9.62) на ділянці ВС визначить рівняння
траєкторії елемента:
Г> Р — ^гРсв^е гпсг/
Кс — КЕ =---------С08СС
(9.63)
ш,
о
де Кв - відстань від центра мас вібробункера (точки О) до центра елемента
(точки В).
Після підстановки границь в формулу (9.63) отримаємо:
Кс = Ки - ЬіРлМ.(і _ соз а).
®с
Визначимо сумарне переміщення елемента в радіальному напрямку при
його русі з точки В в точку В (див. рис. 9.46). Підставляючи значення кута
а ~ л, знайдемо:
р р _ 2Кгре§сі
ш,
З цього рівняння знайдемо умову руху елемента, при якому його
траєкторія охоплює центр мас контейнера. Це буде мати місце при Кр 0- Щ°
дає наступне обмеження кутової швидкості:
<	о 2КгРМ
Дана нерівність обмежує кутову швидкість циркуляційного руху робочого
середовища за умови ефективного його перемішування.
Усереднена кутова швидкість робочого середовища складає:
юс =	,
КПС
де Упс “ усереднена швидкість на поверхні робочого середовища;
Кпс - радіус, що відповідає відстані від центра мас вібробункера по
поверхні робочого середовища.
Після підстановки значення кутової швидкості одержимо нерівність, що
обмежує лінійну швидкість на поверхні робочого середовища:
V	,, <2КгРМ^.
Лінійна швидкість на поверхні робочого середовища пов’язана з
параметрами вібробункера та деталі. Обмеження на характерний розмір
деталі має вигляд [121]:
СФ___т_У ЬФ
2 І 2 2
ть©	тЬ/|	пфсо
412
Розділ 9- Математичні моделі прогресивних технологічних процесів
При виконанні цієї нерівності буде забезпечене ефективне перемішування
робочого середовища, а отже, рівномірна обробка всієї поверхні деталі.
Розглянемо переміщення елемента робочого середовища при його русі
поблизу поверхні (ділянка ЕР на рис. 9.46). Під дією Архімедової сили
елемент робочого середовища (деталь) зміщується вгору і піднімається на
поверхню робочого середовища. У першому наближенні можна вважати, що
опір середовища пропорційний відносній швидкості зсуву елемента в
горизонтальному напрямку з коефіцієнтом пропорційності Су. Швидкість
переміщення елемента в горизонтальному напрямку може бути прийнята у
вигляді лінійної залежності від радіуса обертання робочого середовища. При
цьому рівняння рівноваги в проекціях на осі координат набудуть координат:
О = Су8уУу; Ч = о)су,
де Су - коефіцієнт опору елемента при його русі нагору;
у - відстань від центра обертання до елемента;
Ух, Уу - проекції швидкостей елемента на осі координат.
З огляду на те, що
~ = у.:	“'V,;	С-<Г;	3,-сі;
визначимо диференціальне рівняння траєкторії руху елемента:
Кур*§бебх = убу ,	(9.64)
де ку = Х¥е/(суае8у) - постійна, яка залежить від форми деталі;
бс - характерний розмір деталі.
Виконавши інтегрування рівняння (9.64) знайдемо:
2КурМх = у2 - у2 ,
де уо - початкова відстань елемента від осі обертання рідинно-деформованого
тіла робочого середовища.
Після перетворень визначимо траєкторію руху елемента:
У = 7у» + 2КуРе§аех 	(9.65)
Із (9.65) випливає, що траєкторія руху елемента відповідає параболі.
Знайдемо умову досягнення елементом, що знаходиться в центрі
вібробункера, поверхні робочого середовища. При цьому
У = Ур>
де ур - відстань від центра вібробункера до поверхні.
Із (9.65) визначимо переміщення елемента в горизонтальному напрямку
хр, яке відповідає його виходу на поверхню:
х - ІУг - Уо),
р (2куР;іас)'
Це переміщення повинно бути не більше відстані від центра вібробункера
до його стінки, тобто
Хр < Кв,
413
Струтинський В. Б.
де Кв — половина відстані між стінками вібробункера.
Підставляючи в цю нерівність значення переміщення, одержимо
обмеження на розмір деталі, яке відповідає умові її виходу на поверхню
робочого середовища. Воно має вигляд:
2	2
2КуРе§гв
Це співвідношення визначає розмір деталі, при якому забезпечується її
переміщення з центральної частини робочого середовища па його поверхню.
Забезпечення такого переміщення дозволяє реалізувати раціональне
перемішування робочого середовища, інтенсифікувати процес віброобробки і
забезпечити найбільш рівномірну обробку всієї поверхні деталі.
В процесі віброобробки відбувається не лише поступальне відносне
переміщення деталей і гранул, а й відносне обертальне переміщення
(поворот) деталей.
Визначимо повільне обертальне переміщення деталі в процесі
циркуляційного руху робочого середовища. Для наближеного аналізу будемо
вважати, що при переміщенні деталі вздовж стінки вібробункера вона
котиться по стінці без ковзання (рис. 9.47, г). Вважаючи обертання елемента
рівномірним, визначимо його середню на момент кочення кутову швидкість:
де Ко ~ відстань від центра обертання до стінки контейнера;
По - розмір елемента в напрямку від стінки до центра обертання.
Визначимо співвідношення кутових швидкостей деталі та робочого
середовища:
юр _	।
йс Ц()
Процес віброобробки відбувається ефективно за умови інтенсивного
повороту деталі. Оскільки в основному об’ємі робочого середовища деталь
повертається з кутовою швидкістю циркуляційного руху робочого
середовища, то можна вважати, що процес віброобробки буде ефективним,
якщо відношення кутових швидкостей буде значно не меншим одиниці. Це
буде забезпечено при виконанні обмеження на розмір деталі у вигляді:
О
” к0 ’
де к13 - коефіцієнт, рівний 2..4.
Наведений вище наближений аналіз параметрів циркуляційного руху
деталей доповнює дискретну математичну модель і дозволяє визначити
характерні параметри процесу вібраційної обробки деталі.
Запропонована дискретна модель дозволяє виконати аналіз процесу,
здійснити ефективне узагальнення експериментальних даних та
інтенсифікувати процес вібраційної обробки.
414
Розділ 10. Математичні моделі складних інженерно-фізичних процесів
РОЗДІЛ 10
Математичні моделі складних інженерно-фізичних процесів
10.1. Застосування функції похибок
для моделювання окремих задач гідромеханіки,
теплопередачі та дифузії
Розрахунок параметрів нестаціонарного руху рідини в ламінарному
граничному шарі на поверхнях різної форми здійснюється з використанням
спеціальних функцій. Ця задача зводиться до обчислення функції похибок.
На рис. 10.1 наведені характерні схеми технічних систем, в яких має
► Но =1(0
Рис. 10.1. Технічні системи, в яких мас місце нестаціонарний рух твердої
поверхні відносно рідини: а - обертання вала в масляній ванні;
б — розкручування рідини в центрифузі; в - виникнення течії в кармані
плоского гідростатичного підшипника; г - рух суспензії абразивних
частинок при фінішній обробці (доводці) поверхні
415
Струтинський В. Б.
Рух твердої поверхні у рідині має місце в багатьох технічних пристроях,
зокрема у гідростатичних підшипниках тощо.
Як приклад на рис. 10.2 наведене фото пристрою для підведення рідини
до обертового вала (див. Патент України № 38742. Шпиндельний вузол, кл.
В24В41/04, 1997). Пристрій має втулку, яка встановлена на валу з
утворенням гідростатичних і гідродинамічних підшипників (мають вигляд
лисок).
Рис. 10.2. Пристрій для підведення рідіти до шпинделя верстата
Поверхні, які рухаються в рідині, застосовуються в багатьох прогресивних
технічних пристроях (див. А.с. СССР № 1413309. Струйньїй генератор
импульсов, кл. Р15В21/12, 1988).
Визначимо розподіл швидкостей в’язкої рідини біля площини, яка раптово
приведена у рух.
Рух твердої поверхні відносно рідини відповідає розрахунковій схемі
стінки, яка приводиться в стан руху згідно закону, що відповідає одиничній
ступінчастій функції. Значення швидкості стінки в даному випадку дорівнює:
І) - 1(0 =
10 при г. < 0
Шо при і > 0
(10.1)
Фізична реалізація задачі відповідає випадку, руху рідини біля поверхні
циліндра, раптово приведеного у стан обертання із кутовою швидкістю £го
(рис. 10.1, а). При цьому діаметр циліндра К вважається достаньо великим в
порівнянні з товщиною шару рухомої рідини.
Розподіл швидкостей частинок рідини біля рухомої стінки описується
рівнянням в частинних похідних [44]:
416
Розділ і 0, Математичні моделі складних інженерно-фізичних процесів
он _ 52н
ЗІ Зу2
(10.2)
де и(і, у) - проекція на вісь х швидкості частинки рідини в момент часу і:
розташованої на відстані у від стінки;
V - кінематична в’язкість рідини.
Початкові умови для розподілу швидкостей наступні:
при і < 0 и(0, у) = 0.
Крайові умови для швидкості рідини на стінці мають вигляд:
при у = 0 н(і, у) = и(і, 0) = 110.
Веденням нових змінних у вигляді
Кл) = “!	(10.3)
ІЗ о	2-У VI
рівняння в частинних похідних (10.2) перетворюється у звичайне
диференціальне рівняння для визначення деякої спочатку невідомої функції ї
відносного параметра ц:
сР( п а( п	,
+2гг~—= о.	(ю.4)
ату аг)
Рівняння (10.4) є звичайним нелінійним диференціальним рівнянням
другого порядку.
Для даного рівняння маємо крайові умови:
Кч> -1;	(|05)
при Г] = ОО ІДГ|) = 0.
Розв’язком рівняння (10.4) із крайовими умовами (10.5) є залежність, яка
включає функцію похибок [44]. Даний розв’язок має вигляд:
£(г|) = 1 _ егг(г)).	(10.6)
Розподіл швидкостей частинок рідини біля стінки, раптово приведеної в
рух, визначиться залежністю (10.6) із врахуванням значень змінних (10.3).
Відповідно швидкість частинок рідини в граничному шарі біля стінки:
11(1, у) = Ц,
1 - егп —~=
у2улй
(10.7)
Залежність швидкостей рідини від параметрів задачі, розрахована за
формулою (10.7), наведена в графічному вигляді на рис. 10.3.
Товщина шару рідини, що приведена в рух завдяки руху стінки (товщина
шару рухомої рідини), оцінюється значенням:
(10.8)
Рух рідини біля стінки є одним із видів виникнення граничного шару на
поверхні тіла, що обтікається в’язкою рідиною.
Граничний шар виникає тоді, коли сили інерції в рідині переважають сили
в’язкості. Співвідношення цих сил оцінюється числом Рейнольдса. При
417
Струтинський В. Б.
низьких числах Рейнольдса біля поверхні має місце звичайна течія рідини.
Рис. 10.3. Залежність швидкостей частинок рідини від відстані
до стінки при раптовому приведенні стінки в рух
На рис. 10.4 показана візуалізована картина руху рідини біля
криволінійної поверхні при низьких числах Рейнольдса.
Рис. 10.4. Візуалізована картина течії в’язкої рідини біля твердої
криволінійної поверхні при низьких числах Рейнольдса
Із розгляду картини течії біля стінки випливає, що при малих числах
Рейнольдса граничний шар на твердих поверхнях не утворюється, рух рідини
є однорідним з невеликими значеннями градієнта швидкості.
При високих числах Рейнольдса має місце якісно відмінний характер течії
в основному потоці та в області течії, що безпосередньо межує зі стінкою. На
рис. 10.5 показані візуалізовані картини течії в’язкої рідини в пристроях
гідропривода при високих числах Рейнольдса.
Течія рідини в граничному шарі представляє собою складний
гідродинамічний процес. Процес може супроводжуватись відривом граничного
шару від стінки (позиція 2 на рис. 10.5) або виникненням зворотних течій
рідини в околі (позиція 3 на рис. 10.5).
Розроблено ряд технічних пристроїв гідро автоматики, які дозволяють
керувати параметрами граничного шару. Зокрема, це - пристрої, в яких у
граничний шар подається рідина під тиском (див. А.с. СССР № 1562548.
Сопло гидравлического отруйного устройства, кл. Р15С5/00, 1990).
418
Розділ 10. Математичні моделі складних інженерно-фізичних процесів
Рис. 10.5. Течія рідини при високих числах Рейнольдса з утворенням
граничного шару при обтіканні виступу (а) та при русі рідини
в дифузорі (б): 1 — граничний шар; 2 — відрив граничного шару;
З ~ зворотна течія рідини в граничному шарі
Відсмоктування рідини з граничного шару дозволяє значно знизити
інтенсивність відривних і кавітаційних явищ, підвищити ефективність
пристроїв гідро автоматики (див. А.с. СССР № 1657781. Приемное сопло
отруйного усилителя, кл. Р15С5/00, 1991).
Іноді для цієї мети застосовують пристрої з пористими стінками каналів, у
яких рухається рідина (див. А.с. СССР № 1335738. Преобразователь сопло -
заслонка,. кл. Р15СЗ/02, 1987).
Математичне моделювання процесів, що мають місце в граничному шарі,
відзначається значною складністю [76, 78]. Але деякі задачі аналізу течії в
граничному шарі вирішуються порівняно просто. Зокрема, це стосується
розрахунку швидкостей у нестаціонарному ламінарному граничному шарі па
поверхні циліндра, еліпсоїда або клина, що рухаються. Розвиток течії в
нестаціонарному граничному шарі рідини на поверхні цих тіл виражається
через функцію похибок [44].
Схема виникнення і розвитку течії в нестаціонарному граничному шарі
рідини на поверхні довільного виду показана на рис. 10.6.
На самій твердій поверхні швидкість частинок рідини дорівнює нулю. По
об’єму граничного шару (обмежено пунктирною лінією на рис. 10.6, с)
швидкість різко збільшується від 0 до максимального значення Со(х). Це
максимальне значення відповідає потенціальній течії нев’язкої рідини.
Для нестаціонарного граничного шару розподіл швидкостей в його
перерізі залежить не тільки від просторових координат, а й від часу. Це
ілюструється графіками, показаними на рис. 10.6, б.
Нестаціонарний рух в’язкої рідини в граничному шарі визначається
рівнянням в частинних похідних. Це рівняння зміни швидкості в граничному
419
Струтинський В. Б,
шарі має вигляд [44]:
5п <32и
	 _ у--
а----------су2
(10.9)
Рис. 10.6. Схема виникнення течії в граничному шарі (а)
та розвиток течії в граничному шарі на твердій поверхні (б)
в різні моменти часу і/ < і?: ( _ потенціальна область течії;
2 - граничний шар біля твердої поверхні
Швидкість рідини ц в граничному шарі визначається, зокрема, швидкістю
потенціального потоку на межі граничного шару. Швидкість потенціального
потоку рідини залежить від поздовжньої координати х, тобто Ио = Іїо(х).
Врахування значення цієї швидкості здійснюється через крайові (граничні)
умови диференціального рівняння (10.9). Граничні умови для швидкості
рідини мають вигляд:
при у = 0 и = 0;
при у = да ц = И0(х).
Розв’язок рівняння (10.9) з даними крайовими умовами виражається
через функцію похибок:
п(х,у,і) = П0(х)" еНІ —Д===-1.	(10.10)
у 2-у VI )
В першому наближенні цей розв’язок відповідає як плоскому, так і
осесиметричному руху рідини в граничному шарі.
Розглянемо ряд характерних прикладів розрахунку нестаціонарного руху
рідини в граничному шарі, що виникає при обтіканні рідиною тіл різної форми.
На рис. 10.7 наведено схему плоскої течії біля поверхні циліндра, який
раптово набув швидкості Уо.
При русі циліндра на його передній поверхні від точки 0 до точки В виникає
граничний шар. На задній поверхні циліндра за точкою В утворюється область
відриву потоку, в якій має місце інтенсивне вихроутворенпя.
420
Розділ 10. Математичні моделі складних інженерно фізичних процесів
Рис. 10.7. Схема утворення граничного шару при раптовому русі циліндра:
1 - граничний шар; 2 - відривна область течії; 3 ~ нерухома рідина
Швидкість потенціальної течії рідини на межі граничного шару біля
передньої поверхні циліндра, який раптово набув швидкості Уд, визначається
залежністю [44]:
и0(х)= 2У0 • §іп — ,
(10.11)
де Уц - швидкість, якої раптово набув циліндр;
х - довжина дуги від критичної точки 0 до перерізу граничного шару, в
якій визначаються швидкості.
Враховуючи, що в залежності (10.11) координата х = гоф, із (10.10)
одержимо формулу для розрахунку розподілу швидкостей в граничному шарі
на поверхні циліндра:
(10.12)
ц(ф,у,і) = 2У0 • 8ІПф • егп —~= .
}
Розрахунок за формулою (10.12) відповідає результатам багаточисельних
експериментів [44] для перерізів граничного шару від критичної точок 0 до
точки його відриву (точки В).
Аналогічна залежність має місце для еліптичного циліндра, раптово
приведеного в рух в напрямку більшої півосі а (рис. 10.8).
Розподіл швидкостей в граничному шарі на передній поверхні еліптичного
циліндра визначається формулою:
(10.13)
ц(ф,у,і) =	.?.---„=Г • ег/—у
< Ь2 12/у
V а
де а та Ь - більша та менша півосі еліпса.
Формула (10.13), одержана для еліптичного циліндра, є узагальненням
421
Струтинський В.Б.
залежності (10.12) і співпадає з нею при а = Ь.
Рис. 10.8. Схема течії навколо еліптичного циліндра,
раптово приведеного в стан руху
Практично важливим випадком є розрахунок параметрів нестаціонарного
граничного шару на поверхні клина, що обтікається потоком рідини. На
рис. 10.9, а показана схема течії біля клина, який рухається в нерухомій рідині.
Рис. 10.9. Схема течії в’язкої рідини біля плоского клина (а)
та візуалізована картина течії біля клина (б)
Обтікання клина, як видно із візуалізованої картини течії (рис. 10.9, б), є
безвідривним. Хоча в потоці рідини перед клином наявні відривні та
кавітаційні області [78].
В багатьох технічних пристроях застосовуються елементи розподілу
рідини у вигляді клина (див. А.с. СССР № б) 723358. Струйное
гидрораспределительное устройство, кл. Р04Р5/00, 19917.
Математичне моделювання характеристик таких пристроїв представляє
собою актуальну задачу. Нижче наведено нескладну математичну модель, яка
служить для розрахунку параметрів течії біля клина.
В граничному шарі на клиновій поверхні (див. рис. 10.9, а) розподіл
422
Розділ 10. Математичні моделі складних інженерно-фізичних процесів
швидкостей потенціального руху рідини визначається залежністю [44]:
и(х) = У0-хга,	(10.14)
де т ~ параметр, який зв’язаний із кутом клина а наступним
співвідношенням:
т =
(10.15)
(10.16)
характеристик
СССР № 1439304. Гидравлический
характеризується усередненими
швидкостей. При цьому поперечна
за поздовжню складову и. Такий
1-А
2л
Розподіл швидкостей в граничному шарі знайдено із (10.10) з використанням
значення швидкості потенціального руху рідини у вигляді (10.14). Швидкість
рідини у нестаціонарному граничному шарі на поверхні клина:
и(х,у,і) = Ч • хт • ег^^=| .
Спеціальні функції дають можливість аналізу
турбулентного руху рідини. Зокрема, розрахунок розподілу швидкостей на
межі двох турбулентних потоків зводиться до обчислення функції похибок.
На рис. 10.10 наведені візуалізовані картини течії в стуменях та в області
течії на межі турбулентного струменя, який розповсюджується в камері,
заповненій рідиною.
Турбулентні струмені, що розповсюджуються в камерах обмежених
розмірів, дають можливість реалізувати різноманітні керуючі функції в
елементах гідро автоматики (див. А.с.
струйньїй з лемент, кл. Е15С1/08, 1988).
Турбулентний шар змішування
значеннями поздовжньої та поперечної
складова швидкості V набагато менша
характер турбулентного руху рідини має назву вільної турбулентності.
Узагальненням даного виду течії є змішування двох паралельних
турбулентних потоків. На рис. 10.11 наведена ідеалізована схема руху рідини
в шарі змішування двох паралельних турбулентних потоків, які мають різні
усереднені швидкості Ц) та П2.
Для плоского турбулентного руху рідини, що відповідає “вільній”
турбулентності, рівняння, яке дає зв’язок між поздовжньою н та поперечною
V складовими усереднених швидкостей частинок рідини має вигляд [44]:
ои	с'и	32и
и----ь V— = є—х-,
ох	су	су
де є - еквівалентна турбулентна кінематична в’язкість рідини;
х, у - поздовжня та поперечна координати.
Еквівалентна турбулентна в’язкість для даного випадку визначена
наближеною залежністю. В’язкість залежить від різниці швидкостей та
відстані від початку області змішування до поточного перерізу потоку.
є~х(И1-и2).	(10.18)
(10.17)
423
Струтинський В. Б.
а)	б)
в)
Рис. 10.10. Візуалізовані картини течії турбулентних потоків:
а, б - струмені з різними значеннями швидкості; в - турбулентний шар
змішування на межі струменя
Рис. 10.11. Схема змішування двох паралельних турбулентних потоків
та епюри усереднених поздовжніх проекцій швидкостей частинок рідини
в різних перерізах області змішування
Розв’язок рівняння руху рідини (10.17) із врахуванням (10.18)
представляє собою залежність, що включає функцію похибок:
де а - емпірична константа, значення якої о ~ 13,5.
(10.19)
424
Розділ 10. Математичні моделі складних інженерно-фізичних процесів
Функція похибок дає можливість знайти загальний вид розв’язку деяких
практично важливих задач теплопровідності та молекулярної дифузії.
Зокрема, задача теплопровідності (молекулярної дифузії) напівобмеженого
масиву при раптовій зміні температури на його поверхні вирішується з
використанням функції похибок [58].
Розглянемо напівобмежений масив речовини (рис. 10.12), який має
нескінченну протяжність від точки 0 в напрямках х і у.
Рис. 10.12. Схема напівобмеженого масиву для задачі
теплопровідності (а) та молекулярної дифузії (б)
Рівняння нестаціонарної теплопровідності в масиві має вигляд:
ао а2о
— — а —у-,
ді. бх2
(10.20)
де а - коефіцієнт температуропровідності;
і - час;
6 - відносна температура, 0 = Т - ТР;
Тр - фіксована (початкова) температура в кожній точці напівобмеженого
масиву і навколишнього середовища.
В початковий момент часу температура на межі масиву змінюється за
законом, що відповідає одиничній ступінчастій функції:
[0 при і < 0
0. =1
|Та - Тр при г > 0
Рівняння молекулярної дифузії в напівобмеженому масиві має
аналогічний (10.20) вигляд:
5С	а2с
- • ’
сЛ	ОХ
(10.21)
де С - концентрація речовини в кожній точці масиву;
В - коефіцієнт молекулярної дифузії.
Зміна концентрації на межі масиву (х = 0) в початковий момент часу
також відповідає одиничній ступінчастій функції:
425
Струтинський В. Б.
Сх.0 = С-"<1’-
Розв’язок рівняння теплопровідності (10.20) при вказаних умовах має
вигляд:
е = т-тр =(Та-Тр)-
1 - егп
(10.22)
На рис. 10.13 наведені графіки залежностей температури в різних точках
напівобмеженого масиву від поздовжньої координати в різні моменти часу,
розраховані за допомогою пакету МаіЬСАІ).
Рис. 10.13. Графіки залежностей температури в точках масиву
від поздовжньої координати (а) та від часу (б):
криві 1—3 відповідають послідовним моментам часу,
криві 4~6 - послідовно зростаючим значенням координати х
Розв’язок рівняння дифузії (10.21) має вигляд, аналогічний (10.22) при
заміні значень постійних, що входять у (10.22). Відповідно аналогічний вигляд
мають залежності концентрації речовини в масиві від поздовжньої координати та
від часу при молекулярній дифузії речовини в масиві.
426
Розділ 10. Математичні моделі складних інженерно-фізичних процесів
10.2. Математичне моделювання пристрою формування
струменя води установки для отримання металевого порошку
із розплавленого струменя металу
Математичне моделювання пристрою формування струменя води
установки для отримання металевого порошку із розплавленого струменя
металу виконане з використанням аналітичного розв’язку диференціального
рівняння в частинних похідних, іцо включає гіперболічні функції.
Виготовлення деталей методом порошкової металургії базується на
формуванні заготовки деталі із дрібнодисперсного металевого порошку з
подальшим спіканням одержаної заготовки. Одним із методів одержання
металевого порошку є розпилення струменя розплавленого металу при
взаємодії його із кільцевим струменем води. Розпилення здійснюється в
спеціальному пристрої (рис. 10.14).
Патрубок для подачі
рідкого металу
Рис. 10.14. Схема пристрою для одержання металевого порошку
шляхом розпилення струменя розплавленого металу
кільцевим водяним струменем
427
Струтинський В,Б.
Пристрій (див. А.с. СССР № 1514481. Устройство для получения
металлического порошка, кл. В22 Р9/08, 1989) включає заливну лійку 1,
корпус 2 із кришкою 8. Втулка 5 та сферична вставка 3 утворюють конічне
сопло, через яке витікає кільцевий конічний струмінь води під високим
тиском (10 МПа). Струмінь води взаємодіє із струменем розплавленого
металу, який витікає з лійки 1. При цьому метал розпилюється на
дрібнодисперсний металевий порошок.
Якість розпилення оцінюється одержанням порошку з частинками
приблизно однакового розміру. Якість розпилення залежить в основному від
рівномірності товщини по периметру та відсутності збурень струменя води.
Формування струменя води здійснюється в кільцевому сопловому насадку
з криволінійними стінками. Насадок являє собою конфузор із складною
залежністю площі перерізу конфузора від довжини.
В результаті виконаних попередніх теоретичних і експериментальних
досліджень встановлено, що найкращу якість розпилення забезпечує
пристрій, в якому закон зміни площі перерізу конфузора відповідає оберненій
функції, тобто площа перерізу конфузора зменшується обернено пропорційно
відстані від входу в конфузор до поточного перерізу.
Рух всіх частинок рідини в такому конфузорному каналі відбувається в
одному напрямку, напрямку до деякої точки (полюса) [46, 58]. Це
підтверджується результатами експериментів по візуалізації течії рідини в
конфузорі [76]. На рис. 10.15 наведені фото візуалізованої течії рідини в
конфузорах з різними кутами конфузорності.
В конфузорному пристрої виникає рух рідини з двома якісно відмінними
між собою ділянками. Основна частина рідини утворює ядро потоку, що
знаходиться посередині конфузора. В ядрі потоку рідина рухається в
напрямку до полюса О. В кожному окремому перерізі потенціального ядра
потоку частинки рідини мають однакову швидкість [78, 81].
Схема полярного руху рідини в напрямку до полюса відповідає
потенціальній течії в ядрі потоку з утворенням ламінарного граничного шару
на стінках конфузора. При цьому розрахункова схема течії відповідає
плоскому конфузорному каналу з прямолінійними стінками (рис. 10.16).
В зонах, що безпосередньо межують зі стінками конфузора, течія рідини
визначається рівнянням граничного шару. Диференціальні рівняння
стаціонарного плоского руху рідини в граничному шарі мають вигляд [44]:
би	би	тт/ ч <Ш(х)	б’и	би	бу
+	=	+	тот + —= 0,	(10.23)
бх	бу	ах	бх	ох	су
де и, V - проекції швидкості рідини в граничному шарі на осі координат х і у;
Ц(х) - швидкість потенціальної течії рідини на межі граничного шару;
V - кінематична в’язкість рідини.
428
Розділ 10. Математичні моделі складних інженерно-фізичних процесів
Потенціальна течія рідини в ядрі конфузорного каналу описується
залежністю [44]:
=	(10.24)
х Ьр,,х
де С] - постійна величина, яка залежить від витрати рідини в потенціальному
ядрі потоку конфузорного каналу;
О,)П - витрата рідини в потенціальному ядрі потоку;
Ь - товщина конфузора;
Рп ~ кут конфузорності потенціального ядра потоку.
|
І
І
І
а)	б)
Рис. 10.15. Візуалізовані картини течії рідини в конфузорах
з утворенням граничного шару на його стінках при куті конфузора:
а - 90’: б - 60"; в - 15'; г — 60' із гальмуванням рідини в граничному шарі
Для інтегрування рівнянь граничного шару (10.23) введемо нову змінну
координату та функцію течії:
ц = —	,	\|/(х,у) =-д/ус^ • і(т]).	(10.25)
X V V
429
Струтинський В.Б.
Рис. 10.16. Схема течії рідини в конфузорному пристрої,
де є потенціальне ядро потоку та граничні шари на стінках конфузора
При цьому проекції швидкості частинок рідини в граничному шарі
визначиться як:
І— П (,
УС|----1 .
х
Підставивши значення проекцій швидкості (10.26) в рівняння граничного
рівняння
и = 11 • і';
(10.26)
шару (10.23), одержимо звичайне нелінійне диференціальне
третього порядку для визначення невідомої функції £:
сі3!	і п
—+ _ — +1 = 0.
ГІГ]
Дане рівняння має наступні крайові (граничні) умови:
при г] = 0
при Г] = со
Розв’язком рівняння (10.27) є точна аналітична залежність
включає гіперболічні функції:
£'= 0;
£' = 1, £’ = 0 .
11
= 3£Ь2	+ АгШ- - 2.
л/2 ЇЗ
Підставивши значення величин в першу формулу (10.26),
проекцію швидкості рідини в граничному шарі у вигляді:
и = ида2

-2 ,
(10.27)
[44], яка
(10.28)
одержимо
(10.29)
де [3 - кутова координата, що вимірюється від стінки конфузорнсго каналу;
430
Розділ 10. Математичні моделі складних інженерно-фізичних процесів
II - швидкість руху рідини в потенціальному ядрі потоку.
Швидкість руху рідини в потенціальному ядрі потоку визначається
формулою (10.24) і складає:
(,0-30)
Товщина граничного шару на стінці конфузора наближено складає:
5 = 3,0-	(10.31)
ї х/ ол
Витрата рідини в перерізі граничного шару визначиться інтегруванням
проекції швидкості (10.29) по товщині граничного шару:
в
= Ь |и<іу = 2,22
0
(10.32)
р
Загальна витрата рідини в конфузорі визначається сумою витрат у
потенціальному ядрі та у двох граничних шарах. Після перетворень одержимо:
( І Не "і
Оо =0оп+2-0сл =Ьу Кеп+4,44/уі ,	(10.33)
(10.34)
де число Рейнольдса потенціального ядра потоку визначається за формулою:
Ке = О™
п Ьу
Сумарний кут звуження конфузора із врахуванням наявності гранични:
шарів:
(10.35)
Ро=Рп+2-.
X
Підставивши значення величин із (10.31) та (10.34) в (10.35), виразимо
кут конфузора через число Рейнольдса потенціального ядра потоку:
—	\2
Л _1
9
Ке„
Ро Ке,
(10.36)
= 9 —
Дана формула дозволяє знайти число Рейнольдса потенціального ядра
потоку за заданим кутом конфузора.
Для знаходження гідравлічних характеристик конфузора використаємо
рівняння імпульсів. Виділимо елементарний об’єм рідини довжиною сіх (див.
рис. 10.16). Складемо рівняння імпульсів для даного об’єму в проекції на вісь
конфузора [81]:
<ц + <іртр +ар„ -ар = о.	(іо.з7)
де сі.) - диференціал осьової проекції імпульсу;
Ртр - проекція на вісь конфузора сил тертя рідини на стінках;
Рн - проекція на вісь конфузора сил нормального тиску на його стінки;
431
Струтинський В. Б.
сІР - диференціал проекції на вісь конфузора сил тиску в перерізі
конфузора.
Осьова проекція імпульсу в перерізі конфузора визначається інтегралом:
'Р/2 _	6
З - -2Ьр | 112хсо5рбр +
о	о
(10.38)
Після підстановки значення швидкості а із формули (10.29), інтегрування
та перетворення одержимо:
Шляхом диференціювання залежності (10.39) знайдемо:
сії = 4-' 2РЬу2 'і 8ІП“ +	С05—
х І Рп ;	2 К Рп ;	2
(10.39)
(10.40)
Проекція па вісь конфузора сил тертя на стінках виділеного об’єму:
бРтр = 2Ьтсо8-убх .	(10.41)
В цю формулу входить дотичне напруження на стінці конфузора т.
Дотичне напруження одержане шляхом диференціювання залежності (10.29):
би	2 ру2 [(Ке
т = ру-—
ау у = о 4з х н Р„
т = ру-—
(10.42)
Підставивши значення дотичного напруження із (10.42) в формулу
(10.41), одержимо проекцію сили тертя на стінках виділеного об’єму
конфузора у вигляді:
бРтр =Х--5^1Р^Щ~со8-^с1х.	(10.43)
тр 73 X2 рп )	2
Проекція на вісь конфузора сил тиску на стінках:
ЗРи = 2(р + бр) • Ь • зіп -у бх ,
де р - тиск в перерізі конфузора;
бр - приріст тиску на довжині бх.
Приріст тиску бр є величиною нескінченно малою і ним можна
знехтувати. При цьому проекція на вісь конфузора сил тиску на його стінках
буде визначатися залежністю:
6РН = 2р • Ь • зіп-у бх .	(10.44)
Проекція на вісь конфузора сил тиску в його перерізі буде визначатися
інтегруванням по площі перерізу сил нормального тиску і складатиме:
432
Розділ 10. Математичні моделі складних інженерно-фізичних процесів
№	о
Р = 2Ь | рх • сов рдр = 2Ьрх • кіп—.
о
Знайдемо диференціал даного виразу:
сі Р = 2Ь 8іп ~ [хсір + рсіх].
(10.45)
(10.46)
Підставивши знайдені значення величин (10.40), (10.43), (10.44), (10.46)
в рівняння імпульсів (10.37), одержимо залежність диференціала тиску від
координати, що вимірюється по довжині конфузора:
сір =
, • Рн
51"т Ж
4М (Ке.
І 2
2,98 (
і;е —
2 З
сіх.
(10.47)
Тиск в поточному перерізі конфузора буде знайдено інтегруванням даної
залежності по довжині конфузора:
X
Р = Рк + рР >
де рк - тиск на виході конфузора;
хк - відстань від полюса до вихідного перерізу конфузора.
Підставивши в цю залежність значення диференціалу тиску з формули
(10.47) і виконавши інтегрування, визначимо тиск в початковому перерізі
конфузора (прийнято рк = 0):
р =	1 — і Ке2
Ро 2вцрп; п
(§о ~ О
(10.48)
де Бо = хк*Ро - ширина конфузора на його виході;
8о - відношення площ перерізу на вході та виході конфузора.
Визначимо, як звичайно, зв’язок між витратою рідини і перепадом тиску
на конфузорі у вигляді квадратичної залежності:
Р0=цйЬВ0 &,	(10.49)
У Р
де ро - коефіцієнт витрати конфузора.
Підставивши в цю залежність значення витрати і перепаду тиску,
одержимо формулу, яка визначає коефіцієнт витрати конфузора у вигляді:
4,44 + Д Кеп	8»5Іп^
Цо = 'цпі -------------Т—в----------------------ІП ' (10'50)
6,0 + д/рп Кеп і (52 _ Л 8ІП + КЄп . 2 98 С05 Ь.
Результати розрахунків за формулою (10.50) наведені на рис. 10.17.
433
Струтинський В.Б.
Розрахунок за формулою (10.50)
Рис. 10.17. Схема пристрою для формування кільцевого струменя води (а)
та результати математичного моделювання коефіцієнта витрат
конфузора у порівнянні з експериментальними даними (6)
При протіканні рідини в конфузорі основні втрати енергії мають місце в
граничному шарі на стінках. Втрати енергії характеризуються дисипативною
функцією [44]. Для випадку плоского руху рідини у граничному шарі
дисипативна функція рівна:
\\ = 2ру
(5нУ 1 (би\
їм+2^; *руЬуГ
(10.51)
Після підстановки значення похідної швидкості згідно (10.29) у формулу
(10.51) та після перетворень одержимо дисипативну функцію у вигляді:
(10.52)
Сумарні втрати енергії у всьому об’ємі граничного шару за одиницю часу
визначаються інтегруванням дисипативної функції (10.52) по всьому об’єму
граничного шару Відповідно сумарні втрати енергії виражаються
інтегралом:
хт окґґхта Л 2,48рЬу3(8д - 1)рц Ке2 [Ке“
= 2Ь ДМДхау =	.	(10 53)
XV	ОІ)Д0Рп	V РП
Потужність потоку рідини, яка підводиться до конфузора, знаходиться
розрахунковою формулою:
N0 = Ро'Оо-
Відповідно коефіцієнт корисної дії конфузора визначається у вигляді:
434
Розділ 10. Математичні моделі складних інженерно-фізичних процесів
Ло =!- — = !-
4,96
(4,44 + 7МЧ
2,98 Пц
(10.54)
Результати розрахунків ККД за формулою (10.54) наведеш на рис. 10.18.
Рис. 10.18. Результати математичного моделювання характеристик
конфузора: /а$ - коефіцієнт витрат конфузора; ур - коефіцієнт
корисної дії конфузора; 8 - товщина граничного шару на стінці;
[Ктах] ~ максимально допустима висота мікронерівностей проточної
частини конфузора
Із результатів розрахунків випливає, іцо коефіцієнт корисної дії
конфузора для чисел Рейнольдса більших за 5000 складає 0,85...0,95.
Режим руху рідини в граничному шарі залишається ламінарним за умови,
що стінки конфузора є гідравлічно гладкими. Ця умова виконується, якщо
максимальна висота мікронерівностей Ктах на поверхні конфузора менша
деякого значення [44], а саме:
ЮОу
тах < у
Підставивши значення швидкості II в потенціальному ядрі потоку із
залежності (10.30), одержимо обмеження на максимальну висоту
мікронерівностей стінок конфузора:
ктах <[Ктах]=100- -~,
Ке0
де В - поточна ширина конфузора.
Результати розрахунків за цією формулою також наведені на рис. 10.18.
435
Струтинський В. Б.
10.3. Застосування рядів із спеціальних функцій
при моделюванні задач гідравліки та теплофізики
Застосування рядів із спеціальних функцій при моделюванні задач
гідравліки та теплофізики дозволяє розраховувати параметри процесів
гідродинаміки і теплофізики в різних технічних системах.
Зокрема, розподіл швидкостей при ламінарному русі рідини в
прямокутному каналі описується функціональними рядами, складеними із
гіперболічних та тригонометричних функцій [58].
Для прямокутного каналу зі сторонами 2а і 2Ь розподіл осьових
швидкостей при ламінарному русі рідини визначається залежністю:
и(у,х) =
16 • Ар • а2
тг\р
£(2п-1)3
, (2п - 1)лг
сп~--------—
1 _ 2а
г(2п-1)яу
1 2а
(10.56)
2а
де Ар - перепад тиску на одиницю довжини каналу;
V, р - кінематична в’язкість та густина рідини;
у, г ~ координати точки, в якій розраховується швидкість;
а, Ь - розміри каналу.
Епюри осьових швидкостей в різних шарах прямокутного каналу, що
відповідає залежності (10.56), наведені на рис. 10.19.
Рис. 10.19. Епюри осьових швидкостей в різних шарах прямокутного
каналу, в якому має місце ламінарний рух в’язкої рідини
436
Розділ 10. Математичні моделі складних інженерно-фізичних процесів
Значення середньої швидкості в прямокутному каналі також визначається
функціональним рядом, який включає функцію тангенс гіперболічний:
Ар • а2 Цсср“ Зур	„ 192-а -А 1 2а )
Наступний приклад математичного моделювання гідродинамічного процесу
стосується побудови профілю каналу, в якому протікає рідина, за умови
відсутності відривних та вихрових явищ в каналі. Побудова профілю каналу
здійснюється з використанням спеціальних функцій (ортогональних поліномів)
(див. розділ 2.3.4). Використання поліномів Ерміта дає можливість вирішити
практично важливу задачу проектування профілю каналу, по якому рухається
рідина без вихроутворення та дисипації енергії [76].
Безвихровий рух ідеальної рідини в осесиметричному каналі довільної
форми описується рівнянням Лапласа для потенціалу швидкостей ф в
циліндричній системі координат [44]:
(10.58)
де х - координата, що вимірюється по осі каналу;
г - поточний радіус: Ф _ потенціал швидкостей.
Якщо задане значення швидкості рідини на осі симетрії, тобто У0(х), то
значення проекції швидкостей частинок рідини, що задовольняє рівнянню
Лапласа, буде мати вигляд [44]:
Ч =$ = Ух(х>г)=Е^Г17-л2-г2пУ0(2п)(х);	(10.59)
5х	2 • (п!)
Ч =	= Ч(х,г) = £	• Г2п• Ур-^х),	(10.60)
от	2 -(и!)
де Ух, Уу - проекції швидкостей на осі х та у відповідно;
х, г - координати, в якій визначаються відповідні проекції швидкості.
Значення функції течії при наявному осесиметричному русі рідини в
каналі визначається залежністю:
(10.61)
п=1	’ (М
У формули (10.59)-(10.61) входять похідні відповідного порядку
функціональної залежності осьової швидкості Уо від поздовжньої координати х:
(10.62)
ах
Використовуючи залежності (10.59)-(10.61) можна будувати осесиметричні
канали різноманітного виду з потенціальним (безвихровим) рухом нев’язкої
437
(10.64)
(10.65)
виражені
(10.66)
Струтинський В. Б.
рідини. Профіль каналу визначиться з рівняння \|/(х, г) = Соизі.
Приймемо, що значення проекції осьової швидкості на осі каналу
відповідає виразу, який включає функцію похибок:
У0(х) = 0,55 + 0,45* ег£(х).	(10.63)
При цьому швидкість частинок рідини на осі симетрії каналу змінюється
від 0,1 при х = -оо до 1 при х = +оо.
Послідовні похідні функції У0(х) визначаються шляхом диференціювання
залежності (10.63), що включає функцію похибок, і мають вигляд:
" ' ' Дї <1х- ' '
Похідні визначаються через поліноми Ерміта (див. розділ 2.3.4).
Поліноми Ерміта відповідають залежності наступного виду:
Н.(х) = (- 1)" • є"’ 
Відповідно значення послідовних похідних осьової швидкості,
через поліноми Ерміта, мають вигляд:
У0'п+,,(х) = (-!)’• 0,90 •-—•Нп(х),
>/2л
де Нп(х) - поліном Ерміта степеня п.
Підставивши це значення в залежності (10.59)—(10.61) знайдемо проекції
швидкостей в перерізі каналу. Форма твірної лінії цього осесиметричного
каналу одержана як розв’язок рівняння:
\р(х, г) = СОП8І,
де значення функції течії прийняте у вигляді (10.61).
На рис. 10.20 наведена форма каналу, розрахована за даною залежністю
та профілей осьових проекцій швидкостей в перерізах каналу.
Рис. 10.20. Профіль каналу, що відповідає розрахунковому полю
швидкостей нев’язкої рідини, та профілі повздовжніх швидкостей
в різних перерізах каналу
438
Розділ 10. Математичні моделі складних інженерно-фізичних процесів
Наступним прикладом математичного моделювання складного
гідродинамічного процесу є розрахунок нестаціонарного ламінарного руху
в’язкої рідини в циліндричному трубопроводі.
В результаті математичного моделювання визначено розподіл швидкостей
нестаціонарного руху в’язкої рідини в довгому циліндричному трубопроводі
при раптовій зміні перепаду тиску на його кінцях. Математична модель
включає функціональні ряди, які містять функції Бесселя [44, 58].
На рис. 10.21 наведена схема круглого трубопроводу, в якому зміна
перепаду тиску Ар являє собою деяку функцію часу £(х).
Рис. 10.21. Схема трубопроводу, в якому має місце нестаціонарна течія
в’язкої рідини під дією ступінчастої зміни перепаду тиску
Диференціальне рівняння нестаціонарного ламінарного руху в’язкої
рідини постійної густини в нескінченно довгій циліндричній трубі круглого
перерізу згідно [44] має вигляд:
5У	(д-\Т	1
------V • ----4* — *
ді.---І Зг"	г
(10.67)
де V - кінематична в’язкість; р - густина рідини; V = У(г, і) - значення
поздовжньої швидкості в перерізі трубопроводу на відстані г від осі
трубопроводу в момент часу Ь.
Рівняння (10.67) розв’язане для раптової зміни перепаду тиску у
трубопроводі. Перепад тиску задано у вигляді одиничної ступінчастої функції:
£(£) =
Ар
Т
'Ар
•1(0= 1
при
0 при £
і>0
< 0
(10.68)
де 1 - довжина трубопроводу.
Згідно [44] розв’язок виражається рядом, що включає функції Бесселя. В
результаті знаходиться швидкість частинок рідини в кожній точці каналу:
¥^,0=4-^
4ур1
х	( хЛ2
8ІехР Г4
к-1	\ Го
(10.69)

439
Струтинський В. Б.
де Хк ~ корені функції Бесселя першого роду нульового порядку 5о(Х) = 0;
5о,	5і ~ бесселеві функції першого роду нульового і першого порядків.
Перші два доданки в квадратних дужках (10.69) відповідають усталеному
(при І -> оо) руху рідини і визначають параболічний профіль швидкостей
(параболу Пуазейля). Сума в квадратних дужках визначає нестаціонарну
складову профілю швидкості в циліндричному каналі.
Результати розрахунків профілів швидкостей в діаметральних площинах
каналу для двох різних моментів часу і наведені на рис. 10.22.
Рис. 10.22. Результати розрахунків профілів швидкості
при нестаціонарному русі в’язкої рідини в циліндричному каналі
для двох різних моментів часу І
Математичні моделі на базі спеціальних функцій дозволяють виконати
аналіз складних процесів магнітної гідродинаміки. Наступний приклад
ілюструє використання спеціальних функцій (функцій Бесселя) для
математичного моделювання процесів магнітної гідродинаміки.
За допомогою функціональних рядів, складених із модифікованих
функцій Бесселя, описано рух електропровідної рідини в круглому
трубопроводі при дії зовнішнього магнітного поля [58].
Розглянемо круглий трубопровід радіуса Ко, поміщений в магнітне поле,
по якому тече електропровідна рідина (рис. 10.23). Ззовні на рідину діє
магнітне поле, напруженість якого постійна (Но = соті) і направлена вздовж
осі у. Індукція зовнішнього магнітного поля Во = цН0 також постійна і має
такий же напрямок.
Розподіл швидкостей в перерізі трубопроводу визначається залежністю,
яка включає модифіковані функції Бесселя Іо(х), .... Іп(х) та їх похідні по
аргументу х, а також гіперболічні та тригонометричні функції.
440
Розділ 10. Математичні моделі складних інженерно-фізичних процесів
Рис. 10.23. Схема трубопроводу, по якому тече електропровідна рідина,
на яку діє зовнішнє магнітне поле
Залежність швидкості в перерізі трубопроводу має вигляд:
<у) =	• "МЙ • іо(и • к)- к • г0(н • к)1 +
І Н а [_10{гу
+	І2п (н • К) - К • І2п(Н • К)]со8(2п0) ,
її п=1 І2пЩ)
ТТ ККо	Ж- •
де и0 =	— - коефіцієнт, що має розмірність швидкості;
'•'Р
... ср Ар	.
К =-----=	- - градієнт тиску по довжині трубопроводу;
йх 1
Ко - радіус трубопроводу;
V - кінематична в’язкість рідини; р - густина рідини;
У	г
¥ = — - відносна координата; К =---------- відносний радіус;
Ко	Ко
Н =	, де На = ВЙКЙ - число Гартмана;
2	\ ур
(10.70)
о - коефіцієнт електропровідності рідини; 0 = агссоз— .
г
На осі симетрії трубопроводу (при г = 0) значення швидкості дорівнює:
(10.71)
441
Струтинський В.Б.
Випадок, коли магнітна індукція Во 0, відповідає граничному значенню
швидкості у вигляді:
1ітІ)(г,у) = ——2-(1-К2),	(10.72)
Н-»0	4ур
що співпадає з параболою Пуазейля.
Розрахунок профілів швидкостей в площині ® = 0 наведено на рис. 10.24.
Рис. 10.24. Профіль швидкостей електропровідної рідини в площині 0-0,
розрахований за формулою (10.70) для різних значень числа Гартмана
(10.73)
Наступні приклади математичних моделей відповідають практично
важливим задачам теплопровідності.
Нестаціонарне температурне поле циліндра описується функціональним
рядом, складові якого включають функції Бесселя. Розподіл відносних
температур в об’ємі круглого стрижня, що нагрівається чи охолоджується,
описується диференціальним рівнянням в частинних похідних [120]:
д&	ґа2® і а®4]
51 бг2	Г бг )
де а - коефіцієнт температуропровідності;
® = Т(г, О - Тц - відносна температура, що представляє собою різницю
температур в точках стрижня та температури навколишнього середовища;
Т(г, і) - температура в точці стрижня на відстані т від осі в момент часу і;
То - постійна температура зовнішнього середовища;
а - коефіцієнт температуропровідності.
Радіус стрижня позначимо то, а його довжину будемо вважати нескінченно
великою у порівнянні з радіусом.
Значення відносних температур при зміні температури зовнішнього
середовища на величину ®а знаходяться за формулою [120]:
С \	> аі
т г “ті~
Л  т, — • е
І] їм
®(г,е) = @а£—
(10.74)
442
Розділ 10. Математичні моделі складних інженерно-фізичних процесів
де ті - нескінченна кількість коренів рівняння:
(10.75)
•М™)
Ві = — г0 - критерій Біо;
к
А - коефіцієнт теплопровідності матеріалу стрижня.
Результати розрахунків нестаціонарного температурного поля в циліндрі
наведені на рис. 10.25.
Рис. 10.25. Результати розрахунків нестаціонарного температурного поля
в циліндрі, що охолоджується
Другий приклад рішення задачі теплопровідності полягає в розрахунку
конвективної тепловіддачі. Конвективна тепловіддача рідини в
циліндричному трубопроводі визначається функціональними рядами,
складеними із функцій Бесселя.
Нагріта рідина, що рухається в циліндричному трубопроводі при ламінарному
режимі руху, має закон розподілу швидкостей у вигляді параболи:
(10.76)
де г0 - радіус трубопроводу;
г - поточний радіус;
Ус - середня швидкість в перерізі трубопроводу.
Розподіл температури по об’єму рухомої рідини залежить від радіуса
1-
V = 2УС
443
Струтинський В.Б.
трубопроводу г та відстані вздовж труби х. Залежність відносної температури
в кожній точці труби від просторових координат має вигляд [120]:
30	2 і г і
@(х,г) = ®а£ т / ч • Л> Иі “ х
х ехр<
X
2г0
' ґ 2 у	(	2 \
(Ре)2 • 1 -	+ 4|Л2 - Ре • 1 - іу І
< го )	У г<> )
(10.77)
де ®(х, г) = Т(х, г) - То - різниця температур в точці потоку з координатами
х, г відносно температури стінки каналу То;
®а(х, г) = Та(х, г) - То - різниця температур в початковому перерізі
потоку на вході у трубопровід;
Ці - послідовні корені функції Бесселя першого роду нульового порядку
(корені рівняння 5о(ц) = 0);
Іо. -Ь| ~ функції Бесселя першого роду відповідно нульового і першого
порядку;
2У г„
Ре = —— - критерій Пекле, складений для середньої по перерізу
а
трубопроводу швидкості Ус та коефіцієнта температуропровідності рідини а.
Розрахунок температурного поля в діаметральному перерізі трубопроводу
наведено на рис. 10.26.
2 г/го
Рис. 10.26. Температурне поле при русі рідини в трубопроводі
з кснвективною тепловіддачею до стінок трубопроводу
444
Розділ 11. Символьні та дискретні моделі просторового турбулентного руху рідини
РОЗДІЛ 11
Символьні та дискретні моделі просторового
турбулентного руху рідини
11.1. Знаходження символьних математичних моделей векторного
поля просторового турбулентного струменевого потоку
за результатами експериментальних вимірів
В багатьох технічних пристроях має місце розповсюдження та взаємодія
потужних просторових турбулентних потоків обмежених розмірів. Це
стосується, наприклад, пристрою “струменева трубка” та його модифікацій
(див. А.с. СССР № 144108.5. Струйньїй гидроусилитель, кл. Г15ВЗ/00,
1988). При математичному моделюванні робочих процесів таких пристроїв
необхідно визначити реальні параметри векторного поля швидкостей рідини в
різних перерізах турбулентних потоків. Звичайно векторне поле визначається
за результатами експериментальних вимірів. Експериментальне визначення
проекцій швидкостей здійснюється в дискретних точках турбулентного
потоку. Для одержання символьних залежностей, що описують векторне поле
швидкостей, значення вимірів у окремих точках апроксимуються
відповідними аналітичними залежностями.
В багатьох практично важливих технічних пристроях (див., наприклад,
А.с. СССР №	1541432. Струйномеханический преобразователь, кл.
Г15СЗ/02, 1989) розміри високошвидкісних (порядку 100 м/с) обмежених
турбулентних потоків є невеликими (порядку 1 мм). Для експериментального
визначення поля швидкостей в таких потоках застосована спеціальна
методика [76]. Методику розглянемо на прикладі визначення потоку маси
(масової витрати) та гідродинамічного напору в обмеженому високонапірному
струмені рідини довільної (складної) форми.
При проведенні експериментів використана спеціальна гідравлічна
установка, схема якої показана на рис. 11.1.
Експериментальна установка дозволяє сформувати високонапірний
просторовий турбулентний струмінь довільної форми чи систему двох
перпендикулярних або зустрічно направлених струменів.
Високонапірний струмінь рідини формуються в сопловому пристрої 2. Цей
пристрій має насадки різної форми, зокрема для формування прямокутного,
овального кільцевого або струменів іншої форми. Форма струменя також
може змінюватись безпосередньо в'самій камері.
Одиночний струмінь чи система двох струменів, що розповсюджуються в
445
Струтинський В.Б.
камері, деформується за допомогою спеціальних дефлекторів 3. Для цього
використовуються механічні дефлектори різноманітної форми, а також керуючі
струмені рідини, що формуються в сопловому пристрої 1.
Рис. 11.1. Принципова схема експериментальної установки, призначеної
для вимірів векторного поля швидкостей просторових високонапірних
турбулентних потоків: 1,2- соплові пристрої; 3 - дефлектор; 4 - трубка
для виміру гідродинамічних параметрів потоку; 5 - манометр; 6 - мірний
бак для визначення витрат рідини; 7, 8 - регульовані об’ємні гідронасоси
Вимірювання гідродинамічних параметрів здійснюються трубкою 4, яка може
змішуватись в трьох напрямках. Вимірювання положення трубки здійснюються за
допомогою індикаторів годинникового типу з точністю ±0,001 мм.
Камера (рис. 11.2), в якій розповсюджуються струмені, виконана
446
Розділ 11. Символьні та дискретні моделі просторового турбулентного руху рідини
прозорою і дозволяє здійснювати спостереження взаємодії струменів.
Високонапірні струмені мають звичайно невеликі розміри (~1 мм).
Діаметр вимірювальної трубки з метою виключення облітерації в її проточній
частині вибирається не менше 0,3 мм. Тому розміри потоку, який
вимірюється, і розміри трубки є величинами одного порядку. Цю обставину
необхідно враховувати при визначенні поля швидкостей.
Рис. 11.2. Фото камери, в якій проводились експериментальні вимірювання
вектора швидкості та гідродинамічного напору в обмежених високонапірних
турбулентних струменях рідини розміром порядку 1 мм
Установка (див. рис. 11.1) дозволяє виконати точкові вимірювання
значень переносу маси (об’ємної витрати рідини) в перерізі трубки або виміри
значень усередненого гідродинамічного тиску в перерізі трубки [76].
Точкові вимірювання значень переносу маси здійснюються вимірюванням
об’ємних витрат рідини в перерізі трубки тоді, коли трубка з’єднана із
мірним баком 6. Витрати рідини в перерізі трубки визначаються як потік
вектора швидкості:
<3(у,х)= Дч(у,2)-сіо,	(п
$
де 5 = тгсІу/4 - площа перерізу трубки діаметром сіт;
у(у, г) ~ розподіл швидкостей потоку рідини в перерізі трубки.
Швидкість частинок рідини в перерізі трубки не є постійною.
Для врахування змін швидкості в перерізі розглянемо спрощену схему
447
Струтинський В. Б.
течії в околі торця трубки, коли швидкість змінюється лише в одному
напрямку так, як це показано на рис. 11.3.
Для врахування змін швидкості по перерізу трубки встановимо залежність
швидкості від координати у вигляді ряду Тейлора. Розклад в ряд здійснимо в
напрямку координати у в околі центра трубки. Значення швидкості в точці з
координатою у визначається рядом:
у(у) = уо	0-	(11-2)
“7і! Зу у = 0
де у0 — швидкість в центрі торцевого перерізу трубки;
Ау - відстань від центра до поточної точки перерізу трубки;
(>) 5'уо	....
уу =------ - послідовні похідні швидкості частинок рідини,
Зу' у = 0
визначені в центрі торцевого перерізу трубки.
Рис. 11.3. Врахування впливу нерівномірності розподілу швидкості
в перерізі трубки на результати вимірювань: а - профіль швидкостей;
б — картина течії в трубці; в - залежність витрат рідини в трубці
від її зміщення
Обчислимо подвійний інтеграл (11.1) із врахуванням залежності (11.2).
Перейдемо до полярних координат з центром на осі трубки, а саме до г та <р.
Відповідно поперечна координата:
Ау = І-СО8ф.
Витрата рідини в перерізі трубки визначається інтегралом:
СІ-г
2	СС 4
0 = IIу» +Х^У»)’СО8І(Р'ГІ
0 0 І.	І=1 1-
гскрсіг.
(11.3)
Для обчислення цього інтеграла використано таблиці [19]. Після
обчислень значення подвійного інтеграла одержимо у вигляді [76]:
тліу „	1 (о 1	(4Т
о = у0 • -7і+у• 7—
4	1! (і + 2) ( 2
- + 1 , (11.4)
448
Розділ / /. Символьні та дискретні моделі просторового турбулентного руху рідини
де сІт - діаметр торцевого перерізу трубки;
Г(х) - гамма-функція (див. розділ 2.3.2).
Визначимо витрату рідини в трубці у вигляді ряду Тейлора як функцію,
що залежить від зміщення трубки:
0 =	о’	(11-5)
V! Ау = 0
де Оо ~ значення витрати без врахування зміщення трубки;
0^^ - послідовні похідні виміряного значення витрати при зміщенні
трубки на величину Ау від нульового положення.
При зміщенні трубки значення у0 = У0(у) буде змінюватись у
відповідності з формулою (11.2). Прирівняємо розраховані за формулами
(11.4) та (11.5) значення витрати рідини в трубці:
Ти V!
(Ач)* =
'	4
Ау = 0
(11.6)
Введемо припущення, що ця рівність не залежить від величини зміщення
(Ау). При цьому одержимо зв’язок похідної швидкості та похідної
експериментально виміряного значення витрати рідини в трубці:
уп) = дб) .4/^2
Відповідно із формули (11.4) значення швидкості на осі трубки знайдемо
у вигляді:
40
ПСІ І
Л4Т їїотц 2; и )! и )
(11.7)
Якщо врахувати тільки перші лінійну і квадратичну складові (першу та
другу похідні) залежності зміни витрат від зміщення трубки, одержимо:
„ _	0' О"
ясі2 л7лсІт 4тг7я
(11.8)
Це означає, що фактичне значення швидкості на осі трубки буде меншим
за визначене за виміряним значенню О витрати рідини в трубці. При цьому
зменшення швидкості залежить від першої та другої похідних виміряного
значення витрати рідини в трубці.
Якщо враховувати тільки залежність зміни витрат від першої похідної
значення швидкості, формула (11.8) набуде більш простого вигляду:
ясі2
Коли взагалі не враховувати зміну витрат, то будемо мати наближену
449
Струтинський В. Б.
формулу:
N =	.
Остання залежність не враховує зміни швидкості в перерізі трубки і
використовується звичайно при вимірюваннях швидкостей потоків великого
розміру трубкою малого діаметра [58].
За допомогою трубки також здійснюються вимірювання гідродинамічного
тиску в перерізі турбулентного потоку. Для цього використовується
заглушена трубка, в якій за допомогою манометра вимірюється тиск. Схема
вимірювань показана на рис 11.1, а характер течії рідини в торцевій області
отвору трубки наведений на рис. 11.4.
Рис. 11.4. Картина ліній течії в заглушеній трубці при точкових
вимірюваннях гідродинамічного напору в турбулентних потоках:
а течія при рівномірному розподілі швидкостей; б — течія
при нерівномірному розподілі швидкостей в перерізі трубки
Коли потік рідини на вході в трубку має рівномірний розподіл
швидкостей, то значення тиску р в трубці зв’язане із швидкістю потоку
рівнянням Бернуллі, тобто
р = ру2/2.
Таким чином, для рівномірного потоку швидкість частинок рідини
визначається по виміряному значенню тиску за формулою:
V = у/2р/р .	(11.9)
Якщо розміри трубки мають той же порядок, що і розміри потоку,
необхідно врахувати наявність нерівномірності швидкостей в перерізі трубки.
Для врахування нерівномірності швидкості виконаємо наближений аналіз
процесу. Картина течії для випадку нерівномірного розподілу швидкостей в
перерізі трубки зображена на рис. 11.4, б. Складемо рівняння Бернуллі для
лінії течії АКТ. Із цього рівняння випливає:
УА = 72р/р •	(11.10)
Порівнюючи залежності (11.9) та (11.10), можна зробити висновок, що
у(у) = уа. Розкладемо залежності у(у) та чА у відповідні ряди Тейлора і
450
Розділ 11. Символьні та дискретні моделі просторового турбулентного руху рідини
одержимо рівність:
ЬІ 1!	і=і
де Уд , Уд - значення швидкостей при певному положенні трубки, в якому
у = Уо, а 5у представляє собою відхилення трубки від даного положення.
Будемо вважати, що рівність (11.11) мало залежить від значення
зміщення трубки 8у. Відповідно одержимо відношення між похідними:
У(і) = У^.
Враховуючи дану рівність та формулу (11.11), встановлено, що швидкість
на осі трубки визначається рядом:
V = V* + УУ^Зу)1 •
Використовуючи даний розклад в ряд, визначимо значення швидкості в
точці А:
уа = у‘ + (лУа)' •	(11.12)
Звідси знайдемо:
у’ = У А -Е^у'Р^Ул)1 •	(11.13)
~71!
Визначимо послідовні похідні швидкості через виміряні значення похідних
тиску в об’ємі заглушеної трубки. Похідні визначаються шляхом
диференціювання залежності (11.10) по змінній - тиску р у заглушеній
трубці. Нульова, перша і друга похідні відповідають виразам:
уа =л/2р/р ’	(11.14)
у'а =Д-4-р'; уА =у(А) =	•	(1115)
V р V?	ЇР |_4д/р а/р
Підставивши значення похідних із (11.14) та (11.15) в формулу (11.13) і
обмежуючись трьома складовими ряду Тейлора, одержимо значення
швидкості частинок рідини у вигляді:
у = Д-а/Р-Д'-7=-(ЛУа) + Д- -Ту-уг ’Йл)- (11-16)
УР V р л/р ЇР [47р3 2д/р
Формула (11.16) визначає швидкість в залежності від виміряного
значення тиску в заглушеній трубці та його похідних. В цілому вона
аналогічна залежності (11.10).
У формулу (11.16) входить невідоме значення Дуд, яке залежить від
багатьох факторів. Визначимо його як відносну величину діаметра трубки 6Т:
Лул = хА.
451
Струтинський В. Б.
де % - деякий емпіричний коефіцієнт.
При цьому формула для визначення швидкості частинок рідини на осі
трубки набуде вигляду:
С атХР' сітХ2 .( Р'2 Р'ї)
Із геометричних міркувань (див. рис. 11.4, б)значення коефіцієнта не
може перевищувати величину:
Х = 0...0,5.
Уточнення значення цього коефіцієнта виконане із врахуванням закону
збереження імпульсу в перерізі потоку [76]. Для практичних розрахунків
можна прийняти х = 0,2.
Якщо у формулі (11.17) враховувати лише першу похідну тиску і
знехтувати квадратом похідної з причини його малості, одержимо,
враховуючи значення коефіцієнта х = 0.2:
Ї2 Г г о,іатР'
Формула (11.18) значно простіша за (11.17) і придатна для практичних
розрахунків швидкості по вимірах тиску та його похідної.
Таким чином, встановлено, що при визначенні швидкості через
експериментально виміряне значення тиску в трубці одержане значення
швидкості повинно бути скореговано (зменшено) на деяку величину. Якщо
виміряне значення тиску має суттєву першу похідну, то поправка
здійснюється в залежності від похідної (градієнта) тиску згідно формули
(11.18). При наявності суттєвого значення другої похідної тиску потрібно
враховувати поправку на другу похідну згідно формули (11.17).
Одержані формули дають змогу здійснити точкові вимірювання
гідродинамічних параметрів у перерізі струменевого потоку обмежених
розмірів (порядку 1 мм). Для визначення нормальної проекції швидкості в
перерізі потоку використовувалась наступна методика. При вимірюваннях
трубка (діаметр трубки 0,3 мм) зміщувалась в двох напрямках у та г.
Зміщення проводилось дискретно на певні невеликі значення кроку (0,2 мм)
від значень у = уо, г = го до значень у = уп, г = гт. При цьому здійснювалось
дискретне сканування всього перерізу потоку (рис. 11.15).
В процесі експериментів вимірюється тиск в заглушеній трубці або
витрати рідини через неї. Результати вимірювань тиску (або витрат рідини)
заносяться в таблицю у відповідності із покроковою зміною координат трубки
при її переміщенні в перерізі потоку.
452
Розділ 11. Символьні та дискретні моделі просторового турбулентного руху рідини
Рис. 11.5. Схема сканування трубки при вимірюванні гідродинамічних
параметрів по перерізу потоку (а) та таблиця із виміряними
значеннями тиску (б) у вузлах прямокутної сітки
Одержаний масив значень тиску р^ утворює матрицю (рис. 11.5, б),
елементи якої є множиною дискретних значень гідродинамічного параметра
(тиску або витрат рідини в трубці). Математична обробка одержаної множини
дискретних значень дає можливість знайти фактичні значення швидкості у
всіх точках перерізу потоку та побудувати символьну математичну модель
фактичних значень швидкості. Це здійснюється наступним чином:
•	Шляхом інтерполяції сплайнами (див. розділ 7.1) масив дискретних
значень тиску рц описується символьною залежністю у вигляді функції двох
змінних Р(х,у).
453
Струтинський В. Б.
•	Знаходиться градієнт цієї функції §га<1[Р(у,2)] та визначається
максимальне значення похідної по напрямку функції Р(у,г). Методика
визначення градієнта і похідної за напрямком наведена у розділі 2.2. За
максимальним значенням градієнта (похідної) в кожному вузлі (і, р перерізу
потоку, використовуючи формулу (11.17) чи (11.18), знаходяться значення
швидкості. Обчислення здійснюються у всіх точках перерізу. З метою
спрощення обчислень доцільно знаходити значення швидкості в тих же
точках, де вимірювався тиск, тобто у вузлах перерізу потоку.
•	Одержаний масив значень швидкостей шляхом інтерполяції сплайнами
описується символьною залежністю. Дана залежність визначає неперервне
значення швидкості у всіх точках перерізу потоку у вигляді символьної
функції двох ЗМІННИХ V = у(у,г).
Знаходження швидкостей турбулентних потоків, згідно розробленої
методики, здійснене для різноманітних просторових турбулентних потоків.
Нижче наведені характерні високонапірні струменеві потоки, для яких
визначено розподіл швидкостей в перерізах [79].
Рис. 11.6 відповідає вимірам профілю швидкості в різних перерізах
круглого турбулентного струменя. Там же наведені ізотахи швидкостей в
перерізах струменя.
а)	б)
Рис, 11.6. Експериментально визначені профілі швидкостей в різних
перерізах круглого турбулентного струменя (а) та ізотахи (лінії рівних
значень осьових проекцій швидкості) в перерізі струменя (б)
Лінії рівних значень швидкості (ізотахи) в перерізі струменя є зручним
засобом аналізу просторових турбулентних потоків. Для круглого струменя
ізотахи являють собою концентричні кола.
Узагальненням круглого струменя є струмінь еліптичної форми.
В результаті експериментальних вимірювань одержана символьна
нелінійна математична модель, яка описує розподіл усереднених швидкостей в
перерізі високонапірного турбулентного еліптичного (круглого) струменя, у
вигляді:
454
Розділ 11. Символьні та дискретні моделі просторового турбулентного руху рідини
у(у>2) = у0/[1 + а,(у - у0)2 + а2(г-г0)2],	(11.19)
де Уо - швидкість на осі струменя в точці з координатами (уо> хо)!
«і, «2 ~ постійні коефіцієнти математичної моделі (для круглого струменя
аі = а2)> визначені за результатами експериментів.
Формула (11.19) одержана як результат апроксимації (див. розділ 7.2)
дробово-раціональною функцією одержаних значень швидкостей струменя.
Розроблена методика була застосована для аналізу високонапірних
турбулентних струменів складної форми. Такі струмені використовуються в
багатьох технічних пристроях, зокрема, в гідравлічних струменевих
підсилювачах [79] (див. А.с. СССР ?<<? 1470994. Струйньїй гидроусилитель,
кл. Р15СЗ/10, 1988; А.с. СССР № 1245780. Струйньїй дифференциальньїй
усилитель, кл. Р15СЗ/14, 1986; А.с. СССР № 1439305. Струйньїй
гидроусилитель, кл. Р15СЗ/10, 1988).
Нижче наведені експериментальні результати по визначенню
гідродинамічних параметрів потоків різної форми.
На рис. 11.7 наведені лінії рівних значень швидкості (ізотахи) в перерізі
подвійного струменевого потоку, який одержаний із круглого струменя його
деформацією двома клиновими дефлекторами.
1.7 мм
Рис. 11.7. Результати експериментальних вимірювань розподілу
швидкостей в перерізах подвійного потоку, утвореного деформацією
круглого струменя, сформованого в сопловому пристрої діаметром 2 мм:
а - ізотахи в перерізі на відстані 1,7 мм від торця сопла;
б - на відстані 3,3 мм; в - на відстані 6,9 мм
Подвійні високонапірні струмені застосовуються в ряді високоефективних
пристроїв гідро автоматики (див., наприклад, А.с. СССР № 1530832.
Пульсатор, кл. Р15В21/12, 1989).
455
Струтинський В. Б.
На рис. 11.8 подані лінії рівних значень осьових проекцій швидкості
(ізотахи) в перерізах Т-подібного турбулентного струменевого потоку, який
одержано деформацією круглого струменя спеціальним дефлектором у
вигляді площини, до якої прилягають дві сфери (рис. 11.8, а).
Рис. 11.8. Схема (а) дефлектора для формування Т-подібного
турбулентного струменевого потоку та ізотахи цього потоку виміряні
в перерізах, розташованих на відстані 0,45 (б), 2,15 (в) та 5,55 мм (г)
від торцевої поверхні дефлектора
Одержані експериментальні дані оброблені згідно вищенаведеної
методики. В результаті знайдені символьні математичні моделі, які
визначають профілі швидкостей в різних перерізах подвійного та Т-подібного
потоків. Моделі одержані у вигляді нелінійних функцій:
у(г)= уДі-а^)2,	(11.20)
де У() - швидкість струменя в точці локального максимуму епюри швидкостей;
а.) - постійний емпіричний коефіцієнт;
г - відстань від точки локального максимуму до точки, в якій визначається
швидкість.
Вимірювання гідродинамічних параметрів потоків здійснені для потоків
складної просторової форми, зокрема для конічних потоків. Такі потоки
утворюються в технічних пристроях, що мають зустрічно направлені насадки
(див. А.с. СССР № 1305645. Струйньїй стабилизатор расхода жидкости,
кл. С05В7/06, 1986; А.с. СССР № 1661725. Струйньїй стабилизатор
скорости гидропривода, кл. 605В7/03, 13/44, 1991). На рис. 11.9 наведені
ізотахи швидкостей в перерізах симетричних конічних потоків різного виду.
Симетричні конічні турбулентні потоки (див. рис. 11.9) мають
характерний вигляд криволінійного конуса. Кут конуса залежить від
співвідношення струменя і насадки і складає звичайно а =30°... 150°.
456
Розділ 11. Символьні та дискретні моделі просторового турбулентного руху рідини
а)
б)
в)
Рис. 11.9. Профілі радіальних проекцій швидкостей в перерізах
осесиметричних високонапірних турбулентних потоків, що мають місце
при взаємодії круглого струменя з трубчастою насадкою: а - сопло,
в якому формується струмінь, входить в трубчасту насадку;
б - сопло знаходиться на відстані від насадки і діаметр струменя менший
діаметра насадки; в - діаметр струменя більший діаметра, насадки
В результаті вимірювань і подальшої обробки експериментальних даних з
побудовою нелінійної математичної моделі встановлено, що профілі проекції
швидкостей в перерізах конічного потоку мають характерну форму, близьку
до кривої Гауса.
Аналогічний вигляд мають профілі швидкостей асиметричних конічних
турбулентних потоків (рис. 11.10).
Знайдемо символьні нелінійні математичні моделі (див. розділ 7.2) для
апроксимації експериментально визначених дискретних значень радіальних
проекцій швидкості в циліндричних перерізах конічного потоку. Один з
варіантів моделі відповідає кривій Гауса і має вигляд:
457
Струтинський В, Б.
де и, а - постійні величини; К - радіус циліндричного перерізу; х - осьова
координата; хо - точка, в якій досягається максимум швидкості в перерізі
потоку.
а)
б)	в)
Рис. 11.10. Профілі швидкостей в перерізах конічних
асиметричних турбулентних потоків, які формуються при. дії
ексцентрично розташованого круглого струменя на трубчасту
насадку: а - діаметр струменя набагато більший діаметра
насадки; б - діаметр струменя дорівнює діаметру насадки;
в — діаметр струменя менший за діаметр насадки
В результаті проведеного комплексу експериментів встановлено, що форма
обмежених турбулентних потоків може бути досить складною, а схеми течії
самими різноманітними. В той же час профілі швидкостей в перерізах потоків
відповідають певним достатньо простим нелінійним математичним моделям. Із
результатів обробки експериментальних даних встановлено, що профілі
швидкостей можуть бути описані математичними моделями, базисні функції
яких мають наступний вигляд:
•	експоненціальна базисна функція: (р0](г) = е " !г,	(11.21)
де г - просторова координата, що вимірюється вздовж лінії в плоскому чи
криволінійному перерізі потоку; сс, та г0 - постійні параметри. Коли
параметри задані як константи маємо лінійну математичну модель, якщо
параметри визначаються за результатами вимірювань, то модель є
нелінійною;
•	обернено-квадратична базисна функція: <р1і (г) = 1/[1 + а^г - г0 )2 ;
•	поліноміальна базисна функція: <р2і (г) = 1-	~	>
458
Розділ 11. Символьні та дискретні моделі просторового турбулентного руху рідини
В цю залежність входить нова змінна £ = а^г - г0);
•	ірраціональна базисна функція: Ф3і(г)= 1 -а4-^(г*-г^)^ ;
•	базисна функція, яка включає гіперболічні функції:
ФьСО = 1 - Йі2[аі(г - і'о)2];
•	базисна функція, що включає функцію похибок:
Фзі(0 = 1 - ег£(а([1 - рХг - г0)]) 
Всі вищенаведені базисні функції дають близький результат розрахунків.
Близькість профілю швидкостей струменевого потоку до кривої Гауса не є
випадковою. Це випливає із фундаментальних закономірностей роботи
складних технічних систем. Турбулентні струменеві потоки є стохастичними
системами, які само впорядковуються під дією численних факторів
різноманітного характеру. Тому їх характеристики тісно пов’язані із законами
розподілу випадкових величин.
Розглянемо інтегральну енергетичну характеристику струменевого потоку
у вигляді сумарного імпульсу струменя:
; - 0руМз .
5
де р - густина рідини; V - швидкість в поточній ділянці сіз потоку; 3 ~
загальна площа потоку.
В залежності від розподілу швидкості в перерізі потік може бути більш
компактним або розмитим. Для встановлення міри компактності потоку
введемо моменти розсіяння імпульсу потоку у вигляді:
Ц№х-хо)2ру2а5; ст2 |/(у-у„)2рУ2гі8,	(11.22)
де хо, уо _ координати центра потоку.
Не зменшуючи ступеня узагальнення подальших висновків, будемо
розглядати плоский струменевий потік товщиною Зх.
Значення швидкості в струмені визначимо через базисну функцію (11.21)
у вигляді:
V = ут-Ф()=Угае^-^ ,
де Ут - максимальна швидкість в перерізі потоку.
Підставивши дане значення швидкості у формулу (11.22), знайдемо
розсіяння імпульсу потоку у вигляді:
у 2
Сту = -р Д(у - Уо )2Фоі(у)йу ,	(11.23)
5
Де Фоі(у) = е 2“*'у	•
Моменти розподілу параметрів за своєю математичною суттю відповідають
459
Струтинський В. Б.
моментам розподілу неперервних випадкових величин, а саме дисперсії
випадкових величин.
В теорії ймовірностей [10, 60] доведена наступна теорема: при
фіксованому розсіянні о2 (визначеного формулою (11.23)) випадкового
параметра <р01 функціонал виду
Н = -}<рОі(у)-1п[ф(П(у)]ду	(11.24)
має екстремум тоді, коли параметр ф01 розподілено за нормальним законом.
Знайдемо втрати енергії у перерізі струменевого потоку. Розглянемо
окремий випадок такого потоку, а саме ламінарний плоский потік.
Втрати енергії визначаються дисипативною функцією [44], вигляд якої
відповідає формулі (10.51). Таким чином, для плоского струменя товщиною
5х втрати енергії в одиницю часу складуть:
ДЦ = 5х  |ру|”	(1у .	(11.25)
Знайдемо похідну швидкості в перерізі струменя використовуючи
залежність (11.21):
= -2Уп1а(у - у0)' е а(>	.
от
Визначимо квадрат частинної похідної:
2
= 4У>2(у - уо)2 • е2а(>,’УоГ = 2У2аф01(у)- 1п[ф01(у)].
Підставивши значення квадрату похідної швидкості у формулу (11.25),
встановимо, що втрати енергії в перерізі струменя пропорційні:
ДЦ~- /фоі(у)-1п[фш(у)Иу.
— X
Ця залежність відповідає функціоналу (11.24).
Звідси випливає, що профіль швидкостей потоку у вигляді кривої Гауса
забезпечує мінімум функціоналу, який визначає втрати енергії в одиницю
часу для перерізу плоского струменевого потоку.
Розглянута методика ефективно застосовувалась при дослідженнях
процесів у складних технічних системах гідроавтоматики (див., наприклад,
А.с. СССР № 1566106. Струйньїй гидроусилитель, кл. Г15С1/20, 1990).
На основі даної методики розроблені теоретичні основи принципово нової
елементної бази гідро автоматики [76, 78, 79].
( ау')
V <5у ;
460
Розділ //. Символьні та дискретні моделі просторового турбулентного руху рідини
11.2.	Математичні моделі процесів переносу у вигляді дискретних
множин значень інтегральних параметрів
Різноманітні математичні моделі систем і процесів у розподілених та
зосереджених параметрах використовують фундаментальні закони переносу.
Найбільш широко застосовуються закони переносу імпульсу, тепла та
речовини (дифузії). При формуванні законів переносу оперують
інтегральними характеристиками деяких фізичних параметрів, що визначені у
вигляді скалярного чи векторного поля в евклідовому просторі. Для
декартової прямокутної системи координат х, у, г, яка характеризується
одиничними ортами і , ] , к , скалярне поле задається скалярною функцією
точки, що відповідає радіусу-вектору г :
г = іх + іу + кх .
Скалярна функція точки, яка визначає поле, записується у вигляді:
<р(г) = ф(х,у,г).
Векторне поле представляє собою векторну функцію точки:
Г(г)= іРх(х.у,2,) + ]Ру(х,у,г,) + кГ7(х,у,г,).	(11.26)
Прикладами скалярних функцій поля є змінна густина рідини чи
деформованого тіла в кожній точці об’єму, що займає рідина чи пружне тіло.
Скалярною функцією описується поле температур або концентрації речовини
в об’ємі. Векторні поля утворюють швидкості частинок рухомої рідини V ,
градієнти температур чи концентрацій речовини в деякому об’ємі.
Закони переносу встановлені для обмеженої частини простору, який має
назву контрольного об’єму XV і обмежується довільною просторовою
замкненою поверхнею 8. Цю поверхню називають контрольною. Вона
обмежує контрольний об’єм рідини в даний момент часу. Переміщуючись у
просторі, контрольний об’єм протікає через свою контрольну поверхню.
Візьмемо в просторі, заповненому рідким середовищем, елементарну
ділянку сіо з ортом нормалі п , який прикладений до зовнішньої частини
поверхні. Загалом площа всієї контрольної поверхні:
3=]7<Ь.	(11.27)
5
На поверхні 8 визначені інтегральні характеристики скалярного або
векторного поля. Зокрема, в процесах переносу використовується інтегральна
характеристика у вигляді потоку вектора. Потік вектора швидкості
(1128)
з	$
де крапкою позначено скалярний добуток V • п = Уп.
461
Струтинський В. Б.
Потік вектора визначається як поверхневий інтеграл скалярного добутку
вектора (в даному випадку вектора швидкості) на нормаль до контрольної
поверхні або як інтеграл від нормальної проекції вектора в кожній точці
контрольної поверхні.
Потік вектора має конкретний фізичний зміст в залежності від
розглянутої векторної функції, для якої визначені процеси переносу.
Наприклад, розглядається масова витрата рідини з інтенсивністю витрат:
8-рУ,	(11.29)
де р - густина; V - швидкість рідини.
Потік О5 вектора § визначає масову витрату (перенос) рідини через
контрольну поверхню 8:
65 = #8 • псЬ = ДрУ/о .	(1130)
З	8
Наступний приклад стосується задачі теплопровідності. Визначається
перенос тепла в одиницю часу в області з відомим розподілом температури.
Розподіл температури відповідає скалярній функції просторових координат
Т(г) = Т(х,у,х).
Перенос тепла описується потоком вектора-градієнта температури:
= [|ї[8га<і(Т)]п<Ь ,	(11.31)
8
де X “ коефіцієнт теплопровідності середовища;
[8гай(Т)]п = 8га4(Т) • її = — •- проекція градієнта температури на нормаль
5п
до елемента поверхні (Іа.
Аналогічно переносу тепла описується перенос речовини за рахунок
механізмів молекулярної дифузії.
Розглянемо закономірності та характеристики процесів переносу в
загальному вигляді.
Добуток скалярних і векторних величин виду
<рУ • гі(1с>
визначає перенос скалярної фізичної величини (р через елементарну ділянку
контрольної поверхні СІСТ .
Скалярний добуток вектора швидкості на орт нормалі
V • п = Уп
відповідає нормальній проекції швидкості. Добуток У„сісг визначає секундну
об’ємну витрату рідини через елементарну ділянку до.
Інтеграл по контрольній поверхні 8 (замкнутій чи незамкнутій)
Ф=/Иаст	(11.32)
462
Розділ 11, Символьні та дискретні моделі просторового турбулентного руху рідини
визначає перенос фізичної величини <р через поверхню 8. Перенос величини
<р відповідає потоку вектора швидкості V , помноженому на величину ер .
В суцільних рідких середовищах має місце перенос різноманітних
фізичних величин. Зокрема, такими величинами можуть бути константи,
наприклад, ер = 1, скаляри, вектори (наприклад, вектор питомої кількості
руху <р - рУ або скаляр - питома кінетична енергія рідини <р = рУ2/2 ).
Для вищеназваних фізичних величин одержимо потоки векторів швидкості
(витрати) фп, імпульсу Іп та переносу кінетичної енергії Еп. Вони
визначаються інтегралами:
Оп = {[У-шіа; Іо = ДрУ(у-й)ба;
,г2 ,	.	(11.33)
8
Для замкненої контрольної поверхні 8 визначені фундаментальні рівняння
гідродинаміки в інтегральній формі, які включають вищевказані значення
інтегралів витрат, імпульсу та кінетичної енергії.
Рівняння збереження маси в інтегральній формі має вигляд:
4 Я|р^+(ц-34)
IV	8	IV
де 8 - контрольна поверхня;
XV - контрольний об’єм, обмежений контрольною поверхнею 8;
р - густина рідини в об’ємі;
І(] - інтенсивність розподілених в об’ємі XV джерел маси;
І - час.
Для стаціонарного руху рідини при відсутності джерел маси в об’ємі
рівняння збереження маси (11.34) має вигляд:
ЯРу> = °.	(1135)
8
Дане рівняння відповідає рівнянню нерозривності суцільного середовища і
трактується як рівність нулю потоку маси через контрольну поверхню, тобто
маса рідини, яка видаляється з об’єму через контрольну поверхню, дорівнює
масі рідини, яка попадає в контрольну поверхню. Це має місце для
довільного проміжку часу.
Рівняння зміни кількості руху в інтегральній формі, записане для
замкнутої контрольної поверхні 8, має вигляд:
>гаху + Дрпао-^^руаху-ДрУУпао = °,	(11.3б)
IV	8	XV	8
де Р - вектор, який визначає інтенсивність зовнішніх масових сил в
463
Струтинський В. Б.
контрольному об’ємі XV;
р„ - вектор, що визначає тиск в кожній точці контрольної поверхні 8;
V - вектор швидкості в кожній точці виділеного об’єму;
Уц - як і раніше, нормальна проекція вектора швидкості в точці
контрольної поверхні 5.
Для стаціонарного потоку при відсутності зовнішніх масових сил рівняння
(11.36) зміни кількості руху в інтегральній формі (рівняння імпульсів) має
вигляд:
= Др¥Уп<Ь.	(Ц.37)
8	8
Дане векторне рівняння відповідає трьом скалярним рівнянням відносно
проекцій векторів на осі координат, які і використовуються при аналізі
гідродинамічних процесів.
Рівняння зміни моменту кількості руху встановлює співвідношення між
моментами кількості руху елементів рідкого середовища:
Ш?х Рдг =Д|г х(ррд\¥+ ||гхрпаст,	(11.38)
(, “*- у	з
де знак х - визначає векторний добуток векторів;
г - радіус-вектор довільної точки в середині контрольного об’єму XV.
Рівняння зміни кінетичної енергії в інтегральній формі відповідає закону
збереження енергії стосовно контрольного об’єму:
А|ДРУІа\у=]ДрГ.уалу+ Др„ .¥60+ /Дміп<П¥. (11.39)
XV 2	XV	8	XV
де Ьііп - інтенсивність потужності внутрішніх сил, які викликають дисипацію
енергії в середині контрольного об’єму.
Наведені вище рівняння гідродинаміки в інтегральній формі, а саме:
рівняння збереження маси (нерозривності) (11.34), рівняння зміни кількості
руху (11.36) і моменту кількості руху (11.38) та рівняння переносу
кінетичної енергії (11.39), дають змогу розробити математичні моделі
різноманітних процесів гідромеханіки, гідравліки, тепломасопереносу та
інших. Ці рівняння мають багато практичних застосувань і широко
використовуються в інженерній практиці.
При розробці математичних моделей процесів переносу із застосуванням
рівнянь гідродинаміки в інтегральній формі виникає проблема обчислення
інтегралів по поверхні та об’єму. В більшості випадків це обчислення неможливе
в символьному вигляді. Часто обчислення інтегралів настільки ускладнює
математичну модель, що її розробка і використання стають недоцільними.
Для ілюстрації цього положення розглянемо типову задачу гідромеханіки,
що описує розповсюдження ізольованого струменя рідини в обмеженій камері.
464
Розділ 11. Символьні та дискретні моделі просторового турбулентного руху рідини
На рис. 11.11 наведено ряд візуалізованих картин течії в камері, що
відповідають даній задачі.
Рис. 11.11. Візуалізовані картини течії ізольованого струменя в камері
обмежених розмірів: а~г — симетрична течія рідини; д, е — течія при
наявності перепаду тиску між верхньою та нижньою частинами камери
465
Струтинський В. Б.
Течія рідини при розповсюдженні струменя в камері відзначається
значною складністю. Наявні різноманітні фізичні явища, зокрема порушення
суцільності рідини (кавітація) (рис. 11.11, а, в), відрив потоку,
вихроутворення (рис. 11.11, д, є).
Не дивлячись на складність явищ, що мають місце при розповсюдженні
обмежених турбулентних кавітуючих потоків рідини, дана задача
гідромеханіки підлягає достатньо точному математичному моделюванню при
застосуванні фундаментальних законів переносу. Для цього необхідно
виділити відповідний контрольний об’єм та контрольну поверхню.
На рис. 11.12 наведені розрахункові схеми, що відповідають
візуалізованим картинам течії (рис. 11.11, г) та (рис. 11.11, е). Пунктиром
виділені контрольні об’єми. Дані контрольні об’єми використані для
застосування рівнянь гідромеханіки в інтегральній формі. На рисунку
показані епюри швидкостей на контрольній поверхні та потоки векторів
інтегральних параметрів рухомої рідини.
а)
Рис. 11.12. Принципові схеми течії турбулентного струменя в обмеженій
камері: а - симетрична течія; б - несиметрична течія в камері
при наявності перепаду тиску
б)
На рисунку також показані потоки векторів переносу імпульсу по
ділянках кожної контрольної поверхні. Контрольні поверхні визначені
контурами АВСБЕР (рис. 11.12, а) та АВСВЕРНК (рис. 11.12, б). Там же
наведені профілі швидкостей на ділянках контрольної поверхні.
Для застосування законів переносу треба визначити інтегральні параметри
течії на контрольній поверхні. Виконати обчислення кратних інтегралів в
замкненому аналітичному вигляді для даних контрольних поверхонь
практично неможливо. Одержаний результат буде дуже складним і не матиме
практичної цінності. Труднощі обчислення інтегралів обумовлені складною
466
Розділ 11. Символьні та дискретні моделі просторового турбулентного руху рідини
формою контрольної поверхні, а також складним видом залежностей, що
описують зміну гідродинамічних параметрів по контрольній поверхні. Це
випливає із загальної складності задач, які підлягають математичному
моделюванню за допомогою рівнянь гідродинаміки в інтегральній формі.
Одержана математична модель у вигляді набору кратних інтегралів від
функцій кількох змінних буде мати ряд незручностей, вона громіздка і мало
придатна для аналізу процесів переносу.
З метою спрощення математичного моделювання запропоновано
здійснювати обчислення кратних інтегралів наближеними методами,
використовуючи дискретні математичні моделі - аналоги інтегралів у вигляді
масивів значень інтегральних параметрів переносу. В результаті розроблена
ефективна дискретизована математична модель процесів переносу в
обмежених потоках складної форми. Особливо ефективним є дискретизація
інтегральних параметрів процесів при розробці математичних моделей
просторових турбулентних високонапірних потоків обмежених розмірів. Дана
модель придатна для використання в багатьох практично важливих задачах
гідромеханіки, гідравліки, теиломасопереносу.
Дискретизована математична модель інтегральних параметрів процесу
переносу описує неперервні інтегральні залежності функцій кількох змінних
кінцевими сумами. Зокрема, потік вектора, записаний у формі дискретного
аналога, має вигляд:
ф = Дф(у-п)до == 22 |]ф(У-п)сісг,	(11.40)
8	1 = 1 Д5,
де - число ділянок (точок), на які розбивається область інтегрування;
Д8] - площа 1-її ділянки.
Число ділянок вибирається виходячи із необхідної точності розрахунків.
Для 5%-ої точності число ділянок К’і > 20. Ділянки можуть мати різну форму
і різне значення інтегрального параметра процесу переносу. Розподіл плоскої
чи криволінійної контрольної поверхні на ділянки здійснюється за
спеціальною методикою (див. розділ 6.1).
Особливо просто дискретизація інтегральних параметрів потоку
здійснюється у випадку, коли підінтегральна функція має постійне значення в
області інтегрування. Це відповідає, наприклад, припущенню про
рівномірність розподілу швидкості рідини в області потоку або припущенню
про однакову температуру чи концентрацію речовини в перерізі потоку.
Розглянемо область, де наявні обмежені просторові потоки рідини.
Обмежений потік характеризується формою та розподілом швидкості в
перерізі потоку. Спочатку розглянемо випадок рівномірного розподілу
швидкості в перерізі потоку довільної форми. Цей випадок, зокрема,
відповідає вільному струменю ідеальної рідини. На рис. 11.13 наведено ряд
467
Струтинський В.Б.
перерізів таких потоків.
Для потоків з постійним значенням швидкості при рівномірному розподілі
параметра <р інтеграл від цього параметра буде пропорційним площі
елементарної ділянки. Доцільно розбивати потік на елементарні ділянки
однакової площі, при цьому значення інтеграла по кожній ділянці буде
однаковим. На рисунку наведена схема формування елементарних ділянок та
відповідні ділянкам точки рівного значення інтегрального параметра. Цим
параметром можуть бути витрата рідини, імпульс, перенос кінетичної енергії,
а також потік тепла чи масовий дифузійний потік речовини.
Рис. 11.13. Форми перерізів прямокутного (а), трикутного (6),
ромбічного (в), трапецієвидного (г), круглого (д) та криволінійних (е~к)
вільних струменів рідини з рівномірним розподілом швидкостей в перерізі
струменя та розбивка перерізу струменя на рівновеликі по площі
елементарні ділянки: 1 - контур, що обмежує струмінь; 2 - точка
рівного значення інтегрального параметра процесу переносу;
З - ділянка, якій відповідає точка; 4 — контур, по якому виконується
інтегрування; 5 ~ ділянки з від’ємними значеннями площі; 6 — точка
від’ємного значення параметра
Покладемо, що ділянки, на які розбито потік, мають однакову площу:
Д8, = сопхе = §/Ц| ,
де N1 - загальне число ділянок.
Доцільно ділянки вибирати конгруентними (подібними) формі потоку.
Ділянки можуть мати різну форму і площу. Бажано вибирати ділянки
468
Розділ 11. Символьні та дискретні моделі просторового турбулентного руху рідини
рівновеликі по площі. Потоки з криволінійною формою контуру можна
розбити на криволінійні ділянки. В деяких випадках треба проводити
розбивку перерізу потоку на кілька груп ділянок з різною площею, або
вводити ділянки з “від’ємною” площею так, як показано на рис. 11.13, к. При
розбивці на ряд груп ділянок вводяться вагові коефіцієнти по окремих групах
точок рівного значення інтегрального параметра.
Для знаходження інтегрального параметра процесу переносу по деякій
площі визначають контур інтегрування. Тоді потік вектора через частину
площі 5, обмеженої контуром інтегрування (як приклад показано на
рис. 11.13, а позицією 4), що включає X ділянок, буде визначено сумою:
1=1
де Ху - загальне число ділянок.
Ця формула виступає еквівалентом формули обчислення подвійного
інтеграла. Процес інтегрування замінюється підрахунком числа точок, які
попадають у виділений контур, що охоплює частину площі 8.
Для потоків, у яких гідродинамічний параметр ф або швидкість V є
змінним по перерізу, також застосовується дискретизація потоку вектора. При
цьому доцільно взяти елементи площі різної величини, але з постійним
значенням потоку вектора для кожного елемента. Оскільки параметр ф має
різні значення по площі, то розміри і форма елементарних ділянок
інтегрування будуть різними в різних частинах перерізу потоку. Розміри
окремої ділянки вибираються за умови:
ДфУ, ЙО =	= С0Г18І ,	(Ц.42)
де Ф - загальне по контрольній поверхні значення потоку;
Му - загальне число елементарних ділянок, на які розбита поверхня.
Звичайно форму і величину ділянки А8, вибирають методом послідовних
наближень, досягаючи умови (11.42).
Дискретизація інтегрального параметра процесу переносу здійснена для
складних турбулентних потоків рідини різної форми. На рис. 11.14 показані
дискретні математичні моделі розподілу інтегральних параметрів в
поперечному перерізі потоку для круглого та квадратного турбулентних
струменів рідини.
Із рисунка випливає, що точки рівного значення параметра (витрати,
імпульсу, переносу кінетичної енергії) для реального турбулентного потоку
рідини розташовані нерівномірно. В місцях, де значення швидкостей є
максимальними (центр потоку), точки розташовані густіше, по периферії
потоку точки розташовані рідко.
469
Струтинський В.Б.
а)	б)
Рис. 11.14. Розбивка круглого (а) та квадратного (б) турбулентного
струменя рідини на елементарні ділянки та відповідні їм точки рівного
значення інтегрального параметра (витрат рідини) в перерізі потоку
Дискретизація інтегральних параметрів особливо ефективна для потоків
складної форми. На рис. 11.15 наведено результат дискретизації параметрів у
турбулентному струмені складної форми. На рис. 11,15, а показано точки
рівного значення витрат для потоку з криволінійним поперечним перерізом.
На рисунку також наведені ізотахи струменю і перерізи (показані цифрами
1-5). Розподіл швидкостей частинок рідини в цих перерізах описується
складними залежностями (див. рис. 11.15, б). Ці залежності в цілому
відповідають кривій Гауса, яка показана на рисунку пунктирною лінією.
Набір точок, який є дискретним аналогом інтегрального параметра
потоку, дозволяє знаходити довільні характеристики потоку. На рис. 11.16
наведено масив точок, який в дискретній формі описує розподіл інтегрального
параметра в перерізі деякого турбулентного потоку рідини складної форми.
За даним масивом точок знаходяться всі характеристики турбулентного
потоку. Наприклад, для знаходження розподілу швидкостей в деякому' напрямку
по перерізу потоку виділяється вузький шар у цьому перерізі. Для знаходження
характеристик потоку у виділеному шарі товщиною А вводиться фізична
координата г, яка змінюється вздовж шару від -оо до поточного значення г.
Підраховується кількість точок, які знаходяться в інтервалі (-оо, г). Будується
ламана лінія, що визначає кусково-постійний процес зміни параметра в
залежності від координати г. Дана залежність Ф (рис. 11.16, б) апроксимується
плавною кривою з використанням розглянутих раніше методів (див. розділ 7.2).
Диференціювання одержаної символьної моделі дозволяє знайти значення
диференціального параметра (швидкості) ф = в шарі шириною А .
470
Розділ //. Символьні та дискретні моделі просторового турбулентного руху рідини
2 ММ
Рис. 11.15. Дискретизація інтегрального параметра в перерізі
турбулентного потоку складної форми (а) та профілі швидкостей в
радіальних перерізах потоку (б). Цифрами 1-5 позначені перерізи та
відповідні їм профілі швидкостей
Крім інтенсивності (значення) диференціального параметра , потік
складної форми характеризується моментами розподілу інтенсивності по
перерізу потоку. Моменти визначаються інтегралами:
= “’ч')ксіа’	(11.43)
де г, - координата, що вимірюється в перерізі потоку;
тю ~ середнє (центроване) значення координати;
і, к - індекси, які визначають номери відповідних моментів.
Моменти за своїм фізичним змістом аналогічні моментам, що
характеризують плоскі перерізи в механіці матеріалів. Зокрема, моменти
першого порядку визначають центр потоку виконанням умови:
т'і = 0 •
471
Струтинський В. Б.
Рис. 11.16. Дискретна математична модель інтегрального параметра
в перерізі довільного турбулентного потоку (а) та знаходження
диференціальних параметрів потоку у виділеному шарі (б)
Відповідно, для знаходження центра потоку параметра ер (координат хо,
Уо) використовуються рівняння:
пі* =	||(х - х0)(рсіст = 0 ;
1 5	(11.44)
т' = —Я<У-Уо)фсЬ = О.
Таким чином знаходяться центри потоків векторів переносу речовини,
імпульсу, кінетичної енергії чи температури.
Моменти другого порядку характеризують розсіяння інтегральних
параметрів відносно центра потоку. Вони аналогічні дисперсіям випадкових
472
Розділ 11. Символьні та дискретні моделі просторового турбулентного руху рідини
величин в теорії ймовірностей:
ф лі
ту = ф'Л(У“Уо)2<р(1ст-
(11.45)
Раніше було визначено розсіяння імпульсу струменевого потоку (див.
формулу (11.22)). Розсіяння імпульсу є моментом другого порядку переносу
кількості руху в перерізі струменя.
Моменти третього порядку характеризують асиметрію розподілу
відповідного параметра в перерізі потоку. їх використання надзвичайно
ефективне при встановленні тенденцій виникнення асиметрії характеристик
технічних пристроїв, в яких використовуються струменеві потоки.
Одержання більш точних інтегральних характеристик процесів, що
протікають у високонапірних струменях, здійснюється з використанням
моментів четвертого та вищих порядків. Момент четвертого порядку
характеризує баланс вкладу центральної та периферійної частини струменя у
формування інтегральної характеристики процесу переносу.
Використовуючи дискретизовані математичні моделі для обчислення
подвійних інтегралів, можна спростити знаходження моментів. Відповідно
обчислюються значення моментів розподілу величини ф в перерізі потоку.
Для обчислення моменту к-го порядку розподілу параметра <р по координаті
Г; застосовується наступна формула:
Д8,
(Н . ».
к 1 = 1	Д8,	1 Vі /
Щ“ = ----г;-----1--- = --> ІГ -
1=1 д8,
(11.46)
де № — число точок рівного значення інтегрального параметра, на які розбито
весь потік; г; - координата і-ої точки рівного значення параметра.
Дискретизована математична модель процесу переносу може бути
ефективно використана для розв’язку рівнянь гідродинаміки в інтегральній
формі та для знаходження узагальнюючих характеристик гідродинамічних
процесів у технічних системах механіки.
473
Струтинський В. Б.
11.3. Дискретна математична модель відхилення просторового
турбулентного струменя
Дискретна математична модель інтегральних параметрів, використана в
фундаментальних законах переносу, є ефективним засобом встановлення
закономірностей процесів, що мають місце в обмежених турбулентних
потоках. Зокрема розглянуто процес відхилення просторового турбулентного
струменя іншим струменем або механічним дефлектором.
а)
д)
Рис. 11.17. Візуалізовані картини течії в області взаємодії
двох струменів у плоскій камері (а—г) та відповідні візуалізованим
картинам лінії течії (е-з), що відображають послідовне збільшення
швидкості керуючого струменя
Дискретизація потоків вектора імпульсу дала можливість вирішити задачу
розрахунку взаємодії двох просторових турбулентних струменів.
Такі задачі часто виникають при математичному моделюванні пристроїв
474
Розділ 11. Символьні та дискретні моделі просторового турбулентного руху рідини
гідроавтоматики (див. А.с. СССР № 1231292. Струйньїй распределитель
жидкости, кл. Г15С1/18, 1986).
Гідродинамічні процеси, які мають місце при взаємодії струменів,
відзначаються значною складністю. Точне врахування всіх особливостей цих
процесів не є доцільним з причини значного ускладнення математичної
моделі [103]. Тому виконано спрощений розрахунок характеристик процесів,
який базується на дискретизації інтегральних параметрів струменів.
Для обгрунтування розрахункових схем виконані попередні
експериментальні дослідження. В результаті встановлені якісні особливості
процесу відхилення плоского струменя, які є основою для розробки
дискретної математичної моделі процесу відхилення просторового струменя.
На рис. 11.17 наведено фото візуалізованих картин течії в області
взаємодії двох струменів в плоскій камері. Нижче на рисунку показані
картини ліній течії, що відповідають фото.
При малих значеннях швидкості керуючого струменя (рис. 11.17, а, д)
рідина із керуючого струменя ежектується в периферійну частину основного
струменя. При збільшенні швидкості керуючого струменя течія в області
взаємодії струменів стає нестійкою. При цьому можливе утворення замкнутої
вихрової області (рис. 11.17, б, е). При подальшому підвищенні швидкості
керуючого струменя утворюється зворотний струмінь (рис. 11.17, в, ж).
Можливі такі специфічні гідродинамічні явища, як кавітація, яка виникає
біля стінок сопла або вихрової зони (рис. 11.17, г, з).
Поля швидкостей та тиску в області взаємодії струменів відзначаються
значною складністю. В області наявні обмежені потоки рідини зі значними
градієнтами швидкості. Епюри швидкостей та статичного тиску в області
взаємодії струменів наведені на рис. 11.18.
а)	б)
Рис. 11.18. Епюри швидкостей (а) та тиску (б) в області взаємодії
двох струменів у плоскій камері, що відповідають течії, показаній
на рис. 11.17, г, з
475
Струтинський В. Б.
Із аналізу наведених експериментальних даних випливає, що в області
взаємодії струменів мають місце складні гідродинамічні явища.
Гідродинамічні параметри в області взаємодії струменів характеризуються
складними залежностями, мають розриви та неоднозначність.
Взаємодія просторових турбулентних струменів супроводжується ще
більш складними процесами ніж плоских потоків. Проведені експерименти
дали можливість встановити кількісні та якісні закономірності процесу
взаємодії струменів. При взаємодії двох турбулентних просторових струменів
(рис. 11.19) утворюється складна система вторинних потоків [76].
Процес взаємодії струменів характеризується виникненням системи
відривних потоків та вторинних течій. Керуючий струмінь Пк, натікаючи на
основний струмінь По, розділяється на два потоки П( та Щ (рис. 11.19, б).
Ці потоки охоплюють контур основного струменя Ьо від критичної точки О до
точок відриву А, В. Гідродинамічний тиск на контурі Ьо основного струменя
змінюється від максимального значення (в точці О) до нуля (в точці А). Під
дією гідродинамічного тиску основний струмінь стискається в площині осей
струменів і розширюється в перпендикулярному напрямку. При обтіканні
рідкого контуру Ьо (основного струменя) в ньому індукуються вторинні
вихрові потоки, які формуються у вигляді двох симетричних струменів П3 та
Гід. Ці струмені направлені до критичної точки О. Відривні потоки 1Ц та Щ
під дією сил ежекції основного струменя відхиляються в напрямку осі
основного струменя і формують периферійні частини результуючого
струменя. Частина рідини із потоків Гф та Щ нижче по течії втягується в
контур ОСНОВНОГО струменя 3 утворенням ДВОХ зустрічних ПОТОКІВ П5 та 11(5
(див. рис. 11.19, в). Ці потоки взаємодіють між собою в критичній точці О( і
стимулюють вихроутворення у вигляді потоків П7 та ІЦ і П9 та IIю- Ці
потоки нижче по течії утворюють два симетричних вихрових шнури, які з
часом сповільнюються і затухають на відстані 3...4 діаметрів від зони
взаємодії струменів. В результаті взаємодії струменів утворюється
результуючий струмінь складної форми. Експериментально визначені ізотахи
поздовжніх швидкостей цього струменя, наведені на рис. 11.20.
В результаті експериментів обгрунтована фізична розрахункова схема
взаємодії двох просторових струменів (рис. 11.21).
Для визначення кількісних параметрів відхилення та деформації струменя
розглянемо спрощену модельну задачу. Виділимо нескінченно тонкий шар в
площині осей струменів. Цей шар обмежується областю АВСО. Товщину
шару приймемо за одиницю. Будемо вважати, що на ділянці ВС області
АВСІЗ статичний тиск постійний і дорівнює гідродинамічному напору
керуючого струменя. Ділянки ВС і АГ) виділеної контрольної поверхні АВСП
є криволінійними. Апроксимуємо дані ділянки дугами кола.
476
Розділ 11. Символьні та дискретні моделі просторового турбулентного руху рідини
Рис. 11.19. Результати експериментальних вимірювань параметрів
турбулентних вторинних потоків, що виникають при взаємодії двох
перпендикулярних круглих турбулентних струменів: а - профілі
швидкостей в площині осей струменів; б - відривні потоки в площині
осі керуючого сопла; в - течія в перерізі струменя на відстані одного
діаметра від торця сопла; г — течія в перерізі потоку на відстані
2-х діаметрів від торця сопла
477
Струтинський В. Б.
Рис. 11.20. Ізотахи повзовжніх швидкостей результуючого струменя,
який утворився при взаємодії двох турбулентних круглих струменів.
Ізотахи в перерізі на відстані 1 діаметр від торця сопла (а),
2 діаметри (б) та 4 діаметри (в). Пунктиром показані розрахункові
значення ізотах
Запишемо рівняння імпульсів (11.36) в проекціях на осі координат.
Враховуючи стаціонарність задачі та відсутність масових сил з рівняння
(11.36) залишаться лише другий та четвертий доданки.
В проекції на вісь х рівняння імпульсів для виділеного в площині осей
струменів шару одиничної товщини має вигляд:
РуоУо -Р^,Уе/2 = Дх ’	(11.47)
де Уо, Уу - швидкості відповідно в основному і керуючому струменях;
Уо - ширина основного струменя;
Уе - проекція криволінійного контуру ВС на вісь у;
Дх - проекція на вісь х імпульсу у виділеному об’ємі на ділянці СВ.
Із геометричних співвідношень для дуги кола ВС випливає:
УЕ = Ху(1-СО8Є0)8ІПЄ0,	(11.48)
де єо - кут відхилення струменя;
Ху - ширина керуючого струменя.
Рівняння імпульсів в проекції на вісь у має вигляд:
1ху - рууху/2 ,	(11.49)
478
Розділ 11 Символьні та дискретні моделі просторового турбулентного руху рідини
де 5ху - проекція на вісь у імпульсу результуючого струменя на ділянці СО.
Рис. 11.21. Розрахункова схема взаємодії двох круглих струменів (а)
та зміщення точок рівних значень імпульсу основного струменя
під дією керуючого струменя (б)
Кут відхилення результуючого струменя визначимо через проекції
імпульсів результуючого струменя у вигляді:
є0 = агсі§ОХу/ Іх).	(11.50)
Підставивши значення проекцій імпульсів із рівнянь (11.47) та (11.49),
знайдемо:
є0 = агс!§
(11.51)
Визначений за цією формулою кут відхилення струменя відповідає
відхиленню рідкого шару в площині осей струменів. Розрахунок відхилення в
площині осей відповідає експериментальним даним.
В інших площинах значення кута відхилення буде іншим. Для визначення
кута відхилення в інших площинах використаємо математичну модель
479
Струтинський В.Б.
струменя у вигляді дискретної множини точок рівних значень імпульсів.
Інтегральний параметр - імпульс основного струменя - розбивається на
дискретну сукупність точок (див. розділ 11.3). Ці точки для основного
струменя показані в його перерізі (див. рис. 11.21, а). Кожна і-та точка
характеризується координатами у;, г,. Всього роглянуто і — 0...П-1, тобто п
точок з імпульсами А}0 - ]0/п .
Розглянемо окремо кожну і-ту точку рівних значень імпульсів. Приймемо,
що тангенс кута відхилення, який відповідає даній точці, змінюється в
залежності від її розташування відносно площини осей. Залежність тангенса
кута від відстані розкладемо в ряд Тейлора і, обмежуючись першою
складовою ряду, одержимо лінійну залежність тангенса кута відхилення від
координати точки 2,. Відповідно кут відхилення буде:
єОІ =агс^Ц1-ку2^£є0},	(11.52)
де ку - деякий постійний коефіцієнт.
Складемо рівняння імпульсів для половини потоку з одного боку від
площини осей. В проекціях на вісь у рівняння імпульсів набуде вигляду:
іі/2	г	,
5у/2 = Елі0-[1-к^Ж,	(11.53)
де 1у - імпульс керуючого струменя;
АІО - імпульс, що відповідає одній точці рівного значення імпульсу
(11.54)
основного струменя.
Із даного рівняння знайдемо значення коефіцієнта:
і _ п ґі ) Аг
у~4 хс1^Дгі-
Підставивши значення коефіцієнта із (11.54) в (11.52), знайдемо кут
відхилення кожної точки з імпульсом Дфу
.	4	2. • П ‘
єОІ = агсі§ 1 - -і—-
/ЇХ
у/ І=1
(11.55)
Для визначення відхилення точки в напрямку осі г зробимо аналогічні
розрахунки. Врахуємо, що в області взаємодії струменів має місце
підвищення тиску. Приймемо, що на ділянці АВ (див. рис. 11.21, а) тиск
змінюється лінійно від нуля (в точці А) до значення, що відповідає
гідродинамічному напору керуючого струменя. Із врахуванням цього
припущення визначимо сумарну силу тиску на ділянку АВСВ:
рг = рУуу0ху/б = 1ууоху/(б8у),	(11.56)
де 8у - площа керуючого струменя.
На кожну і-ту елементарну точку, що відповідає певній частині струменя
буде діяти деяка еквівалентна сила Р2І в напрямку осі г. Залежність цієї сили
від відстані до площини осей розкладемо в ряд Тейлора. Обмежуючись
480
Розділ 11. Символьні та дискретні моделі просторового турбулентного руху рідини
лінійними складовими ряду, одержимо:
Р2і = к2Уі2іРг,
де кг - постійний коефіцієнт.
Із рівняння рівноваги для половини струменя одержимо:
п/2
Рг=£Рн-	(11.57)
Підставимо в рівняння (11.57) значення сили і з (11.56) одержимо:
/п/2
кг=у£уіг,.	(11.58)
Використовуючи знайдене значення коефіцієнта (11.58), із формули
(11.56) визначимо еквівалентну силу, що діє на кожну і-ту точку імпульсу
основного струменя:
хох, /Й
Ргі=-^-Ч„УЛ/2>Л-	(11.59)
Визначимо відхилення елементарної точки струменя в напрямку осі г. Для
цього складемо рівняння імпульсів в проекціях на вісь г:
Рлі = АЛ0 • Ш 	(11.60)
Підставивши значення величин, одержимо кут відхилення кожної точки у
вертикальному напрямку:
є, = агс'су
УохуЩІу
б8у)0
(11.61)
За значеннями кутів відхилення в напрямках осей у і х знайдемо зміщення
кожної точки рівного імпульсу по перерізу струменя. Зміщення в двох
напрямках буде визначено через кути відхилення:
ДУі = х • 1§єОІ; Аг, =х-і§єі.	(11.62)
На рис. 11.21, б наведені розрахункові зміщення точок рівного імпульсу
круглого струменя при його відхиленні. Зміщення точок відповідає зміні
форми струменя, який набуває витягнутої форми.
Розрахункові значення ізотах (пунктирні криві) загалом відповідають
результатам експериментів (див. рис. 11.20, б). Деякі відхилення
розрахункових і експериментальних даних мають місце на периферійних
ділянках результуючого струменя.
Таким чином, використання дискретної математичної моделі дало
можливість виконати теоретичне узагальнення та розрахунок складного
гідродинамічного процесу взаємодії двох просторових турбулентних
високонапірних струменів рідини.
Аналогічно розраховане відхилення турбулентного потоку механічним
дефлектором. Цей процес має місце в багатьох технічних пристроях. Зокрема, це
пристрої гідравлічної автоматики і гідроприводу (див. А.с. СССР № 1399534.
481
Струтинський В. Б.
Струйньїй усилитель, кл. Е15СЗ/10, Е15ВЗ/00, 1988; А.с. СССР № 1643826.
Гіадравлический струйньїй усилитель, кл. Р15СЗ/10, 1990).
Визначення шляхом розрахунку процесу відхилення високонапірного
турбулентного струменя представляє собою практично важливу задачу. Ця
задача стосовно відхилення турбулентного струменя механічним дефлектором
вирішена з використанням дискретної математичної моделі.
Для обгрунтування розрахункової схеми і основних припущень виконані
попередні експериментальні дослідження. На рис. 11.22 наведені візуалізовані
картини течії при взаємодії струменя з механічним дефлектором в плоскій
камері, а на рис. 11.23 - лінії течії що відповідають візуалізованій картині.
а)	б)	в)
Рис. 11.22. Візуалізовані картини течії в області взаємодії струменя
рідини з дефлектором в плоскій камері; фото а, б, в відповідають
послідовному збільшенню подачі рідини в струмені
Із результатів експериментів випливає, що на поверхні дефлектора наявна
критична точка, в якій швидкість рідини дорівнює нулю. Мають місце
зворотні потоки, відривні та кавітаційні явища. На поверхні дефлектора
виникає ламінарний або турбулентний граничний шар, в якому швидкість
рідини наростає від нульового до максимального значення. Експериментальні
лінії течії та профілі швидкостей при взаємодії струменя з дефлектором
наведені на рис. 11.23 [80].
Для розробки загальної математичної моделі виконано аналіз плоскої
модельної задачі. Побудована математична модель процесу відхилення
плоского струменя рідини призматичним дефлектором. Для цього розглянута
плоска розрахункова схема (рис. 11.24, а).
482
Розділ 11. Символьні та дискретні моделі просторового турбулентного руху рідини
Рис. 11.23. Експериментальні лінії течії та профілі швидкостей в області
взаємодії турбулентного струменя з механічним дефлектором
Плоска модельна задача відповідає обтіканню клинового дефлектора
струменем нескінченної товщини. Дана модельна задача відповідає деяким
реальним технічним пристроям (див. А.с. СССР № 1335737. Струйно-
механический преобразователь, кл. Р15СЗ/02, 1987; А.с. СССР № 1373918.
Струйно-механический преобразователь, кл. Р15СЗ/02, 1987).
Рис. 11.24. Розрахункова схема (а), що відповідає плоскій модельній задачі
відхилення потоку клиновим дефлектором, та порівняння розрахунків
з експериментальними даними (б)
б)
483
Струтинський В. Б.
На розрахунковій схемі (див. рис. 11.24, а) будемо вважати, що розміри
струменя набагато більші за розміри клина. Розподіл швидкостей в перерізі
струменя в першому наближенні приймемо рівномірним. Враховуючи високі
значення швидкості в струмені, можна розглянути задачу обтікання у
відповідності зі схемою, коли в основному потоці в’язкість не враховується, а на
поверхні дефлектора в’язкість проявляється в утворенні граничного шару. Будемо
вважати течію рідини в основному потоці потенціальною. При обтіканні клина
швидкість потенціальної течії рідини визначена залежністю [44]:
Уе=Цт,	(11.63)
де § - координата, що вимірюється вздовж клина;
к - постійний коефіцієнт;
т - показник степеня, який зв’язаний із кутом клина наступною
залежністю:
т = є3/(л-єг7),	(11.64)
де Єз - половина кута клина.
Приймемо, що тиск за дефлектором (в точці В) дорівнює нулю. Із цієї
умови на основі інтеграла Бернуллі знайдемо
рУо РСах
2	2
або
У0=Чтах-
Враховуючи цю рівність і залежність (11.63), одержимо:
к^=У0.
Із даної залежності визначимо невідомої коефіцієнт:
к = ч0-^:х.	(11.65)
Відповідно значення швидкості потенціальної течії рідини біля поверхні
дефлектора буде визначатися степеневою функцією від координати ф
^=^гааХ	(И.66)
де £тах - загальна довжина рефлектора в напрямку струменя;
ч0 - швидкість рідини в струмені.
Використовуючи значення швидкості (11.66), із інтеграла Бернуллі [44]
знайдемо розподіл тиску на поверхні дефлектора:
Визначимо сумарну силу тиску на ділянці АВ шляхом інтегрування:
ш.б8>
І 2"> -1
Швидкість в граничному шарі рідини на поверхні клина згідно [44]
484
Розділ 11. Символьні та дискретні моделі просторового турбулентного руху рідини
визначається залежністю:
и = уа • £'(л),
де €(т]) - деяка функція безрозмірного параметра:
П =	7(т + 1ЬС/(^тах) і
(11.69)
(11.70)
V - кінематична в’язкість рідини;
С, - координата, що вимірюється від поверхні дефлектора
перпендикулярно їй.
Функція ( є розв’язком диференціального рівняння:
')р	/	х
Г + £Г + ^М1-Г2)=0.	(11.71)
я
Це рівняння розв’язане чисельним методом. Знайдено значення функції Кр)
та її похідних і' і Г. Значення другої похідної Г при ц = 0 використане для
знаходження дотичних напружень в граничному шарі на поверхні дефлектора.
Для невеликих кутів дефлектора є3 = 0..30° значення другої похідної на стінці
апроксимовано лінійною математичною моделлю виду:
Г(о)= 0,5 + 0,8т .
(11.72)
І 2 |(т + !)ург^
Д ї 8Е 	(11.73)
кліпах/ і ^тах
За значенням другої похідної знайдене дотичне напруження на стінці
дефлектора:
Зт~1 ,___________
т =	= (1 + 1,6т
С = 0
Сумарна сила тертя на ділянці АВ розрахована як інтеграл дотичного
напруження по площі дефлектора:
т = "'Т та? = ру^(°’25 + 0’4т) [(т + 1)у	(!! 74)
о	Зт + 1	\ у(^тах
Для визначення кута відхилення струменя дефлектором складемо
рівняння імпульсів у проекціях на осі координат х та у (див. рис. 11.24, а)'.
Зо - Т СО8 Є(, - Р 8ІП єе = ,1Х
-г . т •	(11.75)
РСО8Є, ~ 1 81П Ее = лу
З системи (11.75) визначено кут відхилення струменя єд:
= К/К 
Розв’язавши систему рівнянь (11.75), знайдемо кут відхилення струменя
плоским клиновим дефлектором:
V
аі - а2Л -----
Е0 = агсі£-------------------------------,	(11.76)
у,	І V
- а212є,3 • з-—----аф§єе
(ітах	V ^дЧтах
485
Струтинський В. Б.
де постійні величини:
Є=СО8Є,	Л + 0,6єл 8ІПЄ-
а1 = —----- ; а7 = ——--------г.~ .	.
* + е5	я + 2єг ^/(1 - єа/л)/2
Розраховані за формулою (11.76) значення кута відхилення струменя
наведені на рис. 11.24, б. На цьому ж рисунку показані і експериментальні
дані для випадку взаємодії прямокутного струменя з плоским дефлектором.
Одержана формула дає близькі до експериментальних даних розрахункові
значення і її можна використати при розробці математичної моделі процесу
відхилення просторового (об’ємного) струменя.
Розглянемо процес взаємодії об’ємного струменя з дефлектором. При
натіканні струменя на дефлектор має місце не тільки відхилення, а й деформація
(сплющення) струменя. Струмінь набуває вигляду, показаного на рис. 11.25.
Рис. 11.25. Розрахункова схема (а) для розробки дискретної математичної
моделі процесу відхилення просторового турбулентного струменя
механічним дефлектором та схема зміщення точок рівного імпульсу
струменя при його відхиленні (б)
486
Розділ 11. Символьні та дискретні моделі просторового турбулентного руху рідини
Розрахунок деформації струменя здійснений з використанння дискретної
математичної моделі струменя у вигляді масиву точок рівного імпульсу. Вони
показані на розрахунковій схемі (рис. 11.25). Розміри струменя набагато менші
за розміри дефлектора. Тому для визначення зміщення точок в напрямку осі у
можна в першому наближенні використати результати розрахунків по плоскій
модельній задачі. При цьому відхилення точки в напрямку осі у визначиться
через кут відхилення єо, розрахований за формулою (11.76).
Для визначення розширення струменя в напрямку осі 2 розглянемо сили,
що діють на кожну точку. Будемо вважати, що в площині симетрії (ділянка
АВС) тиск рідини розподілено таким чином, що в перерізі ділянки (лінія
С'А') тиск змінюється за лінійним законом. При цьому сумарна сила тиску в
напрямку осі 2 складає:
„	<’"г	1	1,. РуоУп£т«єл(Зл - Є,,)'СО8Є=
Р = І р • -• СО8£а(^ =	(11.77)
о 5	6л(л +є,Д
де відстань 1 = А'С'.
На кожну елементарну ділянку струменя, яка відповідає і-тій точці з
координатами (уі, у), буде діяти сила в напрямку осі г. Ця сила призводить
до розширення струменя в напрямку осі 7.. Силу, що діє на елементарну
ділянку струменя у вигляді точки, визначимо як
X = кгУі2іРг.	(11.78)
Підсумовуючи сили по всіх елементарних ділянках, що знаходяться по
один бік від площини симетрії, та прирівнюючи суму до загальної сили,
знайдемо величину постійного коефіцієнта:
/ п/2
к2 =1/£уЛ-	(11.79)
Проекцію імпульсу кожної елементарної точки струменя в напрямку осі 2
визначимо із рівняння імпульсів в проекціях на вісь 2
1 =Р .
Відповідно кут відхилення точки буде рівного значення імпульсу в
напрямку, паралельному площині дефлектора:
є і = агсІ§(Ріг)/}іх .
Враховуючи, що імпульс і-тої точки
Лх =Л/П
і підставивши значення сили із (11.78), а коефіцієнт к2 - із (11.79), знайдемо
кут відхилення і-ї точки:
Є;
, Р12п
= агсІ§—— = агсі§
Зо
Уц^тахЄг(Зл-еа)со8£г
6л(тг + у.)
(11.80)
Знайдені значення кутів відхилення дозволяють розраховувати зміщення
і-ї точки рівного імпульсу в двох напрямках:
487
Струтинський В.Б.
Ауі = х-1§є0, Д/і = хЧдєі,
де х - відстань від дефлектора до поточного перерізу потоку.
На рис. 11.25, б наведено розрахункове зміщення точок рівного значення
імпульсу круглого струменя при відхиленні його плоским дефлектором. За
цими точками встановлена форма струменя після відхилення. Розрахунок
відповідає експериментальним даним (рис. 11.25, б).
Застосування дискретної математичної моделі відхилення струменя
дефлектором дало можливість розраховувати кількісні параметри процесу. Дана
модель є ефективніш інструментом дослідження даного надзвичайно складного
гідродинамічного процесу. Дискретна модель рекомендується до застосування при
аналізі пристроїв гідро автоматики, в яких використовуються високонапірні
струменеві потоки обмежених розмірів.
Розглянута вище методика математичного моделювання процесу відхилення
струменів узагальнюється на струмені двофазної рідини. Такі струмені мають
широке застосування в технічних пристроях (див. А.с. СССР № 1164475.
Струйньїй генератор колебаний, кл. Р15С1/22, 1985); А.с. СССР № 1004673.
Гидравлический генератор колебаний, кл. Р15С1/22, 1982).
Розроблені генератори коливань мають аналогові струменеві підсилювачі,
охоплені додатними зворотними зв’язками. У гідравлічних * магістралях
зворотних зв’язків встановлені струменеві ежектори, в які подається газова
фаза. При цьому керуючі струмені підсилювачів мають газорідинну структуру
випадкового характеру.
Розробка математичної моделі такого струменя базується на дискретизації
гідродинамічних параметрів окремо рідинної та газової складових струменя.
Густина рідини на три порядки вища густини газу. Тому значення
інтегральних параметрів (імпульсу кінетичної енергії) газової складової
струменя набагато менші відповідних значень рідинної складової. Це дає
можливість значно спростити математичну модель струменя.
Дискретизація інтегральних параметрів двофазового струменя якісно не
відрізняється від дискретизації рідинного струменя. Відмінність, яка полягає
у наявності багатозв’язної області інтегрування, нівелюється в силу специфіки
розробки дискретної точкової математичної моделі.
Для розглянутого двофазового струменевого потоку дискретна сукупність
точок змінюється випадковим чином. Випадкових змін в основному зазнають
координати точок рівного значення інтегрального параметра. Певною мірою
випадковим чином змінюється і загальна кількість точок, які описують
інтегральний гідродинамічний параметр у всьому перерізі потоку.
488
Розділ 12. Математичне моделювання динамічних коливальних процесів
РОЗДІЛ 12
Математичне моделювання динамічних коливальних процесів
12.1.	Символьна комплексна математична модель детермінованих
та стохастичних процесів у динамічних системах
Всі технічні пристрої складаються з різноманітних систем, що виконують
певні функції. В системах мають місце динамічні процеси, які відповідають
послідовній зміні стану системи. Характеристики процесів визначаються
складною взаємодією різноманітних факторів і характеризуються, як
правило, закономірностями випадкового характеру.
З розвитком обчислювальної техніки все більшого значення набувають
універсальні символьні математичні моделі, придатні для опису різноманітних
технічних систем та процесів [16, 18. 75, 82-87, 90-92, 100-107, 113].
Універсальна комплексна математична модель побудована на базі методів
теорії автоматичного керування, що застосовуються для технічних систем з
лінійними чи квазіліиійними характеристиками [73]. При цьому структура
моделі визначається взаємодією ряду операторів, які трансформують
параметри системи в загальному випадку стохастичшім чином.
Вхідні параметри системи
ХДО, .... Хи(0,
що є незалежними функціями часу і, трансформуються операторами входу
системи В । за схемою
В^Н).
Дана схема означає дію оператора В^ на вхідний параметр Хр
Для кожного вхідного параметра Х^(О відповідний оператор входу В,
визначається сукупністю ш коефіцієнтів
Цо, Ці’ °Іт
та оператором дифференціювання
В = (і/сіі.
У більшості практично важливих випадків оператори входу лінійної чи
квазілінійної моделі технічної системи можуть бути зведені до поліноміальних
залежностей наступного виду:
В/Ь?О) = Ьр + Ь}1О + ... + Ь.ПіВ'", ] = 1,..., ц,	(12.1)
причому т має конкретне цілочисленне значення для кожного і-го вхідного
параметра, аре цілим числом, яке визначає число входів системи.
Вихідні параметри системи
489
Струтинський В.Б.
Уі(О, .... ¥і(0, ..., УЛО
є результатом дії на них власних операторів системи за адитивною схемою:
АІУІ(О =	і = 1,(12.2)
де V - ціле число, яке відповідає числу виходів системи, які підлягають
математичному моделюванню і є виходом моделі.
Для кожного вихідного параметра УДО відповідний власний оператор
моделі А; визначається сукупністю п коефіцієнтів
аі0> аі1, ••і аіп
та оператором дифференціювання
о - а/аі.
Власні оператори математичної моделі системи з лінійними чи
квазілінійними характеристиками звичайно мають вигляд поліномів:
АДа^В) = аілЕ)п +... + аиО + аі0, і = 1,..., V,	(12.3)
а п є деяким цілим числом, заданим для номеру вихідного параметра і.
Операториий комплекс (12.2) із врахуванням залежностей (12.1) та
(12.3) визначає зв’язок вихідних та вхідних параметрів системи у вигляді
сукупності лінійних диференціальних рівнянь:
<1”Уі	V _
а, ---4-... + а, <-+ а;п і • — / Ь ІПХ і 4* Ь и ——— 4-... 4- Ь.
аг> .1	.0 . .ц 1° ; аі
І = 1, 2, ..., V.
Вираз (12.4) дає в аналітичному вигляді комплексну математичну модель
технічної системи, яка включає вектори зовнішніх
вхідних {Х^(О}М та вихідних {У,;(0}у
параметрів та сукупність внутрішніх параметрів системи
аі0> аі1, ••>аіп> і — 1> 2, ..., V, Ьц> ..., Ь^п, і — 1, 2, ..., ц.
Математична модель зображена графічно у вигляді блок-схеми на рис. 12.1.
<1гаХ0
<Дт Г (12.4)
Вектор входів	Х|(1)3г	Математична модель системи, яка залежить від оператора диференціюван- ня О та детермінованих чи випадкових внутрішніх параметрів системи: а.о, аіь ..., а,„, і = 1, 2,..., V, Цо. Ці,..., Ь]П, і — 1,2,.... ц	Вектор виходів	
{Хдї)}и			Уі(П	
				{¥і(І)К
				
	Хц(і)У(і)		¥у(і)	
Рис. 12.1. Блок-схема комплексної символьної математичної моделі
детермінованих та стохастичних динамічних процесів
у технічних системах
490
Розділ 12. Математичне моделювання динамічних коливальних процесів
Не знижуючи ступеня узагальнення математичної моделі приймемо як
перший варіант, що диференціальне рівняння (12.4), що описує процеси в
системі, має нульові початкові умови.
Диференціальне рівняння (12.4) допускає перетворення по Лапласу. За
нульових початкових умов для вхідних і вихідних параметрів перетворення
по Лапласу рівняння (12.4) має вигляд:
(аіп8'’+... + аі18 + аі0)¥і(8) = ^(Ь^+Ь,8 + ... + Ь^8т)Хі(8),
^=1	VI 2.37
І = 1, 2, ..., V.
де 8 - оператор Лапласа;
¥)(5) ~ зображення по Лапласу вихідного параметра ¥,(1);
Х,(3) - зображення по Лапласу вхідного параметра Х^(0.
Вираз (12.5) являє собою алгебраїчний аналог диференціального рівняння
(12.4) і співпадає з операторною формою запису математичної моделі у
вигляді (12.2), якщо покласти, що оператор диференціювання В = сі/<11
відповідає оператору Лапласа 8.
Комплексна математична модель технічної системи (12.5) може бути
подана у вигляді матрично-векторної залежності:
{¥і(8)}„ = ті](8)]ц„х{Хі(8)}р,	(12.6)
де {Х^(8)}ц - вектор зображень по Лапласу незалежних вхідних параметрів
технічної системи, що моделюються;
{¥((8)}у - вектор вихідних (залежних) параметрів системи, поданий у
вигляді своїх зображень по Лапласу;
\Уф8) = \¥і|(Ьр аі( 8) - компонента прямокутної матриці трансформуючих
(передавальних) функцій технічної системи, яка залежить від параметрів гц, та
від оператора Лапласа 8.
Диференціальне рівняння (12.4), як правило, має початкові умови,
відмінні від нульових. Цей варіант задачі є загальним.
В такому випадку математична модель буде мати вигляд системи
диференціальних рівнянь (12.4) та сукупності початкових умов.
Початкові умови задачі визначаються для деякого моменту часу
і = +0
і складають для кожного вихідного параметра ¥;(!) набір констант:
¥/<„ = ¥[(0)
гі¥(і)
<11
= Х'(0)
1=0
=¥і<л',)(0).

Аналогічно для вхідного параметра технічної системи ХфО початкові
умови мають вигляд набору постійних величин:
ХЇ0І = Х,(0);
; ц=о -1
сІХ/О
<11
= х/(0);
а^’х/о
аг-1
=х/т~,)(о).
491
________________Струтинський В.Б.______________________________
Перетворимо диференціальне рівняння (12.4) по Лапласу із врахуванням
наявності ненульових початкових умов. Розглянемо ліву частину рівняння.
Перетворення її по Лапласу, згідно з [23], має вигляд:
аіп[зп  ¥/8) - З”'1 • ¥/0) - З"’2 • ¥[(0) - ... - 3 • ¥і(п’2)(0) - ¥і(п~°(0)] +
+ аіп_1[зп~' • У-(8) - 8" 2 • ¥,(0) - ... -8-¥і(і,“3)(0)-¥і(^2)(0)]+...+
+ аі2 [з2 • ¥і (8) - 8 • ¥( (0) - ... - ¥'(0)]+а п [8 • ¥( (8) - ¥( (0)] + аі0 [¥, (8)].
Після групування одержимо ліву частину рівняння (12.4) у вигляді:
(аіпЗп + ... + аі13 + аі0)¥і(8)-аіп„)8п-1 -а,,,.^”'2 -...-аі232 -а^З-а^.
В цьому виразі коефіцієнти а^,..., аі0 залежать від початкових умов і
зв’язані з ними співвідношеннями:
аіп-і =аіП -\<0>; аіП-2 = аі„'¥'<0) + аіп-і•••;
аіП - аіп •¥(п-°(0) + аіп_1 • ¥(п~2>(0) + ... +аі1-¥і(0).
Розглянемо один із виразів під знаком суми в правій частині рівняння
(12.4). Перетворення його по Лапласу має вигляд:
ьДзт •х/8)--зт-1 -х/о)-5т 2 •х;(о)-...-х^,)(о)]+
+ Ь ;го_, [З"1'1 • ХД8) -... - Х^т - 2> (0)] +... + Ь (0).
Після групування праву частину перетвореного по Лапласу рівняння
(12.4) запишемо у вигляді:
£(ЬР + Ьл8 + ...+ Ь)тЗт)хі(5) + Рю + РиЗ + + РІМ. ,8м"1,
і=і
де М - найбільший із порядків похідних всіх ненульових початкових умов
вхідних параметрів, які входять в праву частину рівняння (12.4).
З метою спрощення одержаних виразів об’єднаємо значення коефіцієнтів:
Ріо+Иіо^Ьіо; + схп = ЬИ; ...; рІМ + аІМ = ЬіМ;
Ьіп = аіп при п > М.
Перетворене по Лапласу диференціальне рівняння (12.4) з врахуванням
наявності ненульових початкових умов вхідних і вихідних параметрів
запишеться у вигляді:
(аіп8п +...+ аи8 + аі0)¥і(8) = £(ья + Ьи8 +... + Ь^8га)х/8) +
і=і
-ЬіпЧ3"-1+Ьіп_28"~2+...+ Ьі18 + Ьі().
Із аналізу цього алгебраїчного рівняння можна зробити висновок, що
початкові умови рівнозначні існуванню деякого додаткового (фіктивного)
вхідного параметру Х0(О. Його дія може бути визначена із операторного
рівняння:
(аіп8п+... +аи8 + а-0)¥і0(8) = (ЬІП3П~1 + Ьіп_23"-2 +... + Ь^З +	,
А.0\О/
492
Розділ 12. Математичне моделювання динамічних коливальних процесів
де Хд(8) - зображення по Лапласу додаткового вхідного параметра Хц(ї.).
Визначимо трансформуючу функцію, яка відповідає даному рівнянню:
Уіо<5) _	(§) = Ьі„_18п“1 +... + Ьн8 + Ьі0
Х0(8) і0 (аіп8" +... + аи8 + аі0)х0(8) '
Додатковий вхідний параметр Хо(0 може бути вибраний у вигляді деякої
довільної функції часу. Доцільно вибирати його в найпростішій формі,
зручній для аналізу. Приймемо, що додатковий вхідний параметр має вигляд
одиничної ступінчастої функції:
Хо(О = 1(0.
Тоді перетворення по Лапласу додаткового вхідного параметра буде:
Х0(8) = 1.
0	8
Враховуючи назване перетворення, одержимо трансформуючу функцію:
V/. (8) = Ц-'5"1 +--- + Ьі|5 + Ьір)8
(аіП8п + •• + а.,8 + аі0)
залежність
яка звичайно має місце тільки для вхідного параметру Хо(0, що представляє
собою одиничну ступінчасту функцію.
Компоненти матриці трансформуючих функцій, що входить в
(12.6), виражаються через оператори математичної моделі:
Для операторів поліноміального виду (12.1) і (12.3)
трансформуючу функцію у вигляді дробово-раціональної функції:
, , Ью + Ь.,8 + ... + Ьіт8т
ПГ	___2І____________
іп8" + ...+” ап8 + аі0
одержимо
(12.7)
Комплексна математична модель технічної системи (12.6) із врахуванням
(12.7) допускає графічну інтерпретацію у вигляді структурних блок-схем. На
рис. 12.2 наведені схеми, що відповідають математичним моделям, які
визначають різні вихідні параметри системи.
Структура математичних моделей є однотипною і включає базовий блок
(рис. 12.2, г), який трансформує вхідний параметр X, у відповідну складову
вихідного параметра У,. Базовий блок відповідає базовій підсистемі
модельованої технічної системи.
Математична модель (12.5) (12.6) має властивості адитивності по всіх
вхідних параметрах для кожного виходу та суперпозиції вхідних параметрів,
тобто незалежності моделювання впливу окремого вхідного параметра на
вхідний параметр. Це дає можливість при математичному моделюванні
розглядати окремо кожну пару параметрів вхід-вихід, що обумовлює розгляд
сукупності окремих (цху) математичних моделей системи виду:
493
Струтинський В.Б.
¥і(к) = ^(8)^(8), і = 1, 2, ..., V, з = 1,2, ..., ц, (12.8)
де \¥ц(8) - трансформувала функція від і-то вхідного параметра до і-го
вихідного параметра.
Х/8)
г)
Рис. /2.2. Інтерпретація комплексної математичної моделі динамічних
процесів технічних систем у вигляді набору структурних блок-схем (а~в)
та базовий блок в структурі математичної моделі (г)
Математична модель у вигляді (12.8) відповідає базовому блоку
структури (див. рис. 12.2, г).
Кожна математична модель із сукупності (12.8) може застосовуватись при
довільних вхідних параметрах-функціях часу, як детермінованих, так і
випадкових. Модель встановлює однозначну залежність вихідного параметру
від вхідного. Модель залежить тільки від набору постійних коефіцієнтів Ь,,
аі; які представляють собою детерміновані або випадкові величини.
Для аналізу математичної моделі виду (12.8) доцільно застосовувати
частотні методи. При цьому використовуються частотні характеристики
системи, що відповідають її трансформуючій функції. Всі необхідні частотні
характеристики знаходяться наступним чином.
Трансформуюча функція ХУ^(8) шляхом формальної підстановки
8 —» ісо (о - частота, і = -У-7 - уявна одиниця) переводиться у форму
частотної трансформуючої функції У/фзш), іцо є комплексно-значною
функцією дійсного аргументу ю. Використовуючи (12.7), після підстановки
частоти одержимо:
ш /. ч + 1Ьлсо + ... + ГЬ^ют
ХУДіюІ = —------------------------
іпаіпгоп+... +іап®+ аі()
(12.9)
494
Розділ 12. Математичне моделювання динамічних коливальних процесів
За значенням частотної трансформуючої функції (12.9) знаходяться її
модуль та аргумент. Модуль представляє собою значення амплітудно-
частотної характеристики базового блоку математичної моделі:
\¥ц(со) = то<і[\Уц(ісо)].	(12.10)
Аргумент у своєму головному значенні відповідає фазово-частотній
характеристиці:
ц/і](со) = Аг§[\У^()®)].	(12.11)
Відповідно частотна трансформуюча функція як комплексна величина
запишеться в показниковій формі:
ХУц()®) = [^()®)]-ехр[]ц/іі(со)].	(12.12)
За значенням частотної трансформуючої функції (12.9) знаходяться її
дійсна та уявна частини. Дійсна частина визначає собою дійсну амплітудно-
частотну характеристику базового блоку моделі:
Иі/й) = Веа1[ХУц(>)].	(12.13)
Уявна частина частотної трансформуючої функції відповідає уявній
амплітудно-частотній характеристиці:
Уу(а) = Іпі[и^(і®)].	(12.14)
Відповідно частотна трансформуюча функція як комплексна величина
запишеться в алгебраїчній формі:
\Уу(і(о) = Ц/ш) + і-Уі/и).	(12.15)
Між частотними характеристиками існують залежності, що випливають із
означення форм запису комплексних величин.
Модуль та аргумент комплексного числа виражаються через дійсну та
уявну його частину наступними залежностями:
ц/^(и) = агсі§ [Уц(®)/1_ф(с))].
Дійсна та уявна частини комплексного числа виражаються через його
модуль та аргумент відповідно наступним залежностям:
Ц/ш) = ХУц(о)-со8[т|/ц(о))];	(12 17)
Уц(ю) = ХУ^(<в)-8іп[\|/ц(®)]-
Таким чином, комплексна математична модель розглядається як система
функціональних залежностей (частотних характеристик), що одержані із
трансформуючих функцій. Модель доцільно подати у графоаналітичній
формі. Для базової підсистеми, що відповідає блоку (рис. 12.2, г) і
співвідношенню (12.8) графо-аналітична форма математичної моделі
зображена на рис. 12.3.
Одержані залежності та співвідношення є основою для математичного
моделювання як детермінованих, так і стохастичних динамічних процесів, що
мають місце у технічних системах, зокрема системах механіки.
Процес моделювання технічної системи полягає у знаходженні вихідних
495
Струтинський В.Б.
параметрів системи по заданих вхідних параметрах.
х/о
		¥,(8)
)¥у(8)->А¥Уб(д)	{иу((о),^Ц(®)} {%’у(а),^(®)}	¥.0)

Рис. 12.3. Графоаналітична форма математичної моделі
базової підсистеми
Моделювання детермінованих динамічних процесів здійснюється з
використанням детермінованих функціональних залежностей. У цьому
випадку всі величини, що входять у формули (12.4)-(12.17), є
детермінованими і представляють собою константи чи функції часу. В
технічних системах мають місце різноманітні вхідні параметри-функції часу.
Детерміновані вхідні параметри утворюють дві різнорідні групи. Перша
це усталені вхідні параметри, а друга - це параметри, які різко змінюються в
часі. Моделювання систем при дії даних груп параметрів здійснюється двома
принципово різними способами.
Розглянемо усталені детерміновані вхідні параметри технічних систем.
Типовим усталеним вхідним параметром є гармонічна функція:
Х/і) = Ха'8Іп((0І),
де ха - амплітудне значення параметра, що не залежить від часу;
со - кругова частота гармонічної функції;
сої - фаза усталеного гармонічного процесу.
Для базового блока моделі (див. рис. 12.3) з вхідним параметром у
вигляді гармонічної функції вихідний параметр також є гармонічною
функцією і визначається функціональною залежністю:
¥;(1) = ха-\\^^(<ю)-8ііі[озі + Уі^(со)].	(12.18)
Враховуючи співвідношення (12.16) та (12.17), залежність (12.18) може
бути також записана у вигляді:
Уфі) = ха-[ (^((о)-008(01 + Уу(со),8іп(оІ].	(12.19)
Узагальненням усталеного вхідного параметру є функціональна залежність, у
вигляді полі гармонічної функції, що описана гармонічним рядом:
к
Хі(О = Ххак’М^о^ + Фок)-	(12.20)
к=1
де К - число членів ряду (простих гармонік);
«о ~ базове значення частоти;
хак - амплітуда к-ї гармоніки;
Фок ~ початкова фаза к-ї гармоніки.
Залежність (12.20) представляє собою відрізок ряду Фур’є з постійною
496
Розділ 12. Математичне моделювання динамічних коливальних процесів
складовою, що дорівнює нулю. Такою залежністю можуть бути описані
різноманітні періодичні та неперіодичні вхідні параметри (див. розділ 4.2).
Вхідні параметри, що мають особливості типу стрибка (сходинки) не
можуть бути точно описані рядом (12.20) в силу явища Гібса (див. розділ
4.2.2). Тому для таких вхідних параметрів застосовується інша методика
моделювання.
Узагальнений усталений детермінований вхідний параметр, який
відповідає гармонічному ряду (12.20), може бути поданий у більш
компактному вигляді:
к
’5іп(®Л),	(12.21)
к=1
де введені нові значення частоти та часу згідно формул:
©к = кюо; їк = І + уок/(ко)о)-	(12.22)
Для кожного доданка суми (12.21) справедлива залежність (12.19). Тому
вихідний параметр, що відповідає входу у вигляді (12.21), визначиться рядом:
к	,	1
¥і 00 = ЕХк • Рц(®к) • С08(® Дк ) + Ч/ик ) • 5іп(сокІк)] .
кН
Підставивши значення частоти та часу із (12.22) у дану формулу,
одержимо залежність вихідного параметру від часу у вигляді:
уі (0 = Е Хак ' {[иіз(к®0)] • С08(ко>д +	) + |уіз(кшк)] • 8Іп(кйД + уок)} •
к —1
(12.23)
Враховуючи співвідношення (12.16) та (12.17), залежність (12.23) може
бути записана у формі:
к	,
¥і(0 = Ехак •^(ка)о)-8Іп[к(оД +уок + Уі](к<М	(12.24)
к=1
Формули (12.23) і (12.24) дозволяють виконати розрахунок вихідного
параметра системи при довільних усталених вхідних параметрах.
Розглянемо моделювання детермінованих систем, вхідні параметри яких
різко змінюються в часі. Такі вхідні параметри представляють собою
розривні функції (див. розділ 2). Дані вхідні параметри системи допускають
ідеалізацію та зведення до одиничної ступінчастої функції (див. розділ 2.3.5).
Використаємо асиметричну одиничну ступінчату функцію:
, ч ҐО при І < 0
КО = (
[1 при і > 0
Разом з одиничною ступінчастою функцією використовується її символічна
похідна у вигляді одиничної імпульсної функції (дельта-функції Дірака):
, „	[0 при 1^0
8(0 = (
[0...оо...0 при 1 = 0
497
Струтинський В.Б.
причому для дельта-функції виконується інтегральна норма:
+СО
/8(0 = 1.
-оо
Розглянемо моделювання системи, вхідний параметр якої виражається
через одиничну ступінчату функцію, тобто
Х;(0 = Ха-1(6,	(12.25)
де ха - постійне (амплітудне) значення вхідного параметра.
В цьому випадку вихідний параметр представляє собою перехідну
функцію системи Н(О [6].
Зображення по Лапласу ступінчастої функції (12.25) має вигляд:
Х/8) = ха/8.
Відповідно до математичної моделі системи у вигляді (12.8) знаходиться
зображення по Лапласу перехідної функції:
Н(8) = ¥і(8) = ха-\¥ч(8)/8.	(12.26)
Значення перехідної функції може бути знайдене як обернене
перетворення Лапласа виразу (12.26), тобто
Н(0 = Ь-Чха’Х¥і/(8)/8].
Іноді більш доцільно знаходити перехідну функцію за дійсною
амплітудно-частотною характеристикою [6]. При цьому знаходження
перехідної функції зводиться до обчислення інтегралу:
т,л\ 2х, \т / А 8ІГКВІ .
Н(і) = —-	------сію.	(12.27)
Розглянемо моделювання системи при вхідному параметрі у вигляді
одиничної імпульсної функції:
Х/Ю = ха-8(0.
В цьому випадку вихідний параметр представляє собою імпульсну
характеристику динамічної системи (вагову функцію) \\ (с).
Зображення по Лапласу імпульсної характеристики [6] з точністю до
множника співпадає з трансформуючою функцією системи, тобто
ду(8) = ¥і(8) = ха-¥/ц(8).	(12.28)
У відповідності з (12.28) значення імпульсної характеристики може бути
знайдене як обернене перетворення Лапласа трансформуючої функції:
= іЛха-\¥ц(8)].
Імпульсну характеристику також можна знайти за дійсною амплітудно-
частотною характеристикою шляхом інтегрування [6]:
ш(і) = ПцДа) • со8(юі:)сІ<0 .	(12.29)
\ 71 /о
Інтеграли, що входять в праві частини формул (12.28) та (12.29),
звичайно знаходяться чисельними методами з використанням засобів
математичних пакетів, причому верхня межа інтегрування вибирається дещо
498
Розділ 12. Математичне моделювання динамічних коливальних процесів
більшою за смугу пропускання частот системи.
Математичне моделювання стохастичних динамічних процесів у
технічних системах здійснюється в залежності від характеру випадкових змін
параметрів чи коефіцієнтів математичної моделі.
Ці процеси виникають під дією зовнішніх і внутрішніх факторів
випадкового характеру. їх моделювання може здійснюватись різними
методами в залежності від місця дії випадкового фактора. Якщо суттєвою є
дія випадкових вхідних параметрів системи, то математичне моделювання
здійснюється з використанням детермінованої математичної моделі з
випадковими вхідними параметрами. Коли превалюючими випадковими
чинниками є зміна внутрішніх параметрів системи, то моделювання
здійснюється за допомогою стохасіичної математичної моделі із змінними
випадковим чином коефіцієнтами та детермінованими вхідними параметрами.
Загальним випадком є моделювання динамічних процесів у технічній
системі при одночасному врахуванні випадковості зміни внутрішніх параметрів
системи при випадкових вхідних параметрах.
Розглянемо математичне моделювання технічної системи при
детермінованих внутрішніх і випадкових зовнішніх вхідних параметрах.
В даному випадку вхідні та вихідні параметри системи представляють
собою стохастичні функції часу. Математичне моделювання таких систем
полягає у знаходженні статистичних характеристик випадкових вихідних
параметрів. Моделювання здійснюється з використанням детермінованих
математичних моделей.
Із загальної математичної моделі (12.6) випливає матрично-векторне
співвідношення, що зв’язує зображення по Лапласу випадкових функцій часу,
які описують вхідні та вихідні параметри технічної системи:
Х/(О та ¥і’(0.
Це співвідношення системи з детермінованими внутрішніми параметрами
має вигляд матрично-векторної рівності і є загальною математичною моделлю,
призначеною для моделювання випадкових процесів:
{<(8)}у = [^(8)]уих{х/(3)}и,	(12.30)
де знаком “*” позначені випадкові величини, що представляють собою
компоненти векторів вихідних і вхідних параметрів.
Дана математична модель, як і співвідношення (12.6), має властивості
адитивності. Тому моделювання технічної системи полягає в розгляді
сукупності стохастичних математичних моделей, що зв’язують пари
випадкових процесів вхід-вихід, а саме:
<(8) = ^(8)’Х/(5), і=1,2,..,у, і = 1,2, ., щ (1231)
Стохастичні вхідні параметри системи (О представляють собою
499
Струїпгшський В. Б.
випадкові процеси і можуть мати різні статистичні характеристики.
Розглянемо, як приклад практично важливий вид вхідного параметра системи
у вигляді гаусівського стаціонарного ергодичного випадкового процесу [6].
Такі процеси характеризуються своїми статистичними характеристиками,
зокрема кореляційною функцією:
Мт) = І™	+ тМі ,	(12.32)
де хо^(і) ~ конкретне значення (реалізація) випадкового вхідного параметра
*
Х| (і), подане у вигляді центрованої випадкової функції часу з достатньо
протяжною областю визначення в часі.
Кореляційна функція (12.32) може мати різний вигляд в залежності від
особливостей випадкового процесу [63]. Для вхідного процесу у вигляді
“білого” шуму кореляційна функція відповідає дельта-функції:
Кх/т) = ох2-5(т),	(12.33)
*
де сух2 - дисперсія випадкового вхідного параметра (0.
Для випадкового процесу у вигляді кусково-лінійної ламаної лінії [3]
кореляційна функція має вигляд:
КХ](т) = ох2-е-“М,	(12.34)
де а - деяка постійна величина.
Для опису випадкових вхідних параметрів використовують також
кореляційні функції виду:
КХ](т) = ох2-е'<і!т‘-со.фг або
Кх/т) - СТх2,Є'“^^(сО8(Рт)+-^-8Іп(р |т|)),	(12.Зо)
де а, р - постійні величини.
Для вхідного параметра у вигляді центрованого гаусівського ергодичного
процесу закон розподілу густини ймовірності Р(Хр значень вхідного
параметра є нормальним:
7	1	(~ х2
Р(Х])= 7==ехР „ 2' 	(12.36)
охл/2л 2ох
Іншою статистичною характеристикою випадкового вхідного параметра є
спектральна щільність процесу 8х^(со), яка зв’язана з кореляційною функцією
перетворенням Фур’є. Кожній кореляційній функції відповідає спектральна
щільність (спектр) вхідного параметра:
8^(и) = 2°]КДт) • сої(<от)сіт .	(12.37)
о
Спектр випадкового вхідного параметра може бути неперервним або
лінійчатим. Для неперервного спектра формула (12.37) визначає неперервну
500
Розділ 12. Математичне моделювання динамічних коливальних процесів
парну функцію з нескінченною областю визначення.
Лінійчатий спектр відповідає наявності у спектральній щільності
особливостей типу дельта-функції.
Наприклад, процес у вигляді “білого” шуму (12.33) має спектральну
щільність, постійну у всьому діапазоні частот:
8х(со) = Сопзі.
Спектральні щільності, що відповідають кореляційним функціям (12.34),
(12.35) мають вигляд відповідно:
а + со
8ч(ю) = а • ст2 
8 (®) = -Е М
Ч	О X
1
а2 + (р - <о)2
2р - <в
а2 + (р + со)2
2р + со
(12.38)
а2 + (Р - ю)2 а2 + (р + со)2
Всі спектральні щільності, які визначені за допомогою виразів (12.38), є
дробово-раціональними функціями квадрата частоти.
Кореляційні функції та спектральні щільності визначаються звичайно за
результатами експериментів,
наближений характер масиву
кожну спектральну щільність
функцією виду:
С / х Р(о)
де Р(со) І р(ю) - поліноми відносно частоти со.
Оскільки спектральна щільність є парною затухаючою функцією при
ю -» ао, то поліноми включають в себе тільки парні степені частоти, при цьому
степінь полінома чисельника завжди менший степеня полінома знаменника.
Коефіцієнти поліномів є дійсними числами. Відповідно всі корені
чисельника і знаменника спектральної щільності завжди розташовані
симетрично відносно дійсної та уявної осей на площині комплексної змінної.
Враховуючи вищесказане, спектральну щільність можна розкласти на
прості дроби [44]. Тоді спектральна щільність довільного процесу:
^21)
+ У ,   •—У---у ,
л а, + со
де перша сума відповідає четвірці комплексно спряжених коренів знаменника
Р(со), а друга сума - парі чисто уявних коренів знаменника.
Приводячи дроби під знаком першої суми до спільного знаменника,
одержимо:
Тому вони відомі приблизно. Враховуючи
значень спектральної щільності, практично
можна апроксимувати дробово-раціональною
с / \	Р(со) у- О
4 Ю	0(и)	Л ?’
а - у (со - о0) а + у (со + со0)
2тг а2 + (со- со0)2 а2+(со + соц)
аі
501
Струтинський В. Б.
о / -) _ Р(ю) _ у. Р(а + ую0)р2 + (а - у©0)©2 у 2Р . а1
4 Ш 0(й) о,ад7,Ио Р4+2(а2-©2)©2+©4	71 а2 4-Го2’
де константи зв’язані між собою співвідношенням: р2 = а2 + ©о2-
В залежності від значення параметра у вид дробу в першій сумі може бути
різним. Підставивши у формулу два характерні значення: у = 0 та у - а/©о,
будемо мати суму:
\	V-1 Ра	р' 4- го
я Р +2(а2 -ю2)©2 4-ю
у Р	2р2а	у 2Р оц
о.ТрД я (р4 + 2(а2 - ©о)©2 4- го4) ті а2 4- ©2
При цьому друга сума даної формули відповідає спектральним
щільностям диференційованих випадкових функцій, які мають похідні з
обмеженою дисперсією.
Враховуючи, що кореляційна функція зв’язана зі спектральною щільністю
співвідношенням [6]:
1 х
К(т) = — |8(ю)сО8ЮТЙ07 ,
71 о
в загальному випадку одержимо значення кореляційної функції:
Кх}(т) - ^Ре а'ТІ + £РеО|ТІСО5©0Т4- Ре’“іТ|(сО8©0Т 4- — 8ІП©0|т|) .
О,а	О,а,аі0	О,а,я0	®о
Це означає, що кореляційну функцію кожного стаціонарного випадкового
процесу можна представити у вигляді лінійної комбінації кореляційних
функцій трьох типових випадкових процесів, причому один з них відповідає
випадковому процесу, похідна якого має обмежену дисперсію.
Запишемо формулу для суми спектральних щільностей у вигляді:
О,а,о0
аР
Я
1 ! 1
а2 4- (© - ©())2 а2 4- (© 4- ©д)
-у аР	2©0 - ю 2©и 4-го	у 2Р а
шДа2	+ (ф-с),У	а2 4- (ю + ю2)	££ я	а2 +	©2 ’
Цю формулу можна інтерпретувати як суперпозицію дії вхідних сигналів
у вигляді білого шуму зі спектральною щільністю
8о(©) = СопяЬ = 2л
на динамічні системи з відповідними трансформуючими функціями.
Доданкам першої суми відповідають динамічні системи, які мають
трансформуючі функції наступного виду:
XV (8) —	+ 0
Р Т282 +~-8 + 1
Р2
502
Розділ 12. Математичне моделювання динамічних коливальних процесів
це Ті= 1/р - постійна часу трансформуючої функції (р = д/а2 + «>„ ).
Доданкам другої суми відповідають коливальні ланки динамічних систем,
що мають трансформуючі функції наступного виду:
Х¥2(8) =	\.
Р Т282 +~8 + 1
р2
Доданкам третьої суми відповідають аперіодичні ланки динамічних систем
з трансформуючими функціями виду:
\¥3(8) = Ж--------—.
3 V лР тз5 +1
Таким чином, довільний стаціонарний випадковий вхідний параметр
технічної системи може бути представлений як результат дії широкополосного
випадкового процесу з постійним значенням спектральної щільності ("білого"
шуму) на деяку динамічну підсистему.
Детермінована технічна система, на вхід якої подається стаціонарний
ергодичний вхідний параметр зі спектральною щільністю 8х^(ш), на своєму
виході має також стаціонарний ергодичний випадковий параметр зі
спектральною іцільнісю [6]:
8уі(со) = |5¥. ,(]со)|2-8х/со),	(12.39)
де [\¥..(]ш)|2 ~ квадрат модуля частотної трансформуючої функції.
Ця залежність має місце при всіх і = 1, 2, ..., V, і = 1, 2, ..., ц.
Кореляційна функція, що відповідає спектральній щільності (12.39),
визначається інтегралом:
— |8уі(и)с°8С0Т<1т.	(12.40)
л о
Окремо знаходиться дисперсія випадкового вихідного параметра:
ст2і =-|8у(ю)сіа).	(12.41)
71 о
Вона представляє собою постійну величину і є інтегральною статистичною
характеристикою випадкового вихідного параметра.
Розглянемо математичне моделювання технічної системи при
детермінованих вхідних параметрах і випадкових змінах внутрішніх
параметрів.
В більшості практично важливих задач можна вважати, що внутрішні
параметри системи мають незначні випадкові флуктуації (відхилення)
відносно деяких середніх значень. Для їх визначення використаємо набір
випадкових чисел. Схема математичного моделювання при цьому відповідає
методу Монте-Карло [25].
503
Струтинський В.Б.
Згідно з методом Монте-Карло, приймемо, що флуктуації коефіцієнтів
математичної моделі є функціями сукупності к незалежних випадкових
величин з певними законами розподілу:
§1*.	(12.42)
В більшості практично важливих задач математичного моделювання ці
величини можна вважати незалежними від часу. Тоді розрахункові випадкові
внутрішні параметри математичної моделі визначаться функціональними
залежностями, що включають випадкові величини:
аі0 = аіо(§1> Й2,	40= Ь^О(§1, §2, 8кЛ
(12.43)
*	7 *	*	Як	«*,✓**	Як
аїп- §2>	Ціт” ЬітОзЬ •••» §к/-
Враховуючи, що формули (12.43) визначають нескінченну кількість
(1 = 1, 2, ..., Е -» да)
можливих значень коефіцієнтів, диференціальне співвідношення між вхідним
і вихідним параметрами (12.4) набуде вигляду:
<1"%,	. ау, V V к гі"хі к
*'	,11	,01 ,1	2_, ,01 .) Л!	ЛП| аіт
і = 1, 2, ..., V, 1 = 1, 2, ..., Ь—>ос.
(12.44)
В рівнянні (12.44) індексом 1 позначена 1-та реалізація набору випадкових
величин, що визначають коефіцієнти математичної моделі. Причому значення
коефіцієнтів рівняння не залежать від часу, а реалізація вихідного параметра
Уіі є звичайною детермінованою функцією часу.
Диференціальне рівняння (12.44) є узагальненням формули (12.4) і
визначає сукупність детермінованих УцН) функцій, що є окремими
реалізаціями випадкового вихідного параметра. Для рівняння (12.44) мають
місце всі положення, встановлені для детермінованих моделей, зокрема
формули (12.18)-(12.31), якщо їх розглядати для кожної окремої реалізації
випадкових внутрішніх параметрів системи.
Із співвідношення (12.6) з урахуванням (12.44) випливає справедлива для
кожної реалізації внутрішніх параметрів детермінована математична модель
системи у вигляді матрично-векторної залежності:
{¥п(8)}у = [Х¥іЯ(8)]иух{Х/8)}и, 1 = 1, 2, ..., Е -> оо, (12.45)
де вираз у квадратних дужках представляє собою матрицю трансформуючих
функцій, що відповідає 1-й реалізації коефіцієнтів математичної моделі.
Математична модель (12.45) має властивості адитивності, як і загальна
модель (12.6). Тому при моделюванні достатньо розглянути одну пару
параметрів вхід-вихід.
Якщо вхідний параметр системи являє собою детерміновану гармонічну
функцію часу виду (12.18), то згідно (12.19), реалізація відповідного
504
Розділ 12. Математичне моделювання динамічних коливальних процесів
вихідного параметра в функції часу має вигляд:
¥і](0 = Ха-[Ц)|(ю)-со8(а)0 + Уііі(<л)-8іп((оі)],	(12.46)
де	Уііі(й)) - значення дійсної та уявної характеристик, що
відповідають 1-й реалізації випадкових коефіцієнтів моделі.
Залежність (12.46) визначає вихідний параметр як лінійну функцію двох
випадкових величин Ьф] та У^р
Згідно з [10], математичне сподівання ¥и(і) та дисперсія о2уі(0 даної
лінійної функції визначаються формулами:
¥іі(0 = Ха-[ц(<В) •со8(оп)+ У(ю)*8іп(<ві)];	(12.47)
0^(1.) =	• [ооц(со)- со82(®і) + аУІІ(®)’ 8іп2(сій)+ 2с:о8((Щ)- 8іп(со0* соу{иі?Уи|],
(12.48)
де 1)ц,Уц _ математичні сподівання значень дійсної та уявної амплітудно-
частотних характеристик;
стуі^(®) ” дисперсії значень дійсної та уявної амплітудно-частотних
характеристик при частоті ®;
соу{Ціі; Уц} - кореляційний момент (коваріація) випадкових значень
дійсної та уявної частотних характеристик.
Ці величини знаходяться шляхом обробки статистичних вибірок,
складених із значень частотних характеристик, що відповідають окремим
реалізаціям сукупності коефіцієнтів математичної моделі. Відповідно
вибіркові значення математичних сподівань дисперсій та кореляційного
моменту дійсної та уявної характеристик:
Ц>) = 1 • ЕцДш); Уу(®) = |  І»);
<=^70X0-0:	(12.49)
“Ф.лУ	- Ч).
Кореляційний момент (коваріація), що визначений останньою формулою
(12.49), може бути виражений через коефіцієнт кореляції:
Рш- =соу{иірУц}/(сим -оу..).
Випадкові дійсна та уявна амплітудно-частотні характеристики утворюють
у своїй комбінації комплексну випадкову функцію, що відповідає частотній
трансформуючій функції системи. Відповідно 1-та реалізація частотної
трансформуючої функції буде:
\УіЛ0®) = Циі(со) + і УіН(®).	(12.50)
Математичним сподіванням значень цієї випадкової функції є
комплексно-значна детермінована функція дійсного аргументу ®:
505
Струтинський В.Б.
\УмО<0)=иіі((о)+]УіХсо).	(12.51)
Формула (12.50) визначає систему двох взаємозалежних випадкових
величин. Ці величини мають певний закон розподілу. Для складних технічних
систем значення випадкових величин залежить від великої кількості
параметрів. Тому закон розподілу, як правило, відповідає нормальному. При
цьому густина ймовірності значень частотної трансформуючої функції:
ехр
іНіМ]=—
2	„	'	2	’ /А1 РНЧГ
аеу	стіл; СТ\\|	ф
На рис. 12.3 наведено графічну інтерпретацію двомірного закону
розподілу випадкових значень частотної трансформуючої функції.
Закон розподілу характеризується еліпсами рівної ймовірності, рівняння
яких визначаються залежностями:
= Сопві.
Еліпси рівної ймовірності також наведені на рис. 12.3. Вони відображають
розсіяння значень частотної трансформуючої функції відносно її
математичного сподівання.
Рис. 12.3. Густина ймовірності розподілу значень частотної
трансформуючої функції
Півосі еліпса розташовані під кутом а до дійсної осі:
1
а = — агсс§
2рцу ‘
2
506
Розділ 12. Математичне моделювання динамічних коливальних процесів
Визначимо випадковий вихідний параметр технічної системи при дії
детермінованого вхідного параметра загального виду (12.20), (12,21).
Окрему реалізацію вихідного параметра одержимо узагальненням
формули (12.24), в якій значення характеристик Ю;) та Хф є реалізаціями
відповідних випадкових величин:
к г	/	і
ХіСО = Ехак • Ріл(к®о)- со5(к®(ф + \Иок)+ уЦк®о)' 8іп(кюоі + \|/Ок)]. (12.52)
к-1
Залежність (12.52) є лінійною функцією випадкових величин Цц та У^.
Її математичне сподівання буде визначатися формулою:
к ,	_ ,
Уіі(0 = УХк чЛіі(к(Х’<Мк“<Л +УоїХ у%к(ксоо)* 8іп(ксо0і + \рок)1- (12.53)
к-1
Для знаходження дисперсії функціональної залежності (12.54) будемо
вважати значення характеристик на різних частотах некорельованими. Тоді
К г
нЦі) = ХрЦЬйо)' С082(кю01 + уоь) + сфц(к(00)- 8ігі2(кшоі + шок) +
к-1
+ фіп[2(к®оі + шок)]- соуХ/Х].
(12.54)
Формули (12.53) і (12.54) визначають статистичні характеристики
випадкових вихідних параметрів при детермінованих вхідних параметрах і
випадкових змінах внутрішніх параметрів системи.
Розглянемо математичне моделювання технічної системи при одночасних
випадкових вхідних параметрах і випадковій зміні внутрішніх параметрів
системи.
Як і раніше, внутрішні параметри (коефіцієнти) математичної моделі
будуть визначені залежностями (12.43).
Диференціальне співвідношення між випадковими вхідним і вихідним
параметрами розглядається для всіх І реалізацій внутрішніх параметрів і буде
мати вигляд аналогічний (12.44), а саме:
сіпу.’ ау.; .	ах* атх*
аЛІ-Л + ... + а„Хк + а у = ук.Х; + ЬИІ--------1 + ... + Ьіт. --
аг і1 аі 01 11 £ 'гі‘ ] аі ]т| аіт (12.55)
і = 1, 2, ..., V, 1 = 1, 1 = 1, 2, ..., Ь оо,
де X*) = Х*фі) - випадковий вхідний параметр у вигляді стохастичної
функції часу;
¥*іі = ¥*і|(і) ~ випадкова функція, що визначає вихідний параметр, для
1-тої реалізації випадкових внутрішніх параметрів системи.
Диференціальне співвідношення (12.55) є подальшим узагальненням формул
(12.4) та (12.44). Воно визначає сукупність стохастичних функцій часу ¥*ц(0,
які відповідають випадковому вихідному параметру для конкретної реалізації
507
Струтинський В. Б.
набору внутрішніх параметрів.
Для рівняння (12.55) мають місце всі положення, встановлені для моделей з
детермінованними внутрішніми параметрами при випадкових вхідних параметрах,
а саме: залежності (12.30)—(12.41), якщо їх визначити для кожної окремої
реалізації випадкових внутрішніх параметрів системи.
Із співвідношення (12.30) випливає математична модель системи у вигляді
матрично-векторної залежності, що зв’язує зображення по Лапласу
стохастичних функцій часу ¥*п(О та Х*((О:
{¥и’(8)}у = [\¥ц)(8)]уцх{Х;(8)}ц,	1=1,2. ...,Ь->оо,	(12.56)
де матриця трансформуючих функцій відповідає залежності (12.45).
Відповідно до даної моделі (12.56), встановлюється зв’язок між
спектральними щільностями стохастичних вхідного та вихідного параметрів.
Математична модель у вигляді (12.56) є узагальненням моделі (12.45) в
тому, що (12.56) визначає не один вектор вихідних параметрів, а нескінченну
сукупність (Ь -> оо) векторів випадкових вихідних параметрів.
Враховуючи адитивність моделі можна в (12.56) розглядати лише одну
пару компонент векторів входу і виходу, а саме:
¥Н8) = \УІЯ(8)-Х;(8),	(12.57)
і =1,2, ..., у; .і =1 , 2, ..., ц; 1 = 1, 2, ..., Б-» оо.
Розглянемо знаходження стохастичного вихідного параметра для практично
важливого випадку, коли вхідний параметр є стаціонарним ергодичним
випадковим процесом. Тоді для вхідного параметра, як показано раніше, мають
місце залежності (12.32)-( 12.38), що визначають кореляційну функцію, закон
розподілу густини ймовірностей та спектральну щільність вхідного параметра.
Будемо вважати, що спектральна щільність вхідного параметра
ХфО визначається функціями 8х^(и).
Тоді згідно з (12.57), спектральні щільності для всіх Б реалізацій вихідного
параметра визначаться залежністю [6]:
8уі1(ш)= |\¥^](і®)| 2-8х/®),	/юсяї
 4 О	14 4 Т	(12.58)
і = 1, 2, ..., у; 1=1,2, ..., Б -> оо,
яка включає ІА¥і^()и)|2	- значення квадрата модуля частотної
трансформуючої функції для 1-ої реалізації.
Залежність (12.58) є узагальненням формули (12.39) в тому, що вона
визначає не одну спектральну щільність як (12.39), а нескінченну сукупність
спектральних щільностей, що відповідає нескінченній сукупності реалізацій
вихідних параметрів - випадкових функцій часу.
За значеннями сукупності спектральних щільностей вихідного параметра
знаходиться сукупність кореляційних функцій:
508
Розділ 12. Математичне моделювання динамічних коливальних процесів
1 30
Куй(т) = - Кп(со)- соа(®т)- а® ,
я о
а також дисперсій окремих реалізацій вихідного параметра:
(12.59)
(12.60)
Підставивши в (12.60) значення (12.58) спектральної щільності окремої
реалізації вихідного параметра, знайдемо:
стуіі Д^іііС®)]2	’ 1 = 1. 2, .... Ь-> оо. (12.61)
71 о
Значення дисперсій, що визначаються для окремих реалізацій формулами
(12.60) та (12.61), утворюють статистичну вибірку при
1 = 1, 2, ..., Ь,
де Ь - число розглянутих реалізацій.
Із цієї статистичної вибірки знаходиться математичне середнє значення
дисперсії для всіх Ь реалізацій:
= тЕаиі •	<12.62)
1-І
Об’єднуючи (12.61) та (12.62) і змінюючи черговість операцій, одержимо:
<4і = - /1“- Е К0®^		(12.63)
Я о [Ь і,.
Вираз у фігурних дужках при Ь -> оо являє собою математичне сподівання
квадрата модуля частотної трансформуючої функції для частоти и і
визначається формулою:
'	(12.64)
ь 1=1
Тоді математичне середнє значення дисперсії:
 М®) а® •
71 о
Визначимо розсіяння дисперсії (дисперсію дисперсії) вихідного параметра.
Згідно із статистикою (12.61), після центрування значення дисперсії як
випадкової величини розсіяння значень дисперсії знайдено у вигляді:
1	1- /	—г
< = • (12-65)
Підставивши в формулу (12.65) значення величини із (12.61), (12.63) та
(12.64), після перетворень знайдемо:

8ХІ(ю) • сі®.
Вираз в фігурних дужках даної формули являє собою дисперсію виходу
509
Струтинський В. Б.
математичної моделі, квадрат модуля частотної трансформуючої функції якої
представляє собою різницю дійсного квадрата модуля для 1-ї реалізації та
математичного сподівання квадрата модуля, визначеного залежністю (12.64),
а саме:
.	17 і	17 .'1 1 ' і-'  2
=	-|’%(>)| •	(12.67)
Об’єднуючи залежності (12.66) та (12.67), знайдемо розсіяння дисперсії
вихідного параметра у вигляді:
де дисперсія для 1-ї реалізації визначена формулою:
—	1 “і-ї	|2
71 0
Формули (12.62)—(12.68) визначають інтегральні статистичні
характеристики вихідного параметра.
З метою розширення аналізу ці характеристики доповнені сукупністю
інтегральних спектральних характеристик вихідного параметра. Ансамбль
реалізацій спектральних щільностей вихідного параметра визначено
залежністю (12.58). Відповідно математичне середнє спектральної щільності
при частоті ш складає:
—•	і і	. 2
м®)=гіКМ5»-
ь 1=і
Із врахуванням залежності (12.64), що визначає математичне сподівання
квадрата модуля частотної трансформуючої функції, одержимо математичне
середнє спектральної щільності у вигляді:
8УІ(®)-|\¥М(3©)!2 -8х/(о).
(12.69)
Аналогічно визначиться дисперсія спектральної щільності
параметра при фіксованій частоті:
1
вихідного
І9$уі(о)) — *
Ь-1
іікм2 -ко-
—-і2
|2
8>),
де у фігурних дужках знаходиться дисперсія квадрата модуля
трансформуючої функції:
1
частотної
Е р	-----------,2
І |\¥у1(»|2 -|^(»|2

Таким чином, дисперсія спектральної щільності вихідного параметра
технічної системи в функції частоти буде:
О5УІ(®) - Отею(®)- 82хД(о) .	(12.70)
Залежності (12.69) та (12.70) дозволяють визначити спектральну
510
Розділ 12. Математичне моделювання динамічних коливальних процесів
щільність вихідного параметра технічної системи як випадкову функцію
частоти з відповідними статистичними характеристиками, а саме:
математичним середнім спектральної щільності та дисперсією спектральної
щільності, причому ці величини є функціями частоти. Спектральна щільність
вихідного параметра залежить як від статистичних характеристик вхідного
параметра, так і від статистичних характеристик частотної трансформуючої
функції системи, тобто від зміни випадкових внутрішніх параметрів.
З метою апробації комплексної стохастичної математичної моделі
виконано розрахунок спектральної щільності вихідного параметра динамічної
системи металорізального верстата при випадкових вхідних параметрах і
випадкових змінах внутрішніх параметрів токарного верстата [85].
Вхідним параметром системи є флуктуація сили різання, що має вигляд
широкополосного випадкового процесу, вихідним - динамічна похибка
обробки. На рис. 12.4 наведено результати розрахунків у порівнянні з
експериментальними даними [16].
Встановлено, що закон розподілу значень спектральної щільності при
фіксованій частоті, близький до нормального:
„ 1
Реу, = —г=--------ехр-
л/2я • О5УІ(®)
УІ,(<о) - 8УІ((о)
2О5уі(ю)
Рис. 12.4. Порівняння розрахунку спектральної щільності прискорень
стохастичного коливального процесу з результатами експерименту:
1 - експеримент; 2 - діапазон розрахункових значень спектральних
щільностей; 3 - закон розподілу значень спектральної щільності
Із порівняння розрахункових та експериментальних значень спектральних
щільностей випливає їх кількісна та якісна відповідність. Деяке зміщення
розрахункового спектра над експериментальною кривою пояснюється
неврахованими при розрахунках нелінійними дисипативними властивостями
динамічної системи верстата.
511
Струтинський В. Б.
12.2. Спектральні характеристики стохастичних динамічних ударних
навантажень в ланцюговій крутильній системі привода головного
руху верстата
В динамічній системі верстата діє рад внутрішніх стохастичних збурень
значної інтенсивності. Ці збурення представляють собою суттєво
нестаціонарні випадкові процеси. Динамічна система верстата відзначається
значною складністю. Розглянемо кінематичну схему токарно-гвинторізного
верстата (рис. 12.5).
Рис. 12.5. Кінематична схема токарно-гвинторізного верстата
моделі КА-280, на якій виділено кінематичний ланцюг привода головного
руху, що включає основні джерела динамічних вібраційних навантажень
Джерела внутрішніх стохастичних збурень знаходяться, зокрема, в
зубчастих передачах і мають вигляд імпульсних (ударних) навантажень.
512
Розділ 12. Математичне моделювання динамічних коливальних процесів
Найбільші імпульсні навантаження виникають в приводі головного руху який
передає основну частину потужності електродвигуна (кінематичний ланцюг
привода виділено штриховкою). Імпульсні навантаження мають вигляд
випадкових збурень, що виникають, в люфтових (зазорних) ланках приводів
головного руху верстата.
В приводі головного руху наявна велика кількість рухомих інерційних
елементів, які мають значну кінетичну енергію. Інерційними елементами є
вали, зубчасті колеса, муфти. З’єднання між ними мають зазори, які
вимірюються сотими і десятими частками міліметра. Всі деталі головного
руху знаходяться у складній динамічній взаємодії. Компактне розташування
привода призводить до додаткових взаємних впливів його елементів один на
одного і збільшує інтенсивність вібраційного поля верстата.
Складність аналізу таких систем ілюструється наведеним нижче зовнішнім
виглядом частини привода головного руху (рис. 12.6)
Рис. 12.6. Загальний вигляд 'частини привода головного руху верстата
(стрілкою <- показано шпиндель)
Блоки зубчастих коліс, які знаходяться на обертових валах, мають
обмежені переміщення в межах зазорів шліцьових з’єднань і можуть
зміщуватися один відносно одного.
При взаємодії зубчастих коліс виникають складні процеси контактних
деформацій, виникнення знакозмінних нелінійних сил тертя, динамічного
перерозподілу інтенсивних поверхневих навантажень но поверхні зуба,
деформації зубів та перерозподілу зусиль, що діють на окремі зуби передачі.
513
Струтинський В. Б.
Тому внутрішні динамічні навантаження виникають в основному в зубчастих
передачах, які зв’язують вали привода. При роботі верстата навантаження
діють одночасно із процесами різання і обумовлюють виникнення
стохастичних коливальних процесів у шпиндельній групі верстата [74].
Враховуючи значну складність динамічної системи при математичному
моделюванні, прийнята схема суперпозиції неперервних і розривних
випадкових процесів. Проведено кількісний аналіз окремо дії найбільш
суттєвих (імпульсних) навантажень в зубчастих передачах та оцінено їх
сумарний вплив на зміну кінематичних та динамічних параметрів привода
головного руху.
В процесі роботи верстата шпиндель має випадкові зміни (флуктуації)
кутової швидкості. Вони визначаються в основному імпульсними (ударними)
навантаженнями, що виникають в приводних зубчастих передачах. При
наявності неточностей виготовлення і монтажу в деяких парах зубців мають
місце зазори або переспряження зубців. Це призводить до появи імпульсних
навантажень значної інтенсивності в динамічній системі верстата.
Розглянемо динамічну систему приводу головного руху, яка відповідає
виділеній (див. рис. 12.5) частині приводу. Динамічна система представлена
як ланцюгова система, на яку діють імпульсні навантаження в різних точках
по довжині ланцюга. Навантаження виникають хаотично в залежності від
взаємного положення зубчастих коліс. Навантаження визначаються
закономірностями випадкового характеру. їх оцінка зв’язана із значною
складністю. Для визначення динамічних навантажень проведено теоретичний
аналіз параметрів стохастичних ударних навантажень. Розроблена нелінійна
математична модель для визначення параметрів імпульсних навантажень в
коробці швидкостей верстата. При розробці математичної моделі прийнято
ряд припущень.
Враховуючи короткочасність дії імпульсу, можна знехтувати рухом валів
привода в поперечному до осі обертання напрямку і розглянути ланцюгову
нелінійну крутильну систему привода головного руху (рис. 12.7).
Рис. 12.7. Ланцюгова крутильна система привода головного руху з
виділеною ділянкою, що включає інерційні елементи (П і III), між якими
виникають імпульсні (ударні) навантаження
514
Розділ 12. Математичне моделювання динамічних коливальних процесів
Імпульс навантаження виникає при перерозподілі точок контакту зубців
передачі між ланками кінематичного ланцюга П і Ш. Шестерня П є кінцевою
ланкою першої (лівої) частини кінематичного ланцюга приводу головного
руху, початковою ланкою якого є ротор електродвигуна. Зубчасте колесо Ш є
початковою ланкою другої (правої) частини кінематичного ланцюга приводу
головного руху, кінцевою ланкою якого є власне шпиндель верстата.
При зміні точок контакту зубців в приводі виникають інтенсивні імпульсні
навантаження. Враховуючи значні статичні крутні моменти, які мають місце в
приводі в першому наближенні, можна знехтувати особливостями закону
розподілу по довжині кінематичного ланцюга сил інерції та розглянути привід
головного руху як два зосереджені інерційні елементи, причому перший
відповідає приведенню лівої частини кінематичного ланцюга до ротора
електродвигуна, а другий - приведенню правої частини кінематичного
ланцюга до шпинделя верстата. Ідеалізована приведена схема крутильної
системи показана на (рис. 12.8).
Рис. 12.8. Схема виникнення ударних навантажень
у зубчастій передачі привода головного руху
На схемі показані два інерційні елементи П (привод) і Ш (шпиндель).
Передача моменту здійснюється зусиллями, які діють в точках контакту
зубців А і В почергово.
На ідеалізованій схемі показана лише одна пара зубців (1п та 1ш) із
зазором, яка здійснює передачу моменту від зубчастого колеса П до колеса
Ш. В реальних умовах передача моменту здійснюється кількома парами
зубців. Наявність кількох точок контакту в передачі із зазором не змінює
принципово механізму перерозподілу навантажень між окремими зубцями
передачі. Тому для обґрунтування механізму виникнення імпульсних
навантажень та математичного опису його закономірностей прийнята
515
Струтинський В. Б.
спрощена (ідеалізована) схема, наведена на рис. 12.8.
Припинення контакту зубців у точці А призводить до вибірки зазору в точці
В. В результаті чого виникає контакт зубців 2п і 2ш в точці В. Рух валів передачі
під час зміни точок контакту зубців має три якісно відмінні фази. Перша фаза
відповідає зміні зусилля в контакті зубців Іп та 1ш (точка А) від номінального
значення до нуля. Зусилля в передачі, а також крутний момент М змінюється при
цьому від номінального до мінімального (можливо і нульового) значення. Друга
фаза відповідає повороту' валів в межах зазору між зубцями. Третя фаза руху
має місце під час контакту зубців 2п і 2ш в точці В. Вона характеризується
зміною моменту від мінімального до номінального значень. Друга фаза руху може
виникати одночасно з першою та третьою фазами. Вона може проявлятися
незначним чином. Якщо шпиндель навантажений значними силами різання, то
виникають пружні деформації зубців, що викликає зменшення модуля зміни
моменту М під час зміни точок контакту зубців. Відповідно поворот валів під час
другої фази руху буде незначним, але загальний механізм зміни крутного
моменту зберігається.
Розглянемо характер зміни крутного моменту в різних фазах руху. На
рис. 12.9 наведені можливі реалізації закону зміни моменту в передачі.
Показані на рисунку випадки відповідають різним геометричним параметрам
та умовам роботи зубців передачі.
Випадок, показаний на рис. 12.9, а, відповідає зубчатій передачі із
зазором між зубцями, коли момент навантаження на шпинделі незначний, а
крутний момент на валу електродвигуна мінімальний (момент холостого
ходу). Випадок, показаний на рис. 12.9, б, відповідає реальній зубчастій
передачі із зазором при довільному навантаженні шпинделя, а випадок,
показаний на рис. 12.9, в, - передачі з переспряженням зубців. Останній
характеризується ударом зуба 2п по зубу 2ш в той момент, коли ще наявні
контакт зубців Іп та 2п (див. рис. 12.8).
Для математичного опису зміни моменту під час удару використаємо
узагальнені функції, зокрема одиничну ступінчасту функцію:
, х /1 при і > Тк
' к' [0 при і <ТК ’
Зміна моменту в зубчатій передачі при цьому визначається залежністю:
М = Мн - ДМ-1(і - Тк) + АМ-1[1 - (Тк + ДО],
де Тк - час, при якому має місце зміна моменту;
АМ - амплітуда імпульсного крутного моменту;
ДІ - тривалість імпульсного навантаження.
Прийнято, що амплітуда імпульсу для передачі із зазором АМ > 0, а для
передачі, в якій наявні переспряження зубців, - АМ < 0.
Обмежимось розглядом дії на динамічну систему лише випадкових
516
Розділ 12. Математичне моделювання динамічних коливальних процесів
центрованих імпульсних навантажень. Графік зміни імпульсного крутного
моменту в часі наведено на рис. 12.9, г.
г)
Рис. 12.9. Зміна крутного моменту, що діє в окремій зубчастій передачі
привода головного руху при наявності зазорів передачі: а - ідеалізований
випадок, коли наявна повна відсутність контакту зубців у межах зазору;
б - випадок імпульсного зменшення крутного моменту з причини наявності
зазору в передачі; в - імпульсне збільшення крутного моменту з причини
наявності переспряження зубців передачі; г - центрований імпульсний
випадковий процес крутного моменту в зубчастій передачі
Випадковий імпульсний крутний момент відповідає послідовності
імпульсів нескінченно малої ширини. Періодичність імпульсів відповідає
частоті ударів і.г (Гц), що співпадає із зубцевою частотою передачі:
г п • 7,„	,	.
(12.71)
де п - число обертів вала за хвилину;
хп - число зубців зубчастого колеса, розташованого на валу.
Відповідно визначимо період дії ударів:
Т = 1 = 60
• п • гп
Тривалість ударного імпульсу АІ є незначною, тому приймемо, що ширина
ударного імпульсу є постійною для серії ударів, а амплітуди імпульсів є
517
Струтинський В. Б.
випадковими величинами. Позначимо математичне сподівання амплітуд
через ДМ , а дисперсію - через Оди- Ці параметри визначаються статистичною
обробкою серії імпульсів відповідно за формулами:
______________	4 к
ДМ = ^£дМк;	(12.72)
К к=і
і К	____
В,м=-£(ЛМк-АМ)\	(12.73)
К. к=1
де К - загальне число імпульсів у розглянутій серії;
ДМк ~ амплітуда к-го імпульсу.
Розглянемо дві окремі динамічні підсистеми крутильної динамічної
системи привода головного руху (рис. 12.10), на які діє імпульсний-момент
виду:
М = -ДМ-1Ц - Тк) + ДМ-1Ц - (Тк + ДО,	(12.74)
де Тк - час зміни моменту.
Рис. 12.10. Приведені до зубчастого зчеплення динамічні підсистеми
лівої частини привода головного руху і шпинделя верстата
(правої частини головного руху)
Для динамічної підсистеми шпинделя (Ш) рівняння зміни кутової
швидкості під дією імпульсного моменту має вигляд:
Іш + ьш®ш = -дм при Тк < і < Тк + Ді,	(12.75)
ск
де 5Ш - приведений до шпинделя момент інерції всієї даної підсистеми;
Ьш ~ приведений коефіцієнт опору підсистеми;
сош - зміна кутової швидкості шпинделя за рахунок імпульсного
навантаження.
Рівняння (12.75) має нульові початкові умови, тобто
при і = Тк сош = 0.
Розв’язок рівняння (12.75) для проміжку часу
518
Розділ 12. Математичне моделювання динамічних коливальних процесів
Тк < і; <	+ Ді
буде мати вигляд:
дмГ.
сіі...(і) =----1-е “
ш
/,\ ДМ
сош(0 = ——
п„,
В момент час.у, що відповідає кінцю дії ударного імпульсу,
і —	+ Лі
одержимо значення кутової швидкості підсистеми шпинделя у вигляді:
(12.76)
Знак мінус означає, що під дією імпульсного навантаження шпиндель
набуває додаткової кутової швидкості, протилежної напрямку свого
постійного обертання.
Для динамічної підсистеми електродвигуна (П) (рис. 12.10) рівняння
зміни кутової швидкості має вигляд:
Л~- + Ьпи„ = ДМ ,	(12.77)
аі
де )п - момент інерції частини приводу головного руху що знаходиться зліва
від передачі, приведений до ротора двигуна;
ЬГІ - постійна, яка враховує як механічні, так і електричні втрати в
електромеханічній системі.
Для приводу головного руху з двигуном постійного струму, згідно з [39]:
Ь,.=Ьм+^Фв,	(12.78)
де Фв - магнітний потік збудження якоря електродвигуна;
Се, Ст - постійні величини, які визначають характеристики двигуна;
Я я - активний опір обмотки якоря;
Ьм - приведений коефіцієнт опору в підшипниках приводу.
Для привода, який має асинхронний двигун, коефіцієнт опору складає:
2 т т2
ь" = ь"+гїїГ^'	<12 79)
де Шв - коефіцієнт взаємної індукції;
Яо - амплітуда синусоїдальної зміни напруги збудження;
Кр, Кс ~ електричні опори ротора та обмоток статора відповідно.
Рівняння (12.77) має нульові початкові умови і його розв’язок для
< 1 < Тк + Лі
запишеться у вигляді:
519
Струтинський В. Б.
В момент часу, який відповідає завершенню дії імпульсного навантаження,
С =	+ Аі
значення кутової швидкості підсистеми електродвигуна складе
ДМ
СОП(0 = —-
1 - Є )я
(12.80)
Залежності (12.76) та (12.80) визначають кутові швидкості підсистем в
кінці дії імпульсного навантаження. Кутова швидкість шестерні П в цей час
(рис. 12.10) збільшується, а кутова швидкість зубчатого колеса Ш
зменшується. При цьому має місце вибір зазору та нове імпульсне
навантаження (удар) в зубчастій передачі.
Розглянемо загальну динамічну систему приводу головного руху яка
приведена до вала електродвигуна. Під час вибірки зазору загальна динамічна
система складається із двох автономних приведених підсистем (рис. 12.10). В
момент часу, коли зазор вибрано, дві системи з’єднуються в одну так, як це
показано на рис. 12.11. Для подальшого аналізу ці системи приводяться до
одного вала (вала електродвигуна).
Після вибору зазору в ланцюговій системі привода головного руху виникають
хвильові явища. їх врахування представляє окрему задачу і не розглядається в
рамках даного дослідження. Вважається, що протяжність кінематичних ланцюгів
; іриводу головного руху невелика,
що дозволяє знехтувати хвильовими
процесами.
Рис. 12.11. Схема приведення окремих елементів системи
привода головного руху до одного вала
Приведені до вала електродвигуна моменти інерції обох підсистем в
момент удару складають:
ҐП	..
1 тя Т = Т н|"	= Т -і2
п 1 Л Ш ш	Ш 1 ’
)
(12.81)
де і - загальне передавальне число від вала електродвигуна до шпинделя;
®пш - номінальна частота обертання шпинделя;
520
Розділ 12. Математичне моделювання динамічних коливальних процесів
сонд ~ номінальна частота обертання вала електродвигуна.
Після удару в момент часу І > Ти + ЛІ момент інерції системи буде:
л = 5Ш  І2 + Уп 	(12.82)
Кутові швидкості приведених підсистем до удару складають
Он та (Ощ = —.	(12.83)
і
Знайдемо загальну кутову швидкість системи після вибору зазору. Із
закону збереження моменту кількості руху при пружному ударі випливає
співвідношення:
Лп ~ Лш = (Лп + Лш) <Вко>	(12.84)
де сако - загальна кутова швидкість системи після удару.
Підставляючи в (12.84) значення величин із (12.81) та (12.83), одержимо:
Після підстановки в дану формулу кутових швидкостей із (12.76) та
(12.80) знайдемо:
(12.85)
®ко
Із аналізу цієї формули випливає, що кутова швидкість системи після
удару може бути або додатною, або від'ємною, тобто може збільшуватись або
зменшуватись в залежності від місця розташування передачі, в якій
виникають імпульсні навантаження.
Запишемо формулу (12.85) у спрощеному вигляді. Розкладаючи
експоненту в ряд згідно з формулою
ег ® 1 + г,
одержимо лінійну складову кутової швидкості:
дм/^-і-^!Л(і-і)-ді
Враховуючи, що час зміни моменту Ді є дуже малим, можна вважати, що
після удару всі маси динамічної системи приводу набувають невеликого
приросту кутової швидкості, який може бути додатним або від’ємним в
залежності від параметрів зубчастої передачі та місця її розташування в
приводі. Якщо для передач із зазором удари відбуваються в передачах,
близьких до електродвигуна, то множник в дужках менший нуля, якщо удар
має місце, ближче до шпинделя - множник додатній.
Значення кутової швидкості, якої набуває шпиндель після удару, є
випадковою величиною, що залежить від випадкової зміни моменту та
521
Струтинський В. Б.
тривалості удару. Позначимо математичне сподівання кутової швидкості <иКС) ,
а дисперсію значень кутової швидкості ВиКО.
Розглянемо рух приводу головного руху після дії удару. Динамічна
модель приводу наведена на рис. 12.11, б. Рівняння зміни кутової швидкості
приводу має вигляд:
5-^—- + Ьик=0,	(12.86)
а і.
де Ь - постійна, яка визначається залежностями (12.78) або (12.79) з
урахуванням коефіцієнтів опору у всій динамічній системі; 5 - момент інерції
системи, який відповідає формулі (12.82).
Рівняння (12.86) має випадкові початкові умови
при і = Тк + ДЬ, ш = гоко.
Загальний розв’язок рівняння (3.16) із врахуванням початкових умов
складає:
®к(0 = “ко-є ' к)-	(12.87)
Введемо нові позначення в рівнянні (12.87). Постійна часу крутильної
динамічної системи приводу головного руху:
З
Постійна часу включає приведені до вала електродвигуна коефіцієнт
опору Ь та момент інерції 1. Вона враховує місце дії удару в приводі
головного руху верстата.
Введемо також інтенсивність імпульсної зміни швидкості приводу:
Рк =®коу>	(12.88)
яка в силу залежності (12.85) є випадковою величиною. Тоді рух приводу
після дії імпульсного навантаження визначиться формулою [74]:
Юк=А<Х.е т .	(12.89)
Імпульсні навантаження в зубчастій передачі діють в приводі періодично з
частотою (2 (формула (12.71)) і викликають сумарну зміну' кутової
швидкості, яку можна визначити користуючись принципом суперпозиції.
Відповідно значення кутової швидкості в момент часу € складає:
।	('-У
ю(О=тХОк-е ~т“,	(12.90)
де сума береться для всіх значень і > Т^.
Залежність (12.90) визначає зміну кутової швидкості системи під дією
імпульсних навантажень, які відбуваються лише в одній зубчастій передачі.
Зміна кутової швидкості в часі представляє собою випадковий процес,
522
Розділ 12. Математичне моделювання динамічних коливальних процесів
схематична реалізація якого для однієї зубчастої передачі наведена на
рис. 12.12.
Рис. 12.12. Характерна реалізація випадкового процесу зміни
кутової швидкості шпинделя під дією імпульсних навантажень,
що діють в одній зубчастій передачі
Наявні на графіку миттєві зміни кутової швидкості пояснюються
введенням припущення про абсолютно пружні удари і відсутність пружних
хвиль в динамічній системі приводу головного руху верстата. Враховуючи,
що миттєві ступеневі зміни кутової швидкості невеликі, можна вважати ці
припущення обґрунтованими і прийняти, що розрахунковий випадковий
процес зміни швидкості відповідає реальному процесу.
В приводі головного руху наявний ряд зубчастих передач, які генерують
випадкові зміни кутової швидкості. Загальна кутова швидкість елементів
привода відповідає суперпозиції збурені, кутової швидкості від кожної
зубчастої передачі і визначається сумою:
а>£(0 =	,
де М - загальне число зубчастих передач у приводі.
Реалізація випадкової зміни сумарної кутової швидкості відповідає сумі
випадкових процесів. Визначимо окремо кожен випадковий процес і знайдемо
його спектральні характеристики згідно з методикою [60].
Розглянемо проміжок часу (з, і), причому 8 -> -оо. Кутову швидкість, яка
спричинена імпульсними навантаженнями, що мають місце в проміжку часу
(з, 0, позначимо ®3(0. Приймемо, що число ударів, що мало місце за даний
проміжок часу, в середньому складало ц ударів в одиницю часу. Удари є
рідкими подіями, тому величина ц мала. Число ударів в одиницю часу ц
відповідає частоті імпульсів (12.71). Тому:
Число ударів можна вважати розподіленим за законом Пуассона (закон
рідких подій), причому математичне сподівання цього розподілу:
X = |і(1 - з).
Визначимо випадкову подію ет, яка відповідає числу ударів т = 0, 1, 2,...
523
Струтинський В. Б.
за проміжок часу (з, і). Ймовірність цієї події:
Р(ет)— • ;....., ш = 0, 1,2,...
т!
Для проміжку часу (з, і) при кількості ударів т кутова швидкість
приводу визначається залежністю:
і ,п XX"
<05а)=-Х<Зк-е т .	(12.91)
і к-.-1
Дана залежність є основою для розрахунків випадкового процесу зміни
кутової швидкості. Розрахунки виконані в програмному середовищі
МаїЬСАІ). Випадкові параметри приводів задавались вбудованими
функціями, що генерують послідовності випадкових чисел з нормальним
законом розподілу.
Одержані розрахункові типові реалізації зміни кутової швидкості
(рис. 12.13) охоплюють діапазон флуктуації кутової швидкості, ширина якого
складає 2...6 % від номінальної кутової швидкості.
Рис. 12.13. Розрахункові реалізації випадкового процесу флуктуації
кутової швидкості шпинделя металорізального верстата
Таким чином, абсолютні значення флуктуації кутової швидкості шпинделя
є незначними. Вони несуттєво впливають на кінематичні характеристики
приводу головного руху. В той же час вплив зміни кутової швидкості на
динамічні властивості верстата є досить значним. Причиною цього є імпульсні
навантаження в приводі, а також ймовірність співпадання циклічної зміни
кутової швидкості із резонансними частотами верстата. Для визначення
впливу зміни кутової швидкості на динаміку верстата визначені спектральні
характеристики випадкового процесу флуктуації кутової швидкості шпинделя.
Для цього виконано аналіз залежності (12.91). Розглянемо всі можливі
випадки наявності кількох ударів в одиницю часу (ш = 1, 2, З,...).
Знайдемо математичне сподівання випадкової функції со5(0:
524
Розділ 12. Математичне моделювання динамічних коливальних процесів
м[®5(1)] = ^Р(ет)м[ш5(і) | ет],
т=0
(12.92)
де М[а>5(О|ет] - умовне математичне сподівання випадкової функції ©§(1) за
умови здійснення події ет.
Умовне математичне сподівання розраховується на основі формули
(12.90) шляхом знаходження статистичного середнього по всіх можливих
значеннях інтенсивності ударів фк та всіх можливих моментах ударів Тк при
фіксованому числі ударів, що діють в інтервалі часу (§, 1).
Враховуючи незалежність випадкових величин ф« і Тк, одержимо:
Г	1	1 ІП
м[®5(1) І ет] = — М фк
1 К = 1
<ь-ть)~|	1 т	Г (і-тк)
е т =-£м[фк]-Ме т
-* к=і
(12.93)
К = 1
Математичне сподівання експоненціальної функції:
(і-т)
М
е 
 Ргк(тМт ,
де Ртк(т) - густина ймовірності випадкової величини Тк-
Цю густину Ймовірності приймемо ПОСТІЙНОЮ Ртк(^) “ 1/(1 - з), оскільки
моменти ударів розподілені в проміжку часу (з, і) рівномірно.
Таким чином, математичне сподівання експоненціальної функції:
М
е т
1
1-8
І (1-Х)	гр
[е т сіт = —— 1-е
•’	1-8
(12.94)
Позначивши математичне
одержимо:
сподівання інтенсивності удару
М[фк] = д,
(1-$)
ПІ
= !_е
1-8
(12.95)
Т
Використовуючи значення (12.95),
сподівання випадкової функції ®5(і):
м[и,(ф У
1  ‘ ті-а-й
знайдемо з (12.92)
під 1-е
(1-5)
математичне
Після перетворення даної залежності одержимо:
(І-5)
1-е" т
[ц(і-з)Г'
(ш -1)!
М[®5(О]= цде ца'5)
V №
Враховуючи, що експоненціальна функція відповідає ряду:
X п
е-П,
п=о п!
одержимо, підставивши замість г = ц(1 - з):
525
Струтинський В. Б.
[ца-з)г1
(т -1)!
Таким чином, математичне сподівання кутової швидкості складе:
м[и5(О]= цц 1-е т
(12.96)
В граничному випадку з -> -оо значення математичного сподівання кутової
швидкості визначається залежністю:
М[о5а)]=ца.	(12.97)
Знайдемо кореляційну' функцію кутової швидкості. Для цього розглянемо
значення величин у два моменти часу і і 1'. Для V > І з формули. (12.90)
одержимо:
Т ’	(12.98)
1 Тк<1
Сума в правій частині (12.98) може бути розділена на дві складові.
Відповідно знайдемо:
і	дди і	а'-т„)
Н() = ^дк-е г +± ^Рь.е т .	(12 99)
‘ Тк<г	і Ь<Ть<Г
З формули (12.99), враховуючи (12.90), випливає:
С-і	<Г-Т|.>
<в(1') = а(0 • е т +-1 ^(\-е т •	(12.100)
Другий доданок в (12.100) не залежить від <о(0, тому що він включає
інші випадкові величини. Тому кореляційна функція дорівнює кореляційному
моменту величин:
®(0е т та и(0.
Відповідно значення кореляційної функції флуктуацій кутової швидкості
шпинделя складе:
Коа,1') = о[а(0]-е”т .	(12.101)
Знайдемо дисперсію кутової швидкості О[<в(0]. Дисперсія (умовна)
випадкової функції <о3(Т) за умови, що в приводі діє іп ударів за час (з, 0,
дорівнює сумі дисперсій доданків у формулі (12.91) (внаслідок незалежності
доданків). Знайдемо дисперсію одного доданку. Його центральний момент
другого порядку:
м{ [®5(і)Г}= М
2<і-Ть)
т
= М^]-Ме"
(12.102)

Математичне сподівання інтенсивності ударів дорівнює ц. Дисперсію
інтенсивності ударів позначимо П. Тоді
526
Розділ 12. Математичне моделювання динамічних коливальних процесів
М[0к] = ч2+О.
Математичне сподівання експоненціальної функції
2(1-ТК)
е“ т
знайдемо за формулами (12.93) та (12.94), в яких замість
Т -> Т/2.
(12.103)
Відповідно значення математичного сподівання експоненціальної функції:
2(Ь-5)>
Є т
Т
2(1 - з)
М
Є т
(12.104)
В результаті одержимо умовну
умови, що за час (з, і) в приводі діє т ударів:
20-8) \
1 - е т -
ш(д2 ч- Р) 
2Т(1 - з)
дисперсію кутової швидкості а>5(0 за
тд2
(Г^7
1-е
(12.105)
2
Дисперсія випадкової кутової швидкості:
Після підстановки значень величин із (12.105) одержимо:
2Т(і - з)
_2Н25)'\
1-е” Т
іп=0
тд2
(і - з)2
[ц(і-8)]т-Є-Ца-5>
т
Після спрощення, відповідно до формул (12.95) та (12.96), знайдемо:
р[м5(0]=	 р) • 1-е’ т -	1-е“т	.	(12.106)
1 5 -1 2Т	] і)
В граничному випадку з —> -<х> значення дисперсії кутової швидкості
визначається залежністю:
Р[®(О] =	•	(12.107)
Використовуючи значення дисперсії, одержимо кореляційну функцію
кутової швидкості приводу, приведеної до вала електродвигуна відповідно
при дії ударних імпульсів лише в одній зубчастій передачі у вигляді:
В (1,0 =	.+ Е>).е V.	(12.108)
соч '	2Т
Якщо В < І, то відповідно в степені експоненти зміниться порядок
доданків і тому для всіх значень і' і І будемо мати:
К (1,0 =	+21.е	(12.109)
и	2Т
де ц - число імпульсних навантажень в одиницю часу (частота навантажень);
д - математичне сподівання інтенсивності ударних імпульсів;
527
Струтинський В. Б.
В - дисперсія інтенсивності імпульсів, що діють у зубчастій передачі;
Т - постійна часу.
Всі ці параметри залежать від місця виникнення імпульсного
навантаження, тобто від місця розташування зубчастого зчеплення в приводі
головного руху.
В приводі наявний ряд зубчастих передач. Тому кутова швидкість
шпинделя визначається сумою випадкових змін кутової швидкості,
обумовлених ударами в різних передачах.
Будемо вважати зміни кутової швидкості, що мають місце під дією
імпульсних навантажень у різних передачах некорельованими. При цьому
кореляційна функція буде визначатися наступною формулою:
5=1
де 2 - число послідовно з’єднаних передач в приводі головного руху;
щ - частота навантажень в фій передачі;
ц, , В, - математичне сподівання та дисперсія інтенсивності імпульсів;
Т: - постійна часу, визначена для даної передачі.
Формула (12.110) дозволяє визначити кореляційну функцію випадкових
флуктуацій кутової швидкості вала електродвигуна, який є початковою
ланкою приводу головного руху.
Кутова швидкість шпинделя як випадкова функція часу пов’язана з
випадковою кутовою швидкістю вала електродвигуна лінійною залежністю:
=	(12.111)
де і - передавальне число, визначене як і в формулах (12.81)-(12.83).
З (12.110), (12.111) випливає залежність для знаходження кореляційної
функції кутової швидкості власне шпинделя металорізального верстата:
2 і2п«г,(а? + В,)
= У--------------^--е 1 ,	(12.112)
ши	120Т^
де п5,	- число обертів за хвилину і число зубців зубчатої передачі, в якій
відбуваються імпульсні навантаження.
Таким чином, математична модель кореляційної функції флуктуації
кутової швидкості відповідає лінійній математичній моделі, базисні функції
якої є експонентами, а число складових математичної моделі дорівнює числу
зубчастих передач в приводі головного руху верстата.
Визначимо кореляційну функцію кутового прискорення шпинделя.
Прискорення зв’язане з кутовою швидкістю диференціальною залежністю:
Р - ао)ш
ш сік 
528
Розділ 12. Математичне моделювання динамічних коливальних процесів
Відповідно кореляційна функція кутового прискорення згідно з [60]:
КШВ(М') =
д2кшю(и')
Виконуючи операцію подвійного диференціювання у формулі (12.102) по
змінних І та V, як це зроблено в [60], одержимо залежність, яка включає
дельта-функцію:
кшеа,о = І і2.пЛ5.^+Ь2
шє £	120Тг
2
+ — • 5(4 - і') ,
Т.
(12.113)
1
— • е
Т
де 8(1 - В) - одинична імпульсна функція (дельта-функція Дірака).
Із аналізу кореляційних функцій кутової швидкості шпинделя (12.112) та
кутового прискорення (12.113) випливає, що вони залежать лише від різниці
т = і - і',
тобто відповідають стаціонарним випадковим процесам. Тому кореляційні
функції можна записати у вигляді:
і2пе2^(д2 +Р4)
120'18
тг
Є -
і\2^(д2+Рр
ШЕ £1	120Т,
—-є + — • 8(т)
Т	Т
= Е
5 = 1
Цим кореляційним функціям відповідають
відповідно кутової швидкості
8 <ю) = У +Е>Р .	1
ш“ £	120л (І + Т^в2)
та кутового прискорення шпинделя
і2щ2Дд2 +Р.)
ше	120л	’ (Т2ш2 +1)'
спектральні щільності
(12.114)
(12.115)
Дані залежності дозволяють сформувати практично важливі висновки, які
використовуються для опису спектральних характеристик кутової швидкості
шпинделя. З формули (12.114) випливає, що для низькочастотної області в
діапазоні частот:
а» <— (Т(?ю2 « 1) для всіх = 1, ..., 7.
спектральну щільність флуктуацій кутової швидкості допустимо вважати
постійною величиною, що не залежить від частоти:
2 і2П-2
8,„щ(и) = ЕцЕт~ +Г)Р = СоП5І •	(12.116)
529
Струтинський В.Б.
Для зони високих частот спектра вібрацій привода головного руху, що
відповідають частотам
Ш > -- (Т2И2 » 1) ДЛЯ ВСІХ = 1,	7
Те
із формули (12.115) випливає, що спектральна густина флуктуацій кутового
прискорення шпинделя може вважатись постійною із значенням:
2 і2п 2
5.-Лм)	+Г)Р = Соп^-	(12.117)
1211л Ц
Таким чином, із теоретичного аналізу випливає, що спектральна
характеристика флуктуації кутової швидкості шпинделя металорізального
верстата, які виникають під дією імпульсних навантажень в зубчастих
передачах приводу головного руху, відповідає кореляційній функції у вигляді
суми експоненціальних складових (формули (12.112)), причому кількість
доданків суми дорівнює числу зубчастих передач приводу головного руху, а
інтенсивність зміни доданків визначається частотою обертання зубчастих
коліс та числом зубців передач.
Для аналізу низькочастотних коливальних процесів спектр флуктуацій
кутової швидкості може бути прийнятий відповідним “білому шуму” з
постійною спектральною щільністю (формула (12.116)), причому
інтенсивність спектра залежить від суми інтенсивностей випадкових
імпульсних навантажень в усіх зубчастих передачах.
Для аналізу високочастотних коливальних процесів доцільно
використовувати математичну модель у вигляді спектральної щільності
кутового прискорення шпинделя (формула (12.117)), що відповідає “білому
шуму”, інтенсивність якого залежить, зокрема, від інерційних та
дисипативних параметрів приводу головного руху.
Таким чином, при математичному моделюванні динамічних процесів
верстата випадкові збурення в зубчастих передачах можна визначити
адитивним набором випадкових процесів у вигляді “білого шуму”. Для
моделювання низькочастотних процесів “білий шум” визначає флуктуації
кутової швидкості, а для моделювання високочастотних процесів - флуктуації
кутового прискорення. Кількість цих випадкових процесів відповідає числу
зубчастих передач в приводі головного руху.
При моделюванні динамічної системи верстата в кожній зубчастій передачі
необхідно помістити джерело стохастичних збурень, статистичні
характеристики якого відповідають “білому шуму”. Реалізація даного методу
виконана в математичній моделі, наведеній нижче (див. розділ 12.4). Це
значно спрощує математичну модель і дає можливість виявити вплив окремих
зубчастих передач на динамічні процеси, що мають місце при роботі верстата.
530
Розділ 12. Математичне моделювання динамічних коливальних процесів
12.3. Структурна математична модель динамічної системи
шпиндельно-супортної групи верстата
Динамічна система верстата при математичному моделюванні розділена на
чотири основні підсистеми: шпиндельну групу, супортну групу, процес різання та
систему привода головного руху [39, 84].
На рис. 12.14 зображено загальний вигляд та конструктивну схему
шпиндельної групи токарного верстата.
а)
Рис. 12.14. Загальний вигляд (а) та конструктивна схема шпиндельної
групи токарного верстата (б), з параметрами динамічної системи
531
Струтинський В. Б.
Шпиндель, на якому знаходиться зубчасте колесо приводної передачі,
встановлений на підшипниках кочення у корпусі передньої бабки. При
обробці заготовки на шпиндель будуть діяти зусилля з боку приводної
передачі, а на заготовку - динамічна сила різання. Дані силові фактори
змінюються під час обробки. Тому при аналізі динаміки розглянуто вплив
динамічних складових цих силових факторів на коливання шпинделя [84].
Під дією динамічної складової рп в приводній передачі та динамічної
складової р сили різання шпиндель буде зміщуватись в підшипникових
опорах і деформуватись (згинатись), що показано викривленою пружною
лінією осі шпинделя (див. рис. 12.14, б).
Математична модель шпиндельної групи включає в себе систему рівнянь,
які описують коливання пружної системи при відповідних припущеннях. В
рівняння входять параметри системи, які показані на конструктивній схемі
шпиндельної групи верстата (див. рис. 12.14, б): <р0, ф0, <р0 - динамічна
складового кута повороту приводного вала та її похідні; с(рп, -
еквівалентна крутильна жорсткість та еквівалентний коефіцієнт опору
приводу головного руху; <р , <рп - динамічні складові кута повороту
шпинделя та вала приводної передачі відповідно; ЬфШ - еквівалентний
коефіцієнт опору підшипників; р, рп ~ динамічна складова відповідно сили
різання та зусилля в приводній передачі; „І - приведений момент інерції
шпинделя; уш - переміщення заготовки в зоні різання; рк, а - кутові розміри;
х, у, 2, - осі координат.
Розглянемо переміщення шпинделя в горизонтальній площині (хоу).
Переміщення у вертикальній площині мало впливають на точність обробки
деталі і тому в першому наближенні їх можна не враховувати.
На рис. 12.15 показана схема зміщення та деформації шпинделя в
горизонтальній площині, а також - вигляд та переріз шпинделя, які
пояснюють дію на шпиндель навантажень від динамічної складової рп зусилля
в приводній передачі.
В процесі поперечних коливань шпинделя він деформується, що
проявляється в зміні форми пружної лінії шпинделя (рис. 12.15, а).
Додатково шпиндель переміщується за рахунок деформатпвності опор.
Деформативність опор обумовлена: по-перше, відносним переміщенням
деталей підшипників; по-друге, переміщенням в контактах між внутрішніми
кільцями підшипників і шпинделем; по-третє, переміщенням в контактах між
зовнішніми кільцями підшипників та обоймами, встановленими в корпусі
передньої бабки; по-четверте, деформаціями корпусних деталей, в яких
встановлені обойми підшипників, відносно корпусу. На розрахунковій схемі
деформативність опор показана еквівалентними жорсткостями опор С(ш, сзш
та еквівалентними дисипативними коефіцієнтами опор й1ш і Й2Ш.
532
Розділ 12. Математичне моделювання динамічних коливальних процесів
Рис. 12.15. Схема переміщення та деформації шпинделя при його
поперечних коливаннях (а), динамічна модель крутильних коливань
шпинделя (б) і схема дії сили різання на заготовку (в): 1іш<р ~
еквівалентний коефіцієнт опору підшипників; с^ш, с?ш - еквівалентні
жорсткості відповідно задньої та передньої опор шпинделя;	_
еквівалентні коефіцієнти опору відповідно задньої та передньої опор
шпинделя; ру, р,р - проекції на вісь у динамічних складових відповідно сили
різання та зусилля в приводній передачі; сіп, <1% - діаметри ділильного кола
відповідно шестерні та зубчастого колеса приводної передачі; <1 -
номінальний діаметр обробленої поверхні заготовки в зоні різання; уш —
переміщення шпинделя разом із заготовкою в зоні різання; р, рп - динамічна
складова відповідно сили різання та зусилля в приводній передачі; а; - кут
зачеплення приводної передачі; с^, Ії(рп - відповідно еквівалентна крутильна
жорсткість та еквівалентний коефіцієнт опору приводної зубчастої
передачі; <р, срп - динамічна складового кута повороту відповідно
шпинделя та вала приводної передачі; а(і) — зміна припуску
оброблюваної деталі в функції часу; а, ф;, - кутові розміри;
] - приведений момент інерції шпинделя
533
Струтинський В.Б.
Пружна система шпинделя, яка здійснює поперечні коливання, у
спрощеному вигляді представлена еквівалентною одномасовою динамічною
моделлю, приведеною до точки дії сили різання [43]. На рис. 12.16 показана
еквівалентна і приведена одно масові динамічні моделі шпинделя.
Рис. 12.16. Еквівалентна одномасова динамічна модель поперечних
коливань шпинделя (а) і приведена одномасова динамічна модель
шпинделя (б): Сіш - еквівалентна жорсткість задньої опори шпинделя;
с2ш ~ еквівалентна жорсткість передньої опори шпинделя; !і]ш,	~
коефіцієнти опору відповідно задньої та передньої опор шпинделя;
Ні, К? — динамічні складові реакцій відповідно задньої та передньої
опор шпинделя; ру, ру] - проекції на вісь у динамічної складової
відповідно сили різання і зусилля в приводній передачі; тш — приведена
до зони різання маса шпинделя; уш - поперечні переміщення шпинделя разом
із заготовкою в зоні різання; сш - еквівалентна жорсткість шпинделя;
1іш - еквівалентний коефіцієнт опору при поперечних коливаннях
шпинделя; - деформативність шпинделя в зоні різання; є? ~
деформативність шпинделя в зоні різання при дії зусилля в приводній
передачі рур 11, І2, Із ~ осьові геометричні розміри шпинделя
Розрахункова схема еквівалентної одномасової системи шпинделя
(рис. 12.16, а), що здійснює поперечні коливання, включає в себе приведену
масу шпинделя тш та пружну систему шпинделя, яка представлена у вигляді
невагомої пружної балки, розміщеної на пружних опорах з демпфуванням.
Маса шпинделя тш приведена до зони різання та розміщена в точці
прикладення сили різання р.
Приведена одномасова система шпинделя (рис. 12.16, б) включає в себе
масу тш, розташовану на пружній опорі, яка характеризується еквівалентною
жорсткістю сш та еквівалентним коефіцієнтом опору Ьщ. До маси тш
534
Розділ 12. Математичне моделювання динамічних коливальних процесів
прикладені: ру - проекція на вісь сили різання р та ру( - проекція на вісь у
динамічної складової р„ зусилля в приводній передачі. При цьому проекція
динамічної складової рУ| зусилля в приводній передачі міняє свій напрямок
дії відповідно з умовами приведення.
Рівняння поперечних коливань шпинделя, складене для приведеної одно
масової динамічної моделі шпинделя (рис. 12.16, б), має вигляд:
тшуш +Ьшуш + — уш = р-8іпа+^р„ -зі^а, +рк),	(12.118)
еі	еі
де е1 = <3уш/і3ру - СОП8І = 1/сш - деформативність шпинделя разом із
заготовкою в зоні різання при прикладенні сили в зоні різання;
е2 = Зуш/ф у1 ~ деформативність шпинделя разом із заготовкою в зоні
різання при прикладенні сили в приводній передачі;
тш - приведена до зони різання маса шпинделя;
йш ~ еквівалентний коефіцієнт опору шпинделя;
уш - переміщення шпинделя разом із заготовкою в зоні різання в
напрямку осі у;
р ~ динамічна складова сили різання;
рп - динамічна складова зусилля в приводній передачі;
а - кут між динамічною складовою р сили різання та віссю г;
а। - кут зачеплення в приводній передачі;
Рк - кут розміщення шестерні приводної передачі відносно осі у.
Перетворимо рівняння поперечних коливань шпинделя (12.118) по
Лапласу при нульових початкових умовах [6]:
<	і \
тш®2 +ЬШ8 + — -уш(3) = р(5)‘5Іпа + ?„($)• —"ЛіКсц +Рк), (12.119)
І	є,)	е1
де 8 - оператор Лапласа;
Уш(3) ~ зображення по Лапласу переміщення шпинделя разом із
заготовкою в зоні різання;
р(з) - зображення по Лапласу динамічної складової сили різання;
р„(з) ~ зображення по Лапласу динамічної складової зусилля в приводній
передачі шпинделя.
Введемо позначення для комплексів параметрів, що називаються
постійними часу:
Ті = 7тшеі > Т2 = Ьше1.	(12.120)
Перетворимо рівняння (12.119) з урахуванням позначень (12.120):
(Т,282 +Т>8 + 1)-уш(8) = Є( • 8ІП а • р(з) + е2 -зйИоц +Рк)-р„(8).	(12.121)
Це рівняння в операторній формі описує поперечні коливання шпинделя у
горизонтальній площині.
535
Струтинський В. Б.
Розглянемо поперечно-кутові (крутильні) коливання шпинделя навколо
осі обертання (див. рис. 12.15, б). При складанні рівнянь, які визначають
крутильні коливання шпинделя, він розглядається як абсолютно тверде тіло,
встановлене на підшипниках. Підшипники мають певний опір, який враховано
введенням еквівалентного коефіцієнта опору (в’язкого тертя) ЬШФ .
Рівняння крутильних коливань шпинделя:
т.. ,
Іф = р — соз а - р„ СО8 а, - Ь^ф,
(12.122)
де І - приведений момент інерції шпинделя та приводної передачі;
ЬШ(р - еквівалентний коефіцієнт опору підшипників шпинделя;
б - номінальний діаметр обробленої поверхні заготовки в зоні різання;
бк - діаметр ділильного кола зубчастого колеса приводної передачі;
Ф - динамічна складова кута повороту шпинделя, що представляє собою
відхилення кута повороту шпинделя від номінального (усталеного) значення,
яке визначено обертанням шпинделя зі сталою частотою.
Будемо вважати, що приведений момент інерції привода головного руху
набагато більший моменту інерції шпинделя. Це означає, що крутильні
коливання шпинделя загалом мало впливають на коливання валів привода. З
врахуванням цього, рівняння, що описують вплив привода головного руху на
динамічні параметри шпинделя, має вигляд:
Рп-усоз»! =Сч>п(фп -фо) + МФп - Фе)’	(12.123)
де сі, - діаметр ділильного кола шестерні приводної передачі;
сФП - еквівалентна крутильна жорсткість приводної передачі;
1іфП ~ еквівалентний коефіцієнт опору приводної передачі;
Фо - динамічна складова кута повороту приводного вала, визначена як
відхилення кута повороту вала від номінального (усталеного) значення;
Фи - динамічна складова кута повороту шестерні приводної передачі.
Зв’язок між динамічними складовими кутів повороту шпинделя та
шестерні приводної передачі одержимо у спрощеному вигляді як кінематичне
співвідношення:
ф = ішф„.	(12.124)
де іш - передавальне відношення приводної передачі.
Підставимо значення кута повороту шестерні із залежності (12.124) в
рівняння привода (12.123). Після перетворення одержимо:
Рп—соза, =-^-ф + —ф-сфПф0 -ЬфПф0.	(12.125)
2	іщ іщ
Перетворимо рівняння крутильних коливань шпинделя (12.122) по
Лапласу при нульових початкових умовах:
536
Розділ 12. Математичне моделювання динамічних коливальних процесів
(12.126)
ь
фВ ііфН
(12.127)
ти ш
СІЗ2 + Ь Шфз) • ф(з) + рп (з) • —у ’ соз а4 = р(з) •• соз а,
де з - оператор Лапласа;
ф(з), рп(з), р(з) - зображення по Лапласу динамічних складових відповідно
кута повороту шпинделя, зусилля в приводній передачі та сили різання.
Перетворимо рівняння привода (12.125) по Лапласу:
рп(3)’ 4г  с°з а
2
де ф0(з) - зображення по Лапласу динамічної складової кута повороту
приводного вала.
З рівняння (12.127) знайдемо значення динамічної складової кута
повороту шпинделя в функції оператора Лапласа та зображень по Лапласу
динамічних складових зусилля в приводній передачі рп та кута повороту
приводного вала <рд:
а,.
--соз а
“(рп ч>п'
<оп , ^фП
фП { ^фП
ш
(12.128)
(12.129)
ш
Спростимо дане рівняння шляхом перетворення та скорочення:
. сІг
іш-усоза,
Й) = Рп(5)-----' Фо(®)-
сфп + М
Підставимо значення динамічної складової кута повороту шпинделя з
формули (12.129) в (12.126):
1Ш—СО8(Х| ,
Оз2 + ь з)... 2 —-----+ -^-соза,
сф„ + ЬфПз 2
4соза - іш0з2 + ЬфШз) • ф0(з).
(12.130)
Перетворимо рівняння (12.130) з метою його спрощення:
Міш ^-С08а,52 + (Ьфшіш -у-созоц + ЬГ?І, ^соза^з +
+	— соза,] • рп(з) = (с„ГІ + ЬфПз) • р(з)- -^соза -
- ішзСІ8 + ЬфП) • (сфП + ЬфПз) • ф0(з).
Приведемо рівняння (12.131) до стандартного вигляду,
теорії автоматичного керування [6]. Для цього кожний доданок поділимо на
вираз сфП—созсц . Відповідно одержимо:
(12.131)
прийнятому в
537
Струтинський В. Б.
. ^фП
1 + —— 8
СфП
<1со8а .	_ 2ішЬШф
(ІкСозоц сіксо8а
Ь.
• 1 + -— 8 |- “""“8 + 1
< Сфп
к ^фШ

ДЛ52 + МД^Л,5+1 • Рп(8) =
Сфп^к	СфП
5-ф0(з).
(12.132)
Введемо позначення для постійних часу та коефіцієнтів передачі, які
визначають крутильні коливання шпинделя:
гр2 _ «Нщ^ц . гр ___	^к^фл , -у _ ^фп
1 кі ~ Т~ ’	1 к2 ~	’	1 п -	;
Сфп^к	Сфл	^©п
гр 3	СІ СО8 СС _	.ц.	^Фи^шф
1 І і ’ І^рл 1	’ ^ОП 1
ЬШф	<1ксо8а(	сіксозоц
С урахуванням введених позначень величин, рівняння (12.132) прийме
вигляд:
(Тк2,82 + Тк28 + 1) • р„(8) = Крп(1 + Т„8) • р(8)-Ко„(1 + Т„8)(1 + Т;5)5 • ф0(з). (12.133)
Звідси визначається значення зображення по Лапласу динамічної
складової рп(з) зусилля у приводній передачі:
р„(0 =	‘ ко"	'<Ро^- (12134)
Цкі8 + 1к25’ + Ч	Цкі5 + Хк25 + V
Підставимо в рівняння поперечних коливань шпинделя (12.121) значення
динамічної складової зусилля в приводній передачі рп з формули (12.134):
(т282 + т28 + 1)уш (я) = Є! 8ІП ар(з) +
+ е2 8іп(а, + рк)Крп ----(1+.р2	р(8)_
'1к1Я + £к25 +
, ч (і+т^а+тч)	п
-е28іп(а1 +Рк)К0П—2-2-—---------(12.13о)
(Тк18 + Тк28 + 1)
Із рівняння (12.135) після перетворень знаходимо переміщення шпинделя
разом із заготовкою у зоні різання. Подамо його у вигляді залежності від
динамічної складової р сили різання і від динамічної складової <р0 кута
повороту приводного вала. Одержимо символьну математичну модель
шпиндельної групи токарного верстата у вигляді:
Уш(5)=5^ші-р(з)-^ш2-<Ро(3)>	(12.136)
де А¥ш1 и'ш2 - трансформуючі функції шпинделя відповідно по силі різання і
по куту повороту приводного вала. Вони знаходяться із (12.135):
кш1	Кш2(1 + Тп8)
ШІ ” (т282 + т28 + 1) + (т282 + Т28 + 1)(тку + тк28 + 1) ’	<12-137>
(1 + ТЛ8У1 + Тхк
^ш2 ~ -^шЗ /гр2 2 т'	2 тг	Ті’	(12.138)
(Т, 8 + Т28 + ЦТк182 + Тк28 + 1)
538
Розділ 12. Математичне моделювання динамічних коливальних процесів
В формулах (12.137), (12.138) позначені коефіцієнти передачі:
КШ1 =е18іпа ; Кш2 =е2Крп§іп(а1+рк);
Кш3 = е2Коп 8іп(а, +рк).
Символьна залежність (12.136) із врахуванням (12.137) та (12.138) в
операторному вигляді описує динамічні коливальні процеси, які протікають у
шпиндельній групі верстата при різанні. Відповідно до символьної
математичної моделі побудована структурна математична модель (структурна
схема) динамічної системи шпиндельної групи верстата (рис. 12.17).
а)
б)
Рис. 12.17. Базова структурна схема (а) і блок-схема (б) динамічної
системи шпиндельної групи верстата. На схемі в зображеннях по Лапласу
вказані: р(з) - динамічна складова сили різання; <р^з) — динамічна складова
кута повороту приводного вала; уш(з) - переміщення шпинделя разом із
заготовкою в зоні різання; ^Ш2 ~ трансформуючі функції шпинделя
відповідно по силі різання та куту повороту приводного вала
Окремі блоки математичної моделі відповідають складовим
трансфер муючих функцій (12.137) та (12.138).
Входами структурної математичної моделі шпиндельної групи служать
динамічна складова р(з) сили різання (зображення по Лапласу динамічної
складової сили різання) та динамічна складова <р0(х) кута повороту вала
приводної подачі (зображення по Лапласу динамічної складової кута
повороту вала).
Виходом структурної схеми шпиндельної групи є горизонтальне
переміщення уш(з) шпинделя разом із заготовкою в зоні різання (зображення
по Лапласу переміщення шпинделя разом із заготовкою в зоні різання) [84].
539
Струтинський В. Б.
Математична модель супортної групи верстата розроблена для плоского
руху різця в площині, перпендикулярній осі шпинделя [16, 18, 90, 113].
Супортна група токарного верстата (рис. 12.18) являє собою складну
просторову систему, яка включає десятки деталей, між якими наявні
прецизійні рухомі та нерухомі з’єднання.
Рис. 12.18. Загальний вигляд супортної групи верстата
Деталі супорта мають значні масу та жорсткість. При дії сил різання
пружна система супорта деформується. Деформації в основному виникають в
контактах між деталями і мають суттєво нелінійний характер.
В першому наближенні прийнято, що пружна система супорта є
однорідною та ізотропною і допускає зосередження своїх інерційних,
дисипативних та деформативних параметрів в деякій точці, рух якої
здійснюється в площині, перпендикулярній осі шпинделя [90]. Конструктивна
схема супорта, що відповідає даному припущенню, показана на рис. 12.19.
При обробці заготовки коливання супорта спричиняються зміною сили
різання в часі. Розглянемо зміну положення вершини різця у процесі
коливань супорта. В загальному випадку супорт як плоска динамічна
коливальна система має три ступені вільності [39]. Для математичного опису
переміщень вершини різця будемо розглядати дані переміщення в системі
головних ортогональних координат £-Г] [51]. Це дозволяє значно спростити
систему рівнянь та обмежитись розглядом динамічної системи супорта як
системи з двома ступенями вільності. Осі головних ортогональних координат
співпадають з напрямками головних жорсткостей супорта [55].
У даній системі координат динамічна система супорта інтерпретується у
вигляді двомасової динамічної системи (рис. 12.20), яка здійснює незалежні
540
Розділ 12. Математичне моделювання динамічних коливальних процесів
коливання вздовж осей та т], що співпадають з напрямками головних
жорсткостей С} та пружної системи супорта.
Рис. 12.19. Конструктивна схема супорта токарного верстата:
р - динамічна складова сили різання; су, с2 - еквівалентні жорсткості
пружної системи супорта в напрямку осей координат у і г;
1іу, кг ~ еквівалентні коефіцієнти опору пружної системи супорта
при коливаннях у напрямку осей координат у і г; с^ - еквівалентна
крутильна жорсткість пружної системи супорта; 1і^: - еквівалентний
коефіцієнт опору супорта при поперечно-кутових коливаннях;
у, система головних ортогональних координат, що співпадає
з напрямками головних жорсткостей пружної системи супорта;
а, [і - кутові розміри, що характеризують напрямки головних
жорсткостей та напрямок дії сили різання
В математичній моделі супорта при розгляді його коливань маса супорта
врахована у вигляді двох масових коефіцієнтів (приведених мас) пі) та пі2,
які представляють собою масу супорта, приведену до вершини різця (зони
різання) при коливанні супорта відповідно вздовж осей £ та г]. Приведені
маси ті та пі2 здійснюють незалежно одна від одної коливання вздовж осей £
та ц. При цьому приведені жорсткості відповідають головним жорсткостям С]
та с-2 супорта. Дисипативні властивості механічної системи визначаються
приведеними коефіцієнтами опору супорта Ф та 112-
541
Струтинський В. Б.
Рис. 12.20. Еквівалентна розрахункова схема супорта: р, система
головних ортогональних координат, що співпадає з напрямками головних
осей жорсткості пружної системи супорта; С/, с-, — головні жорсткості
супорта; ти у - масові коефіцієнти (приведені маси), що представляють
собою масу супорта, приведену до вершини різця (зони різання) при
коливаннях супорта відповідно вздовж осей т], ф Іір її? ~ приведені
коефіцієнти опору супорта; р — динамічна складова сили різання;
а, р - кутові розміри, що визначають положення головних осей
та орієнтацію сили різання
Відповідно до розрахункової схеми (рис. 12.20) для двох ступенів
вільності, які відповідають переміщенням у напрямках та г| складені
рівняння динаміки, що описують коливання вершини різця:
т^ + Ь^ + с^ = Р-СО8 0І	(12 139)
т2п,+ Ь2Г| + с2г| = р-зіпр] ’
де ту, пі2 - масові коефіцієнти (приведені маси);
Ьі, 1г_> - приведені коефіцієнти опору супорта;
С(, с-) - головні жорсткості супорта;
Т] - переміщення вершини різця вздовж головних осей жорсткості;
Г], ті - відповідно проекції швидкості та прискорення вершини
різця на осі £ та т];
542
Розділ 12. Математичне моделювання динамічних коливальних процесів
р - динамічна складова сили різання;
а - кут між динамічною складовою сили різання та вертикальною віссю (г);
р - кут між динамічною складовою сили різання та віссю ц.
Перетворимо диференціальні рівняння системи (12.139) по Лапласу при
нульових початкових умовах Результати перетворення, які мають вигляд
алгебраїчних рівнянь запишемо в стандартній формі, прийнятій в теорії
автоматичного керування [6]:
(ТД82 + Тг.,8 +1) •	= р(з) • £21Р
с’
(Тфп + !> + !)	Р(5)-^.
(12 140)
де р(«) -
зображення по Лапласу динамічної складової сили різання;

г](г>) - зображення по Лапласу переміщення вершини різця в
напрямках головних осей ц та р.
Постійні часу, введені в системі рівнянь (12.140), зв’язані з параметрами
динамічної системи супорта наступними співвідношеннями:
Т,,, -= гШ2/с2 ;	Т,|2 = Ь2/с2 .
(12.141)
Із системи рівнянь (12 140) визначимо в зображеннях по Лапласу
переміщення вершини різця в напрямку головних осей жорсткості супорта'
= фУ
7ТТЛ—Л 74 ‘ РЬ);
(	+ Кп8 + 1)
(Т,у + Тп25 +1) ’
(12.141)
(12.142)
Переміщення вершини різця в інших напрямках лінійно залежить від
переміщень в напрямках головних осей.
Вхідним параметром для динамічної системи супорта є зміна сили
різання. Вихідним параметром супорта, який впливає на похибку обробки, є
переміщення вершини різця вздовж нормалі до поверхні різання, яке
відповідає зміщенню вершини різця вздовж осі у.
Із геометричних міркувань визначимо зміщення вершини різця вздовж осі
у в залежності від переміщень вершини різця в напрямках головних осей
жорсткості:
у, = т] • софа + р) - С, • 8іп(а + р).	(12 143)
Після перетворень даної залежності по Лапласу і підстановки переміщень
вздовж головних осей жорсткості, згідно з (12.141) та (12 142), одержимо
переміщення вершини різця в зображення по Лапласу.
543
Струтинський В Б
і \ .чіп В • соз(а + В)	1	/
У1'8)- с2	ГТ2с2а_Т 0.1.11
сс>8 Р • зіп(а + р)
(12.144)
С1
Із цього рівняння визначимо загальну трансформуючу функцію супорта’
у.(я)	К,.<	К,
= ^7Т =	----А ~	—7? '	(12.145)
р(8)	(ТГ),8 +ІП,8 + 1) (І, ,8 +Т(-,8 + 1)
де К^, Кс2 ~ коефіцієнти передачі, які визначені через головні жорсткості
супорта та кутові розміри:
__ 8ІП Р • С08(а + р)	_ СО8 Р • 8Іп(а + р)
К., -	;	-	.
с2	с2
На рис. 12.21, а показана структурна математична модель, яка відповідає
трансформуючій функції \¥с, визначеній з рівняння (12.145).
Рис. 12.21. Структурна схема (а) і блок-схема (б) математичної моделі
супорта. В зображеннях по Лапласу вказані: р(з) - динамічна складова
сили різання; ус(з) — переміщення вершини різця в напрямку осі у;
Ну - трансформуюча функція динамічної системи супорта
Аналіз динаміки процесу різання виконано із врахуванням інерційних і
дисипативних характеристик процесу. Математична модель динаміки процесу
різання складена у прощеному вигляді згідно з методикою [39].
В діапазоні частот до 105 Гц процес різання може бути описаний
диференціальним рівнянням, в якому врахована залежність динамічної
складової сили різання рк від зміни припуску в часі у4:

У і
„ СІу. „2 СІ2\'. !
+ 3 —- + Т —ф- І
07 сії ар сію ;
(12.146)
де рк - динамічна складова сили різання, обумовлена зміною корпусу,
Уі - зміна припуску в залежності від часу;
Тр - постійна часу процесу різання (згідно з [39], порядок значення
постійної складає близько Тр = 5-Ю"4 с);
Тар, Тау - постійні коефіцієнти, які враховують особливості геометрії,
544
Розділ 12. Математичне моделювання динамічних коливальних процесів
кінематики та динаміки процесу різання;
Кр - коефіцієнт передачі процесу різання.
Перетворимо рівняння (12.146) по Лапласу при нульових початкових
умовах і одержимо алгебраїчне співвідношення:
(Тр8 + !)-р4(8)= Кр(Т2рз2 +Таї8 + 1)-у1(8).	(12.147)
Звідси знайдемо трансформуючу функцію процесу різання:
_уДз) Кр(Тй2р82+Тку8 + 1)
”	Р((5)	Тр8 + 1
(12.148)
Структурна схема процесу різання, яка відповідає математичній моделі
(12.148), зображенії на рис. 12.22, а.
а)
б)
Рис. 12.22. Структурна схема математичної моделі динаміки процесу
різання (а), блок-схема моделі процесу (б) та схема суматора,
що враховує випадкові флуктуації сили різання (в), які мають місце в
процесі обробки реальної деталі В зображеннях по Лапласу позначені:
у/з) - зміна припуску; рфз) - динамічна складова сили різання,
обумовлена зміною припуску; ра(з) — незалежна випадкова складова,
(флуктуація) сили різання.; р(з) - результуюча динамічних складових
сили різання; V/? - трансформуюча функція процесу різання
При обробці заготовки сила різання змінюється під дією різноманітних
факторів Зокрема, має місце температурна флуктуація сили різання, зміна
сили різання з причини неоднорідності структури заготовки та інше. Зміна
сили різання носить, як правило, випадковий характер і не залежить від
зміни припуску. Тому можна вважати, що сила різання є сумою динамічної
складової сили різання рДз), що визначається зміною припуску, та
незалежної випадкової динамічної складової сили різання р„(з). Отже
р(з) = рй(з) + Рі(з).
545
Струтинський В. Б,
Це рівняння інтерпретоване на структурній схемі (рис. 12.22, в) у вигляді
суматора, що дозволяє в математичній моделі врахувати наявність випадкових
флуктуацій сили різання.
Загальна математична модель динамічної системи шпиндель-супортної
групи верстата одержана об’єднанням моделей окремих підсистем, а саме:
моделі шпиндельної групи, супортної групи і процесу різання.
Зміна припуску у* залежить від форми заготовки, деформації шпинделя
разом із заготовкою та переміщення супорта.
Пружна система верстата має високу жорсткість. Але під дією сил різання
виникають невеликі деформації елементів динамічної системи. Вони особливо
проявляються при обробці протяжних маложорстких деталей.
На рис. 12.23 показано процес обробки деталі на токарному верстаті.
Рис. 12.23. Схема динамічних переміщень шпинделя та супорта в процесі
обробки деталі на токарному верстаті. Стрілкою А показане пружне
горизонтальне переміщення деталі, стрілкою Б - переміщення різця,
які виникають внаслідок дії сичи різання
Під дією сил різання мають місце складні просторові переміщення деталі
та різця На точність обробки впливають в основному горизонтальні проекції
переміщень (показані стрілками А і Б на рис. 12 23).
Розглянемо закономірності зміни взаємного положення різця і
оброблюваної заготовки, що мають місце при коливальних процесах в
динамічній системі верстата при різанні.
546
Розділ 12. Математичне моделювання динамічних коливальних процесів
Із геометричних міркувань (рис. 12.24) випливає, що зміна припуску в часі:
У і ~ а “Ус “Уш-
де а - відхилення форми заготовки від номінального значення;
ус - динамічна деформація (переміщення) вершини різця внаслідок
коливальних процесів у супортній групі верстата;
уш - переміщення шпинделя разом із заготовкою в зоні різання.
Рис. 12.24. Схема зміни взаємного положення різця та заготовки
при коливаннях елементів пружної системи верстата: уш - переміщення
шпинделя разом із заготовкою; ус — переміщення вершини різця внаслідок
деформативності супорта; А — загальна динамічна похибка обробки;
ао — номінальний діаметр заготовки; а - відхилення форми заготовки
відносно номінального значення; у і - зміна припуску в часі
В процесі обробки заготовки відбуваються складні переміщення елементів
динамічної системи верстата. Під дією сил різання змінюється взаємне
положення супорта та шпинделя. Разом з цим відбуваються додаткові зміни
взаємного положення шпинделя і супорта з причини, наприклад,
температурних деформацій різця тощо. Ці зміни не залежать від коливань
елементів пружної системи верстата. Тому фактична зміна припуску
визначиться із врахуванням незалежної складової зміни взаємного положення
різця та заготовки:
Ус =а-Ус “Уш “УР>	(12.149)
де а - відхилення припуску від номінального значення;
ус - переміщення вершини різця внаслідок деформацій супорта;
уш - переміщення шпинделя разом із заготовкою в зоні різання;
ур - незалежна складова зміни взаємного положення різця та заготовки,
яку можна зміною розмірів різця.
547
Струтинський В.Б.__________________________
Переходячи від залежності (12.149) до зображення її по Лапласу,
отримаємо:
У і (§) = а(з) - ус(з) - уш(§) - Ур(з) •	(12.150)
Визначимо похибку обробки А, що виникає за рахунок динамічних
деформацій супорта і шпинделя, з врахуванням додаткової зміни розмірів. У
зображеннях по Лапласу одержимо динамічну похибку обробки:
д(в) = У с (8) + У ш (8) + У Р (з)-	(12.151)
Об’єднуючи рівності (12 150) та (12.151), одержимо:
уДз) = а(з)-Д(8).	(12.152)
Залежності (12.151) та (12.152) зображені у вигляді суматорів
(рис. 12.25). Знак “-".біля ус(з) враховує, що переміщення вершини різця є
протилежним додатному напрямку, прийнятому на рис. 12.20 та у формулі
(12.144).
Рис. 12.25. Графічне зображення суми деформацій супорта і шпинделя (а)
і схема формування фактичної зміни припуску (б). У зображеннях по
Лапласу вказані: ушС^) — переміщення шпинделя разом із заготовкою;
ус(з) - переміщення вершини різця; ур(з) - додаткова незалежна зміна
взаємного положення різця та заготовки; ДСГ) - динамічна похибка
обробки; у;($) ~ зміна припуску; а(з) - зміна в часі форми заготовки
Для визначення загальної структурної математичної моделі динамічної
системи шпиндельно-супортної групи верстата розглянемо в комплексі всі
блок-схеми математичних моделей окремих підсистем верстата (рис. 12.26).
З’єднуючи відповідні входи і виходи окремих блок-схем математичних
моделей динамічних підсистем, отримаємо загальну структурну блок-схему
математичної моделі динамічної системи верстата (рис. 12.27).
Виконаємо деталізацію структурної схеми математичної моделі динамічної
системи верстата. Замість трансформуючих функцій блоків \Ур, \УС, XV,,,
підставимо їх структурні схеми і одержимо загальну структурну схему
математичної моделі динамічної системи токарного верстата (рис. 12.28).
548
Розділ 12. Математичне моделювання динамічних коливальних процесів
а)
д)
Рис. 12.26. Блок-схеми математичних моделей окремих динамічних
підсистем верстата: а - суматор, що визначає фактичну зміну припуску;
б - блок-схема математичної моделі процесу різання; в - суматор, що
враховує випадкові флуктуації сили різання; г - блок-схема математичної
моделі динамічної системи суппорта; д - суматори, що визначають
залежність динамічної похибки обробки від переміщень шпинделя та
супорта; е - блок-схема математичної моделі шпиндельної групи верстата
Рис. 12.27. Загальна структурна схема математичної моделі динамічної
системи шпиндельно-супортної групи токарного верстата, одержана
об’єднанням блок-схем окремих динамічних підсистем. У зображеннях
по Лапласу вказані: а(з) - зміна форми заготовки; уфз) - зміна припуску;
рфс) - динамічна складова сили різання, обумовлена зміною форми
заготовки; ра(з) - незалежна складова (флуктуація) сили різання;
ус(з) — переміщення вершини різця; ут(з) - переміщення шпинделя разом
із заготовкою; Ур($) - незалежна зміна взаємного положення різця
та. заготовки; 3(з) — похибка обробки; (р0 - динамічна складового кута
повороту приводного вала; р(з) - результуюча сили різання
549
Струтинський В. Б.
Рис. 12.28. Структурна математична модель, шр включає підсистеми
шпиндельної ( ХУШ) та супортної (XVс) груп і процесу різання ( \Х'р)
Структурна математична модель відповідає динамічній системі верстата, що
об’єднує всі основні її елементи: супорт, шпиндель, процес різання. Основним
входом моделі є зміна форми заготовки (а). Додатковими входами є випадкова
складова сили різання (ра) та зміна розмірів різця (ур). Виходом структурної
математичної моделі є динамічна складова похибки обробки деталі (А).
Структурна математична модель може бути зображена у вигляді блок-
схеми (рис. 12.29).
Рис. 12.29. Блок-схема математичної моделі динамічної системи
шпиндельно-супортної групи верстата
Структурна математична модель має додатковий вхід фо у вигляді
динамічної складової кута повороту вала приводної передачі шпинделя.
Цей вхід служить для зв’язку структурної математичної моделі із моделлю
привода головного руху. Формування моделі привода головного руху та
загальної математичної моделі здійснене у розділі 12.4.
Структурна математична модель динамічної системи шпиндельно-
супортної групи верстата є основою для розробки візуальної математичної
моделі в системі 8ІМІЛЛМК пакету МАТЬАВ.
550
Розділ 12. Математичне моделювання динамічних коливальних процесів
12.4. Аналіз стохастичних процесів в динамічній системі верстата
з використанням структурної математичної моделі
Розроблена структурна (візуальна) математична модель верстата дозволяє
визначити основні характеристики коливальних процесів. Модель була
застосована для аналізу стохастичних процесів в динамічній системі токарно-
гвинторізного верстата мод. КА280. Вона враховує особливості коливальних
процесів у шпиндельній та супортній групах, в приводі головного руху при
наявності стохастичних входів та імітаційного стохастичного навантаження
силами різання.
Розроблена стохастична математична модель динамічної системи верстата
враховує основні інерційні, дисипативні та деформативні властивості
елементів і вузлів верстата при різанні. Модель включає як свої складові
розглянуті раніше (див. розділ 12.2, 12.3) моделі окремих підсистем верстата.
При розробці моделі всі переміщення в динамічній системі верстата
приведені до зони різання. З метою спрощення моделі розглянуто
переміщення лише в площині оуг, які є суттєвими з точки зору визначення
динамічної точності обробки (рис. 12.30).
Рис. 12.30. Суттєві напрямки динамічних переміщень при обробці деталі,
які впливають на точність обробки
551
Струтинський В. Б.
Для розглянутої площини переміщень використана спрощена
розрахункова схема динамічної системи верстата (рис. 12.31).
Динамічна система верстата розділена на чотири підсистеми: підсистема
привода головного руху; підсистема шпиндельної групи; процес різання;
динамічна підсистема супорта. Математична модель шпиндельно-супортної
групи та процесу різання одержана в розділі 12.3 у вигляді блокової
структурної моделі (див. рис. 12.29).
Рис. 12.31. Принципова схема динамічної системи токарного верстата
Виходом даної математичної моделі є динамічна похибка обробки А, яка
визначена у вигляді функціональної залежності від часу А(0 та відповідного
зображення по Лапласу А(з). Модель має два входи: а(0 відповідає імітаційному
навантаженню у вигляді випадкової зміни контуру заготовки; представляє
собою динамічну складову кута повороту приводного вала шпинделя. Для цих
входів також визначені зображення по Лапласу а(з) і д>о(з).
Останній вхід <ро(к) є виходом математичної моделі динамічної підсистеми
привода головного руху.
В процесі виконання досліджень розроблена математична модель привода
головного руху. З метою спрощення моделі привод головного руху розглянуто
у вигляді лінійної ланцюгової крутильної системи (див. рис. 12.31). Система
включає всі обертові маси, починаючи з ротора електродвигуна і закінчуючи
приводним валом шпинделя. Нелінійні властивості системи враховані як
стохастичні збурення (крутні моменти М;), що діють на кожний інерційний
552
Розділ 12. Математичне моделювання динамічних коливальних процесів
елемент крутильної системи. Стохастичні збурення та їх спектральні
характеристики визначені раніше у розділі 12.2.
Розглянемо окремо кожний інерційний елемент крутильної системи
привода головного руху верстата (рис. 12.32).
Рис. 12.32. Принципова схема лінійної ланцюгової крутильної
динамічної системи привода головного руху верстата
з виділеним інерційним елементом.
Рівняння динаміки, що відповідає виділеному і-му інерційному елементу,
має вигляд:
+(фм "ФіКі + (Фм -ФЛ ~(Фі -ФілКі "(Фі -Фі+і)Ьі+і
аг
(12.153)
де Фі(О, Фі-і(О, Фі+і(О ~ динамічні складові кутів повороту послідовно
з’єднаних і-го, (і-І)-го та (і+1)-го інерційних елементів в функції часу (0;
З,	- приведений момент інерції і-го інерційного елемента;
сі-1> сі+1 _ коефіцієнти жорсткості пружних зв’язків і-го інерційного елемента
із сусідніми елементами ланцюгової системи;
Ь-і-і, ф+і ~ коефіцієнти дисипативних зв’язків і-го інерційного елемента із
сусідніми елементами ланцюгової системи;
Ь;- коефіцієнт опору підшипників і-го елемента (при їх наявності);
М, - збурюючий момент (в загальному випадку - стохастична функція часу),
іцо діє на і-й інерційний елемент.
Після перетворення диференціального рівняння (12.153) по Лапласу за
нульових початкових умов одержимо алгебраїчне співвідношення між
зображеннями по Лапласу кутів повороту трьох інерційних елементів:
[ 3;82 + (Ьм + Ь.. + Ьі+1)з + (сі_1 + С| + сі+1)] • Фі(з) =
- М( + (Ьмз + см)’ф|_|(з) + (йі+15 + сі+1)*фі+і(з),	(12.154)
де фі(з), Фі./в), Фі+іЬ) ~ зображення по Лапласу кутів повороту і-го, (і-І)-го
та (і+1 )-го інерційних елементів;
8 - оператор Лапласа.
Із алгебраїчного рівняння (12.154) знаходиться взаємозв’язок зображення
по Лапласу кута повороту і-го інерційного елемента та зображень по Лапласу
кутів повороту сусідніх елементів:
553
Струтинський В. Б.
«І;8 4"	4- 11  + Ь.^^8 4- Сі_і 4~ С| + СІ4^
; _і 8 4” С, «	/\
+ 7~ї-  а -—г~Чг“Ґ'^------------------Фі-іООч-
1,8 4- (Пі-і + Пі 4- Пі + . )8 4- СЬ] 4- С: 4- Сі + 1
,	Ь, н 18 4- С.+1	✓ \
т <12-155)
Графоаналітичне зображення даної залежності (рис. 12.33) дає окремий
блок математичної моделі ланцюгової крутильної системи привода головного
руху, що відповідає і-му інерційному елементу.
Рис. 12.33. Структурна схема математичної моделі, що описує коливання
одного інерційного елемента ланцюгової крутильної системи
Окремі блоки математичної моделі, що описують коливання кожного
елемента ланцюгової системи привода, з’єднуються послідовно. Зв’язки між
блоками, включаючи зворотні зв’язки, об’єднуються відповідно утворюючи
послідовну ланцюгову структуру (рис. 12.34).
Рис. 12.34. Об’єднання блоків математичної моделі ланцюгової крутильної
системи привода головного руху
Виходом даної математичної моделі є динамічна складова кута повороту
вала приводної передачі шпинделя еро, а входами - динамічна складова кута
повороту шпинделя <р (зворотний зв’язок) та динамічна складова кута
повороту вала електродвигуна <ре.
554
Розділ 12. Математичне моделювання динамічних коливальних процесів
На кожну масу системи діють випадкові збурення у вигляді крутних
моментів
Мь .... Ми, Мі, Мж, Мп.
Ці випадкові збурення при математичному моделюванні задаються
стохастичними процесами, спектральні характеристики яких відповідають
“білому шуму”, інтенсивність якого визначена в розділі 12.2, де показано, що
для високочастотної області спектра спектральна густина флуктуацій кутового
прискорення інерційного елемента, приведеного до шпинделя верстата, може
вважатись постійною із значенням:
2 і2п 7
Зш» = І^-(чЬЦ) = соп51,	(12.156)
де іц, 2^ - число обертів за хвилину і число зубців зубчастої передачі, в якій
відбуваються імпульсні навантаження;
<Р - математичне сподівання інтенсивності імпульсів;
ЇХ - дисперсія інтенсивності імпульсів;
Т? - постійна часу, що визначається з приведеного до зубчастої передачі, в
якій відбуваються імпульсні навантаження моменту інерції та податливості;
і - передавальне число від поточної зубчастої передачі до шпинделя верстата.
Відповідно сума відносно рідких в часі імпульсних стохастичних
навантажень в кожній зубчастій передачі може бути описана випадковим
моментом із постійним спектром, інтенсивність якого визначено виходячи із
інерційного навантаження, яке відповідає випадковому процесу зміни
кутового прискорення шпинделя.
Розроблені структурні математичні моделі підсистем привода головного
руху та шпиндельно-супортної групи в своїй сукупності утворюють загальну
модель. Відповідно створена структура (візуальна) математична модель
динамічної системи верстата. При розробці використані засоби системи
візуального математичного моделювання 8ІМІЛПМК пакету МАТЬАВ.
Загальний вигляд розробленої 8-моделі верстата наведено на рис. 12.35.
Модель призначена для розрахунку стохастичних коливальних процесів
що виникають при спеціальних імітаційних навантаженнях верстата силами
різання та здійснення кореляційного і спектрального аналізу системи
випадкових коливальних процесів. Вона включає ряд блоків. Зокрема:
ІТПіШІОП
ехр'иаїаіюп1 ~~
Іоадіп^я
блок-модель імітаційного навантаження силою різання, що формується у
вигляді випадкового процесу, який відповідає профілю поверхні спеціальної
заготовки, що обробляється;
555
Струтинський В.Б.
Бузіет _
таіп ро\\ег
тогіоп
модель багатомасової ланцюгової крутильної системи приводу головного руху;
а* р
Вупатіс ~
ргос гех
стохастичну модель процесу різання;

Зукіет “
яіррогі
модель супорта як динамічної системи з двома ступенями вільності;
’р
»Е **
8уйет —
зріїїдеї
математичну модель шпиндельної групи, що враховує поперечні та крутильні
коливання шпинделя.
Рис. 12.35. Блок схема візуальної математичної моделі (5-моделі) динамічної
системи токарно-гвинторізного верстата КА280
Імітаційне навантаження верстата здійснено силами різання, що
виникають при обробці заготовки спеціального профілю [92, 106]. Спеціальне
імітаційне навантаження дозволяє задати випадковий вхід на динамічну
систему верстата, який суттєво впливає на процеси в динамічній системі
верстата. Випадковий вхід формується при обробці заготовки із спеціально
556
Розділ 12. Математичне моделювання динамічних коливальних процесів
розрахованим профілем поверхні, яка забезпечує випадкове імітаційне
навантаження. Використано випадковий вхід у вигляді кусково-постійного
випадкового процесу Пуассона. Синтез випадкового процесу Пуассона
здійснено за спеціальною програмою (рис. 12.36).
ОКЮШ:=1 і'=1..1Чтах х := гроІ5( N т ах, х$) у := гпогіЦМтах,2 с=у Ьітах=50
-і	.	хз-180
—-—	Мтах	і
800 \ ~V і	\ і	І	,  •
Ц := і£ х^хз,0 0000001,-е 1~ р Ц еіу'=	г :=-- _е 7 180
**	і = 1	к = 1	1 г 7Г
у Гі ;= аи§теп(іу,х|/) уйі:= аизтепіїуЦІі)
ХУКІТЕРКІЧ'ТГІу ргп)':= уїїі
Рис. 12.36. Програма розрахунку параметрів спеціального профілю заготовки,
що відповідає випадковому процесу Пуассона, та реалізація випадкового процесу
у вигляді кусково-постійної форми контуру заготовки
Розроблена і виготовлена заготовка зі складним ступінчастим профілем,
що має змінний крок. Відстань між виступами та впадинами ступенів
розподілена за законом Пуассона (закон рідких випадків), а висота ступенів
та глибина западин - за нормальним законом. Параметри розподілу Пуассона
та нормального розподілу визначені розрахунком на ЕОМ в програмному
середовищі МаЙіСАВ (див. рис. 12.36).
За результатами розрахунків контуру розроблені креслення заготовки із
профілем, що відповідає випадковому процесу Пуассона (рис. 12.37).
За розробленими кресленнями виготовлена заготовка із профілем, що
відповідає випадковому процесу Пуассона (рис. 12.38).
При обробці цієї заготовки виникає складова сили різання, що здійснює
імітаційне стохастичне навантаження на динамічну систему верстата.
Інтенсивність прийнятого стохастичного навантаження набагато перевищує
власну стохастичну складову (збурення) сили різання, що виникає за рахунок
технологічних факторів.
557
Струтинський В. Б.
Рис. 12.37. Креслення заготовки для імітації стохастичного навантаження
на динамічну систему верстата у вигляді процесу Пуассона
Моделювання стохастичної складової процесу різання, що має місце при
генерації випадкового імітаційного навантаження, яке відповідає процесу
Пуассона, здійснюється за допомогою блока 8-моделі системи 8ІМІЛПМК,
зображеного на рис. 12.39.
Блок-модель включає три структурні підблоки:
БідгіаІ
Оепегаіог
РРРР
оо — ~
блок формування базових прямокутних імпульсів;
558
Розділ 12. Математичне моделювання динамічних коливальних процесів
ітііраштаї -
Егот Еііе
блок введення значень імітаційного навантаження із файлу, сформованого за
координатами реального контуру заготовки;
ВапФитііе<і _
ШКІіе М0І5ЄІ
блок формування випадкового збурення, що відповідає мікрогеометрії
контуру заготовки, математична модель якого прийнята у вигляді «білого
шуму».
Рис. 12.38. Спеціальна заготовка із профілем, що відповідає випадковому
процесу Пуассона, використана для генерації стохастичного імітаційного
навантаження на динамічну систему верстата
Для задання фактичного контуру заготовки виконано натурні вимірювання
контуру перерізу виготовленої заготовки. Висота ступенів та їх крок занесені в
файл ігпііраа'.таї, і в подальшому вони слугують вхідними параметрами в блоці
Ггот Рііе 8-моделі імітаційного навантаження (рис. 12.39).
Модель процесу різання (рис. 12.40) від входу
у вигляді зміни припуску до виходу ’
(ІЗ	Р
у вигляді динамічної складової сили різання включає два основні блоки:
-10^5з+1
2’10'^45+1	-
Ггапгїег Геп ргос геї
559
Струтинський В. Б.
блок, який визначає трансформуючу функцію процесу різання;
ІІпИогт йагчіопі ~
ИитЬег
блок, який формує адитивну випадкову складову сили різання.
Рис. 12.39. Структура 8-моделі для математичного моделювання
імітаційного навантаження на динамічну систему верстата
Рис. 12.40. Візуальна стохастична математична модель процесу різання,
сформована у вигляді 8-моделі
Випадкова складова процесу різання задана у вигляді кусково-постійного
випадкового процесу із рівномірним законом розподілу амплітуди.
Блок-схема математичної моделі супорта відповідає поступальній
динамічній системі з двома степенями вільності від входу
С2_)" у вигляді сили різання до виходу 1 )
Р	ус
у вигляді зміщення вершини різця в напрямку поперечної подачі (рис. 12.41).
Модель включає два динамічних блоки, які визначають коливання
вершини різця в напрямках головних осей жорсткості. Кожен блок відповідає
динамічній підсистемі з відповідною трансформуючою функцією.
560
Розділ 12. Математичне моделювання динамічних коливальних процесів
Тгзп^ег Рсп (мс2
Рис. 12.41. Візуальна математична модель супорта верстата,
сформована у вигляді 8-моделі
Коефіцієнти трансформуючих функцій визначено через еквівалентні маси
та головні жорсткості супортної групи, як це вказано в розділі 12.3.
Блок - модель шпиндельної групи верстата, визначена для динамічної
системи з двома степенями вільності від двох входів
СЇЗ" у вигляді сили різання та СЮ
р	ю
динамічної складової кута повороту приводного вала до виходу
ї
уе
у вигляді радіального переміщення заготовки в напрямку поперечної подачі.
Структурна модель наведена на рис. 12.42.
Рис. 12.42. Візуальна математична модель шпиндельної групи верстата,
сформована у вигляді 8-моделі
Модель шпиндельної групи включає п’ять динамічних блоків - трьох
з’єднаних в ланцюг від входу у вигляді сили різання та двох послідовно
з’єднаних блоків від входу у вигляді динамічної складової кута повороту
561
Струтинський В. Б.
приводного вала.
Всі динамічні блоки мають складові у вигляді коливальних та
пропорційних або форсуючих ланок. Постійні часу та коефіцієнти
демпфування у трансформуючих функціях визначені через еквіваленті маси
та жорсткості так, як це зроблено у розділі 12.3.
Візуальна математична модель, яка відповідає приводу головного руху,
показана на рис. 12.43.
Рис. 12.43. Візуальна математична модель привода головного руху
верстата, що відповідає ланцюговій крутильній багатомасовгй системі,
сформована у вигляді 8-моделі
Входом моделі є блок
ЇОгее
8иЬ§у5Іеггі
який моделює навантаження в електромеханічній системі електродвигуна
приводу. Виходом моделі є блок
562
Розділ 12. Математичне моделювання динамічних коливальних процесів

у вигляді динамічної складової кута повороту шестерні приводної передачі.
Модель включає чотири динамічні підсистеми, які відповідають групам
рухомих деталей (шестерень, напівмуфт, ділянок валів, шківів) на кожному з
валів коробки швидкостей верстата. Ці підсистеми сформовані у вигляді блоків:
зузіет екК-гет, тоск-1 зуЦет уа!2, тосіеі зузіет уаІЗ, тосіеі кузіет уа!4.
Кожна з чотирьох динамічних підсистем привода головного руху має по
два додаткові входи:
Вап(і-кітйе4
ШЬііе Моізеб
ЦпИопп Напдот
КитЬеН
що відповідають збуренням у зубчастих передачах привода головного руху.
Ці входи моделюють високочастотні та низькочастотні збурення у кожній
зубчастій передачі.
Розглянемо окремо кожен блок математичної моделі. Блок
ЇОГ5Є -
моделює навантаження на привод з боку системи електродвигуна приводу
головного руху. Даний блок (їог.че) сформовано у вигляді підсистеми,
зображеної на рис. 12.44.
ЗідпаІ
Оепегаіог
Рис. 12.44. Візуальна математична модель для реалізації
навантажень системи електродвигуна приводу головного руху верстата,
сформована у вигляді 5-моделі
Ця структурна модель включає блок
563
Струтинський В.Б.
&
Зілє 'іЛ’-зке
формування матриці коефіцієнтів (амплітуд, частот, та початкових фаз)
розкладу в ряд Фур’є неперервного детермінованого навантаження на привод
з боку електродвигуна [66].
При моделюванні процесів в електродвигуні використовується 14 гармонік
розкладу. Вони враховують зусилля, що виникають за рахунок відцентрових сил
при обертанні ротора та інших рухомих деталей (зокрема, тіл кочення підшип-
ників), перемагнічування активного заліза обмоток, пульсації магнітного потоку у
повітряних зазорах, похибок форми підшипників кочення двигуна: радіальні
зазори в підшипниках; хвилястість доріжок підшипників; похибки форми тіл
кочення (розмірності, гранності), а також похибки монтажу підшипників.
Зазначені 14 гармонік формуються як один детермінований векторний
вхід (див. рис. 12.44), який в подальшому об’єднується суматором. До цього
об’єднаного векторного входу додаються випадкові входи
Впітогт Капсіот
НитЬеґІ
Вап<3-Ьітііа<і уа
«ЛіНе Ноігеб
які моделюють випадкові збурення в електромережі та в підшипниках
електродвигуна. Також додаються
трикутні
Нерезііпд
Зедиепсе
та прямокутні
0000
оо
ЗідпаІ
Оепегаіог
імпульсні навантаження, що виникають в електродвигуні.
Математична модель електродвигуна є одним із блоків математичної моделі
привода головного руху. Загалом модель привода головного руху включає чотири
блоки, які відповідають чотирьом динамічним підсистемам привода.
Структурні математичні моделі вказаних чотирьох динамічних підсистем
включають однотипні модулі, зображені на рис. 12.45 прямокутниками.
Динамічні підсистеми включають вхідні блоки
Вап<М_ітйес1
‘йУЬііе Ноігеб
ЦпИогт Вапйот
НитЬеИ
які служать для формування випадкових збурень в з’єднаннях вал-втулка.
Муфти та механізми перебору відповідають ручним перемикачам
Кожний однотипний блок динамічних підсистем відповідає одній масі, яка
здійснює крутильні коливання. Візуальні математичні моделі всіх блоків
однотипні і розрізняються лише значеннями коефіцієнтів (рис. 12.46).
564
Розділ 12. Математичне моделювання динамічних коливальних процесів
а)
Рис. 12.45. Структурні математичні моделі чотирьох динамічних
підсистем привода головного руху: а - підсистема “вал електродвигуна —
пасова передача”; б - підсистема “вал її з механізмом реверсу”;
в, г — підсистеми валів III і IV
565
Струтинський В. Б.
Рис. 12.46. Візуальна математична модель динамічної крутильної коливальної
системи шківа як приклад типової математичної моделі елемента крутильної
динамічної підсистеми привода головного руху
Математична модель динамічної крутильної коливальної системи шківа
включає три незалежні входи та один вихід, зокрема визначає:
М1
вхід, що відповідає випадковому збуренню від коливань пасів пасової
передачі;
СїЗ" -
«з
вхід у вигляді кута повороту вала електродвигуна;
(~3~> _
12
вхід, що відповідає зворотному зв’язку у вигляді кута повороту шківа на валу
коробки швидкостей. Вихід моделі
її
визначає кут повороту шківа.
Математичної модель динамічної крутильної коливальної системи шківа
має три паралельні ланцюги, в яких знаходяться трансформуючі функції.
Перший ланцюг (від входу у вигляді збурення) має трансформуючу функцію,
що відповідає коливальній ланці з власного частотою, рівною парціальній
частоті коливання шківа. Другий і третій ланцюги включають таку ж
коливальну ланку, послідовно з’єднану з пропорційною та форсуючою
ланками. Вони відповідають впливу сусідніх коливальних систем
(електродвигуна та шківа на валу коробки швидкостей).
566
Розділ 12. Математичне моделювання динамічних коливальних процесів
Параметри останніх динамічних ланок, які утворюють динамічну систему
привода головного руху, визначені шляхом розрахунку і задані в
математичній моделі конкретно для кожного однотипного блоку динамічної
підсистеми, яка відповідає одній масі, що здійснює крутильні коливання.
За результатами математичного моделювання верстата з імітаційним
навантаженням здійснено кореляційний та спектральний аналіз [47] динамічної
похибки обробки деталі. Для реалізації вказаного аналізу до математичної
моделі включено систему блоків, що реалізують стандартні процедури аналізу
пакету ЗІМИЬШК (рис. 12.47).
Рис. 12.47. Графічний, супровід розрахунків: кореляційний та. спектральний
аналізи результатів математичного моделювання верстата
Блок побудови графіків (Зсоре) здійснює виведення у графічному вигляді
(рис. 12.48) динамічної похибки обробки деталі (верхній графік) та імітаційного
навантаження у вигляді фрагмента заготовки (нижній графік).
Зсореї
Рис. 12.48. Графічний супровід процесу моделювання шляхом виведення
графіків динамічної похибки обробки та імітаційного навантаження
у вигляді функції часу
Блоки знаходження спектральної густини потужності (рис. 12.49, а) та усе-
редненої по ансамблю реалізацій спектральної пютини потужності (рис. 12.49, б)
визначають спектральні характеристики динамічної похибки обробки.
567
Струтинський В. Б.
б)
Рис. 12.49. Результати розрахунків спектральної густини потужності (а)
та усередненої по ансамблю реалізацій спектральної густини потужності (б)
динамічної похибки обробки
Блок знаходження усередненої спектральної густини потужності призначено
для виведення на екран та аналізу стохастичного імітаційного навантаження.
Блок-аналізатор спектра (рис. 12.50) з усередненням по множині
реалізації (Ауегафпд Зресігит Апаїугег) здійснює спектральний аналіз двох
випадкових процесів. Для динамічної похибки обробки та імітаційного
навантаження будується амплітудно-частотна (середній графік) та
фазочастотна характеристика (нижній графік).
Блок знаходження взаємної кореляційної функції входу та виходу
зображений на рис. 12.51. Він встановлює кореляційний зв’язок між
випадковими процесами імітаційного навантаження та динамічної похибки
обробки деталі.
Блок спектрального аналізу (рис. 12.52) окремої реалізації (Зресігит
Апаїугег) здійснює спектральний аналіз двох випадкових процесів без
усереднення по ансамблю реалізацій. Для динамічної похибки обробки та
568
Розділ 12. Математичне моделювання динамічних коливальних процесів
імітаційного навантаження будується амплітудно-частотна (середній графік)
та фазочастотна характеристика (нижній графік).
А/егзбіпд
ЗресЯгат
Аіаіугег
Рис. 12.50. Результати роботи блока-аналізатора спектра
з усередненням по множині реалізації
Рис. 12.51. Знаходження взаємної кореляційної функції
стохастичного входу і виходу математичної моделі
Зресіпт
Аізіугег
Рис. 12.52. Блок спектрального аналізу окремої реалізації двох випадкових
процесів: імітаційного входу та динамічної похибки обробки
569
Струтинський В.Б.
Блок знаходження автокореляційної функції (Аиіо Соггеїаіог) похибки
обробки деталі здійснює розрахунок і виведення у графічному вигляді
фрагменту реалізації випадкового процесу (рис. 12.53, верхній графік) та
відповідної йому автокореляційної функції (нижній графік).
Рис. 12.53. Результати математичного моделювання автокореляційної функції
динамічної похибки обробки
Результати математичного моделювання порівнювались із
експериментальними даними, одержаними безпосередньо вимірюваннями
вібраційних параметрів токарно-гвинторізного верстата КА280 при його
імітаційному стохастичному навантаженні [92, 104, 105, 107].
Методика експериментальних досліджень включала ряд вимірювань
вібраційних параметрів верстата. Зроблені вимірювання параметрів вібрацій
шпиндельної групи, супорта та різця. Вимірювання зроблені комплектом
апаратури, що дозволяє виконати комплексний аналіз стохастичних
вібраційних параметрів верстата.
Схема розміщення датчиків при визначенні вібраційних характеристик
верстата наведена на рис. 12.54.
Для вимірювань параметрів вібрацій використано комплект апаратури, що
включає: датчики віброприскорень типу КО45; підсилювач-вимірювач
вібрацій КоЬоігоп з каскадом подвійного інтегрування вхідного сигналу;
16-канальний магнітограф; аналізатор параметрів вібрацій.
Загальний вигляд використаної апаратури показаний на рис. 12.55.
Апаратура дозволяє здійснити вимірювання вібраційних параметрів
верстата в діапазоні від 0 до 50 кГц. Визначено реалізації випадкових
процесів, що відповідають віброприскоренням деталей верстата. Шляхом
інтегрування одержано записи віброшвидкостей, а шляхом подвійного
інтегрування - вібропереміщення.
Одержані реалізації вимірювань вібрацій оброблені за допомогою
аналізатора параметрів вібрацій. Визначено спектри віброприскорень,
віброшвидкостей та вібропереміщень.
570
Розділ- 12. Математичне моделювання динамічних коливальних процесів
Рис. 12.54. Схема визначення вібраційних параметрів верстата та розміщення
датчиків на верстаті: 1 - блок датчиків для вимірювання трьох компонент
віброприскорень різня; 2 - датчики для вимірювань вібрацій супорта;
З, 4 - датчики для вимірювань вертикальної та горизонтальної складових
віброприскорень передньої опори шпинделя
Рис. 12.55- Загальний вигляд апаратури
для визначення вібраційних параметрів верстата
571
Струтинський В.Б.
Вібраційні параметри різця визначались різними методами.
Віброприскорення вимірювались датчиками, встановленими безпосередньо на
бокових поверхнях різця (див. рис. 12.23). Проекції сил різання
вимірювались трикомпонентним динамометром (рис. 12.56).
Рис. 12.56. Трикомпонентний динамометр
для визначення складових сили різання
Для контролю за роботою апаратури безпосередньо перед проведенням
експериментальних досліджень виконувались контрольні вимірювання параметрів
вібрацій із графічною індикацією результатів вимірювань (рис. 12.57).
Рис. 12.57. Контрольні вимірювання параметрів вібрацій
з поточною графічною індикацією результатів вимірювань
572
Розділ 12. Математичне моделювання динамічних коливальних процесів
Для порівняння результатів математичного моделювання з
експериментальними даними виконувались паралельні вимірювання
параметрів віброакустичного сигналу і математичного моделювання
динамічних процесів верстата 3 метою підвищення надійності результатів
порівняльного аналізу використовувалась паралельна обробка
експериментальних даних і результатів моделювання в режимі реального часу
(рис. 12 58).
Рис. 12.58. Порівняння експериментальних даних (комп’ютер зліва)
та результатів математичного моделювання (комп’ютер справа)
при моделюванні в режимі реального часу
Типовий визначений експериментально спектр вертикальних
віброприскорень різця мас кілька резонансних зон і охоплює діапазон частот
до 10 кГц (рис. 12.59, а).
При вимірюваннях встановлено, що найбільш суттєвими за рівнем
потужності, є вібрації в діапазонах: 0,2..0,6; 1..1.2; 2..З та 5,8..6,4 кГц.
Спектр вертикальних віброприскорень різця, визначений в результаті
математичного моделювання (рис. 12 59,	б), в цілому відповідає
експериментальному. Визначені за результатами математичного моделювання
резонансні області складають: 0,8..1,2; 2..2,2; 2,4..З кГц, що відповідає
результатам експериментів
Розроблена математична модель дає змогу розрахувати спектри середнього
діапазону частот (до 3 кГц) Точність визначення резонансних зон складає
близько 10 %. Враховуючи складність динамічної системи верстата, гаку
точність моделі можна вважати задовільною
Розроблена візуальна математична модель [106] відзначається
універсальністю, надійністю роботи та достатнім рівнем точності розрахунків.
573
Струтинський В Б
Вона рекомендується для дослідження показників динамічної якості верстата.
51ор
РІоі:
РарегГ
РеесІ І
Рис. 12.59. Експериментально виміряний спектр вертикальних
віброприскорень різця (а) та спектр, визначений в результаті
математичного моделювання (б)
Використання розробленої математичної моделі дає змогу оцінити вплив
всіх інерційних, дисипативних та деформатпвних параметрів па
віброакустичні характеристики верстата. Змінюючи окремо деякий параметр
або комплекс параметрів можна ціле направлено змінювати динамічні
властивості верстата в потрібному частотному діапазоні.
Розділ 12. Математичне моделювання динамічних коливальних процесів
12.5. Теоретичне узагальнення експериментально визначених
спектральних характеристик стохастичних динамічних
процесів верстатів
Математичний опис спектра динамічного віброакустичного процесу
верстата здійснено за результатами експериментальних вимірювань
вібраційних параметрів. В результаті експериментальних вимірювань знайдено
спектральні щільності віброакустичного сигналу. Вони мають характерний вигляд із
значною кількістю резонансних піків (див. рис. 12.59, а).
Будемо вважати, що спектральна щільність описується дробово-
раціональною функцією частоти, тобто
5^ = ТГГ	(12.160)
де Н(<в) і 2(ш) - деякі поліноми, що залежать від частоти со.
Оскільки спектральна щільність є парною функцією, то поліноми В (о) і
Х(ш) включають лише парні степені частоти, тобто от ,	, ...
В монографії (60] доведено, що за таких умов поліноми чисельника і
знаменника представляють собою добутки деяких комнлексно-спряжених функцій
частоти Ь та д, тобто
ег„і н(®) _ ь0®)-ь(-і®)
Із даної залежності випливає, що спектральна щільність рівна:
з(й)=фф.
ЧІІ®)
Будемо вважати динамічну систему верстата квазілінійною системою
автоматичного управління, що має певне кінечне число (І) стохастичних
збурюючих входів
Х,(ї) (і = 1, 2, 3, ..., І).
Позначимо через ¥'(8] трансформуючу функцію від входу X, до виходу
¥. Тоді зображення по Лапласу вихідного сигналу (8 - оператор Лапласа):
¥(8) = І\¥і(8)Хі(8).	(12.162)
І = 1
Введемо формуючий фільтр для і-го входу Х;, який визначає випадковий
вхід через одиничний стохастичний сигнал Х0(і), що відповідає “білому
шуму”. Одиничний стохастичний сигнал є випадковим процесом, спектральна
щільність якого постійна, тобто
80(го) = сопзі = 80.
575
Струтинський В.Б.
Трансформуючу функцію формуючого фільтра для і-го входу позначимо:
/с\ Х^(8)
=	(12.163)
Враховуючи (12.163), із (12.162) одержимо зображення по Лапласу
вихідного сигналу. Воно буде мати вигляд:
¥(8) = Х^(8)^ІО(8)-Х0(8).	(12.164)
і-1
Враховуючи, що зображення по Лапласу одиничного стохастичного
сигналу є однаковим для кожного входу, із (12.164) визначимо загальну
трансформуючу функцію динамічної системи верстата для виходу ¥ у
вигляді:
= ^у(8) = ІХ(8)- ^і0(8).	(12.165)
Загальну трансформуючу функціюіз (12.165) як трансформуючу функцію
квазілінійної системи можна подати у кількох формах, зокрема у вигляді
дробово-раціональної функції:
ГсЛ Ко +К.8 + ... + К 8"
^у(5) = -^7...............’	(12.166)
О І».. І	Т І
де Ко , К(, ..., КП1 - коефіцієнти передачі динамічної системи;
Тп , ..., Т( - постійні часу транформуючої функції;
т і п - цілі числа (звичайно п > т).
Поліноми, які входять в чисельник і знаменник трансформуючої функції
(12.166), розкладемо на множники. В результаті отримаємо формулу, яка
описує загальну трансформуючу функцію:
ПО + 45 + ^32)
"’(5)=к'ПЯхЙ’	<12,67>
де тіц > т2ц >	, Т2у - коефіцієнти складових розкладу; К - загальний
коефіцієнт передачі динамічної системи верстата.
Під знаками добутку у формулі (12.167) знаходяться множники, кожний з
яких відповідає парі комплексно-спряжених коренів поліномів відповідно
чисельника і знаменника.
Визначимо комплексні спряжені корені полінома, що знаходяться в
знаменнику трансформуючої функції. Для цього маємо рівняння:
Т2у82 + Тіу8 + 1 = 0 ,
звідки
-Т1у±/т*-4<
VI, 2
576
Розділ 12. Математичне моделювання динамічних коливальних процесів
Після перетворення цієї залежності одержимо значення коренів:
5VI, 2 ~ т
-1 ф
2
4
І = 7-1,
(12.168)
Т
де 9, =—— - постійна, яка залежить від співвідношення коефіцієнтів.
При наявності в чисельнику чи знаменнику трансформуючої функції лише
одного дійсного кореня із пари коренів, визначених залежністю (12.168),
відповідно коефіцієнт т2ц або Т,„ буде дорівнювати нулю.
Приймемо, що трансформуюча функція е відношенням деяких поліномів р
та ср тобто
\Уу(8) = к-||1.	(12.169)
Враховуючи залежність (12.167) із (12.169), одержимо:
'р(3) = П(1 + Ч2-”>М
Ч(3) = П(1 + Т..3 + ТМ	(12.170)
Знайдемо квадрат модуля частотної трансформуючої функції:
р(іо>)р(-І(о)
ч(і®)  ч(-1®)'
(12.171)
К(Я2 = к2
Підставивши значення 8 -»)со в формули (12.169) і (12.170), із
залежності (12.171) одержимо:
пініл
(12.172)
Цей квадрат модуля з точністю до множника 80 дорівнює спектральній
щільності вихідного сигналу [6]:
8у(ш) = )\Уу(>)|2-80,	(12.173)
Враховуючи, що залежність (12.172) включає лише парні степені частоти
о, спектральну щільність вихідного сигналу визначимо в функції квадрата
частоти () = от :
ПМі-ЧМе1]
3'<0)=к’' 5“' Йі-йоЬт’о]= кг'5" ’ПГ+к-2ті)5+т*оП 
(12.174)
Спектральну щільність 8у(0) (12.174) розкладемо на прості дроби. Для
цього знайдемо корені полінома, який знаходиться в знаменнику функції.
577
Струтинський В. Б.
Пара коренів визначається як розв’язок рівняння:
Т^оМт^-2Т22у)(2 + 1 = 0.
Остаточно пара коренів рівняння (12.175) буде визначена як
Лі'2	21м
Після перетворень та скорочень в (12.176) знайдемо пару
спряжених коренів рівняння (12.175) у вигляді:
02
VI,2
Х2у
(12.175)
(12.176)
комплексно-
(12.177)
2
2
т
де через 0,. позначене відношення постійних часу: 0,, = —.
Аналогічно корені чисельника спектральної щільності,
формулою (12.174), знайдені у вигляді:
0 =
яка визначена
02	02
1—У-±	1——
2 V 2
(12.178)
Т
де 0 = —— представляє собою відношення постійних часу.
Комплексні спряжені корені знаменника спектральної щільності подамо у
вигляді алгебраїчної форми комплексного числа:
0у1,2 = «V ± Л ’
де дійсна та уявна складові коренів визначаються через значення коефіцієнтів:
а.
Раніше введені коефіцієнти
формулами:
1
' к V 2
визначаються
через
складові коренів згідно з
т2 -
2
1
І 2 аі
Т2у
©V =-Г=
\2
Аналогічно для комплексно-спряжених
алгебраїчну форму запису у вигляді:
Оці,2 = ац ± ІЬц ,
де значення дійсної та уявної частин кореня чисельника визначені формулами:
(12.179)
коренів чисельника одержимо
0 І 02
Ьц =2-ф-А 1—
и Ч ]	2
2 [. 0,
а„ = —5- 1-~
М Т2	2
Для цих залежностей маємо співвідношення між коефіцієнтами:
= 21
2
578
Розділ 12. Математичне моделювання динамічних коливальних процесів
би
т2н=-
аН 2
2
і.8!
ан
(12.180)
2
Р
1
V
Коли співмножник полінома в знаменнику трансформуючої функції із
пари коренів має лише один дійсний корінь, тоді параметр
Т2у = 0
і значення кореня буде знайдене з рівняння 1 +	= 0 .
Відповідно розв’язок даного рівняння:
1	1
(Хз ~ т2 ~ т2	(12.181)
Му	^Зу
Аналогічно визначається дійсний корінь чисельника. При Т2ц = 0 :
1 + Т^ = 0 ;
1
<2мз = -фГ = %3	(12.182)
або
Т3ц = ацз 
Використовуючи знайдені значення коренів знаменника, здійснимо
розклад спектральної щільності (12.174) як дробово-раціональної функції від
квадрата частоти ( О = (о2) на прості дроби. З метою спрощення розкладу
будемо вважати, що знаменник спектральної щільності не має кратних
коренів. Це обмеження не є принциповим, оскільки спектральна щільність
визначена наближено за результатами експериментів і для її опису
використовується наближена математична модель.
Згідно з [42], розклад дробово-раціональної функції на прості дроби має
вигляд:
де перша сума відповідає набору дійсних коренів знаменника ( 0УЗ ), а друга
сума включає доданки, кожен з яких відповідає одній парі комплексно-
спряжених коренів знаменника ( РУ) 2 ).
Виконаємо перетворення у формулі (12.183) підставивши в неї замість
значення частоти. Одержимо:
§ .(ю) = у _лкі + у________________________.
'	^'(В2+_1_ И2 + 2(- ау)“2 ++ Ьу	(12.184)
ті
Введемо нові коефіцієнти згідно з формулами:
579
Струтинський В.Б.
ау3 = ~ і	Ру = — Оа2 + Ь2
УО гр '	г V	і у V	V
Відповідно дійсна та уявна складові коренів знаменника:
а = Р2-а2; Ь = л/(р2 + а2Т^(р2 -а?,Т •
а2
а2 + Ь2 - а
(12.185)
(12.186)
Із врахуванням нових позначень одержимо розклад спектральної щільності на
прості дроби (12.184) у вигляді:
Уз ® + а„3 Г|,2 (о*
Виконаємо перетворення в чисельнику дробу під знаком другої суми у
формулі (12.187):
(12.187)
а
^-у /
ау
-а2-В2
(12.188)
Позначимо постійні величини:
ТА	N у 2
= я—— ;
О2у
Відповідно визначимо параметри:
= ОзлЛ;
<«•<»>
З використанням нових позначень формула (12.187) для визначення
спектральної щільності набуде вигляду:
е 6,-Л - V Рзуау/Л , V______Р^>^' + Ру)________
¥	“Ґа^+ю2	+ 2(а2 -р2,)ш2 + (а2у +р27
+ у Ріуау(со2 +Иу +Р9
ІЇг а>4 + 2(а2 - В2 )и2 + (а2 + р$У ‘
(12.190)
Всі три вирази під знаками суми у формулі (12.190) можуть бути записані
в узагальненому вигляді як одна базисна функція математичної моделі:
2
(12.191)
-
а
О3^ — Му3л .
де:
- для першої суми у (12.190) (р., = 0, уу = 0) і базисна функція:
(Ру3(<й) = <р(Оу,ау,0,0,сй) = -?;^Р^-ї;	(12.192)
Тії ОСу "г р КО
580
Розділ 12. Математичне моделювання коливальних процесів
-	для другої суми у формулі (12.190) (уу = <д /ру) базисна функція:
ґ	а
=	= у->	=
= ^------------------------------	(12.193)
я о?+2(сф-р^)и2+(сф+р^
-	для третьої суми у формулі (12.190) (уу = 0) базисна функція:
Ф1х,(со) = ф(И¥, ау, Р„, у, =0, со) =
. ог+сф+р(	(12.194)
л ш4 + 2(оф - р()ю2 + (а2 + РуУ
Не дивлячись на різний вигляд базисних функцій (12.193) та (12.194)
вони дають подібні результати розрахунків. На рис. 12.60 наведено дві
базисні функції, побудовані за допомогою пакету МаійіСАГ).
Рис. 12.60 Результати розрахунків базисних функцій
математичних моделей
Базисні функції ф1у(ш) та ф2ч,(ю), визначені формулами (12.193) та
(12.194), окремо допускають розклад на прості дроби у вигляді:
Р2у<А
2тг
(12.195)
Ф2х
——Гл---------- ---__£Д--------
а; т (сі - В,,)2 сф+(ш + Р7)2
(12.196)
Базисні функції мають екстремуми по параметру и. Для знаходження
екстремуму базисної функції ф2у(а>) знайдемо похідну залежності (12.196) по
параметру и і прирівняємо її до нуля. Одержимо рівняння:
581
Струтинський В Б
400і н-4®(сс2-р“)= 0 .	(12.197)
Звідси знаходимо значення частоти, при якій має місце екстремум:
®е2	-«V 	(12.198)
Для практично важливого випадку ру»а, маємо:
сое2»РУ.	(12.199)
Знаходження екстремуму базисної функції <рІУ(<о) здійснено з
використанням математичного пакету МаДтСАВ 2000 Нижче наведено
фрагмент документа МаїЬСАП, що здійснює знаходження похідної
залежності (12.194) та її коренів:
0 Р (а + V  Ю(а2 + Р2)+ (« - У • Р)®2
<1® (а2 + р2^ + 2(а2 - Р*')в2 + ©4
0
1
-а2 -р2 +2(а2р2 +р4)ї 2
- -а2 -р2 -2(а2р2 +р4^ 2
(12.201)
За фізичною суттю задачі корінь є дійсним і додатнім. Тому за корінь
треба взяти другу компоненту одержаного вектора, що знаходиться в правій
частині формули (12.201). Відповідно значення кореня буде:
ЙС1 = дРсс2 - р2 + 27«Ж + РІ 	(12.202)
Для практично важливого випадку, коли РУ»ау маємо:
®еІ«РУ.	(12.203)
Таким чином, встановлено, що обидві базисні функції мають близькі
582
Розділ 12. Математичне моделювання коливальних процесів
екстремуми, які визначаються умовами (12.198) та (12.202).
Ця обставина використана для знаходження коефіцієнтів математичної
моделі. З метою спрощення моделі із розгляду виключаються безрезонансні
складові, які відповідають базисній функції ф3у(ш). При цьому математична
модель спектральної щільності в загальному вигляді:
8у(®) = -££ф^Ок,ак,0к,уік,и),
71 к=0 І=1
де Уік = 0 , у2к = ак/0к .
Узагальнений вираз спектральної щільності:
ч 6Л - 1V V Р* • Ьк + УікРк)(ак + РкУ + (<*к ~ УікРкК1
(12.204)
(12.205)
Цей вираз являє собою нелінійну математичну модель спектральної щільності
випадкового процесу вихідного параметра динамічної системи верстата.
Математична модель включає три групи коефіцієнтів Г)к , ак , 0к і залежний
від них коефіцієнт ук. Ці коефіцієнти визначаються за експериментальними
спектрами віброприскорень чи спектра акустичного сигналу.
При визначенні коефіцієнтів враховуються характерні особливості
математичної моделі, зокрема точки екстремумів базисних функцій.
Розроблений метод визначення коефіцієнтів полягає в наступному.
Використовується одержана експериментально спектральна щільність
віброприскорень чи рівня звукового тиску. На рис. 12.61 наведена типова
експериментальна спектрограма віброприскорень корпусу шпиндельної бабки
токарно-гвинторізного верстата КА-280.
Рис. 12.61. Експериментальна спектрограма віброприскорень корпусу
шпиндельної бабки верстата КА-280
583
Струтинський В.Б.
Із аналізу спектрограми випливає, що частотний діапазон
віброакустичних впливів, суттєвих за рівнем віброприскорень, складає
0...5 кГц. В межах даного частотного діапазону мають місце декілька
десятків резонансних піків спектральної щільності. Для кожного з цих
піків шляхом підбору знаходяться резонансні частоти, що наближено
(див. формули (12.199) та (12.203)) відповідають коефіцієнтам Рк
математичної моделі. Для спектрограми, наведеної на рис. 12.61, знайдені
значення окремих резонансних частот складають:
Ро = 3000	р9=450	Рзз= 1650	Р41 = 1420
Рі= 1450	Рю = ИО	Рз4 = 1550	Р42= 1320
Р2 = 5000	Р15 = 1940	р35=40	3.54=2120
Р3 = 1000	Р16= 2280	Р36=70	Р55=950
Р4 = 840	Рзо = 2200	Рз? = 170	Р61=750
р7=1520	Рзі = 1750	Рз8= 2070	
Р8=650	Рз2 = 1840	Рз9=20Ю	
Визначені коефіцієнти (Зк використовуються для знаходження інших
коефіцієнтів моделі - ак, Ок .
Нижче наведено ряд знайдених коефіцієнтів, що відповідають рис. 12.61.
а0 = 1550	О0 = 2,5	а32 = ЗО	О32 =0,05
а( = 650	О! = 0,9	«зз = ЗО	О33 = 0,05
а2 = 1000	О2 = 1,7	«34 = ЗО	О34 = 0,05
а3 = 1050	Вз=0,9	«35 = ЗО	О35 = 0,025
а4 = 25	О4 = 0,14	«36= Ю	О36= 0,006
а7 ~ 70	О7 = 0.25	«37 = 20	О37= 0,015
а8 = 40	О8= 0,15	«38 = 20	О38 = 0,035
а9 = 90	О9= 0,35	«39 = 20	О39 = 0,025
040= 45	О10 = 0,07	а41 = 20	О4) = 0,025
аІ5 = 60	Пі5= 0,25	а42 = 20	О42 = 0,025
«іб = 40	0.56=0,11	«54 = 20	054 = 0,02
а30 = ЗО	О3о=0,05	«55 = 20	О55 = 0,035
«зі = 30	О31 = 0,06	«61 = 40	О61 = 0,025
Спочатку знаходиться наближена математична модель, яка включає лише
базисні функції <р2к(<о) (формула (12.193)). Для цієї моделі за коефіцієнтами
Рк підбираються коефіцієнти ак і В2к із умови, щоб одержана математична
модель наближено відповідала вихідній спектральній щільності.
Підібрані значення коефіцієнтів, що відповідають рис. 12.61, наведені
нижче у вигляді масивів пакету МаіЬСАВ:
584
Розділ 12. Математичне моделювання динамічних коливальних процесів
	0
0	1,55-Ю3
1	650
2	1-Ю3
3	1,05-103
4	25
5	25
6	ЗО
7	70
8	40
9	90
10	45
11	20
12	40
13	40
14	25
15	60
	0
0	3-Ю3
1	1,45103
2	5-Ю3
3	1-Ю3
4	840
5	1-Ю3
6	1,24103
7	1,52-103
8	650
9	450
10	240
11	2,63-Ю3
12	2,96-103
13	3,45-103
14	3,94-103
15	1,94-Ю3
	0
0	2,5
1	0,9
2	1,7
3	0,9
4	0,14
5	0,14
6	0,14
7	0,25
8	0,15
9	0,35
10	0,07
11	0,09
12	0,18
13	0,17
14	0,08
15	0,25
Всього для спектра, зображеного на рис. 12.61, визначено 283 резонансні
частоти і відповідно 283 коефіцієнти рк, ак і В2к.
Нижче (рис. 12.62) наведені результати розрахунків спектра
віброприскорень за знайденою наближеною математичною моделлю:
N := 282	к:=0..М	Гк:= —
Рк
зАоУ-^УО Лак+Ук*Рк)*|(«к)2 +ФкУ]+(аІІ-Гк	<12-206>
Рис. 12.62. Результати розрахунків спектра віброприскорень
за наближеною математичною моделлю
585
Струтинський В. Б.
Експериментальні спектрограми, як правило, будуються в
логарифмічному масштабі по осі абсцис так, як це показано на рис. 12.61.
Ця обставина не є суттєвою. Для переходу від логарифмічного масштабу
до дійсного значення спектральної щільності використовують наближену
математичну модель.
На рис. 12.63 наведено розрахунок дійсних значень спектральної
щільності, одержаний шляхом потенціювання наближеної математичної
моделі:
соє := 0.008
—-У о,
/ \	СОЄ
Ь(<в) := 0.00036 * 10і
(«і+ТкДк)каД
(12.207)
Ь(1000)= 1.822 * 10~3	Ь(5000)= 5.322 »1(Г4
Рис. 12.63. Порівняння спектральних щільностей, зображених
відповідно в логарифмічному (суцільна крива)
і лінійному (пунктирна крива) масштабах по осі ординат
Із порівняння кривих в різних масштабах випливає, що залежності мають
близькі значення і використання логарифмічного масштабу не є суттєвим.
Одержана раніше наближена математична модель (12.206), яка включає
базисні функції лише одного виду, є досить неточною. Для її уточнення
вводиться друга частина математичної моделі. Початково вважається, що
®2, =	= Ок/2 ,
і виконуються обчислення з подальшим уточненням значень коефіцієнтів.
Уточнення значень коефіцієнтів здійснено методом найменших квадратів.
Знайдені уточнені значення коефіцієнтів моделі мають вигляд:
586
Розділ 12. Математичне моделювання динамічних коливальних процесів
	0
0	1.55103
1	650
2	1-103
3	1,05103
4	25
5	25
6	ЗО
7	70
8	40
9	90
10	45
11	20
12	40
13	40
14	25
15	60
	0
0	3-Ю3
1	1,45103
2	5-Ю3
3	1-Ю3
4	840
5	1-Ю3
6	1,24-Ю3
7	1,52-Ю3
8	650
9	450
10	240
11	2,63-Ю3
12	2,96-103
13	3,45-Ю3
14	3,94-103
15	1,94103
	0
0	0,518
1	0,258
2	0,491
3	0,194
4	0,036
5	0,03
6	0,04
7	0,071
8	0,045
9	0,095
10	0,02
11	0,027
12	0,042
13	0,037
14	0,024
15	0,056
	0
0	1,774
1	0,656
2	1,256
3	0,695
4	0,103
5	0,1
6	0,103
7	0,176
8	0,119
9	0,273
10	0,05
11	0,064
12	0,134
13	0,136
14	0,06
15	0,189
Всього визначено 283 пар коефіцієнтів В1к і О2к.
Результати розрахунків спектра віброприскорень за уточненою моделлю
наведені нижче (рис. 12.64).
812(о) := - * У О1 *	1~у1к *Рк)*^)2 + (Рк)2]+(«к + УІк *Рк)*®2 +
71 к=°_ к І. ^Хк)2 + фку ] + 2 * Іаі)2 ~ (ркУ]♦ ш2 + о4 ]
+ 02
(12.208)
(ак +Ук *Рк)*ІкУ + ФкУІ-ь(“к + Ук *Рк)*<»2
. ІкУ +(РкУ] + 2*І«к)2-Фк)2]*®2+®4
Рис. 12.64. Результати розрахунків спектра віброприскорень
за уточненою математичною моделлю
587
Струтинський В. Б.
Знаходження кореляційної функції стохастичного динамічного процесу
верстата виконано шляхом перетворення Фур’є знайденого аналітичного
виразу процесу (12.208) спектральної щільності віброакустичного параметра.
За спектральною щільністю випадкового процесу знаходиться кореляційна
функція (автокореляційна функція). Згідно [60], спектральній щільності виду
(12.208) відповідає кореляційна функція у вигляді добутку експоненціальної
та тригонометричних функцій:
N1 2
к(т)= ЕІЖ •е’акМ ‘ММ+П “5іп(РкМ)]	(12.209)
к=0 і=1
Результати розрахунків згідно даної залежності наведено нижче
(рис. 12.65).
К(т):= £П1к *е~акН ♦[созфь *т) + уік ♦»іп(рк ♦ |т|)]+
(12.210)
+ О2к * е”“к|ТІ * |со8(рк * т) + ук * 8Іп(рк * (ті)].
перетворення математичної моделі експериментально визначеного
спектра віброприскорень (графіки мають різні масштаби)
588
Розділ 12. Математичне моделювання динамічних коливальних процесів
Із аналізу кореляційної функції випливає, що стохастичний коливальний
процес має незначний ступінь кореляційного зв’язку між сусідніми точками
для інтервалів часу, більших 0,1 мс. Кореляційна функція характеризується
суттєвою коливальністю протягом значного проміжку часу (до 3 мс).
Визначення кореляційної (автокореляційної) функції здійснено також за
допомогою вимірювань безпосередньо на працюючому верстаті. Для цього
використаний аналізатор спектра ЗІ 1220.
Виміряні експериментальні автокореляційні функції (рис. 12.66) в цілому
аналогічні одержаним в результаті математичного моделювання.
шязззяи $и»ег ижшаяки
Зеїесі Ріо* Сопігої орііоп
ЕгеЄX е
30-МЯК-2000
Рис. 12.66. Коваріаційна (автокареляційна) функція віброприскорення
вертикальних коливань різця, знайдена за допомогою безпосередніх
вимірювань на верстаті
ЕХІТ
09 : 49:35
Кореляційна функція характеризується значною коливальністю. На
графіку кореляційної функцій віброприскорень простежуються
короткоперіодичні складові. Період цих складових близько 0,2 мс при періоді
довгоперіодичних складових коливань близько 10 мс.
Основний процес затухання кореляційної функції відбувається за період
часу близько 5 мс. Це відповідає затуханню функції, наведеної на рис. 12.65.
За експериментальними вимірами встановлені динамічні характеристики
динамічної системи верстата. Характеристики знаходилися з використанням
апаратурної обробки виміряних параметрів вібрацій. Виміряні параметри
(віброприскорення, віброшвидкість, вібропереміщення) згруповані попарно з
утворенням окремих ланцюгів «вхід-вихід» Сформовані різні пари «вхід-
вихід», наприклад, вхід - віброприскорення кришки передньої опори
шпинделя, вихід - вертикальна складова віброшвидкості різця. Для кожної
пари «вхід-вихід» визначені частотні та часові характеристики. Зокрема,
знайдені імпульсні характеристики верстата \у(і). Вони представляють собою
реакцію динамічної системи верстата на ударне навантаження у вигляді
589
Струтинський В.Б.
дельта-функції Дірака. Експериментально визначена імпульсна
характеристика для входу у вигляді сили, направленої перпендикулярно до
осі шпинделя, та виході у вигляді вертикального переміщення різця наведена
на рис. 12.67.
Рис. 12.67. Імпульсна характеристика динамічної системи верстата
при вході у вигляді сили, направленої перпендикулярно осі шпинделя,
і виході у вигляді вертикального переміщення різця
За імпульсною характеристикою знайдено час перехідного процесу -
38 мс. Коливальність перехідного процесу - 8 (число повних коливань за час
перехідного процесу). Період коливань складає 4,3..4.6 мс, що відповідає
превалюючій власній частоті коливань різця (близько 230 Гц). На імпульсній
характеристиці простежується високочастотна складова власних коливань
супорта з періодом 0.3 .0.4 мс, що відповідає другій резонансній частоті
супортної групи, яка знаходиться в діапазоні 2500..3300 Гц. Імпульсна
характеристика має низькочастотну складову незначної амплітуди з періодом
15..17 мс (частота 58..66 Гц). Ця складова відповідає низькочастотному
резонансу динамічної системи супортної групи.
Одержана спектральна щільність випадкового стохастичного параметра
динамічної системи верстата описана математичною моделлю у вигляді суми
нелінійних базисних функцій. Використовуючи дану математичну модель,
знайдена еквівалентна трансформуюча функція динамічної системи верстата.
Перетворимо математичну модель спектральної щільності до виду
дробово-раціональної функції, тобто запишемо спектральну щільність у
вигляді відношення двох поліномів:
с / X Ну(й))
=	(12.211)
Чисельник і знаменник цієї формули виражається через відомі
коефіцієнти математичної моделі згідно з формулами:
590
Розділ 12. Математичне моделювання динамічних коливальних процесів
ху(и)=7гп[(ак +РЇ +2(ак -й)®2 +®4];
к=о	(12.212)
Ну(ш)=8у(©)Ху(а>).
В чисельнику і знаменнику знаходяться деякі
відповідно 4т і 4п. Таким чином
Я (п) . ну(®) _ Ьо+Ь2®2+- + ь2т(о4т
ЬИИЬ2у(Ю)-ч1Х'+... + ^+Чо-
поліноми степенів
(12.213)
При знаходженні цих поліномів за допомогою ЕОМ виникають певні
обчислювальні труднощі. Вони пов’язані з високим порядком чисел, які
відповідають коефіцієнтам ак, рк та частоті со . Порядок цих величин ( ак,
рк, со) складає 103. Відповідно четверта степінь цих величин має порядок
10 і2. Добуток врахованих 283 складових математичної моделі дає порядок
чисел ~103396; шо набагато перевищує можливості персонального комп’ютера
(ЮЗбО) Навіть врахування значно меншого числа складових (61 резонансний
пік) приводить до появи чисел з порядком 10732, які не можуть бути
обчислені на персональних ЕОМ.
Для вирішення даної обчислювальної проблеми введені масштабні
множники цм для значень коефіцієнтів і частоти. Масштабні множники
вводяться для певного обмеженого діапазону частот [ со, , со2 ].
При цьому чисельник, а відповідно, і знаменник (12.212), для визначення
спектральної щільності набирають вигляду:
Ну(<о)=Н^ •ХцшУ(«)=рГ •8У(«>)-2ИМУ|— К
Масштабні множники не впливають на знаходження коренів чисельника
спектральної щільності, але дозволяють зняти обчислювальну проблему,
пов’язану з високими порядками величин.
Обчислення виконані в пакеті МаїЬСАП і наведені нижче (рис. 12.68). Для
діапазону частот со = 0...600 с-1 використано масштабний множник цо = 12000.
Враховано 61 суттєву резонансну частоту спектральної щільності:
591
Струтинський В.Б.
к:=0..61	ц:= 12000	ак:=^-	Рк:=^
44-їїк)2	-№)*«? И
Н(<в):= г(ш)*8(ш).
(12.214)
Рис. 12.68. Графіки поліномів, що визначають чисельник і знаменник
спектральної щільності в діапазоні частот 0..600 с'1
Для знаходження коренів полінома чисельника спектральної щільності
використана наступна методика. Масштабний множник не впливає на корінь
чисельника, тому:
Н¥(®)=^-НишУМ = 0.	(12.215)
Враховуючи (12.215), знаходиться корінь рівняння:
Нца¥| —1 = 0.	(12.216)
їм
Для цього обчислюються значення Н у — , (і - 0,.п).
1М(
Потім здійснюється апроксимація цих точок поліномом за допомогою
спеціальної вбудованої функції пакету МаїЬСАІ).
Функція 1іп£іі знаходить набір коефіцієнтів полінома. Використовуючи
коефіцієнтами за допомогою вбудованої функції Роїугооіз знаходять корені
полінома. Звичайно враховуються лише ті корені, дійсна складова яких
592
Розділ 12. Математичне моделювання динамічних коливальних процесів
належить вибраному інтервалу зміни со = [а>1, со2 ] •
В наведеному нижче фрагменті документа МаіЬСЛО визначено корені
чисельника, які належать інтервалу зміни ш = 0...600 с'1. Цей фрагмент є
продовженням документа МаЦіСАВ (12.214).
п:=0..И ухп
п-600
11-ц
у0„ :=Н
п-600
11 -ц
срої := 1іп£іІ(ух,уО,Гт)
	<1			0			
	X		0	0.191			0
	X2		1	0.181		0	-7.744+4.636
	3		2	0.154		1	-7.744-4.636
			3	0.121		2	-7.887-10-3
Рт(х) :=	X		4	0.092		3	0.016+0.019
	х3	у0 =	5	0.07	роїугооб (срої) =	4	0.016-0.019
	х6		6	0.051		5	0.036-5.594-10-3
	X7		7	0.033		6	0.036+5.594-Ю-з
	х,8		8	0.027		7	0 266
			9	0.063		8	0.809-10.334
	X’'		10	0.193		9	0.809+10 334
	к,		11	0.471			
Аналогічним чином знайдені масиви коренів чисельника в інших
діапазонах зміни частоти и. Всього розглянуто сім частотних діапазонів, які
наведені в позиціях наступних таблиць (розмірності величини дані в Гц).
Ьк1 =
	0
0	-1.479-104+8.854-10-3
4 1	-1.479-104—8.854-103
2	-15.064
3	30.484+37.123
4	30.484-37.123
5	68.885-10.684
6	68.885+10.684
7	508.634
8	1.546ЮЗ-1.974Ю4
9	1.546 103+1.974 104
	0
0	-67.138
1	-95.547
2	-203.509
3	-288.011
4	-663.785
5	-795.668
6	-932.545
7	-1.055-104
8	-1.166-104
9	-1.273-Ю4
	0
0	1.248-103
1	1.372-103-126.111
2	1.375-103-132.584
3	1.664-103-261.933
4	1.675-103-273.417
5	2.05-103-57.756
6	2.116-103-221.577
7	2.119-103-256.377
8	2.513-103-145.138
9	2.514-103-140.139
593
Струтинський В. Б.
Ьк4 =
	0
0	1.325103
1	1.457 103-133.871
2	1.46-103-140.743
3	1.766-103-278.052
4	1.779-103-290.243
5	2.176 103-61.31
6	2.246-10-3-235.213
7	2.249-103-272.155
8	2.668-103-154.069
9	2.668-103-148.763
Ьк5 =
	0
0	-1.564-103
1	1.722-103-149.668
2	1.725-103-156.367
3	2.066-103-325.108
4	2.098-103+299.324
5	2 435-103+232.082
6	2.568-103-383.269
7	2.772-103+293.415
8	3 003-103-214.142
9	3.085-103-90.999
пкб =
	
0	-1.892-юЙ
1	2.084-103-181.119
2	2.088-103+189.227
3	2.5-103-393.428
4	2.538-1ОЗ-362.225І
5	2 946-103+280.8531
6	3.108-10-3-463.811
7	3.354-103+355.0741
8	3.634-103-259.143
9	3.734-103+110.122|
Ьк7 =
	0
0	2.188-103
1	2.409-10-3-212.504
2	2 413-103+222.469-
3	2.895-Ю-З-433.0761
4	2.915-10-3+452.87
5	3.531 10-3-437.768
6	3.588-103+466.077
7	4.009-103-211.645
8	4.14-103+196.286
9	4 274-10-3-42.709
Позначимо знайдені т коренів чисельника, із яких є комплексні спряжені
Оці,2 І ДІЙСНІ , ЯК
®ці,2 =	± К;
«цз=ацз (аи = акІ ,ьи = ЬЬ; ).
(12.217)
Дійсні та уявні частини коренів визначаються засобами пакету МаіЬСЛВ і
роздруковані у вигляді наступних таблиць:
	0
0	0
1	30.484
2	68.885
ЗІ	1.372-10-3
4	1.664-103
5	1.664-103
6	2.05-103
7	2.119-103
8І	2.514-Ю3
9	1.766-103
10	2.176-103
11	2.249-103
12	2.668-103
13	1.722-1О3
14	2.066-103
15	2.435-103
	0
0	01
1	37.123
2	10.684
3	126.111
4	261.933
5	261.933
6	57.756
7	256.377
8	140.139
9	278.052
10	61.31
11	272.155
12	148.763
13	148.668
14	325.1081
15	232.082
594
Розділ 12. Математичне моделювання динамічних коливальних процесів
Використовуючи одержані значення коренів, за формулами (12.180)
знайдемо коефіцієнти складових чисельника трансформуючої функції:
	к:= ЄЬк:		□..27; 11 р +	ТЬ2к :=і 1	. (аЬкУ КУ		1	£ цььку £й:=-	*(аЬк) . + 2*(аЬкУ £ 2 ’		(12.218)		
ТЬ2 =		0	еь =		0	!ф =		0			
	0	0		0	1,414		0	0,707	тзь =		0
	1	0,194		1	0,923		1	0,461		0	0
	2	0,169		2	0,154		2	0,077		1	3,881
	3	0,038		3	0,092		3	0,046		2	9,775
	4	0,034		4	0,156		4	0,078		3	14,266
	5	0,034		5	0,156		5	0,078		4	16,971
	6	0,031		6	0,028		6	0,014		5	25,764
	7	0,031		7	0,121		7	0,06		6	28,208
	8	0,028		8	0,056		8	0,028		7	30,538
	9	0,033		9	0,156		9	0,078		8	32,483
	10	0,03		10	0,028		10	0,014		9	34,142
	11	0,03		11	0,121		11	0,06		10	35,683
	12	0,027		12	0,056		12	0,028		11	39,545
	13	0,034		13	0,087		13	0,043		12	43,502
	14	0,031		14	0,156		14	0,078		13	46,776
	15	0,029		115	0,095		15	0,048			
За	значеннями параметрів ак					та рк	за формулами (12.186) знаходяться				
дійсні та уявні складові комплексних коренів знаменника спектральної щільності:
а2к := [ФкУ “ (“кУ| 1	 Ьгк :=	+ (ак/1 ~(акУГ  (12219)
аг =		0	Ьг =	1°
	0	р,934		0 1,316
	1	0,238		1 Ю,267
	2	3,397		2 1,416
	3	0,015		3 Ю,297
	4	0,1		4 5,945 10-3
	5	0,141		5 7,078-10-3
	6	0,218		6 0,011
	7	0,326		7 коз
	8	0,06		8 |7,361-Ю-з
	9	0,028		9 кои
	10	7,867-10-3		103,058 10-3
	11	1,24		110,015
	12	1,685		120,034
	із	2,197		130,039
	14	0,532		140,028
	15	0,029		15р,033
595
Струтинський В. Б.
Остаточно комплексні корені знаменника знайдені розрахунком
	0
	0.934+1.316
0	0.238+0.267
1	3.397+1 416
2	0.015+0.297
3	0.1+5,945-10 з
4	0.141+7.078- ІО-з
5	0.218+0,011
6	0.326+0,03
7	0.06+7,361-10-3
8	0.028+0,011
9	7.867-1О-3+З.О58-1О-3
10	0.979+0,015
11	1.24+0,034
12	1.685+0,039
13	2.197+0,028
14	0.532+0,033
За значеннями коренів знаменника спектральної щільності за формулами
(12.179) знаходяться коефіцієнти складових знаменника трансформуючої
функції:
Тг2к :=---;	02к ;= _^=^=== 
агк • |Ьгк / + 2 • (агк У ]
р ' (ЬгкУ (12.220)

02
Т'
Числові значення коефіцієнтів знаменника трансформуючої функції
наведено нижче
Тх2 =
	0
0	1.036
1	2.272
2	0.736
3	0.808
4	4.473
5	3.758
6	3.03
7	2.47
8	5.772
9	8.178
10	15.178
11	1.429
12	1.27
13	1.089
14	0 954
15	1.937
	0
0	0.998
Г1	0.879
2	04
3	1.411
4	0.06
5	0.05
6	0.048
7	0.092
8	0.123
9	0.4
10	0.375
11	0.015
12	0.027
13	0.023
14	0.013
15	0.062
	0
0	0.499
1	0.439
2	0.2
3	0.705
4	0.03
5	0.025
6	0.024
7	0 046
8	0.062
9	0.02
10	0 187
11	7.605-Ю-з
12	0.014
13	0.012
14	6.345-10-3
15	0.031
596
Розділ 12. Математичне моделювання динамічних коливальних процесів
Остаточно математична модель динамічної системи верстата у вигляді
частотної трансформуючої функції буде мати вигляд:
ті 13
П12,,)2 (і-шУ +2-^Ь„ -ТЬ2„  і  © +1} П(ТЗЬші * <0 + 1)
== -----ш-у-----------------“----1------ 
П1М)2 - (і • о)2 + 2 Чгп • Т?2П - і  ш +1]
п=0
(12.221)
де числові значення коефіцієнтів визначені залежностями (12.218) та (12.220).
За виразом (12.221) знаходяться частотні характеристики динамічної
системи верстата (рис. 12.67). Зокрема, дійсна та уявна амплітудно-частотні
характеристики:
Іі(ш) := Ке(\У(ш)); У(со) := Іт(\У(ш)).	(12.222)
201	(—————।	;
со
Рис. 12.69. Розрахункові значення амплітудно-частотної (а)
і дійсної та уявної амплітудно-частотних (6) характеристик
Частотні характеристики дозволяють визначити резонансні частоти,
інтенсивність резонансних піків та інші властивості динамічної системи верстата.
Узагальнюючою частотною характеристикою є амплітудно-фазова частотна
характеристика. Вона побудована в координатах [и(со), )У(®)] (рис. 12.70).
Амплітудно-фазова частотна характеристика має складний вигляд із
значним числом резонансних петель, які часто накладаються одна на одну.
Дана характеристика відповідає динамічній системі верстата, на яку діє
узагальнюючий стохастичний вхід.
597
Струтинський В. Б.
Рис. 12.70. Амплітудно-фазова частотна характеристика верстата,
знайдена за експериментально визначеним спектром, віброприскорень
і визначена при різних масштабах при осях координат
Узагальнений вхід дає можливість встановити загальні динамічні
властивості верстата. Для виявлення конкретних особливостей системи,
зокрема резонансних областей по відповідних входах, результати
математичного моделювання доповнені експериментальними вимірами
амплітудно-фазових частотних характеристик. Амплітудно-фазові частотні
характеристики визначені зо допомогою аналізатора спектра 81 1220.
Із виміряних значень характеристик випливає, що в динамічній системі
верстата мають місце значні резонансні явища, які проявляються в істотних
викидах на графіках амплітудно-фазових частотних характеристик (рис. 12.71).
Виміряні характеристики мають складний вигляд і зливаються в області
малих амплітуд.
Для виявлення характеру зміни характеристики виконане збільшення
ділянки малих амплітуд. Одержані при цьому графіки характеристики мають
окремі ділянки, визначені в межах чутливості аналізатора спектра. Для їх
практичного використання здійснене згладжування окремих ділянок
598
Розділ 12. Математичне моделювання динамічних коливальних процесів
амплітудно-фазової частотної характеристики.
НВИВЗММ	ЖЯЯЯЯИ8И Егвеге ЗИЗМНВЇЯІ	13-РРК-га00 12:54:16
8е1ес± Р1о± Соп±го1 орііоп Ні ГКв№зГЕН - ГЬч  СЬг/СЬІ Р ркУНг___
і	З'їор І	£±аг1	!	І	"	І І	Рарег	І	І	| рСт т І
І	Р1.Л . І	РЮ1	І______І________і І________________І_______І.. ЬХ_І Т . 1
Рис. 12.71 Експериментально визначені амплітудно-фазові частотні
характеристики динамічної системи верстата: а — для входу у вигляді
віброшвидкості вертикальних коливань деталі та виходу у вигляді
віброшвидкості вертикальних коливань прохідного різця; б - для входу
у вигляді віброшвидкості горизонтальних коливань деталі та виходу
у вигляді віброшвидкості горизонтальних коливань різця; в — для входу
у вигляді віброприскорення горизонтальних коливань опори шпинделя
та виходу у вигляді віброшвидкості вертикальних коливань різця
На рис. 12.72 представлено типову амплітудно-фазову частотну характерис-
тику (частотну трансформуючу функцію) XV()0)) досліджуваного верстата.
Амплітудно-фазова частотна характеристика визначена при вході у
вигляді переміщення деталі та виході у вигляді вертикального переміщення
різця. Вона зображена в координатах своєї дійсної Шл>) та уявної У(ю)
частин.
Приведена амплітудно-фазова частотна характеристика має значну кількість
петлеподібних ділянок різної величини, які відповідають резонансним частотам
динамічної системи. Обвідна характеристики охоплює еліптичну область із
півосями еліпса 0,8..0,9 в напрямку дійсної осі та 1,4.. 1,5 в напрямку уявної осі.
Центр еліпса (точка С) зміщено в перший квадрант графіка на величину близько
0,15 в напрямку як дійсної, так і уявної осей. Еліптична область має приблизно
постійне заповнення графіком амплітудно-фазової частотної характеристики в
зоні, яка приблизно відповідає колу, вписаному в еліпс. Викиди з цієї області
розташовані в четвертому квадранті а також у верхній частині еліпса. Ці викиди
відповідають головним резонансам динамічної системи, які мають місце на
частотах <вр1 = 60 Гц та сорЗ = 3100 Гц. Ці частоти відповідають визначеним
раніше із аналізу імпульсної характеристики супортної групи першій та третій
частотам власних коливань. На характеристиці простежується друга резонансна
частота <ор2 = 220 Гц. Інтенсивність резонансних явищ визначається довжиною
радіуса-вектора, проведеного з початку координат в точках резонансів. Радіус-
вектор дорівнює значенням амплітудно-частотних характеристик ХУ(го). Значення
амплітудно-частотної характеристики на резонансних частотах складає
599
Струтинський В Б.
№(®Р1) = Х¥р1 = 1,3; ХУ(ор2) = Ч¥р2 = 0.85; ШгорЗ) = \¥рЗ = 1,45. Між
першим і другим резонансом знаходиться перший локальний мінімум амплітудно-
частотної характеристики АУмІ = 0.5. Цим пояснюється наявне в експериментах
зниження інтенсивності коливань у низькочастотній області.
б)
Рис. 12.72. Визначена експериментально амплітудно-фазова частотна
характеристика (частотна трансформуюча функція \У(]со)) динамічної
системи верстата): а ~ характеристика, визначена за допомогою
аналізатора спектра коливань; б - та ж характеристика, оброблена
шляхом згладжування за допомогою ЕОМ
Полярний кут, що відраховується від додатного напрямку дійсної осі,
відповідає фазочастотній характеристиці динамічної системи у(ш). Значення
фазочастотної характеристики охоплює діапазон полярних кутів від 0 до бтг,
що відповідає прийнятому частотному діапазону аналізу від 0 до 5000 Гц.
Амплітудно-фазова частотна характеристика є основою для визначення
показників стійкості динамічної системи верстата. Знайдено запас стійкості по
амплітуді АXV = 0,55. Враховуючи складний вигляд характеристики в околі
фазових кутів -180°, можна припустити значні коливання запасу стійкості.
Тому для оцінки запасу стійкості запропоновано використати обвідну
амплітудно-фазової частотної характеристики у вигляді еліпса. При цьому
еквівалентний запас стійкості по амплітуді складає Д\Уе = 0,2 при нульовому
запасі стійкості по фазі.
600
ЛІТЕРАТУРА
1.	Анго А. Математика для електро- и радиоинженеров. - М.: Наука,
1965. - 778 с.
2.	Андронов А.А., Витт А.А., Хайкин С.З. Теория колебаний. -
Физматгиз, 1959. - 540 с.
3.	Бахвалов Н.С. Численньїе методи (анализ. алгебра, обьїкновенньїе
дифференциальньїе уравнения). - М.: Наука, 1973. - 683 с.
4.	Беллман Р. Введение в теорию матриц. - М.: Наука, 1976. - 351 с.
5.	Березин И.С., Жидков И.П. Методьі вичислений. Т. 1-2. - М.:
Наука, 1966. - 545 с.
6.	Бесекерский В.А., Попов Е.П. Теория систем автоматического
регулирования. - М.: Наука, 1972. - 768 с.
7.	Боголюбов Н.Н., Крьілов Н.М. Введение в нелинейную механику. -
Киев, 1937. - 680 с.
8.	Бурек Ян. Адаптивное регулирование процессом врезного
шлифования валов: Дис... докт. техн. наук. - К.: КПИ, 1997. - 349 с.
9.	Ван-дер Поль Б., Бреммер Г. Операционное нечисленне на основе
двухетороннего преобразования Лапласа. - М.: Иностранная литература,
1952. - 420 с.
10.	Венцель Е.С. Теория вероятностей. - М.: Наука, 1969. - 576 с.
11.	Гельфанд И.М., Шилов Г.Е. Обобіценньїе функции и действия над
ними. - М.: Физматгиз, 1959. - 630 с.
12.	Гідроприводи та гідропневмоавтоматика:	Підручник /
В.О. Федорець, М.Н. Педченко, В.Б. Струтинський та ін. - К.: Вища шк.,
1995. - 463 с.
13.	Гельфанд И.М. Лекции по линейной алгебре. - М.: Наука, 1971. -
531 с.
14.	Гультяев А. Имитационное моделирование в ереде ХАішіохуз. -
С-Пб.: КОРОНАпринт, 1999. - 288 с.
15.	Гурвиц А., Курант Р. Теория функций. - М.: Наука, 1968. - 443 с.
16.	Гуржій А.М. Математичне моделювання стохастичних коливальних
процесів металорізальних верстатів та їх оцінка по статичних критеріях.
Дис... докт. техн. наук. - К.: КПІ, 1995. - 299 с.
17.	Гутер Р.С., Овчинский Б.В. Злементьі численного анализа и
математической обработки результатов опьіта. - М.: Наука, 1970. - 432 с.
18.	Даниленко О.В. Способи формоутворення та верстатне обладнання
для обробки полігональних поверхонь з криволінійними ділянками: Дис...
канд. техн. наук. - К.: КПІ, 1996. - 298 с.
19.	Двайт Г.Б. Таблицьі интегралов и другие математические
601
формули. - М.: Наука, 1983. - 172 с.
20.	Демиденко Е.З. Линейная и нелинейная регрессии. - М.: Финансьі
и статистика, 1981. - 302 с.
21.	Деч Г. Руководство к практическому применеиию преобразования
Лапласа и г-преобразования. - М.: Наука, 1971. - 375 с.
22.	Дьяконов В.П. МаґЬСАВ 8/2000' Специальньїй справочник. -
С-Пб., Москва, Харьков, Минск, 2000. - 590 с.
23.	Диткин В.А, Прудников А.П., Операциошюе нечисленне. - М.:
Вьісшая школа, 1975. - 408 с.
24.	Дьяконов В.П., Абраменкова И.В. МАТЬАВ 5.0/5.3. Система
символьной математики. - М.: Нолидж, 1999. - 633с.
25.	Ермаков С.М. Метод Монте-Карло и смежньїе вопросьі.' - М.:
Наука, 1975.- 471 с.
26.	Ермаков С.М., Михайлов Г.А. Статистические моделирование. -
М.: Наука, 1982. - 520 с.
27.	Жушма В.Б., Корінь Р.К., Мовчан Т.В., Писаренко Ю.В.,
Путилов ТО.В. Хвилькове перетворення: неперервна версія “Сопііпиоиз
хеаееіеі Тгап/огт” // Злектороника и связь. Научно-технический журнал
№ 6. - Т. 2. - К., 1999. - С. 288-301.
28.	Залманзон Л.А. Преобразование Фур’є, Уолша, Хаара и их
применение в управлений связи и других областях. - М.: Наука, 1989. - 496 с.
29.	Зельдович Я. Б., Мьішкис А.Д. З лементи прикладной математики. -
М.: Наука, 1965. - 616 с.
ЗО.	Згуровский М.З., Новиков А.Н. Анализ и управление односторонними
физическими процесами. - К.: Наукова думка, 1996. - 326 с.
31.	Зоммерфельд А. Дифференциальньїе уравнения в частньїх
производньїх. - М.: Иностраиная литература, 1950. - 475 с.
32.	Ісаханов Г.В., Чорний С.М. Чисельні методи розв’язування задач
будівництва. - К.: Вища школа, 1995. - 374 с.
33.	Калиткин Н.Н. Численньїе методи. - МлНаука, 1978. - 512 с.
34.	Ковальов В.Д. Основи теорії розрахунку та проектування
гідравлічних опорних вузлів верстатного устаткування: Дис... докт. техн.
наук. - К.: КПІ, 2001. - 424 с.
35.	Колмогоров А.Н. К обоснованию метода наименьших квадратов /
Успехи математических наук. - 1946. - Т. 1. - Вьш. 1 - С. 57-70.
36.	Коллатц Л.	Функциональньїй анализ	и вьічислительная
математика. - М.: Мир, 1969. - 780 с.
37.	Кочин Н.Е.	Векторнеє нечисленне и	начала тензорного
исчисления. - М.: Изд-во АН СССР, 1961. - 520 с.
38.	Курант Р., Гильберт Д. Методи математической физики. Т. 1. - М.:
Гостехиздат, 1951. - 537 с.
602
39.	Кудинов В.А. Динамика станков. - М.: Машиностроение, 1967. -
360 с.
40.	Кузнєцов Ю.М., Луців І.В., Дубиняк С.А. Теорія технічних систем:
Навчальний посібник. - Тернопіль: ТДТУ, 1997. - 310 с.
41.	Колмогоров А.Н., Фомин С.В. Злементьі теории функций и
функционального анализа. - М.: Наука, 1989. - 624 с.
42.	Корн Г., Корн Т. Справочник по математике для научньїх
работников и инженеров. — М.: Наука, 1973. - 831 с.
43.	Левин А.И. Математическое моделирование в исследованиях и
пректировании станков. - М.: Машиностроение, 1978. - 184 с.
44.	Лойцянский Л.Г. Механика жидкости и газа. - М.: Наука, 1973. -
847 с.
45.	Лаврентьев М.А., Шабат Б.В. Методи теории функций
комплексного переменного. - М.: Наука, 1965. - 673 с.
46.	Лаврентьев М.А., Шабат Б.В. Проблемні гидродинамики и их
математические моделі!. - М.: Финансьі и статистика, 1983. - 304 с.
47.	Мзнли Р. Анализ и обработка зависей колебаний. - М.:
Машиностроение, 1972. - 368 с.
48-	Марпл-мл	С.Л. Цифровой спектральний анализ	и	его
приложения. - М.: Мир, 1990. - 584 с.
49.	Марчук Г.И. Методи вьічислительной математики. - М.: Наука,
1980. - 537 с.
50.	Математика. Большой знциклопедический словарь. - М.: Большая
российская знциклопедия, 2000. - 848 с.
51.	Металлорежущие станки: Учебник / Под ред. В.З. Пуша. - М.:
Машиностроение, 1985. - 256 с.
52.	Мак-Кракен Р., Дорн У. Численньїе методи и программирование на
Фортране. - М.: Мир, 1977. - 584 с.
53.	Мьшікис А.Д. Математика для втузов: Специальньїе курси. - М.:
Наука, 1971. - 520 с.
54.	Натансон И.П. Теория функций вещественной переменной. - М.:
Физматгиз, 1957. - 470 с.
55.	Орликов М.Л. Динамика станков. - К.: Вища школа., 1989. - 272 с.
56.	Очков В.Ф. МаіЬСАВ 7 Рго для сгудентов и инженеров. - М.:
Компьютер Пресе, 1998. - 380 с.
57.	Петренко В.А. Теоретичні основи вдосконалення металорізального
обладнання для тропіків і субтропіків.: Дис... докт. техн. наук. - К.: КПІ,
1999. - 455 с.
58.	Повх И.Л. Техническая гидромеханика. - Л.: Машиностроение,
1969. - 524 с.
59.	Потемкин В.Г. МАТЬАВ: Справочное пособие. - М.: Диалог
603
МИФИ, 1998. - 351 с.
60.	Пугачев В.С. Введение в теорию вероятностей. - М.:Наука, 1968. -
368 с.
61.	Пчельник Б.К. Специальньїе раздельї вьісшей математики. - М.:
Вьісшая школа, 1973. - 464 с.
62.	Плис А.И., Сливина Н.А. МАТНСАВ 2000 математический
практикум для зкономистов и инженеров. - М.: Финансьі и статистика,
2000. - 655 с.
63.	Попович М.Г., Ковальчук О.В. Теорія автоматичного керування. -
К.: Либідь, 1997. - 544 с.
64.	- Потемкин В.Г., Рудаков П.И. МАТЬАВ 5 для студентов. - М.:
Диалог МИФИ, 1999. - 447 с.
65.	Радченко С.Г. Математическое моделирование технологических
процессов в машиностроении. - К.: ЗАО Укрспецмонтажпроект, 1998. - 258 с.
66.	Решетов Д.Н., Портман В.Т. Точность металорежущих станков. -
М.: Машиностроение, 1986. - 336 с.
67.	Саленко О.Ф. Підвищення точності гідрофікованих приводів подач
верстатів з ЧПУ: Дис... канд. техн. наук. - К.: КПІ, 1994. - 247 с.
68.	Самарский А. А. Математическое моделирование - интеллектуальное
ядро информатики. - М.: Наука, 1998. - 244 с.
69.	Сигорский В.П. Математический аппарат инженера. - К.: Техніка,
1975. - 768 с.
70.	Смирнов В.И. Курс вьісшей математики в пяти томах. - М.: Наука,
1967. - 652 с.
71.	Смит Д.М. Математическое и цифровое моделирование для
инженеров и исследователей. - М.: Машиностроение, 1980. - 271 с.
72.	Снеддон И. Преобразования Фурье. - М.: Иностранная литература,
1955. - 580 с.
73.	Струтинський В.Б. Комплексна математична модель детермінованих
та стохастичних динамічних процесів у технічних системах / Вістник
Національного технічного університету України “КІП". Серія
“Машинобудування”. - 1998. - № 33. - С. 115-135.
74.	Струтинський В.Б. Математична модель спектральних характеристик
флуктуацій кутової швидкості шпинделя металорізального верстата / / Вісник
Житомирського інженерно-технологічного інституту. - 1999. - № 9. - С. 5-25.
75.	Струтинський В.Б. Математичне моделювання привода переміщення
стола металорізального верстата, що описується жорсткою системою
диференціальних рівнянь з випадковими коефіцієнтами // Збірник
наукових праць ХДТУ. Високі технології в машинобудуванні. Вип. 2. -
Харків: ХДТУ, 1999. - С. 82-87.
76.	Струтинский В.Б. Развитие и совершенствование злементарной базьі
604
и методов струнного управлення гидроприводом: Дис... докт. техн. наук. -
К.: КНИГА, 1989. - 332 с.
77.	Струтинский В.Б. Расчет характеристик вьісоконапорньїх течений на
основе численного интегрирования уравнений течения идеальной жидкости
// Вестник КПИ. Серия Машиностроение, ВЬШ. 23. - 1986. - С. 35-42.
78.	Струтинский В.Б., Бочаров В.П., Вадах В.Н., Таможний П.П.
Расчет и проектирование устройств гидравлической струйной техники. - К.:
Техника, 1987. - 127 с.
79.	Струтинский В.Б., Бадах В.Н. В помощь лектору и пропагандисту.
Разработка и применение струйньїх устройств с некруглими струями для
авиационного гидропривода. - Общество “Знание” Украинской ССР, 1989. -
37 с.
80.	Струтинский В.Б., Бочаров В.П., Коновалов В.Н. Моделирование
течений в устройствах гидроавтоматики на ЗВМ. - В кп.: Пневматика и
гидравлика. Приводні и системи управлення. Вьт. 13. - М.: Машиностроение,
1987. - С. 46-52.
81.	Струтинский В.Б., Бочаров В.П., Бадах В.Н. Влияние гидромехани-
ческих иараметров в канале на внешние гидравлические характеристики сопл
гидравлических струйньїх злементов. - Вопросьі надежности гидравлических
систем летательньїх аппаратов. - Киев: КНИГА, 1988. - С. 23-28.
82.	Струтинский В. Б., Гейчук В.Н. Методические указания к
лабораторной работе “Определение на ЗВМ характеристик злементарньїх
динамических звеньев систем автоматического управлення станков” по курсу
“Теория автоматического управлення”. - К.: КПИ, 1991. - 32 с.
83.	Струтинский В.Б., Гейчук В.Н., Даниленко А.В., Лепетюк А.Л.
Методические указания к лабораторной работе “Математическое моделирование
гидропривода металлорежущего станка” по курсу “Математическое
моделирование станков и станочньїх комплексов”. - К.: КПИ, 1991. - 28 с.
84.	Струтинский В.Б., Гейчук В.Н., Даниленко А.В., Чикин С.В.,
Протасов С.В. Методические указания к лабораторной работе “Расчет на
ЗВМ частотних характеристик динамической системи токарного станка” по
курсу “Математическое моделирование станков и станочньїх комплексов”. -
К.: КПИ, 1991. - 40 с.
85.	Струтинський В.Б., Гуржій А.М. Математичне моделювання
стохастичних коливальних процесів у динамічній системі токарного верстату
// Тези доповідей П-го міжнародного симпозіуму українських інженерів-
механіків у Львові. - Львів, 1995. - С. 78-85.
86.	Струтинский В.Б., Гуржий А.Н., Лопаткина Н.Н. Математическая
модель случайного процесса позиционирования прецизионного механического
привода // Вестник НТУУ “КПИ” серия “Машиностроение”. - Киев,
1999. - № 32. - С. 44-56.
605
87.	Струтинський В.Б., Гуржій А.М., Лопаткіна Н.Н. Аналіз
стохастичних динамічних процесів у технічних системах методом Монте-
Карло з використанням частотних характеристик // Весник НТУУ “КПИ”.
Серия “Машиностроение”. - С. 108-112.
88.	Струтинський В.Б., Гуржій А.М., Лопаткіна Н.Н. Стохастическая
математическая модель для исследования динамических процессов позиционньїх
приводов металлорежущих станков /,/ Праці міжнародної науково-технічної
конференції, присвяченої 100-річчю механіко-машинобудівного факультету КПІ
“Прогресивна техніка і технологія машинобудування, приладобудування
зварювального виробництва”. - Том 1. - Київ, 1998. - С. 124-129.
89.	Струтинський В.Б., Даниленко О.В., Дем’яненко С.К. Аналіз
точності вертикально-фрезерного верстата з ЧПК // Вестник НТУУ
“КПИ”. Серия “Машиностроение”. - 2000. - № 39. - С. 48-54.
90.	Струтинський В.Б., Даниленко О.В. Визначення динамічних вла-
стивостей пружної системи супорта токарного верстата за допомогою
стохастичної математичної моделі // Вісник Житомирського інженерно-
технологічного інституту. - 1999. - № 10. - С. 22-27.
91.	Струтинський В. Б., Даниленко А. В. Стохастична математична
модель гідравлічного приводу металорізального верстата / / Вестник НТУУ
“КПИ”. Серия “Машиностроение”. - 1999. - № 36. - С. 14-19.
92.	Струтинський В.Б., Кравець А.М., Дем’яненко С.К. Спектральний
аналіз форми поверхні, одержаної при обробці заготовок зі спеціальним
профілем // Вісник Житомирського інженерно-технологічног інституту. -
2000. - № 14. - С. 54-63.
93.	Струтинский В. Б., Лопаткина Н.Н. Расчет статистических
характеристик точности позиционирования прецизионного механического
привода // Вестник НТУУ “КПИ”. Серия “Машиностроение”. - 1999. -
№ 34. - С. 241-247.
94.	Струтинський В.Б., Лопаткіна Н.М. Застосування функціональних
рядів на базі спеціальних функцій для математичного опису мікро- і
макрогеометрії деталей типу тіл обертання / / Вісник Житомирського
інженерно-технологічного інституту. - 1999. - № 10. - С. 13-18.
95.	Струтинский В.Б., Лопаткина Н. Н. Определение точностнмх па-
раметров привода позиционирования металлорежущего станка на основе
стохастической математической модели / / Праці міжнародної науково-технічної
конференції, присвяченої 100-річчю механіко-машинобудівного інституту КПІ
“Прогресивна техніка і технологія машинобудування, приладобудування
зварювального виробництва”. - Том 1. - Київ, 1998. - С. 124-129.
96.	Струтинський В.Б., Петренко В.А. Закономірності виникнення
резонансних режимів під дією випадкових ударних навантажень (статистичні
резонанси) і їх негативний вплив на роботу верстатного обладнання // Вісник
606
Житомирського інженерно-технологічного інституту. - 1998. - № 7. - С. 60-66.
97.	Струтинский В.Б., Петренко В.А. Совершенствование металлорежуще-
го оборудования для торпиков и субтропиков. - Кировоград: КИСМ. - 236 с.
98.	Струтинський В.Б., Саленко О.Ф., Приходько В.П.,
Загорянський Г.М. Математичне моделювання електрогідравлічних приводів
подач верстатів з ЧП: Навчальний посібник для студентів спеціальностей
1201 та 1202 “Технологія машинобудування” та “Металорізальні верстати і
інструмент”. - Кременчук, 1994. - 138 с.
99.	Струтинський В. Б., Саленко О.Ф. Техніка та технологія
гідроструменевої обробки. - К.: ВІПОЛ, 1998. - 252 с.
100.	Струтинский В.Б., Троян И.А. Математическое моделирование
привода зажима заготовки металлорежущего станка / / Вестник КПИ. Серия
“Машиностроение”. Вьш. 31. - 1995. - С. 115-119.
101.	Струтинский В.Б., Турусбеков З.Т. Оценка параметров случайньїх
ударних пагрузок в динамических системах металлорежущих станков //
Вестник НТУУ “КПИ”. Серия “Машиностроение”. - Киев, 1997. - № 32. -
С. 44-47.
102.	Струтинский В.Б , Турусбеков З.Т. Статистические характеристики
случайньїх нагрузок, возникающих в динамической системе токарного
многошпиндельного автомата / / Вестник НТУУ “КПИ”. Серия
“Машиностроение”. - Киев, 1997. - № 32. - С. 98-103.
103.	Струтинський В.Б., Федорец В.А., Новик Н.А. Численний расчет
на ЗВМ характеристик турбулентного течения жидкости в злементах
струйной техники // Вестник КПИ. Серия “Машиностроение”. Вьш. 25. -
1988. - С. 75-82.
104.	Струтинский В.Б., Шевченко А.В., Даниленко А.В., Джаалук Али.
Исследование виброакустических характеристик токарно-винторезньїх
станков // Вестник НТУУ “КШ”. Серия “Машиностроение”. - Киев,
2000. - № 34. - С. 112-121
105.	Струтинский В.Б., Шевченко А.В, Джаалук Али. Расчет параметров
стохастических колебаний токарно-винторезного станка с помощью системні
визуального математического моделирования / / Материальї докладов
научно-технической конференции. Технология машиностроения. Проблеми и
перспективи. - Севастополь, 2000. - С. 70-74.
106.	Струтинський В.Б., Шевченко О.В., Кравець О.М., Джаалук Алі.
Математичне моделювання вібраційних характеристик токарно-гвинторізного верстата
КА-280 на основі імітаційного стохастичного навантаження /,/ Вестник НТУУ
“КШ”. Серия “Машиностроение”. - Киев, 2000. - № 39. - С. 133-146.
107.	Струтинский В.Б., Шевченко А.В., Даниленко А.В , Джаалук Али.
Анализ виброакустических характеристик станков на основе нелинейной
математической модели спектров виброускорений / / Сборник научньїх
607
трудов. Технологи» машиностроения. Проблеми и перспективи. - Донецк:
ДонГУ, 1999. - Вьш. 8. - С. 140-148.
108.	Светлицкая В.А., Стасенко И.В. Сборник задач по теории
колебаний. - М.: Вьісшая школа, 1973. - 454 с.
109.	Тимошенко С.П., Янг Д.Х., Уивер У. Колебанпя в инженерном
деле: Пер. с англ. Л.Г. Корнейчука. - М.: Машиностроение, 1985. - 472 с.
110.	Трантер Д. Интегральние преобразования в математической
физике. - М.: Гостехиздат, 1956. - 460 с.
111.	Тихонов А.Н., Арсенин В.Я. Методи решения некорректньїх задач:
Учебное пособие для ВУЗов. - М.: Наука, 1986. - 299 с.
112.	Тихонов А.Н., Кальнер В.Д., Гласко В.Б. Математическое
моделирование технологических процессов и метод обработки задач в
машиностроении. - М.: Машиностроение, 1990. - 264 с.
113.	Фам Тхань Там. Совершенствование токарно-револьверного станка
путем снижения динамических нагрузок на шпиндельний у зел: Дис... канд.
техн. наук. - К.: КПИ, 1996. - 175 с.
114.	Фихтенгольц Г.М. Курс диффереициального и интегрального
исчисления. Т. І—III. - М.: Наука, 1969. - 675 с.
115.	Форсайт Дж., Малькольм М., Маулер К. Машинньїе методи
математических вичислений. - М.: Мир, 1980. - 455 с.
116.	Федорець В.О., Педченко М.Н., Струтинський В.Б., Федорець О.О.,
Яхно О.М., Єлісєєв Ю.В. Технічна гідромеханіка, гідравліка та
гідропневмопривод: Підручник. - Житомир: ЖІТІ, 1998. - 412 с.
117.	Ферстер 3., Ренц Б. Методи корреляционного и регрессионного
аиализа. Руководство для зкономистов: Пер. с ием. и предисл.
В.М. Ивановой. - М.: Финансьі и статистика, 1981. - 302 с.
118.	Хемминг Р.В. Численньїе методи. - М.: Наука, 1972. - 540 с.
119.	Шефтель З.Г. Теорія ймовірностей. - К.: Вища школа, 1994. - 192 с.
120.	Шорнії С.Н. Теплопередача. - М.: Вьісшая школа, 1964,- 490 с.
121.	Зрнани Фернандеш Манузль Исследования технологического
процесса вибротермической обработки деталей из литейньїх сплавов
алюминия: Дис... канд. техн. наук. - К.: КПИ, 1994. - 182 с.
122.	Янке Е., Змде Ф., Леш Ф. Специальньїе функции (формули,
графики, таблицьі). - М.: Наука, 1968. - 670 с.
608
ЗМІСТ
Вступ ..........................................   .	.	. .	. З
Розділ 1. Основні поняття та визначення..................................... 5
1	1. Технічні системи та їх робочі процеси.............................. 5
1	2 Математичні моделі процесів та систем............................... 9
Розділ 2. Математичні моделі процесів на основі символьних функціональних
залежностей...........................................................   19
2	1. Обчислення та перетворення символьних функціональних залежностей 19
2 11. Обчислення залежностей засобами пакету МаїЬСАО............... 19
2.12 Побудова та аналіз плоских графіків	....	26
2 1 3. Побудова об’ємних графіків поверхонь та діаграм ....	31
2 2 Символьні залежності із диференціальними операціями	...	36
2 2 1 Символьні диференціювання та інтегрування . .	. .	36
2 2.2. Дослідження процесів з використанням диференціальних
операцій........................................................... 42
2 2 3 Диференціальні оператори поля .	...	...... 54
2	3. Символьні моделі процесів у вигляді спеціальних функцій .	.	64
2.3.1 Елементарні трансцендентні та спеціальні функції ...	64
2.3.2. Інтегральні функції гамма-функція та зв’язані з нею функції	69
2.3.3. Функції Бесселя ...	. .	.	.	73
2.3 4. Ортогональні поліноми .	.	....... 80
2 3 5 Типові розривні функції ....	...	.	. .	84
2.3.6 Символічні імпульсні функції...............................   93
Розділ 3. Система 8ІМІЛЛМК для моделювання процесів та систем .	99
З	1. Загальна характеристика системи................................... 99
З 1.1. Принципи побудови системи, приклади 8-моделей	99
3.1	2. Бібліотека модулів (блоків) 81М11ИИК ...	.	...	104
3.2	Основні розділи бібліотеки, характеристика модулів . .	. .	105
3 2 1. Зошсез - вхідні модулі (джерела)	.	.	....	105
З 2.2 Розділ 8іпкк - вихідні модулі (отримувачі) ....	107
3 2 3 Сопііпиоиз - аналогові блоки ....	........... 109
З 2 4. Вічсгеїе та ЕипсНопз & ТаЬІез - дискретні модулі, функції та
таблиці................................... .	.	..... 113
З 2.5. МаІЬ - модулі для реалізації математичних операцій ....	116
З 2 6. Попііпеаг - модулі, що реалізують нелінійні функції . .	119
З 2.7 ЗфііаІ & Зузіет - модулі для формування структури системи 122
3.2.8 Сопігої 8уДет ТооІЬох, ЗіаЬеПоіу та Зіпіиііпк Ехігаз - модулі
зв’язку між системами, візуалізація процедури моделювання і а
модулі обробки сигналів.......................... ...	.	129
Розділ 4. Математичні моделі процесів у вигляді функціональних рядів .	131
4	1. Числові послідовності, функціональні ряди ....	....... .	131
4 11. Визначення числових послідовностей та функціональних рядів .	131
4 12 Ряди Тейлора та Маклорена ....	........ . .	135
609
4 13. Ряди, складені з функцій Бесселя ...	............... 138
4.2 Особливі властивості рядів Фур’є............................ .	140
4 2.1. Ряди Фур’є. Загальні положення . .	....................... 140
4.2 2. Ряди Фур’є для розривних функцій Явище Гібса ...	. .	149
1.2 3 Некоректно поставлені задачі щодо нескінченного ряду Фур’є та
їх регуляризації...........................................   157
4.3 Застосування рядів Фур’є при аналізі процесів у технічних системах . .	162
4 3.1. Гармонічний аналіз процесів.......................... ...	162
4.3.2 Спектральний аналіз процесів................................. 176
Розділ 5. Операторні математичні моделі, визначені в лінійному просторі . . .	192
5.1. Елементи теорії лінійних операторів................................ 192
5.1.1 Відношення еквівалентності, лінійний простір, базис ...	192
5 1.2 Лінійні оператори та їх характеристики .	..."	200
5 2 Операції з векторами і матрицями в пакеті МаїЬСАВ................... 204
5.2 1. Алгебраїчні операції з векторами і матрицями ............... 204
5.2.2. Вбудовані функції пакету МаіЬСАВ для роботи з матрицями та
векторами................................................     218
Розділ 6. Дискретні математичні моделі процесів............................ 232
6.1 Формування дискретних математичних моделей . .	........... 232
6 1.1 Знаходження дискретних множин значень неперервного процесу 232
6.1 2 Дискретизація процесів з розривами або особливостями типу
дельта-функції...................................................... 239
6.2 Аналіз дискретних моделей шляхом інтеї ральшіх перетворень .. .	.	.248
6 2.1 Дискретне перетворення Фур’є . .	. .	.	........ 248
6.2.2. Дискретне перетворення Лапласа, г-перетворения, хвилькове
(^ауеІеО перетворення .	.	....	.... 252
6.3 Аналіз і синтез дискретних модельних процесів ...................... 255
6.3 1. Процеси у вигляді числових послідовностей ............. ...	255
6.3.2. Ступінчасті та імпульсні дискретні процеси ....	........ 258
Розділ 7. Знаходження символьних математичних моделей за дискретними
моделями процесів........................................ .	.	. .	264
7	.1 Інтерполяція та екстраполяція засобами пакету МаїЬСАВ ...	. .	264
7.1.1.	Лінійна та поліноміальна інтерполяція.................. ...	264
7	1.2. Інтерполяція сплайнами . .	.................. .	.	272
7.1.3.	Прогнозування параметрів процесів методом екстраполяції . . .	280
7	2 Апроксимація дискретних множин значень процесу.........	.	. .	287
7.2.1. Принципи і критерії апроксимації Метод найменших квадратів .	287
7 2 2. Розробка лінійних математичних моделей ...	.	295
7 2 3 Нелінійні математичні моделі дискретних процесів . .	.	308
Розділ 8. Математичні моделі простих механічних коливальних систем	. .	315
8	і. Визначення прогинів та критичної частоти обертання пружних
протяжних деталей з розподіленою масою ...	............ 315
8.2	. Розрахунок параметрів високочастотних коливань гільзи шпинделя
координатно-розточувального верстата..................................   321
8.3	Розрахунок параметрів коливань гнучких масивних протяжних тіл із
610
розподіленою масою .	...... ...	. .	326
8 4 Поперечні коливання стрижнів із розподіленою масою без врахування
втрат енергії................................. ....	331
8 5 Коливання круглої мембрани ....	....	338
8 6 Математичне моделювання позиційних приводів металорізальних верстатів
з використанням символьної математичної моделі ...	...	342
Розділ 9. Математичні моделі прогресивних технологічних процесів
механічної та фізико-технічної обробки деталей ....	...	355
9.1	Математичний опис мікро- і макроіеометрії деталей типу тіл обертання .	355
9.2	. Спектральний аналіз форми поверхні, одержаної в результаті обробки
на т окарному верстаті .	.	.	.......... .	.	363
9 3 Дискретизована математична модель для визначення ефективності процесу
обробки поверхонь інструментом інтегральної дії .................. 379
9.4 Дискретна математична модель процесу вібраційної обробки деталей	391
Розділ 10. Математичні моделі складних інженерно-фізичних процесів ...	415
10.1. Застосування функції похибок для моделювання окремих задач
гідромеханіки, теплопередачі та дифузії.......	............ 415
10 2. Математичне моделювання пристрою формування струменя води для
отримання металевого порошку із розплавленого струменя металу	427
10 3 Застосування рядів із спеціальних функцій лрп моделюванні задач
гідравліки і теплофізики	.	436
Розділ 11. Символьні та дискретні моделі турбулентного руху рідини . .	445
11 1 Знаходження символьних математичних моделей векторного поля
просторового турбулентного струменевого потоку за результатами
експериментальних вимірів ...	...	445
11.2. Математичні моделі процесів переносу у вигляді дискретних множин
значень інтегральних параметрів	461
11 3 Дискретизована математична модель відхилення просторового
турбулентного струменя .....	.	474
Розділ 12. Математичне моделювання динамічних коливальних процесів .	489
12.1 Символьна комплексна математична модель детермінованих та
стохастичних процесів у динамічних системах . .	...	489
12 2 Спектральні характеристики стохастичних динамічних ударних
навантажень в ланцюговій крутильній системі привода головного руху
верстата .	. .	...	....	.	. .	.	512
12 3. Структурна математична модель динамічної системи шпиндельно-
супортної групи верстата . .	. .	.	.	531
12 4 Аналіз стохастичних процесів в динамічній системі верстата з
використанням структурної математичної моделі ...	. .	551
 12 5 Теоретичне узагальнення експериментально визначених спектральних
характеристик стохастичних динамічних процесів верстатів . .	575
Література ....	. .	. .	...	.......... .	.601
611
Василь Борисович Струтинський
МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ ПРОЦЕСІВ
ТА СИСТЕМ МЕХАНІКИ
Підручник
Редактор
Комп'юіерний набір та верстка
Макетування
Кушнірук Л. О.
Мясникова Н.Л.
Кушнірук Л. О.
Кондратенко В. В.
Підписано до друку 06 11 2001 р Формат 70x100 1 /16. Папір офсетний. Гарнітура РегеїЬигф
Ум. друк арк 64,42. Наклад 1000 скз Зам./&ІЧ9
Житомирський шжснерію-техно логічний інститут
10005, м Житомир, вуд Черпяховського, 103