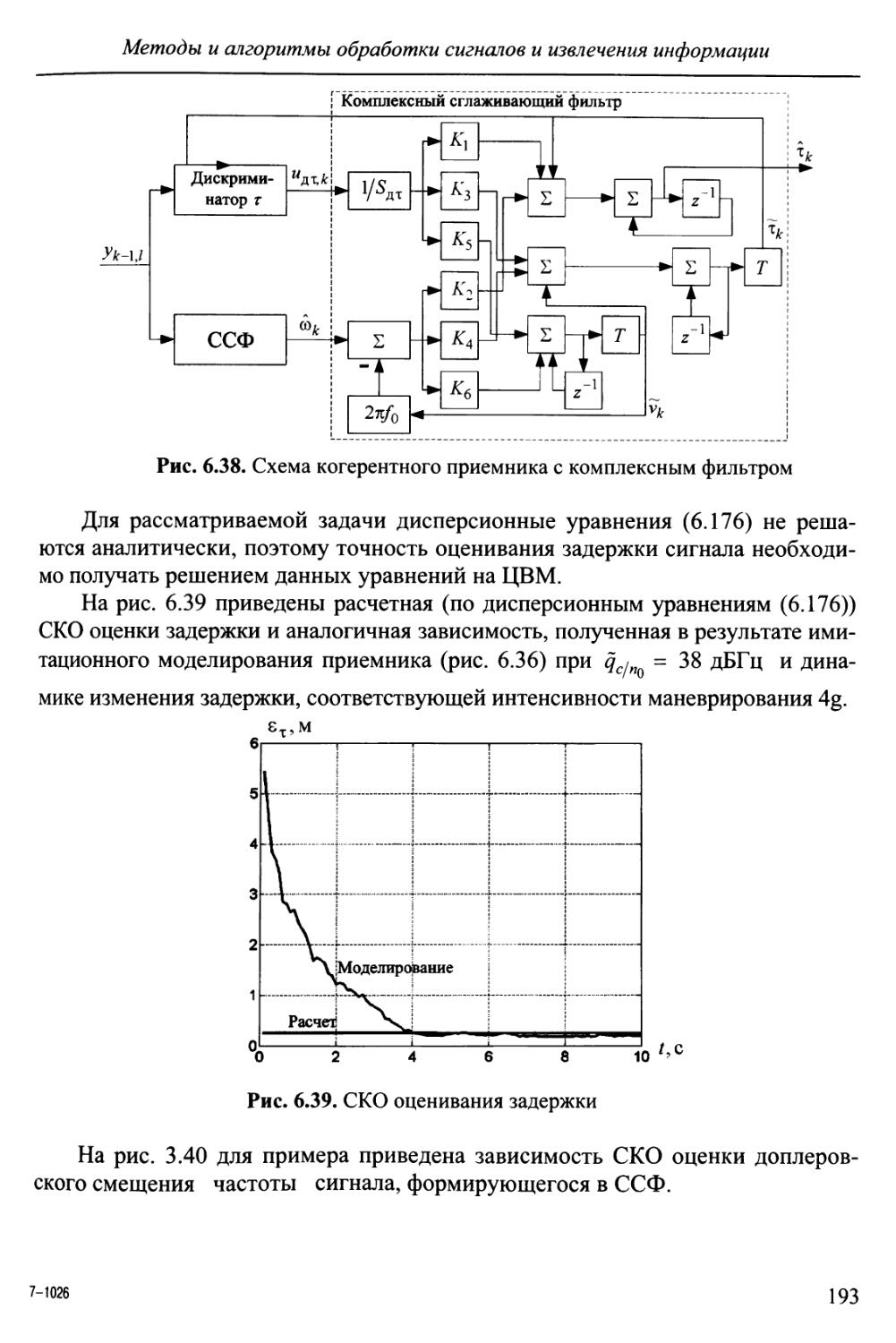
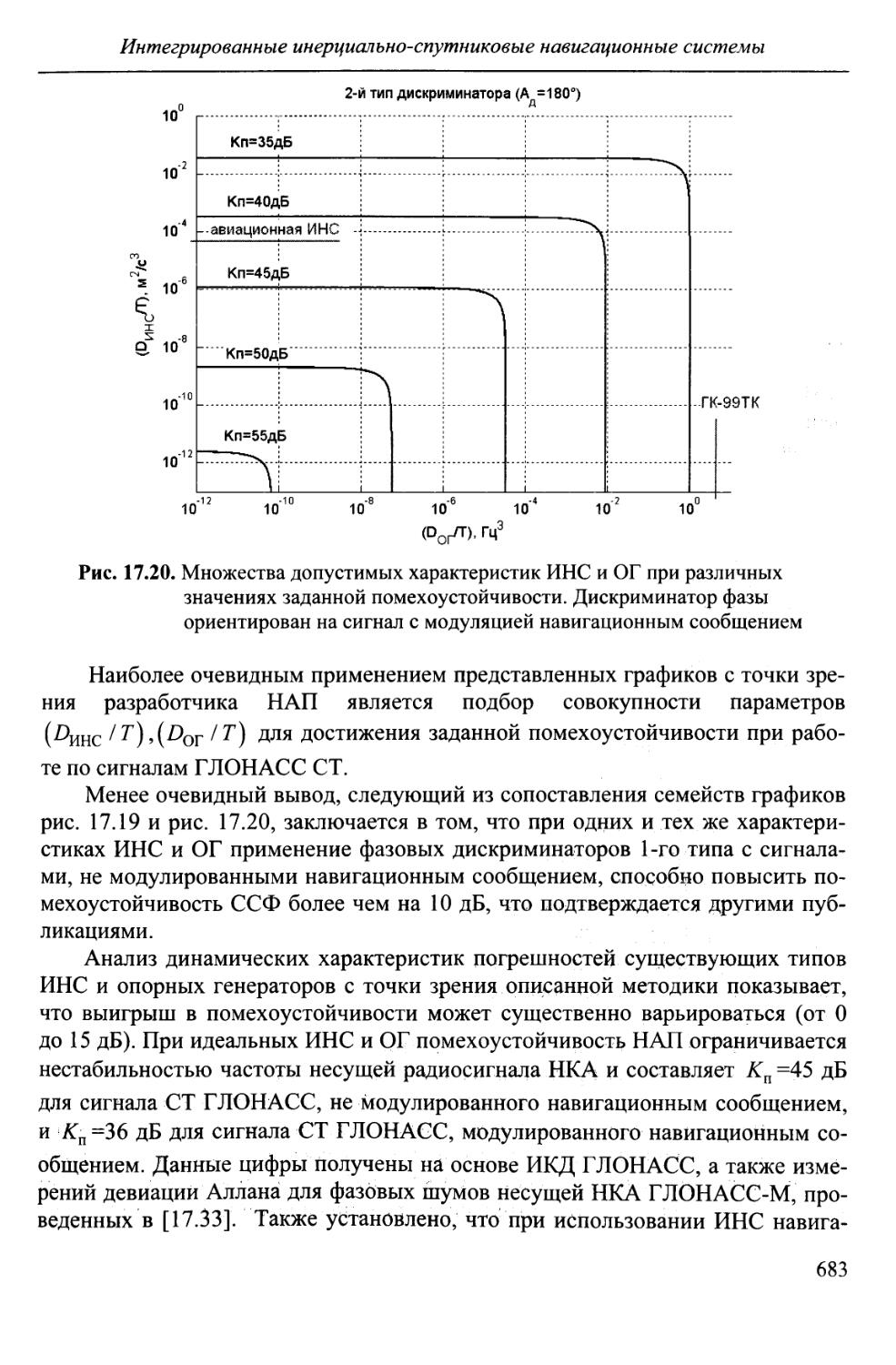
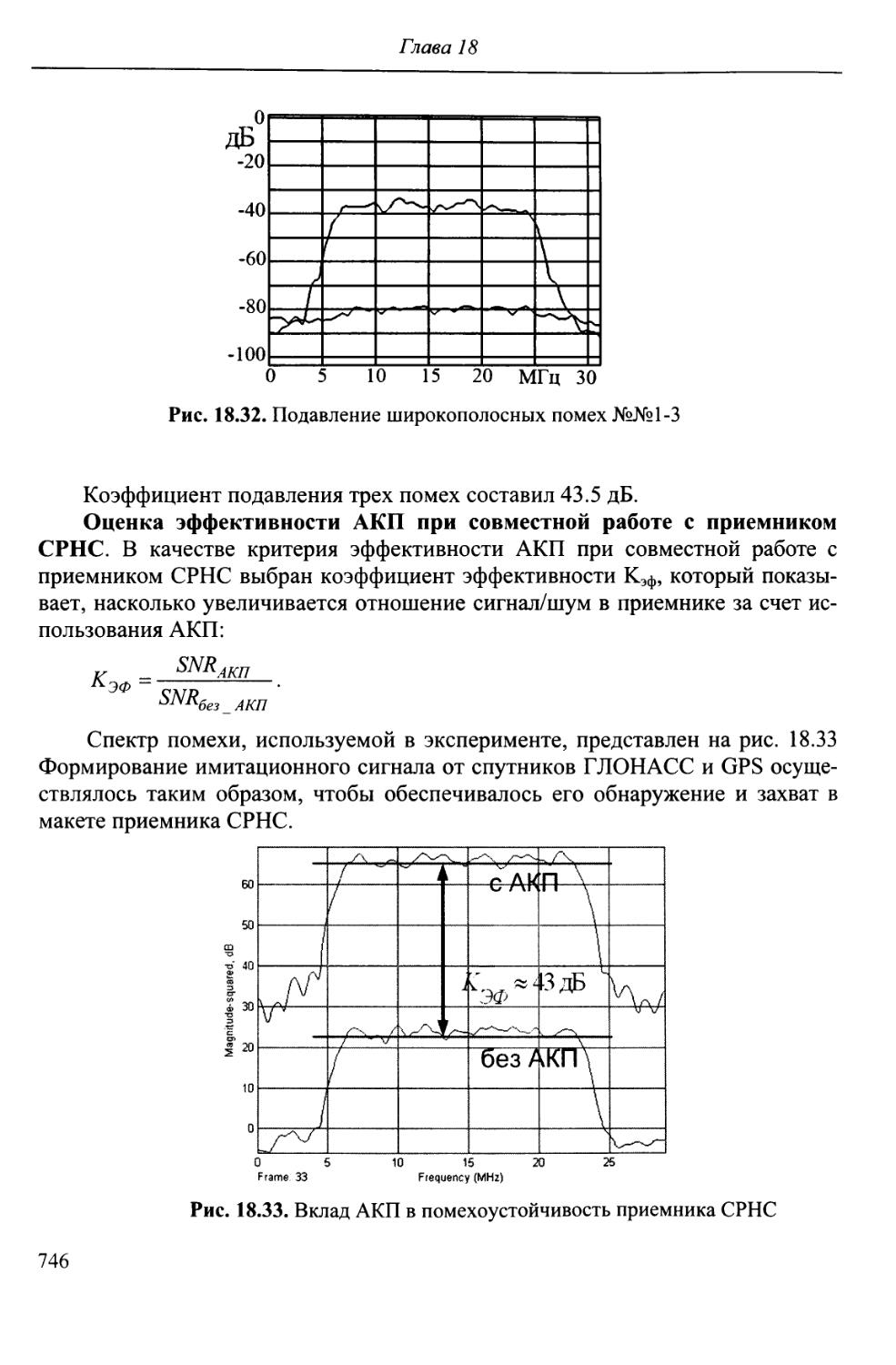
Author: Перова А.И. Харисов В.Н.
Tags: авиация и космонавтика летательные аппараты ракетная техника космическая техника междупланетные соединения (междупланетные полеты) космонавтика (аэронавтика) искусственные спутники глонасс
ISBN: 978-5-88070-251-0
Year: 2010
▲
принципы построения и функционирования
'¥ ?
РАДИОТЕХНИКА
ГЛОНАСС
принципы построения и функционирования
Издание четвертое
перераб. и доп.
Под редакцией
А И. Перова, В. К Харисова
Издательство «Радиотехника»
Москва, 2010
УДК 629.78
Г63
ББК 39.67
Авторы:
Р.В. Бакитько, Е.Н. Болденков, Н.Т. Булавский, В.В. Дворкин, B.C. Ефи-
менко, В.Е. Косенко, В.Я. Нартов, А.И. Мерой, А.Е. Перьков, В.В. Тюбалин,
Ю.М. Урличич, В.Н. Харисов, В.Е. Чеботарев, А.Ю. Шатилов
Г63 ГЛОНАСС. Принципы построения и функционирования / Под ред. А.И.
Перова, В.Н. Харисова. Изд. 4-е, перераб. и доп. - М: Радиотехника, 2010. 800 с, ил.
ISBN 978-5-88070-251-0
Изложены принципы построения спутниковой радионавигационной системы (СРНС)
ГЛОНАСС, даны ее системные характеристики и основные характеристики подсистем
космических аппаратов, наземного контроля и управления, навигационной аппаратуры потребителей,
а также дифференциальных дополнений СРНС. По сравнению с предыдущим изданием
существенно переработан материал по направлениям совершенствования технологий
спутниковой навигации с учетом новых перспектив по введению сигналов с кодовым разделением и
материал по интегрированным инерциально-спутниковым навигационным системам. Добавлены
материалы по использованию сигналов СРНС для определения угловой ориентации объектов и
частотно-временной режекции узкополосных помех в аппаратуре потребителей, а также приему
сигналов в условиях многолучевости, быстрому поиску сигналов и результаты последних
исследований в области пространственно-временной обработки навигационных сигналов,
принимаемых на фоне пространственно распределенных помех.
Для широкого круга специачистов, занимающихся разработкой, производством и
эксплуатацией аппаратуры потребителей СРНС ГЛОНАСС. Может быть полезна студентам,
аспирантам и преподавателям высших учебных заведений при изучении дисциплин
радиотехнического профиля.
УДК 629.78
ББК 39.67
ISBN 978-5-88070-251-0
© Авторы, 2010
О Издательство «Радиотехника», 2010
ПРЕДИСЛОВИЕ
(к четвертому изданию)
Спутниковые радионавигационные системы (СРНС), наряду с системами
мобильной связи, стали неотъемлемой частью человеческой деятельности.
Технологии спутникового координатно-временного обеспечения используются
в различных технических системах, быту, науке и образовании, в экономике и
т.д. Для реализации потребностей в высокоточном координатно-временном
обеспечении разработаны, созданы и введены в эксплуатацию СРНС
ГЛОНАСС (Россия), GPS (США), а в настоящее время разрабатываются
аналогичные системы GALILEO (Европейский Союз), Compass (Китай).
Важность проблем глобального координатно-временного обеспечения
регулярно подчеркивается руководством России. Принято Постановление
Правительством Российской Федерации от 9 июня 2005 г. № 365 «Об оснащении
космических, транспортных средств, а также средств, предназначенных для
выполнения геодезических и кадастровых работ, аппаратурой спутниковой
навигации ГЛОНАСС или ГЛОНАСС/GPS», издан Указ Президента РФ от 17 мая
2007 г. № 638 «Об использовании глобальной навигационной спутниковой
системы ГЛОНАСС в интересах социально-экономического развития РФ», а во
исполнение этого указа Правительство РФ выпустило Постановление от 30
апреля 2008 г. № 323 об утверждении Положения о полномочиях федеральных
органов исполнительной власти по поддержанию, развитию и использованию
ГЛОНАСС, принято Постановление Правительства Российской Федерации от
25 августа 2008 г. № 641 "Об оснащении транспортных, технических средств и
систем аппаратурой спутниковой навигации ГЛОНАСС или ГЛОНАСС/GPS".
В феврале 2008 г. в РФ принята «Концепция развития навигационных сигналов
глобальной навигационной системы ГЛОНАСС», в которой определена
необходимость совершенствования системы ГЛОНАСС.
Учитывая сказанное, понятен постоянно возрастающий интерес к основам
и принципам построения СРНС. Поэтому редакторы и авторы издания книги
«ГЛОНАСС. Принципы построения и функционирования» [В.1] решили
подготовить очередное (четвертое) издание книги, переработав и дополнив его рядом
новых разделов.
Книга состоит из введения и трех разделов основного материала,
разделенных на 19 глав.
Во вводной части содержатся исторические сведения о СРНС ГЛОНАСС,
характеризующие этапы развития технологий спутниковой навигации.
В разделе 1 (гл. 1—8) помещены материалы, описывающие общие
принципы построения СРНС; законы орбитального движения искусственных
спутников Земли; шкалы времени, используемые в СРНС и принципы их
синхронизации; методы решения навигационных задач; используемые радиосигналы и
навигационные сообщения, передаваемые в них; принципы построения прием-
3
Предисловие
ников сигналов СРНС. Дополнены главы по перспективным навигационным
сигналам, оптимальным алгоритмам обработки сигналов и информации в
приемнике. Существенно расширена глава по помехоустойчивости аппаратуры
потребителей.
В разделе 2 (гл. 9—13) изложены конкретные сведения о структуре и
основных характеристиках СРНС ГЛОНАСС и ее подсистем. Дано подробное
описание подсистемы космических аппаратов, наземного сегмента и
аппаратуры потребителей. Расширено описание бортовой аппаратуры навигационных
спутников, в которое включено описание моделей навигационных спутников и
бортовой аппаратуры межспутниковых измерений.
В разделе 3 (гл. 14—19) рассмотрены вопросы развития СРНС ГЛОНАСС
в части перспектив модернизации навигационной системы и излучаемых
сигналов, в том числе с кодовым разделением. Добавлена новая глава по
использованию сигналов СРНС для определения угловой ориентации объектов.
Существенно переработаны главы по интегрированию аппаратуры спутниковой и
инерциальной навигации и по принципам построения и алгоритмам обработки
сигналов в адаптивных антенных решетках для приемников спутниковой
навигации. Добавлена глава по методам и алгоритмам частотно-временной режек-
ции узкополосных помех.
В книге принята нумерация рисунков и формул по главам. Список
литературы приведен в конце каждой главы и включает только те источники, на
которые даны ссылки в тексте.
Предполагается, что материалы книги могут быть использованы при
подготовке других изданий (учебников для высших и средних специальных
учебных заведений, справочников, руководств по эксплуатации, технических
описаний аппаратуры), при разработке вопросов взаимодействия аппаратуры
потребителей и других технических средств подвижных объектов, при отработке
планов радионавигационного обеспечения стран и регионов, постановке курсов
лекций в системе учебных заведений и программ повышения квалификации
специалистов.
Книга рассчитана на специалистов в области навигации и смежных
дисциплин таких, как штурманское обеспечение, геодезия и картография,
землеустройство, мониторинг земной поверхности; аспирантов и студентов
соответствующих высших и средних учебных заведений.
В написании книги участвовали: Р.В. Бакитько (п. 11.7, 14.1—14.2);
Е.Н. Болденков (п. 6.2, гл. 19), Н.Т. Булавский (п. 6.6, гл. 15); В.В. Дворкин
(п. 12.8.2, 14.3); B.C. Ефименко (гл. 18); В.Е. Косенко (п. 11.6, 11.7); В.Я. Нартов
(гл. 9, 10); А.И.Перов (гл. 1—5, 7—13, 16, 17, 19, п. 6.1—6.5, 11.1—11.5, 11.7,
12.1—12.7, 14.1—14.2); А.Е. Перьков (п. 15.2—15.4); В.В. Тюбалин (п. 9.3,
11.1—11.5, п. 14.1); Ю.М. Урличич(п. 11.7, 12.8.2, 14.1—14.3); В.Н. Харисов (гл.
6,8, 15, 18); В.Е. Чеботарев (п. 11.6, 11.7); А.Ю. Шатилов (п. 16.1—16.2, гл. 17).
Редактирование книги выполнено А.И. Перовым, В.Н. Харисовым.
4
Методы решения навигационных задач
В организации работы и подготовке материалов книги активное участие
приняли следующие организации: кафедра автоматизированных систем
радионавигации и радиосвязи ВВИА им. проф. Н.Е. Жуковского; кафедра
радиотехнических систем Московского энергетического института (технического
университета); ОАО «Российские космические системы».
Авторы будут признательны читателям за предложения и замечания по
улучшению содержания книги, которые следует направлять по адресу: 103031,
Москва, Кузнецкий мост, д. 20/6. Изд-во «Радиотехника». E-mail:
info@radiotec.ru — Радиотехника; alexp@aha.ru — Перов А.И.; vhar@list.ru —
Харисов В.Н.
Авторы
5
ВВЕДЕНИЕ я
Исторические сведения
Материалы данного раздела во многом заимствованы из [В.2].
4 октября 1957 г. в Советском Союзе был запущен первый в истории
человечества искусственный спутник Земли (ИСЗ) [В.2, В.З]. Измерения доплеров-
ского сдвига частоты передатчика этого ИСЗ на пункте наблюдения с
известными координатами позволили определить параметры движения этого
спутника [В.З]. Решение обратной задачи, т.е. определение координат пункта приема
сигнала, излученного с ИСЗ с известными координатами, по измерениям доп-
леровского сдвига принятого сигнала положило начало развитию спутниковых
радионавигационных систем (СРНС) [В.З, В.4].
Как свидетельствует [В.4], первое научно обоснованное предложение об
использовании ИСЗ для навигации родилось в Ленинграде еще до запуска
первого советского ИСЗ, в период проведения под руководством профессора
B.C. Шебшаевича в Ленинградской военно-воздушной инженерной академии
(ЛВВИА) им. А.Ф. Можайского в 1955—1957 гг. исследований возможностей
применения радиоастрономических методов для самолетовождения.
Материалы исследований докладывались в октябре и декабре 1957 г. на
межведомственной конференции и семинаре [В.5].
Научные основы низкоорбитальных СРНС были существенно развиты в
процессе выполнения исследований по теме «Спутник» (1958—1959 гг.),
которые осуществляли ЛВВИА им. А.Ф. Можайского, Институт теоретической
астрономии АН СССР, Институт электромеханики АН СССР, два морских НИИ
и Горьковский НИРФИ. Работы проводились с участием крупных
специалистов по аналитической механике (чл.-корр. АН СССР А.И. Лурье) и расчетам
орбит (проф. П.Е. Эльясберг). В коллективах этих организаций по проблеме
активно работали Ю.В. Батраков, Е. Д. Голиков, В.П. Заколодяжный, Э.А. Жи-
жемский, М.М. Кобрин, А.А. Колосов, Л.И. Кузнецов, В.Ф. Проскурин,
А.Н. Радченко, Н.К. Сергеев, Б.А. Смольников, Е.Ф. Суворов, В.А. Фуфаев,
Г.И. Черепанов, Е.П. Чуров, В.И. Юницкий и др. [В.З]. Основное внимание при
этом уделялось вопросам повышения точности навигационных определений,
обеспечения глобальности, круглосуточности применения и независимости от
погодных условий.
Проведенные работы позволили перейти в 1963 г. к
опытно-конструкторским работам над первой отечественной низкоорбитальной системой,
получившей в дальнейшем название «Цикада».
В создании этой системы приняли участие: Научно-производственное
объединение прикладной механики (НПО ПМ) — головная организация по систе-
6
Введение
ме в целом и по разработке навигационных спутников (НС); Российский
научно-исследовательский институт космического приборостроения (РНИИ КП) —
головная организация по радиотехническому комплексу системы, разработке
бортовой космической и наземной радиотехнической аппаратуры, а также
бортовой аппаратуры морских судов; Российский институт радионавигации и
времени (РИРВ) — разработчик бортовой космической аппаратуры
синхронизации и навигационной аппаратуры ряда типов морских судов, а также другие
предприятия космической, радиотехнической и судостроительной отраслей
промышленности СССР.
Генеральный конструктор космических систем навигации и связи
академик М.Ф. Решетнев в 1992 г. описал в [В.2] следующие этапы развития СРНС.
«Полномасштабные работы по созданию отечественной навигационной
спутниковой системы были развернуты в середине 60-х годов, а 27.11.1967
года был выведен на орбиту первый навигационный отечественный спутник
(«Космос-192»). Спутник и ракета-носитель были разработаны и изготовлены
Красноярским научно-производственным объединением прикладной механики.
Навигационный спутник обеспечивал непрерывное в течение всего
времени активного существования излучение радионавигационного сигнала на
частотах 150 и 400 МГц. Среднеквадратическая погрешность местоопределения по
этому спутнику составляла 250.. .300 м.
В 1979 г. была сдана в эксплуатацию навигационная система 1-го
поколения «Цикада» в составе четырех НС, выведенных на круговые орбиты высотой
1000 км, наклонением 83° и равномерным распределением плоскостей орбит
вдоль экватора. Она позволяет потребителю в среднем через каждые 1,5...2 ч
входить в радиоконтакт с одним из НС и определять плановые координаты
своего места при продолжительности навигационного сеанса до 5.. .6 мин.
В ходе испытаний было установлено, что основной вклад в погрешность
навигационных определений вносят погрешности передаваемых спутниками
собственных эфемерид, которые определяются и закладываются на спутники
средствами наземного комплекса управления. Поэтому, наряду с
совершенствованием бортовых систем спутника и
корабельной приемоиндикаторной аппаратуры, разработчиками системы
серьезное внимание было уделено вопросам повышения точности определения и
прогнозирования параметров орбит навигационных спутников.
Была отработана специальная схема проведения измерений параметров
орбит средствами наземно-комплексного управления, разработаны методики
прогнозирования, учитывающие все гармоники в разложении геопотенциала.
Большой вклад в повышение точности эфемерид навигационных
спутников внесли результаты работ по программе геодезических и геофизических
исследований с помощью специальных геодезических спутников «Космос-842» и
«Космос-911», которые были выведены на навигационные орбиты.
7
Это позволило уточнить координаты измерительных средств и вычислить
коэффициенты согласующей модели геопотенциала, предназначенной
специально для определения и прогнозирования параметров навигационных орбит. В
результате точность передаваемых в составе навигационного сигнала
собственных эфемерид была повышена практически на порядок и составляет в
настоящее время на интервале суточного прогноза примерно 70...80 м, а средне-
квадратическая погрешность определения морскими судами своего
местоположения уменьшилась до 80... 100 м.
Для оснащения широкого класса морских потребителей разработаны и
серийно изготавливаются комплектации приемоиндикаторной аппаратуры
«Шхуна» и «Челн». Последняя имеет возможность работы и по спутникам
американской радионавигационной системы «Транзит».
В дальнейшем спутники системы «Цикада» были дооборудованы
приемной измерительной аппаратурой обнаружения терпящих бедствие объектов,
которые оснащаются специальными радиобуями, излучающими сигналы
бедствия на частотах 121 и 406 МГц. Эти сигналы принимаются спутниками
системы «Цикада» и ретранслируются на специальные наземные станции, где
производится вычисление точных координат аварийных объектов (судов,
самолетов и др.).
Дооснащенные аппаратурой обнаружения терпящих бедствие спутники
«Цикада» образуют систему «Коспас». Совместно с американо-фран-ко-
канадской системой «Сарсат» они образуют единую службу поиска и спасения,
на счету которой уже несколько тысяч спасенных жизней.
Успешная эксплуатация низкоорбитальных спутниковых навигационных
систем морскими потребителями привлекла широкое внимание к спутниковой
навигации. Возникла необходимость создания универсальной навигационной
системы, удовлетворяющей требованиям всех потенциальных потребителей.
Выполнить требования всех классов потребителей низкоорбиталь-ные
системы в силу принципов, заложенных в основу их построения, не могли.
Перспективная спутниковая навигационная система должна была обеспечивать
потребителю в любой момент времени возможность определять три
пространственные координаты, вектор скорости и точное время. Для получения
потребителями трех пространственных координат беззапросным методом требуется
проведение измерений навигацион-ного параметра не менее чем до четырех
спутников, при этом одно-временно с тремя координатами местоположения
потребитель опреде-ляет расхождение собственных часов относительно шкалы
времени спутниковой системы.
Исходя из принципа навигационных определений, выбрана структура
спутниковой системы, которая обеспечивает одновременную в любой момент
времени радиовидимость потребителей, находящимся в любой точке Земли, не
менее четырех спутников, при минимальной общем их количестве в системе.
Это обстоятельство ограничило высоту орбиты навигационных спутников 20
8
Введение
тыс. км (дальнейшее увеличение высоты не ведет к расширению зоны
радиообзора, а следовательно, и к уменьшению необходимого количества спутников в
системе). Для гарантированной видимости потребителем не менее четырех
спутников, их количество в системе должно составлять 18, однако оно было
увеличено до 24-х с целью повышения точности определения собственных
координат и скорости потребителя путем предоставления ему возможности
выбора из числа видимых спутников четверки, обеспечивающей наивысшую
точность.
Одной из центральных проблем создания спутниковой системы,
обеспечивающей беззапросные навигационные определения одновременно по
нескольким спутникам, является проблема взаимной синхронизации спутниковых
шкал времени с точностью до миллиардных долей секунды (наносекунд),
поскольку рассинхронизация излучаемых спутниками навигационных сигналов в
10 не вызывает дополнительную погрешность в определении местоположения
потребителя до 10... 15 м.
Решение задачи высокоточной синхронизации бортовых шкал времени
потребовало установки на спутниках высокостабильных бортовых цезиевых
стандартов частоты с относительной нестабильностью 110 и наземного
водородного стандарта с относительной нестабильностью ЬЮ-14, а также
создания наземных средств сличения шкал с погрешностью 3...5 не.
С помощью этих средств и специального математического обеспечения
производится определение расхождений бортовых шкал времени с наземной
шкалой и их прогнозирование для каждого спутника системы. Результаты
прогноза в виде поправок к спутниковым часам относительно наземных
закладываются на соответствующие спутники и передаются ими в составе цифровой
информации навигационного сигнала. Потребителями, таким образом,
устанавливается единая шкала времени. Расхождение этой шкалы с наземной
шкалой времени системы не превышает 15...20 не.
Второй проблемой создания высокоорбитальной навигационной системы
является высокоточное определение и прогнозирование параметров орбит
навигационных спутников.
Достижение необходимой точности эфемерид навигационных спутников
потребовало проведения большого объема работ по учету факторов второго
порядка малости таких, как световое давление, неравномерность вращения
Земли и движение ее полюсов, а также исключение действия на спутник в
полете реактивных сил, вызванных негерметичностью двигательных установок и
газоотделением материалов покрытий.
Для экспериментального определения параметров геопотенциала на
орбиты навигационных спутников были запущены два пассивных ИЗС «Эталон»
(«Космос-1989» и «Космос-2024»), предназначенных для измерения
параметров их движения высокоточными квантово-оптическими измерительными
средствами. Благодаря этим работам достигнутая в настоящее время точность
9
эфемерид навигационных спутников при прогнозе на 30 ч составляет: вдоль
орбиты — 20 м; по бинормали к орбите — 10 м; по высоте — 5 м (среднеквад-
ратическая ошибка (СКО)).
Летные испытания высокоорбитальной отечественной навигационной
системы, получившей название ГЛОНАСС, были начаты в октябре 1982 г.
запуском спутника «Космос-1413» ...»
В 1995 г. было завершено развертывание СРНС ГЛОНАСС до ее штатного
состава (24 НС). В 1999—2002 гг. состав группировки существенно сократился
в результате вывода из эксплуатации отработавших свой ресурс спутников и
недостаточным финансированием новых запусков. В настоящее время
действует федеральная целевая программа «Глобальная навигационная система», в
рамках которой орбитальная группировка системы ГЛОНАСС к 2008 г. должна
быть доведена до установленной численности (18—24 космических аппаратов).
Спутниковая радионавигационная система ГЛОНАСС запатентована в
Соединенных Штатах Америки [В.6].
В рассматриваемый период времени в США также проведены
интенсивные разработки СРНС. В 1958 г. в рамках создания первого поколения
атомных ракетных подводных лодок «Полярис» была создана система
«Транзит» (аналог СРНС «Цикада»), введенная в эксплуатацию в 1964 г. [В.З].
В начале 70-х годов начаты работы по созданию СРНС второго поколения
— GPS/«HaBCTap» (аналога отечественной системы ГЛОНАСС). Спутниковая
радионавигационная система GPS полностью развернута и введена в
эксплуатацию в 1995 г.
С 2007 г. в РФ принят ряд директивных документов, направленных на
ускорение развития технологий спутниковой навигации, в том числе издан Указ
Президента РФ от 17 мая 2007 г. № 638 «Об использовании глобальной
навигационной спутниковой системы ГЛОНАСС в интересах социально-
экономического развития РФ», а во исполнение этого указа Правительство РФ
выпустило Постановление от 30 апреля 2008 г. № 323 об утверждении
Положения о полномочиях федеральных органов исполнительной власти по
поддержанию, развитию и использованию ГЛОНАСС, принято Постановление
Правительства Российской Федерации от 25 августа 2008 г. № 641 "Об
оснащении транспортных, технических средств и систем аппаратурой спутниковой
навигации ГЛОНАСС или ГЛОНАСС/GPS". В феврале 2008 г. в РФ принята
«Концепция развития навигационных сигналов глобальной навигационной
системы ГЛОНАСС», в которой определена необходимость
совершенствования системы ГЛОНАСС.
В соответствии с решениями директивных органов РФ основными
направлениями дальнейших работ в области СРНС являются:
создание и внедрение перспективных технологий навигационно-
временного обеспечения на основе систем спутниковой навигации во все
сферы человеческой деятельности (экономику, быт, науку и технику);
10
Введение
модернизация СРНС ГЛОНАСС с целью обеспечения ее характеристик на
уровне зарубежных аналогов и конкурентоспособности на мировом рынке
навигационных услуг;
развитие, в том числе в регионах РФ, дифференциальных подсистем
СРНС;
развитие сотрудничества с различными международными и зарубежными
организациями и фирмами в области расширения использования возможностей
навигационной системы ГЛОНАСС для широкого круга потребителей;
совершенствование нормативно-правовой базы в области навигационно-
временного обеспечения на территории РФ.
Работы в указанных направлениях ведутся в соответствии с требованиями,
выдвигаемыми различными потребителями (воздушными, морскими и
речными судами, наземными и космическими средствами, топогеодезическими,
землеустроительными и другими службами).
Литература
8.1. ГЛОНАСС. Принципы построения и функционирования/ Под ред. А.И.
Перова, В.Н. Харисова. — М.: Радиотехника, 2005.
8.2. Глобальная спутниковая навигационная система ГЛОНАСС/ Под ред. В.А.
Болдина, А.И. Перова, В.Н. Харисова. — М.: ИПРЖР, 1998.
8.3. Решетнев М Ф. Развитие спутниковых радионавигационных систем// Инф.
бюллетень НТЦ «Интернавигация», 1992, п. 6—10.
8.4. Parkinson В. W. A History of Satellite Navigation// Navigation (USA), Spring,
1995, vol. 42, no. 1, pp. 109—164.
B.5. Шебшаевич В. С. Развитие теоретических основ спутниковой радионавигации
ленинградской радиокосмической школой// Радионавигация и время, РИРВ, 1992, № 1,
pp. 6—9.
8.6. Шебшаевич В. С. Основные возможности использования ИСЗ для
радионавигации самолетов: Докл. на семинаре ЛВВИА 25.12.57// Информационный
сборник. — Л., 1958, № 33.
8.7. Pat. 5,331,329 (US), Jul. 19. 1994, Int. CI.5 G01S 5/02$ H04B 15/00. Satellite-
aided Radio Navigationing Metod and Radio Navigation System Therefor.
11
Глава 1
Р а з д е л 1
ОБЩИЕ ПРИНЦИПЫ ПОСТРОЕНИЯ СПУТНИКОВЫХ
РАДИОНАВИГАЦИОННЫХ СИСТЕМ
Глава 1
СТРУКТУРА СПУТНИКОВЫХ
РАДИОНАВИГАЦИОННЫХ СИСТЕМ
1.1. Общие сведения
Основными требованиями к спутниковой радионавигационной системе
второго поколения ГЛОНАСС являются:
глобальность навигационно-временного обеспечения потребителей, т.е.
потребитель, находящийся в любой точке околоземного пространства, должен
иметь возможность определения своих координат;
непрерывность навигационно-временного обеспечения, т.е. возможность
определять координаты потребителя в любое время суток;
неограниченность числа потребителей системы;
высокая точность навигационно-временных определений (НВО), под
которыми понимают вычисление трех пространственных координат потребителя,
трех составляющих его вектора скорости и текущего времени.
Удовлетворение первого требования обеспечивается выбором параметров
орбит навигационных спутников (искусственных спутников Земли) и их
расположением на орбитах.
Для решения проблемы неограниченности числа потребителей системы
была выбрана концепция независимой навигации, предусматривающая
выполнение НВО непосредственно в аппаратуре потребителя [1.1, 1.2], а в рамках
этой концепции использован метод пассивных (беззапросных) дальномерных и
доплеровских измерений по сигналам нескольких НС.
Концепция независимой навигации и пассивные измерения, дополненные
непрерывным излучением сигналов с НС, решают задачу непрерывности
навигационно-временного обеспечения потребителей.
Высокая точность НВО достигается за счет использования сложных
радиосигналов, излучаемых с НС; правильного выбора рабочего созвездия НС,
т.е. тех НС, сигналы которых принимаются в обработку при НВО; излучения
сигналов с НС с достаточной мощностью; использования высокоточной
информации о параметрах движения НС; оптимизации алгоритмов обработки
сигналов в аппаратуре потребителей (АП) и рядом других факторов.
12
Структура спутниковых радионавигационных систем
Реализация перечисленных методов и подходов, обеспечивающих
выполнение основных требований к СРНС, возможна в сетевой структуре СРНС,
включающей три основные подсистемы [1.3, 1.4] (рис. 1.1):
космических аппаратов (ПКА), состоящую из навигационных спутников
(космический сегмент);
контроля и управления (ПКУ) (наземный командно-измерительный
комплекс или сегмент управления);
навигационная аппаратура потребителей (НАП) СРНС (сегмент
потребителей).
HQ+i
Подсистема
космических
аппаратов
НС,
4-
НС,
Н-2
Подсистема
контроля и
управления
Функциональные
дополнения
(дифференциаль-
ные структуры)
НС,
|+/
Навигационная
аппаратура
потребителей
Рис. 1.1. Глобальная спутниковая радионавигационная система
В последнее время в структуру СРНС часто включают еще одну
подсистему, которую называют функциональным дополнением СРНС (рис. 1.1). Данная
подсистема позволяет расширить функциональные возможности СРНС и
улучшить ее потребительские характеристики [1.4] (подробнее см. в гл. 12).
Приведем более подробную характеристику основных подсистем СРНС.
1.2. Подсистема космических аппаратов
Подсистема космических аппаратов СРНС состоит из определенного числа
навигационных спутников (штатно 24 НС). Основные функции НС —
формирование и излучение радиосигналов, необходимых для навигационных
определений потребителей СРНС, контроля бортовых систем спутника
подсистемой контроля и управления СРНС. В состав аппаратуры НС включают
радиотехническое оборудование (передатчики навигационных сигналов и
телеметрической информации, приемники данных и команд от ПКУ, антенны, блоки
ориентации), ЭВМ, бортовой эталон времени и частоты (БЭВЧ), солнечные ба-
13
Глава 1
тареи и т. д. Бортовые эталоны времени и частоты обеспечивают практически
синхронное излучение навигационных сигналов всеми спутниками, что
необходимо для реализации режима пассивных дальномерных измерений в
аппаратуре потребителей.
Навигационные сигналы спутников являются сложными сигналами,
позволяющими точно измерять дальность и доплеровское смещение частоты,
которые, кроме того, переносят навигационное сообщение. Сложный
радиосигнал получается в результате цифровой фазовой модуляции (манипуляции)
гармонического колебания кодовой последовательностью, которую называют
дальномерным кодом. Передаваемое навигационное сообщение является
цифровым и содержит информацию о параметрах движения НС {эфемеридная
информация) и некоторую дополнительную {служебную) информацию. Основная
часть навигационного сообщения спутника готовится в наземной ПКУ и
передается по радиолинии на борт спутника. И только небольшая его часть
формируется непосредственно бортовой аппаратурой.
В бортовой аппаратуре предусмотрено формирование двух типов
дальномерных кодов: стандартной и высокой точности. В НАП гражданских
потребителей обрабатывается сигнал с дальномерным кодом стандартной точности.
Для использования сигнала с кодом высокой точности требуется санкция
военных органов [1.2, 1.3].
Выбор состава и конфигурации орбитальной группировки НС
обеспечивает заданную рабочую зону, непрерывность НВО, возможность реализации
различных методов НВО и т. д. Например, увеличение в СРНС ГЛОНАСС высоты
полета НС примерно до 20 000 км позволило принимать сигналы каждого
НС на значительных территориях. А использование 24 НС, расположенных
на определенных орбитах, формирует сплошное, с точки зрения наземного и
авиационного потребителя, радионавигационное поле (глобальную рабочую
зону).
В современных СРНС ГЛОНАСС/GPS большое внимание уделяется
взаимной синхронизации НС по орбитальным координатам и излучаемым
сигналам, что обусловило применение к ним термина «сетевые СРНС».
1.3. Подсистема контроля и управления
Наземная подсистема контроля и управления выполняет следующие
основные задачи [1.5]:
эфемеридное и частотно-временное обеспечение НС;
мониторинг радионавигационного поля;
радиотелеметрический мониторинг НС;
командное и программное радиоуправление функционированием НС.
Под эфемеридным обеспечением понимают определение и прогноз
параметров движения всех НС с помощью наземных средств и передачу этой ин-
14
Структура спутниковых радионавигационных систем
формации («закладка») на НС с целью ее последующей передачи в
навигационном сообщении потребителям.
Частотно-временное обеспечение означает определение и прогноз
отклонений бортовых шкал времени НС от системной шкалы времени и «закладка»
на борт НС частотно-временных поправок (ЧВП) с целью последующей их
передачи в навигационном сообщении потребителям.
Излучаемые с НС непрерывные радиосигналы образуют в околоземном
пространстве радионавигационное поле. Мониторинг радионавигационного
поля в ПКУ осуществляется с целью обеспечения потребителей навигационными
радиосигналами гарантированного качества, реализующими требуемую
точность НВО. При выявлении сигналов НС, не удовлетворяющих заданным
требованиям, принимаются меры по выявлению и устранению возникших
дефектов или исключению этих сигналов из процедур НВО.
При штатной комплектации ПКУ состоит из
координационно-вычислительного центра (КВЦ), станций траекторных измерений и управления
(СТИ), системного (наземного) эталона времени и частоты.
Периодически при полете НС в зоне видимости СТИ происходит
наблюдение за спутником, что позволяет с помощью КВЦ определять и
прогнозировать эфемеридную и другую необходимую информацию. Затем эти данные
закладывают в память бортовой ЭВМ и передают потребителям в навигационном
сообщении.
Синхронизация различных процессов в СРНС обеспечивается с помощью
высокостабильного (атомного) системного эталона времени и частоты,
который используется, в частности, в процессе юстировки бортовых эталонов
времени и частоты навигационных спутников СРНС.
1.4. Навигационная аппаратура потребителей
Навигационная аппаратура потребителей предназначена для приема и
обработки радиосигналов НС с целью определения необходимой потребителям
информации (пространственно-временных координат, направления и
скорости, пространственной ориентации и т.п.). В состав НАП входят антенна с
равномерной диаграммой направленности в верхнюю полусферу;
высокочастотный приемник, осуществляющий фильтрацию и разделение сигналов, и
вычислитель, решающий задачу НВО. Обычно используют двухэтапное решение
задачи НВО. На первом этапе формируют оценки параметров радиосигнала —
задержки и доплеровского смешения частоты, и извлекают из сигнала
навигационное сообщение, содержащее, в том числе, информацию о параметрах
движения НС. На втором этапе рассчитывают координаты потребителя и
составляющие его вектора скорости.
В зависимости от типа НАП (носимая человеком, авиационная, морская,
автомобильная, геодезическая и т.д.) в ней реализуются дополнительные сер-
15
Глава 1
висные функции, например, привязка к карте местности, движение по
заданному маршруту, определение положения потребителя относительно заданной
точки и др.
Области использования НАП СРНС неуклонно расширяются и в
настоящее время охватывают авиацию, мореплавание, железнодорожный и
автомобильный транспорт, геодезию и картографию, геодинамику и сейсмологию,
военное дело, космонавтику, сельское хозяйство, системы связи и
телекоммуникаций и т.д.
1.5. Особенности формирования эфемеридной
информации в среднеорбитальных СРНС
Способ функционирования среднеорбитальных СРНС ГЛОНАСС, GPS
позволяет отнести их к радиомаячным навигационным средствам, где роль
маяков выполняют НС. Однако они отличаются от традиционных
радиомаячных систем ближней и дальней навигации (РСБН, РСДН) [1.6] тем, что
координаты маяков (НС) постоянно меняются, причем с достаточно большой
скоростью. Непрерывное высокоточное определение координат НС представляет
собой сложную задачу.
Координаты НС могут быть определены в общем случае либо в ПКУ, либо
непосредственно на спутнике (самоопределяющиеся НС) [1.1]. При разработке
СРНС ГЛОНАСС предпочтение отдано первому подходу. Это связано с тем,
что существуют хорошо апробированные на
практике методы и средства решения этой проблемы в наземных условиях.
В современных СРНС управление НС осуществляется с ограниченных
территорий и, следовательно, не обеспечивается постоянное взаимодействие сети НС
с ПКУ. В связи с этим выделяют два этапа решения данной задачи [1.2]. На
первом этапе в ПКУ измеряют координаты спутников в процессе их пролета в
зоне видимости и вычисляют параметры их орбит. Эти данные прогнозируются
на фиксированные {опорные) моменты времени, например на середину каждого
получасового интервала предстоящих суток, до выработки следующего
прогноза. Спрогнозированные координаты НС и их производные (эфемериды)
передаются на НС, а затем в виде навигационного (служебного) сообщения —
потребителям. На втором этапе в аппаратуре потребителя по этим данным
осуществляется последующее прогнозирование координат НС, т.е.
вычисляются текущие координаты НС в интервалах между опорными точками
траектории. Процедуры первичного и вторичного прогнозирования координат
проводят при известных закономерностях движения НС.
В отличие от самоопределяющихся НС [1.1], рассмотренный вариант
функционирования СРНС обеспечивает упрощение аппаратуры спутников за
счет усложнения структуры и аппаратуры ПКУ.
16
Структура спутниковых радионавигационных систем
1.6. Требования различных потребителей к спутниковым
радионавигационным системам
В п. 1.1 приведены основные требования к СРНС ГЛОНАСС,
сформулированные на этапе разработки системы. После введения системы в
эксплуатацию и при непрерывном расширении сфер ее применения в интересах
различных потребителей возникла необходимость введения ряда новых требований и
конкретизации (уточнения) отдельных требований.
Следуя [1.7], введем следующие дополнительные характеристики СРСНС:
доступность {готовность), мерой которой является вероятность
работоспособности радионавигационных систем перед выполнением той или иной
задачи и в процессе ее выполнения;
целостность, мерой которой является вероятность выявления отказа в
течение времени, равного заданному или меньшего;
непрерывность обслуживания, мерой которой служит вероятность
работоспособности системы в течение наиболее ответственных отрезков времени
движения (выполнения задачи).
Требования к навигационному обеспечению различных гражданских
объектов, реализуемому, в частности, с помощью СРНС, впервые в РФ
сформулированы, обобщены и приведены в Российском радионавигационном плане [1.8],
подготовленном с участием специалистов заинтересованных ведомств и служб.
Они учитывают также положения документов таких международных
организаций, как ИКАО (Международная организация гражданской авиации), ИМО
(Международная морская организация), а также ряда национальных
радионавигационных планов других стран, например, США [1.9].
Требования к навигационному обеспечению воздушных судов
Эти требования определяются, в первую очередь, необходимостью
обеспечения безопасности полетов воздушных судов (ВС) в условиях сложившейся
структуры деления воздушного пространства. В соответствии с этим
рассматриваются различные этапы полета: по трассам, воздушным линиям, вне трасс, в
аэродромной или аэроузловой зоне, взлет, заход на посадку и посадка, пробег
по взлетно-посадочной полосе (ВПП) и руление по рулежным дорожкам.
В табл. 1.1 приведены требуемые СКО определения плановых координат и
высоты полета ВС (абсолютной — по трассам и местным линиям,
геометрической — при заходе на посадку) [1.8].
Требуемые показатели даны для основных решаемых задач таких, как
маршрутный полет, полет в зоне аэродрома, специальный полет, заход на
посадку. Для задачи захода на посадку по категориям ИКАО указаны высоты над
ВПП, на которых должна осуществляться проверка точностных характеристик.
Требования к доступности зависят от этапов полета и интенсивности
воздушного движения. Численные значения доступности при маршрутных поле-
17
Глава 1
тах составляют 0,999...0,99999; при полете в зоне аэродрома и некатегориро-
ванном заходе на посадку — 0,99999. Требования по доступности для захода на
посадку и посадки по категориям ИКАО соответствуют требованиям к
системам инструментальной посадки. Численные значения их близки к единице
[1.8].
Требования к целостности для маршрутных полетов, полетов в зоне
аэродрома и некатегорированному заходу на посадку составляют 0,999 при
допустимом времени предупреждения соответственно 10, 10 и 2 с, а для захода на
посадку и посадки по I, II и III категориям ИКАО — 0,999999, 0,9999999 и
0,9999999995 при допустимом времени предупреждения не более 1 с [1.8].
Таблица 1.1. Требования к точности определения координат
и высоты полета ВС
Решаемые задачи
Маршрутный полет
Полет в зоне аэродрома
Специальные полеты
(разведка полезных
ископаемых, поиск и спасение и др.)
Некатегорированный заход
на посадку
Заход на посадку :
по I категории, #=30 м
по II категории, //=15 м
| по III категории, Я=2,4 м
Зоны полета
Над океаном (безори-
ентирная местность)
Трассы шириной 20 км
Трассы шириной 10 км
Местные воздушные
линии:
I категории
II категории
—
—
Точность
(С!
координат
5800
2500
1250
500
250
200
1...10
50
4,5...8,5
2,3...2,6
2,0
определения
КО), м
высоты
30...40
30...40
30...40
30...40
30...40
1,5...2
0,7...0,85
0,2...0,3 |
В [1.10—1.12] приведены несколько иные требования, основанные на
концепции требуемых навигационных характеристик (ТНХ или RNP),
развиваемой ИКАО (табл. 1.2).
18
Структура спутниковых радионавигационных систем
Таблица 1.2. Требования к точности выдерживания траектории
захода на посадку
[Категория
I
II
III
Туннель
Внутренний
Внешний
Внутренний
Внешний
Внутренний
Внешний
Вероятность
решения задачи
0,95
(1... 3,3) 10~7
0,95
(1... 3,3) Ю-8
0,95
(1 ... 1,5) Ю-9
Границы
уклонений, м
боковых
± 40
± 121
±21
±64
±15
±46
вертикальных
±12
±37
±4,6
±14
±1,5
±4,6
Высота НА
м, более
60
60
30
30
15
15
Требования к точности боковых и вертикальных уклонений при категори-
рованных заходах на посадку представляются в виде границ внешнего и
внутреннего «туннелей», внутри которых должен оставаться снижающийся по
глиссаде самолет с заданными вероятностями. Границы «туннелей»
представляют собой предельные значения суммы погрешностей определения координат
(в боковом канале) и высоты, а также соответствующих ошибок управления.
Сравнение численных значений, приведенных в табл. 1 и 2, показывает, что
они не противоречат одно другому.
В [1.12, 1.13] даны несколько иные значения надежностных характеристик
(табл. 1.3) захода на посадку по категориям ИКАО, уровни которых, однако,
соответствуют приведенным выше из [1.8].
Таблица 1.3. Требования к надежности при заходе на посадку
по категориям ИКАО
Кате-
И гория
I
II
III
Доступность
0,9975
0,9985
0,999
Целостность
Г<6с
1...3,3-10"7
Т<2с
1... 3,3 10"8
Т<\ с
1... 1,5 Ю-9
Непрерывность
1 -10-5 в течение 15 с
1 • 10"4 в течение 150 с
1... 1,4-Ю-6в течение 15 с
1... 1,4 Ю-5 в течение 165 с
1... 4,0 10"6 в течение 30 с
Высота Н,
м, более ||
60
30
15
1 I
19
Глава 1
Требования, приведенные в табл. 1.1—1.3, относятся к точности и
надежности определения координат на различных этапах полета ВС. Следует
отметить, что совершенствование процедур и методов управления полетом может
привести к обоснованию и формулировке требований к точности определения
составляющих скорости и, возможно, времени. Это, в частности, относится к
разработке и использованию алгоритмов управления движением
конфликтующих ВС в задаче предотвращения столкновений ВС в воздухе, а также в
задаче предупреждения столкновений ВС с наземными объектами и для
обеспечения более комфортных условий посадки.
Требования к навигационному обеспечению морских судов
Требования к навигационному обеспечению морских судов (МС),
предъявляемые сейчас и к СРНС, вытекают из необходимости обеспечения
безопасности и экономичности плавания, которые зависят от районов и этапов
судовождения [1.8]:
открытое море (океан);
прибрежные зоны (на удалении менее 50 миль от берега);
узкости, входы в порты и гавани;
акватории портов.
Международные требования к точности и надежности навигационного
обеспечения морских судов в зависимости от районов плавания определяются
ИМО. Требования к навигационному обеспечению судоходства при входах в
порты, гавани, в узкостях и акваториях портов определяются
соответствующими национальными администрациями.
В табл. 1.4 приведены обобщенные требования к навигационному
обеспечению морских судов [1.8].
Следует отметить, что приведенные требования находятся в состоянии
перманентных корректировок и уточнений, в основном, в сторону их
повышения. Это объясняется постоянно возрастающей ценой навигационных ошибок,
особенно в условиях роста тоннажа танкеров, опасности и стоимости
последствий возможных экологических катастроф из-за столкновений с препятствиями
и посадками на мель. Велика также роль определения точного местоположения
при проведении народнохозяйственных работ на шельфе таких, как
геологоразведка и добыча полезных ископаемых.
Для обеспечения надежности и экономичности движения МС пока не
сформулированы требования к определению скорости и времени. Однако
представляется, что качественное решение задачи проводки большегрузных танкеров в
узкостях, посадки ВС (вертолета) на палубу МС в условиях сильного волнения и
шторма может быть осуществлено лишь при получении качественной
информации о горизонтальных и вертикальной составляющих скорости МС.
20
Структура спутниковых радионавигационных систем
Таблица 1.4. Требования к точности и надежности определения
координат морских судов
Решаемая задача
Плавание в открытом море
(океане)
1 Плавание в прибрежной зоне
Прохождение узкостеи, заходы
в порты
Маневрирование впортах
Картография и океанография
| Геологоразведка, добыча
полезных ископаемых
Погрешность
определения
(СКО), м
1400...3700
100...60
Менее 20
8
0,25...5
1...5
Доступность
0,99
0,99...0,997**
0,99...0,997**
0,997
0,99
0,99
Целостность
0,99
0,99
0,99
0,99
0,9...0,99
0,9...0,99 I
* Допустимое время предупреждения находится в пределах единиц
секунд — единиц минут в зависимости от задачи и типа МС
| ** Значения 0,997 относятся к МС большого тоннажа |
Добавим, что точная корректировка шкалы времени МС может позволить
эффективно решать задачи обеспечения надежного опознавания, связи и т.д., а
для решения задачи буксировки по морю высотных платформ для добычи
полезных ископаемых может потребоваться и информация о пространственной
ориентации объекта с точностью (СКО) до единиц — долей угловых минут.
Требования к навигационному обеспечению судов речного флота
Требования к навигационному обеспечению плавания судов по рекам и
озерам в первой редакции Российского радионавигационного плана не были
сформулированы [1.8] и в настоящее время находятся в стадии обоснования.
Предварительно они могут быть определены по аналогии с требованиями к
навигационному обеспечению МС при плавании в прибрежной зоне (СКО
определения координат 100...460 м, доступность и целостность соответственно
0,99...0,997 и 0,99) и при прохождении узкостеи и маневрировании в портах
(СКО определения координат менее 8...20 м, доступность и целостность
соответственно 0,99...0,997 и 0,99). Для речных судов помимо определения точного
местоположения важно иметь и базу данных с цифровым описанием фарватера
и различного рода препятствий, отмелей, порогов, рифов и т. д.
Требования к навигационному обеспечению наземных объектов
К наземным объектам относятся автомобильный и железнодорожный
транспорт, объекты геологоразведывательных подразделений, топогеодезиче-
21
Глава 1
ских и землеустроительных служб. Для обычных транспортных средств
требуемая СКО определения координат находится в пределах единиц метров —
единиц километров [1.8], причем при необходимости, например для
обеспечения точной ориентировки в городе, соответствующая точность равна
единицам — первому десятку метров. При этом определение точного
местонахождения должно комбинироваться с использованием базы данных (БД) городской
застройки.
Учитывая возможности навигационного обеспечения с помощью НАП
СРНС, в качестве современного требования для автомобильного транспорта
следует считать СКО определения местонахождения, равную 10...50 м.
Требования геологоразведки и добычи полезных ископаемых, а также
привязки наземных радиосредств составляют 1 ...5 м, а необходимая СКО
проведения топогеодезических и землеустроительных работ — 0,01 ...5 м.
Требования к надежности определения места наземных объектов, как
правило, не заданы [1.8]. Исключение составляют требования по доступности для
геологических работ, добычи полезных ископаемых и геодезической привязки,
которая составляет 0,95.
С учетом условий, при которых используются наземные средства,
специальные требования к определению скорости, как правило, не выдвигаются.
Однако ряд служб и систем нуждаются в едином точном времени. Такая
необходимость возникает при управлении разнесенными в пространстве объектами;
при испытаниях, синхронизации систем связи, опознавания; проведении
тонких научных исследований и т.д. Требуемая точность может составить десятки
(и даже единицы) наносекунд (по крайней мере в относительном режиме).
При строительстве и топогеодезических работах в ряде случаев также
требуется информация о пространственной ориентации объектов в условиях
ограниченной видимости с СКО до единиц — долей угловых минут.
Требования к навигационному обеспечению космических средств
Точность навигационного обеспечения космических средств задана на
уровне 300...3000 м при доступности 0,95...0,997 [1.8] и, по-видимому, будет в
дальнейшем уточняться до нескольких десятков (и возможно, единиц) метров
при решении, например, задачи экстренной посадки на наземный аэродром в
условиях категорий ИКАО (см. табл. 1.1). Довольно высокие требования
предъявляются к точности определения скорости (на уровне нескольких
сантиметров в секунду), которая необходима, в частности, при сближении и
стыковке космических средств.
Литература
1.1. Сетевые спутниковые радионавигационные системы/ Под ред. /7. Я.
Дмитриева, В. С. Шебшаевича. —М.: Транспорт, 1982.
22
Структура спутниковых радионавигационных систем
1.2. Спутниковые радионавигационные системы. 4.1. Основы функционирования
подсистем/ Под ред. В. К Харисова. — М: Изд-во ВВИА им. Н.Е. Жуковского, 1997.
1.3. Глобальная спутниковая навигационная система ГЛОНАСС// Интерфейсный
контрольный документ. Редакция 5.0. — Москва, 2002.
1.4. Сетевые спутниковые радионавигационные системы/ Под ред. В. С Шебшае-
вича. — М: Радио и связь, 1993.
1.5. Волков К М, Иванов К Е., Салищев В. А., Тюбалин В. В. Глобальная
спутниковая радионавигационная система ГЛОНАСС// Успехи современной
радиоэлектроники, 1997, № 1, с. 31—46.
1.6. Ярлыков М.С. Статистическая теория радионавигации. — М: Радио и связь,
1985.
1.7. Глобальная спутниковая радионавигационная система ГЛОНАСС/ Под ред.
В.А. Болдина, АЛ. Перова, В.К Харисова. — М.: ИПРЖР, 1999.
1.8. Российский радионавигационный план// НТЦ «Интернавигация». — М., 1994.
1.9. Федеральный радионавигационный план США// МТ и МО США, 1999.
1.10. Материалы особого совещания по связи/производству полетов 27.3 —
7.4.95//ИКАО Л 995.
1.11. All Weather Operations Panel (AWOP)// 15 Meeting, Montreal, ICAO, 26.9. —
12.10.1994.
1.12. Kelly R. Jy Davis J. Required Navigation Performance (RNP) for Pre-cision
Approach and Landing with GNSS Application// Navigation (USA), 1994, no. 1, pp. 1—30.
1.13. Blomenhofer K, Meyer-Hilberg J. Availability and Accuracy During Precision
Approaches and Automatic Landings// 5-th Intern. Conf. on Differential Satellite Navigation
Systems, St. Petersburg, 1996, Add., Paper l 43.
23
Глава 2
Глава 2
ВРЕМЯ. ШКАЛЫ ВРЕМЕНИ
Определение координат потребителя в СРНС тесно связано с понятием
времени, т.к. основано на измерении времени распространения радиосигнала
между двумя пространственно разнесенными точками (НС и потребитель). В
современной физике все явления и события описываются в пространстве-
времени, которое имеет три пространственных и одно временное измерения.
Существуют различные динамические модели пространства-времени.
Наиболее простая модель базируется на принципах классической механики и законах
Ньютона [2.1]. Такая модель пространства-времени лежит и в основе теории
спутниковой радионавигации.
Согласно первому закону Ньютона изолированная материальная точка
движется по прямой линии с неизменной скоростью. Другим словами, за
равные интервалы At временного измерения материальная точка перемещается на
одинаковые отрезки пространственного измерения (прямой линии). Таким
образом, одни и те же события (перемещения на одинаковые отрезки прямой
линии) происходят через равные временные интервалы. Для описания такой
ситуации можно ввести понятие «идеального, равномерно текущего времени», а
для его обозначения использовать символ t. Момент наступления какого либо
события А будем обозначать как tA .
Каждое событие, происходящее в пространстве-времени, может быть
идентифицировано его описанием, как, например, это сделано выше. Однако
удобнее, рассматривая событие как точку в пространстве-времени, приписать
ему числовой код, который должен однозначно характеризовать положение
точки в четырехмерном пространстве-времени. Такой числовой код принято
называть пространственно-временной координатой, которая задается в
некоторой четырехмерной координатной системе. Описание пространственных
координат и координатных систем будет приведено в гл. 3. В данной главе
рассматривается временная координата и различные временные координатные
системы, которые исторически принято называть шкалами времени. Подчеркнем,
что шкала времени водится для обеспечения возможности определения
количественного значения времени, под которым будем понимать число,
определенное для каждого момента времени. Такое число будем называть временем по
шкале или просто временем, если изложение ведется для одной шкалы
времени. Для обозначения текущего времени для шкалы «Ь » будем использовать tb ;
для обозначения момента наступления какого либо события А для рассматри-
24
Время. Шкалы времени
ваемой шкалы будем использовать tA; количественное значение времени для
момента наступления события А на шкале « Ъ » будем обозначать Тъ иъА).
Для задания шкалы времени может использоваться любой периодически
повторяющийся процесс: вращение Земли, движение Земли вокруг солнца,
излучение атомов при их переходе между разными энергетическими уровнями,
гармонический сигнал электрического генератора и др.
Сформировав ту или шкалу времени для нее необходимо определить
(задать) единицу меры времени, которая далее используется далее для
количественного определения времени на шкале. Используемые на практике единицы
мер времени описаны в п. 2.1, 2.2.
В технике, наряду с понятием «шкала времени» с соответствующим
определением количественного значения времени на этой шкале, часто
используется понятие часы. Наиболее полно определение часов дано в [2.2]:
«...количественное значение времени всегда осуществляется с помощью часов,
под которыми понимается совокупность средств и действий, направленных на
определение количественного значения времени на основе наблюдения за
фазой некоторого периодического процесса». Для определения количественного
значения времени используется понятие показаний часов. Данные определения
часов и показаний часов практически эквивалентны приведенным выше
определениям шкалы времени и времени на шкале. Однако во многих литературных
источниках термин «часы» используется в более узком смысле. В настоящей
книге, как правило, будет использоваться понятие шкалы времени с заданной
на ней системой количественного определения времени, включающей единицу
измерения времени.
В п. 2.1, 2.2 приведена краткая характеристика наиболее широко
используемых шкал времени [2.1, 2.3—2.4] и используемых в них единиц времени.
2.1. Астрономические шкалы и единицы времени
Исторически возникшая в астрономии шкала всемирного времени задается
вращением Земли вокруг своей оси. При этом единицей времени являются
сутки — интервал времени, за который Земля делает один полный оборот вокруг
своей оси относительно какой-либо фиксированной точки отсчета на небесной
сфере для наблюдателя, расположенного на одном и том же меридиане. Сутки
делятся на 86400 равных интервалов, а длительность единичного интервала
называют секундой. В зависимости от выбранной точки отсчета (точка весеннего
равноденствия, центр видимого диска Солнца, «среднего Солнца» и т. д.) сутки
отличаются по длительности и имеют разное название. Звездные сутки Т3
(звездный период обращения Земли) отсчитываются между двумя
последовательными верхними положениями (кульминациями) точки весеннего
равноденствия. Интервал времени от момента верхней кульминации этой точки, выра-
25
Глава 2
женный в долях Г3, называют звездным временем. Обычно время, измеренное
на данном меридиане, называется местным временем данного меридиана, т. е.
в рассматриваемом случае местным звездным временем меридиана. Местное
звездное время S измеряется часовым углом t точки весеннего
равноденствия у (точки Весны или точки Овна) относительно местного небесного
меридиана L (рис. 2.1). На рисунке показан вид северного полушария небесной
сферы сверху, где PN — Северный полюс. Часовой угол аналогичен
географической долготе, отсчитывается от небесного меридиана наблюдателя по
часовой стрелке и измеряется в часовой мере — часах, минутах, секундах.
L/ \
Ъ™У~уЛ t(S) \
/ Небесный
Лг^ экватор
Рис. 2.1. Определение местного звездного времен
Звездное время можно выразить в угловых значениях. Поскольку за 1 ч
Земля поворачивается на 15°, местному звездному времени, например,
о
S- 2 ч 3 мин 1 с соответствует угол, равный 30 45'15".
Для точных расчетов следует учитывать также, что ось вращения Земли
совершает медленное периодическое колебательное движение, состоящее из
прецессии (движение по конусу) и нутаций (небольшие колебания) оси. Из-за
прецессии и нутаций точка Весны перемещается. Если учитывается только
прецессионное движение, то получаются среднее (равномерное) звездное время
и средние звездные сутки. Если же учитывается и нутация, то получается
истинное звездное время. Местное звездное время, измеренное на Гринвичском
меридиане, называется обычно гринвичским звездным временем Sr.
Истинные солнечные сутки Ги отсчитывают по нижним кульминациям
центра видимого диска Солнца («истинного Солнца»). Из-за неравномерности
движения Земли по орбите и непараллельности осей ее суточного и годичного
вращения Ги непостоянно, поэтому в повседневной жизни за основную
единицу времени принимают средние солнечные сутки Т , которые отсчитываются
26
Время. Шкалы времени
по нижним кульминациям «среднего Солнца» — гипотетической точки,
рассчитанной в предположении ее равномерного движения по орбите. «Среднее
Солнце» совершает один полный оборот по небесному экватору за то же
время, как и настоящее Солнце по эклиптике, и проходит точку весеннего
равноденствия одновременно с Солнцем. Интервал времени от момента нижней
кульминации «среднего Солнца», выраженный в долях Тср, называется
средним солнечным временем или средним временем. Местное среднее время
измеряется часовым углом «среднего Солнца» относительно местного меридиана,
увеличенным на 12 ч. Значение Тср соответствует среднему значению ТИ
за год.
Подсчитано, что 24 ч звездного времени равны примерно 23 ч 56 мин
4,091 с среднего времени, т. е. Т3 « 86 164,091 с среднего времени.
Из-за неравномерности суточного вращения Земли звездные и солнечные
сутки незначительно изменяются. Для точных расчетов введено равномерно
текущее время — эфемеридное (предвычисленное) время ЕТ. Это —
равномерно текущее время ньютоновой механики. Шкала эфемеридного времени
задается орбитальным движением тел Солнечной системы. Основная единица
измерения эфемеридного времени — тропический год в фундаментальную
эпоху 1900, январь 0, 12 ч, то есть промежуток времени между
последовательными прохождениями центра истинного Солнца через среднюю точку
весеннего равноденствия в эпоху 1900, январь 0, 12 ч. Эфемеридная секунда равна
1/31556925.9747 части тропического года для начальной эпохи. Эфемеридные
сутки содержат 86 400 эфемеридных секунд.
2.2. Атомные шкалы и единицы времени
С появлением молекулярных и атомных стандартов частоты возникла
принципиально новая, не зависящая от вращения Земли и движения тел
Солнечной системы, физическая шкала времени — атомная. Определяемое по
атомной шкале время, называют атомным временем AT {Atomic Time). В
1967 году Международный комитет мер и весов постановил принять за
единицу измерения времени в Международной системе единиц (СИ) атомную
секунду, равную интервалу времени, в течение которого совершается 9192631770
колебаний, соответствующих резонансной частоте энергетического перехода
между уровнями сверхтонкой структуры основного состояния атома цезия—
133 при отсутствии внешних воздействий [2.5]. Атомная секунда выбиралась
таким образом, чтобы ее продолжительность была максимально близка к
продолжительности эфемеридной секунде. Атомная секунда соответствует эфеме-
ридной с относительной погрешностью±2-1 (Г9. Осреднение показаний
различных атомных эталонов времени позволило создать шкалу международного
атомного времени TAJ {International Atomic Time).
27
Глава 2
2.3. Универсальные шкалы времени и шкалы времени,
используемые в СРНС
На шкале всемирного времени среднее солнечное время на меридиане
Гринвича называется всемирным временем UT {Universal Time). Это время
содержит год, месяц, число, час, минуту и секунду. Первые три величины от-
считываются по общепринятому (григорианскому) календарю, остальные —
по местному среднему времени на Гринвичском меридиане tUT . Данная
система отсчета введена в 1928 г. III Генеральной ассамблеей Международного
астрономического союза.
Всемирное время tUT измеряется часовым углом «среднего Солнца»
относительно Гринвичского меридиана, увеличенным на 12 ч. Так как движение
полюсов Земли обусловливает изменение положения меридианов, по степени
учета возмущающих факторов различают следующие разновидности
всемирного времени: UT0 — всемирное время, получаемое в результате текущих
астрономических измерений относительно мгновенного Гринвичского
меридиана (т.е. определенного по мгновенному положению полюсов Земли); UT1
— всемирное время среднего Гринвичского меридиана, рассчитанное с
учетом движения полюсов, оно является основой для измерения времени в
повседневной жизни; UT2 — отличается от UT1 сезонными поправками; UT1R
— отличается от UT2 поправками на приливы.
Заметим, что UT равно местному среднему времени минус
географическая долгота места наблюдателя L; ST (гринвичское звездное время) равно
местному звездному времени S минус L, при этом восточная долгота L
положительна, западная отрицательна.
Шкала универсального координированного времени UTC {Universal
Coordinated Time) — является составной шкалой, в основе которой лежит
атомная шкала времени, показания времени на которой корректируются с
учетом данных относительно вращения Земли. Коррекция осуществляется
периодически (с периодом 0,5...2,5 г.) на 1 с так, чтобы разность
(UT1—UTC) не превышала 0,9 с. Сигналы UTC передаются по
радиовещательным сетям и обычно используется в повседневной жизни. Достоинства
UTC — сравнительно высокая равномерность шкалы, присущая атомному
времени; привязка к естественным природным процессам (восход, заход), что
характерно для солнечного времени. Различные страны формируют и
поддерживают собственные шкалы универсального координированного времени.
Так, например, в США формируется шкала UTC(USNO) на базе ансамбля
(около 50 шт) цезиевых стандартов, показания на которой поддерживаются с
точностью не более 50 не относительно показаний международного стандарта
UTC. В РФ поддерживается национальная шкала UTC(SU), показания
которой смещены на +3 часа относительно показаний UTC.
28
Время. Шкалы времени
Поясное время ZT. Это время содержит год, месяц и число, которые от-
считываются аналогично всемирному времени UT, часы, минуты и секунды
— как местное среднее время основного (центрального) географического
меридиана рассматриваемого часового пояса tu по формуле ZT = UTC+ An , где
An — номер часового пояса. Поясное время введено в большинстве стран с
1884 г., в России — с 1919 г. При этом поверхность Земли была разделена на
24 часовых пояса, центральные меридианы которых отличаются по долготе
на 15° (1 ч). Для Москвы An = 2 . Достоинство поясного времени — удобство
использования в повседневной жизни, так как не требует уточнения времени
при соответствующих перемещениях вдоль параллели.
Местное декретное время. Это время отличается от поясного времени
ZT на декретную добавку Д/дкр, устанавливаемую для каждой местности
законодательным порядком. В СССР это время существовало до 1981 г. В
настоящее время в России действует система летнего времени.
Летнее время. Это время tn = ZT+ 2 ч. Обычно летнее время действует
ежегодно с 2 ч ночи последнего воскресенья марта до 3 ч ночи последнего
воскресенья сентября, когда вводится зимнее время /зим . Оно соответствует
существовавшему ранее декретному времени с добавкой Д/дкр= 1 ч, т. е.
'зим = ZT+ 1ч. Декретное (летнее) время часового пояса с An = 2 называют
московским летним временем.
Юлианский период. Полное обозначение заданных моментов времени с
помощью рассмотренных систем отсчета не всегда удобно и требует
использования как минимум четырех чисел — год, месяц, число и часы с
десятичными долями, поэтому на практике применяют систему отсчета, называемую
юлианским периодом, удобство которой состоит в том, что счет текущего
времени ведется в днях (средних солнечных сутках с десятичными долями).
Все дни в этом периоде пронумерованы по порядку независимо от принятой
календарной системы, номера года, месяца и т. д.
Счет дней, называемых юлианскими днями (JD), ведется от полудня 1
января 4713 г. до н.э. {начало юлианского периода) до заданного момента
времени, Общая длительность юлианского периода составляет 7980 лет.
Юлианское столетие содержит 36 525 средних солнечных суток. Любой
момент времени в этой системе отсчета выражается числом, в котором целая
часть — число юлианских дней, прошедших до последнего среднего
гринвичского полудня, а дробная часть — интервал времени (в долях Тс — средних
солнечных суток), прошедший от этого полудня до рассматриваемого
момента времени.
29
Глава 2
Пересчет даты общепринятого календаря в юлианскую дату (JD)
производят по справочным таблицам или расчетным формулам. Так, для периода
1990—1994 гг. пересчет заданного момента всемирного времени UT к
юлианской дате JD можно выполнить по формуле [2.7]
f лэ = 2440000 + gkl + n + tm - 0,5 ,
где /ит — часы, минуты и секунды всемирного времени, соответствующие
заданному моменту времени и пересчитанные в доли Гс; к, 1,п — год, месяц и
число по общепринятому календарю; gkl — число, определяемое на начало
каждого месяца этого периода по данным таблицы
1 Год
1990
1991
1992
1993
1994
Число gkl по месяцам
1
7892
8257
8622
8988
9353
2
7923
9288
8653
9019
9384
3
7951
8316
8682
9047
9412
4
7982
8347
8713
9078
9443
5
8012
8377
8743
9108
9473
6 1
8043
8408
8774
9139
9504 1
1 Год
1990
1991
1992
1993
1994
Число gkl по месяцам
7
8073
8438
8804
9169
9534
8
8104
9469
8835
9200
9565
9
8135
8500
8866
9231
9596
10
8165
8530
8896
9261
9626
11
8196
8561
8927
9292
9657
12 I
8226
8591
8957
9322
9687 |
Например, в юлианском периоде момент московского времени 9 ч 48
мин 1 января 1985 г. обозначается числом: 2 446 066,783 333 JD.
Для удобства начало отсчета юлианских дней иногда смещают на момент
времени (эпоху), например, ноль часов всемирного времени 1 января 1900
г. (JD=2 415 020,0) — на полночь 17 ноября 1858 г., смещая при этом начало
отсчета вперед на 2400000,5 JD (это начало модифицированного юлианского
периода, дни которого обозначают MJD); на полдень 1 января 2000 г.
(JD=2 451 545), обозначаемый J20-00.
30
Время. Шкалы времени
2.4. Локальные шкалы времени в СРНС
СРНС является пространственно-распределенной системой, включающей
наземный сегмент управления, навигационные спутники и аппаратуру
потребителей, с зоной действия, охватывающей все околоземное пространство. Для
обеспечения высокоточных НВО все подсистемы СРНС должны
функционировать в единой шкале времени (ШВ). Реализовать это требование на практике
не представляется возможным, так как для его выполнения в каждой
подсистеме необходимо использовать однотипные высокоточные стандарты частоты,
которые, к тому же, должны быть синхронизированы с высокой точностью.
Поэтому в современных СРНС выделяются несколько ШВ, отличающихся
стабильностью: системная шкала времени (СШВ); бортовая шкала времени
(БШВ) НС; шкала времени потребителя (ШВП).
Локальная шкала времени задается некоторым стандартом частоты
(опорным генератором), который формирует высокостабильное колебание
"or (0 = ^0 sin{Зл/н.ог* + <Ро)> (2.1)
где /Hi0r — номинальная частота опорного генератора (ОГ); (р0 — начальная
фаза; t — собственное время ОГ, которое задает соответствующую шкалу
времени (часы). Показания часов возрастают на номинальное значение
периода 1//н ог каждый раз, когда полная фаза Ф(/) = 2л:/н ort + щ возрастает на 2п.
Системная шкала времени непосредственно или косвенно используется
для временной привязки основных процессов во всех подсистемах СРНС. Она
формируется и поддерживается наиболее стабильными квантовыми
системными эталонами времени и частоты (СЭВЧ) наземного
командно-измерительного комплекса, высокая стабильность которых обеспечивается, во-
первых, водородным стандартом частоты, который формирует единицу
системного времени с относительной погрешностью 5-Ю"14 [1.2], и, во-вторых,
специальными инженерно-техническими и алгоритмическими решениями.
Уход формируемой таким образом системной шкалы времени составит 3 мкс
за год.
Бортовая шкала времени каждого спутника, к которой привязываются
излучаемые им радиосигналы, формируется квантовыми (цезиевыми)
бортовыми стандартами частоты с относительной нестабильностью частоты
(1...5) 10"13. Они раб отают в более неблагоприятных условиях, чем СЭВЧ,
поэтому в процессе работы неизбежно возникает расхождение между БШВ и
СШВ.
Шкала времени потребителя формируется, как правило, кварцевым
стандартом частоты, устанавливаемым в каждом приемнике. Современные требо-
31
Глава 2
вания к относительной нестабильности частоты КГ9...КГ11 в зависимости от
назначения и класса приемника.
Между шкалами времени СШВ, БШВ, ШВП существуют расхождения,
которые изменяются во времени. Поэтому важное место в СРНС отводится
проблеме временной синхронизации шкал времени. Однако прежде чем
переходить к идеологии и процедурам синхронизации шкал времени, рассмотрим
вопрос нестабильности частоты и времени в ОГ и ее описание.
2.5. Нестабильность частоты и времени
в опорных генераторах
Соотношение (2.1) описывает идеальный ОГ, который формирует строго
гармонический сигнал. На выходе реального ОГ формируется сигнал, который
в общем случае может быть записан в виде [2.8]
иог (t) = U0 sm((27rfHOrt + <р0) + ф(г) + <p(t)), (2.2)
где </){t) — достаточно медленный систематический уход фазы сигнала,
обусловленный влиянием внешних факторов (температура, влажность, давление,
магнитное поле, ускорение и др.) и старением элементной базы; cp(t) —
случайные флуктуации фазы сигнала, вызываемые различными шумами (тепловым,
дробовым или фликкер-шумом), источниками которых служат электронные
компоненты. Здесь и далее будем полагать, что амплитуда U0 формируемого
колебания постоянна, т.е. не учитываем амплитудные флуктуации сигнала.
Систематические уходы фазы ф(г) могут быть достаточно точно
измерены, спрогнозированы на некоторый промежуток времени и использованы для
синхронизации шкал времени (об этом более подробно — в п. 2.5).
Здесь же остановимся на случайных изменениях фазы <p(t). Обозначим
для удобства номинальную частоту ОГ как v0 = /н ог и запишем (2.2) без учета
систематического ухода фазы, полагая для простоты р0 = 0,
uor{t) = U0sm(27rv0t + (p(t)) = U0s^(t)). (2.3)
При отсутствии отклонений фазы q>(t) имеем, как отмечалось в п. 2.3,
идеальную ШВ. При наличии таких отклонений и принятом определении
приращения времени получаем реальную шкалу времени потребителя:
tn=t + -±-!- = t + t'(t)9
2tiv0
32
Время. Шкалы времени
где t'{t) = p-L. (2.4)
Из (2.3) запишем выражение для мгновенной частоты ОГ:
, v 1 d<b(t) 1 dcp(t)
^=Тх*-^т^- (2-5)
Введем мгновенное относительное отклонение (относительная
нестабильность) частоты ОГ Sv{t), которое определим как
*„(,)_2kW_,=^=_!_**)
v0 v0 2ttv0 dt
(2.6)
Дифференцируя (2.4) по времени и принимая во внимание (2.6), получаем
-±± = Svm(t). (2.7)
at
Таким образом, нестабильность времени t'{t) определяется относительной
нестабильностью частоты ОГ.
Нестабильность частоты ОГ можно описывать в частотной и временной
областях.
Описание нестабильности частоты ОГ в частотной области
Так как <p(t) и Sv0T (t) являются случайными функциями, то для описания
их статистических характеристик принято использовать корреляционные
функции и спектральные плотности мощности [2.7, 2.8]. Более просто и
корректно данный аппарат используется для стационарных процессов, поэтому
будем полагать, что на рассматриваемых ограниченных интервалах времени
исследуемые случайные процессы являются стационарными.
Пусть pAv(r) = A/[Av(f)Av(f--r)l — корреляционная функция
случайного процесса Av(t). Тогда двухсторонняя спектральная плотность мощности
данного процесса определяется как преобразование Фурье от корреляционной
функции
Положим C±v(i) = d<pj{2ndt). Тогда для спектральной плотности
мощности относительного отклонения частоты Svm (t) с учетом (2.6) запишем
2-1026
33
Глава 2
**„(/) =-2-М/)'
(2.8)
В то же время, используя известное соотношение между спектральной
плотностью мощности процесса и его производной и учитывая (2.6), имеем
s*y (/) = Т"^2^ S* О = /2^ ^'
(2л-)
где Sp(f) —спектральная плотность мощности фазы #>(f)
Из сопоставления (2.8) и (2.9) получаем
,2
(2.9)
S*,Jf) = {f/vo) S,(f).
(2.10)
В технических характеристиках ОГ, как правило, приводятся
экспериментально снятые характеристики спектральной плотности мощности фазовых
шумов Sy(f). Тогда, используя (2.10), можно рассчитать спектральную
плотность мощности относительной нестабильности частоты.
При теоретических исследованиях спектральную плотность мощности
SSv (/) часто [2.1, 2.8, 2.9] аппроксимируют полиномом от /, содержащим
пять членов:
■V, (/)=!>«/",
(2.11)
а=-2
где значения констант ha, а = -2,2 зависят от типа ОГ, а точнее — от вида
спектральной плотности SSv (/).
Представление спектральной плотности мощности в виде (2.11)
соответствует модели относительного отклонения частоты Sv0T(t) в виде взвешенной
суммы различных типов независимых шумов, которые вносят
соответствующий вклад в итоговую нестабильность. В табл. 2.1 приведены данные типы
шумов и соответствующие им значения параметра а .
Таблица 2.1. Типы шумов, вносящих вклад в нестабильность ОГ
| Тип шума
Белый фазовый шум
Фазовый фликкер-шум
Белый частотный шум
Частотный фликкер-шум
Шум случайного блуждания (винеровский
1 шум) частоты
a J
2
1
0
-1
-2
34
Время. Шкалы времени
Напомним, что под белым шумом понимают случайный процесс с
постоянной (равномерной) спектральной плотностью мощности на всех частотах;
фликкер-шум имеет спектральную плотность мощности, меняющуюся в
зависимости от частоты как \/f в области низких частот / > fmin; винеровский
процесс определятся как интеграл от белого шума, а, следовательно, его
спектральная плотность мощности пропорциональна 1//2 .
Заметим, что моделью (2.11) можно пользоваться лишь в ограниченной
области частот /min < / < /max так, чтобы дисперсия относительного
отклонения частоты ОГ была конечной и соответствующей реальным измерениям.
Описание нестабильности частоты ОГ во временной области
Вариация Алана используется для описания статистических свойств
относительной нестабильности частоты во временной области. Прежде всего
отметим, что мгновенная частота ОГ vor(t)9 определяемая соотношением (2.5), не
может быть реально измерена, так как любой измеритель измеряет некоторое
усредненное значение. Поэтому рассмотрим среднее значение мгновенной
частоты на некотором интервале [tk9tk + т]:
tk+r tk+r
у
УОГ
('U-=7 borW* = v0+^ JM*)*- (2-12>
tk 'k
С учетом (2.12) и (2.6) запишем выражение для среднего значения
относительной нестабильности частоты, определенной для того же временного
интервала,
lk+T
Подставляя правую часть выражения (2.6) в (2.13), получаем
М = '('*")-'('*). (2.14)
2лу0т
Числитель в (2.14) представляет собой набег (приращение) фазы на
интервале времени [tk9tk + г].
Параметр 5vk является случайной величиной, поэтому можно говорить о
его среднем значении и дисперсии. Полагая процесс 5vk эргодическим,
введем выборочное среднее значение и выборочную дисперсию (несмещенную):
35
Глава 2
i^
И*.Ф£2>"'
**=■
^(^^) = {{^-^(^,r))2) = ^-T|:(^-(^(iV,r)})2, (2.15)
где N — число отсчетов в выборке.
Вариация Алана определяется как усредненная по времени (операция ( })
выборочная дисперсия (2.14) при N = 2 , т.е.
,2'
<й(о=(«£(2.г))-(£и*-Й>' Ки*"-*")2)- <2Л6>
2
*=i v к=\ J
2
Смысл вариации Алана (2.16) заключается в том, что рассматривается
дисперсия двойных (вторых) приращений фаз. Сначала вычисляются
приращения фаз на интервале времени т для двух соседних интервалов (8v\ и
dvi), а затем вычисляется приращение для вычисленных первых разностей
(Sv2 - Sv\).
Можно показать [2.7], что вариация Алана связана со спектральной
плотностью относительного отклонения частоты соотношением
Ст11(г) = 2к„(/)^Ш//. (2.17)
Отметим, что преобразование SSv (/)—>0"ал(г) в соответствии с (2.17)
является однозначным, однако обратное преобразование не является
однозначным. Другими словами, зная спектральную плотность относительных
отклонений частоты ОГ, можно вычислить вариацию Алана, но, зная вариацию
Алана, нельзя однозначно восстановить спектральную плотность
относительных отклонений частоты.
Для модели спектральной плотности относительных отклонений частоты
(2.11) при условии 0</</тах вычисление по формуле (2.17) приводит к
следующему результату [8]:
<U(0 = *J^?-M + 2AL1ln(2) + AT +
О 2\Т\
(2ет)Т[з(2 + Ц2^И)-Ц2))] + ^
36
Время. Шкалы времени
Данное выражение позволяет анализировать влияние различных типов
шумов (см. табл. 2.1) на вариацию Алана и ее изменение при изменении
усреднения г.
2.6. Синхронизация шкал времени в СРНС
Синхронизация системной шкалы времени и UTC(SU). Показания
системной шкалы времени ГЛОНАСС привязывается к шкале Госэталона
Всемирного координированного времени РФ UTC(SU), причем между этими
шкалами времени существует постоянный сдвиг на целое число часов,
обусловленный особенностями функционирования ПКУ:
'ГЛОНАСС =tUTC(SU) +03 4 00 МИН.
Показания системной шкалы времени корректируется одновременно с
коррекциями на целое число секунд показаний шкал UTC, планово
проводимыми Службой Всемирного времени [1.2]. Эти коррекции осуществляются в
00 ч 00 мин 00 с в полночь с 30 июня на 1 июля или с 31 декабря на 1
января по мере необходимости.
Текущая привязка СШВ к UTC(SU) осуществляется с погрешностью, не
превышающей 1 мкс.
Синхронизация бортовых шкал времени НС осуществляется в ПКУ в
результате сверки показаний с показаниями СШВ и коррекцииазаний
(непосредственной и алгоритмической) [1.4, 1.5].
Сверка шкал времени в СРНС позволяет определить значение ухода БШВ
относительно СШВ. В зависимости от процедуры нахождения величины
псевдодальности до /-го НС различают пассивные (СРНС GPS) и активные (СРНС
ГЛОНАСС) методы сверки шкал времени. Активный (запросный) метод более
прост и позволяет получать более точные результаты, но требует установки
дополнительной аппаратуры.
В процессе сверки по принятым в ПКУ навигационным сигналам от
каждого НС по данным навигационного сообщения определяется значение
времени в БШВ на момент излучения сигнала спутником /£lub • При приеме сигнала
в ПКУ определяется расчетное время приема в БШВ в соответствии с
формулой
где Д/рас — время распространения сигнала от /-го НС до ПКУ; Д/р э —
уход БШВ из-за релятивистских эффектов, рассчитываемый с точностью до
единиц наносекунд (см. п. 7.4); Д/ат— сдвиг определяемой БШВ из-за
рефракции радиоволн в атмосфере (см. п. 7.3); Дгап— прочие аппаратурные бор-
■XI
Глава 2
товой аппаратуры и приемника потребителя) и методологические
погрешности (см. п.7.6). Для этого в ПКУ осуществляются высокоточные определения
составляющих А/рас Atp э, AtaT, Atan с использованием дополнительных
инструментальных средств.
Уход БШВ относительно СШВ определяется при сравнении расчетного
времени t^B с известным системным временем /сшв приема того же
сигнала.
Коррекция БШВ производится при ее уходе относительно СШВ,
превышающем допустимые значения. Коррекция выражается в совмещении
временных интервалов в БШВ и СШВ (процедура фазирования БШВ) и (или) в
уточнении их оцифровки (процедуры коррекции кода БШВ на целое число единиц
времени). Фазирование обеспечивает точность совмещения шкал времени до
десятков наносекунд.
Длительные наблюдения за расхождением БШВ и СШВ позволяют
установить его закономерность и прогнозировать на требуемый момент времени с
соответствующей точностью. В СРНС ГЛОНАСС/GPS, управляемых с
ограниченных территорий, необходимость прогнозирования БШВ и ее ухода
обусловлена тем, что непосредственная коррекция БШВ (воздействие системы
управления на БШВ) может производиться только эпизодически, когда НС
находится в зоне видимости СТИ. Прогнозирование систематической
составляющей ухода обеспечивает возможность осуществления алгоритмической
коррекции БШВ, при которой задается модель ухода БШВ, а корректировке
подлежат ее параметры, т.е. частотно-временные поправки, которые
закладываются в память ЭВМ спутника с помощью специальных станций ПКУ и в
дальнейшем передаются потребителям совместно с эфемеридной
информацией. Более подробно алгоритмический метод коррекции БШВ описан в п. 7.7.
Синхронизация шкалы времени потребителя. Нахождение
потребителем бортового времени НС и соответственно системного времени СРНС
осуществляется с использованием навигационной информации, передаваемой в
излучаемом НС радиосигнале. При этом может быть реализовано несколько
способов синхронизации шкалы времени потребителя, отличающихся
точностью [1.6]: расчет поправки к шкале времени потребителя на основе псевдо-
дальномерных измерений; использование меток времени, передаваемых в
навигационном сигнале; применение дальномерных кодов, передаваемых в
навигационном сигнале НС.
Первый способ основывается (в первом приближении) на том, что
информация, полученная потребителем в сигналах НС, используется как для
расчета текущего ухода БШВ относительно СШВ, так и для привязки ШВП к
СШВ при нахождении поправки к ШВП (временной координаты потребителя
/'). Этот способ наиболее широко распространен и обеспечивает точность
временных измерений не хуже 1 мкс. Второй способ основывается на том, что
38
Время. Шкалы времени
данные о текущем спутниковом времени (метка времени НС) и о прогнозе
ухода БШВ в опорные моменты времени относительно СШВ передаются
потребителям в навигационном сообщении. Точность привязки ШВП в этом
случае определяется неопределенностью знания дальности от НС до
потребителя. Третий способ аналогичен предыдущему и отличается в основном видом
информации, используемой в сигнале НС.
Литература
2.1. Одуан К., Гино Б. Измерение времени. Основы GPS. — М: Техносфера, 2002.
2.2. Поваляев А.А. Спутниковые радионавигационные системы: время, показания
часов, формирование измерений и определение относительных координат. — М:
Радиотехника, 2008.
2.3. Хренов Л.С., ГолубИ.Я. Время и календарь. — М.: Наука, 1989.
2.4. Астрономический ежегодник СССР на 1989 год.—Л.: Наука, 1987, т. 68.
2.5. Астрономический календарь. Ежегодник, переменная часть, 1990/ Под ред.
Д.Н. Пономарева . — М: Наука, 1989.
2.6. Воздушная навигация и аэронавигационное обеспечение полетов/ Под ред.
Н.Ф. Миронова. —М: Транспорт, 1992.
2.7. Кантор Л.Я., Тимофеев В.В. Спутниковая связь и проблемы геостационарной
орбиты. — М.: Радио и связь, 1988.
2.8. Рютман Ж. Характеристики нестабильности фазы и частоты сигналов
высокостабильных генераторов: итоги развития за 15 лет// ТИИЭР, т. 66, № 9, 1978.
2.9. Global Positioning System: Theory and Applications, vol.1 / Edited by B.W. Par-
kinson, J.J. Spilker. — Washington, AIAA, 1996.
39
Глава 3
Глава 3
ТРАЕКТОРНОЕ ДВИЖЕНИЕ
НАВИГАЦИОННЫХ СПУТНИКОВ
3.1. Системы координат, используемые в СРНС
Геоцентрическая инерциалъная система координат
Для описания движения навигационного спутника используются законы
ньютоновской механики, которые справедливы в инерциальной системе
координат, т.е. неподвижной или двигающейся с постоянной скоростью. В качестве
такой системы координат в СРНС используется геоцентрическая инерциалъная
система координат OX0Y0Z0, начало координат которой расположено в центре
масс Земли (рис. 3.1).
Рис. 3.1. Геоцентрическая инерциальная система координат
Плоскость X0OY0 лежит в плоскости экватора Земли, причем ось ОХ0
направлена в точку весеннего равноденствия — точку Весны или точку
Овна у (у — астрономический знак созвездия Овна), которая лежит на линии
пересечения плоскости экватора Земли и плоскости орбитального движения
Земли вокруг Солнца (рис. 3.2). Ось OZ0 дополняет прямоугольную систему
координат до правой, т.е. направлена вдоль оси вращения Земли в сторону
Северного полюса. Так как центр Земли вращается вокруг Солнца и, следовательно,
имеет некоторое ускорение (центростремительное), то, строго говоря, данная
система координат является квазиинерциальной, и в ней необходимо
учитывать определенные релятивистские эффекты.
40
Траекторное движение навигационных спутников
Рис. 3.2. Линия весеннего равноденствия
Геоцентрическая система координат, связанная с Землей
Положение объектов (точек), находящихся на Земле, удобно описывать в
системе координат, неподвижной относительно Земли. В качестве такой
системы используется геоцентрическая декартова система координат OXYZ,
центр которой совмещен с центром масс Земли, ось OZ совпадает с осью OZ0
инерциальной системы координат OX0Y0Z0 (т.е. направлена по оси вращения
Земли в сторону Северного полюса), ось ОХ лежит в плоскости земного
экватора и связана с Гринвичским меридианом G , ось OY дополняет систему
координат до правой (рис. 3.3). Данная декартова система координат жестко связана
с Землей и вращается вместе с ней относительно геоцентрической
инерциальной системы координат OX0Y0Z0 с угловой скоростью щ. В СРНС
ГЛОНАСС геоцентрическая подвижная система координат определена как
ПЗ-90 [3.1], а в СРНС GPS — WGS-84 [3.2].
Рис. 3.3. Геоцентрическая подвижная система координат
41
Глава 3
В процессе суточного вращения системы координат OXYZ ось ОХ
периодически проходит точку Весны. Интервал времени между двумя такими
последовательными моментами соответствует звездным суткам, а интервал времени,
отсчитанный от момента прохождения точки Весны, определяет звездное
время (см. п. 2.1). Поскольку это время дается для Гринвичского меридиана, оно
является гринвичским звездным временем. Поэтому угол у/т на рис. 3.3
соответствует гринвичскому звездному времени Sr.
Для геоцентрической системы координат, связанной с Землей, кроме
декартовых {x,^,z} можно ввести сферические координаты {г,ф9Л} (рис. 3.4),
где г — радиус точки с декартовыми координатами {.x,jy,z}, ф и Я —
соответственно геоцентрические широта и долгота этой точки, причем возрастание
долготы Я определяется в направлении на восток от Гринвичского меридиана.
Рис. 3.4. Декартовы и сферические координаты
Связь между декартовыми и сферическими координатами определяется
соотношениями
jc = rcos(^)cos(A), у = rcos(^)sin(A), r = rsin(A),
r = yjx2+y2+z2 , tg(A) = y/x, tg^) = z/y]x2+y2 .
(3.1)
(3.2)
Геодезическая система координат
Так как Земля имеет форму эллипсоида, использование определенных
выше сферических координат {г,^,Я} для точек, находящихся на Земле и
околоземном пространстве, не очень удобно. Поэтому вводят эллипсоидальную сис-
42
Траекторное движение навигационных спутников
тему координат, которую часто называют геодезической. В данной системе
координат точка П задается координатами [Н,Ь,В] (рис. 3.5), где Н —
геодезическая высота; L — геодезическая долгота; В — геодезическая широта.
Рис. 3.5. Земной эллипсоид и эллипсоидальная система координат
Геодезическая широта точки П определяется как угол между нормалью к
поверхности эллипсоида и плоскостью экватора. Геодезическая долгота
L точки П определяется как угол между плоскостью Гринвичского меридиана
и плоскостью меридиана, проходящего через точку П (положительное
направление счета долгот — от Гринвичского меридиана к востоку).
Геодезическая высота Н определяется как расстояние по нормали от
поверхности эллипсоида (которую называют местной вертикалью) до точки 77.
В эллипсоидальной системе координат используется физическая модель
Земли в виде эллипсоида (рис. 3.5) с большой полуосью а, лежащей в
экваториальной плоскости, и малой полуосью Ъ. Основные параметры земного
эллипсоида и некоторые геодезические константы приведены ниже.
Основные геодезические константы
Угловая скорость вращения Земли, рад/с-1 7292115 Ю-11
Геоцентрическая константа гравитационного поля Земли
с учетом атмосферы, м с" 398600,4410
Геоцентрическая константа гравитационного поля
атмосферы Земли, mj с" 0,35 10
Скорость света, м с"1 299 792 458
Коэффициент (С20) при второй зональной гармонике разложения
геопотенциала в ряд по сферическим функциям -1082,63 • Ю-6
43
Глава 3
Параметры общего земного эллипсоида
Большая полуось, м 6 378 136
Знаменатель сжатия 1 : 298,257
Гравитационное ускорение на экваторе Земли, мГал 978 032,8
Поправка к гравитационному ускорению на уровне моря,
обусловленная влиянием земной атмосферы, мГал - 0,9
Связь между геодезическими координатами {#,£, В) точки пространства и
декартовыми координатами {jc,^,z} определяется формулами [3.3]
х = (N + H)cosBcosL, y = (N + #)cosi?sinL,
z = U\-e2))N + H~\smB, (3.3)
где N = a/\l 1-е2 sin2 В — радиус кривизны в точке местной вертикали Я;
е = \]\-Ъ21а2 = v2а-а2 — эксцентриситет эллипсоида; а = \-b/а —
параметр сжатия эллипсоида.
Обратные преобразования имеют вид
tg(B) =
у
Л . ..2l N + H
х + у
V
^/^7
tg(L) = y/x, Н = ^ ' -N. (3.4)
cos{B)
Локальная декартова система координат
Декартову систему координат можно задавать в любой точке Р Земли или
околоземного пространства. При этом начало системы координат Ол
определяется в точке Р. Плоскость ХлОлУл является касательной плоскостью к
земному эллипсоиду, причем ось ОлХп ориентирована на север, а ось ОлУл — на
восток. Ось Ол2л совпадает с местной вертикалью, и при ее ориентации в
зенит (вверх) получаем левостороннюю, а при ее ориентации в надир (вниз) —
правостороннюю системы координат.
На рис. 3.6 для примера приведена левосторонняя локальная декартова
система координат. Координаты точки в локальной системе координат могут
задаваться декартовыми {xn,yn,zn} или сферическими {d,f?,&} координатами, где
d — дальность, /? — азимут, 3 — зенитный угол.
44
Траекторное движение навигационных спутников
L . [*п>Уп>2п)
У » лп
Рис. 3.6. Локальная левосторонняя
система координат
Рис. 3.7. Декартова система
координат, связанная с ЛА
Декартова система координат, связанная с подвижным объектом
При решении задач навигации летательных аппаратов (ЛА) часто
используют декартову правостороннюю систему координат OXcYcZc 9 связанную с
летательным аппаратом (рис. 3.7). Начало координат данной системы
располагается в центре масс ЛА, ось ОХс направлена вдоль строительной оси к фюзеляжу,
ось OYc лежит в плоскости крыльев, а ось OZc направлена по нормали к
плоскости XcOYc. Положение ЛА в пространстве задается тремя углами: крена у ,
тангажа р и рыскания а , которые характеризуют вращение ЛА относительно
осей ОХС9 OYc и OZc соответственно.
Преобразование декартовых систем координат
Пусть имеем две декартовы правосторонние системы координат OXxYxZx и
OX2Y2Z2, начала которых совмещены, и задана некоторая точка Р9
координаты которой в одной системе координат определяются вектором \х = \хх ух zx\ , a
в другой системе координат — вектором х2 = \х2 у2 z2\ .
Преобразование вектора X! в вектор х2 может быть описано выражением
Х2 "" ^1 Х1 '
(3.5)
где Uj2 — матрица преобразований, которая описывает три последовательных
вращения системы координат OXxYxZx на угол ах относительно оси ОХх
45
Глава 3
(рис. 3.8), на угол а2 относительно оси OYx, на угол аъ относительно оси OZ{
и которую иногда называют матрицей направляющих косинусов или матрицей
вращений. Поэтому можно записать
Uf=U3(af3)U2(flf2 ^(а,),
где
и,Ц)=
и3(«з) =
10 0
0 cos(aj) sin(a1)
0 -sin(a,) cos(orj)
cos(or3) ^п{аз) 0|
-sin(<z3) cos(or3) 0
0 0 1
, U2(a2) =
cos(ar2) 0 -sin(a2)
0 1 0
sin(a2) 0 cos(or2)
-v,,-v;
(3.6)
(3.7)
Рис. З.8. Последовательные повороты системы координат
Для правосторонних систем координат углы вращения а{ положительны,
если они соответствуют движению против часовой стрелки для наблюдателя,
46
Траекторное движение навигационных спутников
смотрящего с положительно направления соответствующей оси на начало
координат (рис. 3.8).
Матрица вращений U? обладает следующими свойствами
(u,2)TU12=I,det(u12) = l, (3.8)
где I — единичная матрица.
Соотношения (3.8) справедливы и для матриц (3.7), описывающих
вращение относительно одной из осей.
Если центры систем координат не совпадают, то преобразование вектора
координат точки из одной системы в другую дается выражением
x2=c + //U2x1? (3.9)
где с — вектор смещения начала координат OXxYxZx относительно OX2Y2Z2;
ju — скалярный фактор, отражающий возможное изменение длины
единичного вектора при переходе из одной системы координат в другую.
3.2, Уравнения невозмущенного траекторного движения
навигационного спутника в инерциальной
системе координат
Под невозмущенным (кеплеровым) движением спутника понимают его
движение под действием только силы притяжения Земли (одного
притягивающего центра) [3.4]. В соответствии со вторым законом
Ньютона движение центра масс спутника в инерциальной системе координат OXoY0Zo
описывается уравнением
mg = F, (ЗЛО)
где т — масса спутника; g — вектор центростремительного ускорения; F —
вектор силы притяжения Земли.
По закону всемирного тяготения сила притяжения Земли
F = k Mm/г2 = /и т/г2,
где к = 6,672- Ю-1' м3/кгс2 — универсальная гравитационная постоянная;
М = 5,974242 1024 кг — масса Земли; г — расстояние от центра Земли до
спутника; ju = kM = 3,9860044-1014 м3/с2 — геоцентрическая гравитационная
постоянная Земли.
47
Глава 3
С учетом соотношения g = d2r/dt2 , где производная по времени
понимается как полная производная в инерциальнои системе координат, уравнение
движения (ЗЛО) принимает вид
т-
dt2
= F.
Пространственная траектория невозмущенного движения спутника в
проекциях на оси инерциальнои системы координат OXqY^Zq описывается
уравнениями
(3.11)
d х0 х0 d у0 у0 d z0 z0
,2 " 3 ' i2 " 3 ' /2 ^ 3
dr Г dr Г dr Г
Здесь x0, yQ, z0 — текущие координаты спутника (проекции радиус-
х0 + у0 + z0 .
Уравнения (3.11) описывают траекторию движения спутника, которую
принято называть орбитой.
3.3. Классические элементы орбиты спутника
В соответствии с первым законом Кеплера траектория НС, движущегося в
центральном поле тяготения, лежит в неподвижной (относительно
инерциальнои системы координат) плоскости (орбитальной плоскости), проходящей
через центр тяготения, и представляет собой кривую второго порядка, в одном из
фокусов которой находится центр притяжения (Земля).
Ориентацию орбитальной плоскости характеризуют ее положением
относительно экваториальной плоскости XOY(рис. 3.9).
Плоскость орбиты НС
Орбита НС
Рис. 3.9. Ориентация орбитальной плоскости
48
Траекторное движение навигационных спутников
Линию пересечения этих плоскостей называют линией узлов. Узлами
орбиты спутника являются точки пересечения орбиты с экваториальной
плоскостью. Узел U , соответствующий движению спутника из южной небесной
полусферы в северную, называют восходящим, а узел D, соответствующий
движению из северной небесной полусферы в южную, — нисходящим.
Положение орбитальной плоскости относительно экваториальной
характеризуется двумя орбитальными элементами — долготой восходящего узла О.
и наклонением орбиты i. Угол Q отсчитывается в экваториальной плоско-
скости от оси ОХ до линии узлов и изменяется в диапазоне от 0 до 360°.
Угол i определяется как угол между экваториальной и орбитальной
плоскостями и изменяется в диапазоне от 0 до 180°. При i = 90° орбиту называют
полярной, при /«90° — приполярной, при / = 0° — экваториальной, при
0</<90° —наклонной.
Уравнение орбиты спутника в орбитальной плоскости в полярной системе
координат (г0, 3) с центром, совпадающим с центром Земли, имеет вид
r = p/(\ + ecos(3-30)), (3.12)
где р — фокальный параметр; е — эксцентриситет; 30 — угол между
положительным направлением полярной оси и фокальной осью.
Данное уравнение является уравнением конического сечения — кривой
второго порядка, один из фокусов которой совпадает с центром полярной
системы координат. При 30 = 0 полярная ось направлена от центра к ближайшей
вершине кривой (3.12), а при 30 -п — в противоположную сторону. В
дальнейшем для определенности будем полагать 30 = 0. Угол 3 называют
истинной аномалией.
При е - 0 орбита спутника является кругом; при 0 < е < 1 — эллипсом,
степень вытянутости которого определяется орбитальными параметрами р и
е; при е = 1 — параболой; при е > 1 — гиперболой. Для НС характерны
эллиптические орбиты, т. е. 0 < е < 1.
На рис. 3.10 приведена эллиптическая орбита спутника в орбитальной
плоскости. В одном из фокусов (О) находится Земля. Прямую линию,
проходящую через фокусы эллипса, называют линией апсид. Точки пересечения этой
линии с эллипсом называют апсидами. Ближайшую к силовому центру (точке
О) вершину кривой называют перицентром, а удаленную вершину (которая
имеется только у эллипса) — апоцентром. В зависимости от того, вокруг
какого небесного тела движется спутник, апсиды орбиты получают собственные
названия: при движении вокруг Земли — перигей и апогей. Ориентация орбиты
49
Глава 3
в орбитальной плоскости характеризуется углом перигея (аргументом) сои
между направлением на перигей и линией узлов.
нс(г = /7,а = 9о°)
Эллиптическая орбита НС
Линия узлов
Рис. 3.10. Эллиптическая орбита спутника
Размеры орбиты спутника можно характеризовать различными
комбинациями следующих параметров:
а = p/ll -е2) = (гА + гп )/2 — большая полуось эллипса;
Ъ = ау]\ -е2 — малая полуось;
d - ае = (гА - гп )/2 — линейный эксцентриситет;
где гА=ОА, гп = ОП — апогейное и перигейное расстояние соответственно.
Иногда апогейное и перигейное расстояния выражаются как
rA=R3+HA, гп=Д3+Яп,
где R3 =6371 км — радиус Земли; НА,НП — высоты апогея и перигея
относительно поверхности Земли.
3.4. Движение спутника по невозмущенной орбите
Пять параметров орбиты Q, i, соп, /?, е постоянны и не меняются при
движении спутника по орбите, а шестой параметр 3(t) (истинная аномалия)
характеризует положение спутника на орбите в каждый момент времени t,
который часто называют эпохой.
Другим широко распространенным орбитальным элементом является
время г прохождения спутником характерной точки орбиты, например перигея
т = tn (поэтому иногда т называют временем перигея). Используя этот эле-
50
Траекторное движение навигационных спутников
мент, положение НС на орбите в произвольный момент времени t
определяется с помощью уравнения Кеплера:
t-T = J—(E-esinE), (3.13)
где Е — эксцентрическая аномалия НС, определяемая из соотношения
Геометрический смысл параметра Е можно уяснить из рис. 3.11, на
котором, кроме эллиптической орбиты НС, приведена гипотетическая круговая
орбита. Для точки Нх круговой орбиты, имеющей одинаковую с НС абсциссу, и
определяется угловой параметр Е.
Эллиптическая орбита НС
Рис. 3.11. Определение эксцентрической аномалии
Движение спутника по эллиптической орбите, в отличие от
движения по круговой орбите, является неравномерным, т. е. d&fdt ^ const, а
зависит от положения спутника на орбите. Чтобы использовать удобное
равномерное движение, т.е. движение с постоянной угловой скоростью, вводят
угловой параметр М — средняя аномалия для момента времени / {средняя
аномалия эпохи t)\
M = 360(t-t0)/T = n(t-r)9 (3.15)
где /0 — какой-либо определенный (начальный) момент времени, например
t0 = r ; п = 360°/Т = \Jju/a3 — среднее движение НС или средняя угловая
скорость НС.
Дифференцируя (3.15) по времени, получаем другое определение среднего
движения:
Глава 3
n = dM/dt. (3-16)
В отличие от г, вычисление М сохраняет смысл и при круговых орбитах.
Если истинная аномалия 9 определяет истинное положение НС на орбите, то
параметр М характеризует гипотетическое положение НС при условии
равномерного орбитального движения с угловой скоростью, равной средней
скорости п. Поэтому в соответствии с (3.15) М — угол между линией апсид и
направлением на предполагаемое положение НС на орбите, в котором он
находился бы при равномерном движении. Чем меньше отличие орбиты НС от
круговой, тем больше соответствует средняя угловая скорость п истинной угловой
скорости и тем ближе значения Ми «9.
С учетом (3.15) уравнение Кеплера (3.13) можно представить в виде
M = E-esmE. (3.17)
Тогда для каждого заданного момента времени t рассчитывается средняя
аномалия М по формуле (3.15), которая используется в (3.17) для вычисления
эксцентрической аномалии Е. При этом решение равенства (3.17) проводится
итерационным методом. Зная Е, из уравнения (3.14) можно определить
истинную аномалию &(t).
В процессе расчетов параметров движения НС по почти круговым орбитам
(при е—»0) возникают вычислительные трудности, для устранения которых
используются преобразованные параметры. Например, вместо элементов е, соп
используются элементы: q = ecosсоп, к = esin con [3.1].
3.5. Уравнения невозмущенного движения спутника
в инерциальной системе координат
с использованием орбитальных элементов
Получим уравнения движения спутника в геоцентрической прямоугольной
системе координат OX0YoZo, переходя от орбитальных координат к инерциаль-
ным. В плоскости орбиты положение НС в каждый момент времени дается
полярными координатами (г, 9). Введем геоцентрическую декартову систему
координат OXorYorZor, центр которой совмещен с центром Земли, плоскость
XorOYor совмещена с орбитальной плоскостью, ось ОХог направлена вдоль
линии апсид в сторону перигея; ось OYor расположена перпендикулярно оси
ОХог так, что при повороте оси ОХог на 90° против часовой стрелки ее
направление совпадет с направлением оси OYor; ось OZor дополняет систему
координат до правосторонней. В такой системе координат положение НС
задается вектором \or =|rcos(9) rsin(«9) оГ .
52
Траекторное движение навигационных спутников
Перейдем от системы координат OXorYorZor к инерциальной системе
OX0Y0ZQ в результате трех последовательных вращений: на угол -а)п
относительно оси OZor; на угол -/ относительно оси ОХог; на угол -Q относительно
оси OZor. Тогда для вектора координат x0=|jc0 y0 z0|T НС в инерциальной
системе координат в соответствии с (3.5), (3.6) можно записать
х0 = и3(-а)и1(-0и3(-^п)хог,
где матрицы U^*), U3(*) определяются в соответствии с (3.7), или в
развернутом виде
х0 =r[cos(i9 + ^n)cosQ-sin(i9 + ^n)sinQcos/l;
у0 = г [cos(i9 + о)п )sin Q + sin (*9 + о?П )cosQcosi];
z0 =rsin(i9 + ^?n)sin/. (3.18)
В эти уравнения входят пять постоянных геометрических параметров
(эксцентриситет е, фокальный параметр р, углы соп, /, Q), не меняющихся при
движении спутника по орбите и характеризующих форму и размеры
эллиптической орбиты и ее ориентацию в пространстве. Текущее положение
спутника на орбите, как отмечалось выше, характеризуется шестым параметром —
истинной аномалией 3. Из (3.18) видно, что можно ввести другой обобщенный
параметр, характеризующий положение спутника на орбите, и = о)п + 3 ,
который называют аргументом широты спутника. Он измеряется от восходящего
узла (по аналогии с углом перигея о)п).
Дифференцируя (3.18) по времени, получаем
—9- = VXo =^^-K^sin(^n+l9)cosQ+cos(^n+^)sinQcos/);
~^ = Vyo =Kro^-K^sin(^n+l9)sinn-cos(^n+i9)cosQcos/);
^ = ^o=^0- + ^cosK+^)sin/, (3.19)
dt ° u r
где V = drjdt = ■Jju/p es*n & —радиальная составляющая вектора V
скорости спутника (рис. 3.5); Vu = rd&jdt = yjju/p (1 + г cos «9) — трансверсальная
составляющая вектора V (рис. 3.10).
Ориентация орбитальной плоскости НС в инерциальном пространстве
определяется начальными условиями орбитального полета. Начальная точка ор-
53
Глава 3
биты НС и вектор скорости НС (как в начальной точке, так и в любой другой)
должны лежать в этой плоскости. Форма орбиты определяется значением и
направлением скорости, сообщаемой НС в начальной точке его свободного
полета. Для движения НС по круговой орбите высотой НА относительно Земли
необходимо, чтобы начальная скорость Vu0 соответствовала круговой скорости
VKp на этой высоте и была направлена перпендикулярно радиусу-вектору г .
Можно показать (приравняв возникающую центробежную силу и силу
тяготения), что VKp = J/uJr , где r = R3+HA.
При гипотетической орбите с r = R3 значение VKp =28500 км/ч = = 7,91
км/с — первая космическая скорость (Vx).
Если высота орбиты НА= 1000 км, что соответствует СРНС типов
"Транзит", "Цикада", то VKp = 7,35 км/с; при #А=19 100 км (СРНС ГЛОНАСС, GPS)
VKp « 3,95 км/с; при #А=35 809 км (геостационарные НС) V^ « 3,076 км/с .
При использовании круговых орбит НС движется с постоянной угловой
скоростью, что существенно упрощает расчеты и прогнозирование его
координат в ПКУ и в приемниках сигналов СРНС.
Для создания эллиптической орбиты необходимо, чтобы V^ < VUH <Vn.
Здесь Vn ~ l,41Kj = 40 300 км/ч = 11,2 км/с — вторая космическая скорость. В
этом случае в зависимости от координат начальной точки и от угла между VWH
и г эллипс может занимать в орбитальной плоскости разное положение
относительно Земли.
Скорость движения НС по эллиптической орбите в общем случае [3.1]
VU3Jl = yj/i(2/r - 1/я). Видно, что скорость максимальна в перигее и минимальна
в апогее.
При движении по эллиптической орбите угловая скорость движения НС
меняется во времени, что усложняет расчеты по прогнозированию движения.
Однако движение по таким орбитам более экономично по энергетическим
затратам и позволяет при выборе соответствующих параметров орбиты (/\гА,гп)
обеспечить почти круглосуточное использование НС для навигационных
определений в заданном районе.
Так, НС с сильно вытянутыми эллиптическими орбитами предусмотрено
использовать при формировании региональных СРНС, в которых апогей
орбиты располагается над заданным районом. При этом НС будет находиться
максимальное время над этим районом. Но в бортовой аппаратуре СРНС в данном
случае могут возникать сложности в связи с необходимостью учета большого
динамического диапазона сигналов НС и значительной неравномерности пара-
54
Траекторное движение навигационных спутников
метров орбитального движения. Кроме того, эллиптические орбиты
характеризуются меньшей стабильностью.
При рассмотрении движения НС на эллиптических орбитах часто
оперируют таким параметром, как секториальная скорость VCK, под которой
понимают площадь сектора эллипса, описываемого радиусом-вектором НС в
единицу времени.
Из решения уравнений (3.12) следует, что VCK — величина постоянная для
любой точки орбиты:
._ 1 2d& 1 г—
Это соответствует второму закону Кеплера. Время полного оборота
радиус-вектора НС
T = S3JVCK=2xJ7JJi, (3.20)
где S3Jl = пab — площадь эллипса.
Часто используются более простые соотношения для круговой и
эллиптической орбит:
T = S494yl(rA/R3f ; Г = 1,6586-1(Г4я3/2 ,
где a, rA, R3 выражены в км, Т— в мин.
Период обращения НС, вычисленный по (3.20), называют сидерическим
или звездным, и он равен временному интервалу между двумя
последовательными прохождениями НС одной и той же точки орбиты, например перигея.
Очевидно, что интервал времени между двумя последовательными
прохождениями НС одного и того же меридиана, называемый синодическим периодом,
вследствие вращения Земли несколько больше (при совпадении направления
вращения НС и Земли).
Период обращения Т можно получить также из соотношения
т\1тг =а\/а2 >
где а{ и а2 — большие полуоси орбит двух НС; Тх и Т2 — периоды их
обращения.
Это соответствует третьему закону Кеплера.
В зависимости от периода обращения НС подразделяют на суточные при
Т = Т3 (звездные сутки или звездный период обращения Земли вокруг своей
оси) и на синхронные — при периоде Т, кратном звездным суткам. В свою
очередь, суточные НС, орбитальная плоскость которых лежит в плоскости эк-
55
Глава 3
ватора, называют геостационарными, так как они неподвижны относительно
одной из точек экватора.
В СРНС "Транзит", "Цикада" период обращения НС Т = 105 мин; в СРНС
ГЛОНАСС Т =11,2 ч ; в GPS Т =12 ч ; у геостационарных НС Т = 23 ч 56 мин
04,1 с. Видно, что синхронный спутник системы GPS один раз в сутки
проходит над одной и той же точкой поверхности Земли.
3.6. Общая характеристика возмущенного движения
навигационных спутников
В реальных условиях траекторного движения НС на него, кроме основной,
центральной силы притяжения Земли, действуют разнообразные
дополнительные возмущающие силы. И хотя они малы по сравнению с основной, их
длительное воздействие приводит к отклонениям (возмущениям) реальной орбиты
от расчетной (кеплеровой), которыми при построении СРНС нельзя
пренебречь.
Основными источниками возмущения орбит навигационных спутников
являются [1.6, 3.5—3.6]:
возмущения гравитационного поля вследствие несферичности Земли и
неравномерности распределения ее массы;
притяжение со стороны Луны и Солнца;
сопротивление среды при движении НС;
давление светового излучения Солнца и прочие физические факторы.
Расчеты показывают [3.5], что возмущенная орбита НС в общем случае не
будет эллиптической, и истинные параметры орбитального движения НС
отличаются от параметров, рассчитанных по формулам невозмущенного (кеплеро-
ва) движения.
При анализе возмущенного движения НС принято считать, что НС в
каждый момент времени находится на той невозмущенной (эллиптической)
орбите, которая рассчитана с учетом прекращения в этот момент действия
возмущающих сил. Это означает, что в отличие от невозмущенного движения
элементы возмущенной орбиты НС непостоянны. Их изменение происходит
непрерывно, но каждому моменту времени и каждой точке возмущенной
траектории соответствует своя кеплерова орбита, которую называют оскулирующей,
а ее орбитальные элементы — оскулирующими. Тогда истинную траекторию
НС можно представить в виде огибающей оскулирующих траекторий,
построенных для различных моментов времени. Положение НС в пространстве может
быть определено в любой момент времени при решении известных уравнений
для орбитальных элементов /(/), Q(/), соп (/), e(t), p(t), &(t). При этом можно
исследовать влияние на траекторию НС приведенных возмущающих факторов,
а также различных моделей конфигурации Земли.
56
Траекторное движение навигационных спутников
Все наблюдаемые возмущения орбит разделяют на вековые и
периодические. Вековые приводят к непрерывным медленным изменениям элементов
орбиты НС, периодические повторяются через определенный интервал времени,
в зависимости от длительности которого их подразделяют на коротко- и дол-
гопериодические. Они обусловлены периодическим характером траекторного
движения и аппроксимацией возмущающих факторов (аномалий поля
тяготения, конфигурации Земли).
Детальное изучение возмущений, вызываемых нецентральностью поля
тяготения Земли, показало, что при определенных допущениях вековые
изменения орбитальных элементов /, р, е отсутствуют, а периодические изменения
им присущи.
За один оборот НС значения параметров i и р совершают несколько
колебаний, причем амплитуда i максимальна при / = 45° или / = 135°, а для
полярной и экваториальной орбит периодическими возмущениями можно
пренебречь. В свою очередь, амплитуда р максимальна для полярных орбит и
равна нулю для экваториальных. Периодические возмущения параметра е
носят сложный гармонический характер. У параметра а могут наблюдаться
небольшие вековые уходы, пропорциональные уходу перигея, а также
периодические возмущения. Следует отметить, что изменения большой полуоси
орбиты не зависят от ее наклонения.
Орбитальная плоскость и сама орбита вращаются (прецессируют) в инер-
циальном пространстве. Вековой уход долготы восходящего узла за один
оборот НС составляет [3.6] AQ = -2;r zcosi/ljup2), где £ = 2,634 1025 м5/с —
коэффициент, учитывающий конфигурацию Земли.
Из приведенного соотношения следует, что скорость прецессии орбиты
зависит от наклонения i и фокального параметра р , поэтому в первом
приближении вековой уход АГ2у полярных орбит отсутствует, а у экваториальных
максимален (при р-const). При прямом движении НС 1/<90°) восходящий
узел перемещается к западу (в сторону уменьшения Q), при обратном (i > 90° J
— к востоку (в сторону увеличения Q.).
Периодическими возмущениями величины Q. можно пренебречь.
Вековой уход аргумента перигея за один оборот НС в первом
приближении равен Асо = 7r£pcos2 i-lyijup2).
Вековое движение перигея при / = 0 и 180° максимально, а для
построения стабильных (в орбитальной плоскости) орбит можно выбирать значения
ix = 63°29'06" или i2 = 116°35'54", которые обеспечивают Аа? « 0. Если / < ix или
57
Глава 3
i > i2, то перигей прецессирует в направлении движения НС, а при /, < /' < i2 —
навстречу движению НС.
Наиболее существенные периодические возмущения аргумента перигея
имеют такой же характер, как и аналогичные возмущения эксцентриситета е
(гармонические с периодом, равным периоду обращения НС, и периодом, втрое
меньшим), но со сдвигом по фазе на 90°.
Изменение периода обращения НС характеризуется драконическим
периодом ТПТ), определяемым как время полета НС от экватора до экватора. При на-
клонении орбиты / = 60 и 120° имеем Гдр = Т .
Описанные возмущения орбитальных элементов приводят к возмущениям
радиуса-вектора НС и, следовательно, высоты полета. Эти возмущения носят
такой характер, что высота НС как бы отслеживает изменения размеров Земли:
над экватором высота увеличивается, а над полюсом уменьшается.
Обобщая приведенные результаты анализа влияния нецентральности поля
тяготения Земли, можно констатировать следующее.
Полярные орбиты отличаются стабильностью орбитальной плоскости
(отсутствуют возмущения Q, /) и сравнительно большими изменениями формы
орбиты и ее ориентации в орбитальной плоскости.
Экваториальные орбиты отличаются сравнительно стабильной формой
орбиты, но положение ее в орбитальной плоскости и самой плоскости может
быть нестабильным.
Наклонные орбиты, характерные для средневысотных СРНС ГЛОНАСС,
GPS (/«60°), отличаются относительной стабильностью параметров:
аргумента перигея, характеризующего положение орбиты в плоскости движения, и
периода обращения.
Исследования возмущений (вековых и долгопериодических) почти
круговых орбит с периодом обращения, равным приблизительно 12 ч
(двенадцатичасовые НС СРНС ГЛОНАСС, GPS), показали, что периоды колебаний
элементов /, Q могут составлять десятки и сотни лет, в зависимости от начальных
значений /0, Q0; причем для /0, не слишком близких к 0 и 90°, амплитуда
долгопериодических колебаний составляет 1 ... 2°. Для них влияние сжатия
Земли на возмущения примерно в 10 раз больше влияния Луны и Солнца.
Кратко охарактеризуем влияние других возмущающих сил.
При высотах полета НС более 1000 км (например, средневысотные СРНС
ГЛОНАСС, GPS) эффект атмосферного торможения невелик и им можно
пренебречь.
Известные данные о влиянии Луны и Солнца на эволюцию орбит НС
свидетельствуют о том, что возмущающее ускорение из-за притяжения Луны
примерно в 2 раза больше влияния Солнца. Для средневысотных СРНС возмуще-
58
Траекторное движение навигационных спутников
ния из-за влияния Луны и Солнца превосходят соответствующие возмущения,
обусловленные аномалиями силы тяжести Земли.
Для расчета возмущенных пространственных координат НС и их
производных аппаратура потребителя получает от НС периодически обновляемые
оскулирующие элементы и поправки к ним. Такая процедура соответствует
предъявляемым требованиям к точности и простоте расчетов в приемниках
сигналов СРНС.
3.7. Приближенные уравнения возмущенного движения
в геоцентрической подвижной системе координат
В геоцентрической подвижной системе координат ПЗ-90, жестко
связанной с Землей, определяются координаты потребителей. Для этого необходимо
иметь координаты и составляющие скоростей НС в этой же системе координат.
Известно [3.7], что уравнения движения материальной точки в инерциальнои и
подвижной системах координат различны вследствие различий в нахождении
производной по времени.
Положение некоторой точки в пространстве, например центра масс
спутника, определяется геоцентрическим радиусом-вектором г. Компонентами
этого вектора в геоцентрических системах координат OX0Y0Zo и OXYZ служат
координаты его конца, которые соответственно равны x0,y0,z0 и x,y,z.
Координаты конца радиус-вектора г в указанных системах координат описываются
различными функциями.
Производная по времени радиуса-вектора г в некоторой геоцентрической
системе координат определяется как вектор (V или Уг в рассматриваемых
системах координат), проекции которого на оси этой системы координат равны
производным от проекции самого радиуса вектора на те же оси
clx* с/у* dz^} Ж7 [dx dy dz\ ч
—-,-^-,—-> и V„ =<—,—,— > соответственно).
dt dt dt J [ dt dt dt J
Производную, взятую в инерциальнои системе координат, называют
полной^ в других системах координат — локальной. Полная производная г по
времени определяет вектор V абсолютной скорости в инерциальнои системе
координат. Локальная производная определяет вектор относительной
скорости в подвижной системе координат, например Vr в системе координат OXYZ.
Связь между полной dr/dt и локальной dx/dt производными
определяется формулой [3.7]
dx dx /о -> 1 ч
— = — + <*>wxr, (3.21)
dt dt
59
Глава 3
где cdw — вектор абсолютной угловой скорости подвижной системы
координат относительно инерциальнои; х — знак операции векторного умножения.
Выражение (3.21) является общим и справедливо для любого вектора.
В соответствии с (3.21) для описания движения в геоцентрической
подвижной системе координат OXYZ необходимо в уравнениях движения (3.11),
записанных для инерциальнои системы координат, перейти от полной второй
производной d2rjdt2 к локальной производной. Применив дважды (3.21),
получим
-f = —f+ 2cowxVr+cowx(cowxr). (3.22)
dr dt
Первое слагаемое в правой части уравнения определяет относительное
ускорение, т. е. ускорение в подвижной системе координат, второе слагаемое —
кориолисово ускорение, третье — переносное ускорение от вращательного
движения подвижной системы координат относительно инерциальнои.
Так как система координат OXYZ жестко связана с Землей и вращается
вместе с ней относительно оси вращения OZ, вектор cow для нее имеет
компоненты {0, 0, (щ).
С учетом (3.22) уравнение движения материальной точки (спутника) (3.11)
в системе координат OXYZ, связанной с Землей, принимает вид
^f + 2cowxVr+cowx((owxr) = -, (3.23)
at m
где F — вектор внешних сил, действующих на НС.
При рассмотрении невозмущенного движения НС внешней силой является
центральная сила притяжения Земли (3.10).
Уравнения возмущенного движения НС, приводимые ниже, полученные на
основе (3.23) и используемые при расчетах в СРНС ГЛОНАСС, кроме
центральной силы притяжения Земли учитывают дополнительную силу,
обусловленную полярным сжатием и характеризуемую гармоникой С20, а также
лунно-солнечные гравитационные возмущения:
dx dy dz
dt x* dt yt dt
dt ~ Гз* + 2С20~
vx,
(
1-
5z2
' r1
+ cu^x + lo^V + x
ЛС '
60
Траекторное движение навигационных спутников
dK
dt
y=_ILy+Lc ""<
I г
5z
2\
V
+ о4у-2а^Ух+улс,
dV.
И
ца{
2 (
dt
— ^Г^ ' t-ОЛ 7 %
3 - ■ - -20 —J"
г I г
5z
2\
+ Z
лс '
(3.24)
где ае — экваториальный радиус Земли.
При интегрировании уравнений (3.24) лунно-солнечные гравитационные
ускорения {*лс,.улс, 2ЛС} полагаются постоянными величинами на интервалах
±15 мин.
При дальнейшем изложении знак «~» у производных по времени в
подвижной системе координат опустим.
3.8. Зоны и время видимости навигационных спутников
К основным характеристикам НС относят зону обзора, зону видимости,
продолжительность наблюдения, орбитальную конфигурацию сети НС и др. На
рис. 3.12 приведена геометрическая схема, поясняющая основные определения.
А
Рис. 3.12. Зона обзора НС
Зона обзора НС представляет собой участок земной поверхности, на
котором можно осуществлять наблюдение за НС, прием его сигналов. Центром
зоны обзора является подспутниковая точка 03, называемая географическим
местом спутника (ГМС).
Координаты {географические широта и долгота) ГМС могут быть
рассчитаны по формулам
61
Глава 3
#> = arcsin(sinw sin/), Л = Q-Sr +arctg(tgw cos/) + Q/,
где /, и, Q — орбитальные элементы; Sr — гринвичское звездное время;
tl = AQ/T— угловая скорость прецессии узла орбиты. Зона обзора ограничена
линией истинного горизонта в точке НС, поэтому ее размер зависит от высоты
Лш1х НС. Размер зоны обзора характеризуется углом /?тах (град) или
соответствующей ему дугой А03, которая называется радиусом зоны обзора Rq [km].
Из рис. 3.12 следует
Дшх=Ш-СС08 [R3/(R3+HA)],
^=^/^«/57,3 = 111,19/?^. (3.25)
Приемники сигналов СРНС обеспечивают заданную точность измерений в
зоне обзора, ограниченной радиогоризонтом, который поднят для пользователя
на угол а « 5 ... 10° (угол маски). В этом случае зона обзора определяется углом
/?<Лпах>гДе
р = arccos \_R3 cosa/(R3 + ЯА)] - а . (3.26)
Площадь зоны обзора So6 = 2tzR\ (l -cos/?^ax ]. Тогда относительная
площадь обзора So6/S3 = sin2 (Д^/2\, где S3 = 4лR% — площадь земного шара.
Для существующих СРНС рассмотренные выше параметры имеют
следующие значения:
"Цикада", "Транзит" — J3°max~30°, Д0«3400 км, So6/S3^3,S % при
ЯА «1000 км, а = 10°;
ГЛОНАСС (GPS) — /?;ах «75,52°, R0 * 8400 км, So6/S3*30 % при
ЯА «19 100 км, а = 10°.
При увеличении высоты НС до ЯА « 40 000 км радиус зоны обзора
изменяется незначительно (R0 « 9 400 км), а затраты на формирование такой
орбиты возрастают существенно.
Рассмотренная выше зона обзора соответствует фиксированному моменту
времени (мгновенная зона обзора).
У нестационарных НС мгновенная зона обзора, перемещаясь по
поверхности Земли, образует зону обзора в виде полосы шириной 2Rq . Ее осью является
совокупность ГМС — трасса НС. Заметим, что трасса НС не поднимается
выше географической широты #>тах = /.
62
Траекторное движение навигационных спутников
Установим условия видимости НС для наблюдателя, расположенного в
точке 03, лежащей на трассе НС (рис. 3.13). Область небосвода СС, в
которой НС наблюдается из точки 03 от момента восхода г до момента захода
г , называют зоной видимости (геометрической зоной видимости), для
которой справедливы соотношения (3.25), (3.26).
Рис. 3.13. Время нахождения НС в зоне видимости
Из рис. 3.13 видно, что максимальный угловой радиус зоны видимости
(дуга А'С)
А'С = /Гтах=пссо* [R3/(R3+HA)].
С учетом радиогоризонта угловой радиус зоны обзора уменьшается
р = arccos [j?3 cosa/(R3 + НА)] - а . Здесь угол а иногда называют
минимально допустимой высотой.
Продолжительность сеанса связи с НС tBm (в пределах видимости НС)
определяется разностью (гвых - гвх) и зависит от угла /? (т. е. от высоты
полета НС или периода его обращения Т).
Для круговой орбиты tBm = 2/3/v = Tpfn, где v = InjT — угловая
скорость обращения спутника.
Для СРНС "Цикада", "Транзит" гвид=18 мин при #А= 1000 км, а = 0°, а
для СРНС ГЛОНАСС tBm * 300 мин.
Если потребитель находится в стороне от трассы НС, то
продолжительность наблюдения спутника уменьшается.
63
Глава 3
Навигационные алгоритмы, реализованные в навигационной аппаратуре
современных СРНС, обычно ориентированы на прием сигналов от нескольких
НС одновременно. Наблюдение в любой точке рабочей зоны СРНС
одновременно нескольких НС обеспечивается путем оптимального выбора стабильной
пространственно-временной структуры (конфигурации) сети НС — числа,
ориентации и формы орбит; числа НС на каждой из них; взаимного
расположения орбит и спутников на них. Обычно число НС в сети превышает
минимально необходимое за счет резервных НС.
Литература
3.1. Иванов КМ. и др. Баллистика и навигация космических аппаратов. — М:
Машиностроение, 1986.
3.2. Охоцимский Д.Е., Сихарулидзе ЮТ. Основы механики космического полета. —
М: Наука, 1990.
3.3. Аппаратура радионавигационных систем ГЛОНАСС и GPS. Системы
координат. Методы перевычислений координат определяемых точек// Государственный
стандарт РФ (проект), Госстандарт России, 1997.
3.4. Основы теории полета и элементы проектирования спутников Земли/ Под ред.
М.К. Тихонравова. — М.: Машиностроение, 1974.
3.5. Вашковьяк М.А. Об эволюции почти круговых орбит 12-часовых ИСЗ//
Космические исследования, 1985, т. XXIII, вып. 1,с. 3—16.
3.6. Бородовщина Т.В. и др. Структура возмущений орбитального движения
навигационных ИСЗ типа НАВСТАР// Космические исследования, 1985, т. ХХШ, вып. 5, с.
713—719.
3.7. Бромберг П.В. Теория инерциальных систем навигации. — М.: Наука, 1979.
64
Глава 4
МЕТОДЫ РЕШЕНИЯ НАВИГАЦИОННЫХ ЗАДАЧ
4.1. Общие сведения
Основным содержанием навигационной задачи в СРНС является
определение пространственных координат потребителя, составляющих вектора его
скорости, а также текущего времени [4.1—4.3]. Поэтому в результате решения
навигационной задачи должен быть определен расширенный вектор состояния
потребителя П, который в инерциальной геоцентрической системе координат
OX0Y0Z0 можно представить в виде П = \ху z t Vx Vy Vz\ , где x9y9z —
координаты потребителя; Vx Vy Vz — составляющие вектора скорости потребителя;
t — текущее время (в той или иной временной шкале).
Элементы вектора состояния П недоступны непосредственному
измерению с помощью радиосредств. У принятого радиосигнала могут измеряться те
или иные его параметры, например задержка или доплеровское смещение
частоты. Измеряемый в интересах навигации параметр радиосигнала называют
радионавигационным (РНП), а соответствующий ему геометрический параметр
— навигационным (НП) [4.1]. Поэтому задержка сигнала т и доплеровское
смещение частоты /д являются радионавигационными параметрами, а
соответствующие им дальность до объекта Д и радиальная скорость сближения
объектов V - Д служат навигационными параметрами, связь между которыми
дается соотношениями
Д = сг, Гр=/дЯ,
где с — скорость света; Я — длина волны излучаемого НС сигнала.
Геометрическое место точек пространства с одинаковым значением
навигационного параметра называют поверхностью положения [4.3]. Пересечение
двух поверхностей положения, каждая из которых соответствует своему
навигационному параметру с заданным значением, определяет линию положения —
геометрическое место точек пространства, для которых два заданных
навигационных параметра имеют одинаковые значения. Местоположение
определяется координатами точки пересечения трех поверхностей положения или двух
линий положения. В ряде случаев (из-за нелинейности поверхностей
положения) две линии положения могут пересекаться в двух или более точках. При
этом однозначно найти местоположение можно только, используя
дополнительную поверхность положения или иную информацию о местоположении
объекта.
3-1026
65
Глава 4
Проиллюстрируем сказанное для* плоского случая. Пусть в точке А
(рис. 4.1) расположен источник излучения сигнала, а в качестве
радионавигационного параметра выбрана задержка сигнала тх. В рассматриваемом
случае имеем лишь линию положения, которой является окружность радиуса
/?! = стх. Пусть в точке Б излучается другой сигнал, а в качестве
радионавигационного параметра также выбрана задержка сигнала г2. Линией положения
для второго радионавигационного параметра также является окружность
радиуса R2 = ст2. При соответствующих значениях Rx и R2 две окружности
пересекаются в двух точках — С и Д. Следовательно, местоположение
определяется неоднозначно. Если ввести дополнительную информацию, например,
«местоположение объекта — выше линии, соединяющей точки А и Б, то
местоположение определятся однозначно — точка С.
Рис. 4.1. Линии положения на плоскости
Для решения навигационной задачи, т. е. для нахождения вектора
потребителя П, используют функциональную связь между навигационными
параметрами и компонентами вектора потребителя. Соответствующие
функциональные зависимости принято называть навигационными функциями.
Конкретный вид навигационных функций обусловлен многими факторами: типом НП,
характером движения НС и потребителя, выбранной системой координат и т.д.
Навигационные функции для пространственных координат потребителя
можно получить с помощью различных разновидностей дальномерных, разно-
стно-дальномерных, угломерных методов определения координат и их
комбинаций. Для записи навигационных функций, включающих составляющие
вектора скорости потребителя, используют соответствующие методы определения
скорости объекта.
4.2. Дальномерный метод
Наиболее простой дальномерный метод навигационных определений
[4.1—4.7] основан на измерениях дальности Д, между /-м НС и потребителем.
66
Методы решения навигационных задач
В этом методе навигационным параметром является дальность Д , а
поверхностью положения — сфера с радиусом Д и центром, расположенным в центре
масс /-го НС. Уравнение сферы имеет вид
Дг =
(Х;-х)2+(у{-у)2 +(zt-zY
1/2
(4.1)
Здесь Xj, yt, z{ — известные на момент измерения координаты /-го НС (с
учетом его перемещения за время распространения сигнала); х9 у, z —
координаты потребителя.
Местоположение потребителя, т. е. координаты х9 y9 z, определяются как
координаты точки пересечения трех поверхностей положения, другими
словами трех сфер. Поэтому для реализации дальномерного метода необходимо
измерить дальности (4.1) до трех НС, т. е. / = 1,3.
Таким образом, для дальномерного метода навигационная функция
представляет собой систему из трех уравнений вида (4.1). Ввиду нелинейности
такой системы уравнений возникает проблема неоднозначности определения
координат потребителя, устраняемая с помощью известной потребителю
дополнительной информации (ориентировочные координаты потребителя, его
радиальная скорость и т. д.).
В классической механике при использовании (4.1) неявно
подразумевается, что все величины берутся в один и тот же момент времени tk . В СРНС
ситуация несколько иная, т.к. дальность Д1 определяется по результатам
измерения задержки т1=Д11с (где с —скорость света) радиосигнала при его
распространении от /-го НС до потребителя. Положим, что потребитель и НС
работают в единой шкале времени t, и с борта НС излучается сигнал, огибающая
которого приведена на верхнем графике рис. 4.2.
Сигнал с НС
|ш=рчр
Сигнал у потребетеля
fyizd~lF
\
Время распространения Т
м
Рис. 4.2. Временная диаграмма излучения и
приема навигационного сигнала
Такой вид огибающей соответствует дальномерному коду сигналов,
используемых в СРНС, поэтому в дальнейшем вместо огибающей сигнала будем гово-
67
Глава 4
рить о дальномерном коде. В момент времени tx имеем некоторую фазу
излучаемого дальномерного кода (верхний график на рис. 4.2). В этот момент
времени НС и потребитель имеют координаты х/(/1) = {^-(/1), .уД^), zi{h)\ и
\(tx) = ix(tx), y(t\), z(tx)} соответственно. В момент времени t2 сигнал с фазой
дальномерного кода, соответствующей моменту времени tx, достигнет
приемника потребителя (нижний график на рис. 4.2).
В этот момент времени НС и потребитель имеют координаты х,(/2) и
х(/2). Задержка сигнала в приемнике измеряется в момент времени t2 и
определяется временным интервалом между моментами времени tx и t2, т.е.
ri(t2) = t2 -tx. За время, равное длительности интервала г,(/2) сигнал
«проходит» расстояние
Д, (<2) = от, (/2) = [(*, (,,)-х(,2))2 + (у,(/, )-y(h )f + (z,(»,)-*(/,))2] "2 .(4.2)
Таким образом, в СРНС дальность Дх (/) = crz (?) является геометрической
дальностью между точкой, в которой находился НС в момент излучения сигнала
('изл =' ~ ri (0 )> и точк°й, в которой находится потребитель в момент времени t.
Подставляя в (4.2) выражение для связи между tx, t2 и г, (?2), приведенное
выше, и заменяя в полученном выражении t2 на текущее время t, запишем
r|.(/) = k(/-r|.(0)-x(0||/^ (4-3)
где | *| — евклидова норма вектора [4.8].
Соотношение (4.3) является нелинейным уравнением относительно г, (/) в
отличие от алгебраической формулы (4.2) и может использоваться для
получения более точных оценок задержек сигналов в СРНС.
4.3. Псевдо дальномерный метод
В СРНС ввиду большого разноса передающей и приемной позициями
фиксация моментов излучения и приема сигнала не может выполняться в одной
шкале времени, как это полагалось на рис. 4.2. Время излучения сигнала с
борта НС определяется в бортовой шкале времени ?БШВ, а время приема сигнала
— в шкале времени потребителя /швп . При этом в СРНС решается задача
определения длительности интервала между моментами времени (t^B — момент
излучения некоторой фазы дальномерного кода с борта НС и ^вп — момент
68
Методы решения навигационных задач
приема той же фазы дальномерного кода у потребителя), заданными в
различных шкалах. Для такого интервала времени используется термин псевдо
задержка. Если TjjpU™11) — значение времени на ШВП в момент времени
/JJjBn , а ^л IS3) — значение времени на БШВ в момент времени ^вп , то
значение псевдо задержки определяется соотношением
КСпНр(Сп)-МСв). <4-4>
Если теперь определить линейную величину соотношением
ту/.ШВП \ ~ЛШВП\ (л с\
то, имея смысл дальности (расстояния), параметр Д не является дальностью в
обычном понимании, т.е. дальностью между двумя точками в пространстве.
Поэтому для Д, определенному с использованием (4.4), (4.5), используется
термин псевдо дальность.
Отметим, что в (4.4), (4.5) моменты времени /™В и ^ВП не является
независимыми, а взаимосвязаны через одну и ту же фазу дальномерного кода
радиосигнала (на излучение и при приеме).
Если шкалы времени ?БШВ и /швп абсолютно совпадают (т.е. совпадают
единицы времени, идеально синхронизированы моменты наступления одного и
того же события и совпадают значениям времени на этих шкалах для
совпадающих моментов времени), то эти шкалы времени будем называть идентичными.
В реальности шкалы времени различаются. Поэтому рассмотрим процесс
вычисления псевдо задержки (4.4) в этом случае. Для этого воспользуемся
методикой [2.2], которая иллюстрируется рис. 4.3. На данном рисунке по
горизонтальной оси откладывается абсолютное равномерное время /, а по
вертикальной оси — равномерные значения Т показаний шкалы.
Положим для простоты, что ШВП идентична абсолютно равномерной
шкале времени. Тогда функция Гшвп (?), описывающая показания времени на
ШВП, может быть отражена на рис. 4.3 прямой линией под углом 45°. Пусть
характеристики БШВ отличаются от характеристик ШВП, что приводит к иной
зависимости TEU1B(t). Полагая время на БШВ равномерным, на рис. 4.3
функция ГБШВ (/) будет соответствовать прямой линии, наклоненной под углом,
отличным от 45°. При этом моменты времени, для которых показания на данной
шкале соответствуют значениям, отложенным по вертикальной оси на рис. 4.3,
смещаются относительно аналогичных моментов времени ШВП (вертикальные
стрелки вниз на рис. 4.3).
69
Глава 4
■ швп
ШВП
[БШВ
*изл *ист
Рис. 4.3. Временная диаграмма для расчета псевдо задержки
с неидентичными шкалами времени
Пусть / — время приема сигнала, для которого из рис. 4.3 значение
времени TjuBnf'np) на ШВП. Пусть tmjl — время излучения фиксированной фазы
дальномерного кода сигнала, прием которой осуществился в момент времени
/пр. Моменту времени 7ИЗЛ, как видно из рис. 4.3, соответствуют значения
времени Тшвп (/изл) и ГБШВ (/изл) на шкалах времени ШВП и БШВ соответственно.
Истинное значение оценки задержки должно измеряться в одной шкале
времени, например ШВП, и равно
Гист (/пр ) = ТшВП (/пр ) ~ ^LIJBn (/изл ) >
а рассчитанное в соответствии с (4.4) —
г ('пР) = Тшвп (>пР) - ТБШВ (tmn). (4.6)
Вводя Г(/пр) = Гшвп (*изл) - ТБШВ (tmjl), запишем (4.6) в виде
^(Ч) = ГИСТ(Ч) + Г(Ч)' (4-7)
из которого следует, что различие характеристик ШВП и БШВ приводит к
ошибке Тд^пр) в оценке псевдо задержки.
Положим, что БШВ для всех НС идентичны друг другу, что может быть
достигнуто в результате взаимной синхронизации этих шкал и коррекции
показаний времени на них. Тогда, с учетом (4.4), (4.6), (4.7) выражение для псевдо
дальности Д1 u™n ] относительно /' го НС можно записать в виде
70
Методы решения навигационных задач
Д(СП) = Д/иСТ(СП) + ^'= (4-8)
- \{х, (<«БГ) - *(СП ))2 + (л ('-»в') - у{>7п ))' + {*, ('«Г) - *(С ))2 + я ■
где Д' = сГ(С")-
Данное выражение является основой псевдо дальномерного метода
определения координат потребителя и отличается от (4.1) наличием
дополнительного параметра Д' и отличием моментов времени, для которых определяются
координаты потребителя и НС.
Так как псевдо дальномерный метод основан на измерениях псевдо
дальностей, в качестве навигационного параметра выступает Д{. Поверхностью
положения по-прежнему является сфера с центром в точке центра масс НС, но
радиус этой сферы изменен на неизвестную величину Д'. Измерение псевдо
дальностей до трех НС приводит к системе трех уравнений с четырьмя
неизвестными х9у9г9Д'. В решении этой системы уравнений возникает
неопределенность, для устранения которой необходимо провести дополнительное
измерение, т. е. измерить псевдо дальность до четвертого спутника. Полученная
таким образом система четырех уравнений имеет точное решение.
Следовательно, местоположение потребителя при измерениях псевдо дальностей
определяется как точка пересечения четырех поверхностей положения.
Необходимость нахождения в зоне видимости четырех НС предъявляет
достаточно жесткие требования к структуре сети НС, которые выполняются
только для среднеорбитальных СРНС. При использовании низкоорбитальных
СРНС параметры орбитальной группировки НС (высота орбит, число
спутников, их расстановка) обычно обеспечивают периодическую видимость в зоне
потребителя лишь 1 ... 2 НС, поэтому определение местоположения в этих
СРНС может осуществляться не в реальном времени, а лишь после
проведения последовательных измерений нескольких линий положения по сигналам
одного НС.
Псевдо дальномерный метод не накладывает жестких ограничений на
значение параметра Д' = ct' (пропорционального смещению ШВП) и позволяет
одновременно с определением местоположения вычислять смещение шкалы
времени потребителя.
4А. Разностно-дальномерный и псевдо разностно-
дальномерный методы
Метод основан на измерении разности дальностей или псевдо дальностей
от потребителя до нескольких НС.
71
Глава 4
При использовании дальностей (4.1) в разностно-дальномерном методе
формируются три разности АД у = Д1 - Ду до трех НС. Навигационным
параметром в этом случае является АД у. Поверхности положения определяются из
условия АД у = const и представляют собой поверхности двухполостного
гиперболоида вращения, фокусами которого являются координаты опорных точек /
и j (центров масс /- иу-го НС). Расстояние между этими опорными точками
называют базой измерительной системы. Если расстояния от опорных точек
(НС) до потребителя велики по сравнению с размерами базы, то гиперболоид
вращения в окрестности точки потребителя практически совпадает со своей
асимптотой — конусом, вершина которого совпадает с серединой базы.
При использовании псевдо дальностей (4.7) также формируются три
разности Atf^f™^ Для которых псевдо дальности
Д \^ВП) > Д] (^ВП) определяются в приемнике в один и тот же момент вре-
ШВП БШВ БШВ.
мени t^ , но моменты излучения /изл ', /изл J соответствующих сигналов
для различных НС различны. В этом случае метод называю псевдо разностно-
дальномерным.
Точность определения координат потребителя при использовании псевдо
разностно-дальномерного метода, как будет показано в гл. 6, совпадает с
точностью определения этих координат псевдо дальномерным методом.
Недостатком метода является то, что в нем не может быть измерено
смещение Д', а, следовательно, и смещение шкалы времени потребителя.
4.5. Радиально-скоростной (доплеровский) метод
Метод предназначен, прежде всего, для определения составляющих
вектора скорости потребителя и основан на измерении доплеровских смещений
частот сигналов, принимаемых от трех НС: /Д|. =-Д/Д , / = 1,3, где Я, — длина
волны несущего колебания /-го радиосигнала, Д — радиальная скорость
сближения потребителя и / -го НС.
В классической механике выражение для Д может быть получено
дифференцированием (4.1) по времени
Д =[(*,.-*)(*,. -Х) + (У; -У)(Ъ -у) + (Ъ-2)(1;-2)]/Д; . (4.9)
Введем вектор скорости /-го НС V, = |*. y{ i,.|T, вектор скорости потреби-
IIT
х у z\ , и вектор направляющих косинусов
72
Методы решения навигационных задач
С,=
*i-* Уг~У Zi~A
Дг Mi Mi
(4.10)
характеризующий направление на / -й НС из точки расположения потребителя.
Тогда (4.9) можно записать в виде
A=CT(V,.-V). (4.11)
При известных векторах С,-, V,, / = 1,3 и трех измерениях Д из (4.11)
однозначно определяется вектор скорости потребителя V .
Вектор направляющих косинусов может быть определен, например, по
дальномерным измерениям (4.1).
Другой возможный подход основан на измерениях радиальных скоростей
Д в течение некоторого времени At и их интегрировании
t+At
N,(t)= |д,(г)Л = Д,(* + Д0-Д,(/). (4Л2>
В результате определяются «новые эквивалентные измерения» Nt[t)9
соответствующие разностно-дальномерному методу, но с той лишь разницей, что
разности дальностей формируются по измерениям дальностей для одного и
того же НС для различных моментов времени.
Действительно, если за время At перемещением потребителя можно
пренебречь, то из (4.12) следует
1 / *У
^(') = {й(' + Д')-^)2+(^(' + д')->')2+(2/(' + А')-г)2} -
-{{xl(,)-x)2+{yl(t)-yf+(zl{l)-zf)m. (4.13)
Отсюда видно, что, зная координаты трех НС в моменты времени t и
t + At и вычислив Ni по (4.12), можно определить координаты точки
потребителя {.x,^,z}.
Недостатком данного метода измерения координат потребителя является
невозможность их проведения в реальном масштабе времени. Кроме того, в
средневысотных СРНС реализация РСМ затруднена ввиду медленного
изменения радиальной скорости, что приводит к малым значениям разностей в (4.12).
Это обусловило применение РСМ в таких СРНС только для определения
составляющих скорости потребителя.
Недостатком РСМ при определении скорости потребителя является
необходимость наличия высокостабильного эталона частоты, так как любая
нестабильность частоты приводит к неконтролируемому изменению доплеровского
73
Глава 4
смещения частоты, а, следовательно, к дополнительным ошибкам измерения
составляющих скорости потребителя.
Так же, как и в п. 4.2, применительно к СРНС данный метод должен быть
несколько модифицирован.
Рассмотрим соотношение (4.2), определяющее измеряемую в СРНС
дальность. Дадим приращение времени 8t2. При этом возникают приращения
координат потребителя 8х, 8 у, 8z и приращение времени 8tx, т.к. в момент
времени t2 + St2 принимается другая фаза дальномерного кода (по сравнению с
фазой, принимаемой в момент времени t2), которой соответствует другой
момент излучения tx + 8tx. Приращение времени 8tx, в свою очередь, приводит к
приращению координат НС 8xi, 8yi, Szt. В итоге, изменяется и дальность
Д1 (t2+8t2) = Д/ (t2) + 8Д1 (t2). Определим радиальную скорость соотношением
Д,(,г)= lim ^1. (4.14)
Тогда, используя (4.2), можно получить формулу, аналогичную (4.11)
A(/2) = C7(/2)(Vi(/1)-V(/2)), (4.15)
где
k('i)-*('2) УМ~У(*г) ^M-z(t2)\
С/Ы =
Д/('2) Д/('2) Д,-('2)
(4.16)
Радиальной скорости сближения (4.14) соответствует доплеровское
смещение частоты
кг (h) = -Д, (h )А = -С? (Г2)(V, (/,) - V(f2 ))/Д, . • (4.17)
принимаемого сигнала относительно номинального значения ft частоты
несущего колебания.
4.6. Псевдо радиально-скоростной (псевдо доплеровский) метод
Так же, как и в п. 4.4, при отсутствии единой шкалы времени в точках
излучения и приема радиосигнала, в точке излучения сигнала используется
бортовая шкала времени ?БШВ< / -г0 НС, а в точке приема сигнала — шкала
времени потребителя /швп . При этом, в СРНС соотношением (4.8) вводится понятие
псевдо дальности Д (fJjJBn).
74
Методы решения навигационных задач
Воспользуемся методикой определения производной по времени,
описании
пр
ной в предыдущем пункте, а именно, дадим приращение времени д fJJJBn, on
ределим производную
Д.(,швп)= ,im Щ** L llm ИДД'пр ) с6Т{ь )
^'1ПР ) ЛШВП vrt ЛШВП ЛШВП J ЛШВП ^ о,ШВП
<вп-о Л£Ш| <вп-о
(4.18)
Первое слагаемое в (4.18) соответствует определению (4.14). Поэтому,
учитывая (4.15), (4.16), можно записать выражение
lim
ЦТ-*> Stnp
rrj /.ШВП\
°"Л1Ч ;_ст/ШВП\/у/БШВЛ у/,ШВП\\
о.ШВП ~^'Ч"Р ДМИЗЛ ) v\>p jj
Учитывая, что в (4.18) Тд^811] — значение смещения ШВП
относительно БШВ /-го НС в момент времени ^вп приема сигнала, а нестабильность
ШВП описывается (2.7), можно записать
lim
?т>( ,швп\
"пр LcSv (/ШВП) = Г(/ШВП)
г,ШВП ""от^пр ) v \'пр j'
где £v0T — относительная нестабильность частоты ОГ, формирующего ШВП.
Таким образом, соотношение (4.18) можно записать в виде
Л, (Свп)=с] (Свп )(v- ('«Г) - v(Cn Ж(СП) • <4-19>
Параметр Д ('™ВП) = ^ КВП) называю псевдо скоростью, а
соответствующий ей параметр
Л,=г,(С)Л <4-20>
— псевдо доплеровским смещением частоты.
Можно показать, что
, , дт(гшвп)
/Д,('ШВП) = /ГВ-^ШГ1. И.21)
где /БШВ — номинальное значение частоты несущего колебания / -го НС в его
шкале времени.
Так же, как и в п. 4.5, интегрируя выражение для псевдо скорости (4.19) на
интервале времени At, получаем разность псевдо дальностей,
соответствующих двум моментам времени. Если на интервале времени At можно пренеб-
75
Глава 4
речь изменением смещения Д', то полученный после интегрирования
результат будет равен разности дальностей, соответствующих двум моментам
времени, т.е. будем иметь тот же результат, что и в разностно-дальномерном методе.
4.7. Разностно-радиально-скоростной метод
Сущность данного метода заключается в определении трех разностей
дд = д. - д. двух радиальных скоростей НС. С учетом (4.11) запишем
Atf,=CT(V,-V)-C}(V,.-V).
При этом разности можно вычислять относительно одного или
относительно различных НС. По существу, при вычислении разностей могут
использоваться и псевдо скорости Д1, так как при таком вычитании компенсируется
неизвестное смещение Ц\ (в предположении, что это смещение одинаковое
для различных спутников).
Поверхности положения представляют собой поверхности тела вращения,
фокусами которых являются координаты центров масс /-го иу'-го НС.
Как и для «дальномерных» методов, точность определения составляющих
вектора скорости в разностно-радиально-скоростном методе совпадает с
точностью определения тех же составляющих в псевдо радиально-скоростном
методе (см. гл. 6).
Достоинством разностно-радиально-скоростного метода является его
нечувствительность к нестабильностям эталонов частоты и другим
неконтролируемым смещениям частоты, а его недостатком — невозможность оценки
нестабильности эталонов частоты.
4.8. Комбинированные методы
Помимо перечисленных основных методов определения компонент
вектора состояния потребителя П возможны комбинированные методы,
использующие кроме СРНС дополнительные измерители координат, имеющиеся у
потребителя. Так, в дальномерном методе при наличии у потребителя
измерителя высоты Н можно вместо измерений трех дальностей до НС ограничиться
измерением двух дальностей. В этом случае навигационная функция будет
включать два уравнения вида (4.1), а третье необходимое уравнение дает
измеритель высоты:
{R3+H)2=x2+y2+z2.
Другой вариант использования комбинированных методов заключается в
замене совокупности одновременных измерений на комбинацию одновремен-
76
Методы решения навигационных задач
ных и последовательных измерений или на совокупность только
последовательных измерений, например, определение координат потребителя радиально-
скоростным методом (4.4). В качестве другого примера можно привести псев-
додальномерный метод, который можно реализовать, заменив четыре
одновременных измерения по четырем НС на два последовательных измерения по
двум НС или на четыре последовательных измерений до одного НС.
Аналогичные комбинации возможны и для других методов.
4.9. Определение ориентации с помощью СРНС
До сих пор рассматривалась классическая задача определения координат и
вектора скорости потребителя. С развитием СРНС и совершенствованием
методов и аппаратуры приема и извлечения информации из радиосигналов
возникают потребности и возможности решения более сложных задач. Одной из
таких задач является определение ориентации потребителя (летательного
аппарата, морского судна или иного протяженного объекта). Решение этой задачи
может заключаться в следующем. В двух точках потребителя (двух точках
палубы корабля) А и В, расположенных на расстоянии d одна от другой
(рис. 4.4), устанавливают два приемника сигналов СРНС. Пространственная
ориентация линии АВ относительно системы координат, связанной с
потребителем (связанной системы координат, например, корабельной) известна.
Рис. 4.4. Схема определения ориентации
Ориентация линии АВ определяется направляющими косинусами
cosy/x=(xb-xa)/d, cosy/y=(yb-ya)/d, cosy/z =(zb -za)/d ,
77
Глава 4
фиксирующими положение вектора АВ относительно геоцентрической
системы координат OXYZ.
Пусть приемники, расположенные в точках А и В, измеряют дальности
Да1 и ДЬ1 до навигационного спутника НС] с известными координатами
{*i,;>i,z1}. Рассмотрим угол /\ (см- Рис- 4.3), для которого с учетом
соотношения <Л«ДаХ, <1«ДЬХ можно записать
со8Г1*(Дв1-Дм)/^- (4-22>
С другой стороны, угол^ — это угол между векторами АВ и АНС].
Следовательно, косинус этого угла можно выразить через направляющие косинусы
этих векторов [4.8] соотношением
cos п = Mxi cos Vx + Му\ cos Vy + Mzi cos Vz > (4-23)
где juxl9 juvl, juzl — направляющие косинусы вектора AHCj, которые могут
быть определены в приемнике сигналов, находящемся в точке А.
Уравнение (4.23) содержит три неизвестных величины — направляющие
косинусы cosi//x, cosy/y , cosi//z. Для их определения необходимо иметь три
таких (независимых) уравнения, которые можно получить, например, проведя в
точках А и В аналогичные измерения еще по двум НС и записав соотношения,
аналогичные (4.22):
<W2 «(Да2 - ДЪ1 )/d, cosy3 * (Даз - Дьъ )/d (4-24)
и аналогичные (4.23):
cos/2 = /лх2 cosy/x + fiy2 cosy/у + /uz2 cosy/z,
cos уъ = jux3 cos y/x + /луЪ cos y/y + //z3 cos y/z. (4.25)
Соотношение (4.22—(4.25) позволяют составить систему трех уравнений:
(Да\ ~ Дь\ )ld = Mxl <X>Wx + /Iyl COSy/у + Цл COSy/z ,
(Да2 ~ Ды )ld = МХ2 C0S V.r + My2 COS Vy + Mz2 C0Wz »
(Даъ ~ Дьъ)ld = Мхз cosy/x + /луЪ cosy/y + juz3 cosy/z (4.26)
и решить ее, определив направляющие косинусы и пространственную
ориентацию линии АВ и, соответственно, потребителя.
Иногда задачу упрощают, используя уравнение связи
cos2 у/х + cos2 у/у + cos2 y/z = 1
вместо одного из уравнений в (4.26), т.е., используя сигналы только от двух
навигационных спутников.
78
Методы решения навигационных задач
Для решения задачи высокоточного определения ориентации потребителя
вместо дальномерных измерений можно использовать фазовые измерения в
точках А и В или относительные фазовые измерения в данных точках.
Так как разность фаз сигналов, принимаемых в точках АиВ,
А<р1=2я{Да1-ДЬ1)/Л, (4.27)
то, измерив такие разности по сигналам трех НС
А^2=2^(Д,2-Д,2)/А, Аъ=2я(Да3-Дьз)/А9
соотношения (4.26) для определения ориентации потребителя можно
представить в виде
АщА/(2Ы) = juXi cos^x + Myi c°Wy + Mzi cos^z > i = U • (4-28)
Однако следует отметить, что для использования (4.27), (4.28) необходимо
решить проблему неоднозначности фазовых измерений. Более подробно
данная проблема описана в гл. 16.
Литература
4.1. Шкирятов В. В. Радионавигационные системы и устройства. — М.: Радио и
связь, 1984.
4.2. Гришин Ю. П., Ипатов В. Я., Казаринов Ю. М. и др. Радиотехнические
системы/ Под ред. Ю. М Казаринова. — М.: Высшая школа, 1990.
4.3. Ярлыков М С. Статистическая теория радионавигации. — М.: Радио и связь,
1985.
4.4. Ярлыков М С, Болдин В. А., Богачев А. С. Авиационные радионавигационные
устройства и системы. — М.: Изд-во ВВИА им. Н.Е. Жуковского, 1980.
4.5. Пестряков В. Б., Кузеков В. Д. Радиотехнические системы. — М: Радио и
связь, 1985.
4.6. Виницкий А. С Автономные радиосистемы. — М: Радио и связь, 1986.
4.7. Теоретические основы радиолокации/ Под ред. В. Е. Дулевича. — М.: Сов.
радио, 1978.
4.8. Корн Г., Корн Г. Справочник по математике. — М.: Наука, 1968.
79
Глава 5
Глава 5
РАДИОСИГНАЛЫ И НАВИГАЦИОННЫЕ
СООБЩЕНИЯ В СПУТНИКОВЫХ
РАДИОНАВИГАЦИОННЫХ СИСТЕМАХ
5.1. Требования, предъявляемые к сигналам в СРНС
В СРНС осуществляется непрерывное излучение сигналов со всех
находящихся в эксплуатации НС. При этом на вход приемника потребителя
поступают сигналы от всех видимых НС. Для решения задачи навигационных
определений принимаемые сигналы должны иметь такую структуру, чтобы их
можно было разделить и достаточно точно измерить параметры радиосигнала
(задержку, доплеровское смещение частоты, фазу). Отсюда вытекают два
основных требования, предъявляемых к радиосигналам:
возможность их эффективного разделения в приемнике;
обеспечение высокой точности измерения параметров сигнала.
Первое требование реализуется за счет использования того или иного
метода разделения сигналов [5.1—5.3]: частотного, временного, кодового и др.
Наилучшее разделение п сигналов достигается при использовании
ортогональных сигналов. В этом случае при условии точной синхронизации сигналов
методы временного, частотного и кодового разделения эквивалентны. В
современных СРНС используются два метода разделения сигналов: в СРНС
ГЛОНАСС — частотное, в СРНС GPS, Galileo — кодовое.
При частотном разделении сигналов, каждому из них отводится своя
полоса частот, а спектр сигнала должен быть достаточно компактным (в идеале —
строго полосовым). Так как реализация строго полосовых сигналов
практически невозможна, реальные сигналы имеют частично перекрывающиеся
спектры, что определяет их неортогональность и взаимное влияние сигналов друг
на друга при их приеме и обработке, т.е. приводит к внутрисистемным
помехам. Уровень внутрисистемных помех в СРНС ГЛОНАСС оценивается на
уровне 54 дБ [5.4].
При кодовом разделении каждый сигнал излучается на одной и той же
частоте и модулируется своим индивидуальным кодом, причем используемые
коды должны быть по возможности ортогональны между собой.
Неортогональность кодов приводит к ошибкам при разделении сигналов (внутрисистемные
помехи). В СРНС GPS в качестве таких кодов (для сигналов стандартной
точности) используются коды Голда, для которых уровень внутрисистемных
помех оценивается величиной 21,6 дБ [5.4].
Основные навигационные параметры, определяемые в СРНС, — дальность
и скорость движения потребителя. Соответствующими им радионавигацион-
80
Радиосигналы и навигационные сообщения в СРНС
ными параметрами (параметрами радиосигнала) являются задержка г сигнала
и доплеровское смещение частоты /д. Поэтому для высокоточного
определения координат и параметров движения потребителя необходимо обеспечить
высокую точность измерения г и /д сигнала.
Из статистической теории оценивания параметров сигнала [5.1,5.2]
известно, что минимальные среднеквадратические ошибки <тг, af оценки задержки
J Д
и доплеровского смещения частоты при приеме сигнала s{t) с известной
начальной фазой на фоне некоррелированного гауссовского шума с
односторонней спектральной плотностью N0 при раздельном их измерении определяются
соотношениями
где q = E/N0 — отношение сигнал/шум;
т
Е= \s2(t)dt — энергия сигнала за время наблюдения Т ;
о
" т -|1/2
ij(2*/)V(0<*
(5.1)
а =
р=
— эффективная длительность сигнала;
-,1/2
±\(2*f)2\S(ff df
—оо
Т
эффективная ширина спектра сигнала;
£(/) = b(f)e xln^ dt — спектральная плотность сигнала.
о
Как видно из (5.1), требования к повышению точности измерения
задержки сигнала и доплеровского смещения частоты противоречивы. Для
повышения точности измерения задержки необходимо расширять спектр сигнала, а для
повышения точности измерения доплеровского смещения частоты следует
увеличивать длительность сигнала.
Данное противоречие разрешается при рассмотрении задачи совместной
оценки т и /д, для которой при выполнении условия
j-
% St
■dt = 0
(5.2)
одновременный максимум точности оценки задержки и доплеровского
смещения частоты соответствует минимуму произведения
81
Глава 5
°"г^/д = У(2?а/?) •
(5.3)
Следовательно, повышения точности совместных оценок задержки
сигнала и доплеровского смещения частоты можно достигнуть за счет увеличения
произведения ар-В^ которое получило название база сигнала. При
выполнении условия (5.2) справедливо неравенство ар > 1/2 — соотношение
неопределенности. Данное соотношение показывает, что сигнал не может иметь
одновременно произвольно малую длительность и произвольно малую ширину
спектра. Таким образом, одним из основных требований к радиосигналам в
СРНС является большая база сигнала.
5.2. Математическое описание радиосигналов
В СРНС используют узкополосные радиосигналы, под которыми
понимают сигналы, у которых полоса занимаемых частот значительно меньше, чем
несущая частота.
Пусть вещественный сигнал s(t) имеет двустороннюю спектральную
плотность S(f), приведенную на рис. 5.1.
\Н/)\
/о
/о
/
Рис. 5.1. Спектральная плотность вещественного сигнала
Сформируем из s(t) сигнал £(/), у которого спектральная плотность
сосредоточена только в области положительных частот, а его мощность равна
мощности исходного сигнала. Спектральную плотность такого сигнала можно
записать как
S{f) = 2u{f)S(f), (5.1)
1, /^0,
— единичная ступенчатая функция.
/<0,
Искомый сигнал s(t) может быть получен как обратное преобразование
Фурье от (5.1)
где „(/) = {£
82
Радиосигналы и навигационные сообщения в СРНС
—00
Сигнал s(t) называется аналитическим сигналом для s(t), и он
представим в виде
s(t) = s(t) + is(t),
00 / \
1 Л V ( Т I
где s(t) - — -^-dr — преобразование Гильберта.
-оо
Аналитический сигнал s(t) является полосовым сигналом на несущей
частоте /0.
Можно получить соответствующий этому сигналу низкочастотный сигнал
s0(t) путем сдвига спектра частот S(f) влево на величину /0, Поэтому для
спектра такого сигнала S0(f) можно записать
4 (/М(/ +/о)-
Эквивалентное представление во временной области имеет вид
~s0(t) = [s(t) + is(t)yt2^'. (5.2)
В общем случае низкочастотный сигнал £0(0 — комплексный, и его
можно представить в виде
s0(t) = x(t) + iy(t). (5.3)
Подставляя (5.3) в (5.2) и приравнивая действительные и мнимые части
левой и правой частей равенства, получаем соотношения
s(t) = x(t)cos(27rf0t)- y(t)sin(27rf0t), (5.4)
s(t) = x(t)cos(27rf0t) + y(t)sm(2nf0t). (5.5)
Выражение (5.4) является желательным представлением полосового
сигнала. Низкочастотные сигнальные компоненты x{t) и y(t) можно
рассматривать как сигналы, модулирующие по амплитуде соответствующие несущие
cos(2;r/0/) и sin(2;r/0/). Поскольку эти несущие находятся в квадратуре
(сдвинуты по фазе по 90°), компоненты x(t) и y(t) называют квадратурными
компонентами полосового сигнала.
Сигнал (5.4) можно записать в виде
83
Глава 5
s{t) = Re[(x(/) + \y(t))e2^'~\ = Re[t/, (/)ei2jr/or] , (5-6)
где
Us(t) = U(t)J«\ (5.7)
U(t) = Jx2(t) + y2(t), (5.8)
#>(/) = arctg
fy(t))
x(t)
(5.9)
Низкочастотный сигнал £/s(/) называют комплексной огибающей
вещественного сигнала s(t), U(t) — огибающей (вещественной) сигнала s(t),
<p(t) — фазой сигнала s(t).
Важными характеристиками радиосигналов являются корреляционная
функция (КФ) и спектральная плотность мощности. Корреляционная функция
для низкочастотного сигнала Us (t) определяется выражением
1 Т
R{t)= lim— \u*s(t)Us(t + T)dt, (5.10)
-Т
где « » обозначает комплексное сопряжение.
Спектральная плотность мощности определяется как преобразование
Фурье от корреляционной функции (5.10)
N
ии
(/)= \R{ryn^dr. (5.11)
При т = 0 из (5.10) получаем /?(0) = Ри, где
т
Ри=— \u*s{t)Us(t)dt = — ju2(t)dt - (5.12)
-т -т
мощность комплексной огибающей Us (t).
Часто удобно вместо корреляционной функции (5.10) оперировать с
нормированной корреляционной функцией
P(t) = R(t)/Pu. (5.13)
Наряду с корреляционной функцией сигнала (5.10) часто представляет
интерес рассмотрение взаимной корреляционной функции двух сигналов s(t) и
u(t), имеющих комплексные огибающие Us(t) и Uu(t) соответственно. Вза-
84
Радиосигналы и навигационные сообщения в СРНС
имная корреляционная функция (ВКФ) комплексных огибающих
(низкочастотных сигналов) определяется соотношением
1 Т
R»W = tZ2T \^{t)Uu{t^r)dt. (5.14)
-т
Заметим, что корреляционную функцию сигнала (5.10) иногда называют
автокорреляционной функцией.
5.3. Фазоманипулированные сигналы в СРНС
Как следует из § 5.1, в СРНС для получения высокой точности измерения
радионавигационных параметров (задержки и доплеровского смещения
частоты) сигнала целесообразно использовать сигналы с большой базой В » 1.
Такие сигналы называют шумоподобными (ШПС) [5.6, 5.7] или сложными
сигналами в отличие от простых с В = 1.
Шумоподобные сигналы можно получить в результате дополнительной
модуляции радиосигнала. Различные виды ШПС можно разбить на частотно-
модулированные; многочастотные; фазоманипулированные; дискретные
частотные (сигналы с кодовой частотной модуляцией, частотно-манипулирован-
ные сигналы); дискретные составные частотные и др.
В современных СРНС используют фазоманипулированные сигналы [1.2,
1.4], в которых сигнал длительностью Тс (период функции модуляции)
разбивается на L элементов с длительностью гэ = Тс IL . При этом база сигнала
В = Тс/тэ = L, а эквивалентная ширина спектра А/э=\/тэ в В раз шире, чем у
исходного сигнала. Так, фазоманипулированный сигнал стандартной точности
в СРНС ГЛОНАСС имеет параметры: Тс=\ мс, г3~2 мкс, база сигнала
В = Тс /гэ = 511; сигнал стандартной точности GPS имеет параметры: Тс = 1 мс,
гэ * 1 мкс и базу В = Тс/тэ= 1023.
Фазоманипулированные сигналы обеспечивают достаточно высокую по-
мехоустоичивостъ приемника сигналов, под которой понимают возможность
работы аппаратуры в условиях воздействия помех. Повышенная скрытность
работы с фазоманипулированными сигналами обеспечивается тем, что при
равных мощностях и длительности сигнала (т. е. при равных энергиях)
спектральная плотность мощности фазоманипулированного сигнала в В раз
меньше, чем у аналогичного сигнала без фазовой манипуляции. Одновременно
высокие характеристики помехоустойчивости и скрытности обеспечивают
достаточный уровень помехозащищенности приемников таких сигналов.
Хорошая разрешающая способность фазоманипулированных сигналов
обусловлена тем, что они имеют корреляционные функции с узкими пиками по
осям г и /д, ширина которых обратно пропорциональна А/э и гэ. Более под-
85
Глава 5
робно корреляционные свойства фазоманипулированных сигналов будут
рассмотрены далее.
5.3.1. Общие свойства бинарных фазоманипулированных сигналов
Под фазовой манипуляцией понимают дискретное изменение фазы
несущего колебания через заданные временные интервалы гэ. В общем случае
изменение фазы сигнала может проводиться на конечное число разных фазовых
углов. В простейшем случае используют два таких угла: 0 и п, а
соответствующий вид манипуляции называют бинарной (двоичной) фазовой
манипуляцией (ФМ-2 или в иностранной литературе BPSK — binary phase shift keying). В
CPHC ГЛОНАСС/GPS /Galileo используют сигналы ФМ-2.
Сигнал с бинарной фазовой манипуляцией может быть записан в виде
s(t) = Acos^co0t + ^&(t)-^(p0>), (5.15)
где А — амплитуда сигнала; а>0 — несущая частота; <р0 — начальная фаза;
3(t) — функция фазовой манипуляции. При бинарной фазовой манипуляции
типичный вид 3(t) приведен на рис. 5.2 а).
«о
о %-
-► /
1
1
1
0
-1 -
.*(')
0
ъ
а) б)
Рис. 5.2. Функция бинарной фазовой манипуляции
Так как изменение фазы сигнала на тс эквивалентно умножению
амплитуды на -1, сигнал (5.15) можно записать в виде
s(t) = Ah(t)cos(o)0t + (p0), (5.16)
где функция амплитудной модуляции h(t) приведена на рис. 5.2 б).
Для сигнала (5.16) комплексная огибающая записывается в виде
Us (t) = Ah(t)ti<pQ, а огибающая сигнала — U(t) - Ah(t).
В CPHC используют периодические сигналы ФМ-2, у которых на
длительности периода Гс укладывается L символов длительностью r3=Tc/L. При
86
Радиосигналы и навигационные сообщения в СРНС
этом функция /?(/) также является периодической, и на длительности одного
периода Тс она может быть описана соотношением
с
L
mo=Z^o(^(*-ik), (5-17)
где go (0 — импульс с единичной амплитудой и длительностью гэ, ак = ±1.
Последовательность символов А = {axa1...ak...aL) называют кодовой после-
довашельносшью, которую в СРНС принято называть дальномериым кодом, а
функцию h{t) — функцией дальномерного кода, т.к. по задержке огибающей
принятого сигнала, пропорциональной функции //(/), измеряется дальность
потребителя относительно навигационного спутника.
В цифровой технике для формирования кодовых последовательностей
используют символы 0 и 1. Такую последовательность будем обозначать
A.a=(ala2..xxk...aL).
Соответствие между значениями символов двух последовательностей ак и
ак и фазой закона фазовой манипуляции ФМ-2 сигнала определяется
следующим образом:
фаза закона фазовой манипуляции 0 л
символ кодовой последовательности:
о* 1 -•
с„ О 1
Спектральные свойства ФМ-2 сигналов определяются спектральной плот-
00
ностью S0(f) = \gQ{t)t~xl7r^dt импульса g0(t) и типом кодовой последова-
—00
тельности А . Для одиночного прямоугольного импульса
. , ч sin(2л fr^ 12)
М/) = Гэ 2ж/т12 ;ехр(-12;г/гэ/2).
Нормированная корреляционная функция прямоугольного импульса
описывается соотношением
Ро(т) = \ л I | ' (5-18)
[ 0, при |г|>гэ,
а спектральная плотность мощности, рассчитанная по (5.11), —
87
Глава 5
#0 (/)=*,
($\п(тт/т^
(5.19)
Спектральная плотность функции дальномерного кода h(t) (5.17) имеет
вид
5А(/) = 50(/)Х«*ехр(-1(Л-1)2^/гэ). (5.20)
Сумма в правой части (5.20) является спектральной плотностью кодовой
последовательности А , которую обозначим как
L
к=\
Тогда спектральную плотность функции дальномерного кода h(t) можно
представить в виде произведения:
W) = W)H(f). (5.21)
Выражение (5.22) удобно тем, что можно сначала отдельно найти
спектральные плотности S0(f) и //(/), а затем, перемножив их, — спектральную
плотность функции h(t), которая с точностью до амплитуды А является
спектральной плотностью огибающей ФМ-2 сигнала (5.16).
Рассчитаем нормированную КФ огибающей сигнала (5.16),
рассматриваемого на длительности периода Тс. С учетом (5.10), (5.12) и фиксированной
длительности Т = 71 запишем
'с
jh(t)h(t + r)dt т
!*(,)
2ТС
dt ~т<
Тс L
1 fv^ ^i
= ^F J 2^ак8о(*-(к-1)т->)2*ат8о(*-('п-\)т3+т)с11 =
IT -
c _r k=\ m=\
1 r
. L L
1 Гс
гдер0(г-(ш-А:)гэ) = — jg0{t ~(k-l)T3)g0(t-(m-\)T3+T)dt. (5.22)
88
Радиосигналы и навигационные сообщения в СРНС
С учетом (5.18) р0 отлично от нуля при выполнении условия
т-(т-*)тэ<тэ. (5.23)
Рассмотрим значения сдвига г в пределах длительности одного символа
кода тэ. В этом случае в соответствии с (5.23) следует положить т = к, а для
нормированной КФ получаем выражение
Ph{T) = PoiT)> M^V
При |г| > гэ, как правило, рассматривают не всю КФ (5.21), а ее значения
при временных сдвигах на целое число дискрет хэ. Поэтому введем
дискретный параметр ц = 1,2,... и рассмотрим значения нормированной КФ в моменты
времени х = (ихэ. Из условия (5.23) получаем неравенство \л-(т-к)<\,
которому удовлетворяет лишь два целочисленных значения: \i = m-k и \л = т-к + \.
Учитывая, что при первом значении \х имеем р0 = 1, а при втором — р0 = 0,
приходим к следующему выражению для нормированной КФ огибающей
ФМ-2 сигнала
PhM = j^akak+M- (5-24)
Таким образом, нормированная КФ огибающей ФМ-2 сигнала в
дискретных точках сдвига т = цтэ определяется корреляционными свойствами кодовой
последовательности А .
Выше рассмотрен случай, когда принимается сигнал на интервале времени
Тс, поэтому все приведенные формулы, в том числе и для КФ, лучше называть
спектрами и КФ «отрезка» сигнала или, как иногда говорят в литературе, для
«апериодического режима работы».
Кроме апериодического режима возможен также периодический режим,
когда сигнал излучается непрерывно, и он модулирован по фазе кодовой
последовательностью А с периодом Тс=Ьхэ. Для периодического режима
нормированная КФ огибающей ФМ-2 сигнала имеет вид
1 L
L k=\
и число слагаемых в сумме равно L (в отличие от (5.24)).
Итак, нормированная КФ огибающей ФМ-2 сигнала (5.24), (5.25)
определяется корреляционными свойствами кодовой последовательности.
Если взять случайную кодовую последовательность, у которой значения
соседних символов независимы между собой, а каждый из символов
случайным образом с равными вероятностями может принимать значения ± 1, и
положить в соответствии с определением (5.10) Тс -> оо, то, как показано в [5.8], и
89
Глава 5
из (5.25) следует ph(ju) = 0 при //*0. Следовательно, нормированная КФ
огибающей при использовании такой кодовой последовательности
описывается (5.18), а спектральная плотность мощности — соотношением (5.19).
На практике используют псевдослучайные кодовые последовательности
(ПСП), которые по своим свойствам близки к описанной выше абсолютно
случайной последовательности, но формируются на базе регулярных структур
(алгоритмов) и, поэтому, легко воспроизводимы. Существуют различные
псевдослучайные кодовые последовательности с хорошими корреляционными
свойствами: М-последовательности; кодовые последовательности Кассами, Барке-
ра; последовательности Лежандра и Якоби и др. В настоящее время СРНС
ГЛОНАСС используются М-последовательности, поэтому рассмотрим
основные определения и свойства таких последовательностей.
5.3.2. М-последовательности. Основные свойства
Наиболее распространенными и хорошо изученными являются
рекуррентные линейные циклические кодовые последовательности, которые
формируются в результате циклических перестановок некоторого кодового слова
[Ъх Ь2 ...6„_1), элементы Ъ{ которого принимают одно из возможных значений из
заданного алфавита (при использовании двоичного алфавита — это 0 и 1).
Устройством, реализующим циклические перестановки, является многоразрядный
(поразрядный) сдвигающий регистр [5.7, 5.8], состоящий из п последовательно
соединенных двоичных элементов памяти, состояние которых передается
(сдвигается) на последующие элементы под действием тактовых импульсов.
Чтобы после п тактовых импульсов регистр не оказался «пустым», в схему
вводится элемент обратной связи, осуществляющий логическую операцию над
содержимым п разрядов регистра. Полученный результат поступает на первый
разряд. Схема такого регистра приведена на рис. 5.3, где btj — состояние /-го
регистра нау-м такте работы (другими словами, z-й элемент кодового слова
нау-м такте); f\p\j,b2j,...,bnj) — логическая функция в цепи обратной связи.
Наиболее распространены и изучены регистры с линейной обратной сея-
зъю, в которых f(blj,b2j,...,bnj) представляет собой сложение по модулю 2
(mod 2) всех или некоторых выходов регистров.
г>К
—5 гг-ij-^
J ffh h h ) L
| J\°lj02j—Dnf \*
Рис. 5.З. Схема и - разрядного сдвигающего регистра с обратной связью
90
Радиосигналы и навигационные сообщения в СРНС
Суммирование по mod 2 обозначается © , а умножение по mod 2
этому для регистра с линейной обратной связью получаем
/(^Л^-^ ®{c„®b„j),
где с{ — коэффициенты, принимающие значения 0 или 1.
Суммирование двоичных Умножение двоичных
чисел по mod 2: чисел по mod 2:
е
0
1
0
0
1
Т~|
1
0
®
0
1
0
0
0
Т1
0
1
Последовательность на выходе ^-разрядного сдвигающего регистра всегда
периодична, причем ее период L < 2п. В случае линейного сдвигающего
регистра наибольший период Z,max = 2п -1. Любая выходная последовательность,
имеющая такой период, называется последовательностью максимальной
длины или М-последовательностью. Для каждого значения п существуют
линейные последовательности максимальной длины.
М-последовательности имеют ряд замечательных свойств. Одно из них
(свойство уравновешенности) [5.9] состоит в том, что в периоде
последовательности (длиной Imax) число нулей и единиц отличается на единицу. При
использовании двоичного алфавита символов (0 и 1 или -1 и 1) число единиц
в последовательности равно 2п~х, а число нулей 2п~х -1.
Другое свойство — свойство корреляции: если последовательность
почленно сравнивать с любым ее циклическим сдвигом на длительности периода
этой последовательности, то число совпадений меньше числа несовпадений на
единицу, т. е. число совпадений равно 2п~х -1, а число несовпадений 2п~х.
Следующее важное свойство — сумма (по mod 2) двух М-после-
довательностей, сдвинутых одна относительно другой, является
М-последовательностью. Это является следствием того, что сдвинутые
М-последовательности можно получить с помощью одной и той же схемы.
Часто для описания работы сдвигающего регистра (рис. 5.1) с линейной
обратной связью (5.20) используют характеристический многочлен (или
порождающий полином) [5.3, 5.9]:
В(х) = спх" +сп_ххп~Х +... + qjt + l. (5.27)
Из теории М-последовательностей известно [5.3, 5.5—5.7], что
характеристический многочлен в(х) степени п должен быть, во-первых, неприводимым,
т.е. его нельзя представить в виде произведения многочленов меньших
степеней, а во-вторых, он должен быть первообразным (примитивным) относитель-
<8>, по-
(5.26)
91
Глава 5
но двучлена xL +1, т. е. характеристический многочлен должен делить х +1
без остатка. Если характеристический многочлен является первообразным, то
он неприводим. Известно, что если L-2k -1, то многочлен xL + 1
представляется как произведение неприводимых полиномов степени не выше к. Каждый
из этих полиномов, а также их произведения могут быть использованы как
порождающие полиномы. Известны таблицы [5.6] неприводимых многочленов
до степени к = 34.
Рассмотрим корреляционные свойства огибающей сигнала,
использующего в качестве кодовой последовательности М-последовательность. Согласно
общему свойству (5.24) при |г| < г3 нормированная корреляционная функция
ph(r) описывается формулой (5.17). В соответствии с отмеченным выше
общем свойстве корреляции, периодическая КФ (5.25) кодовой М-
последовательности (5.25) при //^0 равна ph(ju) = -l/L, где L число
символов кодовой последовательности. Учитывая периодичность кодовой
последовательности, а, следовательно, и функции h(t) (с периодом Гс),
нормированная КФ Рь(т) также является периодической с периодом Тс. Принимая во
внимание данные факты можно записать выражение для нормированной КФ
аМ=7+Т £ М*+Ю> (5-28)
/=-00
где Ро(т) определяется (5.17).
График корреляционной функции (5.28) приведен на рис. 5.4.
■ 1/L
Рис. 5.4. Нормированная корреляционная функция огибающей
сигнала, использующего М-последовательность
Спектральная плотность мощности функции ph(r) получается в
результате преобразования Фурье от (5.28) [5.13]
92
Радиосигналы и навигационные сообщения в СРНС
Mfh-ji
где S(x) =
S(f) + (L + l)^smc2
1, при х = О,
Ща
f
j=-00
Lt.
э У
(5.29)
О, при х * О.
На рис. 5.5 приведен трафик спектральной плотности мощности
нормированной корреляционной функции ph(r) при Тс= 1 мс, /,=511 (характеристики
кодовой последовательности для СРНС ГЛОНАСС).
Частота, МГц
Рис. 5.5. Спектральная плотность мощности Рь(т)
Как следует из (5.29) спектр Nh (/) — дискретный. Для иллюстрации
этого факта на рис. 5.6 приведен более детальный спектр Nh(f) (рис. 5.5) в
районе / = 0 Гц.
20
хЮ
о
о
х
э-
§15
и
н
о
о
X
5 ю
с
к
(в
Ф
-3 -2-1 0 1
Частота, кГц
Рис. 5.6. Спектральная плотность мощностиNh(f) в районе/ = 0Гц
93
Глава 5
Из графика следует, что дискретные спектральные компоненты следуют с
частотой 1 кГц, а мощность спектральной компоненты на частоте / = 0 Гц в L
раз меньше мощности соседних компонент.
5.3.3. Последовательности Голда
В статье Голда Р. [5.10] предложены последовательности, получившие его
имя, которые широко используются в спутниковой навигации (GPS, Galileo) и в
системах связи с кодовым разделением сигналов.
Дальнейшее изложение базируется на материалах [5.11].
Пусть имеем бинарную М-последовательность {<?,} длины (периода)
L = 2п -1. Введем операцию децимации с индексом децимации v , где v
взаимно прост с L, которая означает выбор каждого v -го символа at<v\
последовательности {at) и запись выбранных символов друг за другом в новую
последовательность {Д}, где Д = а^.
Введем два варианта взаимосвязанных параметров п и v :
1) п — нечетное число, v = 2s +1, a s — взаимно просто с п;
2) п — четное число, не кратное четырем, v - 2s +1, a s — четно и
взаимно просто с п/2.
Для указанных сочетаний параметров справедливы следующие
утверждения:
индекс v взаимно прост с длиной L исходной последовательности;
новая последовательность {Д} также является М-последовательностью
длины (периода) L.
Ансамбль последовательностей Голда {g,} формируется по следующему
правилу:
^)=«/ФДчД = и I,
g^2)=ft-k- (5.30)
Из (5.30) следует, что в ансамбле содержится К = L + 2 = 2n +1
последовательностей Голда.
Формирование последовательностей Голда реализуется устройством,
схема которого приведена на рис. 5.7.
94
Радиосигналы и навигационные сообщения в СРНС
Генератор ПСП 1
{а,
Генератор ПСП 2
Ш
>
Задержка
на к тактов
А
►
р /
т
е
Lk\
\8i ^
\Л+2\
\ Т moa/ |«i |
W
Рис. 5.7. Схема устройства, формирующего последовательность Голда
Для последовательностей Голда боковые лепестки нормированной
периодической КФ принимает лишь три возможных значения, причем для первого
варианта —
Рр (т)'
P(L + l)-\ -V2(L + 1)-1 1
, — , -jt, /и = 1,2,...,1-1,
а для второго варианта —
/^(rojej—*— , —*— , --ф m = \,2,...,L-\.
На рис. 5.8 приведена нормированная КФ последовательности Голда при
и =7, L=127, v=9, 5=3, характеристический полином исходной М-по-
следовательности В(х) = 1 + х + х2 + х3 + х1.
1-
ас
х
ос
со
1.2
1г
0.8 г
о
£ 0.61
0)
CL
CL
S 0.4
ГС
(О
X
CD
о
CL
I о
О
I
-0.2
—1 1 1
fflffffj
1 1
20 40 60
Число элементов сдвига
80
Рис. 5.8. Нормированная корреляционная функция последовательности Голда
95
Глава 5
Для данной последовательности Голда боковые лепестки нормированной
КФ принимают три возможных значения:
/^(т)е{0,118, -0,134, -0,00787}, /и = 1,2,..., 126.
Нормированная ВКФ последовательностей Голда также принимает три
возможных значения, приведенные выше.
5.3.4. Последовательности Касами
Принцип формирования последовательностей Касами близок к принципам
формирования последовательностей Голда [5.11]. По-прежнему,
рассматривается М-последовательность [аг) длины L = 2п -1, но у которой п = 2р —
четное число. В результате децимации с индексом v = 2Р +1 сформируем
последовательность {Д} = !#;/ Л. В данном случае значение v не взаимно просто с
периодом L. Поэтому, последовательность {Д} имеет период, значение
которого является делителем L. Доказано, что при соблюдении некоторых условий
на начальное значение последовательности [at) «короткая»
последовательность {Д} является бинарной М-последовательностью длины ЬХ=2Р -\.
Ансамбль последовательностей Касами {kst)периода L формируется по
следующему правилу:
fo}*)=a/©A_t,* = l,2,...,Z1,
Ь
ft+i) _
а,
(5.31)
Из (5.31) следует, что в ансамбле содержится К = Ь{+\ = 2Р
последовательностей Кассами, т.е. существенно меньше, чем последовательностей Голда.
Формирование последовательностей Касами реализуется устройством,
схема которого приведена на рис. 5.9.
Генератор ПСП на
базе л-разрядного
регистра
<«.)
К1
Генератор ПСП на
базе л/2-разрядного
регистра
Задержка
на к тактов
ь
w
1
©
ы
►
{/%}
?
mod 2
Рис. 5.9. Схема формирования последовательности Касами
96
Радиосигналы и навигационные сообщения в СРНС
Для последовательностей Касами боковые лепестки нормированной
периодической КФ принимает лишь три возможных значения
, ( ЛУ^-1 -Vo^1)-1 il 1? , ,
Рр\т)&\ ~г ' —-j ' -ТГ» m = l,2,...,L-\.
На рис. 5.10 приведена нормированная КФ последовательности Касами
при и =8, Z,=255, к =17, /? =4.
0 20 40 60 80
Число элементов сдвига
Рис. 5.10. Нормированная корреляционная функция последовательности Касами
Для данной последовательности Касами боковые лепестки нормированной
КФ принимают три возможных значения:
^(m)e{0,0588, -0,0667, -0,00392}, от = 1,2,...,126.
Нормированная ВКФ для последовательностей Касами также принимает
три указанных выше значения.
5.4. Фазоманипулированные сигналы с модуляцией
на поднесущих частотах
Фазоманипулированные сигналы, рассмотренные в п. 5.3, имеют
спектральную плотность мощности, сосредоточенную в области несущей частоты
сигнала (характеристика рис. 5.5, перенесенная на несущую частоту сигнала). В
то же время, как следует из (5.1) более высокая точность измерения задержки
сигнала достигается, если спектр сигнала имеет форму, у которой максимумы
смещены к краям занимаемого диапазона частот (более подробно см. п. 5 ).
Такая форма спектральной плотности мощности может быть получена при
использовании бинарной модуляции на поднесущих частотах [12]. В англоязыч-
I 1
to 0.8
X
X
о
к 0.6
ф
Q.
Q.
О
«0.4|
СО
X
X
(О
8 0.2
Q.
S
S
Q.
■? о
4-1026
97
Глава 5
ной литературе данный тип модуляции называется binary offset carrier (BOC)
[5.13,5.14].
Под модуляцией BOC(fsub,fchip} понимается бинарная модуляция на под-
несущих частотах, при которой fsub — частота отстройки поднесущих, fchi
— частота следования символов (чипов) кода. Обычно, частоты fsub, fchi
выбираются кратными некоторой «базовой» частоте /с (например, в GPS
fc =1,023 МГц), т.е. fsub = mfc, fchip = nfc. Тогда для обозначения модуляции на
поднесущих частотах используется сокращенная запись ВОС(т,п). Отметим,
что аналогичное обозначение используется для фазовой манипуляции BPSK(ri),
что соответствует скорости следования символов кода fchi = nfc.
Для формирования поднесущих используются функции sign (cos (2;т/^?))
или sign (sin (2xfsubty)9 т.е. колебание меандрового типа. Здесь sign(x) —
знаковая функция, принимающая значения ±1 в зависимости от знака аргумента
jc. В СРНС GPS, Galileo и перспективной СРНС ГЛОНАСС используется
функция sign (sin (27rfsubt))t
В п. 5.3.1 отмечалось, что для случайной непериодической кодовой
последовательности функция амплитудной модуляции сигнала с фазовой
манипуляцией BPSK(fl) (5.16) описывается выражением
00
£=-оо
в котором гэ =l/(w/c), значения ак соседних символов независимы между
собой, а каждый из символов случайным образом с равными вероятностями
может принимать значения ± 1, а нормированная КФ описывается (5.18).
Для нормированной КФ справедливо соотношение
+00
Ро(Т)= \ёвР5к(')йвР8к(* + т)Ж>
+00
8вр5к(<) = \ л \gBPSK(t)dt = \
О при иных t* J
при 0<7<гэ,
при иных /,
Последнее условие означает, что модулирующий сигнал
+00
к=-оо
98
Радиосигналы и навигационные сообщения в СРНС
имеет единичную мощность. Далее будут рассматриваться именно такие
модулирующие сигналы. Спектральная плотность мощности такого сигнала
описывается (5.19).
Для модуляции ВОС функция g[t) определяется выражением
Ёвос{*) = §вр5к(*)ы&*(ыъ(м/Ъ +^))> (5-33)
где rs =\/(2fsub) = l/(2mfc) — длительность половины периода модулирующей
гармонической функции, у/ — начальная фаза модулирующей функции.
Как отмечалось выше, обычно используется у/ = О или у/ = ж 12, а в СРНС
используется у/ = О, что и полагается далее.
Введём параметр к = тэ/т5 = 2m/n.
Спектральная плотность мощности модулирующего сигнала единичной
мощности с модуляцией ВОС (5.33) и у/ = О определяется выражением [5.13]
NBoc(f) =
/э
•sinc2(^///3)tg2
/
2fs;
при чётном к,
lcos^/ТЛ) *(*Л .. ,
^tg — — , при нечетном к.
(5.34)
В СРНС используется ВОС модуляция при кратных значениях т = рп , т.е.
2р\г\
ВОС(рп,п), р = \,2,.... Введём целочисленный параметр v =
, где [х]
функция взятия целой части числа. Тогда корреляционную функцию сигнала с
модуляцией ВОС(рп,п) можно записать в виде [5.14]
Рвос(т) =
(-1)
v+l
—(-у2 + 2vp + v-p) -—Up - 2v +1)
при r<r,
О, при иных т.
(5.35)
На рис. 5.11 приведены графики спектральной плотности мощности
сигналов с модуляцией BOC{m,ri) и /с =1,023 МГц, занимающих одинаковую
полосу частот А/=8/с = 8,184 МГц.
Из рисунка видно, что, варьируя значения параметров пят, можно
формировать различную форму спектральной плотности мощности модулирующего
сигнала, а, следовательно, и фазоманипулированного сигнала в целом.
99
Глава 5
tf(/)xl07
J fife
Рис. 5.11. Спектральные плотности мощности
сигналов с модуляцией ВОС{т,п)
5.5. Сравнительный анализ потенциальной точности оценки задержки
сигналов с различными законами фазовой манипуляции
В общем случае потенциальная точность оценки задержки сигнала s(t),
принимаемого на интервале времени [0,Г] в аддитивной смеси с белым гаус-
совским шумом с двусторонней спектральной плотностью N0/2, определяется
соотношением (5.1), в котором
Р =
00
U(2*ff\s(f)\2df
1/2
— эффективная ширина спектра сигнала; S(f)
сигнала;
(5.36)
спектральная плотность
Е= \s2(t)dt= \\S(f)\ df—энергия сигнала за время наблюдения Т .
О -оо
В реальном приёмном устройстве принимаемая аддитивная смесь сигнала
и шума фильтруется в радиочастотном тракте приёмного устройства с полосой
пропускания А/. Данная фильтрация приводит к искажению спектра сигнала
s(t) и спектра шума n(t). При этом будут изменяться значения параметра /3
(5.36) и дисперсии ошибки оценки задержки.
Для получения более адекватных характеристик точности оценки
задержки в реальной аппаратуре при расчете эффективной ширины спектра (5 можно
использовать соотношение (5.36) с учётом полосы пропускания радиочастотно-
100
Радиосигналы и навигационные сообщения в СРНС
го тракта [5.15]. При этом коэффициент передачи A^(j/) тракта будем
полагать идеально прямоугольным с единичным усилением в пределах полосы
пропускания А/ и нулевым за пределами полосы пропускания.
С учётом этого допущения соотношение (5.36) примет вид
/о+А/72 /0+Л//2
/?2=i J (2xf)2\s(ff df, E= J \s(ffdf. (5.37)
/О "А//2 /0-Л//2
Так как потенциальная точность оценки задержки не зависит от несущей
частоты сигнала, то расчёт можно проводить для комплексной огибающей
сигнала. Кроме того, учитывая наличие нормировки в (5.37), можно перейти от
квадрата модуля спектральной плотности сигнала \S(f)\ к соответствующей
спектральной плотности мощности N(f) комплексной огибающей сигнала.
Поэтому, запишем (5.37) в виде
А//2 А//2
/?2=- | (2xff N(f)df , Ps = J N(f)df. (5.38)
s -A/72 -A/72
где N(f) — спектральная плотность мощности комплексной огибающей
сигнала.
Рассмотрим сигнал с модуляцией BPSK(m). Спектральная плотность
мощности комплексной огибающей сигнала определяется (5.19). Полагая в (5.38)
А/ = 2mfc , гэ = 1//э = \j(mfc), где /с = 1,023 МГц, рассчитаем сначала
+Д/72
PIpsk= \ (2яff-sine2(7rf/f3)df=(2mfcf.
Л
Мощность комплексной огибающей сигнала в полосе частот А/ равна
+nf 1 ( f \ 2 *r
Ps,BPSK(m) = \ -7-sinc2 n^— \df = - [sine2 (x)dx = 0.903 .
, mfo
-mf0
V "У0 )
Подставляя данные соотношения в (5.38), получаем
Ав(-)-1-»074(2О2.
Рассмотрим сигнал с модуляцией ВОС{п,п). Спектральная плотность
мощности комплексной огибающей сигнала определяется (5.34). На рис. 5.12
приведена спектральная плотность мощности комплексной огибающей сигнала с
модуляцией ВОС(\, 1).
101
Глава 5
t 5(/)(xlO"7)
Рис. 5.12 Спектральная плотность мощности комплексной
огибающей сигнала с модуляцией ВОС{\, 1)
Сигнал с модуляцией ВОС(п, п) занимает полосу А/ = Anfc. Рассчитаем
параметр
We
Р2вос(п,п)= \ (2тг/)2—-sine
-2nfc Jc
Л
j_
nf
\ J
4'
с J
\
2 nfr
о J
df=l.5(4nfcf
Мощность комплексной огибающей сигнала в полосе частот А/ равна
rs,BOC(
2nfc
f
n
f
tg
nfc) I 2 nfc
* f
# = 0.8557
с J
Подставляя данные соотношения в (5.38), получаем Рвос(п,п) = 1 -753(4w/0) .
Сопоставим точность оценки задержки для сигналов BPSK(m) и ВОС{п, и),
занимающих одинаковую полосу частот, т.е. т = 2п.
Рассмотрим сигналы с полосой 8,184 МГц (8/с). Это сигналы BPSK(4) и
ВОС (2,2), Для которых получаем Рврщл) =1-1074-(8/с)2>
Рвос{п,п) = 1.753(8у^.) . В этом случае отношение дисперсий ошибок оценок
задержки равно:
_ aBPSK(4) _ РвоС(2,2) _
В
7 7
°50С(2,2) PbPSK(4)
= 1.583
Таким образом, использование сигнала с модуляцией ВОС(п,п) позволяет
уменьшить дисперсию ошибки оценки задержки в 1,583 по сравнению со
случаем использования сигнала с модуляцией BPSK{2n). Выигрыш по СКО оценки
составляет р = 1,258 раза.
102
Радиосигналы и навигационные сообщения в СРНС
Рассмотрим сигнал с модуляцией ВОС{рп,п). Провести интегрирование в
(5.38) в общем виде не удаётся, но его можно осуществить в частных случаях.
Рассмотрим сигнал с модуляцией ВОС(3,\), занимающий полосу частот
Д/ = 8/с (по-прежнему, полагаем /с= 1,023 МГц).
Расчеты параметра Рвос{ъ,\) по приведенной выше методике дают
следующий результат
Рвоф,\) -2(2Л)
(
22 +
18.9л/3
тс
Мощность комплексной огибающей сигнала в полосе частот Af равна
s,BOC(3
+4fc
-4/с
fc
sine
7Т
f_
fc
&
bfcj
# = 0.82
Подставляя данные соотношения в (5.38), получаем
/&с(з,1)=2-439(2/с)2
(
22 +
18.9л/з
тс
Выигрыш по дисперсии ошибки оценки задержки при использовании
сигнала с данным типом модуляции по сравнению со случаем использования
сигнала, имеющего модуляцию BPSK{4) (занимающим ту же полосу частот) равен
в = <*ДРЯ:(4) = РЮС{Ъ,Х) _ 1 162?
авос(ъ,\) Pbpsk(a)
Аналогичный выигрыш при использовании сигнала с модуляцией
ВОС[2,2) (также занимающим полосу частот А/ = 8/с)равен
В =
_ ^BPSK^) _ РвОС{2,2) _
= 2.819.
GBOC{2,2) РвРБЩ)
Таким образом, из сигналов с модуляцией BPSK(4), BOC(2,2) и
ВОС(3,\), занимающих одинаковую полосу (см. рис. 5.11), наибольшую
точность оценки задержки обеспечивает использование сигнала с модуляцией
ВОС(Ъ,\). Выигрыш по СКО оценки задержки для данного сигнала составляет
103
Глава 5
1,68 раза по сравнению с сигналом, имеющим модуляцию £0С(2,2), и 2,11
раз по сравнению с сигналом, имеющим модуляцию BPSK(4).
Рассмотрим сигналы, занимающие полосу частот А/ = 16/с, а именно
сигналы с модуляцией BPSK(S), 50С(4,4), 50С(6,2) и 50С(7,1). Спектральные
плотности мощности комплексной огибающей для данных сигналов приведены
на рис. 5.13.
t 5(/)(xl0-7)
///о
Рис. 5.13. Спектральные плотности мощности комплексных
огибающих сигналов с полосой с модуляцией
BPSK(S)9 ВОС{ЛА\ ВОС(6,2) и ВОС(79\)
Для сигнала с модуляцией ВОС(6,2) параметр РВос{б,2) определяется
следующими соотношениями
+8/с
д
ВОС(6,2)
J (2*/)
Sfc
2 1.2
smc
2*/с
( Г \
п-
V
(
df =2(4 fj
44-
18,973
п
Мощность комплексной огибающей сигнала в полосе частот А/ равна
rs,BOC{6,2)
+8/с
-8/с
1 • 2
sine
2/с
/^ / \
/_
2/с
я--
V ^с/
tg'
\—J-
1б2/сУ
^ = 0,823.
Подставляя данные соотношения в (5.38), получаем
P2BOC(6,2)=2M4fc)
44-
18,9л/3
л*
Сравнивая дисперсию ошибки оценки задержки для сигналов с
модуляцией 50С(6,2) и БОС(4, 4), получаем
104
Радиосигналы и навигационные сообщения в СРНС
D _ аВОС(4,4) РвОС(6,2) _ 0 00
В-—2 -^2 ~2'89-
(У
РВ0С(4,<
ВОС(6,2) ГВОС(4,4)
Выигрыш по СКО оценки задержки равен 4в = 1,7 раза.
При сопоставлении сигнала с модуляцией 50С(6,2) с сигналом, имеющим
модуляцию BPSK(S)9 получаем
aBPSK(%) _ Рвос{б,:
аВОС(6,2) PbPSK{%)
Выигрыш по СКО оценки задержки равен 4в - 2,249 .
Для сигнала с модуляцией ВОС{1,\) расчеты дают следующие результаты
+8 Ус / \ / \
Мос<ю= J (2^/)2|sinc2 №- № §^# = 913(4/с)2,
2 = aBPSK(%) = РВ0С(6,2) = 5 05g
-8/с fc
+8/с
^,i?oc(7,i) = J "7"sinc
-8/с Л
V -/с У
с У
5/;
V Л У
tg2
f г \
*_у
2 7/с
# = 0.801,
с J
/&С(7Д)=П4.1(4/С)2.
Сравнивая дисперсии ошибок оценки задержки для сигналов с
модуляциями ВОС(7,1) и 5<9С(4,4), получаем
в = °ДОС(4,4) = РвОСУЛ) = ^ Q98
аВОС(7,1) РвОС(4,4)
Выигрыш по СКО оценки задержки составляет V5 = 2.02 раза.
При сопоставлении сигнала с модуляциями ВОС(1,\) с сигналом,
имеющим модуляцию BPSK(S), получаем следующие результаты
2 = ffM(8) = Рвосдл) = 6 4735
3"Я0С(7,1) PbPSK(%)
Выигрыш по СКО оценки задержки равен v5 = 2.54.
5.5. Навигационные сообщения в СРНС
5.5.1. Общие сведения
Передаваемое в радиосигналах навигационное сообщение предназначено
для проведения потребителями навигационных определений и планирования
105
Глава 5
сеансов навигации. По своему содержанию навигационное сообщение,
передаваемое каждым НС, содержит оперативную и неоперативную навигационную
информацию (НИ) [1.2, 1.6].
Оперативная информация (ОИ) относится к тому НС, с борта которого
передается данный навигационный радиосигнал, и содержит данные:
эфемериды НС, т. е. координаты и параметры движения спутника на
фиксированный момент времени;
сдвиг шкалы времени НС относительно системной шкалы времени;
относительное отличие несущей частоты излучаемого радиосигнала от
номинального значения;
код метки времени, необходимой для синхронизации процесса извлечения
навигационной информации в аппаратуре потребителя.
Неоперативная информация (НОИ) содержит альманах системы,
включающий:
данные о состоянии всех НС системы (альманах состояния);
сдвиг шкалы времени каждого НС относительно шкалы времени системы
(альманах фаз);
параметры орбит всех НС системы (альманах орбит);
поправку к шкале времени системы относительно UTC.
Навигационное сообщение формируется в цифровой форме. Для этого
каждый передаваемый информационный параметр подвергается квантованию по
уровню. Каждому уровню квантования ставится в соответствие кодовая
комбинация нулей и единиц. Систему соответствий между дискретными
значениями параметра и кодовыми комбинациями называют кодом. Кодовую
комбинацию, соответствующую квантованному значению какого-либо параметра,
называют словом.
В СРНС навигационное сообщение передается в виде потока цифровой
информации (ЦИ). Скорость передачи информации в СРНС ГЛОНАСС
составляет 50 бод. Структурно поток ЦИ формируется в виде непрерывно
повторяющихся суперкадров длительностью 2,5 мин, каждый из которых можно
рассматривать как одно сообщение. Структура сообщения (передаваемой
информации) оптимизируется таким образом, что объем суперкадра относительно
невелик (в СРНС ГЛОНАСС — 7 500 бит). В суперкадре передается полный
объем неоперативной информации для всех НС. Каждый суперкадр состоит из
пяти кадров. Каждый кадр состоит из 15 строк и содержит полный объем
оперативной информации для конкретного НС и часть альманаха. Вся
передаваемая информация представляется в виде слову каждое из которых занимает
определенное место в строке. Информационная строка кадра содержит 100 бит
информации. В СРНС GPS скорость передачи ЦИ также составляет 50 бод,
структура потока цифровой информации аналогична и имеет следующие
параметры: длительность суперкадра — 12,5 мин; объем суперкадра — 37 500 бит;
в суперкадре 5 кадров по 5 строк каждый.
106
Радиосигналы и навигационные сообщения в СРНС
5.5.2. Помехоустойчивое кодирование навигационной
информации
С целью повышения достоверности передачи/приема навигационных
данных по каналу связи НС—потребитель используют помехоустойчивое
кодирование, суть которого заключается во введении избыточности (дополнительных
символов) в передаваемый поток данных [5.5,5.16]. При помехоустойчивом
кодировании используются не все возможные кодовые комбинации, а только
некоторые из них, т. е. весь код обладает избыточностью относительно той части,
которая применяется для кодирования информации. Оставшаяся часть кода
может быть направлена на обнаружение возможных ошибок и их устранение,
т.е. на повышение достоверности приема данных.
Правило преобразования исходного потока символов в новый поток
определяет метод помехоустойчивого кодирования.
Существует большое многообразие методов помехоустойчивого
кодирования [5.5,5.11,5.16], которые можно подразделить на два принципиально
отличающихся класса:
1. Использование блоковых кодов, при котором исходный непрерывный
поток символов в кодере разбивается на блоки одинакового объема из к
символов. Все дальнейшие операции производятся над каждым блоком отдельно и
независимо от остальных блоков. Каждому входному блоку из к символов
ставится в соответствие (по тому или иному правилу) блок из п выходных
символов (п>к), которые и передаются по каналу связи.
2. Непрерывное кодирование, при котором исходный непрерывный поток
символов подвергается обработке (как правило, с использованием
рекуррентных процедур) в кодере без какого либо предварительного разбиения его на
отдельный фрагменты, но с введением избыточности.
Блоковые коды
Пусть имеем к информационных символов (битов источника), которые
нужно передать двоичным кодовым словом А-\ах,а2,...,а^ ) длины L6n>k .
Из к битов источника можно сформировать 2к = М кодовых комбинаций,
которые все полагаются возможными. Каждой (из М) кодовой комбинации
источника ставится в соответствие кодовое слово А, в котором к двоичных
символов являются информационными, (/,бл-&) символов — избыточными.
Таким образом, получаем М кодовых слов длины L6jl, совокупность которых
называется блоковым кодом.
Почти все блоковые коды относятся к разделимым, кодовые комбинации
которых состоят из двух различающихся частей: информационной и
проверочной. Информационные и проверочные разряды во всех кодовых комбинациях
107
Глава 5
разделимого кода всегда занимают одни и те же позиции. Разделимые
блоковые коды условно обозначают в виде (L6}l,k).
Важными характеристиками блоковых кодов являются:
скорость кода г = k/L6n ;
избыточность w = (L6jl - k)/L6jl ;
кодовое расстояние (или расстояние Хемминга); расстоянием d между
двумя кодовыми комбинациями называют число позиций, в которых эти
комбинации имеют разные символы; расстояние между различными
комбинациями конкретного кода может быть различным; минимальное расстояние dmin
между кодовыми комбинациями называют кодовым расстоянием;
число обнаруживаемых и исправляемых ошибок.
Если код используется только для обнаружения ошибок кратностью а, то
необходимо и достаточно, чтобы минимальное расстояние dn^n > а +1. Чтобы
можно было исправить все ошибки кратности а и менее, необходимо иметь
dmm>2a + \.
Важным классом блоковых кодов являются коды Хемминга, которые
исторически появились раньше многих других. Число символов слова кода
Хемминга определяется соотношениями Ь6л = 2п -1; к = 2п -1 - п , где п — целое
положительное число. Данные коды являются линейными циклическими
кодами и формируются на основе к разрядного регистра сдвига, охваченного
обратной связью, в цепи которой использованы сумматоры по mod 2 (рис. 5.3).
Сначала в к ячеек регистра сдвига помещается блок информационных
символов, затем замыкается обратная связь и производится Ь6л сдвигов. Первые к
символов, снимаемых с выхода, будут информационными, а остальные L6jl -к
символов — проверочными. Кодовое расстояние dm[n = 3, поэтому коды
Хемминга исправляют одиночные ошибки в кодовом слове.
Коды Хемминга используются для помехоустойчивого кодирования
данных в СРНС ГЛОНАСС (см. гл. 11).
Сверточные коды
При сверточном кодировании последовательность информационных
символов подвергается линейному преобразованию (суммированию по mod 2
некоторых компонент последовательности), такому, что каждой совокупности из
к входных (информативных) символов ставится в соответствие п > к
выходных символов. Таким образом, скорость сверточного кода равна г = к/п.
Линейное преобразование последовательности информационных символов
реализуется на базе / = рк разрядного регистра сдвига, где р — целое число, и п
сумматоров по mod 2.
108
Радиосигналы и навигационные сообщения в СРНС
Параметр / • п/к называется длиной кодового ограничения и характеризует
количество выходных символов, на которые оказывает влияние любой входной
информационный символ.
Рассмотрим простейший (но часто используемый на практике) случай
к = 1, п = 2 (скорость кода г = 1/2), р = 3. Возможная схема сверточного
кодера для этого случая приведена на рис. 5.14 а).
а0,а1э...
а^о^
filfi,
а)
б)
Рис. 5.14. Схема формирования сверточного кода с к = \ 9 и = 2, р = 3,
а) несистематического, б) систематического
В выходной последовательности сверточного кодера рис. 5.14 а)
отсутствует «в чистом виде» исходная информационная последовательность a0,al9....
Такой сверточный код называют несистематическим. Систематическим свер-
точным кодом является такой код, для которого в выходной
последовательности кодовых символов содержится без изменения исходная информационная
последовательность а0,аи.... Схема систематического сверточного кодера
приведена на рис. 5.14 б).
Как и в случае блочных кодов, корректирующая способность сверточного
кода определяется кратностью а исправляемых ошибок. При сверточном
кодировании для исправления всех ошибок кратности а и менее, необходимо
иметь dL > 2а +1, где dL — минимальное свободное расстояние, определяемое
как минимальное расстояние по Хеммингу между последовательностями
сверточного кода на длине кодового ограничения.
Турбокоды
Турбокоды по своей сути являются параллельно-каскадными сверточными
кодами [5.11]. Схема, поясняющая принцип формирования турбокода,
приведена на рис. 5.15 при использовании систематического сверточного кода со
скорость г = 1/2 .
109
Глава 5
a0,al9...
w
w\
w
Сверточвый 1
кодер |
Перемежитель
J Сверточный 1
Л w
Ад1,,
Pt,P\
Мультиплексор
p,
Рис. 5.15. Схема формирования турбокода с использованием
систематического сверточного кода с г = 1/2
В схеме формирования турбокода присутствуют два идентичных
систематических сверточных кодера. На вход первого сверточного кодера поступает
исходная информационная последовательность а0,ах,..., а с его выхода
снимается последовательность проверочных символов ySjJ,/?/,.... На вход второго
сверточного кодера подается последовательность символов, формируемая из
исходной информационной последовательности а09al9... в результате ее пере-
межения в пределах блоков фиксированной длины Ln . С выхода данного коде-
ра снимается последовательность проверочных символов /?0 , Д ,.... Выходная
последовательность турбокодера формируется в результате мультиплексирова-
11 О *У
ния последовательностей а0,аи..., /?0?Л ,••• > Ро >Р\ >•• •
5.6. Модуляция радиосигнала навигационным
сообщением
5.6.1. Относительная фазовая манипуляция
Сформированное тем или иным образом цифровое (навигационное)
сообщение &HC(t) с длительность информационных символов гнс должно быть
передано с помощью излучаемого навигационным спутником радиосигнала. Как
отмечалось в п. 5.3 в СРНС используются фазоманипулированные
радиосигналы, для которых при передаче навигационного сообщения #нс (?) можно
записать выражение
s(t) = Acos(co0t + x&HC(t) + <p0). (5.39)
На приемной стороне для демодуляции навигационного сообщения может
использоваться фазовый детектор (ФД), в котором реализуется умножение
принятого сигнала (5.39) на опорный сигнал sou (t) = cos (a?0t + <роп), где <роп —
начальная фаза, и выделение постоянной составляющей (рис. 5.16).
ПО
Радиосигналы и навигационные сообщения в СРНС
Рис. 5.16. Схема фазового детектора
Если на интервале интегрирования гс значение цифрового символа равно
в, на выходе фазового детектора формируется сигнал
^=^ccos(^on-^o)-
(5.40)
Если фаза опорного сигнала сроп стабильна на всем интервале наблюдения,
то из (5.40) однозначно определяется информационный символ в . Однако,
если фаза (роп по каким-либо причинам изменится на ±п, то знак определяемого
параметра в изменится на обратный. Это явление называют обратной
работой ФД. Очевидно, что такой режим работы фазового детектора недопустим,
так как с момента перехода на обратную работу последовательность символов
вк\ к = \, 2 ... будет приниматься неправильно до тех пор, пока не
произойдет следующий скачок фазы на ±тт .
Одним из путей устранения явления обратной работы ФД на приемной
стороне является отказ от классического вида противофазных ФМ-сигналов и
переход к относительной фазовой манипуляции (ОФМ) — методу русского
ученого Н.Т. Петровича.
Суть метода заключается в том, что отсчет фазы для каждого
информационного символа &к; k = U 2 ... производится не относительно начальной (для
данного сеанса приема) фазы, а относительно фазы предыдущей посылки.
Пусть <pj — фаза у-и посылки, a q)j_x — фаза (j-l )-й посылки. Так как для
противофазного ФМ сигнала &л = = {0 или тт\ , разность фаз между двумя
соседними посылками может также принимать только два значения
А(р =
<Pj-9j-\
0, если q>j =<Pj_l9
л", если <pj = g)j_x + 7Т .
(5.41)
Из (5.41) видно, что если скачок фазы опорного сигнала произойдет в
пределах (j-l )-й посылки, то соответствующий импульс на выходе ФД
"раздробится" на две части с разной полярностью. Можно показать [5.8], что в ре-
111
Глава 5
зультате такого эффекта возможен ошибочный прием двух соседних
символов. Если скачок фазы произойдет точно на границе двух посылок, то
неправильно будет принят лишь один символ. Таким образом, перескок фазы
опорного сигнала на ±п при приеме ОФМ-сигнала приводит к появлению только
локальных ошибок, а не к переходу на обратную работу в течение длительного
времени, как это имеет место при приеме ФМ сигнала.
Относительную фазовую манипуляцию можно рассматривать как
дополнительную перекодировку исходной последовательности двоичных символов
Го
& =
при к-\ 2, ... Действительно, пусть Зк\ к = 1, 2,
последовательность символов, полученная после перекодирования. Тогда в соответствии
с принципом формирования ОФМ совпадение двух символов ^ и Зк_х
означает передачу исходного символа Зк = О, а в противном случае, когда
символы Зк и Зк_{ различны, — передачу символа Зк = 1. Формально это можно
записать в виде алгоритмов:
Эк_х®Эк=Эк, (5.42)
Уь- ~ Уь-
*к-\-
(5.43)
Алгоритм (5.43) используется для перекодировки исходного потока
Зк\ к-\, 2,... символов в поток Зк; к = \, 2, ..., соответствующий ОФМ, а
алгоритм (5.26) — для обратного перехода от Зк; к = 19 2, ... к исходному потоку
символов Зк; к = 1, 2, ... Оптимальный прием сигналов с ОФМ реализует
устройство, приведенное на рис. 5.17, где УЗ — устройство задержки. Как
следует из рисунка, приемное устройство состоит из двух частей: устройства
оптимального приема противоположных сигналов (обведено штриховой линией) и
устройства перекодировки последовательности Зк;к = 1, 2, ... в исходную
последовательность Зк\ к-\ 2, ...
мфд
Рис. 5.17. Схема оптимального приемника сигнала с ОФМ
112
Радиосигналы и навигационные сообщения в СРНС
Наличие второго устройства, дополнительного к ФД, приводит к
изменению (увеличению) вероятности ошибочного решения для всей схемы по
сравнению с приемом ФМ-сигнала. Энергетический проигрыш ОФМ-метода по
сравнению с ФМ не превосходит 1 дБ.
5.6.2. Фазовая манипуляция радиосигнала
Сформированное тем или иным образом цифровое сообщение #нс(7)
должно быть передано с помощью излучаемого навигационным спутником
радиосигнала. Как отмечалось в п. 5.3 в СРНС используются фазоманипули-
рованные радиосигналы, в которых для расширения спектра (с целью
обеспечения хорошей точности измерения задержки огибающей сигнала)
используется манипуляция фазы сигнала на п бинарной кодовой
последовательностью, которую называют дальномерным кодом. Обозначим эту
последовательность #дк(/). Два цифровых потока #дк(/), 3HC(t) формируются на борту
НС синхронно, т.е. фронт каждого символа навигационного сообщения i9HC (/)
совпадает с фронтом первого символа дальномерного кода 3ДК (/)
периодической последовательности Аа =(axa2~.ak...aL). Итоговая цифровая
последовательность b(t), поступающая на модулятор гармонического сигнала,
формируется в результате сложения по mod 2 двух указанных последовательностей
b{t) = 9№{t)®3K{t). (5.44)
Излучаемый НС радиосигнал описывается соотношением
s(t) = Acos{a>Qt + 7ib(t) + <р0). (5.45)
Учитывая, что b{t) — поток символов 0 и 1, (5.45) можно записать в виде
s(*) = Ahw (O^c {t)cos(co0t + <p0), (5.46)
где hm {t) — функция амплитудной модуляции дальномерным кодом; huc (t)
— функция амплитудной модуляции навигационным сообщением. Обе этих
функции принимают значения ±1 на длительностях тэ дальномерного кода и
гнс навигационного сообщения соответственно.
5.7. Синхронизация в приемнике сигналов СРНС
Для приема сигналов с ОФМ, близкого к оптимальному, необходимо
реализовать когерентный прием сигнала [5.13, 5.17], т. е. использовать фазовую
113
Глава 5
синхронизацию^ которая осуществляется путем использования системы
слежения за фазой сигнала (ССФ). Более подробно вопросы построения ССФ
рассмотрены в гл. 6.
При демодуляции двоичных символов навигационного сообщения в
приемнике необходимо выделить импульсы символьной (тактовой) частоты,
определяющие границы принимаемых символов, т. е. осуществить тактовую
синхронизацию. Ввиду случайного характера передаваемой информации
спектр радиосигнала не содержит составляющей тактовой частоты. Поэтому
информацию о тактовой частоте можно выделить только из сигнала, в котором
модулирующие посылки меняют свое значение, т. е. при смене принимаемых
символов от 0 к 1, и наоборот. Так как смена 0 и 1 имеет неравномерное
распределение, то могут появиться длительные интервалы времени, когда
отсутствует смена значений символов. При этом время установления тактовой
синхронизации (нахождение правильной фазы символьной частоты) может
существенно возрастать. Для устранения этого явления можно использовать
дополнительный синхрокод, который складывается по mod 2 с символами
навигационных данных. В СРНС ГЛОНАСС в качестве такого кода используется бид-
воичный (манчестерский) код с длительностью посылки гсм = гнс/2 (частота
100 бод). Благодаря бидвоичному кодированию всегда осуществляется
практически равномерное распределение переходов от 1 к 0 и наоборот, в том
числе при передаче длинных массивов навигационных данных с преобладанием
одинаковых символов. Это позволяет облегчить условия и уменьшить время
установления тактовой синхронизации в приемнике.
Кроме тактовой синхронизации в приемнике необходимо определить
границы кодовых слов или некоторой совокупности (блоков) слов, т. е.
осуществить цикловую синхронизацию [5.8]. В СРНС ГЛОНАСС в качестве таких
блоков приняты строки навигационного сообщения. Цикловую синхронизацию
обеспечивают с помощью специальных синхросигналов, которые в аппаратуре
ГЛОНАСС получили название «код метки времени».
Сигналы навигационного сообщения, дальномерного кода, тактовой и
цикловой синхронизации связаны по фазе между собой (синхронны). Это
достигается путем их формирования от одного синтезатора тактовой частоты.
Литература
5.1. Перов А.И. Статистическая теория радиотехнических систем. — М.:
Радиотехника, 2003.
5.2. Тихонов В.К, Харисов В.Н. Статистический анализ и синтез радиотехнических
устройств и систем. — М: Радио и связь, 1991.
5.3. Борисов В.А., Калмыков В /?., Ковальчук Я.М. и др. Радиотехнические системы
передачи информации. — М: Радио и связь, 1990.
5.4. Pat. 5,331,329 (US), Jul. 19. 1994, Int. CI.5 G01S 5/02$ H04B 15/00. Satellite-aided
Radio Navigationing Metod and Radio Navigation System Therefor.
114
Радиосигналы и навигационные сообщения в СРНС
5.5. Проксис Дж. Цифровая связь/Пер. с англ. под ред. Д.Д. Кловского. — М:
Радио и связь, 2000.
5.6. Варакин Л.Е. Системы связи с шумоподобными сигналами. — М.: Радио и
связь, 1985.
5.7. Шумоподобные сигналы в системах передачи информации/ Под ред. В.Б. Пе-
стрякова. — М.: Сов. радио, 1973.
5.8. Forssell В. Radionavigation systems. — Artech House, 2008.
5.9. Цифровые методы в космической связи/ Под ред. В.И. Шляпобергского. — М:
Связь, 1969.
5.10. Gold R.. Optimal binary sequences for spred specrum multiplexing// IEEE trans.
Inform. Theory, vol.13, 1967.
5.11. Ипатов В.П. Широкополосные системы и кодовое разделение сигналов.
Принципы и приложения. — М.: Техносфера, 2007.
5.12. Ярлыков М.С. Характеристики меандровых сигналов (ВОС-сигналов) в
спутниковых радионавигационных системах нового поколения// Радиотехника, 2008, №2,
с. 61—75.
5.13. Understanding GPS. Principles and applications/ Edited by D. Kaplan, C.J. Hegar-
ty. Second edition. — Artech House, 2006.
5.14. Borre K., Akos D.M., Bertelsen PN., Rinder P., Jensen S.H. A software-defined
GPS and Galileo receiver/ A single-frequency approach. — Birkhauser Boston, 2007.
5.15. Перов А.И., Болденков Е.К Сравнительный анализ характеристик приема
сигналов спутниковых навигационных систем с модуляцией BPSK{ri) и BOC(mfri)ll
Радиотехника, 2008, №7, с. 26—32.
5.16. Спилкер Дж. Цифровая спутниковая связь. — М: Связь, 1979.
5.17. Тихонов В. И. Оптимальный прием сигналов. — М.: Радио и связь, 1983.
115
Глава 6
Глава 6
МЕТОДЫ И АЛГОРИТМЫ ОБРАБОТКИ СИГНАЛОВ
И ИЗВЛЕЧЕНИЯ НАВИГАЦИОННОЙ ИНФОРМАЦИИ
В АППАРАТУРЕ ПОТРЕБИТЕЛЕЙ
6.1. Общие сведения
Навигационная аппаратура потребителей (НАП) предназначена для
выполнения следующих основных функций: прием сигналов от навигационных
спутников; выбор рабочего созвездия, т. е. выбор тех находящихся в зоне
радиовидимости навигационных спутников, сигналы которых будут
использоваться для навигационно-временных определений; извлечение информации из
навигационного сообщения, передаваемого в радиосигналах; определение век-
тора состояния потребителя П = \х у z t Vx Vy Vz .
К современным СРНС предъявляются высокие требования по точности
НВО. Это обусловливает необходимость рассмотрения методов оптимальной
обработки сигналов и извлечения информации при построении НАП. Так как
принимаемые от навигационных спутников сигналы Sj (?Д (/)) (где j — номер
НС; k(t) — вектор параметров сигнала) являются случайными (кавзислучай-
ными) процессами, а их прием осуществляется на фоне внутреннего шума
приемника, задача определения вектора потребителя является статистической, и
для ее решения необходимо использовать статистическую теорию приема и
обработки сигналов [5.1, 5.2, 5.4]. По своей сути навигационная задача
определения вектора состояния потребителя П(/) относится к задаче оценивания в
текущем времени координат и составляющих вектора скорости объекта по
наблюдениям сигналов от источников излучения с известными координатами.
Известно [5.1, 5.2, 5.4], что квазиоптимальными системами оценивания
меняющихся во времени процессов являются следящие системы. При любом
выборе оцениваемого в следящей системе вектора состояния \{t) (это может
быть вектор состояния потребителя П(/) или любой другой вектор) он должен
быть связан с вектором параметров сигнала к , т.е. Цх(/)). Поэтому слежение
за вектором состояния х(/) трансформируется в слежение за вектором
параметров сигнала ^(t). Так как в общем случае параметры X входят в
сигнальную функцию Sj(t,X) (в радиосигнал) нелинейно, радиотехнические следящие
системы являются принципиально нелинейными системами. Это влечет за со-
116
Методы и алгоритмы обработки сигналов и извлечения информации
бой два существенных обстоятельства: во-первых, необходимо «захватить
сигнал» на устойчивое сопровождение по отслеживаемому параметру; во-вторых,
возможен срыв режима устойчивого сопровождения. Первый фактор приводит
к необходимости получения предварительных оценок значений параметров
сигнала, которые, с одной стороны, должны быть достаточно грубыми, а с
другой стороны, их точность должна быть достаточной для осуществления захвата
сигнала на сопровождение по данному параметру. Таким образом, можно
говорить о двух этапах в получении текущей оценки вектора состояния
потребителя П(/): этап предварительной (грубой) оценки значений параметров сигнала
и этап формирования точных текущих оценок параметров сигнала и
соответственно вектора потребителя. Первый этап называют поиском сигнала по
соответствующим параметрам, второй — текущим оцениваем (фильтрацией)
вектора состояния.
Общая постановка задачи синтеза оптимального приемника (оптимальных
алгоритмов обработки сигналов) формулируется следующим образом. Пусть на
вход приемника СРНС поступает реализация y(t), представляющая собой
аддитивную смесь сигнала s(t,k,&,\i) и помехи n[t)\
Сигнальная функция ^(/Д(п(/),/),19(г),ц(/)] в наблюдаемой реализации
y[t) в задаче спутниковой навигации состоит из нескольких сигналов,
соответствующих различным НС:
N
7=1
где у: — случайный параметр, принимающий значение 1 или 0 и
характеризующий наличие или отсутствие сигнала от j -го НС в наблюдаемой
реализации; Я. ■ — вектор радионавигационных параметров сигнала у'-го
НС, т.е. тех параметров, из которых извлекается информация о
координатах и параметрах движения потребителя; цу — вектор параметров
сигнала, в которых не содержится какая-либо навигационная
информация, поэтому их можно считать неинформативными; 3j — дискретный
параметр, несущий дополнительную навигационную информацию
(навигационное сообщение).
Радионавигационными параметрами X в СРНС являются (см. гл. 4)
задержка сигнала г, доплеровское смещение частоты /д или фаза сигнала
117
Глава 6
(p(t) = 2n \fA(y)dv (при приеме одновременно нескольких сигналов в (6.2)
имеем г•,/„,-, q>j\j = \,N). Радионавигационные параметры сигнала в свою
J " J J
очередь зависят от вектора состояния П потребителя, т.е. г (П), /Д(П),
(р(И). К неинформативным параметрам ц относится, например, амплитуда
сигнала А и его начальная фаза р0 . Аддитивную помеху n(t) в (6.1) часто
полагают белым гауссовским шумом (БГШ) с нулевым математическим
ожиданием и двусторонней спектральной плотностью N0/2. Сигнальная функция от
у-го НС может быть описана соотношением
( ' "1
= ^y(r"ry(0)cos ^jt + 2*\f*onj(v)dv + <PQj > (6-3)
V о )
где ^4у—амплитуда сигнала; hMJ(t-Tj(t)) —функция модуляции дальномер-
ным кодом и навигационным сообщением; a>0J — несущая частота; (p0J —
случайная начальная фаза сигнала.
Задача синтеза оптимального приемника (оптимальных алгоритмов
обработки сигналов и информации в приемнике) формулируется как отыскание
такой системы (алгоритмов), которая в результате обработки наблюдений (6.1) в
каждый текущий момент времени / формирует оценку П(/) вектора состояния
потребителя с минимальной дисперсией ошибки оценивания.
Как отмечалось выше, задача синтеза оптимальных алгоритмов обработки
сигналов и информации в приемнике разбивается на две самостоятельных
задачи: синтез алгоритмов поиска сигналов по тем или иным параметрам и
синтез алгоритмов текущего оценивания (фильтрации) вектора состояния
потребителя. Первая задача решается методами теории оценивания случайных
параметров (случайных величин) сигналов [5.1—5.3, 6.1], вторая — методами
теории оптимальной фильтрации случайных процессов [5.1—5.3].
6.2. Поиск сигналов по задержке и частоте
Основной задачей режима поиска сигналов является формирование
предварительной (грубой) оценки его параметров. Данная задача решается на
ограниченном интервале времени Т , длительность которого определяется, с одной
стороны, требуемой точностью формирования соответствующих оценок, а с
118
Методы и алгоритмы обработки сигналов и извлечения информации
другой стороны, условием постоянства оцениваемых параметров или малости
их изменения.
Для стандартных значений мощности навигационного (полезного) сигнала
в СРНС ГЛОНАСС/GPS и внутреннего шума приемника удовлетворительные
характеристики точности предварительных оценок параметров сигнала
достигаются при времени обработки сигнал одного НС Т ~ 5... 10 мс. Для таких
интервалов времени задержка и доплеровское смещение частоты сигнала
меняются незначительно, т.е. их можно считать константами. При этом сигнал на
входе приемника (6.1) на интервале времени /е^о^+Г] может быть
представлен в виде
N
7=1
где n{t) — БГШ с нулевым математическим ожиданием и двусторонней
спектральной плотностью N0/2 (N0 — реальная физическая одностороння
спектральная плотность внутреннего шума приемника).
Зададим априорное статистическое описание случайных величин,
входящих в (6.4).
Амплитуда сигнала А- на входе приемника в общем случае априорно не
известна. Однако диапазон возможных значений амплитуды невелик и
составляет 10... 15 дБ. Поэтому при решении ряда задач синтеза оптимальных
алгоритмов обработки амплитуду А- можно полагать известной. При более
корректном подходе А- следует считать случайной величиной, распределенной по
законам Рэлея (при отсутствии ярко выраженной детерминированной
составляющей сигнала) или Раиса (при наличии детерминированной и случайной
составляющих сигнала) [5.1].
Начальные случайные фазы (p0j распределены равномерно на интервале
[-я\;г],т.е. pap(<poJ) = \/27T,j = lN.
Диапазон возможных значений доплеровских частот зависит от геометрии
взаимного движения НС и потребителя и скорости движения последнего.
Максимальное значение проекции вектора скорости НС на направление НС—
потребитель — не более 800 м/с, что соответствует доплеровскому смещению
частоты А/д =800/0,2 = 4 кГц. С учетом возможного движения потребителя
обычно полагают, что диапазон возможных значений доплеровского смещения
частоты равен ± 5 кГц, т.е. А/да/7 = 10 кГц. Зададим равномерное распределение
частоты Доплера в пределах этого диапазона, т.е. рар (/допу) = УУДопар •
119
Глава 6
Параметр у ■, имеющий значение 1 или 0, определяет наличие или
отсутствие сигнала j -го НС в принимаемом сигнале. Реально в зоне видимости
конкретного потребителя находится не более двенадцати НС. Следовательно,
половина значений параметров у., j = \,N равно единице, а половина — нулю.
Но потребитель обычно не знает какие НС (с каким номером) находятся в поле
его видимости. А так как с номером НС связано значение несущей частоты
излучаемого сигнала, то эта информация весьма существенна для работы
приемника. Поэтому, строго говоря, необходимо оценивать значение параметра у • и
соответствующее значение несущей частоты a>0j. Однако, учитывая то, что в
СРНС ГЛОНАСС используется частотное разделение сигналов, а в приемнике
организуется 24 приемных канала, настроенных на соответствующие несущие
частоты сигналов НС и имеющих согласованные со спектрами сигналов
частотные полосы пропускания, в (6.4) можно полагать, что N =12, у • =1, j = 1,12 ,
а несущие частоты co0j, j = 1,12 известны.
Рассмотрим более подробно вид модулирующей функции /^(/-Гу) в
(6.4). Как отмечалось в гл. 5, в СРНС ГЛОНАСС используются фазоманипули-
рованные на п сигналы, в которых модулирующая последовательность
образуется в результате сложения по модулю 2 двух цифровых
последовательностей: дальномерного кода #дк(^) и кода навигационного сообщения i9HC(f)
(рис. 6.1).
*дкк
->* t
»нс(0
s—
! *нс к
"НС
Рис. 6.1. Временные диаграммы кодовых последовательностей
Начало формирования двух кодовых последовательностей
синхронизировано по времени (момент времени /и). Длительность элементарного символа
120
Методы и алгоритмы обработки сигналов и извлечения информации
дальномерного кода гэ= 1/511 мс, а длительность символа кода
навигационного сообщения гнс = 20 мс.
Так как изменение фазы сигнала на п соответствует изменению знака
амплитуды сигнала, кодовым последовательностям &т (/) и i9HC (/) фазовой
манипуляции соответствуют аналогичные последовательности амплитудной
модуляции /*дк (/) и GHC (/) с заменой значений символов 0 —> 1, 1 -> -1 и заменой
операции суммирования по модулю 2 кодов #дк(*) и i9HC(?) на операцию
умножения кодов hnK (/) и Л^с (/). Таким образом, для модулирующей функции
/^ (г) можно записать выражение hMJ(t) = hJlKJ(t)h}iCJ(t). При задержке
сигнала на время Tj получаем h^j и - т}\ = //дку и - tA^j (t -тЛ. Строго говоря,
модулирующая функция /*м7(*) задается в бортовой шкале времени у-го НС, а
следовательно, функция вида /z^(t-тЛ также определена в БШВ. Сигнал же
на входе приемника (6.4) должен быть описан в шкале времени потребителя,
так как в этой шкале времени проводится его прием и вся дальнейшая
обработка. Учет этого фактора приводит к тому, что в модулирующую функцию
hujit-Tjj, стоящую в (6.4), в действительности входит не истинная задержка
сигнала г ■, а псевдозадержка fj. Однако для простоты терминологии в
дальнейшем в данном разделе будем говорить просто о задержке и доплеровском
смещении частоты.
Измерение задержки сигнала основано на обработке огибающей сигнала,
т.е. дальномерного кода hmj {t), который является периодическим (см. п. 5.3) с
периодом Гкод = 1 мс (для дальномерного кода стандартной точности).
Следовательно, временная задержка сигнала однозначно может быть определена
лишь при ее изменении в пределах одного периода, поэтому статистические
характеристики случайной задержки также целесообразно задавать в пределах
периода Гкод. Зададим равномерный закон распределения задержки в пределах
этого периода, т.е. рар (гу) = 1/ГК0Д , j = l9N .
Так как в приемнике реализуется раздельная обработка сигналов каждого
НС, то в дальнейшем будем рассматривать поиск сигнала лишь в одном из
каналов приема, для которого входной сигнал имеет вид
j;(r) = ^/2M(/-r)cos(^ + 2^ + ^0) + w(r), te[t0J0+T]. (6.5)
Положим сначала, что время наблюдения сигнала Т « гнс, а начальный
момент t0 выбран так, что на интервале наблюдения Т отсутствует момент
121
Глава 6
времени tHck -г(см. рис. 6.1), когда возможна смена символов #нс(/)
навигационного сообщения. При такой формулировке задачи неопределенность
значения символа навигационного сообщения соответствует неопределенности по
фазе: 0 или к , которую можно отнести к неопределенности значения начальной
фазы (р0 . Поэтому наблюдения (6.5) на интервале времени t е[/0,/0 +Г] можно
записать в эквивалентном виде:
^(?) = ^ДД?-Г)С08(^0/ + 2Я/Д/ + ^0) + А7(/) = 5(^Г9/Д^0)9 (6.6)
где ф0 — случайная начальная фаза, распределенная равномерно на интервале
[-л-,л-]
В (6.6) информативными параметрами являются задержка г и доплеров-
ское смещение частоты /д сигнала, а начальная фаза <р0 является
неинформативным параметром (амплитуду А полагаем известной). Следовательно,
предварительной оценки подлежат только параметры г и/д.
Из теории оптимального оценивания случайных параметров сигнала [5.1,
5.2] следует, что максимум апостериорной информации (информации,
учитывающей проведенные наблюдения) о случайных параметрах сигнала
содержится в апостериорной плотности вероятности (АПВ) р[т,/д,ф0 Г/0+ I, где
YJ°*T = {y(t)9t е [/0,/0 + 7*]} — наблюдаемая реализация.
Используя формулу Байеса, запишем
Здесь с — нормировочная константа.
Так как нас интересуют оценки только параметров г и / , рассмотрим
АПВ р[т,/д \Ytto+T I, которая получается из (6.7) интегрированием по ф0 :
л
р{т<Мсг)= \p^n\Y'VT)d^=
л
= СРар(т)РаРШ \р(^+Т\т>иФь)РарШ<*Фь
(6.8)
-л
При фиксированных значениях т,/д,ф0 функционал плотности
вероятности наблюдаемой реализации (6.6) имеет вид
122
Методы и алгоритмы обработки сигналов и извлечения информации
ИС^'Л^оНехр
— J s(t,Tja,p0)^y(t)--s(t,T,fa,p0)jdt
= с2 ехр
'о
tQ+T
— \y(t)s(t,T,f„fa)dt\.
(6.9)
'о
При записи последнего равенства учтено, что т,/Д,ф0 являются
неэнергетическими параметрами, таким образом, второе слагаемое, стоящее под знаком
экспоненты в (6.9), пропорционально энергии сигнала и соответствующий
сомножитель можно отнести к константе.
Подставив (6.9) в (6.8) и выполнив интегрирование по ф0 , получаем
^(г'/д|С0=Сз^(г)^^)/оигх(г)
>
(6.10)
где 10 (х) — функция Бесселя нулевого порядка от мнимого аргумента;
Х(Г,г,/д) = ^//2(Г,г,/д) + ^2(Г,г,/д) (6.11)
— огибающая сигнала на выходе согласованного фильтра (коррелятора);
tQ+T
/(Г,г,/Д)= | ^(/)Ада(/-г)со8Ц/ + 2^/д/)Л,
'о
tQ+T
Q(T,r,fa)= J y(t)hw(t-T)sm(a>0t + 2xfat)dt (6.12)
'о
— синфазная и квадратурная компоненты соответственно.
Квадратурные компоненты /(Г,г,/Д) и £>(Г,г,/д) формируются на
выходах двух корреляторов (рис. 6.2).
cos(co0t + 2nfat)
Синфазный коррелятор
Я<)
КЛ<~Т)
х
Н X
J
'(Wj
Квадратурный коррелятор
х
X
I
efru/д)
яп(т0г + 2я/дГ)
Рис. 6.2. Схемы синфазного и квадратурного корреляторов
123
Глава 6
Заметим, что в (6.12) y(t) рассматривается только как функция времени,
так как является принятой реализацией наблюдений. В схеме рис. 6.2 сигналы
/?дк(/-г), cos(tf>0/ + 2;r/^) и sin(&>0/ + 2;rJ^/) формируются соответствующими
опорными генераторами (дальномерного кода и гармонического колебания) с
соответствующими значениями параметров г и/д.
Располагая АПВ (6.10), можно вычислить любые оценки задержки т и до-
плеровского смещения частоты /д. Обычно рассматривают оценки,
соответствующие максимуму АПВ, т.е.
{иН»-'/>(г,/д|СГ), (6.13)
где max"1 обозначает функцию, обратную функции нахождения максимума.
Заметим, что поскольку априорные плотности вероятности распределения
параметров г и /д приняты равномерными в заданных диапазонах Атар и
А/д^, их роль при нахождении оценок (6.13) сводится к фиксированию
двумерной области [Атар,А/дар 1, в которой задаются возможные изменения г и
Уд при поиске экстремума АПВ. Поэтому, если у потребителя есть достаточно
точная априорная информация о возможных значениях г и /д, то
соответствующая двумерная область ГДг^Д/д^] будет более узкой, что облегчает
поиск экстремума.
С учетом сделанного замечания, выражения (6.10), а также того факта, что
/0(х) является монотонной функцией своего аргумента, решение (6.13) можно
записать в эквивалентном виде:
{г,/д} = max"' ЛГ(Г,г,/д). (6.14)
При практической реализации решающего правила (6.14) область
ГДга/,,Д/дд/Л возможных значений параметров г и /д дискретизируется,
например, по г с шагом Sr = ATap/NT и по /д с шагомSfa =Afaap/Nf . При
таком подходе поиск по непрерывным аргументам в (6.14) заменяется более
простой процедурой перебора по конечному числу значений двух аргументов г ■,
j = l,NT и /д/, i = \,Nf.
Другим практическим приближением относительно строгого решающего
правила (6.14) является отказ от нахождения истинного максимума, а поиск
такого значения х(т,т,/Л, которое больше некоторого заданного порога h.
124
Методы и алгоритмы обработки сигналов и извлечения информации
Значение порога выбирается близким к максимальному значению Хтах . Такая
процедура позволяет в 2 раза уменьшить число рассматриваемых значений
каждого из аргументов т и /д. Кроме того, при таком подходе решающее
правило (6.14) заменяется на более простые операции определения значения
огибающей X\T9Tj9fJxonj) для последовательных значений Tj9fuJ и сравнения по-
лученного значения с порогом /п . В качестве решения, т.е. оценок т9/Д,
принимаются такие значения, при которых наблюдается превышение порога, т.е.
Х(т,т,/Д)>1п. (6.15)
Таким образом, получается известная процедура поиска сигнала в
двумерной области параметров гх/д. Решение (6.14) и вытекающее из него решение
(6.15) предусматривают параллельный поиск, так как в них фигурирует одна и
та же реализация Г/0+г. На практике параллельный поиск сигнала в каждом из
каналов приема часто заменяют последовательным поиском с сохранением
одновременного (т.е. по сути параллельного поиска по сигналам всех НС) поиска
по всем каналам приема. Схематично схема последовательного поиска сигнала
по г и /д в одном канале приема приведена на рис. 6.3. Ячейка разрешения с
номером {/,у} соответствует использованию опорного сигнала со значениями
задержки гу и доплеровского смещения частоты /д/.
5х
Ячейка разрешения
Начало поиска
(ожидаемое значение
доплеровского
смещения частоты)
6
4
2
-> 1
3
/
/
J
1
А
|J
hi
J Д*
т
Nz - число элементов поиска по задержке
Последовательность поиска по частоте
г»
ё
<j
2
о
с
о
с
со
I
S
О
Рис. 6.3. Схема поиска сигнала по двум параметрам
125
Глава 6
Для обоснования выбора размеров ячейки разрешения St и Sfa
рассмотрим преобразование регулярной (сигнальной) составляющей входного сигнала
y(t) при формировании огибающей х1т,т,/А в обнаружителе (6.15).
Положив в (6.12) n(t) = О, запишем
t0+T
1(Т)= |^Лдк(/-г)со8(Ц+©д)г + й)-А№(/-г)сов((<ц,+<эд)/)л =
'о
tQ+T
= - J ^k(^-^")^k('-^)cos((^-^) t + <pQ)dt. (6.16)
'о
Введем корреляционную функцию дальномерного кода
t+T
P(Ar) = J \КЛ<-*ЖЛ*-*)Ж^т = т-т,
t
обозначим Ао)д =сод-сЬд и представим (6.16) в виде
а'0+т
1{Т) = - \ (h№(t-r) haK(t-T)-p(AT))cos((a)a -&л) 1 + ф0) dt +
'о
+ Ар^т)_ jcos^_^t + ^dt (617)
'о
В первом слагаемом (6.17) подынтегральная функция
haK(t-z) haK(t-z)-p(At)является быстро меняющейся функцией с нулевым
средним, а функция cosUcd^ -соа) t + фА — медленно меняющаяся. Поэтому
значение первого интеграла близко к нулю, и можно записать
'о
Ао(Ат)
= —+—^(sin(A^(?0+r) + ^0)-sin(A^0+^0)). (6.18)
Проделав аналогичные выкладки для квадратурной составляющей, запи-
0{Т) = ^^(со5(Асоа(^+Т) + ф0)-со5(Асо^0+ф0)). (6.19)
126
шем
2Да>д
Методы и алгоритмы обработки сигналов и извлечения информации
Подставляя (6.18), (6.19) в (6.11) и выполняя необходимые
преобразования, получаем
Х(Т) = —
р{Ат)™№)
(6.20)
При А/д=0, Аг = 0 имеем максимальное значение Х(Т), причем
Х2(Т)~Е , где Е = А2Т/2 — энергия сигнала на интервале времени Т . При
возрастании А/Д или Л г значение Х(Т) уменьшается, что приводит к
ухудшению условий обнаружения сигнала, параметры которого (г и /д)
соответствуют краям ячейки разрешения. Следовательно, размеры 8т и 3/Д ячейки
разрешения можно выбирать из условия допустимого ухудшения
характеристик обнаружения в указанных выше условиях. Так, допуская двукратное
уменьшение мощности квадрата огибающей Х2{Т), получаем условия:
St « 0,4гэ, £/д « 2/(ЗГ). На практике часто полагают St = 0,5гэ, 3/Д =2/(37').
Важным обстоятельством является то, что шаг поиска по частоте обратно
пропорционален времени интегрирования в корреляторе Т. Этот факт является
одним из существенных ограничений на выбор конкретного значения данного
параметра. При просмотре требуемой зоны поиска по частоте Af число
анализируемых ячеек разрешения по частоте прямо пропорционально времени
интегрирования в корреляторе: Nf = А/Дар/8/Д = kAfAapT. Число анализируемых ячеек
разрешения по задержке равно NT -Тс/6т = кхТ/гэ. Следовательно, общее число
анализируемых ячеек при поиске Nn0HCK = NfNT = кА/ДарТ2 /тэ, т.е.
пропорционально квадрату времени интегрирования в корреляторе. Поэтому, удвоение
времени интегрирования в корреляторе, дающее 3 дБ выигрыша по отношению
сигнал/шум, повышает вычислительные затраты при поиске сигнала в 4 раза.
Величина порога /п в алгоритме обнаружения (6.15) выбирается из
заданных характеристик правильного обнаружения и ложной тревоги (вероятность
принятия решения о наличии сигнала в наблюдениях при фактическом их
отсутствии). Для большей наглядности приводимых пояснений положим, что
St = t3, 6/д = 1/Т , а возможные значения параметров т и /д сигнала
совпадают с значениями гу и /д/, которые соответствуют центрам ячеек разрешения
(рис. 6.3). В этом случае при приеме сигнала с параметрами г., /д/
составляющая огибающей Х(Т), обусловленная воздействием полезного сигнала в
ячейке с номером [ij], будет максимальной и определяется по формуле (6.20).
Аналогичные составляющие для других ячеек (с номерами
127
Глава 6
{s,p}, s ф i и/илир ф j) будут либо равны нулю (при рФ j), либо близки к
нулю (при р = j и s*i ). Первое обстоятельство обусловлено тем, что функция
sinixAf Т)
— равна нулю при ДЛ Г =1,2,3»... , а второе — тем, что корреляцион-
я¥ят
ная функция дальномерного кода р(Дг) = 1/511 (в 511 раз меньше, чем
значение, определяемое (6.20)) при Аг = гэ, 2гэ, ....
Таким образом, можно считать, что при последовательном просмотре всех
ячеек сигнал (наблюдаемый на фоне шума) находится лишь в одной ячейке, а
во всех других ячейках присутствует только шум. Следовательно, при анализе
каждой ячейки разрешения (с номером {/,т}) решается классическая задача
обнаружения сигнала S(t,rm,fmnl^0) с известными параметрами гш,/д/ и
случайной фазой ф0 в соответствии с оптимальным алгоритмом (6.15).
Характеристики обнаружения для сформулированной задачи описаны,
например, в [5.1]. Отсчеты 1(Т) = 1 и Q(T) = Q, сформированные в момент
времени Т в соответствии с алгоритмом (6.12), являются гауссовскими
случайными величинами с математическими ожиданиями
М[/] = m, = AT cos(^0)/2, M[Q] = Шд = AT sin (ф0)/2
и равными дисперсиями:
Dj=DQ=D = N0T/4. (6.21)
Величины I и Q можно считать практически независимыми, так как
взаимная корреляционная функция между ними приближенно равна нулю.
Поэтому при наличии сигнала плотность вероятности р1 (X) случайной величины
X = yjl2 + Q2 определяется законом Раиса:
( X2 + (0,5AT)2) J2АХ^
N0T
'о
^0 J
Х>0
N0T/2
При отсутствии сигнала случайные величины I и Q также независимы и
распределены по нормальному закону с нулевыми математическими
ожиданиями и одинаковыми дисперсиями (6.21). Поэтому плотность вероятности
Ро(Х) случайной величины X будет рэлеевской:
р0(Х) = ехр
uv ' N0T
( 2Х2\
~N0Tj
Вероятность ложной тревоги определяется выражением
128
Методы и алгоритмы обработки сигналов и извлечения информации
'п In
( 2Х2Л
Рт = jV0 (X)dX = J—exp -— \dX = exp
Wj
f i2\
(6.22)
где /0 = laI^D = ln/yjN0T/4 — нормированная величина порога
Для вероятности правильного обнаружения запишем
Х2+(0,5АТ)
Роб = \р\ {X)dX = J— exp
( -2 ,,пеА^2} /. .„ч
00
■J'
иехр
( u2+2E/N0} (
к
\2Е
N0T/2
\
2АХ
dX =
и
N,
du
(6.23)
о J
где Е = A2T/2 — энергия сигнала на интервале времени Т .
Как видно из (6.23), вероятность правильного обнаружения зависит только
от отношения сигнал/шум q = E/N0 и от уровня нормированного порога /0,
который, в свою очередь, определяет вероятность ложной тревоги (6.22).
При использовании в задаче обнаружения критерия Неймана—Пирсона
задается вероятность ложной тревоги рлт, для которой из (6.22)
определяются величина нормированного порога /0 и соответствующая вероятность
правильного обнаружения /?об.
На рис. 6.4 приведены рассчитанные по данной методике вероятности
правильного обнаружения как функции отношения сигнал/шум q = lOlog(^r) [дБ]
для различных значений вероятности ложной тревоги.
-2
Роб
Рлт = 0,5 /»лт = 0,1 pm=W
?,ДБ
Рис. 6.4. Характеристики обнаружения
5-1026
129
Глава 6
Из рисунка следует, что при относительно небольших допустимых
вероятностях ложной тревоги (рят <10"3) для обеспечения вероятности правильного
обнаружения ро6 >0,9 необходимо иметь достаточно большое значение
отношения сигнал/шум # = 10... 12 дБ.
В спутниковой навигации энергетические характеристики условий приема
сигналов часто характеризуют отношением
4c/n0=Pc/No = A2/2N0=E/{N0T),
которое определяет отношение мощности сигнала к мощности внутреннего
шума в полосе 1 Гц. При этом формула для вероятности правильного
обнаружения принимает вид
Роб
■J-
ехр
u2+2Tqc/
\
"о
{иу]2Т<1с/п0) du
(6.24)
Зависимости (6.24), аналогичные тем, что даны на рис. 6.4, приведены на
рис. 6.5 при принятом выше значении Т = 1 мс и qcj4 = lOlogfg^ j. Для
обеспечения тех же характеристик обнаружения, которые обсуждены выше,
необходимо иметь qcin = 40...42 дБ, что обеспечивается лишь при хороших
условиях приема сигнала.
go ^с/ио'ДБГч
Рис. 6.5. Характеристики обнаружения
При приеме слабых сигналов необходимо увеличивать значение
отношения сигнал/шум за счет увеличения времени накопления Т до 10 мс и более.
Характеристики обнаружения, приведенные на рис. 6.4, 6.5, получены для
случая, когда параметры сигнала г и /д совпадают с параметрами опорного
130
Методы и алгоритмы обработки сигналов и извлечения информации
сигнала, соответствующего центру ячейки разрешения. Если параметры
сигнала соответствуют краям ячейки разрешения, то, как следует из (6.20),
возникают потери мощности сигнала, зависящие от размера ячейки разрешения,
которые приводят к ухудшению характеристик обнаружения.
При увеличении времени наблюдения Т с целью повышения значения
отношения сигнал/шум и улучшения характеристик обнаружения следует
помнить о том, что одновременно необходимо уменьшать размер ячейки
разрешения по частоте Sfa, а это приводит к увеличению времени поиска сигнала.
Другая проблема, возникающая при увеличении времени наблюдения
существенно более, чем 1 мс, заключается в том, что навигационный сигнал,
кроме модуляции дальномерным кодом haK(t), модулирован навигационным
сообщением /г„с (?). При Т » 1 мс даже при идеальной синхронизации ШВП и
БШВ возникают ситуации, когда на интервале наблюдения появляется
скачкообразное изменение значения информационного символа ^. Правило
обнаружения (6.15) не предусматривает возможность такого скачка и,
следовательно, не является оптимальным в этих условиях. Возникающие при этом потери в
характеристиках обнаружения можно оценить, рассчитав сигнальную
составляющую, аналогично тому, как это было сделано в (6.16)—(6.20), но полагая,
что в момент времени /0 + tx (tY<T) происходит скачок фазы входного сигнала
на к . Полагая для простоты выкладок А г = 0 , в этом случае имеем
'o+'i
l(T,tY)= j AhlK(t-r)cos((u)0+a)a) f + ^0)cos((u>0 +d)a) t) dt +
'o
t0+T
+ J ЛйдкС'-фЦЦ+^д) f + ;r + ^0)cos((u>0+u>fl) t) dt =
(2sin(A^(/0+^) + ^0)-sin(A^(?0+r) + ^0)-sin(A6y/0+^0)),
2Aa>a
A
Q{TA) = ——[2cos(A^(/0+^) + ^0)-cos(A^(/0+r) + ^0)-
2Aa>,
д
-cos(Auy0+^0)],
^2(6-4cos(A^1)-4cos(A^(r-/1)) + 2coS(A^r))
X [1,^) = ——г . (6.25)
4А*>д
При отсутствии скачка фазы внутри интервала наблюдение (6.25)
принимает максимальное значение:
131
Глава 6
*L (г)=~'г1мп(Ай>дГ/2)
sin
(6.26)
Д
Введем нормированную характеристику / (tx, Асод) =
= X2 (Т^19Аа)Л)/Х^ (7\Дюд). При ЛбУд= 0 из (6.25), (6.26) получаем
зависимость y(f1,0) = | 1 — 2— I , из которой видно, что при tx - Г/2 значение функции
f(t\,0)= 0, т.е. если символ навигационного сообщения изменяется в середине
интервала накопления, полезный сигнал на выходе блока выделения
огибающей отсутствует, при этом обнаружитель выдаст ложное решение — пропуск
сигнала. При Асод ф 0 сигнал на выходе блока выделения огибающей не равен
нулю, но его значение будет существенно меньше максимального (до 10 дБ и
более по мощности), и сигнал также не будет обнаружен.
Таким образом, увеличение времени наблюдения приводит к увеличению
вероятности того, что за это время произойдет смена значения символа
навигационного сообщения, что может привести к пропуску сигнала в обнаружителе.
Решение задачи синтеза оптимального обнаружителя при возможных
случайных скачках фазы сигнала за время наблюдения приводит к очень сложным
алгоритмам обработки сигнала, которые не реализуются на практике.
В СРНС ГЛОНАСС мощность навигационного сигнала у поверхности
Земли равна - 160 дБВт (см. п. 11.2.2). Для обнаружения такого сигнала с
хорошими характеристиками достаточно выбрать время интегрирования в
корреляторе Г=1...2мс. Однако, к современной аппаратуре потребителей часто
предъявляются более жесткие требования, например работа при мощности
принимаемого сигнала - 140 дБВт и менее (например, в помещениях, лесистой
местности и т.д.). Для обнаружения сигнала в таких условиях необходимо
увеличивать время интегрирования в корреляторе. Однако, с одной стороны, как
отмечалось выше, этому мешает наличие у навигационного сигнала модуляции
навигационным сообщением, а с другой стороны, при этом существенно
возрастет число анализируемых ячеек при поиске, а, следовательно, и время
поиска сигнала. Одним из возможных (и часто используемых) подходов к решению
данной проблемы является накопление выходных отсчетов X(7V,) или их
квадратов, т.е.
R^X2(T9tt). (6.27)
При вычислении отсчетов X{Tjt) пропадает фазовая информация,
поэтому последующее накопление таких отсчетов (или их квадратов) часто
называют некогерентным накоплением. Эффективность некогерентного накопления
132
Методы и алгоритмы обработки сигналов и извлечения информации
ниже, чем эффективность прямого увеличения времени интегрирования в
корреляторе (без учета влияния навигационного сообщения). Так, например, при
увеличении времени интегрирования в корреляторе в 2 раза отношение
сигнал/шум в отсчетах X2{2T,t^) увеличивается на 3 дБ, а при некогерентном
суммирования двух отсчетов X2{Tj^) отношение сигнал/шум в
сформированном отсчете R составляет лишь 2 дБ. Но при этом вычислительные затраты
возрастают не в 4 раза, а только в два. Учитывая это обстоятельство, часто в
приёмной аппаратуре при поиске сигнала время интегрирования в корреляторе
выбирается равным 1...2 мс с последующим некогерентным накоплением
выходных отсчетов коррелятора.
Рассмотрим характеристики обнаружения сигнала при использовании
некогерентного накопления квадратов выходных отсчетов коррелятора.
Положим для простоты анализа 3/Д = 1 / Т, St = гэ, а возможные значения
частот и задержек входного сигнала совпадают с центрами ячеек разрешения.
В этом случае опорные сигналы в корреляторах, используемых для различных
ячеек разрешения по частоте, являются ортогональными за счёт выбора шага
по частоте, а сигналы, используемые для различных ячеек разрешения по
задержке, — близки к ортогональным за счёт корреляционных свойств дально-
мерного кода. Систематическая составляющая на выходе коррелятора,
соответствующего ячейке разрешения, параметры опорного сигнала которой
совпадают с истинными значениями, будет максимальной и определяться
выражением (6.27), а в остальных ячейках — близкой к нулю.
При этом случайные составляющие в разных ячейках будут
некоррелированны за счёт ортогональности опорных сигналов. Можно считать, что сигнал
находится в одной из ячеек анализа, а в остальных присутствует только шум. В
каждой из ячеек анализа решается задача принятия решения о наличии сигнала
с известными значениями параметров г и со и случайной начальной фазой.
Величины 1{Т) и Q(T) являются независимыми гауссовскими
случайными с математическими ожиданиями M[l]= M[Q] = m = ATcos(<pQ)/2, и
дисперсиями Dj =Dq=ct2 = N0T/4.
При накоплении квадратов выходных отсчетов корреляторы в
соответствии с 6.27) в ячейке, где присутствует сигнал, случайная величина R
подчиняется нецентральному j2 распределению, для которого плотность вероятности
определяется выражением
м*у- га1
1_Г е>2)'М/
V ст
2
133
Глава 6
2NH-i
где s2 = У\ т2 = NHA2T2 J2. В ячейках, где отсутствует сигнал, случайная
величина R подчиняется центральному х1 распределению с плотностью
вероятности
Ро(х) =
2^
2N»a2N»r(NH)
xNH-l e-x/(2^)
где T{NH) = £°° yN»~l e~y dy = (NH -1)
Вероятность ложной тревоги для одной ячейки равна
Рлт = 1 Po(x)dx,
где h величина порога сравнения. Вводя нормированную величину
и = х I (2<т21, запишем выражеиние для вероятности ложной тревоги в виде
К T(NH)
где hQ=h/\ 2а2
Вероятность правильного обнаружения рассчитывается по формуле
Л>б = I Р\ (x)dx = JH f J J e~{u+L)jNH-\ {JluL^du ,
meL = s2/(2cr2) = 2qc/noNJ.
Приведённая выше вероятность ложной тревоги получена для одной
ячейки. Однако ячеек анализа Afn0HCK =N^NT, поэтому общая вероятность ложной
тревоги будет выше, и в предположении независимости накопленных в разных
ячейках величин определяется выражением
Задав вероятность ложной тревоги Рят для всей процедуры поиска, можно
рассчитать вероятность ложной тревоги рят в одной ячейке разрешения и
рассчитать величину порога, а затем — вероятность правильного обнаружения роб.
Описанные выше результаты получены в предположении совпадения
параметров входного сигнала с параметрами опорного сигнала в одной из ячеек.
В реальности параметры входного сигнала всегда будут рассогласованы с
параметрами опорного в пределах ячейки разрешения, что приведёт к
определённым потерям в отношении сигнал/шум и, следовательно, в значении вероятно-
134
Методы и алгоритмы обработки сигналов и извлечения информации
сти правильного обнаружения. Кроме того, величина указанных потерь будет
зависеть от шага разрешения по частоте и задержке. Чем меньше шаг
разрешения, тем меньше будет потерь, но тем больше будет вычислительных затрат.
Поэтому в каждом конкретном случае разработчик должен искать оптимум,
который будет зависеть от способа реализации поиска сигнала. В ряде случаев
лучше поступиться величиной потерь ради снижения вычислительных затрат, а
потери скомпенсировать увеличением времени накопления сигнала.
В качестве примера рассмотрим обнаружение сигнала ГЛОНАСС
стандартной точности. Шаг поиска по задержке зададим равным 8т = гэ/2, таким
образом, на периоде дальномерного кода имеем 1022 ячеек анализа по
задержке. Диапазон смещения частоты определим равным ±10 кГц. Шаг поиска по
частоте определим как 8fA = 1 / Т. Вероятность ложной тревоги для всей
процедуры поиска зададим равой Рлт =0,1. Время интегрирования в корреляторе
рассмотрим различной: 1, 2 и 5 мс. Подберем количество накапливаемых
выходных отсчётов коррелятора так, чтобы при различных временах
интегрирования в корреляторе получалась одинаковая вероятность правильного
обнаружения. Расчеты показывают, что примерно одинаковая вероятность
правильного обнаружения достижима при следующих сочетаниях параметров: NH = 30
при Г = 1 мс; NH = 10 при Т = 2 мс; NH = 4 при Т = 5 мс. Результаты расчёта
вероятности правильного обнаружения роб от отношения сигнал шум qcj для
трех рассмотренных ситуаций приведены на рис. 6.6: кривая 1 — NH = 30,
Т = 1 мс; кривая 2 — NH = 10, Т = 2 мс; кривая 3 — NH = 4, Т = 5 мс.
1.0
0.8
0.6
0.4
0.2
0.0
28 30 32 34 36 38
Т= 1 мс, Nh = 30 Т= 5 мс, Nh = 4
Т=2мс, Nh=10
Рис. 6.6. Характеристики обнаружения
135
Глава 6
6.3. Общие принципы построения следящих систем
в аппаратуре спутниковой навигации
6.3.1. Навигационный приемник с двухэтапной обработкой
сигналов
В аппаратуре СРНС используются псевдодальномерный метод
определения координат потребителя и псевдо радиально-скоростнои метод определения
его вектора скорости. Псевдо дальности и псевдо скорости соответствуют
радионавигационные параметры сигнала — псевдо задержка (ПЗ) т и псевдо до-
плеровское смещение частоты /д (ПДСЧ). Поэтому для реализации выбранных
методов навигационных определений необходимо измерять указанные
параметры сигнала. Таким образом, на базе общих принципов радионавигационных
определений постулируется следующая процедура:
измерение псевдо задержек г, и псевдо доплеровских смещений частот
/д; для сигналов четырех НС / = 1,4 (как минимум);
по измеренным значениям fit /д/, / = 1,4 и известным характеристикам
движения НС {x^y^z^ = \t, {Vxi,Vyi,Vzi\ = V/9 / = 1,4 расчетным путем
вычисляются координаты потребителя {.x,>\z} = x и составляющие вектора скорости
[vx,vy,vz} = \.
Реализация данного положения в приемнике сигналов СРНС приводит к
двухэтапной обработке:
на первом этапе измеряют псевдо задержки, псевдо доплеровские
смещения частот принятых сигналов и извлекается навигационная информация
(передаваемая в радиосигнале) о характеристиках движения (значениях
на втором этапе, используя результаты измерений первого этапа
обработки, вычисляют координаты и составляющие вектора скорости потребителя.
Функциональная схема приемника сигналов СРНС с двухэтапной
обработкой приведена на рис. 6.7.
Сигналы, излучаемые находящимися в зоне видимости НС, принимаются
антенной и поступают на вход высокочастотного (ВЧ) приемника. Таким
образом, на входе ВЧ-приемника имеем
п
MBx(0 = Z5'(f'f"A/) + "(0' (6-28)
;=1
где
136
Методы и алгоритмы обработки сигналов и извлечения информации
V
Антенна
Блок первичной
обработки
«к (О
ВЧ-приемник
ы
Блок слежения
за параметрами
сигнала
I
4)
»
НС
Блок
вторичной
обработки
ih)
vfc)
Блок поиска
сигнала
i j
Рис. 6.7. Функциональная схема приемника с двухэтапной обработкой сигналов
(
= Aihm(t-fi)hHCi(t-fi)cos
u)0it + 27rjfai(v)dv + (p0i
о )
V
— принимаемый от / -го НС сигнал с амплитудой А, несущей частотой щ,
случайной начальной фазой p0i, псевдо задержкой г; и псевдо доплеровским
смещением частоты /д/; n{t) — внутренний БГШ приемника с односторонней
спектральной плотностью N0.
Основные требования к ВЧ-приемнику заключаются в обеспечении
линейности преобразования сигналов в заданном динамическом диапазоне и
фильтрации непреднамеренных помех таких, например, как сигналы других систем,
работающих в близких диапазонах (например, систем мобильной связи,
радиоастрономии, отдельных гармоник телевизионных каналов вещания и т.д.),
индустриальные помехи и др. Существует большое разнообразие различных
вариантов построения ВЧ-приемников.
Так как в СРНС ГЛОНАСС используется частотное разделение сигналов,
а, следовательно, сигнал i -го НС имеет свою несущую частоту co0i, то в ВЧ-
приемнике можно организовать многоканальную обработку (ВЧ-фильтрацию)
входного сигнала (6.28) с целью выделения сигнала каждого НС для
последующей оценки его параметров. Схема такого ВЧ-приемника приведена на рис. 6.8,
где обозначено: МШУ — малошумящий усилитель с коэффициентом шума
&ш = 2,5...3; ПФ1 — полосовой фильтр с шириной полосы пропускания A/j =
50...60 МГц; СМ1 — первый смеситель, переносящий сигналы на
промежуточную частоту примерно 160 МГц; ПФ2 — полосовой фильтр с шириной
полосы пропускания A/j= 15...20 МГц; СМ2 — первый смеситель, переносящий
137
Глава 6
сигналы на промежуточную частоту порядка 4 МГц; КПФ/ — канальные
полосовые фильтры с шириной полосы пропускания Af2 « 1,2 МГц; АЦШ —
канальные аналого-цифровые преобразователи с шагом дискретизации
Td = tj -1 :_x, типичное значение которого составляет около 0,25-10 с.
ПФ2
СМ2
—^
КПФ1
КПФ2
•
КПФл
АЦП1
АЦП2
У1
Уг
^
•
АЦПя
•
У„
Рис. 6.8. Схема ВЧ-приемника с многоканальной фильтрацией сигналов
На выходе ВЧ-приемника формируется вектор
цифровых сигналов, состоящий из сигналов каждого из п видимых НС, где
rijhl = l9n — независимые дискретные БГШ с нулевыми математическими
ожиданиями и равными дисперсиями а^ = NQ/(2Td).
В данной главе не будут рассматриваться вопросы квантования сигналов
по уровню, поэтому в дальнейшем под Уи7) будем понимать сигналы, дискре-
тизированные только по времени.
Сигналы y[tj) подаются в блок первичной обработки, в котором
проводится поиск по задержке и частоте. После того, как принимается решение об
обнаружении сигнала в некоторой ячейке поиска, включаются системы
слежения за указанными параметрами. На выходах следящих систем формируются
*Ы = |*И'*) *Л*к) - K(h)
оценки векторов
Uh)=\lM) lAh) ...L(tk)
и
(псевдозадержек и псевдодоплеровских
частот) в моменты времени tk такие, что tk -tk_x =T»Td. В этом же блоке
138
Методы и алгоритмы обработки сигналов и извлечения информации
выделяется навигационная информация, содержащаяся в кодовой
последовательности GHCi (t - fi), т.е. формируются оценки 9НС.
Сформированные на выходе блока первичной обработки оценки т(^),
fa[tk) и внс (ж,-,V,-,/ = \,п\ подаются в блок вторичной обработки, где на их
основе вычисляются оценки координат х(^) и вектора скорости V(^)
потребителя, а также точное значение текущего времени.
Отметим, что современные приемники строятся не по схеме рис. 6.8, а по
схеме, приведенной на рис. 6.9.
«вх(')
МШУ
ПФ1
СМ1
ПФ2
СМ2
ПФЗ
"W
АЦП
Я4)
►
Рис. 6.9. Схема ВЧ-приемника с одноканальной фильтрацией сигналов
В этой схеме совокупность всех навигационных сигналов фильтруется в
полосовом фильтре ПФЗ с полосой пропускания - 12 МГц (что соответствует
полосе частот сигналов СРНС ГЛОНАСС в диапазоне частот Ы) и
подвергается аналого-цифровому преобразованию, а частотное разделение сигналов
осуществляется многоканальном корреляторе (см. п. 13.3).
63.2. Формирование оценок информационных процессов
на основе следящих систем
Вследствие движения потребителя и НС псевдо задержка fit Л- =fy и
ПДСЧ j^f Л = / . изменяются во времени, поэтому для формирования
соответствующих оценок целесообразно использовать теорию оптимальной
фильтрации. Синтез оптимальных приемников СРНС на основе теории оптимальной
фильтрации требует серьезной специальной подготовки исследователя и
достаточно сложен в понимании. Поэтому в настоящей книге, ориентированной на
широкий круг читателей, изложение будет вестись в несколько упрощенном
виде, базирующимся на основных результатах теории оптимальной
фильтрации, т.е. опускаем строгий вывод этих результатов. Читатель, интересующийся
подробным выводом тех или иных результатов, может обратиться к
соответствующей специальной литературе [5.1, 5.2].
Теория оптимальной фильтрации основана на статистическом описании
наблюдаемых у у и информативных процессов, а ее основной задачей является
нахождение апостериорной плотности вероятности plkjAY£ ) информативных
139
Глава 6
процессов при заданном априорном описании динамики изменения и
проведенных наблюдениях Y/ = {у15у2?--^Уу} •
Задача получения оценок информативных процессов, переносимых
радиосигналом, относится к классу задач нелинейной фильтрации, решение которой
может быть получено в том или ином приближении. Наиболее часто
используется гауссовское приближение АПВ /?lkJY/l. В этом случае оптимальная
(квазиоптимальная) оценка процесса А, • формируется следящей системой,
обобщенная схема которой приведена на рис. 6.10.
у(<
,-.»•/) „
■ ■ - -^
ДИСКрИмипши^
i
i
/
ид*(8**) .
«onlO'M
Фильтр
Генератор
опорного сигнала
h
h
Рис. 6.10. Обобщенная схема следящей системы
Отсчеты yUjt'kA наблюдаемого процесса в моменты времени tj
(следующие с шагом дискретизации Td) поступают на вход дискриминатора, на
второй вход которого поступает опорный сигнал и0П(/-Д ■], сформированный
для экстраполированного на момент времени t- значения к- оцениваемого
параметра. Дискриминатор — это устройство, сигнал на выходе которого
идк(3'кк) пропорционален рассогласованию 8Хк-Хк-;кк между значениями
оцениваемого параметра X,, соответствующими входному и опорному
сигналам. В теории оптимальной фильтрации [5.1, 5.2] (и в теории оценки
постоянных параметров [6.1, 6.2]) при приеме сигнала на фоне гауссовского белого
шума процесс на выходе дискриминатора определяется соотношением
/аь/(у1мд)У|
ид*(**) =
дк
А, — Ki
(6.30)
где Yj ={у*_1,1'У*-1,2>"-'У*-1,л/} — отрезок реализации наблюдений на
интервале времени [^к-\,\^к-\,м^» где для инДекса времени использована двойная
нумерация tk0=kMTd=kT, T = MTd, tkJ=tkfi+lTd=kT + lTd, tkM=tk+l0;
140
Методы и алгоритмы обработки сигналов и извлечения информации
/(YjM,X, j — функция от наблюдаемого отрезка реализации Y^1 и
оцениваемого процесса X.
В (6.30) производная от скаляра по вектору понимается как вектор-строка,
т.е. df(x)/dx = \df(x)/dxl df(x)/dx2... д/(х)/дхп\. Более полно формулы
дифференцирования по векторному аргументу можно найти в [6.3].
Из (6.30) следует, что в дискриминаторе проводится накопление
наблюдений на интервале Т = MTd, длительность которого должна быть много меньше
времени корреляции процесса >.(/) (который при этом можно полагать
неизменным на данном интервале, т.е. X, = const), но много больше времени
корреляции аддитивного шума (что делает операцию равновесного накопления
близкой к оптимальной).
Вид функции /(Y^4 Д] зависит от принимаемой при синтезе
статистической модели сигнально-помеховой обстановки, набора оцениваемых
параметров и ряда других факторов и будет конкретизирован в п. 6.3.3 для различных
типов задач. Здесь же отметим, что, если все параметры сигнала, кроме
оцениваемых, известны, то /(У/^Д] является функцией правдоподобия
наблюдаемого отрезка реализации piY^4 \k\9 которая определяется выражением
p(Y/>)~exp |у(^_,^
(6.31)
где Dn' — матрица дисперсий аддитивных шумов наблюдений.
Напомним, что функцией правдоподобия называется условная плотность
вероятности наблюдаемой реализации YXM при заданных значениях
оцениваемых параметров X, рассматриваемая как функция этих параметров [5.1].
Так как в приемниках СРНС оцениваемые параметры сигнала (псевдо
задержка т , псевдо доплеровское смещение частоты /д, навигационное
сообщение i9HC) являются неэнергетическими, функцию правдоподобия можно
представить в виде
(м \
р(\1м\х) = сехр \^(tk_u,xJa,Kc)^ny{tk-ii)
V/=i
(6.32)
так как второе слагаемое под знаком экспоненты в (6.31) представляет собой
энергию сигнала, и оно может быть отнесено к константе с .
141
Глава 6
Структура фильтра обобщенной следящей системы рис. 6.9 определяется
динамикой изменения информативного процесса Хк. Поэтому при синтезе
оптимальной следящей системы необходимо задать априорную модель изменения
данного процесса, для чего используют его описание в пространстве
состояний. Введем п -мерный вектор \к, связанный с процессом Хк соотношением
Хк = сх^ , где с — матрица соответствующего размера. Зададим линейную
модель изменения вектора состояния:
x^Fx^+G^, (6.33)
где %к_х — дискретный БГШ с нулевым математическим ожиданием и
матрицей дисперсий D^.
С учетом (6.33) структуру фильтра в контуре следящей системы рис. 6.9
можно описать соотношениями
^к = СХк ' ^к = СХк '
*к = Fi*-i + к*ид* {h). Ч = Fi*_i, (6-34)
где Хк — текущая (фильтрационная) оценка информативного процесса; Хк —
экстраполированная (с момента времени tk_l0 на момент времени tkfi) оценка
того же процесса; Кк — матрица весовых коэффициентов фильтра (в общем
случае меняющихся во времени).
Генератор опорного сигнала в схеме рис. 6.8 формирует сигнал иоп (*уЛу) >
необходимый для работы дискриминатора. Вид опорного сигнала определяется
используемым типом дискриминатора.
63.3. Когерентная и некогерентная обработка сигналов в приемнике
В теории приема и обработки сигналов различают когерентную и
некогерентную обработку. При когерентной обработке сигналов оценивается фаза
принимаемого сигнала, а полученная оценка используется при формировании
опорных сигналов дискриминаторов. При некогерентной обработке фаза
сигнала не оценивается, а оценивается только несущая частота (что эквивалентно
оцениванию доплеровского смещения частоты). Навигационный приемник с
когерентной обработкой сигналов позволяет получить более высокую точность
НВО, чем некогерентный приемник, а некогерентный приемник имеет
большую помехоустойчивость, чем когерентный приемник [6.4].
Оценки псевдо дальностей и псевдо скоростей в приемнике сигналов
СРНС могут быть получены как при когерентной, так и при некогерентной
обработке сигналов. Выделение же навигационного сообщения, закодированного
142
Методы и алгоритмы обработки сигналов и извлечения информации
в фазе сигнала, возможно лишь в когерентном режиме, в котором
обеспечивается необходимый уровень синхронизации по фазе сигнала. После выделения
навигационного сообщения из принятого сигнала, оно хранится в
долговременной памяти приемника. Так как данная информация обновляется
достаточно редко (1 раз в 15 мин), то после ее выделения можно использовать
некогерентный режим работы приемника.
При когерентном и некогерентном режимах работы приемника
изменяются структуры дискриминаторов следящих систем, поэтому необходимо
рассматривать раздельно синтез приемников с когерентной и некогерентной
обработкой сигналов.
6.3.4. Синтез дискриминаторов следящих систем
Так как приемник СРНС содержит идентичные каналы слежения за
сигналами всех видимых НС, в дальнейшем будем рассматривать синтез следящих
систем для одного из накалов, опуская при этом для простоты индекс /
принадлежности к соответствующему каналу. При этом наблюдаемый процесс
будет скалярным, т.е. в (6.32) необходимо полагать >>(/уД Л. Кроме того, для
простоты терминологии и обозначений, вместо псевдозадержки т (и
соответствующей ей псевдодальности) и псевдодоплеровского смещения частоты /д
будем говорить просто о задержке г и доплеровском смещении частоты /д.
6.3.4.1. Синтез дискриминаторов когерентных приемников
Поставим задачу синтеза приемника, в котором автономно оценивается
задержка х огибающей и текущая фаза ср сигнала. При таком подходе
переменные г и ср полагаются независимыми, поэтому можно ввести вектор
информативных параметров X = | т ср |т.
При синтезе дискриминатора в соответствии с определением (6.30)
необходимо выбрать временной интервал \tk_xxjk_XM\^ на котором вектор
оцениваемых параметров X можно считать постоянным. Положим, что такой
интервал длительностью Т выбран. Тогда представим сигнальную функцию,
входящую в наблюдения на данном временном интервале, в виде
s(h-ij) = Ah&(h-ij-Tk-u)^ +<Pk-u)> (6-35)
где сои — промежуточная частота сигнала на выходе ВЧ-приемника (рис. 6.7).
Отметим, что в (6.35) информативные параметры тк_хх, <рк_х^х заданы на
момент времени tk_xx и предполагаются постоянными на интервале
143
Глава 6
[>£_i,1'^-i,m] • При переходе от момента времени tk_lM =tk к моменту tkl
происходит изменение данных параметров в соответствии с моделью марковского
процесса (6.33), так что в момент времени tkl будет иметь место новое
значение параметров, которое не меняется в течение следующего интервала
['*дЛ,м] ИТ-Д-
При синтезе дискриминатора параметры А,о)п полагаем известными,
параметры т,(р — оцениваемыми, а символ навигационного сообщения Знс —
случайной величиной, которая может принимать значения 0 или 1 с равными
априорными вероятностями рар (.9НС = 1) = = рар (i9HC = 0) = 1/2 . Отметим, что на
интервале наблюдения |Д_иЛ-1,м] случайная величина Зис полагается
неменяющейся.
Наличие случайного параметра при синтезе дискриминатора следящей
системы предполагает использование в качестве функции /(YXM,Х\
усредненной по этому случайному параметру функции правдоподобия (6.32), т.е.
f{YxM ^)-pap(&HC=\)p(YlM\X,^c=l) + Pap(^c= 0)p(YlM\X,&HC=0) =
( Г м
= с
ехр
—^у{*к-и)*(*к-и>т><РЛс =0) +
\ап 1=1
-1
М
+ еХР —£>'('*-и)5('*-и'Г'^,9нс =0)
'л /=1
(6.36)
При записи (6.36) учтено, что с изменением значения символа
навигационного сообщения «9НС изменяется знак сигнальной функции (6.35).
Сумму двух экспонент в (6.36) можно выразить через функцию
гиперболического косинуса, поэтому
. м \
/(r/'AJ^ch — ^(^И^.г.Мнс =0)
'п 1=1
(6.37)
Подставляя (6.37) в (6.30) и выполняя дифференцирование по X , получаем
м
ид*{h) = th\ —^у(*к-ц)ЬЛк{h-u ~ fk)cos(u)n^_M + фк)
\an i=\
м
jf>('*-i./)
'п /=1
&('*-l,/>f*>&Ac=°)
V
дк
(6.38)
144
Методы и алгоритмы обработки сигналов и извлечения информации
В (6.38) формально использованы экстраполированные оценки fk, фк, в
которых индекс «к» обозначает к-й интервал наблюдения. Поэтому следует
конкретизировать в соответствии с каким алгоритмом следует формировать эти
экстраполированные оценки. Исходя из принятого описания (6.35), в качестве
искомых экстраполированных оценок следует использовать fk_xl, ^-i,i •
Действительно, в момент времени tk_x обрабатывалась выборка наблюдений
Ч-г\ ' содержащая информацию о значениях информативных параметров
r*-2,i' %-2,i • В результате обработки данной выборки в следящей системе
формируются оптимальные оценки тк_21, фк-2\ ■ При переходе от момента
времени tk_2M = tk_x к моменту tk_xx происходит изменение информативных
параметров, которые становятся равными тк_х,, <рк_х х, и выборка наблюдений
Yk~x\M содержит именно эти значения информативных параметров. Так как в
системе сформированы лишь оценки тк_2Х, фк_2Х, в опорном сигнале для
корреляторов на интервале времени [^-i,1'^-i,m] можно использовать либо эти
оценки, либо экстраполированные на момент времени tk_xx оценки, т.е. тк_хх,
фк_хх . Последний вариант более предпочтителен, так как он частично
«отрабатывает» изменение информативных параметров между моментами времени
tk_i и tk_x j, что и вытекает из теории оптимального синтеза. Поэтому в
приводимых далее алгоритмах под тк, фк, будем понимать экстраполированные
оценки тк_и, фк_хх.
Формула (6.38) описывает векторный дискриминатор, включающий
фазовый дискриминатор (ФД) и дискриминатор задержки огибающей сигнала
(ДЗО). Рассмотрим данные дискриминаторы подробнее.
Фазовый дискриминатор
Фазовый дискриминатор соответствует второй компоненте в (6.38) и
описывается выражением
( А М ^
\а" 1=1
1 ^ / М*к-Ц,Тк,ФкЛс=0)
яЪу[к-и)—*—
145
Глава 6
. м \
= -th| —^y(tk-ij) К*{1к-и -4)cos(o)ntk_ul +фк)
ап 1=1
А м
*—^у(*к-и) лда('*-и "f*)sinK'*-i,/ +Фк)-
ап 1=1
X
(6.39)
Схема фазового дискриминатора, определяемого формулой (6.39),
приведена на рис. 6.11.
Фазовый дискриминатор формируется на базе синфазного и квадратурного
корреляторов, сигналы на выходах которых определяются соотношениями
А м
'п 1=\
М
Синфазный коррелятор
Ак-и)
X
X
h
м
X
/=1
th(.)
Квадратурный коррелятор
х
X
^дк ('*-!,/ _ Ч )
м Qk
; 1 '
х
МДф('*)
sin(fV*-u+$;fc)
(6.40)
Рис. 6.11. Схема фазового дискриминатора
В схеме рис. 6.10 сигналы /гдк (tk_u -тк),sin[a>ntk_xtl + фк), cos(a>ntk_xl + фк)
подаются с генераторов опорных сигналов: генератора дальномерного кода и
перестраиваемого генератора гармонического колебания.
Функция th(x), входящая в (6.39), приведена на рис. 6.12.
Из рисунка следует, что при малых значениях аргумента (|х|<0,5)
th(x)« х, и ФД описывается соотношением
"дЛ'*) = -Ш- (6.41)
При |дг| > 2 имеем th(x)« sign(x), а для ФД справедливо представление
uaip{tk) = -Qksign(lk). (6.42)
146
Методы и алгоритмы обработки сигналов и извлечения информации
Рис. 6.12. Функция гиперболического тангенса
Дискриминатор задержки огибающей сигнала
Данный дискриминатор соответствует первой компоненте в (6.38) и
описывается выражением
( А М
А
\
ИдгЫ = Н~ХИ'*Ч/)М
\ап Ы
М
хЗ-ЕЯ'*-и)
дЬм{*к-\,1-*к)
'п /=1
дт
cos(o)ntk_u+pk).
(6.43)
Дифференцирование /гдк(**_!,/ -?к) п0 задержке часто заменяют
вычислением конечной разности. Введем расстройку Аг и запишем
^дк[h-u -Ч) К,(tk_u -(fk + AT/2))-haK(tk_ul-(fk-AT/2))
~ ——— .
дт At
С учетом данного представления схема ДЗО может быть представлена в
виде, приведенном на рис. 6.13.
Компоненты
А м
*Е,к = —2М'*-1,/)М'*-и "(f* +Ar/2))cos(<Vb.u +фк)
и
'п /=1
М
h,k =—^У(*к-и)}1А*к-и ~(fk -Ьт/2))со&(а#к_ц+фк)
Gn 1=1
(6.44)
147
Глава 6
У
(?*-!,/)
ЬЯк(*к-и-*к)
X
cos((antk_u +ц>к)
X
X
L
,/,(*)
м
I
/=1
1Е,к
. А
М
I
/=1
'/,,*
X
1/Дт
иАгк)
Лдк(^-1,/-(^-ЛГ/2))
Рис. 6.13. Схема дискриминатора задержки огибающей сигнала
соответствуют опережающему (early) кДК^к_{1-(fk + Ат/2)) и
запаздывающему (late) hm(tk_xl -(fk -Дг/2)) опорным сигналам соответственно.
Дискриминатор задержки огибающей включает в себя три ветви обработки
входного сигнала, в которых используются три типа корреляторов. В первой
ветви на основе синфазного коррелятора формируется 1к (синфазная
компонента), идентичная той, что использовалась в ФД (рис. 6.9). В двух других
ветвях используются аналогичные синфазные корреляторы, но с опережающим и
запаздывающим опорными сигналами дальномерного кода. На выходах данных
корреляторов имеем опережающую 1Ек и запаздывающую ILk синфазные
компоненты.
Таким образом, основой формирования дискриминаторов когерентного
приемника являются корреляторы, использующие те или иные опорные
сигналы.
В схемах дискриминаторов рис. 6.10, 6.12 используются
экстраполированные оценки тк , фк информативных параметров, выражения для которых могут
быть получены, например, из соотношений (6.34), описывающих
сглаживающий фильтр следящей системы. Более подробно этот вопрос обсужден в
п. 6.3.5.
Как и для ФД, функция th(x), входящая в (6.43), может быть
аппроксимирована более простыми функциями при малых и больших значениях аргумента.
При I/J < 0,5 ДЗО может быть описана соотношением
uJXT{tk) = Ik(lEk-ILk)/Ar,
(6.45)
148
Методы и алгоритмы обработки сигналов и извлечения информации
а при \lk | > 2 — выражением
u*T{tk) = (h,k-h,k)^{Ik)/*T. (6.46)
Комбинированный фазовый и частотный дискриминаторы
При определении дискриминатора в (6.30) полагалось, что на интервале
накопления Т информативные параметры сигнала к не меняются. Для
дискриминатора задержки огибающей данное требование достаточно хорошо
выполняется для типичных значений времен накопления Г« 1...5 мс. Так, при
взаимной скорости сближения потребителя и НС Vc6 = 500 м изменение
дальности за 1 мс будет составлять всего 0,5 м. Иная ситуация имеет место при
построении фазового дискриминатора. Максимальное значение доплеровского
смещения частоты в СРНС полагается равным |/д|=5 кГц. В этом случае
изменение фазы сигнала за 1 мс составляет Юя", т.е. весьма существенно. Поэтому
для работы с требуемыми временами накопления (1 мс и более) необходимо
использовать несколько модифицированную методику синтеза
дискриминаторов. Один из возможных подходов заключается в следующем.
Положим, что в общем представлении сигнальной функции (6.29) на
интервале времени Т = [tk_xl,tk_lM] доплеровское смещение частоты постоянно и
равно /д к_х. Тогда можно записать
*('*Ч/) = ^Лда(^ +(Рк-и +^.k^{l-\)Td),
(6.47)
ГДе ^д;Ы,1=И;И1-
В (6.47) фаза (рк_хх не меняется на интервале длительностью Т , а
допущение о неизменности доплеровского смещения частоты связано с
пренебрежением второй производной по времени от задержки сигнала, пропорциональной
ускорению потребителя относительно НС. Полагая данное ускорение 50 м/с2,
рассчитаем погрешность аппроксимации фазы:
8ср = ттаТ2/л = 0,785 ■ 10"3рад (0,045 град).
Следовательно, допущение о постоянстве доплеровского смещения
частоты на интервале Т правомерно.
Включим (DjykA 1 в число информативных параметров, т.е. положим
I it
Х = \т <р о)Д . Тогда в соответствии с определением (6.30), кроме фазового
дискриминатора и дискриминатора огибающей сигнала, необходимо
рассматривать частотный дискриминатор, для которого, используя (6.38), можно записать
149
Глава 6
&{*к-ч>ч>Фк>в>а*>&ж =0) _
'п 1=1
М
хттХИ'*-1.')-
'п 1=1
дсо„
= -th
С Л м
А
-тТ^Л1к-и)кА^-и-^)С05{^Л-и + Фк+^а,к(1-1)^)
М
^и /=1
(6.48)
Здесь, как и в предыдущих разделах, под экстраполированными на к-й
такт оценками тк , эд., юАк следует понимать значения fk_ltl, фк_хх, u^-i.i .
Существенным отличием (6.48) от выражений (6.39), (6.40) для ФД и
(6.43), (6.44) для ДЗО является то, что фаза сигнала перестраиваемого опорного
генератора гармонического колебания меняется линейно на интервале
накопления, т.е. экстраполируется по линейному закону на каждый текущий момент
времени. Это обстоятельство и позволяет более корректно проводить
накопление в дискриминаторе на более длительных интервалах времени.
Схема частотного дискриминатора, описываемого соотношением (6.48),
приведена на рис. 6.14.
С08(а>п/*_и+^+<5дЛ(/-1)7^)
У('к-и)
X
X
I
/=1
th(*)
Н X
X
(/-Ifo
X
м
I
Ок
X
ияА'к)
Лдк(*к-и -?к)\ sin(<V*-U +Фк+^аА1-1)7^)
Рис. 6.14. Схема частотного дискриминатора когерентного приемника
Заметим, что при использовании представления сигнала (6.47) и вектора
информативных параметров X = I г ср сол\ дискриминаторы фазы и задержки
сигнала описываются соотношениями (6.39), (6.40) и (6.43), (6.44)
соответственно, в которых для гармонических функций вместо фк необходимо исполь-
150
Методы и алгоритмы обработки сигналов и извлечения информации
зовать Фк-ii + £>д;Ы1 (/-1)7^ . Аналогичные изменения необходимо сделать и в
схемах рис. 6.9, 6.10.
6.3.4.2. Синтез дискриминаторов некогерентных приемников
Для синтеза дискриминаторов следящих систем некогерентных
приемников полагают, что информативными параметрами являются задержка г и доп-
леровское смещение частоты /д, которые на интервале [f*_i,i>'*-i,A/]
полагаются постоянными. Тогда сигнальную функцию можно представить в виде
. s{tk_u) = Ahm [tk_u - тк_1Л )cos(co0tk_u + a>Kk_hl (/ - \)Td + л9т + <рк_и), (6.49)
где (рк_хх — фаза сигнала, обусловленная взаимным движением НС и
потребителя к моменту времени tk_u .
Как и выше полагаем, что символ служебного сообщения 19нс на
рассматриваемом интервале наблюдения принимает значения 0 или 1 с равными
вероятностями. Введем допущение о том, что начальная фаза <рк_ц для каждого
тактового интервала является случайной величиной, распределенной
равномерно на интервале [0,2;г]. Тогда можно ввести случайную фазу
фкА = 7rSHC + Фк-ц, которая для интервала накопления также является
случайной величиной, распределенной равномерно на интервале [0,2л-]. С учетом
этого (6.49) можно представить в виде
s{h-u) = АК* [h-u "тк-\л)c°s(*V*-u + ®д;*-1,1 il-\)Td+ Фк-\) • (6-5°)
Информативными параметрами в (6.50) являются задержка г и доплеров-
ское смещение частоты соА. Случайная фаза фк_х является неинформативным
параметром, поэтому используемая для определения дискриминаторов
некогерентного приемника функция/(У^Я) в (6.30) определяется в результате
усреднения функции правдоподобия (6.32) по случайной фазе фк_х. Выполнив
такое усреднение, получаем
/(у]м\л) = сх10(х(Т,тк_11,^к_и))^ (6.51)
где сх — нормировочная константа; Х = \ т соа ; 10(х) — функция Бесселя
нулевого порядка от мнимого аргумента;
Х(Ч-1Л >*>д;*-1,1 ) = у[^ (г*-1,1 >®д;*-1,1 ) + Q2 [Tk-U ><»Кк-\,\ ) i (6-52)
151
Глава 6
м
(6.53)
Q(Tk-i,i >*V-u) = 4Zj'(/h/ ) Ада ('*-u ~ r*-u )sinK'*-u + ^;*-u (7 - O7*) •
°"л /=1
(6.54)
Частотный дискриминатор некогерентного приемника
Соотношение для частотного дискриминатора (ЧД) получается
дифференцированием (6.51) по соЛ:
'п 1=1
М
мд«('*) =
/,(х(^ЛЛ))дХ(^А*)
(6.55)
I0(x(rk,cb^)) <Ч
где /i(^) — функция Бесселя первого порядка от мнимого аргумента;
^д,* "* ^кк-и ' г£ "^ г£-1,1
На рис. 6.15 приведена зависимость отношения /, (х)/10 (х) от аргумента л;.
ЛМЛоМ
1
0.9
0.8
0.7
0.6
0.5J
0.4
0.3
0.2
0.1
I 1 1 '
10
15
20
Рис. 6.15. Зависимость функции Ix (jc)//0(jc) от аргумента х
При х < 1 (малое значение отношения сигнал/шум) справедливо
приближенное равенство
Ii(x)/l0(x)*x/29 (6.56)
и (6.55) преобразуется к виду
x{rk^k)dx{fk^k)
uzco Vk ) ~ " =
2 о(о„
152
Методы и алгоритмы обработки сигналов и извлечения информации
/(г*»а,д,*)—^—-+Q(Tk^a,kr
дсо„
да>„
(6.57)
При большом отношении сигнал/шум (jc> 10Справедливо приближенное
равенство
/,(^(r,^))//0(^^))*l. (6-58)
и (6.55) может быть представлено как
дХ(тк,а>а>к)
МД«Ы
дсо„
X(fk>*Ak)
дсо„
дсо„
, (6.59)
где
м
а/(^*)=-^^
'п /=1
М
бсоя °п 1=1
(6.60)
Схема частотного дискриминатора, описываемого соотношениями (6.56),
(6.57), приведена на рис. 6.16.
Кк('к-1,1 ~fk)\ со&(ао1к_и+&Л^(1-1)Та)
i'k-v)
X
X
sin(fi>0/fc-l,/+^,Jfc(/-1)7^)
>п /=1
Зп Ы
б(**Лл)
X
7*
-I'(h^jk)
Q'(h>ti*,k)
X
X
UA<oitk)
Рис. 6.16. Схема частотного дискриминатора некогерентного приемника
153
Глава 6
Дискриминатор следящей системы за задержкой
огибающей сигнала некогерентного приемника
Соотношение, описывающее дискриминатор задержки огибающей сигнала
в некогерентном приемнике, получается дифференцированием (6.51) по г и
имеет вид
цдг('*)=, (v(~ ~ \\ Тт * ( }
При большом отношении сигнал/шум с учетом (6.58) получаем соотношение
, ч дХ(тк,б)„Л
»,гЫ- дт ■ (662>
Как и в когерентном приемнике, вычисление производной в (6.62) можно
заменить вычислением конечной разности
,, ч х(^к,тк+Ат/2)-Х(^к,тк-Ат/2)
"А*к)=— -г > (6-63)
где Х(а>Лук,тк ±Ar/2) = yjl2(^k,fk ±Ar/2) + Q2(d>^kJk ±Дг/2),
l(cba>k,fk ±Ат/2) =
А М
= "^Х>;(^-1'/)/гДк(^-М-(^±Аг/2))СО8(<У0^-1./+Йд,Л/-1)Гс/)'
Gn /=1
Q(a>^k,fk±Ar/2) =
А М
ап 1=1
Схема дискриминатора задержки огибающей сигнала, описываемая
выражениями (6.62)—(6.64), приведена на рис. 6.17.
При малом отношении сигнал/шум справедливо приближение (6.56), и
выражение для оптимального дискриминатора может быть представлено в виде
„ /. 1 ,,1в*2(МЬ) -У2КдЛ+Аг/2)-Х2(шд,,Л-Аг/2)
Схема такого дискриминатора приведена на рис. 6.18 и отличается от
схемы рис. 6.17 лишь видом нелинейной функции выходных блоков.
154
Методы и алгоритмы обработки сигналов и извлечения информации
sm(a0tk_u+ZdJc(l-\)rd)
>Л
kk-ij)
X
X
X
X
cos(a)o/t_u + adJc {l-\)Td)
hifk)
X
X
А М
CT* /=1
A M
Qsifk)
1
yff+6
2 At
m
СТл /=l
*M
M
°IU
SM
Ш+Ш
2Ar
IT
лДк(^-ц-(^-Аг/2))
*«Е('*-и-Й+Ат/2))
*—|"дтЫ
Рис. 6.17. Схема дискриминатора задержки огибающей сигнала
некогерентного приемника при большом отношении сигнал/шум
sm(fflo'*-i,/+ s<a ('- * W
У
(?*-!,/)
X
X
i
cos(co0/jt_u +^d,k(l~])rd)
X
X
X
X
A M
CTn /=1
hifk)
A M
QE{tk)
1
Ц +§l
2Дт
м
*n Ы\
h(tk)
M
°lis
QM
1
Il+Ql
2Лх
T~
*—I мдтЫ
A -
Лдк(/*-ц-(^+Аг/2))
Рис. 6.18. Схема дискриминатора задержки огибающей сигнала
некогерентного приемника при малом отношении сигнал/шум
Глава 6
6.3.4.3. Синтез дискриминаторов с оптимальным накоплением
Классическое определение дискриминаторов в соответствии с (6.30) тесно
связано с теорией оценивания постоянных параметров сигнала [5.1, 6.2], что и
обусловливает требование постоянства информативных (оцениваемых)
параметров на интервале накопления Т. Как отмечалось в п. 6.3.4.1, в ряде задач
это приводит к ограничению длительности интервала накопления. В то же
время, в аппаратуре спутниковой навигации представляют интерес достаточно
большие времена накопления (до величины длительности символа
навигационного сообщения — 20 мс), что в рамках определения (6.30) не может быть
сделано без потери качественных характеристик слежения. Выход из данной
ситуации дает теория комбинированной калмановско-винеровской фильтрации
[5.1, 6.5] в интерпретации для нелинейных задач фильтрации. Данная теория
позволяет синтезировать квазиоптимальные дискриминаторы, в которых
допускается произвольное изменение информативных параметров на интервале
накопления Т .
Строгий вывод соотношений для дискриминаторов с оптимальным
накоплением достаточно сложен и громоздок, потому здесь не приводится (его
можно найти в указанной выше литературе). Поясним суть получающихся
результатов на примере синтеза фазового дискриминатора для когерентного
преемника. В этом случае функция f\YxM,1Л, входящая в определение
дискриминатора (6.30), задается выражением
( 1 м Л
где весовая функция ^{tk-ihh-i) зависит от динамических свойств следящей
системы (типа сглаживающего фильтра, полосы пропускания и др.); она равна
1 при / = М и убывает при уменьшении /. Смысл данной функции
заключается в постепенном «забывании» более давних наблюдений, т.е. их
использовании с меньшим весом.
Фазовый дискриминатор при данном подходе описывается выражением
( А м ^
\а" 1=1
А М
Прежде всего, следует отметить, что, поскольку при синтезе не
накладывается требование постоянства информативных параметров (задержки г и фазы
<р) на интервале накопления, они полагаются меняющимися, например, в соот-
156
Методы и алгоритмы обработки сигналов и извлечения информации
ветствии с заданным априорным описанием (6.33). При этом в дискриминаторе
(6.61) опорные сигналы в каждый момент времени tk_xl формируются для
экстраполированных на данный момент времени значений задержки fk_xl и фазы
фк_х i, причем закон экстраполяции определяется теми же априорными
уравнениями (6.33). Аналогичная ситуация имела место при синтезе
комбинированного фазового и частотного дискриминатора, приведенного выше.
Если время накопления Т в (6.61) существенно меньше величины,
обратно пропорциональной полосе пропускания следящей системы, то
^{h-u^k-i)" 19 и (6.61) переходит в соотношение (6.37) и следующие из него
формулы (6.39), (6.40) для ФД с той лишь разницей, что в (6.61)
информативные параметры опорного сигнала экстраполируются на каждый текущий
момент времени tk_y , а не на момент tk_xx. Этот факт часто используют при
построении реальных следящих систем.
6.3.5. Выделение навигационного сообщения
Навигационное сообщение Эяс передается в радиосигнале (6.29) путем
модуляции его фазы двоичными символами длительностью 20 мс,
формирование которых синхронизировано с циклами формирования дальномерного кода.
Выделение символов #нс осуществляется при когерентном режиме работы
приемника. После захвата сигнала на сопровождение по дальномерному коду
приемник входит в синхронизм, в том числе по тактам приема символов
навигационного сообщения. После этого символы навигационного сообщения
могут быть выделены в соответствии с алгоритмом
Г N
1, если ^^(^и^Vu0^k(?-Vi^)C0S(^-U +<PP-hv)>0>
L=\ "' (6-66)
0, если ]Г>;(tp_Xv,Лр_1у)/*дк(t-fp_hv)cos(o)0tp_Xv + фр_Ху)<0.
[ v=\
В (6.66) суммирование по индексу v осуществляется на интервале, равном
длительности символа навигационного сообщения Гнс = NTd = 20 мс. Поэтому
моменты времени tp отстоят друг от друга также на 20 мс, т.е. tp - tp_x = Гнс.
Отметим, что в соответствии с (6.66) оценка символов навигационного
сообщения формируется с использованием экстраполированной оценки фазы
фрЛ v, формируемой в схеме слежения за фазой сигнала.
157
Глава 6
6.3.6. Синтез сглаживающих фильтров
В п. 6.3.2 отмечалось, что структура сглаживающего фильтра определяется
моделью изменения информативного процесса, за которым ведется слежение.
В частности, если процесс описывается уравнением (6.33), то оптимальный
сглаживающий фильтр описывается уравнениями (6.34). Однако для получения
действительно оптимального сглаживающего фильтра необходимо определить
не только его структуру, но и задать оптимальные значения коэффициентов
усиления. Определить такие значения можно по следующей упрощенной
методике.
Рассмотрим для простоты следящую систему за одним из параметров
сигнала Л, который отображается в пространстве состояний п -мерным вектором
х, так что Л = сх , где с = |l 0 0 ... 0|т . Дискретная следящая система в этом
случае может быть описана уравнением
\ = СХк > К ~ С*к >
*к = ¥Ч-\ + Кк"*к (h) > Ч = *Vi» (6-67)
где идк(1к) — процесс на выходе дискриминатора.
Представим процесс на выходе дискриминатора в виде
u,k(ik) = u(lkJk) + rjk, (6.68)
где и(Лк9ХА = М[илк(ХА] — среднее значение процесса на выходе
дискриминатора; т]к — флуктуационная составляющая выходного процесса.
Представление (6.68) является статистическим эквивалентом
дискриминатора, в котором зависимость и( Хк 91к), рассматриваемая как функция
аргумента sk = Л - Л, называется дискриминационной характеристикой, а дисперсия
Dn = М[щ ] при £я = О — флуктуационной характеристикой дискриминатора.
Принимая во внимание (6.24) и вводя операторный коэффициент передачи
К(р) фильтра в контуре следящей системы, представим структурную схему
следящей системы в виде, приведенном на рис. 6.19.
I Лаг
ki
u(xk,lk)
I
к(р)
Кг
Рис. 6.19. Структурная схема следящей системы
158
Методы и алгоритмы обработки сигналов и извлечения информации
При большом отношении сигнал/шум на входе следящей системы ошибка
слежения SXk = Ak - Як мала и не выходит за пределы линейного участка
дискриминационной характеристики, которая в этом случае может быть
представлена в виде U(Ak9Xk) = SRsXk, где £д — крутизна дискриминационной
характеристики. Таким образом, при большом отношении сигнал/шум следящую
систему можно линеаризовать и представить в виде, приведенном на рис. 6.20.
I
—►
*д
—►
I
у — —
—►
к(р)
1к
г——►
X
ад
X
У ' '1
Рис. 6.20. Структурная схема линеаризованной Рис. 6.21. Структурная схема
следящей системы эквивалентной следящей системы
В линеаризованной схеме флуктуационный процесс rjk можно
пересчитать на вход линеаризованной схемы, что приводит к эквивалентной схеме
рис. 6.21, в которой для дисперсии эквивалентного шума fjk справедливо
представление D^ -D^ S^.
В схеме рис. 6.20 ук — эквивалентные линейные наблюдения, из которых
последующий линейный фильтр формирует оценку Як информативного
процесса. Следовательно, можно ставить задачу синтеза оптимального линейного
фильтра, который формирует соответствующую оценку с минимальной
дисперсией ошибки. Таким оптимальным фильтром будет фильтр Калмана, в
котором определяется матрица дисперсий ошибок фильтрации и требуемые
оптимальные коэффициенты усиления.
Переход от синтезированной таким образом оптимальной системы
фильтрации (рис. 6.19) к исходной (рис. 6. 17) и определение оптимальной структуры
и параметров сглаживающего фильтра осуществляется выполнением
аналогичных обратных процедур.
Для применения данной методики необходимо располагать
статистическими характеристиками дискриминатора (крутизной и флуктуационной
характеристикой), которые должны быть получены в аналитическом виде.
Проиллюстрируем применение данной методики.
6.3.6.1. Оптимальный фильтр третьего порядка для следящей
системы за фазой сигнала
Зададим априорную модель изменения фазы сигнала уравнениями
159
Глава 6
9к = <Рк-\ + Тс°к-\ > о)к = сок_х + Tvk_x, vt = vt4 + 4^_,, (6.69)
где %9£ — дискретный БГШ с дисперсией D^ .
Рассмотрим ФД вида (6.41), в котором в опорном сигнале будем
использовать линейную экстраполяцию фазы на интервале накопления (данный вопрос
обсуждался в п. 6.3.4.3). Фазу входного сигнала также будем считать
меняющейся линейно на том же интервале. В Приложении к гл. 6 приведен расчет
статистических характеристик ФД данного типа, из которого следуют
следующие соотношения (см. (П6.19), (П6.22)):
U(e9) = 2q2c/noT2p2 (eT )sin(2*„ + ^r)sinc2 (eJ/2),
Dn=*UnJ3P2(er)s™2(*»T/2)
i<p
1 +
2qc/noTp2(eT)smc2(eJ/2)
(6.70)
(6.71)
где ет=т-т, е(р=(р-ф, р{ет) = -^С№^к_и -rk)Gm(tk_u -zk) — корре-
ляционная функция дальномерного кода; qcj =PC/N0 .
Отметим, что дискриминационная характеристика (6.70) оказывается
смещенной, т.е. при е =0 имеем £/(0)*0. Ноль дискриминационной
характеристики формируется в точке е -0 , sa=0.
Определим крутизну дискриминационной характеристики соотношением
Дифференцируя (6.70) по е и полагая ^ = 0 получаем следующее
выражение для крутизны дискриминационной характеристики:
2 гг2 2/ \ • 2
Saf> = ^с/поТ V (ет )sinc2 (eaT/2).
Тогда для дисперсии шума эквивалентных наблюдений получаем
\ =
1
^c/nJP 2(er)smc2(eJl2)
1 +
1
(6.72)
(6.73)
2qclnJp2(eT)smc2(sJl2)
Из (6.73) видно, что ошибки оценки частоты san задержки огибающей ет
сигнала приводят к снижению эквивалентного отношения сигнал/шум:
Яс/п0 = Чс/щР1 К )sinc2 (sJll),
(6.74)
которое и определяет дисперсию шума эквивалентных наблюдений. При этом
(6.73) можно записать в эквивалентном виде:
160
Методы и алгоритмы обработки сигналов и извлечения информации
\ =
\
2Яс1тТ
(
1 +
21с/»0Т
(6.75)
Рассмотрим теперь синтез фильтра Калмана для эквивалентных наблюдений:
Ук=<Рк+*?1>,к>
полагая, что модель изменения фазы задается уравнениями (6.65).
Фильтр Калмана для рассматриваемой задачи определяется уравнениями
Фк=Фк+К\,к(Ук-Фк)> Фк=Фк-1+тб>к-\>
6)к=сЬк+К2к(ук-фк), a>k=a)k_x+Tvk_x,
h = П-i + Къл{Ук ~Фк), (6.76)
Klk = »п,к/\ , К2Л =Dlu/D^ , Ки =DIU/D^ , (6.77)
где Dy, i9j = 1,3 — элементы матрицы Dx дисперсий ошибок фильтрации
вектора х = | ср со v |т, удовлетворяющей уравнениям
D"1, = D"1, + НТН/Д^ , Ьхк = FDX ^F* + GGT£^, (6.78)
где Ь k — матрица дисперсий ошибок экстраполяции вектора х;
F =
1 Т 0
0 1 Т
0 0 1
, G =
0
0
1
, Н = |1 0 0 .
(6.79)
В установившемся режиме коэффициенты усиления и матрица дисперсий
ошибок фильтрации постоянные, т.е. имеем стационарную систему
фильтрации. Аналитическое решение для установившихся значений дисперсий ошибок
фильтрации для рассматриваемой дискретной задачи (6.78) невозможно.
Однако такое решение удается найти для аналогичной задачи фильтрации в
непрерывном времени. Отличие решений для непрерывной и дискретной задач при
Т = 1 мс не превышает 1% , поэтому вполне допустимо рассматривать решение
дисперсионных уравнений для непрерывной задачи. Соответствующие
непрерывные дисперсионные уравнения в установившемся режиме имеют вид
2Оп-°ф1- = 0,О11+Г\г-?^ = 0,О1г
£п£и=о,
Л<р
2D.
23
Чф Чф Лф
= 0,5,
<9ф
Лф
=о,
6-1026
161
Глава 6
где S^ =Д, T.S^ =D^ T — двусторонние спектральные плотности
формирующего шума и шума наблюдения.
Решение данной системы уравнений имеет вил
/ с \1/6 / \1/2
A,=^=2(vi) '^=D»=¥A) • (6-80)
а для коэффициентов усиления непрерывной системы фильтрации получаем
выражения
^н,=2(^/^)1/6=2</33,
Кн2 = 2(^ /^),/3 = 2^з3, *н3 = (^ /^ ) V2 -
(6.81)
Коэффициенты усиления для дискретной системы фильтрации
определяются соотношениями
КЛ = К„,Т, К-у = /Г„->Г , К-, - Л^Г
'Hi
h2j
^h3j
(6.82)
Для расчета численных значений дисперсий ошибок фильтрации
необходимо задать диапазон возможных значений спектральной плотности Sg
формирующего шума в модели изменения фазы сигнала. В [6.6] показано, что при
некоторых допущениях справедливо соотношение S^ = 2ava [рад с" ], где <jv ,
а — среднеквадратическое значение (СКЗ) ускорения и его ширина спектра
для модели ускорения в виде случайного процесса с экспоненциальной
функцией корреляции rv (г) = al ехр(-|г|а).
Учитывая также, что фаза связана с линейной координатой (выраженной в
метрах) коэффициентом пропорциональности 2я/Л «33 м"1, можно рассчитать
значения спектральной плотности S^ , соответствующие заданному средне-
квадратическому значению ускорения ста, выраженному в м/с2. В табл. 6.1
приведено соотношение численных значений Sg и оа для от =0,1 с"
Таблица 6.1. Соответствие между Sz и <7а
-1
СКЗ ускорения <та,
\ м/с2
1
40
1 100
Значения S* , с 5
9
2,18-103 1
3,48 105
2Д8106 |
На рис. 6.22 приведены расчетные значения минимальной СКО фильтра-
162
Методы и алгоритмы обработки сигналов и извлечения информации
ции фазы сигнала в зависимости от СКЗ ускорения для различных значений
qctn при нулевой расстройке по задержке (£Т = 0).
СКОф,град
10о а„,м/с
Рис. 6.22. Зависимости СКО оценки фазы сигнала
Из приведенных зависимостей следует, что при типичных значениях
Яс1п = 30...45 дБГц СКО оценки фазы не превышает 14°, т.е. ошибка слежения
лежит в пределах линейного участка дискриминационной характеристики, что
подтверждает справедливость линеаризации следящей системы.
Ошибки слежения по задержке сигнала, как следует из (6.73), приводят к
возрастанию эквивалентного шума наблюдений. Однако при типичных
значениях ошибки слежения по задержке огибающей сигнала 10... 15 м такое
возрастание несущественно и слабо влияет на ошибку слежения за фазой сигнала.
На рис. 6.23 приведены зависимости СКО оценивания доплеровской
частоты в схеме ССФ.
СКО/9Гц
оя, м/с
100 *'
Рис. 6.23. Зависимости СКО оценки доплеровского смещения частоты
163
Глава 6
Одной из важных характеристик следящих систем является их шумовая
полоса пропускания (в дальнейшем для краткости «полоса пропускания»), которая
для линейной системы в непрерывном времени определяется соотношением
00
д/сс = 1—гт Ik Hi®) I dot, (6.83)
Jcc 2тгКуХ(0))\ уХУ ; I
где К Л)со) — коэффициент передачи системы от входа «у» к оценке «Я»
информативного процесса.
Запишем уравнения линейной непрерывной следящей системы за фазой
сигнала, которые получаются из (6.76) при Т —> 0,
&=&+Кй1(у(1)-Ф)' ™=*+к.Л№-Ф).
4jL = Kmi(y(l)-Q, (6.84)
где коэффициенты усиления Ки1,Кн2,Кн3 определяются в соответствии с (6.81).
Из (6.84) определяем операторный коэффициент передачи
Куф(р)= f»>P2+f2«P + K«> . (6.85)
Подставляя (6.85) в (6.83), рассчитаем полосу пропускания системы
слежения за фазой сигнала:
K„iK„t +Л„т -A„iA„
д^- _ "-h2jvh! ^ jvh2 jvh1j нЗ
или, с учетом (6.75),
А/ссф=7</з=0^33</з3. (6.86)
о
На рис. 6.24 приведены графики оптимальной полосы пропускания ССФ в
зависимости от СКЗ ускорения вдоль линии потребитель—НС для различных
значений qcj при нулевой расстройке по задержке (ег = 0). Из приведенных
зависимостей следует, что для динамичных объектов (оа > 20 м/с2)
оптимальное значение полосы пропускания А/ССФ > 20 Гц.
При заданных полосе пропускания А/ССФ и односторонней спектральной
плотности Np эквивалентного шума наблюдений fj (t) (в непрерывном
времени) можно рассчитать дисперсию флуктуационной ошибки оценки фазы по
формуле [6.7]
164
Методы и алгоритмы обработки сигналов и извлечения информации
4/ссф>гч
ал,м/с
Рис. 6.24. Зависимости полосы пропускания ССФ
Учитывая, что Л^, = £b IT, и используя (6.75), формулу (6.87) можно
записать в виде
1
п _ 4/ссф
Ф-ошр ,
Яс/гщ
(
1 +
24с/поТ
(6.88)
Известно, что следящая система третьего порядка имеет зоны устойчивой
и неустойчивой работы. Поэтому необходимо анализировать ССФ с фильтром
третьего порядка на устойчивость. Так как непрерывная и дискретная системы
слежения могут иметь разные характеристики устойчивости, проанализируем
на устойчивость дискретную систему (6.76). Операторный коэффициент
передачи такой системы
К9Ф-
Kx(z -1)| + K2T(z -1) + КЪГ
(z-\f +(z-l)2(Kl+K2T) + {z-\) (К2Т + К3Т2) + К,Т2
Использование алгебраического критерия устойчивости [6.7] дает
следующую систему неравенств:
К3>0, K3<4KjT2 , К3<2К2/Т, КЪ<КХК21Т,
8-4ATJ -2К2Т + КЪТ2 > 0. (6.89)
При задании коэффициентов усиления в форме (6.81), (6.82) система
уравнений (6.89) приводится к виду Ъ<КХЦЪ <0,842/Г, а учитывая (6.80),
для полосы пропускания ССФ можно записать
0<А/сСФ<0,7/Г. (6.90)
165
Глава 6
Для часто используемого значения Т = 1 мс граничное значение полосы
пропускания равно 700 Гц, что существенно превышает значения, приведенные
на рис. 6.24.
Перейдем от линеаризованной системы (6.76) к нелинейной ССФ. Для
этого представим (6.76) в виде
Фк=Фк+-Г-\^1у<р{Ук-^к)\ Фк=Фк-\+Т<»к-1,
Sa<P
4=&k+-Z2-\_SA<p(yk-Vk)\ й>к=й>к-1+ТП-1>
0,1 ' s
s„
**=**-,+-^|>«Лл-А)]- (6.91)
Далее, учитывая, что Sap(yk -фк) — линеаризованный статистический
эквивалент дискриминатора, заменим его исходным нелинеаризованным
эквивалентом ия(р^к =и(<рк,фк) + т]^к , и вводя обозначения Кх = Кх/8а<р , К2 = K2/Sa<p,
Къ =K3/S — коэффициенты усиления сглаживающего фильтра, представим
(6.91) в виде
Фк=Фк+ К\ид<р,к » Фк = Фк-\ + Т®к-\ »
Щ=а)к+К2ид^, G}k=a)k_x+Tvk_x,
П=П-\+Кзия<р,к> (6-92)
что соответствует представлению (6.34).
Для корректного использования описанной методики необходимо
располагать реальным значением q^^ в текущем сеансе работы и значением
амплитуды А навигационного сигнала. В принципе, величина qc, может быть
измерена в приемнике, что часто и реализуется. Но величина А или (что
эквивалентно) величина мощности Рс навигационного сигнала неизвестны. В то же
время, Рс может меняться в пределах ~ 10... 15 дБ. Неопределенность значения
амплитуды сигнала вынуждает отказаться от использования коэффициента
А/(т1 при формировании квадратурных компонент в (6.40). Это не сказывается
на значении дисперсии эквивалентного шума наблюдений (6.73), но приводит
к тому, что крутизна дискриминационной характеристики становится
пропорциональной квадрату амплитуды навигационного сигнала. Это обстоятельство
может приводить к нарушению устойчивости ССФ. Из (6.91) следует, что
«параметр» Sa(p ъ ССФ определяет два фактора. Во-первых, его расчетное значение,
166
Методы и алгоритмы обработки сигналов и извлечения информации
которое обозначим как 5,д^расч, определяет значение коэффициентов усиления
сглаживающего фильтра К{ = ^/^pac4 , К2 =^2/S^pac4 , Къ = К3/5дррат •
Данное значение выбирается проектировщиком и закладывается в
соответствующее программное обеспечение. Во-вторых, есть истинное значение 5Д^,
которое определяется реальной мощностью принимаемого сигнала, и на
которое проектировщик влиять не может. С учетом данных обстоятельств и
принятых обозначений перепишем (6.91) в виде
Фк=Фк+к\ „ ^ (h-Pk)> Фк=Фк-\+Т<»к-\>
^д^расч
щ=а)к+К2 Д<р {ук~Фк)> 4=4-i+Ttk-i,
^д#>расч
П=П-1+К3-^-{ук-фк). (6.93)
Из (6.93) следует, что в процессе работы в ССФ формируются несколько
отличные (от проектируемых) значения коэффициентов усиления. Введем
параметр x = Sa<p/Sa<pp!lC4 и рассмотрим устойчивость системы (6.91). Выполнив,
как и выше, необходимые вычисления, в дополнение к условию устойчивости
(6.90) получаем условие x = Sa9/Sa(ppaC4 > 1/4. Таким образом, для обеспечения
устойчивости ССФ расчетное значение Sa<ppaC4 должно быть взято меньшим,
чем 45^ min, где Sa(pmin определяется минимальным значением мощности
навигационного сигнала, при котором приемник может работать.
Отметим, что приведенные результаты справедливы лишь для
дискриминатора (6.41). Для других типов дискриминаторов ситуация может быть иной. В
частности, для дискриминатора вида иД<р =arctg(£)//) отсутствует зависимость
крутизны дискриминационной характеристики от мощности сигнала НС, а также
описанная выше проблема.
6.3.6.2. Оптимальный фильтр второго порядка для следящей
системы за задержкой огибающей сигнала
При синтезе сглаживающего фильтра второго порядка априорная модель
изменения задержки сигнала задается уравнениями
Тк = Ч-\ + Tvr,k-\ > Vr,* = Vr,k-\ + &,*-1 > (6-94)
где £r k — дискретный БГШ с дисперсией D^ .
167
Глава 6
В Приложении к гл. 6, например, для дискриминатора задержки сигнала
(6.65) получены следующие выражения для дискриминационной и флуктуаци-
онной характеристики:
U(sr) = 2q2c/noT2smc2{s(0T/2)(p2(sT-Tj2)-p2(sT+Tj2))/AT, (6.95)
Dn =
4<4/3 sine2 (^772)
дг
1 +
<Jc/n0Ts'mC4£coT/2)
(6.96)
где €т=т-т; Аг = гэ — расстройка между «опережающим» и
запаздывающим каналами ДЗО.
Как и в (6.74), введем эквивалентное отношение сигнал/шум:
Яс/п0=<1с/п0йпС2(£(ОТ/2).
Крутизна дискриминационной характеристики получается
дифференцированием (6.95) по ет в точке sx = 0 :
1 дет
= 4q2/noT2sinc2{s(0T/2)/T2 ,
а дисперсия шума эквивалентных наблюдений
дет
(
Пт 4а', Т
1 +
acjnJ )
(6.97)
(6.98)
Запишем эквивалентное наблюдение
Ук=Ч+Ъ,к>
где fjzk — ДБГШ с дисперсией (6.98), и синтезируем фильтр Калмана, полагая,
что модель изменения задержки определяется уравнениями (6.94). Уравнения
оптимальной фильтрации имеют вид
4=4 + Ки{Ук -Ч)» fk = Ч-\ + Пт,к-\.
Кк = V-i + K2Jk(yk -тк), (6.99)
*u = Au/^r ' Чк =Dn,k/D^r , (6.100)
где Dy, i,j = \,2 — элементы матрицы Dx дисперсий ошибок фильтрации
вектора х = | г vr | , которая удовлетворяет уравнениям, аналогичным
(6.78), с заменой Dfl -> D~ , D, -> D, и
168
Методы и алгоритмы обработки сигналов и извлечения информации
1 Т
0 1
, G =
0
1
F= L G= L H= 1 0
Как и в задаче фильтрации фазы сигнала, для расчета дисперсии ошибки
фильтрации задержки сигнала целесообразно рассмотреть дисперсионные
уравнения в непрерывном времени, которые в установившемся режиме дают
следующие алгебраические уравнения:
^,-^ = 0,^-^1 = 0,^-^ = 0,
\ *ч ч
где Sg =Dg /T9Sfj =ЩТ — двусторонние спектральные плотности
формирующего шума и шума наблюдения.
Решение данной системы уравнений имеет вид
Dn =DT =(4^X),/4, D22 =DVr =(4SlS^r)V\ (6.101)
а для коэффициентов усиления непрерывной системы фильтрации получаются
выражения
*н! = (45^ /% f = (2КИ2 f , КИ2= (Sfr /^ f . (6.102)
Коэффициенты усиления непрерывной и дискретной систем фильтрации
связаны соотношениями, аналогичными (6.82).
Спектральную плотность Sg формирующего шума можно задавать через
дисперсию аа ускорения вдоль линии потребитель—НС приближенным
соотношением Sg =gI/p,yjxs /?«1...4 с"1.
На рис. 6.25 приведены графики СКО оценки задержки сигнала
(выраженные в метрах) в зависимости от СКЗ ускорения аа для различных значений
qcj . Ошибка оценки задержки не превышает 30 м, т.е. лежит в пределах
линейного участка дискриминационной характеристики, что подтверждает
допустимость использованной при анализе линеаризации следящей системы.
Рассчитаем полосу пропускания следящей системы. Для этого запишем
уравнения линейной непрерывной следящей системы за задержкой сигнала,
которые получаются из (6.99) при Т —> 0 :
^ = *г+ *.,(*(')-*). % = К.г(№-*)> <6-103>
где коэффициенты усиления Кн1,Кн2 определяются в соответствии с (6.102).
169
Глава 6
СКОх,м
80
loo G"M/C
20 40 60
Рис. 6.25. Зависимости СКО оценки задержки огибающей сигнала
Подставляя (6.104) в (6.83), рассчитаем полосу пропускания системы
слежения за задержкой сигнала (ССЗ):
4/ссз -
Кн1 + К}
н2
ЛК„
.7^*0,537^7.
(6.105)
т 4л/2
На рис. 6.26 приведены графики оптимальной полосы пропускания ССЗ в
зависимости от СКЗ ускорения вдоль линии потребитель—НС для различных
значений qcin . Из рис. 6.26 следует, что оптимальные значения полосы
пропускания ССЗ лежат в пределах 0,5...4 Гц, что существенно меньше полосы
пропускания ССФ. Это обусловливает большую помехоустойчивость ССЗ по
сравнению с ССФ.
АГссз^Ц
100
<Vm/c
Рис. 6.26. Зависимости полосы пропускания ССЗ
170
Методы и алгоритмы обработки сигналов и извлечения информации
Дисперсия флуктуационной ошибки оценки задержки сигнала
определяется выражением, аналогичным (6.87), которое с учетом (6.98) принимает вид
D,
ф.ошг ~ t
4/cc^2f1 + _2_^
c/nQ
Я с/по'
(6.106)
Дискретная следящая система второго порядка (в отличие от
аналогичной непрерывной системы) может быть в неустойчивом состоянии. Условия
устойчивости дискретной системы даются соотношениями
К^О, К2>0, 4-2К1-К2Т>0, (6.107)
из которых с учетом (6.102), (6.103) следует
¥ССЗ=0,534К^<^~^- (6.108)
Типичные значения полос пропускания, приведенные на рис. 6.25,
удовлетворяют условию (6.102), что обеспечивает устойчивость ССЗ.
Переход от синтезированной оптимальной линейной системы фильтрации
к соответствующей нелинейной системе осуществляется так же, как это
делалось для ССФ, и приводит к уравнениям
Тк = *к + ^\илт,к 9 ?к " Тк-\ + TvTfk_{ ,
Кк =^к-\+К2илт,к> "дт,к =U{Tk,fk) + TJTik, (6.109)
где K^K^S^ , К2=К2/5ЛТ — коэффициенты усиления сглаживающего
фильтра.
Эффект влияния расчетного значения крутизны дискриминационной
характеристики от истинного значения, формирующегося в соответствии с
истинным значением мощности принимаемого навигационного сигнала,
описанный при анализе ССФ, имеет место и в данном случае. Вводя параметр
х = 5дг/5дг , подставляя его в условия устойчивости (6.107) и выполнив
необходимые преобразования, получаем следующее соотношение, определяющее
устойчивость ССЗ:
A/CC3=0,53V^„2 <^ ■
При больших значения х условия на устойчивость ССЗ достаточно
жесткие. Однако, если обеспечить х < 1, то можно пользоваться приближением
(6.108), для реализации которого необходимо £дграсч выбирать из условия
максимально возможной мощности принимаемого навигационного сигнала.
171
Глава 6
6.3.6.3. Оптимальный фильтр второго порядка для следящей
системы за частотой сигнала
При синтезе линейной следящей системы за фазой сигнала использовалась
модель изменения фазы (6.69), которая включает соответствующую модель
изменения частоты, а именно,
Щ = *Ъ-1 + Tsk-\ > vk = vk-\ + 4p,*-i • (6.110)
Данная модель является моделью второго порядка, т.е. такой же, что
модель (6.94) для задержки сигнала. Следовательно, структура фильтра Калмана
для фильтрации частоты сигнала определяется теми же соотношениями (6.99),
(6.100), что и в случае фильтрации задержки. Для дисперсий ошибок
оценивания и коэффициентов усиления остаются справедливыми формулы (6.101),
(6.102), в которых необходимо провести замену Sg -»5^ , S^ ->S^ . При
этом спектральная плотность формирующего шума S^ = 2<7va [рад с" ], а
спектральную плотность эквивалентных линейных наблюдений, под которыми в
данном случае надо понимать ук = сок + fjwk, необходимо рассчитать для того
или иного типа частотного дискриминатора. В Приложении к гл. 6 приведен
расчет статистических характеристик некоторых типов ЧД. Например, для ЧД
(П6.63) справедливы следующие выражения:
и(еа>) = 4Яс/П0т Р K)sinc {£Jl2)™{£J)> £а=а>-а>,
\=1WVW
1 +
21c/nJP2{Sr)
(6.111)
(6.112)
где для простоты выкладок положили етк = ет к_х.
Крутизна дискриминационной характеристики получается
дифференцированием (6.111) по еф с последующим приравниваем sw = 0:
*Дй,=4<40:гУ(*г),
а дисперсия шума эквивалентных наблюдений —
i+
1
V» ггЪ _ _2
Т Яс/щР М
V
2<1с/п0Р {£Т)Т
1
Т qc/no
1 +
1
Щщ7 )
(6.113)
(6.114)
где q'cj^ =qci„0p (sT) —эквивалентное отношение сигнал/шум.
Рассчитаем СКО ошибки измерения частоты f = (oj{ln) по формуле
CKO/=jD; = jASfrSi/(2*) [см. (6.101), где S^ = Д^Г; S^ =г{Ъс$ а\
172
Методы и алгоритмы обработки сигналов и извлечения информации
На рис. 6.27 приведены графики зависимостей СКО измерения частоты в
зависимости от СКЗ ускорения вдоль линии потребитель—НС для различных
значений <7с/„0 ПРИ нулевой расстройке по задержке (еТ = 0). Из графиков видно,
что величина ошибки оценки частоты не превышает 20 Гц, т.е. лежит в пределах
линейного участка дискриминационной характеристики.
Сопоставление графиков, приведенных на рис. 6.27, с аналогичными
графиками рис. 6.22, полученными для оценки доплеровского смещения частоты в
схеме ССФ когерентного приемника, показывает, что точность оценки частоты
в некогерентном приемнике существенно хуже (примерно в 10 раз), чем в
схеме ССФ когерентного приемника.
СКО/;Гц
аа,м/с
Рис. 6.27. Зависимости СКО оценки частоты сигнала
Полоса пропускания системы слежения за частотой (ССЧ) сигнала
определяется выражением (6.105), а графики зависимости А/Ссч от величины СКЗ
ускорения приведены на рис. 6. 28.
4Гссч-гч
оа, м/с1
Рис. 6.28. Зависимости полосы пропускания ССЧ
173
Глава 6
Для дисперсии флуктуационной ошибки оценки доплеровского смещения
частоты, используя (6.87), (6.114), можно записать
п _ 2А/ССЧ
ф. ош со
2(1'с1щТ
Сглаживающий фильтр для ССЧ описывается уравнениями,
аналогичными (6.106), а именно,
^=^-l+^2*W> »aa>1k=U(0>k>&k) + r!a>,k> (6-П5)
где Kl=Kl/Saa}, K2=K2/Sa(0 — коэффициенты усиления сглаживающего
фильтра.
6.3.6.4. Сглаживающий фильтр комбинированной фазо-частотной
системы слежения в когерентном приемнике
В п. 6.3.4.1 рассмотрен вариант построения следящей системы за фазой
сигнала когерентного приемника с использованием двух дискриминаторов:
фазового и частотного. Для синтеза сглаживающего фильтра в этом случае также
можно использовать методику, основанную на введении эквивалентных
наблюдений. Однако при этом ее обобщить с учетом того факта, что в
комплексной системе статистические характеристики дискриминаторов могут зависеть
от различных ошибок слежения.
Поэтому рассчитаем сначала статистические характеристики фазового и
частотного дискриминаторов. Рассмотрим случай малого отношения
сигнал/шум и выберем дискриминатор (6.41), дискриминационная и флуктуацион-
ная характеристики которого описываются выражениями (6.70), (6.71), которые
приведем еще раз:
идр(ер) = 2д^Т2рЦег)вт(2ер+еют)8тс2(е<^/2)9 (6.116)
^=8^/„0^V2(^)sinc2(^r/2)
П(р
1+ 1
2Яф0ТР (*r)sinc (sj/l)
(6.117)
Частотный дискриминатор комбинированной системы слежения
описывается соотношением (6.48), которое при малом отношении сигнал/шум
принимает вид (П6.38). Статистические характеристики такого дискриминатора
рассчитаны в Приложении к гл. 6 [формулы (П6.39), (П6.40)]:
Uaa{sw) = 4q2c/noT3p2(£T)cos(s4p+e{0T/2)smc(sJ/2)x
х—p[cos(s, + sJl2)smc(sJl2) - cos(*„ + sj)], (6.118)
£j
174
Методы и алгоритмы обработки сигналов и извлечения информации
^.4*</*гН4-*п2М+—.
4с/v
(6.119)
Из (6.116), (6.118) видно, что дискриминационные характеристики зависят
от ошибок рассогласования как по фазе ер, так и по частоте £(0. Причем лишь
при одновременном выполнении условий s = 0, еф = 0 имеем «глобальный
ноль» векторной дискриминационной характеристики \](sq>,£(0) = \U:i^ £/ДЙ)| .
Зависимость дискриминационных характеристик двух рассматриваемых
дискриминаторов от двух ошибок £ и £а говорит о том, что по сути эти
дискриминаторы нельзя называть фазовыми или частотными. Оба они являются
комбинированными «фазочастотными». Более наглядно это проявляется, если
линеаризовать М^у^еЛ при малых ошибках £р и £(0. В этом случае (6.116),
(6.118) можно записать в виде
Ua(p * 2q2c/noT2 (is, + £j) = 5д1 (ер + sj/l) ,
^i=4^r2sinc2(^r/2), (6.120)
ила - 4^Г3 (ер/2 + ejfi) = Sa2 (ep + 2еаТ/3),
*л2 = 2q^T3Cos(£p+£J/2)sinc(eJ/2). (6.121)
Из (6.120), (6.121) следует, что структуры двух дискриминаторов
идентичны, а отличаются они лишь коэффициентами при ошибках по фазе и частоте.
С учетом представлений (6.120), (6.121) процессы на выходах фазового и
частотного дискриминаторов можно представить в виде
uapjc = $я\ \£<p,k + eo),lJ/2) + Ч9,к »
«W =sii{£<p,k +2ettttkT/3) + tjattkt (6.122)
где tjPtk, t] к — дискретный БГШ с дисперсиями (6.117), (6.119).
Шумы 77^,*» *1а>,к на выходах фазового и частотного дискриминаторов
оказываются коррелированными. Взаимная дисперсия для них рассчитана в
Приложении к гл. 6 (П6.45):
1
а
ЦрЧа
= 4^Г4
1 +
24W
(6.123)
Для линеаризованной модели (6.122) введем следующие эквивалентные
наблюдения, приведенные к оцениваемым параметрам:
175
Глава 6
У\,к =<Рк+ <°кт/2 + П\,к > У2,к = <Рк + ЩТ/3 + fj2k ,
где fjxk , fj2k — ДБГШ с дисперсиями, равными
(6.124)
Dm=-
D.
$<р
я<Р
П\Й2
Ч/п0^
Ч/пот
1 +
1 +
Ч/пТ
А* =
D.
фсо
'JXCO
Ч/nJ
1 +
24с/п0Т
ч
с/V
(6.125)
При записи (6.125) для упрощения соотношений использовано
приближение sinc(£-<y71/2)~l.
Из (6.124), (6.125) следует, что эквивалентные наблюдения У\£,у2,к
практически равноценны как по информационным компонентам <рк, сок, так и по
дисперсиям аддитивных шумов. Поэтому два дискриминатора (6.122) можно
рассматривать как две ветви комбинированного фазо-частотного дискриминатора.
Синтез фильтра Калмана для эквивалентных наблюдений (6.124) и модели
динамики изменения фазы (6.69) приводит к следующим уравнениям
оптимальной фильтрации:
Фк =Фк +К\1,к(У1,к ~(Фк +«>кТ/2)) + К\2,к(У2,к -(Фк+ЩТ/З)),
сок=сЪк +К21к(у]к -(фк +щТ/2)) + К22к(у2к -(фк +ЩТ/3)),
Ук =4-1 +K3\,k(hk -(9k+&kT/2)) + K32tk(y2tk -(фк+2сокТ/3)),
Фк = Фк-\ + т&к-\>Щ = &к-\ + тП-\ ■ (6-126)
Здесь Kijk, / = 1,3, У = 1,2 —элементы матрицы К к коэффициентов
усиления, для которой справедливы выражения
(6.127)
К£ -Dx,/tHR7
D:V=D:V+HTR^H, Dvt=FDvt_,FT+GGTZX
(6.128)
х,к **x,k ^ 1Ж **-rj " ' **х,к ЛЛ*х,к-1К' TUU ^^<р
где Dtj, i,j = 1,3 — элементы матрицы Dx дисперсий ошибок фильтрации
вектора х = | (р со v | ; Ьхк — матрица дисперсий ошибок экстраполяции вектора х;
F =
1 Т 0
0 1 Т
0 0 1
,G =
0
0
1
>R7 -
П\П2
,Н
1 Г/2 О
1 2Г/3 О
(6.129)
Комбинированная система слежения (6.126) имеет преимущества перед
автономной системой ССФ (6.76) лишь при достаточно больших временах нако-
176
Методы и алгоритмы обработки сигналов и извлечения информации
пления сигнала в корреляторах. На рис. 6.29 приведены зависимости СКО
фильтрации фазы в комбинированной и автономной СФФ при qc,n = 37 дБГц
и Т= 10 мс. Как видно, точность фильтрации фазы в комбинированной ССФ
повышается на 20.. .30 %.
На рис. 6.30 приведены аналогичные зависимости СКО фильтрации
доплеровского смещения частоты сигнала. Точность фильтрации доплеровского
смещения частоты в комбинированной ССФ повышается на 10...20 %.
Приведенные значения выигрышей в точности фильтрации фазы и доплеровского
смещения частоты слабо зависят от отношения сигнал/шум qc, при его
изменении в диапазоне 30...50 дБГц. При увеличении времени накопления Т в
корреляторах приемника величины выигрышей возрастают.
СКОф> град
с„,м/с
100 а
Рис.6.29. Зависимости СКО фильтрации фазы сигнала
СКО/9Гц
ад, м/с
20 40 60 80 100 я'
Рис. 6.30. Зависимости СКО фильтрации доплеровской частоты сигнала
177
Глава 6
Учитывая, что в (6.126)
Уг,к ~{Фк + 2щТ/3) = (<рк-фк) + 2(&к -щ)Т/3 + fj2= ep>k + 2£(йкТ )Ъ + т}2
а также, формулы (6.122), уравнения (6.126) преобразуем к виду
Фк=Фк+ KU,k Ua<p,k/Sjx\ + К\2,к uaco,k/Sn2 '
Щ =">к+К2\,к ua<p,klSa\ +K22,kUboJ<lSn2 >
^к = $к-\ + КЪ1,к "д^,А:/^д1 + Кз2,к илсо,к/^д2 »
Фк = Фк-\ + ТЩ-\ » Щ = 4-1 + Th-\ ■ (6.130)
Уравнения (6.130) описывают комбинированную ССФ, схема которой
приведена на рис. 6.31.
У
('*-!,/)
^дк yk-\J ~*к)
Фазовый
дискриминатор
>д1
Частотный
дискриминатор
й
•е-
Е
<Рк
в>к
Перестраиваемый
генератор
Рис. 6.31. Схема комбинированной ССФ
Кроме описанного выше, возможен другой подход к синтезу
сглаживающего фильтра комбинированной ССФ. Преобразуем (6.120), (6.121) к виду
Uj,<pK2^c/noT2(2£^+£(0T) = SaU£<p+Sal2£(0,
San=^c/noT2,Sal2=2q2c/noT\ (6.131)
^дсо - 4<40Г3 (ejl + eJli) = 5д21*, + Sr22sw ,
£Д21 = 2д2е/Я0Т>, Sal2 = 4q2c/nJ4/3 . (6.132)
РдП ^д12
Введем матрицу крутизны Sa
Sn2\ ^д22
, вектора ид =
мр
и
асо
щ =
^<Р,к
Тогда (6.122) можно записать в векторном виде:
'со
178
Методы и алгоритмы обработки сигналов и извлечения информации
"а,к=$л*к+Чк- (6ЛЗЗ)
Теперь можно ввести векторное эквивалентное наблюдение
ук=Вхк+щ, (6.134)
-1 i it ~ |1 0 0|
где ти=8дти, х = | 9 со v \ ; Н= ^ .
Отличие эквивалентных наблюдений (6.134) от (6.124) заключается в том,
что наблюдение фазы срк и частоты сок разделено, т.е. ухк включает только
9k** hjk —только сок.
Корреляционная матрица шума % эквивалентных наблюдений
^-h
i-l
Щ - &ц R7sfl -
ЧЫ«Т)
Яс/г-Т
/«О
2Г2/3 -Т
-Т 2
(6.135)
Уравнения оптимальной фильтрации вектора состояния х по
наблюдениям (6.134) имеют такой же вид, что и (6.126)—(6.128) с заменой Н и R^ на Н
и ГЦ соответственно.
Решение дисперсионных уравнений для рассматриваемого варианта
комбинированной системы фильтрации приводит к тем же результатам, что и в
рассмотренном ранее случае (рис. 6.27, 6.28).
Запишем уравнения (6.126) в векторном виде:
хк=хк+кк(ук-тк). (6.136)
Преобразуем (6.136)
(6.137)
Уравнение (6.137) описывает нелинейную комбинированную ССФ, схема
которой приведена на рис. 6.32.
, Лдк (1к-и - Ч)
У('к-и)
Фазовый
дискриминатор
Частотный
дискриминатор
•е-
о
<Рк
Фк
Перестраиваемый
генератор
Рис. 6.32. Схема комбинированной ССФ
179
Глава 6
Отличие данной схемы от той, что приведена на рис. 6.30, заключается в
наличии матричного преобразователя S"1, стоящего после фазового и
частотного дискриминаторов, и иными коэффициентами усиления в сглаживающем
фильтре (при идентичной структуре самих сглаживающих фильтров).
6.3.6.5. Сглаживающий фильтр комплексной системы слежения
за задержкой огибающей и доплеровской частотой сигнала
в некогерентном приемнике
В некогерентном приемнике осуществляется слежение за задержкой
огибающей сигнала и доплеровским смещением частоты. Следовательно, имеем
два соответствующих дискриминатора и можно вести два эквивалентных
наблюдения
Кк =Тк+ Чт,к > Уа>,к =0)к+ Чсо,к > (6-138)
где fjT k — шум эквивалентного наблюдения по задержке огибающей сигнала,
который получается в результате пересчета шума с выхода дискриминатора
задержки; rj^k — ШУМ эквивалентного наблюдения по частоте, который
получается в результате пересчета шума с выхода частотного дискриминатора.
В Приложении к гл. 6 приведен расчет дискриминационных и флуктуаци-
онных характеристик дискриминатора задержки огибающей и частотного
дискриминатора некогерентного приемника, например, формулы (П6.90), (П6.92) и
(П6.66), (П6.67), которые для удобства приведем еще раз:
2£
U(sT) = ^—s\nc2{sJl2){p\sT-rj2)-p\sT + rj2)),
\ =
4^, Г3 sine2 (^772)
At4
1 + -
2c/»0rsinC {£JI2)
U(e*) = Aq1cjlJ2p{stjk) p(eVtk_l)sinc2 (^,_^/2)sin(^_1r),
Dn„ =16Я3с/п0т3р{£г,к)р{£т,к-\)
1 +
2^c/n0TP(£r,k)p{Sr,k-l)
(6.139)
(6.140)
(6.141)
(6.142)
Из (6.139) и (6.141) находим крутизны дискриминационных
характеристик, полагая А г = гэ:
*дг = 2q2c/nJ2 sine2 (еаТ/2)/т2э , Saa = Ц2С,ЩТЪ р2 (ет),
180
Методы и алгоритмы обработки сигналов и извлечения информации
используя которые, а также (6.140) и (6.142), рассчитаем дисперсии
эквивалентных шумов наблюдений по задержке огибающей и доплеровскому
смещению частоты сигнала:
% = „_ ^:„„2
4qc/nJsmc2(sJ/2)
(
1 +
^/«o^sinc2(^r/2)
DR =
1
*• g^TV(sT)
1 +
^c/nJP Ю
(6.143)
(6.144)
Для синтеза комплексной системы фильтрации примем модель изменения
задержки сигнала (6.94) и учтем, что в (6.138) cok = 2nf0vrk . Тогда уравнения
оптимальной комплексной фильтрации могут быть записаны в виде
4=4+ К\,к (Ут,к ~Ч) + К2,к (Уа>,к ~ Щ-1 ) » h = 4-Х + Т$т>к-\ >
*т,к = *т,к-\ + ^3,* (Ут,к -?к) + К4,к [Усо,к ~ <*>к-1) » 4-1 = 2т/(А-1 ,
% = Ai,*/Ajr ' 4k=^kDn,klDna .
*з,* = Аг,*/ % . ^4,* = 2^/0D22i, /Z^ , (6.145)
где Д , i,j = \,2 — элементы матрицы Dx дисперсий ошибок фильтрации
вектора х = | г vr
В уравнениях (6.145) удобно перейти от эквивалентных наблюдений
частоты сигнала yw k к эквивалентным наблюдениям скорости изменения
задержки yvk = у at / (2л fо) • При этом уравнения (6.145) принимают вид
Ч=*к+ К\,к (Ут,к ~?к) + К2,к (yv,k ~ П-1)> fk = ^-i + 7vr>t_!,
*г.* = V,,*-! + ^3,* [У г,к -h) + &4,к {Уу,к - Ук-1) > (6-146)
К\,к =DU,k/DfjT » ^2,* =Dl2,k/Dnv '
*3.* = A2,*/Afr > ^4.* = ^22,*/^ > (6Л47)
г*^=^/(И)2.
Как и в рассмотренных выше задачах фильтрации, для расчета дисперсий
ошибок фильтрации в комплексном фильтре (6.146) целесообразно рассмотреть
дисперсионные уравнения в непрерывном времени, которые в установившемся
режиме дают следующие соотношения:
181
Глава 6
DnD21 _q
ч
£ A2A2 ^22^22 _Q
где Se =DeT,Sf: =DjjT,Sjj =D^T —двусторонние спектральные плотности
формирующего шума и шумов эквивалентных наблюдений.
Решение данной системы уравнений имеет вид
AiyCT = ^r^,(1 + 2^)/(1 + ^)' A2yCT=^/(i + V?)>
A2ycx=^r^(1 + 2^)/(1 + ^)' (6Л48)
где S^=S^/(27rf0f , p = Sl/s4rS% — безразмерный параметр.
Как следует из (6.148), точность фильтрации зависит от значения
параметра р. В табл. 6.2 приведены значения данного параметра для приемников
СРНС для аа = 1 м/с2 (S4r=\ mV1).
Таблица 6.2. Численные значения параметра р
Яс/п0. ГЦ
1 1(Г
103'7
| 104'5
S^,m2c
258
24
2,9
S^.mV1
1,3
0,19
0,028
~Р
6,5 Ю-3
1,5 10"3
2,7-Ю"4 J
Из табл. 6.2 следует, что в реальных ситуациях всегда имеем р«\ и
формулы (6.132) можно записать в более простом виде
(6.149)
А
Пуст ~ \j^fjT^fjv » А2уст ~Sjjv » ^22 уст ~V^r^
^
Из (6.149) видно, что дисперсия ошибки оценки задержки не зависит от
динамики движения потребителя и определяется уровнем шумов
эквивалентных наблюдений (табл. 6.3).
Таблица 6.3. СКО оценки задержки сигнала
1 Чс/п0»ГЦ
1 СКОг, м
103
3,6
103'7
1,3
104'5 1
0,5
182
Методы и алгоритмы обработки сигналов и извлечения информации
Сопоставление данных значений с СКО оценки задержки сигнала в
автономной ССЗ (рис. 6.23) показывает, что в комплексной системе фильтрации
выигрыш по точности оценки задержки составляет 6... 10 раз.
Из (6.149) следует, что СКО оценки скорости изменения задержки
(радиальной скорости сближения) не зависит от уровня шума в эквивалентных
наблюдениях задержки сигнала, а определяется только динамикой движения
потребителя (параметром Sg ) и уровнем шума в эквивалентных наблюдениях
доплеровской частоты. Это означает, что при формировании оценки vTk нет
особой необходимости использовать сигналы с выходов двух
дискриминаторов, а достаточно использовать лишь сигнал с выхода частотного
дискриминатора, т.е. второе уравнение в (6.130) определять в виде
vT,k = vr,t-i + KAk (y^k - vk_x). (6.150)
На рис. 6.33 приведены зависимости СКО оценки доплеровского смещения
частоты (радиальной скорости сближения) в зависимости от интенсивности
ускорения потребителя при различных значениях отношения сигнал/шум.
Сравнение зависимостей рис. 6.33 и 6.27 показывает, что на рис. 6.26 СКО
меньше. Обусловлено это тем, что в рассматриваемой задаче слежение за
частотой сигнала осуществляется более простым фильтром первого порядка
(6.149). Однако, учитывая свойство автономности слежения за частотой
сигнала от слежения за задержкой сигнала в комплексном фильтре, можно взять
более сложную модель изменения задержки сигнала (например, модель третьего
порядка типа (6.69)), из которой получится система слежения за частотой
сигнала второго порядка.
СКО f9 Гц
°0 20 40 60 80 100 <Vm/c
Рис. 6.33. Зависимости СКО оценки частоты сигнала
При этом точность оценки доплеровского смещения частоты будет
близка к той, которая приведена на рис. (6.25), а точность оценки задержки сигнала
183
Глава 6
будет по-прежнему определяться (6.149), т.е. только уровнем шумов
эквивалентных наблюдений.
Для коэффициентов усиления непрерывной комплексной системы
фильтрации, соответствующей (6.146), получаем выражения
v _ Aly<rr _ prz /ТГ— £ _ А 2 уст _Л
Ан1-—" -у] 1Ъг)уГЪ ' Ан2~—" -^
^*=^-^К- (6.151)
Коэффициенты усиления для дискретной системы фильтрации
определяются соотношениями
Выше было показано, что СКО оценки задержки не зависит от динамики
движения потребителя и определяется только уровнем шумов эквивалентных
наблюдений. Рассчитаем составляющие данной ошибки, обусловленные
шумами дискриминатора задержки и частотного дискриминатора. Для этого
определим частные шумовые полосы пропускания от входов эквивалентных
наблюдений утк и yvk до оценки задержки сигнала тк :
лл=-Ч-
"-if
1_ r ^нфЦ+^н4| deo _KHl
1 °f \)<»Кн2+Кн4\ da _ К*2+Кн4/Ки]
о (jco) + }(й(Кн1+Кн4) + Кн1Кн<
4Кн1(\ + Кн4/Кн1)
(6.152)
(6.153)
Учитывая, что в соответствии с (6.151) Кн2 =1, формулу (6.153) можно
записать в более простом виде: A/v = 1/(4ЛГн1).
Теперь для дисперсии флуктуационной ошибки оценки задержки сигнала
запишем
0^=2*/^ +2А/^ =*н1^г/2 + ^/2*н1 .
Из табл. 6.2 и (6.151) следует, что Ки1 «0,1...0,14 с"1, следовательно
А/г =0,025...0,35 Гц, А/„ =2,5... 1,8 Гц"1. Сопоставление шумовой полосы
пропускания по входу эквивалентных наблюдений задержки сигнала в
комплексной системе фильтрации с аналогичной шумовой полосой пропускания в
автономной системе слежения за задержкой сигнала (рис. 6.24) показывает, что она
184
Методы и алгоритмы обработки сигналов и извлечения информации
существенно (-в 100 раз) меньше, что и обусловливает повышение точности
оценки задержки сигнала в комплексном измерителе.
6.3.6.6. Комплексный фильтр слежения за задержкой огибающей
и фазой сигнала когерентного приемника
В когерентном приемнике можно организовать комплексную фильтрацию
задержки и фазы сигнала, позволяющую существенно повысить точность
оценки задержки сигнала за счет дополнительных высокоточных (хотя и
неоднозначных) фазовых измерений.
Оставаясь в рамках используемого подхода раздельного синтеза
дискриминаторов и сглаживающего фильтра, полагаем, что сформированы два
дискриминатора: задержки огибающей и фазы сигнала. В качестве первого из
дискриминаторов рассмотрим, например, (6.45), статистические характеристики
которого определяются (П6.75), (П6.76) и имеют вид (при Дгэ = гэ)
U{£T) = 4q2c/noT2cos2(^) p(er) (P(sT-Tj2)-p(eT+Tj2)),
\=16я1/п0Т3оов2(е<р)
(
1 +
1
(6.154)
(6.155)
2<7cM)7W(^)
Крутизна дискриминационной характеристики (6.154)
S^T=Sq2c/noT2 cos2 (s^/t,.
Введем эквивалентное наблюдение по задержке:
Ут,к = тк + *?т,к '
где Tj k — шум эквивалентного наблюдения по задержке огибающей сигнала,
дисперсия которого
( ^ ^
(6.158)
(6.156)
(6.157)
* Si 4qc/nJ cos2(*,)l 2дс/поТсо82(£<р)
1 +
Статистические характеристики фазового дискриминатора рассмотрены в
п. 6.3.6.1, поэтому воспользуемся (6.73) и запишем дисперсию эквивалентного
шума по фазе:
1
ВП„=\ „_2
' 2qclnTp2(eT)
1 +
1
2Яс/п0тР2^т)
Эквивалентное наблюдение по фазе имеет вид
У9,к =<Рк+ Лср,к>
(6.159)
(6.160)
185
Глава 6
где fj k —дискретный БГШ с дисперсией (6.159).
Так как фаза сигнала связана с его задержкой, удобно ввести параметр,
аналогичный задержке, соотношением rd = <р/2л/0 , где /0 — несущая частота
сигнала. При этом наблюдения (6.160) можно преобразовать к виду
yrd,k = Td,k+'ird,k> (6Л61)
где fj к — дискретный БГШ с дисперсией
а
Аы =
п<р
1
(
1 +
1
laclnJP (£т)
(6.162)
(2*/0Г 2{2nU)qclnTp\eT)\
Можно показать, что при нулевых ет = 0 и ех - 0 шумы эквивалентных
наблюдений (6.157) и (6.161) некоррелированны.
Изменение задержки сигнала во времени, по-прежнему, будем описывать
соотношениями (6.94), а изменение rd определим уравнением
Td,k=Td9k-l+TvT9k-l> С6-163)
где параметр vrk_x — скорость изменения задержки, которая определяется
вторым уравнением в (6.94). Полагаем, что в начальный момент времени
выполняется условие rd0 = г0.
Такой выбор переменных состояния и взаимосвязь между ними
соответствуют методу дополнительной переменной, более подробное описание которого
будет приведено гл. 15.
Введем вектор состояния х^ =
-d9k
, изменение которого во
времени описывается общим уравнением (6.33), где следует положить
F =
1 Т 0
0 1 0
0 Т 1
,G =
0
1
0
, D«=D«
Для сформулированной задачи оптимальной фильтрации вектора
состояния хк по наблюдениям (6.157), (6.161) уравнения оптимального фильтра Кал-
мана имеют вид
4=4+ Кик (yTtk -fk) + К2к [учк - fdtk),
*tjk = vr,*-i + K3Jc (yT>k -fk) + K4^k (yTdtk - fd<k),
4k = *d,k + Ks,k (Ут,к -h)+K6,k [y4,k - 4k).
186
Методы и алгоритмы обработки сигналов и извлечения информации
Ч = h-\ + TKk-\> fd,k = *d,k-\ + т^т,к-\» (6-!64)
^1,A = Dll,k/DrjT » ^2,* =D\3,k/DfjTd > ^3,* =D\2,k/DfjT » К4,к =D23,k/DijTd »
^ = Аз.*/Я > *5,* = Аз,*/%, ' (6Л65)
где Дуд? /,7 =1,3 — элементы матрицы дисперсий ошибок фильтрации DxA:,
которая описывается матричными уравнениями
D^D-'+H^'H, D^FD^F'+GG^, (6.166)
в которых Dx к — матрица дисперсий ошибок экстраполяции вектора х,
Н
1 0 0
0 0 1
»D» =
' Ч
о а
о
Vrd
Решение дисперсионных уравнений в установившемся режиме показывает,
что Ai,yCT = Аз.уст' те- дисперсия ошибки фильтрации задержки огибающей
становится равной дисперсии ошибки фильтрации аналогичного параметра по
фазовым измерениям. Для получения количественной оценки данной
дисперсии перейдем, как и выше, к дисперсионным уравнениям для непрерывной
задачи фильтрации. В этом случае для установившегося режима из
дисперсионных уравнений Риккати можно записать
2Dn-
Ч4 А2, '
V5»
fD}
Чг
12
= 0, D22-
ГРпРп {РиРпЛ
ltd J
2 ^
v
Лт
= 0
Hrd )
= о,
(6.167)
Ird J
где ^ =DijT, S^ = D^T , S4r = D(t jT .
Решение системы уравнений (6.167) имеет вид
Dn=D33= 12
S4r\SnrSnrd)
*V2^'
4rd
(6.168)
При записи последнего приближенного равенства учтено, что S^ » S^ ,
так как спектральная плотность эквивалентного шума по задержке огибающей
обратно пропорциональна квадрату частоты повторения символов дальномер-
ного кода (~ 2 МГц), а спектральная плотность эквивалентного шума по
дополнительной переменной — квадрату несущей частоты сигнала (~ 1,6 ГГц).
187
Глава 6
Из (6.168) следует, что результирующая точность оценки задержки
определяется потенциальной точностью фазовых измерений. Однако следует еще раз
подчеркнуть, что это соответствует установившемуся режиму, т.е. t —> оо. Для
рассмотрения поведения оценок в переходном режиме необходимо проводить
математическое моделирование нелинейной комплексной системы фильтрации.
Перейдем от линейных уравнений (6.164) к нелинейным уравнениям по
методике, описанной в п. 6.3.6.1:
Ч = Ч + К\,к "дг,*/5^ + К2,к Uw,k/(4Sa,<p) >
VT,k = $т,к-1 +КЪ,к Uar,k/Sa,r + К4,к ид<р,к/(<ЧА,р) »
Фк=Фк + ^5,Л иат,к /Sr,t + К6,к иа<р,к /Sw >
Ч = fk-l + Т\,к-\> Фк = Фк-\ + ТЩУт,к-1 > (6Л69)
где иатк — процесс на выходе дискриминатора задержки огибающей (6.45);
S — крутизна его дискриминационной характеристики (6.156); иЛ(рк —
процесс на выходе фазового дискриминатора (6.41); S^ — крутизна его
дискриминационной характеристики (6.72); фк — оценка фазы сигнала в кольце ССФ.
Приведем результаты моделирования нелинейной комплексной системы
фильтрации (6.168) при qcj =45 дБ, Т = 1 мс и динамике изменения ускорения
вдоль линии визирования, соответствующей 0,5g.
На рис. 6.34 приведена реализация ошибки оценки составляющей rd, из
которой следует, что СКО составляет около 2 мм. Расчетное значение СКО
фильтрации rd, полученное по дисперсионным уравнениям (6.166), составляет 1,9 мм.
8Т<ГМ
0.01
0.008
0.006
0.004
0.002
0
-0.002
-0.004
-0.006
-0.006
О 5 10 15"' 2025 Эб'""~Э5 40 ',С
Рис. 6.34. Реализация мгновенной ошибки оценки rd
На рис. 6.35 приведена реализация ошибки оценки составляющей г .
188
J i i I i L
Методы и алгоритмы обработки сигналов и извлечения информации
8т,м
10 15 20 25 30 35 40 Ь
/,С
Рис. 6.35. Реализация мгновенной ошибки оценки г
Как видно из рисунка, к 40-й секунде ошибка равна примерно 12 см.
Расчетное значение СКО фильтрации т , полученное по дисперсионным
уравнениям (6.166) составляет 13 см. При дальнейшем увеличении времени наблюдения
ошибка оценки г стремиться к ошибке оценки rd как по дисперсионным
уравнениям (6.166), так по реальным реализациям ошибок.
Для сравнения ошибок фильтрации задержки сигнала в синтезированном
комплексном фильтре и в автономном измерителе задержки на рис. 6.36
приведена реализация ошибки оценки г в автономном измерителе при тех же
реализациях шумов наблюдения и формирующего шума, что и для
комплексного измерителя. Как видно из рисунка, ошибка в автономном измерителе
существенно (в 10... 15 раз) больше, чем в комплексном измерителе. При
увеличении времени наблюдения выигрыш в точности фильтрации в комплексном
измерителе по сравнению с автономным возрастает.
8Т?М
~0 5 10 15 20 25 30 Э5 40 ',с
Рис. 6.36. Реализация мгновенной ошибки оценки г
189
Глава 6
Оценки составляющих г и rd в комплексном измерителе могут быть
дополнительно обработаны в соответствии с алгоритмом, описанным в п. 15.4.2.
Суть этого алгоритма заключается в том, что в процессе решения задачи
фильтрации оценивается число периодов неоднозначности фазовых измерений,
которое используется для дополнительной совместной об-работки полученных
оценок т и id. В результате формируется итоговая сгла-женная оценка. На
рис. 6.37 приведена реализация такой сглаженной оценки, полученная для
приведенных выше (рис. 6.33, 6.35) результатов моделирования. Из рисунка видно,
что после 20-й секунды точность оценки задержки сигнала составляет около
1,2 мм, т.е. соответствует ошибке оценки задержки по фазовым измерениям.
8Х?М
0.2г
0.1 [
Г
-о.г[
-о.з[
-0.4h
-0.5^
-0.б1
"°,7Г
-0.81-
' If™ "
j II
- j-W
|„Ж~
II-
Г
H
I
1
j.—
1Ш wJ. jl . ^»...—. ■-
r ] ]
• ]
T j
—1~ {--
: j
—j \- —
| {
! ;
i i i
r
—-* fr "
i •
j—
- —-j
•- -}""
!
!
i i i
„.J
A
—A
10
15 20
25
30
35
40
t,c
Рис. 6.37. Реализация сглаженной ошибки оценки задержки сигнала
6.3.6.7. Комплексный фильтр слежения за задержкой
огибающей с поддержкой оценки доплеровской
частоты сигнала когерентного приемника
Извлечение информации о задержке сигнала из его фазы связано с
проблемой неоднозначности фазовых измерений, что требует специальных
методов синтеза сглаживающих фильтров, один из которых описан в предыдущем
разделе. В то же время, в системе слежения за фазой сигнала достаточно точно
оценивается доплеровское смещение частоты сигнала, пропорциональное
производной задержке сигнала по времени (радиальной скорости сближения).
Причем такая оценка является однозначной. Этот факт позволяет ставить и
решать задачу синтеза комплексного фильтра слежения за задержкой огибающей
с поддержкой оценки доплеровской частоты сигнала когерентного приемника.
Рассмотрим более подробно эту задачу.
Положим, что для когерентного приемника проведен синтез оптимальной
системы слежения за фазой сигнала с использованием модели изменения фазы
(6.69). Оптимальная ССФ при этом описывается уравнениями (6.91).
190
Методы и алгоритмы обработки сигналов и извлечения информации
Для системы слежения за задержкой огибающей сигнала выполнен синтез
временного дискриминатора, например, в той же форме, что и в п. 6.3.6.6.
Следовательно, эквивалентное наблюдение по задержке описывается выражением
(6.157), т.е.
Л,*=г*+?7а, (6.170)
в котором дисперсия шума наблюдения определяется выражением (6.158).
Учитывая, что для полной фазы сигнала (f>(t) справедливо выражение
^(/) = 2я-/0г(?), где /0 — частота несущего колебания, а модель изменения
фазы соответствует (6.69), для модели изменения задержки сигнала моно записать
Ч = Ч-i + Tvk-i» vk = vk-\ + TYk-\ > У к = Ук-\ + 6,*-1 > (6.171)
где %ук —дискретный БГШ с дисперсией Д* =D^ /(2тг/0) .
Связь между частотой со в модели изменения фазы (6.69) и скоростью v в
(6.171) дается соотношением со = 2;r/0v.
В ССФ формируется оценка частоты со, которую представим в виде
Щ=<°к+11а>,к> (6.172)
где сок — истинное значение частоты; г)фк — погрешность оценки.
Будем рассматривать (6.172) как дополнительное наблюдение при синтеза
сглаживающего фильтра синтезируемой системы ССЗ, для которого введем
новое (принятое для эквивалентных наблюдений) обозначение
y»,k=2xfovk+r?a>,k- (6Л73)
Для дальнейшего использования (6.173) необходимо задать статистические
характеристики процесса г/^ . Строго говоря, процесс г\ю^ является
коррелированным с достаточно сложной функцией корреляции. Учет этого
обстоятельства приводит к сложной процедуре синтеза оптимального фильтра на фоне
коррелированной помехи. Поэтому введем допущение о некоррелированности
процесса rja k, а его дисперсию положим равной дисперсии ошибки оценки
/ \1/2
частоты в ССФ (6.80): D^ = Ms^S^ J .
Таким образом, получаем задачу синтеза оптимальной оценки задержки
сигнала тк , описываемой моделью (6.171), при наблюдении процессов (6.170),
(6.173).
Введем вектор состояния \к =\тк vk yk\T, изменение которого во времени
описывается общим уравнением (6.33), где следует положить
191
Глава 6
F =
1 Т 0
0 1 0
0 0 1
,G =
О!
О
1
■D4=D4,-
Тогда уравнения оптимального фильтра Калмана для оценки вектора х^
имеют вид
h = Ч + к\,к (Рт,к ~fk) + К2,к [Усо,к ~ 2xf0vk),
Vr>* = Vr>jfc + КЪ,к {Ут,к -?к) + К4,к [у<о,к ~ 2*/<>V* ) ,
У к = Ук-\ + К5,к (Ут,к ~ч) + Кб,к (у<о,к - 2*/<Л) >
h = Ч-\ + Пт,к-\ >*т,к= Кк-\ + тУк-\> (6Л 74)
*5,к = Аз^/% . V = ^fo^k/D^ , (6.175)
где Д,^, i,y = 1,3 — элементы матрицы дисперсий ошибок фильтрации Dx/t,
которая описывается матричными уравнениями
D"1, = D"1, + Н^Н , Dx , = FDX ,_,FT + GGTD^ ;
Dxk — матрица дисперсий ошибок экстраполяции вектора х;
Н =
Перейдем от линеаризованных уравнений фильтрации (6.174) к
нелинейным уравнениям, включающим отсчеты идтк с выхода временного
дискриминатора, по методике, описанной в п. 6.3.6.3,
h =fk +Kuujxr^klSjxr +Кг,к{Усо,к -2*foVk)>
vT,k = vr,A + КЪчкиЛТчк /5Дт + К4к (у^к - 2/т/0^),
Гк =h-i +*5,*Идг,*/5дг + *6,*(>W -2^/о^)- (6Л7?)
На рис. 6.38 приведена схема когерентного приемника, включающего ССФ
и комплексный фильтр слежения за задержкой огибающей с поддержкой
оценки доплеровской частоты сигнала.
(6.176)
1 0 0
0 2л-/0 0
, 1>й =
' П
°ь
0
0
DJ
192
Методы и алгоритмы обработки сигналов и извлечения информации
Комплексный сглаживающий фильтр
Ук-\,1
Дискриминатор г
4ахк\
У5ДТ
КЛ
А\
к^и
ССФ
(Ок
ГЦ
КА
11
"ЁТЦТ
2л/0
^
т*
ч
Ч'>
vk
Рис. 6.38. Схема когерентного приемника с комплексным фильтром
Для рассматриваемой задачи дисперсионные уравнения (6.176) не
решаются аналитически, поэтому точность оценивания задержки сигнала
необходимо получать решением данных уравнений на ЦВМ.
На рис. 6.39 приведены расчетная (по дисперсионным уравнениям (6.176))
СКО оценки задержки и аналогичная зависимость, полученная в результате
имитационного моделирования приемника (рис. 6.36) при <7с/„о = 38 дБГц и
динамике изменения задержки, соответствующей интенсивности маневрирования 4g.
ет,м
2\-
1 1 ' 1
i j !
уМоделироЬание j
Расчет! \J
1 -J»—^ ■—^ja 1 , m | ■. -i
i j
— ч
i i i :—
10 l>
/,c
Рис. 6.39. СКО оценивания задержки
На рис. 3.40 для примера приведена зависимость СКО оценки доплеров-
ского смещения частоты сигнала, формирующегося в ССФ.
7-1026
193
Глава 6
8/?Гц
1.2
1
0.8
0.6
0.4
02
°0 2 4 6 8 10 7
Рис. 6.40. СКО оценивания частоты
Сопоставление СКО оценивания задержки в рассматриваемом алгоритме
(рис. 6.39) с аналогичной СКО, полученной для алгоритма комплексной
обработки сигналов с выходов дискриминаторов задержки и фазы (рис. 6.35),
показывает, что при использовании оценки частоты несколько снижается точность
оценки задержки. Тем не менее, по сравнению с СКО оценки задержки в
автономной ССЗ (~ 6 м) синтезированная комплексная система фильтрации дает
существенное повышение точности (более чем в 10 раз).
6.4. Алгоритмы вторичной обработки (навигационные алгоритмы)
6.4.1. Вторичные наблюдения
В результате первичной обработки радионавигационных сигналов в
заданные моменты времени tk формируются оценки радионавигационных парамет-
А
ров (псевдозадержки fik и псевдодоплеровского смещения частоты /ац) в
общем случае для всех видимых спутников (i = \,N). Данные оценки можно
представить в виде
^* =*/.*+«г/,*» (6Л78)
/д/,*=/да+ЛА*. (6.179)
где г,, /д/ — истинные значения псевдозадержки и псевдодоплеровского
смещения частоты; nTi, п^ — погрешности их оценок, полученных на этапе
194
Методы и алгоритмы обработки сигналов и извлечения информации
первичной обработки сигналов. Оценки fik и fAik иногда называют сырыми
измерениями.
Конечной целью навигационной задачи является получение оценки векто-
ра потребителя 11 = \х у z t Vx Vy Vz\ , включающего его координаты {x^z} в
той или иной системе координат, время t и составляющие вектора скорости
{Vx9Vy9Vz}.
Так как ft и /д/ связаны известными соотношениями (4.3), (4.7) с
координатами потребителя {x,^,z} и составляющими его вектора
скорости!^, Vy9Vz}, т.е. fi(x9y9z) и /д/(*,у9z,Vx,Vy,Vz), то в результате
дополнительной обработки сырых измерений (6.178), (6.179) можно получить оценки
координат {xk9yk9zk} и составляющих вектора скорости {Vx,Vy,Vz}
потребителя. Такая обработка называется вторичной, а соответствующие алгоритмы —
алгоритмы вторичной обработки или навигационные алгоритмы (так как на
их выходе формируется итоговое решение навигационной задачи).
Используя терминологию теории оптимального оценивания, соотношения
(6.178), (6.179) в дальнейшем будем называть вторичными наблюдениями, для
которых введем обозначения
>V=fa+"rU> i = UN9 (6.180)
^Л/.*=/^*+иЛ*'/ = 1^' (6Л81)
Таким образом, итоговая навигационная задача является задачей
получения оценок вектора потребителя по имеющимся векторным вторичным
наблюдениям при условии наличия информации о параметрах движения
(координатах и векторах скорости) навигационных спутников, которая формируется в
приемнике потребителя в результате декодирования навигационного
сообщения из принятых радиосигналов.
Если на этапе первичной обработки использовались автономные следящие
системы за задержкой огибающей и фазой сигнала, т.е. вторичные наблюдения
(6.180), (6.181) являются измерениями двух независимых датчиков, то их
можно использовать для получения уточненных оценок псевдодальности и
псевдодоплеровского смещения частоты. Такие алгоритмы будем называть
алгоритмами вторичного сглаживания оценок псевдо дальности и псевдодоплеровского
смещения частоты. В этом случае, кроме вторичных наблюдений (6.180), (6.181),
можно использовать и оценку псевдофазы сигнала, формируемую в ССФ,
Уъ.к=Фик+пт19к> * = ЪЯ- (6.182)
195
Глава 6
6.4.2. Алгоритмы вторичного сглаживания оценок псевдо дальности
6.4.2.1. Вторичное сглаживания оценок псевдо дальности
оценками псевдо доплеровского смещения частоты
Положим, что приемник имеет следящую систему за задержкой дально-
мерного кода и следящую систему за фазой сигнала. На выходе ССЗ в моменты
времени tk с временным шагом Т формируются оценки псевдозадержки
сигнала тк, т.е. имеем вторичные наблюдения (6.180), а с выхода ССФ рассмот-
рим оценки псевдодоплеровского смещения частоты }лк, т.е. имеем вторичные
наблюдения (6.181).
Положим, что с некоторого момента времени tk = tko (т.е. к = к0)
необходимо организовать алгоритм совместной обработки вторичных измерений
(6.180), (6.181) с целью получения более точной оценки псевдодальности и
псевдоскорости. Нормируя (6.180), (6.181) на соответствующие константы
(скорость света с и длину волны несущего колебания Я), перейдем от наблюдений
псевдозадержки и псевдодоплеровского смещения частоты к наблюдениям
псевдодальности и псевдоскорости, т.е. запишем уравнения наблюдения в виде
Уя,к = *к + Чл > Уу,к = Ъ + "у* ■ (6-1 83)
Здесь ^ к и Пу к некоррелированны между собой, но каждый из них
коррелирован во времени, причем их корреляционные функции существенно
отличаются. Поэтому при строгом подходе к синтезу оптимальных алгоритмов
вторичного сглаживания (оценивания) Rk и Vk необходимо использовать
теорию оптимальной фильтрации на фоне коррелированных помех [5.1, 5.2].
Однако при этом получаются достаточно сложные алгоритмы фильтрации.
Рассмотрим упрощенный подход к синтезу, полагая процессы п^к и Пу к
некоррелированными во времени, а их дисперсии Dn„, Dn„ равны дисперсиям оце-
R V
нок псевдодальности и псевдоскорости, формирующихся на выходах ССЗ и
ССФ соответственно.
В качестве модели изменения псевдодальности можно использовать либо
модель второго порядка, аналогичную (6.94), либо модель третьего порядка,
аналогичную (6.171). Рассмотрим модель третьего порядка (с целью
последующего сравнения получающихся в данном разделе результатов с
результатами, приведенными в п. 6.3.6.7)
h = h-x + TVk-x, У к = Vk-x + Щ-i, ак = ак_х + $-ак_х, (6.184)
где %ак — дискретный БГШ с дисперсией D. .
196
Методы и алгоритмы обработки сигналов и извлечения информации
Уравнения (6.183), (6.184) описывают стандартную постановку задачи
оптимальной линейной фильтрации. Введем вектор состояния хк =
Д* У к "к
изменение которого во времени описывается общим векторным уравнением
(6.33), где следует положить
F =
1 Т 0
0 1 0
0 0 1
,G =
0
0
1
• D«=zv
Векторные уравнения наблюдения имеют вид
ук=Шк+пк,
(6.185)
где Н =
1 О О
О 1 О
. Dn =
А.
О
О А.
Тогда уравнения оптимального фильтра Калмана для оценки вектора \к
имеют вид
4=4 +к1к (у^ - 4)+ки [y9Jk - Pk), 4 = 4_,+rvk_x,
h=?k+къ,к {ук,к - 4)+Чк (уу,к -h)Jk=h-\+щ-\.
а-к=ак+ К5к (yRk -4) + K6Jc[yu - fk), (6.186)
^1,* =D\\,klDnR ' K2,k =Dl2,k/Dny » КЪ,к =Dl2,k/DnR » K4,k =D22,k/Dny »
4k = Dm/DnR , K6>k = D2Xk/Dn^ , (6.187)
где Dyk9 /,y = l,3 — элементы матрицы дисперсий ошибок фильтрации Dxk,
которая описывается матричными уравнениями
D"i =D-\ +HTD-H , Dx, =FDxJtlFT +GGT£^ , (6.188)
в которых D к — матрица дисперсий ошибок экстраполяции вектора х.
Вторичное сглаживание, как следует из (6.186), осуществляется
комплексной (для вторичных наблюдений псевдодальности и псевдоскорости) линейной
следящей системой.
На рис. 6.41 приведена зависимость СКО оценки псевдодальности,
полученная в результате моделирования алгоритма (6.186)—(6.188) совместно с
моделями ССЗ и ССФ для когерентного приемника и оптимальными
сглаживающими фильтрами третьего порядка в каждой из следящих систем при qc, =
=38 дБГц и динамике изменения задержки, соответствующей интенсивности
197
Глава 6
маневрирования 4g. Прямой линией на том же рисунке приведено значение
СКО оценки псевдодальности, формируемой на этапе первичной обработки.
ет,м
г + —
Первичная обработка
Вторичное сглаживание
\ - I
/,с
~0 2 4 6 8 10 '
Рис. 6.41. СКО оценивания задержки
Как видно, вторичное сглаживание псевдодальности позволяет
существенно повысить точность ее оценивания. В то же время, сопоставление
зависимости рис. 6.41 с аналогичной зависимостью, приведенной на рис. 6.39 и
полученной для комплексированной системы фильтрации псевдозадержки и псев-
додоплеровского смещения частоты на первичном уровне, показывает, что
точность оценивания псевдодальности при комплексировании на первичном
уровне выше (примерно в 3 раза), чем при комплексной обработке на
вторичном уровне.
Точность оценки доплеровского смещения частоты (радиальной скорости
сближения) в алгоритме (6.186) не улучшается по сравнению с точностью
фильтрации той же частоты в ССФ. Это говорит о том, что в оптимальной ССФ
достаточно корректно и полно извлекается информация о фазе и доплеровском
смещении частоты сигнала, если их изменение соответствует принятой при
синтезе модели (6.69). Если истинное изменение фазы сигнала отлично от того,
для которого проводился синтез, то при вторичном сглаживании возможно
повышение точности оценивания доплеровского смещения частоты. Однако в
рамках одной комплексной следящей системы (6.186) это не всегда удается
сделать. Так, если задержка и фаза сигнала изменяются в соответствии с
полиномом второго порядка, для повышения точности вторичного
сглаживания доплеровского смещения частоты необходимо сужать полосу пропускания
комплексной системы фильтрации по оценке частоты, что негативно
сказывается на точности сглаживания псев до дальности. Для повышения точности
сглаживания обеих компонент можно поставить дополнительную
узкополосную следящую систему, на вход которой подавать только вторичные
наблюдения псевдодоплеровского смещения частоты (6.181). Пример возможного по-
198
Методы и алгоритмы обработки сигналов и извлечения информации
вышения точности оценки псевдодоплеровского смещения частоты в
дополнительной следящей системе иллюстрируется зависимостью, приведенои на
рис. 6.42, где дана усредненная по 50 реализациям характеристика СКО оценки
частоты при ускорении а = 5 мс2 и ^ =38 дБГц.
6/, Гц
2
1.8
1.6
1.4
1.21
1
0.6
0.6
0.4
10 *>с
1XL_^
I j —"I ""I 1
II1 ' 5 '
I > i i
111 ! !
LI j. j 1 j.
II s I i '
E::±:::izzizziTd
Рис. 6.42. СКО оценивания доплеровского смещения частоты
На рис. 6.43 для сравнения приведена зависимость СКО оценивания
псевдодоплеровского смещения частоты в ССФ при тех же входных
воздействиях.
е/,Гц
/,с
Рис. 6.43. СКО оценивания доплеровского смещения частоты в ССФ
Из сопоставления графиков следует, что выигрыш по точности (СКО)
может составлять около 30 раз.
199
Глава 6
6.4.2.2. Вторичное сглаживания оценок псевдо дальности
приращениями оценок фазы
Кроме рассмотренного выше алгоритма вторичного сглаживания
псевдодальности оценками псевдодоплеровского смещения частоты в литературе
описаны алгоритмы вторичного сглаживания псевдодальности оценками фазы,
а точнее, приращениями оценок фаз на соседних интервалах.
Рассмотрим две оценки псевдофазы фк и фк_х. Из уравнений оптимальной
фильтрации фазы сигнала, например (6.92), можно записать выражение
к -фк-\=тЧ-\ +*i*W • (6Л89)
Если определить новое вторичное наблюдение
Уыр=<Рк ~Фк-\=тК-\ +К\ид<р,к> (6-190)
то оно отличается от наблюдения доплеровской частоты (6.179) множителем
2тгТ и вторым слагаемым. Из теории оптимальной фильтрации известно [5.1,
5.2], что при высокой точности фильтрации процесс w A является
некоррелированным. Тогда, разделив (6.190) на 2пТ и представив его в виде
Уь<р,к-\ =УА<р,к-\/(2ЛТ) = А-\ +"/,*-!, (6-191)
получаем вторичное наблюдение, полностью идентичное (6.181). Поэтому
далее можно использовать алгоритм оптимального вторичного сглаживания,
описанный в п. 6.4.2.1.
Отличие такого алгоритма оптимального сглаживания оценок
псевдодальности, от аналогичного алгоритма, описанного в п. 6.4.2.1, в том, что на его
вход подается иной процесс (с другой точки сглаживающего фильтра ССФ).
Моделирование данного алгоритма сглаживания показывает, что его
характеристики близки к характеристикам описанного ранее алгоритма.
Приведем еще один (упрощенный) алгоритм вторичного сглаживания
оценок псевдодальности приращениями оценок фаз.
Пусть имеем вторичное наблюдение псевдодальности
Уя,к=*к+"я,к> * = 0,1,2,..., (6.192)
и вторичное наблюдение приращений оценок фаз (6.191), приведенной (путем
нормировки на Я) к радиальной скорости
Уу9к=Ук+"у,к> * = U,... . (6.193)
Процессы пкк, Пу к, как и выше, полагаем некоррелированными во
времени и между собой и имеющими дисперсии Dr и Dr соответственно.
200
Методы и алгоритмы обработки сигналов и извлечения информации
Положим, что на рассматриваемом временном интервале допустимо
линейное представление
Rk=Ro+kTV09 (6.194)
где Rq = const; V0 = const.
Подставляя (6.194) в (6.192) и (6.193), получаем
У&9к=Ъ+кТУ0+пк9к9 * = 0,1,2,..., (6.195)
Уу9к=Го+»у9к>к = 1>2>- <6Л%)
Рассмотрим совокупность наблюдений (6.195), (6.196) на интервале
времени [0, А:] и получим оптимальные оценки RQk9 VQk для данной совокупности
наблюдений.
Из (6.196) найдем оптимальную оценку скорости
и подставим ее в (6.195) вместо V0 в каждое из наблюдений у^ ., j е [0, А:]:
к
В (6.180) второе слагаемое в правой части является известной функцией
времени, поэтому оценка псевдодальности, формируемая на основе
рассматриваемой совокупности наблюдений, определяется выражением
к ( .к \ \ к \ к
~{Ц у*; -jHyv^ ГГЙ^Л ~ 2^Х" * (6Л99)
й - 1
°>к~к +
/=0 v=\
Поставляя (6.197), (6.199) в (6.194), получаем выражение для оценки
псевдодальности в к -й момент времени
к , к
I ж—\ I т—\ ж—\ I 1
=i~rJlyR,i - jX^+Z^,v =^7jZ^+ -J^yyy ■ (6-20°)
/=0 v=\ v=l /=0 v=l
По аналогии с (6.200) запишем выражение для оценки псевдодальности в
(Л: — 1) -й момент времени:
Комбинируя (6.200), (6.201), запишем рекуррентное выражение
201
Глава 6
/=0 v=\
к в 1 у* У*,,* , 1
= 4,. + ^(^ - 4*)+^(»,* - Щ*-1)>
(6.202) где
kk=h-ik-i+TV0^ (6.203)
— экстраполированная оценка псевдодальности.
Из (6.202), (6.203) следует, что с течением времени (возрастание значения
к) второе слагаемое в (6.202) имеет все меньший и меньший вес, так что
информация, получаемая из псевдодальномерных измерений, становится все
менее существенной, и в установившемся режиме оценка псевдодальности
осуществляется лишь по приращениям фазовых измерений.
На рис. 6.44 приведены результаты моделирования алгоритма (6.202),
(6.203) в той же ситуации, в которой были получены результаты
моделирования алгоритма (6.186), (6.187) (см. рис. 6.40). Из зависимостей рис. 6.41 и
6.44 видно, что упрощенный алгоритм, описанный в данном разделе,
незначительно (< 5 %) уступает по точности (СКО) комплексному алгоритму
сглаживания.
9
8
7
6
5
4
3
2
1
О 2 4 6 8 10 #>с
Рис. 6.44. СКО оценивания псевдодальности
В [6.8] описан алгоритм сглаживания дальномерных измерений фазовыми,
который получается из (6.202), (6.203) при отбрасывании третьего слагаемого в
(6.202), а вместо оценки (6.197) используется текущее измерение (6.196). Такой
алгоритм оценивания (сглаживания) описывается рекуррентным уравнением
202
Методы и алгоритмы обработки сигналов и извлечения информации
К* ~ h-\,k-\ +Уу,к-1 +J^i\yR,k ~[Rk-i,k-\ +Уу,к-\))-
=*тт^+*тт(^-+^-)- (6204)
В приведенных алгоритмах вторичной обработки формируется оценка
псевдодальности, в которой реализовано дополнительное сглаживание
погрешностей, обусловленных внутренним шумом приемника, но которая, по-
прежнему, содержит все остальные составляющие погрешности определения
псевдодальности такие, как ионосферная, тропосферная, расхождение шкал
времени НС и потребителя, релятивистские, погрешности многолучевости и
др. (см. гл. 7).
6.4.3. Одношаговый алгоритм вторичной обработки
Как отмечалось в п. 6.4.1, итоговая навигационная задача является задачей
получения оценок вектора потребителя по имеющимся векторным вторичным
наблюдениям при условии наличия информации о параметрах движения
(координатах и векторах скорости) навигационных спутников, которая формируется
в приемнике потребителя в результате декодирования навигационного
сообщения из принятых радиосигналов.
Решение этой задачи оценивания во многом определяется принимаемыми
при ее решении моделями оцениваемых и мешающих процессов.
Использование различных моделей приводит к различным алгоритмам обработки.
Наиболее простым является алгоритм, основанный на независимой
обработке каждой совокупности наблюдений (6.178), (6.179) в заданный момент
времени tk.
Учитывая определение псевдодальности и псевдоскорости, запишем
(6.183) в виде
У** =Мхк>Ук>2к) + Д'+ "*,*> (6-205)
^=^(^^М'^) + ^ + ^,,. (6.206)
где R(xk,yk,zk), v(Vxk,Vyk,Vzk) — истинные дальность и скорость
сближения / -го НС и потребителя; Д' = ct'; V = Л/'; t', /' — смещение часов и
частоты опорного генератора приемника потребителя относительно бортовых
эталонов частоты и времени; [xk,yk,zk\ — координат потребителя, например,
в геоцентрической вращающейся системе координат (ПЗ-90 или WGS-84);
iK,k»Vyjc»К,к} — составляющие вектора скорости потребителя в той же
системе координат.
203
Глава 6
Рассмотрим задачу оценки координат потребителя {xk,yk,zk} и смешения
часов t'k по вторичным наблюдениям (6.205), i = \,N. Полагаем, что
погрешности nR k имеют нулевое математическое ожидание.
Введем вектор состояния х = |х^гД'|т, вектор вторичных наблюдений
Ук,к ~
nRbk nR2,k -nRN,k
\УкькУкък-У~к„,к\ и вект°Р погрешностей П/ц =
Линеаризуем вторичные наблюдения yRk (6.205) относительно некоторой
априорной оценки хк = \хк ук zk Д'к | :
у^=ь(^)+й(^Ж-^)+п^' (6-207>
где
dh(xk)
///(х,) = /га(х,)+д;;н(х,) =
(6.208)
*к=*к
Здесь и далее принято определение производной от скаляра /(х) по
вектору как вектор-строка [6.3]:
#(х)
dx
df df df
dxx dx2
dx,
n\
из которого следует соотношение
df
j|/1(x)/2(x).../m(x)[T =
dx
dfx
dxy
dx„
dfm
df
m
dx.
dxr
Введем векторы ошибок Ay ~Rk = yRk -h(xk), Axk=xk-xk и
представим (6.207) в виде
АУ/Ц=ЙАх*+п/Ц- (6-209)
Ставим задачу нахождения такой оценки Ахк, которая минимизирует
квадратичную форму:
е2 = (АУ*,* - ЙАх* Г (АУ/Ц " ЙАх*) • (6-210)
204
Методы и алгоритмы обработки сигналов и извлечения информации
Решение задачи ищем путем прямого дифференцирования s по Ахк и
приравнивания нулю полученной производной:
де1
= -2HT(Ays>t-HAx4)
О
Дх^ =Ах^
Полагая, что матрица (ЙТН) невырожденная, находим решение данного
уравнения:
Дх, ЦЙТН)-1 НтДУ/а , (6.211)
где ДхЛ = xk-xk,a xk — искомая оценка вектора состояния.
Можно показать [6.8], что решение (6.211) является необходимым и
достаточным условием минимума квадратичной формы (6.210).
Из (6.211) получаем
х,=х,+(нтн)_,НтДу^. (6.212)
Если известна матрица D = M[n^kn^k] дисперсий погрешностей
вторичных наблюдений (6.207), то вместо (6.193) можно использовать алгоритм
Axk =(htD-;h)_1 НХ;Ду^ , (6.213)
который получается, если в показатель качества (6.210) ввести весовую матри-
«уК ■
Рассмотрим матрицу Й(хЛ). Используя определения (6.208), запишем
-cos^) -cos(^) -cos(^) 1
-COs(tf2) -COs(/?2) ""cos(^2) 1
H(M
-cos(a^) -cos(^) -cos (7^) 1
(6.214)
где (Xj, Д, yi — направляющие косинусы линии визирования потребитель—i
й НС, которые определяются соотношениями
cos
(«<)■
xi,k xk
Ri,k
,COS(A):
Уик-Ук
R'i,k
, cos(^-) =
zi,k zk
Kk
Rlk=i(xi,k-*k) +{Уц~Ук) +{zi,k-zk) •
(6.215)
Если априорная оценка хк вектора состояния недостаточно хорошая, то
соотношения (6.211), (6.213) можно рассматривать как первую итерацию, яв-
205
Глава 6
ляющуюся исходной точкой для последующих итераций (при выполнении
замены ху =хк), которые продолжаются до тех пор, пока ошибка оценивания
вектора состояния не станет достаточно малой.
Соотношения, аналогичные (6.211), (6.213), можно записать и для задачи
оценки составляющих вектора скорости потребителя по результатам обработки
вторичных наблюдений (6.206). При этом в навигационных функциях (4.7),
связывающих псевдоскорости с составляющими вектора скорости
потребителя, вместо истинных координат потребителя {x,^,z} следует использовать
оценки {jc,^,z} , полученные описанным выше методом (например, (6.212)).
6.4.4. Фильтрационные алгоритмы вторичной обработки
Недостатком одношагового алгоритма вторичной обработки является то,
что в нем не учитывается информация о координатах потребителя,
составляющих его вектора скорости, смещении ШВП, уходе частоты опорного
генератора, полученная на предыдущих тактах работы приемника. Кроме того, в нем
нельзя использовать оценку доплеровского смещения частоты, полученную в
ССФ для улучшения точности оценки координат потребителя. Устранение
данных недостатков достигается при использовании фильтрационных
алгоритмов вторичной обработки.
Суть фильтрационных алгоритмов заключается в том, что принимается
некоторая априорная модель изменения оцениваемого вектора состояния хк в
дискретном времени tk. Далее с использованием этой априорной модели и
результатов вторичных наблюдений в моменты времени tk организуется слежение
за изменяющимся во времени вектором состояния. Искомая следящая система
строится на базе теории оптимальной фильтрации, поэтому такие алгоритмы и
называют фильтрационными. В них учитывается вся предыстория изменения
вектора состояния, что приводит к повышению точности формируемых оценок.
Модель динамики вектора состояния
Из теории оптимальной фильтрации [5.1, 5.2] следует, что модель
динамики изменения вектора состояния во многом определяет как структуру, так и
свойства синтезированной системы фильтрации. Чем точнее априорная модель
отражает реальные свойства фильтруемого процесса, тем выше точность
фильтрации. Поэтому для различных приложений (геодезия, автомобильный
транспорт, мореплавание, авиация и др.) целесообразно использовать
различные модели для повышения точности определения координат потребителя.
Учитывая это обстоятельство, а также то, что данная книга не предполагает
детального рассмотрения всех возможных вариантов приложений, ниже в качест-
206
Методы и алгоритмы обработки сигналов и извлечения информации
ве примера приводится лишь одна из возможных моделей, ориентированная на
подвижного потребителя.
Как и в предыдущем разделе, будем полагать, что координаты потребителя
{xk,yk,zk) определяются в геоцентрической вращающейся системе координат,
а динамику их изменения определим уравнениями
хк = хк-\ + ^К,к-\» Vxjc ~ Vx,k-\ + Тахк_х, ахк = ахкЛ + Т%хк_х,
У к = Ук-i + TVy,k-\ > vy,k = vy,k-i + Tay,k-i * ay,k = ay,k-\ + T%y,k-\»
Zk = Zk-\ + TVz,k-\ » Vz,k = Vz,k-\ + Taz,k-\ » az,k = az,k-\ + T%z,k-\»
где 4Xtk-i>€yjt-i>€z,k-i — независимые ДБГШ с нулевыми математическими
ожиданиями и дисперсиями D^ ,D^ ,D^ соответственно.
Так как вторичные наблюдения (6.205, (6.206) содержат смещения часов
t' = Д'/с и опорного генератора /' = V'/А , необходимо задать модель
изменения данных параметров.
Модели смещения часов
В гл. 2 приведены общие соотношения (2.6), (2.7) для смещения часов
t'{t), которые для удобства запишем еще раз:
dt'it)
~^1 = Sv0T{t), (6.217)
^м-2-Н?1. (6-218)
2^/н.ог dt
где /н ог — номинальная частота опорного генератора; <p(t) — отклонение
(флуктуации) фазы ОГ от идеальной (линейной); Sv0T — относительная
расстройка частоты ОГ.
Из (6.217) следует, что для конкретизации модели смещения часов
необходимо задать модель изменения относительной расстройки частоты Sv0T.
Данная модель во многом определяется типом используемого ОГ. В технических
описаниях к серийно выпускаемым ОГ задаются характеристики
кратковременной и долговременной нестабильности ОГ. При выборе параметров
следящих систем навигационного приемника большее значение имеет
кратковременная нестабильность ОГ, которая и будет рассмотрена ниже.
Как отмечалось в п. 2.4, кратковременная нестабильность частоты ОГ
характеризуется спектральной плотностью фазовых шумов S (/). В техниче-
207
Глава 6
ских условиях на ОГ задается спектральная плотность Sn<p(f) циклической
фазы <pn(t) = (p(t)/(2K) в виде, приведенном в табл. 6.4, например, для ОГ
ГК68-ТС-ДЗ фирмы «МОРИОН» /н ог = 10 МГц.
Таблица 6.4. Спектральная плотность фазовых шумов
Значение
частоты, Гц
1
10
100
Значение спектральной плотности
шумов, дБ/Гц
-80
-120
-140
Учитывая (2.10) и определение циклической фазы, можно записать
^„(/И^/А^Чл/)-
(6.219)
В табл. 2.1 приведены различные составляющие шума, которые принято
использовать для характеристики спектральной плотности SSv, (/)
относительной нестабильности частоты ОГ. Для синтеза следящих систем методами
теории оптимальной фильтрации модель смещения часов должна быть
марковской, поэтому модель изменения относительной расстройки частоты также
желательно иметь марковскую. В табл. 2.1 к таким моделям относятся белый
фазовый шум, белый частотный шум и шум случайного блуждания частоты.
Поэтому можно предложить следующие модели для описания процесса Sv0T (t):
а) модель Sv0T(t) в виде белого гауссовского шума с равномерной
двусторонней спектральной плотностью Nv = SSv (0)/2
<Чт (0=&('); (6-22°)
б) модель Sv0T(t) в виде винеровского процесса, для которого
справедливо уравнение
~5Г = £('). (6-221)
где двусторонняя спектральная плотность формирующего шума N*
выбирается из заданных характеристик спектральной плотности фазовых шумов для
конкретного типа ОГ;
в) модель Sv0T(t) в форме экспоненциально коррелированного процесса,
описываемого уравнением
(6.222)
208
Методы и алгоритмы обработки сигналов и извлечения информации
где ау — константа, характеризующая ширину спектра флуктуации частоты ОГ;
%y(t) — БГШ с односторонней спектральной плотностью Ng .
Модель (6.222) является некоторым обобщением модели (6.221),
позволяющим учесть спадание спектральной плотности флуктуации относительной
частоты ОГ на больших частотах.
Для ОГ, характеристики которого приведены в табл. 6.4, спектральная
плотность фазовых шумов в области частот 1...10 Гц, попадающих в полосу
частот пропускания систем слежения за фазой сигнала, спадает на 40 дБ, что
соответствует зависимости спектральной плотности от частоты как I//4 .
Такой характер спадания спектральной плотности соответствует модели (6.205)
для относительной нестабильности частоты ОГ.
Переход к моделям смещения часов в дискретном времени получается в
результате интегрирования соответствующих непрерывных уравнений на
интервале временной дискретизации. Так, для модели (6.217), (6.221)
соответствующие уравнения имеют вид
*'к = *к-1 + TSvot*-\ + £',*-! > <Чт,* = <Чт,*-1 + &,*-! > (6.223)
где|*=|4/\* &9к
AflLll \ = N.
likil\-"zf
(6.224)
— дискретный БГШ с матрицей дисперсий
г3/з t2/i\
Т2/2 Т |
Для получения более устойчивых для вычислений алгоритмов фильтрации
целесообразно в вектор состояния объединять составляющие, приведенные к
одному диапазону численных значений. Поэтому вместо смещения часов tf
введем смещение по дальности Д' = ct\ где с — скорость света, и запишем
уравнения (6.207), (6.208) в эквивалентном виде:
Д[ = д;_, + TVU + £д',*-1, К = VU + Zvjc-i> (6-225)
где $* = &.* tf*
M[^k] = Q^=c2N4f
(6.226)
дискретный БГШ с матрицей дисперсий
Г3/3 T2/l
Т2/2 Т
i iT
Введем вектор состояния \к =\хк Vxk ук Vyk zk Vzk Д[ Vk\ и вектор фор-
%х,к Ьу,к 4z,k %k
мирующих шумов §хк =
нение
хк = ^xk-l + ^\,к-\'
, для которого можно записать урав-
(6.227)
209
Глава 6
где
F =
F, О О О
О Ц О О
О О F, о|
О О О F,
G =
О
о
о
о
G,
О
о
о
о
G,
О
о
о
о
G,
|1 Т
0 1
.G,=
0
1
,G2 =
1 Ol
0 1
м
\Ъ\&,к J - R^ -
D
0
0
0
0
0
0
0
0
D
0
0
0
0
(6.228)
У К,к Уу2,к ■•■yVN,k
т
Модель вторичных наблюдений
Запишем вторичные наблюдения (6.205), (6.206) в векторном виде:
I lT
ГДе Ук,к=\УЁьк Уя2,к ■■■Уя]М,к\ >Уу,к =
hR Ы = ^ Ы \ К ) - hRN (Xk )
hR, Ы=[ (*,■ -х)2 +U -yf +(z> ~zf] +Д'>
hAxk)=\byx {ч) h2(хк) -hN(**)| ;
h u\Axi~x) (х,~х)+{у-у) (ц-Я+(*»-*) (*,•-*) n
(6.229)
(6.230)
(6.231)
(6.232)
Синтез алгоритмов вторичной обработки
Для вторичных наблюдений (6.229), (6.230) аддитивные помехи п^, п^,
формируемые в темпе работы следящих систем по задержке и фазе (частоте)
сигнала (1...10 мс), являются коррелированными процессами. Поэтому, если
вторичную обработку информации осуществлять в том же темпе, то для
синтеза соответствующих алгоритмов необходимо использовать теорию
оптимальной фильтрации при коррелированных шумах наблюдения [5.1, 5.2]. Однако на
210
Методы и алгоритмы обработки сигналов и извлечения информации
практике так не делают ввиду того, что информацию потребителю о его
координатах нет необходимости выдавать чаще, чем 1 раз в секунду. Поэтому
алгоритмы вторичной обработки также целесообразно реализовывать с тем же
темпом (1 Гц), при котором шумы вторичных наблюдений можно считать
некоррелированными.
При некоррелированных шумах вторичных наблюдений (6.229), (6.230)
задача фильтрации вектора состояния хк, изменение которого во времени
происходит в соответствии с (6.216), (6.225), может быть решена на основе
расширенного фильтра Калмана [5.1, 5.2], описываемого уравнениями
хк ~ Хк + Ux,k
V kn R-l(yk-h(xk)), x,=Fx,_]5
D^ = Di +
дх
ах
r;
DX)A=FDX,FT+GR^GT,
ах
(6.233)
(6.234)
где ук =
\Уй,к
\Уу,к
у h* =
hR,k
hv,k
у Пк =
UR,k
nv,k\
R.=^[n*<] =
D
aR
0
0
D
nv
xk —
текущая оценка вектора состояния; хк — экстраполированная оценка вектора
состояния; Dx к — матрица дисперсий ошибок фильтрации вектора хк ; Dxk —
матрица дисперсий ошибок экстраполяции.
В алгоритме (6.233) обрабатываются как наблюдения дальности (6.229),
так и наблюдения скорости (6.230). Следовательно, получаем комплексный
фильтр обработки, имеющий наилучшие характеристики точности фильтрации
вектора состояния. В принципе, наблюдения (6.229) и (6.233) можно
обрабатывать в раздельных фильтрах. Так, рассматривая вектор состояния хк,
описываемый уравнениями (6.216), (6.225), а в качестве наблюдений используя
только (6.229), получаем следующие уравнения фильтрации:
Хк ~ хк + Dx,*
V
дх
D»i (У^ "ьл (**))» ** = Fi*-i»
/
К,к
DA=D"'t +
-1
'х,к
V
дх
•я
/
дх
(6.235)
(6.236)
DX)^FDX,FT+GR^GT
Точность фильтрации вектора состояния в алгоритме (6.235)—(6.236)
хуже, чем в алгоритме (6.233)—(6.234).
211
Глава 6
Аналогично можно записать алгоритм вторичной обработки вторичных
наблюдений по скорости (6.230). Однако при этом надо исключить координаты
потребителя и смещение часов из вектора состояния, т.е. ввести вектор
гк=\ Vxk Vyk Vzk Vk\ , а в определении функций (6.232) вместо координат
потребителя [xk,yk,zk] использовать их экстраполированные оценки
йк =\хк ук zk\T, формируемые в соответствии с (6.235). Итоговый алгоритм
фильтрации имеет вид
ъь =z.k +D
г,к
дМг*»й*)У
dz
ЪпЦу^-К^к >«*))>
(6.237)
Di=D"i +
дЬу(*к>*к)\ ,л-1 дК{ч^к)
дг
D
6Ж, = DK.A + Rf , R,=
zyk
D,
о
о
nF
о
о д
iv
dz
0
0
0 А
iz
0
о
о
0 0 czN^fT
(6.238)
6.5. Одноэтапная обработка сигналов в приемниках СРНС
6.5.1. Общие сведения
В предыдущих разделах рассматривались приемники СРНС с двухэтапной
обработкой сигналов, которая логично вытекает из псевдо дальномерного
метода, описанного в п. 4.3, и включает этап оценки параметров радиосигналов
(псевдо дальностей, псевдо фаз и псевдо доплеровских смещений частоты) и
этап оценки координат потребителя и составляющих его вектора скорости. В то
же время, используемые для синтеза оптимальных алгоритмов обработки
сигналов методы, позволяют сразу решать задачу формирования оценок
координат потребителя по наблюдениям высокочастотных сигналов НС [6.9, 6.10].
При этом получается единый алгоритм обработки всех принятых сигналов НС,
в котором нельзя выделить отдельные алгоритмы оценки параметров
радиосигнала и координат потребителя, поэтому такую обработку сигналов
называют одноэтапной.
На вход схемы обработки поступают сигналы с выхода ВЧ-приемника
(6.239)
y(o)=k(0'fi'Ai)+,,yi> •••' 5п{1]>?п>/Лп)+п]п
212
Методы и алгоритмы обработки сигналов и извлечения информации
Так как псевдо задержки ft и псевдо доплеровские смещения частот fAi,
/ = l,w зависят от вектора потребителя П = \х у z Д' Vx Vy Vz V'\ , введем
обозначения гДП), /Д/(П).
Как отмечалось в п. 6.3.2, используемая для синтеза алгоритмов обработки
сигналов теория оптимальной фильтрации приводит к следящей системе (в
общем случае многомерной), обобщенная схема которой приведена на рис. 6.8.
В данной схеме оценке подлежит обобщенный вектор к информативных
процессов. Существенным требованием при синтезе оптимального алгоритма
является необходимость того, чтобы к отображался в пространстве состояний
многомерным марковским процессом.
Учитывая данное обстоятельство, определим в качестве вектора к
отображение вектора потребителя в пространстве состояний. В п. 6.4.3.2 введен
|т
, описываемый
уравнениями (6.216), (6.225). Положим к = \. Для синтеза оптимального одноэтапного
алгоритма обработки можно использовать методику, описанную в п. 6.3.
Учитывая, что синтез алгоритма обработки сигналов в когерентном и
некогерентном приемниках проводится по разному, рассмотрим в качестве примера
синтез более простого алгоритма для некогерентного приемника.
6.5.2. Синтез одноэтапного алгоритма обработки сигналов
для когерентного режима работы
На входе приемника имеем совокупность сигналов всех видимых НС
(6.28). Положим, что радиочастотный блок приемника имеет структур,
приведенную на рис. 6.7, и на его выходе формируются векторные наблюдения
(6.29). Запишем данные наблюдения для интервала времени [^-i,1'^-i,m]
У(*к-и) = «('t-u .*»*•)+ n*-U' (6-24°)
W*i('*4/>fi,*-i>U,*-i) =
= Aihm,i (h-u ~ Ъ,к-\ )Kc,i*-\ cos(fi>n/k-\,i+^ni,k-\lTd + Фик-\) (6-241)
— навигационный сигнал / -го НС, пк_у — вектор независимых дискретных
БГШ с матрицей дисперсий Dn.
Как и в п. 6.3, параметры Г/,/Д1-,^,^ каждого из принимаемых сигналов
полагаем постоянными на интервале наблюдения Г^_1,1Л-1,м] •
213
Глава 6
Согласно методике, изложенной в п. 6.3, синтез многомерной следящей
системы, в которой обрабатываются наблюдения (6.240) с цель формирования
оценок вектора состояния \к, может быть разделен на синтез многомерного
дискриминатора и синтез интегрированного сглаживающего фильтра.
6.5.2.1. Синтез многомерного дискриминатора с когерентной
обработкой
При синтезе многомерного дискриминатора используется общее
выражение (6.30), в котором в качестве функции f\\^,\\ необходимо использовать
функцию правдоподобия для наблюдений (6.240), для которой справедливо
представление (6.32).
В когерентном режиме работы приемника оцениваемыми параметрами
сигнала являются псевдо задержки fi и псевдо фазы ф{ принятых сигналов
(/ = 1,и), поэтому введем векторы оцениваемых параметров v, = |f, ф§
навигационных сигналов.
Как и выше, символы навигационного сообщения hHCi к_х рассматриваются
как случайные величины, принимающие значения ±1, что соответствует
изменению фазы сигнала на ±тг В п. 6.3.4 было показано, что при приеме
одиночного сигнала усреднение функции правдоподобия по случайным значениям
символа навигационного сообщения дает функцию /(Y^ Д] вида (6.37). При
синтезе многомерного дискриминатора одноэтапного алгоритма обработки
усреднение функции правдоподобия необходимо выполнить по значениям
символов навигационных сообщений всех видимых сигналов. Запишем функцию
правдоподобия (6.32) в виде
( и \
P^lv^cexp ^
/=i
( * м-\
/=1
= *]^ехр — ^-^
\Gn 1=0
(6.242)
Усредняя (6.242) по значениям символов h^Qik_x, получаем
V°" /=o
(6.243)
Введем обозначение
214
Методы и алгоритмы обработки сигналов и извлечения информации
А
м-\
h(va_i(x*_,)) = — ^у(*к-и)Ьдм('*-и -*u-i (*k-i))c°sK'*-u + ф{.к_х (х*_,)),
ап 1=0
(6.244)
и запишем (6.243) в виде
p(Y1M|v,_1) = /(Y1M,x,.1) = cnch(//(va_1(x,_1))).
(2.245)
i=i
В одноэтапном алгоритме обработки срузу ищется оценка вектора
состояния потребителя х, поэтому функцию правдоподобия (6.245) необходимо
рассматривать как функцию аргумента х. Поэтому многомерный дискриминатор
следует определять выражением
«**-i(**-i) =
ain/^x,.,)
ах
Хк-\ _ Хк-\
(6.246)
Учитывая функциональную зависимость \k_l =g(xA._]), представим
(6.246) в виде
/ / / >\\т
^-i(Vi) = S
/=1
дх
д\п(р(\1м\хк_1))
dv,
(6.247)
J
Определим многомерный дискриминатор по параметрам сигнала / -го НС
соотношением
и
да-i
av,.
(6.248)
Выполнив дифференцирование в (6.248), запишем
ида-1 = th(/;(x*-i)j
dft
дф1
(6.249)
Здесь 1Ау1к_х(\к_х)\, описываемый (2.244) в точке экстраполированной
оценки v, к_1 [хк_]), — синфазный коррелятор для сигнала / -го НС.
Введем квадратурный коррелятор для сигнала / -го НС соотношением
А/-1
Qi(va_i (i*_i)) = -jXУ('к-и)нщ(h-v ~Кк-\{Ч-\))sin(*>Л-1,/ + Й,*-1 (x*-i))
'и /=0
215
Глава 6
Тогда (2.248) можно записать в виде
ufla4=th(//(va_1(xifc.1)))
ОТ: V
(6.250)
Из данного выражения следует, что по сигналу каждого спутника
формируется два дискриминатора: задержки огибающей (дальномерного кода) и
фазовый дискриминатор. При этом в фазовом дискриминаторе опорный сигнал
берется в точке экстраполированной на момент времени tk_x фазы, а на
интервале [^_i,^-i,A/-i] фззъ опорного сигнала не меняется. Последнее
обстоятельство при больших временах накопления сигнала в дискриминаторе приводит к
нарастанию фазовой ошибки к концу интервала накопления и, как следствие, к
ухудшению точности фильтрации. Для устранения этого недостатка фазу
опорного сигнала можно менять линейно по закону
где d)Jxk — оценка псевдо доплеровской частоты, которая может
формироваться в сглаживающем фильтре следящей системы.
В качестве дискриминаторов задержек огибающих (дальномерных кодов)
и фазовых дискриминаторов принимаемых сигналов НС могут использоваться
различные типы дискриминаторов когерентных приемников, описанные в
п. 6.3.4.
В описание многомерного дискриминатора (6.247) входят матрицы
dvik_l(\k_]) ~ /
—! = НЛ\к_1), которые будем называть матрицами связи, т.к. они оп-
дх
ределяют связи радионавигационных параметров сигналов v и навигационных
параметров х потребителя.
Для расчета этих матриц необходимо конкретизировать вектор состояния
\к. Определим для когерентного приемника вектор состояния в виде
i it
*к =\хк У к Ч D'k vx,k vy,k vz,k К ax ay az R^| » где {xk,yk,zk} — координаты
потребителя в геоцентрической вращающейся системе координат, связанной с
Землей (ПЗ-90); {VXtk>Vy,k>K,k} — составляющие вектора скорости потребителя
в той же системе координат; {ах,ау,аА — составляющие вектора ускорения
потребителя; D'k =ct' — смещение по дальности, обусловленное расхождением
шкал времени НС и потребителя; Vk = Я/д' — смещение по скорости
сближения, обусловленное нестабильностью частоты опорного генератора;
216
Методы и алгоритмы обработки сигналов и извлечения информации
r>
Rd\ Rd2 -Rein
— вектор дополнительных переменных, характеризующий
задержку (дальность Rd2), связанную с фазой сигнала
Ai Ai
(6.251)
Функциональная зависимость f{ (х) определяется выражением (см. (4.8))
f, = ^J(x-xt)2 +(у-У1)2 +(z-zi)2 + Д'), (6.252)
где {jc^j^z,.} — координаты /-го НС, которые полагаем известными, т.к.
информация о них передается в навигационном сообщении; Д' = ctf — смещение
по дальности, обусловленное расхождением шкал времени НС и потребителя;
с — скорость света.
Учитывая структуру выражения (6.247) (то, что параметр v, входит в чис-
лител одного сомножителя и знаменатель другого), можно под v,- понимать
любой вектор, ему пропорциональный. Поэтому положим для дальнейшего
рассмотрения vz =
Mi Rdi , полагая Rdi (t0) = Д, (t0)
Представим вектор состояния в виде xk -
х0=\хугДГ, xv=\Vx Vy Vz V'\ , xa =
ax ay az
xD,k xV,k xa,k^d\ » гДе
подвектора координат,
скорости и ускорения.
Тогда, для матрицы связи можно записать выражение
Н,(х)
0v, (х)
дх
ад(»)
ах
дх
= .
ады
dxD
О
0 0 0
0 0 L,
(6.253)
где дДЫ =,(„,) _С08(д) _со8(Г/) 1|,
ах
D
Lt =|0 0 ... 1... 0| — вектор-строка, на /-1 позиции которой стоит
единица, а на остальных — 0.
Введем векторные дискриминаторы дальностей (задержек огибающих), и
«дополнительных переменных (фаз) для сигналов всех НС
и
аД,к
и
и
... и.
адьк "яД,к - "аД„,к
217
Глава 6
u
ДЛ«/,*
Ujxkdx,k lijxRd2,k ~'UixRdn,k
= -diag(2^)|w^^ идф1шк -идфп9к
= -diag(2^)uflW, (6.254)
где diag(2^/A/), / = 1,л — диагональная матриц, на главной диагонали
которой на пересечении / -й строки и / -го столбца стоят элементы 2л/Xt, а все
остальные элементы равны нулю.
Соответствующие типы дискриминаторов и^д к, иЛф к описаны в п. 6.3.4.
Запишем сумму, стоящую в (6.247) в виде
_vfdva(**-,)v
ид,А:-1 ~ Zj
Ы
'(p(Y,"lxt-,))
8v
У
/
uaxD,k-l
ид\у,к-\
идх0Л-1
"дЙ^Д-!
(6.255)
Из (6.253)-(6.255) следуют представления дискриминаторов по
координатам и дополнительным переменным
ЦДХ£)Д
ид\у,к
Ыдх,к иду,к идг,к идО\к
= Hu
дД,к
идУх,к идУу,к идУ2,к ыдУ\к
= о,
и
д*аЛ
Ыдах,к идауМ Ыда2,к
= о,
U
aRdJc
a,Rd\,k aRcJ2,k '" aRdn<k
= -diag(2;r/4-)ii^,
(6.256)
где
H =
-cos(#,) -cos($) -cos^) 1
-cos(«2) -cos(/?2) -cos (ft) 1
-cos(a„) -cos(#,) -cos(r„) 1
(6.257)
Обобщенная схема многомерного дискриминатора когерентного
приемника с одноэтапной обработкой сигналов приведена на рис. 6.45.
Отметим, что в соответствии с (6.255) вектор выходных отсчетов
дискриминатора ид формально содержит составляющие по всем компонентам
вектора состояния \к , ряд из которых тождественно равен нулю.
218
Методы и алгоритмы обработки сигналов и извлечения информации
!йд(х*-1)
*(**-! )
yfo-u)
(**-l)
Блок дискриминаторов
дальностей (задержек) до НС
шяД
Нт
и
—».
Блок фазовых дискриминаторов
др
-diag(2*/4)
■дк.
I
о
Рис. 6.45. Обобщенная схема многомерного дискриминатора когерентного
приемника с одноэтапной обработкой сигналов
6*5.2.2. Синтез интегрированного сглаживающего фильтра
Для синтеза сглаживающего фильтра многомерной следящей системы
когерентного приемника с одноэтапной обработкой сигналов будем использовать
методику линеаризации многомерного дискриминатора с последующим
использованием теории оптимальной линейной фильтрации эквивалентных
наблюдений, приведенных к оцениваемым параметрам [5.1].
Представим идд в виде
■W-i = иЯ, (*А.*-1)+ hjt-i' (6-258)
где Un.\£n.k-\\ — дискриминационная характеристика дискриминаторов
дальности; £д. k-i — ШУМ на выходе того же дискриминатора;
А
£д к = Д Jti- ~ Д',А:-1 — ошибка оценки псевдо дальности.
Линеаризуем дискриминационную характеристику Uд \£д к_х) и
представим (6.258) в виде
где S у, — крутизна дискриминационной характеристики.
Соотношения (6.259) линейны по ошибкам оценки псевдо дальности, но
они нелинейны относительно ошибок оценки координат потребителя
ех,к-\ ~ хк-\ ~ *к-\ ' еу,к-1 = Ук-\ ~ Ук-\ ' ez,k-l ~ Zk-\ ~ 2к-\ » еЦ\к-\ ~ Дк-\ ~ Дк-\ ■
Это второй тип нелинейности в многомерном дискриминаторе. Разложим
I л 1т
ошибку бд к_х в ряд в точке оценки i^., =\xk_l yk_x zk_x Дк_А и ограничимся
линейными членами разложения
219
Глава 6
' £Ху
£Vx £v £v £г И ДИа-
^ = & *** + "ду *>*+ & ^ + с^'* "
= -cos(al-)fx>t -cos(^)fM -cos(^.)^ +^д^.
Следовательно, в результате вторичной линеаризации (2.259) получаем
»W-i = 5дД- (_cos(^)^-i "С08(Д>^-i -cos(r,-k,*-i +£д\к-\) + £дьк-
Введем вектора ошибок ех =\sx £у £z £д
тональную матрицу (HaglS д ], на главной диагонали которой на пересечении
/ -й строки и / -го столбца стоят элементы 5" д , а все остальные элементы
равны нулю. Тогда для вектора и л к можно записать выражение
I |Т
где %пк\^п к %д к — €д к\ > а коРРеляЦионная матрица этого шума равна
Линеаризация дискриминатора по дополнительной переменной
соответствует линеаризации фазового дискриминатора, для которого можно записать
выражение
Подставляя (6.260), (6.261) в (6.256), получаем
идй„,*-1 =-diag(^A)(-diag(2^^//^)^^1 + ***-,)■ (6-262)
Преобразуем (6.262) к виду
(н^Кд, )Й)"' «д,0,*-1 = «.„.t-i +(нТ0!а8(5дД. )й)"' Й^_,,
diagf(2*5ДЙ /Д,. )2)] uakj д_, = %к_, - (diag(2^; /Я,))"' ^_, .(6.263)
Введем эквивалентные наблюдения по координатам
Ух0>к-\ = XD,£-1 + 4xDJc-l '
Уй,д-1=й^-1+%,,_,, (6.264)
220
Методы и алгоритмы обработки сигналов и извлечения информации
где 4Xrf>jt-i> %.*_! — ДБГШ с дисперсиями
\-i
м[лХсп;о] = К,1с=(н'<На8(5дД)н)" HTR^ft(rdiag(sajH) ,(6.265)
При одинаковых крутизнах дискриминационных характеристик и уровней
шумов на выходах дискриминаторов в каналах слежения за сигналами НС,
(6.265), (6.266) упрощаются
Л
R
'Д
Пх0
ы
(Нтй)\ R„=diag
V*
[2^тг)
4 =
Запишем уравнения, описывающие изменение вектора состояния
xk ук zk Д'к Vxk Vyk Vzk Vk ax ay az RTd\ . Модель изменения координат
потребителя зададим уравнениями (6.216), модель смещения Д',
пропорционального смещению часов t', — уравнениями (6.225), а модель вектора
дополнительных переменных запишем в виде
R<a = R<a-i + rv*-i> Vk = Нхк* + diag(a,.)vHC>jfc,
i iT
где diag(A,-) = \cos(at) cos(Д) cosfo )|, VHC = |VHC] VHC2 ... VHCw | .
В векторном виде динамические уравнения имеет вид
XD,k = XD,fc-l + T*V,k-\ '
^=х^_1+Гха>,_1+7Б^ог,к_1,В = |0 О О 1|т,
Ха,к ~ Ха,к-\ + ^эа,к-1 >
*d,k = R^-i + THxy^ + rdiag(A,-) Vhc^, . (6.266)
Заметим, что динамические уравнения (6.266)и уравнения наблюдения
(6.263) линейны относительно вектора состояния хк =
xD,k xV,k Xa,k^d
Уравнения оптимальной фильтрации вектора состояния хк , описываемого
уравнениями (6.266), по эквивалентным наблюдениям
Уы =
11
Ух ,к-\ ® ® У A k-i ' где два «нулевых» наблюдения соответствуют
наблюдениям векторов \vk и \ак имеют вид [5.1]
221
Глава 6
Ч=Ч+ ЪхЛЩ {ук -xk) = xk+ Kku^k =xk+ К^ид^ ,
** = F*A:-i> к* = Dx^Rfj , K^ =Sa Кк,
Di = Di + R^1 , Dx, = FDX?,FT + GR^GT,
(6.267)
(6.268)
где йд^ =(yt-i) = Sfl ид^ — нормированный к единичной крутизне
многомерный дискриминатор.
Схема приемника с одноэтапной обработкой сигналов в когерентном
режиме приведена на рис. 6.46.
Блок пересчета
^Лг—1
y{'*-v)
йд&-1)
Кх*ч)
(Vl)
L*-l
к
*-i
Интегрированный
сглаживающий фильтр
Блок дискриминаторов
дальностей (задержек) до НС
U
дД
Нт
и
Д*д
Блок фазовых дискриминаторов
U
ДР
diag(2*/4)
U
дК<*
I
£
u
A*-l
4-1
Рис. 6.46. Схема приемника с одноэтапной обработкой сигналов
в когерентном режиме
На выходе схемы приемника с одноэтапной обработкой сигналов
формируется оценка вектора состояния потребителя x^_j.
6.5.3. Синтез одноэтапного алгоритма обработки сигналов
для некогерентного режима работы
В некогерентном режиме работы, также как и в когерентном режиме,
многомерная следящая система состоит из многомерного дискриминатора и
интегрированного сглаживающего фильтра. Рассмотрим раздельно синтез
многомерного дискриминатора и интегрированного сглаживающего фильтра.
222
Методы и алгоритмы обработки сигналов и извлечения информации
6.5.3.1. Синтез многомерного дискриминатора
При синтезе многомерного дискриминатора используется общее
выражение (6.30), в котором в качестве функции /(Y^.x) необходимо использовать
усредненную по начальным фазам принимаемых сигналов функцию
правдоподобия. Рассмотрим данную процедуру более подробно. Запишем функцию
правдоподобия при известных начальных фазах сигналов
( М / ч\
/>(YiM|xM) = exp| ^sT(^_u,^
v/=i
(6.269)
где Sjyk_u,f/A._j,f^k-i»0ijt-\)-
= А К [h-u - h,k-\ )cos(o>nt■ k-U+a>utk-JTd + Sik_x7i + pa_,). (6.270)
При синтезе многомерного дискриминатора параметры сигнала т(,/Д^ф{
полагаем постоянными на интервале накопления Г .
Подставляя (6.270) в (6.269) и усредняя полученное выражение по
случайным фазам ф1,к_х, i = \,n, получаем
(6.271)
/=1
где с — нормировочная константа; 10 (х) — функция Бесселя нулевого
порядка от мнимого аргумента;
^ : ~ " (6.272)
х(ъ*-\ ixk-i ) A.-.*-i (x*-i)) = fiH*k-i)+QHxk-\)»
А М
h (x*-i) = ;^2я {^-u)hm [*к-Ч - fijk-\ (x*-i ))cos(fl\,/ft_lf/ + й)да_! (хА_,)lTd) ,
(6.273)
'п 1=1
м
Qi(x*-i) = -tZ^[*к-и)К*[h-u -hjk-\(x*-i))sin(^/t-y + *W-i (x*-i)lTd)
'n l=\
(6.274)
Процесс на выходе многомерного дискриминатора описывается
выражением
идЛх*Н
d\nf(YxM,x)
дх
х = х
(6.275)
к-1
223
Глава 6
С учетом представления (6.269) выражение (6.275) можно преобразовать к
виду
/=1 7o(^(^(^-l)'^/(^-l)))t
+
да>„:
Д.1
дх
(6.276)
vx,k vyJk vZtk vi
Введем два подвектора xDk = \xk yk zk Д'к\ и xvk =
Так как псевдо задержки fi{хк_х), i = \,n зависят только от xD, a псевдо доп-
леровские частоты coai, i = \,n —только от xv , многомерный дискриминатор
(6.276) распадается на две группы дискриминаторов, для которых введем
соответствующие подвекторы
, (6.277)
" /1(хДгДх,_0^дДх,_0))ахДгДх^_1))ргг.(хд,_1)У
= у 7i (xi (*/ (**-i )Л» fe-i))) dx> (< (*vjc-i))(duAi (x w)V
Приведем дискриминаторы (6.277), определенные для псевдо задержки
Tj(xk_{) и псевдо доплеровского смещения частоты <уд/, к дискриминаторам
по псевдо дальности и псевдо скорости, учитывая, что V = dftjdt = -Ао)Л/(2я)
и Д = гс :
и
п
ч
( г,
X,
Д.(хд) -2л^(хк)
Л\
V V
I
дХ,
rM*Dp
(
Д*£)Д /ш^ ( ( fj
'О
X
V
#(iD) -2^(xr)
^
V
f г.
Л;
ад
ады'
дх
D )
, (6.278)
h *i
\\
Д(хд) -2^.(xF)^_f-2^(xK)^
дХ;
I
/лт?
U
ДХК,£
' /
/^ 77
/=1
А) */
Д,(х0) -2^.(xF)
>Л
А-
ак.
^•(М
ах
у )
Из (4.1), (4.9) следует
224
Методы и алгоритмы обработки сигналов и извлечения информации
Щч)
дх
= \-cos(aj) -cos(fii) -cos (ft) ll,
D
Щ(*у)
дх
= \-cos(ai) -cos($) -cos(ft) ll,
V
где cos (a,-), cos (/?,-), cos (%) — направляющие косинусы линии z'-й НС-
потребитель.
Определим частные дискриминаторы псевдо дальности
X
A(*z>) ~2*Шу)
А-
и
W
JJ
дХ;
ЛЫ
дД-
( ( 77
V
Д.(х0) -2*Г,(хк)
^
V
А-
ад
(6.279)
и псевдо скорости
( ГК(*
'1
W I/ =
ЛА
A(xD) -2^(xF)])_f-2^.(xF)^
А
ах
А-
/ f;
X
v с А
>л
дК
(6.280)
характеризующие обработку сигнала каждого из видимых навигационных
спутников.
Тогда, учитывая определение (6.214), соотношения (6.277) можно записать
в виде
и
д*о,£
U
дху,к
идх,к иду,к unz,k идД\к
идУх,к uaVv,k uaVz,k ипУ\к
HTu
аД,к
HTu
ч,У,к '
(6.281)
где \д =
U и U гг
и
*Дп
и*А ыч,у2
и
чЛ
Из (6.281) следует, что многомерный дискриминатор по вектору координат
потребителя \Dk - \хк ук zk Д'к |т строится на основе дискриминаторов
дальности (задержки сигналов) по каждому НС и матрицы направляющих косинусов
Н, а многомерный дискриминатор по составляющим вектора скорости потре-
i iT
бителя Xyj=\Vxk V к Vzk Vk\ —на основе дискриминаторов скорости (доп-
леровских смещений частот) по каждому НС и той же матрицы направляющих
косинусов Н. В качестве частных дискриминаторов дальности и скорости (за-
-1026
225
Глава 6
держки и доплеровского смещения частоты) можно использовать любой из
дискриминаторов для некогерентного приемника, описанных в п. 6.3.4.
Обобщенная схема многомерного дискриминатора некогерентного
приемника с одноэтапной обработкой сигналов приведена на рис. 6.47, где
коммутатор выполняет функцию преобразования входных векторов иДХ£) и идх^ в
вектор ид
иах идУх ияу uaVv uaz uaVz иаД' uaV
и фактически сводится к
коммутации входов и выходов.
y(fc-u)
-►
uflftfc-l)
т 1
Tfe-l)
Г
Блок дискриминаторов
дальностей (задержек) до НС
—^
У
Г \
Г
Блок дискриминаторов скоростей
(до
нлеровских част
от)
пД
йт
нт
иЛ1
ЦДХИ
Коммутатор
U™
д
►
Рис. 6.47. Обобщенная схема многомерного дискриминатора
некогерентного приемника с одноэтапной обработкой
6.5.3.2. Синтез сглаживающего фильтра
Для синтеза сглаживающего фильтра многомерной следящей системы
некогерентного приемника с одноэтапной обработкой сигналов также можно
использовать методику линеаризации многомерного дискриминатора с
последующим использованием теории оптимальной линейной фильтрации
эквивалентных наблюдений, приведенных к оцениваемым параметрам. Однако для
приемников с одноэтапной обработкой данная процедура оказывается более
сложной, чем в случае приемников с двухэтапной обработкой.
Прежде всего следует отметить, что многомерный дискриминатор,
приведенный на рис. 6.46, содержит два типа нелинейностей. Одна из них
обусловлена нелинейной связью псевдо задержки (псевдо дальности) и псевдо
доплеровского смещения частоты (псевдо скорости) с радиосигналом. В схеме рис.
6.46 этот тип нелинейности характеризует блоки дискриминаторов дальности и
скорости. Для линеаризации этих блоков используем тот же подход, что и в
п. 6.5.2.2. Представим и * и и „ в виде
и
= UnX£n:k) + Zn
и
д Д,-,* ~ Д, ^Д,,к ' ^Mt,k ' "n,Vhk -"Ъ y°Vi,k
= Uvi£v,k) + 4l
Vhk>
(6.282)
226
Методы и алгоритмы обработки сигналов и извлечения информации
где U'* {вд k), Uy{£y k) — дискриминационные характеристики
дискриминаторов дальности и скорости соответственно; £*. к9 %у к — шумы на выходах
тех же дискриминаторов; £д к = Д1к - Д1к , £у к = Vik - Vlk — ошибки оценки
псевдо дальности и псевдо скорости. Примеры расчета статистических
характеристик различных типов дискриминаторов приведены в Приложении к гл. 6.
Линеаризуем дискриминационные характеристики L/д (£„ к), Uy (£у к) и
представим (6.282) в виде
иЛДпк = 5дД,*Д,,* +£д,,* > UjxVhk =SjxVtSVhk +%Vhk > (6.283)
где S jj ,S у — крутизны соответствующих дискриминационных характери-
стик.
Соотношения (6.283) линейны по ошибкам оценок псевдо дальности и
псевдо скорости, но они нелинейны относительно ошибок оценок координат
потребителя exJk =xk-xk, syJk =Ук-ук> ezJc =zk-zk, effJk = Д'к-Дк. Это
второй тип нелинейности в многомерном дискриминаторе. Разложим ошибку
ч у к ч Дк
и ограничимся линейными
£д к в ряд в точке оценки \Dk = =
членами разложения
_ ЗД,*{*р,к) ЗД,* (**>,*) ВД.*(*Д.*)
^ —^; *** +~^к *у* +~^к *** +£*>к =
= -cos{ai)sxk -cos(Pi)eyk -cos(^)^ +£д;к- (6.284)
Для ошибки по скорости £у к из определения псевдо скорости
V, = -cosfa.) (Гх - Гх>,)-cos(Д.) (Vy - Vy4) -cosfo) {Vz - Vzj) + V непосредст-
венно имеем
Syik=-cos(at) sVxk -сов(Д) ^it -cos(fi) eVz%k +srk . (6.285)
Следовательно, в результате линеаризации (6.283) получаем
\дьк =5ддД"С08(а|-) ^~C0S(A) *M-COs(ft) *^+*^ + ^,*'
ujxvhk =SjXvi(-C0S(ai) £vx* -сов(Д.) ^ -cosfo) ^ + %,*) +£^-(6.286)
^ %^ 8VZ SV
T
и
Введем векторы ошибок гХ[) =\ех sy sz едЛ , £%v = ~
диагональную матрицу diag(5Afi), на главной диагонали которой на пересече-
227
Глава 6
нии / -й строки и / -го столбца стоит элемент 5Д,-, а все остальные элементы
равны нулю. Тогда для векторов ич ^ и ич у можно записать выражения
ид^=с11а8Кд()Й£^+^'
u^=diag(1S^)H£XK+^,
(6.287)
гДе^/7^ =
Д,к
%Дък £д2,к - %ДпМ
' ^v к ~
У,к
<*уьк ^У2,к
£
К*
Подставляя (6.287) в (6.281), получаем
иДЛоД==Н^а8(5дД)йе1о+ЙЧ;Ж4,
"дv.* = Ur<Hag(Slf:) Ш1у + Н%,к. (6.288)
Введем эквивалентные наблюдения координат потребителя и
составляющих вектора скорости
Ух0,* = *D,k + По,к , fxv,k = *V,k + %,* » (6-289)
где ^^(HMiagl^^.JH^H^,
%,* = (HTdiag(s^ )й)'' Й%4 . (6.290)
Уравнения эквивалентных наблюдений, в принципе, дают решение
искомой задачи линеаризации и могут быть использованы для синтеза линейного
фильтра Калмана (совместно с уравнениями (6.216), (6.225), описывающими
динамику изменения вектора состояния).
Учитывая, что (6.289) получается из (6.288) в результате умножения на
матрицы В^ =JHTdiag(S^£ )Н) и By =IHTdiag(5' у]Н1 , преобразуем схему
многомерного дискриминатора рис. 6.44 в схему, приведенную на рис. 6.48.
В данной схеме на выходе коммутатора при малых ошибках слежения
имеем процесс йд^ = (хк - хк) + цк, компоненты которого упорядочены в
соответствии со структурой информативного вектора \к . После такого
упорядочивания можно вести вектор эквивалентных наблюдений ук = \к + цк, для
которых алгоритм оптимальной фильтрации вектора \к запишем в виде
1
**=**+ Dx,*Rn (У* - *) = Ч + КкК,к >
*к - F^-i> Кк - DxкК^ ,
Di = 6^ + R^1 , DXft = FDSiAFT + GR^GT
(6.291)
(6.292)
228
Методы и алгоритмы обработки сигналов и извлечения информации
ykk-u)
"^
»д(**-1)
*(**-!)
т ?
Блок дискриминаторов
дальностей (задержек) до НС
^~
1
г \
»д^
г
Блок дискриминаторов скоростей
(доплеровских частот)
ид£
Нт
ид*в
нт
идхг
BD
BF
"д*0
"дхк
►
Коммутатор
йд,*
-—►
Рис. 6.48. Модифицированная схема многомерного дискриминатора
некогерентного приемника с одноэтапной обработкой
В данной схеме на выходе коммутатора при малых ошибках слежения
имеем процесс йд^ = [\к - \к) + цк , компоненты которого упорядочены в
соответствии со структурой информативного вектора \к . После такого
упорядочивания можно вести вектор эквивалентных наблюдений ук = \к + цк, для
которых алгоритм оптимальной фильтрации вектора \к запишем в виде
**=**+ Dx,*Rf| (У* " *) = Ч + К*йД,
Л'
(6.291)
(6.292)
Таким образом, схема некогерентного приемника с одноэтапной
обработкой сигналов имеет вид, приведенный на рис. 6.49.
yfet-u)
Блок дискриминаторов
дальностей (задержек) до НС
ЛлД
Многомерный дискриминатор
U
Н1
■ДХд
В
D
жДХд
Блок дискриминаторов скоростей
(доплеровских частот)
(О
Лч-\)
*д<р
Н1
и
Дхк
Вт
и
ДХИ
I
£
U
д,*
'(**-!)
Блок пересчета
**-1 -»*(**-! )>**-! ->йд^*-1)
к.
Интегрированный
сглаживающий фильтр
ч
Рис. 6.49. Схема некогерентного приемника с одноэтапной обработкой
229
Глава 6
В этой схеме осуществляется совместная фильтрация всех компонент
вектора хк . Однако заметим, что изменение вектора состояния по координатам
х,у ,z ,Z)' описывается независимыми уравнениями (6.216), (6.225), а
эквивалентные наблюдения ук также представлены в виде независимых наблюдений
отдельных компонент. Поэтому возникает вопрос о возможности раздельной
фильтрации компонент вектора состояния по каждой из координат. Если бы
шумы % эквивалентных наблюдений по каждой из координат были
независимыми, то оптимальное решение распалось бы на совокупность четырех
независимых фильтров. Наличие же коррелированности шумов наблюдений приводит
к тому, что оптимальным является интегрированный фильтр (6.291)—(6.292),
осуществляющий совместную обработку всех наблюдений. Однако учет
корреляции наблюдений несущественно повышает точность фильтрации вектора
потребителя, поэтому можно использовать раздельную фильтрацию различных
координат вектора потребителя. В этом случае при незначительной потере в
точности фильтрации достигается существенное сокращение вычислительных
затрат за счет упрощения дисперсионных уравнений (6.292).
При таком подходе, например, при синтезе фильтра по координате х
необходимо использовать априорные уравнения
хк = х^ + TVxJk_x, VXtk = VxM_x + r&>jw , (6.293)
и эквивалентные наблюдения
Ух,к = Хк + ПХ,к * УУх,к = V4 + 4VxJk ■ (6-294)
Аналогичные соотношения можно записать для синтеза фильтров по
координатам х, у, z, Д'.
Синтез оптимальных фильтров в постановке задачи (6.293), (6.294)
приведен в п. 6.3.6.5 (уравнения (6.146), (6.147)). При этом необходимо лишь
вычислить соответствующие значения дисперсий шумов эквивалентных наблюдений
(6.294).
В схеме приемника (рис. 6.48) в этом случае вместо одного
интегрированного сглаживающего фильтра будут стоять четыре более простых
сглаживающих фильтра для фильтрации каждой из координат х, у, z, Д'.
6.6. Прием сигналов в условиях многолучевости
Целью написания данного параграфа является стремление авторов
привлечь внимание отечественных специалистов к проблеме обеспечения
качественного приема сигнала в условиях многолучевости, которая в настоящее
время в отечественной литературе не рассматривается на должном уровне. Тем не
менее, ошибки, связанные с многолучевостью, являются одной из
составляющих, присущих навигационным измерениям и, как будет показано ниже, без
230
Методы и алгоритмы обработки сигналов и извлечения информации
использования специальных методов борьбы могут достигать вполне заметной
величины, превышая по абсолютному значению все остальные составляющие
ошибки.
Разумеется, в рамках столь короткого параграфа невозможно рассмотреть
вопрос с необходимой глубиной, поэтому ниже представлен только краткий
экскурс в проблему с рассмотрением основных положений.
6.6.1. Общая характеристика многолучевости
Под многолучевостью (multipath) понимаются условия, когда в точке
приема навигационного сигнала помимо прямого существует еще один или
даже целый ряд отраженных лучей. Наличие отраженных, задержанных по
времени прихода, сигналов приводит к искажению формы корреляционного
пика сигнала и, как следствие, к смещению в оценке истинной задержки. Так,
ниже на рис. 6.50 представлены формы корреляционного пика для случая
одного отраженного луча с амплитудой в два раза меньше амплитуды прямого
луча (мощность отраженного луча на 6 дБ ниже мощности прямого луча) и
задержкой, равной половине длительности элементарного символа (чипа) кода.
На правом графике представлена форма пика для случая, когда фаза прямого и
отраженного сигналов совпадают, на левом - для случая, когда фазы
противоположны (по оси X отложена задержка сигнала в длительности элементарного
импульса кода).
1.2 /Ч 1.2
1 / \ 1
08 / \ 0.8
0.6 /
04 /
0.2 /
0 *
-0.2
-2 -1 0
Рис. 6.50. Формы корреляционного пика
Из графиков видно, что форма корреляционного пика искажается вполне
заметно, приводя к смещению оценки задержки для синфазных сигналов —
вправо, для противофазных — влево относительно истинного значения
задержки. Компенсация такого смещения требует использования специальных
подходов и алгоритмов обработки сигналов.
231
Глава 6
Для количественной оценки влияния эффектов многолучевости на
точность оценки задержки сигналов в мировой практике используется так
называемая огибающая многолучевости (multipath envelope). Это характеристика,
показывающая зависимость ошибки смещения оценки задержки прямого
сигнала от задержки отраженного сигнала при фиксированном соотношении
амплитуд прямого и отраженного лучей. Обычно амплитуду отраженного луча
выбирают в два раза меньше, чем амплитуду прямого. Форма огибающей
многолучевости в существенно степени зависит от построения приемной
аппаратуры и используемых в ней алгоритмов обработки сигнала. На рис. 6.51
представлены зависимости ошибки оценки задержки в условиях
многолучевости для случая стандартного широкого коррелятора, когда стробы смещены
друг относительно друга на длительность элементарного импульса ПСП
сигнала.
Ошибка оценки задержки, чипы кода
0.3
0.2
0.1
о
-0.1
-02
-0.3
-0.4
Задержка отраженного луча, чипы
Рис. 6.51. Ошибка оценки задержки
Верхняя часть графика соответствует ошибке в оценке задержки для
случая синфазности прямого и отраженного сигналов, нижняя — противофазным
сигналам. Ошибки оценки задержки при других фазовых соотношениях лежат
в пределах области, ограниченной верхней и нижней линиями графика
(отсюда название — огибающая). Из графика видно, что для рассмотренных выше
условий, ошибка в оценке задержки сигнала может достигать значений,
равных четверти от длительности чипа кода. То есть для сигнала ГЛОНАСС СТ,
имеющего длительность чипа около 2 мкс, ошибки могут достигать значений
0.5 мкс, что составляет порядка 150 м в пересчете на дальность. Очевидно,
что если не применять специальных методов борьбы, ошибки многолучевости
могут превышать по абсолютному значению все остальные составляющие
ошибки задержки (ионосферные, тропосферные и др.)
Поиск эффективных методов борьбы с многолучевостью ведется с начала
90-х годов. Условно их можно разбить на две группы:
232
Методы и алгоритмы обработки сигналов и извлечения информации
- антенные методы;
- алгоритмы цифровой сигнальной обработки.
Наиболее известными антенными методами борьбы с многолучевостью
являются:
- использование choke-ring антенн [6.12], обеспечивающих подавление
отраженных сигналов от подстилающей поверхности и отражающих
объектов, расположенных ниже плоскости антенны;
- использование фазированных антенных решеток (ФАР) (см. гл.18, а
также [6.13, 6.14]), способных фокусироваться на спутник, обеспечивая
подавление отраженных лучей с любых других направлений.
Choke-ring антенны довольно габаритны, малоэффективны в условиях,
когда отражающие поверхности расположены выше плоскости антенны, а
ФАР слишком дороги для широкого использования. Поэтому наиболее
действенными методами борьбы с многолучевостью считаются алгоритмы
цифровой сигнальной обработки непосредственно в навигационном приемнике. С
начала 90-х годов таких алгоритмов разработано настолько много, что
описать или хотя бы перечислить их в рамках данного параграфа просто не
представляется возможным. Достаточно взглянуть на эволюцию алгоритмов
борьбы с многолучевостью, разработанных и лицензированных канадской фирмой
NovAtel:
- Narrow Correlator (1992), [6.15,6.16]
- Multipath Eliminating Technique (1994), [6.17]
- Multipath Eliminating Delay Lock Loop (MEDLL) (1996), [6.18]
- Pulse Aperture Correlator (РАС) (1999), [6.19]
- Multipath Mitigating Technique (MMT), [6.20, 6.21]
- Vision Correlator (2005), [6.22]
Наиболее простыми и, поэтому, широко используемыми в настоящее
время в аппаратуре являются Narrow [6.15, 6.16] и Strobe [6.17] (или Duble-
Delta) Correlators. Огибающая многолучевости для этих двух типов
корреляторов представлен ниже на рис. 6.52 а, б.
Из графиков видно, что использование даже таких простых методов
позволяет существенно снизить влияние многолучевости. Strobe Correlator
позволяет практически полностью решить проблему с компенсацией смещения
оценок в условиях многолучевости для больших задержек, тем не менее, при
малых задержках отраженного сигнала проблема сохраняется, а остаточные
смещения оценки задержки могут составлять десятки метров.
233
Глава 6
Ошибка оценки задержки (Narrow Correlator), чипы кода
и.иь
0 04
0.02
0
■0.02
■0.04
•0.06
т 1 Л
/
7
\
\
\ \
\
)
/
/
0 0.5
1 1
Задержка отраженного луча, чипы
а)
0.5 1
Задержка отраженного луча, чипы
б)
Рис. 6.52. Ошибка оценки задержки
6.6.2. Оптимальные алгоритмы приёма в условиях многолучёвости
Оптимальные алгоритмы приёма основаны на рассмотрении суммы
прямого aQS(t-r0) и отражённых сигналов atS(T-rz) i = l,/w как единого суммар-
т
ного сигнала S1(t,£,a) = ^a*S(t-ri) = aH S(t,£), где аТ ^[^.щ.^а^ —
комплексные амплитуды сигналов, гг = [ г0, г,.. .г„ ] — задержки сигналов
^r(M) = [^(?~"ro)'^(?_ri)-^(?"rw)]5 мощность S(t-Tt) принята равной
единице. В этом случае задача синтеза сводится к оцениванию не только
параметров т0,а0 прямого сигнала, но и всех задержек и комплексных амплитуд
отражённых сигналов.
Как уже отмечалось, решение такой задачи рассматривалось в целом ряде
работ с использованием разных методов, приближений и математических
аппаратов. Наиболее полным решением является подход, при котором осуществ-
234
Методы и алгоритмы обработки сигналов и извлечения информации
ляется постоянное слежение за всеми параметрами сигнала г и а . Из-за
увеличения систем слежения он является и самым сложным. Однако в этом случае
ошибка оценки а может становиться столь малой, что характеристики
слежения за г будут близки к характеристикам приёма при полностью известных а .
Это аналогично квазикогерентному (когерентному) приёму.
Мы приведём здесь другой более простой подход, приводящий алгоритму
приёма, вполне доступному для реализации в современных приёмниках.
Особенность его в том, что здесь не осуществляется слежение за а , а используется
его оценка, полученная только на основе текущих измерений (на основе
очередных значений выхода корреляторов). В противоположность полному
«когерентному» алгоритму, будем называть такой алгоритм «некогерентным». Мы
покажем, что оба алгоритма дают несмещённые оценки х_, отличаясь только
дисперсией шумовой составляющей.
Рассмотрим интервал группирования сигнала длиной Г = 1...10мс,
кратный периоду сигнала, и будем считать параметры г и а постоянными на этом
интервале. Это, конечно, предполагает компенсацию заметной (по сравнению с
XIТ) расстройтки по частоте. Подход к подстройке фазы и частоты для этой
задачи будет рассмотрен далее.
Получим оценку параметра а по наблюдению
Z(t) = aHS(t,r) + n(t), te(0J)
(6.295)
Здесь £(0 — комплексное наблюдение, n{t) — комплексный БГШ со
спектральной плотностью N0 , т.е.функционал правдоподобия (ФП) реализации
т
равен р(% | г,а) = с • ехр\ -—— |^(/) -анS{t, r)|
оценки максимума правдоподобия
dt
•
Ставится задача найти
(b«) = max=1s/7(^|r,«) = max-1 --— fe{t)-aHS{tA dt\ . (6.296)
Найдём сначала максимум по а при фиксированном г . Подстановка а в
(6.296) позволит получить компактное выражение для алгоритма оценивания
г . Дифференцирование ln(p(£o I !»(*)) по ^ Дает
'т
jS(t,T)[4(t)-aHS{t,T)\ dt
= q(i)-K(L)a,
235
Глава 6
1 f *
где введены обозначения q(f) =— \S(t,r)•£, {t)dt для корреляционного инте-
N0 J
1 с
грала,£(£,£) = — \S{t,b)S{t,l2)Hdt — для корреляционной матрицы
сигналу J
лов S(t,£) и, кроме того, для сокращения записи обозначено к(т) = К(т_,т_).
Заметим, что это выражение для дискриминатора системы слежения за а
для «когерентного» алгоритма. Оно основано на использовании выходов I и Q
обычных корреляторов / и Q, так как q(z) = 1 + jQ.
Приравнивание производной нулю даёт оценку комплексных
коэффициентов для «некогерентного» алгоритма
a = K~l{r_)q{t_). (6.298)
Подстановка а в (6.296) даёт
Z(r) = Relq"(т)а --анК(т)а 1 = -qH(г )£_1 (T)q(r). (6.299)
Физический смысл этого выражения становится очевиден, если
представить его как корреляционный интеграл от произведения наблюдения £(0на
оценку £Е(/,_г) = о;я£(/,г) суммарного сигнала
«я т Лт
Z(r) = —— \S(t,r)^ (t)dt = — рхОМ^ (t)dt, т.е. в стандартном для задач оце-
2 J 2 J
о о
нивания виде.
Алгоритмы оценивания или слежения за т_ должны быть основаны на
максимизации этого выражения. Например, алгоритм фильтрации г в
гауссовом приближении имеет вид [13]
din
т = f + М
Р(4(к+\)Т \*к)
дт
(6.300)
где М — матрица коэффициентов усиления, рассчитываемая из уравнения
Риккати; т — экстраполированная оценка т_.
Допустимо приближение р{^кт+Х)т \ т_) * Р(4(к+\)т I LA) те- использование в
(6.300) производной от Z(_r) .
Выражение для производной Z(r) несложно получить, однако возможно
использовать ставший в приёмниках СРНС стандартным подход с заменой
производной по времени конечной разностью. Например, для производной по т0
236
Методы и алгоритмы обработки сигналов и извлечения информации
dZ(f) ^ Z(ff)+S,Tl,..Tm)-Z(T0 -S9fl9..fm)
дт0 ~ 28
Несмотря на несколько большую , чем в обычных дискриминаторах,
сложность выражения для Z(r) , оно не должно вызывать чрезмерных
сложностей в реализации, так как формируется один раз за время Т, т.е. с частотой
доли килогерца. Основные вычисления в быстром темпе вычисляются в обычных
корреляторах, где формируются q(£ + S)9 q{t)9 я(т_-8). Число корреляторов
теперь в (т + \) раз больше, чем в обычных дискриминаторах, но для
современных многокорреляторных приёмников это не следует считать проблемой.
Элементы матрицы К(т) получаются расчётным путём на основе
автокорреляционной функции сигнала и вычисляемых оценок задержек.
В некоторых случаях удобно перейти от вектора гг =[го>г1—ги] к другим
переменным [г0,Al5...Aw], где А, = г,- -г0, / = 1,/и. Основная причина в том, что
динамика запаздываний А, отражённых лучей от прямого много меньше, чем
динамика задержки прямого сигнала. Это позволяет уменьшить полосы
фильтров слежения за дельта и тем самым ошибку оценивания вектора
A = [A1,A2,...Awf.
Функциональная схема, реализующая алгоритм, изображена на рис. 6.53.
>kW
Фильтр
ФАП
Early
корреляторы
Prompt
корреляторы
Late
корреляторы
q(ik+s):
а(ь)
arg
qfe-s).
Q.
О
I-
Ш
I
S
s
Q.
gZ„(lk)/52
Фильтр
т
CXok
Рис. 6.53. Функциональная схема оптимального приемника
Здесь уместно вернуться к замечанию об оценке частоты и фазы прямого
сигнала. Оптимальная оценка фазы прямого сигнала по наблюдению на
интервале длиной Т, фактически, была определена при получении а (3).
Синтезированный оптимальный алгоритм оценивал комплексные амплитуды всех
составляющих суммарного сигнала, т.е. и амплитуду и фазу прямого сигнала. В
частности, оценка фазы прямого сигнала
237
Глава 6
ф0 = arctg(lm(dQ)/Re(d0)). (6.301)
Такая оценка по наблюдению на интервале Т является основой
эффективных систем слежения за фазой и частотой сигнала, как это показано в схеме
рис. 6.52, где входной сигнал предварительно умножен на ет^*\ где ^0(7) —
экстраполированная оценка фазы по наблюдениям на предыдущих интервалах,
осуществляемая в ФАПЧ. Это умножение убирает сдвиг частоты сигнала, т.е.
обеспечивает оговоренные ранее условия постоянства комплексных
коэффициентов. В этом случае выражение (6.301) для ф0 описывает дискриминатор с
линейной дискриминационной характеристикой, основанный на синфазном
I = Re(d0) и квадратурном Q = lm(a0) корреляционном интеграле,
оценивающий фазовую ошибку S<pQ =<р0-ф0 оценки комплексной амплитуды прямого
сигнала а0. Особенность в том, что а0 согласно (6.298) — это не
корреляционный интеграл для прямого сигнала, а взвешенная сумма корреляционных
интегралов для прямого и отражённых сигналов. Получаемая в этом случае оценка
фазы сигнала, оптимизированная для учёта отражений, может оказаться особо
полезной для измерителей угловой ориентации и вообще для приёмников с
использованием фазовых измерений.
6.6.3. Дискриминационная характеристика
Дискриминационная характеристика (ДХ) является основной
характеристикой дискриминатора и в значительной степени определяет свойства
следящей системы в целом. Дискриминационная характеристика f(s) - это
зависимость сигнальной составляющей на выходе дискриминатора от ошибки
слежения. При этом ошибки по другим параметрам сигнала считаются равными ну-
= 1
s=0
лю. Иногда удобно нормировать ДХ так, чтобы
Нас интересует прежде всего ДХ по задержке г0 прямого сигнала, т.е.
зависимость среднего значения выхода дискриминатора по г0 от ошибки оценки
прямого сигнала s = fQ-r0 при А, - А, = 0, / = 1, т
_д
т=\м\
^{qH(L)K-l(t)q(T)}
го-го=£
д=д
Для упрощения поменяем местами операции взятия производной и
математического ожидания, и учтём, что q(f) = К0(т_,т) + п(т)
M{qH (т)-К-\т)-д(т)} = ан К? (т,т)К-\т)а +
238
Методы и алгоритмы обработки сигналов и извлечения информации
+М[анК$ (т,т)К-1 (£)и(г)} + М[пн (т)К~1 (г)л(г)} .
Второе и третье слагаемые равны нулю, так как М{п(т)) = 0. Четвёртое
слагаемое равно
м{пн(т)К-1(т)п(т)} = K~\i)M\in{i)nH'(£)} =
= Тг{к~\1)К (T)} = Tr{lm+l} = (m + \).
Здесь /w+1 — единичная матрица (w + l)x(m + l), использовано свойство
следа матрицы Тг(АВ) = Тг(ВА), а также известное свойство корреляционных
интегралов
М<\ [s(t9T)n(t)dtJ \s(t9r)• n{t)dt\ I = N0 Ь(/,г)5'я(f, f)df
Естественно, производная от четвёртого слагаемого также равна нулю. В
результате
2 \ 0£ С£ Jr0-r0=^
(6.302)
где учтено, что К(т) = К(А), т. е. не зависит от г0 и £.
Несложно увидеть выполнение главного свойства ДХ /(0) = 0. Оно
обеспечивает отсутствие смещения оценки задержки прямого сигнала. Для
доказательства заметим, что при г = г выполняется К0 (г, г) = К{т), т.е.
т=\аИ
дк£(т,т_) + дК0(ьт)
де
де
а.
Теперь достаточно воспользоваться известным свойством
взаимокорреляционных функций К(ХХ,'k2) = KT(k2,'kl), откуда
дК£(т,т)_ дК0(т,т)
дБ
дБ
и
т=\ан
дК0(Ьт) | дК0(т,т)
дБ дБ
а
д=д
(6.303)
239
Глава 6
Теперь очевидно, что для любых а и А ДХ при f0 = г0 обращается в нуль,
смещение оценки задержки отсутствует, сравнение с другими алгоритмами по
огибающей многолучевости теряет смысл, так как она здесь стягивается в
точку (в начало координат).
Вид ДХ для некогерентного алгоритма в условиях воздействия одного
отраженного луча (т=1) при а0 = 1, ах = 0.5 представлен на рис. 6.53. Здесь же
приведены дискриминационные характеристики других алгоритмов для тех же
условий. По оси абсцисс отложена ошибка оценки задержки отраженного луча,
отнесенная к длительности чипа.
~^— Narrow Correlator I
Double Delta
Некогерентный
-0.5 h
-i.ol
-1.sL
-1.5 -1 -0.5 0 0.5 1 1.5
Рис. 6.53. Дискриминационные характеристики
Из рисунка видно, что ДХ для некогерентного алгоритма свойством
нечетности не обладает. Однако при т0 = т0 среднее значение выхода
дискриминатора некогерентного алгоритма равно нулю при всех А , в том числе малых,
в отличие от других алгоритмов.
Подчеркнем, что речь идет о систематической составляющей ошибки,
которую труднее всего уменьшить другими способами. Флуктуационная
составляющая ошибки в некогерентном алгоритме остается и даже возрастает. Обычно для
ее учета используют флуктуационную характеристику дискриминатора, или
спектральную плотность шума дискриминатора, как в параграфах главы. Такой
подход справедлив в более простых случаях, но не проходит в нашей задаче с
многими параметрами, где шумы разных дискриминаторов коррелированны.
Проще воспользоваться другим распространенным подходом, удобным именно в
случае множества параметров сигнала, а именно найдем дисперсию ошибки на
выходе дискриминатора на основе неравенства Рао-Крамера [6.24].
240
Методы и алгоритмы обработки сигналов и извлечения информации
6.6.4. Потенциальные характеристики точности
Рассмотрим сначала характеристики приёма для случая, когда амплитуды
и фазы прямого и отражённого сигналов известны, т.е. для «когерентного»
приёма. Очевидно, что высокоточное слежение за комплексными амплитудами
всех составляющих суммарного сигнала, т.е. реализацию оптимальных
алгоритмов, может обеспечить лишь приближение к таким характеристикам.
Поэтому уместно рассматривать их как потенциальные. Оптимальный алгоритм
для обработки наблюдения на интервале (О, Т) в этом случае хорошо известен
т = max l <
-i-Re jmSL(t,bq)dA-^- ^,т,а)\ dt
(6.304)
или во введённых выше обозначениях
г = тах-1 \ке{дн(т)а}--анК~1(А)а
(6.305)
Известно, что матрица ковариаций ошибки такой оценки удовлетворяет
границе Рао-Крамера, которую для сигнала на фоне шума можно записать как
-1-1
Rr*N0
I дт
о -
дт
п#
dt
= N0-J-\
(6.306)
причём пока оценка лежит в пределах линейного участка ДХ выполняется знак
равенства.
Учитывая, что dSY(t,£,a)/dTi =a* -dSit-T^/dTj получаем внутри
квадратных скобок (т +1) х (т +1) -матрицу J, элементами которой являются
Jy=aiaj \ \ 1) ' dt = aiaj—-— \S{t-Tl)S{t-vJ)dt =
J дт; дт,- дт:дт: J
о
' J о
-or,- а, —;——— = -a; (Xjp (Л,у)
-t~j
dtjdTj
Здесь р(т) = \S(t) • S(t + T)dt — корреляционная функция сигнала, и для
о
сокращения записи обозначено р\т) = д2р(т)/дт2 , Atj = т{ - г •.
Для получения более конкретных результатов ограничимся простым
случаем одного отражённого сигнала m = 1. Тогда, пользуясь формулой Крамера
для обращения матриц и учитывая, что //(А) = р\-А), получим
241
Глава 6
RT * -Щ
|a0|V(0) alaxp\b)
a0a*lP"(A) k|V(0)
-M
|«o|2N2|V(0))2 -(р\А))2\-а,щр\А) \a0\2 p"(0) J
h|V(0) -cclaxPn{A)
(6.307)
В частности, дисперсия ошибки оценки времени прихода прямого сигнала
по наблюдению на интервале (0,Г) равна
Я0 =
Nn
А»
\a0\2(-p\0))(\-[p"(A)/p\0)f) \-[p\A)lp\0)f '
(6.308)
Первый сомножитель здесь - дисперсия ошибки оценки запаздывания для
сигнала в отсутствии отражений D0 =
Nn
— [6.24]. Второй сомножи-
КГС-/Л0))
тель показывает увеличение ошибки за счёт многолучёвости и представляет
наибольший интерес.
К сожалению, использовать для исследования стандартную для сигналов
ГЛОНАСС модель с прямоугольными фронтами не удаётся, так как она
приводит к дисперсии ошибок, равной нулю, как при наличии отражений, так и при
их отсутствии. Следующей по простоте моделью является «трапецеидальная»
модель сигнала с линейными фронтами. В ней сигнал S(t) при смене символов
кодовой последовательности &к_{ и &к описывается в пределах длительности
к -1 и &-того элементов сигнала как
S(t) = A\
2 НИ^(_!^ -,ее*
7
(-1)0*,
(-1)0*-1
t>(k-\)Te+-±
t<(k-\)re+^-
\t-(k-\)re\<^
7
Здесь ту — длительность фронта сигнала; те — длительность элемента
сигнала; А — амплитуда, величина, которая в нашем случае должна
обеспечивать условие единичной мощности сигнала. Производная от такого сигнала
равна
dS(t) _ 2А
dt
(-1) *~,е0*, \t-(k-\)те\ < —, т.е. имеет вид прямоугольных
7
импульсов в пределах фронтов сигнала и равна нулю вне фронтов.
242
Методы и алгоритмы обработки сигналов и извлечения информации
Корреляционная функция для прямоугольных импульсов хорошо известна,
поэтому легко увидеть, что
-Р\т)=\-
dS(t)dS(t-r)
dt
dt
dt = n^
f—1
/
1ф
\
1
•ф)
\T\<T
f
(6.309)
где nc — число смен знака на интервале Т.
Если период кодовой последовательности равен Т, то пс = 1,
наприте
мер, пс = 255 для кода стандартной точности ГЛОНАСС.
Подстановка(6.309) в (6.308) даёт нам DT =D0, A > Гу, т.е. при
использовании оптимального алгоритма наличие отражённого сигнала не ухудшает
точности синхронизации при временах запаздывания отражённого сигнала
больших длительности фронта сигнала.
При меньших задержках А < Гу получим
Я0=А>
1
7 = ZV
7
1
1-
1-
7j
А2_А
7
Согласно этому выражению при малых гу/Д, дисперсия ошибки
возрастает обратно пропорционально Д/гу . Например, при запаздывании, равном
половине фронта сигнала, дисперсия увеличивается в 4/3 раза, что
эквивалентно ухудшению отношения с/ш на 1 дБ.
Длительность фронта сигнала ГЛОНАСС обратно пропорциональна
ширине полосы аналоговой части приёмника Тф=\/А/. Следовательно,
эффективность работы алгоритма существенно зависит от ширины полосы
приёмника. Расширение полосы Д/ может обеспечивать эффективный приём при
малых запаздываниях отражённого сигнала. Например, для подавления
алгоритмом отражённых сигналов, запаздывающих на 15 м относительно прямого
требуется Д/ > 1 / Д * 20МГц .
6.6.5. Характеристики «некогерентного» алгоритма обработки
Теперь найдем дисперсию ошибки оценки задержки для «некогерентного»
алгоритма, ограничившись одним лучем т=1. Матрица R ковариаций ошибок
оценки всех параметров т_, а сигнала получается вполне аналогично
243
Глава 6
R>
fds^{t) ds\{t)^
дт>
да" J
-l
1 т1
-
Nn J
dSz(t)
дт
S (t,r)
dS (t) „
1 s" (t,D
Здесь В=
дт'
( 0 а0р'А)
WiPa О
Nn
(I в^х
уВН А;
с =
1 Ра
Ра 1
так как р(0) = 1,
уо (0) = 0,рд =/?(Л), рд =—— = .
дт дт
Для обращения блочной матрицы воспользуемся формулой Фробениуса,
согласно которой
(А В^
С D
{А - BD~lCyl -A~XB[D - СА~ХВ}
-D~1c(a - BD~XC) [D - СА~хВу1
-Л
Отсюда матрица ковариаций ошибок оценки т0,т{
No
г (
Nn
-Pi
(р'а)2
\ (
2
v-1
а.
о
пп (Ра) -Ра
Ра '
1
-Ы
«0«1
Qr0flfj
-Ра
(Р'а)2 Ра
1
ы
-Pi-
1
(Р'а)2
а.
(6.310)
Сравнение с формулой (6.307) для случая известных а показывает, что
(Ра)2 '"ч2
они совпадают при замене -р0 = -р$
~„ . „» (Ра) -pJPq
2 > Ра~ Ра 2 '
1-(рд) 1-(рл)
Такая замена учитывает потери, связанные с отказом от слежения за
амплитудами и фазами прямого и отражённого сигналов.
244
Методы и алгоритмы обработки сигналов и извлечения информации
На рис. 6.55 приведены зависимости дисперсий ошибки оценки задержки
когерентного и некогерентного алгоритмов от задержки отраженного сигнала.
4.5
4.0
3.5
3.0
2.5
2.0
1.5
1.0
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
Относительная задержка отраженного сигнала
Рис. 6.55. Зависимости дисперсий ошибки оценки задержки
По оси абсцисс отложена задержка отраженного сигнала, отнесенная к
длительности чипа. По оси ординат дисперсии ошибок, отнесенные к
дисперсии ошибки оценки в отсутствии многолучевости. Как видим, ошибки
когерентного алгоритма отличаются от ошибок алгоритма при отсутствии
отражений только в области запаздываний, близких к длительности элемента (в
отличие от модели с прямоугольными сигналами) или меньших длительности
фронта (0.1 в нашем случае). Ошибки «некогерентного» алгоритма
незначительно отличаются в области задержек, больших длительности фронта, и
заметно больше ошибок в отсутствии многолучевости при малых задержках (в
1.5 раза при А = Гу /2). Тем не менее, учитывая, что речь идет только о флук-
туационных ошибках, которые можно устранить сглаживанием в фильтрах,
использование поддержки от несущей, характеристики некогерентного
алгоритма следует считать удовлетворительными.
Таким образом, если не принимать специальных мер, ошибки, связанные с
многолучевостью, могут превышать все другие составляющие ошибки оценки
задержки. Известны алгоритмы, обеспечивающие существенное уменьшение
влияния многолучевости, прежде всего, для больших задержек отраженных
лучей. Устранение ошибки, связанной с многолучевостью, при любых задержках
удается на основе оптимальных алгоритмов, основанных на оценивании всех
параметров приходящего суммарного сигнала.
245
Глава 6
Приложение к гл. 6
Статистические характеристики дискриминаторов
В основе формирования дискриминаторов различных типов лежат
синфазные / и квадратурные Q компоненты, которые формируются на выходах
соответствующих корреляторов. Поэтому сначала рассчитаем статистические
характеристики данных сигналов.
П6.1. Статистические характеристики синфазных и квадратурных
компонент корреляторов когерентного приемника
На вход приемника в моменты времени tk_xl ^]tk_xxJk_XM^ поступают
наблюдения
у{*к-и) = АКк{*к-и -^-i,/)cos(^n^-i,/ +^нс*-1 +9к-ч) + пк-и> (П6Л)
где пк_х 1 — дискретный БГШ с нулевым математическим ожиданием и
дисперсией а2п = N0/(2Td); Td — шаг дискретизации по времени.
В когерентном приемнике при формировании различных дискриминаторов
используются синфазная и квадратурная компоненты (6.40), которые запишем
в виде
А м
h =—^у(*к-и) лдк('*-и -*к-и)с™(<»п*к-и +Фк-и)>
Gn /=l
А М
Qk =—^у(*к-и) Адк(^-и -^-i,/)sin(®„^.u + фк-и), (П6.2)
Gn /=1
где тк , фк — задержка и фаза соответствующих опорных сигналов.
При расчете статистических характеристики сигналов (П6.2) будем
полагать, что на интервале накопления Т = MTd:
задержки тк_Х1 и ткЛ1 навигационного и опорного сигналов меняются
несущественно, так что тк_и = тк_хх, тк_Х1 = тк_и ;
фазы <рк_ц и фк_х1 навигационного и опорного сигналов меняются
линейно, а именно рк-ц =pk-U+(l-l)Td(ak_U9 фк_и = = Pk-hl+(l-l)Td&k_ll.
Сигналы (П6.2) содержат регулярную и флуктуационную составляющие,
поэтому могут быть представлены в виде
h=^h] + I^k=h+I^k>Qk=M[Qk} + Q^k=Qk+Q^k- (П6.3)
246
Методы и алгоритмы обработки сигналов и извлечения информации
Для регулярных составляющих сигналов запишем
А2М
°и /=1
хЛдк('*-1,/ -^-u)C0S(^A-l,/ +^-U +(^-1)ГЛ-и)да
it
{ Лдк ('" **-i )cos(*y + cok_x (t - tk_x) + ж&жк_х + (pk_x):
2A2 tk'
No ,
= — J Лдк (' ~ ^-1 ) ^дк (' ~ 4-Х )C0S(^ + ^ (f - tk_x ) + 7lSmk_x ) dt =
'k-\
А2 %
=—Kck-\ I КЛ*-Тк-\) M'-f*-i)cos(s+^('->*-i)) <h, (П6.4)
fk-\
где £w = o)k_x - wk_x, £p = (pk_x - фк_х — ошибки по частоте и фазе; hHck_x = ±1
— функция модуляции навигационного сообщения.
Введем корреляционную функцию дальномерного кода p[sz) =
'к
= J \кЛ*-тк-\ЖЛ*-?к-№> £т=тк_х-тк_х. Так как hm(t) является М-
*к-\
последовательностью, p(sT) не зависит от фактического значения tk_x.
С учетом введенной функции p(zT) преобразуем интеграл, входящий в
(П6.4), к виду
'*
{ К (> - 4-х) К (> - 4-х )cos(^ + ею (t - tk_x)) dt =
*k-\
*k
= j*p(€T)cos(s(p+ ea{t-tk_x)) dt
<k-i
+ J[Лдк(*'4-х) hw('"4-х)"p(*T)]cos(^ +ea(t-tk_x)) dt. (П6.5)
*k-\
247
Глава 6
Второе слагаемое в (П6.5) представляет собой интеграл от произведения
быстро меняющейся знакопеременной и медленно меняющейся функции,
поэтому его значение близко к нулю. Следовательно, (П6.4) приводится к виду
h =
N,
Кк-\р{£т) l^s(e<p + £co{t-tk_l))dt =
'к-\
i \ i i \sin(£cJ72)
Кск-\Р{£т)™*[£<р+£Л2)-
eJT/2
'СО
= 2Яс1щТКск-\Р{£тУ™{£<р + £Л2)^С{£Л2) »
sin(£(0T/2)
(П6.6)
где sinc(£C0T/2) =
£,JI2
'со
Проделав аналогичные выкладки для квадратурной составляющей,
получаем
^ -А1Т
Qk =—^—Кск-1Р(£т)™(£<р + £J'/2)sinc(^7'/2)
Nt
= ~2(1с1щТКск-\р{£г )sin(^ + ejjl)smc{€jl2)
(П6.7)
Рассчитаем дисперсию флуктуационной составляющей синфазной
компоненты:
D,=M[llk] =
А ы
= — М
м
м
^nk_uhm{tk_u-fk_u)cos{a>ntk_u +фк_и +(l-\)Tdd>k_u)x
/=1
хХл*-иАдк(^-1,у -fk-i,i)cos(e>ntk-i,j +Фк-ц +{j-])Tc,a>k-x,x)
A2 wi
-tX^k ('*-».' ~ fk~U )COs2 {<°п*к-и + Pk-l,l +(l~ O^A-U ) =
Gn 1=1
A2T/N0=2qc/nT.
(П6.8)
Дисперсия флуктуационной составляющей квадратурной компоненты
рассчитывается аналогично и оказывается равной £>7 , т.е.
%=*>Ь=А2Фо=Ыс/ЯвТ.
(П6.9)
248
Методы и алгоритмы обработки сигналов и извлечения информации
Взаимная дисперсия флуктуационных составляющих синфазной и
квадратурной компонент
А2 М
= -тХАда ('*-!./ "^-uHsK'jt-i,/ +&-i,i +(/-1)гА-и)х
xcos(fiy*_u + &_и +(/-l)r^_u)sin(u;n^_u +^Ч1 +(/-1)%_1>1)*0.
При формировании дискриминаторов задержки огибающей используются
опережающие IEk, QEk и запаздывающие ILk, QLk компоненты,
отличающиеся от рассмотренных выше сигналов тем, что опорный сигнал с дальномер-
ным кодом формируется со сдвигом дальномерного кода на +Дг/2 [см. (6.44)].
Такой сдвиг не влияет на дисперсии флуктуационных составляющих таких
сигналов (что явно следует из (П6.8)), поэтому можно записать
% = % =%Ф =%Ф -^т1Щ = 2ЧфТ. (П6.10)
Флуктуационные составляющие /£ф k и QE^k, как и IL^k и QL$k, некор-
релированы между собой, т.е. м[/£ф^£фЛ] = 0 , м[/1ф^фД] = 0.
Взаимная дисперсия одноименных (либо синфазных, либо квадратурных)
компонент
%Ь» =%ФЙФ =p(*T)A2T/N0±2<]c/„Jp(AT). (П6.11)
Для взаимных дисперсий смещенных (опережающих или запаздывающих)
компонент с одноименными несмещенными компонентами справедливо
соотношение
%ЧФ'Ф = %ц* = Р(Дг/2)Л2гМ, = 2Чс/„Тр(Ат/2). (П6.12)
При расчете, например, регулярной составляющей 1Ек в (П6.4) вместо
КЛ*~тк-\) наД° подставить hm(t-(rk_x + А г/2)). При этом в (П6.5) вместо
/?(£г) будет стоять р{ег -Ат/2), что ведет к замене аналогичных функций в
(П6.6) и (П6.7). Следовательно, для регулярных составляющих опережающих и
запаздывающих компонент можно записать
W =^rKck-A£r + Ar/2)cos(*„ +^r/2)sinc(^r/2) =
= ^cin,TK,k-xP{sr + Ar/2)cos(^ + eJl2)*mc(sJll). (П6.13)
249
Глава 6
— —А^Т
QE(L),k=—7~ /2Hot-iP(^r + AV2)sin(^ + ^7,/2)sinc(^r/2) =
= -2qc/nJhHCk_lp(sT+Ar/2)sm(£(p+sMT/2)smc(eu)T/2). (П6.14)
П6.2. Статистические характеристики синфазных и квадратурных
компонент корреляторов некогерентного приемника
В некогерентном приемнике формирование синфазной и квадратурной
компонент коррелятора определяется выражениями (6.53), (6.54), которые для
удобства приведем еще раз:
1{Ч-1\>«>кк-1,\) =
А М
= —Х^(^-и)ЛДк(^Ч,/-^д)с08(^о^Ч,/+^д;^л(/-1)^)'(П6Л5)
ап Ы
Q{jk-\,\ >*>д;*-1,1 ) =
А М
Gn /=1
Отличие (П6.15), (П6.16) от аналогичных выражений (П6.2) для
когерентного приемника заключается в отсутствии в опорных гармонических
колебаниях слагаемого фк_ц . Учитывая это обстоятельство, нетрудно убедиться в том,
что статистические характеристики синфазной (П6.15) и квадратурной (П6.16)
составляющих некогерентного приемника могут быть получены из
статистических характеристик соответствующих составляющих когерентного приемника,
если в последних положить фк_ц = 0 .
Поэтому для средних значений (П6.15), (П6.16) имеем
h =2<1с/п0тКск-\р(£т)СО5(<Рк-и +*u7/2)sinc(*ft7/2),
Qk =-2Яс/поТКск-\р(£т)™{<Рк-и +^/2)sinc(^r/2). (П6.17)
Дисперсии квадратурных составляющих (П6.15), (П6.16) равны дисперсиям
квадратурных составляющих когерентного приемника (П6.9).
250
Методы и алгоритмы обработки сигналов и извлечения информации
П6.3. Статистические характеристики фазовых дискриминаторов
В п. 6.3.4.1 показано, что при значении аргумента jc<0,5 функция
th(jc) = л: и оптимальный фазовый дискриминатор описывается формулой
(6.41). При этом из (6.39) следует, что x = Ik . Понимая в приведенном выше
условии под значением х математическое ожидание М[/^], с учетом (П.6.6)
при £Т=е =£^=0 получаем условие применимости данной аппроксимации:
qc/noT <0,25. (П6.18)
Данное условие в дальнейшем будем использовать для определения
понятия «малое» значение отношения сигнал/шум, т.е. при выполнении (П6.18)
будем говорить о малом значении отношения сигнал/шум.
Для определения термина «большое» значение отношения сигнал/шум
будем использовать условие \х\ > 2 (см. (6.42)), что в соответствии с принятой
выше методологией приводит к формуле
W*1- <П619)
Заметим, что, поскольку приемники СРНС нормально функционируют при
qci >102'8 Гц (qcin >28 дБГц), при Т> 1 мс практически всегда
выполняется условие (П6.16), т.е. приемник работает при большом отношении
сигнал/шум.
Фазовый дискриминатору оптимальный при малом
отношении сигнал/шум
При малом отношении сигнал/шум оптимальный фазовый дискриминатор
определяется формулой
uap(tk) = -IkQk, (П6.20)
А М
h =—ХИ'*-и) Ада ('*-!.' -^-uH^iA-u +&-u).
А М
Qk =—ZH'*-u) hAh-\j -h-\M^nh-u +Фк-\,\)- (П6-21)
Gn /=1
Учитывая принятые в п. П6.1 определения задержек и фаз у принятого и
опорного сигналов, рассчитаем статистические характеристики ФД (П6.20),
под которыми будем понимать дискриминационную £/(^,) = м[мдД^)]и
251
Глава 6
ч\2
(иЛЛ'к)-и(9>>Ф))
^=0
характеристики, где
флуктуационную Dn = М
£ср=<Р-Ф-
Рассчитаем дискриминационную характеристику (ДХ)
u(e(p) = -M[(Tk+I^k)(Qk+Q^k)] =-TkQk =
= 2q2c/nJ2p2(sr)sm(2e(p+su)T)smc2(su)T/2). (П6.22)
Для времен накопления Т= 1...5 мс выполняется условие £&Т<0,6рад и
(П6.22) можно упростить:
U(e<p) = 2q2c/noT2p2(sT)sm(2s<p). (П6.23)
Флуктуационная характеристика ФД (П6.20) определяется соотношением
\=м
\hQ$,k+ Qk^,k+ i$,kQ$ jc)
S=0
= Ik2DQh+Q2D,+DIDQh =
= Sq3c/T3p2(eT)smc2(sJ/2)
1 +
1
2^/^V(^)sinc2(^r/2)
Ф Aj> бф
. (П6.24)
При f^r < 0,6 рад формула (П6.24) упрощается:
flr^W
1 +
1
Чч7^ К)
(П6.25)
Фазовый дискриминатор, оптимальный при большом
отношении сигнал/шум
При выполнении условия (П6.19) (большое отношение сигнал/шум)
оптимальный дискриминатор описывается формулой (6.42), а именно
^('*) = -0*sign(/t), (П6-26)
где Ik, Qk — по-прежнему, описываются выражениями (П6.21);
1, jc>0,
jc<0 "
При большом отношении сигнал/шум с большой вероятностью можно
полагать sign (4) = sign (/д.) = /гнсАг_1, поэтому (П6.26) можно записать в виде
sign(jf) = |ji
252
Методы и алгоритмы обработки сигналов и извлечения информации
мдД'*) = ^X^(/*-w)Aw(^-U~f*-u)sinKr*-U+^-l,l)-
ап 1=1
Тогда дискриминационная и флуктуационная характеристики определяются
как
U(s^) = -hHck_lQk=2qc/^Tp(sr)sm(s9+s(0T/2)sinc(sJ/2), (П6.27)
\ = % = A2T/No = 2аФ0 Т. (П6.28)
Фазовый дискриминатор в виде отношения квадратурной
и синфазной составляющих
В описанных выше дискриминаторах, полученных из статистического
синтеза при известной амплитуде сигнала, крутизна дискриминационной
характеристики зависит от амплитуды принимаемого сигнала. А так как крутизна
дискриминационной характеристики определяет коэффициент усиления по
контуру следящей системы и, следовательно, полосу ее пропускания, то
последняя также зависит от амплитуды принимаемого сигнал. При возможном
(5... 15 дБ) изменении мощности принимаемого сигнала данное обстоятельство
может быть нежелательным, поэтому бывает целесообразно использовать ФД,
в которых крутизна не зависит от амплитуды принимаемого сигнала. Одним из
возможных типов таких дискриминаторов описывается выражением [6.11]
ua<p{h) = -Qk/h- (П6.29)
Рассчитаем статистические характеристики данного дискриминатора при
большом отношении сигнал/шум. Представим (П6.29) в виде
%Л^)=-^т=~и^- (П630)
Принимая во внимание малость отношения «шум/сигнал», запишем для
функции и2 приближенное выражение:
и2 =—= т^«1-4/а ,
2 A \ + U L ф/
а функцию и, представим в виде
h h h
Подставляя данные представления в (П6.30) и пренебрегая членами второго
порядка малости (по величине отношения шум/сигнал), запишем
253
Глава 6
«„(o=-f-f4f- (гш1)
lb lb lb lb
lk 1k Jk 1k
Из (П6.31) с учетом (П6.6)—(П6.9) получаем статистические
характеристики ФД:
Як
1_
'** 2qcjnTp2 (er )sinc2 (^r/2)cos4 (ep + sj/l) \
u(s<p) = -^ = tg(e<p+sJ/2), (П6.32)
lb
D„ =
£<p=0
= ; J- 7 • (П6.33)
2qc,nTp2 (sT )sinc2 (eJ/2)cos4 (eJ/2)
Крутизна дискриминационной характеристики (П6.32) действительно не
зависит от амплитуды принимаемого сигнала.
П6.4. Статистические характеристики частотных дискриминаторов
Частотный дискриминатор когерентного приемника
Частотный дискриминатор (ЧД) для когерентного приемника определяется
формулой (6.48), которую запишем в виде
( А М Л
»аА*к) = -Щ -тХИ'*-и) M'*-U -fk-u)™s(a)ntk_hl +фк_х +d)akAlTd)
\ап /=1
А М
Х^Х[И'*-МК7_0ГАк (>*-!,/ -r*-l,l)sin(^*-U +Фк-1Л +^д;Ыл(/-1)7>)]-
(П6.34)
[ИМ
-А м
°п 1=1
Обозначим
м
°п Ы\
xsin(^Irit_u + фк_и +&Kk.u{l-l)Td)] П6.35)
и рассчитаем статистические характеристики данного процесса:
-А2 М
I' = MlI'k]=—rllhAtk-ij-Tk-u) Кск-АК(*к-и-ч-и) (/-i)^x
xsin(^n^_u +фк_и + &Kk.u(l-l)Td)*
254
Методы и алгоритмы обработки сигналов и извлечения информации
А2К 'V
* NCk~l J A«('-r*-i)A„('-**-i) (t-tk_x)sm{e(p + s0)(t-tk_l))dt =
N0 ,
*k-\
A2h T<
No
p(£T)jvsb(€<p+£6)v)dv =
A Th k-iPM^^ + ^r/2)sinc(^r/2)-cos(*„ + ej)] =
N0*a>
1(1с1щТ2Кск-\Р{^г)
S,J
'CO
[cos(e, + sJll)smc(eJl2)-cos(^ + ej)\. (П6.36)
Ч=М[^-Т)Мт\ \ )Ч«(')«И] ('-'*->) (r-/t.,):
vJTo, , ,
xsin(uy + ^АЧ + а>лМ (t-tk_x))sm{a)nv + фк_х + а>лМ (v -tk_x)) dtdv =
( \2 tk
= I —I J-|-(^ " ^*-l )2 Sin2 ЦГ+ %_!+<*., (/-/*_!))* =
Л2Г3 2
,3
= -qc/nJ. (П6.37)
3iV0 3^c/"° V '
Оптимальный частотный дискриминаторпри
малом отношении сигнал/шум
Рассмотрим случай малого отношения сигнал/шум (П6.18), при котором
(П6.34) можно заменить приближенным соотношением
«д«Ы=ад. <П6-38)
Дискриминационная характеристика ЧД (П6.38) определяется аналогично
(П6.22), а именно
иМ=V' = *&b7V K)cos(s+€Л2У™{£Л2)*
x-L[cos(^ + eJl2)*wz(eJl2) - cos(^ + *вг)] . (П6.39)
На рис. П6.1 приведена нормированная к (4д2/„оГ3p2 (ет))
дискриминационная характеристика (П6.39) при е9 = О. Апертура дискриминационной
характеристики (по первым нулям) А^ = ±/г/Г.
255
Глава 6
-0.1
-0.2
^о^^рад
-10 -8 -6 -4 -2 0 2 4 6 8 10
Рис. П6.1. Нормированная дискриминационная характеристика ЧД
Флуктуационная характеристика ЧД (П6.38) определяется выражением
a,.='*4+/,2/VV4
:\gl/H0TVM\l +
^=0,^=0
2Яс/поТР2(£т)
(П6.40)
Оптимальный частотный дискриминаторпри
большом отношении сигнал/шум
При большом отношении сигнал/шум формула (П6.34) может быть
представлена приближенным выражением
«д»(^) = 818п(/*)/* *^с*-Л» (П6.41)
из которого с учетом (П6.36), (П6.37) следуют соотношения для
статистических характеристик ЧД:
"(*»)= Яс,И° у g [cos(gy+^r/2)sinc(gfl>r/2)-cos(gy+gfl>r)].(n6.42)
Ч«) 1^с/"0
(П6.43)
Нормированная к 2qc/noT2p(£T) дискриминационная характеристика
(П6.39) при £у=0 приведена на рис. П6.2. Апертура дискриминационной ха-
256
Методы и алгоритмы обработки сигналов и извлечения информации
рактеристики А^ «±/г/0,7Г , что несколько больше, чем апертура
дискриминационной характеристики, приведенной на рис. П6.1.
ик
0.5 г
0.41
0.3 [
0.1
°Г
-0.1
-0.2Ь
-о.з[
-°-6ю
-в -6 -4
0 2
6 8 10
ешГ,рад
Рис. П6.2. Нормированная дискриминационная характеристика ЧД
Взаимная дисперсия шумов на вы ходах фазового
ичастотного дискриминаторов когерентного
приемника
Рассчитаем взаимную дисперсию шумов на выходах фазового и
частотного дискриминаторов когерентного преемника.
При большом отношении сигнал/шум, принимая во внимание (П6.26) и
(П6.41), запишем
\пш=м{^лМ
2А
\2
N,
М
о У
'к
'k-i
'к
*k-i
^=0,^=0
= Яс/поТ2.(П6Л4)
При малом отношении сигнал/шум дискриминаторы фазы и частоты
описываются выражениями (П6.20), (П6.38), следовательно, получаем
V» =м[-(7^ф>* +е*7«м +7фЛ^)х
(П6.45)
:(vj
<М +h^jc +^ф
5аАм)
^=о,%=о
= 4q3c/nJ4p2(sT)
1 +
2ЧфТр {ет)
9-1026
257
Глава 6
Оптимальный частотный дискриминатор некогерентного
приемника
Оптимальный дискриминатор некогерентного приемника описывается
выражением (6.55), которое представим в виде
"дДО = —Ь"? : и— ^ • (П6.46)
где ^(iV-U'^;£-u) — огибающая сигнала на выходе согласованного фильтра
(коррелятора), которая описывается формулами (6.52)—(6.54).
Дифференцируя (6.52) по соа, получаем
м*»('*) = 7л^ : ^Т7^ : \х (П6-47)
где I'(fk_u,&Kk_hl) =
А м
Gn 1=1
6'(rjt-uA*-i,i) =
. л/
= — ^У('к-1,1 ) (/ " !)ГЛк [h-\,l - Ч-\,\ )COS(^0^-1,/ + ®д;*-1,1 (' - О7^ ) •
(П6.48)
Оптимальный частотный дискриминаторпри
малом отношении сигнал/шум
При малом отношении сигнал/шум (П6.15) справедливо приближенное
равенство
Il(x)/l0(x)^x/2, jc«1, (П6.49)
и (П6.47) можно заменить приближенным выражением
[7(г,а>д)/>(г,£Рд) + б(г,а>д)б>(г,£Рд)]
"д<у 1Л J * ;
Г = Г*-1,1»Й,Д =£0Кк-\,\
(П6.50)
258
Методы и алгоритмы обработки сигналов и извлечения информации
Для дискриминационной характеристики в этом случае справедлива
формула
, ч [7(г^д)7'(г^д)+е(г^д)б'(г^д)1
^) = L : ~
\T = Tk-u>0)a=6>Kk-i,i
(П6.51)
Средние значения I(fk-\,\*®Kk-\,\)> 6(^*-i,i'^»;*-i,i) 0ПРеДеляются
формулами (П6.17). Выражение для I'{jk-\,\^a;k-\,\) получается из (П6.36) заменой
£ на Фк-\,\ (аналогично тому, как это было сделано при получении формул
(П6.17)),т.е.
J, = 4/noT% '""M^fa-u +^/2)sinc(^r/2)-cos(^_u +ej)\
(П6.52)
Рассчитаем
A2 M
= ~f^fyiK \*к-1,1 ~ Tk-\,\ ) Кск-\Кк yk-\J ~ ?k-\,\) V~4^dx
Gn 1=1
xcos(^n^_u +(pk_u +u)a.kAA(l-\)Td)cos(o)ntk_ll +a>a.k_u(l-\)Td)*
A2 U '*■
Л "нск-1
*k-\
\К(*-Тк-\)К(*-Ч-\)(*-Ъ^
2 T
= ^S^p(£r)jvcos(<pk_u + eav) dv= (П6.53)
^o
= A2TK'k-lP{£\-sm(<pk_u +^r/2)sinc(^r/2) + sin(^_1>1 + ej)\ =
= 2^r4t_,p(gf)^n(ft[| +^r)_sin(fti| +^r/2)sinc(^r/2)].
6to*
Подставляя (П6.52), ( П6.53) и (П6.17) в (П6.51) и выполняя необходимые
преобразования, получаем
259
Глава 6
и(^)=
2(Jc/noT P (^r)sinc(^r/2)
е,.Т
[sinc(^r/2)-cos(^r/2)] . (П6.54)
График зависимости нормированной к 2q^noT3p2(£r) дискриминационной
характеристики (П6.54) приведен на рис. П6.3. Апертура дискриминационной
характеристики Д^ « ±2л/Т.
uv
0.15
0.1
0.06
-0.05
-o.ib
-10 -8 -6 -4 -2 0 2 4 6 8 10 £со^'Рад
Рис. П6.3. Дискриминационная характеристика ЧД
Флуктуационная характеристика ЧД (П6.47) определяется соотношениями
1
D„ =-M
£»=0
+2b/^6' + ЩАё + 2РщОщ ), (П6.55)
где дисперсии флуктуационных составляющих D? , Dh определяются фор-
*ф Уф
мулой (П6.9), a ZX-, и Dh< — (П6.37).
*ф Уф
Рассчитаем взаимные дисперсии флуктуационных составляющих
Dm=M
\h-!')(&-о)
(
2А
а ^ 'к
v^o
| |Ч"('Ж](>-л-,)><
'к-\ 'к-\
xsin(*y + юдЫ (г -^ч ))sin(a)av + о)йкЛ (v -tk_x)) dtdv = (П6.56)
260
Методы и алгоритмы обработки сигналов и извлечения информации
2А
2 *к
Nn
J (/ -tk_x )sin2 (cont + a>aM (t -tk_x)) dt =-A2T2/2N0 = -qcjnT2 .
'*-i
Аналогично рассчитывается
DLn'=A2T2/2N0=qc/T2.
%0
(П6.57)
Подставляя (П6.9), (П6.37), (П6.56), (П6.57) в (П6.55) и выполняя
несложные преобразования, получаем
( . \
Dn.=^l/noT5p2(sT)
1 +
1
Чс/nJP (еТ)
(П6.58)
Оптимальный частотный дискриминаторпри
большом отношении сигнал/шум
При большом отношении сигнал/шум допустимо приближение
/, (x)/l0 (х)«1, и оптимальный ЧД может быть представлен в виде
"д«('*):
[1(т,а>Д)1'(т,соа) + ё(т,соД)ё'(т,соа)}
JP(T,a>a) + Q2(T,a>a)
т = т
*-1Л'^д "^д;*-М
(П6.59)
Для расчета дискриминационной и флуктуационной характеристик в
первом приближении можно полагать
JI'T&vJp+Q2
(П6.60)
При этом дискриминационная характеристика ЧД (П6.59) определяется
выражением
I-F + Q-Q' 2tfc/^rV(Osign(sinc(^7y2))
и{еа)= L'V-
I2+Q2
х[зтс(еаТ/2)-соз(еаТ/2)].
sS
х
(П6.61)
График нормированной к 2qcj T2p(sT) дискриминационной
характеристики (П6.59) приведен на рис. П6.4. Апертура дискриминационной
характеристики Д » ±2.86л-/Г.
261
Глава 6
0.3
0.2
0.1
0
-0.1
-0.2
н
j
V-i
i
! ■'■■"! !
| ) j /\
s ( / I
f [-■/■ { )
i i i i
' ' ' 1
1 -V] -
i i I---V--
1 { \ -
i 1 I ..
-10 -8
-4-2 0 2 4 6 8 10 &m
ет^,рад
Рис. П6.4. Дискриминационная характеристика ЧД
Для флуктуационной характеристики с учетом (П6.56), (П6.57) запишем
6
°пы=^сЫТър2{ет)
1 +
1
Яс/щТр (sT)
(П6.62)
Частотный дискриминатор некогерентного приемника
с временным сдвигом квадратурных компонент
Квадратурные компоненты Ik и Qk некогерентного приемника,
формируемые в момент времени tk, зависят от фазы ^_j(1 принимаемого сигнала.
Аналогичные компоненты Ik+l и Qk+l, соответствующие моменту времени
tk+l, зависят от соответствующего значения фазы <рк х. Так как приращение
фазы А<р = (ркх -(рк_\Х за заданный интервал времени определяет доплеровскую
частоту, обрабатывая квадратурные компоненты для двух соседних моментов
времени, можно получить информацию о доплеровской частоте принимаемого
сигнала. Следовательно, на этом принципе могут быть сформированы
частотные дискриминаторы. Один из возможных типов таких ЧД описывается
соотношением [4.2, 6.11]:
uw{tk) = h+\{?k,u®Kk,\) 64^4'^-u)-4+i(^,i'^,i)^(f*-i.i'^-u)-
(П6.63)
Запишем соотношения (П6.17) для различных моментов времени:
4+1 =24c/nJKckP{sr,k)™s{<Pk,\ +^r/2)sinc(^a772)'
262
Методы и алгоритмы обработки сигналов и извлечения информации
Qk+i=-2ac/noThHckp(£T,k)s™{<Pk,i +£a>,kT/2)si™(£{UtkT/2),
~1к=2Яс1щТКск-\р{£г,к-\У^{(Рк-\,\ +£со,к~\Г12)^с{£со,к-\Т12)у
Uk = -2adnJKck-iP{£r,k-\ )sin(%_ltl + е^_<Г l2)smc(eaJk_xT/2). (П6.64)
Тогда для дискриминационной характеристики получаем выражение
UM = 4Яс/п0Т2р{^к )p{sTjt.l )sinc(^r/2)sinc(^_1r/2) x
x[-cos(^, +£u)tkT/2)sin(<pk_u +£(0k_xTl2) +
+ cos(^_u +£(0k_lT/2)sin(<pkl + £(okT/2)\.
Положим, что 8юк = s^^i. Тогда, учитывая
Фк,\ ~ Фк-и = Т£(о,к-\' формула (П6.65) приводится к виду
^(^) = 4^c/«orV(^)/?(^-i)sinc2(fu)>it_1r/2)sin(^_1r)
График нормированной к 4^^r2/7(^r,*)/?(ffr,*-i) Дискриминационной
характеристики (П6.64) приведен на рис. П6.5. Ширина апертуры
дискриминационной характеристики А^ « ±ж/Т. Заметим, что крутизна
дискриминационной характеристики, приведенной на рис. П6.5, существенно больше, чем
крутизна аналогичных характеристик, приведенных на рис. П6.3, П6.4.
(П6.65)
соотношение
(П6.66)
-1
_i |_
-10 -8
-4 -2 0 2 4 6 8 10
еш7\рад
Рис. П6.5. Нормированная дискриминационная характеристика ЧД
Флуктуационная характеристика ЧД определяется выражением
263
Глава 6
D„ =M
'/со
(h+iQ^k+Qkh,
к+\ +1фМ&ф,к ~
"Абф,*+1 ~Qk+\Ifrk "^ф,*бф,Л+1 j
^=0
i6^%/V(^)^(^a-i)
1 +
2^/„/p(^)^(^-i)
(П6.67)
П6.5. Статистические характеристики дискриминаторов
задержки сигнала
Дискриминатор задержки огибающей сигнала когерентного приемника
В когерентном приемнике оптимальный дискриминатор задержки сигнала
в общем случае описывается (6.43), а при использовании технологии
опережающих и запаздывающих квадратурных компонент — соотношением (6.45)
при малом отношении сигнал/шум и формулой (6.46) при большом отношении
сигнал/шум. Рассмотрим данные типы дискриминаторов раздельно.
Дискриминатор задержки огибающейпри
большом отношении сигна л/ш у м
Как и выше, под термином «большое отношение сигнал/шум» понимаем
условие (П6.19). Оптимальный дискриминатор в этом случае описывается
соотношением
"*r{h) = {h,k-ht)sw{h)- (П6.68)
Принимая во внимание (П6.38) и (П6.13), запишем выражение для
дискриминационной характеристики
= 2qc/noTcos(s(p+£u}T/2)smC(sJ/2) (p(sT - Ат/2)-р(ет + А г/2)) .
(П6.69)
При выполнении условия eJT «1 формула (П6.69) упрощается:
U{zT) = 2qc/noTcos(s<p) (p(er -Ат/2)-р(ет + Аг/2)). (П6.70)
Дискриминационные характеристики оптимального ДЗО (П6.69), (П6.70)
в когерентном приемнике зависят от ошибки слежения по фазе s , что
является недостатком данного типа дискриминатора.
264
Методы и алгоритмы обработки сигналов и извлечения информации
График нормированной к 2gc/„o7,cos(^) дискриминационной
характеристики (П6.71) приведен на рис. П6.6 (при Аг = гэ). Апертура
дискриминационной характеристики Аг = +3/2гэ.
uv
1
0.8
0.6 h
0.4
0.2h
0
-0.2
-0.4
-0.6
-0.8
-1
-1.5 -1
-Об
0.6 1 1.6
ех/т,
Рис. П6.6. Нормированная дискриминационная характеристика ДЗО
Флуктуационная характеристика ДЗО (П6.68) определяется соотношением
вщ=и
(4ф -h*)2\ =%ф +% -20,гф,,ф =^Г(1-р(Дг)).(П6.71)
При часто используемом значении Дг = гэ имеем /?(Дг)«0, и (П6.71)
принимает вид
Dnr=4^/nJ- (П6.72)
Дискриминатор задержки огибающей
при малом отношении сигна л/ш у м
При малом отношении сигнал/шум (П6.18) оптимальный дискриминатор
описывается соотношением
ujxr(tk) = Ik(IE,k-IL9k)>
(П6.73)
из которого можно записать выражение для дискриминационной
характеристики
U(er) = T(TE-IL) = 4q2c/noT2 cos2 (ep + sj/l) x
xsinc2 (£aT/2)p(er) (p(er - Ar/2)-p(er+ At/2)) . (П6.74)
265
Глава 6
При выполнении условия е^Т «1 формула (П6.74) принимает вид
1/(^ = 4^^ (П6.75)
График нормированной к Aq2c,n^T2 cos2 (zA дискриминационной
характеристики (П6.75) при Ат = тэ приведен на рис. П6.7. Апертура
дискриминационной характеристики Аг =±гэ, т.е. в 1,5 раза меньше, чем у
дискриминационной характеристики, приведенной на рис. П6.6.
0.5
0.25k
-0.25
-ОД
-2 -1.6 -1 -0.6
0.5 1 1.5
6Х/Х,
Рис. П6.7. Нормированная дискриминационная характеристика ДЗО
Флуктуационная составляющая на выходе дискриминатора (П6.73)
^дг,ф ""^£ф
^/,ф + ^£^ф ~ ^//ф + Aj/^ф ~~ А^/,ф '
Поэтому для флуктуационной характеристики можно записать выражение
\=м
[МДг.ф]
ег=0
= 16?,
с/п0-
1 +
1-р(Аг)
(П6.76)
Модифицированный дискриминатор задержки
огибающей при большом отношении сигнал/шум
Для устранения зависимости дискриминационной характеристики (П6.74)
ДЗО (П6.73) от ошибки слежения за фазой сигнала е соотношение (П6.73)
надо дополнить аналогичным слагаемым, но включающим квадратурные
компоненты, т.е.
*V ('*) = h [h,k ~ hjc) + Qk {QE,k ~ QL,k) •
(П6.77)
266
Методы и алгоритмы обработки сигналов и извлечения информации
При этом в выражении для дискриминационной характеристики также
появляется второе слагаемое, совпадающее по форме с (П6.74) за исключением
сомножителя cos \е9 + €аТ/2], вместо которого будет сомножитель
sin2 ye9 + s^T/lj. В итоге для дискриминационной характеристики получается
выражение
VM = 4Яс/п/2sine2(eJll)p(eT) (р(ет-Ат/2)-р(ет+Ат/2)). (П6.78)
Флуктуационная характеристика ДЗО (П6.77) в два раза больше, чем в
предыдущем случае:
(П6.79)
А,г=з2<4ог3
и*-р(**)
V 2^/»оГ
Дискриминатор задержки огибающей сигнала некогерентного
приемника
В некогерентном приемнике ДЗО в общем случае описывается
выражением (6.61), а при большом значении отношения сигнал/шум — формулой (6.62).
Дискриминатор задержки огибающейпри
большом отношении сигна л/ш у м
Рассмотрим ДЗО (6.62) с учетом представления производной по задержке
в виде конечной разности (6.63)—(6.64)
ил У к ) - — '
где
*(*>«*-l,l'f*-l,l + AT/2) = ^E(L),k =
= ,Jil(L)A&Kk-U'fk-i,i +AT/2) + Q2E(L),k{^k-U^k-u +Ar/2) ; (П6.81)
h{L),k(&Kk-U>?k-l,l+AT/2) =
A M
= —^у(^-и)Ипк{h-u ~{h-\,\ + Ar/2))cos(a^/ft_lf/ + а>Д.к_и(l-l)Td);
(П6.80)
Ar
Gn 1=1
&(£),* (®«*-U»f*-l,l+Ar/2) =
A M
= -^^у('к-и)Ь№{'к-и ~{fk-ii +Ar/2))cos(^0^_u + &Kk_u(l-l)Td).
267
Gn l=\
Глава 6
При большом отношении сигнал/шум представим огибающую ХЕщк
приближенным соотношением
XE{L),k ~ XE{L) + XE(L)$ ' (П6.82)
где
*E(L) = ^E(L) + Qe(L) ' (П6.83)
h(L)h(L),^ + Qe(l)Qe(l),<\>
~? ~ 2
h{L) + Qe(L)
a IE(LyQE(L\ определяются формулами (П6.13), ( П6.14).
С учетом представления (П6.82)—( П6.84), рассчитаем
дискриминационную характеристику ДЗО (П6.80):
^£(1),Ф = /-- ' (116.84)
U{sT) = (V/J +Ql- A2 + Ql )/д г
= 2<7с/^Г|япс(*даГ/2)|(|/>(*г -Ar/2)|-|/?(fr +Лг/2)|)/Дг. (П6.85)
Вид нормированной дискриминационной характеристики (П6.85) такой
же, что и на рис. П6.6.
Формулу (П6.84) для флуктуационной составляющей представим в виде
xe(l)$ = с17ОД,ф + ciQe(l)$ ' (П6.86)
где
q - ._ '_ =, с2 - _=. (116.87)
У 7£(i) + Qe(l) YE{l) + &e(l)
При расчете флуктуационной характеристики ДЗО полагается ег = О. В
этом случае (П6.87) представляется в виде q = cos(^_,л), с2 = sin(^_j j), а для
флуктуационной характеристики с учетом (П6.10)—( П6.12) получаем
выражение
^=Ч/„оГ/Аг2. (П6.88)
Дискриминатор задержки огибающейпри
малом отношении сигна л/ш у м
При малом отношении сигнал/шум выражение (6.61) может быть
представлено в виде
268
Методы и алгоритмы обработки сигналов и извлечения информации
/ 1 дХ2(тк,о)ак) X2Fk-X2Lk
и (tk) = V a'k> * —^ ^. (П6.89)
аУи 2 дт 2Ат }
Дискриминационная характеристика такого дискриминатора определяется
выражением
i/W=[(7i + g)-(7/+g)]/Ar = .
_2q2c/noT2 sine2(sJll) |
Дг
-(/>2 (sr - Ar/2) - p2 (sT + Ат/2)). (П6.90)
r . ~ 2q2c/noT2smc2(eJ/2)
График нормированной к —— дискриминационной ха-
Ат
рактеристики (П6.81) приведен на рис. П6.8. Апертура дискриминационной
характеристики Аг = +3/2гэ.
и„
1
0.8I-
0.6^
0.4Н
0.2^
°Г
-0.2^
-0.4 [
-0.6 [
-0.81-
-1
-2 -1.5 -1 -0.6 0 0.5 1 1.5 2
БхЛз
Рис. П6.8. Нормированная дискриминационная характеристика ДЗО
Флуктуационная характеристика для данного дискриминатора может быть
рассчитана для произвольного отношения сигнал/шум:
°*-и
2/Аф+'1ф+2&&ф+е1Ф-
ф т^£ф
2
(П6.91)
-2/£/£ф - /1ф - 2&&ф - Йф)
16,4,7V (Ar/2)sinc2(gu,r/2)
<4Ат2 =
At'
1 +
2qc/nJp2(AT/2)smc2{£J/2)
269
Глава 6
При А г = тэ формула (П6.91) упрощается и принимает вид
Ад3с/яоТ3 sine2 (£аТ/2)
* Аг2
Литература
6.1. Сосулин Ю.Г. Теория обнаружения и оценивания стохастических сигналов. —
М: Сов. радио, 1978.
6.2. Куликов Е.И., Трифонов АЛ. Оценка параметров сигнала на фоне помех. —
М: Сов. радио, 1978.
6.3. Первачев СВ., Перов А.И. Адаптивная фильтрация сообщений. — М.: Радио и
связь, 1991.
6.4. Перов А.К, Болденков Е.Н., Григоренко Д.А. Упрощенная аналитическая
методика оценки потенциальной помехоустойчивости оптимальных следящих систем
приемников спутниковой навигации// Радиотехника. Радиосистемы, 2002, № 7, с. 106—
112.
6.5. Перов А.К, Харисов В.К Уменьшение вычислительной сложности
алгоритмов в приемоиндикаторах СРНС на основе комбинированной калмановско-
винеровской фильтрации// Радиотехника. Радиосистемы, 1996, № 1, с. 120—125.
6.6. Перов A.M., Болденков Е.Н. Анализ помехоустойчивости системы ФАП
приемника сигналов спутниковых радионавигационных систем// Радиотехнические
тетради, № 24, 2002, с. 46-50.
6.7. Первачев СВ. Радиоавтоматика. — М.: Радио и связь, 1982.
6.8. Седж Э. П., Меле Дж. Теория оценивания и ее применение в связи и
управлении. — М.: Связь, 1976.
6.9. Харисов В.Н., Яковлев А.И., Глущенко А.Г. Оптимальная фильтрация
координат подвижного объекта// Известия АН СССР. Радиотехника и электроника, 1984, т. 29,
№10.
6.10. Харисов В.Н., Горев А.П. Исследования одноэтапного алгоритма навигаци-
онно-временных определений для приемника СРНС// Радиотехника. Радиосистемы,
2001, №4, с. 49—58.
6.11. Understanding GPS: Principles and Applications/ Ed. by E.D. Kaplan. Artech
House, Inc., Norwood, Massachusetts, 1996.
6.12. Filippov D., Tatarnicov J., Ashjaee A.., Astakhov I,. Sutiagin. The First Dual-
Depth Dual-Frequency Choke Ring, ION GPS-98, NASHVILLE, TENNESSEE,
SEPTEMBER 15-18, 1998, pp. 1035-1040.
6.13 Moelker D-J. Multiple Antennas for Advanced GNSS Multipath Mitigation and
Multipath Direction Finding, ION GPS-97, KansasCity, Missouri, September 16-19, 1997,
pp.541-550.
6.14. Ray J.K. Use of Multiple Antennas to Mitigate Carrier Phase Multipath in
Reference Stations, ION GPS-99, Nashville, TN, 14-17 September 1999, pp.269-279
6.15. Fenton P.B., Falkenberg, Ford Т., Ng K.t and Van A J. Dierendonck. NovAtePs
GPS Receiver-The High Performance OEM Sensor of the Future, ION GPS-91, Fourth
Inters/sine2 (*„^
(П6.92)
270
Методы и алгоритмы обработки сигналов и извлечения информации
national Technical Meeting of the Satellite Division of the Institute of Navigation,
Albuquerque, NM, September 11-13, 1991, pp. 49-58.
6.16. Van DierendonckAJ. et.al. Theory and Performance of Narrow Correlator
Spacing in a GPS Receiver// Journal of The Institute of Navigation, vol. 39, no. 3, Fall 1992.
6.17. Garin Z,., Rousseau, J-M. Enhanced Strobe Correlator Multipath Rejection for
Code & Carrier, ION-GPS 1997, KansasCity, Missouri, September 16-19, 1997, pp.569-578.
6.18. Townsend B.R., Fenton PA. Practical Approach to the reduction of Pseudorange
Multipath Errors in a LI GPS Receiver, in Proceedings of ION GPS-94 Salt Lake City, Sep.
20-23, 1994.
6.19. Van Nee R., Fenton P., Townsend B.R.. The Multipath Estimating Delay Lock
Loop Approaching Theoretical Accuracy Limits," presented at the IEEE Position, Location
and Navigation Symposium, Las Vegas, Nevada, April 11-15, 1994.
6.20. Jones J., Fenton P., Smith. B. Theory and Performance of the Pulse Aperture
Correlator. Internet: http://www.novatel.ca, June 9, 2004.
6.21. Weill L. Achieving Theoretical Accuracy Limits for Pseudoranging in the
Presence of Multipath, in Proceedings of ION GPS-95, pp. 1521-1530.
6.22. Weill L. Multipath Mitigation Using Modernized GPS Signals: How Good Can it
Get, in ION GPS 2002, Portland, Oregon, Sep. 2002, pp. 24-27.
6.23. Fenton P., Jones J. The Theory and Performance of NovAtel Inc.'s Vision
Correlator, ION GNSS 2005, Long Beach, CA.
6.24. Тихонов В.И., Харисов В.К Статистический анализ и синтез
радиотехнических устройств и систем. — М.: Радио и связь, 2004.
271
Глава 7
Глава 7
ИСТОЧНИКИ ПОГРЕШНОСТЕЙ И ТОЧНОСТЬ
НАВИГАЦИОННО-ВРЕМЕННЫХ ОПРЕДЕЛЕНИЙ
В СПУТНИКОВЫХ НАВИГАЦИОННЫХ СИСТЕМАХ
Под навигационно-временными определениями понимают формирование
оценок координат, составляющих скорости потребителя и текущего времени в
результате обработки радиосигналов, принимаемых от НС. Рассматривая в
качестве базовой аппаратуру потребителя с двухэтапной обработкой сигналов,
можно констатировать, что точность НВО определяется двумя типами
погрешностей: погрешностями, возникающими на этапе первичной обработки, и
погрешностями, соответствующими этапу вторичной обработки. Так как при
первичной обработке формируются оценки псевдо дальностей и псевдо скоростей,
погрешности для данного этапа — это погрешности определения псевдо
дальности и псевдо скорости. На этапе вторичной обработки оценки псевдо
дальностей и псевдо скоростей пересчитываются в оценки координат потребителя,
поэтому погрешности этого этапа определяются факторами, влияющими на
эффективность такого пересчета. Рассмотрим два указанных типа
погрешностей более подробно.
7.1. Составляющие погрешности определения псевдо дальности
при использовании дальномерного метода
Суть псевдо дальномерного метода (см. п. 4.3) заключается в определении
псевдо дальности Д = ст через время распространения сигнала
г (С") = гпр (С") - т™ («2°) от НС до потребителя, где Г„р (г™) - зна-
чение времени на ШВП в момент времени f JJjBn (момент излучения некоторой
фазы дальномерного кода с борта НС), Гизл М™в) — значение времени на
БШВ в момент времени ^вп (момент приема той же фазы дальномерного
кода у потребителя).
При этом в п. 4.3 полагалось, что момент излучения сигнала с НС — это
одновременно и момент его формирования, а радиосигнал распространяется в
свободном пространстве. При таком определении псевдо дальность (расчетная)
определяется соотношением
д(Сп)-К('пГп)-^(Св))=аст(Свп)+Д'. an
272
Источники погрешностей и точность НВО
где ДистИпр ) — геометрическая дальность между точной, из которой
излучался сигнал, и точкой, в которой он принимается; Д' — погрешность
определения истинной геометрической дальности, обусловленная сдвигом шкал
времени НС и потребителя (см. (4.7)).
В приемнике формирование оценки псевдо дальности (измеренной псевдо
дальности) основано на измерении момента приема заданной фазы дальномер-
ного кода и расчете ее запаздывания относительно момента формирования той
же фазы дальномерного кода на борту НС, информация о котором извлекается
из навигационного сообщения. Определенная таким образом псевдо дальность
отличается от той, которая постулируется формулой (7.1), что обусловлено
рядом физических и технических факторов. Отклонения измеренной псевдо
дальности от расчетной (7.1) будем называть погрешностями определения
псевдо дальности.
При распространении сигнала по трассе НС—потребитель он проходит
ионосферу и тропосферу, которые существенно влияют на время
распространения сигнала. Возникающие при отклонения измеренной псевдо дальности от
расчетной будем обозначать Stmiic и St^onc — ионосферная и тропосферная
погрешности. Подробное описание данных погрешностей приведено в п. 7.3.
Вращение источника излучения сигнала по орбите с высотой примерно
25 тыс. км приводит к ряду релятивистских и гравитационных эффектов,
влияющих на определение времени распространения сигнала от НС до
потребителя. Погрешности данного типа обозначим как Stpr3, а их краткое
обсуждение приведено в п. 7.4.
При работе приемника в условиях, отличных от «свободного
пространства», на его вход, кроме сигналов НС, могут поступать переотраженные от
местных предметов (а также от подстилающей поверхности) сигналы. Это
приводит к смещению измеряемого в преемнике положения максимума
корреляционной функции опорного сигала с поступившей смесью входных сигналов, т.е.
к возникновению погрешности в оценке времени приема сигнала, а
следовательно, и в оценке псевдо дальности. Данный вид погрешности StMnpc
называют погрешностью многолучевого распространения. Анализ эффектов
многолучевого распространения дан в п.7.5.
При обработке сигналов в приемнике возникают также погрешности
(ошибки) в оценке псевдо дальности, среди которых выделяют два типа: погрешность,
связанная с групповой задержкой сигнала в высокочастотном тракте приемника,
и погрешность, обусловленная следящими системами за задержкой кода и фазой
сигнала. Обозначим погрешности, вносимые приемником, как Stnpc.
В бортовой аппаратуре в инерционных цепях формирования
высокочастотного сигнала возникает групповое его запаздывание, что приводит к отста-
273
Глава 7
ванию момента излучения «заданной» фазы дальномерного кода относительно
момента ее формирования в генераторе кода и, соответственно, к отличию
реального момента излучения относительно того, которое передается в
навигационном сообщении. Погрешность данного типа обозначим как 8tm,
Итоговая погрешность определения псевдо дальности определяется как
сумма частных составляющих погрешностей и может быть представлена в виде
$Д = КопС + £'тропс + Лмлрс + Stw>c + 5t*vC + Stm + £Д > С7-2)
где £д — прочие составляющие погрешности определения псевдо дальности,
не входящие в описанные выше.
С учетом описанных типов погрешностей для измеренной псевдо
дальности (оценка псевдо дальности) можно записать выражение
Д = Д + ЯД = Дист (f ™п ) + Д' + ЗД. (7.3)
7.2. Составляющие погрешности определения псевдо скорости
В СРНС псевдо скорость ^определяется по доплеровскому смещению
частоты принятого сигнала.
Доплеровское смещение частоты принимаемого узкополосного сигнала
относительно частоты излученного сигнала обусловлено взаимным
перемещением источника излучения и приемника сигнала. Если частота излучаемого
сигнала /0, то частота принимаемого сигнала fn определяется известным
соотношением [7.1]
v-l
/п ~Л
( v У ( v Л
/о
1-^
V с J
(7.4)
LT-P
V
где Vp — скорость относительного движения вдоль линии НС—потребитель,
положительное значение которой соответствует увеличению расстояния между
объектами.
Для доплеровского смещения частоты из (7.4) получаем
Л=Л-/о-/Д = -^ = -Нг, (7.5)
с Л Л at
где Д — расстояние между источником излучения и приемником.
Полная фаза принимаемого сигнала с частотой (7.4) при Vp = const
фп (0 = <Ро + fafndt = (p0+ Ixfy + 2л-// , (7.6)
о
где ср0 — начальная фаза.
274
Источники погрешностей и точность НВО
При известной частоте /0 оценку доплеровского смещения частоты
принимаемого сигнала в приемнике можно получить, если сформировать опорное
колебание cos(#>0on + Inf^t) = cos(Oon (?.)), измерить разность фаз
ДФ(0 = Фп(0-фоп(0 = ^о-^оп+2/г/д/ (7.7)
и вычислить производную по времени от данной разности
1 dA<&(t)
^й-r1- (7-8)
Учитывая (7.7) и (7.8), запишем выражение для оценки скорости,
формируемой в приемнике
-Xdb<S>{t)_-l(d<bn(t) d<bm(t)
2тг dt 2/г
\
dt dt
(7.9)
Производные d<S>n(i)ldt и dOm(t)/dt в (7.9) определяют мгновенные
частоты 2я-/нс(?) и 2/г/оп(?) бортового передатчика и опорного генератора
приемника. Так как каждый генератор гармонического колебания обладает
вполне определенной нестабильностью частоты, можно записать выражения
/нс(') = /0+/н'с> /оп(>) = /0+/о'п> (7.Ю)
где /н'с и /0'п — отклонения частот излучаемого сигнала и опорного колебания
приемника от номинальных значений.
Таким образом, при определении радиальной скорости в соответствии с
(7.9) возникает смещение в оценке скорости Р' = Я(/0'П -/н'с)> обусловленное
расхождением частот опорных генераторов НС и потребителя, т.е. фактически
определяется не скорость, а псевдо скорость V = Vp + V'. Можно показать (см.
п. 4.6), что V = dftjdt = cdt'jdt, где t' — расхождение между БШВ и ШВП,
описанное в предыдущем разделе.
Приведенные выше определения доплеровского смещения частоты и
псевдо скорости соответствуют распространению сигнала в свободном
пространстве. Реально сигнал, излученный с НС, проходит слой ионосферы и
тропосферы, поэтому необходимо учесть эффекты, возникающие при распространении
сигнала в реальных средах.
Ионосфера влияет не только на задержку огибающей сигнала, но и на
задержку его фазы. Более подробно эти эффекты будут обсуждены в п. 7.3. Здесь
же лишь констатируем итоговый результат, который гласит: дополнительная
задержка фазы, обусловленная влиянием ионосферы, в первом приближении
совпадает с аналогичной задержкой огибающей Лион , но имеет обратный знак.
275
Глава 7
Однако, поскольку изменение задержки StmH (t) во времени очень медленное,
производная d8tmHjdt очень незначительная, что обусловливает слабое
влияние ионосферы на определение псевдо скорости.
Аналогичная ситуация имеет место при анализе влияния тропосферы на
определение псевдо скорости, поэтому им также пренебрегают.
Релятивистские и гравитационные эффекты оказывают влияние на
точность определения псевдо скорости, что учитывается соответствующей
погрешностью SV .
В приемнике оценка доплеровского смещения частоты принятого сигнала
формируется следящей системой за фазой (или частотой), что приводит к
определенной ошибке, которую обозначим Sf^np.
В результате оценка псевдо скорости (измеренная псевдо скорость) может
быть записана в виде
? = Vp+V + SVpr3 + X8f^p + SVnp04 , (7.11)
где SVnpo4 — прочие составляющие погрешности определения псевдо
скорости, не входящие в описанные выше.
7.3. Влияние среды распространения на параметры сигнала
При определении псевдо дальности и псевдо скорости в п. 7.1, 7.2
полагалось, что электромагнитные волны (сигнал) распространяются со скоростью
света. Это соответствует их распространению в вакууме. Реально сигнал
распространяется в земной атмосфере, характеристики которой отличны от вакуума,
что необходимо учитывать при анализе псевдо дальности и псевдо скорости.
Основными электрическими параметрами среды, в которой
распространяются электромагнитные волны, являются [7.2, 7.3]:
в — относительная диэлектрическая проницаемость;
ju — относительная магнитная проницаемость;
о — удельная проводимость.
Если электрические параметры среды зависят от частоты, то среда
распространения называется диспергирующей, в противном случае — недисперги-
рующей.
В атмосфере выделяют несколько слоев, отличающихся физическими
свойствами [7.2, 7.3]. Нижний слой, простирающийся от поверхности Земли до
высоты около 10 км, называют тропосферой. Слой атмосферы от 60 до 1000 км
называют ионосферой. Тропосфера является недиспергирующей средой, а
ионосфера — диспергирующей.
276
Источники погрешностей и точность НВО
При распространении плоской монохроматической электромагнитной
волны в однородной изотропной среде изменение ее фазы описывается
соотношением [7.1]
<p = cot-kr, (7.12)
где г — радиус-вектор из начала координат в рассматриваемую точку
пространства; k = k 10 — волновой вектор, модуль которого равен к = co/v^ , где
Уф— фазовая скорость, а единичный вектор 10 определяет направление
распространения волны, т.е. перпендикулярен фронту волны. Модуль волнового
вектора к определяет изменение фазы на единице длины пути. Фазовая
скорость Уф характеризует скорость перемещения волнового фронта. В вакууме
Уф = с, в реальной среде v^^c.
Так как электрические параметры недиспергирующей среды не зависят от
частоты, фазовая скорость электромагнитных волн, имеющих различные
частоты одинакова. Поэтому сигнал, представляющий собой совокупность
электромагнитных волн с различными частотами, распространяется в такой среде
как единое целое (группа волн) с единой скоростью.
В диспергирующей среде фазовая скорость различных составляющих
сигнала различна, что приводит к изменениям распространения сигнала как
группы волн. Для характеристики такого изменения вводят понятие групповой
скорости распространения сигнала. Остановимся на понятиях фазовой и
групповой скорости более подробно.
7.3.1. Групповая и фазовая скорости распространения сигнала
Положим, что в (7.12) ось ОХ системы координат направлена вдоль
направления распространения волны. Тогда можно записать
( \
х
v4>
<p(xyt) = cot-y/(a)) = cot-x— = &\ t =йн*-/ф|, (7.13)
где у/(со) называют фазовым запаздыванием, а ^— временем фазового
запаздывания или временем фазовой задержки.
Рассмотрим узкополосный сигнал s(t), передаваемый на несущей частоте
щ, и представим его через преобразование Фурье:
?(/) = Re
ии
eiu»' \s(f)e2*fi<P
(7.14)
где £(/) — спектральная плотность комплексной огибающей сигнала
277
Глава 7
00
(7.15)
При распространении сигнала вдоль оси ОХ после прохождения
расстояния L каждая частотная составляющая сигнала приобретет фазовое
запаздывание у/(со), в общем случае зависящее от частоты. Положим, что в пределах
ширины спектра сигнала зависимость у/(со) относительно у/(щ) можно
приблизительно считать линейной функцией частоты. Тогда разложим у/ (со) в ряд
в точке щ и ограничимся линейными членами разложения:
у/((о) = у/(щ+27г/) = у/(щ) + у/'(а)0)2тг/.
Тогда, полагая, что в точке х-0 излучался сигнал (7.14), для сигнала в
точке x-L можно записать
s(t,L) = Re
00
JW f£( ,\е\2лАе-1{у'{щ)+У''{щ)2л/) „
= Re
}{щ*-у{щ))
\s{f)
^/(t-y'to)) „
(7.16)
В (7.16) интеграл есть не что иное, как огибающая сигнала в точке x-L,
для которой с учетом определения (7.15) можно записать
U(,,L)=)s(f)e,2"/^^df = U(t-^((»0)).
-00
Таким образом, получаем запаздывание комплексной огибающей на время
'г=^'Н)> (7-И)
которое называют временем группового запаздывания сигнала.
Из (7.16) также следует, что фаза высокочастотного заполнения
изменилась на величину у/(со0), поэтому в соответствии с (7.13) время фазового
запаздывания
'ф=И^)М- с7-18)
Вернемся к соотношению (7.13) и запишем более общее выражение для
фазового запаздывания:
1 dx
¥
/ ч СО СОХ
[СО) = Х = €0 .
v^ й"ф
(7.19)
ч
278
Источники погрешностей и точность НВО
Формула (7.19) более общая в том смысле, что она справедлива для случая,
когда фазовая скорость v(j) (jc) зависит от координаты х, что может иметь
место, например, в неоднородных средах.
Из (7.18), (7.19) вытекает еще одно полезное соотношение:
dx
t
сох
(7.20)
W
связывающее фазовую скорость и время фазового запаздывания.
Аналогичное соотношение справедливо для группового времени
запаздывания
dx
t
_ f "*
J v
(v) Г
Подставляя (7.19) в (7.17) и учитывая (7.21), запишем
(7.21)
dco
С dx
со\ —
dx
0)=(Щ
-Jv
(*)г
(7.22)
Положим, что фазовая скорость у^(со) зависит от частоты (дисперсия
волн). Тогда, выполнив дифференцирование по со в (7.22), можно получить
следующее выражение, связывающее фазовую и групповую скорости:
"Ф
ы
v = t
[1 -ЦЧ (®))^ф (a>)lda>\
«уфЮ
1 +
со
dv^ (со)
v^(co) dco
. (7.23)
-iO)=0)Q
В недиспергирующей среде dv^ldco - 0 и из (7.23) получаем vr = v^ .
7.3.2. Коэффициент преломления среды
При распространении электромагнитных волн в однородной среде с
параметрами е, //, а модуль волнового числа к определяется выражением [7.1]
к =
2к
Я V 2
следовательно
^1 + J\ + (6Q<T/tef,
(7.24)
Ч=с/'Щ^й^^Щ2
Наряду с волновым числом к и фазовой скоростью v± широко
используется коэффициент преломления среды
279
Глава 7
^=~ = ^\ + ^ + {б0а/Л£)2. (7.25)
Для сред с малыми потерями бОсг/Ле «1 из (7.25) получаем
пф * ^ф « 4s , (7.26)
поскольку для многих сред выполняется соотношение //«1.
По аналогии с (7.25) можно ввести коэффициент
пг = c/vr . (7.27)
В случае дисперсии волн v(j)(&>) дифференцирование (7.25) по со дает
соотношение
подставляя которое, а так же (7.27), в (7.23), получаем
"г = г-^ ;— * Ч + /—* • (7-28)
г [1-(//^ф)^ф/#] ф #
Коэффициенты преломления иг, т, можно использовать для определения
группового и фазового времен запаздывания. Используя (7.25), (7.27) и (7.20),
(7.21), запишем
1
с
>г =
- J V7, (7.29)
= - \nTdl. (7.30)
с J
С)
В (7.29), (7.30) принятое ранее направление распространении волны по
координате х заменено (для общности) произвольным направлением
распространения /.
7.3.3. Влияние ионосферы на запаздывание сигнала
Ионосфера — область атмосферы, содержащая значительное число
свободных электронов (более тысячи в 1 см3), что обусловливает ее
диспергирующие свойства.
Относительная диэлектрическая проницаемость ионосферы определяется
выражением [7.1]
280
Источники погрешностей и точность НВО
, 3190W
e = l—2 f-, (7.31)
где Ne — концентрация электронов, эл/м3; гэфф— эффективная частота
столкновений электронов с ионами и нейтральными молекулами.
Для дециметровых и более высоких частот v3^ « со, поэтому (7.31)
принимает более простой вид:
80,6W,
е = \ Ц-*-. (7.32)
/2
Подставляя (7.32) в (7.26), получаем
п^^\~Щ6Ме//2 . (7.33)
Для метровых и более коротких длин волн выполняется условие
%0,6Ne/f2 «1, поэтому (7.33) можно записать в упрощенном виде:
«ф*1-40,ЗЛГе//2. (7.34)
Подставляя (7.34) в (7.28), получаем
nr*\ + 40,3Ne/f2 . (7.35)
Рассчитаем групповое время запаздывания сигнала, излучаемого
навигационным спутником, находящимся в зените, при его прохождении ионосферы.
Для НС, находящегося в зените, фактически отсутствует искривление
направления распространения (луча) сигнала, которое присутствует при другом
расположении НС и влияет на время распространения сигнала. Поставляя (7.35) в
(7.30), получаем
*min,HOH
/ 40 л Г
,г=_жж+^ Г #,(/)<//, (7.36)
с cf J
'max, ион
гДе 'max,™»» ^п.ион — верхняя и нижняя границы ионосферы;
^ион =(^тах,ион "'т^ион) — ТОЛЩИНа СЛОЯ ИОНОСферЫ.
Первое слагаемое в (7.36) представляет собой время прохождения сигналом
расстояния ZH0H в вакууме. Следовательно, второе слагаемое дает приращение
времени запаздывания огибающей сигнала, обусловленное ионосферой, т.е.
5, 40'3
*гшп,ион
да f2 J Ne(l)d! = U(nr-\)dl. (7.37)
У I (I)
1 max, ион
281
Глава 7
Аналогично получаем выражение для приращения времени фазового
запаздывания, обусловленного ионосферой,
чшп.ион
^н=^рГ J K(l)dl = -J{n^-\)dl. (7.38)
'max, ион v)
Из (7.37), (7.38) следует, что дополнительное время запаздывания,
обусловленное влиянием ионосферы, определяется зависимостью Ne (/)
электронной концентрации от высоты (высотные профили). Данная зависимость
существенно меняется в течение суток, что приводит к соответствующему
изменению времени запаздывания, которое может составлять примерно 10 не (3 м)
ночью и доходить до 50 не (15 м) днем. Кроме того, Ne(l) существенно
зависит от активности солнца, геомагнитной активности и ряда других факторов,
определяющих уровень ионизации ионосферы.
При распространении сигнала с НС, расположенного под углом
возвышения а относительно потребителя, время запаздывания сигнала в ионосфере
возрастает за счет увеличения длины пути, проходимого сигналом в ионосфере.
Данное увеличение может быть учтено соответствующим коэффициентом ка.
В [7.1] приводится следующее выражение для такого коэффициента:
*„ =
' R3cos[a)
1
а
^3 "■" Л/этах J
R*+h
где R3 — радиус Земли; /гэтах — высота точки над Землей, которой
соответствует максимум концентрации электронов.
Для углов возвышения а = 0...10° дополнительная задержка сигнала,
обусловленная влиянием ионосферы, может возрастать до 3 раз по сравнению со
случаем распространения сигнала из точки зенита, и составляет от 30 не (9 м)
ночью и до 150 не (45 м) днем.
7.3.4. Влияние тропосферы на запаздывание сигнала
Тропосфера является недиспергирующей средой, поэтому групповая и
фазовая скорости сигнала в ней совпадают, и в дальнейшем будем говорить
просто о скорости распространения сигнала.
На скорость распространения сигнала в тропосфере оказывают влияние
нейтральные атомы и молекулы, состояние которых зависит от локальной
температуры, давления и относительной влажности. Диэлектрическая
проницаемость тропосферы для частот ниже 50 ГГц с ошибкой менее 1% по данным
теории и эксперимента описывается выражением [7.1]
282
Источники погрешностей и точность НВО
£т =1 +
Г\,552р 7,45-юУ
V
10"
(7.39)
у
где Т — абсолютная температура, К; р — давление сухого воздуха, Па; е —
давление водяного пара, Па.
Учитывая соотношение (7.28), связывающее диэлектрическую
проницаемость среды с коэффициентом преломления, запишем
WTp=>/^ = J1 +
зЛ
1,552р 7,45-КГе
10
-6
2
Г
ъЛ
1,552р 7,45 -We
\
10
-6
(7.40)
Тогда для времени запаздывания сигнала в тропосфере относительно
времени его распространения в вакууме на основании (7.40) запишем
8и
А1п^*-Л\
1 fO,776£J/1()_6+J_ гЗ,725-103е
Г cJT2
J/10
-6
(7.41)
/ / /
Первое слагаемое в (7.41) отражает влияние давления и температуры
сухого воздуха, а второе слагаемое — влияние влажности и температуры на время
задержки сигнала. Обозначим
N =
■'сух
0,776/71Л_6 АГ 3,725 10"в1Л_6
-ю-°,лг =
10"
Пусть источник сигнала (навигационный спутник) находится в зените
относительно точки расположения приемника, находящейся на высоте hn над
уровнем моря. Тогда интегрирование в (7.41) проводится по высоте h от /^ до
/zmax — максимальная высота тропосферного слоя. Существуют различные
модели, отображающие зависимости Ncyx(h), NbJl(h) от высоты [7.1, 6.11, 7.4].
Наиболее простая модель имеет вид
^сух (А) = NcyK 0 е"'А ,Nm(h) = Nm0 е"'А,
Где Мсухо и NBJ]0 — значения параметров (7.42) на уровне моря;
^*0,12...0,15 км-1.
Если источник излучения сигнала находится не в зените, а под углом места
а над горизонтом, то увеличивается длина пути при интегрировании в (7.41),
что, как и в случае ионосферы, может быть учтено коэффициентом ka,
описываемым соотношением ка = l/sin(«).
283
Глава 7
Задержка сигнала в тропосфере может составлять около 7 не (2 м) для НС,
находящихся в зените, и до 83 не (25) м для НС, расположенных под углом
места а < 5°.
7.4. Влияние релятивистских и гравитационных эффектов
Среднеорбитальная СРНС ГЛОНАСС одна из немногих технических
систем, на характеристики которой оказывают заметное влияние законы общей и
специальной теории относительности Энштейна. Связано это с тем, что, во-
первых, НС движутся по орбитам с достаточно высокими скоростями, во-
вторых, разность гравитационных потенциалов в точках нахождения НС и
потребителя такова, что ей нельзя пренебречь, и, в-третьих, Земля с
находящимися на ней потребителями вращается относительно инерциальной системы
координат, в которой задается движение НС. Остановимся кратко на отмеченных
факторах, следуя [6.11]. Более подробное описание релятивистских эффектов
можно найти в [7.5].
В специальной теории относительности доказывается, что время At',
измеренное между двумя событиями внутри одной инерциальной системы
координат, отличается от времени At, измеренного между теми же событиями, но в
другой инерциальной системе координат, которая движется относительно
первой со скоростью v. Соотношение между двумя интервалами времени
описывается формулой
где с — скорость света.
Аналогичное соотношение справедливо для отрезков длиной As и As', a
именно,
As'
As= , (7.43)
VHv/c)2
Исходя из постулата специальной теории относительности о постоянстве
скорости света в любой инерциальной системе, полагая в (7.43) вместо As
(As') длину волны Л (Я') и принимая во внимание соотношение /Л = с и
/'Л' = с из (7.43), получаем выражение
f = f'^-(v/cf . (7.44)
При v « с из (7.46) получаем приближенное соотношение
284
Источники погрешностей и точность НВО
f-Г-Л
• —^""■ /^/
Г 2
(7.45)
Выражение в правой части (7.45) можно трактовать как отношение
кинетической энергии материальной точки с единичной массой, движущейся со
скоростью v, к квадрату скорости света.
При движении материальной точки в центральном поле тяготения U, как
следует из общей теории относительности, соотношение (7.47) должно быть
дополнено аналогичным эффектом, обусловленным потенциальной энергией
АС/, т.е.
-^-^---1-1 + —. (7.46)
Г 2
\с;
с
Используем соотношение (7.46) для оценки влияния релятивистских
эффектов на характеристики опорного генератора, устанавливаемого на борту НС
и формирующего бортовую шкалу времени. Положим в (7.46): /' — частота
бортового опорного генератора, фиксируемая наблюдателем, находящемся на
НС; / — частота того же опорного генератора, но фиксируемая
наблюдателем, находящимся в точке инерциального пространства, соответствующей
подспутниковой точке на Земле; v — скорость НС в инерциальном пространстве.
В этом случае потенциальная энергия АС/ определяется соотношением
AU= M M
RHC R3
где ju — геоцентрическая гравитационная постоянная Земли; R3 — радиус
Земли; RHC — радиус орбиты НС.
Расчет по (7.48) для рассматриваемых условий и параметров Земли и
орбит НС ГЛОНАСС приводит к следующему результату:
^/^4,36-l(T10. (7.47)
Следовательно, с точки зрения наблюдателя, находящегося на Земле,
частота опорного генератора НС / будет казаться больше, чем частота /',
которую фиксирует наблюдатель, находящийся на НС.
Номинальное значение частоты бортового опорного генератора для
наземного наблюдателя должно соответствовать for0 = 5,0 МГц. Тогда из (7.47)
следует, что реальная частота опорного генератора, находящегося на борту НС,
/Jr =(l-4,36-10-10)/or0 =4,99999999782 МГц, (7.48)
т.е. на 2,18 • 10~3 Гц меньше номинального значения /ог0.
285
Глава 7
Компенсация данного релятивистского эффекта осуществляется
соответствующим смещением частоты опорного генератора при его настройке на Земле.
Другой тип релятивистского эффекта связан с отличием траектории НС от
круговой, что характеризуется эксцентриситетом орбиты е (см. гл. 3). Для
некруговых орбит скорость НС в перигее больше, чем в апогее, а гравитационный
потенциал — меньше. Это приводит к тому, что бортовые часы (БШВ) идут
медленнее в перигее и быстрее в апогее. Временная поправка к времени
бортовых часов, которое соответствует движению НС по круговой орбите, дается
соотношением [7.5]
St. = 2Г(Ч"('и) = 4V^si„(£(,„)), (7.49)
С С
где г(*и) и v(/H) — радиус-вектор положения и скорости НС соответственно
на момент времени tn излучения сигнала; Е[ги) — значение эксцентрической
аномалии на тот же момент времени; а — большая полуось орбиты НС.
В [6.11] отмечается, что погрешность (7.51) может составлять 70 не (21 м).
Поэтому данный релятивистский эффект необходимо компенсировать для
получения высокоточных НВО, что может быть реализовано в аппаратуре
потребителей на основе данных, содержащихся в навигационном сообщении.
Еще один релятивистский эффект связан с вращением Земли. Пусть в
момент времени /и НС находится в точке, соответствующей радиусу-вектору гнс
(в геоцентрической инерциальной системе координат), и излучает сигнал.
Приемник в момент времени ги находится в точке на Земле, которой соответствует
радиус-вектор гп (рис. 7.1).
НС в момент
//7 излучения сигала
Приемник в момент
приема сигала,
Земля
Рис. 7.1. Схема излучения и приема сигнала
286
Источники погрешностей и точность НВО
Пусть приемник неподвижен относительно Земли, а Земля вращается
относительно инерциальной системы координат с вектором угловой скорости
ft3 • За время распространения сигнала г от НС до приемника последний
сместится за счет вращения Земли, и его новый радиус-вектор будет равен
гп + vr, где для вектора скорости можно записать выражение v = ft3 х гп •
Полагая, что скорость распространения сигнала равна скорости света, т.е.
пренебрегая релятивистскими эффектами, можно записать
cr = |rn+vr-rHC|.
Тогда для приращения времени StQ, обусловленного вращением Земли,
справедливо выражение
cStQ=\rn+\r-rHC\-\rn -гнс|. (7.50)
Введем Дг = гп -гнс и запишем для первого слагаемого в (7.50)
приближенное выражение [7.5]
|гп + \т -гнс| « л/Дг • Дг + 2Дг • vr . (7.51)
Учитывая малость второго слагаемого под знаком корня в (7.51), разложим
(7.51) в ряд Тейлора и ограничимся линейными членами
Дг-vr
л/Дг-Аг + 2Аг-уг »|Аг|+ , , • (7.52)
|Дг|
Подставляя (7.51), (7.52) в (7.50) и учитывая, что |Дг|/с = т, получаем
,. Ar-v (rn-rHC)(ft3xrn) nm
dtQ=—— = . (7.53)
с с
Если приемник движется относительно Земли с вектором скорости v0, то
в (7.53) вместо вектора скорости v = П3 х гп следует использовать
v = O3xrn+v0.
Погрешность, обусловленная вращением Земли, может составлять до
100 не (30 м), и ее также необходимо компенсировать для получения высокой
точности НВО.
7.5. Влияние многолучевого распространения сигнала
При работе НАП в городских условиях, а также в любых других
ситуациях, характеризующихся наличием отражающих предметов, на вход приемника,
кроме сигналов НС, поступают переотраженные от местных предметов
сигналы. Переотраженные сигналы имеют, как правило, меньшую, чем у прямого
сигнала, амплитуду, дополнительную задержку огибающей и дополнительное
287
Глава 7
фазовое смещение, которые, кроме того, могут изменяться во времени.
Суммирование всех принятых сигналов на входе приемника приводит к
результирующему сигналу, который флуктуирует по амплитуде, фазе и задержке
огибающей. При достаточно медленных флуктуациях следящие системы
приемника за дальномерным кодом, фазой (или частотой) сигнала сопровождают
мгновенное значение соответствующих параметров, которые отличаются от
истинных значений задержки, фазы (или частоты), т.е. возникает ошибка оценивания
псевдо дальности и псевдо скорости. Кроме того, искажаются формы
дискриминационных характеристик дискриминаторов задержки, фазы (или частоты),
что также негативно сказывается на точности формируемых оценок.
Так как в приемнике осуществляется корреляционная обработка сигналов,
а используемые в ГЛОНАСС фазоманипулированные сигналы некоррелирова-
ны при сдвиге кодовой последовательности на длительность гэ символа даль-
номерного кода, задержка огибающей отраженного сигнала на величину,
большую или равную гэ, не влияет на работу приемника. Поэтому режим
работы НАП с ВТ-кодом меньше подвержен влиянию многолучевости, чем
режим работы с кодом стандартной точности. Указанное обстоятельство можно
использовать для грубой оценки максимально возможной ошибки в оценке
псевдо дальности, обусловленной многолучевым распространением сигнала, а
именно ЗДмлрдпах = с^млР,тах = Тэс > ЧТ0 составляет около 600 м при
использовании кода стандартной точности и около 60 м при использовании ВТ-кода.
Если сигнал приходит от НС, расположенного в Зените, то условий для его
переотражения возникает существенно меньше, чем при приходе сигнала от
НС, находящегося под низким углом места. Поэтому одним из методов
борьбы с многолучевостью является отказ от работы по сигналам НС с малым
углом места. Для отображения этого факта, вводят понятие угла маски, типичное
значение которого составляет 5... 10°. Соответственно антенну преемника
проектируют так, чтобы для углов, меньших угла маски, коэффициент усиления
антенны был меньше, чем для остального сектора углов.
Другой метод борьбы основан на том факте, что с НС излучается сигнал с
правой круговой поляризацией. При переотражении сигнала от местных
предметов характер его поляризации меняется. Поэтому использование приемных
антенн, согласованных с поляризацией прямого сигнала, ослабляет влияние
переотраженных сигналов (примерно на 3 дБ по мощности). Кроме того,
известны разработки специальных антенн, снижающих влияние многолучевого
распространения сигналов [6.11].
Естественным методом борьбы с многолучевостью является поднятие
антенны приемника на максимально возможную высоту, по крайней мере
относительно наиболее существенных отражающих объектов.
Эффективным способом снижения влияния многолучевости на точность
оценки псевдо дальности при работе с сигналом стандартной точности являет-
288
Источники погрешностей и точность НВО
ся использование дискриминатора задержки с узкой апертурой
дискриминационной характеристики. При этом используется то обстоятельство, что, если
разность задержек принятого переотраженного и опорного сигналов
дискриминатора превышает его апертуру, то такой переотраженный сигнал «не
проходит» на выход дискриминатора и, следовательно, не влияет на работу следящей
системы за задержкой сигнала.
Для неподвижных приемников уменьшение влияния многолучевости на
точность определения псевдо дальности может быть достигнуто за счет
дополнительного сглаживания кодовых измерений фазовыми измерениями [7.5] (см.
п. 6.4.2.2).
Отметим, что проблема многолучевости актуальна не только для систем
спутниковой навигации, но и для систем мобильной связи и других
радиотехнических систем, работающих в городских условиях. Поэтому по данной
проблематике велись и продолжаются интенсивные исследования.
7.6. Погрешности, вносимые навигационным приемником
В навигационном приемнике сигналов НС на этапе первичной обработки
формируются оценки псевдо дальности и псевдо скорости на базе следящих
систем за задержкой огибающей и фазы (или частоты) сигнала. Следящие
системы, обладая конечной полосой пропускания, вносят ошибки в оценки
указанных параметров. В гл. 6 проведен анализ этих ошибок для различных
режимов работы приемника и оптимальных алгоритмов обработки сигналов, из
которого следует, что их величина существенно зависит от ряда факторов:
отношения qci мощности сигнала на входе приемника к спектральной плотности
внутреннего шума приемника; режима работы — когерентного или
некогерентного, по сигналам стандартной или высокой точности, одночастотный или
двухчастотный; алгоритмов обработки сигналов и информации; динамики
движения потребителя и др. При этом диапазон погрешностей оценивания
псевдо дальности составляет 0,5...30 м, а псевдо скорости — 0,1... 10 м/с.
Данные погрешности обусловлены внутренним шумом приемника и динамикой
движения потребителя. Кроме данных источников погрешностей в приемнике
есть еще один источник погрешностей оценивания псевдо дальности и псевдо
скорости — опорный генератор.
Погрешности, обусловленные опорным генератором приемника
Как отмечалось в п. 2.4 опорному генератору присуща нестабильность
частоты формируемого гармонического колебания. При этом на
характеристики следящих систем приемника оказывает влияние кратковременная
нестабильность частоты. Нестабильность частоты ОГ приводит к нестабильности
шкалы времени приемника [см. (2.4), (2.7)] и флуктуациям фазы ОГ [см. (2.3),
10-1026
289
Глава 7
(2.6)]. Спектральные характеристики флуктуации фазы существенно зависят от
типа используемого ОГ. Наиболее совершенные ОГ в области частот 1 ... 10 Гц
характеризуются спаданием спектральной мощности фазовых шумов 40 дБ на
декаду. Для таких ОГ относительная нестабильность частоты Svor (t)
описывается формулой (6.221), которую для удобства приведем еще раз:
^ = £,(')■ (7-54)
at
Здесь <$v(t) — БГШ с односторонней спектральной плотностью N* , Гц.
Для определения численного значения N* обратимся к характеристикам
фазовых шумов ОГ, приводимых в техническом паспорте. Как правило,
приводится односторонняя спектральная плотность Sn(p(f) циклической фазы в
диапазоне частот 1.. .1000 Гц (см., например, табл. 6.4). Полагая спадание
спектральной мощности фазовых шумов 40 дБ на декаду, запишем
Sn(p(f) = Sn(p(\)/f4, где Sn<p(\) — значение спектральной плотности при
/ = 1 Гц. Тогда, используя (2.10), запишем
( ^
^„(/) = R МО- (7-55)
Vvo/ )
Используя известное соотношение между спектральными плотностями
процесса и его производной [формулы (7.54), (7.55)], получаем
(2л-)4 SUJ\)
^ 2v2
Для выпускаемых ОГ обычно v0 = 10 МГц, поэтому (7.56) можно
представить в виде
Л^=7,79-10-12^(1). (7.57)
Значение может меняться от Sn<p(\) = \0~1 (-70 dBc) (ГК99 фирмы
«Марион») до 5ЦД1) = 10~10 (-100 dBc) (ГК89-ТС фирмы «Марион»), что
соответствует N4y =7,79-10"19 Гц и N4y =7,79-10"22 Гц.
Принимая модель (7.54) для относительной нестабильности частоты,
рассчитаем дополнительную ошибку в оценке псевдо дальности и псевдо
скорости, которую вносит данная нестабильность. Так как данные ошибки малы
относительно апертуры дискриминационных характеристик дискриминаторов
задержки и фазы, можно использовать линеаризованные модели следящих
систем. Кроме того, для простоты анализа будем рассматривать непрерывные
варианты следящих систем.
290
Источники погрешностей и точность НВО
Рассмотрим линеаризованную следящую систему за задержкой сигнала
(6.103), в которой положим во входном воздействии отсутствует аддитивные
шумы и динамическая составляющая изменения задержки, обусловленная
взаимным перемещением НС и потребителя, а присутствует лишь составляющая,
обусловленная флуктуациями времени t\ т.е. y[t) = t\ где —±1 = Svm (t);
dt
£v0T описывается (7.54).
Следовательно, уравнения фильтрации задержки сигнала можно записать в
виде
£| = vr+tfHl(/'-f), ^ = K»2(t'-r). (7.58)
Дисперсия флуктуационной ошибки оценки задержки т в установившемся
режиме определяется выражением
D£ = — \ ^ = ^_ [с2]. (7.59)
+ }соКн1+Кн:
h1jvh2
Так как в оптимальной следящей системе коэффициенты усиления связаны
между собой выражением (6.102), а полоса пропускания следящей системы
определяется формулой (6.105), то (7.59) можно представить в виде
Л^(0,53)3 0,0526Л^ r 2i
272(Д/ССЗ)3~ (А/ссз)3
D£r = *) ' J = $- [с2]. (7.60)
Рассматривая автономное слежение за задержкой сигнала с полосой
пропускания ССЗ А/ссз = 1 Гц (см. рис. 6.24), из (7.60) при N?y =7,79-Ю-19 Гц
получаем JD£ = 0,2 не (0,06 м), т.е. ошибка достаточно маленькая. Однако,
если мы для повышения помехоустойчивости малоподвижного приемника
выберем полосу пропускания ССЗ А/ссз = 0,2 Гц (см. рис. 6.24), то ошибка,
вносимая ОГ, будет составлять JD£ = 2,24 не (0,72 м), что уже сопоставимо с
динамической и флуктуационной ошибками ССЗ.
Еще большие проблемы возникают, если используется комплексный
фильтр слежения за задержкой огибающей и доплеровской частотой сигнала
(см. п. 6.3.6.5), поскольку в этом случае полоса пропускания следящей системы
может быть еще в несколько раз быть меньше, что приведет к дальнейшему
возрастанию ошибки (7.60).
Рассмотрим влияние нестабильности ОГ на точность оценки доплеровского
смещения частоты в ССЧ некогерентного приемника, полагая, что в ней
используется сглаживающий фильтр в виде двух интеграторов с демпфированием. При
291
Глава 7
этом линеаризованная система фильтрации описывается теми же уравнениями
(6.103), что и выше, однако в этом случае положим входное воздействие
где /нс — частота несущего колебания (например, 1605 МГц).
Запишем уравнения фильтрации доплеровского смещения частоты
^- = h+KHl [fmSvm - /д), ^ = *н1 (fmSv0T - /д). (7.61)
Дисперсия флуктуации доплеровского смещения частоты /д в
установившемся режиме определяется выражением
1 xf и2/н2л^ _^Ч,
2К,
D£f =— f ' ' " ^ -=™-*- [с2]. (7.62)
£f 2л- JI,. v2 . „ „ I2 2Я...
^Hl
Используя соотношения (6.102) между коэффициентами усиления и
формулу (6.105) для полосы пропускания следящей системы, запишем (7.62) в виде
-2-
»*,="""*'"" [Гц2]. (7.63)
/н^^0,187
сеч
9
£/ а/;
Положим /н =1,605 10 Гц, A/CC4=2 Гц (см. рис. 6.26), Л^ =
= 7,79-10"19 Гц. Тогда из (7.63) получаем Ш^ = 0,43 Гц (0,08 м/с). При
сужении полосы пропускания ССЧ до А/ссч = 0,2 Гц (например, при комплек-
сировании с инерциальной системой навигации) ошибка, обусловленная
нестабильностью ОГ, возрастает до уровня ^"=1,37 Гц (0,256 м/с), что
сопоставимо с флуктуационной ошибкой ССЧ.
Рассчитаем ошибку, обусловленную нестабильностью ОГ, в схеме
слежения за фазой сигнала когерентного приемника. Линеаризованная ССФ
описывается уравнениями (6.84). В качестве входного воздействия следует выбирать
y(t) = 27rfHCt'. Поэтому представим (6.84) в виде
^ = а, + К^(2хи-ф), ™-е + Кш1(2*/к?-ф),
^ = *„з(2*/н/-0). (7.64)
Запишем выражение для дисперсии флуктуационной ошибки по доплеров-
скому смещению частоты:
292
Источники погрешностей и точность НВО
00
1 v ' (7.65)
1\()с»)\()со)2Кн1+}соКн2+Кн3\2 ^i^-^l '
Используя соотношения (6.81) между коэффициентами усиления в
оптимальной ССФ и выражение (6.86) для полосы пропускания, представим (7.65) в
виде
КъЪ А/ССФ
Положим, как и в предыдущем случае, /н =1,605-109 Гц, N% =
= 7,79 Ю-19 Гц, а А/ССФ =20 Гц (см. рис. 6.24). Тогда из (7.66) получаем
De =0,347 Гц (0,065 м/с), т.е. такую же ошибку, что и в схеме ССЧ. Как и в
предыдущем случае схемы ССЧ, при сужении полосы пропускания ССФ
ошибка, обусловленная нестабильностью ОГ, возрастает пропорционально
У л/^ссф •
Аналогичные расчеты можно провести для ОГ, имеющих спадание
спектральной плотности фазовых шумов 20 дБ на декаду, т.е. при модели
относительной нестабильности частоты (6.187). Влияние таких шумов на оценку
псевдо дальности примерно такое же, как и описанное выше. Для ССФ
характер зависимости дисперсии ошибки оценки частоты от полосы пропускания
ССФ меняется и описывается соотношением
Я/д=1,2/н2%Д/ССФ, (7.67)
где N4y =1,97-Ю-20 с (при 5ЦД1) = 1(П7 (-70 dBc)).
4
Для /н = 1,605109Гц, Д/ССФ=20 Гц из (7.78) получаем /z^~ = l,l Гц
(0,2 м/с), что в 3 раза больше, чем в рассмотренном выше случае. Однако для
такого типа флуктуации ОГ при сужении полосы пропускания ССФ ошибка
оценки частоты уменьшается.
7.7. Методы снижения погрешностей определения
псевдо дальности и псевдо скорости
Из анализа погрешностей определения псевдо дальности и псевдо
скорости, проведенного в предыдущих разделах, следует, что величина каждой из
составляющих может быть равной от единиц до нескольких десятков метров по
псевдо дальности и от долей до десяти метров в секунду по псевдо скорости.
293
Глава 7
Если не принимать специальных мер по снижению данных погрешностей, то
нельзя ожидать высокой точности НВО.
Рассмотрим некоторые из мер, которые позволяют снизить погрешности
определения псевдо дальности и псевдо скорости.
Компенсация погрешностей бортовой шкалы времени
Одной из существенных составляющих погрешностей определения псевдо
дальности являются погрешности бортовой шкалы времени. Частичная
компенсация данных погрешностей осуществляется в результате накопления
статистических данных по флуктуациям бортового ОГ, которое осуществляется
наземным сегментом контроля и управления. В результате такой обработки
формируются оценки следующих параметров: сдвига шкалы времени и-го НС
относительно СШВ тп\ относительного отклонения уп =(/„ -fm)/fnn
прогнозируемого значения несущей частоты fn и-го НС от номинального значения
fnn этой частоты для того же НС. Значения параметров тп, уп передаются
наземным комплексом управления по линии связи на борт НС, где они
закладываются в навигационное сообщение (более подробно о навигационном
сообщении см. п. 11.4). Обновление данной информации производится каждые 15
мин, поэтому используют обозначения Tn(tb), Yn(tb), где tb — время внутри
текущих суток по шкале UTC(SU)+03 ч 00 мин, к которому относятся
передаваемые значения параметров. В приемнике поправка к БВШ может быть
рассчитана в соответствии с формулой
**(<) = Тп{<ь) + Г„(*ь) ('"'*)■ (7-68)
Отметим, что прогнозируемое значение частоты fn дается с учетом
гравитационного и релятивистского эффектов на момент времени tb (см. п. 7.4).
Кроме (7.68) в приемнике могут быть учтены поправки на релятивистские
эффекты (7.49) и (7.53), при этом итоговая поправка к БШВ будет иметь вид
StwlB=St„+Ste+Sta. (7.69)
Компенсация ионосферной погрешности
Различают методы компенсации ионосферной погрешности для одночас-
тотных приемников, т.е. преемников, работающих только в диапазоне L\, и
для двухчастотных приемников, работающих в диапазонах Ы и L2 .
Наиболее просто проблема компенсации ионосферной погрешности
решается в двухчастотном приемнике. Из всех составляющих погрешности
определения псевдо дальности (7.2) лишь ионосферная погрешность зависит от
частоты. Поэтому, если измерить псевдо дальности Д(/{), Д(Л) на ДВУ* частотах,
294
Источники погрешностей и точность НВО
то в погрешностях этих измерений только ионосферные погрешности будут
различаться, следовательно, можно записать
h (Л) - Д (fi) = c{Stm (/,) - йи (/2)). (7.70)
Запишем формулу (7.37) для группового запаздывания в ионосфере в виде
Лион (/i(2)) = A/f\{2) и подставим ее в(7.70):
АД = ДШ-Д(/г) = с
/,2
\л
fh
= cStmm(fi)
/.
2\
Й,
или
Лион (Л ) =
ьд
А
2\
-1
/:
2
2 )
Для СРНС ГЛОНАСС fjf2 = 9/7 , следовательно к =
(1-л7л2)"
(7.71)
= 1,531.
Вычисленное в соответствии с (7.71) значение 8tmH можно использовать
для коррекции измеренной псевдо дальности в диапазоне с частотой fx.
Ошибки в оценке ионосферной задержки в соответствии с (7.71) опреде-
ляются погрешностями оценки АД, которая, в первом приближении,
определяется ошибками оценок псевдо дальностей (в диапазонах L\ и L2),
обусловленными шумом приемника. Полагая их дисперсии <Тдф равными в двух
диапазонах, запишем выражение для дисперсии ошибки ионосферной задержки:
4„„„=Чф*2А2-
Для стационарных объектов за счет дополнительного усреднения оценки
псевдо дальности по времени флуктуационная ошибка сгдф может быть
сделана менее 1 м. Следовательно, среднеквадратичное значение ошибки оценки
ионосферной погрешности может быть <т# < 2 м. Эта ошибка является
одновременно и ошибкой компенсации ионосферной задержки (остаточной
ошибкой после компенсации).
В одночастотном приемнике недоступна дополнительная информация,
характеризующая состояние ионосферы, поэтому здесь возможно лишь
использование той или иной модели ионосферы. Основная проблема при таком
подходе заключается в том, что состояние ионосферы очень изменчиво и зависит
от многих факторов. Поэтому невозможно предсказать с высокой точностью
распределение концентрации электронов по высоте. Однако оказалось, что
можно создать относительно грубую модель ионосферы, которая описывается
незначительным числом параметров и позволяет скомпенсировать около 50%
295
Глава 7
общей погрешности. Такая восьмипараметрическая модель была разработана
[7.6] применительно к системе GPS. При этом с СРНС GPS данные восемь
параметров передаются в навигационном сообщении, что позволяет относительно
просто реализовать процедуру компенсации в приемнике. В дальнейшем были
разработаны более сложные модели ионосферы [7.7]. Однако их использование
не позволяет осуществлять компенсацию ионосферной погрешности лучше,
чем на 75% . В навигационном сообщении СРНС ГЛОНАСС информация о
состоянии ионосферы не передается, поэтому для реализации компенсации
ионосферной погрешности в одночастотном приемнике необходимо использовать
дополнительную внешнюю информацию о параметрах ионосферы.
Компенсация тропосферной погрешности
Для компенсации тропосферной погрешности используется та или иная
модель тропосферы. Одна из широко используемых моделей, предложенная в
[7.4], определяется формулой
0,002277f (1255 . п\ _ 2, Л „
где Т — температура в Кельвинах в месте расположения приемника; р —
атмосферное давление в миллибарах; е — парциальное давление водяного пара в
миллибарах; а — угол места НС, для которого рассчитывается поправка; В и
SR — корректирующие члены, зависящие от высоты h расположения
приемника и утла а , для которых существуют специальные таблицы [7.4].
Известны и другие, более сложные модели тропосферы, например [7.8].
Использование моделей тропосферы позволяет скомпенсировать до 90 %
общей погрешности так, что остаточная погрешность может составлять < 0,2 м
для сигналов НС, находящегося в зените.
Снижение погрешностей, обусловленных многолучевостью
Методы снижения погрешностей определения псевдо дальности,
обусловленных многолучевым распространением, обсуждены в п. 7.5, поэтому просто
перечислим их:
неиспользование при обработке сигналов, приходящих с направлений,
ниже угла маски;
поднятие антенны выше наиболее существенных отражающих объектов;
использование антенн с правой круговой поляризацией;
использование дискриминаторов задержки с узкой апертурой
дискриминационной характеристики.
Снижение погрешностей, обусловленных приемником
Основным средством снижения погрешностей оценивания псевдо
дальности и псевдо скорости в приемнике является оптимизация алгоритмов и уст-
296
Источники погрешностей и точность НВО
ройств обработки сигналов и информации. Так, говоря об оптимизации
устройств обработки сигналов, можно иметь в виду:
использование прецизионных малошумящих входных усилителей,
позволяющих снизить (на 1,5...2 дБ) мощность внутреннего шума приемника;
использование высокостабильных опорных генераторов, например, с
уровнем спектральной плотности фазовых шумов (циклической фазы), равной
-100 ...-ПО дБ на частоте 1 Гц;
использование аналого-цифровых преобразователей с большим, чем два,
числом уровней квантования;
использование полосовых фильтров в высокочастотной части приемника с
высокой избирательностью и т.д.
Если говорить об оптимизации алгоритмов обработки информации, то
можно отметить следующие направления:
оптимизация структуры и параметров следящих систем за задержкой
огибающей, фазой и частотой с учетом динамики конкретного потребителя;
адаптация следящих систем к отношению сигнал/шум на входе приемника;
использование комплексных следящих систем, совместно
обрабатывающих сигналы с выходов дискриминаторов дальности, фазы и частоты;
совместное использование кодовых (по огибающей) и фазовых измерений
для НВО;
переход от идеологии построения приемников с двухэтапной обработкой к
приемникам с одноэтапной обработкой;
использование дифференциальных методов НВО, при которых устраняются
многие медленно меняющиеся коррелированные составляющие погрешностей;
комплексирование алгоритмов обработки сигналов навигационного
приемника и других навигационных систем потребителя, в первую очередь инер-
циальной системы навигации (ИНС).
Некоторые из отмеченных направлений частично рассмотрены в гл. 6.
Вопросы более полного использования фазовых измерений в НАП, наряду с
кодовыми, будут рассмотрены в гл. 15. Дифференциальные режимы работы НАП
СРНС излагаются в гл. 12. Проблемы комплексирования НАП ГЛОНАСС и
ИНС рассматриваются в гл. 17.
7.8. Бюджет погрешностей определения псевдо дальности
и псевдо скорости
Подводя итог анализу погрешностей определения псевдо дальности и
псевдо скорости, приведем итоговую таблицу отдельных составляющих
общей погрешности, которую принято называть бюджетом погрешностей. В
приводимой ниже табл. 7.1 полагается, что все составляющие погрешностей
являются некоррелированными между собой случайными величинами с гаус-
совским законом распределения, имеющими нулевые математическое ожида-
297
Глава 7
2
ние и дисперсию а8д . Поэтому дисперсия общей ошибки определяется как
сумма дисперсий отдельных составляющих. Приводимые в таблице значения
отдельных составляющих соответствуют остаточным значениям погрешностей,
т.е. предполагается, что в приемнике приняты меры по снижению
погрешностей определения псевдо дальности и псевдо скорости, описанные в п. 7.7.
Погрешность, вносимая приемником, дается для автономно работающего одно-
частотного стационарного (неподвижного) приемника с двухэтапной
обработкой сигналов, при приеме сигнала от НС, находящегося в зените. Учитывая
данный комментарий, величина общей (итоговой) погрешности в табл. 7.1, 7.2 имеет
смысл потенциальной, т.е. предельно достижимой в реальной аппаратуре.
Таблица 7.1. Бюджет погрешностей определения псевдо дальности
Источник погрешности
Часы спутника
Ионосфера
Тропосфера
Многолучевость
Приемник
Прочие
| Суммарная погрешность
°8Д ' М
2
4 !
0,5
2,5
1,5 !
2
5,7
Таблица 7.2. Бюджет погрешностей определения псевдо скорости
Источник погрешности
Бортовой ОГ
Релятивистский эффект
Многолучевость
Приемник
Прочие
Суммарная погрешность
о8у, м/с
0,04
0,001 |
0,01
0,08
0,01
0,09
7.9. Погрешности, вносимые на этапе решения
навигационной задачи
Оценки псевдо дальностей и псевдо скоростей, полученные на этапе
первичной обработки по четырем или более видимым НС, используются для
расчета оценок координат и вектора скорости потребителя, составляющего суть
вторичной обработки информации (см. п. 6.4) в приемнике (или решения
навигационной задачи). При проведении необходимых расчетов используется
298
Источники погрешностей и точность НВО
информация о координатах и составляющих вектора скорости (эфемериды)
каждого НС, которая извлекается из навигационного сообщения. Точность этой
эфемеридной информации непосредственно влияет на точность НВО. Кроме
того, при пересчете оценок псевдо дальностей в координаты потребителя
осуществляется преобразование погрешностей определения псевдо дальностей в
погрешности определения координат потребителя. При этом происходит
ухудшение точности определения координат потребителя по сравнению с
точностью определения псевдо дальностей, зависящее от геометрии расположения
потребителя и НС, сигналы которых принимаются в обработку.
Для количественной оценки данного эффекта используют понятие
геометрического фактора.
7.9.1. Погрешности эфемеридного обеспечения
Одной из основных задач наземного сегмента контроля и управления
является формирование предсказанных на заданные моменты времени tb значений
эфемерид всех НС и передача их на НС, где они закладываются в
навигационное сообщение. Подробное описание процедур формирования и закладки
эфемеридной информации приведено в п. 11.6. В данном разделе рассматривается
лишь точность эфемеридной информации и ее влияние на точность НВО.
При проведении экспериментальных исследований под эфемеридными
погрешностями понимают: 81 — трансверсальная (по касательной к траектории);
дг — радиальная; 8п — нормальная (по нормали к плоскости, образуемой
векторами <Я, Sr).
В [7.5] приведены результаты экспериментальных исследований эфеме-
ридных погрешностей для НС GPS, под которыми понимают погрешности
предсказанных значений эфемерид (закладываемых в навигационное
сообщение) относительно точно измеренных значений. Итоговые результаты данных
исследований приведены в табл. 7.3.
Таблица 7.3. Экспериментальные значения эфемеридных погрешностей
Тип погрешности
Радиальная aSr
\ Нормальная а8п
Трансверсальная о81
Среднеквадратичное
значение, м
0,8
3,0
6,3
К сожалению экспериментальных данных по определению эфемеридных
погрешностей для НС ГЛОНАСС в настоящее время нет. Поэтому в дальнейшем
будем полагать, что они несущественно отличаются от данных для НС GPS.
299
Глава 7
Определенные выше эфемеридные погрешности принято пересчитывать в
эквивалентную ошибку определения псевдо дальности. Обусловлено это тем,
что погрешности определения псевдо дальностей все равно пересчитываются
через геометрический фактор в погрешности определения координат
потребителя, поэтому нет смысла пересчитывать отдельно погрешности эфемеридного
обеспечения. Общая формула для пересчета эфемеридных погрешностей в
погрешности определения псевдо дальности имеет вид
ад'ф = Wsr + кш (<т1 + а%), (7.72)
где коэффициенты kr,ktgопределяют вклад соответствующих ошибок в
итоговую ошибку и зависят от взаимного положения НС и потребителя.
В [7.5] рассчитаны усредненные (по различным угловым положениям НС
и потребителя) значения этих коэффициентов: kr =0,959,&,g =0,0204.
Используя данные табл. 7.3 и приведенные значения коэффициентов, получаем
приведенную к псевдо дальности погрешность, обусловленную эфемеридными
погрешностями £Дэф = 1,27 м. Это значение отличается, например, от
аналогичного значения (ЗДэф = = 4 м), приведенного в [6.11]. Поэтому, для
дальнейшего анализа примем среднее из данных двух значений, т.е. £Дэф = 2,6 м.
Добавляя данную погрешность в табл. 7.1, получаем интегрированный бюджет
погрешностей определения псевдо дальности (табл. 7.4).
Таблица 7.4. Интегрированный бюджет погрешностей
определения псевдо дальности
Источник погрешности
Эфемериды
Часы спутника
Ионосфера
Тропосфера
Многолучевость
Приемник
Прочие
Суммарная погрешность
°8Д ' М
2,6
2
4
0,5
2,5
1,5
2
6,2
7.9.2. Геометрический фактор в СРНС
В п. 6.4.3 при рассмотрении одношагового алгоритма вторичной
обработки информации получено соотношение (6.211), связывающее ошибки опреде-
300
Источники погрешностей и точность НВО
ления вектора состояния потребителя х = |х j>z Д'|т с ошибками определения
вектора псевдо дальностей Ду^ = Д - Д , которое имеет вид
Ах = (нтЙ)"1НтАуд, (7.73)
где Н — матрица направляющих косинусов (6.214).
Рассчитаем корреляционную матрицу ошибок Ах :
(Ах-М[Ах] ) (Дх-М[Дх] )Т] =Н-1КошДН-т=(йтКо-;дн)"1,
(7.74)
(ауд-м[ауд])(ауд-м[аУд] Т
КОШ,Х=М
ГДе Кош,Д = М
корреляционная
матрица погрешностей определения псевдо дальностей (в дальнейшем будем
полагать М[Ах] = М[уд ] = 0).
Диагональными членами корреляционных матриц Rom д и ROUI x являют-
ся дисперсии определения псевдо дальностей (<т~ , i = \,N) и пространствен-
но-временных координат потребителя (а\, <у2, а\, &2П,).
Из (7.74) следует, что соотношение между погрешностями определения
псевдо дальностей и пространственно-временных координат потребителя
зависит только от вида матрицы направляющих косинусов Н, т. е. от геометрии
взаимного расположения НС и потребителя. Таким образом, важным условием
достижения высокой точности навигационных определений в СРНС является
такое взаимное пространственное расположение рабочего созвездия НС и
потребителя, при котором обеспечивается требуемая точность НВО при заданном
уровне погрешностей измерения псевдо дальностей. На этом выводе основана
концепция коэффициента геометрии КГ, являющегося мерой уменьшения
точности навигационных определений в СРНС из-за особенностей
пространственного расположения НС и потребителя (в иностранной литературе
используется обозначение GDOP (geometric delution of precision).
Количественная характеристика КТ вводится для случая, когда
погрешности определения псевдо дальностей до НС равновелики и некоррелированы. В
этом случае матрица Rom д = cr^I, a (7.86) принимает вид
Кош,х=^ал(нтн)"\ (7.75)
где сГдал — дисперсия погрешностей определения псевдо дальностей; I —
единичная матрица соответствующего размера.
301
Глава 7
Отсюда видно, что дисперсии погрешностей определения координат
потребителя и смещения шкалы времени (диагональные элементы матрицы
R0UIX) являются функциями диагональных элементов матрицы (Йтн) .
Положим о2АЬЛ = 1 и рассчитаем СКО определения положения потребителя в
четырехмерном (пространственно-временном) пространстве:
<гт=[<т2х+о*+<г1+<т2д.~\ =[tr(RonitX)] , (7.76)
где tr(*) обозначает след матрицы.
Сопоставляя (7.75) и (7.76), видим, что можно ввести коэффициент
К =
( Г
tr
v
(Щ
V/2
(7.77)
который определяет величину пространственно-временной ошибки
определения положения потребителя и который называют коэффициентом геометрии.
Выше для большей наглядности было положено <тдал = 1. В общем случае
при сГдзл ф 1, сохраняя определение (7.77) и учитывая (7.75), можно записать
КГ =[<т2х+<т2у+<т22 +4'] "V^ • (7-78)
При выборе орбитальных параметров НС на этапе разработки подсистемы
НС, а также при выборе рабочего созвездия в приемнике, коэффициент
геометрии (7.77) полагают основным критерием.
Коэффициент геометрии Кг может быть представлен в другом виде:
K2=Kla+K2J9 (7.79)
tl 2 2~\ ^^ /
сгх + <7у + gz J /о"дал > Ktj =сгд'/(7дал — пространственный
(PDOP) и временной (TDOP) коэффициенты.
Пространственный коэффициент геометрии, в свою очередь, можно
разделить на две составляющие, характеризующие точность определения положения
потребителя СРНС в горизонтальной и вертикальной плоскостях:
^г.п - ^г.г + ^г.в » (7.80)
где КТ г = \ах + ау I /°'Дал-> ^ч.в =<тг/(Таал —горизонтальный (HDOP) и
вертикальный (VDOP) коэффициенты.
302
Источники погрешностей и точность НВО
Наиболее важной характеристикой СРНС является точность определения
метоположения, поэтому чаще используются параметры КГ п (PDOP),
£rr(HDOP)H £rB(VDOP).
Использованные выше приближения (несмещенность,
некоррелированность погрешностей и др.) искажают значения погрешностей НВО для
реальных ситуаций, когда необходимо учитывать множество неслучайных, в общем
случае неравноточных составляющих и центрированных случайных
составляющих, имеющих неравные дисперсии и произвольные коэффициенты авто- и
взаимокорреляции. Тем не менее, использование определенного выше
коэффициента геометрии находит широкое применение.
Можно показать, что минимальное значение Кг и= 1,5 достигается в
случае, когда потребитель находится в центре правильного тетраэдра [6.11]. Для
наземного потребителя минимальное значение Кг п = 1,63 достигается тогда,
когда один НС находится в зените, а три других равномерно расположены в
горизонтальной плоскости. Таким образом, для минимизации КТ п необходимо
максимизировать объем тетраэдра.
Характеристики стандартной орбитальной конфигурации спутников в
СРНС ГЛОНАСС таковы, что они с вероятностью 99,9 % и более
обеспечивают в глобальной рабочей зоне видимость в любом 24-часовом интервале
четырех и более спутников, при этом четыре спутника обеспечивают PDOP < 6 (в
случае использования "угла маски", равного 5°). При этом среднее значение
HDOP =1,5, a VDOP =2,2.
Значения геометрических факторов, обеспечиваемых орбитальной
группировкой, и вероятности видимости PN заданного числа спутников N в СРНС
ГЛОНАСС [7.9] приведены в табл. 7.5.
Таблица 7.5. Геометрический фактор в СРНС
Параметры
pv
|hdop, ктт
VDOP, Кгв
|tdop, кг(
PDOP, КГП
GDOP, Кг
1 !—!_J
Число видимых НС (N) ||
4
1
1,41
2,0
1,13
2,45
2,69
5
1
1,26
1,75
1,03
2,16
2,39
6
1
1,15
1,7
1,03
2,05
2,3
7
1
1,03
1,61
0,95
1,91
2,13
8
0,91
0,95
1,6
0,93
1,86
2,08
9 1
0,58 |
0,89 J
1,55 J
0,91 |
1,79 J
2,01 |
303
Глава 7
Эти данные можно использовать для оценки точности определения
координат местоположения потребителя в горизонтальной (режим двумерных
измерений или 2-D) и вертикальной плоскостях, в трехмерном пространстве
(режим трехмерных измерений или 3-D) и т. д.
Так, используя потенциальное значение суммарной погрешности
определения псевдо дальности, приведенную в табл. 7.4, можно рассчитать
потенциальную погрешность определения пространственного положения (сферическая
ошибка) потребителя, например, для 4 НС сгсфпот =АТшП<тдал = 15,2 м.
Аналогичные ошибки определения координат потребителя в горизонтальной
плоскости и по высоте: агор пот = Кттст^ = 8,7 м, <7верт иот = Кг встдал = 12,4 м.
Литература
7.1. Радиоэлектронные системы: основы построения и функционирования.
Справочник/ Под ред. Я.Д Ширмана. — М: ЗАО «МАКВИС», 1998.
7.2. Грудинская Г. П. Распространение радиоволн. — М.: Высшая школа, 1975.
1 .Ъ. Долуханов М. П. Распространение радиоволн. — М.: Связь, 1972.
7.4. GuochangXu. GPS. Theory, Algorithms and Application. — Springer-Verlag,
Berlin, 2003.
7.5. Global Positioning System: Theory and Application/ Edited by B.W. Parkinson, J.J.
Spilker Jr. — AIAA. Inc., Washington, vol. 1, 1996.
7.6. Llewellyn S.K., Bent R.B. Documentation and Description of the Bent Ionospheric
Model/ AFCRL-TR-73-0657, AD 772733, 1973.
7.7. BilitzaD., Rawer K. and others. International Reference Ionosphere—Past, Present
and Futuer: Electronic Density/ Advances in Space Research, vol. 13, no. 3 1993.
7.8. Hofmann-WellenhofB., Lichtenegger #., Collins J. GPS theory and Practice. —
Springer-Press, Wien, 1997.
7.9. Bazarov Y. Introduction to Global Navigation Satellite System//AGARD ECTURE
SERIES 207. System implications and innovative applications of satellite navigation. NATO
AGARD, 1996.
304
Помехоустойчивость аппаратуры потребителей
Глава 8
ПОМЕХОУСТОЙЧИВОСТЬ АППАРАТУРЫ
ПОТРЕБИТЕЛЕЙ
8.1. Общие определения и подходы
Радиоприемная аппаратура спутниковой навигации, как и любая другая
радиоаппаратура, подвержена воздействию радиопомех естественного и
искусственного происхождения. Различают помехи, спектр которых расположен в
полосе частот спутниковых сигналов, и помехи, спектр которых расположен
вне указанной полосы частот (внеполосные помехи). Для борьбы со вторым
типом помех в приемнике используют известные методы частотной селекции в
высокочастотном тракте, поэтому их воздействие на приемник во многом
определяется характеристиками соответствующих полосовых фильтров. Данный
тип помех не рассматривается в настоящей книге. Помехи, спектр которых
находится в полосе частот спутниковых сигналов, воздействуют непосредственно
на основной тракт обработки навигационного сигнала (обнаружитель,
следящие системы) и на характеристики режимов обнаружения и слежения за
параметрами сигнала. Поэтому в дальнейшем будем рассматривать именно такие
помехи.
Под помехоустойчивостью приемника понимают его способность
работать в условиях воздействия внешних помех. В качестве характеристики
помехоустойчивости часто принимают граничное (наибольшее) значение
отношения мощности помехового сигнала к мощности полезного сигнала Кп = РП /Рс,
при котором система еще может решать целевую задачу (в рассматриваемом
случае выполнять навигационно-временные определения) с заданными
характеристиками. Здесь Рс— мощность полезного сигнала, Рп — мощность помехи
в полосе частот полезного сигнала. Параметр Кп, который иногда называют
коэффициентом подавления, удобно характеризовать в децибелах, поэтому
введем КП = 101g(ATn) дБ.
При отсутствии внешних помех приемник работает в условиях воздействия
только внутреннего шума приемника, спектральная плотность которого
определяется выражением N0=kT0Km, где к = 1,38-10"23 Вт-с/К — постоянная
Больцмана; Т0 = 290 К — температура; Кш — коэффициент шума приемника.
Обычно полагают Кш = 2,5(КШ = 4 дБ), что дает значение N0 = 1 • 1020 Вт- с или
Л^0 =101g(iV0)= -200 дБВт/Гц.
305
Глава 8
В условиях отсутствия внешних помех приемник сигналов СРНС
характеризуется отношением мощности сигнала к спектральной плотности
внутреннего шума приемника (отношение сигнал/шум) qc,n =PC/N0 Гц или
4с/*0=101фсМ)) ДБГЦ-
Наиболее просто помехоустойчивость приемника рассчитывается для
внешней шумовой помехи. В этом случае на входе приемника действует
внутренний шум приемника со спектральной плотностью N0 и «внешний» шум со
спектральной плотностью Nn. Так как эти шумы не коррелированны, то их
воздействие равноценно воздействию одного эквивалентного шума со
спектральной плотностью N3= N0+ Nn .
Однако, воздействие различных типов помех на навигационный приемник
различно, что приводит разным значениям коэффициента подавления Кп.
Поэтому, говоря о конкретном значении коэффициента подавления, корректно
упоминать для какого типа помехи оно приводится.
8.2. Методика оценки помехоустойчивости навигационного приемника
В целях анализа помехоустойчивости навигационный приемник может
быть представлен обобщенной схемой, приведенной на рис. 8.1.
V
Антенна
Блок первичной обработки
В режиме слежения за сигналами
"вх(')
ВЧ-приемник
'W:
I Многоканальный
коррелятор
Блок
I дискриминаторов
Блок
сглаживающих
фильтров
N
Блок поиска
сигнала
В режиме допоиска сигналов
Рис. 8.1. Обобщенная схем навигационного приемника
для анализа помехоустойчивости
Помехи, спектр которых расположен в полосе частот навигационных
сигналов, воздействуют, прежде всего, на блок поиска сигналов и на следящие
системы за параметрами навигационных сигналов. И в том и другом случаях,
первым блоком, на котором сказывается воздействие помех, является
многоканальный коррелятор. Поэтому, сначала необходимо проанализировать
воздействие помех на коррелятор.
306
Помехоустойчивость аппаратуры потребителей
8.2.1. Методика оценки влияния помех на коррелятор
В общем случае на вход приемника поступает сигнал
^вх(0 = ^нав(0 + ^п(0 + ^ш(0' (8-1)
где smB(t) — сигнал от навигационного спутника; sn(t) — помеховый
сигнал; 5Ш (?) — внутренний шум приемника, который полагается гауссовским с
равномерной спектральной плотностью N0 в полосе пропускания А/пр
высокочастотной части приемника.
Каждый канал многоканального коррелятора строится по схеме,
приведенной на рис. 8.2, где Ik, Qk — синфазная и квадратурная компоненты
(см. (6.40)); т, ф — оценки задержки и фазы сигнала, формируемые
соответствующими следящими системами; Т —время накопления в корреляторе; h{t) —
дальномерный код сигнала, на прием которого настроен данный коррелятор.
'вх
(')
<?(<)
кТ
J
h(t-T)sin(2nft + <p)
h(t - x)cos(27i// +ф)
кТ
J
(к-\)Т
Qk
h
Рис. 8.2. Схема коррелятора
В дальнейшем удобно рассматривать одну из ветвей коррелятора рис. 8.2,
например синфазную, и в непрерывном времени (с целью упрощения
математических выкладок). Схема такого коррелятора приведена на рис. 8.3.
'вх
(')
X
Jon
(')
J
'.(Г)
Рис. 8.3. Упрощенная схема коррелятора
На первый вход коррелятора поступает входной сигнал (8.1), в общем
случае содержащий: навигационный сигнал sHaB (t), шумовую компоненту sm (t),
обусловленную внутренним шумом приемника, и помеховый сигнал sn (?).
307
Глава 8
Для сигналов, используемых в КНС, для навигационного сигнала
справедливо представление
где /с, срс, гс, Рс — несущая частота, фаза, задержка и мощность
принимаемого навигационного сигнала.
На второй вход коррелятора подается опорный сигнал son(t), в качестве
которого в НАП СРНС используется сигнал, являющийся копией
принимаемого навигационного сигнала. Поэтому, при отсутствии ошибок слежения за
задержкой, фазой и частотой можно записать
*оп (0 = A(^rc)cos(2^/cr+ %(/)). (8.3)
Сигнал на выходе коррелятора в момент времени tk определяется
выражением
h = J *вх (>Кп (t)dt = J 5BX (t)sm (t)dt = /навД + /шД + /nJt, (8.4)
'*-i -г/2
Г/2
где /нав^ = 5оп(05нав(0^ —полезная составляющая, обусловленная прие-
-Т/2
мом навигационного сигнала;
Т/2
AiU = 5оп(05ш(0^ —шумовая составляющая, обусловленная внут-
-Т/2
ренним шумом приемника;
Т/2
1пк = sou[t)sn{t)dt — помеховая составляющая, обусловленная дейст-
-Т/2
вием дополнительной помехи.
В отсутствие внешних помех отношение мощности полезной составляю-
л [~ 7 ~I
щей (/нав>А) к дисперсии Dm = М\ (/ш>*)~ шумовой составляющей на выходе
коррелятора определяет качество работы НАП. Поэтому введем параметр
GUn=(W)7Du.» (8-5)
который для краткости будем называть отношением сигнал/шум на выходе
коррелятора.
При нулевых рассогласованиях опорного сигнала относительно входного
навигационного по фазе, частоте и задержке полезная составляющая на выходе
коррелятора рис. 8.3 определяется выражением (см. п. П6.1)
308
Помехоустойчивость аппаратуры потребителей
1™,к=Щт/2. (8.6)
Соответственно, дисперсия шумовой составляющей равна
Dm = N0T/4 . (8.7)
Подставляя (8.6), (8.7) в (8.5), получаем
Qc/ui=2PcT/N0=2qc/nJ. (8.8)
Отметим, что с теории спутниковой навигации условия работы НАП
принято характеризовать параметром qc, . Из (8.8) следует, что введенная
характеристика Qdui пропорциональна отношению qcjn^. Поэтому, при отсутствии
дополнительных помех с точки зрения влияния отношения сигнал/шум qc, на
характеристики НАП можно использовать параметр Qc/U1.
При действии дополнительной внешней помехи на выходе коррелятора
формируется новая помеховая составляющая 1пк, которую будем
характеризовать средним квадратом Dn = Ml I^k . В этом случае будем характеризовать
условия работы НАП отношением, аналогичным (8.5), но с учетом
дополнительной помеховой составляющей, т.е.
е„ш+„,=^-. (8.9)
которое можно преобразовать к виду
2с/(ш+п) = г, ' г, ~ Т. Г?- (8-1°)
Параметр <2с/(ш+п) будем называть отношением сигнал/помеха+шум на
выходе коррелятора.
Из (8.10) следует, что влияние дополнительной помехи на отношение
сигнал/помеха+шум на выходе коррелятора можно характеризовать коэффициентом
Kn/C^AW)2- (8-П)
По своей сути это — отношение мощности помеховой составляющей на
выходе коррелятора к мощности полезной составляющей на том же выходе.
Учитывая, что (/нав,*) ~^с и Ai ~^п> W ^п — мощность помехового
сигнала, (8.11) можно представить в виде
^п/с=?п/А/с- (812)
где qnic = РП/РС — отношение помеха/сигнал на входе НАП.
309
Глава 8
В (8.11) первый сомножитель дп/с характеризует влияние мощности
помехового сигнала, а второй сомножитель кпи — влияние структуры помехового
сигнала и ее параметров на коэффициент Кп/С. В настоящей статье основное
внимание уделяется анализу коэффициента knu .
Другая возможная характеристика воздействия помехового сигнала на
коррелятор может быть введена, если (8.9) представить в виде
Qc/m
.с/(ш+п) i + D /D
1 ^ ^п / ^ш
(8.13)
Из (8.13) следует, что влияние дополнительной помехи на отношение сиг-
нал/помеха+шум на выходе коррелятора можно характеризовать коэффициентом
Knlm=DjDm, (8.14)
оценивая его значение относительно единицы.
8.2.2. Методы расчета помеховой составляющей на выходе коррелятора
Спектральный метод расчета среднего квадрата помеховой
составляющей на выходе коррелятора
Рассмотрим общее выражение для корреляционного интеграла
Г/2 оо
/= f x(t)y(t)dt= \x(t)Y(t)dt, (8.14)
-Г/2 -ж
где
x(t) = lx^ при -Tl2^tuTl2*
U [ О при t<-T/2; t>T/2. '
Y(t) = \yM ПРИ "Г/2^Г/2'
U [ О при г<-Г/2; t>T/2.'
Введем обратное преобразование Фурье
00 00
*(/)= \sx{f)S'* df, у(»)= \sv(f)e2"* df.
—00 —00
и подставим данные соотношения в (8.14)
00 00 00 00
/= \ \sx(f)J2K*df \sY{vy2^dvdt= jsx(f)S*Y(f)df.
—оо —оо —оо —оо
Полагая теперь x(t) = sn (t), y(t) = son (t), запишем
310
(8.15)
Помехоустойчивость аппаратуры потребителей
ц,- p,„(/)$L (/)<*■
(8.16)
Расчет среднего квадрата помеховой составляющей на выходе
коррелятора методом комплексных амплитуд
Общие соотношения метода комплексных амплитуд приведены в п. 5.2
По-прежнему рассматриваем вычисление корреляционного интеграла
(8.14), в котором положим
x(t) = ^xh(t)cos(27rf0t + <px) (8.17)
— узкополосный сигнал.
Введем комплексный сигнал
X(t) = Ax(t)^2jrfy9 (8.18)
где Ах (t) = aXR (/) + ]aXI (t) — комплексная амплитуда (огибающая).
При <рх = 0 имеем aXI (t) = О и
В дальнейшем для простоты будем полагать <рх = О .
Определим вторую функцию в (8.14) соотношением
>;^r^^/) = ^(?-r)cos(2^(/0+^/)^^). (8.19)
Обозначим комплексные амплитуды сигналов X(t) и Y(t) (8.15) как
Ax(t) и AY(t,r,(p,8f), ъ спектральные плотности комплексных амплитуд как
Skx (/) и SAy (/) = 5iy (f,r9<p9Sf) соответственно.
Введем
00 ОС'
^(/)= \AY(t,T = 0,<p = 0,Sf = 0yi2*ftdt= jhy(t)e-'*2*ftdtt (8.20)
-00 -00
Соответствующую сигналу (8.19) при нулевых расстройках по задержке, фазе и
частоте относительно сигнала (8.17).
Запишем выражение для спектральной плотности комплексной амплитуды
£• (f,r,<p,Sf) через спектральную плотность 5^ (/) с учетом свойств
сдвигов по фазе, частоте и задержке
SMr(f,T,9,Sf) = sX(f-S/y^->^'. (8.21)
Выразим (8.14) через комплексные амплитуды
311
Глава 8
/= jx(t)Y(t)dt = JRe[x(t)]Re[Y(t)]dt = -Re\ \ Ax(t)A*Y(t)dt
-oo —oo |_— oo
Рассмотрим
oo x oo oo
\AX (t)A'r (t)dl = \ \sAx (/У2'* df Jfs; (v)e-*™ dvdt =
(8.22)
-00 —00
00
= jsAx(f)s\(fW
(8.23)
Подставляя (8.23) и (8.21) в (8.22), получаем соотношение
2
J -■ 00
/= jx(t)Y(,)d, = Ue в"" }s^(/)S»;(/-<J/)e'2^V/
(8.24)
Для мощности помеховой составляющей на выходе коррелятора теперь
можно записать выражение
А,=
1
Re
jl
в"* fo (/)5?* (f-Sf)J2*'Tdf
(8.25)
Формула (1.26) учитывает возможные сдвиги сигналов на входах
коррелятора по фазе, частоте и задержке, а также различие кодовых конструкций
навигационного и помехового сигналов.
8.3. Анализ внутрисистемных помех при использовании различных
типов навигационных сигналов с кодовым разделением
Как отмечалось в гл. 5 в настоящее время в СРНС ГЛОНАСС
используются навигационные сигналы с модуляцией ФМ-2 (BPSK), а в перспективе, в
соответствии с «Концепцией развития навигационных сигналов глобальной
навигационной системы ГЛОНАСС», будут использоваться сигналы с модуляцией
на поднесущих частотах {ВОС{т,п)) и кодовым разделением сигналов.
Рассмотрим уровень внутрисистемных помех при использовании сигналов с
модуляциями BPSK(n) и ВОС{т,п) при использовании принципа кодового
разделения сигналов. Напомним (см. п. 5.4), что при использовании обозначений
BPSK(n) и ВОС{т,п) подразумевается наличие некоторой «базовой» частоты
fc (например, в GPS fc =1,023 МГц), так что частота отстройки поднесущих
частот — fsub = mfc, а частота следования символов кода — fchip = nfc.
В соответствии с описанной в п. 8.1 методикой анализ внутрисистемных
помех будем проводить, рассчитывая коэффициент Кп/С (8.11), характери-
312
Помехоустойчивость аппаратуры потребителей
зующий отношение мощности помеховои составляющей на выходе
коррелятора к мощности полезной составляющей на том же выходе.
Для навигационного и помехового сигналов, поступающих на вход
приемника, используем представление
s(t) = U(t)cos(27rft + <р), (8.26)
где U(t) — огибающая сигнала; /, ср — частота и фаза сигнала.
Пусть приемник принимает навигационный сигнал с заданным типом
модуляции. Работая в режиме навигационных определений, приемник следит за
задержкой и фазой принятого сигнала, формирую при этом опорный сигнал
где h(t) — функция модуляции навигационного сигнала; гоп — задержка
огибающей опорного сигнала; /оп, срои — частота и фаза опорного сигнала.
Пусть на коррелятор действует внутрисистемная помеха, для которой
запишем
sn(t) = Un(t)cos(2xfnt + q>n)9 (8.27)
где Un (t) — огибающая помехового сигнала; /п, срп — частота и фаза помехи.
На выходе коррелятора имеем сигнал
Т Т
/п = рп(0*вп(0Л = 2^(0^-гоп)со8(2Я2угс„/ + А%п)Л, (8.28)
о о
где Д/сп =/оп -/п, АсрСП =<роп -<ри.
Здесь и далее для определенности будем полагать Т = ТС, где Тс — период
дальномерного кода.
Так как cos(2^Acn//4-A^cn) — медленно меняющаяся функция по
сравнению с g(t) = U(t)h(t), преобразуем (8.28) к виду
т( т \
/n=i|^(0M^-^on)-^J^WM?-^on)^^os(2M/cn^A^cn)^ +
ov о J
т т
+^lu(t)h(t-Ton)dtjcos(2xAfcnt + A<pcn)dt =
2Т
о о
т т
2Т
Г 1
= ^\u{t)h(t-Ton)dt\cos(27rAfcnt + Acpcn)dt =
о
313
Глава 8
1 sm(xAfcnT)
I
cos(xbfcnT + A<pQn)\u{t)h(t-Ton)dt. (8.29)
2 *bfmT o
При отсутствии расстроек между помеховым и опорным сигналами
д/сп = 0 > д^сп = 0, гоп = 0 соотношение (8.29) принимает вид
т
In=\\u(t)h(t)dt (8.30)
о
и соответствует максимальному значению помеховои составляющей на выходе
коррелятора.
8.3.1. Анализ внутрисистемных помех при использовании сигналов
с модуляцией BPSK(w)
Положим, что НАП работает по навигационному сигналу с модуляцией
BPSKin), и помеха имеет такую же структуру. Положим для определенности:
частота следования символов дальномерного кода fchip = nfc, длительность
периода дальномерного кода Т, число символов на периоде кода L = fchipT,
длительность символа дальномерного кода тс = 1//сыр •
Рассмотрим сначала случай, когда А/сп = 0, А<рсп = 0, гоп = 0. Отметим,
именно такой случай рассматривается во всех учебниках и монографиях при
анализе внутрисистемных помех.
Для помехи, согласованной по ширине спектра с навигационным
сигналом, представление (8.27) конкретизируем в виде
*n(0 = >/^^Wcos(2;r/n^ + %),
где Рп — мощность огибающей помехи; hn(t) — функция модуляции помехи;
№bn(') = U(t).
Для функции модуляции навигационного сигнала запишем
L
А(0 = Е^о(^-(У-1)гс), (8.31)
7=1
где go (0 — импульс с единичной амплитудой и длительностью тс;
[1
bj: = < — последовательность символов модулирующего кода,
а для огибающей помехи имеем
314
Помехоустойчивость аппаратуры потребителей
tf(0=V^E^<*o('-0"-ikn)-
(8.32)
/=i
Подставляя (8.31), (8.32) в (8.30) и выполнив интегрирование, получаем
о '=1 У=1
=^?ZI6nA/J?o('-('-i)^)?»('-(/-i)^)<* =
:=1 у=1
М (М)ге '=1
(8.33)
В (8.33) произведение bt=bnibci, i = \,L представляет собой случайную
последовательность из элементов, принимающих с равными вероятностями
значения ±1. При этом для используемых в СРНС ГЛОНАСС псевдослучайных
последовательностей М[бг] = 0, и символы Ъ{ и bj некоррелированы при i±j,
т.е. Mlbjbjj = ^ij■, где Stj —символ Кронекера.
Учитывая данное обстоятельство, из (8.33) следует, что 1п является
суммой большого числа L независимых случайных величин, поэтому на
основании центральной предельной теоремы можно утверждать что, случайная
величина /п распределена по нормальному закону с нулевым математическим
ожиданием и дисперсией
Рт1
L ^
2Х<^,/
2
/=1 )
Рт1
i=\
tfc
L + M
Pnr2cL _ PJ2
PT
4£ 4/c
(8.34)
chip
2 X KKKjKj
Из (8.34) следует, что при заданной мощности помехи РП и фиксированном
времени интегрирования в корреляторе Т дисперсия помеховои составляющей
на его выходе зависит только от частоты следования fchip символов кода.
Аналогичный расчет для полезной (сигнальной) составляющей дает
выражение £>нав =РсТ/4. Следовательно, для коэффициента (8.12) получаем
К
п/с
Яп/с
/с
(8.35)
chip
315
Глава 8
Рассмотрим теперь влияние задержки огибающей опорного сигнала т <тс
относительно помехового сигнала. Учтем этот факт в (8.33)
О '=1
Т L L
У=1
= ^ГУУ^о('-г-(«--1)гс)^о(^-(У-1К>* =
2 0 '=1 7=1
2 4-?
i(rc-r)
/r^
\А,/ { gl^-ii-^dt + b^A, \ g20(t-(i-\)rc)dt
(i-l)rc /(rc-r)
Тогда для мощности помеховой составляющей на выходе коррелятора
запишем
Р
2-М
( L
ХКА,/ (Тс ~Т) + *A,,/+A,i )
V/=l
L r-
(8.36)
X (6пА/(Гс"Г)) +(г*п,,-+А,|)
Ы
РпГ2сЬ
1-2—+ 2
^
Vrc /
Первый сомножитель в (8.36) совпадает с (8.34), поэтому проанализируем
второй сомножитель. Полагая г случайной величиной с равно распределенной
на интервале [0,гс], получаем, что второй сомножитель также является
случайной величиной. На рис. 8.4 приведена плотность вероятности распределе-
ния случайной величины и = 1 - 2х + 2х^ при равномерном распределении
х = т/тс на интервале [0,1].
Среднее значение данной плотности вероятности равно 0,67, а наиболее
вероятное значение — 0,51.
Следовательно, среднее значение (8.36) равно
Aw =
0,67Рпт2Ь_РпТ2 l
4 4L 1,5
а наиболее вероятное —
а
п,вер
_0,5lPnr2L ^PJ2 l
4 ~ 41 2
316
Помехоустойчивость аппаратуры потребителей
0.7 0.8
Значение и
Рис. 8.4. Плотность вероятности распределения случайной величины и
Таким образом, учет реально существующих расстроек огибающих (даль-
номерных кодов) у навигационного (и опорного) и помехового сигналов
приводит к уменьшению дисперсии помеховои составляющей на выходе
коррелятора в 1,5 ... 2 раза.
8.3.2. Анализ внутрисистемных помех при использовании
сигналов с модуляцией ВОС(т, п)
Для НАП, работающей по сигналам с модуляцией ВОС(т,п) (см. п. 5.4),
внутрисистемные помехи также имеют модуляцию ВОС(т,п). Сигналы с
данным типом модуляции также описываются (8.26).
Рассмотрим модуляцию ВОС(рп, п). Введем нумерацию кодовой
последовательности помехи bni, i = l,L, L = \/(nfc) и аналогичную нумерацию
кодовой последовательности опорного сигнала bcj , j = \,L . Тогда при отсутствии
рассогласований А/сп = 0, Д#>сп = 0, топ = 0 соотношение (8.30) принимает вид
7" =^ ji^^o(r-(/-l)/(<))sign(sin(2^/c0)x
0 '=1
xIX>go (' "О'" Щп/с))**&(*м(2ярф))й =
У=1
= ^-JLbn,iKi ^o(0(sign(sin(2^^0))2^=^Z^nA, • (8-37)
1 /=1 о 1 ы\
317
Глава 8
запишем
Теперь для дисперсии помеховои составляющей на выходе коррелятора
тем
(8.38)
1
Dn=-M
Put
Г L \
V ;=1 )
1 -у 1
PJ"
4L
Формула (8.38) полностью совпадает с (8.34), полученной для случая
воздействия на НАП, работающей по сигналу с модуляцией BPSK(«), такой же фа-
зоманипулированной помехи.
Введем временную задержку г между кодами помехового и опорного
сигналов и запишем выражение для помеховои составляющей на выходе коррелятора
7" = *Г jiXso (' -(*-1)/«))sign(sin(2^«/cr))х
О '=1
L
x2^o(^-r-(i-l)/(«/c))sign(sin(2^»i/c(/-r)))A =
7=1
(8.39)
'■=1 У=1 О
xg0(t-т-(j-l)/(nfc))sign(sin(2xpnfc(t-r)))dt.
Рассмотрим случай р = 1. В этом случае (8.39) преобразуется к виду
[р~ L
7" =^y-ZfenA,< }sign(sin(2^/c0)sign(sin(2^/c('-0))^- (8-4°)
Интеграл в (8.40) разбивается на два интеграла
J
'с
= sign(sin(2^«/c/))sign(sin(2^«/c(?-r))W^ =
п
гс/2-г
= 2
sign (sin (27rnfct)"j dt-2 [sign (sin (2ят?/с/)) dt.
0 о
При 0 < г < гс/2, где гс = nfc, получаем J = (тс - 2т) - 2г , подставляя
которое в (8.40), получаем
^ =^1>пДМ1-3*)-W)-
1 /=1
Тогда для дисперсии помеховои составляющей на выходе коррелятора
получаем выражение
318
Помехоустойчивость аппаратуры потребителей
Рт1
P^lL
V 1=1 )
J) >7"»2
(1-6x + 10jc2) = -2—(1-6jc + 10jc2).
(8.41)
Первый сомножитель в (8.41) совпадает с (8.38), поэтому проанализируем
второй сомножитель. Полагая, как и выше, г случайной величиной
равномерно распределенной на интервале [0,гс], получаем, что второй сомножитель
также является случайной величиной. На рис. 8.5 приведена плотность
вероятности распределения случайной величины и = 1 - 6х +1 Ох2 при равномерном
распределении х - т/тс на интервале [0,0.5].
* 0.14
I 0.121
ш
& 0.1
и
s 0.08 f
о
о
I о.об \
О
Q.
4>
ю 0.04
и
I-
о
о
о
с;
0.02
0
0.2
0.4 0.6
Значение и
0.8
Рис. 8.5. Плотность вероятности распределения случайной величины и
Среднее значение и равно 0,33, а наиболее вероятное значение и = 0,1.
Рассмотрим случай тс/2<т<тс. В этом случае получаем
J= (-гс +2S) + 2S , S = t-tc/2 , a (8.39) принимает вид
/n=^-t^(*c/H + ')-^+i(2-3x))
£> =5iZL(5-14jc + 10jc2)
Тогда для дисперсии помеховой составляющей на выходе коррелятора
получаем выражение
РГ
AL
Расчеты показывают, что плотность вероятности распределения случайной
величины и = 5 - \4х +10* при равномерном распределении jc = т/тс на
интервале [0.5,1] совпадает с плотностью вероятности, приведенной на рис. 8.3.
319
Глава 8
Следовательно, среднее значение (8.41) равно
А,
J,61Pnr2cL = PJ2 l
'п'ср 4 41 3'
а наиболее вероятное
а
0,5\Pnr2L^PJ2 1
п,вер
4 41 10
Таким образом, учет реально существующих расстроек огибающих (даль-
номерных кодов) у навигационного (и опорного) и помехового сигналов
приводит к уменьшению дисперсии помеховои составляющей на выходе
коррелятора в 3 ... 10 раз, т.е. существенно больше, чем для сигналов с модуляцией
BPSK.
Рассмотрим случай р = 2 . При этом (8.40) преобразуется к виду
[р~ L *с
7п =:VL2X'"*C-/ Jsign(sin(4^if/e0)sign(sin(4^c(/-r)))A. (8.42)
i=l о
Расчеты по описанной выше методике приводят к следующему результату
при 0<г<гс/4
а
Dn =
В.т.
п*с
м\
V PS2
Y,bn,(bCJ(\-lx)-bCJ+lx) =-^-{\-Ых + 50х2)
i=\
fret
(l - 14jc + 50jc2 ) = 5£-(l _ \4X + 5Qjc2 ).
(8.43)
На рис. 8.6 приведена плотность вероятности распределения случайной
величины и = \-\4х + 50х2 при равномерном распределении х = т/тс на
интервале [0,0.25].
0.12
0.2
0.4 0.6
Значение и
0.8
Рис. 8.6. Плотность вероятности распределения случайной величины и
320
Помехоустойчивость аппаратуры потребителей
Среднее значение и равно 0,292, а наиболее вероятное значение «=0,03.
При тс/4<т<гс/2 получается выражение
РгТ2(5
D =
41
--9jc + 34*2
8
На рис. 8.7 приведена плотность вероятности распределения случайной
5 2
величины и = — 9л:+ 34* при равномерном распределении х на интервале
8
[0.25,0.5].
0.12
х
ф
i
0.1
о 0.08
Со
а.
s
о 0.06 \
х
о
й 0.04 \
Л
&
S 0.02 \
о
0.2 0.4 0.6 0.8
Значение и
Рис. 8.7. Плотность вероятности распределения случайной величины и
Среднее значение и равно 0,208, а наиболее вероятное значение и = 0,04.
При тс/2<т<Згс/4 получаем выражение
Dn~^
РпТ2 (1
м
Л
— 8х + 34х , л: = S/tc ,
2 J
1 2
а распределение случайной величины и = — 8х + 34х совпадает с тем, что
приведено на рис. 8.7.
При Згс/4<т<тс получаем выражение
D =5iL-\--\\x + 50x2
п 4L U
а распределение случайной величины и = — 1 ljc + 50jc2 совпадает с тем, что
8
приведено на рис. 8.6.
Итоговая (суммарная) плотность вероятности значений и при изменении
х = TiTc на интервале [0,1] приведена на рис. 8.8.
11-1026
321
Глава 8
0.4 0.6
Значение и
Рис. 8.8. Плотность вероятности распределения случайной величины и
Среднее значение и равно 0,25, наиболее вероятное - 0,04.
Следовательно, среднее значение (8.43) равно
Д
_^61Pnr2cL_PJ2 1
пср 4 41 4'
а наиболее вероятное
_0,5\Pnr2L^PJ2 l
п'вер 4 ^ 41 25'
Таким образом, учет реально существующих расстроек огибающих (даль-
номерных кодов) у навигационного (и опорного) и помехового сигналов
приводит к уменьшению дисперсии помеховой составляющей на выходе
коррелятора в 4 ... 25 раз.
Аналогично могут быть рассчитаны дисперсии помеховых составляющих на
выходе коррелятора для других значений р для помех с модуляцией ВОС(/?и, п).
8.3.3. Анализ внутрисистемных помех с учетом расстройки помехового
и навигационного сигнала по частоте
В п. 8.1.1, 8.1.2 анализировались внутрисистемные помехи для ситуаций,
когда частоты опорного и помехового сигналов совпадают. В данном разделе
оценим влияние расстройки по частоте между указанными сигналами, полагая,
что между кодовыми последовательностями сигналов отсутствуют временные
сдвиги или они кратны длительности символа кода.
Положим для определенности, что НАП работает по навигационному
сигналу с модуляцией BPSK{ri), и помеха имеет такую же структуру. Кроме того,
следуя [8.3], рассмотрим «предельный» случай совершенно случайных кодов,
322
Помехоустойчивость аппаратуры потребителей
когда каждый /' -й (i = \,L, L — длина кодовой последовательности) символ bj
каждой кодовой последовательности (8.31), (8.32) является независимой от
всех других символов случайной величиной, принимающей с равной
вероятностью значения ±1.
При наличии частотной расстройки Асот между навигационным сигналом
и помехой будем рассматривать два коррелятора приемника: синфазный и
квадратурный. На выходе синфазного коррелятора имеем помеховую
составляющую, аналогичную (8.28),
/п =- )U(t)h(t)cos(Aa>cnt)dt, (8.44)
о
а на выходе квадратурного коррелятора имеем
т
Qn = -±ju(t)h(t)sin(Aa>cnt)dt. (8.45)
о
Подставим (8.31), (8.32) в (8.44) и выполним необходимые
преобразования, аналогичные (8.33)
[Р~ 7Tv4 L~l
7" = V" IIX/So(> - JTe)2X,So(*~ jrc)cos(Ao)cnt)dt =
oj=o j=o
= ^Е*пА/ J ™s(Acocnt)dt =
J=0 JTc
= ^sincf ^)XU) cos( A^cn (j + 0-5)rc). (8.46)
1 У z ) j=o
Учитывая, что Асосп = 2лА/сп обусловлено различием доплеровских
смещений частот навигационного и помехового сигналов, значение которых
|A/lJ<5-103 Гц, a |rJ<2-l(T6 с, можно положить sine —2IL-£- «1 и записать
| J СП I | С | I ^ I
V 1 )
(8.46) в виде
7п = ^ZV/c/ cos(Aa>cn (j + 0.5) тс) = B^bnjbcj cos( Acocn {j + 0.5) rc ),
(8.47)
щеВ = ^тс/2.
Для квадратурного коррелятора аналогичные вычисления для (8.45)
приводят к выражению
323
Глава 8
L-\
Qn =B^bnJbCJsm(Acocn(j + 0.5)Tc)
y=0
(8.48)
В (8.47), (8.48) произведение bnjbcj, j = \,L представляет собой
последовательность из элементов, принимающих значение ±1. Обозначим эту новую
последовательность bj = bn jbc;. Легко убедиться, что последовательность bj в
статистическом смысле ничем не отличается от последовательностей Ьп , и
Ьс , а именно: bj, j-\,L принимают значения ± 1 с равными вероятностями,
т.е. Л/ГбЛ = 0, и символы bt и bj некоррелированы при i*j, т.е.
, где Sy — символ Кронекера. Отсюда, в частности, следует, что
M[ln] = M[Qn] = 0, M[l2n+Q2n] = Pnr*L/4, (8.49)
т.е. мощность «огибающей» помеховой составляющей на выходе квадратурных
корреляторов не зависит от расстройки навигационного и помехового сигналов
по частоте.
Отметим, что (8.49) совпадает с выражением (8.34), полученным для
мощности помеховой составляющей синфазного коррелятора при отсутствии
расстроек по частоте между навигационным и помеховым сигналом.
Обозначим /3 = Аа>сптс=27гА/сптс«7г и введем вектор v = |/n/2? Qn/B\T,
для которого запишем корреляционную матрицу
R = M
w
аи ап
а\2 а22
(8.50)
где
ап=М
\^bjCos(fi(j + 0.5))
1-1
=Z^cos2H-/+o-5))
7=0
f L-\ \
L + ^cos(2/?(y + 0.5))
y=0
a,-, = M
42
L-\
J
L-\
£>,. cos(/?(y + 0.5)j£bj sin(fi(j + 0.5))
.7=0 7=0
= ^cos(/?(y + 0.5))sin(/?(y + 0.5)) = -2]siii(2/?(y + 0.5))
7=0
7=0
324
Помехоустойчивость аппаратуры потребителей
а22=М
2>ysin(/?(y + 0.5))
\j=o
L-\
= 2>in2(/?(y + 0.5)) =
У=0
( L-\ \
L-^cos(2/?(y + 0.5))
I 7=0
(8.51)
Для преобразования сумм, входящих в (8.51), в компактные соотношения,
рассмотрим комплексное число при J3 ф 0
i-i
i-i
£сЦ2/»(уЧ0.5)) + 8]>(2М + О.5)) = £е,,«>«">=е!>2>!
Z.-1 Z.-1
i2/?(y+0.5)_ Ар \^J2fij
j=Q
j=0
j=0
y=0
= e1/? * =е'^—^—i = —y-^-(cos( J3LUisin /?Z))
1-e'2^ sin(/?)- sin(ytf) V V^ } УН п
С учетом данного выражения (8.50) записываются в виде
*п=т
Г
L +
sin
(/?£)
V
sin(/?)
COS
(PL)
\
> «12 =
У
1 sin(/7L)
2 sin(/?)
sin
(^).
a22=T
^ sin(/?Z,) . ^
V
/
sin(/?)
а для матрицы (8.50) получаем выражение
2
(
1 +
sin
(/И)
Z,sin(/?)
cos(fiL) sin (/?/,)
sin(/?Z,) -cos(/?Z)
= ^(l + cA),
(8.52)
где введены обозначения
sin(/?Z,) sin(/?Z,) . .
c=1щщ* "7z-=sinc(/?z)=sm<2«Af^ •
A =
со8(2лД/спГ) sin(2/rA/cnr)
sin(2M/cnr) -со§(2лА/спГ)
(8.53)
Icos (/?/,) sin(/?L)
|sin(/?Z,) -cos(/?Z)|
I — единичная матрица, Т = Lrc.
Отметим, что след матрицы R равен tr(R) = L и не зависит от расстройки
навигационного и помехового сигналов по частоте, что соответствует (8.49).
Определитель корреляционной матрицы R равен
325
Глава 8
R =
UJ
(l-c2)>0
Напомним, что случай (5 - О, при котором с -1, соответствует отсутствию
расстройки по частоте между навигационным и помеховым сигналами, который
был рассмотрен в предыдущих разделах, поэтому здесь не рассматривается.
В п. 8.3.1, что вследствие того, что 1П и Qn являются суммой большого
числа L независимых случайных величин, поэтому на основании центральной
предельной теоремы каждая из них починяется нормальному распределению с
нулевым математическим ожиданием, а дисперсии этих распределений в
соответствии с (8.52), (8.53) равны
PnT^L (1 + 8тс(2лА/спГ)со§(2лА/спГ))
4 2
Я/ =■
DQ» =
PycL (1-8тс(2л-А/спГ)со8(2М/спГ))
(8.54)
4 2
Также, как и в п. 8.3.1, 8.3.2, полагая А/сп случайной величиной с равно
распределенной на интервале [0,4] кГц, получаем, что вторые сомножители в
(8.54) также являются случайными величинами. На рис. 8.9 приведена
плотность вероятности распределения случайной величины
и = (l + sinc(2^^)cos(2^x))/2 при равномерном распределении х = А/спТ на
интервале [0,4].
0.2
£ 0.18
z
ш
§0.16
о-0.14
о
со
о-0.12
0.1
о
о
X
0 0.08
о.
О)
S 0.06
I-
1 0.04
I-
^ 0.02 \
I
I ! 1 1
i 1 1
[ : iJ
0 0.2 0.4
\ 1
!
\ J
0.6 0.8 1
Значение и
Рис. 8.9. Плотность вероятности распределения случайной величины и
326
Помехоустойчивость аппаратуры потребителей
Среднее значение данной плотности вероятности равно 0,5.
Следовательно, среднее значение (8.54) равно
Dr
_0,5Pnr2cL_PJ2 l
/п.ср 4 4L 2
Плотность вероятности
распределения случайной величины
и = (l -sine(2тгх)cos(2я\х))/2 аналогична той, что приведена на рис. 8.7,
следовательно Dn co =Dj cn.
Получим еще ряд статистических характеристик, представляющих
интерес. Для двумерного вектора v = |vj v2| с учетом (8.49) можно записать
совместную плотность вероятности в виде
P(vi,v2) =
1
J l\
i —1 I it
v-, R Vi Vt
(8.55)
2^|R| "I 21
Для нахождения R-1 воспользуемся тем, что матрица А в (8.52) является
матрицей отражения [8.4]: она симметрична, имеет собственными числами 1 и
-1, ее определитель равен -1, и, кроме того, А = I. Поэтому можно записать
R'1 =-(1 + сАу1 =-[1-сА + {сА)2 ~{сА)3 +•••] =
L 1
= £(l-cA){l + c2+c4 + ...} = f-iT(l-cA) = ^]lf(I-cA)
(8.56)
При выводе (8.56) учитывалось, что в фигурных скобках имеем сумму
элементов геометрической прогрессии с знаменателем \с2\ < 1.
Получим выражение для плотности вероятности «огибающей» для
квадратурных компонент V! и v2. Для этого воспользуемся стандартной методикой
перехода к полярным координатам v} = Acoscp, v2 = Asmq> [8.4]. В результате
перехода к новым переменным получим
р(А,<р) =
2*V|R|
А
ехр
4R
LA
(Acosp Asin(p)(l-cA)
Asin<p
expj—:—j-(l-c(cos(^L)cos2^ + sin(/?L)sin2^>n
2^7[R| I 4|R|
LA
expJ ——7-^(1 — ^008(2^ — ^2:))
2^ I 4|R|
A>0.
(8.57)
327
Глава 8
Плотность вероятности А = aJv,2 + v\ находится интегрированием (8.57) по <р
LA
/ А\ А \ 4R
R
cLA
ехр<—:—rQos(2(p- /3L)>d(p
4R
(8.58)
Интеграл в (8.58) выражается через модифицированную функцию Бесселя
нулевого порядка [4]. Окончательное выражение для плотности вероятности
р(А) принимает вид
( . \
Р(А)=-
2А
,7П^
■ехр
L
■(l-ef
А2с
.(1-е»)
,Л>0.
(8.59)
При нулевой расстройке по частоте распределение стремится к
одностороннему нормальному p(A) = 2N(0,L), A>0, а при увеличении
расстройки распределение быстро сходится к рэлеевскому закону
р(А) = —ехр
Проведенный анализ для сигналов с модуляцией BPSK{n)
распространяется и на случай сигналов с модуляцией ВОС{т,п), т.к. при отсутствии расстроек
по задержке дальномерных кодов навигационного и помехового сигналов
выражения для помеховых составляющих на выходах синфазного и
квадратурного корреляторов совпадают с аналогичными выражениями для случая приема
сигналов с модуляцией BPSK{n) (см. (8.37)).
8.4. Анализ воздействия различного типа помех на НАП,
работающую по различным типам навигационных
сигналов с кодовым разделением
Рассчитаем мощность помеховой составляющей на выходе коррелятора
(рис. 8.3), когда на его вход поступает помеховый сигнал с одним видом
модуляции, а на его другой вход подается опорный сигнал с другим типом
модуляции, используемом в той или иной навигационной системе с кодовым
разделением сигналов.
В качестве помехового сигнала выберем фазоманипулированный сигнал с
модуляцией BPSK{ri), а в качестве навигационного сигнала — сигнал с
модуляцией ВОС{т,п).
Кроме того будем полагать, что ширина спектра помехи равна ширине
спектра навигационного сигнала. Для фазоманипулированной помехи,
согласованной по ширине спектра с навигационным сигналом, тсп = l/((n + m)f0).
328
Помехоустойчивость аппаратуры потребителей
Рассмотрим сначала случай отсутствия расстроек между помеховым и
опорным сигналами A/cn = 0, А<рсп = О, гоп = 0.
В рассматриваемом случае в (8.30) следует положить
м
U(t) = y[K^bn>iu(t-(i-\)Tcn),
L
^(0=Z^M(?"(-/"1)^)sign(sin(2;r*))' (8-60)
7=1
где тс=\/(п/с).
Отметим, что для рассматриваемых типов модуляции выполняется
условие р = т/п — целое число, поэтому тс = p/(mfc).
Подставим (8.60) в (8.30), полагая, как и выше, что между кодами
опорного сигнала и помехи отсутствует временной сдвиг
0 i=l
L
xZ^w(?~(-/'"1)A'?/o))sign(sin(2^m/0/))^. (8.61)
7=1
Из соотношения между длительностью тс символов дальномерного кода
опорного сигнала и длительностью тСП символов кода помехи следует, что то
на длительности кода тс укладывается (1 + /з) символов кода помехи, а
следовательно, М = (1 + p)L .
Введем двойную нумерацию кодовой последовательности помехи bnvl,
v = 1,/L , / = 1,(1 + р) и запишем
Гр~ т*^ \+р
/"=2т-ЕХ^»('-(("-1)0+р)+'-0/((»+'»)л)):
0 v=\ 1=1
*£Ьс,]и(* -U-l)/(nf0))sign(sin(2Kmf0t))dt =
У=1
[=- l 1+р {(J-l)(l+p)+lhu
2 J=l /=1 ((j-l)(\+P)+l-l)rcn
x sign (sin (2xmf0t))dt. (8.62)
329
Глава 8
^ -
Рассмотрим случай модуляции ВОС(рп,п). Положим р -1 (модуляция
ВОС(и,и)). Тогда на длительности символа тсп укладывается половина периода
синусоиды, и интеграл в (8.62) равен
((v-l)2+/)rcn
J u(t-((v-l)2 + l-\)/((n + m)fQ))^^^
((„-l)2+/-l)rcn
и получаем
Тогда для мощности помеховой составляющей на выходе коррелятора
запишем
Рт1
Х^уКу,1-\у,2)
W=i
R.T.
7=1
PnT;n2L_PnTcuT_PJz _РпГ 1
4L
СП
4L 2
(8.63)
где Lcn=2L — число символов кода помехового сигнала на длительности
интервала накопления Т .
Заметим, что для навигационного сигнала с модуляцией BPSK(w) и
согласованной фазоманипулированной помехи, т.е. помехи с той же модуляцией
BPSK(ft), дисперсия помехи на выходе коррелятора определяется аналогичным
соотношением (8.34) при L = Lcn, т.е. эффективность воздействия
фазоманипулированной помехи на НАП, работающей по сигналам с модуляциями
ВОС(п,п) и BPSK(2a), одинаковая.
Рассмотрим влияние рассогласования по задержке между кодами опорного
и помехового сигналов. Для этого запишем
/n=^JlIZV./«('-r-((l'-1)2 + /-l)/((« + '»)/c))x
О "=1 Ы
L
x^bCJu(t-(j-\)/(mf0))sign(sin(2Kmfct))dt =
7=1
=JT-tt*cjt^/j»('-'-(("-02+'-0/((»+'»)/e))x
v=l j=\ l=\ о
xM(f-(y-l)/(w/0))sign(sin(2/rm/c?))tffr =
330
Помехоустойчивость аппаратуры потребителей
= , 2Х/ К А М+К**г М+Ws (0)>
(8.64)
" 7=1
где Л(г)= j M(^-r)sign(sin(2^w/oO)^ = rcn-r = rcn(1-x)'
2гсп-г
•М*") = J «(^-(^cn-^))sign(sin(2^w/0?))^ = 2r-rcn=rcn(2x-l),
тгп-т
2г,
(8.65)
У3(г)= j w(?-(2rcn-r))sign(sin(2^/w/0r))^ = -rcnx,
2гсп-г
где х = т/тсп.
Подставляя (8.65) в (8.64), получаем
'п = hBfi-iLbcJ Кл (I-*)* Kj,2 (2* - 1) - ^+1,,х]
7=1
Тогда для дисперсии помеховои составляющей на выходе коррелятора
запишем выражение
\2'
D ££сп_М
f
^bc,j [bn,j,l (l~X) + Kj,2 i2x ~ 0 " *n,;+l,l*]
Vy=i
^S^y (^,i (1 - *)2 + ^ (2* ~ О2 + *2W) =
7=1
= 5E£-^(1_3x + 3x2) = ^l-3x + 3x2)
4Z
(8.66)
СП
На рис. 8.10 приведена плотность вероятности распределения случайной
величины и = 1 - Зх + Зх2 при равномерном распределении х = т/тс на
интервале [0,1].
Среднее значение данной плотности вероятности равно 0,5, а наиболее
вероятное значение и = 0,26.
Следовательно, среднее значение (8.66) равно
РТ2 1
п 4т:сп 2
331
Глава 8
-0.12
0.1
z
CD
с;
Ф
сС
ш
Q.
й 0.08
Q.
S
о 0.06
g
g-0.04
m
о 0.02
о
с;
0.3 0.4 0.5 0.6 0.7 0.8 0.9
Значение и
Рис. 8.10. Плотность вероятности распределения
случайной величины и
Положим, что р = 2 (модуляция ВОС(2и,и)). Тогда на длительности сим-
вола дальномерного кода опорного сигнала тс = — укладывается р +1 = 3
"/о
символа кода помехи (длительностью тсп) и р = 2 периода функции
sin(2/rw/0).
Проделав выкладки, аналогичные выше приведенным, получим выражение
для мощности помеховой составляющей на выходе коррелятора
D„
Рт1
16
( L Л
-%LI^(^+^)=
j=\
Pnr2nL _ PntcnT _ PJ2 \_PJ2 1
8
24
41
СП
4L 18
(8.67)
где Lcn=3L — число символов кода помехового сигнала на длительности
интервала накопления Т .
В (8.67) первый сомножитель характеризует мощность помехового
сигнала на выходе коррелятора, если опорный сигнал имеет модуляцию BPSK(3fl),
т.е. такую же, что и у помехового сигнала. Следовательно, при постановке фа-
зоманипулированной помехи НАП, принимающей навигационный сигнал с
модуляцией ВОС(2я,и), уровень помеховой составляющей на выходе
коррелятора в 6 раз меньше, чем в случае приема НАП сигнала с модуляцией
BPSK(3^).
332
Помехоустойчивость аппаратуры потребителей
Учет рассогласования по задержке между кодами опорного и помехового
сигналов, проделанный аналогично тому, как это сделано выше, приводит к
следующему выражению для дисперсии помеховои составляющей на выходе
коррелятора
D,'%£-«(* = Фс.)-
(8.68)
СП
Функции Dn (х) для различных интервалов изменения аргумента
приведены ниже
1) 0<jc<0,25, w(jc) = 0,5-jc + 10jc2;
2) 0,25 <jc< 0,5, w(jc) = 1,5-4jc + 6jc2;
3) 0,5 <x< 0,75, w(x) = 3,5-8jc + 6jc2;
4) 0,75<jc<1, w(jc) = 9,5-19jc + 10jc2.
Анализ показывает, что плотности вероятности распределений случайной
величины и для первого и четвертого диапазонов изменения аргумента х и
для второго и третьего диапазонов совпадают и приведены соответственно на
рис. 8.11 и 8.12 (при равномерном распределении аргумента х на
соответствующих интервалах).
* 0.35
S
Z
ш
§ 0.3|
О)
5 0.25 [
(О
Q.
? 0.2 \
о
о
I 0.15
О
а
О)
ш 0.1
I-
х 0.05
5
С
%
0.15 0.2 0.25 0.3 0.35 0.4
Значение и
Рис. 8.11. Плотность вероятности распределения
случайной величины и при 0 < х < 0,25 и 0,75 < х < 1
333
Глава 8
к 0.4
s
1 0.35[
ф
8. o.3h
2.0.25
8 0.2
Z
I-
§0.15
0)
m
d 0.1
o
=E 0.05
о
с;
*
25
0.3 0.35
Значение и
0.4
Рис. 8.12. Плотность вероятности распределения
случайной величины и при 0,25 < х < 0,5 и 0,5 < х < 0,75
Для плотности вероятности, приведенной на рис. 8.11 среднее значение
равно 0,19, а для плотности вероятности, приведенной на рис. 8.12 среднее
значение — 0,29.
На рис. 8.13 приведена общая плотность вероятности распределение
случайной величины и, для которой итоговое среднее значение равно 0,25.
0.2
z
О)
с;
О)
§0.15
с
о
со
а
0.1
о
о
X
тс
о
а.
О)
л 0.05 (
о
о
X
о
с;
I
) (
—I
I
i
).2
I
I
0
i 1
.4 0
i 1 1
: ]
6 0.8 1
Значение и
Рис. 8.13. Плотность вероятности распределения
случайной величины и
334
Помехоустойчивость аппаратуры потребителей
Таким образом, усредненное (по всем возможным) значение дисперсии
помеховой составляющей на выходе коррелятора равно
РТ2 1 РТ2 1
Г) _ Л Пх , _ Пх 1_
п 4L„„ *4 41 12
(8.69)
"'СП
Отметим, что значение дисперсии помеховой составляющей на выходе
коррелятора (8.69) в 2,7 раза меньше, чем аналогичное значение в (8.34).
Следовательно, при одной полосе занимаемых частот постановка фазоманипули-
рованной помехи НАП, работающей по сигналу с модуляцией BPSK(3ft), более
эффективна, чем постановка той же помехи НАП, работающей по сигналу с
модуляцией ВОС(2л,и) в 2,7 раза (на 4,3 дБ).
Из сравнительного анализа соотношений (8.34), (8.38), (8.63), (8.67), (8.69)
и др. следует, что для дисперсии помеховой составляющей на выходе
коррелятора можно записать обобщенное выражение
Dn
4Lcn к
(8.70)
в котором коэффициент к принимает различные значения в зависимости от
типа помехи, типа навигационного сигнала, по которому работает НАП, учета
или неучета временного смещениям между кодами помехового и опорного
сигналов и ряда других факторов.
В табл. 8.1 приведены значения к для некоторых типов модуляций
опорного сигнала ВОС{рп,п) и BPSK(w) как при отсутствии сдвигов по задержке и
частоте у опорного о помехового сигналов, так и при наличии таких расстроек.
В последнем случае при расчетах проводилось усреднение по возможным
значениям указанных расстроек при постановке фазоманипулированной помехи,
согласованной по ширине спектра с опорным (навигационным) сигналом.
Таблица 8.1 Значения к для некоторых типов навигационных сигналов
при постановке фазоманипулированных помех
Тип модуляции
опорного сигнала
ВОС(1,1)
ВОС(15,10)
ВОС(10,5)
ВОС(15,2.5)
Значение к
При отсутствии
расстроек г
1
3,2
5,65
9,1
При наличии
расстроек г
3,85
5,7
7,41
9,52
Аналогичные расчеты значений коэффициента к по описанной методике
можно сделать и для других сочетаний типов помехового и навигационного
сигналов.
335
Глава 8
8.5. Помехоустойчивость режимов поиска и захвата сигнала
В режиме поиска и захвата сигнала, как отмечалось в п. 6.2, проводится
обнаружение сигнала в каждой ячейке поиска. При этом характеристики
обнаружения определяются отношением сигнал/шум q = E/N0 , где Е — энергия
полезного сигнала (см. рис. 6.4). Положим время накопления сигнала в
обнаружителе Г = 0,01 с, а мощность сигнала на входе приемника Рс = -160 дБВт,
что соответствует гарантированной минимальной мощности сигнала [1.3].
Следовательно, при отсутствии внешних помех q^^ = 40 дБГц. Пусть
теперь на входе приемника действует внешняя шумовая помеха со спектральной
плотностью Nn . Вводя эквивалентный шум со спектральной плотностью N3 =
= N0 + Nn, рассмотрим характеристики обнаружения сигнала на фоне этого
эквивалентного шума. Зададим требования к вероятности ложной тревоги и пра-
вильному обнаружению соотношениями рлт =10" , /?об =0,9.
На рис. 8.14 приведена характеристика обнаружения для
рассматриваемых параметров, из которой следует, что приемник обеспечивает требуемые
характеристики при <7с/„экв ^ 28 дБГц. Рассчитаем коэффициент подавления,
соответствующий данному условию,
4/с*"
к =Рп=К¥с_
" Рс Рс
1
1
ас/пэкв ас/щ
44_ = 10з,2
^с/"экв
т.е. Кп = 32 дБ, где А/с — полоса частот спутникового сигнала (для сигнала с
дальномерным кодом стандартной точности Afc « 1 МГц).
Роб
40 Ъ/и^ДБГц
Рис. 8.14. Зависимость вероятности правильного обнаружения при Т = 0,01 с.
336
Помехоустойчивость аппаратуры потребителей
При увеличении времени накопления сигнала в обнаружителе
коэффициент подавления будет увеличиваться, что соответствует повышению
помехоустойчивости. Снижение требований по вероятности ложной тревоги или
вероятности правильного обнаружения также приводит к повышению
помехоустойчивости режима обнаружения, а, следовательно, и режима поиска и
захвата сигнала.
8.6. Методика приближенной оценки помехоустойчивости
следящих систем
Наиболее полно помехоустойчивость следящих систем характеризуется
вероятностью срыва слежения за заданное время. Строгое математическое
решение данной задачи основано на теории марковских процессов, а более
точное — на решении задачи о достижении границ многомерным марковским
процессом [8.1]. Использование данного математического аппарата требует
высокой квалификации от исследователя и существенных временных затрат.
Поэтому для инженерных расчетов можно рекомендовать упрощенную
методику аналитической оценки потенциальной помехоустойчивости следящих
систем [8.2], приводимую ниже.
Использованный выше термин потенциальной помехоустойчивости
отображает два фактора. Во-первых, помехоустойчивость оценивается для
шумовой помехи, которая является наименее эффективной с точки зрения срыва
режима слежения по сравнению с другими помехами (узкополосными,
импульсными, фазоманипулированными и т.д.). Во-вторых, помехоустойчивость
рассчитывается для оптимальных (по структуре и параметрам) следящих систем.
Достоинства данного подхода:
задается статистические описание параметра сигнала, за которым ведется
слежение, что более адекватно реальным процессам (в классической теории
следящих систем динамические воздействия задаются в виде полиномов той
или иной степени, что является более грубым описанием);
в оптимальной системе, во-первых, минимизируется суммарная ошибка
слежения, что правильно отражает целевое назначение навигационного
приемника — достижение высокой точности оценивания координат и составляющих
вектора скорости потребителя, а во-вторых, для каждого типа потребителя
(неподвижного, мало подвижного, интенсивно маневрирующего,
высокодинамичного и т.д.) определяется свое оптимальное значение полосы пропускания
следящей системы (СС), которая во многом и определяет ее помехоустойчивость.
Суть упрощенной методики заключается в следующем. При малых
ошибках слежения s(tk) = £k -X(tk)-X(tk) за параметром сигнала Я (здесь Я -
оценка параметра сигнала, формируемая следящей системой) мгновенную
ошибку et можно считать гауссовской случайной величиной с нулевым мате-
337
Глава 8
матическим ожиданием и дисперсией D£ . Следовательно, можно рассчитать
вероятность того, что абсолютное значение мгновенной ошибки слежения
будет больше заданных значений smax :
р(^)=21^Ч^;р- (8-71)
Помехоустойчивость следящей системы будем оценивать по значению
спектральной плотности внешней помехи (а, следовательно, и
соответствующего ей значения Кп), при которой вероятность выхода мгновенной ошибки е
слежения за апертуру дискриминационной характеристики
&Ua=[-Uamax,Uamax] не превышает заданной величины рзад. Полагая,
например, Рзад = 4>55" Ю 2 из (8-71), находим условие для определения Кп:
^^дтах/2- (8.72)
Таким образом, для оценки помехоустойчивости СС необходимо
рассчитать дисперсию ошибки D£ в зависимости от спектральной плотности Nn
дополнительной шумовой помехи и найти такое ее значение, при котором будет
выполняться граничное условие (8.72).
Для расчета дисперсии D€ можно воспользоваться методикой
линеаризации следящей системы, описанной в п. 6.3.6.
8.7. Помехоустойчивость автономной системы слежения
за фазой сигнала
Рассмотрим ССФ третьего порядка с дискриминатором (6.41). В
п. 6.3.1.6 проведена линеаризация такой ССФ и получены выражения для
дисперсии шума эквивалентных (линейных) наблюдений (6.75) и дисперсии
ошибки фильтрации фазы (6.80) в оптимальной следящей системе. Положим для
простоты, что ошибка слежения по задержке отсутствует, т.е. ет = 0. Такой
режим работы ССФ будем называть автономным.
Параметры оптимальной ССФ выбираются при отсутствии
дополнительных внешних помех, т.е. дисперсия D~ шума эквивалентных наблюдений при
выборе оптимальных коэффициентов усиления системы (6.81), (6.82)
рассчитывается в соответствии с (6.75) для заданного значения q. . При этом ССФ
имеет вполне конкретную полосу пропускания Д/сСФ (6.86), графики
зависимости которой от интенсивности ускорения потребителя а г 2п для различ-
м/с
:]
ных значений ^ приведены на рис. 6.24.
338
Помехоустойчивость аппаратуры потребителей
Рассмотрим воздействие на приемник дополнительной шумовой помехи со
спектральной плотностью Nn. При этом на синтезированную следящую
систему (6.76) (или в непрерывном варианте (6.84)) будет воздействовать
эквивалентный аддитивный шум, дисперсия D- которого определяется (6.75) с
заменой q'c/^ на яс/Пэкв . Для линейной системы можно рассчитать дисперсию
ошибки фильтрации D^ по известной методике [8.4]. Динамическая ошибка
фильтрации
|2
°>-i\
MJ
M3+^HiO*>)2+^H2i*> + ^H3
■da> =
(ia>f
Ж
5/3 '
нЗ
где коэффициенты усиленияКн{,Кн2 ,Кн3 определяются в соответствии с (6.81).
Для флуктуационной ошибки можно записать
<rl=2Dl{Nn)TAfcc<t>. (8.73)
Следовательно, для суммарной ошибки фильтрации получаем
d*=
*ЩЛК)ТЬ/ссф
(8.74)
3(^„з)5/3
В (8.74) подчеркнута зависимость дисперсии D^ (Nn) аддитивного шума
от спектральной плотности внешней помехи Nn, которая позволяет рассчитать
помехоустойчивость ССФ. В соответствии с описанной в п. 8.6 методикой КП
определяется при достижении дисперсией ошибки фильтрации D9 значения,
удовлетворяющего условию (8.72). Для рассматриваемой ССФ из
дискриминационной характеристики (6.70) определяем Uamax = njl. Следовательно,
условие (8.72) принимает вид JD^ < /г/4. Подстановка в данное условие формулы
(8.74) и решение полученного неравенства относительно Nn дает следующую
формулу для расчета коэффициента подавления ССФ:
Кп =ТА/с{у]2В/Т + \-\-\/(дс/поТ)), (8.75)
/
где В =
D.
>£
^шор
3(*нз)
5/3
4/ссф> °<рпоР=(я/4)2> а А/ссф определяется в
соответствии с (6.86).
На рис. 8.13 приведены зависимости помехоустойчивости оптимальной
автономной ССФ, синтезированной для заданных значений интенсивности уско-
339
Глава 8
рения потребителя ста и отношения сигнал/шум.
Отметим, что каждой паре значений аа и qc, соответствует свое
значение полосы пропускания ССФ (см. рис. 6.24). Поэтому изменению аа по оси
абсцисс на рис. 8.15 соответствует изменение А/сСФ .
О 20 40 60 80 100а*'
Рис. 8.15. Коэффициент подавления автономной ССФ
Из графиков рис. 8.15 видно, что для динамичных потребителей
(cra>4g) помехоустойчивость ССФ составляет 36...37 дБ, а для слабо
динамичных (cra<0,5g) получаем Кп «39...40 дБ. При увеличении ширины
спектра сигнала А/с, как следует из (8.75), помехоустойчивость ССФ
пропорционально увеличивается. Так, при приеме сигнала с ВТ-кодом
помехоустойчивость возрастает в 10 раз.
Из проведенного анализа видно, что при принятой методике расчета
помехоустойчивости следящей системы существенными являются два фактора:
структура сглаживающего фильтра следящей системы, определяющая
операторный коэффициент передачи замкнутой следящей системы, и дисперсия
эквивалентных линейных наблюдений, приведенных к параметру, за которым
ведется слежение. Поэтому в дальнейшем при расчете помехоустойчивости будут
анализироваться в основном эти факторы.
8.8. Помехоустойчивость автономной системы слежения
за частотой сигнала
Рассмотрим следящую систему за частотой сигнала некогерентного
приемника, описанную в п. 6.3.6.3 и использующую сглаживающий фильтр второго
порядка. Для такой системы в линеаризованном режиме установившиеся
значения коэффициентов усиления ССЧ и дисперсий ошибок фильтрации определя-
340
Помехоустойчивость аппаратуры потребителей
ются формулами (6.101), (6.102). Рассмотрим частотный дискриминатор
некогерентного приемника (П6.63), для которого дисперсия эквивалентных
наблюдений определяется соотношением (6.114). Для автономной ССФ полагаем sT - 0.
Динамическая ошибка фильтрации частоты определяется соотношением
|2
•2-iJ
Ы
(ifi>) +KHlico + KH2
■dco =
4<р
м2
2л/2^н3/22 '
где коэффициенты усиления Ки1, Кн2 определяются в соответствии с (6.102).
Флуктуационная ошибка фильтрации частоты при воздействии внешней
шумовой помехи описывается выражением, аналогичным (8.73),
°l=2Dl(Nn)TAfcC4-
Следовательно, дисперсия ошибки фильтрации частоты при воздействии
внешней шумовой помехи определяется соотношением
D„ = _ * .,. + 2D* (Nn)TAfCC4, (8.76)
СО
2j2(K„2f
из которого получается следующее выражение для коэффициента подавления
ССЧ:
КП = TAfc (JB/T + 1 -1 - \/(qc/no T)),
(8.77)
(
где В =
D.
сопор
2^(KH2f2
Т /4/ссч> D<onop={K/2T) >a 4/ссч
определяется в соответствии с (6.105).
Зависимости потенциальной помехоустойчивости автономной ССЧ
приведены на рис. 8.16.
10"
10*в
ю*7
10*в
ю*5
10м
ю43
avn
\-
1д».-1^
\\ \з
- V-—s
-^
%
\
h ]
с/по =45fBr^
^"^^V^i
^" I **^
„0 =30дрГц
i i
i
1
4
^£/50.
!
1^*—•*
_j
=37дБГц
| *—^
"4---- - -
0 20 40 60 80 100 °а
Рис. 8.16. Коэффициент подавления автономной ССЧ
341
Глава 8
Из сопоставления зависимостей рис. 8.14 и 8.13 следует, что
помехоустойчивость ССЧ на 7.. .9 дБ выше, чем помехоустойчивость ССФ.
8.9. Помехоустойчивость автономной системы слежения
за задержкой сигнала
Рассмотрим некогерентный приемник. Так как в ССЗ используется
сглаживающий фильтр второго порядка, т.е. такой же, как и в ССЧ, отличие
анализа помехоустойчивости ССЗ от помехоустойчивости ССЧ состоит лишь в
отличии соотношений для дисперсии шума эквивалентных наблюдений, которая в
рассматриваемом случае определяется формулой (6.98). Для автономной
системы слежения за задержкой сигнала полагаем еф = О.
Следуя методике, описанной в двух предыдущих разделах, можно
получить следующее выражения для коэффициента подавления ССЗ
кп =
ТА/С
(j\6B/T + \-\-4/(qc/noT)),
(8.78)
(
где В =
а
%
г пор
2j2(KH2f
Т1 А/ссз > Япор=(3Гэ/4)2> а А/ссз
определяется в соответствии с (6.105).
Зависимости потенциальной помехоустойчивости автономной ССЗ
приведены на рис. 8.17. Сопоставление этих зависимостей с аналогичными,
приведенными на рис. 8.16, показывает, что помехоустойчивость автономной ССЗ
на 2 дБ ниже помехоустойчивости автономной ССЧ.
20 40 60 80 100
Рис. 8.17. Коэффициент подавления автономной ССЗ
<Vm/c
342
Помехоустойчивость аппаратуры потребителей
8.10. Помехоустойчивость приемника с учетом взаимного
влияния следящих систем
В приемниках сигналов СРНС следящие системы взаимосвязаны, что, в
частности, обусловливает зависимость дисперсий шумов эквивалентных
наблюдений по одному из параметров, за которым ведется слежение, от ошибок
оценивания другого параметра, слежение за которым осуществляется другой
следящей системой. Такая взаимосвязь следящих систем влияет на их
помехоустойчивость, поэтому в данном разделе анализируется помехоустойчивость
приемников СРНС с учетом взаимного влияния различных подсистем.
8.10.1. Помехоустойчивость некогерентного приемника
В некогерентном приемнике имеем две следящие системы: за задержкой и
частотой сигнала. В п. 6.3.6.2 и 6.3.6.3 показано, что дисперсия шумов
эквивалентных наблюдений, приведенных к задержке сигнала, зависит от
эквивалентного значения сигнал/шум qc, - qcj sine2 (sC0T/2), а дисперсия шумов
эквивалентных наблюдений, приведенных к доплеровской частоте — от
Яс/п0 =Яс/п0Р2(st)> гДе £т и £со — ошибки слежения за задержкой и
доплеровской частотой соответственно. Из приведенных выражений видно, что учет
ошибок слежения приводит к снижению эквивалентного отношения
сигнал/шум, а, следовательно, и к снижению помехоустойчивости ССЧ и ССЗ.
При расчете помехоустойчивости приемника с учетом взаимного влияния
следящих систем будем полагать s / ч = //)г/ ч , где Д-и) — дисперсия ошибки
фильтрации соответствующего параметра, определяемая из дисперсионных
уравнений соответствующей следящей системы.
На рис. 8.18 приведена зависимость коэффициента подавления ССЧ с
учетом влияния на ее характеристики ошибки слежения за задержкой сигнала.
о 20 40 ео во 1оо а*'
Рис. 8.18. Коэффициент подавления ССЧ
343
Глава 8
Сопоставление данных зависимостей с аналогичными зависимостями,
приведенными на рис. 8.16, показывает, что помехоустойчивость ССЧ
снизилась на 4 дБ.
На рис. 8.19 приведены зависимости коэффициента
помехоустойчивости ССЗ с учетом влияния на нее ССЧ. Сопоставление данных зависимостей с
аналогичными, приведенными на рис. 8.17, показывает, что ССЧ слабо влияет
на помехоустойчивость ССЗ.
Рис. 8.19. Коэффициент подавления ССЗ
Из сопоставления зависимостей, приведенных на рис. 8.18 и 8.19, следует,
что помехоустойчивость некогерентного приемника определяется
помехоустойчивостью ССЧ и составляет 38...41 дБ для динамичных потребителей
(оа > 4g ) и 41.. .45 дБ для слабо динамичных потребителей (аа < 0,5g).
8.10.2. Помехоустойчивость когерентного приемника
В когерентном приемнике осуществляется слежение за задержкой и фазой
сигнала. Аналогично тому, как это сделано в предыдущем разделе, можно
показать, что система слежения за фазой сигнала слабо влияет на
помехоустойчивость системы слежения за задержкой сигнала. Поэтому рассмотрим лишь
влияние ССЗ на помехоустойчивость ССФ.
Как следует из (6.73) и (6.74), влияние ошибки слежения по задержке £т
приводит к изменению эквивалентного отношения сигнал/шум в соответствии
с формулой qlj = qc/„0p2 (sT) - На рис. 8.20 приведены зависимости
коэффициента подавления ССФ с учетом влияния ССЗ. Из сопоставления данных
зависимостей с аналогичными, приведенными на рис. 8.15, следует, что
помехоустойчивость ССФ уменьшилась на 1,5...2 дБ.
344
Помехоустойчивость аппаратуры потребителей
Помехоустойчивость когерентного приемника определяется
помехоустойчивостью ССФ и составляет 34...36 дБ для динамичных потребителей
(аа > 4g ) и 38.. .40 дБ для слабо динамичных потребителей (аа < 0,5g).
Рис. 8.20. Коэффициент подавления ССФ
Помехоустойчивость когерентного приемника на 4...5 дБ ниже
помехоустойчивости некогерентного приемника.
8.11. Помехоустойчивость комплектированных следящих систем
В комплексированных следящих системах в сглаживающем фильтре
обрабатываются сигналы с выходов двух или более дискриминаторов. Описанная
выше методика расчета помехоустойчивости может быть использована и в
этом случае. Проиллюстрируем это на примере комплексированной следящей
системы по задержке и доплеровскому смещению частоты некогерентного
приемника, описанной в п. 6.3.6.5.
Линеаризованная следящая система описывается уравнениями (6.146),
коэффициенты усиления данной системы — соотношениями (6.147), а дисперсии
ошибки фильтрации в установившемся режиме — формулами (6.148). В
табл. 6.2 проиллюстрировано, что для реальных уровней сигнала и динамики
движения потребителей параметр р«1 и дисперсии ошибок фильтрации
могут быть представлены в упрощенном виде (6.149). При этом уравнения
оптимальной фильтрации (6.150) также упрощаются, и оценка скорости изменения
задержки сигнала (доплеровского смещения частоты) формируется только по
сигналам с выхода частотного дискриминатора.
Следовательно, помехоустойчивость кольца слежения за частотой сигнала
не зависит от характеристик кольца слежения за задержкой. Зависимости
коэффициента подавления для ССЧ в рассматриваемом случае приведены на
345
Глава 8
рис. 8.21. Сравнение данных зависимостей с аналогичными, приведенными на
рис. 8.18, показывает, что помехоустойчивость несколько снизилась.
Объясняется это тем, что в рассматриваемом случае принято описание изменения доп-
леровской частоты уравнением первого порядка [см. (6.94)], и соответственно в
комплексной следящей системе кольцо слежения за частотой также имеет
первый порядок [см. (6.146)] (сглаживающий фильтр первого порядка), в то
время как в п. 8.10.1 рассматривалось описание доплеровской частоты
уравнением второго порядка. В связи с этим следует отметить, что повышение
помехоустойчивости следящей системы с увеличением порядка сглаживающего
фильтра наблюдается и в других типах следящих систем (за фазой и задержкой
сигнала).
ю4-6
104J
10*
103'9
10з.78
1036
кп
-V-V
- -
! ; ! f
~ t " Г"" "; "Т
! : 1 '■
.^&/я^|*1ЁЭД__ I
. I X. \tS^ "Т^^—-^j
---~$^~- ^^S**^^^ _4- -----
i i i i
20
40
60
80
100 °*>м/с
Рис. 8.21. Коэффициент подавления кольца слежения за частотой
На рис. 8.20 приведены графики коэффициента подавления для кольца
слежения за задержкой сигнала.
кп
юг
SM
10
,5.16
iff
.6.15
Iff
Д14
10'
k5.13
10'
,5.12
| дс/„0={45дБГц
1 у^-^дВГтг
-■^7—фолвгд
100 а"'м/с
0 20 40 60 60
Рис. 8.20. Коэффициент подавления кольца слежения за задержкой
346
Помехоустойчивость аппаратуры потребителей
Из графиков следует, что помехоустойчивость кольца слежения за
задержкой практически не зависит от интенсивности маневрирования потребителя.
Это вполне согласуется с тем, что, как отмечено в п. 6.3.6.5, при р «1
дисперсия ошибки фильтрации задержки сигнала не зависит от интенсивности
ускорения потребителя [см. (6.134)]. Помехоустойчивость также слабо меняется
при изменении отношения сигнал/шум.
Как и выше, помехоустойчивость приемника с комплексированной
следящей системой определяется помехоустойчивостью кольца слежения за
частотой сигнала.
Приведенные в данной главе зависимости коэффициента подавления для
различных типов следящих систем можно использовать для расчета
критического отношения сигнал/внутренний шум tfc/^кр, при котором приемник еще
работает с заданными потребительскими характеристиками. Для численного
расчета данного параметра следует использовать соотношение
Чс/по кР = А/с /Кп ИЛИ Я с/по кр = 10 l0g(4fc ) " К •
Так, для сигнала стандартной точности А/с « 1 МГц, и для значения
коэффициента подавления Кп= 38 дБ (приемник с комплексированной системой
слежения, мощность входного сигнала Рс=-170 дБВт) получаем Яс/п0кр =
=22 дБГц.
Литература
8.1. Перов А.И., Болденков Е.Н., Бакитько Р.В. Анализ влияния межсистемных
помех на аппаратуру потребителей спутниковых радионавигационных систем//
Радиотехника. 2009. № 1, с. 20-28.
8.2. Перов А.И. Анализ внутрисистемных помех в спутниковых
радионавигационных системах с кодовым разделением сигналов при использовании различных
навигационных сигналов// Радиотехника. 2009. № 7, с
8.3.Харисов В.Н., Булавский Н.Т., Хамматов P.P. Распределение случайных помех
множественного доступа// Радиотехника. 2009. № 7, с
8.4. Голуб Дж., Ван Лоун Ч. Матричные вычисления/ Пер. с англ. - М.: Мир, 1999.
8.5. Тихонов В.И., Харисов В.Н. Статистический анализ и синтез
радиотехнических устройств и систем. - М.: Радио и связь, 2004.
8.5. Тихонов В.К, Миронов В.А. Марковские процессы. - М.: Сов. радио, 1977.
8.6. Перов А.И., Болденков Е.А., Григоренко Д.А. Упрощенная аналитическая
методика оценки потенциальной помехоустойчивости оптимальных следящих систем
приемников спутниковой навигации// Радиотехника, 2003, № 7, с. 78-87.
347
Глава 9
Р а з д е л 2
СПУТНИКОВАЯ РАДИОНАВИГАЦИОННАЯ
СИСТЕМА ГЛОНАСС
Глава 9
ОБЩИЕ СВЕДЕНИЯ О СПУТНИКОВОЙ
РАДИОНАВИГАЦИОННОЙ СИСТЕМЕ ГЛОНАСС
9.1. Структура и основные характеристики
Отечественная сетевая среднеорбитальная СРНС ГЛОНАСС (ГЛОбальная
НАвигационная Спутниковая Система) предназначена для непрерывного и
высокоточного определения времени, пространственного (трехмерного)
местоположения, а также вектора скорости движения космических, авиационных,
морских и наземных потребителей в любой точке Земли или околоземного
пространства. В настоящее время она состоит из трех подсистем:
1) подсистема космических аппаратов, состоящая из навигационных
спутников ГЛОНАСС на соответствующих орбитах;
2) подсистема контроля и управления, состоящая из наземных пунктов
контроля и управления;
3) подсистема навигационной аппаратуры потребителей.
Навигационные определения в аппаратуре потребителей системы
ГЛОНАСС осуществляются на основе беззапросных измерений псевдо
дальностей и радиальных псевдо скоростей до четырех или более спутников
ГЛОНАСС (или трех спутников при использовании дополнительной
информации) с учетом информации, содержащейся в навигационных сообщениях,
передаваемых в радиосигналах этих спутников. Для решения навигационной задачи
из навигационного сообщения извлекаются данные о параметрах движения
навигационных спутников на соответствующие моменты времени. В результате
обработки этих данных в НАП обычно определяются три (две) координаты
потребителя, величина и направление вектора его земной (путевой) скорости,
текущее время (местное или в шкале Госэталона Координированного Всемирного
Времени UTC(SU), или по другому, иТС(ГЭВЧ) (ГЭВЧ — Государственный
эталон времени и частоты).
Разработчиком системы ГЛОНАСС в целом, в том числе НС и
программного обеспечения управления НС, является Научно-производственное
объединение прикладной механики. Разработчиком бортовой аппаратуры НС
ГЛОНАСС, подсистемы контроля и управления, а также отдельных образцов
НАП является Российский научно-исследовательский институт космического
348
Общие сведение о СРНСГЛОНАСС
приборостроения. Он же — обладатель патента на СРНС ГЛОНАСС [В.6].
Генеральным заказчиком системы ГЛОНАСС являлись Военно-космические
силы (ВКС) Министерства обороны (МО) РФ, которые длительное время
осуществляли управление системой ГЛОНАСС и информирование потребителей о ее
состоянии (через Координационный научно-информационный центр (КНИЦ
ВКС МО РФ)). В настоящее время управление системой ГЛОНАСС
осуществляется Космическими войсками РФ.
Основным документом, содержащим описание структуры и наиболее
общих характеристик навигационных сигналов и сообщений системы, служит
интерфейсный контрольный документ ГЛОНАСС [1.3].
Основные характеристики СРНС ГЛОНАСС (а также аналогичной
американской системы GPS) приведены в табл. 9.1 [1.3, 9.1].
Таблица 9.1. Системные характеристики СРНС ГЛОНАСС (GPS)
и Параметр, способ
[Число НС (резерв)
Число орбитальных плоскостей
Число НС в орбитальной плоскости
Тип орбит
Высота орбит, км
Наклонение орбит, град
Драконический период обращения НС
Способ разделения сигналов НС
Несущие частоты навигационных
радиосигналов, МГц: L\
12
Период повторения дальномерного кода
(или его сегмента)
Тактовая частота дальномерного кода, МГц
Скорость передачи цифровой информации
(соответственно СИ- и D- код), бит/с
Длительность суперкадра, мин
Число кадров в суперкадре
Число строк в кадре
Система отсчетов времени
Система отсчета координат
Тип эфемерид
1
ГЛОНАСС
24(3)
3
8
Круговая(^0±0,01)
19100
64,8+0,3
11ч 15 мин 44 с ±5 с
Частотный
1598,0625...1609,3125
1242,9375...1251,6875
1 мс
0,511
50
2,5
5
15
UTC(SU)
ПЗ-90.02
Геоцентрические
координаты и их
производные
GPS 1
24(3) 1
6
4
Круговая
20145
55 (63)
11 ч 56,9 мин
Кодовый
1575,42
1227,6
1 мс (С/А-
код)
7дн (Р-код)
1,023(С/А-
код) 1
10,23 (P(Y)-
код)
50
12,5
25
5
UTC(USNO)
WGS-84
Модифицированные
кеплеровы
элементы |
349
Глава 9
Точность определения координат потребителя существенно зависит от
условий распространения сигнала в атмосфере, маневренности потребителя,
алгоритмов обработки сигналов в НАП и ряда других факторов, которые
подробно обсуждены в гл. 7. Там же приведены потенциальные характеристики
точности, которые для удобства сведены в табл. 9.2.
Таблица 9.2. Потенциальные точностные характеристики
СРНС ГЛОНАСС
Г Параметр
[Сферическая ошибка по
координатам, м
Ошибка по координатам в
горизонтальной плоскости, м
Ошибка по координатам в
вертикальной плоскости, м
Сферическая ошибка по
скорости, м/с
1 Время, мкс
Точность (lg) 1
15
8,5
12,5
0,2
1 1
В перспективе на базе СРНС ГЛОНАСС предполагается создание Единой
глобальной системы координатно-временного обеспечения (ЕС КВО) [9.2].
Кроме СРНС эта система будет включать: Государственную систему Единого
времени с эталонной базой страны; Государственную систему и службу
определения параметров вращения Земли; систему наземной и заатмосферной
оптической астрометрии; космическую геодезическую систему и т. д. Считается,
что возможности существенного повышения точности навигационных
определений связаны с созданием глобальной системы отсчета, использующей
самоопределяющиеся навигационно-геодезические спутники без привлечения
измерений с поверхности Земли [1.1, 1.4].
9.2. Этапы развертывания
Теоретические предпосылки к созданию отечественной СРНС впервые
были сформулированы [В.5] еще до запуска первого ИСЗ в рамках
исследований, проводимых группой сотрудников ЛВВИА под руководством В. С. Шеб-
шаевича в 1955—1957 гг., что свидетельствует о приоритете отечественной
науки в разработке идеологии СРНС.
Первый НС («Космос-192») отечественной низкоорбитальной спутниковой
навигационной системы («Цикада»), предназначенной для нединамичных
потребителей, был выведен на орбиту в 1967 г. А уже через год были проведены
научные исследования по обоснованию, целесообразности и возможности соз-
350
Общие сведение о СРНС ГЛОНАСС
дания Единой СРНС (Единой Космической Навигационной Системы),
способной удовлетворить потребности любых наземных, морских, воздушных и
космических потребителей с высокой точностью НВО. В качестве такой СРНС
была разработана сетевая СРНС ГЛОНАСС (1972—1982 гг.).
Развертывание созвездия НС велось поэтапно. Первый спутник СРНС
ГЛОНАСС (Космос 1413) был запущен 12 октября 1982 г. К середине 1995 г.
всего было запущено 65 НС ГЛОНАСС, а к 1 января 2004 г. — 86, большая
часть из которых к настоящему времени уже выведена из эксплуатации.
Этапы создания полного орбитального созвездия ГЛОНАСС
иллюстрируются данными, приведенными в табл. 9.3 [9.3].
Таблица 9.3. Этапы развертывания СРНС ГЛОНАСС
1
Номер
1 1
1 *
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
1 28 |
Номер,
Космос
2
1413
1490
1491
1519
1520
1554
1555
1593
1594
1650
1651
1710
1711
1778
1779
1780
1838
1839
1840
1883
1884
1885
1917
1918
1919
1946 !
1947
1948
Дата
запуска
3
12.10.82
10.08.83
10.08.83
29.12.83
29.12.83
19.05.84
19.05.84
04.09.84
04.09.84
18.05.85
18.05.85
25.12.85
25.12.85
16.09.86
16.09.86
16.09.86
24.04.87
24.04.87
24.04.87
16.09.87
16.09.87
16.09.87
17.02.88
17.02.88
17.02.88
21.05.88
21.05.88
21.05.88
Дата начала
работы
4
15.11.82
03.09.83
31.08.83
07.01.84
15.01.84
13.06.84
18.06.84
22.09.84
28.09.84
28.06.85
14.06.85
24.01.86
24.01.86
19.10.86
19.10.86
19.10.86
-
-
-
12.10.87
12.10.87
07.10.87
-
-
-
15.06.88
15.06.88
15.06.88
Окончание работы/
состояние
5
12.01.84
05.07.84
27.09.84
27.09.84
30.06.86
16.08.85
25.10.85
28.11.85
04.09.86
08.11.85
09.08.87
28.02.87
16.05.87
20.02.87
15.07.88
15.06.88
аз
аз
аз
06.06.87
30.08.88
01.02.89
аз
аз
аз
10.05.90
19.03.91
11.06.91
Номер
блока
6 ||
i I
2
2
3
3
4
4
5
5
6
6
7
7
8
8
8
9
9
9
10
10
10
11
11
11
12
12
12 |
351
Глава 9
Продолжение табл. 93.
1 1
29
30
31
32
33
-
34
35
-
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
1 69
2
1970
1971
1972
1987
1988
1989*
2022
2023
2024*
2079
2080
2081
2109
2110
2111
2139
2140
2141
2177
2178
2179
2204
2205
2206
2234
2235
2236
2275
2276
2277
2287
2288
2289
2294
2295
2296
2307
2308
2309
2316
2317
2318
2323
3
16.09.88
16.09.88
16.09.88
10.01.89
10.01.89
10.01.89
31.05.89
31.05.89
31.05.89
19.05.90
19.05.90
19.05.90
08.12.90
08.12.90
08.12.91
04.04.91
04.04.91
04.04.91
30.01.92
30.01.92
30.01.92
30.07.92
30.07.92
30.07.92
17.02.93
17.02.93
17.02.93
11.04.94
11.04.94
11.04.94
11.08.94
11.08.94
11.08.94
20.11.94
20.11.94
20.11.94
07.03.95
07.03.95
07.03.95
24.07.95
24.07.95
24.07.95
4
11.10.88
11.10.88
11.10.88
01.02.89
01.02.89
эгс
04.07.89
17.06.89
эгс
20.06.90
17.06.90
11.06.90
01.01.91
29.12.90
28.12.90
28.04.91
28.04.91
04.05.91
24.02.92
22.02.92
18.02.92
19.08.92
29.08.92
25.08.92
14.03.93
25.08.93
14.03.93
04.09.94
18.05.94
16.05.94
07.09.94
04.09.94
07.09.94
11.12.94
15.12.94
16.12.94
30.03.95
05.04.95
05.04.95
26.08.95
22.08.95
22.08.95
07.01.96
5
21.05.90
31.08.89
01.11.91
14.03.93
16.02.92
-
25.01.90
18.11.89
-
23.04.94
27.07.94
18.08.92
17.03.94
29.10.93
09.06.96
29.09.94
06.01.92
26.02.92
09.01.93
23.05.97
25.10.96
27.06.97
29.06.94
18.05.96
09.03.94
30.06.97
27.07.97
05.03.99
30.07.99
24.07.97
05.11.98
24.08.99
13.08.00
04.09.99
27.07.99
27.10.99
10.09.99
21.11.00
17.07.97
03.12.98
24.01.01
03.02.01
13.08.00
6 |
^ 1
13
13
14
14
14
15
15
15
16
16
16
17
17
17
18
18
18
19
19
19
20
20 1
20
21
21
21
22
22
22
23
23
23
24
24
24
25
25
25
26
26
26 |
352
on
a:
t5
CO
m
CO
чо
m
Ur
со
(N
k--
CM
о
о
on
CN
ON
ON
N"
о
чо
CN
in
ON
CN
i-h
h1"
2324
о
r-»
r-
(N
_
О
о
со
CN
чо
ON
^
О
00
*-н
m
ON
CN
^^
T|-
2325
r-
r-
CN
X
3
Я
я
H
я
ON
ON
,_-i
О
ON
(N
m
ON
CN
«—•
Tf
^
2362
CN
r-
00
CN
X
Я
я
ет дан
я
ON
ON
1-Н
О
ON
CN
00
ON
CN
1-H
О
CO
2363
CO
r-
00
CN
CN
О
1—H
о
1-H
CO
ON
ON
CN
О
00
1—H
00
ON
CN
^^
О
CO
2364
^fr
r-
00
CN
3
я
ет дан
я
1—Н
о
1-Н
о
in
о
00
ON
CN
*"~'
о
со
2374
m
г-
омер
Д
ты/
або
сх
чание
Окон
5
sr
Я
К[
о1
Дат
CD
пока ||
ю
я
я
05
°
<->
°
о
Н
ю
cd
п
ГС1
^
с!
cd
со
АСС
§ aci
И
о
К
ГТЮ1
<L>1
2
ON
CN
k^
о
о
^
CN
°
О
'"^
*—i
in
о
о
о
о
со
1-Н
со
00
г-
ЧО
г-
ON
CN
ЧО
О
ON
О
CN
1-Н
О
О
1-Н
•—«
Tj-
о
о
о
о
со
1—Н
г-
00
г-
г-
г-
ON
CN
in
О
CN
^fr
O
О
1-H
*~1
1-Н
CN
О
о
о
со
1—Н
00
00
Г-
00
г-
О
СО
г^
о
00
О
in
CN
CN
О
i—i
О
тг
о
1—Н
о
CN
i-h
о
ON
00
Г-
ON
Г-
о
со
VO
О
Г-
о
ON
О
СО
о
CN
О
со
1—Н
1—4
О
CN
1-Н
о
1-Н
Г-
О
00
СО
Г-
о
о
1-Н
о
со
о
i-h
о
^н
CN
CN
О
CN
in
CN
1-Н
ON
С^
00
1—Н
СО
ЧО
о
ON
О
^fr
CN
СО
о
^н
О
1-Н
СО
CN
О
CN
in
CN
CN
On
Г-
CN
00
со
VO
о
ON
о
со
CN
СО
о
i-h
О
Г-Н
СО
CN
О
CN
Ш
CN
СО
ON
Г-
СО
00
CN
СО
г-
о
Tj-
о
ON
1—Н
Tj-
о
CN
О
CN
О
со
о
CN
О
1—Н
тг
ON
Г^
Tj-
00
CN
СО
ON
О
in
О
1-Н
О
Tt
о
1—1
о
ON
CN
СО
о
CN
О
1-Н
in
ON
Г-
in
00
CN
СО
ON
О
ЧО
О
00
1-Н
тГ
о
CN
*-н
00
О
СО
о
CN
О
*-"
о
г^
vo
00
СО
со
00
О
in
о
Tj-
о
in
о
CN
О
VO
CN
Т|"
О
CN
ЧО
CN
ЧО
ON
г-
г-
00
СО
СО
00
О
ЧО
О
чо
«—<
in
о
CN
О
чо
о
Tf-
о
CN
ЧО
CN
Г-
ON
t^
00
00
со
со
+
in
о
О
1-Н
Г-
о
Tf-
о
CN
ЧО
CN
CN
1-Н
Г*-
ON
00
ТГ
со
г-
о
г-
о
ON
О
ЧО
О
1-Н
О
CN
CN
in
О
CN
in
CN
00
ON
Г-
О
On
tj-
со
+
vo
О
00
О
1-Н
со
in
о
CN
in
CN
СО
1-Н
с^
ON
Tiro
+
чо
О
00
О
г-Ч
СО
in
о
CN
in
CN
Tf
1-Н
Г-
CN
on
ш
со
+
г-
о
ТГ
о
со
о
ЧО
О
CN
in
CN
in
1—Н
r^
со
ON
in
со
+
г-
о
о
•—«
CN
•—*
ЧО
О
CN
in
CN
ЧО
1—Н
Г-
Tj-
On
m
со
+
г-
о
Tj-
о
со
о
чо
о
CN
in
CN
Г-
1-Н
г-
in
ON
ЧО
СО
+
Г-
о
CN
^н
т1-
О
г-
о
о
чо
CN
00
1-Н
Г-
чо
ON
ЧО
со
+
г-
о
*-н
^н
г^
CN
Г-
о
о
VO
CN
ON
1-Н
Г-
г-
о\
ЧО
со
+
г-
о
1-Н
1-Н
in
CN
Г-
О
о
ЧО
CN
О
CN
Г^
00
ON
Г-
СО
+
оо
о
CN
О
ОО
О
Г-
о
CN
in
CN
1-Н
CN
Г-
ON
On
Г-
со
+
00
о
1-Н
о
in
CN
Г-
О
CN
Ш
CN
CN
CN
Г^
О
о
г-
со
+
оо
о
^н
о
CN
CN
Г-
CN
CN
in
CN
СО
CN
Г-
О
00
СО
+
00
О
О
^н
чо
CN
00
О
ON
О
in
CN
Tf
CN
Г-
CN
О
00
CO
+
00
О
^н
1-Н
in
о
00
О
ON
О
in
CN
in
rN
t^
CO
о
00
CO
+
00
о
1—1
i-H
CO
1—1
00
о
ON
О
in
CN
vo
CN
c--
О
On
CO
+
ON
О
*—<
о
г-
1—1
00
о
CN
«—•
in
CN
r^
CN
r^
in
О
On ON
CO CO
+ +
ON ON
О О
-н CN
О О
О CN
CN ^
00 00
О О
CN CN
1-Н 1—< II
in in
CN CN
00 ON
CN CN
Г- Г-
ЧО Г-
О О
8
ci
Глава 9
Здесь в графе «Окончание работы/состояние» показаны даты окончания
работы спутника; знаком + отмечены рабочие спутники орбитальной
группировки на 11.09.09 г.; аз — аварийный запуск; эгс — эталонный геодезический
спутник.
В соответствии с указом Президента РФ от 24 сентября 1993 г. началось
официальное использование системы ГЛОНАСС с промежуточным созвездием
спутников. Штатная эксплуатация ГЛОНАСС началась в конце 1995 г., когда
сеть НС объединила 24 рабочих спутника. Считается, что такое созвездие
имеет некоторую избыточность, так как, например, даже 22-спутниковое созвездие
ГЛОНАСС, созданное к середине 1995 г., обеспечивало непрерывное
навигационное поле в течение суток. При этом потребители могли наблюдать от 5 до
8 спутников.
В 1996 г. Правительство России [9.4] подтвердило сделанное на 10-й
Аэронавигационной конференции ИКАО предложение о предоставлении
мировому авиационному сообществу канала стандартной точности системы
ГЛОНАСС, обеспечивающего определение координат с характеристиками
точности, показанными в табл. 9.4 [1.5].
Таблица 9.4. Точностные характеристики СРНС ГЛОНАСС,
гарантируемые разработчиком
Параметр
Ошибка по координатам в
горизонтальной плоскости, м
Ошибка по координатам в верти-
1 кальной плоскости, м
Точность (1 а) ||
максимальная
солнечная
активность
60
100
минимальная
солнечная
активность ||
30
50
В отличие от системы GPS, в СРНС ГЛОНАСС не предполагается
использования каких-либо методов загрубления точности (режим селективного
доступа в GPS). Кроме того, Россия принимает все меры для обеспечения
целостности и надежности обслуживания и полагает, что она будет в состоянии
представить уведомление по крайней мере за 6 лет до прекращения обслуживания.
Система ГЛОНАСС с полностью развернутой группировкой НС
характеризуется вероятностью обеспечения навигационных определений не хуже 0,947
в непрерывном навигационном поле с точностью, указанной в табл. 9.4 (в
Российском радионавигационном плане 1994 г. [9.5] приведены несколько
отличающиеся данные; точностные характеристики определения плановых
координат, высоты и времени (1 <т) равны соответственно 30 м, 30 м и 1 мкс, а
доступность системы — 0,98). Значение HDOP в этом случае для 93 %
потребителей будет менее двух.
354
Общие сведение о СРНСГЛОНАСС
Расчетный ресурс спутников «Глонасс» первой модификации составлял не
менее трех лет. Запускаемые в настоящее время НС «Глонасс-М» имеют ресурс
не менее 5 лет, что позволяет повысить надежность системы в целом. За счет
использования на НС «Глонасс-М» технологии межспутниковых измерений
значительно повысится время автономной работы орбитальной группировки и
другие ее характеристики. Точностные характеристики определения плановых
координат, высоты и времени (1 а) составят соответственно 10 м, 10 м и
десятки наносекунд (более подробно о «Глонасс-М» см. гл. 11).
9.3. Система координат, используемая в СРНС ГЛОНАСС
Эфемеридная информация, передаваемая потребителям ГЛОНАСС в
составе служебной информации конкретного НС, содержит координаты фазового
центра передающей антенны данного НС в геоцентрической системе координат
ПЗ-90 (см. гл. 3). Эта система координат, как и принятая в СРНС GPS система
координат WGS-84 [8.1], является декартовой системой координат, связанной с
Землей, т.е. ее центр «О» находится в центре масс Земли, ось OZ направлена к
Северному полюсу, плоскость XOY лежит в плоскости экватора, о ось ОХ
лежит в плоскости Гринвичского меридиана. До 1993 г. в СРНС ГЛОНАСС
использовалась система координат СГС-85 [9.6].
Несмотря на схожесть систем координат ПЗ-90 (OXYZ) и WGS-84 (AUVW),
они различаются в некоторых важных параметрах. Принято сводить эти
различия к некоторому повороту системы относительно оси Z или Y и смещению
начала координат (рис. 9.1).
Рис. 9.1. Системы координат ПЗ-90, WGS-84
Соотношения, характеризующие переход от координат в системе ПЗ-90 к
системе WGS-84, можно представить в виде [9.1]
355
Глава 9
X
У
Z
=
0
0
4 м
+
1 -3-10"6 о|
3 10
о
-6
1
о
Смещение координат точки на земной поверхности в двух указанных
системах координат оценивается по результатам измерений как не превышающее
15 м (в среднем 5 м).
В 2008 году в системе ГЛОНАСС была введена модернизированная версия
системы координат: ПЗ-90.02 (Распоряжение Правительства РФ от 20.06.07
№ 1911?).
При модернизации общеземной системы координат ПЗ-90 были
максимально использованы данные об установлении общеземных систем координат,
полученные отечественными и международными научными организациями из
многолетних наблюдений искусственных спутников Земли и космических
объектов. На основании этих данных в модернизированной системе координат
ПЗ-90.02 изменены долготная ориентировка и линейный масштаб. Они
приближены к значениям, принятым в системе координат Международной земной
сети (ITRF).
Ниже приведены формулы преобразований между различными системами
координат (значения координат даны в метрах).
Преобразование координат из референцной системы СК-42 в систему
ПЗ-90
ПЗ-90
1
+3,1998-10
-1,6968-10"
-6
-3,1998-10"
1
0
+1,6968-10"
0
1
X
У
Z
+
СК-42
25
-141
-80
Преобразование координат из референцной системы СК-95 в систему
ПЗ-90
X
У
Z
=
ПЗ-90
X
У
z
+
СК-95
25,0
-130,94
-81,76
Преобразование координат из системы координат WGS-84 в систему
ПЗ-90
= (l + 0,12-10-6)
ПЗ-90
1 +0,9696 10"ь 0|
-0,9696-10"6 1 0|
0 0
WGS-84
1,10
0,301
0,90
356
Общие сведение о СРНСГЛОНАСС
Преобразование координат из системы координат ITRF-2000 в систему
ПЗ-90.02
ПЗ-90.02
X
У
Z
+
ITRF-2000
0,36
-0,08
-0,18
Преобразование координат из системы ПЗ-90 в систему
ПЗ-90.02
= (l-0,22-10"6)
ПЗ-90.02
1
,6303-1О"6
0
-0,6303-10"ь
1
0
0
0
1
ПЗ-90
-1,07
-0,03|
0,02
Обратное преобразование координат из системы ПЗ-90.02 в систему
ПЗ-90
:(l + 0,22-10"6)
ПЗ-90
1 +0,6303-10"6 0
-0,6303-Ю-6 1 0
о
о
+
ПЗ-90.02
-1,07
-0,03
0,02
9.4. Частотно-временное обеспечение. Шкалы
системы ГЛОНАСС
времени
Частотно-временное обеспечение реализуется системой синхронизации
ГЛОНАСС, которая обеспечивает формирование единой системной шкалы
времени, синхронизацию бортовых шкал времени каждого НС с СШВ, расчет
частотно-временных поправок, определение расхождения СШВ относительно
шкалы Государственного эталона координированного всемирного времени
UTC (SU), расчет поправок БШВ к СШВ, закладку поправок на борт НС
(дважды в сутки) для передачи их потребителям в составе навигационного
сообщения. (Общие сведения о единицах мер времени, системах отсчета и шкалах
времени приведены в гл. 2.).
Система синхронизации включает в свой состав [1.3]:
1. Цезиевые БЭВЧ НС, обеспечивающие формирование и хранение БШВ
НС. Суточная относительная нестабильность частоты составляет 5-Ю-13 для
НС «Глонасс» и 110~13 для НС «Глонасс-М». Точность взаимной
синхронизации бортовых шкал времени НС «Глонасс» составляет 20 не (1 а), а спутников
«Глонасс-М» — 8 не.
357
Глава 9
2. Центральный синхронизатор (ЦС) системы, обеспечивающий
формирование СШВ с помощью водородных стандартов частоты с суточной
нестабильностью частоты не хуже 1...5 10-14 и относительной нестабильностью частоты
не хуже 110"13. Для системы GPS эти параметры имеют значения 3 10"14 и
1 • 10 соответственно (для одного из этапов использования системы).
3. Аппаратуру привязки, обеспечивающую определение расхождения
СШВ и UTC(SU), которое не должно превышать 1 мс (1 <т). Погрешность
привязки этих шкал не должна превышать 1 мкс (1 а).
4. Систему контроля фаз (СКФ), осуществляющую активные и пассивные
измерения дальности до всех НС и передачу результатов измерений на центр
управления системой (ЦУС) для сверки БШВ и СШВ.
5. Контрольные станции, обеспечивающие контроль и управление БШВ и
передачу ЧВП на НС.
6. Программные средства вычислителей ЦУС, обеспечивающие
согласованную работу подсистем, периодическое определение ухода БШВ
относительно СШВ, расчет и прогнозирование ЧВП для НС. При этом учитываются
влияние релятивистских и гравитационных эффектов на формирование БШВ
(см. п. 7.4).
Частотно-временные поправки рассчитываются на каждом витке НС и
закладываются на борт НС два раза в сутки. ЧВП представляют собой два
параметра линейной аппроксимации смещения БШВ относительно СШВ (см. п.
7.7), при этом погрешность прогноза БШВ на 12 ч составляет в среднем 14 не.
В НС «Глонасс-М» используются более стабильные цезиевые стандарты
частоты, которые обеспечивают погрешность прогноза БШВ на 12 ч, равную 5 не.
Шкала системного времени ГЛОНАСС корректируется одновременно с
плановой коррекцией на целое число секунд шкалы Координированного
всемирного времени UTC. Коррекция шкалы UTC на ±1с проводится
Международным бюро времени (BIH/BIPM) по рекомендации Международной службы
вращения Земли (IERS). Коррекция шкалы UTC производится, как правило, с
периодичностью один раз в год (в полтора года) в конце одного из кварталов: в
00 ч 00 мин 00 с в полночь с 31 декабря на 1 января — 1-й квартал (или с 31
марта на 1 апреля — 2-й квартал, с 30 июня на 1 июля — 3-й квартал, с 30
сентября на 1 октября — 4-й квартал) и осуществляется одновременно всеми
пользователями, воспроизводящими или использующими шкалу UTC.
Следовательно, между СШВ ГЛОНАСС и UTC (SU) не существует сдвига
на целое число секунд. Благодаря этому сокращается объем информации при
передаче потребителям величины расхождения СШВ и UTC(SU). Между
системным временем ГЛОНАСС и UTC(SU) существует постоянный сдвиг на
целое число часов, обусловленный особенностями функционирования ПКУ:
'глонасс = UTC(SU) + 03 ч 00 мин.
358
Общие сведение о СРНС ГЛОНАСС
В перспективе предполагается снизить погрешность взаимной
синхронизации фаз сигналов НС до 15 не за 24 ч, а также провести согласование СШВ
GPS и ГЛОНАСС. Согласование этих ШВ основывается на высоких
характеристиках шкалы UTC (SU) [8.10].
Спутники «Глонасс-М» передают два коэффициента (В 1 и В2) для
перехода к шкале всемирного времени UT1 (см. п. 2.2) и поправку xGps для перехода к
шкале времени системы GPS. Точность определения поправки Tops не хуже
30 не (СКО).
Литература
9.1. ICD-GPS-2000.
9.2. Шебшаевич В. С. Этапы становления и проблемы развития спутниковых РНС
в СССР// Вопросы радиоэлектроники. Сер. ОВР, вып. 8, 1991.
9.3. www.glonass-center.ru (Интернет).
9.4. Письмо министра транспорта РФ Президенту Совета ИКАО/ Компьютерный
бюллетень BBS КНИЦ ВКС РФ.
9.5. Российский радионавигационный план. — М.: НТЦ «Интернавигация», 1994.
9.6. Характеристики системы ГЛОНАСС: качество измерений и
функционирование системы/ Пер. П. Мишра и др. ION GPS-96. Компьютерный бюллетень BBS
КНИЦ ВКС РФ.
359
Глава 10
Глава 10
НАЗЕМНЫЙ СЕГМЕНТ
(ПОДСИСТЕМА КОНТРОЛЯ И УПРАВЛЕНИЯ)
10.1. Назначение и состав подсистемы контроля и управления
10.1.1. Общие сведения
Наземный сегмент СРНС ГЛОНАСС — подсистема контроля и
управления, предназначенная для контроля правильности функционирования,
управления и информационного обеспечения сети спутников системы и состоящая из
следующих взаимосвязанных стационарных элементов [1.3, 9.3, 10.1]: центра
управления системой ГЛОНАСС; центрального синхронизатора; контрольных
станций (КС); системы контроля фаз; квантово-оптических станций (КОС);
аппаратуры контроля поля (АКП).
Схема наземного сегмента ГЛОНАСС приведена на рис. 10.1.
на спутники
ЦС
-измерения ► -команды -н- #-*• -время
—*■ - телеметрия ► - измерения
Рис. 10.1. Схема наземного сегмента с направлением
движения потоков информации
Наземный сегмент выполняет следующие функции:
проведение траекторных измерений для определения, прогнозирования и
непрерывного уточнения параметров орбит всех НС;
временные измерения для определения расхождения бортовых шкал
времени всех НС с системной шкалой времени ГЛОНАСС, синхронизация шкал
времени НС с временной шкалой центрального синхронизатора и службы единого
времени путем фазирования и коррекции БШВ НС;
формирование массива служебной информации (навигационных
сообщений), содержащего спрогнозированные эфемериды, альманах и поправки к
бортовой шкале времени каждого НС и другие данные, необходимые для
формирования навигационных кадров;
360
Наземный сегмент (подсистема контроля и управления)
передача (закладка) массива служебной информации в память ЭВМ
каждого НС и контроль за его прохождением;
контроль по телеметрическим каналам за работой бортовых систем НС и
диагностика их состояния;
контроль информации в навигационных сообщениях НС, прием сигнала
вызова ПКУ;
управление полетом НС и работой их бортовых систем путем выдачи на
спутники временных программ и команд управления; контроль прохождения
этих данных; контроль характеристик навигационного поля;
определение сдвига фазы дальномерного навигационного сигнала НС по
отношению к фазе сигнала центрального синхронизатора;
планирование работы всех технических средств ПКУ, автоматизированная
обработка и передача данных между элементами ПКУ.
В автоматизированном режиме решаются практически все основные
задачи управления НС и контроля навигационного поля.
Система
отображения
информации
1
АРМ
оператора
Группа
управления
аппаратурой
_ ^ _
АРМ
I Группа 1
баллистического
обеспечения
полета
Группа
планирования
сеансов связи
1 Группа 1
обработки
телеметрической
1 информации 1
1 Группа 1
обмена
с внешними
абонентами
1 ; * i
АРМ
АРМ
АРМ
АРМ
+ + + + + +
Локальная сеть обмена данными
#
ЭВМ
1
Средства i
сопряжения !
+ * W j
Подсистема связи:
с абонентами КС i
Система
отображения
информации
III*;
АРМ
1 АРМ 1
администратора
1 сети |
Сервер
| базы данных |
1 АРМ 1
администратора
[ базы данных |
Сервер
1 печати |
Резервный
тракт связи Л
Группа
управления
аппаратурой
1 +
| АРМ
оператора
АРМ
+ т
Связь
J
Группа
эксплуатации
Группа общего
оперативного
управления
Командование
♦ t *
АРМ
АРМ
АРМ
♦ 1 1
Локальная сеть обмена данными
i
? ?
! эвм
; 1
i Средства
! сопряжения
Информационный
центр
t
1 АРМ 1
администратора
1 сети 1
t t
1 АРМ
администратора
базы данных
Сервер
печати
/П
Рис. 10.2. Схемы локальной вычислительных сетей ЦУС (а) и КС (б)
361
Глава 10
С использованием специального математического обеспечения в сетях ЭВМ
решаются следующие задачи (10.2, а, б): планирование работы ПКУ с НС и
формирование программы работы для средств ЦУС и других элементов; расчет
баллистической информации для планирования и управления НС; командно -
программной информации; обработка телеметрической информации; контроль
навигационного поля; обработка траекторных измерений и прогнозирование
пространственного положения НС и расхождение их шкал времени с временной
шкалой системы.
На приведенных схемах АРМ — автоматизированное рабочее место.
Основные функции элементов ПКУ заключаются в следующем.
10.1.2. Центр управления системой
Центр управления системой [1.1, 1.4] соединен каналами
автоматизированной и неавтоматизированной связи, а также линиями передачи данных со
всеми элементами ПКУ, планирует и координирует работу всех средств ПКУ на
основании принятого для ГЛОНАСС ежесуточного режима управления
спутниками в рамках технологического цикла управления. При этом ЦУС собирает и
обрабатывает данные для прогноза эфемерид и частотно-временных поправок,
осуществляет с помощью так называемого баллистического центра расчет и
анализ пространственных характеристик системы, анализ баллистической
структуры и расчет исходных данных для планирования работы элементов ПКУ.
Информацию, необходимую для запуска спутников, расчета параметров их
орбитального движения, управления ими в полете, ЦУС получает от системы
единого времени и эталонных частот, системы определения параметров
вращения Земли, системы мониторинга гелио- и геофизизической обстановки [10.2].
Центральный синхронизатор, взаимодействуя с ЦУС, формирует шкалу
времени ГЛОНАСС, которая используется для синхронизации процессов в
системе, например, в системе контроля фаз. Он включает в свой состав группу
водородных стандартов.
10.1.3. Контрольные станции
Контрольные станции (станции управления, измерения и контроля или
наземные измерительные пункты) по принятой схеме радиоконтроля орбит
осуществляют сеансы траекторных и временных измерений, необходимых для
определения и прогнозирования пространственного положения спутников и
расхождения их шкал времени с временной шкалой ГЛОНАСС, а также собирают
телеметрическую информацию о состоянии бортовых систем спутников. С их
помощью происходит закладка в бортовые ЭВМ спутников массивов служебной
информации (альманах, эфемериды, частотно-временные поправки и др.),
временных программ и оперативных команд для управления бортовыми системами.
362
Наземный сегмент (подсистема контроля и управления)
Траекторные измерения осуществляются с помощью радиолокационных
станций, которые запросным способом определяют дальность до спутников и
радиальную скорость. Дальномерный канал характеризуется максимальной
ошибкой около 2...3 м. Процесс измерения дальности до спутника совмещают
по времени с процессом закладки массивов служебной информации,
временных программ и команд управления, а также со съемом телеметрических
данных со спутника.
^^^ - КС ЦУС - центр управления системой
ml - КОС АКЛ - аппаратура контроля поля
^ -КСС-командная станция слежения СКФ - система контроля фаз
ЦС - центральный синхронизатор
Рис. 10.3. Наземный сегмент СРНС ГЛОНАСС
Для эфемеридного обеспечения с КС в ЦУС ежесуточно выдается по
каждому спутнику по 10... 12 наборов (сеансов) измеренных текущих
навигационных параметров объемом примерно 1 Кбайт каждый.
В настоящее время для обеспечения работ ГЛОНАСС могут
использоваться КС, рассредоточенные по всей территории России (рис. 10.3). Часть КС и
других элементов наземного сегмента ГЛОНАСС осталась вне территории
России (в странах СНГ) и может быть использована лишь при наличии
соответствующих договоренностей. Размещение сети КС выбрано с учетом
существующей инфраструктуры управления НС и из условий надежного решения
задач траекторных измерений для всей орбитальной группировки.
Такая сеть КС обеспечивает закладку на спутники системы высокоточных
эфемерид и временных поправок 1 раз/сут (возможна закладка 2 раз/сут).
363
Глава 10
В случае выхода из строя одной из станций возможна ее равноценная
замена другой, так как сеть КС обладает достаточной избыточностью и в
наихудшей ситуации работу системы может обеспечивать ЦУС и одна станция,
однако интенсивность ее работы будет очень высокой.
При планировании работы КС на сутки определяются основные и
резервные станции для проведения сеансов измерений с необходимой
избыточностью. Контрольные станции имеют тройное резервирование по аппаратуре
(один комплект рабочий, второй — в резерве, третий — профилактические
работы). Коэффициент готовности средств ПКУ в сеансе измерений и закладки
информации на борт спутника близок к единице.
Описанная сеть КС отличается от аналогичной структуры СРНС GPS тем,
что обеспечивает высокое качество управления орбитальной группировкой
только с национальной территории. КС ГЛОНАСС могут использоваться для
обеспечения функционирования других космических средств.
10.1.4. Квантово-оптические станции
Квантово-оптические станции предназначены для периодической
юстировки радиотехнических каналов измерения дальности КС с помощью
лазерного дальномера. В этих целях на каждом спутнике размещены специальные
лазерные отражатели. Применение КОС обеспечивает высокоточное измерение
параметров движения спутников ГЛОНАСС. В РФ разработаны три
отечественные лазерные станции слежения или КОС: лазерная дальномерная система
«Гео-ИК»; КОС «Эталон»; КОС «Майданак» (Узбекистан).
Всего в России было сооружено 20 таких комплексов. Станция «Гео-ИК»
является частью спутниковой геодезической системы «Гео-ИК», которая
используется для определения земных координатных систем и моделей
гравитационного поля Земли. Эти модели являются основой для высокоточных
определений орбит спутников ГЛОНАСС.
Квантово-оптические станции типа «Эталон» и «Майданак» используются
для корректировки радиолокационных измерений и в процессе определения
орбит в ГЛОНАСС. Второе поколение КОС «Эталон» позволяет определять
положение спутников, видимых по отраженному вниз солнечному свету (со
звездной величиной менее, чем 13), на максимальной высоте 20000 км.
Погрешность измерений дальности при интервале усреднения в 15 с составляет
около 1,5.. .2 см, а углового положения — 2 ... 3" .
Квантово-оптическая станция «Майданак» представляет собой
многофункциональный комплекс, который позволяет измерять дальность до
космических объектов на высотах до 40 000 км (со звездной величиной 16).
Максимальная угловая ошибка определения положения спутника имеет порядок от
0,5 до 1...2", а дальномерная ошибка — не более 1,5... 1,8 см. Наиболее
эффективно лазерные станции работают в ночное время при хорошей видимости.
364
Наземный сегмент (подсистема контроля и управления)
10.1.5. Система контроля фаз
Система контроля фаз обеспечивает контроль (сверку) сигнала,
излучаемого спутником с целью измерения фазового и частотного сдвига
бортовых эталонов времени и частоты относительно эталона ЦС. Эта информация
необходима для синхронизации фаз навигационных сигналов, излучаемых
всеми спутниками ГЛОНАСС. Такая процедура производится с помощью
контрольного навигационного приемника СКФ. В процессе сверки (для
определения сдвига бортовой шкалы времени) принятые дальномерные сигналы
спутника сравниваются с опорными сигналами, полученными от
высокостабильного (относительная нестабильность порядка 10~13) эталона частоты ЦС.
В результате сравнения измеряется псевдо дальность PR(t) = /?(/) + A(t),
где R{t) — дальность от СКФ до спутника; A(t) — ошибка ее измерения,
обусловленная, в частности, рассогласованием фаз между бортовым
стандартом времени и частоты и ЦС. В связи с тем, что псевдо дальность является
измеряемой величиной, и учитывая максимальную ошибку R(t), значение A{t)
можно определить с точностью 3...4 м. В дальнейшем A{t) можно усреднить
на длительном интервале, экстраполировать на заданный момент времени
(t + T) и привести к соответствующей размерности для коррекции, например,
шкалы времени и частоты бортового эталона.
Результаты измерений, проводимых в СКФ, автоматически передаются в
ЦУС для расчета поправок к фазе и частоте бортового эталона, входящих в
навигационные сообщения соответствующего спутника. Сверка фаз дальномер-
ных сигналов выполняется 1 раз/сут для каждого спутника. Параметры для
синхронизации бортовой шкалы времени обновляются 2 раз/сут, поэтому вклад
ошибки из-за сдвига фазы дальномерного сигнала спутника в результирующую
ошибку измерения псевдо дальности может составить не более 5 ... 6 м.
10.1.6. Аппаратура контроля поля
Аппаратура контроля поля представляет собой высокоточную НАП,
располагаемую на контрольных станциях и имеющую высокоточную
геодезическую привязку. Она обеспечивает непрерывный контроль характеристик
навигационного обеспечения (в частности, точностных характеристик координатно-
временного обеспечения, которые должны поддерживаться с достаточно
высокой достоверностью — с вероятностью не хуже 0,997, а также характеристик
целостности) с помощью системы ГЛОНАСС на территории России.
Для оценки качества работы ГЛОНАСС предусматривается: диагностика
работы основных бортовых систем спутников; контроль точности решения на-
365
Глава 10
вигационной задачи и качества информации, содержащейся в навигационных
сообщениях спутников.
Диагностику бортовых систем спутника можно осуществлять на АКП,
например по результатам его самоконтроля, которые передаются в
навигационном кадре. В случае обнаружения неисправности, влияющей на качество
навигационного сигнала, признак непригодности данного спутника для
навигационных определений потребителей (соответствующее значение параметра "5"
навигационного кадра) автоматически включается в состав навигационного
сообщения спутника не позднее, чем через одну минуту после обнаружения
неисправности. Это позволяет потребителям исключить неисправный спутник из
процедуры навигационных определений.
Контроль качества навигационного обеспечения системой ГЛОНАСС
ведется АКП, в основном, в двух режимах: контроля НС и контроля поля.
Режим контроля НС предусматривает непрерывное сравнение измеренных
значений псевдо дальностей и псевдо скоростей с их прогнозируемыми
значениями для всех видимых спутников ГЛОНАСС (одновременно в зоне
радиовидимости АКП может находиться до 8 ... 11 спутников). За время сеанса связи от
каждого спутника принимаются и контролируются данные, содержащиеся в
навигационных кадрах, а также осуществляется измерение с помощью его
сигналов первичных навигационных параметров (псевдо дальности и псевдо
скорости). После окончания сеанса связи в АКП выполняется автономный анализ
полученной информации и контролируется отсутствие сигнала вызова ПКУ.
При отрицательном результате проверки спутника об этом автоматически
сообщается в ЦУС с указанием конкретных причин, где принимаются
необходимые меры по устранению неисправностей, ограничивающие или временно
исключающие использование спутника по целевому назначению. Выход из
строя отдельных спутников ГЛОНАСС не приводит к заметному ухудшению
точностных характеристик навигационного поля системы, так как группировка
спутников имеет необходимую избыточность по числу НС.
Режим контроля навигационного поля предусматривает решение
навигационной задачи по каждому оптимальному созвездию спутников над
соответствующим АКП. Эта процедура включает в себя также сравнение эталонных
координат с текущими результатами определения местоположения по данному
созвездию и выполняется непрерывно по автономному плану. Результаты
навигационных определений (а при отрицательных данных контроля и
измерительная информация, используемая в этом сеансе) передается в ЦУС для
оценки текущих характеристик навигационного обеспечения, анализа причин
аномальных характеристик и принятия решения по дальнейшему варианту
функционирования системы. В такой ситуации могут быть предприняты следующие
меры: передача на борт спутника команды, формирующей в составе кадра
навигационной информации признака непригодности НС для использования его
сигналов потребителями системы ГЛОНАСС; проведение с использованием те-
366
Наземный сегмент (подсистема контроля и управления)
леметрического канала работ с аппаратурой спутника по отысканию в ней
неисправностей; пересчет и перезакладка на борт спутника навигационной
информации; выполнение сеанса навигационных измерений с данным спутником с
помощью другой аппаратуры АКП.
Перечисленных видов контроля с учетом избыточности орбитальной
группировки обычно достаточно для поддержания требуемых характеристик
навигационного поля.
В СРНС ГЛОНАСС, в отличие от GPS, осуществляется раздельное
решение задач эфемеридного и частотно-временного обеспечения.
10.2. Эфемеридное обеспечение
Эфемеридное обеспечение поддерживается комплексом технических и
программных средств, выполняющих радиоконтроль орбит спутников с
нескольких наземных КС, обработку результатов траекторных измерений и
расчет эфемеридной информации (ЭИ), передаваемой далее с помощью
загрузочных станций на спутник.
Высокая точность расчета эфемерид (определение и структура эфемерид
НС ГЛОНАСС описаны в п. 11.4.2) обеспечивается соответствующей
точностью измерительных средств, внесением поправок на выявленные
методические погрешности, применением в процессе расчета эфемерид не только
текущих траекторных измерений, но и накапливаемых за недельный срок. При этом
дальномерные данные, получаемые от станций слежения за спутниками,
периодически калибруются, что обеспечивает высокое качество траекторных
измерений в системе ГЛОНАСС.
В ближайшем будущем планируется переход на новые технологии,
включающие межспутниковые угломерно-дальномерные измерения, что обеспечит
качественный скачок в координатно-временном обеспечении потребителей.
10.2.1. Особенности формирования эфемеридной информации
в ГЛОНАСС
Система ГЛОНАСС создавалась в условиях, когда уровень
фундаментальных исследований в области геодезии, геодинамики и геофизики не
обеспечивал требуемую точность эфемеридного обеспечения системы. Был
проведен комплекс работ по обоснованию путей решения этой проблемы через
построение согласующих моделей движения спутников, параметры которых
определяют в процессе решения задачи баллистико-навигационного
обеспечения системы.
Исследования показали, что необходимо отказаться от типовых
острорезонансных (например, с периодом обращения спутника 12 ч, как в СРНС GPS,
когда период вращения Земли вокруг своей оси равен двум периодам обраще-
367
Глава 10
ния спутника) орбит спутников. В процессе моделирования уравнений траек-
торного движения спутников это повышает устойчивость их решений и
ослабляет корреляции между параметрами отдельных уравнений (моделирующих,
например, изменение геопотенциала, координат измерительных средств,
радиационного давления). Кроме того, оказалось, что наивысшая точность балли-
стико-эфемеридного обеспечения системы при решении многомерной
навигационной задачи с расширенным вектором состояния обеспечивается при
обработке измеренных текущих навигационных параметров на инервале 8 суток.
Переход от острорезонансных орбит был осуществлен путем увеличения числа
витков спутника (по сравнению с GPS) до 16... 17 на интервале 8 суток. Число
спутников в системе выбрано равным 24 с равномерным распределением по
трем орбитальным плоскостям. Все спутники системы фазируются таким
образом, что на больших временных интервалах они имеют один след на
поверхности Земли. Это обеспечивает высокую баллистическую устойчивость системы и
относительно высокую точность и простоту расчетов траекторий. Опыт
эксплуатации системы показал, что при обеспечении начального периода
обращения спутника с точностью не хуже 0,1 с на протяжении заданного срока
активного существования спутника его положение в системе корректировать не нужно.
В настоящее время в системе ГЛОНАСС используется запросная
технология эфемеридного обеспечения, когда исходной информацией для расчета
эфемерид служат данные измеренных текущих параметров (ИТП) спутников,
поступающие в ЦУС от контрольных станций по программам межмашинного
обмена через вычислительную сеть. Ежесуточно осуществляется 10... 12 сеансов
передачи информации по каждому спутнику.
10.2.2. Типовые операции управления
Процесс эфемеридного обеспечения реализуется в ходе отработки типовых
операций управления ПКУ, который предполагает решение следующих задач:
предварительная обработка ИТП; расчет начальных условий на начало каждого
интервала работы; определение параметров движения; расчет и формирование
ЭИ и альманаха системы; апостериорная оценка точности формирования ЭИ;
оперативная и камеральная оценка возможности использования измерений КС
и временной информации в интересах эфемеридного обеспечения системы;
обработка и прогнозирование параметров вращения Земли (ПВЗ).
Рассмотрим подробнее отдельные операции управления.
Предварительная обработка ИТП. Цикл управления в ЦУС начинается с
запроса сеансов связи с КС для получения наборов ИТП и предварительной
обработки этой информации. При этом выполняются следующие операции:
дешифровка и анализ ключевых, технологических, калибровочных и
информационных посылок наборов (массива) данных; расчет априорных навигационных
функций; преобразование информационных параметров, полученных в резуль-
368
Наземный сегмент (подсистема контроля и управления)
тате дешифровки массивов, в значения навигационных параметров; коррекция
измерений массивов ИТП с учетом поправок на распространение
измерительного сигнала в ионосфере и тропосфере Земли; формирование и запись
массивов ИТП в базу данных.
Время решения задачи предварительной обработки информации для
первого сеанса составляет 1,5 мин.
Расчет начальных условий. Для расчета начальных условий спутника на
начало мерного интервала осуществляется считывание из БД исходных
начальных условий, настройка математической модели движения спутника,
расчет параметров движения спутника на заданное время численным методом
интегрирования и запись полученных кинематических параметров движения в
БД. В типовой операции управления интервал прогнозирования составляет
около двух витков.
Определение параметров движения. После подготовки начальных
условий, проведения измерений и решения задачи определения параметров
движения спутника на восьмисуточном интервале производится уточнение
расширенных начальных условий, включающих кинематические параметры
движения, коэффициенты модели движения и измерений. В задаче определения
параметров движения реализован итерационный метод Ньютона, при этом число
итераций равно 3.. .4.
Формирование эфемерид. Полученные в ходе предыдущей операции
начальные условия используют для расчета эфемеридной информации
(кинематические параметры движения спутника и составляющие действующего на
него возмущающего ускорения), которая записывается в базу выходных данных.
Из нее формируется служебная информация в заданном виде (форме) и
передается на КС для закладки на борт спутника. Высокая точность расчета
траектории движения спутника достигается в основном за счет разработки адекватной
модели движения спутников, описываемой системой дифференциальных
уравнений и учитывающей следующую совокупность сил: притяжение Земли (с
учетом аномалий), Луны и Солнца; воздействие лунно-солнечных приливных
вариаций геопотенциала, давление солнечного излучения. Основным
фактором, определяющим характер движения спутника, является геопотенциал,
возмущающая часть которого задает общую эволюцию орбиты. Действие
остальных возмущающих факторов примерно в 1000 раз меньше воздействия
геопотенциала.
Задача определения начальных условий движения спутника, а также
расширенного вектора состояния решается на основе математической обработки
измерений, полученных на восьмисуточном интервале наблюдений методом
наименьших квадратов (см. п. 6.4.3), который в настоящее время является
основным методом статистического оценивания траектории движения спутника
[10.3].
369
Глава 10
Формирование альманаха. Расчет альманаха (определение альманаха и
его структура описаны в п. 11.4.3) в системе ГЛОНАСС осуществляется на
заданном интервале с шагом расчета 1 сутки. Информация альманаха системы
предназначена, в частности, для выбора потребителем созвездия спутников, по
которым определяется местоположение. Результаты расчетов записываются в
базу выходных данных. Из них формируется служебная информация и
передается на КС для закладки на борт спутника.
Оценка точности эфемерид. В процессе проведения типовых операций
управления производится неоперативное оценивание точностных
характеристик эфемерид, ежесуточно уточняемых для каждого спутника. С учетом
уточненных на данных технологических сутках опорных эфемерид рассчитывают
эталонные (осредненные на интервале измерения) кинематические параметры
движения и вычисляют максимальные отклонения оцениваемых опорных
эфемерид, прогнозируемые на 30 ч, относительно эталонных. Вектор
максимальных отклонений записывается в БД и используется при вычислении
выборочных оценок точности эфемеридного обеспечения за определенный интервал
времени для отдельных спутников или всей системы в целом.
Оценка возможности применения КС. Контроль возможности
использования КС в интересах эфемеридного обеспечения осуществляется в два этапа.
На первом этапе оперативно (ежедневно) после окончания выполнения
типовых операций управления оценивается качество работы КС как по составу
всей орбитальной группировки, так и в течение десятисуточного интервала
предыстории.
На втором этапе — неоперативно (ежемесячно) в конце каждого месяца.
На этом этапе более углубленно оценивается качество работы КС, так как
оцениваемый интервал берется равным не менее месяца, и принимается решение о
дальнейшем использовании данной КС в ПКУ ГЛОНАСС.
Определение параметров вращения Земли. Для обеспечения СРНС
ГЛОНАСС параметрами вращения Земли в системе организовано оперативное
определение координат полюса Земли, эксцесса длительности суток по данным
измерений КС на основе совместного уточнения ПВЗ и вектора состояния
системы. Специально разработанные методики позволяют определить и всемирное
время в процессе эфемеридного обеспечения системы. Точность получаемых
результатов оценивается для координат полюса на уровне 15...20 см, для
длительности земных суток — 0,5 мс и для всемирного времени — 1 мс.
Регулярное определение ПВЗ по данным наблюдений НС в режиме оперативной
службы осуществляется наземным комплексом ГЛОНАСС с 1984 г.
Получение этих данных методически и организационно тесно связано с
технологией информационного обеспечения спутников ГЛОНАСС, что
определяет высокую надежность и оперативность определений, однородность и
равномерность распределения данных, а также приемлемую для практических
применений точность получаемых значений ПВЗ. Однако это привносит неко-
370
Наземный сегмент (подсистема контроля и управления)
торую специфику в технологию определения ПВЗ. В первую очередь — это
региональное размещение КС исключительно на территории России и
особенности орбитального построения системы.
Определение ПВЗ проводится в процессе технологического цикла
управления спутниками ГЛОНАСС, предусматривающего проведение ежесуточных
вычислений орбит спутников и ПВЗ по данным наблюдений каждого спутника
за предшествующие 8 суток. В каждом таком решении получают оценки трех
значений ПВЗ — двух координат полюса Хр, YP и скорости вращения Земли
(эксцесса длительности суток D). Текущие значения координат полюса и
скорость вращения Земли уточняются в процессе обработки наблюдений методом
наименьших квадратов на восьмисуточном интервале. Этот интервал
обеспечивает наилучшее усреднение и компенсацию неучтенных возмущений.
Всемирное время определяют при сопоставлении результатов текущих
определений орбит спутников с их эфемеридами, вычисленными с
использованием данных ПВЗ, согласованных на некоторую начальную эпоху с данными
Международной службы вращения Земли. Таким образом, при выполнении
каждого суточного технологического цикла получают п реализаций оценок
всех четырех параметров:^, YP, D и (UT1—UTC), где п — число
спутников. Усреднение этих данных с исключением аномальных значений дает
возможность получить более точные оценки суточных значений ПВЗ, которые и
составляют ряды данных ПВЗ, определяемых в ПКУ. Обработка результатов
ежесуточных определений ПВЗ осуществляется в ЦУС еженедельно.
Полученные результаты передают в вычислительный центр Государственных
определений ПВЗ, где используют для вывода срочных и окончательных значений
ПВЗ и публикуют в Бюллетене серии Е Госстандарта РФ.
Рассмотренные задачи эфемеридного обеспечения решаются в
автоматизированном режиме. Требуемая достоверность служебной информации и
значительное снижение нагрузки по анализу результатов и нештатных
ситуаций достигается включением в пакет помимо основных указанных задач по
обработке ИТП программных модулей по контролю входной и выходной
информации, а также промежуточных расчетов.
10.2.3. Технология определения траектории движения спутника
Технология обработки ИТП и определения траекторий движений
спутников ГЛОНАСС включает несколько вариантов в соответствии с требованиями к
точности нахождения и прогнозирования эфемерид спутника, предъявляемыми
на различных этапах полета, и составом измерений. К таким этапам можно
отнести: выведение спутника на орбиту; приведение и постановка спутника в
системную точку с заданными значениями периода обращения и угловым
положением в системной плоскости.
371
Глава 10
В типовых операциях управления ПКУ ГЛОНАСС предусмотрено
использование измерений КС в запросном режиме с двумя разновидностями ДН
бортовой антенной системы — всенаправленной и узкой. В первом случае
точностные характеристики измерений запросной дальности находятся в пределах от
сотен метров до десятков километров. Такие измерения выполняют только на
первом этапе полета НС.
Проведение измерений во втором случае определяет начало операций по
приведению и постановке спутника в заданную системную точку. Требования к
точности определяют, исходя из необходимой точности коррекции орбит по
периоду обращения или точности постановки в системную точку с заданными
периодом обращения и угловым положением (0,1 с по периоду обращения и
0,1° по угловому положению).
Определение параметров движения спутника производится по запросным
измерениям дальности и радиальной скорости в два этапа. На первом этапе
определяются параметры движения спутника по измерениям радиальной
скорости с последующей переработкой этих измерений с использованием
уточненных по ним начальных условий движения. На втором этапе вычисляются
параметры движения спутника по измерениям дальности и радиальной скорости.
Параметры движения спутника на участках приведения и постановки
спутника в системную точку находят на мерных интервалах
продолжительностью 14 витков. Технология эфемеридного обеспечения на этапе
штатной эксплуатации основана на использовании высокоточных измерений
дальности КС и включает предварительную обработку измерений
(расшифровка данных измерений КС с последующим устранением неоднозначности
измерений дальности, калибровкой, приведением измерений к центру масс
спутника для компенсации выноса бортовой антенны, учетом ионосферной и
тропосферной рефракции).
Поправка, учитывающая влияние условий распространения сигнала в
тропосфере, рассчитывается по данным метеоусловий в районе КС.
Решение проблемы высокоточных определений орбит возможно при
создании высокоточных математических моделей движения и измерений, на
точность которых влияют следующие факторы: геофизические, определяемые
погрешностью задания системы координат и гравитационного поля Земли;
геодинамические, связанные с нахождением координат полюса и неравномерности
вращения Земли; а также факторы, обусловленные учетом негравитационных
возмущений в модели движения. В основе таких моделей лежит понятие
согласующих моделей, которые представляют собой системы геофизических
параметров и параметров, определяющих математическую модель движения НС по
данным обработки навигационных измерений. Они не являются
фундаментальными, а пригодны только для конкретных орбит и позволяют при
наличии высокоточных измерений параметров движения НС и достаточно
полном описании действующих на них сил уменьшить влияние погрешностей оп-
372
Наземный сегмент (подсистема контроля и управления)
ределения геофизических и геодинамических факторов на точность
определения эфемерид конкретного НС за счет уточнения координат измерительных
пунктов, параметров гравитационного поля Земли, параметров вращения Земли
и включения координат КС и других параметров согласующей модели в состав
расширенного вектора состояний НС.
При решении задач определения и прогнозирования движения спутника
эфемериды рассчитываются путем численного интегрирования
дифференциальных уравнений движения комбинированным методом Рунге—Кутта и
Адамса в координатной системе, заданной средним экватором и
равноденствием эпохи начала бесселева года (в 1975 г.). В правых частях дифференциальных
уравнений учитываются основные возмущающие силы. Гравитационное поле
Земли представлено разложением в ряд по сферическим функциям до гармоник
степени 8 включительно. При моделировании расчетных аналогов измерений
учитываются уходы полюса и поправки ко времени за счет неравномерности
вращения Земли.
При выводе спутника из системы требование к точности нахождения
параметров движения определяют, исходя из необходимости надежного
вхождения в связь со спутником. В этом случае параметры движения спутника
определяют на мерных интервалах длительностью не менее четырех витков не реже
одного раза в месяц. В состав уточняемых параметров при этом включаются
только кинематические.
Литература
10.1. Состав ГЛОНАСС// Компьютерный бюллетень BBS КНИЦ ВКС РФ, 1996.
10.2. Bazarov Y. Introduction to Global Navigation Satellite System// AGARD
LECTURE SERIES 207. System implications and innovative applications of satellite
navigation, NATO AGARD, 1996.
10.3. Губин 5. А., Клюев Н. Ф., Костылев А. А. и др. Основы радионавигационных
измерений/ Под ред. Я. Ф. Клюева. — М.: Изд-во Мин. обороны, 1987.
373
Глава 11
Глава 11
ПОДСИСТЕМА КОСМИЧЕСКИХ АППАРАТОВ
Приводимые в п. 11.1. ..11.5 сведения соответствуют Интерфейсному
контрольному документу [1.3].
11.1. Орбитальные характеристики спутников
В соответствии с целевым назначением система ГЛОНАСС имеет в своем
составе подсистему космических аппаратов (навигационных спутников),
которая представляет собой орбитальную группировку из 24 спутников. Спутники,
излучая непрерывные радионавигационные сигналы, формируют в
совокупности сплошное радионавигационное поле на поверхности Земли и в
околоземном пространстве, которое используется для навигационных определений
различными потребителями.
Структура сети спутников такова, что в каждой точке земной поверхности
и околоземного пространства, в которой находится потребитель, в любой
момент времени в зоне видимости находится одновременно не менее четырех
спутников, взаимное расположение и качество сигналов которых обеспечивает
ему возможность координатно-временных измерений с заданными
характеристиками. Требование по количественному составу орбитальной группировки
обусловлено тем, что заданные точностные характеристики навигационного
обеспечения могут быть получены в системе ГЛОНАСС при наличии в
орбитальной группировке, например, 21 спутника (по семь спутников в каждой
орбитальной плоскости), а остальные обеспечивают "горячий" резерв и высокую
устойчивость системы.
Спутники ГЛОНАСС размещаются на трех практически круговых
орбитах, высоты которых — 18 840... 19 440 км (номинальное значение составляет
19 100 км), что позволяет отнести ГЛОНАСС к среднеорбитальным СРНС.
Номинальные значения других параметров орбит НС ГЛОНАСС приведены в
табл. 9.1.
Точность приведения спутника в заданную (рабочую) точку орбиты
составляет: по периоду обращения 0,5 с; по аргументу широты Г; по
эксцентриситету ±0,01; по наклонению орбиты ±0,3°.
Орбитальные плоскости разнесены по долготе восходящего узла на 120°
(рис. 11.1). При полном созвездии НС в каждой орбитальной плоскости
равномерно размещается по 8 спутников с номинальным сдвигом в 45° по истинной
аномалии (которую в [1.3] называют «аргументом широты» со). Спутники в
соседних орбитальных плоскостях сдвинуты на 15° по значению истинной
374
Подсистема космических аппаратов
аномалии. Нумерация орбитальных плоскостей осуществляется по
направлению вращения Земли, а нумерация позиций (так называемых рабочих точек
орбиты или орбитальных точек) в последовательности спутников на орбите на
определенный момент времени — против их движения. Спутники,
занимающие эти позиции, часто обозначаются с помощью соответствующих
(системных) номеров, совпадающих с номером позиции, несмотря на известную
неоднозначность данного термина. При этом спутники с системными номерами
1...8 располагаются в первой орбитальной плоскости, 9... 16 — во второй и
17...24 — в третьей соответственно. На рис. 11.1 приведено расположение НС
по орбитальным плоскостям и рабочим точкам на 20.01.96 г.
Частотный канал
Р749[19] ,,/
/ 14/ 770[9]
Номер рабочей точки ^/764ГШ /
^ / 15/780[4]
11 759[21] /
/ l6d 775[22] /
'769[2] / 17/760[24
/ ?76[6] 1?/
" То/ " У'ЩТбГ
У 781[9] /
П / 19/777[3]
'V 785[4] /
12 / 767[22]
Плоскость 1
13/782[6]
Плоскость 2
Рис. 11.1. Распределение НС по орбитальным плоскостям на 20.01.96 г.
Номинальные значения Q абсолютных долгот восходящих узлов
идеальных орбитальных плоскостей, зафиксированных на 0 ч 00 мин 00 с 1.01.83 г.
(московского декретного времени), равны 25Г15'00"+ +120° (/-1), где / = 1,3
— номер орбитальной плоскости. Идеальные значения истинных аномалий НС
с системными номерами j = N + S и j = N + \6 отличаются от истинных
аномалий НС с номерами j = N и j = N + 8 соответственно на 15°, где N = 1, 8 и
составляют на 0 ч 00 мин 00 с 1.01.83 г. (московского декретного времени)
,9 = й> = 145026'37" + 150(27-3./ + 25/), где j — системный номер НС;
/ = entier((y -1) / 8) — целая часть числа (*).
Состояние орбитальной группировки ГЛОНАСС на 11.09.09 г. показано в
табл. 11.1, где «+» означает штатную работу.
375
Глава 11
Таблица 11.1. Состояние орбитальной группировки
Номер
НС
1 ^
713
714
715
716
717
718
719
720
721
722
723
724
725
726
727
728
1 729
Номер
орбитальной
плоскости/точки
Г/07
3/24
3/23
2/14
2/15
2/10
3/17
3/20
3/19
2/13
2/09
2/11
3/18
3/21
3/22
1/03
1/02
1/08
Состояние
спутника
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
Номер
частотного
канала 1
05 1
02
03
-7
00
-7
04
02
03
-2
-2
00
"3
04
-3
05
-4
06 1
Расположение НС, приведенных в табл. 11.1, по орбитальным плоскостям
и рабочим точкам приведено на рис. 11.2.
При полностью развернутой группировке интервал повторяемости трасс
движения НС и зон радиовидимости НС наземными потребителями составляет
17 витков (7 сут 23 ч 27 мин 28 с).
Таким образом, спутники СРНС ГЛОНАСС не имеют резонанса с
вращением Земли. Период обращения спутников подобран таким образом, что
приблизительно за 8 суток они совершают 17 оборотов вокруг Земли. При этом
начало каждого витка смещается относительно поверхности Земли
приблизительно на 21° по долготе. Каждые восемь суток спутник проходит над одними
и теми же точками на поверхности Земли. За счет смещения спутников внутри
орбитальных плоскостей все они движутся относительно поверхности Земли
практически по одному и тому же следу (полосе). Это свойство обеспечивает
высокоточное определение орбит спутников и ПВЗ при использовании
региональной ПКУ.
376
Подсистема космических аппаратов
Распределение НС по орбитальным плоскостям на 11.09.2009
Частотный канш
Широта
Номер
ГЛОНАСС
225
180
Номер рабочей точки
Плоскость 1 Плоскость 2
Плоскость 3
Рис. 11.2. Распределение НС по орбитальным плоскостям на 11.09.09 г.
Орбитальная группировка спутников ГЛОНАСС с несинхронными почти
круговыми орбитами более стабильна по сравнению с группировкой спутников
GPS с синхронными 12-ти часовыми орбитами.
г
1
0,75
0,5
0,25
2
/
/ /
1
1 ' ' - / /
1 1 ■ t I L.
//777 /
//U-f-7
I 1 : i 1 / .
it' l J—-"^
II:.' /-——T
I ' ' ' / /
1 1 : t 1 1 -
/ / ; ' / l~~^~^
//:•.'/ /
' :' •' / /
/ . / / /
' if I
f ! I I
■ 1 I I
/ til
л ' 1
^ N=9HC
^ 6HC
^ 5HC
^ 4HC
1
4 PDOP
Рис. 11.3. Статистические характеристики орбитального созвездия ГЛОНАСС
Рассмотренная структура орбитальной группировки позволяет обеспечить
практически непрерывное и глобальное покрытие земной поверхности и около-
377
Глава 11
земного пространства (включая ближний космос) навигационным полем с
заданными характеристиками.
Доступность спутников в системе ГЛОНАСС на широтах более 50° выше,
чем в системе GPS. Это связано с большим значением наклонения орбит
спутников ГЛОНАСС. На рис. 11.3 приведены [1.5, 10.2] расчетные зависимости
вероятности, с которой пространственный фактор ухудшения точности место-
определения (PDOP, см. п. 7.9.2) принимает заданное значение (для угла маски,
равного 5°, и при нахождении в зоне видимости потребителя N спутников).
Сравнительные характеристики ПКА систем ГЛОНАСС, GPS показаны
на рис. 11.4 [11.1] для полных созвездий. Эти данные дополняют сведения о
характеристиках доступности СРНС ГЛОНАСС, приведенных в табл. 7.5.
Р
0,4
0,3
0,2
0,1
5 6 7 8 9 10 N
Рис. 11.4. Статистические характеристики полных
орбитальных созвездий GPS и ГЛОНАСС
Орбитальная структура спутников ГЛОНАСС характеризуется высокой
устойчивостью и не требует дополнительных коррекций в течение всего срока
активного существования НС. Так, максимальные уходы НС относительно
идеального положения на орбите не превышают ±5° на интервале в 5 лет, а средняя
скорость прецессии орбитальных плоскостей составляет 0,59251 1(Г3 рад/с.
Кроме того, структура сохраняет свои функциональные качества при выходе из
строя одновременно до 6 НС (по два в каждой плоскости).
Поддержание структуры ПКА осуществляется выведением новых
навигационных спутников при снижении общего числа НС в любой плоскости менее
восьми. Запуск в заданную плоскость орбиты осуществляется по групповой
схеме (три спутника одновременно) с помощью ракеты носителя ПРОТОН с
космодрома «Байконур». Использование групповой схемы выведения приводит
к тому, что в каждой плоскости могут находиться избыточные
работоспособные НС, которые переводятся в нештатный способ функционирования, когда
целевая (навигационная) аппаратура выключена, и возможна профилактика
378
GPS
S
ЛОНАСС
1
L
Подсистема космических аппаратов
систем, так как обеспечивающие системы поддерживают штатную ориентацию
НС, заданный тепловой режим и энергоснабжение.
Схема выведения НС включает: выведение космической головной части на
промежуточную круговую орбиту высотой около 200 км; переход на
эллиптическую орбиту с перигеем примерно 200 км, апогеем около 19 100 км и
наклонением 64,3°; переход на круговую орбиту высотой 19 100 км.
В общем случае эксплуатация спутника предполагает следующие этапы
полета:
выведение спутника на орбиту после отделения его от разгонного блока
продолжительностью от 5 до 12 витков; здесь производится проверка
работоспособности всех бортовых систем;
приведение и постановка спутника в системную точку с заданными
периодом обращения и угловым положением в системной плоскости
(продолжительность этого этапа — от одной недели до одного месяца и определяется угловым
положением спутника в точке выведения на орбиту и системной точкой
спутника);
штатная эксплуатация спутника;
нахождение спутника вне системы (например, при проведении
профилактических и восстановительных работ по командам с ПКУ).
Реконфигурация рассмотренной орбитальной группировки ГЛОНАСС
допускается в связи с ограниченными запасами топлива для двигательных
установок спутника только в крайних случаях и проводится в целях оптимизации
структуры и используемых частот (в целях повышения точности
навигационных определений и обеспечения электромагнитной совместимости с другими
системами). Орбитальные маневры проводятся на этапе установки новых
спутников после их выведения на орбиту. При этом один НС остается в точке
выведения, а два других разводятся в соседние рабочие точки (предварительно
возможен перевод уже функционирующих НС в новую рабочую точку).
11.2. Радиосигналы в СРНС ГЛОНАСС
11.2.1. Виды используемых сигналов
Каждый спутник системы ГЛОНАСС излучает фазоманипулированные
навигационные радиосигналы в диапазоне Ы (~1600 МГц) и L2 (-1250 МГц).
В СРНС ГЛОНАСС используется частотное разделение сигналов различных
спутников в каждом из диапазонов. При этом спутники ГЛОНАСС,
находящиеся в противоположных точках орбиты (антиподные НС), т.е. невидимые
приземными потребителям одновременно, обычно передают навигационные
радиосигналы на одинаковых частотах (см., например, рис. 11.2), что позволяет
более рационально использовать частотный диапазон.
379
Глава 11
В СРНС GPS, в отличие от СРСН ГЛОНАСС, сигналы всех НС в каждом
из частотных диапазонов L\ и L2 излучаются на одной несущей частоте, при
этом используется кодовое разделение сигналов, т.е. сигнал каждого НС имеет
свой дальномерный код.
В радиолинии частотного диапазона L\ спутники системы ГЛОНАСС
излучают навигационные радиосигналы двух типов: стандартной и высокой
точности (СТ- и ВТ-сигнал соответственно), которые позволяют выделить два
соответствующих канала навигационного обслуживания — каналы
стандартной и высокой точности.
Сигнал стандартной точности предназначен для использования
гражданскими потребителями, и предоставляемое им обслуживание доступно всем
владельцам аппаратуры потребителей ГЛОНАСС. Сигнал высокой точности
модулирован специальным кодом и не рекомендован к использованию без
согласования с МО РФ, поэтому рассматриваемые каналы можно называть
открытыми и закрытыми. Иногда в иностранной литературе применительно к
указанным навигационным каналам используют обозначения CSA (Channel of
standard accuracy) и СНА (Channel of high accuracy) соответственно.
В отличие от сигнала стандартной точности системы GPS в системе
ГЛОНАСС не предусматривается его принудительное загрубление, хотя
иногда применительно к нему используется обозначение ПТ-сигнал (сигнал
пониженной точности). Однако имеющиеся более низкие по сравнению с ВТ-
сигналом характеристики точности можно отнести к этапу выбора параметров
сигнала при разработке системы, что не связано с политикой поставщиков
навигационного обслуживания в системе ГЛОНАСС на этапе ее эксплуатации.
Поэтому всем пользователям ГЛОНАСС доступны измерения координат
местоположения и скорости с высокой точностью. В дальнейшем более подробно
будут рассмотрены структура и характеристики СТ-сигнала, передаваемого в
диапазоне LX. В радиолинии диапазона L2 с НС «Глонасс» в настоящее время
передается только ВТ-сигнал, поэтому гражданские потребители не могут
использовать метод двухчастотной компенсации ионосферных погрешностей.
Этот существенный, с точки зрения гражданских потребителей, недостаток
присущ и системе GPS.
В декабре 2003 г. с космодрома «Байконур» был запущен НС новой
модификации «Глонасс-М». Он передает навигационный СТ-сигнал не только в
диапазоне Ы, но и в диапазоне L2. Параметры СТ-сигнала в диапазоне L2
полностью аналогичны параметрам СТ-сигнала в диапазоне Ы, излучаемого
этим же НС.
Отличие СТ-сигналов в диапазонах L1 и L2 НС «Глонасс-М» от СТ-
сигнала в диапазоне Ы НС «Глонасс» состоит только в некоторых
дополнительных параметрах навигационного сообщения. Остальные параметры
(мощность сигнала у поверхности земли, структура сигнала и др.) идентичны. Более
подробно о системе ГЛОНАСС с НС «Глонасс-М» — в гл. 14.
380
Подсистема космических аппаратов
11.2.2. Характеристики излучаемых навигационных радиосигналов
Частотные каналы. В системе ГЛОНАСС номинальное значение рабочих
частот радиосигналов НС: /ц = fQi + k/Sft, где / = 1,2 — номер диапазона
частот; к = 1,24 — номер частотного канала (литер); fQl = 1602 МГц; /02 =
= 1246 МГц; A/i = 562,5 кГц; А/2 = 437,5 кГц. Отношение fkL11 Л* = 7 / 9.
Канал £ = 0 не предназначен для использования потребителями системы
ГЛОНАСС. Он применяется наземной подсистемой управления для проверки
резервных спутников на орбите при восполнении орбитальной группировки.
Сведения о распределении частотных каналов к = 1,24 между спутниками,
расположенными в орбитальных рабочих точках с номерами т = 1,24, содержатся в
альманахе системы. В табл. 11.2 показано соответствие номинальных значений
несущих частот /ц для двух диапазонов каналам к = 1,24 .
Таблица 11.2. План частот
Номер
|канала
-07
-06
-05
-04
-03
-02
-01
00
01
02
1 03
Частота, МГц
П
1598,0625
1598,625
1599,1875
1599,75
1600,3125
1600,875
1601,4375
1602,0
1602,5625
1603,125
1603,6875
L2
1242,9375
1243,375
1243,8125
1244,25
1244,6875
1245,125
1245,5625
1246,0
1246,4375
1246,875
1247,3125
Номер
канала
04
05
06
07
08
09
10
11
12
13
Частота, МГц ||
Ы
1604,25
1604,8125
1605,375
1605,9375
1606,5
1607,0625
1607,625
1608,1875
1608,75
1609,3125
12 ||
1247/75" 1
1248,1875
1248,625
1249,0625
1249,5
1249,9375
1259,375
1250,8125
1251,25
1251,6875
Навигационные СТ-сигналы с тактовой частотой 511 кГц занимают в
частотном диапазоне Ы полосу шириной (1598,0625... 1609,3125)+ 0,511 МГц.
Внеполосные излучения каждым НС за пределами полосы, отведенной для
навигационных радиосигналов ГЛОНАСС, не превышают -40 дБ относительно
мощности Р немодулированной несущей. Навигационные ВТ-сигналы с
тактовой частотой 5,11 МГц занимают в частотном диапазоне сигналов Ы полосу
шириной (1598,0625... 1609,3125) +5,11 МГц. Соотношение спектральных
характеристик сигналов в системах ГЛОНАСС и GPS показано на рис. 11.5.
381
Глава 11
ш
GPS
ГЛОНАСС
Канал 1 .... Канал 12
А
2 МГц
СТ-сигнал
W* (С/А-код)
\ ВТ-сигнал
(Р-код)
1 МГгГЧ
1
1575,42
СТ-сигнал
ВТ-сигнал
1598,0625
*« ►!
/
1609,3125
20 МГц 10 МГц
Рис. 11.5. Спектральные характеристики сигналов ГЛОНАСС и GPS
Все радиосигналы (стандартной и высокой точности в диапазонах L\ и
L2), формируемые на борту каждого НС, когерентны, так как формируются от
общего БЭВЧ. При этом спектральная плотность фазовых шумов
смодулированной несущей такова, что схема слежения за фазой сигнала с односторонней
шумовой полосой 10 Гц обеспечивает точность слежения за фазой несущей не
хуже а= 0,1 рад.
Номинальное значение частоты БЭВЧ с точки зрения потребителя,
находящегося на поверхности Земли, равно 5 МГц. Для компенсации
релятивистских эффектов (см. п. 7.4) частота, формируемая БЭВЧ, смещена
относительно 5 МГц на А/ = 2,18 10"3 Гц (соответствует номинальной высоте НС,
равной 19 100 км). Фактические значения рабочих частот сигналов каждого НС
могут отличаться от номинальных значений /ц на относительное значение, не
превышающее ±2 -10~11.
В настоящее время предусматривается поэтапное изменение частотного
диапазона ГЛОНАСС с тем, чтобы с 2005 г. все находящиеся в эксплуатации
навигационные спутники системы ГЛОНАСС использовали в качестве рабочих
только каналы частот к = -7...+6. Более подробно об изменении плана частот
— в гл. 14.
Характеристики поляризации излучаемых сигналов. Спиральные
антенные элементы спутников ГЛОНАСС формируют радиосигнал, который
имеет правую круговую поляризацию. При этом коэффициент эллиптичности
по полю не хуже 0,7 в обоих диапазонах излучения и в секторе излучения ±19°
относительно оси симметрии диаграммы направленности (ДН) бортовой
передающей антенны НС. Эти параметры сигнала учитываются при
конструировании приемных антенн потребителей СРНС и при учете поляризационных потерь
сигнала в радиолинии.
382
Подсистема космических аппаратов
Характеристики модуляции сигналов. В системе ГЛОНАСС
используются сложные фазоманипулированные сигналы (общие сведения приведены в
п. 5.4). Фазовая манипуляция несущей осуществляется на п радиан с
максимальной погрешностью не более ±0,2 рад. Для манипуляции используется
цифровая последовательность 0 и 1, представляющей собой сумму по mod 2
трех цифровых последовательностей: дальномерного кода, символов
навигационного сообщения и М-кода (манчестерский код, или иначе, меандровая
последовательность).
В зависимости от качества модуляции может измениться стандартный вид
излучаемого сигнала, что обусловливает появление потерь при
корреляционной обработке сигналов в аппаратуре потребителя, которые часто называют
корреляционными потерями. Наибольшие корреляционные потери, вызванные
искажением формы псевдослучайного двоичного сигнала в приемнике,
составляют не более 0,2 дБ, а обусловленные неидеальностью модулятора
передатчика НС — 0,6 дБ [1.3].
Групповая задержка радиосигнала в аппаратуре НС. Групповая
задержка радиосигнала в аппаратуре НС обусловлена зависимостью фазовой
характеристики передающего тракта от частоты (фазочастотная характеристика).
Данная групповая задержка определяется как задержка между излучаемым
радиосигналом (измеряется в фазовом центре передающей антенны НС) и
выходным сигналом бортового стандарта частоты. Считается, что
детерминированная составляющая групповой задержки радиосигнала потребителю не важна,
так как может быть заранее скомпенсирована, и не влияет на ошибки
определения системного времени. Максимальное значение случайной составляющей
групповой задержки радиосигнала в бортовой аппаратуре НС «Глонасс» не
превышает ± 8 не, а для НС «Глонасс-М» — ± 2 не.
Внутрисистемные помехи. В зоне видимости потребителя СРНС всегда
находится более четырех спутников, каждый из которых излучает
радиосигналы. Так как спектры сигналов не являются строго ограниченными по частоте
функциями, при обработке сигнала одного из спутников сигналы других
спутников мешают и их относят к внутрисистемным помехам. Уровень последних
зависит от используемых типов сигналов и принятого в системе метода
разделения сигналов.
В системе ГЛОНАСС используется частотное разделение сигналов.
Частотный разнос между номинальными значениями несущих частот в диапазоне
L\ равен 562,5 кГц и выбран таким образом, что с учетом длительности
элементарной посылки сигнала гэ =1/511 мс помеховые радиосигналы от
спутников, находящихся в зоне радиовидимости, могут мешать приему
обрабатываемого сигнала только вторыми и последующими лепестками спектра. При этом
доля мощности одного ближайшего по частоте помехового сигнала
относительно полезного составляет примерно 2 • 10~5, т. е. не превышает - 48 дБ, что
и определяет уровень внутрисистемных помех СРНС ГЛОНАСС.
383
Глава 11
Внутрисистемные помехи в СРНС GPS существенно больше. В GPS
используется кодовое разделение сигналов, и уровень внутрисистемных помех
определяется значением максимального бокового лепестка кроскорреляцион-
ной функции используемых кодов. Для кодов Голда длиной 1023 элемента,
применяемых в GPS, уровень максимального бокового лепестка относительно
величины полезного сигнала составляет примерно 7 • 10~3 (-21,6 дБ).
Энергетические характеристики навигационной радиолинии.
В [1.3] определено, что мощность радиосигнала, принимаемого
потребителем от НС «Глонасс», на выходе приемной линейно поляризованной антенны с
коэффициентом усиления + 3 дБ и при угле места 5° составляет не менее
минус 161 дБВт для частотного диапазона Ы .
Формирование такого сигнала обеспечивается при следующих основных
характеристиках навигационной радиолинии:
мощность сигнала передатчика Pt = 64 Вт (18 дБВт);
коэффициент усиления передающей антенны спутника Gt = 10 дБ (по
центру ДН) и G,=12 дБ (в углах ±15°);
эффективная мощность излучаемого сигнала PGmjl = PtGt=2S и 30 дБВт
для двух указанных направлений соответственно;
потери в свободном пространстве IF=201g (Я/4лR)дБ» 184,2 дБ (для
угла места НС 5°) и 182,2 дБ (для угла места 90°) для Я « 18,6 см (средняя
часть диапазона частот системы ГЛОНАСС);
затухание в атмосфере LaT « 2 дБ;
поляризационные потери Ьтл * 1 дБ;
прочие потери 1пр«3...4 дБ.
Таким образом, мощность сигнала на входе приемной антенны
Рант =PGmsl -LF -LaT -Ьпол -Lnp «-161...-163 дБВт (для угла места спутника
5°). При коэффициенте усиления антенны Ga = + 3 дБ на ее выходе (а,
следовательно, на входе высокочастотной части приемника) получаем
^вх=^ант^а*-159...-161дБВт.
В теории спутниковой навигации энергетические характеристики условий
приема сигналов в аппаратуре потребителя принято характеризовать
параметром qcjnQ = Рвх /N0 , представляющим собой отношение мощности полезного
сигнала на входе высокочастотной части приемника Рвх к спектральной
плотности (односторонней) внутреннего шума приемника N0. Учитывая, что
N0 =ккшТ0, где Г0 =290К, к = 1,38-Ю-23 — постоянная Больцмана; кш— ко-
384
Подсистема космических аппаратов
эффициент шума приемника, и полагая кш =2,5, получаем N0 =-201,5 дБВт/Гц;
Яс/по = Ю1°ё(<7с/ио ) = -161 + 201,5 = 40,5 дБГц.
Мощность радиосигнала, принимаемого потребителем от НС «Глонасс-
М», на выходе приемной линейно поляризованной антенны с коэффициентом
усиления +3 дБ и при угле места 5° составляет не менее -161 дБВт для частот
диапазона Ы и не менее -167 дБВт для частотного диапазона L2 с
последующим доведением до уровня не менее -161 дБВт.
На рис. 11.6 приведены зависимости минимальной мощности сигнала в
частотных диапазонах 1Л и L2, принятого потребителем, находящимся на
поверхности Земли, от угла возвышения НС [1.3].
Угол возвышения НС, град
30 45 60
Н 1 Ь
-168
Рис. 11.6. Зависимости минимальной мощности сигнала от угла возвышения НС
Наблюдаемое экспериментально увеличение уровня принимаемого
сигнала может быть обусловлено следующими причинами: отклонением высоты НС
от номинального значения; ошибками угловой ориентации НС; изменением
коэффициента усиления передающей антенны НС по азимутальным
направлениям и по частотному диапазону; вариациями выходной мощности
передатчика НС из-за технологических причин, колебаний температуры и т. д.;
уменьшением потерь при распространении радиосигнала в атмосфере.
Полагают [11.2], что максимальный уровень принимаемого радиосигнала
НС «Глонасс» не превышает -155,2 дБВт (потери в атмосфере 0,5 дБ,
погрешность угловой ориентации НС Г в сторону увеличения мощности сигнала).
11.3. Характеристики модулирующих последовательностей
Навигационный радиосигнал, передаваемый каждым НС, представляет
собой многокомпонентный фазоманипулированный сигнал.
13-1026
385
Глава 11
Для получения высокой точности измерений задержки сигнала
излучаемый сигнал модулируется дальномерным кодом стандартной точности (СТ-
код), представляющим собой периодическую последовательность
максимальной длины (см. п. 5.4.2). Для диапазона L\ тактовая частота формирования
дальномерного кода /дк =511 кГц (скорость передачи символов 511 кбит/с),
период повторения Гдк= 1 мс.
Для передачи навигационной (служебной) информации используется
модуляция двоичной последовательностью (кодом служебной информации (СИ-
код)) с тактовой частотой /си = 50 Гц (скорость передачи символов 50 бит/с).
Для обеспечения безошибочной работы фазового демодулятора в
приемнике сигналов СРНС передаваемый сигнал подвергается относительной
фазовой манипуляции (см. п. 5.6.2), а для обеспечения процессов синхронизации в
приемнике (см. п. 5.7) вводятся:
модуляция меандровым колебанием (М-кодом) с тактовой частотой /мк =
= 100 Гц (скорость передачи символов 100 бит/с);
код метки времени (МВ-код), представляющий собой двоичную
псевдослучайную последовательность (М-последовательность) с тактовой частотой
/мв = ЮО Гц (скорость передачи символов 100 бит/с).
Упрощенная схема формирования модулирующей последовательности в
ГЛОНАСС показана на рис. 11.7, где ФОК — формирователь относительного
кода. Из рисунка видно, что модулирующий навигационный сигнал (двоичная
последовательность) формируется двумя способами.
В первом происходит сложение по mod 2 трех двоичных сигналов:
дальномерного кода стандартной точности (СТ-код); кода служебной информации
(СИ-кода); меандрового колебания (М-кода).
Результирующая двоичная последовательность поступает на модуляцию
несущего колебания в течение 1,7 с каждого двухсекундного интервала
спутникового времени.
МВ-код
Гмв =10мс
Н,Гси, Ил 1«
Навигационные
данные at
1
Тси = 20 мс
К модулятору
Тмк=10мс
СТ-код
TW=X3=\/51\MQ
Рис. 11.7. Схема формирования модулирующей последовательности
В течение оставшихся 0,3 с этого интервала модулирующая
последовательность формируется сложением по mod 2 двух последовательностей:
дальномерного СТ-кода и кода метки времени (МВ-кода).
386
Подсистема космических аппаратов
Рассмотрим особенности формирования указанных двоичных
последовательностей.
Дальномерный СТ-код представляет собой М-последовательность
(псевдослучайная последовательность (ПСП)). Эта сравнительно короткая ПСП
(длина L=511 элементов) обеспечивает быстрый поиск дальномерного сигнала
и приемлемую точность измерения дальности до НС. Порождающий полином
СТ-кода Яст (х) = 1 + х5 + х9 .
Схема, поясняющая принцип формирования дальномерного кода ПСП и
различных синхроимпульсов, показана на рис. 11.8.
Синхроимпульсы Эталонная частота 5 МГц
/0Г=5МГц
(7^=200 не)
Формирователь
синхроимпульсов
У0Г=5МГц)
:10
l^ifTW^
Сброс в "0"
/«=0,511 МГц
Регистр сдвига генератора ПСП
Ф*
4
JE1
Установка в *
« яоооо I—
Тригер |
[синхронизации 1
Строб-импульсы 7М с
от эталона частоты НС
±
Тригер I
ситроншащпп
щн
Синхроимпульсы Т=Ю мс
Ы 8 Ы 9 U
_т_
у
ПСПк
модулятору
к процессору
Синхроимпульсы Т-\ мс
к процессору
Рис. 11.8. Схема формирования дальномерного кода
Как видно из рисунка, последовательность двоичных сигналов ПСП
снимается с седьмого разряда девятиразрядного регистра сдвига. Начальным
символом в периоде ПСПД является первый символ в группе 111111100,
повторяющийся через 1 мс.
Код служебной (навигационной) информации (СИ-код) представляет
собой преобразованную цифровую последовательность навигационных
данных, передаваемых аппаратурой НС потребителям системы ГЛОНАСС.
Навигационные данные ai (рис. 11.7) подвергаются помехоустойчивому
кодированию (см. п. 5.5.2) в соответствии с кодом Хэмминга (85,77) (кодовое
расстояние равно четырем). Выходные символы Ъг кодера преобразуются в
относительный код по правилу (5.25) С( =bi®Ci_l , где Cz — последовательность
символов в относительном коде (длительность рассматриваемых символов
Гси=20 мс). Таким образом, в канале передачи навигационной информации
используется ОФМ-сигнал, что исключает явление обратной работы, когда
символы цифровой информации, соответствующие 1, идентифицируются как
символы, соответствующие 0, и наоборот.
387
Глава 11
Результирующая двоичная последовательность навигационного
сообщения (названная здесь Dl-код), содержащая информационные и проверочные
символы в так называемом бидвоичном коде (Тт =10 мс), образуется, как
видно из рис. 11.7, после сложения по mod 2 последовательности символов Ci
в относительном коде (СИ-код) с меандровым колебанием (М-код с
длительностью символа 7"мк=10 мс). М-код обеспечивает, в частности, простоту
синхронизации по СИ-коду, содержащему серии одинаковых двоичных символов
(нулей или единиц). Сигналы тактовых частот СТ-, МВ-, СИ-, М-кодов и другие
синхросигналы получены делением эталонной частоты БЭВЧ for = 5 МГц, что
обеспечивает когерентность формируемых последовательностей.
Код метки времени (ПСП MB, МВ-код) представляет собой укороченную
ПСП с порождающим полиномом вида Вмв (х) = 1 + хъ + х5.
Длина ПСП MB равна тридцати символам с длительностью Гмв = =10 мс
каждый. Эта характерная двоичная последовательность имеет вид
111110001101110101000010010110. Она используется как двухсекундная метка
времени, так как задний фронт ее последнего символа ПСП в излученном
навигационном радиосигнале является меткой времени и соответствует окончанию
очередного двухсекундного интервала времени от начала суток в БШВ. Эта
метка позволяет осуществлять строчную синхронизацию, а также устранять
неоднозначность дальномерных измерений.
Первый символ служебной информации в каждой строке всегда
соответствует «0». Он является "холостым" с точки зрения передачи навигационных
данных, но дополняет укороченную ПСП MB предыдущей строки до полной
(неукороченной) ПСП.
Синхронизация кодовых последовательностей осуществляется
синхроимпульсами с периодами следования 1 мс, 10 мс и 1 с. На рис. 11.9 приведены
временные соотношения между данными синхроимпульсами и символами
дальномерного кода стандартной точности.
Синхро-
■ .импульсы
»| Т=1 с
Юме
±
и
II
1
Синхро-
> t
[ИМ1
1с
пульсы
ЩЩ ШI i IJ11L,, i 111111111
1=511 символов; 7^= 1 с
ran
o|o|o
0 0
S7J
СТ-код(511
ы
ТМОмс
Синхро-
импулъсы
периода
СТ-кода
символов)
> t
-* \<-ту =1,9569 мке
Рис. 11.9. Временные соотношения между СТ-кодом и синхроимпульсами
388
Подсистема космических аппаратов
ш
Синхроимпульсы 7^=10 мс
-►*
Oi
ш
Меандр 7^=10 мс
in
i i i
liiii
Символы служебной
1 1
информации 7^=20 мс
Символы кода D1 7^=10 мс
-> t
-> t
1 1
+ U
ш
Символы МВ-кода
1,7 с
*н-
Гм,=10 мс
0,3 с
-> t
| __ 85 символов СИ-кода, сложенного по mod 2 с меандром 130 символов МВ-кода^
->f
Четные секунды шкалы времени спутника
Рис. 11.10. Формирование символов навигационной информации,
кода D1 и кода метки времени
Рис. 11.10 иллюстрирует формирование символов навигационной
информации (СИ-кода), кода D\, формирующегося в результате сложения по mod 2 СИ-
кода меандрового колебания (см. рис. 11.7), и кода метки времени (МВ-кода).
11.4. Навигационные сообщения в СРНС ГЛОНАСС
11.4.1. Общие сведения
По своему содержанию навигационные сообщения, передаваемые каждым
НС ГЛОНАСС, содержат оперативную и неоперативную навигационную
информацию (НИ). Иногда применительно к ним используют термин «служебные
сообщения» или «служебная информация» (СИ). Потребителям ГЛОНАСС они
необходимы для планирования и осуществления навигационных определений.
т
Оперативная информация
Номер строки в кадре (1 ... 15)
Время начала кадра в пределах суток (ч, мин, с)...
Опорное время ОИ
Относительный сдвиг частоты сигнала
Сдвиг БШВ относительно СШВ тп
Координаты НС (ПЗ-90) XnJniZn
Составляющие скорости НС Xn,Yn,Zn
Уп
389
Глава 11
Составляющие ускорения НС
Возраст ОИ
Признаки исправности; смены ОИ;/6; кадра
Неоперативная информация (альманах)
Календарный номер суток (4 г.)
Поправка СШВС к ШВ ГЭВЧ (на начало NA)
Номер НС
Номер (литер) частоты НС
Долгота первого восходящего узла (ПЗ-90)
Момент прохождения восходящего узла
Поправка к среднему наклонению (63°)
Поправка к среднему драконическому периоду об
ращения НС (12 час)
Скорость изменения драконического периода
Эксцентриситет
Аргумент перигея
Грубый сдвиг БШВ
Признак состояния НС
Оперативная НИ (ОИ) относится к данному НС и содержит: оцифровку
меток времени спутника; оценки сдвига БШВ относительно СШВ и отличия
несущей частоты излучаемого радиосигнала от номинального значения;
эфемериды и др.
Неоперативная НИ содержит альманах системы: данные о состоянии
всех НС (альманах состояния), оценки сдвига БШВ каждого НС относительно
СШВ (альманах фаз), параметры орбит всех НС системы (альманах орбит),
сдвиг шкалы времени системы ГЛОНАСС относительно UTC (SU) и др.
Поток НИ состоит из непрерывно повторяющихся суперкадров, кадров и
строк (рис. 11.11). На рисунке использованы следующие сокращения: КХ —
код Хэмминга; MB — метка времени. В нижней части рисунка показан порядок
нумерации разрядов служебных сообщений.
Границы строк, кадров и суперкадров у различных НС синхронны с
погрешностью не более 2 мс. Структура передаваемой навигационной
информации в СРНС ГЛОНАСС оптимизирована таким образом, что объем суперкадра
весьма невелик 7 500 бит, из них 620 резервные (в GPS 37 500 и 2 750 бит
соответственно). Каждый суперкадр состоит из кадров, в нем передается полный
объем неоперативной информации альманаха для двадцати четырех НС.
Ш,П2, ПЗ
N
А
с
.А
н
tA
:А
at:
at:
<
с
390
Подсистема космических аппаратов
Каждый кадр состоит из 15 строк и содержит полный объем ОИ для
конкретного НС (строки 1 ... 4) и четверть альманаха. В пределах суперкадра ОИ и
строка 5 (системные данные) в каждом кадре повторяются. Структура
навигационного кадра (с 1-го по 4-й) показана на рис. 11.11. Здесь заштрихованные
области представляют собой резерв, предусмотренный на случай изменений и
дополнений в структуре навигационного сообщения
Номер кадра
в суперкадре
I
II
III
IV
V
Номер
строки
в кадре
1
4
■А
* 2с
■ ►
1.7с (85 бит) 'Г 0.3 с
0
0
0
Оперативная
НИ для
передающего НС
КХ
кх
кх
MB
MB
MB
Неоперативная НИ -jc
(альманах)
15
1
4
0
0
0
0
для НС с № 1...5
Оперативная
НИ для
передающего НС
кх
кх
кх
кх
MB
MB
MB
MB
Неоперативная НИ
(альманах)
15
1
4
0
0
0
0
для НС с№ 6... 10
Оперативная
НИ для
передающего НС
кх
кх
кх
кх
MB
MB
MB
MB
Неоперативная НИ зс
(альманах) =-
15
1
2
3
0
0
0
0
для НСс№ 1...15
Оперативная
НИ для
передающего НС
кх
кх
кх
кх
MB
MB
MB
MB
Неоперативная НИ
(альманах)
15
1
4
0
0
0
0
для НС с№ 16..20
Оперативная
НИ для
передающего НС
кх
кх
кх
кх
MB
MB
MB
MB
Неоперативная НИ
(альманах)
для НС с №21...24
14
15
0
0
85
Резерв
Резерв
84 9
кх
кх
8...1
MB
MB
1...30
i
)c
1
r
i
)cx5 =
>,5 мин
1
f
Номер разряда
в строке
Информационные символы
в относительном
бидвоичаом коде
Символы кода Хемминга Метка
в относительном времени
бидвоичном коде
Рис. 11.11. Структура суперкадра навигационного сообщения ГЛОНАСС
391
Глава 11
Информационная строка кадра длительностью 2 с (100 бит) разделена, как
показано на рис. 11.11, на две части. В первой части строки (1,7 с) содержится
навигационная информация (85 бит), преобразованная в относительный код и
сложенная по mod 2 с меандровым колебанием (бидвоичныи относительный
код D\). Во второй части строки (0,3 с) в качестве последовательности
навигационных данных используется ПСП MB (МВ-код), состоящая из 30 символов
длительностью 10 мс.
В каждой строке старшие 77 разрядов (передаются первыми) содержат
информационные символы (85-й символ обеспечивает реализацию
последовательного относительного кода и равен 0), а младшие 8 разрядов —
проверочные символы. Они способствуют исправлению одиночных ошибок и
обнаружению двойных ошибок (и большего четного числа) в строке.
11.4.2. Эфемериды НС ГЛОНАСС
Рассмотрим, следуя [1.3], подробнее содержание эфемеридной
информации, приведенной на рис. 11.12 для кадров 1...4 и на рис.
11.13 для 5-го кадра.
Nn<U
Х„ (tb)
X„(tb)
кх
MB
УпОь)
УоОъ)
Уп(1ь)
КХ
MB
Zn(tb)
Zn(tfe)
Zn(tb)
КХ
MB
NT
КХ
MB
КХ
MB
*-\
Ai\
KX
MB
ATA
ATA„
KX
MB
KX
MB
ATAn
ДТ \ '
KX
MB
Ai\
KX
MB
ДТА
ATAn
KX
MB
b\
Ai\
KX
MB
ATA
ДТАП
KX
MB
KX
MB
16 .A
ATA„
AT\ H'
KX
MB
Рис. 11.12. Структура навигационных кадров 1...4
392
Подсистема космических аппаратов
Рис. 11.13. Структура 5-го навигационного кадра
Слово т — номер строки в навигационном кадре. Число разрядов этого
слова — 4; цена младшего разряда — 1; диапазон значений — 0... 15.
Слово tk (ч, мин, с) — время начала кадра внутри текущих суток,
исчисляемое в шкале бортового времени НС. В пяти старших разрядах передается
число целых часов, прошедших с начала текущих суток; в шести средних —
число целых минут; в младшем — число тридцатисекундных интервалов,
прошедших с начала текущей минуты. Начало суток по бортовому времени
совпадает с началом очередного суперкадра.
Число разрядов этого слова — 12; цена младшего разряда — 1 (для часов и
минут) и 30 (для секунд); диапазон значений — 0...23 (для часов), 0... 59 (для
минут) и 0...30 (для секунд).
Слово Вп — содержит три двоичных разряда. Аппаратурой потребителя
анализируется только старший разряд. Передача в нем 1 свидетельствует о
непригодности данного НС для навигационных измерений.
Слово tb — порядковый номер временного интервала внутри текущих
суток по шкале системного времени ГЛОНАСС, к середине которого относится
передаваемая в кадре оперативная информация; длительность данного
временного интервала и, следовательно, максимальное значение слова tb
определяются значением слова PL
Слово Р1 — признак смены ОНИ (смена ОНИ производится с интервалом,
определяемым словом Р1). Этот признак сообщает интервал времени Atb меж-
393
Глава 11
ду значениями tb (мин) в данном и предыдущих кадрах. Значениям Р1, равным
00, 01, 10 и 11, соответствуют значения tb = 0, 30, 45 и 60 мин.
Слово Р2 — признак смены. Он представляет собой признак нечетности
«1» или четности «0» порядкового номера (Ь) 30(60) — минутного текущего
отрезка времени, середина которого оцифрована числовым значением слова tb.
Слово РЗ — признак, состояние «1» которого означает, что в данном кадре
передается альманах для пяти, а состояние «0» — для четырех НС.
Слово Еп (сут) — характеризует "возраст" оперативной информации,
представляет собой интервал времени, прошедший с момента расчета
(закладки) оперативной информации до момента времени tb для а?-го НС. Это слово
формируется на борту НС. Число разрядов в этих словах — 5; цена младшего
разряда — 1; диапазон значений — 0.. .31.
Слово yn(tb) — относительное отклонение прогнозируемого значения
несущей частоты излучаемого навигационного радиосигнала п -го НС от
номинального значения на момент времени tb:
где f„(tb) — прогнозируемое значение несущей частоты излучаемого
радиосигнала п -го НС с учетом гравитационного и релятивистского эффектов на
момент времени tb\ fHn — номинальное значение несущей частоты. Число
разрядов этого слова — 11; цена младшего разряда — 2-40; диапазон значений
— ± 2'30.
Слово п — номер НС, излучающего данный навигационный сигнал и
соответствующий его рабочей точке внутри орбитальной группировки
ГЛОНАСС.
Слово rn(tb) (с) — сдвиг БШВ а?-го НС tn относительно СШВ /с, равный
смещению по фазе ПСП дальномерного кода излучаемого радиосигнала и-го
НС относительно системного опорного сигнала на момент времени tb,
выраженный в единицах времени:
гД'*) = 'Д'б)-'Д'б)-
Число разрядов этого слова — 22; цена младшего разряда — 2"30;
диапазон значений — ± 2~9.
Слова Xn(tb),Yn(tb) ,Zn(tb) (км) — координаты п-го НС в геодезической
системе координат ПЗ-90 на момент времени tb.
Число разрядов в этих словах — 27; цена младшего разряда — 2~п ;
диапазон значений — ±2,7 • 104.
394
Подсистема космических аппаратов
Слова Xfn{tb),Y^{tb),Zfn{tb) (км/с) — составляющие вектора скорости я-го
НС в геодезической системе координат ПЗ-90 на момент времени tb. Число
разрядов в этих словах — 24; цена младшего разряда — 2"20; диапазон
значений — ±4,3.
Слова X^(tbXY^(tb),Z^(tb) (км/с2) — составляющие ускорения п-го НС в
геодезической системе координат ПЗ-90 на момент времени tb, обусловленные
действием Луны и Солнца. Число разрядов в этих словах — 5; цена младшего
разряда— 2~30; диапазон значений — ± 6,2 10~9.
Параметры эфемерид НС периодически определяются подсистемой
контроля и управления и закладываются на все спутники системы.
Среднеквадратические значения погрешностей передаваемых
местоположения и скорости спутников в орбитальной системе координат при суточном
прогнозе приведены в табл. 11.3.
Таблица 11.3. Погрешности передаваемых координат и скорости НС
Составляющая
погрешности НС
Вдоль орбиты
По бинормали к орбите
1 По радиус-вектору
СКО погрешности определения: |
местоположения, м
«Глонасс»
20
10
5
«Глонасс-М»
7
7
1,5
скорости, см/с 1
«Глонасс»
0,05
од
0,3
«Глонасс-М»
0,03
0,03
0,2 |
Для вычисления эфемерид НС на момент измерений навигационных
параметров используются следующие соотношения для определения времени в
шкале UTC(SU)
где t — время излучения сигнала по бортовой шкале времени НС; тс, т„, у,
tb — параметры определены выше.
В НС «Глонасс-М» дополнительно передается следующая информация.
Слово Р — признак режима работы НС по частотно-временной
информации (ЧВИ). Значения признака:
00 — ретрансляция параметра гс, ретрансляция параметра tgps ;
01 — ретрансляция параметра гс, размножение параметра rGPS на борту
НС;
10 — размножение параметра гс на борту НС, ретрансляция параметра
TGPS '■>
395
Глава 11
11 — размножение параметра гс на борту НС, размножение параметра
tgps на борту НС.
Слово Р4 — признак того, что на текущем интервале времени tb
средствами ПКУ на НС заложена (1) или не заложена (0) обновленная эфемеридная
или частотно-временная информация.
Передача обновленной эфемеридной и частотно-временной информации
осуществляется только после окончания текущего интервала tb9 на котором
произошла закладка ПКУ новых данных.
Слово NT — текущая дата, календарный номер суток внутри
четырехлетнего интервала, начиная с 1 -го января високосного года. Алгоритм пересчета от
номера суток внутри четырехлетнего интервала к общепринятой форме даты
(чч.мм.гг.) приведен в [1.3].
Слово FT — фактор точности измерений, характеризующий в виде
эквивалентной ошибки прогнозируемую ошибку измерения псевдо дальности,
обусловленную набором данных (эфемеридная и частотно-временная
информация), излучаемых в навигационном сообщении на момент времени tb (см.
табл. 11.4).
Таблица 11.4. Соответствие значения слова FT и прогнозируемой
ошибки измерения псевдо дальности
Значения слова FT
0
1
2
3
4
5
6
7
Точность <т, м
1
2
2,5 !
4
5
7
10
12
Значения слова FT
8
9
10
11
12
13
14
[ 15
Точность ст, м
14
16
32
64
128
256
512
не используется |
Слово Атп — смещение излучаемого навигационного радиосигнала
диапазона L2 относительно навигационного радиосигнала диапазона Ь\ для п -го НС:
где tL2Ji\ — аппаратурные задержки в соответствующих диапазонах,
выраженные в единицах времени.
Слово М — модификация НС, излучающего данный навигационный
сигнал. Символ «00» означает НС «Глонасс», «01» — НС «Глонасс-М».
396
Подсистема космических аппаратов
Слово 1п —признак недостоверности кадра я-го НС; 1п = О
свидетельствует о пригодности спутника для навигации; /Л=1 означает факт непригодности
данного спутника для навигации.
Отметим, что в словах, числовые значения которых могут принимать
положительные и отрицательные значения, старший разряд является знаковым,
символ «О» соответствует знаку «плюс», а символ «1» — знаку «минус».
11.4.3. Альманах системы ГЛОНАСС
Рассмотрим подробнее содержание альманаха системы, приведенного на
рис. 11.12 и 11.13.
Слово тс (с) — поправка к СШВ ГЛОНАСС относительно UTC(SU).
Поправка дана на начало суток с номером NA . Число разрядов этого слова — 28;
цена младшего разряда — 2~21; диапазон значений — ± 1.
Слово тс с увеличенным значением количества разрядов с 28 до 32 и
ценой младшего разряда слова до 2~31 ( т.е. до 0,46 не) передается в
навигационном сообщении спутника «ГЛОНАСС-М». Слово расположено в 5-, 20-, 35-,
50- и 65-й строках суперкадра с 38-го по 69 разряды.
Слово пА — условный номер НС в системе, который соответствует
занимаемой спутником рабочей точки орбиты (см. п. 11.1). Число разрядов этого
слова — 5; цена младшего разряда — 1; диапазон значений — 1 ... 24.
Слово НА — литер несущей частоты радиосигнала, излучаемого НС с
номером пА . Число разрядов этого слова — 5; цена младшего разряда — 1;
диапазон значений — 1 ... 31.
Отрицательные значения номера несущей частоты в кадре обозначаются в
соответствии с табл. 11.5
Таблица 11.5. Обозначение отрицательных значений номера несущей
частоты в кадре навигационного сообщения
Номер несу-
1 щей частоты
-01
-02
-03
1 -04
Значение слова Н„А
31
30
29
28
Номер
несущей частоты
-05
-06
-07
Значение слова
пА
27
26
25
Слово NA (сут) — календарный номер суток внутри четырехлетнего
периода, начиная с високосного года, к которым относятся поправки тс и дан-
397
Глава 11
ные альманаха системы (альманахи орбит и фаз). Число разрядов этого слова
— 11; цена младшего разряда — 1; диапазон значений — 1 ... 1461.
Слово ЯА (полуцикл) — долгота в системе координат ПЗ-90 первого
внутри суток с номером NA восходящего узла орбиты спутника с номером п. Чис-
—20
ло разрядов этого слова — 21; цена младшего разряда — 2 ; диапазон
значений — ± 1.
Слово tAn (с) — ближайшее к началу суток с номером NA время
прохождения первого внутри этих суток восходящего узла орбиты спутника с номером
пА . Число разрядов этого слова — 21; цена младшего разряда — 2"5;
диапазон значений —0...44100.
Слово AiA (полуцикл) — поправка к среднему значению наклонения
орбиты (/ = 63°) для спутника с номером пЛ на момент tAn . Число разрядов этого
слова — 18; цена младшего разряда — 2~20; диапазон значений — ± 0,067.
Слово АТА (с/виток) — поправка к среднему значению драконического
периода обращения (Г=43 200 с) НС с номером пА на момент времени tAn.
Число разрядов этого слова — 22; цена младшего разряда — 2~9; диапазон
значений — ±3,6 • 103.
Слово АГ„ (с/виток ) — скорость изменения драконического периода
обращения с номером пА . Число разрядов этого слова — 7; цена младшего
разряда — 2~14; диапазон значений — ± 2-8.
Слово еА — эксцентриситет орбиты НС с номером пА на момент времени
tAn. Число разрядов этого слова — 15; цена младшего разряда — 2-20;
диапазон значений — 0 ... 0,03.
Слово соА (полуцикл) — аргумент перигея орбиты НС с номером пА на
момент времени tAn. Число разрядов этого слова — 16; цена младшего разряда
— 2-15; диапазон значений — ±1.
Слово тА (с) — грубое значение сдвига БШВ НС с номером пА
относительно СШВ на момент времени tAn. Это слово равно смещению ПСП дально-
мерного кода излучаемого радиосигнала относительно номинального
положения, выраженному в единицах времени. Число разрядов этого слова — 10; цена
младшего разряда — 2"18; диапазон значений — ±1,9 • 10"3.
Слово СА — обобщенный признак состояния НС с номером пА на момент
закладки неоперативной информации (альманаха орбит и фаз). Нулевое
значение указывает на непригодность НС для навигационных определений. Число
398
Подсистема космических аппаратов
разрядов этого слова — 1; цена младшего разряда — 1; диапазон значений —
0... 1.
В НС «Глонасс-М» дополнительно передается следующая информация.
Слово rGPS — поправка на расхождение системных шкал времени
GPS( TGPS) и ГЛОНАСС ( Тптонасс ) в соответствии с выражением
Tgps ~~ ^глонасс = Д^ + tgps ,
где AT — целая часть, a rGPS — дробная часть расхождения шкал времени,
выраженного в секундах. Целая часть расхождения AT определяется
потребителем из навигационного сообщения системы GPS.
Слово N4 — номер четырехлетнего периода, первый год первого
четырехлетия соответствует 1996 году.
Слово М* — признак модификации п НС; «00» — «Глонасс», «01» —
«Глонасс-М».
Слова В\ и В2 — коэффициенты линейного полинома для определения
величины AUT1 расхождения всемирного UT1 (время Гринвичского меридиана
с учетом движения полюса) и координированного времени UTC(SU)
государственного стандарта Российской Федерации:
AUT1 = UT1 - UTC(SU).
Слово В\ — величина AUT1 на начало суток с номером NA, измеряется в
секундах.
Слово В2 — скорость изменения параметра AUTl, измеряется в секундах
за средние солнечные сутки (с/ссс):
AUT\=B\+B2(NT-NA).
Слово КР — признак ожидаемой секундной коррекции шкалы UTC на
величину ±1 с, как показано в табл. 11.6.
Таблица 11.6. Значения слова КР
Ykp
loo
101
[и
Информация о секундной коррекции UTC
В конце текущего квартала коррекции UTC не будет
В конце текущего квартала будет коррекция на плюс 1с.
В конце текущего квартала будет коррекция на минус 1 с. |
Признак КР помещается в навигационный кадр не позднее, чем за 8
недель до проведения коррекции. Однако решение о предстоящей коррекции
может быть принято раньше, чем за 8 недель. Поэтому с начала квартала до
принятия решения передается признак 10 (решение ещё не принято), а после
принятия решения передаётся один из трех перечисленных признаков.
399
Глава 11
Если потребитель определяет дальность до НС и радиальную
составляющую скорости НС на основе передаваемой неоперативной информации, то
погрешности измерений соответствующим образом зависят от «возраста» этих
данных:
возраст НИ, сут 1
погрешность определения (1а):
дальности, км 0,83
радиальной скорости, м/с 0,33
11.4.4. Резервные разряды в суперкадре
Дальнейшая совершенствование передаваемых навигационных сообщений
в системе ГЛОНАСС может проводится с учетом имеющегося резерва в
массиве данных. Он представляет собой запасные разряды в соответствующих
строках суперкадра служебной информации. Номера этих строк и разрядов
показаны в табл. 11.7.
Таблица 11.7. Резервные разряды
| Номер строки
1,16,31,46,61
2,17,32,47,62
3,18,33,48,63
4,19,34,49,64
5,20,35,50,65
74
[75
Номер резервного разряда |
^79-80
65-69
68
27-29,35-48
37
9-57
10-80 1
11.4.5. Контроль достоверности навигационных данных
Проверка качества навигационных данных может осуществляться
различными способами. Рассмотрим способ, заключающийся в контроле достоверности
данных, передаваемых в каждой строке. Он основывается на известных
свойствах кода Хэмминга и заключается в обнаружении и исправлении одиночных
ошибок (неправильный прием одного разряда строки), а также в обнаружении
двойных и большего четного числа ошибок. Как известно, каждая строка
представляет собой 85-разрядный код, где старшие 77 разрядов содержат
информационные символы, а младшие 8 разрядов — проверочные. Для исправления
однократных ошибок в вычислителе формируются по определенному закону [5.8—
5.9] контрольные суммы С, (/ = 1 ... 7), а для обнаружения двукратных и
большего четного числа ошибок формируется общая контрольная сумма СЕ. Путем
обработки этих сумм по соответствующему правилу принимается решение о нали-
10
2
0,7
20
3,3
4,2
400
Подсистема космических аппаратов
чии или отсутствии ошибок и их исправление. Более подробно алгоритм
проверки достоверности информации в строке описан в [1.3].
11.5. Контроль целостности СРНС ГЛОНАСС
Контроль целостности радионавигационного поля СРНС заключается в
контроле качества излучаемых НС навигационных радиосигналов и качества
передаваемой ими навигационной информации с целью поддержания высокой
достоверности навигационных измерений и/или предупреждения потребителей
о состоянии системы. Известно несколько способов контроля целостности.
Кратко рассмотрим некоторые из них применительно к системе ГЛОНАСС.
Самоконтроль бортовых систем НС. На спутниках системы ГЛОНАСС
осуществляется непрерывный автономный контроль (само-контроль)
функционирования основных бортовых систем. При обнаружении непарируемых
нарушений нормального функционирования этих систем, влияющих на качество
излучаемого спутником навигационного радиосигнала и достоверность
передаваемого навигационного сообщения, на спутнике формируется признак его
неисправности, который передается потребителю системы в составе оперативной
информации навигационного сообщения. Дискретность передачи такого
признака составляет 30 с. Максимальная задержка от момента обнаружения
неисправности до момента передачи соответствующего признака не превышает 1
мин. В НС «Глонасс-М» предусмотрено уменьшение данной задержки до 10 с за
счет введения признака 1п и увеличения оперативности изменения признака Вп.
Недостатки этого канала контроля заключаются в его неполноте.
Например, средства самоконтроля рассчитаны на обнаружение не всех возможных
нарушений в работе каждой бортовой системы НС; неисправности самих
средств контроля не обнаруживаются и не сопровождаются передачей
соответствующего сообщения потребителям; искажение эфемерид не может быть
обнаружено на самом НС и т. д.
Наземный контроль. Качество навигационного поля ГЛОНАСС
контролируется специальной аппаратурой, входящей в состав ПКУ, — аппаратурой
контроля поля (АКП). После соответствующего отказа бортовой аппаратуры
спутника АКП обеспечивает формирование признака его неисправности в
альманахах системы всех НС не позднее, чем через 16 ч. Дискретность передачи
данного признака в служебных сообщениях НС «ГЛОНАСС» составляет
2,5 мин.
В соответствии с этими двумя способами контроля навигационного поля
ГЛОНАСС в служебных сообщениях каждого НС передаются два типа
признаков исправности (неисправности): Вп — его нулевое значение означает
пригодность данного НС для проведения навигационных определений
потребителями системы; Сп — совокупность (/7 = 1,24) этих обобщенных признаков
отражает состояния всех НС системы на момент закладки НИ (альманахи орбит и
401
Глава 11
фаз). Значение признака Сп = О указывает на непригодность спутника с
системным номером п для проведения навигационных определений потребителями
системы. Значение признака Сп = 1 указывает на пригодность этого спутника.
Признаки первого типа передаются каждым НС в составе оперативной
информации, а признаки второго типа — в составе неоперативной информации.
Время, необходимое для формирования и доставки потребителям признаков Вп
(до 1 мин) значительно меньше, чем для признаков Сп (до 16 ч), но
формирование признаков Сп основано на более глубоком анализе качества
навигационного поля системы ГЛОНАСС. В связи с этим потребители системы должны
при принятии решения об использовании сигналов конкретного НС
анализировать значения обоих признаков. Решающее правило приведено в табл. 11.8.
Известны подходы к решению проблемы контроля целостности, свободные от
недостатков, связанных с неприемлемой задержкой в оповещении
потребителей. Они, в частности, предусматривают использование дифференциальных
измерений и своевременного оповещения потребителей об отказах НС с
помощью каналов связи (например, через дополнительные геостационарные ИСЗ).
Таблица 11.8. Решающее правило при анализе
контроля целостности
Значения признаков
!____ в*-
0
0
1
1 1
сп
0
1
0
1
Пригодность НС для
целей навигации |
-
+ 1
-
-
Автономный контроль целостности в приемнике (RAIM). Потребители
СРНС могут использовать избыточность навигационной информации,
получаемой в НАП СРНС от сети НС, для контроля качества навигационного поля, т. е.
для обнаружения и идентификации отказавшего НС, например, принимая
сигналы от пяти спутников ГЛОНАСС, можно организовать процедуру
навигационных определений только по четырем из них. Выбирая разные комбинации
четырех рабочих из пяти видимых спутников, можно получить пять наборов
координат потребителя, которые позволяют с высокой достоверностью судить о
наличии отказавшего НС, а при большем числе спутников — и о его номере.
Известно много способов реализации концепции RAIM, отличающихся,
например, алгоритмом формирования достаточной статистики, выбором
решающего правила, минимально необходимым числом НС, степенью
использования априорных сведений, достоверностью полученных результатов,
использованием избыточности измерений и т. д.
402
Подсистема космических аппаратов
Требования к вероятности правильного обнаружения РП0 наличия отказа
НС алгоритмом RAIM весьма разнообразны. Так, в соответствии с одним из
существующих стандартов (TSO С-129), введенным в США, в случае
превышения погрешности определения местонахождения с помощью аппаратуры
потребителей СРНС типа GPS некоторого предельного значения (защитный
порог AI), алгоритм RAIM должен обнаружить отказ НС с вероятностью
Рпо =0,999.
Учитывая значение частоты существенных (погрешность местоопределе-
ния превышает 500 м при PDOP < 6) отказов (А=3 в год) и полагая, что треть
потребителей пострадает от этого отказа, можно определить вероятность Рно
появления у потребителя в течение одного летного часа необнаруженной с
помощью RAIM погрешности, превышающей значение защитного порога,
/>Н0=8[А/(3-365.24)](1-РП0).
Эксплуатационная готовность устройства, реализующего алгоритм RAIM,
зависит от многих факторов (числа используемых НС, угла маски спутников,
координат потребителя и т. д.). Самая высокая степень готовности («99 %)
обеспечивается при полете по маршруту, когда защитный порог AL « 3,6 км, а
самая низкая (90 ... 95 % на средних широтах) — при некатегорированном
заходе на посадку, когда AL « 0,55 км. Эти данные соответствуют случаю
использования вспомогательных данных от баровысотомера. Как видно, даже в
этом случае эксплуатационная готовность не достигает 100%. Поэтому такое
оборудование должно использоваться в качестве дополнительного.
Бортовая автономная система контроля целостности (AAIM).
Потребители СРНС могут использовать и избыточность навигационной информации,
получаемой от различных бортовых навигационных датчиков
(радиотехнических и нерадиотехнических), для контроля качества навигационного поля
ГЛОНАСС, т. е. для обнаружения и идентификации отказавшего НС.
Трудность реализации такой концепции часто связана со сравнительно большой
погрешностью измерений с помощью типовых бортовых навигационных
датчиков и необходимостью соответствующих аппаратных и/или программных
доработок бортового оборудования.
Заметим, что иногда с грубыми ошибками в дальномерных измерениях,
вызванными соответствующими отказами НС, целесообразно бороться не
исключением сигнала отказавшего спутника, а использованием избыточных
навигационных определений.
11.6. Навигационные спутники системы ГЛОНАСС
Навигационные спутники являются основным элементом системы
ГЛОНАСС и предназначены для выполнения следующих функций:
1) навигационное обеспечение:
403
Глава 11
- непрерывное излучение высокостабильных навигационных
радиосигналов в дециметровом диапазоне волн (L диапазон);
- прием, хранение, формирование и передача навигационной информации
(данных);
- формирование оцифрованной высокостабильной бортовой шкалы
времени, хранение и передача в навигационном сигнале;
2) автономное эфемеридно-временное обеспечение:
- проведение межспутниковых измерений и обмен результатами
измерений;
- обработка результатов межспутниковых измерений, расчет и
прогнозирование эфемерид и частотно-временных поправок;
- информационный обмен между КА результатами межспутниковых
измерений и навигационными параметрами;
- прием данных о параметрах вращения Земли;
3) управление, контроль и баллистическое обеспечение:
- ретрансляция или излучение сигналов для радиоконтроля орбиты
спутника и определения поправок к бортовой шкале времени;
- прием, квитирование, дешифрирование и отработка радиокоманд;
- прием, запоминание и отработка временных программ управления
режимами функционирования спутника на орбите;
- формирование телеметрических данных о состоянии бортовой
аппаратуры и передача их в наземный комплекс управления;
- прием и отработка кодов коррекции и фазирования бортовой шкалы
времени;
- выработка и передача сигналов «Вызов наземного комплекса
управления» при сбое или выходе важных контролируемых параметров за пределы
нормы;
- анализ состояния бортовой аппаратуры (совместно с наземным
комплексом управления) и выработка управляющих команд;
- ретрансляции запросных лазерных сигналов наземных квантово-
оптических средств.
Реализация вышеперечисленных функций на спутнике возлагается на
следующую аппаратуру и системы: бортовой целевой комплекс, бортовой
комплекс управления, обеспечивающие бортовые системы (коррекции, ориентации
и стабилизации, электропитания, терморегулирования) и конструкцию.
Конкретная комплектация приборами аппаратуры и систем зависит от типа
навигационного спутника.
В системе ГЛОНАСС используются следующие типы навигационных
спутников: «Глонасс», «Глонасс-М» и «Глонасс-К», отличающиеся
номенклатурой решаемых задач, аппаратурным составом, техническими
характеристиками и ресурсом.
404
Подсистема космических аппаратов
11.6.1. Навигационный спутник "Глонасс"
Навигационный спутник Тлонасс" разработан в НПО ПМ (г. Красноярск)
и изготавливался в ПО «Полет» (г. Омск).
Бортовой целевой комплекс реализует целевую задачу спутника "Глонасс"-
непрерывное излучение в сторону Земли высокостабильных
радионавигационных сигналов в двух диапазонах частот L\ и L2 . В бортовой целевой комплекс
входит следующая аппаратура: бортовой источник навигационных
радиосигналов, антенно-фидерная система, бортовое синхронизирующее устройство.
Принципы построения и функционирования вышеуказанной аппаратуры
приведены в п. 11.6.5.
Бортовой комплекс управления совместно с наземным комплексом
управления решает задачи управления, контроля и баллистического обеспечения.
При этом на наземный комплекс управления возлагается задача формирования
программы работы спутника с помощью радиокоманд и временных программ
по результатам анализа телеметрической информации со спутника, проведение
измерений параметров орбиты спутника и сверки времени, прогнозирование
движения спутника и ухода его шкалы времени с проведением расчета и
закладки на спутник эфемеридно-временной информации. В бортовой комплекс
управления входят:
бортовая аппаратура командно-измерительной системы,
системы телеконтроля,
специализированная вычислительная машина, обеспечивающая отработку
временных программ и эфемеридно-временной информации.
Система телеконтроля формирует и передает по командной радиолинии
телеметрическую информацию о состоянии спутника, при нахождении его как
непосредственно в зоне радиовидимости наземных средств, так и на протяжении
всего витка его движения путем запоминания значимых событий и
сопутствующей им телеметрической информации. Дополнительно в бортовом комплексе
управления реализована аппаратная логика управления спутником при
возникновении аварийных ситуаций с формированием признака «вызов наземного
комплекса управления». Этот признак передается по командной радиолинии.
В целях обеспечения высокой точности измерений осуществляется
калибровка радиолиний спутника с помощью оптической ретрорефлекторной
антенной системы, предназначенной для пассивного отражения оптических сигналов
наземных квантово-оптических средств.
Система коррекции спутника предназначена для коррекции орбиты
спутника и формирования управляющих моментов системы ориентации. Система
коррекции состоит из двигательной установки и блока управления.
Двигательная установка формирует импульсы коррекции с помощью двух двигателей
коррекции и управляющих моментов по трем осям с помощью 24-х двигателей
ориентации (основные и резервные). Рабочим телом двигателей является гид-
405
Глава 11
разин. Высокая точность выдачи импульсов коррекции параметров орбиты
позволяет удерживать спутник в системной точке в заданных пределах (±5° по
аргументу широты) без последующих коррекций в течение всего срока
функционирования спутника.
Система ориентации и стабилизации обеспечивает непрерывную
ориентацию спутника на Землю (продольная ось спутника с антеннами) и на Солнце
(панелей солнечной батареи), периодическую ориентацию по вектору
скорости. При этом на время ориентации по вектору скорости штатная ориентация
на Солнце прекращается. Ориентация спутника осуществляется с
использованием электромаховиков, которые требуют периодической их разгрузки по мере
накапливания кинетического момента. Для снижения возмущений на движение
спутника по орбите разгрузка электромаховиков осуществляется с помощью
электромагнитов, управляемых по сигналам магнитометра. В целях снижения
влияния магнитных полей спутника магнитометры установлены на выносной
штанге.
Система электропитания формирует электропитание бортовой
аппаратуры с постоянным стабильным напряжением качестве генератора
энергии используется солнечная батарея на кремниевых фотопреобразователях,
а в качестве аккумулятора — никель-водородная батарея.
Система терморегулирования обеспечивает тепловой режим приборов в
термоконтейнере с использованием одноконтурной (газовой) схемы с жалюзи,
а приборов на антенном блоке — с использованием непосредственного
излучения тепла в окружающее космическое пространство. Излучательным
радиатором одноконтурной схемы является часть поверхности термоконтейнера,
эффективное излучение которой регулируется переменным положением створок
жалюзи. Высокая точность регулирования положения створок жалюзи
позволяет стабилизировать температуру газа в термоконтейнере с точностью 5°С,
что повышает стабильность атомного стандарта частоты.
Основу конструктивно-компоновочной схемы спутника составляет
силовой термоконтейнер, внутри которого размещена часть приборов. На нижней
части основания термоконтейнера крепятся элементы системы отделения, а на
верхней части термоконтейнера размещен антенный блок. Навигационные
передатчики, как наиболее тепловыделяющие элементы, вынесены на антенный
блок и расположены вблизи излучателей антенн. На время выведения
спутников на орбиту панели солнечных батарей уложены в ромбическую форму,
оптимальную для размещения трех КА в цилиндрической зоне полезного груза
обтекателя ракеты-носителя. После выведения на орбиту осуществляется
раскрытие солнечных батарей и их непрерывная ориентация на Солнце с
помощью электроприводов. Штанга магнитометра во время размещения спутника в
зоне полезного груза ракеты-носителя сложена и раскрывается после его
выведения на орбиту.
406
Подсистема космических аппаратов
Выведение спутников на орбиту осуществляется по групповой схеме
(одновременно три спутника) с космодрома "Байконур" с помощью ракеты-
носителя "Протон" с разгонным блоком. Время выведения на орбиту не
превышает 7 часов.
Отделение трех спутников от разгонного блока осуществляется
одновременно с закруткой каждого спутника с угловой скоростью около 27 град/с
вокруг поперечной оси. Такой режим отделения выбран исходя, с одной стороны,
из обеспечения безударного отделения трех спутников от разгонного блока и, с
другой стороны, обеспечения равномерной засветки солнечных батарей,
находящихся в сложенном положении и получения на борту спутника
электроэнергии, достаточной для поддержания режима ожидания.
Глобальная навигационная спутниковая система ГЛОНАСС в 1993г. была
принята в эксплуатацию с орбитальной группировкой из 12 спутников
«Глонасс», а в 1995 г. была развернута орбитальная группировка штатного состава
из 24 спутников. Характеристики спутника «Глонасс» приведены в табл. 11.9, а
его конструкция схематично приведена на рис. 11.14.
Таблица 11.9. Характеристики спутника «Глонасс»
1 N
1
2
3
4
5
6
7
Г I
\ТЛ
1<П
LllI
Параметры
Эффективная изотропная излучаемая
мощность навигационного сигнала, дБВт
в углах ±19°
в углах ±15°
в углах 0°
Руточная нестабильность сигнала
Точность ориентации, град:
Тяга двигателей, Н:
Суммарный импульс для коррекции, Не
Рабочая мощность солнечных батарей, Вт
Рабочая энергоемкость аккумуляторных
батарей, Вт/час
Диапазон терморегулирования, °С:
стандартов частоты
газа в термоконтейнере
Ресурс спутника, лет
Масса спутника, кг.
Энергопотребление аппаратуры спутника, Вт
Величина
22(F1),21(F2)
27 (F1), 19 (F2)
25 (F1), 19 (F2)
5хКГ13
0,5 (на Землю)
5 (на Солнце)
5(коррекция)
0,1 (ориентация)
90 000
1600
1800
(15...30)±5
0...40
3
1415
1000 1
407
Глава 11
Солнечные
батареи
Жалюзи системы
терморегулирования
Двигательная
установка
Антенный блок
Навигационная
антенна
Магнитометр
Гермоконтейнер
Рис. 11.14. Навигационный спутник Тлонасс"
11.6.2. Навигационный спутник "Глонасс - М"
Навигационный спутник "Глонасс-М" разработан и изготавливается в
НПО ПМ (г. Красноярск).
Навигационный спутник "Глонасс-М" имеет по сравнению со спутником
"Глонасс" лучшие целевые и эксплутационные характеристики, увеличенный
ресурс работы.
Бортовой целевой комплекс доработан в следующей части.
В первую очередь модернизирован навигационный радиосигнал:
1) полоса используемых частот смещена влево L\ = (1598,0625 ... 1605, 375)
±5,11 МГц, L2 = (1242,9375 ... 1248,625) ± 5,11 МГц;
2) увеличена мощность излучения в два раза на частоте диапазона L2 ;
3) установлены режекторные фильтры, уменьшающие внеполосное
излучение в диапазонах частот (1610,6 ... 1613,8) МГц и (1660,0 ... 1670,0) МГц до
уровня, приведенного в рекомендациях 769 МККР;
4) на частотах L\ и L2 излучаются двухкомпонентные сигналы СТ и ВТ,
содержащие цифровую информацию и дальномерный код для измерений
дальности; кроме того, повышена информативность навигационного сигнала за счет
размещения в резервных разрядах навигационного кадра дополнительной
информации, в том числе:
1) расхождение шкалы времени систем GPS и ГЛОНАСС;
408
Подсистема космических аппаратов
2) признак недостоверности навигационного кадра (передается с
дискретностью 4 с);
3) признак ожидаемой секундной коррекции шкалы UTC-UT1 (за 8 недель
до коррекции);
4) возраст эфемеридно-временной информации.
За счет использования цезиевых атомно-лучевых трубок и обеспечения их
высокоточной термостабилизации снижена относительная нестабильность
частоты навигационного сигнала до 1 • 10~13, а за счет повышения точности
ориентации солнечных батарей на Солнце снижен уровень неучтенных активных
сил, воздействующих на спутник до уровня 5 • 10~10 м/с2.
В результате реализации вышеперечисленных мероприятий улучшены
точностные характеристики навигационных определений по спутнику «Гло-
насс-М» примерно в 2 раза.
Для повышения автономности спутника на нем размещена аппаратура
межспутниковых измерений и информационного обмена (принципы работы
изложены в разделе 11.6.5).
Бортовой комплекс управления построен на основе бортовой ЦВМ,
обеспечивающей информационную увязку с приборами по шинам MIL-STD-1553 В
и решающей задачи управления, диагностики, обработки информации
межспутниковых измерений, расчета и формирования эфемеридно-временной
информации.
Принципы построения и функционирования обеспечивающих систем
сохранены, однако изменился приборный состав, их конструктивное исполнение
и технические характеристики. Это привело к существенному изменению
конструктивно-компоновочной схемы спутника «Глонасс-М» по сравнению со
спутником «Глонасс». Из состава спутника исключен магнитометр, включение
электромагнитов осуществляется по программе, рассчитываемой бортовой
ЦВМ. Уменьшен в два раза запас рабочего тела для коррекции орбиты, что
было обосновано результатами эксплуатации спутника «Глонасс». Уменьшено
количество двигателей ориентации в 2 раза за счет перехода от схемы
формирования управляющего момента с помощью двух двигателей к схеме однодви-
гательной. Возникающая при этом возмущающая сила на центр масс КА
учитывается при проведении коррекции орбиты.
Конструктивная схема спутника «Глонасс-М» построена на основе
использования унифицированной космической платформы связных спутников
разработки НПО ПМ. При этом сохранена ромбическая схема укладки солнечных
батарей на время выведения спутника на орбиту и способ их отделения.
Спутник Тлонасс-Ми выводится по групповой схеме — одновременно 3
спутника с космодрома "Байконур" с использованием ракеты-носителя
"Протон" и разгонного блока.
На рис. 11.15 схематично приведена конструкция спутника «Глонасс-М».
409
Глава 11
Рис. 11.15. Навигационный спутник Тлонасс-Мм
Первый летный образец спутника Тлонасс-М", разработанный и
изготовленный в НПО ПМ, был запущен в составе комбинированного блока (вместе с
двумя спутниками Тлонасс") в 2003 г. Последующими запусками спутника
Тлонасс-М" в 2004 г. (один КА), 2005 г. (два спутника) были завершены
летные испытания модернизированного спутника и они были переданы в опытную
эксплуатацию. Запуском в 2006 г. трех спутников Тлонасс-М" началось
интенсивное восстановление штатной орбитальной группировки.
При запланированном темпе запусков — 6 спутников в год будут
обеспечены сроки развертывания штатной орбитальной группировки из 24 спутников
в 2010 г.
Характеристики спутника «Глонасс-М» приведены в табл. 11.10.
Таблица 11.10. Характеристики спутника «Глонасс-М»
\~н
1
Lj
Параметры
Эффективная изотропная излучаемая
мощность навигационного сигнала, дБхВт
в углах ±19°
в углах ±15°
в углах 0°
Суточная нестабильность сигнала
Величина
26(F1),21(F2)
30(F1),23(F2)
28(F1),21(F2)
1хКГ13 J
410
Подсистема космических аппаратов
1
4
[ь
1 6
7
[7
[9
Г10
и
Точность ориентации, град:
Тяга двигателей, Н:
Суммарный импульс для коррекции, Не
Рабочая мощность солнечных батарей, Вт
Рабочая энергоемкость аккумуляторных
батарей, Вт/час
Диапазон терморегулирования, °С :
стандартов частоты
газа термоконтейнера
Ресурс спутника, г
Масса спутника, кг
Энергопотребление спутника, Вт
0,5 (на Землю)
2 (на Солнце)
5(коррекция)
0,1 (ориентация)
45000
2200
2300
(15...30)±1
0...40
7
1415
1270
11.6.3. Навигационный спутник "Глонасс-К"
Навигационный спутник "Глонасс-К" разрабатывается в НПО ПМ
(г. Красноярск).
Навигационный спутник мГлонасс-Ки имеет следующие отличительные
особенности в сравнении со спутником мГлонасс-Мм:
а) вводится третья частота в L диапазоне для повышения надежности
навигационных определений;
б) увеличен срок функционирования КА;
в) уменьшена масса спутника;
г) дополнительно размещена аппаратура спасения терпящих бедствия;
д) реализованы мероприятия, снижающие уровень воздействия немодели-
11 О
руемых сил до 5х 10" м/с ;
е) применена негерметичная конструктивная схема приборного отсека.
Спутник «Глонасс-К» создается на базе конструктивно-компоновочной
схемы с использованием коробчатого негерметичного приборного отсека из со-
топанелей. Все приборы размещены на внутренних поверхностях сотопанелей,
которые одновременно являются радиаторами-излучателями.
Тепловой режим приборов обеспечивается пассивным способом —
непосредственным сбросом тепла от приборов теплопроводностью через сотопа-
нель в окружающее космическое пространство путем излучения. Для
исключения переохлаждения используется теплоизоляция, электрообогреватели,
тепловые трубы. Для атомных стандартов частоты организована местная
прецизионная термостабилизация радиаторов излучателей в диапазоне ±0.5°С с помощью
управляемых обогревателей.
411
Глава 11
В штатном режиме поддерживается непрерывная ориентация спутника на
Землю (продольная ось спутника с антеннами) и на Солнце (панелей солнечной
батареи), периодическая ориентация по вектору скорости. При этом на время
ориентации по вектору скорости штатная ориентация на Солнце прекращается.
Ориентация обеспечивается с помощью электромаховиков, периодически
разгружаемых электромагнитами.
Система коррекции спутника «Глонасс-К» подобна системе коррекции
спутника «Глонасс-М» и выполняет задачи создания управляющих моментов
для реализации начальных режимов ориентации и выдачи импульсов
коррекции для приведения спутника в системную точку, удержания в ней и перевода
в другую системную точку. Бак для хранения рабочего тела размещен вблизи
центра масс спутника внутри негерметичного приборного отсека. Имеется
возможность снимать бак для автономной его заправки рабочим телом. Высокая
точность выдачи импульсов коррекции в процессе приведения спутника в
заданную системную точку позволяет удерживать спутник в заданных пределах
по аргументу широты без коррекций в течение всего срока функционирования.
Система электропитания на основе никель-водородных аккумуляторов и
арсенид-галиевых солнечных батарей формирует электропитание бортовой
аппаратуры постоянным стабильным напряжением 27^ В и мощностью
непрерывно на теневых и солнечных орбитах.
Бортовой комплекс управления на основе бортовой ЦВМ обеспечивает
информационную увязку с приборами по шинам MIL-TD-553 и решает задачи
управления, диагностики, обработки информации межспутниковых измерений,
расчета и формирования эфемеридно-временной информации.
Первые спутники Тлонасс-К" запланировано выводить с космодрома
"Байконур" по комбинированной схеме, т.е одновременно два спутника
"Глонасс-М" и один спутник "Глонасс-К".
Характеристики спутника «Глонасс-К» приведены в табл. 11.11, а его
конструкция схематично приведена на рис. 11.16.
Таблица 11Л1. Характеристики спутника «Глонасс-К»
VW
1
\2
Гз~
Параметры
Эффективная изотропная излучаемая
мощность навигационного сигнала, дБхВт
в углах ±19°
в углах ±15°
в углах 0°
Суточная нестабильность сигнала
Точность ориентации, град:
Величина
26(F1),21(F2,F3)
30(Fi),23(F2,F3)
28(F1),21 (F2,F3)
1х1(Г13о.е
0,5 (на Землю)
1 (на Солнце)
412
Подсистема космических аппаратов
4
[5
[6
7
8
9
Гю
[ и
Тяга двигателей, Н:
Суммарный импульс для коррекции, Не
Рабочая мощность солнечных батарей, Вт
Рабочая энергоемкость аккумуляторных
батарей, Вт/час
Диапазон терморегулирования, °С :
стандартов частоты
приборов
Срок активного существования спутника,
лет
Масса спутника, кг
Энергопотребление спутника, Вт
0,1 (коррекция) 1
0,1 (ориентация)
45000
2750
2800
(15... 20) ±6,5
-20...50
10
995
1400 1
Приборный
Навигационная
антенна
Антенны системы
спасания
Солнечные
батареи
Двигательная
установка
Датчики ориентации
на Солнце и Землю
Рис. 11.16. Навигационный спутник Тлонасс-К"
11.6.4. Пассивный спутник "Эталон"
Спутник "Эталон" был разработан для отработки согласующей модели
геопотенциала для орбит системы ГЛОНАСС. На спутнике реализован только
оптический (лазерный) метод измерения дальности.
Спутник "Эталон" разработан в НПО ПМ и изготовлен в ПО «Полет». По
своему конструктивному исполнению он представляет собой тяжелое пробное
тело сферической формы, внешняя поверхность которого покрыта призматиче-
413
Глава 11
скими светоотражателями (для отражения лазерного луча) и светорассеиваю-
щей (диффузно) поверхностью между ними для наблюдения в телескоп за
спутником в отраженных лучах Солнца. Такая форма спутника позволяет
снизить воздействие на него неучтенных активных сил негравитационной
природы, что обеспечивает достаточно точное исследования всех гармоник
гравитационного поля.
Спутники "Эталон" (рис. 11.17) были выведены на орбиты системы
ГЛОНАСС (круговая орбита высотой -20000 м, наклонение -65°)
одновременно со спутниками системы ГЛОНАСС в составе комбинированного блока
(два спутника «Глонасс» и один спутник «Эталон»): 10 января 1989 г. (Эталон-
1) и 31 мая 1989г. (Эталон-2).
Рис. 11.17. Общий вид спутника «Эталон»
При заданном сроке активного существования 5 лет спутники «Эталон»
продолжают работать уже сверх гарантийных сроков без ухудшения
эксплуатационных характеристик более 20 лет.
В настоящее время они используются международным сообществом для
решения ряда фундаментальных задач геодезии и динамики Земли:
Характеристики спутника «Эталон» приведены в табл. 11.12.
Таблица 11.12. Характеристики спутника «Эталон»
ПчГ
1.
2.
3.
4.
5.
6.
8.
Наименование
Эффективная площадь, м
Угловая ширина диаграммы (по уровню 0,5), угл. сек
Расстояние от геометрического центра до плоскости
наиболее вероятного отражения, мм
Масса спутника, кг
Геометрические размеры спутника, мм
Отклонение центра масс спутника от геометрического
центра сферы, мм
Максимальная визуальная звездная величина
Величина
0,010 ±0,0016
8,6
558 ± 44
1344,5 ±0,8
1294 1
1,2
+ 11,5 __
414
Подсистема космических аппаратов
11.6.5. Особенности построения навигационного спутника
Навигационный спутник в космической навигационной системе
используется как радионавигационная точка с известными координатами, излучающая
высокостабильный навигационный сигнал, охватывающий весь земной шар и
околоземное космическое пространство. Это вносит специфические требования
к построению спутника в целом и его составных частей.
Навигационные антенны размещаются таким образом, чтобы их фазовый
центр находился на минимальном расстоянии от продольной оси спутника,
которая совмещается с центром масс спутника и совпадает с радиус-вектором
орбиты.
Для атомных стандартов частоты созданы комфортные условия
эксплуатации (в первую очередь прецизионная термостабилизация) и обеспечиваться
экранирование от воздействия магнитных полей.
Учитывая важность высокоточного прогнозирования движения спутника
по орбите на длительный период (более суток), уделено внимание учету всех
активных сил негравитационной природы, воздействующих на спутник. Часть
факторов, имеющих регулярный характер, моделируются при прогнозировании
движения спутника. Факторы, имеющие случайный характер воздействия и не-
поддающиеся моделированию, существенно ограничены (до 5x10" м/с ).
Для этого разработаны и реализованы специальные мероприятия по
снижению уровня их воздействия, а именно:
а) по системе ориентации и стабилизации:
, реализуется высокая точность ориентации солнечных батарей на Солнце
(1-2°);
для разгрузки электромаховиков в штатном режиме работы спутника
используется электромагнитная система управляющих моментов;
б) по двигательной установке:
для снижения утечек рабочего тела через сопла двигателей (в
выключенном состоянии) до уровня 0,025 см3/с используется последовательная пара
запорных клапанов в гидротракте;
в) по конструкции:
обеспечена высокая герметичность замкнутых объемов (0,01—0,001 мкм
мм.р.ст./с);
используются материалы на внешних поверхностях с низким уровнем
испарения (потеря массы < 1%);
поддерживается высокая стабильность конфигурации спутника в течение
всего времени его функционирования на орбите;
создана модель деградации значений оптических коэффициентов внешних
поверхностей корпуса спутника и солнечных батарей;
г) по системе терморегулирования:
создана температурная модель внешнего контура спутника;
415
Глава 11
создана модель работы створок жалюзи или реализуется их экранирование
от солнечного светового давления.
В системе ГЛОНАСС обеспечена высокая стабильность орбитальной
структуры за счет:
а) отличия периода обращения от половины звездного периода на 45 мин;
б) ассиметричного расположения абсолютных долгот восходящих узлов
спутников с целью обеспечения их минимального отклонения от прецессирую-
щих с постоянной скоростью орбитальных плоскостей идеальной структуры;
в) реализации среднего периода обращения каждого спутника на сроке его
активного существования, равного среднему драконическому периоду в
идеальной структуре.
Это позволило удерживать взаимные уходы спутников по аргументу
широты в допустимых пределах (<5°) за весь срок активного существования
спутника без коррекции параметров орбиты при условии высокоточной коррекции
параметров орбиты.
11.6.6. Логика функционирования навигационного спутника
В процессе функционирования спутник последовательно находится в
следующих режимах работы: выведение на орбиту, ожидание после выведения на
орбиту, начальной ориентации, дежурное функционирование, ввод штатного
функционирования, штатное функционирование.
В процессе выведения спутника вся его аппаратура выключена,
задействованы специальные цепи (непосредственно от аккумуляторной батареи)
электрообогрева датчиков ориентации на Солнце.
На всем интервале движения спутника от опорной орбиты до конечной (на
переходном эллипсе) разгонный блок осуществляет пространственные
развороты для обогрева спутника солнечными лучами.
После выведения спутников на заданную орбиту (за время не более 7 ч) по
команде, выдаваемой разгонным блоком непосредственно после остановки
двигателей, включаются электропитание некоммутируемых шин питания и
дежурные схемы спутников. Через 15 с после этого система управления
разгонным блоком выдает команду на отделение спутников. Эта операция
осуществляется для трех спутников синхронно с их закруткой (с угловой скоростью не
более 27 град/с). Процесс отделения спутников контролируется с помощью
телеметрической системы разгонного блока. На каждом спутнике при его
отделении формируется команда «Контакт отделения», по которой он переводится
в режим ожидания, в котором при прохождении спутником зоны
радиовидимости средств наземного комплекса управления (НКУ) обеспечивается прием
команд управления и передача телеметрических данных. Длительность работы
спутника в режиме ожидания — до трех суток.
416
Подсистема космических аппаратов
Перевод спутника в режим начальной ориентации происходит в зоне
радиовидимости наземных средств в следующей последовательности: раскрытие
солнечных батарей и штанги магнитометра; успокоение спутника; начальная
ориентация спутника на Солнце и начальная ориентация спутника на Землю.
В режиме успокоения осуществляется торможение вращательного
движения спутника с помощью двигательной установки с одновременным
разворотом панелей солнечных батарей для выставки крыльев активной поверхностью
в одну сторону и установкой их в плоскости, совпадающей с продольной осью
спутника.
В режиме начальной солнечной ориентации осуществляется разворот
спутника вокруг продольной оси с помощью двигателей маховиков до
попадания Солнца (диаграмма прибора ножевидной формы) и разворот вокруг
поперечной оси до совмещения нормали к солнечной батареи с направлением на
Солнце. После завершения этой операции осуществляется закрутка вокруг оси,
ориентированной на Солнце для создания возможности длительного
пребывания (до трех суток) в состоянии с благоприятным энергоснабжением спутника.
Режим начальной ориентации на Землю проводится в зоне
радиовидимости НКУ на участках, где угол между линями «Солнце—спутник» и
«спутник—Земля» составляет (90±18)°. При этом обеспечивается торможение
вращения спутника и его разворот с помощью управляющих
двигателей—маховиков вокруг направления, ориентированного на Солнце до
попадания Земли в поле зрения прибора ориентации на Землю. После этого
включается режим одновременного слежения за Солнцем и Землей и спутник
переводится в режим дежурного функционирования. В этом состоянии организуется
ввод спутника в штатное функционирование, который начинается с приведения
спутника в заданное положение на орбите (рабочую системную точку). Эта
операция осуществляется в несколько этапов: определение параметров орбиты
и формирование программы приведения; выдача импульсов коррекции для
обеспечения требуемой скорости смещения спутника относительно
номинальной орбиты; пассивное движение спутника по орбите в заданном направлении;
выдача импульсов, обеспечивающих торможение движения спутника и
приведение спутника в заданное положение на орбите; проведение измерений
параметров орбит.
После завершения всей программы приведения спутника в заданное
положение с требуемой точностью производится окончательное уточнение
параметров орбиты, высокоточная синхронизация бортовой шкалы времени, расчет
временных программ и эфемеридно-временной информации, закладка их на
спутник. После этого спутник может использоваться по целевому назначению.
При штатной эксплуатации управление спутником организуется по
типовым циклограммам управления с использованием командной радиолинии.
Типовые циклограммы управления формируются в виде массива командно-
программной информации, закладываемой на спутник. Это обеспечивает про-
14-1026
417
Глава 11
граммное управление спутником на длительных интервалах времени с
соответствующим увеличением интервалов радиоконтактов с спутником для
управления. Для навигационных спутников необходимо постоянное проведение
высокоточных измерений орбиты и сверки времени, расчет и закладку на спутник
эфемеридно-временной информации (практически на каждом витке).
Вывод из целевого использования спутника осуществляется при
возникновении аварийных ситуаций, приводящих к кратковременному нарушению
целевого функционирования спутник, а также после возникновения необратимых
отказов, исключающих возможность целевого применения спутник. К
основным признакам аварийных ситуаций КА кратковременного типа относятся:
недопустимое снижение энергоемкости аккумуляторных батарей, отсутствие
ориентации на Солнце, сбой в работе бортовой ЦВМ, непрохождение команд и
служебной информации, отсутствие телеметрической информации. В этом
случае автоматически КА переводится в режим обеспечения живучести:
1) поддержание положительного энергобаланса переводом спутник в
режим минимального потребления (выключение целевой аппаратуры) и
гарантированного энергосъема с солнечных батарей в нештатном режиме ориентации
(аварийная закрутка спутник, реализация режима автономной ориентации на
Солнце);
2) поддержание теплового режима приборов спутник в расширенных
допусках по температуре, допустимой для сохранения их работоспособности.
Аварийная ситуация на борту спутник регистрируется телеметрической
аппаратурой (время события, информационная посылка) и запоминается с
последующей передачей по командной радиолинии сигнала «вызов НКУ» при
вхождении спутника в зону радиовидимости наземных средств.
Пропадание навигационного радиосигнала является достаточным
признаком оперативного вмешательства средств НКУ в работу спутника.
При возникновении аварийных ситуаций на спутнике необратимого типа
принимается решение о прекращении его обслуживания.
11.7. Бортовой радиотехнический комплекс спутника
11.7.1. Бортовой источник навигационных радиосигналов
Бортовой источник навигационных радиосигналов (БИНРС) предназначен
для формирования и излучения высокостабильных навигационных
радиосигналов в двух частотных диапазонах — L\, L2 (а в перспективе и в диапазоне L3).
Радиосигнал диапазона L\ модулирован по фазе кодом дальности и
навигационными данными (эфемеридная информация, поправки времени, частоты и
фазы бортового стандарта частоты). Радиосигнал диапазона L2 модулирован
только кодом дальности и предназначен для исключения влияния
ионосферной рефракции на точность измерений навигационных параметров военными
418
Подсистема космических аппаратов
потребителями. В перспективе в данном диапазоне будет излучаться сигнал
для гражданских потребителей (более подробно в гл. 14).
Обобщенная схема БИНРС приведена на рисунке 11.18 и включает:
формирователь навигационного кадра (ФНК);
формирователь навигационного сигнала (ФНС);
контроллер магистрали мультиплексного канала обмена (МКО);
синтезатор несущих частот диапазонов II и L2 ;
четырехканальный усилитель мощности диапазона Ы ;
двухканальный усилитель мощности диапазона L2 ;
12-элементная антенная система (активная фазированная антенная решетка
(АФАР)).
Взаимодействие БИНРС с другими бортовыми системами осуществляется
по стандартному МКО.
Магистраль МКО
Контроллер
магистрали
МКО
Управление
частотой
л.
I
Формирователь
навигационных
кадров
Диагностика
управления
резервом
Синтезатор
несущих
частот
/ы
Н\
Н2
III
НЪ
Формирователь
навигационных
радиосигналов
т
4-х канальный
усилитель
мощности
I
I
-Лт
-1 сек
-БШВ
2-х канальный
усилитель
мощности
I
12-ти элементная антенна
Рис. 11.18. Обобщенная схема БИНРС
Формирователь навигационного кадра выполняет следующие функции:
прием от бортового цифрового вычислительного комплекса (БЦВК)
массивов навигационной информации;
хранение принятых массивов навигационной информации (навигационный
суперкадр (НСК) в течение 30 или 60 мин (в зависимости от текущего периода
смены оперативной информации);
циклическое формирование навигационных кадров НСК СТ (HI), НСК
ВТ(Н2) и кадров дополнительной информации НЗ из хранящихся в ОЗУ
прибора массивов НСК СТ и НСК ВТ в течение 30 или 60 мин (в зависимости от
текущего периода смены оперативной информации);
419
Глава 11
выдача в аппаратуру формирования навигационных радиосигналов
сформированных навигационных кадров ИСК СТ, НСК ВТ и НЗ;
прием от БЦВК и выдача в аппаратуру БИНРС команд управления;
хранение информации о текущей конфигурации бортовой аппаратуры;
периодическое считывание из аппаратуры БИНРС телеметрической
информации;
диагностику работы приборов для автономного управления комплексом;
прием от БСУ бортовой шкалы времени;
привязку к БШВ выдаваемых НСК СТ, НСК ВТ и НЗ;
контроль монотонности БШВ;
прием от БЦВК специализированной пользовательской информации, ее
преобразование и выдачу в аппаратуру БИНРС для передачи потребителю.
Обмен данными между ФНК и БЦВК осуществляется в двух основных
форматах обмена, предусмотренных ГОСТ26765.52-87 и MIL-STD-1553В.
Обмен данными по МКО для каждого типа массивов осуществляется либо
периодически (загрузка навигационных кадров, считывание телеметрической
информации), либо по мере возникновения необходимости (выдача команд
управления, формирование специальной информации).
Загрузка массивов НСК СТ и НСК ВТ осуществляется с периодом 30 или
60 мин. Период загрузки определяется текущим периодом размножения ОИ в
БЦВК. Информация о текущем периоде размножения ОИ (признак Ш)
содержится в массивах (в структуре кадров) НСК СТ и НСК ВТ. Данный признак Р\
(Atb) считывается прибором ФНК из загружаемых массивов НСК СТ и НСК
ВТ и определяет время следующей загрузки массивов НСК СТ и НСК ВТ
(время, когда прибор ФНК ожидает следующей загрузки данных массивов).
Любой обмен данными по МКО инициируется бортовым цифровым
вычислительным комплексом (БЦВК). ФНК принимает командное слово и,
декодировав свой адрес, определяет тип команды, содержащейся в «команде
управления» или «команде обмена». Если принятая команда — «команда
управления», то ФНК выполняет ее, если это «команда обмена», то принимает пакет
данных (записывает в свое встроенное оперативное запоминающее устройство
(ОЗУ) в область, соответствующую принятому под адресу) или выдает пакет
данных (из области ОЗУ, соответствующей принятому подадресу).
Принятые от БЦВК массивы (НСК СПТ и НСК ВТ) на очередной период
излучения (период смены оперативной информации) хранятся в ОЗУ ФНК в
течение всего периода излучения. При этом в ОЗУ ФНК для хранения каждого
массива НСК СТ и НСК ВТ отведено по две зоны. Из одной зоны, в которой в
данный момент находится ОИ на данный период излучения, производится
чтение пакетов. Вторая зона содержит ОИ предыдущего периода, и в эту зону
производится запись очередного массива ОИ на следующий период излучения.
Таким образом, эти зоны периодически (с периодом смены ОИ) меняются
своими функциями: из первой — чтение, а во вторую — запись, и наоборот, в
420
Подсистема космических аппаратов
первую — запись из второй. Это необходимо для того, чтобы в любой момент
времени, исключая время после включения питания до первой загрузки ОИ, в
ОЗУ ФНК находилась в полном объеме ОИ для формирования полного НСК
СТ и НСК ВТ. Смена зоны ОЗУ (внутреннего указателя адресов) производится
автоматически при успешном завершении режима штатной загрузки пакетов
НСК СТ и НСК ВТ.
Помехоустойчивое кодирование строк НСК СТ и НСК ВТ с добавлением
избыточных разрядов (код Хемминга) осуществляется на аппаратном уровне.
Затем также на аппаратном уровне потенциальные коды НСК СТ и НСК ВТ
преобразуются в относительные бидвоичные коды. Кроме того, к каждой
строке НСК СТ добавляется метка времени, представляющая собой усеченную М-
последовательность длинной 30 бит (см. п. 11.4). Последовательные
относительные бидвоичные коды НСК СТ и НСК ВТ выдаются с тактовой частотой
100 Гц (Гмк = 10 мс) и 50 Гц (Гси =20 мс) и привязываются к внутренним
тактовым сеткам 1 Гц (Т = 1 мс) и 500 Гц (Т = 2 мс).
Функциональная схема формирователя навигационного сигнала приведена
на рисунке 11.19.
Л Г
^1
"1
#1
w
Генератор
ПСПСТ
тт
/эт 1с
Н\
""■"Р
/2>Г
^1
Ml
t
1 ^
г
гт\
ГКЛ
11У ivi
i
г>
i
<J
г
\л*>
Г»Г
1 W\
\
1 V
i
i
г
А Г
т
гт \гъл
НУ
]/иш
Г" ~" ^
Н2
Щ
Генератор
ПСПВТ
тт
Лт 1С
НЪ
щ
|/l2_
1 w
Рис. 11.19. Функциональная схема ФНС
Выходные сигналы генераторов ПСП СТ и ПСП ВТ перемножаются с
соответствующими информационными последовательностями (#1,//2,#3) и
поступают на входы квадратурных фазовых модуляторов Ml и М2.
Сформированные модулированные колебания поступают на предварительные усилители
мощности (ПУМ) и далее на выходы блока.
синтезаторы частот диапазонов L\ и L2 ;
фазовые модуляторы (ФМ) на каждый из диапазонов;
формирователь модулирующих сигналов (ФМС).
421
Глава 11
Структурная схема ФНС приведена на рисунке 11.20 и включает три
основных функциональных узла:
/ог=5 МГц
1с
Инф. от ФНК
11
н о со
2 2 о
§ la
tV
" Л Управление ЛГ
" fn
:4
ФАПЧ
ФНЧ
ФД
ГУН2
и:
:576
:4 [■
ФНЧ
t
ФД
|фАПЧ
ГУНЗ [
1
:448
ФМ/,1
ttt
/1 0/т
ФМ12
-►
УС
УС
Вых/,1
Вых/,2
■^^
m
V2 02УЬ
Рис. 11. 20. Структурная схема ФНС
Синтезатор частот выполнен по схеме фазовой автоподстройки частоты
(ФАПЧ). Частоты выходных сигналов, формируемых в диапазонах L\ и L2,
определяются соотношениями:
/гун1 =(/ог :Ю)# = (1420 - 1427'5) МГ^ А/ = 0,5 МГц,
где N = (2841 ... 2855) соответствует номерам НС от -7 до +4,
/гунг Ц/гущ :128):4-576 = (1597,5 ... 1605,9375) МГц, А/= 0,5625 МГц,
что соответствует диапазону частот Ы ,
/гун2 =(/ГУН] : 128):4-448 = (1242,5 ... 1249,0625) МГц, А/ = 0,4375 МГц,
что соответствует диапазону частот L2 .
Потенциальный код установки частоты после команды разрешения смены
литеры поступает от формирователя навигационного кадра на управляющие
цепи делителя (:N),n ФАПЧ перестраивается на необходимую частоту.
Фазовый модулятор представляет собой квадратурный ФМ, состоящий из
двух бинарных фазовых модуляторов, квадратурного устройства расщепления
фазы на (+45° и -45°) канала несущей частоты и выходного синфазного
сумматора двух модулированных сигналов. Он имеет два дифференциальных входа
для модулирующих сигналов, по каждому из которых осуществляется
независимая бинарная модуляция (манипуляция) фазы несущей частоты. После
суммирования двух фазоманипулированных сигналов формируется выходной
сигнал с квадратурной модуляцией с фазовым дискретом 0, 90, 180 и 270°. Для
обеспечения минимальных взаимных временных рассогласований
навигационных радиосигналов модулирующие сигналы перед подачей на входы модуля-
422
Подсистема космических аппаратов
торов синхронизируются сигналом тактовой частоты, формируемым в
генераторе тактовой частоты. Изменение разности задержек выходных сигналов ФНС
в диапазонах Ы и L2 не превышает 1 не.
Формирователь модулирующих сигналов, структурная схема которого
приведена на рисунке 11.21, включает:
входной преобразователь формата входных сигналов;
генератор тактовой частоты fT = 5,11 МГц;
генераторы ПСП ВТ и ПСП СТ;
регистр памяти начальной фазы ПСП ВТ;
регистр памяти НЗ;
делитель на 10;
логические схемы формирования выходных сигналов.
/ог=5 МГц
1 с
Сигналы
управления
H2
НЗ
HI
^-
^
^
^
-^»
-^
Генератор
тактовой
частоты
Входной преобразователь
формата информационных
сигналов
1с
Сигналы
управление
H2
НЗ
HI
у
Г
:10
^~
^
^-
1 ^
-►
"■"' ""^
Генератор
пспвт
t *
_J
Рагистр памяти
начальной фазы
пспвт
Рагистр памяти
НЗ
Генератор
пепет
^-
^
\
г
е
ф
i
{
пспвт
- - w-
/т=5,11МГц _
►
ПСП ВТ ® Н2_
— ^
ПСПСТ 0Н1^
^~
Рис. 11. 21. Структурная схема ФМС
Формирователь модулирующих сигналов принимает от ФНК
информационные сигналы (#1,#2,#3), формирует временные стробы ПСП СТ и ПСП ВТ,
привязывает информационные сигналы к временным стробам ПСП СТ и ПСП
ВТ, осуществляет прием и хранение значения кода начальной фазы ПСП ВТ,
формирует итоговые модулирующие последовательности для каналов L\ и L2 .
Синтезатор тактовой частоты /т = 5,11 МГц работает по принципу
прямого синтеза с фазированием по фазе. Система ФАПЧ имеет максимальную
ошибку слежения за фазой ± 1,08°. Петля слежения за фазой сигнала 5,11 МГц
обеспечивает флуктуации фронта сигнала 0,6 не за 1 мс, при этом сгДг =0,2 не
за 1 с.
423
Глава 11
Сигнал ПСП СТ складывается по модулю 2 с символами навигационной
информации Н\ (100 бит/с). Сигнал ПСП СТ0Н1 является модулирующим
для фазового модулятора несущей частоты диапазона Ы (а в перспективе и
диапазона 12).
Аналогичная процедура выполняется для ПСП ВТ и символов
навигационной информации #2.
Технические характеристики БИНРС:
а) диапазон частот 1597—1621 МГц (канал L1), 1241—1261 МГц (канал L2);
б) излучаемая мощность 64—80 Вт (канал L1), 20-40 Вт (канал L2);
в) энергопотребление не более 530 Вт;
г) масса не более 88 кг.
11.7.2. Антенно-фидерная система навигационной радиолинии
Антенно-фидерная система предназначена для передачи электромагнитной
энергии навигационных сигналов на частотах Ь\ и L2 в заданном направлении
и включает в себя: излучатели (12 шт.), блок делительный (4 шт.), делитель,
кабели.
Конструктивно антенно-фидерная система представляет собой решетку,
состоящую из двух групп спиральных излучателей: центральной (4 излучателя)
и периферийной кольцевой (8 излучателей на кольце диаметром 850 мм).
Излучатели объединены в четыре излучающих модуля, каждый из которых
состоит из трех излучателей (один из центральной группы и два ближайших из
периферийной) и делительного блока. Такая антенная решетка обеспечивает
одновременную работу на частотах Ы и L2, подавление побочных излучений, а
также оптимальное распределение энергии в диаграмме в целях обеспечения
равенства парциальных сигналов при приеме на поверхности Земли (в центре
диаграммы усиления антенны меньше на 2 дБ, чем на краю диаграммы).
11.7.3. Бортовая аппаратура межспутниковых измерений
Межспутниковые измерения и информационный обмен предназначены для
решения задач автономного эфемеридно-временного обеспечения, передачи
информации о целостности системы ГЛОНАСС, глобального оперативного
управления и контроля функционирования навигационных спутников (НС).
Для решения данных задач на борту НС начиная с «Глонасс-М»
устанавливается бортовая аппаратура межспутниковых измерений (ВАМИ), которая
должна выполнять следующие функции:
формирование и передача широкополосных измерительных сигналов
(ШИС) для приема их на всех НС «Глонасс», находящихся в зоне
радиовидимости излучающего аппарата;
424
Подсистема космических аппаратов
прием ШИС от всех излучающих НС, находящихся в зоне радиовидимости
принимающего аппарата;
измерение временного сдвига принимаемых ШИС относительно местной
шкалы времени и измерение псевдо дальностей и псевдо скоростей;
передача и прием измерительной и эфемеридно-временной информации.
Обобщенная схема БАМИ приведена на рис. 11.22.
Сигнал на частоте
2212.5 МГп ^
Команда «Вкл-Выкл»
Усилитель
мощности
К передающей
антенне
Команда «Запирание»
Сигнал на частоте
2212,5 МГц
1
Калибровка
задержки
Входное
устройство
приемника
От приемной
антенны
Рис. 11. 22. Обобщенная схема БАМИ
Все функции формирования сигнала, приёма сигналов и измерения
временных сдвигов сосредоточены в одном конструктивном узле — блоке
формирования и обработки сигналов. Это позволяет минимизировать относительные
аппаратные задержки ШИС и их нестабильности.
Функции блока формирования и обработки сигналов:
формирование несущей частоты сигнала;
формирование модулирующих кодовых последовательностей;
модуляция несущей частоты;
усиление и преобразование частоты принимаемого сигнала;
обработка принимаемого сигнала (обнаружение, выделение, фильтрация);
измерение задержки принимаемого сигнала относительно местной шкалы
времени;
запоминание результатов измерений;
демодуляция и декодирование информационных символов из принятого
радиосигнала;
обмен данными с внешними абонентами (БЦВМ) по интерфейсу
мультиплексного канала обмена;
диагностика и управление реконфигурацией выходных усилителей
мощности и малошумящим усилителем приемного тракта.
Для уменьшения ошибки, связанной с нестабильностью параметров
выходного усилителя мощности, в системе предусмотрена цепь калибровки всего
приемного тракта (за исключением малошумящего усилителя, который при
работе передатчика блокируется для защиты от выгорания).
425
Глава 11
Диапазон частот, циклограмма работы, структура цикла
Для ВАМИ определен диапазон 2200 ... 2225 МГц. В основу работы
системы положено временное разделение приема и передачи сигналов, поэтому
здесь используется одна рабочая частота /н =2212,5 МГц (13,56 см) для
приема и передачи при условии обеспечения защиты входных цепей
приемника от мощного сигнала передатчика.
Система ВАМИ работает в симплексном режиме циклами по 20 с:
5 с — передача (вещание всем НС);
15 с — прием.
Циклы повторяются в течение 5 мин. Далее следует 10-минутный перерыв.
В системе используется принцип кодового и временного разделения
сигналов различных НС. Все 24 НС разбиты на 4 группы по 6 НС. Каждой группе
выделен фиксированный временной интервал для работы в режиме передачи.
Внутри группы сигналы НС различаются кодами, модулирующими сигнал
несущей частоты. Таким образом, на передачу одновременно работают 6 НС,
каждый своим модулирующим кодом.
В каждом цикле приема (передачи) сигнала НС в ВАМИ осуществляется
включение/выключение приемника (передатчика), обнаружение и захват
сигнала по частоте и модулирующему коду (синхронизация), измерение псевдо
дальности/псевдо скорости и выделение информационных символов.
Реализация этих режимов при работе ВАМИ на прием отображена в виде циклограммы
на рис. 11.23. Аналогичная циклограмма соответствует и режиму передачи
сигнала.
Включение
приемника
i
Т
1 ВК.1
Обнаружение и
синхронизация
^ ^
Т
1 вхожд
Измерение и
выделение информации
Выключение
приемника
i i
Т
1 инф
Т
1 вы к л
L J I I I _U'
"^ jc ^ Односекундные метки
Рис. 11. 23. Временная циклограмма режимов работы на прием (передачу)
Таким образом, весь цикл приема/передачи длительностью 5 с содержит
защитные интервалы (длительностью Гвкл / ГВЬ1КЛ) между
включением/выключением приемника/передатчика и приемом/передачей радиосигнала,
интервал обнаружения/синхронизации (длительностью Гвхожд) и интервал
(информационный, длительностью Гинф) измерения псевдо дальности/псевдо
скорости и выделения передаваемой информации. Начало каждого цикла
приема/передачи синхронизировано с односекундными метками времени (см.
рис. 11.22).
426
Подсистема космических аппаратов
В качестве сигнала в режимах обнаружения/синхронизации и
измерения/выделения передаваемой информации планируется использовать фазома-
нипулированный на к сигнал с полосой частот 10 ... 20 МГц.
Длительность и структура информационного сообщения выбраны такими,
чтобы обеспечивалась передача необходимого объема данных. Кроме того,
необходимо перед передаваемой информацией вводить признак типа
информации. Различают следующие типы: измерительная, эфемеридно-частотная,
программная. Длительность символа информационного сообщения гинф
планируется равной примерно 1 мс.
Для обеспечения заданных требований по вероятности ошибки приема
одного символа Рош=10~6 при заданной энергетике радиолинии используется
сверточное кодирование потока информационных символов по схеме (Я =2/3,
К =7), где число входных символов кодирующего устройства — 2, число
выходных символов — 3, длина кодового ограничения — 7.
Энергетика межспутниковой радиолинии
Диаграмма направленности антенны ВАМИ конусообразная с провалом
направленным на центр Земли, что обеспечивает одинаковую мощность
сигналов, принимаемых от всех видимых спутников. В табл. 11.13 приведены
значения коэффициента усиления GA (по мощности) антенны в зависимости от угла
а , отсчитываемого от оси, направленной от НС к центру Земли.
Таблица 11.13. Характеристики диаграммы направленности антенны
а, град
| GA(a),gb
37
+5,2
50
+3,3
60
_+}±_
70
-2Д_
80
-8,J_
85
-14,1
87
-18,5 1
Положим, что НС движутся по идеальным невозмущенным орбитам.
Ввиду симметрии такой орбитальной группировки, изменение дальности между
некоторым (например № 1) и остальными НС будет одинаковым, вне
зависимости от того, относительно какого НС определяются дальности. На рис. 11.24
приведены зависимости изменения взаимной дальности между НС № 1 и НС
№ 9—16, которые не находятся в одной орбитальной плоскости с НС № 1.
Из рис. 11.24 следует, что максимальная дальность между НС равна
Лпмх=5,26-107м.
Затухание сигнала на максимальной дальности (по мощности)
TS __ х ИЗЛ =
зат ~ р
ч-20
Ы 42
= 4,210"z" (-193,7 дБ).
max
427
Глава 11
> R, тыс. км
15000 20000 25000 30000 35000 40000
Рис. 11.24. Графики изменения взаимных дальностей между НС
Расстояние между НС № 1 и другими НС может быть представлено как
функция угла а соотношением Rx - Rmax cos [a).
Тогда для затухания сигнала от / -го НС можно записать выражение
К =
(П.1)
COS^(tf)
Расчеты по (11.1) с учетом данных табл. 11.13 показывают, что в
диапазоне углов 37 ... 85° значение K3aTi *<-184,5 дБ для всех /.
Если задать мощность сигнала на выходе РПДУ 70 Вт (+18,5 дБВт) и
приведенную температуру шума приемника 300 К (-203 дБВт/Гц), на входе
приемника будем иметь qc* =31 дБ/Гц. Следовательно, параметры приемника
ВАМИ в режиме поиска, обнаружения, захвата на сопровождение и
сопровождения сигнала должны оптимизироваться для qcin =37 дБ/Гц, или с учетом
запаса в 3 дБ — для qc/nQ =34 дБ/Гц.
Аппаратура приема и обработки сигналов
Аппаратура приема и обработки сигналов ВАМИ строится аналогично АП
навигационных радиосигналов СРНС ГЛОНАСС (рис. 13.1) и включает:
антенну, радиочастотный блок, синтезатор частот, АЦП и цифровой вычислитель.
Радиочастотный блок включает входное устройство приемника (ВУП)
(рис. 11.22) и радиоприемник.
Входное устройство приемника предназначено для усиления сигнала,
приходящего от антенны, ослабления сигнала передатчика в режиме излучения
428
Подсистема космических аппаратов
(защита МШУ), ввод в тракт приема нормированного сигнала от передатчика
для калибровки.
Обобщенная схема ВУП приведена на рис. 11.25.
От антенны
УАт
ОгРПДУ
калибровка
МШУ
*■
Ат
▼
НО
КРП
Рис. 11. 25. Обобщенная схема ВУП
Управляемый аттенюатор (УАт), установленный непосредственно перед
малошумящим усилителем (МШУ), служит для ослабления сигнала,
поступающего от усилителя мощности передающей части антенны системы
межспутниковых измерений в режиме излучения («Передача»). Вносимые
ослабления УАт: в режиме излучения — не менее 20 дБ; в паузе — не более 0,5 дБ.
Малошумящий усилитель имеет коэффициент шума около 1 дБ.
Суммарный коэффициент усиления МШУ не менее 34...50 дБ, что обеспечивает
компенсацию потерь в кабеле и сумматорах-разветвителях.
Направленный ответвитель (НО), стоящий после МШУ, служит для ввода
«Калибровочного сигнала» от усилителя мощности передающей части БАМИ в
тракт приемника через аттенюатор (Ат) с ослаблением сигнала на 30 дБ.
Радиоприемник. В радиоприемнике осуществляется усиление
радиосигналов, понижение частоты сигнала, фильтрация шумов и внеполосных помех
(зеркальных и соседних каналов приема).
Схема радиоприемника приведена на рис. 11.26.
От ВУП
Чувч
ПФ1
CMi
г
ПФ2
см2
Г
НЧФ
К АЦП
/onl I /оп21
Рис. 11. 26. Схема радиоприемника
В радиоприемнике осуществляется двукратное понижение частоты
входного сигнала. Первый смеситель переносит сигнал на первую промежуточную
частоту /пр1 » 142,5 МГц (/оп1 «2070 МГц), а второй — на вторую
промежуточную частоту /пр2 « 14,5 МГц (/оп1 * 156 МГц).
Полосовые фильтры (ПФЬ ПФ2) имеют полосы пропускания Д/Пф, ~
« 50 МГц, А/Пф2 * 20 МГц, а низкочастотный фильтр (НЧФ) — Д/нчф ~ 24 МГц.
429
Глава 11
Общее усиление радиоприемника около 90 дБ, и оно распределяется по
тракту следующим образом: УВЧ — 20 дБ, У! — 40 дБ, У2 — 30 дБ.
Аналого-цифровой преобразователь БАМИ использует 2-битное
квантование сигнала с частотой fd = 52 МГц.
Многоканальный коррелятор. В БАМИ используется кодовое
разделение сигналов, принимаемых от шести одновременно излучаемых НС, поэтому
необходимо сформировать шесть групп корреляторов, соответствующих шести
каналам обработки. Схема корреляторов одного канала обработки аналогична
приведенной на рис. 13.7.
Аппаратура приема и обработки сигналов БАМИ работает в двух режимах:
обнаружение/синхронизация и измерение/извлечение информации. В режиме
обнаружение/синхронизация корреляторы работают с временем накопления
3,15 мс, а в режиме измерение/извлечение информации время накопления
составляет 1 мс.
Поиск и обнаружение сигналов. Поиск и обнаружение сигнала
осуществляется по задержке и доплеровскому смещению частоты на интервале
времени То6н « 0,6 с. Поиск по задержке производится с шагом, равным половине
длительности символа ПСП St - гэПСПВ/2 « 0,4 мкс, а поиск по частоте с
шагом 66 Гц при 8fA = 132 Гц.
Для обеспечения требуемых характеристик обнаружения (Рп « 3 • 10~2) и
неопределенности по частоте ±66 Гц алгоритм обнаружения может
заключаться в вычислении огибающей сигнала на выходе согласованного фильтра
(коррелятора) Хк (Т) = yjl% (Г) + Ql (Т) (где Т « 3,15 мс) с последующим
накоплением отсчетов Хк(Т) для к = \9К.
Измерение псевдо дальности и псевдо скорости. В БАМИ требуется
реализовать достаточно высокую точность измерения псевдо дальности и
псевдо скорости с целью обеспечения требуемого уровня погрешностей эфемерид в
МГНСС ГЛОНАС.
При построении следящих систем за псевдо задержкой и псевдо фазой
сигнала необходимо учитывать характер взаимного движения НС, каждый из
которых движется по слабо возмущенным траекториям. Изменение взаимных
дальностей приведено на рис. 11.24, а изменение взаимных скоростей и
ускорений — на рис. 11.27 и 11.28 соответственно.
Из рис. 11.27, 11.28 следует, что на интервалах измерения псевдо
дальности и псевдо скорости (Гинф =3,6 с) изменение взаимной скорости между НС
можно считать линейным с максимальным значением производной (ускорени-
ем) 3...4 м/с .
430
Подсистема космических аппаратов
aV,m/c
60001
5000 {
Рис. 11.27. Графики изменения взаимных скоростей между НС
30 Т
25 \
20
15 +
ю4
А а, м/с
4000 8000
10
!i
И
11
12
Л 14 15
16
И
И
l I
12000 16000 20000 24000 28000 32000 36000 40000
t,c
Рис. 11.28. Графики изменения взаимных ускорений между НС
Таким образом, изменение взаимной дальности между НС может
описываться уравнениями
dR r, dV da .
— = V , = а, — = 0.
dt dt dt
Для такой модели изменения дальности с целью минимизации
динамической ошибки слежения необходимо строить следящую систему по дальности с
астатизмом третьего порядка.
Кроме того, учитывая высокие требования по точности измерения псевдо
дальности и псевдо скорости, целесообразно использовать когерентную ком-
431
. _^^^ Глава 11
плексную систему слежения за задержкой и фазой сигнала, например такую,
которая описана в п. 6.3.6.7 (рис. 6.36). Параметры комплексной следящей
системы необходимо рассчитывать на отношение сигнал/шум qc/rl0 =34...37 дБГц.
При этом в качестве фазового дискриминатора можно использовать (6.42)
(оптимальный для большого отношения сигнал/шум), а в качестве
дискриминатора задержки — (6.46) (или (6.63)).
Для уменьшения ошибки оценивания доплеровской частоты
(пропорциональной оценке псевдо скорости) в ССФ можно использовать достаточно
широкую полосу пропускания (ДГССФ = 30...40 Гц) с целью уменьшения
динамической ошибки оценивания, а снижение итоговой флуктуационной ошибки
можно обеспечить вторичным сглаживанием оценок псевдодоплеровской
частоты, например, используя алгоритм, описанный в п. 6.4.2.1.
Итоговые оценки псевдо дальности и псевдо скорости формируются в
конце интервала измерения псевдо дальности/псевдо скорости и используются
далее в сети НС для уточнения эфемерид НС.
Алгоритмы обнаружения и оценивания псевдо дальности и псевдо
скорости реализуются процессором, входящим в состав блока формирования и
обработки сигналов (см. рис. 11.22).
Аппаратура передачи сигналов
Аппаратура передачи сигнала (АПС) предназначена для формирования
кодовых псевдослучайных последовательностей, предназначенных для измерения
дальности между НС, генерирования колебания несущей частоты, модуляции
несущего колебания и усиления мощности сформированного радиосигнала до
требуемого уровня. Обобщенная схема АПС приведена на рис. 11.29, где
обозначено: БФОС — блок формирования и обработки сигналов; БФКП — блок
формирования кодовых последовательностей; БФСП — блок формирования
сигнала передатчика; УМ — усилитель мощности.
Сигналы ]
управления i
БФОС
БФКП
БФСП
1
1
1
V
1
УМ
К антенне
^
Рис. 11.29. Обобщенная схема аппаратуры формирования сигналов
Блок формирования кодовых последовательностей содержит набор
регистров и постоянных запоминающих устройств, которые в совокупности
формируют необходимые ПСП. Все временные и структурные параметры ПСП
задаются и контролируются процессором, входящим в состав БФОС.
Блок формирования сигнала передатчика выполняет функции
генерирования колебания несущей частоты, модуляции несущего колебания и его
усиления. Схема БФСП приведена на рис. 11.30.
432
Подсистема космических аппаратов
ncili| |ПСП2
/ог-5МГц, 1 .„ 1 ^|ттфЛ
|^| .Z | ^| 1V*VA
1 1
Синтезатор 1
:885
УГ \
+
i r
41
КФМ
к ум
!2/ст
Рис. 11.30. Схема блока формирования сигнала передатчика
Блок формирования сигнала передатчика состоит из синтезатора на основе
схемы ФАПЧ, квадратурного фазового модулятора (КФМ) и усилителя (У).
Выходная частота синтезатора
/синт=885/ог/2 = 2212,5 МГц.
Ослабление паразитных дискретных составляющих в спектре выходного
сигнала в полосе частот ± 200 МГц должно быть не менее 70 дБ относительно
уровня сигнала несущей частоты, а уровень шумовых составляющих — не более:
-75 дБ/Гц при отстройке на 100 Гц;
-85 дБ/Гц при отстройке на 1,0 кГц;
-90 дБ/Гц при отстройке на 10,0 кГц.
Для исключения скачков фазы выходного модулированного сигнала на /г
использован квадратурный фазовый модулятор. На два квадратурных входа
модулятора поступают две одинаковые ПСП (ПСП} и ПСП2), сдвинутые друг
относительно друга на половину символа. В результате скачки фазы выходного
сигнала модулятора не будут превышать л/2. Следовательно, глубина
паразитной амплитудной модуляции выходного сигнала БФСП не превысит 30%,
что важно для обеспечения нормального режима работы усилителя мощности.
Усилитель БФСП поднимает мощность выходного сигнала до 10 мВт.
Выходной усилитель мощности аппаратуры передачи сигналов,
конструктивно вынесенный из БФОС (см. также рис. 11.22), имеет следующие параметры:
центральная частота 2212,5 МГц;
полоса пропускания ± 20 МГц;
выходная мощность не менее 75 Вт (70 Вт на входе антенны);
коэффициент усиления 39 дБ.
Среднее за цикл энергопотребление БАМИ не более 65 Вт, масса приборов
БАМИ не более 25 кг.
11.7.4. Бортовое синхронизирующее устройство
Бортовое синхронизирующее устройство предназначено для решения
следующих задач: непрерывной выдачи высокостабильных синхрочастот в
системы спутника; формирования, хранения и выдачи бортовой шкалы времени.
Он обеспечивает формирование сигналов стандартной точности и сетки
импульсов синхрочастот, Гц:
433
Глава 11
fl
f?
и
f4
и
n
5 000 000
200 000
50 000
10 000
1000
100
f?
U
и
f,0
fll
Сигнал частоты fx формируется в виде гармонического, остальные в
импульсном виде. Кроме того, БСУ формирует сигналы временных интервалов.
Оцифровка времени производится 32-разрядным двоичным последовательным
кодом с частотой 100 Гц.
В состав БСУ входят атомный стандарт частоты (3 комплекта) и
устройство формирования синхрочастот и шкал времени.
Атомный стандарт частоты состоит из цезиевого генератора, атомно-
лучевой трубки и системы автоподстройки частоты. Цезиевый генератор
предназначен для генерирования колебаний с частотой 5 МГц. Атомно-лучевая
трубка совместно с системой автоподстройки частоты служит для
стабилизации высокостабильных колебаний частоты 5 МГц.
В состав устройства формирования синхрочастот и шкал времени входят
блоки синусоидальных усилителей и устройство формирования. С атомного
стандарта частоты высокостабильный сигнал частоты 5 Мгц поступает на блок
синусоидальных усилителей, а затем к внешним потребителям и на устройство
формирования, которое выдает потребителям сетку синхрочастот и код времени.
Работает БСУ в штатном или в дежурном режимах. В дежурном режиме
аппаратура обеспечивает выдачу сетки частот, необходимой аппаратуре
спутника на этапах ожидания, начальной ориентации, приведения в точку, при
хранении спутника на орбите, в аварийной ситуации. В этом режиме в качестве
задающего используется кварцевый генератор. При штатном функционировании
аппаратура обеспечивает выдачу сигналов высокой стабильности. В штатный
режим спутник включается по командам с ПКУ после окончания проверок
аппаратуры спутника.
Если расхождение бортовой и наземной шкал времени превышает
установленную норму, то по команде с ПКУ производится фазирование и
коррекция бортовой шкалы. При выходе из строя эталона частот потребителю
выдается сигнал «недостоверность фазы». Переход из штатного режима в дежурный
производится по командам блока управления спутника.
Технические характеристики БСУ:
Номинальное значение выходной частоты, МГц
Точность хранения шкалы времени, не
Относительная нестабильность стандарта частоты за сутки ...
50
10
1
1/60
1/1800
5
20
(1...5)-10"13
434
Подсистема космических аппаратов
Ослабление дискретных боковых составляющих спектра
выходного сигнала в полосе ± 20 кГц по отношению
к основной составляющей 5 МГц, дБ более 90
Масса, кг 107
Энергопотребление, Вт 100
11.7.5. Бортовой комплекс управления
В состав БУК входят следующие системы и приборы: бортовая аппаратура
командной системы (АКС); бортовой цифровой вычислительный комплекс;
бортовая телеметрическая система (БТС); блок управления (БУ).
Аппаратура командной системы предназначена для выполнения
следующих задач: измерения параметров орбиты спутника в радио и оптическом
диапазонах (совместно с ПКУ); исполнения разовых команд для управления
системами спутника; обработки временных программ выдачи навигационной
информации; приема, формирования и передачи сигналов бортовой шкалы
времени; передачи телеметрической информации; ретрансляции информации
обмена между наземными средствами.
Конструктивно АКС состоит из блоков НЧ, ВЧ, криптозащиты, антенно-
фидерной системы и комплекта оптических уголковых отражателей. Антенно-
фидерная система содержит слабонаправленные антенны на прием и передачу
и направленную передающую антенну, которая используется при штатной
ориентации спутника.
Бортовой цифровой вычислительный комплекс предназначен для решения
следующих задач: запоминания и обработки навигационной информации;
формирования навигационных кадров и выдача их в БНП; контроля состояния
БНП и переключения его комплектов; запоминания и выдачи кодов временных
программ и скачков в командноизмерительную систему; приема,
формирования и выдачи сигналов «Вызов наземного комплекса управления»;
автономного тестового контроля работоспособности аппаратуры БЦВК с выдачей
сообщения по телеметрическим каналам; формирования и передачи «отчета БЦВК»
по навигационному каналу при аварийной ситуации в БЦВК и снятии спутника
с эксплуатации (для анализа ситуации на наземных станциях); пересчета
информации об изменении задержки дальномерного сигнала и переключения
комплектов БНП; формирования в навигационном кадре признака
непригодности спутника к использованию потребителями при отказе БУ.
Блок управления спутника обеспечивает включение спутника после
выведения на орбиту, выдачу питания на пиропатроны для раскрытия механических
систем после отделения спутника от ракеты-носителя. Он распределяет
питание между всеми электроприборами, обеспечивает совместную работу
подсистем при проведении режимов коррекции, разгрузки управляющих маховиков, а
435
Глава И
также управление системами спутника в аварийных ситуациях при потере
ориентации или отказах системы электропитания.
Технические характеристики БКУ:
Скорость записи информации, Гц
Время готовности после подачи питания, мин
Интервал отработки информации, сут
Максимальный темп отработки временных программ,
программа/с
Диапазон частот
Точность сверки времени, мс
Скорость приема, Гц :
разовая команда
временная программа
Погрешность измерительной линии, м:
радиодиапазон
оптический диапазон
Число временных программ
Число телеметрических каналов
11.7.6. Система ориентации и стабилизации
и другие вспомогательные системы
Система ориентации и стабилизации предназначена для решения
следующих задач: успокоение спутника и обеспечение начальной ориентации на
Солнце и на Землю; ориентация продольной оси спутника на центр Земли,
солнечных батарей на Солнце; ориентация вектора тяги двигателей коррекции
орбиты по вектору скорости (на время выдачи импульса коррекции).
В спутниках ГЛОНАСС используется активная трехосная система
ориентации и стабилизации (СОС) с управляющими маховиками и реактивной
системой разгрузки. В состав СОС входят чувствительные (блок измерения
угловых скоростей, приборы ориентации на Землю и Солнце, приборы солнечной
ориентации по каналу рыскания, магнитометры) и исполнительные
(электромеханический исполнительный орган, привод вращения панелей солнечных
батарей, электромагнитные устройства, маховик стабилизирующий, двигательная
установка, блок управления) элементы.
Работает СОС в следующих режимах: успокоения; начальной ориентации
на Солнце; закрутки вокруг поперечной оси; начальной ориентации на Землю;
ориентации на Землю; ориентации при проведении коррекции.
Солнечные батареи спутника выполнены в виде четырех плоских
прямоугольных панелей, объединенных попарно в два крыла, расположенных
симметрично плоскости стабилизации (XOY). Крылья солнечных батарей враща-
1000
3
30
2
см
0...2
100
1000
3
03
1000
512
436
Подсистема космических аппаратов
ются вокруг оси (OZ), перпендикулярной плоскости стабилизации и
направлены на Солнце в процессе штатной эксплуатации. Перевод каждого спутника в
заданную точку орбитальной структуры (системную или рабочую точку)
проводится с помощью спутниковой двигательной установки (два симметричных
блока) коррекции.
С целью создания необходимых климатических условий для аппаратуры НС
используется цилиндрический герметичный контейнер, являющийся
одновременно основной несущей конструкцией НС и радиационной поверхностью. Для
снижения возмущающих воздействий на движение НС от реактивной струи
исходящего из термоконтейнера газа его герметичность повышена на порядок по
сравнению с аналогичными. На днище контейнера крепятся различные блоки и
антенно-фидерная система. В сложенном положении спутник представляет
собой ромбическую призму.
Характеристики систем спутника:
Система ориентации и стабилизации
Точность ориентации, град:
продольной оси 0,5 ... 1
солнечных батарей 5
вектора тяги 5 ... 11
Система коррекции
Тяга двигателей, Н:
коррекции 5
стабилизации 0,1
Суммарный импульс, Н 90000
Система электропитания
Рабочая мощность солнечных батарей, Вт 1250
Рабочая емкость аккумуляторных батарей, Ач(Втч). 45(1260)
Выходное напряжение, В 27 ± 1
Система термолегулирования
Диапазон термолегулировапния, °С :
стандартов частоты п$ 30) ± 1
термоконтейнера 0 40
двигательной установки 5 40
Энергопотребление, Вт 36
Спутник ГЛОНАСС
Срок активного существования, г 3 ... 5
Длительность непрерывной работы, сут 1415 ... 1485
Масса (конструкции), кг 237
Энергопотребление (среднесуточное), Вт 1000
437
Глава 11
11.7.7. Функционирование бортовых систем спутника ГЛОНАСС
В процессе функционирования спутник последовательно находится в
следующих режимах работы: ожидание после выведения на орбиту; начальной
ориентации; приведения в расчетную точку; штатного функционирования.
После выведения спутников на заданную орбиту (за время не более 5 ч) по
команде, выдаваемой разгонным блоком непосредственно после остановки
двигателей, включаются электропитание некоммутируемых шин питания и
дежурные схемы спутников. Через 15 с после этого система управления
разгонным блоком выдает команду на отделение спутников. Эта операция
осуществляется для трех спутников синхронно с их закруткой (с угловой скоростью не
более 27 град/с). Процесс отделения спутников контролируется с помощью
телеметрической системы разгонного блока. На каждом спутнике при его
отделении формируется команда «Контакт отделения», по которой он переводится
в режим ожидания, в котором при прохождении спутником зоны
радиовидимости наземных средств ПКУ обеспечивается прием команд управления и
передача телеметрических данных. Длительность работы спутника в режиме
ожидания — до трех суток.
Перевод спутника в режим начальной ориентации происходит в зоне
радиовидимости наземных средств в следующей последовательности: раскрытие
солнечных батарей и штанги магнитометра; успокоение спутника; начальная
ориентация солнечных батарей на Солнце и спутника — на Землю.
В процессе успокоения осуществляется торможение вращательного
движения спутника с помощью двигательной установки и разворот панелей
солнечных батарей для выставки крыльев активной поверхностью в одну сторону
и установки их в плоскости, совпадающей с продольной осью спутника.
В режиме начальной солнечной ориентации осуществляется разворот
спутника вокруг продольной оси с помощью двигателей маховиков до
попадания Солнца в поле зрения приборов ориентации на Солнце с последующим
переводом в закрутку вокруг оси, ориентированной на Солнце.
Режим начальной ориентации на Землю проводится в зоне
радиовидимости ПКУ на участках, где угол между линями «Солнце—НС» и «НС—Земля»
составляет (90 ± 18)°. При этом обеспечивается торможение вращения
спутника и его разворот с помощью управляющих двигателей — маховиков вокруг
направления, ориентированного на Солнце до попадания Земли в поле зрения
прибора ориентации на Землю. После этого включается режим слежения за
Солнцем и Землей.
Приведение спутника в заданное положение на орбите осуществляется в
несколько этапов: определение параметров орбиты и формирование программы
приведения; выдача импульсов коррекции для обеспечения требуемой
скорости смещения спутника относительно номинальной орбиты; пассивное
движение спутника по орбите в заданном направлении; выдача импульсов, обеспечи-
438
Подсистема космических аппаратов
вающих торможение движения спутника и приведение спутника в заданное
положение на орбите; проведение измерений параметров орбит.
После завершения всей программы приведения спутника в заданное
положение с требуемой точностью производится окончательное уточнение
параметров орбиты, высокоточная синхронизация БШВ, расчет временных
программ и закладка их на спутник. После этого спутник может использоваться по
целевому назначению.
Литература
11.1. Ivanov N., Salischev V., Vinogradov A. Ways of GLONASS system advancing//
ION GPS-95, 1995, pp. 991 — 1011.
11.2. Глобальная спутниковая навигационная система ГЛОНАСС/ Интерфейсный
контрольный документ. Редакция 5.0. — М.: КНИЦ, 2002.
11.3. Глобальная космическая навигационная система Глонасс: исторические
аспекты создания. / Космонавтика и ракетостроение. - М: ЦНИИ МАШ, 2004. - №
4(37).-С. 21-28.
11.4. Глобальная космическая навигационная система Глонасс: Перспективы
развития. / Космонавтика и ракетостроение. - М: ЦНИИ МАШ, 2004. - № 4(37).- С. 29-36.
439
Глава 12
Глава 12
ДИФФЕРЕНЦИАЛЬНЫЕ РЕЖИМЫ СПУТНИКОВОЙ
РАДИОНАВИГАЦИОННОЙ СИСТЕМЫ ГЛОНАСС
Использование СРНС ГЛОНАСС в стандартном режиме удовлетворяет
требованиям широкого круга потребителей. В то же время для ряда
приложений (например, заход на посадку воздушных судов по категориям ИКАО,
маневрирование морских судов в «узкостях», использование для решения топоге-
одезических, гидрографических и других задач) необходимы более высокие
точности и достоверности координатного и навигационно-временного
обеспечения. Они могут быть получены при использовании специальных режимов
работы СРНС, одним из которых является дифференциальный режим (ДР).
12.1. Принципы организации дифференциальных режимов
работы СРНС
В основе ДР лежит свойство пространственно-временной коррелированно-
сти погрешностей измерений радионавигационных параметров сигналов НС,
проведенных в различных точках пространства в близкие моменты времени.
Суть ДР заключается в измерении и компенсации коррелированных
постоянных и медленно меняющихся во времени и пространстве составляющих
погрешностей измерений РНП, т.е. измерений псевдо задержки дальномерного
кода, псевдо доплеровской частоты и псевдо фазы принимаемых сигналов НС.
Измерение псевдо задержки дальномерного кода в дальнейшем для простоты
будем называть измерением псевдо дальности, а измерение псевдо
доплеровской частоты — измерением псевдо скорости.
Для реализации ДР штатное оборудование СРНС необходимо дополнить
рядом технических средств, совокупность которых можно рассматривать как
дифференциальную подсистему (ДПС), которая является функциональным
дополнением СРНС.
В простейшем случае для организации ДР необходимо использовать два
приемника сигналов НС (рис. 12.1), один из которых (опорная измерительная
станция (ОИС)), как правило, неподвижный и расположен в точке с
известными координатами, другой (навигационная аппаратура потребителя) может
находиться в движении. Если ОИС и НАП находятся достаточно близко друг к
другу, то измерения псевдо дальности, выполненные приемником ОИС и
НАП для одного и того же НС будут содержать одинаковые значения медленно
меняющихся составляющих погрешностей измерений (ионосферной,
тропосферной, релятивистской и т.д.). Если для расчета координат ОИС и НАП
использовать измерения псевдо дальностей по одному и тому же созвездию НС,
440
Дифференциальный режим СРНС ГЛОНА С С
-$-
НС,
4-
НС,
V'
|оис
=i
ПС |
Дифференциальные поправки
->v
^
ккс
НАЛ
Траектория
движения
Рис. 12.1. Принцип организации ДР
то ошибки определения их координат, обусловленные указанными выше
медленно меняющимися погрешностями измерений, также будут одинаковыми.
Поскольку координаты ОИС известны точно, сравнивая их значения с
значениями координат, вычисленными по принятым сигналам НС, можно определить
величины этих систематических ошибок, которые называют дифференциальны-
ми поправками (ДП). Передавая эти ДП в НАП по той или иной линии связи,
можно использовать их для коррекции координат потребителя. Совокупность
ОИС и передающих средств будем называть контрольно-корректирующей
станцией (ККС).
Возможны два варианта реализации ДР, в первом из которых на ОИС для
заданного созвездия НС по принятым от них сигналам определяются оценки
координат ОИС, которые сравниваются с известными истинными значениями.
По результатам сравнения формируются ДП к координатам, которые
передаются потребителям для коррекции его координат. Такой подход прост идейно,
но требует, чтобы каждая из обслуживаемых НАП работала по тому же
созвездию НС, что довольно сложно реализуемо на практике. Поэтому такая
идеология ДР не нашла широкого распространения на практике.
Другой подход к организации ДР основан на измерениях псевдо
дальностей по всем видимым НС на ОИС и сравнении их значений с «ожидаемыми
значениями» псевдо дальностей, которые заранее вычисляются по известным
координатам ОИС и рассчитанным на момент измерений координатам
каждого из видимых НС. Расчеты координат НС проводятся по эфемеридным
данным НС, передаваемым по широковещательным сетям или предварительно
извлеченным из принятых сигналов НС. При таком подходе в качестве ДР
передаются погрешности измерения псевдо дальностей НС, а в НАП также
корректируются измерения псевдо дальностей. При этом для определения своих
координат потребитель может выбирать любое созвездие, обеспечивающее ему
441
Глава 12
наилучшую точность их определения. Даная идеология организации ДР
используется в большинстве современных ДПС СРНС. В дальнейшем будет
рассматриваться только данный вариант ДР.
В зависимости от используемых типов первичных измерений можно
выделить три разновидности ДР. Первая из них основана на использовании при
организации ДР «сырых» измерений псевдо дальностей и псевдо скоростей для
каждого НС. Во втором варианте используются измерения псевдо дальностей и
измерения псевдо фаз, которые используются для сглаживания псевдо дально-
мерных измерений (см. п. 6.4.2.2). Данные два подхода иногда называют
общим термином стандартный (обычный) ДР. Третья разновидность ДР связана
исключительно с использованием измерений фазы несущей и называется
высокоточный ДР. Основная направленность данного типа ДР связана с проблемой
разрешения неоднозначности фазовых измерений. Для большинства
практических приложений достаточно использования стандартного ДР, и лишь для
прецизионных приложений, например в геодезии, требуется использование
высокоточного ДР.
Дифференциальные подсистемы СРНС, основанные на использовании
одной ККС и передающие одну {скалярную) поправку для суммарной
погрешности измерения псевдо дальности (или сглаженной фазовыми измерениями
псевдо дальности) и одну поправку для суммарной погрешности измерения
псевдо скорости для каждого НС, называют локальными ДПС (ЛДПС).
Дальность зоны обслуживания ЛДПС составляет, как правило, до 300 км.
Для расширения зоны обслуживания ДПС несколько ЛДПС могут быть
объединены в единую сеть, в которой скалярные дифференциальные поправки,
формируемые соседними ККС, дополнительно сглаживаются и поставляются
конечному пользователю. Такую сетевую ДПС называют региональной
(РДПС), и ее рабочая зона может составлять от 300 до 2000 км. В РДПС
обеспечивается более однородное в пределах региона качество НВО потребителей.
Однако при этом усложняется аппаратура ККС. Кроме того, возникает
дополнительная временная задержка в обеспечении потребителя
дифференциальными поправками.
При использовании сетевой структуры ДПС есть возможность
формирования не просто скалярных поправок для каждого НС, а вектора поправок,
составляющие которого соответствуют отдельным составляющим погрешностей
измерения псевдо дальностей (псевдо скоростей и/или псевдо фаз). Такой тип ДПС
называют широкозонной ДПС (ШДПС) (рис. 12.2).
Широкозонная ДПС состоит из нескольких ККС и базовой станции.
Каждая ККС, непрерывно принимая сигналы от всех видимых НС, определяет
вектор поправок, включающий, например [6.8], поправку к БШВ каждого НС, три
составляющих ошибок положения каждого НС и параметры модели
ионосферной задержки сигналов НС. Формируемые каждой ККС поправки
соответствуют геометрическому местоположению ККС в сети. Сформированная на ККС
442
Дифференциальный режим СРНС ГЛОНА СС
Ионосфера
Базовая станция
Рис. 12.2. Широкозонная ДПС
информация передается на головную станцию, где рассчитываются итоговый
вектор дифференциальных поправок, включающий трехмерные поправки к
эфемеридам всех НС, находящихся в зоне видимости всех ККС сети, поправки
к БШВ тех же НС и восемь параметров модели ионосферной задержки
сигналов НС. Кроме того, на головной станции оцениваются сдвиги шкал времени
каждой ККС сети относительно опорной шкалы времени. Сформированный
вектор дифференциальных поправок передается потребителям по сетям связи.
Протяженность зоны обслуживания ШДПС составляет порядка 5000 км.
Состав оборудования ДПС СРНС в значительной степени зависит от
назначения, размеров обслуживаемой рабочей зоны, применяемых методов
измерения РНП и формирования ДП, каналов передачи ДП потребителям и
используемых для передачи форматов.
Для передачи ДП могут использоваться традиционные (например, в УКВ-
диапазоне), спутниковые, сотовые и специальные каналы радиосвязи, а также
навигационные каналы других радионавигационных систем (типа «ЛОРАН-С»,
«ЧАЙКА») и СРНС. Для морских потребителей наиболее целесообразным
считается использование для передачи ДП каналов морских радиомаяков (РМ) в
средневолновом диапазоне.
12.2. Математические модели для дифференциальных режимов
Измеренная в НАП в момент времени t псевдо дальность (оценка псевдо
дальности) до / -го НС может быть представлена в виде (см. (7.3))
443
Глава 12
Д-(0=А(о+ад-(0=Д/(0+(д^«(о-д^Р(о)^+ад-(0- (121)
где
ДДО = [ЫО"*('))ЧМ')"^')) +Ы')-*(')) ] (12.2)
— геометрическая дальность между / -м НС с координатами xi9 yi9 zi и НАП с
координатами х9 у9 z; ATUCi[t) — смещение БШВ НС относительно
системного времени; АГпр (/)— смещение ШВП относительно системного времени;
ад(0 = адион(0+адтРоп(0+адпР(0+^(0' (12.3)
где ЗДШН — погрешность измерения псевдо дальности, обусловленная
влиянием ионосферы; ВДтроп — погрешность измерения псевдо дальности,
обусловленная влиянием тропосферы; 5Д — погрешность измерения псевдо
дальности, обусловленная приемником; £д — прочие составляющие
погрешности определения псевдо дальности, не входящие в описанные выше.
Пусть ОИС находится в точке с известными координатами
{хоп, уоп, zon} = хоп. Тогда геометрическая дальность между ОИС и /-м НС в
момент времени t0 определяется выражением
1/2
ДопД'<>)= Ы'оЬ*оп) +(tt('o)->;oii) +(Z/('o)-Zon)"
(12.4)
В момент времени t0 на ОИС измеряется псевдо дальность Д0п,/(/о)> для
которой справедливо выражение (12.1). Поэтому для скалярной поправки
Apt (?0,хоп) к измерению псевдо дальности можно записать
Ад('о>*оп) = Д^^
(12.5)
Дифференциальные поправки А/?,-(*0,хоп) формируются на ККС для всех
видимых НС (/ = 1, N) и передаются потребителям.
Поскольку время формирования поправок t0 на ОИС не совпадает с
временем их применения t в НАП, для улучшения качества коррекции можно
использовать экстраполированную поправку к псевдо дальности
аа(^хоп)-А/7/(г0,хоп) + АД(?0,хоп)(/^г0), (12.6)
где АД (t9 хоп) = dApi (/, хоп )/dt t=t характеризует скорость изменения
дифференциальной поправки во времени.
444
Дифференциальный режим СРНС ГЛОНАСС
В НАП измеренные псевдо дальности (12.1) корректируются полученными
ДП, в результате чего формируется скорректированная оценка псевдо
дальности:
Д,корр (>>Х) = Д (>>Х) + АЛ {t,*on ) =
= Д, (/) + (АГНС, (t) - ДГнс, (0) + (^пр,оп (') - А^пр (t))c +
+ (*Аюн М - <?ДИОн (^Хоп )) + (^on (f.x) - «УД^ (/,Х0П )) +
+ (Wnp,HAn (') " <?ДпР,оп (>)) + (*Д,НАП (0 " *Д,оп (0) > С12"7)
где «~» обозначает экстраполированные на момент времени t составляющие
погрешностей, формирующиеся в соответствии с (12.6).
Структура скорректированной псевдо дальности (12.7) аналогична
структуре измеренной в НАП псевдо дальности с той лишь разницей, что вместо
абсолютных значений тех или иных составляющих погрешности входят
соответствующие разности между значениями этих составляющих, измеренными в
НАП и на ОИС, т.е. остаточные (после компенсации) значения погрешностей.
При малых значениях At = t-t0 и Ах = х-хоп остаточные ионосферные,
тропосферные погрешности и смещение бортовой шкалы времени практически
раны нулю, и погрешность скорректированной оценки псевдо дальности
определяется только шумовыми составляющими приемников НАП и ОИС и
смещением их шкал времени.
Из (12.7) вытекает ряд рекомендаций, которые необходимо учитывать при
использовании ДР в НАП. Прежде всего, любые дополнительные коррекции
псевдо дальностей или псевдо скоростей в НАП не должны противоречить
идеологии формирования ДП на ОИС. Это означает, что при использовании ДР
в НАП нельзя делать произвольных дополнительных коррекций измеренных
псевдо дальностей, так как это может нарушить условия компенсации тех или
иных составляющих погрешности измерения псевдо дальности
дифференциальными поправками. Так, если в НАП провести частичную коррекцию
ионосферной погрешности по данным, передаваемым по широковещательным
сетям, то использование ДП приведет не к компенсации ионосферной
погрешности, а к ее частичному восстановлению. Другая рекомендация заключается в
том, что в НАП при решении навигационной задачи должны использоваться те
самые эфемеридные данные, что и на ОИС. Так как эфемеридные данные
периодически обновляются, то использование соответствующих эфемерид в НАП
и тех, для которых рассчитаны передаваемые ДП, должно быть согласовано.
При установке ОИС необходимо следить за тем, чтобы при ее работе не
возникали дополнительные погрешности измерения псевдо дальностей, которые
отсутствуют у НАП. К таким дополнительным погрешностям относятся, напри-
445
Глава 12
мер, погрешности многолучевого распространения навигационных сигналов.
Поскольку при распространении ДП по линиям связи возникает задержка
сигнала, зависящая от расстояния между ОИС и НС, необходимо решать проблему
согласования времени формирования ДП и времени их использования в ПАП
(например, использовать экстраполированные поправки (12.6)).
Из формулы (12.5) для скалярной поправки А/7Д?0,хоп) видно, что можно
выделить различные медленно меняющиеся составляющие, например,
смещение БШВ АГНСj (t) и ионосферную погрешность £ДИ0Н (/,х). Поэтому на ОИС
можно формировать отдельные поправки для каждой из указанных
составляющих суммарной погрешности и передавать их потребителю. Таким
образом, получается векторная поправка, т.е. поправка, состоящая из нескольких
составляющих.
Для высокоточного ДР используются измерения псевдо фаз на ОИС и в
НАП. Сигнал от / -го НС на входе приемника может быть записан в виде
где щ = 2л ft — несущая частота сигнала / -го НС; ф0 — начальная фаза
излучения, которую для простоты положим нулевой.
Введем текущую полную псевдо фазу, полагая для простоты рассуждений
ф0=0:
(p(t) = colT(t) = 27rNi+$(t), (12.9)
где Nt — целое число периодов (частоты ft) полной фазы; ^(/)<2/г —
«дробная часть» периода фазы высокочастотного заполнения.
В когерентном приемнике сигналов НС осуществляется слежение за фазой
сигнала (12.8), и в контуре следящей системы формируется оценка дробной
части фазы, т.е. ф .
Пусть на ОИС проведены измерения псевдо дальности (12.1) и псевдо фазы
(12.9) для / -го НС. Тогда, подставляя (12.1) в (12.9), запишем
Ц- Д. (г) = ^(Д, (/) + (АГнс, (0 - АГпр (t))c + ОД (0) = 2^оис) + Й (0
ИЛИ
Щ± = д, (,) + (Д7-нс _, (,) - ДГпр (,))с + 6Д, (I) - ЛГ/(оис)Л, (12.10)
где Л^оис) — целое число периодов полной фазы сигнала с частотой ft,
принятого на ОИС.
Из (12.10) видно, что фазовые измерения зависят, во-первых, от
погрешностей (ATnci^-AT^^fjc + Sfi^t), характерных и для псевдо дальномерных
446
Дифференциальный режим СРНС ГЛОНАСС
измерений (12.1), а во-вторых, от параметра ^оис\, определяющего неодно-
значность фазовых измерений. Действительно, поскольку ф{{)<2л, измерив
ф из (12.9), нельзя определить точное значение псевдо дальности Д , если
неизвестно Nt. Поэтому А^оис) иногДа называют параметром неоднозначности
фазовых измерений. Заметим, что если в приемнике сигналов СРНС обеспечива-
ется слежение за фазой сигнала без перескоков оценки фазы (f>(t) на целое число
периодов, то параметр Л^оис\ остается постоянным в процессе слежения.
Из сравнения (12.1) и (12.10) следует, что они принципиально отличаются
наличием (или отсутствием) параметра неоднозначности Nt.
Из этого факта вытекает отличие высокоточного от стандартного ДР, а
именно: в высокоточном ДР на ОИС формируются не только
дифференциальные поправки псевдо дальности и псевдо скорости, но и оценка параметра
неоднозначности Л^(оис) Фазовых измерений, которая также должна
передаваться потребителю.
Из (12.10) видно, что для установления однозначности и высокой точности
определения дальности Д{ по фазовым измерениям ф{, необходимо оценить
погрешность (дГнс/(/)-ДГпр(/мс + <!>Д (/) (которая есть не что иное, как
погрешность дальномерных измерений), параметр неоднозначности Nt и вычесть
эти оценки из ф . Поэтому, принимая в качестве указанных оценок полученные
от ОИС поправки А/?,- (/), АД (/) и А^//кксч, в НАП можно сформировать
скорректированное значение псевдо фазы по формуле
= д. (О+(дгнс, (/') - дгнс, (/'))+(дгпР)ОП (0 - дгпр (ф +
+(адИОн (О - *JL (о)+(адтроп (О - ^хроп (о)+
-ь(едпр,НАП (О - ^„р,оп ('')) + КнАП (О " *Д,оп ('')) "
-Кнап)Л-^(оис)Л)» (12.11)
где /' — время проведения измерений в НАП; AN; = ^.(НАП)Я; ^(0ис)Л _
разность параметров неоднозначности фазовых измерений по линиям НС—
ОИС и НС—НАП соответственно.
447
Глава 12
ьсли нс находится в плоскости, перпендикулярной линии НАП—ОИС и
проходящей через середину этой линии, то ДАТ, = 0 (при условии небольших
расстояний между НАП и ОИС).
12.3. Пространственно-временные характеристики
дифференциальных поправок
Характерной особенностью дифференциальных режимов является то, что
дифференциальная поправка Ap(t0,xon) формируется в одной точке
пространства (с координатами хоп) и в один момент времени (t0), а используются они в
другой точке пространства и в другой момент времени. Наименьшая
погрешность измерений при использовании ДР получается, если НАП расположена в
той же точке, что и ОИС, а измерения в НАП проводятся в тот же момент
времени, в который формируются ДП. В этом случае поправка Д/?(/0,хоп)
является наилучшей в том смысле, что поправки Ap(t,x), полученные от ОИС,
расположенных в других точках (с координатами х), и сформированные в другой
момент времени (t), будут приводить к худшим результатам коррекции
измерений псевдо дальности в НАП.
Представим теперь обратную ситуацию: НАП находится в точке с
координатами х, измерения проводятся в момент времени t, а от ОИС получены
поправки Ap(t0,xon). Для такой НАП поправка Ap(t,x) (при ее наличии) была
бы наилучшей, а поправка Д/?(/0,хоп) будет хуже. Разложим Ap(t0,xon) в ряд
Тейлора в точке (t,x) и ограничимся линейными членами разложения
М,0,*оп)*ДрМ + М^(хоп-х) + ^(,0-,). (12.12)
Здесь первое слагаемое в правой части равенства является наилучшей
поправкой для рассматриваемой НАП, а два вторых слагаемых характеризуют
отклонение принятой от ОИС поправки от наилучшей. Причем первое слагаемое
соответствует ухудшению, обусловленному различием пространственного
положения ОИС и НАП. Такое ухудшение называют пространственным декор-
релирующим фактором. Второе слагаемое (из указанных двух) обусловлено
отличием времени использования ДП от времени ее формирования, а
соответствующее ухудшение ДП называют временным декоррелирующим фактором
Разные составляющие погрешностей дальномерных измерений могут
иметь свойства либо пространственной, либо временной декорреляции, либо и
той и другой одновременно. Например, ионосферная погрешность обладает
свойствами пространственной и временной декорреляции, а погрешность,
обусловленная расхождением шкал времени НС и потребителя, характеризуется
лишь временной декорреляцией.
448
Дифференциальный режим СРНС ГЛОНАСС
12.4. Дифференциальные поправки к погрешностям
эфемеридного обеспечения
При измерении псевдо дальности до / -го НС и рассмотрении погрешности
ее измерения используется представление (12.1), в которое входит
геометрическая дальность Mj(t)9 определяемая выражением (12.2). Представим (12.2) в
виде
Д-=|^НС,-ГНАП| = Ь?(^НС/-ГНАП). (12ЛЗ)
где RHC — радиус-вектор /-го НС в системе координат, связанной с Землей
(рис. 12.3); гЯАП —радиус-вектор НАП; h, —единичный вектор вдоль линии
НАП—НС/, представляющий собой вектор направляющих косинусов (6.149)
данной линии.
дк;
Роис,/
Рис. 12.3. Геометрическая схема
Подставляя (12.13) в (12.1), получаем
А(') = Ь?(*нс, -Гнап) + (а^сЛО-А7,пр(0) c + SMt(t). (12.14)
Измерения псевдо дальности (12.4), проведенные для четырех НС (/ = 1,4),
используются для решения навигационной задачи, т.е. для нахождения
вектора координат потребителя Гндп . При этом используется эфемеридная
информация, т.е. данные о координатах НС (векторе RHC ), передаваемые в
навигационном сообщении.
Эфемеридная информация характеризуется некоторой погрешностью,
которую можно представить в виде вектора ошибок AR, (рис. 12.3). Эти ошибки
приводят к ошибкам оценки координат потребителя, поэтому естественно
стремление снизить влияние данного типа ошибок измерений.
15-Ю26 449
Глава 12
Решение данной проблемы привело к формированию в составе векторных
поправок соответствующей составляющей — поправка погрешности эфеме-
ридного обеспечения.
Выразим из (12.4) информацию о координатах потребителя:
h>HAn =hjRHc; "Д(0 + (А7нс,«(0-А7,пр(0)с + ад,-(0. <12Л5)
где RHC = RHC + AR, — эфемеридная информация, переданная в
навигационном сообщении.
Подставим выражение для Йнс в (12.15) и запишем полученное
выражение в виде
Ь-Гнап =h[RHC/ -(Д(0-Ь^;) + (аГнс,(0-А7;р(0) с + ЗД^). (12.16)
Из (12.16) следует, что если измерение псевдо дальности скорректировать
на величину Ap3^t=h]ARi9 то скорректированному измерению
Д.кор(0 = Д"(0~ ААф/ соответствует представление
Д,кор(') = ь/ (rhc,. -rHAn) + (AW0-A7Tnp(')) * + *#/(')> (12.17)
которое не содержит погрешностей передаваемых эфемерид и может
использоваться для расчета более точных значений координат потребителя.
Поправка Д/т^Д^х) погрешностей эфемеридного обеспечения
подвержена факторам декорреляции по времени и по пространственным координатам.
Рассмотрим последний из данных факторов.
Как и в п. 12.3, положим, что поправка Д/7Эф/(*о>гоис) формируется на
ОИС, имеющей координаты хоп (определяются вектором гоис (рис. 12.3)), в
момент времени t0. Пусть НАП расположена в точке с координатами х,
которые определяются вектором гНАП =гоис+Дг (рис. 12.3). Тогда для поправки
ААф/('о>гоис) справедливо представление (12.12), из которого следует, что
пространственный декоррелирующий фактор, т.е. ухудшение
корректирующего свойства поправки в зависимости от пространственного удаления
потребителя от ОИС, определяется выражением
дДАфД'о^оис), ч АОт51,/,оис
'пр. декор ~ Z V ГОИС ГНАП ) " "лк/ -
АДф.декор = ^ (ГОИС -rHAn) = -AR« ~^ Аг » (12Л8>
гоис ^гоис
Учитывая определение вектора направляющих косинусов:
_ Роис,/ _ ^нс,/-гоис
h/.OHC
Роис,/
^НС,; Г0ИС
450
Дифференциальный режим СРНС ГЛОНА СС
и выполнив дифференцирование в (12.18), получаем
ЛАф.декор = _AR^ ^Г^ЛГ = ТГ~~Л(ЛГ " (Л1*Т,1'-,ОИС ) Ь/,ОИС ) =
AR/d
' дг,
оис
Роис,/
Р0ИС,г
(12.19)
где вектор d = Ar -(ArTh/ оис J h, оис представляет собой проекцию вектора Дг
на нормаль к линии ОИС—НС„ лежащую в плоскости, образованной
векторами Роис,/ и h/ •
Используя неравенство Коши—Шварца, для (12.19) можно записать
AAiP.
пр.декор
<
AR,
Роис,/
<
AR,
Аг
Роис,/
(12.20)
Из (12.19), (12.20) следует, что с увеличением расстояния |Аг| между ОИС
и НАП возрастает влияние пространственного декоррелирующего фактора для
поправок эфемеридного обеспечения.
12.5. Бюджет погрешностей определения псевдодальности
в дифференциальном режиме
В результате использования дифференциального режима в СРНС
снижаются отдельные составляющие погрешностей в интегрированном бюджете
погрешностей определения псевдо дальностей (см. табл. 7.4).
В табл. 12.1 приведены ожидаемые значения погрешностей в этом случае,
заимствованные из [6.8]. Приведенные данные соответствуют положению
потребителя в радиусе 50 км от ККС.
Таблица 12.1. Интегрированный бюджет погрешностей
определения псевдо дальности при использовании ДР
Источник погрешности
Эфемериды
Часы спутника
Ионосфера
Тропосфера
Многолучевость
Приемник
Итого
а8Д ' М
0
0,7
0,5
0,5
1,4
0,6
3,7
451
Глава 12
При большем удалении потребителя от ККС необходимо учитывать
пространственные и временные декоррелирующие факторы, рекомендуемые
значения которых приведены в табл. 12.2.
Таблица 12.2. Пространственные декоррелирующие факторы
Источник погрешности
Эфемериды
Ионосфера
АЛф.декор>м/1(Юкм
< 0,05
<0,2
12.6. Контроль целостности СРНС в дифференциальных
подсистемах
Одним из важных требований к системам глобальной навигации, как
отмечалось в п. 1.6, является целостность, под которой понимают способность
системы своевременно выявлять и предоставлять потребителю информацию об
отказах в системе. В системе ГЛОНАСС предусмотрен контроль целостности,
основные способы реализации которого описаны в п. 11.5. Однако время
информирования потребителей о произошедших в системе отказах с
использованием только средств системы не удовлетворяет требованиям ряда важных
приложений, например, гражданской авиации. Поэтому существует потребность в
дополнительных, независимых методах и средствах контроля целостности
СРНС.
Одним из возможных подходов к решению данной проблемы является
создание сети наземных станций мониторинга, основная задача которых —
выявление отклонений от штатного функционирования СРНС и оперативное
информирование об этом пользователей.
Другой подход основан на использовании имеющихся или создающихся
дифференциальных подсистем для дополнительного контроля целостности
СРНС. В основе такой возможности лежит аналогичность проводимых
измерений. Так, на ККС осуществляется прием и обработка сигналов всех НС, в
результате чего формируются оценки координат ККС, которые сравниваются с
точно известными координатами. Отклонение характеристик сигнала того или
иного НС от стандартных приводит к изменению оценок координат, что
фиксируется и может быть использовано для набора статистических данных о
характеристиках сигналов, излучаемых НС. Наличие сети ККС позволяет
организовать дополнительную совместную обработку данных, полученных на каждой
ККС, что повышает качество контроля целостности. Совмещение функций
формирования дифференциальных поправок и контроля целостности в
ДПС полезно также и в интересах исключения передачи недостоверных
поправок потребителям.
452
Дифференциальный режим СРНС ГЛОНА СС
В качестве характеристик целостности могут использоваться следующие
параметры:
вероятность выявления отказа в течение времени, равного заданному или
менее;
время обнаружения отказа — интервал времени между фактом
наступления отказа и фактом его обнаружения;
частота отказов на заданном интервале времени;
допустимые значения ошибок при решении навигационной задачи.
При осуществлении контроля целостности решаются следующие задачи:
оценивание в реальном времени ошибок измерения псевдо дальностей по
сигналам всех НС;
оценивание точности определения горизонтальных и вертикальных
составляющих координат с учетом лишь погрешностей эфемерид, частотно-
временных поправок и текущей геометрии НС;
оценивание точности определения горизонтальных и вертикальных
составляющих скорости с учетом лишь погрешностей эфемерид, ЧВП и текущей
геометрии НС;
оценивание отношения сигнал/шум по сигналам всех НС;
контроль количества наблюдаемых НС;
поддержка баз данных, содержащих перечисленные выше параметры;
фиксация ситуаций, когда НС функционирует аномально.
Результаты контроля целостности передаются потребителям в форме
«рекомендаций» о целесообразности использования сигналов того или иного НС
для решения навигационной задачи. Данная информация передается вместе с
дифференциальными поправками по соответствующим каналам связи.
12.7. Форматы данных, используемые при передаче
информации в дифференциальных подсистемах
Для передачи данных, формируемых в ДПС, разработано и используется
несколько форматов данных. Наиболее широко, в том числе и в России,
используется стандарт RTCM SC-104, предложенный Специальным Комитетом
104 (Special Committee 104) Радиотехнической комиссии по мореплаванию
(Radio Technical Commission for Maritime Services) США [12.1, 12.2] и
поддержанный Международной ассоциацией маячных служб. Существует несколько
версий данного стандарта:
версия 2.0 включает дифференциальные поправки для кодовых измерений
псевдо дальности и скорости изменения псевдо дальности по сигналам СРНС
GPS;
версия 2.1 дополнительно включает ДП для измерений псевдо фазы и
сырых измерений;
453
Глава 12
версия 2.2 дополнительно к данным версии 2.1 включает аналогичные
поправки для измерений по сигналам СРНС ГЛОНАСС;
версия 2.3 учитывает последние изменения в технологии спутниковой
навигации, в том числе выключение режима селективного доступа в СРНС GPS.
Далее приводятся основные сведения о стандарте RTCM версии 2.2,
базирующиеся на [12.2]. В стандарте предусмотрена передача ДП,
предназначенных для коррекции следующих составляющих ошибок навигационно-
временных измерений по сигналам НС GPS и ГЛОНАСС:
ошибки прогнозирования эфемерид спутников;
ошибки прогнозирования часов спутников;
ошибки ионосферных задержек;
ошибки тропосферных задержек на опорной станции;
искусственные ошибки, вносимые технологией селективного доступа (SA)
(только GPS);
дифференциальные ошибки тропосферных задержек;
ошибки фазовых измерений;
смещения часов ККС.
Кроме того, в данный стандарт включены оценки точности
навигационных измерений, данные альманаха, информация о состоянии НС
(годен/негоден для использования) и «возрасте» данных, использованных ККС.
Стандарт допускает использование сообщений, содержащих иную
(произвольную) информацию.
В стандарте RTCM передаваемые данные представляются в виде
сообщений различного типа. Типы сообщений различаются или по частоте их
передачи, или по типу пользователя, для которого они предназначены, или в
зависимости от того, являются они или нет данными для коррекции ошибок или
данными альманаха. Каждый тип сообщения имеет индивидуальный номер (один
из 64). Несколько базовых типов сообщений определены в их окончательной
форме. Несколько других определены в предварительной форме;
производители оборудования, применяющие этот стандарт, осведомлены о том, что они
могут быть изменены после натурных испытаний. Большое число типов
сообщений остались неопределенными, но зарезервированы для будущего
использования в предполагаемых приложениях.
Все RTCM-сообщения передаются в виде последовательности 30-битовых
слов. При этом различные типы сообщений могут включать различное число
слов. Например, типичное сообщение для передачи ДП для 6 НС включает
примерно 16 слов. Каждое слово содержит 24 информационных бита и 6
проверочных. В качестве помехоустойчивого кодирования слова используется
блочный код Хэмминга (32,26) (см. п. 5.5.2), а проверка правильности
принятого слова осуществляется по той же схеме, что и при извлечении
навигационного сообщения в GPS.
454
Дифференциальный режим СРНС ГЛОНАСС
Каждое РТСМ-сообщение начинается заголовком, включающим два слова,
структура которых и передаваемые в них данные приведены в табл. 12.3.
Таблица 12.3. Структура первых двух слов сообщения
Слово
Первое
слово
1 Второе
слово
Состав слова
Преамбула
Номер типа сообщения
Идентификатор ККС
Проверочные биты
Модифицированный Z-
отсчет
Текущий номер сообщения
в последовательности
Число слов в сообщении
Состояние станции
Проверочные биты
Число
бит
8
6
10
6
13
3
5
3
6
Цена младше-
_горазряда
-
1
1
-
0,6 с
1
1
-
-
1 1
Диапазон
изменения |
-
1...64
1...1023
|
0..3599,4 с
0...7
0...31
1...8
_- |
Модифицированный Z-отсчет представляет собой опорное время для
данных сообщения, которое соответствует времени GPS или ГЛОНАСС, в
зависимости от принадлежности данных сообщения той или иной системе.
В табл. 12.4 приведены типы сообщений, их номера и текущее состояние
их использования.
Дадим краткую характеристику основных типов сообщений для СРНС
GPS, приведенных в табл. 12.3. Аналогичные по назначению типы (31...36)
используются для передачи ДП по сигналам СРНС ГЛОНАСС.
Сообщение 1 типа предназначено для передачи ДП псевдо дальности
&Pi(t0) и скорости изменения ДП псевдо дальности Apt (t0) для всех НС,
видимых на ККС. Для каждого НС передаются данные, приведенные в табл. 12.5.
Таблица 12.4. Типы сообщений
[Номер
U типа
1
2
3
4
5
6
и 1
Назначение
Дифференциальные поправки псевдо дальности
GPS
Приращение дифференциальных поправок
псевдо дальности GPS
Параметры опорной станции GPS
Опорный эллипсоид опорной станции
Техническое состояние созвездия GPS
Нулевой кадр GPS
Альманах радиомаяков GPS
Текущее
состояние 1
Постоянное
Постоянное
Постоянное
Экспериментальное
Постоянное
Постоянное
Постоянное ]
455
Глава 12
18
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23...30
31
32
33
34
35
36
37
38...58
59
160...63
Альманах псевдо литов [
Установка частных поправок GPS |
Дифференциальные поправки для Р-кода
Поправка в диапазоне L2 для С/А-кода
Параметры псевдолитной станции 1
Параметры наземной передающей станции
Время недели GPS
Сообщение об ионосферной (тропосферной)
задержке
Специальное сообщение GPS
Эфемериды GPS
Нескорректированные на «кинематике реального
времени» фазы несущей
Нескорректированные на «кинематике реального
времени» псевдо дальности
Поправки фазы несущей на «кинематике реального
времени»
Высокоточные поправки псевдодальности
Расширенные параметры опорной станции
Не определены
Дифференциальные поправки GLONASS
Параметры опорной станции GLONASS
Техническое состояние созвездия GLONASS
Установка частных поправок GLONASS или
нулевой кадр GLONASS
Альманах радиомаяков GLONASS
Специальное сообщение GLONASS
Сдвиг системного времени GNSS
Не определены
Сообщения о собственности
Многоцелевое использование
Экспериментальное
Постоянное
Зарезервировано
Зарезервировано
Зарезервировано
Экспериментальное
Экспериментальное
Экспериментальное
Постоянное
Экспериментальное
Постоянное
Постоянное
Экспериментальное
Экспериментальное |
!
Экспериментальное
1
Экспериментальное
Экспериментальное 1
Экспериментальное
Экспериментальное
Экспериментальное
Экспериментальное
Экспериментальное
1
Постоянное
Зарезервировано |
Таблица 12.5. Данные, передаваемые для каждого НС в сообщении 1 типа
Данные
ДП псевдо дальности
Скорость изменения ДП псевдо
| дальности
Оценка ожидаемой погрешности
скорректированной псевдо
дальности
| Номер спутника
Число
бит
16
8
2
5 __ь
Масштабный к-т
0,02 или 0,32 м
0,002 или 0,032 м/с
-
1
Диапазон
изменения J
±655,34 или I
±10485,44 м
±0,254 или
±4,064 м/с
2 состояния
1...32 1
456
Дифференциальный режим СРНС ГЛОНАСС
Масштабный коэффициент (МК)
Признак принадлежности
посылки данных (ПППД)
1 Итого
1
8
_40
1 2 состояния
Смотри спецификацию сигналов GPS I
Передаваемые дифференциальные поправки Apt[t0), ЛД(/0)
соответствуют моменту времени /0= модифицированный Z-отсчет (см. табл. 12.3). Коды
использования масштабных коэффициентов приведены в табл. 12.6.
Дифференциальные поправки псевдо дальности на текущий момент
времени t рассчитывается в соответствии с (12.6).
Таблица 12.6. Коды масштабных коэффициентов
Код
0
1
Число
(0)
(1)
Значение
Коэффициент масштабирования для поправки псевдо дальности
0,02 м, а для поправки скорости изменения дальности 0,002 м/с
Коэффициент масштабирования для поправки псевдо дальности
0,32 м, а для поправки скорости изменения дальности 0,032 м/с |
Таблица 12.7. Коды ожидаемой погрешности скорректированной
псевдо дальности
[Код
1
г ■ ■■■ ■■ ■
00
01
10
Lu
Число
(0)
(1)
(2)
ш 1
Дифференциальная ошибка на уровне
одной сигмы, м |
<1
> 1 и < 4
> 4 и < 8
>8 [
Оценка ожидаемой погрешности скорректированной псевдо дальности
SD в аппаратуре потребителя определяется в соответствии с табл. 12.7.
Структура сообщения 1 типа приведена на рис. 12.4.
Слово 3
МК
SD
Номер НС
ДП псевдо дальности
Проверочные
символы
Слово 4
Скорость
изменения ДП
псевдо дальности _
ПППД
МК
SD
Номер НС
Проверочные
символы
457
Глава 12
Слово 5
ДП псевдо дальности
Скорость изменения ДП
псевдо дальности
Проверочные
символы
Слово 6
пппд
мк
sb
Номер
НС
ДП псевдо дальности
(страшие байты)
Проверочные
символы
Слово 7
ДП псевдо
дальности (младшие
байты)
Скорость изменения
ДП псевдо дальности
ПППД
Проверочные
символы
Слово 8
Слово N+2
Скорость изменения ДП
псевдо дальности
ПППД
Заполнение
Проверочные
символы
Рис. 12.4. Структура сообщения 1 типа
Из рис. 12.4 видно, что в сообщении 1 типа каждое слово имеет один из
пяти форматов (см. слова 3...7), за исключением последнего слова в
сообщении. Из табл. 12.4 следует, что для представления данных по каждому НС
необходимо 40 бит. При разном числе видимых НС не всегда требуется точно
целое число слов. Поэтому могут появиться слова, которые надо дополнять
восемью или шестнадцатью битами до полного кадра. Для этого в конце сообщения
предусмотрена позиция «Заполнение».
Признак принадлежности посылки данных (см. табл. 12.4)
идентифицирует временную привязку передаваемых в сообщении данных к
соответствующему навигационному сообщению GPS, которое использовалось ККС. Он
включается в сообщение 1 типа для того, чтобы пользователь мог
проконтролировать тот факт, что НАП и ККС используют одни и те же данные «часов НС» и
эфемеридной информации.
Сообщение 2 типа имеет тот же формат, что и на рис. 12.4. Оно является
альтернативой сообщению 1 типа и содержит поправки, соответствующие
старым данным «часов НС» и эфемеридной информации. Это сообщение
предназначено для ситуаций, когда оборудование пользователя не может
немедленно декодировать новые данные эфемерид спутников в спутниковых
сообщениях и использует старые данные, т.е. возникает ситуация, когда
пользователь и ККС используют различные эфемериды.
Сообщение 9 типа отличается от сообщений 1 типа лишь тем, что в нем
передается информация не для всех НС, находящихся в зоне видимости ККС, а
458
Дифференциальный режим СРНС ГЛОНА СС
для некоторой их части. Данный тип сообщений может использоваться в тех
случаях, когда требуется различная скорость обновления ДП по различным НС.
Сообщения 18,19,20 и 21 типов предназначены для передачи ДП для
фазовых измерений (в иностранной литературе для одного из возможных режимов
фазовых измерений используют термин «кинематика реального времени»
(RTK — Real Time Kinematic)). Эти сообщения имеют заголовок из трех слов.
Первые два слова имеют такую же структуру, что и в описанных выше
сообщениях. Третье слово включает поле «Расширение времени измерений»,
которое увеличивает разрешение по времени, дающееся модифицированным Z-
отсчетом во втором слове. После заголовка из трех слов каждое сообщение
содержит два слова для каждого НС, так что общая длина сообщения составляет
30(3+7V), где N — число НС, видимых на ККС. Два слова сообщений 18 и 19
типов включают данные «сырых» измерений псевдо фазы и псевдо дальности,
выполненные на ККС. Аналогичные слова сообщений 21 и 22 типов содержат
данные измерений, скорректированные по эфемеридной информации,
содержащейся в навигационном сообщении. Кроме указанных данных, два
информативных слова содержат следующие идентификаторы:
номер НС;
принадлежность поправок диапазонам Ы или L2 ;
принадлежность поправок сигналам с С/А- или Р- кодам (кодам
стандартной или повышенной точности СРНС GPS);
принадлежность измерений фазы несущей частоты полной или половине
длины волны L2;
качество данных;
данные о перескоках фазы, зафиксированных при измерениях.
12.8. Примеры построения дифференциальных подсистем
12.8.1. Морские локальные дифференциальные подсистемы
Морская ДПС (МДПС) СРНС предназначена для обеспечения
возможности реализации дифференциального режима в НАП СРНС с целью повышения
точности и надежности навигационных определений морских потребителей и
эффективного их использования для повышения безопасности судоходства
вблизи берегов, в узкостях, зонах разделения путей, на подходах к портам и в
районах стесненного маневрирования.
Для морских потребителей считается наиболее целесообразным применять
для передачи дифференциальных сообщений (ДС) каналы морских РМ в
средневолновом диапазоне. В состав МДПС входят локальные ККС, создаваемые
на базе РМ, или их сети. МДПС СРНС GPS для передачи ДС использует
несколько сот из существующей сети морских радиомаяков. Их рабочая зона
охватывает практически все важнейшие районы судоходства.
459
Глава 12
Международными организациями (Международной морской организацией
(ИМО), Международной организацией маячных служб (МАМС),
Международной электротехнической комиссией (МЭК), Международным союзом
электросвязи (МЭС)), а также национальными морскими службами и, в первую
очередь, Радиотехнической комиссией для морских служб США (RTCM)
разработаны документы, определяющие требования к судовой аппаратуре СРНС и к
МДПС СРНС, которые должны быть учтены при создании судовой
аппаратуры и оборудования ККС ДПС СНС ГЛОНАСС и GPS [12.1—12.11].
Основные требования к составу и функциональным характеристикам ККС
МДПС СРНС ГЛОНАСС и GPS изложены в [12.12, 12.13].
На рис. 12.4 приведена структурная схема варианта ККС МДПС на базе
морского радиомаяка.
Морской радиомаяк
1-й полукомплект
▲ А
Опорная станция
(ДГЛОНАСС/DGPS)
с МФС модулятором
(основной комплект)
Станция интегрального
контроля
(основной комплект)
Т
2-й полукомплект
?? 11
Опорная станция
(ДГЛОНАСС/DGPS)
с МФС модулятором
(резервный комплект)
А
▼
Станция интегрального
контроля
(резервный комплект)
Контрольная станция
(на базе IBM PC)
Рис. 12.4. Типовая схема ККС
В состав ККС входят:
РМ с антенной системой, имеющий основной и резервный полукомплекты
передающего устройства;
основной и резервный комплекты опорной станции (ОС);
основной и резервный комплекты станции интегрального контроля (СИК);
контрольная станция.
В случае необходимости может применяться удаленная
контрольно-управляющая станция. Резервный полукомплект передающего устройства
радиомаяка, а также резервные ОС и СИК находятся в режиме горячего резерва, чтобы в
случае отказа в основном оборудовании обеспечить возможность
оперативного переключения для замены его на резервное оборудование без нарушения
работы НАП в дифференциальном режиме.
460
Дифференциальный режим СРНС ГЛОНАСС
Для выполнения своих функций ККС МДПС должна решать следующие
задачи:
одновременный приём и обработку аппаратурой ОС и СИК
навигационных сигналов стандартной точности (СТ-кодов ГЛОНАСС и С/А- кодов GPS) в
диапазоне LX всех находящихся в зоне видимости спутников СРНС ГЛОНАСС
и GPS, а также приём и обработку аппаратурой СИК сигналов
дифференциальных сообщений в диапазоне работы радиомаяков;
измерение псевдо дальностей по всем принимаемым сигналам СРНС
ГЛОНАСС и GPS, а также сравнение передаваемых и принимаемых
дифференциальных сообщений и их временную привязку к системной шкале СРНС
ГЛОНАСС (GPS);
выработку ДП к измеренным псевдо дальностям по всем принимаемым
сигналам СРНС и формирование дифференциальных сообщений в
соответствии со стандартом RTCM SC-104, в которые входят ДП, информация о
целостности и другие данные, необходимые для обеспечения нормального
функционирования ДПС;
передачу дифференциальных сообщений в диапазоне частот 283,5...325
кГц с использованием модуляции минимальным фазовым сдвигом (МФС)
(класс излучения G1D);
контроль качества и регистрацию передаваемых дифференциальных
сообщений;
непрерывный анализ качества навигационных полей СРНС ГЛОНАСС и
GPS и регистрацию данных о них;
формирование и выдачу информации о качестве навигационных полей и
дифференциальных сообщений;
непрерывный контроль качества функционирования элементов ККС в
рабочем режиме;
обмен информацией между элементами ККС с использованием
стандартизованных сообщений RSIM;
автоматическое переключение оборудования ККС в случае отказа с
основного на резервный комплект.
Для решения указанных выше задач ОС ККС должна иметь геодезическую
привязку и оснащаться:
высокоточной, многоканальной НАП СРНС, обеспечивающей прием
сигналов всех наблюдаемых спутников;
вычислительным комплексом для определения ДП и формирования
дифференциальных сообщений в формате RTCM SC-104, а также для обеспечения
возможности выполнения ОС своих функциональных задач;
модулятором для модуляции МФС излучаемых передатчиком радиомаяка
сигналов по закону соответствующих дифференциальных сообщений;
средствами связи с СИК, КС и другими объектами.
Опорная станция обеспечивает вычисление ДП к измеренным псевдо
дальностям по навигационным сигналам всех видимых НС, формирование ДС
461
Глава 12
в стандартном формате RTCM SC-104 и модуляцию высокочастотного сигнала
по их закону. Для успешного выполнения своих функций ОС должна
оснащаться:
высокоточной, многоканальной приемной аппаратурой СРНС, антенна
которой имеет геодезическую привязку и обеспечивает прием сигналов всех
наблюдаемых спутников;
вычислительным комплексом для определения ДП, формирования ДС и
выполнения других необходимых функций;
модулятором для модуляции МФС высокочастотного сигнала по закону
соответствующих ДС, который усиливается радиомаяком для передачи
потребителям;
средствами связи.
При обмене данными с другим оборудованием ККС должна
обеспечиваться совместимость с форматом RSIM. Приемная аппаратура СРНС,
вычислительный комплекс и MSK-модулятор для удобства использования
некоторыми фирмами изготовляются в виде моноблока.
Станция интегрального контроля предназначена для контроля
правильности передачи дифференциальных сообщений потребителям, для контроля
качества навигационных полей СРНС и сравнительной оценки расчетных и
измеренных значений псевдо дальностей до каждого НС, а также эталонных и
вычисленных с использованием ДП координат места, анализ которых позволяет
оценивать точность выработанных ОС дифференциальных поправок. Для связи
с другими устройствами должно быть предусмотрено не менее трех
последовательных портов RS-232. Ввод и переустановка исходных данных должны
обеспечиваться с помощью клавиатуры на передней панели с возможностью
отображения параметров на дисплее. Пороговые значения контролируемых
параметров и период времени для срабатывания сигнала тревоги устанавливаются в
соответствии с требованиями стандарта на МДПС. В случае превышения
значения одним из контролируемых параметров заданных порогов оборудование
СИК немедленно вырабатывает и передает сигнал тревоги на ОС и КС.
Одновременно решается задача контроля целостности рабочего созвездия спутников
СРНС ГЛОНАСС и GPS для оценки работоспособности этих систем.
Станция интегрального контроля предназначена также для контроля
качества сигналов дифференциальных сообщений формируемых ОС и полного
контроля за ее работой. Совместная работа ОС и СИК позволяет исключать из
дифференциальных сообщений ошибки, вызываемые сбоями в работе
аппаратуры НС, в том числе в период закладки на него новых данных. Станция
интегрального контроля должна оснащаться высокоточной, многоканальной НАП
СРНС, антенна которой имеет геодезическую привязку; аппаратурой приема
дифференциальных сообщений; вычислительным комплексом и средствами
связи. При обмене данными с другим оборудованием ККС должна
обеспечиваться совместимость с форматом RSIM.
462
Дифференциальный режим СРНС ГЛОНАСС
Контрольная станция предназначена для обеспечения возможности
оперативного контроля состояния и управления функционированием ККС с
заданными характеристиками. Она построена на базе современного компьютера с
программным обеспечением для контроля и управления ОС, СИК и РМ, а
также для регистрации данных.
Существует несколько вариантов использования КС. Одна станция может
использоваться в составе одной ККС или в составе их сети. Контрольная
станция может находиться в одном месте с ОС и СИК или на некотором удалении
от них. При совместном размещении КС может состоять из компьютера с
программным обеспечением или быть интегрирована в оборудование ОС или
СИК. При такой интеграции отпадает необходимость применения RSIM-
сообщений, так как они идентичны используемым в оборудовании
вычислительных комплексов ОС и СИК.
Контрольная станция как элемент ККС особенно важна для морских
пользователей, предъявляющих высокие требования к СРНС. Возможности
контроля состояния системы с помощью КС минимизируют перерывы в
обслуживании при возникновении сбоев и нарушениях нормальной работы МДПС за счет
оперативного оповещения морских пользователей информацией о состоянии
СРНС и МДПС. КС должна обеспечивать хранение данных о состоянии
системы с целью их анализа и выработки корректирующих воздействий
операторами системы. Она оснащается вычислительным комплексом и средствами связи
с ОС и СИК для обмена данными, выработки и передачи управляющих сигналов.
Контрольная станция обеспечивает возможность установки и при
необходимости переустановки параметров оборудования ККС МДПС СРНС,
текущего контроля функциональных и технических характеристик ее при
оперативном оповещении потребителей об отказах или выходе параметров за
допустимые пределы, а также дистанционного управления работой ОС и СИК. Роль КС
заключается в подтверждении работоспособности ОС, определении параметров
передаваемых сообщений и контроле работы ККС МДПС. Наличие КС в
составе ККС МДПС особенно необходимо в случае применения ее в стесненных
условиях плавания, где требуются высокие доступность, точность, надежность и
целостность системы. Контрольная станция производит управление ККС путем
начальной или повторной установки параметров оборудования ОС и СИК. При
этом осуществляется выбор режимов работы, порогов для выработки сигналов
тревоги, интервалов регистрации данных, графика передачи необходимых
дифференциальных сообщений и т.д. Она обеспечивает также контроль и
управление работой ККС МДПС практически в реальном масштабе времени.
Контрольная станция принимает информационные сигналы от радиомаяка, ОС
и СИК и на программном уровне обеспечивает контроль за параметрами ОС и
РМ, а также управляет их работой, включая изменения характеристик передач,
переустановку данных, конфигурирование системы и регистрацию данных.
463
Глава 12
Радиомаяк с антенной системой обеспечивает передачу сигналов,
модулированных по закону дифференциальных сообщений спутниковых
навигационных систем ГЛОНАСС/GPS, потребителям. Он имеет основной и резервный
каналы и согласуется со всеми типами антенн морских радиомаяков.
Радиомаяк оборудован системой автоматического регулирования, системой
дистанционного управления с помощью компьютера, системой контроля и диагностики,
а также бесперебойным источником питания.
Комплекс оборудования ККС должен полностью удовлетворять
международным и национальным требованиям, в том числе:
радиомаяк должен обеспечивать работу с антенной, имеющей круговую
диаграмму направленности в азимутальной плоскости;
радиомаяк должен иметь основной и резервный полукомплекты, а также
систему автоматики, контролирующую исправную работу и переключение на
резервный полукомплект с настройкой антенного контура;
радиомаяк должен обеспечивать непрерывную передачу
дифференциальных сообщений со скоростью 50, 100 или 200 бит/с в частотных диапазонах,
предназначенных для морской навигации: от 283,5 до 315 кГц в регионе 1 и
от 286 до 325 кГц в регионах 2 и 3; при этом должны быть использованы
несущие частоты радиомаяков кратные 500 Гц для обеспечения при разделении
частот минимальной интерференции соседних каналов и их совместимость;
радиомаяк должен обеспечивать непрерывную передачу
дифференциальных сообщений с компактным спектром за счет применения для передачи
двоичных данных модуляции МФС (класс излучения G1D); при этом занимаемая
полоса частот при скорости передачи 200 бит/с и 100 бит/с соответственно
не должна быть больше 236 Гц и 120 Гц для 99% мощности;
сигналы дифференциальных сообщений должны передаваться на
основной частоте или на поднесущей и излучаться одновременно с излучением
сигнала пеленгования;
мощность излучения РМ должна обеспечивать рабочую зону действия ДПС
с учетом получения заданных доступности, точности и надежности
навигационных определений и обычно не превышает 80... 100 Вт;
дальность действия РМ (при Ризл = 80 Вт) при работе на антенну с
действующей высотой не менее 18 м, емкостью 290... 1100 пФ и сопротивлением
2...6 Ом должна быть не менее 300 км с обеспечением напряженности поля в
точке приема 50 мкВ/м для сигналов пеленгования и не менее 600 км для
приема дифференциальных сообщений с уровнем сигнала 5 мкВ/м;
защитное соотношение параметров полезного и мешающего сигналов для
Европейской зоны приведены в табл. 12.8 для полосы пропускания шириной
4кГц (± 2 кГц); при их расчете минимальный уровень полезного сигнала,
принимаемого в рабочей зоне РМк, который содержит информацию о
дифференциальных сообщениях, должна быть не менее 75 мкВ/м;
464
Дифференциальный режим СРНС ГЛОНА СС
Таблица 12.8. Защитные соотношения параметров
Разделение
несущих частот между
сигналами ОС и
помехой, кГц
0,0
0,5
1,0
1,5
[2,0
Требуемое соотношение сигналов ОС и по- 1
мех при работе, дБ |
Ненаправленные
морские и аэромаяки
15
-25
-45
-50
-55
Радиомаяки, 1
транслирующие
ДП |
15
-25
-36
-42
-47
кадры передаваемой информации, формируемые опорной станцией
должны соответствовать требованиям RTCM SC-104;
работа СИК должна обеспечивать обработку сигналов с уровнями на
входе от -160 до -153 дБВт, принимаемых от всех видимых НС с углами
возвышения над горизонтом более 7,5°;
при размещении СИК на опорной станции, нормальная работа ее должна
обеспечиваться при напряженности электрического поля сигналов на входе от 1
до 24В/м и напряженности магнитного поля от 0,18до4мА/м.
В настоящее время в эксплуатации находится несколько сот ККС МДПС
СРНС GPS. Их рабочая зона охватывает прибрежные районы морей и океанов
большинства государств. Согласно принятой в США программе развития
МДПС СРНС GPS введено в эксплуатацию более 50 ККС, зона действия
которых охватывает все прибрежные воды США, часть из них размещена в Канаде,
что позволяет обеспечить высокоточными навигационными измерениями
внутренние водные пути Великих озер и реки Святого Лаврентия. В США полные
эксплуатационные характеристики МДПС СРНС GPS достигнуты в 1999 г. За
счет распространения ее рабочей зоны на всю территорию США создана
Национальная дифференциальная подсистема GPS с двойным покрытием рабочей
зоной всей территории США. С вводом российской ККС МДПС СРНС на базе
радиомаяка «Шепелевский» акватория всего Балтийского моря от порта Санкт-
Петербурга до Датских проливов покрыта рабочей зоной МДПС СРНС GPS.
Работа по созданию сети ККС МДПС СРНС ГЛОНАСС/GPS в России
проводится по линии Минтранса в Арктике и на внутренних водных путях и по
линии МО РФ в морских прибрежных районах Российской Федерации.
Разработана и утверждена Министерствами транспорта и обороны РФ
Межведомственная программа по оборудованию побережья морей Российской
Федерации ККС МДПС СНРС ГЛОНАСС/GPS. Предлагаемое оснащение позволит
удовлетворить не только потребности общего мореплавания, но и нужды других
потребителей в прибрежных районах. В интересах морских потребителей на побе-
465
Глава 12
режьях морей Российской Федерации предусмотрена установка более 30 ККС с
зоной действия, охватывающей все прибрежные воды и устьевые участки Волги,
Дона, Невы, Енисея и других рек, а также Ладожского и Онежского озер.
Разработана отечественная аппаратура для ККС МДПС СРНС
ГЛОНАСС/GPS в составе комплекса оборудования типа СН-3500М (КБ
«НАВИС») и радиомаяка «Янтарь - 2М» (АО «ТЕХНОМАРИН»),
обеспечивающая определение ДП, независимое формирование ДС СРНС ГЛОНАСС и
ДС СРНС GPS и возможность их последовательной или параллельной
передачи потребителям в стандартном формате RTCM SC-104.
Первая ККС МДПС СРНС ГЛОНАСС/GPS размещена в районе порта
Новороссийск. Опорная станция с помощью 28 канальной аппаратуры СРНС
принимает сигналы всех видимых спутников ГЛОНАСС и GPS, производит
выработку дифференциальных поправок, формирует дифференциальные сообщения
в стандартном формате RTCM SC-104 и модулирует ими высокочастотные
сигналы, которые радиомаяк усиливает и излучает в эфир. СИК с помощью 28-
канальной аппаратуры СРНС принимает сигналы всех видимых спутников
ГЛОНАСС и GPS, а также с помощью встроенного приемника — сигналы
дифференциальных сообщений, и проверяет нахождение контролируемых
параметров в допустимых пределах. Данные о нормальном функционировании
подтверждают нормальную работу. При выходе контролируемых параметров
за допустимые пределы формируется сигнал тревоги. Контрольная станция
построена на базе IBM-совместимого компьютера с программным обеспечением
контроля и управления ОС, СИК, РМ и связи с удаленной контрольно-
управляющей станцией RSIM Software «CONTROL STATION NAVIS». Она
принимает информацию о работе системы, определят места отказов,
вырабатывает соответствующие управляющие сигналы, производит установку и
изменения параметров оборудования, принимает решения о работоспособности
спутников, сохраняет информацию о работе ККС и т.д. Удаленная контрольно-
управляющая станция, находящаяся в Новороссийске, через модемную линию
связи позволяет оператору производить все действия по управлению и
контролю так же, как при использовании КС. В ходе испытаний ККС погрешность
определения координат на удалениях до 100 км не превышала 1 м (для Р=95%).
В настоящее время в России находятся в эксплуатации пять ККС МДПС СРНС
ГЛОНАСС/GPS, использующих оборудование типа СН-3500М и радиомаяки
«Янтарь - 2М». Они установлены на побережьях Азовского, Черного,
Балтийского и Каспийского морей.
12.8.2. Перспективная российская дифференциальная подсистема
Общие положения
Как отмечалось в п. 12.1, для организации ДР на территории больших
регионов можно использовать сетевую структуру ДПС (региональную ДПС),
466
Дифференциальный режим СРНС ГЛОНА СС
объединяющую несколько локальных ДПС (радиусом 150...200 км). Для
построения этим способом непрерывного поля высокоточных поправок (т.е. ДП с
малой остаточной погрешностью коррекции) в крупных регионах требуется
развернуть непрерывную сеть из большого числа ККС и аппроксимировать
поправки от соседних ККС для сглаживания ошибок коррекции в пределах
рабочей зоны региона. Поскольку точный закон изменения поправок в
произвольной точке между ККС неизвестен и меняется по мере движения спутника, для
расчета аппроксимации можно воспользоваться только простейшим
полиномом первого порядка. Это затрудняет получение высокоточной
дифференциальной коррекции в произвольной точке не только региональной зоны, но и в
пределах локальной рабочей зоны отдельно взятой ККС. К тому же, для
каждой точки региона соотношение погрешностей региональных и локальных
поправок будет зависеть от расстояния до ближайшей ККС. Поэтому для каждой
точки рабочей зоны потребителю самому придется выбирать наиболее точные
поправки. Отсюда возникает необходимость использования в единой системе и
региональных поправок, и всего множества локальных поправок, а задачу
выбора наиболее точных из них переложить на НАП потребителя.
Из-за перечисленных проблем единая система получается громоздкой и
сложной, а конечная НАП — дорогой. Так, например, это потребует
размещения на территории РФ около 2000 геодезически привязанных ККС, в том числе
в труднодоступных районах, и объединения их с помощью сложных и дорогих
каналов связи в единую сеть.
Кроме того, объединение отдельных ЛДПС в рамках одной системы
приводит к необходимости решать следующие сложные технические вопросы:
работа на общий канал связи одновременно нескольких ККС требует их
селекции в канале и усложнения как самого канала связи, так и аппаратуры
потребителя;
различие в алгоритмах работы обслуживаемой НАП требует включения в
общие дифференциальные поправки ионосферной и (или) тропосферной
коррекции для одних потребителей и исключения ее для других;
при проектировании канала связи приходится закладывать максимальный
трафик с учетом обслуживания наиболее «быстрого» потребителя, однако
большинство пользователей устроила бы существенно меньшая загрузка
канала связи, поэтому можно было бы существенно снизить затраты на создание и
обслуживание как канала связи, так и конечного терминала пользователя;
для мобильного потребителя по мере его движения необходимо
организовать процесс переключения между отдельными локальными зонами, который
по существующей концепции возлагается на аппаратуру потребителя; это
существенно усложняет НАП и повышает ее стоимость, требуя введения единого
аппаратно-программного стандарта на канал связи.
Другим недостатком использования описанного выше способа построения
РДПС является то, что при этом невозможно использовать имеющийся парк
467
Глава 12
НАП, и потребуется как доработка самой НАП, так и дополнительная
установка на уже эксплуатируемых объектах пользователей сложных и дорогих
терминалов специализированных каналов связи с последующим проведением
полного комплекса повторных испытаний нового оборудования при штатном
размещении на объекте. В итоге требуется снятие с эксплуатации всего парка
действующих объектов и их дооборудование.
Экономические и технические расчеты, проведенные РНИИ космического
приборостроения, показывают нецелесообразность использования такой схемы
для создания единой дифференциальной подсистемы Российской Федерации.
Поэтому предложен иной вариант создания Российской дифференциальной
подсистемы (РДП), который является развитием методов высокоточной широкозонной
навигации. Подсистема обеспечивает повышение качества, достоверности и
точности навигационного обслуживания потребителей всех классов, а также
минимизирует затраты на создание такой системы. Предлагаемая концепция использует:
действующую версию космического сегмента СРНС ГЛОНАСС и GPS;
ограниченную сеть из 10... 12 (минимум) автономных станций сбора
информации (ССИ) для покрытия единой системой всей территории РФ; при этом
не требуется точной синхронизации шкал времени и частот опорных
генераторов ССИ и, следовательно, отпадает необходимость в высокоточном
метрологическом обеспечении;
новые методы обработки измерений и получения корректирующей
информации, а также методы ее адаптации под требования конкретного потребителя
без дополнительной загрузки последнего;
действующие на территории РФ информационные технологии и каналы
связи для доставки корректирующей информации конечному пользователю.
Повышенная точность и достоверность навигационного обслуживания
потребителя в РДП обеспечивается за счет:
точного расчета ДП для каждого выбранного центра из множества зон
групповой высокоточной навигации, вплоть до местоположения отдельного
потребителя;
неизменности погрешности определения местоположения в пределах всей
рабочей зоны (Российской Федерации),
снятия погрешностей эфемеридно-временного обеспечения (ЭВО) СРНС в
реальном масштабе времени;
компенсации погрешностей распространения сигналов НС
непосредственно в ДПС;
возможности использования действующего парка НАП (дифференциальной
НАП, недифференциальной НАП) с повышенной точностью определения
местоположения (соответственно в дифференциальном и абсолютном режимах).
Новая система позволяет включить уже действующие ЛДПС в единую
непрерывную зону высокоточной навигации без изменения их ведомственной
принадлежности и штатного регламента работы, а также оперативно включать
468
Дифференциальный режим СРНС ГЛОНАСС
и исключать отдельные ЛДПС из структуры действующей системы по мере
необходимости.
Дополнительным преимуществом является возможность создания на базе
новой концепции единой навигационно-информационной сети,
обеспечивающей решение прежде несовместимых разнородных задач навигации в рамках
одной системы. Как следствие достижений современных информационных
технологий, система обеспечивает простую наращиваемость, доступность и
легкость адаптации под меняющиеся индивидуальные требования конечных
пользователей.
Особыми преимуществами вновь создаваемой РДП являются:
легкость расширения рабочей зоны до глобальной (без доработки уже
функционирующих сегментов системы);
возможность обеспечения высокоточной дифференциальной коррекции
вне зоны досягаемости традиционных ККС;
оперативное включение (или исключение) в состав системы закрытых и
узконаправленных широкополосных каналов связи специального назначения
для обслуживания специальных потребителей, без оповещения об этом
остальных пользователей системы.
Принципы построения и работы РДП
Структура навигационного обслуживания в РДП приведена на рис. 12.5.
Космический
сегмент СРНС
7S
Радионавигационные сигналы
Коррекция
ЭВО
Наземный
сегмент СРНС
с
Базовые
радионавигационные
параметры
Данные от системы
мониторинга ГЛОНАСС
^
it
*
Дифференциальная |
НАП L
Ограниченная
сеть ССИ
Дифференциальная \ j
V НАП V
7%
Корректирующая
информация
—jyA
Обработка . ^
информации I—А
Адаптация , к! тг
, у Каналы связи
информации —Л
Дифференциальная подсистема
Рис. 12.5. Структура навигационного обслуживания
Концепция РДП определяет использование сети станций сбора информации
(ССИ), которые в отличие от опорных измерительных станций, входящих в
состав ККС, не решают задач выработки ДП, а лишь проводят измерения псевдо
дальностей Д у (tk) и псевдо скоростей VtJ(tk) (а при необходимости и псевдо
469
Глава 12
фаз Д7(^)), где / = 1,л {п —число видимых НС); j = l,N (N — число ССИ).
Кроме того, в структуре сети используются базовые станции (БС),
устанавливаемые в «точках координации» и предназначенные для создания зон групповой
высокоточной навигации с использованием относительных кодовых
определений. Число одновременно работающих в системе БС определяется
вычислительной мощностью центра обработки и может быть сколь угодно большим.
Для повышения точности навигационного обслуживания основной массы
потребителей целесообразно снять с них задачу коррекции погрешностей
распространения радиосигнала и включить ионосферные и тропосферные
поправки в состав передаваемой им корректирующей информации. В РДП эта задача
возлагается прежде всего на дифференциальную подсистему. В этом случае
НАП потребителя может быть одночастотной при сохранении точности
определения местоположения. В то же время предлагаемая концепция позволяет
использовать и широко распространенный сегодня метод самостоятельной
коррекции пользователями погрешностей распространения сигнала в
атмосфере на основе двухчастотных измерений и расчета ионосферной и тропосферной
погрешностей по стандартным моделям.
Повышенные требования к достоверности навигационных определений
при решении ответственных задач таких, как управление воздушным
движением в ближней зоне аэропорта и при точном заходе на посадку, управление
морским (речным) транспортом в узких акваториях, организация (синхронизация)
движения мобильных объектов и железнодорожного транспорта, точное
решение с вероятностью не менее 0,995 специальных задач и т.п. предопределяет
необходимость проведения мониторинга навигационного поля. Включение
этой задачи в состав требований на новую систему диктуется основной целью
ее создания — расширением функциональных возможностей конечной НАП.
На первом этапе для решения проблемы мониторинга целесообразно
использовать систему мониторинга ГЛОНАСС, для чего она должна быть
максимально объединена с РДП.
Мониторинг частотно-временных радионавигационных параметров
сигналов НС, а также передаваемых данных, проводится по всем спутникам в зоне
радиовидимости сети ССИ. При выходе значений контролируемых параметров
за пределы зоны априорных допусков потребителям выдается сигнал о
неисправности спутника. Допустимые же отклонения параметров ГЛОНАСС/GPS
компенсируются корректирующей информацией, которая передается в НАП
через дифференциальную подсистему (рис. 12.5).
Для потребителей, оборудованных обычной (не дифференциальной) НАП,
в РДП появляется возможность индивидуальной коррекции по конечному
навигационному параметру (по координатам и скоростям), что позволяет
провести квазидифференциальную коррекцию. При этом корректирующая
информация может вводиться в фильтр комплекса как данные.
470
Дифференциальный режим СРНС ГЛОНА СС
Корректирующая информация
Известные способы коррекции погрешностей СРНС основаны на
определении ДП в априорно известной точке пространства и распространении их
действия на прилежащую область, именуемую рабочей зоной ОИС. В пределах
рабочей зоны максимальная точность коррекции достигается в центре и убывает
к ее периферии, ограничивая тем самым размер рабочей области. Для
построения таким способом в крупных регионах непрерывного поля высокоточных
поправок требуется развернуть в том же регионе непрерывную сеть из ОИС и
аппроксимировать поправки от соседних станций для сглаживания ошибок
коррекции в пределах рабочей зоны региона. Поскольку градиент поля
поправок в произвольной точке между станциями неизвестен и к тому же изменяется
при движении спутника, для аппроксимации можно использовать только
простейший полином первого порядка. Это в принципе затрудняет получение
точной дифференциальной коррекции не только для протяженной (региональной)
зоны, но даже в пределах локальной рабочей зоны отдельной ОИС.
Для точной коррекции погрешностей СРНС в пределах всей зоны
радиовидимости НС в РДП планируется использование новых глобальных скалярно-
векторных поправок (СВП), которые не связаны с местоположением ССИ.
Скалярно-векторные поправки определяются для каждого /-го НС в виде
{АХ/5 AV,, Ад., AVt], где АХУ =|Axf. Ay, Az,|T — вектор поправок к априорным
данным о координатах НС; AV, =
Д^,/ А^,/ *K,i
вектор поправок к
априорным данным о составляющих вектора скорости НС; А/?,-— скалярная
поправка к оценке псевдо дальности; AVt— скалярная поправка к оценке псевдо
скорости. Совокупность поправок {АХ/9 AV,, А/?,, AVt) будем называть
корректирующей информацией.
На рис. 12.6 представлена развернутая схема функционирования РДП.
Космический ч}
сегмент С^НС *
-I-
НС*
п>\
"J*,.
I рЖ'' Центр
(уг^ав^ения СРНС
**, ^ '
' -Базовая стаяци*Я 1
БСо
*вс,|
БЭВЧ
эвч
СРНС
Л а
ССИ,
Г*БС<
R
ССИ,
сси2
RCCH2
ггги,
ж*
ксси
ССИ*
(CCH>
, О:
О:
L6!
Ц Канал связи
1 Векторные поправки
Обработка р————— j
.-- 4 |
^ ^ '■■') 2
( Центр обработкн^! §
.,. "--": ' > О
Скалярные поправки Канал связи г—
Г
у
г><
ж
О г
*g £
§ 1
Рис. 12.6. Схема функционирования РДП
471
Глава 12
Ограниченная сеть ССИ состоит из нескольких независимых, двухчастот-
ных приемников, с высокой точностью привязанных к заданной системе
координат и расположенных на максимально возможном удалении. Их положение
задается известными векторами RCCH , j = \,N . В состав сети входит также
базовая станция, координаты которой известны и задаются вектором RBC . На ССИ
и БС в результате приема и обработки сигналов НС формируются оценки псевдо
дальностей Д. .(^) и псевдо скоростей Vt j(tk),j = 0,N (при необходимости и
псевдо фаз fyjih))- Сформированный набор оценок
'сси,= U,- ...Д„,у -Лу
">7
YBco= Д,,0 ...Д„,о - ^о-^,о > J = IN
по каналам связи передается в Центр обработки, где выполняется расчет СВП
по алгоритму, структура которого приведена на рис. 12.7. Туда же передаются
измеренные отклонения характеристик эталона времени и частоты (ЭВЧ) БС
относительно ЭВЧ СРНС.
Оценки псевдодальностей и
псевдоскоростей от всех ССИ
Цхи, ■■/ = '■*'
1_Е
вход
Вычисление первых разностей
псевдодальностей и
псевдоскоростей всех ССИ
относительно БС
Вычисление вторых разностей
по навигационным спутникам
Расчет векторных поправок
ARl9&Yhi = Un
выход
Оценки псевдодальностей и
псевдоскоростей от БС
¥БСП
Измерение смещения БЭВЧ
относительно ЭВЧ СРНС
Расчет текущих (во времени)
скалярных поправок
Усреднение по времени
скалярных поправок
Ap;.,Af,-,4/;,/=l,H
Рис. 12.7. Структура алгоритма расчета СВП
472
Дифференциальный режим СРНС ГЛОНА СС
Сначала вычисляются первые разности оценок псевдо дальностей и псевдо
скоростей, полученных на всех ССИ, относительно аналогичных оценок, полу-
ченных на БС: Д#,->у- = Д,; - Цц -> у = 1,# , / = 1, и. Далее сформированные
первые разности используются для вычисления вторых разностей по различным
НС: Д2Ду =Д#/,у-A#/j- Во вторых разностях удается устранить
зависимость от координат ССИ, что позволяет вычислить векторные поправки
AXfjAV,-, характеризующие погрешности априорного знания эфемерид НС.
Используя сформированные векторные поправки и измеренные на БС
отклонения характеристик БЭВЧ относительно ЭВЧ СРНС, вычисляют скалярные
поправки к псевдо дальностям и псевдо скоростям Api9 AVt i = \,n, которые в
дальнейшем усредняются по времени на соответствующим образом выбранных
временных интервалах.
Сформированные в Центре обработки СВП по каналам связи передаются в
Центр управления СРНС для коррекции закладываемой на борт НС эфемерид-
ной информации и потребителям СРНС.
Рассмотренные глобальные дифференциальные поправки по сути
представляют собой поправки к эфемеридам НС и частотно-временные поправки.
Точность и достоверность их определения обеспечивается обработкой всех
доступных к моменту принятия решения измерений, собираемых в
квазиреальном времени с сети станций ССИ. В отличие от штатной ЭВИ спутника,
глобальные поправки не имеют жестких ограничений по частоте обновления, что
позволяет значительно сократить время прогноза и получать наиболее точную
ЭВИ в реальном времени. Сами поправки по величине не превосходят
нескольких десятков метров по координатам и нескольких наносекунд по ЧВП, что
сокращает объем передаваемых данных.
Принципиально возможна реализация двух разных систем глобальных
дифференциальных коррекций.
Вариант L Предполагается, что система глобальных дифференциальных
коррекций предназначена для повышения точности ГЛОНАСС.
Распространение глобальных коррекций принципиально возможно даже непосредственно с
самих НС ГЛОНАСС, например, в рамках навигационных сообщений новых
сигналов. В этом случае достаточно передачи небольшого объема данных, а
частота обновления поправок соизмерима с частотой обновления ЭВИ и
составляет 1 раз в 30 мин.
Вариант 2. Полагается, что система глобальных дифференциальных
коррекций предназначена для получения поправок к ЭВИ вне зависимости от
штатного эфемеридно-временного обеспечения ГЛОНАСС. Частота
обновления поправок может быть сколь угодно высокой, вплоть до 1 раза в секунду.
Объем передаваемых данных в такой системе существенно больше.
473
Глава 12
Для получения поправок в Центре обработки в режиме реального времени
проводится уточнение и прогнозирование ЭВИ, а также сбор бортовой ЭВИ.
Согласно опыту IGS при наличии глобальной сети из 12... 18 станций
современные методы обработки позволяют получать и прогнозировать орбиты НС
на интервале до нескольких часов с точностью до 50 см. При этом основная
часть ошибки сосредоточена вдоль орбиты, поэтому вклад эфемерид в
эквивалентную дальномерную погрешность (UERE) составляет не более 20...30 см.
На основании полученных орбит на 30-минутных интервалах,
соответствующих периодам действия штатных эфемерид, происходит уточнение эфемерид в
моделях, предусмотренных документацией на ГЛОНАСС/GPS. Затем на
основании полученных и штатных эфемерид определяются глобальные поправки к
эфемеридам НС. При этом для расчета поправок должны использоваться
эфемериды, получаемые из навигационных сообщений с учетом отсечения
младших разрядов данных повышенной точности. Таким образом, глобальные
поправки к эфемеридам ГЛОНАСС/GPS остаются неизменными на 30-минутном
интервале действия бортовых эфемерид, что существенно сокращает объем
передаваемых данных.
Получение высокоточных эфемерид требует решения сложных краевых
задач на длительных интервалах времени (2...4 суток) с уточнением большого
числа параметров. Решение таких задач требует определенного времени
(возможно, десятков минут), поэтому такие решения должны использоваться в
основном для получения орбит, с использованием которых могут рассчитываться
поправки к ЧВП. С учетом медленного ухудшения точности получаемых орбит
со временем, такие решения должны проводиться 1 раз в 2...6 ч. При условии
доведения стабильности бортовых стандартов НС «Глонасс-К» до
сегодняшнего уровня стандартов GPS создание первого варианта системы глобальных
поправок потребует только таких решений. Полные решения могут проводиться
1 раз в 30 мин перед переходом на новые бортовые эфемериды и ЧВП (прогноз
ЧВП на срок до 1 ч обеспечивает ошибки часов на уровне 0,5 не).
Принципиальная разница между разными вариантами системы глобальных
поправок заключается в сборе и обработке данных. В первом случае
допускается, что измерения собираются и обрабатываются с некоторым запаздыванием, и
при достаточной стабильности часов можно построить систему глобальных
поправок без сбора и обработки измерений в реальном времени. Во втором случае
система сложнее, поскольку она требует обработки данных в реальном времени.
Решения по уточнению орбит одинаковы в обоих вариантах системы, а
решения по уточнению параметров часов отличаются принципиально
используемыми методами оценивания: во втором варианте возможны только
рекуррентные схемы оценивания типа фильтра Калмана.
Получение поправок к ЧВП происходит аналогично поправкам к
эфемеридам. В режиме квазиреального времени с учетом всех доступных измерений
производится уточнение поправок бортовых часов. При этом используются ор-
474
Дифференциальный режим СРНС ГЛОНАСС
биты, по которым рассчитывались поправки к эфемеридам. За счет корреляции
параметров орбит и бортовых часов суммарный вклад ЭВИ в UERE получается
меньше, чем в случае, когда высокоточные эфемериды и ЧВП рассчитывались
независимо, т.е. поправки бортовых часов частично компенсируют неточность
эфемерид. Современные методы обработки позволяют получать поправки
часов на уровне лучше 0,5 не. Таким образом, суммарный вклад ЭВИ в UERE при
условии точного прогноза бортовых часов может составить порядка 20 см.
Точность прогноза часов и, следовательно, частота обновления поправок к
ЧВП в первом варианте системы определяется характеристиками бортовых
стандартов частоты. Для существующих бортовых стандартов ГЛОНАСС
прогнозирование ЧВП с указанной точностью проблематично даже на
относительно коротких интервалах времени (несколько десятков секунд). Поэтому
вероятно, что даже для первого варианта на 30-минутном интервале действия
одного набора ЭВИ потребуется несколько поправок к ЧВП. Минимальный шаг
обновления поправок определяет темп проведения решений по уточнению
параметров бортовых часов. Во втором варианте должно проводиться постоянное
уточнение поправок часов.
Технологический цикл получения глобальных ДП
Штатный технологический цикл ЭВО включает все операции от
проведения измерения до формирования ЭВИ, закладываемой на борт. Функционально
они могут быть разделены на несколько групп:
сбор и предварительная обработка измерений на пунктах сети;
сбор измерений с сети ССИ и их предварительная обработка в Центре
обработки, получение штатной ЭВИ ГЛОНАСС;
уточнение параметров орбит и часов;
формирование высокоточной ЭВИ и расчет глобальных поправок.
Каждая группа задач может решаться в отдельном контуре (рис. 12.8),
что упрощает разработку программного обеспечения и повышает его
надежность.
Рис. 12.8. Структура программного обеспечения
475
Глава 12
Обмен между задачами должен производиться через базу данных (БД),
обеспечивающую одновременный доступ к данным задач из разных групп.
При вычислении ДП для конкретного потребителя на основе данных
нескольких соседних ССИ возможно применение метода линейной аппроксимации
локальных поправок от соседних станций. Такой подход позволяет снизить
влияние декорреляции ошибок измерений между ССИ и потребителем на точность
определения координат.
При реализации метода применимы два подхода. Схематично они
представлены на рис. 12.9.
сси
сси
сси
НАЛ
I ¥
сси
Центр
обработки
Концепция 2
Концепция 1
Рис. 12.9. Подходы к реализации метода линейной аппроксимации
Сущность первого подхода заключается в следующем:
ССИ передают измерительную информацию в Центр обработки по
специальным каналам;
потребитель передает в Центр обработки свои координаты, полученные в
абсолютном режиме;
Центр обработки данных вычисляет и передает потребителю его
«персональные» ДП.
Суть второго метода заключается в следующем:
ССИ излучают ДП в стандартном режиме;
потребитель принимает ДП от нескольких ССИ одновременно.
Первый подход позволяет потребителю использовать простые аппаратно-
программные средства (приемник ДП, построенный на основе стандартных
решений), однако налагает нагрузку на Центр обработки. Кроме того,
вследствие задержек, потребитель может получать поправки, имеющие возраст
10.. .30 с, что несколько ухудшит результирующую точность.
Реализация второго подхода требует разработки перспективных
приемников ДП, обеспечивающих возможность приема сигналов нескольких станций и
ввода приближенных координат потребителя, а также имеющих алгоритм их
совместной обработки. Эта концепция наиболее пригодна для работы в
реальном времени и обеспечения повышения точности определения координат.
476
Дифференциальный режим СРНС ГЛОНА СС
В основе обеих концепций лежит одинаковый математический аппарат,
который строят, исходя из предположения о том, что в некоторой
ограниченной области пространства ошибки измерений псевдо дальности линейно
изменяются в зависимости от координат точки. Область пространства может быть
ограничена тремя-пятью ССИ и иметь протяженность около 500 км.
Пусть ДП/ ., / = 1,л, j = l9N — дифференциальные поправки,
соответствующие / -му НС на j -й ССИ. Пусть первая станция является ведущей, тогда
поправки, вырабатываемые остальными станциями, можно выразить через
поправки первой станции соотношением
ДП,у.=ДП/д + а^ (12.20)
где ai,bi,ci — неопределенные коэффициенты; Xj9y-Zj — координаты у-й
ССИ в некоторой системе координат (например, геодезической).
Вводя векторы
ДДП,. =|(дпи-дпи)... (дп,„-дп/л)|\сН*/ bt c\\
ДХ/ = |(*2 - *i) - (% " *i )Г > АХ = \(у2 - ух) ... (yN - ух )|т,
AZ/=|(z2-^l) - (^V-Zl)|\
систему уравнений (12.20) можно записать в векторном виде:
ДДП(.=|ДХ,. AY, AZ^C-H,.^..
Решение данного векторного уравнения имеет вид
^-(Н^^Н^АДП,.. (12.21)
При использовании описанного подхода возникают остаточные
погрешности измерений, обусловленные использованием линейной аппроксимации
(12.20) нелинейных зависимостей измерений псевдо дальности и псевдо
скорости от пространственных координат. Аналогично тому, как это сделано в
п. 12.5, остаточные погрешности будем разделять по источникам погрешностей
первичных измерений, а именно: эфемеридные, ионосферные и тропосферные
составляющие. Расчеты показывают, что при покрытии ССИ пространственной
области 500x500 км остаточные погрешности могут достигать:
для эфемерид — 10 см;
для ионосферы — 5 см;
для тропосферы — 30 см.
Результирующая остаточная погрешность составит около 33 см. С учетом
ошибок многолучевости и геометрического фактора можно прогнозировать
точность определения координат потребителя на уровне 1...2 м для области
500x500 км.
477
Глава 12
Использование корректирующей информации в РДП
Каждый из рассмотренных выше методов получения поправок и
корректирующей информации имеет и недостатки.
Так, метод выделения скалярной и векторной компонент погрешности дает
минимальную задержку коррекции состояния КНС и обеспечивает
глобальность коррекции, но имеет большую шумовую погрешность определения
корректирующих параметров (СКО ~ 2,0 м).
Метод определения глобальных поправок с помощью уточнения ЭВО и
точной орбиты спутника напротив обеспечивает малую погрешность
определения параметров (СКО ~ 0,3 м). Однако из-за большого объема вычислений время
одного цикла расчета поправок составляет 2...3 ч, что в принципе не позволяет
получить заданную достоверность корректирующей информации при
возникновении внезапных сбоев в КНС.
Метод линейной аппроксимации точечных (локальных) ДП не
обеспечивает глобальности коррекции и имеет низкую точность из-за линейного закона
аппроксимации. К тому же погрешность изменяется в пределах рабочей
области: точность максимальна в точках расположения ККС, но минимальна в
центре области и на ее краях. Однако этот метод в качестве исходных данных
использует поправки, полученные от независимой сети локальных ККС. Для РДП
это положительное качество, поскольку метод полезен для организации RAIM-
функций.
Таким образом, ни один из перечисленных методов самостоятельно
полностью не удовлетворяет требованиям РДП, однако их совокупность позволяет
решить поставленную задачу. Поэтому предложен следующий вариант ком-
плексирования описанных методов:
а) на базе сети ССИ и доступных измерений от глобальной сети станций
IGLOS определяются ЧВП и поправки к ЭВО, т.е. строится точная орбита
спутников;
б) на базе сети станций ССИ (расположенных на территории РФ) строится
обработка с выделением глобальных СВП;
в) на основе ДП, полученных от множества доступных локальных ККС
(ССИ) определяются плоскости положения дифференциальных поправок
между соседними локальными ККС и строится общая поверхность поправок для
региона — территории РФ;
г) для каждой категории пользователей выбирается наиболее подходящий
метод и вычисляются итоговые глобальные ДП;
д) итоговые глобальные ДП пересчитываются в контрольных точках
рабочей зоны РДП в локальные ДП и сравниваются со значениями поправок,
полученных методом линейной аппроксимации. Тем самым в РДП обеспечивается
выполнение функций RAIM (самоконтроля).
Предлагаемое комплексное использование методов рассчитано, прежде
всего, на обслуживание основной массы зарегистрированных пользователей
478
Дифференциальный режим СРНС ГЛОНА СС
РДП. Тем не менее, данная концепция предусматривает и автономное
использование рассмотренных выше методов. Например, метод выделения СВП
целесообразно использовать для организации общедоступного обслуживания на
территориях большой протяженности, мобильных незарегистрированных
категорий пользователей (т.е. пользователей, не имеющих права доступа к
высокоточным поправкам). Метод определения точной орбиты НС может
использоваться для обслуживания пользователей в режиме постобработки при траек-
торных или геодезических измерениях. Метод линеаризации локальных ДП
можно использовать для расширения рабочей зоны локальных ведомственных
дифференциальных подсистем
12.8.3. Широкозонная ДПС WAAS
Основой широкозонных ДПС является глобальная сеть контрольно-
корректирующих станций, информация которых передается в специальный
центр для совместной обработки с целью выработки широкозонных поправок и
сигналов целостности. Примером подобной ДПС может служить система
WAAS — широкозонная система дополнения GPS (Wide Area Augmentation
System). По замыслу заказчика — Федеральной авиационной администрации
США, система предназначена для доведения точности базовой навигационной
системы GPS и уровня целостности и доступности до уровня,
соответствующего требованиям, предъявляемым к основным системам навигации воздушных
судов для всех фаз полета, вплоть до захода на посадку по 1-й категории.
Рабочая зона охватывает в первую очередь весь Северо-Американский континент и,
частично, Северную Атлантику вплоть до Европы.
По своим характеристикам WAAS в состоянии обслуживать наземные и
морские объекты, обеспечивая высокоточную морскую и сухопутную
навигацию, проведение работ на шельфе и т.д.
WAAS состоит (рис. 12.10) из космического и наземного сегментов
[12.14].
Космический сегмент включает геостационарные КА GEO (типа
«INMARSAT») или аналогичные им, предназначенные для:
передачи навигационного сигнала (аналогичного GPS) в диапазоне Ы на
частоте 1575,42 МГц, используемого в качестве дополнительного
навигационного спутника с указанием своей целостности;
ретрансляции сформированных на земле сообщений о целостности всех НС
системы GPS, поправок ЭВО и ЧВП, а также параметров ионосферной модели.
Наземный сегмент включает:
опорные станции (WRS — WAAS Reference Station) мониторинга,
предназначенные для контроля и наблюдения за состоянием навигационного поля;
479
Глава 12
Управление системой
Рис. 12.10. Структура WAAS и выполняемые функции
ведущие станции (WMS — WAAS Master Station), предназначенные для
обработки данных мониторинга и наблюдений WRS и выработки данных об
орбитах НС, целостности СРНС, дифференциальных поправок, оценок
остаточных погрешностей навигационных определений и информации о состоянии
ионосферы для всех НС и КА GEO;
наземные станции (GES — Ground Earth Station), осуществляющие связь
между наземными ведущими станциями и геостационарными КА и
обеспечивающие передачу корректирующих и иных данных, выработанных WMS,
космическому сегменту.
Опорные и ведущие станции, а также наземные станции передачи данных
объединены в единую сеть обработки и передачи данных.
Широкозонная ДПС WAAS имеет свое системное время, которое
привязывается к системному времени GPS с точностью не хуже 50 не. Информация о
смещении времени WAAS относительно UTC передается в служебном
сообщении.
Зарегистрированные пользователи WAAS получают и обрабатывают
следующие данные:
о целостности СРНС GPS, гарантирующие работу по исправным НС;
480
Дифференциальный режим СРНС ГЛОНАСС
дифференциальные поправки и сведения об ионосфере, позволяющие
повысить точность навигационных определений;
дальномерные сигналы от одного или более КА GEO для проведения
дополнительных дальномерных измерений.
КА GEO излучают радиосигналы на несущей частоте 1575,42 МГц
(диапазон Ы ) с фазовой манипуляцией на ж дальномерным кодом с частотой
следования символов 1,023 Мбит/с и кодом навигационной (служебной) информации
с частотой следования 500 бит/с. При этом навигационные данные
формируются со скоростью 250 бит/с, после чего они подвергаются сверточному
кодированию, так что на выходе формируется код с частотой следования 500 бит/с.
Дальномерный код, как и в GPS, является кодом Gold и выбирается из не
занятых в СРНС GPS последовательностей.
На входе приемника потребителя минимальная мощность сигнала WAAS
составляет -161 дБВт, максимальная -155 дБВт, т.е. имеет несколько меньшее
значение, чем для сигналов GPS с С/А-кодом (-160 и -153 дБВт соответственно).
Для формирования ДП в ШДПС WAAS сетью наземных опорных станций
WRS проводится прием сигналов НС GPS и КА GEO, измерения параметров
тропосферы, получение данных топопривязки и калибровки аппаратуры. В
результате обработки принятых сигналов и информации формируются:
оценки псевдо дальностей для всех НС GPS и КА GEO по сигналам
диапазона Ы (С/А-код);
разностные измерения псевдо дальностей по сигналам двух диапазонов
L\ IL2 (без знания Y-кода в L2);
данные навигационных сообщений двух систем (GPS, WAAS) о
параметрах движения спутников;
данные о смешении разностных измерений псевдо дальностей в
диапазонах L\l L2\
данные о положении фазовых центров приемных антенн;
данные по калибровке приемной аппаратуры.
Сформированные данные со всех опорных станций передаются на
ведущие станции WMS для последующей обработки с целью получения
дифференциальных поправок.
При расчете ионосферной ДП используются разностные измерения псевдо
дальностей в диапазонах L\ IL2, данные о смещении разностных измерений и
о положении фазовых центров приемных антенн, а также данные
навигационных сообщений системы GPS о параметрах движения спутников.
Важной задачей WMS является уточнение параметров движения НС GPS и
формирование эфемерид и данных альманаха для КА GEO, которые в
дальнейшем закладываются в навигационное сообщение и передаются
потребителям WAAS. Для решения этой задачи используются следующие данные:
оценки псевдо дальностей для всех НС GPS и КА GEO по сигналам
диапазона L\ (С/А-код);
16-1026
481
Глава 12
разностные измерения псевдо дальностей в диапазонах L\ IL2;
данные навигационных сообщений двух систем (GPS, WAAS) о
параметрах движения спутников;
данные тропосферы;
данные о положении фазовых центров приемных антенн;
данные о смещении разностных измерений псевдо дальностей в
диапазонах L\ IЫ;
полученные и рассчитанные в системе данные об ионосфере.
В результате расчетов определяются:
уточненные данные орбитального движения НС GPS (положение,
составляющие вектора скорости, временной сдвиг и параметры дрейфа БШВ НС GPS
относительно СШВ WAAS);
уточненные данные орбитального движения КА GEO (положение,
составляющие вектора скорости и ускорения, временной сдвиг и
параметры дрейфа БШВ КА GEO относительно СШВ WAAS);
эфемеридные данные КА GEO;
данные альманахов КА GEO.
После получения уточненных параметров орбитального движения НС GPS
и КА GEO вычисляются ДП к эфемеридам НС и КА. При этом раздельно
формируют поправки к медленно- и быстроменяющимся составляющим
погрешностей эфемеридного обеспечения. Для быстроменяющихся составляющих
дополнительно рассчитывается параметр, характеризующий их старение
(деградацию). Кроме того, здесь же формируется оценка ожидаемой
(прогнозируемой) остаточной погрешности оценки псевдо дальности потребителем.
С целью своевременного оповещения потребителей о некорректной
информации, содержащейся в сигналов тех или иных НС GPS и КА GEO, а также
о некорректности переданных ионосферных поправок, проводится автономный
контроль целостности GPS и WAAS с использованием всех доступных
сигналов и информации.
Литература
12.1. Резолюция ИМО А.815(19): 1995. Всемирная радионавигационная система.
12.2. Резолюция ИМО А.915(22): 2001. Политика мореплавания в отношении
будущей ГНСС.
12.3. Рекомендация Международного союза электросвязи (МСЭ). ITU-R.M.823.
Technical Characteristics of Differential Transmissions for Global Navigation Satellite
Systems (GNSS) from Maritime Radio Beacons in the Frequency Band 283.5—315 kHz
in Region 1 and 285—325 kHz in Region 1 and 3, 1995.
12.4. Материалы Международной ассоциации маячных служб (МАМС) «List of
Radionavigation Services, DGNSS Reference and Transmitting Stations in the Maritime Ra-
dionavigation (Radio beacons) Band», issue 5, 1997.
482
Дифференциальный режим СРНС ГЛОНАСС
12.5. Стандарт МЭК 61108-4 «Судовая приемная аппаратура сигналов DGPS и
ДГЛОНАСС морских радиомаяков». Стандарт требований к характеристикам, методы
испытаний.
12.6. Рекомендованный RTCM стандарт «RTCM recommended standards for
differential NAVSTAR/ GPS service», vol. 2.1, RTCM, 1996.
12.7. Рекомендованный RTCM стандарт «RTCM recommended standards for
differential GNSS service», vol. 2.2, RTCM, Paper 15-96/SC104-139, 1996.
12.8. Рекомендованный RTCM стандарт «RTCM recommended standards for
differential GNSS service», vol. 2.3, RTCM, PAPER 136-2001/SC104-STD, 2001
12.9. Рекомендованный RTCM стандарт «RTCM recommended standards for
differential NAVSTAR/GPS Reference Stations and Integrity Monitors (RSIM)», vol. 1.1,
1996.
12.10. ТЭТ Госслужбы Морфлота Минтранса России № МФ-02-22/848-61: 2001 г.
«Морская дифференциальная подсистема СНС ГЛОНАСС/GPS». Назначение, состав,
требования и методы испытаний
12.11. ТЭТ Госслужбы Морфлота Минтранса России № МФ-02-22/848-59: 2001 г.
«Формат передачи дифференциальных поправок по системам ГЛОНАСС/GPS».
Назначение, состав, требования и методы испытаний.
12.12. Уорд К Будущее развитие радиомаяков DGNSS. Навигация 2000. Сборник
трудов Третьей Международной конференции «Планирование глобальной
радионавигации». Москва, 9-11 октября 2000г.
12.13. Доборин М.А., Ратьков КВ., Солощев А.Н. Обзор состояния
дифференциального сервиса ДГЛОНАСС/DGPS. ИНФОРМОСТ? № 2, 2004 г.
12.14. FAA-E-2892B «Wide Area Augmentation System (WAAS)», U.S. Department
of Transportation, Federal Aviation Administration Specification, 1999.
483
Глава 13
Глава 13
АППАРАТУРА ПОТРЕБИТЕЛЕЙ
13.1. Принципы построения аппаратуры потребителей
Навигационная аппаратура потребителей СРНС предназначена для
определения пространственных координат и составляющих вектора скорости
потребителя, текущего времени и других навигационных параметров в результате
приема и обработки радиосигналов, излучаемых навигационными спутниками.
Современная НАЛ является аналого-цифровой системой, сочетающей
аналоговую и цифровую обработку сигналов. Обобщенная схема НАЛ приведена на
рис. 13.1 и включает антенну, радиочастотный блок (РЧБ), синтезатор частот (СЧ)
аналого-цифровой преобразователь (АЦП) и цифровой вычислитель (ЦВ).
\
/ Антенна
Радиочастотный
блок
I
Синтезатор
частот
Аналого-цифровой
преобразователь
i
i
Цифровой
вычислитель
i
{
Потребителю
^
Рис. 13.1. Обобщенная схема аппаратуры потребителя
Антенна выполняет функцию преобразования электромагнитных волн в
электрический сигнал и может состоять из одного или нескольких антенных
элементов с необходимыми блоками электронного управления.
Радиочастотный блок (радиоприемник) предназначен для усиления
принятых сигналов, частотной селекции (фильтрации) полезных сигналов из смеси с
шумами и помехами, понижение несущей частоты принятых сигналов до
заданного значения, которое принято называть промежуточной частотой.
Синтезатор частот формирует набор гармонических колебаний,
необходимых для работы РЧБ, шкалу времени АП и тактовые сигналы,
синхронизирующие работу АЦП и ЦВ.
Аналого-цифровой преобразователь трансформирует аналоговый сигнал,
поступающий с выхода РЧБ, в цифровой сигнал, предназначенный для
последующей обработки в цифровом вычислителе.
Цифровой вычислитель решает задачу извлечения навигационной и другой
информации из принятых и преобразованных в цифровую форму радиосигналов.
484
Аппаратура потребителей
По выполняемым функциям ЦВ часто представляют в виде сигнального
процессора и навигационного процессора (процессора приложений) [7.5]. При
этом сигнальный процессор выполняет задачи первичной обработки сигналов:
распараллеливание обработки входного сигнала на п каналов;
формирование опорных сигналов дальномерного кода и управляемых
опорных генераторов (гармонических колебаний);
корреляционную обработку сигналов в каждом из п каналов;
поиск сигналов по задержке и частоте;
слежение за дальномерным кодом, частотой сигналов и формирование
оценок псевдо дальности, псевдо доплеровской частоты и псевдо фазы;
выделение (демодуляция) навигационных данных (сообщений),
передаваемых в радиосигналах;
оценку отношения сигнал/шум qc, для принимаемых радиосигналов;
привязку шкалы времени потребителя к системной шкале времени СРНС.
Навигационный процессор решает задачи вторичной обработки, в том
числе:
декодирование эфемеридной информации, альманахов и т.д. из
навигационных сообщений;
оценку координат потребителя (в той или иной системе координат) и
составляющих его вектора скорости;
комплексную обработку оценок псевдо дальностей, псевдо доплеровских
частот (и/или псевдо фаз) с данными других измерителей (инерциальных и/или
доплеровских систем навигации и др.);
пользовательские алгоритмы маршрутизации, привязки к опорным точкам,
вывода в заданный район и т.д.
Практическая реализация ЦВ традиционно включает в себя жесткую
аппаратную часть (многоканальный коррелятор) и программируемый вычислитель.
Многоканальный коррелятор представляет собой отдельную микросхему, в
которой реализованы все необходимые для работы НАП корреляторы
(несмещенные, опережающие и запаздывающие, с обычным и суженым стробом и
т.д.), генераторы дальномерных кодов, управляемые опорные генераторы и
схемы управления режимами работы коррелятора. В некоторых типах
микросхем многоканального коррелятора реализуются также петли слежения за
задержкой кода, частотой и фазой сигнала, а также схемы демодуляции
навигационного сообщения. Программируемый вычислитель реализует обработку
отсчетов с выходов многоканального коррелятора, следующих с относительно
невысокой частотой (100... 1000 Гц) с целью решения конечной навигационной
задачи, используя для этого соответствующее программное обеспечение.
В последние годы интенсивно развивается направление, основанное на
полностью программной реализации ЦВ. При этом он может выполняться на
программируемых процессорах общего назначения (в том числе и на
персональных ЭВМ) или на цифровых сигнальных процессорах (Digital Signal Pro-
485
Глава 13
cessor (DSP)). Основным достоинством такого подхода является большая
гибкость при проектировании новых типов НАП, а также широкие возможности
по использованию новых, перспективных алгоритмов обработки сигналов
информации, например, одноэтапных алгоритмов (см. п. 6.5). Кроме того, при
таком подходе снижается стоимость и время разработки НАП.
13.2. Антенна навигационного приемника
Антенна навигационного приемника должна, с одной стороны,
обеспечивать прием сигналов всех видимых НС, а, с другой стороны, по возможности
режектировать переотраженные от местных предметов спутниковые сигналы
(помехи многолучевого распространения) и другие помехи. Поскольку данные
требования противоречивы, к стандартным антеннам предъявляется
компромиссное требование — надежный прием сигналов НС, находящихся выше 5°
над горизонтом (угол маски), в предположении, что помеховые сигналы
приходят с углов места, меньших угла маски. При этом коэффициент усиления
антенны в рабочем секторе углов (0...3600 по азимуту и 5...90° по углу места) не
должен меняться существенно.
Если антенна используется для двухчастотного приемника, работающего в
диапазонах Ы и L2 , то она должна быть широкополосной.
Типичные характеристики антенны (для рабочего диапазона частот
1570... 1625 МГц):
обеспечение работы в тракте с волновым сопротивлением, Ом .. 50
коэффициент стоячей волны (КСВ) не более 2
коэффициент эллиптичности антенны в зените, дБ не менее -3,5
минимальное значение коэффициента усиления G
относительно изотропного излучателя с круговой
поляризацией в меридиональных сечениях (как
функция угла возвышения /?), дБ:
5°>/?>0° -5>G>-7,5
10°>^>5° G>-4,5
15°>/?>10° G>-2,5
/?>15° G>-2.
Обычно используют микрополосковую антенну [12.1], достоинствами
которой являются малые масса и габаритные размеры, простота изготовления и
дешевизна. Такая антенна состоит из двух параллельных проводящих слоев,
разделенных диэлектриком: нижний проводящий слой является заземленной
плоскостью, верхний — собственно излучателем антенны. По форме
излучатель может быть прямоугольником, эллипсом, пятиугольником и т.д. Антенна
рассчитывается для работы на низшей резонансной моде, которая излучается в
486
Аппаратура потребителей
основном в верхнюю полусферу (в направлении вертикальной оси). Микропо-
лосковая антенна имеет диаграмму направленности (ДН), обеспечивающую
всенаправленный прием сигналов правосторонней круговой поляризации в
верхней полусфере.
Часто антенна интегрируется в одном модуле с предварительным
усилителем/полосовым фильтром (ПУ/ПФ) (рис. 13.2), который предназначен для
обеспечения заданного значения коэффициента шума (шумовой температуры)
АП, ограничения частотного спектра шумов, режекции внеполосных помех и
обычно включает устройство защиты входа (УЗ), малошумящий усилитель и
полосовой фильтр (рис. 13.3).
Радиосигнал
К^ Антенный модуль
\ /Антенна
^
W
ПУ/ПФ
—►
МШУ
—►
ПФ
Рис. 13.2. Структура антенного модуля Рис. 13.3. Схема предварительного усилителя
Устройство защиты входа должно предотвращать нарушение функций
последующих радиоэлектронных элементов при поступлении на его вход сигнала
с пиковой плотностью мощности 69 кВт/м в течение 10 мс или непрерывно-
го сигнала с плотностью мощности 348 Вт/м [2.8].
Малошумящий усилитель должен иметь коэффициент шума Кт < 4 дБ,
работать в тракте с волновым сопротивлением Rq= 50 Ом, иметь по входу и
выходу КСВ < 2 и обеспечивать в рабочем диапазоне частот коэффициент
усиления Ку «26...30 дБ. При выполнении данных требований шумы
последующих каскадов радиоприемника практически не влияют на итоговое значение
коэффициента шума АП.
Полосовой фильтр осуществляет фильтрацию сигналов в полосе частот
А/ « 60 МГц (относительно несущей частоты) и подавление шумов и иных
помех, действующих вне данной полосы пропускания. Параметры амплитудно-
частотной характеристики ПФ выбирают в зависимости от требуемого уровня
подавления внеполосных помех.
Потери мощности в устройстве защиты входа составляют 1 дБ, в ПФ
около 2 дБ, так что общие потери в ПУ/ПФ не превосходят 3 дБ.
13.3. Радиоприемник
Основными функциями радиоприемника АП СРНС ГЛОНАСС являются:
487
Глава 13
усиление радиосигналов, фильтрация шумов и внеполосных помех, перенос
сигналов на более низкую (промежуточную) частоту.
Обобщенная схема современного радиоприемника приведена на рис. 13.4.
пенна
ПУ/ПФ
| Радиоприемник
-j-Jcmi
! |
[ /onl 1
Yi
ПФ!
/
CM2
опг!
У2
ФНЧ
АЦП
Рис. 13.4. Схема радиоприемника
В данной схеме осуществляется двукратное понижение частоты входного
сигнала. Первый смеситель переносит сигнал на первую промежуточную
частоту f х « 100...200 МГц, а второй — на вторую промежуточную частоту
/пр2*10...40МГц.
Назначение ПФ) — выделение полезных навигационных сигналов и ре-
жекция внеполосных помех. Поэтому он имеет полосу пропускания
4/пф ~ 14 МГц, соответствующую полосе частот, занимаемых радиосигналами
НС ГЛОНАСС. В качестве таких фильтров широко используются фильтры на
поверхностных акустических волнах. Недостатком данного типа фильтров
является достаточно большое ослабление полезного сигнала (на 20...22 дБ), что
необходимо учитывать при выборе коэффициента усиления усилителя У\ и при
расчете общего коэффициента усиления приемного тракта.
Низкочастотный фильтр, стоящий после второго смесителя предназначен
для подавления сигнальных составляющих суммарной частоты, образующихся
на выходе смесителя. При больших значениях / 2 вместо низкочастотного
фильтра можно использовать соответствующий полосовой фильтр.
Отметим, что радиоприемник на рис. 13.4 является одноканальным и
переносит все радионавигационные сигналы на вторую промежуточную частоту.
Задача частотного разделения радиосигналов различных НС в современных
приемниках решается в блоке корреляторов путем использования различных
несущих частот перестраиваемых опорных генераторов.
Рассмотрим требования к общему усилению сигналов в радиоприемнике.
В п. 11.2.2 отмечалось, что на входе радиоприемника мощность
навигационного радиосигнала составляет -161 дБВт, а спектральная плотность внутреннего
шума равна -201,5 дБВт/Гц (при значении коэффициента шума приемника
Кш = 2,5 дБ). Полоса пропускания радиоприемника определяется полосой
пропускания ПФ] и составляет А/Пф « 14 МГц. Следовательно, мощность шума в
полосе пропускания приемника Рш= -201,5+71,5 = -131 дБВт, а отношение
488
Аппаратура потребителей
сигнал/шум q = \Olog(Pc/Pm) =-161+201,5-71,5 = -31 дБ. Таким образом,
полезный сигнал находится на 31 дБ ниже уровня внутренних шумов приемника.
Из этого факта следует, что общий коэффициент усиления приемника следует
выбирать, ориентируясь на уровень внутреннего шума приемника, а не на
уровень полезного сигнала.
Полагая, что мощность внутреннего шума приемника Рш рассеивается на
согласованной нагрузке Rq = 50 Ом, можно записать
Рш=м[иш(02]/^=</До,
откуда
Сигнал с выхода радиоприемника подается на АЦП (рис. 13.4). Рабочее
значение эффективного напряжения на входе типового АЦП составляет
^ацп =0,1...0,5 В. Так как на входе АЦП действует шумовой процесс, будем
полагать f/дщт =<твх ш дцП. Тогда общий коэффициент усиления
радиоприемника по мощности Ку может быть найден из условия
"ш УЕ ~°вх.ш.АЦП>
Т.е. Кп ^^вх.ш.АЦП/ аиш -°"вх.ш.АЦп/(^ш^о) ' (13.2)
Полагая, Рш =130,5 дБВт, Я0=50Ом, сгвх шАЦП = 0,25 В, получаем К =
= 10 log(ATys) =102 дБ. Данное значение общего коэффициента усиления
включает коэффициенты усиления ПУ, Уь У2 (рис. 13.4) и не включает потери
мощности в УЗ, ПФ, ПФ1 и фильтра нижних частот (ФНЧ) и, возможно, в CMi, CM2.
13.4. Аналого-цифровой преобразователь
Сигнал с выхода радиоприемника подвергается аналого-цифровому
преобразованию, т.е. дискретизации по времени и квантованию по уровню.
При выборе частоты дискретизации по времени обычно исходят из того,
что необходимо правильно воспроизводить суммарный спектр всех сигналов
ГЛОНАСС, который занимает полосу частот около 14 МГц (по первым нулям
спектров крайних сигналов). Поэтому минимальное значение частоты
дискретизации (в соответствии с второй теоремой В.А. Котельникова для
полосовых сигналов) fd = 14 МГц. На практике часто используют более высокое
значение частоты дискретизации (например, 40 МГц).
Для квантования сигналов по уровню в стандартной НАП наиболее часто
применятся бинарное (1-битное) и 2-битное квантование. При бинарном кван-
489
Глава 13
товании используется лишь знак (±, sign) входного аналогового сигнала
u(tk). При 2-битном квантовании используют три пороговых уровня (уровни
сравнения), схематически представленные на рис. 13.5. Если в момент
времени /^ значение входного сигнала u(tk) превышает значение порога L, то на
выходе АЦП формируется кодовая последовательность 00; если §<u{tk)<L,
то формируется код 01; если -L<u(tk)<09 то формируется код 10; если
u{tk) < -L , то формируется код 11.
Аналоговый сигнал
Пороги
Выходные
коды
► 01
ь ПО
w \J\J
—► 10
—► 11
Рис. 13.5. Логика работы 2-битного АЦП
Квантование сигналов по уровню приводит к некоторому ухудшению
характеристик НАП, которое принято характеризовать энергетическими
потерями в значении отношения сигнал/шум, под которыми понимают необходимое
повышение сигнал/шум (выраженное в децибелах), обеспечивающее такие же
характеристики НАП при работе с квантованным сигналом, что и при
отсутствии квантования. Величина потерь П зависит от соотношения уровня
входного сигнала и значения порога L. На рис. 13.6 приведена зависимость величины
потерь от отношения у = £/сгвх.ш.ацп > гДе °"вх.ш.ацп — мощность гауссовского
шума на входе АЦП [2.8]. Минимальные потери (около 0,7 дБ) получаются при
выборе порога L*crBX ш.
0 12 3 4 5
Рис. 13.6. Характеристика потерь 2-битного АЦП
490
Аппаратура потребителей
В прецизионной НАП может использоваться АЦП с существенно большей
разрядностью выходных чисел, например, 12-битное АЦП.
13.5. Опорный генератор и синтезатор частот
Опорный генератор в НАП формирует шкалу времени потребителя. На его
основе строится необходимая сетка частот, используемых в приемнике.
В последние годы существенно возросли требования к ОГ. В конце 90-х
годов вполне удовлетворительным считался ОГ с относительной
нестабильностью частоты 10~7 (вариация Алана, см. п. 2.4). Однако в настоящее время
НАП с таким ОГ не удовлетворяет требованиям многих приложений,
например, для выскодинамичных объектов, интегрированных инерциально-
спутниковых систем навигации и др.
Для улучшения технических характеристик НАП необходимо
использовать высокостабильные ОГ (с кратковременной относительной
нестабильностью частоты 10~ ...10" и ниже), что приводит к существенному
удорожанию приемника. Поэтому при выборе типа ОГ исходят из компромисса между
характеристиками (а, следовательно, и стоимостью) ОГ и НАП в целом.
Более детальное исследование влияния ОГ на работу следящих систем
НАП (например, [13.1]) показывает, что необходимо учитывать не только
относительную нестабильность частоты, но и более полную характеристику —
спектральную плотность фазовых шумов (подробнее — в п. 2.4). В табл. 13.1
приведены значения спектральной плотности циклической фазы для некоторых
типов ОГ, из которых следует, что в существенной для работы следящих
систем области частот / = 1... 100 Гц она может быть различной как по
абсолютному значению, так и по скорости спадания спектральной плотности в
зависимости от частоты. Чем быстрее спадает спектральная плотность, тем лучшие
характеристики режимов слежения в НАП могут быть получены.
Таблица 13.1. Характеристики спектральной плотности
фазовых шумов ОГ
Значение
частоты
/,Гц
1
10
100
ГК99-ТК
S,(/), дБ/Гц
-50
-70
-100
ГК54-ТС
S+ (/), дБ/Гц
-95
-120
-140
ГК68ТС-ДЗ
S,(/), дБ/Гц
-80
-120
-140
Синтезатор частот строится на основе частотного плана, который
определяет выбор промежуточных частот приемника, тактовую частоту АЦП,
тактовую частоту работы вычислителей, необходимые прерывания для работы при-
491
Глава 13
ложений и т.д. Частотный план должен разрабатываться для каждого
конкретного приложения НАП, и при его создании необходимо учитывать требования
к подавлению гармоник биений, возникающих на выходах смесителей, к
воздействию индустриальных и других помех, расположенных в близких
частотных диапазонах, зеркальных помех и др. Важной характеристикой при
разработке синтезатора является минимизация фазовых шумов, порождаемых и
преобразуемых в нем. Так как в синтезаторе необходимые частоты формируются в
результате умножения/деления частоты ОГ в целое число раз, происходит
соответствующее преобразование фазовых шумов ОГ. Таким образом,
проектирование синтезатора может влиять на характеристики НАП.
13.6. Многоканальный коррелятор
Отсчеты сигнала (цифровой сигнал) с выхода АЦП поступают в цифровой
вычислитель (рис. 13.1), где они подвергаются корреляционной обработке в
многоканальном корреляторе.
Из общей теории построения навигационных приемников (см. гл. 6)
следует, что при поиске сигналов по задержке и частоте, и при слежении за теми же
параметрами (в некогерентном режиме) необходимо сформировать сигналы
вида
м
/=1
А/
Й,* = X>;('*-U ) АДК {h-U - */;*-!,/ )sin КЛ-1,/ + ®д/;*-1,1 (7 - 0Г</ ) > О3'4)
/=1
а для слежения при когерентном режиме работы
м
!Uk =X>,(/*-1-/)A«(/*-U "f/;*4,/)cos(^n/^4/ +^;*-и)^ (13'5)
/=1
д/
Qi*=^y{h-u)h*{h-\J~4^ +Й;*-1,/)> (13-6)
/=1
где для индексации времени использована двойная нумерация tk0 = kMTd =
= кТ9 T = MTd, tkJ=tkfi+lTd=kT + lTd9 tkM=tk+l09
y(tk-u) = g
X^(^-U'^^) + A?(^-u) (l3'7)
- /=1 J
— сигнал с выхода АЦП (входной сигнал для коррелятора), в котором g[x] —
функция амплитудного квантования (в дальнейшем для простоты полагаем
492
Аппаратура потребителей
g[x] - х), / = 1,п — номер спутника, г — псевдо задержка, <уд/ — псевдо доп-
леровское смещение частоты; hm(tk_xl -тгк_{1^ — дальномерный код
навигационного сигнала, т1;к_{1 — экстраполированная оценка задержки дальномер-
ного кода сигнала /-го НС; a>ui — промежуточная частота сигнала /-го НС;
Фгк-ц — экстраполированная оценка фазы сигнала /-го НС; *»Д|-.*-ц —
экстраполированная оценка доплеровского смещения частоты сигнала / -го НС.
Соотношения (13.3)—(13.6) описывают обработку входного сигнала в /-м
канале многоканального коррелятора. При этом составляющие Iik , Iik
называют синфазными, a Qik, Qik — квадратурными компонентами.
В многоканальном корреляторе осуществляется частотное разделение
сигналов НС за счет использования разных промежуточных частот coni
перестраиваемых генераторов.
При построении дискриминаторов следящих систем за задержкой сигналов
с использованием методики замены производной сигнальной функции по
задержке вычислением конечных приращений (6.63) необходимо формировать
квадратурные компоненты корреляторов с опережающей и запаздывающей на
Аг/2 функцией /?дк (^-ц ~~*/#-!,/) дальномерного кода, т.е.
М
= ХИ'*-и) Лдк ('*-U -(fi*-v + Ar/2))cos(^n/^_b/ + <&д/;*_,л (/ - \)Td),
1=1
м
= ZH'*-u) Ня*('к-и -(^-i,!+^/2))sin(<yniii,,+fflJi;Hi(/-l)r(/))
1=1
м
JE(L)i,k =^У^к-и) Кь[*к-и ~(fi*-ij + Ar/2))cos(fl^^-w +kk-u)> (13-10)
/=i
л/
беда =ЕЯ'ь-и) Лда('*-и -(Vi^^/2))sinKA-u+fe-u)- (13.11)
/=i
На рис. 13.7 приведена схема, реализующая корреляционные алгоритмы
(13.3)—(13.6), (13.8)—(13.11) для одного канала приема. На рисунке УЦГС —
управляемый цифровой генератор гармонического сигнала; ГДК — генератор
дальномерного кода; УТГ — управляемый тактовый генератор; /ст = 1/гэ —
493
Глава 13
скорость следования символов дальномерного кода; Р — индекс (IP, QP),
используемый для идентификации опорного канала, в котором синфазная и
квадратурная составляющие вычисляются в соответствии с (13.5), (13.6) (или для
некогерентного режима работы — (13.3), (13.4)).
к.
^it-u)
От АЦП
X
X
И х
cos
sin
Сигналы
управления по
фазе (частоте)
Ы УЦГС
fd
ГДК
Накапливающий Z
со сбросом
х
Накапливающий X
со сбросом
X
Т
х
х
Накапливающий Е
со сбросом
Накапливающий Е
со сбросом
Накапливающий £
со сбросом
X
Накапливающий Е
со сбросом
Я?*
Ql
3-битовый регистр сдвига
2/сг
УТГ
Сигналы управления
| по задержке
f
Рис. 13.7. Схема корреляторов одного канала приема
Принцип работы УЦГС описан, например в [6.11]. В зависимости от того,
какие сигналы управления подавать на УЦГС, можно формировать как
корреляторы, соответствующие когерентному режиму приема (13.5), (13.6), (13.10),
(13.11), так и корреляторы, соответствующие некогерентному режиму (13.3),
(13.4), (13.8),(13.9). Генератор дальномерного кода вырабатывает кодовую М-
последовательность (модулирующую функцию /?дк(^-1,/)) с длительностью
элементарного символа гэ = 1 / /ст, положение которой во времени
определяется сигналами управления по задержке; 3-битовый регистр сдвига обеспечивает
формирование hm (tk_xl - (fi;k_y - А г/2 п — опережающей и
hm[tk-ij ~{ji\k-u + Аг/2и — запаздывающей модулирующих функций.
13.7. Алгоритмы первичной обработки сигналов
Отсчеты lEUk,QEukJPi^QPiMJu^Qu,k синфазных и квадратурных
составляющих, сформированные в многоканальном корреляторе в моменты
времени tk по сигналам всех видимых НС / = 1,и, используются в алгоритмах
первичной обработки для поиска сигналов по частоте и задержке и для
непрерывного слежения за задержкой, фазой и/или частотой сигналов НС.
494
Аппаратура потребителей
13.7.1. Алгоритмы поиска и обнаружения
Особенности реализации поиска навигационных сигналов
Общая задача поиска рассмотрена в разделе 6.2. При практической
реализации алгоритмов поиска сигналов различают полный поиск и допоиск, что
обусловлено количеством априорной информации о значениях задержки и доп-
леровского смещения частоты принимаемого сигнала. Полный поиск
используется при отсутствии или достаточно грубой априорной информации о задержке
и доплеровском смещении частоты сигнала. Кроме того, отсутствует
информация текущих эфемеридах и текущем времени в приёмнике. Режим допоиска
используется при наличии информации о значениях задержки и доплеровского
смещения частоты с той или иной точностью. Такая ситуация возникает в двух
случаях. Во-первых, в режиме, так называемого, горячего старта, когда при
включении приемника имеется априорная информация о значениях задержки и
доплеровского смещения частоты либо от внешних источников (в зарубежной
литературе это называется "Aiding", "Assisted GPS"), либо она формируется из
данных сохранённого с прошлого сеанса альманаха системы. Во-вторых, после
срыва слежения за сигналом с целью перезахвата сигнала и повторного
вхождения в режим слежения.
Общая характеристика полного поиска сигналов
Так как в режиме полного поиска отсутствует априорная информация о
задержках, доплеровских смещениях частот сигналов и номерах видимых НС, то
поиск осуществляется во всем диапазоне возможных задержек (равном
длительности периода дальномерного кода), в диапазоне возможных доплеровских
смещений частот, обусловленных движением спутников, движением
потребителя, а также возможными уходами частоты опорного генератора приемника,
для сигналов всех НС.
В качестве примера рассмотрим возможные параметры поиска сигнала
СРНС ГЛОНАСС для наземного потребителя: диапазон доплеровских
частот А/дои = -5 ... +5 кГц, а значение 8/я элементарной ячейки поиска
определяется полосой захвата А/3 системы частотной автоподстройки и составляет
примерно 8/д = А/з = 500 Гц. Число анализируемых ячеек по частоте
Nf = А/дои/8/д = 20. Значение элементарной ячейки поиска по задержке
8т = 0,5гэ = 1/1022 (см. п. 6.2), а число анализируемых ячеек NT = \/8т = 1022 .
Таким образом, общее число анализируемых ячеек Na = N^NT =20440.
В режиме поиска используются квадратурные составляющие IP,QP
(13.3.), (13.4), а задача обнаружения сигнала в элементарной ячейке поиска ре-
Ip+Qp ^h, где h — порог, выбирае-
495
Глава 13
мый из условия обеспечения заданной вероятности правильного обнаружения
(см. п. 6.2).
Длительность интервала накопления сигнала Га при анализе в одной
элементарной ячейке (число накапливаемых отсчетов в (13.3), (13.4) Га = MTd)
зависит от величины отношения сигнал/шум qcin и заданных вероятностей
правильного обнаружения и/или пропуска сигнала: Га « 1 ... 10 мс (см. п. 6.2).
Общая характеристика допоиска при горячем старте
Горячий старт — режим работы приёмника при включении, если доступны
некоторые сведения о параметрах сигнала, в том числе:
• текущее время от часов реального времени приёмника;
• эфемериды и альманахи движения НС, сохранённые с прошлого сеанса;
• последнее местоположение приёмника, определённое при прошлом
сеансе работы;
• информация от внешних источников ("aiding"), которая может включать
текущие эфемериды, текущее время и сигналы точной временной
синхронизации.
Вся эта информация может быть использована для облегчения задачи
поиска. Практически все навигационные приёмники используют первые три
пункта — по текущему времени, выдвинув гипотезу, что текущее
местоположение приёмника не очень сильно отличается от последнего положения, по
альманахам с прошлого сеанса рассчитываются области видимости НС — это
помогает сузить круг поиска среди навигационных сигналов. Кроме того,
может быть рассчитано доплеровское смещение частот сигналов, что в ряде
случаев существенно снижает диапазон поиска по доплеровской частоте.
Более точная информация может быть получена от внешних источников
информации. Так, например, в стандартах сетей связи 3 поколения 3GPP [13.2]
прописан протокол передачи текущих эфемерид НС, координат базовой
станции и временной синхронизации. Однако текущих эфемерид недостаточно,
чтобы решить навигационную задачу, т.к. нужно ещё по фазам наблюдаемых
дальномерных кодов рассчитать псевдо дальности. Расчёт псевдо дальности
предполагает выделение из навигационного сигнала метки времени,
содержащей оцифровку шкалы времени НС и позволяющей разрешить
неоднозначность измерений по задержке. Вместо этой метки можно использовать
синхросигнал сети 3G. В стандарте 3GPP прописано два режима передачи точного
времени. В первом из них ("Coarse aiding") текущее время передаётся с
точностью до 2 с, что, в совокупности с передаваемой оцифровкой времени
позволяет разрешить неоднозначность по задержке. Во втором режиме ("Fine aiding")
время передается с точностью 10 мкс. Этой точности уже достаточно, чтобы
существенно сузить диапазон поиска по задержке.
496
Аппаратура потребителей
Общая характеристика допоиска при восстановлении слежения
При работе АП возможны срывы слежения за параметрами принимаемых
сигналов, что может быть вызвано рядом причин: снижением мощности
принимаемого сигнала, пропадание сигнала из зоны видимости, влияние
внутреннего шума приемка и др. При этом через некоторое время ситуация изменяется
и «потерянный» сигнал вновь может быть найден и взят на сопровождение.
Данная ситуация характерна тем, что в приёмнике присутствуют текущие
эфемериды, приблизительно известно его местоположение, а также известен сдвиг
шкалы времени приёмника. Всё это в совокупности позволяет определить с
высокой точностью задержку и частоту сигнала и ограничиться перебором
нескольких ячеек анализа по задержке и доплеровскому смещению частоты. Эта
задача и решается в режиме допоиска.
Рассмотрим некоторые варианты реализации процедуры поиска сигналов и
возможности ускорения поиска.
Последовательный поиск на корреляторах
Одним из возможных способов реализации поиска является
последовательный поиск с использованием тех же корреляторов, которые впоследствии
используются при слежении за сигналом. Данные корреляторы, несмотря на
простоту формулы (13.3)—(13.11), имеют достаточно сложную структуру,
предполагающую плавную перестройку по фазе, частоте, задержке и скорости кода.
Реализация такого коррелятора требует достаточно много аппаратных
ресурсов, поэтому даже в современной аппаратуре количество подобных
корреляторов ограничено (не более 100). Как следствие этого, процесс поиска
происходит очень медленно. Характеристики данного алгоритма описаны в п. 6.2.
Наиболее простой вариант ускорения поиска в этом случае —
использование внутренних ресурсов корреляторов слежения. Данные корреляторы для
реализации дискриминаторов задержки имеют «опережающие» и
«запаздывающие» компоненты, которые можно использовать для одновременного
анализа нескольких частотных позиций. Если классический коррелятор имеет
«опережающий», «центральный» и «запаздывающий» компоненты, их
использование может ускорить процесс поиска в 3 раза. В современных корреляторах
существует тенденция к увеличению данного набора до 5, 7 и более, что
связано с решением проблемы многолучёвости и слежением за сигналами с
модуляцией ВОС(я,т). Это также позволяет ускорить процесс поиска сигналов.
Поиск с использованием параллельных корреляторов
Наиболее очевидный метод ускорения поиска — распараллеливание, то
есть использование большого количества корреляторов. Использование с этой
целью полноценных корреляторов, аналогичных тем, что используются при
слежении, хотя и возможно, но, во-первых их реализация требует больших
аппаратных ресурсов, а во-вторых, для управления каждым таким коррелятором
497
Глава 13
требуется большая пропускная способность линии обмена с центральным
процессором. В противном случае он может просто не успевать ими управлять.
Поэтому разрабатываются блоки быстрого поиска навигационных
сигналов на основе специализированных версий корреляторов, предназначенных
исключительно для поиска.
Рассмотрим корреляционный интеграл, например (13.3), который
вычисляется для ячейки анализа, соответствующей значениям задержки т{ и допле-
ровского смещения частоты &>Д7
м
А-.У = ^^(^-1,/ ) Лдк (^Аг-1,/ ~ ^/;*-1,/ )cos(^n/^-l,/ + ^ду;*-1Л (7 ~ О7!/) " (13Л2)
/=1
Разобьем интервал интегрирования Т = MTd на Nx участков
длительностью, равной длительности ячейки анализа по задержке Тх = mxTd (T = NXTX9
М = Nxmx), таким образом, чтобы моменты смены символов опорного
дальномерного кода совпадали с границами этих участков. С учетом этого представим
(13.12) в виде
где
тх
v=\
(13.14)
Благодаря принятому разбиению временного интервала Т на подинтерва-
лы Тх значение символов дальномерного кода опорного сигнала постоянно на
каждом из интервалах длительностью Тх, поэтому (13.13), (13.14) можно
представить в виде
Nx-l Nx-\
h,j = 2*1 ^дк Ук-lr+v ~ *i;k-l,l)Pr,j = 2j hwi;rPr,j ' (13.15)
r=0 г=0
где
mx
Prj =7Е*У('к-1,г+у) cos(u,niWK+^i;Hl(r'"x+'/-1)^)- О316)
v=\
В (13.16) выражение под знаком суммирования не содержит
дальномерного кода, поэтому может быть вычислено заранее и сохранено в памяти. Далее
498
Аппаратура потребителей
осуществляется расчёт сумм (13.15) для всех значений задержки fi с учетом
вычисленных значений Рг ,.
Г У J
Схема коррелятора для одной ячейки анализа по частоте, реализующего
алгоритм (13.15), (13.16) для двух квадратурных каналов приведена на рис. 13.8.
Рассчитанные для всех значений частот и задержек корреляционные интегралы
/,. . (и аналогичные квадратурные компоненты Qij) далее используются для
расчёта огибающей (6.11), поиска максимума по fi, /. и принятия решения.
y(tk-i,r+v)
X
cos
v=\
Pr,l
v=\
sin
Генератор
опорной частоты
т
Память
отсчётов
X
X
X
Сумматор
Сдвиговый регистр
Текущая анализируемая частота д).
V
а.
ДК
Генератор
дальномерного
кода
Рис. 13.8. Схема коррелятора для одной ячейки анализа по частоте
Использование предварительного накопления сигнала на интервале
времени Тх снижает темп поступления обрабатываемых отсчётов с исходного,
определяемого частотой дискретизации входного процесса, до величины порядка
1...2 МГц (для СТ-сигналов). Если темп работы блока предварительного
накопления привязан к частоте дискретизации и символьной скорости
используемого дальномерного кода, то перебор по задержке может осуществляться с
отчётами, занесёнными в память на более высокой частоте (эта область на рис. 13.8
выделена пунктирной линией).
Для хранения отсчётов требуется достаточно большой объем памяти,
уменьшить который можно усечением разрядности накапливаемых величин
Prj (на рисунке не показано). Данное усечение разрядности отсчётов будет
вносить некоторые потери, поэтому выбор разрядности представления чисел
должен оптимизироваться под каждое конкретное применение.
Таким образом, использование специализированных поисковых
корреляторов при меньших вычислительных затратах позволяет на порядки ускорить
процесс поиска. Так, например, в чипе SiRFstar IV полноценных каналов
слежения за навигационными сигналами — 48, а блок поиска эквивалентен
499
Глава 13
1000000 корреляторов. При этом получается пропорциональное ускорение
процесса поиска.
Поиск с использованием согласованных фильтров
Алгоритм поиска по задержке можно реализовать в форме согласованного
фильтра (рис. 13.9).
:v('*-i,r+i')
X
cos
I '"X
v=\
r,j
'"X
I
sin
Генератор
опорной частоты
&
+i i+
+
hi
[x
-►|_|_
jf
_L
iff
i—ill
1 El
i—i
WxWxV 4x1
рЕУХ^ЕУ ^SS
Ш
t\[
Ш 1
лЗ
Й,у
Текущая анализируемая частота а>
Рис 13.9. Схема блока поиска с использованием согласованного фильтра
Также как и в предыдущем варианте, входные отсчеты поступают на два
квадратурных канала, где выполняется предварительное накопление сигнала на
интервале времени Тх . Далее в каждом канале используется согласованный
фильтр, состоящий из линии задержки, соответствующего количества
умножителей и ячеек памяти, в которые записываются отсчёты опорного кода.
Результат перемножения проходит через цепочку сумматоров с линиями задержки.
На выходе согласованного фильтра на каждом такте работы формируется
отсчёт, соответствующий корреляционному интегралу, накопленному для одной
ячейки анализа по задержке. При этом для реализации алгоритма (13.15)
необходимо использовать либо параллельное перемножение Nx отсчётов и много-
входовый сумматор, либо последовательные вычисления, но тогда на
вычисление корреляционной суммы для одного значения задержки потребуется Nx
тактов.
Поиск с использованием дискретной свёртки во временной области
Теоретической основой данного подхода является следующий известный
результат. Пусть имеем два дискретных периодичных сигнала с периодом N.
Запишем дискретную свёртку этих сигналов
500
Аппаратура потребителей
N-\
**=£*тЛ-т> ke[0;N-l]. (13.17)
Подставляя в (13.17) представление хк и ук в форме обратного
дискретного преобразования Фурье (ДПФ), запишем
N-\ Л N-\ ,„ Л N-X
w=0 и=0 /=0
£4 лм лм .2я,
-ЬТУУМ„&№. (Ш8)
N2 La La La °х,п^у,1
iV w=0 и=0 /=0
Учитывая, что У^ е
j%m(n-l)
m=0
, запишем (13.18) в виде
О, п ф I.
N-\
lrii л /%Ь
Данное выражение описывает обратное преобразование Фурье от
произведения спектров исходных сигналов и является следствием известной теоремы о
том, что спектральная плотность свёртки сигналов во временной области равна
произведению спектральных плотностей этих сигналов.
Отметим, что представление (13.19) справедливо и для комплексных
сигналов хк, ук .
Рассмотрим то, как можно применить данную теорему для задачи поиска
сигнала.
При поиске необходимо для различных значений задержек г,, i = О, NX -1
вычислить корреляционную сумму (13.15). Для этого опорный сигнал (дально-
мерный код) многократно сдвигается относительно входного сигнала по
задержке на длительность ячейки разрешения по задержке с вычислением
скалярного произведения векторов входного и опорного сигналов. Положим для
простоты рассуждения длительность ячейки разрешения по задержке равной
длительности символа дальномерного кода, а длительность интервала
интегрирования в корреляторе равной периоду кодовой последовательности, т.е.
Тх=тэ, Т = ТС. Тогда Nx =L, где L — число символов дальномерного кода на
длине периода Тс. Рассмотрим первую ячейку анализа / = 1, для которой
последовательность символов дальномерного кода обозначим как Лда1;г =ЛДКГ,
г = 0,1-1. Последовательность символов дальномерного кода для второй
ячейки анализа по задержке получается в результате сдвига аналогичной
последовательности для первой ячейки анализа на одну позицию, поэтому можно запи-
501
Глава 13
сать выражение hm2r =hm\\r+\ =^Дкг+1» '" = 0,1-1. Аналогично для i-й ячейки
анализа по задержке можно записать выражение hAKi.r=haKl.r+i=h
г = 0,1-1. Учитывая сказанное, (13.15) можно записать в виде
Nx-l
*дкг+/
ДКГ+/ >
(13.20)
г=0
Данное выражение отличается от выражения для дискретной свёртки
(13.17) тем, что «второй сигнал» оказывается «развёрнутым» во времени.
Поэтому, подставив опорный сигнал, заранее «развёрнутый» во времени в (13.20),
можно рассчитать все требуемые корреляционные суммы. Таким образом, из
сказанного и соотношения (13.19) получается следующий алгоритм обработки:
рассчитывается спектральная плотность опорного сигнала, развёрнутого
во времени;
рассчитывается спектральная плотность входного сигнала;
выполняется поэлементное перемножение массивов спектральных
плотностей входного и развёрнутого во времени опорного сигнала;
выполняется обратное преобразование Фурье спектральной плотности,
полученной на предыдущем шаге.
Отметим, что «развернуть» во времени опорный сигнал удобно в
спектральной области, выполнив комплексное сопряжение исходной спектральной
плотности.
Структурная схема алгоритма изображена на рис. 13.10.
У(*к-19г+у)
X
cos
—х
I
г,J
[sin
Комплексное
сопряжение
Генератор
опорной частоты
ТУТТ
Текущая анализируемая частота д).
БПФ
Генератор
дальномерного
кода
Рис 13.10. Схема блока поиска с использованием дискретной свёртки
во временной области
Следует отметить, что в описанном алгоритме поиска вычисляется
циклическая свёртка, то есть сигнал сдвигается циклически. Такая процедура хорошо
502
Аппаратура потребителей
подходит для поиска периодических сигналов, которыми являются СТ-сигналы
СРНС ГЛОНАСС.
Если в сигнале используется непериодическая кодовая
последовательность, например сигналы для специальных потребителей, то использование
циклической свёртки неправомерно. Для таких сигналов можно использовать
метод добавления нулей (Zero padding), заключающийся в том, что один из
сигналов заполняет полностью интервал, анализируемый БФП, а другой сигнал
заполняет только половину этого интервала, а его вторая половина заполняется
нулями. В этом случае половина полученного в результате преобразования
сигнала будет содержать требуемые корреляционные суммы. Поэтому, при
использовании данного метода для непериодических требуется удвоенный объём
БПФ.
Описанный алгоритм имеет еще одну особенность. Существует теорема о
том, что спектральная плотность произведения сигнала на комплексный
гармонический сигнал равна частотному сдвигу спектральной плотности сигнала.
Это позволяет упростить поиск сигнала по частоте. Перед предварительным
накоплением сигнал умножается на гармоническое колебание, частота
которого соответствует центральной частоте ячейки поиска по частоте. Далее, после
преобразования Фурье, полученная спектральная плотность циклически
сдвигает по частоте, тем самым перебирая каналы поиска по частоте с шагом 1 / Т.
После этого сформированная спектральная плотность умножается на
комплексно сопряжённый спектр опорного сигнала и выполняется обратное
преобразование Фурье. В данном алгоритме прямое преобразование Фурье
входного сигнала выполняется один раз, а обратное преобразование Фурье
выполняется столько раз, сколько есть частотных каналов. Это дает выигрыш по
вычислительным затратам.
При программной организации поиска описанный алгоритм наиболее
логичен ввиду простоты реализации БПФ. Однако сложность заключается в том,
что наиболее эффективная его реализация требует хранения большого объёма
промежуточных данных, что может наталкиваться на ограниченностью
аппаратных ресурсов НАП.
Поиск с использованием БПФ по частоте
Существует метод быстрого поиска, использующий последовательное
сканирование по частоте и параллельное — по задержке. Для параллельного
поиска по частоте используется БПФ, реализуемое, как правило, программно.
Схема блока поиска, основанного на данном методе, приведена на
рис. 13.11. Входной сигнал умножается на опорный сигнал, представляющий
собой дальномерной код для заданной ячейки разрешения по задержке. Далее
используется коррелятор с квадратурными каналами, предназначенный для
накопления на интервале Т0 = \jbf = m0Td , длительность которого определяет-
503
Глава 13
ся зоной поиска по частоте А/дар . Параметры опорного сигнала, поступающего
на коррелятор, соответствуют значениям задержки и частоты анализируемой
ячейки разрешения. Накопленные на требуемом количестве N, интервалов
длительностью Т0 (равном Nj = Д/дар/£/д , где Sfa — шаг анализа по
частоте) отсчёты поступают на блок БПФ, на выходе которого формируются N,
отсчётов, соответствующих одному значению задержки (одной ячейке поиска
по задержке) и Nj- значениям частоты (ячейкам поиска по частоте).
y(*k-i,r+v)
А
Генератор
дальномерного
кода
т
X
COS
sin
щ
v=\
щ
У=\
Генератор
опорной частоты
Текущее значение задержки
БПФ
Текущая
анализируемая
частота со
J
Рис 13.11. Схема блока поиска с использованием БПФ по частоте
Достоинством данного метода является относительная простота его
реализации в аппаратуре — нужно ввести специальный режим работы коррелятора с
накоплением на интервалах времени Т0 и организовать передачу накопленного
массива в процессор, а остальное можно реализовать программно.
Преимущество использования данного метода по сравнению с методом
последовательного поиска на корреляторах состоит в использовании
эффективного алгоритма БПФ, имеющего вычислительную сложность N-log2(N)
вместо N2 для прямого вычисления корреляционных сумм. Типичный объём
БПФ в таком методе N = 64.. .256. Однако при практической реализации с
учетом разрядности вычисления данный метод может проиграть методу,
указанному выше методу.
Перечисленные выше методы и алгоритмы иллюстрируют лишь
некоторые из возможных подходов к построению блока быстрого поиска. Данные
алгоритмы можно комбинировать друг с другом. В качестве примера на
рис. 13.12 приведена схема алгоритма, представляющего собой комбинацию
согласованного фильтра и БПФ по частоте.
504
Аппаратура потребителей
+ + М А4
БПФ
У('к-1,г+у)
X
COS
v=l
Pr,J
v=\
sin
Генератор
опорной частоты
т
ЖЗ
±
±L
±
н 1><]Ф<НхК *4х
Ч ^Ьмо* л.
Ао AJ А2
А#
Текущая анализируемая частота #),
Рис 13.12. Схема блока поиска с использованием комбинированного алгоритма
Данный алгоритм содержит несколько коротких согласованных фильтров,
процессы с выхода которых подвергаются БПФ и на каждом такте работы на
выходе БПФ формируются все корреляционные суммы по частоте для одного
значения задержки.
Таким образом, возможны различные варианты реализации алгоритма
быстрого поиска. Следует отметить, что основная проблема проектирования
таких алгоритмов заключается не в подборе наиболее подходящей структуры, а
возможностями реализации того или иного алгоритма с учётом аппаратных
ограничений. Основные вопросы при этом: выбор разрядности представления
чисел на каждом из шагов обработки, выбор темпа обработки для отдельных
блоков и оптимизация требований к памяти. Как результат, при правильной
реализации большинство из рассмотренных алгоритмов дают примерно одинаковый
результат по скорости поиска.
13.7.2. Алгоритм работы и схема слежения за фазой сигнала
В когерентном режиме работы НАП осуществляется слежение за фазой
сигнала НС. Подробное описание принципов построения следящих систем, в
том числе и за фазой сигнала (ССФ), приведено в п. 6.3.2, из которого следует,
что ССФ включает фазовый дискриминатор, сглаживающий фильтр и
генератор опорного сигнала.
В п. 6.3.4.1 показано, что в зависимости от условий работы ССФ
оптимальными (с точки зрения обеспечения наилучшей точности слежения)
являются различные типы ФД. В табл. 13.2 приведена итоговая сводка различных
типов ФД и их основные характеристики.
505
Глава 13
Таблица 13.2. Фазовые дискриминаторы и их характеристики
Алгоритм
работы
-Hh)Qp
-s\gn(IP)QP
-hQp
-Qplh
-Arctg(QP/IP)
Зависимость
ДХ от
фазовой ошибки
sin(^)
sin (2дф)
tg(<¥)
8ф
Общие свойства 1
Оптимальный ФД при произвольном отношении]
сигнал/шум. Крутизна ДХ пропорциональна
амплитуде А . Большие вычислительные затраты.
Близок к оптимальному при большом отношении]
сигнал/шум. Крутизна ДХ пропорциональна
амплитуде А . Минимальные вычислительные затраты.
Близок к оптимальному при малом отношении сиг-
нал/шум. Крутизна ДХ пропорциональна А .
Умеренные вычислительные затраты.
Субоптимален, но имеет хорошие характеристики
при большом и малом отношении сигнал/шум.
Крутизна ДХ не зависит от амплитуды А .
Большие вычислительные затраты и необходима
проверка операции деления при ошибке ±90°
(деление на ноль).
Главный угол арктангенса. Оптимален в смысле
оценок максимума функции правдоподобия [5.1,
5.2] при произвольном отношении сигнал/шум.
Крутизна ДХ не зависит от амплитуды А. Наи-
большие вычислительные затраты.
Дискриминационные характеристики ФД приведены на рис. 13.13 (по оси
ординат характеристики нормированы к размерности «градус»).
Ифд, град
90
-Arctg(ft>/^)
90 Sep, град
Рис. 13.13. Дискриминационные характеристики ФД
506
Аппаратура потребителей
Формулы, приведенные в первом столбце табл. 13.2 в дальнейшем будем
называть дискриминирующими функциями.
На рис. 13.14 приведена схема ССФ с одним из возможных типов ФД.
Л-и)|
От АЦП
3-битовый
Рг сдвига }4 fd
X
cos
-/стф
Коррелятор
X
X
Накапливающий!)
со сбросом
X
Накапливающий L
со сбросом
Qp
sin
УЦГС
и
Т
Дискриминирующая
функция
-sign(/P)
X
ид(р,к:
СФ
ф*
соп
ФА: - ФАг-1
Рис. 13.14. Схема ССФ
Данная схема включает в себя корреляторы синфазной 1Ри квадратурной
QP составляющих, блок дискриминирующей функции, сглаживающий фильтр
и блок формирования управляющих сигналов для УЦГС. В приведенной схеме
управление УЦГС осуществляется приращениями оценок фаз, полученных на
соседних тактах работы ССФ.
В качестве сглаживающего (СФ) в ССФ целесообразно использовать
фильтр третьего порядка (6.92). Для слабо динамичных потребителей в ССФ
может использоваться фильтр второго порядка (типа (6.109)).
Для описания ССФ общего вида введем п -мерный вектор состояния \фк ,
полагая при этом фк=Сф\фк, с^=|10 0...0| . Тогда для дискретной ССФ
можно записать следующие дискретные уравнения:
(13.21)
(13.22)
хф,к ~хф,к +^ф идф,к>
хф,к ~ Ффхф,к-1 »
где \фк — текущая оценка вектора состояния; 1^ — экстраполированная
оценка вектора состояния; К^ — вектор-столбец коэффициентов усиления;
Ф^ — переходная матрица сглаживающего фильтра в контуре следящей
системы; иАфк —процесс на выходе ФД. Так, для схемы рис. 13.14 имеем
«W =-sign(/p,*(i^-i)) ft\*(v*-i)- (13-23)
507
Глава 13
Уравнения (13.21), (13.22), рассматриваемые как уравнения линейного
фильтра, на вход которого действует процесс и^фк, описывают сглаживающий
фильтр ССФ, который характеризуются переходной матрицей Ф^ и вектором
Кф коэффициентов усиления.
При наличии дополнительной информации о доплеровском смещении
частоты принимаемого сигнала (например, от внешних измерительных датчиков)
соответствующая оценка #>двн может быть введена в СФ (рис. 13.14), что
позволяет «снять» часть динамического возмущения, действующего на ССФ, и
сузить ее полосу пропускания. Такая процедура позволяет повысить
помехоустойчивость ССФ.
13.7.3. Алгоритм работы и схема слежения за задержкой сигнала
Следящая система за задержкой (ССЗ) сигнала, как и ССФ, включает в
себя дискриминатор, фильтр и генератор опорного сигнала (ГОС).
Для формирования дискриминаторов ССЗ часто используют, как
отмечалось в п. 6.3.4.2, опережающие и запаздывающие квадратурные составляющие
Ie^Qe^l^Ql (13.8), (13.9) (или (13.10), (13.11)). Алгоритмы работы
дискриминаторов ССЗ и их краткая характеристика:
^IE +QE ~\Il +Ql — близок к оптимальному при некогерентном приеме
при большом отношении сигнал/шум; крутизна ДХ (кривая 1 на
рис. 13.15) зависит от амплитуды А ; хорошие характеристики
при модуле ошибки слежения менее 0,5гэ; большие
вычислительные затраты;
— крутизна ДХ (кривая 2 на рис. 13.15) не зависит от
Jll+Ql+yjll+Ql
амплитуды; хорошие характеристики при модуле ошибки
слеже-ния менее 0,5г3; наибольшие вычислительные затраты;
(1Е + QE I - (IL + QL I — близок к оптимальному при некогерентном приеме при
малом отношении сигнал/шум; крутизна ДХ (кривая 3 на рис.
13.15) зависит от А ; хорошие характеристики при модуле
ошибки слежения менее 0,5гэ; умеренные вычислительные
затраты;
508
Аппаратура потребителей
(/£ -IL)lP +(Qe ~Ql)Qp — близок к оптимальному при когерентном приеме
при малом отношении сигнал/шум; хорошие характеристики
(кривая 4 на рис. 13.15) при модуле ошибки слежения менее
0,5гэ; минимальные вычислительные затраты.
-*г-тг
-1,К\ -1% "0,5
Рис. 13.15. Дискриминационные характеристики
дискриминаторов задержки сигнала
Типичная схема ССЗ с одним из типов дискриминаторов задержки
приведена на рис. 13.16.
'(fe-u)
От АЦП
н х
COS
sin
X
г
Сигналы
управления по
фазе (частоте)
УЦГС
fd
т
Н х
гдк
"1Z
*\ X
*\ х
X
Коррелятор
Накапливающий Е
со сбросом
Накапливающий I
со сбросом
0Е
Дискриминирующая
функция
Накапливающий Z
со сбросом
Накапливающий Z
со сбросом
Ql
3-битовый регистр сдвига
И
УТГ
Уст
fd
1лхМ
ay;
СФ
хк ~хк-\
. Генератор опорного сигнала
Рис. 13.16. Схема ССЗ
В схеме рис. 13.16 управление положением опорного сигнала
осуществляется приращением оценки задержки сигнала на соседних тактах работы ССЗ.
509
Глава 13
В качестве сглаживающего фильтра (СФ) в ССЗ часто используют фильтр
второго порядка (6.109).
Следящая система за задержкой сигнала описывается дискретными
уравнениями, аналогичными (13.21), (13.22):
*а=*г,*+кг мдг,*> (13-24)
*а=фА,*-1- (13.25)
При построении комплексных систем слежения за задержкой и доплеров-
ской частотой сигнала в СФ может вводится оценка доплеровской частоты а>Л,
формируемая в ССФ (или в схеме слежения за частотой сигнала (ССЧ)) (см.
п. 6.3.6.5,6.3.6.6).
13.7.4. Алгоритм работы и схема слежения за частотой сигнала
Система слежения за частотой сигнала (ССЧ), которую часто называют
схемой частотной автоподстройки (ЧАП), используется, во-первых, на
промежуточном этапе при переходе из режима поиска сигнала по частоте к режиму
непрерывного слежения по фазе, а во-вторых, в некогерентном режиме работы
НАП. ССЧ включает частотный дискриминатор, сглаживающий фильтр и
перестраиваемый генератор.
Частотный дискриминатор можно сформировать из синфазной и
квадратурной составляющих IP,QP, сформированных для двух моментов времени
tk_x, tk . Алгоритмы работы ЧД данного типа и их краткая характеристика:
Ip(k)QP[k-\)-Ip(k-l)QP{k) — близок к оптимальному при малом отно-
шении сигнал/шум; крутизна ДХ (см. рис. 6.3) зависит от А ;
минимальные вычислительные затраты;
[//.We(*-i)-/P(*-i)&W>ign[/7>W6p(*-i)+/p(*-i)e/.W]-
близок к оптимальному при большом отношении сигнал/шум; кру-
тизна ДХ зависит от А ; умеренные вычислительные затраты;
h(k)Qp(k-l)-Ip(k-\)QP(k)
arctg—7-т ; : : : т—г — полный угол арктангенса; оптима-
*IP(k)QP(h-\) + IP(k-l)QP(k)
лен в смысле максимума функции правдоподобия [5.1,5.2] при
произвольном отношении сигнал/шум; крутизна ДХ не зависит от
амплитуды А ; наибольшие вычислительные затраты.
В Приложении к гл. 6 показано, что ширина апертуры дискриминационной
характеристики для большинства типов ЧД обратно пропорциональна времени
510
Аппаратура потребителей
накопления Т в корреляторе. Так, для первого из приведенных выше типов ЧД
Д/ = 1/(2Г) и для получения ширины апертуры частотного дискриминатора
д^ = 500 Гц необходимо выбирать время накопления при формировании
квадратурных составляющих Т = 1 мс.
В п. 6.3.4.2 получены и другие типы ЧД. Однако анализ их статистических
характеристик показывает (см. Приложение к гл. 6), что они имеют худшие
характеристики дисперсии шума, приведенного к оцениваемому параметру, чем
приведенные выше типы ЧД, что в итоге приводит к худшим характеристикам
точности оценки частоты.
Схема ССЧ с одним из типов ЧД приведена на рис. 13.17.
У(*к-и)
От АЦП
^ f лл Коррелятор
3-битовый И -Jct vT/
Рг сдвига \4 fd
X
COS
X
X
Накапливающий Z
со сбросом
Н х
Накапливающий 2
со сбросом
Qp
sin
fc
уцге
ГС
Дискриминирующая
функция
|Блок
задержки на Г
{Блок
задержки на Г
г
X
СФ
со
Д,к
Рис. 13.17. Схема ССЧ
Дискретные уравнения, описывающие ССЧ в пространстве состояний,
имеют вид
Xu>,fc = Xu>,£ + *^-й> им»,к '
Хй>,А ^а)*а>,к-\ •
(13.26)
(13.27)
В ССЧ в качестве сглаживающего фильтра обычно используют фильтр
второго порядка (6.115).
В установившемся режиме ССЧ обеспечивает ошибку измерения допле-
ровского смещения частоты менее 50 Гц, что позволяет системе ССФ захватить
сигнал и перейти на устойчивое слежение за фазой сигнала.
13.7.5. Алгоритмы работы дискретных фильтров
в контуре следящих систем
В следящих системах ССФ, ССЧ и ССЗ могут использоваться различные
типы сглаживающих фильтров. Синтез оптимальных СФ приведен в п. 6.3.6. На-
511
Глава 13
ряду с рассмотрением оптимальных СФ возможны стандартные подходы,
вытекающие из теории автоматического управления. Они кратко приводятся ниже.
Описание дискретных фильтров удобно давать в сравнительном плане
относительно соответствующих аналоговых фильтров, так как работа последних
физически более прозрачна. Поэтому будем придерживаться такого подхода.
Для аналоговых фильтров порядок фильтра определяется порядком
дифференциального уравнения, которым он описывается. Для дискретных
фильтров — порядком соответствующего разностного уравнения.
Дискретные "интеграторы". В непрерывных следящих системах за
подвижными объектами фильтры в контуре следящей системы строят, как
правило, с использованием интеграторов, т. е. звеньев с операторным коэффици-
Кп
ентом передачи К[р)-——, где р =
оператор дифференцирования.
р dt
Схема аналогового интегратора приведена на рис. 13.13, а. Она реализует
операцию х = ——у и включает усилитель с коэффициентом усиления Кш и
интегратор с единичным коэффициентом усиления.
При построении дискретных фильтров аналоговый интегратор заменяют
дискретным эквивалентом. Известны различные схемы замены аналогового
интегратора дискретным, что обусловлено различными формулами численного
интегрирования [13.3]. Наиболее часто используют схемы дискретных
интеграторов, приведенные на рис. 13.18, б—г.
У<!\
w
^ин
—►
1
x(t)
w
_п+
т
—►
£
V
—►
*-4
ч¥
Ук>
W
а
Т
)
►
s [
т_
хк^
V
\2*
W
б)
Ук>
W
Т
—►
^
La Г
i
i
у
ь
w
г
г\
1
J ^
1 La
к
L
*кы
W
в) г)
Рис. 13.18. Схемы аналогового (а) и дискретных (б — г) интеграторов
Здесь z-1 обозначает задержку на один такт Г обработки.
В схеме рис. 13.18, б реализуется дискретный алгоритм численного
интегрирования
■хк=Хк-1+тУк-1> (13-28)
512
Аппаратура потребителей
коэффициент передачи дискретного интегратора (в смысле Z-преобразования)
Т
K(z) =
z-1
(13.29)
Схема рис. 13.18, в описывается разностным уравнением
хк ~ хк-\ + ТУ к »
коэффициент передачи дискретного интегратора
Tz
K(z) =
z-1
(13.30)
а в схеме рис. 13.18, г реализуется алгоритм численного интегрирования
хк=хк-\+т(Ук+Ук-\)12>
коэффициент передачи дискретного интегратора
Т z + \
K(z) =
2z-\
(13.31)
Дискретный фильтр второго порядка. Аналоговый фильтр второго
порядка, используемый в следящих измерителях координат подвижных объектов,
имеет коэффициент передачи
К(Р) =
*ф2(1 + />*ф) Kt
ф2
Uz
УР
ф
(13.32)
где ЛГф2 — коэффициент усиления фильтра; Т^ — постоянная времени
демпфирующего звена.
Схема аналогового фильтра приведена на рис. 13.19, а.
у(0ы
W
кщ
-!-►
~~w
Ук
w
^ф2Г
у>
~w\
Г 1
р
Гф
т
z-1
Тф\
►
Л
S"
L*t
а)
^
W\
—►
1
1 p
x(t)
w
J
I
i
L
T 1
z-l|
4*
w
6)
Рис. 13.19. Схемы аналогового (а) и дискретного (б)
фильтров второго порядка
17-1026
513
Глава 13
Дискретный фильтр второго порядка, соответствующий (13.32),
получается при замене аналогового интегратора дискретным. Так, используя
дискретный интегратор с коэффициентом передачи (13.29), получаем коэффициент
передачи дискретного фильтра второго порядка:
k(z)-K^T( т
Z-1
z-1
+ ТА
Ф
(13.33)
Структурная схема дискретного фильтра второго порядка с
коэффициентом передачи (13.33) приведена на рис. 13.19, б. Аналогично получаются
коэффициент передачи и структурная схема дискретного фильтра второго
порядка при использовании дискретного интегратора с коэффициентом передачи
(13.31).
Дискретный фильтр третьего порядка. Коэффициент передачи
аналогового фильтра третьего порядка
к{Р) =
Кфз(' + ^ф|+К>2)2) *ф,
<\<
-Ur,
ф1
+ ТЛ
ф2
(13.34)
где АГфз —коэффициент усиления фильтра; T^,T^2 —постоянные времени.
Схема аналогового фильтра третьего порядка приведена на
рис. 13.20, а.
y(0w
^■фзг
1
р
?ф1
—►
Т
►
Ь,
W
1
р
т2
уф2
—►
к
"Л
►
1
Р
*(0»
а)
б)
Рис. 13.20. Схемы аналогового (а) и дискретного (б)
фильтров третьего порядка
Укь
W
^фЗГ
-р>
[*>
т
z-1
7ф1
ь
W
£
1
—►
^
W
Т
z-1
т2
уф2
—►
I
к
\.
—►
т
z-1
хк.
W
514
Аппаратура потребителей
Коэффициент передачи дискретного фильтра третьего порядка получается
при подстановке в (13.34) вместо коэффициента передачи аналогового
интегратора соответствующего коэффициента передачи дискретного интегратора.
Подставляя, например (13.29), получаем
K(z) =
К*ъТ(
z-1
Т ( Т
z-1
z-1
4-71, \ + ТА
[Ф1
ф2
(13.35)
Схема дискретного фильтра, имеющего коэффициент передачи (13.35),
приведена на рис. 13.20, б.
Дискретные фильтры в контуре ССФ. Описанные в предыдущих
разделах фильтры второго и третьего порядка могут быть реализованы в различных
следящих системах, в том числе и в ССФ.
Для фильтра второго порядка с коэффициентом передачи (13.33)
переходная матрица Ф^ и матрица коэффициентов усиления К^ в уравнениях (13.21),
(13.22) имеют вид
(13.36)
Для фильтра третьего порядка с коэффициентом передачи (13.35)
переходная матрица Ф^ и матрица коэффициентов усиления Кф имеют вид
ф,=
1 Г
0 1
; к,=
кф\
Кф2
—
^ф2^ф
Фл =
1 Т 0
0 1 Т
0 0 1
; кф =
КФ1
Кф2
Кфъ
=
^ф3^ф2^
^ф3^ф1^
КфЗТ
(13.37)
Дискретные фильтры в контурах ССЗ и ССЧ. В ССЗ и ССЧ
используется в основном фильтр второго порядка с коэффициентом передачи (13.33).
Переходные матрицы и вектор коэффициентов усиления описываются
соотношениями (13.36) с заменой ^—»г или ф^со соответственно.
13.7.6. Алгоритмы управления генераторами опорных сигналов
в следящих системах
Важным элементом следящих систем за задержкой, фазой и частотой
сигнала являются генераторы опорных сигналов, параметры которых управляются
таким образом, чтобы обеспечить требуемые характеристики слежения. Через
ГОС замыкается обратная связь в СС, а используемые в них параметры влияют
на дискриминационные характеристики соответствующих дискриминаторов, а
также на фильтрующие свойства СС.
515
Глава 13
Рассмотрим для примера ССФ. Из алгоритмов оптимальной фильтрации
(например, (П6.2)) следует, что на корреляторы синфазной и квадратурной
компонент на интервале накопления [^_ц,^] необходимо подавать
гармонические колебания
со^{соп1к_и+фк_и), ът(а)п1к_и+фк_и), 1 = \,М,
где
&-1,/=&-1+('-0%Л. (13-38)
Td — временной шаг работы АЦП.
Соотношение (13.38) определяет оптимальный закон управления фазой
перестраиваемого генератора гармонического колебания (УЦГС на рис. 13.14).
Такое управление включает управление по фазе (фк_х) и по частоте (сэк_х). В
гл. 6 статистические характеристики ФД рассчитывались именно для такого
закона управления УЦГС.
На практике для упрощения СС используют более простые законы
управления. Так, на рис. 13.14 управление УЦГС осуществляется только по частоте, а
закон управления определяется приращением оценки фазы за шаг временного
накопления в корреляторе Т . При использовании СФ с характеристиками
(13.36), (13.37) оценка фазы сигнала определяется уравнением
Фк = Фк-\ + Т^к-\ + Кф\иаф,к »
из которого определяем сигнал управления:
Л^^^^ч+^Чм (13-39)
и соответствующий закон изменения фазы УЦГС:
ФуЩС,к,1 =ФуцуС;к + lTdAcoyn,k • (13.40)
Аналогичные выражения можно записать для сигналов управления
задержкой дальномерного кода в ССЗ.
13.7.7. Алгоритм выделения навигационного сообщения
Выделение символов #нс осуществляется в когерентном режиме работы
приемника.
Из общей теории оптимального приема следует (см. п. 6.3.5), что в случае
модуляции сигнала НС только символами навигационного сообщения
(длительностью 20 мс) для оценки информационного символа необходимо
сформировать сигнал (6.66), аналогичный синфазной компоненте коррелятора на
длительности информационного символа (20 мс). Для формирования такого сигна-
516
Аппаратура потребителей
ла необходимо прежде всего осуществить синхронизацию по границам бит
информационных символов (битовую синхронизацию).
В СРНС ГЛОНАСС навигационное сообщение (символы которого
следуют с частотой 50 бит/с) складывается по mod 2 с символами М-кода,
следующими с частотой 100 Гц (см. п. 11.3). Поэтому, прежде чем выделять символы
навигационного сообщения, необходимо выделить символы М-кода, для чего
следует также выполнить битовую синхронизацию М-кода.
Пусть корреляторы АП имеют время накопления Г = 1 мс. Рассмотрим
отсчеты синфазной компоненты коррелятора 1к (следующие с частотой 1 кГц).
Алгоритм выделения символов навигационного сообщения, основанный
на обработке отсчетов 1к, условно представлен функциональной схемой
рис. 13.21.
U
Блок выделения
импульсов тактовой
частоты/^
Блок формирвания
М-кода
Блок выделения
символов М-кода
i
Блок формирования
импульсов
символьной частоты ^си
Сумматор
mod 2
i
Сумматор
со сбросом
Символы навигационного
сообщения
т
Рис. 13.21. Выделение символов навигационного сообщения
Отсчеты 1к с выхода коррелятора поступают в блок выделения импульсов
тактовой частоты М-кода (/м_к =50 Гц). Здесь фиксируются моменты смены
знака отсчетов 1к и после определенной статистической обработки
формируются импульсы тактовой частоты 50 Гц, привязанные к моменту смены знака
символов М-кода. Сформированные импульсы поступают:
в блок формирования М-кода («дискретный генератор» М-кода), который
формирует последовательность +1 или -1, чередующихся с частотой 50 Гц
(т.е. в рассматриваемом варианте с Т = 1 мс формируется по десять +1 или -1);
в блок формирования импульсов символьной частоты (/си = 100Гц),
которые соответствуют границам символов навигационного сообщения
(синхронизация по символам навигационного сообщения);
в блок выделения символов М-кода, в котором формируются «пачки»
отсчетов 1к, соответствующие одному символу М-кода; границы символов
задаются импульсами тактовой частоты 50 Гц, поступающими с одноименного
блока.
517
Глава 13
Выделенные символы М-кода («пачки» отсчетов 1к) поступают в
сумматор по mod 2, где они складываются с импульсами тактовой частоты, в
результате чего снимается модуляция навигационного сообщения М-кодом. Поэтому
на выходе данного сумматора формируются отсчеты 1к, в которых
присутствует модуляция только навигационным сообщением.
Отсчеты 1к поступают в сумматор со сбросом, интервал суммирования в
котором определяется импульсами символьной частоты, которые привязаны к
границам символов навигационного сообщения. Таким образом, в данном
сумматоре производится дополнительное сглаживание флуктуационной
составляющей отсчетов 1к на интервале времени 20 мс. На выходе сумматора
формируется последовательность ±1, следующих с частотой 50 Гц, которая в
дальнейшем подвергается декодированию с целью извлечения эфемеридной и
другой информации, переданной в радиосигнале НС.
13.8. Алгоритмы вторичной обработки информации
На этапе вторичной обработки информации выполняется:
определение координат и вектора скорости потребителя в результате
решения навигационной задачи;
декодирование навигационного сообщения;
другие сервисные функции.
13.8.1. Оценка координат и вектора скорости потребителя
В современной аппаратуре потребителя для получения оценки координат и
вектора скорости потребителя используются сигналы от всех НС, находящихся
в зоне видимости. В п. 6.4.2 показано, что в этом случае наиболее простое
решение получается при использовании метода наименьших квадратов.
Введем вектор состояния потребителя х = \х у z Д'|т в системе координат
OXYZ (см. п. 3.1) и вектор наблюдений оценок псевдо дальностей (формируе-
I л л л IT
мых в блоке первичной обработки) утк -\тхк т1к ... fNk\ . Тогда алгоритм
вычисления оценок вектора состояния потребителя записывается в виде (6.177)
x^x.+^^x^H^^H^x.^-h^^c, (13.41)
где хк — начальная оценка (начальное приближение) вектора хк; h(x^),
Н(хл) = сН(хА) — функции, определяемые в соответствии с (6.173), (6.181); с
— скорость света.
518
Аппаратура потребителей
Для реализации алгоритма (13.41) необходима априорная информация о
координатах спутников на момент проведения вычислений. Такая информация
доступна в АП после декодирования навигационных данных.
Получим соотношения для оценки вектора скорости потребителя. Введем
вектор V =
частот у у к =
V V V V
' х у z
и вектор наблюдений оценок псевдо доплеровских
fl,kfl,k —fN,k
, для которого запишем
(13.42)
где Vc6^ =\Д\}к Дг,к -Дли > Д/,* — скорость сближения (удаления)
потребителя с / -м НС; Я — длина волны радиосигнала; п^ к — вектор погрешностей
оценки псевдо доплеровского смещения частоты.
Учитывая, что
Д. = cos(a,)(^. -^) + cos(#)(^ -Vy) + cos(ri)(vyi -Vy) + V\
где cos(a;), cos($), cos(^) — направляющие косинусы линии потреби-
V V V
Щ У1 Ъ
тель—/-и НС; V, =
(13.42) можно представить в виде
У/,А=(АУа+НУ^)/Я + п/д,
где
cos(tfj) cos(^) cos(^)
|cos(a2) cos(/?2) cos(^2)
— вектор скорости /-го НС; наблюдения
(13.43)
А =
cos(aN) cos(/?^) cos^)
Из (13.43), используя метод наименьших квадратов (см. п. 6.4.2), находим
оценку вектора скорости потребителя
Vt =(HT(it)H(xt))_1H'(xt)(y/>tl-AVa). (13.44)
Если известны дисперсии шумов оценок псевдо дальности и псевдо
доплеровского смещения частоты, то соответствующие матрицы дисперсий шумов
можно учесть в алгоритмах (13.41), (13.44), аналогично тому, как это сделано,
например, в (6.178).
519
Глава 13
13.8.2. Расчет вектора состояния НС на основе
неоперативной информации (альманаха)
Алгоритм расчета параметров движения НС по данным альманаха
используется при выборе оптимального созвездия, расчете целеуказаний для поиска
навигационного радиосигнала выбранного НС. В основу алгоритма положена
модель невозмущенного движения спутников (кеплерово движение см. в гл. 3).
Исходные данные для расчета:
NA — календарный номер суток внутри четырехлетнего периода ot
начала ближайшего високосного года, на которые даны оскулирующие элементы
орбиты НС;
tfn — время прохождения восходящего узла, ближайшего к началу суток с
номером NA, с;
ЯА — долгота восходящего узла в системе координат ПЗ-90 на момент
tin > рад;
АФА — поправка к среднему значению наклонения орбиты на момент tAn,
рад (1^=63°);
АТА — поправка к среднему значению драконического периода
обращения НС, с (Гср = 43200 с);
еА — эксцентриситет орбиты на момент tAn;
сопА — аргумент перигея, рад;
/тек — текущее время, на которое рассчитывается вектор параметров
движения навигационного спутника, с;
NTeK — номер суток внутри четырехлетнего периода, на которое
рассчитывается вектор кинематических параметров.
Координаты движения НС в системе координат ПЗ-90 рассчитывают в
последовательности выполнения следующих шагов [1.3] (индексы А и п
опущены):
1. Определение текущих значений классических (кеплеровских) элементов
и некоторых других элементов орбиты:
i = icp+Ai; Гдр=Гср+АГ; « = 2^/Гдр; a = tfju/n2 ,
где п — среднее движение НС; а — большая полуось орбиты НС; п =
=3,1415926536 ; ju = 398600,44.
2. Внесение поправок на несферичность Земли:
Л*=Л + (Л-^)д/пп,
520
Аппаратура потребителей
о)^=й)П+о)пМПП,
где Д>пп = 86400 (WTeK - NA) + /тек - tA ;
(13.45)
л = -\о
а
Л/2
е
а
cos
(О
я-
180-86400'
6)п=5
v
ч7/2
*■] (5cos2(;)-l) -
a J v w 480-86
тек
86400 '
яе = 6378,136 км — экваториальный радиус Земли.
3. Расчет эксцентрической аномалии на текущий момент времени tT
проводится при рекуррентном решении уравнения Кеплера (3.17):
E^=M + esm(E^).
Средняя аномалия М эпохи /тек определяется в соответствии с
уравнением (3.15):
М = " ('тек~г)>
где г = tx + STU — время прохождения перигея, которое можно определить как
сумму времени прохождения восходящего узла и времени дТп движения НС
от восходящего узла до перигея.
Учитывая привязку времени tA к суткам с номером NA, а времени /тек к
суткам с номером NreK, с учетом (13.36) уравнение для средней аномалии
принимает вид
M = n{Atnn-STn).
Время 8ТП можно определить из уравнений Кеплера (3.14), (3.15), (3.17)
следующим образом. Пусть Еп — эксцентрическая аномалия,
соответствующая истинной аномалии 3 = со*п . Тогда в соответствии с (3.15)
Еп =2Arctg
tg
V2/
(1-е
1 + е
Из уравнения (3.17) для эксцентрической аномалии Еп можно определить
среднюю аномалию:
Mn=En-esin{En). (13.46)
Тогда для интервала времени STn справедливо соотношение
521
Глава 13
О, со*<к,
STn=Mjn + \ \
[Гдр, еап>тг.
Рекуррентное уравнение (13.46) решается с начальным условием
Е^'=М, к = 0,1— ДО тех пор, пока не будет выполняться условие
?<*+1> _£(*)!<3-1 (Г8.
4. Определение вектора состояния НС в орбитальной прямоугольной
системе координат ОХ\Х2, лежащей в орбитальной плоскости с началом в центре
Земли, ось Х\ направлена вдоль фокальной оси к перигею, ось Х2 — по
нормали к фокальной оси:
*г
= а (cos(E<t+1>)-e); x? =<n/TV sin(£<**'»)
Соотношения для составляющих скорости НС в орбитальной системе
координат получаются дифференцированием координат (^1ор,^2Р) по времени (с
учетом (3.17)):
nas'mlE^ +М na\j\-e2 coslis' +M
' l-ecos(£'*+'))' 2 l-ecos(£<*+1>)
5. Пересчет ортов |е°р,е°р| орбитальной прямоугольной системы
координат OXjX2 в инерциальную систему координат ПЗ-90, осуществляется путем
трех последовательных поворотов орбитальной системы координат на углы
&>*, /', Я* (см. (3.7)). Соотношения для проекций орта е°р на оси инерциальной
системы координат могут быть получены также из (3.18) при г = 1, 3 = 0 и
замене долготы восходящего узла Q в инерциальной системе на
соответствующую долготу восходящего узла Я* в системе координат ПЗ-90:
е°хХ = cos &>*cos ^ " s*n ^п s*n ^* cos z>
e°x - cos &>* sin Я* + sin cq*u cos Л* cos /, etx = sin &>* sin /,
а для проекций орта е°^2 аналогичные соотношения получаются из (3.18) при
8 = к12\
е®2 = -sin&>* cos Я* - cos co*n sin Я* cos/,
^2 =-sinfi>*sinA* +С08 69*С08Я*С08/, е^2 = cos&>*sin/.
522
Аппаратура потребителей
6. Преобразование вектора состояния НС из орбитальной системы в
систему координат ПЗ-90. Введем X = |Ar Y Z\T , ef =
0 0 0
ex\ ey\ ez\
т Ло
> e2 =
0 0 0
2*2 S>2 ez2
Тогда вектор координат НС в системе координат ПЗ-90 определяется
соотношением
Преобразование вектора скорости НС из орбитальной системы координат
во вращающуюся систему координат ПЗ-90 проводится в два этапа. Сначала
вектор скорости преобразуется в неподвижную систему координат, ось которой
смещена относительно оси Х0 инерциальной системы координат OXoYoZo на
долготу восходящего узла, равную Л*, в соответствии с формулой
Л. -=: Хл Ci ~г Xj ©2 •
На втором шаге вектор скорости Xs =
Xs Ys Z*
т
из неподвижной
системы координат пересчитывается во вращающуюся систему координат ПЗ-90 в
соответствии с общим правилом (3.21) по формулам
X = XS +щУ , Y = YS -щХ, Z = ZS.
13.8.3. Расчет вектора состояния НС на основе
оперативной информации
Расчеты в НАП проводятся с целью уточнения параметров движения НС
на момент времени tt по данным эфемерид (которые содержатся в разделе
оперативной информации навигационного сообщения), даются на моменты
времени tb и обновляются через каждые 15 мин, поэтому для времени ti
выполняется условие \tb - tt:| < 15 мин.
Процедура пересчета проводится численным интегрированием
дифференциальных уравнений орбитального движения (3.24). Начальными условиями
для интегрирования системы уравнений являются данные эфемерид.
Интегрирование проводится классическим одношаговым методом Рунге—Кутта
четвертого порядка [4.8], когда при разложении нелинейной функции в ряд
удерживаются все члены порядка малости до А4, где А — шаг численного
интегрирования. Для этого метода локальная ошибка имеет порядок А .
При использовании этого метода для решения дифференциального
уравнения первого порядка вида dy/dx = f(x,y) при начальном условии у(х0) = у0
расчеты проводятся по правилу
уп+1=Уп+К0+2К1+2К2+К3/6,
523
Глава 13
где K0=f(x„,y„)A; /С, =/\ хп +-А,уп +-К0 Д;
\ I 2 J
13.8.4. Пересчет координат потребителя из земной
в геодезическую систему координат
Алгоритм оценки навигационных параметров (13.32) формирует оценки
вектора потребителя в геоцентрической системе координат OXYZ, связанной с
Землей. Потребителя во многих случаях интересуют свои координаты в
геодезической системе координат (см. п. 3.1). Поэтому в АП необходимо
осуществить пересчет координат из геоцентрической системы в геодезическую. Общие
формулы связи двух систем координат имеют вид (3.3), (3.4), а пересчет по
этим выражениям может быть реализован следующим вычислительным
алгоритмом [13.3]:
1) определяются исходные данные — координаты х9 у, z в
геоцентрической системе координат OXYZ, выходные данные — координаты В, L, Н в
геодезической системе координат;
2) вычисляется вспомогательная величина
D = ylx2+y2\
3) анализируется значение D:
если D = 09toB = 7tz/(2\z\)9 L = 09
Н = zsinB - а4\-ег sin2 В ,
если D > О, то La - arcsin (у / D) 9 при этом:
если х > О, у > О, то L-La9
если лг<0, у>09 то L-K-La9
если х < О, .у <0 , то Ь = я + Ьа9
если х> О, у < О, то L = 27r-La;
4) анализируется значение z :
если z = 0, то В = О, # = Z) - а, в других случаях находятся
вспомогательные величины г, с, р :
r = >Jx2 +y2 +z2 , c = arcsin(z/r), p = e2a/2r,
реализуется итеративный процесс:
524
Аппаратура потребителей
sx =0 ; b = c + s^ s2 =arcsmipsm(2b)/\]\-e2sm2b J,
если модуль разности \s2 -sx\ < в , где s — требуемая точность
вычислений, то
B = b, H = DcosB + zsmB-a\ll- e2 sin2 В ,
в противном случае полагается s{ = s2 и вычисления повторяются, начиная
с расчета Ь . Во всех случаях выбирается е= 0,000Г'.
После нахождения B,L,H становится известной матрица перехода из
геоцентрической системы координат в прямоугольную горизонтальную, что
позволяет осуществить преобразование составляющих скорости движения
подвижного объекта.
13.9. Использование оптимальных алгоритмов обработки
сигналов и информации в аппаратуре потребителей
Как пример использования оптимальных алгоритмов обработки сигналов и
информации в современной НАП СРНС, описанных в гл. 6, рассмотрим
образцы приемной аппаратуры, выпускаемые Javad Navigation System Co. (Lexon,
Maxtor и др.) и доступные на российском рынке. Эти приемники воплощают в
себе наиболее передовые технологии в области приема и обработки
спутниковых сигналов ГЛОНАСС и GPS. Перечислим основные особенности
реализованных технических решений.
Использование ССФ 3-го порядка для слежения за фазой принимаемых
сигналов, что обеспечивает устойчивое сопровождение спутников при
установке аппаратуры на высокоманевренных объектах.
Использование поддержки схемы слежения за задержкой сигнала (ССЗ)
от схемы ССФ [см. п.6.3.6.5, 6.3.6.6], что позволяет уменьшить ширину
шумовой полосы ССЗ до единиц и даже долей герца и, таким образом, уменьшить
флуктуационные ошибки оценки псевдо дальности до уровня единиц-десятков
сантиметров.
Common (Co-Op) Tracking [0]. Представляет собой несколько упрощенный
вариант одноэтапного слежения за параметрами сигнала [см. п. 6.5, 17.2.2].
Суть алгоритма заключается в разделении динамики фазы сигнала на две
составляющие: быстро- (обусловленную динамикой объекта и нестабильностью
опорного генератора приемника) и медленноменяющуюся (обусловленную
движением спутника и нестабильностью его опорного генератора). Такое
разделение позволяет использовать для слежения за медленноменяющейся
составляющей ССФ с шириной шумовой полосы порядка 2 Гц, а для слежения за
быстроменяющейся составляющей — с полосой порядка 20 Гц. Количество
узкополосных ССФ равно количеству сопровождаемых спутников, широкополос-
525
Глава 13
ная ССФ — одна для всех спутников, и использует для оценки параметров
суммарную мощность принимаемых сигналов. Такой подход позволяет
повысить чувствительность приемника примерно на 10 дБ по сравнению с
традиционно используемым подходом, основанном на использовании для слежения за
каждым из сигналов НС автономных ССФ.
Подавление многолучёвости осуществляется на основе двух подходов,
которые могут использоваться как совместно, так и по отдельности. Первый
подход состоит в использовании специально сконструированной антенны [13.6],
обеспечивающей подавление сигналов, отраженных от земной поверхности и
объектов, расположенных ниже антенны. Однако, данный подход не
обеспечивает подавление сигналов, отраженных от объектов, расположенных над
антенной (высокие здания, деревья и т.п.), поэтому в приемнике осуществляется
дополнительная сигнальная обработка, позволяющая в существенной степени
снизить ошибки оценки параметров сигнала, обусловленных эффектом
многолучёвости.
Дифференциальный режим навигации. Приемник в реальном времени
обеспечивает декодирование корректирующих поправок, передаваемых в
соответствии с форматом RTCM 104 (см. гл. 12), и оценивание координат объекта с
точностью до десятков сантиметров.
Режим RTK (Real Time Kinematic) [13.7] является дальнейшим
расширением режима дифференциальной навигации и позволяет на основе приема данных
об измерениях псевдо дальности и псевдо фазы, выполняемых в базовом
приемнике, в реальном времени оценивать текущие координаты приемника с
точностью до единиц миллиметров в статическом режиме и до единиц
сантиметров в динамическом режиме.
Ы & L2. Приемник может осуществлять слежение за сигналами спутников
в двух частотных диапазонах L\ и L2 , модулированными кодами стандартной
точности С/А, кодами высокой точности Р (режим AS выключен) и криптоза-
щищёнными кодами высокой точности Y (режим AS включен). В последнем
случае используется специальная технология Semicodeless tracking.
Использование измерений в двух частотных диапазонах позволяет выполнить
компенсацию погрешностей, обусловленных задержками сигналов в ионосфере, и тем
самым повысить точность оценки координат в автономном режиме навигации.
Кроме того, применительно к режиму RTK использование двухчастотных
измерений позволяет повысить вероятность правильного разрешения
неоднозначности фазовых измерений, сократить время, необходимое на разрешение
неоднозначности, и повысить точность оценки координат.
GPS & GLONASS. Приемник осуществляет прием как сигналов СРНС GPS,
так и сигналов СРНС ГЛОНАСС в обоих частотных диапазонах (L\ и L2), что
обеспечивает повышение точности, доступности, непрерывности и
целостности НВО, в том числе в городских и других сложных условиях, когда
ограничена радиовидимость НС.
526
Аппаратура потребителей
WAAS & EGNOS. Приемник может осуществлять прием сигналов от
геостационарных спутников SBAS, используя передаваемую корректирующую
информацию для повышения точности оценки текущих координат.
Высокие точность и темп выдачи данных измерений. Приемник может
выдавать данные о текущих измерениях псевдо дальности, полной фазы до
всех радиовидимых спутников, координатах и скорости объекта с темпом до 20
Гц, что позволяет фиксировать траектории объектов (в том числе
высокодинамичных) с высокой детальностью и точностью.
Подавление помех в полосе сигнала. Наряду с GPS/GLONASS
корреляционными каналами JNS chip содержит 6 цифровых настраиваемых режекторных
фильтра, обеспечивающих подавление узкополосных помех в полосе частот
принимаемых сигналов спутников. Общее число подавляемых помеховых
сигналов — до 6. Полоса режекции каждого из фильтров может быть программно
задана в диапазоне от 5 до 80 кГц. Коэффициент подавления помех — до 60 дБ.
Для анализа помеховой обстановки и начальной оценки параметров помеховых
сигналов используются два сканирующих цифровых спектроанализатора с
программируемой разрешающей способностью.
Поставляемое с приемным модулем программное обеспечение
используется для управления приемником в реальном времени, отображения текущей
информации (координат, скорости, видимого созвездия спутников и др.), записи
«сырых» данных в файлы для их последующей обработки.
Литература
13.1. Харисов В.Н., Булавский Н.Т., Горев А.П. Обоснование модели динамики при
синтезе схем слежения для приемников СРНС// Радиотехника. Радиосистемы, 2004,
№7, с. 104—107.
13.2. 3GPP TS 34.171 Assisted Global Positioning System (A-GPS). http://www.3gpp.org
13.3. Цифровые радиоприемные системы: Справочник/ М К Жодзишский,
Р. Б. Мазепа и др. — М.: Радио и связь, 1990.
13.4. Аппаратура радионавигационных систем ГЛОНАСС и GPS. Системы
координат. Методы перевычислений координат определяемых точек. Государственный
стандарт РФ, Госстандарт России, 1997.
13.5. Zhodzishsky M, Yudanov S., Veitsel V.f Ashjaee J. Co-Op Tracking for Carrier
Phase, http://www.javad.com
13.6. Filippov V.f Tatarnicov D., Ashjaee J., Astakhov A., Sutiagin L The First Dual-
Depth Dual-Frequency Choke Ring, http://www.javad.com
13.7. Zhodzishsky M, Vorobiev M, Khvalkov A., Ashjaee J. Real-Time Kinematic
(RTK) Processing for Dual-Frequency GPS/GLONASS, http://www.javad.com
527
Глава 14
Р а з д е л 3
НАПРАВЛЕНИЯ РАЗВИТИЯ ТЕХНОЛОГИЙ
СПУТНИКОВОЙ НАВИГАЦИИ
Глава 14
НАПРАВЛЕНИЯ СОВЕРШЕНСТВОВАНИЯ
РАДИОНАВИГАЦИОННОЙ СИСТЕМЫ ГЛОНАСС
Превращение системы ГЛОНАСС в непрерывно эксплуатируемую
систему предъявляет повышенные требования к надежности функционирования ее
космического и наземного сегментов, совместимости навигационных сигналов
с сигналами других радиотехнических систем, взаимодействия с другими
навигационными системами. Кроме того, необходимо учитывать постоянный рост
требований пользователей к точности навигационного определения и
целостности системы, понимая под целостностью ее способность обеспечивать
предупреждение пользователей о тех моментах времени, когда система в целом
или отдельные НС не должны использоваться для навигационных определений.
Модернизация системы ГЛОНАСС проводится и будет проводиться в
дальнейшем по следующим направлениям:
улучшение совместимости с другими радиотехническими системами;
повышение точности навигационных определений и улучшение сервиса,
предоставляемого пользователям;
повышение надежности и срока службы бортовой аппаратуры спутников и
улучшение целостности системы;
развитие дифференциальной подсистемы.
14.1. Модернизация ГНС ГЛОНАСС
В 2008 году были официально утверждены новые требования к глобальной
навигационной системе (ГНС) ГЛОНАСС. Требования относятся как к составу
системы, так и к значению ее основных параметров. Выполнение требований
должно осуществляться последовательно за 4 этапа:
Этап 1. Обеспечение непрерывной навигации на территории Российской
Федерации.
Этап 2. Обеспечение глобальной непрерывной навигации.
Этап 3. Доведение основных тактико-технических характеристик ГНС
ГЛОНАСС до уровня, обеспечивающего конкурентоспособность ГНС
ГЛОНАСС.
Этап 4. Дальнейшая модернизация ГНС ГЛОНАСС. Требования этапа 4
528
Направления совершенствования СРНСГЛОНАСС
определяются при формировании программы по поддержанию, развитию и
использованию системы ГЛОНАСС на 2012 - 2020 годы.
В состав ГНС ГЛОНАСС должны входить:
1. Космический комплекс (глобальная навигационная спутниковая система)
ГЛОНАСС в составе:
• орбитальная группировка навигационных космических аппаратов
(ОГ НКА);
• наземный комплекс управления КА, включающий систему
синхронизации (СС).
2. Комплекс функциональных дополнений глобальных навигационных
спутниковых систем (КФД ГНСС) в составе:
• широкозонная система дифференциальных коррекций и
мониторинга (СДКМ) навигационных полей ГНС;
• региональные и локальные дифференциальные системы (входят
функционально).
3. Система апостериорного высокоточного определения эфемерид и
временных поправок системы ГЛОНАСС.
4. Средства фундаментального обеспечения (СФО) ГНС ГЛОНАСС
(входят функционально):
• комплекс средств определения и прогнозирования параметров
вращения Земли;
• комплекс средств формирования UTC(SU);
• комплекс средств уточнения фундаментальных астрономо-
геодезических параметров.
5. Навигационная аппаратура потребителей.
Система ГЛОНАСС должна отвечать следующим основным требованиям.
1. Обеспечить решение задач координатно-временного и навигационного
обеспечения в абсолютном режиме для неограниченного количества
стационарных и мобильных потребителей непрерывно на всей поверхности Земли и
до высот 2000 км, и дискретно — до высот 40000 км.
2. Обеспечить решение задач координатно-временного и навигационного
обеспечения в дифференциальном режиме для неограниченного количества
стационарных и мобильных потребителей непрерывно на территории
Российской Федерации в зонах действия функциональных дополнений.
3. Погрешность определения пространственных координат и времени
потребителя для непрерывного поля в государственной системе координат и
времени в системной шкале ГЛОНАСС за счет «космического сегмента» по
сигналам с СТ-кодом (без учета ошибок в среде распространения и ошибок приемной
аппаратуры) в реальном времени в абсолютном режиме без использования
информации от функциональных дополнений с вероятностью 0,95 на любом
суточном интервале времени на этапе штатной эксплуатации системы в пределах всей
области обслуживания СРНС ГЛОНАСС при PDOP=2 должна составлять:
529
Глава 14
по положению
по скорости
по времени
Этап 1
12.4 м
0.027 м/с
30.7 не
Этап 2
7.0 м
0.02 м/с
13.3 нс
Этап 3
2.8 м
0.013 м/с
5.3 не
4. Доступность навигационного поля (процент времени, в течение
которого для штатной группировки КА, используемых по целевому назначению,
пространственный геометрический фактор PDOP < 6 на любом 24-часовом
интервале в зоне действия системы) должна быть не хуже 98%.
5. Для полностью развернутой орбитальной группировки космических
аппаратов космического комплекса ГЛОНАСС должна быть обеспечена
целостность навигационного поля с вероятностью 0,99 в соответствии с таблицей:
зона действия
время доставки до потребителя
сигнала целостности
Этап 1
-
-
Этап 2
Россия
Юс
Этап 3
глобально
Юс
6. Для всех КА, используемых по целевому назначению, эквивалентная
погрешность псевдо дальности и псевдо скорости в пространстве за счет ошибок
космического сегмента с вероятностью 0,95 на любом суточном интервале на
этапе штатной эксплуатации космического комплекса при использовании
сигналов с открытым доступом и передаваемой в них эфемеридно-временной
информации не должна превышать:
псевдо дальность, м
псевдо скорость, м/с
Этап 1
6,2
0.013
Этап 2
3,5
0.010
Этап 3
1,4
0.007
7. Расхождение системной шкалы времени ГЛОНАСС с национальной
шкалой всемирного координированного времени UTC(SU) с вероятностью 0.95
не должно превышать:
Этап 1
660 нс
Этап 2
660 нс
Этап 3 !
120 нс
8. Погрешность определения времени потребителем в системной шкале
времени ГЛОНАСС за счет ошибок космического сегмента на любом суточном
интервале на этапе штатной эксплуатации с вероятностью 0.95 не должна
превышать:
530
Направления совершенствования СРНСГЛОНАСС
Этап 1
100 нс
Этап 2
40 нс
Этап 3
12 не
9. Для полностью развернутой группировки НС ГНС ГЛОНАСС
обеспечивается доступность системы не ниже 0,997, целостность 0,99 (10 с).
Совершенствование аппаратуры НС будет проводиться по следующим
направлениям:
введение излучения навигационного радиосигнала в диапазоне ЬЪ
(-1200 МГц);
введение новых сигналов с кодовым разделением;
гарантированное обеспечение излучения радионавигационных сигналов в
течение всего срока активного существования;
срок активного существования НС «Глонасс-М» будет не менее 7 лет,
а НС «Глонасс-К» — не менее 10 лет;
бортовой стандарт частоты, применяемый на НС, должен иметь вариацию
частоты не более 10~13 при времени измерения 1 сутки;
обеспечение возможности размножения на борту эфемеридной и частотно-
временной информации (ЭЧВИ) по исходным данным, передаваемым с
наземных средств управления, а также расчета ЭЧВИ по результатам
межспутниковых измерений;
проведение бортовым комплексом управления анализа состояния бортовой
аппаратуры и выработка управляющих команд для поддержания
работоспособности НС, а также формирование и передача в навигационном сообщении
сигнала «Вызов НКУ», в том числе и в навигационную аппаратуру потребителя
при неисправности, влияющей на качество решения целевой задачи;
среднеквадратические погрешности эфемерид, не должны превышать:
для НС «Глонасс-М»
вдоль орбиты — 5 м,
в боковом направлении — 5 м,
в радиальном направлении — 1 м,
по составляющим вектора скорости — 0,02; 0,02; 0,17 см/с соответственно;
для НС «Глонасс-К»
вдоль орбиты — 3,5 м,
в боковом направлении — 3,5 м,
в радиальном направлении — 0,5 м,
по составляющим вектора скорости — 0,02; 0,02; 0,17 см/с соответственно.
Указанные выше точности должны обеспечиваться на интервале штатного
и автономного функционирования для полностью развернутой орбитальной
группировки с межспутниковыми измерениями (работа с бортовой
аппаратурой межспутниковых измерений (ВАМИ)) и закладке информации о
параметрах вращения Земли. При работе без ВАМИ указанная точность обеспечивается
531
Глава 14
на интервале между очередными закладками. Автоматизированное управление
НС (АСУ НС), их информационное обеспечение, контроль и поддержание
параметров навигационного поля реализуются входящим в состав АСУ наземным
комплексом управления (НКУ) с соответствующим специальным
программным обеспечением во взаимодействии с бортовым управляющим комплексом.
Вероятность выполнения этих задач — не менее 0,99.
Наземный комплекс управления обеспечивает решение следующих
основных задач:
управление навигационными спутниками орбитальной группировки;
эфемеридно-временное обеспечение НС с заданной точностью, при этом
точность измерения текущих навигационных параметров при решении задач
ЭВО должна быть не хуже (СКО) 0,17 м по псевдодальности (0,03 м при
измерениях по фазе несущей) и 0,17.. .0,3 м по дальности;
мониторинг технического состояния НС и качества излучаемых
навигационных сигналов;
мониторинг характеристик навигационного поля;
поддержание структуры навигационного поля путем своевременного
восстановления работоспособности НС после кратковременных отказов или
перевода НС в рабочее состояние из числа находящихся в орбитальном резерве;
закладка командно-программной и специальной информации и контроль за
ее прохождением с проверкой на достоверность;
прием и автоматизированную обработку телеметрической информации;
проведение сеансов измерения текущих навигационных параметров;
сверка, фазирование и коррекция бортовой шкалы времени;
организация информационного обмена между элементами НКУ;
обеспечение привязки БШВ к СШВ с погрешностью (СКО) не более
1.. .2 не на момент измерения;
измерение дальности до НС с ошибкой (СКО) не более 1.. .3 м.
Отметим, что управление и эфемеридно-временное обеспечение НС
должно осуществляться в режиме обычного (неавтономного), полуавтономного (с
размножением ЭИ и ЧВП на борту) и автономного (с обновлением 1 раз в
10... 15 суток информации о ПВЗ) функционирования.
Для решения приведенных выше задач в состав НКУ будут входить:
модернизированный Центр управления системой (ЦУС-М);
существующие и модернизированные командно-измерительные системы
(КИС);
квантово оптические станции;
средства информационно-телеметрического обеспечения;
система связи и передачи данных между ЦУС-М и всеми элементами
наземного комплекса управления;
беззапросные измерительно-вычислительные системы;
закладочно-измерительные станции.
532
Направления совершенствования СРНСГЛОНАСС
Поскольку орбитальная группировка, кроме штатно функционирующих
24 НС, может содержать до трех резервных НС и до шести НС, находящихся в
режиме выведения на орбиту, НКУ должен обеспечивать управление,
информационное обеспечение и контроль орбитальной группировки в составе до
33 НС.
Для обеспечения улучшенных характеристик СРНС ГЛОНАСС
необходимо улучшать характеристики системы синхронизации, в том числе:
стандарты частоты, входящие в состав центрального синхронизатора,
должны иметь относительное среднеквадратическое отклонение частоты не
более 1(Г14 при времени измерения 1 сутки;
среднеквадратические погрешности взаимной синхронизации сигналов НС
в течение интервалов автономного функционирования при штатной работе (с
ВАМИ) не должны превышать 3...4 не; при работе без ВАМИ — 8 не на 12-
часовом интервале после закладки.
В результате определение и прогнозирование расхождения СШВ
относительно ШВ Госэталона должно осуществляться с погрешностью (СКО) не
более 0,3 мкс.
14.2. Сигналы ГНС ГЛОНАСС
14.2.1. Концепция развития навигационных сигналов ГНС ГЛОНАСС
В феврале 2008 г. в РФ была принята «Концепция развития
навигационных сигналов глобальной навигационной системы ГЛОНАСС», в которой
определена необходимость развития навигационных сигналов. Основными
целями такого развития являются:
обеспечение интересов национальной безопасности в области спутниковой
навигации;
повышение конкурентоспособности системы ГЛОНАСС;
удовлетворение возрастающих требований потребителей;
международная интеграция спутниковых навигационных систем.
В Концепции определено, что «в соответствии с интересами национальной
безопасности РФ и расширением использования аппаратуры спутниковой
навигации гражданскими потребителями при развитии навигационных сигналов
необходимо обеспечить сохранение навигационных сигналов, обеспечивающих
работоспособность существующего парка аппаратуры спутниковой навигации
(АСН). Кроме того, для сохранения паритета в области спутниковой навигации
необходимо совершенствовать параметры существующих навигационных
сигналов и вводить новые более совершенные навигационные сигналы, поскольку
параметры сигналов и их количество в значительной степени определяют
характеристики спутниковой навигационной системы в целом».
533
Глава 14
В марте 2008 была создана рабочая группа по координации развития
навигационных сигналов ГНС ГЛОНАСС, в которую вошли ведущие специалисты
в области спутниковой навигации и разработчики системы, бортовой
аппаратуры и аппаратуры потребителей. Результатом работы этой группы принятая
«Концепция развития навигационных сигналов глобальной навигационной
системы ГЛОНАСС» была доработана и к моменту сдачи данной монографии в
издательство разработан проект второй редакции «Концепции развития
навигационных сигналов глобальной навигационной системы ГЛОНАСС»,
утверждение которой планируется в конце 2009 г. Ниже приводятся основные
положения данной концепции.
Требовании к навигационным сигналам системы ГЛОНАСС
Навигационные сигналы ГНС ГЛОНАСС должны удовлетворять всему
спектру требований специальных потребителей и потребителей социально-
экономической сферы. Основными требованиями являются:
точность навигационных определений;
оперативность навигационных определений;
простота аппаратного построения АСН (простота технологии обработки
сигнала);
устойчивость к помехам;
электромагнитная совместимость с навигационными сигналами других
ГНСС;
взаимодополняемость с навигационными сигналами аналогичных
навигационных спутниковых систем;
возможность независимого использования сигналов с санкционированным
и открытым доступом;
информативность навигационного сообщения в навигационных сигналах;
возможность компенсации погрешностей измерений, привносимых средой
распространения;
высокая вероятность декодирования служебной и навигационной
информации;
высокая эффективность алгоритмов раскрытия неоднозначности фазовых
измерений в АСН;
высокие потребительские качества АСН, использующей новые сигналы.
Соответствие параметров существующих навигационных сигналов
требованиям потребителей
Существующие сигналы системы ГЛОНАСС с частотным разделением не
полностью отвечают перечисленным выше требованиям потребителей.
Для выполнения требований современных и перспективных потребителей,
оптимальная совокупность навигационных сигналов для перспективных НКА
системы ГЛОНАСС должна состоять из независимых сигналов с частотным, а
534
Направления совершенствования СРНСГЛОНАСС
также кодовым разделением, как для специальных потребителей, так и
потребителей в социально-экономической сфере.
Международная интеграция спутниковых навигационных систем
В настоящее время заключено межправительственное соглашение между
США и Европейским Союзом об использовании близких по параметрам
сигналов с кодовым разделением в диапазонах Ы (-1.6 ГГц) и L5 (-1.1 ГГц).
Планируют подобную работу и другие разработчики глобальных и
региональных навигационных спутниковых систем и их функциональных
дополнений.
Международная интеграция ГНС в части сигналов с открытым доступом
при гарантиях совместимости ГНС позволит:
реализовать разработку комбинированной навигационной аппаратуры
потребителей для приема навигационных сигналов ГНСС, работающих в близких
частотных диапазонах, без значительного усложнения ее аппаратного
построения и повышения затрат на производство;
повысить надежность и качество предоставления навигационных услуг
потребителям.
В настоящее время складываются благоприятные условия для вхождения
российской ГНС ГЛОНАСС в мировой рынок спутниковых навигационных
технологий, которые обусловлены:
осознанием мировым сообществом потребителей преимуществ
совместного использования ГНС;
повышенным интересом потребителей и производителей навигационной
аппаратуры к системе ГЛОНАСС, связанным с развитием орбитальной
группировки системы и повышением точностных характеристик ГНС ГЛОНАСС;
гарантиями Российской Федерации и многолетней практикой
предоставления потребителям на безвозмездной основе навигационных сигналов с
открытым доступом ГНС ГЛОНАСС.
Анализ тенденций международной интеграции ГНС определяет
целесообразность введения в системе ГЛОНАСС новых навигационных сигналов с
открытым доступом и кодовым разделением, близким по параметрам к
навигационным сигналам систем GPS и GALILEO.
Введение этих сигналов в дополнение к уже существующим
навигационным сигналам ГНС ГЛОНАСС позволит дополнительно привлечь широкий
круг потребителей к эффективному использованию системы ГЛОНАСС не
только в Российской Федерации, но и за рубежом.
Состав навигационных сигналов системы ГЛОНАСС
Существующие навигационные сигналы
Существующая орбитальная группировка системы ГЛОНАСС состоит из
космических аппаратов «ГЛОНАСС-М», которые излучают четыре
навигационных сигнала:
535
Глава 14
сигнал LIOF с открытым доступом и частотным разделением в диапазоне /Л;
сигнал L20F с открытым доступом и частотным разделением в диапазоне 12;
сигнал L1SF с санкционированным доступом и частотным разделением в
диапазоне L1;
сигнал L2SF с санкционированным доступом и частотным разделением в
диапазоне L2.
Новые навигационные сигналы
Современные и прогнозируемые требования к навигационным услугам для
специальных и гражданских потребителей, тенденции развития ГНС и
направления их интеграции, состав излучаемых сигналов КА системы ГЛОНАСС в
настоящее время, существующее закрепление частотных диапазонов за
спутниковыми навигационными системами позволяют рассматривать
целесообразность реализации в ГНС ГЛОНАСС следующих новых навигационных
сигналов:
сигнал L1SC с санкционированным доступом и кодовым разделением в
диапазоне L1;
сигнал ЫОС с открытым доступом и кодовым разделением в диапазоне II;
сигнал L2SC с санкционированным доступом и кодовым разделением в
диапазоне L2;
сигнал L20C с открытым доступом и кодовым разделением в диапазоне L2;
сигнал L3SC с санкционированным доступом и кодовым разделением в
диапазоне 13;
сигнал ЬЗОС с открытым доступом и кодовым разделением в диапазоне L3;
сигнал LSOC с открытым доступом и кодовым разделением в диапазоне 15.
Основные параметры новых навигационных сигналов с кодовым
разделением
Все навигационные радиосигналы с кодовым разделением сигналов НКА
системы ГЛОНАСС представляют собой сложный шумоподобный сигнал.
Навигационный сигнал ЫОС с открытым доступом и кодовым
разделением в диапазонеЫ
Гарантированный уровень мощности сигнала у поверхности Земли не
менее минус 158 дБВт.
Несущая частота сигнала 1599,972 МГц.
Ширина спектра -20 МГц.
Навигационный сигнал ЫОСМ с открытым доступом и кодовым
разделением в диапазоне Ы GPS
Гарантированный уровень мощности сигнала у поверхности Земли не
менее минус 158 дБВт.
Несущая частота сигнала 1575,42 МГц.
Ширина спектра -16 МГц.
536
Направления совершенствования СРНСГЛОНАСС
Навигационный сигнал L20C с открытым доступом и кодовым
разделением в диапазоне L2
Гарантированный уровень мощности сигнала у поверхности Земли не
менее минус 158 дБВт.
Несущая частота сигнала 1248,06 МГц.
Ширина спектра -20 МГц.
Навигационный сигнал L30C с открытым доступом и кодовым разделе-
нием в диапазоне L3
Гарантированный уровень мощности сигнала у поверхности Земли не
менее минус 158 дБВт.
Несущая частота сигнала 1202,25 МГц.
Ширина спектра -20 МГц.
Навигационный сигнал L50C с открытым доступом и кодовым
разделением в диапазоне L5
Гарантированный уровень мощности сигнала у поверхности Земли не
менее минус 158 дБВт.
Несущая частота сигнала 1176,45 МГц.
Ширина спектра -20 МГц.
Навигационный сигнал L1SC с санкционированным доступом и кодовым
разделением в диапазоне Ы
Гарантированный уровень мощности сигнала у поверхности Земли не
менее минус 158 дБВт.
Несущая частота сигнала 1599,972 МГц.
Ширина спектра -20 МГц.
Навигационный сигнал L2SC с санкционированным доступом и кодовым
разделением в диапазоне L2
Гарантированный уровень мощности сигнала у поверхности Земли не
менее минус 158 дБВт.
Несущая частота сигнала 1248,06 МГц.
Ширина спектра -20 МГц.
Навигационный сигнал L3SC с санкционированным доступом и кодовым
разделением в диапазоне L3
Гарантированный уровень мощности сигнала у поверхности Земли не
менее минус 158 дБВт.
Несущая частота сигнала 1202,025 МГц.
Ширина спектра -20 МГц.
Для новых сигналов с кодовым разделением значения несущей частоты,
ширины спектра и гарантированного уровня мощности у поверхности Земли
могут уточняться при:
изменении (уточнении) тактико-технических требований к системе
ГЛОНАСС;
537
Глава 14
двухсторонних международных частотных согласованиях (в случае
необходимости);
проведении международной частотной координации в Международном
союзе электросвязи.
Подробно параметры новых навигационных сигналов системы ГЛОНАСС
с кодовым разделением (структура сигналов, состав передаваемой в них
цифровой информации) будут определяться в процессе их проектирования.
Планируемый эффект от реализации новых навигационных сигналов
системы ГЛОНАСС
Реализация новых навигационных сигналов на КА системы ГЛОНАСС
обеспечит ее конкурентоспособность с действующими и перспективными
навигационными спутниковыми системами, а также повысит надежность и
качество предоставления навигационных услуг.
Система ГЛОНАСС приобретет новые возможности, имея в своем
арсенале навигационные сигналы, как с частотным, так и с кодовым разделением. Это
позволит любым группам потребителей использовать для решения своих
специфических задач необходимую комбинацию сигналов. Необходимо отметить,
что таких возможностей не предоставляет ни система GPS, ни одна из
создаваемых систем, в том числе GALILEO.
Введение новых навигационных сигналов в диапазонах /Л, L2, L3 и L5 с
кодовым разделением позволит расширить частотный диапазон для работы
ГНС ГЛОНАСС за счет использования части частотного диапазона ГНС GPS и
GALILEO, а также обеспечить высокоточные навигационные определения в
режиме реального времени.
Использование навигационных сигналов с частотным и кодовым
разделением в диапазонах ранее выделенных Международным союзом электросвязи
для работы ГНС ГЛОНАСС (XI, L2, L3) позволит сохранить независимость
системы ГЛОНАСС от ГНС GPS и GALILEO и гарантировать потребителям
качественное навигационное обслуживание.
Этапность реализации новых сигналов системы ГЛОНАСС
Модернизация навигационных сигналов должна проводиться
сбалансировано с модернизацией парка АСН.
Этапы разработки и реализации новых навигационных сигналов в системе
ГЛОНАСС следующие.
Этап 1. (2009 - 2010 годы). КА «Глонасс-М» излучают навигационные
сигналы LIOF, L20F, L1SF, L2SF с открытым и санкционированным доступом
в частотных диапазонах Ы (-1.6 ГГц) и L2 (-1.24 ГГц) . Осуществляется
разработка перспективных навигационных сигналов, состава передаваемой в них
цифровой информации, в том числе методов управления доступом к
навигационным сигналам с учетом всех требований Минобороны России.
538
Направления совершенствования СРНСГЛОНАСС
На основании тактико-технических требований к глобальной
навигационной системе ГЛОНАСС, настоящей Концепции, а также документов по
структуре сигналов и составу передаваемой цифровой информации, выпускаются
Интерфейсные контрольные документы.
Этап 2. (2010 - 2020 годы). На КА серии «Глонасс-К» дополнительно
вводятся новые навигационные сигналы L1SC, ЫОС, L2SC, L30C с кодовым
разделением каналов.
Этап 3. (после 2020 г.) На КА серии «Глонасс-КМ» дополнительно
вводятся новые навигационные сигналы L3SC, ЫОСМ, L20C, L50C. При этом
состав вводимых на данном этапе сигналов, их основные параметры будут
уточняться по результатам использования системы ГЛОНАСС на первых двух
этапах, а также с учетом достигнутого к 2020 году уровня теоретических,
технических и технологических вопросов дальнейшего развития ГНС.
14.2.2. Частотный план для сигналов с кодовым разделением
В целях международной интеграции и унификации спутниковых
навигационных систем целесообразно сигналы с кодовым разделением формировать
аналогично тому, как это делается в ГНС GPS и Galileo. В этих системах
навигационные сигналы формируются от опорного генератора с номинальной
частотой 10,23 МГц. На борту спутников ГЛОНАСС используется опорный
генератор с номинальной частотой /оп = 5 МГц. Один из вариантов формирования
необходимых частот для сигналов с кодовым разделением приведен на
рис. 14.1.
/оп = 5МГц /опк =10,23 МГц /о =1,023 МГц
ОГ 5 МГц
Синтезатор
10,23 МГц
:10
Синтезатор
несущей Ы
/h,L1
►
Синтезатор
несущей 12
/н,.
12
Синтезатор
несущей 13
/н,
13
Формирователь
дальномерных
кодов
Рис. 14.1. Схема синтеза частот
В данной схеме используется синтезатор частот преобразующий частоту
/0П = 5 МГц в частоту /опк = 10,23 МГц, из которой далее формируются все
необходимые частоты для сигналов с кодовым разделением.
539
Глава 14
14.2.3. Навигационный сигнал ЬЗОС
В диапазоне 13 для ГНС ГЛОНАСС отведен диапазон частот
1190.35... 1212.23 МГц (полоса частот 21,88 МГц). Один из вариантов
навигационного сигнала ЬЗОС, обсуждаемый в рамках указанной выше рабочей
группы, может иметь следующие характеристики:
несущая частота f 1Ъ = 1174/0= 1201,002 МГц;
способ модуляции — фазовая манипуляция на 180°;
модулирующий сигнал: сумма по модулю 2 ПСП с частотой следования
символов /дк= \0/0 = 10,23 МГц (/0= 1.023 МГц) и цифровых данных со
скоростью передачи 50 Бод, синхронизированных с ПСП;
ширина спектра ~ 20,46 МГц.
14.2.4. Навигационный сигнал ЫОС с модуляцией ВОС(6,4)
Один из рассматриваемых вариантов сигналов в частотном диапазоне Ы
ГЛОНАСС является сигнал с модуляцией ВОС(6,4). Напомним (см. п. 5.4), что
под модуляцией BOC(fsub9fchip) понимается бинарная модуляция на поднесу-
щих частотах, при которой fsub — частота отстройки поднесущих, fchi —
частота следования символов (чипов) кода. Обычно, частоты fsub, fchi
выбираются кратными некоторой «базовой» частоте /0 (в нашем случае
/0 =1,023 МГц), т.е. fsub = mf0 , fchip = nf0 . Тогда для обозначения модуляции на
поднесущих частотах используется сокращенная запись ВОС(т,п).
При разработке сигналов с кодовым разделением в частотном диапазоне
Ы ГЛОНАСС необходимо учитывать ограничения, обусловленные близостью
частотного диапазона, отведенного для радиоастрономии: 1610,6... 1613,8 МГц,
и необходимостью обеспечения определенных требований по внеполосным
излучениям в данном диапазоне. Сигналы с модуляцией ВОС{т,п) имеют
характерные «провалы» мощности спектральных составляющих, находящихся после
лепестков спектра с максимальной мощностью, что позволяет выбором несущей
частоты сигнала обеспечить такую ситуацию, когда указанные «провалы»
мощности спектральных составляющих будут приходиться на частотный диапазон
радиоастрономии. При этом надо дополнительно обеспечить ширину «провала»
мощности спектральных составляющих, не менее ширины частотного диапазона,
отведенного для радиоастрономии, равного A/PA =3,2 МГц. Данному условию
удовлетворяют сигналы с модуляцией Я0С(7,3.5), Z?0C(5,2.5), Z?0C(6,4)
ширина частотных «провалов» которых приведена в табл. 14.1.
540
Направления совершенствования СРНС ГЛОНАСС
Таблица 14.1. Ширина частотных «провалов»
Модуляция сигнала
ВОС(7,3.5)
\ВОС(5,25)
ВОС(б,4)
Ширина частотного
«провала», МГц
7,16
5,15
4,09
Рассмотрим сигнал с модуляцией ВОС(6,4) и рассчитаем несущую
частоту сигнала так, чтобы, с одной стороны, «провалы» мощности спектральных
составляющих попадали на диапазон радиоастрономии, а, с другой стороны,
чтобы несущие частоты были кратны опорной частоте /0. В результате расчета
получаем /н11 = 1564 /0 = 1599,972 МГц.
На рис. 14.2 приведена спектральная плотность мощности
рассматриваемого сигнала с единичной мощностью.
1.57
1.58
1.59 1.6 1.61
Частота, Гц
1.62
х 10
1.63
9
Рис. 14.2. Спектральная плотность мощности сигнала L10C
Из рис. 14.2 видно, что в частотном диапазоне радиоастрономии имеет
место существенное снижение мощности спектральных компонент
навигационного сигнала. На рис. 14.3 зависимость спектральной плотности мощности
сигнала ЫОС в частотном диапазоне радиоастрономии приведена в увеличенном
масштабе.
541
Глава 14
х 10'
10
1.6105 1.611 1.6115 1.612 1.6125 1.613 1.6135 1.614
Частота, Гц х 109
Рис. 14.3. Спектральная плотность мощности сигнала L10C
в частотном диапазоне радиоастрономии
14.3. Система глобального мониторинга СРНС
14.3.1. Необходимость создания расширенной системы мониторинга
систем ГЛОНАСС/GPS
Широкое использование спутниковых радионавигационных систем и
существенное расширение круга их пользователей обусловливает повышенные
требования не только к параметрам точности системы, но и к целостности
самой системы и достоверности получаемой от нее навигационной информации.
Между тем разработанная еще в 70—80-х годах идеология построения средне-
орбитальных навигационных систем не позволяет кардинально повысить
целостность системы и поднять достоверность навигационных определений.
Внутрисистемный мониторинг целостности не отвечает требованиям
оперативности, поскольку между моментом возникновения неисправности НС и
моментом установки признака «не здоров» в навигационном сообщении может
пройти несколько часов. Поэтому для любой навигационной системы проблема
точного и оперативного мониторинга навигационных параметров останется
актуальной.
Полученные результаты последних исследований показали, что наиболее
точное определение параметров эфемеридно-временного обеспечения
навигационных систем и точная реконструкция текущего состояния среды
распространения радиосигналов в виде многомерной пространственно-временной
модели с высокой разрешающей способностью возможны только при организа-
542
Направления совершенствования СРНСГЛОНАСС
ции измерений на пространственно разнесенных пунктах. При этом
оптимальные характеристики достигаются при организации глобальной системы
мониторинга. По предварительным расчетам, размещение станций первичных
измерений только на территории РФ приведет к снижению потенциально
достижимых характеристик, а именно:
оперативность оповещения потребителя снизится примерно на 10... 15 %
(за счет предварительного накопления выборки измерений при восходе
спутника);
точность определения погрешностей распространения сигнала над
приграничными областями РФ уменьшится на 20...25 % (из-за потери почти 50 %
томографических срезов ионизированных областей Земли и пропуска из-за этого
локальных неоднородностей среды распространения навигационных сигналов).
Однако перечисленные недостатки проявляются в относительно узких
приграничных областях РФ и не являются катастрофическими. Поэтому вполне
допустимо развертывать систему мониторинга ГЛОНАСС/GPS только на
территории РФ. В дальнейшем возможно наращивание уже развернутой системы
путем дополнительного глобального размещения станций первичных
измерений или использования в действующей системе информации от доступных
источников «сырых» измерений, расположенных вне территории РФ.
Таким образом, главная цель служб мониторинга — выявление ситуаций
нештатного функционирования СРНС и своевременное информирование о них
пользователей.
Настоятельная необходимость создания Российской системы мониторинга
навигационных полей ГЛОНАСС/GPS определяется ужесточением требований
к достоверности получаемых потребителем навигационных определений, а
также резким сокращением допустимого времени реакции на возможные
неисправности в СРНС. Кроме того, развертывание подсистем ионосферного и
тропосферного мониторинга позволяет совместить решение проблемы
мониторинга трасс распространения навигационных сигналов и выявления их аномальных
зон с решением проблемы точной компенсации погрешностей распространения
навигационных сигналов, что в конечном счете повышает точность
определения местоположения потребителя.
14.3.2. Основные задачи системы мониторинга СРНС
Главной задачей системы мониторинга является оценивание (мониторинг)
качества функционирования СРНС ГЛОНАСС и GPS.
Система должна осуществлять два типа мониторинга: оперативный и
апостериорный.
Основным назначением оперативного мониторинга является скорейшее
предупреждение потребителя о возникновении нарушений в
функционировании СРНС.
543
Глава 14
Таким образом, задачами «оперативного мониторинга» является:
оценивание в реальном времени ошибок измерения псевдо дальностей по
сигналам НС ГЛОНАСС и GPS;
информирование потребителей о величинах этих ошибок.
Мониторингу подвергаются только гражданские сигналы СРНС
ГЛОНАСС и GPS.
Погрешности измерений по сигналам СРНС содержат следующие
составляющие:
погрешности вследствие влияния ионосферы;
погрешности вследствие влияния тропосферы;
погрешности эфемерид НС;
погрешности частотно-временных параметров НС.
Задачей оперативного мониторинга (ОМ) является оценка совокупного
влияния погрешностей, вносимых наземным и космическим сегментами систем
ГЛОНАСС и GPS, т.е. его функция — учет влияния лишь погрешностей
эфемерид и ЧВП, поскольку они влияют на точность навигации всех потребителей,
принимающих сигналы данного НС, в то время как погрешности вследствие
влияния тропосферы и ионосферы имеют локальный характер.
Потребителю должны передаваться оценки суммарного влияния
погрешностей эфемерид и ЧВП на измерения псевдо дальности для конкретного НС.
Целесообразно передавать оценки в дискретном виде, для чего можно
использовать слово длиной 4 бита (16 градаций).
Информация оперативного мониторинга должна доставляться
потребителю по имеющимся каналам связи, однако необходимо стремиться к
обеспечению универсальности аппаратуры всех групп потребителей, находящихся в
различных частях земного шара. Для этих целей наиболее подходит передача
данных через спутник.
Задачей потребителя после получения результатов оперативного
мониторинга (оценок ошибок измерения псевдо дальностей) является принятие
решения о том, вводить или нет измерение по данному НС в обработку, и если
вводить, то с каким весом.
Задачи «апостериорного мониторинга» (AM)):
получение через заданный интервал времени апостериорных оценок
следующих параметров:
вертикальной задержки навигационных сигналов вследствие влияния
ионосферы в диапазоне Ы,
вертикальной задержки навигационных сигналов вследствие влияния
тропосферы,
погрешностей бортовых эфемерид НС ГЛОНАСС и GPS,
погрешностей бортовых ЧВП НС ГЛОНАСС и GPS,
различия шкал системного времени ГЛОНАСС и GPS;
544
Направления совершенствования СРНСГЛОНАСС
оценка статистических характеристик (математического ожидания и СКО)
следующих параметров по результатам наблюдения на суточном интервале:
отношения сигнал/шум по НС ГЛОНАСС и GPS,
различия шкал системного времени ГЛОНАСС и GPS,
количества наблюдаемых НС ГЛОНАСС и GPS,
точности определения горизонтальных и вертикальных составляющих
координат с учетом лишь погрешностей эфемерид, ЧВП и текущей
геометрии НС,
точности определения горизонтальных и вертикальных составляющих
скорости с учетом лишь погрешностей эфемерид, ЧВП и текущей
геометрии НС,
поддержка баз данных, содержащих вышеперечисленные параметры;
фиксирование ситуаций, когда НС функционирует аномально.
Оценки погрешностей бортовых эфемерид и ЧВП для каждого НС
ГЛОНАСС и GPS могут представляться в виде графиков, имеющих
определенный интервал.
По истечении суток должны строиться графики погрешностей бортовых
эфемерид и ЧВП, полученные по более точным эфемеридным данным,
являющимся результатом обработки большего количества информации.
Оценка различия шкал системного времени ГЛОНАСС и GPS может быть
представлена в виде графика, имеющего определенный интервал.
Статистические характеристики (математическое ожидание и СКО) могут
представляться в виде таблиц, полученных по результатам обработки данных,
собранных в течение суток.
Для каждого параметра, обработанного на суточном интервале, должна
строиться гистограмма распределения.
Аномальным считается такое функционирование НС, когда суммарное
влияние погрешностей эфемерид и ЧВП превышает некоторый предел. При
обнаружении факта аномального функционирования НС необходимо
фиксировать значения оценок суммарного влияния погрешностей эфемерид и ЧВП с
интервалом 1 с.
Результаты апостериорного мониторинга должны храниться в базах
данных, доступ к которым со стороны потребителя может быть осуществлен через
Internet.
В целях обеспечения избирательного доступа к базам данных должен быть
реализован механизм авторизации потребителей.
14.3.3. Структура системы мониторинга целостности СРНС
Система мониторинга целостности может состоять из следующих
компонентов:
пунктов мониторинга (ПМ);
18-1026
545
Глава 14
центра глобального мониторинга (ЦГМ);
линий связи между ПМ и ЦГМ;
подсистемы информационного обмена;
станции закладки (СЗ) информации на борт НС.
Задачей ПМ является сбор измерений, позволяющих производить оценку
качества функционирования систем ГЛОНАСС и GPS. Основным компонентом
ПМ является станция мониторинга, в состав которой входит навигационный
приемник ГЛОНАСС/GPS, обладающий способностью производить измерения
по НС ГЛОНАСС и GPS в диапазонах LI/L2 по фазе кода и несущей.
Задачами ПМ являются:
формирование и передача в ЦГМ массивов сырых измерений по фазе кода
и несущей в диапазонах LX/L2, а также эфемеридно-времен-ной информации,
передаваемой в навигационных сообщениях;
формирование и передача в ЦГМ результатов измерения
метеорологических параметров, служащих для оценки вертикальной тропосферной задержки.
Измерения по фазе кода и несущей в диапазонах LX/L2 должны
производиться с частотой 1 Гц и каждую секунду передаваться в ЦГМ. Эфемеридно-
временная информация должна передаваться в ЦГМ по мере ее обновления.
Оценки значений метеорологических параметров должны формироваться
по результатам измерения и передаваться в ЦГМ с интервалом 15 мин.
Аппаратные средства ПМ должны обеспечивать надежное и
бесперебойное функционирование.
Центр глобального мониторинга предназначен для выполнения
следующих задач:
сбора измерительных данных с пунктов мониторинга соответствующего
региона;
выполнения функций оперативного мониторинга по формированию
индекса целостности «In»;
передачи с помощью станции закладки значения индекса целостности «In»
на борт НС «Глонасс-К»;
контроля содержания сообщения целостности, передаваемого с борта НС
индекса целостности «In» в диапазоне 1200 МГц;
ведения баз данных измерений, поступивших в ЦГМ, и результатов ОМ;
приема команд по управлению и иной информации.
Задача оперативного мониторинга решается в ЦГМ на основании оценок
совокупного влияния ошибок эфемерид и ЧВП, получаемых по данным,
поступающим от сети ПМ. Результатом оперативного мониторинга является
формирование индекса «In» для каждого НС ГЛОНАСС и GPS. Значения индекса «In»
должны передаваться на станции закладки, откуда они могут закладываться на
борт НС «Глонасс-К» или на борт других спутников, предназначенных для пере-
546
Направления совершенствования СРНСГЛОНАСС
дачи информации целостности потребителям. Кроме того, передача индекса
«In» должна производиться по выделенной линии в ЦУС ГЛОНАСС.
Центр глобального мониторинга несет на себе основную нагрузку по
управлению работой системы мониторинга и обработке данных. В ЦГМ
стекаются все потоки информации от различных частей системы мониторинга.
В общей формулировке задачами ЦГМ являются:
проведение апостериорного мониторинга;
проведение контроля результатов оперативного мониторинга, полученных
наПМ;
хранение и предоставление потребителям результатов оперативного и
апостериорного мониторинга;
обеспечение связи со всеми ПМ в составе системы;
обеспечение связи с ЦУС ГЛОНАСС.
Задача контроля результатов оперативного мониторинга решается в ЦГМ
на основании оценок совокупного влияния ошибок эфемерид и ЧВП,
получаемых по данным, поступающим от ПМ.
Задача апостериорного мониторинга решается в ЦГМ на основании
«сырых» измерительных данных, эфемеридно-временной информации, значений
вертикальной тропосферной задержки, поступающих от сети пунктов
мониторинга.
По результатам обработки данных сети ПМ в ЦГМ рассчитываются
уточненные значения эфемерид и ЧВП и оцениваются их погрешности. «Возраст»
таких оценок не должен превышать 15 мин.
Кроме того, для решения задач апостериорного мониторинга в ЦГМ
следует использовать данные об уточненных эфемеридах и ЧВП НКА,
полученные в результате обработки измерений в течение более длительного интервала
времени (по истечении суток).
В целях обеспечения глобальности мониторинга в ЦГМ должны
использоваться результаты измерений, полученных международной сетью станций IGS
и IGLOS, публикуемые в Internet.
Результаты оперативного и апостериорного мониторинга, полученные в
ЦГМ, должны заноситься в базы данных и храниться в течение срока
существования системы мониторинга.
Часть результатов апостериорного и оперативного мониторинга ЦГМ
должен предоставлять потребителям посредством доступа в Internet.
Как отмечалось в п. 14.4.1, наилучшие характеристики системы
мониторинга могут быть получены при размещении ПМ по поверхности Земли таким
образом, чтобы в любой момент времени каждый спутник ГЛОНАСС или GPS
находился в зоне видимости одного из них. Однако на первой стадии вполне
допустимо развертывать систему мониторинга ГЛОНАСС/GPS только на
территории РФ. При этом на размещение ПМ накладывается ряд дополнительных
ограничений.
547
Глава 14
Пункты мониторинга целесообразно размещать в крупных населенных
пунктах (в этом случае имеется возможность использовать инфраструктуру
этих населенных пунктов для организации работы ПМ); среди крупных
населенных пунктов целесообразно выбрать те, в которых имеются открытые
пункты РАН или Госстандарта (на базе этих пунктов могут быть организованы ПМ с
гораздо меньшими затратами); ПМ должны быть разнесены по территории
России максимально широко.
Для примера на рис. 14.4 приведена схема возможной структуры системы
мониторинга, а также показано предполагаемое расположение ПМ, ЦГМ на
территории РФ. На рис. 14.4 номерами обозначены пункты, относительно
которых в настоящее время достигнута договоренность о размещении
аппаратуры ПМ.
Рис* 14.4. Схематическая структура системы мониторинга:
1 — Москва; 2 — Ловозеро; 3 — Минск; 4 — Кисловодск;
5 — Новосибирск; 6 — Тикси; 7 — Билибино;
8 — Хабаровск; 9 — Бидары (Забайкалье)
Расчеты показывают, что при размещении ПМ только на территории РФ
каждый из НС будет находиться под наблюдением около 50% времени, т. е.
примерно каждые 6 ч НС будет выпадать из наблюдения.
Если вести речь об обеспечении глобального мониторинга, то необходимо
размещать пункты мониторинга за рубежом. В настоящее время наиболее
перспективным видится размещение пунктов в Республике Беларусь и Индии.
Если планы по размещению ПМ в этих государствах будут реализованы, то
вероятность наблюдения НС хотя бы с одного из ПМ возрастет примерно до 65%,#а
вероятность наблюдения НС хотя бы с двух ПМ возрастет примерно до 55%.
548
Направления совершенствования СРНСГЛОНАСС
14.3.4. Предоставление потребителям доступа к результатам
работы системы мониторинга
Результатом оперативного мониторинга являются значения индекса «In».
Доступ к этой информации должен обеспечиваться в режиме, максимально
приближенном к режиму реального времени. Для этих целей можно
использовать сигнал НС «Глонасс-К», излучаемый в диапазоне 1Ъ (см. п. 14.2).
Для получения доступа к этой информации потребитель должен быть
оснащен навигационным приемником, обладающим способностью принимать
соответствующий сигнал. Такой подход целесообразен, поскольку не требует
использования специальных телекоммуникационных ИСЗ, позволяя реализовать
в рамках одной системы функции нескольких.
Информация, содержащая результаты оперативного мониторинга, должна
закладываться на борт НС «Глонасс-К» средствами, входящими в систему
мониторинга.
Кроме того, доступ к результатам оперативного мониторинга должен
предоставляться посредством Internet с помощью специализированного сайта.
Доступ к результатам апостериорного мониторинга должен
предоставляться посредством Internet. На специализированном сайте потребителям
должен быть обеспечен доступ к результатам мониторинга, полученным за весь
период работы системы, а также к результатам, получаемым в течение текущих
суток.
В настоящее время представляется целесообразным размещение на сайте
следующей информации:
значений индекса «In» для каждого НС;
значений индекса «Q1» для каждого НС;
оценок погрешностей эфемерид и ЧВП для каждого НС;
значений ионосферной задержки для диапазона Ы ;
значений тропосферной задержки;
о наличии и характере аномальных ситуаций, возникших за период
функционирования системы мониторинга.
В дальнейшем возможна корректировка состава предоставляемой
информации.
Отдельные потребители могут быть подписаны на рассылку с желаемой
периодичностью в электронном виде или на бумажных носителях бюллетеней,
содержащих сводку необходимых параметров. Состав параметров должен
оговариваться отдельно.
При необходимости, в ЦУС ГЛОНАСС должны поставляться результаты
мониторинга, оговариваемые отдельным протоколом.
549
Глава 14
14.3.5. Характеристики канала, передающего информацию о
целостности с борта НС «Глонасс-К»
Для передачи данных о целостности предполагается использовать
аппаратуру спутника «Глонасс-К» в режиме ретрансляции данных, т.е. в режиме
реального времени. Это означает, что оперативность доставки информации через
линию «ПМ—ЦГМ—СЗ—борт «Глонасс-К»— потребитель» зависит в
основном от различных временных задержек в каналах передач данных. Основная
задержка будет иметь место при сборе данных от ПМ в ЦГМ, поскольку для
этих целей предполагается использовать специализированные Internet-каналы.
Задержки передачи информации в этом канале не превышают 1...1,5 с, так что
суммарная задержка по доставке информации потребителю не превысит 5...6 с.
В СТ-сигнале диапазона L3 навигационное сообщение будет передаваться
125 бит/с при использовании дополнительного кода со скоростью 250 бит/с. С
учетом этого можно предложить:
в нечетных строках передавать навигационную информацию, аналогичную
той, которая содержится в СТ-сигнале диапазона L\ (эфемериды по данному
НС и часть альманаха системы);
в четных строках передавать информацию мониторинга и информацию
для потребителей расширенной (глобальной) дифференциальной подсистемы.
Длительность каждой строки составляет 1 с.
Передаваемая информация целостности «стареет» во времени, при этом
скорость старения зависит, в первую очередь, от характера самой информации.
В задаче мониторинга наиболее важными являются случаи, когда в реальности
происходит ухудшение целостности навигационной системы.
При передаче данных о целостности можно выделить два типа информации:
медленно меняющаяся информация о целостности;
быстро меняющаяся информация о целостности.
Под медленно меняющейся информацией понимают изменение оценок
ошибок измерения псевдо дальностей вследствие естественных причин,
связанных:
с ухудшением эфемеридного обеспечения НС (увеличение времени после
закладки опорных эфемерид);
с ухудшением условий навигационных измерений (НС находится вблизи
местного горизонта).
Под быстро меняющейся информацией понимают изменение оценок
ошибок измерения псевдо дальностей вследствие возникновения какой-либо
неисправности на борту НС:
сбой в работе бортового цифрового вычислительного комплекса НС;
сбой в работе бортового стандарта частоты НС.
Изменение медленно меняющейся информации происходит за десятки
минут и это не создает особых проблем при доставке данных о целостности по-
550
Направления совершенствования СРНС ГЛОНАСС
требителю. Причем сами изменения имеют небольшую величину. В этом
случае достаточно обеспечить обновление информации о целостности с темпом
один раз в несколько минут.
Совершенно другая картина обстоит с быстро меняющейся информацией.
Во-первых, само изменение, т.е. неисправность, происходит практически
мгновенно или всего за одну или несколько секунд. Во-вторых, величина
скачкообразного изменения может иметь огромное значение. Здесь уже может идти речь
о необходимости как можно быстрее информировать потребителя о
неисправности спутника. И в этом случае информация о целостности может устареть
всего за секунду.
14.3.6. Оценка надежности системы мониторинга
Для оценки надежности системы примем следующие исходные данные. В
состав системы входят девять пунктов мониторинга и центр глобального
мониторинга.
Связь между центром глобального мониторинга и пунктами мониторинга
осуществляется по специализированным каналам Internet.
Оборудование ПМ включает в себя: станцию мониторинга (состоящую из
двух комплектов), метеостанцию, высокостабильный стандарт частоты (по
одному на каждый полукомплект станции мониторинга).
Высокостабильный стандарт частоты может входить в состав не всех
пунктов мониторинга. Кроме того, его наличие не влияет существенно на
характеристики всей системы. При этом наличие и исправность метеостанции
также не влияет существенно на характеристики всей системы.
Станция мониторинга в составе ПМ имеет дублированную структуру.
В табл. 14.2 приведен перечень устройств станции мониторинга в составе
ПМ и интенсивности отказов отдельных устройств, полученные на основании
данных о надежности приборов-аналогов.
Таблица 14.2. Интенсивность отказов компонентов станции мониторинга
1 Наименование составной части
1 Антенно-фидерное устройство
I Малошумящий усилитель
Приемник ГЛОНАСС/GPS:
радиочастотное устройство
устройство цифровой обработки
навигационный процессор
1 вторичный источник питания
Интенсивность отказов X106 1/ч ||
0,01
0,48
8,5
13,0
10,0
5Л 1
551
Глава 14
Некоторые ПМ могут быть совмещены со станциями закладки
информации на борт НС.
Расчет интенсивности отказов антенного модуля, представляющего собой
последовательное соединение узлов, выполнен по структурной схеме
надежности на основании данных о результатах эксплуатации приборов-аналогов,
разработанных или использовавшихся ранее.
В состав антенного модуля входят: опорно-поворотное устройство с
зеркальной системой (ОПУ ЗС); облучатель; ИД A3 и ИД УМ, ДУ A3 и ДУ УМ;
аналого-цифровые преобразователи волноводных трактов A3 и УМ; частотный
преобразователь A3 и частотный преобразователь УМ; блок усиления.
Так как ОПУ ЗС и облучатель с волноводным трактом представляют собой
пассивное механическое устройство, интенсивность отказов ОПУ ЗС
принимается равной нулю.
В табл. 14.3 приведен перечень устройств из состава антенного модуля и
интенсивности отказов отдельных устройств.
Таблица 14.3. Интенсивность отказов компонентов станции закладки
| Наименование составной части
ИД A3
ИД УМ
ДУ A3
1 ДУУМ
АЦП ВТ A3
АЦП ВТ УМ
Част, преобразователь A3
Част, преобразователь УМ
1 Блок управления
Интенсивность отказов X1061 /ч |
43,4783
43,4783
0,143
0,143
22,4392
22,4392
112,67
112,67
2,643 |
Наработка на отказ системных блоков компьютеров и мониторов,
используемых в составе ПМ и ЦГМ, в соответствии с ТУ составляет 46000 и 12000 ч
соответственно.
Оборудование ЦГМ включает: сервер сбора информации с ПМ, сервер
выделенной линии с ЦУС ГЛОНАСС, аппаратные средства базы данных,
аппаратные средства AM, аппаратные средства ОМ, аппаратные средства
визуализации результатов, Internet-сервер обслуживания потребителей, аппаратные
средства подготовки данных для Internet.
Оборудование в составе ЦГМ и ПМ должно обеспечивать непрерывную
автоматическую круглосуточную работу с обслуживанием по
предусмотренному в его эксплуатационной документации регламенту и возможность
«горячей» замены при проведении профилактических и ремонтных работ.
552
Направления совершенствования СРНСГЛОНАСС
Исходя из задач, решаемых системой мониторинга целостности СРНС
ГЛОНАСС/GPS, целесообразно отдельно рассматривать нарушение функций
оперативного и апостериорного мониторинга.
Критерием отказа, заключающегося в нарушении функций ОМ, является
совокупность событий, приводящая к любому из шести нижеприведенных
состояний:
выход из строя четырех и более дублированных станций мониторинга из
девяти;
выход из строя СЗ на двух и более ПМ;
выход из строя станции закладки (отказ четырех и более антенных
модулей) на одном ПМ;
выход из строя станции закладки (отказ четырех и более антенных
модулей) на одном ПМ и более двух дублированных станций мониторинга;
выход из строя аппаратных средств ОМ в ЦГМ и более двух
дублированных станций мониторинга.
Критерием отказа, заключающегося в нарушении функций AM, является
совокупность событий, приводящая к любому из четырех приведенных ниже
состояний:
выход из строя четырех и более дублированных станций мониторинга из
девяти;
отказ аппаратных средств базы данных на любом из ПМ;
отказ сервера выделенной линии ЦУС, длящийся более одного часа;
отказ сервера системы сбора измерений в ЦГМ, длящийся более одного
часа.
В качестве показателей надежности, характеризующих способность
системы выполнять функции ОМ и AM, выбраны вероятность безотказной работы и
коэффициент готовности в соответствующих режимах.
Расчет показателей надежности выполнен в РНИИ Космического
приборостроения с использованием разработанного для этих целей программного
обеспечения. Результаты расчета вероятности безотказной работы (Р) и
коэффициента готовности (Кг) системы в режиме ОМ на срок активного существования
10 лет для различных времен восстановления приведены в табл. 14.4.
Таблица 14.4. Характеристики надежности выполнения функции ОМ
* воет ? Ч
\р
[Кг
24
0,8557
0,99998
i " =
12
0,9316
0,999995
6
0,9661
0,999999
2
0,9887
1 0,9(9) 1
Т~ 1
0,9956 1
1 0,9(9) 1
Результаты расчета вероятности безотказной работы (Р) и коэффициента
готовности (Кг) системы в режиме AM на срок активного существования 10 лет
для различных времен восстановления и времени восстановления серверов вы-
553
Глава 14
деленной линии в ЦГМ равном одному часу и тридцати минутам приведены в
табл. 14.5 и 14.6 соответственно.
Таблица 14.5. Характеристики надежности выполнения функции AM
V 1 восст~~ 1 Ч)
\ 1 воет ? Ч
\р
\Кг
24
0,8637
0,9995
5
12
0,9228
0,99956
6
0,9562
0,99957
2
0,9782
0,9995
8
1 1
0,9830
0,9995
_9
Таблица 14.6. Характеристики надежности выполнения функции AM
(Твосст=30 МИН)
1 -* воет ? Ч
|р
кг
24
0,8736
0,9997
5
12
0,9333
0,99976
6
0,9671
0,99977
2
0,9894
0,9997
8
1 ]
0,9942
0,9997
_9
Из приведенных результатов расчетов видно, что при принятых
допущениях система демонстрирует высокую надежность. В то же время
надежностные характеристики системы очень чувствительны к параметрам процедуры
восстановления работоспособности, и сокращение времени ремонта резко
увеличивает вероятность безотказной работы.
554
Навигационно-временные определения, основанные на фазовых измерениях
Глава 15
НАВИГАЦИОННО-ВРЕМЕННЫЕ ОПРЕДЕЛЕНИЯ,
ОСНОВАННЫЕ НА ФАЗОВЫХ ИЗМЕРЕНИЯХ
Навигационно-временные определения, основанные на фазовых методах
измерения, характеризуются высокой точностью. Потенциальная точность
(СКО) оценки задержки г = const по фазе несущей частоты fQ определяется
соотношением ат =l/(2?rqf0) [5.1], где q1 — отношение энергии сигнала к
спектральной плотности аддитивного шума наблюдения. При рабочих
значениях q2 ^10 имеем <тг « l/(20/0) = 7"0/20, т. е. СКО составляет сотые доли
периода несущей частоты радиосигнала. Такая высокая точность определяет
значительный интерес к фазовым методам измерения. В настоящее время
наиболее активно эти методы используются для решения задач геодезии.
Перспективным является их применение для высокоточной навигации, например для
определения пространственной ориентации и автоматизации управления
объектами, в частности, автоматизации посадки ЛА.
15.1. Описание измерений первичных радионавигационных
параметров, выполняемых в приемнике СРНС
При решении радиотехнических задач достаточно широкое
распространение получила практика, когда влияние взаимного расположения и перемещения
объектов учитывается в огибающей радиосигнала через задержку
распространения, а в высокочастотном заполнении — через доплеровскую частоту и фазу.
Вместе с тем, вся информация о местоположении объекта во многих
радиотехнических системах, в том числе и в СРНС, заключена именно в задержке
распространения. При этом сигналы разных частотных каналов имеют
одинаковую задержку, но различные фазы и доплеровские сдвиги. Таким образом,
применение стандартного описания сигналов в многочастотных системах
таких, как ГЛОНАСС, усложняет решение задач НВО. Более адекватным
является подход, основанный на описании как огибающей, так и высокочастотного
заполнения сигналов с помощью временных сдвигов.
Ниже рассматривается понятие сигнального времени, близкое к понятию
«эпохи сигнала». Полезность данного понятия состоит в том, что описание
преобразования сигнала в процессе излучения и распространения на его основе
не использует знания формы сигнала. В практическом плане это позволяет
учесть эффекты движения объекта и нестабильность опорного генератора для
несинусоидальных и вообще непериодических сигналов, где понятия фазы, до-
плеровской частоты и т.п. теряют смысл. Сведение эффектов распространения
555
Глава 15
к сигнальному времени вместо обычных описаний на основе доплеровской
частоты и фазы сигнала позволяет более просто описывать сложные сигналы.
Что касается использования фазовых измерений для высокоточной оценки
координат потребителя, то данная задача требует очень глубокого понимания и
высокой точности описания измерений первичных РНП, осуществляемых
приемником СРНС, и здесь понятие сигнального времени играет важнейшую роль.
15.1.1. Понятие сигнального времени
Рассмотрим данное понятие применительно к СРНС. Здесь передатчик
(навигационный спутник), а в общем случае и приемник, перемещаются в
пространстве, что является существенным источником случайности времени
принимаемых радиосигналов. Предположим сначала, что шкалы времени ОГ
приемника t и передатчика НС tf синхронизированы с системной ШВ
t(t3) = tf{t3) = t3 (начала отсчета всех ШВ совмещены и нестабильности нет).
Индекс «э» означает «эталонный» (в СРНС СШВ может рассматриваться в
качестве эталонной). Для простоты рассмотрения влияние на распространение
сигнала ионосферы и тропосферы учитывать не будем.
НС с координатами Хг(/) излучает в свободное пространство сигнал
ST(t)) (индекс «Г » — от английского «transmitter», далее индекс «R » — от
английского «receiver»). Прохождение сигнала по радиоканалу кроме
изменения амплитуды сигнала всегда приводит к сдвигу во времени (другие
искажения сигнала пока не рассматриваются). В результате в момент времени t в
точке XR (/) принимается сигнал
SR(t) = AST(tT(t))9 (15.1)
где А — амплитудный множитель; tT{t) — момент излучения сигнала
(элемента сигнала), который принимается в момент / (в случае точной
синхронизации шкал времени tT(t) представляет собой сигнальное время).
Задержка распространения сигнала r{t), принимаемого в момент t, выражается через
основное время / и время излучения tT:
r(t) = t-tT(t)9 (15.2)
т.е. рассмотрения, основанные на tT и r{t), эквивалентны. Задержка сигнала
определяется соотношением
||Хп(/)- хЛ/-г(0)|
T^JLJ12—ТЛ—LM? (15.3)
с
556
Навигационно-временные определения, основанные на фазовых измерениях
где с — скорость распространения радиоволн, ||«| — функция определения
длины вектора (расстояния между точками).
В (15.3) учтено, что принимаемый в момент / сигнал был послан в момент
tT </, т.е. из точки Хг(/Г). Для (15.3) можно записать также эквивалентное
выражение
}xR(t) -xT(tT(t)
tT(t) =t
с
Рис. 15.3 графически иллюстрирует определение r(t) для скалярных
функций xR(t) и xT(t)(случай xR(t)>xT(t)).
м
x(t)
*„(t)
xT(tT)
/ В
/^£-~-
cx(t)
XRy
у
0'
Xl/
ctT(t) ct ct 0
Рис. 15.1. Связь координат и сигнального времени
Из точки А, соответствующей моменту приема сигнала, под углом ж/4 с
осью / проводится прямая. Абсцисса точки В пересечения ее с кривой xT(t)
является искомой tT{t). Действительно, треугольник АО'В на рис. 15.1 —
прямоугольный с углом Л-/4, т.е. равнобедренный. Отсюда
c[t-tT(t)] = cz{t) = \0<xR{t)\ = xR(t)-xT(tT(t)),
что эквивалентно (15.2). Рис. 15.1 (справа) графически характеризует
соотношение между временем приема сигнала t, моментом излучения tT[t) и
задержкой сигнала при распространении z(t).
Существование и единственность решения обеспечиваются выполнением
IcMOl
условия ——Ц-1 < 1 для всех / (скорость передатчика меньше скорости света) и
d(ct)
условия tT<t из (15.3). В трехмерном пространстве вместо прямой следует
строить круговой конус с вершиной в точке [ct, XR (t) ] и углом ж/4 с осью t.
557
Глава 15
Такое «геометрическое» построение может служить основой эффективного
алгоритма определения т ^ ' на ЭВМ. В СРНС уравнение (15.1) может
использоваться в режиме начального поиска сигнала НС по задержке, а также при срыве
слежения за НС для его быстрого поиска.
Обратимся теперь к общему случаю, когда время часов приемника и
передатчика не совпадает, т.е. ^ э' \ э)~ э Введем обобщающее сигнальное
t(L)*t'(L) = L /1с 1ч
время, исходя из уже использованного при v э 7 v э' э соотношения (15.1):
SR{t) = AST(ts(t))
(15.4)
t'
Учитывая, что передатчик излучает сигнал в своем времени ' , т.е.
sT(t) = s(r(t))
u; v ;, принимаемый сигнал можно записать в виде
SR(t) = AST(tT(t)) = AS(t'(tT(t)))
где т^ ' представляет собой показание часов приемника, соответствующее
моменту излучения сигнала передатчиком. Сравнение этого соотношения с
(15.4) приводит к выражению для сигнального времени
которое предполагает задание процесса t'(t) и определение процесса tT(t)
согласно выражению (15.2) при заданных XT(t') и ХЛ(/). Рис. 15.1
представляет графический метод определения ts(t), иллюстрируя соотношение
сигнального времени с t'(t) и tT(t).
tx(t)
Рис. 15.2. Сигнальное время
558
Навигационно-временные определения, основанные на фазовых измерениях
Описание сигнального времени возможно и на основе «разностных»
эквивалентов v(t) и A(t) для tT(t) и t'(t), где z(t) определяется выражением
(15.2), а смещение времени передатчика (расхождение «часов» приемника и
передатчика) определяется аналогично A(t) = t-t'(t). Использование rs(t),
r(t) и Д(/) вместо ts(t), tT(t) и t'[t) более привычно и в ряде задач более
удобно.
Из (15.5) и (15.2) получаем эквивалент для (15.5)
ts{t) = t<(tT(t)) = tT{t)-A(tT{t)) = t-T(t)-A(t-r(t)).
Отсюда смещение времени прихода сигнала
В случае наличия рассогласования ШВ приемника и передатчика
выражение (15.3) можно записать в виде
XR(t)-XT(t-T(t)-A(t-T(t)))\\
'с с
В реальных условиях шкалы времени НС и приемника не совпадают с
СШВ г(/э)*/(/э)*/э. Для описания процесса распространения сигнала и
определения сигнального времени введем следующие функции:
^п (?э)= Фэ) ~'э — смещение ШВ приемника t относительно СШВ t3
(эквивалентна введенной выше A(t));
Дне (}э)= 'не (*э) ~ ?э — смещение ШВ НС tHC относительно СШВ 7Э;
Ди(/), Лт(') — задержки сигнала на трассе распространения НС—точка
приема, обусловленные ионосферной и тропосферной рефракцией,
соответственно. Считаем, что Аи (?) соответствует измерению задержки сигнала по фазе
дальномерного кода, т.е. является групповой задержкой сигнала в ионосфере.
При проведении выкладок будем пренебрегать влиянием многолучевости
и задержками сигналов в аппаратуре приемника.
Определим ts (t), используя введенные функции.
Моменту выполнения измерений в аппаратуре приемника t соответствует
момент системного времени /эЛ = t3(t) = t-An(tjR). Тогда момент системного
времени, соответствующий излучению сигнала НС, определяется как
/эГ =t3R -v(t)-AK(t)-Дт(t), где z(t) = R(t)/c — истинная задержка сигнала,
R(t) = /)(Х(/),Хнс(гэГ)) — расстояние между приемником в момент
измерения, имеющим координаты X(t), и НС в момент излучения сигнала Хнс(/эт).
559
XR{t)-XT(t-Ts(t))\
Глава 15
Момент излучения сигнала в ШВ НС ts (t) = t3T + Анс (t3T). Таким образом,
^(0 = ?-Ап(^)-^(0-Аи(0^Ат(0 + АНС^эг).
Тогда для задержки радиосигнала, излучаемого НС и принимаемого в
точке с координатами X в момент времени ty (время отсчитывается по ШВП),
можно записать
|Х(0-Хнс(/Э7>)|
\К) =
ЧК)" хнс [К -r(tv) - AH)V - AT,V - An,v)
(15.6)
С
Здесь Хнс(/э7>) — координаты НС в момент системного времени t3Ty,
соответствующий излучению сигнала.
Решение этого уравнения дает точное значение задержки сигнала, однако в
силу случайного характера Аи, Ат, Ап и r(tv) можно говорить лишь о
некотором приближенном решении уравнения (15.6), точность которого зависит от
количества доступной информации и ее качества. Пусть каким-либо образом
получены оценки параметров AHV, ATV/ и Anv, тогда уравнение (15.6)
преобразуется к виду
X(>v ) " ХНС [К - *v ~ Kv ~ Kv ~ Kv )||
*V =
С
Неизвестное значение величины задержки ту входит в правую и левую
части уравнения (15.7). Геометрически решение этого уравнения
иллюстрируется на рис. 15.2. Наиболее простым методом решения данного уравнения
является метод последовательных приближений, суть которого состоит в
следующем: на первом шаге ту полагают равным нулю и, используя правую часть
уравнения (15.7), находят первое приближение для ту. Найденное
приближение снова подставляют в правую часть (15.7) и получают новое приближение
для ту . Количество итераций зависит от требуемой точности оценки
координат. При практической реализации алгоритмов НВО обычно достаточно двух-
трех итераций [15.13].
Следует отметить, что в стандартном режиме функционирования
приемника СРНС, когда осуществляется слежение за фазой дальномерного кода,
достаточно хорошим приближением для вычисления r(ty) является измеренное
значение псевдозадержки rm(ty). При этом итеративных вычислений не тре-
560
Навигационно-временные определения, основанные на фазовых измерениях
буется (достаточно одной итерации) и T[ty) определяется как
ЫМ -XHc('v-r„3 ('vMhcJI
м =
(15.8)
где
Тт(к) = К Ч(0 = Г(0 + Ап,у - AHC,v + AHv + \v +«vi(15.9)
is {tv) — оценка эпохи сигнала (сигнального времени), соответствующая
принимаемому сегменту дальномерного кода; Днс — смещение БШВ НС относи-
тельно СШВ; Анс — оценка соответствующего смещения, определяемая с
использованием эфемеридных данных; nv — дискретный БГШ,
характеризующий ошибки измерений.
Для оценки точности данного приближения вычислим разность между
истинным значением задержки t(tv) и значением f(tv), получаемым с
использованием выражения (15.8). Для этого разложим правую часть (15.8) в ряд
Тейлора в точке tl=tv-r(tv)- Дп>„ - Диу - AJV:
4<v) - Хне [tv ~ г„з (tv) - Дне,, )|| |х(/„) - Хнс [С )||
+
eT[v(c)-VHc(C)(l-W/)]
*тМ
c-eJVHC(C){\-Sf/f)
АК. „
<W*r('v) +
АК,
с-К
'НО
НО
+ ■
'HC,v '
где V = dX/dt и VHC=dXHC/<# —скорости приемника и передатчика (НС); е
— направляющий вектор от передатчика Хнс(?*1 к приемнику X(/v); Sf/f
— относительная нестабильность генератора приемника; AVr — радиальная
составляющая скорости относительного перемещения приемника и передатчи-
ка' ^но — радиальная скорость передатчика; SHC n =DHC n-DHC n — ошибка
синхронизации БШВ по эфемеридным данным.
Таким образом, величину ошибки при вычислении t(tv) по (15.8)
приближенно можно определить по формуле
8T = T(tv)-r(tv)*—^HC,v
(15.9)
561
Глава 15
Поскольку AVr = 10 ...10 м/с, a SHCv не превышает 20 не, ошибка
вычисления r(tv) с использованием (15.8) не превышает 10~13...10~14с, что составляет
единицы—десятки микрометров и вполне достаточно при решения
практических задач, связанных с обработкой фазовых измерений.
Связь сигнального времени с частотно-временными характеристиками
принимаемого сигнала. Традиционно, описание радиосигнала в системах с
подвижными объектами основано на понятиях доплеровской частоты, фазы и
случайной задержки. Введение сигнального времени обобщает эти понятия.
Рассмотрим опять случай, когда ШВП приемника t и передатчика НС tf
совпадают. При излучаемом радиосигнале ST(t) = f(t)cosa>0t принимаемый
радиосигнал согласно (15.1) имеет вид
5л(г) = ^5г(/г(/)) = ^/(/г(фо8^г(0 , (15.10)
или с использованием г(/)
^(r) = ^/(/-r(/))cos^(r)=:^/(/-r(r))cos[^ + ^(0] ■
Из (15.10) и (15.2) следует, что:
полная фаза сигнала y/{t) = co0tT (f);
круговая частота co{t) = dy/(t)/dt = щ dtT/dt;
доплеровская фаза <p[t) - у/[t) - co^t = co0[tT (t)-tj = -a>0r(t);
доплеровская частота coJl(t) = d<p(t)/dt -co(t)-co0=co0(dtT/dt-\), т.е. все
радиотехнические параметры выражаются через tT(t). Формула для dtTjdt
получается дифференцированием обеих частей (15.3) (с учетом (15.2)):
dtT = х [XR(t) - XT{tT)J[vR(t) - VT(tT) dtTjdt]
dt c\\xR(t) -XT(tT)\\
откуда следует
djj_ = \-tJyR{t)/c n)
dt 1- eTVT(tT(t))/c
Здесь VRT =dXRT/dt — скорости приемника и передатчика; е —
направляющий вектор от передатчика XT[tT) к приемнику XR{t); eTV — скалярное
произведение е и V, совпадающее в данном случае с проекцией V на е, т.е.
радиальная составляющая V . Частота co(t) отличается от (15.11) лишь
множителем со0. Для доплеровской частоты получаем
562
Навигационно-временные определения, основанные на фазовых измерениях
0)a(t) = co(t)-co0=u)0
a?0AVr(t)/c
ет
[УгЫО)-У*(0]
[l-SVT(tT(t))/c]\
(15.12)
[1- VTrlc]'
Здесь AFr(/) = eT[ Vr(rr(r))-V^(/)1 — радиальная составляющая
относительной скорости; VTr [tT (/)) — радиальная составляющая скорости передатчика.
Формула (15.12) уточняет привычную формулу для доплеровской частоты
/э(0 = М0 = ауг(0
/о Юо С
Уточнение связано с более точным учетом в (15.3) положения передатчика
в момент излучения tT, т.е. XT[tT)9 но не Хг(/). Из (15.12) следует, что при
заданной разности скоростей приемника и передатчика доплеровский эффект
зависит дополнительно от скорости передатчика. Однако обычно это не
принципиально, так как ||Vr| = 102...103м/с, т.е. |Vr|/c«0.3-10"6...0.3-10"5, и
поправкой можно пренебречь. Аналогично пренебрегают поправкой более высо-
кого порядка (V/c) « V/c, появляющейся при дополнительном учете
релятивистского эффекта.
В общем случае, когда шкалы времени приемника и передатчика не
совпадают с СШВ, в выражениях вместо tT(t) необходимо использовать
ts(t) = t'(tT(t)). Дифференцирование ts(t) по / дает выражение
dts(t) dt\tT(t))dtT(t)
dt dtT dt
(15.13)
Из (15.13) при необходимости можно легко получить выражения для
частоты принимаемого радиосигнала: co{t) - co0 dts (t)/dt и др.
15.1.2. Модели фазовых и кодовых измерений в СРНС
Рассмотрим модели кодовых и фазовых измерений (ФИ), осуществляемых
приемником СРНС.
Псевдозадержка сигнала оту'-го НС в аппаратуре приемника определяется
как г/ (t) = t- tJs (t), где / — момент снятия отсчета, определяемый в ШВ
приемника; tJs{t) — сигнальное время (соответствует моменту излучения прини-
563
Глава 15
маемого элемента сигнала от у-го НС, определяемому в его БШВ). Выше было
показано, что
// (/) = t - т* (/) - Ап (t3R) - Д{ (?) - Д j (t) + Д'нс (t{T),
где tj (t) = RJ (t)jc — истинная задержка сигнала; RJ (?) =
= D(X(r),X^c(^rj) — расстояние между приемником в момент измерения
Х(/) и j-м НС в момент излучения сигнала Х^су{т\\ Ап — смещение ШВП
относительно СШВ; А^с — смещение ШВ у-го НС ^с относительно СШВ;
Д^ и AJT — ионосферная и тропосферная задержки сигнала на трассе
распространения (j -й НС)—(точка приема).
Таким образом, псевдозадержка сигнала определяется как
г/ (0 = tj (J) + А{ (0 + Д> (0 + Дп (гэЛ) - AJHC (t3T).
Псевдодальность до j -го НС можно представить в виде
p>(0 = cr/(0 = ^(0 + c(A>(0 + Ai(0 + An(^)-Aic(^))- (15.14)
Проводя аналогичные выкладки для измерений, выполняемых в
приемнике по фазе несущей, можно легко получить следующее выражение для
псевдофазы принимаемого сигнала:
^(') = ^ + /У(^(')-ДУ.(') + Ал(',«)-Айс(«/г)) + *у, (15.15)
где AJ — длина волны, соответствующая несущей частоте сигнала fJ,
излучаемого 7-м НС; kJ — некоторое целое, характеризующее неоднозначность
фазовых измерений.
Здесь и ниже в качестве единицы измерения псевдофазы рассматривается
цикл высокочастотного колебания соответствующей частоты, так как данный
формат наиболее часто используется приемниками СРНС для выдачи
потребителю данных о фазе принимаемых сигналов. В условиях отсутствия срывов
слежения в схеме ССФ параметр к] является постоянным во времени,
поэтому в выражении (15.15) его зависимость от времени не рассматривается.
Помимо зависимости от несущей частоты сигнала fJ, выражение (15.15)
отличается от (15.14) знаком при A„(f). Связано это с тем, что ионосфера
является диспергирующей средой, знак задержки в которой меняется в
зависимости от измеряемого параметра радиосигнала НС — фазы огибающей или несу-
564
Навигационно-временные определения, основанные на фазовых измерениях
щей. В первом случае учитывается групповая скорость распространения
радиоволн F, во втором — фазовая V^ . Соответственно в первом случае
задержка А^ положительная (измеренная дальность больше истиной), а во втором -
отрицательная (см. п. 7.3.1).
На практике измерения псевдодальности и псевдофазы, выполняемые
приемником СРНС, содержат инструментальные ошибки, объясняемые, в первую
очередь, влиянием внутренних шумов приемника. Тогда модели измерений
можно представить в виде
й(/)=^(0+с(д{(0+^(0+Ап(^)-д^с(^))+«^(0.
^Л0=^+/у(А;т(0-А7и(0+^(^)-4с(4))+^+<(0^/=и,^,
где njD(t) и nJ9{t) представляют собой БГШ, характеризующие шумы
измерений; N — количество радиовидимых в момент времени t навигационных
спутников.
Измерение РНП в приемнике СРНС выполняется в дискретные моменты
времени tv, привязанные к ШВ приемника, обычно с постоянным интервалом
накопления сигнала А/. В дискретном времени модели измерений
псевдодальности и псевдофазы можно представить в виде
й.к=й(^)=^+с(а^+д^+Ап,и-а;нс.к)+<к. 05.16)
где nJDv и п^у представляют собой эквивалентные дискретные БГШ с
нулевым математическим ожиданием и дисперсиями DD и Dp соответственно. При
этом dAxj\ «Dd, что объясняется высокой точностью слежения за фазой
сигнала, которая в существующих образцах аппаратуры СРНС составляет
сотые доли длины волны. При использовании выражений (15.16) и (15.17)
следует понимать, что А и А^с у относятся к соответствующим моментам
времени f3R,v =K- An,v И 'э7> = *3R9v ~Tl- Kv ~ Aiv '
Выражения (15.16) и (15.17) могут быть использованы для построения
алгоритмов автономных НВО, однако наличие в наблюдениях систематических
погрешностей А£, Af и AJHC, даже при использовании для их компенсации
сложных математических моделей, в настоящее время позволяет получать
оценки координат потребителя с точностью не лучше единиц...десятков мет-
565
Глава 15
ров. Для ряда практических задач такой точности недостаточно. Вместе с тем,
относительное постоянство величин задержек AJM, AJT и А^с во времени и
пространстве позволяет использовать измерения, выполняемые вторым
приемником СРНС, для компенсации данных составляющих погрешности. Это
является основой дифференциального режима (режима относительных
определений) в СРНС (см. гл. 12).
15.1.3. Модели наблюдений радионавигационных параметров
в СРНС, используемые для высокоточных НВО
Для реализации метода относительных измерений необходимо, чтобы
отсчеты наблюдений относились к одному моменту времени. На практике
отсчеты наблюдений снимаются в ШВ приемников, смещение которой относительно
ШВ системы является случайным и, следовательно, неодинаковым для
различных приемников. Современные приемники СРНС осуществляют
синхронизацию собственной ШВ относительно СШВ с точностью до половины
миллисекунды. Следовательно, даже если рассмотреть задачу приема сигналов двумя
приемниками на общую антенну, то взаимное смещение их ШВ может
достигать миллисекунды, а за это время НС, движущийся с большой скоростью (для
среднеорбитальных СРНС около 3 км/с), проходит расстояние вдоль орбиты в
несколько метров, что эквивалентно изменению дальности до единиц-десятков
сантиметров. Следовательно, при простом вычитании измерений одного
приемника из измерений другого получаемая разность содержит
некомпенсированные ошибки, обусловленные различным положением НС в моменты
излучения принимаемых элементов сигнала. Поэтому перед получением разности
отсчетов наблюдений их необходимо привязать к единой ШВ, в качестве
которой наиболее целесообразно рассматривать ШВ приемника потребителя.
Пусть измерения РНП выполняются в точках А и В. Координаты Хв точки
В считаем известными (опорная станция). С целью сокращения выкладок все
преобразования будем рассматривать только над измерениями
псевдодальностей, учитывая, что над измерениями псевдофазы выполняются аналогичные
преобразования.
Суть коррекции сводится к следующему. Вычтем из наблюдений
псевдодальности в базовой точке расстояние до НС, рассчитываемое с
использованием эфемеридной информации на момент времени, соответствующий моменту
приема сигнала приемником:
Н в (>*) = Й в ('*) - d{xb, х£с (tfTtV)) =
566
Навигационно-временные определения, основанные на фазовых измерениях
где A-Lv — ошибки, обусловленные неточностью эфемеридного обеспечения.
Пусть к v-му моменту выполнения измерений каким-либо образом
найдена приближенная оценка вектора относительных координат приемников АХК
(для алгоритма фильтрации относительных координат такой оценкой является
экстраполированное значение вектора АХ). Приближенная оценка координат
приемника в точке А ХАу = = Хв + АХУ. Если истинное значение координат
потребителя в момент выполнения измерений XA(ty) = XAv, то при
небольшой величине X^v -X^ J (до 1 км) можно записать
Д(х^,х{,с(/Э^
где GJ(ty) = GJy =dD{xAv,X{lc(t^Tv)\/dXA — направляющие косинусы
вектора, направленного из точки ХАу на j -й НС в момент времени ty .
Разность ХАу - ХАу можно представить в виде
^ачу ~^а,у = ХАчУ -Хв + Хв -ХАу = АХУ -/±ХУ ,
и тогда, подвергая измерения в точке А преобразованию
Й4^) = ^Л?")-^(^'Хнс(4,)) + С^АХг,
получаем
«(A{{tt) + Ai(<t) + Д„(^,„) + *Ц$ ) " Afc(&, )) + 4{>" ) ■
Погрешности A;J, AJT, A-L и А^с сильно коррелированы по времени и
пространству. Таким образом, выполняя рассмотренные выше преобразования
над измерениями псевдодальности и псевдофазы для всех радиовидимых в
обеих точках приема НС и находя их разность получаем следующие модели для
первой разности измерений РНП в СРНС:
Aft,v=A&(/v) = GJAXl,+cA;v+«i)fV, j = l..,N, (15.18)
A#t„ = A{i(ty) = GiAXjAJ +cA;v +kl + <,,. (15.19)
Здесь все наблюдения приведены к единой ШВ tv=t„ ', АХК — вектор
относительных координат приемников; АП — взаимное смещение их шкал времени;
к{ характеризует неоднозначность разности измерений псевдофазы; п^ и
567
Глава 15
nicp — дискретные БГШ с нулевыми математическими ожиданиями и
дисперсиями 2DD и IDy (считается, что оба приемника выполняют измерения с
одинаковой точностью).
Модели (15.18) и (15.19) получили широкое распространение в
отечественной и зарубежной литературе под названием первые разности измерений.
Их использование позволяет строить высокоточные алгоритмы определения
относительных координат при расстоянии между приемниками до 10... 15 км.
Данное ограничение связано с появлением в (15.18) и (15.19) при увеличении
расстояния между точками приема остаточных погрешностей, соизмеримых по
абсолютной величине с ошибками измерения псевдофазы. Эти погрешности
обусловлены неполной компенсацией составляющих задержки сигнала в
ионосфере и тропосфере при формировании разностей измерений.
15.1.4. Методика проверки точности математических моделей
измерений радионавигационных параметров в СРНС
Качество функционирования алгоритмов НЕЮ в СРНС на основе фазовых
измерений в существенной степени определяется адекватностью
математической модели описания РНП реальным измерениям, выполняемым в приемнике.
Критичность алгоритмов фильтрации к точности моделей обусловлена малыми
флуктуационными ошибками псевдофазовых измерений, которые в
современных приемниках СРНС имеют порядок единиц миллиметров. Как известно,
измерения РНП содержат ряд систематических погрешностей, обусловленных
дисперсионностью среды распространения, нестабильностью ОГ, ошибками
эфемеридного обеспечения. Величина этих погрешностей на несколько
порядков превышает величину флуктуационных ошибок. Систематические
погрешности могут быть исключены из наблюдений за счет использования режима
относительной навигации (дифференциального режима), однако точность их
компенсации ухудшается с увеличением расстояния между точками приема.
Это приводит к наличию в наблюдениях остаточных погрешностей,
обусловливающих отклонение измерений РНП от их моделей, и, как следствие — к
неправильному функционированию алгоритмов. Существует ряд других причин,
приводящих к ошибкам в моделях измерений, например, влияние шумов мно-
голучевости, неправильное вычисление координат опорных точек (положения
НС в момент излучения сигнала) и др. Ниже предлагается методика проверки
точности моделей измерений РНП. Практические исследования показывают,
что использование методики позволяет существенно сократить время,
затрачиваемое на поиск причин неработоспособности алгоритмов НВО и их
устранение. Идея методики была подсказана А.А. Поваляевым в 2000 году.
Как отмечалось, измерения РНП в СРНС можно описать уравнениями
568
Навигационно-временные определения, основанные на фазовых измерениях
^v=V(tv,X) + c{^v-^v+biv+^v) + njDv, (15.20)
^'v=zy(/v,X)^4/^(AniV-AiC(V+A(Xv) + *y'+<v.y = l.-^,(15.21)
где j обозначает номер НС; N — число НС, радиовидимых в момент
выполнения измерений tv ; DJ (tv,X) — расстояние между j -м НС в момент излучения
и точкой приема с координатами X; А^, А^ — ионосферная и тропосферная
задержки сигнала на трассе распространения у'-й НС—точка приема; Ап —
смещение ШВ приемника относительно СШВ; AJHC — смещение ШВ у-го НС
относительно СШВ; с — скорость распространения электромагнитных волн в
свободном пространстве; fJ = c/AJ — несущая частота излучаемого j -м НС
сигнала; Я; — длина волны излучения; kJ — целое число, характеризующее
неоднозначность захвата фазы; подстрочный индекс v говорит о том, что
соответствующая величина рассматривается в момент времени tv ; nD и п^ —
дискретные БГШ с дисперсиями DD и D9 соответственно (Dp « DD).
Выражение (15.20) описывает измерение псевдодальности, выражение (15.21) —
измерение псевдофазы. Единица измерения псевдодальности — метры, псевдофазы
— циклы (единицы длин волн).
Если координаты точки приема X известны точно, то, вычисляя на основе
эфемеридной информации расстояние до НС DJ (^,X) и вычитая его из
измерений, получаем
?£>, к = #> v " & (tv, X) = с( An,v - AyHC,v + Kv + Aiv + Aiv ) + nD, v »
= kj + fJ (An,v - Анс,к + Aiv + ALv ~ Kv) + "is»
где AJ3 — характеризует погрешности, обусловленные неточностью эфемерид-
ного обеспечения.
Погрешности Анс, А^, А{ и А{ являются сильно коррелированными по
времени и пространству, следовательно, при наличии измерений в двух точках
с точно известными координатами для разности измерений можно получить
ArjJDv = cA*nv +п^,у, (15.22)
A/7^=M>+/>a;,+<,v. (15.23)
Здесь Д*=Дп1-Ап2 - взаимное смещение ШВ приемников; AkJ =kJnX -kJn2;
569
Глава 15
п/ю и пА<р — дискретные БГШ с дисперсиями 2DD и ID^ соответственно
(считается, что измерения РНП в каждой точке и по всем НС выполняются с
одинаковой точностью).
Величина А* определяется характеристиками ОГ приемников и, как видно
из (15.22) и (15.23), является одинаковой для всех НС. Для исключения ее из
наблюдений один из НС выбирается базовым, и его наблюдения вычитаются из
наблюдений, полученных по другим НС. Пусть в качестве базового выбран НС,
стоящий в списке первым. Тогда получаем
VA»/SfV=A7S.v-A'7D,v=»JADiv, <7 = 2,..,7V, (15.24)
VA<V, = A<v - Ai/i,, = VM4 А/*ДП,, +*W > (15.25)
где VAkq = Akq - Akl; Afq = fq - fl; nVAD и n^A(p — дискретные БГШ с
дисперсиями 4DD и 4D(p соответственно.
Отметим, что шумы в различных каналах становятся коррелированными с
коэффициентом корреляции 0,5. При практической реализации в качестве
базового рекомендуется выбирать НС с максимальным углом возвышения, так как в
большинстве случаев измеряемые по нему РНП обладают наилучшей точностью.
Проанализируем выражения (15.24), (15.25). В случае отсутствия ошибок
процесс, полученный выполнением описанных выше действий над
измерениями псевдодальностей, должен представлять собой реализацию дискретного
БГШ. В случае выполнения измерений в высоком темпе с дискретностью 1с и
меньше возможно наличие корреляции между отсчетами, однако
математическое ожидание процесса всегда должно быть равно нулю. Если измерения,
выполняемые по всем НС, равноточные, то дисперсия процесса в 4 раза превышает
дисперсию измерений. Это может быть использовано для оценки точности измерений РНП
при синтезе алгоритмов НВО. Некомпенсированные и остаточные ошибки
приводят к наличию в (15.24) систематического смещения, сравнительно
постоянного во времени. Таким образом, отличие математического ожидания
процесса (15.24) от нуля является показателем отклонения модели от истинных
значений измеряемых РНП.
Рассмотрим выражение (15.25). В случае определения РНП по сигналам
СРНС GPS имеем Afq - 0 (так как все НС излучают сигналы с одинаковой
несущей частотой)и
VA/^VM^^,. (15.26)
Точность фазовых измерений в приемниках СРНС составляет сотые доли
от длины волны принимаемого радиосигнала. Следовательно, мгновенные
отклонения полученной реализации (15.26) от целого числа VAkq не должны
превышать десятой доли цикла, а реализация случайного процесса
570
Навигациоино-временные определения, основанные на фазовых измерениях
VArj^ - VA77jK , где [x]z представляет собой операцию округления числа
jc до ближайшего целого, должна представлять собой дискретный БГШ с
нулевым математическим ожиданием и дисперсией, в 4 раза превышающей
дисперсию измерения псевдофазы.
В силу высокой точности фазовых измерений различного рода ошибки
существенно сказываются на характеристиках процесса (15.26), вследствие
чего он является надежным индикатором причин, по которым тестируемые
алгоритмы могут быть неработоспособны.
Обратимся теперь к случаю, когда РНП определяются по сигналам СРНС
ГЛОНАСС. Здесь Afq =(/^ -/1)-562.5 кГц, где lq и /, — литеры частот,
соответствующие <дг-му и базовому НС. Величину А* можно оценить, используя
(15.22):
1 N
7=1
В большинстве случаев точности полученной оценки (сгд ~ 10-8 с)
недостаточно для компенсации второго слагаемого в (15.25), так как величина
остаточного члена в выражении
VA/^VA^-A/^
может достигать десятых долей цикла с учетом того, что максимальный разнос
частот в СРНС ГЛОНАСС А/тах = 24 • 562,5 кГц = 1,35 • 107 Гц
(Д/тах<7д «1,35 107 Гц-КГ8 с = 0,135). Поэтому, используя (15.23), на основе
методики дополнительной переменной получаем алгоритм оценки взаимного
смещения ШВ приемников:
A^=A;),+RAkRk1(k-k),k = mm-1[(k-k)TR^(k-k)
где1(к)=(к-к)ТЯк1(к-к); RAk=-FDA; Rk =FDAFT +ID,;
FT=[/!.../"]; к = А^,-РА^;ДЛ;=[А7;...А7;];
DA — дисперсия оценки A* v; D — удвоенная дисперсия ошибок
псевдофазовых измерений; I — единичная матрица.
Среднеквадратическое отклонение получаемой оценки составляет порядка
10~10...10-11 с. Этого вполне достаточно для компенсации ее в (15.25), при этом
характеристики получаемой реализации сходны с характеристиками (15.26).
571
Глава 15
На рис. 15.3 и 15.4 представлены реализации (15.24) и (15.25), полученные
в результате применения описанной методики к записям РНП, сделанным в
ходе эксперимента, который подробнее описан в п. 15.4.3.2.
Псевдодал ьность ,м
200
Q
| 0 02 h
* о
600 т fooo
П севдофаз а, цикл ы
12D0
1400 t с
< -0 02
> чО.ОЗ ,,
-004 р
-О05
0 200 400 8CD Ш0 1000 1200 1400 t, с
Рис. 15.3. Вторые разности РНП, измеряемые по сигналам GPS
П сеед од ал ьн ость, м
0 200 400 600 800 1000 1200 1400 t, с
Рис. 15.4. Вторые разности РНП, измеряемые по сигналам ГЛОНАСС
Рис. 15.3 соответствует разностям псевдодальностей и псевдофазы для НС
СРНС GPS с системными номерами 2 и 7, рис. 15.4 — для НС СРНС
ГЛОНАСС с системными номерами 4 и 6. Аналогичные результаты
получаются и по другим НС. Видно, что математическое ожидание реализаций равно
нулю, что позволяет сделать вывод об адекватности математических моделей
(15.20), (15.21) реальным измерениям, выполняемым в приемнике.
572
Навигационно-временные определения, основанные на фазовых измерениях
15.2. Методы разрешения неоднозначности фазовых
измерений на уровне вторичной обработки
15.2.1. Общие подходы к разрешению неоднозначности
фазовых измерений
Для исключения из первых разностей измерений составляющей,
обусловленной взаимным смещением шкал времени, в качестве наблюдений в
алгоритмах оценки относительных координат часто используют вторые разности
измерений, когда из первой разности измерений одного спутника вычитается
первая разность измерений другого спутника. Однако это не позволяет
устранить неоднозначность ФИ. Одним из путей решения проблемы
неоднозначности является применение третьих разностей — приращения двойных
разностей за некоторое время. Известны результаты использования третьих
разностей для обработки данных от приемников, работающих по сигналам
ГЛОНАСС [15.1]. Недостатком этого подхода является длительное время
наблюдения (порядка 20 мин) для получения оценки вектора относительных
координат с сантиметровой точностью.
Методы разрешения неоднозначности (РН) ФИ могут быть
классифицированы по типу используемой в этих целях информации. Такая информация
может представлять собой априорные оценки координат; оценки координат с
помощью навигационных средств иного типа; измерения по огибающей
радиосигнала (псевдодальности); избыточность измерений псевдодальности и
псевдофазы за счет использования второго частотного канала, совместной оценки
относительных координат по измерениям более чем от шести НС или
использования наземных псевдоспутников.
В зависимости от изменения расположения точек аппаратуры
потребителей методы разрешения неоднозначности классифицируют как статические,
кинематические и «в движении» (On-the-Fly, OTF). Статические методы
разрешения неоднозначности применяют при неподвижных приемниках, а два
других метода - при изменении положения приемников во время сеанса
определения их относительных координат. В кинематических методах разрешение
неоднозначности осуществляется в начальный момент времени при
размещении приемников в точках с известными координатами, а в методах OTF — в
процессе взаимного перемещения.
Наиболее эффективные процедуры РН основаны на избыточности
фазовых измерений, когда число измерений фазы больше числа неизвестных
параметров (координат). В последние годы этот подход привлек наибольшее
внимание. Проиллюстрируем общую идею использования избыточности фазовых
измерений на примере определения местоположения объекта на плоскости.
Пусть измерения осуществляются в точке А с координатами хА9 уА. На
рис. 15.5, а приведен чертеж приема одного сигнала с направления Nx в пред-
573
Глава 15
положении плоского фронта приходящей волны. В точке А полная фаза
сигнала Фа\ ~ Фа\ + кЛ\, где кА1 — число целых циклов фазы принимаемого сигнала,
характеризующее неоднозначность измерений; фАХ — дробная часть полной
фазы.
В результате измерений определяется только фАХ = срАХ - кАХ = const. Имея
данные одного измерения, нельзя однозначно определить две неизвестные
координаты хА, уА точки А. Приведенные линии положения являются
геометрическим местом точек всех возможных решений.
Рис. 15.5. Влияния избыточности фазовых измерений
На рис. 15.5, б приведен аналогичный чертеж при приеме двух сигналов с
различных направлений NY и N2 в общем случае с различными частотами (т.е.
отличающимися длинами волн л\ и А^). В точке А проводят два измерения
<f>A\=<PAl-kAl=C0nstl И Фл2=<РА2-кА2=<Я>п&2- (15.17)
Решению этой системы уравнений соответствуют точки пересечения
прямых на рисунке. Формально, с точки зрения определения координат, имеем два
неизвестных параметра хА, уА и два уравнения для их определения, т.е.
минимально необходимое число измерений. Однако проблема в том, что
неизвестные параметры хА, уА входят лишь в одно из слагаемых каждого уравнения
574
Навигационно-временные определения, основанные на фазовых измерениях
(15.27), так как неоднозначность измерений от координат не зависит. В
результате имеем фактически четыре неизвестных параметра: хА, уА, кАХ,кА1, что и
приводит к неопределенности решения.
Если теперь ввести дополнительное измерение (при формальном
определении задачи нахождения координат являющееся избыточным), то, как видно
из рис. 15.5, в, в ограниченной окрестности точки А все три линии фА1 = const,
пересекаются в одной точке. Однако проведение избыточных измерений не
снимает проблему неоднозначности решения, так как каждое новое (/-е)
измерение содержит дополнительное неизвестное kAi. Избыточные измерения
расширяют окрестность вокруг искомого решения, в которой отсутствуют другие
возможные решения. В этом и состоит эффект избыточности измерений.
Избыточность фазовых измерений в СРНС требует соответствующего
числа НС и (или) использования сигналов второго частотного канала. Решение
общей задачи НВО в дифференциальном режиме на основе фазовых измерений
предполагает видимость пяти и более НС. Это может быть обеспечено при
совместном применении обеих систем в рамках единой системы GNSS или при
использовании псевдоспутников.
При измерениях в двух частотных каналах и пренебрежимо малом
остаточном ионосферном смещении возможно приведение измерений
псевдозадержек высокочастотного заполнения (псевдофаз) на частотах каналов Ы и
L2 к эквивалентным измерениям псевдозадержек на частотах биения
/д = (f\ ~ fi )/2 и /z = (/1 + /2 )/2 • Для правильного разрешения
неоднозначности при этом способе необходимо (но не достаточно), чтобы ошибка измерения
двойных разностей псевдодальностей была меньше половины длины волны
полуразностной частоты /д (например, для СРНС GPS, равной 63 см).
Другой подход к разрешению неоднозначности сводится к целочисленной
максимизации функции неоднозначности, выбранной из характера
периодичности сигналов НС по фазе [15.2]. Для малых базовых линий (линий,
соединяющих две точки в пространстве), когда можно пренебречь остаточными
ионосферными погрешностями, в [15.2] предложена функция неоднозначности
L(x)=ES2>sNAV'w.'» -AVD^ (х))Д.) •
k=\ m=\ i=\
где X = Х^ - Х5 — вектор базы, т. е. относительных координат двух точек;
AV7/p - наблюдения, соответствующие вторым разностям; AVZ) — вторые
разности дальностей.
Использовать приведенную функцию неоднозначности для решения
задачи оценки вектора базы крайне сложно в силу значительных вычислительных
затрат для расчета L{X) при всех возможных значениях параметров. Однако,
575
Глава 15
как отмечалось, измерения псевдофазы в приемниках СРНС выполняются с
достаточно высокой точностью, поэтому каждый локальный пик
апостериорной плотности вероятности ^(X) = c-pjl(X)} может быть аппроксимирован
гауссовой плотностью вероятности (более подробно данный вопрос рассмотрен
ниже), что позволяет свести задачу разрешения неоднозначности к задаче
целочисленной минимизации квадратичной формы:
L(k) = (k - k)T Rj;1 (k - k), (15.28)
где k — предварительная оценка вектора целочисленных смещений,
задаваемое на множестве действительных чисел; Rk — матрица дисперсий оценки
вектора целочисленных смещений.
Задача целочисленной минимизации L(k) в общем случае может быть
выполнена только через процедуру перебора целочисленных комбинаций. В
[15.3] отмечено, что для разрешения неоднозначности при использовании
аппаратуры геодезического типа, работающей по пяти-семи НС и
осуществляющей измерения по сигналам двух частотных каналов необходим перебор
105...109 целочисленных комбинаций.
Повышение достоверности разрешения неоднозначности и уменьшение
числа целочисленных комбинаций при переборе возможно путем сглаживания
измерений псевдодальности (или их разностей), полученных по огибающей
сигнала, более точными измерениями, полученными по фазе. Такой подход с
использованием калмановской фильтрации позволяет существенно уменьшить
шумовую составляющую измерений псевдодальности по огибающим (carrier
(phase) smoothing) [15.7] (см. п. 6.4.2.).
15.2.2. Беспереборные процедуры разрешения неоднозначности
Как отмечалось в предыдущем параграфе, во многих методах разрешения
неоднозначности возникает проблема целочисленной оптимизации, решение
которой основано на переборе целочисленных комбинаций. Ниже будут
рассмотрены беспереборная процедура разрешения неоднозначности, а также
один из способов оценки достоверности получаемого решения. Вероятность
неправильного разрешения неоднозначности является монотонной функцией
определителя матрицы Rk из (15.28), т.е. с уменьшением определителя будет
уменьшаться вероятность неправильного разрешения неоднозначности [15.5,
15.16, 15.17]. Избыточность фазовых измерений и тот факт, что точность
фазовых измерений на один-два порядка выше точности измерений по огибающей
сигнала, приводят к слабой обусловленности матрицы Rk, когда часть
собственных чисел матрицы значительно меньше остальных. Кроме того,
576
Навигационно-временные определения, основанные на фазовых измерениях
?/|Rk| <3c(Rk).., /= 1...и, где п — размерность матрицы. При этом часть осей
эллипсоида (15.28) будет иметь размеры, значительно меньшие остальных. Из
геометрических соображений следует, что поиск точки арифметического
минимума целесообразно осуществлять внутри узкой области пространства в
окрестности центра данного эллипсоида.
Как отмечено в [15.16, 15.17], поиск точки целочисленного минимума
квадратичной формы (15.28) в общем случае должен выполнятся через
процедуру перебора целочисленных комбинаций. Однако, если Rk = diagn(Rk), то
точка целочисленного минимума квадратичной формы (15.28) определяется
через округление до ближайшего целочисленного вектора
k = [k]z> (15.29)
где [•]_ обозначает операцию округления до ближайшего целого.
Действительно, для диагональной матрицы Rk имеем
(k-k)T Rk'(к-к) = £(*,. Ч)7(К*)„ •
Так как каждое слагаемое суммы зависит только от одного элемента
вектора к, то минимум квадратичной формы достигается тогда, когда достигается
минимум каждого слагаемого:
^min-'j^-*,)2:/(*0,}-[*'1-
Сформулируем следующую задачу: найти такую корреляционную матрицу
Rk (при фиксированном значении ее определителя |Rk| = /?), для которой
вероятность правильного разрешения неоднозначности для беспереборной
процедуры [15.5] будет максимальной. Определение такой матрицы дает
направление поиска требуемого преобразования квадратичной формы.
Рассмотрим задачу условной максимизации
Rk =max-1{pnpH (Rk ||Rk | =/?)}, (15.30)
где Рирп — вероятность правильного разрешения неоднозначности:
0,5 0,5 0,5
^пРн(*к)= j~ J- J^(x,0,Rk)</x. (15.31)
-0,5 -0,5 -0,5
Здесь N„(x,m,Rk) обозначает я-мерный гауссовский закон распределения
вектора х со средним значением m и матрицей дисперсий Rk .
19-1026
577
Глава 15
Для решения задачи нахождения условного экстремума (15.30)
воспользуемся методом множителей Лагранжа [15.19], в соответствии с которым
[Рпрн (Rk) - /(|Rk | - /?)] = 0 , что приводит к уравнению
dRk
v 0,5 0,5 0,5
max(PnpH||Rk| = /?)-2r/? Rk = J... J... j xxTNn(x,0,Rk)dx .
^ k -0,5 -0,5 -0,5
Легко проверить, что его решением является матрица
Rk=I„# (15.32)
— частный случай диагональной матрицы. При такой матрице поверхность,
задаваемая (15.28), представляет собой многомерную сферу. Подставляя
(15.32) в (15.31), можно вычислить максимальную вероятность
правильного разрешения неоднозначности:
Рпрн=(2ф(о,5/Щ-\)\
Полученный результат показывает, что для повышения эффективности
беспереборной процедуры разрешения неоднозначности (повышения
вероятности правильного разрешения неоднозначности) необходимо искать такое
преобразование координат m = Uk , при котором в новой системе координат
уравнение (15.28), принимающее вид
(т - Uk)T (URklT)"1 (m - Uk) = const,
задавало сферу. При этом обязательным требованием является взаимно
однозначное отображение целочисленных точек при преобразовании U .
Необходимое и достаточное условие этого — унимодулярность (равенство определителя
по абсолютному значению единице) и целочисленность матрицы U .
Следовательно, матрица U не может быть построена на множестве собственных
векторов матрицы Rk k, что, как известно, обеспечивает приведение квадратичной
формы к диагональному виду. Поэтому можно лишь требовать близости в
некотором смысле преобразованной матрицы URkUT к |Rk|l„ (коэффициент
при In n равен |Rk|, так как унимодулярное преобразование не изменяет
значения определителя матрицы). Из всех симметричных положительно
определенных матриц размера пхп с одинаковым определителем /3 матрица у[р \п будет
иметь минимальный след. Таким образом, в качестве меры близости двух
матриц можно выбрать след матрицы и свести задачу нахождения целочисленной
унимодулярной матрицы U к задаче целочисленной минимизации:
578
Навигационно-временные определения, основанные на фазовых измерениях
U = min"irtr(uRkuT)|w(/. eZ, |u| = l]
Решение данной задачи можно осуществить на основе подхода,
предложенного в [15.18], заключающегося в том, что итоговое преобразование,
задаваемое матрицей U, разбивается на последовательные элементарные
преобразования u(m):
и=ПиН'
{ш}
где {т} обозначает множество последовательных преобразований, а каждая
матрица u(m) обеспечивает некоторое уменьшение следа преобразованной
матрицы. При этом
u(m)=I„+e(m)GZ„„,
где е(т) — целочисленная матрица, все элементы которой, кроме элементов
т-то столбца, равны нулю, причем e(m) mm = 0.
Рассмотрим матрицу Rk =u(m)RkuT(m) и аналогично процедуре
Грамма—Шмидта представим ее след
tr(Rk)=(Rk)„m+£((*»)„+2Wm)UR"L+(«(-)£ («*)-)=
/=1
=(Rk) +Y
v K?тт / *
1=1
(M„-^+(RjJ(*(™)L + (RkL'
2\
(Rk)
(Rk)
V V к)тт J
Поскольку матрица е(т) целочисленна, величина tr(Rkj будет
минимальной, когда элементы m-го столбца е(т) (кроме элемента (е(т) тт)
(Rk)
(««.=-
'mi
(«О.
mm
С учетом этого результата алгоритм нахождения матрицы преобразования
U состоит из следующих шагов:
1) задают начальные условия (Rk = Rk, R = Rk, U = In );
2) последовательно для т= \...п вычисляют
u(m) = I„+e(m).
Для каждого m находят (переопределяют матрицы):
579
Глава 15
Rk =u(m)RkuT(m); U = u(m)U;
3) сравнивают следы матриц Rk и R. Если tr(Rk) < tr(R), то выполняют
переопределение R = Rk и осуществляют возврат к шагу 2. В противном
случае алгоритма завершен.
Анализ эффективности представленной процедуры беспереборного
разрешения неоднозначности рассмотрен в [6.11] на примере задачи синхронизации
разнесенных в пространстве генераторов по сигналам СРНС, где показано, что
наличие избыточных измерений позволяет радикально повысить достоверность
разрешения неоднозначности фазовых измерений.
Следует отметить, что рассмотренная процедура поиска матрицы
преобразования U не является единственной. В [15.20] представлен еще один
алгоритм вычисления матрицы U, в ряде случаев обеспечивающий более
качественную диагонализацию матрицы Rk, однако требующий более высоких
вычислительных затрат.
15.3. Применение методов оптимальной фильтрации для синтеза
алгоритмов навигационно-временных определений,
основанных на фазовых измерениях
15.3.1. Метод дополнительной переменной
Общим подходом к оцениванию случайных процессов в радиотехнических
системах являются методы оптимальной фильтрации [15.1, 15.2, 15.5],
позволяющие определить апостериорную плотность вероятности оцениваемых
параметров и процессов, на основе которой могут быть получены те или иные их
оценки. Использование методов оптимальной фильтрации в задачах вторичной
обработки навигационной информации достаточно традиционно [15.6, 15.13].
Применение тех же методов для синтеза оптимальных алгоритмов первичной
обработки, включающих извлечение информации из фазы несущей частоты,
затруднено в связи с возникающей многомодальностью апостериорной плотности,
обусловленной наличием периодической функции в наблюдениях. Для
получения итоговых алгоритмов фильтрации в условиях полимодальности
апостериорного распределения предлагались различные подходы [15.6—15.18,
15.22—15.24]. Наиболее конструктивные результаты получаются при
использовании метода дополнительной переменной (МДП), впервые предложенного в
[15.9], а применительно к задачам навигационных определений — в
[15.10—15.14]. Основное преимущество использования МДП для
аппроксимации АПВ заключается в учете регулярности распределения локальных
максимумов АПВ в некотором расширенном пространстве состояния, что дает
возможность получить простую аппроксимацию полимодальной апериодической
580
Навигационно-временные определения, основанные на фазовых измерениях
АПВ и тем самым значительно уменьшить количество оцениваемых
параметров. Кроме того, применение данной методики в случае использования
гауссовой аппроксимации АПВ позволяет свести задачу разрешения неоднозначности
измерений к задаче поиска точки целочисленного минимума квадратичной
формы, которая, как показано в п. 15.2.1, может быть решена беспереборным
методом. Все вышеперечисленное позволяет эффективно использовать МДП
для построения высокоточной оценки параметров сигналов в реальном времени.
Для задачи фильтрации задержки сигнала т по огибающей и фазе несущей
частоты суть МДП заключается в следующем. Вместо одной переменной х,
входящей в описание огибающей и фазы сигнала, рассматривают две
переменные {z,rd}, одна из которых т связывается с огибающей, а вторая rd — с
фазой сигнала, т. е. для сигнальной функции полагается
S(t,T,rd) = A(t - r)coso)0 (t - rd).
Тождественность двух переменных в исходной задаче учитывается в
априорном распределении
PPr{T>Td) = Ppr(T)s(T-Td)> (15.33)
где ррг (г) — априорная плотность распределения задержки.
В дальнейшем рассматривается апостериорная плотность вероятности
(АПВ) р (T,rd) расширенного вектора T = [r,rd]T. Так как априорная
плотность (15.33) содержит £-функцию, то, как показано в [15.9], апостериорная
плотность также содержит эту функцию, т.е. имеет вид
P{r,Td) = Cp2{T,Td)S{T-Td). (15.34)
Типичный вид функции р2 ij^d) приведен на рис. 15.6.
Рис. 15.6. Апостериорная плотность вероятности в
методе дополнительной переменной
581
Глава 15
Наличие в (15.34) 5-функции отражено на рисунке секущей плоскостью
T-rd. Пересечение этой плоскости с поверхностью Pii^^d) c точностью до
нормировочного множителя совпадает с искомой апостериорной плотностью
p(r) = p2(T,Td)\Td=T, (15.35)
т.е. имеет многопиковый характер. Поверхность/^(г,rd) более регулярна, чем
р(г). Ее зависимость по т определяется огибающей сигнала и при
используемых сигналах унимодальна. По переменной rd вид Piij^d) имеет
многопиковый характер, но эта многопиковость строго периодична:
Рг{?*та) = Pi{T^Td +7о)> гДе ^о — период повторения ВЧ-сигнала, и ее легко
учесть.
Достаточно подробный вывод различных алгоритмов фильтрации,
основанных на МДП, приведен в [15.11], поэтому ниже дается краткая сводка
основных результатов синтеза и некоторые примеры, иллюстрирующие их
применение.
15.3.2. Оценка задержки одночастотного когерентного
радиосигнала
На вход приемника поступает аддитивная смесь когерентного радиосигнала
S(t-r) = A(t-T)cos(27rf0(t-T)) и белого гауссовского шума n(t) с нулевым
средним и двусторонней спектральной плотностью N0/2:
£(t) = S(t-T) + n(t). (15.36)
Время наблюдения Т »Т0= \/f0 . Априорные сведения о задержке
задаются ее плотностью вероятности ррг (г).
Плотность вероятности, входящая в (15.34), имеет вид
/?2(^^) = ^r(^)exp{^(^)cos^0(rJ-//(r))}, (15.37)
где Х[т) = yjx^ (г) + Х52 (г) — огибающая на выходе согласованного фильтра;
2Т
Хс(т) = — fat) A(t - r)cos(o)0t)dt;
"о0
2T
ХЛТ) = — J4(t)A(t-T)sm((o0t)clt;
0 о
/#(г) = (lM, )arg(Xc (t),Xs (г)), (15.38)
582
Навигационно-временные определения, основанные на фазовых измерениях
arg(jc,>>) - аргумент комплексного числа х + iy
Плотность р2(г>г</) приведена на рис. 15.6. Учитывая характер данной
плотности, предлагается ввести аппроксимацию одного из периодических
фрагментов в расширенном пространстве т=|г rd\T двумерной нормальной
плотностью в соответствии с методикой гауссовской аппроксимации [15.1] с
последующим периодическим продолжением по rd :
ЫГ)=СХ^2 Т>
к=-оо
Md+kT0
,R
где
//0=max l[^r(r)exp(jT(r))]
(15.39)
(15.40)
— оценка задержки сигнала по огибающей; jud =//(//0) — оценка задержки
сигнала по фазе ВЧ (\o)0jud\ <л);
Rl=-
дт
др2(х)
дт
Н>"0 Mdf
-д2[х(т) + Ыррг(т)]/дт2 0
0 ^X(t)jt = Mq
Максимумы плотности (15.39) расположены в точках с координатами
Аппроксимация для апостериорной плотности р(т) получается из (15.34),
(15.35) и может быть представлена в виде
оо
Р(т) = Z^(r'f(*)'*r)' Pk=cNl(k,k,Rk),
к=-оо
где
f = (R22^0+Rn(Md+kT0))/(Rn+R22); к = (ц0 -Md)/To ;
Rr - Rl \R2l/{Rl 1 + Л22 ) '■> Rk={RU+ Л22 )/Т0 •
(15.41)
(15.42)
Выбирая в качестве оценки задержки сигнала значение, соответствующее
максимуму АПВ, и полагая, что нормальные плотности в сумме (15.42) не
перекрываются, получаем
г = г(*); k = max~l Nl(k,k,Rk) = mm~lUk-kf =[£] . (15.43)
583
Глава 15
Уравнения (15.34), (15.40), (15.42), (15.43) дают решение поставленной
задачи.
В приведенном алгоритме с учетом (15.41) оценка задержки формируется
как взвешенная сумма оценок, полученных по огибающей (15.40) и фазе (15.38)
сигнала, причем в последней учитывается оценка целого числа периодов
ВЧ. Оптимальную оценку задержки можно представить в несколько ином виде,
если в (15.41) подставить выражение для jud из( 15.42), что приведет к
соотношению
f = Mo+Rn(k-k)T0/{Rn+R22), (15.44)
из которого следует, что оценка задержки, полученная по огибающей сигнала,
уточняется по результатам оценки числа периодов неоднозначности. Из
(15.43), (15.44)видно, что главный максимум АПВ р(х) совпадает с
максимумом p2(r,rd) по дополнительной задержке, ближайшим к оценке задержки,
полученной по информации из огибающей и априорным сведениям. Обе
приведенные трактовки эквивалентны. Однако при выводе более общих
алгоритмов, которые будут рассмотрены ниже, удобнее использовать представление
(15.44).
15.3.3. Оценка задержки двухчастотного когерентного
радиосигнала
Рассмотрим задачу оценивания задержки двухчастотного когерентного ра-
2
диосигнала S(t -т) = A(t - г) / ^cos\27rfj (t - т) \, принимаемого на фоне БГШ.
Этот сигнал относится к классу сигналов, содержащих несколько
периодических зависимостей от оцениваемых параметров, и его можно записать как
£(/,г,У\(т),<р2(т)), где q(r) = -2;r/jr ; %(r) = -2^/2r. Функция £(•)
периодична по <Pi(t) и ^(г) . Такое представление является основой общей
постановки задачи.
Аналогично (15.37), при времени наблюдения Т »l/|/j - f2\ АПВ
задержки р(т) описывается выражением
H0=c/v(r)exP
X^(r)cos©y(r-//y(r))[f
U=1
где Xj(г) = >/4 (г)+ 4 (');
584
Навигационно-временные определения, основанные на фазовых измерениях
X^(T)^ — jy(t)A(t-T)cos(a)jt) dt\ XsJ(t) = — jy(t)A(t-T)sva(a)jt) dt;
/,y(r) = (l/u>y)arctg(Xsy(r)/Xcy(r)).
На рис. 15.7, а приведена
реализация (кривая 7) АПВ задержки
двухчастотного сигнала с
смодулированной несущей, полученная
моделированием. Кривая 3 соответствует
плотности вероятности при отказе от
информации, содержащейся в фазе
высокочастотного заполнения.
Моделирование выполнялось при
А2Т/М0=4, fj=gjf09 ft =7,
£2=9,Л=100МГц.
Из рисунка видно, что
отсутствует регулярность расположения
максимумов АПВ. Применение
аппроксимаций, основанных на одномо-
довом характере огибающей АПВ,
очевидно, невозможно.
В соответствии с методом
дополнительной переменной вводим
расширенный вектор т= r,r^ rd2\ .
Выполнив шаги, аналогичные
приведенным в п. 15.3.2, приходим к
выражению для аппроксимации АПВ
(подробный вывод — в [15.11])
-3,3310* -1,6710~9 О
а)
1,6710 ъ.с
3,33-10
1,6710 J
-9 Ь^"
-з,ззю Y
-3,33-Ю9 ""1,67-10 9
1,6710 Гё1Л
6)
Рис. 15.7. Апостериорные плотности
вероятности
оо оо
к\=-оок2=-со
где f = ^)+Rr|kRj;1(k-k); к = [к\ к2]т; к =
(15.45)
Mp-Mdi Mo~Md2
585
Глава 15
RT -Ru- RjkRk RLk; Rr -
Г *и
Rr|k
Rr|k]
Rk
; Rr=TRTT;
(15.46)
T =
1 0 0
1/7] -1/7] 0
\/T2 0 -1/7V
д2(Хх(т) + Х2(т))
Rk =
дт2
0
0
0
0
*taM 0
0
со-
■X2(r)
t = Mo
/i0, judl, jud2 — параметры распределения p2 (г), аналогичного (15.39).
Как видно из(15.45), дискретное распределение p^ki аппроксимировано
дискретизированной двумерной нормальной плотностью.
Оценка задержки сигнала по критерию максимума АПВ при не слишком
больших RT определятся как положение максимума Л^(г,г (к),Лг) по г при
(к), максимизирующем ркхк2 = /\ (к),
т = f (к), к = тах/>к (к) = mirT1 Г(к-к)Т Rkl (к - к) 1. (15.47)
При получении оценки в соответствии с (15.47) необходимо провести
целочисленную минимизацию квадратичной формы. Так как матрица Rk
недиагональная, то в общем случае необходимо осуществлять перебор
целочисленных комбинаций [к\ к2\
На рис. 15.7, а кривой 2 дана аппроксимирующая функция р(т),
вычисленная согласно (15.45), (15.46). Вертикальной линией отмечено положение
оценки задержки по критерию максимума АПВ, выполненной в соответствии с
(15.46). Можно отметить хорошее качество аппроксимации, так как она точно
задает высоты и положения локальных максимумов АПВ.
На рис. 15 7, б приведена карта сечений равного уровня р2(т)) по
дополнительным задержкам rdu rd2 . Большим уровням сечений соответствуют
более светлые тона. На рисунке показано, как сечением гиперплоскостью,
соответствующей S{rd2-rdx) (прямая Td2=rdl на рис. 15.7, б), периодические по
Td\xd\ и rd2 максимумы р2(т) формируют нерегулярные максимумы АПВ за-
586
Навигационно-временные определения, основанные на фазовых измерениях
держки. Наглядно демонстрируется насколько МДП упрощает работу с
многомодальными АПВ, многопиковый характер которых обусловлен наличием в
наблюдаемом сигнале периодических функций оцениваемого параметра.
15.3.4. Общая задача оценки параметров при наличии в
наблюдениях периодических функций
До сих пор рассматривалась задача оценки задержки х по огибающей и
фазе радиосигнала, т.е. фактически задача синтеза алгоритма первичной
обработки с учетом фазовых измерений. Однако метод дополнительной переменной
универсален и может успешно применяться для многих других задач синтеза, в
том числе синтеза алгоритмов вторичной обработки. Приведем общее решение
задачи синтеза алгоритма оценки вектора X с размерностью q, априорные
сведения о котором задаются априорной плотностью вероятности ррг (X).
Имеем N-мерный вектор наблюдений (N>q)
§ = 8(т0(Х),т^(Х)) + п, (15.48)
где п — вектор гауссовских ошибок с нулевым средним и корреляционной
матрицей Vn.
Сигнальная функция, входящая в (15.48), зависит от X через две группы
функций т0(Х) и тДх), причем зависимость от каждого мго элемента
вектора Гр,-(X) является периодической с периодом Ti9i= l...n (n<N):
s(x0(X),%(X) + Tk) = S(x0(X),^(X)),
где к — целочисленный вектор; Т = diag„ (7]).
Введение однозначной зависимости сигнала от X через т0(Х) не является
обязательным и отражает особенности навигационных приложений.
Представление уравнения наблюдения в виде (15.48) охватывает
большинство задач радионавигации на основе фазовых измерений, в том числе и задачу
дифференциальных НВО в СРНС на уровне вторичной обработки.
В соответствии с МДП введем вектор дополнительных переменных
xd = Ху (X), элементы которого будем полагать независимыми один от другого
и от вектора оцениваемых параметров X. Полагая априорное распределение
каждой i-и компоненты вектора дополнительных переменных равномерным на
периоде длительностью Th запишем соотношение для априорной плотности
вероятности расширенного вектора Хр =Гхт rTd 1 :
587
Глава 15
Ppr{Xp) = PPr(X)YlpPr(rdi)=PPr{X)flVTi . (15.49)
Исходя из (15.48), выражение для апостериорной плотности вероятности
расширенного вектора оцениваемых параметров запишем в виде
p(Xp) = cjPpr(Xp)^ft,S(Xp),Vn),
где S(Xp) — сигнальная функция, входящая в (15.48), но представленная как
функция расширенного вектора Хр.
Плотность вероятности р(Хр) — строго периодическая функция вектора
дополнительных переменных, поэтому, как и в рассмотренных выше задачах,
достаточно аппроксимировать один из периодических ее фрагментов. В
соответствии с методикой гауссовского приближения запишем
аппроксимирующую функцию
р(хр)=с£...£...£ n
к] =-оо kj =-oo к м =-оо
(
N
ux*j
\
,R
(15.50)
где
Rn
R
max
хр
R
/>К),
0<р
Щ<р
R
<р
д
(
дХг
д
дХг
Лп(р(Хр))
х=ц0
Так как искомая АПВ р(Х) определяется из АПВ расширенного вектора
р(Х) при xd = тф(Х), то для получения искомой аппроксимирующей плотности
р(Х) необходимо аналогичную процедуру проделать с (15.50), т. е.
р(х)=с £...£...£ n
к^ =-оо kj =-oo kft =-oo
N
VL
Мх)
Ио
R
(15.51)
Таким образом, найдена аппроксимация полимодальной АПВ с негауссов-
ским описанием ее локальных максимумов, что обусловлено наличием
функции тф(Х). Однако для многих задач НВО допустимо использовать линейное
приближение зависимости тф(Х) от вектора оцениваемых параметров в
окрестности оценки Но, полученной на основе информации из однозначных
измерений и априорных сведений. Полагая
тДХ)*тДцо) + Н(Х-Цо), (15.52)
588
Навигационно-временные определения, основанные на фазовых измерениях
где Н = Лр(ц0)/г?Х, подставляя данное соотношение в (15.51) и выполняя
необходимые преобразования, получим
00 00 00
Р(*)= Z -X - Z л(к)^(хД(к),Кх),
к] =-оо kj=-<x) /гдг=-оо
^(k) = ^„(k,k,Rk). (15.53)
Здесь
X(k) = ji0+Rx|kR,;,(k-k), к = Т-1(^-тДц0));
RX|k = R0 -RXkRkRXk> RXk =(R0^-RoHT)T >
Rk =t-1 [hr0ht -hr0^ -r;^ht +r^]t-1 . (15.54)
Выражение для итоговой оценки вектора X по критерию максимума АПВ
при условии, что локальные максимумы р(Х) практически не перекрываются
(что выполняется при малых значениях корреляционной матрицы Rxik),
записывается аналогично (15.47):
X = Х(к), к = max"1 рк (к) = min"1 Г (к - к)Т R;;1 (к - к)1. (15.55)
15.3.5. Задача фильтрации при наличии в наблюдениях
периодических функций
При рассмотрении в предыдущих параграфах задачи оценки
предполагалось, что оцениваемые параметры постоянны за время наблюдения. Однако
при больших временах наблюдения это допущение не выполняется, т. е.
оцениваемые параметры следует считать меняющимися во времени. В этом случае
следует рассматривать задачу фильтрации случайных процессов [15.1, 15.2,
15.5].
Задачу фильтрации в условиях присутствия в наблюдении периодических
функций оцениваемых параметров сформулируем следующим образом.
Требуется выполнить оценку ^-мерного вектора Xv, который является марковским
процессом. Для простоты представления методики синтеза данный процесс
будем считать также гауссовским. Так как в аппаратуре реализуется дискретная
обработка отсчетов наблюдаемых процессов, динамику оцениваемого вектора
зададим разностным уравнением
Xv=AXv4+nXtV, (15.56)
589
Глава 15
где nx v — дискретный белый гауссовский шум с нулевым средним и
матрицей дисперсий Dx; v — номер отсчета времени.
Векторное уравнение наблюдения для дискретного времени имеет вид
§v=S(v,x0(Xv),^(Xv)) + nv, (15.57)
где s(v,T0(Xv),Tp(Xv)) — функция, периодическая по аргументу х<р(Ху); пу
— дискретный белый гауссовский шум с нулевым средним и матрицей
дисперсий Dn.
Расширение вектора оцениваемых параметров для решения задачи синтеза
осуществляется так же, как в предыдущем разделе:
При этом априорная плотность вероятности определяется выражением
(15.49).
Для новой дополнительной переменной необходимо записать уравнение
состояния, характеризующее ее изменение во времени. Для этого представим
Vv=Vv_1+^(Xv)-x^(Xv_1). (15.58)
Разлагая функцию т^(Хк) в ряд в окрестности точки Xv_jXv.i
(аналогично (15.42)), выражение (15.58) запишем в виде
*d,v = Vi + HAXv i + Anx,v > (15-59)
гдеН = Л^(Х„_1)/^Х.
Используя (15.56) и (15.59), запишем уравнение динамики для
расширенного вектора:
Xp^Gp^Xp^J + n^, (15.60)
X.
nXv — гауссовский шум с нулевым средним и матрицей диспер-
где npv =
сий Dpv =
я
А
я
А
D,
VT
^-мерная единичная матрица.
Задачу фильтрации расширенного вектора состояния, описываемого
уравнением (15.60) при наблюдениях (15.57), можно решать известными методами
оптимальной нелинейной фильтрации [15.1, 15.5]. Аналогично тому, как это
было сделано в п. 15.3.4, можно доказать, что АПВ /?(v,Xp J строго
периодична по элементам вектора xd, поэтому аппроксимация АПВ может быть задана
через аппроксимацию одного из ее периодических фрагментов.
590
Навигационно-временные определения, основанные на фазовых измерениях
Оценку параметров гауссовской аппроксимации одного из максимумов
АПВ p(v,Xp) можно получить с помощью расширенного фильтра Калмана:
HP,v = Gp,v (lV-i) + R^V (^ -%GP)V, (np>vM))),
r;1 =(ap<vr,_1a^ +dPi,)_1 +Hjvn-1H,,
(15.61)
где Hp=[n5ni] — оценка вектора Xp; s(*,GPfi,(nPf„_,)) — сигнальная
функция, входящая в (15.57), но представленная как функция в точке
экстраполированной оценки расширенного вектора:
Hv = Gp,v (l»p,v-l ) > \,v = ^Gp,v (Цр.и-1 )/^Хр >
H^^S^.Gp^Hp,,.,))/^.
Периодическое продолжение локального максимума дает аппроксимацию
АПВ pv(Xp) в тождественном (15.50) виде.
Искомая АПВ ру{Ху) получается из /\,(Хру) на основе общего
принципа МДП (15.34), т.е. ру(Ху) = ру(Хр,у)
, тем самым осуществляет-
\Xd -X(p\X>v)
ся переход к соотношению, аналогичному (15.51) и соответствующему
моменту времени v:
uu yjo vu
/T
£j =-oo Л • =-oo Лдг =-оо
Ho,v
>RK
K(x,)j'L^v+Tk_
Далее, как и в задаче оценивания (п. 15.3.4), линеаризуем т^(Ху) в точке
оценки ц0 (оценки вектора Х^), формируемой фильтром Калмана (15.51):
xp(Xv)«xff(xv) + Q(xv-Xv)9
а корреляционную матрицу представим в виде
■R =
1*0 ^0<р
Ro?
R
<р
После проделанных преобразований апостериорная плотность ру(Х)
записывается в виде, аналогичном (15.53):
591
Глава 15
оо оо оо
/V(X„)= X -Z - Z Pk(k)^(XK,Xv(k),Rx),
/q =-oo fc • =-oo /гдг =-oo
Pk(k) = ^(k,k,Rk),
где
X,(k) = Ho,v+RX|kRk1(k-k); к = Т-,(ц^-тДц0)1/));
RX|k = R0 ~RXkRk RXk ' RXk =(R0^-RoQT)T >
Rk =T-1[QR0QT-QR0^-R^QT+R^]T-1. (15.62)
Итоговые оценки вектора состояния Xv и целочисленного вектора к,
понимаемые как оценки максимума АПВ, определяются в соответствии с (15.55).
Полученный алгоритм фильтрации процесса Ху состоит из уравнения фильтра
Калмана и процедуры итоговой оценки, включающей процедуру разрешения
неоднозначности, реализуемую посредством беспереборной процедуры или, в
общем случае, через процедуры перебора целочисленных комбинаций.
Процедура итоговой оценки по виду совпадает с задачей оценки постоянных
параметров, рассмотренных в ряде известных статей [15.16, 15.17].
Главное отличие предложенного алгоритма фильтрации от задач оценки
по критерию максимума правдоподобия [15.16, 15.17] заключается в
значительном улучшении качества разрешения неоднозначности с увеличением
времени фильтрации. За счет введенной в МДП жесткой связи динамики
изменения Xv и %d дисперсии ошибок оценки Xv с выхода фильтра Калмана со
временем будут существенно уменьшены по сравнению с ошибками оценки
Xv, полученной только по огибающим сигналов. Не менее важен и другой
эффект фильтрации: корреляционная матрица ошибок фильтрации
неизменяющегося во времени вектора xdv-x(p{Xv) с увеличением времени фильтрации
уменьшается, стремясь к нулю. Следовательно, Rk также стремится к 0.
Поэтому с увеличением времени фильтрации повышается достоверность
разрешения неоднозначности и уменьшается объем области перебора
целочисленных комбинаций при решении задачи целочисленной минимизации. Этот
эффект позволяет в ряде случаев отказаться от переборных алгоритмов
разрешения неоднозначности и повышает эффективность рассмотренной выше
беспереборной процедуры.
592
Навигационно-временные определения, основанные на фазовых измерениях
15.3.6. Модифицированный алгоритм фильтрации с разрешением
неоднозначности методом дополнительной переменной
Как отмечалось, для описания неоднозначности измеряемых параметров
вводят целочисленный параметр неопределенности к, характеризующий
отклонение истинного значения параметра от его оценки. Вместе с тем, к
является параметром АПВ и непосредственно не присутствует в принимаемом
сигнале, поэтому при использовании МДП в одноэтапных алгоритмах и на этапе
первичной обработки в качестве дополнительных переменных
рассматриваются параметры АПВ, эквивалентные параметрам, оцениваемым по однозначным
измерениям. В СРНС такими параметрами являются псевдозадержки сигналов
различных НС. На этапе вторичной обработки в СРНС параметры
неоднозначности непосредственно входят в состав измерений псевдофазы сигналов НС,
что позволяет осуществлять их оценивание. Кроме того, фазовым измерениям
свойственны перескоки, характеризуемые скачкообразным изменением к,
поэтому включение параметров неопределенности в состав оцениваемых
параметров позволяет корректно ставить и решать задачу оценки параметров при
наличии перескоков в ФИ.
Ниже рассмотрен алгоритм фильтрации с разрешением неоднозначности
методом дополнительной переменной, ориентированный на этап вторичной
обработки. Алгоритм ориентирован на фильтрацию векторного параметра X
при наличии неоднозначных измерений в дискретном времени и может быть
легко распространен на случай фильтрации в непрерывном времени.
Пусть в результате измерений на v -м шаге фильтрации доступны два
случайных вектора:
§v=S^(Xv) + n^, (15.63)
n,=S^(XJ + k,+n7,v- (15-64)
где $v=[6 -£N]T, Цу=[т ••• *?м]т> Xv=[*i -*JT;
kv=[A:1 ... км\ ; n^v=yn^x ... «^J ; n^^ =^nnl ... nnM j ;
£,. eZ, / = 1,...,M, L<N < M, v = \,..,T;
S^V(XV) и S7V(XV) — векторные функции параметра X; n^ и n^ —
векторы дискретных белых гауссовских шумов, характеризующих шумы
измерений, причем дисперсия измерения компонент вектора ц значительно меньше
дисперсии измерения компонент вектора ^ (D « D^).
Уравнение (15.63) описывает однозначные измерения параметра X, а в
уравнение (15.64) входит неоднозначность, описываемая целочисленным
вектором к. Сразу отметим, что модели измерений псевдодальности и псевдофа-
593
Глава 15
зы, выполняемые в СРНС, описываются выражениями, подобными (15.63) и
(15.64) (см. п. 15.1.3).
Динамика параметра X описывается уравнением
Х,=ФДх,-1) + пХд/, (15.65)
где ФУ(ХГ_1) — векторная функция параметра X; nXv — вектор
формирующих дискретных БГШ с нулевым математическим ожиданием и
корреляционной матрицей Dx .
При отсутствии срывов в схемах слежения за фазой сигнала значение
вектора к сохраняет свое значение постоянным во времени и может быть описано
следующим уравнением состояния:
kv=kvM. (15.66)
Для описания динамики вектора к могут использоваться любые, сколь
угодно сложные модели, позволяющие учитывать наличие перескоков (cycle
sleep) в фазовых измерениях, однако данные модели не являются частью
рассматриваемого метода и поэтому здесь не приводятся.
В общем случае априорные сведения о X, и к задаются смешанной
плотностью вероятности ррг(Х,к). Значение к для различных каналов в
значительной степени связано с конструктивными особенностями схем захвата и
слежения и в большинстве случаев весьма неопределенно. Однако существуют
алгоритмы фильтрации при наличии неоднозначных измерений, в которых
априорная информация о значении к , задаваемая общем случае законом
распределения pk(k), может оказаться существенной. Например, если в начальный
момент осуществлять приведение неоднозначных измерений Т| к интервалу
[0,1) (т.е. 0 < (kpr + S^ (Xpr и < 1), то значения к сильно коррелированны с X,
а диапазон возможных значений к определяется априорной
неопределенностью знания X.
Для синтеза алгоритма фильтрации вместо вектора к введем вектор км,
который по физическому смыслу соответствует переменным к в выражении
(15.64), но в отличие от них, компоненты вектора kR не являются
целочисленными, а принимают непрерывное множество значений. Вектор км в
соответствии с (15.66) также является постоянным во времени. В соответствии с МДП
априорная плотность вероятности /? (X,kR) выбирается так, чтобы
выполнялось равенство /? (X,k) = cp (X,kR = к), где с — нормировочная константа.
В данной постановке для определения параметров АПВ с использованием
уравнений наблюдения (15.63), (15.64) и уравнений состояния (15.65), (15.66)
можно применить методику локальной гауссовской аппроксимации [15.1]. То-
594
Навигационно-временные определения, основанные на фазовых измерениях
гда параметры АПВ определяются с использованием уравнений расширенного
фильтра Калмана
R;1 = (AVRVATV + % )_1 + H* V/!H„,
где XPtV =[xj kR>v,] ; §л„ =[§J ijj] ;
~дФ1У(Ху)/дХу jo"
(15.67)
(15.68)
H„ =
R. =
asj^J/ax, | о
asj(V)/ax,,|i
Rx [R
Xk
Rxk ! Rk
• A =
¥.,=
0
Dx, JO
........ _^__
V^ представляет собой корреляционную матрицу шумов измерений.
Апостериорная плотность вероятности р (X,kR) является нормальной.
Получение АПВ р (Х,к) при целочисленном к осуществляется простым
переходом pps(X,k) = cpps(X, kR =k). Совместную АПВ pps(X,k) можно
преобразовать к виду
Pps{X,k) = p(X\k)p{k),
где ^(x|k) = ^(x,mx(k),Rx(k), />(k) = ctf(k,kR,Rk),
mx(k) = X + RXkRk1(k-kR), (15.69)
Rx|k =Rx~RxkRk Rxk • (15.70)
Апостериорная плотность вероятности параметра X определяется
выражением
00 00
Р(Х)= £ ... £ p(k)Ar(x,mx(k),Rx|k).
*i=-°° *л/=-°°
Если дисперсия оценок компонент вектора к удовлетворяет соотношению
Rk//«1 (i= \...M), то оценка вектора X будет определяться согласно
следующему решающему правилу:
595
Глава 15
X™ = mx (к), к = max"1 p(k), (15.71)
v ' к
где "РН" при X означает, что оценка выполняется после разрешения
неоднозначности измерений.
В качестве оценки X выбирют mxfk) (выражение (15.69)), где к —
целочисленный вектор, обеспечивающий максимум р(к), что эквивалентно
минимуму квадратичной формы (к - kR J R^1 (к - км J. Точность получаемой оценки
будет определяться выражением (15.70).
Аналитического выражения для нахождения к не существует, определе-
ние к осуществляется посредством целочисленной минимизации
квадратичной формы.
Искомая оценка Хрн =mx(k], согласно (15.69), включает два слагаемых.
Первое представляет собой оценку параметра X, получаемую из уравнений
расширенного фильтра Калмана, и содержит составляющие погрешности,
обусловленные неточным знанием вектора параметров неопределенности к. В этом
отношении второе слагаемое является компенсационным, так как в случае
точного определения вектора к позволяет полностью исключить эти погрешности из
X, получив, тем самым, высокоточную оценку параметра X. Точность получае-
мой оценки при безошибочном определении вектора к характеризуется
выражением (15.70).
15.4. Алгоритмы навигационно-временных определений
при использовании фазовых измерений
15.4.1. Постановка задачи синтеза алгоритма
навигационно-временных определений
Рассмотрим задачу синтеза алгоритма фильтрации относительных
координат двух приемников. Рассмотрение данного алгоритма актуально в связи с
развитием и широким использованием в настоящее время режима
дифференциальной навигации в СРНС.
Представим модели измерений (15.22), (15.23) в матричном виде:
A^=HvXP>v+nv, (15.72)
где Ag =[A^V ... A#,v А&у ... Д#„] ; < =
п
D,v
П
N
П
D,v n<py
-<л
596
Навигационно-временные определения, основанные на фазовых измерениях
XPv = АХ* Vj aj А* и Sv kj — расширенный вектор состояния,
включающий параметры взаимного перемещения НАП AXV , V„ и av, смещение их
ШВ Ап v и £v, а также параметры неоднозначности псевдофазовых измерений
kT-IV kN 1-
н„ =
Gv
Gj
0tfx3
®7Vx3
®Nx3
®Nx3
C Otfxl 1 ®NxN
* 1 ®Л^х1 J Itf
J G -
КГ-КУ
G* =
I
#
(G')Т/Я" ... (G?)T/l"] ; cT = [c ...c]; Г = [/ .../„];
единичная матрица размерности N , где TV — количество
радиовидимых НС; шум наблюдений имеет корреляционную матрицу V^.
Динамику относительных координат, смещения ШВ и вектора параметров
неоднозначности опишем выражением
(15.73)
^Р,у - ^Р,у^Р,у-\ + ПР,у >
где А^ =
м{пРл,
\ К
®NxN
UP,v} =
"NxN
*N J
1>P.v =
'■> nPv -[nZv®lxNJ '
^Z>v "ПхЛГ
0
ЛМ1 ОухА'
15.4.2. Общая методика синтеза алгоритмов НВО с использованием
фазовых измерений в СРНС на этапе вторичной обработки
Синтез алгоритмов НВО в СРНС на этапе вторичной обработки может
быть выполнен на основе модифицированного алгоритма фильтрации с
разрешением неоднозначности методом дополнительной переменной. Решение этой
задачи можно разбить на ряд этапов.
1. Модификация уравнений наблюдений (15.72), состоящее в замене
целочисленного вектора параметров неоднозначности к непрерывнозначным
вектором кк с целью упрощения алгоритмов нахождения параметров АПВ.
2. Определение АПВ векторного параметра Хр. С учетом линейности
уравнений наблюдения (15.72) и состояния (15.73) параметры АПВ
определяются с использованием уравнений фильтра Калмана:
Хл„ = APtVXp,y-i + R„HJV (А^ - HvАл„ХЛ1М)
597
Глава 15
R;1 = (XPvRv ATPfV + DPv )"1 + HTV V^ lH
3. Определение параметров для аппроксимации АПВ. На этом этапе
осуществляется обратная замена вектора kR на целочисленный вектор к и АПВ
представляется в виде p(Z,k) = cp ps(Z,kR =k)= = cp(z|k)p(k).
4. Итоговая оценка вектора относительных координат и взаимного
смещения ШВ объектов выполняется на основе определения вектора параметров не-
однозначности псевдофазовых измерений k = max Рук) путем целочислен-
k
ной минимизации квадратичной формы. Оценка вектора параметров
z: =
V
AKl V; aj An>v Sv
определяется как ZPVH = ZV + RzkRk* (к -kRv J, где
Zv и kRv — оценки параметров АПВ, получаемые из уравнений фильтра
Калмана; Rk и RZk — корреляционная матрица ошибок оценки вектора
неопределенности kR и взаимная корреляционная матрица ошибок векторов Z и
kR соответственно.
Следует отметить, что в стационарном режиме корреляционная матрица
ошибок фильтрации Rv Rv является постоянной или слабоменяющейся,
поэтому при разрешении неоднозначности нет необходимости рассчитывать заново
матрицу преобразования координат U в каждый момент времени. Достаточно
взять матрицу преобразования, рассчитанную на предыдущем такте. Кроме
того, в общем случае в качестве начального значения при вычислении матрицы
Vv на v -м шаге может быть взята \]у_} из предыдущего шага. Использование
подобного подхода позволяет существенно сократить вычислительные затраты,
связанные с расчетом матрицы U.
15.4.3. Результаты экспериментальных исследований
Экспериментальное исследование алгоритмов с использованием
данных, записанных приемником Trimble 4000SSE
Условия проведения эксперимента. Эксперимент проводился 17 октября
1993г. в г. Менделеево Московской обл. на аппаратуре АО «Прин» (Москва).
Осуществлялась запись измерений РНП по сигналам НС в двух частотных
диапазонах (L\ и L2). При записи РНП два приемника TRIMBLE 4000SSE были
размещены в двух фиксированных точках (под точкой размещения приемника
здесь и далее будем понимать координаты фазового центра антенны
приемника) с точно известными координатами (далее будем обозначать их А и В, точку
В будем считать базовой). Дискретность снятия отсчетов РНП составляла 15 с.
Координаты точек в геоцентрической системе координат WGS-84:
598
Навигационно-временные определения, основанные на фазовых измерениях
хА = 2844650,425 м, уА =2161039,687 м, zA = 5266366,966 м, высота антенны
hA = 0,848 м; хв = 2845453,477 м, ув = 2160937,391 м, zB = 5265976,262 м,
hB = 0,349 м, что соответствует относительным координатам фазовых центров
антенн Ах = 802,829 м, Ду =-102,465 м, Az =-391,117 м и длине базовой
линии г = 898,892 м. В точке А запись РНП производилась с 9 ч 31 мин 30 с до 14
ч 6 мин 15 с, в точке В — с 10 ч 28 мин 00 с до 13 ч 28 мин 30 с. За время сеанса
записи в радиовидимости находились от 4 до 6 НС СРНС GPS с системными
номерами: 1, 7, 14, 15, 18, 19, 22, 24, 25, 29.
Отсчеты РНП содержатся в двух файлах, полученных от приемников в
точках А и В. РНП представляют собой псевдодальности и полные фазы на частотах
II и 12 (коды С/А и Р соответственно, Ll= 1575,42 МГц, L2 = 1227,6МГц)
для всех радиовидимых в момент снятия отсчетов НС СРНС GPS. Здесь и далее
единица измерения псевдодальности - метры, псевдофазы — циклы
(количество длин волн).
Алгоритм оценки относительных координат. Учитывая небольшое
расстояние между точками приема сигналов для первой разности измерений
псевдодальности и псевдофазы можно записать следующие выражения:
дЙ1,у = GjJAX, + cA*nv + nj^Xv , j = \,..,N,
A%D2,v = G^AX^ + c(A^v + AAn,v ) + nAD2,v >
nA<plv >
Д#2>„ =Gi/SXy/AL2 +/l2(a;,v + Дап,„) + ^2 +
где индексы 1 и 2 соответствуют измерению РНП по сигналам НС на частотах
Ы и 12 соответственно; АХУ — вектор относительных координат
приемников, соответствующих моменту выполнения измерений tv;
GJV =ldDixB(tv),XJuc(t3Tv))/дХ I — вектор-строка направляющих косину-
сов из точки В нау'-й НС; Ап — взаимное смещение ШВ приемников; Д^ —
дополнительное смещение, обусловленное различием задержек сигналов
различных частот в аппаратуре приемника; kJAl и kJA2 — параметры
неоднозначности псевдофазовых измерений; п^, п]^2, п}^ х и п[ 2 — дискретные БГШ,
характеризующие шумы измерений.
Использование того факта, что все НС в СРНС GPS излучают сигналы с
одинаковой несущей частотой, позволяет, выбрав один из НС базовым и вычтя
его измерения из измерений остальных НС, получить вторые разности
наблюдений, исключив тем самым составляющие погрешностей, обусловленные
599
Глава 15
влиянием взаимного смещения ШВ приемников и аппаратурной задержкой
сигналов. Получаем
VA^^VG^+^u,,
VA^^VG^AX^W,,
VA$,„ = VGlДХ„/Л£1 + k$Al + 4A<phv ,
VA^2v = VG;AX,A2 + k*A2 + л*д„2>„ , q = 2...N,
где VG^ =G^ -Gxv — вектор-строка направляющих косинусов для вторых
разностей (разность векторов направляющих косинусов на q-и спутник и первый
спутник, выбранный в качестве базового); k$Ai = к\{ - к\{, / = 1,2 ; «vadiv >
"vad2v > wva^iv и ^va^2v —эквивалентные дискретные БГШ для второй
разности наблюдений.
При получении первых и вторых разностей дисперсия шумов наблюдений
увеличивается, а шумы в каналах становятся коррелированными с
коэффициентом корреляции 0,5.
Представим уравнения наблюдения в матричном виде:
где К =[VA&i,v VA&2.V VA&.v VA^2,v] ;
^/?,v = [АХу kvAl ^VA2J >
т Г т т т т
nv -\_nVADl,y nVAD2,i- nVA<p\,v nVAp2,vJ>
М{пк} = 0, A/jnX} = V„;
(15.74)
H„ =
VGV, ] 0 i 0"
VGJALI jlfo
VG„/^2 | 0 } I
; v„ =
__
0
\j
(
__
0
) j
E^2
4 * = j>
E, , = <! ' '; I — единичная матрица; VGJ =
2, /' * У
'j
(VGJ)T,..,(VG^)T
При формировании матрицы шумов наблюдения Vv принималась гипотеза
о том, что измерения псевдодальности и псевдофазы для сигналов всех НС на
600
Навигационно-временные определения, основанные на фазовых измерениях
одной частоте выполняются с одинаковой точностью и, кроме того, измерения
псевдодальности и псевдофазы некоррелированы. Вместе с тем в настоящее
время широкое распространение получили алгоритмы первичной обработки в
СРНС, в которых измерение псевдодальности выполняется с использованием
фазовой поддержки от схемы ССФ. В этих условиях гипотеза о
некоррелированности измерений псевдодальности и псевдофазы несправедлива, что нужно
учитывать при синтезе алгоритмов вторичной обработки при высоком темпе
снятия данных от приемников. В рассматриваемом нами эксперименте
корреляция измерений псевдодальности и псевдофазы не наблюдалась.
Учитывая, что во время эксперимента приемники были неподвижны,
уравнение состояния для вектора относительных координат можно записать в
виде AXV = AX^.j.
В наблюдениях псевдофазы, записанных в ходе эксперимента, перескоки
отсутствуют, что позволяет записать следующее уравнение для вектора
параметров неоднозначности: кУД/> = куд/ у_х, / = 1,2 .
Таким образом, динамика вектора параметров X имеет вид
X^=X„,v-.- (15-75)
Уравнение наблюдения (15.74) в совокупности с уравнением состояния
(15.75) позволяет синтезировать алгоритм фильтрации относительных
координат двух неподвижных приемников. Согласно методике, изложенной в п.
15.4.2, на первом этапе целочисленные векторы kVAll/ и kVA2 v заменяются не-
прерывнозначными векторами кш у и кМ2 , и согласно уравнениям
фильтрации Калмана, определяются параметры АПВ pps (AX,kR1,kR2) = Pps fap):
RF = Rv,_i + HvV^ Hv .
На втором этапе вводится обратная замена векторов kR1>v и kR2,v на
целочисленные куд1 и кУД2 , выполняется разрешение неоднозначности и
вычисление оценки относительных координат с использованием однозначных
фазовых измерений.
Учитывая, что приемники СРНС, способные выполнять измерения РНП на
частотах LX и L2 , достаточно дороги и недоступны широкому кругу
пользователей, рассмотрим алгоритм, использующий измерения только по сигналу С/А-
кода на частоте L\.
Использование выражений (15.74) и (15.75) позволяет легко получить
уравнения наблюдения и состояния для случая выполнения измерения РНП
только по сигналам НС на частоте II в СРНС GPS. Имеем
601
Глава 15
%v -HyXpfV +nv ,
x =x
PS
V,v-1 '
(15.76)
(15.77)
где К = [VA^,,„VA^ltV ] ; XTPtV = [AXTV к* Д1 ]; nj = [n
VADl,v nVApl
l,vj;
M{n,,} = 0; A/{nv<} = Vv; HK =
VGJ4, J I
;vv =
ED
D\
0
0
ЕД
Vi
Уравнения (15.76) и (15.77) используются для синтеза алгоритма
фильтрации относительных координат в той же последовательности, что и при синтезе
алгоритма с использованием измерений РНП на обеих частотах.
Экспериментальное исследование алгоритмов. При использовании
экспериментальных данных функционирование алгоритмов рассматривалось на
выборке из файлов наблюдений длиной 600 отсчетов. Определение дисперсий
измерений РНП выполнялось с использованием методики, изложенной в п.
15.1.4. На основе анализа полученных реализаций вторых разностей
псевдодальностей и псевдофазы были выбраны следующие дисперсии измерений:
псевдо дальности по сигналу с частотой L\ DDX =0,9м ; псевдодальности по
сигналу с частотой L2 DD2=0,5m2; псевдофазы на обеих частотах
^1=^2=Ь6-10"3цикл2.
На рис. 15.8 приведены результаты функционирования алгоритма,
использующего измерения на двух частотах, по оценке относительных координат точек
приема. Пунктирной кривой изображена ошибка фильтрации ех = Ах - Ахи без
разрешения неоднозначности, сплошной - после разрешения неоднозначности.
cos И
-о.кв
Рис. 15.8. Оценка относительных координат при использовании
измерений РНП на двух частотах
602
Навигационно-временные определения, основанные на фазовых измерениях
На рис. 15.9 приведены аналогичные кривые для алгоритма, использующего
измерения только на частоте L\. Отметим, что правильное разрешение
неоднозначности при двухчастотных измерениях произошло значительно раньше, чем
при использовании измерений на одной частоте.
т —\ i ~ 1 •—I 1
Рис. 15.9. Оценка относительных координат при использовании
измерений РНП на одной частоте
Из графиков видно, что наличие избыточности измерений за счет
использования сигналов НС на частоте L2 позволяет на порядок сократить время,
затрачиваемое на разрешение неоднозначности ФИ. Разрешение
неоднозначности при использовании измерений РНП на двух частотах осуществляется после
обработки 3...5 отсчетов наблюдений. В целом экспериментальные
исследования подтверждают возможность вычисления относительных координат
объектов при использовании ФИ в СРНС с точностью в единицы миллиметров.
Экспериментальное исследование алгоритмов с использованием
данных, записанных с приемника GG-24 Ashtech
Условия проведения эксперимента. Запись данных осуществлялась 18
ноября 1998 г. в г. Менделеево Московской обл. в течение 30 мин с 14 ч 14 мин
34 с по 14 ч 44 мин 42 с двумя примениками СРНС GG-24 фирмы Ashtech.
Приемники были размещены в двух фиксированных точках на крыше
административного здания. Относительные координаты фазовых центров антенн
составляли Ах = -7,389 м, Ау= 4,175 м, Az = -1,694 м и длине базовой линии
г = 8,655 м. Дискретность снятия отсчетов РНП составляла At = 1с. За время
сеанса записи в зоне радиовидимости находились от 4 до 9 НС СРНС GPS с
системными номерами: 2, 5, 7, 9, 15, 21, 23, 26, 27 и от 4 до 5 НС СРНС
ГЛОНАСС с системными номерами: 4, 6, 13, 15, 22. Отсчеты РНП содержатся в
двух файлах и представляют собой псевдодальности и полные фазы, измерен-
0Л5
<
-flft*
г о
-АОК
603
Глава 15
ные по сигналу стандартной точности, для всех радиовидимых в момент снятия
отсчетов НС.
Алгоритм оценки относительных координат. В ходе эксперимента
измерение РНП выполнялось по сигналам НС как СРНС ГЛОНАСС, так и СРНС
GPS. Рассмотрим последовательно алгоритмы фильтрации относительных
координат с использованием одной из систем, а затем совместно по двум
системам.
Алгоритм фильтрации относительных координат с использованием
сигналов НС СРНС ГЛОНАСС. Первую разность измерений
псевдодальности и псевдофазы можно записать в виде
где Nr — количество радиовидимых в момент выполнения измерений НС
СРНС ГЛОНАСС.
Остальные параметры уравнений аналогичны рассмотренным выше. При
записи уравнений считалось, что разности дополнительных задержек сигналов
различных частот в аппаратуре приемника пренебрежимо малы, поэтому в
выражениях не учитываются.
Модели состояния для относительных координат /SXV и параметров
неоднозначности к[г в условиях отсутствия перескоков по-прежнему задаются
уравнениями
AXv=AXv_l9 кАГу = A:ArvM , j = \9..9Nr.
Модель динамики относительного смещения ШВ приемника А* опишем
гаусс-марковской моделью второго порядка
К =АаК-\+ПАу>
где \у =
An,v ^ПТ
Ад =
' пдк — вектор дискретных БГШ с
1 At
О (1-адД*)
нулевым математическим ожиданием и матрицей дисперсий DA .
Учитывая, что в приемнике GG-24 используется кварцевый ОГ, то
параметры модели можно выбрать равными аА =КГ2с-1 и Ds = 10-8 с-2, где D5
— дисперсия формирующего шума для скорости изменения относительного
смещения ШВ 5. Остальные элементы матрицы DA определяются через D5 с
использованием известных формул [15.3].
В векторно-матричном виде уравнения наблюдения и состояния имеют вид
J^ = UvXPtV+nvt (15.78)
604
Навигационно-временные определения, основанные на фазовых измерениях
*-p,v - Ax*-p,v-\ + nx,v '
(15.79)
где С =[A&.v *%,.v]->XTp.v = [*% Av klv];
А,=
Gl =
[l
0
lo
0
Ад
О
О
О
I
;Н„ =
"G, 1 с | О'
Gkv | f | I
/° i ... i /° 1
т
; ст =
о
п
;Г =
\£i"i
[тр
,/Л]
о 1
(с',)т... (eft)*!; gJ =[(Gi.iV)T/4 ... (g£)7^T;
^A,v -|_^Д1> — ^\r>J > nv ~[nAD,v nA^,v J ^ n*v ~|_0,nAv,OJ;
M{nX} = V;M{nxX,} = ^;^ =
Го
0
0
0
DA
0
0
0
0
; v =
Щ> 1 О
о Тш
<p
Уравнения (15.78) и (15.79) используются для синтеза алгоритма
фильтрации относительных координат приемников в соответствии с п. 15.4.2.
На рис. 15.10 приведены результаты функционирования алгоритма по
оценке относительных координат приемников с использованием измерений НС
СРНС ГЛОНАСС.
04 hi
в 02 И
К
я
«"«■у ■**■>■»»■
1200 1400 t, с
Рис. 15.10. Оценка относительных координат при использовании
измерений РНП по сигналам ГЛОНАСС
Пунктирной линией на рис. 15.10 изображена ошибка фильтрации
ех = Ах - Ахи без разрешения неоднозначности, сплошной — после разрешения
неоднозначности.
605
Глава 15
Алгоритм фильтрации относительных координат с использованием
сигналов НС СРНС GPS. Уравнения наблюдения для РНП, измеряемых по
сигналам НС СРНС GPS, имеют вид
Д£/
Dv
■ Gi&Xy+cA'uy+nito,
Д#„ = GlАХ,/Я + /Д*я„ + к{ 4-nJAw, у = l,..,tf,
где N — количество радиовидимых в момент выполнения измерений НС
СРНС GPS; / и Я — частота и длина волны сигнала соответственно.
В векторно-матричном виде
где £ = [д^ Д£.„]; х;,„ =[ДХ; A, k^]; kA>„ = [*',„ ...*£„J;
н„ =
g; =
[G,
[ct
с
f
0"
I
;ст =
■[k)t»(<
С
(Г
1
> Gv =
;fT =
КГ/
Г/
0
-i/i
••• 0
?
i...(g?)V4
nJ=[nW пд^]; Af{nvnj} = v =
ш
Z)
о
о ю
р
Динамика вектора параметров X v описывается выражением (15.79).
Синтез алгоритма выполняется на основе общей методики синтеза алгоритмов
НВО при использовании ФИ п. 15.4.2.
На рис. 15.11 представлены результаты функционирования алгоритма по
оценке относительных координат между приемниками с использованием
измерений НС СРНС GPS.
а.41
S 0.2
~аш2
Рис. 15.11. Оценка относительных координат для измерений РНП по сигналам GPS
606
Навигационно-временные определения, основанные на фазовых измерениях
Пунктирной линией на рис. 15.11 изображена ошибка фильтрации
относительной координаты Ах без разрешения неоднозначности, сплошной — после
разрешения неоднозначности.
Алгоритм фильтрации относительных координат на основе
совместного использования сигналов НС обеих систем. Для синтеза алгоритма
фильтрации относительных координат с использованием измерений РНП по
сигналам РНП обеих систем используются модели наблюдения и состояния
(15.78), (15.79), где
К =[Aft,v Ы£г,у]\ ХТЛУ =[АХ^ А, к^];
Л -Гл* S А Т-к -IV kN к1 lcNr7-
н,=
G* =
cT =
Гс„
_GJ
с
f
0"
I
; Gv-
(dj ... (G?)T (G[,J .. (eft)''
{Glf/Л ... (Gf )T/l (C',)7^ ... (С#)У4
IT
lp
с
0
lo
...
...
...
с
0
0
с
0
с
...
...
...
с
0
с
;fT =
71
0
0
-j/1
••• | 0
1
... о
Л
0
Л
...
...
...
/Л1
0
/Л J
[I^D
0
0 1
Wv\
A =
[I
0
0
0
A*
AA
0
0"
0
I
' K X
"0
0
0
0
К
0
0"
0
0
Га 1 n~l Гт* ! л~1
> Ад =
Ад
о
и
~7
;»;=
л
0 0
L 1 J L 1 J
В состав вектора оцениваемых параметров включена разность
аппаратурных задержек сигналов НС СРНС GPS и ГЛОНАСС в приемнике,
обусловленная значительным различием частот излучаемых сигналов в обеих системах.
Отличием аппаратурных задержек сигналов различных НС в СРНС ГЛОНАСС
по-прежнему пренебрегаем.
На рис. 15.12 представлены результаты функционирования алгоритма по
оценке относительных координат на основе совместного использования измере-
607
Глава 15
ний РНП, выполняемых по сигналам СРНС ГЛОНАСС и GPS (пунктирная
кривая соответствует алгоритму фильтрации Ах с использованием ФИ без
разрешения неоднозначности, сплошная — после разрешения неоднозначности ФИ).
02 И
[f ' ■"" ""Т тш'
1;:' >\
II* * *
111 и. ,,
~Т~~"
J.
1 -1
.„ч,.у,.„*,1'а,.||,1Г|,м,*,мГ.,..^..и,*. .Т т.»
L„w. , , i
— г №,п
... 1
*"" "1 ~"'Г|"
L
1
1
1
J
G.002
1400 t с
Рис. 15.12. Оценка относительных координат при использовании
измерений РНП по сигналам ГЛОНАСС и GPS
Анализ характеристик, полученных в ходе экспериментального
исследования алгоритмов, показывает, что использование ФИ для дифференциального
режима НВО в СРНС позволяет вычислять координаты потребителя с
точностью до единиц миллиметров, при этом для разрешения неоднозначности
необходимо от 40 до 200 отсчетов наблюдений. Время, затрачиваемое на
разрешение неоднозначности определяется величиной ошибок измерений РНП и
наличием избыточных измерений. Увеличение числа измерений за счет
использования измерений на двух частотах или совместного использования сигналов
НС СРНС ГЛОНАСС и GPS позволяет существенно (на один-два порядка)
сократить время, необходимое на разрешение неоднозначности ФИ.
Алгоритмы фильтрации относительных координат с
использованием вторых разностей измерений аппаратуры
ГЛОНАСС и GPS
Если для измерений псевдофазы от НС GPS получение вторых разностей
наблюдений не составляет труда, то получение вторых разностей для
измерений псевдофазы от НС ГЛОНАСС затруднено, из-за различия несущих частот
сигнала от разных НС.
608
Навигационно-временные определения, основанные на фазовых измерениях
Представим уравнение наблюдения первых разностей фаз в единицах
измерения дальности в виде
Можно использовать следующий способ получения вторых разностей для
СРНС ГЛОНАСС. Пусть в качестве базового выбран НС, стоящий в списке
первым. Тогда из уравнений наблюдений на первых разностях получаем
наблюдения на вторых разностях
VA#„>V = VGf)VAX, +c + Zfkir -ЯХг +<,v -<.„ У = 2.JVr . (15.80)
Уравнение для вторых разностей измерений псевдофаз ГЛОНАСС
содержит слагаемое А/к^- - Я^к1АГ , коэффициенты при параметрах
неоднозначности /гдр равны длинам волн сигналов соответствующих НС ГЛОНАСС. Про-
1 с
изведем замену Я/, в [15.80] на А/ = /^ —, где Aq = — ; с - скорость света; F0
- наибольший общий делитель (НОД) для несущих частот сигналов СРНС
/
f
ГЛОНАСС; а, = —, /р - несущая частота i-ro НС. Для сигналов СРНС
1 /_i
ЛрЛдр Яр^др - Aq
(«i^ir-^ir) = Щ
axat v ' ад
ГЛОНАСС в диапазоне частот L1 НОД равен 562500, а а, =2540 + /, / = 1,24
Тогда,
При этом необходимо, чтобы разность ахк1^ - а^)^ = mt принадлежала
множеству целых чисел, а НОД{а{, ах) = 1
Такой подход позволяет согласованно привести псевдофазу СРНС
ГЛОНАСС к единому масштабу с сохранением целочисленности параметров
неоднозначности.
Такой способ формирования вторых разностей для измерений аппаратуры
потребителя от спутников ГЛОНАСС был проверен при исследовании
алгоритма двухсторонней интерполяции для относительных определений в СРНС с
использованием фазовых измерений [15.23].
Суть алгоритма двусторонней интерполяции состоит в вычислении
параметров движения в момент времен / по всей совокупности траектории
наблюдения доступной на момент времени Т > t. В задачах текущей фильтрации
оценивание связано с вычислением АПВ p(x\g ), ас помощью алгоритма
двухсторонней интерполяции вычисляется аппроксимация АПВ p(x\g )
20-1026
609
Глава 15
Эксперимент осуществлён с помощью двух двухчастотных приемников
фирмы Javad Positioning Sistems, один из которых был установлен на
автомобиле, второй в навигационной опорной точке. При этом производилась запись
данных на внутреннюю память приемников СРНС. Накопление
экспериментальных данных осуществлялось в ходе серии поездок, по выбранному участку
трассы. Всего было выполнено 20 проходов в направлениях «туда и обратно».
По итогам выполненных экспериментов получены траектории движения
автомобиля в системе координат геодезического репера опорной точки ENU (Е -
направление на восток, N - на север, U - вертикальное направление). Для
исключения влияния качества управления автомобилем на характер изменения
измеренной траектории, а также с учетом того, что погрешность измерения
вертикальной координаты приемником СРНС в 1.5 -г- 2.0 раза больше, чем
погрешность измерения плановых координат, последующий анализ проводится
только для вертикальной составляющей траектории движения автомобиля. В
горизонтальной плоскости плавность построенной траектории для
прямолинейного участка трассы определяется как погрешностями измерений, так и
ошибками управления, причем ошибки управления значительно превосходят
погрешности измерений. В вертикальной плоскости график изменения высоты
включает только практически погрешности измерений и профиль выбранного
для экспериментов участка трассы.
На рис. 15.13 приведены графики оценок профиля движения автомобиля
для нескольких проходов, полученных с помощью разработанного алгоритма.
Разброс оценок вертикальной составляющей траектории при нескольких
проходах не превышает 2 сантиметров, что можно объяснить вибрацией в
вертикальной плоскости при движении автомобиля.
1600 1700 1800 1900 2000 2100 2200 2300 2400 2500 fll
Рис. 15.13. Оценка профиля движения автомобиля в вертикальной плоскости
по измерениям РНП сигналов ГЛОНАСС и GPS
610
Навигационно-временные определения, основанные на фазовых измерениях
Представленный способ формирования вторых разностей не является
единственным. В [15.22] А.А. Поваляевым рассмотрен иной способ
формирования вторых разностей измерений псевдофаз спутников ГЛОНАСС
Заключение
В силу ограничений на объём 15 главы многие вопросы связанные с
использованием фазовых измерений в СРНС не рассмотрены. В частности
опущены вопросы, связанные с формированием измерений псевдозадержек и
псевдофаз в аппаратуре потребителя при различных способах коррекции
показаний часов приёмника. Не рассмотрены также вопросы компенсации
атмосферных погрешностей измерений при относительных определениях. Эти
вопросы подробно рассмотрены в монографии 2008 года [15.22]. Её автор А. А.
Поваляев один из российских пионеров использования фазовых методов в
спутниковых радионавигационных системах. Значительной составляющей этой
книги является обобщением мирового и личного опыта автора в области
обработки неоднозначных фазовых измерений для относительных определений в
СРНС.
Литература
15.1. Тихонов В.И. Нелинейные преобразования случайных процессов. — М.:
Радио и связь, 1986.
15.2. Поваляев А.А., Тюбалин В.В., Хвалъков А.А. Определение относительных
координат по радиосигналам системы ГЛОНАСС//Радиотехника, 1996, №4, с. 48—51.
15.3. Frie E., Beulter G. Rapid static positioning based on the fast ambiguity resolution
approach// FARA : theory and result. Manuscripta Geodetica, 1990, vol. 15.
15.4. Euler H.J., Landau H. Fast GPS Ambiguity Resolution on-the-fly for Real-Time
application// Proc. 6 International Geod. Symposium on Precise Positioning with the GPS,
Ohio, 1992, pp. 712-719.
15.5. Хорн Р., Джонсон Ч. Матричный анализ. — M.: Мир, 1989.
15.6. Пензин КВ. Синтез структуры многошкальных многопараметрических
систем// Радиотехника и электроника, 1990, т. 25, №11.
15.7. Jonge P.J., Tiberius С J. A new GPS ambiguity estimation method based on
Integer least squares// Proc. DNS94, 1994.
15.8. Graas F. GNSS Augmentation for high precision navigation servis// AGARD
lecture seris 2007, 1996.
15.9. AIpach D.L., Sorenson KW. Recursive Bayesian Estimation Using Gaussian
Sum pproximation// Automatica, 1971, vol. 7.
15.10. Харисов В.Н. Нелинейная фильтрация при полимодальном апостериорном
распределении// Изв. АН СССР. Сер. Техническая кибернетика, 1985, № 6.
15.11. Харисов В.Н., Новоселов 0.Ф. Общее решение задачи фильтрации
координат в дифференциальном режиме спутниковых радионавигационных систем//
Радиотехника, 1996, № 7, с. 65—69.
15.12. Харисов В.К, Перъков А.Е. Алгоритмы фильтрации при фазовых
измерениях// Радиотехника, 1997, № 7, с. 90—101.
611
Глава 15
15.13.Харисов В.Н., Булавский Н.Т. Экспериментальное исследование алгоритма
фильтрации относительных координат в СРНС NAVSTAR с использованием фазовых
измерений// Радиотехника, 1998, №7.
15.14.Харисов В.Н., Булавский Н.Т. Фильтрация относительных координат в
СРНС ГЛОНАСС: подход на основе сигнального времени// Радиотехника, 1999, №7.
15.15.Харисов В.Н., Булавский Н.Т. Беспереборный алгоритм синхронизации на
основе фазовых измерений// Радиотехника, 2000, №7, с. 75-79.
15.16. Харисов В.Н., Павлович Е.В. Усовершенствованный алгоритм расчета
времени распространения сигналов СРНС// Радиотехника, 1997, №7.
15.17. Розов Л.С., Собцов Н.В. Задача фильтрации в условиях неоднозначных
измерений// Радиотехника и электроника, 1980, т. 25, № 9.
15.18. Поваляев А. А. Вычисление характеристик качества и синтез
многошкальных измерительных устройств, осуществляющих оценку по критерию
максимального правдоподобия// Радиотехника и электроника, 1978, т. 23, № 1.
15.19. Пензин К. В. Алгоритмы оперативной обработки многошкальных
измерений по критерию максимального правдоподобия// Радиотехника и
электроника, 1990, т. 25, № 1.
15.20. Кнут Д. Искусство программирования на ЭВМ. Т.2. — М.: Мир, 1977.
15.21. Lenstra А.К., Lenstra H.W., Lovasz L. Factoring Polynomials with Rational
Coefficient// Mashematische Annalen, 1982, p. 515-534.
15.22. Поваляев А. А. Спутниковые радионавигационные системы: время, показания
часов, формирование измерений и определение фазовых координат. М.: Радиотехника,
2008 г.
15.23. Харисов В.Н., Перъков А.Е., Крючков Л.А., Звеков СТ. Реализация
алгоритма двухсторонней интерполяции для относительных определений в СРНС с
использованием фазовых измерений // Радиотехника, 2006, №7.
612
Определение угловой ориентации по сигналам СРНС
Глава 16
ОПРЕДЕЛЕНИЕ УГЛОВОЙ ОРИЕНТАЦИИ ПО СИГНАЛАМ
СПУТНИКОВЫХ РАДИОНАВИГАЦИОННЫХ СИСТЕМ
В п. 4.9 описана задача определения углов ориентации линии с
использованием сигналов СРНС. В настоящей главе рассматривается более общая
задача определения углов ориентации объекта по сигналам СРНС.
16.1. Синтез оптимального алгоритма оценки углов ориентации
объекта по сигналам СРНС
Постановка задачи
Рассмотрим устройство определения угловой ориентации (УОУО),
включающее, например, 4 антенных элемента (рис. 16.1), лежащих в одной
плоскости и расположенных в точках А, В, С, D [1]. На рис. 16.1 для определен
положено AB = AC = BD = CD = l.
Рис. 16.1. Схема расположения антенных элементов УОУО
Введем систему антенную координат AXaYaZa (ACK), связанную с
плоскостью расположения антенных элементов так, как показано на рис. 16.1.
Антенные элементы установлены на жесткой конструкции, положение
которой известно относительно собственной (связанной) системы координат
объекта (ССК). Другими словами, положение системы координат AXaYaZa
относительно ССК известно.
Введем 2 декартовых системы координат (СК):
- геоцентрическую подвижную СК OX0Y0Z0 (ЦГСК) рис. 3.3), связанную с
центром Земли, ось ОХ которой совпадает с Гринвичским меридианом;
- локальную (ЛСК, рис. 16.2), центр которой расположен в точке Ol,
находящейся на поверхности земной сферы и характеризующейся (геодезической)
613
Глава 16
долготой L и (геодезической) широтой В ; оси OlXl и OlYl направлены на
восток и север соответственно, а ось 0LZL направлена вдоль радиус-вектора Земли.
1
1 о
X \.
— \ 1 ]
Рис. 16.2. Локальная система координат
Положение ССК относительно ЛСК задается углами Эйлера а,р,у,
которые примем в качестве искомых углов ориентации объекта.
В ССК положение линий, связывающих точки расположения антенных
—сек
элементов, задано, поэтому введем направляющий вектор т -и линии 1^ ,
\£ск\-1 и ее длину 1т (в общем случае т = \9М). Здесь и далее символ « »
обозначает вектор единичной длины, верхний индекс обозначает систему
координат.
Пусть в ЦГСК заданы координаты J видимых навигационных спутников
ХЦГСК .7-7
XSj , J - I,*/ .
Для определения углов ориентации a = lax,ay,az\ рассмотрим 4 линии
(рис. 16.1): АВ, AC, BD , CD , которые принято называть базовыми.
Положим, что для каждой из указанных линий в результате обработки
навигационных сигналов, принятых в двух точках, расположенных на концах
линии, измерены разности фаз А^ ■, Д^2,у, д^з,у > д#Чу этих сигналов для
каждого у-го НС (у = 1,У ). Считаем, что в процедуру формирования разности фаз
входит процедура разрешения неоднозначности фазовых измерений (например,
одним из методов, описанных в гл. 15) и компенсация паразитных фазовых
набегов в антенно-фидерном и радиочастотном трактах приемника, т.е. полагаем,
что в А<рт ., т -1,4 входят только ошибки фазовых измерений в
навигационных приемниках.
Далее удобно работать с разностью фаз, выраженной в единицах длины
(например, в метрах), т.е.
614
Определение угловой ориентации по сигналам СРНС
<j=^mJ, (16.1)
где Л, — длина волны несущего колебания для j -го НС.
Так как измерение фаз в НАП проводится с ошибками, то при
формировании эквивалентных измерений для синтеза алгоритма оценки углов ориентации
также возникает ошибка, так что модель таких измерений может быть записана
в виде
yd(mJ)=dmJ+SdmJ> С16'2)
где Sdmj — погрешность измерений, которая связана с погрешностями
измерений фаз в навигационных приемниках соотношением
SdmJ=^-S<pmJ. (16.3)
Для измерений (16.2), проведенных для т базовых линий по J
спутникам, необходимо синтезировать оптимальный алгоритм формирования оценок
углов ориентации а,/3,у.
Решение задачи синтеза
Найдем функциональную зависимость между измеряемыми первыми
разностями dmj и углами ориентации а,/3,у .
Введем направляющий вектор линии визирования у'-го спутника в ЦГСК
ЦГСК _ ЦГСК
-ЦГСК _ XSJ xnomp ^ j 6 4^
Г
ЦГСК _ ЦГСК
xS,j xnomp
Поскольку дальность до спутника существенно больше размеров антенной
системы, то для каждой точки антенной системы г^гск будет одинаковым.
Рассмотрим косинус угла emj между у'-й линией визирования и т-й
базовой линией (рис. 16.3).
******
С*НС
/.
Рис. 16.3. Схема определения угла между вектором базовой
линии и направлением на НС
615
Глава 16
Из геометрической схемы рис. 16.3 запишем
cos(emJ) = dmJ/!m. (16.5)
С другой стороны, косинус втj определяется как скалярное произведение
направляющих векторов линии визирования и базовой линии, т.е.
cos(^) = f^^)T-U
цгск
(16.6)
Приравнивая правые части (16.5) и (16.6), получим выражение для
измеряемых разностей фаз
JmJ=L{lurcK)TlurcK, (16.7)
где \^гск — направляющий вектор базовой линии, записанный в ЦГСК.
Переход от заданного по условию \£ск к \^гск определяется матричным
оператором поворота UcckK > так чт0
где
V%™ =\Jx(ex)\Jy(ey)Vz(ez) =
1 О О
О cos(^) -sin(ex)
О sin(^) cos(^)
cos(^) 0 sin(^)
О 1 О
-sin(ev, J 0 cos(evJ
cos(e2) -sin(e,) 0
sin(e2) cos(ez) 0
0 0 1
(16.9)
где ex, ey , ez — углы Эйлера между ССК и ЦГСК.
Подставляя (16.8), (16.9) в (16.7), получаем явную зависимость
измеряемых разностей фаз от углов Эйлера между ССК и ГЦСК
ГССК
dm,j =lm(r?rCK)T Vx(ex)Vy(ey)Vz(e2)tf
(16.10)
Связь между углами Эйлера, определенными относительно ГЦСК, и
углами Эйлера, определенными относительно ЛСК дается выражениями:
а = ех-тг/2 + В, fi = e y = ez-nl2-L. (16.11)
Подставляя (16.11) в (16.10), получаем
a + l.B}Vy{fi)Vzlr + l + LjJcc
m = l,4, y = l„/. (16.12)
616
Определение угловой ориентации по сигналам СРНС
Для синтеза оптимального алгоритма оценивания воспользуемся методом
максимального правдоподобия.
Сформируем вектор измерений для однозначных разностей фаз по всем
базовым линиям и всем видимым спутникам
У</ =
Ус1(\Х) -yd(M9J)
(16.13)
IIT
а Р у\ , и представим
вектор измерений (16.13) в виде
y^=h(y) + n, (16.14)
где п — вектор ошибок измерения разностей фаз с матрицей дисперсий
М nnT =D„, где D„ — диагональная матрица с равными элементами а2п\
h(\|/) определяется из (16.12)
( -гг \ ( „ \
h(v) =
1^ГЦСК)Ти*
а + ^-В
2
71
Vy(/3)Vz\r + - + L\\
сек
/М(г/^)ТШ
/
а + — -В
2
\
п
Vy(j3)Vz\r + - + L
сек
1М
(16.15)
В соответствии с методом максимального правдоподобия запишем
условие нахождения оптимальной оценки
dta(p(y,|iK)) (аь(у)
<3\|/
А1
5\|/
D»!(^-hW)
= 0,
(16.16)
\j/ = i|/
где ^(у</|ч/) — условная плотность вероятности распределения случайного
вектора у^ при фиксированном значении ц/.
Решение уравнения (16.6) можно найти итерационным методом. Пусть
у £_! — решение, найденное на (£ -1) -м шаге итерации. Тогда решение на
k -м шаге итерации дается соотношением
V* = **-i + (HI-1 (V*-i )Н,_! (V*-, ))_1 Щ_, (♦*_! К1 (у, - h(v,_1)) , (16.17)
где
H*-l(M'Ar-l) =
d\\f
(16.18)
Рассмотрим произвольную m-ю строку матрицы Н. На основании (1.66),
(1.69) запишем выражение
617
Глава 16
H(/i,*) =
d\\f
л
\
dUx\a + — -B
da
Vy{j3)Vz
im(*rKf
m^J > I 2 ) dp
Y + — + L
2
ГССК
J
^ )
1я(гГ*)ТЦх
dVz
ж
at--BJVy{/3)- ^
T + - + L
\ Z J
TCCK
Используя (16.9), (16.11), находим производные
аш
a + — В
2
да
О
О -sin
О
а + В
2
К
\
dVy(fi)
д/3
О cos a + В
{ 2
-sin(ytf) 0 cos(/?)
0 0 0
-cos(^) 0 -sin(/?)
О
( * Л
-cos a + В
I 2 )
-sin a + В
I 2 )
dVz
(
Y + — + L
2
Л
ду
sin
V
71 Л ( П т
y + — + L -cos / + — + L
2 ) V 2
cos
/ + — + L
V
(
sin
У
О
У
Y + — + L
v 2 )
О
О
0|
о
(16.19)
(16.20)
Выражения (16.17)—(16.20) определяют алгоритм определения углов
ориентации а,/3,у по однозначным измерениям разностей фаз принятых антенной
системой навигационных сигналов.
16.2. Потенциальная точность определения углов ориентации
В теории оценивания параметров сигналов (функций) используют понятие
потенциальной точности оценок максимального правдоподобия, под которой
618
Определение угловой ориентации по сигналам СРНС
понимают нижнюю границу Рао-Крамера для дисперсии эффективной оценки,
которая определяется выражением
D
у, пот
м
_д_
d\\i
31п(р(у„|ч0)'
5\|/
-1
= ht(Vhct)d;1h(M/hct)
\|/ = \|/
ист
(16.21)
Введем скалярную характеристику точности определения углов
ориентации в виде среднеквадратической ошибки (СКО)
у/,пот
,пот "*" >#,пот ~*~ ^/,пот
=7^
(16.22)
Потенциальную точность определения углов ориентации объекта будем
характеризовать параметром <х^пот (16.22).
Из (16.17)—(16.22) следует, что СКО определения углов ориентации
объекта зависит от многих факторов (параметров тактической ситуации):
абсолютных значений углов ориентации, от числа обрабатываемых навигационных
сигналов, от геометрического фактора, соответствующего обрабатываемым
сигналам НС и др.
Рассмотрим параметры тактической ситуации как случайное событие, т.е.
будем полагать, что случайными величинами являются: число видимых НС,
параметры а,р,у угловой ориентации объекта, положение начала координат
ЛСК, эпоха t движения НС. Тогда тактическая ситуация, характеризуемая
набором указанных параметров также является случайным событием. Реализации
каждого такого случайного события соответствует вполне определенное
значение СКО (У¥. Задавая априорные вероятности возможных тактических
ситуаций, например равновероятные, можно построить гистограмму распределения
значений а. Результаты расчета такой гистограммы для 40000
равновероятных тактических ситуаций приведены на рис. 16.4 при ап = 1 мм, из которого
следует, что наиболее вероятное значение aw равно (7^= 1,7...2,1 угл. мин., а
95% значений aw лежит в диапазоне 1,3 < &¥ < 4 угл. мин.
Представляет интерес рассмотреть гистограммы распределения значений
<j¥ раздельно для ситуаций, когда работа осуществляется по всем видимым НС
и когда работа проводится только по 4 НС. На рис. 16.5, 16.6 приведены
соответствующие гистограммы (отметим, что по всем остальным параметрам
тактической ситуации сохраняется случайность их значений).
619
Глава 16
120?-
«100'
с 80;
60^
т
о
§ 40
С
oL
а , угл. мин. на 1 мм погрешности о
Рис. 16.4. Гистограмма распределения значений о¥
100
90
1 во
х
ш
f 70
I 60
О
1 50^
О 30:
с
20
10
о
0 5
2.5
о , угл. мин. на 1 мм погрешности о
Рис. 16.5. Гистограмма распределения значений сг
при работе по всем видимым НС
lilift
12 3 4 5
а , угл. мин. на 1 мм погрешности^
Рис. 16.6. Гистограмма распределения значений <т^
при работе по четырем НС
620
Определение угловой ориентации по сигналам СРНС
Из рис. 16.5, 16.6 следует, что наиболее вероятные значения СКО оценки
углов ориентации при работе по всем видимым НС лежат в диапазоне
1,3 < о у < 1,8 угл. мин, а при работе по 4-м НС — 1,9 < о^ < 3 угл. мин.
В проведенном выше анализе рассчитывалась СКО оценки углов
ориентации в соответствии с определением (16.22). Полагая дисперсии ошибок
оценивания углов ориентации а,р,у равными, можно записать
Тогда, при оп -1 мм наиболее вероятные значения СКО оценки одного
угла ориентации лежат в диапазоне:
- 0,75 < оw < 1,04 угл. мин при работе по всем видимым НС;
- 1,1 < Су < 1,73 угл. мин при работе по 4-м НС.
16.3. Оптимальная фильтрация разности фаз двух сигналов СРНС,
принятых в пространственно разнесенных точках
Для определения углов ориентации объекта по сигналам СРНС, как следует
из (16.1), (16.2), необходимо измерить разность фаз двух сигналов, принятых в
пространственно разнесенных точках. Для этого в существующей аппаратуре
сначала измеряются фазы принятых сигналов в каждой точке, затем
формируются соответствующие разности, которые далее подвергаются той или иной
обработке в соответствии с решаемой задачей. Такой подход не является
оптимальным с точки зрения теории оптимального приема сигналов, что неизбежно ведет
к ухудшению характеристик используемых алгоритмов. Поэтому, рассмотрим
синтез оптимального алгоритма относительных фазовых измерений по сигналам
СРНС, принимаемых в двух пространственно разнесенных точках [2].
Постановка задачи синтеза
Пусть в системе координат (СК) OXYZ задана базовая линия АВ рис. 16.7.
Пусть в точке S} с координатами {x^^Zj} находится навигационный
спутник, излучающий радиосигнал.
Ориентацию линии АВ в СК OXYZ можно характеризовать
направляющими косинусами
cos(ax) = (xb-xa)/l9 cos(ay) = (yb-ya)/l9 cos(az) = (zb-za)/l,
где ax,ay,az — углы, определяющие положение базовой линии в
пространстве, [xa,ya,za), {хь9Уь>2ь} — координаты точек А и В соответственно; / —
длина базовой линии.
621
Глава 16
S *sHCi(xi,yi,zi)
B(xb,yb,zb)
Рис. 16.7. Геометрическая схема прима сигнала в двух точках
Пусть в точках А и В расположены приемники сигналов НС. При /« DaX,
можно полагать Da, « Db x, и направляющие косинусы НС относительно точек
А и В одинаковы и равны
У"х1 =
_Х\~Ха .. _У\~Уа .. _Z\~Za
£>
> y"vi =
£>
Mzi
Введем единичные
D
a,\
векторы
u =
cos(ax) cos(ay} cos(az)
Инс, _
Mxi Myi Mzi
Пусть точка Ob делит базовую линию АВ пополам. Для сигнала,
приходящего от НС в точку Оь , запишем выражение
s0(t) = Ahmt(t-T0)cos((a>c+a)jy)t + xSttc+(p0), (16.23)
где А — амплитуда; сос — несущая частота сигнала; соЛ — доплеровское
смещение частоты, обусловленное движением точки Оь базовой линии; г0 — задержка
огибающей сигнала, q>0 — постоянная составляющая фазы сигнала, включающая
начальную фазу излученного сигнала, задержки сигнала в передающей аппаратуре
НС, по трассе распространения и др., haK(t) — дальномерный код сигнала, ^с
— навигационные данные, принимающие значение 0 или 1.
В точках А и В принимаемые сигналы сдвинуты по фазе на угол ±у/ , где
¥
Я
(16.24)
622
Определение угловой ориентации по сигналам СРНС
т.е. можно записать
^в^)^ЛКЛ(-ТвУ^{{^с+^ + ^с+П-¥)^ (16.25)
Отметим, что в (16.25) задержки дальномерного кода тл , тв в точках А и
В различные.
Разность фаз сигналов, принимаемых в точках А иВ равна А<рАВ = 2у/ .
В точках А и В радиосигналы (16.25) принимаются на фоне независимых
белых гауссовских шумов nA{t), nB(t) с равными двусторонними
спектральными плотностями N0/2
yA(t) = SA(t) + nA(t)9 yB(t) = SB(t) + nB(t). (16.26)
Поставим задачу синтеза оптимального приемника следующим образом:
по наблюдениям (16.26) необходимо сформировать оптимальную оценку y/{t),
полагая, что задержка дальномерного кода известна. Последнее допущение
введено исключительно с целью упрощения выкладок и акцентирования
внимания на особенностях оценки разности фаз сигналов А(рАВ.
Синтез оптимального алгоритма фильтрации
Для синтеза оптимального алгоритма фильтрации воспользуемся теорией
оптимальной фильтрации информационных процессов. В гл. 6 показано, что
оптимальная система фильтрации включает оптимальный дискриминатор и
оптимальный фильтр.
Оптимальный дискриминатор описывается соотношением (6.30), в
котором вид функции /I У/^Д] зависит от принимаемой при синтезе
статистической модели сигнально-помеховой обстановки, набора оцениваемых
параметров и ряда других факторов.
Применительно к рассматриваемой задаче у (/) = |>^^ (/) yB(t)^, а в каче-
IIT
у/ а>Л .
Обозначим в (16.23) ф = я$нс +<р0. При этом ф, рассматриваемая для
сигнала на интервале длительности Т, является случайной величиной с
равномерным законом распределения на интервале [ -ж, /г ].
Таким образом, в рассматриваемой задаче имеем вектор информативных
случайных параметров "к и неинформативный случайный параметр ф, которые
являются неэнергетическими параметрами.
Аналогично тому, как это делалось в гл. 6, рассматриваем алгоритм
обработки в дискретном времени с шагом дискретизации Td, вводя двойную индек-
623
Глава 16
сацию отсчетов времени tk0=kMTd=kT, T = MTd, tkl = tkfi+lTd =kT + lTd,
h,M - h+xfi
В дискретном времени на интервале [**_,,/*] сигнал (16.23) представим в
виде
Ч ('*-!,/ ) = АКк ('*-!,/ " T0,k-\ )C0S(*>A-1,/ + ®д,*-1 (/ ~l)Td+ фк_х ) ,
где фк_х — начальная фаза сигнала для рассматриваемого интервала времени,
которая при синтезе алгоритма фильтрации рассматривается случайной
величиной с равномерным законом распределения на интервале \-к, п\
Сигналы sA (tk_n), sB (tk_ij) при этом записываются следующим образом
SA У к-IJ ) = ^дк ук-1,1 ~ ТА,к-\ ) Х
xcos(fi>c^_,л + соак_х (/-1)7^ + фк_х + [у/к_х + (ovk_x (/-\)Td)).
SB yk-\,l ) = ^Kk yk-U ~ TB,k-\ ) X
xcos(<yc^-i,/ +<»a,k-\(l-l)Td +4-i -(Vk-i + *V,*-i(/-~1)r</))'(16-27)
где положено y/k_xl = y/k_x + a>wk_x (/ - \)Td .
С учетом (16.27) запишем выражение для условной плотности вероятности
наблюдений YXM на интервале времени [^-i»'*] при фиксированных значениях
X, и ф
( Л М
р(\М\К-\'Фк-\) = с^Р \—^Ут(*к-1,1)*('к-ц>Ч-1'Фк-\)
v°"« /=i
(16.28)
где s(tk_xh'k^ = \sA(tk_xh'k,^^ sA{tk_xl,X^"i , с —константа, не зависящая
от к и ф, а2п = N0/(2Td) — дисперсия аддитивных дискретных белых шумов в
наблюдениях y(tk_xl).
Подставляя (16.27) в (16.28), запишем
Г А м
xcos(fi)c^_u +(®д,*_1 +fiV,*-i)(/-1)7rf + V*-i +Фк-\) +
624
Определение угловой ориентации по сигналам СРНС
А М
ап 1=1
(16.29)
Так как фаза ф является неинформативным параметром, следуя
стандартной методике синтеза, усредним (16.29) по фк_х
( * \
-Л \ W
(16.30)
(16.31)
где 10 (х) — функции Бесселя нулевого порядка от мнимого аргумента;
X \^к-\) = Хс\}'к-\) +Xs\^k-\)^
м
Хс (К-1) = YjVa {*к-и)Ьт {* ~ ТА )™*{<»А-и + (&Л,к-1 + %,к-1 )(l~l)Td+ ¥k-\ ) +
+Ув{*к-и)Ь№к-тв)со*(а>с^_и +{coJlk_x-o)¥k_x)(l-\)Td ~¥к-\)) ,
м
xs (h-i) = Yj{yA{*к-И)hw(' -та)sin(^A-i,/ + K,*-i + %,k-\)(l-l)Td+ ¥k-\) +
+Ув (fk-i,i)h№ (' ~ ta )sin(<yA-i,/ + (®д,*-1 - %,k-i ){l ~l)Td- ¥k-\))>
(16.32)
Представим (16.32) в виде
^c(Vl) = (/U+^2,*)cos(^-l)-(Q,it-62,*)sin(n-l)»
^, (*•*-! ) = (/U-/2.*)sin(^-l) + (ft,t+02,* J008^*-!)» ^16-33)
где
м
h,k =^Уа (tk-u)лда('"ta)c°s(u>A-i,/ + (fi^., + cowk_x)(/-1)7>),
/=1
^^S^^-wJ^K^-^W^c^+^t^+^it-lK'-l)^)»
/=1
Й.* = Цуа [h-u )Лдк (' - *A)*™{a>c*k-\ji + K*-i + fiV,t-i )(7 - 0^)»
/=1
^=2^(^-1'/)^K(/"rs)sinK^-u+(^,^+^^-i)(/-1)^)- (16-34>
/=1
625
Глава 16
Отметим, что корреляционные интегралы (16.34) необходимо вычислять в
единой шкале времени.
Подставляя (16.33) в (16.31) и проделав необходимые преобразования,
получаем
X2{kk_l) = 2(llk+Qlk+Ilk+Qlk) +
+2cos(2^_1)(/u/2>ft + QhkQ2k) + 2sm(2yxk_l)(lllcQ2l( -I2,kQlk). (16.35)
Для получения структуры дискриминаторов оптимального приемника в
(6.30) вместо /(у^д) необходимо использоватьр(У$* \к), описываемую
(16.30).
Оптимальный дискриминатор разности фаз
Дискриминатор для оценки фазы у/ получается дифференцированием
(16.30) по у/ и описывается выражением
"" I0(A.x(it)/ai)ai д¥ '
где 1\(х) — функции Бесселя первого порядков от мнимого аргумента; кк —
экстраполированная оценка вектора к .
Рассмотрим дискриминатор (16.36) более подробно.
При большом отношении сигнал/шум q = E/N0 »1, где Е — энергия
сигнала на интервале времени Т , справедливо соотношение Ix (x)/l0 (х) = 1, и
выражение (16.36) можно заменить эквивалентным выражением
w=4-r^- (16-37)
<7п ду/
Известно, что оценка максимального правдоподобия некоторого
параметра, в нашем случае у/ , определяется из условия
*wM
= 0. (16.38)
Дифференцируя (16.34) по у/ и подставляя полученный результат в
(16.35), получаем
о-„Х^ГД]
Из данного выражения находим
626
Определение угловой ориентации по сигналам СРНС
1ё(2^) = Ц^#Ж^##|- (16-39)
Из (16.39) следует
2у/ = arctg
^иЮ^Ю+а^Юбг^Ю.
±тпу т = 0,1,2,.... (16.40)
Рассмотрим теперь (16.37) при некоторой произвольной оценке у/ . Тогда,
с учетом (16.39), запишем
«W = ^Гм (tg(2^)cos(2*/)-sin(2|/)) =
= /sin(2^-2^), (16.41)
где у — нормирующий множитель.
Следовательно, оценка у/ сходится к оценке максимального
правдоподобия у/.
Представим (16.37) в виде
*W =r[-sin(2n-i)(/u/u +Q\,kQ2,k) + ^s(2ipk_l)(ilkQ2k -i2.kQu)\
где у/ — экстраполированная оценка; у — коэффициент.
Коэффициент у можно отнести к коэффициенту усиления следящей
системы за разностью фаз. Поэтому в дальнейшем будем рассматривать
дискриминатор разности фаз в виде
«W =-sin(2^-i)(7U^ +a*62,t) + cos(2^*-i)(/i.*62.* -h.kQi,k) -(16.42)
Схема дискриминатора разности фаз у/ , соответствующая (16.42),
приведена на рис. 16.8.
Рассчитаем дискриминационную характеристику дискриминатора (16.42).
Используя статистическое описание составляющих Ilk, I2k, Qlk, Q2k,
приведенных в п. П6.1, и выполнив необходимые преобразования, получаем
U(e¥) = 4<40Г2 sinc(^7/2)sinc(^Br/2)sin(2(^ + ^r/2))' (1643)
где е¥=у/-у>, е^ = й>д-й>д, е^ =a)w-d)w,
^в=К-^)-(Ад-^)=Ч"Ч-
627
Глава 16
КкУк-\,1~тА)
yJ(k-\j)
X
cos (a>ctk_u + (&ък-\ + <V*-1 )(l-1)Td)
sin(ec/Jk_1>/ +(<fc_i + йуАг_1)(/-Г)Гс/)
x
i
>>n(2^fc_i)
/=1
Af
Z
a
.Ы
^
A
i
L
^рс('*-М-гв)
X
Af
Z
Af
Z
Ы
а
X
J
X
X
T
. A
X
T
X
j
i
L
A
w
A
c°8(2v%-i)
cos^A-i,/ + (<*-! -^.it-iJC-1)7!/)
Рис. 16.8. Схема дискриминатора разности фаз
Флуктуационная характеристика дискриминатора (16.42) описывается
соотношением
v2
\ = 4^0^3 (sinc(^r/2) + sinc(^fir/2))
1 +
^07'(sinc(^r/2) + sinc(^r/2))
(16.44)
Для синтеза сглаживающих цепей следящей системы зададимся моделью
изменения фазы у/ динамическими уравнениями
¥к = ¥к-\ + т%,к-\> %,к = %,к-\ + Т£¥,к-\> V* = -Sa-i + ^,*-i' О6-45)
где 4ш к-\ — дискретный белый гауссовский шум с нулевым математическим
ожиданием и дисперсией а2 .
Для синтеза сглаживающих фильтров следящих систем можно
воспользоваться методикой эквивалентных наблюдений (см. п. 6.3.6), основанной на
линеаризации дискриминационной характеристики дискриминатора (16.43).
Полагая е = О и линеаризуя (16.43), представим (16.42) в виде
628
Определение угловой ориентации по сигналам СРНС
^д^ж5д^(^~^0 + ^Л=(5д^^+^л)-^д^' (16.46)
где rj — флуктуационная составляющая на выходе дискриминатора разности
фаз, которую будем полагать дискретным БГШ с нулевым математическим
.2
ожиданием и дисперсией <т3
Цу '
Введем эквивалентное наблюдение фазы у/к
У¥%к =Vk+rl,/,9k/Sw =Vk+n¥^ (16.47)
где п¥к =7^,*:/£ду, — БГШ с нулевым математическим ожиданием и
дисперсией
*2 -st2
"у/
Лу/
/SJX¥ -
^Яс/nJ
sine
sincta772)sinc(£<»fi7V2)
X .
1 +
?c/«0r(sinc(^7'/2) + sinc(^B7'/2))
Отметим, что разность фаз в точках А и В равна АрАВ = 2ц/ , а
эквивалентное наблюдение данной разности фаз записывается в виде
УА<р,к = ЬфАВ,к + ПА<р,к »
где дисперсия шума равна
r^=4^/5L=.
1
fy / ДУ
A4clnJ
sinc(gfl>i<7T/2) + sinc(ga>itr/2)
smc(^7'/2)sinc(ge,i|7'/2)
X
1 +
^/«or(SinC(^7,/2) + SinC(^:r/2))
(16.48)
Положим sine(e T/2j = smc(sWbTll\ = 1. Тогда (16.48) принимает вид
пА<р
1с/щ>Т
1 +
^с/щТ
(16.49)
Сопоставим (16.49) с (6.75), которое описывает дисперсию шума
эквивалентных наблюдений
У\,к=(Р1,к+%,к
(16.50)
629
Глава 16
при оптимальной оценке фазы сигнала в одном приемнике (см. п. 6.3.6.1). Из
сопоставления следует, что дисперсия (16.49) шума эквивалентных
наблюдений разности фаз в 2 раза больше, дисперсии шума (6.75). Если теперь взять
второе наблюдение, аналогичное (16.50), но полученное другим приемником, и
сформируем разностное наблюдение
Уьък = Кк - hk = (<Р\Л - <Pi]k) + 7дЛ* >
то дисперсия шума ffA к будет совпадать с дисперсией (16.49).
Известно [1], что дисперсия шума эквивалентных наблюдений
характеризует потенциальную точность однократной оценки соответствующего
параметра. Следовательно, можно констатировать, что в синтезированном
дискриминаторе разности фаз (16.42) реализуется такая же потенциальная точность
однократной оценки разности фаз как и в системе, состоящей из двух
оптимальных дискриминаторов «абсолютных» фаз. В то же время, т.к. динамика
изменения у/к слабее динамики изменения «абсолютных» фаз (Р\{2\к > то
оптимальная полоса пропуская следящей системы за у/к меньше оптимальная полоса
пропуская следящей системы за д\^к > чт0 приводит к повышению точности
«фильтрационной» оценки у/к по сравнению с точностью аналогичной оценки
ф\(2\к • Кр°ме того, повышается помехоустойчивость следящей системы за у/к.
Для эквивалентных наблюдений (16.47) и априорных уравнений
измерений у/к (16.43) можно записать алгоритм фильтрации в векторном виде
*к -*к +K*(jV,* ~Н**)' **~F*
К,=Вх*нУ/<7*
Аг-1 »
(16.51)
Di=Di+HTHr2/^, Dx,=FDaiFT+GGV2 ,
(16.52)
где Д , i,j = 1,3 — элементы матрицы Dx дисперсий ошибок фильтрации
вектора х
тора х;
¥ %
'¥
; Ьхк — матрица дисперсий ошибок экстраполяции век-
1 Т 0
0 1 Т
0 0 1
, G =
0
0
1
Н=1 0 0
С учетом (16.46), (16.47) уравнение (16.51) можно записать в виде
x*=x*+K**wAV' **=FVi- (16-53)
630
Определение угловой ориентации по сигналам СРНС
Дискриминационная (16.43) и флуктуационная (16.44) характеристики
дискриминатора разности фаз (16.42) получены при известных значения
задержек тА и тв. Если данные задержки неизвестны, но оцениваются
соответствующими следящими системами, а сформированные оценки тА , тв
используются при формировании опорных сигналов в корреляторах (16.34), то
дискриминационная и флуктуационная характеристики дискриминатора разности фаз
будут описываться следующими соотношениями
U(e¥) = 4q2c^T2p(eTA)p(eTB)smC(e^
(16.54)
\ =4^/»o7,3(/?(^)sinc(^:r/2) + ^(^)sinc(^r/2)) х
1 +
Яс/щ>т(р(еТА )sinc(s(0AT/2) + p(sTB )sinc(^r/2))
где еТА =та-та, €Тв =тв-тв,
(16.55)
Оптимальный дискриминатор доплеровского смещения частоты
Дискриминатор для оценки частоты соД получается дифференцированием
(6.29) по <уд и описывается выражением
и
aci),k
h{A-x{ik)lc72n)dx{ik)
I0(A-X(ik)/a2n) <Ч
которое по форме аналогично (6.55).
Полагая как и выше q »1, можно записать
и
а.со,к
dx(ik)
дсоП
Дифференцируя (16.30) по а>Д 9 запишем
и
дсо,к
x(r,ik)
'и
dL
i,*
дбо„
+ GJ
dQ
U
и*
дй)„
+ 1
dU
dQ2
2,к , ^ "\£2,к
2,* ~Z + У2,к ~Z
oco„ дб)„
+ cos(2^4) /u
dl
2,k
дй)„
+ 1
dl
2,k
\,k
do)„
+ Й
6Q.
U
Xk
da>„
+ Q:
dQu
2,k
dco,
д J
(16.56)
631
Глава 16
дсод дсоа
do)n do)n
(16.57)
Первый сомножитель в (16.57) может быть отнесен к коэффициенту
усиления следящей системы за частотой, поэтому в дальнейшем будем
рассматривать частотный дискриминатор вида
и
( dL, dQLk w di2jc _ Л dQu ^
до),к
Ч,к
да>„
+ 0
и
+ /о
+ Qi
а^д дсоД да)д ,
+
+ COS
(2¥к-\)
дГ
2,к . r &h,k
+ Л
дсоД дсоД
+ 61
%,* . Л ОД,* '
5,*
■ + 02
'-ч Z^L + K /*ч
+ sin
/,. J, ^2, a/u а#и а/2.
а<»д э^уд
д /
\
у
. (16.58)
Рассчитаем дискриминационную характеристику дискриминатора (16.57).
Используя статистическое описание составляющих 1]к, 11к, Qlk, Q2k,
приведенных в п. П6.1, и выполнив необходимые преобразования, получаем
:(^г/2),
^(ч)=4<4.г:
sine
'®Л
-(sinc(^7/2)-cos(^r/2))
+
+ ^ / ;(sinc(^r/2)-cos(^r/2)) +
SinC^"r/2^inc(^r/2)cos(2^ +(е„А -^B)r/2)-cos(2^ +^7-/2-^7-)) +
sine
(^г/2)
'й>Л
(sinc(^r/2)cos(2^ + (s^ -^B)r/2)-cos(2^ +^Г-^вГ/2))
(16.59)
Полагая sv «1, £ ^«l, я Г«1 формулу (16.59) можно привести к
виду
U
(чН*
г2 ^2
с/«о
6 (^ + ^ )
12c/rJA
'°>Л*
(16.60)
из которого следует, что дискриминационная характеристика имеет
устойчивую точку равновесия.
632
Определение угловой ориентации по сигналам СРНС
Крутизна дискриминационной характеристики (16.59) определяется из
(16.60) как
Зъ-Щ£- (16-61)
Следовательно, эквивалентные наблюдения для доплеровского смещения
частоты записываются в виде
^=®д+^*/^=®д+%,*, (16.62)
где 7]^ к — флуктуационный процесс на выходе частотного дискриминатора
(16.58).
Приведем без вывода выражение для дискриминационной характеристики
оптимального дискриминатора доплеровского смещения частоты для случая,
задержки сигналов тЛ , тв в точках А и В неизвестны и оцениваются
соответствующими следящими системами, а сформированные оценки тА , тв
используются в опорных сигналах корреляторов (6.34),
1ч W
U\e„ ) = 4a2c/nJ2
p2(eT)smc(ewT/2)/ , u
ьсоА
+
Ь(0В
Ьо)В
-cos(2^+^r/2-^r)) +
+ P{etMs )HV/*)(sinc(^//2)cos(2gy +(% _£jr/2).
-cos(2^+^r-^r/2))].
Для синтеза сглаживающих цепей следящей системы за доплеровским
смещением частоты будем использовать эквивалентные наблюдения (16.62), а
в качестве модели изменения доплеровскои частоты воспользуемся моделью
второго порядка (6.110)
Ю^к = ®д,*-1 + Теа>,к-1 > 8со,к = 8(о,к-\ + %а>,к-\ > (16.63)
где £^_1 — дискретный БГШ с нулевым математическим ожиданием и
дисперсией а] .
ho)
633
Глава 16
Напомним, что сод описывает динамику движения точки Оъ (см. рис. 16.7).
Поэтому дисперсию о1 формирующего шума в (16.51) необходимо выбирать
с учетом данного факта. Фаза у/ , в соответствии с (16.43) характеризует
динамику изменения параметра угловой ориентации а базовой линии. Поэтому
дисперсию о формирующего шума в (6.43) необходимо выбирать с учетом
данной динамики, которая в ряде приложений может быть существенно
меньше динамики движения точки Оь .
В сформулированной постановке задачи синтеза для оптимальной оценки
а> к справедливы уравнения (16.46), (16.47), в которых надо полагать ymJk
вместо уш и, al вместо al , al вместо al , х =
*>д е„
F =
1 Т\
О 1
, G =
, Н =
s*» °
(16.64)
16.4. Оптимальный навигационный приемник для устройства
определения углов ориентации объекта по сигналам
спутниковых радионавигационных систем
Рассмотрим устройство определения угловой ориентации (УОУО) по
сигналам СРНС, описанное в п. 16.1, в котором для оценки разностей фаз
используем оптимальный алгоритм, описанный в п. 16.3.
В качестве опорной точки Оъ , относительно которой будет рассматриваться
вращательное движение объекта, определим точку А, в которой принимаемый
навигационный сигнал описывается соотношением (16.23) [3]. Заметим, что
точка Оь является «воображаемой» точкой и может быть выбрана в любом месте.
В точках В, С, D принимаемые навигационные сигналы описываются
выражениями
sB (t) = AhaK (t -тв)cos((^c + сод)t + ж\с + cp0 -у/в),
sD(t) = Ahm(t-td)cos((o)c + coa)t + л&нс + р0 -y/D). (16.65)
Далее рассматриваются пары сигналов sA(t) и sB(t); sA(t) и sc(t);
sA(t) и sD (t). Поэтому положим измеряемые разности фаз по сигналам
каждого j -го НС (j = 1, п):
634
Определение угловой ориентации по сигналам СРНС
A<P\j = Vbj > A(Pij = Vcj > A(Pij = Vdj • (16.66)
Для каждой из этих пар сигналов можно использовать алгоритм
оптимальной фильтрации разностей фаз двух сигналов, описанный в п. 16.3.
Приведем кратко такой алгоритм применительно, например, к первой паре
сигналов SA(t) и SB[t) при приеме одного навигационного сигнала.
Алгоритм слежения за разностью фаз двух сигналов
Следящая система за разностью фаз у/ сигналов включает дискриминатор
разности фаз и сглаживающий фильтр. Дискриминатор разности фаз у/
описывается выражением (16.42), а следящая система за разностью фаз описывается
уравнениями (16.47), (16.48).
Алгоритм слежения за доплеровской частотой опорной точки
Для слежения за доплеровской частотой опорной точки А можно
использовать алгоритм слежения, описанный в п. 16.3 для каждой из пар точек А-В,
А - С, A-D. При этом частотный дискриминатор, например, для пары точек
А-В будет описываться выражением
и
А-В
Д(о,к
1
А-В
(М
/
81
А,к
А,к
дсо„
+ Q
dQ.
А,к
А,к
да>„
+ 1
д!
В,к
В,к
дсоп
+ Qu
dQB,k
дсо„
■ +
+ COS
[2¥в,к-\]
(
81
'А,к
В,к
8со„
+ 1
81
В,к
дсо,
А,к ,п д0в,* , ^ 8QAjk
+ УА,к^— + Ув,к
Л
8со„
8а>,
+sin
(2ftB,k-l)
%
[А,к
В,к
+ У В,к ~*В,к
81
В,к
д J
Л
8со„ дсо,
8сэ„ 8а>„
Q
А,к
)
.(16.67)
Аналогичные выражения записываются для других пар точек с заменой
индекса « В » на индексы « С » и « D » соответственно.
Линеаризуем каждый из дискриминаторов (16.55)
КЛ * Sav К " *>д ) + ni~k .
где п£~кв , п^~кс, п^~к° — дискретные БГШ с нулевыми математическими
ожиданиями и дисперсионной матрицей м\n^n^l = Dn<y.
Введем эквивалентные наблюдения
Й»,* = *>д + Й»Г/» Й»,* = ®д + Й£*С» Л»,* = ®д + й^» (16-69)
635
Глава 16
где nAJ = n^B/Sa0), hAJ = nAJjSAa , hif = n£?/snttf - дискретные БГШ
с нулевыми математическими ожиданиями и дисперсионной матрицей
м\
кк
Введем усредненное наблюдение
1 3
гДе Па к = n£~kB + ni~k + йа~к° — ДБГШ с дисперсией Вя , которая
рассчитывается стандартным образом по известной дисперсионной матрице Dn .
Для эквивалентного наблюдения (16.70) и модели изменения доплеров-
ской частоты (16.63), также, как и в п 16.3, для оптимальной оценки а)ак
справедливы уравнения (16.46), (16.47), в которых надо полагать у^к вместо у¥к,
сод е^ I , а матрицы F , G, Н
определяются формулами (16.64).
al вместо al , al вместо crl , х
Синтез алгоритма слежения за задержками сигналов, принимаемых
в двух точках пространства, с учетом алгоритмов слежения
за разностью фаз сигналов
Известно (см. п. 6.3.6.7), что в следящих системах за задержкой дальномер-
ного кода целесообразно использовать поддержку от следящей системы за фазой
(или доплеровским смещением частоты) сигнала. Использование такого подхода
в рассматриваемой задаче имеет особенность, обусловленную раздельным
слежением в точке В за относительной фазой у/ и доплеровским смещением
частоты, обусловленным движением точки В относительно точки А.
Сигнал, принимаемый в точке А, описывается (16.23), для которого
задержка тА определяется выражением тА= [^(f)d/, а для производной
с о
задержки по времени имеем
(16.71)
^__*>д(0
dt со,
с
Данное уравнение является стандартным при описании задержки сигнала,
используемом при синтезе соответствующих следящих систем, поэтому
алгоритм оптимального оценивания задержки сигнала в точке А описывается,
например, (6.177).
636
Определение угловой ориентации по сигналам СРНС
Для сигнала, принимаемого в точке В, с учетом представления сигнала в
форме (16.65), задержка тв определяется выражением
t \
1
'-о
тв=-—\ к (0Л-
¥в
, а для производной получаем
drB= о>д(0| dytB= а>д(/)-дуд(р^
Л &>с Л сос
Уравнение (17) описывает динамику изменения тв и должно учитываться
при синтезе следящей системы за задержкой тв .
Один из возможных вариантов синтеза заключается в том, что в (16.72)
вместо истинных значений а>Д и #> используются их оценочные значения сЬД
и <у , которые формируются в следящей системе за фазой ^ ив аналогичной
системе слежения за доплеровским смещением частоты соЛ (см. предыдущий
раздел). Погрешности измерений я)д и & учитываются в (16.72) введением
дополнительного формирующего шума £ . Поэтому, модель изменения тв в
дискретном времени может быть записана в виде
т
тв,к=тв,к-\ +—{д)л,к -%в,к) + £тв,к> (16-73)
шс
гдеМ(4,*) = ^,.
При синтезе следящей системы за задержкой а>д1с и <o¥Bjc полагаются
известными процессами.
С учетом (16.73) следящая система за задержкой тв описывается
соотношениями
т
?В,к =?В,к+КтЛт,к > ?В,к=?В,к-1 +— К,* -%в*)> (16Л4)
Кт,к =DT,kSjy,r/anT »
D~\ = D;\ + Sl/crl , DTjc = DvJk_x + % , (16.75)
где идт к — процесс на выходе дискриминатора задержки сигнала, для
которого можно использовать одно из известных представлений (см. п. П6.5); Sa т —
крутизна дискриминационной характеристики дискриминатора задержки; агп
— дисперсия шума эквивалентных наблюдений задержки сигнала.
637
Глава 16
Аналогичные следящие системы за задержками сигналов необходимо
использовать в приемниках, находящихся в точках С и D.
Суммируя приведенные выше результаты, структурная схема
навигационного приемника для устройства определения углов ориентации объекта по
сигналам спутниковых радионавигационных систем может быть представлена
в виде, приведенном на рис. 16.9.
УА^к-ц)
о
БКЛ
а
J\E>Q\E
hb'QiL
Ув
('*-!,/)
БКД
т.
Qi
hE'QlE
hL,QlL
Ус
('*-!,/)
БКС
а
Не'Оъе
Нь>0ьь
Уо(1к-и)
БКД
♦ А
а
hE>Q'
АЕ
1al*Qal
ЧД сол
СФсо,
ВДХЛ
СФХЛ
AAA
ЕД
ФД \|/в
СФ
VB
ЧД со7
вд
хя
СФтв
ФД ус
СФ
ч>с
ЧД сог
ВД
^с
СФ
хс
ЕИ
ФД
Уд
СФ
УД
ЧД сог
ВД г.
о
СФ
lD
Юг
"Ч
(О
Ув
Ув
^
со
Ус
VC
t
со
ч^
Уд
4£>
Рис. 16.9. Схема навигационного приемника для устройства определения углов
ориентации объекта по сигналам спутниковых радионавигационных систем
На рис. 16.9 обозначено: БК — блок корреляторов, ВД — временной
дискриминатор, ФД — дискриминатор разности, фаз, ЧД — частотный
дискриминатор, СФ — сглаживающий фильтр.
638
Определение угловой ориентации по сигналам СРНС
Оценка эффективности синтезированных алгоритмов проводилась на
математической модели навигационного приемника, созданной в среде
имитационного моделирования Matlab.
Условия моделирования: длина базовой линии 1т = 2 м; модель движения
НП — по спирали с одновременным вращением вокруг оси со скоростью
10 градусов в секунду; отношение сигнал/шум qc, =PC/N0 = 40 дБГц; полоса
пропускания следящей системы за разностью фаз — 2 Гц; полоса пропускания
следящей системы за доплеровским смещением частоты — 10 Гц;
На рис. 16.10 а), б) приведены реализации ошибок слежения за разностью
фаз у/ на одной базовой линии и доплеровским смещением частоты соД в
отсутствие преднамеренных помех.
а)
б)
Рис. 16.10. Реализации ошибок слежения за у/ и я>д в отсутствие
преднамеренных помех
639
Глава 16
Среднеквадратическая ошибка слежения за разностью фаз равна е¥= 2.5
градуса, а доплеровским смещением частоты ^г^ = 10 Гц.
Положим теперь, что на входе приемника действует шумовая полосовая
помеха с мощностью Рп в полосе частот навигационного сигнала. Введем
отношение помеха/сигнал qujc -Рп/Рс и положим #п/с= 38 дБ и положим
среднюю динамику изменения разности фаз у/ . На рис. 16.11, 16.12 приведены
реализации ошибок слежения за у/ и а>д в этом случае.
400
а)
б)
Рис. 16.11. Реализации ошибок слежения за у/ и а>д при воздействии
преднамеренных помех
Из данных рисунков следует, что СКО оценки у/ и а>а составляют
соответственно е¥ = 35 градуса, sf =120 Гц.
640
Определение угловой ориентации по сигналам СРНС
При дальнейшем увеличении qnjc наблюдается срыв слежения за у/ .
Таким образом, помехоустойчивость синтезированного алгоритма обработки
составляет 38 дБ. Анализ помехоустойчивости обычной НАП, у которой полоса
пропускания ССФ равна 20 Гц, составляет 28 дБ (результат получен на той же
математической модели) (см. также п. 8.7). Таким образом, повышение
помехоустойчивости в синтезированном алгоритме составляет 10 дБ.
При высокой динамике изменения разности фаз помехоустойчивость
синтезированной системы снижается до 35 дБ, а выигрыш по помехоустойчивости
по сравнению с обычной НАП составляет 8 дБ.
Литература
16.1. Перов А.К, Шатилов А.Ю. Оценивание углов ориентации объекта с
использованием спутниковых радионавигационных систем// Радиотехнические тетради, № 37,
2008, с. 53-56.
16.2. Перов А.И., Корогодин И.В. Оптимальное оценивание угла прихода сигнала
с неизвестной начальной фазой двумя разнесенными приемниками// Радиотехнические
тетради, №37, 2008, с. 57-61.
16.3. Перов А.И., Корогодин И.В. Комбинированная когерентно-некогерентная
система определения углов ориентации объекта по сигналам спутниковых
радионавигационных систем// Радиотехника, 2009. № 7, с. 33-40.
21-1026
641
Глава 17
Гл а ва 17
ИНТЕГРИРОВАННЫЕ ИНЕРЦИАЛЬНО-СПУТНИКОВЫЕ
НАВИГАЦИОННЫЕ СИСТЕМЫ
Одним из перспективных направлений развития навигационных
комплексов является создание интегрированных инерциально-спутниковых
навигационных систем (ИСНС), в которых совместно обрабатываются сигналы инерци-
альной навигационной системы (ИНС) и НАП СРНС. Основной целью
интеграции ИНС и НАП СРНС является объединение измерителей,
функционирующих на различных физических принципах, в единый комплекс,
обладающий более высокими характеристиками точности, помехоустойчивости,
непрерывности и надежности по сравнению с отдельными измерителями.
Повышение эффективности в ИСНС обусловлено тем, что ИНС и СРНС являются
взаимно дополняющими [17.1,2.8, 6.11], что отражено в табл. 17.1.
Таблица 17.1. Характеристики ИНС и СРНС
\ Характеристика
Автономность
Необходимость
начальной выставки и
калибровки
Характер ошибок
Возможность
отсутствия
навигационных определений
Темп выдачи данных
Возможность резер-
| вирования
СРНС
Нет
Нет
Относительно высокий
уровень шумов,
стационарный процесс
Да
Низкий (1... 10 Гц)
Неэффективно
ИНС 1
Да
Да
Малый уровень шумовой
составляющей,
нестационарный
процесс
Нет
Высокий
(10... 1000 Гц)
Эффективно
При совместной обработке сигналов ИНС и НАП СРНС в ИСНС
сохраняются достоинства каждой из подсистем и в значительной степени снижается
влияние их недостатков.
Преимуществами интегрированной ИСНС по сравнению с автономными
измерителями являются [17.1, 2.8, 6.11]:
повышение надежности;
642
Интегрированные инерциалъно-спутниковые навигационные системы
снижение стоимости за счет снижения требований к инерциальным датчикам;
более высокая степень резервирования;
высокая точность определения координат, составляющих вектора
скорости, углов ориентации и угловой скорости;
обеспечение непрерывности высокоточных навигационных определений;
высокий темп выдачи данных.
17.1. Принципы построения интегрированных
инерциально-спутниковых навигационных систем
Максимального выигрыша от интеграции навигационных измерителей
можно достичь, решив соответствующую задачу синтеза, что позволяет найти
оптимальную структуру и характеристики ИСНС. Теоретическим базисом
такого синтеза является теория оптимальной фильтрации [1.6, 5.1, 5.2], в которой
данное направление получило название комплексной фильтрации (комплекси-
рование измерителей).
В наиболее общем виде задача синтеза комплексной системы фильтрации
может быть сформулирована следующим образом. Пусть Х^ — вектор
состояния в момент времени tk, подлежащий оцениванию (фильтрации) и
включающий координаты потребителя, составляющие его вектора скорости и
ускорения, углы ориентации и соответствующие угловые скорости, заданные,
например, в инерциальной системе координат. Инерциальный датчик (ИНС)
измеряет некоторые компоненты вектора состояния X (обычно это составляющие
векторов ускорения и угловой скорости), поэтому можно записать
Уинсд= Mx*) + fU> (17Л)
где h — векторная функция соответствующей структуры; г\ — вектор
погрешностей измерений.
На вход НАП СРНС поступают радиосигналы S.(X,f), j = hN от всех
видимых НС
jM=ХМ*')+«(').
которые в НАП СРНС подвергаются усилению, фильтрации и аналого-
цифровому преобразованию (см. гл. 13). В результате имеем отсчеты
спутниковых наблюдений в моменты времени tk_Xi =tk_l+iTd, i = \,n, где Td —
шаг дискретизации,
643
Глава 17
N
УС?НС ук-Ц )- 2~i^J (^*-1./Л-1,|-) + nk-\,i»
(17.2)
7=1
где пк_и — внутренний шум НАП.
В (17.1), (17.2) для простоты полагаем, что измерения ИНС и входные
сигналы НАП СРНС синхронизированы.
Задавая динамику изменения вектора X во времени, задачу синтеза
комплексной системы фильтрации можно сформулировать как получение наилуч-
шей оценки Х^ (например, в смысле минимума дисперсии ошибки
фильтрации) при совместной обработке наблюдений (17.1) и (17.2). В результате
синтеза получается схема оптимальной ИСНС, приведенная на рис. 17.1.
V
Антенна
НАП СРНС
ИСНС
Радиочастотный
блок
Аналого-цифровой
преобразователь
ИНС
Акселерометры
и гироскопы
Компенсация
инструментальных
ошибок
^срнс(Д-и)
Интегрированная
система обработки
Уине,* f
i j
Рис. 17.1. Схема оптимальной ИСНС (первый вариант)
На рис. 17.1 в блоке НАП СРНС отображены только антенна,
радиочастотный блок и АЦП, а интегрированная система обработки является общие для
НАП и ИНС.
В теории оптимальной фильтрации показано [5.1, 5.2], что при
определенных условиях вместо наблюдений (17.2) можно использовать достаточную
статистику:
(17.3)
/=1
где S(XkJttkti) = \sl(Xktfttkti) ...SN(XkJ,tkJf — вектор опорных сигналов.
Выражение (17.3) есть не что иное, как векторный коррелятор. При таком
представлении эквивалентных наблюдений в НАП СРНС схема оптимальной
ИСНС принимает вид, приведенный на рис. 17.2.
644
Интегрированные инерциалъно-спутниковые навигационные системы
В данной схеме в блок НАП СРНС, кроме антенны, радиочастотного блока
и АЦП, входит многомерный коррелятор, а комплексный фильтр является
общим для НАП и ИНС.
IV
Антенна
Радиочастотный
блок
Аналого-цифровой
преобразователь
ИНС
Акселерометры
и гироскопы
Компенсация
инструментальных
ошибок
НАПСРНС1
йене
1£
Многомерный
коррелятор
iУ иней
j
Укорр,/г
Комплексный
фильтр
Рис. 17.2. Схема оптимальной ИСНС (второй вариант)
Если в схеме рис. 17.2 в комплексный фильтр не подавать сигналы с ИНС,
то оставшаяся часть схемы (антенна, радиочастотный блок, АЦП, многомерный
коррелятор и комплексный фильтр) есть ни что иное, как навигационный
приемник с одноэтапной обработкой сигналов (см. п. 6.5). Следовательно, можно
сказать, что схема рис. 17.2 (и эквивалентная ей схема рис. 17.1) реализует комплек-
сирование ИНС и НАП СРНС с одноэтапной обработкой сигналов.
Описанный принцип построения комплексной системы фильтрации,
основанный на обработке исходных сигналов (17.1) и (17.2) (или эквивалентных
сигналов (17.3)) в отечественной литературе [5.2] называют комплексированием
по входам (входным сигналам). Иногда схему комплексирования рис. 17.2
называют глубокоинтегрированной, так как в ней уровень совместной обработки
сигналов СРНС и ИНС неразделим настолько, что нельзя выделить раздельных
каналов обработки сигналов СРНС и ИНС с формированием соответствующих
оценок координат потребителя. Разработанные на основе данного подхода
ИСНС обладают характеристиками точности и помехоустойчивости, близкими
к потенциальным [17.2—17.5].
Реализация алгоритма комплексирования по схеме рис. 17.2 достаточно
сложна, так как требует отказа от классического построения навигационного
приемника, основанного на двухэтапной обработке сигналов. Чтобы сохранить
традиционную структуру НАП и дополнить ее интегрированием с ИНС, были
разработаны упрощенные алгоритмы комплексирования.
На рис. 17.3 приведена обобщенная схема НАП СРНС с двухэтапной
обработкой сигналов.
645
Глава 17
V
Антенна
ii
РЧ-канал и
корреляторы
ССЗ, ССФ (ССЧ)
Урнги
Фильтр вторичной
обработки НАП
LHATU
>
[^П^^ичная обработка сигналов^
Рис. 17.3. Схема НАП с двухэтапной обработкой
В приемнике с двухэтапной обработкой сигналов в качестве
эквивалентных наблюдений НАП СРНС, которые используются для синтеза алгоритма
комплексной обработки, могут быть взяты оценки радионавигационных
параметров сигнала (задержки, доплеровского смещения частоты), которые на рис.
17.3 обозначены как уРНП^, или оценки навигационных параметров Хк,
которые обозначим как урщ к. Для таких эквивалентных наблюдений можно
записать выражения
Урнп,*=г(х*) + прнп,*> (17-4)
Унпл=вх*+Пнп,*> (17.5)
где пРНП к, пнп к — погрешности оценивания радионавигационных и
навигационных параметров.
Если при синтезе комплексного алгоритма фильтрации использовать
наблюдения ИНС (17.1) и эквивалентные наблюдения СРНС (17.4), то в результате
получается схема ИСНС, приведенная на рис. 17.4.
v
Антенна
ИСНС
Г"
£
РЧ-канал и
корреляторы
ССЗ, ССФ (ССЧ)
I [^Первита^обработка f|
НАП СРНС
В
Урнп?Ад фильтр вторичной
обработки НАП
ИНС
Акселерометры
и гироскопы
Компенсация
Ц инструментальных
ошибок
AL
Комплексный
фильтр ИСНС
i Уинс,£ Л
Алгоритм
счисления ИНС
Ь^НАГи
\ ХИСНС,А:
=0
Рис. 17.4. Схема ИСНС с комплектованием по выходам оценок РНП
646
Интегрированные инерциально-спутниковые навигационные системы
Другая схема комплексирования (рис. 17.5) получается, если в качестве
эквивалентных наблюдений СРНС использовать (17.5).
В схемах рис. 17.4, 17.5 формируется три типа оценок: Хинс k — оценки,
формируемые только ИНС; XHCHC/t — оценки, формируемые интегрирован-
ной системой ИСНС; XHASlk — оценки, формируемые НАП СРНС, ком-
плексированной с ИНС (в НАП вводятся оценки Хиснс k). Отметим, что состав
вектора ХНАП k отличается от состава векторов Хиснс k и Хшс k, так как в
него не входят углы ориентации и соответствующие угловые скорости.
V
Антенна
ИСНС
JE
РЧ-канал и
корреляторы
ССЗ,ССФ(ССЧ)
Перв^чнадобработка
НАП СРНС
Урнпл
Фильтр вторичной
обработки НАП
В
•ХнАП,*
ИНС
Акселерометры
и гироскопы
Компенсация
инструментальных
ошибок
Комплексный
фильтр ИСНС
IX-
ЖНС,Лг
| Уине,*-
Алгоритм
счисления ИНС
!х
инс,*
:>
Рис. 17.5. Схема ИСНС с комплексированием по выходам оценок НП
Характерной особенностью схем рис. 17.4, 17.5 является то, что в блоки
первичной обработки НАП СРНС вводятся оценки Хиснс k, сформированные в
комплексном фильтре ИСНС. Такое комплексирование позволяет сузить
полосы пропускания следящих систем (ССЗ, ССФ и ССЧ), что приводит к
повышению помехоустойчивости НАП СРНС. Данный тип комплексирования иногда
называют комплексированием на первичном уровне.
Описанный и реализованный в схемах рис. 17.4, 17.5 принцип построения
комплексной системы фильтрации, основанный на обработке оценок РНП
(17.4) или НП (17.5), формируемых в НАП СРНС, в отечественной литературе
[5.2] получил название комплексирования по выходам (выходным оценкам
НАП СРНС). Разработанные на основе данного подхода ИСНС [17.6—17.10]
обладают характеристиками точности и помехоустойчивости, несколько
худшими, чем при использовании принципа комплексирования по входам.
Практическая реализация схем комплексирования рис. 17.4, 17.5 требует
доработки блоков первичной обработки сигналов НАП СРНС с целью введения
647
Глава 17
в них соответствующих оценок Хиснс ^ и изменения параметров следящих
систем (ССЗ, ССФ, ССЧ). Если при комплексировании ИНС и НАП СРНС
желательно не затрагивать структуру АП, то, как видно из рис. 17.4, 17.5, можно
положить В = 0, т.е. разорвать соответствующую связь между оценками
Хиснс к и блоком первичной обработки НАП. При этом получаются схемы
комплексирования, приведенные на рис. 17.6, 17.7, которые иногда называют
схемами с комплексированием на вторичном уровне, так как в них не
затрагиваются блоки первичной обработки сигналов с НАП СРНС.
v
Антенна
йене
г;
AL
РЧ-канал и
корреляторы
ССЗ, ССФ (ССЧ)
Ц НАП СРНС
Урнпл
I ^Первичная обработка
Фильтр вторичной
обработки НАП
(АНАП,Лг
ИНС
Акселерометры
и гироскопы
Компенсация
^ инструментальных
ошибок
Комплексный
фильтр ИСНС
1 УИНС,А: Ц
!х
йене,*
Алгоритм
счисления ИНС
X
ИНС,Аг
>
Рис. 17.6. Схема ИСНС с комплексированием на вторичном уровне
«сырых» измерений НАП СРНС
V/ Антенна
ИСНС
гг--
i
И
РЧ-канал и
корреляторы
ССЗ, ССФ (ССЧ)
I Шрвивдэдобработга
НАП СРНС
Урнги
Фильтр вторичной
обработки НАП
ИНС
Акселерометры
и гироскопы
Компенсация
инструментальных
ошибок
Комплексный
фильтр ИСНС
iУина* fT
Алгоритм
счисления ИНС
^НАП,А
=>
XwcHC,£
^с
LHHC,Ar
Рис. 17.7. Схема ИСНС с комплексированием на вторичном уровне
с использованием оценок координат НАП СРНС
В приведенных схемах комплексная обработка осуществляется только на
вторичном уровне и не затрагивает уровень первичной обработки НАП СРНС.
648
Интегрированные инерциалъно-спутниковые навигационные системы
В этом случае помехоустойчивость НАЛ не изменяется по сравнению с
автономной НАЛ, а лишь повышается точность формирования оценок НП.
Большинство современных ИСНС используют именно такую схему комплексиро-
вания[2.8, 17.11—17.13].
Наконец, наиболее простой схемой комплексирования ИНС и НАП СРНС
является коррекция данных ИНС оценками навигационных параметров ХНАП k,
сформированных в НАП (рис. 17.8).
V/ Антенна
]Г
1?=
РЧ-канал и
Ifc.
корреляторы
N
ССЗ,ССФ(ССЧ)
1 [ Первичная обработка
1 \к
НС
Акселерометры
и гироскопы
,,
Компенсация
инструментальных t
ошибок 1
ИСНС
п» НАП СРНС
||УРНП,*
:
1
1
I Уинеа
i
i
j
Фильтр вторичной
обработки НАП
ь
Блок коррекции
п
Алгоритм
счисления ИНС
■-|
1 Iх НАП,*
У
1хиснс\*
ч
■ хинс,л-
. ...^
Рис. 17.8. Схема ИСНС с коррекцией ИНС
В зарубежной литературе описанные выше схемы комплексирования
классифицируются следующим образом [17.4]:
разомкнутая (uncoupled)— рис. 17.8;
слабосвязанная (loosely coupled)— рис. 17.6, 17.7;
тесносвязанная (tightly coupled)— рис. 17.4, 17.5;
глубокоинтегрированная (deeply integrated, ultra tightly coupled) — рис. 17.3.
Основные особенности (достоинства) описанных схем комплексирования
ИНС и НАП СРНС приведены в табл. 17.2.
Таблица 17.2. Сравнительная характеристика схем комплексирования
I Тип
1 комплексирования
Разомкнутый
1 Слабосвязанный
"с"ый
Основные особенности
Ограниченность ошибок оценок местоположения и
скорости, наличие информации об ориентации и
угловой скорости, минимальные изменения в бортовой
аппаратуре
Все перечисленные качества разомкнутой схемы,
выставка и калибровка ИНС в полете
Все перечисленные качества слабосвязанной схемы, 1
повышение помехоустойчивости |
649
Глава 17
Глубокоинтегрированный
Обеспечение характеристик точности и
помехоустойчивости, близких к потенциальным.
Требует существенной перестройки НАП СРНС и вы-
соких вычислительных затрат
Первые три из приведенных в табл. 17.2 типов комплексирования ИНС и
НАП СРНС могут быть реализованы с использованием существующих моделей
НАП, ИНС и навигационных процессоров. Однако следует отметить, что для
более полного использования открывающихся возможностей интеграции НАП
СРНС и ИНС целесообразно создание специализированных датчиков для
инерциальной и спутниковых систем, изготовленных на одной
технологической и конструктивной базе. Последняя из рассмотренных схем в табл. 17.2
(глубокоинтегрированная) в обязательном порядке требует разработки единого
приемоизмерительного инерциально-спутникового модуля [17.2, 17.4, 17.5].
В слабо- и тесносвязанных, а также в глубокоинтегрированной схемах
комплексирования итоговая оценка ХИСНСА: может использоваться в НАП
СРНС в режиме допоиска сигналов НС для сокращения области поиска по
задержке и доплеровскому смещению частоты.
17.2. Синтез алгоритмов комплексирования НАП СРНС/ИНС
Как отмечалось, практически все алгоритмы комплексирования НАП
СРНС/ИНС могут быть получены с использованием теории оптимальной
фильтрации [5.1, 5.2]. В рамках данной теории существует множество
подходов к синтезу конкретных алгоритмов, фактическое различие которых
заключается в выборе вектора состояния оцениваемых компонент и в составе
используемых наблюдений (измерений). В настоящем разделе рассматривается
один из возможных подходов, основанный на задании вектора состояния в
подвижной СК, связанной с Землей (ПЗСК), а в качестве ИНС —
бесплатформенная ИНС (БИНС), широко используемая на современных летательных
аппаратах [17.1].
17.2.1. Модернизированный вариант комплексирования
Описанная в п. 17.1 постановка задачи синтеза комплексной системы
фильтрации с использованием наблюдений (17.1)—(17.5) предполагает
использование стандартного аппарата теории оптимальной фильтрации. В то же время
при синтезе алгоритмов комплексирования НАП СРНС/ИНС можно
использовать модернизированный вариант комплексирования [5.1, 5.2], суть которого
заключается в следующем.
Пусть имеем спутниковое наблюдение
650
Интегрированные инерциалъно-спутниковые навигационные системы
Ус?нс,к=3{Лк) + "к> О7-6)
где Лк = схк — фильтруемый процесс, который в пространстве состояний
отображается векторным марковским процессом хк 9 и наблюдение ИНС
Уинс,к=Лк+ек> О7-7)
где ек в общем случае — коррелированный процесс, который в пространстве
состояний также отображается некоторым марковским процессом гк:
Выразим формально Як из (17.7):
Лк=Уинс,к-ек (17-8)
и подставим полученное выражение в (17.6):
^срнс,*=5(^инс,*-^) + л*- О7-9)
В представление (17.9) входят наблюдения j>cphc,*> ^инс,* и случайный
процесс ек, поэтому можно рассматривать задачу фильтрации процесса ек по
заданным наблюдениям (17.9), полагая ушс,к известной функцией времени.
Теоретическое обоснование такого подхода, получившего название
модернизированный вариант комплексирования, приведено в [5.2].
При использовании модернизированного варианта комплексирования
основной акцент делается на задании модели ошибок ИНС (модели изменения sk).
В отличие от оптимального алгоритма комплексирования,
модернизированный алгоритм, во-первых, не требует априорного знания модели движения
подвижного объекта, точное задание которой часто неоднозначно. Во-вторых,
упрощается схемная реализация алгоритма. При этом по точности получаемых
оценок модернизированный вариант комплексирования близок к оптимальному.
17.2.2. Синтез тесносвязанного алгоритма комплексирования
НАП СРНС/ИНС
В качестве примера синтеза тесносвязанного алгоритма по схеме рис. 17.2
можно взять [17.29]. Особенностями рассматриваемого алгоритма являются:
учет различного темпа поступления данных от ИНС и СРНС;
некогерентная обработка сигналов СРНС.
Постановка задачи
Рассмотрим задачу синтеза комплексной системы фильтрации сигналов
СНС и ИНС, когда темп поступления данных от двух систем различный.
На рис. 17.9 приведена временная диаграмма поступления входных данных:
651
Глава 17
V*,i 1пМХ" tn*j
| i i i i | 1 ► /
'n,0,0 *„,1,о '" *n,k,0 """ ln,(M-\)fi 'и+1,0,0
Рис. 17.9. Временная диаграмма поступления входных данных
Td — шаг работы АЦП приемника СРНС, tnkj=nTj+kT + jTd, j = l,J,
к = 19М, 'м/,у='я+1ао> W=W+i,o> T — вРемя накопления сигналов в
корреляторах приемника СНС, 7} — шаг работы (темп формирования
измерительных сигналов) ИНС.
В моменты времени tnkj наблюдения на выходе АЦП приемника СНРС
имеют вид
= АУ°д*(*п9к9)f -<*,o)cos fflAw +<*,y + ^Ghc,* +^o К (17.10)
где ,4V — амплитуда сигнала v -го навигационного спутника (НС); Сушк —
символ навигационного сообщения v -го НС, принимающий значения ±1 pi не
меняющий своего значения на любом из интервалов Г^д ^„,*,у ] >
п = var 9k = var; GRK\tn^kj) — дальномерный код с периодом 1 мс и числом L
символов на периоде повторения, при этом на каждом из интервалов
L'«,t,i'^,Jt,yJ > п = var > ^ = var укладывается целое число периодов кода, а
моменты времени t к1, и = var, к = var совпадают с началом соответствующего
периода кода; тк — задержка дальномерного кода v -го НС, которая при
синтезе полагается неизменной на каждом из интервалов Г^*!,^*./] > w = var,
к = var; covc ~ несущая частота v -го НС; <рк . — фаза сигнала, обусловленная
взаимным перемещением v -го НС и потребителя, которую при синтезе
полагаем меняющейся линейно на каждом из интервалов и„^,^ Л , tf = var,
к - var, т.е.
<*,у=<*,1+(У-1)7,</<и.*.1; <17-п)
652
Интегрированные инерциалъно-спутниковые навигационные системы
$ — случайная начальная фаза сигнала v -го НС; пп k . — дискретный белый
гауссовский шум (ДБГШ) с нулевым математическим ожиданием и дисперсией
<j2 =N0/(2Td), где N0 — спектральная плотность внутреннего шума
приемника.
В моменты времени /„00, n = vzr проводятся измерения ИНС, которые
включают измерения углов Эйлера %п = \у/ 3 <р\
(17.12)
где гп =
'у
~'Э
<р
— вектор погрешностей измерении гироскопов, и
измерения акселерометров (более подробно см. прил. П17.2)
УиА,«=и(^^^)[а«+2ПхУ«-8т(хЛ + п^^
где \п = \х у z
V =\V V V , а =
п х,п у,п z,n\ ' п
^х,п у,п az,n
(17.13)
векторы
координат, скорости и ускорения потребителя в геоцентрической
прямоугольной системе координат, связанной с Землей; П = [0 О Q3]T — вектор
угловой скорости вращения Земли; пап — вектор погрешностей измерений
акселерометров, включающий независимые ДБГШ с равными дисперсиями а\а\
gT(xw) = gr(xw)-nx(nxxw) —удельная сила тяжести, gr(x„) —вектор
интенсивности гравитационного поля Земли; где V{y/b&^(p) — матрица
преобразований, которая описывает три последовательных вращения системы
координат на углы Эйлера, так что
и(^,^) = и3(^)и2(^)и1(^), и,(1/) =
1 О О
О cos(^) sin(^)
О -sin(^) cos(^)
cos(#>) sin(#>) 0
-sin(#>) cos(#>) 0
0 0
1
cos (.9) 0 -sin (.9)
V2{3) = \ 0 10, U3(p) =
sin(,9) 0 cos (5)
В дальнейшем при синтезе будет использоваться модифицированный
метод комплексирования, когда в измерениях гироскопов оцениваются
погрешности £„ измерений (17.12), а измерения акселерометров (17.13)
преобразуются к виду
yHA,«-U(yHr)„-£w)[a„+2nxVw-gT(x„)] + na;W. (17.14)
653
Глава 17
Введем описание изменения информационных (оцениваемых) процессов.
Для смещения часов и частоты ОГ будем использовать соотношения /' = D'/c,
f = V'/AV , с — скорость света, \ — длина волны несущего колебания
сигнала v -го НС. Введем вектор D' = \D' V'\t , для которого запишем уравнение
V'n,k,j = ^D'Vn,k,j-l + GD'^D';n,k,j-\» (17.15)
где FD. =
1 ТА
Dl.=%'
О 1
о о
> GD- -
, iD-->n^j-\ — вектор ДБГШ с матрицей дисперсией
О ТА
, где Nt , — двусторонняя спектральная плотность
непрерывного шума ОГ.
Ошибки измерения гироскопов определим уравнениями
Еи = FffЕл-1 + Gs^e,n-\»
(17.16)
где Е =
К
> Еу, -
¥
¥
> F.9 -
9
9
;е,=
ф
;рИ
G,=
G7 0
О G,
О
О
;f7 =
1 т,
О 1
F7 О О
О F7 О
О О F,
> ъ£,п-\ \^{//,п-\ ъЗ,п-\ ъ<р,п-\
;G7 =
IU 1 I
О О G7|
вектор независимых ДБГШ с равными дисперсиями D^ .
Изменение координат вектора потребителя зададим векторным уравнением
X„,j; = Fxx«,*-i + Gx^X;wA._,, (17.17)
где Х =
х,
х,
xz
; Хх -
X
к
ах
» Л-у —
У
УУ
ау
xz =
z
у,
az
;fx =
о о
О О F.
* X
О F
Gx =
X
О
о
0
*х
0
0
0
G,
;fx =
1 Т 0
0 1 Т
0 0 1
; Gx -
0
0
1
» £х;л,*-1 ~
£х;п,к-\
€у\п9к-1
— вектор
независимых ДБГШ с равными дисперсиями D^ .
Для решения задачи вторичной обработки потребуются уравнения
изменения вектора X с темпом 7}, которые аналогичны уравнениям (17.17) при
замене Г -> 7} и £>^ -> D| = D^T/Tj .
654
Интегрированные инерциально-спутниковые навигационные системы
В [17.29] показано, как с использованием уравнений (17.15), (17.17)
получены уравнения для вектора R^-i =
nV т/К V
лп,к-1 yR;n,k-\ aR;n,k-l
(где Rlk_x —
псевдо дальность до v -го НС, V^nk_x — псевдо скорость), которые имеют вид
**л,* ~^R^n,k-\ + ^ R^R;n,k-l >
где Рл =
Иго
0 1 Г
0 0 1
» GR -
0 0
1 0
0 1
> $R\n9k-\ ""
£>а\п,к-\
(17.18)
— вектор независимых
ДБГШ с матрицей дисперсий D^ =
N,D,T О
О D,
Синтез комбинированного комплексного алгоритма фильтрации
Так как наблюдения от разных датчиков поступают неравномерно, то
рассмотрим пошаговое преобразование апостериорных плотностей вероятности
n>k,j _
(АПВ). Обозначим как Yjfy =
у n,k,j
'hco.o.i
Y "
-'ИНС!
вектор наблюдений, включающий
наблюдения сигналов навигационных спутников (17.10) на интервале времени
г 0,0,1» tn,k,j J и наблюдения ИНС на интервале \jx ,tnj.
Пусть в момент времени tn00 имеем вектор наблюдений YJ'qj0 , по
которому сформирована АПВ p(a„|y0w;0*j°) вектора Aw=|x;oo Ej00 D£0>0|T,ko-
торую будем полагать гауссовской с вектором средних значений \п и
матрицей апостериорных дисперсий DA n .
Так как векторы Хп k, D'nk функционально связаны с Rvn, то можно
рассчитать апостериорную оценку R^
К = ij(x„ ~ *нс,и f + (уп - /НС;п f + (z„ - zHC;„ f + D'n, (17.19)
К;п =-cos(av)V^n -cos(j3v)Vy\n -cos(yv)Vz\n+K , (17.20)
aVR;n=-COS(av)ax;n -C0S(&K;« ~ C0S(/vK;w, (17.21)
и соответствующую ей матрицу дисперсий ошибок оценивания D6 с эле-
ментами
655
Глава 17
DL,n = НЛ;Х, Df = H,DVx;wHT, , Day;n = ЯуЬч;пН1,
DRVv;n = DVRv;n ~ HvDxV;«Hn > DRav;n ~ Dakv;n " HvDxa;X ,
DVav;n=DaVv;n=HvDVwHv>
Hv=\-cos(ay) -cos(j3y) -cos(/v) l|;
Dx;,=^
^;n=M
DxV;« = M
(x„ -i„)(x„ -x„)T], DVx;„ =m|(vx;w - Vx;„)(vx;„ - Vx;n)
\**х;и ^xjw/^x;/? **х;л /
» Dxa;« = M
1Хл ХяД х;л х;л]
(Vx;„ - Vx;„ Дах;„ - ax;„ J
x =Ijc v z D'|T V =Ik F V V
Лп г« >л *n n\ ' T x;w х,л .у,л z,w л
(Хл ХлДах;л ах;л)
DVa;„ - M
**x;w
ax,n ay,n az,n °l
(17.22)
Вектору оценок R„ с матрицей дисперсий ошибок оценивания D^
можно ассоциировать с АПВ piRyn Yq q^0 I, соответствующей моменту времени
Чо.о ■
Рассмотрим отрезок времени Г^олЛду]- На этом отрезке времени имеем
только наблюдения реализации Jhc/j'oY (только по НС), задержка сигнала
полагается постоянной и равной тупОХ =^o,i/c' a Ф333 меняется линейно (17.11)
2"Ko,j ,у
2*Koj
<о,у = <o,o,i + (j - 1)^<«,о,1> гДе <о,у = Г^* <о,у = -
Рассмотрим эволюцию плотности вероятности (ПВ) p(Ry„ Y0"oj°l на
интервале времени [\,o,i Л,о,у ] > так как на этом интервале времени
R^ = const = R^)0,i > т0 ПРИ фиксированном значении навигационного сообщения
можно записать уравнения
656
Интегрированные инерциалъно-спутниковые навигационные системы
Л\*у Iv"'0'0 у n>°>J п \-1т(лу lv">°'0>l n(v n&J\\>v a \
P^rtAl |*0,0,1 ^НСл.ОД »инс;л,А^""^^ллД1|ж0Д1 jP^HCnAl |К",0Д >иж;п,к ] >
р(Ки\>&)- 1р(Ко4<?)р{КМ\Ко,о)<П:ао . (17.23)
Рассматривая случай некогерентного приема сигнала, определим
изменение фазы сигнала 5V(^0J,<00,^0J) на интервале времени [/яД1,/яДУ]
соотношением
ж
VnAj +^°ясЛ +<Ро=Фп,ОЛ +U-l)Td0)d-M>
(17.24)
где начальная (для данного тактового интервала) фаза несущей ф£.ох + ф$ и
случайная фаза, обусловленная навигационным сообщением, объединены в
одну случайную фазу с равномерным распределением на интервале [-;г,;г]. При
этом полагаем, что значение ф„01 для каждого интервала и^д Лл,у ] является
независимой случайной величиной. Тогда после усреднения по такой
случайной фазе уравнения, аналогичные (17.23), принимают вид [5.1]
^(^л.ОД^йд ) = ^(R«,0,l|Yo!o,i )/>(^НСяД1 |R«,0,l)>
р{Км\К»?)= jp(Ko4<f)p{KoA\Ko,o)^Vn,o,o . (17-25)
где p(yHcUi* |r«,o,i ) = Vo {Un,o,J)» 7о (*) ~ Функция Бесселя нулевого порядка,
1 J
Us-n,0,J =—^yc;n,0JAVGw{tn,0J-Tn,k)COS{a>ctnAj + Л>£и,0,1)
1 J
Uc;nAJ =~l2l,y^nAjAVGJyKyn,Q,J"С^Ц^А, + Д/^и.ОД )
°"« 7=1
Полагая в (17.25) АПВ гауссовской и связывая R^0)i c задержкой дально-
мерного кода, из уравнений (17.25) следуют уравнения для моментов АПВ
^o(^)0,y(FR<o,o))
K,0J - R",1,0 - FRR«,0,0 + DR„,„,i,c
dRy
(17.26)
D
Rv;«.i,o
657
Глава 17
(F^Rv;«,0,0^+G^Gi) +
dSv (>?n,0,l>®и,0,у ) I _2 f My (»f«,0,l>*£,0,7 )
dR,
<9R,
Rv;w,0,0 R^;« '
(17.27)
Уравнения (17.26), (17.27) могут решаться рекуррентно на всех интервалах
времени \tnk\JnkJ~\, к = 0,М-2, так как на данных интервалах поступают
только измерения от НС (17.10).
Рассмотрим интервал времени \tnM_xx,tnM_\A. На этом интервале на
внутренних точках имеем только измерения от НС, а в последний момент
времени tnM_\j = '„+1до имеем измерения от НС и от ИНС.
Рассмотрим АПВ
Py^nM-hJ \X0,0,\ »/НСи,А/-1,1 ' ИНС »^л,А/-1,1/
-lm(~Qy |vw,M-l,0\ (y n,M-\,J у "+l||jv ~v \_
-Кр^ЧпМ_и\Х001 )Py*HCn,M-l,l >7ИНС |кл,М-1,У'¥ЯЛ/-1,1 j~
-1т(иу |Vw,A/-l,0\ lу n,M-\,j\nV rnv \ v
-KpyS.n M_j^ | «0,0,1 jPynCnM-U l^nM-U'rnM-U)
*P(Ymc
Введем ПВ
и+1
R
(17.28)
Р\^п,M-I J \X0,0,\ '/HCw,M-l,l >Ги,Л/-1,1^-
= ^p^RwjV/_1J|Y001 ]/?^нси|а/-1л |r«,m-U'^,a/-u J> (17.29)
а для плотности вероятности plR^M-i.yh^o.'of1'0) запишем выражение,
аналогичное (17.25)
p(R«,M-i,y|Yo,b,i j= J/,(^Ii,A/-i,o|Xjo,i Jp(r«,m-i,i|r«,a/-i,o)<^rH,m-i,o -(17.30)
Усреднив (17.29), (17.30) по случайной фазе Йм_ц, сформировавшейся
на начало интервала накопления \tnM_^\,tnM_XJ~\ (с учетом параметра
навигационного сообщения), получим уравнение, аналогичное (17.21)
п(пх |vn,A/-l,0 у п,М-М\_ jL,(пУ IV«,M-1,0\ ~(у п,М-и\тъУ \
/7^I1/i,A/-U|I0,0,l »/НСи,Л/-1,1 )~ KP\K'n,M-\,J \Х0,0Л jPynCnM-l^l |K«,A/-l,J j '
Ру^пм-м \хо,о,1 ]-
658
Интегрированные инерциалъно-спутниковые навигационные системы
- J/7(R«,A/-l)o|Y0,b,l ' )р(^я,А/-и|Ки,А/-1,о)б^и,А/-1,0 » (17.31)
где Р\УЯСп\м-\,\ \^п,м-и ) = ^о(^п,м-и) •
Из уравнений (17.31) следует, что и для интервала времени
Ги,л/-1,1»'л,А/-1„/] можно использовать рекуррентные уравнения оценивания
(17.26)—(17.27) и в итоге сформировать оценку WM_XJ и соответствующую
ей матрицу дисперсий DR M .
Рассмотрим теперь вектор
it | it
-Vх IYT Fx
" Ля+1,А/-1,У Un+\,M-U Ля+1,Л/-1,У
Л«+1 =
Vх П'т FT
ли+1,0,0 ип+1,0,0 ^и+1,0,0
и апостериорную плотность
п( Л lv"'°'° V И.А/-1.У v n+l\
Py\+l\x0,0,\ »/НСя,0,1 '7ИНС ) •
Напомним, что в момент времени f„00 мы располагали АПВ pl\n Kfif)
с вектором средних значений Л„ и матрицей апостериорных дисперсий Т)Ап.
Для спутниковых измерений YHC^['l'J можно ввести достаточные
координаты (обобщение понятия достаточных статистик) &Уп>М-и> ^й «Л/-1У
v = \,т, каждая из которых соответствует АПВ p\RvnM-\,jРнс^й 1"/)» которую
полагаем гауссовской. Информация о векторе Хя+1д0 (входящем в вектор
Ли+1), содержащаяся в спутниковых наблюдениях Знс^ол"1"7» буДет полностью
входить в оценки RjJ>A/-i,y» ^r •„ м-\ j » П0ЭТ0МУ проведем замену
^НС л ,0,1 ""> Кя,А/-1,У' *% ;и,М-1,У ' V ~ X»W
и рассмотрим р(ля+1 ^о^ДУинс^1 Дя,м-1,у^й ;w мч у), для которой запишем
уравнения, аналогичные (17.30),
P^w+1|Y0)'0ji ,^инс 'R«,M-i,y»DRv/;„)M-i,yv/ = l'^j =
= ^(л„+,|Yй7)p(^'инc"t^R;«ч^.Ч;»,«-U^' = i^|Y„",•o0,•,^Л„+1),
Р(Л„+,|У„";„°;)= |р(л„|У0",Ь°;10)р(л„+1|л„)</Л„ . (17.32)
659
Глава 17
Векторы R^A/-i,y > v = 1,1я являются случайными независимыми от такта к
такту величинами, каждая из которых имеет гауссовскии закон распределения
с математическим ожиданием R^M_U и дисперсией Dft м_{у так, что
можно записать выражение
^л,А/-1,У = ^nM-lJ + ^w+l > (17.33)
где цуп+] — гауссовскии случайный вектор с матрицей дисперсий.
Алгоритм формирования оценок R^maj идентичен алгоритму
оценивания R^A/_!y (17.26)—(17.27), с той лишь разницей, что для каждого
временного интервала \Jn0l,tnM^j А он решается независимо, т.е. с априорными
данными
loo 0 0|
RH,0,0 - ° >
D
Rv\nfifi
О оо О
О 0 оо
(17.34)
Для формирования оценки R^-u можно использовать алгоритм
(17.26)—(17.27) первичной обработки сигналов в приемнике СНС. В уравнении
(17.26) можно выделить дискриминатор и фильтр [5.1]. Дискриминатор
описывается выражением:
^ln(/0(^,^(R^y)))V
U
</,*+!
dRv
(17.35)
При малых ошибках фильтрации вектора Rvnk0, что имеет место на
практике, выражение (17.35) можно записать в линеаризованном виде
(17.36)
и17 -Kv
ua;n,kJ ~ эд
vv -Vv
snc;n,k,J ' R;n,k,J
0
где ynjl;njj , yUc;ntk9j — эквивалентные линеаризованные измерения
псевдодальности и псевдоскорости для v -го НС; S\ — матрица крутизн
дискриминационной характеристики.
Приравнивая (17.34) и (17.35), выразим эквивалентные измерения упд.пк j ,
УпъпМ В ВИДе
660
Интегрированные шерциалъно-спутниковые навигационные системы
v =
J экв;л,/г,У
Утщ',п,к^
Упс;п,к^
= н
(Ч)"
51п(/0(^,л,у(^м)))Т
dRv
+ R«,/t,j
, (17.37)
где Н =
1 о о!
|о 1 о|'
Можно показать [5.1], что вектор эквивалентных наблюдений может быть
представлен в виде
r3Ks;nAJ=nKk,J+<K*n,ic;> k = 0,M-U (17.38)
где Иэкв;и,*,у — ДБГШ с матрицей дисперсий Dn не коррелированны по
времени и имеют закон распределения, близкий к гауссовскому.
Так как эквивалентные наблюдения Уэкв;и,*,./ ■> сформированные в
соответствии с алгоритмом (17.37), линейны относительно вектора Rvnk j (см. (17.38)),
то для оптимального оценивания этого вектора можно использовать фильтр
Калмана
R«,/t,J = FRR!U-1,./ + ^Rv;n,k,J \Ужв;п,к^ ~ HFRRw,*:-U ) »
K.,U =(F«4;»,MFR +GRD^GTRr' +HT<„H (17.39)
с начальными условиями (17.34) для каждого временного интервала
|_^Ai>^,M-i,y>J •
Итоговые оценки R^m-i,j> v = 1,/w формируются с темпом 7} в моменты
времени f0,M-u> tXM_XJ, ..., tnM_XJ, ... и используются для формирования
оценок вектора Л„ 0 0 на этапе вторичной обработки информации.
Введем обобщенный вектор измерений
i Iх
Xt+i ~ \\Унсп+\) — (Унся+ij (Уиа^+i) 9
для которого запишем обобщенное уравнение
Y,+1=f(Aw+1) + ^+1, (17.40)
где M[q;+1qB+1] = De.
Вектор Ли+, описывается линейными уравнениями (17.15)—(17.17),
которые можно обобщить в одно векторное уравнение
661
Глава 17
К+\ = или + г$АуП,
(17.41)
где U =
Fx
0
0
0
*Ь-
0
0
0
F,
> %А,п
^X;w
%D';n
%£,П
; г = !
5Х О О
О GD О
О О G,
;A/[^^A>„] = D
$л
Теперь, учитывая стандартную структуру уравнений (17.32) для АПВ,
запишем уравнения фильтрации
Л„+1 - Ая+] + DA)W+1
ет(ли+,)'
ал
(уи+,-г(ля+1)),
(17.42)
Ln+1
ил
Я ?
D
Л.л+1
шл,иит+го5АГт
-1
+
5f(Aw+1)
ал
d:
*(ля+,)
v-1
ал
(17.43)
Матрица дисперсий ошибок оценивания Ол>я+1 вектора Лл+1 содержит
матрицы дисперсий ошибок оценивания Dv ;я+1, Dv ;л+1, Da ;я+1, DxV;„+1,
Dxa;*+i> Dva*+i> которые на следующем такте работы [f„+iAi, *„+!,<>,■/] ПРИ
приеме только сигналов СРНС используются в соответствующих
соотношениях (17.22) в качестве априорных дисперсий.
Схема комбинированной комплексной инерциально-спутниковой системы
навигации с некогерентным режимом работы навигационного приемника
приведена на рис. 17.10.
Как видно из рис. 17.10, в блоке вторичной обработки не используются
оценки псевдодальностей и псевдоскоростей (вектора R^), формируемые в
блоке первичной обработки, что отличает данную систему от классического
двухэтапного приемника. В синтезированном алгоритме в блоке вторичной
обработки используются оценки Rv, которые формируются по наблюдениям,
полученным лишь на последнем интервале Г^д^^дЛ. Это вполне
соответствует идеологии работы оптимальных систем фильтрации, в которых
коррекция экстраполированных оценок проводится также только по последнему
отрезку наблюдений, а информация извлеченная из всех предыдущих
наблюдений, входит в экстраполированную оценку. Заметим также, что в блок
вторичной обработки подаются не только оценки псевдодальностей ^ и
псевдоскоростей VVR , но и ускорений а\. Использование оценок Rv (вместо к ) приво-
662
Интегрированные инерциалъно-спутниковые навигационные системы
дит, кроме того, к изменению параметров аддитивного шума х{п+х в (17.33),
которые в существенной степени определяют параметры комплексного фильтра
Калмана в блоке вторичной фильтрации. Во-первых, отметим, что шум цуп+1 —
некоррелированный во времени, в то время как погрешность у^+1 оценки
RJ+1 = Rvn+l + yvn+l является коррелированным процессом. Во-вторых, дисперсия
шума цуп+1 существенно (на порядок и более) больше дисперсии погрешности
ууп+1, а данная дисперсия определяет коэффициенты усиления комплексного
фильтра в блоке вторичной обработки.
Ус;п,к,)
Г
О.
О
»-
к
&
о.
о
т
о
а
"d*
У
Ч&
Фильтр
первичной
обработки
R' =
Rv
Блок первичной обработки I
(же
v -и канал
приемника СНС
УПСЭ
Фильтр 2
формирования
оценок
Rv
Т
инс
Акселерометры
Гироскопы
Угы/,=<Р + А<Р
Кл
Блок пересчета
к;=Г(х>)
D^(x,D',dJ
D:
л„
РФК
вторичной
обработки
X
V
а
Vх
D' =
Е =
Ду
+ф ►
X,D'
i I
Рис. 17.10. Схема комбинированной тесносвязанной инерциально-спутниковой
системы навигации
Другим существенным отличием синтезированного алгоритма от
известных является то, что в блок первичной обработки вводится не только оценка
проекции ускорения (или скорости) на линию потребитель—НС, а весь вектор
RJJ оценок (включающий проекции ускорений, скоростей и сами псевдо даль-
663
Глава 17
ности), полученный в результате пересчета оценок координат, вектора
скорости, вектора ускорений и параметров нестабильности опорного генератора,
сформированных в блоке комплексной вторичной обработки. Это позволяет
скомпенсировать часть динамических возмущений, действующих на следящие
системы блока первичной обработки (обусловленных динамикой движения
потребителя и нестабильностями опорного генератора), что, в свою очередь,
позволяет сузить полосы пропускания следящих систем. Причем это сужение
полос пропускания задается не произвольно разработчиком, а определяется
пересчетом дисперсионных уравнений из блока вторичной обработки в блок
первичной обработки в соответствии с (17.22), что автоматически учитывает
точностные характеристики работы блока вторичной обработки и геометрию
расположения НС.
17.2.3. Синтез алгоритма комплексирования на вторичном уровне
(слабосвязанный алгоритм)
Описанная в п. 17.2.2 постановка задачи синтеза глубоко
интегрированного алгоритма комплексирования НАП СРНС/ИНС с небольшими изменениями
может быть использована для синтеза алгоритма комплексирования НАП
СРНС/ИНС на вторичном уровне (слабо связанного алгоритма).
На выходе блока первичной обработки сигналов в НАП СРНС, формиру-
ются оценки псевдо дальности и псевдо скорости Дк и псевдо скорости V^ по
всем видимым НС, которые при синтезе будем рассматривать как спутниковые
измерения. Вектор измерений от / -го НКА можно записать
Усрнси _
А,
и
а
Уц+Ук
+
п,
п,
nai,k
пс i,k
(17.33)
где / = I...N; ппд;к,ппс1к — взаимно независимые дискретные БГШ с диспер-
сиями (тпд/ и с7пс/соответственно; D[ — систематическая ошибка измерения
дальности, вызванная рассогласованием часов спутника и потребителя; Vfk —
систематическая ошибка скорости, вызванная уходом частоты задающего
генератора в приемнике СРНС;
Д/=>/(*,--*)2+(У1 -yf +(zi~z?
— истинное значение дальности до / -го НС;
(Xi-x).(yxi-Vx) + (y.-y).[Vyi-Vy) + (Zi-z)\Vyi-Vy)
(17.34)
V; =
^{xi-x)2+{yi-yf+{zi-z)7
(17.35)
664
Интегрированные инерциалъно-спутниковые навигационные системы
— истинное значение радиальной скорости спутника относительно
потребителя; X = [xj>z]T, V = [FJC VyvA — координаты и компоненты вектора
скорости объекта в ПЗСК; {xi9yi9zi9Vxi9Vyi,Vzi\ —эфемериды / -го НС той же СК.
Для синтеза ИСНС используем такую же БИНС, как и в п. 17.2.2, которую
также будем характеризовать погрешностями угловой ориентации и угловых
скоростей:
«=fc «»('КWj.v.(')=|>* v4 vsJ
Измерения БИНС описываются соотношениями (17.12), (17.13).
Зададим вектор состояния в ПЗСК в виде 5i = [xT VTaT£T v;J , где, как и
раньше
X = [xTA]T,V = [vTKA]\a = an.
Динамика изменения вектора состояния к во времени описывается
формулами (17.16), (17.17), которые можно представить в обобщенном векторно-
матричном виде линейным уравнением
^=^и+СЛи, (17.36)
что является несомненным достоинством рассматриваемого подхода.
Синтез комплексного алгоритма
Для синтеза алгоритма комплексной вторичной обработки, как и в п.
17.2.2, будем использовать модифицированный вариант комплексирования.
Введем вектор наблюдений
У*
т т т т
УСРНС1,* УСРНС2,А: — УСРНСА/,* УИА,*
(17.37)
гДе Уиа,* определяется (17.25), т.е. при X = Уиг _£ •
Используя для синтеза комплексной системы фильтрации расширенный
фильтр Калмана [5.1, 5.2], запишем уравнения
*кк — Кк + Е
ds(ik)'
дк
N-'^-S^)), (17.38)
^к-\ - F^jt-i»
665
Глава 17
e^1=(fe,_1f+g,gi)"4
*WN-,(*(**P
дк
дк
(17.39)
где кк и кк — текущая и экстраполированная оценки вектора состояния на
к -м шаге; Ек — матрица дисперсий ошибок фильтрации;
N =
°"пд1
0
0
0
0
0
0
0
„2
0 •
0
0
0 •
0
0
0
„2
" °пдМ
0
0
0
0
0
0
0
_2
°псМ
0
0
0
0
0
0
0
„2
°уа
0
0
0
0
0
0
0
_2
0
0
0
0
0
0
0
crl
уа
— матрица дисперсий шумов наблюдений;
Vx{\) + V}
S(k) =
(17.40)
Дм(Х) + Д'
U{yHr-£}[a + 2<onxV-g(X)]
— векторная сигнальная функция.
В [5.1] показано, что нелинейный расширенный фильтр Калмана можно
представить в виде дискретной следящей системы, содержащей многомерный
дискриминатор и фильтр. Рассмотрим такое представление для алгоритма
(17.38).
|Т
Введем вектор v =
Хт D' Vх V ат е1
, от компонент которого явно
зависит сигнальная функция (17.40). Данный вектор связан с вектором состояния "к
соотношением v = ск, где с — матрица размером 14 х 17. Запишем выражение
для производной от сигнальной функции:
ЩХ) dS(ck)dv dS(ck)
дк
dv дк
dv
(17.41)
666
Интегрированные инерциалъно-спутниковые навигационные системы
С учетом (17.41) алгоритм комплексной фильтрации (17.38) можно
представить в виде схемы, приведенной на рис. 17.11, в которой выделен
дискриминатор и сглаживающий фильтр.
У*
Дискриминатор
.м
чР
L
S(cv,)
-►
I dv ) IT
i
^
i [
Г Сглаживающий фильтр
! ♦
ИЕ*сТ
z-1
V
L
*Vl
**-1
Рис. 17.11. Схема комплексной системы фильтрации на вторичном уровне
В соответствии с [5.1] многомерный дискриминатор описывается
выражением
ид,* =
ds(dk)
dv
N-'(yk-S(c¥Xk)),
(17.42)
для которого можно ввести статистический эквивалент вида
uUJt=U(v-v) + Cft, (17.43)
где U(v-v) = m[u;iA.] — дискриминационная характеристика
(рассматривается при фиксированной расстройке Av = v-v); С>к — флуктуационный
процесс на выходе дискриминатора, дисперсия которого определяет флуктуацион-
ную характеристику. Дискриминационная характеристика определяет
сходимость оценок вектора состояния к истинным (или смещенным) значениям.
Дискриминационная характеристика U(v-v) является векторной
функцией векторного аргумента, анализ которой в общем случае достаточно
сложен. Поэтому широко используется подход, основанный на анализе данной
функции в сечениях по тому или иному аргументу при нулевой расстройке по
другим аргументам, т.е. представление U(v-v) в виде набора зависимостей
v /v,-v,=0
при j*m
Ниже приведены ДХ по координатам потребителя в ПЗСК, по скорости и
ускорению потребителя в этой же СК, а также по ошибкам углов ориентации
[17.22]. Для наглядности приводимые выражения для ДХ записаны для малых
ошибок фильтрации (т.е. в линеаризованном виде). Так как координаты x,y,z
667
Глава 17
равноценны, выражения для ДХ по любой из компонент какого-либо вектора
будут иметь сходную запись с ДХ по остальным компонентам того же вектора.
Дискриминационная характеристика по координате:
•2( Зх2) ^({Xi-x)2
Ях
Ъ,(х-х) =
1 И'
^уа^
+
1
R'
+
/=i
гЛ п2
°1аД?
(Ух;-Ух)2-{Ух1-Ух)(х,-~х)^
(х-х);
по скорости:
F*vx(Uvx-Vx)) =
м
(xj-x)'
^-» гЛ п2
(Ух-К)
по ускорению:
^K"5*) = —гК"а*);
по угловой ошибке:
уа
~2 ~2
ак^х + а«
>ю
U4
.3-2
где Л — расстояние от объекта до центра Земли; /л = Gm3 =4 10 м с
Из приведенных выражений следует, что многомерный дискриминатор
имеет устойчивую точку равновесия при А, = А,. Кроме того, учитывая, что в
представлении дискриминационной характеристики в виде U(v-v) =
= Sfl(v-v) параметр 8Д определяет ее крутизну, в приведенных выражениях
можно выделить крутизны дискриминаторов по соответствующим параметрам
и исследовать их поведение в различных тактических ситуациях. Такой анализ
показывает, что в рассматриваемом алгоритме комплексной фильтрации
крутизны ДХ имеют конечные значения при любых физически осуществимых
условиях.
17.2.4. Синтез алгоритма коррекции ИНС от НАЛ СРНС
(разомкнутый алгоритм)
Схема ИСНС, соответствующая данному алгоритму, изображена на
рис. 17.8. Синтез разомкнутого алгоритма представляет наибольший интерес с
точки зрения повышения точности ИСНС в автономном режиме работы, когда
сигналы СРНС недоступны. Идея повышения точности заключается в оценива-
668
Интегрированные инерциально-спутниковые навигационные системы
нии и компенсации погрешностей ИНС. В периоды наличия сигналов СРНС
происходит оценивание погрешностей ИНС, а в периоды отсутствия - их
экстраполяция. Компенсация погрешностей выходных данных ИНС
осуществляется непрерывно.
Постановка задачи
С выходов НАП СРНС и ИНС поступают измерения координат и скорости
потребителя в дискретном времени, которые можно представить векторами
[СРНС,*
Bk+nB,k
Lk+nL,k
^E,k + nVE,k
^N,k + nVN,k
[инс,/
Bi+SBt
Li+SLt
УN4 + SVN,i
(17.44)
h-\ ~ Tcphc — темп
\hk+nh,k
где k — момент времени измерения в шкале СРНС; tk
измерений от СРНС; /— момент времени измерения в шкале ИНС;
tt -fM = ТШС — темп измерений от ИНС; В — географическая широта; L —
географическая долгота; VE — восточная составляющая вектора скорости; VN
— северная составляющая вектора скорости; h — высота; пв — ДБГШ с
нулевым математическим ожиданием и СКО, равным ав = -—-—-
нулевым математическим ожиданием и СКО, равным crL =
■ nL — ДБГШ с
Л,
{R3+h)cos{B)'
— средний радиус Земли; сх — СКО измерений горизонтальных координат в
НАП; nh — ДБГШ с нулевым математическим ожиданием и СКО, равным <rh
(определяется из спецификации НАП); nVE, пш — независимые ДБГШ с
нулевыми математическими ожиданиями и СКО, равными оу (определяется из
спецификации НАП); SB ,SL — погрешности определения географической
широты и долготы в ИНС; 8VE , 8VN — погрешность определения восточной и
северной составляющей вектора скорости в ИНС.
Будем приближенно считать, что моменты измерений ИНС и СРНС
когерентны, т.е., если tk =/,-, то tk+l =ti+M, М = ТСРИС/ТШС- целое число. Отме-
тим, что обычно Гинс «с Тстс, а М имеет порядок 10 ... 10 .
В периоды сбоя СРНС результирующая точность навигационных
определений будет определяться точностью экстраполяции погрешностей ИНС SB,
SL , SVE , SVN . Чем корректнее будет выбрана их динамическая модель, чем
669
Глава 17
точнее заданы её параметры, тем выше окажется точность экстраполяции
погрешностей ИНС, а, следовательно, и результирующая точность определения
координат и скорости. В данном случае использована модель (П 17.22),
описанная в приложении П17.2.
Ставится задача по измерениям (17.44) и с использованием
математической модели (П 17.22) получить фильтрационные оценки горизонтальных коор-
динат (В, L) и вектора скорости (VE, VN) потребителя с темпом Гинс.
Синтез алгоритма
Воспользуемся модернизированным вариантом комплексирования,
описанным в п. 17.2.1. Сформируем вектор измерений погрешностей ИНС на
основе (17.44):
Х&,* ~
(*ИНС,£,* ~*СРНС
(*ИНС,Д,* ~*СРНС
\У\\}\СУЕ,к ~ *СРНС
(ч
\\HC,VN,k 'СРНС
-Yr
,L,k )\&з + ^срнс,* )cos\Yc?RC,B,k)
,B,k)(R3 +hc?HC,k)
,VE,k )
,VN,k )
AEk
ANk
8VEJk
WN,k
ПЕ,к
nN,k
nVE,k
nVN,k\
,(17.45)
где 1инс,1,*» *инс,д,* — измерения долготы и широты от ИНС; 5cphc,l,*>
*cphc,zu — измерения долготы и широты от СРНС; УШСУЕк , УИнс,™,* _ из"
мерения восточной и северной составляющих скорости от ИНС; Ус?иСуЕк,
7CPHCPW^ — измерения восточной и северной составляющих скорости от
СРНС; ^срнс,* — измерения высоты от СРНС;
пЕ9к = nLJk \R3 + hc?HC,k )C0S(YC?UC,B,k ) i nN9k " nB9k \R3 + ^CPHC,*: ) ■
Отметим, что YAk формируется только в моменты выдачи измерений от
СРНС.
Введем вектор состояния
X =
rsh
sh
АЕ AN 8VT 8VS" Ф^ Ф^ Ф
n
'N
up
0)l
(О
W
СО,
up
(17.46)
и решим задачу его оценивания по измерениям (17.45) методами теории
оптимальной нелинейной фильтрации. Для достижения наилучшей точности
экстраполяции погрешностей ИНС, входящих в х, целесообразно выбрать
наибольший темп фильтрации — 77инс, а моменты счета фильтра привязать к
моментам выдачи измерений от ИНС, несмотря на то, что \Ак поступает с более
редким темпом Тстс.
670
Интегрированные инерциалъно-спутниковые навигационные системы
Задача фильтрации вектора х решена в виде расширенного фильтра Кал-
мана, общие уравнения которого приводятся, например, в [5.1]. В ходе решения
этой задачи были приняты допущения, связанные с тем, что в модели (П 17.22)
использовались не истинные высота и компоненты вектора скорости, а их
оценки. Также было учтено то, что измерения YA k поступают не в каждый
такт работы фильтра. В итоге, окончательный алгоритм фильтрации вектора х
можно изложить следующим образом.
1. Рассчитывается экстраполированная оценка вектора состояния х.
Уравнения для отдельных компонент х имеют вид:
\ up,i-\)
\l + ^upJ-\)
8V* =^_1 -gT4>NM -^-&Ю.Х9
2
2
2
8V& =W&-x+&*Ej-\ +^j-&ej-i>
T-8VNi_x я
ф£,/ = ф£,м - -, гт- + a>E,i-\T> ®е; = Щ,г-\>
T-SVEi_x „
®N,i = фм;-1 ~ ~, гт- + (*>N,i-\T, coNi = coNi_x,
(Rs+hi)
®uP; = ®uP,i-\ + ®up,i-iT> &uP; = ®uP<i-\»
*£,/ = YmCVEj ~ ^Nj' ^Nj = YmC,VN,i ~ ^N,i» (17.47)
где символ «~» означает экстраполированную оценку с предыдущего шага; «л»
— оценку; Т = Гинс .
2. Рассчитывается экстраполированная оценка матрицы дисперсий фильтра
Ё,- =FME/F£i + G Q Gt, (17.48)
где
671
Глава 17
1
I
F,-i =
1
1 ° т ° ° о (ww-,-^-,)r
0 10 Г 0 0 -(Ws.m-^-.K
0 0 1 0 0 -gT 0
0 0 0 1 gT 0 0
-Т
ft О О 1 л (
(*,+Vi)
)
0 0 7 ^— 0 0 1 0
0 0 0 0 0 0 1
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
/j;_, — грубая оценка высоты, которую можно получить,
последнее актуальное измерение hcmCk;
G =
1 0 0 0 0 0 0
0 0 0 0 0 0
0 -gT/2 0 0 -gT2/4 0
\-gTI2 0 0 -gT2/4 0 0
1 0 0 Г/2 0 0
0 10 0 Г/2 0
0 0 10 0 Г/2
0 0 0 1 0 0
0 0 0 0 1 0
0 0 0 0 0 1
?
0
0
0
ill
2
T
0
0
1
0
0
0
0
-gT2
2
0
0
T
0
0
1
0
например,
0
0
0
0
0
0
T
0
0
1
?
взяв
Q = diag (<7ф, <r|, crj, <7^, <rj, <rj) - диагональная матрица размером 6x6.
3. Если в / -й момент времени поступило измерение от СРНС, то
выполняется шаг оценивания вектора состояния и его матрицы дисперсий:
К, =Ё,Н7 (н,Ё,Нт +N)"1, Е, =(l10 -К.Н, )Ё,-,
x/=x/+K/-(YA,-S/(x/)), (17.49)
где УД; определяется (17.45), 110 —единичная матрица размером 10 х 10,
672
Интегрированные шерциалъно-спутниковые навигационные системы
»,(*,) =
Щ
ANt
ti^NS ~ ®up,i * ^CPHC,F£,i
H,=
as,(xy)
Si,-
, N = diag(c7j,o-J,of ,of)
— диагональная матрица.
4. Если в / -й момент времени измерений от СРНС не поступало, то
х,=х„ Е,.=Ё,.. (17.50)
5. Пункты 1—4 повторяются циклически для последующих моментов
времени.
Таким образом, реализуется оценивание погрешностей ИНС. Теперь,
чтобы найти уточнённые оценки координат и скорости потребителя, необходимо
из измерений ИНС вычесть оценки соответствующих погрешностей.
Поскольку в модели погрешностей ИНС (П 17.22) компоненты SVEi, SVNi зависят от
истинного значения вектора скорости, то такой расчет несколько усложняется.
Кроме того, следует учесть переход от смещений к востоку и северу Д£, AN в
метрах к смещениям по долготе и широте 8L ,8В в радианах. Опуская вывод,
приводим окончательные выражения для оценок координат и скорости
потребителя на выходе алгоритма:
fy ~ ^инс,я,1
ДМ-
и = к
Д£,
VEJ =
VN,i =
YHHC,VE,i - 8Ve,\ ~®up,i \J\mC,VN,i ~ ^N,i)
(1+<нм) '
Y\mC,VN,i - ^N,i + ®up,i (YUHC,VE,i - $VE,i)
(17.51)
Уравнения (17.45)—(17.51) полностью описывают предложенный
алгоритм комплексирования. Из п. 3 и 4 следует, что алгоритм учитывает
измерения СРНС по мере их поступления. При этом не обязательно, чтобы измерения
от СРНС приходили через равные промежутки времени. В частности,
допускаются длительные перерывы этих измерений, что часто бывает на практике из-за
затенения сигналов СРНС, резких маневров объекта, или радиопомех. В этом
случае погрешности ИНС компенсируются за счет экстраполяции с
использованием ранее оцененных параметров модели этих погрешностей.
22-1026
673
Глава 17
17.3. Точность и помехоустойчивость интегрированных
инерциально-спутниковых систем навигации.
Основными целями, преследуемыми при разработке ИСНС, являются:
повышение точности навигационных определений в комплексном режиме
работы ИСНС;
повышение точности навигационных определений в автономном режиме
работы ИСНС после компенсации погрешностей инерциальных датчиков в
комплексном режиме;
повышение помехоустойчивости НАП СРНС и ИСНС в целом.
17.3.1. Точность интегрированных инерциально-спутниковых
систем навигации в комплексном режиме
В настоящее время большинство производимых интегрированных
ИНС/СРНС систем использует идеологию комплексирования на вторичном
уровне. Краткий обзор разработок ИСНС данного типа и достигнутые в них
характеристики точности НВО описаны в п. 17.4, а здесь приведем оценку
потенциальных характеристик точности НВО в комплексированных на
вторичном уровне ИНС/СРНС системах, которые базируются на результатах
математического моделирования алгоритма, описанного в п. 17.2.3.
Приводимые ниже результаты соответствуют следующим исходным данным:
временной интервал дискретной обработки Td = 1 мс (соответствует
времени накопления сигнала в корреляторах НАП СРНС);
число спутников, сигналы которых используются для решения
навигационной задачи,10;
величина геометрического фактора PDOP = 1,48;
высота полета 2000 м, продольная скорость 250 м/с, поперечное ускорение
45 м/с2;
отношение сигнал/шум qcj = 40 дБГц;
среднеквадратическая погрешность измерений акселерометров
ava =0,006 м/с2;
среднеквадратическая погрешность измерения псевдо дальности <тпд = 6 м;
среднеквадратическая погрешность измерения псевдо скорости сгпс =1 м/с;
среднеквадратическое значение формирующего шума в модели динамики
V£ — сту£ =3,6-10"5 рад/с;
среднеквадратическое значение флуктуации частоты опорного
генератора, пересчитанное к флуктуациям скорости, оу< =0,0014 м/с.
В качестве критерия точности оценки координат потребителя
принимаются сферические ошибки оценок (СФО) по координатам
674
Интегрированные инерциалъно-спутниковые навигационные системы
£ф,х = V(* " х? +(У- yf + (z " f f
и скорости потребителя
Чу = yj(rx-K)2+{vy-?y)2+{K-K)2 •
На рис. 17.12 приведена зависимость СФО по оценке координат для
интегрированной ИНС/СРНС системы. График отражает только флуктуацион-
ную и динамическую составляющие погрешности координат.
Систематические погрешности определения координат в СРНС (см. гл. 7) не учитываются.
есфА">м
25
20
15
10
5
"0 10 20 30 40 50 '» и
Рис. 17.12. СФО по оценке координат в слабосвязанном алгоритме
Из рисунка видно, что СФО имеет порядок 3-х метров, что практически
согласуется с величиной шумовой ошибки в автономной НАЛ с некогерентной
обработкой сигналов. Отметим, что систематические погрешности координат в
СРНС оказываются много больше, но не могут быть скомпенсированы за счет
ИНС из-за аналогичного низкочастотного характера. Таким образом, комплек-
сирование с ИНС оказывается малоэффективным средством повышения
точности координатных определений, что подтверждается множеством других
публикаций.
На рис. 17.13 а, б приведены зависимости СФО по оценке скорости
потребителя для интегрированной и автономной некогерентной НАП
соответственно.
Регулярная составляющая СФО оценки скорости в интегрированной
системе 0,29, а в автономной 0,33 м/с. Среднеквадратические значения СФО
соответственно равны 0,06 и 0,12 м/с.
Из приведенных зависимостей следует, что в некогерентной ИСНС
достигается повышение точности оценки скорости — в 1,5...2 раза. По ряду
публикаций, например [17.3], известно, что аналогичные когерентные алгоритмы
675
Глава 17
обеспечивают повышение точности оценивания скорости в 8... 10 раз. Таким
образом, более предпочтительным режимом приема сигналов в ИСНС является
когерентный.
ес<ьг,м/с
', с
3.5,
3
2.5
2
1.5|
1
0.5|
ЕсфГ*м/с
1l л\ Л hiLJ \ A j 11, ! ,ii> I. * ;Ц. 11. fl
L iLU ul, jIlUlu inl ki I faikii .U I. h,i.iiil U
10
20
30
40
50
t- с
a) 6)
Рис. 17.13. СФО по оценке скорости в комплексной (а) и автономной (б) НАП
при некогерентной обработке сигналов.
Комплексирование на вторичном уровне позволяет повысить не только
точность оценивания координат и скорости, но и точность оценивания угловых
координат. Для примера на рис. 17.14, а, б приведены зависимости ошибок
определения угловой ориентации в автономной БИНС типа MEMS и в ИСНС.
£сф^, утл.мин
4000
3500
3000
2500
2000
1500
1ПЛП
1UUU
500
п
всфу >тл
мин
- ~ ~у^
I
I
j /
/ i
/
/
■ ~ ■
^<-^4S^4- J
- \ \J
i
i
?~ 1
i
i 1
10
20
30
40
50
/. С
50 '
a) 6)
Рис. 17.14. СФО оценки угловых координат в БИНС (а) и ИСНС (б)
Дальнейшее повышение точности оценивания угловых координат возможно
при использовании тесносвязанной схемы ИСНС (см. п. 17.2.1). Это достигается
за счет применения более полных моделей ошибок ИНС, включающих ошибки
676
Интегрированные инерциалъно-спутниковые навигационные системы
параметров ориентации и ошибки их производных. На рис. 17.15 приведены
соответствующие зависимости ошибок оценивания углов ориентации, полученные
в результате моделирования алгоритма, описанного в п. 17.2.2 [17.29].
160
20 40 60 80 100 120 140
t, с
Рис. 17.15. СФО оценки угловых координат в тесносвязанной ИСНС
В [17.23] разработаны и реализованы в виде программного обеспечения
оригинальные алгоритмы оценивания погрешностей углов ориентации БИНС,
точность определения которых, полученная в результате летных испытаний,
составила Г (1а) для углов крена и тангажа и 10' (1а) для угла курса, что
согласуются с результатами [17.3]. Высокая точность определения параметров
ориентации продемонстрирована в [17.20], где СКО ошибок углов ориентации
составило 2'...4' в зависимости от вида использованной информации
(позиционная, позиционно-скоростная). На рис. 17.16 а), б) приведены зависимости
ошибок углов ориентации и результаты калибровки гироскопов,
опубликованные в [17.23].
0.104
DOS
1
000
-006-
•UI0-
*й!5.
1
I
l_i—4—-Ы
- Яо11 rate
•Р*с* rate
■Yaw rate
-4-
«U—U
4-
II..
4 -I | U
4 1 1 L
I I I I
4 J i L
i i i i
500
400 BOO
Time (sec}
aoo
5000
is
1J0-
04-
Q4-
04
0J2
0Л
4*2
ЯА
«0*
\
\ j
■J i
\
..^__..—
, -
Г j
|
R0g
Prtcfc
Yaw
h.A i J - L ' „j '.
It \r\ i
IMJ
1 1 i
1 * i
-1 1 ■ 1
1 i ,,. j
, /Щ-х*.,-
' | .Ль-
fr/VV'j>4
i i
i i
1 ■ 1 ■ 1 ■ 1
200
400 «CO
Time i*#c)
6O0
1000
4 б;
Рис. 17.16. СКО оценки угловых координат в глубокоинтегрированной ИСНС
677
Глава 17
17.3.2. Точность интегрированных инерциально-спутниковых
систем навигации в автономном режиме
Результатом высокой точности определения параметров модели ошибок
ИНС является возможность сохранения высокоточной навигации в течение
длительных интервалов времени при затенении сигналов НС, воздействии
преднамеренных помех с уровнем выше порогового и т.п. На рис. 17.17 а, б
представлены результаты работы слабосвязанного алгоритма ИСНС,
описанного в п. 17.2.3, в условиях долговременного отсутствия сигналов навигационных
спутников при использовании ИНС низкой точности (типа MEMS).
абсолютная ошибка координат, м
1200
1000
800
600 Ь
400
200
0 ' 50 100 150 200 250 300 350 400 450 tc
б)
Рис. 17.17. Характеристики слабосвязанного алгоритма ИСНС
при пропадании сигнала СРНС (автономный режим)
678
Интегрированные инерциально-спутниковые навигационные системы
Ряд алгоритмов ИСНС (например, как в п. 17.2.4) разрабатывается
специально для повышения точности автономных навигационных определений во
время сбоя СРНС. В табл. 17.3 приведены обобщенные результаты
моделирования и эксперимента алгоритма из п. 17.2.4. Для сравнения даны характеристики
дрейфов автономной БИНС. Эксперимент проводился на автомобиле,
использовалась аппаратура БИНС ГЛ-1Д производства ЗАО «НПК Электрооптика».
Таблица 17.3. Рост погрешностей автономных навигационных
определений во время сбоя СРНС
[ Рост погрешности
за 1000 сек(2а)
Координаты, м
| Скорость, м/с
Моделирование
автономная
БИНС
3000
2
после комплек
сирования
70
0,2
Эксперимент |
автономная
БИНС
600
1
после комплек
сирования
150
0,7 |
По данным таблицы можно констатировать экспериментально
подтвержденное повышение точности координатных определений в 4 раза.
Моделирование же показывает потенциально достижимое повышение точности в 40 раз.
Подобное расхождение результатов эксперимента и моделирования вытекает из
упрощения выбранной модели ошибок ИНС. Также в эксперименте наблюдается
уменьшение выигрыша в сокращении скорости роста ошибок по сравнению с
моделированием, что объясняется рядом дестабилизирующих факторов:
отсутствие синхронизации измерений СРНС и ИНС;
наличие рычага между приёмной антенной СРНС и центром
чувствительности ИНС;
вибрация корпуса автомобиля и неровность дороги, приводящие к появлению
дополнительных высокочастотных составляющих в погрешностях ИНС;
погрешность математической модели ошибок ИНС.
Результаты работы современных ИСНС с ИНС высокого класса точности в
условиях долговременного отсутствия сигналов НС представлены на рис. 17.18
для аппаратуры LN-200G [17.25].
Ошибка по широте, м
Рис. 17.18. Характеристики аппаратуры LN-200G при
долговременном отсутствии сигналов НС
679
Глава 17
В табл. 17.4 представлены точностные характеристики ИСНС LN-200G
при долговременном отсутствии сигналов НС [17.12]. К сожалению, сведения о
примененном алгоритме отсутствуют.
Таблица 17.4. Точностные характеристики ИСНС LN-200G
| Интервал времени отсутствия сигналов НС, с
Точность определения координат, м
горизонтальная
вертикальная
Точность определения составляющих скорости, м/с
ГбО
16,8
15,9
[2,1
300
95
61
3,0
17.3.3. Помехоустойчивость интегрированных
инерциально-спутниковых систем навигации
В Российской Федерации официальные требования к помехоустойчивости
НАП СРНС, в том числе и ИСНС, отсутствуют. Типовые требования к
помехоустойчивости ПАП СРНС и ИСНС, соответствующие зарубежным стандартам,
приведены в табл. 17.4 [17.26].
Таблица 17.4. Требования по помехоустойчивости НАП СРНС
Тип НАП СРНС
Когерентная автономная
Некогерентная автономная
1 Некогерентная ИСНС
Помехоустойчивость
для СТ-сигнала, дБ |
24
31
55
1 1
Основными факторами, ограничивающими помехоустойчивость НАП
СРНС, являются [17.15], [17.30]:
кратковременная нестабильность частоты опорных генераторов НАП и
НКА;
дрейф погрешностей измерений ИНС.
Как было показано в гл. 8, наиболее уязвимой для помех является система
ССФ. Поэтому для оценки помехоустойчивости ИСНС достаточно рассчитать
только помехоустойчивость системы ССФ. В [17.30] приведена методика
расчета помехоустойчивости комплексной системы ССФ при наличии скоростной
поддержки от ИНС. Показано, что полоса (и помехоустойчивость) такой
комплексной системы ССФ/ИНС не зависит от динамики движения носителя НАП,
но определяется лишь динамикой уходов частоты ОГ и динамикой
погрешностей скорости ИНС. Причем параметры динамики ОГ (S0T) и динамики по-
680
Интегрированные инерциально-спутниковые навигационные системы
грешностей скорости ИНС (SliHC) сведены к единому суммарному параметру
динамического возмущения S^ = iSHHC + Sor . Ниже дана методика расчета
предельной помехоустойчивости системы ФАП при заданном параметре S^.
1. Исходные данные:
/0 — несущая частота радиосигнала;
AFC — полоса сигнала;
А/ог (') [Гц], 'начала -' - 'конца — экспериментальная выборка дрейфов
частоты ОГ относительно несущей f0;
<^инс (') [м/с]> 'начала -' - 'конца — экспериментальная выборка
погрешности скорости ИНС в проекции на ту ось, где динамика погрешности
наибольшая;
Ал — апертура ДХ дискриминатора фазы (360° — 1 тип, 180° — 2 тип);
Ts — длительность интервала преддетекторного накопления в
корреляторе (для дискриминатора фазы, учитывающего смену символа навигационного
сообщения).
2. По выборкам Afor(/), ^инс(') определяется спектральная плотность
эквивалентного суммарного шума динамических возмущений 52 :
s _1
11 ^./t i Dr\r +1
Т
(2л-) Dor +
Ашс
(17.52)
где £>ог - дисперсия приращений (в Гц2) процесса А/ог(г) за интервал
дискретизации Т ; £>инс - дисперсия приращений (в м2/с2) процесса SVUUC (?)
за интервал дискретизации Т .
3. Искомое значение предельной помехоустойчивости (Кп) при
использовании дискриминатора фазы, не учитывающего смену символа навигационного
сообщения (Ащ = 2/г), выражается формулой
Kn=(AaCA)i-AFc.J^-, (17.53)
где СА = 0,076.
4. Искомое значение предельной помехоустойчивости при использовании
дискриминатора фазы, учитывающего смену символа навигационного
сообщения (Аа = ж), выражается формулой
681
Глава 17
Kn=AFcTs-
И +
2(4Л)з
(17.54)
где СА = 0,076.
Применение изложенной методики, например, к сигналам ГЛОНАСС СТ
(AFC =1,022 МГц, /0=1600 МГц, Ts=\0 мс) дает графики рис. 17.19—17.20.
Каждый график является кривой, которая ограничивает сверху область
допустимых значений характеристик ИНС (Бшс/Т) и ОГ (Dor/71). Координаты
любой точки, лежащей под кривой, представляют пару допустимых значений
указанных параметров для данной помехоустойчивости. На каждом рисунке
представлено по 5 кривых для пяти наиболее актуальных значений
помехоустойчивости. Данные рис. 17.19 и 17.20 отличаются различным выбором типа
дискриминатора фазы.
Ю
ю
-2
ш2
ю1
10J
-о ю~1
2
£ ю2
-р
ОТ ю3
..,4-4.
10
ю5
10е
1-й тип дискриминатора (А =
360°)
КП=35ДЬ -г -------- i -- : -;
L _ - - __ А i_- -Т^к J
Кп=40дБ : .... .]
:;;:::::;::..:;:;;:;;:;::;:^;;::;;;;;:::;::;;;;:::::::i::::::::::::::::::::::::::i:::::::::i
:::::::::::::::::::::::::::^::::::::::::::::::::::::::i:::::::::T^:::::::::::::::::::::::
г ; X ;
пппшипшпшшш[П|ШИПИПНММПИП!П|ШПИП1шт|Н:Ш!ПМ,
:::::::::: Кп=45дБ :::^:::::::::::::::::::::::Е:::::::::::::::::^
ППППМ1МПМММП = М = 1пММП^ПГЦ- = = !1ПП1П = ^Ч--
Г г Т
„ ...Кп=50дБ .-[..—.-=-
.авиационная ИНС_Ч_
р:::::::::::::::::::::::::с:П
Кп=55дБ г-
"'^^w !"
\ •
1 i
[_::::::гк-в
Е:::::::::::::
г *
I !
Г •
I i
этк:
f-- :.л.._
•
|==!==z=:=j:==;=!;;;:
[ '
;
[ •
I i
,
:::::::::::::::::!
•
i
j
■
h::::E::::::::::5
1
|
i
10
10
10
(D0f7T). lV
Рис. 17. 19. Множества допустимых значений характеристик ИНС и ОГ при различных
значениях заданной помехоустойчивости. Дискриминатор фазы
ориентирован на сигнал без модуляции навигационным сообщением
682
Интегрированные инерциалъно-спутниковые навигационные системы
10°
ю2
ю-4
со
„у
5. ю"6
J 10"
1010
ю-12
2-й тип дискриминатора (А =180°)
Кп=35дБ
Кп=40дБ
-авиационная ИНС -
Кп=45дБ
Кп=50д
Кп=55д
Б
5
^
I
Л
;
\
"^V
Л
;
;
i
...fK-Q^T^
10
,-12
10
10
10
10
10'
10
(оОГп), r4d
Рис. 17.20. Множества допустимых характеристик ИНС и ОГ при различных
значениях заданной помехоустойчивости. Дискриминатор фазы
ориентирован на сигнал с модуляцией навигационным сообщением
Наиболее очевидным применением представленных графиков с точки
зрения разработчика НАП является подбор совокупности параметров
(Ашс /^)>(Лэг /^) для достижения заданной помехоустойчивости при
работе по сигналам ГЛОНАСС СТ.
Менее очевидный вывод, следующий из сопоставления семейств графиков
рис. 17.19 и рис. 17.20, заключается в том, что при одних и тех же
характеристиках ИНС и ОГ применение фазовых дискриминаторов 1-го типа с
сигналами, не модулированными навигационным сообщением, способно повысить
помехоустойчивость ССФ более чем на 10 дБ, что подтверждается другими
публикациями.
Анализ динамических характеристик погрешностей существующих типов
ИНС и опорных генераторов с точки зрения описанной методики показывает,
что выигрыш в помехоустойчивости может существенно варьироваться (от 0
до 15 дБ). При идеальных ИНС и ОГ помехоустойчивость НАП ограничивается
нестабильностью частоты несущей радиосигнала НКА и составляет Кп=45 дБ
для сигнала СТ ГЛОНАСС, не модулированного навигационным сообщением,
и АГП =36 дБ для сигнала СТ ГЛОНАСС, модулированного навигационным
сообщением. Данные цифры получены на основе ИКД ГЛОНАСС, а также
измерений девиации Аллана для фазовых шумов несущей НКА ГЛбНАСС-М,
проведенных в [17.33]. Также установлено, что при использовании ИНС навига-
683
Глава 17
ционного класса точности, помехоустойчивость ИСНС потенциально может
быть ограничена скорее из-за фазовых шумов несущей радионавигационного
сигнала (и пользовательского ОГ), чем из-за динамики ошибок ИНС.
Одной из существующих тенденций является отказ от высокой точности
измерения радионавигационных параметров в угоду повышения
помехоустойчивости приема сигналов НС. Это достигается за счет использования
некогерентных схем приема сигналов НС, что приводит к дополнительному
повышению помехоустойчивости приблизительно на 6 дБ (см. гл. 8).
Следует отметить три основных достоинства, которыми обладают
интегрированные инерциально-спутниковые навигационные системы:
введение скоростной информации с выхода интеграционного фильтра
НАП СРНС/ИНС в схемы слежения за сигналом НС позволяет обеспечить
сужение шумовых полос и поднять пороговое отношение помеха/сигнал;
принципиально различный характер спектров погрешностей скорости в ИНС
и НАП СРНС позволяет эффективно производить фильтрацию этих погрешностей
и повышать таким образом точность определения скорости в 2... 10 раз.
использование моделей ошибок ИНС, включающих параметры ориентации,
позволяет существенно повысить точность определения параметров
пространственной ориентации и обеспечивает сохранение высокоточных навигационных
определений в течение длительных интервалов отсутствия сигналов НС.
17.4. Обзор современных интегрированных
инерциально-спутниковых навигационных систем
На сегодняшний день лидирующие позиции на рынке инерциально-
спутниковой навигации занимают ведущие мировые производители авиони-
ки: Litton, Honeywell, Boeing, Rockwell Collins, Systran Donner [17.8—17.10].
Большое внимание разработкам ИСНС уделяется и в России, где на первый
план выходит продукция предприятий ФНЦП «Раменское
приборостроительное конструкторское бюро» (г. Жуковский), ЗАО «НПК Электрооптика» (г.
Москва), ЦНИИ «Электроприбор» (С-Петербург), Пермской НППК (г.
Пермь) [17.21, 17.27, 17.28].
Основную массу производимых сегодня интегрированных систем
составляют ИСНС с комплексированием на вторичном уровне (слабо связанное
комплексирование).
В ЦНИИ «Электроприбор» разработана миниатюрная ИСНС «Мини-
навигация-1», которая предназначена для малых судов, летательных
аппаратов и наземных транспортных средств. «Мининавигация-1» состоит из
бесплатформенного инерциального измерительного модуля на волоконно-оптических
гироскопах и миниатюрных акселерометрах, микровычислителя и приемника
спутниковых навигационных систем GPS/ГЛОНАСС, установленных в едином
корпусе. Основные характеристики системы приведены в табл. 17.5 [17.21].
684
Интегрированные инерциалъно-спутниковые навигационные системы
Таблица 17.5. Характеристики ИСНС «Мининавигация-1»
1 1
J Предельные погрешности определения: |
J координат, м
скорости, м/с
углов качки и рыскания, град
составляющих угловой скорости, град/с
энергопотребления, Вт
габаритных размеров, мм
массы, кг
15
од
0,2
од
50
260x160x90
4
Другая российская фирма — ФНЦП «Раменское приборостроительное
конструкторское бюро» — ведущий российский разработчик интегрированных
комплексов, систем и приборов бортового радиоэлектронного оборудования —
представляет интегрированные навигационные системы: инерциально-
спутниковую систему ИСС-1, лазерную инерциально-спутниковую систему
ЛИНС-2000, инерциальную систему ИНС-2000, работающую с приемником
СНС, и навигационную систему определения ориентации БКВ-95 [17.11, 17.27].
Инерциальная навигационная система ИСС-1 разработана на основе
инерциальной гироскопической платформы и сервисной электроники. Система
обеспечивает определение и выдачу пилотажно-навигационных параметров и
предназначена для комплексов наведения различных типов летательных
аппаратов. Она интегрируется со спутниковыми навигационными системами GPS
и ГЛОНАСС (табл. 17.6).
Таблица 17.6. Характеристики ИСНС ИСС-1
Г. ■■■■-■ 1. ., ■■ '-■■■■■ =^^ ■■ ,_,_. ■'—■" ■ '
Погрешности:
1 координат, м
относительной скорости, м/с
крена и тангажа, град
истинного курса, утл. мин/ч
Время готовности, мин
1 Потребляемая мощность, Вт
1 Габаритные размеры, мм
Масса, кг
1 Интерфейс
ИНС
5 400 м/ч
I2'4
0,1
йене
100
0,8
0,1 1
12 1
15 (с гирокомпасированием) 1
10 (по заданному курсу)
200
400x240x230
18
В стандарте RS-422, 614 кГц |
685
Глава 17
Лазерная инерциально-спутниковая система ЛИНС-2000 (совместный
продукт ФНПЦ РПКБ (Россия) и фирмы Thales (Франция)) разработана для новых
и модернизируемых российских самолетов и соответствует российским и
зарубежным стандартам. Малогабаритная бесплатформенная инерциальная
навигационная система создана на базе блока чувствительных элементов на
кольцевом лазерном трехосном гироскопе фирмы Thales и электроники РПКБ.
Система обеспечивает определение и выдачу пилотажно-навигационных
параметров, интегрируется со спутниковыми навигационными системами GPS и
ГЛОНАСС. Основные технические характеристики приведены в табл. 17.7.
Таблица 17.7. Характеристики ИСНС ЛИНС-2000
Погрешности:
координат, м
| относительной скорости, м/с
крена и тангажа, град
| истинного курса, угл. мин/ч
Время готовности, мин
| Потребляемая мощность, Вт
| Габаритные размеры, мм
1 Масса, кг
Интерфейс
инс
1800 м/с
1,8
од
ИСНС
30
0,2
ОД 1
7,8 1
4 (с гирокомпасированием)
0,5 (по заданному курсу) |
90
280x178x178
9
Мультиплексный канал
информационного обмена в соответствии с
ГОСТ 26765.52-87 и MIL STD-
1553 В - 8 линий для приема и 3
линии для передачи
последовательного кода в соответствии с
ГОСТ 18977-79 и ARINC-429
Инерциальная навигационная система ИНС-2000 выполнена в виде
моноблока, состоящего из гиростабилизированной платформы на базе динамически
настраиваемых гироскопов, сервисной электроники, вычислителя, блока
интерфейса и спутниковой навигационной системы. В состав системы входит
антенное устройство спутниковой навигационной системы. Система ИНС-2000
обеспечивает определение и выдачу пилотажно-навигационных параметров и
предназначена для новых и модернизируемых вертолетов и самолетов.
Основные технические характеристики приведены в табл. 17.8.
686
Интегрированные инерциально-спутниковые навигационные системы
Таблица 17.8. Характеристики ИСНС ИНС-2000
1 Погрешности:
1 координат, м
| относительной скорости, м/с
1 крена и тангажа, град
| истинного курса, у гл. мин/ч
1 Время готовности, мин
| Потребляемая мощность, Вт
| Габаритные размеры, мм
1 Масса, кг
Интерфейс
инс
3700 м/с
2,0
0,1
ИСНС
40
0,2
0,1 1
18
15 (с гирокомпасированием) |
150
385x264x195
21
Мультиплексный канал информационного
обмена в соответствии с ГОСТ 26765.52-87 и
MILSTD-1553 В 8 линий для приема и 3
линии для передачи последовательного кода в
соответствии с ГОСТ 18977-79 и ARINC-429 |
Навигационная система определения ориентации БКВ-95 представляет
собой малогабаритную навигационную систему, разработанную на базе
динамически настраиваемых гироскопов, силиконовых акселерометров и
обслуживающей электроники. Навигационная система БКВ-95 корректируется
с помощью спутниковых навигационных систем GPS и ГЛОНАСС.
Основные технические характеристики приведены в табл. 17.9.
Таблица 17.9. Характеристики ИСНС БКВ-95
Погрешности:
| координат, м
| относительной скорости, м/с
| крена и тангажа, град
J истинного курса, угл. мин/ч
Время готовности, мин
| Потребляемая мощность, Вт
| Габаритные размеры, мм |
| Масса, кг |
ИНС
5000 м/с
6,0
0,5
ИСНС
200
0,6
0,5
1,5
15 (с гирокомпасированием) |
80
420x133x194
^5 |
Ведущими мировыми производителями авионики по заказу Министерства
обороны США разработаны и поставлены в серийное производство несколько
образцов тесно связанных ИСНС, к которым с высокой степенью
достоверности можно отнести следующие изделия: P-MIGITSII, M-MIGITSII, C-MIGITSIII
(Boeing, Rockwell Collins), LN-200G, LN-270 (Litton), P-764G (Honeywell)
[17.11,17.7,17.24,17.8—17.10].
687
Глава 17
Высокоточная помехоустойчивая ИСНС P-MIGITSII разработана по заказу
ВВС США в соответствии с требованиями директивы [17.26].
При проектировании ИСНС основной акцент был сделан на разработку
миниатюрного, маломощного, дешевого, помехоустойчивого комплекса
СРНС/ИНС, обладающего высокими точностными характеристиками для
широкого спектра приложений.
Конструктивно в состав P-MIGITSII входят цифровой блок твердотельных
инерциальных датчиков, включающий кварцевые датчики угловой скорости и
кварцевые акселерометры, и 5-канальный ПСН военного назначения AN/PSN-11.
В качестве навигационного процессора, решающего подавляющее число задач в
ИСНК P-MIGITS II используется высокопроизводительный сигнальный процессор
TMS320C31 производства компании Texas Instruments. Часть задач
предварительной обработки сигналов инерциальных датчиков возложена на
специализированные сигнальные процессоры SPROC, выполненные по технологии ASIC.
Основные характеристики P-MIGITS II приведены в табл. 17.10.
Таблица 17.10. Характеристики ИСНС P-MIGITS II
Погрешности:
координат, м
относительной скорости, м/с
крена, тангажа, курса, мрад
Вибрация
Габаритные размеры, мм
Ударные нагрузки
Максимальные скорости
Максимальные ускорения
Интерфейс
Гинс
<1800м/ч
—
2,5...3+£
J = 1...3 град/ч
ИСНС
<16
0,2
2,5...3
kg
90x102x120
20 g, 11 мс J
12 000 м/с, ЮОО град/с
15 g
RS-232, NMEA 0183, AMRAAM
Интегрированные инерциально-спутниковые системы LN-250, LN-260,
LN-270 разработаны Litton Systems Inc и предназначены для широкого спектра
приложений (ВВС, ВМС, СВ, высокоточное оружие). При их разработке
основное внимание уделялось снижению массогабаритных характеристик,
потребляемой мощности, повышению надежности, точности и помехоустойчивости.
Основные характеристики ИСНС LN-270 приведены в табл. 17.11.
Одной из значимых разработок Litton Systems Inc является
помехоустойчивая, высокоточная ИСНС LN-200G, разработанная по заказу ВВС США.
Характеристики ИСНС LN-200G приведены в табл. 17.12.
688
Интегрированные инерциально-спутниковые навигационные системы
Таблица 17.11. Характеристики ИСНС LN-270
| Погрешности:
1 координат, м
1 относительной скорости, м/с
| крена, тангажа, курса, мрад.
| Потребляемая мощность, Вт
1 Габаритные размеры, мм
1 Вибрация
| Ударные нагрузки
| Макс, эксплуатац. хар-ки
1 Интерфейс
ИНС
<4000 м/ч
—
—
ИСНС ~~|
<10
0,2
ОД
<25
3200 куб. см
8,1 g
86 g, 8Mc;21g,40MC
13 g /с, 1000 град/с, 1500 град/с2
GPS MIL-STD-1553,SS-US-200,GRAM
i 1
Таблица 17.12. Характеристики ИСНС LN-200G
| Погрешности:
| координат, м
1 относительной скорости, м/с
| крена, тангажа, курса, град.
| Потребляемая мощность, Вт
1 Габаритные размеры, мм
1 Вибрация
| Ударные нагрузки
1 Макс, эксплуатац. хар-ки
1 Интерфейс
ИНС
—
—
—
ИСНС
<10
0,1
0,2...0,35
< 17
5000 куб. см
15 g
90 g, 6 мс
13 g, 1000 град/с
RS-422, ARTNC 429, RS-485 |
Конструктивно LN-200G включает бесплатформенный инерциальный
измерительный блок LN-200, состоящий из волоконно-оптических гироскопов и
кварцевых микромеханических акселерометров, и 12-канальный двухчастот-
ный GPS-приемник военного назначения. LN-200G является первой ИСНС,
удовлетворяющей требованиям директив GRAM/SAASM.
17.5. Синхронизация измерений в инерциально-спутниковых
навигационных системах
В рассмотренных примерах синтеза алгоритмов работы ИСНС (п. 17.2)
предполагалось, что измерения навигационных параметров в ИНС и НАП
СРНС осуществляются синхронно, либо в кратные моменты времени.
Соблюдение этого условия на практике крайне важно. Ошибки определения векторов
координат и скорости из-за рассинхронизации можно найти по формулам
689
Глава 17
'Хт,к
IS
к -> ьУт,к
IS
Lt»
(17.55)
где tis — время задержки между моментом актуальности измерений от ИНС и
моментом актуальности измерений от СРНС (время рассинхронизаци); А^ и
V^ — средние за интервал дискретизации значения ускорения и скорости
объекта соответственно. Формулы даны в практическом приближении, что tis
много меньше времени корреляции ошибок скорости в ИНС.
В частности, из (17.55) следует, что для динамичных объектов со
среднеквадратичным ускорением 5g (на которых применение ИСНС особенно
актуально) время рассинхронизации rIS не должно превышать 100 мкс для
достижения декларируемой среднеквадратичной погрешности оценивания
скорости порядка 1 см/с.
Без наличия специальных средств синхронизации в аппаратуре ИСНС
выполнить данное требование невозможно, а при наличии таких средств
требование tis < 100 мкс выполняется с большим запасом.
Существуют различные способы синхронизации измерений. В качестве
примера приведем здесь наиболее простой способ синхронизации по
аппаратному сигналу метки времени (MB). На рис. 17.21 изображена схема связей
основных узлов ИСНС, учитывающая синхронизацию измерений.
Устройство
| синхронизации
1 ОГ
ИНС
-^
^
Метка
времени
Интерфейс
НАЛ
СРНС
ОГ
>
информационного
обмена
Рис. 17.21. Схема связей основных узлов ИСНС
с учетом синхронизации измерений
Необходимым условием при построении ИСНС является организация
электрического сигнала метки времени, поступающего от НАП СРНС в ИНС,
как показано на схеме рис. 17.21. Активный фронт электрического импульса
MB формируется в момент осуществления навигационных измерений по
СРНС. Устройство синхронизации, входящее в состав ИНС, принимает сигнал
MB и измеряет время задержки каждого отсчета измерений инерциальных
датчиков относительно последнего активного фронта MB. Эта информация
«подмешивается» к инерциальным измерениям и поступает на вход комплексного
алгоритма обработки, который использует её для привязки спутниковых и
инерциальных измерений к единой шкале времени.
690
Интегрированные инерциалъно-спутниковые навигационные системы
Приложение к гл. 17
Основы инерциальной навигации
Функциональное предназначение любой ИНС состоит в получении
информации о траекторном и угловом движении объекта. Конструктивно в состав
ИНС входят триады измерительных датчиков (акселерометров, гироскопов) и
вычислитель, реализующий алгоритм счисления (алгоритм вычисления
координат (линейных и угловых) путем интегрирования соответствующих
производных).
В основе принципа функционирования ИНС лежит использование законов
Ньютона. Для тела массой т, движущегося в центральном поле тяготения
Земли под действием некоторой внешней силы F , можно записать закон
Ньютона в инерциальной системе координат (см. п. 3.1):
F + mg(r) = iii—, (П17.1)
где г — радиус-вектор центра масс подвижного объекта; g(r) —
гравитационное ускорение; d2r/dt2 = аи — ускорение тела в инерциальной системе
координат (ИСК).
Введем вектор ускорения ак = ¥/т и запишем (П17.1) в виде
aK=aH-g(r). (Ш7-2)
В теории инерциальной навигации ускорение ак принято называть
кажущимся ускорением [17.1, 17.14], и именно оно измеряется акселерометрами,
т.е. является выходным сигналом акселерометра.
При записи (П17.2) не делалось никаких предположений о траектории
акселерометра, но оно дает явное представление о зависимости выходного
сигнала акселерометра от текущего местоположения объекта (от вектора г ).
П17.1. Алгоритм бесплатформенной ИНС
Алгоритм БИНС дает способ получения координат и вектора скорости по
измерениям датчиков ускорения (акселерометров) и датчиков угловой скорости
(гироскопов). В состав БИНС входят 3 акселерометра и 3 гироскопа,
образующих инерциальный измерительный блок (ИИБ). Оси чувствительности каждой
триады датчиков ортогональны и совпадают с осями собственной системы
координат объекта.
Таким образом, на вход алгоритма БИНС поступают измерения:
*к,с,* — вектора кажущегося ускорения в центре чувствительности ИИБ,
собственная система координат объекта, м/с2;
691
Глава 17
iock — вектора угловой скорости в центре чувствительности ИИБ,
собственная система координат объекта, рад/с.
Измерения поступают в дискретном времени с периодом дискретизации
Т ; индекс к — номер отсчета.
Будем полагать, что измерения ак с к и ю" ^ уже прошли компенсацию
инструментальных погрешностей датчиков. (Компенсация инструментальных
погрешностей включает устранение температурного дрейфа нуля, линеаризацию
передаточной характеристики, масштабирование, ортогонализацию осей
чувствительности и т.п. по каждому датчику. Рассмотрение этих вопросов выходит
за рамки данного материала.)
Кроме того, для обеспечения измерений по вертикальной оси необходима
грубая оценка высоты над референц-эллипсоидом НЬк от других средств
навигации.
Выходными (счисляемыми) параметрами БИНС являются:
В, L, Н — геодезические широта, долгота и высота соответственно;
— вектор скорости в локальной системе координат
^,* =
Ч* ve,k vd,k
«север-восток-низ»;
R , Р, Y — углы крена, тангажа и рыскания соответственно.
Для корректной работы алгоритма необходима задать начальные значения
всех счисляемых параметров.
Используем распространенный аппарат кватернионов для представления
ориентации в алгоритме (см. приложение П17.3). В этом случае механизм
счисления ориентации выражается рекуррентным уравнением [17.31]:
qa=(M*®q;.*-i®A">
(П17.3)
где q^ — кватернион поворота осей ЛСК к осям ССК (выполняемого
относительно ЛСК), что соответствует преобразованию координат из ССК в ЛСК;
■(ИИ
А и
* =
cos
Рк
/2
Pi,k
Ik II
Р\к
Ikl
sin(M/2)
sin(M/2)
ли /ди . ди \
P*=(«>c,*-i+e>c,*)
2
(П17.4)
692
Интегрированные инерциально-спутниковые навигационные системы
А£ — кватернион малого поворота объекта за малый интервал времени
tk_x...tk относительноинерциальногопространства;
\зк — кватернион поворота ЛСК относительно инерциального
пространства за счет вращения Земли и движения объекта над криволинейной
поверхностью земного эллипсоида;
Аз,* =
cos(HI/2)
чин
Q
2,к
т
Q
3,к
т
sin(||ftjj||/2|
sin(|njj|/2|
Slk «
cos
(4Ц
+
ve,k
a
vn,k
Г
a
(Bk) + e2 cos2 (Bk)
и \
l-0.5e2sin2'5 ^ Hk
a
J
f> N\
l-I^sin2'*^-2—2'** Hk
2
a
-sin(4)«3
T,
(П17.5)
где щ — угловая скорость вращения Земли; а — большая полуось земного
эллипсоида; е2 — квадрат эксцентриситета земного эллипсоида; Вк, Нк, vnk ,
vek — экстраполированные оценки широты, высоты и горизонтальных
компонент вектора скорости на момент времени к:
{^k-iT + An,k.rT2/2)
Нк ~ Нк-\ ~ Vd,k-\T ~ Ad,k-\ ' ~Г ' Вк ~ Вк-\ + / i —- г _ »
2 аЦ\-е2 sin2 {Вк_х)+Нк
Vn,k ~ Vn,k-\ + An,k-\T ' Ve,k ~ Ve,k-\ + \k-\T \
(П17.6)
л л
Ап9 Ае — оценки горизонтальных составляющих вектора ускорения.
Вычислив qc/t, можно найти оценки углов крена (Rk), тангажа (Рк) и
рыскания (Yk) пользуясь соотношениями (П 17.40) (см. приложение П17.4). В
нулевой момент времени необходимо задать кватернион начальной ориентации
qj0. Информация о начальной ориентации берется из процедуры гирокомпас-
сирования, или из внешних источников, для чего могут пригодиться
соотношения обратного пересчета из углов Эйлера в кватернионы (П 17.38).
693
Глава 17
Измерения акселерометров пересчитываются в локальную систему
координат с помощью счисленного на текущий момент кватерниона ориентации
о
а
к,л,к
<к®
О
а
к,с,&
® (<*)*■
(П17.7)
От измеренного кажущегося ускорения в ЛСК ак л к переходят к собст-
А | А А Л I 1
венному ускорению объекта в ЛСК АлА. = \Апк Аек Adk\ путем
компенсации ускорения свободного падения и центростремительного ускорения:
Аа=^-еК^*Л4), (П17.8)
где
§(ЯМД,УЛ.*)*
О
-g0R + V к + V„ к / ч 2 / 5 \ 2
(* + ям)
д =
а
1-е2 sin2 (4)
(П17.9)
g0 — ускорение свободного падения у поверхности Земли; Ньк — оценка
высоты над референц-эллипсоидом, полученная другими средствами навигации
(например, НАП СРНС, баровысотомер, радиовысотомер+карты рельефа).
Необходимость ввода оценки высоты НЬк от других измерителей (а не
использование оценки Нк из алгоритма БИНС) вызвана известной
нестабильностью вертикального канала ИНС [17.13].
Для получения оценок координат Вк, Lk, Нк и вектора скорости \пк не-
обходимо проинтегрировать Ал к тем или иным методом численного
интегрирования. С этой целью традиционно используется метод Рунге-Кутта 4-го
порядка. Также, при малых Г (меньше 0,01 с), допустимо применять метод
трапеций. Запишем выражения для получения оценок координат и вектора
скорости пользуясь методом трапеций:
Vn,k =Kk~\ +(Кк + *njc-\)~Z> А к =Нк-Х -(v^ +Vrfjt-i)-T»
694
Интегрированные инерциалъно-спутниковые навигационные системы
°k = Bk-\
аЦ\-е2*т2(Вк_х) + Нк '
(Vek+Vek-l)-T/2
4=4-1 + / / ч • (П17.10)
^l-e2sin2(4) + ^j-cos(4)
Описанный алгоритм основан на приближенных методах численного
решения дифференциальных уравнений и поэтому имеет собственную
погрешность. В связи с этим его не рекомендуется использовать в автономных
высокоточных БИНС. Однако при работе в составе ИСНС, алгоритм показывает
высокую эффективность.
П17.2. Модели ошибок БИНС
В п. П 17.1 приведены общие алгоритмы, описывающие работу
«идеальной» БИНС, т.е. системы в которой инерциальные датчики не имеют
инструментальных и методических погрешностей и начальные условия для
алгоритмов счисления координат заданы точно. В реальных условиях невозможно
задать начальные условия абсолютно точно, а измерения инерциальных датчиков
всегда содержат погрешности, для которых необходимо задавать те или иные
модели.
Модель измерений инерциальных датчиков.
В наиболее общем виде, модель измерений инерциальных датчиков можно
определить следующим образом
{р)(Ма*па{Чс) + *а+"а+™а8{<))> (П17.11)
Ac"=^(p)(Me,fIM,(«c") + £e+na,+wge(aICiC)), (П17.12)
где акс- вектор истинного кажущегося ускорения в центре чувствительности
инерциального измерительного блока (ИИБ) (собственная система координат
объекта); со" - вектор истинного значения угловой скорости в центре
чувствительности ИИБ (собственная система координат объекта); Ка(р) -
операторный коэффициент передачи, отвечающий за инерционность акселерометров,
АГа(у-2л-/)| =1; Ка>(р) ' операторный коэффициент передачи,
отвечающий за инерционность гироскопов, KM(j-2^f)\ _ =1; Мв, М^ - матрицы
масштабных коэффициентов и перекосов осей акселерометров и гироскопов;
fm, fn(0 - векторные функции нелинейностей передаточных характеристик ак-
695
Глава 17
селерометров и гироскопов; га9 г^ — векторы смещений нулей
акселерометров и гироскопов; па, п^ — шумы измерений; wag - функция, учитывающая
влияние вращений вокруг условного центра масс на выходные сигналы
акселерометров; wga - функция, учитывающая влияние линейных ускорений на
показания датчиков угловой скорости.
При изготовлении ИИБ выполняется частичная компенсация нелинейно-
стей fna,fna)9 а также кросс-чувствительности акселерометров и гироскопов,
выраженной функциями wag и wga. При синтезе алгоритмов,
соответствующие погрешности полагаются несущественными. Также обычно считается, что
полоса пропускания инерциальных датчиков много шире полосы пропускания
интеграционного фильтра, поэтому Ка(р)^\, К0){^р)^\. И, наконец, внедиа-
гональные элементы матриц Ма, М^ зачастую полагаются нулевыми из-за
плохой наблюдаемости. Таким образом, модель измерений инерциальных
датчиков можно записать в упрощенном виде
ак,с=МАс+£а+па, (П17.13)
шси=МХ+^ + п.. (П17.14)
В табл. П17.1 приведены значения параметров модели ошибок типового
ИИБ. В качестве «типового» взят блок Honeywell HG1700 [17.34], ставший
классическим в зарубежных публикациях. HG1700 построен на кольцевых
лазерных гироскопах и является инерциальным блоком тактического класса
точности. К сожалению, среди отечественной продукции невозможно выделить
столь же распространенного ИИБ.
Таблица П17.1. Характеристики модели ошибок ИИБ HG1700
1 Параметр
Значение 1
Гироскопы |
Смещение нуля гироскопа (СКО), град/ч
СКО набега угловой ошибки гироскопа за интервал времени,
1 7/ч
1 СКО шума гироскопа, мкрад
1 Точность масштабного коэффициента гироскопа (СКО)
Точность привязки осей гироскопов к осям блока (СКО),
мкрад
Неортогональность осей гироскопов (СКО), мкрад
2 1
од
80
1,5-10"4
500
100 |
Акселерометры \
1 Смещение нуля акселерометра (СКО), Mg
J 1
696
Интегрированные инерциалъно-спутниковые навигационные системы
———— ^^—^—^—^— III ——■_
ГСКО набега ошибки скорости акселерометра за интервал
времени, MKg /л/Гц 1
1 СКО шума акселерометра, м/с
Г Точность масштабного коэффициента акселерометра (СКО)
1 Точность привязки осей акселерометров к осям блока (СКО),
мкрад
Неортогональность осей акселерометров (СКО), мкрад
1 ^^—— = , !
150
0,0024
5-Ю-4
500
100
Модель ошибок выходных навигационных параметров в ПЗСК
Приведем одну из возможных моделей ошибок ИНС, ориентированную на
применение в ПЗСК. Модель дается в непрерывном времени и учитывает
только составляющие погрешности датчиков еа, гф, па, п^.
Счисленные координаты гп, вектор скорости Vn и матрица ориентации
U" определяются с ошибками и, учитывая малость ошибок, могут быть
записаны в виде
гп=гп+Л, (П17.15)
Vn=Vn+^V, (П17.16)
Ucn=Uj(l-[yx]), (П17.17)
где дг — ошибка координат; д\ — ошибка по скорости; [ух] — матрица
векторного произведения, соответствующая вектору у ошибок углов
ориентации:
' 0 -Уъ Уг
[ух] =
Уъ
-Уг
0 -ух
Ух 0
Учитывая (П 17.31)—(П 17.33), для линеаризованной модели ошибок ИНС
запишем
(П17.18)
Л-2[^х]п^У + исп[аК)Сх]у + исп(£а+па), (П17.19)
dSr _
dt
dSV
--SV,
ffk
dt
dr„
=-№*l
T + «*+n«.
(П17.20)
697
Глава 17
Здесь [аксх]
вектору ак с;
"О
L Jn
(Ш7.21)
матрица векторного произведения, соответствующая
Oh,
О
О О
о о
oh, — угловая скорость вращения Земли;
g„ = gn (гп) - ftj x П„ х гп — вектор ускорения силы тяжести,
включающий гравитационное и центробежное ускорения.
Приведенная выше линеаризованная модель ошибок ИНС может быть
использована при синтезе алгоритмов комплексирования НАП СРНС/ИНС. Эта
модель не претендует на общеупотребительный характер ее применения, но
демонстрирует общие принципы получения моделей ошибок ИНС [17.1, 17.12,
17.13].
Модель ошибок выходных навигационных параметров в ИСК.
В [17.32] предложена математическая модель ошибок ИНС в дискретном
времени. Модель предназначена для прогнозирования шулеровских дрейфов
ИНС на длительных интервалах времени, поэтому её область применения
ограничивается ИСНС, построенными на базе ИНС высокого и среднего класса
точности (до 20 км за час). Вертикальный канал в модели не рассматривается.
Достоинством модели является её простота и независимость от типа ИНС
(платформенной или бесплатформенной).
Математическая запись рассматриваемой модели дается в виде
SL; =
Д£;
SB;=-
AN;
' (*3+/;;)cos(2?,)' ' (Я3+/>,)'
T
Щ = Д£м +
Щ = ДЛГМ +
(1 + <м)
Т
(1 + <м)
(sVnh ,+Ф ■ ,V„ +Ф2 iVr \
у" E,i-\ T ^up,i-V N,i ^ ^up,i-r E,i J '
(л'Й-
ф
upJ-\v EJ
v^+ф
up,i-VN
..)>
rsh
sh
Wej = SV™ + Фир,Ую, SVNJ = SV™ - Фир,ГЕ>1,
дУ^=8У^_х-ёТФМ4_х ~^-coN,_x
rsh ?j,sh . _™. . gT'
^=^-,+^Фад +
О)
2
gT
n,
<JW,/ •>
E,i-\
n,
ФЕ,1 '
698
Интегрированные инерциалъно-спутниковые навигационные системы
Т ■ SVN м
Ф£,,- = ФЕ,1-\ - ,R + /\ + <»ES-\T + ПфЕ; ,
T-8VEi_x
фм; = фм;-\ ~ ,R +h^ + <»N,i-\T + "<i>N,i.
Фир,1 = Фцр,/-1 + ^.i-l7, + «Фцр,/> *V' = ЮирМ + ncmp,i >
®E,i = °>E,i-\ + ncoE,i > °>N,i = &NJ-1 + "vNj ■ (П17.22)
где / — номер отсчета; Т — интервал дискретизации модели; g — ускорение
свободного падения в диапазоне рабочих высот; R3 — средний радиус Земли;
h — высота; В — широта;
Д£,AN , 8VsEh, SVfl1, Фир, ФЕ, Ф# , соир,G)E,a)N — параметры модели из
которых можно выделить: 8L, 8 В — погрешности долготы и широты
соответственно; AE,AN — восточная и северная составляющие погрешности
координат в метрах; Ф — погрешность угла курса; 8VEh, 8V^h — шулеровские
погрешности восточной и северной составляющих скорости; пФМ, пФЕ, пф
— независимые ДБГШ с нулевыми математическими ожиданиями и
дисперсиями <Тф ; naN, псоЕ, п — независимые ДБГШ с нулевым математическими
ожиданиями и дисперсиями <т^.
Величины (Уф и <т^ являются обобщением динамики погрешностей инер-
циальных датчиков и могут быть подобраны для каждого конкретного случая.
Так, для авиационной ИНС с уходом порядка 10 км / час эти значения
составили о£=1,2-1(Г157\ crl = 0 [17.32].
Несмотря на приведенные примеры, вряд ли можно сформулировать
общие рекомендации по выводу модели ошибок ИНС. Наиболее полная модель
измерений инерциальных датчиков (П17.11)—(П17.12) практически непригодна
для такого вывода из-за своей сложности. Для каждого конкретного случая
структура и параметры модели ошибок подбираются опытным путем и
являются результатом математического моделирования, экспериментальных
исследований и эксплуатации.
При использовании для синтеза оптимальных ИСНС теории оптимальной
фильтрации для описания моделей смещения нулей, ошибок масштабных
коэффициентов акселерометров и гироскопов обычно выбирают модели в виде
случайных констант [17.14, 17.19] или экспоненциально-коррелированных
процессов первого порядка [17.16, 17.19]. Для описания ошибок углов
ориентации используются модели второго порядка [17.2, 17.3, 17.11, 17.16].
699
Глава 17
П17.3. Кватернионы
В математике кватернионы рассматриваются как гиперкомплексные числа
вида
Ч = 41+?2* + ?з] + ?4к> (П17.23)
где qx ...q4 — действительные числа, a i, j, к — мнимые единицы такие, что
i2 =j2 =k2 =-1, ij = -ji = k, jk = -kj = i, ki = -ik = j.
Алгебра кватернионов впервые была введена ирландским физиком и
математиком У.Р. Гамильтоном в 1843 г применительно к механике. Важным
свойством кватернионов является способность описывать вращения в
трехмерном пространстве в виде точек на поверхности четырехмерной сферы. С
появлением бесплатформенных ИНС кватернионы быстро стали общепринятой
формой представления ориентации в подобных системах. Также кватернионы
нашли широкое применение в компьютерной анимации.
Векторно-матричные представления кватеронионов
Кватернион может быть представлен кватернион-вектором q, или же
изоморфной ему кватернион-матрицей Q. Реже используется
преобразованный вид кватернион-матрицы Q.
q =
Я\
Яг
Яъ
Яа
<+ Q =
Я\
Яг
Яъ
Ял
-Яг
Я\
Яа
~Яъ
-Яъ
~Яа
Я\
Яг
~Яа
Яъ
-Яг
Я\
,Q =
Я\
Яг
Яъ
Яа
-Яг
Я\
-Яа
Яъ
-Яъ
Яа
Я\
-Яг
-Яа
-Яъ
Яг
Я\
(П17.24)
Операции над кватернионами
I |Т | |Т
Если & = \аха2аъ а4\ > b = Z^ Z>2 63 64 - кватернионы, то сложение а и
b определяется обычными правилами векторно-матричного сложения
.ai+bi
a + b =
а2 +b2
аъ+Ьъ
а4 +Ь4
(П17.25)
Произведение двух кватернионов а и b определяется как
\axbx -a2b2 -аъЪъ -a4bA
\а2Ьх + ахЬ2 - аАЬъ + аъЬЛ
\аъЬх + а4Ь2 + ахЬъ -а2Ь4\'
\а4Ьх -аъЪ2 + а2Ъъ + ахЬ4\
a®b = A b = B а =
(П17.26)
700
Интегрированные инерциалъно-спутниковые навигационные системы
где <S> — операция кватернионного произведения; А, В — соответствующие
матричные представления кватернионов а и b .
Из (П 17.26) следует, что произведение кватернионов не коммутативно
a<g>b*b<8)a, (П17.27)
однако свойства ассоциативности и дистрибутивности выполняются:
а®Ь ®с = (а®Ь)®с = a®(b®c),
a<8>(b + c) = a<S>b + a<g>c,
(sa)®b = a®(db) = s(a®b), (П17.28)
где с — кватернион-вектор; s — скалярный множитель.
Сопряжение. Если q — кватернион вида (П17.24), то сопряженный ему
кватернион q* определяется как
q*=k -Чг -Ь -Яа\Т- (П17.29)
Через операцию сопряжения определяется норма кватерниона:
HI = Vq®q* = Vq*®q = h\ + <& + я1 + я1 (пп.з.8)
Инверсия. Если q - ненулевой кватернион вида (П 17.3.2), то обратный ему
кватернион q-1 определяется как
*
Ч"'=-^Т- (П17.30)
IN»2
Дифференцирование произведения кватернионов. Производная по
скалярному параметру t от произведения кватернионов дается в виде
(a(f)®b(f))'=a'(f)®b(f) + a(/)®b'(f). (П17.31)
При взятии производной по кватернион—вектору справедливы следующие
соотношения.
я я
—(a®b) = B, — (a®b) = A,
dav } дЪК J
—(a<g>b®c) = D, D<->d = (c®a), (П17.32)
дЬ
где D — кватернион—матрица результата произведения d = (с <8> а).
Представление вращений
При изложении кватернионного представления вращений удобно
воспользоваться понятием вектора вращения. По определению, вектором вращения
является такой вектор, направление которого задает ось вращения, абсолютная
701
Глава 17
длина численно равна углу поворота, а направление вращения определяется по
правилу правой руки. Обозначим вектор вращения как р = \рх р2 /?3 .
Кватернион, описывающий тот же самый поворот, что и вектор р,
определяется как [П17.13]
cos(||p|/2)
def
q(p) =
о-ОМИ
gHIPIN
os-(IHI/2)
(П17.33)
Пусть требуется повернуть «обычный» вектор v = Ivj v2
вокруг
вектора вращения р на угол ||р||. С привлечением аппарата кватернионов
решение данной задачи имеет вид
0
\w\
\w2
\w3
= q(p)(g)
0
vi
v2
V3
®q(p),
(П17.34)
где w,,w2,w3 —компоненты результирующего вектора w = \w{ w2 w3| .
Если поворот вектора v осуществляется в виде серии нескольких (и)
вращений, заданных векторами pj,p2...p„, то компоненты результирующего
вектора w будут находиться как
О
w
Wo
W->
= q(p„)®-.®q(Pi)®
о
®q*(t>l)®...®q*(pn).
(П17.35)
Следовательно, кватернион полного поворота в результате серии
вращении р!,р2...р„ вычисляется как
qz=q(p«)®-"®q(p2)®q(Pi)-
(П17.36)
В инерциальной навигации один элементарный поворот соответствует
одному отсчету сигнала с выхода триады датчиков угловой скорости, а текущая
702
Интегрированные инерциалъно-спутниковые навигационные системы
ориентация является результатом серии таких поворотов относительно
начального момента времени.
Широкое применение кватернионов вызвано тем, что они лишены
недостатков, присущих другим формам представления вращений и ориентации.
Конкретизируем суть данного вопроса.
Кватернионы и векторы вращения. Недостаток векторов вращения
заключается в том, что при представлении серии вращений р1,р2...р„
результирующий вектор вращения рЕне является простой функцией от pl9p2...pw . В ква-
тернионном представлении данная проблема решается относительно просто
путем последовательного умножения соответствующих кватернионов (П 17.36).
Кватернионы и матрицы преобразования координат. Недостаток матрицы
преобразования координат заключается в том, что она содержит большее число
параметров - 9, тогда как кватернион содержит только 4 параметра.
Кватернионы и углы Эйлера. Углы Эйлера по своей природе разрывны.
Например, малое изменение положения объекта при тангаже около 90°
приводит резкому изменению углов крена и рыскания, их скачкам на 180°.
Кватернион же является непрерывной функцией ориентации объекта (малый поворот
влечет малое изменение кватерниона).
П17.4. Математические соотношения между различными формами
представления ориентации
При разработке алгоритмов работы систем навигации можно пользоваться
различными формами представления ориентации объекта. К ним относятся:
- углы Эйлера;
- матрица преобразований координат (матрица направляющих косинусов);
- кватернион;
- вектор вращения.
Задание ориентации предполагает введение однозначного преобразования
координат между ССК объекта и целевой СК. В качестве целевой будем
рассматривать локальную систему координат (ЛСК) «север-восток-низ», как
наиболее частый в навигационной практике случай. В этом случае углы Эйлера,
задающие ориентацию объекта, называются углами крена (R), тангажа (Р) и
рыскания (Y) (раздел 3.1, рис. 3.7).
1. Если заданы углы R , Р и Y , то матрица преобразований координат из
ССК в ЛСК рассчитывается по формуле [17.13]
и; =
су • ср -cr -sy + sr-cy-sp sr-sy + cr-cy- sp
sy cp cr-cy + srsy- sp -sr -cy + crsysp
-sp sr -cp cr- cp
(П17.37)
703
Глава 17
где cr = cosR, sr = s'mR, cp = cosP, sp = smP, cy = cosY, sy = sinY . Индексы
систем координат: «л»-ЛСК, «с»-ССК.
Кватернион поворота, рассчитывается по формуле
\cR-cPcY + sRsP-sY\
< =
sRcPcY-cRsPsY
cRsPcY + sRcPsY
cRcPsY-sRsPcY
(П17.38)
R R P P Y Y
где cR = cos—, sR = sin —, cP = cos—, sP = sin—, cY = cos—, s7 = sin—.
2 2 2 2 2 2
Запись q£ означает кватернион поворота осей ЛСК к осям ССК
(выполняемого относительно ЛСК), что соответствует преобразованию координат из
ССК в ЛСК.
2. Если задана матрица преобразований координат из ССК в ЛСК -
uj =
ц.1
UU
^3,1
^1.2
и2Л
U3,2
V*
U2,3
иъ,ъ
то углы крена, тангажа и рыскания рассчитываются по формулам
Д = а1ап2(*У3,2>£/з,з)>
ж
~2
P = atan2^(t/U) +(U2A) ,tf3,i
F = atan2(^/21,f/11),
где atan2(j\*) — функция вычисления полного угла арктангенса.
i |Т
3. Если задан кватернион поворота q£ -\qx q2 q3 Я4\ »
то углы крена, тангажа и рыскания рассчитываются по формулам
R = atan2l2(qiq2+q3q4),(\-2(q22 +qlfjY
P = arcsm(2(qiq3-q2q4)),
Y = atm2(2(qiq4+q2q3),(\-2(q23 + q\
(П17.39)
= 1,
(П 17.40)
704
Интегрированные инерциалъно-спутниковые навигационные системы
Матрица преобразований координат из ССК в ЛСК рассчитывается по
формуле
и; =
2 2 2 2
Я\ + Я2~Яъ -Ча
2(Я2Яз+Я\Я4)
2{я2Я4-Я\Яъ)
2{Я2Яъ~Я\Я4)
2 2 2 2
Я\ + Яъ ~Я2~Я4
2{Я\Я2 + ЯъЯ4)
2(Я\Яз+Я2Я4)
ЧЯ3Я4-Я1Я2)
я1+я1-я1~я1
(П17.41)
4. Если в ЛСК задан вектор поворота осей ЛСК к осям ССК,
1 |Т
Рс=|А Р2 Ръ\ , то соответствующий кватернион поворота рассчитывается
по формуле
где
<£
cos
А
Рс
Р2
Рс
Ръ
(\Ф)
sin(|p;|/2)|
sin(NII/2)
sin(||P;||/2)
(П 17.42)
у]р? + р% + р\ — абсолютная величина утла поворота.
Литература
17.1. Бабич О.А. Обработка информации в навигационных комплексах. — М:
Машиностроение, 1991.
17.2. Харисов В.К, Горев А.П. Синтез тесно связанного алгоритма инерциально-
спутниковой навигации// Радиотехника. Радиосистемы, 2000, № 7, с. 80—86.
17.3. Харисов В.Н., Горев А.П. Исследования характеристик алгоритма глубокой
интеграции СРНС/ИНС//Радиотехника. Радиосистемы, 2001, №7, с. 56—63.
17.4. Richard E. Philips, George T. Schmidt. GPS/INS Integration/ AGARD Lecture
Series 207. System Implementation and Innovative of Satellite Navigation, 1996, pp. 9.1—9.18.
17.5. Dornheim M.A. Cold War Lab Applies Strengths to New Missions// Aviation week
and space technology, 2002, July, pp. 149—152.
17.6. Martin M., Detterich B. The World's Smallest Military INS/GPS//
PMIGITS™ II. ION—GPS, 1998.
17.7. Bruner C.P. LN—200G First SAASM based tactical grade INS/GPS navigator//
ION-GPS, 2000.
23-1026
705
Глава 17
17.8. www.honeywell.com
17.9. www.rockwellcollins.com
17.10. www.systron.com
17.11. Управление и наведение беспилотных маневренных летательных аппаратов
на основе современных информационных технологий/ Под ред. М.Н. Красилыцикова
и ГГ Серебрякова, - М: ФИЗМАТЛИТ, 2003.
17.12. Farrell J.A., Barth М. The Global Positioning System & Inertial Navigation. —
NY: McGraw-Hill, 1999.
17.13. Global Positioning Systems, Inertial Navigation, and Integration, with MATLAB.
— NY: John Wiley & Sons, 2001. Co-authors M.S.Grewal, L.R. Weill and A.P. Andrews,
17.14. Hong S., Chang Y. Estimation of alignment errors in GPS/INS integration// ION-
GPS, 2002.
17.15. Kreye C, Eissfeller В., WinkelJ. Improvements of GNSS Receiver Performance
Using Deeply Coupled INS Measurements// ION-GPS, 2000.
17.16. Salychev O, Voronov O., Cannon M., Lachapeele G. Low cost INS/GPS
integration: Concepts and testing/ Proceedings of National Technical Meeting, The Institute of
Navigation, Anaheim, С A, 2001.
17.17. Ярлыков M.C., Кудинов A.T. Анализ субоптимальных алгоритмов
обработки сигналов интегрированной аппаратуры потребителей спутниковых
радионавигационных систем ГЛОНАСС и GPS// Радиотехника, 1999, №2, с. 56—65.
17.18. Ярлыков М.С, Пригонюк Н.Д. Бортовая инерциально-спутниковая система
для навигации и посадки самолетов/ Сборник статей и докладов под ред. В.Г. Пешехо-
нова. — Санкт-Петербург: Изд-во ЦНИИ «Электроприбор», 2001.
17.19. Дмитриев СП., Степанов О.А. Неинвариантные алгоритмы обработки
информации инерциальных навигационных систем/ Сборник статей и докладов под ред.
В.Г. Пешехонова. — С.-Петербург: ЦНИИ «Электроприбор», 2001.
17.20. Дмитриев СП., Степанов О.А., Кошаев Д.А. Исследование способов ком-
плексирования данных при построении инерциально-спутниковых систем/ Сборник
статей и докладов под ред. В.Г Пешехонова. — С.-Петербург: ЦНИИ
«Электроприбор», 2001.
17.21. www.elektropribor.spb.ru.
17.22. Перов A.M., Шатилов А.Ю. Сравнительный анализ характеристик двух
алгоритмов комплексной вторичной обработки информации в инерциально-спутниковых
навигационных системах// Радиотехника. Радиосистемы, 2003, № 7, с. 88—98.
17.23. Salychev О, Voronov О., Cannon M, Lachapeele G. Low cost INS/GPS
integration: Concepts and testing/ Proceedings of National Technical Meeting. The Institute of
Navigation, Anaheim, С A, 2003.
17.24. Martin M., Detterich B. The World's Smallest Military INS/GPS: P-
MIGITS™ II/ ION-GPS, 1998.
17.25. Bruner C.P. LN-200G First SAASM based tactical grade INS/GPS navigator//
ION-GPS, 2000.
17.26. Guidelines for the global positioning system. Receiver application module/
Headquarters, Space and Missile Systems Center, NAVSTAR GPS Joint Program Office,
1997.
706
Интегрированные инерциалъно-спутниковые навигационные системы
17.27. www.rpkb.ru
17.28. www.ppk.perm.ru
17.29. Перов А.И., Шатилов А.Ю. Синтез комбинированного алгоритма
комплексирования на первичном и вторичном уровнях в инерциально-спутниковои системе
навигации//Радиотехника. Радиосистемы, 2005, № 7, с. 4—14.
17.30. Шатилов А.Ю. Методика расчета помехоустойчивости комплексной ФАП
в НАП СРНС/ИНС// Радиотехника. 2009. № 7, с. 19-25.
17.31. Salychev O.S. Applied Inertial Navigation: Problems and Solutions. - Moscow,
BMSTU Press, 2004.
17.32. Шатилов А.Ю. Алгоритм комплексирования приёмника СРНС и ИНС по
разомкнутой схеме// Радиотехника. 2008. № 7, с. 19-25.
17.33. Anja Hesselbarth, Lambert Wanninger. Short-term Stability of GNSS Satellite
Clocks and its Effects on Precise Point Positioning.// ION GNSS 21st Techical Meeting of the
Satellite Division, 16-19, September 2008, Savannah, GA.
17.34. http://www.navsys.com/Papers/0409001 .pdf
707
Глава 18
Глава 18
ПРОСТРАНСТВЕННО-ВРЕМЕННАЯ ОБРАБОТКА
СИГНАЛОВ В АППАРАТУРЕ ПОТРЕБИТЕЛЕЙ
Навигационная аппаратура потребителей часто работает в условиях
воздействия помех, приходящих с направлений, отличных от направлений
прихода спутниковых сигналов. Наиболее эффективным способом повысить
помехоустойчивость НАП СРНС в этом случае является пространственная
обработка сигналов (ПОС), которая предполагает использование антенной решетки
(АР), служащей датчиком пространственных различий приходящих сигналов.
Используя эти различия, ПОС способна обеспечить дополнительное (к
«собственным» возможностям приемника) подавление помех на 30.. .50 дБ и более.
18.1. Принцип пространственного подавления помех
Разработка антенных устройств пространственной обработки сигналов,
которые часто называют антенными компенсаторами помех (АКП), для НАП
СРНС ведется довольно давно и опирается на методы пространственно-
временной обработки сигналов (ПВОС) [18.15, 18.20, 18.18].
Рис. 18.1. Идея пространственной обработки (компенсатор помех)
Работа пространственного компенсатора помех базируется на двух
эффектах. Во-первых, используется пространственная избирательность антенны, то
есть способность по-разному усиливать сигналы, приходящие с разных
направлений. Это качество антенн характеризуют диаграммой направленности
(ДН) - зависимостью усиления от угла прихода сигнала. Сигналы, попадающие
в максимум ДН, усиливаются. Гораздо больший эффект достигается тем, что
сигналы, попадающие в минимум ДН (в «нуль»), могут существенно
ослабляться.
Имея в виду эти качества антенны, следует управлять ДН так, чтобы
направлять ее нули в сторону источников помех (ИП) ("нуль на помеху").
708
Пространственно-временная обработка сигналов в аппаратуре потребителей
Управлять антенной можно механически или электронно. Особенно
просто осуществить электронное управление антенной решеткой (АР), состоящей
из нескольких антенных элементов. Такое управление можно выполнять,
изменяя комплексные весовые коэффициенты р, с которыми складываются выходы
антенных элементов (рис, 18.1).
Чем больше антенных элементов в решетке, тем больше степеней свободы
для создания новых глубоких «нулей» ДН. В принципе, число таких нулей на
единицу меньше числа элементов антенны [8.15].
Итак, главная задача такой обработки, не усилить сигнал, а подавить
помеху. Подавляя помеху, можно существенно улучшить отношение
сигнал/помеха и обеспечить условия для приема полезного сигнала.
Вторая идея обеспечивает простой механизм управления ДН.
На первый взгляд для подавления помех обязательно знать направления
прихода помехи и сигнала, а также и структуру антенной решетки.
На самом деле, если помеха - как в случае СРНС - значительно мощнее
полезного сигнала, а компенсатор имеет структуру рис. 18.2, существенно
подавить помеху и улучшить условия приема полезного сигнала можно,
используя простой критерий минимума выходной мощности.
11Ц вЫХ
Рис. 18.2. Структура компенсатора
При этом алгоритму адаптации "не нужно знать", откуда приходит
помеха. Достаточно лишь так подстраивать коэффициент(ы) р, чтобы мощность на
выходе сумматора уменьшалась.
Существует несколько эффективных алгоритмов, способных выполнить
такую минимизацию. Однако, такие алгоритмы адаптации не гарантирует
наилучшего выходного отношения сигнал/помеха, т.к. сигналы от НС могут
случайно попасть в провал ДН, где будут ослаблены.
Особенности задачи пространственного подавления помех
для защиты НАП СРНС
Первые пространственные компенсаторы помех применялись для
повышения помехозащищенности радиолокаторов. Известно, что ДН РЛС имеет
достаточно узкий главный лепесток, в котором находится цель, и широкую
зону боковых лепестков. Поскольку задача заключалась в том, чтобы подавить
\г
ее
X
709
Глава 18
источники помех, действующие из зоны боковых лепестков, такие
компенсаторы назвали «компенсаторами боковых лепестков (КБЛ)».
В отличие от типовых радиолокационных задач для приемников СРНС
требуется защитить сигналы, приходящие от нескольких (не менее 4-х)
навигационных спутников из разных точек небесной сферы. Поскольку, как правило,
спутников, доступных приемнику СРНС больше четырех, какие-то из них
можно и потерять, но приемник при этом решит поставленную задачу.
Другая особенность - сигнал от спутника очень слабый, т.к. спутник
далеко. Эта специфика задачи приводит к существенным отличиям в реализации
компенсатора для СРНС от КБЛ.
18.2. Алгоритм оптимальной пространственно-временной обработки
Модель наблюдения.
Используя комплексную форму описания сигналов и помех [18.2], можем
записать наблюдение на выходе антенной решетки
$g=Htsg(bg) + Cgnt+n0t9 (18.1)
где С,=
С1 ~'Ск - CL
, Н и Cj. — векторы фазовых распределений
сигнала и А>й помехи на элементах антенны; й — БГШ, моделирующий
источники внешних помех; п0, — вектор независимых БГШ, описывающий
внутренние шумы в каналах.
Если ввести обозначение для суммарного шума
п,=С,п(+п0;> (18.2)
то уравнение наблюдения (18.2) приобретает вид
!,=НЛ(Х;) + пг (18.3)
Получим оптимальный алгоритм определения параметров к сигнала
St(k) на основе многоканального наблюдения §,(/) на некотором временном
интервале t = 1, Т. Величина интервала Т не имеет особого значения, но для
определенности можем принять ее соответствующей 1 мс - основному
интервалу как ГЛОНАСС, так и GPS.
Ограничимся рассмотрением оценки к по максимуму правдоподобия.
Существенно более общий подход, основанный на рассмотрении задачи
фильтрации, дан в [18.7, 18.16] и приводит к структуре рис. 18.3. Функционал
правдоподобия /?(£, | X) с учетом комплексного характера фигурирующих в
уравнении для \t векторов имеет вид [18.7, 18.15]
710
Пространственно-временная обработка сигналов в аппаратуре потребителей
(2-я-) |V| L 2 J
где V — корреляционная матрица суммарных шумов (18.2), а верхний индекс
(•)* означает операцию эрмитова сопряжения.
Учитывая независимость шумов п, в разные моменты времени
функционал наблюдения всей совокупности наблюдений $J на интервале равен
pktT\k) = Ylp(lt\X). (18.5)
v > t=\
Оценка i. = max-1 p(tl \ X) при подстановке (18.4), (18.5) соответствует
л
минимуму суммы в показателе экспоненты
т
" ■ —1
k = min
£[§, -Щ (X)]* V1 |\ - HS, (X)] [= max"1 ReJHV1^^ (*)}.
(18.6)
l*=i
Обозначив
Ъ=Н*У%, (18.7)
получаем, что оценка X соответствует оценке по максимуму корреляционного
интеграла
JU max^Rej^^S^H, (18.8)
который представляет привычный алгоритм обработки сигнала во временной
области.
Наблюдения с выходов элементов антенны %t входит в алгоритм (18.6)
лишь объединенным в эквивалентное наблюдение rjt, которое, следовательно,
является достаточной статистикой от вектора %t. Выражение (18.8)
представляет оптимальный алгоритм пространственной обработки в многоэлементной
антенной решетке.
Обозначив p = V_1H, записываем алгоритм (18.8) в виде взвешенной
суммы выходов элементов АР
m
;=1
причем весовые множители в сумме (18.9) являются комплексными числами.
711
Глава 18
Понятно, что оценка к не изменяется при умножении р на произвольное
положительное (некомплексное) число. Поэтому иногда удобно рассматривать
Р в виде [18.7,18.15]
P = DV1H,
Z) = l/H*V"1H.
Так как в этом случае
PH = h*v1h/h*v1h = i,
(18.10)
(18.11)
ТО
(18.12)
где иэ/ — эквивалентный шум с дисперсией
Dn = М{пэ(п*э(} = М{р*пэ/п;гр} = P*Vp = H*V"! W^H/H^V^H = l/H^V^H,
что совпадает с (18.11).
Принципиально, что характеристики оптимальной оценки параметра 1
при многоканальном наблюдении эквивалентны характеристикам оценивания
X, при одноканальном наблюдении (18.12).
/
Пространственный"]]" Временной
фильтр м фильтр
л
ОФ
Х\
■>сз
L L^_JL
Рис. 18.3. Схема оптимального алгоритма ПВОС
Результирующий оптимальный алгоритм пространственно-временной
обработки представлен на рис. 18.3 в виде последовательно соединенных
оптимального пространственного фильтра (ОПФ) и временного фильтра. При более
общих постановках задачи, включающих меняющиеся во времени параметры
сигнала и параметры Н, и V,, характеризующие пространственное
расположение АР, НИСЗ и источников помех, в структуре оптимального алгоритма
меняется только вид временного фильтра [18.7, 18.16].
Прежде чем анализировать оптимальный пространственный фильтр
рассмотрим антенный компенсатор помех.
712
Пространственно-временная обработка сигналов в аппаратуре потребителей
18.3. Классический антенный компенсатор помех
В классическом антенном компенсаторе помех (АКП) [18.20, 18.15]
выделяют основную антенну, выход которой содержит полезный сигнал и помехи, и
дополнительные (компенсационные) антенны, которые не должны содержать
полезного сигнала. Структура компенсатора имеет вид рис. 18.4.
О-
В»2
1,
*7
■KZ)
Вых
а
Рис. 18.4. Структура компенсатора
В компенсаторе сигнал основного канала подается на сумматор с
единичным весом, а колебания компенсационных каналов взвешиваются, исходя из
помеховой обстановки. При этом цель подстройки весовых коэффициентов а -
обеспечить минимальную мощность шума на выходе (минимальную
дисперсию Dn колебания //).
Выражение для а можно найти из условия D (а) = min :
Dn(a) = M
V(l «)
v«/
ГП
va/
(Vn
VV21
V "^
v12
'22/
(1 a)
= Vn+a V21+V12a + a V22a
Откуда, дифференцируя по a
d/da(Dn(aj) = Vl2+a\2
22
и приравнивая результат нулю, получаем
-1--*
a = -V2Vr2=-V^V21. (18.13)
Если Bxl, Вх2 схемы рис. 18.4 подключены к антеннам, такая компенсация
эквивалентна формированию нулей в ДН на все источники приходящих
сигналов, в связи с чем для этих схем даже используется термин Адаптивный
формирователь нулей (АФН) [18.9], а в иностранной литературе [18.15, 18.21] —
miller. Такой компенсатор помех часто используется в радиолокации как
компенсатор боковых лепестков [18.20, 18.15].
Коэффициент подавления. Качество работы компенсатора принято
характеризовать [18.20, 18.18] коэффициентом подавления, который определяется
713
Глава 18
как отношение дисперсии шума в основном канале к дисперсии шума на
выходе АКП
*п=7Г (18.14)
п
Учитывая, что D^. = Vx {, и приведенные выше соотношения, получаем
^=(V_1)n=Kl,"Vl2-V22l-V21'T-e-
Кп =
11
^11 %2 '^22 '^21
Выражение для Кп упрощается, если вместо матрицы V ковариаций
шумов в каналах использовать матрицы коэффициентов корреляции шумов р,
т.е., V = оро, где
a = diag(<Tl,...am) = diag(yl^,...yl^yp = {pij}, ij = 1,/и,ptj =M[ninj\/aiGJ .
В частности,
v\ l = °\Р\ 1 = °\ » так как Pi, = 1, / = 1, /я ,
V21=V,2 =<т1а2р21,где <s2=diag(cr2,...crm), р2Х = (р2\,Ръь-Рт\) >
v22 = «2Р22<*2 » гДе (Р22 ),,• = Л/» ,'»-/ = 2' т
При этом
*п =
of - ofpj^ (a2P22a2 ) <*2 1 " P21P22P2I
Существенно, что коэффициент подавления зависит только от
коэффициентов межканальной корреляции шумов. В частности, для одного опорного
канала АКП (двухэлементной АР)
к —L—J—
п ~—i—а~—i—[Г*
l-\Pi2\ 1-\Pl\
Замечание 1. Отметим, что экспериментально коэффициент подавления
можно оценить, подав на входы компенсатора рис. 18.4 одно и то же колебание
и замерив в установившемся режиме отношение мощностей D& lDn .
Выражение для коэффициента подавления через р^~ Рп характеризует
"качество" каналов, интегрально учитывая действие декоррелирующих
факторов: межканальной корреляции (коэффициент корреляции р собственно поме-
ховых колебаний Хи и X2t в каждой из антенн) и внутренних шумов. Эти
714
Пространственно-временная обработка сигналов в аппаратуре потребителей
факторы в (18.16) несложно разделить. Если внутренний шум в каналах
отсутствует, то коэффициент подавления (18.16) примет вид:
*по=—|-т. (18.17)
1-И
Если, напротив, р = 1, коэффициент подавления определяется лишь
внутренними шумами:
_(\ + Р1)(\ + Р2)
Кит — —; —, (18.18)
где Pt = Dx. ID . Оно следует из (18.17) если учесть, что
. |2 DXDX,
С учетом (18.18), (18.19) выражение (18.16) можно представить в виде:
111 Х ' +-L. (18.20)
Выражение для коэффициентов подавления Кш можно представить виде
111 I 111 ЛОЛп
= + - = + , (18.21)
Кп \ + Рх 1 + Р2 \} + Р2)\}\ +Pi) Китг Киш2 ^пш,^пш2
где £пш. = l/(l + i?) — коэффициент подавления при наличии шума только в
1-м канале. При интересных для практики больших отношениях Pi - Dx lDn.
выражение упрощается
1111 1
КП /> Р2 (Dx/Dn\ {Dx/Dn)2
Отсюда следует, что Киш, а следовательно и Ки, всегда меньше
отношения помеха/внутренний шум в любом из каналов АКП. В типовых условиях,
когда отношения помехи к внутреннему шуму в каналах равны получаем
m~2Dn '
Эти соотношения ограничивают значение коэффициента подавления при
не слишком большой мощности помехи по сравнению с уровнем внутреннего
шума. Однако это ограничение исчезает при наиболее важных для подавления
больших уровнях помехи. Физика этого явления довольно проста, и часто
формулируется как «помеха подавляется до уровня внутреннего шума». Действи-
715
Глава 18
тельно, смесь помехи с мощностью Dx с шумом в основном канале при
идеальной коррелированности помех в каналах компенсатора будет подавлена до
уровня
DY+D„ DY+D„
If D \
Щ,
= 2D,
п
Так как внутренний шум с мощностью Dn в основном канале не может
быть компенсирован, то остаток мощности Dn предлагается трактовать как He-
скомпенсированную часть помехи. Более детальный анализ показывает, что на
самом деле помеха в этом случае почти полностью компенсируется, однако при
этом на выход АКП добавляется внутренний шум опорного канала с
мощностью Dn. В итоге мощность шумов на выходе АКП увеличивается по меньшей
мере в 2 раза или на 3 дБ.
Выше отмечалось, что с точки зрения создания условий для приема
полезного сигнала, структура АКП оптимальна только тогда, когда полезный сигнал
присутствует лишь в основном канале. Тем не менее, он нашел широкое
применение в качестве устройства подавления помех на входе ПСН. Например, в
разработанном фирмой Raytheon антенном компенсаторе помех GAS-1,
описываемом далее, в 7 элементной решетке центральный антенный элемент
образует основной канал компенсатора, а расположенные вокруг него равномерно по
окружности радиусом Я/2 6 элементов-вспомогательные каналы АКП.
Оснс вные причины такой подмены оптимального пространственного
фильтра компенсатором помех заключаются, прежде всего, в относительной
сложности реализации электронной фокусировки на НИСЗ. Такая фокусировка
требует весьма точной юстировки амплитудных и особенно фазовых
характеристик элементов АР. Кроме того, хотя положение НИСЗ в земной системе
координат известно достаточно точно, ориентация АР на подвижных объектах
изменяется в довольно широких пределах. Поэтому для реализации
оптимального пространственного фильтра в современных приемниках типа GPS-
приемника Lockheed Martin G-STAR™ [18.24] в блок антенной решетки
приходится ставить специальные гироскопы, определяющие ориентацию АР. Во-
вторых, оптимальный пространственный фильтр предполагает фокусировку на
каждый НИСЗ.
С другой стороны, АКП реализует основную составляющую оптимальной
пространственной обработки — режекцию помех, по сравнению с которой роль
фокусировки, собирающей полезные сигналы от небольшого числа отдельных
элементов АР, заметно меньше. При этом алгоритмы АКП не требуют знания
направлений на источник помех, а извлекают необходимую информацию из
корреляционных характеристик помех. Это следует из алгоритма оптимальной
пространственной обработки (18.7), куда входит только корреляционная
матрица помех на выходах элементов АР. Далее, в условиях СРНС АКП гаранти-
716
Пространственно-временная обработка сигналов в аппаратуре потребителей
рованно не настраивается на подавление полезных сигналов. Дело в том, что
приходящий полезный сигнал оказывается на 15 и 30 дБ ниже уровня
внутреннего шума, поэтому даже в отсутствии внешних помех он не будет
формировать нули в направлении на НИСЗ.
Наконец, анализ структуры ОПФ (см. п. 18.4) подчеркивает важную роль
АКП ивтеорииПВОС.
Замечание 2. Легко увидеть, что классический компенсатор получается
путем минимизации выходного шума ряКр при ограничении 1^=1. Иногда
предлагается другой вариант компенсатора, минимизирующего выходной шум
ряКр при ограничении |р|| = 1 - Можно показать, что такой компенсатор (в
отличие от классического) при отсутствии помех формирует провал ДН на
полезный сигнал.
Замечание 3. В [18.28] предложен вариант построения пространственных
фильтров с линейными ограничениями. Такой подход позволяет задавать
направления, в которых нужно дополнительно формировать провалы и
максимумы ДН. К сожалению, рациональное задание таких ограничений требует
установления детерминированного соответствия между физическим трехмерным
пространством и пространством векторов H=f(#,ar). Это предполагает
фазирование антенной решетки и существенно усложняет реализацию.
В дальнейшем при исследовании характеристик пространственной
обработки мы будем рассматривать параллельно как оптимальный
пространственный фильтр, так и АКП.
18.4. Структура оптимального пространственного фильтра
Проанализируем структуру ОПФ. В нашем анализе выбраны
представления, подчеркивающие фундаментальную роль АКП как важнейшей
составляющей ОПФ.
В выражении для алгоритма оптимальной пространственной обработки
(18.7) легко увидеть две ее главные составляющие. Первая и основная для
работы в условиях помех составляющая пространственной обработки — режек-
ция помехи, отражаемая в выражении (18.7) умножением вектора наблюдения
с выходов АР на матрицу V-1, содержащую все пространственно-временные
характеристики помехи,
5r/=V-V (18.23)
Вторая составляющая алгоритма пространственной обработки —
объединение полезных сигналов, содержащихся во всех компонентах £ . Она
осуществляется умножением £ , на вектор Н*, т.е.
717
Глава 18
т
/=1
Множитель, Н* сопряженный множителю Hz во входном наблюдении,
обеспечивает равенство фаз полезных сигналов при сложении. В пространстве
такое когерентное сложение эквивалентно фокусированию антенны в
направлении на источник излучения полезного сигнала, т.е. НИСЗ.
В отличие от АКП, который только формирует нули в ДН на ИП, ОПФ
выполняет еще и фокусировку на полезный сигнал. Схемы с такими
характеристиками в зарубежной литературе [18.15, 18.21, 18.24] называются Beamformer,
а в нашей [18.9] — адаптивные формирователи лучей.
Приведенная интерпретация пространственного фильтра отображается
схемой рис. 18.5.
пространственный фильтр
Режекция помехи
Ы
V
**
Фокусировка на НИСЗ
н*
Пг
Рис. 18.5. Структура пространственного фильтра
Одно из преимуществ такого представления связано с необходимостью
одновременного приема сигналов от множества НИСЗ. В структуре рис. 18.5
это приводит только к размножению блока фокусировки для различных Н,.
При этом первый наиболее сложный блок режекции помех оказывается общим
для всех НИСЗ.
Процедуру режекции в схеме рис. 18.5 можно представить в виде
параллельных АКП, причем в АКПк в качестве основного элемента берется k-й ан-
теннный элемент. Этот факт следует из очевидного равенства
v"^ = [(i о o)v^ .. (о о \)\~l$J.
Схема ОПФ рис. 18.6 подчеркивает фундаментальную роль АКП в ПВОС.
Полезным для дальнейшего будет и другое представление оптимального
алгоритма пространственной обработки на основе АКП. Основное отличие от
предыдущей схемы состоит в том, что здесь операция фокусировки
предшествует операции режекции (компенсации) помех.
718
Пространственно-временная обработка сигналов в аппаратуре потребителей
ПРОСТРАНСТВЕННЫЙ ФИЛЬТР
Н
АКП
1
АКП
2
h
L
^Фокусировка]
наНИСЗ
а
41
|Фокусировка|
наНИСЗ
Пг
Фокусировка]
наНИСЗ
Рис. 18.6. Схема пространственного фильтра
Сконструируем невырожденное представление вектора %( таким образом,
чтобы полезный сигнал сфокусировался на одном, пусть первом, выходе
преобразователя и отсутствовал на остальных т-\ выходах. Например, оно
может описываться матрицей П, зависящей только от взаимного расположения
АР и НИСЗ
П
н7|н|
... Gm_x
в которой первая строка равна сопряженному вектору Н с нормировочным
множителем 1/Н , а остальные пг-\ строк составлены из векторов
G,, / = 1, w-1, ортогональных Н, т.е. G, H = 0. Например, в качестве G,
могут использоваться m -1 строка матрицы
РН=1-НН
У(н*н),
представляющей оператор проектирования на подпространство, ортогональное
вектору Н,т.е., РнН = 0.
Т
Очевидно, что ПН=(1 0 ... 0) и значит
|,=Щ,=П[Ш,(Х) + П,] =
О
уЬ
St(k) + nt.
(18.24)
Из (18.24) следует, что полезный сигнал собран в первом элементе вектора
4,. Остальные выходы преобразователя Щ, содержат только шумы
719
Глава 18
n,, / = 2, т. Так как эти шумы коррелированны с шумом первого выхода, то
интуитивно ясно, что выходы с номерами 2, т можно использовать для
компенсации й,, т.е. напрашивается дальнейшая конструкция обработки типа
т
^=|»+Ха*^=^+а*^'
(18.25)
/=2
век-
где (* = {#,}, / = 2, т, at - некоторые комплексные числа, а §2/ = (й")
тор, составленный из компенсационных выходов преобразователя (18.24).
Важно заметить, что преобразование (18.25) изменяет лишь уровень шума
на выходе rjt, не искажая сигнал и оставляя его мощность фиксированной. В
этих условиях выбор вектора а из условия минимума мощности выходного
шума обеспечит максимум отношения сигнал/шум (ОСШ).
В [18.3] показано, что минимум дисперсии rjt достигается при
а = -V^1 * V21, где V22 = М (|2/ • |2,}, V21 = М ||2/ • lu} > a оптимальный алгоритм
пространственной обработки (18.10) приводит к тому же результату. Это
означает, что если полезный сигнал присутствует только в одном канале
наблюдения, то оптимальный пространственный фильтр совпадает с корреляционным
компенсатором помех.
Структуру оптимального пространственного фильтра в общем случае
можно представить в виде рис. 18.7.
пространственный фильтр
Электронная
фокусировка
п
Рис. 18.7. Структура оптимального пространственного фильтра
В пространстве первый этап преобразований приводит к электронному
формированию m антенн. Первая антенна, представленная выходом §,,
сфокусирована в направлении на НИСЗ. Остальные т-1 антенны, напротив, имеют в
направлении на НИСЗ нуль в диаграмме направленности. Это следует из
выражения Ошибка! Источник ссылки не найден., конкретнее из требований к
весам G* • Н = 0, / = 2, т. Отсутствие сигнала в компенсационных выходах |2
720
Пространственно-временная обработка сигналов в аппаратуре потребителей
гарантирует полезный сигнал в первом канале £и от подавления при сложении
с полезными сигналами в других каналах с неудачными фазовыми
соотношениями при компенсации в АР.
18.5. Характеристики алгоритмов пространственной обработки сигналов
Наиболее распространенным критерием помехозащищенности ПСН
служит максимальное отношение мощности помехи J к мощности сигнала S на
входе приемника, при котором приемник остается в рабочем режиме. Для
помех с шириной спектра, большей, чем у сигнала, для определения мощности
необходимо задать полосу частот. Для военных GPS приемников принято
использовать полосу частот помехи по первым нулям спектра сигнала, т.е.,
например, для P(Y) кода ширина полосы В=20,46 МГц. Обычное обозначение
этого критерия J/S (от английского jammer to signal).
Полезно отметить, что отношения J/S на выходе пространственного
фильтра и АКП справедливы для помехи произвольного вида. Это следует из
того, что они зависят только от мощностей и межканальных ковариации смесей
помеха+шум, содержащихся в полосе А/с.
Помимо J/S естественно характеризовать эффективность
пространственной обработки сравнением отношений J/S на входе и выходе
пространственного фильтра. Обе эти характеристики зависят от помеховой обстановки и
направления прихода полезного сигнала.
Ниже приведена методика расчета J/S для оптимального
пространственного фильтра и АКП, которая иллюстрируется примером для семиэлементной
плоской антенной решетки (АР), аналогичной используемой в GAS-1.
Координаты элементов антенной решетки
Структура антенной решетки задана матрицей AR, в которой в /-том
столбце записаны декартовы координаты x,y,z /-го антенного элемента (АЭ)
(rf=l/2)
'о 0 (л/з</)/2 (>/3</)/2 0 -(л/3</)/2 -[-fed]/!
AR = |0 d d/2 -d/2 -d -d/2 d/2 |. (18.26)
0 0 0 0 0 0 0
Для простоты предполагалось, что элементы АР всенаправленные.
В типовой обстановке на входе антенной решетки полезный сигнал (ВТ-
код системы ГЛОНАСС) имеет уровень -160дБВт. Для приемника
навигационных сигналов принято два уровня порогового отношений J/S 50дБ и 54дБ.
Впрочем, зависимость от порогового отношения J/S приемника
навигационных сигналов исследуется отдельно.
721
Глава 18
Рис. 18.8. Расположение антенных элементов в решетке
В зоне приема действуют от 1 до 8 постановщиков помех. Их
характеристики сведены в табл. 18.1.
Таблица 18.1. Характеристики постановщиков помех
Отн. J/S (дБ)
Азимут (град)
Угол места (град)
90
55
-18
90
75
5
90
95
9
90
ПО
15
90
145
19
90
190
12
90
210
13
90
233
2
При моделировании принято два уровня попарного рассогласования КЧХ
приемных каналов, соответствующие коэффициентам подавления 30 и 40дБ.
Для компенсатора основным (главным) каналом назначен центральный АЭ
в 7-элементной АР.
Расчет векторов Нк и Ck
Для определения вектора амплитудно-фазовых распределений сигнала НА
необходимы направление прихода сигнала, координаты АЭ и их ДН.
Направление прихода сигнала можно задать единичным вектором из
выбранного АЭ к источнику
R(y/,y) = (cos(y/)cos(y) sin(y/)cos(/) sin(/))r. (18.27)
Вектор от выбранного элемента решетки (его координаты в данном случае
(0 0 0) ) к к-му элементу легко получить как разность координат этих
элементов. В данном случае это просто к-й столбец матрицы AR, т.е. АК<к>
H(^,/) = (^(^,r)exp{-2^(AR<",R(^,/))} ... F7(^,r)exp{-2^y(AR<T>,R(^,y))})T'.
(18.28)
722
Пространственно-временная обработка сигналов в аппаратуре потребителей
Здесь Fk(y/,y) — амплитудно-фазовая диаграмма направленности А>го
АЭ; (•,•) — скалярное произведение.
Аналогично вычисляется вектор амплитудно-фазовых распределений к-то
источника помехи Ск
ck{y/,y) = [Fx{y,,y)exv{-2Kj(AR<x>,Kk{y/,y))) ... F1(y/,y)exv{-2xj(AR<1>,Rk{y/,y))\) ■
(18.29)
Суммарная матрица помех
V = N0+f PkCkC?. (18-30)
к=\
При равных по уровню внутренних шумах в каналах, т.е., N0 = N0l
выражение для суммарной матрицы помех и внутренних шумов имеет вид
V/N0=I + ZPk/N0ckck .
(18.31)
к=\
Отношение J/S.
Найдем связь J/S с введенными ранее параметрами сигнально-помеховой
обстановки. Для этого рассмотрим выходы пространственно-временного
фильтра и АКП.
Для перехода к J/S будем считать, что V — матрица ковариаций смеси по-
меха+шум в Д/с, например, для сигнала стандартной точности ГЛОНАСС,
А/с=1МГц.
Если колебание ^ = Hsk + nk подвергается в пространственном фильтре
весовой обработке с весом р, то на выходе этого фильтра отношение J/S равно
отношению мощности помехи
J= M[\ р\ \2] = M\fi\n*l] = p*M[n^n/]p = pVp
2
к мощности сигнала
*
S = М[\ р Usk |2 ] = М[Р*Н | sk |2 Н*р] = М
* 9 * о
р нг=5|р нр
Оптимальное отношение J/S на выходе оптимального пространственного
фильтра получается при Р, удовлетворяющем (18.10), и равно (в дБ)
.//%^) = -101og
HV,r)v ХЩуг,у)
~(S),
dB
(18.32)
Если в качестве уровня отсчета взять внутренний шум, то (18.32)
преобразуется в выражение
7/%^) = -101og
К*(у,у)(У/М0) 1Щу,у)
-(s/N0)dB
(18.33)
723
Глава 18
Аналогичное соотношение для АКП можно получить при
P = cV'(l 0 .. 0)г:
J/5(^,r)=((v-,)ii)^-201og|(i о .. o)(\/N0)->H(y,yy)\-(S/N0)dB.
(18.34)
Коэффициент эффективности пространственной обработки.
Естественно характеризовать эффективность пространственной обработки
сравнением отношений J/S на входе и выходе пространственного фильтра
^=J/SBX/J/SBbIX. (18.35)
Однако поскольку входное отношение
т
(•//5)вх=Е^/жо1^г-|н,г^0
к=\
при равномерной диаграмме направленности элементов АР практически не
зависит от пространственного расположения сигнала, то зависимость КЭф от
направления прихода полезного сигнала отличается от зависимости J/SBbIX только
множителем. В рассматриваемом примере Кэф=78.5 - J/SBbIX
Некоторые результаты расчета.
Графики зависимостей в координатах (азимут (у/), угол места(/)),
построенные по (18.34), показывают, каковы условия приема навигационного сигнала,
приходящего с различных углов. В общем случае эти условия различны.
Трехмерный график зависимости J/S от углов для случая двух ПП показан
на рис. 18.9.
0.8 0,6 0,4 0.2 0 -0.2 4X4 43,6 -0.8
Рис. 18.9. Трехмерный график зависимости J/S
724
Пространственно-временная обработка сигналов в аппаратуре потребителей
Графики зависимостей J/S{y/,y) можно строить в разных координатах.
На рис. 18.10 представлены графики для пяти первых постановщиков
помех из 8 представленных в табл. 18.1.
Компенсатор
90
270
ОПТИМАЛЬНЫЙ
90
0 180
а)
КОМПЕНСАТОР
90
ОПТИМАЛЬНЫЙ
90
г)
Рис. 18.10. Графики зависимостей J/S(y/,y)
725
Глава 18
Видно, что в зоне, близкой к направлениям на ПП отношение J/S
существенно возрастает (формируются нули на помехи). В остальных направлениях
помеха существенно подавлена (J/S - мало) и возможен прием сигналов от
НИСЗ.
Если действует лишь один ПП контурный график J/S в проекции на
небесную полусферу для компенсатора и оптимального алгоритма имеет вид
рис. 18.10 а), б). Видно, что в этой диаграмме в направлении на источник помех
формируется глубокий провал, а в остальных направлениях обеспечивается
достаточно высокое отношение сигнал/помеха+шум (ОСПШ).
Видно, что оба фильтра формируют не только "правильный" (с азимутом
55°), но и ложный провал, который может помешать нормальному приему
сигналов от некоторых спутников. Однако провал для оптимального алгоритма
этот существенно меньше.
При воздействии 3-х ИП в диаграмме формируется 3 провала на все ПП
(рис. 18.10 в), г)). ОПФ имеет превосходство относительно компенсатора,
однако в данной конкретной сигнально-помеховой обстановке визуально это
трудно зафиксировать.
18.6. Формирование весовых коэффициентов
В реальности параметры сигнально-помеховой обстановки (СПО)
неизвестны, и структуры как ОПФ так и АКП необходимо дополнить схемой оценки
вектора весовых коэффициентов (ВВК) р , которую называют блоком адаптации.
Согласно выражению (18.10), эти коэффициенты зависят от матрицы кова-
риаций выходов элементов АР. Значения этой матрицы можно найти в
зависимости от азимута и угла места источников помех относительно АР согласно
формулам (18.35)—(18.37). Однако на практике эти углы неизвестны, и, кроме
того, такой подход предъявляет очень высокие требования к юстировке АЭ, их
диаграмм направленности и пр. Гораздо проще, оказывается, определять кова-
риации выходов АЭ непосредственно. Множество различных алгоритмов
адаптации в ОПФ или АКП в той или иной форме основаны на нахождении
эмпирических оценок ковариаций
Оказывается, такой подход обеспечивает достаточно высокую точность их
оценивания даже в условиях реальной динамики помеховой обстановки.
Алгоритмы адаптации можно разделить на прямые и следящие [18.20,
18.15 , 18.18]. Прямые алгоритмы связаны с вычислением корреляционной
матрицы помех, являются оптимальными [18.15, 18.3] и обеспечивают
минимальное время адаптации. Функционирование следящих алгоритмов
предполагает относительно медленные изменения пространственно-временной СПО и
обычно требуют большего времени на адаптацию. Однако оптимальные
следящие алгоритмы также обеспечивают минимальное время адаптации.
726
Пространственно-временная обработка сигналов в аппаратуре потребителей
В работе [18.13] синтезированы оптимальные алгоритмы адаптации для
режима захвата в условиях быстрых изменений СПО. Их характеристики
можно считать потенциальными для этих условий. На практике рационально
использовать квазиоптимальные алгоритмы различной степени сложности.
18.6.1. Оптимальный «следящий» алгоритм
Оптимальный «следящий» алгоритм описан в [18.8, 18.12]. Наблюдения на
выходах и-элементной антенной решетки представим в виде [18.15, 18.7]:
£*=Н*-^(Я*) + пА, * = 1,2... (18.36)
Здесь Hk — известный комплексный «-вектор, описывающий
амплитудно-фазовое распределение полезного сигнала на антенных элементах; sk(kk)
— комплексная амплитуда выборки полезного сигнала; п^ — дискретный
комплексный белый гауссов шум (КБГШ), описывающий отсчеты суммарного
шума в элементах решетки, причем
M{nknHM} = 2VkSMk. (18.37)
Оптимальный алгоритм должен оценить параметр к по наблюдению
(18.36) в условиях шумов с неизвестной матрицей V (18.37). В нелинейной
фильтрации этот алгоритм сводится к формированию апостериорной плотно-
сти вероятности (ПВ) р{Х,\), т.е., требует дополнительной оценки п
вещественных параметров, определяющих эрмитову матрицу V . Уменьшение
числа параметров может быть получено выделением достаточной статистики в
наблюдение 18.36).
Выполним преобразование (18.24) ц-
.42 J
= Щ (рис. 18.11)) наблюдения
(18.36) с матрицей П = Гн/||Н|2, В
вектору.
, где (и-1)х« матрица В ортогональна
пр'осТранственНьГй фильтр
Фокусировка!
4Х
п
л
оо
АК
т
\~
12*
щ н 1
Ч Блок
^адаптации
П
щ
ВРЕМЕННОЙ
ФИЛЬТР
X,
Рис. 18.11. Схема устройства
727
Глава 18
В [18.12] показано, что оптимальный фильтр информационного параметра
может быть представлен блок-схемой (рис. 18.11), где важнейший блок оценки
вектора ак (блок адаптации) является фильтром Калмана с вектором состояния
\к =[tt*;Va£], в который включен вектор скорости изменения ак9 а модели
динамики и наблюдения иллюстрируются рис. 18.12.
п
Ак
Я+)
Ф
*-i
ц<
Л
к-\
Модель динамики
а,
Й
п,
Oit
Модель наблюдения
Пи
Рис. 18.12. Схема устройства
В результате алгоритм оценки вектора состояния Л можно представить
схемой на рис. 18.13.
П
Чт,
X
зг
X
а,
R
ак
Xh=<+>
А,
•*-
!<Н^р
Ль
Рис. 18.13. Схема устройства
Основное отличие от стандартной схемы автокомпенсатора заключается,
во-первых, в том, что оцениваются не только собственно весовые векторы а,
но и весь вектор переменных состояния Л, то есть и производные от а. Во-
вторых, в алгоритме формируется матрица дисперсий Rak, играющая роль
коэффициентов усиления петли слежения за Л, вместо обычного для
градиентного метода выбираемого априори скалярного коэффициента усиления.
Характеристики адаптации оптимального следящего компенсатора
представлены на рис. 18.14.
На этом же графике приведена кривая адаптации традиционного
следящего градиентного фильтра для оценки а . Сравнение с градиентным алгоритмом
показывает существенный выигрыш оптимального алгоритма для всех
моментов времени.
Использование фильтра даст существенный выигрыш при наличии
динамики ак. В этом случае точность экстраполяции существенно возрастает и от-
728
Пространственно-временная обработка сигналов в аппаратуре потребителей
счеты \k можно брать реже. Оценки выигрыша оптимального фильтра
представлены в [18.11].
ОСШ от времени
30
л 25
з
?20
<
%.
S 15
2
ш
а5
О
О 100 200 300 400 500
Время (Такт)
Рис. 18.14. Характеристики адаптации
18.6.2. Оптимальный неследящий алгоритм
Вывод этого алгоритма рассмотрен в [18.13]. При выводе мы
ориентировались на интервал тк, на котором параметры СПО S = Sk = (Hk,Vk) (Hk —
"сигнальный11 вектор; Ук — корреляционная матрица помех), а также
информационный параметр Хк можно считать неизменными. Такая простейшая
модель может адекватно описывать режим захвата или "сопровождения", если
пространственно-временной алгоритм будет оптимальным, т.е. быстрым, и
обеспечит захват на указанном интервале. Величина тк оценивается
статистическим моделированием с расчетом на наибольшую динамику.
Адекватность выбора модели для информационного параметра
подтверждается тем, что для описания его динамики на интервалах порядка 1 мс
вполне подходит модель "квазислучайного" процесса [18.16].
В соответствии с принятой методикой синтеза [18.16], в режиме захвата
вводятся априорные плотности параметров Sk и кк, а в режиме
сопровождения — дополняются их связью параметров СПО на соседних (при марковской
динамике) интервалах.
В любом случае важно иметь адекватную информационную модель для
параметров СПО. В зависимости от того, используется ли направление на
навигационный спутник (НС) или нет, можно выделить две ситуации. Первая
соответствует случаю, когда обработка начинается в условиях полной априорной
Фильтр Калмана
—f~ Градиент
729
Глава 18
неопределенности относительно параметров СПО. Вторая — когда параметр
Н^, соответствующий направлению на НС, известен с высокой точностью, а
матрица \к — полностью неизвестна. Вторая ситуация может считаться
основной в СРНС и в дальнейших разработках следует ориентироваться именно
на нее. Однако нами использовались алгоритмы [18.13], полученные для
первого варианта СПО, а также для других возможных ее модификаций.
18.6.3. Алгоритм с разделением пространственного и
временного операторов
Оптимальный алгоритм, синтезированный в [18.10,18.13], является
пространственно-временным, поскольку временную обработку для вычисления
основной статистики требуется вести в каждом антенном канале. Реализация
такого алгоритма - вопрос ближайшего будущего. Однако уже сейчас можно
реализовать незначительно уступающий ему по характеристикам
квазиоптимальный алгоритм, которому соответствует схема на рис. 18.15
Рис. 18.15. Схема устройства
Здесь использованы обозначения
L
~ % Ч if.
W = 2_\v\v — тхт матрица;
v=\
, L L
Основная функция этого алгоритма — вычисление статистики Н* W Q^ и
ее максимизация. Вся структура распадается на пространственный и временной
фильтры.
730
Пространственно-временная обработка сигналов в аппаратуре потребителей
Векторные отсчеты ^ в цифровом виде поступают на вход
пространственного фильтра. Как показывает анализ на модели, для вычисления
выборочной корреляционной матрицы W не обязательно использовать все отсчеты,
выбранные с частотой Котельникова или чуть выше (как это сделано в
стандартных реализациях GPS-приемников), которая необходима для временной
обработки. Отсчеты можно взять реже (децимация).
Выход пространственного фильтра — набор скаляров Н* W"1^,
поступающих на временной скалярный фильтр — коррелятор. Эта функция
полностью возлагается на приемник СРНС.
18.6.4. Характеристики адаптации
На рис. 18.16 показаны типовые "кривые адаптации" - зависимость
коэффициента подавления на выходе блока пространственной обработки от
времени накопления для оптимального алгоритма (схема на рис. 18.15) и для
классического компенсатора помех. Видно, что оптимальный алгоритм сходится до
уровня "потенциальный КП0Д-ЗдБ" примерно за 4 • п тактов (где п — число
каналов пространственной обработки), что соответствует теоретическому
уровню. Классическому алгоритму требуется несколько тысяч тактов.
Рис. 18.16. Характеристики адаптации
731
Глава 18
18.7. Технологический прорыв в пространственной
компенсации помех
Разработка антенных компенсаторов помех (АКП) имеет долгую историю.
Упомянем лишь имена создателей АКП Уидроу Б. (1957 год) в США и Шир-
мана Я.Д. (1958 год) в СССР.
Отметим, что теоретический уровень подавления 40-50дБ и более (см.
п. 18.5) и достижимый в реализованных устройствах, как правило, до
недавнего времени существенно различались. Более того, достигнутый в 70-х годах
уровень глубины подавления порядка 20—25 дБ оказался своеобразным
техническим порогом, который многие сочли пределом. В течение нескольких
десятилетий разрабатываемые для радиолокации или связи отечественные и
зарубежные образцы АКП имели глубину подавления в этом диапазоне. Развитие
цифровой элементной базы также не оказало существенного влияния.
Прорыв произошел в середине 90-х годов. Выдвинутые МО США
требования повышения помехоустойчивости аппаратуры пользователя GPS военного
назначения привели к необходимости создания АКП с резко увеличенной
глубиной подавления помехи. Целым рядом организаций (MITRE, MIT Lincoln
Laboratory, Raytheon и др.) были проведены исследования по преодолению
предела в уровне подаления. Так, в работе Mitre [18.22] выделены основные
декоррелирующие факторы, которые приведены в табл. 18.2 (приведен
примерный уровень того или иного ограничения, достижимый для современных
технологий):
Таблица!8.2. Основные декоррелирующие факторы
Фактор
Нелинейности каналов
Амплитудное и фазовое рассогласование
ЧХ приемных каналов (с коррекцией)
Взаимное влияние антенных элементов
Нелинейность
Характеристики АЦП
число разрядов (12р-14р)
"джиттер"
Кп, дБ J
70 J
45
70 J
70 J
66...78 I
70 1
В результате были сделаны выводы: 1) о наиболее узком месте при
реализации АКП — неидентичности ЧХ приемных каналов и 2) о возможности
достижения в АКП уровня подавления в 45...50 дБ.
732
Пространственно-временная обработка сигналов в аппаратуре потребителей
Были определены и пути достижения такого результата. Основным
принципом явилось использование цифрового диаграммообразования, при котором
выходы всех элементов антенной решетки селектируются по частоте и
усиливаются до уровня АЦП. Вся дальнейшая обработка осуществляется на
цифровом уровне. Преодоление порога потребовало изменения или
совершенствования не одного, а целого ряда технологических решений, причем, как в
аналоговой, так и в цифровой части АКП.
В аналоговой части это, прежде всего:
- выравнивание задержки в трактах приема (до 0.1 не);
- обеспечение идентичности АЧХ и ФЧХ трактов приема (размах
разностей АЧХ разных каналов лучше 0.2 дБ, размах разностей ФЧХ — 1.2 °);
- линейность трактов усиления (АЦП - 12... 16 разрядов, IP3 ~ lOdBm).
В цифровой части это:
- высокоточное формирование квадратур;
- адаптивные корректирующие фильтры для компенсации неидентичности
частотных характеристик трактов приема;
- усовершенствование алгоритмов формирования весовых коэффициентов
для корректирующих фильтров и компенсационного цифрового суммирования.
К концу 90-х годов целый ряд фирм разработали АКП нового поколения с
глубиной подавления 40 дБ и более (Raytheon, Lokheed Martin, Rockwell Collins
и др.). К настоящему времени множество образцов АКП широко используются
во всех видах военной техники.
18.8. Экспериментальная проверка компенсаторов помех для
приемников спутниковой навигации
18.8.1. Экспериментальная проверка двухканального
компенсатора помех
В параграфе представлены результаты экспериментальной проверки
макета АКП с двухэлементной АР для GPS-приемника «Jupiter» [18.5]. Компенсатор
рассчитан на защиту открытого С/А-кода в диапазоне Ы.
Компенсатор выполнен по классической схеме с управлением весовыми
коэффициентами на высокой частоте и цифровым вычислением самих
коэффициентов.
Проверка макета Компенсатора с двухэлементной АР имела целью
экспериментально оценить практически достижимую эффективность макета АКП
при воздействии узкополосной и широкополосной помехи.
Схема эксперимента показана на рис. 18.17.
В качестве показателя эффективности Компенсатора использован
известный коэффициент подавления (Кп) - отношение входной мощности помехи к
733
Глава 18
мощности шума на выходе суммарного канала. Этот показатель является
критерием классического Компенсатора - именно его максимизирует эта схема.
В эксперименте оценивалось два значения коэффициента подавления .
В первом случае коэффициент подавления оценивался при подаче одного
и того же колебания на вход обоих каналов минуя антенны. Фактически при
этом определялись потенциальные возможности АКП.
Рис. 18.17. Схема эксперимента
Второе значение оценивалось при излучении помехи из пространства, т.е.
в условиях переотражений от местных предметов. Это значение Кп условно
можно назвать «реальным».
Практически значения коэффициента подавления измерялись с помощью
спектранализатора. Эпюры, соответствующие измерению Кп для
узкополосной и широкополосной помехи, показаны на рис. 18.18 и рис. 18.19
соответственно. В эксперименте дополнительно оценивался коэффициент
эффективности, т.е., отношение ОСШ (отношения сигнал/шум) на входе Компенсатора к
ОСШ на его выходе. ОСШ оценивалось по данным GPS-приемника,
предварительно откалиброванного с помощью имитатора спутниковых сигналов фирмы
«НАВИС».
734
Пространственно-временная обработка сигналов в аппаратуре потребителей
£43 12:12:16 RPR 08, 2Й04
Ref -10.0 dBm fitter; 0 dB
Srnpi
Log
10
dB/
Мкгд 0 Hz
-5717 dB
Center 1.575420 GHz
Res BH 30 kHz УВН 30 kHz
Span 5.000 MHz
Sweep 16.7 msec
Рис. 18.18. Эпюры СПМ для гармонической помехи
I&3 12:10:31 APR 08, 2004
Ref -25.0 dBm fltten % dB
Smpl
Log
10
dB/
Мкгд 950 kHz
-45.99 dB
Mi
ц
KaJ
w
/
/J
/
f\b^
("^
ЛАд^
JKA
<//\,
TK. I *vs-{
\Л)
i
ЧЪ
*\/Л
,%aAu
AV-4
у V'
Й
""Aw
уц
*-*A--*
'^\Д
'\
X
^
A
V
л
A
i
/V _
flvg
VflSB
SCFC
flfi
Center 1.575420 GHz
Res BW 30 kHz
Span 5.000 MHz
Sweep 16.7 msec
VBW 30 kHz
Рис 18.19. Эпюры СПМ для полосовой помехи
735
Глава 18
Полученные в эксперименте результаты сведены в табл. 18.3
Таблица 18.3. Коэффициенты подавления
Тип помехи
широкополосная
узкополосная
ПОКАЗАН
Потенциальный Кп
45 дБ
57 дБ
Реальный Кп
27 дБ
44 дБ
ЕЛЬ 1
Коэф. эффективности 1
24 дБ
Сравнительно низкое значение «реального» коэффициента подавления
объясняется наличием переотражений помехового колебания в условиях
эксперимента. В реальных приложениях условия приема сигналов могут быть
лучше, чем в нашем эксперименте. Во всяком случае, специально для исключения
переотражений оценивался коэффициент подавления АКП в безэховой камере.
При этом по широкополосной помехе достигнут Кп = 38дБ.
Таким образом, исследование экспериментального макета АКП,
созданного на основе доступной элементной базы и современных схемотехнических
решений, показало возможность практического достижения значений
коэффициента подавления 30..45дБ.
18.8.2. Экспериментальные исследования возможности повышения
характеристик подавления путем коррекции ЧХ
Анализ частотных характеристик аналоговых трактов АКП. Для
исследований в макете АКП взяты 4 экземпляра полосовых фильтров серии ФП-
478 одного из главных российских разработчиков фильтров на ПАВ. Трансвер-
сальные фильтры этой серии [18.26, 18.25] выпускаются на двунаправленных
штыревых преобразователях и обладают следующими характеристиками:
центральная частота 140МГц; полоса пропускания 22,97 МГц; избирательность
56дБ; ослабление сигнала в полосе фильтра 21 дБ.
По своим потребительским качествам данные фильтры не уступают
лучшим мировым аналогам. Однако критерии, по которым отбираются фильтры,
не учитывают их применение в АКП, где, прежде всего, важна повторяемость
(идентичность) частотных характеристик экземпляров фильтра.
Экспериментальные исследования частотных характеристик выполнены на
базе макета четырехканального АКП. В макете один из каналов (первый)
считается основным, остальные (компенсационные) поочередно сравниваются с
ним. На рис. 18.23 показаны амплитудно-частотные характеристики (АЧХ)
аналоговых трактов первого и второго каналов.
Из рис. 18.23 видно, что коэффициент усиления в рассматриваемых двух
каналах значительно отличается (около 5 дБ). Тем не менее, данное отличие не
736
Пространственно-временная обработка сигналов в аппаратуре потребителей
уменьшает коэффициент подавления, так как алгоритм компенсации
выравнивает усиление в каналах.
20 ;-
АЧХ каналов 1 и 2
-20!
Ш ^40
t» ,*,
T\hX:V\
If
-1ЙП
'00 ПО 120 130 140 150 160 170 180 190
Частота, МГц
Рис. 18.20. АЧХ аналоговых трактов первого и второго каналов
Разность АЧХ каналов 1 и 2 в полосе сигнала ДР=18МГц представлена на
рис. 18.21.
Разность АЧХ каналов в полосе сигнала
4.6
Рис. 18.21. Разность АЧХ каналов 1 и 2 в полосе сигнала
Как показано в [18.19] гарантированное значение коэффициента
подавления АКП в случае воздействия наихудшей помехи определяется размахом раз-
24-1026
737
Глава 18
ности характеристик АЧХ и ФЧХ каналов приема в полосе сигнала. Размах
АЧХ и размах ФЧХ определяются, соответственно, по формулам.
A^12=max|^12(/)|-min|^12(/)|,
A^12=max(arg(^12(/)))-min(arg(^12(/))), (18.40)
где Kn(f) = Kl(f)-K2(f) — разность комплексных частотных
характеристик каналов 1 и 2, arg( ) — аргумент комплексного числа.
В табл. 18.4 представлены экспериментально полученные значения
размаха разности АЧХ в полосе сигнала для всех компенсационных каналов и
значения коэффициента подавления для наихудшей помехи.
Таблица 18.4. Размах разности АЧХ каналов
к
анал
2
3
4
Размах АЧХ
в дБ
0,6
0,9
0,9
Предельный
^П АЧХ ' Д"
29,3
25,7
25,7
Видно, что без устранения неидентичности АЧХ коэффициент подавления
не достигает ЗОдБ для наихудшей помехи.
Аналогичное влияние на предельные значения коэффициента подавления
оказывает несовпадение фазочастотных характеристик трактов. В табл. 18.5.
показана величина постоянной задержки в каждом компенсационном канале, а
также величина неравномерности ФЧХ (относительно основного канала) после
устранения постоянной задержки.
Таблица 18.5. Размах ФЧХ каналов после устранения постоянной задержки
Канал
2
з
4
Разность
задержек,
НС
1,253
0,243
0,837
Размах ФЧХ в
градусах после
устранения задержки
5,2
2,9
4,1
Кп дБ
до
юстировки
26,9
31,3
28,9
Кп дБ
после
юстировки
32,5
31,6
30,8
Как показано в табл. 18.5, коэффициент подавления может быть повышен
устранением разности постоянных задержек между основным и
компенсационными каналами АКП. Из приведенных в таблицах значений коэффициентов
подавления видно, что даже после проведения юстировки коэффициент
подавления не превышает 29,ЗдБ (канал №2).
738
Пространственно-временная обработка сигналов в аппаратуре потребителей
18.8.3. Анализ возможностей повышения характеристик
подавления путем коррекции ЧХ
Дальнейшее повышение коэффициента подавления возможно путем
применения корректирующих фильтров. Применение корректирующих фильтров
обеспечивает дополнительную подстройку каналов, обеспечивая уменьшение
расхождения их частотных характеристик. На рис. 18.22 показана структурная
схема двухканального компенсатора с корректирующим фильтром.
хатп 1
<(осно&нйй| ^
Р**
%тж2
l|WI.W.lJ*WJI*iJlJ>.WJ.l|l.ll.lWIJW^fc
нвддрззур
'тт^^''\>гчф
77*1 Т
'■'IHJ,
F4
*•-
vinwiffunww..^ ,.„.„„,.,„,™^™OT^.OT„,™,™,,„,„^..,.„„.w,r., 1^.
»•<_
T *^
_. ifcj
""■ f^l
КорФ*ть?р
—43—►■
m
-Г 7^
Е*ЮЙ ЙОД#Ш№£0е
Выход
компенсатора
1 ^
з ^
i^*
Рис. 18.22. Компенсатор с корректирующими фильтрами
По структуре корректирующий фильтр представляет собой КИХ фильтр с
переменными коэффициентами. Определение коэффициентов корректирующих
фильтров производится при одинаковом сигнале на входе всех каналов
компенсатора в установившемся режиме.
На рис. 18.23 представлены |^12(/)| (пунктирной линией) и
аппроксимирующие её АЧХ корректирующих фильтров длиной 5 и длиной 64.
-4.6
-4J9
-5l4
АЧХ корректор, фильтров
при L=5 и L=64
130 132 134 136 13В 140 142 1
Частота, МГц
146 148 ISO
Рис. 18.23. АЧХ корректирующих фильтров
739
Глава 18
Как видно из рис. 18.23, АЧХ корректирующего фильтра приближается к
разностной АЧХ основного и компенсационного каналов. В табл. 18.6
представлены значения коэффициента подавления для разных длин
корректирующего фильтра в компенсационных каналах.
Таблица 18.6. Влияние длины корректирующего фильтра
на коэффициент подавления
Канал
2
3
4
L=l
32,5
31,6
30,8
L=5
37,3
38,.0
37,1
L=9
38,1
39,0
39,7
L=16
38,4
41,4
40,8
L=128
46,7
50,0
50,3
L=256
47,5
51,0
51,1
На рис. 18.24 представлена зависимость коэффициента подавления от длины
фильтра для различных компенсационных каналов представлена графически.
49
ГЛ mi
"О
35
25
Коэффициент подавления
i
:.д...
--//--■
// :
i
i 1 i i i :
"Ш~х
i i i i i i i
--Li
/] M.
—i i i
i :
У : '
.': 1 J
f :
4 -i—
j ;
"т-:ту:т
i—* i—« i i i
2 3 4 567 Ю
1Q0O
шДлинаи линии
Рис. 18.24. Зависимость коэффициента подавления от длины
корректирующего фильтра
Для зависимости характерно наличие участка резкого возрастания Кпод при
малых длинах порядка 3...10, далее имеется участок относительно медленного
возрастания Кподот длины фильтров в диапазоне 10...60, и новый участок
быстрого возрастания Кпод, соответствующий увеличению длины фильтра от 60 до
120. Этот рисунок может быть использован при выборе порядка
корректирующего фильтра учитывая, что увеличение порядка фильтра приводит к
существенному росту аппаратных затрат на его реализацию.
740
Пространственно-временная обработка сигналов в аппаратуре потребителей
18.8.4. Экспериментальные исследования цифрового АКП
для приемника СРНС
В [18.1] представлены результаты экспериментальных исследований
макета цифрового четырехканального АКП.
Основные цели исследования:
оценка достижимого уровня эффективности подавления помех в
различной сигнально-помеховой обстановке (СПО);
оценка эффективности АКП при совместной работе с приемником СРНС.
Стенд для экспериментальных исследований АКП. Экспериментальные
исследования цифрового четырехканального АКП проводились в
лабораторных условиях на стенде. Структурная схема стенда представлена на рис. 18.25.
На входах цифрового четырехканального АКП формируется помеха,
поступающая с генератора помех через делитель мощности. АКП включает в себя
Аналоговую часть и Блок электронного подавления помех (БЭПП). Аналоговая
часть реализует прием и предварительную фильтрацию сигнала, перевод на
промежуточную частоту и подачу на четыре 12-ти разрядных аналого-
цифровых преобразователя (АЦП).
Е
Делитель
мощности
Генератор
помех
1 f
Осциллограф
Имитатор
сигнала
СРНС
к*
О
8
3
о
2
А
§
£
Ф
АКП
Аналогов, часть ■ | £ЭПП
ВЧ-ПЧ 1
АЦП1 j~W
ВЧ-ПЧ 2
АЦП2
ВЧ-ПЧ 3
АЦПЗ
ВЧ-ПЧ 4
АЦП4
±
Анализатор
спектра
н
Делитель
мощности
FPGA
I—
U
X
ф
с
о
S
о.
о
Н ЦАП
LVDS
ЧТ
4N
\fTV
л
JTAG j\
Специали-
зир. прм.
СРНС
С
ПЭВМ
^Т
Рис. 18.25. Структурная схема стенда
БЭПП представляет собой цифровой квадратурный компенсатор на
промежуточной частоте.
Сигнал с выходов аналоговой части подается на АЦП, переводится в
цифровой вид и поступает на вычислитель, реализованный на ПЛИС. В
вычислителе формируются квадратуры сигналов, осуществляется коррекция частотных
характеристик каналов обработки и компенсация помех. После вычислителя
741
Глава 18
сигнал преобразуется в цифро-аналоговом преобразователе (ЦАП) для анализа
на спектроанализаторе или в цифровом виде передается в ПЭВМ для анализа и
обработки. Подача сигнала на приемник СРНС может осуществляться на
промежуточной частоте двумя способами: с выхода ЦАП через модулятор в
аналоговом виде или непосредственно в цифровом виде.
Для оценки эффективности работы АКП совместно с приемником СРНС
используется Имитатор сигнала СРНС. Сигнал СРНС подмешивается в
основной канал компенсатора в цифровом виде. Для приема сигнала на выходе АКП
использовался макетный образец приемника СРНС ГЛОНАСС/GPS
(разработка ФГУП «НИИ КП»). Особенностью приемника является наличие цифровых
входов для подачи сигнала на корреляторы непосредственно в цифровом виде.
В условиях отсутствия возможности применения специальных мер (без-
эховая камера и пр.) для проведении экспериментальных исследований в
лабораторных условиях с формированием помеховых воздействий от нескольких
пространственно разнесенных источников разработана методика эмуляции
сигнально-помеховой обстановки.
Методика эмуляции сигнально-помеховой обстановки для
экспериментальных исследований АКП. Сутью методики является запись в
цифровом виде нескольких независимых реализаций помех, прошедших аналоговые
тракты АКП, формирование в реализациях помех пространственных различий
в соответствии с пространственным расположением помех и подача их после
сложения на вход вычислителя для компенсации. Последовательность работы с
Цифровым макетом АКП и эмулятором СПО представлена на рис. 18.26.
Г
Этап 1, запись отсчетов помехи
Аналог,
часть
ШАЦП2
Ген-р
АЦП1
АЦПЗ
X
ф
5
С
Ъ
АЦП4
5
6
FPGA
ПЭВМ
(HDD,
Workspace)
n
Этап 2- Моделирование на эмуляторе СПП
Реализации пространственно
разнесенных
помех на выходах
АЦП
ПЭВМ
(HDD,
Workspace)
выход АКП
-ян*
Эмуляция
СПО
N
FPGA N.
|/|(вАКП)[—|/
Фазовое
распределение
по«ек на АР
Параметры
СПО
_ _ j
Рис. 18.26. Последовательность работы с макетом АКП и эмулятором СПО
Я/2
—м
При пространственной компенсации помех
на входе АКП стоит четырехэлементная
антенная решетка (АР), структура которой показана
на рис. 18.27.
Учет амплитудно-фазовых распределений
Cs(9,(p) помех на элементах АР осуществлялся
Рис. 18.27. Структура антенной „ Лп Л
оешетки АКП согласно методике, изложенной в п. 18.4.
742
Пространственно-временная обработка сигналов в аппаратуре потребителей
Дальнейшие результаты приведены для параметров СПО, заданных
табл. 18.7.
Таблица 18.7. Исходные данные
Номер ИП
Отн. J/No (дБ)
Азимут (град)
Угол места (град)
1
40
5
10
2
40
170
15
3
40
260
5
4
40
100
12 |
Экспериментальная оценка эффективности подавления помех в АКП.
В качестве показателя эффективности АКП использован коэффициент
подавления (К„) - отношение мощности помехи на входе АКП к мощности
некомпенсированного остатка на выходе АКП.
Измерения производились для комбинаций одновременного воздействия
одной, двух и трех помех на входе АКП. Далее помехи будут называться по
номерам из табл. 18.7, например «Помеха №2».
Эффективность подавления узкополосных помех. Спектры
используемых помех представлены на рис. 18.28. Частота помех в полосе частот АКП
выбрана из условий раздельного наблюдения в спектре. Пространственное
расположение помех задано табл. 18.7.
1
1 1
г
0 1
А
уф
(
> 1
I
J
Jf\
**%/"
0 1
v~~
\
I «
1
V
V
5 2
Wn
J№J
V4^
0 M
9 1
\
V
T
Гц 30
1 I
n
1
Ш
ГТвв
1
1
\
w\
ij
'm
МГц 30
10
15 20 МГц 30
Рис. 18.28. Спектры узкополосных помех, используемых в эксперименте
743
Глава 18
На рис. 18.29 представлены спектры помехи №2 (слева) и ее
нескомпенсированного остатка (справа). Коэффициент подавления составил 43.6 дБ.
о
дБ
-20
-40
-60
-80
-100
рта
\/Я^ VLJ—
ГУ
О 5 10 15 20 МГц 30
О
дБ
-20
-40
-60
-80
-100
1
1-ЛЛ
/
Ал 1 ^
vj
V v \
V 1
V
п
о
10 15 20 МГц 30
Рис. 18.29. Подавление помехи №2
На рис. 18.30 представлены спектры одновременно действующих с разных
направлений помехи № 1, помехи №2 и помехи №3 на входе алгоритма
компенсации и нескомпенсированного остатка на выходе. Коэффициент подавления
составил 42.25 дБ.
МГц 30
1
0 !
У
7^
/
> 1
*л /\
Y v vr
0 1
■п. j^
«^■^тг
5 2
^Zk
0 M
К
\v
V
[Гц 30
Рис. 18.30. Подавление трех помех с разных направлений
(помеха №1 + помеха №2+ помеха №4)
Результаты эксперимента при воздействии других комбинаций помех
представлены в табл. 18.8 в сравнении с результатами имитационного
моделирования. Для имитационного моделирования использовалась модель АКП,
разработанная в среде Simulink Matlab. В качестве входных воздействий в модели
использовались те же отсчеты помех, которые использовались в эксперименте.
744
Пространственно-временная обработка сигналов в аппаратуре потребителей
Таблица 18.8. Результаты эксперимента
Комбинация
помех
Кп эксперимент
Среднее по
эксперименту
Кп
моделирование
Среднее по
моделированию
1 помеха
№1
42.7
№2
43.6
№3
42.3
№4
42.54
42.6
43.10
45.7
44.09
44.51
44.3
2 помехи
№1+
№2
42.32
№1 +
№3
41.03
№2+
№4
40.6
41.4
41.91
40.11
41.09
41.1
3 помехи
№1 +
№2+
№3
42.25
№1 +
№2+
№4 |
40.05
41.3
42.88
42.91
42.9
Эффективность подавления широкополосных помех. Для
формирования широкополосной помехи использовался векторный генератор Agilent
N9310A, на модуляционные входы I и Q которого подается псевдослучайная
последовательность с шириной спектра 20 МГц. На выходе генератора стоит
аналоговый фильтр с полосой пропускания 20 МГц.
На рис. 18.31 представлены спектры широкополосной помехи №2 на входе
АКП и нескомпенсированного остатка на выходе АКП.
0
ДБ
-20
-40
-60
-80
-100
Рис. 18.31. Подавление широкополосной помехи №2
Коэффициент подавления помехи составил 44 дБ.
На рис. 18.32 представлена ситуация подавления трех широкополосных
помех (№№1-3), действующих на входе АКП.
и/
Г/
Е2:
0
■J
5 1
0 1
Ч 7
0 М
ПГп Ч
О
745
Глава 18
15 20 МГц 30
Рис. 18.32. Подавление широкополосных помех №№1-3
Коэффициент подавления трех помех составил 43.5 дБ.
Оценка эффективности АКП при совместной работе с приемником
СРНС. В качестве критерия эффективности АКП при совместной работе с
приемником СРНС выбран коэффициент эффективности Кэф, который
показывает, насколько увеличивается отношение сигнал/шум в приемнике за счет
использования АКП:
кэф -
SNR
АКП
SNR
без АКП
Спектр помехи, используемой в эксперименте, представлен на рис. 18.33
Формирование имитационного сигнала от спутников ГЛОНАСС и GPS
осуществлялось таким образом, чтобы обеспечивалось его обнаружение и захват в
макете приемника СРНС.
60
50
ф 30
| 20
10
Г
I
-еЛШ
ЭФ
43 дР
"бёзТОТТ
Ьл
ы
0 5
Frame: 33
10 15
Frequency (MHz)
20
25
Рис. 18.33. Вклад АКП в помехоустойчивость приемника СРНС
746
Пространственно-временная обработка сигналов в аппаратуре потребителей
Отношение мощности сигнала к спектральной плотности внутреннего
шума в полосе сигнала S/N0 = -20 дБ, отношение мощности помехи к мощности
внутреннего шума задается в диапазоне J/N0 - 20...40дБ .
Количественная оценка вклада АКП в помехоустойчивость приемника
оценивается по факту захвата навигационного сигнала. Коэффициент
эффективности измерялся как отношение мощности помехи на входе приемника
СРНС при включенном режиме компенсации к мощности помех при
выключенном режиме компенсации при условии, что в обоих случаях приемник
уверенно захватывает навигационный сигнал. На рис. 18.36 показаны спектры
помехи для этих случаев.
Из рисунка видно, что коэффициент эффективности составил примерно
43 дБ.
18.9. Известные устройства пространственного подавления помех
GAS-1 [18.30], разработанный фирмой Raytheon (Raytheon Systems
Limited) для ВВС США, Великобритании и др. стран.
GPS Antenna System-1 (GAS-1) - антенный подавитель помех, имеющий
две основные модификации: с 4-элементной (PAGAN) или 7-элементной
антенными системами. 4-элементная антенная система хорошо видна на
рис. 18.37 справа. 7-элементная антенная система (справа позади на рис. 18.37)
включает одну основную антенну в центре и 6 вспомогательных антенн,
расположенных на расстояниях 1/2 длины волны от основной антенны и друг от
друга. Левее антенн на рис. 18.34 представлен модули антенной электроники АЕ.
Рис. 18.34. 7-элементная антенная система
747
Глава 18
Основные характеристики GAS-1, такие как достижимый коэффициент
подавления, время адаптации и коэффициент шума нам неизвестны.
Известными общими сведениями можно считать:
диапазон частот — Ы и L2;
максимальное число подавляемых помех — 6;
число выходов — 2 на частоте 173.9МГц (по одному на L\ и L2) и до 2 на
радиочастоте;
алгоритм определения весовых коэффициентов — градиентный спуск;
Подавление помех проводится только по выходам на промежуточной
частоте 173.9 МГц. На радиочастотных выходах осуществлено только усиление и
предварительная частотная селекция. Отсюда для использования GAS-1
требуются специальные приемники. Общие требования к таким приемникам
военного назначения приведены в GPS-GRAM-001 — Руководство (рекомендации)
для прикладного приемного модуля ПМВ (GRAM) системы GPS. Известны
следующие типы приемников, работающие с GAS-1. Это: CVR ЗА, MAGR IF и
GEMII.
Размеры блока АЕ — 304.8ммх214.4ммх57.6мм, что составляет объем —
3.8 литра.
Модификацией GAS-1 является PAGAN, разработанная той же фирмой
и фактически отличающаяся от GAS-1 только числом антенн (4 вместо 7) и
соответствующим уменьшением весов, габаритов и стоимости. Компенсатор
PAGAN способен подавлять до 3 постановщиков помех.
GSTAR™ — пространственно-временной помехозащищенный GPS-
приемник [18.23], разработанный фирма Lockheed Martin вместе с Rockwell
Coliins. Компенсатор приемника использует критерий максимума отношения
сигнал/шум. Этот критерий требует не только направлять нули на ИП, но и
максимум — на источники навигационных сигналов. Заявленные параметры
проекта — обеспечить работу системы в динамично изменяющейся помеховой
обстановке при отношении помеха/сигнал до 120 дБ с коэффициентом
подавления 60 дБ за счет пространственно-временной обработки и пороговом
отношении помеха/сигнал 60 дБ за счет тесносвязанного комплексирования с ИНС.
Модульность и масштабируемость системы должны обеспечить широкий
спектр применений.
Цифровой компенсатор помех (DAGR,MIDAS) [18.29] производства
фирмы Rockwell Collins использует критерий минимума дисперсии
выходного шума и обеспечивает коэффициент подавления до 40дБ. Он реализуется в
лвух вариантах — 2-х и 4-хканальном и имеет два выхода — цифровой и ВЧ.
Варианты исполнения компенсатора MIDAS представлены на рис. 18.35.
Система имеет 24 канала обработки сигналов GPS и способна
поддерживать одновременное отслеживание диапазона L\ от 12 спутников.
Приемник с IGAS способен управлять 12-ю лучами диаграммы
направленности (ДН) в соответствии с современной концепцией «all-in-view» обеспе-
748
Пространственно-временная обработка сигналов в аппаратуре потребителей
чивает расширенное покрытие созвездия спутников, для получения наилучших
навигационных характеристик посредством увеличения отношения сигнал-
шум.
Рис. 18.35. Компенсатор MIDAS
Управление максимумом ДН подразумевает использование оптимального
пространственного фильтра (ОПФ), а управление нулями ДН - АКП.
IGS-352 и IGS-355 [18.27] — системы точного позиционирования, с
возможностью подавления 2 или 5 ИП (рис. 18.36). Разработанное фирмой
Integrated Guidance Systems LLC, это семейство продуктов является результатом
объединения приемников GPS военного назначения фирмы Rockwell Collins и
технологии Honeywell создания микро электромеханических систем и
навигационных устройств.
,_.^.. Mfit,
**
Рис. 18.36. Система точного позиционирования IGS-352
Использование глубокой интеграции и тесно-связанного комплексирова-
ния, широкие возможности сопряжения с ЭВМ (интерфейсы 2 порта — 400
Мбит 1ЕЕЕ-1394Ь, 1 порт — асинхронный RS-422, 2 порта — RS-422
настраиваются как 1 SDLC, 4 разрядный программируемый LVCMOS), малые размеры
и масса (объем 655 см , вес 0,68 кг), поддержка работоспособности при J/S до
95 дБ (в режиме слежения) обеспечивают устройствам возможности для
широкого применения.
Литература
18.1. Быстраков СТ., Головин П.М., Ефименко B.C., Пастухов А.В., Харисов В.Н.
Экспериментальные исследования цифрового антенного компенсатора помех для
приемника СРНС// Радиотехника №7, 2008.
749
Глава 18
18.2. Ван Трис Г. Теория обнаружения, оценок и модуляции. В 3-х т./ Пер. с англ.
под ред. В.Т.Горяинова. — М.: Сов. радио, 1977.
18.3. ГЛОНАСС.Принципы построения и функционирования/ Под ред. А.И.
Перова, В.Н. Харисова. — М.: Радиотехника, 2005.
18.4. Давыденко И.Н., Ефименко B.C., Охрименко А. Е., Папушой В.И., Пучило
А.В., Романов А.В., Токарев А.В., Харисов В.Н. Результаты экспериментальной
проверки макета компенсатора помех для приемника спутниковой навигации// Радиотехника,
№7, 2004.
18.5. Ефименко B.C., Харисов В.Н, Давыденко И.Н, Папушой В.И, Модель
компенсатора помех с коррекцией частотных характеристик каналов// Радиотехника, №7,
2003.
18.6. Ефименко B.C., Харисов В.Н. Оптимальная фильтрация в задачах
пространственно-временной обработки и ее характеристики// Радиотехника и электроника, т.32,
№8, 1987.
18.7. Ефименко B.C., Харисов В.Н. Оптимальная фильтрация в задачах
пространственно-временной обработки и ее характеристики// Радиотехника и электроника, т.32,
№8, 1987.
18.8. Ефименко B.C., Харисов В.Н. Адаптивная пространственно-временная
фильтрация при многоканальном приеме// Радиотехника и электроника, т.32, № 9,
1987.
18.9. Ефименко B.C., Харисов В.Н. Адаптивные формирователи лучей для
повышения помехоустойчивости приемников СРНС// Радиотехника, №7, 2008.
18.10. Ефименко B.C., Харисов В.Н. Потенциальные характеристики адаптации
пространственно-временной обработки для СРНС// Радиотехника, №7, 2002.
18.11. Ефименко B.C., Харисов В.Н., Котов А.А. Характеристики
автокомпенсатора с оптимальным формированием весовых коэффициентов// Радиотехника, №7, 2009.
18.12. Ефименко B.C., Харисов В.Н., Котов А.А. Калмановская фильтрация
весовых коэффициентов адаптивной антенной решетки// Радиотехника, №7, 2009.
18.13. Ефименко B.C., Харисов В.Н. Алгоритмы оптимальной фильтрации при
пространственно-многоканальном приеме в условиях быстрых изменений сигнально-
помеховой ситуации// Радиотехника. (Приложение к журналу) Пространственно-
временная обработка сигналов в системах радиосвязи, 1992..
18.14. Монзиго Р.А., Миллер ТУ. Адаптивные антенные решетки. Введение в
теорию/ Пер. с англ. под ред. В.А. Лексаченко. — М.: Радио и связь, 1986.
18.15. Тихонов В.И., Харисов В.Н. Статистический анализ и синтез
радиотехнических устройств и систем. - М: Радио и связь, 1991.
18.16. Уидроу Б., Стирнс С. Адаптивная обработка сигналов: Пер. с англ. — М:
Радио и связь, 1989.
18.17. Харисов В.Н, Быстраков С.Г., Пастухов А.В., Сизов Р.Н Метод задания
требований к неидентичности каналов компенсаторов помех// Радиотехника, №7, 2007.
18.18. Ширман Я.Д., Манжос В.Н. Теория и техника обработки радио-
локационной информации на фоне помех. - М.: Радио и связь, 1981.
18.19. Carlson S.G., Popeck C.A., Stockmaster М.Н., McDowell CE. Rockwell Collins'
Flexible Digital Anti-Jam Architecture — ION GPS/GNSS 2003.
750
Пространственно-временная обработка сигналов в аппаратуре потребителей
18.20. Moulin D., Solomon M.N., Hopkinson TM, Capozza Р.Т., Psilos J. High-
Performance RF-to-Digital Translators For GPS Anti-Jam Applications. ION-1999.
18.21. G-STAR (Spatial Temporal Anti-Jam Receiver) http://www.aeronautics.ru.
18.22. G-STAR GPS Anti-Jam Solutions.// Lockheed Martin.
www.lockheedmartin.com/data/assets/4031 .pdf.
18.23. http://www.mniirs.org/prod/filters/filters.ppt.
18.24. http://www.mniirs.org/prod/filters/fp-478.html.
18.25. http://www.igsllc.com/docs/IGS%20Brochure%200509.pdf.
18.26. Frost O.L., III "An Algorithm for Linearly Constrained Adaptive Array
Processing". Proc IEEE,Vol.60,№8,August 1972,pp. 926-935.
18.27. The compact GAS-1 System, http://www.raytheon.co.uk.
751
Глава 19
Глава 19
ЧАСТОТНО-ВРЕМЕННАЯ РЕЖЕКЦИЯ
УЗКОПОЛОСНЫХ ПОМЕХ
19.1. Теоретическое обоснование методов частотно-временной
компенсации помех
Рассмотрим один канал обработки НАП, в котором навигационный сигнал
s{tk,\k,&k) принимается на фоне помехового сигнала sn(tk,Xnk) и
внутреннего шума приемника пк , т.е. наблюдаемый процесс имеет вид
yk=s(tk,\k,3k) + su(tk^k) + rik, (19.1)
где Хк — параметры навигационного сигнала (задержка, фаза, доплеровская
частота); Зк — цифровое сообщение навигационного сигнала; Хпк —
параметры помехового сигнала; пк — дискретный белый гауссовский шум с
дисперсией сг^.
Если помеховый сигнал известен точно, т.е. sn(tk,Xnk\ — известная
детерминированная функция своих аргументов, то для исключения влияния
помехового сигнала на прием и результаты обработки навигационного сигнала
достаточно сформировать разностный сигнал
1к=Ук-Зп{ч,Кк) = *{*к,ЧА)+пк> О9-2)
который и подвергать дальнейшей обработке.
Вычитание помехового сигнала sn(tk,XnA из наблюдений ук, по сути,
является компенсацией одной из составляющих аддитивной смеси (19.1),
поэтому методы борьбы с влиянием помеховых сигналов, использующие
принцип (19.2), иногда называют компенсационными методами.
На практике помеховый сигнал не бывает точно известным. В этом
случае для использования компенсационного метода необходимо сформировать
некоторую оценку помехового сигнала £П('*АП>*)> а вместо (19.2)
использовать выражение
%=Л-^п(^Дп,*)- О9'3)
Из теории оптимального приема и обработки сигналов следует [5.1, 5.2],
что при аддитивном взаимодействии полезного сигнала, помехи и белого гаус-
совского шума (19.1) принцип компенсации (19.3) является неотъемлемым ат-
752
Частотно-временная режекция узкополосных помех
рибутом подавляющего большинства оптимальных алгоритмов обработки при
различных моделях сигналов, помех и изменения их параметров.
Все многообразие компенсационных методов приема полезных сигналов
на фоне мешающих основано на том, как сформировать оценку помехового
сигнала •*„(/* ЛПч*) • При этом существенную роль играет априорная
информация о структуре и параметрах помехового сигнала. Чем больше априорной
информации, тем выше точность компенсации помехи.
Рассмотрим более подробно три наиболее часто используемых
компенсационных методов и алгоритмов приема полезных сигналов на фоне мешающих.
19.1.1. Метод оптимальной оценки параметров помехи
Данный метод базируется на использовании теории оптимальной
фильтрации [5.1, 5.2], в рамках которой полезный s(tk9Xk,3k) и помеховый $П(/*ЛП,*)
сигналы задаются в виде детерминированных функций времени и своих
параметров Хк,Зк и Хпк соответственно, которые, в свою очередь, описываются
многомерными марковскими процессами.
Применительно к спутниковой навигации навигационный сигнал
описывается соотношением
где А — амплитуда сигнала; \к =(гк,(рк); тк — задержка огибающей;
йдк (/*,**) — функция модуляции дальномерным кодом; hHC(tk.rk,9k) —
функция модуляции навигационным сообщением.
Для иллюстрации рассматриваемого метода и вытекающих из него схем и
алгоритмов обработки в качестве помехового сигнала рассмотрим
узкополосную помеху, для которой зададим достаточно простое описание
^п(^Дпд) = ЛК)с05(^Л+^)^ О9'5)
где Хик =(Auk,<puJc);Au(tk), (pnk — случайные амплитуда и фаза, которые
описываются в общем случае многомерными марковскими процессами.
Положим для простоты их описание в виде одномерных марковских процессов
где а ап — параметры, характеризующие скорость изменения амплитуды и
фазы помехи; дА^\9 Z^k-i —дискретные белые гауссовские шумы.
На вход НАП поступают отсчеты (19.1). Используя аппарат теории
оптимальной фильтрации, ищется алгоритм оптимального оценивания
расширенного вектора состояния \хк = [к] Зк Хтпк
753
Глава 19
В [19.1] приведен синтез оптимального алгоритма фильтрации. В [19.2]
приведены сведения об аппаратной реализации схем НАП, базирующихся на
данном методе.
Обобщенная схема НАП, реализующая данный метод, приведена на
рис. 19.1.
Компенсация
помехи
УК
f-Hs
А-
Блок памяти
М отсчетов ykJ
j=l М
+
X
Блок формирования опорных
навигационных сигналов
Блок корреляторов
для навигационных
сигналов
3
ЕЖЖ
х
it
К=
R,
Л
МДФс.*+1
МДтсД+1
А-
X
Т
Й
ДЛЯ
zZ
Блок корреляторов
помеховых сигналов
X
*(.)
'ве
III
о
8
о
Ч*+.
*
На решение
навигационной
задачи
1=
a g F
МД<РцД+1
Мд4„*+1
I *§
в в S
I ё I
i s в
Е I I
ц * а
Ч*+1
Блок формирования опорных
помеховых сигналов
£
Рис. 19.1. Обобщенная схема НАП, реализующая метод оценки параметров помехи
На рис. 19.1 компенсация помехи осуществляется в соответствующем
сумматоре путем вычитания из входного сигнала ук оценки сигнала помехи
sn (tkXn9k) • При этом оценка сигнала формируется в виде $п ltk,Хпк ) =
= Д, (tk)cos(coutk + фик), т.е. с использованием оценок параметров сигнала
(амплитуды и фазы), для чего в структуре НАП организованы соответствующие
кольца слежения за параметрами помехового сигнала.
19.1.2. Метод адаптивных трансверсальных фильтров
Трансверсальный фильтр (ТФ) - это линейный фильтр с конечной
импульсной характеристикой, обобщенная схема которого приведена на рис. 19.2.
754
Частотно-временная режекция узкополосных помех
Ук
Уы-\\ -1
Ук-2
-| ► •••
-1
Ук-п
Pi
А*
А*
V ^г ^г
• а ■
1
Л]
т
Е
г.
Рис. 19.2. Обобщенная схема трансверсального фильтра
Сигнал на выходе ТФ описывается выражением (при /?0 = 1)
п
ъ = Ук -^fith-i =Ук - КТЪ-\.„>
/=1
(19.6)
где Р*т = Д* Д^ ••• Р*п\ —вектор весовых комплексных коэффициентов
линейного оператора; ¥к-\,п=\Ук-1 Ук-2 — Л-иГ —вектор комплексных
отсчетов наблюдений на предшествующих (текущему к -у) п тактах.
Структура сигнала (19.6) полностью соответствует принципу компенсации
(19.3), при этом оценка помехи формируется в виде
С цель получения наилучшей компенсации помехи вектор весовых
комплексных коэффициентов р„ выбирается таким образом, чтобы
минимизировать мощность остаточной помехи в (19.6). Как будет показано в п. 19.3, при
существенном превышении мощности помехи над мощностью полезного сиг-
нала оптимальные коэффициенты р„ определяются соотношением
P„=Rv'Ry«> (19-7)
где RY=M[Yi_,,„Y;:,,„] (19.8)
— автокорреляционная матрица входного вектора, рассчитанная для п
предшествующих текущему моменту времени отсчетов;
*ул=Ч*м*п*-1.я] (19-9)
— вектор взаимной корреляции отсчета входного отсчета в к -й момент
времени с входным вектором, рассчитанным для п предшествующих текущему
моменту времени отсчетов.
755
Глава 19
При реализации алгоритма (19.7)—(19.9) определения вектора весовых
коэффициентов ТФ вместо математического усреднения используют усреднение
по временным выборкам, т.е.
1
1
l'=l 1=1
Схема адаптивного ТФ (АТФ) приведена на рис. 19.3.
(19.10)
i
у к ■ г
L
-
▼
i
1
т
Блок
i
,-1
i _._-_. 4 |
Ук
1
вычисления ы
i i
W --1
* ^^i ^
f ,''' 1
К х \
ховых коэффициентов li—(
Л 2 -1 ■. \Ук n !
1
r t
i
Рис. 19.3. Обобщенная схема адаптивного трансверсального фильтра
19.1.3. Метод режекции помехи в частотной области на основе БПФ
Данный метод основан [19.3] на следующих операциях над сигналом:
- преобразование выборки \к =|v^ yk_x ... vA._„|T временного сигнала в
частотную область с использованием дискретного преобразования Фурье
(ДПФ)
XY(frj = Ui) = F(Yk): (19.11)
- оценка спектра помехи Хп(/,..v = l,w?). которое выполняется
определением тех спектральных составляющих Л'п (/,-). для которых наблюдается
превышение заданного порога h, т.е.
(19.12)
\А\ (./г)|> /?, v = lm:
- вычитание из спектра входного сигнала Xvl/7,y = 1.«) оценки спектра
помехи Xn(/l'.,v' = l,w), т.е.
"56
Частотно-временная режекция узкополосных помех
X^{fjJ = \,n) = X^{fJJ = U)-kn{fv,v = \.m)- (19.13)
- преобразование спектра \AfjJ-\,п\ во временную область с
использованием обратного дискретного преобразованмя Фурье (ОДПФ)
ik=F-l(\(fjJ=u)). (19.14)
Так как ОДПФ является линейной операцией, то, подставляя (19.13) в
(19.14), можно записать
Y*=F
-1
(xY(/y,y = l,/f)-Xn(/v,v = l,w))
= F-,(xY(/y.J = l,«))-F-,(xn(/.,v = b;i)) = S'A-Vn.^ (19-15)
где
Yn^=F-] Xn(/V,v = l,m
(19.16)
является оценкой помехи.
Формула (19.15) является векторной записью принципа компенсации
(19.3), в котором оценка помехи формируется в соответствии с алгоритмом
(19.11)—(19.14).
Обобщенная схема устройства, реализующего данный метод, приведена на
рис. 2.4.4.
Ук
Блок формирования
выборки Y*
ДПФ
Блок оценки
спектра помехи !
—^ ОДПФ —к
J
Преобразователь
YA M* п^к „<1-
т
Рис. 19.4. Схема устройства режекции помехи в частотной области
19.1.4. Краткая характеристика методов и устройств
частотно-временной компенсации помех
1. Компенсатор с оптимальной оценкой параметров помехи
Для эффективной работы данного типа компенсатора необходимо
предварительно решить задачи грубой оценки параметров помехи (частоты и
мощности), для чего схему компенсатора рис. 19.1 необходимо дополнить
устройствами оценки частоты и мощности, что приводит к существенному усложнению
компенсатора с точки зрения его практической реализации. В то же время, при
757
Глава 19
наличии таких устройств данный тип компенсатора обеспечивает наиболее
эффективное подавление узкополосной помехи и работоспособность НАП при
отношениях qu/c = Ри/Рс < 100...120 дБ.
Другим недостатком использования данного типа компенсатора является
то, что может эффективно работать лишь в условиях действия одной помехи.
Для обеспечения работы в условиях воздействия нескольких мощных помех
необходимо использовать соответствующее число следящих систем за помехо-
выми сигналами, причем при слежении за каждой помехой необходимо
использовать принципы компенсации других помеховых сигналов, т.е.
необходимо строить комбинированную следящую систему с взаимными
перекрестными связями. В такой системе возможны неустойчивые режимы работы,
Кроме того, существенно возрастает сложность компенсатора.
2. Компенсатор на базе трансверсалъного фильтра
Данный тип компенсатора эффективно работает при воздействии помех с
шириной спектра А/п < 1...5 кГц. При этом в ТФ необходимо использовать
примерно п > 200 отводов линии задержки. Такой ТФ обеспечивает работу
НАП при отношениях ^П//С=РП/РС< 80...90 дБ. При возрастании ширины
спектра помехи до 10 кГц и более для эффективной работы ТФ потребуется
более 800 отводов линии задержки, что в настоящее время сложно реализовать
на практике.
Компенсатора на базе ТФ обеспечивает работу НАП при воздействии
небольшого числа т узкополосных помех (т < 3). При увеличении числа помех
для их эффективного подавления потребуется достаточно большое число
отводов линии задержки (я>1600).
3. Компенсатор в форме режекторного фильтра в частотной области
Основным достоинством данного типа компенсатора является простота
его практической реализации. Другим достоинством является то, что алгоритм
его работы практически не меняется (а, значит, и не усложняется) при
воздействии нескольких помех. Данный компенсатор обеспечивает работу НАП при
отношениях qnjc = Рп/Рс < 60...70 дБ при воздействии до 10 помех, общая
протяженность спектра которых не превышает 10% ширины спектра полезного
сигнала.
19.2. Синтез и анализ трансверсального фильтра
Описание наблюдений
Пусть на вход приемника в дискретном времени (с шагом дискретизации
Т^) поступает аддитивная смесь полезного сигнала и нескольких
гармонических помех
758
Частотно-временная режекция узкополосных помех
т
Ук
-Sc,k +2-iKl,k +^k >
(19.17)
ы
где sck — комплексный полезный сигнал; snlk = 4,/ Q^l7r^lTdk+<Pl> — 1-й
комплексный помеховый гармонический сигнал; пк— комплексный дискретный
белый гауссовский, для которого Л/ГяАл]М = 20^; a2 = N0/(2Td); N0
—односторонняя спектральная плотность мощности внутреннего шума приемника.
При этом Рс = А2с/2 , Рп1 = 4i/2 , qc/no = Pc/N0 = A2C/2N0 .
Алгоритм компенсации помех
Рассмотрим алгоритм компенсации помехи в форме линейного оператора
[19.4], аналогичного (19.2),
п
ь = у k -^fih-i =h - КТ%-и
Пк
(19.18)
/=1
Соотношение (19.18) описывает линейный фильтр с конечной импульсной
характеристикой, в котором значение параметра п определяет порядок
линейного фильтра (или число отводов линии задержки в реализации).
Введем вектора
Sc;k-l,n
Sn;*-1,«
*с,*-1 Sc,k-2 ••• sc,k-n\ ' Пк-\,п ~ \nk-l nk-2
m m m
2_/n/,*-l ^^n/,*-2 "• / ^nhk-n
1=1 1=1 l=\
IT
nk-n\ '■>
Тогда можно записать векторное наблюдение Yk_ln в виде
^к-\,п = К;к-\,п + *п;*-1,и + Щ-1,п = *с;к-\,п + ^п;*-1.и '
где
%п;к-\,п - Sn;k-l,n + пк-1,п
— помеховая составляющая вектора наблюдений.
(19.19)
(19.20)
Для к -го отсчета имеем
m
К,к=^Ш,к+"к-
(19.21)
i=\
Оптимальные весовые коэффициенты
Подставим (19.19) в (19.17)
т
П = *а +!>'-* +"k -&Т{***-и+Клп) = \к -K\k-u +ек(Ь„),(\922)
i=i
Ik
759
Глава 19
где
(19.23)
/=i
— составляющая процесса /^, обусловленная помеховыми сигналами
(включая внутренний шум приемника).
Определим оптимальный вектор р„ таким образом, чтобы
минимизировалось математическое ожидание квадрата ошибки
г,...
Мр»)1
min Л/
= min Л/
Р..
[>■
= mm
£inJ +2a; -2£^1ЛАл/[г;;4.11Й]ри+КтА/[^_и^.и] ря
/=1 I /=1
Выполнив минимизацию, находим
-1|
P«=Rz'R
Zv
где
Rz = A/
7 7*т
(19.25)
(19.26)
— автокорреляционная матрицч помехового вектора, рассчитанная для п
предшествующих гекуше.м\ моменту времени отсчетов;
!I,A-1.//
= м
-n,*^n;*-Uj '
(19.27)
/=i
Последнее равенство в (19.27) записано с учетом некоррелированности
шумов приемника.
Из (19.19), (19.20) следует, что компоненты помехового вектора Zn;kAn
отличаются от аналогичных компонент наблюдаемого вектора Yk^n
слагаемым sn;A:4 „, соответствующим навигационному сигналу. Так как нарушение
работы НАП происходит при воздействии достаточно мощных помех
(<7пс = ^i/^ - 30 дБ), то с точки зрения эквивалентности значения мощности
процессов в (19.19), (19.20) можно в первом приближении заменить Ъ^.к_Хп на
^'к-\м - те* вместо Rz , RZv рассматривать
Rv =A/
у у*Т
1 п;Аг—1.А/ * п;к-),п
(19.28)
?Ы)
Частотно-временная режекцчя узкополосных помех
RY» =М[КЛ;*-1.Й].
(19.20)
Тогда для весовых коэффициентов р,; можно использовать соотношение,
аналогичное (19.25),
P„=RyR
V^jt •
(19.30)
Выражения (19.28)—( 19.30) удобны тем. что в них входят только отсчеты
принимаемой реализации (19.17).
Коэффициент передачи трансверсалъного фильтра
Линейный фильтр (19.18) можно характеризовать коэффициентом
передачи. Применим к (19.18) Z преобразование
Т1 = у-^и-1у={\-^;2-1)у. (19.31)
1=1 1=1
Тогда, для операторного коэффициента передачи получаем выражение
A:(z) = (1-]£AV'). (19.32)
ы
Коэффициент передачи в частотной области получается в результате под-
становки z = e
,т.е.
(19.33)
/=i
Рассчитаем коэффициент передачи ТФ, оптимального при воздействии
одной гармонической помехи. Для матрицы Rz (19.26) в этом случае
справедливо выражение
Rz = 4
1
р
-1
Ап-2)
. (и-1) .(п-г)
ру ' fr '
1
+ 2<т;1,г,
(19.34)
-\2nfnTd
где р = е
Введем вектор v =
ношения
(при этом р* = р х), \п — п -мерная единичная матрица.
1 р ... ^~»Г
, для которого можно записать соот-
761
Глава 19
VV =
1
Р
1 Р
-(«-1)
-1
.(и-1) .(и-2)
Таким образом, (19.34) можно представить в виде
Rz=^n2vv*T+2(Tw2Iw.
Рассчитаем
R
Zsr
= л2
р р
р
= Кру ■
Г("-1)
Лп-2)
(19.35)
(19.36)
Таким образом, для оптимального вектора весовых коэффициентов Ри
получаем выражение
-1 ^ / \-i
P„=(A2vv*T+2c7„2I,,)~ A>pv = (qnvx*T+lnJ qnpv,
(19.37)
где qn =
— отношение помеха/шум.
2<т2 N0/(2Td)
Выполнив обращение матрицы в (19.37), получаем
$п=ЯпР
(
1 —
апп
v = _^_v.
nqn+\) nqa +1
(19.38)
Подставляя (19.38) в (19.33), получаем формулу для коэффициента
передачи оптимального ТФ
Значение коэффициент передачи на частоте помехи (/ = /„) равно
1 ЛГ"1 ;?я-о/7\ п . 1 1
(19.39)
*(/ = ЛН
= 1
yj2*0lTd =1 «
Из данного соотношения следует, что глубина провала АЧХ на частоте
помехи увеличивается с увеличением порядка фильтра п и величины
отношения помеха/шум qn.
Положим для определенности, что ТФ работает на промежуточной частоте
НАП 4,5 МГц. Частота помехи /п =4,52604 МГц, fd = \/Td =44 МГц,
«7п=10-1оё(<7п) = 60дБ.
762
Частотно-временная режекция узкополосных помех
На рис. 19.5 приведена амплитудно-частотная характеристика (АЧХ)
квадрата модуля £(/) коэффициента передачи при л =2.
4.5 5
Частота, Гц
х10°
Рис. 19.5. Амплитудно-частотная характеристика ТФ при и =2
Как видно из рис. 19.5 АЧХ имеет провал на частоте помехи, величиной
минус 125 дБ. В то же время, такой фильтр подавляет входной сигнал, в том
числе навигационный, в полосе частот 2 МГЦ на 18...20 дБ.
На рис. 19.6 приведена АЧХ при «=140.
4.5 5
Частота, Гц
х10°
Рис. 19.6. Амплитудно-частотная характеристика ТФ при «=140
В данном случае существенно улучшились условия приема навигационного
сигнала в основной полосе частот и хорошее подавление узкополосной помехи.
763
Глава 19
Анализ мощности помех на выходе трансверсалъного фильтра
Рассчитаем дисперсию помеховой составляющей Е^ (19.23) выходного
процесса (19.18)
= D, -R*/ R7R7, ,
(19.40)
где D- = Л/
-k
"n,k
Подставляя (19.35), (19.36) в (19.40), получаем
D =A2 + 2<72-q»P
nqn + 1
v*\/> = 2<7„2
1 +
1
/I + 1/^п
(19.41)
В (19.41) первое слагаемое — мощность аддитивного шума; второе
слагаемое характеризует дополнительную помеху, обусловленную наличием
гармонической помехи в наблюдениях (19.17), т.е. это остаточная помеха после
компенсации.
Из (19.41) следует, что даже при п = 1 дисперсия помехи увеличивается не
более, чем в 2 раза. При увеличении порядка п ТФ дисперсия шумового
процесса на его выходе асимптотически стремится к значению дисперсии шумовой
помехи.
Искажение навигационного сигнала на выходе ТФ
Неравномерность коэффициента передачи ТФ в полосе частот,
занимаемых навигационным сигналом (см. рис. 19.5—19.6) приводит к искажению
полезного сигнала. Проанализируем эти искажения.
Запишем навигационный сигнал в комплексной форме:
Л'а = ЛЛкАс*е
где h k — значение текущего символа дальномерного кода; 1\ск — значение
текущего символа навигационного сообщения; S<pc = cocTd — приращение фазы
сигнала на длительности интервала дискретизации; ф — начальная фаза сигнала.
с,и
Для помехи запишем аналогичное выражение
_ A '('Pn.O^Vn^)
Sn.k - Лп е
где ё(рп=соиТс
d
г ii 11 а
Используя данные обозначения, перепишем выражения для
коэффициентов ТФ (19.38) в виде
764
Частотно-временная режекция узкополосных помех
к =
Яи
Q-lS(Pn Q-'l2S(Pn
,-\nS(pn
j[n ^-i^>n/
> Pi =-^-ге
nqn+\
nqn+\
Подставим данные выражения в (19.18), полагая, что аддитивные шумы и
помеховый сигнал отсутствуют,
п
Ik = Пек = ^с,к ~ 2и& ^с,А-/ ~
Пк
= Асе
{<pcfi+8(pck)
i=l
^зк.кКск
Чп
"йк,к-1Пнс,кЧ е
Из полученного выражения следует, что искажение полезного сигнала на
выходе ТФ зависят от порядка фильтра п, характеристик дальномерного кода
Идкк и разности частот навигационного сигнала и помехи.
Положим для простоты анализа /п = /с. На рис. 19.7 приведена реализация
процесса на выходе ТФ с п - 44. На том же рисунке приведена огибающая
процесса на входе ТФ (пропорциональная реализации дальномерного кода).
t, МКС
0123456789 10
Рис. 19.7. Процесс на выходе ТВФ при «=44 ( nTd=\ мкс)
Из рис. 19.7 видно, что сигнал сильно искажён. В данном примере на вход
ТФ был подан сигнал с дальномерным кодом, имеющим длительность
элементарного символа тэ * 1 мкс, а частота дискретизации составляет 44 МГц.
Следовательно, длительность импульсной характеристики фильтра составляет
Тф=\ мкс, т.е. длительность интервала накопления в фильтре примерно равна
длительности символа ПСП. При /п = /с имеем
( п \
1к
= А е'^с-0+<%с*)/г
нс,к
<7п
■£*'
Из данного выражения следует, что на участке, где символы ПСП не
изменяются, сигнал оказался полностью подавлен, т.к. в ТФ с заданной длительно-
765
Глава 19
стью импульсной характеристики на данном участке сигнал оказывается чисто
гармоническим. На тех участках, где происходит смена символов ПСП, ТФ не
подавляет сигнал. Отсюда следует, что, увеличивая длительность интервала
накопления, можно снижать искажение сигнала в фильтре. Для иллюстрации
этого на рис. 19.8 приведена реализация процесса на выходе ТФ при «=176.
<.мкс
0123456789 10
Рис. 19.8. Процесс на выходе ТВФ при п =176 (nTd =4 мкс)
Оценим потери энергии полезного сигнала при прохождении ТВФ в
случае совпадения частот помехи и сигнала.
~ 1 А2
ъ _ * ■ * — с
1 1 гс | 1 " 1
qn+\/nn^ \qn+\/nn<-f )
(19.42)
Отметим, что первое слагаемое в полученном выражении определяет
мощность навигационного сигнала на входе ТВФ, а, следовательно, два вторых
слагаемых определяют его искажение.
На рис. 19.9 приведены рассчитанные по (19.42) характеристики
искажения мощности навигационных сигналов ГЛОНАСС с НТ- и ПТ-кодами и
сигнала GPS с С/А-кодом в зависимости от порядка п ТФ.
■Рвых/^вх,ДБ
о
п
16 32 64 128 256 512 1024 2048
Рис. 19.9. Зависимости искажения мощности
навигационных сигналов на выходе ТФ
766
Частотно-временная режекция узкополосных помех
Из графиков рис. 19.9 следует, что допуская потери мощности полезного
сигнала на выходе ТФ не более 3 дБ, необходимо использовать ТФ порядка
п> 140.
Синтез адаптивного трансверсалъного фильтра
Из проведенного выше анализа следует, что оптимальные весовые
коэффициенты ТФ определяются числом и параметрами воздействующих на его
входе помех. В практических задачах данные характеристики сигнально-
помеховой обстановки неизвестны. Поэтому необходимо строить адаптивные
ТФ (АТФ). В литературе описаны различные алгоритмы адаптации ТФ,
которые могут быть разбиты на две большие группы: градиентные алгоритмы
адаптации; прямые алгоритмы адаптации.
Ниже остановимся на прямых алгоритмах адаптации, суть которых
заключается в расчете оценочных значений требуемых корреляционных матриц по-
мех, т.е. RY и RY .
В соответствии с определениями (19.28), (19.29) требуемые
корреляционные матрицы должны рассчитываться как средние значения корреляционных
произведений векторов наблюдений. Полагая аддитивные шумы в
наблюдениях эргодическими, заменим вычисление среднего по ансамблю реализаций
вычислением выборочного среднего по времени, т.е.
R -lVv(,/) Y*T(l/) R -IVv^ П9 43^
В (19.43) вектора Y^' можно формировать последовательно в каждый
очередной момент времени tk , что можно записать, как ^-к-\ n ~ ^n-,v-\,n •>
Уа1 = Ущу • При этом каждый последующий вектор содержит п -1 компонент
предыдущего вектора, но сдвинутых по индексу в структуре вектора.
Отметим, что алгоритм адаптации (19.43) не зависит от структуры помехо-
вого сигнала, а, следовательно, не изменяется, если на входе приемника
действует одна или несколько гармонических помех, или какая либо узкополосная
помеха.
Результаты моделирования адаптивного ТФ
Моделирование АТФ проводилось в имитационной среде MATLAB при
следующих условиях: канал приема сигнала диапазона L1; энергетика
радиоканала qcin = 40 дБ; промежуточная частота сигнала, поступающего на вход
ТФ — 5 МГц; несущая частота помехи /п =5,1 МГц; частота дискретизации
АЦП fd = 44 МГц.
767
Глава 19
Положим qn,c- 50 дБ, число отводов линии задержки п = 1200, число
отсчетов, по которым производится вычисление корреляционных матриц L = 2400.
На рис. 19.10 а) приведена спектральная плотность мощности (СПМ)
процесса на входе АТФ, на которой присутствуют равномерный внутренний шум и
гармоническая помеха на частоте 5.1 МГц, а на рис. 19.10 б) — аналогичная
характеристика приведена для спектральной плотности процесса на выходе АТФ.
150
"100
-60
- V |
V -"-.""?$- ■
5
^^:'Т^-^^ЗДР^р
1сГ is"
Частота, МГц
20
25
с
О
Vf
-50'
0
РР
ЩЩрщ
5
ш^^ш
10 15
Частота, МГц
20
25
а) б)
Рис. 19.10. Спектральная плотность процесса на входе и на выходе АТФ
при п = 1200, L-2400
Из сопоставления двух рисунков видно, что гармоническая помеха
эффективно подавлена.
Для иллюстрации эффективности процесса адаптации рассчитаем
коэффициент передачи АТФ, который устанавливается в нем после завершения
режима адаптации. На рис. 19.11 приведена соответствующая характеристика.
ш 20 г- --
| 10
го
I о
О)
я-10
1-20
|-30
£-40
&-50
о
j^-60
гз
£-70
-80
4.5
5.5
Частота, МГц
Рис. 19.11. Амплитудно-частотная характеристика АТФ
при воздействии 1 помехи и п= 1200, 1=2400
768
Частотно-временная режещия узкополосных помех
Из рис. 19.11 следует, что на частоте помехи /п =5,1 МГц в АТФ
сформировался провал АЧХ, глубиной ~ 60 дБ, что и позволило эффективно подавить
помеху.
Рассмотрим ситуацию, когда на входе НАП воздействуют три
гармонические помехи с частотами: /п1 = 4,5 МГц, /п2 = 4,7МГц, /п1 = 4,9 МГц. На
рис. 19.12 а), б) и рис. 19.13 приведены характеристики подавления помех в
АТФ при qn/c = 70 дБ п = 2400.
140
150
100
10 15
Частота» МГц
-50^
20
10 15
Частота» МГц
20
25
а)
б)
Рис. 19.12. Спектральная плотность процесса на входе и на выходе АТФ
при воздействии 3 помех и п = 1200, L = 2400
Рис. 19.13. Амплитудно-частотная характеристика АТФ
при воздействии 3 помех и п= 1200, /,=2400
Реальные помехи отличаются от идеальных гармонических помех ввиду
конечной ширины спектра реальных сигналов. Рассмотрим «идеальную»
полосовую помеху, которая состоит из набора синусоид, частоты которых компактно
25-1026
769
Глава 19
заполняю заданную полосу частот Afn . При этом мощность помехи
определяется как Ри = SnAfu , где Sn — СПМ помехи в заданной полосе частот А/п . При
заданной мощности помехи увеличение полосы занимаемых ее частот приводит к
снижению уровня СПМ.
Положим полосу частот, занимаемых помехой, А/п= 10 кГц, и #п/с=100 дБ.
На рис. 19.14 а), б) и рис. 19.15 приведены характеристики АТФ для
рассматриваемого случая.
100
ш
* 80
х 60
О
ш
да
о.
/~\Л
-fit
-20^
455
4 65
Частота, МГц
455
4.6
Частота» МГц
4.65
а)
б)
Рис. 19.14. Спектральная плотность процесса на входе и на выходе АТФ
при воздействии помехи с полосой частот 10 кГц и п = 1200, L = 2400
Частота, МГц
Рис. 19.15. Амплитудно-частотная характеристика АТФ при воздействии
помехи с полосой частот 10 кГц и п = 1200, L = 2400
Из приведенных зависимостей следует, что АТФ успешно подавляет
помеху с полосой частот 10 кГц и qnjQ = 100 дБ.
770
Частотно-временная режекция узкополосных помех
Из проведенного исследования можно сделать следующие выводы:
Алгоритм адаптации трансверсального фильтра (19.443) эффективно
работает как при воздействии одной или нескольких гармонических помех, так и
при воздействии полосовых помех с шириной спектра, как минимум, до 10 кГц.
Для эффективного подавления помех целесообразно использовать ТВФ
достаточно большого порядка п> 200. 3. Адаптивный ТФ подавляет узкополосные
помехи, мощность которых по отношению к навигационному сигналу может
составлять до 100 дБ и более. При уменьшении ширины спектра помехи
эффективность ее подавления возрастает, а требования к необходимому значению
порядка фильтра п уменьшаются.
19.3. Режекция узкополосных помех в частотной области на основе БПФ
В п. 19.1.4 описана последовательность операций, реализующих метод ре-
жекции узкополосных помех в частотной области на основе БПФ. Обобщённая
структурная схема устройства, реализующего данный метод, изображена на
рис. 19.16.
.
Ук
"^
X
^
БПФ
Y„
^
Вырезание
помех
Y„
—►
ОБПФ
Г
Ук
^
Весовое окно
Рис. 19.16. Структурная схема устройства режекции узкополосных помех
Суть данного способа заключается в том, что входная реализация
аддитивной смеси широкополосного навигационного сигнала и узкополосной помехи
подвергается преобразованию Фурье. После такого преобразования
спектральные составляющие, соответствующие узкополосной помехе, представляют
собой узкий компактный спектр, существенно превышающий спектральные
составляющие, соответствующие навигационному сигналу. Подавление помехи
осуществляется удалением указанных выше мощных спектральных компонент.
После этого осуществляется обратное преобразование Фурье к оставшимся
спектральным компонентам, в результате чего формируется сигнал с
подавленной узкополосной помехой.
Математически операции можно выразить следующим образом:
Yn = /Wk У к ехР {~11якп1Щ — преобразование Фурье над входной реали-
зацией ук ;
771
Глава 19
Yn
0> \Y„\>h,
... — сравнение спектральных компонент с порогом и
Yn-> \Yп\ ^ "
удаление мощных компонент;
N-X
ук = 2^ fnwp{i27tknlN) — обратное преобразование Фурье,
л=0
где h — порог, выбираемый исходя из уровня аддитивного шума; wk —
весовое окно, речь о котором пойдёт ниже, в простейшем случае wk = 1; N —
объём дискретного преобразования Фурье (ДПФ).
В отличие от непрерывного преобразования Фурье, ДПФ оперирует с
конечной выборкой временных отсчетов входного сигнала. Математически это
можно представить, как предварительное умножение входного сигнала на
стробирующую функцию
[1, te[09T]9
w(t) =
i г i (19-44)
[о, /е[о,г],
где Т = TdN — длительность интервала анализа ДПФ; Td — шаг
дискретизации по времени.
Рассмотрим непрерывный сигнал u(t) = w(t)y(t). Произведению двух
сигналов во временной области соответствует свёртка их спектров в частотной
области. Следовательно, для спектральной плотности процесса ii{t) можно
записать
Su(f)= \sw(Z)Sy(f-S)dt. (19.45)
-00
Для функции w{t) (19.44) имеем
*„(/) = Г *g^exp{-i;r/r} (19.46)
Если в качестве y(t) положить гармонический сигнал, т.е.
y{t) = Aexpii2^f0t\, спектральная плотность которого представляет собой
дельта-функцию Sy (со) = AS(2тг/0), то (19.45) принимает вид
sin(/r(/'-/п)Т) . ч ,
Su(f) = T \у /°' ;ехр{-1л-(/-/„)г}. (19.47)
Таким образом, данная спектральная плотность процесса и(*)уже не будет
представлять собой дельта-функцию, а её форма повторит форму спектральной
плотности весового окна (19,46).
772
Частотно-временная режекция узкополосных помех
При использовании дискретных во времени функций и ДПФ вместо
непрерывных спектральных плотностей (19.44)—(19.47) рассчитываются
дискретный спектральные компоненты для частот /ДПф)И = п/Т, где п — целое
число. В этом случае, для частот входного сигнала, кратных значениям 1/Т
(т.е. fm = m/T при целых m), «нули» функции (19.47) будут совпадать с
частотами ДПФ /дпф,и • В результате, помеха с такой частотой будет отображаться
на спектре только одним отсчётом (рис. 19.17).
/, МГц
Рис. 19.17. Дискретный спектр смеси белого шума и гармонического
сигнала с частотой, кратной 1/Г
Если частота /0 окажется не кратной 1/Г, то при преобразовании (19.47)
спектр отобразится целым "пьедесталом", имеющим спад 6 дБ на октаву и
максимальный уровень боковых лепестков достигает -13 дБ (рис. 19.18).
/, МГц
Рис. 19.18. Дискретный спектр смеси белого шума и гармонического
сигнала с частотой, не кратной 1/Г
773
Глава 19
Подавление таких помех в частной области затруднено — нужно вырезать
множество отсчётов спектра.
Решение данной проблемы известно давно и заключается в
предварительной весовой обработке наблюдений. Смысл данной обработки сводится к
умножению входного сигнала на некоторую весовую функцию, длительность
которой равна длительности интервала анализа ДПФ. Входной сигнал
умножается теперь на сигнал — "весовое окно", подбираемый таким образом, чтобы его
спектр имел более быстрое спадание боковых лепестков, чем функция
"sin(x)/x". Это позволяет уменьшить "пьедестал" в частотной области. В
качестве примера можно рассмотреть весовое окно Ханна:
wh(k) = cos \n .
Спектральная плотность данного окна имеет вид:
Swh(f) = 0.5Sw(f) + 0.25(Sw(f-VT) + Sw(f + VT)), (19.48)
где Sw(f) —спектральная плотность прямоугольного окна (19.46).
Спектральная плотность (19.48) имеет спад 18 дБ на октаву и
максимальный уровень боковых лепестков минус 31 дБ.
Ценой данной обработки является снижение отношения сигнал/шум в
результате снижения эффективной длительности анализируемого сигнала
(огибающая произведения двух сигналов становится не постоянной (рис. 19.19)).
: ; .' - мкс
-20 '■ - - ' - - - -; -- J *■
О 20 40 60 80 100
Рис. 19.19. Произведение входного процесса на весовое окно Ханна
Для рассматриваемого окна Ханна снижение отношения сигнал/шум
составляет 1,3 дБ.
Известны различные типы весовых окон, предназначенных для весовой
обработки сигналов перед ДПФ. Параметры некоторых из них приведены в табл. 19.1.
774
Частотно-временная режекция узкополосных помех
Таблица 19.1. Весовые окна и их параметры
Название
окна
Вид весовой функции и>(&)
Макс, уро
вень бок.
леп., дБ
Потери
по с/ш,
дБ
Прямо
мо-
уголь-
ное
-13
О
Барт-
летта
\-2t[k]
-27
-1,1
Хэм-
минга
0.54 + 0.46 cos(2^[A:])
-43
-2,2
Ханна
cos2 (л?[&])
-31
1,3
Парзе-
на
\-6t[kf+6\t[kf, \t[k]\<N/4
[2(1 -|/[А:]|)3, N/4 < \t[k]\ <N/2
-53
■1,7
Блэк-
мена
0.42-0.5 cos 2л--
k \ _ (. к ^
N-\
+ 0.08 cos 4л--
V N-l
-58
-2,8
Тьюки
2
1,
I
2
1 + cos
(2n k-\ \
r N-l
-7C
при k<-(N-l) + l,
при -(N-l) + l<k<N—(N-l),
(2ж 2ж к-1
1 + cos ж
\r r N-l ,
,при — ~(N-\)<k.
-13
(при г
0.2),
-21
(при г
0.8)
-0.5
-1.2
Аналогичная ситуация происходит при обработке полосовых помех. На
рис. 19.20 изображён дискретный спектр при наличии на входе помехи с
полосой 1 МГц при использовании прямоугольного весового окна.
/. МГц
0 5 10 15 20 25
Рис. 19.20. Спектр смеси шума и помехи для прямоугольного весового окна
775
Глава 19
Как и на рис. 19.19, виден широкий пьедестал. Аналогичный график при
использовании весового окна Ханна изображён на рис. 19.21. На данном
графике спектр полосового шума чётко ограничен, что позволяет эффективно еого
вырезать.
/, МГц
Рис. 19.21. Спектр смеси шума и помехи для окна Ханна
19.4. Сравнение эффективности алгоритма режекции узкополосных
помех в частотной области и трансверсального фильтра
Для оценки качества работы алгоритма режекции узкополосных помех в
частотной области и трансверсального фильтра рассмотрим следующие
показатели:
• дисперсия разности процесса на выходе режекторного фильтра и чистого
сигнала:
D£=M
{*?k-sk)(i?k-sk)
• степень искажения полезного сигнала, определяемая, как:
Nd
YXh's*k\
r = l-*=o
k=0
(19.49)
где §k — чистый сигнал, обработанный фильтром;
• отношение сигнал/помеха на длительности интервала дискретизации qdn.
Ниже приводятся результаты анализа воздействия гармонической помехи
при qn =105 дБГц и разном значении параметра N, определяющего порядок
776
Частотно-временная режекция узкополосных помех
режекторного фильтра (или объём ДПФ). При отсутствии дополнительной
гармонической помехи отношение мощности сигнала к мощности помехи на
интервале дискретизации составляет qdn =-25.3 дБ, дисперсия суммарного по-
мехового сигнала до обработки составляет D£ = 2345, отношение
сигнал/помехи на интервале дискретизации до обработки составляет минус 70 дБ.
В системе на основе ДПФ использовано весовое окно Парзена.
Таблица 19.2. Характеристики рассматриваемых алгоритмов
N
1
2
4
8
16
32
64
128
256
512
1024
2048
Трансверальный фильтр
странсе
18.7
16.1
14.8
14.0
13.6
13.3
13.2
13.2
13.0
13.0
12.9
12.6
г
трансе
0.81
0.72
0.53
0.28
0.14
0.07
0.04
0.02
0.02
0.02
0.04
0.09
Чс1п ' ДБ
<*/л трансе
-35.7
-32.7
-29.8
-27.3
-26.3
-25.6
-25.6
-25.5
-25.4
-25.4
-25.5
-25.4
БПФ
D£
£ДПФ
-
-
-
7.7
12.2
13.8
13.5
14.0
14.2
13.3
13.1
12.8
ГДПФ
-
-
-
0.98
0.94
0.86
0.66
0.46
0.37
0.35
0.33
0.34
4с1пДПФ > ДБ
-
-
-
-38.5
-37.0
-34.7
-30.4
-28.7
-28.2
-27.3
-27.1
-26.9
Из анализа приведенной таблицы можно сделать вывод о том, что при
больших значениях N оба алгоритма демонстрируют сходные характеристики.
При малых N трансверсальный фильтр предпочтительней.
Следует заметить, что при практической реализации данных алгоритмов
по ряду показателей всё же более удачным оказался алгоритм на основе БПФ.
Реализация трансверсального фильтра с коэффициентами большой разрядности
требует очень много ресурсов, сопоставимых с двумя преобразованиями
Фурье. Кроме того, алгоритм с трансверсальным фильтром требует вычисления и
адаптации коэффициентов усиления, для чего требуется достаточно мощный
сигнальный процессор, в то время, как для второго алгоритма коэффициенты
рассчитывать не надо. И третье — расчёт коэффициентов требует достаточно
много времени (на экспериментальном образце с процессором ADSP21262
Share и фильтром 2048 отводов требовалось несколько десятков миллисекунд
[19.4]). За это время параметры реальной помехи могут измениться и коэффи-
777
Глава 19
циенты "устареют". Алгоритм на основе БПФ не имеет задержки на
адаптацию, поэтому пригоден для обработки помех, близких к гармоническим на
интервале анализа БПФ (порядка сотен мкс). Это позволяет обрабатывать ряд
узкополосных помех с изменяющимися параметрами.
Литература
19.1. Перов А.И. Синтез оптимального алгоритма обработки сигналов в приемнике
спутниковой навигации при воздействии гармонической помехи// Радиотехника.
Радиосистемы, 2005, № 7, с. 36-42.
19.2. . Zhodzishsky M. In-Band Interference Suppression for GPS/GLONASS/ GPS
ION-98.
19.3. Бакитъко Р.В., Полыциков В.П., Шилов А.К, Хацкелевич Я.Д., Болден-
ков Е.Н. Использование весовых функций для предварительной обработки шумопо-
добных сигналов при наличии сильных интерференционных помех// Радиотехника.
2006, №6, с. 13-17.
19.4. Перов А.К, Болденков Е.Н. Исследование адаптивных трансверсальных
фильтров для приемников спутниковой навигации при воздействии узкополосных
помех// Радиотехника. 2006, № 7, с. 98-105.
778
Список сокращений
Список
АКП — аппаратура контроля поля
АКС — аппаратура командной
системы
АКП — антенный компенсатор
помех
АКЦ — автономный контроль
целостности
AM — апостериорный мониторинг
АП — аппаратура потребителей
АПВ — апостериорная плотность
вероятности
АПС — аппаратура передачи
сигнала
АР — антенная решетка
АРУ — автоматическая регулировка
усиления
АСУ — автоматизированное
управление
Ат — аттенюатор
АФАР — активная фазированная
антенная решетка
АЦП — аналого-цифровой
преобразователь
АЭ — антенный элемент
ВАМИ — бортовая аппаратура
межспутниковых измерений
БВЧ — блок высокой частоты
БГШ — белый гауссовский шум
БД — база данных
БИНРС — бортовой источник
навигационных радиосигналов
БИНС — бесплатформенная инер-
циальная навигационная система
БТС — бортовая телеметрическая
система
БУ — блок управления
БУК — бортовой управляющий
комплекс
БС — базовая станция
БСУ — бортовое
синхронизирующее устройство
БФКП — блок формирования
кодовых последовательностей
БФОС — блок формирования и
обработки сигналов
БФСП — блок формирования
сигнала передатчика
БЦВК — бортовой цифровой
вычислительный комплекс
БЦОС — блок цифровой
обработки сигналов
БШВ — бортовая шкала времени
БЭВЧ — бортовой эталон времени
и частоты
ВВИА — военно-воздушная
инженерная академия
ВВК — вектор весовых
коэффициентов
ВВС — военно-воздушные силы
ВКС — военно-космические силы
ВПП — взлетно-посадочная полоса
ВС — воздушное судно
ВТ — высокая точность
ВУП — входное устройство
приемника
ВЧ — высокочастотный
ГДК — генератор дальномерного
кода
ГЛОНАСС — глобальная
навигационная спутниковая система
ГОС — генератор опорного сигнала
ГЭВЧ — Государственный эталон
времени и частоты
ДЗО — дискриминатор задержки
огибающей
ДН — диаграмма направленности
779
Список сокращений
ДП — дифференциальные
поправки
ДПС — дифференциальная
подсистема
ДР — дифференциальный режим
ДС — дифференциальное сообщение
ДХ — дискриминационная
характеристика
ИКАО — Международная
организация гражданской авиации
ИМО — Международная морская
организация
ИНС — инерциальная
навигационная система
ИСК — инерциальная система
координат
ИСНС — инерциально-спутни-
ковая навигационная система
ИСЗ — искусственный спутник
Земли
ИТП — измеренные текущие
параметры
КВЦ —
координационно-вычислительный центр
КИС — командно-измерительная
система
ККС —
контрольно-корректирующая станция
КМ — квадратурный модулятор
КНИЦ — Координационный
научно-информационный центр
КОС — квантово-оптическая
станция
КПП — коэффициент подавления
помехи
КПФ — канальный полосовой
фильтр
КС — контрольная станция
КФ — корреляционная функция
КФМ — квадратурный фазовый
модулятор
КХ — код Хемминга
ЛА — летательный аппарат
ЛВВИА — Ленинградская военно-
воздушная инженерная академия
ЛДПС — локальная
дифференциальная подсистема
ЛСК — локальная система
координат
МАМС — Международная
ассоциация маячных служб
MB — метка времени
МГНСС — модернизированная
глобальная навигационная
спутниковая система
МДП — метод дополнительной
переменной
МДПС — морская
дифференциальная подсистема
МК — масштабный коэффициент
МКО — мультиплексный канал
обмена
МО — Министерство обороны
МС — морское судно
МСМ — метод сравнения
местоположения
МСД — метод сравнения
дальностей
МФС — минимальный фазовый
сдвиг
МШУ — малошумящий усилитель
МЭК — Международная
электротехническая комиссия
МЭС — Международный союз
электросвязи
НАП — навигационная аппаратура
потребителей
780
Список сокращений
HBO — навигационно-временные
определения
НИ — навигационная информация
НКУ — наземный комплекс
управления
НО — направленный ответвитель
НП — навигационный параметр
НС — навигационный спутник
НСК — навигационный суперкадр
ОГ — опорный генератор
ОЗУ — оперативное запоминающее
устройство
ОИ — оперативная информация
ОИС — опорная измерительная
станция
ОМ — оперативный мониторинг
ОПФ — оптимальный
пространственный фильтр
ОС — опорная станция
ОСШ — отношение сигнал/шум
ОФМ — относительная фазовая
манипуляция
ПВАО —
пространственно-временная адаптивная обработка
ПВЗ ^- параметры вращения Земли
ПВОС — пространственно-
временная обработка сигналов
ПД — псевдодальность
ПДСЧ — псевдодоплеровское
смещение частоты
ПЗ — псевдозадержка
ПЗСК — подвижной система
координат, связанная с Землей
ПКА — подсистема космических
аппаратов
ПКУ — подсистема контроля и
управления
ПМ — пункт мониторинга
ПОС — пространственная
обработка сигналов
ПППД — признак принадлежности
посылки данных
ПСП — псевдослучайная
последовательность
ПУ — предварительный усилитель
ПУМ — предварительный
усилитель мощности
ПФ — полосовой фильтр
ПЧ — промежуточная частота
РАН — Российская академия наук
РДП — Российская
дифференциальная подсистема
РДПС — региональная
дифференциальная подсистема
РМ — радиомаяк
РН — разрешение неоднозначности
РНП — радионавигационный
параметр
РСБН — радионавигационная
система ближней навигации
РСДН — радионавигационная
система дальней навигации
РСМ — разностно-скоростной
метод
РФ— Российская Федерация
РЦМ — региональный центр
мониторинга
РЧБ — радиочастотный блок
СБИС — сверхбольшая
интегральная схема
СВП — скалярно-векторные
поправки
СЗ — станция закладки
СИ — служебная информация
СИК — станция интегрального
контроля
СК — система координат
СКЗ — среднеквадратическое
значение
781
Список сокращений
СКО — среднеквадратическая
ошибка
СКФ — система контроля фаз
СМ — смеситель
СОС — система ориентации и
стабилизации
СПМ — спектральная плотность
мощности
СПО — сигнально-помеховая
обстановка
СРНС — спутниковая
радионавигационная система
СС — следящая система
ССЗ — следящая система за
задержкой сигнала
ССИ — станция сбора информации
ССК — связанная (с объектом)
система координат
ССФ — следящая система за фазой
сигнала
СТ — стандартная точность
СТИ — станция траекторных
измерений и управления
СУ — схема управления
СФ — сглаживающий фильтр
СФО — сферическая ошибка
СЧ — синтезатор частот
США — Соединенные штаты
Америки
СШВ — системная шкала времени
СЭВЧ — системный эталон
времени и частоты
У — усилитель
УАт — управляемый аттенюатор
УЗ — устройство защиты
УКВ — ультракороткие волны
УС — усилитель
УТГ — управляемый тактовый
генератор
УЦГС — управляемый цифровой
генератор гармонического сигнала
ФАПЧ — фазовая автоподстройка
частоты
ФД — фазовый дискриминатор
ФИ — фазовые измерения
ФМ — фазовый модулятор
ФМС — формирователь
модулирующих сигналов
ФНК — формирователь
навигационного кадра
ФНС — формирователь
навигационного сигнала
ФНЧ — фильтр низкой частоты
ЦВ — цифровой вычислитель
ЦГМ — центр глобального
мониторинга
ЦИ — цифровая информация
ЦС — центральный синхронизатор
ЦУС — центр управления системой
ЦФЛ — цифровой формирователь
лучей
ЧАП — частотная автоподстройка
ЧВИ — частотно-временная
информация
ЧВП — частотно-временные
поправки
ЧД — частотный дискриминатор
ШВ — шкала времени
ШВП — шкала времени
потребителя
ШДПС — широкозонная
дифференциальная подсистема
ШИС — широкополосный
измерительный сигнал
ШПС — шумоподобный сигнал
ЭВМ — электронная
вычислительная машина
ЭВО — эфемеридно-временное
обеспечение
782
Список сокращений
ЭВЧ — эталон времени и частоты
ЭИ — эфемеридная информация
AT — Atomic Time (атомное время)
DSP — Digital Signal Processor
(цифровой сигнальный процессор)
ECEF — Earth-centered Earth-fixed
(геоцентрическая система
координат, связанная с Землей)
ЕТ — эфемеридное время
GDOP — geometric delution of
precision (геометрический фактор
ухудшения точности местоопределения)
GES — Ground Earth Station
(наземные станции)
GIC — GPS Integrity Channel
(канал целостности GPS)
GNSS — Global Navigation Satellite
System (глобальная навигационная
система)
GPS — Global Positioning System
(Глобальная система
позиционирования)
JD — юлианская дата (день)
HDOP — horizontal delution of
precision (горизонтальный фактор
ухудшения точности
местоопределения)
LSR — least squares residuals
(невязки по методу наименьших
квадратов)
MSS — maximum solution separation
(метод максимального отличия
решения)
OTF — on-the-fly (в движении)
PDOP — position delution of
precision (фактор ухудшения точности
определения пространственного
положения)
RAIM — Reseiver Integrity
Monitoring (автономный контроль
целостности)
RTK — Real Time Kinematic
(кинематика реального времени)
RTCM — Radio Technical
Commission for Maritime Services
(Радиотехническая комиссия для морских
служб)
SA — selective availability
(селективный доступ)
TAI — International Atomic Time
(международное атомное время)
TDOP — time delution of precision
(фактор ухудшения точности
определения времени)
VDOP — vertikal delution of
precision (вертикальный фактор
ухудшения точности местоопределения)
UERE — User Equivalent Range
Error (эквивалентная дальномерная
погрешность)
UT — Universal Time (Всемирное
время)
UTC — Coordinated Universal Time
(Всемирное координарованное
время)
UTC(SU) — шкала Госэталона
Всемирного координарованного
времи
WAAS — Wide Area Augmentation
System (широкозонная система
функционального дополнения)
WMS — WAAS Master Station
(WAAS ведущие станции)
WRS — WAAS Reference Station
(WAAS опорные станции)
ZT — поясное время
783
ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ 3
ВВЕДЕНИЕ 6
Литература 11
Р а з д е л 1. ОБЩИЕ ПРИНЦИПЫ ПОСТРОЕНИЯ
СПУТНИКОВЫХ РАДИОНАВИГАЦИОННЫХ
СИСТЕМ 12
Глава 1. Структура спутниковых радионавигационных
систем 12
1.1. Общие сведения 12
1.2. Подсистема космических аппаратов 13
1.3. Подсистема контроля и управления 14
1.4. Навигационная аппаратура потребителей 15
1.5. Особенности формирования эфемеридной информации
в среднеорбитальных СРНС 16
1.6. Требования различных потребителей к спутниковым
радионавигационным системам 17
Литература 22
Г л а в а 2. Шкалы времени 24
2.1. Астрономические шкалы и единицы мер времени 25
2.2. Атомные шкалы и единицы времени 27
2.3. Универсальные шкалы времени и шкалы времени,
используемые в СРНС 28
2.4. Локальные шкалы времени в СРНС 30
2.4. Нестабильность частоты и времени в опорных генераторах 32
2.5. Синхронизация шкал времени в СРНС 36
Литература 38
Г л а в а 3. Траекторное движение навигационных спутников .... 40
3.1. Системы координат, используемые в СРНС 40
3.2. Уравнения невозмущенного траекторного движения НС в
инерциальнои системе координат 47
3.3. Классические элементы орбиты спутника 48
3.4. Движение спутника по невозмущенной орбите 50
3.5. Уравнения невозмущенного движения НС в инерциальнои
системе координат с использованием орбитальных элементов . 52
784
3.6. Общая характеристика возмущенного движения
навигационных спутников 56
3.7. Приближенные уравнения возмущенного движения в
геоцентрической подвижной системе координат 59
3.8. Зоны и время видимости навигационных спутников 61
Литература 64
Г л а в а 4. Методы решения навигационных задач 65
4.1. Общие сведения 65
4.2. Дальномерный метод 66
4.3. Псевдо дальномерный метод 68
4.4. Разностно-дальномерный и псевдо разностно-дальномерный
метод 71
4.5. Радиально-скоростной (доплеровский) метод 72
4.6. Псевдо радиально-скоростной (псевдо доплеровский) метод ... 74
4.7. Разностно-радиально-скоростной метод 76
4.8. Комбинированные методы 76
4.9. Определение ориентации с помощью СРНС 77
Литература 79
Г л а в а 5. Радиосигналы и навигационные сообщения
в спутниковых радионавигационных системах 80
5.1. Требования, предъявляемые к радиосигналам в СРНС 80
5.2. Математическое описание радиосигналов 82
5.3. Фазоманипулированные сигналы 85
5.3.1. Общие свойства бинарных фазоманипулированных сигналов 86
5.3.2. М-последовательности. Основные свойства 90
5.3.3. Последовательности Голда 94
53.4. Последовательности Касами 96
5.4. Фазоманипулированные сигналы с модуляцией
на поднесущих частотах 97
5.5. Сравнительный анализ потенциальной точности оценки
задержки сигналов с различными законами фазовой
манипуляции 100
5.5. Навигационные сообщения в СРНС 105
5.5.1. Общие сведения 105
5.5.2. Помехоустойчивое кодирование навигационной
информации 107
5.6. Модуляция радиосигнала навигационным сообщением 110
5.6.1. Относительная фазовая манипуляция 110
5.6.2. Фазовая манипуляция радиосигнала 113
5.7. Синхронизация в приемнике сигналов СРНС 113
Литература 114
Г л а в а 6. Методы и алгоритмы обработки сигналов и
извлечения навигационной информации 116
6.1. Общие сведения 116
6.2. Поиск сигналов по задержке и частоте 118
6.3. Общие принципы построения следящих систем
в аппаратуре спутниковой навигации 136
6.3.1. Навигационный приемник с двухэтапной
обработкой сигналов 136
6.3.2. Формирование оценок информационных процессов
на основе следящих систем 139
6.3.3. Когерентная и некогерентная обработка сигналов
в приемнике 142
6.3.4. Синтез дискриминаторов следящих систем 143
6.3.4.1. Синтез дискриминаторов когерентных
приемников 143
6.3.4.2. Синтез дискриминаторов некогерентных
приемников 151
6.3.4.3. Синтез дискриминаторов с оптимальным
накоплением 156
6.3.5. Выделение навигационного сообщения 157
6.3.6. Синтез сглаживающих фильтров 158
6.3.6.1. Оптимальный фильтр третьего порядка
для следящей системы за фазой сигнала 159
6.3.6.2. Оптимальный фильтр второго порядка для
следящей системы за задержкой огибающей
сигнала 167
6.3.6.3. Оптимальный фильтр второго порядка для
следящей системы за частотой сигнала 172
6.3.6.4. Комплексный фильтр слежения за фазой и
частотой сигнала в когерентном приемнике 174
6.3.6.5. Комплексный фильтр слежения за задержкой
огибающей и доплеровской частотой сигнала
в некогерентном приемнике 180
6.3.6.6. Комплексный фильтр слежения за
задержкой огибающей и фазой сигнала
когерентного приемника 185
786
Оглавление
6.3.6.7. Комплексный фильтр слежения за задержкой
огибающей с поддержкой оценки доплеровской
частоты сигнала когерентного приемника 190
6.4. Алгоритмы вторичной обработки (навигационные
алгоритмы) 194
6.4.1. Вторичные наблюдения 194
6.4.2. Алгоритмы вторичного сглаживания оценок
псевдо дальности 196
6.4.2.1. Вторичное сглаживания оценок псевдо дальности
оценками псевдо доплеровского смещения частоты 196
6.4.2.2. Вторичное сглаживания оценок псевдо дальности
приращениями оценок фазы 200
6.4.3. Одношаговый алгоритм вторичной обработки 203
6.4.4. Фильтрационные алгоритмы вторичной обработки 206
6.5. Одноэтапная обработка сигналов в приемниках СРНС 212
6.5.1. Общие сведения 212
6.5.2. Синтез одноэтапного алгоритма обработки сигналов
для некогерентного режима работы 213
6.5.2.1. Синтез многомерного дискриминатора с
когерентной обработкой 214
6.5.2.2. Синтез интегрированного сглаживающего фильтра 219
6.5.3. Синтез одноэтапного алгоритма обработки сигналов
для некогерентного режима работы 222
6.5.3.1. Синтез многомерного дискриминатора 223
6.5.3.2. Синтез сглаживающего фильтра 226
6.6. Прием сигналов в условиях многолучевости 230
6.6.1. Общая характеристика многолучевости 231
6.6.2. Оптимальные алгоритмы приёма в условиях
многолучевости 234
6.6.3. Дискриминационная характеристика 238
6.6.4. Потенциальные характеристики точности 241
6.6.5. Характеристики «некогерентного» алгоритма обработки 243
Приложение к гл. 6. Статистические характеристики дискриминаторов 246
П6.1. Статистические характеристики синфазных и квадратурных
компонент корреляторов когерентного приемника 246
П.6.2. Статистические характеристики синфазных и
квадратурных компонент корреляторов некогерентного
приемника 250
П6.3. Статистические характеристики фазовых дискриминаторов 251
П6.4. Статистические характеристики частотных дискриминаторов 254
787
По.5. Статистические характеристики дискриминаторов
задержки сигнала 264
Литература 270
Г л а в а 7. Источники погрешностей и точность
навигационно-временных определений в СРНС 272
7.1. Составляющие погрешности определения
псевдо дальности 272
7.2. Составляющие погрешности определения псевдо скорости .... 274
7.3 Влияние среды распространения на параметры сигнала 276
7.3.1. Групповая и фазовая скорость распространения сигнала . 277
7.3.2. Коэффициент преломления среды 279
7.3.3. Влияние ионосферы на запаздывание сигнала 280
7.3.4. Влияние тропосферы на запаздывание сигнала 282
7.4. Влияние релятивистских и гравитационных эффектов 284
7.5. Влияние многолучевого распространения сигнала 287
7.6. Погрешности, вносимые навигационным приемником 289
7.7. Методы снижения погрешностей определения
псевдо дальности и псевдо скорости 293
7.8. Бюджет погрешностей определения псевдо дальности и
псевдо скорости 297
7.9. Погрешности, вносимые на этапе решения
навигационной задачи 298
7.9.1. Погрешности эфемеридного обеспечения 299
7.9.2. Геометрический фактор в СРНС 300
Литература 304
Г л а в а 8. Помехоустойчивость аппаратуры потребителей 305
8.1. Общие определения и подходы 305
8.2. Методика оценки помехоустойчивости навигационного
приемника 306
8.2.1. Методика оценки влияния помех на коррелятор 307
8.2.2. Методы расчета помеховой составляющей на выходе
коррелятора 310
8.3. Анализ внутрисистемных помех при использовании различных
типов навигационных сигналов с кодовым разделением 312
8.3.1. Анализ внутрисистемных помех при использовании
сигналов с модуляцией BPSK{ri) 314
8.3.2. Анализ внутрисистемных помех при использовании
сигналов с модуляцией ВОС(т, п) 317
8.3.3. Анализ внутрисистемных помех с учетом расстройки
помехового и навигационного сигнала по частоте 322
8.4. Анализ воздействия различного типа помех на НАП,
работающую по различным типам навигационных
сигналов с кодовым разделением 328
8.5. Помехоустойчивость режимов поиска и захвата сигнала 336
8.6. Методика приближенной оценки помехоустойчивости
следящих систем 337
8.7. Помехоустойчивость автономной системы слежения за
фазой сигнала 338
8.8. Помехоустойчивость автономной системы слежения за
частотой сигнала 340
8.9. Помехоустойчивость системы слежения за задержкой
сигнала 342
8.10. Помехоустойчивость приемника с учетом взаимного
влияния следящих систем 343
8.10.1. Помехоустойчивость некогерентного приемника 343
8.10.2. Помехоустойчивость когерентного приемника 344
8.11. Помехоустойчивость комплексированных следящих систем . 345
Литература 347
Р а з д е л 2. СПУТНИКОВАЯ РАДИОНАВИГАЦИОННАЯ
СИСТЕМА ГЛОНАСС 348
Г л а в а 9. Общие сведения о спутниковой радионавигациннои
системе ГЛОНАСС 348
9.1. Структура и основные характеристики 348
9.2. Этапы развертывания 350
9.3. Система координат, используемая в СРНС ГЛОНАСС 355
9.4. Частотно-временное обеспечение. Шкалы времени системы
ГЛОНАСС 357
Литература 359
Глава 10. Наземный сегмент
(подсистема контроля и управления) 360
10.1. Назначение и состав подсистемы контроля и управления 360
10.1.1. Общие сведения 360
10.1.2. Центр управления системой 362
10.1.3. Контрольные станции 362
10.1.4. Квантово-оптические станции 364
10.1.5. Система контроля фаз 365
10.1.6. Аппаратура контроля поля 365
10.2. Эфемеридное обеспечение 367
10.2.1. Особенности формирования эфемеридной
информации в ГЛОНАСС 367
10.2.2. Типовые операции управления 368
10.2.3. Технология определения траектории движения
спутника 371
Литература 373
Г л а в а 11. Подсистема космических аппаратов 374
11.1. Орбитальные характеристики спутников 374
11.2. Радиосигналы в СРНС ГЛОНАСС 379
11.2.1. Виды используемых сигналов 379
11.2.2. Характеристики излучаемых навигационных
радиосигналов 381
11.3. Характеристики модулирующих последовательностей 385
11.4. Навигационные сообщения в СРНС ГЛОНАСС 389
11.4.1. Общие сведения 389
11.4.2. Эфемериды НС ГЛОНАСС 392
11.4.3. Альманах системы ГЛОНАСС 397
11.4.4. Резервные разряды в суперкадре 400
11.4.5. Контроль достоверности навигационных данных 400
11.5. Контроль целостности СРНС ГЛОНАСС 401
11.6. Навигационные спутники системы ГЛОНАСС 403
11.6.1. Навигационный спутник "Глонасс" 405
11.6.2. Навигационный спутник Тлонасс - М" 408
11.6.3. Навигационный спутник Тлонасс-К" 411
11.6.4. Пассивный спутник "Эталон" 413
11.6.5. Особенности построения навигационного спутника ... 415
11.6.6. Логика функционирования навигационного спутника . 416
11.7. Бортовой радиотехнический комплекс спутника 418
11.7.1. Бортовой источник навигационных радиосигналов 418
11.7.2. Антенно-фидерная система 424
11.7.3. Бортовая аппаратура межспутниковых измерений 424
11.7.4. Бортовое синхронизирующее устройство 433
11.7.5. Бортовой комплекс управления 435
11.7.6. Система ориентации и стабилизации и другие
вспомогательные системы 436
11.7.7. Функционирование бортовых систем спутника 438
Литература 439
790
Глава 12. Дифференциальные режимы спутниковой
радионавигационной системы ГЛОНАСС 440
12.1. Принципы организации дифференциальных режимов 440
12.2. Математические модели для дифференциальных режимов ... 443
12.3. Пространственно-временные характеристики
дифференциальных поправок 448
12.4. Дифференциальные поправки к погрешностям
эфемеридного обеспечения 449
12.5. Бюджет погрешностей определения псевдо дальности
в дифференциальном режиме 451
12.6. Контроль целостности СРНС в дифференциальных
подсистемах 452
12.7. Форматы данных, используемые при передаче
информации в дифференциальных подсистемах 453
12.8. Примеры построения дифференциальных подсистем 459
12.8.1. Морские локальные дифференциальные подсистемы .. . 459
12.8.2. Перспективная Российская дифференциальная
подсистема 466
12.8.3. Широкозонная ДПС WAAS 479
Литература 482
Г л а в а 13. Аппаратура потребителей 484
13.1. Принципы построения аппаратуры потребителей 484
13.2. Антенна навигационного приемника 486
13.3. Радиоприемник 487
13.4. Аналого-цифровой преобразователь 489
13.5. Опорный генератор и синтезатор частот 491
13.6. Многоканальный коррелятор 492
13.7. Алгоритмы первичной обработки сигналов 494
13.7.1. Алгоритм поиска и обнаружения 495
13.7.2. Алгоритм работы и схема слежения за фазой сигнала .. 505
13.7.3. Алгоритм работы и схема слежения за задержкой
сигнала 508
13.7.4. Алгоритм работы и схема слежения за частотой
сигнала 510
13.7.5. Алгоритмы работы дискретных фильтров
в контуре следящих систем 511
13.7.6. Алгоритмы управления генераторами опорных
сигналов в следящих системах 515
13.7.7. Алгоритм выделения навигационного сообщения 516
13.8. Алгоритмы вторичной обработки информации 518
13.8.1. Оценка координат и вектора скорости потребителя ... 518
13.8.2. Расчет вектора состояния НС на основе
неоперативной информации (альманаха) 520
13.8.3. Расчет вектора состояния НС на основе оперативной
информации 523
13.8.4. Пересчет координат потребителя из земной
в геодезическую систему координат 524
13.9. Использование оптимальных алгоритмов обработки
сигналов и информации в аппаратуре потребителей 525
Литература 527
Р а з д е л 3 НАПРАВЛЕНИЯ РАЗВИТИЯ ТЕХНОЛОГИЙ
СПУТНИКОВОЙ НАВИГАЦИИ 528
Г л а в а 14. Направления совершенствования системы ГЛОНАСС 528
14.1. Модернизация ГНС ГЛОНАСС 528
14.2. Сигналы ГНС ГЛОНАСС 533
14.2.1. Концепция развития навигационных сигналов
ГНС ГЛОНАСС 533
14.2.2. Частотный план для сигналов с кодовым разделением . 539
14.2.3. Навигационный сигнал L30C 540
14.2.4. Навигационный сигнал LIOC с модуляцией ВОС(6,4). 540
14.3. Система глобального мониторинга СРНС 542
14.3.1. Необходимость создания расширенной системы
мониторинга систем ГЛОНАСС/GPS 542
14.3.2. Основные задачи системы мониторинга СРНС 543
14.3.3. Структура системы мониторинга целостности СРНС . . 545
14.3.4. Предоставление потребителям доступа к результатам
работы системы мониторинга 549
14.3.5. Характеристики канала, передающего информацию
о целостности с борта НС «Глонасс-К» 550
14.3.6. Оценка надежности системы мониторинга 551
Глава 15. Навигационно-временные определения, основанные
на фазовых измерениях 555
15.1. Описание измерений первичных радионавигационных
параметров, выполняемых в приемнике СРНС 555
15.1.1. Понятие сигнального времени 556
15.1.2. Модели фазовых и кодовых измерений в СРНС 563
792
Оглавление
15.1.3. Модели наблюдений радионавигационных параметров
в СРНС, используемые для высокоточных НВО 566
15.1.4. Методика проверки точности математических
моделей измерений радионавигационных параметров
в СРНС 568
15.2. Методы разрешения неоднозначности фазовых
измерений на уровне вторичной обработки 573
15.2.1. Общие подходы к разрешению неоднозначности
фазовых измерений 573
15.2.2. Беспереборные процедуры разрешения
неоднозначности 576
15.3. Применение методов оптимальной фильтрации для
синтеза алгоритмов навигационно-временных определений,
основанных на фазовых измерениях 580
15.3.1. Метод дополнительной переменной 580
15.3.2. Оценка задержки одночастотного когерентного
радиосигнала 582
15.3.3. Оценка задержки двухчастотного когерентного
радиосигнала 584
15.3.4. Общая задача оценки параметров при наличии в
наблюдениях периодических функций 587
15.3.5. Задача фильтрации при наличии в наблюдениях
периодических функций 589
15.3.6. Модифицированный алгоритм фильтрации с
разрешением неоднозначности методом
дополнительной переменной 593
15.4. Алгоритмы навигационно-временных определений
при использовании фазовых измерений 596
15.4.1. Постановка задачи синтеза алгоритма
навигационно-временных определений 596
15.4.2. Общая методика синтеза алгоритмов НВО с
использованием фазовых измерений в СРНС
на этапе вторичной обработки 597
15.4.3. Результаты экспериментальных исследований 598
Литература 611
Г л а в а 16. Определение угловой ориентации по сигналам
спутниковых радионавигационных систем 613
16.1. Синтез оптимального алгоритма оценки углов ориентации
объекта по сигналам СРНС 613
793
16.2. Потенциальная точность определения углов ориентации .. . 618
16.3. Оптимальная фильтрация разности фаз двух сигналов
СРНС, принятых в пространственно разнесенных точках ... 621
16.4. Оптимальный навигационный приемник для устройства
определения углов ориентации объекта по сигналам
спутниковых радионавигационных систем 634
Литература 641
Г л а в а 17. Интегрированные инерциально-спутниковые
навигационные системы 642
17.1. Принципы построения интегрированных инерциально-
спутниковых навигационных систем 643
17.2. Синтез алгоритмов комплексирования НАП СРНС/ИНС .... 650
17.2.1. Модернизированный вариант комплексирования 650
17.2.2. Синтез тесносвязанного алгоритма комплексирования
НАП СРНС/ИНС 651
17.2.3. Синтез алгоритма комплексирования на вторичном
уровне (слабосвязанный алгоритм) 664
17.2.4. Синтез алгоритма коррекции ИНС от НАП СРНС
(разомкнутый алгоритм) 668
17.3. Точность и помехоустойчивость интегрированных
инерциально-спутниковых систем навигации 674
17.3.1. Точность интегрированных инерциально-
спутниковых систем навигации в комплексном
режиме 674
17.3.2. Точность интегрированных инерциально-
спутниковых систем навигации в автономном режиме . 678
17.3.3. Помехоустойчивость интегрированных
инерциально-спутниковых систем навигации 680
17.4. Обзор современных интегрированных инерциально-
спутниковых систем навигации 684
17.5. Синхронизация измерений в инерциально-спутниковых
навигационных системах 690
Приложение к гл. 17. Основы инерциальной навигации 691
П17.1. Алгоритм бесплатформенной ИНС 692
П17.2. Модели ошибок БИНС 695
П17.3. Кватернионы 700
П17.4. Математические соотношения между различными
формами представления ориентации 703
Литература 705
794
Глава 18. Пространственно-временная обработка сигналов
в аппаратуре потребителей 708
18.1. Принцип пространственного подавления помех 708
18.2. Алгоритм оптимальной пространственно-временной
обработки 710
18.3. Классический антенный компенсатор помех 713
18.4. Структура оптимального пространственного фильтра . 717
18.5. Характеристики алгоритмов пространственной обработки
сигналов 721
18.6. Формирование весовых коэффициентов 726
18.6.1. Оптимальный «следящий» алгоритм 727
18.6.2. Оптимальный неследящий алгоритм 729
18.6.3. Алгоритм с разделением пространственного и
временного операторов 730
18.6.4. Характеристики адаптации 731
18.7. Технологический прорыв в пространственной компенсации
помех 732
18.8. Экспериментальная проверка компенсаторов помех
для приемника спутниковой навигации 733
18.8.1. Экспериментальная проверка двухканального
компенсатора помех 733
18.8.2. Экспериментальные исследования возможности
повышения характеристик подавления путем
коррекции ЧХ 736
18.8.3. Анализ возможностей повышения характеристик
подавления путем коррекции ЧХ 739
18.8.4. Экспериментальные исследования цифрового АКП
для приемника СРНС 741
18.9. Известные устройства пространственного подавления помех 747
Литература 749
Глава 19. Частотно-временная режекция узкополосных помех . . 752
19.1. Теоретическое обоснование методов частотно-временной
компенсации помех 752
19.1.1. Метод оптимальной оценки параметров помехи .... 753
19.1.2. Метод адаптивных трансверсальных фильтров 754
19.1.3. Метод режекции помехи в частотной области на
основе БПФ 756
19.1.4. Краткая характеристика методов и устройств
частотно-временной компенсации помех 757
19.2. Синтез и анализ трансверсального фильтра 758
19.3. Режекция узкополосных помех в частотной области
на основе БПФ 771
19.4. Сравнение эффективности алгоритма режекции
узкополосных помех в частотной области
и трансверсального фильтра 776
Литература 778
Список сокращений 779
ОГЛАВЛЕНИЕ 784
796
Справочное пособие
ГЛОНАСС
Принципы построения и функционирования
Изд. 4-е, перераб. и доп.
Под редакцией
Перова Александра Ивановича
и Харисова Владимира Назаровича
Корректура автора
Изд. № 2. Сдано в набор 11.11.2009.
Подписано в печать 18.01.2010. Формат 70x100 1/16.
Бумага офсетная. Гарнитура Тайме.
Печать офсетная
Печ. л. 50. Тираж 700 экз. Зак. № 1026.
Издательство «Радиотехника».
107031, Москва, К-31, Кузнецкий мост, д. 20/6.
Тел./факс: (495) 621-48-37; 625-78-72, 625-92-41.
e-mail: info@radiotec.ru
www. radiotec.ru
Отпечатано в ООО ПФ «Полиграф-Книга»
160001, г. Вологда, ул. Челюскинцев, д. 3.
ВНИМАНИЕ !
Издательство «Радиотехника» представляет
Ежегодник
Спутниковые системы связи и вещания
Главный редактор Ю. А. Подъездков
Научно-технический справочно-аналитический журнал «Спутниковые
системы связи и вещания» призван информировать читателей о текущем
состоянии и перспективах развития спутниковых систем, их технических
характеристиках и возможностях. Для читателей он является своеобразным
проводником в мире спутниковой связи.
Выпуски журнала кроме основных разделов (системы фиксированной
связи, вещания и передачи данных на основе геостационарных ИСЗ; системы
подвижной и персональной связи со спутниками на низких, средних и
геостационарных орбитах; проекты широкополосных систем связи, вещания и
передачи данных; системы передачи данных и управления космическими
аппаратами и космические платформы спутников связи, вещания и
передачи данных, приложение со сведениями о размещении ИСЗ связи на
геостационарной орбите и подробный предметный указатель), содержат и
другую информацию, актуальную на данный момент времени.
Подписаться на Ежегодник
«Спутниковые системы связи и вещания» (два выпуска)
можно непосредственно в Издательстве «Радиотехника» по адресу:
107031, Москва, Кузнецкий мост, 20/6,
в любом отделении связи по каталогу «Роспечать»
(подписной индекс 46499).
По всем вопросам обращайтесь по тел./факс:
(495) 621-48-37, 625-92-41.
e-mail: info@radiotec.ru
http: //www.radiotec.ru/
с
принципы построения и функционирования
Изложены принципы построения спутниковой
радионавигационной системы (СРНС) ГЛОНАСС, даны ее системные
характеристики и основные характеристики подсистем космических
аппаратов, наземного контроля и управления, навигационной
аппаратуры потребителей, а также дифференциальных дополнений СРНС.
По сравнению с предыдущим изданием существенно переработан
материал по направлениям совершенствования технологий
спутниковой навигации с учетом новых перспектив по введению
сигналов с кодовым разделением и материал по
интегрированным инерциально-спутниковым навигационным системам.
Добавлены материалы по использованию сигналов СРНС для
определения угловой ориентации объектов и частотно-
временной режекции узкополосных помех в аппаратуре
потребителей, а также приему сигналов в условиях многолучевости,
быстрому поиску сигналов и результаты последних исследований
в области пространственно-временной обработки
навигационных сигналов, принимаемых на фоне пространственно
распределенных помех.
Для широкого круга специалистов, занимающихся разработкой,
производством и эксплуатацией аппаратуры потребителей СРНС
ГЛОНАСС. Может быть полезна студентам, аспирантам и
преподавателям высших учебных заведений при изуч-нии
дисциплин радиотехнического профиля.
ISBN 978-5-88070-251-0
Издател «д * « от^ ника"
Тел./- -9241
е- » •" ec.ru
• diotec.ru
с о о n h n к I n
ВНИМАНИЕ I
Издательство «Радиотехника» представляет
Ежегодник
Космическая съемка Земли
Стремительное развитие космических и информационных технологий обусловили
кардинальное изменение в начале нового тысячелетия ситуации в области
космической съемки Земли. Перестав быть прерогативой исключительно военных
ведомств, космические системы съемки Земли превратились в привлекательный
объект капиталовложений для многих коммерческих фирм и организаций, а высокий
спрос на снимки, полученные из космоса, привел к тому, что сейчас в мире на
разных этапах реализации находятся более 50 программ и проектов,
предусматривающих разработку и использование спутников дистанционного зондирования
Земли (ДЗЗ).
Представляет собой самое полное и подробное справочно-аналитическое издание
из когда-либо выпускавшихся по данной тематике.
В ежегоднике, рассчитанном на широкий круг читателей, в доступной и
систематизированной форме изложены материалы по:
действующим и перспективным системам ДЗЗ за рубежом и в России;
характеристикам и особенностям эксплуатации аппаратуры оптической и
радиолокационной съемки с высоким, средним и низким разрешением;
состоянию рынка космических снимков;
применению данных ДЗЗ и многим другим вопросам.
Для облегчения восприятия информации все тексты снабжены поясняющими
рисунками и таблицам. Несколько разделов издания отведены под справочные
данные, дающие читателю возможность получить представление о принципах
ведения космической съемки и позволяющие ему ориентироваться в применяемой
терминологии и аббревиатурах.
Подписка по каталогам:
«Роспечать» - индекс 81175,
«Пресса России» - индекс 44778,
а также непосредственно в Издательстве «Радиотехника» по адресу:
107031, Москва, Кузнецкий мост, 20/6.
Тел./факс: (495) 625-9241, 625-78-72, 621-4837.
http: //www.radiotec.ru
E-mail: info@radiotec.ru