Author: Перова А.И. Харисова В.Н. Болдина В.А.
Tags: авиация и космонавтика летательные аппараты ракетная техника космическая техника междупланетные соединения (междупланетные полеты) космонавтика (аэронавтика) космос космонавтика спутники издательство ипржр система глонасс
ISBN: 5-88070-004-6
Year: 1998
ГЛОБАЛЬНАЯ СПУТНИКОВАЯ
РАДИОНАВИГАЦИОННАЯ СИСТЕМА
ГЛОНАСС
Под редакцией
В. Н. Харисова, А. И. Перова, В. А. Болдина
Москва ИПРЖР 1998
УДК 629.78
ББК 39.67
Г-52
Авторы:
В. А. Болдин, В. И. Зубинский, Ю. Г. Зурабов,
Н. Е. Иванов, А. В. Карпейкин, В. Я. Нартов,
И. Н. Мищенко, А. И. Перов, А. Е. Перьков,
Ю. А. Соловьев, В. А. Удалой, В. Н. Харисов,
В. М. Хроленко, М. С. Ярлыков
Глобальная спутниковая радионавигационная система ГЛОНАСС/ По;
Г-52 ред. В. Н. Харисова, А. И. Перова, В. А. Болдина. — М.: ИПРЖР, 1998.
— 400 с. : ил.
ISBN 5-88070-004-6
Изложены принципы построения спутниковой радионавигационно
системы (СРНС) ГЛОНАСС, даны ее системные характеристики, а такж
основные характеристики подсистем космических аппаратов, наземног
сегмента и сегмента потребителей.
Предназначена для широкого круга специалистов, занимающихся раз
работкой, производством и эксплуатацией аппаратуры потребителе
СРНС ГЛОНАСС; может быть полезна также студентам и преподавателя:
высших учебных заведений при изучении дисциплин радиотехническог
профиля.
ISBN 5-88070-004-6
® 000”Лаборатория дистанционных измерений”, 1991
ПРЕДИСЛОВИЕ
Российская спутниковая радионавигационная система (СРНС) второго
поколения ГЛОНАСС продемонстрировала высокие точностные характеристи-
ки определения координат, скорости и времени воздушных, космических,
морских и наземных подвижных средств. В настоящее время она находится в
начале широкого практического освоения.
Система в состоянии обеспечить существенное повышение безопасности
движения транспортных средств, наиболее экономичное решение задачи ос-
воения удаленных, слабо изученных территорий и акваторий морей и океанов,
регулярность функционирования буровых и добывающих платформ на шельфе
и в открытом море, быстрый поиск и спасение терпящих бедствие и решать
многие другие задачи.
Наряду с аналогичной американской GPS (НАВСТАР) система ГЛО-
НАСС планируется международными организациями в качестве составной час-
ти перспективной глобальной навигационной спутниковой системы GNSS-1,
отличающейся большей точностью и надежностью.
Система ГЛОНАСС по точности использования предоставляемых миро-
вому сообществу сигналов превосходит аналогичные показатели GPHC GPS в
режиме селективного доступа. Одновременно самим своим существованием
ГЛОНАСС побуждает правительство США отказываться от ограничений на
использование системы GPS.
Эти обстоятельства предопределяют весьма устойчивый интерес различ-
ных специалистов, владельцев и эксплуатанционщиков транспортных средств,
геодезистов и землеустроителей к системе, ее элементам, возможностям и ха-
рактеристикам.
Необходимо отметить, что аналогичный интерес к СРНС GPS удовлетво-
ряется достаточно большим количеством изданий, среди которых “Интер-
фейсный контрольный документ GPS”, три больших монографии общим объе-
мом свыше 3000 страниц, ряд описаний системы и ее характеристик и ряд ру-
ководств по практическому применению системы.
Работа по популяризации и распространению информации о GPS допол-
няется регулярно проводимыми с 1984 г. компанией NAVTECH, а также позд-
нее — Группой AGARD НАТО специальными курсами лекций по системе и ее
применениям. Значительный вклад в дело распространения информации о
GPS вносит также периодический журнал “GPS World”.
В то же время по СРНС ГЛОНАСС опубликован сравнительно неболь-
шим тиражом “Интерфейсный контрольный документ ГЛОНАСС”. Часть ма-
териалов изложена в монографии В. С. Шебшаевича и др. “Сетевые спутнико-
вые радионавигационные системы”, которая стала уже библиографической
редкостью. Большое внимание в ней уделено системе GPS. Кроме того, про-
шедшее с момента последнего издания время обусловило необходимость су-
щественного обновления книги, многих корректировок и дополнений мате-
риалами статей и докладов, которые публикуются на регулярно проводящихся
конференциях и симпозиумах по спутниковым навигационным системам.
Таким образом, написание и издание специальной книги по СРНС
ГЛОНАСС представляется вполне актуальной и оправданной. Инициатором
написания такой книги выступил научно-технический центр “Интернави-
гация”.
Книга включает теоретические разделы, призванные предоставить чита-
телю в сжатом виде основы теории навигационных определений с использова-
нием навигационных спутников, материалы по облику и характеристикам сис-
темы ГЛОНАСС и ее элементов, по аппаратуре потребителей и применению
системы для навигации подвижных объектов и определения места и времени
наземными пользователями.
Книга состоит из введения и трех разделов основного материала, разде-
ленных на 16 глав.
Во вводной части содержатся исторические сведения о СРНС ГЛОНАСС
и требования, предъявляемые потребителями к спутниковым радионавигаци-
онным системам.
В разделе 1 (гл. 1—7) помещены материалы, формулирующие общие
принципы построения СРНС-,-методы решения навигационных, задач и оценки
точности определения навигационных параметров, используемые радиосигна-
лы, сообщения, методы кодирования информации.
Во разделе 2 (гл. 8—12) излагаются сведения о принципах построения и
структуре СРНС ГЛОНАСС и ее подсистем, приводятся характеристики сис-
темы и подсистем (подсистема космических аппаратов, наземный сегмент, ап-
паратура потребителей), рассматриваются вопросы использования системы
авиационными, морскими и наземными потребителями, описываются алго-
ритмы обработки сигналов и информации в аппаратуре потребителей и дается
информация о современных образцах такой аппаратуры.
В разделе 3 (гл. 13—16) рассматриваются вопросы развития СРНС ГЛО-
НАСС в части реализации дифференциального режима, фазовых методов из-
мерений, комплексной обработки и интегрирования информации СРНС ГЛО-
НАСС, GPS и других, в том числе автономных, средств, а также контроля це-
лостности сигналов системы.
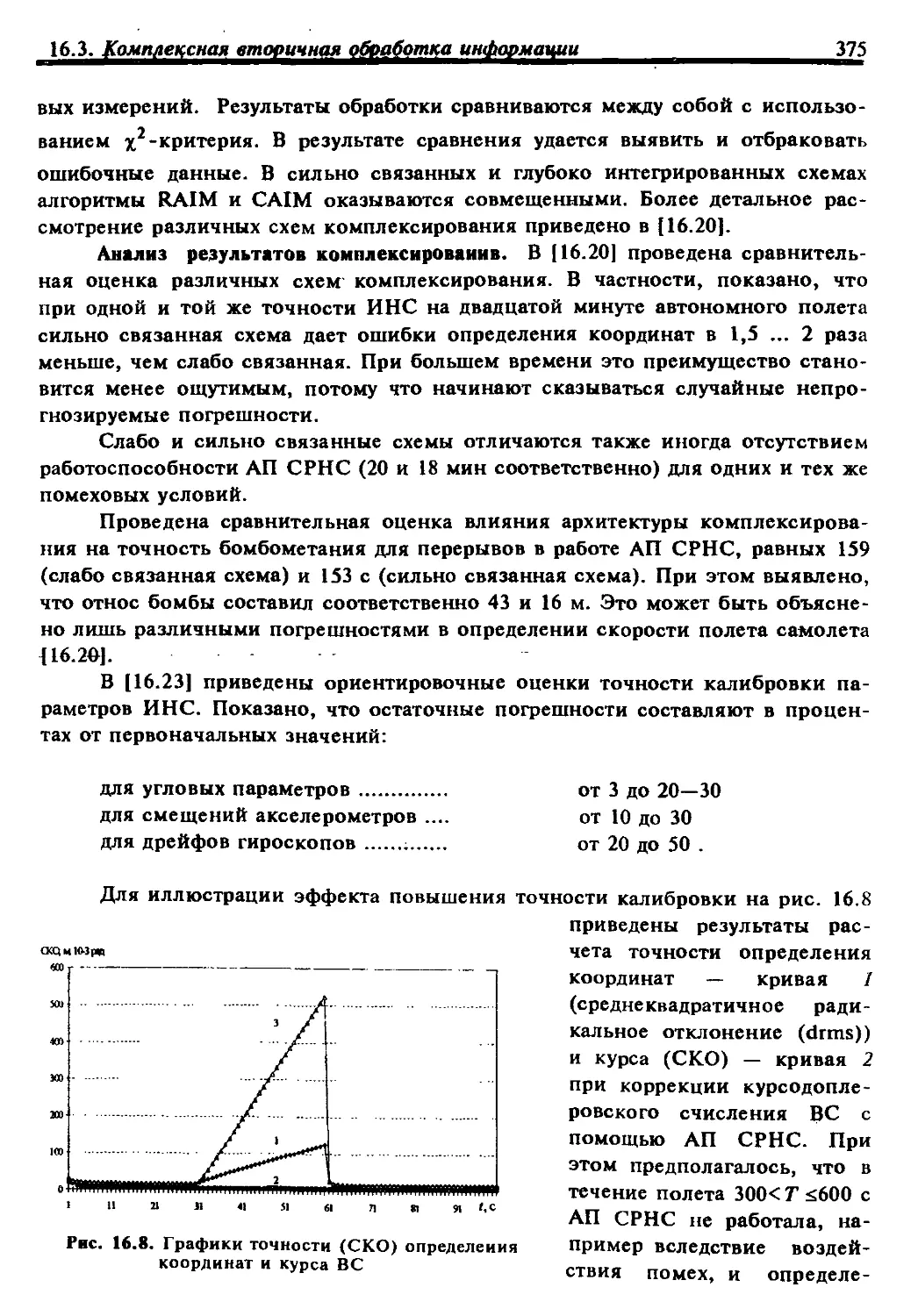
В книге принята сквозная нумерация рисунков и формул по главам.
Список литературы приводится в конце каждой главы и включает только те
источники, на которые даются ссылки в тексте.
Предполагается, что материалы книги могут быть использованы при
подготовке других изданий, таких, как учебники для высших и средних специ-
альных учебных заведений, справочники, руководства по эксплуатации, техни-
ческие описания аппаратуры, а также при разработке вопросов взаимодейст-
вия аппаратуры потребителей и других технических средств подвижных объек-
тов, при отработке планов радионавигационного обеспечения стран и регио-
нов, постановке курсов лекций в системе учебных заведений и программ по-
вышения квалификации специалистов.
Книга рассчитана на специалистов в области навигации и смежных дис-
циплин, таких как штурманское обеспечение, геодезия и картография, земле-
устройство, мониторинг земной поверхности, аспирантов и студентов соответ-
ствующих высших и средних учебных заведений. Немало полезного в ней мо-
гут найти члены экипажей речных, морских и воздушных судов, работающих в
сложной навигационной обстановке.
В написании книги участвовали: В. А. Болдин (гл. 7, п. 12.8.3, § 12.9);
В. И. Зубинский (п. 12.8.4); Ю. Г. Зурабов (п. 12.8.2); Н. Е. Иванов (гл. 13);
А. В. Карпейкин (гл. 16); И. Н. Мищенко (п. 12.8.2); В. Я. Нартов (гл. 1—3,
7-10, п. 12.8.1); А. И. Перов (гл. 2-6, § 12.1-12.7, п. 12.8.4, § 12.9, гл. 14);
А. Е. Перьков (гл. 14); Ю. А. Соловьев (введение, § 11.1, 11.2, п. 12.7.5, §16.3);
В. А. Удалой (гл. 9); В. Н. Харисов (гл. 4-6, 8, § 12.1-12.7, гл. 14, 15);
В. М. Хроленко (п. 12.8.1); М. С. Ярлыков (§ 16.1, 16.2).
Редактирование книги выполнено В. Н. Харисовым, А. И. Перовым,
В. А. Болдиным.
Авторы выражают благодарность В. И. Денисову, А. И. Задорожному,
Ю. Г. Милову, Ю. В. Медведкову и Ю. А. Меркулову, оказавшим содействие в
опубликовании книги. В организации работы и подготовке материалов книги
активное, участие приняли следующие организации^ Отделение --Интернави-
гация” Международной Академии информатизации; Российское космическое
агентство; кафедра автоматизированных систем радионавигации и радиосвязи
ВВИА им. проф. Н.Е. Жуковского; кафедра радиотехнических систем Мос-
ковского энергетического института (технического университета); ООО “Лабо-
ратория дистанционных измерений”, Российский общественный институт на-
вигации. Материалы книги широко использовались при чтении лекций по со-
ответствующим курсам в ВВИА им. проф. Н.Е. Жуковского и в Московском
энергетическом институте (техническом университете).
Авторы будут признательны читателям за предложения и замечания по
улучшению содержания книги, которые следует направлять по адресу: 103031,
Москва, Кузнецкий мост, д. 20/6, ИПРЖР; E-mail: zaoiprzhr@glasnet.ru —
ИПРЖР; vhar@orc.ru — Харисов В. Н.; alexp@aha.ru — Перов А. И.
Авторы
6
Введение
ВВЕДЕНИЕ
1. Исторические сведения
Развитие отечественной спутниковой радионавигационной системы
(СРНС) ГЛОНАСС имеет уже практически сорокалетнюю историю, начало
которой положено, как чаще всего считают, запуском 4 октября 1957 г. в Со-
ветском Союзе первого в истории человечества искусственного спутника Зем-
ли (ИСЗ) [В.1, В.2]. Измерения доплеровского сдвига частоты передатчика
этого ИСЗ на пункте наблюдения с известными координатами позволили [В.2]
определить параметры движения этого спутника.
Обратная задача была очевидной: по измерениям того же доплеровского
сдвига при известных координатах ИСЗ найти координаты пункта наблюдения
[В.2, В.З].
В то же время, как свидетельствует [В.З], первое научно обоснованное
предложение об использовании ИСЗ для навигации родилось в Ленинграде
еще до запуска первого советского ИСЗ, в период проведения под руково-
дством проф. В. С. Шебшаевича в Ленинградской военно-воздушной инже-
нерной академии (ЛВВИА) им. А. Ф. Можайского в 1955—1957 гг. исследова-
ний возможностей применения радиоастрономических методов для самолето-
вождения [В.З]. Материалы исследований докладывались в октябре и декабре
1957 г. на межведомственной конференции и семинаре [В.4].
Научные основы низкоорбитальных СРНС были существенно развиты в
процессе выполнения исследований по теме “Спутник” (1958—1959 гг.), кото-
рые осуществляли ЛВВИА им. А. Ф. Можайского, Институт теоретической
астрономии АН СССР, Институт электромеханики АН СССР, два морских
НИИ и Горьковский НИРФИ. Работы проводились с участием крупных спе-
циалистов по аналитической механике (чл.-корр. АН СССР А. И. Лурье) и
расчетам орбит (проф. П. Е. Эльясберг). В коллективах этих организаций по
проблеме активно работали Ю. В. Батраков, Е. Д. Голиков, В. П. Зако-
лодяжный, Э. А. Жижемский, М. М. Кобрин, А. А. Колосов, Л. И. Кузнецов,
В. Ф. Проскурин, А. Н. Радченко, Н. К. Сергеев, Б. А. Смольников, Е. Ф. Су-
воров, В. А. Фуфаев, Г. И. Черепанов, Е. П. Чуров, В. И. Юницкий и др.
[В.З]. Основное внимание при этом уделялось вопросам повышения точности
навигационных определений, обеспечения глобальности, круглосуточности
применения и независимости от погодных условий.
Проведенные работы позволили перейти в 1963 г. к опытно-конструк-
торским работам над первой отечественной низкоорбитальной системой, по-
лучившей в дальнейшем название “Цикада”.
В создании этой системы приняли участие: Научно-производственное
объединение прикладной механики (НПО ПМ) — головная организация по
системе в целом и по разработке навигационных спутников (НС); Российский
научно-исследовательский институт космического приборостроения (РНИИ
КП) — головная организация по радиотехническому комплексу системы, раз-
работке бортовой космической и наземной радиотехнической аппаратуры, а
также бортовой аппаратуры морских судов; Российский институт радионави-
гации и времени (РИРВ) — разработчик бортовой космической аппаратуры
синхронизации и навигационной аппаратуры ряда типов морских судов, а
также другие предприятия космической, радиотехнической и судостроитель-
ной отраслей промышленности СССР.
Спутниковая радионавигационная система ГЛОНАСС запатентована в
Соединенных Штатах Америки [В.5].
Вот что писал в 1992 г. о решении этой задачи Генеральный конструктор
космических систем навигации и связи академик М. Ф. Решетнев [В.Ц: “Пол-
номасштабные работы по созданию отечественной навигационной спутнико-
вой системы были развернуты в середине 60-х годов, а 27.11.1967 года был вы-
веден на орбиту первый навигационный отечественный спутник (“Космос-
192”). Спутник и ракета-носитель были разработаны и изготовлены Красно-
ярским Научно-производственным объединением прикладной механики .
Навигационный спутник обеспечивал непрерывное в течение всего вре-
мени активного существования излучение радионавигационного сигнала на
частотах 150 и 400 Мгц. Среднеквадратическая погрешность местоопределения
по этому спутнику составляла 250 ... 300 м.
В 1979 г. была сдана в эксплуатацию навигационная система I-то поко-
ления “Цикада” в составе 4-х навигационных спутников (НС), выведенных на
круговые орбиты высотой 1000 км, наклонением 83° и равномерным распреде-
лением плоскостей орбит вдоль экватора. Она позволяет потребителю в сред-
нем через каждые полтора-два часа входить в радиоконтакт с одним из НС и
определять плановые координаты своего места при продолжительности нави-
гационного сеанса до 5 ... 6 мин.
В ходе испытаний было установлено, что основной вклад в погрешность
навигационных определений вносят погрешности передаваемых спутниками
собственных эфемерид, которые определяются и закладываются на спутники
средствами наземного комплекса управления. Поэтому наряду с совершенст-
вованием бортовых систем спутника и корабельной приемоиндикаторной ап-
паратуры, разработчиками системы серьезное внимание было уделено вопро-
сам повышения точности определения и прогнозирования параметров орбит
навигационных спутников.
Была отработана специальная схема проведения измерений параметров
орбит средствами наземно-комплексного управления, разработаны методики
прогнозирования, учитывающие все гармоники в разложении геопотенциала.
Большой вклад в повышение точности эфемерид навигационных спутни-
ков внесли результаты работ по программе геодезических и геофизических
исследований с помощью специальных геодезических спутников “Космос-842”
и “Космос-911”, которые были выведены на навигационные орбиты.
8 Введение
Это позволило уточнить координаты измерительных средств и вычислить
коэффициенты согласующей модели геопотенциала, предназначенной специ-
ально для определения и прогнозирования параметров навигационных орбит.
В результате точность передаваемых в составе навигационного сигнала собст-
венных эфемерид была повышена практически на порядок и составляет в на-
стоящее время на интервале суточного прогноза величину ® 70 ... 80 м, а
среднеквадратическая погрешность определения морскими судами своего ме-
стоположения уменьшилась до 80 ... 100 м.
Для оснащения широкого класса морских потребителей разработаны и
серийно изготавливаются комплектации приемоиндикаторной аппаратуры
“Шхуна” и “Челн”. Последняя имеет возможность работы и по спутникам
американской радионавигационной системы “Транзит”.
В дальнейшем спутники системы “Цикада” были дооборудованы прием-
ной измерительной аппаратурой обнаружения терпящих бедствие объектов,
которые оснащаются специальными радиобуями, излучающими сигналы бедст-
вия на частотах 121 и 406 Мгц. Эти сигналы принимаются спутниками систе-
мы “Цикада” и ретранслируются на специальные наземные станции, где про-
изводится вычисление точных координат аварийных объектов (судов, самоле-
тов и др.).
Дооснащенные аппаратурой обнаружения терпящих бедствие спутники
“Цикада” образуют системы “Коспас”. Совместно с американо-франко-ка-
надской системой “Сарсат” они образуют единую службу поиска и спасения,
на счету которой уже несколько тысяч «пасенных жизней.
Успешная эксплуатация низкоорбитальных спутниковых навигацион-
ных систем морскими потребителями привлекла широкое внимание к спутни-
ковой навигации. Возникла необходимость создания универсальной навига-
ционной системы, удовлетворяющей требованиям всех потенциальных потре-
бителей: авиации, морского флота, наземных транспортных средств и косми-
ческих кораблей.
Выполнить требования всех указанных классов потребителей пизкоорби-
тальные системы в силу принципов, заложенных в основу их построения, не
могли. Перспективная спутниковая навигационная система должна обеспечи-
вать потребителю в любой момент времени возможность определять три про-
странственные координаты, вектор скорости и точное время. Для получения
потребителей трех пространственных координат беззапросным методом требу-
ется проведение измерений навигационного параметра не менее чем до четы-
рех спутников, при этом одновременно с тремя координатами местоположения
потребитель определяет и расхождение собственных часов относительно шка-
лы времени спутниковой системы.
Исходя из принципа навигационных определений, выбрана структура
спутниковой системы, которая обеспечивает одновременную в любой момент
времени радиовидимость потребителей, находящимся в любой точке Земли, не
менее четырех спутников, при минимальной общем их количестве в системе.
Это обстоятельство ограничило высоту орбиты навигационных спутников
3
20 тыс. км, (дальнейшее увеличение высоты не ведет к расширению зоны ра-
диообзора, а, следовательно, и к уменьшению необходимого количества спут-
ников в системе). Для гарантированной видимости потребителем не менее че-
тырех спутников, их количество в системе должно составлять 18, однако оно
было увеличено до 24-х с целью повышения точности'определения собствен-
ных координат и скорости потребителя путем предоставления ему возможно-
сти выбора из числа видимых спутников четверки, обеспечивающей наивыс-
шую точность.
Одной из центральных проблем создания спутниковой системы, обеспе-
чивающей беззапросные навигационные определения одновременно по не-
скольких спутникам, является проблема взаимной синхронизации спутнико-
вых шкал времени с точностью до миллиардных долей секунды (наносекунд),
поскольку рассинхронизация излучаемых спутниками навигационных сигналов
в 10 нс вызывает дополнительную погрешность в определении местоположе-
ния потребителя до 10 ... 15 м.
Решение задачи высокоточной синхронизации бортовых шкал времени
потребовало установки на спутниках высокостабильных бортовых цезиевых
стандартов частоты с относительной нестабильностью 1-Ю-*3 и наземного
водородного стандарта с относительной нестабильностью 1 • 10-14, а также
создания наземных средств сличения шкал с погрешностью 3 ... 5 нс.
С помощью этих средств и специального математического обеспечения
производится определение расхождений бортовых шкал времени с наземной
шкалой и их прогнозирование для каждого спутника системы. Результаты
прогноза в виде поправок к спутниковым часам относительно наземных закла-
дываются на соответствующие спутники и передаются ими в составе цифровой
информации навигационного сигнала. Потребителями таким образом устанав-
ливается единая шкала времени. Расхождение этой шкалы с наземной шкалой
времени системы не превышает 15 ... 20 нс.
Второй проблемой создания высокоорбитальной навигационной системы
является высокоточное определение и прогнозирование параметров орбит на-
вигационных спутников.
Достижение необходимой точности эфемерид навигационных спутников
потребовало проведения большого объема работ по учету факторов второго
порядка малости, таких как световое давление, неравномерность вращения
Земли и движение ее полюсов, а также исключение действия на спутник в по-
лете реактивных сил, вызванных негерметичностью двигательных установок и
газоотделением материалов покрытий.
Для экспериментального определения параметров геопотенциала на ор-
биты навигационных спутников были запущены два пассивных ИЗС “Эталон”
(“Космос-1989” и “Космос-2024”), предназначенных для измерения парамет-
ров их движения высокоточными квантово-оптическими измерительными
средствами. Благодаря этим работам достигнутая в настоящее время точность
эфемерид навигационных спутников при прогнозе на 30 ч составляет: вдоль
орбиты -- 20 м; по бинормали к орбите — 10 м; по высоте 5 м (СКО).
10
Введение
Летные испытания высокоорбитальной отечественной навигационной
системы, получившей название ГЛОНАСС, были начаты в октябре 1982 г. за-
пуском спутника “Космос-1413”...”
В 1995 г. было завершено развертывание СРНС ГЛОНАСС до ее штат-
ного состава (24 НС). В настоящее время предпринимаются большие усилия
по поддержанию группировки.
Разработаны самолетная аппаратура АСН-16, СНС-85, АСН-21, наземная
аппаратура АСН-15 (РИРВ), морская аппаратура “Шкипер” и “Репер” (РНИИ
КП) и др. [В.6, В.7].
Работы по созданию спутниковых радионавигационных систем осущест-
влялись помимо НПО ПМ (руководители работ М. Ф. Решетнев, А. Г. Коз-
лов, Г. М. Чернявский, В. Ф. Черемисин) коллективами РНИИ КП (руко-
водители работ Л. И. Гусев, М. И. Борисенко, Н. Е. Иванов, В. А. Салищев),
РИРВ (руководители работ П. П. Дмитриев, А. Ф. Смирновский, Ю. Г. Гужва,
А. Г. Геворкян, Ю. М. Устинов, С. Н. Клюшников, И. В. Кудрявцев, Г. С. Це-
ханович, Б. В. Шебшаевич, В. Ю. Кутиков) при активном участии руководите-
лей и специалистов министерства общего машиностроения (ныне Российское
космическое агентство) Ю. П. Коптева, Ю. Г. Милова и Ю. В. Медведкова,
научно-исследовательскими учреждениями министерств обороны, гражданской
авиации, морского флота, Управления по геодезии и картографии и др. [В.З].
Основным заказчиком и ответственным за испытания и управление сис-
темами являются Военно-космические силы РФ.
Механизм государственного контроля и координации работ по СРНС
ГЛОНАСС осуществляется на межведомственной основе Координационным
Советом, созданным в соответствии с Постановлением Правительства РФ
№ 237 от 7 марта 1995 г. Рабочим органом Координационного совета опреде-
лен научно-технический центр “Интернавигация”.
В рассматриваемый период времени в США также проведены интенсив-
ные разработки СРНС. В 1958 г. в рамках создания первого поколения атом-
ных ракетных подводных лодок “Полярис” была создана система “Транзит”
(аналог СРНС ’’Цикада”), введенная в строй в 1964 г. [В.8].
В начале 70-х годов начаты работы по созданию СРНС второго поколе-
ния — ОР8/“Навстар” (аналога отечественной системы ГЛОНАСС). Спутни-
ковая радионавигационная система GPS полностью развернута в 1993 г.
В соответствии с Постановлением Правительства РФ № 237 от 7 марта
1995 г. основными направлениями дальнейших работ являются [В.9|:
модернизация СРНС ГЛОНАСС на основе модернизированного спутника
ГЛОНАСС-М с повышенным гарантийным сроком службы (пять лет и более
вместо трех в настоящее время) и более высокими техническими характери-
стиками, что позволит повысить надежность и точность системы в целом;
внедрение технологии спутниковой навигации в отечественную эконо-
мику, науку и технику, а также создание нового поколения навигационной
аппаратуры потребителей, станций дифференциальных поправок и контроля
целостности;
разработка и реализация концепции российской широкозонной диффе-
ренциальной подсистемы на базе инфраструктуры Военно-космических сил и
ее взаимодействия с ведомственными региональными и локальными диффе-
ренциальными подсистемами, находящимися как на территории России, так
и за рубежом;
развитие сотрудничества с различными международными и зарубежными
организациями и фирмами в области расширения использования возможно-
стей навигационной системы ГЛОНАСС для широкого круга потребителей;
решение вопросов, связанных с использованием совместных навигаци-
онных полей систем ГЛОНАСС и GPS в интересах широкого круга потреби-
телей мирового сообщества [В.9]: поиск единых подходов к предоставлению
услуг мировому сообществу со стороны космических навигационных систем;
согласование опорных систем координат и системных шкал времени; выра-
ботка мер по недопущению использования возможностей космических навига-
ционных систем в интересах террористических режимов и группировок.
Работы в указанных направлениях ведутся в соответствии с требования-
ми, выдвигаемыми различными потребителями (воздушными, морскими и
речными судами, наземными и космическими средствами, топогеодезически-
ми, землеустроительными и другими службами).
2. Требования к спутниковым радионавигационным
системам
До последнего времени создание СРНС осуществлялось в соответствии с
требованиями, определяемыми их первоначальным целевым предназначением.
Общими при этом были качественные требования глобальности, независимо-
сти от гидрометеорологических условий, подстилающей поверхности, рельефа
местности, окружающей растительности, застройки, времени суток и года, не-
прерывности, неограниченной пропускной способности, практической незави-
симости от высоты над поверхностью земли и других условий движения опре-
деляющегося объекта, помехозащищенности и др.
Изучение потребностей гражданских пользователей также указывает на
необходимость иметь эти свойства. Однако использование СРНС в интересах
местоопредсления и навигации гражданских объектов (самолетов и вертоле-
тов, морских и речных судов, автомобилей, топопривязчиков и др.) выдвигает
и новые более высокие требования, вытекающие’из необходимости обеспече-
ния безопасности и экономичности движения, а также решения специальных
задач (наблюдение, аэрофотосъемка, поиск полезных ископаемых, поиск и
спасение терпящих бедствие транспортных средств и людей).
Требования к точностным характеристикам, таким как среднеквадрати-
ческие ошибки (СКО) определения навигационных параметров, показателям
надежности навигационного обеспечения и др., следующие:
12
Введение
доступность (готовность), мерой которой является вероятность работо-
способности радионавигационных систем (РНС) перед выполнением той или
иной задачи и в процессе ее выполнения;
целостность, мерой которой является вероятность выявления отказа в
течение времени, равного заданному или менее;
непрерывность обслуживания, мерой которой служит вероятность работо-
способности системы в течение наиболее ответственных отрезков времени
движения (выполнения задачи).
Требования к навигационному обеспечению различных гражданских объ-
ектов, осуществляемому, в частности, с помощью СРНС, впервые в нашей
стране сформулированы, обобщены и приведены в Российском радионавига-
ционном плане [В. 10], подготовленном с участием специалистов заинтересо-
ванных ведомств и служб. Они учитывают также положения документов таких
международных организаций, как ИКАО (Международная организация граж-
данской авиации), ИМО (Международная морская организация), а также ряда
национальных радионавигационных планов других стран, например, США
IB.11].
Требования к навигационному обеспечению воздушных судов
Эти требования определяются в. пер„вую_рчередь_ необходимостью обеспе-
чения безопасности полетов воздушных судов (ВС) в условиях сложившейся
структуры деления воздушного пространства. В соответствии с этим рассмат-
риваются различные этапы полета: по трассам, воздушным линиям, в аэро-
дромной или аэроузловой зоне, взлет, заход на посадку и посадка, пробег по
взлетно-посадочной полосе (ВПП) и руление по рулежным дорожкам.
В табл.1 приведены требуемые СКО определения плановых координат и
высоты полета ВС (абсолютной — по трассам и местным линиям, геометриче-
ской — при заходе на посадку) [В. 10].
Требуемые показатели даны для основных решаемых задач, таких как
маршрутный и специальный полеты, полет в зоне аэродрома, заход на посад-
ку. Для захода на посадку по категориям ИКАО указаны высоты над ВПП, на
которых должна осуществляться проверка точностных характеристик.
Требования к доступности зависят от этапов полета и интенсивности
воздушного движения. Численные значения доступности при маршрутных
полетах составляют 0,999 ... 0,99999; при полете в зоне аэродрома и некатего-
рированном заходе на посадку — 0,99999. Требования по доступности для за-
хода на посадку и посадки по категориям ИКАО соответствуют требованиям к
системам инструментальной посадки. Численные значения их близки к едини-
це [В. 10].
Требования к целостности для маршрутных полетов, полетов в зоне аэ-
родрома и некатегорированному заходу на посадку составляют 0,999 при до-
пустимом времени предупреждения соответственно 10, 10 и 2 с, а для захода
на посадку и посадки по I, II и III категориям ИКАО — 0,999999,
0,9999999 и 0,9999999995 при допустимом времени предупреждения не более
1 с [В. 10].
Таблица 1. Требования к точности определения координат
и высоты полета ВС
Решаемые задачи Зоны полета Точность определения (СКО), м
координат ВЫСОТЫ
Маршрутный полет Над океаном (безориен- тирная местность) Трассы шириной 20 км Трассы шириной 10 км Местные воздушные ли- нии: I категории II категории 5800 2500 1250 500 250 30 ... 40 30 ... 40 30 ... 40 30 ... 40 1 30 ... 40 1
Полет в зоне аэродрома — 200
Специальные полеты 1 (разведка полезных иско- 1паемых, поиск и спасение 1и др.) 1 ... 10
ЦНекатегорированныЙ заход 1 на посадку 50
Заход на посадку : по I категории, /7=30 м по II категории, /7=15 м но III категории, /7=2,4 м I1 1 1 4,5 ... 8,5 2,3 ... 2,6 2,0 1,5 ... 2 0,7 ... 0,85 “ 0,2 ... 0,3
В [В. 12—В. 14] приведены несколько иные требования, основанные
на концепции требуемых навигационных характеристик (ТНХ или RNP), раз-
виваемой ИКАО. Эти требования пока находятся в процессе обоснований и
согласований, поэтому здесь они приводятся лишь для иллюстрации подходов
и возможных уровней значений, утвержденных в будущем (табл.2).
Таблица 2. Требования к точности выдерживания траектории
захода на посадку
Категория Туннель Вероятность решения задачи Границы уклонений, м Высота Н, м, более
боковых вертикальных
I Внутренний Внешний 0, 95 (1 ... 3,3)-10'7 ± 40 ± 121 ±12 ±37 60 60
II Внутренний Внешний 0,95 (1 ... 3,3) 10“8 ±21 ± 64 + 4,6 ±14 30 30
III Внутренний Внешний 0,95 (1... 1,5) • 10-’ ±15 ±46 ±1,5 ±4,6 15 15
Требования к точности боковых и вертикальных уклонений при катего-
рированных заходах на посадку представляются в виде границ внешнего и
внутреннего “туннелей”, внутри которых должен оставаться снижающийся по
глиссаде самолет с заданными вероятностями.
*14 ' 1 ‘ . Bl 1ение
Границы “туннелей” представляют собой предельные значения суммы
погрешностей определения координат (в боковом канале) и высоты, а также
соответствующих ошибок управления. Сравнение численных значений, приве-
денных в табл. 1 и 2, показывает, что они не противоречат одно другому.
В [В. 14—В. 15] даны несколько иные значения надежностных характери-
стик (табл. 3) захода на посадку по категориям ИКАО, уровни которых однако
соответствуют приведенным выше из |В.1О].
Требования, приведенные в табл. 1—3, относятся к точности и надежно-
сти определения координат на различных этапах полета ВС. Следует отме-
тить, что совершенствование процедур и методов управления полетом мбжет
привести к обоснованию и формулировке требований к точности определения
составляющих скорости и, возможно, времени. Это, в частности, относится к
разработке и использованию алгоритмов управления движением
Таблица 3. Требования к надежности при заходе
на посадку по категориям ИКАО
Категория Доступ- ность Целостность Непрерывность Высота Н, I м, более 1
I 0,9975 Г < 6 с (1... 33) 10”7 1-10~5в течение 15 с 1-104 в течение 150 с 60
11 0,9985 Г<2с (1 ... 33) КГ8 (1 ... 1,4) • 10^ в течение 15с (1 ... 1,4)-10~5 в течение 165 с 30-
III 0,999 Т< 1 с (1... 1,5)109 (1 ... 4)-КГ6 в течение 30 с 15
конфликтующих ВС в задаче предотвращения столкновений ВС в воздухе, а
также в задаче предупреждения столкновений ВС с наземными объектами и
для обеспечения более комфортных условий посадки.
Требования к навигационному обеспечению морских судов
Требования к навигационному обеспечению морских судов (МС),
предъявляемые сейчас и к СРНС, вытекают из необходимости обеспечения
безопасности и экономичности плавания, которые зависят от районов и эта-
пов судовождения [В. 10]:
открытое море (океан);
прибрежные зоны (на удалении менее 50 миль от берега);
узкости, входы в порты и гавани;
акватории портов.
Международные требования к точности и надежности навигационного
обеспечения морских судов в зависимости от районов плавания определяются
ИМО. Требования к навигационному обеспечению судоходства при входах в
) J - i L. ). > y ; xJ
порты, гавани, в узкостях и акваториях портов определяются соответствующи-
ми национальными администрациями.
В табл. 4 приведены обобщенные требования к навигационному обеспе-
чению морских судов [B.1OL Необходимо отметить, что приведенные требова-
ния находятся в состоянии перманентных корректировок и уточнений, в ос-
новном, в сторону их повышения. Это объясняется постоянно возрастающей
ценой навигационных ошибок, особенно в условиях роста тоннажа танкеров,
опасности и стоимости последствий возможных экологических катастроф из-
за столкновений с препятствиями и посадками на мель. Всем памятны катаст-
рофы с танкерами “Экссон Валдис” и “Находка”. Последняя помимо загряз-
нения района катастрофы привела к серьезному напряжению при обеспечении
жизни всего региона Камчатки. Огромный общественный резонанс вызвала
катастрофа пассажирского судна “Адмирал Нахимов”, повлекшая за собой
смерть сотен людей, которой можно было бы избежать при более совершен-
ном навигационном обеспечении.
Таблица 4. Требования к точности и надежности определения
координат морских судов
Решаемая задача Погрешность опреде- ления (СКО), м Доступность Целостность*
Плавание в откры- том-море (океане) 1400 ... 3700 0;99 0,99
Плавание в при- брежной зоне 100 ... 60 0,99 ... 0,997“ 0.99
Прохождение узко- стей, заходы в порты менее 20 0,99 ... 0,997“ 0,99
Маневрирование в портах 8 0,997 0,99
Картография н океанография 0,25 ... 5 0,99 0,9 ... 0,99
Геологоразведка, добыча полезных ископаемых 1 ... 5 0,99 0,9 ... 0,99
* Допустимое время предупреждения находится в пределах единиц секунд — единиц минут в зависимости от задачи и типа МС 1 •* Значения 0,997 относятся к МС большого тоннажа
Велика также роль определения точного местоположения при проведе-
нии народнохозяйственных работ на шельфе, таких как геологоразведка и до-
быча полезных ископаемых.
Для обеспечения и экономичности движения МС пока не сформулиро-
ваны требования к определению скорости и времени. Однако представляется,
что качественное решение задачи проводки большегрузных танкеров в узко-
стях, посадки ВС (вертолета) на палубу МС в условиях сильного волнения и
шторма может быть осуществлено лишь при получения качественной инфор-
мации о горизонтальных и вертикальной составляющих скорости МС.
Добавим, что точная корректировка шкалы времени МС может позво-
лить эффективно решать задачи обеспечения надежного опознавания, связи и
16 Введение
т. д., а для решения задача буксировки по морю высотных платформ для добы-
чи полезных ископаемых может потребоваться и информация о пространст-
венной ориентации объекта с точностью (СКО) до единиц — долей угловых
минут.
Требования к навигационному обеспечению судов речного флота
Требования к навигационному обеспечению плавания судов по рекам и
озерам в первой редакции Российского радионавигационного плана не были
сформулированы [В. 10] и в настоящее время находятся в стадии обоснования.
Предварительно они могут быть определены по аналогии с требования-
ми к навигационному обеспечению МС при плавании в прибрежной зоне
(СКО определения координат 100 ... 460 м, доступность и целостность соот-
ветственно 0,99 ... 0,997 и 0,99) и при прохождении узкостей и маневрирова-
нии в портах (СКО определения координат менее 8 ... 20 м, доступность и
целостность соответственно 0,99 ... 0,997 и 0,99). Для речных судов помимо
определения точного местоположения важно иметь и базу данных (БД) с циф-
ровым описанием фарватера и различного рода препятствий, отмелей, поро-
гов, рифов и т. д.
Требования к навигационному обеспечению лаземвых объектов
К наземным объектам относятся автомобильный и железнодорожный
транспорт, объекты геологоразведывательных подразделений, топогеодезиче-
ских и землеустроительных служб. Для обычных транспортных средств требуе-
мая СКО определения координат находится в пределах единиц метров — еди-
ниц километров [В. 10], причем при необходимости, например обеспечения
точной ориентировки в городе, соответствующая точность равна единицам —
первому десятку метров. При этом определение точного местонахождения
должно комбинироваться с использованием БД городской застройки.
Учитывая возможности навигационного обеспечения с помощью СРНС,
в качестве современного требования для автомобильного транспорта следует
считать СКО определения местонахождения, равную 10 ... 50 м.
Требования геологоразведки и добычи полезных ископаемых, а также
привязки наземных радиосредств составляют 1 ... 5 м, а необходимая СКО
проведения топогеодезических и землеустроительных работ — 0,01 ... 5 м.
Требования к надежности определения места наземных объектов, как правило,
не заданы [В. 10]. Исключение составляют требования по доступности для гео-
логических работ, добычи полезных ископаемых и геодезической привязки,
которая составляет 0,95.
С учетом условий, при которых используются наземные средства, специ-
альные требования к определению скорости, как правило, не выдвигаются.
Однако ряд служб и систем нуждаются в едином точном времени. Такая
необходимость возникает при управлении разнесенными в пространстве объ-
ектами; при испытаниях, синхронизации систем связи, опознавания; прове-
дении тонких научных исследований и т. д. Требуемая точность может соста-
вить десятки (и даже единицы) наносекунд (по крайней мере в относительном
режиме). .
При строительстве и топогеодезических работах в ряде случаев также
требуется информация о пространственной ориентации объектов в условиях
ограниченной видимости с СКО до единиц — долей угловых минут.
Требования к навигационному обеспечению космических средств
Точность навигационного обеспечения космических средств (КС) задана
на уровне 300 ... 3000 м при доступности 0,95 ... 0,997 [В. 10] и, по всей види-
мости, будет в дальнейшем уточняться до нескольких десятков (и возможно,
единиц) метров при решении, например, задачи экстренной посадки на на-
земный аэродром в условиях категорий ИКАО (см. табл. 1). Достаточно высо-
кие требования предъявляются к точности определения скорости (на уровне
нескольких сантиметров в секунду), которая необходима, в частности, при
сближении и стыковке космических средств.
Литература
В.1. Решетнев М. Ф. Развитие спутниковых радионавигационных систем// Инф.
бюллетень НТЦ "Интернавигация”, 1992, с. 6—10.
В.2. Parkinson В. W. A History of Satellite Navigation// Navigation (USA), Spring,
1995, vol. 42, no. 1, pp. 109—164.
B.3. Шебшаевич В. С. Развитие теоретических основ спутниковой радионавигации
ленинградской радиокосмической школой// Радионавигация и время, РИРВ, 1992, № 1,
с. 6-9.
В.4. Шебшаевич В. С. Основные возможности использования ИСЗ для ра-
дионавигации самолетов: Докл. на семинаре ЛВВИА 25.12.57// Информационный сбор-
ник, Л., 1958, № 33.
В.5 Pat. 5,331,329 (US), Jul. 19. 1994, Int. Cl.5 G01S 5/02$ H04B 15/00. Satellite-
aided Radio Navigationing Metod and Radio Navigation System Therefor.
B.6. Кудрявцев И. В., Клюшников С. Н. и др. Результаты испытаний аппаратуры по-
требителей системы ГЛОНАСС// Радионавигация и время, РИРВ, 1992, № 1, с. 57—59.
В.7. Кудрявцев И. В., Клюшников С. Н, Федотов Б. Д. Перспективная авиационная
спутниковая аппаратура потребителей, работающая по сигналам систем ГЛО-
НАСС/GPS// Радионавигация и время, РИРВ, 1992, № 1, с. 60—63.
В.8. Макода В. С. Тенденции развития спутниковых навигационных систем в
США// Навигация и гидрография, ГОСНИНГИ, 1995, № 1, с. 26—128.
В.9. Гусев Ю., Лебедев М. Перспективы развития спутниковой навигационной сис-
темы ГЛОНАСС и ее интеграция с зарубежными навигационными средствами//Тр. Меж-
дународной конференции “Глобальная радионавигация”, М., 1995, с. 5.1—5.13.
В.10. Российский радионавигационный план// НТЦ “Интернавигация”, М., 1994.
В.И. Федеральный радионавигационный план США// МТ и МО США, 1994.
В.12. Материалы особого совещания по связи/производству полетов 27.3 —
7.4.95// ИКАО, 1995.
В.13. All Weather Operations Panel (AWOP)// 15 Meeting, Montreal, ICAO, 26.9. —
12.10.1994.
B.14. Kelly R. J, Davis J. Required Navigation Performance (RNP) for Pre-cision Ap-
proach and Landing with GNSS Application// Navigation (USA), 1994, no. 1, pp. 1—30.
B.15. Blomenhofer H., Meyer-Hilberg J. Availability and Accuracy During Precision Ap-
proaches and Automatic Landings// 5-th Intern. Conf, on Differential Satellite Navigation
Systems, St. Petersburg, 1996, Add. vol., Paper № 43.
Раздел 1
ОБЩИЕ ПРИНЦИПЫ ПОСТРОЕНИЯ СПУТНИ-
КОВЫХ РАДИОНАВИГАЦИОННЫХ СИСТЕМ
Г л а в а 1
Структура спутниковых радионавигационных
систем
1.1. Общие сведения
Структура, способы функционирования и требуемые характеристики
подсистем СРНС во многом зависят от заданного качества навигационного
обеспечения и выбранной концепции навигационных измерений [1.1 —1.6].
Для достижения таких важнейших качеств, как непрерывность и высокая точ-
ность навигационных определений, в глобальной рабочей зоне в составе со-
временной СРНС типа ГЛОНАСС и GPS функционируют три основные под-
системы [ В.2, 1.5} (рис. 1.1):
Рис. 1.1. Глобальная спутниковая радионавигационная система
космических аппаратов (ПКА), состоящая из навигационных ИСЗ (в
дальнейшем ее называем сетью навигационных спутников (НС) или космиче-
ским сегментом);
\.2.11рдсистема космических аппаратов ’' 1 1 19
контроля и управления (ПКУ) (наземный командно-измерительный
комплекс (КИК) или сегмент управления);
аппаратура потребителей (АП) СРНС (приемоиндикаторы (ПИ) или сег-
мент потребителей). Разнообразие видов приемоиндикаторов СРНС обеспечи-
вает потребности наземных, морских, авиационных и космических (в преде-
лах ближнего космоса) потребителей.
Основной операцией, выполняемой в СРНС с помощью этих сегментов,
является определение пространственных координат местоположения потреби-
телей и времени, т. е. пространственно-временных координат (ПВК). Эту опе-
рацию осуществляют в соответствии с концепцией независимой навигации,
предусматривающей вычисление искомых навигационных параметров непо-
средственно в аппаратуре потребителя [1.4, 1.6]. В рамках этой концепции в
СРНС выбран позиционный способ определения местоположения потребите-
лей на основе беззапросных (пассивных) дальномерных измерений по сигна-
лам нескольких навигационных искусственных спутников Земли с известны-
ми координатами.
Выбор концепции независимой навигации и использование беззапрос-
ных измерений обеспечили возможность достижения неограниченной пропу-
скной способности СРНС. По сравнению с зависимой навигацией, не преду-
сматривающей процедуры вычислений ПВК в ПИ СРНС, произошло усложне-
ние аппаратуры потребителей. Однако современные достижения в области
технологий сделали возможной реализацию таких подходов при решении про-
блемы навигационных определений в СРНС.
Высокая точность определения местоположения потребителей обуслов-
лена многими факторами, включая взаимное расположение спутников и пара-
метры их навигационных сигналов. Структура космического сегмента обеспе-
чивает для потребителя постоянную видимость требуемого числа спутников.
В настоящее время считается целесообразным введение в состав СРНС
региональных дополнительных систем, обеспечивающих реализацию наиболее
строгих требований потребителей 11.5]. Эти структуры позволяют существенно
повысить точность обсерваций, обнаруживать и идентифицировать нарушения
в режимах работы СРНС, недопустимое ухудшение качества ее функциониро-
вания и своевременно предупреждать об этом потребителей, т. е. они могут
осуществлять контроль целостности системы и поддерживать режим диффе-
ренциальных измерений (см. гл. 11) [1.5].
1.2. Подсистема космических аппаратов
Подсистема космических аппаратов СРНС состоит из определенного
числа навигационных спутников. Основные функции НС — формирование и
излучение радиосигналов, необходимых для навигационных определений по-
требителей СРНС, контроля бортовых систем спутника подсистемой контроля
и управления СРНС С этой целью в состав аппаратуры НС обычно включают:
радиотехническое оборудование (передатчики навигационных сигналов и те-
20 Глава!. Стру.гур» спутниковых радионавигационных систем
леметрической информации, приемники данных и команд от КИК, антенны,
блоки ориентации), ЭВМ, бортовой эталон времени и частоты (БЭВЧ), сол-
нечные батареи и т. д. Бортовые эталоны времени и частоты обеспечивают
практически синхронное излучение навигационных сигналов всеми спутника-
ми, что необходимо для реализации режима пассивных дальномерных измере-
ний в аппаратуре потребителей.
Навигационные сигналы спутников содержат дальномерные компоненты
и компоненты служебных сообщений. Первые используют для определения в
аппаратуре потребителей СРНС навигационных параметров (дальности, ее
производных, ПВК и т. д.), вторые — для передачи потребителям координат
спутников, векторов их скоростей, времени и др. Основная часть служебных
сообщений спутника подготовлена в наземном командно-измерительном ком-
плексе и передана по радиолинии на борт спутника. И только небольшая их
часть формируется непосредственно бортовой аппаратурой.
Дальномерные компоненты навигационных сигналов содержат две со-
ставляющие, отличающиеся обеспечиваемой ими точностью. навигационных
определений (стандартной и более высокой). В аппаратуре гражданских потре-
бителей обрабатывается сигнал стандартной точности. Для использования сиг-
нала высокой точности требуется санкция военных органов [1.2, 1.6J.
Выбор состава и конфигурации орбитальной группировки НС может
обеспечить заданную-рабочую зону; возможность реализации различных мето-
дов навигационно-временных определений (НВО), непрерывность и точность
НВО, диапазон изменения параметров радиосигналов НС и т. д. Например,
увеличение высоты полета НС современных средневысотных СРНС до при-
мерно 20 000 км позволяет принимать сигналы каждого НС на значительных
территориях (приблизительно на половине поверхности Земли). И тогда не-
сколько НС, расположенных на определенных орбитах, могут формировать
сплошное, с точки зрения наземного и авиационного потребителя, радиона-
вигационное поле (глобальную рабочую зону).
Соответствующие характеристики сигналов НС и способы их обработки
позволяют проводить навигационные измерения с высокой точностью.
В современных СРНС типа ГЛОНАСС и GPS большое внимание уделя-
ется взаимной синхронизации НС по орбитальным координатам и излучаемым
сигналам, что обусловило применение к ним термина “сетевые СРНС”.
1.3. Наземный командно-измерительный комплекс
Подсистема контроля и управления представляет собой комплекс назем-
ных средств (командно-измерительный комплекс — КИК), которые обеспечи-
вают наблюдение и контроль за траекториями движения НС, качеством функ-
ционирования их аппаратуры; управление режимами ее работы и параметрами
спутниковых радиосигналов, составом, объемом и дискретностью передавае-
мой со спутников навигационной информации, стабильностью бортовой шка-
лы времени и др.
21
Обычно КИК состоит из координационно-вычислительного центра
(КВЦ), станций траекторных измерений и управления (СТИ), системного
(наземного) эталона времени и частоты (СЭВЧ).
Периодически при полете НС в зоне видимости СТИ, происходит на-
блюдение за спутником, что позволяет с помощью КВЦ определять и прогно-
зировать координатную и другую необходимую информацию. Затем эти данные
закладывают в память бортовой ЭВМ и передают потребителям в служебном
сообщении в виде кадров соответствующего формата.
Синхронизация различных процессов в СРНС обеспечивается с помо-
щью высокостабильного (атомного) системного эталона времени и частоты,
который используется, в частности, в процессе юстировки бортовых эталонов
времени и частоты навигационных спутников СРНС.
1.4. Навигационная аппаратура потребителей СРНС
Приемоиндикаторы СРНС, состоящие из радиоприемника и вычислите-
ля, предназначены для приема и обработки навигационных сигналов спутни-
ков с целью определения необходимой потребителям информации (прост-
ранственно-временных координат, направления и скорости, пространственной
ориентации и т. п.).
Пространственное положение потребителя обычно определяется в прие-
моиндикаторе в два этапа: сначала определяются текущие координаты спутни-
ков и первичные навигационные параметры (дальность, ее производные и др.)
относительно соответствующих НС, а затем рассчитываются вторичные —
географическая широта, долгота, высота потребителя и т. д.
Сравнение текущих координат потребителей с координатами выбранных
навигационных точек (точек маршрута, реперов и т. п.) позволяет сформиро-
вать в ПИ сигналы для управления различными транспортными средствами.
Вектор скорости потребителя вычисляют путем обработки результатов измере-
ний доплеровских сдвигов частоты сигналов НС с учетом известного вектора
скорости спутника. Для нахождения пространственной ориентации потребите-
ля в приемоиндикаторе СРНС осуществляются разностные измерения с ис-
пользованием специальных антенных решеток.
1.5. Взаимодействие подсистем СРНС в процессе
определения текущих координат спутников
Способ функционирования современных СРНС позволяет отнести их к
радиомаячным навигационным средствам. Однако необходимость постоянного
определения текущих координат НС и выбора из них видимых потребителю
НС и рабочего созвездия исправных НС существенно отличает СРНС от тра-
диционных радиомаячных РНС (РСБН, РСДН), в которых координаты радио-
маяков известны и постоянны. Непрерывное нахождение текущих координат
22 Г л а в a 1. Огруктура спутниковых ркущонавипщионных систем
НС, движущихся с большими изменяющимися во времени скоростями, пред-
ставляет собой сложную задачу.
Координаты НС могут быть определены в общем случае на КИК или не-
посредственно на спутнике (самоопределяющиеся НС) [1.4J. В настоящее вре-
мя отдается предпочтение первому подходу. Это связано с тем, что существуют
хорошо апробированные на практике методы и средства решения этой про-
блемы в наземных условиях. В современных СРНС управление НС осуществ-
ляется с ограниченных территорий и, следовательно, не обеспечивается по-
стоянное взаимодействие КИК и сети НС. В связи с этим Выделяют два этапа
решения этой задачи [1.6]. На первом этапе в аппаратуре КИК измеряют ко-
ординаты спутников в процессе их пролета в зоне видимости и вычисляют па-
раметры их орбит. Эти данные прогнозируются на фиксированные (опорные)
моменты времени, например на середину каждого получасового интервала
предстоящих суток, до выработки следующего прогноза. Спрогнозированные
координаты НС и их производные (эфемериды [1.2]) передаются на НС, а затем
в виде навигационного (служебного) сообщения, соответствующего указанным
моментам времени, потребителям. На втором этапе в аппаратуре потребителя
по этим данным осуществляется последующее прогнозирование координат НС,
т. е. вычисляются текущие координаты НС в интервалах между опорными точ-
ками траектории. Процедуры первичного и вторичного прогнозирования коор-
динат проводят при известных закономерностях движения- НС.
В отличие от самоопределяющихся НС [1.4], рассмотренный вариант
функционирования СРНС обеспечивает упрощение аппаратуры спутников за
счет усложнения структуры КИК с целью достижения заданной надежности.
Заметим, что в навигационное сообщение НС КИК, кроме того, закла-
дывает альманах [1.2] — набор справочных сведений о всей сети НС, в том
числе загрубленные эфемериды НС, которые обычно используются для опреде-
ления видимых потребителю НС и выбора рабочего созвездия, обеспечиваю-
щего высокое качество НВО. Темп обновления точной эфемеридной инфор-
мации (ЭИ) значительно выше, поэтому ее часто называют оперативной ЭИ в
отличие от долговременной ЭИ в альманахе.
Литература
1.1. Волков Н. М., Иванов И. Е., Салищев В. А., Тюбалин В. В. Глобальная спутни-
ковая радионавигационная система ГЛОНАСС// Успехи современной радиоэлектрони-
ки, 1997, № 1, с. 31-46.
1.2. Глобальная спутниковая навигационная система ГЛОНАСС// Интерфейсный
контрольный документ. — М.: ВКС РФ, 1995.
1.3. Шебшаевич В. С. Введение в теорию космической навигации. — М.: Сов. ра-
дио, 1971.
1.4. Сетевые спутниковые радионавигационные системы/ Под ред. Л. П. Дмитрие-
ва, В. С. Шебшаевича. — М.: Транспорт, 1982.
1.5. Сетевые спутниковые радионавигационные системы/ Под ред. В. С. Шебшае-
вича. — М.: Радио и связь, 1993.
1.6. Спутниковые радионавигационные системы. 4.1. Основы функционирования
подсистем/ Под ред. В. Н. Харисова. — М.: Изд-во ВВИА им. Н.Е. Жуковского, 1997.
/
. V
23
Глава 2
Шкалы времени
2.1. Единицы мер времени
Приведем основные понятия, относящиеся к единицам мер времени, ко-
торые используют для временной привязки сигналов СРНС, пространствен-
ного положения НС и т. д. [2.1—2.7].
Рассмотрим две группы единиц отсчета времени — астрономические и
неастрономические. Основной астрономической единицей времени являются
сутки (86 400 с) — интервал времени, за который Земля делает один полный
оборот вокруг своей оси относительно какой-либо фиксированной точки от-
счета на небесной сфере для наблюдателя, расположенного на одном и том же
меридиане. В зависимости от выбранной точки отсчета (точка весеннего рав-
ноденствия, центр видимого диска Солнца, "среднего Солнца" и т. д.) сутки
отличаются по длительности и имеют разное название. Звездные сутки Т3
(звездный период обращения Земли) отсчитываются между двумя последова-
тельными верхними положениями (кульминациями) точки весеннего равно-
денствия. Интервал времени от момента верхней кульминации этой точки,
выраженный в долях Т3, называют звездным временем. Обычно время, изме-
ренное на данном меридиане, называется местным временем данного меридиана,
т. е. в рассматриваемом случае местным звездным временем меридиана. Мест-
ное звездное время S измеряется часовым углом t точки весеннего равноден-
ствия у (точки Весны или точки Овна) относительно местного небесного
меридиана L (рис. 2.1). На рисунке показан вид северного полушария небес-
ной сферы сверху, где Рц — Северный полюс. Часовой угол аналогичен гео-
графической долготе, отсчитывается от небесного меридиана наблюдателя по
часовой стрелке и измеряется в часовой мере — часах, минутах, секундах.
Звездное время можно выразить и в угловых значениях с учетом того,
Рис. 2.1. Определение местного
звездного времени
что за 1 ч Земля поворачивается на 15®,
например местному звездному времени
S = 2 ч 3 мин 1 с соответствует угол,
равный 30°45'15".
Для точных расчетов следует учи-
тывать также, что ось вращения Земли
совершает медленное периодическое ко-
лебательное движение, состоящее из пре-
цессии (движение по конусу) и нутаций
(небольшие колебания) оси. Из-за пре-
24 Гл а в а 2. Шкалы времени^
цессии и нутаций точка Весны перемещается. Если учитывается только пре-
цессионное движение, то получаются среднее (равномерное) звездное время и
средние звездные сутки. Если же учитывается и нутация, то получается ис-
тинное звездное время. Местное звездное время, измеренное на Гринвичском
меридиане, называется обычно гринвичским звездным временем S.
Истинные солнечные сутки Тя отсчитывают по нижним кульминациям
центра видимого диска Солнца ("истинного Солнца"). Из-за неравномерности
движения Земли по орбите и непараллельности осей ее суточного и годичного
вращения Тя непостоянно, поэтому в повседневной жизни за основную еди-
ницу времени принимают средние солнечные сутки Гср, которые отсчитывают-
ся по нижним кульминациям "среднего Солнца" — гипотетической точки, рас-
считанной в предположении ее равномерного движения По орбите. "Среднее
Солнце" совершает один полный оборот по небесному экватору за такое же
время, как и настоящее Солнце по эклиптике, и проходит точку весеннего
равноденствия одновременно с Солнцем. Интервал времени от момента ниж-
ней кульминации "среднего Солнца", выраженный в долях Гср, называется
средним солнечным временем или средним временем. Местное среднее время изме-
ряется часовым углом "среднего Солнца" относительно местного меридиана,
увеличенным на 12 ч. Значение Тс$ соответствует среднему значению Тк
за год.
Подсчитано, что 24 ч звездного времени равны примерно 23 ч 56 мин
4,091 с среднего времени, т. е. Т3 » 86 164,091 с среднего времени.
Из-за неравномерности суточного вращения Земли звездные и солнеч-
ные сутки незначительно изменяются. Для точных расчетов введено равномер-
но текущее время — эфемеридное (предвычисленное) время ЕТ, где единица
меры времени — эфемеридная секунда, рассчитывается как 1/86400 доля сред-
ней продолжительности времени в определенный день 1900 г.
Создание сверхстабильных атомных эталонов частоты (времени) позво-
лило перейти к неастрономическому способу измерения времени и ввести ис-
кусственную единицу меры времени, не зависящую от особенностей вращения
Земли, — атомную секунду, близкую к эфемеридной. Атомная секунда принята
в качестве единицы измерения времени XIII Генеральной конференцией но
мерам и весам в 1967 г. Атомная секунда равна интервалу времени, в течение
которого совершается 9 192 631 770 колебаний, соответствующих резонансной
частоте энергетического перехода между уровнями сверхтонкой структуры ос-
новного состояния атома цезия—133 при отсутствии внешних воздействий
[2.4, 2.6[.
Атомная секунда является основой шкалы атомного времени АТ и при-
нята в настоящее время за единицу времени в системе СИ (вместо эфемерид-
ной секунды). Осреднение показаний различных атомных эталонов времени
позволило создать шкалу международного атомного времени TAI.
1 >!!!>)! !
2.2. Системы отсчета времени, используемые в СРНС 25
2.2. Системы отсчета времени, используемые в СРНС
Всемирное (гринвичское среднее солнечное) время UT (Universal Time).
Это время содержит год, месяц, число, час, минуту и секунду. Первые три ве-
личины отсчитываются по общепринятому (Григорианскому) календарю, ос-
тальные — по местному среднему времени на Гринвичском меридиане .
Эта система отсчета введена в 1928 г. III Генеральной ассамблеей Междуна-
родного астрономического союза.
Всемирное время /ру измеряется часовым углом "среднего Солнца" от-
носительно Гринвичского меридиана, увеличенным на 12 ч. Так как движение
полюсов Земли обусловливает изменение положения меридианов, то по степе-
ни учета возмущающих факторов различают следующие разновидности все-
мирного времени: UT0 — всемирное время, получаемое в результате текущих
астрономических измерений относительно неуточненного поправками Грин-
вичского меридиана; UT1 — всемирное время среднего Гринвичского мери-
диана, рассчитанное с учетом движения полюсов. Оно является основой для
измерения времени в повседневной жизни; UT2 — отличается от UT1 сезон-
ными поправками; UT1R — отличается от UT2 поправками на приливы.
Заметим, что UT равно местному среднему времени минус географиче-
ская долгота места наблюдателя Г; 5^ (гринвичское звездное время) равно
местному звездному времени 5 минус L, при этом восточная долгота L по-
ложительна, западная — отрицательна.
Всемирное координированное время UTC. Его обычно используют в по-
вседневной жизни, измеряется по атомным часам, показания которых перио-
дически (с периодом 0,5 ... 2,5 г.) корректируются на I с так, чтобы разность
(UT-UTC) не превышала 0,9 с. Сигналы UTC передаются по радиовещатель-
ным сетям. Разность (TAI-UTC) составляла +• 25 с на 1 января 1990 г. Досто-
инства UTC — сравнительно высокая равномерность шкалы, присущая атом-
ному времени; привязка к естественным природным процессам (восход, за-
ход), что характерно для солнечного времени.
Поясное время ZT. Это время содержит год, месяц и число, которые от-
считываются аналогично всемирному времени UT, часы, минуты и секунды —
как местное среднее время основного (центрального) географического мери-
диана рассматриваемого часового пояса /п по формуле ZT = UTC+Ди , где Ди
—номер часового пояса. Поясное время введено в большинстве стран с 1884 г.,
в России — с 1919 г. При этом поверхность Земли была разделена на 24 часо-
вых пояса, центральные меридианы которых отличаются по долготе на 15°
(I ч). Для Москвы Ди = 2 . Достоинство поясного времени — удобство исполь-
зования в повседневной жизни, так как не требует уточнения времени при со-
ответствующих перемещениях вдоль параллели.
Местное декретное время. Это время отличается от поясного времени ZT
на декретную добавку Д/^р , устанавливаемую для каждой местности законода-
26 ч ______ Г л а в а 2. Шкалы времени
J^BSSSS^^S ВВМВЯЯВЗНХГ ^ПВВВ^В^В ^^ВВМ^ПН^Р \^^аам*ц* *"^ESS5SflBB^^^* ^фВЙЙЕЯ^ВЯВ
1 ' 1
тельным порядком. В СССР это время существовало до 1981 г. В настоящее
время в России действует система летнего времени.
Летнее время. Это время гл = ZT+2 я. Обычно летнее время действует
ежегодно с 2 я ночи последнего воскресенья марта до 3 я ночи последнего
воскресенья сентября, когда вводится зимнее время /зим. Оно соответствует
существовавшему ранее декретному времени с добавкой Д/дКр=1 ч, т. е.
/зим =ZT + 1 ч. Декретное (летнее) время часового пояса с Лп = 2 называют
московским летним временем. Очевидно, что, например, в ноябре московское
время равно UTC+2 ч+1 ч, в мае — UTC+2 ч+2 ч.
Юлианский период. Полное обозначение заданных моментов времени с
помощью рассмотренных систем отсчета не всегда удобно и требует использо-
вания как минимум четырех чисел — год, месяц, число и часы с десятичными
долями, поэтому на практике применяют систему отсчета, называемую юлиан-
ским периодом, удобство которой состоит, в частности, в том, что счет теку-
щего времени ведется в днях (средних солнечных сутках с десятичными доля-
ми). Все дни в этом периоде пронумерованы по порядку независимо от при-
нятой календарной системы, номера года, месяца и т. д.
Счет дней, называемых юлианскими днями (JD), ведется от полудня
1 января 4713 г. до н. э. {начало юлианского периода) до заданного момента
времени. Общая длительность юлианского периода составляет 7 980 лет.
Юлианское столетие содержит 36 525 средних солнечных суток. Любой момент
времени в этой системе отсчета выражается числом, в котором целая часть —
число юлианских дней, прошедших до последнего среднего гринвичского по-
лудня, а дробная часть — интервал времени (в долях Тс — средних солнечных
суток), прошедший от этого полудня до рассматриваемого момента времени.
Пересчет даты общепринятого календаря в юлианскую дату (JD) произ-
водят по справочным таблицам или расчетным формулам. Так для периода
1990—1994 гг. пересчет заданного момента всемирного времени UT к юлиан-
ской дате JD можно выполнить по формуле [2.5] fjD = 2440000 +
+8kl +n+t[jr -0,5 , где /ит — часы, минуты и секунды всемирного времени, со-
ответствующие заданному моменту времени и пересчитанные в доли Тс; k, I, п
— год, месяц и число по общепринятому календарю; gu число, определяемое
на начало каждого месяца этого периода по данным таблицы
Год Число gfri по месяцам
1 2 3 4 5 6
1990 7892 7923 7951 7982 8012 8043
1991 8257 9288 8316 8347 8377 8408
1992 8622 8653 8682 8713 8743 8774
1993 8988 9019 9047 9078 9108 9139
1994 9353 9384 9412 9443 9473 9504
Год Число g£j по месяцам I
7 8 9 10 11 12
1990 8073 8104 8135 8165 8196 8226
1991 8438 9469 8500 8530 8561 8591
1992 8804 8835 8866 8896 8927 8957
1993 9169 9200 9231 9261 9292 9322
| 1994 9534 9565 9596 9626 9657 9687
Например, в юлианском периоде момент московского времени 9 ч
48 мин 1 января 1985 г. обозначается числом: 2 446 066,783 333 JD .
Для удобства начало отсчета юлианских дней иногда смешают на мо-
мент времени (эпоху), например, ноль часов всемирного времени 1 января
1900 г. (JD=2 415 020,0 ); на полночь 17 ноября 1858 г., смещая при этом на-
чало отсчета вперед на 2 400 000,5 JD (это начало модифицированного юлиан-
ского периода, дни которого обозначают MJD); на полдень 1 января 2000 г.
(JD=2 451 545), обозначаемый J20-00.
2.3. Шкалы времени СРНС
Спутниковая радионавигационная система является пространствейно-
временной системой с зоной действия, охватывающей все околоземное про-
странство, и функционирует в собственном системном времени. Важное место
в СРНС отводится проблеме временной синхронизации подсистем. Так, про-
странственно-временная привязка всех НС определяет заданную орбитальную
конфигурацию сети НС. Временная синхронизация важна и для обеспечения
заданной последовательности излучения сигналов всех НС. Она обусловливает
возможность применения пассивных дальномерных (псевдодальномерных) ме-
тодов измерений. При этом все подсистемы СРНС должны функционировать в
единой шкале времени (ШВ).
На практике реализовать это требование не реально, так как для его вы-
полнения в каждой подсистеме необходимо использовать однотипные высоко-
точные эталоны времени и частоты (ЭВЧ). Поэтому в современных СРНС вы-
деляются несколько ШВ, отличающихся стабильностью: системная ШВ
(СШВ); бортовая ШВ (БШВ) НС; шкала времени потребителя (ШВП).
Системная ШВ непосредственно или косвенно используется для времен-
ной привязки основных процессов во всех подсистемах СРНС. Она формиру-
ется и поддерживается наиболее стабильными датчиками времени, входящими
в подсистемы СРНС, — квантовыми системными эталонами времени и часто-
ты (СЭВЧ) наземного командно-измерительного комплекса, высокая стабиль-
ность которых обеспечивается специальными инженерно-техническими и ал-
горитмическими решениями. Например, при использовании системного эта-
лона, который воспроизводит единицу системного времени с относительной
погрешностью 110 13 , уход формируемой системной шкалы времени соста-
вит 3 мкс за год.
)
28
Г лава 2. Шкалы «ремейк
Бортовая ШВ спутника, к которой привязываются соответствующие на- '
вигационные сигналы НС, формируется квантовыми бортовыми ЭВЧ (БЭВЧ). .
Они работают в более неблагоприятных условиях, чем СЭВЧ, поэтому неиз- |
бежно расхождение между БШВ и СШВ. Шкала времени потребителя наибо- '
лее нестабильна и смещена относительно СШВ и БШВ, так как формируется
и поддерживается кварцевым опорным генератором, входящим в комплект
ПИ.
2.4. Синхронизация шкал времени
Командно-измерительный комплекс (КИК) обеспечивает синхрониза-
цию шкал времени всех НС путем их сверки и коррекции (непосредственной
и алгоритмической) [1.4, 1.5[.
Синхронизация бортовых шкал времени НС. Сверка шкал времени в
СРНС позволяет определить значение ухода БШВ относительно СШВ. В про-
цессе сверки по принятым на КИК навигационным сигналам НС измеряется
значение времени в БШВ на момент излучения сигнала спутником
В момент его приема расчетное время по БШВ
^БШВ ~ ^БШВ + ^рас + ^р.э + Л^ат + ^апп >
где Л/рас — время распространения сигнала от z'-ro НС до КИК; Д/р э — уход
БШВ из-за релятивистских эффектов, рассчитываемый с точностью до единиц
наносекунд; Д/ат — сдвиг определяемой БШВ из-за рефракции радиоволн в
атмосфере; Д/апп ~ прочие аппаратурные и методологические погрешности.
Уход БШВ относительно СШВ определяется при сравнении вычислен-
ного и скорректированного ZBUIB с известным системным временем tc.
В зависимости от процедуры нахождения величины дальности до z-ro НС
различают пассивные (СРНС типа GPS) и активные (СРНС типа ГЛОНАСС)
методы сверки ШВ. Активный (запросный) метод более прост и позволяет по-
лучать более точные результаты, но требует установки дополнительной аппа-
ратуры.
Коррекция БШВ производится обычно при ее уходе относительно СШВ,
превышающем допустимые значения. Коррекция выражается в совмещении
временных интервалов в БШВ и СШВ (процедура фазирования БШВ) и (или)
в уточнении их оцифровки (процедуры коррекции кода БШВ на целое число
единиц времени). Фазирование обеспечивает точность совмещения ШВ до
десятков наносекунд.
Длительные наблюдения за расхождением этих ШВ позволяют устано-
вить его закономерность и прогнозировать на требуемый момент времени с
соответствующей точностью. Прогнозирование систематической составляющей
ухода обеспечивает возможность осуществления алгоритмической коррекции
рЩВ, когда определяется модель ухода БШВ и ее параметры, т.е. частотно-
временные поправки, которые закладываются в память ЭВМ спутника с по-
мощью специальных станций КИК и в дальнейшем передаются потребителям
совместно с эфемеридной информацией.
В современных СРНС, управляемых с ограниченных территорий, необхо-
димость прогнозирования БШВ и ее ухода обусловлена тем, что непосредст-
венная коррекция БШВ (воздействие системы управления на БШВ) может
производиться только эпизодически. Кроме внутрисистемной синхронизации
КИК обеспечивает привязку и (или) определение ухода СШВ относительно
какой-либо общепринятой системы отсчета времени, например UTC.
Синхронизация шкалы времени потребителя. Нахождение потребителем
бортового времени НС и соответственно системного времени СРНС осуществ-
ляется с помощью навигационных сигналов, принятых от НС. При этом может
быть реализовано несколько способов синхронизации шкалы времени по-
требителя, отличающихся точностью [1.6]: расчет поправки к шкале времени
потребителя на основе псевдодальномерных измерений; использование меток
времени, передаваемых в навигационном сигнале; применение дальномерных
кодов, передаваемых в навигационном сигнале НС.
Первый способ основывается (в первом приближении) на том, что ин-
формация, полученная потребителем в сигналах НС, используется как для
расчета текущего ухода БШВ относительно СШВ, так и для привязки ШВП к
СШВ при нахождении поправки к ШВП (временной координаты потребителя
/'). Этот способ наиболее широко распространен «и обеспечивает точность
временных измерений не хуже 1 мкс. Второй способ основывается на том, что
данные о текущем спутниковом времени (метка времени НС) и о прогнозе
ухода БШВ в опорные моменты времени относительно СШВ передаются
потребителям в навигационном сообщении. Точность привязки ШВП в этом
случае определяется неопределенностью знания дальности от НС до потреби-
теля. Третий способ аналогичен предыдущему и отличается в основном видом
информации, используемой в сигнале НС.
Литература
2.1. Аситрономический ежегодник СССР на 1989 год. — Л.: Наука, 1987, т. 68.
2.2. Астрономический календарь. Ежегодник, переменная часть. 1990/ Под
ред. Д. И. Пономарева . — М.: Наука, 1989.
2.3. Хренов Л. С., Голуб И. Я. Время и календарь. — М.: Наука, 1989.
2.4. Воздушная навигация и аэронавигационное обеспечение полетов/ Под ред.
Н. Ф. Миронова. — М.: Транспорт, 1992.
2.5. Кантор Л. Я., Тимофеев В. В. Спутниковая связь и проблемы геостационар-
ной орбиты. — М.: Радио и связь, 1988.
2.6. Справочник пилота и штурмана гражданской авиации/ Под ред. И. Ф. Васи-
на. — М.: Транспорт, 1988.
2.7. Скубко Р. А., Мордвинов В. Г. Спутник у штурвала. — Л.: Судостроение, 1989.
о
Глава 3
Траекторное движение навигационных спутников
3.1. Системы координат, используемые в СРНС
Движение ИСЗ происходит по законам небесной механики под действи-
ем инерции и сил притяжения Земли [3.1, 3.2]. Для описания такого движени^
гспользуется геоцентрическая инерциальная система координат OXqYqZq, свя
’.анная с Землей (рис. 3.1) [3.11]. Начало координат расположено в центра
ласе Земли. Ось OXq лежит в плоскости экватора и направлена в точку весен-'
гего равноденствия — точку Весны или точку Овна у (у — астрономический
нак созвездия Овна). Ось OZq направлена вдоль оси вращения Земли в сторону,
«верного полюса. Ось OYq дополняет прямоугольную систему координат до пра-
вой. Другой системой координат, используемой в спутниковой радионавига
гии, является геоцентрическая подвижная система OXYZ, например ПЗ-90 [1.2f
з СРНС ГЛОНАСС или WGS-84 в GPS [1.4]. Центр этой системы координат
~акже расположен в центре масс Земли. Ось OZ совпадает с осью OZq инерци
гльной системы координат ОАо YqZq и направлена вдоль оси вращения Земли. №.
торону Северного полюса Руу. Ось ОХ лежит в" плоскости земного экваторав:
-вязана с Гринвичским меридианом G. Плоскость OXZ определяет положени.
гуль-пункта принятой системы отсчета долгот. Ось OY дополняет систему ко-
>рдинат до правой.
Угол ср г между осями ОХ и OXq соответствует гринвичскому звездном?
зоемени 5, и определяется звездными датой и временем на Гринвичском ме
’нс. 3.1. Геоцентрические системы
координат
ридиане [3.8, 3.9, 2.7]:
= 5Г = 50 +®з/(1 + v3),
где со з = 15 °/ч = 7,292115 • КГ5 рад/ч -
угловая скорость вращения Земли; 50 -
гринвичское звездное время (угол межд
осями OXq и ОХ) на момент tg (ноль Че
сов всемирного времени) в заданную дате
град; t — всемирное время заданной дать
на которое рассчитывается угол \pr; v3
= 0,002737909 — коэффициент связь
звездных и солнечных суток.
3.1. Системы координат, используемые в СРНС
31
Вычисление гринвичского (среднего) звездного времени Sg на момент
/0 может быть проведено с помощью формулы Ньюкома [1.3, 2.Ц:
So =64ч15мин0,54841с + 8640184,812866СТ + 0,093104сТ2 - 6,2С- 106T3,
где Т = (JDo-2451545)/36525 — время, измеренное в долях юлианского столе-
тия (36525JD) и отсчитываемое от момента времени (эпохи) 12 ч всемирного
времени UT1 на 1 января 2000 г. (JD=2 451 545,0) до момента tg; JDo — время
t0, выраженное в юлианских днях.
Ось ОХ в процессе суточного вращения периодически проходит точку
Овна. Интервал времени между двумя такими последовательными моментами
соответствует одним звездным суткам. Солнечные сутки отсчитываются по по-
ложению солнца и имеют большую продолжительность из-за движения Земли
по орбите.
В геоцентрической подвижной системе координат формируется инфор-
мация о движении спутников, которая передается в навигационном сообще-
нии потребителю. В этой же системе координат на этапе вторичной обработки
информации в аппаратуре потребителя рассчитываются координаты самого
потребителя.
Однако потребителя в большей степени интересуют такие координаты
как высота, широта и долгота, которые
относятся к геодезической системе коор-
динат. Геодезические координаты точки
связаны с физической моделью Земли в
виде эллипсоида рис. 3.2 с большой по-
луосью а, лежащей в экваториальной
плоскости, и малой полуосью Ь. Основ-
ные параметры земного эллипсоида и
некоторые геодезические константы при-
ведены ниже:
Основные геодезические
Угловая скорость вращения Земли, рад/ с'1 ................... 7292115 -10-11
Геоцентрическая константа гравитационного поля Земли
с учетом атмосферы, м’ с'2 .................................. 398600,44 109
Геоцентрическая константа гравитационного поля
атмосферы Земли, и1 с'2...................................... 0,35•109
Скорость света, м с’1........................................ 299 792 458
Коэффициент ( Cjo ) при второй зональной гармонике разложения
геопотенциала в ряд по сферическим функциям ..................... - 1082,63 • 10~4
32 Глава! Траекторное движеми наангв^иовных Аутянь^
Параметры общего земного эллипсоида:
Большая полуось, м......................................... 6 378 136
Знаменатель сжатия........................................ 1 : 298,257
Гравитационное ускорение на экваторе Земли, мГал ......... '978 032,8
Поправка к гравитационному ускореиию.на уровне моря, обусловленная
влиянием земной атмосферы, мГал.................................... - 0,9
Геодезическая широта В точки П определяется как угол между нормаль*
к поверхности эллипсоида и плоскостью экватора. Геодезическая долгота 1
точки П определяется как угол между плоскостью начального меридиана t
плоскостью меридиана, проходящего через точку П (положительное направле
ние счета долгот — от начального меридиана к востоку). Геодезическая высот
Н определяется как расстояние по нормали от поверхности эллипсоида д<
точки П.
Найденные в ходе навигационных определений прямоугольные геоцен,
трические координаты {x,y,z} потребителя должны быть преобразованы в гео-
дезические координаты {В,£,27}.
Указанные координаты связаны соотношениями (3.3 ]
!
х = (N + H)cosBco&L ; у = (N + H)cosBsinL ; z = ^l-e2j^ + K-jsinB, (3.1)
где
N = a/Vl-e2sin2 В ; (3.2)
e = Jl- Z>2/a2 = V2a - a2 — эксцентриситет эллипсоида; a = l-bla — пара-
метр сжатия эллипсоида. '
3.2. Уравнения невозмущенного траекторного движения
НС в инерциальной системе координат
Под невозмущенным (кеплеровым) движением спутника понимают его дви
жение под действием только силы притяжения Земли, т. е. одного притяги
вающего центра [3.10]. В соответствии со вторым законом Ньютона движени
центра масс спутника в инерциальной системе координат OXqIqZo описывает
ся уравнением
mg = F, (3(.3
где т — масса спутника; g — вектор центростремительного ускорения; F -
вектор силы притяжения Земли.
По закону всемирного тяготения сила притяжения Земли
шсси .)ские э^Линты ^)биты с.^тники
F = У.Мт!г2 = цт/г2 ,
(3.4)
[где к = 6,672 • 10"п м3/кгс2 — универсальная гравитационная постоянная;
। Х = 5,974242 1024 кг — масса Земли; г — расстояние от центра Земли до спут-
ника; p = kAf = 3,9860044 10м м3/с2 — геоцентрическая гравитационная посто-
1янная Земли.
I С учетом соотношения g = rf2r/rf/2 , где производная по времени понима-
кется как полная производная в инерциальной системе координат, уравнение
[движения (3.3) принимает вид
rf2r -
m—г- = F.
dt2
системы координат OXqYqZq описывается
инерциальной
Пространственная траектория невозмущенного движения спутника в
проекциях на оси
уравнениями:
d2x0 xp
di2 g r3 ’
rf2>0 „ Уо .
di2 г3
d2Zo _ Zp
rf/2 - Ur3
(3.5)
Здесь х0, у0> Zo ~ текущие координаты спутника (проекции радиус-вектора г
на оси координат); г = + у% +Zq
Уравнения (3.5) описывают траекторию движения спутника, которую
^тринято называть орбитой.
3.3. Классические элементы орбиты спутника
В соответствии с первым законом Кеплера любая траектория летатель-
Ного аппарата (ЛА), движущегося в центральном поле тяготения, лежит в не-
подвижной (относительно инерциальной системы координат) плоскости
^орбитальной плоскости), проходящей через центр тяготения, и представляет
«кривую второго порядка, в одном из фокусов которой находится центр притя-
жения (Земля).
| Ориентацию орбитальной плоскости характеризуют ее положением от-
носительно экваториальной плоскости XOY (рис. 3.3). Линию пересечения
Ьтих плоскостей называют линией узлов. Узлами орбиты спутника являются
кочки пересечения орбиты с экваториальной плоскостью. Узел U , соответст-
вующий движению спутника из южной небесной полусферы в северную назы-
34
Глава 3. Траекторное движение навигационных спутников
Рис. 3.3. Ориентация орбитальной
плоскости
вают восходящим, а узел D, соот-
ветствующий движению из север-
ной небесной полусферы в южную
— нисходящим.
Положение орбитальной
плоскости относительно экватори-
альной характеризуется двумя ор-
битальными элементами — долготой
восходящего узла Q и наклонением
орбиты i . Угол Q отсчитывается
в экваториальной плоскости от
оси ОХ до линии узлов и изменя-
ется в диапазоне от 0 до 360°.
Угол । определяется как угол между
экваториальной и орбитальной плоскостями и изменяется в диапазоне от 0 до
180°. При i = 90° орбиту называют полярной, при i » 90° —' приполярной, nps
i = 0 ° — экваториальной, при 0 < i < 90° — наклонной.
Уравнение орбиты спутника в орбитальной плоскости в полярной систе-
ме координат ( 9) с центром, совпадающим с центром Земли, имеет вид
.... 1
г = p/(l + е cos(9 - Эо)), (3.6)!
где р — фокальный параметр; е — эксцентриситет; 90 — угол между положи!
тельным направлением полярной оси и фокальной осью. |
Данное уравнение является уравнением конического сечения — криво;
второго порядка, один из фокусов которой совпадает с центром полярной сис-:
темы координат. При Эо = 0 полярная ось направлена от центра к ближайше!
вершине кривой (3.6), а при Эо = л — в противоположную сторону. В даль!
нейшем для определенности будем полагать Эо =0. Угол Э называют истину
ной аномалией.
При е = 0 орбита спутника является кругом; при 0 < е < 1 — эллипсом
степень вытянутости которого определяется орбитальными параметрами р F
е ; при е = 1 — параболой, при е > 1 — гиперболой. Для навигационных спут
ников характерны эллиптические орбиты, т. е. 0 < е < 1.
На рис. 3.4 приведена эллиптическая орбита спутника в орбитально|
плоскости. В одном из фокусов (О) находится Земля. Прямую линию, прохо;-
дящую через фокусы эллипса называют линией апсид. Точки пересечения это|1
линии с эллипсом называют апсидами. Ближайшую к силовому центру (точк!
О) вершину кривой называют перицентром, а удаленную вершину (котора!
имеется только у эллипса) — апоцентром. В зависимости от того, вокруг како-
3.4. Параметры движения НС по невозмущенной орбите
35
го небесного тела движется спут-
ник, апсиды орбиты получают
собственные названия: при дви-
жении вокруг Земли — перигей и
апогей. Ориентация орбиты в ор-
битальной плоскости характери-
зуется углом перигея(аргументом)
сод между направлением на пе-
ригей и линией узлов.
Рис. 3.4. Эллиптическая орбита спутника
Размеры орбиты спутника мож-
но характеризовать различными ком-
бинациями следующих параметров:
а = р/(1 - е21 = (гА + г^)/2 — большая полуось эллипса;
b = fyl - е2 — малая полуось;
d = ае = (гА - Лт)/2 — линейный эксцентриситет;
где Га = СИ, Гд = ОП — апогейное и перигейное расстояние соответственно.
Иногда апогейное и перигейное расстояния выражаются как
га=лз + ^а; 'й = Я3+Яп>
(3.7)
где /?з = 6371 км — радиус Земли; НА, Яд — высоты апогея и перигея отно-
сительно поверхности Земли.
3.4. Параметры движения НС по невозмущенной орбите
Пять параметров орбиты Q, С <вп, р, е постоянны и не меняются при
движении спутника по орбите, а шестой параметр Э (истинная аномалия) ха-
рактеризует положение спутника на орбите в каждый фиксированный момент
времени tk . Время tk , т. е. время, в которое спутник находится в некоторой
точке орбиты, часто называют эпохой.
Другим широко распространенным орбитальным элементом, который
фиксирует положение спутника на эллиптической орбите, служит время т
прохождения спутником характерной точки орбиты, например перигея т •= /п
'поэтому иногда т называют временем перигея). Используя этот элемент, опре-
деляют положение НС на орбите в произвольный момент времени / с помо-
чью уравнения Кеплера [3.8, 3.9]:
t - т = - esin£) , (3.8)
36 ___ Г л а р.а З. Тряектд£ид^двмжение на»нг>циоиных сдутников_
где Е — эксцентрическая аномалия НС, определяемая например из соотноше
ния
(3.9)
Геометрический смысл параметра Е легко уяснить из рис. 3.5, на ко-
тором кроме эллиптической орбиты НС приведена гипотетическая круговая
орбита. Для точки Hi круговой орбиты, имеющей одинаковую с НС абсциссу,
и определяется угловой параметр Е.
Движение спутника по эллиптической орбите, в отличие от движения по
круговой орбите, является неравномерным, например при 6S/5Z # const, а зави-
сит от положения спутника на орбите. Для того чтобы использовать удобное
равномерное движение, т. е. движение с постоянной угловой скоростью, вво-
дят угловой параметр М — средняя аномалия для момента времени t {средняя
аномалия эпохи t):
M = 36C(t-t0)/T = ri(t-x), (3.10)
где to — какой-либо определенный (начальный) Момент времени, например
t0 — т ; п = 360°/г = Jp/o3 — среднее движение НС или средняя угловая ско-
рость НС.
Дифференцируя (3.10) по времени, получаем другое определение сред-
него движения
п = dM/dt.
(3.11)
В отличие от т вычисление М сохраняет смысл и при круговых орби-
тах. Если истинная аномалия Э определяет истинное положение НС на орби-
те, то параметр М характеризует
Рис. 3.5. Определение эксцентри-
ческой аномалии
гипотетическое положение НС при условии
равномерного орбитального движения с уг-
ловой скоростью, равной средней скорости
и. Поэтому в соответствии с (3.10) М —
угол между линией апсид и направлением на
предполагаемое положение НС на орбите, в
котором он находился бы при равномерном
движении. Чем меньше отличие орбиты НС
от круговой, тем больше соответствует сред-
нее движение п истинной угловой скорости
и тем ближе значения М и 9 .
3.5. Уравнения невозмущенного Овцжения ЙС (с орбитальными элементами,, 37
С учетом (3.10) уравнение Кеплера (3.8) можно представить в следую-
щем виде:
M = E-esinE. (3.12)
В процессе расчетов параметров движения НС по почти круговым орби-
там е -> 0 возникают вычислительные трудности, для устранения которых ис-
пользуются преобразованные параметры. Например, вместо элементов е, <оп
используются элементы: 9 = есово>п» Jt = esino>n [3.1].
3.5. Уравнения невозмущенного движения НС
в инерциальной системе координат
с использованием орбитальных элементов
Запишем уравнения движения спутника в геоцентрической прямоуголь-
ной системе координат OXgtgZg, переходя от орбитальных координат (г, 9) к
инерциальным. Переход осуществляется тремя последовательными поворотами
орбитальной системы координат на углы <вп, i, П. В результате такого пере-
хода получаются уравнения:
х0 = rjcos(9 +<on)cosQ -sin(3 + <on)sinQcosi|;
Уд = r|cos(9 +<on)sinQ + sin(9 + <on)cosQcosij; Zg = rsin(3 +<Bn)sini, (3.13)
где г определяется уравнением (3.6).
В эти уравнения входят пять постоянных геометрических параметров
(эксцентриситет е, фокальный параметр р, углы <вп, i, Q), не меняющихся
при движении спутника по орбите и характеризующих формуй размеры эл-
липтической орбиты и ее ориентацию в пространстве. Текущее положение
спутника на орбите, как отмечалось выше, характеризуется шестым парамет-
ром — истинной аномалией 9. Из (3.13) видно, что можно ввести другой
обобщенный параметр, характеризующий положение спутника на орбите,
и = о>П +3, который называют аргументом широты спутника. Он измеряется
от восходящего узла (по аналогии с углом перигея <оп).
Дифференцируя (3.13) по времени, получаем:
= 1% = V/g ~ vu (sin(o> п + 9) cos П + cos(o> п + 9) sin Q cos i) ;
~~~ = Vyo =V,g^-- Vu(sin(w n + 3) sin Q - cos(o> n + 3) cos Q cos i); (3.14)
38
Х^л^а^а^З^Т^аекто^ное^дмжение^нагагеционных^сн^таиков.
— = Г7„ = — + Уи cosfcon + э)Sin <,
20 Ф г и \ 11 / ’
где И =-21= /Й} +Г2 +И2 = Jp/p е sin & — радиальная составляющая вектора
и и» ¥ А0 Л0 Ч)
i
V скорости спутника (рис. 3.5); Vu = г— = 7й/р(1 + ecosS) — трансверсальная
составляющая вектора V скорости спутника (рис. 3.5).
Ориентация орбитальной плоскости НС в инерциальном пространстве
определяется начальными условиями орбитального полета. Начальная точка
орбиты НС и вектор скорости НС (как в начальной точке, так и в любой дру-
гой) должны лежать в этой плоскости. Форма орбиты определяется значением
и направлением скорости, сообщаемой НС в начальной точке его свободного
полета. Для движения НС по круговой орбите высотой ЯА относительно Зем-
ли необходимо, чтобы начальная скорость Кц0 соответствовала круговой ско-
рости Ккр на этой высоте и была направлена перпендикулярно радиусу-
вектору г. Можно показать (приравняв возникающую центробежную силу и
силу тяготения), что Икр = -Jh/p , где r.= R3
При гипотетической орбите с г = Л3 значение Икр = Kj = 28500 км/ч =
=7,91 км/с — первая космическая скорость.
Если высота орбиты ЯА = 1000 км, что соответствует СРНС типов
“Транзит”, “Цикада”, то Икр = 7,35 км/с; при ЯА=19 100 км (СРНС ГЛО-
НАСС, GPS) — Икр ~ 3,95 км/с; при ЯА =35 809 км (геостационарные НС)
— Ккр я 3,076 км/с .
При использовании круговых орбит НС движется с постоянной угловой
скоростью, что существенно упрощает расчеты и прогнозирование его коорди-
нат в КИК и в бортовых приемоиндикаторах СРНС.
Для создания эллиптической орбиты необходимо Ккр < Vun < Иц, где
® l,41Pi= 40 300 км/ч = 11,2 км/с — вторая космическая скорость. В этом
случае, в зависимости от координат начальной точки и от угла между VUH и
г эллипс может занимать в орбитальной плоскости разное положение относи-
тельно Земли.
Скорость движения НС по эллиптической орбите в общем случае [3.1]
^.эл = 7и(2/'' - 1/а) Видно, что скорость максимальна в перигее и минимальна
в апогее.
При движении по эллиптической орбите угловая скорость движения НС
меняется во времени, что усложняет расчеты по прогнозированию движения.
Однако движение по таким орбитам более экономично по энергетическим за-
3.5. Уравнения невозмущенного движения ЯС (с орбитальными элементами) 39
тратам и позволяет при выборе соответствующих параметров орбиты (i, rA,/ti)
(3.7) обеспечить почти круглосуточное использование НС для навигационных
определений в заданном районе.
Так, например, НС с сильно вытянутыми эллиптическими орбитами
предусмотрено использовать при формировании региональных СРНС, в кото-
рых апогей орбиты располагается над заданным районом. При этом НС будет
находиться максимальное время над этим районом. Но в бортовых приемоин-
дикаторах СРНС в данном случае могут возникать сложности в связи с необ-
ходимостью учета большого динамического диапазона сигналов НС и значи-
тельной неравномерности параметров орбитального движения. Кроме того,
эллиптические орбиты характеризуются меньшей стабильностью.
При рассмотрении движения НС на эллиптических орбитах часто опери-
руют таким параметром, как секториальная скорость Иск, под которой пони-
мают площадь сектора эллипса, описываемого радиусом-вектором НС в еди-
ницу времени.
Из решения уравнений (3.7) следует, что Кск — величина постоянная для
любой точки орбиты:
1 2 1
— г --- = —
2 Л 2
Три -
Это соответствует второму закону Кеплера. Время полного оборота ра-
диус-вектора НС
r = S.M/Vn = 2r^UTv-^ (3.15)
где 5эл = nab — площадь эллипса.
Часто используются более простые соотношения для круговой и эллип-
тической орбит |1.6|:
Т = 84,4,/(7л/Лз)3 ; Т = 1,6586 10 4а3/2 .
где а, гА, Л3 выражены в км; Г — в мин.
Период обращения НС, вычисленный но (3.15), называют сидерическим
или звездным и равен временному интервалу между двумя последовательными
прохождениями НС одной и той же точки орбиты, например перигея. Вполне
очевидно, что интервал времени между двумя последовательными прохожде-
ниями НС одного и того же меридиана, называемый синодическим периодом.
вследствие вращения Земли несколько больше (при совпадении направления
вращения НС и Земли).
40
Гл а в а 3. Траекторное движение навигационных спутников
Период обращения Т можно получить также из соотношения
где и oj — большие полуоси орбит двух НС; 7\ и 7’j — периоды их об-
ращения.
Это соответствует третьему закону Кеплера.
В зависимости от периода обращения НС подразделяют на суточные при
Т = Т3 (звездные сутки или звездный период обращения Земли вокруг своей
оси) и на синхронные — при периоде Т , кратном звездным суткам. 3 свою
очередь, суточные НС, орбитальная плоскость которых лежит в плоскости эк-
ватора, называют геостационарными, так как они неподвижны относительно
одной из точек экватора.
В СРНС “Транзит”, “Цикада” период обращения НС Т=105 мин; в
СРНС ГЛОНАСС [3.7] Г = 11,2 ч ; в GPS Г =12 ч ; у геостационарных НС
Г =23 ч 56 мин 04,1 с [1.5]. Видно, что синхронный спутник системы GPS
один раз в сутки проходит над одной и той же точкой поверхности Земли.
3.6. Общая характеристика возмущенного движения НС
В реальных условиях траекторного движения НС на него действуют кро-
ме основной, центральной силы притяжения Земли, разнообразные дополни-
тельные возмущающие силы. И хотя они малы по сравнению с основной, их
длительное воздействие приводит к отклонениям (возмущениям) реальной ор-
биты от расчетной кеплеровой, которыми при построении спутниковых нави-
гационных систем нельзя пренебречь.
Основными источниками возмущения орбит НС являются [3.5, 3.7, 3.8]:
возмущения гравитационного поля вследствие несферичности Земли и
неравномерности распределения ее массы,
притяжение со стороны Луны и Солнца,
сопротивление среды при движении НС,
давление светового излучения Солнца и прочие физические факторы.
Расчеты показывают [3.5], что возмущенная орбита НС в общем случае
не будет эллиптической, и истинные параметры орбитального движения НС
отличаются от параметров, рассчитанных по формулам невозмущенного (кеп-
лерова) движения.
При анализе возмущенного движения НС принято считать, что НС в ка-
ждый момент времени находится на той невозмущенной (эллиптической) ор-
бите, которая рассчитана с учетом прекращения в этот момент действия воз-
мущающих сил. Это означает, что в отличие от невозмущенного движения
элементы возмущенной орбиты НС непостоянны. Их изменение происходит
непрерывно, но каждому моменту времени и каждой точке возмущенной тра-
ектории соответствует своя кеплерова орбита, которую называют оскулирую-
3.6. Общая характеристика еозл<уи4еииого движения НС^41
щей, а ее орбитальные элементы — оскулирующими. Тогда истинную траекто-
рию НС можно представить в виде огибающей оскулирующих траекторий, по-
строенных для различных моментов времени. Положение НС в пространстве
может быть определено в любой момент времени при решении известных
уравнений для орбитальных элементов i(t), шп(г), ^(0, • При этом
можно исследовать влияние на траекторию НС приведенных возмущающих
факторов, а также различных моделей конфигурации Земли.
Все наблюдаемые возмущения орбит разделяют на вековые и периодиче-
ские. Вековые приводят к непрерывным медленным изменениям элементов
орбиты НС. Периодические повторяются через определенный интервал време-
ни, в зависимости от значения которого их подразделяют на коротко- и долго-
периодические. Они обусловлены периодическим характером траекторного
движения и аппроксимацией возмущающих факторов (аномалий поля тяготе-
ния, конфигурации Земли).
Детальное изучение возмущений, вызываемых нецентральностью поля
тяготения Земли, показало, что при определенных допущениях вековые изме-
нения орбитальных элементов i, р, е отсутствуют, а периодические изменения
к[м присущи.
За один оборот НС значения параметров i и р совершают несколько
колебаний, причем амплитуда i максимальна при i = 4S“ или < = 135°, а для
полярной и экваториальной орбит периодическими возмущениями можно
пренебречь. В свою очередь, амплитуда р максимальна для полярных орбит и
равна нулю для экваториальных. Периодические возмущения параметра е но-
сят сложный гармонический характер. У параметра а могут наблюдаться не-
большие вековые уходы, пропорциональные уходу перигея, а также периоди-
ческие возмущения. Следует отметить, что изменения большой полуоси орби-
ты не зависят от ее наклонения.
Орбитальная плоскость и сама орбита вращаются (прецессируют) в
инерциальном пространстве. Вековой уход долготы восходящего узла за один
оборот НС АО = - 2я ecos/Дц/г) , где с = 2,634 Ю25 м5/с — коэффициент, учи-
тывающий конфигурацию Земли.
Из приведенного соотношения следует, что скорость прецессии орбиты
зависит от наклонения i и фокального параметра р , поэтому в первом при-
ближении вековой уход АЙ у полярных орбит отсутствует, а у экваториаль-
ных максимален (при р = const ). При прямом движении НС ^ <90°) восходя-
щий узел перемещается к западу (в сторону уменьшения О ), при обратном
(< > 90°) — к востоку (в сторону увеличения О ).
Периодическими возмущениями величины О можно пренебречь.
Вековой уход аргумента перигея за один оборот НС составляет в первом
приближении А«=ле(5соя2/ 1)/(цр2).
42 ____Г л а в a 3. Траекторноедвижение навигационных спутников
з ~~ Г > •/" ’ ”
Вековое движение перигея при /=0 и 180° максимально, а для построе-
ния стабильных (в орбитальной плоскости) орбит можно выбирать значения
I) = 63°29’06" или <2 = 116°35'54" , которые обеспечивают А® ® 0 . Если i < q
или 1 > i2, то перигей прецессирует в направлении движения НС, а при
< 1 < i2 — навстречу движения НС.
Наиболее существенные периодические возмущения аргумента перигея
имеют такой же характер, как и аналогичные возмущения эксцентриситета е
(гармонически с периодом, равным периоду обращения НС, и периодом, втрое
меньшим), но со сдвигом по фазе на 90° .
Изменения периода обращения НС характеризуется драконическим пе-
риодом Тдр, определяемым как время полета НС от экватора до экватора. При
наклонении орбиты i = 60 и 120° имеем Гдр = Т .
Описанные возмущения орбитальных элементов приводят к возмущени-
ям радиуса-вектора НС и, следовательно, высоты полета. Эти возмущения но-
сят такой характер, что высота НС как бы отслеживает изменения размеров
Земли: над экватором высота увеличивается, а над полюсом уменьшается.
Обобщая приведенные результаты анализа влияния нецентральности по-
ля тяготения Земли, можно констатировать следующее.
Полярные орбиты отличаются стабильностью орбитальной плоскости
(отсутствуют возмущения О , 1 ) й сравнительно большими йзмёнёниямИ фЗр-
мы орбиты и ее ориентации в орбитальной плоскости.
Экваториальные орбиты отличаются сравнительно стабильной формой
орбиты, но положение ее в орбитальной плоскости и самой плоскости может
быть нестабильным.
Наклонные орбиты, характерные для средневысотных СРНС ГЛОНАСС,
GPS (1»60°), отличаются относительной стабильностью параметров — аргу-
мента перигея, характеризуюшего положение орбиты в плоскости движения, и
периода обращения.
Исследования возмущений (вековых и долгопериодических) почти кру-
говых орбит НС с периодом обращения, равным приблизительно 12 ч (две-
надцатичасовые НС СРНС ГЛОНАСС, GPS), показали, что периоды колеба-
ний элементов I , О могут составлять десятки и сотни лет, в зависимости от
начальных значений iq, Qq; причем для i0, не слишком близких к 0 и 90°,
амплитуда долгопериодических колебаний составляет 1 ... 2°. Для них влияние
сжатия Земли на возмущения примерно в 10 раз больше влияния Луны и
Солнца.
Кратко охарактеризуем влияние других возмущающих сил.
При высотах полета НС более 1000 км (например, средневысотные
СРНС ГЛОНАСС, GPS) эффект атмосферного торможения невелик и им мож-
но пренебречь. 4
3,7. Лгиолиженныеу/.авнения возмущенного иаижепия
Известные данный о влиянии лДгы и солнца эволкдию ор.йт НС
свидетельствуют о том, что возмущающее ускорение из-за притяжения Луны
примерно в 2 раза больше влияния Солнца. Для средневысотных СРНС воз-
мущения из-за влияния Луны и Солнца превосходят соответствующие возму-
щения, обусловленные аномалиями силы тяжести Земли.
Для расчета возмущенных пространственных координат НС и их произ-
водных аппаратура потребителя получает от НС периодически обновляемые
оскулирующие элементы и поправки к ним. Такая процедура соответствует
предъявляемым требованиям к точности и простоте расчетов в приемоиндика-
торах СРНС.
3.7. Приближенные уравнения возмущенного движения
в геоцентрической подвижной системе координат
В геоцентрической подвижной системе координат ПЗ-90, жестко связан-
ной с Землей, определяются координаты потребителей. Для этого необходимо
иметь координаты и составляющие скоростей НС в этой же системе коорди-
нат. Известно [3.6], что уравнения движения материальной точки в инерци-
альной и подвижной системах координат отличаются вследствие различного
нахождения производной по времени.
Положение некоторой точки в пространстве, например центра масс
спутникА,_о5тределяе_т.ся геоцентрическим радиусом - вектором г . Компонента-
ми этого вектора в геоцентрических системах координат OXqYqZq и OXYZ слу-
жат координаты его конца, которые соответственно равны x0,y0,zo и x,y,z
Координаты конца радиус-вектора г в указанных системах координат описы-
ваются различными функциями.
Производная по времени радиуса-вектора г в некоторой геоцентриче-
ской системе координат определяется как вектор (Vro или Уг в рассматривае-
мых системах координат), проекции которого на оси этой системы координат
равны производным от проекции самого радиуса вектора на те же оси
[dx0 dy0 dzo ] \dx dy dz\ .
( = <—t2-,—и Vr =<-;-• соответственно).
1 dt dt dt J [ dt dt dt j
Производную, взятую в инерциальной системе координат, называют пол-
ной, в других системах координат — локальной. Полная производная г по вре-
мени определяет вектор Vr(j абсолютной скорости в инерциальной системе ко-
ординат. Локальная производная определяет вектор относительной скорости в
подвижной системе координат, например Уг в системе координат OXYZ.
Связь между полной dr/dt и локальной dr/dt производными определяет-
ся формулой [3.6]
dr dr
л = л+ю'"хг- <3-,6)
44
Глава). Траекторное движение навигационных спутников
где ®т — вектор абсолютной угловой скорости подвижной системы координат
относительно инерциальной; х — знак операции векторного умножения. Вы-
ражение (3.16) является общим и справедливо для любого вектора.
В соответствии с (3.16) для описания движения в геоцентрической под-
вижной системе координат OXYZ необходимо в уравнениях движения (3.3),
записанных для инерциальной системы координат, перейти от полной второй
производной cPr/dt1 к локальной производной. Применив дважды (3.16), по-
лучим
^Г = “^Г + 2®т xVr+<om х(®т хг). (3.17)
Первое слагаемое в правой части уравнения определяет относительное
ускорение, т. е. ускорение в подвижной системе координат, второе слагаемое
— кориолисово ускорение, третье — переносное ускорение от вращательного
движения подвижной системы координат относительно инерциальной.
Так как система координат OXYZ жестко связана с Землей и вращается
вместе с ней относительно оси вращения OZ, то вектор ®т для нее имеет
компоненты {О, 0, ®з}. ....... __
ч
С учетом (3.17) уравнение движения материальной точки (спутника)
(3.3) в системе координат OXYZ, связанной с Землей, принимает вид
-^-+2eB х V,+ея х(шв хг) =—, (3.18)
где F — вектор внешних сил, действующих на НС.
При рассмотрении невозмущенного движения НС внешней силой явля-
ется центральная сила притяжения Земли (3.4).
Уравнения возмущенного движения НС, приводимые ниже, полученные
на основе (3.18) и используемые при расчетах в СРНС ГЛОНАСС, кроме цен-
тральной силы притяжения Земли учитывают дополнительную силу, обуслов-
ленную полярным сжатием и характеризуемую гармоникой , а также лун-
но-солнечные гравитационные возмущения:
_ и • с?? — V -- - V •
dt х’ dt dt~ ’
rfP", Ц 3 рв2 f 5z21 2 о rz
—rL = —TX+^C^-f-x 1-^- +®|x + 2®3Ky +хлс;
ш r3 2 г \ г )
= + у ле; (3.19)
«• г 2. ГЭ \ < J
3.8. Основные навигационные характеристику НС
45
л
(, 5z2^ -
гр—2* +?лс>
где ае — экваториальный радиус Земли.
При интегрировании уравнений (3.19) лунно-солнечные гравитационные
ускорения {хлс, улс, глс} полагаются постоянными величинами на интервалах
±15 мин.
При дальнейшем изложении знак у производных по времени в под-
вижной системе координат будет опускаться.
3.8. Основные навигационные характеристики НС
К основным навигационным характеристикам НС относят зону обзора,
зону видимости, продолжительность наблюдения, орбитальную конфигурацию
сети НС и др. На чертеже (рис. 3.6) поясняются основные определения.
Зона обзора НС представляет собой участок земной поверхности, на ко-
тором можно осуществлять наблюдение за НС, прием его сигналов. Центром
зоны обзора является подспутниковая точка Оз, называемая географическим
местом спутника (ГМС).
Координаты ГМС (географические широта и долгота) могут быть рассчи-
таны по формулам:
<р = arcsin(sinu sin»); X = Q-Sr +arctg(tg« cos/) + Qi,
где i, и, Q — орбитальные элементы НС; 5r — гринвичское звездное время;
Q = t&l/T — угловая скорость прецессии узла орбиты. Зона обзора ограничена
линией истинного горизонта в точке НС, поэтому ее размер зависит от вы-
соты НС ( Яд ). Размер зоны обзора ха-
рактеризуется углом ртах [град] или
соответствующей ему дугой ЛО3, кото-
рая называется радиусом зоны обзора
Ло [км]. Из рис. 3.6 видно, что
Ртах = arccos [/г3/(Я3 + ЯА)];
Л) = ЛзРт^/57,3 = HUJP^ . (3.20)
Бортовые приемоиндикаторы
СРНС обеспечивают заданную точность
измерений в зоне обзора, ограниченной
радиогоризонтом, который поднят для
Рис. 3.6. Зона обзора НС
46 Г л а в a 3- Траекторное движение навигационных спутников
пользователя на угол а «5 ... 10® (угол маски). В этом случае зона обзора оп-
ределяется утлом р < Рим , где
Р = arccos [Л3 cosa/(^3 + Я А)] - а .
(3.21)
Площадь зоны обзора 5^ = 2it/l3|l-cos Ртах)- Тогда относительная пло-
щадь обзора 5об/5з = sin2(Pmax/2), гДе *5з = 4лЛj — площадь земного шара.
Для существующих СРНС рассмотренные выше параметры имеют сле-
дующие значения:
“Цикада”, “Транзит” — Ртах “30®, Rq « 3400 км, /S3 и 3,8 % при
ЯА « 1000 км, а = 10® ;
ГЛОНАСС (GPS) - Ртах «75,52®, Rq « 8400 км, Яоб/^з » 30 % при
ЯА «19 100 км, а = 10®.
При увеличении высоты НС до ЯА «40 000 км радиус зоны обзора из-
меняется незначительно (До «9 400 км), а затраты на формйровайие такой ор-
биты возрастают существенно.
Рассмотренная выше зона обзора соответствует фиксированному момен-
ту времени (мгновенная зона обзора).
У нестационарных НС мгновенная зона обзора, перемещаясь по поверх-
ности Земли, образует зону обзора в виде полосы шириной 2Яо- Ее осью яв-
ляется совокупность ГМС — трасса НС. Заметим, что трасса НС не поднима-
ется выше географической широты Фтах =' •
Установим условия видимости НС для наблюдателя, расположенного в
точке О3, лежащей на трассе НС (рис. 3.7). Область небосвода СС, в которой
Рис. 3.7. Время нахождения НС
в зоне видимости
НС наблюдается из точки О3 от момента
восхода ти над горизонтом до момента за-
хода т , называют зоной видимости
тх
(геометрической зоной видимости), для ко-
торой справедливы соотношения (3.20),
(3.21). Из рис. 3.6 видно, что максимальный
угловой радиус зоны видимости (дуга Л'С')
А'С' = Ртах = arccos [7?з/(я3 + ЯА)].
С учетом радиогоризонта угловой ра-
5
) > > > > , „
3.8. Основные нависйционнь.. харак. Jpucmu. )НС
диус зоны обзора уменьшается 0 = arccos [Л3 cosa/(/?3 + Яд)] ~ а • Здесь угол а
называют минимально допустимой высотой.
Продолжительность сеанса связи с НС (в пределах видимости НС)
определяется разностью (чвщ-^щ) и зависит от угла 0 (т. е. от высоты полета
НС или периода его обращения Т).
Для круговой орбиты /вдд = 20/v = = 70/я, где v = 'lxlT— угловая ско-
рость обращения спутника.
Для СРНС “Цикада”,“Транзит” получаем /щщ = 18 мин при Яд =1000 км,
а = 0°, а для СРНС ГЛОНАСС /«щ « 300 мин .
Очевидно, что если потребитель находится в стороне от трассы НС, то
продолжительность наблюдения спутника уменьшается.
Навигационные алгоритмы, реализованные в бортовых приемоиндикато-
рах современных СРНС, обычно ориентированы на прием сигналов от не-
скольких НС одновременно. Наблюдение в любой точке рабочей зоны СРНС
одновременно нескольких НС обеспечивается путем оптимального выбора
стабильной пространственно-временной структуры (конфигурации) сети НС
— числа, ориентации и формы орбит; числа НС на каждой из них; взаимного
расположения орбит й спутников на них. Обычно число НС в сети превышает
•минимально необходимое за счет резервных НС.
Литература
3.1. Иванов Н. М. и др. Баллистика и навигация космических аппаратов. — М.:
Машиностроение, 1986.
3.2. Охоцимский Д. Е., Сихарулидзе Ю. Г. Основы механики космического полета.
— М.: Наука, 1990.
3.3. Аппаратура радионавигационных систем ГЛОНАСС и GPS. Системы коорди-
нат. Методы перевычислений координат определяемых точек// Государственный стандарт
РФ (проект), Госстандарт России, 1997.
3.4. Попович П. Р., Скребушевский Б. С. Баллистическое проектирование космиче-
ских систем. — М.: Машиностроение, 1987.
3.5. Вашковъяк М. А. Об эволюции почти круговых орбит 12-часовых ИСЗ// Кос-
мические исследования, 1985, т. XXIII, вып. 1, с. 3—16.
3.6. Бромберг П. В. Теория инерциальных систем навигации. — М.: Наука, 1979.
3.7. Бородовицина Т. В. и др. Структура возмущений орбитального движения на-
вигационных ИСЗ типа НАВСТАР// Космические исследования, 1985, т. ХХШ, вып. 5,
с. 713-719.
3.8. Волосов П. С. и др. Судовые комплексы спутниковой навигации. —Л.: Судо-
строение, 1986.
3.9. Инженерный справочник по космической технике/ Под ред. А. В. Солодова.
— М.: Воениздат, 1969.
3.10. Основы теории полета и элементы проектирования спутников Земли/ Под
ред. М. К. Тихонравова. — М.: Машиностроение, 1974.
3.11. Субботин М. Ф. Введение в теоретическую астрономию. — М.: Наука, 1968.
48
Глава 4
Методы решения навигационных задач
4.1. Общие определения
Основным содержанием навигационной задачи (НЗ) в СРНС является
определение пространственно-временных координат потребителя, а также со-
ставляющих его скорости 11.4, 4.1], поэтому в результате решения навигаци-
онной задачи должен быть определен расширенный вектор состояния потре-
бителя П, который в инерциальной системе координат можно представить в
виде II = |х у z 1Г х у г|т • Элементами данного вектора служат пространствен-
ные координаты (х, у, г) потребителя, временная поправка V шкалы времени
потребителя относительно системной ШВ, а также составляющие вектора ско-
рости (х, у, г).
Элементы вектора потребителя недоступны непосредственному измере-
нию с помощью радиосредств. У принятого радиосигнала могут измеряться те
или другие его параметры, например задержка или доплеровское смещение
частоты. Измеряемый в интересах навигации параметр радиосигнала называют
радионавигационным (РНП), а соответствующий ему геометрический параметр
— навигационным (НП) [4.1], поэтому задержка сигнала т и его доплеровское
смещение частоты /ДО11 являются радионавигационными параметрами, а соот-
ветствующие им дальность до объекта Д и радиальная скорость сближения
объектов Ир служат навигационными параметрами. Связь между этими пара-
метрами дается соотношениями:
Д ~ ст, Ир - /цен X.,
где с — скорость света; X. — длина волны излучаемого НС сигнала.
Геометрическое место точек пространства с одинаковым значением на
вигационного параметра называют поверхностью положения 14.3]. Пересечение
двух поверхностей положения определяет линию положения — геометрическое
место точек пространства, имеющих два определенных значения двух навига-
ционных параметров. Местоположение определяется координатами точки пе-
ресечения трех поверхностей положения или двух линий положения. В ряде
случаев (из-за нелинейности) две линии положения могут пересекаться в двух
точках. При этом однозначно найти местоположение можно, только используя
дополнительную поверхность положения или иную информацию о местополо-
жении объекта.
4.2. Дальномерный метод
49
Для решения навигационной задачи, т. е. для нахождения вектора потре-
бителя П, используют функциональную связь между навигационными пара-
метрами и компонентами вектора потребителя. Соответствующие функцио-
нальные зависимости принято называть навигационными функциями. Конкрет-
ный вид навигационных функций обусловлен многими факторами: видом НП,
характером движения НС и потребителя, выбранной системой координат и т.д.
Навигационные функции для пространственных координат потребителя
можно определить с помощью различных разновидностей дальномерных, раз-
ностно-дальномерных, угломерных методов и их комбинаций. Для получения
навигационных функций, включающих составляющие вектора скорости потре-
бителя, используют радиально-скоростные методы.
4.2. Дальномерный метод
Наиболее простой дальномерный метод навигационных определений
[4.1—4.7] основан на пассивных (беззапросных) измерениях дальности Д: ме-
жду /-м НС и потребителем. В этом методе навигационным параметром явля-
ется дальность Д1, а поверхностью положения — сфера с радиусом Д1 и цен-
тром, расположенным в центре масс 1-го НС. Уравнение сферы
Л = [(*/ - х}2 + (у,- - у)2 + (it - z)2] '
(4.1)
Здесь*,-, у(, Z, — известные на момент измерения координаты Z-ro НС (с уче-
том его перемещения за время распространения сигнала); х, у, z — координа-
ты потребителя.
Местоположение потребителя, т. е. координатых, у, z . определяют как
координаты точки пересечения трех поверхностей положения, другими слова-
ми трех сфер. Поэтому для реализации дальномерного метода необходимо из-
мерить дальности (4.1) до трех НС, т. е. i = 1,3.
Таким образом, для дальномерного метода навигационная функция
представляет собой систему из трех уравнений вида (4 I). Ввиду нелинейности
такой системы уравнений возникает проблема неоднозначности определения
координат потребителя, устраняемая с помощью известной потребителю до-
полнительной информации (ориентировочные координаты потребителя, его
радиальная скорость и т. д.).
В (4.1) неявно подразумевается, что все величины должны быть взяты в
один и тот же момент времени. Однако координаты спутника привязаны к
бортовой шкале времени, а потребитель измеряет задержку сигнала и опреде-
ляет свои координаты в своей шкале времени (ШВП). Если шкалы времени
БШВ и ШВП идеально синхронизированы, то проблем не возникает. При на-
личии расхождения Г шкал времени возникает смешение Д’ = ct' измеренной
50
Г л а в a 4. Методы решения навигационных задач
дальности относительно истинной и точность определения местоположения
потребителя падает, поэтому недостатком метода является необходимость
очень точной привязки шкал времени НС и потребителя. Уменьшить влияние
этого фактора можно, установив у потребителя высокостабильный эталон вре-
мени (частоты) и периодически проводя его калибровку по БШВ. Однако вы-
сокостабильные эталоны времени достаточно дороги и не могут быть исполь-
зованы у массового потребителя. Создание относительно дешевых высокоста-
бильных эталонов времени (частоты) — трудная техническая проблема, поэто-
му в настоящее время более широко применяют псевдодальномерный метод.
4.3. Псевдодальномерный метод
Под псевдолальностью от i-ro НС до потребителя понимают измеренную
дальность Дизм/ до этого НС, отличающуюся от истинной дальности Д/ на
неизвестную, но постоянную за время определения навигационных параметров
величину Д' [4.1, 4,5). Таким образом, для псевдодальности до /-го НС мож-
но записать
Г 2 2 ,-|1/2
Диэм/= Д/+ Д'= [(*/-*) +(>'/-1') +(?/-z)j +Д'.
(4.2)
В псевдодальномерных методах (ПДМ), основанных на измерениях псев-
додальностей, в качестве навигационного параметра выступает ДИЗм/- Поверх-
ностью положения по-прежнему является сфера с центром в точке центра
масс НС, но радиус этой сферы изменен на неизвестную величину Д'. Изме-
рение псевдодальностей до трех НС приводит к системе трех уравнений с че-
тырьмя неизвестными (х,у,г,Д'). В решении этой системы уравнений возни-
кает неопределенный параметр, и для устранения возникшей неопределенно-
сти необходимо провести дополнительное измерение, т. е. измерить псевдо-
дальность до четвертого спутника. Полученная таким образом система четырех
уравнений имеет точное решение, и, следовательно, местоположение потреби-
теля при измерениях псевдодальностей определяется как точка пересечения
четырех поверхностей положения.
Необходимость нахождения в зоне видимости четырех НС предъявляет
достаточно жесткие требования к структуре сети НС, которые выполняются
только в среднеорбитальных СРНС. Параметры же орбитальной группировки
НС низкоорбитальных СРНС (высота орбит, число спутников, их расстановка)
обычно обеспечивают периодическую видимость в зоне потребителя 1 ... 2 НС,
поэтому определение местоположения в этих СРНС может осуществляться не
в реальном времени, а лишь после проведения последовательных (обычно до-
плеровских) измерений нескольких линий положения по сигналам одного НС.
4.4. Разностно-дальномерный метод
Псевдодальномерный метод не накладывает жестких ограничений на
значение погрешности Д' = ct' (погрешности временной шкалы) и позволяет
одновременно с определением местоположения вычислять отклонение шкалы
времени потребителя.
4.4. Разностно-дальномерный метод
Метод основан на измерении разности дальностей от потребителя до од-
ного или нескольких НС. По своей сути этот метод аналогичен псевдодально-
мерному, так как его целесообразно использовать только при наличии в даль-
номерных измерениях неизвестных сдвигов Д', т.е. когда фактически прово-
дятся измерения псевдодальностей. Разностно-дальномерный метод (РДМ) ис-
пользует три разности &Ду = Дизм/ - Днзм j Д° четырех НС, так как при посто-
янстве Д' за время навигационных определений разности псевдодальностей
равны разностям истинных дальностей, для определения которых требуется
лишь три независимых уравнения. Навигационным параметром является !\Ду .
Поверхности положения определяются из условия &Ду = const и представляют
собой поверхности двухполостного гиперболоида вращения, фокусами послед-
него являются координаты опорных точек i и j (центров масс г- и /-го НС).
Расстояние между этими опорными точками называют базой измерительной
системы. Если расстояния от опорных точек (НС) до потребителя велики по
сравнению с размерами базы, то гиперболоид вращения в окрестности точки
потребителя практически совпадает со своей асимптотой — конусом, вершина
которого совпадает с серединой базы.
Точность определения координат потребителя, как будет показано в гл.6,
совпадает с точностью определения этих координат псевдодальномерным
методом.
Недостатком разностно-дальномерного метода является то, что в нем не
может быть измерено смещение Д' , а следовательно, и смещение шкалы вре-
мени потребителя.
4.5. Радиально-скоростной (доплеровский) метод
Метод основан на измерении трех радиальных скоростей перемещения
потребителя относительно трех НС. Физическойвюсновой радиально-скорост-
ного метода (РСМ) является зависимость радиальной скорости точки относи-
тельно НС от координат и относительно скорости НС. Дифференцируя (4.1)
по времени, получаем
Л = [(*/ - *)(*/ - *) + (л- - ’ $]1Д1 (4-3)
52 Г Л а в a 4. Методы реисиид навигацирцдых мдич
Здесь компоненты {(х( -x),(yf -y),(z( -z)} характеризуют вектор относительной
скорости; Д[ — относительные координаты потребителя.
Из (4.3) следует, что для определения компонент (x,y,z) вектора скоро-
сти необходимо знать: векторы координат Х( = {xz, ylt Zi}m скорости
Уде/ = {*/, У1> Z/} трех (/ = 1,3) НС, а также координаты потребителя {x,y,z}.
Последние можно получить, если измерить радиальные скорости Д/ в течение
некоторого времени Д/, а затем вычислить интеграл
/+д/
Nt = f Д,(/)Л = + Д/) - Д,(/) . (4.4)
t
В результате интегрирования определяются “новые эквивалентные” из-
мерения Nt, соответствующие разностно-дальномерному методу с той лишь
разницей, что разности дальностей формируются для одного и того же НС, но
в различные моменты времени.
Действительно, если за время Д/ перемещением потребителя можно
пренебречь, то из (4.4)
------------------------------------------------------------------------ - »
= {(*/(' + М - х)2 + Ы1 + М - у)2 + (?/(' + М - z)2}Z -
- {(*/(') - х)2 + (tt(') - у? + (z/W - z)2} ' (4-5)
Отсюда видно, что, зная координаты / = 1,3 НС в моменты времени t и
t + Д/ и проведя измерения Nt , можно определить координаты точки потре-
бителя.
Недостатком данного метода измерения координат потребителя является
невозможность их проведения в реальном масштабе времени. Кроме того, в
средневысотных СРНС реализация РСМ затруднена ввиду медленного измене-
ния радиальной скорости, что приводит к малым значениям разностей в (4.5).
Это обусловило применение РСМ в таких СРНС только для определения со-
ставляющих скорости потребителя.
Другой возможностью получения информации о координатах {х, у, z}
является использование радиально-скоростного метода совместно с одним из
известных (описанных выше) “дальномерных” методов.
Недостатком РСМ при определении скорости потребителя является не-
обходимость наличия высокостабильного эталона частоты, так как любая не-
стабильность частоты приводит к неконтролируемому изменению лоплеров-
4.6. Псевдоррдиально-скорортной метоф 53
ского смещения частоты, а, следовательно, к дополнительным ошибкам изме-
рения составляющих скорости потребителя.
4.6. Псевдорадиально-скоростной метод
Псевдодоплеровский метод (аналогичен псевдодальномерному методу
при определении координат потребителя) позволяет определять вектор скоро-
сти потребителя в присутствии неизвестного смещения частоты сигнала, на-
пример из-за нестабильности эталона частоты. При наличии такого смещения
Д1 выражение для радиальной скорости можно представить в виде двух сла-
гаемых
А,, д. л - - *> -у) ~ ~ - ЯГ <«)
Для нахождения вектора скорости потребителя Vp = {х, у, z} и поправ-
ки Д[ =Х/УДоп/ необходимо провести измерения по четырем НС и решить
систему четырех уравнений вида (4.6). Для ее решения потребуются знания
дальностей Д( и координат {х, у, z} потребителя. Эта информация может
быть получена, например из псевдодальномерных измерений (4.2).
4.7. Разностно-радиально-скоростной метод
Сущность данного метода заключается в определении трех разностей
ЬДц = Д( - Д) двух радиальных скоростей НС. При этом разности можно вы-
числять относительно одного или относительно различных НС. По существу,
при вычислении разностей могут использоваться и пссвдорадиальные скорости
Дизм/, так как ПРИ таком вычитании компенсируется неизвестное смеще-
ние Д1 ( в предположении, что это смещение одинаковое для различных спут-
ников). Навигационные параметры
[(х, - х)(х, - х) 4. (у, - y\yt - у) + (Zl - z)(zf - г)]
ДД- = 1----------------------------------1 _
Д/ Г
[Ь - х)(ху - х) + (уу - y\yj - у) + (zj - z)(z7 - z)]
Д)
Поверхности положения представляют собой поверхности тела враще-
ния, фокусами которого являются координаты центров масс i- и у-го НС.
54 Г л а в a 4. Методы решения навигационных зтджч
К
Так же как и для “дальномерных” методов, точность определения со-
ставляющих вектора скорости в разностно-радиально-скоростном методе сов-
падает с точностью определения тех же составляющих в псевдорадиально-
скоростном методе (см. гл. 6).
Достоинством разностно-радиально-скоростного метода является его
нечувствительность к нестабильностям эталонов частоты и другим неконтро-
лируемым смещениям частоты, а его недостатком — невозможность оценки
нестабильности эталонов частоты.
4.8. Комбинированные методы
Помимо перечисленных основных методов определения компонент век-
тора потребителя П возможны комбинированные методы, использующие кро-
ме СРНС дополнительные измерители координат, имеющиеся у потребителя.
Так, в дальномерном методе при наличии у потребителя измерителя высоты
Н можно вместо измерений трех дальностей до НС ограничиться измерением
двух дальностей. В этом случае навигационная функция будет включать два
уравнения вида (4.1), а третье необходимое уравнение дает измеритель высоты:
(Я3 + Н)2 =x2+y2+z2-
' ” ..................... /
Другой аспект использования комбинированных методов заключается в
замене совокупности одновременных измерений на комбинацию одновремен-
ных и последовательных измерений или на совокупность только последова-
тельных измерений, например определение координат потребителя разностно-
скоростным методом (4.5). В качестве другого примера можно привести псев-
додальномерный метод, который можно реализовать, заменив четыре одновре-
менных измерения по четырем НС на два последовательных измерения по
двум НС или на четыре последовательных измерений до одного НС.
Аналогичные комбинации возможны и для других методов.
4.9. Определение ориентации с помощью СРНС
До сих пор рассматривалась классическая задача определения координат
и вектора скорости потребителя. С развитием СРНС и совершенствованием
методов и аппаратуры приема и извлечения информации из радиосигналов
возникают потребности и возможности решения более сложных задач. Одной
из таких задач является определение ориентации потребителя (летательного
аппарата, морского судна или иного протяженного объекта). Решение этой
задачи может заключаться в следующем (4.8].
В двух точках потребителя (двух точках палубы корабля) А и В, располо-
женных на расстоянии d одна от другой (рис. 4.1), устанавливают два прием-
ника сигналов СРНС. Пространственная ориентация линии АВ относительно
^.Определение ориентации с помолцью СРНС
55
системы координат, связанной
с кораблем (связанной систе-
мы координат) известна. По-
этому знание ориентации ли-
нии АВ эквивалентно знанию
ориентации связанной системы
координат корабля.'
Ориентация линии АВ
определяется направляющими
косинусами cosy*, cosy^,,
cosvj/j, фиксирующими поло-
жение вектора АВ относитель-
но геоцентрической системы
координат OXYZ.
Пусть приемники, распо-
ложенные в точках А к В, из-
меряют дальности Дл и ДЬ\ до навигационного спутника HCi с известными
координатами {xj, yi, Zj}. Тогда разность фаз сигналов, принимаемых в точ-
ках А и В
Aq>! = 2я(Дв1-ДИ)Д,
(4.7)
где X — длина волны излучаемого НС сигнала. Параметр A<pi связан с уг-
лом yi между вектором АВ и вектором SlM, соединяющим середину базы АВ
и навигационный спутник HCj соотношением
cosy! = A<p!X/(2ju/).
(4-8)
С другой стороны угловой параметр Yi связан с направляющими косину-
сами cosx|*x, cos»|/y, cosvj/j выражением
cosyi.= Их! совфх + cos^j, +рг1 cos\pz,
(4.9)
где Pxi, Hii — коэффициенты, определяющиеся известными соотноше-
ниями через координаты HCi и точки М, которые могут быть вычислены на
основе дальномерных измерений До1 и Дм.
Уравнение (4.9) содержит три неизвестных величины — направляющие
косинусы cos^x» cos^y, cos»|/j. Для их определения необходимо иметь три
таких (независимых) уравнения, которые можно получить, например проведя в
58 Г л а в a 5. Радиосигналы и навигационные сообщения в СРНС
j2ntS(t,i)^^-dt = 0 ‘ (5.2)
минимальное значение произведения
ата f = l/(gI 2ap) (5.3)
Следовательно, повышения точности совместных оценок задержки сиг-
нала и доплеровского смещения частоты можно достигнуть за счет увеличения
произведения ар = В, которое получило название база сигнала. При выполне-
нии условия (5.2) справедливо неравенство сф £ 1 / 2 — соотношение неопреде-
ленности. Данное соотношение показывает, что сигнал не может иметь одно-
временно произвольно малую длительность и произвольно малую ширину
спектра. Таким образом, основным требованием к радиосигналам в СРНС яв-
ляется большая база сигнала.
Другое существенное требование — обеспечение мнргостанционного
доступа. При определении навигационных параметров потребитель должен
принимать сигналы от различных спутников, в том числе и одновременно, по-
этому у потребителя должна быть возможность одновременного доступа к сиг-
налам от различных спутников. Проблема многостанционного доступа решает-
ся путем временного, частотного или кодового разделения, сигналов, напри-
мер, в спутниковой навигационной системеОРЗиспользуется кодовое разде-
ление, в СРНС ГЛОНАСС — частотное.
Известно, что при ортогональности сигналов и их точной синхрониза-
ции методы временного, частотного и кодового разделения эквивалентны. Это
объясняет использование различных способов разделения сигналов в совре-
менных СРНС.
5.2. Функция неопределенности и выбор формы сигнала
Потенциальная точность измерений параметров сигнала достигается на
выходе оптимального приемника. В случае приема сигнала на фоне некорре-
лированного гауссовского шума оптимальный приемник представляет собой
согласованный фильтр или коррелятор. Коррелятор — это устройство, вычис-
ляющее корреляцию между входным и опорным сигналами. Отсюда возникает
интерес к корреляционным функциям сигналов.
Под корреляционной функцией р сигнала S(t) понимают [5.1, 5.4]
I «> | со
p(v) = - f S(t)S(t -v)dt = — f С(/Х(/)е*2^ df, (5.4)
-00 —co
где <?(/) — спектр сигнала; * — знак комплексного сопряжения.
Корреляционные функции принято выражать через комплексную ампли-
туду сигнала. Пусть имеем сигнал
5,2. Функция неопределенности и eiyffop Формы сигнала 59
S(t) = /i(/)cos(<i)o/ + <₽(/)) •
где й(/), <₽(/) — амплитудная и фазовая модуляция; <о0 — несущая частота
сигнала.
Комплексная амплитуда такого сигнала
Us(t) = A(/)exp(i<p(/)). (5.5)
Тогда корреляционную функцию (5.4) можно представить в виде
p(v) = 57 ]us(t)u;(t-v)dt.
— со
Здесь v — произвольный временной сдвиг.
Корреляционную функцию (5.4) иногда называют автокорреляционной
функцией, для подчеркивания ее отличия от взаимной корреляционной рю
функции, которая определяется соотношением, аналогичным (5.4), но в каче-
стве второй подынтегральной функции берется функция S^Z-v) любого дру-
-гого сигнала (вместо 5(/- v)), т. е.
1 “
Pbs(v) = 7 f - v)dt. (5.6)
— CO
Если в (5.4) под v понимать задержку сигнала т и ввести доплеровский
сдвиг частоты /доп, то для корреляционной функции можно записать [5.21
ш dt
р(т,/дол) = 57 JUs(tyj^t - т) е- 2^°"' dt = -----------------. (5.7)
-00
Функцию р(т, /До11) называют функцией неопределенности. Эту функцию
широко используют при выборе наилучшей формы сигнала.
Функция неопределенности обладает следующими свойствами:
наибольшее значение функция неопределенности принимает при
т = /доп =0> р(0,0) = 1; (5.8)
объем тела неопределенности р2(т,/доп) не зависит от вида сигнала
f 1р2(т-/доп)^/дОП = 2я. (5.9)
62 Г л а в а 5. Радиосигналы и навигационные сообщения СРНС
Соответствие между начальными фазами ФМн радиосигнала и значения-
ми символов ак и а.к кодовой последовательности:
Начальная фаза сигнала ................ О я
Символ кодовой последовательности:
Спектральные свойства ФМн сигналов определяются спектром импульса
и0(/) и кодовой последовательностью А. Обозначим спектр импульса
Go(o>) = j u0(t)e~‘mtdt. Для прямоугольного импульса
О
, . sinfcoT, / 2) , .
<70(и) = тэ ---—- ехр(- iитэ / 2). '
<отэ /2 ' ’
Спектр комплексной огибающей ФМн сигнала имеет следующий вид
L
б(и) = 1/с(7о(и) ak ехр(- i(k - 1)итэ). (5.12)
*=1
Сумма в правой части (5.12) является спектром кодовой последовательно-
сти А, которую обозначим как Я(и) = £ ak ехр(- i(fc - 1)а>тэ). Поэтому спектр
*=1
ФМн сигнала можно представить в виде произведения
С7(и) = г/сС70(ш)Я(со). (5.13)
Выражение (5.13) удобно тем, что можно сначала отдельно найти спек-
тры б0(и) и //(<>), а затем, перемножив их, — спектр ФМн сигнала. Анализи-
руя различные кодовые последовательности, можно исследовать отдельно их
спектры.
Спектр (5.13) определяет свойства сигнала в частотной области. Во вре-
менной области свойства сигнала описываются корреляционной функцией
р(т) = TF f - 0тэ) Ё^свда«о('-(т~ 0тэ)^ =
= 1 ml
= *Л«/яРо(т-(т“*)тэ)’ <5/,4)
L k~lm=l
где корреляционная функция видеоимпульса
1 w
Ро(т) = — J«o(z -(* - 1)тэ)"о(/ -(w - 0гэ + т)» (5.15)
Тэ -00
для прямоугольного видеоимпульса
5.4. Фазоманипулированные сигналы 63
PoW=-Tf«o(0«oe+^=|i!’,t|/T3) при!т!~Тэ: (516)
о [о при Н > Тэ.
С учетом (5.16) в соотношении (5.14) должно выполняться неравенство
т - (т - k)t3 < тэ . (5.17)
На практике, как правило, рассматривают не всю корреляционную
функцию (5.15), а ее значения при временных сдвигах на целое число дискрет
тэ поэтому введем дискретный параметр ц - 1,2 ... и рассмотрим значения
корреляционной функции в моменты времени т = ртэ. Из условия (5.17) полу-
чаем неравенство р-(т-к)<1, которому удовлетворяет лишь два целочислен-
ных значения р = т- к и ц = т - к + 1. Учитывая, что при первом значении ц
имеем ро = 1, а при втором ро =0, приходим к следующему выражению для
корреляционной функции ФМн сигнала
1
р(1‘) = V • <5-18>
1 Ы -
Таким образом, корреляционная функция ФМн сигнала в дискретных
точках сдвига т = ртэ определяется корреляционными свойствами кодовой по-
следовательности А (5.11).
Выше рассмотрен случай, когда принимается один импульс ФМн сигна-
ла, поэтому все приведенные формулы, в том числе и для корреляционных
функций лучше называть спектрами и корреляционными функциями одиноч-
ного ФМн импульса или, как иногда говорят в литературе, для “апериоди-
ческого режима работы”.
Кроме апериодического режима возможен также периодический режим,
когда сигнал излучается периодически с периодом, равным длительности пер-
вичного немодулированного сигнала хс - 1лэ . Фактически периодический ре-
жим работы соответствует непрерывному излучению высокочастотного коле-
бания Uс cos(<oqZ) , а модуляция его осуществляется периодической кодовой
последовательностью с длиной периода L и длительностью одиночного ви-
деоимпульса тэ . Для периодического режима Корреляционная функция ФМн
сигнала
1 L
(5.19)
L k-A
и число слагаемы в сумме равно L (в отличие от (5.18)).
64
Г л а в a 5. Радиосигналы н навигационные сообщения в СРНС
__________- •-*** * ' ' f .. -?• • ___g^-J-L - Ш-111ЧЦ . -
Итак, корреляционная функция ФМн сигнала (5.18), (5.19) определяется
корреляционными свойствами кодовой последовательности. Существуют раз-
личные кодовые последовательности с хорошими корреляционными свойства-
ми: кодовая последовательность Баркера; ^-последовательности; последова-
тельности Лежандра и Якоби и др. В СРНС используются А/-последова-
тельности, поэтому рассмотрим определения и основные свойства таких по-
следовательностей.
5.4.2. Af-последовательности. Основные свойства
Наиболее распространенными и хорошо изученными являются рекур-
рентные линейные циклические кодовые последовательности, которые формиру-
ются в результате циклических перестановок некоторого кодового слова
\t>i b2 ... йл-1), где элементы bt кодового слова принимают одно из возможных
значений из заданного алфавита (при использовании двоичного алфавита —
это 0 и 1). Устройством, реализующим циклические перестановки, является
многоразрядный (п-разрядный) сдвигающий регистр (5.6, 5.7], состоящий из п
последовательно соединенных двоичных элементов памяти, состояние которых
передается (сдвигается) на последующие элементы под действием тактовых
импульсов. Чтобы после п тактовых импульсов регистр не оказался “пустым”,
в схему вводится элемент обратной связи, осуществляющий логическую опе-
рацию над содержимым п разрядов регистра. Полученный результат поступает
на первый разряд. Схема такого регистра приведена на рис. 5.1, где bf J — со-
стояние z-го регистра на у'-м такте работы (или, другими словами, /-й эле-
мент кодового слова на у'-м такте), f(blj,b2j,...,b„j^ — логическая функция в
цепи обратной связи. Наиболее распространены и изучены регистры с линей-
ной обратной связью, в которых /(ft| j, b2 j.., b„ j j представляет собой сложе-
ние по модулю 2 (mod 2) всех или некоторых выходов регистров. Суммирова-
ние по mod 2 обозначается как ©, а умножение по mod 2 — как 0, поэтому
для регистра с линейной обратной связью получаем
/(^1,у Л,у,у) = (q ® bij)®(c2 0 hj) ©....© (с„ ©Z>„.y), (5.20)
где с, - коэффипис!/ты, принимающие значения 0 или 1.
Суммирование двоичных чисел по mod 2:
Рис. 5.1. Схема п- разрядного сдвигаю-
щего pciистра
ф 0 1
0 0 1
1 1 0
Умножение двоичных чисел по mod 2:
0 1
0 0 1
1 0 1
65
5.4. Фазоманипулированные сигналы
Последовательность на выходе л-разрядного сдвигающего регистра всегда
периодична, причем ее период L < 2я . В случае линейного сдвигающего ре-
гистра наибольший период £тах = 2я - 1. Любая выходная последователь-
ность, имеющая такой период, называется последовательностью максимальной
длины или М-последовательностью. Для каждого значения п существуют ли-
нейные последовательности максимальной длины.
М-последовательности имеют ряд замечательных свойств. Одно из них
(свойство уравновешенности) [5.6] состоит в том, что в периоде последова-
тельности (длиной Lmax) число нулей и единиц отличается на единицу. При
использовании двоичного алфавита символов ( 0 и 1 или —1 и 1) число еди-
ниц в последовательности равно 2я'1, а число нулей 2я-1 - 1.
Другое свойство — свойство корреляции: если последовательность по-
членно сравнивать с любым ее циклическим сдвигом на длительности перио-
да этой последовательности, то число совпадений меньше числа несовпадений
на единицу, т. е. число совпадений равно 2я-1 - 1, а число несовпадений 2я-1.
Следующее важное свойство — сумма (по mod 2) двух Л/-последо-
вательностей, сдвинутых одна относительно другой, является Af-после-
довательностью, вследствие того, что сдвинутые ЛТ-последовательности можно
получить с помощью одной и той же схемы.
Часто для описания работы сдвигающего регистра рис. 5.1 с линейной
обратной связью (5.20) используют характеристический многочлен (или порож-
дающий полином) [5.6, 5.7]
5(х) = с„хП + сл_1хя"'+. . ,+сцх + 1. (5.21)
Из теории Af-последовательностей известно [5.4—5.7], что характеристи-
ческий многочлен 5(х) степени п должен быть, во-первых, неприводимым,
т.е. его нельзя представить в виде произведения многочленов меньших степе-
ней, а во-вторых, он должен быть первообразным (примитивным) относи-
тельно двучлена xL + I, т. е. характеристический многочлен должен делить
xL +1 без остатка. Если характеристический многочлен является первообраз-
ным, то он является и неприводимым.
Известно, что если L = 2k - 1, то многочлен х1' +1 представляется как
произведение неприводимых полиномов степени не выше к . Каждый из этих
полиномов, а также их произведения, могут быть использованы как порож-
дающие полиномы. Известны таблицы [5.4] неприводимых многочленов до
степени к = 34 *
В п. 5.4.1 было показано, что корреляционные свойства сигнала зависят
от корреляционных свойств кодовой последовательности, поэтому рассмотрим
корреляционные свойства ^-последовательностей. Прежде всего согласно от-
меченному выше общему свойству корреляции можно сказать, что периодиче-
66
Г л а в а 5. Радиосигналы и навигационные сообщения СРНС
ская автокорреляционная функция кодовой ^-последовательности (5.19) имеет
боковые лепестки, равные -\/ L (где L длительность последовательности).
Вид периодической корреляционной функции приведен на рис. 5.2, а.
Апериодическая автокорреляционная функция, т. е. корреляционная
функция (КФ), вычисленная в соответствии с (5.18), существенно отличается
от периодической КФ. Ее типичный вид приведен на рис. 5.2, б. Из рисунка
видно, что боковые пики у непериодической КФ существенно больше, чем у
периодической КФ. Максимальное значение боковых пиков близко к 1 / -Jl .
Для непериодической КФ ^-последовательности можно вычислить статисти-
ческие характеристики, такие как среднеквадратическое значение боковых ле-
пестков, среднее значение их модулей и др. Расчеты показывают, что такие
характеристики для Af-последовательностей близки к аналогичным характери-
стикам случайных последовательностей, поэтому ЛГ-последовательности часто
называют псевдослучайными последовательностями (ПСП).
5.5. Навигационные сообщения в СРНС
5.5.1. Общие сведения
Передаваемое в радиосигналах навигационное сообщение предназначено
для проведения потребителями навигационных определений и планирования
сеансов навигации. По своему содержанию навигационное сообщение, переда-
ваемое каждым НС, содержит оперативную и неоперативную навигационную
информацию (НИ) 11.2, 4.5].
Оперативная информация (ОИ) относится к тому НС, с борта которого
передается данный навигационный радиосигнал, и содержит данные:
эфемериды НС, т. е. координаты и параметры движения спутника на
фиксированный момент времени;
сдвиг шкалы времени НС относительно системной шкалы времени;
относительное отличие несущей частоты излучаемого радиосигнала от
номинального значения;
5 5. Навигационные сообщения в СРНС________________________________ 67
иш ' 1111,1 ...
код метки времени, необходимой для синхронизации процесса извлече-
ния навигационной информации в аппаратуре потребителя.
Неоперативная информация (НОИ) содержит альманах системы, т. е.:
данные о состоянии всех НС системы (альманах состояния);
сдвиг шкалы времени каждого НС относительно шкалы времени системы
(альманах фаз);
параметры орбит всех НС системы (альманах орбит);
поправку к шкале времени системы относительно UTC (SU).
Навигационное сообщение формируется в цифровой форме. Для этого
каждый передаваемый информационный параметр подвергается квантованию
по уровню. Каждому уровню квантования ставится в соответствие кодовая
комбинация нулей и единиц. Систему соответствий между дискретными зна-
чениями параметра и кодовыми комбинациями называют кодом. Кодовую ком-
бинацию, соответствующую квантованному значению какого-либо параметра,
называют словом.
В СРНС навигационное сообщение передается в виде потока цифровой
информации (ЦИ). Скорость передачи информации в СРНС ГЛОНАСС со-
ставляет 50 бод. Структурно поток ЦИ формируется в виде непрерывно повто-
ряющихся суперкадров длительностью 2,5 мин, каждый из которых можно рас-
сматривать как одно сообщение. Структура сообщения (передаваемой инфор-
мации) оптимизируется таким образом, что объем суперкадра относительно
невелик (в СРНС ГЛОНАСС — 7 500 бит). В суперкадре передается полный
объем неоперативной информации для всех НС. Каждый суперкадр состоит из
5 кадров. Каждый кадр состоит из 15 строк и содержит полный объем опера-
тивной информации для конкретного НС и часть альманаха. Вся передаваемая
информация представляется в виде слов, каждое из которых занимает опреде-
ленное место в строке. Информационная строка кадра содержит 100 бит ин-
формации. В СРНС GPS скорость передачи ЦИ также составляет 50 бод,
структура потока цифровой информации аналогична и имеет параметры: дли-
тельность супсркадра — 12,5 мин; объем суперкадра — 37 500 бит; в суперкад-
ре 5 кадров по 5 строк каждый.
5.5.2. Помехоустойчивое кодирование навигационной информации
Для кодирования информации могут быть использованы различные коды
15.6—5.9 ] — простые (безызбыточные) и помехоустойчивые коды. К простым
кодам относятся, например, двоичный натуральный, симметричный двоично-
числовой, код Грея [5.6, 5.7]. Под помехоустойчивыми понимают колы, обла-
дающие избыточностью и позволяющие обнаруживать и исправлять ошибки,
возникающие при передаче из-за действия помех. В безызбыточном коде ис-
пользуются все возможные кодовые комбинации, поэтому ошибочный прием
лишь одного символа приводит к ошибочному приему всей кодовой комбина-
ции, так как различные кодовые комбинации могут отличаться только по од-
ной позиции. Это приводит к относительно низкой достоверности приема ин-
<j>8 л л а в а J. Радиосигналь. и иа»и1ициоиныу сообщу^ня » С. НС
формации. У помехоустойчивых кодов используются не все возможные кодо-
вые комбинации, а только некоторые из них, т. е. весь код обладает избыточ-
ностью относительно той части, которая применяется для кодирования ин-
формации. Оставшаяся часть кода может быть направлена на обнаружение
возможных ошибок и их устранение, т. е. на повышение помехоустойчивости.
Известны различные методы помехоустойчивого кодирования [5.8—5.10],
один из которых основан на использовании корректирующих кодов.
В настоящее время наибольшее распространение в практических систе-
мах получили двоичные равномерные корректирующие коды, так как они облада-
ют хорошими корректирующими свойствами и их реализация сравнительно
проста. Двоичные равномерные коды делят на блочные и непрерывные.
В СРНС используются блочные коды, когда цифровая информация пере-
дается в виде отдельных кодовых комбинаций (блоков) равной длины. Коди-
рование и декодирование каждого блока осуществляется независимо. Почти
все блочные коды относятся к разделимым, кодовые комбинации которых со-
стоят из двух различающихся частей: информационной и проверочной. Ин-
формационные и проверочные разряды во всех кодовых комбинациях разде-
лимого кода всегда занимают одни и те же позиции. Разделимые коды обычно
условно обозначают в виде (£6лЛ), где £бл — общее число позиций в блоке;
к — число информационных позиций.
Разделимые коды бывают систематические (или линейные) и несистема-
тические. Особенность систематических (линейных) кодов заключается в том,
что проверочные символы образуются различными линейными комбинациями
информационных символов. Систематические коды обстоятельно изучены.
Наиболее известны среди них циклические. Формирование циклических ко-
дов было рассмотрено в п. 5.4.2. Важными циклическими кодами являются
коды Хемминга, которые появились (исторически) раньше многих. Для них
найдены сравнительно простые методы реализации. Коды Хемминга исправ-
ляют одиночные ошибки в кодовом слове. Число символов слова кода Хем-
минга определяется соотношениями £6л =2л-1; к = 2” -1-п.
Основные параметры корректирующих кодов:
избыточность w = (£бл - к}/L6„ ;
кодовое расстояние (или расстояние Хемминга). Расстоянием d между
двумя кодовыми комбинациями называют число позиций, в которых эти ком-
бинации имеют разные символы. Расстояние между различными комбинация-
ми конкретного кода может быть различным. Минимальное расстояние r/min
между кодовыми комбинациями называют кодовым расстоянием;
число обнаруживаемых и исправляемых ошибок. Если код используется
только для обнаружения ошибок кратностью а , то необходимо и достаточно,
чтобы минимальное расстояние c/min > а + 1 . Чтобы можно было исправить все
ошибки кратности а и менее, необходимо иметь dmm > 2а + 1 .
5.6. Модуляция раоиосигнала навигационным сообщением
)
5?
5.6. Модуляция радиосигнала навигационным сообщением
5.6.1. Фазовая манипуляция радиосигнала
Сформированное тем или иным образом цифровое сообщение должно
быть передано с помощью излучаемого навигационным спутником радиосиг-
нала. Такая передача осуществляется путем модуляции одного из параметров
радиосигнала цифровым сообщением. Из теории статистической обработки
информации известно |5.2, 5.3], что наибольшей помехоустойчивостью обла-
дают противоположные сигналы, т. е. сигналы, взаимная корреляционная
функция (5.6) которых равна —1. При наличии аддитивного белого шума веро-
ятность ошибочного приема таких сигналов
рош =1-ф(72£/ЛГо)<
(5.22)
1 2
гле Ф(х) = -=|е ' dt — интеграл вероятности [5.11]; Ао/2 — односторонняя
V* о
спектральная плотность аддитивного шума.
Одним из широко используемых видов противоположных сигналов яв-
ляются фазоманипулированные сигналы с манипуляцией фазы на л. При ФМн
информация о передаваемой цифровой последовательности заложена в фазе
сигнала, так что на интервале времени [0, тс], где тс — длительность инфор-
мационного символа (для ГЛОНАСС тс = 20 мс), для радиосигнала можно за-
писать
5(г) = Uc соь(ш0/ + Отс ыро) = 0L/c cos(o0/ + <po); S = {0, 1} ; 0 = {1, -1}. (5.23)
Демодуляция ФМн сигнала на приемной стороне осуществляется с по-
мощью фазового детектора (ФД), в котором происходит умножение принятого
сигнала (5.23) на опорный сигнал 5011 (г) = cos(mQt + <pOII), где <pon — начальная
фаза, и выделение постоянной составляющей (рис. 5.3). На выходе фазового
детектора
«фд = 0£/с cos(<p011 -ФО).
Если фаза <роп опорного сигнала ста-
бильна на всем интервале наблюдения, то из
(5.24) однозначно определяется информа-
ционный символ 0 . Однако, если фаза <р0)1
но каким-либо причинам изменится на ±л,
(5.24)
Ене. 5.3. Структурная схема
фазовою детектора
70 Г л а в a 5. Радиосигналы и навигационные сообщения СРНС
то знак определяемого параметра 9 изменится на обратный. Это явление
называют обратной работой ФД. Очевидно, что такой режим работы фазо-
вого детектора недопустим, так как с момента перехода на обратную работу
последовательность символов 9fc; к = 1, 2... будет приниматься неправильно
до тех пор, пока не произойдет следующий скачок фазы на ±л .
5.6.2. Относительная фазовая манипуляция
Одним из путей устранения явления обратной работы ФД на приемной
стороне является отказ от классического вида противофазных ФМн-сигналов
и переход к относительной фазовой манипуляции (ОФМ) — методу русского
ученого Н. Т. Петровича.
Суть метода заключается в том, что отсчет фазы для каждого информа-
ционного символа 9fc; к = 1, 2... производится не относительно начальной
(для данного сеанса приема) фазы, а относительно фазы предыдущей посылки.
Пусть фу — фаза j -й посылки, a фу1 — фаза (у-1)-й посылки. Так как для
противофазного ФМН сигнала 9л = {0 или л}, то разность фаз между двумя
соседними посылками может также принимать только два значения:
I I (°>
Дф =|ФУ -Фу-1| = I
если Фу=Фу1;
если фу = фу । + л .
(5.25)
Из (5.25) видно, что, если скачок фазы опорного сигнала произойдет в
пределах (у-1)-й посылки, то соответствующий импульс на выходе ФД
“раздробится” на две части с разной полярностью. Можно показать [5.7], что в
результате такого эффекта возможен ошибочный прием двух соседних симво-
лов. Если скачок фазы произойдет точно на границе двух посылок, то непра-
вильно будет принят лишь один символ. Таким образом, перескок фазы опор-
ного сигнала на ±л при приеме ОФМ-сигнала приводит к появлению только
локальных ошибо!к, а не переход — на обратную работу в течении длитель-
ного времени, как это имеет место при приеме ФМн-сигнала.
Относительную фазовую манипуляцию можно рассматривать как допол-
нительную перекодировку исходной последовательности двоичных символов
[0
9* = j при к = 1, 2... Действительно, пусть 9fc: к = 1,2... — последователь-
ность символов, полученная после перекодирования. Тогда в соответствии с
принципом формирования ОФМ совпадение двух символов 9* и 9fc_! означа-
ет передачу исходного символа 9* =0, а в противном случае, когда символы
И &к-1 различны, передачу символа 9t =1. Формально это можно запи-
сать в виде алгоритмов:
5.7- Синхронизация в СРНС ГЛОНАСС
71
(5.26а)
(5.266)
Алгоритм (5.266) используется для перекодировки исходного потока
к = 1, 2... символов в поток к = \, 2..., соответствующий ОФМ, а
алгоритм (5.26а) — для обратного перехода от к = 1, 2 ... к исходному по
току символов Sfc; к = 1, 2 ... Оптимальный прием сигналов с ОФМ реализу-
ет устройство, приведенное на рис. 5.4, где УЗ — устройство задержки. Как
следует из рисунка, приемное устройство состоит из двух частей: устройства
оптимального приема противоположных сигналов (обведено штриховой ли-
нией) и устройства перекодировки последовательности к = 1, 2 ... в ис-
ходную последовательность к = 1, 2 ...
Наличие второго устройства приводит к изменению (увеличению) веро-
ятности ошибочного решения для
всей схемы по сравнению с (5.22),
справедливой для приема ФМн-
сигнала. Данная вероятность опреде-
дя_ется выражением [5.7]
Рис. 5.4. Схема оптимального прием-
ника сигнала с ОФМ
Рот ОФМ а 2^1 “ )] •
Энергетический проигрыш ОФМ-
метода по сравнению с ФМн не пре-
восходит 1 дБ.
5.7. Синхронизация в СРНС ГЛОНАСС
Для приема сигналов с ОФМ, близкого к оптимальному, необходимо
реализовать когерентный прием сигнала [5.7, 5.10], т. е. использовать фазовую
синхронизацию (ФС), которая осуществляется путем использования системы
фазовой автоподстройки (ФАП). Более подробно вопросы построения ФАП
будут рассмотрены в гл. 6.
При демодуляции двоичных символов навигационного сообщения в при-
емнике необходимо выделить импульсы символьной (тактовой) частоты, опре-
деляющие границы принимаемых символов, т. е. осуществить тактовую син-
хронизацию. Ввиду случайного характер? передаваемой информации спектр
радиосигнала не содержит составляющей тактовой частоты. Поэтому инфор-
мацию о тактовой частоте можно выделить только из сигнала, в котором мо-
дулирующие посылки меняют свое значение, т. е. при смене принимаемых
символов от 0 к 1 и наоборот. Так как смена 0 и 1 имеет неравномерное рас-
72 1 Хла1 15. Pat Ьсигна |иМ8 Баннон )е сооб >иия УНС
пределение, то могут появиться длительные интервалы времени, когда отсут-
ствует смена значения символов. При этом время установления тактовой син-
хронизации (нахождение правильной фазы символьной частоты) может суще-
ственно возрастать. Для устранения этого явления можно использовать допол-
нительный синхрокод, который складывается по mod 2 с символами навигаци-
онных данных. В СРНС ГЛОНАСС в качестве такого кода используется бид-
воичный (манчестерский) код с длительностью посылки тс м = тс / 2 (частота
100 бод). Благодаря бидвоичному кодированию всегда осуществляется практи-
чески равномерное распределение переходов от 1 к 0 и наоборот, в том числе
при передаче длинных массивов навигационных данных с преобладанием оди-
наковых символов. Это позволяет облегчить условия и уменьшить время уста-
новления тактовой синхронизации в приемнике.
Кроме тактовой синхронизации в приемнике необходимо определить
границы кодовых слов или некоторой совокупности (блоков) слов, т. е. осу-
ществить цикловую синхронизацию (ЦСХ) [5.7]. В СРНС ГЛОНАСС в качестве
таких блоков приняты строки навигационного сообщения. Цикловую синхро-
низацию обеспечивают с помощью специальных синхросигналов, которые в
аппаратуре ГЛОНАСС получили название “код метки времени”.
Сигналы навигационного сообщения, дальномерного кода, тактовой и
цикловой синхронизации связаны по фазе между собой (синхронны). Это дос-
тигается путем их формирования от одного синтезатора тактовой частоты.
Более подробно конкретная реализация системы синхронизации в СРНС
ГЛОНАСС будет описана в гл. 10.
Литература
5.1. Тихонов В. И., Харисов В. II. Статистический анализ и синтез радиотехниче-
ских устройств и систем. — М.: Радио и связь, 1991.
5.2. Тихонов В. И. Оптимальный прием сигналов. — М.: Радио и связь, 1983.
5.3. Перов А. И. Оценка параметров сигнала. — М.: Изд-во МЭИ, 1997.
5.4. Варакин Л. Е. Системы связи с шумоподобными сигналами. — М.: Радио и
связь, 1985.
5.5. Шумоподобные сигналы в системах передачи информации / Под ред. В. Б.
Пестрякова. — М.: Сов. радио, 1973.
5.6. Цифровые методы в космической связи/ Под ред. В. И. Шляпобергского. — М.:
Связь, 1969.
5.7. Борисов В. А., Калмыков В. В., Ковальчук Я. М. и др. Радиотехнические систе-
мы передачи информации. — М.: Радио и связь, 1990.
5.8. Кларк Дж., Кейн Дж. Кодирование с исправление ошибок в системах цифро-
вой связи; Пер с англ. — М.: Радио и связь, 1987.
5.9. Пенин П. И. Системы передачи цифровой информации. — М.: Сов. радио,
1976.
5.10. Спилкер Дж. Цифровая спутниковая связь. — М.: Связь, 1979.
5.11. Корн Г., Корн Т. Справочник по математике. — М.: Наука, 1961.
Гл а в a 6
Методы и алгоритмы обработки сигналов
и извлечения навигационной информации
6.1. Общие сведения
Аппаратура потребителя предназначена: для приема сигналов от навига-
ционных спутников; выбора рабочего созвездия, т. е. выбора тех находящихся
в зоне радиовидимости навигационных спутников, из сигналов которых будет
извлекаться навигационная информация; определение вектора потребителя
П'=1хугД'Ух Vy Vz rf.
К современным СРНС предъявляются высокие требования по точности
навигационных определений. Это обусловливает необходимость рассмотрения
методов оптимальной обработки сигналов и извлечения информации при по-
строении приемоиндикаторов. По своей сути навигационная задача определе-
ния вектора потребителя П' является задачей оценивания координат объекта
(в общем случае подвижного) по наблюдениям сигналов от источников излу-
чения с известными координатами. Математическим аппаратом, позволяющим
проводить синтез оптимальных систем оценивания координат объекта, служит
теория оптимальной фильтрации [5.1, 6.1, 6.9—6.12].
Общая постановка задачи формулируется следующим образом. Пусть на
вход приемника СРНС поступает реализация y(t), представляющая собой ад-
дитивную смесь сигнала S(/, I, Э,ц) и помехи n(z):
у(0 = 5(Л1(П'),9,И)+л(0. (6.1)
Сигнальная функция 5(/,Х(1Г), 9,ц) в наблюдаемой реализации y(f) может
состоять из одного или нескольких сигналов, соответствующих, например
различным навигационным спутникам,
5(/,Х(П'),&>и)= ^ДЛХу(П'),9у-.И/), (6.2)
/=1
где Ху- — вектор радионавигационных параметров сигнала от у-го НС, т. е. тех
параметров, из которых извлекается навигационная информация; цу- — вектор
параметров сигнала, в которых не содержится навигационная информация,
поэтому их можно считать неинформационными; 9у — дискретный параметр,
74 Г л а в a 6. Методы и мго^игмьцобработки сигналов и извлечения НИ
несущий дополнительную навигационную информацию. Радионавигационны-
ми параметрами X. в СРНС являются (см. гл. 4) задержка сигнала т и допле-
ровское смещение частоты /доп (при приеме одновременно нескольких сигна-
лов в (6.2) запишем ту, fnon j', J' = 1»ЛГ)- Радионавигационные параметры сиг-
нала в свою очередь зависят от вектора И’ потребителя, т. е. т(П'), /доп(П')-
К неинформационным параметрам ц относится, например, амплитуда сигнала
А. Аддитивную помеху л(/) часто полагают белым гауссовским шумом с нуле-
вым математическим ожиданием и матрицей двусторонних спектральных
плотностей No /2. Сигнальная функция от j-го НС может быть описана соот-
ношением
Sj(t) = Ahj(t-ty)cos((<o0 + 2л/доп j)l +<Ру),
(6.3)
где А — амплитуда сигнала; hj(t - т) — модулирующая функция, обусловлен-
ная модуляцией дальномерным кодом и передачей навигационного сообщения;
Фу — случайная начальная фаза сигнала.
Задача синтеза оптимальной системы фильтрации формулируется как
отыскание такой системы, которая в результате обработки наблюдений (6.1) в
каждый текущий момент времени t формирует оценку П'(1) вектора потреби-
теля с минимальной дисперсией ошибки оценивания.
Теория оптимальной фильтрации позволяет решить сформулированную
задачу в общем виде [6.3]. Однако получающиеся при этом алгоритмы фильт-
рации достаточно сложны и в настоящее время не реализуются в существую-
щих приемоиндикаторах.
Для упрощения аппаратуры потребителя задачу получения оценок век-
тора П'(/) разбивают на два этапа обработки [1.4, 4.3, 6.4|: первичную и вто-
ричную.
На этапе первичной обработки решается задача фильтрации радионави-
гационных параметров сигнала, а на этапе вторичной обработки вычисляются
оценки вектора потребителя с использованием полученных на первом этапе
оценок радионавигационных параметров и соответствующих навигационных
функций.
6.2. Алгоритмы первичной обработки
Хорошо известно [5.1, 6.1, 6.10|, что успешное решение задачи фильт-
рации параметров радиосигнала возможно лишь в том случае, когда начальная
ошибка между истинным значением фильтруемого параметра и его оценкой
достаточно мала. Это обусловлено нелинейностью радиотехнической системы
6.2. Алгоритмы первичной обработки ; > 75
фильтрации и связанной с этим необходимостью “захвата” сигнала на устой-
чивое слежение за фильтруемым параметром. В связи с этим в радиотехниче-
ских системах, в том числе и радионавигационных, различают два режима: по-
иск сигнала и фильтрация (измерение) параметров. В режиме поиска сигнала
осуществляется грубая, и в то же время достаточная для дальнейшего захвата
системой фильтрации, оценка параметров сигнала (задержки и частоты), а в
режиме фильтраций параметров реализуется непрерывное и точное их из-
мерение.
Поиск сигнала и фильтрация его параметров проводят по каждому НС
отдельно, поэтому в дальнейшем рассматриваются алгоритмы обработки толь-
ко одного сигнала, опуская при этом, для удобства записи, индексу.
6.2.1. Алгоритмы поиска сигналов по задержке и частоте
С позиций теории статистического оценивания [5.2, 5.3] задача поиска
I у. !т
сигнала является задачей оценки его параметров X = |т УдОП| , которые прини-
маются постоянными за время наблюдения [0,7’] и выбираются из конечной
области [X-min Лшах]- Обычно возможные значения X полагаются равновероят-
ными. В этих условиях в качестве оптимальных оценок X чаще всего рассмат-
ривают оценки максимального правдоподобия [5.2, 5.3], т. е.
X = шах 1 иф^х), (6.4)
где — уловная плотность вероятности наблюдаемой на интервале
[0,7’] реализации Yf] = {у(/), /е[0, Т][ при заданных значениях X.
Il Т
т /аоп| амплитуду А и фа-
зу <р сигнала можно считать случайными неинформационными параметрами.
Поэтому, как следует из общей теории оценок параметров сигнала [5.2. 5.3],
для условной плотности вероятности можно записать
2ла>
И^Го^х) = ] | И-(гог|Х,ф, л) ^ор(ч>)^ор(А) dA <Лр, (6.5)
где — условная плотность вероятности наблюдаемой реализации
при фиксированных значениях параметров X, А, <р ; W^ap(<р), ИЛ,,,]/!) — априор-
ные распределения фазы и амплитуды сигнала соответственно, для которых
будем полагать (Гар(<р) = (ре[0, 2л]; ГИар(Л) = Л~ехр| - Ле[0,оо].
2к а£А V 1о1А)
76
Г л а в a 6. Методы и алгоритмы обработки сигналов и извлечения НИ
Подставляя данные выражения в (6.5) и выполняя интегрирование, по-
лучаем, что условная плотность вероятности И^У^х) является монотонной
функцией достаточной статистики А'2(7’,Х), которая определяется соотноше-
ниями:
т
Х2(Т, X) = I2(T. X) + Q2(T, X); I(T, X) = J у(/) Л(г - t)cos ((«о + 2^)/) dt;
О
т
Q(T,X) = Jу(/) й(/-т)ьш((<о0 +2л/доп)/) dt.
О
(6.6)
Здесь ,Y(f,X) — огибающая на выходе согласованного фильтра; 7(/,Х), С(/,Х) —
соответственно синфазная и квадратурная составляющие.
С учетом отмеченной выше монотонности зависимости условной плот-
ности вероятности И^У^х) от достаточной статистики Х2(Т, X) для оптималь-
ной оценки (6.4) можно записать
Х = игах1 Х2(Т,Х).
(6.7)
Нахождение (поиск) решения в соответствии с (6.7) предполагает пере-
бор всех возможных значений из области определения [Хпцп.Хщах]- Для этого
при практической реализации алгоритма поиска область возможных значе-
ний задержек [Tmm.tmax] и доплеровских смещений частоты [/допmin,/допmax]
дискретизируется, т. е. считается, что параметры т и /доп могут принимать
дискретные значения ; i = l,)Vt и faonj, j = f В целях получения оцен-
ки (6.7) для каждой из пар , /доп j } вычисляется А'(т, г,,/доп j) > а в качестве
оптимальной оценки |т,/доп | выбирается та пара, которой соответствует зна-
чение максимальное т>/Доп) • При одновременном определении
х(т, т(,/доп у) для всех возможных сочетаний {ч,/допу}; i = 1,(VT ; J = \,Nf
говорят о параллельном поиске, что требует NxiV[ идентичных каналов обра-
ботки. Реализация приемоиндикаторов с такой обработкой проблематична.
Поэтому используют иные алгоритмы поиска, основанные на параллельно-
последовательном или последовательном просмотре области возможных зна-
чений т и /доп . Другим фактором, используемым в целях упрощения аппара-
туры потребителя, является замена процедуры вычисления и запоминания всех
6,2- Алгоритмы первичной обработки
77
возможных значений А'(7’, т(,/допу| с последующим выбором максимального из
них на алгоритм обнаружения сигнала в анализируемой ячейке. При этом в
простейшем случае некогерентный обнаружитель, вычисляющий статистику
х(т, т/,/доп/), последовательно анализирует ячейки из зоны неоп-
ределенности по задержке и доплеровскому смещению частоты. Найденное
значение т,-,/допу) сравнивается с пороговым и принимается решение о
наличии или отсутствии сигнала. При принятии решения об отсутствии сигна-
ла осуществляется переход к следующей ячейке анализа, а при положительном
решении вырабатывается команда на переход в режим непрерывного сопрово-
ждения по т и /доп . Если следящие системы по задержке и доплеровской час-
тоте успешно захватывают сигнал на сопровождение, то принимается решение
о прекращении поиска, в противном случае процедура поиска возобновляется.
Упрощенная схема устройства поиска приведена на рис. 6.1. Входная
реализация после предварительного усиления, понижения частоты до проме-
жуточной и усиления усилителем промежуточной частоты (УПЧ) поступает на
умножители каналов формирования синфазной / и квадратурной Q состав-
ляющих.
По команде блока управления поиском в синтезаторе частот устанав-
ливается частота fwj, такая, что = /11₽, где fs = /0 + /доп j — частота
сигнала, принятого от НС; /пр — промежуточная частота усилителя промежу-
точной частоты (УПЧ). Блок управления поиском выдает также команды в
блок управления задержкой кода для формирования задержки т; опорного
сигнала, соответствующей анализируемой ячейке. Синтезатор частот выраба-
тывает опорное колеба-
ние cos(<oС1)у). На выхо-
де генератора кода ПСП
вырабатывается модули-
рующая функция
соответствующая задан-
ной кодовой последова-
тельности (дальномерно-
му коду) и сдвинутая на
т,-. На выходе первого
умножителя формируется
опорный сигнал h(t - т,) х
х cos^<oCH jt^, который по-
Входной
сигнал
J~x j____' Интиретор
) | "со сбросом
-----• п/2 ' !-
' 'Г
Интегратор
со сбросом
|Т " “I
। Генератор |
| кода ПСП Г
> Блок управ-
ления задерж-
1 кой кода
ступает на умножитель
Синтезатор
частот
, генератор
рдения сдвигом
Блок
управления
поиском
H Пороговое j
устройство j
Рис. 6.1. Схема системы поиска сигнала
т
<г
П Гл а в а 6. Методы и алгоритмы обработки сигналов и излечения НИ
канала формирования синфазной составляющей I, а сдвинутое на я/2 коле-
бание поступает на умножитель канала формирования квадратурной состав-
ляющей Q. Напряжения с выходов умйожителей поступают на интеграторы
со сбросом, начало и конец интегрирования в которых определяется коман-
дами, поступающими от блока управления задержкой кода. В момент сброса (в
конце интервала интегрирования) напряжение с выходов интеграторов посту-
пает на блок формирования квадрата огибающей I2 + Q2 , а затем на порого-
вое устройство, в котором принимается решение об обнаружении
(необнаружении) сигнала. Данные об обнаружении сигнала передаются в блок
управления поиском, где принимается решение о последующем поиске или
переходе в режим непрерывного сопровождения.
6.2.2. Алгоритмы фильтрации фазы, задержки сигнала
и оценки дискретного параметра
В отличие от алгоритма поиска сигнала, где реализуется некогёрентная
обработка принимаемого сигнала, в режиме фильтрации информационных па-
раметров используется квазикогерентная обработка [5.1, 5.2], т. е. совместная
фильтрация, информационных параметров и фазы сигнала (неинформацион-
ного параметра).
Для решения задачи синтеза оптимальной системы фильтрации радиона-
вигационных параметров сигнала представим описание сигнала (6.3) в виде
5(z) = Ah(t - т) cos((<o0 + Зя/доп )t + <po) = ЛАд-кС* - т) cos(<o0f + 9(/ - т)л + ф(/)) , (6.8)
где йдк(1) — модулирующая последовательность, соответствующая дальномер-
ному коду (5.10), один период (длительностью 1тэ) которой описывается
Адк(0= 2>*ио(/-(*_1)тэ); 'б[0,£тэ].
(6.9)
Параметр 9 в (6.8), описывающий навигационное сообщение, пред-
ставляет собой последовательность нулей и единиц, смена которых проис-
ходит в фиксированные моменты времени tk , такие, что tk - tk_x = Тси - const.
Данную последовательность удобно представлять в виде однородной марков-
ской цепи с матрицей перехода tty =0,5; i,j = 0,1 .
Фазу ф(/) можно описать компонентой в общем случае многомерного
марковского процесса хф(г), т. е. ф(г) = сфхф(г), где сф = | 1 0 0 ... 0 |т — п-
мерный вектор; х(/) описывается векторным уравнением
6.2. Алгоритмы первичной обработки
79
~ ®фхф + >
(6.10)
где ₽ф, Сф— матрицы размера лхл и лхт соответственно; цф(/) — т-
мсрный вектор белых гауссовских шумов с нулевыми математическими ожи-
даниями и матрицей спектральных плотностей Nn9/2.
Наиболее часто используются модели
<КО = ПФ0. <611>
что соответствует сф = 1, £ф = 0, 6ф = 1;
Лр /л
0 1 0
что соответствует сф = | 1 0 |т; F9 - 0 0 ; с, = 1
(6.12)
= со
Лйф ^*ф / \
i = ^Г=Е*; -F = n’w
(6.13)
что соответствует
Сф =1 1 00 |т;
Аналогичное представление в виде компоненты многомерного марков-
ского процесса принимается для описания изменения во времени задержки т
сигнала, т. е. т = с’хх,
= FTxt +GTnT(z), (6.14)
где FT, GT — матрицы размера йхй и п х т соответственно; цт(/) — т- мер-
ный вектор белых гауссовских шумов с нулевыми математическими ожида-
ниями и матрицей спектральных плотностей N^/2. Шумы qt(/) и цф(/) по-
лагаются некоррелированными.
Общее решение задачи оптимальной непрерывно-дискретной фильтра-
ции, т. е. совместной фильтрации параметров сигнала, одни из которых меня-
ются непрерывно, а другие — дискретно, дано в {6.2]. Конкретизация общих
соотношений в рассматриваемой задаче приводит в* комплексной системе
фильтрации, включающей дискриминаторы задержки и фазы сигнала и сгла-
живающие фильтры для оценок задержки и фазы {6.7, 6.8]. В комплексной
системе фильтрации каждая из оптимальных оценок тиф формируется после
обработки сигналов с выходов двух дискриминаторов (задержки и фазы). Од-
80 Глава 6. Методы и алгоритмы обработки сигналов и извлечения НИ
нако это приводит к достаточно сложной системе, поэтому на практике оцен-
ку задержки сигнала формируют по сигналам временного дискриминатора, а
оценку фазы — по сигналам фазового дискриминатора, т. е. перекрестные свя-
зи между “разноименными” оценками и дискриминаторами не учитываются.
Уравнения оптимальной фильтрации без учета указанных перекрестных связей
и при выполнении условия > 2 (при работе приемоиндикаторов в
реальных условиях) имеют следующий вид:
-#=F’X
+ RTcT2ziyj1 th-
I Hv)aak(v - ?) cos(“ov +
«*
x y(r) ........-— cos(co0/+ <p); t
Лч> V -
—— = F x
dt ф ф
th-
- R^/tVo1
2/4
T7~ f Hv)Aa к (v - ?) cos(“ оv + tydv
/о tk
x у(0Ад. к (t - *) sin(“ о t + <p); t e , tk+1 ];
если | y( v)/ifl к (v - r) cos(co q v + <p)dv > 0 ;
‘k
6t+i
если j y(u)hn K (v - r) cos(<o 0 v + <pjdv < 0 ,
‘k
(6.15)
(6.16)
(6-17)
где th(«) — функция гиперболического тангенса; R, и R? - матрицы диспер-
сий ошибок фильтрации векторов хт и хф соответственно, которые удовле-
творяют уравнениям Риккати
-^ = FTRz +rtftT -IR^^cjR,;
= f9rq + rqf; +g(Pnwg; - ir^s^-'cJr,, ,
(6.18)
(6.19)
где 5ДТ , 5Дф — крутизны дискриминационных характеристик дискриминатора
задержки сигнала и фазового дискриминатора.
Уравнение (6.15) описывает канал оценки задержки сигнала т = с^хт;
(6.16) — канал оценки фазы сигнала ф = сфхф; (6.17) — оценку дискретного
параметра (6.18)—(6.19) — коэффициенты усиления в системе.
6.2. Алгоритмы первичной обработки 81
Схема следящего измерителя, описываемого уравнениями (6.15)—(6.17)
приведена на рис. 6.2, где Кх = RT ст, Кф = Яф сф — векторы коэффициентов
усиления сглаживающих фильтров каналов оценки задержки и фазы сигнала.
Канал оценки задержки сигнала включает дискриминатор задержки,
сглаживающий фильтр и генератор кодовой последовательности. Дискримина-
тор задержки сигнала вырабатывает напряжение, пропорциональное рассогла-
сованию истинного значения -задержки т и его оценочного значения т.
Структура сглаживающего фильтра определяется принятой моделью изменений
задержки (6.14). Генератор кода формирует кодовую последовательность,
сдвинутую на время, равное оценке т задержке сигнала, и последовательность
Эйд - £)/ai. Последнюю часто формируют в виде конечной разности двух
сдвинутых исходных кодовых последовательностей в соответствии с алго-
ритмом
дйд.к(< ~ т) йдк(/ - т + Ат / 2) - йд к(/ - т - Ат / 2)
Эт Ат
где Ат — интервал, равный длительности тэ элементарной посылки.
Рис. 6.2. Схема следящего измерителя
82 Г л а в a 6. Методы и алгоритмы обмбрткисвгн^довмизвлечения НИ
Канал оценки фазы (система фазовой автоподстройки ФАП) включает
фазовый дискриминатор (ФД), сглаживающий фильтр и генератор сигнала
(ГС) с частотой /о- В отличие от обычного [5.7, 5.9] фазовый дискриминатор
в данной схеме включает два перемножителя. Среднее значение напряжения
на выходе первого и второго перемножителей
1/1 » -cos(a>0Z + Эя + <p)sin(<oot +ф) = 0,5sin(8n + ф - ф);
U2 >» яп(Эя +ф- ф)соб(Эя +ф-ф) = 0^яп2(ф- ф).
(6.21)
Таким образом, ФД приведенной схемы имеет стандартную дискримина-
ционную характеристику вида яп2Дф.
Заметим, что в оптимальной системе фильтрации фазы сигнала в начале
дискретной посылки (t = tk) коэффициент усиления петли ФАП близок к ну-
( 2/4 t
лю, так как limth----fy(v)/iaK(v-tJcos^qZ+ $)dv =0, а в конце посылки бли-
*-»** lk )
зок по модулю к единице, так как в реальных условиях эксплуатации
I Л2Тси / No > 21 и, следовательно,
10^ ^Jt+1
thМ— fy(v)AaK(v-?)cos(<i>0r + $)dv »±1.
И» tk
Структура сглаживающего фильтра канала оценки фазы определяется
принятой моделью изменения фазы (6.10), например, для модели (6.12) сгла-
живающий фильтр представляет собой два интегратора и демпфирующее зве-
но. Приведенная на рис. 6.2 схема системы фильтрации устойчива при усло-
вии захвата сигнала каналом оценки фазы и вхождения в синхронизм. По-
следнее обеспечивается лишь в том случае, если начальное расхождение частот
принимаемого сигнала и ГС не превышает полосы захвата системы ФАП.
Обычно после режима писка априорная неопределенность по несущей частоте
ДСс ю500Гц, что превышает полосу захвата ФАП (4СЗХ »50 Гц), поэтому непо-
средственно после режима поиска сигнала предусматривается дополнительный
режим автоматической подстройки частоты (АПЧ), реализуемый с помощью
системы частотной автоподстройки (ЧАП).
Для построения системы ЧАП необходимо иметь частотный дискрими-
натор, напряжение на выходе которого пропорционально разности частот Д/с г
принимаемого сигнала и ГС. Такой частотный дискриминатор можно сформи-
ровать алгоритмически, обрабатывая сигналы /(/) и С(/), поступающие на
вход второго умножителя фазового дискриминатора. Действительно, проинтег-
6'2- Алгоритмы первичной обработки
83
рируем 2 раза I(t) и Q(t) на последовательных интервалах времени + Г] и
[tk+T,tlc+2T]:
tk+T tk+2T tk + T tk±2T
/*4 = P('P'; ha= M')*; Gfc,i= ew = fePK (6.22)
>k 1k+T tk tk + T
Для меняющихся во времени фазы <р(/), ее оценки ф(/) и достаточно ма-
лых интервалов времени Т можно записать
Д<р(/) «; Аф(/) « 2чГдоп/, (6.23)
1 ftp
где /доп ~ -
2л 81 t = tk
/доп
1 Эф
2л 8t
Тогда, с учетом (6.21)—(6.23), имеем
Cfc.t ю ТТУ—РМ8* + ММ+ 2я^.г7’) - cos(sk + Дф(4))];
^я^Ус.г1 J
Ct,2 » гяд/Ч008^* + ММ+4я^с гГ) “ cos(s’c + ММ+ 2я^с гГ)]
1кЛ “ 2лд/~[М8* + ММ + 2®Ус.г7’) - Sin(8jt + ММ)] >
Л,2 « [sin(&7r + Дф(М + 4xVciT)- «п(»л + Лф^) + 2xA/cr7j] •
(6.24)
Определим процесс на выходе частотного дискриминатора выражением
«/ = Ik,lQk2 -Jk^Qk,l-
(6.25)
Подставляя (6.24) в (6.25) и выполняя необходимые преобразования, по-
лучаем
, J sin(xA/c тТ)
f « sin(2Wc.rT
(6.26)
Выражение (6.26) описывает характеристику частотного дискриминаци-
онную, вид которой приведен на рис. 6.3. Такая дискриминационная характе-
ристика обеспечивает устойчивое слежение по частоте если начальная
ошибка лежит в пределах ее главного лепестка, т. е.
|ДГС.г| < Полагая, что
после режима поиска диапазон неопределенности по частоте составляет
Д/с =500Гц, находим требуемое время интегрирования Т = 1 мс.
84 Глава 6. Методы и алгоритмы обработки сигналов и извлечения НИ
Ряс. 6.3. Характеристика частотного
дискриминатора
Следящая система частотной
автоподстройки замыкается через
сглаживающий фильтр, в качестве
которого обычно используют фильтр
второго порядка с операторным ко-
эффициентом передачи К(р) =
Л70(1 + р7ф)
= —1—s----L , где Ко — коэффициент
Р
усиления фильтра; Гф — постоянная
времени.
6.3. Алгоритмы вторичной обработки
В результате первичной обработки радионавигационных сигналов оцени-
ваются (измеряются) радионавигационные параметры (задержка т, и допле-
ровское смещение частоты /доп/) Для каждого из НС (7 = 1,4.) выбранного ра-
бочего созвездия. Как отмечалось в гл. 4, радионавигационные параметры свя-
заны с параметрами потребителя через соответствующие навигационные
функции. В СРНС используются псевдодальномерные методы определения
координат (см. § 4.3) и псевдорадиально-скоростной метод определения со-
ставляющих скорости потребителя. Для реализации этих методов необходимо
измерять радионавигационные параметры относительно четырех НС, а в каче-
стве навигационных функций использовать соотношения (4.3), (4.6).
Для решения нелинейных уравнений (4.3), (4.6) можно применять как
прямые, так и итерационные алгоритмы решения нелинейных задач.
Прямые алгоритмы можно использовать для начального определения
вектора П*(/) при значительной априорной неопределенности относительно
координат потребителя. Они дают практически точное решение системы, со-
ставленной из i уравнений с I неизвестными.
6.3.1. Итерационные алгоритмы определения координат
Итерационные алгоритмы можно использовать для уточнения априорных
значений координат потребителя путем отыскания поправок к ним в процессе
последовательных приближений.
Суть итерационных алгоритмов решения систем из п уравнений вида
h(u) = O,
(6.27)
6.3. Алгоритмы вторичной обработки 85
где и — вектор размерности п, заключается в следующем [5.11]. Уравнение
(6.27) приводят к виду
и = <р(и).
(6.28)
Выбирают некоторое начальное приближение и вычисляют последо-
вательные приближения
i(7+1) =ф(и{7)); j=0,I, 2...
(6.29)
Итерационный процесс продолжается до достижения требуемой точно-
сти решения.
Имеется много способов приведения уравнения (6.27) к виду (6.28). Ши-
роко используется метод Ньютона, как наиболее просто реализуемый и быстро
сходящийся. В этом методе функцию h(u) раскладывают в ряд в точке с
использованием лишь линейного члена разложения
(6.30)
Здесь и в дальнейшем в книге принято определение производной от ска-
ляра /(х) по вектору как вектор—столбец
#(х) _ # # df
dx dx\ dx-i dx„
Полагая, что матрица невырожденная, получаем уравнение
типа (6.29) **
(6.31)
86 _ Г л а в а 6. Методы и алгоритмы обработки сигналов и извлечения НИ
Вычисленное таким образом значение в принимают в качестве нового
значения итерационной процедуры, т. е. в^+1» = и.
Проиллюстрируем последовательности итерационных расчетов для зада-
чи определения координат потребителя в псевдодальномерном методе, где оп-
ределяемыми параметрами являются в = х = |ху z Д'|т ; исходными данными —
координаты НС х(, у/, z-t; / = 1,4; начальные приближения координат потреби-
теля А у’0’, z^, Д'^ ; измеренные на этапе первичной обработки дально-
сти Дизм /; ‘ - И до четырех НС
Дтм1 = Дизм/ + П/> (6.32)
где ДИЗ„/=Д/+Д'; Д/ =[(х,-х)2+(у,--у)2+(z(-z)2] 7 . (6.33)
Определим функцию йДх, у, z, Д’) = Дизм/ ~ ДИзм(- Тогда, вводя векторы
Дизм “ |Дизм1 Дизм 2 ДизмЗ ^изм4| > Дизм — |Дизм1 -^изм2 ДизмЗ Дизм4Г. ДЛЯ про-
изводной (6.30) можно записать
Лт(в)/ац = -^%^, (6.34)
а уравнение (6.31) при и -> х преобразовать к виду
(6.35)
Элементы матрицы <ЭДиЗМ/<5х определяются соотношениями
5Дизм/(*>У.г,Д') xt-x 5Дизм,(х,у,г,Д') У!-у
Эх Д1 * ' ду Д1
ЭДИЗм1(х,УЛ,Д’) Z/-Z 5Дизм/(х.у,г,Д')
-------* = —=-cosy,; ---—--------= 1, (6.36)
oz---------------------------------------------------------------Д, дД
где а/( pj, у,- — направляющие косинусы радиуса-вектора, соединяющего по-
требителя и /-й НС.
Для нулевого приближения значений координат потребителя
х(°)) yl0), j(0), Д^ ВЫЧИСЛЯЮТ Дизм/ (А у(°), Z(O), Д'(о)) по (6.33) и элемен-
ты матрицы производных (6.34) по (6.36). Далее по (6.35) находят первое при-
ближение хС), у’1’, z^\ Д'^ , которое используют в качестве начального для
6 3. Алгоритмы вторичной обработки
87
второго приближения. Затем вся процедура повторяется. Вычисления заканчи-
ваются когда выполняются условия
|Х(ЛЧ _х(1)|<8х- pH) _y(j)|<;8ji;p) |д.(М) _ 8д.,
где 8Х, 6^, 8г, 8д. — заданные погрешности нахождения координат.
6.3.2. Определения координат при избыточности измерений
Итерационный алгоритм определения координат (6.31) получен в пред-
положении невырожденности матрицы дЬт(х^)/йх. Применительно к задачам
навигационных определений это означает, что число определяемых парамет-
ров потребителя должно быть равно числу измерений, например, в рассмот-
ренном выше примере определялось четыре параметра потребителя
{ х, У> Z, Д‘ }и использовались измерения псевдодальностей до четырех НС. В
то же время потребитель часто работает в условиях, когда в зоне видимости
находится более четырех НС, и в приемной аппаратуре возможно получить
большее число измерений N > 4. Физически понятно, что обработка большего
числа измерений должна повысить точность, поэтому желательно иметь соот-
ветствующий алгоритм определения координат потребителя при избыточности
измерений.
Такой алгоритм может быть найден при решении задачи оценивания по
методу наименьших квадратов [6.6].
Суть метода заключается в следующем. Имеем вектор измерений у раз-
мерностью У, который линейно зависит от вектора постоянных оцениваемых
параметров х размерностью л , т. с.
y=Hx + q, (6.37)
где ц — вектор ошибок измерения.
Ставим задачу нахождения такой оценки й параметров, которая ми-
нимизирует квадратичную форму
с2 = (у - Нх)т(у - Нх). (6.38)
Решение задачи ищем путем прямого дифференцирования г.2 по х и
приравнивания нулю полученной производной
---= -2Нт(у-Нх) . =0.
<Эх v 'х = х
Полагая, что матрица 1НТН1 невырожденная, находим решение данного
уравнения
88
.Гдвва <L Методы и алгоритмы обржботкясигиалови извлечения, НИ
х = (нтн) ‘нту . (6.39)
Можно показать (6.6], что решение (6.39) является необходимым и дос-
таточным условием минимума квадратичной формы (6.38).
Применим данную процедуру к задаче навигационных определений
при использовании псевдодальномерного метода. В этом методе измеряют-
ся псевдодальности Диам/• * = ЬN до Nспутников (6.32), а определению
подлежит вектор х = |х у z Д'|т •
Объединим все измерения ДЮЫ) в одно векторное
Дизм — Дизм (х) + Л • (6.40)
Пусть х0 — некоторое начальное приближение искомого вектора х.
Разложим функцию Дизм(х) в ряд в точке х0 и ограничимся линейными чле-
нами разложения
Диэм(х) — Дизм(хо)
ЭДизм(хо)
дх
(6-41)
Определим в качестве вектора у измерений в (6.37) разность
У ~ Дизм Дизм (хо)
ЭДизм(хо) -
------5--- х0 •
дх
Подставив (6.41) в (6.40), с учетом (6.39) запишем
дДизм(хо)
дх
х +1) .
У =
Сопоставляя данное соотношение с (6.37), получаем, что матрица Н
для рассматриваемой задачи определяется соотношением
ЭДизм(хо)
дх
(6.42)
Н =
Теперь задача навигационных определений полностью формализована в
виде (6.37). Поэтому, используя решение (6.39) этой задачи по методу наи-
меньших квадратов и переходя к исходным обозначениям, получаем
х = (нтн)-1нту = - ДИзм(хо) + Нх0) =
= х0 + (нтн) * Нт^Диам - Дизм(х0)), (6.43)
где Н — матрица, определяемая выражением (6.42), а ее компоненты вычис-
ляют аналогично тому, как это было сделано в (6.36).
•^б^^Алго^тмывщоричроИоб/аботки, • j ' ‘ ~ . . . ।. 89
Уравнение (6.43) позволяет определить оценку х вектора потребителя,
имея начальное грубое приближение х0 и измерения псевдодальностей Дизм1
до # навигационных спутников.
Если число измерений совпадает с числом определяемых параметров и
матрица Н невырожденная, то уравнение (6.41) преобразуется к виду
х = х0 + Н-1(ДИЗМ - Дизм(х0)), (6.44)
т. е. полностью совпадает с (6.35).
При неравноточных измерениях в (6.37), определяемых корреляционной
матрицей м{гщт} = Rn, для получения оптимальных оценок используется
квадратичная форма вида
г2 =(y-Hx)TRn1(y^Hx), (6.45)
а выражение (6.39) для оптимальной оценки принимает вид
х = (htR~1h)-1 HTR-‘y . (6.46)
Аналогичным образом изменяется и уравнение (6.44)
х = х0 +(htR-1h)’*HtR-1(Ah3M - Дизм(х0)) . (6.47)
6.3.3. Сравнение точности оценок координат потребителя,
полученных псевдодальномерпым и разностпо-
дальномерным методами
При использовании псевдодальномерного метода определения координат
потребителя оценивается вектор х = |ху?Д'|т. В общем случае, когда изме-
ряются псевдодальности (6.40) до У спутников и измерения неравноточны,
решение задачи по методу наименьших квадратов определяется общим уравне-
нием (6.47) или эквивалентным уравнением (см. (6.43))
х = (htR“1h)’1HtR“1^h3M - Дизм(хо) + Нхо).
Представим вектор х в виде х = | хт Д' | * где х = |хуг|т. Тогда измере-
ния (6.40) можно представить
Дизм ~ Д + Д' I + И j
адт(х0)
90 Г л а в a 6. Методы и алгоритмы обработки сигналов и извлечения НИ^
где Д = |Д1Дг- д#Г — вектор истинных дальностей до спутников ( Д/ оп-
ределяется соотношением (6.33)), 1 = | 1 1... 1 |т — ^-мерный вектор, состоя-
щий из единиц.
С учетом введенного вектора х преобразуем матрицу Н (6.42) к виду
H=|G l|, (6.48в)
где
— матрица размера Nx3. (6.486)
Теперь уравнение (6.5) с учетом определения компонент вектора ДИзм
(6.33) можно записать в виде
х - - д(й0) + (Я0). (6.49)-
Из этого уравнения видно, что оценка вектора х потребителя не зави-
сит от начальной оценки Дй смещения Д'.
Напомним, что оценка (6.49) является оптимальной оценкой, которая
минимизирует квадратичную форму (6.45). Запишем данную квадратичную
форму с учетом введенного вектора х и представлений (6.48 а, 6)
е2 =(у-Сх-Д'1)1К-1(у-Сх-Д'|), (6.50а)
где
У = Диам -Д(х0) + Сх0. (6.506)
Рассмотрим разностно-дальномерный метод определения координат по-
требителя. Согласно этому методу (см. § 4.4) из измерений (6.40), с целью ис-
ключения зависимости от смещения Д', формируются разностные измерения,
например типа
= Дизм/ -Дизм1 = Д/-Д1+П/ -ПН » = 2,ЛГ, (6.51)
где Д, по-прежнему определяются соотношением (6.33).
В векторной форме разностные измерения (6.51) принимают вид
ДДизм - ВДизм - ВД + Вт] ,
6.3- Алгоритмы вторичной обработки
91
где
- 1 1 0 ... О
- 1 О 1 ... О
- 10 0 ... 1
матрица размером (N - 1).х .
Заметим, что если все разностные измерения (6.51) формировать относи-
тельно j-го, а не относительно первого, то положение 1 и -1 в каждой строке
матрицы В изменится, но в строке, по-прежнему, будет одна 1 и одна -1. По-
этому при любых разностных измерениях BI = 0 , где 0 обозначен TV-мерный
вектор, элементами которого являются нули.
Разложим функцию Д(х) в ряд в точке некоторой начальной оценки х0
Д(х) = Д(хо)
дДт(хр)
дх
(х - х0) = Д(хо) + G(x - х0),
где G— матрица, определяемая формулой (6.486).
Для задачи разностно-дальномерных измерений квадратичная форма
(6.45) принимает вид
е2 = (у - BGx)T(BRnB)’ '(у - BGx),
(6.52а)
где
У = ВДиэм - ВД(х0) + BGx0 • (6.526)
Оптимальная оценка х по методу наименьших квадратов определяется
соотношением (6.46) или в развернутом виде
х = |gtBt(bR,1Bt)“1BG^ GTBT(BRnBTp'y =
= [GTBT(BRnBT)-,BGl GTBT(BRnBT) *В^ДИЗМ - д(х0) + Gxo). (6.53)
Покажем, что оценка координат потребителя (6.534) может быть получе-
на и из псевдодальномерного метода. Для этого Ледем матрицу
Т =
gtbt(br4b) ’bg] ствт(ввпв) ’в
(lTR-1l)‘*lTR-1
(6.54)
92 Глава 6, Методы и алгоритмы обработки сигналов и извлечения НИ
Пусть Т-1 — псевдообратная матрица [5.11], так что Т-1Т = ТтТ"т = I,
где I — единичная N х N матрица.
Рассмотрим квадратичную форму (6.50 я) для псевододальномерного
метода и представим ее в виде
е2 = (у - Gx - Д' 1)t(t’T-t)r-*(т'*т|(у - Gx - Д' 1) =
= (ТУ - TGx - ТД' |)1(Т»ЛТТ)-1(ТУ - TGx - ТД' 1).
Прямой подстановкой (6.54) можно показать, что
(6-55)
л-i = GTBT(BRnBT) *BG 0
’ 0 lTR-‘l
Ty-TGx-ТДЧ
Рту-Х
YT(y-Gx)'
Таким образом, квадратичная форма (6.55) представляется в виде двух
слагаемых
с2 =(x-pTy)TGTBT(BRnBT) 1BG(x-pTy) + [^'-YT(y-Gx)]2|TR"1l. (6.56)
Оптимальная оценка вектора потребителя х = | хт Д'| ищется путем ми-
нимизации квадратичной формы (6.55) или, что то же самое, (6.56). Но в
(6.56) первое слагаемое не зависит от параметра Д', поэтому выполним ми-
нимизацию в два этапа
гшпе2(х,Д') = тт(гшпе2(х,Д'
v ' ' v I ГТ' '
(6.57)
Выполняя минимизацию- по Д'
пипе2(х, Д') = пип (Д' - 7т(у - Gx)|2|TRn’l ,
получаем
Д' = Тт(у-6х) (6.58)
для каждого значения х .
Выбирая оптимальную оценку в виде (6.58) и выполняя минимизацию в
(6.57) по х
min е2(х, Д') = min(x - рту) GTBT(BRnBT j Bg(x - pTyj,
3 Алгоритмы вторичной обработки
93
^находим
х = Рту = ^GTBT(BRnB)-1BGj 1GIBT(BRnB)’1By =
= ГСТВ1(ВВЛВТ)’1ВС СТВТ(ВВПВ1)'1В(ДИЗМ -Д(хо) + 6хо)-
(6.59)
Так как оценка Д' должна определяться для каждого значения х в со-
ответствии с (6.58), то решение общей задачи минимизации (6.57) включает
оценку (6.59) и оценку Д' в соответствии с алгоритмом
Оценка вектора состояния потребителя (6.59) получена как оптимальная
для псевдодальномерного метода и в точности совпадает • с оценкой (6.53),
найденной для разностно-дальномерного метода. Следовательно и точности
этих оценок совпадают.
Совершенно аналогичное доказательство можно выполнить для псевдо-
радиально-скоростного и разностно-радиально-скоростного метода, что гово-
рит о том что эти-методы также имеют одинаковую точность навигационных
' определений.
Литература
6.1. Перов А. И. Оптимальная нелинейная фильтрация. — М.: Изд-во МЭИ, 1987.
6.2. Тихонов В. И., Харисов В. Н., Смирнов В. А. Оптимальная фильтрация дискрет-
но-непрерывных процессов// Радиотехника и электроника, 1978, т. 23, № 7, с. 1441 —
1452.
6.3. Харисов В. Н., Яковлев А. И., Глущенко А. Г. Оптимальная фильтрация коорди-
нат подвижного объекта//Радиотехника и электроника, 1984, т. 29, № 10, с. 1939—1947.
6.4. Губин В. А., Клюев Н. Ф., Костылев А. А. и др. Основы радионавигационных
измерений// Под ред. II. Ф. Клюева. — М.: Изд-во Мнн. обороны, 1987.
6.5. Аоки М. А. Оптимизация стохастических систем. — М.: Наука, 1971.
6.6. Седж Э. П., Меле Дж. Теория оценивания н ее применение в связи н управ-
лении. — М.: Связь, 1976.
6.7. Харисов В. Н., Эфендиев Р. Н., Нартов В. Я. Синтез оптимальных измери-
телей радионавигационных параметров РСДН// Статистическая раднотехннка. Научно-
методические материалы/ Под ред. А. И. Яковлева. — М.: Изд-во ВВИА им. Н.Е. Жуков-
ского, 1985.
6.8. Никитин А. В., Нартов В. Я. Оптимальный прием сигналов РСДН// Стати-
стическая радиотехника. Научнр-методнческие материалы^ Под ред. Л. А. Ершова. — М.:
Изд-во ВВИА им. Н.Е. Жуковского, 1986.
94 ? ! > ) '' ' _ ) )
Г л а в а 7
Источники погрешностей и точность
навигационно-временных определений в СРНС
Навигационная задача, решаемая в аппаратуре потребителя СРНС, в
простейшем случае заключается в определении пространственно-временных
координат П* = |хугД’|т. В настоящее время известно много вариантов опре-
деления вектора П*(/). В дальнейшем будем рассматривать традиционные под-
ходы, сводящиеся к двухэтапной процедуре обработки информации с исполь-
зованием минимально необходимого объема одновременных измерений (число
уравнений равно числу неизвестных координат потребителя).
Двухэтапность процедуры навигационных измерений предполагает нали-
чие двух независимых этапов обработки сигналов НС. На этапе первичной об-
работки проводят измерения навигационных параметров (Д, Д и т. д.), ко-
торые лишь функционально связаны с вектором состояния П*(/). На этапе
вторичной обработки полученные параметры подвергают преобразованиям на
основе навигационных алгоритмов с целью расчета вектора П*(т).
На точность определения потребителем СРНС координат местоположе-
ния, высоты, скорости, времени и других параметров влияет множество фак-
торов. Они связаны с особенностями первичных и вторичных навигационных
измерений, с характеристиками используемых сигналов, среды распростране-
ния и т. д. Рассмотрим основные источники погрешностей этих измерений
применительно к псевдодальномерному методу НВО.
Основное соотношение (4.2), используемое при рассмотрении псевдо-
дальномерных измерений в СРНС, записано в упрощенном виде, так как даль-
номерная погрешность бдал/ представлена лишь одной составляющей Д'. Од-
нако существуют и другие составляющие дальномерной погрешности, которые
в зависимости от причины их происхождения можно разделить на три группы:
погрешности 5Дцс/, вносимые на i-м НС или КИК; погрешности 5Д1Т,, вно-
симые на трассе распространения сигнала /-го НС; погрешности 6ДПИ, вно-
симые в ПИ СРНС.
Таким образом, в общем виде (4.2) запишем 11.4—1.6, 7.4]
Дизм/ ~ Д/ + ®дал/ ~ Mi + Д + 5ДнС/ + ^Дтр/ + йДпИ • (?• О
Для удобства анализа влияния различных факторов на качество навига-
ционно-временных определений обычно вводят так называемые эквивалент-
ные погрешности измерения дальности и скорости (ЭПД и ЭПС) [7.5], обу-
^7Л. L )решно< )и, внос кые на С и Кя У ) ) ) ) 95
словленные некоррелированными составляющими погрешностей измерения
псевдодальности и скорости ее изменения. В зарубежной литературе их назы-
вают UERE (User Equivalent Range Error) и UERRE (User Equivalent Range
Rate Error). Вторичные навигационные определения удобно характеризовать с
помощью коэффициентов геометрии (геометрических факторов) Кг, обозна-
чаемых еще как разнообразные DOP (Dilution of precision).
7.1. Погрешности, вносимые на НС и КИК
Первая группа погрешностей обусловлена в основном несовершенством
частотно-временного и эфемеридного обеспечения НС.
7.1.1. Погрешности частотно-временного обеспечения
Погрешности частотно-временного обеспечения НС возникают вследст-
вие несовершенства процедур сверки и хранения бортовой шкалы времени
НС. Они проявляются, например, в смещении фаз излучаемых дальномерных
кодов и меток времени, что приводит к погрешностям измерения расстояния
до спутника и расчета его координат. Например, временной сдвиг в 1 мс мо-
жет привести к эквивалентной дальномерной погрешности в 300 км.
Смещение БШВ определяется, в частности, характеристиками стабиль-
ности частоты опорного генератора БЭВЧ, расположенного на НС, и задерж-
ками в аппаратуре НС. Для типовых БЭВЧ изменение дисперсии ошибки
формирования БШВ, вызванное смещениями частоты ОГ между моментами
коррекции (с2), можно аппроксимировать следующим образом [1.4, 1.6, 7.6,[:
для рубидиевых БЭВЧ ст2(/) = 10-20(/-/*.) +1,44 • 10'24(/- i^)2 ;
для цезиевых БЭВЧ ст2(/) = 2,5 • 10-21(/ - tk) + 5,76 • 10-26(г - ,
где t — текущее время; tk — время коррекции БЭВЧ.
Отсюда видно, что СКО сдвига БШВ составляет примерно 9 нс через 2 ч
и 25,4 ... 108 нс через сутки после коррекции (25,4 для цезиевых и 108 нс для
рубидиевых БЭВЧ).
Командно-измерительный комплекс СРНС корректирует БШВ таким об-
разом, чтобы СКО сдвига БШВ не превосходила 10 ^с. Кроме того, на КИК
формируется модель ухода БШВ в промежутках между аппаратной коррекцией.
Ее параметры передаются потребителям в служебном сообщении НС для обес-
печения алгоритмической коррекции БШВ. В качестве модели может исполь-
зоваться полином второй степени. При этом непрогнозируемые отклонения
формируемой на борту НС БШВ относительно ШВС могут достигать 1 нс на
интервале в 1 ч.
Достижение высоких точностных характеристик СРНС возможно лишь
црн тщательном учете релятивистских и гравитационных эффектов (РГЭ) [1.4].
Они обусловлены различием и изменением гравитационного потенциала в
точках расположения спутника и потребителя, а также различием их скоро-
стей. Игнорирование этих особенностей средневысотных СРНС может при-
вести к погрешностям НВО, сравнимым с точностными характеристиками та-
ких систем. Реализация прецизионного беззапросного способа измерений,
предусматривающего определение времени и частоты, требует учета следую-
щих РГЭ: поперечного доплеровского эффекта, гравитационного сдвига часто-
ты эффектов, связанных с пересчетом моментов излучения и приема сигна-
лов, вращением используемых систем координат и др.
Для компенсации влияния наиболее существенных из указанных эффек-
тов частоту БЭВЧ несколько уменьшают относительно номинала (на 4,55 х
х 10~3 Гц в СРНС GPS) [1.2, 7.7]. Коррекция остаточного влияния этих РГЭ
осуществляется потребителями с помощью соответствующей поправки к БШВ,
рассчитываемой на основе служебных данных НС,
Д1ргэ = feja sin Е.
Здесь F = -ijyi / с2; у — геоцентрическая (универсальная) гравитационная
постоянная Земли; с — скорость-света;- а и е — большая полуось, и эксцен-
триситет орбиты спутника; Е — его эксцентрическая аномалия [Т-.7].
7.1.2. Погрешности эфемеридного обеспечения
Эфемеридные погрешности навигационно-временных определений вы-
званы неточностью определения параметров орбит НС на КИК и непрогнози-
руемыми смещениями НС относительно экстраполированной орбиты. По-
грешности эфемерид i-ro НС образуют вектор С] = |д/ ЛЬ Дг|т, составляющими
которого служат трансверсальная Д/, бинормальная Д6 и радиальная Дг [1.4,
1.5]. Их значения составляют величины порядка 0,6 ... 10 м для СРНС GPS.
Так же, как и погрешности часов спутника, эти параметры можно пересчитать
в соответствующую (эфемеридную) компоненту эквивалентной дальномерной
погрешности ЭПД, представляющую собой проекцию вектора С] на линию
визирования НС—ПИ. При этом наибольшие из них (продольные и попереч-
ные) входят в погрешность вычисления дальности с коэффициентом, обычно
не превышающим 0,25, а радиальные 0,6 ... 2 м практически полностью входят
в дальномерную погрешность. В СРНС GPS среднеквадратическое значение
эфемеридных составляющих ЭПД составляет примерно 1 м [7.8]. В СРНС
ГЛОНАСС суммарная составляющая ЭПД, вносимая на КИК и НС (включая
погрешности часов спутника, эфемеридные и другие компоненты), не превы-
шает 9,2 м (наиболее пессимистическая оценка) [1.1, 7.9].
"^ 7;2. *~чгрешн' yiu, вн' умые н трассе \C-nor -ебител \________ \______ ч_____97
|ВЯВИвИ^Ж фИВМВВПВБ |ВЯИНВПЯ№ |СЯЮИв ^вякяяваяг. pBKtSKBtBBL ptSSBSS^^^K. feCSBBSKBBt
Достоверность передаваемых со спутника частотно-временных поправок
и эфемерид зависит также от срока, прошедшего с момента их закладки в па-
мять бортовой ЭВМ, т.е. от "возраста” данных, например, погрешность опре-
деления местоположения потребителя по данным альманаха составляет 900 м
t- (1 ст ) при “возрасте” данных альманаха 1 день, 1200 м — 1 неделя и 3600 м —
2 недели (большие значения погрешностей могут иметь место в период затме-
ний и коррекции орбиты) 11.1, 1.4].
Зависимость точности навигационных данных спутника от интервала
обмена информацией между КИК и спутником будет значительно снижена
при реализации режима межспутниковых измерений в следующем поколении
средневысотных СРНС (типа ГЛОНАСС-М и GPS со спутниками типа Block
II R) [7.8, 7.12].
Кроме указанных выше выделяют еще один вид погрешности дальномер-
ных измерений — групповую задержку навигационного сигнала в аппаратуре
спутника [7.10], представляющую собой задержку между выходным навигаци-
онным сигналом и выходным сигналом бортового эталона времени и частоты.
Различают случайную и систематическую составляющие групповой задержки.
Информация для компенсации систематической составляющей содержится в
служебном сообщении НС (параметры коррекции бортовой шкалы времени).
Случайная составляющая входит в дальномерную погрешность и не превышает
3 нс (2 а) для СРНС GPS. Отличие групповых задержек Р(У)-сигналов диапа-
зонов Ы и L2 должно быть не выше 15 нс (абсолютное среднее значение) со
случайными флуктуациями не более 3 нс (2а ) J7.7] .
7.2. Погрешности, вносимые на трассе НС—потребитель
Вторая группа погрешностей вызвана неточным знанием условий рас-
пространения радиоволн в атмосфере Земли. В атмосфере вылеляют несколько
слоев, отличающихся своими свойствами [1.4, 7.2, 7.3]. Нижний слой, распо-
ложенный над поверхностью Земли, называют тропосферой, высота которой
8 ... 10 км в полярных широтах, 10 ... 12 км в средних и 16 ... 18 км в тропи-
ках. Слой атмосферы от 60 ... 90 км до 500 ... 1000 км называют ионосферой.
Эти два слоя оказывают заметное влияние на качество навигационных изме-
рений в СРНС, которое проявляется в основном в дополнительных задержках
сигнала, возникающих из-за рефракции сигналов спутника (искривления трас-
сы распространения радиоволн) при прохождении атмосферы Земли.
7.2.1. Тропосферные погрешности
Основная составляющая тропосферной погрешности навигационных оп-
ределений в СРНС обусловлена наличием тропосферной рефракции. Рефрак-
ция сигналов СРНС в тропосфере вызвана неоднородностями и изменением ее
диэлектрической проницаемости и соответственно показателя преломления с
изменением высоты. Дополнительная задержка сигнала НС в тропосфере мо-
98 Г л а в a 7. Источники погрешностей и точность HBQ в СРНС
жет достигать 8 ... 80 нс (экспериментальные данные для СРНС GPS) [7.8]. В
связи с тем что для диапазона волн, в котором работают современные СРНС
типа ГЛОНАСС и GPS, тропосфера не является диспергирующей средой
(тропосферная рефракция не зависит от частоты сигнала), устранение этой
задержки двухчастотным способом не осуществляется. Однако значение тро-
посферной погрешности зависит от факторов, которые достаточно точно из-
вестны и прогнозируются (взаимные координаты НС и ПИ, температура, дав-
ление, влажность воздуха). Для средних метеоусловий
К 57
где Kt — параметр, характеризующий состояние тропосферы; р — угол места
(возвышения) НС; п — коэффициент преломления радиоволн; ST — длина
тропосферного участка радиотрассы.
Тропосферу с точки зрения влияния на ее коэффициент преломления, а
значит, и на тропосферную задержку, рассматривают как смесь сухого воздуха
и водяных паров. Для каждой из этих компонент в отдельности значения ко-
эффициента преломления хорошо известны. Зная содержание водяных паров в
соответствии с известными закономерностями можно определить значение
коэффициента преломления для смеси. Кроме того, относительные погрешно-
сти прогноза Tponoi ферных задержек по среднему показателю преломления в
точке приема, не превышают 8 ... 10 %. Поэтому используемые в СРНС моде-
ли тропосферы позволяют уменьшить эти погрешности до единиц наносе-
кунд.
Значения тропосферной рефракции, так же как и ионосферной достига-
ют максимума при малых углах возвышения спутника (0,2° или 25 м при угле
возвышения 5°) |3.9, 7.3, 7.8]. Это объясняется большой длиной трассы, про-
ходимой радиосигналами в атмосфере в такой ситуации. Для уменьшения
влияния атмосферных погрешностей в аппаратуре потребителей осуществляет-
ся обработка сигналов только тех спутников, которые находятся над горизон-
том выше, чем некоторый угол — ’’угол маски”. Обычно этот угол составляет
5 ... 10° в зависимости от качества используемых в приемоипдикаторе СРНС
алгоритмов компенсации атмосферных погрешностей.
При компенсации атмосферной рефракции периодичность расчета кор-
ректирующих поправок потребителем определяется скоростью изменения со-
ответствующих задержек, которая в обычных условиях не превышает 10 м/ч.
7.2.2. Ионосферные погрешности
Рефракция сигналов СРНС в ионосфере вызвана неоднородностями и
изменением ее диэлектрической проницаемости с изменением высоты. Допол-
7.2. Погрешности^. вносим^) на пц, )се НС )отреб
ель
нительная задержка в ионосфере А/Ион сигнала НС с частотой f по сравне-
нию с задержкой сигнала при прямолинейном распространении оценивается
[1.4, 7.8]
А^ион
А В С А
f2 * /3 + /“ + ”И /2 ’
(7.2)
где А, В , С — коэффициенты, характеризующие свойства среды распростра-
нения радиоволн. Для сигналов средневысотных СРНС вторым и третьим
слагаемыми можно пренебречь (для частоты у = 1,5 ГГц их значения оценива-
ются как в/f3 < 0,08 ИС и с//4 <0,25 нс).
В связи с тем что ионосфера является диспергирующей средой, знак за-
держки меняется в зависимости от измеряемого параметра радиосигнала НС —
фазы огибающей или несущей. В первом случае учитывается групповая ско-
рость распространения радиоволн Ррруп , во втором — фазовая 1фаз. Соответ-
ственно в первом случае дополнительная задержка АГИОН положительная (из-
меренная дальность больше истинной), а во втором — отрицательная.
Значение задержки изменяется в широких пределах в зависимости от
района Земли, где расположен ПИ, времени суток, года, солнечной и геомаг-
нитной активности и Т. д., и составляет 5 ... 500. нс [1.1, 7.2]-. Среднее значе-
ние А/ион на частоте средневысотной СРНС (1,6 ГГц) составляет 5 ... 10 нс
ночью и 30 ... 50 нс днем для углов места НС уцс, близких к 90°, а при
Унс<15° возрастает в 2 ... 3 раза. Современные исследования подтверждают
влияние ионосферы только днем и наиболее сильно на низких широтах Земли.
Считается, что эти погрешности необходимо учитывать, если требуется полу-
чить точность нахождения плановых координат больше 8 м [1.6].
В настоящее время известны следующие методы определения и учета
А/ион : моделирование условий на трассе распространения сигналов НС; двух-
частотное измерение; избыточные одночастотные измерения.
Метод моделирования трассы. Этим методом рассчитывают атмосферную
(в данном случае ионосферную) задержку с использованием известных функ-
циональных зависимостей ее значения от параметров атмосферы на соответст-
вующем участке радиотрассы. Используемые при этом соотношения должны
быть оптимальны по критериям точности и приемлемо^сложности. Такой
подход широко применяют в одночастотной (гражданской ) аппаратуре поль-
зователей СРНС. Коэффициент А, входящий в соотношение (7.2) и зависящий
от интегральной (полной) концентрации A/Mp свободных электронов на ионо-
сферном участке трассы, известна лишь приблизительно, поэтому расчеты
А/ион носят ориентировочный характер. Так, параметры модели ионосферы,
100.
Г пав а 7 • Источники погрешность.? и точи фть HL 7 в СР. 1
передаваемые в служебных данных НС СРНС, позволяют уменьшить ионо-
сферную погрешность приблизительно наполовину. В стационарных условиях
при использовании даже сложных многопараметрических моделей сильная из-
менчивость значения N3np в зависимости от многих факторов не позволяет
прогнозировать се с точностью выше 70 ... 80 % [1.6|.
В качестве типового примера приведем алгоритм расчета Л/Ио11 в GPS
[7.7]. Ионосферная задержка аппроксимируется соотношением вида Л/Ион =
= Д1‘н + Д/дн- Здесь Л/н = 5 нс — суточная константа (соответствующая ночным
условиям); Д/дн = cos ^2тг (/ - ) / Т№ j — переменная составляющая за-
держки (соответствующая дневной ионосфере); Лда, Т^, =50 400 с — ам-
плитуда, период и фаза составляющей задержки; t — местное время в точке
расположения потребителя, рассчитанное на основе полученного со спутника
системного времени и ориентировочных координат потребителя.
Для вычисления параметров Лда, Тт используют полиномы третьей
степени:
Лдн=Е«/Ф'; 7’ДН=Х₽/Ф',
i I
где а,-, р( — коэффициенты модели ионосферы, передаваемые для каждого
спутника в навигационном сообщении; Ф1 — геомагнитная широта подионо-
сферной точки (проекции на земную поверхность точки максимальной иони-
зации трассы НС—потребитель, расположенной на высоте около 350 км). Пе-
риод обновления данных коэффициентов в служебном сообщении спутника
обычно составляет 10 сут, но может быть уменьшен, например, в случае по-
вышенной солнечной активности, когда характеристики ионосферы значи-
тельно меняются. Параметр Ф' определяется потребителем для каждого ви-
димого спутника на основании известных ориентировочных координат потре-
бителя и спутника.
Приведенный алгоритм справедлив для усредненных в глобальном мас-
штабе значений основных составляющих вариаций задержки. Он обеспечива-
ет ориентировочно 50 %-ю компенсацию подобных компонент. Здесь не учи-
тываются, например, суточные вариации, которые могут составлять 20 ... 25 %,
и региональные в приэкваториальной зоне и в высоких (более 75°) широтах,
особенно ночью и во время авроральных возмущений.
Двухчастотный метод. Коррекцию псевдодальномерных измерений мож-
но осуществлять по следующему правилу. Сначала необходимо измерить псев-
додальности Диэм/(/1) и ДизмД/г) Д° '-го НС на двух частотах /j и /2, а за-
тем вычислить разность задержек этих сигналов на трассе [1.6, 7.8|
7 2. л. Грешно. \u, ено )мые hl \pacce 'С—поп }бител ) ) ) 101
_**_ -г—-*! ыт^м—е=^>' ' " " 1 ..--ддгааат;
бГион =(Дизм/(/2)- Дизм/(/1))/с, равную разности дополнительных групповых
задержек в ионосфере Л/ИОН1 и Д*ион2 иа этих частотах. В результате можно
записать соотношение
Мион
- S/ ((f / f V - 11 1 ~ П’546 бГиои
- Ь'ионЦ/1 / Л) ’J ~ |lj53l 8ГИО11
для GPS;
для ГЛОНАСС,
где Л/Л =77/60 «1,283 (для GPS) и fi/f2 =9/7^1,2857 (для ГЛОНАСС), -
значения которые используют для коррекции пссвдодальности Дизм/ на час-
тоте ft.
Рефракционные составляющие имеют и погрешности измерения скоро-
сти потребителя в СРНС. По аналоши с вышесказанным можно осуществить
вычисление и компенсацию дополнительного доплеровского сдвига сигнала в
ионосфере А/ион .- Для этого необходимо вычислить разность 8/ измеренных
иссвдодоплеровских сдвигов на частотах f и fi /-го НС, равную разности до-
полнительных сдвигов на этих частотах А/ИО111 и Д/Ион2, и подставить ее в со-
отношение
/ и ч\-1 [3,534 8/
А/ион! =8/(/2/(/!-/2)) » ’ /
( •Эу-' о/
для GPS;
для ГЛОНАСС,
которое используют для коррекции пссвдодоплсровского сдвига на частоте / .
Остаточная погрешность двухчастотного метода, вызванная используе-
мыми допущениями, пропорциональна 1/япуцс и равна 1 ... 2 м при
YIIC <10° . В лучшем случае она составляет десятки сантиметров (1.4, 7.5|.
Рассматриваемый метод теоретически наиболее точный, однако требует
высокоточных измерений на двух частотах, что значительно усложняет аппа-
ратуру потребителя. Кроме того, рассмотренная методика устранения ионо-
сферных погрешностей приводит к значительному возрастанию важнейшей
составляющей погрешности, обусловленной радиошумами, которую трудно
скомпенсировать.
Метод избыточных одночастотных измерений. В этом случае проводятся
измерения по сигналам нескольких НС (обычно более восьми). Здесь за счет
усреднения пространственных характеристик ионосферы можно достичь зна-
чительного снижения ее влияния на точность измерения координат потреби-
телей. Для стационарного потребителя такая методика дает выигрыш в точно-
сти на несколько порядков.
Ионосфера может вызывать также вращение плоскости поляризации
j02 _Г л а в а 7. Источники ногрешяустей и точность НВО СРНС~
линейно поляризованных сигналов (эффект Фарадея), что приводит к появле-
нию дополнительных потерь энергии сигнала {7.3], для уменьшения которых в
СРНС применяют антенны с круговой поляризацией.
7.2.3. Погрешности из-за многолучевости
На приемную антенну аппаратуры потребителя СРНС может поступать
не только прямой сигнал от навигационного спутника, но и множество пере-
отраженных сигналов от земной и морской поверхностей и близлежащих объ-
ектов, например зданий. Для авиационного потребителя СРНС задержка отра-
женного сигнала может составлять 2/3 ... 160 мкс для спутника, находящегося
в зените; при небольших углах возвышения спутника это значение уменьшает-
ся на порядок. Уровень отраженного сигнала может быть соизмеримым с пря-
мым сигналом. Это приводит к существенным искажениям полезного сигнала
и к погрешностям в схемах слежения за параметрами этого сигнала
(задержкой, частотой и фазой). Эти погрешности во многом зависят от взаим-
ного расположения спутника, приемной антенны и отражающих объектов.
Экспериментальные исследования показали большой разброс значений даль-
номерной погрешности из-за многолучевости, которая составляет 0,5 ... 2 м в
лучшем случае (при использовании специальных антенн) и до 100 м в худшем,
в городских условиях с высотными зданиями. Использование в последней си-
туации приемников сигналов стандартной точности (С/А-сигналов СРНС GPS
или СТ-сигналов СРНС ГЛОНАСС) с узкополосными корреляторами может
снизить погрешности на порядок. Кроме того, использование высокоточных
сигналов (например, Р(У)-сигналов СРНС GPS или ВТ-сигналов СРНС ГЛО-
НАСС) позволяет снизить погрешности из-за многолучевости в среднем до
1 ... 3 м и в наихудшей ситуации до 8 м (1 а ) J7.8],
В наиболее неблагоприятных ситуациях может произойти срыв слежения
в следящих схемах, особенно в фазовых.
7.3. Погрешности, вносимые приемоиндикатором СРНС
К дальномерным погрешностям, обусловленным аппаратурой потребите-
ля, можно отнести погрешности слежения за моментом прихода (временного
положения) сигнала спутника, при этом основной вклад вносят шумовые и
динамические погрешности схем слежения за задержкой огибающей (ССЗ) и
несущей ( ЧАП и ФАП) сигналов спутников.
Шумовая и динамическая погрешности. Типовая некогерентная схема
слежения за задержкой, использующая огибающую спутникового сигнала
(двоичную псевдослучайную последовательность), может характеризоваться
шумовой погрешностью с СКО [1.1, 1.4. 7.5, 7.8]
7 3. Погрешности, вносимые приемоиндикатором СРпЬ
!
/ \ 1/2
<т = гэ(д,/(Р/^) + BtBrl(PlN0)2) .
Здесь тэ — длительность элементарного символа ПСП дальномерного кода
(Хэ к0,1 мкс, что эквивалентно 29,32 м, для Р(У)-кода и тэ мкс (293,2 м)
для С/А-кода СРНС GPS и соответственно тэ »0,2 мкс (58,71 м) и тэ =2 мкс
(587,084 м) для ВТ- и СТ-кода системы ГЛОНАСС); В, — односторонняя ши-
рина полосы пропускания замкнутой ССЗ; Вг — односторонняя ширина поло-
сы пропускания тракта промежуточной частоты; P/Nq — отношение мощно-
сти сигнала к спектральной плотности шума на входе приемника (расчетное
значение равно 38,4 дБГц для С/А-кода GPS и 39 ... 44 дБГц для СТ-кода
СРНС ГЛОНАСС). При использовании ССЗ с т -качанием следует учитывать
дополнительные потери до 6 дБ. Погрешности квантования измеряемой
дальности могут составлять 0, 27 м и 2,66 м с учетом шага квантования, рав-
ного 1/64 тэ .
С учетом этого типовая погрешность ПИ (1 ст ), обусловленная шумами
и квантованием, составляет приблизительно 0,2 ...1м и 1,5 ... 10 м (для P(Y)
и С/А-кода СРНС GPS соответственно), и 5 ... 15 м для СТ-кода СРНС ГЛО-
НАСС.
Динамическую составляющую дальномерной погрешности ПИ можно
оценить как сдин = 1,12 т / 4В2 . Это соотношение справедливо для установив-
шегося режима ССЗ второго порядка при квадратичном законе изменения за-
держки сигнала т.
Суммарное значение аппаратурной составляющей дальномерной погреш-
ности ((nJ, + Сдан)1/2 =0,1 тэ при полосе В,=3 Гц и Р/ =30 дБ Гц.
Шумы приемника и квантование оказывают влияние и на качество из-
мерений в ССН. Типовые значения таких погрешностей составляют (I ст) для
схемы ФАП порядка 1,2 мм при слежении за С/А-сигналом и 1,6 мм для P(Y)-
сигнала.
Способы уменьшения погрешностей. Ряд составляющих дальномерной
погрешности, входящих в (7.1), в течение ограниченного интервала времени
можно считать общими (коррелированными) для потребителей СРНС, распо-
ложенных в обширных районах рабочей зоны (районах пространственно-
временной корреляции погрешностей). Поэтому, определив эти данные в про-
извольной точке указанного района, можно использовать их в течение време-
ни корреляции для коррекции дальномерных измерений в других точках.
Такой способ навигационных измерений % СРНС называют дифференци-
альным. Он имеет много разновидностей (см. гл. 11).
Погрешность дальномерных измерений в дифференциальных режимах
СРНС существенно зависит от пространственного разноса потребителей и
временного интервала между моментами расчета поправки и ее использова-
! j
104 Глава?. Источники погрешностей и точность НВО * СРНС ;
ния. В лучшем случае она может уменьшаться с обычным режимом работы
СРНС от нескольких до десятков раз. При типовых погрешностях эфеме-
рид (например СРНС GPS) 10 м и удалениях точек измерения D 5 30 км и
D <, 2000 км использование дифференциального режима снижает погрешности 4
измерений до значений не более 1,5 см и 1м соответственно. Такие значения 1
существенно меньше аппаратурных погрешностей и погрешностей, возникаю- '
щих при распространении радиоволн.
Реализация в приемоиндикаторах СРНС фазовых методов измерений,
отличающихся беспрецедентно высокой точностью, позволяет достигнуть ка-
чественно нового уровня навигационного обеспечения потребителей. Основ-
ная проблема при фазовых измерениях — их неоднозначность. Уменьшить ее
влияние, а в ряде случаев и устранить, можно при использовании избыточных
измерений. Более подробно эти вопросы анализируются в гл. 14.
Номинальная точность определения ПВК получается на основе одно-
кратных измерений псевдодальностей до четырех НС. Повышение точности
достигается также статистической обработкой результатов навигационных оп-
ределений П*(/) и (или) измерений радионавигационных параметров ( т, /дап и
т. д.). В неподвижном ПИ можно усреднять получаемые координаты по ко-
нечному объему выборки или рекуррентно. При этом от длительност!! интер-
вала усреднения Д/ср зависит степень .устранения тех или иных составляющих
погрешностей: при Д/ср=10 с ... 1 мин усредняются быстро флуктуирующие-
шумы вычислений, приемника и атмосферы, погрешности из-за многолучево-
сти распространения и т. и.; при Д1ср = 1 ч ... 1 сут — медленно меняющиеся
погрешности БЭВЧ и прогноза координат НС, фазовые сдвиги в ионосфере и
тропосфере.
В подвижном ПИ применяются алгоритмы статистического сглаживания
быстро флуктуирующих погрешностей на основе известной информации о мо-
дели динамики потребителя и измерений. Обычно в этих целях используются
различные разновидности фильтра Калмана, причем размерность вектора со-
стояния подвижного потребителя, как правило, не менее восьми (три коорди-
наты, три составляющие скорости, систематические погрешности фазы и час-
тоты ОГ ПИ).
Дополнительное расширение вектора состояния целесообразно, напри-
мер, за счет учета трех составляющих ускорения (для высокодинамичных по-
требителей), а также параметров погрешностей бортовых пилотажно-навига-
ционных датчиков. Положительный эффект достигается при учете в модели
измерений не только пссвдодальностей, но и результатов доплеровских изме-
рений (дсльта-псевдодальностей), используемых для измерений не только ско-
рости, но и дальности. При этом обеспечивается слабая чувствительность на-
вигационных алгоритмов к динамике потребителя и снижаются требования к
производительности вычислителей ПИ.
>05
Д. Геом hpuveci & Лакп ) в
^жмевмк»апшмавпяаппза1к^виа
7.4 Геометрический фактор в СРНС
Рассмотрим основные соотношения, характеризующие влияние взаим-
ного расположения НС и потребителя на точность навигационных определе-
ний в СРНС. Для этого запишем уравнение, связывающее погрешности опре-
деления первичных и вторичных навигационных параметров. Такое уравнение
''можно получить из итерационного алгоритма (6.31) вторичной обработки на-
вигационной информации. Действительно, конкретизируя (6.31) в задаче на-
вигационных определений, можно записать х(у+1> - х^ = 8ОШ = |8х 8у 8z 8#’|т —
вектор ошибок определения координат потребителя; = 8дал =
= |ЗДизм1 8Дизм2 ЗДизмЗ 8Дизм4|Т— вектор ошибок измерения дальностей до НС.
Линейность (6.31) позволяет записать
«ош = Н 'бдал ,
Тогда корреляционная матрица ошибок определения ПВК потребителя
может быть записана в виде
Кош = лфош ~«ош) («ОШ -п»ош)Т| = Н-^данН1 = (irR^Il)’1, (7.3)
где йдал = Л/|(бдал - Мдал) (8дал - Шдал)7} — корреляционная матрица погреш-
ностей измерения псевдодальностей; шош, шдад — соответственно векторы
математических ожиданий погрешностей 8оши 8дал. В дальнейшем будем счи-
тать П1ош тдал~ 0.
Диагональными членами корреляционных матриц йдал и Rolu являют-
ся дисперсии определения псевдодальностей (а?._,, i = l,4) и ПВК (а| а?,
Выражение (7.3) подтверждает вывод о том, что соотношение между по-
грешностями определения первичных и вторичных навигационных параметров
зависит только от вида матрицы градиентов Н, т. с. от геометрии взаимного
расположения НС и потребителя. Таким образом, важным условием достиже-
ния высокой точности навигационных определений в СРНС является такое
10ol
Г.,) ва 7 Источи м ногр
взаимное пространственное расположение рабочего созвездия НС и потреби-
теля, при котором обеспечивается требуемая точность ПВК при заданном
уровне погрешностей измерения псевдодальностей. На этом выводе основыва-
ется концепция коэффициента геометрии Кт, являющегося мерой уменьше-
ния точности навигационных определений в СРНС из-за особенностей про-
странственного расположения НС и потребителя (в иностранной литературе
используется обозначение GDOP — геометрический фактор ухудшения место-
о пределения).
Количественная характеристика вводится для случая, когда погреш-
ности определения псевдодальностей до четырех НС равновелики и некорре-
лированы. В этом случае матрица
йдал = стдал1 > Чдал - стдал (нтН
где оды — дисперсия измерения псевдодальностей; I — единичная матрица
соответствующего размера.
Отсюда видно, что дисперсии погрешностей местоопределения и кор-
рекции бортового времени являются функциями диагональных элементов мат-
рицы Приняв =1 и считая СКО определения положения потре-
бителя в четырехмерном (пространственно-временном) пространстве
anB=[^+^+a?+a^.j’/2=[tr(Roul)],/2 ,
можно определить коэффициент геометрии
Kr = [trflCH)'1] 7 , (7.4)
где «{•) ~ след (trace) матрицы.
В общем случае
[ 7 7 7 7 /
О*+стг +стд ] /стаал • (7.5)
При выборе орбитальных параметров НС на этапе разработки подсисте-
мы НС, а также выбора рабочего созвездия, Кг (7.4) является основным кри-
терием. Коэффициент геометрии Кг (7.5) может быть представлен в другом
виде
I
Ге^^етричес/сии (patcjnop e CPHC
v2 _ jf2 . jr2
Л г “ лг.п + лг/»
где *г.п =[’х + ау +стг],/2/’дм . ^гг =од-1авлл ~ пространственный (PDOP)
и временной (TDOP) коэффициенты.
Пространственный коэффициент геометрии, в свою очередь, можно раз-
делить на две составляющие, характеризующие точность местоопределения
потребителя СРНС в горизонтальной и вертикальной плоскостях;
*?.п =*г2г+*?.»,
(7-7)
где Кгг = [oi+о^]1/2/одал , Кг.в = ог/Стдал — горизонтальный (HDOP) и вер-
тикальный (VDOP) коэффициенты.
Наиболее важной характеристикой СРНС является точность местоопре-
деления, поэтому чаще используются параметры Kr „ (PDOP) и Kr T (HDOP).
Используемые приближения (несмещенность, некоррелированность погрешно-
стей и др.) искажают значения погрешностей НВО для множества реальных
ситуаций, когда необходимо учитывать множество неслучайных, в общем слу-
чае неравноточных составляющих, и центрированных случайных составляю-
щих, имеющих неравные дисперсии-и произвольные коэффициенты авто- и
взаимокорреляции.
Такой расширенный состав погрешностей РНП можно учитывать с ис-
пользованием корреляционно-геометрических факторов, которые отражают
особенности также и традиционных геометрических факторов КТ [7.1].
Можно показать, что минимальное значение АГгп=1,5 достигается в
случае, когда потребитель находится в центре правильного тетраэдра [1.4, 7.8].
Для наземного потребителя минимальное значение АГгг = 1,63 достигает-
ся тогда, когда один НС находится в зените, а три других равномерно распо-
ложены в горизонтальной плоскости (КТ1 =0,577; = 1,732). Таким образом,
для минимизации Кг необходимо максимизировать объем тетраэдра.
В современных СРНС влияние кратковременных (5 ... 30 мин) периодов
"плохой геометрии" четырех НС на Кт может быть снижено, например, при
использовании потребителем высокоточного бортового ОГ или высотомера в
этот промежуток времени.
Характеристики стандартной орбитальной конфигурации спутников в
СРНС GPS таковы, что они с вероятностью 99,9 % и более обеспечивают в
глобальной рабочей зоне видимость в любом 24-часовом интервале четырех и
более спутников, при этом четыре спутника обеспечивают PDOP $6 (в случае
использования “угла маски”, равного 5°). При этом среднее значение
HDOP =1,5, a VDOP =2,2 [7.8].
108
Г л а в а 7. Источники погрешностей и точность НВО в СРНС
Значения геометрических факторов, обеспечиваемых орбитальной груп-
пировкой, и вероятности видимости Р# заданного числа спутников Анс в
СРНС ГЛОНАСС (7.9] приведены в табл. 7.1.
Таблица 7.1 Геометрический фактор в СРНС
Параметры Число видимых НС ( Nnc )
4 5 6 7 8 9
Pn 1 1 1 1 0,91 0,58
HDOP, Kr.r 1,41 1,26 1,15 1,03 0,95 0,89
VDOP, Kr„ 2,0 1,75 1,7 1,61 1,6 1,55
TDOP, KTt 1,13 1,03 1,03 0,95 0,93 0,91
PDOP, KrI1 2,45 2,16 2,05 1,91 1,86 1,79
GDOP, KT 2,69 2,39 2,3 2,13 2,08 2,01 j
Эти данные можно использовать для оценки точности определения ко-
ординат местоположения потребителя в горизонтальной (режим двумерных
измерений или 2-D) и вертикальной плоскостях, в трехмерном пространстве
(режим трехмерных измерений или 3-D) и т. д.
Литература
7.1. Котяшкин С. И. Определение ионосферной задержки сигналов в одночастот-
ной аппаратуре потребителей спутниковой системы навигации NAVSTAR// Зрубежная
радиоэлектроника, 1991, № 1, с. 85—95.
7.2. Грудинская Г. П. Распространение радиоволн. — М.: Высшая школа, 1975.
7.3. Долуханов М. П. Распространение радиоволн. — М.: Связь, 1972.
7.4. Болдин В. А. Зарубежные глобальные системы навигации. — М.: Изд-во ВВИА
им. Н.Е. Жуковского, 1986.
7.5. Бортовые устройства спутниковой радионавигации/ Под ред. В. С. Шебшаеви-
ча. — М.: Транспорт, 1988.
7.6. Новиков И. А. и др. Использование спутниковой радионавигационной системы
NAVSTAR для синхронизации шкал времени//3арубежная радиоэлектроника, 1985, №11.
7.7. ICD-GPS-200.
7.8. Understanding GPS: principles and application, Elliotte Kaplan editor. — Artech
House Publish ERs. Boston-London, 1996.
7.9. Bazarov Y. Introduction to Global Navigation Satellite System//AGARD LECTURE
SERIES 207. System implications and innovative applications of satellite navigation. NATO
AGARD, 1996.
7.10. Глобальная спутниковая навигационная система ГЛОНАСС//Интерфейсный
контрольный документ. — М.: Главкосмос, 1988.
7.11. Spilker J. J. GPS signal structure and performance characteristics// Navigation,
1978, vol. 25, № 2.
7.12. Feairheller S. The Russian GLONASS System. US Air Force// Russian study/ION
GPS-94, 1994, pp. 293-302.
7.13. Lachapelle G. Navigation accuracy for absolute positioning// AGARD lecture Se-
ries 207. System Implication and Innovative Applications of Satellite Navigation, 1996,
no. 4-1.
109
Раздел 2
СПУТНИКОВАЯ РАДИОНАВИГАЦИОННАЯ
СИСТЕМА ГЛОНАСС
Глава 8
Общие сведения о спутниковой
радионавигационной системе ГЛОНАСС
8.1 Структура и основные характеристики
Отечественная сетевая среднеорбитальная СРНС ГЛОНАСС (ГЛОбаль-
ная НАвигационная Спутниковая Система) предназначена для непрерывного и
высокоточного определения пространственного (трехмерного) местоположе-
ния, вектора скорости движения, а также времени космических, авиационных,
морских и наземных потребителей в любой точке Земли или околоземного
пространства. В настоящее.время она состоит из трех подсистем:
подсистема космических аппаратов (ПКА), состоящая из навигационных
спутников ГЛОНАСС на соответствующих орбитах;
подсистема контроля и управления (ПКУ), состоящая из наземных пунк-
тов контроля и управления;
аппаратуры потребителей (АП).
Навигационные определения в ГЛОНАСС осуществляются на основе
беззапросных измерений в аппаратуре потребителей псевдодальности и ради-
альной псевдоскорости до четырех спутников (или трех спутников при ис-
пользовании дополнительной информации) ГЛОНАСС, а также с учетом при-
нятых навигационных сообщений этих спутников. В навигационных сообще-
ниях, передаваемых с помощью спутниковых радиосигналов, содержится ин-
формация о различных параметрах, в том числе и необходимые сведения о по-
ложении и движении спутников в соответствующие моменты времени. В ре-
зультате обработки этих данных в АП ГЛОНАСС обычно определяются три
(две) координаты потребителя, величина и направление вектора его земной
(путевой) скорости, текущее время (местное или в шкале Госэталона Коорди-
нированного Всемирного Времени L)TC(SU) или, по другому, иТС(ГЭВЧ)
(ГЭВЧ — Государственный эталон времени и частоты).
Разработчиками системы ГЛОНАСС в целом, в том числе НС и про-
граммного обеспечения управления НС является Научно-производственное
объединение прикладной механики. Разработчиком системы ГЛОНАСС, в том
числе подсистемы контроля и управления, бортовой аппаратуры НС и аппара-
туры потребителей является Научно-исследовательский институт космиче-
НО Г л а в а 8. Общие сведения о СРНС ГЛОНАСС
ского приборостроения. Генеральный заказчик системы ГЛОНАСС — Военно-
космические силы МО РФ, которые и осуществляют в настоящее время управ-
ление системой ГЛОНАСС и информирование потребителей о ее состоянии
(через Координационный научно-информационный центр (КНИЦ ВКС МО
РФ)). Основным документом, содержащим описание структуры и наиболее
общих характеристик навигационных сигналов и сообщений системы, служит
интерфейсный контрольный документ ГЛОНАСС [1.2].
Основные характеристики СРНС ГЛОНАСС приведены в табл. 8.1 — 8.3
[1.1, 1.2, 1.6, 7.9, 8.2, 8.4, 8.5], где для сравнения приведены сведения об аме-
риканской средневысотной СРНС GPS [7.8|. В табл. 8.1 приведены общесис-
темные характеристики СРНС ГЛОНАСС. В табл. 8.2 приведены как стандарт-
ные значения характеристик СРНС, так и их оценки на основе данных, полу-
ченных в 1993—1995 гг. Последние показаны в скобках, причем для С/А-кода
(кода стандартной точности) значения приводятся для вариантов работы (с
SA/без SA (SA — Selective Availability — селективный доступ) ).
Таблица 8.1. Системные характеристики СРНС ГЛОНАСС
Параметр, способ ГЛОНАСС GPS
Число НС (резерв) Число орбитальных плоскостей Число НС в орбитальной плоскости Тип орбит Высота орбит, км Наклонение орбит, град Драконический период обращения НС Способ разделения сигналов НС Несущие частоты навигационных радиосиг- налов, МГц: /Л L1 Период повторения ПСИ (дальномерного кода или его сегмента Тактовая частота ПСИ, МГц Скорость передачи цифровой информации (соответственно СИ- и D- код), бит/с Длительность суперкадра, мин Число кадров в суперкадре Число строк в кадре Система отсчетов времени Система отсчета пространственных координат Тип афемсрид 24 (3) 3 8 Круговая) е =0+0,01) 19100 64,8±0,3 11ч 15 мин 44 с +5 с Частотный 1602,5625...1615,5 1246,4375...1256,5 1 мс 0.511 50 2.5 5 15 Ul C(SU) ПЗ-ЧО Гсоцен1рические координаты и их производные 24 (3) 6 4 Круговая 20145 55 (63) 11ч 56,9 мин Кодовый 1575,42 1227,6 1 мс (С/А-код) 7 дн (Р-код) 1,023 (С/А-кол) 10,23 (Р,У-код) 50 12,5 25 5 UTC(USNO) WGC-84 Модифициро- ванные кенле- ровы элементы
В табл. 8.3 приведены типовые данные погрешностей для СРНС ГЛО-
НАСС как для более (в скобках), так и для менее точного варианта экспери-
ментальных измерений, а так же для СРНС GPS (в скобках дан типовой диа-
пазон изменения).
8 1. Структура и основные характеристики
111
Таблица 8.2. Точностные характеристики СРНС
Параметр Точность измерений
GPS (/*=0,95) ГЛОНАСС (/*=0,997)
Горизонтальная плоскость, м 100 (72/181 (С/А код) 300 (Р=0,9999) (С/.А-код) 18- (Р-, Y-код) 60 (СТ-код) (39)
Вертикальная плоскость, м 156 (135/34) (С/А-код) 28 (Р-, Y-код) 75 (СТ-код) (67,5)
Скорость, см/с < 200 (С/А-код ) 20 (Р-, Y-код) 15 (СТ-код)
Ускорение, мм/с2 8 (С/А-код) <19 (С/А-код ) —
Время, мкс 0,34 (С/А-код ) 0,18 (Р-, Y- код) 1 (СТ-код)
В настоящее время на базе ГЛОНАСС предполагается создание Единой
глобальной системы координатно-временного обеспечения (ЕС КВО) |8.7].
Кроме СРНС эта система включает:
Государственную систему Единого времени с эталонной базой страны;
Государственную систему и службу определения параметров вращения
Земли;
систему наземной и заатмосфсрной оптической астрометрии;
космическую геодезическую систему и т. д.
Считается, что возможности существенного повышения точности навигацион-
ных определений связаны с созданием глобальной системы отсчета, ис-
пользующей самоопределяющиеся навигационно-геодезические спутники без
привлечения измерений с поверхности Земли 11.4, 1.5].
Таблица 8.3. Погрешности СРНС ГЛОНАСС.
Источи и к погрешности, м Дальномерная погрешность
ГЛОНАСС СТ-код GPS
- 1 ГСр= Ю с Р-.Y-код С/А-код
Эфемериды и БЭВЧ 9.2 9.2 Tn 3,6
Ионосферная рефракция 10 10 0,01 7
Тропосферная рефракция 2 2 0,7 0,7
Многолучевость 3 1 I.S 1,2
Другие 1.5 1
Приемом иди кагор 13 5 0 24 |
Типовое затрубление (SA) - - 0,0 1,5
Суммарная СКО эфемерид 20.6 (8 .. 10) 14.7 4,1 (1.4..0,6) 8,1 (7 ... 14) (без SA) 25 (30,3 .. 40) (с SA)
112
Г л_ ав_а8.Общиесведеиия о СРНС ГЛОНАСС
8.2 . Этапы развертывания
Теоретические предпосылки по созданию отечественной СРНС впервые
были сформулированы [В.4] еще до запуска первого ИСЗ в рамках исследова-
ний, проводимых группой сотрудников ЛВВИА под руководством В. С. Шеб-
шаевича в 1955—1957 гг., что свидетельствует о приоритете отечественной
науки в разработке идеологии СРНС.
Первый НС отечественной низкоорбитальной СРНС, предназначенной
для нединамичных потребителей, был выведен на орбиту в 1967 г. А уже через
год были проведены научные исследования по обоснованию, целесообразности
и возможности создания Единой СРНС (Единой Космической Навигационной
Системы), способной обеспечить потребности любых наземных, морских, воз-
душных и космических потребителей с повышенной точностью. В качестве
такой СРНС была разработана сетевая СРНС ГЛОНАСС (1972—1982 гг.).
Развертывание созвездия НС велось поэтапно. Первый спутник СРНС
ГЛОНАСС (Космос 1413) запущен 12 октября 1982 г. К середине 1995 г. всего
было запущено 65 НС ГЛОНАСС, большая часть из которых к настоящему
времени уже выведена из эксплуатации.
Этапы создания полного орбитального созвездия ГЛОНАСС иллюстри-
руются данными, приведенными в табл. 8.4 [7.12, 8.3, 8.9—8.11].
Таблица 8.4. Этапы развертывания СРНС ГЛОНАСС
Номер п.п Космос, номер Дата запуска Дата начала использова- ния Состояние Номер блока
1 2 3 4 5 6
1 1413 12.10.82 10.11.82 30.03.84 1
2 1490 10.08.83 02.09.83 29.10.85 2
3 1491 10.08.83 31.08.83 09.06.88 2
4 1519 29.12.83 07.01.84 28.01.88 3
5 1520 29.12.83 15.01.84 16.09.86 3
6 1554 19.05.84 05.06.84 16.09.86 4
7 1555 19.05.84 09.06.84 17.09.87 4
8 1593 04.09.84 22.09.84 28.11.85 5
9 1594 04.09.84 28.09.84 16.09.86 5
10 1650 18.05.85 06.06.85 28.11.85 ь
11 1651 18.05.85 04.06.85 17.09.87 6
12 1710 25.12.85 17.01.86 06.03.89 7
13 1711 25.12.85 20.01.86 17.09.87 7
14 1778 16.09.86 17.10.86 05.07.89 8
15 1779 16.09.86 17.10.86 24.10.88 8
16 1780 16.09.86 17.10.86 12.10.88 8
17 1838 24.04.87 - аз 9
18 1839 24.04.87 - аз 9
19 1840 24.04.87 - аз 9
20 1883 16.09.87 10.10.87 06.06.88 10
21 1884 16.09.87 09.10.87 20.08.88 10
22 1885 16.09.87 05.10.87 07.03.89 10
23 1917 17.02.88 - аз 11
24 1918 17.02.88 - аз 11
8,2. Этапы развертывания
113
Продолжение табл. 8.4.
Г 1 2 3 4 5 6
1 25 1919 17.02.88 аз и
26 1946 21.05.88 01.06.88 10.05.90 12
27 1947 21.05.88 03.06.88 18.09.91 12
28 1948 21.05.88 03.06.88 18.09.91 12
29 1970 16.09.88 20.09.88 21.05.90 13
- 1971 16.09.88 28.09.88 30.08.89 13
30 1972 16.09.88 03.10.88 12.08.92 13
31 1987 10.01.89 01.02.89 03.02.94 14
32 1988 10.01.89 01.02.89 17.01.92 14
33 1989* 10.01.89 ЭГС 14
- 2022 31.05.89 04.07.89 23.01.90 15
34 2023 31.05.89 15.06.89 18.11.89 15
35 2024» 31.05.89 ЭГС - 15
36 2079 19.05.90 20.06.90 17.08.94 16
37 2080 19.05.90 17.06.90 27.08.94 16
38 2081 19.05.90 11.06.90 20.01.93 16
39 2109 08.12.90 01.01.91 10.06.94 17
40 2110 08.12.90 29.12.90 20.01.94 17
41 2111 04.04.91 28.12.90 15.08.96 17
42 2139 04.04.91 28.04.91 14.11.94 18
43 2140 04.04.91 28.04.91 04.06.93 18
44 2141 30.01.92 04.05.91 16.06.92 18
45 2177 30.01.92 24.02.92 29.06.93 19
46 2178 30.01.92 22.02.92 4- 19
47 2179 30.01.92 18.02.92 4- 19
48 2204 30.07.92 19.08.92 4- 20
49 2205 30.07.92 29.08.92 27.08.94 20
50 2206 30.07.92 25.08.92 26.08.96 20
51 2234 17.02.93 14.03.93 17.08.94 21
52 2235 17.02.93 25.08.93 + 21
53 2236 17.02.93 14.03.93 4- 21
54 2275 11.0494 04.09.94 4- 22
55 2276 11.04.94 18.05.94 4 22
56 2277 11.04.94 16.05.94 4 22
57 2287 11.08.94 07.09.94 4 23
58 2288 11.08.94 04.09.94 4 23
59 2289 11.08.94 07.09.94 г 23
60 2294 20.11.94 11.12.94 4- 24
61 2295 20.11.94 15.12.94 + 24
62 2296 20.11.94 16.12.94 4 24
63 2307 07.03.95 30.03.95 4 25
64 2308 07.03.95 05.04.95 4 25
65 2309 07.03.95 05.04.95 4 25
66 2316 24.07.95 26.08.95 4 26
67 2317 24.07.95 22.08.95 4 26
68 2318 24.07.95 22.08.95 4 26
69 2323 14.12.95 07.01.96 4 27
70 2324 14.12.95 резерв -г 27
71 2325 14.12.95 18.01.96 т 27
Здесь все даты даны для Московского времени (UTC+03 ч 00 мин); в графе
“состояние" показаны даты снятия спутника с использования, а знаком + от-
мечены рабочие спутники орбитальной группировки; аз — аварийный запуск;
эгс — эталонный геодезический спутник. Таким образом, полная орбитальная
группировка была развернута в составе 24 работающих и одного резервного
спутников.
Г л а в a 8. Общие сведения о СРНС ГЛОНАСС
В соответствии с указом Президента РФ от 24 сентября 1993 г. началось
официальное использование системы ГЛОНАСС с промежуточным созвездием
спутников. Штатная эксплуатация ГЛОНАСС началась в конце 1995 г., когда
сеть НС объединила 24 рабочих спутника. Считается, что такое созвездие име-
ет некоторую избыточность, так как, например, даже 22-спутниковое созвез-
дие НС ГЛОНАСС, созданное к середине 1995 г., обеспечивало непрерывное
навигационное поле в течение суток. При этом потребители могли наблюдать
от 5 до 8 спутников.
В 1996 г. Правительство России [8.4] подтвердило сделанное на 10-й Аэ-
ронавигационной конференции ИКАО предложение о предоставлении канала
стандартной точности системы ГЛОНАСС мировому авиационному сообщест-
ву, обеспечивающего определение координат с характеристиками точности,
показанными в табл. 8.2. В отличие от системы GPS, здесь не предполагается
использования каких-либо методов загрубления точности. Кроме того, Россия
принимает все меры для обеспечения целостности и надежности обслужива-
ния и полагает , что она будет в состоянии представить уведомление по
крайней мере за 6 лет до прекращения обслуживания.
Оценить широкие возможности ГЛОНАСС даже при неполном созвездии
можно рассмотрев приведенные в табл. 8.5 характеристики зоны действия
ГЛОНАСС для авиационных потребителей на промежуточном этапе разверты-
вания (12 НС на двух орбитах) (8.1] .
Таблица 8.5. Характеристики зоны действия
| Характеристики зоны действия Географичес- кая широта потребителя Трехкоор- динатные определения Двухкоорди- I натные определения |
I Часть одновременно обслужи- | ваемого пространства >±50" < ±50" 92 60 100 98
| Суммарная продолжительность I навигационных определений в 1 сутки, не менее (часы) > +50" < +50" 18 ... 20 13 ... 15 24 21
1 Длительность максимального 1 перерыва в навигационных опре- 1 делениях, ч в сут, не более > +50° < +50" 2 <5 0
Система ГЛОНАСС с полностью развернутой группировкой НС характе-
ризуется вероятностью обеспечения навигационных определений не хуже 0,947
в непрерывном навигационном поле с точностью, указанной в табл. 8.2 (в
Российском радионавигационном плане 1994 г. [В.9| приведены несколько от-
личающиеся данные. Точностные характеристики определения плановых коор-
динат, высоты и времени (1 ст) равны соответственно 30 м, 30 м и 1 мкс, а
доступность системы — 0,98). Значение HDOP в этом случае для 93 % потре-
бителей будет менее двух.
Расчетный ресурс спутника системы ГЛОНАСС составляет не менее трех
лет. После 2000 г. [7.12| планируется развернуть модернизированную систему
115
8.3. Система координат, используемая в СРНС ГЛОНАСС
рЛОНАСС-М. Ресурс ее НС составит не менее 5 лет, что позволит повысить
надежность системы в целом. За счет межспутниковых измерений 17.12] зна-
чительно повысится время автономной работы орбитальной группировки и
другие характеристики. Точностные характеристики определения плановых
координат, высоты и времени (1а) составят соответственно 10 м, 10 м и де-
сятки наносекунд |В. 10, 7.12]. (Болес подробно о ГЛОНАСС-М см. гл. 13).
8.3 Система координат, используемая в СРНС ГЛОНАСС
Эфемеридная информация, передаваемая потребителям ГЛОНАСС в со-
ставе служебной информации конкретного НС, содержит координаты фазового
центра передающей антенны данного НС в геоцентрической системе коорди-
нат ПЗ-90 (см. гл. 3). Эта система координат также как и принятая в СРНС
GPS система координат WGS-84 |7.8] относится к декартовым системам типа
ECEF (Earth-centered Earth-fixed, т. е. начало координат расположено в центре
масс Земли и направления осей связаны с Землей). До 1993 г. в СРНС ГЛО-
НАСС использовалась система координат СГС-85 [8.5, 8.6|.
Несмотря на схожесть систем координат ПЗ-90 и WGS-84, они, тем не
менее, различаются в некоторых важных параметрах. Принято сводить эти
различия, например к некоторому пово-
роту системы относительно оси Z или Г
и смещению начала координат (рис. 8.1).
Соотношения, характеризующие
v переход от координат в системе ПЗ-90 к
* системе WGS-84, можно представить в
виде ]8.1]
Рис. 8.1. Системы координат Смещение координат точки па зем-
ной поверхности в двух указанных систе-
мах координат оценивается по результатам измерений как нс превышающее
15 м (в среднем 5 м).
8.4 . Частотно-временное обеспечение.
Шкалы времени системы ГЛОНАСС
Частотно-временное обеспечение реализуется системой синхронизации
(СС) ГЛОНАСС, которая обеспечивает формирование единой системной шка-
лы времени (СШВ), синхронизацию БШВ (бортовых шкал времени) каждого
ПС с СШВ. расчет частотно-временных поправок (ЧВП). определение расхож-
116 Глава 8. Общие сведення о СРНС ГЛОНАСС
дения СШВ относительно шкалы Государственного эталона координирован-
ного всемирного времени UTC (SU), расчет поправок к СШВ, закладку попра-
вок на борт НС (дважды в сутки) для передачи их потребителям в составе на-
вигационного сообщения. (Общие сведения о единицах мер времени, системах
отсчета и шкалах времени приведены в гл.2.)
Система синхронизации включает в свой состав 11.1, 1.2, 8.10|:
I. Цезиевые БЭВЧ НС, обеспечивающие формирование и хранение БШВ
НС. Точность взаимной синхронизации бортовых шкал времени НС составля-
ет 20 нс (1а) .
2. Центральный синхронизатор (ЦС) системы, обеспечивающий форми-
рование СШВ с помощью водородных стандартов частоты с суточной неста-
бильностью частоты не хуже 5 10 14 и относительной погрешностью частоты
не хуже 1-Ю'13. Для системы GPS эти параметры имеют значения 3 10 14 и
ЫО'12, соответственно (для одного из этапов использования системы).
3. Систему контроля фаз (СКФ), осуществляющую активные и пассив-
ные измерения дальности до НС и передачу результатов измерений на центр
управления системой (ЦУС) для сверки БШВ и СШВ.
4. Аппаратуру привязки, обеспечивающую одновременные измерения по
сигналам одного НС для определения расхождения СШВ и UTC(SU). Расхож-
дение между СШВ и UTC(SU) не должно превышать 1 мс (1а). Погрешность
привязки этих шкал не должна превышать 1 мкс (1а ).
5. Контрольные станции, обеспечивающие контроль и управление БШВ
и передачу ЧВП на НС.
6. Программные средства вычислителей ЦУС, обеспечивающие согласо-
ванную работу СС, периодическое определение ухода БШВ относительно
СШВ, расчет и прогнозирование ЧВП для НС. При этом учитываются влияние
релятивистских и гравитационных эффектов на формирование БШВ.
Частотно-временные поправки рассчитывают па каждом витке НС в виде
двух параметров линейной аппроксимации расхождения БШВ относительно
НС на тридцати- (шестидесяти ) минутном интервале и закладываются дважды
в сутки (ориентировочно каждые 12 ч) на борт каждого НС.
Шкала времени каждого спутника ГЛОНАСС? может эпизодически под-
вергаться коррекции с целью того, чгобы отличие этой шкалы от шкалы вре-
мени цен трального хронизагора не превышало +1 нс. В этом случае в течение
времени, необходимого наземному комплексу для проведения сверки и фор-
мирования поправок, в навигационном сообщении передаются признаки, >а-
прещающие использование этого спутника для целей навигации.
В сетевых СРНС' годность взаимной синхронизации фаз дальномерных
сигналов НС является основным показателем частотно-временных определе-
ний. Она характеризуется точностью привязки каждой БШВ к СШВ на интер-
вале примерно 12 ч и зависит, в основном, от стабильности БЭВЧ и погреш-
ности определения ухода БШВ относительно СШВ по измерениям СКФ.
8.4. Частотно-временное обеспечение. Шкалы времени системы ГЛОНАСС 117
В случае использования БЭВЧ на основе квантовых' стандартов частоты
с атомными лучевыми трубками, характеризующихся относительной погреш-
ностью ио частоте не более 7 - 10 12 и суточной нестабильностью частоты не
более 5 10~13, и проведения сверки шкал времени (определения ухода БШВ) с
погрешностью не более 5 нс (1а ), обеспечивается точность взаимной синхро-
низании сигналов НС порядка 20 ... 23 нс на интервале 12 ч. Алгоритмическая
коррекция дополняется аппаратной коррекцией при уходе БШВ более 1 мс.
Шкала системного времени в ГЛОНАСС корректируется одновременно с
коррекциями на целое число секунд шкал UTC (SU), проводимыми Службой
Всемирного времени. Коррекции шкал UTC необходимы для их согласова-
ния с астрономической шкалой UT1 всемирного времени. Указанная коррек-
ция СШВ ГЛОНАСС осуществляется в 00 ч 00 мин 00 с в полночь с 30 июня
на 1 июля или с 31 декабря на 1 января. О планируемом проведении секунд-
ной коррекции СШВ ГЛОНАСС сообщается заблаговременно.
Следовательно, между СШВ ГЛОНАСС и UTC (SU) нс существует сдвига
на целое число секунд. Благодаря этому сокращается объем информации при
передаче потребителям величины расхождения СШВ и UTC(SU). Между сис-
темным временем ГЛОНАСС и UTC(SU) существует постоянный сдвиг на це-
лое число часов, обусловленный особенностями функционирования ПКУ:
^ГЛОНАСС = UTC(SU)+ 03 ч 00 мин.
В перспективе предполагается снизить погрешность взаимной синхрони-
зации фаз сигналов НС до 15 нс за 24 ч, а также провести согласование СШВ
GPS и ГЛОНАСС. Согласование этих ШВ основывается на высоких характе-
ристиках шкалы UTC (SU) [8.10|.
Литература
8.1. Misra 1‘ A’. Integrated use ol GPS and GLONASS in civil aviation //Mil LL. Hi
let net.
8.2. fans, j wp/75. icao, i9,ss.
8.3. История запусков no программе ГЛОНАСС// Компьютерный бюллетень BBs
КНИЦ ИКС РФ.
8 4. Письмо министра транспорт РФ llpeiH.-tenri c-uiera ИКАО// Компьютерньп
ок.ллетень BBS КНИЦ ИКС РФ.
S5. Характеристики системы ГЛОНАСС, качество тимереннй и функционирование
сипемы/ Пер. //. Мишра и др. ION GPS-96. Компьютерный бюллетень BBS КНИЦ
ИКС РФ
8.6. Функционирование ГЛОНАСС в 1995 году Резулыагы моииторинiа/ Пер
// Мишра и др. Mil LL. Компьютерный бюллетень BBS КНИЦ ВКС РФ.
8.7. Шебшаевич В. С. Этапы становления и проблемы развития спутниковых РН<
в СССР// Вопросы радиоэлектроники. Сер. ОВР. 1991. вып. 8.
8.8. GNSSP/2-WP/70. ICAO, 1995.
8.9. GLONASS Development History// Mil LL GG. Internet.
8.10. балясников В. II. и tip. Современное состояние и перспективы развития час-
тотно временного обеспечения системы IJIOHACC// Вопросы радиоэлектроники Сен
ОВР. 1991. вып. 8.
118
Глава 9
Наземный сегмент
(подсистема контроля и управления)
9.1. Назначение и состав подсистемы контроля и управления
9.1.1. Общие сведения
Наземный сегмент системы ГЛОНАСС — подсистема контроля и управ-
ления (ПКУ), предназначена для контроля правильности функционирования,
управления и информационного обеспечения сети спутников системы ГЛО-
НАСС, состоит из следующих взаимосвязанных стационарных элементов [1.1,
1.4, 1.5, 7.9, 9.1, 9.2]: центр управления системой ГЛОНАСС (ЦУС); централь-
ный синхронизатор (ЦС); контрольные станции (КС); система контроля фаз
(СКФ); кванто-оптические станции (КОС); аппаратура контроля поля (АКП).
Наземный сегмент выполняет следующие функции:
проведение траекторных измерений для определения и прогнозирования
и непрерывного уточнения параметров орбит.всех спутников;
временные измерения для определения расхождения бортовых шкал вре-
мени всех спутников с системной шкалой времени ГЛОНАСС, синхронизация
спутниковой шкалы времени с временной шкалой центрального синхрониза-
тора и службы единого времени путем фазирования и коррекции бортовых
шкал времени спутников;
формирование массива служебной информации (навигационных сообще-
ний), содержащего спрогнозированные эфемериды, альманах и поправки к
бортовой шкале времени каждого спутника и другие данные, необходимые для
формирования навигационных кадров;
передача (закладка) массива служебной информации в память ЭВМ каж-
дого спутника и контроль за его прохождением;
контроль по телеметрическим каналам за работой бортовых систем спут-
ников и диагностика их состояния;
контроль информации в навигационных сообщениях спутника, прием
сигнала вызова ПКУ;
управление полетом спутников и работой их бортовых систем путем вы-
дачи на спутники временных программ и команд управления; контроль прохо-
ждения этих данных; контроль характеристик навигационного поля;
определение сдвига фазы дальномерного навигационного сигнала спут-
ника по отношению к фазе сигнала центрального синхронизатора;
планирование работы всех технических средств ПКУ, автоматизирован-
ная обработка и передача данных между элементами ПКУ.
В атоматизированном режиме решаются практически все основные зада-
9.1- Назначение и состав подсистемы контроля ц .управления
119
чи управления НС и кон-
троля навигационного поля.
С использованием
специального математиче-
ского обеспечения в сетях
ЭВМ решаются следующие
задачи (рис. 9.1, 9.2, a, ff):
планирование работы ПКУ
...—► - измерения
* команды
* время
-------* - телеметрия -----------* - измерения
с НС и формирование
программы работы для
средств ЦУС и других
элементов; расчет бал-
листической информа-
ции для планирования
и управления НС, ко-
мандно - программной
информации; обработка
телеметрической ин-
формации; контроль
навигационного поля;
обработка траекторных
измерений и прогнози-
рование пространст-
венного положения НС
и расхождение их шкал
времени с временной
шкалой системы.
На приведенных
схемах АРМ — автома-
тизированное рабочее
место.
Основные функ-
ции элементов ПКУ за-
Рис. 9.1. Схема наземного сегмента с направле-
нием движения потоков информации
Рие. 9.2. Схемы локальной вычислительных
сетей ЦУС (а) и КС (6)
ключаются в следую-
щем.
9.1.2 Центр управления системой
Центр управления системой [1.4, 1.5| соединен каналами автоматизиро-
ванной и неавтоматизированной связи, а также линиями передачи данных
со всеми элементами ПКУ, планирует и координирует работу всех средств
120 Г л а в а 9. Наземный сегмент(подснстем» контроля и управления)
ПКУ на основании принятого для ГЛОНАСС ежесуточного режима управле-
ния спутниками в рамках технологического цикла управления. При этом ЦУС
собирает и обрабатывает данные для прогноза эфемерид и частотно-временных
поправок, осуществляет с помощью, так называемого, баллистического центра
расчет и анализ пространственных характеристик системы, анализ баллистиче-
ской структуры и расчет исходных данных для планирования работы элемен-
тов ПКУ.
Информацию, необходимую для запуска спутников, расчета параметров
их орбитального движения, управления ими в полете, ЦУС получает от сис-
темы единого времени и эталонных частот, системы определения параметров
вращения Земли, системы мониторинга гелио- и геофизизической обстановки
[7.9,9.Ц.
Центральный синхронизатор, взаимодействуя с ЦУС, формирует шкалу
времени ГЛОНАСС , которая используется для синхронизации процессов в
системе, например, в системе контроля фаз. Он включает в свой состав группу
водородных стандартов.
9.1.3. Контрольные станции
Контрольные станции [1.4, 1.5] (станции управления, измерения и кон-
троля или наземные измерительные пункты) по принятой схеме радйокб'нт-
роля орбит осуществляют сеансы траекторных и временных измерений, необ-
ходимых для определения и прогнозирования пространственного положения
спутников и расхождения их шкал времени с временной шкалой ГЛОНАСС, а
также собирают телеметрическую информацию о состоянии бортовых систем
спутников. С их помощью происходит закладка в бортовые ЭВМ спутников
массивов служебной информации (альманах, эфемериды, частотно-временные
поправки и др.), временных программ и оперативных команд для управления
бортовыми системами.
Траекторные измерения осуществляются с помощью радиолокационных
станций, которые определяют запросным способом дальность до спутников и
радиальную скорость. Дальномерный канал характеризуется максимальной
ошибкой около 2 ... 3 м. Процесс измерения дальности до спутника совмеща-
ют по времени с процессом закладки массивов служебной информации, вре-
менных программ и команд управления, со съемом телеметрических данных
со спутника.
Для эфемеридного обеспечения с КС в ЦУС ежесуточно выдается по
каждому спутнику по 10 ... 12 наборов (сеансов) измеренных текущих навига-
ционных параметров объемом примерно 1 Кбайт каждый.
В настоящее время для обеспечения работ ГЛОНАСС могут использо-
ваться КС, рассредоточенные по всей территории России (рис. 9.4). Часть КС
и других элементов наземного сегмента ГЛОНАСС осталась вне территории
России (в странах СНГ) и может быть использована лишь при наличии соот-
ветствующих договоренностей. Размещение сети КС выбрано с учетом сущсст-
9.1. Назначение и состав подсистемы контроля иугчювления
121
Рис. 9.4. Наземный сегмент СРНС ГЛОНАСС
вуюшей инфраструктуры управления НС и из условий надежного решения за-
дач траекторных, измерений для всей орбитальной группировки.
Такая сеть КС обеспечивает закладку на спутники системы. 1 раз/сут вы-
сокоточных эфемерид и временных поправок (возможна закладка 2 раз/сут).
В случае выхода из строя одной из станций возможна ее равноценная
замена другой, так как сеть КС обладает достаточной избыточностью и в наи-
худшей ситуации работу системы может обеспечивать ЦУС и одна станция,
однако интенсивность ее работы будет очень высокой.
При планировании работы КС на сутки определяются основные и ре-
зервные станции для проведения сеансов измерений с необходимой избыточ-
ностью. Контрольные станции имеют тройное резервирование по аппаратуре
(один комплект рабочий, второй — в резерве, третий — профилактические ра-
боты). Коэффициент готовности средств ПКУ в сеансе измерений и закладки
информации на борт спутника близок к единице.
Описанная сеть КС отличается от аналогичной структуры СРНС GPS
тем, что обеспечивает высокое качество управления орбитальной группиров-
кой только с национальной территории. КС ГЛОНАСС могут использоваться
для обеспечения функционирования других космических средств.
9.1.4. Кванто-оптические станции
Кванто-оптическая станции предназначены для периодической юсти-
ровки радиотехнических каналов измерения дальности КС с помощью лазер-
ного дальномера. В этих целях на каждом спутнике размещены специальные
лазерные отражатели. Применение КОС обеспечивает высокоточное измере-
ние параметров движения спутников ГЛОНАСС. За последние 20 лет разрабо-
' х I )
122 I Л а в а у. Наземный сегмент(подсистема контроля и управления)
таны три отечественные лазерные станции слежения или КОС: лазерная даль-
номерная система Гео-ИК; КОС Эталон; КОС Майданак (Узбекистан).
Всего в России было сооружено 20 таких комплексов. Станция Гео-ИК
является частью спутниковой геодезической системы Гео-ИК, которая ис-
пользуется для определения земных координатных систем и моделей гравита-
ционного поля Земли. Эти модели являются основой для высокоточных опре-
делений орбит спутников ГЛОНАСС.
Кванто-оптические станции типа Эталон и Майданак используются для
корректировки радиолокационных измерений и в процессе определения ор-
бит в ГЛОНАСС. Второе поколение КОС Эталон позволяет определять поло-
жение спутников видимых по отраженному вниз солнечному свету (со звезд-
ной величиной менее, чем 13) на максимальной высоте около 20000 км. По-
грешность измерений дальности при интервале усреднения в 15 с составляет
около 1,5 ... 2 см и углового положения — 2 ... 3" .
Кванто-оптичекая станция Майданак представляет собой многофунк-
циональный комплекс, который позволяет измерять дальность до . космиче-
ских объектов на высотах до 40 000 км (со звездной величиной 16). Макси-
мальная угловая ошибка определения положения спутника имеет порядок от
0,5 до 1 ... 2", а дальномерная ошибка — не более 1,5 ... 1,8 см.
Наиболее эффективно лазерные станции работают в ночное время при
хорошей видимости. _ ___. . ___
9.1.5. Система контроля фаз
Система контроля фаз обеспечивает контроль (сверку) сигнала, излучае-
мого спутником с целью измерения фазового и частотного сдвига бортовых
эталонов времени и частоты относительно эталона ЦС. Эта информация необ-
ходима для синхронизации фаз навигационных сигналов, излучаемых всеми
спутниками ГЛОНАСС. Такая процедура производится с помощью контроль-
ного навигационного приемника СКФ. В процессе сверки (для определения
сдвига бортовой шкалы времени) принятые дальномерные сигналы спутника
сравниваются с опорными сигналами, полученными от высокостабильного
(относительная нестабильность порядка 10-13) эталона частоты ЦС.
В результате сравнения измеряется псевдодальность PR(t) = А(/) + Л(/), где
Л(/) — дальность от СКФ до спутника; Л(/) — ошибка ее измерения, обуслов-
ленная, в частности, рассогласованием фаз между бортовым стандартом вре-
мени и частоты и ЦС. В связи с тем, что псевдодальность является измеряе-
мой величиной, и учитывая максимальную ошибку A(f), значение Л(г) можно
определить с точностью 3 ... 4 м. В дальнейшем Л(/) можно усреднить на дли-
тельном интервале, экстраполировать на заданный момент времени (t + T) и
привести к соответствующей размерности для коррекции, например, шкалы
времени и частоты бортового эталона.
y.L Назначение и состав подсистемы контроля и упеадления 123
Результаты измерений, проводимых в СКФ, автоматизировано переда-
ются в ЦУС для расчета поправок к фазе и частоте бортового эталона, входя-
щих в навигационные сообщения соответствующего спутника. Сверка фаз
дальномерных сигналов выполняется 1 раз/сут для каждого спутника. Пара-
метры для синхронизации бортовой шкалы времени обновляются 2 раз/сут,
поэтому вклад ошибки из-за сдвига фазы дальномерного сигнала спутника в
результирующую ошибку измерения псевдодальности может составить не бо-
лее 5 ... 6 м.
9.1.6. Аппаратура контроля ноля
Аппаратура контроля поля представляет собой высокоточную аппаратуру
потребителей, располагаемую на контрольных станциях и имеющую высоко-
точную геодезическую привязку, и обеспечивает непрерывный контроль харак-
теристик навигационного обеспечения (в частности, точностных характери-
стик координатно-временного обеспечения, которые должны поддерживаться
с достаточно высокой достоверностью — с вероятностью не хуже 0,997, а так-
же характеристик целостности) с помощью системы ГЛОНАСС на территории
России.
Для оценки качества работы ГЛОНАСС предусматривается: диагностика
работы основных-бортевых систем-спутников; контроль точности решения на-
вигационной задачи и качества информации, содержащейся в навигационных
сообщениях спутников.
Диагностику бортовых систем спутника можно осуществлять на АКП,
например по результатам его самоконтроля, которые передаются в навигаци-
онном кадре. В случае обнаружения неисправности, влияющей на качество
навигационного сигнала, признак непригодности данного спутника для нави-
гационных определений потребителей (соответствующее значение параметра
”В” навигационного кадра) автоматически включается в состав навигацион-
ного сообщения спутника нс позднее, чем через одну минуту после обнаруже-
ния неисправности. Это позволяет потребителям исключить неисправный
спутник из процедуры навигационных определений.
Контроль качества навигационного обеспечения системой ГЛОНАСС ве-
дется аппаратурой АКП, в основном, в двух режимах*&онтроля НС и контроля
поля.
Режим контроля НС предусматривает непрерывное сравнение измерен-
ных значений псевдодальностей и псевдоскоростей с их прогнозируемыми
значениями для всех видимых спутников ГЛОНАСС (одновременно в зоне ра-
диовидимости АКП может находиться до 8 ... 11 спутников). За время сеанса
связи от каждого спутника принимаются и контролируются данные, содержа-
щиеся в навигационных кадрах, а также осуществляется измерение с помощью
его сигналов первичных навигационных параметров (псевдодальности и
124 Глава 9. Наземный сегмент(нодсистема контроля и управления)
псевдоскорости). После окончания сеанса связи в АКП выполняется автоном-
ный анализ полученной информации и контролируется отсутствие сигнала вы-
зова ПКУ.
При отрицательном результате проверки спутника об этом автоматиче-
ски сообщается в ЦУС с указанием конкретных причин, где'принимаются не-
обходимые меры по устранению неисправностей, ограничивающие или вре-
менно исключающие использование спутника по целевому назначению. Вы-
ход из строя отдельных спутников ГЛОНАСС не приводит к заметному ухуд-
шению точностных характеристик навигационного поля системы, так как
группировка спутников имеет необходимую избыточность по числу НС.
Режим контроля навигационного поля предусматривает решение навига-
ционной задачи по каждому оптимальному созвездию спутников над соответ-
ствующим АКП. Эта процедура включает также сравнение эталонных коорди-
нат с текущими результатами местоопределения по данному созвездию и вы-
полняется непрерывно по автономному плану. Результаты навигационных оп-
ределений (а при отрицательных данных контроля и измерительная информа-
ция, используемая в этом сеансе) передается в ЦУС для оценки текущих ха-
рактеристик навигационного обеспечения, анализа причин аномальных харак-
теристик и принятия решения по дальнейшему варианту функционирования
системы. В такой ситуации могут быть предприняты следующие меры; переда-
ча на бррт спутника команды, формирующей в составе кадра навигационной
информации признака непригодности НС для использования его Сигналов по-
требителями системы ГЛОНАСС; проведение с использованием телеметриче-
ского канала работ с аппаратурой спутника по отысканию в ней неисправно-
стей; пересчет и перезакладка на борт спутника навигационной информации;
выполнение сеанса навигационных измерений с данным спутником с помо-
щью другой аппаратуры АКП.
Перечисленных видов контроля с учетом избыточности орбитальной
группировки обычно достаточно для поддержания требуемых характеристик
навигационного поля.
В СРНС ГЛОНАСС, в отличие от GPS, осуществляется раздельное реше-
ние задач эфемеридного и частотно-временного обеспечения.
9.2. Эфемеридное обеспечение
Эфемеридное обеспечение поддерживается комплексом технических и
программных средств, выполняющих радиоконтроль орбит спутников с не-
скольких наземных КС, обработку результатов траекторных измерений и рас-
чет эфемеридной информации (ЭИ), передаваемой далее с помощью загрузоч-
ных станций на спутник.
Высокая точность расчета эфемерид (определение и структура эфемерид
НС ГЛОНАСС описываются в п. 10.4.2) обеспечивается соответствующей точ-
ностью измерительных средств, внесением поправок на выявленные методиче-
ские погрешности, применением в процессе расчета эфемерид не только те-
1.2, Эфемеридное обеспечение
125
кущих траекторных измерений, но и накапливаемых за недельный срок. При
этом дальномерные данные, получаемые от станций слежения за спутниками,
периодически калибруются, что обеспечивает высокое качество траекторных
измерений в системе ГЛОНАСС.
Предполагается, что такие традиционные методы управления будут ис-
пользоваться до 2000 г. В дальнейшем будет осуществляться переход на новые
технологии, включающие межспутниковые угломерно-дальномерные измере-
ния, что обеспечит качественный скачок в координатно-временном обеспече-
нии потребителей (7.12, 9.3].
9.2.1. Особенности формирования эфемеридной
информации в ГЛОНАСС
Система ГЛОНАСС создавалась в условиях, когда уровень фундамен-
тальных исследований в области геодезии, геодинамики и геофизики не обес-
печивал требуемую точность эфемеридного обеспечения системы. В этих усло-
виях был проведен комплекс работ по обоснованию путей, решения этой про-
блемы через построение согласующих моделей движения спутников, парамет-
ры которых определяют в процессе решения самой задачи баллистико-
навигационного обеспечения системы.
Исследования показали, что необходимо отказаться от типовых остро-
резонансных (например, с периодом обращения спутника равным 12 ч, как в
СРНС GPS, когда период вращения Земли вокруг своей оси равен двум перио-
дам обращения спутника) орбит спутников, так как в процессе моделирования
уравнений траекторного движения спутников это повышает устойчивость их
решений и ослабляет корреляции между параметрами отдельных уравнений
(моделирующих, например, изменение геопотенциала, координат измеритель-
ных средств, радиационного давления). Кроме того, оказалось, что наивысшая
сочность баллистико-эфемеридного обеспечения системы при решении мно-
гомерной навигационной задачи с расширенным вектором состояния обеспе-
чивается при обработке измеренных текущих навигационных параметров на
интервале 8 сут. Переход от острорезонансных орбит был осуществлен путем
увеличения числа витков спутника (по сравнению с GPS) на интервале 8 сут
до 16 ... 17. Число спутников в системе бранолравным 24 с равномерным рас-
пределением по трем орбитальным плоскостям. Все спутники системы фази-
руются таким образом, что на больших временных интервалах они имеют один
след на поверхности Земли. Это обеспечивает высокую баллистическую устой-
чивость системы и относительно высокую точность и простоту расчетов траек-
торий. Опыт эксплуатации системы показал, что при обеспечении начального
периода обращения спутника с точностью не хуже 0,1 с на протяжении задан-
ного срока активного существования спутника его положение в системе кор-
ректировать не нужно.
В настоящее время в системе ГЛОНАСС используется запросная техно-
логия эфемеридного обеспечения, когда исходной информацией для расчета
126 Г л а в a 9. Наземный сегмеит(подсистема контроля и управления)
эфемерид служат данные измеренных текущих параметров (ИТП) спутников,
поступающие в ЦУС от контрольных станций по программам межмашинного
обмена через вычислительную сеть. Ежесуточно осуществляется 10 ... 12 сеан-
сов передачи информации по каждому спутнику.
9.2.2. Типовые операции управления
Процесс эфемеридного обеспечения реализуется в ходе отработки типо-
вых операций управления ПКУ, который предполагает решение следующих
задач: предварительная обработка ИТП; расчет начальных условий на начало
каждого интервала работы; определение параметров движения; расчет и фор-
мирование эфемеридной информации (ЭИ) и альманаха системы; апостериор-
ная оценка точности формирования ЭИ; оперативная и камеральная оценка
возможности использования измерений КС и временной информации в инте-
ресах эфемеридного обеспечения системы; обработка и прогнозирование па-
раметров вращения Земли (ПВЗ).
Рассмотрим подробнее отдельные операции управления.
Предварительная обработка ИТП. Цикл управления ЦУС начинается с
запроса сеансов связи с КС для получения наборов ИТП и предварительной
обработки этой информации. При этом выполняются следующие операции:
дешифровка и анализ ключевых, технологических, калибровочных и информа-
ционных посылок наборов (массива) данных; расчет априорных навигацион-
ных функций; преобразование информационных параметров, полученных в
результате дешифровки массивов, в значения навигационных параметров; кор-
рекция измерений массивов ИТП с учетом поправок на распространение из-
мерительного сигнала в ионосфере и тропосфере Земли; формирование и за-
пись массивов ИТП в БД.
Время решения задачи предварительной обработки информации для пер-
вого сеанса составляет 1,5 мин.
Расчет начальных услоанй. Для расчета начальных условий спутника на
начало мерного интервала осуществляется считывание из БД исходных на-
чальных условий, настройка математической модели движения спутника, рас-
чет параметров движения спутника на заданное время численным методом ин-
тегрирования и запись полученных кинематических параметров движения в
БД. В типовой операции управления интервал прогнозирования составляет
около двух витков.
Определение параметров движения. После подготовки начальных усло-
вий, проведения измерений и решения задачи определения параметров движе-
ния спутника на 8-ми суточном интервале производится уточнение расширен-
ных начальных условий, включающих кинематические параметры движения,
коэффициенты модели движения и измерений. В задаче определения парамет-
ров движения реализован итерационный метод Ньютона (см. п. 6.3.1), при
этом число итераций равно 3 ... 4.
^9.2. Эфемеридное .обеспечение 127
Формирование эфемерид. Полученные в ходе предыдущей операции на-
чальные условия используют для расчета эфемеридной информации (кинема-
тические параметры движения спутника и составляющие действующего на
него возмущающего ускорения), которая записывается в базу выходных дан-
ных. Из нее формируется служебная информация в заданном виде (форме) и
передается на КС для закладки на борт спутника. Высокая точность расчета
траектории движения спутника достигается в основном за счет разработки
адекватной модели движения спутников, описываемой системой дифференци-
альных уравнений и учитывающей следующую совокупность сил: притяжение
Земли (с учетом аномалий), Луны и Солнца; воздействие лунно-солнечных
приливных вариаций геопотенциала, давление солнечного излучения (см.
§ 3.7). Основным фактором, определяющим характер движения спутника, яв-
ляется геопотенциал, возмущающая часть которого задает общую эволюцию
орбиты. Действие остальных возмущающих факторов примерно в 1 000 раз
меньше воздействия геопотенциала.
Задача определения начальных условий движения спутника, а также
расширенного вектора состояния, решается на основе математической обра-
ботки измерений, полученных на восьми суточном интервале наблюдений ме-
тодом наименьших квадратов (см. п. 6.3.2), который в настоящее время явля-
ется основным методом статистического оценивания траектории движения
спутника [1.4, 1.5, 6,4].
Формирование альманаха. Расчет альманаха (определение альманаха и
его структура описываются в п. 10.4.3) и системы ГЛОНАСС осуществляется
на заданном интервале с шагом расчета 1 сут. Информация альманаха системы
предназначена, в частности, для выбора потребителем созвездия спутников, по
которым определяется местоположение. Результаты расчетов записываются в
базу выходных данных. Из них формируется служебная информация и переда-
ется на КС для закладки на борт спутника.
Оценка точности эфемерид. В процессе проведения типовых операций
управления производится неоперативное оценивание точностных характери-
стик эфемерид, ежесуточно уточняемых для каждого спутника. С учетом уточ-
ненных на данных технологических сутках опорных эфемерид рассчитывают
эталонные (осредненные на интервале измерения) кинематические параметры
движения и вычисляют максимальные отклонения оцениваемых опорных эфе-
мерид, прогнозируемые на 30 ч, относительно эталонных. Вектор максималь-
ных отклонений записывается в БД и используется при вычислении выбороч-
ных оценок точности эфемеридного обеспечения за определенный интервал
времени для отдельных спутников или всей системы в целом.
Оценка возможности применения КС. Контроль возможности использо-
вания КС в интересах эфемеридного обеспечения осуществляется в два этапа.
На первом этапе оперативно (ежедневно) после окончания выполнения типо-
вых операций управления оценивается качество работы КС как по составу
всей орбитальной группировки, так и в течение десяти суточного интервала
предыстории.
128__ Г л а в a 9. Наземный сегмент(подсистема контрола н управления) j
На втором этапе — неоперативно (ежемесячно) в конце каждого месяца.!
На этом этапе более углубленно оценивается качество работы КС, так как
оцениваемый интервал берется равным не менее 1 мес, и принимается решет <
ние о дальнейшем использовании данной КС в ПКУ ГЛОНАСС.
Определение параметров вращения Земли. Для’-. обеспечения ГЛОНАСС
параметрами вращения Земли в системе организовано оперативное определе-
ние координат полюса Земли, эксцесса длительности суток по данным изме-
рений КС на основе совместного уточнения ПВЗ и вектора состояния систе-
мы. Специально разработанные методики позволяют определить и всемирное
время в процессе эфемеридного обеспечения системы. Точность получаемых
результатов оценивается для координат полюса на уровне 15 ... 20 см, для дли-
тельности земных суток — 0,5 мс и для всемирного времени — 1 мс. Регуляр-
ное определение ПВЗ по данным наблюдений НС в режиме оперативной
службы осуществляется наземным комплексом ГЛОНАСС с 1984 г.
Получение этих данных методически и организационно тесно связано с
технологией информационного обеспечения спутников ГЛОНАСС, что опре-
деляет высокую надежность и оперативность определений , однородность и
равномерность распределения данных, а также приемлемую для практических
применений точность получаемых значений ПВЗ. Однако это привносит неко-
торую специфику в технологию определения ПВЗ. В первую очередь — это
региональное размещение КС исключительно на территории России и особен-
ности орбитального построения системы.
Определение ПВЗ проводится в процессе технологического цикла управ-
ления спутниками ГЛОНАСС, предусматривающего проведение ежесуточных
вычислений орбит спутников и ПВЗ по данным наблюдений каждого спутника
за предшествующие 8 сут. В каждом таком решении получают оценки трех
значений ПВЗ — двух координат полюса Хр, Yp и скорости вращения Земли
(эксцесса длительности суток D). Текущие значения координат полюса и ско-
рость вращения Земли уточняются в процессе обработки наблюдений методом
наименьших квадратов на 8-ми суточном интервале. Этот интервал обеспечи-
вает наилучшее усреднение и компенсацию неучтенных возмущений.
Всемирное время определяют при сопоставлении результатов текущих
определений орбит спутников с их эфемеридами, вычисленными с использо-
ванием данных ПВЗ, согласованных на некоторую начальную эпоху с данными
Международной службы вращения Земли. Таким образом, при выполнении
каждого суточного технологического цикла получают п реализаций оценок
всех четырех параметров: Хр, Yp, D и (UT1—UTC), где п — число спутни-
ков. Усреднение этих данных с исключением аномальных значений дает воз-
можность получить более точные оценки суточных значений ПВЗ, которые и
составляют ряды данных ПВЗ, определяемых в ПКУ. Обработка результатов
ежесуточных определений ПВЗ осуществляется в ЦУС еженедельно. Получен-
ные результаты передают в вычислительный центр Государственных опреде-
лений ПВЗ, где используют для вывода срочных и окончательных значений
Эфемеридное обеспечение 129
' ПВЗ и публикуют в Бюллетене серии Е Госстандарта РФ.
Рассмотренные задачи эфемеридного обеспечения решают в автоматизи-
4рованном режиме. Требуемая достоверность служебной информации и значи-
тельное снижение нагрузки по анализу результатов и нештатных ситуаций дос-
тигается включением в пакет помимо основных указанных задач по обработке
ИТП программных модулей по контролю входной и выходной информации, а
также промежуточных расчетов.
9.2.3. Технология определения траектории движения спутника
Технология обработки ИТП и определения траекторий движения спут-
ников ГЛОНАСС включает несколько вариантов в соответствии с требования-
ми к точности нахождения и прогнозирования эфемерид спутника, предъяв-
ляемым на различных этапах полета, и составом измерений.
К таким этапам можно отнести : выведение спутника на орбиту; приве-
дение и постановка спутника в системную точку с заданными значениями пе-
риода обращения и угловым положением в системной плоскости.
В типовых операциях управления ПКУ ГЛОНАСС предусмотрено ис-
пользование измерений КС в запросном режиме с двумя разновидностями ДН
бортовой антенной системы — всенаправленной и узкой. В первом случае
точностные характеристики измерений запросной дальности находятся в пре-
делах от сотен метров до десятков километров. Такие измерения выполняют
только на первом этапе полета НС.
Проведение измерений во втором случае определяет начало операций по
приведению и постановке спутника в заданную системную точку. Требования
к точности определяются, исходя из необходимой точности коррекции орбит
по периоду обращения или точности постановки в системную точку с задан-
ными периодом обращения и угловым положением (0,1 с по периоду обраще-
ния и 0,1° по угловому положению).
Определение параметров движения спутника производится по запросным
измерениям дальности и радиальной скорости в два этапа. На первом этапе
определяют параметры движения спутника по измерениям радиальной скоро-
сти с последующей переработкам этих измерений с использованием уточнен-
ных по ним начальных условий движения. На втором этапе вычисляют пара-
метры движения спутника по измерениям дальности и радиальной скорости.
Параметры движения спутника на участках приведения и постановки
спутника в системную точку находят на мерных интервалах продолжительно-
стью 14 витков. Технология эфемеридного обеспечения на этапе штатной экс-
плуатации основана на использовании высокоточных измерений дальности КС
и включает предварительную обработку измерений (расшифровка данных из-
мерений КС с последующим устранением неоднозначности измерений даль-
ности, калибровкой, приведением измерений к центру масс спутника для ком-
пенсации выноса бортовой антенны, учетом ионосферной и тропосферной
рефракции).
5 — 3291
130 Гл а в а 9- Наземный сегмент(подсистема контроля и управлеиия) !
Поправка, учитывающая влияние условий распространения сигнала в!
тропосфере, рассчитывается по данным метеоусловий в районе КС.
Решение проблемы высокоточных определений орбит возможно при.
создании высокоточных математических моделей движения и измерений, на|
точность которых влияют следующие факторы: геофизические, определяемые*
погрешностью задания системы координат и гравитационного поля Земли;
геодинамические, связанные с нахождением координат полюса и неравномер-
ности вращения Земли; а также факторы, обусловленные учетом нсгравита-
ционных возмущений в модели движения.
В основе этих методов лежит понятие согласующих моделей, которые
представляют собой системы геофизических параметров и параметров, опреде-
ляющих математическую модель движения НС по данным обработки навига-
ционных измерений. Такие модели не являются фундаментальными и пригод-
ны только для конкретных орбит, и позволяют при наличии высокоточных
измерений параметров движения НС и достаточно полном описании дейст-
вующих на них сил уменьшить влияние погрешностей определения геофизиче-
ских и геодинамических факторов на точность определения эфемерид кон-
кретного НС за счет уточнения координат измерительных пунктов, параметров
гравитационного поля Земли, параметров вращения Земли и включения коор-
динат КС и других параметров согласующей модели в состав расширенного
вектора состояний НС.
При решении задач определения и прогнозирования движения спутника
эфемериды рассчитывают путем численного интегрирования I дифференциаль-
ных уравнений движения комбинированным методом Рунге—Кутта и Адамса в
координатной системе, заданной средним экватором и равноденствием эпохи
начала бесселева года (в 1975 г.). В правых частях дифференциальных уравне-
ний учитываются основные возмущающие силы. Гравитационное поле Земли
представлено разложением в ряд по сферическим функциям до гармоник сте-
пени и порядка 8 включительно. При моделировании расчетных аналогов из-
мерений учитываются уходы полюса и поправки ко времени за счет неравно-
мерности вращения Земли.
При выводе спутника из системы требование к точности нахождения па-
раметров движения определяются исходя из необходимости надежного вхож-
дения в связь со спутником. В этом случае параметры движения спутника оп-
ределяют на мерных интервалах длительностью не менее четырех витков не
реже одного раза в месяц. В состав уточняемых параметров при этом включа-
ются только кинематические.
Литература
9.1. Состав ГЛОНАСС// Компьютерный бюллетень BBS КНИЦ ВКС РФ, 1996.
9.2. Наземный контур управления // Компьютерный бюллетень BBS КНИЦ
ВКС РФ.
9.3. Kasantsev К The GLONASS and GLONASS-M programs// ION GPS-95, 1995,
pp. 985—990.
Г л а в a 10
Подсистема космических аппаратов
10.1. Орбитальные характеристики спутников
В соответствии с целевым назначением система ГЛОНАСС имеет в сво-
ем составе подсистему КА (навигационных спутников), которая представляет
собой орбитальную группировку из 24 спутников. Спутники, излучая непре-
рывные радионавигационные сигналы, формируют в совокупности сплошное
радионавигационное поле на поверхности Земли и в околоземном пространст-
ве, которое используется для навигационных определений различными потре-
бителями.
Структура сети спутников такова, что в каждой точке земной поверхно-
сти и околоземного пространства в любой момент времени находится одно-
временно не менее четырех спутников, взаимное расположение и качество
сигналов которых обеспечивает ему возможность координатно-временных из-
мерений с заданными характеристиками. Требование по количественному со-
ставу орбитальной группировки основывается на том, что заданные точност-
ные характеристики навигационного обеспечения могут быть получены в сис-
теме ГЛОНАСС при наличии в орбитальной группировке, например, 21
спутника (по семь спутников в каждой орбитальной плоскости), а остальные
обеспечивают “горячий” резерв и высокую устойчивость системы.
Спутники ГЛОНАСС размещаются на трех практически круговых орби-
тах. Высота каждой орбиты составляет 18 840 ... 19 440 км (номинальное зна-
чение составляет 19 100 км), что позволяет отнести ГЛОНАСС к среднеорби-
тальным СРНС. Номинальные значения других параметров орбит НС ГЛО-
НАСС приведены в табл. 8.1.
Точность приведения спутника в заданную (рабочую) точку орбиты со-
ставляет: по периоду обращения 0,5 с; по аргументу широты 1°; по эксцентри-
ситету ±0,01; по наклонению орбиты ±0,3°.
Орбитальные плоскости разнесены по долготе восходящего узла на 120°
(рис. 10.1). При полном со'ЗЪездии НС в каждой орбитальной плоскости рав-
номерно размещаются по 8 спутников с номинальным сдвигом по аргументу
широты 45°. Спутники в соседних орбитальных плоскостях сдвинуты на 15°
по аргументу широты. Нумерация орбитальных плоскостей осуществляется по
направлению вращения Земли, а нумерация позиций (так называемых рабочих
точек орбиты или орбитальных точек) в последовательности спутников на ор-
бите на определенный момент времени — против их движения. Спутники
занимающие эти позиции часто [1.2] обозначаются с помощью соответствую-
щих (системных) номеров, совпадающих с номером позиции, несмотря на из-
вестную неоднозначность этого термина. При этом спутники с системными
132
Г л а в a 10. Подсистема космических аппаратов
Плоскость 1 Плоскость 2 Плоскость 3
Рис. 10.1. Распределение НС по орбитальным
плоскостям
номерами №1 ... №8 распола-
гаются в первой орбитальной
плоскости, № 9 ... 16 — во
второй и № 17 ... 24 — в
третьей, соответственно.
Номинальные значения
абсолютных долгот восходя-
щих узлов идеальных орби-
тальных плоскостей, зафикси-
рованных на 0 ч 00 мин 00 с
1.01.83 г. (московского дек-
ретного времени), равны
О = 251’15'00" + 120’(/-1) , где
/ = 1,3 — номер орбитальной
плоскости. Идеальные значения аргументов широты НС с системными номе-
рами J = N+S и j = А+16 отличаются от аргументов широты НС с номерами
j' = N и j = N +8, соответственно, на 15’, где N = 1, 8 и составляют на
0 ч 00 мин 00 с 1.01.83 (московского декретного времени) величины <о =
= 145’26'37" + 15’(27 - 3/ + 25, где j
системный номер НС, J* =
= entier(/- 1 / 8) — целая часть числа (*).
Таблица 10.1. Состояние орбитальной группи-
ровки на 04.04/10.07.97
НС № Номер орби- тальной плос- кости/точки Состояние спутника Номер час- тотного канала
769 1/8 +/-25.06.97 2
756 3/21 +/-27.06.97 24
759 1/7 +/-30.06.97 21
757 1/2 +/-09.05.97 5
758 3/18 +/-30.06.97 10
760 3/17 4- 24
761 3/23 -01.04.97/+ 3
767 2/12 4- 22
770 2/14 4- 9
775 2/16 4- 22
762 1/4 4- 12
763 1/3 4- 21
764 1/6 4- 13
765 3/20 4- 1
766 3/22 4- 10
777 3/19 + 3
780 2/15 4- 4
781 2/10 4- 9
785 2/11 4- 4
776 2/9 4- 6
778 2/9 Резерв 11
782 2/13 + 6 1
\
Состояние орбиталь-
ной группировки ГЛОНАСС
на 4.04/10.07.97 показана в
табл. 10.1 [10.1], где матема-
тический знак “+” — штат-
ная работа НС; —
временное выведение НС из
применения и дату этого
события.
С учетом приведенных
данных, интервал повторяе-
мости трасс движения НС и
зон радиовидимости НС на-
земными потребителями со-
ставляет 17 витков (7 сут
23 ч 27 мин 28 с).
Таким образом, спут-
ники СРНС ГЛОНАСС не
имеют резонанса с вращени-
ем Земли. Период обраще-
ния спутников подобран та-
10.1. Орбитальные характеристики спутников
133
ким образом, что приблизительно за 8 сут они совершают 17 оборотов вокруг
Земли. При этом начало каждого витка смещается относительно поверхности
Земли приблизительно на 21° по долготе. Каждые восемь суток спутник про-
ходит над одними и теми же точками на поверхности Земли. За счет смеще-
ния спутников внутри орбитальных плоскостей все они движутся относитель-
но поверхности Земли практически по одному и тому же следу (полосе). Это
свойство обеспечивает высокоточное определение орбит спутников и ПВЗ при
использовании региональной ПКУ.
Таким образом, орбитальная группировка спутников ГЛОНАСС с несин-
хронными почти круговыми орбитами более стабильна по сравнению с груп-
пировкой спутников GPS с синхронными 12-тичасовыми орбитами.
Рассмотренная структура орбитальной группировки позволяет обеспе-
чить практически непрерывное и глобальное покрытие земной поверхности и
околоземного пространства (включая ближний космос) навигационным полем
с заданными характеристиками.
Доступность спутников в системе ГЛОНАСС на широтах более 50° выше,
чем в системе GPS. Это связано с большим значением наклонения орбит
спутников ГЛОНАСС. На рис. 10.2 приведены (1.5, 7.9( расчетные зависимо-
сти вероятности пространственного фактора ухудшения точности местоопре-
деления (PDOP см. § 7,4) в пределах зоны действия системы (для угла маски,
равного 5° и использования не менее N спутников).
Сравнительные характеристики ПКА систем ГЛОНАСС, GPS показаны
на рис. 10.3 (10.2| для полных созвездий. Эти данные дополняют сведения о
характеристиках доступности СРНС ГЛОНАСС, приведенные в табл. 7.1.
Орбитальная структура спутников ГЛОНАСС характеризуется высокой
Рис. 10.2. Статистические характеристики
орбитального созвездия
ГЛОНАСС
Рис. 10.3. Статистические характерис-
тики полных орбитальных
созвездий GPS н ГЛОНАСС
Г л а в a 10. Подсистема космических аппаратов
устойчивостью и нс требует дополнительных коррекций в течение всего срока
активного существования НС. Так максимальные уходы НС относительно иде-
ального положения на орбите не превышают ±5° на интервале в 5 лет, а сред-
няя скорость рецессии орбитальных плоскостей составляет 0,59251 х
х 10~3 рад/с. Кроме того, структура сохраняет свои функциональные качества
при выходе из строя одновременно до 6 НС (по два в каждой плоскости).
Поддержание структуры ПКА осуществляется выведением новых навига-
ционных спутников при снижении общего числа НС в любой плоскости ме-
нее восьми. Запуск в заданную плоскость орбиты осуществляется по группо-
вой схеме (три спутника одновременно) с помощью ракеты носителя ПРОТОН
и разгонного блока ДМ с космодрома Байконур. Использование групповой
схемы выведения приводит к тому, что в каждой плоскости могут находиться
избыточные работоспособные НС, которые переводятся в нештатный способ
функционирования, когда целевая (навигационная) аппаратура выключена, и
возможна профилактика систем, так как обеспечивающие системы поддержи-
вают штатную ориентацию НС, заданный тепловой режим и энергоснабжение.
Схема выведения НС включает: выведение космической головной части
на промежуточную круговую орбиту высотой около 200 км; переход на эллип-
тическую орбиту ,с перигеем примерно 200 км, апогеем около 19 100 км и
наклонением 64,3°; переход на круговую орбиту высотой 19 100 км.
В общем случае эксплуатация спутника предполагает следующие этапы
полета:
выведение спутника на орбиту после отделения его от разгонного блока
продолжительностью от 5 до 12 витков; здесь производится проверка работо-
способности всех бортовых систем;
приведение и постановка спутника в системную точку с заданными пе-
риодом обращения и угловым положением в системной плоскости; продолжи-
тельность этого этапа от одной недели до одного месяца и определяется угло-
вым положением спутника в точке выведения на орбиту и системной точкой
спутника;
штатная эксплуатация спутника;
нахождение спутника вне системы (например, при проведении профи-
лактических и восстановительных работ по командам с ПКУ).
Реконфигурация рассмотренной орбитальной группировки ГЛОНАСС
допускается в связи с ограниченными запасами топлива для двигательных ус-
тановок спутника только в крайних случаях и проводится в целях оптимиза-
ции структуры и используемых частот (в целях повышения точности навига-
ционных определений и обеспечения электромагнитной совместимости с
другими системами). Орбитальные маневры проводятся на этапе установки
новых спутников после их выведения на орбиту. При этом один НС остается в
точке выведения, а два других разводятся в соседние рабочие точки
(предварительно возможен перевод уже функционирующих НС в новую рабо-
чую точку).
10.2. Радиоси-лалы в ~-РНС'Гл 135
10.2. Радиосигналы в СРНС ГЛОНАСС
10.2.1. Виды используемых сигналов
Каждый спутник системы ГЛОНАСС излучает фазоманипулированные
навигационные радиосигналы в диапазоне £1 и £2. Основное отличие сигна-
лов в системе ГЛОНАСС от сигналов системы GPS заключается в значении
рабочей частоты, законе формирования и параметрах модулирующих двоичных
последовательностей. В системе ГЛОНАСС используется частотное разделение
(FDMA) сигналов различных НС в каждом из диапазонов при едином даль-
номерном коде. В отличие от этого в системе OPS сигналы спутников, излу-
чаемые на одной частоте, различаются по дальномерному коду (CDMA). Спут-
ники ГЛОНАСС, находящиеся в противоположных точках орбиты (анти-
подальные НС), т. е. не видимые потребителям одновременно, обычно пере-
дают навигационные радиосигналы на одинаковых частотах, что позволяет ра-
ционально использовать частотный диапазон. Из табл. 10.1 видно, что такие
спутники имеют системные номера отличающиеся на четыре, например, тре-
тий и седьмой спутники в первой орбитальной плоскости, использующие два-
дцать первый частотный канал.
В радиолинии частотного диапазона £1 спутники системы ГЛОНАСС
излучают навигационные радиосигналы двух типов: стандартной и высокой
точности (СТ- и ВТ-сигнал, соответственно), которые позволяют выделить два
соответствующих канала навигационного обслуживания — каналы стандартной
и высокой точности.
Сигнал стандартной точности предназначен для использования граждан-
скими потребителями и предоставляемое им обслуживание доступно всем вла-
дельцам аппаратуры потребителей ГЛОНАСС. Сигнал высокой точности мо-
дулирован специальным кодом и не рекомендован к использованию без согла-
сования с МО РФ, поэтому рассматриваемые каналы можно называть откры-
тый и закрытый. Иногда в иностранной литературе применительно к указан-
ным навигационным каналам используют обозначения CSA (Channel of
slandart accuracy) и CHA (Channel of high accuracy), соответственно.
В отличие от сигнала стандартной точности системы GPS в системе
ГЛОНАСС не предусматривается его принудительного загрубления, хотя ино-
гда и используется применительно к нему обозначение ПТ-сигнал (сигнал по-
ниженной точности). Однако имеющиеся более низкие ио сравнению с ВТ-
сигналом характеристики точности можно отнести к этапу выбора параметров
сигнала при разработке системы и не связаны с политикой поставщиков нави
гационного обслуживания в системе ГЛОНАСС на этапе ее эксплуатации. В
связи с этим всем пользователям ГЛОНАСС доступны измерения координат
местоположения и скорости с беспрецедентно высокой (даже по отношению к
открытому каналу системы GPS) точностью. В дальнейшем более подробно
рассматривается структура и характеристики СТ-сигнала передаваемого в диа-
пазоне £1 .
136 Глава 10. Подсистема космических аииаратоЙ1
В радиолинии диапазона L2 в настоящее время передается только ВТ-]
сигнал, поэтому гражданские потребители не могут использовать метод двух-]
частотной компенсации ионосферных погрешностей. Этот существенный, Я
точки зрения гражданских потребителей, недостаток присущ и системе GPS. И
ближайшем будущем разработчики системы ГЛОНАСС-М предполагают обес-
печить передачу открытого сигнала стандартной точности и на частоте £2
19.3] (более подробно о системе ГЛОНАСС-М см. ,гл. 13).
10.2.2. Характеристики излучаемых навигационных радиосигналов
Частотные каналы. В системе ГЛОНАСС номинальное значение рабочих'
частот радиосигналов НС: , где i =1,2 — номер диапазона час-
тот; к =0,24 — номер частотного канала (литер); /01 =1602 МГц; /о2 =
=1246 МГц; Д/i =562,5 кГц; Д/^ =437,5 кГц. Отношение f£2 //ц = 7/9.
Канал к = 0 не предназначен для использования потребителями системы,
ГЛОНАСС. Он применяется наземной подсистемой управления для проверки^
резервных спутников на орбите при восполнении орбитальной группировки.!
'* __ I
Сведения,о распределении частотных каналов /с = 1,24 между спутниками, рас-2
положенными в орбитальных рабочих точках с номерами т —1,24 содержат-,
ся в альманахе системы. В табл. 10.2 показано соответствие номинальных зна-
чений несущих частот для двух диапазонов каналам к =1,24.
Навигационные СТ-сигналы с тактовой частотой 5Й кГц занимают в
частотном поддиапазоне £1 полосу шириной (1602,5625...1615,5)±0,511 МГц.
Таблица 10.2. План частот
Номер канала Частота, МГц Номер канала Частота, МГц
LI £2 L1 L2
00 1602,0 1246,0 13 1609,3125 1251,6875
01 1602,5625 1246,4375 14 1609,875 1252,125
02 1603,125 1246,875 15 1610,4375 1252,5625
03 1603,6875 1247,3125 16 1611,0 1253,0
04 1604,25 1247,75 17 1614,5625 1253,4375
05 1604,8125 1248,1875 18 1612,125 1253,875
06 1605,375 1248,625 19 1612,6875 1254,3125
07 1605,9375 1249,0625 20 1613,25 1254,75
08 1606,5 1249,5 21 16138125 1255,1875
09 1607,0625 1249,9375 22 1614,375 1255,625
10 1607,625 1259,375 23 1614,9375 1256,0625
11 1608,1875 1250,8125 24 1615,5 1256,5
12 1608,75 1251,25 - - -
НД)!& Радиосигналы в СРНС ГЛОНАСС
137
Внеполосные
^лучения каждым
ИС за пределами
Полосы, отведенной
для навигационных
радиосигналов ГЛО- .
НДСС, не превыша-
ют -40 дБ относи-
тельно мощности Р
немодулированной
ресущей. Навигаци-
онные ВТ-сигналы с
тактовой частотой
5,11 МГц занимают
В частотном поддиа-
пазоне L1 полосу
Рис. 10.4. Спектральные характеристики сигналов
шириной (1602,5625 ... 1615,5)±5,11 Мгц. Соотношение спектральных характе-
ристик сигналов в системах ГЛОНАСС и GPS показано на рис. 10.4.
В первом приближении считают, что у каждого НС радиосигналы диапа-
зонов L1 и L2 когерентны, так как формируются от.общего БЭВЧ, При этом
спектральная плотность фазовых шумов немодулированной несущей такова,
что схема слежения с односторонней шумовой полосой 10 Гц обеспечивает
точность слежения за фазой несущей не хуже а =0,1 рад.
Номинальное значение частоты БЭВЧ с точки зрения потребителя, на-
ходящегося на поверхности Земли, равно 5 МГц. Для компенсации релятиви-
стских эффектов частота, формируемая БЭВЧ, смещена относительно 5 МГц
на =-2,18-10"J Гц (соответствует номинальной высоте, равной 19 100 км).
Фактические значения рабочих частот сигналов каждого НС могут отличаться
от номинальных значений на относительное значение, не превышающее
±210“п.
В настоящее время предусматривается поэтапное изменение частотного
диапазона ГЛОНАСС с тем, чтобы с 2005 г. все находящиеся в эксплуатации
навигационные спутники системы ГЛОНАСС использовали в качестве рабочих
только каналы частот к= -7 ... +4, причем каналы +5 и +6 — лишь как техно-
логические в ограниченные периоды времени (при восполнении ПКА). Более
подробно об изменении плана частот см. гл. 13.
Характеристики поляризации излучаемых сигналов. Спиральные антен-
ные элементы спутников ГЛОНАСС формируют радиосигнал, который имеет
правую круговую поляризацию [1.21. При этом коэффициент эллиптичности
по полю не хуже 0,7 в секторе излучения ± 19° относительно оси симметрии
ДН бортовой передающей антенны НС. Эти параметры сигнала учитываются
138 Глава 10. Подсистема космических аппаратом!
при конструировании приемных антенн потребителей СРНС и при учете поля-1
ризационных потерь сигнала в радиолинии. J
Характеристики модуляции сигналов. В системе ГЛОНАСС используются
сложные фазоманипулированные сигналы (общие сведения приведены Я
§ 5.4). Две составляющие сигнала на частоте LI манипулируются по фазе на’
± 180°. Для модуляции каждой составляющей используется своя модулирую-1;
щая двоичная последовательность (код). В завйсимости от качества модуляции
может измениться стандартный вид излучаемого сигнала, что обуславливает’
появление потерь при корреляционной обработке сигналов в аппаратуре по-
требителя.
Наибольшие корреляционные потери, вызванные: искажением формы
псевдослучайного двоичного сигнала в приемнике, составляют — не более
0,2 дБ; неидеальностью модулятора передатчика НС — 0,6 дБ [1.2].
Корреляционные потери определяются как разность между мощностью
сигнала, излучаемого передатчиком НС в отведенной полосе, и мощностью
сигнала, принятого идеальным корреляционным приемником в той же полосе
частот. Корреляционные потери имеют наибольшее значение тогда, когда
принимаемый сигнал имеет несущую на краях диапазона (соответствующую
каналам Jt=l или к =24).
Групповая задержка радиосигнала в аппаратуре НС. Система ГЛОНАСС
характеризуется беспрецедентно высокой точностью навигационных измере-
ний. Это стало возможным благодаря учету различных факторов, вклад кото-
рых в общую погрешность измерений находится даже на наносекундном уров-
не. При этом требуется использование новых технологий измерения. Одна из
таких составляющих погрешности измерений в СРНС — Групповая задержка
сигнала в бортовой аппаратуре спутника, которая определяется [1.2] как за-
держка между излучаемым радиосигналом (в фазовом центре передающей ан-
тенны спутника) и выходным сигналом БЭВЧ и не превышает 8 нс (случайная
составляющая). Считается, что детерминированная составляющая групповой
задержки радиосигнала потребителю не важна, так как может быть заранее
скомпенсирована, и не влияет на ошибки определения системного времени.
Внутрисистемные помехи. В зоне видимости потребителя СРНС всегда
находится более четырех спутников, каждый из которых излучает радиосигна-
лы. При обработке сигнала одного из спутников сигналы других спутников
мешают и их относят к внутрисистемным помехам. Уровень последних зависит
от принятого в системе метода разделения сигналов.
В системе ГЛОНАСС используется частотное разделение сигналов. Час-
тотный разнос между номинальными значениями несущих частот в диапазоне
LI равен 562,5 кГц и выбран таким образом, что, как следует из (5.13)—(5.16)
с учетом длительности элементарной посылки сигнала тэ =1/511 мс, помехо-
вые радиосигналы от спутников, находящихся в зоне радиовидимости, могут
помешать приему обрабатываемого сигнала только вторыми и последующими
лепестками спектра. При этом доля мощности одного ближайшего по частоте
д.2. Радиосигналы в СРНС ГЛОНАСС 139
Етомехового сигнала относительно полезного составляет примерно 2-Ю-5, т. е.
Врт превышает -48 дБ, что и определяет уровень внутрисистемных помех СРНС
Едонасс.
If Внутрисистемные помехи в СРНС GPS существенно больше. В GPS ис-
пользуется кодовое разделение сигналов и уровень внутрисистемных помех
^определяется значением максимального бокового лепестка кроскорреляцион-
'дгой функции используемых кодов. Для кодов Голда длиной 1023 элемента,
применяемых в GPS, уровень максимального бокового лепестка относительно
[величины полезного сигнала составляет примерно 7 103 (-21,6 дБ).
Характеристики навигационной радиолинии. В системе ГЛОНАСС для по-
требителя с изотропной антенной [1.1, 1.2J ориентировочные значения основ-
ных характеристик навигационной радиолинии:
мощность сигнала передатчика Pt = 64 Вт;
коэффициент усиления передающей антенны спутника Gt =10 дБ (по
’центру ДН) и 6, = 12 дБ (в углах ±15°);
эффективная мощность излучаемого сигнала Ризл = PtGt = 28 и 30 дБ Вт
для двух указанных направлений, соответственно;
потери в свободном пространстве Lp =20 1g (Х/4лА) дБ ® 184. дБ (для
угла места спутника 5°) и 182 дБ (для угла места 90°) для X. « 18,6 см (средняя
часть диапазона частот системы ГЛОНАСС);
затухание в атмосфере L„ ~0,5 дБ (для угла места спутника 5°) и
0,1 дБ (для угла места спутника 90° );
мощность принимаемого сигнала Рг = РИМ - LF - L„ - -154,5 дБВт (для
угла места спутника 5°) и -154,1 дБВт (для угла места спутника 90°). Здесь
приведены ориентировочные значения, так как не учтены некоторые потери:
из-за рассогласования в антенных трактах 0 ... 8 дБ; поляризационные потери
— примерно 1 дБ, а также коэффициента усиления приемной антенны потре-
бителя — несколько децибел;
спектральная плотность шума на входе ПИ No=kT&-2OO дБВт/Гц, где
к= 1,38-10 33 Втс/К — постоянная Больцмана; Т—эквивалентная шумовая
температура;
энергетический потенциал радиолинии Pr / = 45,5 дБГц (для угла
места спутника 5°) и 45,9 дБГц (для угла места спутника 90°);
отношение сигнал/ш^ в символе Ес / No= 28,5 дБ (для угла места
спутника 5°) и 28,9 дБ (для угла места спутника 90°), где Ес = Рг / /си —
энергия сигнала, /си = 50 Гц — частота следования символов служебной ин-
формации в сигнале спутника ГЛОНАСС.
140 Г л а в a 10. Подсистема космических аппаратов^
Гарантированный минимум уровня радиосигнала НС, принимаемого ац-
паратурой потребителя, в диапазоне L1 составляет не менее -161 дБВт. Он
определяется как мощность радиосигнала на выходе приемной изотропной
линейно поляризованной антенны (потери 3 дБ) при угле места 5°.
Увеличение уровня принимаемого сигнала обусловлено со следующими
причинами: отклонением высоты НС от номинального значения; ошибками
угловой ориентации НС; изменением коэффициента усиления передающей
антенны НС по азимутальным направлениям и по частотному диапазону; ва-
риациями выходной мощности передатчика НС из-за технологических причин,,
колебаний температуры и т. д.; уменьшением потерь при распространении ра-
диосигнала в атмосфере.
Зависимость минимальной мощности сигнала на Рт выходе изотропной
линейно поляризованной приемной антенны, находящейся на поверхности 1
Земли, от угла возвышения а НС приведена на рис. 10.5. Этот график по- j
строен при следующих допущениях:
Рис. 10.5. Зависимость принимаемой
мощности от угла возвышения
потери за счет распространения !
радиосигнала в атмосфере L„ = 2 дБ;
i
погрешность угловой ориента- ;
ции продольной оси НС на центр
Земли составляет 1° в сторону
уменьшения радиосигнала (после то-
го, как НС будет застабилизирован в
заданном орбитальном положении,
погрешность его ориентации не пре-
вышает ± 1° ). )
Можно считать, что макси-
мальный уровень принимаемого ра-
диосигнала не превысит -155,2 дБВт
(потери в атмосфере 0,5 дБ, погреш-
ность угловой ориентации НС 1° в
сторону увеличения сигнала).
10.3. Характеристики модулирующих последовательностей
Навигационный радиосигнал, передаваемый каждым НС, представляет
собой многокомпонентный фазоманипулированный сигнал.
Для получения высокой точности измерений задержки сигнала излучае-
мый сигнал модулируется дальномерным кодом стандартной точности (СТ-
код), представляющим периодическую последовательность максимальной дли-
ны (см. п. 5.4.2). Для диапазона L1 тактовая частота формирования дально-
мерного кода /ст =511 кГц, период повторения Т„ к = 1 мс.
10.3. Характеристики модулирующих последовательностей
141
Для передачи навигационной (служебной) информации используется мо-
дуляция двоичной последовательностью (кодом служебной информации (СИ-
код)) с тактовой частотой /си ~ 50 Гц.
Для обеспечения безошибочной работы фазового демодулятора в прием-
нике сигналов СРНС передаваемый сигнал подвергается относительной фазо-
вой манипуляции (ОФМ) (см. п. 5.6.2), а для обеспечения процессов синхро-
низации в приемнике (см. § 5.7) вводятся:
модуляция меандровым колебанием (М-кодом) с тактовой частотой /*„ =
=100 Гц (тактовая синхронизация);
код метки времени (MB-кода), представляющий собой двоичную ПСП
(ПСП МВ) с тактовой частотой fm = 100 Гц.
Упрощенная схема формирования модулирующей последовательности в
ГЛОНАСС показана на рис. 10.6, где ФОК — формирователь относительного
кода. Как видно из этого рисунка, модулирующий навигационный сигнал
(двоичная последовательность) формируется двумя способами.
В первом происходит сложение по mod 2 трех двоичных сигналов: даль-
номерного кода стандартной точности (СТ-код); кода служебной информации
(СИ-кода); меандрового колебания (М-кода).
Результирующая двоичная последовательность поступает на модуляцию
несущего колебания в течение 1,7 с каждого двухсекундного интервала спут-
никового времени.
В течение оставшихся 0,3 с этого интервала модулирующая последова-
тельность формируется сложением по mod 2 двух последовательностей: даль-
номерного СТ-кода; кода метки времени (МВ-кода).
Фазовая манипуляция несущей осуществляется на к радиан с макси-
мальной погрешностью не более ±0,2 рад. Указанные результирующие двоич-
ные последовательности используются для манипуляции одной из квадратур-
ных составляющих сигнала спутника на верхней частоте. Другая квадратурная
составляющая сигнала манипулируется двоичной последовательностью, обра-
зованной из специального высокоточного дальномерного кода (закон его фор-
мирования известен только потребителям, имеющим санкцию МО РФ) и соот-
ветствующей последовательности навигационных данных.
Рассмотрим особенности формирования указанных двоичных последова-
тельностей.
Рис. 10.6. Схема формирования модулирующей последовательности
МВ-код
7"мв = 10 мс
142 f
.Г л в J 10. П-, Систем. косми'. .<хихх. .Врагов
Дальномерный СТ-код представляет собой ^-последовательность. Эта^
сравнительно короткая ПСП ( длина £=511 элементов) обеспечивает по ана-J
логии с С/А-кодом в системе GPS быстрый поиск дальномерного сигнала uj
приемлемую точность измерения дальности до НС с соответствующей неодно-'
значностью. Порождающий полином СТ-кода 5ст(х) = 1 + х5 + х9.
Схема, поясняющая принцип формирования дальномерного кода ПСПД
и различных синхроимпульсов, показана на рис. 10.7.
Эталонная частота 5 МГц
/си=0,511 МГц
Регистр сдвига генератора ПСПД
Синхроимпульсы ----------------
5 МГц
(7^ 200 цс)^ формирователь
----------синхроимпульсов f
«„-5 МГц)
Установка
:50000
ПСПД
к модулятору
Тригер
' синхронизации
Строб-импульсы 7 = 1
от эталона частоты НС
Синхроимпульсы 7-1 с
к процессору
Синхроимпульсы Г=10 мс
к процессору
Тригер
* :иихР°низадии
Рис. 10.7. Схема формирования дальномерного кода
Как видно из рисунка, последовательность двоичных сигналов ПСПД
снимается с седьмого разряда девятиразрядного регистра сдвига. Начальным
символом в периоде ПСПД является первый символ в Группе 111111100, по-
вторяющийся через 1 мс.
Код служебной (навигационной) информации (СИ-код) представляет со-
бой преобразованную цифровую последовательность навигационных данных,
передаваемых аппаратурой НС потребителям системы ГЛОНАСС. Как видно
из рис. 10.6, навигационные данные а? подвергаются помехоустойчивому ко-
дированию (см. п. 5.1.2) в соответствии с кодом Хэмминга (85,77) (кодовое
расстояние равно четырем). Выходные символы bt кодера преобразуются в
относительный код по правилу (5.29) С, = £>(©С,_| , где С, — последователь-
ность символов в относительном коде (длительность рассматриваемых симво-
лов 7си = 20 мс). Таким образом, в канале передачи навигационной информа-
ции используется ОФМ-сигнал, что исключает явление обратной работы.
Результирующая двоичная последовательность навигационного сообще-
ния (названная здесь, как Д1-код), содержащая информационные и провероч-
ные символы в так называемом бидвоичном коде (Тщ= 10 мс), образуется,
как видно из рис. 10.7, после сложения по mod 2 последовательности симво-
pld.3. Характеристики модулирующих послсибвателииостей ' 143
лов Ct в относительном коде (СИ-код) с меандровым колебанием (М-код с
„длительностью символа Тт — 10 мс). Бидвоичный код обеспечивает, в част-
ности, простоту синхронизации по СИ-коду, содержащему серии одинаковых
двоичных символов (нулей или единиц).
Сигналы тактовых частот СТ-, МВ-, СИ-, М-кодов, и другие синхро-
сигналы получены делением эталонной частоты БЭВЧ /ог = 5 МГц, что теоре-
тически обеспечивает когерентность формируемых последовательностей.
Код метки времени (ПСП МВ, MB-код) представляет собой укороченную
ПСП с порождающим полиномом вида Дмв(х) = 1 + х3 +х5 .
Длина ПСП МВ равна тридцати символам с длительностью Тщ, = 10 мс
каждый. Эта характерная двоичная последовательность имеет следующий вид
111110001101110101000010010110.
Она используется как двухсекундная метка времени, так как задний
фронт ее последнего символа ПСП МВ в излученном навигационном радио-
сигнале является меткой времени и соответствует окончанию очередного двух-
секундного интервала времени от начала суток в БШВ. Эта метка позволяет
осуществлять строчную синхронизацию, а также устранять неоднозначность
дальномерных измерений.
Первый символ служебной информации в каждой строке всегда соответ-
ствует <<0>>. Он является "холостым" с точки зрения передачи навигацион-
ных данных, но дополняет укороченную ПСП МВ предыдущей строки до пол-
ной (неукороченной) ПСП.
В излучаемом навигационном радиосигнале границы: двухсекундных
строк, символов цифровой информации, символов меандра, символов ПСП
МВ и символов ПСПД синхронизированы между собой; границы символов
меандра и символов цифровой информации совпадают с передними фрон-
тами начальных символов ПСПД. Временные соотношения между синхроим-
пульсами навигационных данных и дальномерным кодом ПСПД показаны на
рис. 10.8.
Рис. 10.8. Временная диаграмма
144
Г л а в a 10. Подсистема космических аппаратов
10.4. Навигационные сообщения в СРНС ГЛОНАСС
10.4.1. Общие сведения
По своему содержанию навигационные сообщения, передаваемые каж-
дым НС ГЛОНАСС, содержат оперативную и неоперативную НИ:
Иногда применительно к ним используют термин "служебные сообще-
ния" (СС) или "служебная информация” (СИ). Потребителям ГЛОНАСС они
необходимы для планирования и осуществления навигационных определений.
Оперативная НИ относится к данному НС и содержит: оцифровку меток
времени спутника; оценки сдвига БШВ относительно СШВ и относительного
отличия несущей частоты излучаемого радиосигнала от номинального значе-
ния; эфемериды.
Неоперативная НИ содержит альманах системы: данные о состоянии всех
НС (альманах состояния), оценки сдвига БШВ каждого НС относительно
СШВ (альманах фаз), грубые параметры орбит сети НС (альманах орбит),
сдвиг ШВ относительно UTC (SU).
Оперативная информация
Номер строки в кадре (1 ... 15) т
Время начала кадра в пределах суток (Ч, МИН, с). ч
Опорное время ОИ ч
Относительный сдвиг частоты сигнала Уп
Сдвиг БШВ относительно СШВ
Координаты НС (ПЗ-90)
Составляющие скорости НС
Составляющие ускорения НС
Возраст ОИ Е„
Признаки исправности; смены ОИ; tb ; кадра . . Ill, П2, ИЗ, П4
Неоперативная информация (альманах)
Календарный номер суток (4 г.)
Поправка СШВС к ШВ ГЭВЧ (на начало ДС4)
Номер НС пА
Номер (литер) частоты НС
Долгота первого восходящего узла (ПЗ-90) . .
Момент прохождения восходящего учла . tA
Поправка к среднему наклонению (63°) ... А'.'1
Поправка к среднему драконическому периоду лта
обращения НС (12 час)
Скорость изменения драконического периода .
Эксцентриситет .... еИ
Аргумент перигея .
Грубый сдвиг БШВ . . .
Признак состояния НС с;
10,4. Навигационные сообщения в СРНС ГЛОНАСС 14.
Поток НИ состоит из непрерывно повторяющихся суперкадров, кадров i
строк (рис. 10.9). На рисунке использованы следующие сокращения: КХ — кот
Хэмминга, соответственно; МВ — метка времени. Снизу на рисунке показаг
порядок нумерации разрядов служебных сообщений.
Границы строк, кадров и суперкадров у различных НС синхронны с по-
грешностью не более 2 мс. Структура передаваемой навигационной информа-
ции в СРНС ГЛОНАСС оптимизирована таким образом, что объем суперкадщ
весьма невелик 7 500 бит, из них 620 резервные (в OPS 37 500 и 2 750 бит
Номер кадра в суперкадре Номер строки в кадре 4 2 С » 0,3 с
1.7с (85 бит)
I I 0 Оперативная КХ МВ 30 с
0 НИ для КХ МВ
4 0 передающего НС КХ МВ
Неоперативная НИ (альманах)
15 0 для НС с № 1...5 КХ МВ
II 1 0 Оперативная КХ МВ
0 НИ для КХ МВ 30 с х 5 = •2,5 мин
4 0 передающего НС КХ МВ
Неоперативная НИ (альманах)
15 0 для' НС с № 6... 10 КХ МВ
III 1 0 Оперативная КХ МВ
0 НИ для КХ МВ
4 0 передающего НС КХ МВ
Неоперативная НИ (альманах)
15 0 для НС с № 1...15 КХ МВ
IV 1 0 Оперативная КХ МВ
2 0 НИ для КХ МВ
3 0 передающего НС КХ МВ
Неоперативная НИ (альманах)
15 0 для НС с № 16..20 КХ МВ
V 1 0 Оперативная КХ МВ
0 НИ для КХ МВ
4 0 передающего НС КХ МВ
Неоперативная НИ (альманах) для НС с № 21 ...24
14 0 Резерв КХ МВ
15 0 Резерв КХ МВ
85 84 9 8...I 1...30 1 1 Г” f ” ”Т к1
Номер — рязрядп в сетке . Информационные Символы Метка символы кода Хэмминга времени в огноситепыЮм В.ОТНОСИТЕЛЬНОМ ... бидвонЧИОМ коде бияаоичйом Коде :
Рис. 10.9. Структура суперкадра навигационного сообщения ГЛОНАСС
> ) ) ) . !
146 i л а в a 10. Подсистема космических аппаратов
соответственно). Каждый суперкадр состоит из кадров, в нем передается пол-
ный объем неоперативной информации альманаха для двадцати четырех НС.
Каждый кадр состоит из 15 строк и содержит полный объем ОН для
конкретного НС (строки 1 ... 4) и четверть альманаха. В пределах супсркадра
ОН и строка 5 (системные данные) в каждом кадре повторяются.
Структура навигационного кадра (с I по 4-й) показана на рис. 10.10.
Здесь заштрихованные области представляют собой резерв, предусмотренный
на случай изменений и дополнений в структуре навигационного сообщения.
Информационная строка кадра длительностью 2 с (100 бит) разделена,
как показано на рис. 10.9, на две части. В первой части строки (1,7 с) со-
держится, навигационная информации (85 бит), преобразованная в относи-
тельный код и сложенная по mod 2 с колебанием (бидвоичный относительный
кол £>1 ). Во второй части строки (0,3 с) в качестве последовательности нави-
гационных данных используется ПСП МВ (MB-код), состоящая из 30 симво-
лов длительностью 10 мс.
В каждой строке старшие 77 разрядов (передаются первыми) содержат
информационные символы (85-й символ обеспечивает реализацию последова-
тельного относительного кода и равен <<0>>), а младшие 8 разрядов прове-
рочные символы. Они способствуют исправлению одиночных ошибок и обна-
ружение двойных ошибок (и большего четного числа) в строке.
10.4.2. Эфемериды НС ГЛОНАСС
Рассмотрим, следуя [1.2|, подробнее содержание зфемерилной информа-
ции приведенной на рис. 10.10.
Слово т — номер строки в навигационном кадре. Число разрядов этою
слова —I; цена младшего разряда -• I; диапазон значений 0 ... 15.
Слово (ч. мин. с) —время начала кадра внутри текущих с-уюк. исчис-
ляемое в шкале бортового времени НС. В пяти старших разрядах исредае.ся
число целых часов, прошедших с начала текущих суток; в шести средних
число целых минут; в младшем — число трилнатисекундных интервалов, про
шедших с начала текущей минуты. Начало суток ио бортовому времени сог.лл
дает с началом очередного супсркадра.
Число разрядов этого слова — 12; цена младшего разряда - 1 (для часов
и минут) и 30 (для секунд); диапазон значений - 0 ... 23 (для часов), О . 5'ч
(для минут) и 0 ... 30 (для секунд).
Слово — содержит три двоичных разряда. Аппаратурой потреби|еля
анализируется только старший разряд. Передача в нем <<!>> свидетельствует
о непригодности данного НС для навигационных измерений.
Слово th (мин) — время внутри текущих суток но шкале НТС(ГЭВЧ) '
Ь 03 ч 00 мин. к которому относится передаваемая в кадре ОН. Число ра зря
лов - 7; цена младшего разряда — 15; диапазон значений 15 . 1425.
}.4. На. Рацион. }е сооб, )ния в )НС УНАСС ) ) ) )47
стрики 1 ' "1 С(>.) > ЭД) КХ * МВ
2 т * 4 | (Й| ЭД) “ ЭД| > r.w г КХ 1 МВ
(»2 ')"^3 т \ "Ц 41,,) ЭД) > г,(з.) КХ • МВ
(пЗ'Г'^ т г. w “ [ . ] г. [: ; КХ е МВ
5 т * N" "| г,а [ КХ 1 МВ
6 т * ,U | Лл. 11 | Л'. 11 £Л И КХ 1 МВ
(С. ')><Г т 4 г,| ЛТ\ г1|лгд ’ |я\ 5 Щ КХ 1 МВ
8 1:ЬЧ 10 лл. ” | л/л. г. " КХ 1 МВ
9 т * а>Л. 1 /* *, 2’| и|лгд. ’ g КХ * МВ
10 т 4 [] "л '1 ? 10 Л'. 71 | л'. '* сА п КХ ’ МВ
11 т 4 а>Ля 1 ЭД !j ЛТ‘. !!|згл. 7 |н\ 1 |_ КХ ‘ МВ
12 т 4 U - 1 - лл. 11 | '• зл. » кх 1 МВ
13 т 4 1 ЛТ\ !!|агл. 7 |н". ’ Р КХ 1 МВ
14 т 4 IP 1 ' 10 Л". 21 | '• в КХ ’ МВ
15 т 4 0) \ | ЭД 7,| ЛЭД а|лГл. 7 j"'. ' кх 1 МВ
Рис. 10.10. Структура навигационного кадра
Слово П1 — признак смены ОИ (смена ОИ производится с интервалом,
определяемым словом П1). Этот признак сообщает интервал времени \th меж-
ду значениями th (мин) в данном и предыдущих кадрах. Значениям П1, рав-
ным 00. 01, 10 и 11, соответствуют значения 1Ь~ 0, 30, 45 и 60 мин.
Слово П2 — признак смены. Он представляет собой признак нечетности
<<!>> или четности <<0>> порядкового номера (b) 30(60) — минутного те-
кущего отрезка времени, середина которого оцифрована числовым значением
слова if,.
Слово ИЗ — признак, состояние <<!>> которого означает, что в данном
кадре передается альманах для пяти, а состояние <<0>> — ,ыя четырех НС.
Слово у— относительное отклонение прогнозируемого значения
несущей частоты излучаемого навигационного радиосигнала и-го НС от но-
минального значения на момент времени tb
" fnn^/fnn •
1 ле /„(//,) - прогнозируемое значение несущей частоты излучаемого радио-
сигнала a-ю НС с учетом гравитационного и релятивистского эффектов на
148 Г л а;в а 10- Подсдст-ема жосмнчаекнх аппаратов^
момент времени Г*; fm — номинальное значение -несущей частоты. Число
разрядов:этого слова -- 11; цена младшето::разряда — 2'w; диапазон значений
- ±2 ’°.
Слово t„(tb) (р)—сдвиг :БП(В л-го НС t относительно СШВ tn, равный
смещению по фазе ПСПД излучаемого радиосигнала п -го НС осиосительнс
системного опорного сигнала на момент времени t„, выраженный а» единица}
времени
t„(tb)^tc(tb) -tn(tb).
Число разрядов этого слова — 22; цена младшего разряда — 2-30; диапа-
зон значений — ± 2~30.
Слова X„(tb), Y„(tb), Z„(tb) (км) — координаты л -го НС в геодезической
системе координат ПЗ-90 на момент времени fb.
Число разрядов в этих словах — 27; цена младшего разряда — 2“н ; диа-
пазон значений — ± 2,7 • 104 .
Слова X„(tb),Y„(tb),Z„(tb) (км/с) —составляющие вектора скорости л-го
НС в геодезической системе координат ПЗ-90 на момент времени tb. Число
разрядов в этих словах — 24; цена младшего разряда — 2-20; диапазон значе-
ний — ±4,3.
Слова X„(tb),Y„(tb),Z„(tb) (км/с2) — составляющие ускорения л-го НС в
геодезической системе координат ПЗ-90 на момент времени tb, обусловлен-
ные действием Луны и Солнца. Число разрядов в этих словах — 5; цена млад-
шего разряда — 2“30; диапазон значений — ±6,2-10“9.
Слово Еп (сут) — характеризует "возраст" оперативной информации,
представляет собой интервал времени, прошедший с момента расчета (зак-
ладки) оперативной информации до момента времени tb для л -го НС. Это
слово формируется на борту НС. Число разрядов в этих словах — 5; цена
младшего разряда — 1; диапазон значений — 0 ... 31.
Параметры эфемерид НС периодически определяются подсистемой ПКУ
и закладываются на все НС. Погрешности прогнозирования положения и век-
тора скорости НС в орбитальной системе координат:
Составляющие
погрешности (1а); ..... Вдоль орбиты По бинормали По радиус-вектору
местоположение, м .. 20 10 5
скорость, см/с .... 0,05 0,1 0,3
40.4. Навигационные сообщениям C^HCXAs^JtACd
х49
Погрешность синхронизации бортовых шкал времени НС между собой
составляет 20 нс (1 а ).
Для вычисления эфемерид НС на момент измерений навигационных па-
раметров используются следующие соотношения для определения времени в
шкале UTC(SU)
tuTC(SU) = t + te + xn(tb) - y(M (f~ tb)>
где t — время излучения сигнала по бортовой шкале времени НС; тс, т„, у ,
tb — параметры определены выше.
10.4.3. Альманах системы ГЛОНАСС
Рассмотрим подробнее содержание альманаха системы, приведенного на
рис. 10.11.
Слово tc (с) — поправка к СШВ ГЛОНАСС относительно UTC(SU).
Поправка дана на начало суток с номером N*. Число разрядов этого слова —
28; цена младшего разряда — 2~27 ; диапазон значений — ±1.
Слово Na (сут) —календарный номер суток внутри четырехлетнего пе-
риода, начиная с високосного года, к которым относятся поправки тс и дан-
ные альманаха системы (альманахи орбит и фаз). Число разрядов этого слова
— 11; цена младшего разряда — 1; диапазон значений — 1 ... 1461.
Слово пл — условный номер НС в системе, который соответствует за-
нимаемой спутником рабочей точки орбиты. Число разрядов этого слова — 5;
цена младшего разряда — 1; диапазон значений — 1 ... 24.
Слово Н„ — литер несущей частоты радиосигнала, излучаемого НС с
номером пл. Число разрядов этого слова — 5; цена младшего разряда — 1;
диапазон значений — 1 ... 24.
Слово (полуцикл) —долгота в системе координат ПЗ-90 первого
внутри суток с номером восходящего узла орбиты спутника с номером п.
Число разрядов этого слова — 21; цена младшего разряда — 2-20; диапазон
значений — ±1.
Слово (с) — ближайшее к началу суток с номером время прохо-
ждения первого внутри этих суток восходящего узла орбиты спутника с номе-
ром пл. Число разрядов этого слова — 21; цена младшего разряда — 2-5; диа-
пазон значений — 0 ... 44100.
Слово Д/л (по^уцикл) —поправка к среднему значению наклонения ор-
биты (| = 63°) для спутника с номером пл на момент tf*. Число разрядов
150
Г л -i в а .10. Пвдсис'уема кссмичевжих 'ампарии'ов
этого слова — .18; цена младшего разряда - 2 20; диапазон значений -
±0,067.
Слово &ТА (с/виток) - поправка к среднему значению дрдкоиического
периода обращения (7’=43 200 с) НС с номером пл на момент времени
Число разрядов этого слова — 22; цена младшего разряда — 29; диапазон зна-
чений — ±3,6-10‘20.
Слово ДТ"/ (с/виток2) — скорость изменения драконического периода
обращения с номером пл. Число разрядов этого слова — 7; цена младшего
разряда — 2~14; диапазон значений — ± 2~8.
Слово еА — эксцентриситет орбиты НС с номером пл на момент вре-
мени Число разрядов этого слова — 15; цена младшего разряда — 2-20;
диапазон значений — 0 ... 0,03.
Слово (полуцикл) —аргумент перигея орбиты НС с номером пл на
момент времени 1^. Число разрядов этого слова — 16; цена младшего разряда
— 2~15; диапазон значений — ±1.
Слово т„ (с) —грубое значение сдвига БШВ НС с номером пА относи-
тельно СШВ на момент времени Это слово равно смещению ПСПД излу-
чаемого радиосигнала относительно номинального положения, выраженному в
единицах времени. Число разрядов этого слова — 10; цена младшего разряда —
2'18 ; диапазон значений — ±1,9-10"3 . )
Слово СА — обобщенный признак состояния НС с номером пл на мо-
мент закладки неоперативной информации (альманаха орбит и фаз). Нулевое
значение указывает на непригодность НС для навигационных определений.
Число разрядов этого слова — 1; цена младшего разряда — 1; диапазон значе-
ний — 0 ... 1.
Если потребитель определяет дальность до НС и радиальную составляю-
щую скорости НС на основе передаваемой неоперативной информации, то
погрешности измерений соответствующим образом зависят от "возраста" этих
данных:
Возраст НИ, сут ................
Погрешность определения (1а):
дальности, км ..................
радиальной скорости, м/с ...
1 10 20
0,83 2 0,33
3,3 0,7 4,2
Высокое качество эфемеридного и частотно-временного обеспечения, а
также формат дальномерного кода ГЛОНАСС обеспечивают высокую точность
10.5. Контроль целостности СРНС ГЛОНАСС
151
измерения дальности до НС (1 а = 7 м), соизмеряемую с точностью канала
стандартной точности (С/А-кода) GPS без применения режима загрубления
(SA) (1 а = 4 м). При этом у малодинамичного потребителя ошибки местона-
хождения в настоящее время равны; 20 м (2а) в горизонтальной плоскости и
примерно 36 м в вертикальной плоскости, что составляет приблизительно 1/5
часть заявленных погрешностей систем ГЛОНАСС и GPS (С/А-код) [8.2].
10.4.4. Резервные разряды в суперкадре
Дальнейшая совершенствование передаваемых
Таблица 10.3. Резервные разряды
I Номер строки Номер резерв- ного разряда
1,16,31,46,61 2,17,32,47,62 3,18,33,48,63 4,19,34,49,64 5,20,35,50,65 6,8,10,12,14,21,23,25,27,29,36,38, 40,42,44,,51,53,55,57,59,66,68,70,72 7,9,11,13,15,22,24,26,28.30,37,39, 41,43,45,52,54,56,58,60,67,69,71,73 74,75 79-80 65-69 65-68 9-48,54-58 9-41 78-79 9 9-80
навигационных сообще-
ний в системе ГЛОНАСС
может проводится с уче-
том имеющегося резерва
в массиве данных. Он
представляет собой за-
пасные разряды в соот-
ветствующих строках
суперкадра служебной
информации. Номера
этих строк и разрядов
показаны в табл. 10.3.
10.4.5. Контроль достоверности навигационных данных
Проверка качества навигационных данных может осуществляться раз-
личными способами. Рассмотрим способ, заключающийся в контроле досто-
верности данных передаваемых в каждой строке. Он основывается на извест-
ных свойствах кода Хэмминга и заключается в обнаружении и исправлении
одиночных ошибок (неправильный прием одного разряда строки), а также об-
наружении двойных и большего четного числа ошибок. Как известно, каждая
строка представляет собой 85-разрядный код, где старшие 77 разрядов содер-
жат информационные символы, а младшие 8 разрядов — проверочные. Для
исправления однократных ошибок в вычислителе формируются по определен-
ному закону (5.8—5.10| контрольные суммы С, (/ = 1 ... 7), а для обнаружения
двукратных и большего четного числа ошибок формируется общая контроль-
ная сумма Cj-. Путем обработки этих сумм по соответствующему правилу
принимается решение о наличии или отсутствии ошибок и их исправление.
10.5. Контроль целостности СРНС ГЛОНАСС
Контроль целостности радионавигационного поля СРНС заключается в
контроле качества из.т^аемых НС системы навигационных радиосигналов и
качества передаваемой ими служебной информации с целью поддержания вы-
сокой достоверности навигационных измерений и/или предупреждения нотре-
152 Г л а в a 10. Подсистема космических аппаратов
1
бителей о состоянии системы. Известны несколько способов контроля цело-
стности. Кратко рассмотрим некоторые из них применительно к системе
ГЛОНАСС.
Самоконтроль бортовых систем НС. На спутниках системы ГЛОНАСС
осуществляется непрерывный автономный контроль (самоконтроль) функцио-
нирования основных бортовых систем. При обнаружении непарируемых нару-
шений нормального функционирования этих систем, влияющих на качество
излучаемого спутником навигационного радиосигнала и достоверность переда-
ваемого навигационного сообщения, на спутнике формируется признак его
неисправности, который передается потребителю системы в составе оператив-
ной информации навигационного сообщения. Дискретность передачи такого
признака составляет 30 с. Максимальная задержка от момента обнаружения
неисправности до момента передачи соответствующего признака не превышает
1 мин. В дальнейшем планируется уменьшить это время до 10 с.
Недостатки этого канала контроля заключаются в его неполноте, напри-
мер, средства самоконтроля рассчитаны на обнаружение не всех возможных
нарушений в работе каждой бортовой системы НС; неисправности самих
средств контроля не обнаруживаются и не сопровождаются передачей соответ-
ствующего сообщения потребителям; искажение эфемерид не может быть об-
-наружецо на самом НС и т. д.
Наземный контроль. Качество навигационного поля ГЛОНАСС“Контро-_
лируется и специальной аппаратурой из состав ПКУ — аппаратурой контроля
поля (АКП). После соответствующего отказа бортовой аппаратуры спутника
АКП обеспечивает формирование признака его неисправности в альманахах
системы всех НС не позднее, чем через 16 ч. Дискретность передачи данного
признака в служебных сообщениях НС ГЛОНАСС составляет 2,5 мин.
Однако, оба указанных метода контроля целостности навигационного
поля ГЛОНАСС не обеспечивают требуемой полноты проверок и своевремен-
ности оповещения потребителей.
В соответствии с этими двумя способами контроля навигационного поля
ГЛОНАСС в служебных сообщениях каждого НС передаются два типа призна-
ков исправности (неисправности): Вп — его нулевое значение означает при-
годность данного НС для проведения навигационных определений потребите-
лями системы; С„ — совокупность (л = 1,24) этих обобщенных признаков от-
ражает состояния всех НС системы на момент закладки НИ (альманахи орбит
и фаз). Значение признака С’„= 0 указывает на непригодность спутника с сис-
темным номером п для проведения навигационных определений потребителя-
ми системы. Значение признака С„ = 1 указывает на пригодность этого спут-
ника.
Признаки первого типа передаются каждым НС в составе оперативной
информации, а признаки второго типа — в составе неоперативной информа-
ции. Время, необходимое для формирования и доставки потребителям призна-
ков В„ (до 1 мин) значительно меньше, чем для признаков С„ (до 16 ч), но
10.5. Контроль целостности СРНС ГЛОНАСС
153
формирование признаков Сп основано на более глубоком анализе качества
навигационного поля системы ГЛОНАСС. В связи с этим потребители систе-
мы должны при принятии решения об использовании сигналов конкретного
НС анализировать значения обоих признаков. Решающее правило приведено в
табл. 10.4. Известны подходы к решению
проблемы контроля целостности,
свободные от недостатков свя-
занных с неприемлемой задерж-
кой в оповещении потребителей.
Они, в частности, предусматри-
вают использование дифферен-
циальных измерений и своевре-
менного оповещения потребите-
лей об отказах НС с помощью
каналов связи (например, через
приемнике (RAIM). Потребители
Таблица 10.4. Решающее правило при ана-
лизе контроля целостности
Значения признаков Пригодность НС для целей навигации
В„ с„
0 0 -
0 1 +
1 0 -
1 1 +
дополнительные геостационарные ИСЗ).
Автономный контроль целостности в
СРНС могут использовать избыточность навигационной информации, полу-
чаемой в приемоиндикаторе СРНС от сети НС, для контроля качества навига-
ционного поля, т. е. для обнаружения и идентификации отказавшего НС, на-
пример, принимая сигналы от пяти спутников ГЛОНАСС, можно организовать
процедуру навигационных определений только по четырем, из них. Выбирая
разные комбинации четырех рабочих из пяти видимых спутников, можно по-
лучить пять наборов координат потребителя, которые позволяют с высокой
достоверностью судить о наличии отказавшего НС, а при большем числе спут-
ников и о его номере.
Известно много способов реализации концепции RAIM, отличающихся,
например, способом формирования достаточной статистики, выбором решаю-
щего правила, минимально необходимым числом НС, степенью использова-
ния априорных сведений, достоверностью полученных результатов, использо-
ванием избыточности измерений и т. д.
Требования к вероятности правильного обнаружения Рпо наличия отказа
НС алгоритмом RAIM весьма разнообразны. Так, в соответствии с одним из
существующих стандартов (TSO С-129), введенным в США, в случае превыше-
ния погрешности определения местонахождения с помощью аппаратуры по-
требителей СРНС типа OPS некоторого предельного значения (защитный по-
рог Д£), алгоритм RAIM должен обнаружить отказ НС с вероятностью
РПО =0,999.
Учитывая значение частоты существенных (погрешность местоопределе-
ния превышает 500 м при PDOP < 6) отказов в настоящее время (Х=3 г1) и
полагая, что треть потребителей пострадает от этого отказа, можно определить
вероятность Рт появления у потребителя в течение 1-го летного часа необна-
руженной с помощью RAIM погрешности, превышающей значение защитного
порога, Рно = 8 [х/(3 • 365 • 24)] (1 - />по).
»54 ) J ' 'f' л^а j 10- 'll дсистек Zkocmm Ами*. лцивгок.
1,1 I ..... " II I! ।... Г Fg|
Эксплуатационная:готовнасть устройства, ::реализуюлцего “алгоритм RAIN]
зависит от многих “факторов (числа используемых НС, угла маски спутников
координат потребителя и т. д.). Самая высокая степень готовности (~99
обеспечивается при полете по маршруту, когда защитный порог составляв
AL~3,6 км, а самая низкая (90 ... 95 % на средних широтах) — при некатего-
рированном заходе на посадку, когда Д£ ®0,55 км. Эти данные соответствуют
случаю использования вспомогательных данных от баровысотомера. Как вид-
но, даже в этом случае эксплуатационная готовность не достигает 100 %. По-
этому такое оборудование должно использоваться в качестве дополнительного.
Бортовая автономная система контроля целостности (AAIM). Потребите-
ли СРНС могут использовать и избыточность навигационной информации,
получаемой от различных бортовых навигационных датчиков
(радиотехнических и нерадиотехнических), для контроля качества навигаци-
онного поля ГЛОНАСС, т. е. для обнаружения и идентификации отказавшего
НС. Трудность реализации такой концепции часто связана со сравнительно
большой погрешностью измерений с помощью типовых бортовых навигацион-
ных датчиков и необходимостью соответствующих аппаратных и/или про-
граммных доработок бортового оборудования.
Заметим, что иногда с грубыми ошибками в дальномерных измерениях,
вызванными соответствующими отказами НС, целесообразно бороться не
исключением сигнала отказавшего спутника, а использованием^ избыточных
навигационных определений.
10.6. Бортовая аппаратура спутников ГЛОНАСС
10.6.1. Назначение бортовой аппаратуры
Навигационные спутники являются основными элементами системы
ГЛОНАСС. Их аппаратура предназначена для выполнения следующих функ-
ций, обеспечивающих высокое качество координатно-временных измерений :
излучения высокостабильных навигационных радиосигналов двух типов
— стандартной точности (СТ или CSA) без преднамеренного ухудшения харак-
теристик и высокой точности (ВТ) в дециметровом диапазоне волн ;
приема, хранения, формирования и передачи навигационной информа-
ции (данных);
формирования, оцифровки, хранения и передачи сигналов времени;
ретрансляции или излучения сигналов для радиоконтроля орбиты спут-
ника и определения поправок к бортовой шкале времени;
приема, квитирования, дешифрирования и отработки разовых команд;
приема, запоминания и отработки программ управления режимами
функционирования спутника на орбите;
формирования телеметрических данных о состоянии бортовой аппарату-
ры и передача их в ПКУ;
ДО.6. Буртовая аппаратура спутников Г^ЬНАСС
! 155
приема и отработки кодов коррекции и фазирования бортовой шкалы
времени;
выработку и передачу сигналов “Вызов наземного комплекса управле-
ния” при сбое или выходе важных контролируемых параметров за пределы
нормы;
анализ состояния бортовой аппаратуры (совместно с ПКУ) и выработка
управляющих команд.
Навигационный спутник ГЛОНАСС имеет две модели, отличающиеся
номенклатурой решаемых задач, аппаратурным составом, точностными харак-
теристиками и сроком активного существования. В настоящее время в штат-
ной орбитальной группировке находятся НС первого поколения — ГЛОНАСС.
Навигационный спутник второго поколения —- ГЛОНАСС-М — в настоящее
время находится на стадии испытаний
и после летных проверок будет исполь-
зован для замены спутников ГЛОНАСС
в орбитальной группировке. Внешний
вид спутника показан на рис. 10.11.
В системе ГЛОНАСС предусмот-
рены режимы применения: номиналь-
ный (штатный) и профилактический. В
номинальном режиме. НС находится в
составе орбитальной группировки и из-
лучает навигационные сигналы. В про-
филактическом режиме НС выводится
из группировки для проведения про-
Рис. 10.11. Навигационный спутник
филактических работ.
10.6.2. Состав спутника
На борту спутника находятся: бортовой навигационный передатчик
(БНП); хронизатор (БХ); управляющий комплекс (УК); системы ориентации и
стабилизации (СО), коррекции, электропитания; терморегулирования; борто-
вые средства заправки и обеспечения среды; элементы конструкции и кабель-
ная сеть.
Для обеспечения надежности основные системы навигационного спут-
ника дублируются. Рассмотрим основные элементы бортовой аппаратуры НС
ГЛОНАСС.
10.6.3. Бортовой навнгапнониый передатчик
Бортовой навигационный передатчик предназначен для формирования и
излучения высокоста^ильных радионавигационных сигналов в двух диапазонах
волн L1 и £2 .
156 Г ла в а 10. Подсистема космических аппаратов
Навигационный сигнал диапазона £1 содержит код дальности, бортовую
шкалу времени и навигационные данные (эфемеридная информация, поправки
времени, частоты и фазы бортового стандарта частоты). Навигационный сиг-
нал диапазона L2 содержит только код дальности и предназначен для исклю-
чения влияния ионосферной рефракции на точность измерений навигацион-
ных параметров военными потребителями.
Бортовой навигационный передатчик включает в свой состав аппаратуру
формирования навигационных сигналов и антенно-фидерные устройства. Ап-
паратура формирования навигационных сигналов конструктивно выполнена из
отдельных блоков, основные из которых (формирователь навигационных сиг-
налов) расположены внутри гермоконтейнера.
Для контроля аппаратуры установлены амплитудные и сигнальные теле-
метрические датчики, сигналы с которых поступают на телеметрическую сис-
тему. Амплитудные датчики характеризуют наличие и уровень высокочас-
тотной мощности на выходах усилителей. Переключение комплектов приборов
и блоков аппаратуры можно производить подачей команды на прибор или ав-
томатически по результатам анализа состояния амплитудных датчиков, про-
водимого в бортовой аппаратуре обработки и запоминания информации.
Антенно-фидерная система (АФС) предназначены для передачи электро-
магнитной энергии навигационных сигналов на частотах £1 и L2 в заданном
направлении. Антенно-фидерное устройство включает следующие элементы:
излучатели (12 шт.); блок делительный (4 шт.); делитель; кабели.
Конструктивно АФС представляет собой решетку, состоящую из двух
групп спиральных излучателей: центральной (4 излучателя) и периферийной
кольцевой (8 излучателей на кольце диаметром 850 мм).
Излучатели объединены в четыре излучающих модуля. Каждый модуль
состоит из трех излучателей (один из центральной группы yl два ближайших из
периферийной) и делительного блока. Такая антенная решетка обеспечивает
одновременную работу на частотах £1 и £2, подавление побочных излучений,
а также оптимальное распределение энергии в диаграмме в целях обеспечения
равенства парциальных сигналов при приеме на поверхности Земли.
Технические характеристики БНП:
Диапазон частот, МГп: канал £1 1597 ... 1621 канал £2 1241 ... 1261 Коэффициент усиления, дБ: канал £1 по центру 10 в углах ± 15° ... 12 в углах 8 канал £2 по центру 9 в углах ±15° ... 11 в у глах +19° - • 9 Выходная мощность, дБВт: канал £1 64 Канал £2 10 Эффективная излучаемая мощность, Вт: канал £1 30 канал £2 21 Энергопотребление, Вт 530
&$.Лортовая аппаратура спутников ГЛОНАСС
10.6.4. Бортшбй хронизатор
Бортсшой хронизатор предназначен для решения следующих задачгно-
^рерывной:аыдачи:нысокостяБильных синхрочастот в системы спутника; сфор-
мирования, хранения и выдачи бортовой шкалы времени.
Он обеспечивает формирование сигналов стандартной точности и сетки
“ импульсов синхрочастот (Гц):
- Сигнал /1 формируется fi 5 000 000 A. 50
fl. 200 000 fa. 10
/в виде синусоиды, остальные h SO 000 h. 1
в импульсном виде. Кроме fi. 10 000 fio. 1/60
«того, хронизатор формирует fs. 1000 fll 1/1800
сигналы временных интерва- fi. 100
' лов. Оцифровка времени про-
изводится 32-разрядным двоичным последовательным кодом с частотой
Д00 Гц.
В состав бортового хроиизатора входят: атомный стандарт частоты
(3 комплекта); устройство формирования синхрочастот и шкал времени.
Атомный стандарт частоты состоит из кварцевого генератора, атомно-
лучевой трубки и системы автоподстройки частоты. Кварцевый генератор
предназначен для генерирования колебаний с частотой 5 Мгц. Атомно-лучевая
трубка совместно с системой автоподстройки частоты служит для формирова-
ния высокостабильных колебаний частоты 5 Мгц.
В состав устройства формирования синхрочастот и шкал времени вхо-
дят блоки синусоидальных усилителей и устройство формирования. С атом-
ного стандарта частоты высокостабильный сигнал частоты '5 Мгц поступает на
блок синусоидальных усилителей, а затем к внешним потребителям и на уст-
ройство формирования, которое выдает потребителям сетку синхрочастот и
код времени.
Бортовой хронизатор работает в штатном или в дежурном режиме. В де-
журном режиме аппаратура обеспечивает выдачу сетки частот, необходимой
аппаратуре спутника на этапе ожидания, начальной ориентации, приведения в
точку, при хранении спутника на орбите, в аварийной ситуации. В этом режи-
ме в качестве задающего генератора используется кварцевый генератор. При
штатном функционировании аппаратура обеспечивает выдачу сигналов высо-
кой стабильности. В штатный режим спутник включается по командам с ПКУ
после окончания проверок аппаратуры спутника.
В случае, если расхождение бортовой и наземной шкал времени превы-
шает установленную норму, по команде с ПКУ производится фазирование и
коррекция бортовой шкалы. При выходе из строя эталона частот потребителю
'выдается сигнал ’’недостоверность фазы”. Переход из штатного режима в де-
журный производится «во командам блока управления спутника.
1S8 Г л а а а 10. Педсистема жосмитеских аппарате^.:
Тад х ни ч:о с к и е ха р:я к те р и с т и к и БХ:
Номинальное значение выходной частоты, МГц ............................ ::5 4
“Точность хранения .шкалы времени, нс .................................. 20
Относительная нестабильность стандарта частоты аахутки .... 5)1013 -
Ослабление::дискретаых::боковых:составляювдих.спектра
выходного сигнала в полосе ±20 кГц по отношению
к основной составляющей 5 МГц, дБ ................................ более 90
Масса, кг............................................................. 207
^Энергопотребление, .13 т.............................................. 100
10.6.5. Борт«1и<й1 управляющий комплекс
В состав БУК входят следующие системы и приборы: бортовая аппарату-
ра командной системы (АКС); бортовой вычислительный комплекс (БВК);
бортовая телеметрическая система (БТС); блок управления (БУ).
Бортовая аппаратура командной системы предназначена для выполнения
следующих задач: измерение параметров орбиты спутника в радиодиапазоне и
в оптическом диапазоне (совместно с ПКУ); исполнение разовых команд для
управления системами спутника; обработка временных программ, выдачи на-
вигационной информации; приема, формирования и передачи сигналов бо-
товойшкалы времени; передачи телеметрической информации; ретрансляции
информации обмена между наземными средствами. ’ - - _
Конструктивно АКС состоит из блоков НЧ, ВЧ, криптозащиты, АФС и
комплекта оптических уголковых отражателей. АФС содержит слабонаправ-
ленные антенны на прием и передачу, и направленную передающую антенну.
Направленная антенна используется при штатной ориентации спутника.
Бортовой вычислительный комплекс предназначена для решения сле-
дующих задач: запоминание и обработка навигационной информации, форми-
рование навигационных кадров и выдача их в БНП; контроль состояния БНП
и переключения его комплектов; запоминание и выдача кодов временных
программ и скачков в командно-измерительную систему; прием, формирова-
ние и выдача сигналов “Вызов наземного комплекса управления”; автономный
тестовый контроль работоспособности аппаратуры БВК с выдачей сообщения
по телеметрическим каналам; формирование и передача “отчета БВК” по на-
вигационному каналу при аварийной ситуации в БВК и снятии спутника с
эксплуатации (для анализа ситуации на наземных станциях); пересчет инфор-
мации об изменении задержки дальномерного сигнала и переключение ком-
плектов БНП; формирование в навигационном кадре признака непригодности
спутника к использованию потребителями при отказе БУ.
Блок управления спутника обеспечивает включение спутника после вы-
ведения на орбиту, выдачу питания на пиропатроны для раскрытия механиче-
ских систем после отделения спутника от ракеты-носителя. Он распределяет
питание между всеми электроприборами, совместную работу подсистем при
проведении режимов коррекции, разгрузки управляющих маховиков, а также
управление системами спутника в аварийных ситуациях при потере ориента-
ции или отказах системы электропитания.
ЧО.о.Борто^ая-аппи^атура^.^тникс- ^ГЛОН. }С
Технические характеристики БУ:
Бортовой вычислительный комплекс
Скорость записи информации, Гц............................ 1000
Время готовности после подачи питания, мин .................. 3
Интервал отработки информации, сут......................... 30
Максимальный темп отработки ВП, программа/с ................. 2
Аппаратура комаидпой системы
Диапазон частот............................................. СМ
Точность сверки времени, мс ............................... 0 ... 2
Скорость приема, Гц :
разовая команда......................................... 100
временная программа.............................. 1000
Блок управлепия
Погрешность измерительной линии, м:
радиодиапазои ............................................ 3
оптический диапазон .................................. 0,3
Число ВП ................................................. 1000
Число телеметрических каналов ............................. 512
10.6.6. Система ориентации и стабилизации
и другие вспомогательные системы
Система ориентации и стабилизации предназначена для решения сле-
дующих задач: успокоение спутника и обеспечение начальной ориентации на
Солнце й на Землю; ориентация продольной оси спутника, на .центр Земли,
солнечных батарей на Солнце; ориентация вектора тяги двигателей коррекции
орбиты по вектору скорости (на время выдачи импульса коррекции).
В спутниках ГЛОНАСС используется активная трехосная система ори-
ентации и стабилизации с управляющими маховиками и реактивной системой
разгрузки. В состав СО входят чувствительные (блок измерения угловых ско-
ростей, приборы ориентации на Землю и Солнце, приборы солнечной ориен-
тации по каналу рыскания, магнитометры) и исполнительные
(электромеханический исполнительный орган, привод вращения панелей сол-
нечных батарей, электромагнитные устройства, маховик стабилизирующий,
двигательная установка, блок управления) элементы.
Система ориентации и стабилизации работает в следующих режимах: ус-
покоения; начальной ориентации на Солнце; закрутки вокруг поперечной оси;
начальной ориентации на Землю; ориентации на Землю; ориентации при про-
ведении коррекции.
Солнечные батареи спутника выполнены в виде четырех плоских прямо-
угольных панелей, объединенных попарно в два крыла, расположенных сим-
метрично плоскости стабилизации (XOY). Крылья солнечных батарей враща-
ются вокруг оси (OZ), перпендикулярной плоскости стабилизации и направле-
ны на солнце в процессе штатной эксплуатации. Перевод каждого спутника в
заданную точку ддбитальной структуры (системную или рабочую точку) про-
водится с помощью спутниковой двигательной установки (два симметричных
блока)коррекции.
160 ........... 1. г ла в а 10. Подсистема космических аппаратов^।
С целью создания необходимых климатических условий для аппаратуры
спутника используется цилиндрический герметичный контейнер, являющийся
одновременно основной несущей конструкцией спутника и радиационной;
поверхностью. Для снижения возмущающих воздействий на движение спутни-
ка от реактивной струи исходящего из термоконтейнера газа его герметичность
повышена на порядок по сравнению с аналогичными. На днище контейнера
крепятся различные блоки и АФС. В сложенном положении спутник представ-
ляет собой ромбическую призму.
Характеристики систем спутника:
Система ориептации и стабилизации
Точность ориентации, град:
продольной оси ..................................... 0.5 1
солнечных батарей ............................................... 5
вектора тяги ..................................... 5 ... 11
Система коррекции
Тяга двигателей, Н:
коррекции ..................................................... 5
стабилизации .................................................. 0,1
Суммарный импульс, Н ........................................... 90000
Система электропитания
Рабочая мощность солнечных батарей, Вт .......................... 1250
Рабочая емкость аккумуляторных батарей, Лч(Втч) ............. 45(1260)
Выходное напряжение, В .............................. 27 ± 1
Система термолегулироваиня
Диапазон термолегулировапния, °C:
стандартов частоты ................................. (15 ... 30) ± 1
термоконтейнера.................................. 0 ... 40
двигательной установки .......................... 5 ... 40
Энергопотребление, Вт............................................. 36
Спутник ГЛОНАСС
Срок активного существования, г......................... 3 ... 5
Длительность непрерывной работы, сут...................... 1415 ... 1485
Масса (конструкции), кг .......................................... 237
Энергопотребление (среднесуточное), Вт .............. 1000
10.6.7. Функционирование бортовых систем спутника ГЛОНАСС
В процессе функционирования спутник последовательно находится в
следующих режимах работы: ожидание после выведения на орбиту; начальной
ориентации; приведения в расчетную точку; штатного функционирования.
После выведение спутников на заданную орбиту (за время не более 5 ч)
по команде, выдаваемой разгонным блоком непосредственно после остановки
двигателей, включается электропитание некоммутируемых шин питания и де-
журные схемы спутников. Через 15 с после этого система управления разгон-
ным блоком выдает команду на отделение спутников. Эта операция осуществ-
ляется для трех спутников синхронно с их закруткой (с угловой скоростью не
более 27 %). Процесс отделения спутников контролируется с помощью те-
леметрической системы разгонного блока. На каждом спутнике при его отде-
лении формируется команда “Контакт отделения", по которой он переводится
ld.6. Бортовая аппаратура спутников ГЛОНАСС
161
цости наземных средств ПКУ обеспечивается прием команд управления и пе-
редачи телеметрических данных. Длительность работы спутника в режиме
ожидания до трех суток.
Перевод спутника в режим начальной ориентации происходит в зоне ра-
диовидимости наземных средств в следующей последовательности: раскрытие
солнечных батарей и штанги магнитометра; успокоение спутника; начальная
ориентация солнечных батарей на Солнце и спутника — на Землю.
В процессе успокоения осуществляется торможение вращательного дви-
жения спутника с помощью двигательной установки и разворот панелей сол-
нечных батарей для выставки крыльев активной поверхностью в одну сторону
и установки их в плоскости, совпадающей с продольной осью спутника.
В режиме начальной солнечной ориентации осуществляется разворот
спутника вокруг продольной оси с помощью двигателей маховиков до попада-
ния Солнца в поле зрения приборов ориентации на Солнце с последующим
переводом в закрутку вокруг оси, ориентированной на Солнце.
Режим начальной ориентации на Землю проводится в зоне радиовидимо-
сти ПКУ на участках, где “Солнце—НС—Земля” составляет (90±18)°. При
этом обеспечивается торможение вращения спутника и его разворот с помо-
щью управляющих двигателей — маховиков вокруг направления, ориентиро-
ванного на Солнце до попадания Земли в поле зрения прибора ориентации на
Землю. После этого-включается режим слежения за Солнцем и Землей .
Приведение спутника в заданное положение на орбите осуществляется в
несколько этапов: определение параметров орбиты и формирование програм-
мы приведения; выдача импульсов коррекции для обеспечения требуемой ско-
рости смещения спутника относительно номинальной орбиты; пассивное дви-
жение спутника по орбите в заданном направлении; выдача импульсов, обес-
печивающих торможение движения спутника и приведение спутника в задан-
ное положение на орбите; проведение измерений параметров орбит.
После завершения всей программы приведения спутника в заданное по-
ложение с требуемой точностью производится окончательное уточнение пара-
метров орбиты, высокоточная синхронизация БШВ, расчет временных про-
грамм и закладка их на спутник. После этого спутник может использоваться
по целевому назначению.
Литература
10.1. Состояние ОГ ГЛОНАСС// Компьютерный бюллетень BBS КНИЦ ВКС РФ.
10.2. Ivanov N., Salischev V., Vinogradov Л. Ways of GLONASS system advancing
// ION GPS-95, 1995, pp. 991-1011.
162
Г л а ев а 11
Особые режимы работы спутниковых
радионавигационных систем
11.1. Дифференциальный режим СРНС ГЛОНАСС
11.1.1. Определение дифференциального режима СРНС
Дифференциальный режим радионавигационных систем первоначально
разрабатывался применительно к РНС типа ЛОРАН и ОМЕГА. Существенна
роль российских ученых (В. С. Шебшаевич и др.) в разработке основ диффе-
ренциального режима СРНС ГЛОНАСС [11.1].
В основе метода дифференциальной навигации лежит относительное по-
стоянство значительной части погрешностей СРНС во времени и й простран-
стве. Необходимость использования дифференциального режима СРНС опре-
деляется стремлением удовлетворить наиболее жестким требованиям навига-
ционного обеспечения таких задач, как посадка ВС по категориям ИКАО, мо-
реплавание в проливных зонах и узкостях и т. п.
Уже первые эксперименты [1Г.2, 11.3] Показали Возможность снижения
ошибок (СКО) определения координат по системе GPS с 20 до 5 м и высоты с
40 также до уровня 5 м.
Дифференциальный режим СРНС предполагает наличие как минимум
двух приемоизмерителей АП1 (контрольно-корректирующая станция) и АП2
(потребитель) в двух точках 1 и 2 пространства, причем АП1 геодезически
точно привязан к принятой системе координат (ПЗ-90 или )WGS-84). Разности
между измеренными АП1 и рассчитанными в нем значениями псевдодально-
стей “видимых” НС, а также разности соответствующих псевдоскоростей по
линии передачи данных (ЛПД) передаются АП2, в котором они вычитаются из
измеренных АП2 псевдодальностей (ПД) и псевдоскоростей (ПСК). Если по-
грешности определения ПД слабо изменяются во времени и пространстве, то
они существенно компенсируются переданными по ЛПД поправками. В даль-
нейшем будем рассматривать коррекцию ПД.
Основными слабо меняющимися погрешностями определения ПД в
СРНС являются: ошибки синхронизации НС; погрешности за счет ошибок
эфемеридного обеспечения НС; нескомпенсированные ионосферные погреш-
ности.
Ошибки синхронизации НС постоянны в пространстве и весьма ста-
бильны на рассматриваемых временных интервалах. Уход БЭВЧ НС порядка
10“мили 1013 за время порядка 15 мин изменяет ошибки ПД пренебрежимо
мало (от 3 мм до 3 см).
ц.1. Дифференциальный режим СРНС ГЛОНАСС
163
Эффект погрешностей эфемеридной информации (ЭИ) может быть оце-
[ен следующими моделями.
Первая модель основана на прямом вычислении ошибки ПД, как функ-
ции ошибок ЭИ. Из предыдущих разделов следует, что ошибки определения
ДД объекта с координатами x,y,z, как функции ошибок координат /-го НС
дх/,Ду/,Д?/> могут быть записаны в виде
Щ = (х-XjjAx, / Dt + (у-yt)byt /У + (г- u)bzt / Д •
(П.1)
Рассчитаем 8Д как функцию удаления L потребителя от контрольно-
“ корректирующей станции (ККС) для /-го НС СРНС ГЛОНАСС со сфериче-
скими координатами Dt = 20 094 км; 4=49,2°; 3/= 53,7° относительно ККС.
В этом случае
х( = £>, sin 4 cos 3(; yf = Д cos 4 cos 3,; z^ZJ/SinS,.
(11.2)
Координаты x, у, z ККС равны нулю. Рассчитывается ошибка е =
8Д(8) - 8Д(0). Результаты расчетов сведены в табл. 11.1 (1-и 2-я строки) -для
4 = (дх2 + Ду2 + Дг2)*/2 = 20; 100 м.
Таблица 11.1. Пространственная изменчивость погрешностей определения
ПД за счет неточности ЭИ
№ модели 4 > м Погрешность для функции удаления L , км 1
25 0.01 50 0,02 100 200 300 500 900 1
1 20 0,04 0,08 0,12 0,2 0,36
1 100 0,05 0,1 0,2 0,4 0,6 1 1,8
2 20 0,025 0,05 0,1 0,2 0,3 0,5 0,9
2 100 0,125 0,25 0,5 1 1,5 2,5 4,5
2 1000 1,25 2,5 5 10 15 25 45 |
Вторая модель впервые предложена в [11.3] и дает несколько завышен-
ные (верхние ) границы е( как функции dh L, Dt'.
г1 5 Ldj / Dt .
(11.3)
Результаты соответствующих расчетов также приведены в табл. 11.1
(строки 3, 4, 5).
Соотношениями.!) и (11.3) характеризуют пространственную изменчи-
вость ошибок определения ПД, обусловленных погрешностями ЭИ. Эта из-
менчивость в первом приближении описывается линейной функцией и растет
Г л а -;, а 11. Особые режимы работы CPHEjj
И.4
явояжв
с ростом расстояния между ККС и потребителем. ::В то .же время, данные 3-'
4-й строк (табл. ИЛ) показывают, -что::эта изменчивость -ire ’превышает 0,2
1 м при df‘= 20 и 1Q0 м ссответстиенно, и £5.200 км.
Пятая строка таблицы характеризует изменчивость погрешностей ПД зЛ
счет ЭИ при использовании для определения места альманаха, возраст котоЗ
рого составляет несколько десятков часов (1.2]. Одновременно можно утвер-j
ждать, что, если использование аналогичного альманаха, возраст которого со-!
ставляет 1 сут, приводит к ошибкам определения ПД порядка 830 м [1.2], то;
при линейном нарастании ошибки за 1 мин изменчивость ЭИ составит при-!
мерно 0,6 м.
Изменчивость во времени и пространстве ионосферных погрешностей,?
обусловленных запаздыванием сигнала при прохождении в ионосфере, харак-:
теризуется корреляционной функцией, которая имеет времена и пространст-
венные радиусы корреляции на уровне, соответственно, нескольких часов и
тысяч километров [11.4]. Поэтому, на интервале в несколько единиц минут и
сотен км ионосферные погрешности можно полагать достаточно стабильными.
Согласно ]11.5], уровень ионосферных погрешностей составляет от 10 до
40 м и достигает минимума при максимальном угле места визируемого НС.
В [11.5, 11.6] приведены конкретные количественные характеристики
временной изменчивости ошибок ПД СРНС ГЛОНАСС, обусловленных ионо-
сферными погрешностями. Так, через 1 мин изменчивость еоетавяяет 0,1
0,2 м (СКО), а через 6 мин — 0,3 ... 1,4 м.
После коррекции псевдодальностей алгоритм определения навигацион-
ных параметров АП2 будет аналогичным используемому в номинальном режи-
ме СРНС.
11.1.2 . Точностные возможности дифференциального режима
Погрешность определения i-й псевдодальности в дифференциальном ре-
жиме может быть записана в виде
bDt- bDie + 8D//on + bD^ - 8Д(я1,
(114)
где 8Pfe и 8РЙОЛ — остаточные погрешности за счет эфемеридных и ио-
носферных ошибок, 8Р/л2 и — соответственно шумовые погрешности
АП2 и АП1, включающие погрешности приемоиндикатора, обусловленные
внутренними и внешними шумами, ошибки за счет многолучевости и особен-
ностей распространения радиоволн в тропосфере.
Если их считать чисто случайными и взаимонезависимыми, соответст-
вующая дисперсия может быть записана в виде
аи - CTie +aUon +alnl + CT4n2 > (11-5)
f t, I. Дифференциальный режим СРНСГЛОНАСС
165
не а/г, Стдол. ст*|2 — дисперсии соответственно 8Z)fe, 8Лйол, 6DM, bDM.
Предполагая взаимную независимость и одинаковые статистические ха-
актеристики погрешностей (11.4) для различных i, получим соотношения
^ля точности определения координат потребителя (среднеквадратическая сфе-
рическая погрешность, СКОсф)
Исф = (11.6)
и временной поправки
- «rt aD Ic >
(П-7)
где ид -°a определяется соотношением (11.5); — расхождения между
шкалой времени СРНС и шкалами времени АП1 и АП2 соответственно;/Ггп,
KIt — пространственный и временной коэффициенты геометрии (см. § 7.4).
В [11.7] впервые опубликованы экспериментальные результаты, подтвер-
ждающие возможность использования практически линейной зависимости
погрешности (СКОсф) местонахождения как функциирасстояния L и возрас-
та t дифференциальной поправки, которая может быть представлена в виде
стсф(Л^) = Осфо + v/ + bL,
(И.8)
где Стсфо =2,28 м; v = 1,32 • 10 3 м/с; 6= 0,000438 м/км.
Обработка экспериментальных данных показала, что СКО аппроксима-
ции с помощью (11.8) может характеризоваться для псевдодальности следую-
щим соотношением:
о - cnfl - er,/T-L/lA
°апп — и(ц* с J >
(И-9)
где ст0= 3,66 м; Т = 3847 с; Lc = 122,84 км.
При сравнительно низких <т2е, основными составляющими,
влияющими на точность определения местонахождения в дифференциальном
режиме, могут быть нескомпенсированные ионосферные ошибки.
В этом случае ошибки определения координат по системе ГЛОНАСС с
вероятностью 95^> (по уровню р=2а ) будут [11.5]
РглонО) = (Ро + (а№ / 2)2)1/2.
(11.10)
166
Глава И. Особые режимы работы СРНС
Здесь ро=О,4м; ej = 0,00014 м/с2.
Для сравнения приведем соответствующее соотношение для GPS [11.5]
Рсду(0 = (Ро + (°1/2 / 2)2 + (“2/2 / 2)2)*^2,
(П Н) -
где в2=0,0И м/с2. Различие в (11.10) и (11.11) определяется эффектом режи-
ма селективного доступа в GPS.
Соотношения (11.6)—(11.11) показывают, что точность определения мес-
та и времени в дифференциальном режиме СРНС в значительной степени за-
висят от точности измерений РНП в ККС и аппаратуре потребителя, от рас-
стояния между ККС и потребителем, от возраста поправок, а также от коэф-
фициентов геометрии Кгп, KIt.
Последние в значительной степени зависят от числа видимых НС, отно-
сительно которых определяются псевдодальностн. Если оно составляет 4 ... 5,
то Кгп, KTt могут составлять 2 ... 4 и даже более. Если количество НС, сиг-
налы которых принимаются приемниками ККС и потребителя, больше 10, то
^г.п> не превосходят единицы.
При полностью скомпенсированных ионосферных и эфемеридных по-,
грешностях основными источниками ошибок остаются шумовые составляю*-
щие, которые при измерениях задержек по коду составляют единицы метров, а
при измерениях по фазе составляют единицы сантиметров и даже миллимет-
ров. Для авиационных объектов дополнительным существенным источником
ошибок является многолучевость. Ее эффект частично характеризуется соот-
ношением (11.9).
11.1.3. Дифференциальные подсистемы СРНС
Дифференциальные подсистемы (ДПС) СРНС ГЛОНАСС и GPS подраз-
деляют на широкозонные, региональные и локальные. Следует отметить, что
это деление является несколько условным [11.8]. В частности, в ряде случаев
трудно указать различие между региональными и локальными ДПС, особенно
тогда, когда последние связаны в сети. С другой стороны, и сеть региональных
ДПС по существу также может образовать широкозонные ДПС.
Создание ДПС ведется в соответствии с требованиями, выдвинутыми
национальными радионавигационными планами и требованиями или стандар-
тами таких международных организаций, как ИКАО, ИМО и др. Ряд требова-
ний сформулирован во вводной части книги, например, к точности и надеж-
ности навигационного обеспечения различных этапов полета самолета.
Широкозонные ДПС СРНС. Основой ШДПС СРНС является сеть ККС,
информация которых передается в центр управления для совместной обработ-
ки с целью выработки общих поправок и сигналов целостности. Размер рабо-
чей зоны ШДПС составляет порядка 5 000 км. Выработанные сигналы целост-
К>(1.1. Дифференциальный режим СРНС ГЛОНАСС 167
• цости и корректирующие поправки передаются по ЛПД, возможности которых
должны соответствовать размерам зоны, обеспечиваемой ШДПС.
Широкозонные ДПС СРНС GPS и ГЛОНАСС является, например, сис-
•<Тема EGNOS (European Geostationary Navigation Overlay Service), разрабаты-
ваемая фирмами Thomson-CSF, Sextant и Syseca (co сроком окончания предва-
рительных работ в декабре 1997 г.) и рассматриваемая совместно с аналогич-
ной американской системой WAAS в качестве составной части будущей гло-
бальной навигационной спутниковой системы GNSS-1 {11.9].
Корректирующая информация EGNOS должна передаваться потребите-
лям через геостационарные НС INMARSAT-III: AORE ( Atlantic Ocean Region
East), расположенный в точке 15,5° западной долготы, и IOR ( Indian Ocean
Region ), расположенный в точке 64° восточной долготы. INMARSAT-III по-
мимо КИ передают и навигационный сигнал, подобный сигналу НС GPS
(11.10].
Для обеспечения работы НС INMARSAT-III используются четыре свя-
занные между собой станции, один центр контроля и управления и две стан-
ции для обеспечения связи ’’Земля—НС”. Данные измерений, контролирую-
щих положение НС, передаются в центр для обработки, результаты которой
через ЛПД передаются затем для точного эфемеридного обеспечения.
Важное место в системе EGNOS занимает служба контроля целостности,
которая не более чем в течение 10 с предупредит потребителя о выходе нави-
гационного сигнала из допустимых границ, если это произойдет.
Предполагаемая точность определения координат ШДПС EGNOS со-
ставляет 2,5 ... 5 м, что значительно лучше точности номинального режима
СРНС ГЛОНАСС и тем более GPS.
Предполагается поэтапный ввод в строй различных компонентов ШДПС
EGNOS. Начало развертывания службы геостационарного дополнения системы
GPS относится к 1998 г., средства контроля целостности и обеспечения КИ
будут развертываться в 1998—2000 гг. Предварительной работоспособности
предполагается достичь в 1999 г., а полная работоспособность будет достигну-
та в 2002 г. [11.10].
Планируется также сопряжение ШДПС EGNOS с дополнительными ре-
гиональными системами, особенно в северных широтах [11.10].
В [11.11] приведены результаты экспериментальных исследований точно-
сти ШДПС RACAL Skyfix System в составе трех ККС, расположенных в горо-
дах Кадис (Испания), Хаммерфест (Норвегия) и на острове Кипр с аппарату-
рой потребителя, установленной в городе Абердин (Шотландия). При этом
показана возможность определения плановых координат и высоты с точно-
стью (СКО) 2,6 ... 2,7 и 3 м соответственно.
Региональные ДПС СРНС. Региональные ДПС СРНС предназначены для
навигационного обеспечения отдельных регионов континента, моря, океана.
Протяженность рабочей зоны может составлять от 400 ... 500 до 2 000 км. Ре-
168 Г л а в a 11. Особые режимы работы СРИСаИ
гиональные ДПС (РДПС) могут иметь в своем составе одну или несколькЯ
ККС, а также соответствующие средства передачи КИ и сигналов целостносдцЯ
Примером РДПС являются ДПС Starfix фирмы Фугро [11.12]. Эти подЛ
системы имеют дальность свыше 2 000 км. Сеть таких ДПС образована 60-jfl
наземными ККС и четырьмя НС INMARSAT и охватывает все континенты, зЛ
исключением части Африки и Азии (Россия), а также акватории прилегающих]
морей и океанов. Заявленная точность местоо пределе ни я (с вероятностью!
0,95) 1 ... 2 м на дальностях до 1 000 км и 3 м на удалениях, превышающих!
2 000 км [11.13]. J
Другим примером служат Средневосточные региональные ДПС [11.14],]
охватывающие зоны Персидского залива, Красного и Средиземного морей,]
Суэцкого канала и Гибралтара, по которым проходят важнейшие пути транс-й
портировки нефти со Среднего и Ближнего Востока в Европу. ;
Достижимая точность РДПС иллюстрируется результатами эксперимен-
тальной работы [11.15], в которой показана возможность определения геоцен-
трических координат по системе ГЛОНАСС для потребителя в городе Лидсел
(Англия) и ККС вблизи города Абердин (Шотландия) с точностью (СКО)?
3,4 ... 7,9 м, по СРНС ГЛОНАСС и GPS — с точностью 3 ... 7,4 м и по систе-
ме GPS — с точностью 2,5 ... 4,4 м. При этом задержки в передаче КИ состав-4
ляли от 5 до 70 с (для GPS — в среднем 20 с, для ГЛОНАСС —- 17 с). Не-
сколько худшие характеристики точности использования СРНС ГЛОНАСС ав-
торами объясняются недостаточной калибровкой соответствующих радио-
каналов.
Локальные ДПС СРНС. Локальные ДПС СРНС имеют максимальные
дальности действия от ККС до 50 ... 200 км. Локальные ДПС обычно включа-
ют одну ККС, аппаратуру управления и контроля (в том числе контроля цело-
стности) и средства передачи данных. '
К настоящему времени определились три основных класса ЛДПС :
морские ЛДПС для обеспечения мореплавания в проливных зонах, узко-
стях и акваториях портов и гаваней в соответствии с требованиям ИМО [11.1];
авиационные ЛДПС для обеспечения захода на посадку и посадки ВС по
категориям ИКАО;
локальные ДПС для геодезических, землемерных и других специальных
работ [11.16].
Морские ЛДПС, использующие в качестве средств ЛПД всенаправленные
средневолновые радиомаяки (РМ) с дальностью до 200 км, размещены, в част-
ности, по периметру острова Исландия (11.17], по побережью Италии [11.18] и
в ряде других мест. Предполагается [11.19], что сеть таких ЛДПС, работающих
по системам ГЛОНАСС и GPS, будет охватывать также все побережье России
и акватории прилегающих морей. В настоящее время отдельные средства про-
ходят предварительную проверку на Балтике.
Среднеквадратическая ошибка определения координат (с вероятностью
более 0,95) при совместном использовании СРНС ГЛОНАСС и GPS составит
от 2 до 4,5 м; надежность обслуживания и доступность составят соответствен-
Hfcl. Дифференциальный режим СРНС ГЛОНАСС ,......................169
цо более 0,9997 и 0,998 при времени предупреждения об отказе меньше 10 с
(11.201.
f В качестве примера авиационной ЛДПС можно привести системы
P92O/D93O фирмы DASA (ФРГ) 111.21,11.22], работающие по СРНС GPS. Ап-
паратура D920 сертифицирована в соответствии со специальной категорией I,
система D930 в состоянии удовлетворить требованиям I и П-й категорий
ИКАО. Радиус действия этих систем доходит до 37 км.
Система D920 включает ККС с монитором СРНС, УКВ ЛПД с монито-
ром (стандарт RTCA/DO-217), а также общий монитор для контроля и управ-
ления.
Система имеет отказоустойчивую конструкцию и сертифицирована для
Критических ситуаций по соответствующим стандартам. Программное обеспе-
чение сертифицировано по требованиям RTCA/DO-178B.
Для того, чтобы удовлетворить жестким требованиям посадки самолетов,
ЛДПС имеет в своем составе монитор целостности со следующими функция-
ми: обнаружение и исключение аномальных сигналов и ошибок, влияющих на
измерительные каналы; аттестация дифференциальных ошибок определения
дальности потребителя посредством сравнения некоррелированных показаний
приемников; обнаружение и исключение перескоков фазы при слежении за
фазой несущей; контроль передаваемых сообщений перед и после их излуче-
ния в эфир.
Общие характеристики ЛДПС D92O следующие; частота выдачи поправок
точность лучше 1,1 м; 1 ... 4 Гц; целостность 1 ... ЗЮ’8; доступность 0,98; не-
прерывность 1... 3,8-Ю’5. Имеется встроенный контроль, осуществляется ав-
тономное функционирование с теленаблюдением, а также взаимодействие со
службами УВД.
Важный, распространенный и весьма перспективный класс ЛДПС со-
ставляют системы геодезического обеспечения с дальностью не более 50 км и
сантиметровой—дециметровой точностью (11.23, 11.24]. Как правило, их ис-
пользование допускает серьезную обработку измерений после того, как эти
измерения проведены. Кроме того, они почти в обязательном порядке реали-
зуют алгоритмы слежения за фазой несущей частоты сигнала (более подробно
см. п. 11.3.3). В то же время требования непрерывности, доступности и цело-
стности для таких систем могут быть существенно ослаблены.
Имеются и весьма специфические применения ЛДПС СРНС, например,
для контроля за перемещением автомашин инкассаторов в системе Инкомбан-
ка г. Москвы (Выставка АО “ПРИН” на семинаре AGARD, 3—4 марта 1997 г.,
МАИ, Москва).
Контрольно-корректирующие станции ДПС СРНС. К настоящему времени
выпущено значительное число конкретных типов ККС. Ниже будут описаны
лишь некоторые из них, что позволит дать общее представление о принципах
построения и другой аппаратуре аналогичного назначения.
170 , Г л а на 11. Особые режимы работы СРНС 1
В Российском НИИ космического приборостроения (РНИИ КП) разра-|
ботана 24-канальная станция мониторинга радионавигационных полей СРНС
ГЛОНАСС и GPS и определения дифференциальных поправок [11.25].
Станция предназначена для решения следующих задач:
непрерывного слежения за всеми “видимыми” НС ГЛОНАСС и GPS с
сохранением в памяти компьютера всей полученной приемниками измери-
тельной и другой цифровой информации;
непрерывного проведения в реальном времени навигационных определе-
ний по созвездиям только НС ГЛОНАСС, только НС GPS и НС ГЛОНАСС и
GPS;
анализа составляющих погрешностей навигационных определений;
контроля качества передаваемых НС навигационных радиосигналов и
навигационных сообщений и контроля целостности;
формирования дифференциальных поправок к навигационным радиосиг-
налам “визируемых” НС и признаков исправности этих НС.
В состав станции входят: антенно-усилительный модуль; четыре 4-ка-
нальных ГЛОНАСС/GPS приемных устройства; четыре цифровых сигнальных
процессора DSP-25U; компьютер обработки данных IBM PC 486.
Одноплатный сигнальный процессор (СП) DSP-25U выполнен на базе
микропроцессора TMS 320 С25. Станция сопряжена с внешним стандартом
частоты 5 МГц и подключена к внешнему источнику постоянного тока на-
пряжением 27 В.
Приемное устройство состоит из блоков аналоговой и цифровой обра-
ботки сигналов, блока управления каналами, блока стабилизации напряжения
и частоты, вторичного источника питания.
Функционирование ККС предполагается в автономном режиме, для чего
предусмотрены телеметрирование приемного устройства в реальном времени и
запись поступающей информации, а также возможна работа под наблюдением
оператора.
Спирально-полосковая широкополосная антенна позволяет принимать
сигналы СРНС GPS и ГЛОНАСС в зоне обзора ± 85° относительно вертикали.
МикроЭВМ (сигнальный процессор) DSP-25U управляется работой при-
емных устройств; платы DSP-25U вставлены в свободные слоты IBM PC 486.
Программное обеспечение (ПО) ККС включает:
ПО СП DSP-25U, призванное управлять аппаратной частью приемника и
цифровой обработкой сигналов;
ПО управляющего компьютера, предназначенное для управления СП,
предварительной обработки и накопления данных измерений и навигационных
сообщений НС и формирования дифференциальных поправок;
ПО обработки, анализа и графического представления данных телемет-
рии (уровней сигналов и шумов в каналах приема, времени поиска сигналов и
т. д.), расчетных дальностей и скоростей (по фазе и коду), их разностей с из-
меренными значениями (невязок), погрешностей ежесекундных и осредненных
17<
Навигационных определений плановых координат и высоты с анализом гео-
метрии созвездий.
Данные управляющего компьютера могут передаваться по интерфейсу RS
232 в другой компьютер или в ЛПД. Стандартный интерфейс ККС позволяет
яерез линии связи объединить несколько таких станций в единую сеть с вза-
имным обменом информацией внутри сети. Совместная обработка информа-
ции, полученной на различных ККС сети, позволяет исключить зависимость
точности поправок от удаления потребителя от ККС в регионе, охватываемом
сетью.
Контрольно-корректирующая ЛДПС D920/930 включает антенный блок,
СРНС монитор, приемник СРНС GPS с линейным модемом, который работает
на оптоволоконный кабель, связывающий приемник с монитором контроля и
управления ЛДПС. Этот монитор включает VHF 900 приемник, с помощью
которого осуществляется контроль передаваемых поправок, магнитофон, тер-
минальный сервер, блок наземной обработки, модемы и принтер. Предусмот-
рена возможность дополнения ККС приемником, работающим по геостацио-
нарному НС. GPS-приемник с 12 каналами параллельного слежения осуществ-
ляет слежение за С/А кодом; фазовые и кодовые измерения проводят с часто-
той 10 Гц, время первого отсчета не более 5 мин, время восстановления сле-
жения менее 30 с после перерывов 10 ... 60 с, среднее время безотказной рабо-
ты более 20 000 ч.
Российским институтом радионавигации и времени создана ККС “Зверь-
М” для упомянутых выше морских ЛДПС, работающая по СРНС ГЛОНАСС и
GPS [11.19, 11.26]. Аналогичная ККС разработана на Украине НИИ “Квант”
(г. Киев) и заводом Оризон (г. Смела). Такие ККС рассчитывают по данным
приемников сигналов СРНС ГЛОНАСС и GPS поправки, преобразуют их в
стандартные сообщения ( в соответствии со стандартом RTCM SC-104) и по-
дают их на модулятор передатчика-радиомаяка [11.1].
Фирмой “3S Navigation” изготовлен 12-канальный приемник СРНС
“ГЛОНАСС” и GPS, также работающий в составе ККС и имеющий вес при-
мерно 3 кг, что позволяет рассчитывать на создание переносной аппаратуры
ККС.
Интересное решение предложила фирма Фугро, разработав, так называе-
мую, виртуальную базовую ККС, которая для выработки оптимальных попра-
вок использует данные всех находящихся в непосредственной близости ККС,
что и позволяет получить высокие заявленные точности местонахождения.
При этом общий вес такой станции не превышает 1,5 кг.
Линии передачи данных ЛДПС. Для морских ЛДПС самым экономичным
решением, как уже отмечалось, является использование в качестве ЛПД все-
направленным средневолновых радиомаяков, работающих в диапазоне 283,5 ...
325 кГц. При этом применяют манипуляцию с минимальным фазовым сдви-
гом (MSK). Возможная скорость передачи данных от 25 до 100 бод. Скорость
передачи поправок для СРНС ГЛОНАСС составляет 25 бод, при работе с
СРНС GPS без селективного доступа и с селективным доступом скорости пс-
J
172 Г л а в a 11. Особые режимы работы CPHfe
।
редачи составляют соответственно 50 и 100 бод. Такая манипуляция не мешас
выполнению основной задачи РМ — определению направления.
Для помехоустойчивого кодирования используются корректирующие кп
ды Рида-Соломона. Основной недостаток выбранной ЛПД — подверженное*
помехам, например из-за разрядов статического электричества в осадка
(дождь, снег и т. д.) [11.26].
Корректирующая информация морских ЛДПС передается в соответстви!
с общепринятым стандартом RTCM SC-104, разработанным первоначально дщ
GPS Специальным комитетом 104 (Special Commitee 104) Радиотехнически
комиссии по мореплаванию (Radio Technical Commission for Maritime) США
поддержанном МАМС (Международной Ассоциацией Маячных служб). ВерсгЦ
2.2 этого стандарта создана, чтобы учесть использование дифференциальное^
режима и СРНС ГЛОНАСС [11.20, 11.27]. Последующее изложение основанг
на этом материале.
Формат RTCM SC-104 предусматривает использование 30-битовых слов;
из них 24 бита являются информационными, следующие за ними 6 бит -х
’’контрольные”. Каждое сообщение имеет заголовок из двух слов, следующи1.
за ним слова передаваемых данных специфичны для каждого конкретного тип;
сообщения.
Поправки и неоперативная вспомогательная информация передаются ft
качестве непрерывного потока сообщений, состоящих из отдельных информа-'
ционных кадров. Одно сообщение включает АГ+2 слова. Сообщения с данными
СРНС ГЛОНАСС сгруппированы в блок из семи типов (табл. 11.2).
Таблица 11.2. Основные сообщения ЛДПС СРНС
ГЛОНАСС/GPS
Номер типа сообщения GPS Наименование Номер типа 1 сообщения j ГЛОНАСС
1 Поправки GNSS (для всех “видимых” НС) 31
3 Параметры ККС 32
5 Исправность созвездия 33
6 Нуль-кадр 34(N=0wm 7)1
7 Альманахи РМ 35
9 Подгруппа “быстрых” поправок GNSS (взамен типов 1 или 31) 34 (N>1)
3 16 Специальное сообщение 36 1
Формат и содержание сообщений о поправках ГЛОНАСС идентичнь
формату и содержанию соответствующих сообщений GPS. Однако имеютс
некоторые отличия, связанные с несколько иной структурой координат и врс
менной шкалы СРНС ГЛОНАСС, а также с содержанием информационны
кадров навигационного сообщения ГЛОНАСС.
!»! Дифференциальный режим СРНС ГЛОНАСС
173
видимых
лишь для подгруппы из этих
координатах ККС в системе
идентичны сообщению 3 для
Имеются также отличия в заголовках сообщений. Сообщение 31 (N>1)
Етит корректирующие поправки для всех “видимых” НС. В отличие от
ения 31 сообщение 34 содержит поправки
иых” НС, общим числом не более девяти.
! Сообщение 32 содержит информацию о
ДЗ-90. Формат и содержание этого сообщения
J2PS, но координаты в сообщении 3 представлены в системе WGS-84.
Сообщение 34 (Т—0 или 1) используется для вспомогательных целей
[обес печения непрерывности передачи), например, когда ККС не готова по-
бить другую информацию, для синхронизации в некоторых специфических
иучаях и т. д.
j Сообщение 35 предусмотрено для РМ, передающих поправки для СРНС
piOHA.CC, содержит информацию о местонахождении, частоте несущей и
^оне действия РМ, и используется для того, чтобы облегчить восприятие сиг-
рала РМ потребителем.
Координаты РМ передаются в системе координат ПЗ-90. Каждый РМ
передает также информацию о двух или трех близлежащих РМ сети. Зона дей-
ствия РМ характеризуется расстоянием от РМ, на котором отношение сиг-
вал/шум в полосе сигнала превышает 7 дБ в 99,9 % времени данного сезона.
Радиомаяк идентифицируется в соответствии с положениями МАМС.
Сообщение 36 идентично сообщению типа 16, но информация о безо-
пасности навигации будет передаваться как на русском, так и на английском
языках.
Частота передачи различных типов сообщений:
3
5
6
7
16
34(31)
32
33
34
35
36
Номер сообщения:
9(1) — передается настолько часто, насколько возможно
(примерно каждые 15 ... 20 с)
дважды в час (по истечении каждой 15 и 45-й мин)
в пятую минуту каждого часа и через каждые 15 мин после
по мере необходимости
в седьмую минуту каждого часа и каждые 15 мин после
в случае необходимости
каждые 50 ... 60 с
дважды в час (в 16 и 45-ю мин каждого часа)
в шестую минуту каждого часа и затем каждые 15 мин
по мере необходимости ^=0 или 1)
в восьмую минуту каждого часа
по мере необходимости
В случае кратковременного отсутствия поправок для любой системы и
информации об отказе ККС и РМ будет передаваться сообщение 6 (34) (N < 2)
или сообщение 16 (36) с указанием вида отказа в заголовке.
Одновременно информация об отказе РМ и ККС будет передаваться
близлежащим РМ посредством сообщений 7 (35). В результате время между
обнаружением отказа и передачей предупреждения о нем не превысит 10 с
[11.28].
174 Глава 11. Особые режимы работы СРЦ|
Как уже отмечалось, ряд систем использует каналы системы INMARSAT]
(WAAS, EGNOS, RACAL Skyfix, Fugro Starfix). Здесь для ориентировки приве-Я
дем их некоторые характеристики применительно к системе Starfix [11.29]. Я
Линия передачи данных INMARSAT работает на частоте близкой к!
1600 МГц, скорость передачи 600, 1200, 2400 бод, надежность линий 0,9997,
вероятность искажения бита 10-5. Формат данных находится в соответствии со
стандартом RTCM-104 версии 2.0. Для системы Starfix используются сообще-
ния 1, 3, 16 (дифференциальные поправки, параметры ККС и специальное со-
общение). Время подготовки сообщения 1 составляет менее 4 с.
К настоящему времени отсутствует согласованное мнение, поддержан-,
ное ИКАО, относительно формата сообщений и радиоканала для авиационных 1
ЛДПС. Однако применительно к задаче захода самолета на посадку по специ- :
альной категории I Радиотехнической комиссией по авиации США подготов- '
лен Стандарт RTCA/DO-217 по минимальным характеристикам авиационных
систем [11.30]. В соответствии с этим стандартом разработан ряд конкретных -
систем [11.21, 11.22], которые прошли испытания, и предполагается использо-
вать их для обеспечения полетов гражданской авиации.
Соответствующая ЛПД использует УКВ диапазон частот 112 ... 118 МГц.
Формат общего сообщения ЛПД включает: служебную последовательность;
информационный массив; корректирующую кодовую последовательность"
(FEC-Forward Error Correction) и вспомогательные символы.
Передаваемое частное сообщение о поправках содержит (бит), например:
идентификатор блока ошибки дифференциальных
сообщения — 8 дальностей пользователя —— 6
идентификатор ККС — 24 поправки на одну ПД — 16
резервное слово 2 номера НС 6
тип сообщения 6 возраст данных \ поправки на одну ПСК кодовую корректирующую 8
длину сообщения модифицированный — 8 12
Z-отсчет — 13 группу ошибку ускорения — 24 3
При 12 НС общий размер такого сообщения составит 664 бит.
Используется относительная фазовая модуляция несущей со сдвигом По
фазе на тс/4 (всего восемь положений). При этом один символ передаваемой
информации представляется одним сдвигом фазы, чему соответствует двоич-
ное число из 3 бит (код Грея). Например, 001 соответствует единице и фазо-
вому сдвигу тс/4 и т. д.
Служебная последовательность (85 бит) позволяет бортовому приемнику
правильно демодулировать сообщение. В передатчике она способствует стаби-
лизации уровня мощности и синхронизации, содержит резервный символ, ин-
формацию о длине сообщения и корректирующую группу служебной последо-
вательности.
Служебная последовательность защищается укороченным кодом Хэм-
минга, способным корректировать ошибку 1 бит и обнаруживать 75 из 300
pl A. Дифференциальный режим СРНС ГЛОНАСС 175
возможных парных ошибок. Информационный массив (общий объем до 1.776)
защищается укороченным кодом Рида-Соломона (225,249). Этот код способен
^справлять до трех ошибочных символов. Он формируется из 8-битовых слов с
помощью кодирующей последовательности (FEC).
После кодирования сообщение подвергается скрэмблированию данных.
Все общее сообщение передается внутри интервала длительностью
500 мс. Восемь таких интервалов составляют один подкадр общего временного
календаря TDMA (Time Division Multiple Access). Скорость передачи данных
достигает 2400 бод.
Система, соответствующая специальной категории I (SCAT-I), внутри
Одного подкадра не использует более двух интервалов. Для обеспечения захода
на посадку по категориям I, II, III может использоваться и более двух интер-
валов в зависимости от требований, предъявляемых этими системами.
Для создания ЛПД применительно к ЛДПС посадки по категории III
рассматриваются альтернативные варианты радиоканалов.
Считается, что дифференциальные поправки для всех “видимых” НС
должны передаваться с частотой 1 Гц, сигналы целостности и положительной
идентификации — с частотой 2 Гц, и данные о состоянии ВПП — с частотой
1/20 Гц. Однако общий формат сообщения о поправках, приведенный выше,
остается неизменным (11.31]. Увеличивается лишь на 8 бит корректирующая
"кодовая группа (до 32); Предполагается также, что сообщение р целостности
будет иметь длину до 272 бит, а сообщение о состоянии ВПП т- до 1000 бит.
В то же время считается, что возможности ЛПД должны быть таковыми,
чтобы учитывать любые изменения в формате, например, за счет включения:
дифференциальных сообщений СРНС ГЛОНАСС; поправок фазы несущей;
формата данных DGNSS-2 (т. е. DGNSS еще более далекого будущего).
Помимо УКВ диапазона 108 ... 118 Min рассматривался и диапазон MLS
5000 ... 5250 МГц, а также модифицированный С-диапазон [11.31]. Использо-
вание УКВ диапазона, как правило, не требует размещения на самолете новых
антенных устройств, однако необходимо обеспечение больших отношений
сигнал/шум по сравнению с С-диапазоном и диапазоном MLS.
Кроме того, этот диапазон уже занят другими средствами (VOR/ILS), по-
этому возможное его использование требует серьезных организационно-
плановых мероприятий. Очевидно также, что использование канала MLS зави-
сит от судьбы этой системы.
Авторы ]11.31] считают, что использование УКВ-диапазона, хотя и яв-
ляется на первый взгляд более привлекательным, уступает возможностям ис-
пользования модифицированного С-диапазона.
Существует еще одно предложение к облику канала передачи КИ регио-
нальных дифференциальных подсистем СРНС ГЛОНАСС/GPS. Имеется в виду
радиоканал передающих станций импульсно-фазовых радиотехнических сис-
тем дальней навигации Лоран-С/Чайка. Эти станции работают в длинноволно-
вом диапазоне радиоволн на частоте 100 кГц. С использованием передатчиков
Лоран-С в качестве основного средства ЛПД создана РДПС СРНС GPS Eurofix
176 Г л а в a 11. Особые режимы работы СРНСй
[11.32]. Радиус действия системы с одной станцией достигает порядка 1000 од,:
Как показано в [11.33], точность определения координат такой РДПС может
составить 5 м. Оценки [11.32] показали, что ЛПД на основе станций РСДЩ
могут обеспечить эффективную скорость передачи данных от 15 до 30 бод^
поэтому возможно дополнение РДПС Eurofix и возможностями использова-
ния СРНС ГЛОНАСС. При этом целесообразно применять асинхронный
DGPS/DniOHACC формат данных, в нем сообщение о поправках для одного
НС имеет длину в 45 бит [11.33].
Бортовая аппаратура дифференциального режима СРНС. Как уже отмеча-
лось, основной алгоритм навигационных определений в дифференциальном
режиме после ввода и учета поправок не отличается от алгоритма навигацион-
ных определений в номинальном режиме, поэтому в настоящее время большая
часть бортовой аппаратуры (БА) СРНС ГЛОНАСС и GPS разработки послед-
них лет признается пригодной к использованию в обоих режимах. Для реали-
зации дифференциального режима дополнительно должны быть предусмотре-
ны возможности ввода дифференциальных поправок в соответствии с приня-
тыми стандартами: для морской — RTCM SC-104, для авиационной —
RTCA/DO-217, ARIN С-419/429 и др.
В качестве примера можно привести бортовую аппаратуру “Интер-А”
разработки МКБ “Компас” [11.34], GNSS-12 фирмы “3S Navigation”, DN-12,
Sensor II фирмы Аштек) [11.35—11.37]. -
Приемник сообщений с поправками и другой КИ, как правило, разра-
батывается и производится отдельно, но на согласованной основе. В качестве
примеров можно указать приемники сигналов PM MX 41R фирмы Leica и Nav
Beacon XL фирмы Trimble [11.38—11.39].
11.1.4. Разновидности дифференциального режима СРНС
Существует ряд признаков классификации разновидностей дифференци-
ального режима: тип основных измерений: фаза кода или фаза несущей часто-
ты сигнала; вид коррекции: коррекция псевдодальности (ПД) и псевдоскоро-
сти (ПСК) или навигационных параметров, вычисляемых на их основе; место
коррекции: у потребителя или в каком-нибудь центре; средства передачи кор-
ректирующей информации.
В соответствии с этими признаками кратко охарактеризуем некоторые
распространенные разновидности ДР, которые отличаются от основного, опи-
санного в предыдущих разделах.
Дифференциальный режим с коррекцией координат. Согласно [1.5], ме-
тод коррекции координат в ДР может использоваться в том случае, когда оп-
ределения координат ДС и потребителем осуществляются по одному и тому же
созвездию НС.
В этом случае дифференциальная поправка Д11д.п = Пдп-Пдп, где
Пд„, Пдп — оцененные в процессе текущих измерений и точно известные
177
11.1. Дифференциальный режим СРНС ГЛОНАСС
к
IK"
заранее векторы координат (геодезических, геоцентрических или Гаусса—
Крюгера) дифференциальной станции. Поправка ДПЛ„ является линейным
Преобразованием основных погрешностей, описанных в § 11.1. Потребитель,
измерив свои координаты П, использует эту поправку для их уточнения, при-
меняя соотношение П = П - ДПд11.
Дифференциальный режим с коррекцией координат требует незначи-
тельного объема передаваемой информации: например, по три поправки к
координатам и к скоростям вместо 16 поправок к ПД и 16 поправок к ПСК.
Он может использоваться потребителем на сравнительно небольших удалени-
ях от ДС и в сравнительно небольшие промежутки времени, а также для одно-
типной приемной аппаратуры СРНС ДС и определяющегося объекта . При
смене созвездия НС ДС в принудительном порядке должно меняться и созвез-
дие НС у потребителя.
Дифференциальный режим с использованием относительных координат.
Во многих случаях, когда точная геодезическая привязка дифференциальных
станций затруднена, дифференциальный режим может быть реализован при
использовании относительных координат.
Если два объекта 061 и 062 определяют свои прямоугольные координа-
ты П] = |xi yi ?i|T и П2 = |х2 У2 Z2|Tс помощью АП СРНС в номинальном режи-
ме работы, то вектор координат 062 относительно 061 (вектор относительных
координат) запишем в виде
П21 = |х21 У21 ?21|Т>
(11.12)
где х21 = х2 - хь у21 = у2 - ус, Z21 = <2 - Zi. •
Поскольку погрешности ДП( (/ = 1, 2), как и в методе коррекции коор-
динат, являются результатом линейного преобразования всех ошибок опреде-
ления псевдодальностей, то, очевидно, в результате такой операции вычита-
ния одинаковые квазисистематические ошибки, обусловленные особенностями
распространения радиоволн в ионосфере, неточностью эфемеридной инфор-
мации и синхронизации, исключаются.
Точность метода использования относительных координат также в пер-
вом приближении эквивалентна точности стандартного дифференциального
режима СРНС [1.5, 11.40J.
С учетом (11.8), (11.9), среднеквадратическое сферическое отклонение
при относительном местонахождении 062 может быть ориентировочно оцене-
но соотношением:-
I 2 2 ( \2 2 2
^сф21 ~ ^сфл! + ^сфл2 ^у^сфО + v/ + bLj + п Сдпл
178 Г л а в a 11, Особые режимы работы СРНС^
где асфпЬасфи2 — СКОсф местонахождения 061 и 062, обусловленные ошиб-
ками за счет шумов приемников, помех, тропосферы и многолучевости; L
ч
расстояние между 061 и 062; t— задержка между определениями 061 и 062;-
^сфО > v и b определены в (11.8); оапп — (11.9); Кт„ — пространственный
коэффициент геометрии.
Также, как и метод коррекции координат, метод использования относи-
тельных координат в случае прямого расчета по соотношениям (11.12) будет
эффективен только на сравнительно небольших взаимных удалениях при рабо-
те АП1 и АП2 по одному и тому же созвездию НС. В передаваемое сообщение
должны при этом включаться координаты и скорости Об, а также номера НС
используемого созвездия.
Возможен вариант, когда в передаваемое сообщение входят ПД и ПСК
объекта, и расчет П?1 может проводиться на основе разностей ПД и ПСК.
Дифференциальный режим с использованием псевдоспутников. Одна из
разновидностей ДР создается тогда, когда передаваемые дифференциальной
станцией сигналы с поправками и другой информацией привязаны к местной
шкале времени. Поскольку при учете дифференциальных поправок шкала вре-
мени потребителя также оказывается привязанной, к шкале времени ДС, при-
нятые потребителем сигналы ДС являются источником информации о взаим-
ной дальности и скорости между потребителем и ДС.
В частном случае ДС может излучать сигнал, аналогичный сигналу НС,
тогда ее называют псевдоспутником. Сигналы ДС могут быть весьма информа-
тивными, например, случай размещения ДС под глиссадой, по которой захо-
дит на посадку самолет. Вопросы оптимального размещения псевдоспутников
для ДПС СРНС рассмотрены в fl 1.40]. '
Использование псевдоспутников призвано скорректировать возможно
плохие геометрические факторы ГЛОНАСС и GPS, если они, возникают.
В качестве критерия в [11.40] использовался взвешенный коэффициент
геометрии WD0P - (2А"ГВ + Кт г)/3 , где Кт я, К1Т — вертикальный и горизон-
тальный коэффициенты геометрии соответственно (см. § 7.4).
Разработанная в [11.40] программа расчетов на ЦВМ позволила дать
предложения по оптимальному размещению одного и двух псевдоспутников
относительно аэропорта Сан-Франциско. При этом снижены значения макси-
мально возможных Кт в и Kt г для СРНС GPS (21 НС) от 15,6 до 2,26 и от
7,71 до 2,36 соответственно. В случае двух псевдоспутников максимально воз-
можный Кгв — 1,66.
11.2. Интегрирование СРНС ГЛОНАСС и GPS
Одним из важнейших направлений совершенствования и развития СРНС
ГЛОНАСС является ее интегрирование со спутниковой радионавигационной
pfl.2. Интегрирование CPHG ГЛ&ЯАСС и GPS 179
системой GPS [11.41—11.42]. Основные цели интегрирования — повышение
Точности и надежности (доступности, непрерывности обслуживания и целост-
ности) навигационных определений.
Наиболее важные предпосылки, облегчающие интегрирование:
общность принципов баллистического построения обеих систем (высота
орбиты 20 000 км, наклонение орбит — 60°, период обращения НС — 12 ч,
общее число НС — 24 и др.);
близкий частотный диапазон (1 600 МГц — II и 1 200 МГц — 12), а
также сигнально-кодовые конструкции, использующие фазовую манипуляцию
'и псевдослучайные последовательности;
схожесть принципов синхронизации и измерения навигационных пара-
метров;
малое различие в используемых системах координат;
практическая одновременность создания и совершенствования СРНС
ГЛОНАСС и GPS;
готовность Правительств США и России предоставить системы для ис-
пользования различными потребителями мирового сообщества.
Точностные аспекты использования НС только СРНС ГЛОНАСС, приве-
дены на рис. 10.2, где отображены зависимости вероятности Р наблюдения за-
данного числа НС СРНС ГЛОНАСС как функций пространственного коэф-
фициента геометрии Л5ГП В табл. 7.1 приведены по материалам [7.9] анало-
гичные характеристики, но с указанием соответствующих значений коэффици-
ентов геометрии: Kr (GDOP), пространственного Krn (PDOP), горизонталь-
ного !Tr.r(HDOP), вертикального ^frB(VDOP) и временного ^fr,(TDOP).
Сравнительные характеристики систем НС ГЛОНАСС , GPS и/или со-
вмещенного созвездия ГЛОНАСС/GPS показаны на рис. 11.1, а для полных
созвездий [10.2] и на рис. 11.1, б для созвездий с тремя отказавшими спутни-
ками (угол маски 73°)18.2[. Эти данные дополняют сведения о характеристи-
а)
б)
Рис. 11.1. Статистические характеристики орбитальных созвездий
180
Глава 11. Особые режимы работы СРНС
ках доступности СРНС ГЛОНАСС, приведенные в табл. 7.1. Как видно вд
графиков, объединение существующих средневысотных СРНС ГЛОНАСС ц
GPS обеспечивает существенное повышение возможностей высококачествен^
ных навигационных определений .
Интересно проследить тенденцию улучшения коэффициентов геометрии!
при дальнейшем увеличении числа наблюдаемых спутников. В табл. 11.3 при-'
ведены усредненные значения геометрических факторов для района Москвы.
Таблица 11.3. Зависимость геометрических факторов
от числа НС
Число НС
8 НС ГЛОНАСС_______
10 НС ГЛОНАСС______
Все НС (ГЛОНАСС+GPS)
TDOP
0,80
0,72
VDOP
1,34
1,24
0,84
______Коэффициенты
HDOP
1,03
0,84
0,58
Из таблицы следует, что использование всех НС ГЛОНАСС и OPS по-
зволяет в 2 раза улучшить коэффициенты геометрии по сравнению с исполь-
зованием восьми НС системы ГЛОНАСС.
В табл. 1L4 приведены также усредненные по времени СКО плановых
координат и высоты в- номинальном и дифференциальном режимах с селек-
тивным доступом. Из табл. 11.4 следует, что использование НС GPS в номи-
нальном режиме с селективным доступом в дополнение к НС ГЛОНАСС
приводит к повышению точности лишь на 5 ... 10 % по координатам и на 8 %
Таблица 11.4. Точности определения координат и высоты
с помощью СРНС ГЛОНАСС и GPS
1 Режим, число НС Координаты СКО, м ) Высота СКО, м
Все НС ГЛОНАСС, и* 9,0 13,5
16 НС ГЛОНАСС+GPS (S/А), н 8,5 12,6
Все НС ГЛОНАСС+GPS (S/А), и 8,4 12,5
Все НС ГЛОНАСС, д* 1,8 2,6
16 НС ГЛОНАСС+GPS,д 1,36 1.9
Все НС ГЛОНАСС+GPS (S/А), д 1.24 1,82
“н" и “д" — номинальный и дифференциальный режимы СРНС
по высоте. Предполагалось, что точности измерения псевдодальностсй ГЛО-
НАСС и GPS в номинальном режиме равны 10 и 30 м соответственно.
В дифференциальном режиме точности определения псевдодальностей пред-
полагались равными 2 м для обеих СРНС. В дифференциальном режиме при-
влечение измерений GPS приводит к повышению точности по координатам и
высоте в 1,3 ... 1,5 раза.
^Д1.2. Яитегрироеаике СРЯС ГДРЯЛСС w GPS 181
Необходимо заметить, что для потребителей, первоначально ориентиро-
ванных на OPS, использование сигналов СРНС ГЛОНАСС дает практически
троекратное повышение точности.
Вопросы повышения надежности навигационного обеспечения при со-
вместном использовании НС ГЛОНАСС и GPS исследованы меньше. Наибо-
лее полно представлены результаты обширного моделирования процесса на-
вигационных определений [11.43]..
В табл. 11.5 приведены, полученные в [11.43] оценки при использовании
только НС GPS и ГЛОНАСС+GPS.
у Таблица 11.5. Доступность и максимальная продолжительность
нерабочего состояния в различных режимах полета
Режим полета Доступность СРНС, % Максимальная продолжитель- ность нерабочего состояния, мин
GPS GPS+ ГЛОНАСС GPS+ ГЛОНАСС GPS GPS+ ГЛОНАСС GPS+ ГЛОНАСС
Полет по маршруту 98,58 100 100 35 0 0
Аэродромная зона 96,53 99,99 100 70 15 30
Некатегориро- ваниый заход на посадку 67,26 98,99 100 0 0 0 I
При моделировании в [11.43] использовался базовый алгоритм, рабо-
тающий с измерениями не менее чем от 6 НС и исключающий из решения не-
кондиционный сигнал. Анализ доступности проводился по группировке GPS
из 24 НС и группировке ГЛОНАСС также из 24 НС, а также по действующей
на декабрь 1994 г. группировке ГЛОНАСС (15 НС). Факт доступности устанав-
ливался в том случае, если при нарушениях подавался сигнал тревоги с веро-
ятностью не менее заданной в течение пролета указанного предельного участ-
ка при заданном максимально допустимом уровне вероятности ложной тре-
воги. При моделировании использовались исходные данные, сведенные в
табл. 11.6
Таблица 11.6. Условия определения доступности
Режим полета Предельный участок, км Максимально допус- тимая частота ложной тревоги, 1 /ч Минимальная ве- | роятность обнару- 1 жения отказа 1
Полет по маршруту 3,7 0,00003 0,999 |
Аэродромная зона 1,85 0,00003 0,999 I
Некатегорированный заход на посадку 0,555 0,00003 0,999 9
182 Глава 11. Особые режимы работы СРЩ^д
Как следует из табл. 11.5 совместное использование СРНС GPS и ГЛО-Я
НАСС приводит к существенному повышению доступности особенно для не-1
категорированного захода на посадку (с 67 до 100 %). При этом также исклк$Я
чаются нерабочие состояния, максимальные длительности которых при ис-1
пользовании только GPS составляют 35 ... 295 мин. Необходимо заметить, что!
здесь используется несколько необычное понимание доступности системы,.
Последняя, по существу, проявляется в виде функции целостности (см. “Тре-
бования к СРНС”).
Совместное использование СРНС ГЛОНАСС и GPS поддерживается ин-
тенсивной разработкой аппаратуры потребителей, принимающей и обрабаты-'
вающей сигналы обеих систем. В качестве примеров можно указать создание?
приемоиндикаторов “ИНТЕР-А”(МКБ “Компас”), АСН-21 (РИРВ), АСН-221
(совместная разработка DASA и РИРВ), GNSS-200 (3S Navigation) и др. [11.34,'
11.44—11.46].
Осуществлена также разработка ряда образцов контрольно-корректи-
рующих станций дифференциальных подсистем СРНС [11.25] и версии стан-
дарта RTCM для передачи корректирующих сообщений применительно к
СРНС GPS и ГЛОНАСС [11.27].
С совместным использованием GPS и ГЛОНАСС связано и создание ев-
ропейской широкозонной дифференциальной системы E6NOS (см. § 11.1)
[11.9, 11.10]. Это же направление реализуется в концепции создания россий-~
ских ДП [11.8].
Совместное применение обеих систем оказывается возможным благодаря
близости используемых систем координат: ПЗ-90 в ГЛОНАСС и WGS-84 в
GPS, а также благодаря имеющимся соотношениям перехода от одной системы
координат к другой [3.3, 11.47]. В частности, геоцентрические координаты
х, у, z двух любых систем А яВ связаны между собой векторно-матричным
уравнением: ,
(11.13)
где т, го, (i = x,y,z), Дх,Ду,Аг — известные элементы (параметры) преобразо-
вания координат [11.47].
Одно из используемых преобразований из ПЗ-90 в WGS-84 приведено в
§ 8.3. В то же время эти параметры нуждаются в уточнениях, что является од-
ной из задач дальнейших совместных исследований специалистов России и
США.
В заключение отметим, что интегрирование и совместное использование
СРНС ГЛОНАСС и GPS обеспечивают также резервирование навигационного
обеспечения на случай непредвиденных форс-мажорных обстоятельств, свя-
,2. Интегрирование СРНС ГЛОНАСС, и GPS
183
данных, например, с террористической деятельностью, земными катаклизмами
Ьк ДР-
Литература
11.1. Шебшаевич В. С., Балов А. В., Химулин В: И. Развитие дифференциального
, метода навигационных определений в спутниковой РНС ГЛОНАСС // Радионавигация
и время, РИРВ, 1992.
11.2. Teasley S., Hoover W., Johnson C. Differential GPS Navigation// IEEE PLAN’S-
/«0,1980, pp. 9—16.
j 11.3. Beser J, Parkinson B. The Application of Navstar Differential GPS in the Civilian
, Community// Navigation (USA), 1982, vol. 29, no. 2, pp. 107—136.
; / 11.4. Конрад Д. Анализ ошибок систем навигационных спутников// Управление в
" космосе. Тр. III Межд. симпозиума ИФАК по автоматическому управлению в мирном
использовании космического пространства, т. 1, М.: Наука, 1972.
11.5. Vroeijenstijn В., Offermans G. et al. Wide Area DGNSS Service Using Existing LF-
transmitters// Proc, of DSNS-96, St. Petersburg, 1996, Paper № 9.
11.6. Chistyakov V., Filatchenkov S., Khimulin V. Parameters of Differential GLON-
ASS/GPS Service on the Base of Russian Marine Radiobeacons// Proc, of DSNS -95, April,
* 1995.
11.7. Philips R. Relative and Differential GPS// System Implications and Innovative
Applications of Satellite Navigation, AGARD Lecture Series 207, 1996, pp. 5.1—5.22.
11.8. Ilkaev G., Filatchenkov S. et al. The Main Principles of Russia’s DGNSS Devel-
opment// Proc, of DSNS-96, St. Petersburg, 1996, Paper № 56.
11.9. Глобальная навигационная спутниковая система, GNSS// НТЦ ’’Интерна-
вигация”, 1997.
“ ' 11.10. GouniP., Job- A. Design- and operation of thc Euridis Ranging System// Proc.
DSNS-96, St. Petersburg, 1996, Paper № 5.
11.11. Ashkenazi У-, Chen W. et al. High Precision Wide Area DGPS// Proc, of DSNS-
96, St. Petersburg, 1996, Paper № 8.
11.12. Orpen Ole. Recent Developments in the Gugro Starfix DGPS Service// Proc. Of
DSNS-96, St. Petersburg, 1996, Paper № 33.
11.13. Stafix Global Coverage — 2000 km Range// Рекламный проспект фирмы Fu-
\ gro, 1996.
11.14. El-Sadawy II. The Middle East Regional DGPS Networks, or Wide Area Aug-
mentation System// Proc, of DSNS-96, St. Petersburg, 1996, Paper № 59.
11.15. Walsh D., Capaccio S. et al. Real Time Differential Positioning Using GPS and
GLONASS// Proc, of DSNS- 96, St. Petersburg, 1996, Paper № 11.
11.16. Кутиков В. Ю., Сошин М. П. и др. Перспективная аппаратура дифференци-
альной геодезической подсистемы спутниковых РНС “ГЛОНАСС” и GPS// Радионавига-
ция и время, РИРВ, 1992.
11.17. Thorstainsson S., Gunnarsson Т., Gudmundsson G. Icelands's Network of Differ-
ential GPS Radiobeacons// Proc, of DSNS-96, St. Petersburg, 1996, Paper № 61.
11.18. Lauro-Cetena G. DGPS for Marine Applications: Ship Performance Monitoring
System found the Italian Coast// Proc. DSNS-96, St. Petersburg, 1996, Paper № 22.
11.19. Аншаков А. В. Состояние и перспективы оборудования морей в Российской
Федерации аппаратурой дифференциальных систем ГЛОНАСС/GPS на базе круговых
морских радиомаяков// Тр. Межд. конф. “Глобальная радионавигация", М., 1995, с.
6.1—6.8.
11.20. Filatchevkov S., Khimulin К., Chistakov V., Bazarov Y. Broadcast Standard for
Russian Maritime DGPS/DGLONASS Service// Proc, of DSNS-96, St. Petersburg, 1996, Pa-
per № 21.
11.2d Blomenhofer H., Mattissek A. The New DASA-NFS Ground Station Family for
Use in Civil Aviation// Proc, of DSNS-96, St. Petersburg, 1996, Paper № 17.
11.22. Differential GNSS for Safe and Accurate Landings// Рекламный проспект фир-
мы DASA, 1996.
11.23. Wild U. The automated GPS Network in Switzerland (AGNES) for Navigation
and Geodesy: Concept and First Test Results// Proc, of DSNS-96, St. Petersburg, 1996, Paper
№ 60.
184______________________________________Глава 11. Особые режимы работы СРНС
аввВЕВЯнаЯМВЯВВНЯНааИНаВВВВ|аВЯ|^НЯНаНаВВННВ|а|аВВНННа|ВНааЯ^НВМВаИМВдВаВВВЖВВаВН^НЯЯа)аЕВаЕКВа^!!аВВ>вада!аВаЯааааааям^|
11.24. Dolier Н. An Open Cellular Concept for a RTDGPS Reference Network in Aus-
tria// Proc, of DSNS-96, St. Petersburg, 1996, Paper № 62.
11.25. Салищев В. А., Дворкин В. В., Виноградов А. А., Букреев А. М. Станция мони-
торинга радионавигационных полей систем ГЛОНАСС-GPS и определения дифференци-
альных лолравок//Радиотехника, 1996, №1, с.89— 93.
11.26. Янг Д. Основные направления проектирования и внедрения системы радио-
маяков DGPS/MSK с широкой областью применения// Межд. конф. “Планирование гло-
бальной радионавигации”, М., 1995, с. 6.37—6.53.
11.27. Kalafus R., Beser J. New RTCM SC-104 Differential GNSS Standards// Proc, of
DSNS-96, St. Petersburg, 1996, Paper № 19.
11.28. RTCM Recommended Standards for Differential GNSS Service. Third Draft,
Future version 2.2, December. 1995.
11.29. Starfix DGPS Virtual Base Station// Рекламный проспект фирмы Fugro, 1996.
11.30. Minimum Aviation System Performance Standards DGNSS Instument Approach
System: Special Category I (SCAT-I). Change № 1 to RTCA/DO- 217 // RTCA Inc., July
1994.
11.31. Offermans G., Zaaijer M., Meijer M. Evaluation of DGNSS Datalinks for Cat-IH
Landings// Proc, of DSNS-96, St. Petersburg, 1996, Paper № 13.
11.32. IVilligen D. van, Offermans G. et al. Eurofix: GNSS Augmented Loran-C&Loran-
C Augmented GNSS// Proc, of the 1995 Nat. Tech. Meeting of the Inst, of Navigation.,
Anakeim. CA, 1995.
11.33. Andersen. J. A Prototype Loran Augmented GPS// Proc. Of the 1995 Nat. Tech.
Meeting of the Inst. Of Navigation., Anaheim, CA, January 18—20 1995.
11.34. Навигационный датчик спутниковых радионавигационных систем ГЛО-
НАСС и GPS для гражданской авиации “Иитер-А”// Рекламный проспект НТЦ
“Интериавигация”.
11.35. Приемник GNSS-12, Рекламный проспект фирмы 3S Navigation, 1995.
11.36. Приемник-Sensor II, Рекламный проспект фирмы Ashtech, 1996.
11.37. Нриемник-DN-12, Рекламный-проспект фирмы Ashtech, 1996.
11.38. MX41R DGPS Beacon Receiver, Рекламный проспект фирмы Leica, 1996.
11.39. Nav Beacon XL, Рекламный проспект фирмы Trimble, 1996.
11.40. Parkinson В. Я'., Fitzgibbon К.Т. Optimal Locations of Pseudolites for Differential
GPS// Navigation (USA), Winter 1986-1987, vol. 33, no. 4, pp. 259-283.
11.41. Greenspan R.L. Global Navigation Satellite System// AGARD Lecture Series 207,
System Implications and Innovative Applications of Satellite Navigation, NATO, 1996, pp.
1.1-1.9.
11.42. Гусев Ю., Лебедев M. Перспективы развития спутниковой навигационной
системы ГЛОНАСС и ее интеграция с зарубежными навигационными средствами// Тр.
Межд. конф. “Глобальная радионавигация”, М., 1995.
11.43. Ван Дайк К. Использование спутниковых радионавигационных систем для
обеспечения требуемого уровня характеристик глобальной навигационной спутниковой
системе// Радиотехника, 1996, № 1, с. 77—82.
11.44. Кудрявцев И. В., Клюшников С. И, Федотов Б. Д. Перспективная авиацион-
ная спутниковая аппаратура потребителей, работающая по сигналам систем ГЛОНАСС-
GPS// Радионавигация и время, РИРВ, 1992. № 1, с. 60—63.
11.45. Кинкулькин И. Е. Интегрированная аппратура потребителей космических ра-
дионавигационных систем//Радиотехника, 1996, № 1, с. 86—89.
11.46. Beser J. Integrated GPS/ GLONASS User Equipment// AGARD Lecture Series
207, System Implications and Innovative Applications of Satellite Navigation, NATO, 1996,
pp. 3.1—3.28.
11.47. Бойков В. В., Галазин В. Ф. и др. Опыт создания геоцентрической системы
координат ПЗ-90// Геодезия и картография, 1993, № 11.
185
Глава 12
Аппаратура потребителей
12.1. Принципы построения и функционирования
аппаратуры потребителей
Аппаратура потребителей (приемоиндикаторы CPHCJ предназначена для
текущего време-
и обработки ра-
определения пространственных координат, вектора скорости,
ни и других навигационных параметров в результате приема
диосигналов, принятых от НС.
На вход ПИ поступают сигналы от НС, находящихся в
зоне радиовиди-
мости. Так как для решения навигационной задачи необходимо измерить
псевдодальности и псевдоскорости относительно, как минимум, четырех НС
(см. гл.4), то ПИ должен быть многоканальным (от 4 до 12 каналов в обычных
и более 12 в совмещенных ГЛОНАСС и GPS ).
Современные ПИ являются аналого-цифровыми системами, сочетающи-
ми аналоговую и цифровую обработку сигналов. Переход на цифровую обра-
ботку осуществляется на одной из промежуточных частот, при этом имеет ме-
стотенденция к повышению этой промежуточной частоты.
Так как приемоиндикаторы СРНС имеют множество возможных приме-
нений (наземное, авиационное, морское, космическое и др.), то при их разра-
ботке необходимо основываться на создании унифицированных узлов с мини-
мальной номенклатурой, из которых в дальнейшем можно конструировать ПИ
различного применения.
Основа типового вариаггга ПИ — два конструктивно раздельных блока:
антенный (АБ) и приемовычислитель (ПВ).
В антенном блоке (рис. 12.1) сово-
купность сигналов НС, принятых антен-
ной, предварительно усиливается и
фильтруется во всей полосе (от 1570 до
1625 МГц в совмещенных ПИ) несущих
частот НС в предварительном усилителе
(ПУ) с полосовым фильтром (ПФ).
Конструктивно приемовычисли-
тель выполнен в виде блока, в котором
расположены модули вторичных источников питания и платы — приемокорре-
лятора^навигационного вычислителя и интерфейсного устройства (рис. 12.2).
Вход ПВ через фидерную линию соединен с выходом антенного блока. В ана-
логовом приемнике АПр сигналы усиливаются, фильтруются и переносятся с
несущей частоты на промежуточную (понижение частоты). В аналого-циф-
ровом преобразователе АЦП аналоговый сигнал преобразуется в цифровую
форму.
Рис. 12.1. Структурная схема
антенного блока
Глава
12. Аппаратура потребителей^
Рис. 12.2. Схема приемовычислителя
В корреляторе (КОР) в цифровой форме формируются отсчеты синфаз-
ных 1(к) и квадратурных Q(k) отсчетов, аналогичных (6.6), которые являются
основой работы алгоритмов поиска сигналов по задержке и частоте, слежения
за ПД, фазой сигнала и выделения навигационного сообщения. ~ -
Навигационный вычислитель НВ является цифровым процессором, в ко-
тором реализуется вычислительный процесс и управление работой ПИ. Нави-
гационный вычислитель удобно представить в виде сигнального процессора
СП, реализующего алгоритмы первичной обработки квадратурных составляю-
щих (см. § 6.2), и навигационного процессора НП, реализующего алгоритма
низкочастотной обработки (первичной и вторичной).
Интерфейсное устройство ИУ предназначено для обеспечения взаимс-
действия приемоиндикатора с внешними устройствами, какими, например, ка*
пульт управления и индикации (ПУИ). В авиационных приемоиндикаторах И'
подключается непосредственно к магистрали НВ, что позволяет обеспечит,
работу в соответствии с существующими ГОСТ, а также дает возможность рее
лизации протокола взаимодействия с внешними устройствами. Дополнителен
в состав ИУ входят два усилителя У, формирующих признак отказа ПИ и сит
налы дискретного управления, а также 8-разрядный регистр Рг, принимающий
сигналы дискретного управления. Этот регистр доступен для чтения со сторо
ны НВ. Последний, в зависимости от находящейся в регистре информации
выбирает тот или иной режим работы.
12.2. Антенный блок
В качестве антенны можно использовать [12.1] микрополосковук
(МПА), что обусловлено ее малой массой и габаритными размерами, пр,-
стотой изготовления и дешевизной. Микрополосковая антенна состоит из дву.
параллельных проводящих слоев, разделенных диэлектриком: нижний пров,-
Антенный блок 187
г-----------------------------------------------------
дящий слой является заземленной плоскостью, верхний — собственно излуча-
телем антенны. По форме излучатель может быть прямоугольником, эллипсом,
Пятиугольником и т.д.. Антенна рассчитывается для работы на низшей резо-
нансной моде, которая излучается в основном в верхнюю полусферу (в на-
правлении вертикальной оси). Микрополосковая антенна имеет ДН, обеспе-
чивающую всенаправленный прием сигналов правосторонней круговой поля-
ризации в верхней полусфере.
Типичные характеристики антенны (для рабочего диапа-
зона частот 1570 ... 1625 МГц):
Обеспечение работы в тракте с волновым
сопротивлением, Ом .................................... 50
Коэффициент стоячей волны КСВ .......................... не более 2
Коэффициент эллиптичности антенны в зените, дБ ......... не менее -3,5
Минимальное значение коэффициента усиления G
относительно изотропного излучателя с круговой
поляризацией в меридиональных сечениях (как
функция угла возвышения р ), дБ:
5° >р>0°................. —5 > G >-7,5
10° > р > 5°..................... G > -4,5
15° > р > 10° ................... G > -4,5
р>15° _............................ " G>-2
Предварительный усилитель ПУ должен работать в тракте с волновым
сопротивлением 50 Ом, иметь по входу и выходу КСВ < 2, обеспечивать в ра-
бочем диапазоне частот коэффициент усиления Ку » 30 дБ и коэффициент
шума Кш < 4 дБ.
Полосовой фильтр ПФ осуществляет фильтрацию сигналов в полосе час-
тот А/ = 60 МГц. Один из вариантов построения ПУ/ПФ приведен на
рис. 12.3.
Рис. 12.3. Схема предварительного усилителя/полосового фильтра
Такая схема со включением двух ПФ, имеющих потери до 2 дБ каждый,
после первого и второго усилительных каскадов позволяет реализовать мини-
мально возможный Кш и обеспечивает необходимую избирательность и ли-
нейность АУ в рабочей полосе частот при воздействии внеполосных помех.
При потерях в кабеле до 13 дБ, коэффициенте шума Кш S4 дБи коэф-
фициенте усиления Ку и 30 дБ, добавка шумов на входе ПУ/ПФ не превы-
шает 5 %. Потери на устройстве защиты входа Уз и двух фильтрах Ф1 и Ф2 не
» i i I : .
188 Глава 12. Аппаратура потреойтелей л
превосходит 5 дБ. Активные элементы У1, У2, УЗ должны обеспечивать сум-’
марный коэффициент усиления не менее 35 дБ.
Устройство защиты входа Уз может быть выполнено на полосковых pin- -•
диодах, выдерживающих входную мощность 1 Вт. При этом уровень проходя- *
щей мощности не будет превосходить единиц милливат, что не выведет из
строя вход ПУ. Потери на устройстве защиты не превышают 0,6 дБ.
В качестве фильтров Ф1 и Ф2 могут быть использованы полосовые
фильтры на встречных стержнях, имеющие потери -2 дБ. Установка двух ПФ
в схеме на рис. 12.3 обеспечивает необходимую полосу пропускания 60 Мгц
по уровню -3 дБ.
Соединение антенны со входом ПУ/ПФ осуществляется непосредственно
через проходной контактный штырек антенны. На выходе ПУ/ПФ имеется ра-
диочастотный соединитель, к которому подключается коаксиальный кабель,
соединяющий АБ с ПВ.
12.3. Приемник
Приемник является многоканальным устройством, в котором, как отме-
чалось выше, проводится аналоговое усиление сигналов, фильтрация и преоб-
разование частоты несущей сингалов НС (понижение частоты), а также преоб-
разование аналогового сигнала в цифровую форму. Так как в ГЛОНАСС сиг-
нал от каждого спутников имеет свою несущую частоту, то каждый канал дол-
жен быть настроен на частоту сигнала одного из НС и селектировать частоты
сигналов других НС. Схема такого приемника приведена на рис. 12.4.
В схеме использовано трехкратное понижение частоты сигналов НС (в
некоторых ПИ используется двухкратное понижение частоты). Первое пони-
Рис. 1Z.4. Схема приемника
1в9
жение частоты до уровня /пр1 =200 Мгц проводится в общем для всех приня-
тых сигналов смесителе CMq. После общего усиления и фильтрации сигналов
в усилителе промежуточной частоты УПЧц с полосой пропускания для совме-
щенного ПИ Д/уп0 и 60 МГц, сигнал поступает в N каналов, в каждом из ко-
торых проводится второе преобразование частоты (до значения /пр2 =40 МГц),
ориентированное на прием сигнала от конкретного НС. Полосу пропускания
канального УПЧ1 Л/уП. = 500кГц выбирают таким образом, чтобы выделялся
сигнал одного из НС и селектировались сигналы других НС. Третье пониже-
ние частоты проводят до уровня /пр3 = 4 МГц.
Опорные сигналы, поступающие на смесители, формируются синтезато-
ром частот из опорной частоты /оп опорного генератора ОГ. Управление ра-
ботой синтезатора частот осуществляется по сигналам, поступающим от на-
вигационного вычислителя. Опорный генератор — это устройство, во многом
определяющее качество работы присмоиндикатора в целом. От ОГ в значи-
тельной степени зависят такие параметры, как время получения первого от-
счета, точность определения координат потребителя, надежность ПИ, уровень
потребления энергии, масса и габариты аппаратуры.
Типичным представителем ОГ, использование которых соответствует
требованиям, предъявляемым к ПИ, является кварцевый генератор опорного
напряжения “Астра”, с характеристиками:
Габаритные размеры, мм ................................... 34x4x24
Питающее напряжение (при мощности <0,35 Вт), В ........... 12
Суммарная мощность, потребляемая во время включения, Вт... не более 0,35
Выходная мощность (при частоте 10 МГц), мВт .............. 350
Фазовые шумы (прн 10 Гц), дБГц ........................... 120
Относительная стабильность частоты ....................... 1 • 10-7
На выходе приемника аналоговые сигналы частоты /11рз = 4 МГц в ана-
лого-цифровых преобразователях (АЦП) преобразуются в цифровую форму.
12.4. Коррелятор
Коррелятор КОР в цифровой форме формирует отсчеты синфазных Ц-. ।
и квадратурных Сги составляющих в соответствии с дискретным аналогом
алгоритмов (6.6)
*
хи
Льи = - ^k,i}^lnfnifk.i +Vk.l} - (12.1)
/ = 1
Л'н
Qk>\ = Е/(Ц./)Л(Ц./ - +?с/)- (12.2)
190 Гл а в а 12. Аппаратура потребителей Я
где y(tk,i) — цифровые отсчеты сигнала с выхода АЦП в дискретные моменту!
времени tkJ = (KHTd)k + Tdi (Td=l/fd — шаг дискретизации по времени);!
-Tfc./) — модулирующая функция дальномерного кода; к — индекс, со- 1
ответствуюший моменту времени tk = (K„Td)k; К„ =Т„ /Td — число накапли- ।
ваемых отсчетов; xkt, <fk l — экстраполированные на момент времени tkt i
оценки задержки и фазы сигнала, которые определяются выражениями <
4,1 = 4 + 4^;
(12.3)
ФА/ — ФА , (12.4)
где хк, хк, <fk, <вдоп t — оценки задержки, скорости изменения задержки, фазы
и скорости изменения фазы соответственно в тактовые моменты времени fk.
Здесь и далее для простоты изложения рассматривается один канал обработки.
Как отмечалось в гл. 6, составляющие I и Q необходимо формировать
как в режиме поиска сигналов по частоте и задержке, так и в режиме слеже-
ния за этими параметрами. В режиме поиска сигналов данные составляющие
формируются в соответствии с (12.1), (12.2) при фиксированных значения
оценок т, <одоп на интервале анализа Та = KHTd, то в режиме слежения дан-
ные оценки меняются во времени. В режиме слежения необходимо сформиро-
вать дискриминаторы по фазе и задержке сигнала. Если для формирования
фазового дискриминатора (см. уравнения (6.16)) можно использовать квадра-
турные компоненты I и Q, описываемые (12.1), (12.2); то для дискриминато-
ра задержки сигнала, в соответствии с (6.15), (6.20), кроме этих составляющих
необходимо дополнительно сформировать смещенные на ±Дт / 2 составляю-
щие. Обычно полагают Дт = тэ, где тэ длительность элементарной посылки
дальномерного кода (для ГЛОНАСС тэ = 1/511 мс. Синфазную и квадратурную
составляющие, формируемые с опережением относительно опорного момента
времени, будем обозначать Ig, Qe (Е — early), а с запаздыванием — Ik, Q/
(L — late), и для них можно записать выражения, аналогичные (12.1), (12.2)
/je.A+1 = 1>('а/) Фи " + ! 2)cos(2’l/n3zA,/ + ФА/) : (12-5)
1=1
Кн
Оя.А+1 = ЕИ'а./) л(?А/ - 4,1 + 4/ 2)sin(2^n3Zjti, +ФА./); (12.6)
^12.5, Навигационный вычислитель 191
Ib.k+l = Zy^k.l^'k.l ~*к,1 ~тэ / 2)cos|2n/n3/jt/ +<pt,/); (12.7)
Ol.hi = - *k,i - тэ / 2)sin(24fn3/tt/ +Ф*,/). (12.8)
Схема коррелятора, реализующего алгоритмы (12.1)—(12.8), приведена
на рис. 12.5, где ЦГС — цифровой генератор сигнала; /ст = 1/тэ; Р— индекс
(Zp, Qp), используемый для идентификации опорного канала, в котором син-
фазная и квадратурная составляющие вычисляются в соответствии с (12.1),
(12.2); Д$ / Т„ — приращение фазы за один такт; Дг / Т„ — приращение за-
держки за один такт.
Принцип работы цифрового генератора сигнала ЦГС описан, например в
[12.2|. Генератор кода ГК вырабатывает дальномерный код (модулирующую
функцию ф/*. / - т*,/)) с длительность элементарного символа тэ =1/ /ст, на-
чало формирования которого сдвинуто на tj.(; 3-битовый регистр Рг сдвига
обеспечивает формирование опережающей f^tk i - , + тэ / 2) и запаздываю-
щей h(tkfl - - тэ / 21 опорных функций.
Накапливающий £ ____ [£
со сбросом_____
Накапливающий £
со сбросом
ЕН
Рис. 12.5. Схема коррелятора
Накапливающий £
со сбросом_____
Накапливающий £ 1 Qg
____со сбросом____j
Накапливающий £ ____ Qp
___со сбросом ]
Накапливающий £
со сбросом
12.5. Навигационный вычислитель
Навигационный вычислитель решает следующие задачи: цифровая обра-
ботка синфазной и квадратурной составляющих I, Q для решения задач по-
иска сигналов по задержке и частоте, а также слежения за фазой и задержкой
192 Г л а в a 12. Аппаратура потребителей^
сигнала (алгоритмы первичной обработки); преобразование радионавигацион-
ных параметров в навигационные (алгоритмы вторичной обработки); дсмоду.
линия навигационного сообщения; форматирование и дешифрация эфемерид- ;
ной информации; расчет прогнозируемых значений ошибок; накопление и
хранение альманаха.
Навигационному вычислителю переданы также диспетчерские функции
управления первичной обработкой, что необходимо из-за наличия многих
спутников в зоне видимости и возможности работы по всем или части НС. В
современных и перспективных ПИ, работающих по сигналам НС двух систем
ГЛОНАСС и GPS возникает дополнительная необходимость управления рабо-
той по двум системам.
Структурно (см. рис. 12.2) НВ включает два процессора: сигнальный и
навигационный. Типичная схема навигационного вычислителя приведена на
рис. 12.6. В качестве вычислительного ядра, например в навигационном про-
цессоре может использоваться микропроцессор (МП) KU8O386EX и арифмети-
ческий сопроцессор N80387SX, работающие на частоте 25 МГц (минимальные
требования). Возможно использование и более мощных процессоров 486, 586
и других серий. Сигнальный процессор значительно производительнее, чем
навигационный. Оперативное запоминающее устройство ОЗУ, объемом бо-
лее 128 К, может быть выполнено, например, на двух микросхемах
SRM2O1OO-7O. Постоянное запоминающее устройство ПЗУ, объемом 256 К,
может быть выполнено на микросхемах PA28F400BX (типа “флэш”).
Применение данного типа г-------— -------> >-------------।
памяти позволяет ВО время рабо- [ Два мп -- т—Сопроцессор j
ты ПИ организовывать режим за- ________
писи информации в ПЗУ, где Г ' ’
J U. J »• К интерфейсному
обеспечивается се хранение. i ~ 1 Г I ус-пюйстау
ПЗУ ОЗУ
Алгоритмы обработки сигналов и | ! | _ ]
информации в НВ будут рассмот-
рены в следующих двух разделах. Рис. 12.6. Структурная схема НВ
12.6. Алгоритмы первичной обработки информации в АП
Отсчеты синфазных и квадратурных составляющих IQp, Ip,Qp, Il,Qi. >
сформированные в корреляторе, через интерфейс поступают в навигационный
вычислитель для дальнейшей обработки. Приемоиндикатор работает в двух
основных режимах: поиска и обнаружения сигналов по частоте и задержке и
непрерывного слежения.
12.6.1. Алгоритм поиска и обнаружения
Общая идеология поиска и обнаружения сигналов описана в и. 6.2.1. Так
как в ПИ имеется несколько частотных каналов, то поиск сигналов для нес-
Алгоритмы первичной обработки информации в .ill ' 1 i>3
кольких спутников можно проводить параллельно. Процедура поиска сигнала
для каждого спутника заключается в последовательном просмотре возможных
значений задержек и доплеровских смещений частоты сигнала. Для СРНС
ГЛОНАСС диапазон доплеровских частот Д/пон =-5 ... +5 кГц, а значение
8/Чоп элементарной ячейки поиска определяется полосой захвата /\f3 системы
частотной автоподстройки и составляет примерно 8/доп = Д/, = 500 Гц. Число
анализируемых ячеек по частоте Nу = ДГдоп/8/доп = 20. Значение элементарной
ячейки поиска по задержке равно длительности тэ =1/511 мс элементарной
посылки, а число анализируемых ячеек равно числу элементов кодовой по-
следовательности дальномерного кода, т. е. Л\ =511. Таким образом общее
число анализируемых ячеек Аа = N= 10 220.
В режиме поиска используются квадратурные составляющие lp,Qp
(12.1.), (12.2), а задача обнаружения сигнала в элементарной ячейке поиска
решается в соответствии с алгоритмом [p+Qp>h, где h — порог, выбирае-
мый из условия обеспечения заданной вероятности правильного обнаружения.
Длительность интервала накопления сигнала Тн при анализе в одной
элементарной ячейке (число накапливаемых отсчетов в (12.1), (12.2)
Гн = ) составляет Тн и 1 ... 2 мс.
12.6.2. Алгоритм работы и схема слежения за фазой сигнала
Реализуемый в ПИ алгоритм слежения за фазой сигнала близок к опти-
мальному алгоритму (6.16) и отличается от него тем, что он дискретный, а не
непрерывный, и в нем используются постоянные коэффициенты усиления.
Другой особенностью практической реализации схем ФАП является использо-
вание различных типов дискриминаторов.
В одном из вариантов дискриминаторов вместо функции гиперболиче-
ского тангенса используется знаковая функция
sign(x) =
при х > 0;
при х < 0.
(12.9)
Эго обусловлено тем, что в реальных условиях ПИ работает при отно-
шениях сигнал/шум <7 2 = 30 ... 38 дБ Гц, когда выполняется условие
,. \1А . . , .. . •)., i [! при 9 = 0;
Jy(v) ^(v-tJcos (<.>ov + 4>) | ( нри 9 = 1,
где тс = 1 мс — длительность периода дальномерного кода.
194 Глав а 12. Аппаратура потребителей^
Для формирования выходных отсчетов дискриминатора используюг
синфазную и квадратурную составляющие 1р(к), Qp(k) (12.1), (12.2) с индек-
сом Р, накопление которых проводится на интервале времени Т„ = =
= I ... 2 мс, так что
{Р,к>1 = Е-к('*,/) ~^.')cos (2лЛз'с/ +?*,/); (12.10)
1--Л
Хн
QpjcA = Е^-') - T*')sin (2”/пЗ^^ (12.11)
С учетом (12.9), (12.11) уравнения , описывающие работу оптимальной
дискретной следящей ФАП, принимают вид
х<р,*Я = х<рЛ+1 + КФ Sign(/P fc+1) Одли; (12.12)
*Ф,Ы=ФфХфЛ’ (12.13)
где ч>£ = СфХф£, сф = | 1 0 0...0 |т (см. п. 6.2.2), а размерность определяется при-
нятой моделью изменения фазы (6.10)—(6.13); Кф — вектор-столбец коэффи-
циентов усиления; Фф— переходная матрица фильтра в контуре следящей
системы, которая также определяется моделью изменения фазы (6.10) —(6.13),
ХфЛ+1 — экстраполированная оценка.
Схема следящего кольца ФАП приведена на рис. 12.7.
Как следует из (12.12) и рис. 12.7 дискриминатор системы ФАП описы-
вается выражением
'W = QP.k гк * си h- приемника i ! г*! t.x г i л q х 1- *| х sinl.... 1 Ц1С ] (12.14) Ат(1) Дискриминатор кольца ФАП [' ' ” v"' 1р г “ ; _ ,1 Накапливающий L Г • >1 sign(/p): ; со сбросом | [ ; з ; - - ^Q,, * г | « 1*1 Накапливающий £ J * I—J ф -- I ; СО сбросом J 1 J : [ j | wnp3 [ * 1 U-J t . ... J
Рис. 12.7. Схема следящей ФЛП
12-6. Алгоритмы первичной обработки информации в АП
195
Применяют и другие типы дискриминаторов [7.8] табл. 12.1, где ампли-
туда А = yip + Qp
Таблица 12.1. Дискриминаторы систем ФАП
Алгоритм работы Зависимость ДХ от фазо- вой ошибки Общие свойства
sin(8<p) Близок к оптимальному при большом отношении сигиал/шум. Крутизна ДХ пропорциональна ампли- туде А . Минимальные вычислительные затраты.
ipQp sin(2&p) Близок к оптимальному при малом отношении сиг- нал/шум. Крутизна ДХ пропорциональна А2 . Уме- ренные вычислительные затраты.
Qp / lP tg(8<p) Субоптимален, ио имеет хорошие характеристики при большом и малом отношении сигнал/шум. Кру- тизна ДХ не зависит от амплитуды А . Большие вычислительные затраты и необходима проверка операции деления при ошибке ±90° (деление на ноль)
A rctg(C?p / Ip) 8ф Главный угол арктангенса. Оптимален в смысле оценок максимума функции правдоподобия (5.2. 5.3] при произвольном отношении сигнал/шум. Крутизна ДХ не зависит от амплитуды А . Наи- большие вычислительные затраты.
Дискриминационные ха-
рактеристики представленных
в табл. 12.1 дискриминаторов
приведены на рис. 12.8, где по
оси ординат значения отсчетов
ДХ приведены в угловой мере.
Следящая система ФЛП
(рис. 12.7) включает дискри-
минатор, фильтр и цифровой
генератор сигнала. Алгоритмы
и структуры фильтров, исполь-
(уемых в ФЛП будут подроб-
но описаны в и. 12.6.5.
Гис. 12.8. Дискриминационные характеристики
фазовых дискриминаторов
12.6.3. Алгоритм работы и схема
за задержкой сигнала
Следящая система за задержкой
ФЛН , включает дискриминатор, фильтр
слежения
(ССЗ) сигнала, также как и система
и генератор опорного сигнала (ГОС).
196 . Г л а в a 12. Аппяратуряпотребителе^jg
Оптимальный алгоритм фильтрации задержки сигнала в непрерывной'
времени приведен в гл. 6 (6.15). В ПИ используются дискретные алгоритму
фильтрации. <
Для формирования дискриминаторов ССЗ используют, как отмечалось
выше, опережающие и запаздывающие. квадратурные составляющие 1в(к),
QE(k),Ii(k),Qi(k) (12.5)—(12.8). Алгоритмы работы дискриминаторов ССЗ и их
краткая характеристика:
7^1+cl - + @1 —
JIe + Qe + <Й
(fE +&е)~(г1 +@1) —
крутизна ДХ (кривая 1 рис. 12.9) зависит от амплиту-
ды А; хорошие характеристики при модуле ошибке
слежения меиее 0,5тэ; большие вычислительные затра-
ты;
крутизна ДХ (кривая 2 рис. 12.9) не зависит от ам-
плитуды; хорошие характеристики при модуле ошибке
слежения менее 1>5тэ; наибольшие вычислительные
затраты;
крутизна ДХ (кривая 3 рис. 12.9) зависит от А? ; хо-
рошие характеристики при модуле ошибке слежения
менее 0^тэ; умеренные вычислительные затраты;
Це -1е)г£ + (Qe - Ql)Qp —
дискриминатор использует три типа квадратурных
компонент Еу-L, f~; Хорошиехарактеристики (кривая
4 рис. 12.9) при модуле ошибке слежения менее
0,5тэ; минимальные вычислительные затраты.
Наиболее часто применяют дискриминатор, соответствующий второй
строке, ввиду его независимости от амплитуды сигнала и широкого диапазона
возможных ошибок, не приводящих к срыву слежения.] Однако этот дискри-
минатор характеризуется большими вычислительными затратами. Уменьшения
этих затрат можно достигнуть, используя некоторые аппроксимации {7.8].
Дискретный алгоритм вычисления оценок задержки сигнала записывают
в виде
Рис. 12.9. Дискриминационные характеристики
дискриминаторов задержки сигнала
ХгЛ+1 = ФЛ.* > (12.15)
где Фт — переходная матрица
фильтра в контуре следящей
системы, которая определяется
моделью изменения задержки
сигнала.
Схема ССЗ с дискримина-
тором (имеющим ДХ, изобра-
женную кривой 2 на рис. 12.9)
приведена на рис. 12.10.
Рис. 12.10. Схема ССЗ
Структура и алгоритмы работы фильтра в контуре следящей системы будут
^рассмотрены в п. 12.6.5.
12.6.4. Алгоритм работы и схема системы
частотной автонодстройки
Система частотной автоподстройки используется налроме.жуточно.м эта-
пе при переходе из режима поиска сигнала по частоте к режиму непрерывного
слежения по фазе (см. § 6.2). Следящая ЧАП включает частотный дискримина-
тор и сглаживающий фильтр. В гл. 6 было показано (6.22)—(6.26), что частот-
ный дискриминатор ЧД можно сформировать из синфазной и квадратурной
^составляющих I, Q, сформированных для двух моментов времени tk. Ал-
горитмы работы частотных дискриминаторов и их краткая характеристика:
IP(k-\)Q(k)-IP(k)QP(k-l) -
[/ДЛ - 1)<2(Л) - IP(k)QP(k - 1)] х
х sign[/p(fc - IQ(fc) + IP(k)QP(k -1))|
arcte ie(k-l)QP(k)-IP(k)QP(k-l)
IP(k-\)Qp(k) + IP(k)QP(k-\)
близок к оптимальному при малом отношении
сигнал/шум; крутизна ДХ (см. рис. 6.3) зависит
от А2 ; минимальные вычислительные затраты;
близок к оптимальному при большом отио-
— шеиии сигнал/шум; крутизна ДХ зависит от
А2 ; умеренные вычислительные затраты;
полный угол арктангенса; оптимален в смыс-
ле максимума функции правдоподобия
[5.2,5.3] при произвольном отношении сиг-
нал/шум; крутизна ДХ ие зависит от ампли-
туды Л наибольшие вычислительные затраты.
В § 6.2 было показано, что для получения ширины апертуры частотного
дискриминатора Д/дОп=500Гц необходимо выбирать время накопления при
формировании квадратурных составляющих Гн = 1 мс.
198
Г л а в a 12. Аппаратура потребителей
Схема системы ЧАП приведена на рис. 12.11. Система ЧАП в устано-
вившемся режиме обеспечивает ошибку измерения доплеровского смещения
частоты менее 50 Гц, что позволяет системе ФАП захватить сигнал и перейти,
на устойчивое слежение за фазой сигнала.
Рис. 12.11. Схема ЧАП
12.6.5. Алгоритмы работы дискретных фильтров
в контуре следящих систем
В следящих системах ФАП, ЧАП и ССЗ могут Использоваться различные
типы фильтров [±2.4]. Наибольшее применение в ПИ СРНС-нолучили фильт-
ры второго и третьего порядков. Описание дискретных фильтров удобно да-
вать в сравнительном плане относительно соответствующих аналоговых
фильтров, так как работа последних физически более прозрачна. Поэтому бу-
дем придерживаться такого подхода.
Для аналоговых фильтров порядок фильтра определяется порядком диф-
ференциального уравнения, которым он описывается. Д^я дискретных фильт-
ров - порядком соответствующего разностного уравнения.
Дискретные ‘‘интеграторы”. В непрерывных следящих системах за под-
вижными объектами фильтры в контуре следящей системы строят, как прави-
ло, с использованием интеграторов, т. е. звеньев с операторным коэффициен-
К d
том передачи K(p) = —BSL, где р s ---оператор дифференцирования. Схема
р at
аналогового интегратора приведена на рис. 12.12, а. Она реализует операцию
Ан1,
х = р у и включает усилитель с коэффициентом усиления Кт и интегра-
тор с единичным коэффициентом усиления.
При построении дискретных фильтров аналоговый интегратор заме-
няют дискретным эквивалентом.
Известны различные схемы замены аналогового интегратора дискрет-
ным, что обусловлено различными схемами численного интегрирования [12.5].
Наиболее часто используют схемы дискретных интеграторов, приведенных
на рис.12.12, б —г. Здесь z~l обозначает задержку на один такт Т№ обработки.
6- Алгоритмы первично» обработки рнфорлации^в АЛ_
199
В схеме на рис. 12.12, б реали-
зуется дискретный алгоритм числен-
но го интегрирования
а)
хк ~ хк-1 + ТдсУк-i,
(12.16)
коэффициент передачи дискретного
интегратора (в смысле Z-преобразо-
ванця)
б)
(12.17)
Схема на рис. 12.11, в описыва-
ется разностным уравнением
«)
хк = Хк-Л + ГДС>Ч,
коэффициент передачи дискретного
интегратора
г)
Рис. 12.12. Схемы аналогового (а) и
дискретных (б—г) интег-
раторов
ад-И
(12.18)
а в схеме на рис. 12.11, г реализуется алгоритм численного интегрирования
хк = xk-i + Т№(Ук + Zt-i) / 2,
коэффициент передачи дискретного интегратора
*(<) =
Где Z + 1
2 Z — 1
(12.19)
Дискретный фильтр второго порядка. Аналоговый фильтр второго по-
рядка, используемый в следящих измерителях координат подвижных объектов,
имеет коэффициент передачи
р1 р \р
(12.20)
Г л а в а 12. Аппаратура потребителе.
200
И»П
где А"ф2 — коэффициент усилен.
б)
Рис. 12.13. Схема аналогового (а) и
дискретного (б) фильтров
второго порядка
фильтра; Гф — постоянная времени,
демпфирующего звена. Схема аналоге*]
вого фильтра приведена на рис.12.13, а.
Дискретный фильтр второго по-
рядка, соответствующий (12.20) при за-
мене аналогового интегратора соответ-
ствующим дискретным. Так, например,
используя дискретный интегратор с ко-
эффициентом передачи (12.17), полу-
чаем коэффициент передачи дискретно-
го фильтра второго порядка в виде
2^дс ( 7дс + 7
(12.21)
Структурная схема дискретного фильтра второго порядка с коэффи-
циентом передачи (12.21) приведена на рис. 12.13, б. Аналогично получаются
коэффициент передачи и структурная схема дискретного фильтра второго
порядка при использовании дискретного интегратора с коэффициентом пере-
дачи (12.19).
Дискретный фильтр третьего порядка. Коэффициент передачи аналого-
вого фильтра третьего порядка
+ О’Тфг) 1
К(р) =------------j----------
Р
(12.22)
где Кфз — коэффициент усиления фильтра; Гф!,Гф2 — постоянные времени.
Схема аналогового фильтра третьего порядка приведена на рис. 12.14, а.
Коэффициент передачи дискретного фильтра третьего порядка получает-
ся при подстановке в (12.22) вместо коэффициента передачи аналогового ин-
тегратора соответствующего коэффициента передачи дискретного интегратора.
Подставляя, например (12.17), получаем
г/_\ -^ФЗ^дс ( Где [Гдс |.т2 I
z_i L-iljTf
(12.23)
Схема дискретного фильтра, имеющего коэффициент передачи (12.23)
приведена на рис. 12.14, б.
Дискретные фильтры в контуре ФАП. Описанные в предыдущих разделах
фильтры второго и третьего порядка непосредственно могут быть реализова-
^12.6. Алгоритмы первичной обработки информации в АЛ
201
ны в оптимальной ФАП, опи-
сываемой уравнением (12.12).
гТогда для фильтра второго
порядка с коэффициентом пе-
редачи (12.21) переходная мат-
рица Фф и матрица коэффи-
циентов усиления Кф в урав-
нениях (12.12) имеют вид
б)
Рис. 12.14. Схемы аналогового (а) и дискретного
(б) фильтров третьего Порядка
^Ф1 _ Афг^дс^ф
^ф2 ^ф2^дс
(12.24)
шаг дискретной обработки следует положить равным Т№ = Тн.
При этом ЦГС должен между тактовыми моментами времени tk осу-
ществлять линейную экстраполяцию фазы в соответствии с алгоритмом
Ф*,< = *ik,i = *l,k + '2rf*2,lt > (12.25)
а в тактовые моменты времени, в соответствии с уравнением (12.12), коррек-
тировать фазу на величину .
В реальных системах делают несколько иначе. Цифровой генератор сиг-
нала управляется только “некоторой частотой” — “приращением оценки фа-
зы за шаг дискретизации”, которую обозначим как Д<о* = . Частота ЦГС
в момент времени
®k.i =o>np3 +®k +‘Td^k> (12.26)
где ДйЛ = (ф*и -$*)/Тн = x2k + ЛГф2?фИдфЛ . (12.27)
Таким образом, Ф в схеме на рис. 12.7 должен формировать оценку <5 в
соответствии с уравнением (12.27) совместно с уравнением для х2 *
*2Л+1 = х2,к + ЛГф2“д к+1 = *2Л + ^ф 2гн“д Jt+1 • (12.28)
Схема такого фильтра приведена на рис. 12.15.
202
Рис. 12. IS. Схема фильтра в контуре
ФАП второго порядка
Тдс
1
О
О
т
•дс
1
Кф =
*Ф1
АфЗ
Глава 12. Аппаратура потребителей -
Если в следящем контуре системы
ФАЛ необходимо использовать фильтр,
третьего порядка с коэффициентом
передачи (12.23), то при построении
оптимальной системы переходная мат-
рица Фф и матрица коэффициентов
усиления КфВ уравнениях (12.12) имеют
вид
ЯГ»2 'Т*
Аф37ф27дс
^фЗ^фЛс
^фЗ^дс
(12.29)
ф =
1
О
О
где, так же как и выше, следует положить Гдс = Тн. В оптимальной ФАП
третьего порядка экстраполяция фазы внутри тактового интервала длительно-
стью Тн в ЦГС должна осуществляться в соответствии с (12.26), а в тактовые
моменты времени необходимо осуществлять коррекцию фазы на величину
^»1“д<р,4+ь ГД6 определяется из (12.29).
На практике, как правило, используют алгоритм управления ЦГС в фор-
ме (12.26), в котором га определяется выражением
“ _ *2,4 + ^ф3^ф2ИДФ,* ’
дополнением уравнениями
*2,4+1 = *2,4 +Аф2Ид4+1 = *2,4 + Гн*3,4 + ^фЗ^ф^нИд 4 + 15
*3,4+1 = *3,4+-^<рЗ“д4+1 =*3,4 +^фЗ?н«д4+1-
(12.30)
(12.31)
Схема фильтра приведена на рис. 12.16.
Ряс. 12.16. Схема фильтра Ф в контуре
ФАП третьего порядка
Дискретные фильтры в
контуре ССЗ. В ССЗ сигнала
используется в основном
фильтр второго порядка с ко-
эффициентом передачи (12.21).
Для ССЗ справедливы те же по-
ложения, что и для ФАП, опи-
санные выше. При построении
оптимальной схемы необходи-
мо использовать уравнения
(12.15) с переходной матрицей
|Г12.6. Алгоритмы первичной обработки информации в АП 203
к
И матрицей коэффициентов усиления вида (12.24), а управление генератором
опорного сигнала осуществлять в режиме экстраполяции (12.25) внутри такто-
‘ вого интервала с коррекцией задержки в тактовые моменты времени.
При другом построении ССЗ, например как в схеме, рис. 12.10, управле-
ние генератором опорного сигнала осуществляется “приращением задержки за
такт”. Принимая для такого сигнала управления обозначение , можно за-
писать, аналогично (12.26)
у*., = Д?/Тн = ТНХ2Л + ^«дгл/Ги . (12.32)
(
Следовательно фильтр в контуре ССЗ имеет структуру, приведенную на
рис. 12.15.
Дискретные фильтры системы ЧАП. В следящей системе ЧАП на
рис. 12.11 используется фильтр второго порядка. Управление работой ЦГС
• осуществляется частотой
ю k,t - ю прЗ + доп к >
где йдоп* — оценка, формируемая указанным фильтром второго порядка.
Следовательно коэффициент передачи фильтра в контуре ЧАП описыва-
ется выражением (12.21) а его структурная схема приведена на рис. 12.13, б.
12.6.6. Выбор параметров дискретной следящей системы
Обобщенная структурная схема следящих систем ПИ. Выбор параметров
следящих систем (СлС) необходимо выбирать в результате анализа следящей
системы в целом, для чего ее необходимо представить в виде .обобщенной схе-
мы. В отличие от классических схем следящих систем, описанных в [12.3],
для следящих систем ПИ СРНС их удобно представить в виде, показанном
на рис. 12.17.
Дискриминатор следящей системы включает обобщенный коррелятор и
накопитель сигнала. На один
вход коррелятора поступают от-
счеты входного сигнала с шагом
временной дискретизации Td , на
другой вход — экстраполирован-
ная оценка фильтруемого пара-
метра А. = стх с тем же ша-
гом Td.
Выходные отсчеты корре- Рис. 12.17. Схема обобщенной следящей системы
204 Г л а в a 12. Аппаратура потребителей Д
лятора накапливаются (суммируются) на интервале времени Ти = и в|
тактовые моменты tk сформированные отсчеты и^к поступают на фильтр,!
который формирует с тактом Ти оценки х вектора состояния. I
Как следует из п. 12.6.5, в следящих системах возможно использование 1
различных экстраполяторов, что приводит к изменению свойств СлС, поэтому j
этот блок в схеме на рис. 12.17 выделен отдельно. Кроме стандартной опера-i
ции выделения информации о рассогласовании истинного значения отслежи-
ваемого параметра и его оценки, дискриминатор выполняет усреднение i
(накопление) выходных отсчетов коррелятора на интервале времени Тн . До-".
полнительное усреднение в контуре СлС также приводит к изменению ее
свойств.
С учетом отмеченных фактов для корректного анализа свойств СлС не
могут быть непосредственно использованы классические методы анализа дис-
кретных следящих систем [12.3]. Их необходимо незначительно модифициро-
вать.
Линеаризация дискриминатора следящей системы. Из рис. 12.17 следует,
что дискриминатор дискретной СлС состоит из двух блоков: коррелятора —
нелинейного безинерционного блока (НББ), выделяющего с шагом 7^ работы
АЦП сигнал, пропорциональный рассогласованию-истинного значения от-
слеживаемого параметра и его оценки, и накопителя (на интервале
Гн = КнТа ) — инерционного звена.
Процесс на выходе НББ в дискретные моменты времени tj =
= Т^) описывается соотношением
“HEBj = -Ajj + тц, (12.33)
где ГдДХу — среднее значений процесса на выходе НББ, которое явля-
ется функцией разности истинного значения Aj фильтруемого параметра и его
экстраполированной оценки Xj; цу — случайная составляющая выходного
процесса, имеющая нулевое математическое ожидания, и часто принимаемая
[12.3] в виде дискретного белого гауссовского шума с дисперсией .
Типичный вид функции ГдДАу-Ау). которую часто называют дискри-
минационной характеристикой (ДХ) дискриминатора [12.3], приведен на рис.
12.18. Дискриминационная характеристика имеет достаточно протяженный
линейный участок, на котором происходит основной устойчивый режим рабо-
ты следящей системы. Полагая, что ошибка слежения Aj - Aj мала и не вы-
ходит за пределы линейного участка ДХ, разложим в ряд функцию
^1X6. Алгоритмы первичной обработки информации в АП
205
(1234)
*
где 5Д j — крутизна ДХ.
Положим, что представление
(12.34) справедливо для каждого
момента времени tj = tky, i = 1, Кн ,
соответствующего интервала нако-
бления сигнала. Тогда, для накоп-
ленного отсчета на выходе дискри-
минатора можно записать
Рис. 12.18. Дискриминационная
характеристика
ид.к+1 = Fa^-'k - *4) + Hjt, (12.35)
где щ — флуктуационная составляющая суммарного отсчета; £д(Х* - Х*) —
регулярная составляющая, для которой, с учетом (12.34), справедливо линеа-
ризованное выражение
F^-'k~ -**)’ (12-36)
где
5д=Хн5дУ; (12.37)
1 *н 1 Ан~
Ъ-'к = 1^-k-lJ ; Ь'к = — •
Ан 1=1 Ан /=1
(12.38)
С учетом (12.35)—(12.38) эквивалентная структурная схема следящей
системы может быть представлена в виде, показанном на рис. 12.19, где
У* + 1 = Ч + ^k/sn
(12.39)
— эквивалентное входное воздействие, приведенное к эквивалентному Х'к
фильтруемому параметру, изменение кото-
рого описывается в тактовые моменты
времени tk; K(z) — коэффициент переда-
чи фильтра в контуре СлС; /Гэк(г) — коэф-
фициент передачи эквивалентного экстрапо-
лятора (с учетом (12.38).
Дискретную СлС на рис. 12.19 можно
анализировать известными методами [12.3].
Рис. 12.19. Эквивалентная струк-
турная схема
я
206 Г л а в а 12. Аппаратура потребителе*^
Эквивалентны* экстраполятор. При использовании оптимального* изме-
ригеля экстраполяция оценки информационного процесса осуществляется в
соответствии с алгоритмом (12.25), поэтому для эквивалентной экстраполиро-;
ванной оценки (12.38) справедливо выражение
^'к = ^к-l +ЬТн^к-1’
где
М*н +1)/2/Гн.
(12.40)
(12-41)
При КИ » 1 получаем b « 0,5 .
В следящих измерителях (см. рис. 12.7, 12.10) используется другой тип
экстраполятора (12.26), (12.27). Однако можно показать [12.5], что и для него
эквивалентный экстраполятор приводится к аналогичному выражению (12.40)
с тем же коэффициентом b (12.41).
Выбор параметров следящей системы второго порядка. Основными харак-
теристиками следящих систем являются: устойчивость, порядок астатизма,
шумовая полоса пропускания, динамическая ошибка в установившемся режи-
ме, флуктуационная ошибка.
Сразу отметим, что все рассматриваемые ниже следящие системы имеют
астатизм второго порядка, поэтому они имеют в установившемся режиме
[12.3] нулевые динамические ошибки при постоянном и линейно меняющемся
процессе Х(/) и отличную от нуля постоянную ошибку при изменении Ц/) по
квадратичному закону.
Сводка основных характеристик СлС второго порядка приведена в
табл. 12.2, где СлС Н — непрерывная следящая система, т. е. система, рабо-
тающая в непрерывном времени; СлС ДО — классическая дискретная следящая
система без накопления процесса на выходе дискриминатора, работающая с
шагом Тдс = ТИ; СлС Д1 — оптимальная дискретная следящая система с накоп-
лением процесса на выходе дискриминатора и с экстраполятором типа (12.25);
СлС Д2 — дискретная следящая система с накоплением и экстраполятором
типа (12.26), (12.27).
В выражении для шумовой полосы пропускания СлС Д2 в числителе
второго сомножителя опущены слагаемые порядка т£. и Т^., слабо влияющие
на значение шумовой полосы, в выражении для динамической ошибки в уста-
новившемся режиме а — абсолютное значение второй производной в описа-
нии входного воздействия Ц/).
Термин оптимальный здесь используется условно. Действительно оптимальный изме-
ритель с накоплением (группированием) наблюдений [12.20] должен реализовывать
весовое накопление с оптимальными весами.
Kfr2»6. Алгоритмы первичной обработки информации в АЛ
207
F Таблица 12.2. Характеристики следящих систем второго порядка
Характеристика
Тип LJL Устойчивость Шумовая полоса пропускания Z/m Динами- ческая ошибка
н >0. Тф >0 1 + Krf 47ф а
ДО *Гс>0, 7ф >0 К 4 Aq < 1 1 Тда(27ф + Т№) 1 2 + 2<r0Tj - З^ГфТда 27ф 4 - 2К„ТфТх - КД* а
Д1 К>0, Тф>7’да(1-4) * Tw(27i + Тж) 1 2(Тф + 7’дс(4-1))Х 2 + 2<r07j - З^ТфГ„ + ЛГ07^(1 - b) 4-2*Г07ф7’да-*Г„7’2(2*-1) а К'
Д2 К„>0, тф >тк Ко< М4Г*(1-*)+7’«) I 2(7ф + 7дс(1+ЛГ0Гф2)(Л-|)) Х 2 + 2<Г07ф2 « + 2ЛГ^ГЖ(1 - Ь} 4 - 2*Г„Тф7’ю(2Л - 1) - KTl(2b - 1) а К'
Уравнения, описывающие приведенные в табл. 12.2 следящие системы,
имеют следующий вид:
непрерывная система СлС Н
= *2 + *i н(Я0 - *i); = ^2н(Л0 - *i);
X = xj; Х1н = Х07ф; Х2Н = Х0,
где Ко = SnK$2 — коэффициент усиления следящей системы; 5Д — крутизна
ДХ (12.37); Хф2, 7ф — параметры фильтра второго порядка (12.20);
дискретная система Сл С ДО
k*+i=*i,*+i; Ь*+1 = *1,*+ь
*!,* + ! = *1,* + Тдс*2,* + Х\(ук11 - ; *!,* + ! = Xi k + ГдсХг,* ;
*2,Ы - *2.* + - *1^+1) ; Ki = ХоТфТдс ; К2 = КОТХ ;
208 Глава 12. Аппаратур» потребителей^
дискретная система СлС ПЛ
* •*+! = *!,*+!> = *1,*+Ь *!,*+! = *1,* + *?ДС*2,* ;
+ l = *l,k + Тдс*2,* + А1(у*+1 -Х1,* + 1);
* 2Л+1 = *2, к + ^2(У*+1 _ *1Л+1) !
дискретная система СлС Д2
* -к + 1 = *!,* + !; b-k + i = *!,* + !; *!,* + ! = *l,Jt + ЬТц/г^Хк i
* M+i = *i,* + ГдсХз,*; *2,*+i = *2,к + - Х1,*+1);
* 3,* + 1 = *2,* + 1 +^l(i’*+l ~ *1,4+1) / ^дс •
Как следует из табл. 12,X при используемом темпе дискретной фильтра-
ции к 1 ... 5 мс шумовые полосы всех следящих систем достаточно близки,
и, в первом приближении, можно пользоваться более простой формулой для
аналоговой СлС. Накопление отсчетов на выходе дискриминатора на тех же
интервалах ТИ = Гдс ... 5 мс так же слабо влияет на характеристики следя-
щих систем. Следящие системы с оптимальной экстраполяцией (12.25) имеют
лучшие характеристики, чем используемые на практике, более простые с точ-
ки зрения реализации, СлС с экстраполятором типа (12.38).
Конкретные значения параметров следящих систем за фазой, частотой и
задержкой сигнала выбирают на основе приведенных соотношений в зависи-
мости от действующих на следящую систему динамических возмущений и
входного отношения сигнал/шум (значение обобщенного параметра Ко?ф час'
то полагают равным примерно 1,5). Данные характеристики могут существенно
различаться в зависимости от конкретных приложений, например, для приме-
нений ПИ в области геодезии, характерно отсутствие значительных динамиче-
ских возмущений, что позволяет выбирать узкую полосу пропускания СлС,
снижая тем самым флуктуационные ошибки. Авиационные ПИ могут работать
в условия существенных динамических возмущений, обусловленных маневри-
рованием ЛА, что приводит к необходимости расширять полосу пропускания
СлС.
Выбор параметров следящей системы третьего порядка. Сводка основных
соотношений, характеризующих следящие системы третьего порядка приведе-
Ии&6. Алгоритмы первичной обработки информации в АЛ 209
Цдя в табл. 12.3. Типы следящих систем те же, что и в предыдущем разделе,
ьдоичем все они обладают астатизмом третьего порядка. Это приводит наличию
Кгличной от нуля.динамической ошибки слежения в установившемся режиме
Ещшь при кубичном изменении отслеживаемого процесса, т. е. Х(/) = cP .
i
; Таблица 12.3. Характеристики следящих систем третьего порядка
Тип СлС Характеристика 8
Устойчивость Шумовая полоса пропуска- ния Д/ш Динами- I ческая 1 ошибка 1
Н 7*1 >0, Т’ф2>0 ^>~Г •фИф2 А - 1) ' В С I ^0 I
ДО Tv>TK/2, Тф2>Тю/2 ъ > Т L 'фНф2 2К-КОТФ1ТК(ЗК^1Т^^2') ^2-К0^гТк) с I *0 1
Д1 Гф1>Тю(М-4),Гф2>7с+в/2 С= 7^(4Ь - 3) , D = 47’ф1Твс(1 - д) Р > 1 1 2(Т^Тк(Ь-1))" 2А-А0Гф1Гдс(зА0Гф1Гфг2 + 2) С 1 I
В таблице в выражениях для устойчивости и шумовой полосы пропус-
кания дискретных СлС опушены слагаемые ТдС и более высоких порядков,
слабо влияющие на характеристики при используемых на практике временах
дискретной обработки.
Линеаризованные уравнения, описывающие работу приведенных в
табл. 12.3 следящих систем третьего порядка, имеют следующий вид:
непрерывная система СлС Н
77 = *2 + ^1н(Я0 - *i);
г 7^- = *з +
77 = *зн(Я0-*1); * = *i;
^2н = А\)7фь ^зн = *о.
210 Г л аз а 12. Аппарату№*
потребителей
где ^о=^5дЛфЗ --коэффициент усиления следящей системы; Л’д ---крутизн!
ДХ (12.37); Хфз, Тф!, Тф2 — параметры фильтра третьего порядка (1222);
дискретная система СлСНО
^к И = *ЦЫ ; + 1 = XlJt + l; =" Тлс*2,* ;
*\,к + Т;ц:*2,к + ^1(УкИ -*1Л+1); *4 = ^О^ф^ф^’дс J
* 2,* + 1 = *2,к + 7дс*3,* + ^з(Ук +1 - *1/11 + 1) i %2 = ^О^ф^дс !
^3,к+1 = *3.* + ^з(й+1 “ ЧЪ1) ! *3 = ^оТдо ;
дискретная система СлС ПА
^* + 1=х1,*+Ь ^Л+1 = *1Л+ь х1,*+1 = *l,Jt + ^де*2,* 1
* 1,*+1 = *1.к + 7дс*2,* + ^1(зТ + 1 ~*1,* + 1);
* 2,t + l = *2,к + Здо*3,4 + ^(i't+l - *!/* + !) J
у
* 3,*+1 = ^3,к +^з(>4<.1 - *1.*»1) ;
дискретная система СлС Til
Л -*«-1 =*!,* + ! J ^-* + 1 = *|,* + Ь -*!.*11 = \к +ЬТ№хз к ;
* !,* + ! = Х\,к +7дс*3,к ; *2Л + 1 = ^2,к + ТК-Х^ + Х2(у* + 1 - Х],**])!
^3,* + 1 = *2,* + 1 + ^1(14 + 1 -*!,*+!)/Тдс J *4Л+1 = *4,* + ^з(Л+1 ~ *l,*tl)-
Как отмечалось в п. 12.6.5, фильтры третьего порядка используются в
системах ФАП. Недостаток таких фильтров — возможная неустойчивость ра-
боты. Типичные значения параметров фильтра [7.8]: Хо = 12079,214 с’3;
7ф] = 0,048 с; Тф2 = 0,0675 с; Д/ш = 18 Гц.
' 12.7- Алгоритмы вторичной обработки информации, в АЛ
211
МНВ
12.6.7. Алгоритм выделения навигационного сообщения
Данный алгоритм является дискретным аналогом непрерывного алгорит-
ма (6.17), т.е.
S*+1 = sign(//>iJt+1),
(12.42)
где /рд+i определяется выражением (12.10).
12.7. Алгоритмы вторичной обработки информации в АП
На этапе вторичной обработки информации осуществляется:
определение координат и, в случае необходимости, вектора скорости
потребителя в результате решения навигационных уравнений см. гл.6);
демодуляция навигационного сообщения;
форматирование и дешифрация эфемеридной информации и др.
12.7.1. Демодуляция навигационного сообщения
На выходе блока оценки навигационного сообщения, работающего в со-
ответствии с алгоритмом (12.42), формируется непрерывный поток символов
навигационного сообщения, модулированный меандровым колебанием кодом
и скаженный шумами. Для выделения навигационного сообщения необходимо
сгладить шумы, синхронизировать принятый поток цифровой информации и
снять модуляцию бидвоичным кодом. Данные преобразования иллюстрируются
схемой, приведенной рис. 12.20.
Блок 1 выделения импульсов тактовой частоты /мк бидвоичного кода по
информации о моментах смены полярности поступающих символов осуществ-
ляет символьную синхронизацию и выделяет импульсы символьной частоты
бидвоичного кода 100 Гц, синхронные с границами десятимиллисекундных
символов. Эти импульсы с выхода
блока/ поступают на вторые вхо-
ды блока 2 выделения кода метки
времени и блока 3 выделения
бидвоичного кода. Они использу-
инотся для определения десятимил-
лисекундных интервалов накоп-
ления (интегрирования) отдель-
ных символов, искаженных шу-
мом, которые поступают на пер-
вые входы этих блоков.
В блоке 2 поступающие
Нис. 12.20. Схема блока демодуляции нави-
гационного сообщения
212 Гл а в а 12. Аппаратура потребителем
символы после сглаживания шумов подвергаются согласованной фильтращЛ
кода метки времени (см. § 9.3). В результате выполнения этой операции выдсЯ
ляется импульс, синхронный с задним фронтом последнего тридцатого симвй!
ла кода метки времени и совпадающий с двухсекундной меткой. Я
Импульс метки времени с выхода блока 2 в качестве синхронизирующего
импульса поступает на вторые входы генератора меандра 4 и блока 6 выделеЛ
ния импульсов частоты /си = 50 Гц навигационного сообщения, на первые!
входы которых поступают импульсы символьной частоты бидвоичного кош
100 Гц с выхода блока 1. Генератор 4 из импульсов частоты 100 Гц вырабаты-1
вает меандровое колебание той же частоты, а блок 6 формирует импульсц;
символьной частоты навигационных данных 50 Гц. j
Меандровое колебание с выхода блока 4 поступает на второй вход сум-1
матора 5 по mod 2, на первый вход которого поступают десятимиллисекундные
символы бидвоичного кода после их сглаживания в блоке 3 выделения бидво-
ичного кода. В сумматоре 5 в результате сложения по mod 2 символов бидво-
ичного кода и меандрового колебания осуществляется восстановление двоич-
ных символов навигационных данных. Эти символы для дополнительного
сглаживания поступают в блок 7 выделения символов навигационных данных.
Фиксация интервалов сглаживания (интегрирования), равных 20 мс. Осущест-
вляется импульсами символьной частоты навигационных данных 50 Гц, кото-
рые поступают из блока б. — - — -...- .
Выходной сигнал блока 7 в виде потока отфильтрованных навигацион-
ных данных поступает для дальнейшей дешифрации. Туда же с выхода блока 2
поступают синхронизирующие импульсы двухмиллисекундной метки времени.
12.7.2. Алгоритм оценки навигационных параметров
В современной аппаратуре потребителя для получения оценки навигаци-
онных параметров используются сигналы от всех спутников, находящихся в
зоне видимости. В п. 6.3.2 было показано, что в этом случае необходимо ис-
пользовать оценки по методу наименьших квадратов. Обозначая, как и в гл.6,
через х=|хухД|т — вектор потребителя (для простоты в вектор потребителя
не включены компоненты вектора скорости) в системе координат OXYZ
(см. § 3.1), соответствующие алгоритмы для вычисления оценок запишем в
виде (6.44)
i = х0 + (Нт(хо)н(хо))“‘нт(хо)(дизм - Дрс(*о)), (12-43)
где Хц — начальная оценка вектора потребителя; Дизн — измерения псевдо-
дальностей до НС, полученные на этапе первичной обработки; Дрс(хо) — рас-
1 i I I I .1 } f ।
Дэ.7. Алгоритмы вторичной обработки информации в АЛ 213
Кяетные дальности до НС, вычисленные для оценочных значений хр координат
потребителя в соответствии с формулами (6.33)
Г Г •> 7 ,-|М2
Дрс/(*о) = Д/(хо)+Д'; Л(*о) = [(х'-*о) +(у,-Л) + (z<-Zo) J . (12.44)
где Xi,yi,Zi —координаты z-ro НС.
Матрица Н(х0), входящая в (12.43), определяется в соответствии с (6.43),
-(6.36) в точке х0 оценочных значений координат потребителя.
Для реализации алгоритма (12.43) необходима информация о координа-
тах спутников на момент проведения вычислений. Такую информацию полу-
чают при обработке эфемеридной информации, которая доступна потребителю
после дешифрации навигационных данных.
12.7.3. Расчет вектора состояния НС на основе
неоперативной информации
Алгоритм расчета параметров движения НС по данным альманаха ис-
_пользуется при выборе оптимального созвездия, расчете целеуказаний для по-
иска навигационного радиосигнала выбранного НС. В основу алгоритма поло-
жена модель невозмущенного движения спутников (кеплерово движение
см. гл. 3).
. Исходные данные для расчета:
\ Д'7* — календарный номер суток внутри четырехлетнего периода от на-
чала ближайшего високосного года, на которые даны оскулируюшие элементы
орбиты НС;
— время прохождения восходящего узла, ближайшего к началу суток
с номером Na , с;
— долгота восходящего узла в системе координат ПЗ-90 на момент
- рад;
Д1Л — поправка к среднему значению наклонения орбиты на момент
ML, Рад ('ср =63°);
АТ’/ — поправка к среднему значению драконичсского периода обраще-
ния НС, с (Тср = 43 200 с);
е„ — эксцентриситет орбиты на момент /Д ;
<опл — аргумент перигея, рад;
214 ) Г л a i , 12. Ai iipaTyp. лотреб )елёД
tTeK — текущее время, на которое рассчитывается вектор параметре!
движения навигационного спутника, с; Я
— номер суток внутри четырехлетнего периода, на которое рассчЯ
тывается вектор кинематических параметров. Я
Координат движения НС в системе координат ПЗ-90 рассчитывают в по«
следовательности выполнения следующих шагов [1.2] (индекса Лип опу,
щены): !
1. Определение текущих значений классических (кеплеровских) элемен-
тов и некоторых других элементов орбиты
» = «ср + Д'; Т№ = Гср + ДГ ; п = ; а = ^р/л2 , |
где л — средние движение НС; а — большая полуось орбиты НС; х =
=3,1415926536 ; ц = 398600,44;
2. Внесение поправок на несферичность Земли
X. = X + (х — <°з^Д^пп , <оп = <оп + “пД^пп >
/ v7/2
где Д'™ =86400 (^ек-ДГ'1)+ ; X =-10 cos(0 18Q . g6400 ;
z \7/2
йп=5|—j (5cos2(j)-l)-----------; )
п ко J \ U /180-86400 J
ae = 6378,136 km — экваториальный радиус Земли.
3. Расчет эксцентрической аномалии на текущий момент времени 7тек
проводится при рекуррентном решении уравнения Кеплера (3.12).
= М +esinK(A:).
Средняя аномалия М эпохи /тек определяется в соответствии с уравне-
нием (3.10)
М п («тек _ t) ,
где т = /к+8Тп — время прохождения перигея, которое можно определить
как сумму времени прохождения восходящего узла и времени 8ТП движения
НС от восходящего узла до перигея.
вто чной о
' Млгори
21.'
Учитывая привязку времени ty к суткам с номером NA, а времени
к суткам с номером N-r^, с учетом (11.9) уравнение для средней анома-
йи принимает вид
М - п (д/ш| 8 Т„).
Время 8ТП можно определить из уравнений Кеплера (3.9), (3.10), (3.12)
Удадующим образом. Пусть Е„
— эксцентрическая аномалия, соответствую-
щая истинной аномалии S =to„. Тогда в соответствии с (3.9)
Еп = 2 Arctg
Из уравнения (3.12) для эксцентрической аномалии Еп можно опреде-
лить среднюю аномалию
Mn = En - е sin Еп .
(12.45)
Тогда для интервала времени 8ТП справедливо соотношение (3.10)
8тп = л/п/„ + Г’
(2др, ип
Рекуррентное уравнение (12.45) решается с начальным условием
= М , к = 0,1... до тех пор пока не будет выполняться условие
|£(*+1) _£W| <3.10-8.
4. Определение вектора состояния НС в орбитальной прямоугольной
системе координат OX\Xi — системе координат, лежащей в орбитальной плос-
кости с началом в центре Земли, ось Х\ направлена вдоль фокальной оси к
перигею, ось Х^ — по нормали к фокальной оси;
х,ор = a (cosl^**1) - е) ; х^ = a-Jl - е2 sin .
Соотношения для составляющих скорости НС в орбитальной системе
координат получаются дифференцированием координат (*°р,х°р) по времени
(с учетом (3.12))
216 Г л а в a 12. Аппаратура потребит^
•op _ nosing**1) -op _ najl -е2 cosE^k+l^
*' l-ecos£(*+1) ’ *2 l-ecos£<*+l) ..
<
5. Пересчет ортов {е°р,е°р| орбитальной прямоугольной системы коог
I *2 I ®"
' ' а
динат ОХ1Х2 в инерциальную систему координат ПЗ-90 , осуществляется nj
тем трех последовательных поворотов орбитальной системы координат на угдв
ш‘, i, X*. Соотношения для проекций орта е°р на оси инерциальной систему
координат могут быть получены из (3.14) при 9 = 0 и замене долготы bocxq
дящего узла Q в инерциальной системе на соответствующую долготу восхода
щего узла X* в системе координат ПЗ-90:
е®! = cos ш n cos X* - sin ш „ sin X* cos i;
= cos co n sinX* + sin co „ cosX* cosi; e= sin co „ sin i,
а. для проекций орта e°| аналогичные соотношения получаются из (3.13) при
9 = я/2:
е®2 = -sincoJi cosX* - cos со „ sinX* cosi;
e®2 = - sin co n sinX* + cos co g cosX* cosi; e®2 = cosco „ sini.
6. Преобразование вектора состояния НС из орбитальной системы в сис-
тему координат ПЗ-90.
Введем вектора X = |х у z|T , е° = |e2i e®i e®i| > е° = |ej2 ej2 е®?| Тогда ве-
тор координат НС в системе координат ПЗ-90 определяется соотношением
Х = х°ре®+х°ре®.
Преобразование вектора скорости НС из орбитальной системы коордг
нат во вращающуюся систему координат ПЗ-90 проводится в два этапа. Сначг
ла вектор скорости преобразуется в неподвижную систему координат, ос
которой смещена относительно оси Хо инерциальной системы коордииа”
OXqYqZq на долготу восходящего узла равную X* , в соответствии с формулог
Ш&ЗлАлгоритмы вторичной обработки информации в АП 217
К X' =х1°’е?+х7е«.
Ж* На втором шаге вектор скорости XJ из неподвижной системы коорди-
Кт пересчитывается во вращающуюся систему координат ПЗ-90 в соответ-
ствии с общим правилом (3.16) по формулам
L X = Xs + <n3Y-, Y = Ys-a3X; Z = Zs.
t- 12.7.4. Расчет вектора состояния НС на основе
В оперативной информации
Г Расчет в приемоиндикаторе проводится с целью уточнения параметров
[движения НС на момент времени tt по данным эфемерид, которые содержатся
№ разделе оперативной информации навигационного сообщения, даются на
^моменты времени tb и обновляются через каждые 15 мин, поэтому для вре-
мени t/ определяется как - /(| 5 15 мин.
| Процедура пересчета проводится численным интегрированием диффе-
ренциальных уравнений орбитального движения (3.23). Начальными условия-
ми для интегрирования системы уравнений являются данные эфемерид. Ин-
тегрирование проводится классическим одношаговым методом Рунге—Кутта
четвертого порядка [12.4], когда при разложении нелинейной функции в ряд
(удерживаются все члены порядка малости до А4, где А — шаг численного ин-
тегрирования. Для этого метода локальная ошибка имеет порядок А5.
При использовании этого метода для решения дифференциального урав-
нения первого порядка вида dy/dx = f(x,y) при начальном условии у(х0) = Уо
расчеты проводятся по следующему правилу
Ул<1 =У„ +К0+2К, +2К2+К3/6,
где Ко = A f(x„,y„); Kt = A • Дх„ + у А,у„ + у ;
= А-Дх„ + |д,у„ +|xi);
Х3 - А-/^х„ + А,у„ + —.
12.7.5. Пересчет координат нотребителя из земной
в геодезическую систему координат
Алгоритм оценки навигационных параметров (12.43) формирует оценки
вектора потребителя в геоцентрической системе координат OXYZ, связанной с
218
Землей. Потребителя во многих случаях интересуют свои координаты в геодД
зической системе координат (см. § 3.1). Поэтому в ПИ необходимо осущесм
вить пересчет координат из геоцентрической системы в геодезическую. Общи!
формулы связи двух систем координат имеют вид (3.1)—(3.2), а пересчет цЯ
этим выражения может быть реализован следующим вычислительным алго|
ритмом [12.5]: ?
1) исходные данные координаты х, у, г в геоцентрической системе ко**
ординат OXYZ; выходные данные — координаты В, L, Н в геодезической сис-
теме координат;
2) вычисляется вспомогательная величина
D = ^х2 + у2 ;
3) анализируется значение I):
если D = 0 , то 2? = тсг/(2|г|); L = 0; Я = zsin В - aVl - е2 sin2 В ; '
если D > 0 , то La - arcsin(y / Р);
при этом если х •> 0, у •> если х < 0, у > 0,-roL=La; 0, то L = л - La;
если х < 0, у • если х > 0, у < 0, то L = л + La ; < 0, то L = 2 л - La ;
4) анализируется значение z :
если z=0, то В = 0, Н = D-a;
в других случаях находятся вспомогательные величины г, с, р
г = ух2 + у2 + z2 ; с = arcsin(z / г); р = е2а/2г;
реализуется итеративный процесс
$1=0; Ь = с + ; s2 = arcsin^psin(2i)/Vl - e2 sin2 ij ;
если модуль разности — ^i| < e , где e — требуемая точность вычислений, то
B = b\ Н = Deos В + z&in В - a\l-е2 sin2 В ;
в противном случае полагается j] = s2 и вычисления повторяются, начиная с
расчета Ь. Во всех случаях выбирается с= 0,0001".
|и2.8. Особенности применения CPhb
• После нахождения B,L,H становится также известной матрица перехо-
да из геоцентрической системы координат в прямоугольную горизонтальную,
taro позволяет осуществить преобразование составляющих скорости движения
Подвижного объекта.
12.8. Особенности применения СРНС в различных областях
12.8.1. Особенности применения в авиации
z Соглашение об использовании ГЛОНАСС. Международная организация
гражданской авиации (ИКАО) определила и на своей 10 Аэронавигационной
конференции одобрила концепцию построения перспективной аэронавигаци-
онной системы (FANS), представляющей собой комплексную глобальную сис-
тему связи, навигации и наблюдения/организации воздушного движения
(CNS/ATM) (12.6—12.10]. В этой системе предполагается преимущественное
использование спутниковых технологий для решения задач навигации, связи и
наблюдения и обеспечения беспрецедентного уровня безопасности полетов.
При этом в качестве основной навигационной системы планировалось исполь-
зовать глобальную навигационную спутниковую систему GNSS, которая долж-
на заменить (или отодвинуть на второй план) многие существующие радиона-
вигационные системы ближней и дальней навигации, используемые в настоя-
щее время на различных этапах полета в качестве средств навигации (VOR,
NDB ,Omega и т.д.) для получения пользователями значительных технических
и экономических преимуществ. На этой конференции страны-создатели
(СССР и США) средневысотных СРНС ГЛОНАСС и GPS предложили их для
использования в качестве основных элементов GNSS на безвозмездной основе
на длительный срок (не менее 15 лет с момента полного развертывания систе-
мы ГЛОНАСС и 10 лет для системы GPS).
В настоящее время ведутся работы по определению наилучшего способа
внедрения спутниковых систем для удовлетворения глобальных потребностей,
так как сегодня считается недостаточным, чтобы новые системы отвечали тре-
бованиям какого-то одного государства или региона. Предполагается приме-
нять GNSS совместно с другими бортовыми датчиками (типа ИНС, высотоме-
ров и т.д.), вычислителями воздушных данных, спутниковыми цифровыми ли-
ниями передачи данных в канале между воздушным судном и диспетчером
системы УВД для:
осуществления полетов по более жестким стандартам на требуемые на-
вигационные характеристики, вплоть до RNP1, когда требуется надежное вы-
держивание коридора шириной ± 1 морская миля ;
реализации автоматического зависимого наблюдения, обеспечивающего
контроль воздушного движения при отсутствии наземных РЛС системы УВД;
увеличения пропускной способности воздушного пространства на мар-
шрутах и в районе аэродрома для обеспечения роста воздушных перевозок;
> 1 i
220 Глава 12, Аппаратура потребителе»;
повышения уровня безопасности полетов благодаря уменьшению риска,
связанного с неточностью информации о пространственно-временных коордц.
натах и скорости, и более точному наведению воздушного судна;
возрастания эффективности полетов, снижения их общей стоимости ц
обслуживания за счет экономии полетного времени, топлива, а также средств'
на закупку и эксплуатацию ряда традиционных РНС, используемых в настоя-
щее время для обеспечения полетов на маршрутах, в районе аэродрома, при
заходе на посадку и т. д. Например, США объявило о прекращении своего
участия в обеспечении функционирования РНС Omega после 1 октября 1997 г.
Опубликовано 7 марта 1995 г. Постановление Правительства РФ “О про-
ведении работ по использованию СРНС ГЛОНАСС в интересах гражданских
потребителей”, предусматривающее разработку и внедрение спутниковой ап-
паратуры, в том числе и в целях обеспечения безопасности и эффективности
применения самолетов всех типов.
После проведения большого объема научных исследований и глобальных
испытаний Правительство России передало ИКАО расширенные предложения
от 4 июня 1996 г. о предоставлении, при условии требуемого по законодатель-
ству России выделения необходимых средств, канала стандартной точности
СРНС ГЛОНАСС для использования гражданской авиацией мира, которые
были приняты руководством ИКАО в качестве элементов соглашения между
РФ и ИКАО об использовании ГЛОНАСС. При этом Россия принимает все
необходимые меры для обеспечения целостности и надежности обслуживания,
постоянно информирует ИКАО относительно эксплуатационного состояния
ГЛОНАСС и готова заключить соглашение с ИКАО о применении ГЛОНАСС
мировым авиационным сообществом как элемента GNSS с приведенными в
табл. 8.1 характеристиками определения координат потребителей. Для обеспе-
чения использования GNSS мировой гражданской авиацией Россия в соответ-
ствии с положениями статьи 37 Чикагской конференции всемерно сотрудни-
чает с ИКАО в подготовке надлежащих стандартов и рекомендуемой практики
(SARPS) на GNSS.
Аналогичное соглашение с ИКАО заключили и США после объявления в
1994 г. о вводе в эксплуатацию системы GPS. Однако предоставляемые ею
возможности по точности определения координат и скорости потребителей
существенно (ориентировочно в несколько раз) ниже, чем у системы ГЛО-
НАСС из-за специального загрубления сигнала стандартной точности.
Опыт использования СРНС в гражданской авиации. В настоящее время
многие российские и зарубежные авиационные потребители СРНС ГЛОНАСС
и GPS отрабатывают правила применения этих средств с целью наиболее пол-
ного использования предоставляемых ими преимуществ. Опыт такой деятель-
ности [12.6—12.9] свидетельствует о нескольких способах применения спутни-
ковых систем в авиации. Наиболее часто бортовые приемом иди каторы СРНС
служат в качестве дополнительного средства обеспечения полетов по правилам
ППП и ПВП по маршруту, в районе аэродромов и некатсгорированных захо-
________
job на посадку. В российской гражданской авиации в качестве дополнитель-
ного оборудования разрешено [12.11] применять не только стационарно уста-
навливаемые приемоиндикаторы СРНС, но соответствующие переносные (руч-
gjie) приемоиндикаторы (без расширения ожидаемых условий эксплуатации
воздушных судов).
Полет по приборам с использованием СРНС по маршруту, в районе аэ-
родромов и при посадке без специализированных систем точного (категориро-
ванного) захода на посадку можно осуществлять, если на воздушном судне ус-
тановлено радиоэлектронное оборудование СРНС, одобренное для примене-
ния при полете по приборам. Минимальные требования, которым должно
удовлетворять дополнительное навигационное оборудование СРНС в этом
случае, изложены в [12.12, 12.15]. Требуемая целостность таких операций
обеспечивается с помощью специальных методов в приемоиндикаторе СРНС
(RAIM, см. § 10.5) или другими эквивалентными методами. При воздушных
перевозках для использования СРНС требуется одобренная спецификация
(сертификат). Оборудование СРНС в ] 12.12] разбивается на классы А,В, С.
Оборудование класса А состоит из датчика СРНС и навигационного вы-
числителя в одном блоке с пультом индикации и управления. Приемоиндика-
тор такого класса выполняет функцию RAIM. Оборудование подкласса А1
одобрено для полета по маршруту, в районе аэродрома и при посадке без
средств точного захода (кроме курсовых радиомаяков и упрощенных радио-
средств направленного действия). Оборудование подкласса А2 одобрено только
для маршрутного полета и полета в районе аэродрома.
Оборудование класса В состоит из датчика СРНС, формирующего дан-
ные для комплексной навигационной системы (например FMS). Оборудование
подкласса BI одобрено для полета по маршруту, в районе аэродрома и посадки
без средств точного захода (кроме курсовых радиомаяков и упрощенных ра-
диосредств направленного действия). Оборудование подкласса В2 одобрено
только для полета по маршруту, в районе аэродрома. Оборудование подклассов
В1 и В2 выполняет функцию RAIM. Оборудование подкласса ВЗ требует, что-
бы комплексная навигационная система обеспечивала уровень целостности,
эквивалентный RAIM. Оно одобрено для полета по маршруту, в районе аэро-
дрома и посадки без применения средств точного захода (кроме курсовых ра-
диомаяков и упрощенных ралиосредств направленного действия). Оборудова-
ние подкласса Вытребует, чтобы комплексная навигационная система обеспе-
чивала уровень целостности, эквивалентный RAIM. Оно одобрено для полета
по маршруту и в районе аэродрома.
Оборудование подклассов С1 ... С4 аналогично оборудованию подклассов
В1 ... В4 соответственно. Однако такое оборудование одобрено для установки
на другие классы ВС, где комплексная навигационная система обеспечивает
расширенные связи с автопилотом или пилотажным командным прибором с
целью уменьшения технических ошибок пилотирования.
В ряде случаев приемоиндикаторы СРНС используются и в качестве ос-
новного средства обеспечения полетов. Это относится, например, к полетам
222 ' s Г л a -> a 12. /-ыпарату,.* потрс^^телей^
по океаническим (в воздушном пространстве северной Атлантики, где предь
являются технические требования к минимальным навигационным характеру
стикам) или по проложенным в отдельных районах маршрутам, а также катд
горированных заходов на посадку в условиях полетов по особой (специально^
категории I. Ожидается переход в ближайшее время (начало 1998 г.) на при!
менение СРНС в качестве основного средства радионавигации и в европей ^
ском регионе [12.15]. Для практического использования в таких случаях обыч-|
но рекомендуется система GPS, однако в дальнейшем после представления ц
одобрения документации относительно готовности и надежности системы;
ГЛОНАСС, по аналогии с документацией по GPS, и она будет рекомендована
к использованию.
В зависимости от вида маршрута или этапа полета имеются некоторые
особенности в использовании оборудования СРНС [12.16]. При полете над
океаном ВС, использующие СРНС, должны быть оборудованы проверенными
и исправными альтернативными средствами навигации (такими как, напри-
мер, VOR, NDB, LORAN или Omega), соответствующими маршруту полета.
Активное наблюдение (перекрестные проверки) необязательно а оборудовани-
ем, которое обеспечивает функцию RAIM для контроля целостности. Для та-
ких систем активное наблюдение экипажа требуется только, если работоспо-
собность RAIM утеряна. Вне воздушного пространства США система GPS мо-
жет использоваться как система дальней навигации. В этом случае на маршру-
тах, требующих наличия на борту двух систем дальней навигации, оборудова-
ние СРНС, соответствующее подклассам Al, А2, Bl, В2, С1 или С2, может ис-
пользоваться вместо или в дополнение к другим средствам дальней навигации,
например, как один из блоков двухканальной ИНС или один из блоков двух-
канальной системы Omega. На маршрутах, требующих более одной системы
дальней навигации, система СРНС, обеспечивающая контроль целостности,
может использоваться как система дальней навигации. Активное наблюдение
за прочим оборудованием необходимо только, если функция RAIM не выпол-
няется. Спутниковая РНС может быть не одобрена в других странах. Пилотам
следует убедиться, что использование СРНС разрешено соответствующим су-
веренным государством до того, как использовать СРНС на территории этого
государства.
При полете по внутренним маршрутам ВС должно иметь исправное на-
вигационное оборудование, которое может получать с наземных средств ин-
формацию, необходимую дд^ полета в аэропорт назначения, а также все тре-
буемое дополнительное оборудование. Наземные устройства, необходимые для
этих маршрутов, также должны быть исправны и не должны активно исполь-
зоваться для контроля за оборудованием СРНС, если только функция RAIM
выполняется. Этим требованиям удовлетворяют, например, оборудование
VOR, NDB, TACAN или LORAN-С в дополнение к системе СРНС для полета
по приборам.
Полет по приборам с использованием СРНС в районе аэродрома и стан-
дартная схема вылета и прибытия по приборам должны выполняться так, как
Осос.Аности .римене. ля CPh Iв разя, кых об. стях
)3
«называют существующие процедуры зональной навигации. Воздушное судно
|рлжно иметь исправное и соответствующее маршруту навигационное обору-
звание. Однако нет необходимости использовать наземное оборудование для
Чстивного мониторинга оборудования СРНС, если функция RAIM выпол-
няется.
( Недавно в США была разработана программа выполнения заходов на по-
садку с совместным использованием СРНС GPS и другого оборудования. Она
Предназначена для ускорения внедрения процедур захода по приборам с ис-
пользованием соответствующего оборудования СРНС, VOR, NDB, DME,
JOR/DME, TACAN и т. д. без применения средств точного захода на посадку,
Которые могут исключаться из БД, за исключением случая захода с использо-
ванием курсовых радиомаяков или упрощенных радиосредств направленного
Действия. Программа ограничивается рамками воздушного пространства США.
7Правила захода по приборам с использованием СРНС за пределами США
«должны быть утверждены соответствующими суверенными государствами.
Всякий требуемый запасной аэродром должен иметь одобренную проце-
дуру захода по приборам, отличную от процедур захода по GPS и LORAN-C,
^которая должна быть в рабочем состоянии во время предполагаемого прибы-
?тия ВС.
Программа совместного использования оборудования при заходе на по-
садку состоит из трех этапов (некоторые сведения по этим этапам приводятся
чиже).
Первый этап состоит из подготовительных и исследовательских проце-
дур. Он закончился 17 февраля 1994 г., когда официально'была подтверждена
триемлемость характеристик СРНС GPS для решения задач гражданской
-авиации.
Второй этап характерен тем, что заходы по СРНС выполняются по суще-
••твующим схемам (без включения СРНС в название захода). При этом серти-
вицированное оборудование СРНС может использоваться как основное сред-
тво при полете по приборам в соответствии с существующими процедурами
тез активного наблюдения за навигационными средствами, которые опредсля-
эт используемый заход. Однако, наземные и бортовые средства, требуемые
щя данного захода должны иметься в наличии в рабочем состоянии. При за-
воде нет необходимости в использовании этих средств, если целостность обес-
печивается с помощью RAIM.
Третий этап начался 28 апреля 1994 г., когда были опубликованы первые
юоцедуры захода по приборам, учитывающие использование СРНС (имеющие
«разу “или GPS” в названии). При посадке без средств точного захода не тре-
бовалось наличие и работоспособность наземного навигационного оборудова-
тия на посадочном аэродроме, наблюдение за ним, а также наличие и работо-
способность традиционного бортового радионавигационного оборудования.
Для оборудования СРНС, не использующих RAIM для контроля целостности,
таземное навигационное оборудование и бортовая радиоэлектроника, обеспе-
’ивающие эквивалентный контроль целостности, должны функционировать во
224
Г л а в a 12. Аппаратура потребители
время захода. Для каждого требуемого запасного аэродрома должно функци
пировать традиционное наземное и бортовое навигационное оборудована
определяющее процедуру захода по приборам и маршрут к этому аэродрому, .
Следующим шагом в применении СРНС для гражданской авиации яв
лось самостоятельное использование СРНС при заходе на посадку. В данно
случае не применялись традиционные средства захода. Первые процедуры за
хода с использованием исключительно СРНС GPS были опубликован^
21 июля 1994 г. Требования к бортовому и наземному радиоэлектронному обо,
рудованию при этом заходе такие же, как на третьем этапе программы cobmq
стного захода на посадку. В течение этого времени в воздушном пространств
США применяются процедуры совместного захода (в соответствии с вторым <
третьим этапами) и с использованием только СРНС. Для осуществления по-
летов по приборам с использованием СРНС на борту воздушного судна должзд
иметься соответствующим образом оформленная обновляемая база навигацц^
онных данных. Она должна иметь необходимую точность привязки координа^
В ее состав обычно включают стандартные схемы вылета и прибытия.
Назначение, основные режимы бортовой аппаратуры СРНС. В настоящее
время известно большое число авиационных приемоиндикаторов СРНС, раз-
личающихся по многим признакам: типам используемых СРНС (приемоинди-
каторы ГЛОНАСС, GPS, ГЛОНАСС/GPS); числу каналов обработки сигналов
(одноканальные с последовательной Обработкой сигналов, одноканальные -
мультиплексной обработкой, многоканальные и т. д.); виду обрабатываемых
сигналов (одночастотные, двухчастотные, для обработки открытых или закры-
тых сигналов и т. д.); высоте применения; допустимым динамическим воздей-
ствиям; степени соответствия нормам требований; видам индикаторов и т. д.
Рассмотрим основные св₽
дения о бортовой аппаратур^
СРНС применительно к типовых
приемоиндикаторам, используе
мым в российской авиации. Эте
приемоиндикаторы применяютс
для определения по сигналах
СРНС наиболее важных навигаци
онных параметров, необходимы:
для самолетовождения. К ним от
носятся (рис. 12.21):
географические координаты
самолета (например, в систем,
координат СК-42 или WGS-84);
высота самолета относы
тельно соответствующего эллиг-
соида;
Рис. 12.21. Схема определения пара-
метров самолетовождения
Hgj. Особенности применения СРНС в различных областях 225
tj путевая (горизонтальная составляющая земной скорости) скорость само-
La Кпур (или GS);
I текущее время (UTC или местное время );
•Г фактический путевой угол ФПУ (или ТК);
дальность до очередного или заданного промежуточного пункта маршру-
та (ППМ или WPT) Дц (или DIS);
’ линейное боковое уклонение (ЛБУ или ХТК, STR) самолета относи-
Ьельно линии заданного пути (ЛЗП);
fr'' азимут (пеленг) очередного или заданного ППМ (А или BRG);
|ь. заданный курс полета % (или CTS);
Z курс выхода на ППМ д (или OBS);
; отклонение от заданного курса (или от курса на ППМ) Д\р = \р3 - ч>тек
|яли (TRN).
Здесь 'Утек — текущий курс полета (или HDG); ЗПУ — заданный путе-
вой угол (или DTK).
р Кроме этих параметров с помощью приемоиндикатора можно осущест-
вить расчет множества других штурманских данных (пересчет высот по давле-
нию и плотности воздуха, расчет истинной воздушной скорости по прибор-
ной, расчет направления й скорости ветра, определение углов снижения м на-
бора высоты для вертикального маневра, пересчет параметров из одной систе-
: мы отсчета в другую и т. д.).
Для типовой бортовой аппаратуры СРНС характерны следующие основ-
I ные режимы работы: навигации (NAV); программирования ППМ (WPT);
'программирования маршрутов полета (FPL или RTE); аварийный (NRST);
“Направить на “ (DIR ТО); установки (SET); просмотра текстовых сообщений
(MSG); встроенного контроля; имитации полета.
После включения аппаратуры экипажу необходимо осуществить кон-
троль ее работоспособности или убедиться в его автоматическом выполнении,
осуществить при необходимости инициализацию (ввод исходных данных) и
выбрать режим работы .
Основным режимом работы ПИ в полете служит навигационный режим,
во время которого на индикаторе приемоиндикатора (и/или на пилотажных
индикаторах) отображаются приведенные выше навигационные параметры (в
различных сочетаниях). Они могут отображаться в цифровой и/или графиче-
ской форме. Масштаб, системы координат и единицы отсчета индицируемых
параметров выбираются экипажем в режиме установки. Различные наборы на-
вигационных параметров позволяют осуществлять полет к очередному ППМ
различными способами (путевым, курсовым или маршрутным). Очередной
ППМ выбирается автоматически или вручную. Автоматически очередной ППМ
выбирается из предварительно выбранного экипажем маршрута полета (в ре-
жиме программирования маршрута). Вручную необходимый пункт маршрута
226 Глава 12. Аппаратура потребителей^
выбирается или из БД (выбор в режиме “Направить на“) или из любого пред,
варительно запрограммированного маршрута полета (в режиме программиро-
вания маршрута).
В аварийном режиме на индикаторе отображаются навигационные дан-
ные, необходимые для полета к ближайшему от самолета ППМ любой катего-
рии. Экипаж может выбрать как тип (категорию) ППМ, так и подходящий
ППМ из числа индицируемых ближайших пунктов. Обычно имеется выбор из
20-ти ближайших ППМ любой категории.
В режиме программирования ППМ можно просмотреть и выбрать необ-
ходимый ППМ из имеющихся в электронной БД приемоиндикатора или за-
программировать данные для “своего” (пользовательского) ППМ. В БД хра-
нятся несколько типов ППМ: аэродромы, радиомаяки РСБН (VOR), привод-
ные радиомаяки (NDB), пользовательские (запрограммированные ранее) и т.д.
Обычно в БД хранится информация о всех основных аэродромах и радиомая-
ках, а также от 250 до 1000 пользовательских ППМ. Экипаж должен следить за
качеством и своевременным обновлением БД.
В режиме программирования маршрутов полета экипаж осуществляет
формирование требуемых маршрутов из числа ППМ имеющихся в БД, редак-
тирование ранее введенных маршрутов, их стирание, активизацию любого
маршрута в прямом или обратном направлении, при этом начиная полет с лю-
бого ППМ маршрута. Обычно число программируемых маршрутов доходит до-
20 ... 30 по 20 ... 30 ППМ в каждом.
Для выполнс! ия наземных тренировок по отработке навыков управле-
ния аппаратурой используется режим имитации полета. В этом режиме необ-
ходимо выбрать маршрут полета, установить скорость и в дальнейшем индика-
ция навигационных данных осуществляется как и реальном полете. В режиме
установки можно контролировать работу каналов слежения за сигналами спут-
ников, оценивать точность местонахождения, наблюдать за составом и качест-
вом орбитального созвездия спутников (определять коэффициент геометрии),
оценивать уровень сигналов спутников, осуществлять прогноз орбитальной
группировки и функций RAIM и т. д.
Для оповещения и предупреждения экипажа имеются соответствующие
органы индикации. Кроме того, в режиме просмотра текстовых сообщений
можно вывести на индикатор имеющиеся сообщения консультативного, пре-
дупреждающего или рекомендательного характера. Экипаж оповещается об
отказах аппаратуры и спутника, плохом качестве навигационных определений,
о невозможности выполнять полет ио ППМ и т. д. Большой объем решаемых в
авиационной аппаратуре СРНС задач, их высокое качество свидетельствует о
возможности се использования как основного навигационного датчика, так и
резерва существующих навигационных комплексов. В настоящее время пер-
спективы использования аппаратуры СРНС часто связывают с ее применением
в составе пилотажно-навигационных комплексов в целях коррекции навига-
ционных данных.
J2.8. Особенности применения СРНС в различных областях 227
12.8.2. Особенности применения морскими потребителями
Морскими потребителями СРНС ГЛОНАСС и GPS могут быть транс-
портные и рыболовецкие суда, ледоколы, суда вспомогательного флота и спе-
циального назначения, плавучие средства, используемые для разведки и добы-
чи полезных ископаемых, сухопутные средства, обеспечивающие безопасность
плавания морских и речных судов, а также решение различных задач в при-
брежных зонах. В зависимости от типа и решаемых задач морские потребители
оснащаются различными навигационными системами и средствами, в состав
которых в настоящее время, как правило, входит приемная аппаратура спут-
никовых навигационных систем ГЛОНАСС или GPS.
Надежное навигационное обеспечение имеет важное значение для безо-
пасности плавания судов, их эффективной эксплуатации и предотвращения
экологических бедствий.
Для удовлетворения современным требованиям к навигационному обес-
печению судоходства внедряются качественно новые средства судовождения в
том числе спутниковые системы навигации, системы управления движения
судов, системы автоматизированного контроля за судоходством, интегриро-
ванные навигационные системы, аппаратура электронной картографии.
Требования к оснащению судов оборудованием современных систем за-
ложены в проект новой Гл. 5 Конвенции по охране человеческой- жизни на
морс (СОЛАС), которая будет одобрена ИМО в ближайшее время. Поправки к
Гл. 5 СОЛАС предусматривают обязательное оснащение морских судов прие-
моиндикаторами СРНС, одобренной в соответствие с требованиями ИМО и
МЭК, т. с. ПИ СРНС ГЛОНАСС, СРНС GPS или СРНС ГЛОНАСС/GPS, ра-
ботающей по сигналам обеих систем. Эти требования, согласно проекта, будут
распространятся на суда вместимостью от 150 per. т. Тип судового ПИ СРНС
должен быть одобрен Морской Администрацией страны флага.
В принятой Международной морской организацией (ИМО) в 1983 г. Ре-
золюции А.529(13) содержатся стандарты точности судовождения, которые оп-
ределяют требования, удовлетворяющие нужды общей навигации. При этом
районы плавания для судов, следующих со скоростью до 30 узлов подразделя-
ют на две основные зоны: открытое море и прибрежные районы; подходы к
портам и портовые воды, а также узкости, в которых ограничена свобода ма-
неврирования судов.
В первой зоне они определены указанной Резолюцией и точность судо-
вождения здесь должна быть не хуже 4 от расстояния до ближайшей навига-
ционной опасности, с максимумом в 4 мили при наибольшем допустимом ин-
тервале времени от последней обсервации. Этот интервал определяется по
приводимым в Резолюции графикам и таблицам в зависимости от точности
счисления пути и точности обсервации ио системе.
Во второй зоне требования к точности судовождения зависят от местных
обстоятельств и определяются национальными морскими Администрация ми,
так как имеют свою специфику, которая может формулироваться конкретными
228 Г л а в a 12. Аппаратура потребителе^!
эксплуатационными требованиями к радионавигационному обеспечению даЯ
ного региона и, в частности, характеризуется допустимой погрешностью о пре л
деления места судна. Эта погрешность зависит от соотношения установленнсД
ширины полосы движения судов, их размеров, гидрометеорологических услаа
вий плавания и др. Её значение должнобыть менее Юме вероятностью 95 йЯ
В концепции обеспечения безопасности мореплавания в данном регион^
высокоточные радионавигационные системы должны стать неотъемлемой ча-
стью всего комплекса радиотехнических и визуальных средств навигации. Для
удовлетворения предъявляемым требованиям радионавигационные систему
должны иметь необходимые системные характеристики (точность, доступ^
ность, целостность, надежность и рабочую зону). J
В 1995 г. на 19 Ассамблее ИМО была принята Резолюция А.815(19) по|
Всемирной радионавигационной системе, в которой определены технике--
эксплуационные требования к такой системе и её компонентам и порядок их4
признания ИМО.
Исходя из перспективных возможностей СРНС, связанных с применение
ем дифференциального режима, совместным использованием обеих созданных'
систем ГЛОНАСС и GPS, а также возможным вводом в эксплуатацию их гео-
стационарного навигационного дополнения в составе спутниковой системы-
связи ИНМАРСАТ, ИМО определила основные требования морских потреби-
телей к будущей глобальной навигационной спутниковой системе: 2
Точность системы* (применительно к определению
положения приемной антенны) (не более), м:
абсолютная погрешность .............................. 10 (95 %)
повторяемая погрешность .......................... 14 (95 %)
Целостность системы*(не более):
задержка оповещения, с ......................_........ 10
допустимый предел ухудшения характеристик
системы, м......................................... 25
Доступность системы**(в течение 30 дней)
(более), % ............................................ 99,8
Допустимый предел ухудшения работы
системы (непредвиденные перерывы) (не более), с...... 3
Надежность системы** (не более) (в течение года), % . 99,97
Зона покрытия системы** ............................. глобальная
Дискретность обновления данных о координатах* ....... каждые 2 с
Возможное число потребителей системы** .............. неограниченное
включая судовую приемную аппаратуру
не включая судовую приемную аппаратуру
Минимальные требования морских потребителей к такой системе каса-
ются обеспечения общего мореплавания и прежде всего задач непрерывного
счисления пути на электронных картах, контроля и управления движения по
заданной траектории, зависимого наблюдения за судами, выдачи данных в
средства Глобальной морской системы связи при бедствии и для обеспечения
безопасности (ГМССБ) и использования другими системами.
^12.8. Особенности применения QJPHC в различных областях 229
* Требования, связанные с рыбным промыслом, гидрографическими рабо-
тами и обеспечением других специфических задач (табл. 12.4) могут быть бо-
^ее жесткими чем обеспечивающие общее мореплавание.
Г
Таблица 12.4. Требования к навигационному обеспечению при решении
специальных задач морскими потребителями
Специальные задачи» решаемые на море Точность, м Доступ- ность, % Наибольшая 1 дискретность обсерваций, с I
/ Рыбный промысел: 1
в открытом море 10 ... 100 99,97 10
в прибрежных водах 5 ... 100 99,97 10
в узкостях 5 ... 50 99,97 10
Добыча полезных ископаемых 1 ... 3 99,97 10
Прокладка:
кабелей 1 ... 2 99,97 10
трубопроводов 1 ... 2 99,97 10
Гидрографические исследования 1 ... 10 99,97 10
Установка навигационных средств 1 ... 10 99,8 10
Дноуглубительные работы 1 ... 10 99,8 10
Швартовые операции 1 ... 5 99,97 10
В настоящее время наиболее полно удовлетворяют требования к навига-
- ционному обеспечению судоходства СРНС GPS и ГЛОНАСС при использова-
ний йх в штатном й дифференциальном режимах работы (более подробно о
дифференциальном режиме см. § 11.1). Основными достоинствами их при ис-
пользовании сигналов стандартной точности в штатном режиме работы явля-
ются глобальность рабочей зоны, высокие доступность, точность и надежность
при непрерывности навигационных определений, а в дифференциальном ре-
жиме — возможность повышения точности и надежности навигационных оп-
ределений в рабочей зоне ДП. Погрешности определения местоположения
СРНС ГЛОНАСС и GPS при использовании сигналов стандартной точности в
штатном режиме не превышают соответственно 45 и 100 м, а в дифференци-
альном режиме — Юме вероятностью 95 %. Более высокие точностные ха-
рактеристики СРНС ГЛОНАСС объясняются отсутствием режима селектив-
ного доступа (SA-selectivc availability), который применяется в СРНС GPS в
штатном режиме для загрубления точности при использовании её граждански-
ми потребителями.
Находящиеся в эксплуатации спутниковые навигационные системы
ГЛОНАСС и GPS в 1996 г. одобрены ИМО в качестве компонентов Всемирной
^радионавигационной системы. При одобрении систем ГЛОНАСС и GPS ИМО
отметила неспособность каждой из них обеспечить в штатном режиме точ-
ность, необходимую для безопасной навигации судов на подходах к портам и в
других водах, в которых свобода маневрирования ограничена. Другой отмечен-
ный недостаток этих систем связан с их неспособностью в данное время обес-
печивать оперативное оповещение потребителей о нарушениях в работе сис-
тем или их элементов, которые происходят пока довольно часто.
230
Наиболее рациональным путем устранения указанных недостатков д
улучшения основных характеристик систем ГЛОНАСС и GPS, необходимы!
для расширения их функциональных возможностей, является применена
дифференциального режима (см. § П.рработы этих систем, что позволяв*
добиться повышения точности, надежности и эффективности радионавигаци-
онного обеспечения. В этом режиме погрешности обсервации с вероятностью
0,95 составляют 5 ... 10 м, и он может рассматриваться как наиболее перспек-
тивный для обеспечения плавания в условиях стесненного маневрирования,
включая узкости, каналы и подходы к портам. Важным достоинством реализа-..
ции дифференциального режима (ДР) является возможность обеспечения кон--
троля правильности работы и оперативной передачи потребителям информа-
ции о целостности СРНС.
Для реализации ДР в дополнение к штатным наземным средствам СРНС
создаются дифференциальные подсистемы СРНС, в состав которых входят
опорные, контрольные и при необходимости управляющие станции, исполь-
зующие средства связи для передачи дифференциальных сообщений (ДС) по-.-
требителям и взаимной связи между станциями.
К ДПС для обеспечения надежности судоходства предъявляют следую-
щие требования:
получение информации о месте судна должно производиться непрерывно
И в~реальном~ масштабе времени; — -
погрешность определения места с вероятностью 95 % в обслуживаемой
зоне не должна превышать 10 м, учитывая наличие зон плавания с узкими ка-
налами, малыми глубинами и сложными подходными путями к акваториям
портов;
информация, выдаваемая судоводителю, должна быть однозначной в
пределах зоны действия системы и определять положение судна относительно
оси фарватера или заданной траектории на всем пути плавания, не требуя до-
полнительных расчетов каких-либо параметров;
должна представляться количественная оценка уклонения судна от оси
фарватера или заданной траектории с отображением параметров движения:
продольной составляющей модуля вектора скорости и значения отклонения
курса относительно оси фарватера;
на дисплее ПИ должны йндицироваться результаты расчета маршрутныг
координат: расстояние до точки поворота, боковое отклонение от заданно!
траектории, время плавания до точки поворота и путевой угол.
Суда транспортного, рыбопромыслового, речного флотов, а также суде
других ведомств решают (с точки зрения навигации) аналогичные задачи, по-
этому область применения дифференциального режима системы достаточна
широка.
Для передачи ДС потребителям могут использоваться традиционны^
спутниковые и специальные каналы радиосвязи. Для морских потребителе!
более целесообразны по техническим и экономическим соображениям каналь
морских радиомаяков. Существующая сеть РМ охватывает практически вс:
В применения СРНС в различных областях 231
[редставляют интерес для морских потребителей и сосредо-
эразом в местах интенсивного судоходства. Их функциони-
>ается государственными структурами и координируется ме-
анизациями. Большое число радиомаяков и предполагаемое
\itx широкое использование для передачи дифференциальных поправок требует
новых подходов к их применению. Современная тенденция развития радиома-
ячной службы определяется требованиями и рекомендациями ряда междуна-
. родных организаций. Согласно Регламенту радиосвязи (п. 466), радиомаяки
морской радионавигационной службы, которые работают в диапазоне частот
^283,5 ... 325 кГц, могут передавать дополнительную навигационную информа-
цию, используя узкополосные системы, при условии, что выполнение основ-
ных функций РМ не будет ухудшено. Определены следующие технические ха-
рактеристики средств, обеспечивающих передачу дифференциальных сообще-
ний СРНС GPS и ГЛОНАСС с помощью РМ:
частотные диапазоны, предназначенные для морской навигации в регио-
не 1 — 283,5 ... 315 кГц; в регионах 2 и 3 — 285 ... 325 кГц;
передача сообщений должна осуществляться непрерывно;
скорость передачи данных в сообщении должна быть в пределах 25 ...
200 бод;
для передачи данных должна применяться MSK (Minimum Shift Keying)
модуляция (манипуляция минимальным-фазовым сдвигом), обеспечивающая
представление двоичного нуля и единицы соответственно задержкой или опе-
режением фазы на 90° относительно фазы несущего колебания на интервале
длительностью 1 бит; занимаемая полоса частот при скорости передачи
200 бод должна составлять не более 236 Гц для 99 % мощности и 120 Гц для
скорости 100 бод;
разделение передаваемых несущих частот должно быть кратным 500 Гц
для обеспечения минимальной интерференции соседних каналов и совмести-
мости с полосой разделения каналов морских радиомаяков;
для повышения надежности работы защитные соотношения параметров
полезного и мешающего сигналов должны соответствовать требованиям
МАМС, приведенным в табл. 12.5.
Таблица 12.5. Требования МАМС к параметрам полезного
и мешающих сигналов
Разделение несущих частот между сигналами опорной станции и помехой, кГц Требуемое соотношение сигналов опорной | станции и помех при работе. дБ И
ненаправленных мор- ских и аэромаяков радиомаяков, трансли- 1 рующих дифференци- альные поправки
0,0 15 15
0,5 -25 -25
1.0 -45 -36
1,5 -50 -42
2,0 -55 -47
232 Глава 12. Аппаратура потребителей
На рис. 12.22 приведена типовая схема ДПС СРНС на базе морского
радиомаяка, в состав которой входят опорная и контрольная станции и предуЛ
смотрена связь с управляющей станцией. J
Опорная станция (ОС) обеспечивает вычисление ДП, формирование Дд
в стандартном формате RTCM SC-104 и передачу их по каналам радиомаяков^
потребителям. Для выполнения своих функций ОС должна иметь геодезиче-
скую привязку и оснащаться высокоточной, многоканальной приемной аппа-
ратурой СРНС, обеспечивающей прием сигналов всех наблюдаемых спутников
вычислительным комплексом для определения ДП и формирования ДС, моду-,
лятором для модуляции радиомаячного сигнала по закону соответствующих;
ДС, передатчиком для их передачи потребителям и средствами связи с кон-
трольной и управляющей станциями, а также другими объектами. Приемоин-
дикатор СРНС, вычислительный комплекс и модулятор для удобства исполь-
зования некоторыми фирмами изготовляются в виде моноблока.
Контрольная станция контролирует правильность работы всех наблюдае-
мых спутников системы и ДПС СРНС, а также формирование данных о их со-
стоянии, которые передаются в составе ДС потребителям. Контрольная
Ряс. 12.22. Типовая схема ДПС
станция должна иметь
геодезическую привязку и
оснащаться высокоточной
(многоканальным - ПИ)
приемной аппаратурой
дифференциальных сооб-
щений ДПС СРНС
(ПИДС ДПС), вычисли-
тельным комплексом, а
также средствами связи.
Присмоиндикатор СРНС
и ПИДС ДПС обеспечи-
вают прием сигналов всех
наблюдаемых НС и ОС
ДПС, определение коор-
динат в штатном и ДР,
выдачу всей необходимой
информации в вычисли-
тельный комплекс, кото-
рый контролирует пра-
вильность работы СРНС в
этих режимах и выработ-
ку необходимых данных
как о состоянии наблю-
даемых спутников, так и
ДПС СРНС, для передачи
передачи их на опорную и
К12.8. Особенности применения СРНС в различных, областях 233
^управляющую станции, а также, при необходимости, в центр контроля и
? управления СРНС. Указанную аппаратуру, кроме средств связи, изготавливают
Lp виде моноблока. Для удобства эксплуатации ОС и КС могут совмещаться. В
^состав ДСРНС при наличии нескольких ОС и КС входит управляющая стан-
' ция (УС) для системного контроля и управления. Последняя оснащается вы-
числительным комплексом и средствами связи с ОС и КС для обмена данны-
ми и передачи вырабатываемых управляющих сигналов.
В штатном режиме работы систем морскими потребителями использует-
ся специально разработанная для них приемная аппаратура СРНС, предназна-
/Ченная для приема спутниковых навигационных сигналов с целью выделения
навигационного сообщения, измерения радионавигационных параметров, об-
работки полученных данных и, если необходимо, данных от других навигаци-
онных систем для определения своих координат и решения различных навига-
ционных и сервисных задач. В состав ПИ СРНС в общем случае входят антен-
ное устройство, приемник, устройства обработки и решения навигационных
задач, управления, контроля и сопряжения с другими средствами, а также уст-
ройство отображения информации. В настоящее время разработаны различ-
ные типы судовых ПИ СНС, от небольших (носимых), которые определяют
координаты потребителя и обеспечивают решение простейших навигационных
задач, до устанавливаемых стационарно, удобных в эксплуатации на судах, ко-
^торые обеспечивают решение различных навигационных задач, в том числе с
использованием ДР работы и электронных карт. Они, в зависимости от на-
значения аппаратуры и требуемых её функциональных возможностей отлича-
ются, по основным техническим, эксплутационным и стоимостным характери-
стикам.
На судах широко применяют следующие комплектации ПИ СРНС:
общего типа с соответствующими устройствами приема и обработки
спутниковых сигналов, решения навигационных задач, управления, контроля
и сопряжения с другими средствами, а также отображения информации;
автономного типа с соответствующими устройствами приема и обработ-
ки спутниковых сигналов, решения навигационных задач, управления, кон-
троля и отображения информации;
типа датчика, входящего в состав интегрированной навигационной сис-
темы и включающего соответствующие устройства приема и обработки спут-
никовых сигналов, решения навигационных задач, сопряжения и отображения
информации на выносном дисплее.
Указанные типы аппаратуры конструктивно оформляются в виде основ-
ою го моноблока с выносной антенной, которая устанавливается на судне в
месте, где обеспечивается минимальное затенение принимаемых спутниковых
сигналов, и, если необходимо, дополнительных средств, например для обеспе-
чения воспроизведения электронных карт.
Судовые ПИ СРНС должны удовлетворять требованиям стандартов Меж-
дународной Электротехнической Комиссии (МЭК) к этой аппаратуре МЭК-
1108-1 для ПИ СРНС GPS , МЭК-1108-2 для ПИ СРНС ГЛОНАСС и МЭК-
234 \ . Г л a j 12. Аг уратур ютреб )елей Г
1108-3 для ПИ СРНС GPS/ГЛОНАСС и может устанавливаться на судах, ско-1
рость которых не превышает 50 узлов, с целью обеспечения возможности: 1
определения координат места и решения различных навигационных за-J
дач по спутниковым навигационным сигналам в штатном режиме работы сие-а
темы и при наличии приемника дифференциальных сообщений, обеспечи-
вающего прием и выдачу ДС в стандартной форме в ПИ СРНС в ДР;
выдачи и приема навигационной информации в требуемом объеме для
использования полученных данных при навигационных и сервисных задач.
Для оценки ПИ СРНС с точки зрения их пригодности для решения за-
дач навигации и их потребительских качеств применяют технические и экс-
плуатационные характеристики аппаратуры: точность и дискретность навига-
ционных определений; возможность работы в ДР; функциональные возможно-
сти и решаемые задачи; возможность оценки достоверности вырабатываемых
данных; наличие портов для обмена с внешним оборудованием; объем, харак-
тер и наглядность представления отображаемых данных; простота и удобство
эксплуатации; надежность; помехозащищенность; электромагнитная совмес-
тимость с судовым оборудованием; масса и габаритные размеры; потребляемая
мощность; условия эксплуатации и стоимость.
Морские ПИ СРНС GPS общего типа ведущих фирм мало отличается по
характеру и объему отображаемой информации, а также по техническим и
эксплуатационным характеристикам.
При оценке создаваемых новых типов ПИ СРНС необходимо учитывать,
в первую очередь, характеристики, которые в максимальной степени отвечают
современным и перспективным требованиям к ПИ СРНС данного типа:
прием и совместная обработка сигналов СРНС ГЛОНАСС и GPS для
решения навигационных задач, что позволит повысить точность и надежность
навигационного обеспечения потребителей;
возможность работы в ДР, т. с. наличие в ПИ необходимых алгоритмов
учета дифференциальных поправок, а также канала приема и обработки опре-
деленных типов ДС, формируемых в соответствии со стандартом RTSM SC-104
и принятых для передачи опорными станциями морской диффподсистсмы;
наличие алгоритма автономного контроля целостности (RAIM), обеспе-
чивающего использование избыточной информации для повышения надежно-
сти навигационных определений;
несколько стандартных высокоскоростных портов для информационного
обмена данными с внешними бортовыми устройствами или ЭВМ;
ввод и хранение в памяти ПИ достаточно большого числа путевых точек
и других данных для составления маршрутов плавания и решения других сер-
висных задач.
С учетом этих требований в настоящее время создастся новое поколение
ПИ СРНС с более широкими функциональными возможностями и улучшен-
ными потребительскими характеристиками аппаратуры. При этом большое
внимание уделяется вопросам, реализации дифференциального режима и со-
вместного использования навигационных сигналов обеих систем, что позво-
12. Особе к>сти > еменен. СРНС } разлив их обле кях
2
дяет значительно улучшить основные характеристики, в том числе повысить
точность и надежность навигационных определений, вопросам необходимых
связей с другим оборудованием и решения сервисных задач в том числе с
применением электронных карт.
Многие зарубежные фирмы серийно выпускают различные тины ПИ
СРНС OPS и несколько зарубежных фирм, например, 3S Navigation, Asctcch
Л ряд наших предприятий начали выпуск ПИ СРНС ГЛОНАСС/OPS. В
табл. 12.6 приведены основные характеристики некоторых типов ПИ СРНС
ГЛОНАСС /OPS.
Таблица 12.6. Характеристики некоторых приемоиндикаторов
Характеристики Приемоиндикатор
“ЧЕЛН-4” “БРИЗ-К” “БРИЗ-Н”
Режим работы: стандартный дифференциальный + + + + + +
Число измерительных каналов, ГЛОНАСС/GPS 3/5 14/14 14/14
Время получения отсчета, мин : холодный старт (менее) горячий старт (менее) 3 1 3 3 3 1
Погрешность навигационных опреде- лений (95 %) в стандартном/дифферен- циальном режимах: координат, м (менее) скорости, м/с (менее) поправки времени, .мкс 40/6 0,2 1 40/6 0,4 узла 1 40/6 0.2 1
Алгоритмы решения задач ио всем ви- димым спутникам. ГЛОНАСС GPS I ЛОНАСС/GPS + + + + + +- +- +- +-
Возможность отображения в системе координат, вводимой с любой пульта +- 4- +
Дисплеи 3 строчный ЖКС 4-строчный ЖКС 2-строчный ЖКС
Оценка точности и достоверности 11 рогноз СКП Прогноз СКП Прогноз СКП
Рабочая температура. ЛС: антенны приемоиндикатора -50 ... +50 - 10 ... +50 -40 . . +65 -10 ... +55 -50 . . +55 -10 . . +50
Габаритно размеры, мм антен ны приемоиндикатора 140.x 140х18 0 294x179x19 8 D—158 11=104 210x170x10 0 D 9? Н = 75 160x50x185
Масса, кг: антенны приемоиндикатора 2.5 6,0 0,95 2,4 0,45 1,3
Потребляемая мощность. Вт 15 9 6
Интерфейсы Два порта RS-232 по NNEA 0183 Два порта RS-232 по NNEA 0183 Два порта RS-232 по NNEA 0183
Частота выдачи данных. Гц 1 1 1
j)J___________________J_______s Г а в a i J Аппар /ура п< Дебите.. X 1
Для реализации ДР морскими потребителями кроме ПИ СРНС. в кото- ’
рой предусмотрено обеспечение работы в ДР, требуется еще приемная аппара- ;
тура дифференциальных сообщений СРНС, которая обеспечивает прием и вы- 4
дачу, полученных данных ДС в ПИ СРНС. Некоторые фирмы выпускают ПИ
СРНС и ПИДС ДПС СРНС в виде моноблока, например, фирма Trimble
Navigation — аппаратуру типа NT200D, а фирма Leica — МХ-400 .
Международными организациями МСЭ и МАМС, а также национальны-
ми организациями США разработаны основные нормативные документы ддя
морской ДПС СРНС, регламентирующие основные характеристики опорных,
контрольных и управляющих станций, параметры сигналов и форматы переда-
чи поправок потребителям и сообщений между станциями.
На основе этих документов многие морские страны уже развернули ра-
боты по внедрению морской ДПС. Так в Норвегии, Швеции, Финляндии, Ка-
наде, США и других странах созданы сети опорных станций ДПС с использо-
ванием морских радиомаяков, часть из которых уже находится в эксплуатации.
В настоящее время в эксплуатации находится более 150 и планируется созда-
ние еще более 50 дифференциальных станций.
Морская ДСРНС должна работать непрерывно и передавать потребите-
лям ДС в формате соответствующем стандарту RTCM SC-104, что обеспечива-
ет потребителям возможность надежных навигационных определений в реаль-
ном масштабе времени с интервалами не более 5 ... 10 с. Погрешности опреде-
ления места увеличиваются с увеличением расстояния от опорной станции и
старением ДП, но не должны превышать 10 м в рабочей зоне.
Основные характеристики дифференциальной подсистемы СРНС:
точность — степень соответствия между измеренными координатами
места судна и его истинными геодезическими координатами, которая характе-
ризуется погрешностью определения места;
доступность (готовность) — параметр, который характеризует вероят-
ность обеспечения потребителя необходимой информацией для определения
места судна с заданной точностью и достоверностью за период 30 cvt н рабо-
чей зоне ДСРНС;
рабочая зона -- площадь, в пределах которой возможен надежный прием
сигналов ДС для обеспечения навигационных определений с заданным уров-
нем точности и надежности;
надежность параметр, который характеризует вероятное::, обеспече-
ния излучения минимально допустимого уровня сигнала ДС за заданны!: про-
межуток времени;
целостность — способность системы своевременно обнаруживать свое
неправильное функционирование и оперативно оповещать потребителей о лю-
бых нарушениях её работоспособности. Передача данных о целостности по-
требителям может производится в составе навигационных предупреждении по
традиционным каналам связи и оперативно по каналам самой ДСРНС.
Основные параметры для ДПС, характеризующие целостность.
|j2.8- )обеннс hu при. Мнения >НС в , длинны. Облает j _____L_
предел защиты, равный максимальной погрешности определения коор-
динат потребителем в пределах рабочей зоны дифференциальной подсистемы,
В случае превышения которого должен передаваться потребителю сигнал пре-
дупреждения о неисправности;
время оповещения (подачи сигнала) — максимально допустимое время
между моментом выхода параметров системы за допустимые пределы и момен-
том приема сигнала предупреждения потребителем;
вероятность ошибки обнаружения неисправности работы системы — ве-
роятность того, что погрешности определения места превышают пределы за-
щиты большее время, чем время, в течение которого передается сигнал опо-
вещения;
частота передачи сигнала предупреждения — частота, с которой сигнал
предупреждения повторяется в точке нахождения потребителя.
В России при создании морской ДПС также принята ориентация на ис-
пользование морских радиомаяков для передачи ДС. С этой целью разрабаты-
вается отечественная аппаратура для совместной ДПС СРНС ГЛОНАСС и
GPS, обеспечивающей независимое формирование ДС СРНС ГЛОНАСС и
GPS и их последовательную или параллельную передачу в формате RTCM SC-
104 при наличии соответственно одного или двух каналов передачи данных
потребителям. Для передачи ДС разрабатывается новое поколение РМ, в кото-
рых один канал предназначен для передачи стандартного пеленгационного
сигнала, а другой — для передачи ДС. При использовании такого РМ только
для передачи ДС, один из каналов может использовать для передачи ДС СРНС
ГЛОНАСС, другой — СРНС GPS. В этом случае они должны быть оборудова-
ны аппаратурой, обеспечивающей прием и обработку сигналов СРНС ГЛО-
НАСС и GPS, определение дифференциальных поправок для этих систем,
формирование и передачу с использованием морских РМ потребителям соот-
ветствующих ДС. Если передавать дифференциальные сообщения СРНС ГЛО-
НАСС и GPS последовательно по одному каналу, то для получения заданной
точности нс менее К) м (95 %) с учетом работы СРНС GPS в режиме селек-
тивного доступа допускаются перерывы в передаче ДС СРНС GPS передачей
ДС для СРНС ГЛОНАСС один раз в минуту. В этом случае СРНС ГЛОНАСС
обеспечит указанную точность, но не обеспечит передачу данных о целостно-
сти в заданном интервале оповещения потребителей 10 с. Учитывая это, необ-
ходимо передавать ДС для СРНС ГЛОНАСС по отдельному каналу радиомая-
ка. Такая возможность имеется при одновременной передаче — ДС СРНС
ГЛОНАСС по одному и ДС СРНС GPS но другому каналу двухканальною ра-
диомаяка, т. с. при использовании радиомаяка только для передачи ДС. В
этом случае потребители могут при наличии ПИ СРНС и ПИДС СРНС ис-
пользовать в дифференциальном режиме ту из систем, ДС которой принима-
ются. Для обеспечения работы в ДР одновременно по двум системам необхо-
димо использовать два приемника ДС, каждый из которых выдает необходи-
мые данные в ПИ СРНС, а в ней предусмотрена возможность их одновремен-
ной обработки или специально разработанный для этих целей двухканальный
Л38 ) 1 ) л ав. Д. Аши>атура -ЗтребичуЛеД
приемник ДС. Для полноценной работы СРНС ГЛОНАСС в дифференциальЯ
ном режиме необходимо предусмотреть узкую передачу ДС, чтобы в рабочем
зоне ДПС обеспечивались заданные точность, доступность и целостность. 3
Дифференциальный режим СРНС позволяет значительно повысить то<Л
ность и надежность навигационного обеспечения потребителей, т. е. расшцЛ
рить функциональные возможности использования таких систем. В этом еду-*
чае точность повышается за счет вычисления на опорных станциях и передачи^
потребителям по каналам связи поправок, учитывающих постоянные и мед.?
ленно меняющиеся составляющие ошибок измеряемых радионавигационных;
параметров. Одновременно повышается надежность за счет контроля работо-
способности наблюдаемых спутников системы и ДПС как ее части контроль-
ными станциями ДПС и оперативного оповещения потребителей в составе ДС.
о целостности системы. В рабочей зоне ДПС при этом удовлетворяются самые
жесткие требования к навигационному обеспечению судов в том числе по це-
лостности для наблюдаемых навигационных спутников и самой ДПС.
Существует два подхода осуществления контроля целостности системы
основанные на внутренних и внешних методах контроля (см. § 10.5).
Внутренние методы предполагают использование данных от навигацион-
ных датчиков, расположенных на потребителе, применяя избыточную инфор-
мацию для контроля целостности. Относящийся к ним автономный контроль
целостности в аппаратуре потребителя СРНС (RAIM-Reseiver Integrity
Monitoring) предусматривает использование избыточной информации за счет
приема навигационных сигналов от большего, чем минимально необходимое,
числа спутников, что позволяет, применяя специальные алгоритмы, в зави-
симости от объема избыточной информации, обнаружить наличие или иден-
тифицировать источник неправильной информации. !! первом случае отбрако-
вывают полученные решения навигационных задач, а во втором — отбраковы-
вают измеренные навигационные параметры по сигналам неисправного спут-
ника, которые не должны использоваться для решения навигационных задач.
Для эффективного применения таких алгоритмов необходимо, чтобы приемная
аппаратура СРНС обеспечивала прием к обработку навигационных сигналов
от всех наблюдаемых навигационных спутников, что ведет к некоторому ус-
ложнению её. Особенно успешно задачи такого контроля можно решать при
совместной обработке навигационных сигналов СРНС ГЛОНАСС и OPS за
счет увеличения числа наблюдаемых спутников.
Внешние методы контроля целостности системы связаны с каналом пере-
дачи данных о целостности (OIC-GPS Integrity Channel). Они предусматривают
наличие сети станций контроля целостности для обеспечения контроля рабо-
тоспособности системы в реальном масштабе времени и регионального вычис-
лительного центра управления для обработки данных, полученных от этой се-
ти станций и формирования данных о целостности для передачи их с назем-
ной станции по каналу передачи данных о целостности потребителям. В каче-
стве каналов передачи информации о целостности СРНС GPS и ГЛОНАСС,
обеспечивающих основные требования к ним, предлагаются каналы связи
ОсобенкЛти применения СРНС в ^азличнык областях
239
Берез геостационарные спутники. При использовании канала целостности
Только для передачи информации о целостности и других данных он, как пра-
вило, является узкополосным. В случае передачи необходимых данных в кана-
Ее целостности сигналов, подобных навигационным сигналам GPS и ГЛО-
'ЦАСС, он является широкополосным и обозначается DGIC. При этом обеспе-
чивается передача данных и навигационные измерения. Использование ши-
рокополосного канала целостности в системе регионального геостационарного
дополнения СРНС GPS и ГЛОНАСС позволит улучшить доступность за счет
дополнительных навигационных сигналов, целостность за счет оперативной
^передачи потребителям информации о целостности в составе навигационных
сообщений, а также реализовать ДР широкозонной ДПС при передаче необхо-
димых данных в составе навигационных сообщений. На рис. 12.23 представле-
на схема взаимодействия в этом случае системы INMARSAT в части навигаци-
онного использования с СРНС GPS и ГЛОНАСС.
Основные этапы в программе развития системы INMARSAT для навига-
ционного использования:
ввод в эксплуатацию системы регионального дополнения СРНС GPS и
ГЛОНАСС с использованием на спутниках INMARSAT-3 ретрансляторов на-
вигационного сигнала, формируемого наземной навигационной станцией;
разработка и установка на связных геостационарных спутниках (GEO)
аппаратуры ретрансляторов и формирования навигационного сигнала;
разработка и установка на связных среднеорбитальных спутниках (ГСО)
аппаратуры формирования навигационного сигнала;
разработка аппаратуры автономных упрощенных навигационных спутни-
ков (NLS) и запуск их для проверки основных характеристик.
INMARSAT
GPS ГЛОНАСС
Навигационный сигнал,
передаваемый на спутник
Навигационные
сигналы спутника
\ ''--INMARSAT
Навигационные Потребители
сигналы СРПС^-—
Резервная наземная
навигационная
__ станция
Данные ДПС
Данные
управления
< // 'Сигнал
_временной
синхронизации
Р Основная наземная
j навигационная
|_____станция
I Данные Данные ДПС
{управления
Взаимосвязь по
Х.25
Сигналы
фавления
телеметрии
Центр управления
спутником
INMARSAT
Сеть станций
контроля
_t_____________
Вычислительный
центр
И
Рис. 12.23. Схема взаимодействия спутниковой системы связи INMARSAT
240 Глава 12. Аппаратура потребителевИ
В этом случае на первом этапе создается система региональное дополн^И
ние СРНС GPS и ГЛОНАСС на основе применения геостационарных спутн|^Н
ков INMARSAT-3 при использовании широкополосного канала целостности
для улучшения основных характеристик СРНС OPS и ГЛОНАСС и расширив
ния возможностей их гражданского применения морскими, воздушными и нау!
земными потребителями. На последующих этапах предлагается эволюционный*
подход создания гражданской GNSS с использованием регионального геоста-
ционарного дополнения СРНС GPS и ГЛОНАСС, связных среднеорбитальных
спутников с дополнительной навигационной аппаратурой и упрощенных на-
вигационных спутников при максимальном использовании существующей ин-J
фраструктуры и минимальном изменении навигационных сигналов GPS
ГЛОНАСС для обеспечения совместимости потребительской аппаратуры. Я
Планируют сохранить преемственность навигационных сигналов, чтобы 1
обеспечить возможность использования находящегося в эксплуатации парка ’
аппаратуры потребителей СРНС для реализации существующих функций сис-
тем. Однако потребуются некоторые доработки аппаратуры потребителей для \
реализации их новых функциональных возможностей, например, приема ин-
формации о целостности, ДС и других данных, передаваемых в навигационном :
сообщении навигационного сигнала регионального дополнения СРНС GPS и
ГЛОНАСС, которое по формату отличается от навигационных сообщения сиг-
налов СРНС GPS и ГЛОНАСС. Реализация такой программы позволит создать
гражданскую глобальную навигационную спутниковую систему (GNSS). Рас-
сматриваются различные варианты такой системы на базе системы региональ-
ного дополнения с использованием геостационарных связных спутников, а
также связных среднеорбитальных спутников и упрощенных навигационных
спутников. Гражданская GNSS хотя и будет отличаться от GPS и ГЛОНАСС,
но является их естественным развитием.
Таким образом, применение СРНС ГЛОНАСС и GPS в стандартном и
дифференциальном режимах и их геостационарного регионального дополне-
ния спутниковой системы связи INMARSAT позволяет иметь глобальную и
высоконадежную систему, единую для всех районов мира и нс требующую на-
личия на судах какой-либо дублирующей радионавигационной аппаратуры. По
своим тактико-техническим требованиям с учетом выполнения необходимых
работ по повышению целостности такая система способна полностью удовле-
творить всем международным и национальным требованиям как для плавания
в открытом море, так и в любых судоходных узкостях. Она позволяется обес-
печить надежную и эффективную работу всех судовых навигационных средств,
включая перспективную аппаратуру электронной картографии и управления
судном по траектории. Ее применение на судах позволит не только повысить
безопасность мореплавания, но и получить значительный экономический эф-
фект в результате сокращения пути следования судов, уменьшения расхода то-
плива, предотвращения экологических катастроф и т. д.
Внедрение на морском флоте СРНС и оснащение судов ес приемной ап-
паратурой создает основу для революционных преобразований в навигацион-
Ц2.8- Особенности применения СРНС в различных областях - 241
дой технике и технологии судовождения. На базе глобальной высокоточной и
непрерывно поступающей навигационной информации в ближайшее время на
^орских судах начнется применение следующих комплексов и систем: навига-
ционный комплекс, в состав которого входят ПИ СРНС; системы электрон-
ной картографии (ЭКДИС), управления судном по траектории, зависимого
контроля за судами; аварийный радиобуй системы КОСПАС-САРСАТ с при-
емником СРНС.
Кроме этого, высокоточная спутниковая навигационная аппаратура в бу-
дущем может применяться для выработки данных о курсе судна и абсолютной
скорости движения, что в принципе позволит заменить традиционные указа-
тели курса и скорости (компас и лаг). Указанная аппаратура с дифференци-
альными поправоками может также эффективно использоваться в системах
управления движения судов (СУДС) в портах и узкостях. Возможны и другие
варианты применения спутниковой навигационной аппаратуры морскими по-
требителями, например, для целей общей навигации и проведения гидротех-
нических работ при строительстве новых портов, сооружаемых в этом районе,
при проведении дноуглубительных работ на фарватерах, разведке и добыче
полезных ископаемых.
Вместе с тем следует иметь в виду, что при использовании новой спут-
никовой навигационной техники возможны случаи неправильного ее приме-
нения, в результате чего могут возникнуть аварийные ситуации и даже аварии.
Примером может служить посадка на мель финского пассажирского парома
"Sally Albatross" и американского лайнера “Royal Majesty”, оснащенных самой
современной навигационной техникой. Необходимо помнить, что для эффек-
тивного применения новой техники следует обеспечить соответствующее обу-
чение и тренажерную подготовку судоводителей и снабдить их качественной
технической и эксплуатационной документацией.
12.8.3. Особенности использования наземным транспортом
Проблема автоматизации управления движением наземных транспортных
средств возникла в начале XX века вместе с развитием железнодорожного и
автомобильного транспорта. Наибольшего развития автомати шрованные сис-
темы управления движением получили на железнодорожном транспорте на
основе релейной автоматики УКВ-радиосвязи.
В 70-х годах вопрос об автоматизации управления движением автомо-
бильного транспорта в связи с массовым развитием дорожного движения в
промышленно развитых странах встал особенно остро. Поэтому на мировом
рынке появились системы управления автотранспортом на основе локальных
систем местонахождения объектов и автомобильных УКВ-радиостанций.
Принципиально новые возможности для создания автоматизированных
систем управления транспортными потоками в масштабах городов, регионов и
даже континентов появились в 80-х годах в связи с развитием радиосистем
дальней навигации и дальней радиосвязи: импульсно-фазовых и фазовых ра-
242 . . Г л э в а 12. Аппаратур» потребителей !
дионавигационных систем, систем метеорной радиосвязи и, в особенности,!
спутниковых РНС и спутниковых систец радиосвязи.
Организация движения транспортных средств характеризуется большим»
разнообразием, что требует учета специфики навигационного обеспечения при!
перевозке грузов и пассажиров.
Классификацию видов организации движения наземного транспорта
проводят по различным признакам: в локальном регионе или по проложенным
магистралям и трассам; в составе группы или одиночное движение; по уста-
новленным или произвольным маршрутам; по расписанию или вне установ-
ленного регламента.
Каждый из вариантов организации движения принципиально отличает-
ся один от другого тем, что требует разработки для каждого варианта индиви-
дуальной технологии управления транспортными процессами, основу которых
составляет специфическое навигационное обеспечение с соответствующими
требованиями.
Уровень требований к навигационному обеспечению технических
средств транспортно-дорожного комплекса зависит от того, где используются
результаты определения параметров движения — непосредственно на борту
транспорта или осуществляется дистанционный контроль и управление транс-
портом, например, на диспетчерском пункте.
Навигационное обеспечение наземных транспортных средств необходимо
для реализации информационно-навигационных технологий, используемых
при решении задач контроля в интересах повышения эффективности и безо-
пасности дорожного движения.
Области применения информационно-навигационных технологий диф-
ференцированы по различным группам решаемых задач в транспортно-дорож-
ном комплексе России:
автоматическое обнаружение мест дорожно-транспортных происшествий;
охрана и контроль состояния перевозимых грузов и обеспечение безо-
пасности участников дорожного движения;
управление муниципальным транспортом (автобусы, троллейбусы, трам-
ваи, транспорт жилищно-коммунальных хозяйств, транспорт доставки продо-
вольственных и промышленных товаров населению, пожарная служба, скорая
помощь);
управление технологическим транспортом при строительстве и ремонте
автомобильных дорог;
мониторинг, идентификацию и управление транспортом на карьерных и
терминальных перевозках;
мониторинг, идентификацию и управление перевозками крупногабарит-
ных, высокотоннажных и экологически опасных грузов;
управление транспортом ведомственных и коммерческих организаций
(внутригородские и пригородные перевозки);
управление транспортом магистральных и интермодальных (земля—море,
земля—река и т. п.) перевозчиков.
М2-8. Особенности применения СРНС в различных областях ____ __243
Требования наземных потребителей к точности местоопределения транс-
портных средств зависят от предназначения тех или иных технологий контро-
ля и управления транспортными процессами:
при решении большинства задач, связанных с обеспечением безопасно-
сти движения и организации перевозок пассажиров и грузов в процессе хозяй-
ственной деятельности, требования к точности местоопределения транспорт-
ных средств с погрешностью не хуже 100 м. (предельная погрешность) в на-
стоящее время удовлетворяют потребности автомобильно-дорожной отрасли;
при решении специальных задач (слежение за экологически опасными
грузами, защита от угона и поиск угнанных средств и т. д.) требования к точ-
ности местоопределения являются более высокими — не хуже 5 ... 15 м.
(предельная погрешность).
Требования наземных потребителей к размерам рабочей зоны задаются
исходя их анализа территориально пространственных условий реализации за-
дач, использующих информационно-навигационные технологии:
территория Российской Федерации, территории стран ближнего и даль-
него зарубежья — при организации внутрироссийских и межгосударственных
перевозок;
глобальная зона — при организации интермодальных перевозок, вклю-
чающих перевозку грузов речным и морским транспортом.
Требования к дискретности (темпу) обновления координатной информа-
ции задаются на основании анализа структуры тех или иных технологий:
при контроле и управлении большими группировками (системами)
транспортных средств — не более 1 с ( по каждому транспортному средству,
входящему в состав группировки;
при решении специальных задач — не более 1 с;
при контроле и управлении одиночными транспортными средствами при
их движении в условиях города и по магистрали — 0,5 ... 1 мин.
При формировании требований к доступности наземных потребителей к
радионавигационным системам исходят из критериев решения (достижения)
тех или иных задач, реализуемых при использовании соответствующих техно-
логий контроля и управления транспортными процессами:
при контроле и управлении большими группировками транспортных
средств, а также при решении специальных задач допускается не более I %
сеансов навигации, в которых не выполняются требования по точности. Отсю-
да требования к доступности данной категории транспортных средств к РНС
определяются значением вероятности не менее 0,99;
при контроле и управлении одиночными транспортными средствами до-
пускается доля сеансов, в которых требования по точности не выполняются,
до 5 %, что обуславливает значение требований к доступности РНС для оди-
ночных транспортных средств на уровне 0,95.
Требования потребителей автомобильно-дорожного комплекса к целост-
ности РНС задаются исходя из возможностей парирования в автоматизиро-
ванных системах контроля и управления транспортными процессами тех вре-
j )
244__________
гвовжавопивш
} 1 1 \ )
Глава 12. Аппаратура потребителе^
менных интервалов, на которых потребителям поступает с РНС недостоверная
(ложная) навигационная информация. Противодействовать такой информации
системы управления транспортными процессами могут ограниченное врем!
Именно численное значение возможного времени противодействия ложной
информации в системах диспетчерского контроля и управления с заданным
уровнем вероятности, по истечении которого должно поступать сообщение о
нарушении функционирования РНС, задается в качестве показателя ее це-
лостности.
В существующих системах диспетчерского контроля и управления транс-
портными процессами время, затрачиваемое на обнаружение и доведение до
потребителя сообщений (команд) об исключении из числа действующих лож-
ных источников навигационных сигналов не должно превышать 15 ... 30 с при
вероятности 0,95.
Требования потребителей наземного транспорта к радионавигационным
системам в обобщенном виде представлены в табл. 12.7.
Таблица 12.7. Требования потребителей наземного транспорта
к радионавигационным системам
1 Вешаемые задачи Характеристики
Контроль- и управле- ние движением транс- портных средств Рабочая зона Точность (предель- ная), м Темп обнов^ ления коор- динат, с Доступ- ность Целост- ность, Т *ВОССТ ’ С (Р=0,9)
Большие группировки Территория РФ 100 1 0,99 15 . ..30
Одиночные средства Территория РФ, СНГ 100 30 ... 60 0,95 15 . . 30
При решении спе- циальных задач Территория РФ 5 ... 15 1 0,99 15 . . 30
Удовлетворение приведенных выше требований может быть обеспечено
только при применении АП СРНС.
12.8.4. Особенности использования АЙ СРНС в геодезин
В настоящее время единые системы координат и высот на территорию
России задаются соответственно государственной геодезической сетью (ГГС) и
государственной нивелирной сетью (ГНС).
В 60-х годах были начаты работы по построению и уточнению общезем-
ной геоцентрической системы координат по наблюдениям специализирован-
ных геодезических спутников. Одновременно определялись и геофизические
параметры Земли (ГПЗ). Носителем создаваемой системы координат являют-
ся центры пунктов Космической геодезической сети (КГС), ведущих посто-
янные наблюдения за спутниками. Хронологически последний вывод коорди-
нат пунктов КГС, полученный по наблюдениям спутников системы ГЕОИК, и
р2.8. ^собеииос.яи ирил.~Иеипя ».Х/7С е Р-Хличиы.. Облает. ) 245
согласованных с ними параметров ГПЗ задает систему координат, известную
£ак ПЗ-90 (Параметры Земли 1990 г.).
к В целях общего повышения точности и однородности ГГС в период
,}987—1993 гг. с использованием спутниковой навигационной системы ТРАН-
ЗИТ создана Доплеровская геодезическая сеть (ДГС), включающая 136 пунк-
тов, равномерно распределенных на территории бывшего СССР.
В 1991 г. было завершено общее уравнивание всей астрономо-
геодезической сети (АГС), а в 1995 г. совместное уравнивание КГС в составе
,26 пунктов на всей территории бывшего СССР, ДГС (136 пунктов) и АГС.
В результате точность созданной, по существу новой референцией сис-
темы координат оценивается сейчас следующими точностными характеристи-
ками взаимного положения пунктов в значениях СКО:
для смежных пунктов на расстояниях 10 ... 15 км — 2 ... 4 см по каж-
дой из плановых координат;
на расстояниях 300 км и более ошибки возрастают до 25 ... 80 см по
плановым координатам.
Ошибки взаимного положения пунктов на расстояниях до 300 ... 700 км
в основном определяются ошибками АГС и возрастают с увеличением рас-
стояний. При больших расстояниях значения ошибок в большей мере зависят
не от расстояния между пунктами, а от их расположения относительно пунк-
тов болесточных сетей KFG и ДГС.
По результатам совместного уравнивания точность взаимного положе-
ния любых пунктов КГС оценена СКО 15 ... 20 см по каждой из пространст-
венных координат без учета общих ошибок ориентирования всей системы ко-
ординат ПЗ-90, влияние которых взаимные положения может составить
1 ... 2 м на расстояниях 8 ... 9 тыс. км.
Итогом работ по выполненному уравниванию ГГС должно быть введе-
ние новой референцией системы координат 1995 г. Заметно улучшенная по
сравнению с системой 1942 г. новая система, снимая многие проблемы, тем
не менее не обеспечивает решение многих задач.
В настоящее время решение широкого круга геодезических задач уже
невозможно представить без применения спутниковых радионавигационных
систем глобального обзора типа ГЛОНАСС и GPS. Геодезические методы, ос-
нованные на использовании этих систем, занимают ведущие позиции при по-
строении глобальных и региональных геодезических сетей, определении па-
раметров вращения Земли, решении задач глобальной и региональной геоди-
намики. Геодезические СРНС-определения, благодаря повышенной точности,
оперативности, независимости от погодных условий, отсутствию требований к
взаимной видимости между определяемыми пунктами, практически вытесни-
ли традиционные наземные геодезические методы при построении локальных
сетей как общего назначения, так и сетей, создаваемых для определения де-
формаций земной поверхности природного и технического происхождения.
Все более массовый характер приобретает использование СРНС-аппаратуры
при проведении геодезических и топографических съемок различного назна-
246
Г л а в a 12. Аппаратура потребителей
чения, при геодезической привязке аэроснимков и космических снимков вы- '
сотного разрешения, а также для непосредственной геодезической привязки
положений фотокамер в процессе выполнения аэросъемочных залетов. )
Новые методы координатных определений пока не составляют конку-
ренции по существу только геометрическому нивелированию, а также в ин-
женерно-геодезических работах повышенной точности. При этом основным
фактором, ограничивающим возможности применения спутниковых методов
для определения высот относительно поверхности квазигеоида (нормальных
высот) взамен геометрического нивелирования, по крайней мере низкого и
среднего классов, является не недостаточно высокая возможная точность
спутниковых определений, а отсутствие (пока) достаточно детальной и точ-
ной информации о высотах самой поверхности квазигеоида.
В то же время использование СРНС открывает новые возможности в
решении задач глобальной и региональной геодинамики, характеризующихся
наиболее жесткими требованиями к точности и дальности передачи координат
— 3 мм +5 мм на каждые 1000 км (3 мм + 5 10-8£, где L — расстояние). При
решении задач локальной геодинамики на территориях протяженностью от
нескольких десятков до нескольких сотен километров необходима и достижи-
ма точность 3 мм +1 мм на каждые 10 км.
Повышенные требования к точности возникают и при использовании
спутниковых методов для определения нормальных высот (спутниковое ниве-
лирование). Минимально необходимая при этом точность передачи высот
5 мм + 10 ... 30 мм на каждые 100 км.
Реально достижимая точность методически строго поставленных спут-
никовых определений на коротких (до I ... 2 км) расстояниях соответствует
СКО определения взаимных положений по плановым координатам порядка
0,5 мм и примерно I мм ио высоте. Эгой характеристикой по существу уста-
навливается точностнач граница применимости СРНС-онрсдслсний при ре-
шении задач Hi геодезии. Естественно, что на малых территориях
прозяженпос: до .. тл.л.ьто километров шк-имушество традиционных э.тек-
гроино-он гич-, ских д >.л '.номерных измерений но точности сохраняется и при
определении иформацай >емной поверхности.
В соответствии с Концепцией перевода системы геодезического обеспе-
чения на сн . 1 :’п о.-вые 'сх ты. но.т: отовлепной Федеральной службой е > г. -
ши и картографии России (Роскартография). предусматривается создание
трех новых вилок опорных геодезических сетей: Фундаментальной астрономо-
геодезической сети (ФАРС). Высокоточной геодезической сети (ВГС) и Спут-
никовой ।содезической сети I класса (СГС-1).
Фундаментальная астрономо-геодезическая сеть должна будет включать
50 ... 70 пунктов при расстояниях между пунктами 700 ... 800 км. Из всех
пунктов ФАГС. около 15 должны быть постоянно действующими, а остальные
— периодически переопределяться группами с цикличностью, зависящей от
гсодинамической активности региона. В состав постоянно действующих пунк-
тов должны быть включены часть пунктов КГС, пункты спутниковых наблю-
12.8. Особенности применения СРНС в различных областях
247
дений Российской академии наук (РАН), пункты Службы определения пара-
метров вращения Земли, пункты сверхдлиннобазового радиоинтсрферометри-
деского комплекса “ КВАЗАР-КВО” РАН. Фундаментальная астрономо-
геодезическая сеть, по крайней мере частью постоянно действующих пунктов,
должна быть интегрирована в международные спутниковые сети аналогичного
назначения. Фундаментальная астрономо-геодезическая сеть будет служить
основой для построения более плотных опорных спутниковых сетей и опреде-
ления точных эфемерид спутников и обеспечивать решение задач глобальной
И региональной геодинамики.
Фундаментальная астрономо-геодезическая сеть должна обеспечивать
определение положений пунктов относительно центра масс Земли с СКО не
более 10 ... 20 см при ошибке взаимного положения любых ее пунктов с СКО
не более 2 см в плане и 3 см по высоте с учетом возможных скоростей их
движения из-за деформаций и движений земной поверхности.
Высокоточная геодезическая сеть должна состоять из 500 ... 700 пунктов,
при расстояниях между смежными пунктами 150 ... 300 км в зависимости от
регионов. Созданием ВГС решаются следующие задачи:
точное распространение единой системы координат на всю территорию;
решение задач региональной и локальной геодинамики;
объединение создаваемой плановой, а точнее пространственной системы
координат с высотной основой, задаваемой нивелирными сетями;
определение с использованием гравиметрической информации детальных
точных данных о высотах квазигеоида для практической реализации спутнико-
вого нивелирования.
В рамках программы модернизации системы геодезического обеспече-
ния метод спутникового нивелирования рассматривается как альтернатива ме-
тодам геометрического и тригонометрического нивелирования для определе-
ния нормальных высот. Совместное использование ГЛОНАСС <>PS-измерсний
и нивелирных измерений I и II классов планируется как iineipyMeiri для более
точного распространения единой системы высот на всю терг.и глпы! .граны.
Средне квадрат ическая ошибка ВГС по взаимном', ц.ыиовомх по.юженик;
смежных пунктов должна быть не хуже 3 мм +5-10 i. и i мм + 7 • 10 " L по
геодезической высо те, также с уче том возможны е Cr.oooci г'1 смещения
пунктов.
Спутниковая i голезическая сен. I класса обеспечив.!; • сгуще••'ш- ВГС
целью: создания сети пунктов с благоприятными условиями наблюдений и хо-
рошей доступностью в интересах всех потенциальных пользователей; решения
задач локальной геодинамики; определения данных для сведения результатов
прежних геодезических определений и топографических съемок с результатами
спутниковых определений во вновь формируемой системе геодезического
обеспечения (оценка и учет локальных деформаций существующей ГГС).
Среднее расстояние между смежными пунктами СГС-1 варьируется в за-
висимости от регионов от 50 км с слабо обжитых районах до 30 ... 35 км в
районах с интенсивной хозяйственной деятельностью. В отдельных районах, в
248 Т л :u в а 12. Аппаратура потсдаебитеж^н
том .числе =» районах повышенной сейсмической активности предполагает®;
построение и болас плотной сети. Не реже чем через 70 ... 100 :км зпупкц
СГС-1 должны быть совмстцстш или связаны с пунктами .существующей. .ГГ(3
что позволит устранить или учесть локальные .деформации последней а чае
тично и повысить точность ^взаимного положения ее близких пунктов. В рай
онах повышенной сейсмической активности и особенно в районах сущест-
вующих локальных геодинамических полигонов такое совмещение или при»,
вязка должно иметь большую плотность для лучшего обеспечения связи эпох,
прежних и новых определений. ;
Точность СГС-1 также должна варьироваться в зависимости от регионов’
и предполагать по крайней мере две градации: стандартная, соответствующая
определению взаимных положений смежных пунктов с СКО 5 мм + 2 • 10~7£
по каждой из плановых координат и 7 мм + 3-10-7£ по геодезической высоте,
и повышенная, с СКО взаимного положения смежных пунктов СГС-1 и пунк-
тов СГС-1 относительно всех смежных пунктов ВГС 3 мм + 1- 10Т7Х в плане и
5 мм + 2 -1071 по высоте.
Ориентировочно число пунктов СГС-1 составит 12 ... 15 тыс.
Модернизация всей системы геодезического обеспечения ориентирована
на применение спутниковых геодезических методов как при. создании геоде.-
зической основъг нового качества, так и при ее последующем использовании
потребителями. Центральное место при этом отводится системам ГЛОНАСС
и GPS. Только для построения опорных сетей и выполнения съемок по ос-
новному государственному заказу необходимо несколько сотен геодезических
спутниковых приемников. Общая же потребность в спутниковой геодезиче-
ской аппаратуре, включая всех основных потребителей, ориентировочно оце-
нивается несколькими тысячами комплектов. Совершенно очевидно, что эти
потребности не могут удовлетворяться только аппаратурой зарубежного про-
изводства, тем более ориентированной только на работу по спутникам систе-
мы GPS. И если создание основных опорных сетей и особенно ФАГС, по
крайней мере на начальном этапе, более целесообразно на основе системы
GPS вследствие ее развитой инфраструктуры в виде уже существующих гло-
бальных систем пунктов наблюдений и служб точных эфемерид, то в более
массовых работах технически важно совместное использование обеих систем
GPS и ГЛОНАСС. В то же время геодезическое применение системы ГЛО-
НАСС находится сейчас, по существу, лишь на начальной стадии. Этому есть
несколько причин. В начале разработки и долгое время в последующем ГЛО-
НАСС не рассматривалась как потенциальная система для геодезии, как это
было и с навигационной спутниковой системой первого поколения “Цикада”,
аналогичной системе “Транзит”. Однако основной причиной отставания яви-
лось отсутствие необходимой отечественной электронной базы, пригодной
для реализации точных фазовых измерений, поэтому, в частности, была пре-
кращена разработка GPS/ГЛОНАСС приемника, выполнявшаяся в конце 80-х
^12-8. Особенности применения СРНС в различных областях 249
начале 90-х годов по заказу Главного управления геодезии и картографии
При Совете Министров СССР.
В настоящее время существует только две завершенные разработки гео-
дезических спутниковых приемников, работающих п<? сигналам спутниковой
системы ГЛОНАСС: TRIMBLE 4000 SGL и GG24 фирмы ASHTECH. Двухчас-
тотный приемник 4000 SGL изготовлен в 1995 г. лишь в нескольких опытных
экземплярах, работает только по сигналам спутников ГЛОНАСС и имеет по
девять параллельных каналов для каждого из рабочих диапазонов частот.
О начале продаж приемников GG24 фирмой ASHTECH было заявлено в
марте 1997 г. Приемник — одночастотный, работает по сигналам обеих сис-
тем: на 12 параллельных каналах для каждой системы. Сообщение с данными
о результатах испытаний этого приемника, выполненных в России, содержат-
ся в настоящем сборнике.
В настоящее время по заказу Роскартографии ведется разработка со-
вмещенного геодезического GPS/ГЛОНАСС-приемника, который будет иметь
по 9 двухчастотных каналов для наблюдений спутников каждой из систем.
GPS или ГЛОНАСС. Обе системы очень близки по техническим характе-
ристикам и идентичны по принципам функционирования. Основные характе-
ристики обеих систем, данные о которых потребуются в дальнейшем, приведе-
ны в табл. 8.1.
Для уменьшения занимаемого частотного- диапазона спутники ГЛО-
НАСС, находящиеся в одной орбитальной плоскости, но по разные стороны
Земли и одновременно не видимые, могут работать на одних и тех же литер-
ных частотах, что предусматривается при проведении модернизации системы
до 2005 г.
Прежде чем приступить к сравнению двух систем с точки зрения их гео-
дезического применения остановимся на основных принципах использования
СРНС в геодезии. Во-первых, требуемая точность измерений (1 ... 20 мм) не
может быть достигнута за счет измерения задержки сигнала по коду. Действи-
тельно, из (5.1) следует, что при используемых сигналах с эффективной поло-
сой примерно 1 МГц и реальных отношениях сигнал/шум — 38 дБГц потен-
циальная точность (с учетом только флуктуационных ошибок) измерения ко-
ординат 1 ... 10 м. Во-вторых, кроме флуктуационной ошибки полная ошибка
измерений включает (м):
Космический сегмент
Нестабильность частоты генератора ....................... 6,5
Задержка в бортовой аппаратуре .......................... 1>0
Неопределенность пространственного положения НС ......... 2,0
Другие ................................................ 1,0
Наземный сегмент
Неточность эфемерид ............................... 8,2
Другие ............................................ 1,8
Сегмент пользователя
Ионосферная ошибка ................................ 4,5
Тропосферная ошибка ..................................... 3,9
Шумовая ошибка приемника .......................... 2 9
Многолучевость .................................... 2*4
Другие ............................................
250
Глава 12. Аппаратура потребите^
Таким образом, стандартные методы определения координат в СРНС »
позволяют достигнуть требуемых точностей, поэтому в геодезии использукт
относительные координатные определения (см. п. 11.1.4) по фазовым Изме}>
ниям на несущей частоте.
Непосредственно фазовые измерения эквивалентны измерению ПД с не
определенной составляющей величиной, равной целому числу длин волн нс!
сущей частоты. Ввиду неоднозначности непосредственных фазовых измерений,
их прямое использование целесообразно только для сглаживания менее точ!
ных, но однозначных псевдодальномерных измерений по коду.
Фактически, в приемнике измеряются разности фаз принимаемого спут.
никового сигнала и сформированного в приемнике опорного сигнала.
Пусть имеется единая шкала времени /ив момент времени /ц = 0 с НС,г
имеющего номер 5 излучается сигнал. В i-м приемнике, в момент времени t
определяемая в циклах 2 п полная фаза сигнала
(1246),
-i -
где АГ/(/) — полное число циклов от момента излучения; ф*(/) — дробная
часть фазы (в долях цикла). ... ____
Аналогичное соотношение можно записать для фазы опорного сигнала
fl on (0 ~ on (4 + Ф/ onW •
Слагаемые в правой части равенства имеют тот же смысл, что и г
(12.46), но для опорного сигнала.
Тогда разность фаз сигнала 5-го спутника и опорного сигнала в 7-м пр?
емнике будет
л<₽/(0 = <₽/(0 ~Ф/оп(4 = Ф?(0 _ Ф/оп(0 + = дФ/(0 + Л^н/(0 > (12.47
где ЛфД/) — фактически измеренное (в долях цикла) значение разности фаз
Л/^,(/) = Л/(/)- Nionft) —- неоднозначность фазовых измерений.
Заметим, что при непрерывном слежении за сигналом НС на небольши:
временных интервалах М‘ является постоянной величиной, поэтому в даль
нейшем зависимость от времени будет опускаться.
В идеальном случае (при наличии единой шкалы времени, стабильно!
частоте передатчика и неизменном расстоянии между спутником и приемн?
ком) можно записать
Особенности применения СРНС в различных областях , . 251
f <₽;(/) = фЦ' - = л/ - +Ф0 = <pU') - > <12-48)
гае Фюл — фаза излучаемого сигнала в момент времени t; fs — частота сигна-
ла s-ro спутника; rf = Д//с — задержка распространения сигнала от s-го спут-
ника до /-го приемника (Д* — расстояние между спутником и приемником);
— начальная фаза излучения, которую в дальнейшем для простоты будем
^полагать равной нулю.
? При известной и стабильной частоте опорного сигнала в приемнике и
^Известном моменте излучения сигнала из (12.47), (12.48) следует, что даль-
ность между двумя объектами может быть измерена с точностью до долей дли-
ны волны излучаемого сигнала, т. е. до миллиметров. Этот факт является ос-
новой фазовых измерений. Однако отсутствие единой шкалы времени на борту
НС и у потребителей (приемников), расхождение временных шкал различных
‘Потребителей (приемников), нестабильности излучаемых частот, различие час-
тот излучаемого и опорного сигналов и ряд других факторов приводит к воз-
никновению ошибок измерений. Рассмотрим некоторые из этих источников и
'оценим их влияние.
__ Сначала положим, что все подсистемы (устройства) работают в единой
шкале времени. Как следует из (12.47) измерение разности фаз принятого сиг-
нала и опорного в одном приемнике позволят определять координаты с ошиб-
кой, кратной целому числу Mf длин волн излучаемого сигнала. Если анало-
гичные измерения провести в J-м приемнике (по сигналу с того же s-ro спут-
ника), т. е. измерить Дфу(/) = <pj(/) - фуОп(0 ~ дФу(О + мн у(0 > то Далее можно вы-
числить разность
ДФ»0 = М') - Лф?(') = |ф/(') -Ф/0] -|ф,-.ои(') - Фу оп(')] + I - (12.49)
Первое слагаемое в (12.49) определяет тот факт, что все постоянные
(систематические) погрешности в спутниковом сигнале, например, ионосфер-
ные, тропосферные, задержки в бортовой аппаратуре, исключаются в первых
разностях. Наличие последнего слагаемого в (12.49) приводит к уменьшению
значение неоднозначности измерений. Этот факт служит основой для по-
строения многошкальных измерителей (4.2], в которых путем использования
набора различных опорных частот меняется значение последнего слагаемого в
соответствующих разностях (12.49), что позволяет устранить неоднозначность
фазовых измерений. Однако наряду с положительными свойствами, первая
разность содержит ошибки, обусловленные нестабильностью опорных частот
двух приемников (второе слагаемое в (12.49)).
252 Глава 12. Аппаратура потребителеЙИ
В связи с отмеченным недостатком первых разностей, на практике Я
большинстве случаев используют^ вторые разности фазовых измерений. Прм
этом первые разности представляют собой разности одновременных измерения
двумя приемниками сигнала одного и того же спутника, а вторые разности
представляют собой разности первых, полученных для одной и той же эпохц
наблюдения по разным спутникам. Таким образом, для вторых разностей mo«j
но записать выражение .
д2Ф^(/) = дф*-дф? =[ф?(0-ф?(0]-[фГ(0-ф7(Ф
+ [(К1/ - MSj) - (м?, - М^)], (12.50)
4
из которого следует, что влияние опорных частот приемников исключено. Из!
(12.50) видно, что, если измерения в приемниках проводить синхронно, то;
влияние различие шкал времени приемников также исключается. ~
В реальных условиях частоты приемников и спутников различны, шкалы
времени приемников точно не синхронизированы между собой и шкалами,
спутников. Спутниковые сигналы обрабатываются в приемниках с задержками,
поэтому соотношения (12.49), (12.50) необходимо переписать с учетом этих
факторов. При этом не будем учитывать ошибки шкал времени спутников по
отношению к системной шкале времени, поскольку уже в первых разностях
эти ошибки исключены полностью, если частоты спутников постоянны. Непо-
стоянство частоты спутника может влиять из-за того, что при синхронных на-
блюдениях разнесенными приемниками результаты измерений относятся к
разным моментам выхода сигнала со спутника. Однако эта разновременность
даже при больших расстояниях^ не велика и при необходимости соответствую-
щая поправка может быть вычислена при известном или моделируемом изме-
нении частоты спутникового генератора частоты.
Пусть ts — шкала времени спутника, которую будем полагать одинако-
вой для всех НС, /' — шкала времени /-го приемника, а расхождение между
этими шкалами даемся соотношением № = № + 8tf.
Для фазы опорного сигнала /-го приемника в его шкале времени
4>/on('(/)) = = Z/onGW = Ф/опР'О +//o.,8tf,
(12.51)
где <р/оп(г J — фаза опорного сигнала в шкале времени спутника.
Аналогичное соотношение, но с учетом дополнительной фазовой ошиб-
ки , вызванной запаздыванием сигнала в аппаратуре, можно записать для
фазы принятого сигнала
|р2.,8) Особенности применения СРНС в различных областях 253
•; »?(/'>) = И+/Х +Мп/. (12.52)
Подставляя (12.51) и (12.52) в выражения для первых (12.49) и вторых
12.50) разностей и выполнив необходимые преобразования, получаем сле-
дующие выражения для поправок (ошибок) в шкале времени спутника к соот-
ветствующим разностям измерений фаз, измеренных в шкале времени прием-
ника
(д = [(Л on - АН - (Л on - ЛИ] + (s<pLi J - 8ф5ап /) +
+ (12.53)
(дф«(^))ош =1(4 -ла>^]+(8фа1У-8фй1/)-
-(^У -8Й/) + [(л^('(')) (12-54)
В первых разностях (11.21) влияние ошибок приемников и неоднознач-
ностей фазовых измерений не могут быть разделены, а значение последних не
может быть определена с точностью до цикла, поскольку синхронизация при-
емников невозможна на субнаносекундном уровне. Однако при близости час-
тот спутника и приемников влияние несинхронности шкал времени приемни-
ков может быть существенно снижено.
Во вторых разностях полностью исключается влияние частот приемни-
ков, а влияние несинхронности шкал времени — лишь при равенстве частот
спутников. Влияние задержек в приемниках исключается не только при равен-
стве их для всех спутниковых каналов каждого из приемников, но и при ра-
венстве задержек для “одноименных” каналов разных приемников, даже если
они различны между каналами.
В действительности даже при равенстве спутниковых частот остаточное
влияние несинхронности существует, поскольку имеются не учтенные нами
различия частот из-за доплеровского смешения. Кроме того, несинхронность
должна быть достаточно мала, чтобы можно было относить измерения, полу-
ченные разными приемниками, к одним и тем же положениям спутников.
Практически при приеме сигналов GPS достаточна синхронизация приемни-
ков в пределах 1 мкс.
При наблюдениях спутников ГЛОНАСС, если для измерений по всем
спутникам используется одна и та же опорная частота /оп приемника, влия-
ние несинхронности /- и у-го приемников (расхождение их шкал времени
254 ' ' Г л а в а 12. Аппаратура потребителей I
I
-8^) к фазовому расхождению Поскольку различие час-
тот одновременно наблюдаемых спутников может составлять 6,75 Мгц, то прц
расхождении шкал времени в 1 мкс будет накоплена ошибка в 6,75 цикла, прц
которой теряется даже смысл применения фазовых измерений. Если для фазо-
вых измерений по каждому спутнику на основе общей опорной частоты фор-
мировать свою референцную литерную частоту, подобно тому, как это делает-
ся при формировании спутниковых литерных частот, то влияние несинхрон-
ности приемников будет сведено до того же уровня, что и при использовании
GPS.
Как показывают оценки, полученные на основе частотно-временных ха-
рактеристик радиоэлектронных элементов, зависимость задержек от частот-
ного разнесения сигналов ГЛОНАСС может вносить дополнительную ошибку,
эквивалентную 2...3 мм. Если во всех приемниках используется элементная
база с идентичными характеристиками, то влияние дифференциальных задер-
жек исключается.
Как первые, так и вторые разности неоднозначных фаз представляют
собой линейную комбинацию неразделяемых величин. К тому же, при исполь-
зовании ГЛОНАСС целочисленные значения неоднозначностей, входящие во
вторые разности, отнесены к существенно различным длинам волн, поэтому
необходимо предварительное преобразование выражения (12.53), (12.54) для
приведения к единой размерности всех его составляющих.. Поскольку соотно-
шение между частотами известно, то такое приведение к одной частоте воз-
можно. При этом должны быть скорректированы как накопленное при непре-
рывном слежении с начального до текущего измерения число целых циклов,
так и дробные значения измеренных фаз. Если с первой корректировкой про-
блем не возникает, то для вычисления дробной части необходимо предвари-
тельно с относительно высокой точностью знать разности дальностей до спут-
ников.
Различие длин волн при максимальном разнесении литерных частот
примерно равно 1 мм. Для исправления дробной части с предельной ошибкой
менее четверти цикла (примерно 5 см), критичной с точки зрения последую-
щего корректного разрешения фазовых неодназначностей, достаточно знать
разность дальностей с ошибкой не более 50 длин волн или 10 м. Получение
разностей дальностей с такой точностью по кодовым измерениям не представ-
ляет проблемы. Однако поскольку фазовые неоднозачности по разным спут-
никам во вторых разностях не разделяются, то лальнейшее уточнение разно-
стей дальностей аналитически методом последовательных приближений не-
возможно. Соответственно влияние ошибок вычисления исправленных дроб-
ных отсчетов фаз полностью войдет в результат относительных определений.
Следовательно разность дальностей должна быть известна априори с более вы-
сокой точностью до нескольких длин волн. Это в принципе возможно при ис-
пользовании результатов кодовых измерений, сглаженных по внутренне более
точным измерениям фаз на несущей частоте или при совместном измерении
рвзличиыхоблас^
fei2;8. Особенности применения СРНС в
задержки по задержке кода и фазе (более подробно см. гл. 14). То об-
стоятельство, что в системе ГЛОНАСС, в отличии от GPS, фазы кодовой по-
следовательности и фазы несущей не совмещены и соотносятся произвольно,
в данном случае не существенно. При сопоставлении первых разностей кодо-
вых и фазовых измерений влияние этого несовмещения исключается. Основ-
ная ошибка будет возникать из-за ошибок определения и учета несинхронно-
сти шкал времени приемников. В конечном счете задача будет решена с доста-
точной точностью, если взаимное положение пунктов по кодовым измерениям
будет предварительно определяться с точностью 0,5 ... 1 м. В сложных услови-
ях наблюдений это не всегда может быть гарантировано. Таким образом, час-
тотное разнесение спутниковых сигналов является основным фактором, лими-
тирующим возможности геодезического применения системы ГЛОНАСС, осо-
бенно в сложных условиях наблюдений, когда и кодовые измерения сопровож-
даются значительными ошибками. Отметим, что использование третьих разно-
стей фазовых измерений (дополнительные разности между вторыми разностя-
ми на смежные эпохи наблюдений) приводит к полному исключению фазовых
неоднозначностей, т. е. не снимает проблему, поскольку в сложных условиях
наблюдений полученные по ним решения очень неустойчивы и чувствительны
к переменным систематическим ошибкам измерений.
В навигационном приложении частотное разнесение сигналов спутников
ГЛОНАСС -разработчиками системы рассматривается как ее преимущество.
При использовании для целей точной навигации, наряду со спутниками орби-
тальной группировки, сигналов так называемых, устанавливаемых в районе
портов, работа последних на индивидуальной литерной частоте будет созда-
вать меньшие помехи приему спутниковых сигналов. Здесь, однако, имеет ме-
сто некоторая некорректность аргументации. В действительности это преиму-
щество может быть реализовано, если уже выпускаемая аппаратура без значи-
тельных изменений обеспечивает работу по сигналам псевдоспутников. Если
нет, то обе системы оказываются примерно в равном положении, так как все-
гда возможны разработки СРНС-аппаратуры, работающей с псевдоспутниками
на отличной от основной частоте.
При сравнении двух систем чаще всего указывается на использование в
GPS режимов селективного доступа (Selective Availability (SA)) и дополнитель-
ного кодирования точного кода (режим А-S — Antispoofing), превращающего
открытый P-код, в закрытый Y-код.
Что касается режима А-S, то уже несколько лет назад разработано не-
сколько эффективных способов выделения несущей частоты при отсутствии
информации о точной структуре Y-кода. Причем такие методы, как кросс-
корреляция сигналов, передаваемых с Y-кодированием на обеих частотах
(фирма Trimble), или так называемое Z-слежение (Ashtech), позволяют полу-
чать результаты измерений на полной длине волны несущей частоты и с
меньшими энергетическими потерями, в отличие от давно применямого мето-
да квадратирования сигнала, приводящего к тому же к заметному увеличению
шума, удвоению частоты и, соответственно, к получению измерений на поло-
256
Глава 12. Аппаратура потребителей
винной длине волны несущей. Использование полной длины волны чрезвы-
чайно важно для устранения временных разрывов непрерывности слежения за
фазой и повышения надежности разрешения фазовых неоднозначностей. Все
точные геодезические приемники последних нескольких лет выпуска способ-
ны эффективно работать в условиях включенного режима A-S.
Режим SA предполагает введение искусственных искажений в С/А-код и
одновременно в фазу несущей путем внесения фазовых сдвигов псевдослучай-
ного характера в опорную частоту, используемую для формирования спутни-
кового сигнала. Период изменения этих искажений составляет 5 ... 15 мин, а
влияние этих искажений на ошибки измерения псевдодальностей может дос-
тигать нескольких десятков метров. Режим SA предполагает также возмож-
ность внесения искажений в передаваемые эфемериды спутников. Если, одна-
ко, подходить к оценке с позиций относительных геодезических определений,
то можно утверждать, что работа в этом режиме практически нс сказывается
на точности получаемых результатов.
Работа спутников в режиме SA в части искажений, вносимых в переда-
ваемый спутниковый сигнал, не сказывается на результатах фазовых относи-
тельных определений, поскольку соответствующее влияние исключается уже
на стадии составления первых разностей. Кроме того, оно в значительной ме-
ре исключается и в разностях результатов одновременных С/А-кодовых изме-
рений, выполненных при одних и тех же искажениях кода. Что касается пред-
полагаемых искусственных искажений эфемерид спутников, то автор не рас-
полагает достаточно детальной и достоверной информацией о характере таких
искажений для получения необходимых аналитических оценок. Однако опыт
нескольких лет практической работы ЦНИИГАиК в условиях объявленного
включения режимов SA и А-S показывает, что совместное влияние всех ука-
занных факторов во всяком случае нс приводит к ошибкам более 5 мм+
НЮ 6 L, стандартно объявляемым для двухчастотной геодезической аппара-
туры. Этот вывод подтверждается и определениями на коротких (до несколь-
ких километров) и на средних (30 ... 50 км) базах при продолжительности на-
блюдений от 4 ... 5 мин до нескольких десятков минут или нескольких часов,
и на более длинных (до 150 км) базах при интервалах наблюдений от 2 ... 3 ч
Ю суток. Причем па средних и длинных базах достоверно достигается точ-
ность порядка 3-10 L при использовании только бортовых эфемерид. В от-
ношении возможных искусственных искажений эфемерид эти результаты по-
казывают, что либо эти искажения не столь велики, как предполагается, либо
они вносятся согласованно для всех спутников так, что их взаимные положе-
ния мало или совсем не изменяются и соответственно нс приводят к сущест-
венному понижению точности относительных определений. Впрочем, для по-
лучения повышенной точности всегда есть возможность воспользоваться точ-
ными апостериорными эфемеридами.
В 2 раза меньшая тактовая частота кодов в системе ГЛОНАСС теорети-
чески означает более высокий шумовой уровень пссвдодалыюмерных кодовых
измерений. Однако сам уровень шума но сравнению с другими ошибками
i 12.8. Особенности применения СРНС в различных областях 257
столь мал и к тому же настолько хорошо усредняется, что этот фактор можно
.ле принимать во внимание при сравнении систем. Более того, с учетом влия-
ния режимов SA и А-S преимущество в измерении псевдодальностей очевидно
за системой ГЛОНАСС. Следует, однако, отметить, что в соответствии с по-
следней директивой Президента США о политике использования системы GPS
предполагается отказ от применения ограничивающих режимов в ближайшие
несколько лет.
В аспекте сравнения двух систем целесообразно рассмотреть возможно-
сти определений повышенной точности на коротких базах. Ошибки определе-
ний GPS-аппаратурой можно представить двухкомпонентной формулой типа
(в+/>10-6£) или (a + b ppm), где первый член характеризует случайную со-
ставляющую общей ошибки, не зависящую от длины L определяемой базы,
второе — случайную составляющую, значение которой пропорционально дли-
не базы. Стандартно для двухчастотной геодезической аппаратуры дается фор-
мула (5 мм +1 ppm) для точности определения взаимного положения по пла-
новым координатам. При этом первый член определяется инструментальными
погрешностями, а второй — влиянием внешних условий, в том числе и прежде
всего ошибками бортовых эфемерид.
Для одночастотной аппаратуры дается формула (10 мм +2 ppm). Указан-
ное для двухчастотной аппаратуры разделение составляющих по источникам
происхождения ошибок менее четко. На коротких базах (до нескольких сотен
метров) первый член можно с уверенностью также положить равным 5 мм. Для
таких баз существует и практически подтверждается возможность получения и
существенно более высокой точности, вплоть до субмиллиметрового уровня
при условии малости влияния помех из-за приема переотраженных спутнико-
вых сигналов.
Основным источником инструментальных ошибок является, в прибли-
женной геометрической интерпретации, нссфсричность фазового фронта при-
емной антенны. Значения соответствующих искажений измерений фаз в пере-
счете на линейную меру могут достигать десятка миллиметров. При этом соот-
ветствующие ошибки носят явно выраженный систематический характер в со-
ответствии с характером изменения фазовых характеристик антенны в сфери-
ческой системе координат, связанной с се корпусом. Исходя из близкого по-
добия этих характеристик для разных экземпляров однотипных антенн реко-
мендуется для получения лучшей точности, указанной в формуле, одинаково
ориентировать корпуса антенн при проведении наблюдений. Тогда абсолютное
влияние характеристик антенн частично компенсируется уже при составлении
первых разностей фазовых измерений, благодаря исключению общих ошибок.
Однако нескомпенсированные остаточные значения еще значительны и прак-
тически почти постоянны в связи с очень медленным изменением видимых
направлений на наблюдаемые спутники. Большинство же инструментальных
ошибок с накоплением большого числа измерений эффективно усредняется.
Существует возможность практически полного исключения ошибок ан-
тенн, если выполнять определение базы в два сеанса с обменом приемников
258 Глава 12. Аппаратура потребител&М
между сеансами при соблюдении требования наблюдать одни и те же спутняИ
ки в одних и тех же направлениях. Легко показать, что в этом случае средцмВ
значения параметров базы будут свободны от остаточного влияние оши&И
антенн. Более просто такую возможйость представляет система GPS, поскодЯ
ку у нее в смежных сутках повторяется практически идентичная видимая коЯ
фигурация положений спутников на небесной сфере. Система ГЛОНАСС cyl
щсственно менее приспособлена для применения такой методики, поскольку^
нее повторяемость конфигурации составляет 7 сут. Такая методика обеспечи
вает исключение также и любых других ошибок, постоянных для индивидуалу
ных измерительных каналов, при дополнительном условии наблюдения в обо
их сеансах одних и тех же спутников одними и теми же измерительными ед
налами. ,
Совместное использование систем GPS и ГЛОНАСС. Потенциалы^
близкие возможности обеих систем при геодезических определениях с техни-
ческой точки зрения означают достаточность использования только одной из
них в случае хороших условий наблюдений. В настоящее время система ГЛО-
НАСС занимает менее выгодную позицию лишь по причине существенна
меньшей обеспеченности геодезической аппаратурой пользователей и менее
развитой инфраструктуры, прежде всего из-за отсутствия сети станций посто-
янных фазовых наблюдений (в том числе глобальной) и службы точных эфе-
мерид. Более того, в хороших условиях наблюдений использование совмещен-
ной GPS/ГЛОНАСС-аппаратуры технически и экономически не выгодно, по-^
скольку при очевидно более высокой стоимости, технические возможности:
такой аппаратуры (оперативность и точность определений) практически не
будут отличаться от возможностей односистемной аппаратуры.
Существенно иная ситуация будет при выполнении работ в сложных ус-
ловиях наблюдений: в полузакрытой местности, в залесенных и горных рай-
онах, на городской территории, из под конструкций, частично экранирующих
небесную сферу, в том числе из под геодезических сигналов. Наблюдения в
таких условиях существенно снижает вероятность видимости минимально не-
обходимого числа удовлетворительно распределенных по небесной сфере
спутников в желательном и минимально необходимом интервале времени, дос-
таточном в частности при работе в открытой местности. Многочисленные раз-
рывы в слежении за спутниками, возникающие в результате интерференции
радиоволн при их прохождении сквозь частичные препятствия или вследствие
приема персотраженных сигналов могут приводить не только к необходимости
значительного увеличения продолжительности наблюдений и уменьшению
точности, но и к значительному увеличению вероятности получения грубых
ошибок результатов, часто не выявляемых без обязательных повторных опре-
делений. При этом возможность выбора для обработки только качественных
интервалов наблюдений существенно ограничена из-за многочисленности раз-
рывов и малого числа одновременно наблюдавшихся спутников даже тогда,
когда для получения удовлетворительного результата достаточно было бы ин-
формации на интервале в несколько минут. Чаще всего грубые и не замечен-
to 8. Особенности применения СРЙС в различных, областях
&ме ошибки происходят вследствие пропуска цикла при восстановлении не-
прерывности измерений, смещенных на границах разрыва из-за интерферен-
Sgni, или пропуска цикла по этой же причине при разрешении неоднозначно-
Енс Получение в этих условиях решений не с фиксированными, а с так назы-
ваемыми плавающими неоднозначностями приводит, как правило, к еще худ-
щщм результатам.
• Ограничение по числу спутников с достаточной продолжительностью
непрерывного слежения и влияние переотраженных сигналов существенно
-снижает точность и саму вероятность получения какого-либо положительного
^результата при определении точных координат подвижных объектов, в частно-
сти при проведении аэросъемочных работ.
Несмотря на усилия разработчиков по повышению чувствительности и
избирательной способности GPS-аппаратуры, прогресс в повышении надежно-
сти наблюдений в сложных условиях не очень велик и всегда будет существен-
но ограничен. В этом отношении аппаратура ГЛОНАСС более перспективна
вследствие большей реальной мощности спутникового сигнала и отсутствия
дополнительных искажений в структуре псевдо шумового кода.
В этих условиях наиболее радикальным средством является применение
совмещенной аппаратуры. Часто в качестве фактора, ограничивающего воз-
можность использования такой аппаратуры, указывают на различие шкал вре-
мени обеих систем и используемых систем координат. Поскольку ошибки
шкал времени спутников при относительных определениях полностью исклю-
чаются, то несовпадение систем времени будет отражаться только на опреде-
лении абсолютных координат по смешанному созвездию. Это не столь сущест-
венно, т. к., во-первых, при геодезических работах существуют другие источ-
ники получения достаточно точных исходных абсолютных координат, во-
вторых — вероятность получения псевдодальномерных кодовых измерений по
минимально необходимому числу спутников только одной системы сущест-
венно выше, чем для определения относительных положений по фазовым из-
мерениям, поскольку в этом случае нет необходимости в разрешении неодно-
значности и, следовательно, в непрерывности измерений. Что касается систем
координат WGS-84 и ПЗ-90, то они, как геоцентрические по определению, не
могут значительно различаться. Уже упоминавшееся ранее совместное уравни-
вание АГС, ДГС (система WGS-84) и КГС (ПЗ-90) дало следующий набор па-
раметров координатного преобразования
ПЗ-90 => WGS-84 в (11.13):
Дх — - 0,3 м; Ду =2,2 м; Дг = 1,0 м; ах = - 0,04" ; v = - 0,01" ;
= - 0,07" ; т= - 0,06 ppm.
Знаки угловых элементов даны при положительном вращении против ча-
совой стрелки.
Система WGS-84 при построении ДГС реализована через использование
бортовых эфемерид спутников системы ТРАНЗИТ. Ожидавшаяся средне квад-
ратическая ошибка реализации системы координат WGS-84 по данным обра-
ботки ДГС составила 1,5 ... 2 м.
260
Глава 12. Аппаратура потребителей^
Нечувствительность относительных определений к расхождениям плац
времени и близость систем координат означает, что минимально необходимый
состав наблюдаемых спутников в принципе может быть представлен не только
комбинацией трех спутников одной системы и двух — другой, но и комбина-
циями типа 3+1 и 2+2, поскольку будет допустимо составление вторых разно-
стей фазовых измерений для смешанных пар спутников. Косвенное влияние
расхождений шкал времени все таки будет при расчете координат спутников
на моменты измерений, но здесь вполне достаточно знания расхождений шкал
с точностью до долей миллисекунды.
Основная проблема при работе по смешанным парам спутников будет
связана с приведением вторых разностей фазовых измерений к единой длине
волны несущей частоты. Различие длин волн двух систем примерно 5 мм при-
водит к существенно более жестким требованиям к предварительному знанию
разностей дальностей до спутников, чем при работе только по спутникам
ГЛОНАСС. Даже ошибка на одну длину волны при расчете поправок будет
эквивалентна внесению постоянной ошибки в измерение фазы, по данному
спутнику, равной 5 мм. Естественно усложняется и задача предварительной
оценки разностей дальностей по кодовым измерениям, которая не всегда мо-
жет быть решена. Для получения предварительных значений абсолютных ко-
ординат и синхронизации приемников необходимы будут хотя бы кратковре-
менные одновременные наблюдения четырех «путников одной из систем. ____
При искусственных искажениях бортовых эфемерид в GPS можно ожи-
дать относительно небольшое снижение точности, по сравнению со стандарт-
ной, если обработка будет базироваться на этих эфемеридах. Это будет экви-
валентно влиянию расхождения систем координат такого же порядка. Для ре-
шения задач повышенной точности связь между системами координат должна
быть уточнена. Наиболее реально и быстро это можно сделать путем привязки
каждой из систем к системе ITRF, задаваемой международной Службой опре-
деления параметров вращения Земли (ПВЗ). Для этого достаточно раздельной
попарной координатной связи для нескольких пунктов носителей интересую-
щих нас систем координат с ближайшими пунктами — носителями системы
координат ITRF. В России для такой связи могут быть использованы доста-
точно разнесенные пункты службы определения ПВЗ Менделееве, Иркутск и
Новосибирск после начала работы последнего по программе GPS наблюдений.
В заключение еще раз отметим, что одна из основных проблем при на-
блюдении в сложных условиях, а так же с подвижных объектов состоит в раз-
решении неоднозначностей фазовых измерений. Несмотря на заметные успехи
в разработке соответствующих методов, в том числе и для подвижных объек-
тов, на настоящий момент это самое слабое звено всей технологии. Возмож-
ность разрешения неоднозначности для единичных групп одновременных фа-
зовых измерений коренным образом изменило бы ситуацию как в геодезиче-
ском применении, так и при относительной навигации, обеспечивая субдеци-
метровую точность по таким практически однократным измерениям. Введение
в состав спутниковых сигналов излучения на дополнительной более низкой
|j2.9. Современные образцы аппаратуры потребителей 261
частоте позволило бы разрешить эту проблему достаточно радикально. :Это
р-аст дополнительную ступеньку при переходе от однозначных кодовых изме-
нений к :фазовым::иэм©рениям иа высокой несущей частоте с разрешенной -не-
рднозначностью:бсз-использования аналитических методов и даже :дая ^отдель-
ных измерений, Tie прибегая к их комбинациям в виде первых или вторых раз-
ностей. Другим перспективным направлением разрешения неоднозначности
фазовых измерений-является оптимальная комплексная фильтрация задерж-
ки по-коду и фазе сигнала (см. гл. 14).
12.9. Современные образцы аппаратуры потребителей
Выше было показано, что в зависимости от области применения аппара-
тура потребителей имеет свои особенности, поэтому производители АП всегда
указывают на область применения соответствующего образца. Помимо основ-
ных блоков, таких как антенна, приемник, индикатор, АП может содержать
вспомогательные, обеспечивающих выполнение специальных сервисных функ-
ций, например диагностику узлов транспортного средства, связь с диспетчер-
ским пунктом и т. д.
В табл. 12.8 приведены краткие сведения об основных образцах АП,
производимых российскими предприятиями и работающих по сигналам СРНС
ГЛОНАСС и GES. Болес полная характеристика некоторых образцов АП, при-
веденных в табл. 12.8, дается ниже. Приводимая информация не претендует на
исключительную полноту сведений как по существующим образцам АП, так и
по их характеристикам, а дается для иллюстрации достигнутого уровня в раз-
работке и производстве АП спутниковых радионавигационных систем.
Таблица 12.8. Аппаратура потребителей
Наименование аппаратуры Область примене- ния Разра- ботчик Число кана- лов Точность (в атономном режиме) Мас- са, кг
коорди- нат, м ско- рости, см/с
1 2 3 4 5 6 7
Станция монито- ринга и формиро- вания ДН “Лл ьфа-К" “Гном-М” “Репер-М” “Шкипср-КН” “Грот" Мони- торинг Космос Авиация Геодезия Морфлот и транспорт РНИИ КП 24 6...12 6...12 6. .8 24 12 1...3 90...100 80...90 0,01...0,02 ±2-10 7 L 15...20 25...30 1...2 8...10 12...15 3...5 5...7 6,0 2,5 3,2 3,5 2,5 2,5
АСН-22 Авиация РИРВ 18 25...30 0,4
“Картограф” “Голиаф” “Вертикаль” Геодезия Транспорт Космос НПО пм 6 0,01..0,2 ± НГ6 L 15...20 15...20 3...5 3...5 5,0 2,0 10,0
262
Г л=а в а3.2. Аппаратура потрз№мтел«я^
Продолжение табл. 1.
1 2 3 .4 5 6 7 -Я
“Вевтака№” Космос 15...20 3...5 Ю.ОЛ
НАВИС СИ-3002 НАВИС СИ-3102 НАВИС СИ-3301 Портатив- ная Морфлот Авиация КБ Л НАВИС 14 14 14 15...20 15...20 15...20 О о о 00 00 00 1=3 я 1;6 2;4
НАВИС СН-3202 Геодезия 14 0,02...0,03 ±10*2, - 2;4
“Терминатор” “Интер-А” -Космос Авиация МКБ КОМПАС 12 12 15...17 25...30 8...10 10.30 3:;5 ' 3:3
“Пеленг” Шарта- тивная НИИ “Научный центр” 3 20...23 40...50 1,5
А-744 Авиация Фирма “Катлин” 6 30..35 15...20 .2,0
j “Контроль” Транспорт ::нпп':'В2Р- МОТЕХ 12 15...20 3...5 2,5
МНОГОКАНАЛЬНАЯ СТАНЦИЯ МОНИТОРИНГА И
ФОРМИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ ПОПРАВОК
Разработчик РНИИ космического приборостроения. Назначение — мо-
ниторинг, дифференциальная станция. Число каналов — 24.
Решаемые задачи:
непрерывное слежение за всеми радиовидимыми спутниками ГЛОНАСС
и GPS с сохранением в памяти накопленной информации;
непрерывное проведение в реальном времени навигационных определе-
ний по созвездиям: только спутников ГЛОНАСС, только спутников GPS,
спутников ГЛОНАСС и GPS;
анализ составляющих погрешностей навигационных определений;
контроль качества передаваемых спутниками навигационных радиосиг-
налов и навигационных сообщений;
формирование дифференциальных поправок к навигационным радиосиг-
налам визируемых спутников и признаков исправности этих спутников;
определение расхождения систем геодезических координат ГС-90 и
WGS-84 в точке расположения станции;
исследование стабильности бортовых шкал времени спутников и непре-
рывное слежение за расхождением системных времен ГЛОНАСС и GPS;
выработка дифференциальных поправок в формате RTCM SC-104 для
передачи различным пользователям в локальной области по интерфейсу RS-
232С;
выработка дифференциальных поправок при работе станций в составе
региональной и широкозонной сетей дифференциальной коррекции.
263
2,9- Современные образцы аппарагаурыпотребитедец
X а::р акт е р и с т ик и:
"Погрешности измерения радионавигационных параметров:
по спутникам ГЛОНАСС
по пеепдодальностям, м.............. 1 ... 3
псевдоскоростям.см/с.............. 1 ... 2
по спутникам "OPS (с учетом S/A)
по псевдодальностям, м............... .25 ... 30
:псевдоскоростям,::см/с........... 25 ... 30
.Погрешности единичных абсолютных определений, м:
по созвездиям спутников Т71ПНАСС
по широте и.долготе................. не хуже 5 ... 7
по высоте...................... не хуже 8 ... 10
по созвездиям спутников OPS
по широте и.долготв................. не хуже 25 ... 35
по высоте ..................... не хуже 45 ... 55
Интерфейс, два порта................ "RSt232C
Уславия::»ксплуятации:
Рабочая температура, °C:
приемоиидикагор..................... -40 ... +60
антенна ....................... —40 ...+60
Температура хранения, °C ........... -50 ... +70
Рабочая влажность, % ............... 100 (40°C)
Энергопотребление, Вт............... не более 25
Электропитание (переменное
на частоте тока 50 Гц), В................. 220
Габаритные размеры, мм.............. 345 х 260 х 200
Масса, кг........................... 6
ГРОТ
Разработчик — PH ИИ космического приборостроения. Назначение —
космос. Число каналов —- 12.
Решаемые задачи:
автоматическое, непрерывное, глобальное, всепогодное определение те-
кущих ЗЕ)-координат местоположения и вектора путевой скорости потребите-
ля при работе: по сигналу стандартной точности частотного диапазона £1
ГЛОНАСС; по сигналу высокой точности частотного диапазона L2 ГЛО-
НАСС; по сигналу С/А-кода GPS; при совместной обработке вышеуказанных
сигналов;
индикация на табло текущих Зб-координат местоположения в выбирае-
мой системе координат (СК-42, ПЗ-90, WGS-84) и в выбираемом формате
.264 Г л а;;а а 12. Аппадатура покцебител^
(географических, картографических, в проекции Таусса-—Крюгера), признак^
режима работы.аппаратуры, вводимых невыводимых параметров; 1
интегральная оцепка зожидаемой точности определении текущих Koopjnj
наг;
автоматический прием, хранение, обновление .альманахов ГЛОНАСС ।
GPS;
автоматический тестовый контроль функционирования блоков и узло
аппаратуры, индикация отказавших блоков;
автоматический выбор оптимального с точки зрения ожидаемой точно
сти созве.эдия?НС ГЛОНАСС и GPS при работе вховмещенном режиме;
выдача во внешние устройства определяемых параметров;
выдача во внешние устройства метки времени (импульсный сигнал 1 Гц)15
кода оцифровки МВ, значений поправок на расхождение шкалы времени по-’
требителя относительно шкалы времени ГЛОНАСС и шкал времени ГЛОНАСС
и Госэталона;
ввод сигнала при работе от внешнего высокоточного стандарта частоты и-
времени (5 МГц и 1 Гц);
ввод, обработку, учет корректирующей информации в соответствии с
RTCM SC-104, решение навигационной задачи в дифференциальном режиме.
Дополнительный сервис:
расчет прямой и обратной геодезических задач;- решение треугольника^...
расчет сближения меридианов; перевычисление из зоны в зону и расчет
поправки в дирекционный угол за переход из зоны в зону;
расчет высоты способом барометрического нивелирования;
пересчет прямоугольных координат в геодезические и обратно;
расчет дирекционного угла ориентирного направления по результатам
астрономических наблюдений.
Характеристики:
Точность определения навигационных параметров:
автономный режим:
координат, м:
по НС ГЛОНАСС............... 30
по НС GPS (в режиме S/A) ... 210
дифференциальный режим:
координат, м ................ 3
скорости, см/с:
на стоянке .............. 5
в движении .............. 7
Время определения
(холодный старт), мин..................... 2
Частота обновления координат, с'1 . 1
Интерфейс, два порта .............. RS-232C
Протокол обмена ................... IEC 1162 (NMEA-183)
3i9. Современные образцыгтпаротуры потребителей 265
Условии эксплуатации
Рабочая температура, °C:
присмоиндикятор.................. -40 ... -+60
^антенна.................... -40 ... -1-60
Рабочая::влажноси>, % ............ [00 (40 ®С)
Температура хранения, °C ......... -50 ....+70
Электропитание (переменное
частоте тока 50 Гц), В.............. 220
Энергопотребление, Вт............. не'более 25
Габаритные :размеры, мм.............. 190х 207х:92
Масса, кг......................... 2,5
ШКИПЕР -КН
Разработчик — РНИИ космического приборостроения. Назначение —
морской и речной флот, наземный транспорт. Число каналов — 24.
Решаемые задачи:
непрерывная выработка текущих значений координат и вектора скоро-
сти;
отображение координат в системе ПЗ-90, WGS-84 и на эллипсоиде Кра-
совского;
расчет рекомендуемого курса следования в заданную точку с сигнализа-
цией о прибытии или отклонении от маршрута;
расчет пройденного расстояния от любой точки и времени прибытия в
заданную точку маршрута;
выработка маршрутных координат;
расчет коммерческих задач.
Характеристики:
Точность определения навигационных параметров:
координат, м.................... 15 ... 20
скорости, см/с.............. 3 ... 5
Интерфейс ...................... RS-232C
Протокол обмена ................ NMEA-183
Электропитание (постоянное), В . 9 ... 36
Энергопотребление, Вт........... не более 10
Г Габаритные размеры, мм .............. 190x75x 25
Масса, кг....................... 2,5
РЕПЕР -М
Разработчик — РНИИ космического приборостроения. Назначение —
геодезия. Число каналов — 6 ... 8.
266 Г л а:п а 12. Аппаратура шнжбитй
Рге ш а е м ы е зя д а ч и:
одншфеменная работано сигналам НС ГЛОПАССи Ш’З;
высокоточная геодезическая привязка разнесенных пункто в;
создание геодазичеекиххетей;
оперативное определение абсолютных -координат местоопределения;
возможности-использования:
при'проведении геологических и изыскательских работ;
при-производстве строительных работ;
при топогеодезической съемке на суше, море и:в воздухе;
при прогнозе землетрясений.
X а р;а к т ери с т-и к-и:
Точность определении.длины базовой линии..!,, см:
-между неподвижными пунктами .. 1 ..2:± 2 -10 7 L
..до подвижных объектов....... 30 ±10 6L
Точность оперативного -абсолютного
определения, м.......................... 15
Интерфейс .......................... -«S 232C
Габаритны® размеры, мм...............700 х 75 х 210
Масса, кг...........................1,6
НАВИС СН-3002
Разработчик — Конструкторское бюро “НАВИС". Назначение — пере-
носная. Число каналов — 14.
Решаемыезадачи: \
автоматическое, непрерывное, глобальное, всепогодное определение те-
кущих ЗИ-координат местоположения и вектора путевой скорости потребите-
ля при работе: по сигналу стандартной точности частотного диапазона IA
ГЛОНАСС; по сигналу С/А-кода GPS; при совместной обработке вышеуказан-
ных сигналов;
индикация на табло текущих Зб-координат местоположения в выбирае-
мой системе координат (СК-42, ПЗ-90, WGS-84) и в выбираемом формат*
(географических, картографических, в проекции Гаусса—Крюгера), признако.
режима работы аппаратуры, вводимых и выводимых параметров;
интегральная оценка ожидаемой точности определения текущих коорди-
нат местоположения;
автоматический прием, хранение, обновление альманаха систем ГЛ С
НАСС и GPS;
автоматический тестовый контроль функционирования блоков и узлог
аппаратуры, индикация отказавших блоков;
автоматический выбор оптимального с точки зрения ожидаемой точне
сти созвездия НС ГЛОНАСС и GPS при работе в совмещенном режиме;
выдача во внешние устройства определяемых параметров;
^9. Современные, образцы аппаратуры попц>еб№№лей .2.67
^автоматическое решение навигационной задачи в географической систе-
:Е> координат или, по желанию пользователя, в квазигеографичаской системе
^дцуцшат;
ч :::«вод, заработку, учет корректирующей информации в соответствии с
JCM SC-I04, решение навигационной задачи при работе ев дифференциаль-
ном режиме.
.Дополни т-е льный сервис:
расчет пройденного расстояния; ввод координат до 30 маршрутных то-
:ек; запоминание текущих координат в качестве координат-маршрутной точ-
15 ... 20
1 ... 3
8 ... 10
0,1
..цц расчет расстояния и направления между двумя маршрутными точками или
^текущей точки до любой из маршрутных точек.
Xsa р а к т е р и с тики:
, Точность определения навигационных параметров:
автономный режим:
координат, м........................
дифференциальный режим:
координат, м ..................
скорости, см/с.............
s времени (UTC), мкс ..........
Время определения
(холодный старт), мин ...............,
Частота обновления координат, с-1
Интерфейс, два порта...........
Протокол обмена ...............
Рабочая температура, ®С:
приемоиндикатор...............
антенна ................
не более 3
1
RS-232C
IEC 1162 (NMEA-183)
-10 ... +50
-50 ... +55
Рабочая влажность, % .............. 100 (25 °C)
Температура хранения, °C .......... -60 ... +65
Электропитание (переменное
на частоте тока 50/400 Гц), В........... 110/127/220
Энергопотребление, Вт.............. не более 10
Габаритные размеры, мм............. 187 х 165 х 50
Масса, кг ......................... 2,5
НАВИС СН-3102
Разработчик — Конструкторское бюро “НАВИС”. Назначение — мор-
ской и речной флот. Число каналов — 14.
Решаемые задачи:
автоматическое, непрерывное, глобальное, всепогодное определение те-
кущих ЗО-координат местоположения и вектора путевой скорости потребите-
ля при работе: по сигналу стандартной точности частотного диапазона LI
ГЛОНАСС; по сигналу С/А-кода UPS; при совместной обработке вышеука,——
ных сигналов;
индикация на табло текущих Зб-крординат местоположения и выбиря^
мой хистеме =координат (СК-42, ПЗ-90, WGS-84) и в выбираемом формап
(географических, картографических, в.проекции Гаусса—Крюгера), признаку!
режима работы аппаратуры, вводимых и выводимых параметров; 1
интегральная оценка ожидаемой точности определения текущих коордиЗ
нат; ]
автоматический прием, хранение, обновление альманаха систем FJloJ
НАСС и GPS;
автоматический тестовый контроль функционирования блоков и узлод
аппаратуры, индикация отказавших'Клоков; j
автоматический выбор оптимального ::с точки зрения ожидаемой точно-
сти созвездия НС ГЛОНАСС и GPS npn работе в совмещенном :режиме;
выдача во внешние устройства определяемых параметров;
автоматическое::рсшоиие навигационной задачи в географической систе-
ме координат или, по желанию пользователя, в квазигеографической системе
координат;
ввод, обработку, учет корректирующей информации =в .соответствии с
RTCM ЗЙС-104, решение навигационной задачи при работе в .дифференциаль-
ном режиме;_______ _______ ____________________________ 2
ввод координат :500 маршрутных точек;
ввод 20 маршрутов движения корабля (до'50 маршрутных точек в каждом
маршруте);
запоминание текущих координат в качестве координат маршрутных то-
чек;
растет::расстояиия и направления между двумя маршрутными точками;
сигнализация о подходе к точке с заданными координатами;
движение по маршруту с выработкой параметров отклонения от маршру-
та (сигнализация достижения поворотнойточки и времени прибытия по теку-
щей ::скорости).
Хара кт ери ст и к и:
Точность определения навигационных параметров:
автономный ражим:
координат, м................. 15 ... 20
диффервнциальный-режим:
координат, м ....................... 1 ... 3
скорости, см/.с ............. 10
^времени (UTC), мкс ......... 0,1
:бремя определения
(холодный::старт), мин ................... не более 3
Частота обновления координат, с'1 .... 1
12-9. Современные образцы аппаратуры потребителей
2W
Интерфейс, два порта
Протокол обмена ...
RS-232C
IEC 1162 (NMEA-183)
Рабочая температура, °C:
приемоиндикатор............... -10 ... +50
антенна............... -50 ...+55
Рабочая влажность, % .............. 100 (25 °C)
Температура хранения, °C .......... -60 ... +65
Электропитание (переменное
на частоте тока 50/400 Гц), В............... 110/127/220
Энергопотребление, Вт.............. не более 10
Габаритные размеры, мм ............ 187 х 165 х 50
Масса, кг.......................... 2,5
Рабочие характеристики сохраняются при:
механическом ударе одиночного воздействия с пиковым ускорением
100±20 g, t < 5 мс; предельном пониженном давлении 1,2x104 Па; погруже-
нии в воду до 1 м; воздействии соляного тумана, песка; движении со скоро-
стью до 180 км/ч; поворотах со скоростью до 5 °/с.
НАВИС СН-3203
Разработчик — Конструкторское бюро “НАВИС”. Назначение — геоде-
зия. Число каналов — 14.
Решаемые задачи:
автоматическое, непрерывное, глобальное, всепогодное определение те-
кущих ЗО-координат местоположения и вектора путевой скорости потребите-
ля при работе: по сигналу стандартной точности частотного диапазона £1
ГЛОНАСС; по сигналу С/А-кода GPS; при совместной обработке вышеуказан-
ных сигналов;
индикация на табло текущих Зй-координат местоположения в выбирае-
мой системе координат (СК-42, ПЗ-90, WOS-84) и в выбираемом формате
(географических, картографических, в проекции Гаусса—Крюгера), признаков
режима работы аппаратуры, вводимых и выводимых параметров;
автоматический прием, хранение, обновление альманаха систем ГЛО-
НАСС и GPS;
автоматический тестовый контроль функционирования блоков и узлов
аппаратуры, индикация отказавших блоков;
автоматический выбор оптимального с точки зрения ожидаемой точно-
сти созвездия НС ГЛОНАСС и GPS при работе в совмещенном режиме;
выдача во внешние устройства определяемых параметров;
геодезическая съемка с использованием фазы несущей.
Характеристики:
Точность определения навигационных параметров, мм:
z70
Глава
в относительном режиме
послесеансной обработки ...............
по фазе несущей ................
Интерфейс, два порта..............
Протокол обмена ..................
20 ... 30
3 ... 4
RS-232C
IEC 1162 (NMEA-183)
Рабочая температура, ®С ........... -40 ... +50
Рабочая влажность, % .............. 98 (25 °C)
Температура хранения, °C .......... -60 ... +65
Электропитание, В:
переменное на частоте тока 50 Гц .. 90 ... 240
постоянное ..................... 9 ... 30
Энергопотребление, Вт.............. не более 10
Габаритные размеры, мм ........... 190 х 190x90
Масса, кг.......................... 2,4
НАВИС СН-3301
Разработчик — Конструкторское бюро “НАВИС”. Назначение — авиа-
ция. Число каналов — 14.
Решаем ы е з ад а ч и:
автоматическое, непрерывное, глобальное, всепогодное определение те-
кущих ЗО-координат местоположения и вектора путевой скорости потребите-
ля при работе: по сигналу стандартной точности частотного диапазона LI
ГЛОНАСС; по сигналу С/А-кода GPS; при совместной обработке вышеуказан-
ных сигналов;
индикация на табло текущих Зб-координат местоположения в выбирае-
мой системе координат (СК-42, ПЗ-90, WGS-84) и в выбираемом формате
(географических, картографических, в проекции Гаусса—Крюгера), признаков
режима работы аппаратуры, вводимых и выводимых параметров;
интегральная оценка ожидаемой точности определения текущих коорди-
нат местоположения;
автоматический прием, хранение; обновление альманаха систем ГЛО-
НАСС и GPS;
автоматический тестовый контроль функционирования блоков и узлов
аппаратуры, индикация отказавших блоков;
автоматический выбор оптимального с точки зрения ожидаемой точно-
сти созвездия НС ГЛОНАСС и GPS при работе в совмещенном режиме;
выдача во внешние устройства определяемых параметров;
автоматическое решение навигационной задачи в географической систе-
ме координат или, по желанию пользователя, в квазигеографической системе
координат;
работа с навигационной базой данных;
К&9. Современные образцы аппаратуры потребителей 271
f ввод, обработку, учет корректирующей информации в соответствии с
HlTCM SC-104, решение навигационной задачи при работе в дифференциаль-
Брм режиме.
В Дополнительный сервис:
Г, расчет пройденного расстояния; ввод координат до 30 маршрутных то-
^чек; запоминание текущих координат в качестве координат маршрутной точки;
[.расчет расстояния и направления между двумя маршрутными точками или от
• текущей точки до любой из маршрутных точек.
'' .. Характеристики:
[ Точность определения навигационных параметров:
f автономный режим:
1 координат, м.................. 15 ... 20
дифференциальный режим:
координат, м...................... 1 ... 3
скорости, см/с ............. 10
времени (UTC), мкс ......... 0,1
Время определения
(холодный старт), мин...................... не более 3
Частота обновления координат, с*1 . 1
Интерфейс:
- . два лорта ...........—.... . . RS-232C
один канал вывода .......... ARING 429
Рабочая температура, °C:
приемоиндикатор............. -20 ... +50
антенна..................... -55 ... +55
Рабочая влажность, % .................. 98 (25 °C)
Температура хранения, °C .......... -60 ... +85
Электропитание, В
переменное на частоте тока 400 Гц. 15
постоянное ..................... 27 ± 5
Энергопотребление, Вт.............. не более 10
Габаритные размеры, мм ............ 384 х 159 х 51
Масса, кг ......................... 2,4
ЗЕМЛЕМЕР - Л1
Разработчик — Российский институт радионавигации и времени. Назна
чение — геодезия. Число каналов — 6 (GPS).
Режимы работы:
статические......... “Статика”, “Быстрая статика”, “Реоккупация”
кинематические...... “Стою/иду”, “Кинематика”
272
‘ t . t
Глава 12. Аппаратура потребителей
Статические режимы съемки позволяют определять относительное коор-
динаты неподвижных удаленной и опорной точек; кинематические — коорди-
наты подвижной удаленной точки относительно неподвижной опорной. ч
Решаемые задачи:
определение абсолютных координат опорных точек по данным кодовых
измерений;
определение относительных координат по данным кодовых измерений;
определение относительных координат по данным фазовых измерений в
пяти режимах статической и динамической съемок;
оценка апостериорных погрешностей измерений и точности определе-
ний;
планирование сеансов;
построение временных диаграмм проведенных сеансов;
просмотр и редактирование файлов измерений;
контроль измерений на наличие незарегистрированных контроллером
потерь фазовых циклов и восстановление непрерывных фазовых отсчетов;
графическое представление проекта и его редактирование;
редукция координат к определяемым точкам
WGS-84 в СГС-85 и обратно.
Характеристики:
Точность относительных определений :
в режиме статической съемки, мм:
на базах до 15 км .......................
на базах более 15 км ..........
в режиме кинематической съемки, мм:
на базах до 25 км ..................
Точность абсолютных определений, м .
Интерфейс .........................
Рабочая температура, °C ...........
Рабочая влажность, % ...............
Электропитание (постоянное), В......
Энергопотребление, Вт ..............
Габаритные размеры, мм .............
Масса, кг...........................
и их преобразование из
5 ...
5 ...
10+(1 ... 2)10“61
10+(2 ... 3) ГО-6!
10 ... 30+(1 ...
10 ... 15 (S/A
RS-232C
-20 ... +50
100 (25 °C)
12
не более 10
170x 380x 265
10
2) КГ*!
выключен)
АСН-22
Разработчик — Российский институт радионавигации и времени. Назна-
чение — авиация. Число каналов — 12 (GPS), 6 (ГЛОНАСС).
Решаемые задачи:
автоматическое, непрерывное, глобальное, всепогодное определение те-
кущих ЗО-координат местоположения и вектора путевой скорости потребите-
I ‘ 7 1 » r t t t
12.9. Современные образцы аппаратуры потребителей 27 з
ля при работе: по сигналу стандартной точности частотного диапазона L1
ГЛОНАСС; по сигналу С/А-кода GPS; при совместной обработке вышеуказан-
ных сигналов;
индикация на табло текущих Зб-координат местоположения в выбирае-
мой системе координат (ПЗ-90, WGS-84), составляющих вектора скорости,
признаков режима работы аппаратуры, вводимых и выводимых параметров;
автоматический прием, хранение, обновление альманаха систем ГЛО-
НАСС и GPS;
автоматический тестовый контроль функционирования блоков и узлов
аппаратуры, индикация отказавших блоков;
автоматический выбор оптимального с точки зрения ожидаемой точно-
сти созвездия НС ГЛОНАСС и GPS при работе в совмещенном режиме;
выдача во внешние устройства определяемых параметров;
работа в дифференциальном режиме.
Характеристики:
Точность определения навигационных параметров, м:
стандартный режим-.
в плоскости....................... 25 ... 30
по вертикали ................ 30 ... 38
дифференциальный режим-.
в—плоскости....................... 4 ... 4,5 __
по вертикали ................ 5 ... 6
Точность определения времени, мс .. 0,2
Характеристики сохраняются при:
скорости, м/с ..................... до 4500
ускорения, g.................. до 4
Время определения
(холодный старт), мин................... не более 1,5
Интерфейс ......................... RS-232C
Рабочая температура, °C ........... -40 ... +70
Температура хранения, °C .......... -55 ... +85
Электропитание (постоянное), В .... 5, ± 15
Энергопотребление, Вт.............. не более 7,5
Габаритные размеры, мм ............ 160 х 182x20
Масса, кг.......................... 0,4
ТЕРМИНАТОР
Разработчик — Московское конструкторское бюро “КОМПАС”. Назна-
чение — космос. Число каналов — 12.
Решаемые задачи:
автоматическое, непрерывное, глобальное, всепогодное определение те-
кущих ЗО-координат местоположения и вектора путевой скорости потребите-
274
Г л а в a 12. Аппаратура потребителей
ля при работе: по сигналу стандартной точности частотного диапазона
L1 ГЛОНАСС; по сигналу С/А-кода ОР§; при совместной обработке вышеука-
занных сигналов;
автоматический режим приоритетного выбора навигационных спутников
ГЛОНАСС и, при наличии свободных каналов, навигационных спутников OPS
по принципу All-in-View;
устойчивое определение навигационных параметров при движении с ли-
нейным ускорениями и при скачкообразных изменениях ускорения, характер-
ных для динамики ракетно-космической техники на высотах до 10000 км;
выдача в бортовые устройства и устройства радиотелеметрии навигаци-
онных параметров:
ЗО-координат местоположения объекта,
ЗО-составляющих вектора скорости,
“сырых” радионавигационных параметров (псевдодальности, псевдо-
скорости и т.д.),
системного времени с UTC(SU)/UTS(USNO);
работа в дифференциальном режиме.
Характеристики:
Точность навигационных определений:
координат, м............................ 15 ... 17
скорости, см/с ......... 8 ... W
высоты, м..................... 17 ... 20
времени(иТС), мкс ............ 0,1
Время определения
(холодный старт), мин................... не более 2,5
Частота обновления координат, с-1 . 10
Время повторного захвата при перерыве (с), с:
5 .............;..... 3 ... 5
5 ... 10 ................... 5 ... 15
10 ... 60 ................... 15 ... 30
Максимальная скорость
использования, км/ч .................... 10
Максимальное ускорение, g.......... 20
Максимальный рывок, g/c ........... 20
Максимальная высота................ без ограничений
Интерфейс ......................... RS-232C
Рабочая температура, °C ........... -50 ... +50
Температура хранения, “С .......... -60 ... +50
Рабочая влажность, % .............. 98 (35 °C)
Электропитание (постоянное), В..... 28 ± 9
Энергопотребление, Вт.............. не более 10
Габаритные размеры, мм ............ 220 х 260 * 80
Масса, кг.......................... 3,5
12$. Современные о&азш* аппаратуры потребителей 275
ЛИДЕР
Разработчик — Московское конструкторское бюро “КОМПАС”. Назна-
чение — авиация. Число каналов — 12.
Решаемые задачи:
автоматическое,- непрерывное, глобальное, всепогодное определение те-
кущих ЗВ-координат местоположения и вектора путевой скорости потребите-
ля при работе: по сигналу стандартной точности частотного диапазона Li
ДУГОЙ ACC; по сигналу С/А-кода GPS; при совместной обработке вышеуказан-
ных сигналов;
автоматический режим приоритетного выбора навигационных спутников
ГЛОНАСС и, при наличии свободных каналов, навигационных спутников OPS
по принципу All-in-View;
устойчивое определение навигационных параметров при движении с ли-
нейным ускорениями и при скачкообразных изменениях ускорения, характер-
ных для динамики летательных аппаратов;
выдача в бортовые устройства и устройства радиотелеметрии навигаци-
онных параметров:
ЗВ-координат местоположения объекта,
ЗВ-составляющих вектора скорости,
системного времени с UTC(SU);
работа в дифференциальном режиме.
Характеристики:
Точность навигационных определений:
автономный режим:
координат, м............... 15 ... 30
высоты, м ................. 18 ... 50
скорости, см/с............. 20 ... 25
времени (UTC), мкс ........ 0,3 ... 1
дифференциальный режим:
координат, м............... 1,5 ... 2
Время определения
(холодный старт), мин................. не более 3
Время повторного захвата, с ..... 3 ... 15
Максимальное значения крена
и тангажа, град....................... 30 ... 40
’ Максимальное ускорение, g .......... 20
Максимальный рывок, g/c ......... 8
Интерфейс ....................... RS-232C
Рабочая температура, °C ......... -40 ... +50
Электропитание (постоянное), В... 27
Энергопотребление, Вт............ не более 14
Габаритные размеры, мм ............ 320 х 194x57
Масса, кг........................ 3
276 ) ’ 1 1 л д в(2, Лль-Аятуря-Атребм.^дей
КОНТРОЛЬ
Разработчик — Научно-производственное предприятие “ТЕРМОТЕХ"
Назначение — транспорт. Число каналов — 14. J
Решаемые задачи:
автоматическое определение текущих ЗВ-координат местоположения и
вектора путевой скорости потребителя при работе: по сигналу стандартной^
точности частотного диапазона LI ГЛОНАСС; по сигналу С/А-кода OPS; !
прием с датчиков информации о состоянии окружающей среды (радиа-j
ционном фоне, концентрации газов в атмосфере и т. д.), информации о со-
стоянии систем и агрегатов подвижного объекта, записи ее вместе с собствен-;
ными координатами во внутреннюю энергонезависимую память, отображение’
ее на встроенном (выносном) табло прибора;
передача всей собранной информации по цифровому радиоканалу с ис-
пользованием штатных средств радиосвязи или иными средствами на диспет-
черский пункт;
обмен формализованными сообщениями между диспетчерским пунктом
и транспортными средствами;
дифференциальный режим навигации.
Аппаратура, устанавливаемая на диспетчерском пункте обеспечивает:
в автоматическом режиме:............... -.......... - -
отображение на мониторе IBM-совместимого компьютера электронной
карты или карты графического формата с отображением в реальном масштабе
времени информации о местоположении всех транспортных средств (ТС), на-
ходящихся в системе и информации о их состоянии и состоянии окружающей
среды;
прием и запись информации, получаемой с ТС и событий в системе;
сигнализацию об отклонениях от заданного маршрута контролируемых
ТС, аварийных ситуаций;
воспроизведение с заданным интервалом времени записанной информа-
ции;
в полуавтоматическом режиме:
передачу и прием сообщений всем или отдельным ТС;
составление маршрутов движения ТС, схематичных карт местности и за-
пись их в системные блоки ТС.
Аппаратура, устанавливаемая на транспортных средствах обеспечивает:
автоматический режим работы с отображением в схематичном виде на
табло системного блока местоположения всех ТС в системе;
непрерывное глобальное определение и отображение на табло систем-
ного блока ТС координат местоположения и составляющих скорости движе-
ния в выбранной системе координат (СК-42, СГС-90, WGS-84) координиро-
ванного всемирного времени;
отображение на табло контролируемых параметров среды, движения,
систем и агрегатов со световой и/или звуковой сигнализацией об отклонении
их от заданных значений;
[j2.9> Современные е&р.азяы анлтшпурв? потреиителей
27/
прием и отображение на табло команд и сообщений с диспетчерского
пункта;
запись во внутреннюю съемную энергонезависимую, память (24 ч с ин-
тервалом в 5 с) память с выбираемым интервалом времени значений контро-
лируемых параметров, принимаемых и передаваемых сообщений с привязкой
их ко времени и координатам местоположения ТС;
подтверждение приема сообщений с диспетчерского пункта и передачу
на диспетчерский пункт формализованных сообщений (до 64), определяемых
потребителем;
автоматическую передачу на диспетчерский пункт сигнала “Авария”.
Характеристики:
Точность навигационных определений:
автономный режим:
координат, м ................ 18 ... 20
скорости, см/с......... ..... 8 ... 10
времени (UTC), мкс .......... 0,1
дифференциальный режим:
координат, м...................... 1... 3
Время определения
(холодный старт), мин ................. не более 3
Количество объектов в системе .... до 1024
Скорость опроса объектов, мин..... до 500.
Режим радиообмена: симплекс, двухчастотный симплекс, дуплекс с вре-
менным разделением.
Скорость передачи информации, Кбит/с
Интерфейс.........................
Рабочая температура, °C ..........
Электропитание (постоянное), В....
Энергопотребление, Вт.............
Габаритные размеры, мм ...........
Масса, кг.........................
до 16
RS-232C
-40 ... +50
28 ±9
не более 10
195 х 165 х 105
2
ПЕЛЕНГ
Разработчик — Научно-производственный концерн “НАУЧНЫЙ
ЦЕНТР”. Назначение — портативный. Число каналов — 8.
Решаемые задачи:
работа по сигналам НС ГЛОНАСС и GPS;
автоматическое определение геодезических координат, прямоугольных
координат в проекции Гаусса, высоты в балтийской системе, местного и сис-
темного времени, путевой скорости и составляющих вектора скорости;
определение направления и расстояния до указанных потребителем то-
чек маршрута.
Гл ад а 12. Аппаратура потуеСитай^
.2.7 в
наомп
Х::а р а к т« р ис тики:
Точность навигационных определений:
координат, м.....................
скорости, см/с.................
времени (UTC), мкс ............
Частота обновления координат, ;с*1 .
Время определения
(холодный старт), мин ....................
Интерфейс ..........................
Работая температура, °C ............
Электропитание (постоянное), В......
Энергопотребление, Вт...............
Габаритные размеры, мм..............
Масса, кг...........................
.20 ... 23
40 ... 50
0,9 ... 1
1
-не более .2
RS-232C
40 ... +.50
9 ...:32
нс более 7,5
2955 х 105 х 73
1,5
Литература
12.1. Отчет по ОКР “Интер-А”. “Приемоиндикатор спутниковых навигационных^
систем для гражданской авиации”/ МКБ “Компас”, 1995. 'i
12.2. Цифровые радиоприемные системы: Справочник/ М. И. Жодзишский, Р. Б.:
Мазепа н др. — М.: Радио и связь, 1990.
12.3. 'Первачёв С. Б. Радиоавтоматика. — М.: Радио и связь, 1982.
12.4. Корн Г., Корн Т. Справочник по математике. — М.: Наука, 1968.
12.5. Аппаратура радионавигационных систем ГЛОНАСС и GPS. Системы коорди-
нат. Методы перевычислений координат определяемых точек. Государственный стандарт
РФ (проект), Госстандарт России, 1997.
12.6. GNSSP/ 1.ICAO, 1994.
12.7. GNSSP/ 2.ICAO, 1995.
12.8. FANS(II)/ 3-WP/87, ICAO, 1992.
12.9. FANS(II)/ 4-doc 9623, ICAO, 1993.
12.10. Гриневич А.С. Спутники для авиации//Воздушный транспорт, 1996,с. 38—39.
12.11. О допуске к эксплуатации приемоиндикаторов СНС на воздушных судах
гражданской авиации. ДВТ МТ РФ, ДВ-61-32. 28.03.95.
12.12. TSO С129, 1992.
12.13. AN-CONF/ 10.Doc 9583, ICAO, 1991.
12.14. RTCA No. RTCA/ DO-208, 1991.
12.15. J 20x20. EC, 1997.
12.16. AC 90-94.FAA, 1994.
12.17. Опарин А. И., Алпеев С. В. Методические указания по летной эксплуатации
системы спутниковой навигации. —М.: Изд-во ГосНИИ АН, 1995.
12.18. Бортовые средства радионавигации/ Под ред. В. С. Смирнова. — М.: Воен-
издат, 1993.
12.19. Lachfhtlle G. Navigation Accuracy For Absolute Positioning// System
Implications and Innovative Applications of Satellite Navigation, AGARD Lecture Series 207,
1996.
12.20. Перов А. И. Дискретные следящие измерители с оптимальным группировани-
ем данных// Радиотехника, 1997, № 7. с. 62—66.
279
Р а з д е л 3
НАПРАВЛЕНИЯ РАЗВИТИЯ СПУТНИКОВОЙ
РАДИОНАВИГАЦИОННОЙ СИСТЕМЫ
ГЛОНАСС
Глава 13
Направления совершенствования
системы ГЛОНАСС
Превращение системы ГЛОНАСС в непрерывно эксплуатируемую систе-
му предъявляет повышенные требования к надежности функционирования ее
космического и наземного сегментов и совместимости навигационных сигна-
лов с сигналами других радиотехнических систем. Кроме того, необходимо
учитывать постоянный рост требований пользователей к точности навигаци-
онного определения и целостности системы, понимая под целостностью ее
“способность обеспечивать предупреждение пользователей о тех моментах вре-
мени, когда система не должна использоваться для навигационных определе-
ний.
Модернизация СРНС ГЛОНАСС будет производиться по следующим на-
правлениям:
улучшение совместимости с другими радиотехническими системами;
повышение точности навигационных определений и улучшение сервиса,
предоставляемого пользователям;
повышение надежности и срока службы бортовой аппаратуры спутников
и улучшение целостности системы;
развитие дифференциальной подсистемы.
Навигационные радиосигналы. В настоящее время номинальные значения
несущих частот навигационных радиосигналов ГЛОНАСС в частотных под-
диапазонах £1 и L2 определяются следующими выражениями (10.1):
/и = /о1 +Wi; fn =/02
где к =0 ... 24 — номер литера несущих частот навигационных радиосигналов,
излучаемых НС в частотных поддиапазонах £1 и £2; /01 = 1602 МГц;
/о2 = 1264 МГц; Д/, =562,5 кГц; Д/i = 437,5 кГц; fLilfL1 = 7/9.
Литер к = 0 потребителями системы ГЛОНАСС не используются и слу-
жит для проверки резервных НС на орбите.
280 t л а ь .13. H„ .равлев. > соверш енством. Айя си< Рмы Г. JHACCJ
Таким образом, навигационные радиосигналы спутников ГЛОНАСС
предназначенные гражданским пользователям, занимают в частотном поддиа-3
пазоне L1 полосу 13,5 МГц (рис. 13.1). При этом отмечены помехи, создавав^
мые спутниками ГЛОНАСС (наблюдениям радиоастрономии) в полосе частот*
1610,6... 1613,8 МГц.
Радиоастрономия
1610,6 1613.8
1598,0625 1602 1604,25 1608.75 1615,5
I 1 t » 1 1 I 1 I I i, I I I 1 I 1 I 111 1 I I I I I I I i , I
-7 0 4 5 6 12 16 20 24
/Технологическая частота
____До:995г.....................................................1 , . , I
I Несущие частоты нжчгяционных радносигиялоя*।
~ Технологическая частота
С1995 г. до 1998 г. ,/ . , //
----------------------1 1-----1--1-1---1--1----1-1--1__1_____I_I_L—1------------
I Несущие частоты навигационных радиосигналов
~ / Технологическая частота
С 1998 г. до 2005 г. / ,
1 —1—I—I—I—I—I—I—I—I_________I_I___;
______Несущие частоты навита-_
После 2005 г 1 * * * * * * В иионных радиосигналов
I__1__I__I I___I__।_I—I—I—।—I—1—।----------------------
! ___Несущие частоты навита-__! \ \
I * ииодаых радиосипило. 1 Техналоптчсаме частоты
Несущие частоты, которые имеют ограниченное пользование.
Ряс. 13.1. Распределение частот
Кроме того, решениями WARC-87 и WARC-92 полоса частот
1610,6 ... 1626,5 МГц распределена на первичной основе спутниковой службе
распределения и подвижной спутниковой службе в направлении Земля—
Космос, Полоса частот 1613,8 ... 1626,5МГц распределена подвижной спутнико-
вой службе в направлении Космос—Земля на вторичной основе.
С учетом этого при модернизации системы ГЛОНАСС проводится по-
этапное смещение и сокращение занимаемого системой диапазона частот.
Принцип частотного разделения навигационных радиосигналов сохраня-
ется, но общее число частот будет сокращено до двенадцати. Чтобы исключить
помехи пользователям внутри системы ГЛОНАСС, в модернизированной сис-
теме навигационные радиосигналы спутников, находящихся в противополож-
ных точках орбиты, будут излучаться на одной и той же частоте.
В ходе модернизации системы ГЛОНАСС запланирована следующая
этапность сокращения и смещения занимаемого диапазона частот.
Этап 1 до 1998 г. На этом этапе спутники ГЛОНАСС полностью пре-
кращают передачу радиосигналов £1 в полосе 1610,6 .... 1613,8 МГц (литеры
частот к = 16 ... 20), используемой радиоастрономией.
Находящиеся в эксплуатации спутники ГЛОНАСС будут использовать
литеры частот к = 0 ... 12, 22, 23, 24. Литеры частот к = 13, 14 и 21 будут
иметь ограниченное применение: после запуска спутников на этапе ввода в
эксплуатацию, а также при проведении профилактических работ на орбите.
281
Этап 2 с 1998 по 2005 г. Спутники ГЛОНАСС-М будут излучать несущие
часто с литерами к = 0 ... 12, в порядке исключения иногда может быть ис-
пользована несущая частота с к = 13. В оборудовании модернизированных
спутников ГЛОНАСС-М будут содержаться фильтры, ограничивающие внепо-
лосное излучение в радиоастрономическом диапазоне 1660 ... 1670 МГц в со-
ответствии с рекомендациями 769 ММКР (CCIR) (-238 дБВт/м2Гц).
Этап 3 с 2005 г, В этот период спутники ГЛОНАСС-М будут излучать
для навигации несущие частоты с к = -7 ... 4; несущие частоты с номиналами
,к — 5 и 6 будут использоваться только как технологические при работе спут-
ников с наземным сектором управления. Спутники, которые будут действовать
в этот период, будут содержать фильтры, ограничивающие внеполосное излу-
чение в радиоастрономическом диапазоне 1660 ... 1670 МГц в соответствии с
рекомендациями 769 ММКР (CCIR) (-238 дБВт/м2Гц).
Эталоны частоты. С целью повышения точности навигационного опре-
деления на борту спутников ГЛОНАСС-М устанавливается новый цезиевый
стандарт частоты с максимальной нестабильностью 110~13 в сут. Можно отме-
тить, что максимальная суточная нестабильность частоты эксплуатируемых
генераторов на спутниках ГЛОНАСС составляет 5-10~13.
Двухчастотное иснользоваиие. В настоящее время сигнал, предназначен-
ный для гражданских пользователей, передается только в диапазоне £1. При
этом в период максимальной солнечной активности составляющая погрешно-
сти навигационного определения за счет ионосферной рефракции может дос-
тигать 30 м и более.
Спутники ГЛОНАСС-М будут, излучать сигналы для гражданских пользо-
вателей в двух диапазонах волн L1 и L1, что позволит практически полно-
стью исключить ионосферную погрешность измерения у тех пользователей,
которые оборудованы двухчастотными приемниками. Мощность, излучаемая
на частоте £2, для гражданских пользователей составит 10 Вт; коэффициент
направленного действия антенны в этом диапазоне — 8,8 дБ вдоль оси спут-
ника, направленной на Землю, и соответственно 11 и 9 дБ при углах ±15 и
+ 19° относительно этой оси.
Дальномерный код сигнала для гражданских пользователей в диапазоне
£2 будет формироваться таким же, как и в диапазоне £1, а именно в виде
псевдослучайной последовательности максимальной длины с периодом 1 мс и
скоростью передачи 511 Кбит/с. Образующий полином имеет вид 2?(х) =
= 1 + х5 + х9.
Навигационное сообщение. В связи с передачей дополнительного кода
для гражданских пользователей в диапазоне £2 в навигационное сообщение
спутников ГЛОНАСС-М вводится дополнительный параметр Атп, характери-
зующий разницу аппаратных задержек дальномерных кодов в диапазонах £1 и
£2: Атп>0 при запаздывании дальномерного кода в диапазоне £2 относи-
282 Г л а в а 13. Направления совершенствования системы ГЛОНАСС
j
тельно кода в диапазоне £1 и Дтп < 0 при опережении. Погрешность переда- -
ваемой величины 8тп < 2 10-9 с. ’ ।
В навигационное сообщение спутников ГЛОНАСС-М кроме Дтп вводит- '
ся еще несколько параметров, повышающих надежность навигационного опре- •
деления пользователей.
Спутники ГЛОНАСС передают в навигационном сообщении параметр
тс, характеризующий сдвиг шкалы времени центрального хронизатора систе-
мы, к которой привязаны фазы дальномерных кодов спутников, относительно
шкалы времени UTC(SU) Государственного эталона времени и частоты Рос-
сии, в которой рассчитываются эфемериды навигационных спутников.
Шкала времени UTC(SU) может корректироваться на 1 с один или два
раза в год в соответствии с ходом астрономического времени. Коррекция мо-
жет быть проведена в 0 ч с 31 декабря на 1 января, с 31 марта на 1 апреля, с
30 июня на 1 июля и с 30 сентября на 1 октября.
В навигационное сообщение ГЛОНАСС-М вводится признак ожидаемой
секундной коррекции шкалы UTC(SU). Этот признак будет постоянно нахо-
диться в навигационном сообщении со следующими вариациями:
10 — решение о проведении коррекции времени пока не принято;
00 — коррекции не будет; __
01 — будет коррекция на +1 с;
11 — будет коррекция на -1 с.
В случае намечающейся коррекции шкалы времени UTC(SU) информа-
цию об этом предполагается вводить в навигационное сообщение не менее
чем за 2 мес. до проведения коррекции.
В навигационное сообщение также предполагается ввести признак мо-
дификации спутника:
00 — спутник ГЛОНАСС;
01 — спутник ГЛОНАСС-М.
Совместное использование ГЛОНАСС и GPS. Совместное использование
для навигации двух систем ГЛОНАСС и GPS дает пользователям дополни-
тельные преимущества, главными из которых являются повышение достовер-
ности навигационного определения и улучшение геометрического фактора за
счет увеличения числа доступных спутников в зоне радиовидимости потреби-
теля. Однако для работы по комбинированному созвездию в настоящее время
требуется минимум пять спутников для определения трех координат из-за не-
обходимости вычисления дополнительного неизвестного параметра — разно-
сти фаз дальномерных кодов спутников ГЛОНАСС и GPS. В системе ГЛО-
НАСС-М планируется передавать разность шкал времени GPS и ГЛОНАСС
XCPS-CLN , к которым привязаны фазы дальномерных кодов. Этот параметр
планируется передавать с максимальным диапазоном значений ±1,9-1О~3 с и
ценой младшего разряда 110“9 с.
283
Надежность н целостность. В бортовое оборудование спутников ГЛО-
> НАСС-М вводятся дополнительные резервные приборы и дополнительные пе-
рекрестные связи между приборами для повышения надежности радиоэлек-
тронного оборудования в период активного существования спутников.
В системе ГЛОНАСС контроль целостности навигационного поля осу-
ществляется двумя способами.
Первый способ — на спутниках системы непрерывно производится авто-
номный самоконтроль функционирования основных бортовых систем. В слу-
,-чае обнаружения нарушений, влияющих на качество навигационного радио-
сигнала, в навигационное сообщение автоматически включается признак В„,
говорящий о непригодности данного спутника для навигации. Автономный
контроль состояния бортовых систем обладает высокой оперативностью, одна-
ко средства автономного контроля не могут обеспечить обнаружение всех воз-
можных нарушений функционирования спутника.
Второй способ — качество навигационных сигналов проверяется средст-
вами контроля навигационного поля, входящими в состав наземного комплек-
са управления. При обнаружении отклонений в параметрах навигационных
сигналов, могущих влиять на качество навигационных определений, в состав
навигационного сообщения плодится признак Сп, говорящий о непригодности
.спутника для навигации.
Улучшение целостности системы планируется проводить в направлении
расширения как состава цепей бортовой аппаратуры, охваченных автономным
контролем, так и средств непрерывного мониторинга навигационного поля со
стороны наземных станций.
Для создания расширенной
сети непрерывного мониторинга
навигационного поля с одновре-
менной выработкой дифференци-
альных поправок в Российском
НИИ космического приборострое-
ния разработана станция на основе
многоканального приемника, по-
зволяющего производить прием и
обработку сигналов каждым кана-
лом как спутников ГЛОНАСС, так
и GPS. На рис. 13.2 приведено рас-
пределение плотности веро ятпости
числа радиовидимых сп утников
систем ГЛОНАСС и GPS для пол-
ного состава орбитальных группи-
ровок (24 спутника в каждой сис-
теме). С учетом критерия зффек-
тивность/стоимость станцич. мони-
Рис. 13.2. Плотность вероятности числа
радиовидимых спутников
систем ГЛОНАСС и GPS
284 Глава 13. Направления совершенствования системы ГЛОНАСД
торинга спроектирована на основе 16-канального приемника, каждый из канш
лов которого может принимать сигналы спутников ГЛОНАСС и GPS. я
Станция предназначена для выполнения следующих основных функций^
непрерывного одновременного слежения за 16 спутниками ГЛОНАСС ^
GPS с сохранением в памяти всей принятой и измеренной информации;
непрерывных навигационных определений по созвездиям:
только спутников ГЛОНАСС;
только спутников GPS;
спутников ГЛОНАСС и GPS;
анализа составляющих погрешностей навигационных определений, а
также погрешностей измерений псевдодальностей и псевдоскоростей;
контроля качества передаваемых спутниками навигационных радиосиг-
налов и навигационных сообщений;
формирования сигналов целостности навигационного поля и дифферен-
циальных поправок по визируемым спутникам.
Аппаратурно-программные средства станции обеспечивают ее работу в
атоматизированном режиме, а также при необходимости управления вручную
оператором. Достоверность ее мониторинговых функций подтверждается не-
прерывным контролем функций центральным компьютером станции на основе
телеметрирования параметров приемного устройства в реальном времени без
прекращения приема и обработки информации спутников. Непрерывно кон-
тролируются:
работа схем слежения за задержкой дальномерного кода, частотой и фа-
зой принимаемых сигналов;
уровни шумов и принимаемых сигналов в каждом канале приемника;
состав и содержание принимаемой цифровой (по коду Хемминга и
сравнением соседних по времени кадров информации).
При обнаружении аномальных результатов измерений псевдодальности и
псевдоскорости производится дополнительный анализ качества работы стан-
ции путем включения всех или нескольких каналов на прием сигналов одного
спутника. Обнаружение аномалии всеми каналами одновременно дает возмож-
ность однозначно отнести причины аномалии к нарушениям в навигационном
сигнале.
Аппаратурные средства и программное обеспечение станции монито-
ринга позволяют, кроме того, производить непрерывные измерения шкал вре-
мени ГЛОНАСС и GPS, а также расхождения систем геодезических координат
СГС и WGS в точке расположения станции. Станция вырабатывает дифферен-
циальные поправки по всем визируемым спутникам систем ГЛОНАСС и GPS.
Стандартный интерфейс станции, соответствующий интерфейсам PC/AT
468 DX2, позволяет через линию связи передавать дифференциальные поправ-
ки пользователям, а также передавать любым абонентам все виды информа-
ции, формируемой На станции мониторинга. На основе этого планируется
объединить все размещенные на территории России станции в единую сеть и
обеспечить таким образом выработку сигналов целостности и расхождения
ЙЙЙЙ*
Ькал времени ГЛОНАСС и GPS для передачи их пользователям, а также фор-
мирование дифференциальных поправок, практически не зависящих от степе-
ни удаления пользователя от станции для территории, покрытой этой сетью.
[ Совместное использование систем ГЛОНАСС и GPS в ближайшее время
Должно стать реальным фактором, повышающим надежность и достоверность
навигации гражданских пользователей во всем мире. Анализ двух систем пока-
зывает, что большая часть различий при современном уровне быстродействия
у интеграции компонентов, используемых в навигационных приемниках, лишь
Незначительно усложняет и удорожает комбинированный приемник ГЛО-
HACC-GPS.
, Значение расхождения шкал времени ГЛОНАСС и GPS будет переда-
ваться в составе навигационного сообщения спутников ГЛОНАСС-М. Остает-
ся не определенное до настоящего времени с необходимой точность различие
систем координат WGS и СГС, которое может несколько ухудшить точность
комбинированного местонахождения. Однако при взаимном стремлении к со-
трудничеству расхождение систем координат наиболее точно может быть опре-
делено совместными усилиями специалистов России, США и других заинтере-
сованных стран.
286 Д
Г л а в а 14 1
Навигационно-временные определения, J
основанные на фазовых измерениях I
. — —
й
Навигационно-временные определения, основанные на фазовых метода^
измерения, характеризуются высокой точностью. Например, потенциальна^
точность (СКО) оценки задержки т = const по фазе несущей частоты /о опре^|
t
деляется соотношением ат = l/(2jtgf0) 15-3], где q1 — отношение энергии сий
нала к спектральной плотности аддитивного шума наблюдения. При рабочих
значениях q1 я 10 имеем ат » 1/(20/0) = 7о/20, т- е- СКО составляет сотые доля
периода ВЧ. Такая высокая точность определяет значительный интерес к фа,
зовым методам измерения. В настоящее время наиболее активно.эти метолу
используются для решения задач геодезии (см. п. 12.8.3). Перспективным яв-
ляется их применение для высокоточной навигации, например для определен
ния пространственной ориентации объектов и автоматизации посадки ЛА.
Сигналы НС в точке приема являются квазикогерентными, поэтому фа-
зовые методы в СРНС применяют для решения задач дифференциальных
(относительных) определений (см. § 11.1).
Основная проблема фазовых измерений (ФИ) — их неоднозначность в
целое число циклов (см. п. 12.8.3). Разрешение неоднозначности (PH) можно
выполнять на уровне как первичной, так и вторичной обработки. Сначала
опишем существующие подходы к PH на этапе вторичной обработки радиона-
вигационных параметров. Затем рассмотрим общий подход к синтезу алгорит-
мов НВО (в том числе и алгоритмов первичной обработки), основанных на
ФИ, с помощь методов оптимальной фильтрации.
14.1. Методы разрешения неоднозначности фазовых
измерений на уровне вторичной обработки
При решении задач НВО в СРНС на уровне вторичной обработки в ка-
честве входных (обрабатываемых) процессов, которые в дальнейшем будем на-
зывать наблюдениями, используются измерения ПД, выполняемые автономны-
ми схемами слежения за задержкой огибающей сигналов НС и схемами ФАП.
В дифференциальном режиме для определения относительных координат
и взаимного расхождения шкал времени используют разности измерений ПД
до одного и того же НС для одинаковых моментов времени в разнесенных
точках приема, поэтому для ДР уравнения наблюдений по огибающей и фазе
высокочастотного заполнения запишем в виде
|р4Л, Методы PH ФИ на уровне вторичной обработки .................. 287
* Погк,!,! = бДк,и + Дк,1,1 + nork,lj'< (14-1)
Чфк,1,1 ~ бДк,1,1 +^ljf»lj + Д'к,1,1 + пфк,1,Г> ' = » / = 1,2 , (14-2)
^•де &Дк,1,1 — разность геометрических дальностей в к-й. момент времени между
i-M НС и точкой приема по /-му частотному каналу; &Д', ЬД" — нескомпен-
^Ированные погрешности измерения ПД, обусловленные тропосферой, ионо-
сферой, аппаратурой потребителя и др. (см. гл. 7); Хц — длина волны сигна-
ла, излучаемого /-м НС по /-му частотному каналу; — смещение в целое
.число длин волн (неоднозначность) в фазовых измерениях; лог, Лф — шумо-
вые составляющие измерений ПД по огибающей и фазе сигнала.
Неоднозначность фазовых измерений (НФИ) отражена в (14.2) состав-
ляющей к^тц.
Как отмечалось в п. 12.8.3 для исключения части составляющих погреш-
ностей, входящих в первые разности, в качестве наблюдений берут вторые
разности, уравнения для которых имеют вид, аналогичный (14.1), (14.2). Одна-
ко это не устраняет НФИ. Одним из путей решения проблемы неоднозначно-
сти является применение третьих разностей — приращения двойных разностей
ПД за некоторое время. Известны результаты по использованию в АП, рабо-
тающей по сигналам ГЛОНАСС, третьих разностей [14.1]. Недостатком этого
подхода является длительное время наблюдения (порядка 20 мин) для получе-
ния оценки вектора базы с сантиметровой точностью.
Классификация методов разрешения неоднозначности ФИ может быть
выполнена по используемой в этих целях информации. В существующих сис-
темах ГЛОНАСС и GPS это априорные оценки координат; оценки координат с
помощью навигационных средств иного типа; измерения по огибающей радио-
сигнала; избыточность измерений ПД по фазе высокочастотного заполнения и
огибающей за счет:
второго частотного канала НС;
совместной оценки псевдозадержек ВЧ-заполнения радиосигналов более
чем от шести НС;
наземных псевдоспутников;
изменения пространственного положения спутников во времени.
В зависимости от изменения расположения точек аппаратуры потребите-
лей методы PH классифицируют как статические, кинематические и "в дви-
жении" ( on а Пу). Статические методы PH применяют при неподвижной АП, а
два других метода — при изменении положения точек расположения АП во
время сеанса определения их относительных координат. В кинематических
методах PH осуществляется в начальный момент времени при размещении АП
в точках с известными координатами, а в методах on a fly — в процессе вза-
имного перемещения.
"$8 \ . давя 4. НВГ основ; уые на )азовы ^змере
Наиболее эффективные процедуры PH основаны на избыточности фаза-'
вых измерений, когда число измерений фазы больше числа неизвестных пара-,
метров (координат). В последние годы этот подход привлек наибольшее вни^
мание. Проиллюстрируем общую и^ею использования избыточности фазовых’
измерений на примере определения местоположения объекта в плоскости.’
Пусть измерения осуществляются в точке А с координатами хА, уА. На рис.
14.1, а приведен чертеж приема одного сигнала с направления N^, в предпо-:
ложении плоского фронта приходящей волны. В точке А полная фаза сигнала,
Фл1 = МА1 + Фл1, где Мм = епбег(дл1(хл,ул)/Х1) — число целых циклов фазы!
принимаемого сигнала, характеризующее неоднозначность измерений; '
дробная часть полной фазы.
В результате измерений определяется только ф^] = AfAl - ф^] = const.
Имея данные одного измерения, нельзя однозначно определить две неизвест-
ные координаты хА, уА точки А. Приведенные линии положения являются
геометрическим местом точек всех возможных решений.
На рис. 14.1, б приведен аналогичный чертеж при приеме двух сигналов
с различных направлений и N2 в общем случае с различными частотами
(длины волн А.) и X?). В точке А проводят два измерения
Фд1 = МА1 ~ Фл1 = const]; фл2 = МА2-фд2 = const? . (14.3)
Решению этой системы уравнений соответствуют точки пересечения
прямых на рисунке. Формально, с точки зрения НВО, имеем два неизвестных
параметра хА, уА и два уравнения для их определения, т. е. минимально необ-
ходимое число измерений. Однако проблема в том, что неизвестные парамет-
ры хА, уА входят лишь в одно из слагаемых каждого уравнения (14.3), поэто-
дВйД. Умды 'S ФИ, ^уровне Inopuui. ) оброс Аки ) * 289
5jgy фактически есть четыре неизвестных параметра х^, у л, Mji, М^г, что и
Приводит к неопределенности решения.
S Бели теперь ввести дополнительное измерение (при формальном опреде-
лении задачи НВО — избыточное), то, как видно из рис. 14.1, в, в ограничен-
дбй окрестности точки А три линии ф^/ =const( пересекаются лишь в одной
точке А. Однако проведение избыточных измерений не снимает проблему не-
Ходнозначности решения, так как каждое новое (/-е) измерение содержит и до-
полнительное неизвестное Избыточные измерения расширяют окрест-
ность вокруг искомого решения, в которой отсутствуют другие возможные ре-
шения. В этом и состоит эффект избыточности измерений.
Избыточность фазовых измерений в СРНС требует соответствующего
числа НС и (или) использования сигналов второго частотного канала. Реше-
ние общей задачи НВО в дифференциальном режиме на основе фазовых изме-
рений предполагает видимость пяти и более НС. Это может быть обеспечено
при совместном применении обеих систем в рамках единой системы GNSS
дли путем использования псевдоспутников.
При измерениях в двух частотных каналах и пренебрежимо малом оста-
точном ионосферном смещении возможно приведение измерений псевдоза-
держек высокочастотного заполнения на частотах.каналов £1 и L2 к эквива-
-дентным -измерениям псевдозадержек на частотах биения и
Л =(/1 + /г)/2 • Для правильного PH при этом способе необходимо (но не
достаточно), чтобы ошибка измерения двойных разностей ПД по огибающим в
(14.3) была меньше половины длины волны полуразностной частоты /д
(например, для СРНС GPS, равной 63 см).
Другой подход к разрешению неоднозначности при решении задачи НВО
сводится к целочисленной максимизации функции неоднозначности, выбран-
ной из характера периодичности сигналов НС по фазе [14.2]. Для малых базо-
вых линий (линий, соединяющих две точки в пространстве), когда можно пре-
небречь остаточными ионосферными погрешностями, в [14.2| предложена
функция неоднозначности
к г я-1 .
С?(х) = 5ЕЕ - Д''Д*Л/(х))Д/),
где х = хЛ-хв — вектор базы, т. е. относительных координат двух точек;
Пф— наблюдения, соответствующие вторым разностям; Д"Д — вторые разно-
сти дальностей.
Использовать приведенную функцию неоднозначности для решения за-
дачи оценки вектора базы крайне сложно.
290 Г л а в a 14. ПВО, основанные на фазовых измеренмо^И
Более простое решение задачи PH при малых базовых линиях (|х|« ДлН
получается, если разность геометрических дальностей АД*,/,/ аппроксимирсйИ
жать линейной зависимостью ДД*,/,/ = 8*,/jx*i гДе 8*,!,/ — вектор коэффициент
тов аппроксимации. Объединив наблюдения по всем НС и всем частотным
каналам ((14.1), (14.2) с индексами I, Г) по огибающей и фазе в соответствую^
щие векторные т)огЛ> ЧФЛ размерностью р, а искомые величины: вектор базц
х, расхождение шкал времени, остаточные ионосферные и тропосферные
смещения и др. — в вектор потребителя П размерностью s<p, уравнения ндт
блюдения (14.1), (14.2) можно представить в виде
ЛогЛ = НогЛП* + norjt > ПфЛ ~ Нф^Пд; + Лш + Пф,4 ,
где Ног (Нф) — матрицы наблюдения, определяемые геометрией расположе- |
ния НС, причем rank (Ног(ф])жр; пог, Иф — векторы погрешностей измере-i
ний с нулевыми средними и матрицами дисперсий Уда, Уф, при этом
Уот » Уф; ш — вектор смещений в целое число длин волн; Л = diag„(Xt) —
диагональная матрица е элементами Xj-,- равиыми-длине-волны /-го НС.
Погрешности измерения при больших отношениях сигнал/шум допусти-
мо считать гауссовскими, поэтому, при решении задачи оценки П по крите-
рию максимума правдоподобия [5.1) PH удается свести к задаче целочислен-
ной минимизации квадратичной формы
£(ш) = (ш - m)TRm’ (ш - ш) , (14.4)
где in — среднее значение вектора целочисленных смещений, задаваемое на
множестве действительных чисел; Rra = л'(НфУпН* + Уф)Л~' — матрица,
имеющая смысл матрицы дисперсий ошибок оценки вектора целочисленных
смещений; Vn = (hJtVot’h от)
Задача целочисленной минимизации £(т) в общем случае может быть
выполнена только через процедуру перебора целочисленных комбинаций. В
(14.3] отмечено, что для PH при использовании АП геодезического типа, рабо-
тающей по пяти—семи НС и осуществляющей измерения ПД по двум частот-
ным каналам с помощью закрытого дальномерного кода необходим перебор
105... 109 целочисленных комбинаций. Уменьшение числа комбинаций при
переборе возможно за счет учета слабой обусловленности матрицы Rm.
В.14,2. Беспереборные процедуры разрешения аеоднозк^чности ! 91
П. Значения дисперсий элементов вектора оценки смещений в целое чис-
до длин волн определяются матрицей HorVnHor. Для существующих образ-
цов АП значения диагональных элементов матрицы НогУц11м. находятся в
^диапазоне 5 ... 30. При этом матрица HOTVnHjr вырождена, так как
rank (HorVnHor)'1 = р. -Можно показать, что в соответствии с теоремой Вейля
414.4] матрица Rm слабо обусловлена, т. е. р - s ее собственных чисел будут
|деНьше или равны максимальному собственному числу матрицы Л~'УПЛ4 и
^Меньше остальных собственных чисел матрицы R„, одновременно
? ^Rm I <(Rm)u ; i = 1,п, где п — размерность матрицы Rm.
Известно [14.5], что уменьшение определителя |Rm | приводит к
; уменьшению вероятности неправильного PH. С другой стороны, слабая обу-
, словленность матрицы R„ дает возможность значительного уменьшения
: числа перебираемых целочисленных комбинаций по сравнению с 105 ... 109
[14.4, 14.6].
Повышение достоверности PH и уменьшение числа целочисленных
г комбинаций при переборе возможно путем усреднения m во времени. Для
существующих образцов АП геодезического типа временное усреднение осу-
ществляется в течение нескольких минут. Однако такое усреднение невоз-
можно, например, для задач авиационной навигации.
Альтернативой временному усреднению может служить сглаживание
измерений ДП (или их разностей), полученных по огибающей сигнала, более
точными измерениями, полученными по фазе высокочастотного заполнения.
Такой подход с использованием калмановской фильтрации позволяет суще-
ственно уменьшить шумовую составляющую измерений ПД по огибающим
(carier (phase) smoosing) [14.7].
14.2. Беспереборные процедуры разрешения неоднозначности
Как отмечалось в предыдущем параграфе, во многих методах PH возни-
кает проблема целочисленной оптимизации, решение которой основано на
переборе целочисленных комбинаций. Ниже будет рассмотрена бесперебор-
<гная процедура PH, которая основана на том, что оценивание при наличии в
наблюдении периодических функций имеет смысл лишь при малых вероятно-
стях неправильного PH. Вероятность неправильного PH является монотонной
функцией определителя матрицы Rm (14.4), т. е. с уменьшением определите-
ля будет уменьшаться вероятность неправильного PH [14.11—14.13]. Избы-
точность фазовых измерений приводит к тому, что матрица становится слабо
обусловленной, т. е. среди ее собственных чисел имеются собственные числа,
>2 ? "j . г ya в а У HBC основ» тине на Чазовы? чзмерг
значительно меньшие, чем остальные. Это приводит к тому,
чКЛ’ «(R»)B ; i = 1,п. При этом часть осей эллипсоида (14.4) будет kmcJ
размеры значительно меньше остальных. Из геометрических соображений
ясно, что поиск точки арифметического минимума целесообразно осущесД
лять внутри узкой области пространства в окрестности центра данного э®
липсоида.
Как отмечено в ]14.12], поиск точки целочисленного минимума квадр£
тичной формы (14.4) в общем случае должен выполнятся через процедур
перебора целочисленных комбинаций. Однако, если Rn = diag„ (Ra)u,
точка целочисленного минимума квадратичной формы (14.4) определяет^
через округление до ближайшего целочисленного вектора
т = [ш]г,
(14.5)
где [ш]^
обозначает операцию округления до ближайшего целого.
Действительно, для диагональной матрицы Rm имеем
(m-m)TRi,(m-m) = £(m,-m,)2/(Rm) .
/-1
Так как каждое слагаемое суммы зависит только от одного элемент-
вектора ш, то минимум квадратичной формы достигается тогда, когда дос-
тигается минимум каждого слагаемого
= 1 J = W* ‘
Сформулируем следующую задачу: найти такую корреляционную матри-
цу Rm (при фиксированном значении ее определителя |Rm| = 0), для коп-
рой вероятность правильного PH для беспереборной процедуры [14.5] буде
максимальной. Определение такой матрицы дает направление поиска требуе-
мого преобразования квадратичной формы.
Рассмотрим задачу условной максимизации
R„ =max’1|pnp(R01||RBI| = р)|,
(14.6
где Рпр — вероятность правильного PH.
Полагая погрешности измерений (14.1), (14.2) гауссовскими, для верс-
ятности правильного PH имеем
пыепр ?ре»ед \неодн уучноа
ол од ол
4p(R.)= f - f - fJV„(x,o,R^)dx,
-од -оз -од
(14.7)
je Яя(х,д,И) обозначает и-мерный гауссовский закон распределения вектора
• со средним значением а и матрицей дисперсий R.
Для решения задачи нахождения условного экстремума (14.6) восполь-
уемся методом множителей Лагранжа (5.11], в соответствии с которым
srpkP(RB)-Y(lRB|-₽)] = 0, что приводит к уравнению
max
(MR-I=₽)
RB
ол ол ол
-2уР -2rP)R„= J ... j ... J xxT^(x,O,Rm)tZx.
-ол -ол -ОЛ
Легко проверить, что его решением является матрица
Rm - 1Л^Р (14.8)
F- - . . - ... —
частный случай- диагональной матрицы. -При такой матрице поверхность,
Задаваемая (14.4), представляет собой многомерную сферу. Подставляя (14.8)
& (14.7), можно вычислить максимальную вероятность правильного PH
' Рпр =(2f(0^/^₽)-1)".
Полученный результат показывает, что для повышения эффективности
беспереборной процедуры PH (повышения вероятности правильного PH)
необходимо искать такое преобразование координат q = Um, чтобы в новой
системе координат уравнение (14.4), принимающее вид
(q - Um)T(URmUT)1(q - Um) = L,
задавало сферу. При этом обязательным требованием является взаимно одно-
значное отображение целочисленных точек при преобразовании U . Необхо-
димое и достаточное условие этого — унимодулярность (равенство определи-
теля по абсолютному значению единице) и целочисленность матрицы U .
Следовательно, матрица U не может быть построена на множестве собствен-
ных векторов матрицы Rm, что, как известно, обеспечивает приведение
квадратичной формы к диагональному виду. Поэтому можно лишь требовать
близости в некотором смысле преобразованной матрицы UReUT к |Rm|ln
294 Г д.а в a 14, HRO, основанные на фазовых измерен^
(коэффициент при 1л равен |RB|, так как унимодулярное преобразован
не изменяет значения определителе матрицы). Из всех симметричных под
жительно определенных матриц размера п х п с одинаковым определите;*
р, матрица (/р 1„ будет иметь минимальный след. Таким образом, в качеств
меры близости двух матриц можно выбрать след матрицы и задачу нахожда
ния целочисленной унимодулярной матрицы U свести к задаче целочислен
ной минимизации
U = mm_1Jtr(uRBuT)| Ug е Z, |и| = ±1|.
I
Решение данной задачи можно осуществить на основе подхода, предо
ложенного в [14.15], заключающегося в том, что итоговое преобразований
задаваемое матрицей U разбивается на последовательные элементарные пре-
образования u(m): *
и = п«("»)>
(т)
где {т} обозначает множество последовательных преобразований, а каждая,
матрица а(ш) обеспечивает некоторое уменьшение следа преобразованной;
матрицы. При этом
u(m) = I„+E(m) eZM,
где Е(ш) — целочисленная матрица все элементы которой, кроме элементов,
/и-го столбца, равны нулю, причем ЕСш)^ = 0.
Рассмотрим матрицу R = u(m)RBuT(m) и аналогично процедуре Грам
ма-Шмидта представим ее след
tr(R) = (R.)^ + f ((«.), +2(E(io))fci(RB)fcl +(EB)j>B) J =
-До-.).
Учитывая целочисленность матрицы E(m), величина tr(R) будет mi-
нимальной, когда элементы т-го столбца Е(ш) (кроме элемента (EGn)^
равны
,2. Бесперебышые wQuedvMtj>MDWeHf^He<)dH03Ha4ifi>cmu
295
С учетом этого результата алгоритм нахождения матрицы преобразова
I U состоит из следующих шагов:
1) задают начальные условия: R = Rm; R = Rm; U = In;
2) последовательно для т = 1,л вычисляют
R*. .
_ ; j “ т; i * т;
.Eflun
0; i * /; / “ / “ m;
u(m) e I„ + E(m).
Для каждого m находят (переопределяют матрицы)
R = u(m)RuT(m); U:= u(m)V ;
3) сравнивают следы матриц R и R. Если tr(R) < tr(R), то выполняют
Переопределение R = R и осуществляют возврат к шагу 2. В противном случае
лгоритма завершен.
Эффективность рассмотренной процедуры беспереборного PH проиллю-
стрируем на задаче синхронизации (оценка смещения т’) разнесенных в про-
странстве генераторов по сигналам СРНС [14.11].
Полагается, что проведены три измерения разностейПД: одно цот — по
огибающей сигнала, два других , Цф2 — по фазам ВЧ-сигналов двух час-
тотных диапазонов LI, L2 (длины волн >.], >.2). Неоднозначность измерений
.заключена в двух фазовых измерениях. При использовании в данной задаче
'Методов оптимального оценивания (которые более подробно рассматриваются
зиже) возникает задача целочисленной оптимизации квадратичной формы
m = max”1 рлп(ш) = min_1f(m - m)TR^(m - m)l, (14.9)
-де m = |mj m2|T — вектор целого числа периодов неоднозначности в двух фа-
зовых измерениях;
Пог Пф 1
Пог Пф 2
х2
— вектор предварительных оце-
зок значений числа периодов неоднозначности;
296
Г л а в a 14. НВО, осночанные ня фазовых намерена
„2 „2
_2 . °ОГ ° от
ф + ич
„2 „2
° от _2 , °ог
ф ц
— матрица Дисперсий погрешностей оценки вектб|
т; Стог, °ф — дисперсии погрешностей ошибок измерений по каналам опт
бающей и фаз (последние в двух каналах полагаются равными).
Так как Оот>>стф, то одно из двух собственных чисел матрицы Rm зна
чительно меньше другого. Это видно из рис. 14.2, а, где показана (полученная:
моделированием) реализация эллипса, задаваемого уравнением
(z - m)TRn(z - й) = L
(14.10)
при Оф =0,03 и аот =0,5 м. Значение L соответствует значению доверитель
ной вероятности 0,99. Для определенности истинное значение ш выбранс
-4 -J -2 0 1
равным |0 0|т. Внутри эллипса со-
держится лишь одна целочисленна'
точка |0 0|т, которая, однако, не яь
ляется геометрически ближайшей -
центру эллипса. Геометрически бли-
жайшая к центру эллипса целочис
ленная точка |- 2 - 2|т не попадав
внутрь эллипса.
Рис. 14.2, б, в иллюстрирую
два промежуточных этапа преобр?
зования координат, а на рис 14.2,
изображен эллипс в окончательна
преобразованных координатах
Рис. 14.2. Целочисленная оптимизация
2 J 4 5 б Tj
= Uz =
(14.11
Матрица преобразования I
целочисленная, кроме того, ее о пре
делитель равен единице, поэтом
такое преобразование взаимоодн<
значно для целочисленных точе?
Из рисунка видно, что в новой cik
теме координат эллипс по форм
4 5
7 9
z.
43. Применение методовшипимальнодфильтрации
297
циг близок к окружности. Целочисленная точка | О О |т стала геометрически
Нижайшей к центру эллипса. Теперь в качестве точки целочисленного мини-
ума квадратичной формы (14.9) в новой системе координат можно взять точ-
у* получаемую округлением до ближайшего целого элементов вектора
= Um, т. е.
m = U
9 -5
-7 4
’ Моделирование показывает, что при этом вероятность правильного PH
5удет равна 0,83. Если для оценки помимо огибающей использовать только
фазовые измерения по частоте £1, то вероятность правильного PH при приня-
тых условиях равна 0,15.
- Приведенный пример позволяет сделать вывод, что избыточность фазо-
вых измерений радикально повышает достоверность PH. В этом примере так-
же продемонстрирована возможность использования беспереборной процеду-
ры PH при избыточных фазовых измерениях.
14.3. Применение методов оптимальной фильтрации
для синтеза алгоритмов НВО, основанных
на фазовых измерениях
14.3.1. Метод дополнительной неременной
Общим подходом к оцениванию случайных процессов в радиотехниче-
ских системах являются методы оптимальной фильтрации [5.1, 5.2, 6.1], по-
зволяющие определить апостериорную плотность вероятности оцениваемых
параметров и процессов, на основе которой могут быть получены те или иные
<х оценки. Использование методов оптимальной фильтрации в задачах вто-
зичной обработки навигационной информации достаточно традиционно [1.3,
.4, 14.7]. Применение тех же методов для синтеза оптимальных алгоритмов
первичной обработки, включающих извлечение информации из фазы несущей
частоты, затруднено в связи с возникающей мно гомо дальностью апостериор-
ной пл'отности, обусловленной наличием периодической функции в наблюде-
ниях. Для получения итоговых алгоритмов фильтрации в условиях полимо-
нальности апостериорного распределения предлагались различные подходы
1.3, 4.3 ]. Наиболее конструктивные результаты получаются при использова-
нии метода дополнительной переменной (МДП), впервые предложенного в
14.9], а применительно к задачам навигационных определений — в [14.10,
4.11].
Для задачи фильтрации задержки сигнала г по огибающей и фазе несу-
лей частоты суть МДП заключается в следующем. Вместо одной переменной
298
Г л а в a 14. НВО, осиоваияые на фазовых измерейз
1, входящей в описание огибающей ифазы сигнала, рассматривают две пру
менные {t, т^}, одна из которых т связывается с огибающей, а вторая ТдЛ
с фазой сигнала, т. е. для сигнальной функции полагается •5’(/,т,тУ1
= A(t - т)cosco0^ - trf) •
Тождественность двух переменных в исходной задаче учитывается в ai
риорном распределении ~
Аи(ьч») = Ап(т) Ят-т<»)’
(14.1
где Pan(t) — априорная плотность распределения задержки.
В дальнейшем рассматривается апостериорная плотность вероятное*
(АПВ) р (t, расширенного вектора т = |т xd|т. Так как априорная плотност
(14.12) содержит 8-функцию, то, как показано в [14.9] апостериорная пло*
ность также содержит эту функцию, т.е. имеет вид
I
Ят>М = <Ыт’т<«)8(т_т<0- (14-П
Типичный вид функции />2(1, t</) приведен на рис. 14.3. Наличие
(14.13) 8-функции отражено на рисунке секущей плоскостью т = rd. Пересе-
чение этой плоскости с поверхностью Д2(г»т</) с точностью до нормировоч
ного множителя совпадает с искомой апостериорной плотностью
Я*) = ,
(14.14)
т. е. имеет многопиковый характер. Поверхность />2(T>Td) более регулярна, чем?
Ряс. 14.3. Апостериорная плотность вероятности
в методе дополнительной переменной
Ят)- Ее зависимость по т оп-
ределяется огибающей сигнала
и при используемых сигнала*
унимодальна. По переменно
вид имеет много-
пиковый характер, но эт
многопиковость строго пери»
дична: />2(т, xd) = р2(т, xd +Т0,
где Tq — период повторени
ВЧ-сигнала, и ее легко учест.
Достаточно подробны!
вывод различных адгоритмо-
фильтрации, основанных нв
4.3. Применение методов оптимальной фильтрации 299
ДДП приведен в [14.11], поэтому ниже дается краткая сводка основных ре-
Гьтатов синтеза и некоторые примеры, иллюстрирующие их применение.
14.3.2. Оценка задержки одночастотного когерентного радиосигнала
На вход приемника поступает аддитивная смесь когерентного радиосиг-
нала 5(Г-т) = Л(/-т)соз(2»/о (/-т)) и белого гауссовского шума n(t) с нулевым
-ре дни м и односторонней спектральной плотностью Nq/2
у(/) = 5(Г-т) + л(/). (14.15)
? Время наблюдения » То - V/o • Априорные сведения о задержке за-
даются ее плотностью вероятности />ап(т).
Плотность вероятности, входящая в (14.13), имеет вид
Р2^, Td) = сРап (т) ехр{х(т) cos®0(Td - р(т))|,
4де Х(г) = А^(4 + Х2£т) — огибающая на выходе согласованного фильтра;
9 Гнб о ^нб
Мт) = Jy(4cos(<»o0^; W Jy(/)sin(<»o^;
р(т) = (l/<o0)arctg(xs(T)/jrc(T)). (14.16)
Плотность рг(т>т</) приведена на рис. 14.3. Учитывая характер данной
плотности, предлагается ввести аппроксимацию одного из периодических
врагментов в расширенном пространстве т = |т rj|T двумерной нормальной
лотностью в соответствии с методикой гауссовской аппроксимации [4.3, 5.1]
. последующем периодическим продолжением по
Рг(т) = с £ т,
НО
Рд + тТй
,R
(14.17)
де
РО = тах-1[рап (т)ехр(х(т))] (14.18)
— оценка задержки сигнала по огибающей; pj = р(ро) — оценка задержки
-игнала по фазе ВЧ (|о>оМд| < я);
Г л a p a 14. НВО, осиоваияые на фазовых измереим!
300
амаов
К'1 = {fy}1 =-д2 ЦРг^))/^2
J
= |мо Md|T
= -s2[*(T) + lnPan(T)lM2
0
О
ШпХ(т)
0 4 4Т = Ио
Максимумы плотности (14.17) расположены в точках с координатами
(но. Md+и7о)-
Аппроксимация для апостериорной плотности р(т) получается из
(14.13), (14.14) и может быть представлена в виде
р(т) = Z рт =cNi(m,m,Rm),
т--а>
где
? = (/?22H0 + «11(14 + да70 ))/(«!! + «22) i «т = «И«22/(«П + «22) > (14.19)-
й = (ио - Hrf )/^о ; «т = («и + «гг)/7!? •
(14.20)
Выбирая в качестве оценки задержки сигнала значение, соответствующее
максимуму АПВ, и полагая, что нормальные плотности в сумме (14.17) не пе-
рекрываются, получаем
? = т(т) ; т = max 1 Ni(m,m,Rm) = min 1 (m-m)2 = [ml .
4 ' m v ' zn Lv ' J 1 J Z
(14.21)
Уравнения (14.16), (14.18), (14.20), (14.21) дают решение поставленной
задачи.
В приведенном алгоритме с учетом (14.19) оценка задержки формируется
как взвешенная сумма оценок, полученных по огибающей (14.18) и фазе
(14.13) сигнала, причем в последней учитывается оценка целого числа перио-
дов ВЧ. Оптимальную оценку задержки можно представить в несколько ином
виде, если в (14.19) подставить выражение для из (14.20), что приводит к
соотношению
т = НО + «11(т ~ т)То/(^и + «22) > (14.22)
114-3. Применение методов оптимальной фильтрации 301
из которого следует, что оценка задержки, полученная по огибающей сигнала,
уточняется по результатам оценки числа периодов неоднозначности. Из
((14.21), (14.22) видно, что главный максимум АПВ р(т) совпадает с максиму-
мом />2(т, т</) по Дополнительной задержке, ближайшим к оценке задержки,
полученной по информации из огибающей и априорным сведениям. Обе при-
веденные трактовки эквивалентны. Однако при выводе более общих алгорит-
мов, которые будут рассмотрены ниже, удобнее представление (14.22).
14.3.3. Оценка задержки двухчастотного когерентного радиосигнала
Рассмотрим задачу оценивания задержки двухчастотного когерентного
2
радиосигнала S(t - т) = А(Г - т) £ cos [2xfj(t - т)1 при тех же, что и для рассмот-
ренного выше одночастотного сигнала, наблюдениях (14.15). Этот сигнал от-
носится к классу сигналов, содержащих несколько периодических зависимо-
стей от оцениваемых параметров, и его можно записать как
S{t, т, ч>1(т), ф2(т)), гДе Ф1 (т) = -2я/1т ; q>2 (т) =-2я/2т. Функция 5(») периодична
по Ф1(т) и ф2(т). Такое представление является основой обшей постановки
задачи.
Аналогично (14.4), при времени наблюдения » 1/1/1-Л| АПВ за-
держки р(т) описывается выражением
[ 2 1
Xх) = ФапЬ)ехр1 £Ху(т)со8шу(т-цу(т)Н,
U=1 J
где
I—“----------- 9 Т’нб
Х/(г) = ^(х) + Х2(т); Хс](х) = — f y(/)cos(®/) Л;
” О О
хя j Я') sin(® ?) Л: Н (т) = (Vю i) arcts(xs j (')/xcj ('))
На рис. 14.4, а приведена реализация (кривая 7) АПВ задержки двухчас-
тотного сигнала с немодулированной несущей, полученная моделированием.
Кривая 3 соответствует плотности вероятности при отказе от информации,
содержащейся в фазе высокочастотного заполнения. Моделирование выполня-
лось при: (Л2^)/^ = 4; jj = gjf0; gl = 7 ; g2 = 9; /0 = 108 Гц.
Г ава! НВО,
сноваи 1е на < >овых мерена
Из рисунка видно,
что?
отсутствует регулярности
расположения максимумов
АПВ. Применение аппрок^
' я
симаций, основанных на од-
номодовом характере оги-.
бающей АПВ, очевидно, не-
возможно.
В соответствии с мето-
дом дополнительной пере-
менной вводим расширенный
0 ♦ ♦ 4
а ф е «
0 ♦ ♦ «
4 ф ф.
4 Ф ♦ 4
Ф > Ф ф’
<> Ф Ф Ф|
м .4 Ж 4
вектор т = |т tji • Выпол-
нив шаги, которые были
сделаны в п. 14.3.1, прихо-
дим к выражению для ап-
проксимации АПВ (подроб-
ный вывод приведен в'
[14.11])
Ят)'= S S (Pmljn2 х
ml=-«o т2--«о
о (дно’ г^.с
б)
Рис. 14.4. Апостериорные плотности
X ^(т,х(т1,т2),Ят)); (14.23)
Рт1л>2 = Р№ = сЛГ2(и>й.К|»),
где т = ц0 +Rt|aiR1B1(ni-ffi); ш =
in =
МО ~М41
Т1
НО - МД2
тг
Rt=TRTt; (14.24)
Rj - Ли RT|nRm R^|m ; Rx
ЛП Rt|i»
Rx|m R-
т = 1 1/71 0 -V71 0 0 ; Rm = a2(Xj(r) + х2(т)) 0 0 0 »
at2 0
1/Т2 0 -vr2 0 0 ш22Х2(г) т = МО
Mo, М<л, — параметры распределения />2(т) • аналогичного (14.17).
^14.3--^pMem Jue мет Joe опт Сально, Ънмыпц. \чи ? . ) ) 303
Как видно из (14.23), дискретное распределение рт1<т2 аппроксимирова-
Гно дискретизированной двумерной нормальной плотностью.
-> Оценка задержки сигнала по критерию максимума АПВ при не слишком
; больших определятся как положение максимума Ni(t, T(m), Л,) по т при
Ш, максимизирующем рт\,т2 = Рдс(т)>
/ т = т(т); т = max рдс(т) = min *1 (т - - fi) I. (14.25)
ш т L j
При получении оценки в соответствии с (14.25) необходимо провести
целочисленную минимизацию квадратичной формы. Так как матрица Rm не-
диагональная, то использовать упрощенную процедуру, описанную в § 14.2
нельзя и необходимо проводить перебор целочисленных комбинаций [ml, m2].
На рис. 14.4, а кривой 2 дана аппроксимирующая функция р(т), вычис-
ленная согласно (14.23), (14.24). Вертикальной линией отмечено положение
оценки задержки по критерию максимума АПВ, выполненной в соответствии с
, (14.24). Можно отметить хорошее качество аппроксимации, так как она точно
- -задает высоты и положения локальных максимумов АПВ.
На рис. 14.4, б приведена карта сечений равного уровня pjft) По допол-
нительным задержкам тд, Большим уровням сечений соответствуют более
светлые тона. Рисунок иллюстрирует, как сечением гиперплоскостью, соответ-
ствующей 8(т^2 - т<л) (прямая = ТД1 113 рис. 14-4, б), периодические по Т[ и
т2 максимумы й(х) формируют нерегулярные максимумы АПВ задержки.
14.3.4. Общая задача оценки параметров при наличии
в наблюдениях периодических функций
До сих пор рассматривалась задача оценки задержки т по огибающей и
фазе радиосигнала, т.е. фактически задача синтеза алгоритма первичной обра-
ботки с учетом фазовых измерений. Однако метод дополнительной перемен-
ной универсален и может успешно применяться для многих других задач син-
теза, в том числе синтеза алгоритмов вторичной обработки. Приведем общее
^решение задачи синтеза алгоритма оценки вектора X с размерностью q, ап-
риорные сведения о котором задаются априорной плотностью вероятности
Рап(Х) •
Имеем N - мерный вектор наблюдений (N k q )
у = 8(т0(Х),гф(Х)) + В,
(14.26)
)4 ') ) 1 / а в a НВС Ъсиова же на )ио»ых Ьмещ.
где в — вектор гауссовских ошибок с нулевым средним и корреляцион^
матрицей V„ j
Сигнальная функция, входящая в (14.26), зависит от X через две груц|
функций т0(Х) и тф(х)• причем зависимость от каждого i-ro элемента вектор
Тф/(Х) является периодической с периодом 7}; / = 1,л (n<N)
s(z0(X), тф(Х) + Tm) = s(t0(X), гф(Х)) ,
где m — целочисленный вектор; Т = diag„ (Г/).
Введение однозначной зависимости сигнала от X через то(Х) не являет-
ся обязательным и отражает особенности навигационных приложений.
Представление уравнения наблюдения в виде (14.26) охватывает боль-
шинство задач радионавигации на основе фазовых измерений. Например, для
задачи дифференциальных ИВО на уровне вторичной обработки первых разно-
стей псевдодальностей уравнение наблюдения можно записать в виде
Уот
Уф
Уог ~ GX + Лог > Уф ~ ®*ф(^ф(Х)) *" Вф »
(14.27-
где Уог, уф — И- мерные векторы наблюдений разностей ПД по огибающих-
и фазам высокочастотного заполнения сигналов НС; G — матрица направ-
ляющих косинусов; X — вектор относительных координат, включающие
разность смещений шкал времени аппаратуры потребителей; пог, пф — ве1
торы ошибок; тф(Х) = GX/c — п -мерный вектор разностей псевдозадержек вы
сокочастотного заполнения сигналов НС; 8ф(тф(Х)) — разность выходов измг
рителей псевдозадержек (схем ФАП) по высокочастотному заполнению радио-
сигналов, которая является периодической функцией
8ф(тф(Х))=8ф(тф(х)+Тт).
(14.28
Действительно, схема ФАП работает по высокочастотному заполнении
радиосигнала, который является периодической функцией задержки радиосю
налов. Поэтому очевидно, что выходы схем ФАП периодичны по задержке вы
сокочастотного заполнения радиосигналов. Запись (14.28) альтернативнс
обычно используемой вф(тф(Х)) = GX + Тш , где m — неизвестное смещение -
целое число периодов высокочастотного заполнения. Однако для решения зе
дач оценивания общего вида представление (14.28) более удобно.
В соответствии с МДП введем вектор дополнительных переменны:
>имет |ге мет \в опт Сально. )>ильтр )uu
1 ) 305
= Тф(Х), элементы которого будем полагать независимыми один от другого
^от вектора оцениваемых параметров X. Полагая априорное распределение
дждой <-й компоненты вектора дополнительных переменных равномерным на
периоде длительностью 7}, запишем соотношение для априорной плотности
*''
вероятности расширенного вектора Хр
X
*d
Pan(^t] = Рап(Х)ПРап(т<й) =РалООП •
(14.29)
Из (14.27) выражение для апостериорной плотности вероятности расши-
ренного вектора оцениваемых параметров записывается в виде
1 pQLJ = cpan(Xp)^(y,S(Xp),Vn) ,
S’!,
уде S(XP) — сигнальная функция, входящая в (14.27), но представленная как
-функция расширенного вектора Хр.
ЛП0Т1ЮСТЬ вероятности p^XpJ — строго периодическая функция вектора
дополнительных переменных, поэтому, как и в рассмотренных выше задачах,
достаточно аппроксимировать один из периодических ее фрагментов. В соот-
ветствии с методикой гауссовского приближения запишем аппроксимирую-
щую функцию
00 00 00
р(Хр) = с X- X •••
т 1~-оол^ = -оо mpf = ~oo
Но
Rd + Тш
(14.30)
где
= шах’1 р(хр);
Ар
R1 =
Ro
К0ф
Rfl4>
R<i>
|xd=(id
Так как искомая АПВ р(Х) определяется из АПВ расширенного вектора
р(Хр) при xd = Тф(Х), то для получения искомой аппроксимирующей плотно-
сти р(Х) необходимо аналогичную процедуру проделать с (14.30), т. е.
X
00 00 со
р(Х) = с Х -- X - YNN
=-® «у =-оо
Mo
Rd + Tm|’
(14.31)
306 Глава 14. НВО, осиованные иа фазовых взмеревнжхд
Таким образом, найдена аппроксимация полимодальной АПВ с негаусЛ
совским описанием ее локальных максимумов, что обусловлено наличиеД
функции Тф(Х). Однако для многик задач НВО допустимо использовать щД
нейиое приближение зависимости Тф(Х) от вектора оцениваемых параметров
в окрестности оценки , полученной на основе информации из однозначных!
измерений и априорных сведений. Полагая |
*ф(Х) * тф(но) + Ф (X -цо), (14.32)|
где Ф = <Иф(цо)/ЗХ, и подставляя данное соотношение в (14.31) и выполнив;
необходимые преобразования, получаем
?(Х)= f... £ ... f p«.n(mpV?(x,X(m),Rx);
т 1 = -а>
pftn(m) = c^(m,m,Rm). (14.33)
Здесь
Х(т) = но + Rx|mR» (т -й) > й = т“'(тф(но) - Р</);
Rx|m = R0 _ RxmRmRxm > Rxm = (R0® " Чоф)Т ’
Rro = T-'[0Ro®T - ФВоф - R^®T + Вф]т!. (14.34)
Выражение для итоговой оценки вектора X по критерию максимума
АПВ при условии, что локальные максимумы />(Х) практически не перекры-
ваются (что выполняется при малых значениях корреляционной матрицы
Rx|„), записывается аналогично (14.25)
Х = Х(т); (14.35)
га = max-1 рдп(т) = min~*| (т-m)TR^(m-т)1, (14.36)
n^Z^ mcZ.. I * ’ ' ’
где Zn — л-мерное пространство целых чисел.
14.3. Применение методов оптимальной фильтрации 307
Решение задачи целочисленной оптимизации (14.36) в общем случае, как
отмечалось в § 14.1), достаточно сложно. Ее упрощение получается при избы-
точности измерений, связанных с периодическими функциями, что приводит к
слабой обусловленности матрицы Rm. Это позволяет осуществлять более эко-
номный перебор целочисленных комбинаций § 14.2 и повысить достовер-
ность PH.
" 14.3.5. Задача фильтрации при наличии в наблюдениях
периодических функций
Рассмотренная в предыдущих параграфах задача оценки предполагала,
что оцениваемые параметры постоянны за время наблюдения. Однако при
больших временах наблюдения это допущение не выполняется, т. е. оценивае-
мые параметры следует считать меняющимися во времени, тогда рассматри-
вать задачу фильтрации случайных процессов [4.3, 5.1, 5.2, 6.1].
Задачу фильтрации в условиях присутствия в наблюдении периодических
функций оцениваемых параметров сформулируем следующим образом. Требу-
ется выполнить оценку ^-мерного вектора Хк, который является марковским
процессом. Для простоты представления методики синтеза данный процесс
будем, считать также гауссовским- Так как в АП реализуется дискретная обра-
ботка отсчетов наблюдаемых процессов, то динамику оцениваемого вектора
зададим разностным уравнением
X* =ВХ*_1+пх.*, (14.37)
гДе вх,* — дискретный белый гауссовский шум с нулевым средним и матри-
цей дисперсий Nx; к — номер отсчета времени.
Векторное уравнение наблюдения для дискретного времени имеет вид
У к = S (*, то(Х*). ч(х*)) + п* , (14.38)
где S (Мо(Х*),тф(Х*)) — функция, периодическая по аргументу Тф(Х*)
(14.28); п* — дискретный белый гауссовский шум с нулевым средним и мат-
рицей дисперсий V„.
Расширение вектора оцениваемых параметров для решения задачи син-
теза осуществляется так же, как в предыдущем разделе Хрк =
xd,k ~ тф(Х*;). При этом априорная плотность вероятности определяется вы-
ражением (14.29).
X*
где
308 ? Гл а в а 14. НВО, основанные на фазовых измерениям
Для новой дополнительной переменной необходимо записать уравне-1
ние состояния, характеризующее ее изменение во времени. Для этого представ
вим т
xd,k ~ xd,k-l + тф,*(Х*)-тф,*-1(Х*-1)- (14-39L
Разлагая функцию *ф,*(Х*) в ряд в окрестности точки Х*_1 (аналогично
(14.32)), выражение (14.39) записываем в виде •
*</,* = t</,*-i + ФВХ*_, + Фпх,*,
(14.40)
где Ф«|0тф(Х*_1)/ах| .
Используя (14.37), (14.40), запишем уравнение динамики для расширен-
ного вектора
ХР1* = gp,*(xp,*-j) + Пр,* ,
(14.41)
где
Ц,
“рЛ ф
“х,* — гауссовский шум с нулевым средним и
матрицей диспер-
19
сий VP*(X*_!) = N,
q — 9-мерная единичная матрица.
Задачу фильтрации расширенного вектора состояния, описываемого
уравнением (14.41) при наблюдениях (14.38), можно решать известными мето-
дами оптимальной нелинейной фильтрации [5.1]. Аналогично тому, как это
было сделано в п. 14.3.3 можно доказать, что АПВ д(Ахр) строго периодична
по элементам вектора , поэтому, аппроксимация АПВ может быть задана
через аппроксимацию одного из ее периодических фрагментов.
Оценку параметров гауссовской аппроксимации одного из максимумов
АПВ р(АХр) можно получить с помощью расширенного фильтра Калмана
В₽,* ~ ®р,*(вр,*-1) + R*HJVp'^y^ S^fc,Gp *(pp,j|._i))j;
R*‘ =(Bp,t-iR*-iBJ,*-1+Vp*(gp*-i)j 1
где Цр
r*Ui v
— оценка вектора Хв
M p
(14.42)'
^>®р,*(вр,*-1)) — сигнальная функ-
ция, входящая в (14.38), но представленная как функция в точке экстраполи-
> 14; 3. Применение методов оптимальной Фильтронии 309
грованной оценки расширенного вектора Йр t-i = <*р,*(йрЛ-1);
I
Hfc = (asT(*. Gp,jt(pp,*_1))/axp)T; Bp,*., = (астрЛ(ЦрЛ_1)/ахр)т.
Периодическое продолжение локального максимума дает аппроксимацию
АПВ р*(хр) в тождественном (14.30) виде.
Искомая АПВ р*(Х*) получается из р*(Хр,*) на основе общего прин-
ципа МДП (14.13), т. е. рк (XD к j fv ч, тем самым осуществляет-
' y-d =*ф(хМ
; ся переход к cool эшению, ичному (14.31) и соответствующему моменту
,времени к ,
рк(*к) = с X- Е -
=—«о =—«о iftjy =~°о
х Нол
Хф(хл) ’ Н</л + ’Пи
R
Далее, как и в задаче оценивания, рассмотренной в п. 14.3.3, линеари-
зуем Тф(Х^) в точке оценки Цо* (оценки вектора X*), формируемой фильт-
ром Калма на (14.41),
хф(Х*) ~ тф(х*) + Q (Х* - X*),
а корреляционную матрицу представляем в виде
Ro коф
Коф Вф
После проделанных преобразований апостериорная плотность />*(Х) за-
писывается в виде, аналогичном (14.33):
Р*(Х*)= Е XpAn(»)^,(xjt.Xjt('n),Rx);
= —<Х> со ntff^—оо
Рд.п(«п) = c2V„(m,m,Rm),
где
Х*(ш) = МОЛ + Rx|mR» (ш - й); m = Т ’(тф(нол) - М</л) ;
310 —— Гл а р а14- НИО, о с веянные ч фжзо yt измг
Rx[m - Ro ~ RxmRmRxm > Rxm _ (RoQ Ro<t>)1' >
Rm = t'[qr()Qt - QRoo - RUQT + кфК* •
•*
Итоговые оценки вектора состояния X* и целочисленного вектора щ,
понимаемые как оценки максимума АПВ, определяются в соответствии с
(14.35), (14.36). Полученный алгоритм фильтрации процесса Хк состоит и$
уравнения фильтра Калмана и процедуры итоговой оценки, включающей про-,
цедуру PH, реализуемую с помощью предложенной процедуры беспереборноЦ^
PH или, в общем случае, через процедуры перебора целочисленных комбина-
ций. Процедура итоговой оценки по виду совпадает с для задач оценки посто-
янных параметров, рассмотренных в ряде известных статей [14.8, 14.12—14.14].
Заметим, что полученный алгоритм фильтрации принципиально отличается of
алгоритма, предложенного в [14.8], где оценки ш задействованы в процедуре
фильтрации.
Главное отличие предложенного алгоритма фильтрации от задач оценки
по критерию максимума правдоподобия [14.12—14,14] заключается в значи-.
тельном улучшении качества PH с увеличением времени фильтрации. За счет
введенной в МДП жесткой связи динамики изменения Х& и tjk, дисперсии
ошибок оценки X* с выхода фильтра Калмана со временем будут существенно
уменьшены по сравнению с ошибками оценки X*, полученной только по оги-
бающим сигналов. Не менее важен и другой эффект фильтрации: корреляци-
онная матрица ошибок фильтрации не изменяющегося во времени вектора
т,/,* - тф(Х*) с увеличением времени фильтрации уменьшается, стремясь к ну-
лю. Следовательно, Rm также стремится к 0. Поэтому с увеличением времени
фильтрации повышается достоверность PH и уменьшается объем области пе-
ребора целочисленных комбинаций при решении задачи целочисленной ми-
нимизации. Этот эффект позволяет в некоторых случаях отказаться от пере-
борных алгоритмов PH и повышает эффективность предложенного выше бес-
переборного алгоритма PH.
Задача взаимной синхронизации генераторов. Рассмотрим задачу синхро-
низации разнесенных в пространстве опорных генераторов (часов) [14.11]. Ме-
стоположение точек, в которых расположены генераторы, известно. Такая за-
дача возникает, например, при синхронизации по СРНС навигационных опор-
ных точек в системах навигации. Будем считать, что синхронизация осуществ-
ляется по одному НС с использованием измерений ПД по двум частотным ка-
налам LI и L2.
:-,.„АЗ. Пр^ененйр ^етодоа Зптимсь.бной фиЛтрации
311
е
Уравнения наблюдений с учетом близости точек запишем в виде
Уо =gTX + CT'+«0;
У1 = gTX + с5ф1(т') + л1 = gTX + pi + Л|;
у2 = gTX + с5ф2(т') + л2 = gTX + Р2 + л2
где у/; i =0,2 - разности измерений ПД (i “ 0 — по огибающей; i = 1, 2 —
по фазам высокочастотного заполнения сигналов частотных каналов 1Л и
£2); g — вектор направляющих косинусов; X — известный вектор разностей
координат точек, в которых расположены генераторы; 5ф/(т') — функция,
описывающая периодическую, зависимость выходов ФАП от т'; pj, р2 —до-
полнительные переменные; п — вектор гауссовских ошибок с нулевыми сред-
ними значениями и матрицей дисперсий V = О
О О
(°ф^1)2 О
о (<Тф*2)2
причем
О
«Од *
Пусть т' — гауссовский процесс с экспоненциально коррелированным
ускорением и задается системой разностных стохастических уравнений
х'к =Tjt-i +Tncv'k_l; v'k = vj._i + Тлса'к_\ ; a'k = (1 - аТдс)<4-1 +ло,
где па — белый гауссовский шум с нулевым средним и дисперсией Кя; а —
ширина спектральной плотности ускорения а' в стационарном режиме.
Алгоритмы оптимальной фильтрации, полученные для данной задачи из
общих соотношений (14.33), (14.34), (14.40), (14.41), моделировались на ЭВМ,
при этом полагалось, что время дискретизации равно Тас =0,1 с, отсчеты не-
коррелированы, аф =0,03; <т0 = 2 , а = 0,1 Гц, в стационарном режиме
с <за = 20 м/с2 .
На рис. 14.5, а приведена зависимость дисперсии ошибок оценки пара-
метра с т’ с выхода фильтра Калмана от времени как при использовании из-
мерений задержки по фазе высокочастотного заполнения сигнала, так и при
фильтрации только по измерениям задержки огибающей (штриховая линия).
На рис. 14.5, б показано изменение во времени дисперсий дополнительных
переменных. Видно, что по дополнительным переменным фильтр входит в
стационарный режим через 3 ... 5 с. В силу того, что уровень шумов по кана-
лам измерения фазы во много раз меньше шума измерения задержки огибаю-
312 i
'лава 14. НВО, основанные иа фазовых измере
щей, время вхождения фильтра в
стационарный режим по каналу
дальности значительно больш^
времени вхождения в стационар-'
ный режим по каналам дополни-
тельных переменных. Ошибки
фильтрации дополнительных пе-
ременных быстро становятся
идентичными', тогда нормирован-
ный коэффициент корреляции
ошибок фильтрации дополни-
тельных переменных приближа-
ется к единице, что видно из
рис. 14.5, в.
На рис. 14.6, а представлена
реализация ' текущих ошибок
оценки ст' с выхода фильтра
Калмана как при использовании
Рис. 14.5. Результаты моделирования измерений задержки по фазе, так
и при “работе только по измерение
ям задержки огибающей штриховая линия). На рис 14.6, б представлена реали-
зация ошибок процедуры итоговой оценки ст'. Рис. 14.5 и 14.6 демонстриру-
ют эффект сглаживания измерений дальности по огибающей за счет точных
измерений приращений фазы высокочастотного заполнения радиосигналов.
На рис. 14.7 показаны реализации эллипса (14.10) в преобразованной в
Рис. 14.6. Результаты моделирования
соответствии с (14.11) системе
координат для нескольких зна-
чений времени фильтрации.
Значение L выбрано для дове-
рительной вероятности 0,99999.
Из рисунка видно, как со вре-
менем этот эллипс стягивается в
точку. На рис. 14.8 приведено
изменение во времени вероятно-
сти неправильного PH. Кривая 2
соответствует верхней границе
неправильного PH для перебор-
ных процедур PH [14.16], кривая
1 — вероятности неправильного
PH для используемой беспере-
борной процедуры по геомет-
рически ближайшей целочис-
ленной точке в преобразованной
системе координат, кривая 3 —
; 14.3. Применение методов оптимальной фильтрации
313
Рис. 14.7. Целочисленная оптимизация
Рис. 14.8. Вероятности неправильного PH
нижней границе вероятности неправильного PH для переборных процедур
[14.16]. Из рис. 14.8 видно, что вероятность неправильного PH с увеличением
времени фильтрации стремится к нулю. Кривая 4 на этом же рисунке соответ-
ствует вероятности неправильного PH при использовании измерений фазы
только по каналу П. Сравнение зависимостей 4 й I на рис. 14.8 демонстриру-
ет, как двухчастотный алгоритм радикально повышает достоверность PH. Ав-
тономное РНФИ в каждом канале СРНС на основе измерений задержки оги-
бающей и фазы высокочастотного заполнения требует нескольких минут для
достижения вероятности неправильного разрешения 10-2, тогда как объедине-
ние используемой информации от каналов фазовых измерений обеспечивает
такую же достоверность за 4 с.
Задача относительных дифференциальных измерений. В рассмотренном
выше примере полагалось, что координаты точек, в которых располагаются
генераторы, известны. Рассмотрим применение МДП для решения задачи от-
носительных (дифференциальных) НВО в СРНС [14.10]. Пусть в точках А и В
осуществляется прием квазикогерентных сигналов от одних и тех же N ис-
точников излучения. Векторные уравнения наблюдения в точках А и В запи-
шем в виде, аналогичном (14.38),
Улл - 8 (к, то(к, Хл)>хф(^> Х^) + <ро)+ плл >
Ув,к - S (к,то(к,Хд),Тф(к,Хд) + Фо) + пд* ,
(14.44)
где <ро — вектор начальной фазы, элементы которого независимы и равномер-
но распределены в интервале соответствующего периода 7}.
314 Г л а в a 14. ПВО, основанные на фазовых измерениях»
Считаем, что динамика изменений Хли Хв задана стохастическим!»
уравнениями (14.37) с соответствующими матрицами сноса и диффузии. Л
Введем дополнительные переменные »
= тф(^»Хл)+ <Ро; xd,B = Тф(Л,Хд) + <Ро- 3
Нахождение аппроксимации Pt(X^g) АПВ вектора относительных коор- |
динат Ххд = ХА -Хв при независимости наблюдений в точках А и В и дви- j
жения этих точек осуществляется через решение вспомогательных задач опре-
деления аппроксимаций АПВ Р*(Хл,т</,л) и At(xP>Td,p)> описываемых
(14.33). Вычисление параметров этих аппроксимаций осуществляется с помо-
щью (14.40).
При разносе точек А и В до нескольких километров для задач относи-
тельных НВО в СРНС допустимо считать, что
Тф(*,Хд) - Тф(Л,Х_4) « Фл^лв.к ,
где Ф_А = </Гф(/г.цл)/^Хт ; рА — оценка вектора ХА, получаемая с выхода рас-'
ширенного фильтра Калмана, который используется для расчета параметров
аппроксимации вспомогательной АПВ Р*(хл,т</,л)-
Переход к аппроксимации АПВ Рк(^Ав) осуществляется следующим об-
разом
Рк(Х-Лв) = f f ?*(хл>т</.л)?л(хл + XA£’xd,A + A^AB^Adxd,A •
ХЛ Ч.А
Итоговая аппроксимация АПВ /^(Хдв) может быть представлена в виде
(14.34), при этом оценка вектора Xосуществляется на основе (14.43) и сво-
дится к автономному решению задач определения аппроксимаций вспомога-
тельных АПВ р^(хл,тй л) и рДХд.т^д) в точках А и В.
Для оценки характеристик фильтрационного алгоритма определения от-
носительных координат, синтезированного на основе МДП, между двумя точ-
ками с помощью АП СРНС была выполнена оценка потенциальных характери-
стик PH при работе по созвездию из четырех НС методами математического
моделирования. Моделирование выполнялось при условиях:
доступны измерения ПД по огибающим и фазам высокочастотного за-
полнения обоих частотных каналов НС;
14.3. Применение методов оптимальной фильтрации 315
СКО шума измерения ПД:
по фазе высокочастотного заполнения — 3 % периода;
по огибающим — 3,5 м;
относительная нестабильность шкалы времени АП составляет 10 8;
эффекты многолучевости не учитываются;
расстояние между точками не превышает нескольких километров.
При моделировании оценивались верхняя границы неправильного PH
для бесперсборного алгоритма PH (§ 14.2) и общая верхняя граница непра-
вильного PH [14.16J рис. 14.9. Эти границы вычислялись по матрице Rm,
имеющей смысл корреляционной матрицы дискретизированного нормального
распределения />дс(ш), определяющего мощность локальных максимумов ап-
проксимации АПВ (14.34), или же корреляционной матрицы ошибок оценки
Рис. 14.9. Графики вероятностей неправильного PH
вектора целочисленных смещений измерений ПД в целое число длин волн.
Общая верхняя граница вероятности HP Р^, = - ₽/**}» г«е
Р = min|mTRnl1ni|; ш — целочисленный вектор размерностью 8. Верхняя грани-
ца вероятности неправильного PH для беспереборной процедуры § 14.2 Р^> =
= 1 - P„.p(Rj), где Pn.p(Rrf) вычисляется по (14.7); Rrf — диагональная матрица,
содержащая главную диагональ матрицы URmUT (U —унимодулярная цело-
численная матрица преобразования, получаемая в ходе беспереборной проце-
дуры PH (§ 14.2).
На рис 14.9, а и б приведено распределение верхних границ неправиль-
ного PH для 3000 конфигураций НС при коэффициентах геометрии, находя-
щихся в диапазоне 2 ... 5. Рис 14.9, а соответствует беспереборной процедуре
316 Глава 14. НВО, осиоваииые иа фазовых измерещцД
PH, а рис. 14.9, б — общей. Кривые 1, 2 и 3 получены для времени фильтрЯ
ции, равного 4, 8 и 12 с соответственно. 1
При решении задачи относительных определений по измерениям фаза
высокочастотного заполнения только первого частотного канала НС близкие
характеристики достоверности PH могут быть достигнуты при использовании
измерений от 8 НС.
Приведенные распределения верхних границ вероятностей HP свидетель-
ствуют об эффективности применения МДП для синтеза высокоточных алго-
ритмов НВО в СРНС, а также возможности применения беспереборных про-
цедур.
Литература
14.1. Поваляев А. А.. Тюбалин В. В., Хвалъков А. А. Определение относительных ко-
ординат по радиосигналам системы ГЛОНАСС// Радиотехника, 1996, № 4, с. 48—51.
14.2. Frie Е., Beulter G. Rapid static positioning based on the fast ambiguity resolution
approach// FARA : theory and result. Manuscripta Geodetica, 1990, vol. 15.
14.3. Euler H. J., Landau H. Fast GPS Ambiguity Resolution on-the-fly for Real-Time
application // Proc. 6 International Geod. Symposium on Precise Positioning with the GPS,
Ohio, 1992, pp. 712—719.
14.4. Хорн P., Джонсон Ч. Матричный анализ. — M.: Мир, 1989.
.. 14.5. Пензин К, В. Силтез структуры мкогошкальных многопараметрических сис-
тем// Радиотехника и электроника, 1990, т. 25, № 11.
14.6. Jonge Р. J., Tiberius С. J. A new GPS ambiguity estimation method based on
Integer least squares// Proc. DNS94. 1994.
14.7. Graas F. GNSS Augmentation for high precision navigation servis// AGARD
lecture seris 2007, 1996.
14.8. Alpach D. L., Sorenson 11. Ж Recursive Bayesian Estimation Using Gaussian Sum
pproximation//Automatica, 1971, vol. 7.
14.9. Харисов В. П. Нелинейная фильтрация при полимодальном апостериорном
распределении// Изв. АН СССР. Сер. Техническая кибернетика. 1985, № 6.
14.10. Харисов В. П., Новоселов О. Ф. Общее решение задачи фильтрации коорди-
нат в дифференциальном режиме спутниковых радионавигационных систем// Радиотех-
ника, 1996, № 7, с. 65—69.
14.11. Харисов В. Н., Перъков А. Е. Алгоритмы фильтрации при фазовых измерени-
ях// Радиотехника, 1997, № 7, с. 90—101.
14.12. Розов Л. С., Собцов Н. В. Задача фильтрации в условиях неоднозначных из-
мерений// Радиотехника и электроника, 1980, т. 25, № 9.
14.13. Поваляев А. А. Вычисление характеристик качества и синтез многошкальных
измерительных устройств, осуществляющих оценку по критерию максимального правдо-
подобия// Радиотехника и электроника, 1978, т. 23. № 1.
14.14. Пензин К. В. Алгоритмы оперативной обработки многошкальных измерений
по критерию максимального правдоподобия// Радиотехника и электроника, 1990, т. 25,
№ 1.
14.15. Кнут Д. Искусство программирования для ЭВМ. — М., Мир, 1977, т. 2.
14.16. Пензин К. В. Синтез структуры многошкальных многопарметрических сис-
тем// Радиотехника и электроника, 1990, т. 35, № 11, с . 2317—2326.
- 317
Глава 15
Повышение достоверности навигационно-
временных определений
15.1. Требования к достоверности НВО
Безопасность полетов ЛА во многом зависит от достоверности и целост-
ности навигационных измерений. Под достоверностью навигационной инфор-
мации понимается способность навигационной системы (устройства) поддер-
живать с заданной вероятностью в определенный промежуток времени в ка-
ком-либо районе в требуемых пределах свои характеристики. В Российском
радионавигационном плане (В. 10] введено также понятие доступности, под
которой понимается вероятность получения потребителем в рабочей зоне дос-
товерной информации о своём местоположении в заданный момент времени и
с требуемой точностью.
Целостность навигационной системы является составной и главной ча-
стью достоверности навигационных измерений. Радиотехническая комиссия
по аэронавтике RTCA ввела два определения целостности СРНС (15.1]. Под
-целостностью при использовавши СРНС в качестве вспомогательного навига-
ционного средства понимают способность системы обеспечить своевременное
предупреждение о том, что ее не следует применять для целей навигации. На
практике это требование предполагает, что система должна быть способной
обнаружить свое неправильное функционирование (например, из-за отказа
НС) до того, как ошибка в выходных навигационных параметрах превысит по-
рог, заданный для каждой фазы (этапа) полёта. Целостность при использова-
нии СРНС в качестве единственного (основного) навигационного средства
означает способность системы исключить неверную спутниковую информацию
из последующей обработки до того, как ошибка в выходных параметрах пре-
высит заданный порог [15.2, 15.3], т. е. изолировать отказавший спутник.
Схожее по смыслу определение целостности приведено и в Российском радио-
навигационном плане. Под отказом спутника здесь понимается такое его со-
стояние, при котором использование радионавигационных параметров, опре-
деляемых по сигналу (сигналам) этого НС, ухудшает точность определения
координат и времени потребителем до значения, превышающего заданный
порог.
В последнее время вопросам целостности навигационных систем и на-
вигационного контура (бортового оборудования) уделяется большое внимание,
что делает эту характеристику навигационных систем сопоставимой по своему
значению с точностными характеристиками систем и комплексов. Тем самым
целостность становится одной из основных характеристик, что отмечается в
соответствующих нормативных документах. Так, в документах [15.3—15.5] со-
держится требование обеспечения автономного контроля целостности (АКЦ) в
? S
318 Г ji а в a 15. Повыдеиие достоверности НВдД
приёмоиндикаторе СРНС, т. е. в перспективе СРНС будет применяться Kail
основное навигационное средство. 1
Основные характеристики контроля целостности — способность обнару||
жить недопустимое ухудшение в работе системы (для СРНС это отказавши®
спутник) с заданной вероятностью и время запаздывания с оповещением (от,
момента начала неправильного функционирования системы до момента его
обнаружения). Российский радионавигационный план к численным характери-.
стикам целостности радионавигационных систем относит вероятность опове-
щения потребителей при нарушении работы системы в пределах допустимого
интервала времени, причем для воздушных потребителей целостность радио-
навигационной системы на различных этапах полета должна быть не хуже
0,999. На различных этапах полета порог обнаружения нецелостности СРНС и
время оповещения об этом потребителей будут существенно различаться, так
как они связаны с требованиями к безопасности полетов.
Рекомендуемые (допустимые) и перспективные требования к этим харак-
теристикам в зависимости от фазы полета сформулированы в [15.6, 15.7],
одобрены в [15.4] и сведены в табл. 15.1. Требования Российского радиона*
вигационного плана [В. 10] приведены в табл. 15.2.
Из таблиц видно, что наиболее жесткие требования предъявляются к ре
жиму некатегорированного и категорированного захода на посадку. Под нека
'тёгдрйрдванным заходом на" посадку понимается посадочный маневр, для ВЫ
полнения которого от навигационной системы требуются данные только о го
ризонтальном положении ЛА. Минимальная высота, достигаемая ЛА при нека
тегорированном заходе на посадку, составляет 60 ... 75 м. Для категорировал
ного захода на посадку, когда навигационная система должна обеспечить потре
бителя данными о его пространственном местоположении, эти требования бу
дут еще жестче. Отметим, что для выполнения указанных требований необхс
дима соответствующая точность определения местоположения ЛА (как прав»
ло, на порядок выше предъявляемых требований). Требования к контролю це
Таблица 15.1. Требования к характеристикам
Фаза полёта Океан Внутренние линии Зона аэро- дрома Некате аэриро- ванный заход на посадку
Допустимые
Пороговое значение, морская миля 12,6 2,8 1,7 0,3
Допустимое запазды- вание, с 120 60 30 10
1 Перспективные
Пороговое значение, морская миля 5 1 0,5 0,1
1 Допустимое запазды- 1 ванне, с 30 30 10 6
• J ! ! I I •• > !
/15.2. Пути повышения достоверности НВО в ПИ СРНС 319
Таблица 15.2. Требования Российского навигационного плана
Параметры контроля целостности Полёты Зона Заход на посадку I
по маршруту аэродрома некатегори- рованный категорн- 1 рованиый |
Достоверность 0.9996
Пороговое значение, м 250 ... 8000 200 50 ... 75 2,0 ... 8,5 й
Целостность 0,999 £0,999999 1
лостности СРНС для военных потребителей из-за большой важности решае-
мых задач должны быть не ниже, чем приведённые выше для гражданских по-
требителей.
15.2. Пути повышения достоверности НВО
в приемоиидикаторах СРНС
Спутниковая радионавигационная система представляет собой достаточ-
но сложную систему, нормальное функционирование которой зависит от
многих факторов: своевременной закладки эфемеридной информации, перио-
дической коррекции часов НС, контроля за работоспособностью всех уст-
ройств НС, своевременной корректировки орбит НС и т. п. Все эти факторы в
той или иной степени влияют на точность НВО ицелостность СРНС.’Заклад-
ка оперативной информации [см. гл. 9[ в НС СРНС ГЛОНАСС осуществляется
один раз в 12 ч , а в СРНС GPS — один раз в 24 ч. В промежутке между за-
кладкой информации наземный контрольный сегмент выполняет оперативный
контроль за функционированием НС. Однако такой контроль не может осуще-
ствляться непрерывно из-за ограниченного времени видимости НС наземным
контрольным сегментом. Поэтому контроль целостности целесообразно про-
водить всеми доступными способами: наземным контрольным сегментом
СРНС; геостационарными спутниками (с орбитами, совпадающими с плоско-
стью экватора); аппаратурой контрольных станций и других радионавигаци-
онных систем с последующей передачей информации о целостности НС по-
требителям; собственно в АП.
15.2.1. Факторы, влияющие на целостность СРНС
Ситуации, когда НС нельзя использовать при навигационно-временных
•’определениях, можно разделить на две категории — легко и трудно обнаружи-
мые. К легко обнаружимым ситуациям относятся: пропадание сигнала от НС;
искаженная структура сигнала, не позволяющая потребителю войти в синхро-
низм со спутником; наличие в навигационном (служебном) сообщении НС
признака запрета на использование информации от данного НС для НВО и
т.п. Например, в навигационном сообщении спутников СРНС GPS есть
6-разрядный параметр "Состояние НС". Старший разряд этого параметра пока-
зывает итоговое состояние навигационных данных (0 — все навигационные
320 Глава 15. Повышение достоверности НВО
данные хорошие, 1 — некоторые или все навигационные данные плохие), а
пять младших разрядов характеризуют 32 состояния компонент сигнала. Кроме
того, в строках 4 и 5 кадра совместно с альманахом i-го спутника передается
восьмиразрядное слово состояния этого же НС, причем пять младших разря-
дов по своему содержанию аналогичны передаваемым в первой строке в пара-
метре "Состояние НС", т.е. определяют одно из 32 состояний спутника (эти
состояния могут быть следующими: все сигналы в норме; все или один из сиг-
налов слабые; сигналы не модулируются данными; отсутствие сигнала на од-
ной или обеих частотах; НС временно не работает или не будет работать и
т.п.). Отметим также, что каждая 25-я страница суперкадра в строках 4 и 5 со-
держит совокупную информацию о состоянии всех НС. В СРНС типа ГЛО-
НАСС (см. рис. 10.11, а) в строке 2 есть 3-разрядный параметр Вп, старший
разряд которого характеризует пригодность или непригодность использования
сигналов данного НС для НВО. Такие ситуации потребитель может обнару-
жить без какого-либо дополнительного оборудования и без дополнительных
вычислительных затрат.
К трудно обнаружимым ситуациям относятся отказы НС, внешнее прояв-
ление которых отлично от приведенных выше. Под отказом НС здесь будет
пониматься излучение НС такого сигнала, что при использовании РНП, выде-
ленных из него, в НВО возникают ошибки. Отказы такого типа могут иметь
следующие внешние проявления: сдвиг БШВ НС;-дрейф частоты опорного ге-
нератора спутника; дрейф несущей частоты у излучаемого спутником сигнала;
сход НС с орбиты; неверная эфемеридная информация. Отметим также, что
аналогичное внешнее проявление будет при включении режима селективного
доступа Selective Availability (SA) в СРНС GPS. Такие отказы по-разному ска-
зываются на радионавигационных параметрах. Так, сдвиг бортовой шкалы
времени НС непосредственно сказывается на значении ПД, дрейф частоты ОГ
проявляется сначала в доплеровском сдвиге частоты и только через некоторое
время в значении ПД, дрейф несущей частоты у излучаемого сигнала сказыва-
ется на значениях как ПД, так и доплеровского сдвига частоты и т.д.
В [15.10] приводятся данные о дрейфе бортовых часов и параметрах его
распределения для исправных навигационных спутников СРНС GPS. Так, за
девятимесячный период сдвиг шкалы времени НС (усредненный по всем.спут-
никам) относительно СШВ колеблется от -0,6 до +0,3 мкс (-180 ... 90 м), а
СКО составляет 28 нс (15 нс) за период в 35 (20) дней для рубидиевых и 11 нс
за 24 дня для цезиевых часов. Максимальное же мгновенное отклонение бор-
тового времени спутника от шкалы системного времени может достигать более
100 нс (более 30 м). Уход рубидиевых часов за одну неделю может достигать
60 нс (20 м), а цезиевых — 30 нс (10 м). У неисправных бортовых часов дрейф
и смещение БШВ будут значительны. Отказы такого типа могут вносить суще-
ственные погрешности в НВО, а потребитель не будет знать об этом.
Именно поэтому проблема контроля целостности и разработка алгорит-
мов обнаружения отказов такого типа представляют большой практический
интерес.
F 15.2. Пути повышения доспЙЛерности НВО в ПИ СРНС_ 321
. 15.2.2. Методы контроля целостности СРНС
. В настоящее время контроль целостности в СРНС осуществляется сле-
дующими способами: в аппаратуре НСЗ; наземным контрольным сегментом;
автономно (АКЦ)) (т.е. в аппаратуре потребителя ).
Контроль целостности в аппаратуре НС. При данном способе контроля
целостности требуется до 1 мин для закладки информации о нецелостности в
сообщение НС, что не удовлетворяет требованиям (15.8, 15.11] по времени
оповещения потребителя. Кроме того, существует вероятность того, что схема
самоконтроля бортовой аппаратуры НС будет неисправной и не выдаст сооб-
щение о нецелостности.
Контроль целостности наземным контрольным сегментом. Наземные кон-
трольные станции принимают сигналы от всех видимых НС (из [15.12] извест-
но, что контрольные станции СРНС типа GPS измеряют ПД до видимых спут-
ников каждые 1,5 с и передают их на главную контрольную станцию каждые
6 с) и определенным способом формируют тестовую статистику для каждого
спутника. При превышении тестовой статистики какого-либо НС определен-
ного порога ошибок информация об этом поступает на главную контрольную
станцию, а с нее потребителям [15.13, 15.14]. Для передачи этой информации
нужен отдельный канал связи, так называемый GIC (GPS Integrity Channel —
канал целостности GPS) [15.8, 15.13—15.15]. Такой канал может быть органи-
зован как с главной контрольной станции, так и с НС [15.8, 15.16], кроме то-
го, могут быть использованы и радиомаяки других навигационных систем
[15.17]. При организации GIC через НС предполагается использование 2 ... 4
геостационарных ИСЗ (находятся над экватором на высоте 35 800 км) [15.13],
что увеличивает число НС СРНС, т. е. создает дополнительную избыточность.
Возможно также использование геостационарных спутников наблюдения за
погодой [15.13]. К недостаткам такого способа контроля целостности относят-
ся дополнительные материальные затраты на организацию канала оповещения
о неисправности НС (НС, навигационную информацию от которых нельзя
применять при НВО), а также вывод и обслуживание дополнительных НС или
переоборудование спутников слежения за погодой. Основным же недостатком
такого подхода к контролю целостности является то, что при нем потребители
несвоевременно оповещаются о неисправных НС. Например, существующий
наземный контрольный сегмент GPS может обнаружить факт отказа НС с за-
паздыванием до 15 ... 20 мин, и до 2 ч может потребоваться для передачи со-
общения на спутник и оповещения всех потребителей [15.8, 15.11, 15.18]. Это
связано, как упоминалось выше, с отсутствием непрерывного контроля за со-
стоянием НС, т. с. контроль целостности наземной контрольной частью не
отвечает даже наименее жестким допустимым и перспективным требованиям,
приведенным в табл. 15.1 — 15.2. Особенно сильно это несоответствие заметно
на таких ответственных этапах полета, как заход на посадку (даже некатегори-
рованный).
322 Глава 15. Повышение достоверности НВО
Необходимо отметить, 'что возможно также применение ДР работы
СРНС для контроля целостности. Такой режим существенно повышает точ-
ность НВО за счет компенсации систематических погрешностей (см. § 11.2 и
(15.19, 15.20]). Если на контрольной станции, применяемой для реализации
ДР, реализовать алгоритмы КЦ, то возможна передача информации о целост-
ности спутников по тому же каналу, по которому передается информация ДР.
Если же дифференциальная станция будет излучать сигнал, аналогичный по
структуре сигналам НС, то она может рассматриваться в качестве псевдоспут-
ника, что позволяет получить дополнительную избыточность. Отметим, что
если отказ спутника является медленно меняющейся во времени функцией
или проявляется в виде постоянного смещения (например, как режим селек-
тивного доступа в СРНС NAVSTAR), то применение метода коррекции радио-
навигационных параметров ] 15.21] позволит использовать информацию отка-
завшего НС для НВО. Однако эффективное применение ДР возможно только
в ограниченном районе, при этом требуется специальный канал связи кон-
трольной станции с потребителями, что существенно сужает возможности
контроля целостности.
Еще одним недостатком приведенных выше способов КЦ является про-
явление эффекта многолучевости: один и тот же НС может по разному влиять
на точность НВО для различных потребителей и информация о его целостно-
сти (нецелостности), полученная КС, может оказаться неверной для отдель-
ных потребителей.
Автономный к штроль целостности. Методы АКЦ можно условно разде-
лить на внешние и внутренние. Внешние методы основаны на избыточной
информации, получаемой от других навигационных устройств и систем,
имеющихся в наличии у потребителя, и предполагают комплексную обработку
навигационной информации от ПИ СРНС и других навигационных устройств
и систем. Внутренние методы используют избыточность информации собст-
венно СРНС.
Внешние методы АКЦ. В настоящее время изучено и проработано доста-
точно много вариантов комплексирования ПИ СРНС с другими навигацион-
ными системами (см. гл. 16, ] 15.13, 15.18]). Приведем и коротко охарактери-
зуем следующие варианты комплексирования.
Комплексирование с высотомером. Инструментальная ошибка барометри-
ческого высотомера может достигать 100 м, но так как он измеряет высоту по
давлению воздуха, а значит, сильно зависит от метеоусловий, то различие ме-
жду измеренной и истинной высотами может быть очень большим и в отсутст-
вие компенсации достигать 350 м (15.20].
Результирующая погрешность местонахождения ЛА при использовании
информации от высотомеров велика (в горизонтальной плоскости может пре-
вышать 1 км), что позволяет с их помощью выявлять лишь грубые ошибки'.
Использование радиовысотомеров, измеряющих высоту ЛА относительно зем-
ной поверхности, не всегда возможно, гак как при кренах и тангажах инфор-
15.2. Пути повышения достоверности НВО в ПИ СРНС 323
мация о высоте искажается (пересчет ее к истинной приводит к увеличению
погрешностей) или вообще пропадает.
Комплексирование с высокостабильным стандартом частоты. Сигналы
этого стандарта могут служить в качестве эквивалента части информации, по-
лучаемой от НС СРНС, что расширяет потенциальные возможности системы
При оценке целостности за счет получения избыточной информации, но, од-
нако, не дает 100 %-ной гарантии исключения неисправного НС из НВО.
Кроме того, высокостабильный стандарт частоты достаточно дорог.
Комплексирование с ИНС. Инерциальная навигационная система является
автономным, непрерывно работающим и не подверженным воздействию помех
средством навигации. Существенным ее недостатком является накопление
ошибок с течением времени. Так, за время, равное 1 ч (среднее время, необ-
ходимое наземному контрольному сегменту для оповещения всех потребителей
об отказе НС), ошибка, вызываемая дрейфом гироскопа, превысит допуски
установленные для контроля целостности СРНС. Заметим, что точность опре-
деления координат в комплексной системе СРНС/ИНС (ИНС корректируется
от СРНС, а СРНС контролирует целостность за счет избыточной информации
от ИНС) может составлять 1 ... 3 м и меньше [15.22]. Однако если один из
НС рабочего созвездия потерял целостность до момента включения комплекса
в работу, то обнаружение его нецелостности становится проблематичным.
Комплексирование с РСБН. Приемлемая точность (кроме этапа некатего-
рированного захода на посадку) в данном случае достигается только в ограни-
ченном районе поблизости от наземного радиомаяка РСБН, а с удалением от
него точность НВО ухудшается.
Комплексирование с системой OMEGA. В настоящее время радиотехниче-
ская система OMEGA на ЛА почти не применяется, так как точность НВО по
этой системе (4 ... 8 км) не удовлетворяет современным требованиям. В пер-
спективе систему OMEGA возможно использовать только как дополнительное
к СРНС средство навигации при полетах над океаном.
Комплексирование с РСДН. Точность определения МП ЛА с помощью
РСДН составляет 500 м, что че удовлетворяет перспективным требованиям
(см. табл. 15.1 — 15.2) к целостности для некатсгорированного и категориро
ванного заходов на посадку. Однако точность НВО по РСДН сильно зависи
от атмосферных условий, поэтому для поддержания требуемой точности необ
ходимо регулярно определять поправки и осуществлять коррекцию НВО. Еще
одним недостатком РСДН является ограниченная зона действия.
Комплексирование одновременно с несколькими устройствами и системами.
Это позволит повысить точность НВО, но не решит проблему обеспечения
глобальной зоны действия, а значит, и проблему контроля целостности в лю-
бой точке околоземного пространства.
Таким образом, внешние методы АКЦ не могут полностью удовлетво-
рить требованиям к контролю целостности на всех этапах полета ЛА.
Внутренние методы АКЦ основаны на избыточности информации собст-
венно СРНС, т. с. на наблюдении в ПИ потребителя пяти и более НС. При
324 Г л а в а Ь. Повышение достоверности НВцД
полном развертывании СРНС ГЛОНАСС и GPS такое условие будет выпол-1
няться для каждой отдельной навигационной системы, а в настоящее врем»
это возможно при совместном их применении. Кроме того, возможна ком-я
плексная обработка информации СРНС и объединённой системы связи, на-i
вигации и опознавания (ОСНОД) (в настоящее время данная система ещё не|
развёрнута, поэтому комплексирование ПИ СРНС с ней не рассматривалось^
выше), что, во-первых, создаёт дополнительную избыточность наблюдений и, 4
во-вторых, организует канал связи для передачи информации о целостности*
НС и дифференциальных поправок. В силу одинаковых принципов обеспече-1
ния НВО данное объединение с технической стороны не является сложным, а?
использование НС и навигационных опорных точек от обеих систем позволит’
существенно повысить избыточность навигационной информации. Рассмотрим-
более подробно АКЦ в ПИ СРНС.
15.2.3. Методы автономного контроля целостности
в приемоиндикаторах СРНС
Методы автономного контроля целостности в ПИ делятся на [15.23] ме-
тоды оценок (в зарубежной литературе методы называют snapshot — "момен-
тальный снимок") и фильтрационные (averaging — усреднения).
Методы оценок предполагают сбор и соответствующую обработку всей
необходимой информации в некоторый момент времени. Известны и изучены
следующие алгоритмы АКЦ в ПИ, основанные на данных методах ] 15.23]:
максимального отличия решения (maximum solution separation (MSS))
[15.24]. Сущность алгоритма заключается в следующем. При наличии сигналов
от N НС (N > 4) рассматриваются координаты, полученные по всем комбина-
циям из Л-1 сигналов НС. Максимальное расстояние в горизонтальной плос-
кости между любыми двумя из этих Л решений используется в качестве тесто-
вой статистики;
сравнения дальности (range comparison method) ] 15.25]. Метод сравнения
дальностей (МСД) в некотором смысле подобен MSS. При наличии сигналов
по всем комбинациям из Л-l НС вычисляют координаты потребителя, каждое
значение которых учитывается при прогнозе дальности до НС, сигнал кото-
рого не используется в данном решении задачи НВО. В качестве тестовой ста-
тистики используются разности между спрогнозированными дальностями и
измеренными псевдодальностями до НС;
сравнения местонахождения (position comparison method) [15.25]. Метод
сравнения местоположения (МСМ) в еще большей степени близок к MSS. В
нем вычисляют координаты по всем комбинациям из Л-1 НС, а также по всем
НС. В качестве тестовой статистики применяют разности между полученными
таким образом координатами;
невязки по методу наименьших квадратов (least squares residuals (LSR))
(15.26]. Здесь по ПД до всех видимых НС по методу наименьших квадратов
15.2. hymu повышения достоверности Hob в ПИ СРНС
325
вычисляют координаты, а по ним — прогнозируемые дальности до всех НС.
Разность между прогнозируемыми и измеренными дальностями нужна для
формирования тестовой статистики. По своей сути данный метод близок к
МСД.
Недостатком этих методов является то, что они не учитывают измерений
радионавигационных параметров, полученных ранее, и в силу этого могут об-
наружить факт отказа при достаточно сильном его проявлении, а не в момент
его возникновения (или достаточно близкий к нему интервал времени). Так, с
вероятностью, близкой к единице, известные в настоящее время алгоритмы
АКЦ, основанные на методах оценок, могут обнаружить отказы порядка 400 ...
500 м при СКО измерения ПД 30 м (отношение значения отказа к СКО изме-
рения ПД порядка 10 ... 20). Для улучшения характеристик алгоритмов АКЦ,
основанных на методах опенок, используют также усредненную за определен-
ный интервал времени тестовую статистику, например, в (15.27, 15.28] пред-
ложен алгоритм кумулятивных сумм для обнаружения изменения гауссовской
шумовой последовательности. Для изоляции отказа предложено сформировать
N сумм нормированных значений компонент вектора невязок. Суммирование
выполняют на каждом шаге обработки, начиная с момента обнаружения отказа
НС, а решение об изоляции конкретного НС принимают после превышения
максимальной из сумм определенного порога. Однако такой метод имеет су-
щественный недостаток: обнаружение отказа здесь сильно за висит , от.-геомет-
рического расположения НС. Например, за время t < 10 с данным методом
могут быть обнаружены отказы с абсолютным значением 170 ... 400 м и более
(отношение значения отказа к СКО порядка 6 ... 10) при хорошей и плохой
геометрии расположения НС. Для сравнения, при использовании невязок по
методу наименьших квадратов [15.29] минимальный уровень обнаруживаемых
отказов в таких же условиях значительно выше 300 и 700 м соответственно.
Отметим, что при трехпозиционном обслуживании описанным выше ме-
тодам для обнаружения факта отказа требуются наблюдения как минимум пяти
НС, а для изоляции отказавшего спутника (исключения его из НВО) — шести
и более НС [15.11, 15.25, 15.26, 15.30).
Фильтрационные методы описаны в [15.31, 15.32]. Метод, описанный в
[15.32], предполагает, что отказы НС проявляются в виде линейного нараста-
ния во времени погрешностей измерения ПД. Для оценки таких погрешностей
применяют банк калмановских фильтров, каждый из которых настроен на оп-
ределенный вид нарастания погрешностей. Получаемые при работе фильтра
невязки используют для формирования тестовой статистики. Данный метод
требует значительных вычислений и обнаруживает отказы НС приблизительно
через 5 ... 10 с, а при включении режима селективного доступа (для СРНС ти-
па NAVSTAR) это время увеличивается до 30 ... 40 с. Метод, описанный в
[15.31], основан на предположении, что у отказавшего НС увеличиваются шу-
мы наблюдения. Он не предполагает использования банка фильтров Калмана,
поэтому с точки зрения вычислительных затрат эффективнее метода, описан-
ного в [15.32|, а по характеристикам почти аналогичен ему. Как достоинство
326 Глава 15. Повышение достовериоста НВОд
фильтрационных методов АКЦ следует отметить полное использование ин*
формации о предшествующих моменту контроля целостности измерений и
меньшую вероятность ложной тревоги (15.31]. Недостатком метода [15.32] яв!
ляется слишком жесткая, а метода [15.31] — очень грубая модель отказов НС|
Из изложенного выше следует, что основным достоинством внутренних;
методов АКЦ является высокая оперативность оповещения потребителя о
факте нецелостности (возможно достижение требуемого времени оповещения
потребителя о нецелостности, причём это время зависит лишь от применяем
мого алгоритма КЦ). Однако существующие алгоритмы АКЦ не в полной мере!
отвечают перспективным требованиям [1.4]. Отметим и недостаток АКЦ
усложнение аппаратуры потребителя и значительные вычислительные затраты:
на реализацию алгоритмов КЦ. Но современное развитие технологий и эле-
ментной базы как с точки зрения уменьшения массы и габаритных размеров,
так и с точки зрения увеличения быстродействия, оперативной памяти и дру-
гих показателей позволяет пренебречь данным недостатком. ,
15.2.4. Подходы к процедуре идентификации неисправного НС
Контроль целостности СРНС, как рассматривалось выше, должен не!
только выявить факт неправильного функционирования навигационной сис-
темы, но и идентифицировать (изолировать, т. е. исключить из процесса НВО)
отказавший НС. В [15.11, 15.22, 15.26, 15.30] задачи обнаружения и идентифи-
кации отказа НС разделены, а в [15.25] задача изоляции неисправного спутни-
ка вообще не рассматривается. В этих работах процедура обнаружения отка-
завшего НС основана на наблюдении сигнала от избыточного спутника, а для
изоляции требуется уже два избыточных измерения. Обоснование такого под-
хода приведено, например в [15.11]. Коротко опишем известные процедуры
обнаружения и идентификации неисправного НС.
В [15.26] обнаружение факта отказа спутника ведется на основании
сравнения параметра тестовой статистики rt с порогом обнаружения факта
отказа hd, причем параметр формируется с применением наблюдений от
всех N НС. При /7 > hd принимается решение о наличии неисправности и вы-
числяются параметры rt, использующие наблюдения от N-1 НС (не включает-
ся РНП от /-го спутника). Если г,- меньше порога идентификации ht, а все
остальные rj,j*i, больше, то отказавшим считается i-й спутник, если же еще
несколько параметров меньше порога ht, то считается, что неисправ-
ный НС нельзя идентифицировать.
В [15.22, 15.25] процедура идентификации вообще не рассматривается, а
обнаружение отказа проводится при сравнении максимального параметра тес-
товой статистики rt с порогом обнаружения. Здесь параметр тестовой статис-
• 15.3. Оптимальные алгоритмы АКЦ в ПИ СРНС 327
тики П не использует наблюдения от /-го НС, т. е. при его отказе НВО, по-
лученные без этих наблюдений, будут единственными верными из всех N-1
НВО» на чем и основана процедура обнаружения отказа.
Такой подход к процедурам обнаружения и идентификации отказов
связан с сильным влиянием геометрического расположения спутников отно-
сительно потребителя на ошибки, вносимые каждым спутником в НВО. С
увеличением числа НС, используемых для НВО, общий коэффициент геомет-
рии понижается, что соответственно уменьшает погрешности НВО и позво-
ляет с большей уверенностью обнаруживать и изолировать неисправные НС.
Существенное влияние на правильность принятия решения оказывают также
быстрое изменение геометрического фактора, что связано с высокой динами-
кой как НС, так и авиационных потребителей, и расхождением шкал времени
П1ВП и БШВ. Однако возможно и совместное решение задач обнаружения и
идентификации отказавшего НС. Так, в 115.32] эти задачи заменены задачей
различения гипотез.
Исходя из сказанного целесообразно совмещать процедуры обнаруже-
ния и идентификации неисправного НС, используя при этом все НС рабо-
чего созвездия (все видимые НС), что позволит снизить влияние геометриче-
ского фактора и неточности хода часов потребителя на данные процедуры.
15.3. Оптимальные алгоритмы АКЦ в ПИ СРНС
на основе однократных измерений
15.3.1. Исходные соотношения для задачи АКЦ методами оценок
Из [15.11, 15.33] известно, что среднее время между легковосстанови-
мыми отказами НС (за счет резервирования блоков, узлов и т. п. на самом
спутнике) составляет 10 мес. (7 300 ч). Исходя из этого можно сделать вывод
об очень малой вероятности одновременного отказа двух и более НС, ис-
пользуемых в рабочем созвездии потребителем. Тогда возможен следующий
подход к задаче обнаружения и идентификации отказавшего НС.
Пусть потребитель в момент времени tk имеет N -мерный вектор на-
блюдений от Nспутников
п('а) = А(/Л,П(^)) + по(/*)» (15.1)
под которыми будем понимать измеренные ПД (аналогично (14.1)) или псев-
доскорости, т. е. измерения, полученные на выходе системы первичной обра-
ботки. Тогда в (15.1) A(/fc, П(/к))— вектор истинных значений навигацион-
ных параметров; П(/*) — N-мерный вектор параметров потребителя
(например, гринвичских прямоугольных геоцентрических координат); п0(/*)
328 Глава 15. Повышение достоверностей
S,
— вектор гауссовских случайных величин с характеристиками М{по(4)}«|
м|п0(4)п^(^)| = N0/2 8(/t), присравноточных измерениях N0/2 = ff0/2 I,
I — единичная матрица. |
Теперь можно определить Я+1 гипотезу: Н$ — все спутники исправна
Hi — неисправен i-й спутник, / = l,N Таким образом, задача обнаружена?
и идентификации отказа сводится к известной задаче многоальтернативног»
обнаружения [15.34, 15.35]. Пусть каким-либо способом сформировано отнс
шение правдоподобия (параметр тестовой статистики) 1{ для i-ro НС, тогд
для случая выбора из W+1 гипотезы решающее правило можно записав
[15.34]: <
Но при тах(/Д < h;
Я= 1 . (15.2)
Н{ при тах[/Д > h . *
I
Выражение (15.2) можно записать в более простых обозначениях: *
>и‘
^тах ="Пгах|/;} fa- (15.3’,
* <Hq
Порог h выбирают в соответствии с заданным критерием, в качестве
которого будем использовать критерий Неймана—Пирсона [15.34, 15.35].-
максимизирующий вероятность правильного обнаружения при заданной ве-
роятности ложной тревоги.
15.3.2. Алгоритм АКЦ на основе метода оценок
Конкретизируем соотношение (15.1) для задачи определения координа*
потребителя. Так как рассматривается задача обнаружения при однократны?
измерениях, то временной аргумент для упрощения записи будем опускат^
Тогда наблюдения (15.1) для гипотезы Яо запишем в виде
П = Дизм(П) + п0, (15.4
где П = |хугг|т — вектор параметров потребителя; смещение шкаль-
времени приемоиндикатора относительно системного времени; ДИЗМ(П) -
= |Дизм1(П) Диэм2(Ч) ДиэмАг(П)|Т — вектор измеренных псевдодальностек
, (П) = j(x-Xl)2 +(у-У1)2 +(z-Zi)2 + Ct’ = Д,+ ct’; х1г У1, Zi - грин-
кичские прямоугольные геоцентрические координаты i-го НС.
Р При гипотезе Ht в i-e наблюдение входит дополнительное смещение 5,
характеризующее проявление отказа z-го спутника. Будем полагать, что сме-
щение 8 является гауссовской случайной величиной с нулевым математиче-
ским ожиданием и дисперсией »8. Уравнение наблюдения для гипотезы Ht
запишем в виде
П = Дизм(П) + По +8 I/,
(15.5)
где 1, = |0 0 ... 1 ... 0|т — вектор, у которого единица только на /-Й пози-
ции.
g Из сопоставления (15.5) и (15.4) следует, что отказ НС соответствует
увеличению шума в наблюдении, полученном от этого НС, на Ds, т. е. мож-
записать
:... П = Дизм(П) + п,, (15.6)
где п, — гауссовская случайная величина с характеристиками М{п,}=0;
М (11,117) = ^/2 I +
Разложим функцию ДИЗМ(П) (см. (15.6)), в ряд Тейлора в точке П, со-
ответствующей априорным сведениям потребителя о своем местонахождении,
ограничившись при этом линейными членами разложения,
И — ДИзм(П) + Gc +п,,
(15.7)
где G = (ад;зм(П)/аП) — матрица линеаризации наблюдения, известная как
матрица направляющих косинусов (6.36); е = (п - п) — отклонение вектора
параметров потребителя от априорных значений (от опорной точки). В каче-
стве значений для опорной точки П могут быть использованы данные с вы-
хода стандартного фильтра Калмана после вторичной обработки в приемоин-
дикаторе СРНС или данные от других навигационных систем.
Вводя эквивалентное наблюдение ц = ц - Дизм(п), запишем
П = Ge + п0 — для гипотезы Hq ;
rj = Ge + n( — для гипотезы Ht. (15.8)
330
Гл а в а 15. Повышение достоверности НВО
Учитывая определение отношения правдоподобия
= Р(ц/Я,) Pffi/Я,)
' Р(Ч/ЯО) Р(п/Я0)’
и линеаризацию наблюдений (15.8), получаем выражение для логарифма от-
ношения правдоподобия
In/^n^Do'-D-^-lndD.I/lDoO, (15.9)
где
D, = Я0/2 I+GDeGT + Ds l,IJ; (15.10)
Do = 7V0/2 I + GDeGT; (15.11)
De =M|e£T|— матрица ошибок априорных сведений о векторе параметров
потребителя. ’
Решающее правило в соответствии с (15.3)
, . . Hi _
maxln1 Ро‘ - »7*)ч - !n(|Df |/|Do0} * .
' 1 ' ' '><Н0
ИЛИ
( . \ \>Bi
тах{цт1Од1 - йр
' 1 ' ’ ><HB
(15.12)
Упростим алгоритм (15.12), используя лемму об обращении матрицы
[5.Ц, согласно которой, если Н — вектор; R — матрица, имеющая обратную,
ис — константа, то справедливо соотношение
(r + сННт) = R1
R~1HHTR~1
HTR1H + l/c
Применение данной леммы к (15.10) приводит к результату
D,-1 =(ЯО /2I + GDeGT +Р51/1/т) 1 = (De
' I/ D0 I/ + 1/DS
15.3. Оптимальные алгоритмы АКЦ в ПИ СРНС
331
Из полученного соотношения следует
где
В итоге алгоритм обнаружения (15.12) принимает вид
[, \2] >н‘ II т П >В‘
maxUnT|i>) !• й], или maxllngj} Л2.
' I' ' J <Н0 ' 11
(15.13)
В соответствии с этим алгоритмом формируется взвешенная сумма на-
блюдений от всех спутников (в ней оптимально учитывается геометрия рабо-
чего созвездия и априорные знания потребителя о своем местоположении),
модуль которой сравнивается с порогом. В результате этого сравнения прини-
мается решение об исправности i-ro спутника. Схема алгоритма показана на
рис. 15.1. ......... ... ...........- - - - -
Рассмотрим предельный случай, в котором De » d(gtg) . Это соответ-
ствует ситуации, когда погрешности априорной оценки местоположения по-
требителя значительно больше текущих ошибок оценок измерений РНП.
Используя псевдообращение для pt, получаем
+1/Р8 = (gdeGt/d + l) *1, =
I-G^G + DD-1)/втк »Tl-G(GTG)“*Gt I,.
С математической точки зре-
ния оператор [^1 - g(gtg) *Gt^ име-
ет хорошо известный смысл: это
оператор проектирования, выде-
ляющий ортогональную состав-
ляющую вектора в пространстве
измерений псевдодальностей отно-
сительно гиперплоскости Gs, со-
ответствующий отклонениям псев-
додальностей от допустимых значе-
ний. В целях дальнейшего упроще-
ние. 15.1. Схема оптимального алгоритма
332
Гл а в а 15. Повышение достоверности НВО
ния рассмотрим выражение для наилучшей оценки П по одному измерению
ц (или ц) при условии справедливости гипотезы Но. Из (6.39) следует, что
e = (gtg) GTrj. Тогда оценочное значение псевдодальности (при условии вер-
ности гипотезы Hq)
Дизм(П) = ДИзм(п) + Gi = Дизм(п) + G(GTG)'lGTn .
С учетом этих соотношений выражение, стоящее под знаком шах. в
(15.13) можно записать
цтц = Нтт1 = ~ G(GTG) GTrjj = - Дизм(П)) = П/ - Лизм(й) •
В результате алгоритм (15.13) принимает вид
(I \П >В‘
шах-|т/ ~ Д/изм(11/яг ^2. £15.14)
1 11 ' .....................................................
Таким образом, приходим к алгоритму сравнения отклонения измерен-
ной псевдодальности тц от рассчитанного по всем спутникам для условий ги-
потезы Но значения Д/шм^п) с порогом. Алгоритм (15.14), являющийся част-
ным случаем при упрощении (15.13), оказывается, аналогичен известному ал-
горитму по методу невязок наименьших квадратов [15.26], полученному эмпи-
рическим путем. Подчеркнем, что алгоритм (15.14) соответствует полному от-
брасыванию априорной информации, полученной от любых источников до
проведения проверки. Действительно, в (15.14) используются только данные
измерений, полученные в заданный момент времени tk: измеренное тц и
расчетное Д, (п) значения для условий гипотезы Яо. Моделирование, ре-
зультаты которого приведены ниже, показывает небольшое преимущество ал-
горитма (16.14), перед другими известными [15.25|.
На практике предположение, что ошибки априорной оценки местонахо-
ждения много больше, чем ошибки текущих измерений РНП, которое приво-
дит к алгоритму (15.14), часто не выполняется. В частности, в стандартном
режиме слежения априорные погрешности оценки местонахождения совпада-
ют с ошибками фильтрации и за счет накопления или комплексирования с
ИНС могут быть заметно меньше, чем ошибки оценки координат по одно-
кратному измерению, которые имеют дисперсионную матрицу i(gtg) ' А/о/2.
15.3. Оптимальные алгоритмы АКЦ в ПИ СРНС
333
При этом оптимальный алгоритм (15.13) может иметь заметно лучшие харак-
теристики, чем (16.14), что и показывает моделирование.
15.3.3. Оптимальный алгоритм АКЦ, учитывающий
наблюдения доплеровской частоты
В предыдущем параграфе был синтезирован алгоритм АКЦ, обнаружи-
вающий отказы НС по измерениям ПД. Однако в современных приемоиндика-
торах СРНС производятся также измерения доплеровской частоты. Отметим,
что внешние проявления таких отказов НС, как скачок или дрейф частоты
опорного генератора или несущей частоты, сказываются в первую очередь на
фазовых измерениях и измерениях частоты, и лишь через некоторое время на
измерениях ПД. Поэтому целесообразно использовать эту дополнительную
информацию для АКЦ СРНС.
При гипотезе Но вектор наблюдений ц в момент времени tk описыва-
ется уравнением (15.4). С учетом дополнительных наблюдений доплеровской
частоты векторы, входящие в (15.4), имеют вид (учтем, что доплеровская час-
тота пропорциональна радиальной скорости вдоль линии НС—ПИ)
S(H) =
Дизм(П)
vMM(n)
, где VH3M (П) - |Иизм j ... Уизм n |
вектор наблюдаемых ради-
альных псевдоскоростей (доплеровских частот);
,(п) - - Г„) , Г„) . - Гц ) . V;
”0
“Д
"и
— вектор нормальных белых гауссовских шумов
наблюдения псевдо-
дальностей и псевдоскоростей с M{n0} = 0; М^пд^д,] = N д/2 8, ,;
= Ny /2 8,j .
При гипотезе Ht в наблюдение входят дополнительные смещения (по
псевдо дальности и псевдоскорости соответственно 8д и Ъу для /-го спутни-
ка, так что
И - £>(П) + п0 +8д1/ + 8к1л+/,
(15.15)
где 8д, 8И — гауссовские случайные величины с м{8д} = 0; м|Зд| = Л8д;
М{8р} = 0; м|8р| = DSy ; = |0 0 ... 1 ... 0|т , т.е. единица только на -й
позиции.
ЗЗ^1 .. г " а ва Пову сине д' товерн ути НР~~
Дополнительные смещения в выражении (15.15) соответствуют увеличе-
нию шумов наблюдений по /-му спутнику, поэтому его можно записать сле-
дующим образом
П = 8(П) + п/,
где п, — гауссовская случайная величина с характеристиками М{п,} = 0,
м|и/п, | = ЛГ0/21 + + Dfy *JV+/*лг+* •
Так как основное влияние на точностные характеристики оказывают
флуктуационные шумы, то взаимной корреляцией можно пренебречь. Линеа-
ризовав задачу, получим эквивалентные наблюдения, аналогичные (15.8).
Синтез этого алгоритма проводился по той же методике, что и выше,
поэтому приведем только окончательные выражения. Корреляционная матри-
ца ошибок определяется аналогично выражению (15.11), а матрица
D/ = Л^о/2 I + GDeG = Do + DSjl 1/lf + ^5Kljv+fljv+/ -
Тогда выражение для отношения правдоподобия примет вид
In//= птц)/у, где Ц/ = — вектор с единицами на /-й и
N+i - й позициях; у = + l/DSy .
Итоговый алгоритм обнаружения отказа имеет вид
( - \ >И‘ ( 1>Я/
тах)ЛтР/Р/ п} *з> или птах|т|тр;} й4. (15.16)
' ’ 1 1 ’<Н0
На практике точность априорной оценки местонахождения не всегда
достаточно высока и представляет интерес дальнейшее упрощение алгоритма
(15.16). В предельном случае, когда DE »N0/2 I, т.е. ошибка априорной
оценки местонахождения много больше ошибки текущих измерений, исполь-
зовав псевдообращение для ц/, получим
14 = = 2/AT0(l -G(gtg)-1Gt)|. у+/ = fi,
и (15.16) принимает следующий вид:
тахптЦ, й4. (15.17)
' 1 ’<в0
15.3 )nmuMi ьные a. IpumMt }КЦ в X CPJS
33f
Результаты моделирования показывают, что при отказе по каналу допле-
ровской частоты алгоритм (15.16) работает несколько лучше алгоритма (15.13).
15.3.4. Характеристики оптимальных алгоритмов АКЦ
Рассмотрим результаты моделирования оптимальных алгоритмов АКЦ,
проведенных для потребителя, находящегося в районе Москвы, по реальному
созвездию СРНС типа ГЛОНАСС для двух конфигураций рабочего созвездия:
1) 17 ч 31.03.94 (коэффициент геометрии Кт = 2,58; PDOP = 2,33; HDOP =
=1,80; конфигурация созвездия в полярной системе координат угол возвыше-
ния - азимут показана на рис. 15.2, а; 2) 8 ч 31.03.94 (коэффициент геометрии
Кт = 5,35; PDOP = 4,91; HDOP = 2,55; конфигурация созвездия показана на
рис. 15.2, б. Дисперсия сбоя (для алгоритмов (15.14), (15.16) и (15.17)) была
выбрана в предположении полного отсутствия априорной информации о сбое
(отказе) 6 (т. е. D8 -> оо). Для оптимальных алгоритмов (выражения (15.14) и
(15.16)) корреляционная матрица ошибок измерения координат De бралась
соответствующей стационарному режиму работы фильтра Калмана при вто-
ричной обработке радионавигационной информации. Вероятность ложной
тревоги (вероятность превышения порога для исправного спутника) задавалась
равной 0,004.
Результаты математического моделирования приводятся для следующих
алгоритмов:
алгоритм 1 — МСД;
алгоритм 2 — квазиоптимальный алгоритм (в соответствии с (15.14));
Рис. 15.2. Конфигурации созвездий
336 Глава 15. Повышение достоверности НМйМ
алгоритм 3 — квазиоптимальный алгоритм, учитывающий наблюдения^
доплеровской частоты (в соответствии с (15.17)); 1
алгоритм 4 — оптимальный алгоритм (в соответствии с (15.13)); J
алгоритм 5 — оптимальный алгоритм, учитывающий наблюдения допле-1
ровской частоты (в соответствии с (15.16)).
Результаты моделирования приведены на рис. 15.3. На рис. 15.3, а и б'
показаны зависимости вероятностей обнаружения отказов для спутников 2
(рабочее созвездие 1) и 5 ( рабочее созвездие 2) для алгоритмов 1 (кривые 7) и
2 (кривые 2). Из графиков видно что алгоритмы 1 и 2 имеют практически
одинаковые характеристики (алгоритм 2 (квазиоптимальный) несколько лучще
алгоритма 1 (МСД)), достаточно сильно зависящие от геометрического распо-
ложения НС относительно потребителя (достижение вероятности обнаружения
отказа, близкой к единице, при худшей геометрии (рис. 15.3, б) происходит
при большей по абсолютному значению величине отказа). Так как алгоритм
по МСД не лучше квазиоптимального алгоритма в смысле обнаружения отка-
зов НС, то в дальнейшем он рассматриваться не будет. е
На рис. 15.3, виг (соответственно, спутники 1 и 5 созвездия 1) показа-
ны сравнительные характеристики алгоритмов 2 (квазиоптимальный, кривые
7) и 3 (квазиоптимальный, учитывающий наблюдения доплеровской частоты в
отсутствие отказов по каналу доплеровской частоты, кривые 2, и при отказе
по каналу доплеровской частоты в 10 раз СКО измерения псевдоскорости
(кривая 3 рис. 15.3, г )). Видно, что при хорошем геометрическом расположе-
нии спутника и при отсутствии отказа по каналу псевдоскорости характери-
стики алгоритмов почти идентичны, при наличии отказа по каналу доплеров-
ской частоты характеристики обнаружения отказов у алгоритма 3 несколько
лучше (рис. 15.3, в). Отметим, что при плохом геометрическом расположении
НС характеристики обнаружения у алгоритма 3 значительно хуже (рис. 15.3,
г), что обнаружения отказов объясняется допущениями, использованными
при выводе выражения (15.17), усиливающими влияние геометрического фак-
тора. На рис. 15.3, д (спутник 1 созвездия 1) и 15.3, е (спутник 5 созвездия 2)
даны характеристики обнаружения отказов НС для алгоритмов 2
(квазиоптимальный, кривые 7), 4 (оптимальный, кривые 2) и 5 (оптимальный,
учитывающий наблюдения доплеровской частоты при отсутствии отказов по
псевдоскорости, кривые 7). Рисунки показывают, что алгоритмы 4 и 5 дают
значительный выигрыш в вероятности обнаружения отказов по сравнению с
алгоритмом 2 (т.е. и по сравнению с алгоритмами 1, 3), незначительно разли-
чаясь по характеристикам между собой. Отметим, что алгоритмы 4 и 5 слабо
зависят от геометрического расположения спутников относительно потребите-
ля. Это объясняется оптимальным учетом геометрии расположения НС и ап-
риорных сведений о своем местонахождении (в выражениях для невязок
(15.13) и (15.16) входят взвешенные в соответствии с априорными данными и
геометрическим расположением наблюдения от всех спутников рабочего со-
звездия).
На рис. 15.3, ж (НС 2 созвездия 1), 15.3, з (НС 3 созвездия 2) показаны
характеристики алгоритма 5 (оптимальный, учитывающий наблюдения допле-
•1'5.3. Оптимальные алгоритмы АКЦ в ПИ СРНС
337
Рис. 15.3. Результаты моделирования
338 Г л а в a 15. Повышение достоверности HBQ3
ровской частоты) в зависимости от значения отказа по каналу псевдоскорости,;
Кривые 1 построены при отсутствии отказа по доплеровской частоте; кривы^
2 и 3 — при отказе по псевдоскорости в 5 и 10 СКО ее измерения соответстЗ
венно; кривая 4 рис. 15.3, з — при отказе в 30 СКО. Видно, что с увеличени-
ем значения отказа по каналу доплеровской частоты характеристики обнару-
жения отказа заметно улучшаются.
Из приведенных результатов моделирования следует:
квазиоптимальные ^лгоритмы АКЦ в ПИ ( (15.14) и (15.17)), не учиты-
вающие априорную информацию о местоположении потребителя, обеспечива-
ют незначительное улучшение характеристик обнаружения отказов по сравне-
нию с известными алгоритмами (15.25, 15.26], а в некоторых случаях могут
работать хуже; характеристики обнаружения отказов НС у этих алгоритмов
сильно зависят от геометрического расположения НС относительно потреби-
теля;
алгоритмы (15.13) и (15.16), оптимальным образом учитывающие всю ап-
риорную информацию о местоположении потребителя и геометрическое рас-
положение спутников, имеют ощутимое преимущество в обнаружении отказов
НС; характеристики обнаружения отказов спутников у таких алгоритмов слабо
зависят от геометрии расположения НС;
чем больше априорная точность информации, тем больше выигрыш в
обнаружении отказов спутников;
Оптимальный алгоритм (15.16), учитывающий наблюдения доплеровской
частоты, при отказе по каналу псевдоскорости имеет лучшие характеристики
(в смысле вероятности обнаружения отказа НС), чем оптимальный алгоритм
(15.13).
К достоинствам методов АКЦ, основанных на методе оценок, относится
их простота и возможность технической реализации в уже существующих ПИ
при малых затратах.
Недостатком методов контроля целостности, основанных на методах
оценок, является то, что они обнаруживают отказы спутников не в момент их
возникновения или в близкий к нему момент времени, а после достаточно
сильного их проявления, что может существенно увеличить время оповещения
потребителя о факте отказа одного из НС рабочего созвездия. Кроме того, на
надежность обнаружения и идентификации отказавшего спутника могут вли-
ять выбросы случайных процессов. Для устранения их влияния необходимо
проводить осреднение невязок во времени, что увеличивает временя оповеще-
ния потребителя о факте отказа НС.
15.4. Фильтрационные алгоритмы АКЦ в ПИ СРНС
Как уже говорилось выше, существенного улучшения характеристик ал-
горитмов АКЦ можно достичь за счёт применения методов оптимальной не-
линейной фильтрации. Однако известные методы [15.31, 15.32] не в полной
мере обеспечивают преимущества оптимальной фильтрации, что объясняется
115.4. Фильтрационные алгоритмы АИД в ПИ СРНС 339
Использованием неадекватной модели отказа НС. В [15.37] на основе уравне-
ния Колмогорова—Феллера для разрывных процессов [5.1] разработана мате-
^ятическая модель отказа НС, описывающая широкий круг их реальных отка-
зов, и на её основе синтезирован оптимальный алгоритм фильтрации коорди-
нат и контроля целостности СРНС.
Кратко^ приведём результаты моделирования данного алгоритма, которое
проводилось для потребителя, находящегося в районе Москвы, по реальному
созвездию СРНС ГЛОНАСС для двух конфигураций рабочего созвездия (см.
.рис. 15.2) : рис. 15.4, а—в — НС 2 и рис. 15.4, г— е — НС 5 первого созвездия
(рис. 15.2, а); рис. 15.4, ж — и — для НС 3 второго созвездия (рис. 15.2, б)
„Вероятность ложной тревоги принималась 0,004 порог подбирался
• экспериментально. Кривые / построены для наблюдения, включающего в себя
псевдодальности, кривые 2 — для расширенного наблюдения (в него кроме
• псевдодальностей входит еще и наблюдения доплеровской частоты). Отказ НС
'Имитировался только по каналу наблюдения псевдодальностей. На рис. 15.4, а,
'г и ж показаны кривые вероятности обнаружения отказов НС; на рис. 15.4, б,
[ д из — вероятность идентификации отказавшего НС, а на рис. 15.4, в, е и и
i — среднее время обнаружения отказа навигационного спутника синтезиро-
> ванных алгоритмов в зависимости от нормированной к СКО измерения ПД
^величины отказа по каналу наблюдения ПД.
.— Из рисунков следует:
синтезированный алгоритм имеет значительно лучшие характеристики
. по сравнению с алгоритмами АКЦ, основанными на методах оценок [15.18,
15.23, 15.25, 15.26, 15.29, 15.38], и лучшие, чем у известных фильтрационных
г алгоритмов АКЦ [15.31, 15.32];
характеристики синтезированных алгоритмов АКЦ очень слабо зависят
от геометрии расположения НС относительно потребителя;
с увеличением абсолютного значения отказа среднее время обнаружения
отказавшего спутника уменьшается и достигает 0,006 ... 0,09 с. (при вероятно-
сти обнаружения отказа НС, близкой к единице), а включение в наблюдение
доплеровской частоты, характеризующей радиальную псевдоскорость по линии
потребитель—НС, улучшает характеристики синтезированного алгоритма
АКЦ, особенно это заметно в области малых отказов.
\ Алгоритм проверялся также экспериментально — постобработкой масси-
ва измерений псевдо дальностей, снятых с приемоиндикатора СРНС GPS типа
Geodetic Surveyor ТМ series 4000 на частотах L1 и L2. Запись массива измере-
ний проводилась в г. Менделееве 17.11.93 с 9 ч 31 мин 30 с до 14 ч 6 мин
15,004 с с дискретностью 15 с, причем предполагаемые (прогнозируемые)
ошибки измерения псевдодальности ад, содержащиеся в навигационном со-
общении спутников, используемых при проведении эксперимента, были равны
32 м. Неисправным являлся НС с системным номером 24, хотя формально по
признаку исправности, содержащемуся в навигационном сообщении НС он
является исправным. Включение в процесс НВО спутника с системным номе-
е)
Рис. 15.4. Результаты моделирования
15.4. Фильтрационные алгоритмы АКД в ПЛ СРНС 341
ром 24 происходило в 12 ч 35 мин 0,002 с (в это время для НВО использо-
вались также НС с системными номерами 14, 18, 22, 25 и 29). Эксперимен-
тальные исследования также показали работоспособность синтезированного
алгоритма КЦ. Таким образом, фильтрационный алгоритм АКЦ существенно
улучшает характеристики контроля целостности по сравнению с известными
алгоритмами.
Большие по абсолютному значению отказы спутников (как в проведен-
ном экспериментальном исследовании) вызывают значительные смещения в
оценках координат и сдвига ШВП. После обнаружения и идентификации от-
казавшего НС и, следовательно, исключения его из процесса НВО смещения в
оценке вектора состояния уменьшаются до допустимых значений (стандарт-
ных ошибок оценок в условиях отсутствия отказов НС).
Литература
15.1. Hartmon R. Joint US/USSR Satellite Navigation Studies// GPS Word, 1992,
vol. 3, no 2.
15.2. International Civil Aviation Organization, Fans Committee// FANS-4 Report,
Fourth Meeting, Montreal, May 2-29,1988.
15.3. Report of RTCA Special Commettee-159 on Minimum Aviation System Perform-
ance Standards (MASPS) for Global Positioning.
15.4. ARINC 743 Characteristics, 1989.
15.5. ARINC 743 Characteristics, 1991.
15.6. US Department of Transport, Federal Radionavigation Plan (FRP), DOT-TTSC-
RSPA 84.8, 1984.
15.7. US Department of Transport, Federal Radionavigation Plan (FRP), DOT-TSC-
RSPA-88, DOD-4650.4, 1988.
15.8. Kalafus R. M. GPS Integrity Channel// RTCA Group.
15.9. Interface Control Document: NAVSTAR GPS Space Segment// Navigation User
Interfaces (ICD-GPS-200). Rockwell Intern. Corporation, 1987.
15.10. Withington F. N., Klepcrynski W. J. Operational Results of GPS in Timekeeping
// Navigation, Spring 1988, vol. 33, no. 1.
15.11. Durand J. M., Michal N., Bouchard J. GPS Availability, part 1(11) vaiability of
Service Achievable for Different Categories of Civil Users// Navigation, Spring (Fall) 1990,
vol. 37, no 2 (3).
15.12. Kovach K, Conley R., Satzar. A Novel Approach to GPS Integrity// Navigation,
Summer 1991. vol. 38, no. 2.
15.13. Alison K. Brown. Civil Aviation Integrity Requirements for the Global Position-
ing System// Navigation, Spring 1988, vol. 35, no 1, p. 23—40.
15.14. Brawn G. RAIM and GIC Working Together: Ultimate Solution to the GPS in-
tegrity Problem// Navigation, Summer 1989, vol. 36, no. 2.
15.15. Minimum Aviation System Performance Standard (MASPS) for Global Posi-
tioning System (GPS)// RTCA Paper no. 394-88/SC159-191, October 1988.
15.16. Jargensen P. A. A Suggested Approach for Integrity Monitoring Stations// RTCA
Paper no. 18-87/SC159-72.
15 17. White F. Communications Methods for Disseminating GPS Integrity Data to Air-
craft Using Planned Capability// RTCA Paper no. 303-86/SC159-33.
15.18. Геращенко C. H.t Медведев Л. К. Перспективы объединения возможностей
спутниковых навигационных систем GPS и ГЛОНАСС// Проблемы безопасности поле-
тов, 1992, № 7, с. 3—6.
342 Г л а в a 15. Повышение достоверности HBQ I
15.19. Шебшаевич В. С., Григорьев М. Н. и др. Дифференциальный режим сетевой ‘
спутниковой радионавигационной системы// Зарубежная радиоэлектроника, 1989, № 1,
с. 5-32.
15.20. Brown A. Integrity Monitoring of GPS Using a Barometric Altimeter// RTCA Pa- •
per no. 405-87/SC159-117.
15.21. Kalafus R. M., Van Dierendonck A. J., Pealer N. A. Special Committee 104 rec-
ommendations for differential GPS service// Navigation, 1986, vol. 33, no. 1, pp. 26—41.
15.22. Геращенко С. II., Медведев Л. К. Перспективы объединения возможностей
спутниковых навигационных систем GPS и ГЛОНАСС// Проблемы безопасности поле-
тов, 1992, № 7, с. 3—16.
15.23. Варавва В. Г., Кирейчинкд В. А. Контроль целостности GNSS в бортовых на-
вигационных системах// Проблемы безопасности полетов, 1992 , № 9.
15.24. Brown R. G., Me Burney Р. W. Selfcontained GPS Integrity Chear Using Maxi-
mum Solutions Separation// Navigation, Summer 1988, vol. 35, no. 2.
15.25. Young C. Lee. Analysis of Range and Position Comparison Methods as a Means
to Provide GPS Integrity in the User Receiver// The MITRE Corporation, McLean, Virginia,
1986.
15.26. Parkinson B. W., Axelrad P. Autonomous GPS Integrity Monitoring Using the
Pseudorange Residual// Navigation, Summer 1988, vol. 35, no. 2.
15.27. Nikiforov I. V., Varrava V. G., Kireichikov V. A. Application of Statistical Fault
Detection Algorithms for Navigation Systems Monitoring// Proc. IRAC/IMACS Symp.
SAFEPRO CESS’91, Baden-Baden, 1991, vol. 2, pp. 351—356.
15.28. Varavva V. G., Vinogradov О. V., Kireichikov V. A. Precision Increasing and In-
tegrity Monitoring of Navigation Data for GPS/ Inertial Hybrid Solution// The 18th ICAS
Congr., Beiging, 1992, Paper no; ICAS-92—1.1.2. .
15.29. Sturza M. A. Navigation System Integrity Monitoring Using Redundant Measure-
ments// Navigation, Winter 1988—89, vol. 35, no. 4, pp. 483—501.
15.30. Tsahg IV. L., Stein B. A. A Robust RAIM Scheme Using GPS/GLONASS Sys-
tems// Science Applications International Corporation, Me Lean, VA 22102.
15.31. Brown R. G. Self-Contained GPS Integrity: Trade off Between Selective Avail-
ability and Radial Error to be Protected Against// RTCA Paper no. 408-87/SC159-119.
15.32. Brown G., Patrik Y. C. GPS Failure Detection by Autonomous Means Within the
Cockpit, Electrical Engineering, Iowa State University Ames, Iowa 50011.
15.33. Kalafus R.M. GPS Integrity Channel// RTCA Group.
15.34. Ван Трис. Теория обнаружения, оценок и модуляции: Пер. с англ, под ред.
В. И. Тихонова. Т. 1. — М.: Сов. радио, 1972.
15.35. Миддлтон Д. Введение в статистическую теорию связи. — М.: Сов. радио,
1962, т.2.
15.36. Сосулин Ю.Г. Теория обнаружения н оценивания стохастических сигналов.
— М.: Сов. радио, 1978.
15.37. Харисов В.Н., Карпейкин А.В. Методы нелинейной фильтрации в задаче об-
наружения отказов в спутниковых радионавигационных системах// Радиотехника, 1996 ,
№ 7, с. 115-119.
15.38. Харисов В.Н., Нартов В.Я., Дунчич Я.Г., Карпейкин А.В. Синтез оптимального
алгоритма автономного контроля целостности СРНС// Научно методические материалы
по статистической радиотехнике/ Под ред. Л.А. Ершова — М.: Изд-во ВВИА им. Н.Е.
Жуковского, 1994, с. 100—115.
343
Глава 16
Комплексная обработка информации в
аппаратуре потребителей спутниковых
радионавигационных систем
16.1. Принципы комилексирования
навигационных измерителей
Одной из центральных идей развития аппаратуры потребителей СРНС
является ее функциональное, информационное и аппаратурное объединение с
другими навигационными измерителями в составе интегрированных навигаци-
онных комплексов (НК). Большинство подвижных объектов (воздушных, кос-
мических, морских и т.д.) имеют в составе своего оборудования помимо АП
СРНС ряд других навигационных радиотехнических средств, таких как аппара-
тура радиотехнических систем ближней (РСБН) и дальней (РСДН) навигации,
РЛС, а также автономные нерадиотехнические навигационные системы.
Основными автономными средствами навигации подвижных объектов
являются инерциальные (ИНСУ и инерциально—доплеровские (ИДНС) нави-
гационные системы, курсо—доплеровские и курсо—воздушные системы счис-
ления, а также одометрические системы. ИНС и ИДНС используют на самоле-
тах, вертолетах и морских судах различного назначения, а в последнее время
ИНС также включают в состав наземных геодезических комплексов местооп-
ределения. Курсо—доплеровские системы входят в состав навигационного
оборудования на самолетах и вертолетах, оснащенных радиолокационными
доплеровскими измерителями скорости—сноса (ДИСС) и курсовыми система-
ми (КУС), а также на морских судах, имеющих на борту ультразвуковые
ДИСС. Курсо—воздушные системы применяют на самолетах и вертолетах,
оборудованных КУС и средствами определения воздушной скорости. Кроме
того, многие морские суда оборудуются автономными системами счисления
пути на основе лага и КУС. У ряда наземных подвижных объектов имеются
одометрические системы счисления координат на основе счета числа оборотов
стандартного колеса и разложения полученных результатов на составляющие с
использованием данных КУС. Все воздушные суда имеют также средства изме-
рения баро- и геометрической высоты полета. На некоторых самолетах поми-
мо этого имеется банк данных о высоте рельефа местности. В состав многих
НК различных подвижных объектов входят датчики времени (часы).
Объединение (интеграция) такого оборудования в единый функциональ-
но, структурно и конструктивно взаимосвязанный НК позволяет полнее ис-
пользовать имеющуюся на борту подвижного объекта избыточную информа-
цию, благодаря этому появляется возможность расширить круг решаемых задач
и улучшить качество их выполнения. Повышение уровня и степени интегра-
, ') \ -I
344 ) Гл а. а 16. К лплекс.^я обраузтка иы.юрмации в АП сРНС
ции оборудования в составе НК проявляется в реализации следующих прин-
ципов комплексирования [16.11:
совмещение функций различных радиотехнических систем, приводящее
к появлению совмещенных систем и многофункциональных интегрированных
комплексов;
объединение технических средств, измеряющих одни и те же либо функ-
ционально связанные навигационные параметры.
Применительно к потребителям навигационной информации совмеще-
ние радиотехнических систем, в которых часто используются сложные радио-
сигналы, позволяет создавать многофункциональные комплексы, обладающие
привлекательными конструктивными и эксплуатационными характеристиками.
Примером реализации первого принципа комплексирования могут служить
разрабатываемые многофункциональные системы, которые создаются на базе
существующих однофункциональных систем связи, навигации и опознавания
[16.1]. При втором принципе комплексирования осуществляется совместная
(комплексная) обработка информации нескольких устройств или. систем НК,
определяющих одни и те же либо функционально связанные навигационные
или специальные параметры. Например, с помощью ИНС, РСБН, РСДН,
СРНС и других измерителей имеется возможность с определенной избыточно-
стью находить координаты местонахождения, скорость потребителя и т. д.
Потребность в одновременном.измерении одних и тех же параметров-е
помощью устройств и систем, работающих на различных физических принци-
пах, обусловлена тем, что каждый измеритель в отдельности не удовлетворяет
всем требованиям, которые предъявляются к качеству измерений навигаци-
онных параметров подвижных объектов. В частности, многие современные
РСБН и РСДН не отвечают требованиям точности, помехозащищенности и
дальности действия; СРНС — требованиям помехозащищенности и целостно-
сти; ИНС — требованию точности и т. д.
Цель комплексирования оборудования — объединение различных изме-
рителей в единый комплекс, обладающий белее высокими характеристиками
точности, непрерывности, помехоустойчивости и надежности навигационных
определений по сравнению с отдельными измерителями. Максимального вы-
игрыша от комплексирования навигационных измерителей можно достичь,
решив соответствующую задачу синтеза, что позволяет найти оптимальную
структуру и характеристики системы комплексной обработки информации.
На практике степень интеграции устройств и систем в составе НК до на-
стоящего времени была такова, что комплексное извлечение информации ча-
ще применялось при ее вторичной обработке. Однако неуклонный рост требо-
ваний, предъявляемых к аппаратуре навигационных потребителей СРНС, а
также значительное расширение круга решаемых задач вызывают сегодня все
более острую необходимость комплексирования измерителей и при первичной
обработке информации. Это представляет собой принципиально новую сту-
пень в повышении степени интеграции оборудования в составе НК, т.е. ведет
к появлению НК интегрального типа.
34э
16. ..Прин^Лы комплексирооиния нао^гациенпоц измерителей
Деление на первичную и вторичную обработку сигналов (см. гл. 6) в ап-
паратуре навигационных потребителей по существу является условным. Под
первичной обработкой информации (иногда называемой обработкой сигналов)
понимают поиск, обнаружение, селекцию, преобразование и обработку (в ре-
жиме слежения) входных сигналов навигационных и специальных измерителей
в целях нахождения соответствующих радионавигационных параметров. На-
пример, определение радионавигационных параметров, пропорциональных ПД
и ПСК, в аппаратуре потребителя СРНС относят к первичной обработке ин-
формации. Под вторичной обработкой информации (иногда называемой обра-
боткой данных) понимают выполняемую в ЦВМ обработку выходных сигналов
самих измерителей, результаты которой используют для нахождения и уточне-
ния навигационных параметров. Примером вторичной обработки является вы-
числение в АП СРНС его координат и скорости движения.
Комплексная вторичная обработка информации дает значимый положи-
тельный эффект, когда соответствующие измерители работоспособны, т.е. на
выходах навигационных измерителей имеются достаточно “хорошие”
(естественно, и в таких случаях наблюдаемые с погрешностями) сигналы,
сформированные в результате первичной обработки информации. Реальные
условия применения аппаратуры навигационных потребителей показывают,
что многие измерители, и прежде всего радиотехнические, далеко не всегда
находятся в работоспособном состоянии. В реальных условиях нередко наблю-
дается срыв сопровождения сигналов, в частности в каналах дальности,
из-за многолучевости и действия других помех, захват ложных фазовых доро-
жек и т. д.
Оптимизация алгоритмов при вторичной обработке информации, естест-
венно, мало затрагивает сами измерители. Это характерно для современных
радиотехнических измерителей, во многих из которых еще не в полной мере
реализуются заложенные возможности. Существенного улучшения характери-
стик навигационных и других специальных измерителей можно достичь путем
комплексной первичной обработки информации.
Применительно к интегрированным НК комплексирование устройств и
систем на уровне первичной обработки информации позволяет [4.3]: сократить
время поиска сигналов измерителей; уменьшить или полностью исключить
вероятность ложных захватов следящих измерителей; снизить вероятность
срыва слежения за соответствующими параметрами радиосигналов; повысить
характеристики точности и помехоустойчивости радиотехнических измерите-
лей в режиме слежения; устранить или уменьшить методические погрешности
измерителей; обеспечить режимы квазикогерентного приема и обработки ра-
диотехнических сигналов, что не представлялось возможным в соответствую-
щих некомплексных измерителях, и тем самым значительно повысить их ха-
рактеристики точности; для высокодинамичных потребителей компенсировать
влияние движения объекта на работу измерителей.
Таким образом, комплексирование оборудования в составе НК на уровне
первичной обработки информации имеет целью прежде всего повысить каче-
зчо I ла , a io. «.эмплекс^йя обрь^Отка информации в АП СРНС,
ство функционирования измерителей в аномальных режимах их работы (при
возможных срывах слежения, ложных захватах и т.п.) и, кроме того, улучшить
характеристики точности и помехоустойчивости измерителей в режиме слежек
ния. Наибольший положительный эффект при комплексной первичной обра-
ботке информации может быть достигнут путем решения задач синтеза алго-
ритмов оптимальной и субоптимальной обработки на основе методов марков-
ской теории оценивания случайных процессов [5.1, 16.2, 16.3).
16.2. Комплексная первичная обработка информации
в аппаратуре потребителей СРНС
Применение марковской теории оптимального оценивания дает возмож-
ность получить оптимальные (субоптимальные) алгоритмы и структурные схе-
мы соответствуюших систем приема и комплексной обработки сигналов, а
также выполнить количественную оценку их характеристик. Методы синтеза
указанной теории позволяют сушественным образом учесть наличие информа-
ционной избыточности, характерной для сигналов объединяемых измерителей.
Эти методы обеспечивают продуктивное решение поставленных задач при та-
ких специфичных для комплексирования измерителей особенностях, как при-
сутствие частично окрашенных (коррелированных во времени) шумов наблю-
дения; наличие полимодальности в апостериорном распределении оценивае-
мых процессов (см. гл. 14); необходимость в совместной обработке импульс-
ных и непрерывных сигналов.
Анализ практической реализуемости синтезированных систем приема и
комплексной обработки сигналов в аппаратуре навигационных потребителей
включает исследование работоспособности полученных схем при отклонениях
реальных условий функционирования от расчетных. При их технической реа-
лизации производят упрощения с учетом особенностей современной элемент-
ной базы и оценивают реальные характеристики качества функционирования.
Успехи в технологии создания радиоэлектронной аппаратуры (в том чис-
ле и в диапазоне сверхвысоких частот) на основе использования гибридно-
пленочной технологии, применения приборов с зарядовой связью, приборов
на базе поверхностных акустических волн, развития микропроцессорной тех-
ники и волоконно-оптических линий позволяют на практике реализовать в
АП СРНС оптимальные (субоптимальные) алгоритмы вторичной и первичной
обработки информации.
Исходя из перспектив развития СРНС, в рамках предстоящей интегра-
ции отечественных и зарубежных навигационных систем общего назначения
одно из центральных мест занимает создание интегрированной АП. В зави-
симости от видов объединяемых РНС уместно выделить прежде всего интег-
рированную АП следующих двух типов [16.4): интегрированная АП СРНС
ГЛОНАСС и импульсно-фазовой разностно-дальномерной РСДН типа
Loran—C/Чайка; интегрированная АП СРНС ГЛОНАСС и GPS.
347
16^2.уСомплексная первичная обработка информации в АП СРНС
16.2.1. Оптимизация интегрированной аппаратуры потребителей
радионавигационных систем ГЛОНАСС и Loran—С/Чайка
Важное направление развития навигации вообще представляет собой ин-
теграция отечественных и зарубежных навигационных систем общего приме-
нения. Одним из. путей реализации этого направления является объединение
СРНС ГЛОНАСС и импульсно-фазовой разностно-дальномерной РСДН типа
Loran—С/Чайка [4.3]. Интегрирование этих РНС позволит улучшить доступ-
ность и целостность СРНС в географических районах, которые определяются
пределами рабочих зон, создаваемых цепочками станций РСДН. Объединенная
РНС ГЛОНАСС и Loran—С/Чайка сможет использоваться в качестве основной
корректирующей системы для всех этапов навигации подвижных объектов,
исключая категорированный заход и посадку самолетов, а также маневрирова-
ние судов в акватории порта. Интегрирование РНС ГЛОНАСС и Loran-
С/Чайка предполагает объединение радионавигационных полей и комплекси-
рование АП. Объединение радионавигационных полей состоит в обеспечении
возможности совместного использования навигационных параметров каждой
из объединяемых систем при решении навигационной задачи, для чего прежде
всего необходимо согласование шкал времени СРНС и РСДН, а также приме-
няемых координатных систем.
Построение интегрированной АП предполагает совместное (комплекс-
ное) использование результатов приема радиосигналов по различным каналам
объединенной РНС при решении навигационной задачи.
Оптимизация алгоритмов для подобной совместной обработки радиосиг-
налов СРНС ГЛОНАСС и РСДН Loran—С/Чайка довольно успешно выполня-
ется на основе методов марковской теории оценивания случайных процессов
[16.5, 16.6[. Заметим, что построение указанной интегрированной АП, напри-
мер, для воздушных или космических подвижных объектов никак не исключа-
ет ее дополнительного сопряжения с другими навигационными датчиками и, в
частности, с ИНС, преимущества которого известны [1.5|.
Постановка задачи. Применительно к СРНС ГЛОНАСС в АП на под-
вижном объекте в сеансе навигации принимаются радиосигналы не менее чем
от четырех видимых НС, которые затем используются для вычисления ПД и
ПСК. подвижного объекта относительно НС. Результаты таких вычислений и
эфемеридная информация (ЭИ), принятая от каждого НС, позволяют опреде-
лить (или уточнить) три координаты и три составляющие вектора земной ско-
рости потребителя, а также оценить смещение шкалы времени потребителя
относительно шкалы времени системы [1.5]. Применительно к РСДН Loran-
С/Чайка в АП на подвижном объекте в сеансе навигации принимаются радио-
сигналы от ведущей и двух—пяти ведомых станций, которые используются для
вычисления разностей дальностей или псевдо дальностей относительно назем-
ных станций [4.3].
Для определенности рассуждений и с целью упрощения выкладок пред-
положим, что решается задача нахождения только плановых координат под-
348
Г л а в a 16. Комплексная обработка информации АП СРНС
вижного объекта, например летательного аппарата, по сигналам одного НС
СРНС ГЛОНАСС и одной навигационной станции РСДН Loran—С/Чайка.
Кроме того, полагаем, что для нахождения координат ЛА используются дац.
ные о составляющих его земной скорости с выхода ИНС, оси которой долж-
ным образом ориентированы относительно нормальной земной системы коор-
динат [16.7]. Высота полета ЛА при этом также считается известной. В рамках
создания единого радионавигационного поля РНС ГЛОНАСС и Loran-
С/Чайка применительно к АП предусмотрено приведение их к одной ШВ.
С учетом изложенного на цолуинтервале ро>0 наблюдаются реализации
случайных процессов:
у1(П = 51(г,и1(/),е*)+л1(/); (16.1)
3'2(0 = 52(r,U2(/)) + «2(/); (16.2)
Пз(4) = Н(/*)Х(,к) + «з('*), (16.3)
где yt(/) и у2(/) — наблюдаемые в АП сигналы от НС и РСДН соответственно;
Пз(^) = nrF(f*)|T~ измеренные с помощью ИНС в момент времени tk
значения проекций земной скорости ЛА на горизонтальные оси геодезиче-
ского репера; и 52(») — непрерывный радиосигнал СРНС ГЛОНАСС и
импульсный радиосигнал РСДН Loran-С/Чайка соответственно; лДО, л2(/)
»з('*) ~ взаимно независимые шумы измерений с известными статистически-
ми характеристиками; 1Ц(/) и U2(/) — векторы радионавигационных парамет-
ров сигналов (задержка сигнала, доплеровское смещение частоты и др.), кото-
рые непосредственно входят в сигналы 5^»), 52(») и связаны детерминиро-
ванными, в общем случае нелинейными, функциями с оцениваемым вектором
состояния Х(/),т. е. IJ|(/) = Gt(X(r)), U2(r) = G2(X(/)); ek = &(tk) — дискретный
информационный параметр (служебная навигационная информация), смена
значений которого происходит в моменты времени tk = t0 + кТ^и , к = 0, 1
Теи — длительность передачи символа служебной информации 0* ; Н(/Л.) —5
известная матрица.
Полагаем, что шумы наблюдения n^(t) и и2(0 аппроксимированы ста-
ционарными белыми гауссовскими случайными процессами с нулевыми мате-
матическими ожиданиями и спектральными плотностями jV|/2 и N^jl, а век-
тор помех u3(/t) определяется разностным уравнением [16.6]
16.2. Комплексная первичная обработка информациив АП СРНС
349
«з(М = ®uuu3(^-l) + <®uxX(/fc-l) + r,u,,u(/A:-l). (16.4)
где Фж, и Ги — известные матрицы; жв(4-1) — вектор гауссовских
случайных величин с независимыми значениями, нулевыми математическими
ожиданиями и единичными дисперсиями.
Применительно к рассматриваемому случаю основными навигационными
параметрами всех трех измерителей являются: Дизм1(/), Диэмзй — псевдо-
дальности ЛА—НС и ЛА-РСДН; Кдг(г)и ^(0 — проекции вектора земной
скорости ЛА на горизонтальные оси геодезического репера. Каждый из них
представляет собой определенную известную функцию геодезических коорди-
нат ЛА В и L (см. § 3.1. и [16.6, 16.7]). В силу этого, вектор состояния Х(/).
оптимальные оценки компонент которого должны быть вычислены синтези-
руемой бортовой системой комплексной обработки информации (СКОИ), це-
лесообразно сформировать в геодезической СК, а не в какой-либо из СК, ис-
пользуемых только в СРНС, РСДН или ИНС [16.8].
На основе изложенного вектор состояния имеет вид
Х(/) = L VN VE aN аЕ Vm ^ео Ф “с дл д£ ^рас ^рас |Т, (16.5)
где ащ, аЕ, — проекции векторов земного ускорения и постоянно
составляющей земной скорости ЛА, направленные вдоль осей репера геодези
ческой СК; ср, юс — случайные фаза и уход частоты сигнала СРНС; Дл-, Л
— постоянные составляющие ошибок акселерометров ИНС, обусловленны
погрешностями начальной выставки гироплатформы и нескомпенсированны
дрейфом гироскопов; трас, трас — флуктуации времени запаздывания сигна.
РСДН и его производной, обусловленные нестабильностью скорости распр’
странения радиоволн в атмосфере. Система дифференциальных уравнени
определяющая динамику вектора X(Z) , записывается следующим образом |4
16.6. 16.7]:
dB . dL dVi dVN <1VE
= -(a + n)aN - ац^дг - Гд0) + ^2(a + na[i (t);
= -(a + p)aE - ац(КЕ - Г£о) + ^2(a + ц)а2а na[, (z);
350 Глава 16. Комплексная обработка информации в АП СРНС)
&.0; ^..0;
dt — 2<ХрасТрас арасрас +J^<xpacCJpac ^т'(0 » (16.6)
где Ci и б2 — известные радиусы кривизны применительно к земному эллип-
соиду; а — коэффициент, определяемый аэродинамическими характеристика-
ми ЛА; р — параметр, характеризующий ширину спектра флуктуаций скоро-
сти ветра; о„ — дисперсия флуктуаций ускорения, зависящая от турбулентно-
сти атмосферы, равномерности тяги двигателей и т. д.; а>о — номинальна^
частота сигнала СРНС; с — скорость света; о„ — дисперсия флуктуаций час-
тоты задающего генератора; у — параметр, характеризующий ширину спектра
изменений частоты 65 с ; Nv — параметр, определяющий интенсивность
флуктуаций-фазы <р(/) ; арас и орас — параметры, характеризующие ширину
спектра и интенсивность флуктуаций времени запаздывания сигналов РСДН;
лОдг(^), ио£(4’ ”<р0) и "т'(0 — стандартные взаимно независимые белые гаус-
совские формирующие шумы. i
Анализ характера изменения во времени нелинейных функций, входящих,
в правые части дифференциальных уравнений (16.6), показывает, что они
представляют собой достаточно медленно меняющиеся функции. Поэтому на
интервалах времени, соответствующих длительности пачек радиосигналов
РСДН и символа служебной информации СРНС, система дифференциальных
уравнений (16.6) может быть представлена в виде линейного векторно-
матричного дифференциального уравнения
^ = FX(/) + CW(0 + G^); Х(/0) = Х0, (16.7)
где £(/) — вектор формирующих белых гауссовских шумов с известными ста-
тистическими характеристиками; W(/) — известный вектор, который будем
называть вектором управления; G, С, F — известные матрицы возмущения,
управления и состояния, элементы которых определяются (16.6).
Таким образом, задача оптимального нелинейного оценивания в данном
случае может быть сформулирована следующим образом. Имея априорные све-
16.2. Комплексная первичная
дения о векторе состояния Х(/) (уравнения
блюдениями (16.1) (16.3), требуется определить оценку Bejcnjpa состояния
Х(/), которая должна удовлетворять критерию минимума
апостериорного риска [16.3]
X = X. mjn.|fc^X,xjp^t,X|Y(,()jdx’
(16.8)
где с^Х,Х| — функция потерь; /у, X|Y^j — апостериорная плотность вероят-
ности вектора состояния Х(/), определяемая на основании наблюдений
Y(/) = |Ы0 У20 Пз(0| на отрезке времени 110, t ].
Заметим, что в приведенной постановке для упрощения и большей на-
глядности именно проблем комплексирования различных измерителей, опу-
щена задача оценки дискретного параметра 9* в СРНС. Учет этого параметра
приводит к определенному усложнению теоретических построений. Однако
при необходимости этот фактор можно учесть, аналогично тому, как это сде-
лано в п. 6.2.1, основываясь на общих алгоритмах [6.2]
Оптимальные и субоптимальные алгоритмы системы комплексной обра-
ботки информации АП. Оптимальная оценка вектора состояния Х(/) , как из-
вестно, определяется на основе знания апостериорной плотности вероятности,
которая отыскивается путем решения уравнения Стратоновича [16.2, 16.3] для
апостериорной плотности вероятности оцениваемого процесса. Для получения
практически реализуемых алгоритмов используются те или иные приближения
при решении указанного уравнения. В рассматриваемых задачах благодаря
обоснованному упрощению математических моделей оцениваемых процессов
(16.6) и с учетом специфики шумоподобных сигналов СРНС, импульсных сиг-
налов РСДН и дискретных сигналов ИНС одно из возможных приближенных
решений основано на поэтапном решении уравнения для апостериорной
плотности на каждом из последовательных интервалов времени 7"н =
- Uii ~ ~20 мс, соответствующих длительности пачек импульсных радиосиг-
налов РСДН и длительности символа служебной информации сигналов СРНС
[16.3, 16.6, 16.9]. На отрезке времени f е[д,Д,1] оцениваемый процесс (16.7)
может быть представим в виде
х0 = ®xx(r>4t)x* + Cf ®xx(/>v)w(v)i/v + Gf Фхх0 v)N(v)</r|, (16.9)
>k <k
352
Глава 16v Кчиквлексиая обработка информации в АД СРНВа
1
где Х*=Х(4) — значение оцениваемого вектора в момент времени (*•
Фдх(^4) ~ матрица фундаментальных решений уравнения (16.7), удовлетво-'
ряющая однородному уравнению ч
= ГФхх(Л^); ФИ(4.4) = 1,
где I — единичная матрица.
Полагая, что на предыдущем этапе работы найдена оценка Х(^) процес-
са Х(г), соответствующая моменту времени и сформированная по результа-
там всех предыдущих наблюдений (16.1)—(16.3), ставится задача нахождения
оценки Х(4+1), соответствующей моменту времени 4+j, по наблюдениям
сигналов на отрезке времени [4,4+1]- Двухэтапность решения уравнения,.
Стратоновича на этом интервале заключается в том, что сначала (первый
этап) по результатам наблюдений сигналов (16.1)—(16.2) и априорной инфор-
мации о X(/jt), которая заключается в знании оценки Х(4), ищутся оценки
параметров X* (см. (16.9)), где — апостериорная"
плотность вероятности; = (yi(f), y2(t); t e[4,4+1]} • При этом полагается,
что динамика изменения процесса Х(1) описывается детерминированной /
функцией X(z) = f(/,Xt) от случайных параметров X*, т. е. в представлении .
(16.9) не учитывается последнее слагаемое.
На втором этапе решения уравнения Стратоновича ищется апостериор-
ная плотность вероятности процесса Х(/) в момент времени 4+1 и соответст-
вующая ей оценка X(zt+i) с учетом полученной на первом этапе оценки Х£
для полной динамики изменения оцениваемого вектора (16.9) и наблюде-\
ния (16.3).
Итоговые алгоритмы оценивания получены в [16.3, 16.5, 16.6] и имеют
следующий вид:
1-й этап
X* =Х(4) + К^+1[Ф] +Ф^]; (16.10)
R*|t+i ={к*’-[фГ + Ф?]} (16.11)
16.2.Хол</мзксиая первичная рбрабогпк.а информации* АП СРНС
353
у»4у.с(>(у,М)Ь ъйт
Ф{ = J ——*--т---и = J -^ФдА; »= 1, 2
Гц Ж щ дл
^p,G(r(r,X(^)))] = N/-1{2y/(/)5/[z>H/G,(/,X(^))]-5/2[/,H/G/(/,X(/*))]}; (16.13)
Ф/
(Ф0Т = J
(16.14)
и(0 = |Д„зМ1 Дизм2 Ипм1 Ф «С ХрасГ = °(Х)! U(ft) = U* — обобщенный вектор
радионавигационных параметров, который связан с векторами радионавигаци-
онных параметров Ub U2, входящих в сигналы Sj(*) и 5г(*) (16.1)—(16.2),
соотношениями Uj = HjV, U21 “H^U; VH3M 1Q1 „ псевдоскорость;
aul , _
—Л- = Ln — матрица преобразования.
ЭХ
Анализ изменения элементов матрицы Ъп на интервалах времени интег-
рирования показывает, что для t e\tk,tk +Т„) их можно считать постоянными
и вынести за знак интеграла в (16.12). В таком случае субоптимальный алго-
ритм обработки информации на первом этапе имеет вид
't+i
х1+1 = x(0t) +Кф+Лп f [ф1и + ф2и]Л'-
(16.15)
Заметим, что при периоде повторения пачек импульсов РСДН 7рсдн =
= 100 ... 250 мс и интервалах накопления Гн=20 мс не для каждого периода
\tk,h +7н) в алгоритме (16.15) будут иметь место две составляющие Ф'ш и
Фги- При отсутствии сигнала РСДН на соответствующих периодах в (16.15)
следует полагать Ф= 0.
2-й этап
X(fA: + l) - Х(Г*и) + К(1а: + 1)[пз(^1) -фИ/Пз(М~ФпХХ(/* + 1)];
(16.16)
354 Г л а в a 16. Комплексная обработка информации а АП СРНС.
К*н = [Фххк1|к+1Ф^|Х +ВпХИФлхЛ*|А: + 1Ф^Х + Впч1
Rfc = [фххв1|*+1фхх +вхх]-Kfc+i^xxRtjfc+i^x +вхл]’ (16.17)
где
x(rt+i) = ФххХ’* +^л); (16.18)
S' — переходная матрица управления; Фпх» ®пп> ВчХ ~~ матрицы, определяе-
мые по Фхх, Фци, Н, Г, с помощьюизвестных соотношений [4.3].
Схема бортовой системы приема с комплексной первичной обработкой
применительно к сигналам СРНС, РСДН и ИНС (а также включающая канал
оценки символов служебной информации вк, не рассмотренный выше, но
присутствующий в реальной системе), которая реализует синтезированные
выше алгоритмы, представлена на рис. 16.1, где обозначено: ДС и ДР —
дискриминаторы сигналов СРНС и РСДН соответственно; АЦП — аналого-
цифровой преобразователь; ВВС — блок весового суммирования; ВПК —
блок прямого преобразователя координат, реализующий операцию умножения
на матрицу Ln B (1-5.14); КВИП ----блок выделения информационных пара--
метров; БВДС — блок вычисления дальностей и скорости, осуществляющий
обратное преобразование координат U = G(X); ЦАП — цифроаналоговый
преобразователь; ЛЗ — линия задержки; СКВОИ — схема комплексной вто-
ричной обработки информации, реализующая (16.16), (16.17) и (16.18); УФОС
1 (2) — устройства формирования опорных сигналов СРНС и РСДН соответ-
ственно; БФТИ — блок формирования тактовых импульсов, решающий за-
дачу синхронизации сигналов СРНС и РСДН; БВДП — блок выделения дис-
кретного параметра О* ; БВСИ — блок выделения служебной информации,
содержащейся в параметре 0*; СИ — служебная информация, содержащаяся
в сигнале СРНС; dlB А-, dlLA- <1п-.9Л. d2B=^;
ив CL CB vL oB
du=^dL '’ B = L = L(tk); и = u(rt).
Замечания
1. В алгоритме квазиоптимальной фильтрации (16.10)—(16.18) формиру-
ются две оценки X* и Х(/*.), что, в принципе, не является необходимым.
16.Z. Комплексная первичная обработка информации в АП С&ВС 355
Рис. 16.1. Схема комплексной системы
Качественно это можно проиллюстрировать, подставив (16.10) в (16.18), тогда
Х(4+1) = ^(,*+1) + к(,*+1^’1з(^+1)-ф£/17’1з(4)-фчхХ(гЛ+1)^;
Х(4+1) = ФххХ(1*) + 'PWf/jt) + ®xxR^+1[®i + Ф-2].
12*
356 Глава 16. Комплексная обработка информации в АП СРНС
В приведенных соотношениях осуществляется рекуррентное вычисление
только оценок Х(/*) в результате обработки всех принятых сигналов.
2. Из (16.15) следует, что на интервале времени Т„ накапливаются
(интегрируются) напряжения на выходе дискриминаторов соответствующих
радионавигационных параметров (задержки, частоты и др.). Сформированные
отсчеты далее фильтруются в дискретном фильтре. Такое построение ком-
плексного измерителя дает удовлетворительные результаты при временах на-
копления Т„ = 1 ... 5 мс. При больших временах накопления, как показано в
[16.13], весовое взвешивание в дискретном фильтре (а не в процессе накопле-
ния напряжения на выходе дискриминатора^ приводит к заметному возраста-
нию ошибки фильтрации. Оптимальная процедура построения непрерывно-
дискретного измерителя на комбинированной калмановско-винеровской
фильтрации [16.14], и приводит к весовому взвешиванию в процессе накопле-
ния напряжения на выходе дискриминатора (весовая матрица R(f) стоит под
интегралом в (16.15)).
3. Использование соотношений (16.15)—(16.18) для синтеза бортовой
системы КОИ применительно к сигналам СРНС, РСДН и ИНС позволяет оп-
ределять координаты ЛА как в штатном режиме работы, так и в аномальных
условиях функционирования СРНС и РСДН". В последнем-случае для опреде-
ления текущих координат ЛА могут быть, например, использованы по одной
линии положения от каждой радионавигационной системы. Это обстоятельст-
во является важным фактором непрерывности и надежности навигации ЛА в
условиях, когда имеет место либо работа с ограниченным созвездием НС, ли-
бо большое значение геометрического фактора СРНС или РСДН, либо слож-
ная помеховая обстановка для этих систем. Кроме того, сопряжение АП с
ИНС в соответствии с алгоритмами (16.16)—(16.18) позволяет рационально
сочетать высокую точность определения координат с помощью РНС с высокой
точностью хранения этих координат на небольших интервалах времени путем
использования ИНС.
Так как СРНС, РСДН и ИНС в конечном счете после соответствующих
преобразований координат вычисляют одни и те же величины ( в данном слу-
чае геодезические координаты В и L), то эта информационная избыточность
дает возможность осуществлять автономный контроль целостности интегриро-
ванной РНС.
Подобный контроль целостности РНС позволяет не только выявить факт
неправильного функционирования системы, но и достаточно эффективно
идентифицировать отказавший канал передачи информации с последующей
выработкой команды на соответствующую реконфигурацию структуры интег-
рированной АП.
Точность в помехоустойчивость ннтегрироааниой АП. Потенциальные ха-
рактеристики точности и помехоустойчивости синтезированной интегриро-
ванной АП могут быть вычеслены путем решения уравнений для матрицы апо-
16.2. Комплексная первичная обработка информации е АЛ_СРНС_________35]
стериорных вторых цен-
тральных моментов (16.11),
(16.17). На рис. 16.2—16.3 в
качестве иллюстрации пред-
ставлены некоторые резуль-
таты расчета апостериорной
дисперсии ошибки оце-
нивания геодезической
долготы L места ЛА от па-
раметров
9с = -^сТеиЛ^Ос J
которые характеризуют от-
ношения сигнал/шум в на-
блюдаемых реализациях
уД/) и у2(/) соответствен-
но. В приведенных выраже-
ниях обозначено: Яс и
— амплитуды сигналов
$1(г) и 52(/); ти — дли-
тельность импульса в сигна-
ле РСДН; Nqc и Aop — ин-
тенсивности шумов «1(0 и
б)
Ряс. 16.2. Среднеквадратические ошибки
л2(/). Зависимости дисперсии для геодезической широты места ЛА по су-
ществу являются аналогичными.
Значения параметров элементов матриц, входящих в (16.15), (16.17) и
(16.18), при расчетах выбирались аналогично [16.5, 16.6], что соответствовало
типовым условиям функционирования СРНС,РСДН и ИНС. Анализ зависимо-
стей дисперсий ошибок оценивания геодезических координат В и L в штат-
ных режимах функционирования СРНС (при больших отношениях сиг-
нал/шум qc для СРНС и малых значениях коэффициента геометрии) пока-
зал, что ее комплексирование с РСДН и ИНС выигрыша по точности, как и
следовало ожидать, практически не дает. Для РСДН выигрыш в точности при
таких условиях значителен. При сложной помеховой обстановке или неудач-
ной геометрии СРНС значения дисперсий и при совместной обработке
информации СРНС, РСДН и ИНС несколько меньше по сравнению с соот-
ветствующими дисперсиями для некомплексной обработки сигналов СРНС.
Причем в данном случае, чем больше отношение сигнал/шум qf для РСДН,
тем ощутимее выигрыш в точности (см. рис. 16.2, а и б).
358 >
JTji BJ^J6i^OMIue^Ba^OL^60T^il
m в Ai. СРНС
Так, например, при ?с = 10 5 и qt = 10 потенциальное среднеквадратиче-
ское значение ошибки определения координаты L равно 1,5 м. Кроме того,
результаты расчетов показывают, что при пропадании сигналов одной из рас-
сматриваемых систем в интегрированной АП срыва слежения за информаци-
онными параметрами не происходит, хотя, естественно, качество функциони-
рования бортовой системы КОИ снижается. На рис. 16.3 представлены зави-
симости от отношения сигнал/шум для СРНС qc и для РСДН qt. Как
следует из графиков, при комплексной обработке информации существенно
ослабляется зависимость дисперсии от 9С или q9, причем для СРНС это
особенно характерно в области малых значений qc, а для РСДН во всем диа-
пазоне типовых отношений сигнал/шум 9р.
Синтезированные субоптимальные алгоритмы комплексной первичной
обработки информации для интегрированной АП применительно к радиосиг-
налам СРНС ГЛОНАСС и РСДН Loran—C/Чайка с привлечением данных с вы»
хода ИНС характеризуются наличием перекрестных связей, охватывающих
дискриминаторы и линейные части устройств. Опорные сигналы для каждого
б)
Ряс. 16.3. Зависимости СКО от отношения
сигнал/шум
дискриминатора формиру-
ются на основе управляю-
щих сигналов, представ-
ляющих собой взвешенные
суммы сигналов ошибок по
каналам для СРНС, РСДН и
ИНС.
Комплексная АП хаА
растеризуется высокой точ-
ностью и помехоустойчи-
востью. Анализ характери-
стик качества функциони-
рования показывает, что
выигрыш в точности от
совместной первичной об-
работки сигналов сущест-
венный в условиях
сложной помеховой об-
становки, при больших
значениях геометрического
фактора для СРНС ГЛО-
НАСС или РСДН Loran —
C/Чайка, при работе с ог-
раниченным созвездием
НС и при других аномаль-
35'
16.2, Комплексная первичная обработка ингрормации в АЛ СРНС
ных режимах функционирования интегрированной РНС. Совместное исполь
зование этих навигационных систем при реализации предлагаемых алгоритме
комплексной первичной обработки информации позволяет осуществлять авто
номный контроль целостности РНС и вырабатывать соответствующие команд!
на реконфигурацию структуры интегрированной АП в тех случаях, когда ха
рактеристики той или иной системы выходят за пределы установленных д<
пусков.
16.2.2. Оптимизация интегрированной аппаратуры потребителей
спутниковых радионавигационных систем ГЛОНАСС и GPS
Создание и использование комбинированных приемников, способны
одновременно принимать сигналы СРНС ГЛОНАСС и GPS, знаменует собо
новый, качественно более высокий уровень навигационного обслуживани
воздушных, морских и иного рода потребителей [16.8, 16.10]. Например, ком
бинированные приемники, предлагаемые фирмами Honeywell, Ashtech и дру
гими, при условии интеграции радионавигационных полей, дают возможност
заметно увеличить число принимаемых радиосигналов от различных видимы
спутников, улучшить точность, сократить время до получения первых коорди
нат, повысить целостность и т. д. Для динамичных потребителей весьма важ
ной Наряду с обеспечением высокой точности и помехоустойчивости являете
возможность улучшения характеристики целостности за счет совместного ис
пользования обеих СРНС. В отдельности ни система ГЛОНАСС, ни систем
GPS не обеспечивают требований по целостности, например при применени
их в качестве основного средства навигации воздушных потребителей при за
ходе*на посадку и при посадке [16.11].
Чтобы добиться максимального позитивного эффекта от комплексиров.
ния приемников ГЛОНАСС и GPS, следует выполнить глубокое структурное
функциональное их объединение на уровне обработки радиосигналов, сфо)
мировав на основе решения соответствующей задачи синтеза интегрировав
ную навигационную аппаратуру [16.2]. Системы ГЛОНАСС и GPS очень пох(
жи друг на друга, но содержат ряд особенностей. Так, спутники ГЛОНАС
имеют период вращения 11 ч 16 мин, а у GPS период вращения спутников р
вен 11 ч 58 мин. Другим отличием является то, что в GPS многоканальны
доступ осуществляется с различением сигналов по коду, а ГЛОНАСС име
многоканальный доступ с частотным разделением [1.1]. Как известно, объедг
ненная группировка спутников ГЛОНАСС и GPS в зоне видимости любог
потребителя в каждый момент времени позволяет иметь 10 ... 21 спутник
(см. [1.1, 16.10]).
Для построения интегрированной АП примем типовую схему, котора
содержит несколько входных СВЧ-фильтров, соответствующих числу одновре
менно принимаемых сигналов от всех видимых спутников объединенно
группировки [16.8]. Чтобы обеспечить значительный выигрыш в качеств
функционирования от объединения нескольких измерителей в единую систе
Г л а в a 16. Комплексная обработка информации в АП СРН(\
360
му, особенно в аномальных режимах работы, их комплексирование осуществ-
ляется на уровне первичной обработки информации [4.3]. При построении
интегрированной АП СРНС для динамичных подвижных объектов (наример,
воздушных или космических) предусматривается ее дополнительное сопряже-
ние с ИНС [1.5, 16.7J.
Рассмотрим задачу синтеза оптимальных (субоптимальных) алгорит-
мов приема и комплексной первичной обработки информации АП СРНС
ГЛОНАСС и GPS при дополнительном использовании сигналов с выхода
ИНС. Синтезируемые алгоритмы являются реконфигурируемыми и позволяют
обеспечить наряду с высокой точностью и помехоустойчивостью автономный
контроль целостности СРНС, идентификацию отказавшего канала системы,
выработку соответствующей команды на оперативное изменение структуры
интегрированной АП.
Постановка задачи синтеза оптимального измерителя сигналов СРНС
ГЛОНАСС, GPS н ИНС. Такая постановка задачи формально незначительно
отличается от той, которая была рассмотрена в предыдущем параграфе. При
этом вместо (16.1)—(16.2) будем рассматривать I наблюдений от всех видимых
НС ГЛОНАСС и GPS [16.15]
МО = + (16.19)
где U/(f) = |ДЮМ/ ^изм/Ф/“с/|Т — вектор радионавигационных параметров, от
которых непосредственно зависит радиосигнал i-го НС; ДтМ1, Иизм/ — псев-
додальность и псевдоскорость до 1-го; <p«(f) — случайная фаза сигналов; Sci
— уход частоты задающего генератора соответствующего НС; S/ Jt — дис-
кретный информационный параметр, передающий служебную информацию и
принимающий значения 0 и 1, смена которых происходит в моменты
h =to+^aii М,к = |х.дд- ••• — вектор параметров отказов для
/-го канала измерения; — т-й параметр отказа /-го канала измерения;
Q/ — матрица, определяющая связь вектора с шумами наблюдения.
Полагаем, что параметры ... , принимают значение 0 или 1 в
зависимости от состояния i-ro канала измерения, причем 0 означает отказ
канала, 1 — i-й канал исправен.
Под отказом /-го канала измерения далее понимаем такое его состоя-
ние, которое исключает возможность использования сигнала соответствую-
щего НС из-за недопустимо больших погрешностей определения навигацион-
ных параметров. Каждый такой отказ, если он не выявлен, ведет к нарушению
целостности системы. Причинами возникновения подобных отказов в каналах
измерения могут быть: временное пропадание сигналов /-го НС, ухудшение
стабильности частоты опорного генератора НС, сход НКА с орбиты, сдвиг
16.2. Комплексная лс, ____________________________________________
шкалы времени БШВ, скачкообразное возийсгячнмЙ^й^Й>г« t;*k. (см: ™- 15)-
Каждой из этих причин может соответствовать свой элемент вектора Л/,*, а в
зависимости от причины, вызвавшей нарушение целостности, мрует разли-
чаться вид функций, определяющих зависимость полезного сигнала
S/д) или шума л((г) от вектора параметров Л/4.
При рассмотрении параметров отказов К/* полагаем, что их значения
на соседних тактовых интервалах образуют однородную марковскую цепь с
матрицей вероятностей перехода
₽/,* = {^.vh } = {р(М'*+1) = нМ'*) = v)| 5 И, v = 0; 1
и вектором вероятностей начального состояния Р;,о = |л,1(*о) Р/д(^о)| •
С учетом принятых допущений задача автономного контроля целостно-
сти сводится к получению оценок параметров отказов ; i = 1,1, характери-
зующих состояние информационных каналов видимого созвездия НС.
Выражение (16.19) описывает полезные сигналы СРНС ГЛОНАСС, и
GPS. При этом сигналы от различных НС ГЛОНАСС отличаются номиналь-
ными значениями несущих частот, а сигналы OPS — модулирующими кодовы-
ми последовательностями.
При решении задачи полагаем, что используемые выходные сигналы
ИНС в моменты времени t* имеют вид [4.3, 16.7]
n3('t) = V(r*) + .3(rt), (16.20)
где V(4) = \vx PZ|T — вектор проекций земной скорости ЛА на оси гринвич-
ской системы координат; и3(/*) — вектор погрешностей измерения земной
скорости ЛА в проекциях на оси гринвичской СК, описываемый стохастиче-
ским разностным уравнением [4.3]
= «*3(**-1) '+ -
где Д = |дх Ду Дг|т — вектор постоянных ошибок измерения ускорений в
проекциях на оси гринвичской СК; nu(fjt) — вектор формирующих стандарт-
ных белых гауссовских шумов; аи — параметр, характеризующий ширину
спектра флуктуационных ошибок акселерометров; ои — среднеквадратиче-
ские значения этих погрешностей.
4
3$j Глава 16. Комплексная обработка информации в АП CPHG|
Вектор U(/) радионавигационных параметров связан известным функ-
циональным соотношением (навигационной функцией) U/(f) = G/(X(f)) с веК1
тором оцениваемых параметров потребителя X(f)", в качестве которых примем;
X(f) = |xyz Vx Vy Vz Ат V* *т го* Дт Д'|Т, где x, у, z — координаты ЛА в грин-
вичской СК; А“|ах ау az|T, V„ = |гпх Ип)1 Ипг|Т - векторы проекций уско-
рения и постоянной составляющей земной скорости ЛА на оси гринвичской
системы координат.
Динамику компонент вектора состояния Х(/) можно описать систе-
мой дифференциальных уравнений [4.3, 16.3]
= к •
dt х’
K_v . *Yn. = 0.
dt у’ dt l’ dt ’ dt ’
dA=0. dA'
dt ’ dt
— <oc/ — в>/КИЗМ|/с + /2 Лф,-(/);
~ ~f a>ia>ci
= -(a + p)A -ap(V - V„) + ^a+pH “a(') . (16.21)
где a — коэффициент, определяемый аэродинамическими характеристика-
ми ЛА; р — параметр, характеризующий ширину спектра флуктуаций скоро-
сти ветра; од — дисперсия флуктуаций ускорения, зависящая от турбулентно-
сти атмосферы, флуктуаций тяги двигателей и т. д.; , уШ/ — параметры,
характеризующие нестабильность частоты и ширину спектра флуктуаций час-
тот задающего генератора НС; о* _ дисперсия флуктуаций частоты задающих
генераторов СРНС; пА(/), иф,(0> *>„.(/) — независимые формирующие белые
гауссовские шумы с нулевыми математическими ожиданиями и единичными
интенсивностями.
Система уравнений (16.21) может быть представлена в векторном виде
(16.7).
Субоптимальиые алгоритмы системы комплексной обработки радиосигна-
лов СРНС ГЛОНАСС и GPS. Также как и в предыдущем параграфе решение
задачи синтез субоптимального алгоритма обработки основано на поэтапном
решении уравнения для апостериорной плотности оцениваемого вектора Х(г),
I 16.2. Комплексная первичная oCpafitmuca информации в АП СРНС 363
г
«то Приводит к следующей последовательности операций:
1-й этан
I **+i ^[v>g/(*(v’X(M))»*''.*]
х* = Х(/к)♦ и;мL4fcM f —1---------(16.22)
<=1 /» 5и/
R*l*+1 - R*1
(16.23)
где X*. — оценка вектора состояния на первом этапе; LJ = —— матрица
ЙХ
преобразования, которая постоянна на интервале времени (/*,fjt+il;
F/[l,G/(f(/,X(/Jt)j) Д/Л] = Nr‘{2yf(r>S>[/.Gf(r.Xf/*)),^] - ^.G^Xfc)),^
Для получения оценок параметров отказов >.lk необходимо вычислить
апостериорные вероятности
Ру (^*+1|х*) = Q’(,(/*|x*)c4>
Т *i[v.G/(f(v>X(/t)))A/it = j\
(16.24)
где ty('*lX‘) = Р^к’^-Цк = /|х*) — условная вероятность "состояния Х/д = j;
7 = 0,1 при заданном значении X*; константа С находится из условия норми-
ровки
/ty('*lx*) = Zox*,jp«/(z*-i|x*)-
Квазиоптимальную оценку выбирают как значение параметра отка-
за, для которого апостериорная вероятность (16.24) максимальна
Ч* = ^y.max. Py{tk+l\Kk^ . (16.25)
364 Гл в а 16. -омплек-вая обряботка ьаформацяв в АН СРНС^.
2-й этап ч
На этом этапе вычисляется уточненная по результатам измерений (16.20)
оценка Х(/*+1) вектора состояния потребителя в соответствии с уравнениями,
общий вид которых определяется соотношениями (16.16)—(16.18) с подстанов-
кой в них соответствующих рассматриваемой задаче матриц.
Схема устройства комплексной первичной обработки радиосигналов
СРНС ГЛОНАСС и GPS, реализующего алгоритмы субоптимальный алгоритм
представлена на рис. 16.4. В составе синтезированного устройства можно вы-
делить: схему выделения непрерывных параметров (СВНП); схему контроля
целостности (СКЦ) и схему комплексной вторичной обработки информации
(СКВОИ).
В СВНП осуществляется формирование оценок Xj в соответствии с вы-
ражениями (16.22)—(16.23). Основными элементами СВНП являются: много-
мерные дискриминаторы (МД1 ••• МД2), число которых соответствует числу
одновременно принимаемых сигналов от всех I видимых НС объединенной
группировки; блок управления структурой (БУС), формирующий конфигура-*
цию устройства в соответствии с текущими условиями функционирования;
блок прямого преобразования координат (БППК) и блок весового суммирова-
ния (БВС).
Изменение структуры устройства осуществляется с помощью БУС на
основе оценок параметров.отказа X/jt, поступающих из СКЦ. г
Схема контроля целостности состоит из I идентичных каналов, в каж-
дом из которых осуществляется формирование оценки параметра отказа
для соответствующего информационного канала согласно (16.24). В состав!
каждого канала СКЦ входят корреляционный приемник (КП), блок вычисле-.
ния вероятностей (БВВ) и блок сравнения (БС). КП и БВВ обеспечивают
вычисление апостериорных вероятностей Ру (/^+1 |Х*) согласно выражению
(16.24). В БС на основе полученных значений апостериорных вероятностей в
соответствии с правилом (16.25) принимается решение о значении оценки па-
раметра отказа X/Jt; i = 1,1.
В СКВОИ в соответствии с (16.16)—(16.18) осуществляется формирова-
ние путем совместной обработки оценок X*, сформированных в
СВНП, и наблюдений Пз(^+1), поступающих с выхода ИНС в момент времени
fjt+i. Полученные таким образом оценки Х(г*+1) поступают в блок выделения
навигационных параметров (БВНП), где выделяется информационная компо-
нента вектора состояния, необходимая для решения задач навигации, а также
в блок обратного преобразования координат (БОПК). В последнем согласно
правилу Ц(/) = G/.(X(/)) формируются оценки векторов радионавигационных
параметров Uf(/jt) для всех I каналов, которые затем поступают в устройства
формирования опорных сигналов (УФОС 1 ... УФОС Г) и генераторы сигналов
(ГС 1 ... ГС 7) для формирования опорных сигналов, подаваемых на пере-
множительные устройства соответствующих МД и КП. Для реализации проце-
дур прямого и обратного преобразования координат в БППК, БОПК, а также
в блок формирования матричных весовых коэффициентов R*|fc+1, входящий в
состав БВС, поступает СИ, полученная после приема и обработки радиона-
вигационных сигналов от соответствующих НС. В состав СИ входят значе-
566 Г л а в a 16. Комплекс— обработка информации АП СРНС
ния координат xt, уZi и составляющих скорости НС ^нс^, ^нс.ур
КНС,г, •
Особенностью синтезированного устройства является наличие перекре-
стных связей между каналами обработки сигналов от различных НС на уровне
первичной обработки сигналов. Это обстоятельство обеспечивает высокую по-
мехоустойчивость и точность по сравнению с другими устройствами и позво-
ляет улучшить качество и надежность навигационного обеспечения ЛА осо-
бенно в нештатных условиях функционирования СРНС ГЛОНАСС и GPS.
Оценка показателей качества. Потенциальные характеристики точности
и помехоустойчивости получают при решении уравнений для матриц апосте-
риорных вторых центральных моментов. Рассмотрим две ситуации. В первой
для навигационных определений используется рабочее созвездие из четырех
НС, которое является оптимальным по типовому критерию, состоящему в
отыскании четверки НС, образующей тетраэдр наибольшего объема [см. § 7.4].
Согласно этому критерию наивыгоднейшей считается такая конфигурация;
6}
Рис. 16.5. Среднеквадратические ошибки
при которой один НС
находится в зените по-
требителя, а три осталь-
ные как можно ближе к
горизонту с максималь-
ными взаимными удале-
ниями. Вторая ситуация
соответствовала случаю
информационной избы-
точности (в качестве
примера было принято,
что обрабатываются сиг-
налы от девяти наблюда-
емых НС).
На рис. 16.5, а и б
даны некоторые зависи-
мости СКО стх оценива-
ния координаты х от
времени при различных
от отношениях синал
/шум qt = 2A?z3 I Nt в
расчете на один элемент
ПСП длительностью тэ.
Графики получены при
условии, что помеховая
обстановка во всех кана-
лах считалась одинаковой
16.2. Комплексная первичная обработка информации в АП СРНС 367
(91 = 92 = -=9/*J =9) •
На рис. 16.5, б приведены графики зависимости установившихся значе-
ний СКО оценивания координаты х от отношения q = 10~3... 10“5 , характери-
зующие помехоустойчивость синтезированных алгоритмов.
Анализ данных, представленных на рис. 16.3, а и б показывает, что ис-
пользование информационной избыточности обеспечивает повышение каче-
ства функционирования интегрированной аппаратуры потребителей СРНС
ГЛОНАСС и GPS. При этом заметный выигрыш от комплексирования, кото-
рый составляет 25 %, наблюдается при сложной помеховой обстановке для
функционирования АП СРНС (при ц = 1(Г5). Из рис.16.5, б также видно, что
алгоритмы, в которых для решения навигационной задачи используются до-
полнительные наблюдения, оказываются в меньшей степени зависимыми от
изменения помеховой обстановки.
Введем понятие достоверности автономного контроля целостности Dk —
достоверности, соответствующей оптимальным по критерию максимума апо-
стериорной вероятности оценкам параметров отказов I,-* и оценкам вектора
состояния, оптимальным по критерию минимума СКО [16.16]. Расчеты DK
проводились для абсолютной достоверности контроля, которая определялась
как вероятность принятия правильного решения при контроле [16.16]
Dk = 1_ Рони гДе Рош*~ апостериорная вероятность ошибочных решений при
контроле, равная сумме апостериорных вероятностей ошибок 1- и 2-го рода.
Вычисление рош проводилось с использованием типового статистического мо-
делирования.
На рис. 16.6 представлен график зависимости Dk от отношения сиг-
нал/шум q. Из графика видно, что в штатных условиях функционирования
прелагаемые алгоритмы обеспечивают достоверность контроля, близкую к
единице. Однако в сложной помеховой обстановке достоверность контроля
снижается и составляет
примерно 0,8 для
q = 10“4 и 0,58 для
q ~ 105 . Следует заме-
тить, что качество кон-
троля целостности в
аномальных режимах
функционирования РНС
может быть повышено за
счет использования до-
полнительных других ме-
тодов контроля 116.11].
Рис. 16.6. Достоверность автономного
контроля целостности
368 Глава 16. Комплексная,обработка информации в АП CPH0
При этом используемая в синтезированных алгоритмах информационная
избыточность делает применение таких методов принципиально возможным.
Результаты работы позволяют сделать вывод о целесообразности построения
бортовой интегрированной АП СРНС на базе синтезированных алгоритмов
комплексной первичной обработки, основанных на избыточной информации
от дополнительных НС СРНС ГЛОНАСС и GPS.
16.3. Комплексная вторичная обработка информации
Комплексирование на уровне первичной обработки информации приво-
дит к необходимости перестройки всего приемоиндикатора, что в ряде случаев
не представляется целесообразным. Более просто технически может быть реа-
лизовано комплексирование на уровне вторичной обработки, т.е. после того,
как выделены радионавигационные параметры.
В результате комплексирования на основе вторичной обработки инфор-
мации достигаются:
повышение точности определения координат, высоты, скорости и вре-
мени потребителя;
уточнение углов ориентации (курса, крена и тангажа); оценка и уточне-
ние параметров калибровки навигационных датчиков, таких, как. дрейфы гиро-
скопов, масштабные коэффициенты, смещения акселерометров и др.-; -
обеспечение на этой основе непрерывности навигационных определений
на всех этапах движения, в том числе и при временной неработоспособности
АП в случаях воздействия помех или энергичных маневров ПО;
улучшение характеристик целостности НВО, т. е. способности при со-
вместной обработки информации автономных средств (особенно ИНС) и
СРНС обеспечивать решение задачи бортового автономного контроля целост-
ности (CAIM — Craft Autonomous Integrity Management) в дополнение к кон-
тролю целостности, осуществляемому в приемнике СРНС (RAIM).
Отмеченные эффекты в той или иной мере имеют место во всех схемах
комплексирования АП СРНС с автономными средствами. Кратко охарактери-
зуем различные схемы комплексирования на примере применения АП СРНС с
ИНС на ВС. Их технической основой является наличие в навигационном
комплексе (НК) цифровых вычислителей и стандартных линий информацион-
ного обмена. Для ВС такой обмен осуществляется в соответствии с ГОСТ-
18977-79, РТМ 1495-75 (ARINC -743,429) и ГОСТ.26765.52-87 (MIL/STD-
1553В). Комплексирование достигается в ходе реализации алгоритмов обра-
ботки информации, полученных из следующей задачи.
Постановка задачи. Пусть на выходе системы первичной обработки
СРНС сформирован векторный процесс, который в дальнейшем будем назы-
вать наблюдением,
Чернел = G(x*)+ МсЛ“сЛ + “сл > (16.26)
16.3. Комплексная вторичная обработка информации ____________________369
где G(«) — векторная детерминированная, в общем случае нелинейная функ-
ция, связывающая радионавигационные параметры сигнала U с вектором со-
стояния X, в качестве компонент которого, как отмечалось в предыдущем па-
раграфе, чаще всего являются геодезические широта' В и долгота L, высота
Н над уровнем референц-эллипсоида, составляющие скорости VN,VE,VB в
направлениях восток, север и вверх, поправка к шкале времени f и уход час-
тоты f БЭВЧ по отношению к шкале СРНС, если предполагается синхрони-
зация часов АП с БЭВЧ; Мс k — известная матрица, uc>fc — коррелированная
помеха, которая описывается разностным уравнением
“c,fc = Фс,*“с,*-1 + Пси,* , (16.27)
где Фсд — известная матрица; nc„ifc — дискретный гауссовский белый шум с
нулевым математическим ожиданием и матрицей дисперсий Qc,jt; пс* — дис-
кретный гауссовский белый шум с нулевым математическим ожиданием и мат-
рицей дисперсий Nc k.
Наблюдения сигналов с выходов имеющихся автономных средств описы-
ваются -векторными соотношением
Лас,* = х* + Ма,*иа,*, (16.28)
где
“а,* = Фа,*иа,*-1 +Паи.* (16.29)
— вектор состояния погрешностей автономных средств; Ма^ — известная
матрица; Паы<л — дискретный гауссовский белый шум с нулевым математиче-
ским ожиданием и матрицей дисперсий Qafc; Фа,* — известная матрица, оп-
ределяемая математическими моделями используемых автономных средств.
В качестве автономных датчиков, обеспечивающих наблюдения (16.26),
могут служить ИНС (В,ДЯ.Кдг.Ке.Рд) и БЭВЧ (отсчеты временной шкалы
Т и частота f ).
Задача синтеза алгоритмов комплексной оптимальной обработки может
формулироваться как нахождение наилучшей (в смысле минимума дисперсии
ошибки оценивания) оценки Хк вектора состояния по наблюдениям сигналов
(16.26), (16.28).
Для решения такой задачи в общем виде необходимо задать описание
динамики изменения вектора состояния Хк и, используя известный аппарат
теории оптимальной нелинейной фильтрации [5.1, 15.3], записать уравнения
13 — 3291
^70 Гла1 16, К длекС1 <обр>1 hta мн->рмаци.1 АП С. НШз
для совместной оценки X* и вектора состояния погрешностей измерений, на«1
пример, в форме, предложенной в предыдущем параграфе. Однако на практике
используется иной подход, предполагающий оценку лишь вектора состояния
погрешностей измерений и последующую их компенсацию в (16.28) для повы-
шения точности определяемых навигационных параметров. Теоретическое
обоснование такого подхода дано в (5.3], а суть состоит в следующем.
Обозначим ЧсрНСО’ Идс о ~ реализации наблюдений сигналов (вто-
ричных) СРНС и автономных датчиков. Из (16.28) выразим (формально)
Х* = ПАС,*
и подставим в (16.26)
ПСРНС,* = б(г]АС,* - Ma,*ua,*) + ^c,*uc,*: + “с,* •
(16.30)
(16.31)
Теперь в качестве вектора, подлежащего фильтрации (оцениванию),
можно рассматривать вектор
и*
«а,*
«с.*
для которого на основании (16.27),
(16.29) можно записать обобщенное уравнение состояния
“* = Ф«,*и*-1 + «>,* > (16.32)
где “а,* — вектор гауссовских шумов с нулевыми математическими ожида-
ниями и матрицей дисперсий Q& ,'
Ф.,* =
Ф
*а,1
о
Qa,*
о
о
Qc.fc
"а.*
“au,*
“cu.*
о
ф
; Q* =
0 — матрицы соответствующих размерностей с нулевыми элементами.
При решении такой задачи фильтрации Пас,* можно рассматривать как
известную функцию времени. После получения оптимальных оценок й* нахо-
дим искомые оценки (16.30)
Хк = Пас,* - Ма,к“а,* • (16.33)
Уравнения для оценки с учетом сделанных допущений получаются из
общих уравнений оптимальной фильтрации (5.3] и имеют вид
1UJ; o/поричнил обработка итйчрцациц______________________________ail
jt = ®t|jt-i + к*(псрнс,* - П*)S (16.34)
Hit =^ПАСЛ -Ма,*®а,*|*-1)+ Mc,t"c,fc|fc-1;
=фл-|; (16 35)
к-t = Rt|fc-iH*(HfcRfci*-iH* +N<)'; Rk = rm*-i - K*H*R^ i- <16-36>
Hfc ~(ЦпАсл-маЛиаЛ) + мсЛисЛ)^ =a ;R*|fc-i = ®fcRfc-iOl +Qfc-
В описанном алгоритме осуществляется прогноз оценок коррелирован-
ных погрешностей измерений ufc_i в соответствии с (16.35). При необходимо-
сти прогноз можно осуществлять на любой последующий момент времени
tp , в том числе в случаях неработоспособности АП СРНС в соответствии
с аналогичным алгоритмом
= ФА «’
где Фр — соответствующая матрица прогноза.
Точность прогноза определяется из (15.29), в котором вместо Фк следу-
ет использовать Фр. Коррекция навигационных параметров в этом случае вы-
полняется в соответствии с алгоритмом
X, = Час,, - Ma,p®a,?|*-i • (16.33а)
Алгоритм (16.34)—(16.36) имеет различные модификации: симметричную
ковариационную; информационную; модификацию, использующую квадратные
корни матриц; последовательную во времени и пространстве измерений и т. д.
[16.16]. Все эти формы предназначены для обеспечения вычислительной ус-
тойчивости алгоритмов в бортовых вычислительных машинах с ограниченной
разрядностью и памятью при наличии ошибок моделей, линеаризации нели-
нейностей и т. д. Ряд аспектов применения этих соотношений и настройки
фильтров путем подбора матриц Qk и рассмотрен в ]16.17—16.19].
В авиационных применениях АП СРНС совместно с платформенной
ИНС вектор состояния коррелированных погрешностей часто может иметь вид
13*
372 Глава 16. Комплексная обработка информации в АП СРНС
II = |ДВ Д£ ДЯ t' &Vg &Vg t±Vg f Ф g Фд Фд г-д ед ед...| , (16.37)
где АВ, AL, ДЯ — погрешности измерений ИНС соответственно широты,
долготы и высоты полета; &Vg,&Vg,&Vg — погрешности измерений ИНС со-
ставляющих скорости; Фд,Фе,Фд — погрешности измерений ориентации в
ИНС; Ед>еЕ>еН ~ скорости дрейфов гироскопов; /' и f -— ошибка време-
ни и уход частоты БЭВЧ. При этом предполагается демпфирование вертикаль-
ного канала ИНС с помощью системы воздушных сигналов (СВС).
Следует иметь в виду, что в состав оцениваемых переменных могут так-
же включаться погрешности и масштабные коэффициенты акселерометров;
коэффициенты дрейфов гироскопов; пропорциональных ускорениям, квадра-
там ускорений; температурные коэффициенты; погрешности определения вы-
соты и вертикальной скорости с помощью СВС и т. д.
Если на выходе приемника СРНС находятся измеренные значения псев-
додальностей ДИзм,/и псевдоскоростей Иизм / до i = l,Z НС (1-я схема кор-
рекции), то матрица измерений может быть записана в виде
Hfc=|D*°|, (16.38)
где — матрица частных производных Дизм,/, /’ = 1,/ по ДВ, Д£, ДЯ, /' и
Иизм,/, / = !,/ — по &VN,b.VE,&Vg,f'. При этом ковариационная матрица из-
мерительных шумов в предположении независимости каналов будет диаго-
нальной с дисперсиями измерений ПД и ПСК вдоль главной диагонали:
N* = ^ч,к
Если выходными параметрами АП СРНС являются координаты, высота,
составляющие скорости, поправки к шкале времени и ее уходу (2-я схема кор-
рекции, при которой размерность вектора цсрнс равна 8), то в предположе-
нии отсутствия систематических погрешностей спутниковых определений или,
если последние полагаются неучитываемыми смещениями, матрица 8хя изме-
рений и ковариационная матрица ошибок измерений 8x8 имеют вид
14 О О
О -14 о
= (D*NoDJ
(16.39)
где 14 — единичная матрица 4x4; 0 — нулевые блочные матрицы соответст-
вующих размерностей. При этом предполагается, что для определения выход-
ных параметров АП СРНС использовался метод взвешенных наименьших
квадратов.
[ЬЗ^омплексная^вто^^,
При большом числе />10 обращ
(16.34)—(16.36) требует значительных вычислений
ле используемых спутников коррекцию цел ecog
ме, имея в виду то, что предфильтрация с послед
пространстве обработкой и контроль целостности (RAIM
ся в приемнике СРНС с минимальным участием данных ИНС.
ис-
е-
и и
твлять-
Можно показать, что обе схемы коррекции практически эквивалентны
по точности, если не учитывать возможные ошибки вычислений й влияние
возмущений.
Модификации схем комплексирования с использованием результатов вто-
ричной обработки. Схема описанного комплексной навигационной системы
приведена на рис. 16.7, а и получила название разомкнутой схемы комплексиро-
вания. Если в схеме реализуются связи, обозначенные штриховыми линиями
от вычислителя к ИНС, БЭВЧ и от ИНС к АП СРНС, то ее называют слабо
связанной схемой комплексирования. При этом пунктирная линия от ИНС к АП
СРНС означает передачу приемнику информации ИНС для обеспечения более
быстрого поиска и вхождения в режим слежения, а управляющие воздействия
поступают из навигационного фильтра в саму ИНС для коррекции погрешно-
стей ориентации и ошибок инерциальных датчиков.
Существуют другие схемы, в которых комплексные фильтры вторичной
обработки более сильно связаны со схемами первичной обработки.
Схема рис. 16.7, б дает представление о так называемой сильно связанной
схеме комплексирования, когда спутниково-инерциальная система представляет
собой единую аппаратуру, состоящую из трех модулей (АП СРНС, модуль чув-
ствительных элементов ИНС и модуль вычислителя).
В вычислителе реализуются как основные алгоритмы бесплатформснной
инерциальной системы (БИНС), так и алгоритмы оптимальной последователь-
ной обработки данных БИНС и приемника СРНС с обратными связями для
коррекции счислимых данных. Кроме того, с выхода фильтра оценки дально-
сти и скорости ВС поступают в приемник для ускорения поиска и улучшения
процесса слежения за кодом и частотой.
Если в приемнике СРНС также имеется навигационный фильтр, а БИНС
дает полное решение задачи инерциальной навигации (вплоть до вычисления
координат), то получается схема сильно связанной системы с избыточностью.
Такая архитектура, в частности, реализуется в системах Litton LN-100G и
Honeywell H-764G [16.19, 16.20J.
Схема на рис. 16.7, а предполагает возможность встраивания приемника
СРНС в блок ИНС, что позволяет существенно облегчить обеспечение доста-
точно быстрых связей между двумя устройствами, поскольку внутренние ли-
нии информационного обмена могут иметь более высокое быстродействие,
чем быстродействие, определенное используемыми в настоящее время стан-
дартами.
Если обратиться к материалам предыдущего параграфа, в котором рас-
сматривалась задача комплексирования на уровне первичной обработки, то ее
, I : ! >
374 Г л a 6 a 16. комплексна* обработка информации в АП СРНС
а)
ориентации
ИНС
Вычислитель.
Навигационный
фильтр
В,1,Н,УК,
УеУнГ.Г.
параметры
ориентации
«)
Рис. 16.7. Разомкнутая и слабосвязанная
(а), сильно связанная (б) и глубоко интег-
рированная (в) схемы комплексирования
укрупненная схема может быть
представлена в виде, приведенном
на рис. 16.7, в, которую называют
глубоко интегрированной схемой
[16.8, 16.20). В этой схеме прием-
ник состоит из радиочастотной
части, генератора кодов, корреля-
торов и поисковой части. Вычис-
литель реализует алгоритмы бес-
платформенной ИНС и оптималь-
ной оценки параметров, таких как
©„Д.АДЯ.Илг.Ге.Кя,?,/.
Реализация глубоко интегрирован-
ной схемы требует весьма мощных
вычислителей, поскольку предпо-
лагается довольно высокая раз-
мерность вектора состояния (20 ...
40) в условиях достаточно быст-
рых изменений (для маневренных
самолетов). Это дело отдаленного
будущего (16.20).
Основное . отличие слабосвя-
занной от сильно связанной и глу-
боко интегрированной схем ком-
плексирования состоит в том, что
вместо использования соотношения
(16.33 а) прогноз параметров дви-
жения осуществляется с помощью
реализуемой самой БИНС моделью
динамики движения, причем про-
гнозируемые параметры состояния
используются при формировании
соответствующих внутренних кор-
ректирующих воздействий.
Бортовой автономный кон-
троль целостности CAIM в чистом
виде реализуется в дополнение к
RAIM лишь в разомкнутых и, воз-
можно, слабо связанных схемах
комплексирования и осуществляет-
ся при использовании в навигаци-
онном вычислителе нескольких
фильтров [16.22], которые обраба-
тывают подмножества спутнико-
16.3. Комплексная вторичная обработка информации
375
вых измерений. Результаты обработки сравниваются между собой с использо-
ванием %2-критерия. В результате сравнения удается выявить и отбраковать
ошибочные данные. В сильно связанных и глубоко интегрированных схемах
алгоритмы RAIM и CAIM оказываются совмещенными. Более детальное рас-
смотрение различных схем комплексирования приведено в [16.20].
Анализ результатов комплексироваиив. В [16.20] проведена сравнитель-
ная оценка различных схем' комплексирования. В частности, показано, что
при одной и той же точности ИНС на двадцатой минуте автономного полета
сильно связанная схема дает ошибки определения координат в 1,5 ... 2 раза
меньше, чем слабо связанная. При большем времени это преимущество стано-
вится менее ощутимым, потому что начинают сказываться случайные непро-
гнозируемые погрешности.
Слабо и сильно связанные схемы отличаются также иногда отсутствием
работоспособности АП СРНС (20 и 18 мин соответственно) для одних и тех же
помеховых условий.
Проведена сравнительная оценка влияния архитектуры комплексирова-
ния на точность бомбометания для перерывов в работе АП СРНС, равных 159
(слабо связанная схема) и 153 с (сильно связанная схема). При этом выявлено,
что относ бомбы составил соответственно 43 и 16 м. Это может быть объясне-
но лишь различными погрешностями в определении скорости полета самолета
[16.20].
В [16.23] приведены ориентировочные оценки точности калибровки па-
раметров ИНС. Показано, что остаточные погрешности составляют в процен-
тах от первоначальных значений:
для угловых параметров........ от 3 до 20—30
для смещений акселерометров .... от 10 до 30
для дрейфов гироскопов от 20 до 50 .
Для иллюстрации эффекта повышения точности калибровки на рис. 16.8
Рис. 16.8. Графики точности (СКО) определения
координат и курса ВС
приведены результаты рас-
чета точности определения
координат — кривая I
(среднеквадратичное ради-
кальное отклонение (drms))
и курса (СКО) — кривая 2
при коррекции курсодопле-
ровского счисления ВС с
помощью АП СРНС. При
этом предполагалось, что в
течение полета 300< Т ^600 с
АП СРНС не работала, на-
пример вследствие воздей-
ствия помех, и определе-
376 Глава 16. Комплексиаяобработканифоомацинв АП СРНС
ние координат проводилось в автономном режиме. Общий вектор состояния,
включающий основные погрешности ДИСС и КС, в этом случае имел вид
и = |Дх ДРХ Дих Ду ДРу Ди,, Фх ez|T, где Ах и Ду — погрешности определения
плановых координат х, у; ДИХ, ЛУу к Дих, Лиу — соответствующие погреш-
ности определения скорости (систематические и коррелированные во време-
ни); Фг, ez — ошибка определения курса и уход курсовой системы соответ-
ственно.
Начальные ошибки составили: по координатам 200 м, по обеим состав-
ляющим скорости 0,5 м/с, по курсу и уходу курса 1 ° и 1 °/ ч соответствен-
но. Предполагалась коррекция курсодоплеровского счисления в номинальном
режиме работы СРНС ГЛОНАСС при точности (СКО) определения координат
20 м. Скорость полета вертолета принималась равной 100 м/с.
Из рисунка следует, что после отключения АП СРНС наблюдается на-
растание погрешностей определения местонахождения до 125 м (кривая 1). В
то же время нетрудно видеть, что при отсутствии предварительной коррекции
по СРНС погрешности местонахождения только за счет курсовой ошибки со-
ставили бы за это время примерно 600 м (кривая 3). Столь существенное
улучшение точности в автономном режиме объясняется калибровкой
(оценкой) и компенсацией, в первую-очередь, -курсовой ошибки до уровня
0,005 рад ( 0,28°).
В [16.24] приведены также результаты комплексирования ИНС, АП
СРНС, баро- и радиовысотомера при вторичной обработке информации этих
средств на этапе захода ВС на посадку. Показано, что при точности (СКО)
определения координат и высоты полета порядка 5 ... 7 м (СРНС в дифферен-
циальном режиме) точность (СКО)определения этих параметров вблизи ВПП
повышается до уровня 1 ... 1,5 и 0,2 ... 0,8 м соответственно. Такая точность в
состоянии удовлетворить требованиям II и даже III категорий ИКАО.
Вторичная обработка информации АП СРНС, ИНС и объединенной на-
вигационно-связной системы (ОНСС). ОНСС типа Джитидс [16.25] позволяет
совместно с ИНС осуществлять оценку вектора состояния вида (16.37). При
этом возможно построение комплексной системы, совместно обрабатывающей
все наблюдения на базе общих соотношений (16.33)—(16.36) или упрощенного
варианта, в котором сначала отдельно для наблюдений ИНС + ОНСС в ре-
зультате комплексной обработки в соответствии с (16.33)—(16.36) вычисляют-
ся оценки Xj = |Д L\ Hj VNl VEt КЯ1| . Аналогично находят оценки для наблю-
дений ИНС + СРНС Х2 = |в2 4 VN2 vE2 гя2|т.
Вычисление итоговой оценки определяется условием — одна или две
различных ИНС используются для АП СРНС и ОНСС. При использовании
двух независимых ИНС наилучшая итоговая оценка определяется соотноше-
ниями [16.26, 16.27]:
377
X* = ИхДийДи+кх2,Лл); Rx,* = (Rxu+Rx^f1, (16.40)
где Rx,t — ковариационная матрица погрешностей оценок вектора X/.; Rx/,t >
i = 1, 2 — ковариационная матрица погрешностей оценивания i-го комплекса
(ИНС+ОНСС и ЙНС+СРНС),
Если в состав обоих комплексов входит одна и та же ИНС, то наилучшая
в смысле максимума плотности апостериорных вероятностей оценка получает-
ся из соотношений [16.26]
Xfc = ПАСЛ - “аД ; = Ri(Rl,Jt®lJt + R2,V®2,i) J (16.41)
ИаЛ
«сЛ
Rfc - (Rl,fc + R2Jt Rk|o) ’
(16.42)
где й( к , /=1, 2 — оценки коррелированных погрешностей для двух комплек-
сов, полученные по соотношениям (16.34)—(16.36); R*{q — ковариационная
матрица погрешностей некорректируемой ИНС.
Стремление к интегрированию бортового оборудования и созданию
бортовых интегрированных систем навигации, посадки, связи и опознавания
[16.28], приводит к целесообразности построения единого алгоритма обработ-
ки (фильтра), в задачу которого входит оценка следующего вектора погрешно-
стей и = |дВ АГ ДН... tj /^|т . При этом предполагается работа с одной
ИНС, но с двумя самостоятельными шкалами времени. Для единой временной
шкалы СРНС и ОНСС вместо будут использоваться единые пе-
ременные Г, f. Матрица Н должна учитывать характер измерений СРНС и
ОНСС.
Рассмотренные алгоритмы пригодны и в случае, если вместо ОНСС бу-
дет применяться какая-либо иная система.
Комплексная обработка информации группы объектов, использующих
СРНС. Рассмотренные в гл. 11 вопросы реализации различных разновидностей
дифференциального режима СРНС предполагают использование и обработку
в том или ином виде спутниковой информации группой объектов. В качестве
последних могут быть дифференциальная станция и ПО — потребители ин-
формации СРНС, радиомаяки-псевдоспутники и ВС [16.29], а также просто
группа ПО с АП СРНС, например группа воздушных или морских судов, реа-
лизующих методы относительной навигации [16.30].
Во всех этих ситуациях в том или ином виде имеет место взаимная ком-
пенсация квазисистематических ошибок СРНС, обусловленных неточностью
378 Г л а в a 16. Комплексная обработка информация в АП СРНС
эфемеридной информации, особенностями распространения радиоволн в ио-
носфере и синхронизацией КА. После такой компенсации основными по-
грешностями, определяющими точность навигации взаимодействующих ПО, в
основном оказываются случайные погрешности, обусловленные шумами из-
мерений, помехами, многолучевостью и распространением радиоволн в тропо-
сфере.
Снизить эти погрешности возможно, используя алгоритмы комплексной
обработки информации группы подвижных объектов, которая реализует усло-
вия дифференциального режима. При комплексной обработке учитываются
как квазисистематические, так и случайные составляющие ошибок СРНС.
Введем в соответствии с [16.31] вектор-цараметров движения группы из
I ПО X = |Xj Xj ... Xj| (где Х(, 1 = 1,1 — вектор параметров движения 1-го
ПО), а также общий вектор состояния погрешностей и = |п[ и2 ... и] Uq| (где
uG — вектор квазисистематических погрешностей СРНС, общий для группы
ПО). Это, в частности , могут быть квазисистематические ошибки определе-
ния координат и скорости ПО с помощью СРНС, обусловленные неточно-
стью ЭИ и синхронизации НС, а также особенностями прохождения сигнала
НС через ионосферу.
Модель изменения вектора и* во времени задается обобщенным уравне-
нием (16.32).
Если принять X, = у, Zl Va Vyt Иг/|Т, где (хьу/>г/), (KJtf,P„,Kt,) -
прямоугольные координаты и составляющие скорости 1-го объекта, то вектор
погрешностей можно записать как uf = |дх( &yt fai ЛУу1
Измерения автономных средств описываются уравнением (16.28), а из-
мерения АП СРНС 1-го ПО будем описывать соотношением
ПСРНС/Л = Х/Л + BG,i + “c/jt • (16.43)
Кроме того полагаем, что возможны взаимные измерения, например
взаимной дальности между 1- и j -м ПО
Псрнсц,;),* = G(x/,*>x;.*) + nc(«j),t- (16.44)
В этом случае оптимальная оценка навигационных параметров группы
ПО также может быть получена на основе соотношений (16.33)—(16.36).
Рассмотрим в качестве иллюстрации случай, когда группа состоит из
трех ПО. Так, Х| может характеризовать вектор НП потребителя (в нашем
случае ВС), а Х2 и Х3 характеризуют известные координаты двух стационар-
16.3, Комплексная вторичная обработка информации ->/9
ных дифференциальных станций. В случае, если имеются взаимные измерения
дальности псрнс(1,2) > ПсРНС(1,3) > ПО2 и ПОЗ являются псевдоспутниками.
Предполагается, что на ВС имеются все данные (16.28), (16.43), (16.44)
благодаря использованию ЛПД и передаче по ней результатов измерений
[16.32], а также осуществляется оценка й в соответствии с (16.41). На рис.
16.14 и 16.15 приведены результаты моделирования и оценки точности опреде-
ления прямоугольных координат ВС, заходящего на посадку (х — вдоль ВПП,
у — вбок, z — вверх), т.е. плановых координат и высоты.
Рис. 16.9, а дает представление об изменении СКО определения коорди-
нат в обычном дифференциальном режиме. При этом видно, что за счет
фильтрации случайных ошибок погрешности по всем трем координатам сни-
зились почти в 3 раза и на высоте 30 м (высота проверки точности для I ка-
тегории ИКАО) составили 1,2 ... 1,5 м. Аналогичный результат получен и для
случая вычисления
относительных коор-
динат (по отношению
к ДС—ПО2, точность
(СКО) привязки кото-
рой составила 20 м).
На рис. 16.9, б
представлены резуль-
таты оценки точности
(СКО) определения
относительных коор-
динат ВС и поведение
ошибок для случая,
когда ПО2 и ПОЗ яв-
ляются псевдоспутни-
ками, расположенны-
ми вблизи ВПП. Точ-
ность определения
координат х, у, z в
этом случае на высоте
30 м составляла 0,7 ...
0,8 м. Кривые “дельта
X, Y, Z” характеризу-
ют поведение соответ-
ствующих ошибок
оценивания.
Для описан-
ных выше ситуаций
были приняты сле-
дующие условия мо-
«)
б)
Рис. 16.9. Графики точности (СКО) определения
координат (а) и относительных координат (б)
при посадке ВС
380
Глава 16. Комплексная обработка информации в АП СРНС
делирования: начальные ошибки (СКО) определения координат ВС по осям
х, у составили 50 м, по оси г — Юм, СКО случайных и квазисистематических
погрешностей определения координат АП СРНС составляли 3 и 20 м соответ-
ственно.
На рис. 16. 10 приведены результаты оценки точности определения вза-
имных координат (дальности Ду и азимута Ау) в группе из трех ВС (ПО1,
ПО2 и ПОЗ), осуществляющих поиск терпящего бедствия объекта. Начальные
точности определения абсолютных координат и характеристики ошибок СРНС
были приняты такими же, как и в предыдущих случаях. Точность измерения
взаимных дальностей составляла 30 м. Как видно из рис. 16.10, точность опре-
~Рис. 16.10. Графики точности (СКО) определения
относительных координат при полете
группы нз трех ВС
деления взаимных даль-
ностей после 60 шагов
обработки находится на
уровне 1,1 ... 1,3 м, что
существенно выше точ-
ности определения вза-
имной дальности без
комплексной обработки
информации (3 ... 5 м),
а СКО определения
взаимных азимутов со-
ставляет примерно 0,2°.
Приведенные результа-
ты ни в коей мере не характеризуют весь накопленный опыт в области ком-
плексной обработки информации СРНС и других систем. Они позволяют лишь
сориентироваться в этом вопросе, а также намечают некоторые направления
будущих работ.
Литература
16.1. Коблов В. Л.? Ярлыков М. С. Принципы построения радиоэлектронных ком-
плексов интегрального типа// Радиотехника, 1987, №2, с. 20—27.
16.2. Ярлыков М. С. Применение марковской теории нелинейной фильтрации в ра-
диотехнике. — М.: Сов. радио, 1980.
16.3. Ярлыков М. С., Миронов М. А. Марковская теория оценивания случайных
процессов. — М.: Радио и связь, 1993.
16.4. Денисов В. И. Перспективы развития и использования радионавигационных
систем// Радиотехника, 1996, № 1, с. 53—56.
16.5. Ярлыков М. С., Базаров А. А. Оптимальное комплексирование радионавига-
ционных измерителей на уровне обработки сигналов для каждого из них// Радиотех-
ника, 1991, № 5, с. 52—59.
16.6. Ярлыков М. С., Базаров А. А. Совмещенная аппаратура потребителей спутни-
ковой н гиперболической радионавигационных систем//Радиотехника, 1992, №4,с. 3—13.
16.7. Бабич О. А. Обработка информации в навигационных комплексах. — М.:
Машиностроение, 1991.
16.8. Кинкулькин И.Е. Совмещенная аппаратура потребителей спутниковых радио-
навигационных систем// Радиотехника, 1996, № 1, с. 86—88.
16.3. Комплексная вторичная обработка информации 3
16.9. Ярлыков М. С., Шишкин В. Ю. Оптимизация алгоритмов комплексной об:
ботки импульсных радиосигналов на основе поэтапного решения уравнения Страто,
вича// Радиотехника и электроника, 1992, т. 37, № 2, с. 442—450.
16.10. Ван Дайк К. Использование спутниковых радионавигационных снст
GPS и ГЛОНАСС для обеспечения требуемого уровня . характеристик глобальной нави
ционной спутниковой системы// Радиотехника, 1996, № 1, с. 77—82.
16.11. Денисов В.И. Контроль целостности среднеорбнтальных спутниковых
дионавигацнонных систем// Радиотехника, 1997, № 1, с. 21—25.
16.12. Миронов М.А., Прохоров С.Л. Комплексные радионавигационные системь
раздельной обработкой сигналов// Радиотехника. Радиосистемы, 1996, № 1, с. 108—11
16.13. Перов А.И., Харисов В.Н. Калмановско-винеровская фильтрация фазы сип
ла в приемоиндикаторах спутниковых радионавигационных систем// Радиотехника, 19
№ 7, с. 102-106.
16.14. Перов А.И., Харисов В.Н. Уменьшение вычислительной сложности алгор,
мов в приемниках спутниковых радионавигационных систем на основе комбинирована
калмановско-винеровской фильтрации// Радиотехника, 1996, № 1, с. 120—125.
16.15. Ярлыков М. С., Кудинов А. Т. Повышение качества функционирования сп
ннковых радионавигационных систем за счет использования информационной избыт,
кости// Радиотехника, 1998, № 2, с. 3—9.
16.16. Каминский, Брайсон, Шмидт. Обзор современных методов днскретп
фильтрации, использующих квадратные корни матриц// Зарубежная радноэлектрони1
1973, № 6, с. 37-53.
16.17. Малаховский Р. А., Соловьев Ю. А. Оптимальная обработка информации
комплексных навигационных системах самолетов и вертолетов// Зарубежная радиоэл,
тропика, 1974, № 3, с. 18—39.
16.18. Soltz J.A., Donna J.I., Greenspan R.L. On Option for Mechanizing Integra:
GPS/INS Solutions// Navigation (USA), Winter 1988—1989, vol. 35, no. 4, pp. 443—457.
16.19. Бар-Ицхак И. Й. Новый метод сжатия информации при рекурренти
оценке ошибок инерциальной навигационной системы,// Ракетная техника и космон
тика, 1981, т. 19, № 2, с.. 153-159.
16.20. Phillips Я. Е., Schmidt G. Т. GPS/INS Integration// AGARD Lecture Series 2
System Implications and Innovative Applications of Satellite Navigation, 1996, pp. 9.1—9.18
16.21. Carroll R. W., Mikelson W. A. Velocity Aiding of Noncogerent GPS Receiv
NAECON’77 Record, pp. 311—318.
16.22. Ren Da Ching-Fang Lin. A New Failure Detection Approach and Its Applicati
to GPS Automonous Integrity Monitoring// JEEE Trans, on AES, 1995, vol. 31, no. 1, i
499-506.
16.23. Mueller T., Sun J, Karkalik F., Kessler K. Low-cost GPS/INS Guided Stand
Weapon Study// JEEE PLAN’S-1988, pp. 317-324.
16.24. Веремеенко К. К., Тихонов В. А., Навигационно-посадочный комплекс на
нове спутниковой радионавигационной системы// Радиотехника, 1996, №1, с. 94—99.
16.25. Rome James Н. Enhanced Noise Immunity and Error Control in a Fully In
grated JTIDS/GPS Receiver// IEEE PLAN’S-80, Atlantic City, 1980, pp. 477—493.
16.26. Соловьев Ю. А. Алгоритмы оптимальной двухуровневой обработки инфор:
ции и оценки точности навигационных комплексов// Научно-методические материя
по авиационным радиоэлектронным комплексам. Изд-во ВВИА нм. Н. Е. Жуковско
М., 1984, с. 167-181.
16.27. Carlson N. A. Federated Square Root Filter for Decentralized Parallel Proces
// IEEE Trans, on AES, 1990, vol. 26, no. 3.
16.28. Беляев В. И., Гордиенко Я. С., Лаврентьев В. В., Соловьев Ю. А. Концепд
создания интегрированного оборудования навигации, посадки, связи и наблюден
// Научные чтения, посвященные творческому наследию Н. Е. Жуковского. Изд-
ВВИА им. Н. Е. Жуковского, М., 1997, 20—22.1, с. 27.
16.29. Klass Р. J. KGLS Technique Sharpens GPS Accuracy// Av. Week. May 10, 19
pp. 55-57.
16.30. Nordwall B. D. System to Offer Formation in IFR, Av.Week,1993,voI.138,no 1.
16.31. Соловьев Ю. А. Потенциальная точность совместной оценки координ
группы подвижных объектов// Радиотехника, 1990, № 2, с. 16—18.
16.32. Mashkov А. К, Masalov Р. V. Tchemodoubov A.Y. PRMP: An Efficient G
Measurement Data Protocol for Relative Navigation Systems// Proc, of DSNS-96, St. Pete
burg, May 1996, vol. 2, Poster no. 1.
382
Список сокращений
АБ — антенный блок
АГС — астрономо-геодезическая
сеть
АКП — аппаратура контроля поля
АКС — аппаратура командной сис-
темы
АКЦ — автономный контроль це-
лостности
АЛМ — альманах системы
АП — аппаратура потребителей
АПВ — апостериорная плотность
вероятности
АПр — аналоговый приемник
АПЧ — автоматическая подстройка
частоты
АРМ — автоматизированное рабо-
чее место
АЦП — аналого-цифровой преобра-
зователь
АФС — антенно-фидерная система
БА — бортовая аппаратура
БВК — бортовой вычислительный
комплекс
БД — база данных
БНП — бортовой навигационный
передатчик
БТС — бортовая телеметрическая
система
БУС — блок управления спутником
БУП — блок управления поиском
БХ — бортовой хронизатор
БШВ — бортовая шкала времени
БЭВЧ — бортовой эталон времени
и частоты
ВВИА — военно-воздушная инже-
нерная акадения
ВГС — высокоточная геодезическая
сеть
ВКС — военно-космические силы
ВПП — взлетно-посадочная полоса
ВС — воздушное судно
ВТ — высокая точность
ВЧ — высокая частота
ГГС — государственная геодезиче-
ская сеть
ГЛОНАСС — глобальная навигаци-
онная система
ГМС — географическое место спут-
ника
ГК — генератор кода
ГНС — государственная нивелир-
ная сеть
ГОС — генератор опорного сигнала
ГПЗ — геофизические Параметры
Земли
ГС — генератор сигнала
ГЭВЧ — Государственный эталон
времени и частоты
ДГС — доплеровская геодезическая
сеть
ДИСС — доплеровский измеритель
скорости—сноса
ДН — диаграмма направленности
ДМ — демодулятор
ДП — дифференциальные поправки
ДПС — дифференциальные подсис-
темы
ДР — дифференциальный режим
ДС — дифференциальная станция
ДХ — дискриминационная характе-
ристика
ЕС КВО — Единая глобальная сис-
тема координатно-временного
обеспечения
ЖКС — жидкокристаллический
ИДНС — инерциально-доплеровс-
кая навигационная система
ИКАО — Международная организа-
ция гражданской авиации
383
ИМО — Международная морская
организация
ИНС — инерциальная навигацион-
ная система
ИПРЖР — издательское предпри-
ятие журнала радиотехника
ИС — информационные символы
ИСЗ — искусственный спутник
Земли
ИТП — измеренные текущие пара-
метры
ИУ — интерфейсное устройство
КВЦ — координатно-вычислитель-
ный центр
КГС — Космическая геодезическая
сеть
КИ — корректирующая инфор-
мация
КИК — командно-измерительный
комплекс
ККС — контрольно-корректирую-
щая станция
КНИЦ — Координационный науч-
но-информационный центр
КОР — коррелятор
КОС — кванто-оптические станции
КС — контрольная станция
КСВ — коэффициент стоячей вол-
ны
КСС — командные станции сле-
жения
КУС — курсовая система
КФ — корреляционная функция
КХ — код Хемминга
ЛА — летательный аппарат
ЛБУ —линейное боковое уклонение
ЛДПС — локальная дифференци-
альная подсистема
ЛЗП — линии заданного пути
ЛПД — линия передачи данных
МАМС — Международная Ассо-
циация Маячных служб
МВ — метка времени
МО — Министерство обороны
МП — микропроцессор
МПА — микрополосковая антенна
МС — морское судно
МСД — метод сравнения даль-
ностей
МСП — метод сравнения положе-
ния
МЭК — Международная электро-
техническая комиссия
НББ — нелинейный безынерцион-
ный блок
НВ — навигационный вычислитель
НВО — навигационно-временные
определения
НЗ — навигационная задача
НИ — навигационная информация
НК — навигационный комплекс
НОИ — неоперативная информа-
ция
НП — навигационный параметр
НПО ПМ — научно-производст-
венное объединение прикладной
механики
НС — навигационный спутник
НФИ — неоднозначность фазовых
измерений
ОГ — опорный генератор
ОЗУ — оперативное запоминающее
устройство
ОИ — оперативная информация
ОС — опорная станция
ОФМ — относительная фазовая
манипуляция
ПА — приемная аппаратура
ПВ — приемовычислитель
ПВЗ — параметры вращения Земли
384
С Л4к со< Дцений
ПВК — пространственно-времен-
ные координаты
ПВП — пространственно-времен-
ные параметры
ПД — псевдодальность
ПДМ — псевдодальномерный метод
ПЗУ — постоянное запоминающее
устройство
ПИ — приемоиндикатор
ПИД — приемноиндикатор диффе-
ренциальных сообщений
ПКА — подсистема космических
аппаратов
ПКУ — подсистема контроля и
управления
ПО — программное обеспечение
ППМ — промежуточный пункт
маршрута
ПС — проверочные символы
ПСК — псевдоскорость
ПСП — псевдослучайная последо-
вательность —-------------
ПСПД — псевдослучайная последо-
вательность дальности
ПТ — пониженная точность
ПУ — предварительный усилитель
ПУИ — пульт управления и инди-
кации
ПФ — полосовой фильтр
РАН — Российская академия наук
РГЭ — релятивистские и гравита-
ционные эффекты
РДМ — разностно-дальномерный
метод
РДПС — региональные дифферен-
циальные подсистемы
РДС — региональная дополнитель-
ная система
РИРВ — Российский институт ра-
дионавигации и времени
РЛС — радиолокационная станция
РМ — радиомаяк
PH — разрешение неоднозначности
РНИИ КП — Российский научно-
исследовательский институт косми-
ческого приборостроения
РНП — радионавигационный пара-
метр
РНС — радионавигационная
система
РСБН — радионавигационная сис-
тема ближней навигации
РСДН — радионавигационная сис-
тема дальней навигации
РСМ — разностно-скоростной ме-
тод
РФ — Российская Федерация
СГС — спутниковая геодезическая
сеть
СК — система координат
СКО — среднеквадратическая
ошибка
СКОИ — система комплексной об-"
работки информации
СКОсф — среднеквадратическая
сферическая погрешность
СКФ — система контроля фаз
СлС — следящая система
СМ — смеситель
СО — система ориентации и стаби-
лизации
СП — сигнальный процессор
СРНС — спутниковая радионавига-
ционная система
СС — система синхронизации
ССЗ — следящая система за за-
держкой сигнала
СТ — стандартная точность
СТИ — станция траекторных изме-
рений и управления
СУДС — система управления дви-
жением судов
)
385
СЧ — синтезатор частот
СЭВЧ — системный эталон време-
ни и частоты
США — Соединенные Штаты Аме-
рики
СШВ — системная шкала времени
ТНХ — требуемые навигационные
характеристики
УВД — управление воздушным
движением
УК — управляющий комплекс
УКВ — ультракороткие волны
УПЧ — усилитель промежуточной
частоты
УС — управляющая станция
Ф — фильтр
ФД — фазовый детектор
ФАГС — Фундаментальная астро-
номо-геодезическая сеть
ФАП — фазовая автоподстройка
ФИ — фазовое измерение
ФМ — фазовая модуляция
ФМн — фазовая манипуляция
ФОК — формирователь относи-
тельного кода
ФС — фазовая синхронизация
ЦВМ — цифровая вычислительная
машина
ЦГС — цифровой генератор
сигнала
ЦИ — цифровая информация
ЦС — центральный синхронизатор
ЦСХ — цикловая синхронизация
ЦУС — центр управления системой
ЧАП — частотная автоподстройка
ЧВП — частотно-временные по-
правки
ШВ — шкала времени
ШВП — шкала времени потре-
бителя
ШДПС — широкозонная диффе-
ренциальная подсистема
ШПС — шумоподобные сигналы
ЭВМ — электронная вычислитель-
ная машина
ЭВЧ — эталон времени и частоты
ЭИ — эфемеридная информация
ЭПД — эквивалентная ошибка
дальности
ЭПС — эквивалентная ошибка ско-
рости
АТ — атомное время;
DOP — Dilution of precision ECEF
— Earth-centered Earth-fixed (гео-
центрическая система координат)
ET — эфемеридное время
JD юлианская дата
GDOP — геометрический фактор
ухудшения точности местоопреде-
ления
GPS — Global Positioning System
(Глобальная система позициониро-
вания)
HDOP — горизонтальный фактор
ухудшения точности местоопредс-
ления
MSK — Minimum Shift Keying
(манипуляция с минимальным фа-
зовым сдвигом);
PDOP — пространственный фактор
ухудшения точности местоопреде-
ления
RAIM — Reseiver Integrity Moni-
toring (автономный контроль цело-
стности)
) ) ' >
386 _________________________________
Списсжсоджцений
TAI — шкала международного
атомного времени
ТДМА — Time Division Multiple
Access
TDOP — временной фактор ухуд-
шения точности местоопределения;
UERE — User Equivalent Range
Error (эквивалентная дальномерная
погрешность)
UERRE — User Equivalent Range
Rate Error (эквивалентная погреш-
ность измерения скорости)
UT —Universal Time ( Всемирное
время)
VDOP — вертикальный фактор
ухудшения точности определения
местонахождения
UNC — Coordinated Universal Time
(Всемирное координарованное
время)
ZT — поясное время
387
Предметный указатель
А
Алгоритм(ы)
— АКЦ оптимальные 327
— извлечения навигационной инфор-
мации 213
— итерационные 84
— комплексирования оптимальные
351
— командной системы 159
— обработки первичный 74, 194
---вторичный 84, 213
— обнаружения 76, 194
— определения координат 84
— — — при избыточности измерений
87
— оценки навигационных параметров
214
— поиска сигнала по задержке 75, 194
------по частоте 76, 194
— расчета вектора состояния на осно-
ве неоперативной информации 215
—--------на основе оперативной ин-
формации 219
— разрешения неоднозначности ФИ
беспереборный 291
— фильтрационные АКЦ 338
— фильтрации доплеровского смеще-
ния частоты 199
----задержки сигнала 80, 197
----фазы 78, 195
Алфавит двоичный 64
Альманах 150
— орбит 144
— фаз 144
— формирование 127
Амплитуда сигнала 61, 74
комплексная 59
Аномалия истинная 34
— средняя 36
— эксцентрическая 36
Антенна микрополосковая 188
Аппаратура бортовая НС 156. 226
— контроля поля 118, 123
— потребителей 21, 187, 263
— привязки 116
Апоцентр 34
Апогей 35
Апсиды 34
Аргумент перигея 35
— широты 37
Б
База сигнала 58
Блок антенный 187
— управления 159
В
Вектор состояния потребителя 48, 73
Видеоимпульс прямоугольный 62
Возмущения орбиты вековые 41
— периодические 41
Время всемирное 25
— — координированное 25
— звездное 23
гринвичское 24
— летнее 26
— местное 23
---декретное 25
---звездное 23
— — среднее 24
— перигея 35
— поясное 25
— среднее солнечное 24
— эфемеридное 24
Высота геодезическая 32
— минимально допустимая 47
- полета НС ГЛОНАСС 38
------- GPS 38
Вычислитель навигационный 188
Г
Генератор кода дальномерного 199
Готовность 12
Группировка НС 114, 132
- д
Движение НС невозмущенное 32
----- среднее 36
Двучлен 65
Демодуляция навигационного сообще-
ния 213
Детектор фазовый 69
Дискриминатор доплеровского смеще-
ния частоты 82, 199
— задержки сигнала 81, 198
— фазовый 197
— следящей системы 205
-----линеаризованный 206
Длительность импульса 61
— периода кодовой последовательно-
сти 63
максимальная 65
— посылки 140
— сигнала эффективная 57
— элементарного символа ПСП 140
Долгота восходящего узла 34
— геодезическая 32
Достоверность НИ 317
Доступ многостанциониый 58
Доступность НВО 12, 183
3
Задача навигационная 73
Задержка радиосигнала групповая 138
— — дополнительная в тропосфере 98
-----дополнительная в ионосфере 99
-----дополнительная в АП 102
388
Предметный уммтель
Закон Ньютона 32
— Кеплера 35, 37, 40
— фазовой манипуляции 141
Зона видимости 46
— действия СРНС 114
— обзора 45
----мгновенная 46
И
Избыточность кода 68
Измерения беззапросные 19
— дальности 49
— двухчастотные 289
— псевдодальиости 50
— псевдоскорости 53
— радиальной скорости 51
— фазовые 252, 286
избыточные 288
Идентификация неисправного НС 326
Информация
— навигационная 66
---- неоперативная 67, 144
----оперативная 66, 144
— служебная 141
— телеметрическая 160
— эфемеридная оперативная 22
---- долговременная 22
Интегрирование СРНС ГЛОНАСС и
GPS 180, 282, 359
К
Кадр навигационного сообщения 67, 145
Канал оценки доплеровского смещения
частоты 199
----задержки сигнала 81
----фазы сигнала 81
Код 67
— безызбыточный 67
— блочный 68
— дальномерный стандартной точности
142
— корректирующий 68
----двоичный равномерный 68
— метки времени (МВ-код) 141, 143
— помехоустойчивый 67, 142
— разделимый 68
— Рида—Соломона 174
— систематический 68
— служебной информации 142
— Хемминга 68, 142
Колебание квадратурное 76, 191
— синфазное 76, 191
Комплекс бортовой управляющий 159
— бортовой вычислительный 160
— командно-измерительный 20, 95
Комплексирование СРНС 322
----при вторичной обработке 368
----при первичной обработке 346
----с высотомером 322
----с ИНС 323
----с РСБН 323
----с РСДН 232, 347
Контроль достоверности навигационных
данных 153
— целостности 153
---автономный (RAIM)154, 223, 240
------бортовой (АА1М)155
---наземный 154
Координаты потребителя 49
---абсолютные 94
--относительные 179
---геодезические 219
Коррекция шкал времени 116
Коррелятор 58, 188, 191
косинусы направляющие 86
Коэффициент геометрии 106
— — вертикальный 107
---взвешенный 180
--- временной 107
---горизонтальный 107
---пространственный 106
---стоячей волны 189
— шума 189
— эллиптичности антенны 189
— модели ионосферы 100
— преломления радиоволн 98
Л
Линия апсид 33
— положения 48
— узлов 34
— передачи данных 169, 173 ->
М
Манипуляция фазовая 60, 69, 141
--- относительная 70
Местоположение 48
Метод (ы)
— внешние АКЦ 322
— внутренние АКЦ 324
— двухчастотный 100
— дополнительной переменной 297
— контроля целостности 321
------автономного 324
— моделирования трассы 99
— наименьших квадратов
— Ньютона 85
— определения координат дальномер-
ный 49
------комбинированный 51
------псевдодальномерный 50
— — — псевдорадиально-скоростной
53
—-----радиально-скоростной 51
------разностно-дальномерный 51
— — — разностно-радиально-скорост-
ной 53
---ориентации 54
— относительной фазовой манипуля-
ции 70
— оценок 328
— разрешения неоднозначности ФИ
287
— Рунге—Кутта 130
38
Минимизация целочисленная 290
Многочлен неприводимый 65
— первообразный 65
— характеристический 65
Модель изменения фазы сигнала 79
— согласующая 130
Модуляция амплитудная 59
— меандровым колебанием 141
— фазовая 59
Н
Наклонение орбиты 34
Непрерывность НВО 12
Нутации 23
О
Обеспечение навигационное
— эфемеридное 124
— частотно-временное 115
Обработка сигналов оптимальная 73
--- первичная 74
---вторичная 74, 84
Огибающая на выходе согласованного
фильтра 76
Операции управления типовые 126
Орбита спутника 33
---геостационарная 40
---наклонная 34
---оскулирующая -40
--- полярная 34
--- приполярная 34
---экваториальная 34
Определение вектора состояния потре-
бителя 73
---параметров вращения Земли 128
— — пространственно-временных ко-
ординат 73
— траектории движения НС 129
Отказ спутника 317
Отношение сигнал-шум 57. 139
— правдоподобия 330
Оценка вектора потребителя 74
— возможности применения КС 127
— максимального правдоподобия 75
— оптимальная дискретного параметра
80
---задержки сигнала 80
-------- двухчастотного 301
---фазы сигнала 80
— точности эфемерид 127
П
Параметр (ы)
— дискретный 73
— измеренный текущий 126
— навигационный 48, 51
— орбит 33
— радионавигационный 48, 73
— сжатия эллипсоида 32
— фокальный 34
Период обращения НС 40
— сидерический (звездный) 39
— синодический 39
— юлианский 26
Перигей 35
Перицентр 34
Плоскость орбитальная 33
Плотность вероятности апостериорно
297
Площадь зоны обзора 46
Поверхность положения 48
Погрешности атмосферные 97, 111
— дальномерные 94, 111
— динамические 102
— ионосферные 98, 111, 166
— командно-измерительного компле
са 95
— многолучевости 102, 111
— приемоиндикатора 102, 111
— псевдодальномерные 94
— тропосферные 97, 111
— частотно-времеиного обеспечен и
95
— угловой ориентации 140
— эквивалентные дальномерные 95
— эквивалентные скоростные 95
— эфемеридного обеспечения 96
— шумовые 102
Подсистема контроля и-управления I
109
— дифференциальная 168
— локальная 170
---широкозонная 168
— космических аппаратов 18
Полином порождающий 65, 142, 143
Помеха(и) аддитивная 73
— внутрисистемные 138
Помехоустойчивость 60
Поправки частотно-временные 116
Последовательность кодовая 61
— рекуррентная линейная циклическ
64
--------максимальной длины 65
Поток навигационной информации 14
Преобразователь аналого-цифровой 11-
Прецессия 23
Приемник АП 190
— аналоговый 190
— оптимальный сигнала с ОФМ 71
Приемовычнслитель 187
Приемоиндикаторы СРНС 264
Применение СРНС 221
---в авиации 221
---в геодезии 246
---морскими потребителями 229
--- на транспорте 243
Принцип неопределенности 60
— комплексирования 343
Производная скаляра по вектору 85
Псевдодальность 50
Псевдоспутник 180
390
) Предм. iwft ук Угель
Р
Радиус Земли 32
— зоны обзора 45
Разделение сигналов кодовое 135
--частотное 135
Разрешение неоднозначности ФИ 287
Разряды резервные 152
Распределение амплитуды 75
— начальной фазы 75
Расстояние апогейное 35
— кодовое 68
— перигейное 35
Регистр сдвигающий п-разрядный 64
--с линейной обратной связью 64
Режим дифференциальный 164, 232
— с коррекцией координат 178
— с псевдоспутниками 180
С
Связь обратная линейная 64
Сегмент космический 18
— наземный 19, 118
— потребителей 19
Секунда атомная 24
— звездная 23
— эфемеридная 24
Сигнал база 58
— задержка 74
— длительность эффективная 57
— сложный 60
— стандартной точности 60
— ширина спектра эффективная 57
— фазоманипулированный 60, 61
— энергия 57
— шумоподобный 60
Символы информационные 67, 142
— проверочные 67, 142
Синтез оптимальных алгоритмов 73
— — — при избыточности измерений
87
-----при фазовых измерениях 287
-----фильтрации 80
Синхронизатор центральный 116, 118
Синхронизация тактовая 71
— фазовая 71
— шкал времени 28, 116
— цикловая 72
Система
— вычислительная бортовая 159
— контроля фаз 116, 118, 122
— координат 30, 115
----- геодезическая
-геоцентрическая 30
-— инерциальная 30
подвижная 30
— объединенная иавигационно-связная
376
— ориентации и стабилизации 161
— синхронизации 116
Система слежения дискретная 205
----- второго порядка 208
-----третьего порядка 211
----за задержкой сигнала 197
-----за доплеровским смещением час-
тоты 199
----за фазой сигнала 195
— слежения непрерывная 80
---- второго порядка 209
----третьего порядка 211
— спутниковой связи INMARSAT 241
Скорость НС абсолютная 43
----локальная 43
---- относительная 43
----радиальная 38
---- секториальная 39
---- трансверсальная 38
----угловая 36
— вращения Земли 31, 44
Слово навигационного сообщения 67
Соотношение неопределенности 58
Спектр кодовой последовательности 62
— комплексной огибающей 62
— ФМн сигнала 82
Способ(ы) измерений дифференциаль-
ный 103
— уменьшения погрешностей 103
.Станция. дифференциальная 120
— — контрольно-корректирующая
165, 171
— контрольная 116, 118, 120
— кванто-оптическая 118, 121
— слежения командная 121
Строка НС 67, 146
Сутки звездные 23, 40
— солнечные истинные 24, 31
— — средние 24
Суперкадр навигационного сообщения
67, 145
Схема комплексирования 373
— глубоко интегрированная 374
— разомкнутая 374
— сильно связанная 374
Т
Тело неопределенности 59
Точность измерения 57, 111
— дифференциального режима 166
— потенциальная 57, 286
Требования к достоверности НВО' 317
— навигационному обеспечению воз-
душных судов 12,231
---космических средств 17
---морских судов 14, 231
---наземных объектов 16, 246
---судов речного флота 16, 231
— к радиосигналам 57
- к СРНС 11
ЗУ!
Точность измерения задержки сигнала
---- потенциальная 57
— доплеровского смещения частоты
----потенциальная 57
- НВО 111
У
Угол маски 46
— перигея 35
Узел орбиты 33
— восходящий 34
— нисходящий 34
Уравнение
— канонического сечения 34
— Кеплера 35, 37, 40
— движения НС возмущенное 43
---невозмущенное 37
Усилитель предварительный 187
— промежуточной частоты
Ускорение
— гравитационное Земли 32
--- лунно-солнечное 45
Устройство защиты входа 190
. — интерфейсное 188
Ф
Фаза сигнала 74
— случайная 74
Фактор геометрический L05
Фильтр полосовой 187, 189
— дискретный 200
---второго порядка 201
---третьего порядка 202
---в контуре ФАП 202
---в контуре ССЗ 204
---\в контуре системы ЧАП 205
Фильтрация 74
— оптимальная 74
совместная 6.2.2
непрерывно-дискретная 6.2.2
Функция
— автокорреляционная 59
— взаимная корреляционная 59
— корреляционная 58
---видеоимпульса 62
— — ФМн сигнала апериодическая
63, 66
----ФМн сигнала периодическая 63,
66
— модулирующая 74
— навигационная 49
— неопределенности 59
— сигнальная 73
* X
Характеристика (и)
— дискриминатора задержки 198
---фазового 197
--- частотного 84,
— дискриминационная 206
Характеристика (и) контроля целостно-
сти 318
— модуляции сигналов 138
— модулирующих последовательностей
140
— навигационной радиолинии 139
— оптимальных алгоритмов АКЦ 335
— орбитальные НС ГЛОНАСС 131
— радиосигналов ГЛОНАСС 135
--частотные 136
--поляризационные 137
--спектральные 137
— сравнительные ГЛОНАСС/GPS 181
- СРНС ГЛОНАСС 111
- СРНС GPS 111
Хронизатор бортовой 158
ц
Целостность НВО 12, 283, 317
Центр управления системой 119
Ч
Частота промежуточная 191
— меандрового колебания 141
— метки времени 141
— символьная 141
Частотно-временные поправки 116
Ш
Ширина спектра эффективная 57
Широта геодезическая 32
Шкала времени бортовая 27, 115
--потребителя 27, 115
--системная 27, 115
Шум аддитивный
--гауссовский
— фазовый 191
Э
Экстраполятор 205
— эквивалентный 208
Эксцентриситет 34
— эллипсоида 32
— линейный 35
Элементы орбиты классические 33
— оскулирующие 41
Энергия сигнала 57
Эпоха 35
Эталон времени и частоты бортовой
116
— системный 21
Эфемериды НС 22, 146
39'
С^де^жаниу
СОДЕРЖАНИЕ
ПРЕДИСЛОВИЕ...................................................... 3
ВВЕДЕНИЕ......................................................... 6
1. Исторические сведения . ................. 6
2. Требования к спутниковым радионавигационным системам . . 11
Литература...................................................... 17
Раздел!. ОБЩИЕ ПРИНЦИПЫ ПОСТРОЕНИЯ СПУТ-
НИКОВЫХ РАДИОНАВИГАЦИОННЫХ СИСТЕМ ... 18
Глава 1. Структура спутниковых радионавигационных систем.... 18
1.1. Общие сведения.................................... 18
1.2. Подсистема космических аппаратов................... 19
1.3. Наземный командно-измерительный комплекс........... 20
1.4. Навигационная аппаратура потребителей СРНС......... 21
1.5. Взаимодействие подсистем СРНС в процессе определения
текущих координат спутников............................ 21
Литература................................................... 22
Г л а в а 2. Шкалы времени................................. 23
2.1. Единицы мер времени .............................. 23
2.2. Системы отсчета времени, используемые в СРНС....... 25
2.3. Шкалы времени СРНС................................. 27
2.4. Синхронизация шкал времени......................... 28
Литература................................................... 29
Г л а в а 3. Траекторное движение навигационных спутников.... 30
3.1. Системы координат, используемые в СРНС............. 30
3.2. Уравнения невозмущенного траекторного движения НС
в инерциальной системе координат....................... 32
3.3. Классические элементы орбиты спутника............. 33
3.4. Параметры движения НС по невозмущенной орбите.... 35
3.5. Уравнения невозмущенного движения НС в инерциальной
системе ординат с использованием орбитальных элементов . 37
3.6. Общая характеристика возмущенного движения НС..... 40
3.7. Приближенные уравнения возмущенного движения
в геоцентрической подвижной системе координат........... 43
3.8. Основные навигационные характеристики НС.......... 45
Литература................................................... 47
Г л а в а 4. МЕТОДЫ РЕШЕНИЯ НАВИГАЦИОННЫХ ЗАДАЧ............. 48
4.1. Общие определения.................................. 48
4.2. Дальномерный метод ................................ 49
39.
4.3. Псевдодальномерный метод. .- •......... 50
4.4. Разностно-дальномерный метод . . . ;..4^.. .............. 51
4.5. Радиально-скоростной (доплеровский) метод » . . . 51
4.6. Псевдорадиально-скоростной (псевдодоплеровский) метод . 53
4.7. РазнОстно-радиально-скоростной метод............. 53
4.8. Комбинированные методы........................... 54
4.9. Определение ориентации с помощью СРНС............ 54
Литература ......................................................... 56
Г л а в а 5. Радиосигналы и навигационные сообщения в спутниковых
радионавигационных системах.......................... 57
5.1. Требования, предъявляемые к радиосигналам в СРНС. 57
5.2. Функция неопределенности и выбор формы сигнала..... 58
5.3. Шумоподобные сигналы в СРНС.............................. 60
5.4. Фазоманипулированные сигналы............................. 61
5.4.1. Общие свойства..................................... 61
5.4.2. Af-последовательности. Основные свойства........... 64
5.5. Навигационные сообщения в СРНС........................... 66
5.5.1. Общие сведения..................................... 66
5.5.2. Помехоустойчивое кодирование навигационной
информации............................................ 67
5.6. Модуляция радиосигнала навигационным сообщением .... 69
5.6.1. Фазовая манипуляция радиосигнала................... 69
5.6.2. Относительная фазовая манипуляция.................. 70
5.7. Синхронизация в СРНС ГЛОНАСС............................. 71
Литература.................................................. 72
Г л а в а 6. Методы и алгоритмы обработки сигналов и извлечения на
вигационной информации............................... 73
6.1. Общие сведения................................... 73
6.2. Алгоритмы первичной обработки.................... 74
6.2.1. Алгоритмы поиска сигналов по задержке и частоте . . 75
6.2.2. Алгоритмы фильтрации фазы, задержки сигала
и оценки дискретного параметра.................... 78
6.3. Алгоритмы вторичной обработки.................... 84
6.3.1. Итерационные алгоритмы определения координат ... 84
6.3.2. Определение координат при избыточности
измерений ............................................ 87
6.3.3. Сравнение точности оценок координат потребителя,
< полученных псевдодальномерным и разностно-
дальномерным методами........................................... 89
Литература ......................................................... 93
394
Содержание
Г л а в а 7. Источники погрешностей и точность навигационно-
временных определений в СРНС.................................... 94
7.1. Погрешности, вносимые на НС и КИК..................... 95
7.1.1. Погрешности частотно-временного обеспечения .... 95
7.1.2. Погрешности эфемеридного обеспечения............ 96
7.2. Погрешности, вносимые на трассе НС—потребитель...... 97
7.2.1. Тропосферные погрешности........................ 97
7.2.2. Ионосферные погрешности......................... 98
7.2.3. Погрешности из-за многолучевости............... 102
7.3. Погрешности, вносимые приемоиндикатором СРНС........ 102
7.4. Геометрический фактор в СРНС......................... 105
Литература .................................................... 108
Р а з д е л 2. СПУТНИКОВАЯ РАДИОНАВИГАЦИОННАЯ
СИСТЕМА ГЛОНАСС................................................ 109
Г л а в а 8. Общие сведения о спутниковой радионавигационной системе
ГЛОНАСС........................................................ 109
8.1. Структура и основные характеристики.................. 109
8.2. Этапы развертывания.................................. 112
8.3. Система координат, используемая в СРНС ГЛОНАСС...... 115
8.4. Частотно-временное обеспечение. Шкалы времени
системы ГЛОНАСС.......................................... 115
Литература..................................................... 117
Глава 9. Наземный сегмент (подсистема контроля и управления) . . 118
9.1. Назначение и состав подсистемы контроля и управления . . 118
9.1.1. Общие сведения................................ 118
9.1.2. Центр управления системой..................... 119
9.1.3. Контрольные станции........................... 120
9.1.4. Кванто-оптические станции..................... 121
9.1.5. Система контроля фаз.......................... 122
9.1.6. Аппаратура контроля поля...................... 123
9.2. Эфемеридное обеспечение.............................. 124
9.2.1. Особенности формирования эфемеридной
информации в ГЛОНАСС................................. 125
9.2.2. Типовые операции управления................... 126
9.2.3. Технология определения траектории
движения спутника.................................... 129
Литература..................................................... 130
Глава 10. Подсистема космических аппаратов .................... 131
10.1. Орбитальные характеристики спутников................ 131
10.2. Радиосигналы в СРНС ГЛОНАСС......................... 135
10.2.1. Виды используемых сигналов.................... 135
10.2.2. Характеристики излучаемых навигационных
радиосигналов......................................... 136
10.3. Характеристики модулирующих последовательностей .... 140
10.4. Навигационные сообщения в СРНС ГЛОНАСС.............. 144
10.4.1. Общие сведения............................... 144
10.4.2. Эфемериды НС ГЛОНАСС.......................... 146
10.4.3. Альманах системы ГЛОНАСС...................... 149
10.4.4. Резервные разряды в суперкадре................ 151
10.4.5. Контроль достоверности навигационных данных . . 151
10.5. Контроль целостности СРНС ГЛОНАСС................... 151
10.6. Бортовая аппаратура спутников ГЛОНАСС............... 154
10.6.1. Назначение бортовой аппаратуры ............... 154
10.6.2. Состав спутника............................... 155
10.6.3. Бортовой навигационный передатчик............. 155
10.6.4. Бортовой хронизатор........................... 157
10.6.5. Бортовой управляющий комплекс................. 158
10.6.6. Система ориентации и стабилизации и другие
вспомогательные системы......................... ... 159
10.6.7. Функционирование бортовых систем
спутника ГЛОНАСС ».................................. 160
Литература..................................................... 161
Г л а в а 11. Особые режимы работы спутниковых
радионавигационных систем................................... 162
11.1. Дифференциальный режим СРНС ГЛОНАСС.............. 162
11.1.1. Определение дифференциального режима СРНС 162
11.1.2. Точностные возможности дифференциального
режима ............................................ 164
11.1.3. Дифференциальные подсистемы СРНС.............. 16с
11.1.4. Разновидности дифференциального режима СРНС . 17<
11.2. Интегрирование СРНС ГЛОНАСС и GPS................ 17
Литература............................................... 18
Г л а в а 12. Аппаратура потребителей........................... 18
12.1. Принципы построения и функционирования аппаратуры
потребителей............................................ 18
12.2. Антенный блок....................................... 18
12.3. Приемник............................................ 18
12.4. Коррелятор.......................................... 18
12.5. Навигационный вычислитель............................ 19
^2.6. Алгоритмы первичной обработки информации в АП.... 19
12.6.1 . Алгоритмы поиска и обнаружения................ 19
396 1 Содер-^ание
12.6.2 . Алгоритм работы и схема слежения за фазой
сигнала.............................................. 193
12.6.3 . Алгоритм работы и схема слежения за задержкой
сигнала.............................................. 195
12.6.4 . Алгоритм работы и схема системы частотной
автоподстройки....................................... 197
12.6.5 . Алгоритмы работы дискретных фильтров в контуре
следящих систем...................................... 198
12.6.6 . Выбор параметров дискретной следящей системы . . . 203
12.6.7 . Алгоритм выделения навигационного сообщения ... 211
12.7. Алгоритмы вторичной обработки......................... 211
12.7.1. Демодуляция навигационного сообщения............ 211
12.7.2. Алгоритм оценки навигационных параметров.... 212
12.7.3. Расчет вектора состояния НС нат>снове
неоперативной информации................ ................213
12.7.4. Расчет вектора состояния НС на основе
оперативной информации............................'. 217
12.7.5. Пересчет координат потребителя из земной
в геодезическую систему координат..............’. . . . 217
12.8. Особенности применения СРНС в различных областях . . . 219
12.8.1. Особенности применения в авиации................ 219
12.8.2. Особенности применения морскими потребителями . 227
12.8.3. Особенности использования наземным транспортом . 241
12.8.4. Особенности использования в геодезии............ 244
12.9. Современные образцы аппаратуры потребителей........... 261
Литература....................................................... 278
Р а з д е л 3. НАПРАВЛЕНИЯ РАЗВИТИЯ СПУТНИКОВОЙ
РАДИОНАВИГАЦИОННОЙ СИСТЕМЫ ГЛОНАСС ... 279
Глава 13. Направления совершенствования
системы ГЛОНАСС.................................................. 279
Г л а в а 14. Навигационно-временные определения,
основанные иа фазовых измерениях ................................ 286
14.1. Методы разрешения неоднозначности фазовых измерений
на уровне вторичной обработки........................... 286
14.2. Бесперсборные процедуры разрешения неоднозначности . . 291
14.3. Применение методов оптимальной фильтрации для синтеза
алгоритмов НВО, основанных на фазовых измерениях .... 297
14.3.1. Метод дополнительной переменной................. 297
14.3.2. Оценка задержки одночастотного когерентного
радиосигнала.....................'................... 299
14.3.3. Оценка задержки двухчастотного когерентного
радиосигнала............................................. 301
397
14.3.4. Общая задача оценки параметров при наличии
в наблюдениях периодических функций.................. 303
J.4.3.5. Задача фильтрации при наличии в наблюдениях
периодических функций........................... 307
Литература................................................... 316
Г л а в а 15. Повышение достоверности навигациоиио-временных
определений . . . . ........................................... 317
15.1. Требования к достоверности НВО..................... 317
15.2. Пути повышения достоверности НВО в
приемоиндикаторах СРНС................................... 319
15.2.1. Факторы, влияющие на целостность СРНС......... 319
15.2.2. Методы контроля целостности СРНС.............. 321
15.2.3. Методов автономного контроля целостности
в приемоиндикаторах СРНС............................. 324
15.2.4. Пододы к процедуре идентификации
неисправного НС............................•......... 326
15.3. Оптимальные алгоритмы АКЦ на основе
однократных измерений.................................... 327
15.3.1. Исходные соотношения для задачи АКЦ методом
оценок........................................... 327
15.3.2. Алгоритм АКЦ на основе метода~оценок.......... 328
15.3.3. Оптимальный алгоритм АКЦ, учитывающий
наблюдения доплеровской частоты...................... 333
15.3.4. Характеристики оптимальных алгоритмов АКЦ .... 335
15.4. Фильтрационные алгоритмы АКЦ в ПИ СРНС............. 338
Литература..................................................... 341
Глав Комплексная обработка информации в аппаратуре
потребителей спутниковых радионавигационных систем . . 343
16.1. Принципы комплексирования навигационных измерителей 343
16.2. Комплексная первичная обработка информации
в аппаратуре потребителей СРНС.......................... 346
16.2.1. Оптимизация интегрированной аппаратуры потреби-
телей радионавигационных систем ГЛОНАСС
и Loran—С/Чайка................................ 347
16.2.2. Оптимизация интегрированной аппаратуры
потребителей спутниковых радионавигационных
систем ГЛОНАСС и GPS........................ 359
16.3. Комплексная вторичная обработка информации......... 368
Литература..................................................... 380
Список сокращений.............................................. 382
Предметный указатель........................................... 387
398
_4ИРМЛ СИСТЕМЫ И СРЕДСТВА
Дошлая ) РАДИОНАВИГАЦИИ
Закрытое акционерное общество Фирма "Котлин" образовано в октябре
1992 г. с целью:
разработки научно-технической продукции в интересах Министерства обо-
роны РФ в сжатые сроки и с более низкими затратами за счет малых накладных
расходов;
более эффективного привлечения и использования потенциала академи-
ческой и отраслевой науки.
В 1996 г. "Котлин” вошел в состав Холдинговой Компании “Ленинец” и в
дислокацию Департамента радиопромышленности' Министерства обороннной
промышленности РФ.
Сегодня в Фирме “Котлин” работает более 300 ведущих специалистов и
ученых по всей радионавигационной тематике.
По своей структуре Фирма “Котлин” соответствует отраслевому НИИ, а
его производственные мощности позволяют выполнять наиболее сложные и трудо-
емкие НИОКР. —
-Основное-направление работ лежит — создание~систем и средств высоко-
точного, надежного и достоверного навигационно-временного обеспечения различ-
ных групп потребителей.
Поскольку современной тенденцией развития радионавигации в мире явля-
ется эксплуатация как наземных, так и космических радионавигационных сис-
тем, а также их совместное использование, то основную тематику работ Фир-
мы “Котлин ” условно можно разбить на следующие части :
1. Проведение НИОКР по созданию, модернизации, ремонту и техническо-
му обслуживанию наземных средств дальней радионавигации и бортового радио-
электронного оборудования летательных аппаратов.
2. Проведение НИОКР по созданию аппаратуры спутниковой навигации
различного назначения, а также систем и комплексов на ее основе.
3. Создание различных высокоточных дифференциальных подсистем, объе-
динение существующих навигационных систем, глобальный мониторинг радиона-
вигационных полей.
4. Создание интегрированных приемоизмерителей, работающих по сигна-
лам радионавигационных систем наземного и космического базирования.
5. Создание электронных информационно - управляющих систем контроля
движения объектов на основе объединения систем и средств навигации, радио-
связи и электронных карт.
6. Разработка навигационно — геодезической аппаратуры в интересах фе-
деральной службы геодезии и картографии РФ .
Кроме того, Фирма “Котлин" занимается серийным освоением, некоторых
из видов разрабатываемых изделий, проведением прикладных и поисковых иссле-
дований по альтернативной тематике, а также занимается созданием регио-
нальной сети на территории РФ по сбыту и сервисному обслуживанию аппара-
туры потребителей.
Важным звеном в деятельности Фирмы "Котлин"является сотрудниче-
ство с ведущими зарубежными фирмами по аналогичной тематике, а также про-
ведение работ в рамках межгосударственных соглашений по созданию объединен-
ных радионавигационных цепей на Востоке и Северо-Западе страны.
Тля навигаци- онной аппарату- ры ‘ Число кака* лов Рабочие, сигналы Масса, кг Погрешность nfitiutui координат.»: >. скорости, 1о Время до первого определения (с'альма- нахом), шин Ско- рость dtvct- аая, м/с
Авиаци- онная 18 ГЛОНАСС CPS 2,0 30 м, 0,2 м/с 5 ... 7 м (диф- ференциаль- ный режим ) 1,5 950
Порта- тивная 16 ГЛОНАСС ФН на L1 WAAS EGNOS 0,3 30 м, 0,2 м/с 5 ... 7 м, ( дифферен- циальный режим ) 1,5 950
Геодези-г ческая 42 ГЛОНАСС GPS ФН на L1 и L2 6,4 с ак- *у- j*y- лято- ром 10мм + 1 *106 d нри L до 50 км менее 5 30
Характеристики, обеспечиваемые аппаратурой, соответствуют требова-
ниям стандартов международных организаций.
ФИРМА “КОТЛИН"
ХОЛДИНГОВАЯ КОМПАНИЯ “ЛЕНИНЕЦ”
193019, Россия Телефон: (812) 567-12-68
Санкт-Петербург (812)567-40-76
Обводный канал, д. 14 Факс;. (812)567-12-68
E-mail: cotlin®infapro.spb.su