Author: Маркеев А.П.
Tags: общая механика механика твердых и жидких тел механика теоретическая механика
Year: 1999
Text
А. П. Маркеев
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
Издание второе, дополненное
Допущена Министерством образования РФ
в качестве учебника для студентов
механико-математических специальностей университетов
Редакция журнала
«Регулярная и хаотическая динамика»
Ижевская
республиканская типография
1999
УДК 531@75.8)
ББК 22.21
М26
М26 МаркеевА. П.
Теоретическая механика: Учебник для университетов. —
Москва: ЧеРо, 1999, 572 стр.
ISBN
Книга представляет собой строгое, целостное и компактное
изложение основных задач и методов теоретической механики.
Она значительно отличается от существующих учебников по
теоретической механике как по подбору материала, так и по
способу его изложения. Основное внимание уделено рассмотре-
рассмотрению наиболее содержательных и ценных для теории и прило-
приложений разделов динамики и методов аналитической механики;
статика изучается как раздел динамики, а в разделе кинемати-
кинематики подробно обсуждаются общие основания кинематики систе-
системы; некоторые методические идеи являются новыми в учебной
литературе.
Для студентов механико-математических факультетов уни-
университетов, а также для студентов втузов, обучающихся по спе-
специальности «Механика» и «Прикладная математика», преподава-
преподавателей механики, аспирантов.
Табл. 1. Ил. 177. Библиогр. 9 назв.
ISBN
ББК 22.21
Оригинал-макет подготовлен в редакции журнала
«Регулярная и хаотическая динамика»
http://www.rcd.com.ru
© А. П. Маркеев, 1999
© Редакция журнала «Регулярная
и хаотическая динамика», 1999
Оглавление
Предисловие к первому изданию 12
Предисловие ко второму изданию 14
Введение 15
I КИНЕМАТИКА
Глава I. Кинематика точки и системы
§ 1. Основные понятия, задачи кинематики 19
1. Пространство и время A9). 2. Материальная точка. Механи-
Механическая система B0). 3. Задачи кинематики B0).
§ 2. Кинематика точки 21
4. Векторный способ задания движения точки B1). 5. Коорди-
Координатный способ задания движения точки B1). 6. Естественный
способ задания движения точки B2). 7. Круговое движение B5).
8. Скорость и ускорение точки в полярных координатах B5).
9. Криволинейные координаты B7).
§3. Общие основания кинематики системы 31
10. Свободные и несвободные системы. Связи C1). 11. Ограни-
Ограничения, налагаемые связями на положения, скорости, ускорения
и перемещения точек системы C4). 12. Действительные и вир-
виртуальные перемещения. Синхронное варьирование C7). 13. Чис-
Число степеней свободы D0). 14. Обобщенные координаты D0).
15. Координатное пространство D2). 16. Обобщенные скорости
и ускорения D4). 17. Псевдокоординаты D5).
§ 4. Кинематика твердого тела 47
18. Задачи кинематики твердого тела. Определение простейших
перемещений D7). 19. Векторно-матричное задание движения
твердого тела. Углы Эйлера D9). 20. Движение твердого тела
с неподвижной точкой как ортогональное преобразование E2).
21. Основные теоремы о конечных перемещениях твердого те-
тела E2). 22. Скорость и ускорение твердого тела при поступа-
поступательном движении E6). 23. О мгновенном кинематическом со-
состоянии твердого тела E7). 24. Скорости и ускорения точек
твердого тела в общем случае движения E7). 25. Вращение твер-
твердого тела вокруг неподвижной оси E9). 26. Движение вокруг не-
неподвижной точки F1). 27. Плоское движение тела F3). 28. Ки-
Кинематические инварианты. Кинематический винт F9).
Оглавление
§ 5. Сложное движение точки 71
29. Основные определения G1). 30. Производная от вектора,
заданного своими компонентами относительно подвижной сис-
системы координат G2). 31. Теорема о сложении скоростей G3).
32. Теорема о сложении ускорений (теорема Кориолиса) G4).
§ 6. Сложное движение твердого тела 76
33. Постановка задачи G6). 34. Сложение мгновенно поступа-
поступательных движений G6). 35. Сложение мгновенных вращений
вокруг пересекающихся осей G7). 36. Кинематические уравне-
уравнения Эйлера G8). 37. Сложение мгновенных вращений вокруг
параллельных осей G9). 38. Пара вращений (80). 39. Сложение
мгновенно поступательного и вращательного движений (81).
II ДИНАМИКА
Глава П. Основные понятия и аксиомы динамики
§ 1. Законы (аксиомы) Ньютона. Задачи динамики 85
40. Инерциальные системы отсчета. Принцип относительности
Галилея (85). 41. Первый закон Ньютона (аксиома инерции).
Сила (85). 42. Масса. Второй закон Ньютона (основная аксиома
динамики) (86). 43. Третий закон Ньютона (аксиома взаимо-
взаимодействия материальных точек) (87). 44. Аксиома независимос-
независимости действия сил (закон сложения сил) (87). 45. Активные силы
и реакции связей (88). 46. Силы внешние и внутренние (89).
47. Задачи динамики. Равновесие. Статика (89).
§ 2. Главный вектор и главный момент системы сил 90
48. Главный вектор системы сил (90). 49. Момент силы относи-
относительно точки и оси (91). 50. Главный момент системы сил (92).
§ 3. Работа. Силовая функция. Идеальные связи 93
51. Работа системы сил (93). 52. Элементарная работа сил, при-
приложенных к твердому телу (93). 53. Силовое поле. Силовая
функция. Потенциал (94). 54. Элементарная работа системы сил
в обобщенных координатах. Обобщенные силы (96). 55. Идеаль-
Идеальные связи (98).
Глава III. Дифференциальные вариационные принципы
механики
§ 1. Принцип Даламбера-Лагранжа 102
56. Понятие о вариационных принципах механики A02). 57. Об-
Общее уравнение динамики (принцип Даламбера-Лагранжа) A02).
§ 2. Принцип Журдена 106
58. Принцип Журдена A06).
Оглавление
§3. Принцип Гаусса 107
59. Формулировка принципа Гаусса (принципа наименьшего
принуждения) A07). 60. Физический смысл принципа Гаус-
Гаусса A09). 61. Экстремальное свойство реакций связей A10).
Глава IV. Статика
§ 1. Статика произвольной механической системы 112
62. Общее уравнение статики (принцип виртуальных перемеще-
перемещений) A12). 63. Общее уравнение статики в обобщенных коорди-
координатах A16). 64. Эквивалентные системы сил A21).
§ 2. Статика твердого тела 122
65. Необходимые и достаточные условия равновесия твер-
твердого тела A22). 66. Критерий эквивалентности систем сил,
приложенных к твердому телу A24). 67. О равнодействую-
равнодействующей. Теорема Вариньона A27). 68. Частные случаи условий
равновесия твердого тела A27). 69. Равнодействующая двух
параллельных сил A33). 70. Теория пар A33). 71. Теоре-
Теорема Пуансо A35). 72. Статические инварианты. Динамический
винт A36). 73. Частные случаи приведения системы сил A37).
Глава V. Геометрия масс
§ 1. Центр масс. Момент инерции 140
74. Центр масс A40). 75. Момент инерции системы относитель-
относительно оси. Радиус инерции A40). 76. Моменты инерции относи-
относительно параллельных осей A43).
§ 2. Тензор и эллипсоид инерции 144
77. Моменты инерции относительно осей, проходящих через од-
одну и ту же точку A44). 78. Эллипсоид инерции. Главные оси
инерции A45). 79. Свойства главных моментов инерции A48).
Глава VI. Основные теоремы и законы динамики
§ 1. Основные динамические величины механической системы 150
80. Количество движения системы A50). 81. Главный момент
количеств движения (кинетический момент) системы A50).
82. Кинетический момент твердого тела, движущегося вокруг
неподвижной точки A52). 83. Кинетическая энергия системы.
Теорема Кёнига A54). 84. Кинетическая энергия твердого тела,
движущегося вокруг неподвижной точки A54).
§ 2. Теоремы об изменении основных динамических величин
системы 156
85. Общие замечания о теоремах и законах динамики A56).
86. Теорема об изменении количества движения A57). 87. Те-
Теорема об изменении кинетического момента A59). 88. Теоре-
Теорема об изменении кинетической энергии A66). 89. Основные
теоремы динамики в неинерциальной системе отсчета A71).
Оглавление
90. О теоремах динамики для движения относительно центра
масс A74).
Глава VII. Динамика твердого тела
§ 1. Вращение твердого тела вокруг неподвижной оси 177
91. Уравнение движения. Определение реакций A77). 92. Усло-
Условия, при которых динамические реакции равны статичес-
статическим A79). 93. Уравнение движения физического маятни-
маятника A80). 94. Фазовая плоскость для уравнения движения ма-
маятника A80). 95. Некоторые сведения из теории эллиптических
интегралов и эллиптических функций Якоби A84). 96. Интег-
Интегрирование уравнения движения маятника A86).
§ 2. Движение твердого тела вокруг неподвижной точки . . . 188
97. Дифференциальные уравнения движения твердого тела
вокруг неподвижной точки. Динамические уравнения Эйле-
Эйлера A88). 98. Первые интегралы A90). 99. Стационарные вра-
вращения твердого тела в случае Эйлера A90). 100. Движение
динамически симметричного тела в случае Эйлера. Регуляр-
Регулярная прецессия A91). 101. Геометрическая интерпретация Пу-
ансо A93). 102. Интегрирование уравнений Эйлера A95). 103. О
герполодиях B01). 104. Определение ориентации твердого тела в
абсолютном пространстве для движения Эйлера-Пуансо B02).
105. Уравнения движения тяжелого твердого тела вокруг не-
неподвижной точки и их первые интегралы B03). 106. Основная
формула гироскопии B06). 107. Об элементарной теории гиро-
гироскопа B10).
§ 3. Движение свободного твердого тела 214
108. Дифференциальные уравнения движения свободного твер-
твердого тела B14). 109. Плоское движение тела B18).
§ 4. Движение тяжелого твердого тела, опирающегося на гори-
горизонтальную плоскость 222
110. Общие сведения. Понятие о трении B22). 111. Волчок на аб-
абсолютно гладкой плоскости B23). 112. Влияние трения на дви-
движение волчка B26). 113. Движение однородного шара по плос-
плоскости при наличии трения B27). 114. Об уравнениях движения
тяжелого тела произвольной выпуклой формы B30).
Глава VIII. Элементы небесной механики
§ 1. Задача двух тел 234
115. Уравнения движения B34). 116. Интеграл площадей. Вто-
Второй закон Кеплера B35). 117. Интеграл энергии в задаче двух
тел B37). 118. Интеграл Лапласа B37). 119. Уравнение орбиты.
Первый закон Кеплера B38). 120. Зависимость характера орби-
орбиты от величины начальной скорости. Первая и вторая космичес-
космические скорости B39). 121. Третий закон Кеплера B40). 122. Время
Оглавление
в кеплеровском движении. Уравнение Кеплера B41). 123. Кеп-
леровские элементы орбиты B43). 124. О задаче трех и более
тел B44).
§ 2. Движение твердого тела в центральном ньютоновском гра-
гравитационном поле 245
125. Главный вектор сил тяготения. Гравитационный мо-
момент B45). 126. Уравнения движения тела относительно цент-
центра масс B49). 127. Относительное равновесие твердого тела на
круговой орбите B50). 128. Плоские движения B51).
Глава IX. Динамика системы переменного состава
§ 1. Основные понятия и теоремы 254
129. Понятие о системе переменного состава B54). 130. Теоре-
Теорема об изменении количества движения B55). 131. Теорема об
изменении кинетического момента B56).
§ 2. Движение материальной точки переменного состава . . . 257
132. Дифференциальное уравнение движения B57). 133. Дви-
Движение ракеты вне поля сил B59). 134. Вертикальное движение
ракеты в однородном поле тяжести B60).
§ 3. Уравнения движения тела переменного состава 263
135. Движение вокруг неподвижной точки B63). 136. Вращение
вокруг неподвижной оси B65).
Глава X. Дифференциальные уравнения аналитической
динамики
§ 1. Уравнения Лагранжа (второго рода) 267
137. Общее уравнение динамики в обобщенных координа-
координатах B67). 138. Уравнения Лагранжа B69). 139. Анализ вы-
выражения для кинетической энергии B71). 140. Разрешимость
уравнений Лагранжа относительно обобщеных ускорений B73).
141. Уравнения Лагранжа в случае потенциальных сил. Функ-
Функция Лагранжа B74). 142. Теорема об изменении полной механи-
механической энергии голономной системы B75). 143. Гироскопичес-
Гироскопические силы B77). 144. Диссипативные силы. Функция Рэлея B79).
145. Обобщенный потенциал B80). 146. О составлении уравне-
уравнений Лагранжа для описания движения в неинерциальной сис-
системе отсчета B82). 147. Натуральные и ненатуральные систе-
системы B82).
§ 2. Канонические уравнения Гамильтона 283
148. Преобразование Лежандра. Функция Гамильтона B83).
149. Уравнения Гамильтона B85). 150. Физический смысл функ-
функции Гамильтона B86). 151. Интеграл Якоби B87). 152. Уравне-
Уравнения Уиттекера и Якоби B89).
§ 3. Уравнения Рауса 293
153. Функция Рауса B93). 154. Уравнения Рауса B94).
Оглавление
§ 4. Уравнения движения неголономных систем 295
155. Уравнения движения с множителями связей B95). 156. Урав-
Уравнения Воронца B98). 157. Уравнения Чаплыгина C01). 158. Урав-
Уравнения Аппеля C06). 159. Вычисление энергии ускорений. Ана-
Аналог теоремы Кенига C09). 160. Энергия ускорений твердого те-
тела, движущегося вокруг неподвижной точки C10).
Глава XI. Интегрирование уравнений динамики
§ 1. Множитель Якоби 314
161. Множитель системы уравнений. Дифференциальное урав-
уравнение для множителя C14). 162. Инвариантность множителя.
Последний множитель Якоби C18). 163. Приложение теории
множителя к каноническим уравнениям C24).
§ 2. Системы с циклическими координатами 326
164. Циклические координаты C26). 165. Понижение порядка
системы дифференциальных уравнений движения при помощи
уравнений Рауса C27).
§ 3. Скобки Пуассона и первые интегралы 334
166. Скобка Пуассона C34). 167. Теорема Якоби-Пуассона C35).
§4. Канонические преобразования 337
168. Понятие канонического преобразования C37). 169. Кри-
Критерии каноничности преобразования C40). 170. Ковариант-
Ковариантность уравнений Гамильтона при канонических преобразовани-
преобразованиях C43). 171. Канонические преобразования и процесс движе-
движения C47). 172. Теорема Лиувилля о сохранении фазового объ-
объема C48). 173. Свободное каноническое преобразование и его
производящая функция C48). 174. О других типах производя-
производящих функций C52).
§ 5. Метод Якоби интегрирования уравнений движения .... 358
175. Уравнение Гамильтона-Якоби C58). 176. Уравнение Гамиль-
тона-Якоби для систем с циклическими координатами C60).
177. Уравнение Гамильтона-Якоби для консервативных и обоб-
обобщенно консервативных систем C60). 178. Характеристическая
функция Гамильтона C61). 179. Разделение переменных C63).
180. Теорема Лиувилля об интегрируемости гамильтоновой сис-
системы в квадратурах C67).
§ 6. Переменные действие-угол 371
181. Случай одной степени свободы C71). 182. Переменные
действие-угол в задаче о движении маятника C75). 183. О
переменных действие-угол для системы с п степенями сво-
свободы C79). 184. Переменные действие-угол в задаче двух
тел C81). 185. Элементы Делонэ C85).
§ 7. Канонические преобразования в теории возмущений . . . 388
186. Предварительные замечания C88). 187. Вариация постоян-
Оглавление 9
ных в задачах механики C88). 188. Классическая теория возму-
возмущений C92). 189. О линейных гамильтоновых системах диффе-
дифференциальных уравнений C94). 190. Преобразование Биркгофа.
Приближенное интегрирование гамильтоновой системы уравне-
уравнений вблизи положения равновесия C98).
Глава XII. Теория импульсивных движений
§ 1. Основные понятия и аксиомы 406
191. Ударные силы и импульсы D06). 192. Аксиомы D07).
193. Главный вектор и главный момент ударных импуль-
импульсов D07). 194. Задачи теории импульсивного движения D08).
§ 2. Теоремы об изменении основных динамических величин
при импульсивном движении 409
195. Теорема об изменении количества движения D09). 196. Те-
Теорема об изменении кинетического момента D10). 197. Теорема
об изменении кинетической энергии D12).
§3. Импульсивное движение твердого тела 413
198. Удар по свободному твердому телу D13). 199. Удар по телу
с одной неподвижной точкой D16). 200. Удар по телу с непо-
неподвижной осью D19).
§ 4. Соударение твердых тел 423
201. Коэффициент восстановления D23). 202. Общая задача о
соударении двух абсолютно гладких тел D27). 203. Измене-
Изменение кинетической энергии при соударении абсолютно гладких
тел D31). 204. Прямой центральный удар двух абсолютно глад-
гладких тел D31).
§ 5. Дифференциальные вариационные принципы механики в те-
теории импульсивных движений 435
205. Общее уравнение динамики D35). 206. Принцип Журде-
на D38). 207. Принцип Гаусса D40).
§ 6. Теоремы Карно 444
208. Первая теорема Карно D44). 209. Вторая теорема Кар-
Карно D46). 210. Кинетическая энергия потерянных скоростей в
случае твердого тела D47). 211. Третья и обобщенная теоремы
Карно D50).
§ 7. Теоремы Делонэ-Бертрана и Томсона 451
212. Теорема Делонэ-Бертрана D51). 213. Теорема Томсо-
Томсона D54).
§ 8. Уравнения Лагранжа второго рода для импульсивных дви-
движений 458
214. Обобщенные ударные импульсы D58). 215. Уравнения Ла-
Лагранжа D60). 216. Случай, когда ударные импульсы возникают
только из-за наложения новых связей D62).
10 Оглавление
Глава XIII. Интегральные вариационные принципы меха-
механики
§ 1. Принцип Гамильтона-Остроградского 467
217. Прямой и окольный пути голономной системы D67).
218. Принцип Гамильтона-Остроградского D71). 219. Принцип
Гамильтона-Остроградского для систем в потенциальном поле
сил D73). 220. Экстремальное свойство действия по Гамильто-
Гамильтону D76).
§ 2. Принцип Мопертюи-Лагранжа 482
221. Изоэнергетическое варьирование D82). 222. Принцип
Мопертюи-Лагранжа D83). 223. Принцип Якоби и геодезичес-
геодезические линии в координатном пространстве D86).
Глава XIV. Малые колебания консервативной системы око-
около положения равновесия
§ 1. Теорема Лагранжа об устойчивости положения равновесия 489
224. Устойчивость равновесия D89). 225. Теорема Лагран-
Лагранжа D90). 226. Теоремы Ляпунова о неустойчивости положения
равновесия консервативной системы D92). 227. Стационарные
движения консервативной системы с циклическими координа-
координатами и их устойчивость D94).
§ 2. Малые колебания 499
228. Линеаризация уравнений движения D99). 229. Главные
координаты и главные колебания E02). 230. Колебания кон-
консервативной системы под влиянием внешних периодических
сил E06).
Глава XV. Устойчивость движения
§ 1. Основные понятия и определения 514
231. Уравнения возмущенного движения. Определение устойчи-
устойчивости E14). 232. Функции Ляпунова E15).
§ 2. Основные теоремы прямого метода Ляпунова 517
233. Теорема Ляпунова об устойчивости движения E17).
234. Теорема Ляпунова об асимптотической устойчивости E22).
235. Теоремы о неустойчивости E24).
§3. Устойчивость по первому приближению 527
236. Постановка задачи E27). 237. Теорема об устойчивос-
устойчивости по первому приближению E29). 238. Критерий Рауса-
Гурвица E32).
§4. Влияние диссипативных и гироскопических сил на устой-
устойчивость равновесия консервативной системы 535
239. Влияние гироскопических сил и диссипативных сил с пол-
полной диссипацией на устойчивое положение равновесия голоном-
Оглавление 11
ной системы E35). 240. Влияние гироскопических и диссипа-
тивных сил на неустойчивое равновесие E37).
§ 5. Об устойчивости гамильтоновых систем 543
241. Общие замечания E43). 242. Устойчивость линейных га-
гамильтоновых систем с постоянными коэффициентами E44).
243. О линейных системах с периодическими коэффициента-
коэффициентами E44). 244. Устойчивость линейных гамильтоновых систем с
периодическими коэффициентами E47). 245. Алгоритм норма-
нормализации гамильтоновой системы линейных уравнений с перио-
периодическими коэффициентами E49). 246. Задача о параметричес-
параметрическом резонансе. Линейные гамильтоновы системы, содержащие
малый параметр E50). 247. Нахождение областей параметри-
параметрического резонанса E53). 248. Уравнение Матье E58).
Список литературы 561
Предметный указатель 562
Предисловие к первому изданию
С развитием науки и техники узкоспециальные знания довольно
быстро устаревают. Для решения возникающих принципиально новых
актуальных задач научные работники и инженеры обязательно долж-
должны обладать, помимо необходимой способности к доучиванию и пере-
переучиванию, хорошей подготовкой в области фундаментальных наук. Это
требует постоянного всестороннего совершенствования вузовского об-
образования. Наиболее перспективный путь лежит именно в повышении
значимости общенаучных дисциплин в учебных планах подготовки бу-
будущих научных работников и инженеров, в совершенствовании препо-
преподавания таких фундаментальных дисциплин, как физика, математика
и механика.
Как фундаментальная наука теоретическая механика была и оста-
остается не только одной из дисциплин, дающей углубленные знания о при-
природе. Она также служит средством развития у будущих специалистов
необходимых творческих навыков к построению математических мо-
моделей происходящих в природе и технике процессов, к выработке спо-
способностей к научным обобщениям и выводам.
Усовершенствование курса теоретической механики надо искать в
следующих двух основных направлениях. Во-первых, курс должен быть
строгим, логичным, целостным и компактным; он должен позволять в
краткое время изложить основные понятия и методы теоретической
механики. Во-вторых, в нем не следует уделять много внимания эле-
элементарным вопросам статики и кинематики; надо сконцентрировать
усилия на рассмотрении наиболее содержательных и ценных для теории
и приложений разделов динамики и методов аналитической механики.
Данная книга возникла в результате продолжительной преподава-
преподавательской работы автора на факультете прикладной математики Мос-
Московского авиационного института им. Серго Орджоникидзе. В ее основу
положены лекции, читаемые будущим инженерам-математикам. Содер-
Содержание книги несколько превосходит тот материал, который излагается
на лекциях.
При написании книги преследовались, главным образом, дидакти-
дидактические цели. В качестве будущего вероятного читателя автор видит
прежде всего студента, желающего получить хорошую первоначальную
подготовку по основным задачам и методам теоретической механики.
Автор надеется, что эта книга может оказаться полезной преподавате-
Предисловие к первому изданию 13
лям механики, а также аспирантам и научным работникам в области
прикладной математики и механики.
Данная книга существенно отличается от имеющихся учебников по
теоретической механике для вузов как по подбору материала, так и по
способу его изложения. Содержание книги хорошо видно из оглавления.
Чтобы выявить методические отличия, достаточно, например, ознако-
ознакомиться с изложением статики, важнейших разделов кинематики, вари-
вариационных принципов механики, теории канонических преобразований.
Трудно перечислить те учебники, монографии, статьи, под влия-
влиянием которых сложились методические взгляды автора. Очень важно
здесь также влияние собственного опыта научной и преподавательской
работы автора, научного и педагогического опыта его московских кол-
коллег и друзей. Список литературы, которая наиболее широко использо-
использовалась, дан в конце книги. Некоторые монографии, учебники и статьи
упомянуты в подстрочных замечаниях.
Предисловие ко второму изданию
Настоящее издание книги по сравнению с первым изданием, вы-
вышедшим в 1990 г., имеет следующие отличия.
Добавлена новая глава XII «Теория импульсивных движений» и § 6
главы XI «Переменные действие-угол», расширен п. 95, посвященный
эллиптическим интегралам и функциям, в § 4 главы XI добавлено не-
несколько новых примеров канонических преобразований, а в § 5 этой же
главы — новый п. 178, в котором рассматривается характеристическая
функция Гамильтона.
Кроме того, устранены некоторые замеченные опечатки и погреш-
погрешности изложения.
Автор благодарен читателем за внимание к первому изданию книги
и за доброжелательную критику, которая вполне учтена при подготовке
второго издания.
Введение
Механика — это наука о движении и взаимодействии материаль-
материальных тел. Под движением понимается механическое движение, т. е. изме-
изменение положения тел или частей тела в пространстве с течением вре-
времени. Основанная, как и всякая физическая наука, на наблюдении и
опыте, механика может быть разделена на наблюдательную (опытную)
и теоретическую.
Наблюдательная (опытная) механика входит в различные отделы
экспериментальной физики, астрономии, техники. В ней устанавли-
устанавливается связь между свойствами материальных тел, их движением и
причинами, вызывающими или изменяющими движение. Эти причи-
причины называют силами. Упомянутая связь формулируется в виде законов
движения, которые не являются математическими следствиями каких-
то изначальных истин, а представляют собой индуктивные положения,
основанные на большом числе согласующихся между собой опытных
фактов. Эти положения представляют собой утверждения о свойствах
движения материальных объектов, верные с той или иной точностью.
Теоретическая, или рациональная, механика опирается на некото-
некоторое конечное число законов, установленных в опытной механике, при-
принимаемых за истины, не требующих доказательства — аксиомы. Эти
аксиомы заменяют собой в теоретической механике индуктивные ис-
истины опытной механики. Теоретическая механика имеет дедуктивный
характер. Опираясь на аксиомы как на известный и проверенный прак-
практикой и экспериментом фундамент, теоретическая механика возводит
свое здание при помощи строгих математических выводов.
По Ньютону теоретическая механика «есть учение о движениях,
производимых какими бы то ни было силами, и о силах, требуемых
для производства каких бы то ни было движений, точно изложенное и
доказанное»1.
Теоретическая механика как часть естествознания, использующая
математические методы, имеет дело не с самими реальными матери-
материальными объектами, а с их моделями. Такими моделями, изучаемыми
в теоретической механике, являются материальные точки, системы ма-
материальных точек, абсолютно твердые тела, деформируемые сплошные
среды. В данной книге механика сплошных сред не рассматривается.
1Из предисловия к первому изданию знаменитого сочинения И. Ньютона «Мате-
«Математические начала натуральной философии» (см.: Крылов А. Н. Собрание трудов.
Т. 7, М.; Л.: Изд-во АН СССР, 1936, С. 2).
16
При изучении теоретической механики методически удобно раз-
разделить ее на кинематику и динамику; из динамики часто выделяют
еще статику. В кинематике движение изучается только с геометричес-
геометрической точки зрения; причины, обусловливающие движение, кинематика
не рассматривает. Изучением движения в связи с причинами, вызыва-
вызывающими или изменяющими его, занимается динамика. Как часть дина-
динамики статика изучает те условия, при которых материальные объекты
могут оставаться в покое; к статике относится также разработка спо-
способов эквивалентных преобразований систем сил. Подробнее о задачах,
изучаемых в кинематике, динамике и ее части — статике сказано в
соответствующих главах книги.
Часть I
КИНЕМАТИКА
Глава I
Кинематика точки и системы
§ 1. Основные понятия, задачи кинематики
1. Пространство и время. Механическое движение происходит
в пространстве и времени. В теоретической механике в качестве мо-
моделей реальных пространства и времени принимаются их простейшие
модели — абсолютное пространство и абсолютное время, существова-
существование которых постулируется. Абсолютные пространство и время счита-
считаются независимыми одно от другого; в этом состоит основное отличие
классической модели пространства и времени от их модели в теории
относительности, где пространство и время взаимосвязаны.
Предполагается, что абсолютное пространство представляет со-
собой трехмерное, однородное и изотропное неподвижное евклидово про-
пространство. Наблюдения показывают, что для небольших по размерам
областей реального физического пространства евклидова геометрия
справедлива.
Абсолютное время в теоретической механике считается непрерыв-
непрерывно изменяющейся величиной, оно течет от прошлого к будущему. Вре-
Время однородно, одинаково во всех точках пространства и не зависит от
движения материи.
Движение в его геометрическом представлении имеет относитель-
относительный характер: одно тело движется относительно другого, если расстоя-
расстояния между всеми или некоторыми точками этих тел изменяются. Для
удобства исследования геометрического характера движения в кинема-
кинематике можно взять вполне определенное твердое тело, т. е. тело, форма
которого неизменна, и условиться считать его неподвижным. Движение
других тел по отношению к этому телу будем в кинематике называть
абсолютным движением. В качестве неподвижного тела отсчета обычно
выбирают систему трех не лежащих в одной плоскости осей (чаще все-
всего взаимно ортогональных), называемую системой отсчета, которая
по определению считается неподвижной (абсолютной) системой отсче-
отсчета или неподвижной (абсолютной) системой координат. В кинематике
этот выбор произволен. В динамике такой произвол недопустим. За
единицу измерения времени принимается секунда: 1 с = 1/86 400 сут,
определяемых астрономическими наблюдениями. В кинематике надо
еще выбрать единицу длины, например 1 м, 1 см и т. п. Тогда основные
20 Глава I
кинематические характеристики движения: положение, скорость, уско-
ускорение, о которых будет идти речь дальше, определяются при помощи
единиц длины и времени.
Если некоторый определенный момент принять за начало отсчета
времени, то всякий другой момент времени однозначно определяется
соответствующим числом t, т. е. числом секунд, прошедших между
начальным и рассматриваемым моментом. Это число положительно или
отрицательно, смотря по тому, следует ли рассматриваемый момент
времени за начальным или предшествует ему, т. е. — оо < t < +00.
2. Материальная точка. Механическая система. Под мате-
материальной точкой понимается частица материи, достаточно малая для
того, чтобы ее положение и движение можно было определить как для
объекта, не имеющего размеров. Это условие будет выполнено, если
при изучении движения можно пренебречь размерами частицы и ее
вращением. Можно или нельзя принять материальный объект за мате-
материальную точку, зависит от конкретной задачи. Например, при опреде-
определении положения спутника Земли в космическом пространстве очень
часто целесообразно принимать его за материальную точку; если же
рассматриваются задачи, связанные с ориентацией антенн, солнечных
батарей, оптических приборов, установленных на спутнике, то его нель-
нельзя считать материальной точкой, так как в вопросах ориентации нель-
нельзя пренебрегать вращением спутника и его следует рассматривать как
объект, имеющий конечные, хотя и малые по сравнению с расстоянием
до Земли, размеры.
В теоретической механике материальная точка представляет со-
собой геометрическую точку, наделенную по определению механически-
механическими свойствами; эти свойства будут рассмотрены в динамике. В ки-
кинематике же материальная точка отождествляется с геометрической
точкой.
Геометрическое место последовательных положений движущейся
точки называется ее траекторией. Если при ti < t < ti траектория —
прямая линия, то движение точки прямолинейное, в противном слу-
случае криволинейное. В частности, движение точки на интервале време-
времени t\ < t < ti называют круговым, если на этом интервале траектория
точки лежит на окружности.
Механической системой, или системой материальных точек, или,
для краткости, просто системой мы будем называть выделенную
каким-либо образом совокупность материальных точек.
3. Задачи кинематики. Задать движение точки (системы) —
значит дать способ определения положения точки (всех точек, образу-
образующих систему) в любой момент времени.
Задачи кинематики состоят в разработке способов задания движе-
§ 2. Кинематика точки
21
ния и методов определения скорости, ускорения и других кинемати-
кинематических величин точек, составляющих механическую систему.
v
§ 2. Кинематика точки
4. Векторный способ задания дви-
движения точки. Рассмотрим движение ма-
материальной точки Р относительно некото-
некоторого тела, которое считается неподвижным.
Пусть О — точка, принадлежащая этому те-
телу. Радиус-вектор г движущейся точки Р
относительно О можно задать как вектор-
функцию времени: г = r(t). С течением вре-
времени конец вектора г описывает траекторию точки (рис. 1). Производ-
Производная от г
dt
называется скоростью точки Р. Производная от v
dv _ d2r
dt ~ dt2
Рис. 1
w =
A)
B)
называется ускорением точки Р.
5. Координатный способ задания движения точки. Пусть
Oxyz — неподвижная декартова прямоугольная система координат,
a i,j,k — орты ее осей Ox,Oy,Oz. Тогда вектор-функция r(t) может
быть задана тремя скалярными функциями x(t), y(t), z(t) — коорди-
координатами точки Р:
r(t)=x(t)i+y(t)j +z(t)k.
При этом для скорости имеем выражение
v(t) = -^ = vxi + vyj + vzk,
C)
где vx = x, vy = у, vz = z — проекции скорости v на оси Ox, Oy, Oz.1
Величина скорости v и ее направление определяются равенствами
V = \V
COS
У
D)
v,i)=y, cos(», j) = jj, cos(v,k) = y.
1 Производная по t какой-либо величины, являющейся функцией аргумента t, час-
часто обозначается точкой над соответствующим символом, обозначающим эту вели-
величину.
22
Глава I
Аналогично для ускорения w(t) получаем
w(t) = —jj = wxi + wyj + wzk, E)
где wx = x, wy = у, wz = z — проекции w на оси Ox,Oy,Oz. И тогда
w =
w
cos(w,i) = §, cos(w, j) = yj, cos(w,k) = ^.
F)
A
Рис. 2
Пример 1. Задан закон движения точки Р:
x = acosbt, у = asinbt, z = ct,
где a,b,c — постоянные. Найдем траекторию, ско-
скорость и ускорение точки.
Из первых двух равенств, возведя их в квадрат и
сложив, получим
9 9 9
х +у = а .
Это показывает, что точка движется по поверхности
у цилиндра радиуса а, ось которого совпадает с осью Oz
(рис. 2).
Пусть <р — угол между проекцией О А радиуса-
вектора ОР на плоскость Оху и осью Ох. Тогда
x = acosip, у = asinip, ip = bt,
a z = cip/b. Следовательно, прямая О А равномерно вращается, а точ-
точка Р •равномерно перемещается по образующей АР. Таким образом,
точка Р движется по винтовой линии.
Определим скорость точки Р. Имеем
х = — ab sin bt, у = ab cos bt, z = с;
v = л/х2 +y2 + z2 = Va2b2 + с2.
Величина скорости постоянна, но направление скорости изменяется со
временем.
Найдем ускорение точки. Имеем
x=—ab2cosbt, у = — ab2 sinbt, z = 0;
b2
w = л/х2 + у2 + z2 = ,
cos(w, г) = — cosbt, cos(w, j) = — sinbt,
cos(w,fc)=0.
Ускорение имеет постоянную величину и направлено по внутренней
нормали цилиндра (от Р к В; отрезок РВ параллелен АО).
i 2. Кинематика точки
23
Рис. 3
6. Естественный способ задания
движения точки. Пусть в пространстве
задана кривая, по которой движется точ-
точка Р. Для определения положения точки Р
на ее траектории возьмем произвольную
точку О\ кривой за начало отсчета дуг
и зададим положительное направление от-
отсчета (рис. 3). Каждому положению точ-
точки Р поставим в соответствие свою дуго-
дуговую координату а, аналогично тому как на прямолинейной оси каждой
точке отвечает своя абсцисса. Величина а будет положительной или от-
отрицательной в зависимости от направления отсчета дуг; при этом длина
дуги О\Р равна |<т|. Если а = a(t) — известная функция времени, то
движение точки Р задано. Такой способ задания движения точки на-
называется естественным. При этом мы будем предполагать, что a(t) —
дважды непрерывно дифференцируемая функция.
Получим выражения для скорости и
ускорения точки Р при естественном спо-
способе задания движения. Введем естествен-
естественный трехгранник, образованный единичны-
единичными векторами т, п, 6, составляющими пра-
правую тройку (рис. 4). Векторы тип лежат
в соприкасающейся плоскости траектории в
точке Р и направлены соответственно по ка-
касательной к траектории в сторону положи-
положительного отсчета дуг и по главной нормали
траектории в сторону ее вогнутости, век-
вектор Ъ направлен по бинормали траектории в
точке Р.
Радиус-вектор г точки Р относительно какой-либо фиксированной
точки будет сложной функцией времени: г = r(a{t)). Из дифференци-
дифференциальной геометрии известно, что
п,
Рис. 4
т(а =
dr_
где р — радиус кривизны траектории в точке Р. Используя определе-
определения A) и B) скорости и ускорения, получаем при помощи G)
v=
dr = drda
dt da dt
= ^
dv
dt
dvT
~dt'
v drda __ _
T da dt di
(8)
(9)
24 Глава I
Здесь введено обозначение vT = а. Величина vT положительна, если
точка Р движется в положительном направлении отсчета дуг О\Р, и
отрицательна в противном случае; v = \vT\. Согласно (8), скорость всег-
всегда направлена по касательной к траектории.
Из (9) следует, что ускорение всегда лежит в соприкасающейся
плоскости. Его можно записать в виде
w = wT + wn, wT = ~фт, wn = ^p-n, A0)
где wT — касательное {тангенциальное) ускорение, a wn — нормальное
ускорение точки. Формулы A0) выражают теорему Гюйгенса о разло-
разложении ускорения точки на тангенциальное и нормальное. Тангенциаль-
Тангенциальное ускорение характеризует быстроту изменения модуля скорости, а
нормальное — ее направления.
Величина ускорения определяется равенством
w = у го„ + w^.
Если v = const, то движение точки называется равномерным.
Движение будет ускоренным или замедленным в зависимости от то-
того, возрастает или убывает величина скорости. Так как v2 = v2 = fr2,
то dv2 jdt = 2(jcr. Отсюда следует, что движение будет ускоренным, если
знаки величин а и '& одинаковы, и замедленным, если их знаки проти-
противоположны. Если на интервале времени ii < t < t^ & = 0 (wT = 0),
то на этом интервале движение равномерное. Если на каком-то интер-
интервале wn = 0, a v ф 0, то на этом интервале движение прямолиней-
прямолинейное (р = оо).
Замечание 1. Из соотношений (8) и (9), в частности, следует, что
если вместо одной декартовой системы координат мы возьмем другую
декартову систему координат, неподвижную относительно первой, то
изменится векторное уравнение г = r(t) движения точки Р, но ско-
скорость и ускорение не изменятся.
Пример 1. Используя теорему Гюйгенса, найдем радиус кривизны эл-
эллипса
а2 Ъ2
в произвольной его точке.
Будем рассматривать эллипс как траекторию материальной точ-
точки с законом движения
x = acost, y = bs'mt.
§ 2. Кинематика точки
25
Из равенства
получаем такое выражение для радиуса кривизны:
,,2
р =
V
Учитывая, что
v = л/ж2 + у2 = v a2 sin2 t + b2 cos2 t,
w = л/ж2 + у2 = у a2 cos2 t + b2 sin2 t,
fdv\2_(a2-b2Jsm2tcos2t
получаем следующее выражение для радиуса кривизны как функции t:
(a2 sin2 t + b2 cos2 tf'2
Р =
ab
В частности, в вершинах эллипса, лежащих на оси Ох (для них
t = 0, тг), р = Ъ2/а, а в вершинах, лежащих на оси Оу (для них
t = тг/2, Зтг/2), р = а2/Ь.
7. Круговое движение. Пусть точка
движется по окружности радиуса R. Тогда
(см. рис. 5) а = Rip. Из (8) и A0) следует, что
2
v = Яфт, wT = Rip'r, wn = ^-n = (p2Rn.
Величины ф и ф называются соответственно уг-
угловой скоростью и угловым ускорением ради-
радиуса ОР (см. также п. 25). Введем обозначе-
обозначения ф = и), ф = е. Тогда для величины ускоре-
ускорения точки Р получаем выражение
w = л/го2 + го2 =
Рис. 5
Угол /3 между полным ускорением точки w и ее нормальным ускоре-
ускорением (рис. 5) находится из равенства
При равномерном круговом движении е = 0 и /3 = 0.
26
Глава I
X
Рис. 6
8. Скорость и ускорение точ-
точки в полярных координатах. Пусть
движение точки происходит в заданной
плоскости. Помимо декартовых коорди-
координат x(t), y(t) движение может быть зада-
задано, например, при помощи полярных ко-
координат (рис. 6). Пусть заданы функции
г = r(t), <p = <p(t). Найдем скорость и уско-
ускорение точки Р.
Пусть ег — единичный вектор, направ-
направленный вдоль радиуса-вектора г точки Р
относительно О в сторону возрастания ве-
величины г, a ev — вектор, получающийся из ег поворотом последнего
на угол тг/2 против часовой стрелки. Единичные векторы ег и ev за-
задают направления двух взаимно перпендикулярных осей: радиальной и
трансверсальной соответственно. В системе координат Оху векторы ег
и ev можно записать в следующем виде1:
e'r = (cos tp, sin ip), e^, = (-siniyj, cosiyj). A1)
Так как х = rcosiyj, у = rsiniyj, то в системе координат Оху имеем
v' = (х,у) = (rcosip — гф sin <p, r simp + гф cos <p), A2)
го' = (ж, у) = ((г — гф2) cos<p — (гф + 2гф) simp,
(г — гф2) simp + (гф + 2гф) costp).
A3)
Проекции vr и vv скорости на радиальную и трансверсальную оси
называются соответственно радиальной и трансверсалънои скоростями.
Из A1) и A2) имеем
vr = (v ¦ er) = г, vv = (v ¦ ev) = гф.
Для проекций ускорения аналогично получаем
wr = г — гф2, wv = гф + 2гф.
Пример 1. Движение точки задано в полярных координатах:
г = at, tp = bt (a, b = const).
Найдем траекторию, скорость и ускорение точки.
A4)
A5)
1Здесь, как и всюду в дальнейшем, под векторами мы понимаем векторы-
столбцы. Штрихом обозначается операция транспонирования.
i 2. Кинематика точки
27
Исключив из данных равенств время t, получим уравнение траекто-
траектории г = aip/b. Эта кривая называется спиралью Архимеда; у нее вели-
величина радиуса-вектора пропорциональна величине полярного угла. Далее
имеем
г = а, ф = Ь, г = О, ф = О.
Поэтому радиальная скорость vr постоянна и равна а, трансверсальная
скорость v,p = abt. Для величины скорости получаем v = \ v2 + v2 =
= ал/1 + b2t2. Для радиального и трансверсального ускорений из A5)
получаем выражения wr = —ab2t, wv = 2ab. Величина ускорения опре-
определяется равенством
w =
+w20 = аЬл
9. Криволинейные координаты. В предыдущем пункте мы ви-
видели, что движение точки по плоскости не обязательно задается только
декартовыми координатами; можно, например, задавать движение в по-
полярных координатах. Вообще, всякие три числа qi, qi, q%, однозначно
определяющие положение точки в пространстве, можно рассматривать
как координаты этой точки. Эти числа, в отличие от прямолинейных
декартовых координат, называют криволинейными координатами. Дви-
Движение точки считается заданным, если ее криволинейные координа-
координаты qi (г = 1,2,3) — известные функции времени qi(t).
Связь между декартовыми и
криволинейными координатами за-
задается равенством
г = r(q!, q2,
q3) = xi + yj + zk,
A6)
где x,y,z — функции gb q2, q3, ко-
которые считаем дважды непрерыв-
непрерывно дифференцируемыми. Радиус-
вектор г — сложная функция вре-
времени: г = r(qi(t), q2(t), q3(t)).
Пусть Pq — какая-либо точка
в пространстве, ее криволинейные
координаты обозначим дю, дго? (?зо-
Первой координатной линией, проходящей через Pq, назовем кри-
кривую Г = Г((?1, 520; (?3о); ПОЛуЧЭЮЩуЮСЯ ИЗ A6) При фИКСИроВЭННЫХ
<7г, Gз и при изменении q\ в некотором интервале. Аналогично опре-
определяются вторая и третья координатные линии. Касательную к г'-ой
Рис. 7
28 Глава I
координатной линии в точке Pq называют г-й координатной осью, про-
проходящей через Pq. Единичный вектор i-й координатной оси (рис. 7)
может быть записан в виде
е. = J_dr dr = дх i | ду dz k
1 Hi dq,' dq, dq, dqt dqt '
dr_
2
dx] (dy\ (dz.
\dqij \dqt
Величины Hi называются коэффициентами Ламе. Производные в A7)
вычисляются в точке Pq.
Если векторы е\, ег, ез взаимно ортогональны, то криволинейные
координаты называют ортогональными. Мы будем рассматривать толь-
только ортогональные криволинейные координаты. Найдем проекции vqi
и wqi (г = 1, 2, 3) скорости v и ускорения w точки Р на оси кри-
криволинейной системы координат. Из A), A6), и A7) получаем
где величины vqi вычисляются по формулам
vqi=Hiqi (г = 1, 2, 3). A9)
Для нахождения величины wqi, равной скалярному произведению
w • е,-, заметим, что она, согласно B) и A7), может быть представлена
в виде
w . = — ¦ е, = — (— ¦ —} = — \— (v ¦ —} - v ¦ — (—\\
B0)
Далее,
d (дг\ _ д2г ,
а из A8) получаем
dv _ d2r
Ввиду того, что г — дважды непрерывно дифференцируемая функ-
функция от gi, g2; (?з5 можно менять порядок дифференцирования по qu
§ 2. Кинематика точки 29
(к = 1, 2, 3) и д^. Поэтому из B1) и B2) следует, что
d I дг_\ _ dv^
dt [dqj ~ %•
Кроме того, из A8) вытекает равенство
дл = dv_ B4)
dqt дщ
Используя B3), B4), равенство B0) можно записать в виде
w -JL\A(v.dv\v.dv
W« " Щ [dt [V dqj V
Если теперь ввести обозначение Т = v2 /2, то выражение для wqi можно
записать в следующем окончательном виде:
_ A 2 з^
dqi dqi) ^-1'2'^-
Пример 1. Найдем скорость и ускорение точки в цилиндрической и сфе-
сферической системах криволинейных координат. В случае цилиндрической
системы координат (рис. 8) полагаем qi = r, qi = <p, q% = z, и тогда
х = rcosiyj, у = rsiniyj, z = z; Hr = 1, Hv = r, Hz = 1;
vr = r, vip= гф, vz = z; B6)
T=I(f2+rV+i2); B7)
wr = r — rip2, wv = гф + 2гф, wz = z. B8)
В случае сферической системы координат (рис. 9) q\ = r, qi = f, 9з = в,
и х = г sin в cos tp, у = rsin#sini^, z = г cos в; Hr = 1, Н^ = rsin#,
Нв = г;
vr = f, vv = гитвф, vg = гв; B9)
Т = 1 (> + r2 gin2 0ф2 + Г2^2^ . C0)
wr = г — г sin2 0tp2 — гв2, Wp = r sin вф + 2 sin вгф + 2r cos вфв, C1)
гое = г^' + 2гв - г sin в cos #<^2.
30
Глава I
<P
Рис. 8
Рис. 9
Пример 2. Пусть материальная точка движется равномерно по поверх-
поверхности сферы радиуса а. Точка начинает движение на экваторе, направ-
направление ее скорости v образует с меридианами сферы постоянный угол а.
Найдем уравнение траектории точки (локсодромы), а также момент
времеии т, в который точка достигает полюса сферы.
Положение точки на сфере зададим при помощи координат <р, в
(рис. 9). Из формул B9) имеем
vv = a sin вф, vg = ав.
Без ограничения общности примем, что движение точки начинается
на оси Ох (т. е. при t = 0, <р = 0, в = тг/2), угол в во время движения
уменьшается от тг/2 до 0, а ф > 0.
Так как направление скорости v пересекает меридиан <р = const
под углом а, то ctga = —ve/vv, что приводит к дифференциальному
уравнению
^- = - ctga sin0.
dip
Проинтегрировав это уравнение с учетом упомянутых выше начальных
условий, получим уравнение локсодромы в виде
Так как при в = 0 <р = оо, то локсодрома делает около полюса бесчис-
бесчисленное множество витков. Однако общая длина дуги локсодромы конеч-
конечна. Найдем ее. Имеем
ds = a\Jd02 + sin2 в dtp2 = -a d9\/l
a = -
ad0
cos a"
§ 3. Общие основания кинематики системы 31
Так как вся дуга I локсодромы соответствует изменению в от тг/2
до 0, то I = _ wa—. Поскольку движение точки равномерное, то время
движения т будет равно _. 7га—.
2v cos a
§ 3. Общие основания кинематики системы
10. Свободные и несвободные системы. Связи. Рассмот-
Рассмотрим движение системы материальных точек Pv [и = 1, 2,... ,N) от-
относительно некоторой прямоугольной декартовой системы координат,
предполагаемой неподвижной. Состояние системы задается радиусами-
векторами rv и скоростями vv ее точек. Очень часто при движении
системы положения и скорости ее точек не могут быть произвольны-
произвольными. Ограничения, налагаемые на величины rv и vv, которые должны
выполняться при любых действующих на систему силах, называются
связями. Если на систему не наложены связи, то она называется сво-
свободной. При наличии одной или нескольких связей система называется
несвободной.
Пример 1. Материальная точка может двигаться только в заданной
плоскости, проходящей через начало координат. Если ось Oz декарто-
декартовой системы координат направить перпендикулярно плоскости, в ко-
которой движется точка, то z = 0 — уравнение связи.
Пример 2. Точка движется по сфере переменного радиуса R = fit) с
центром в начале координат. Если х, у, z — координаты движущейся
точки, то уравнение связи имеет вид х2 + у2 + z2 — f2(t) = 0.
Пример 3. Две материальные точки Pi и Рг связаны нерастяжимой
нитью длиной I. Связь задается соотношением I2 — (п — гг) ^ 0.
Пример 4. Материальная точка может двигаться в пространстве,
оставаясь внутри или на границе первого октанта. Связь задается тре-
тремя неравенствами: х ^ 0, у ^ 0, z ^ 0.
Пример 5 (Движение конька по льду). Пусть конек движется по
льду, расположенному в горизонтальной плоскости. Конек будем моде-
моделировать тонким стержнем, одна из точек которого, например С на
рис. 10, во все время движения имеет скорость, направленную вдоль
стержня. Если ось Oz направлена вертикально, х, у, z — координаты
точки С, a if — угол, который образует стержень с осью Ох, то связи
задаются двумя соотношениями: z = 0,y = xtgip.
32
Глава I
О
Рис. 10
В общем случае связь задается соот-
соотношением1 /(rv, vv, t) ^ 0. Если в этом
соотношении реализуется только знак ра-
равенства, то связь называется удерживаю-
удерживающей {двусторонней, неосвобождающей). В
примерах 1, 2, 5 связи удерживающие. Ес-
Если же реализуется как знак равенства,
так и знак строгого неравенства, то связь
называется неудерживающей (односторон-
(односторонней, освобождающей). В примерах 3, 4 свя-
связи неудерживающие. Системы с неудер-
живающими связями в дальнейшем не рассматриваются.
Если уравнение связи можно записать в виде f(rv, t) = 0, не со-
содержащем проекции скоростей точек системы, то связь называется гео-
геометрической (конечной, голономной). В примерах 1, 2 связи геометри-
геометрические. Если же в уравнение связи /(rv, vv, t) = 0 входят проекции
скоростей vv, то связь называется дифференциальной (кинематичес-
(кинематической). Дифференциальную связь /(г„, »„, t) = 0 называют интегрируе-
интегрируемой, если ее можно представить в виде зависимости между координа-
координатами точек системы и временем (как в случае геометрической связи).
Неинтегрируемую дифференциальную связь называют еще неголоном-
ной связью.
Комментарий 1. В примере 5 дифференциальная связь у = xtg ip неин-
тегрируемая. Покажем это. Предположим противное, т. е. что х, у, <р
связаны соотношением f(x, у, <р, t) = 0. Пусть х, у, <р отвечают ре-
реальному движению конька. Вычислим полную производную / по времени
ox ay dip at
Используя уравнение связи, / можно записать в виде
Отсюда, ввиду независимости величин х, ф, получаем равенства
ох
U
ду
1 Обозначением f{rv, vv, t) мы пользуемся для краткой записи функции
/(ri,... , rjv, vi,... , ujv, t). Функция / имеет в общем случае 6iV + 1 аргумен-
аргументов: 3-/V координат ж„, yv, zv точек Р„, 3N проекций их скоростей ж„, уи, Zv и
время t. Функцию / предполагаем дважды непрерывно дифференцируемой.
§ 3. Общие основания кинематики системы 33
Ввиду произвольности угла <р из этих равенств следует, что частные
производные функции / по всем ее аргументам равны нулю, т. е. / не
зависит от х, у, <р, t. Следовательно, предположение об интегрируе-
интегрируемости связи у = xtgip неверно.
Неинтегрируемостъ связи в рас-
рассматриваемой задаче можно показать
без вычислений, а исходя только из
простых геометрических соображений.
Во-первых, из уравнения связи следу-
следует, что в случае ее интегрируемости в
уравнение эквивалентной геометричес-
геометрической связи время t явно не должно вхо-
входить, а угол <р обязательно должен вой-
войти, т. е. эквивалентная геометричес-
геометрическая связь должна записываться в ви-
виде f(x, у, ф) = 0, где функция / не
должна быть тождественно равной нулю при произвольных фиксиро-
фиксированных значениях х, у. Во-вторых, движение конька, при котором его
точка С перемещается по окружности с центром, лежащим на перпен-
перпендикуляре к полозу конька в точке С, не нарушает связи у = xtgip, так
как при таком движении скорость точки С направлена вдоль полоза
конька. Пусть в начальном положении конька х = xq, у = уо, <р = <ро, а
в конечном х = х\, у = у\, <р = <pi. Если связь интегрируема и записы-
записывается в виде f(x, у, tp) = 0, то f(x0, y0, tpQ) = 0 и /(жь уг, fi) = О,
так как уравнение связи должно выполняться в любом положении конь-
конька. На рис. 11 показана одна из многих возможных траекторий точ-
точки С при движении конька из начального положения в конечное. На
этом рисунке ОС0 ± А0В0, ОС ± А'В', ОСХ ± A±B±, O"O ± А"В",
О'С = О'О, О"С\ = О"О. Перемещение конька из начального поло-
положения в конечное происходит так, что точка С конька (обозначенная
на рис. 11 в разных положениях символами Со, С, О, С\) сначала дви-
движется по дуге СотС окружности с центром О, затем по дуге С'пО
окружности с центром О' и, наконец, по дуге ОрС± окружности с цент-
центром О". Если зафиксировать конечные координаты х\, у\ точки С, а
конечное значение угла tpi изменять в некотором интервале, то в этом
интервале f(x\, у\, <р\) = 0. Но, согласно сказанному выше, функция f
не может тождественно равняться нулю при произвольных фиксирован-
фиксированных значениях х, у. Противоречие говорит о неинтегрируемости рас-
рассматриваемой дифференциальной связи.
Если на систему материальных точек не наложены дифференци-
дифференциальные неинтегрируемые связи, то она называется голономной. Если
34 Глава I
же среди связей, наложенных на систему, есть дифференциальные не-
интегрируемые связи, то система называется неголономной.
В дальнейшем, при изучении движения неголономных систем, мы
будем предполагать, что соответствующие им дифференциальные свя-
связи линейны относительно проекций xv, yv, zv скоростей точек систе-
системы. Как геометрических, так и дифференциальных связей, наложен-
наложенных на систему, может быть несколько. Таким образом, в дальнейшем
мы будем изучать движение свободных механических систем или не-
несвободных систем со связями, аналитическое представление которых
имеет вид
fa(rv,t) = O (а = 1,2,..., г), A)
a0v ¦ vv + a0 = О (/3 = 1, 2,...,в). B)
Векторы apv и скаляры ар — заданные функции от п, гг,... , гм и t.
В частных случаях г и s могут быть равными нулю.
Геометрические связи называются стационарными или склероном-
склерономными, если t не входит в их уравнения A). Дифференциальные связи B)
называются стационарными или склерономными, если функции ари не
зависят явно от t, а функции ар тождественно равны нулю. Система
называется склерономной, если она либо свободная, либо на нее нало-
наложены только стационарные связи. Система называется реономной, если
среди наложенных на нее связей есть хотя бы одна нестационарная.
Комментарий 2. В примере 1 рассмотрена голономная склерономная, в
примере 2 — голономная реономная, в примере 5 — неголономная скле-
склерономная системы.
11. Ограничения, налагаемые связями на положения, ско-
скорости, ускорения и перемещения точек системы. Точки несво-
несвободной системы не могут двигаться в пространстве совершенно произ-
произвольно. Их совместимые со связями (допускаемые связями) координа-
координаты, скорости, ускорения и перемещения должны удовлетворять неко-
некоторым соотношениям, вытекающим из уравнений связей A), B).
Пусть задан какой-то момент времени t = t*. Положения систе-
системы, для которых радиусы-векторы rv = г* точек, образующих сис-
систему, удовлетворяют уравнениям геометрических связей A), назовем
возможными положениями системы для данного момента времени.
Связи налагают ограничения и на скорости точек системы. Чтобы
записать эти ограничения в аналитической форме, продифференциру-
продифференцируем обе части A) по времени, считая rv функциями t. Тогда получим
§ 3. Общие основания кинематики системы 35
следующие дифференциальные связи, вытекающие из геометрических
связей A):
v=l
Совокупность векторов vv = v*, удовлетворяющая линейным уравне-
уравнениям B) и C) в возможном для данного момента времени положении
системы, назовем возможными скоростями для этого момента времени.
Для получения аналитического выражения ограничений, налагае-
налагаемых связями на ускорения точек системы, продифференцируем равен-
равенства C) и B) по времени. Имеем1
Е тпг w- + Е
г/=1 <-" г/ v,fi=\ u'i'ulfi v=l
(a = l, 2,... , r),
v=i dt v=13vv (g)
= 0 {0 = 1,2,..., s).
Совокупность векторов wv = w*, удовлетворяющая линейным
уравнениям D) и E) при возможных для данного момента времени
положении и скоростях точек системы, назовем возможными ускорени-
ускорениями для этого момента времени.
Заметим, что величину SN — r — s следует считать положительной,
так как в противном случае ограничения, налагаемые связями, были
бы настолько жесткими, что согласованное со связями движение точек
материальной системы было бы либо вообще невозможным, либо долж-
должно было происходить по заранее заданному закону во времени. Поэтому
число линейных уравнений, определяющих проекции возможных ско-
скоростей и ускорений, превосходит число этих проекций. Следовательно,
для данного момента времени существует бесконечное множество воз-
возможных скоростей v* и возможных ускорений w*.
Пусть в данный момент времени t = t* система находится в каком-
либо положении, определяемом радиусами-векторами rv = г*, и име-
имеет какие-то возможные скорости v* и возможные ускорения w*. Воз-
Возможному в момент t* + At положению системы отвечают радиусы-
векторы г* + Arv точек системы. Величины Arv — возможные переме-
перемещения системы за время At из ее возможного положения, задаваемого
1При получении равенств C)-E) предполагается, что соответствующие произ-
производные функций fa, a/jy и ар существуют и непрерывны.
36 Глава I
радиусами-векторами г* в момент t = t*. Для достаточно малых At
возможные перемещения точек системы можно1 представить в виде
суммы:
Arv = vtAt+\w*v{Atf + ... (i/ = l, 2,..., N). F)
Здесь не выписаны слагаемые, порядок которых относительно At выше
второго. Так как множество возможных скоростей и ускорений беско-
бесконечно, то бесконечно и множество возможных перемещений.
Пренебрежем в F) величинами выше первого порядка относитель-
относительно At; тогда Arv = v*At. Если уравнения C) и B), которым удовлетво-
удовлетворяют возможные скорости v*, умножить на At, то получим систему
уравнений, которой удовлетворяют линейные по At возможные пере-
перемещения:
J2^-Arv + ^At = 0 (a = l, 2,..., г), G)
N
^2 a&v ¦ Arv + apAt = О (/3 = 1, 2,... , s). (8)
Функции apv, ар в (8) и частные производные в G) вычисляются
при t = t*, rv = г*.
Пример 1. Точка Р движется по неподвижной поверхности (рис. 12).
В этом случае возможной скоростью v* будет любой вектор, лежащий
в касательной плоскости к поверхности в точке Р и проходящий через
эту точку. Если пренебречь в F) величинами выше первого порядка от-
относительно At, то Ar = v* At. Любой вектор, построенный из точки Р
и лежащий в касательной плоскости, будет возможным перемещением.
Если поверхность задается уравнением /(г) = 0, то все возможные пе-
перемещения ортогональны нормали к поверхности, т. е. Дг-grad/ = 0.
Пример 2. Точка Р движется по подвижной или деформирующейся по-
поверхности, все точки которой имеют скорости и 2 (рис. 13). В этом
случае возможная скорость уже не лежит в касательной плоскости.
Возможных перемещений опять бесконечное множество. Если пренеб-
пренебречь величинами порядка (At) и выше, то все они получаются добавле-
добавлением вектора uAt к каждому из возможных перемещений предыдущего
примера. В этом случае уже соотношение Аг • grad/ = 0 не выполня-
выполняется при любых Аг.
1Для этого достаточно, чтобы функции rv(t) имели непрерывные производные
третьего порядка включительно.
2Так будет, например, когда поверхность явл;
жется поступательно со скоростью и (см. п. 22).
до третьего порядка включительно.
2Так будет, например, когда поверхность является недеформирующейся и дви-
> 3. Общие основания кинематики системы 37
и
Рис. 12 Рис. 13
12. Действительные и виртуальные перемещения. Син-
Синхронное варьирование. Пусть в момент времени t = t* система на-
находится в положении, задаваемом радиусами-векторами ее точек r*o, a
скорости точек имеют некоторые конкретные возможные значения v*Q.
Если заданы силы, действующие на систему, то, проинтегрировав сис-
систему дифференциальных уравнений движения, можно получить зна-
значения радиусов-векторов rv точек системы для моментов времени t,
следующих за t*. Если обозначить dt приращение времени t — t*, то
приращения радиусов-векторов точек системы можно представить в
виде
r (f* -Л- flf) — r (f*\ — ,,* fit _|_ I?#)* (fitJ 4- (Q)
где w*o — ускорения точек системы при t = t*; многоточием обо-
обозначены величины выше второго порядка относительно dt. Величи-
Величины (9) суть действительные (истинные) перемещения точек системы
за время dt. Действительное перемещение, естественно, является од-
одним из возможных. Если пренебречь членами порядка (dt) и выше,
то действительное перемещение будет дифференциалом функции rv(t),
т. е. rv(t* + dt) — rv(t*) = drv = v*Qdt. В этом случае действительные
перемещения удовлетворяют уравнениям, аналогичным G) и (8):
JV
JV
^2 «a*/ • drv + apdt = 0 (/3 = 1, 2,... , s). A1)
Уравнения A0) и A1) получаются умножением обеих частей уравне-
уравнений C) и B) на dt. Величины dfa/drv, dfa/dt, ар„, ар в A0), A1)
вычисляются при t = t*, rv = r*Q. В дальнейшем под действитель-
действительными перемещениями точек системы за время dt будем понимать их
38 Глава I
бесконечно малые перемещения, линейные по dt; они удовлетворяют
уравнениям A0), A1).
Помимо действительных перемещений, в теоретической механике
принципиальное значение имеют так называемые виртуальные пере-
перемещения. Пусть при t = t* система занимает некоторое свое возмож-
возможное положение, определяемое радиусами-векторами ее точек г*. Вирту-
Виртуальным перемещением системы называется совокупность величин 8rv,
удовлетворяющая линейным однородным уравнениям
N
У J -a • и*",
v=\ V
N
, - 0 (a -
, = 0 (/3 =
1, 2,..
1, 2,...
¦,r),
• , s),
A2)
A3)
где величины dfa/дг^ и apv вычислены при t = t*, rv = r*.
Остановимся на введенном понятии виртуального перемещения
подробнее. Величина 8rv, задается проекциями 8xv, 8yv, 8zv. Так как
число неизвестных 8xv, 8yv, 8zv (у = 1, 2,... , N) превосходит чис-
число уравнений A2), A3), которым они удовлетворяют, то количество
виртуальных перемещений бесконечно. Из A0), A1) и A2), A3) следу-
следует, что для склерономной системы действительное перемещение будет
одним из виртуальных.
Пусть 8xv, 8yv, 8zv — бесконечно малые величины. Из G), (8)
и A2), A3) видно, что множество линейных относительно At воз-
возможных перемещений склерономной системы совпадает с множест-
множеством ее виртуальных перемещений. Можно сказать, что виртуальные
перемещения — это возможные перемещения при «замороженных»
(t = t* = const) связях.
Комментарий 3. В примерах 1 и 2 п. 11 множества виртуальных пере-
перемещений одинаковы и представляют собой совокупность построенных
из точки Р векторов 8г, лежащих в проходящей через Р касательной
плоскости к поверхности, по которой движется материальная точка.
Бесконечно малые приращения 8xv, 8yv, 8zv называются вариация-
вариациями величин хи, yv, zv. Переход при фиксированном t = t* из положения
системы, определяемого радиусами-векторами г*, в бесконечно близ-
близкое положение, определяемое радиусами-векторами г* + 8rv, называ-
называется синхронным варьированием. При синхронном варьировании мы не
рассматриваем процесс движения и сравниваем допускаемые связями
бесконечно близкие положения (конфигурации) системы для данного
фиксированного момента времени.
§ 3. Общие основания кинематики системы 39
Рассмотрим две совокупности возможных перемещений с одним и
тем же значением величины At. Согласно F),
Возможные скорости v*. и возможные ускорения w*. (i = 1, 2) удов-
удовлетворяют уравнениям B) — E). Подставим в C) величины t = t*,
rv = г*, vv = v*t и умножим обе части этого равенства на At, затем
подставим в C) величины t = t*, rv = г*, vv = v*2 и снова умножим
на At. Если теперь из первого результата вычесть второй, то получим
равенства
t
Е it ¦ « " О At = ° (« = 1, 2,... , г). A4)
Аналогично из B) получаются равенства
N
Е afb> ¦ « - О Ai = ° (/3 = 1, 2,... , s). A5)
Если теперь подобную процедуру проделать с уравнениями D) и E)
(только надо будет еще подставить wv = w*. (i = 1, 2), а умножить
на 1/2(Д?) ), то придем к равенствам
N 8f {AtJ N
A6)
f
A7)
(a = l, 2,... , r; /3 = 1, 2,... , s).
40 Глава I
Составим теперь разность двух возможных перемещений:
Ах rv - Д2 г„ = « - О At + « - <) ^- + ... A8)
Если 8vv = v*± —v*2 ф 0, то главная часть величины A8) линейна по At.
Она равна 8vvAt и, согласно A4), A5), удовлетворяет уравнениям A2)
и A3), т. е. совокупность величин
8rv = 8vvAt (v = l,2,...,N) A9)
будет виртуальным перемещением. Синхронное варьирование A9),
предполагающее v*± ф v*2, называется варьированием по Журдену.
Если же v*± = v*2, но 8wv = w^ — w*2 ф 0, то главная часть
разности A8) равна 8wv—ц—. И, так как в A6), A7) все суммы, кроме
первых, при v*± = v*2 обращаются в нуль, главная часть разности A8),
согласно A6), A7) и A2), A3), будет виртуальным перемещением
8rv = \5wv{Atf (i/ = l, 2,..., N). B0)
Такое синхронное варьирование, в котором предполагается, что
v*t = v*2, a w*x ф w*2, называется варьированием по Гауссу.
13. Число степеней свободы. Виртуальные перемещения
8xv, 8yv, 8zv (у = 1, 2,... , N) удовлетворяют г + s уравнениям A2),
A3). Число независимых виртуальных перемещений системы называ-
называется ее числом степеней свободы. Число степеней свободы мы будем
всюду обозначать п. Ясно, что п = 2>N — г — s.
Пример 1. Одна свободная точка в пространстве имеет три степени
свободы.
Пример 2. Система, состоящая из двух точек, связанных стержнем,
движущимся в плоскости, имеет три степени свободы.
Пример 3. Конек, движущийся по льду {пример 5 из п. 10), имеет две
степени свободы.
Пример 4. Материальная точка, движущаяся по подвижной или непо-
неподвижной поверхности, имеет две степени свободы.
Пример 5. Система двух стержней, соединенных шарниром и движу-
движущихся в плоскости {ножницы), имеет четыре степени свободы.
14. Обобщенные координаты. Рассмотрим несвободную систе-
систему со связями A), B). Будем предполагать, что г функций /„ от 2>N
§ 3. Общие основания кинематики системы
41
аргументов ж„, yv, zv (у = 1, 2,... , N) независимы (время t здесь
рассматривается как параметр). В противном случае одна из связей
противоречила бы остальным или была бы их следствием.
Наименьшее число параметров, необходимое для задания возмож-
возможного положения системы, называется числом ее независимых обобщен-
обобщенных координат. Так как функции fa (а = 1,... , г) независимы, то
число обобщенных координат, которое мы будем обозначать то, рав-
равно 3N — г. За обобщенные координаты можно принять то из 3N декар-
декартовых координат ж„, yv, zv, относительно которых можно разрешить
систему уравнений A). Однако, как правило, такой выбор обобщенных
координат практически мало пригоден. Можно ввести любые другие то
независимых величин qx, q2, ••• , Qm, в своей совокупности определя-
определяющих конфигурацию системы. Они могут быть расстояниями, углами,
площадями и т. п., а могут и не иметь непосредственного геометри-
геометрического толкования. Требуется только, чтобы они были независимы, а
декартовы координаты ж„, yv, zv точек системы можно было выразить
через qx, q2, ... , qm и t:
rv = rv(q!, q2, ... , qm, t) [y = 1, 2,... , N).
B1)
Эти функции, будучи подставленными в уравнения A), обращают их в
тождества. Ранг матрицы
дхг/dqi
dxx/dqm
dyx/dqm
dz1/dqm
dxN/dqx ... dxN/dqn
dzNjdqx
dzN/dqn
B2)
равен то. Это следует из того, что среди 3N функций х„, у„, zv из B1)
от т аргументов qx, q2,-.- , qm (t — параметр) имеется то независи-
независимых, через которые могут быть выражены все остальные координаты
точек системы.
Мы будем предполагать, что обобщенные координаты qx,q2, ¦ ¦ ¦ ,qm
выбраны так, чтобы любое возможное положение системы могло быть
получено из B1) при некоторых значениях величин qx, #25--- , qm. Ес-
Если это не удается сделать сразу для всех возможных положений систе-
системы, то обобщенные координаты вводятся локально, т. е. для различных
совокупностей возможных положений вводятся различные системы об-
обобщенных координат.
42 Глава I
Функции B1) будем предполагать дважды непрерывно дифферен-
дифференцируемыми функциями всех своих аргументов. Кроме того, будем счи-
считать, что если система склерономна, то время t не входит в зависимос-
зависимости B1), чего всегда можно добиться соответствующим выбором обоб-
обобщенных координат.
При исследовании конкретных задач механики очень часто совсем
нет необходимости составлять уравнения связей A). Из физической
сущности задачи обычно ясно, как надо выбрать обобщенные координа-
координаты в таком количестве, которое необходимо и достаточно для задания
возможных положений системы. Если же зависимости B1) требуют-
требуются при решении задачи, то они составляются, как правило, с помощью
геометрических соображений.
15. Координатное пространство. Для каждого момента време-
времени t между возможными положениями системы и точками то-мерного
пространства (qi, Чз-,--- , Чт) устанавливается взаимно однозначное
соответствие. Пространство (qi, Чъ-,--- , Чт) называется координат-
координатным пространством (или пространством конфигураций). Каждому воз-
возможному положению системы отвечает некоторая точка координатного
пространства, которую будем называть изображающей точкой. Движе-
Движению системы соответствует движение изображающей точки в коорди-
координатном пространстве.
Близость точек координатного пространства определяется естест-
естественным образом через близость соответствующих положений системы.
Между положениями системы и точками координатного пространст-
пространства устанавливается таким путем взаимно однозначное и непрерывное
соответствие.
Пример 1 (Материальная точка движется по плоскости). Коорди-
Координатное пространство — сама эта плоскость.
Пример 2 (Система N свободных точек в пространстве). Ко-
Координатное пространство есть 3N-мерное евклидово пространство
(xi, 2/i, zi,... , xN, 2/jv, zN).
Пример З (Маятник). Положение маятника, представляющего со-
собой твердый стержень, подвешенный за один из концов к неподвиж-
неподвижной точке, задается углом <р (рис. 14), который примем за обобщен-
обобщенную координату. Поставим в соответствие каждому положению ма-
маятника точку на числовой оси, имеющую координату <р. Такое соот-
соответствие между положениями маятника и точками числовой оси не
будет взаимно однозначным, так как разным точкам оси <р и <р + 2ктт
(к = ±1, ±2,...) соответствует одно и то же положение маятника.
Однозначности можно добиться, выделив на числовой оси полуоткры-
полуоткрытый интервал 0 ^ <р < 2тг. Но при этом нарушается непрерывность
j 3. Общие основания кинематики системы
43
О 2л <Р
О
2л <р
Рис. 14
Рис. 15
соответствия, так как два близких положения маятника, для кото-
которых 1р = 0и1р = 2тт — е,не будут соответствовать близким точкам на
выделенном полуинтервале. Чтобы восстановить непрерывность, нуж-
нужно считать точки ip = О и ip = 2тг тождественными. Наглядно это
можно сделать, «склеив» точки ip = О и ip = 2тг. Полученный геомет-
геометрический образ — окружность и будет координатным пространством
маятника.
Пример 4 (Двойной маятник). Он состоит из двух соединенных шар-
шарниром твердых стержней, один из которых подвешен за свободный ко-
конец к неподвижной точке А (рис. 15). В остальном стержни могут
свободно перемещаться в одной плоскости. За обобщенные координа-
координаты можно принять углы <f и ф, образуемые стержнями с вертикаль-
вертикальным направлением. Каждому положению маятника ставятся в соот-
соответствие два значения <f и ф, определенных с точностью до чисел,
кратных 2тг. Поэтому если мы возьмем в плоскости <р, ф квадрат со
стороной 2тг и отождествим в нем противоположные стороны, то по-
получим координатное пространство двойного маятника. Наглядно это
можно сделать, «склеив» противоположные стороны квадрата. После
первой склейки получится цилиндр, а после второй — искомый геомет-
геометрический образ — тор.
Пример 5 (Две связанные стержнем материальные точки, движу-
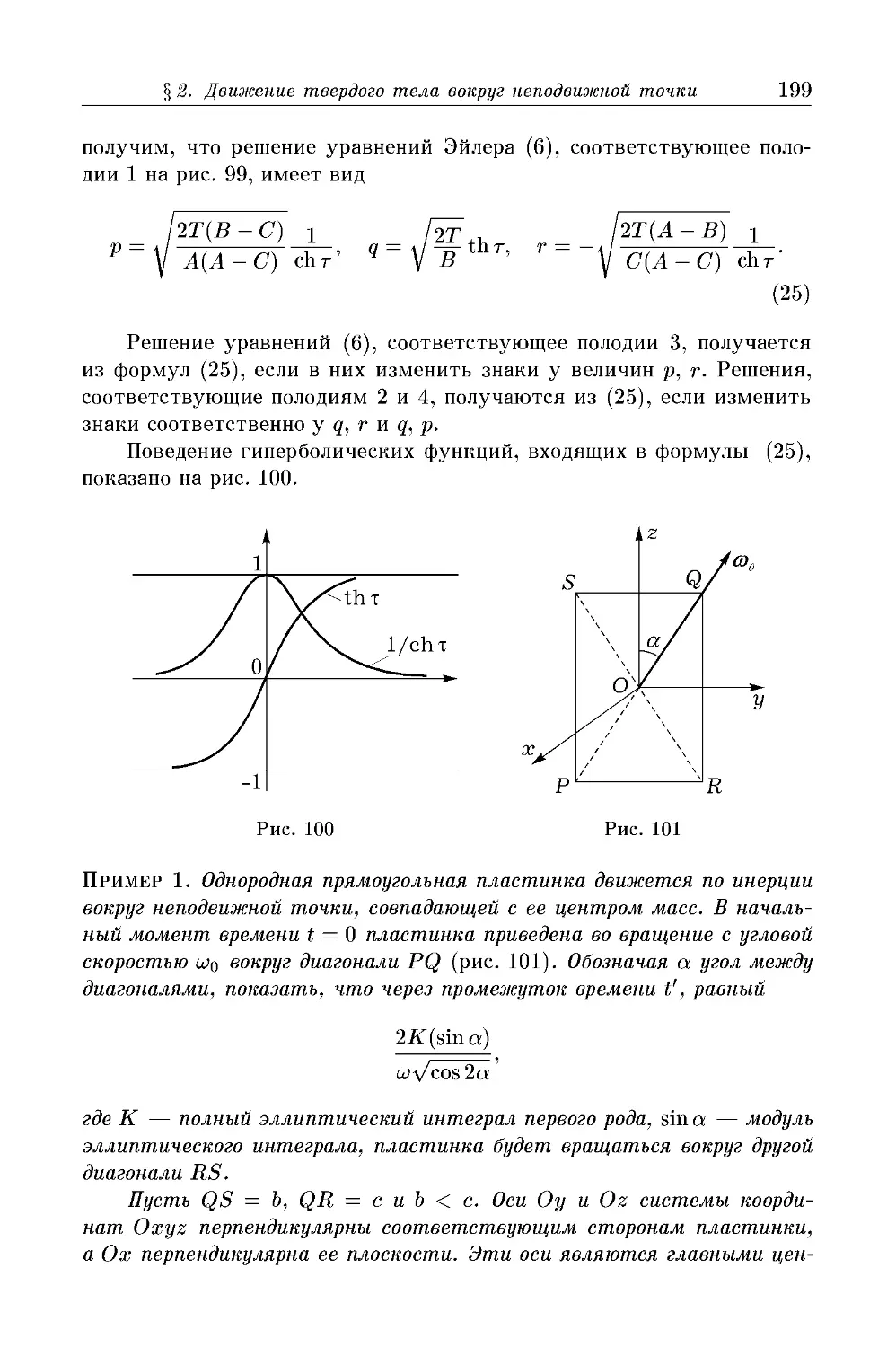
движущиеся по плоскости (рис. 16)). За обобщенные координаты мож-
можно принять декартовы координаты х, у одной из точек и угол ip,
который образует стержень с осью Ох. Координатное пространство
есть слой в пространстве (х, у, ip), заключенный между плоскостя-
плоскостями if = 0 и ip = 2тг, противоположные точки которого отождествлены.
44
Глава I
У"
о
X
Рис. 16
Здесь, в отличие от примеров 3 и 4, наглядное отождествление плос-
плоскостей if = О и if = 2тг путем склеивания получить нельзя.
16. Обобщенные скорости и ускорения. При движении систе-
системы ее обобщенные координаты изменяются со временем. Величины tjj
и ijj (j = 1, 2,... , то) называются соответственно обобщенными ско-
скоростями и обобщенными ускорениями. Скорости и ускорения точек сис-
системы в декартовой системе координат найдем, продифференцировав
сложные вектор-функции времени B1):
= rv =
drv . drv
= l, 2,... , N),
B3)
d2rv . , d2rv
in in о
ov = rv = у -к—q] + У -к—н—qjqk + 2 > -к—Q.47 . „ 9
^ dqj J ^ dqidqhJ *-*< dqjdtJ dt2
B4)
(«/ = !, 2,..., N).
Справедливы следующие равенства, которые будут использованы в
дальнейшем:
drv _ drv
dqk dqk'
A_(drv
dt
drv
(k = l, 2,... , to).
B5)
Первое из этих равенств сразу следует из B3). Второе равенство
легко проверить дифференцированием, если использовать B3) и воз-
возможность изменения порядка дифференцирования функции г„ по ее
аргументам. Последнее возможно, так как г„ предполагается дважды
непрерывно дифференцируемой функцией. Получаем
d (dvv
dt
= ?
d2rv . , d2rv
d2rv . , d2rv drv
dqkdqj 3 dqkdt
dqjdqk 3 dtdqk dqk'
3. Общие основания кинематики системы
45
Запишем в обобщенных скоростях уравнения B) неголономных
связей. Подставив B1) и B3) в B), получим
Е b/3j(qi, 92, • • • , qm, t)qj + bp(qu 9
j=i
(/3 = 1, 2,... , a).
Величины bpj, Ър определяются равенствами
N f)r
qm, t) = 0
к=1
N
(/3=1, 2,..., s; j =
Qr
= 1, 2,... , s).
к=1
заменены
Здесь в векторах apv и скалярах а^ величины т\, г^-, ...,
на их выражения B1).
Для голономной системы обобщенные скорости ijj независимы и
совершенно произвольны. В неголономной системе обобщенные коор-
координаты, как и в голономной системе, могут принимать произвольные
значения, но при этом обобщенные скорости не будут независимы; они
связаны s соотношениями B6).
Чтобы выразить виртуальные перемещения Srv точек системы че-
через вариации Sqj обобщенных координат, надо, в соответствии с п. 12,
отбросить в выражении B3) drv/dt и заменить qj на Sqj, а г„ на Srv.
Тогда получим1
B7)
Для голономной системы вариации Sqj произвольны. В неголономной
же системе они связаны соотношениями, которые получаются из B6)
путем отбрасывания величин Ър и замены qj на Sqj:
= 1,2,..., в).
B8)
Следовательно, число степеней свободы голономной системы совпадает
с числом ее обобщенных координат, а число степеней свободы неголо-
неголономной системы меньше числа то обобщенных координат на количест-
количество s дифференциальных неинтегрируемых связей2.
1Вообще, для любой функции <p(qi, дг,--- , qm, t) имеем Sip = X] я~
j=l "Qj
2Конечно, предполагается, что связи B6) являются независимыми.
46 Глава I
17. Псевдокоординаты. В некоторых задачах динамики, особен-
особенно при изучении движения неголономных систем, бывает удобно ввести
координаты более общего вида, которые получили название псевдокоор-
псевдокоординат. Пусть п — число степеней свободы. Рассмотрим п независимых
линейных комбинаций обобщенных скоростей
т
M (г = 1, 2,..., п). B9)
Коэффициенты c,j — функции q\, Q2,--- , Qnn t. Величины ?Tj имеют
вполне определенный смысл некоторых линейных комбинаций обобщен-
обобщенных скоростей, но сами символы тг^ могут и не иметь смысла, т. е.
правые части в равенствах B9) могут не быть полными производными
по времени от каких-либо функций обобщенных координат и време-
времени. Величины тг; также осмыслены. Это — производные по времени от
правых частей равенств B9). Будем называть символы тг, псевдокоор-
псевдокоординатами, а величины -hi и тг^ — соответственно псевдоскоростями и
псевдоускорениями. Некоторые из тг^ могут быть, в частности, обобщен-
обобщенными координатами qi, тогда соответствующие -hi и тг^ — обобщенные
скорости и обобщенные ускорения.
Величины Cij будем выбирать так, чтобы определитель линей-
линейной системы из то = п + s уравнений B6), B9) относительно ijj
(j = 1, 2,... , то) был отличен от нуля. Разрешив эту систему, полу-
получим
п
Qi = XI d«*< + Si (j = 1, 2,... , то). C0)
»=i
Псевдоскорости ttj могут принимать произвольные значения; если они
заданы, то обобщенные скорости находятся из C0). Величины dij, gj
в C0) — функции q±, q2,.-. , qm, t.
Введем согласованное с B9) обозначение
т
j6qj (i = l,2,...,n). C1)
Формула C1) фактически является определением величин <$тг^. Имен-
Именно, <$ttj — это величина, равная правой части равенства C1), в кото-
которой Sqj — вариации обобщенных координат.
Из C1) и B8) находим выражение Sqj через величины <$тг^
(* = 1, 2,... , п):
П
iSni (i = l, 2,..., то). C2)
§ 4- Кинематика твердого тела 47
Здесь величины Sirt могут принимать произвольные значения.
Найдем нужные для дальнейшего выражения для виртуальных пе-
перемещений Srv точек системы через величины <$ttj. Подставив C2)
в B7), получим
п
Srv = ^2evi67Ti (i/ = l, 2,..., N), C3)
г=1
где введено обозначение
т Я
evi = y^-^dij {у = 1, 2,... , N; i = 1, 2,... , га).
Запишем это выражение несколько иначе. Для этого продифференци-
продифференцируем обе части соотношений C0) по времени и полученное выражение
для ijj подставим в формулу B4), которая примет вид
wv =
где вектор-функции h,, не зависят от псевдоускорений ttj. Отсюда сле-
следует, что
evi=^ {v = \, 2,... , N; i = 1, 2,... , n). C4)
oiTi
Подставив C4) в C3), получим окончательное выражение для 8rv в виде
5rv = ^2-^5жг (v = 1, 2,... , N). C5)
§ 4. Кинематика твердого тела
18. Задачи кинематики твердого тела. Определение прос-
простейших перемещений. Абсолютно твердое тело — это такая ме-
механическая система, у которой взаимные расстояния между точками
постоянны. Очень многие объекты природы и техники моделируются
в теоретической механике системами, состоящими из отдельных мате-
материальных точек и абсолютно твердых тел. Отсюда вытекает важность
изучения их движения. В дальнейшем абсолютно твердое тело будем
для краткости называть просто твердым телом.
48 Глава I
Если в декартовой прямоугольной системе координат точка Р/.
твердого тела имеет радиус-вектор г&, то по определению при лю-
любых г, j величины |г» — г,-| = r,j постоянны во все время движения.
Если помимо связей, обеспечивающих постоянство расстояний r\j, на
твердое тело не наложено никаких других связей, то его называют сво-
свободным твердым телом. Иными словами: свободным называют твердое
тело, на перемещение которого не наложено никаких ограничений. Сво-
Свободное твердое тело является голономнои склерономной системой.
Свободное твердое тело (такое, в котором есть три точки Pi, Р2, Р3,
не лежащие на одной прямой) имеет шесть степеней свободы. В самом
деле, в голономнои системе число степеней свободы и число обобщенных
координат совпадают. Число же обобщенных координат равно шести.
Действительно, чтобы задать положение одной из точек, скажем Pi,
нужно задать три координаты; если это сделано, то положение точ-
точки Рг можно уже будет задать двумя параметрами, так как она может
двигаться только по сфере радиусом r\i с центром Pi; после того как
положения Pi и Р^ зафиксированы, у точки Рз осталась только одна
степень свободы, так как точка при движении должна оставаться на
окружности с радиусом, равным расстоянию от Рз до прямой Р1Р2, и
лежащей в плоскости, перпендикулярной Р1Р2. Итак, число степеней
свободы твердого тела равно шести, как бы ни было велико число N
образующих его точек.
Из приведенных рассуждений следует, что твердое тело с одной не-
неподвижной точкой имеет три степени свободы; если у тела неподвижны
две точки, то оно имеет одну степень свободы. Если свободное твердое
тело представляет собой бесконечно тонкий стержень (или связанные
им две материальные точки), то оно имеет пять степеней свободы.
Задача кинематики твердого тела состоит в разработке способов
задания его движения, а также способов, позволяющих по небольшому
числу кинематических характеристик, общих для всего тела, находить
кинематические характеристики каждой точки тела.
Дадим нужные в дальнейшем определения простейших перемеще-
перемещений твердого тела. Рассмотрим два положения твердого тела, которые
назовем его начальным и конечным положениями. При переходе тела
из начального положения в конечное оно совершает некоторое переме-
перемещение. Будем рассматривать это перемещение, совершенно отвлекаясь
от промежуточных положений, через которые тело проходит во время
движения из начального положения в конечное, и от времени, в течение
которого совершается этот переход. Таким образом, рассматриваемое
перемещение определяется только начальным и конечным положени-
положениями тела; если конечное положение тела совпадает с его начальным
положением, то никакого перемещения нет.
Кинематика твердого тела
49
Перемещение твердого тела, при котором перемещения всех его
точек геометрически равны, назовем поступательным перемещением.
Перемещение твердого тела, при котором его конечное положение
получается из начального путем поворота вокруг неподвижной прямой,
называется вращением (вокруг этой прямой), а сама неподвижная пря-
прямая называется осью вращения.
Винтовым перемещением называется совокупность поступатель-
поступательного перемещения и вращения, в которой поступательное перемещение
происходит вдоль оси вращения.
19. Векторно-матричное за-
задание движения твердого те-
тела. Углы Эйлера. Пусть OaXYZ
— абсолютная система координат
(рис. 17), О — произвольная фикси-
фиксированная точка твердого тела, кото-
которую в дальнейшем будем называть
полюсом, OXYZ — система коорди-
координат, получающаяся из системы ко-
координат OaXYZ при помощи по-
поступательного перемещения, Oxyz
— система координат, жестко свя-
связанная с твердым телом,изучением
движения которого мы занимаемся.
X
Y
Рис. 17
Само тело на рис. 17 не изображено. Пусть Р — некоторая точка те-
тела. Векторы До, Д заданы своими компонентами в системе OXYZ,
а вектор р = ОР — в системе Oxyz; очевидно, что р — постоянный
вектор. Вектор ОР, заданный своими компонентами в системе OXYZ,
обозначим г. Имеет место соотношение
г = Ар,
A)
где А — матрица перехода от системы Oxyz к системе OXYZ.
Положение точки Р тела в абсолютной системе координат задается
равенством
Д = До + Ар.
B)
При движении твердого тела в общем случае изменяется положение по-
полюса О, а также изменяется ориентация тела в абсолютном простран-
пространстве. Поэтому До и А в B) — функции времени; будем их считать
дважды непрерывно дифференцируемыми.
Матрица А, задавая переход от одного ортонормированного бази-
базиса к другому, является ортогональной, т. е. А = А'. Из последне-
последнего равенства следует, что ее элементы связаны шестью независимыми
50
Глава I
соотношениями: сумма квадратов элементов каждой строки (столбца)
равна единице и сумма попарных произведений соответствующих эле-
элементов столбцов (строк) равна нулю. Следовательно, из девяти элемен-
элементов матрицы А независимых только три. Таким образом, матрицу А
можно задать при помощи трех независимых параметров. В зависимос-
зависимости от конкретного выбора этих параметров матрица А будет выглядеть
по-разному. Рассмотрим один из наиболее распространенных способов
задания ориентации твердого тела при помощи углов Эйлера и найдем
соответствующую им матрицу А.
Углы Эйлера вводятся следующим об-
образом (рис. 18). Плоскость Оху пересека-
пересекается с плоскостью OXY по прямой ON,
которая носит название линии узлов. Угол,
составляемый линией узлов с осью ОХ,
обозначается буквой ф и называется углом
прецессии, угол между осями Oz и OZ обо-
обозначается буквой в и называется углом ну-
нутации, угол между осью Ох и линией уз-
узлов обозначается буквой <р и называется уг-
углом собственного вращения.
Три угла ф, в, if не зависят один от
другого и могут быть выбраны совершен-
совершенно произвольно. Если заданы три числа, являющихся значениями уг-
углов ф, в, if, то тем самым однозначно определена ориентация твердого
тела в абсолютном пространстве. Обычно принимается, что 0 ^ ф < 2тг,
0 «С в «С тг, 0 «С if < 2тг.
Переход от системы координат OXYZ к системе Oxyz осущест-
осуществляется при помощи трех последовательных поворотов: на угол -ф во-
вокруг OZ, на угол в вокруг ON и на угол р вокруг Oz. Все повороты
производятся против часовой стрелки, если смотреть с конца соответ-
соответствующих осей поворота.
При первом повороте мы переводим систему координат OXYZ в
промежуточную систему координат OX{Y\Z. Соответствующий пере-
переход задается матрицей Ai:
N
Рис. 18
X
Y
Z
= м
хх
Yx
Z
0
0
Второй поворот осуществляет переход от OX{Y\Z к еще одной про-
промежуточной системе координат OX{YiZ. Соответствующую матрицу
Кинематика твердого тела
51
перехода обозначим
Хг
Ух
Z
= А2
Хх
Y2
z
А2 =
10 0
0 cos# -sin#
0 sin# cos#
И, наконец, третий поворот переводит систему координат OX{Y^z в
систему координат Oxyz. Этому повороту соответствует матрица A3:
Хг
Y2
z
= А3
X
У
z
А3 =
cos (уС — sirup 0
sin ip cos ip 0
0 0 1
агг = cos ф cos tp — sin
ai2 = — cos ф sin ip — sin ф cos ip cos в,
агз = sin ф sin в, а^г= sin ф cos ip + cos ^ sin ip cos ^,
Я22 = - sin ф sin y> + cos ф cos y> cos 0, а2з = - cos ф sin
Матрица А перехода от системы координат Oxyz к системе OXYZ рав-
равна произведению матриц А1А2А3; ее элементы а^- выражаются через
углы Эйлера по следующим формулам:
C)
Отметим, что при в = 0 или в = тг линия узлов O7V и углы if и ф не
определены, а определена только их сумма ip + ф. Эта особенность уг-
углов Эйлера делает их малопригодными для исследования движений, при
которых ось Oz тела может принимать направления, близкие прямой,
проходящей через ось OZ. Избежать этих трудностей можно, приме-
применяя другие углы, определяющие ориентацию тела в абсолютном про-
пространстве, или модифицируя углы Эйлера так, чтобы угол в до оси Oz
отсчитывался не от оси OZ, а, например, от ОХ или OY.
Замечание 2. Мы видели, что конечный поворот системы OXYZ, пе-
переводящий ее в систему Oxyz, задается матрицей А, являющейся про-
произведением трех матриц, задающих последовательные повороты. Но,
так как операция перемножения матриц не обладает свойством ком-
коммутативности, отсюда следует, что конечные повороты твердого те-
тела некоммутативны. Это означает, что в общем случае ориентация
твердого тела, получаемая им в результате двух последовательных ко-
конечных поворотов, зависит от порядка выполнения этих поворотов.
Упражнение 1. Привести конкретный пример некоммутативных по-
поворотов твердого тела.
52 Глава I
20. Движение твердого тела с неподвижной точкой как ор-
ортогональное преобразование. Если во все время движения у твер-
твердого тела остается неподвижной одна точка О, то говорят, что тело
движется вокруг точки О, или совершает сферическое движение.
При движении тела вокруг неподвижной точки О в формуле B)
вектор До постоянен. Пусть при t — 0 оси связанной с телом систе-
системы координат Oxyz совпадают с соответствующими осями неподвиж-
неподвижной системы координат OXYZ. Матрица А будет при этом единичной
матрицей (А = Е) и, согласно A), B), R = г = р, причем выписанные
векторы задаются своими компонентами в одной и той же системе ко-
координат: либо Oxyz, либо OXYZ, что безразлично, так как эти системы
координат при t = 0 совпадают. Мы будем считать, что векторы заданы
в неподвижной системе OXYZ.
Когда тело начнет двигаться, то оно будет «переносить» с собой
вектор р, поворачивая его вокруг точки О. Через какое-то время t
вектор р перейдет в вектор г = A(t)p. Последняя формула определя-
определяет преобразование пространства, в котором выбрана система коорди-
координат OXYZ. Матрица A(t) ортогональна, т. е. АА' = Е. Отсюда и из
правила нахождения определителя произведения квадратных матриц
следует, что (det А) = 1. Следовательно, det А может принимать толь-
только два значения +1 или — 1, но, так как det А в начальный момент равен
единице, стать равным —1 при каком-либо t он не может в силу своей
непрерывности по t.
Таким образом, движение твердого тела вокруг неподвижной точ-
точки задает собственное ортогональное преобразование.
21. Основные теоремы о конечных перемещениях твердого
тела.
Теорема (Эйлера). Произвольное перемещение твердого тела, имею-
имеющего неподвижную точку, можно осуществить посредством вращения
вокруг некоторой оси, проходящей через эту точку.
Доказательство.
Заметим, что утверждение теоремы Эйлера эквивалентно тому,
что у матрицы А есть собственное значение, равное +1. Соответству-
Соответствующий собственный вектор г задает ось вращения.
Действительно, так как г = Аг, то направление этой оси остается
неизменным при движении тела.
Пусть /(А) = det(A — ЛЕ) — характеристический многочлен мат-
§ 4- Кинематика твердого тела 53
рицы А. Чтобы показать, что /A) = 0, рассмотрим следующую цепоч-
цепочку равенств:
/A) = det(A - Е) = det(A' - Е') = det(A - Е) =
= det(A(A - Е)) = det(E - А) = det(-(A - Е)) =
= (-lKdet(A-E) = -
Отсюда следует, что /A) = 0, и теорема доказана.
Теперь найдем упоминаемый в теореме угол поворота^ вокруг оси.
Для этого удобно перейти от системы OXYZ к системе OXYZ, у кото-
которой ось OZ направлена вдоль оси вращения. В этой системе матрица А,
задающая поворот на угол а, имеет вид
А =
cos a — sin a 0
sin a cos a 0
О 0 1
Замечая, что А и А подобны, и пользуясь тем, что у подобных мат-
матриц суммы диагональных элементов совпадают, получаем равенство,
определяющее угол поворота а:
1+2 cos а = ац + a-ii + азз •
Теорема (Шаля). Самое общее перемещение твердого тела разла-
разлагается на поступательное перемещение, при котором произвольно вы-
выбранный полюс переходит из своего первоначального положения в ко-
конечное, и на вращение вокруг некоторой оси, проходящей через этот
полюс. Это разложение можно совершить не единственным способом,
выбирая за полюс различные точки тела; при этом направление и длина
поступательного перемещения будут изменяться при выборе различных
полюсов, а направление оси вращения и угол поворота вокруг нее не за-
зависят от выбора полюса.
Доказательство.
Осуществляется простым геометрическим вычислением. На рис. 19
OaXYZ — абсолютная система координат. Системы координат OXYZ
и O\X\Y\Z\ (не показанные на рис. 19) с началом в двух различных по-
полюсах О и О\ получаются из OaXYZ поступательными перемещени-
перемещениями, определяемыми соответственно векторами Ro и Ro1- Считаем,
что векторы Ro и Ro1 заданы своими компонентами в абсолютной
системе координат OaXYZ. Положение произвольной точки Р тела в
абсолютной системе координат определяется вектором R. Показанные
на рис. 19 векторы p,Pi, 00\ считаем заданными их компонентами в
54
Глава I
системе координат Oxyz, жестко связанной с твердым телом. Имеем
равенства
R = Ro + Ар = Ro + A(OOi + px) =
= Ro
+ Ap-L = ROl + Apx.
Отсюда и следует справедливость теоремы Шаля. Действительно, пере-
перемещение твердого тела можно представить как поступательное, опреде-
определяемое перемещением полюса, плюс вращение, задаваемое матрицей А.
Причем из предыдущего видно, что матрица А не зависит от выбора по-
полюса, но из доказательства теоремы Эйлера следует, что ось вращения
и угол поворота определяются только элементами матрицы А. Посту-
Поступательное же перемещение зависит от полюса. Из приведенного выше
равенства видно, что для разных полюсов О и О\ поступательные пе-
перемещения, задаваемые векторами До и Ro1, связаны соотношением
Упражнение 2. Показать, что результирую-
результирующее перемещение твердого тела не зависит от
порядка, в котором следуют одно за другим со-
составляющие его поступательное перемещение
и вращение.
Теорема (Моцци). Самое общее перемеще-
перемещение твердого тела является винтовым пере-
перемещением.
о
Рис. 19
Доказательство.
Разложим перемещение твердого тела на
поступательное вместе с некоторым полю-
полюсом О и на вращение вокруг полюса. Согласно теореме Шаля, направ-
направление оси вращения и угол поворота вокруг нее не зависят от выбора
полюса. Для удобства вычислений ось OaZ абсолютной системы коор-
координат направим по оси вращения, и пусть в исходном положении тела
соответствующие оси абсолютной OaXYZ и связанной с твердым те-
телом Oxyz систем координат совпадают. Если а — угол поворота, то
матрица А, определяющая ориентацию тела в его конечном положении
относительно абсолютной системы координат, имеет вид
А =
cos a — sin a 0
sin a cos a 0
О 0 1
Кинематика твердого тела
55
Рис. 20
Хо
Yo
Zo
oil _
' RO ~
0
0
Zo
¦> Rq -
Xo
Yo
0
Теорема Моцци будет доказа-
доказана, если в теле найдется такая пря-
прямая, точки которой после переме-
перемещения тела из начального положе-
положения в конечное переместились бы
только вдоль этой прямой. Дейст-
Действительно, выбирая тогда полюса на
этой прямой, мы представим пере-
перемещение твердого тела в виде вин-
винтового перемещения, что и будет
означать справедливость теоремы
Моцци.
Представим вектор До переме-
перемещения полюса (рис. 20) в виде суммы двух векторов До =
где в абсолютной системе координат
Ro =
Пусть Р — точка тела с радиусом-вектором р относительно по-
полюса О. В начальном положении тела р = Д». В конечном положе-
положении тела вектор р в абсолютной системе координат перейдет в век-
вектор До + АД*. Рассмотрим прямую, параллельную оси OZ и проходя-
проходящую через конец вектора Д*. Если при перемещении тела точки этой
прямой переместились вдоль неё самой, то Ro + Ai2* = i2* + Ro. От-
Отсюда следует, что (А — Е)Д„ = —Rq. Если Х„, У*, Z* — компоненты
вектора i2* в системе OaXYZ, то из последнего равенства следуют два
скалярных уравнения, которым должны удовлетворять X*, У*:
(cos а — 1)Х» — sin aY* = Xo, sinaX* + (cos а — 1)У» = Yo-
Величина же Z* может быть произвольной, так как третье скалярное
уравнение удовлетворяется тождественно.
Определитель выписанной системы линейных уравнений равен
4sin2(а/2). Он отличен от нуля, если а ф 0, 2тг, т. е. когда перемеще-
перемещение отлично от поступательного. Таким образом, мы получили в теле
прямую X = X*, Y = Y%, параллельную оси вращения, точки которой
смещаются при перемещении тела вдоль нее самой.
Следствие 1 (теорема Бернулли—Шаля). Самое общее перемеще-
перемещение плоской фигуры в своей плоскости есть либо поступательное пере-
перемещение, либо вращение вокруг точки. Эта точка называется центром
конечного вращения.
56
Глава I
В
A
¦у
QL.
V
'в
х
Y
В,
Рис. 21
0
1
0
0
0
1
1
0
0
Пример 1. Пусть куб движется так, что
три его вершины А, В, С переходят в но-
Е вые положения А\, В\, С\ — также вер-
вершины куба (рис. 21). Выясним, каким прос-
простейшим движением может быть достиг-
достигнут этот переход.
Так как центр куба О при указанном
перемещении остался на месте, то при-
1 менима теорема Эйлера. Свяжем с кубом
систему координат OXYZ, оси которой
перпендикулярны соответствующим гра-
граням куба. В результате перемещения ку-
куба оси OX, 0Y и 0Z перейдут соответ-
соответственно в оси Ох, Оу и Oz (рис. 21). Нетрудно увидеть, что матри-
матрица А, задающая перемещение (поворот) куба, будет такой:
А =
Для собственного вектора г матрицы А, отвечающего собственному
значению Л = 1, имеем г' = A, 1, 1). Угол поворота определяется
уравнением 2 cos Ф + 1 = 0.
Таким образом, указанное перемещение куба достигается враще-
вращением вокруг диагонали DF на угол 120°.
22. Скорость и ускорение твердого тела при поступатель-
поступательном движении. До сих пор при изучении перемещения твердого тела
мы интересовались лишь его начальным и конечным положениями, не
обращая внимания на быстроту перемещения. Теперь будем находить
скорости и ускорения точек твердого тела при его движении.
Движение твердого тела в течение некоторого промежутка време-
времени называется поступательным, если поступательно его перемещение
между положениями, соответствующими двум произвольным момен-
моментам времени из этого промежутка. Примерами поступательных дви-
движений могут служить движение пассажирского лифта в многоэтажных
жилых домах, движение ящика письменного стола при его вдвигании
и выдвигании, движение кабины «колеса обозрения» в парке. В первых
двух примерах поступательное движение прямолинейное (все точки те-
тела движутся по прямым), в третьем примере — криволинейное (точки
тела движутся по криволинейным траекториям — окружностям).
Так как при поступательном перемещении любые две точки тела
Р\ и Рг за время At имеют геометрически равные перемещения
§ 4- Кинематика твердого тела 57
и Д-Кг, то при поступательном движении все точки тела имеют равные
скорости и равные ускорения. Эти одинаковые для всех точек тела ско-
скорости и ускорения называются соответственно скоростью и ускорением
поступательного движения твердого тела. В дальнейшем мы увидим,
что понятия скорости и ускорения твердого тела имеют смысл толь-
только для поступательного движения, так как при движении, отличном
от поступательного, скорости и ускорения различных точек тела, как
правило, неодинаковы.
23. О мгновенном кинематическом состоянии твердого те-
тела. Если в данный момент времени скорости v всех точек твердого
тела равны между собой, то говорят, что тело совершает мгновенно по-
поступательное движение со скоростью v. В частности, если v = 0, то
тело находится в мгновенном покое.
Замечание 3. Здесь речь идет только о распределении скоростей точек
тела в данный момент времени. В частности, ускорения точек тела
совсем не обязаны быть одинаковыми.
Если в данный момент времени точки некоторой прямой в твер-
твердом теле имеют скорости, равные нулю, то говорят, что тело совершает
мгновенное вращение вокруг этой прямой, а прямую называют мгновен-
мгновенной осью вращения.
Замечание 4. В приведенном определении речь идет только о распреде-
распределении скоростей точек некоторой прямой в твердом теле. Мгновенная
ось вращения, в частности, в разные моменты времени может зани-
занимать разные положения и в движущемся теле, и в абсолютном про-
пространстве.
Если в данный момент тело участвует в совокупности двух мгно-
мгновенных движений, поступательном вдоль некоторой оси и вращении
вокруг этой оси, то говорят, что тело совершает мгновенно винтовое
движение. В дальнейшем (в п. 28) будет показано, что самое общее мгно-
мгновенное движение свободного твердого тела является мгновенно винто-
винтовым.
24. Скорости и ускорения точек твердого тела в общем
случае движения. Пусть OaXYZ — неподвижная система коорди-
координат (рис. 17), О — произвольно выбранный полюс, Oxyz — жестко свя-
связанная с твердым телом система координат; система координат OXYZ
получается из OaXYZ поступательным перемещением, определяемым
вектором Ro- Пусть Р — некоторая точка тела, риг — вектор ОР,
заданный своими компонентами в системах координат Oxyz и OXYZ
соответственно.
Теорема. Существует единственный вектор ш, называемый угловой
скоростью тела, с помощью которого скорость v точки Р тела может
58 Глава I
быть представлена в виде
v = vo + ш х г, D)
где vo — скорость полюса О; вектор ш от выбора полюса не зависит.
Доказательство.
Продифференцируем обе части равенства B), учтя сначала, что
вектор р постоянен, а затем воспользовавшись формулой A). Получим
v = Ro + Ар = vo + АА г. E)
Покажем, что матрица АА кососимметрическая. В самом де-
деле, продифференцировав по времени тождество АА' = Е, получим
АА' + АА' = 0. Отсюда АА = —АА'. Применив операцию транс-
транспонирования к обеим частям этого равенства, имеем окончательно
(АА-1)' = -АА' = -АА.
Теперь введем обозначения для элементов кососимметрической
матрицы АА по формуле
0 —ojz шу
UJZ 0 -Ш;
—и>у и>х 0
Если составить вектор ш' = (и>х, шу, ojz) с компонентами, заданными
в системе координат OaXYZ, то результат умножения матрицы АА
на вектор г может быть представлен в виде векторного произведе-
произведения ш х г. Отсюда и из E) следует формула D). Попутно показана
справедливость равенства (называемого формулой Эйлера)
Г = Ш X Г. F)
Мы ввели ш, взяв предварительно в неподвижном пространстве
конкретный базис, задающий систему координат OaXYZ. Из D) по-
получаем, что в этой системе координат ш = У2 rot v. Единственность
ш при заданном полюсе О следует теперь из инвариантности вихря
и независимости v от выбора базиса (см. замечание 1 в п. 6). Неза-
Независимость ш от выбора полюса получаем из того, что компоненты ш
целиком определяются элементами матрицы А и их производными по
времени, а матрица А от выбора полюса не зависит (см. п. 21). Теорема
доказана.
Отметим некоторые следствия, вытекающие из формулы D).
§ 4- Кинематика твердого тела 59
1. В каждый момент времени проек-
ции скоростей любых двух точек твердо- v
го тела на прямую, проходящую через эти
точки, равны между собой. (На рис. 22
v\ coscti = V2 cosa2- Механический смысл
этого равенства весьма прост: в силу того
что Р1Р2 = const, точка Pi не может ни «до-
r> \ тт Рис- 22
гнать» точку Р^-, ни «отстать» от нее.) Дока-
Доказательство следует из того, что согласно D) г>2 = v\ + ш х Р1Р2. Отсю-
Отсюда г>1 • Р1Р2 = г>2 • Р1Р2, или vi cos a± = V2 cos 0:2-
2. Скорости трех точек твердого тела, не лежащих на одной пря-
прямой, вполне определяют скорость любой точки тела. (Очень простое
геометрическое доказательство получается, если использовать следст-
следствие 1.)
3. Если векторы скоростей трех точек твердого тела, не лежа-
лежащих на одной прямой, в некоторый момент времени равны, то тело
совершает мгновенно поступательное движение.
4. Если в данный момент времени скорости двух точек тела равны
нулю, то тело либо находится в мгновенном покое, либо совершает
мгновенное вращение вокруг прямой, проходящей через эти точки.
5. Если скорость некоторой точки тела в данный момент време-
времени равна нулю, то тело находится либо в мгновенном покое, либо в
мгновенном вращении вокруг оси, проходящей через эту точку.
6. Мгновенное движение твердого тела в самом общем случае раз-
разлагается на два движения: поступательное со скоростью, равной ско-
скорости произвольного полюса, и вращение вокруг оси, проходящей через
этот полюс.
Чтобы найти ускорение w точки Р, продифференцируем обе части
формулы D) по времени. Получим
Вектор е = из называется угловым ускорением. Учтя F), формулу для w
можно записать в виде
W = W0 + ? X Г + Ш X (ш X г). G)
Вектор wev = ? х г называют вращательным ускорением,
a woc = ш х (ш х г) — осестремительным ускорением. Таким образом,
ускорение произвольной точки твердого тела складывается из уско-
ускорения полюса, вращательного и осестремительного ускорений. Форму-
Формула G) носит название формулы Ривалъса.
60
Глава I
X
Рис. 23
Рис. 24
25. Вращение твердого тела вокруг неподвижной оси. Пусть
в твердом теле неподвижны две точки О и О\. Прямая, проходящая
через О и О\, будет осью вращения. Ось OZ неподвижной системы ко-
координат и ось Oz системы координат Oxyz, жестко связанной с телом,
направим по оси вращения. Ориентация тела относительно неподвиж-
неподвижной системы координат определяется углом <p(t) между осями ОХ и Ох
(рис. 23). Точки тела, не принадлежащие оси вращения, движутся по
окружностям с центрами на оси вращения и лежащим в плоскостях,
перпендикулярных этой оси. Пусть точка Р тела задана в связанной
системе координат радиусом-вектором р. Тогда
г = Ар,
А =
cos if — sin if 0
cosip 0
0 0 1
Непосредственные вычисления показывают, что
0
ф
0
—ф
0
0
0
0
0
, ш =
0
0
ф
0
0
Ф
Отсюда следует, что угловая скорость ш направлена по оси вращения,
причем так, что если смотреть с конца вектора ш, то вращение те-
тела видно происходящим против часовой стрелки. Угловое ускорение е
также направлено по оси вращения, причем в ту же сторону, что и ш,
если фф > 0, т. е. если вращение ускоренное (этот случай представ-
представлен на рис. 24), и противоположно ш, если фф < 0, т. е. если вращение
замедленное.
§ 4- Кинематика твердого тела 61
Для вычисления скорости и ускорения точки Р примем начало ко-
координат О за полюс. Тогда vo = О и из формулы D) имеем v = ш х г.
Вектор v лежит в плоскости, перпендикулярной оси вращения. Его мо-
модуль v = u>d = \<p\d, где d — радиус окружности, по которой движется
точка Р.
Учитывая, что wo = О, из формулы Ривальса G) получим
w=exr + u>xv. Вращательное ускорение wev = е х г направле-
направлено по касательной к траектории точки Р (к окружности радиуса d);
его модуль wep = ed = \Cp\d (рис. 24). Осестремительное ускорение
woc = ш х v; оно лежит на перпендикуляре, проведенном к оси враще-
вращения из точки Р, и направлено к оси вращения; его модуль woc = w2d.
Отметим, что вращательное ускорение точки Р в случае вращения
тела вокруг неподвижной оси является ее касательным (тангенциаль-
(тангенциальным) ускорением (см. п. 6), а осестремительное ускорение является
нормальным ускорением точки Р. Модуль полного ускорения точки Р
вычисляется по формуле w = d^/e1 + ш4. Угол C между направлени-
направлениями осестремительного и полного ускорений вычисляется по форму-
формуле tg/3 = e/w2.
26. Движение вокруг неподвижной точки. Пусть твердое те-
тело имеет одну неподвижную точку О. Тогда снова vo = 0, wo = 0 и
формулы для о и № те же, что и в случае вращения тела вокруг непо-
неподвижной оси, рассмотренном в п. 25.
Таким образом, в данный момент времени скорости точек тела
таковы, какими они были бы, если бы тело вращалось с угловой ско-
скоростью и> вокруг неподвижной оси, на которой в данный момент вре-
времени лежит вектор и>. Эта ось называется мгновенной осью вращения,
а вектор ш — мгновенной угловой скоростью. Все точки мгновенной
оси вращения имеют скорости, равные нулю. Мгновенная ось враще-
вращения перемещается и в теле, и в абсолютном пространстве. В связи с
этим заметим, что при движении твердого тела вокруг неподвижной
точки (и в общем случае движения свободного твердого тела) и> не яв-
является производной некоторого угла <р, так как нет такого направления,
вокруг которого поворот на угол ip совершается.
При своем движении мгновенная ось вращения описывает в теле
коническую поверхность — подвижный аксоид, а в абсолютном про-
пространстве коническую поверхность — неподвижный аксоид. Вершины
этих аксоидов совпадают с неподвижной точкой О. Аксоиды касаются
один другого по образующей, совпадающей с мгновенной осью враще-
вращения. Можно показать, что при движении тела подвижный аксоид ка-
катится по неподвижному без скольжения.
Годограф вектора ш лежит на неподвижном аксоиде. Так как
е = о», то угловое ускорение е направлено по касательной к годогра-
62
Глава I
Рис. 25
Рис. 26
фу и вовсе не обязательно по мгновенной оси вращения (рис. 25). По-
Положим и> = ше, где е — единичный вектор, коллинеарный и>. Тог-
Тогда ? = ?i + ?2, где вектор ?\ = Сое направлен по мгновенной оси враще-
вращения, а ?2 = toe перпендикулярен ей. Вектор ?i характеризует изменение
ш по модулю, а ?2 — по направлению. Если мгновенная ось вращения
вращается вокруг точки О с угловой скоростью Л, то ?2 = Л х со.
Согласно формуле G), ускорение w какой-либо точки Р тела равно
сумме вращательного и осестремительного ускорений. При этом
Вычислим осестремительное ускорение. Пусть Q — точка на мгновен-
мгновенной оси вращения, в которой ее пересекает опущенный на нее из точ-
точки Р перпендикуляр (рис. 26). Обозначим вектор PQ буквой /. Тогда
woc = и) х (ш х г) = ш2е х (е х г) =
= ш2[е(е -r)-r]= oj2(OQ - г) = ш21.
Таким образом, woc совпадает с тем нормальным ускорением, которое
имела бы точка Р, если бы тело вращалось вокруг мгновенной оси вра-
вращения, как вокруг неподвижной, с угловой скоростью ш.
Следует иметь в виду, что, в отличие от случая вращения тела
вокруг неподвижной оси, при вращении тела вокруг неподвижной точ-
точки wev и woc уже не обязаны быть касательной и нормальной составля-
составляющими ускорения точки Р.
Упражнение 3. Показать, что при движении твердого тела вокруг не-
неподвижной точки вращательная компонента ускорения какой-либо точ-
точки тела совпадает с касательной, а осестремительная компонента — с
нормальной в том и только в том случае, когда эта точка лежит в плос-
плоскости, содержащей ш и ?.
(9)
§ 4- Кинематика твердого тела
63
Пример 1. Диск радиуса За катит-
катится без скольжения по горизонталь-
горизонтальной плоскости, описывая окруж-
окружность радиуса 4а с постоянной уг-
угловой скоростью и>\ и сохраняя
свою плоскость вертикальной. Най-
Найти скорость и ускорение наивысшей
точки диска Р.
Будем представлять себе диск
как основание конуса, движущего-
движущегося вокруг неподвижной точки А (на
рис. 27 показано сечение АРВ этого
со,
У/////////////////////?/.
со
Рис. 27
конуса, скорость центра диска направлена перпендикулярно плоскости
рисунка на читателя).
Ввиду отсутствия скольжения скорость точки В диска равна ну-
нулю. Поэтому угловая скорость со диска направлена по АВ от точки А
к В. Величина угловой скорости может быть найдена из равенств
vo =
= изОС.
Из ААОВ имеем
Поэтому
sina=^, cosa=^, ОС = АО sin а = ^ф-
0 0 О
L
ОС
Далее, vp = и> х АР. Скорость vp перпендикулярна плоскости рисунка
и направлена на читателя, vp = шАР sin 2а = 8u>ia.
Так как модуль угловой скорости постоянен, то угловое ускорение
диска определяется равенством е = u>i x со. Вектор е перпендикулярен
плоскости рисунка и направлен на читателя, е = a>ia>sinGr/2 — а) =
Найдем теперь ускорение точки Р. Имеем w = wBV + woc,
где wev = е х АР, woc = и>21, wev = еАР = 20с^а/3, woc = 40u>la/3.
Вектор wev направлен перпендикулярно АР, лежит в плоскости рисун-
рисунка и составляет с вектором woc угол C = ж — 2а. Следовательно,
w =
1 о V~ 4^97 2
u?c — 2wepwoc cos 2a = —¦=—и){с
64
Глава I
Y,
Or
Рис. 28
27. Плоское движение те-
тела. Движение твердого тела называ-
называют плоским, если все точки тела пе-
перемещаются в плоскостях, параллель-
параллельных некоторой неподвижной плоскос-
плоскости.
Пусть этой неподвижной плоскос-
плоскостью будет координатная плоскость
_^_ OaXY абсолютной системы коорди-
X нат. Каждая прямая, проведенная в те-
теле перпендикулярно плоскости OaXY,
движется поступательно. Поэтому для
определения движения этой прямой достаточно знать движение какой-
либо одной ее точки. Движение же всего тела будет известно, если из-
известно движение любого сечения тела плоскостью, параллельной непо-
неподвижной плоскости OaXY. Следовательно, изучение плоского движе-
движения тела сводится к изучению движения плоской фигуры в ее плоскос-
плоскости.
Плоская фигура, вынужденная двигаться, оставаясь в своей плос-
плоскости, имеет три степени свободы. За обобщенные координаты примем
две координаты Хо, Yo полюса О и угол <р, образованный осью Ох,
жестко связанной с фигурой системы координат с осью ОаХ абсолют-
абсолютной системы координат (рис. 28).
Скорости и ускорения точек плоской фигуры могут быть найдены
по формулам D) и G), справедливым для самого общего случая движе-
движения твердого тела. Остановимся только на некоторых специфических
свойствах плоского движения.
Теорема. Если движение плоской фигуры в ее плоскости в данный мо-
момент времени не является мгновенно поступательным, то в этот мо-
момент времени существует единственная точка С фигуры, скорость
которой равна нулю. Скорости остальных точек таковы, какими они
были бы при мгновенном вращении фигуры вокруг точки С.
Доказательство.
Так как движение не является мгновенно поступательным, то
и> ф 0. В абсолютной системе координат векторы vo, u> и неизвестный
вектор ОС запишем в виде
0
и> =
ОС =
хс
Ус
о
Поскольку скорость vc искомой точки С равна нулю, то для нахождения
(. Кинематика твердого тела
65
ее координат получаем из формулы D) векторное уравнение
vo + u) х ~ОС = О,
которое эквивалентно двум скалярным уравнениям
Хо - фУс = О, Yo + фХс = 0,
откуда получаем Хс = —-Yo, Yc = —Хо, или в векторной форме
ОС =
и> х vo
A0)
Если теперь принять точку С за полюс, то теорема будет полностью
доказана. Точка С называется мгновенным центром скоростей.
Формула A0) дает геометрический способ нахождения мгновен-
мгновенного центра скоростей, если известны угловая скорость ш и скорость
полюса vo. Смотря с конца вектора ш, повернем вектор vo на угол тг/2
против часовой стрелки (рис. 29), затем от точки О в направлении,
которое занял повернутый вектор vo, отложим отрезок длиной vo/u>;
конец С этого отрезка и будет мгновенным центром скоростей.
В
с;
Рис. 29
Рис. 30
Часто вектор со не задан, но известны скорости Va и vb двух то-
точек А и В плоской фигуры. При построении мгновенного центра ско-
скоростей здесь следует рассмотреть следующие возможности.
1) Если va = vb, to движение мгновенно поступательное, так как
из формулы vb = Va + ш х АВ следует, что ш = 0 (здесь мгновен-
мгновенный центр «находится в бесконечности»; терминология оправдывается
тем, что при ф —> 0 величины Хс и Ус неограниченно возрастают по
модулю).
2) Если va ф Vb, но скорость одной из точек, скажем точки А,
равна нулю, то А и есть мгновенный центр скоростей.
66
Глава I
3) Если векторы Va и Vb неколлинеарны (рис. 30), то мгновенный
центр скоростей лежит на пересечении перпендикуляров, проведенных
к векторам va и vb в точках Аи В. Это проще всего показать, опираясь
на свойство проекций скоростей двух точек твердого тела на соединя-
соединяющую их прямую (см. следствие 1 п. 24). Действительно, проекции vc
на С А и С В равны нулю, так как вектор va перпендикулярен С А и vb
перпендикулярен СВ. А поскольку С А и СВ неколлинеарны, то отсюда
следует, что vc = 0.
4) Пусть %>аФ Vb, но вектор va параллелен vb- Случай, когда век-
вектор АВ не перпендикулярен Va (или Vb), невозможен, так как тогда
проекции Va и vb на прямую, проходящую через точки А и В, не будут
равными. Если же вектор АВ перпендикулярен va (и Vb), to мгновен-
мгновенный центр скоростей, как нетрудно проверить, лежит на пересечении
прямой, проходящей через точки А и В, и прямой, проходящей через
концы векторов va и Vb (рис. 31).
А: *?vA А\ -?-vA
В
¦*>'«„
в
с
Рис. 31
При движении тела мгновенный центр скоростей перемещается и в
теле, и в абсолютном пространстве. Геометрическое место его положе-
положений на неподвижной плоскости называется неподвижной центроидой, а
геометрическое место положений мгновенного центра скоростей в са-
самой движущейся плоской фигуре называется подвижной центроидой.
Можно показать, что при движении тела подвижная центроида катит-
катится по неподвижной без скольжения.
Теперь рассмотрим некоторые особенности, касающиеся распреде-
распределения ускорений точек твердого тела при его плоском движении.
Теорема. Пусть плоская фигура движется в своей плоскости. Если в
некоторый момент времени хотя бы одна из величин ф или ф отлична
от нуля, то в этот момент времени существует единственная точ-
точка Q фигуры, ускорение которой равно нулю.
Доказательство.
Пусть заданы ускорение полюса wq, мгновенная угловая ско-
§ 4- Кинематика твердого тела
67
рость ш и мгновенное угловое ускорение е. Требуется найти вектор OQ
такой, чтобы ускорение точки Q было равно нулю. Из формулы G) по-
получаем векторное уравнение для OQ:
0. A1)
Учитывая, что в абсолютной системе координат
wo =
Xo
Yo
0
U) =
0
0
Ф
e =
0
0
Ф
0Q =
Xq
Yq
0
из A1) получаем систему двух линейных уравнений относительно
Xq, Yq:
Из условия теоремы следует, что определитель системы A2) ф2 + ф4
отличен от нуля. Поэтому она имеет единственное решение
Эти формулы можно представить в векторной форме:
OQ =
1
.2 , , ,4
{и?wo + е х wo)-
Точка Q называется мгновенным центром ускорений.
Из A3) следует геометрический способ нахожде-
нахождения мгновенного центра ускорений (рис. 32). Опреде- Q
лим угол Р равенством
Этот угол не зависит от выбора полюса и одинаков
для всех точек тела. Чтобы получить точку Q, надо
вектор wo повернуть на угол C в направлении вра-
вращения фигуры, если вращение ускоренное, и в проти-
противоположном направлении, если вращение замедлен-
замедленное. Затем от полюса О в направлении, которое занял
повернутый вектор wo, надо отложить отрезок OQ,
длина которого вычисляется по формуле
A3)
Рис. 32
OQ =
wo
68
Глава I
Конец Q этого отрезка и будет мгновенным центром ускорений. Рис. 32
соответствует ускоренному вращению фигуры против часовой стрелки.
Если мгновенный центр ускорений Q принять теперь за полюс,
то ускорение любой точки Р в данный момент времени может быть
определено так же, как и при вращении вокруг неподвижной оси, про-
проходящей через Q:
w = wB
Woe
Пример 1. Пусть диск катится по неподвижной прямой без скольжения
и скорость его центра О постоянна (рис. 33). Так как при отсутствии
скольжения скорость точки Р диска, которой он касается неподвиж-
неподвижной прямой, равна нулю, то мгновенный центр скоростей совпадает с
точкой Р. Подвижной центроидой будет обод диска, а неподвижной —
прямая, по которой он катится. Так как скорость точки О постоянна,
то мгновенный центр ускорений совпадает с центром диска.
Рассмотренный пример показывает, в частности, что мгновенный
центр скоростей и мгновенный центр ускорений — это, вообще говоря,
разные точки.
В
У/////////////////////////
Р
Рис. 33
OV/////////7/////
Рис. 34
Пример 2. Тонкий стержень АВ опирается своей точкой Р на прямой
угол, а концом А скользит по горизонтальной направляющей с посто-
постоянной скоростью v. Найдем абсолютную скорость и абсолютное уско-
ускорение точки Р в зависимости от времени, если OP = h и в начальный
момент времени О А = 0 (рис. 34).
Скорость точки Р направлена вдоль стержня. Мгновенный центр
скоростей С будет пересечением перпендикуляров, проведенных к
стержню в его точке Р и к горизонтальной оси в точке А. Пусть
§ 4- Кинематика твердого тела 69
О А = х (х = vt); тогда из ААОР и ААРС имеем
h ' h
Угловая скорость стержня находится из равенства v = шСА, от-
откуда
,, _ v _ vh _ vh
С A h2 + x2 h2 + v2t2"
Вектор ш перпендикулярен плоскости рисунка и направлен к чита-
читателю. Вектор углового ускорения стержня е также перпендикулярен
плоскости рисунка, но его направление противоположно направлению и>
I поскольку -jjj < О ). Модуль углового ускорения определяется равенст-
\ at I
вом е =
f , откуда
at
2v3ht
(h2 + v2t2)
Для модуля скорости точки Р имеем
v2t
vP = шСР = -
Vh2 + v2t2
Поскольку точка А является мгновенным центром ускорений
(v = const), то модуль ускорения точки Р вычисляется при помощи ра-
равенств
28. Кинематические инварианты. Кинематический винт.
Снова вернемся к общему случаю движения твердого тела, рассмот-
рассмотренному в п. 24. В формуле D) для скорости точки Р тела угловая
скорость ш не зависит от выбора точки Р. Вектор ш называют первым
кинематическим инвариантом. В более узком смысле мы будем назы-
называть первым кинематическим инвариантом величину 1\ = ш2. Далее,
из формулы D) следует, что для любых двух точек тела А и В ска-
скалярные произведения их скоростей va и vb на вектор ш одинаковы.
Поэтому проекция скорости точки на направление угловой скорости не
зависит от выбора этой точки. Скалярное произведение скоростей то-
точек тела на его угловую скорость называется вторым кинематическим
инвариантом: 1^ = v ¦ ш.
70
Глава I
\N
Рис. 35
щи поступательного перемещения (рис. 17):
Покажем, что в самом общем случае
движения твердого тела, когда 1^ ф 0, ско-
скорости его точек таковы, как если бы тело
совершало мгновенно винтовое движение.
Для этого, согласно п. 23, надо показать су-
существование такой прямой MN, все точки
которой в данный момент времени имеют
скорости, направленные вдоль этой прямой
и параллельные со.
Пусть выбран какой-либо полюс О и в
данный момент известны его скорость Vo
и угловая скорость тела ш. Пусть они зада-
заданы своими компонентами в системе коор-
координат OXYZ, получающейся из абсолют-
абсолютной системы координат OaXYZ при помо-
vo =
vox
voy
voz
ш =
0JX
Если скорость точки S тела (рис. 35) отлична от нуля и параллельна
вектору и>, то
»o + wx OS = р ш (р ф 0).
Это равенство является векторным уравнением прямой MN. Ес-
Если X, Y, Z — координаты любой точки прямой, то это уравнение в
скалярной форме запишется в виде
vox
— ll>zY)
— usxZ)
СОХ
voz
- wYX)
A4)
= p.
Прямая A4) называется мгновенной винтовой осью тела. Ясно, что
все точки мгновенной винтовой оси имеют одинаковые скорости, рав-
равные проекции скорости любой точки тела на направление и>. Совокуп-
Совокупность угловой скорости со тела и скорости v любой точки мгновенной
винтовой оси называют кинематическим винтом, а число р — пара-
параметром винта. Параметр винта выражается через кинематические ин-
инварианты по формуле
§ 5. Сложное движение точки 71
Кинематический винт называется правым или левым в зависимости от
того, положителен или отрицателен его параметр; рис. 35 соответствует
правому винту.
Пример 1. Пусть в пространстве движется твердое тело и в некото-
некоторый момент времени оказываются известными скорости va, Vb, Vc
трех его точек А{0, 0, 0), В{1, 1, 0), СA, 1, 1); vAB, 1, -3),
Vb@, 3, —1), vc(—l, 2, —1). Найдем положение оси кинематическо-
кинематического винта и его параметр в рассматриваемый момент времени.
Примем точку А за полюс. Тогда Vb = Va + ш х АВ, Vc =
= va + ш хАС. Эти векторные равенства можно записать в виде следу-
следующей совместной системы шести линейных уравнений относительно
компонент шх, шу, шх вектора ш:
—ujz = -2, ujz =2, изх - шу = 2, шу — uiz = -3, uiz - шх = 1, изх - изу = 2.
Решив эту систему, получим
их = 1, шу = -1, шг = 2.
Для кинематических инвариантов Д и 1^ имеем такие значения:
1Х = ш2 = 6, I2 = va • ш = -5.
Таким образом, в рассматриваемый момент времени тело совер-
совершает мгновенно винтовое движение, причем параметр кинематическо-
кинематического винта равен —%. Уравнение мгновенной винтовой оси, согласно A4),
имеет вид
2-2y-z l + 2x-z -3 + х + у =5
=
1-1 2 6"
§ 5. Сложное движение точки
29. Основные определения. Иногда бывает необходимо изучить
движение точки одновременно по отношению к двум системам коор-
координат. Пусть система координат Oxyz движется по любому заданному
закону относительно абсолютной системы координат OaXYZ (рис. 17).
Это значит, что известны движение полюса О и матрица A(t), задаю-
задающая ориентацию осей Ox, Oy, Oz относительно абсолютной системы
координат. Пусть в пространстве движется точка Р. Ее движение по
отношению к системе координат Oxyz называется относительным дви-
движением. Движение трехгранника Oxyz относительно OaXYZ называ-
называется переносным движением. Движение точки относительно системы
72 Глава I
координат OaXYZ, определяемое этими составляющими движениями,
называется ее сложным или абсолютным движением. Задача состоит в
установлении связи между основными кинематическими характерис-
характеристиками движения точки в неподвижной и подвижной системах коорди-
координат.
Абсолютной скоростью va (абсолютным ускорением wa) точки
называется ее скорость (ускорение) относительно абсолютной систе-
системы координат OaXYZ. Относительной скоростью vr (относительным
ускорением wr) точки называется ее скорость (ускорение) относительно
системы координат Oxyz. Переносной скоростью ve (переносным уско-
ускорением we) называется скорость (ускорение) той точки Р', которая
неподвижна в системе координат Oxyz и с которой в данный момент
совпадает движущаяся точка Р. Иными словами, переносная скорость
(переносное ускорение) есть та скорость (ускорение), которую движу-
движущаяся точка Р имела бы в данный момент, если бы она в этот момент
оказалась жестко связанной с подвижной системой координат (т. е. не
совершала бы относительного движения).
30. Производная от вектора, заданного своими компонен-
компонентами относительно подвижной системы координат. Часто при-
приходится встречаться с необходимостью дифференцирования вектора,
заданного своими компонентами в системе координат Oxyz, движу-
движущейся произвольным образом. Скорость изменения этого вектора в
неподвижной системе координат OaXYZ называется его абсолютной
производной, а скорость изменения вектора в системе Oxyz — от-
относительной или локальной производной. Найдем связь между этими
производными.
На рис. 17 ОР = р — вектор, заданный в движущейся системе
координат Oxyz. Тот же вектор ОР, заданный в неподвижной системе
координат OaXYZ, обозначим г. Так как движение системы Oxyz за-
задано, то матрица A(t), определяющая ориентацию подвижной системы
координат относительно неподвижной, известна и
r = A(t)p. A)
Вектор —^ есть абсолютная производная вектора ОР, а вектор
(lib
-? = A(t)-!jj — его относительная производная. Обе производные за-
(ль (ль
даны в системе координат OaXYZ (следует заметить, что вектор -^-
(Хь
задан в системе координат Oxyz).
§ 5. Сложное движение точки 73
Из A) получаем
^р- = Ар + Ар = АА~1г + Ар. B)
Но так как (см. п. 24)
АА~гг = и> х г, C)
где и> — угловая скорость системы координат Oxyz относитель-
относительно OaXYZ, то равенство B) запишется в виде
Если учесть обозначение для относительной производной, то окон-
окончательно получим
Этой формулой устанавливается связь между абсолютной и относи-
относительной производными вектора.
Упражнение 4. Показать, что если угловая скорость и> твердого те-
тела, движущегося вокруг неподвижной точки, неподвижна относитель-
относительно тела, то она неподвижна и относительно абсолютного пространства;
показать, что верно также и обратное.
31. Теорема о сложении скоростей. Связь между относитель-
относительной, переносной и абсолютной скоростями точки устанавливается сле-
следующей теоремой.
Теорема. Абсолютная скорость точки равна сумме переносной и от-
относительной скоростей.
Доказательство.
Заметим, что согласно рис. 17 и формуле A) радиус-вектор точки Р
в абсолютной системе координат равен R = Ro + r. Продифференциро-
Продифференцировав R по времени и воспользовавшись равенством D), получим такое
выражение для абсолютной скорости точки Р:
va = R=Ro+r=vo + u:xr + Ар. F)
Вектор vo + u> х г есть скорость той точки подвижной системы коорди-
координат, в которой в данный момент находится движущаяся точка Р, т. е.
является переносной скоростью ve. Вектор же Ар есть относительная
74 Глава I
скорость iv, заданная в абсолютной системе координат. Следовательно,
равенство F) можно переписать в виде
va = ve + iv- G)
32. Теорема о сложении ускорений (теорема Кориоли-
са). Для получения абсолютного ускорения точки продифференцируем
сначала обе части равенства F) по времени и воспользуемся форму-
формулой D). Имеем
wa = va = vo + uxr + ivxr + Ар + Ар =
(8)
= «io + Exr + wx(wxr + Ар) + Ар + Ар.
Здесь е — угловое ускорение подвижной системы координат Oxyz, a
вектор Ар есть относительное ускорение wr. Перепишем равенство (8)
в виде
wa = wo + exr + u)x(u)xr) + wr + u)x Ар + Ар. (9)
Вектор wo+exr+wx(wxr) есть ускорение той точки подвижной
системы координат, в которой в данный момент находится движущая-
движущаяся точка Р, т. е. является переносным ускорением. Далее, согласно C),
можно написать Ар = АА~гА'р = ш х Ар. Поэтому последние два
слагаемых в (9) одинаковы и равны ш х vr каждое. Следовательно, фор-
формула (9) может быть записана в виде
wa = we + wr + wc, A0)
где wc = 2ш х vr. Вектор wc называется ускорением Кориолйса. Форму-
Формула A0) выражает теорему о сложении ускорений.
Теорема. Абсолютное ускорение точки равно сумме переносного, от-
относительного и кориолйсова ускорений.
Можно сказать, что часть абсолютного ускорения — ускорение Ко-
Кориолйса — связана с изменением абсолютной скорости, обусловленным
двумя причинами: 1) влиянием переносного движения на относитель-
относительную скорость (при ш ф 0 вектор vr поворачивается относительно аб-
абсолютной системы координат за счет вращения подвижной системы
координат); 2) влиянием относительного движения на переносную ско-
скорость (при vr ф 0 положение точки в подвижной системе координат
изменяется и, следовательно, изменяется переносная скорость).
Упражнение 5. Показать, что вклад каждой из указанных причин в
величину кориолйсова ускорения одинаков и равен ш х vr.
I 5. Сложное движение точки
75
Пример 1. В плоскости движутся поступательно два стержня АВ
и CD с данными скоростями Vi и v-i- построим скорость v точки Р
пересечения стержней.
Абсолютная скорость точки Р может быть представлена как
сумма переносной скорости V\ стержня АВ и относительной скорости
в движении точки Р по этому стержню. С другой стороны, ее можно
представить как сумму переносной скорости v^ стержня CD и отно-
относительной скорости точки в ее движении по этому стержню. Отсюда
следует способ построения вектора абсолютной скорости точки Р: че-
через концы векторов Vi и v^ проведем (рис. 36) прямые, параллельные на-
направлениям стержней АВ и CD; точка Р\ пересечения этих прямых и
будет концом вектора РР\, изображающего абсолютную скорость точ-
точки Р.
В
х
А
Рис. 36
Рис. 37
Пример 2. Точка Р движется с постоянной угловой скоростью ш по
окружности радиуса R, вращающейся с той же самой угловой скорос-
скоростью около одного из своих диаметров. Найдем абсолютную скорость и
абсолютное ускорение точки как функции угла (р (рис. 37).
Введем жестко связанную с вращающейся окружностью систему
координат Oxyz, начало которой лежит в центре окружности; плос-
плоскость Oyz совпадает с плоскостью окружности, а ось Oz направлена
вдоль вектора ее угловой скорости ш.
Переносная скорость точки перпендикулярна плоскости окружнос-
окружности: v'e = {—ioRsmip, 0, 0). Относительная скорость направлена по
касательной к окружности: vr' = (О, coRcostp, —coRsimp). Абсолют-
Абсолютная скорость точки Р определяется по формуле G). Имеем
v'a = ujR(— simp, cos<?, — simp),
va =
sin2 (p.
76 Глава I
Переносное ускорение лежит в плоскости окружности и перпен-
перпендикулярно оси вращения: w'e = (О, — uj2Rsm^p, 0). Относительное
ускорение лежит в плоскости окружности и направлено к ее центру:
w'r = (О, — bj2Rsin.(p, —bj2Rcos<p). Кориолисово ускорение wc = 2ш х vr
перпендикулярно плоскости окружности: w'c = (—2bj2Rcos<p, О, 0). Аб-
Абсолютное ускорение точки Р определяется по формуле A0). Имеем
w'a = -w2RBcos(p, 2sin<?, cos<^), wa = oj2Rt/4 + cos2 (p.
§ 6. Сложное движение твердого тела
33. Постановка задачи. Пусть твердое тело движется относи-
относительно системы координат O\X\y\Z\, которая, в свою очередь, движет-
движется относительно неподвижной системы координат OaXYZ. Тогда гово-
говорят, что по отношению к системе OaXYZ тело совершает сложное дви-
движение, которое состоит из названных двух составляющих движений.
Аналогично определяется сложное движение из произвольного числа п
составляющих движений.
Задача изучения сложного движения тела состоит в нахождении
зависимостей между основными кинематическими характеристиками
составляющих движений и сложного движения. Мы будем рассматри-
рассматривать только зависимости между скоростями поступательных движений
и между угловыми скоростями. Для простоты ограничимся только слу-
случаем двух составляющих движений.
34. Сложение мгновенно поступательных движений. Пусть
Vi — скорость мгновенно поступательного движения тела относитель-
относительно системы координат O\X\y\Z\, а «2 — скорость мгновенно поступа-
поступательного движения системы O\X\y\Z\ относительно OaXYZ. Возьмем
произвольную точку Р тела и найдем ее абсолютную скорость va. По
теореме о сложении скоростей (п. 31)
va = ve + vr. A)
Для любой точки Р тела переносной скоростью ve будет скорость г^, а
относительной скоростью vr будет скорость г^. - Поэтому любая точка Р
имеет скорость
Va = fh + V2.
Так как все точки тела имеют в данный момент времени одинаковые
скорости, то сложное движение тела является мгновенно поступатель-
поступательным.
! 6. Сложное движение твердого тела
77
Для случая п составляющих движений аналогично получим мгно-
мгновенно поступательное движение со скоростью
35. Сложение мгновенных вращений во-
вокруг пересекающихся осей. Пусть твердое
тело совершает относительно системы координат
OiXiyiZi мгновенное вращение с угловой скорос-
скоростью u>i, а система OiXiyiZi вращается относитель-
относительно системы OaXYZ с мгновенной угловой скорос-
скоростью о»2- Предположим, что оси составляющих мгно-
мгновенных вращений пересекаются в точке А (рис. 38).
Точка А имеет в данный момент времени ско-
скорость, равную нулю. Следовательно, сложное мгно-
мгновенное движение представляет собой вращение во-
вокруг оси, проходящей через точку А. Найдем его
угловую скорость П. Возьмем произвольную точку Р твердого те-
тела. Для нахождения ее скорости надо в A) положить ve = u>2 x АР,
vr = u>i х АР. Поэтому абсолютная скорость va точки Р равна
»о = «1 х АР + и>2 х АР = (u>i + ш2) х АР.
С другой стороны,
va = ilx АР.
B)
C)
Из B) и C) в силу произвольности АР следует, что
Таким образом, в смысле распределения скоростей точек твердого те-
тела совокупность двух мгновенных вращений вокруг пересекающихся
осей эквивалентна одному мгновенному вращению с угловой скорос-
скоростью, равной сумме угловых скоростей составляющих вращений.
Для случая п составляющих мгновенных вращений вокруг пересе-
пересекающихся осей аналогично можно получить одно эквивалентное враще-
вращение с угловой скоростью
78
Глава I
X
Рис. 39
Рис. 40
Замечание 5. Если два составляющих вращения происходят вокруг од-
одной и той же оси с одинаковыми по модулю, но противоположно направ-
направленными угловыми скоростями, то u»i +u>2 = 0 и наличие этих враще-
вращений не влияет на скорости точек тела, участвующего в сложном дви-
движении. Отсюда, в частности, следует, что ш — скользящий вектор,
т. е. его начало можно перемещать в любую точку линии его дейст-
действия и от этого скорости точек тела не изменятся. Действительно,
пусть тело вращается вокруг некоторой оси с угловой скоростью и>.
Вектор и> приложен в точке А оси вращения (рис. 39). От точки В
оси отложим два вектора u>i и и>2 такие, что со = u»i = — u>2, и рас-
рассмотрим сложное вращение тела вокруг одной оси с тремя угловыми
скоростями ш, u>i, о»2- Согласно сказанному выше, совокупность двух
вращений с угловыми скоростями ш и а»2 не влияет на скорости точек
тела; эти вращения могут быть исключены из системы трех враще-
вращений. Таким образом, вектор и> оказался сдвинутым вдоль оси вращения
на отрезок АВ без изменения скоростей точек тела.
36. Кинематические уравнения Эйлера. Получим выражения
проекций мгновенной угловой скорости твердого тела, движущегося
вокруг неподвижной точки, через углы Эйлера (п. 19) и их производ-
производные. Рассматриваемое тело участвует в сложном движении, состоящем
из трех вращений: с угловой скоростью ф вокруг оси OZ, с угловой
скоростью 6 вокруг линии узлов ON и с угловой скоростью ф вокруг
оси Oz (рис. 40). Мгновенная угловая скорость тела ш равна сумме
угловых скоростей составляющих вращений. Пусть р, q, r — проек-
проекции ш соответственно на оси Ox, Oy, Oz, жестко связанные с телом.
Выражения для р, q, r через углы Эйлера и их производные легко по-
§ 6. Сложное движение твердого тела
79
лучить из рис. 40, на котором вспомогательная прямая ОМ лежит в
плоскости Оху и перпендикулярна линии узлов. Имеем
р = ф sin в sin (р + в cos <р,
q = ф sin в cos ip — 6 sin <p,
r = ip cos в + ф.
D)
Соотношения D) называются кинематическими уравнениями Эйлера.
Они широко применяются при исследовании движения твердого тела.
©,,
С А
А С В
Рис. 41
со
В
Рис. 42
37. Сложение мгновенных вращений вокруг параллельных
осей. Пусть твердое тело совершает мгновенное вращение относитель-
относительно системы координат O\X\y\Z\ с угловой скоростью u>i, а система
координат O\X\y\Z\ вращается относительно абсолютной системы ко-
координат OaXYZ с угловой скоростью а»2 и оси вращения параллельны.
В этом случае очевидно, что в мгновенном сложном движении скорос-
скорости точек тела будут такими же, как в плоском движении. Если взять
какую-либо прямую в теле, параллельную мгновенным осям вращения
составляющих движений, то скорости всех ее точек в данный момент
времени будут одинаконы. Поэтому достаточно рассмотреть скорос-
скорости точек тела, лежащих в какой-либо плоскости, перпендикулярной u»i
и о»2- Пусть эта плоскость пересекает плоскость, в которой лежат u»i
и о;2, по прямой АВ (рис. 41 и 42).
Если векторы u>i и и>2 имеют одинаковые направления, то сложное
движение представляет собой мгновенное вращение с модулем угловой
скорости п = ш\ + и>2', вектор Л лежит в плоскости векторов и>\ и а»2
(рис. 41), параллелен им, направлен в ту же сторону и делит рассто-
расстояние между ними внутренним образом на части, обратно пропорцио-
пропорциональные u>i и а>2, т. е.
= ш2ВС.
E)
80 Глава I
Действительно, для скорости точки С имеем выражение
vc = (Vi х AC + w2x ВС.
Слагаемые векторы в правой части этого выражения параллельны и
противоположно направлены. Но при выполнении равенства E) они рав-
равны по модулю. Поэтому vc = 0. Следовательно, и все точки оси, про-
проходящей через точку С параллельно u>i и и>2, имеют нулевые скорос-
скорости. Сложное движение представляет собой мгновенное вращение вокруг
этой оси.
Для нахождения угловой скорости П сложного движения достаточ-
достаточно рассмотреть скорость одной из точек, не лежащей на мгновенной оси
вращения (скорости всех точек тела вполне определяются скоростями
трех его точек, не лежащих на одной прямой; см. п. 24). Рассмотрим
скорость точки В. С одной стороны, »в = Wi х АВ, а с другой —
«в = fl х СВ. Из равенства
П х СВ = и>х х АВ F)
следует, что u»i и П параллельны и одинаково направлены. Для нахож-
нахождения модуля вектора П приравниваем модули обеих частей равенст-
равенства F):
ПСВ = алАВ. G)
Но, используя E), можно получить, что
АВ = АС + С В = ^СВ + С В = Ш1+г Ш2 СВ. (8)
Из G) и (8) следует, что 12 = ш\ + и>2 ¦
Аналогично рассматривается случай противоположных направле-
направлений u»i и о»2- Примем для определенности, что ш\ > и>2- В этом случае
сложное движение представляет собой мгновенное вращение с угловой
скоростью п = ш\ — u>2'i вектор П расположен в плоскости векторов u»i
и и>2, направлен в сторону большей угловой скорости и делит расстоя-
расстояние между ними внешним образом на части, обратно пропорциональные
модулям u>i и и>2, т. е. олАС = ш2ВС (рис. 42).
38. Пара вращений. Пара вращений есть совокупность двух
мгновенных вращений вокруг параллельных осей с равными по модулю,
но противоположно направленными мгновенными угловыми скоростя-
скоростями.
Плоскость, в которой лежат векторы u>i, и и>2 (a>i = —W2), состав-
составляющие пару вращений, называют плоскостью пары, а расстояние d
между осями мгновенных вращений, соответствующими u»i и а»2, назы-
называют плечом пары (рис. 43). Вектор АВхшг называют моментом пары.
§ 6. Сложное движение твердого тела
81
Покажем, что твердое тело, участвующее в паре вращений, совер-
совершает мгновенно поступательное движение со скоростью, равной момен-
моменту пары. Для этого рассмотрим произвольную точку Р тела и вычислим
ее скорость
V = U>1 X АР + U>2 X ВР = АР X U>2 - ВР X U>2 =
= (АР - В~Р) хш2
Таким образом, пара вращений эквива-
эквивалентна мгновенно поступательному дви-
движению со скоростью v, равной момен-
моменту пары. Вектор v — свободный век-
вектор, так как он может быть приложен
в любой точке тела (все точки тела име-
имеют одинаковую скорость v). Скорость v
перпендикулярна плоскости пары и на-
направлена так, что наблюдатель с кон-
конца v «видит» векторы пары Шх и и>2 ука-
указывающими на вращение плоскости па-
пары против часовой стрелки. Если ввести
обозначение ш = |u>i| = |и>г|, то
v = tod.
А
со Л
со,
В
lABxa2=v
Рис. 43
(9)
Наоборот, всякое мгновенно поступательное движение тела может
быть (бесконечным числом способов) заменено на пару вращений, плос-
плоскость которой перпендикулярна v, а плечо пары d и модули ш\ и и>2,
равные ш, связаны соотношением (9). Направления u>i и и>2 выбирают-
выбираются так, чтобы момент эквивалентной пары был направлен так же, как
вектор v.
39. Сложение мгновенно поступательного и вращательно-
вращательного движений. Пусть твердое тело совершает относительно системы
координат OiXiyiZi мгновенное вращение с угловой скоростью ш, а
система координат OiXiyiZi движется относительно абсолютной сис-
системы OaXYZ мгновенно поступательно со скоростью v. Угол между
векторами ш и v равен а.
Чтобы установить характер сложного мгновенного движения те-
тела, разложим вектор v на две составляющие v\ и V2- Первая состав-
составляющая направлена вдоль вектора ш, а вторая перпендикулярна ему
(рис. 44), vi = vcosa, V2 = vsina. Согласно п. 38, мгновенно по-
поступательное движение можно заменить парой вращений, выбрав со-
соответствующим образом составляющие ее угловые скорости и плечо.
В рассматриваемом случае заменим V2 парой, составленной угловы-
угловыми скоростями u>i = —и>2 = —ш, расположив u>i и и>2 в плоское-
82
Глава I
СО
v,
В
ucos a
В
А,.-
Рис. 44
Рис. 45
ти, перпендикулярной V2, как показано на рис. 44. При этом, соглас-
согласно (9), V2 = vsina = АВ -ш. Мгновенные вращения вокруг одной и той
же оси, проходящей через точку А с равными по модулю, но проти-
противоположно направленными угловыми скоростями u hi>)i, могут быть
отброшены, так как они не влияют на скорости точек тела (см. п. 35).
Останутся только мгновенное вращение с угловой скоростью и>2 и мгно-
мгновенно поступательное движение со скоростью V\, параллельной и>2-
Следовательно, сложное движение будет мгновенно винтовым
(рис. 45). Мгновенная винтовая ось смещена параллельно угловой ско-
скорости тела на расстояние АВ =
. Параметр р кинематического
винта равен
v cos a
и)
. В частном случае, когда а = 0 (вектор v паралле-
параллелен ш), нет необходимости проводить указанные выше преобразования,
так как уже исходная совокупность ш и v образует кинематический
винт. Если а = тг/2 (вектор v перпендикулярен ш), то параметр ки-
кинематического винта равен нулю и сложное движение будет мгновен-
мгновенным вращением с угловой скоростью ш относительно оси, проходящей
через точку В и смещенной параллельно ш от точки А на расстоя-
расстояние АВ = v/ш.
В заключение отметим, что, изучая мгновенное кинематическое
состояние твердого тела, мы видели, что существуют четыре простей-
простейших мгновенных движения тела: покой, поступательное движение, вра-
вращение, мгновенно винтовое движение. Разнообразные движения тела в
природе и технике получаются как непрерывная упорядоченная после-
последовательность этих простейших мгновенных движений.
Часть II
ДИНАМИКА
Глава II
Основные понятия и аксиомы динамики
§ 1. Законы (аксиомы) Ньютона. Задачи
динамики
40. Инерциальные системы отсчета. Принцип относитель-
относительности Галилея. Динамика изучает движение механических систем в
связи с причинами, вызывающими или изменяющими это движение.
Материальная точка в теоретической механике представляет собой
геометрическую точку, наделенную механическими свойствами. Эти
свойства точки определяются законами (аксиомами) дина-
динамики, которые рассмотрены в этом параграфе. Попутно дано определе-
определение некоторых важнейших понятий, которыми оперирует теоретичес-
теоретическая механика.
Основание теоретической механики составляют законы, или ак-
аксиомы, Ньютона. Эти аксиомы представляют собой постулаты, спра-
справедливость которых подтверждается многовековыми наблюдениями и
опытом человечества.
Законы механического движения были сформулированы Ньютоном
по отношению к абсолютному (неподвижному) пространству. Системы
координат, неподвижные относительно этого пространства или движу-
движущиеся относительно него поступательно, равномерно и прямолинейно,
называют инерциальными системами отсчета.
В теоретической механике считается, что инерциальные системы
отсчета эквивалентны во всех механических отношениях. Иными слова-
словами, все уравнения и законы механики не зависят от конкретного выбо-
выбора инерциальной системы отсчета. В этом состоит важнейший принцип
механики — принцип относительности Галилея.
Все аксиомы динамики формулируются по отношению к инерци-
инерциальной системе отсчета.
41. Первый закон Ньютона (аксиома инерции). Сила. Следу-
Следующую аксиому динамики называют первым законом Ньютона
или аксиомой инерции: если на материальную точку не дейст-
действуют силы, то она сохраняет состояние покоя или равномерного и пря-
прямолинейного движения.
Остановимся подробнее на содержании этой аксиомы. Если система
движется только под влиянием внутренних взаимодействий, т. е. взаи-
86 Глава II
модействий точек, входящих в систему, то она называется замкнутой
системой. Конечно, строго говоря, замкнутых систем в смысле данного
определения не существует хотя бы потому, например, что гравитаци-
гравитационное взаимодействие между материальными точками существует, на
каком бы расстоянии одна от другой ни находились эти точки. Точ-
Точность, с которой можно принять ту или иную систему материальных
точек за замкнутую систему, определяется условиями конкретной за-
задачи.
Замкнутая система, состоящая из одной материальной точки, на-
называется изолированной материальной точкой. Ясно, что понятие изо-
изолированной материальной точки также является идеализированным по-
понятием.
Аксиома инерции, фактически, постулирует существование
инерциальных систем отсчета. Именно: существуют такие системы
отсчета, относительно которых изолированная материальная точка
покоится или движется равномерно и прямолинейно. Эти системы от-
отсчета и являются инерциальными.
В действительности инерциальных систем не существует, но с
большой степенью точности за инерциальную систему отсчета мож-
можно принять систему координат с началом в центре Солнечной системы
и осями, направленными на «неподвижные» звезды. Для большинства
технических задач за инерциальную систему отсчета принимают сис-
систему координат, жестко связанную с Землей.
Механическое действие материального объекта на данную матери-
материальную точку состоит в том, что она изменяет свое состояние покоя или
равномерного и прямолинейного движения. Не вдаваясь в физическую
сущность причин, приводящих к появлению ускорения точки, мы гово-
говорим, что если точка движется с ускорением относительно инерциаль-
ной системы отсчета, то на нее действует сила. Именно в этом смысле
мы говорим о существовании силы, приложенной к материальной точ-
точке. Сила есть причина возникновения ускорения точки; она является
количественной мерой механического действия на точку, в результате
которого возникает ускорение этой точки.
42. Масса. Второй закон Ньютона (основная аксиома ди-
динамики). Наблюдение и опыт показывают, что материальные тела об-
обладают «врожденным» свойством, из-за которого тело «с трудом» выво-
выводится из состояния покоя или изменяет свое движение. «Способность»
материальной точки «сопротивляться» изменению ее скорости называ-
называется инертностью.
Количественная мера инертности материальной точки, пропорцио-
пропорциональная количеству вещества, заключенного в этой точке, называется
ее массой. Масса представляет собой основную динамическую характе-
§ 1. Законы (аксиомы) Ньютона. Задачи динамики 87
ристику точки. В динамике материальная точка есть геометрическая
точка, обладающая инертностью, и, следовательно, с динамической сто-
стороны характеризуется своей массой.
Масса является скалярной положительной величиной, обладающей
свойством аддитивности: массы материальных точек складываются
арифметически.
Масса материальной точки считается постоянной величиной, не за-
зависящей от обстоятельств движения. Это свойство массы хорошо под-
подтверждается опытом, если скорость точки мала по сравнению со скорос-
скоростью света и если не учитывать внутриатомные процессы в веществе,
образующем материальную точку. За единицу массы в Международ-
Международной системе единиц принимается масса эталона, хранящегося в Париже.
Единица массы называется килограммом (кг).
Второй закон Ньютона устанавливает связь между массой матери-
материальной точки, приложенной к ней силой и возникающим при этом уско-
ускорением точки. Если т — масса точки, аи — ее ускорение в инерциаль-
ной системе отсчета, то, согласно второму закону Ньютона,
mw = F, A)
где F — сила, приложенная к точке. За единицу силы в Международной
системе единиц принимается такая сила, которая, будучи приложена к
материальной точке массой 1 кг, вызывает ее ускорение в инерциаль-
ной системе координат, равное 1 м/с2. Эта единица называется ньюто-
ньютоном (Н). В дальнейшем считается, что сила F может зависеть только
от положений точек системы, их скоростей и времени, но не зависит
от ускорений точек.
43. Третий закон Ньютона (аксиома взаимодействия ма-
материальных точек). Следующая аксиома постулирует характер взаи-
взаимодействия материальных точек. Если одна материальная точка дей-
действует на другую, то и вторая точка действует на первую, причем
силы, приложенные к каждой из них, равны по величине и направлены
вдоль прямой, соединяющей эти точки, в противоположные стороны.
44. Аксиома независимости действия сил (закон сложения
сил). Опыт показывает, что силы взаимодействия двух материаль-
материальных точек не могут быть изменены возможными действиями на них
других материальных точек, если положение, скорости и физическое
состояние (электрическое, магнитное и т. д.) этих точек остаются
неизменными. Когда точки Pi (г = 1,2,..., к) действуют на одну и
ту же точку Р с силами Fi, то ускорения Wi, которые они вызвали
бы у нее, действуя каждая отдельно, складываются. В этом состоит
аксиома независимости действия сил.
Глава II
Если т — масса точки Р, то согласно формуле A), W{ = ^-F»- По-
Поэтому ускорение w точки Р в соответствии с аксиомой независимости
действия сил вычисляется по формуле
w = w1 + w2 + ... + wk = щ№ + F2 + ... + Fk),
откуда видно, что ускорение w точки Р таково, каким оно было бы,
если бы к ней было приложено не к отдельных сил, а одна сила F,
равная сумме сил Ff.
F = Fx + F2 + ... + Fk.
Это и есть закон сложения сил. Он является эквивалентной формулиров-
формулировкой аксиомы независимости действия сил. Упомянутая сила, действие
которой заменяет действие всех к сил Fi, называется равнодействую-
равнодействующей сил F\, ... , Fk, приложенных к точке Р.
45. Активные силы и реакции связей. Рассмотрим движение
системы N материальных точек Pv (и = 1,2, ... , N) относительно не-
некоторой инерциальной системы отсчета. Пусть rnv — масса точки Pv,
a rv — ее радиус-вектор относительно начала координат. Если систе-
система свободная, то ускорения rv образующих ее точек определяются из
второго закона Ньютона mvrv = Fv, где Fv — равнодействующая сил,
приложенных к точке Pv. Если же система не является свободной, то на
ускорения ее точек наложены вполне определенные ограничения. Эти
ограничения мы рассмотрели в п. 11. Величины
не будут, вообще говоря, удовлетворять уравнениям D) и E) п. 11 для
ускорений, т. е. ускорения wv точек Pv несвободной системы будут
отличаться от их ускорений rv в случае свободной системы. Таким
образом, наличие связей приводит к возникновению у точек системы
дополнительного ускорения wv — rv.
Но, согласно второму закону Ньютона, всякое ускорение точки воз-
возникает за счет действия на нее некоторых сил. В рассмотренном случае
эти силы обусловлены наличием связей. Их называют реакциями свя-
связей. Чтобы не смешивать реакции связей с остальными силами, прило-
приложенными к точкам несвободной системы, назовем эти остальные силы
активными силами. Заметим, что здесь Fv — равнодействующая ак-
активных сил.
Активные силы можно также условно назвать заданными силами;
это те из сил, приложенных к механической системе, которые сохраня-
сохраняются, если связи мгновенно исчезнут. Реакции связей называют иногда
§ 1. Законы (аксиомы) Ньютона. Задачи динамики 89
пассивными силами; они заранее неизвестны и зависят не только от тех
материальных приспособлений, которые реализуют связи, но и от ак-
активных сил и от движения системы.
Обозначив Rv равнодействующую реакций связей, приложенных к
точке Pv, согласно второму закону Ньютона получим mv(wv — rv) = Rv
(у = 1, 2, ... , N). Отсюда и из равенств mvrv = Fv следуют уравнения
движения точек системы
mvwv = Fv + Rv (v = l,2,...,N). B)
Эти уравнения показывают, что с точки зрения динамики несвобод-
несвободную систему можно рассматривать как свободную, движущуюся под
действием активных сил и реакций связей. В дальнейшем при изуче-
изучении движения несвободных систем мы часто будем пользоваться этим
положением.
В механике считается справедливым принцип детерминирован-
детерминированности Ньютона-Лапласа. Согласно этому принципу движение сис-
системы материальных точек является вполне детерминированным: за-
задание начальных положений rvo и скоростей vvo точек единст-
единственным образом определяет их дальнейшее движение, т. е. функ-
функции rv{t) {v = 1,2, ... , N).
46. Силы внешние и внутренние. Совокупность всех сил, при-
приложенных к точкам Pv материальной системы (иногда говорят «сис-
«систему сил»), можно разделить на внутренние и внешние силы. Внут-
Внутренними силами называются силы взаимодействия между точками Pv,
образующими материальную систему. Силы, возникающие благодаря
воздействию на точки Pv материальной системы других материальных
точек, не входящих в эту систему, называют внешними.
Отметим, что деления системы сил на внутренние и внешние силы
и на активные силы и реакции связей не взаимосвязаны.
47. Задачи динамики. Равновесие. Статика. Рассматривая
движение систем в связи с силами, приложенными к образующим их
материальным точкам, динамика ставит целью решение следующих
двух основных задач: 1) по заданным силам найти движение системы;
2) по известному движению системы найти неизвестные силы, прило-
приложенные к точкам системы.
В динамике изучается также частный случай движения — состоя-
состояние равновесия механической системы. Под состоянием равновесия сис-
системы понимается такое ее состояние, когда скорость vv каждой точки
системы равна нулю на протяжении некоторого промежутка времени,
т. е. vv = 0 при ?о ^ t ^ t\\ если при t = to vu = О, то это условие
эквивалентно условию wv = 0 при to ^ t ^ t\. В частности, если to
90 Глава II
равняется нулю, a ti — бесконечности, то материальная система в на-
начальный момент времени находится в состоянии равновесия и остается
в нем все время.
Состояние равновесия механической системы изучается в разде-
разделе динамики, называемом статикой. В статике решаются две задачи:
1) найти условия равновесия механической системы; 2) решить вопрос
о приведении системы сил, т. е. о замене данной системы сил другой, в
частности, более простой, оказывающей то же воздействие на движение
механической системы, что и исходная система сил.
§ 2. Главный вектор и главный момент системы
сил
48. Главный вектор системы сил. Обозначим Fv равнодейству-
равнодействующую всех сил (активных и реакций связей), приложенных к точке Pv.
Сумма
N
R = ?*V A)
называется главным вектором этой системы сил. Пусть Fvx,Fl/y,Fl/z —
компоненты силы Fv в декартовой системе координат Oxyz. Тогда ком-
компоненты Rx,Ry,Rz главного вектора и его направление определяются
в соответствии с формулами
JV JV JV
лх - > ?vx, Ну - > *vy, Hz - у tvz, (Z)
C)
Здесь i, j, k — орты осей Ох, Оу, Oz.
Сила Fv является суммой равнодействующих всех внешних Fi, и
всех внутренних сил F^l\ т. е.
Fv = F& + F^ {v = 1 2, ... , TV). D)
Согласно третьему закону Ньютона силы, с которыми взаимодейству-
взаимодействуют две точки системы, равны по величине и направлены вдоль одной
прямой в противоположные стороны. Поэтому когда мы подставим вы-
выражения D) в A), то в получившейся сумме внутренние силы взаимно
j 2. Главный вектор и главный момент системы сил
91
уничтожаются. Таким образом, главный вектор внутренних сил обра-
обратится в нуль и
N
R =
E)
т. е. главный вектор R системы сил равен главному вектору R^ внеш-
внешних сил.
49. Момент силы относительно точки и оси. Моментом си-
силы F относительно точки О называется вектор
mo(F) = rxF,
F)
и
О.
Рис. 46
где г — радиус-вектор точки приложения силы F от-
относительно точки 0. Из свойств векторного произве-
произведения следует, что модуль момента силы относитель-
относительно точки равен произведению модуля силы на ее пле-
плечо, т. е. на расстояние от точки 0 до линии дейст-
действии силы F. Направлен момент по нормали к плос-
плоскости, проходящей через точку 0 и линию действия
силы F, в ту сторону, откуда «вращение», вызванное
силой, происходило бы против часовой стрелки. Лини-
Линией действия силы F мы называем прямую, на которой
лежит вектор F.
Моментом силы F относительно оси и называет-
называется проекция на эту ось момента силы F относительно
точки, взятой на этой оси. Момент силы F относительно оси и обозна-
обозначается mu(F).
Пусть е — единичный вектор оси и (рис. 46). Возьмем на этой оси
точки О\ и 02- Тогда, согласно определению, mu(F) = (r\ x F)-e, а так-
также mu(F) = (га х F) ¦ е. Составим разность (r\ x F) ¦ е — (rj x F) ¦ е.
Она равна нулю, так как (ri x F) • е — (rj x F) • е = ((ri — гг)х
xF) • е = @102 х F) ¦ е, а векторы 0102 х F и е ортогональны. Тем
самым показана независимость величины mu(F) от выбора точки
на оси.
Пусть Fx,Fy,Fz и х, у, z — компоненты силы F и радиуса-
вектора г точки ее приложения соответственно в декартовой прямо-
прямоугольной системе координат Oxyz с началом в точке 0. Тогда из F)
следует, что момент силы F относительно точки 0 задается в этой
системе координат компонентами
mx(F) = yFz - zFy,
= zFx-xFz, mz(F) = xFy - yFx. G)
92 Глава II
Величины mx(F),my(F) и mz(F) — моменты силы F относительно
осей Ох, Оу и Oz. Из G) сразу следует, что момент силы относительно
оси равен нулю тогда и только тогда, когда линия действия силы и ось
лежат в одной плоскости.
50. Главный момент системы сил. Пусть снова Fv — равно-
равнодействующая всех сил, приложенных к точке Pv механической систе-
системы, аг„ — радиусы-векторы точек Pv относительно точки О. Главным
моментом Мо этой системы сил относительно точки О называется
сумма
N N
MO = Y, mo(Fv) = Y,rvx Fv. (8)
Так же, как и для главного вектора, можно показать, что главный
JV , .
момент внутренних сил равен нулю и Мо = Yl mo(F})e>), т. е. главный
v=\
момент всех сил системы равен главному моменту Мо ее внешних
сил.
Главным моментом Ми системы сил относительно оси и назы-
называется проекция на эту ось главного момента Мо, вычисленного для
какой-либо точки оси. Независимость величины Ми от выбора точки
на оси доказывается так же, как и в случае одной силы в п. 49.
В декартовой системе координат Oxyz главный момент Мо имеет
компоненты, вычисляемые по формулам
N
v=l
N
У^ (zvF
v=l
N
v=l
1 t ТГ \
uz <*vrvy) •>
их v uz) i
"uy - yvFvx).
Величины Mx, My и Mz — главные моменты сил относительно
осей Ох, Оу и Oz.
Направление главного момента определяется формулами
§ 3. Работа. Силовая функция. Идеальные связи 93
§ 3. Работа. Силовая функция. Идеальные связи
51. Работа системы сил. Пусть Fv — равнодействующая всех
сил системы (внутренних и внешних), приложенных к точке Pv,
a drv — смещение точки Pv вдоль ее траектории. Элементарной ра-
работой d'Au силы Fv на перемещении drv называется скалярное произ-
произведение
dl'Av = Fv • drv = Fvxdxv + Fvydyv + Fvzdzv. A)
Элементарная работа d'A всех сил системы получается путем сумми-
суммирования выражений A) по индексу и:
N N
d'A = ^Fv-drv = ^{Fvxdxv + Fvydyv + Fvzdzv). B)
Символ d! указывает на то, что правые части в A) и B) не обязательно
являются полными дифференциалами.
В выражения A) и B) для элементарной работы входит работа как
внешних, так и внутренних сил. Обозначив через d'A^ работу внешних
сил, а через d'A^ — работу внутренних сил, выражение B) можно
записать в виде
Пусть точка Pv совершает конечное перемещение из положения MVo в
положение MVl, описывая дугу MUaMVl, и пусть Fv и drv могут быть
выражены через один и тот же скалярный параметр t (который не обя-
обязательно должен быть временем) так, что положения MVo и MVl точки
отвечают значениям t0 и ti этого параметра. Тогда выражение A) будет
представлено в виде функции параметра t, умноженной на его диффе-
дифференциал, и может быть проинтегрировано по t в пределах от to до t\.
Результат интегрирования называется полной работой Av силы Fv на
рассматриваемом конечном перемещении вдоль пути MUoMVl. Полная
работа всех сил системы представляет собой сумму по и величин А„.
52. Элементарная работа сил, приложенных к твердому
телу. Здесь покажем, что элементарная работа системы сил, прило-
приложенных к твердому телу, определяется лишь работой внешних сил, и
найдем нужное для дальнейшего выражение элементарной работы че-
через главный вектор, главный момент внешних сил и характеристики
мгновенного кинематического состояния тела.
Будем представлять себе твердое тело как механическую систему,
состоящую из N (N ^ 2) отдельных точек Ри, взаимные расстояния
между которыми не изменяются. Пусть Fv — равнодействующая всех
94 Глава II
сил, приложенных к точке Pv тела, которую будем записывать в виде
суммы равнодействующих Fo + F^ всех внешних и внутренних сил,
приложенных к точке Pv.
Пусть О — произвольно выбранный полюс в твердом теле. Ско-
Скорость vv точки Pv относительно неподвижной системы координат опре-
определяется по формуле (см. п. 24)
vv = vo + w x rv,
где vo — скорость полюса, ш — угловая скорость тела. Поэтому сме-
смещение точки Pv вдоль ее траектории равно (vo + и> х rv) dt, где dt —
дифференциал времени. Для элементарной работы системы сил полу-
получим выражение
d'A = ^ Fv • {vo + w x rv) dt = I 53 -Fi/ I • vo dt + ^(u x rv) ¦ Fv dt.
Воспользовавшись свойствами смешанного произведения, перепишем
это выражение в виде
(
d' A = 1^2 Fv \ • vodt
Заменяя Fv на сумму F^' и F^ и учитывая, что главный вектор и
главный момент внутренних сил равны нулю, получаем окончательно
d'A = Д<е> • vo dt + M^ ¦ и dt, C)
где Д(е) и Мо — главный вектор и главный момент внешних сил
относительно точки О.
53. Силовое поле. Силовая функция. Потенциал. Предполо-
Предположим, что на материальную точку, движущуюся относительно инерци-
альной системы отсчета, во всем пространстве или в какой-то его части
действует сила, зависящая от положения точки (и, быть может, от вре-
времени), но не зависящая от скорости точки. В этом случае говорят, что
в пространстве или его части задано силовое поле, а также, что точ-
точка движется в силовом поле. Соответствующие понятия для системы
материальных точек аналогичны.
Силы, зависящие от положения, в механике встречаются очень час-
часто. Такова, например, сила, приложенная к точке, движущейся по го-
горизонтальной прямой под действием пружины, к которой эта точка
прикреплена. Важнейшим примером силового поля в природе является
j 3. Работа. Силовая функция. Идеальные связи
95
гравитационное поле: действие Солнца на планету данной массы вполне
определяется в каждой точке пространства законом всемирного тяго-
тяготения.
Силовое поле называется потенциальным, если существует скаляр-
скалярная функция U, зависящая только от координат хи, yv, zv точек Pv
материальной системы (и, быть может, от времени), такая, что
9U
8U
8U
f — 9U тр _ 8U р _ 8U (,, — л о лп (л\
Функция U называется силовой функцией. Функция П = —U называется
потенциалом, или потенциальной энергией. Функция П определена с
точностью до аддитивной постоянной. Потенциальное поле называется
нестационарным или стационарным в зависимости от того, зависит
функция П явно от времени или нет.
Силы Fv, удовлетворяющие равенствам D), называются потенци-
потенциальными.
Элементарная работа сил стационарного потенциального поля пред-
представляет собой полный дифференциал. В самом деле, из B) и D) полу-
получаем
N
v=l
E)
Поэтому если в рассматриваемой области пространства П является од-
однозначной функцией от xv, yv, zv (и = 1, 2,... , TV), то полная работа
сил потенциального поля при переходе из одного положения системы в
другое не зависит от путей перехода точек из их начальных положений
в конечные. В частности, если все точки системы описывают замкну-
замкнутые пути, то полная работа равна нулю.
Пример 1 (Однородное поле тяжести). Пусть
т — масса точки, g — ускорение свободного па- z'
дения. Тогда (рис. 47)
Fx = 0, Fy = О, FZ = -mg; П = mgz.
Пример 2 (Силовое поле упругой пружи-
пружины). Пусть материальная точка движется
вдоль оси Ох (рис. 48) под действием пружины, к
которой она прикреплена. Если при х = 0 пружи-
пружина не деформирована, то при малых отклонениях
точки можно считать, что со стороны пружины
к ней приложена сила F = —кх (к > 0). В этом случае П = 1/2кх2.
тд
= 1/
96 Глава II
О F Р Пример 3 (Центральное силовое по-
• *¦ • *" ле). Силовое поле называется цен-
центральным, если сила, приложенная к
Рис. 48 движущейся в нем точке, направлена
вдоль прямой, проходящей через задан-
заданный центр — неподвижную точку О. Пусть при этом величина си-
силы зависит только от расстояния от точки до центра. Так как
F(r) = F(r)jr, где г — радиус-вектор точки Р относительно цент-
центра О, то
d'A = F-dr = F(r)^ = \F{r)*f- = F(r)dr = -effl.
Поэтому
П = - / F{r)dr + const. F)
В качестве конкретного примера найдем потенциал для движения точ-
точки массой гиг в ньютоновском гравитационном поле точки массой т\.
т-1/ \ ТО1ТО2 з
В этом случае г (г) = —j —, где j — универсальная гравитаци-
г
онная постоянная. Если считать, что П = 0 при г = оо, то из F)
следует такое выражение для потенциала центрального ньютоновско-
ньютоновского силового поля:
п = _7!^. G)
54. Элементарная работа системы сил в обобщенных ко-
координатах. Обобщенные силы. Пусть Fv — равнодействующая
всех сил, приложенных к точке Pv системы {у = 1, 2,... , N),
a rv — радиусы-векторы точек Pv относительно начала коорди-
координат. Пусть положение системы задается ее обобщенными координата-
координатами qj (j = 1, 2,... , то). Элементарную работу d'A системы сил на
виртуальных перемещениях Srv будем обозначать SA. Найдем выраже-
выражение элементарной работы через обобщенные координаты и их вариа-
вариации Sqj.
Радиусы-векторы точек Pv являются функциями обобщенных ко-
координат и времени, а виртуальные перемещения Srv, выражаются через
вариации 5qj обобщенных координат по формуле B7) п. 16. Поэтому
v=\ v=\
§ 3. Работа. Силовая функция. Идеальные связи 97
Введем обозначение
N Я
^-?: (i = i, 2, ...,т). (9)
Тогда формула (8) запишется в виде
3=1
Величина Qj называется обобщенной силой, соответствующей обобщен-
обобщенной координате qj A, 2, ... , то). В общем случае обобщенные силы
будут функциями обобщенных координат, скоростей и времени.
В практических задачах при вычислении обобщенных сил форму-
формулами (9), как правило, не пользуются. Обычно дают системе такое вир-
виртуальное перемещение, при котором 5qk = 0 для всех к, кроме к = j.
Тогда 5А = 5Aj = QjSqj и
Пусть силы Fv потенциальные с потенциалом П = П(г!/, t). Тогда
и обобщенные силы — потенциальные, причем им соответствует по-
потенциал, полученный из функции n(rv, t), если в ней величины rv
выразить через обобщенные координаты. В самом деле, учитывая E),
имеем
т N т
j=l v=l j=l J
Отсюда следует, что в случае потенциальных сил обобщенные силы мо-
могут быть вычислены по формулам
Qj = ~~сГГ (j = 1, 2, ... , т).
Пример 1 (Материальная точка движется вдоль оси Ох под дей-
действием силы Fx). В этом случае то = 1, обобщенная координата —
абсцисса х точки, 5А = Fx5x, Qx = Fx.
Пример 2 (Твердое тело вращается вокруг неподвижной оси и).
Здесь т = 1, за обобщениую координату примем угол <р поворота те-
тела вокруг оси. Пусть R^ и Мо — главный вектор и главный мо-
момент внешних сил относительно полюса О, выбранного на оси враще-
вращения. Для подсчета величины SA воспользуемся формулой C) п. 52, взяв
98 Глава II
вместо действительного перемещения виртуальное. Последнее возмож-
возможно, так как твердое тело является склерономной механической систе-
системой (п. 18), а для склерономных систем действительное перемещение
является одним из виртуальных (п. 12). Учитывая, что vo = 0, полу-
получим
6А = Д(е) -vodt+ Mo(e) -udt = М
Следовательно,
Здесь Ми — главный момент внешних сил относительно оси и.
Пример 3 (Движение двойного маятника в вертикальной плоскос-
плоскости В ПОЛЕ тяжести (рис. 15)). Пусть стержни, образующие маятник,
имеют одинаковую длину I и одинаковую массу т. Эта система име-
имеет две степени свободы. За обобщенные координаты примем углы if
и -ф, изображенные на рис. 15. Для вычисления потенциала П возьмем
систему координат с началом в точке А и с осью Ах, направленной
вертикально вниз. Тогда, обозначая через Xi и x-i абсциссы центров тя-
тяжести верхнего и нижнего стержней, имеем
П = —mgx\ —
Но Xi = -~ cos ip, X2 = I cos if + -~ cos ip. Поэтому
П = --^mgl{2> cos if + cos-ф),
и для обобщенных сил получаются следующие выражения:
55. Идеальные связи. При движении несвободной системы на
ее точки действуют реакции связей. Пусть Rv — равнодействующая
реакций связей, действующих на точку Р„ системы (у = 1, 2, ... , N).
Связи называются идеальными, если работа SA реакций этих свя-
связей на любых виртуальных перемещениях равна нулю, т. е.
N
^2 R» ¦ $rv = о. (ю)
v=l
Условие идеальности связей не вытекает из их уравнений, оно вводится
дополнительно. Рассмотрим несколько примеров идеальных связей.
j 3. Работа. Силовая функция. Идеальные связи
99
Пример 1 (Материальная точка Р движет-
движется ПО ГЛАДКОЙ ПОВЕРХНОСТИ (ДВИЖУЩЕЙСЯ ИЛИ
неподвижной)). Виртуальные перемещения Sr
лежат в касательной к поверхности плоскости
как в случае неподвижной, так и в случае движу-
движущейся поверхности (см. п. 12). А реакция поверх-
поверхности ортогональна ей (рис. 49). Поэтому 5А =
Пример 2 (Свободное твердое тело). У сво-
свободного твердого тела нет других связей, кроме
тех, которые обеспечивают постоянство взаимных расстояний между
точками, образующими твердое тело. Эти связи действуют на точки
тела посредством сил, которые для твердого тела являются внутрен-
внутренними. Но, согласно п. 52, внутренние силы в случае твердого тела не
совершают работу. Поэтому 5А = 0.
В дополнение к п. 18 мы можем теперь сказать, что свободное твер-
твердое тело представляет собой голономную склерономную систему с иде-
идеальными связями.
Пример 3 (Твердое тело, имеющее одну неподвижную точку
(рис. 50)). В этом случае 5А = 0, так как Sr = 0 (неподвижна точка
приложения реакции связи R).
Пример 4 (Твердое тело, вращающееся вокруг неподвижной оси).
Здесь SA = 0 по той же причине, что и в примере 3.
Пример 5 (Два твердых тела, соединенных в точке О шарниром
(рис. 51)). Здесь Ri = —R2, Sri = Sr^. Поэтому SA = Ri ¦ Sri +
+ R2 • Sr2 = Ri ¦ (Sn - Sri) = 0.
Рис. 50
Рис. 51
Рис. 52
Пример 6 (Два твердых тела, соприкасающихся при движении
гладкими поверхностями (рис. 52)). Относительная скорость точ-
100 Глава II
ки соприкосновения тел лежит в общей касательной плоскости к по-
поверхностям тел в точке их касания. В этой же плоскости лежит раз-
разность 5г1 — 5г2 виртуальных перемещений точек, в которых соприкаса-
соприкасаются тела. Кроме того, как всегда, R\ = — R2, но в рассматриваемом
случае реакции R\ и i?2 перпендикулярны общей касательной плоскос-
плоскости. Поэтому SA = Ri • Sri + R2 • Sr2 = Ri • (Sri — Sr%) = 0.
Пример 7 (Два твердых тела, соприкасающихся при движении
абсолютно шероховатыми поверхностями). По определению это
означает, что относительные скорости точек, которыми соприка-
соприкасаются тела, равны нулю. Следовательно, S(ri — rj) = 0, и поэто-
поэтому SA = Ri ¦ 5п + R2 ¦ Sr2 = Ri ¦ S(n - гг) = 0.
Пример 8 (Две материальные точки, соединенные натянутой иде-
идеальной нитью). Под идеальной нитью понимается не обладающая
массой нерастяжимая нить, которая не оказывает сопротивления из-
изменению ее формы. Для определенности будем считать, что нить пере-
перекинута через неподвижный гладкий стержень А (рис. 53). Так как нить
невесома, то ее реакции 2\ и Т^, приложенные к точкам Pi и Pi, рав-
равны по модулю, Ti = T<i = Т (натяжение нити всюду одинаково). Найдем
работу реакций на виртуальных перемещениях точек. В силу того, что
нить нерастяжима, Sri cos ai = Er2cos«2- Поэтому 5А = Ti ¦ 5ri +
+ T<i ¦ Sr2 = TiSri cos «i — ТгEг2 cos «2 = T(8r\ cos «i — Sr2 cos «2) = 0.
Очень многие механизмы можно трак-
трактовать как сочетание простейших «дета-
«деталей», рассмотренных в примерах 1-8. Од-
Однако в действительности не существует ни
абсолютно гладких, ни абсолютно шерохо-
шероховатых поверхностей, не существует абсо-
абсолютно твердых тел и нерастяжимых ни-
нитей. Поэтому в реальных ситуациях рабо-
работа реакций связей отлична от нуля. Часто
эта работа бывает малой и в допустимом
приближении может считаться равной ну-
нулю. Этот факт и приводит в теоретической
механике к выделению важнейшего класса
связей, названных выше идеальными.
Однако очень часто связи нельзя считать идеальными. Такой слу-
случай встречается, например, когда при движении тела соприкасаются
не абсолютно гладкими участками своих поверхностей и имеет место
относительное скольжение. В этом случае, отнеся силы трения к неиз-
неизвестным активным силам, можно условно считать связи идеальными.
§ 3. Работа. Силовая функция. Идеальные связи 101
Появление новых неизвестных требует тогда привлечения новых экс-
экспериментальных данных, например законов трения скольжения.
В дальнейшем мы будем рассматривать, как правило, только иде-
идеальные связи.
Остановимся на следующем весьма важном обстоятельстве. Упомя-
Упомянутая в п. 47 первая задача динамики для случая несвободной системы
может быть более подробно сформулирована так. Заданы активные си-
силы Fv, приложенные к точкам Р„ материальной системы, массы т„
точек, связи, возможные начальные положения г„0 и скорости vVB то-
точек системы. Требуется найти положения точек г„ и реакции связей Rv
как функции времени. Таким образом, требуется найти QN скалярных
неизвестных.
Для решения этой задачи мы имеем 3N + г + s скалярных уравне-
уравнений: 37V уравнений из векторных уравнений движения B) п. 45 и r + s
уравнений связей A), B) п. 10. Так как число QN больше 37V + г + s
(на число степеней свободы системы п = 2>N — г — s), то сформули-
сформулированная задача неопределенна. Выделением класса систем с идеаль-
идеальными связями мы делаем задачу определенной, так как одно равенст-
равенство A0) эквивалентно п уравнениям. Для их получения нужно в правой
части равенства A0) выразить зависимые из виртуальных перемеще-
перемещений 8х\, 5yi, Szi, ... , Sxn, Si/n, Szn через независимые и затем при-
приравнять нулю коэффициенты при этих независимых виртуальных пе-
перемещениях. Число же последних равно числу степеней свободы, т.е. п.
Глава III
Дифференциальные вариационные
принципы механики
§ 1. Принцип Даламбера—Лагранжа
56. Понятие о вариационных принципах механики. Прин-
Принципами называют, во-первых, некоторые основные начала, на которых
может быть построена какая-либо теория, научная система и т. п., а
во-вторых — законы, основные положения о чем-либо. Под принципа-
принципами часто понимают также точку зрения, убеждения и т. д.
Принципы теоретической механики можно разделить на вариаци-
вариационные и невариационные. К невариационным принципам относятся, на-
например, аксиомы динамики, обсуждавшиеся в §1 предыдущей главы,
а также законы механики, например закон сохранения энергии, закон
всемирного тяготения и т. п.
Вариационные принципы механики представляют собой выражен-
выраженные языком математики условия, которые отличают истинное (дейст-
(действительное) движение системы от других кинематически возможных,
т. е. допускаемых связями, движений. Вариационные принципы делятся
на дифференциальные и интегральные. Первые дают критерий истинно-
истинного движения для данного фиксированного момента времени, а вторые —
на конечном интервале времени.
В этой главе рассматриваются дифференциальные вариационные
принципы механики.
57. Общее уравнение динамики (принцип Даламбера-Лаг-
ранжа). Рассмотрим систему, состоящую из N материальных то-
точек Pv {у = 1, 2, ... , N). Система может быть как свободной, так
и несвободной. В последнем случае связи, наложенные на систему, счи-
считаются удерживающими и идеальными. Пусть Fv и Rv — равнодейст-
равнодействующие всех активных сил и реакций связей, приложенных к точке Р„.
Имеют место следующие уравнения движения (п. 45):
mvwv = Fv + Rv {v = 1, 2, ... , N), A)
где т„ — масса точки Р„, &wv — ее ускорение в инерциальной системе
отсчета.
§ 1. Принцип Даламбера-Лагранжа 103
Поскольку связи идеальны, то для любых виртуальных перемеще-
перемещений 5rv выполняется равенство
N
J2 Ъ, ¦ Srv = 0. B)
v=l
Запишем уравнения A) в виде
Fv - mvwv = -Rv (v=l, 2, ... , N).
Умножим обе части этого равенства скалярно на 8rv и произведем сум-
суммирование по v. Тогда с учетом условия B) получим соотношение
N
^{Fv - mvwv) ¦ 5rv = 0. C)
v=l
Соотношение C) является необходимым и достаточным условием
для того, чтобы движение, совместимое с идеальными связями, отве-
отвечало данной системе активных сил Fv (v = 1, 2, ... , TV). Необходи-
Необходимость условия C) мы только что показали. Предположим теперь, что
некоторое совместимое со связями движение системы удовлетворяет
условию C). Тогда если положить Rv = mvwv — Fv (и = 1, 2, ... , TV),
то получим, что удовлетворяются равенство B) и уравнения движе-
движения A), полученные непосредственно из законов Ньютона.
Соотношение C) характеризует движение всякой системы с иде-
идеальными удерживающими связями по отношению к активным си-
силам Fv и соответствующим (для данного момента времени) виртуаль-
виртуальным перемещениям. Оно получило название общего уравнения динами-
динамики.
Входящие в C) произведения mvwv масс точек системы на их уско-
ускорения, взятые с обратным знаком, называют силами инерции. Приме-
Применяя эту терминологию, можно сказать, что общее уравнение динамики
показывает, что в любой фиксированный момент времени сумма эле-
элементарных работ активных сил и сил инерции на любых виртуальных
перемещениях равна нулю.
Общее уравнение динамики получено в предположении об идеаль-
идеальности связей B). Если же связи таковы, что все или часть их реак-
реакций Gv не удовлетворяют условию B), то можно к системе активных
сил добавить реакции Gv, и уравнение C) примет вид
N
+ Gv - mvwv) ¦ 8rv = 0. D)
104 Глава III
В общем случае силы Gv (или часть из них) неизвестны. Эта неопреде-
неопределенность должна компенсироваться дополнительными данными о фи-
физических свойствах и характере связей, порождающих реакции Gv.
Важным свойством общего уравнения динамики является то, что
оно не содержит реакций идеальных связей.
Соотношение C) на самом деле является не одним уравнением, а
содержит в себе число уравнений, равное п, т. е. числу степеней сво-
свободы системы, которое определяется количеством независимых вирту-
виртуальных перемещений 5х\, 5yi, 5z\, ... , Sxn, Si/n, Szn (cm. п. 55). В
каждом из этих п уравнений отсутствуют реакции связей.
Общее уравнение динамики C) содержит в себе всю информацию
о движении данной механической системы с идеальными удерживаю-
удерживающими связями под действием заданных активных сил. В последующих
главах оно будет положено в основу получения всех основных диффе-
дифференциальных уравнений движения механических систем, голономных
и неголономных.
Общее уравнение динамики называют также дифференциальным
вариационным принципом Даламбера-Лагранжа. Вариационным прин-
принцип называется потому, что в C) входят вариации — виртуальные пе-
перемещения. Название дифференциального принцип носит потому, что в
нем сравнивается данное положение системы с ее варьированным поло-
положением в фиксированный, хотя и произвольный момент времени (син-
(синхронное варьирование, согласно п. 12).
С этой точки зрения принцип Даламбер а-Л а г р а н ж а мо-
может быть сформулирован следующим образом: истинное движение из
всех кинематически возможных выделяется тем, что для него и толь-
только для него в данный момент времени сумма работ активных сил и сил
инерции на любых виртуальных перемещениях равна нулю.
Пример 1. Две материальные точки массой mi и тг (m-i > mi) со-
соединены идеальной нитью, перекинутой через гладкий стержень, и дви-
движутся в поле тяжести в вертикальной плоскости (рис. 54). Найти
ускорения точек.
Пусть xi и Х2 — абсциссы точек mi и т,2 соответственно. Тогда
из общего уравнения динамики C) следует, что
xi + (m2g - т2х2Nх2 = 0. E)
Но так как нить нерастяжима, то имеет место геометрическая
связь xi -\- X2 -\- тгД = const, где R — радиус сечения стержня. Поэто-
Поэтому Sxi = —6x2, Xi = —Х2, и уравнение E) запишется в виде
[(т2 —m\)g— (mi + т2)ж2]5ж2 = 0.
! 1. Принцип Даламбера-Лагранжа
105
Отсюда в силу произвольности виртуального перемещения 8x2 получаем
.. _ 7712 —
Х
пц + т2
g'
О
т
х"
Рис. 54
Пример 2. Найдем дифференциальное уравнение движения плоского ма-
математического маятника. Маятник будем для простоты представ-
представлять в виде точечной массы т, прикрепленной при помощи невесомого
стержня длиной I к точке А, вокруг которой стержень может вра-
вращаться без трения в вертикальной плоскости. Направляя оси Ах и Ау
декартовой системы координат, как показано на рис. 55, получаем
х = I cos (р, у = I sin ip,
8х = —I sin (p 8(p, Sy = I cos ip Sip
x = — I sin (рф — I cos (рф2, у = I cos ip ф — I sin (рф2,
Fx = mg, Fy = 0.
Общее уравнение динамики
дает равенство
(Fx - mx)Sx + {Fy - my)Sy = 0
—ml{gs'm if + I0)8ip = 0,
откуда, ввиду произвольности вариация Sip, следует дифференциальное
уравнение движения маятника
ф + у simp = 0
F)
106 Глава III
Замечание 1. Из общего уравнения динамики C) видно, что оно (а, сле-
следовательно, и движение системы) не изменяется, если вместо систе-
системы сил Fv, взять какую-либо другую систему сил F*, такую, чтобы
элементарная работа обеих систем сил на любых одинаковых вирту-
виртуальных перемещениях была одинакова, т. е.
N
v=l
Fv-5r
N
§ 2. Принцип Журдена
58. Принцип Журдена. Представляет интерес преобразовать об-
общее уравнение динамики таким образом, чтобы прийти к формулам, в
основном эквивалентным уравнению C) п. 57, но имеющим другую
структуру. Так как уравнение C) п. 57, по существу, содержит в себе
все законы движения механических систем с идеальными удерживаю-
удерживающими связями, то эти новые формулы не будут выражением принци-
принципов, существенно новых. Однако они могут дать новую интерпретацию,
обнаруживающую общие свойства движения систем и наложенных на
них связей, которые не могут быть получены из уравнения C) п. 57
непосредственно.
Рассмотрим множество кинематически возможных движений из
возможного положения г* с различными возможными скоростями v*.
Будем сравнивать их одно с другим и с действительным движением из
того же положения в тот же момент времени. Так мы получаем варь-
варьирование по Журдену (п. 12), при котором 8rv = SvvAt, где величина
8vv = v*t — v*2 — разность возможных скоростей в сравниваемых дви-
движениях (эта величина не обязательно является бесконечно малой).
Подставляя это выражение для Srv в общее уравнение динамики C)
и сокращая на At, получаем
N
Y;(Fv ~ mvwv) ¦ 5vv = 0. A)
v=l
Формула A) выражает дифференциальный вариационный принцип Жур-
Журдена. Согласно этому принципу, среди сравниваемых кинематичес-
кинематически возможных в данный момент времени движений (для которых
r*± = r*2, 8vv ф 0) действительное движение выделяется тем, что для
него и только для него выполнено уравнение A).
§ 3. Принцип Гаусса 107
§ 3. Принцип Гаусса
59. Формулировка принципа Гаусса (принципа наимень-
наименьшего принуждения). Вариационные принципы Даламбера-Лагранжа
и Журдена не связаны с понятием экстремальности. Гаусс предложил
замечательную модификацию принципа Даламбера-Лагранжа, которая
вводит в этот принцип понятие минимальности некоторого выражения.
Эта модификация принципа Даламбера-Лагранжа получила название
принципа Гаусса, или принципа наименьшего принуждения.
Для получения математической формулировки принципа Гаусса
будем сравнивать в некоторый момент времени движения, в которых
все точки системы имеют те же возможные положения г* и скорос-
скорости v*, что и в действительном движении. Возможные же ускорения
точек системы в сравниваемых движениях будут отличаться (на вели-
величины, не обязательно являющиеся бесконечно малыми). Такой способ
синхронного варьирования называется варьированием по Гауссу (п. 12).
Если для разности возможных ускорений w^ — w*2 в двух срав-
сравниваемых кинематически возможных движениях ввести обозначе-
обозначение Swv, то, согласно п. 12, 8rv = 1l25wv(\t) . Подставив это значе-
значение виртуального перемещения в общее уравнение динамики C) п. 57
и сократив его на 1/2{\tJ, получим
JV
(FV - mvwv) ¦ 5wv = 0. A)
Замечая, что массы точек т„, постоянны, а силы Fv не зависят от
ускорений точек системы, уравнение A) можно записать в виде
SZ = 0, B)
где введена величина
JV , ч 2
Z = \^mv [щ,-^-\ C)
v=l ^ '
называемая принуждением или мерой принуждения.
Согласно B), величина Z, рассматриваемая как функция возмож-
возможных ускорений, стационарна при значениях ускорений точек системы,
соответствующих действительному движению.
Величина Z не только стационарна, но и минимальна на действи-
действительном движении. В самом деле, пусть wVQ — ускорения точек систе-
системы в их действительном движении, a Zq — соответствующее им значе-
значение величины Z. Тогда, полагая, что в сравниваемом с действительным
108 Глава III
кинематически возможном движении величина wv равна wVo + SwVo,
находим, что
N N
Z - Zo = ^2(mvwVo - FvMwVo + i ^^ mv{8wv0J- D)
v=l v=l
Первая сумма в правой части равенства D) обращается в нуль в силу
уравнения A), а вторая строго положительна, так как не все величи-
величины SwVo (и = 1, 2, ... , N) равны нулю. Поэтому величина Z на
действительном движении принимает наименьшее значение в классе
возможных ускорений системы.
Таким образом, мы получили принцип Гаусса или, как часто
говорят, принцип наименьшего принуждения: среди сравниваемых ки-
кинематически возможных движений (для которых r*t = r*2, v*t = v*2,
Swv ф 0) действительное движение выделяется тем, что для него при-
принуждение Z минимально.
Пример 1. Найдем ускорение точек nil и ni% из примера 1 п. 57, при-
применяя принцип Гаусса. Имеем
Z = ^пц(-и) - gJ + ^m2(w - gJ,
^— = nil (w + g) + m2 (w - g) =0,
П12 — nil
W = : g.
nil + П12
Пример 2. Применяя принцип Гаусса, найдем дифференциальное уравне-
уравнение движения математического маятника (пример 2 п. 57). Функция Z
имеет вид
Z=\m
х —
FXY . Л. F.
т ' l * т
= ^тA2ф2 + 2gl sin tptp) + ^т{12ф4 + 2gl cos рф2 + g2).
Из условия dZ/дф = 0 следует уравнение F) п. 57.
Пример 3. Материальная точка массой т под действием активной
силы F движется по гладкой поверхности, задаваемой уравнением z =
= f(x, у). Найдем дифференциальные уравнения движения точки. Из
уравнения связи имеем
.. df.. 8f.. 82f .2 п 82f .. 82f .2
! 3. Принцип Гаусса 109
Нужно минимизировать величину, равную
(тх - FxJ + (ту - FyJ + (mz - FzJ,
где производная z задана формулой E). Независимыми переменными яв-
являются х и у. Окончательно получаем уравнение
тх -Fx + (mz -Fz)-^=0, my - Fy + (mz - Fz)-J- = 0,
где z следует заменить на правую часть равенства E).
60. Физический смысл принципа
Гаусса. Пусть в момент времени t точки Р„
несвободной механической системы имеют
радиусы-векторы г„ и скорости vv; mv, как
всегда, обозначает массу точки Pv, a Fv —
равнодействующую всех активных сил, при-
приложенных к точке Р„.
В момент времени t+dt точка Pv займет
положение Av (рис. 56). При этом
PVAV = vvdt + ^
Рис. 56
где многоточием обозначены члены выше второго порядка относитель-
относительно (ft.
Если бы в момент времени t система была освобождена от связей
(без изменения Fv, mv, rv, vv), то движение ее точек на интервале
времени dt было бы отличным от движения точек несвободной систе-
системы. Пусть Bv — положение, которое заняла бы точка Р„ в момент
времени t + dt. Тогда
Удаление BVAV точки при несвободном движении от ее положения при
свободном движении вызвано действием связей, принуждающих точки
системы отклоняться от движения, свойственного точкам свободной
системы. Математически это принуждающее воздействие связей мож-
можно характеризовать длиной вектора BVAV. С другой стороны, для того
чтобы сообщить материальной точке какое-то ускорение, необходимо
воздействие тем большее, чем больше (при прочих равных условиях)
ее масса. Поэтому принуждающее воздействие связей на точку естес-
2
твенно оценивать величиной mvBvAv , а для всей системы — суммой
по
Глава III
этих величин по всем точкам Р„ {и = 1, 2, ... , N). Если пренебречь
членами выше четвертого порядка относительно dt, то
у 9 1
mvBvAv = mv(PvAv - PVBV) = j
wv -
Если просуммировать эти величины по всем точкам системы и отбро-
отбросить несущественный множитель У2((Й) , то получим принуждение для
системы в виде
N
Z=~2
wv -
Величина Z является мерой отклонения действительного движения сис-
системы от ее свободного движения. Так как, согласно принципу Гаусса,
величина Z в действительном движении минимальна, то можно ска-
сказать, что несвободная система совершает движение, наиболее близкое
к свободному.
Пример 1. Материальная точка мас-
массой т движется под действием си-
силы тяжести по гладкой прямой, на-
наклоненной к горизонтальной плоскос-
плоскости под углом а (рис. 57). Найдем
ускорение точки, пользуясь тем, что
ее действительное движение наиме-
наименее отклоняется от свободного дви-
движения. Пусть в начальный момент
точка занимает положение Р и име-
имеет скорость, равную нулю. При сво-
свободном движении точка движется по вертикали и за время dt прохо-
проходит расстояние РВ = 1/2g(dtJ. В действительном несвободном движе-
движении по прямой PC точка движется с неизвестным ускорением w и за
время dt проходит расстояние РА = 1/2w{dtJ. Поэтому
У/////////////////////
Рис. 57
С
ВА> =
-2
g{dtJ w(dtJ
¦ sin a =
(w2 — 2gwsina + g2).
Минимум этой величины достигается при w = gs'ma. Это и есть ис-
искомое ускорение.
61. Экстремальное свойство реакций связей. Физический
смысл принципа Гаусса можно выразить и в других терминах. Замечая,
§ 3. Принцип Гаусса 111
что mvwv = Fv + Rv, мы можем переписать выражение для принуж-
принуждения в виде
v=l
Условие того, что величина Z минимальна для действительного движе-
движения, приводит к экстремальному свойству реакций связей: для дейст-
действительного движения реакции связей минимальны (в смысле миниму-
минимума величины F)).
Глава IV
Статика
§ 1. Статика произвольной механической
системы
62. Общее уравнение статики (принцип виртуальных пере-
перемещений). Задачи статики сформулированы в п. 47. В этом параграфе
кратко рассмотрим некоторые основные вопросы статики произволь-
произвольной механической системы с идеальными удерживающими связями. В
следующем параграфе будут подробно изучены вопросы статики твер-
твердого тела, являющегося важнейшим для приложений частным случаем
механической системы.
Рассмотрим несвободную систему материальных точек Р„
(у = 1, 2, ... , N) со связями, задаваемыми уравнениями A), B) п. 10.
Найдем условия, которым должны удовлетворять связи, чтобы система
при г„ = г„0 могла находиться в состоянии равновесия на интервале
времени to ^t^ti. Во-первых, конечно, положения точек, задаваемые
радиусами-векторами г„ = г„0, должны быть возможными на интерва-
интервале to ^ t ^ t\, т. е. на этом интервале должны выполняться тождества
fa(rvo,t)=0 (а=1, 2, ... , г). A)
Во-вторых, из уравнений B)-E) п. 10, 11, задающих ограничения
на скорости и ускорения точек системы, получаем при г„ = г„0,
vv = 0, wv = 0 и t0 ^ t ^ t\ тождества
( .л _ n da0(rVo, t) _ dfa(rvo, t) _ d2fa{rV0, t) _
a(){rvo, t) = 0, jt = 0, jt = 0, —2 = 0
(a = 1, ... , r; /3 = 1, ... , s).
B)
Из A), B) следует, что система при to ^ t ^. t\ может находиться в
состоянии равновесия в каком-либо ее возможном положении г„ = г„0
только тогда, когда связи удовлетворяют условиям
fa(rvo, t) = 0, ap{rVo, t) = 0
(О )
(to^t^h; a = l, 2, ... , г; fi = 1, 2, ... , s).
§ 1. Статика произвольной механической системы 113
Пусть тождества C) выполнены, т. е. состояние равновесия
г„ = г„0 допускается связями, и пусть при t = to имеем г„ = г„0,
vv = 0. Будет ли система при выполнении условий C) находиться в
состоянии равновесия, зависит от приложенных к ней сил.
В основе статики механической системы лежит принцип
виртуальных перемещений, или принцип Лагранжа.
Сформулируем его в виде теоремы.
Теорема. Чтобы некоторое допускаемое идеальными удерживающими
связями состояние равновесия системы действительно было ее состо-
состоянием равновесия на интервале to $C t $C t\, необходимо и достаточно,
чтобы для любого момента времени из этого интервала элементарная
работа активных сил на любом виртуальном перемещении равнялась
нулю, т. е. чтобы выполнялось условие
N
Y,Fv-5rv = {) (to^t^h). D)
v=l
Уравнение D) называется общим уравнением статики.
Доказательство необходимости.
При доказательстве необходимости условия D) для равновесия сис-
системы воспользуемся общим уравнением динамики
N
^2(FV - mvwv) ¦ Srv = 0, E)
v=l
которое справедливо в любой момент времени для систем с идеальными
удерживающими связями. Если при to i^ t i^ ti система находится в
состоянии равновесия, то wv = 0 и из уравнения E) сразу следует
условие D).
Доказательство достаточности более сложно. Мы дадим его да-
далее в п. 158. Здесь только заметим, что это доказательство будет по су-
существу использовать принцип полной детерминированности движения,
т. е. однозначного определения движения системы по начальным поло-
положениям и скоростям образующих ее материальных точек. Следующий
пример показывает, что при отсутствии полной детерминированности
движения принцип виртуальных перемещений может не иметь места.
Пусть материальная точка единичной массы движется вдоль
оси Ох под действием силы F(x) = ах@ (а > 0; 0 < /3 < 1). Урав-
Уравнение движения точки имеет вид
х = ах0. F)
114
Глава IV
Положение равновесия х = О допускается связями; условие D) вы-
выполнено при всех t, так как в положении равновесия F = 0. Тем не
менее точка, находясь при t = 0 в начале координат и имея при этом
нулевую скорость, может не оставаться в нем при t > 0. Действитель-
Действительно, при начальных условиях ж@) = 0, ж@) = 0 уравнение F) помимо
решения х = 0 имеет еще одно решение вида
x(t) = atb,
G)
где
а =
2A
1-/3
Ъ =
1-/3-
Отметим еще, что, так как Ъ > 2, для решения G)
х@) = 0. Это указывает на то, что, если даже уско-
ускорение точки в положении равновесия равно нулю,
все равно точка может не находиться в равновесии
при t > 0, хотя и выполнены условия C) и D). Игно-
Игнорирование этого обстоятельства привело к тому, что
во многих учебниках и научно-методических статьях
доказательство достаточности принципа виртуальных
перемещений либо неполно, либо ошибочно1.
Пример 1. На рис. 58 изображен механизм, состоящий
из стержней, образующих три одинаковых параллело-
параллелограмма. Стержни MN, RS, SL и NQ — цельные, со-
соединенные в точках пересечения шарнирами. Положим,
что точки Aq и А\ соединены нитью; требуется опре-
определить ее натяжение.
Мысленно перережем нить и заменим ее действие приложенной к
точке А\ силой F. Пусть шарнир А\ сдвинется вниз и 8s — его вирту-
виртуальное перемещение. Ввиду цельности стержней MN, RS, SL и NQ
при виртуальном перемещении диагонали всех параллелограммов удли-
удлинятся на одну и ту же величину. Вследствие этого точка А^ сместит-
сместится вниз уже на 25s, a A3 — на 35s.
Приравняв нулю сумму работ силы F и веса Р на виртуальном
перемещении, получим равенство
- F5s = 0.
1Довольно обширную библиографию по этому вопросу см., например, в рабо-
работах: ГеронимусЯ. Л. О принципе виртуальных перемещений // Бюллетень Ясского
Политехи, ин-та, 1963, Т. 9A3), вып. 3-4, С. 251-262; БлюминГ. Д. О принципе вир-
виртуальных перемещений // Изв. АН СССР. МТТ, 1982, №6, С. 22-28.
; 1. Статика произвольной механической системы
115
Р, Д=
Отсюда, ввиду того, что 5s ф 0, следует равенство
F = ЗР.
Пример 2 (Закон Паскаля). Закон Паскаля описывает характер рас-
распространения давления в несжимаемой жидкости: давление на поверх-
поверхность жидкости, произведенное внешними для жидкости силами, пере-
передается ею равномерно во все стороны.
Чтобы проиллюстрировать закон Па-
Паскаля, рассмотрим сосуд, целиком запол-
заполненный несжимаемой жидкостью; в сосу-
сосуде имеются три отверстия, закрытые по-
подвижными поршнями 1, 2 к 3 (рис. 59).
Пусть S, — площадь i-го поршня, a 5U, —
его виртуальное перемещение (i = 1, 2, 3).
Закрепим мысленно поршень 3, тогда
будут двигаться поршни 1 и 2. Определен-
Определенное движение поршня 1 вызовет определен-
определенное движение поршня 2. Объем жидкости,
вдавленной первым поршнем, равен Si5h;
объем жидкости, вошедшей в трубку второго поршня, равен S25l2. Из
условия несжимаемости жидкости имеем Si5h = S25l2.
Составим сумму работ сил Pi и Р2 на рассмотренном виртуаль-
виртуальном перемещении:
Рис. 59
= 0,
= 0.
Отсюда следует, что
±\ ±2
~s~i = s~2-
Аналогично, мысленно закрепляя '%>
поршень 2, можно получить, что
PL = P1
Sl Ss' Рис. 60
т. е. давление на жидкость передается равномерно во все стороны.
Пример 3. У стены здания положены три одинаковые трубы, как пока-
показано на рис. 60. Какую горизонтальную силу F нужно приложить к оси
правой трубы, чтобы удержать трубы в равновесии, если вес каждой
трубы равен Р ?
116 Глава IV
Если правой нижней трубе сообщить виртуальное перемещение
вдоль оси Ох, то работу совершат только две указанные на рис. 60
силы: Р и F. Радиусы-векторы г а и Гв точек их приложения в систе-
системе координат Оху задаются равенствами (а — радиус сечения труб)
г'А = Bа cos а, 2а sin а), г'в = Dа cos а, 0).
На указанном виртуальном перемещении угол а получает приращение
8а. Поэтому
8г'А = 2а5а(— sin а, cos а), 8г'в = AaSa(— sin а, 0).
Приравняв нулю сумму работ сил Р и F на виртуальном перемещении,
получим равенство
P-8rA + F-8rB = 0,
которое с учетом того, что
Р' = @, -Р), F' = (-F, 0),
можно записать в виде
—Р • 2а cos а ¦ 8а + F • 4а sin а ¦ 8а = 0.
Отсюда при 8а ф 0 получаем
F= ±ctg aP.
63. Общее уравнение статики в обобщенных координа-
координатах. Пусть qi, q2, ... , qm — обобщенные координаты системы, а
Qjili 9? t) — соответствующие им обобщенные силы. Уравнение D) в
обобщенных координатах запишется в виде
JV m
Y M, 0, t)8qj = 0. (8)
Если система голономна, то число ее обобщенных координат т сов-
совпадает с числом степеней свободы п и величины Sqj в (8) независимы.
Приравнивая нулю коэффициенты при 8qj в уравнении (8), получаем,
что в положении равновесия системы q = qo (и только в нем) обобщен-
обобщенные силы равны нулю:
Q. = 0 (» = 1, 2, ..., п). (9)
§ 1. Статика произвольной механической системы 117
Равенства (9) образуют систему п уравнений относительно неиз-
неизвестных дю, йо: ••• ) (Ыь задающих положение равновесия системы.
Если все активные силы потенциальны, то, согласно п. 54, из (9)
получаем
Qi = = 0 (i = 12 п)
где П — потенциальная энергия системы. Отсюда следует, что необхо-
необходимые и достаточные условия равновесия голономной системы (с иде-
идеальными удерживающими связями, в потенциальном поле сил) совпа-
совпадают с необходимыми условиями экстремума потенциальной энергии
в рассматриваемом положении равновесия системы.
В частности, если система движется в однородном поле тяжести,
то условия A0) примут вид dzc/dqi = 0 (г = 1, 2, ... , п), где
zc — координата центра тяжести рассматриваемой системы в непо-
неподвижной системе координат с вертикальной осью Oz, т. е. для тяжелой
системы необходимые и достаточные условия равновесия совпадают с
необходимыми условиями экстремальности высоты ее центра тяжести
над горизонтальной плоскостью.
Если система неголономна, то величины Sqj, в (8) не будут неза-
независимы; они связаны s уравнениями B8) п. 16. Среди т величин Sqj
независимыми будут только п (п = m — s) из них. Пусть для определен-
определенности это будут величины Sqi, Sq2, ... , Sqn. Разрешив уравнения B8)
п. 16 относительно 5qn+i, Sqn+2, ••• , Sqm, получим
п
Hn+k = ^2 aki$qi (k = 1, 2, ... , т- п = s), A1)
i=i
где величины aui являются функциями коэффициентов b@j, входящих
в уравнения B8) п. 16. Уравнение (8) после подстановки в него выра-
выражений A1) и приведения подобных членов примет вид
п
^2Q'iSqi = 0, A2)
«=i
где
т—п
piQn+p (г = 1, 2, ..., п). A3)
Так как величины Sqi независимы, то из A2) следует, что
Q\ = 0 (i = I, 2, ... , п). A4)
118
Глава IV
Равенства A4) представляют собой систему п уравнений относитель-
относительно т неизвестных дю,, <7гсь • • • ¦> Что, определяющих положение рав-
равновесия системы. Так как число неизвестных превышает число урав-
уравнений, то в общем случае имеем многообразие состояний равновесия,
размерность которого не меньше числа s неголономных связей.
Отметим, что из A3) и A4) следует, что для неголономной сис-
системы в потенциальном поле сил некоторые или даже все частные про-
производные потенциальной энергии в положении равновесия могут быть
отличными от нуля.
Пример 1. Пусть несвободная материальная точка с неинтегрируемой
связью
движется в силовом поле с потенциалом вида
Тогда т = 3, s = 1, п = 2; ац = 0, «12 = <7i; Qi = —qi (i = 1, 2, 3);
Q[ = — gi, Q'2 = —Q2 — <71<7з- Условия равновесия A4) запишутся в виде
двух уравнений с тремя неизвестными:
=0, q2
= 0.
Отсюда следует, что положения равновесия образуют одномерное мно-
многообразие
qi =0, q2 = 0, q3 = дзо,
где дзо — произвольное число.
Если дзо Ф О? то в положении рав-
равновесия производная dli./dqz отлична от
нуля.
Пример 2. Два одинаковых стержня О А
и АВ весом Р и длиной 2а скреплены шар-
шарниром А. Конец О стержня О А закреп-
лен в неподвижном шарнире, а к концу В
стержня АВ приложена горизонтальная
сила Р/2. Оба стержня расположены в
вертикальной плоскости. Требуется най-
найти углы а и fi при равновесии системы
(рис. 61).
Система имеет две степени свободы и является голономной. За
обобщенные координаты примем углы а и fi. Найдем обобщенные си-
силы Qa и Qp, отвечающие этим обобщенным координатам. В плоскости
§ 1. Статика произвольной механической системы 119
стержней возьмем систему координат Оху, ось Ох которой направим
вертикально вниз. Для активных сил Fc, Fn, Fb и радиусов-векторов
I'd rD, fB точек их приложения имеем
F'c = (Р, 0), F'D = (Р, 0), F'B = (о, f) ;
rc = a(cosa, sin a), r'D = аB cos а + cos/3, 2 sin a + sin fi),
r'B = 2a(cos a + cos fi, sin a + sin fi).
Вычислим элементарную работу активных сил на виртуальном пе-
перемещении системы, отвечающем вариациям 8а и 5/3 обобщенных ко-
координат. Так как
8r'c = a5a(— sin a, cos а),
8r'D = а(—2 sin а • 5а — sin/3 • 5fi, 2 cos a • 5а + cos fi ¦ 5/3),
5r'B = 2a(— sin a • 5a — sin fi ¦ 5fi, cos a • 5a + cos fi ¦ 5fi),
mo
5A= Fc- 5rc + FD ¦ 5rD + FB ¦ 5rB =
= Pa[(cosa - 3sinaMa + (cos/3 - sinfiMfi].
Поэтому
Qa = Pa(cosa — 3sina), Qp = Pa(cosfi — sin/3).
Из условий (9) получаем теперь, что при равновесии системы
tga=|, tg/3=l.
Пример 3. Тяжелое колечко надето на прут, которому придана форма
кривой, определяемой уравнениями
X2 у2 2 _, X У
36 + T + z =1' 6 + f + z = 1'
где ось Oz направлена вертикально вверх. Найдем положения равновесия
колечка.
Пусть виртуальное перемещение колечка задается величинами
5х, 5у, 5z. Продифференцировав уравнения, задающие форму прута, по-
получим, что на виртуальном перемещении должны выполняться условия
= 0, 5х + 2 5у + Q5z = 0.
120
Глава IV
Для положения равновесия элементарная работа PSz (P — вес колеч-
колечка) силы тяжести должна равняться нулю. Поэтому Sz = 0, и преды-
предыдущие два уравнения запишутся в виде
xSx + 4ySy = 0, 8х + 2Sy = 0
или, после исключения 8у,
(х - 2у) 5х = 0.
Это условие должно выполняться при любых 8х, следовательно,
х = 2у.
Принимая во внимание уравнения кривой, по которой изогнут прут,
получим два решения:
l)x = 4,y = 2,z = -±;
Пример 4. Однородный стержень AD опирается концом А на верти-
вертикальную стену, а в некоторой другой точке — на ребро В (рис. 62).
Длина стержня 2а, расстояние точки В от стены Ъ. Найти угол а
при равновесии стержня.
Рассматриваемая система голо-
номна и имеет одну степень свобо-
свободы. Примем угол а за обобщенную
координату. Потенциальная энергия
О
А
х
П = —Рхс, где хс — абсцисса цент-
I'
Рис. 62
У/////////, у ра тяжести стержня:
sin2 a
xq =Ь ctg a — a cos a.
Условие равновесия дП/да = 0 дает
уравнение для а:
+ a sin a = О,
откуда
Ъ
sma= л/5.
Равновесие стержня возможно только в том случае, когда Ь ^ а.
§ 1. Статика произвольной механической системы 121
64. Эквивалентные системы сил. Рассмотрим совокупность
сил (Fi, F2, ... , -F/s), приложенную к некоторой механической систе-
системе. Допустим, что эта совокупность сил в данной механической системе
заменена на совокупность сил (F*, F2*, ... , F*). При этом количество,
точки приложения, величины и направления сил в первой и второй сис-
системах могут быть различными. Движения механической системы под
действием первой и второй систем сил при одинаковых начальных по-
положениях точек системы и одинаковых их начальных скоростях могут
быть одинаковыми, а могут отличаться.
Если две системы сил могут быть заменены одна другой без из-
изменения движения (или состояния покоя) механической системы, то
такие системы сил будем называть эквивалентными.
В частности, если добавление или отбрасывание некоторой системы
сил не изменяет движение механической системы, то говорят, что эта
система сил является уравновешенной или эквивалентной нулю.
Эквивалентность систем сил обозначается символом ~: если две
системы (F±, F2, ... , Fk) и (F*, F2, ... , F{*) эквивалентны, то
пишут (Fu F2, ... , Fk) ~ (*\*, F2*, ... , Ff).
Из общего уравнения динамики следует (см. замечание 1 в п. 57),
что две системы сил эквивалентны тогда и только тогда, когда они
совершают одинаковую работу на любых (одних и тех же для обеих
систем сил) виртуальных перемещениях механической системы.
Выразим этот критерий эквивалентности через обобщенные си-
силы. Пусть Qj и Qj (j = 1, 2, ... , т) — обобщенные силы, отве-
отвечающие первой и второй системам сил соответственно, a SA и 8 А*
— элементарные работы этих систем на виртуальных перемещени-
перемещениях Sqi, Sq2, ... , Sqm. Составим разность
A5)
Для голономной системы величины 6qj независимы. Поэтому, прирав-
приравняв нулю левую часть формулы A5), получим, что системы сил, при-
приложенные к голономной системе, эквивалентны тогда и только тогда,
когда их обобщенные силы совпадают при каком-либо выборе обобщен-
обобщенных координат.
В случае неголономной системы величины Sqj, зависимы. Подста-
Подставив в этом случае величины A1) в A5), приведя подобные члены и
приравняв результат нулю, получим, что в случае неголономной сис-
системы для эквивалентности двух систем сил необходимо и достаточно,
чтобы при каком-то выборе обобщенных координат совпадали величи-
величины Q[ и Q'*, вычисленные для обеих систем сил по формулам A3).
122 Глава IV
Пример 1. Материальная точка Р(х,у) движется в плоскости и
имеет скорость, постоянно направленную на движущуюся точку
Po(xo(t), yo(t)). Уравнение связи имеет вид
У -Vo(t) .
У = 77^. 16
x-xo(t)
При непостоянных хо, уо это — дифференциальная неинтегрируемая
связь. Следовательно, т = 2, s = 1, п = 1.
Пусть к точке Р приложена сила F(yo(t) — у, —x^it) + x). Ей от-
отвечают такие обобщенные силы (qi = x, qi = У)'
Qi=yo(t)-q2, <Эг = -xo(t) + q-i_.
Из уравнения связи A6) следует, что
~yo(t)
аи =
Ях -xo(t)'
Поэтому из формулы A3) имеем Q[ = 0.
Если вместо силы F к точке Р приложена сила F* = kF (k ф 1),
то аналогично получим Q'\ = 0. Поэтому силы F и F* в рассматрива-
рассматриваемой неголономной системе эквивалентны.
Если бы связь A6) отсутствовала, то имел бы место случай голо-
номной системы, а силы F и F* не были бы эквивалентны.
§ 2. Статика твердого тела
65. Необходимые и достаточные условия равновесия твер-
твердого тела. Пусть к твердому телу приложена система внешних сил с
главным вектором R^ и главным моментом Mq относительно произ-
произвольно выбранного полюса. Считая твердое тело свободным, получим
необходимые и достаточные условия его равновесия. Если тело несво-
несвободно, то его можно рассматривать как свободное, мысленно отбросив
связи и заменив их действие на тело реакциями (п. 45). В этом слу-
случае реакции связей, которые обычно являются неизвестными, войдут
в выражения для R^ и М^'.
К свободному твердому телу, как к системе с идеальными связями,
применим принцип виртуальных перемещений, дающий необходимые
и достаточные условия равновесия системы с идеальными удержива-
удерживающими связями. Поэтому наша задача состоит только в том, чтобы
выразить общее уравнение статики D) п. 62 через главный вектор и
главный момент сил, приложенных к конкретной системе — твердому
телу.
§ 2. Статика твердого тела 123
Теорема. Для равновесия твердого тела при to ^ t ^ ti необходимо
и достаточно, чтобы в момент времени to тело покоилось, а главный
вектор R(e*> и главный момент внешних сил Mq относительно про-
произвольно выбранного полюса О при to $C t $C ti равнялись нулю:
Я<е> = О, m?° = 0. A)
Доказательство.
Заметим, что, так как свободное твердое тело является склероном-
склерономной системой, его произвольное действительное перемещение за вре-
время dt является виртуальным. Поэтому, воспользовавшись формулой C)
п. 52, можно элементарную работу сил, приложенных к твердому телу,
на его виртуальном перемещении записать в виде
8 А = R(e) -vodt + Af?° • и dt, B)
где vo — скорость полюса, аи) — угловая скорость тела в момент
времени t (to $J t $J t\). Так как vo и ш — произвольные величины, то
из общего уравнения статики 8А = 0 следуют равенства A). Теорема
доказана.
Если (Fi, F2, ... , Fk) — система внешних сил, приложенных к
твердому телу, а ж», гц, Zi — координаты точек приложения силы F,
(г = 1, 2, ... , к) в декартовой прямоугольной системе координат с на-
началом в полюсе О, то необходимые и достаточные условия равновесия
твердого тела A) запишутся в скалярной форме в виде следующих шес-
шести равенств:
к
^2(yiFiz - ZiFiy) = 0,
1=1
к
^2(ZiFix - XiFiz) = 0, D)
\ (r-F- — 11 F- ) — fl
/ Л г гУ У1 гх > —
i=l
В частных случаях некоторые из шести равенств C), D) могут удов-
удовлетворяться тождественно.
Механическая система, у которой реакции всех наложенных связей
могут быть определены из условий равновесия, получаемых в статике,
124
Глава IV
называется статически определимой, в противном случае — стати-
статически неопределимой. Если рассматриваемое в данном пункте твердое
тело несвободно, то равенства C), D) будут системой уравнений от-
относительно проекций реакций связей. Случай статически определимой
механической системы имеет место лишь тогда, когда число неизвест-
неизвестных проекций не превосходит числа не удовлетворяющихся тождест-
тождественно уравнений системы C), D).
Пример 1. Однородная доска в форме рав-
равнобедренного треугольника ABC (АС =
= ВС) весом Р опирается вершинами на
три координатные плоскости и привя-
привязана за точку С к точке О с помощью
нити СО (рис. 63). Определим натяже-
натяжение Т нити и реакции X, Y, Z в точ-
точках А, В, С. Даны расстояния а, Ь, с и
угол СОу = 7г/4.
На доску действуют пять сил: си-
сила тяжести, натяжение нити и ре-
реакции в точках А, В, С, причем по-
последние, ввиду отсутствия трения, пер-
перпендикулярны соответствующим коор-
координатным плоскостям.
Из геометрических соображений нетрудно получить, что центр
а + Ь а + Ь 2с
3 '
Рис. 63
тяжести доски имеет координаты
3 ' 3
Необходимые и достаточные условия равновесия C), D) запишутся
в виде следующей (совместной) системы шести линейных уравнений
относительно четырех неизвестных X, Y, Z, Т:
-T^f+Y = O, Z-P = O,
Za-Yc- ±
Решив эту систему, получим, что
Хс+±Р(а + Ь)=О, Yb-Xb = O.
X = Y =
ОС
z = p, т=^2ГЬ)Р
Зс
66. Критерий эквивалентности систем сил, приложенных к
твердому телу. Критерий эквивалентности систем сил, приложенных
к произвольной механической системе с идеальными удерживающими
связями, получен в п. 64. Здесь получим критерий эквивалентности для
систем сил, приложенных к твердому телу.
§ 2. Статика твердого тела
125
Теорема. Для того чтобы две системы сил, приложенных к твердому
телу, были эквивалентны, необходимо и достаточно, чтобы они имели
одинаковые главные векторы и главные моменты относительно неко-
некоторого полюса.
Доказательство.
Пусть система сил (F±, F2, ... , Fk) имеет главный вектор R(e~>
и главный момент Mq , а другая система сил (F*, F?, ... , F*) —
главный вектор R*^ и главный момент Mq' Используя формулу B),
составим разность элементарных работ этих систем сил на одинаковых
виртуальных перемещениях тела:
SA - SA* = (Д(е) - Д*(е)) • vo dt + (Мое) - MQ(e)) ¦ и dt.
Согласно определению, для эквивалентности систем сил необходимо и
достаточно, чтобы эта разность равнялась нулю. Отсюда, ввиду произ-
произи Мо =
вольности Vo и ш, следует, что R^ =
Получим связь между главными моментами одной и той же систе-
системы сил, вычисленными относительно разных полюсов. Согласно рис. 64,
имеем
МОг =
ИЛИ
MOl = Mo+0x0 x R.
E)
о
Таким образом, при изменении полюса глав-
главный момент сил меняется на величину, равную
моменту главного вектора (приложенного в ста-
старом полюсе) относительно нового полюса. Отсю-
Отсюда следует, что если у двух систем сил главные
векторы одинаковы и одинаковы главные момен-
моменты относительно какого-либо полюса, то последние
одинаковы и для любого полюса.
Замечание 1. При выполнении условий A) систе-
система сил, приложенная к твердому телу, будет урав-
уравновешенной, или эквивалентной нулю. Это озна-
означает, что любое движение тела не изменится, если к приложенным
к нему силам добавить или отбросить систему сил, удовлетворяющую
равенствам A).
126
Глава IV
У
Пример 1. По ребрам прямоугольного клина действуют силы Fi и F2
(рис. 65), которые требуется заменить эквивалентными им силами F±
и F2*. Величины сил Fi, F2, F± пропорциональны длинам соответству-
соответствующих ребер клина. Найти силу F? ¦
Если а и Ь — длины ребер О А
и АВ клина соответственно, а
f — коэффициент пропорциональ-
пропорциональности (/ > 0), то
Fi = fa, F2 = fa sin a, F? = fb.
Введем систему координат
Oxyz, как показано на рис. 65.
Главный вектор и главный момент
Рис- 65 системы сил (Fi, F2) в этой сис-
системе координат имеют такие компоненты:
Rx = 0, Ry = fa cos a, Rz = 2fas'ma,
Mx = fa2 sin a cos a, My =—fabs'ma, Mz = 0.
Пусть F^, F?y, F%z — компоненты искомой силы F?, a x, у, z —
координаты точки ее приложения. Главный вектор и главный момент
системы сил (F?, F2*) имеют компоненты, задаваемые равенствами
М*х = yF*z - zF*y, M; = zF*x - xF*z, M*z = xF*y - yF*x.
Система трех уравнений, вытекающая из равенства соответству-
соответствующих компонент главных векторов эквивалентных систем сил (F\, F2)
и (F?, F%), позволяет найти компоненты силы F?:
F?x = fb, F?y = fa cos a, F?z = If a sin a.
Эти равенства задают направление силы F2* u ee модуль
71*2 /7?2
2z = V ^1
71*2
Приравняв соответствующие компоненты главных моментов обе-
обеих систем сил и произведя некоторые упрощения, придем к системе
уравнений, определяющей координаты х, у, z точки приложения си-
силы Fi :
2у sin a — z cos a = a sin a cos a; 2ax sin а — bz = ab sin a,
ах cos a — by = 0.
§ 2. Статика твердого тела 127
Эти уравнения определяют не одну точку приложения силы F?, а, как
нетрудно проверить, целую прямую — линию действия этой силы:
2х - Ъ _ 2у - a cos а _ z
Ъ а cos а а sin а '
Линия действия силы F2* проходит через вершину В клина и точку пе-
пересечения диагоналей его нижней грани.
67. О равнодействующей. Теорема Вариньона. Если система
сил (Fi, F2, ... , Fk), приложенная к твердому телу, эквивалентна од-
одной силе R*, то эта сила называется равнодействующей данной системы
сил.
Теорема. Если система сил имеет равнодействующую, то эта рав-
равнодействующая R* равна главному вектору R, а ее момент относи-
относительно произвольного полюса О равен главному моменту Мо данной
системы сил относительно этого полюса.
Доказательство следует из определения равнодействующей и кри-
критерия эквивалентности двух систем сил, приложенных к твердому телу.
Вторая часть приведенной теоремы носит название теоремы Варинь-
Вариньона.
68. Частные случаи условий равновесия твердого тела.
1. Из условий A) следует, что под действием одной, не равной нулю,
силы твердое тело не может находиться в равновесии (хотя бы потому,
что R^ ф 0).
2. Под действием двух сил твердое тело при to ^ t ^ t\ находится
в состоянии равновесия тогда и только тогда, когда оно покоится в
начальный момент t = to, а силы при to ^ t ^ t\, во-первых, равны по
величине и противоположно направлены, а во-вторых, имеют общую
линию действия. Первое требование вытекает из условия R^ = 0,
второе — из условия Mq = 0.
3. Если под действием трех сил Fi, F2, F3 твердое тело находится
в равновесии и линии действия двух сил Fi и F% пересекаются, то все
три силы лежат в одной плоскости и их линии действия пересекают-
пересекаются в одной точке. Это утверждение (которое часто называют теоремой
о трех силах) сразу вытекает из условий A) равновесия твердого те-
тела. В самом деле, из условия R(e~> = 0 следует, что F3 = —(F± + F2), и
поэтому сила F3 лежит в плоскости сил Fi и F2. Замечая теперь, что
моменты сил Fi и F2 относительно точки О пересечения линий их дей-
действия равны нулю, из условия Mq = 0 получаем, что линия действия
силы ^з проходит через точку О.
128
Глава IV
ОУ////Л Q//////,B
Рис. 66
Пример 1. Однородный стержень АВ дли-
длины 21 опирается одним концом на гладкую
вертикальную стенку, а другим концом
упирается в угол В, расстояние О В = а
(рис. 66). Требуется найти направление
реакции в точке В при равновесии стерж-
стержня.
Реакция в точке А ортогональна
стенке, ее линия действия пересекает ли-
линяю действия силы тяжести Р в точке S.
При равновесии третья сила — реакция в
точке В — также проходит через точку S. Из ABCS находим
Замечание 2. Очевидно, что при переносе вектора какой-либо силы
системы вдоль линии его действия главный вектор системы сил и ее
главный момент относительно заданного полюса остаются неизменны-
неизменными. Поэтому из критерия эквивалентности системы сил, приложенных
к твердому телу, следует, что, не нарушая движения тела (и, в част-
частности, его состояния равновесия), можно перенести точку приложения
силы в произвольную точку тела, лежащую на линии действия этой
силы, т. е. сила, приложенная к твердому телу, — скользящий вектор.
4. Системой сходящихся сил называется система сил, линии дейст-
действия которых пересекаются в одной точке.
Теорема. Система сходящихся сил имеет равнодействующую, и эта
равнодействующая проходит через точку пересечения их линий дейст-
действия.
Доказательство следует из предыдущего замечания и закона сло-
сложения сил (п. 44). Пусть О — точка пересечения линий действия сил
системы1. Тогда М^' = 0 и условия A) сводятся к одному векторному
равенству R^ = 0, которое в скалярной форме запишется в виде трех
равенств C).
Пример 2. Полушар весом Р и радиусом г привязан за край нитью к
точке А гладкой вертикальной стены и опирается на стену выпуклой
поверхностью в точке В (рис. 67). Какова длина нити, если в поло-
положении равновесия плоскость лежащего в основании большого круга об-
1 Может оказаться, что точка О не принадлежит твердому телу. Однако это не ме-
меняет наших рассуждений, так как точку О можно считать принадлежащей твердому
телу, мысленно представив ее лежащей на одном из концов невесомого стержня, ко-
который вторым своим концом жестко прикреплен к телу.
i 2. Статика твердого тела
129
разует с вертикалью угол тг/4? Каково натяжение нити и давление
полушара на стену?
На полушар действуют три силы: сила тя-
тяжести Р, давление стены N и натяжение ни-
нити Т. Линии действия сил Р и N пересекают-
пересекаются в точке S. Согласно теореме о трех силах, в
положении равновесия линия действия силы Т
(т. е. направление нити) также должна про-
проходить через точку S. Таким образом, полушар
находится в равновесии под действием систе-
системы сходящихся сил.
В прямоугольном треугольнике OSC
ZSOC = 7г/4 и, так как центр тяжести С
полушара отстоит от центра О окружнос-
окружности большого круга на расстоянии ОС = Зг/8,
OS = OCcosGr/4) = 3\/2r/16.
Обозначим а угол между направлением нити и вертикалью. В
AODS ADOS = тг/4, ZOSD = тг/2 + a, ZODS = тг/4 - а, поэтому
SD
Рис-
sinGr/4)
или
0D
sinGr/2 -\
г
-а)
OS
sin(?r/4 —
3r
а)
= —
cos a 8(Cos a — sin a)
Отсюда следует, что
:а = §( sina = i_, cos а =
8 V л/йо'
Из AABS теперь находим длину нити
SD = ~iirr-
Приравняв нулю суммы проекций сил Р, N и Т на оси системы ко-
координат Вху, получим два уравнения, определяющих натяжение нити
и давление полушара на стену:
Tcosa = P, T sin a = N,
откуда найдем
—
'
N= |
130
Глава IV
Пример 3. Три стержня АО, ВО и СО прикреплены к вертикальной
стене шарнирами и скреплены шарниром в точке О, к которой прикреп-
прикреплен груз весом Р. Стержни АО и ВО расположены в горизонтальной
плоскости и образуют со стеной углы по 60°. Третий стержень СО рас-
расположен в вертикальной плоскости, проходящей через О и середину АВ,
и образует со стеной угол 30°. Определить усилия в стержнях АО, ВО
и СО. Весом самих стержней пренебречь.
Для определения искомых величин рассмотрим равновесие точки
(узла) О. На узел О действуют активная сила Р и реакции Sa, Sb
и Sc стержней, образующие систему сходящихся сил, не лежащих в
одной плоскости.
Условия равновесия запишем в виде равенств C), выбрав систему
координат, как показано на рис. 68. Имеем
^2 Fix = SA cos 60° - SB cos 60° = 0,
Fiy = -SA sin 60° - SB sin 60° - Sc sin 30° = 0,
^2 Fiz = -Sc cos 30° - P = 0.
Решив полученную систему уравнений,
найдем
Величины Sa и Sb положительны, сле-
следовательно, реакции Sa и Sb направлены
так, как показано на рис. 68 (стержни О А и
ОВ растянуты), величина Sc отрицатель-
отрицательна (стержень ОС сжат).
5. Рассмотрим теперь равновесие твер-
твердого тела, к которому приложена плоская
система сил, т. е. система сил, линии дей-
Рис- 68 ствия которых лежат в одной плоскости.
Пусть этой плоскостью будет плоскость Оху. Тогда проекции Fiz сил
на ось Oz и координаты zt, точек их приложения (г = 1, 2, ... , к)
равны нулю и условия C), D) сводятся к трем равенствам
к к к
$^ = 0, $^Fiy = 0, ^2(xiFiy - ViFix) = 0. F)
г=1 г=1 i=l
Таким образом, для равновесия свободного твердого тела при
to ^ t ^ t\ под действием плоской системы сил необходимо и доста-
достаточно, чтобы в момент t = to тело покоилось, а суммы проекций сил
i 2. Статика твердого тела
131
на две координатные оси и сумма моментов сил относительно третьей
оси при to ^ t ^ ti равнялись нулю.
Упражнение 1. Показать, что условия равновесия твердого тела под
действием плоской системы сил могут быть представлены и следую-
следующих, эквивалентных условию F), формулировках: а) суммы моментов
сил относительно каждой из трех произвольных, не лежащих на од-
одной прямой, точек равны нулю (теорема о трех моментах); б) суммы
моментов сил относительно каждой из двух произвольных точек и сум-
сумма проекций сил на произвольную ось, не перпендикулярную прямой,
проходящей через эти точки, равны нулю.
Пример 4. Однородный стержень,
изогнутый под прямым углом, име-
имеющий оба колена одинаковой дли-
длины 21, опирается на край стола дли-
длины АВ = а = 21/5. Найти положе-
положение равновесия и давления Na и Nb
на края стола. Трением пренебречь.
Пусть положение равновесия оп-
определяется величиной а угла ОБА
(рис. 69). Стержень находится в рав-
равновесии под действием плоской сис-
системы четырех сил, показанных на рис. 69; реакции в точках А и В ор-
ортогональны соответствующим коленам стержня. Приравняв нулю сум-
суммы проекций сил на оси, направленные по ОС и 0D, получим
NA = 2Р sin a, NB = 2Р cos a.
Условие равенства нулю суммы моментов сил относительно точки О
дает
! cos a + PI sin a,
Рис. 69
или
sin a + PI cos a = ^
о
^-(sin a — cos2 a) = sin a — cos a.
о
Последнее уравнение имеет три решения. Для первого решения
sina = cos а, «i = ^, NA = NB = л/2Р.
Для второго и третьего решений
cos а) = 1,
2
о
16
= ?-а,
16±5л/7
132
Глава IV
В последних двух равенствах верхний и нижний знаки отвечают соот-
соответственно значениям а = а^, а = аз-
Пример 5. Два одинаковых однородных стержня весом Р каждый со-
соединены шарниром В и прикреплены шарнирами А и С к неподвижной
опоре так, что стержень АВ горизонтален, а стержень ВС образует
с вертикалью угол а (рис. 70). Определить реакции шарниров.
п
y, r. a
Рис. 70
Мысленно уберем шарнир В и рассмотрим равновесие каждого из
стержней в отдельности. На каждый из стержней действуют сила
тяжести и реакции шарниров, которые мы представляем их компо-
компонентами в системе координат Аху, показанной на рис. 70. При этом,
согласно третьему закону Ньютона, реакции Хв, YB шарнира В, дей-
действующие на стержень ВС, должны быть направлены противоположно
реакциям Хв, Yb, действующим на стержень АВ. По величине же
= Х
= Ув
Составим условия равновесия F) для каждого из стержней. Введя
обозначение АВ = ВС = 2а, найдем для стержня АВ
=YB-2a-Pa =
для стержня ВС
2^ = —Pa sin a — Xq • 2a cos a + Yq • 2a sin a = 0.
Из полученной системы шести уравнений с шестью неизвестными най-
найдем
ХА = -Хв = -Хс = -Pig a, YA = YB = \p, Yc = |р.
Направление реакции Ха противоположно указанному на рисунке.
§ 2. Статика твердого тела
133
69. Равнодействующая двух параллельных сил.
Теорема. Две параллельные и одинаково направленные силы Fi и F2
(рис. 71), приложенные к твердому телу, имеют равнодействующую
R* = Fi + F2; эта равнодействующая лежит в плоскости сил F\ и Fi,
и ее линия действия делит отрезок, соединяющий точки Pi и Pi при-
приложения сил, внутренним образом на части, обратно пропорциональ-
пропорциональные величинам Fi и F2. Две параллельные, не равные по величине и
противоположно направленные силы F\ и Fi имеют равнодействую-
равнодействующую R* = Fi + Fi; она направлена в сторону большей силы, лежит
в плоскости сил Fi и Fi, а линия ее действия делит отрезок P\Pi
внешним образом на части, обратно пропорциональные величинам F\
uF2.
Рис. 71
Доказательство.
Если положить R* = F\ + Fi и выбрать точку О так, что
F\ ¦ ОР\ = Fi ¦ OPi, то, согласно п. 66, система двух сил F\ и Fi бу-
будет эквивалентна системе, состоящей из одной силы R* (т. е. R* будет
равнодействующей сил F\ и Fi). Действительно, обе системы сил име-
имеют одинаковые главные векторы R = R* = F\ + Fi и одинаковые
(равные нулю) главные моменты Мо относительно точки О.
70. Теория пар. Пусть параллельные силы Fi и Fi, приложен-
приложенные к твердому телу, равны по модулю и противоположно направле-
направлены (Fi = —Fi). Такую систему сил называют парой сил. Плоскость, в
которой лежат силы F\ и Fi, называют плоскостью пары, а расстоя-
расстояние d между линиями действия сил — плечом пары (d ф 0).
Главный момент сил, составляющих пару, не зависит от точки,
относительно которой он вычисляется. В самом деле, возьмем произ-
произвольную точку О пространства (рис. 72) и найдем главный момент сил
Fi и Fi относительно этой точки:
Мо =
Г2
= (га - п)
Fi = -г\ х
= d x Fi.
ri
134
Глава IV
Отсюда видно, что величина Мо не зависит от точки О.
Векторное произведение М = d
F2 на-
называют моментом пары. Вектор М перпен-
перпендикулярен плоскости пары и направлен так,
что наблюдатель с конца вектора М «видит»
векторы Fi и F2 указывающими на вращение
плоскости пары против часовой стрелки. Если
F — модули сил Fi и F2, то М = dF. Момент
пары — это свободный вектор, и, как будет
рис. 72 видно из последующих теорем этого пункта,
он полностью определяет действие пары на твердое тело.
Теорема. Пара сил не имеет равнодействующей.
Доказательство.
Предположим противное, а именно предположим, что существует
сила R* такая, что (Fi, F2) ~ R*¦ Возьмем произвольную точку О на
линии действия силы R*. Согласно критерию эквивалентности систем
сил, приложенных к твердому телу (п. 66), главный момент Мо сис-
системы сил (Fi, -F2) относительно точки О должен равняться моменту
силы R* относительно той же точки, т. е. должен быть равен нулю. Но
момент Мо равен моменту пары и, следовательно, отличен от нуля.
Противоречие доказывает теорему.
Теорема. Пары сил с равными моментами эквивалентны.
Эта теорема сразу следует из теоремы п. 66 об эквивалентности
систем сил, приложенных к твердому телу, так как у двух пар главные
векторы равны (каждый из них равен нулю), а главные моменты (т. е.
моменты пар) равны по условию.
Следствие 1. Пару сил, приложенную к твердому телу, можно заме-
заменить другой парой в той же плоскости, если при такой замене не из-
изменяется величина момента пары и его направление.
Следствие 2. Пару сил, приложенную к твердому телу, можно перено-
переносить в плоскость, параллельную плоскости пары.
Теорема. Совокупность нескольких пар с моментами Mi
(г = 1, 2, ... , п) эквивалентна одной паре, момент М которой равен
сумме моментов данных пар:
М = Mi + М2 + ... + Мп.
G)
Эта теорема также является следствием теоремы п. 66 об эквива-
эквивалентности систем сил, приложенных к твердому телу.
§ 2. Статика твердого тела 135
Так как для системы пар R^ = О, то условия A) равновесия твер-
твердого тела сводятся к одному векторному равенству М = О, которое на
основании формулы G) запишется в виде трех скалярных равенств
п п п
^Mix = 0, ^Miy = 0, ^Miz = 0. (8)
*=i »=i *=i
Если все пары лежат в одной плоскости или в параллельных плос-
плоскостях, то условия равновесия запишутся в виде одного скалярного ра-
равенства. Например, если плоскости пар перпендикулярны оси Oz, то
условием равновесия будет последнее из равенств (8).
Пример 1. К граням многогранника приложены пары сил, моменты ко-
которых пропорциональны площадям соответствующих граней и направ-
направлены перпендикулярно соответствующим граням внутрь многогранни-
многогранника. Показать, что такая система сил является уравновешенной.
Пусть S — площадь какой-либо грани, а М — модуль момента
соответствующей пары. Тогда М = kS, где к — коэффициент пропор-
пропорциональности (к > 0), одинаковый для всех граней.
Пару, приложенную к рассматриваемой грани, можно заменить эк-
эквивалентной системой сил, действующих по каждой из сторон грани
в направлении движения часовой стрелки, если смотреть со стороны
внешней нормали. Модуль каждой из этих сил равен \j2ka, где а —
длина соответствующей стороны грани.
Если такую процедуру проделать для всех пар, приложенных к гра-
граням многогранника, то вдоль каждого ребра многогранника будут дейст-
действовать две равные по модулю, но противоположно направленные силы.
Следовательно, приложенная к многограннику система пар сил являет-
является уравновешенной.
71. Теорема Пуансо. В предыдущих пунктах были рассмотрены
задачи о приведении системы сил, приложенных к твердому телу, в
частных случаях системы сходящихся сил, параллельных сил и пар.
Теперь рассмотрим задачу о приведении сил в самом общем случае.
Теорема (Пуансо). Произвольная система сил, приложенных к твер-
твердому телу, эквивалентна системе, состоящей из одной силы, приложен-
приложенной в какой-либо точке О тела (центре приведения) и равной главному
вектору R данной системы сил, и одной пары, момент которой равен
главному моменту Мо всех сил относительно точки О.
Справедливость этой теоремы непосредственно следует из крите-
критерия эквивалентности систем сил, приложенных к твердому телу (п. 66).
Следствие 3 (о параллельном переносе силы). Сила, приложенная
в какой-либо точке твердого тела, эквивалентна той же силе, при-
136 Глава IV
ложенной в другой точке этого тела, и паре, момент которой равен
моменту данной силы относительно новой точки приложения.
Пример 1. В точке АB, 2, 2) к твердому телу приложена сила F с
компонентами Fx = 1, Fy = — 2, Fz = 3. Не изменяя действия силы,
перенести ее в новую точку приложении В(—1, 4, 2).
Момент данной силы относительно точки В имеет компонен-
компоненты Мх = -6, Му = -9, Mz = -4.
Следовательно, в результате перенесения получится сила F и пара
с моментом, модуль которого М = л/133, а направляющие косинусы
равны
6 9_ 4
\/Ш' УШ' у/Ш'
72. Статические инварианты. Динамический винт. Главный
вектор R системы сил, являясь суммой всех сил системы, не зависит от
выбора центра приведения. Вектор R называют первым статическим
инвариантом. В более узком смысле будем называть первым стати-
статическим инвариантом квадрат модуля вектора R:
h=R2x+Rl+R2x. (9)
Главный момент системы сил зависит от выбора центра приве-
приведения. Зависимость между главными моментами сил, приложенных
к твердому телу, относительно двух различных центров приведения
определяется формулой E). Из этой формулы следует, что скалярное
произведение главного момента и главного вектора системы сил не за-
зависит от выбора центра приведения. Это произведение называют вто-
вторым статическим инвариантом:
h = Мо- R- A0)
Из существования статических инвариантов следует, что проек-
проекция М* главного момента системы сил на направление главного вектора
не зависит от выбора центра приведения.
Совокупность силы и пары сил с моментом, коллинеарным силе,
называется динамическим винтом, или динамой. По теореме Пуансо
(п. 71), всякая система сил приводится к силе и паре. Возникает вопрос,
нельзя ли так выбрать центр приведения, чтобы плоскость пары сил, о
которой идет речь в теореме Пуансо, была перпендикулярна главному
вектору, т. е. нельзя ли данную систему сил привести к динаме?
Теорема. Если второй статический инвариант отличен от нуля, то
систему сил можно привести к динаме.
2. Статика твердого тела
137
Доказательство.
Предположим, что для некоторого центра О приведения система
сил приведена к силе R и паре сил с моментом Мо, равным главно-
главному моменту системы сил относительно центра О. Выберем какую-либо
неподвижную декартову прямоугольную
систему координат с началом в точке О. /
Пусть Rx, Ry, Rz и МОх, МОу, MOz —
соответственно проекции главного векто-
вектора и главного момента на оси этой систе-
системы координат.
Пусть О* (рис. 73) — новый центр
приведения, а х, у, z — его координаты.
Чтобы убедиться в справедливости теоре-
теоремы, достаточно показать, что центр при-
приведения О* может быть выбран так, что-
чтобы главный момент Мо* был коллинеа-
рен R:
У
Рис. 73
Мо. = PR. A1)
Величина р отлична от нуля, так как из A0) и A1) следует, что
h
P=
а величина 1^ не равна нулю по условию теоремы.
Использовав формулу E), перепишем условие A1) в виде равенства
Мо+0*0 х R=pR
A2)
Это равенство определяет не одну точку О*, а целую прямую, облада-
обладающую тем свойством, что для выбранного на ней центра система сил
приводится к динаме. В скалярной форме уравнение A2) имеет вид
МОх + (zRy - yRz) МОу + (xRz - zRx) MOz + (yRx - xRy)
= p.
A3)
Прямая A3) называется центральной осью системы сил. Еслир >0,
то динамический винт называется правым, если р < 0 — левым.
73. Частные случаи приведения системы сил. Пусть 1^ = 0,
a Ii ф 0. Это возможно, либо когда Мо = 0, либо когда Мо и R орто-
ортогональны. Из критерия эквивалентности системы сил, приложенных к
138
Глава IV
твердому телу, следует, что в первом и во втором случаях система сил
приводится к равнодействующей. Равнодействующая лежит на прямой,
задаваемой уравнением A3) (при р = 0). В частности, если Мо = 0, то
равнодействующая проходит через данный центр приведения О.
Пусть теперь /г = 1\ = 0, а Мо ф 0. В этом случае система сил
приводится к паре с моментом Мо-
Наконец, если /г = 1\ = 0 и Мо = 0, то система сил является
уравновешенной.
В таблице представлены все возможные частные случаи приведе-
приведения системы сил, приложенных к твердому телу. В последнем столбце
таблицы для сравнения указаны соответствующие им аналоги в кине-
кинематике твердого тела.
MOR
фо
= 0
= 0
= 0
R
фо
фо
= 0
= 0
Мо
фо
фв
= 0
фо
= 0
Случай приведения
динамический винт
(динама)
равнодействующая
пара сил
уравновешенная
система сил
Аналог в кинематике
мгновенно винтовое
движение (кинемати-
(кинематический винт)
мгновенное вращение
мгновенно поступа-
поступательное движение
покой
Упражнение 2. Показать, что плоская система сил и система парал-
параллельных сил в пространстве не приводятся к динаме.
Пример 1. К твердому телу приложена сис-
система сил: F\ = 1 Н, направленная по Oz, и
F<i = 1 Н, направленная параллельно Оу, как
указано на рис. 74, где О А = 1 м. привести
эту систему сил к простейшему виду, а так-
также найти наименьшую силу, которую нужно
приложить к точке О, чтобы получающаяся
при этом система трех сил приводилась к рав-
нодействующей.
Для главного вектора и главного мо-
момента имеем R' = @, 1, 1), Мо = @, 0, 1).
Подсчитываем кинематические инварианты:
ф 0, то система сил (Fi, F%)
z
h = R
Рис. 74
= 2, I2 = MOR = 1. Так как
§ 2. Статика твердого тела 139
приводится к динаме. Параметр динамы р = Iijli = Уг- Для момен-
момента М динамы получаем М' = рВ! = (О, У2, 1/2)-
Уравнение A3) центральной оси получает вид
х
0 112'
или z = у, х = У2. Центральная ось проходит через середину отрез-
отрезка О А, ортогональна оси Ох и составляет углы тг/4 с осями Оу и Oz.
Если к данной системе присоединить силу F%, F% = (X, Y, Z),
приложенную в начале координат, то главный момент не изменится,
а для главного вектора получаем R! = {X, Y + 1, Z + 1).
Условие существования равнодействующей Мо • R = 0 приводит
к равенству Z + 1 = 0, откуда Z = —1. Поэтому F^ = (X, Y, —1),
где X, Y произвольны. Величина F3 = V'X2 + Y2 + 1 имеет наименьшее
значение при X = Y = 0. Отсюда следует, что Fs = —F\.
Глава V
Геометрия масс
§ 1. Центр масс. Момент инерции
74. Центр масс. Рассмотрим систему материальных точек Pv
{у = 1, 2, ... , N). Пусть т„ — масса, а г„ — радиус-вектор точки Pv
относительно начала некоторой системы координат Oxyz.
Центром масс системы называется геометрическая точка С про-
пространства, определяемая радиусом-вектором
N
гс = -т-' A)
где М — масса системы,
N
v=l
Центр масс системы называют также ее центром инерции.
75. Момент инерции системы относительно оси. Радиус
инерции. Пусть расстояние точки Pv до некоторой оси и равно pv.
Тогда величина
N
называется моментом инерции системы относительно оси и.
Момент инерции Ju можно записать в виде Мр2; положительная
величина р называется радиусом инерции системы относительно оси и.
Замечание 1. В конкретных задачах при нахождении центра масс и
моментов инерции сплошных тел суммы в выражениях для гс, М, </„
переходят в интегралы.
Упражнение 1. Полярным моментом инерции относительно точки О
называется величина
N
§ 1. Центр масс. Момент инерции
141
Показать, что центр масс системы можно определить как такую точку
пространства, для которой полярный момент инерции наименьший. От-
Отсюда, в частности, следует, что положение центра масс в пространстве
не зависит от конкретного выбора системы координат.
Пример 1. Вычислим моменты инерции однородного прямоугольного па-
параллелепипеда массой т со сторонами а, Ь, с относительно прямых,
проходящих через центр и параллельных ребрам.
Выберем систему координат Oxyz с
началом в центре параллелепипеда, оси
которой параллельны соответствующим
ребрам (рис. 75). Разобьем параллелепи-
параллелепипед на ряд элементарных масс dm в форме
прямоугольных параллелепипедов со сторо-
сторонами dx, dy, dz. Тогда
dm = ^-
abc
dz.
Пусть x, у, z — координаты одной из та-
таких элементарных масс.
Предварительно вычисляем интегралы:
Ol.
Рис. 75
У
х2 dx dy dz =
m
abc
¦c-b-
аналогично
I y2 dm = Y~mb2 и I z2 dm = -т-^
Поэтому для искомых моментов инерции получаем
Jx = J(y2 + z2)dm = ±m(b2 + с2),
Jy = I (z2
±
2)dm = -т-~т(с2 + a2),
/
Jz = /V + V2)dm = ±m(a2 + b2).
±
Чтобы получить момент инерции тонкого однородного стержня
длиной а относительно оси z, перпендикулярной стержню и проходящей
142
Глава V
через его середину, можно взять третье из этих равенств и положить
в нем Ь = 0. Получим
Jz = та2 /12.
Пример 2. Определим момент инерции относительно оси вращения од-
однородной цилиндрической круговой трубки массой т, внутренний радиус
которой равен г, а внешний R (рис. 76).
За элементарную массу dm примем массу ци-
цилиндрического слоя, образуемую двумя коаксиальными
цилиндрами радиусов р и р + dp. Имеем
dm= , ™ „, — ^_2mpdp
Jz = Jp2dm = -J^ Jp3dp= \m{R2
При г = 0 отсюда следует формула для момента
инерции сплошного цилиндра относительно его оси:
Рис. 76
Jz =mR2/2.
Пример 3. Вычислим момент инерции однородного шара массой т и
радиусом R относительно диаметра.
Поместив начало системы координат Oxyz в центре шара, из сим-
симметрии фигуры заключаем, что Jx = Jy = Jz. Обозначим этот одина-
одинаковый для всех диаметров момент инерции шара через J. Тогда
3 J = Jx + Jv + Jz =
у2 + z2)dm.
За элементарную массу dm примем массу сферического слоя, обра-
образуемого двумя концентрическими сферами радиусов р и р + dp. Тогда
dm =
m
Поэтому
J =
¦!/¦
4/ЗтгД3
x2+y2+z2)dm={.^
Пример 4. Найдем момент инерции конуса относительно его оси. Мас-
Масса конуса равна т, радиус основания R.
I 1. Центр масс. Момент инерции
143
г,
z,
С
>Pv(xv,yv,zv)
Рис. 77
Рис. 78
За элементарную массу dm примем массу тонкого диска толщи-
толщиной dz, плоскость которого параллельна основанию конуса и отстоит
от него на расстоянии z (рис. 77). Тогда
dm =
т
l/3irR2h
(h-z)R
h
и для искомого момента инерции получаем
¦/*[
(h-z)R
h
dm =
./<»¦
dz =
76. Моменты инерции относительно параллельных осей.
Момент инерции, очевидно, зависит от выбора оси и. Найдем зави-
зависимость между моментами инерции относительно параллельных осей.
Сначала покажем, что если известен момент инерции Jc относительно
некоторой оси, проходящей через центр масс системы, то момент инер-
инерции Ju относительно любой параллельной оси может быть найден по
формуле
Ju = Jc + Md2,
B)
где d — расстояние между осями1.
Действительно, поместим начало координат в центре масс С, на-
направив ось Cz по оси, относительно которой известен момент инер-
инерции Jc, а ось Су так, чтобы она пересекала ось и, параллельную оси Cz
хЭто утверждение называется теоремой Гюйгенса-Штейнера.
144 Глава V
(рис. 78). Тогда
JV JV
Ju = E тЛх1 + {Vv-d)]=Y<
N / JV
Z n Zl
-2d Y, lmuyu + [Y, «V Ы2-
Первая сумма в полученном выражении есть Jc, вторая сумма об-
обращается в нуль, так как она равна Мус, а для выбранной системы
координат ус = 0, третья сумма равна массе системы М. Справедли-
Справедливость формулы B) доказана.
Из формулы B) следует соотношение
между моментами инерции относительно
любых параллельных осей «i и «2.
JUl=Ju2+M(d21-d22),
где d\ и с?2 — расстояния осей и\ и и^ от
Рис 7Q
гии- 'а центра масс.
Пример 1. Подсчитаем момент инерции тонкого однородного стержня
длиной а и массой т относительно оси z, перпендикулярной стержню
и проходящей через его конец (рис. 79).
Так как (см. пример 1 п. 75) Jc = та2/12, то
Jzi = Jc + т(а/2) = та2 /3.
§ 2. Тензор и эллипсоид инерции
77. Моменты инерции относительно осей, проходящих че-
через одну и ту же точку. Рассмотрим ось и, проходящую через на-
начало системы координат Oxyz. Косинусы углов, образуемых осью и с
осями Ox, Oy, Oz, обозначим соответственно а, /3, j. Тогда (рис. 80)
N N
Jn = ^2 mvpl = ^2 mu[(xl + yl + zl) - (хиа + yvfi + zujJ] =
-2a(ixvyv -
На основании тождества о? + /З2 + j2 = 1 заменяем 1 — а2, 1 — /З2,
1 — 72 соответственно на /З2 +j2, a2 +j2, a2 +/32 и приводим подобные
! 2. Тензор и эллипсоид инерции
145
члены в выражении, стоящем в квадратных скобках. Получаем
Ju = Jxa2 + Jy(i2 + Jzl2 - 2Jxya(i - 2Jxzaj - 2Jyzf3j, A)
где введены следующие обозначения:
N N
Jx — 2—j ^vyVi/ ~r %v)i Jy — 2_^ ^^vKZjj "r Xv),
v=\ v=\
N
jz _ ^ mv(x2v + yl),
B)
N
N
N
XV — / _, туЖуУу, Jxz — / j ТПуХу%У1 Jyz — / y ТЧуУу%у (о)
v=l
v=l
v=l
Величины B), C), очевидно, не за-
зависят от выбора оси и. Величины B)
называются осевыми моментами инер-
инерции: Jx — это момент инерции отно-
относительно оси Ox, Jy — относительно
оси Оу и Jz — относительно оси Oz.
Величины C) называются центробеж-
центробежными моментами инерции. Осевой мо-
момент инерции представляет собой меру
инертности системы при ее вращении
вокруг соответствующей оси. Центро-
Центробежные моменты инерции можно трак- Рис- 80
товать как меру неуравновешенности масс системы: они характеризу-
характеризуют несимметричность распределения масс относительно координатных
плоскостей.
Для различных точек О осевые и центробежные моменты инер-
инерции различны. Они изменяются также при повороте системы ко-
координат Oxyz вокруг рассматриваемой точки О. Можно показать,
что при повороте величины B), C) изменяются в соответствии с
формулами, определяющими симметрический тензор второго ранга.
Матрица J вида
J =
Jxy Jy
Jxz Jv
-Jxz
-J,
Jz
yz
D)
определяет тензор второго ранга, который называют тензором инерции
системы для точки О.
146 Глава V
78. Эллипсоид инерции. Главные оси инерции. Формула A)
допускает наглядную геометрическую интерпретацию. На оси и отло-
отложим по обе стороны от точки О отрезки такой длины ON (рис. 80),
что
ON =
и найдем геометрическое место точек N(x, у, z). Имеем
а = \[Уих, /3 = \[Тиу, 7 = \l~3~uZ.
Подставив эти значения a, fi и j в равенство A), получим
Jxx2 + Jyy2 + Jzz2 - 2Jxyxy - 2Jxzxz - 2Jyzyz = 1. E)
Поверхность второго порядка E) — эллипсоид. Действительно, от-
отрезок ON имеет конечную длину, так как Ju ^ 8 > 0. Исключение со-
составляет предельный случай, когда все точки Ри лежат на одной прямой
(например, случай бесконечно тонкого стержня). Тогда момент инер-
инерции Ju = 0, и эллипсоид инерции превращается в цилиндр.
Эллипсоид E) называется эллипсоидом инерции системы для точ-
точки О. Если точка О совпадает с центром масс, то эллипсоид E) назы-
называется центральным эллипсоидом инерции. При повороте системы ко-
координат Oxyz уравнение эллипсоида инерции меняется. Главные оси
эллипсоида инерции называются главными осями инерции системы для
точки О. В системе координат Ox*y*z*, оси которой направлены по
главным осям эллипсоида инерции, уравнение E) имеет вид
Ах\ + Byl + Czl = 1. F)
В этой системе координат центробежные моменты инерции равны
нулю: Jx,y, = Jx,z, = Jy,z, = 0. Величины А, В, С — моменты инер-
инерции относительно главных осей Ож», Оу*, Oz* соответственно. Они на-
называются главными моментами инерции системы для точки О. Если
точка О совпадает с центром масс, то оси Ож*, Оу*, Oz* называются
главными центральными осями инерции, а величины А, В, С — глав-
главными центральными моментами инерции.
Из аналитической геометрии известно, что для любого эллипсоида
существуют главные оси. Величины А, В, С являются собственными
значениями матрицы D). Если они различны, то главные оси определя-
определяются однозначно. Если эллипсоид инерции для точки О является эллип-
эллипсоидом вращения вокруг оси Oz*, то за его главные оси можно принять
ось Oz* и любые две ортогональные оси, лежащие в экваториальной
плоскости эллипсоида. Если А = В = С, то все оси, проходящие через
точку О, являются для нее главными.
§ 2. Тензор и эллипсоид инерции 147
Если эллипсоид инерции для точки О построен, то момент инер-
инерции относительно какой-либо оси и равен 1/ON2, где ON — отрезок,
соединяющий точку О с точкой пересечения оси и с эллипсоидом. Наи-
Наибольшую величину имеет момент инерции относительно наименьшей
оси эллипсоида, а наименьшую — относительно наибольшей его оси.
Замечание 2. Пусть при каком-либо выборе системы координат Oxyz
не все три центробежных момента инерции равны нулю, а только два
из них, например Jxz — Jyz — 0, a Jxy ф 0. Покажем, что ось Oz будет
главной. Чтобы убедиться в этом, надо показать, что систему коор-
координат Oxyz можно повернуть на такой угол а вокруг оси Oz, что в
повернутой системе координат Ox'y'z уже все центробежные момен-
моменты инерции будут равны нулю. Действительно, пусть система коор-
координат Ox'y'z получается из Oxyz поворотом вокруг оси Oz на угол а
против часовой стрелки, если смотреть со стороны положительного
направления оси Oz. Тогда координаты точки Pv в исходной и поверну-
повернутой системах координат связаны соотношениями
x'v = xvcosa + yv sin a, y'v = —xv sin а + yv cos a, z'v = zv. G)
Используя равенство G) и условие Jxz = Jyz = 0, получаем
N N
Jx'z' = X) mvx'vz'v = Yj mv(xvcosa + yvsm.a)zv =
v=l v=l
/ n \ / n \
= I X) mvxvzv I cos a + I X) mvyvzv I sin a = Jxz cos a + Jyz sin a = 0.
V=i / V=i /
Аналогично получаем, что Jyizi = 0, т. е. центробежные моменты
инерции, которые были равны нулю до поворота системы координат,
остаются равными нулю при любом угле поворота вокруг оси Oz. Вы-
Вычислим теперь третий центробежный момент инерции:
N
Jx'y' = X) mvx'vy'v =
v=l
N
— Yl tnv{xv cos a + yv sina)(—xv sina + yv cos a) =
N \ (N \
E rnv(x2v - yl) sin2a + X) mvxvyv cos2a.
=i / V=i /
Замечая, что
N
= Jy-Jx
v=l
148 Глава V
и приравнивая Jxiyi нулю, получаем уравнение для нахождения угла а:
-7)(Jy - Jx) sin2а + Jxycos2a = О
Если Jx = Jy, то а = тг/4, если же Jx ф Jy, то
1
7Г.
Jy JX
Таким образом, ось Oz, отвечающая общему индексу (в рассмотрен-
рассмотренном случае индексу z) равных нулю центробежных моментов инерции,
является главной осью инерции для точки О.
Упражнение 2. Показать, что если между радиусом основания R од-
однородного прямого кругового конуса и его высотой h выполняется со-
соотношение R = 2h, то эллипсоид инерции конуса для его вершины есть
сфера.
Упражнение 3. Показать, что: а) главная ось инерции остается глав-
главной для всех своих точек тогда и только тогда, когда она является
главной центральной осью инерции; б) если в системе есть ось мате-
материальной симметрии, то эта ось является главной центральной осью
инерции; в) если у системы есть плоскость материальной симметрии,
то любая прямая, перпендикулярная этой плоскости, является главной
осью инерции системы для точки, в которой эта прямая пересекает
плоскость симметрии; г) для однородного тела вращения ось вращения
и любые две взаимно перпендикулярные и перпендикулярные ей оси
образуют систему главных осей инерции.
79. Свойства главных моментов инерции. Не всякий эллип-
эллипсоид может служить эллипсоидом инерции. Действительно, если за оси
Ож», Оу*, Oz* приняты главные оси инерции для точки О, то уравнение
эллипсоида инерции имеет вид F), где
N N
Л = ? mv(ylv + z\v), В = Y, mv(zlv + x\v),
N
С = ? mv{xlv + ylv).
v=l
Главные моменты инерции (как, впрочем, и осевые моменты инер-
инерции B)) удовлетворяют неравенствам треугольника
А + В^С, А + С^ В, В + С^А. (8)
§ 2. Тензор и эллипсоид инерции
149
Проверим первое из этих неравенств. Имеем
JV
А + В = Y, ти(х1„ + y\v + 24,)
= ?
2 ?
= С
2 ?
С
причем знак равенства возможен только для случая, когда все точки
системы лежат в плоскости Ох*у*, т. е. когда z*v = 0 для всех v. Второе
и третье неравенства из (8) проверяются аналогично.
Для графического представления области допустимых значений
моментов инерции введем обозначения вл = Л/В, вс = С/В. Нера-
Неравенства (8) запишутся в виде
Область допустимых значений парамет-
параметров показана на рис. 81 штриховкой. Она
представляет собой бесконечную поло-
полосу, лежащую между параллельными пря-
прямыми в а + 1 = вс и 1 + вс = в а
и расположенную правее и выше пря-
прямой в а + вс = 1. Участки границы об-
области допустимых значений параметров
в а + 1 = вС, вА + вС = 1 И 1 + вС = в А
отвечают системам материальных то-
точек, лежащим соответственно в плоскос-
плоскостях Ох*у*, Ox*z* и Oy*z*. Точка A,0) на
рис. 81, точка @,1) и бесконечно удаленные точки прямых в а + 1 = вс,
1 + вс = вл отвечают системам материальных точек, лежащим соот-
соответственно на осях Oz*, Ох* и Оу*.
Упражнение 4. Показать, что симметрическую матрицу, образован-
образованную элементами Jij (г, j = 1, 2, 3; Jij = Jji), можно рассматривать
как матрицу тензора инерции реального твердого тела тогда и только
тогда, когда одновременно выполняются неравенства1
xi > 0,
где
О
Рис. 81
XlX2X3 - ХХJ|3 - X2J13 ~ X3J12 - 2Jl2Jl3J23 > 0,
J22 + J33 — Jii
J11 + J33 — J22
X3 =
Jll + J22 — J33
'См.: Пеньков В. И., Сарычев В. А. Оптимизация гравитационной системы ста-
стабилизации спутников с одностепенным подвесом на слабоэллиптической орбите, М.:
Ин-т прикладной математики АН СССР, препринт №90, 1974.
Глава VI
Основные теоремы и законы динамики
§ 1. Основные динамические величины
механической системы
80. Количество движения системы. Количеством движения
механической системы называется вектор
N
Q = ^2ml/vl/. A)
N N
Так как Мгс = X) mvf*v, то Mvc = XI mvvv = Q- Таким образом,
Q = Mvc,
B)
Рис. 82
т. е. количество движения системы равно
массе системы, умноженной на скорость ее
центра масс.
81. Главный момент количеств
движения (кинетический момент) сис-
системы. Пусть pv — радиус-вектор точки Pv
системы относительно некоторой точки А,
называемой центром (рис. 82). Моментом
*у количества движения (кинетическим мо-
моментом) точки Pv относительно центра А
называется вектор Kva, определяемый по
формуле
К„а = Р„ х mvvv.
Моментом количества движения (кинетическим моментом) точ-
точки Pv относительно оси называется проекция на эту ось момента коли-
количества движения точки относительно любого выбранного на данной оси
центра. В независимости момента количества движения относительно
оси от выбора центра на этой оси можно убедиться точно так же, как
в п. 49 при определении момента силы относительно оси.
§ 1. Основные динамические величины механической системы 151
Главным моментом количеств движения [кинетическим момен-
моментом) системы относительно центра А называется величина
JV
КА = ^2ри х mvvv. C)
Главным моментом количеств движения (кинетическим момен-
моментом) системы относительно оси называется проекция на эту ось глав-
главного момента количеств движения системы относительно любого вы-
выбранного на данной оси центра.
При изменении центра кинетический момент изменяется. Найдем
зависимость между его значениями для двух различных центров Аи В.
Пусть pvA и pvA — радиусы-векторы точки Pv соответственно отно-
относительно центров А и В. Тогда
N N
КВ = Y, PvB х mvvv = Е {PvA + ВА) Х mvvv =
!/ = 1 !/=1
N N
= Z) PvA x fnvvv + ВА х Yl mvVv = Ка + ВА х Q.
v=l v=l
Таким образом,
Кв = КА + ВАх Q. D)
Установим связь между значениями кинетического момента сис-
системы относительно какого-либо произвольного центра и относительно
центра масс системы. Предварительно введем важное здесь и в даль-
дальнейшем понятие движения системы относительно ее центра масс. Та-
Таким движением называется движение точек системы относительно по-
поступательно движущейся системы координат с началом в центре масс
системы. Эта система координат называется еще кениговой системой
координат.
Покажем, что абсолютный кинетический момент Kq системы от-
относительно центра масс С равен относительному кинетическому мо-
моменту Ксг относительно С. Действительно, пусть vc — абсолютная
скорость центра масс, vv — абсолютная скорость точки Pv системы, vVT
— скорость точки Pv в ее движении относительно центра масс. В силу
того что кенигова система координат движется поступательно, пере-
переносные скорости всех точек системы одинаковы и равны Vq- Поэтому
абсолютная скорость точки Р„, участвующей в сложном движении, бу-
будет определяться формулой
vv = vc + vvr. E)
152 Глава VI
Пусть pvr — радиус-вектор точки Pv относительно центра масс. Тогда
JV
КСг = ^Pvr* mvvvr. F)
v=l
Вычислим теперь абсолютный кинетический момент системы относи-
относительно точки С:
N N
КС = Е Pvr Х mvVv = Е PvrX m,v{vC + Vvt) =
G)
/ N \ N
= I E mvPvr I X VC + E Pvr X ™>vVvr-
\v=l J v=l
Так как центр масс находится в начале кениговой системы координат
N
(Per = 0)? то Е mvPvr = МрСг = 0 и, следовательно, из F), G)
вытекает, что Kq = Ксг-
Замечая, что
N
^2 «VtVr = Mvcr = 0,
v=l
т. е. количество движения системы в ее движении относительно центра
масс равно нулю, из D) получаем, что кинетический момент системы
в ее движении относительно центра масс одинаков для всех точек про-
пространства и, согласно предыдущему, равен Kq-
Поэтому абсолютный кинетический момент системы относитель-
относительно центра О равен сумме ее относительного кинетического момента
(одинакового для всех точек пространства) и момента вектора Q от-
относительно центра О в предположении, что он приложен в центре масс
системы.
82. Кинетический момент твердого тела, движущегося во-
вокруг неподвижной точки. Примем неподвижную точку О тела за
начало системы координат Oxyz, оси которой неподвижны относитель-
относительно тела. Пусть pv — радиус-вектор точки Pv тела относительно нача-
начала координат, его проекции на оси Ox, Oy, Oz обозначим xv, yv, zv.
Проекции мгновенной угловой скорости со тела на те же оси обозна-
обозначим р, q, r.
Вычислим кинетический момент тела относительно точки О. Учи-
Учитывая, что скорость vv точки Pv равна со х pv, имеем
N N N
Ко = ^2р„ х mvvv = ^ Pv x ти(ш х pv) = ^ mvpv x (ш х pv).
§ 1. Основные динамические величины механической системы 153
Используя формулу а х (Ь х с) = Ь(а ¦ с) — с(а ¦ Ъ) для двойного
векторного произведения трех векторов а, Ъ, с, выражение для Ко
можно переписать в виде
N N
Ко = Е ™>„р1ш - Е тЛш • pv)pv =
N N
= Е ™ЛХ1 + vl + *1)ы - Y, mv(pxu + qyv + rzv)pv.
Отсюда получаем следующее выражение для проекции Кох вектора Ко
на ось Ох:
N N
Кох = Е fnv{x2v + yl+ zl)p - Е fnv(pxv + qyv + rzv)xv =
N \ / N \ / N \
E mAvl + zl) )P - \ E fnvxvyv )q - E mvxvzv r.
v=l J \v=l J \v=l J
Аналогично можно выписать выражения для проекций Коу и Koz-
Учтя формулы B), C) п. 77 для осевых и центробежных моментов инер-
инерции, окончательно получим
Кох = Jxp - Jxyq - Jxzr,
кОу = -Jxyp + Jyq - Jyzr, (8)
KOz = -JxzP - JyzQ + JzT-
Эти формулы можно записать более компактно, использовав матрицу J,
определяющую тензор инерции тела для точки О (см. п. 77):
Ко=3ш. (9)
В частном случае, когда оси Ox, Oy, Oz представляют собой глав-
главные оси инерции тела для точки О, матрица J диагональна; ее диа-
диагональными элементами служат главные моменты инерции тела для
точки О, т. е. Jx = A, Jy = В, Jz = С. В этом случае
КОх = Ар, КОу = Bq, KOz = Cr. A0)
Если твердое тело вращается вокруг неподвижной оси, например вокруг
оси Oz, то р = q = 0 и, согласно (8),
Кох = -Jxzr, KOy = -Jyzr, KOz = Jzr. A1)
154 Глава VI
Из A1) видно, что при вращении тела вокруг неподвижной оси направ-
направления оси вращения и кинетического момента тела, вообще говоря, раз-
различны. Они совпадают тогда и только тогда, когда ось вращения явля-
является главной осью инерции тела.
83. Кинетическая энергия системы. Теорема Кёнига. Ки-
Кинетической энергией системы называется величина Т, определяемая по
формуле
T=±f>^- A2)
При вычислении кинетической энергии очень часто используется
следующее утверждение.
Теорема (Кёнига). Кинетическая энергия системы равна сумме ки-
кинетической энергии, которую имела бы материальная точка, располо-
расположенная в центре масс системы и имеющая массу, равную массе систе-
системы, и кинетической энергии движения системы относительно центра
масс.
Доказательство.
Согласно E) и A2), имеем
Так как относительная скорость центра масс Vcr равна нулю, то отсюда
следует, что
N
T=\Mv2c + \Y,mvvlr- A3)
Теорема доказана.
84. Кинетическая энергия твердого тела, движущегося во-
вокруг неподвижной точки. Пусть Oxyz — жестко связанная с те-
телом система координат с началом в его неподвижной точке О и пусть
мгновенная угловая скорость тела со направлена вдоль оси и, косинусы
§ 1. Основные динамические величины механической системы 155
углов которой с осями Ox, Oy, Oz соответственно равны а, /3, j. Тогда
проекции ш на оси Ox, Oy, Oz вычисляются по формуле
р = изо., q = u)[i, r = ujj. A4)
Если dv — расстояние от точки Р„ до оси и, то vv = u)dv и для
кинетической энергии тела имеем выражение
Г = \ ? mvvl
v=l
где Ju — момент инерции тела относительно оси и. Подставив в A5)
выражение для Ju из формулы A) п. 77 и воспользовавшись формула-
формулами A4), получим окончательно
Т = 2 (JxP2 + JyQ2 + Jzr2) - Jxypq - Jxzpr - Jyzqr. A6)
Если оси Ox, Oy, Oz представляют собой главные оси инерции тела
для точки О, то формула A6) принимает вид
T=\{AP2+Bq2+Cr2), A7)
где А, В, С — моменты инерции тела относительно осей Ox, Oy, Oz.
Для твердого тела, вращающегося вокруг неподвижной оси, напри-
например вокруг оси Oz, формула A6) сильно упрощается. Так как в этом
случае р = q = 0, \г\ = и), то
T=\jzu?. A8)
Замечание 1. Между мгновенной угловой скоростью ш твердого тела
и его кинетическим моментом относительно неподвижной точки О
существует простое геометрическое соответствие. Действительно,
из формул (8) и A6) следует, что
Т=\{Ко-ш). A9)
Так как кинетическая энергия движущегося тела положительна, то
отсюда следует, что угол между векторами Ко и и> будет всегда ост-
острым. Используя A9), можно также геометрическим путем найти на-
направление одного из двух векторов ш и Ко, когда задано направление
другого.
Упражнение 1. Пусть известен эллипсоид инерции тела для неподвиж-
неподвижной точки О и задана мгновенная угловая скорость со. Найти направле-
направление и модуль кинетического момента Kq тела относительно точки О.
156 Глава VI
§ 2. Теоремы об изменении основных
динамических величин системы
85. Общие замечания о теоремах и законах динамики. Рас-
Рассмотрим движение системы материальных точек Pv (у = 1, 2, ... , N)
в некоторой инерциальной системе координат. Пусть rnv — масса точ-
точки Р„, a pv — ее радиус-вектор относительно начала координат. Если
система несвободна, то ее можно рассматривать как свободную, если
помимо активных сил, приложенных к точкам системы, учесть реак-
реакции связей. Если затем все силы, приложенные к системе, разбить на
внешние и внутренние, то из аксиом Ньютона получим дифференци-
дифференциальные уравнения движения рассматриваемой механической системы
в виде
mvwv = F^ + F® (v = l,2,...,N), A)
где wu — ускорение точки Pv в инерциальной системе отсчета, a F^
и Fv — соответственно равнодействующие всех внешних и внутрен-
внутренних сил системы, приложенных к точке Pv.
Для исследования движения надо при заданных начальных услови-
условиях проинтегрировать систему уравнений A) и найти зависимость rv от
времени. Это в большинстве случаев невозможно, особенно если число
уравнений A) велико.
Однако при практическом исследовании движения очень часто нет
необходимости изучать систему A), а достаточно знать изменение со
временем некоторых величин, общих для всей материальной системы
и являющихся функциями координат и скоростей точек системы (и,
быть может, времени). Если такая функция при движении системы
остается постоянной, то она называется первым интегралом уравнений
движения A). Использование первых интегралов позволяет упростить
задачу исследования движения системы, а иногда и решить ее до конца.
Самый распространенный прием получения первых интегралов
уравнений A) основан на изучении поведения основных динамичес-
динамических величин системы: количества движения, кинетического момента,
кинетической энергии. Изменение этих величин во времени описывает-
описывается основными теоремами динамики, являющимися непосредственными
следствиями уравнений A). Утверждения, описывающие условия, при
которых некоторые из основных динамических величин остаются по-
постоянными, называются законами сохранения.
§ 2. Теоремы об изменении основных динамических величин системы 157
86. Теорема об изменении количества движения. Сложив
почленно уравнения A), получим
B)
Первая сумма в правой части равенства B) равна главному векто-
вектору Д(е) внешних сил системы, а вторая сумма равна нулю, так как
по третьему закону Ньютона внутренние силы попарно равны и про-
противоположны. Принимая во внимание постоянство массы каждой из
точек системы, равенство B) можно записать в виде
Это равенство выражает теорему об изменении количества движе-
движения системы: производная по времени от количества движения системы
равна главному вектору всех внешних сил системы.
Эту теорему можно представить в интегральной форме. Проинтег-
Проинтегрировав обе части равенства C) от t\ до t2, получим
AQ=Q2-Q1 = J R^dt. D)
ti
Интеграл в правой части формулы D) называется импульсом внеш-
внешних сил системы за время t% — t\. Таким образом, приращение коли-
количества движения за конечное время равно импульсу внешних сил за это
время.
Дифференциальной форме теоремы об изменении количества дви-
движения можно придать другую формулировку. Так как Q = Mvc,
где М — масса системы, a vc — скорость центра масс, то форму-
формула C) с учетом постоянства массы М может быть представлена в виде
равенства
Это равенство означает, что центр масс системы движется так
же, как двигалась бы материальная точка, масса которой равнялась
бы массе системы, под действием силы, равной главному вектору всех
внешних сил системы. Это утверждение называют теоремой о движе-
движении центра масс (центра инерции).
158 Глава VI
Если система замкнута, то R^ = 0 и из C) следует закон со-
сохранения количества движения: при движении замкнутой системы ее
количество движения Q постоянно. На основании равенства E) закон
сохранения количества движения можно сформулировать еще так: ско-
скорость vc центра масс замкнутой системы постоянна. Ясно, что эти
утверждения справедливы и для системы, не являющейся замкнутой,
если только R^ = 0 во все время движения.
Проектируя вектор Q на оси координат, получаем из закона сохра-
сохранения количества движения три первых интеграла:
Qx = ci, Qy = с2, Qz = с3,
или
хс = с[, ус = с'2, zc = с'3,
где Qx, Qy, Qz и хс, Ус, %с — проекции на оси Ox, Oy, Oz со-
соответственно количества движения и скорости центра масс системы,
а с,, c't (i = 1, 2, 3) — произвольные постоянные.
Если проекция главного вектора внешних сил на какую-нибудь од-
одну ось, например на ось Ох, равна нулю, то имеем один первый интег-
интеграл
Qx = const или хс = const.
Пример 1. Два человека стоят на абсолютно гладкой горизонтальной
плоскости на расстоянии а друг от друга. Один из них бросает мяч
массой т, другой подхватывает его через t секунд. С какой скоростью
начнет скользить по плоскости бросивший мяч, если его масса рав-
равна М?
Так как плоскость абсолютно гладкая, то горизонтальная состав-
составляющая главного вектора внешних сил {силы тяжести и реакции плос-
плоскости) равна нулю. Следовательно, проекция количества движения сис-
системы, состоящей из мяча и человека, бросившего мяч, на плоскость
будет постоянна {равна нулю, так как в начальный момент времени
система покоилась).
Пусть v — скорость, с которой начнет скользить человек после
бросания мяча. Замечая, что горизонтальная составляющая абсолют-
абсолютной скорости центра масс мяча равна a/t, получаем равенство
Mv-mj = 0.
Отсюда
v=rna
Mt
Уд
§ 2. Теоремы об изменении основных динамических величин системы 159
Пример 2. Две притягивающиеся по некоторому закону точки одина-
одинаковой массы могут скользить без трения одна по оси Ох, а другая —
по перпендикулярной ей оси Оу (рис. 83). Точки начинают движение
из состояния покоя. Показать, что при любом законе притяжения они
одновременно окажутся в начале координат.
Внешними силами, действующими на
рассматриваемую систему из двух матери-
материальных точек, являются реакции Ni и N2
осей Ох и Оу; эти реакции ортогональ-
ортогональны соответствующим осям. Ввиду того
что каждая из точек вынуждена двигать-
двигаться только вдоль своей координатной оси,
имеем Ni = Fcosa, N2 = Fsina, где F —
модуль силы притяжения точек. Главный
вектор i?(e) внешних сил имеет компонен-
компоненты —N2, —N±, т. е. R^ коллинеарен
вектору СО, имеющему начало в центре
масс С точек, а конец в начале координат.
Так как при t = 0 система покоилась, то,
согласно теореме о движении центра масс,
точка С при t > О будет двигаться вдоль неизменной прямой, прохо-
проходящей через точку О и начальное положение центра масс. Поэтому
материальные точки одновременно достигнут начала координат.
87. Теорема об изменении кинетического момента. Пусть
vv — скорость точки Pv системы в инерциальной системе отсчета,
a rv — ее радиус-вектор относительно начала координат (рис. 82). Возь-
Возьмем произвольную точку А пространства, которая может и не совпа-
совпадать с какой-либо материальной точкой системы во все время движе-
движения. Точка А может быть неподвижной, а может совершать произволь-
произвольное движение; обозначим va ее скорость в выбранной инерциальной
системе отсчета. Пусть pv — радиус-вектор точки Pv, относительно
точки А. Тогда кинетический момент системы относительно точки А
вычисляется по формуле
Рис. 83
JV
а =
mvvv.
F)
v=l
Продифференцировав обе части равенства F) по времени и воспользо-
160 Глава VI
вавшись постоянством величин mv и уравнениями A), получим
N , N
— -v^xm^ + y;,
dt ^—' (ft ^—'
JV , JV
Последняя сумма в этом равенстве равна главному моменту Мд
внешних сил относительно точки А (см. п. 50). Учитывая еще, что,
о о dpv drv drA Д
согласно рис. 82, —г- = —т- -г- = vv — va, а также что 2^ mvvv =
dx dt dt v=\
= Mvc, получаем
Таким образом,
:vA + M{Ae). G)
Если точка А неподвижна, то во все время движения системы Va = 0 и
уравнение G), выражающее теорему об изменении кинетического мо-
момента относительно произвольно движущегося центра, принимает сле-
следующую часто встречающуюся форму:
Уравнение (8) представляет собой теорему об изменении кинетического
момента для неподвижного центра: производная по времени от кинети-
кинетического момента системы относительно неподвижного центра равна
главному моменту внешних сил системы относительно этого центра.
Эту теорему можно представить в интегральной форме. Проинтег-
Проинтегрировав обе части равенства (8) от ti до ?2, получим
= К a, -KAl= I Mfdt. (9)
§ 2. Теоремы об изменении основных динамических величин системы 161
Интеграл в правой части этой формулы называется импульсом
моментов внешних сил за время ?2 — ^1- Таким образом, приращение
вектора кинетического момента системы относительно неподвижно-
неподвижного центра за конечное время равно импульсу моментов внешних сил
относительно этого центра за это время.
Если система замкнута, то МА = 0 и из равенства (8) следу-
следует закон сохранения кинетического момента: при движении замкнутой
системы ее кинетический момент относительно любого неподвижного
центра постоянен:
КА = const. A0)
Если Ках-, Клу, Kaz — проекции вектора К а на соответствующие оси
координат, то из A0) следуют три первых интеграла:
К Ах ~ '"I ? Ay ~~ ^2? КAz ~ ^3?
где Ci (г = 1, 2, 3) — произвольные постоянные. Эти интегралы су-
существуют не только в случае замкнутой системы, но и тогда, когда сис-
система не замкнута, но для некоторого неподвижного центра А МА = 0
во все время движения.
Отметим еще, что если МА = 0 во все время движения, то интег-
интеграл A0) существует не только когда центр А неподвижен, но и в более
общем случае, когда во все время движения радиусы-векторы га и гс
точки А и центра масс системы С относительно начала координат свя-
связаны соотношением га = агс + а, где скалярная величина а и вектор а
постоянны. Действительно, в этом случае va = ctvc и первое слагае-
слагаемое в правой части равенства G) тождественно равно нулю. Поэтому
при МА = 0 существует интеграл A0).
Рассмотренный выше случай неподвижного центра А получается
отсюда при а = 0. Если же а = 1 и а = 0, то га = гс и уравнение G)
примет вид
d-Jr = M(ce\ (И)
откуда следует, что теорема об изменении кинетического момента сис-
системы для неподвижного центра А и для центра масс С имеют одинако-
одинаковый вид: в левой части уравнения стоит производная от кинетического
момента относительно точки (А или С), а в правой — главный момент
внешних сил относительно этой точки. Отметим, что абсолютный кине-
кинетический момент Кс системы относительно центра масс в левой части
уравнения A1) можно заменить на равный ему (см. п. 82) кинетичес-
кинетический момент Ксг системы в ее движении относительно центра масс.
162 Глава VI
Пусть и — некоторая неизменная ось или ось неизменного направ-
направления, проходящая через центр масс системы. Для кинетического мо-
момента Ки системы относительно этой оси из (8) и A1) следует диффе-
дифференциальное уравнение
<^ = М<?\ A2)
где Ми — главный момент внешних сил относительно оси и. Если он
во все время движения равен нулю, то имеем первый интеграл
Ки = const. A3)
Последний вывод допускает обобщение. Именно, справедливо сле-
следующее утверждение. Пусть Ми равен нулю во все время движения.
Тогда для существования первого интеграла A3) необходимо и доста-
достаточно, чтобы проекции скорости центра масс системы и скорости
какой-нибудь точки А оси и на плоскость, перпендикулярную этой оси,
были во все время движения параллельны. Действительно, пусть е —
единичный вектор, направленный вдоль оси и. Умножая обе части ра-
равенства G) скалярно на вектор е и учитывая его постоянство по вели-
величине и направлению, получаем
Но К а • е = Кш, МАе' ¦ е = М„ , поэтому последнее равенство
можно переписать в виде
Если Ми = 0, то величина Ки будет постоянной тогда и только
тогда, когда (vc x va) • е = 0. Если за направление оси Oz принять
направление оси и, то последнее условие эквивалентно тождеству
ХА _ Хс
У А ~ Ус'
означающему параллельность проекций скоростей точек А и С на плос-
плоскость, перпендикулярную оси и, что и требовалось доказать.
Пример 1. Вдоль образующей однородного круглого конуса массой М, ось
которого неподвижна и занимает вертикальное положение, а вершина
обращена вверх, просверлен тонкий канал. Конусу сообщают угловую
§ 2. Теоремы об изменении основных динамических величин системы 163
скорость ujq вокруг его оси и одновременно с этим опускают в верхнее
отверстие канала шарик массы т, не сообщая ему начальной скорос-
скорости. Какова будет угловая скорость конуса в тот момент, когда шарик
выскочит из канала?
Так как внешние силы системы конус — шарик не создают мо-
момента относительно оси конуса, то кинетический момент Kz отно-
относительно оси остается постоянным. В начальный момент времени
Kz = Jzu>o,
а в момент, когда шарик выскакивает из канала,
Kz = Jzlo 2
— его момент
Здесь R — радиус основания конуса, a Jz = -^
инерции относительно оси. Из равенства
Jzu>0 = Jzuj + mR2u>
находим
и> =
ЗМ
3M + 10m u"
Пример 2. На гладкой горизонтальной плоскости находится твердое
тело, имеющее вид тонкого кругового кольца массой М и радиусом R.
Вдоль по кольцу движется точка А массой т с постоянной по модулю
относительной скоростью v. Определить движение этой системы по
плоскости, если в начальный момент и кольцо, и точка находились в
покое.
Так как горизонтальная составляющая
главного вектора внешних сил равна нулю и в
начальный момент времени центр масс С всей
системы покоился, то и в последующем дви-
движении системы он будет оставаться в покое.
Расстояния точки С будут (рис. 84): от цент-
центра О кольца
от точки А
ОС =
АС =
т
М + т
R,
Рис. 84
М
М + т
R.
Таким образом, и центр О кольца, и материальная точка А будут дви-
двигаться по концентрическим окружностям с центром в точке С, причем
164
Глава VI
и О, и А будут всегда находиться в диаметрально противоположных по
отношению к С точках своих траекторий.
Чтобы определить угловую скорость и> вращения кольца, воспользу-
воспользуемся тем, что, в силу равенства нулю главного момента внешних сил
относительно неподвижной вертикальной оси Cz, кинетический мо-
момент системы относительно этой оси постоянен (равен нулю, так
как в начальный момент времени система покоилась). Имеем:
Jcw + m(v + uj ¦ AC) ¦ AC = 0,
где Jc — момент инерции кольца относительно оси Cz. Так как мо-
момент инерции Jo кольца относительно параллельной Cz оси Oz, оче-
очевидно, равен MR2, то, согласно п. 76,
Jc = MR2 + M -ОС2.
Воспользовавшись еще выписанными выше выражениями для АС
и ОС, получим окончательно
V
т(М + т)
М2 + ЪтМ + 2т2 '
Знак минус в полученном выражении для и> указывает на то, что вра-
вращение кольца происходит по часовой стрелке, если смотреть со сто-
стороны положительного направления оси Cz.
Пример 3. Два тонких однородных диска 1
и 2, массы и радиусы которых равны соот-
соответственно nil, f'i uni2, Г2, могут вращать-
вращаться вокруг их ортогональных осей Oz\ и Ozi
(рис. 85). Диск 1 раскрутили до угловой ско-
скорости ш и привели затем в контакт с не-
вращающимся диском 2, причем расстояние
между точкой соприкосновения и осью диска 1
равно а. Через некоторое время (за счет тре-
трения) диски начнут вращаться без проскаль-
проскальзывания. Найти установившиеся угловые ско-
скорости дисков.
Для решения задачи используем интегральную форму теоремы об
изменении кинетического момента. При t = 0 кинетические момен-
моменты KZl и KZ2 дисков 1 и 2 будут соответственно равны:
1
HUM 1 1 1 1 1 1
Z2
СО
1 1 III Mill
О
a
=
;
2
Рис. 85
KZl = JZlw,
= 0,
! 2. Теоремы об изменении основных динамических величин системы 165
а в момент времени At, равный продолжительности процесса установ-
установления движения дисков,
Zl = JZ1U>1,
= JZ2U>2-
Здесь Mi — модуль установившейся угловой скорости, a JZi = -^mi^
— момент инерции i-го диска относительно оси Ozi (г = 1, 2). При-
Приращения кинетических моментов первого и второго дисков соответ-
соответственно равны JZl(iL>i — ui) и Jz.2iL>2- Изменение кинетических моментов
вызвано действием силы трения в точке контакта дисков в течение
времени At. Сила трения, модуль которой F одинаков для обоих дис-
дисков, тормозит первый диск и ускоряет второй. Согласно равенству (9),
имеем
At
-ш) = -а / Fdt, |
о
Добавив сюда еще уравнение
= u2r2,
At
= r2 Fdt.
выражающее условие отсутствия скольжения в установившемся режи-
режиме движения дисков, получим систему трех уравнений относитель-
относительно угловых скоростей дисков u>i, и>2 и модуля импульса силы трения
At
j F dt. Решив ее, найдем:
о
т\аг\
+ т2аг)
Пример 4. Диск массой т и радиусом а
катится по горизонтальной плоскости без
скольжения. Центр тяжести С диска на-
находится на расстоянии Ь от его геометри-
геометрического центра О, момент инерции диска
относительно оси, перпендикулярной плос-
плоскости диска и проходящей через точку С,
равен Jc- Пусть <р — угол между отрез-
отрезком ОС и вертикалью (рис. 86). Соста-
Составить дифференциальное уравнение, описы-
описывающее изменение угла <р со временем.
Для решения задачи воспользуемся те-
теоремой об изменении кинетического момента в форме G). За
'//Лх
У777777777
Рис. 86
166 Глава VI
точку А примем геометрическую точку, которая принадлежит
следу (прямой линии), вычерчиваемому точкой касания диска с
плоскостью. В силу отсутствия скольжения для скорости точ-
точки А в системе координат Axyz (оси Ах, Ау показаны на ри-
рисунке, ось Az направлена перпендикулярно плоскости рисунка на
читателя) имеем: v'A = (аф, 0, 0). Вектор АС имеет компонен-
компоненты: —bsimp, —a + bcosip, О; АС2 = а2 + b2 — 2abcos<p. Для угловой ско-
скорости диска и>, скорости его центра масс vc = и>хАС и кинетического
момента Ка диска относительно точки А имеем:
ш' = (О, О, ф), v'c = ((а — &cos<?>)<?>, —Ьи'икрф, О),
КА = (О, О, ^с + тАС2)ф).
Момент внешних сил относительно точки А создает только сила тя-
тяжести:
М(Ае) = (О, О, -mg6sin<?>).
Проектирование обеих частей векторного уравнения G) на ось Az
приводит к искомому уравнению, описывающему изменение угла <р во
времени:
[Jc + т(а2 + Ъ2 — 2аЬ cos <р)\ф + таЪът<рф2 + mgbsimp = О.
88. Теорема об изменении кинетической энергии. Пусть
точки Р„ системы переместились так, что их радиусы-векторы г„ в
инерциальной системе отсчета получили приращения drv. Найдем, как
при этом изменилась кинетическая энергия системы Т. Так как
JV
т-1Гт v2
v=l
то для дифференциала кинетической энергии имеем такое выражение:
N N
dT = VJ mv vv ¦ dvv = 2_, mvvv • —jT dt =
v=l v=l
N N
= 2^ tnvwv ¦ vv dt = 2^ tnvwv ¦ drv.
Принимая во внимание дифференциальные уравнения A), перепишем
§ 2. Теоремы об изменении основных динамических величин системы 167
последнее равенство в виде
JV
v=l
N N
v=l v=l
Таким образом,
dT = d'A^ + d'A^. A4)
Последнее равенство выражает теорему об изменении кинетичес-
кинетической энергии системы: дифференциал кинетической энергии системы ра-
равен элементарной работе всех сил системы.
Подчеркнем, что, в отличие от двух рассмотренных выше основных
теорем динамики, в теореме об изменении кинетической энергии речь
идет о всех силах системы: как внешних, так и внутренних. Тот факт,
что силы, с которыми взаимодействуют две точки системы, равны по
величине и противоположно направлены, не приводит к равенству нулю
работы d'A^1 внутренних сил системы, так как при подсчете работы
важны и перемещения точек, а они у двух взаимодействующих точек
не обязательно одинаковы. Как мы видели в п. 52, для твердого тела
работа внутренних сил равна нулю, поэтому для него равенство A4)
принимает более простой вид
dT = d'A^. A5)
Проинтегрировав обе части равенства A4) от t\ до t2, получим
интегральную форму теоремы об изменении кинетической энергии
AT = Т2-Т1 =
= f d'A(e) + fd'AW, A6)
т. е. приращение кинетической энергии системы за конечное время рав-
равно работе всех сил системы за то же время.
Пусть все силы системы (внешние и внутренние) потенциальны
и их потенциал П не зависит явно от времени. В этом случае (п. 53)
элементарная работа сил системы будет полным дифференциалом
d'A^ + d'A^ = -da. A7)
Из A7) и A4) следует, что тогда dT + dH = 0.
168
Глава VI
Сумма кинетической и потенциальной энергий называется полной
механической энергией системы. Из последнего равенства следует, что
Е = Т + П = h= const,
A8)
т. е. если все силы системы потенциальны и потенциал не зависит от
времени, то при движении системы ее полная механическая энергия по-
постоянна. Это — закон сохранения механической энергии. Равенство A8)
называется интегралом энергии.
Следует иметь в виду, что для справедливости закона сохранения
механической энергии требование о том, чтобы все силы системы бы-
были потенциальными, не обязательно. Достаточно потребовать, чтобы
потенциальными были силы, работа которых на действительном пере-
перемещении системы отлична от нуля. Например, работа реакций стацио-
стационарных идеальных связей равна нулю, и если остальные силы системы
потенциальны и потенциал не зависит явно от времени, то для такой
системы справедлив закон сохранения механической энергии.
'¦к
2
Рис. 87
Рис.
Пример 1. Тонкий однородный стержень длиной I вращается на шар-
шарнире О в вертикальной плоскости (рис. 87). Какую скорость v нужно
сообщить нижнему концу стержня, чтобы угол наибольшего отклоне-
отклонения стержня от вертикали равнялся тг/2? Помимо силы тяжести и
реакции шарнира на стержень действует постоянный момент mconv,
препятствующий вращению стержня.
Если нижний конец имеет начальную скорость v, то угловая ско-
скорость стержня в начале движения равна v/l. Пусть т — масса стерж-
§ 2. Теоремы об изменении основных динамических величин системы 169
ня. Тогда момент инерции стержня относительно оси вращения ра-
равен Уд mi2, а кинетическая энергия стержня в начальный момент рав-
равна Уг-Узт/2-^//J.
При переходе стержня в горизонтальное положение сила тяжести
совершит работу, равную —mgl/2, а силы сопротивления вращению —
работу — (тг/2)тсоггр. Принимая во внимание интегральную форму тео-
теоремы об изменении кинетической энергии, получим
-mv2 = ^
v = уЗШ +
откуда
Пример 2. На вертикально поставленный винт надета массивная гай-
гайка. Ей сообщена угловая скорость и> такого направления, что гайка
начинает подниматься. На какую высоту поднимется гайка? Трение
отсутствует. Шаг винта h, его радиус г, радиус гайки R (рис. 88).
Пусть v — скорость движения гайки вдоль оси винта в начале дви-
движения. Она найдется из пропорции
V _ U)
h ~ 2тг-
Примем, что гайка имеет форму цилиндра с осевым отверстием ради-
радиуса г. Если т — масса гайки, то ее момент инерции J относительно
оси винта будет определяться равенством
J=\m{R2 + r2).
Пусть высота подъема гайки Н, тогда из интеграла энергии имеем
откуда
27Г2
Пример 3. Цилиндр, который может вращаться вокруг вертикальной
оси АВ, имеет на своей поверхности винтовой желоб; в него вложен
шарик массой т, который можно считать материальной точкой. Най-
Найти относительную скорость и шарика в его движении по желобу и уг-
угловую скорость ш цилиндра при движении системы под действием силы
тяжести, полагая, что масса цилиндра равна массе шарика, радиус ци-
цилиндра а и угол а наклона касательной к винтовой нарезке равен тг/4.
Найти также давление шарика на желоб (рис. 89).
170
Глава VI
А
Если шарик пройдет по вертикали расстояние z,
то его потенциальная энергия уменьшится на величи-
величину mgz. Приравняв ее кинетической энергии системы,
будем иметь
11 2 2
mgz = g • -кгпа ш +
\т
ч 2
— и cos?) +(Msin-^-
или
2gz = |a2w2 -
и2.
Второе уравнение для определения неизвестных uj
и и получим из теоремы об изменении кинетическо-
кинетического момента. Так как внешние силы не дают момен-
момента относительно вертикальной оси и в начальный мо-
момент вся система была неподвижна, то кинетический момент систе-
системы относительно оси АВ постоянен и равен нулю:
-~та2и;
+ т (аш — и cos j) a = 0,
откуда
Заш - V2u = 0.
Решая совместно полученные уравнения для и и и), находим
и, - у »бЛ, ш - ^ .
Пусть N — давление шарика на желоб. Составим уравнение A4)
только для одного цилиндра:
d (н • А"га2а;2) = TV cos ? • а d^>,
ылы, так как dip = u> dt,
та du> = V2N dt.
Но
dw = dwdz = 1 /iLMsin7r
dt dz dt a V 6z 4'
и, следовательно,
AT
mal
\/2
§ 2. Теоремы об изменении основных динамических величин системы 171
89. Основные теоремы динамики в неинерциальной систе-
системе отсчета. Будем теперь изучать движение механической системы
в произвольно движущейся неинерциальной системе отсчета. Абсолют-
Абсолютное ускорение wv точки Р„ системы найдем при помощи теоремы о
сложении ускорений (п. 32):
wv = wvr + wve + wvc (v = 1, 2, ... , TV). A9)
Здесь wvr и wve — относительное и переносное ускорения точ-
точки Р„, a wvc — ее кориолисово ускорение; wvc = 2ш х vvr, где ш
— угловая скорость неинерциальной системы координат относительно
инерциальной, a vvr — относительная скорость точки Р„. Подставив
выражение A9) для абсолютного ускорения в уравнения A), получим
mvwvr = F^ + F^+jve + jvc (i/ = l, 2, ..., TV), B0)
где jve = -mvwve, jvc = -mvwvc = -2mvu> x vvr; величину jve назы-
называют переносной, a jvc — кориолисовой силами инерции.
Таким образом, второй закон Ньютона может быть применен в
неинерциальной системе отсчета, если к силам, приложенным к точкам
системы, добавить еще переносные и кориолисовы силы инерции.
Но полученные в п. 86-88 теоремы динамики вытекали из уравне-
уравнений A). Следовательно, все сформулированные выше теоремы динами-
динамики будут верны и в неинерциальной системе отсчета, если к силам, при-
приложенным к системе, добавить переносные и кориолисовы силы инер-
инерции для ее точек. При этом силы инерции следует формально относить
к внешним силам.
Например, теорема об изменении количества движения в неинер-
неинерциальной системе отсчета выглядит так:
^k = R(e)+Je + Jc, B1)
N
где Qr = ^2 rnvvvr, R^ — главный вектор внешних сил, приложенных
N
к системе, Je = J^ jve — главный вектор переносных сил инерции,
N
Jc = ^2 jvc — главный вектор кориолисовых сил инерции.
Теорема об изменении кинетического момента в неинерциальной
системе отсчета записывается в виде (для неподвижного относительно
неинерциальной системы центра А)
B2)
172
Глава VI
JV
Здесь Каг = S Pv x mvvvri Pv — радиус-вектор точки Р„ относи-
v=\
тельно центра А, МА — главный момент внешних сил, приложенных
к системе, относительно точки A, Majc и Majc — главные моменты
переносных и кориолисовых сил инерции относительно точки А.
Теорема об изменении кинетической энергии Тг системы, соответ-
соответствующей ее движению в неинерциальной системе координат, будет
такой:
Здесь
N
mvvvr,
B3)
B4)
v=l
d'A(e\ d'A^ — элементарная работа внешних и внутренних сил, при-
приложенных к системе, на относительных перемещениях dpv ее точек,
a d'Aje — элементарная работа переносных сил инерции на тех же пе-
перемещениях. В B3) отсутствует работа кориолисовых сил инерции: эта
работа равна нулю, так как кориолисова сила инерции для каждой точ-
точки Р„ перпендикулярна ее относительному перемещению dpv.
Пример 1. При вращении сосуда, наполненного жидкостью, вокруг вер-
вертикальной оси жидкость отбрасывается к стенкам и внутри сосуда
образуется воронкообразная полость, ограниченная поверхностью вра-
вращения (рис. 90). Определить форму этой поверхности.
щ
У
а
У
4Р——
о
— х -
Рис. 90
Рассмотрим какую-нибудь частицу жидкости массой т, распо-
расположенную на ее поверхности; координаты частицы обозначим х и у
(рис. 90). Задача состоит в нахождении зависимости у от х.
Во вращающейся вместе с жидкостью системе координат Оху
частица покоится. Следовательно, равнодействующая силы тяжес-
§ 2. Теоремы об изменении основных динамических величин системы 173
ти Р = mg и переносной силы инерции Je = тш2х (ш — угловая ско-
скорость вращения жидкости) ортогональна поверхности жидкости. Из
рис. 90 находим, что
Но tga = dy/dx, поэтому
dx
Решив это дифференциальное уравнение (с начальным условием
у@) = 0), получим
v- —х2
У ~ 2gX ¦
Следовательно, воронка, образующаяся при вращении сосуда, представ-
представляет собой параболоид вращения.
Пример 2. Материальная точка положена на гладкую горизонтальную
плоскость Оху, вращающуюся вокруг неподвижной вертикальной оси Oz
с постоянной угловой скоростью и>. Точке сообщена некоторая началь-
начальная скорость, лежащая в этой плоскости. Показать, что в относи-
относительном движении точки имеют место следующие равенства:
х2 + у2 — lj2(x2 + у2) = const, (a)
ху — ху + из{х2 + у2) = const. (б)
Во вращающейся системе координат имеем
ш' = @, 0, ш), v'r = (i, у, 0), w'e = (-w2x, -u>2y, 0).
Кинетическая энергия точки в ее относительном движении опре-
определяется равенством
Tr= ±m(x2 + y2).
Для переносной и кориолисовои сил инерции имеем соответственно
(т — масса материальной точки):
j'e = mw2(x, у, 0), jc' = 2тш(у, -х, 0).
Из выражения для переносной силы инерции видно, что она явля-
является потенциальной с потенциалом, определяемым по формуле
±x2 +У2).
174 Глава VI
Внешние силы (сила тяжести и реакция плоскости) перпендику-
перпендикулярны плоскости Оху, в которой происходит движение точки и, следо-
следовательно, работы не совершают. Поэтому из B3) следует, что в от-
относительном движении справедлив интеграл энергии: Тг + ПГ = const,
m. e.
jzm(x2 + у2) - ]ymuJ(x2 + у2) = const.
Этот интеграл с точностью до множителя т/2 совпадает с доказы-
доказываемым равенством (а).
Чтобы показать справедливость равенства (б), воспользуемся те-
теоремой об изменении кинетического момента B2), приняв за центр А
точку О. Обе части векторного равенства B2) будем проектировать
на ось Oz.
Моменты внешних сил относительно оси Oz равны нулю. Пере-
Переносная сила инерции проходит через точку О и, следовательно, тоже
не создает момента относительно Oz. Для момента Mz кориолисовой
силы инерции получаем
Mz = —2ти>(хх + уу).
Замечая, что проекция на ось Oz кинетического момента точки в ее
относительном движении равна т(ху — ху), получаем из B2)
т-т-(ху — ху) = —2тиз(хх + уу),
или
Отсюда следует справедливость равенства (б) на стр. 173.
90. О теоремах динамики для движения относительно
центра масс. В предыдущем пункте мы видели, что основные тео-
теоремы динамики в неинерциальной системе отсчета можно записать в
той же форме, что и в инерциальной. Отличие заключается только в
том, что в формулах, выражающих основные теоремы, появляются до-
добавочные члены, обусловленные неинерциальностью системы отсчета.
Но существует подвижная система отсчета, являющаяся в общем
случае неинерциальной, такая, что для движения в этой системе от-
отсчета теоремы об изменении кинетического момента и кинетической
энергии выглядят точно так же, как и в инерциальной системе. Этой по-
подвижной системой отсчета является кенигова система координат, т. е.
(см. п. 81) поступательно движущаяся система координат с началом в
§ 2. Теоремы об изменении основных динамических величин системы 175
центре масс механической системы. Для теоремы об изменении кине-
кинетического момента мы это видели в п. 87. Рассмотрим теперь теорему
об изменении кинетической энергии.
Из равенств B0), B4) и из того, что переносное ускорение wve для
всех точек одинаково и равно ускорению центра масс we, получаем
dTr =
=
JV
53 т"'<
v=l
N
5^(-^е
v=l
N
vvr • dvvr
N
= 53m*
v=l
\- jve + ju,
N
,wvr ¦ dpv =
=) • dpv =
N
N
(N \ N
53 mvdpv I • «jc + 53 J"c" dPv
v=\ ) v=\
Последняя сумма в этом равенстве обращается в нуль, так как ко-
JV
риолисова сила инерции jvc перпендикулярна dpv. Сумма ^ wivPv рав-
v=\
на нулю из-за выбора начала системы координат в центре масс систе-
N
мы; следовательно, сумма ^ mvdpv также равна нулю. Поэтому окон-
v=\
чательно имеем следующее выражение для дифференциала кинетичес-
кинетической энергии движения системы относительно центра масс:
d-Lip — (ii ./А ~\ (it -ii • ( ^0 )
Таким образом, теорема об изменении кинетической энергии вы-
выглядит точно так же, как и в случае инерциальной системы отсчета.
Отличие заключается только в том, что элементарная работа внешних
и внутренних сил системы вычисляется на перемещениях точек их при-
приложения по отношению к центру масс.
Пример 1. Рассмотрим произвольную механическую систему, движущу-
движущуюся в пустоте в однородном поле тяжести. Перенеся все силы системы
в ее центр масс С, получим равнодействующую Р, равную общему весу
системы. На основании теоремы о движении центра масс (п. 86) мы
можем сказать, что точка С будет описывать некоторую параболу.
Момент внешних сил относительно осей кениговой системы коор-
координат равен нулю. Поэтому кинетический момент Кс системы отно-
относительно центра масс остается постоянным во все время движения.
176 Глава VI
Далее, так как точка приложения равнодействующей внешних сил
— веса Р системы неподвижна в кёниговой системе координат (совпа-
(совпадает с ее началом), то работа внешних сил на относительных пере-
перемещениях системы равна нулю. Поэтому, согласно B5), кинетическая
энергия Тг в относительном движении изменяется только вследствие
действия внутренних сил. В частности, если рассматриваемая меха-
механическая система является твердым телом, то кинетическая энергия
остается постоянной.
Глава VII
Динамика твердого тела
§ 1. Вращение твердого тела вокруг неподвижной
оси
91. Уравнение движения. Определение реакций. Рассмотрим
твердое тело, имеющее две неподвижные точки О и О± (рис. 91).
Пусть F и Fi — реакции связи в точках О и О\, R — главный
вектор активных сил, а Мо — главный их момент относительно точ-
точки О.
Примем точку О за начало непо-
неподвижной системы координат OXYZ, ось
OZ которой направим по оси ОО\. С
телом жестко свяжем систему коорди-
координат Oxyz; ее ось Oz направлена вдоль
оси ОО\. Тело имеет одну степень свобо-
свободы. За обобщенную координату примем
угол <р, образуемый осями ОХ и Ох.
Чтобы получить уравнения, описы-
описывающие движение твердого тела, вос-
воспользуемся теоремами об изменении ко-
количества движения и момента количеств
движения. Обе части соответствующих
этим теоремам уравнения E) п. 86 и
уравнения (8) п. 87 спроектируем на оси
вращающейся системы координат Oxyz. Рис. 91
Для этого воспользуемся формулой E)
п. 30, связывающей абсолютную и относительную производные век-
вектора. Получим:
xvc =
dt
¦ш х Ко = Мо + ООг х
A)
B)
Здесь М — масса тела, ш — его угловая скорость, vc — скорость цент-
центра масс тела; реакция F не вошла в уравнение B), так как ее момент
178
Глава VII
относительно точки О равен нулю. Пусть в связанной с телом системе
координат
R =
R,,
Mo =
U) =
Mx
My
Mz
oc =
xc
Ус
zc
Fx
Ko =
Fly
Flt
Ky
Kz
Очевидно, что р = 0, q = 0, r = ф, и из формул (8) п. 82 следует,
что Кх = -Jxz(jp, Ку = -Зуяф, Kz = Jz(jp, где Jxz, Jyz — центробеж-
центробежные, a Jz — осевой моменты инерции тела для точки О.
Принимая во внимание, что Vc = ш х ОС и обозначая буквой h
расстояние между неподвижными точками тела О и Oi, получим ска-
скалярную форму векторных уравнении A) и B) в виде
C)
Мхсф -
— Rx -
= Ry-
= RZ-
= MX
= My
= M,.
^Fx +
?Fy +
*-Fz +
-hFu
Fix,
Fiy,
Fiz,
n
+ hFix,
z,
Fz
О
•x
системы
Пример
щается
Последнее уравнение не содержит
реакций и является дифференциальным
уравнением вращения твердого тела во-
вокруг неподвижной оси. Остальные пять
уравнений служат для нахождения реак-
реакций. Последняя задача является неопреде-
неопределенной. Действительно, из третьего урав-
уравнения системы C) видно, что нельзя от-
отдельно найти продольные реакции Fz и F\z,
а можно определить лишь их сумму. Эта
сумма не зависит от характера враща-
У тельного движения тела. Поперечные реак-
реакции Fx, Fix, Fy, Fiy находятся из перво-
рис д2 го: второго, четвертого и пятого уравнений
C); они зависят от вращения тела.
1. Равнобедренный прямоугольный треугольпиик OOiA вра-
вокруг вертикальной оси, к которой он подвешен катетом
§ 1. Вращение твердого тела вокруг неподвижной оси 179
00\ = а (рис. 92). Какова должна быть угловая скорость вращения,
чтобы боковое давление на нижнюю опору О равнялось нулю? Треуголь-
Треугольник считать тонкой однородной пластинкой.
Для решения задачи воспользуемся уравнениями C). В рассматри-
рассматриваемом случае
хс =0, ус = а/3, h = а,
Jxz = 0, а для Jyz получаем
а / z \
Jyz = yz dm = -^ / z\ у dy dz =
J a J \J I
a
= Щ [z*dz= \ma2.
о
Далее,
Rx = Ry = 0, Rz = -mg, Mx = -\mga, My = Mz= 0.
Учитывая еще, что по условию задачи Fx = Fy = 0, получаем
уравнения C) в виде
l--'' = Flx, -\таф2=Р1у, 0=-mg+Fz + Flz,
mga- aFly, -^та2ф = aFlx,
Из последнего уравнения следует, что ф = ш = const, т. е. враще-
вращение треугольника происходит с постоянной угловой скоростью.
Исключив из второго и четвертого уравнений величину F\y, при-
придем к соотношению, определяющему величину угловой скорости. Окон-
Окончательно найдем, что
и> = 2^/g/a.
92. Условия, при которых динамические реакции равны
статическим. Если в первом, втором, четвертом и пятом уравнениях
системы C) положить ф = 0, ф = 0, то получим систему уравнений
для определения поперечных статических реакций. Если же тело вра-
вращается, то либо ф, либо ф, либо та и другая из этих величин не будут
равными нулю. Поэтому левые части упомянутых уравнений в общем
случае не будут тождественно равными нулю во все время движения
и, следовательно, динамические реакции отличаются от статических.
180 Глава VII
Найдем условия, при которых динамические реакции равны стати-
статическим. Приравнивая нулю левые части первого, второго, четвертого и
пятого уравнений системы C), получим следующие две пары равенств:
УсФ
ЗхгФ
+ хсф2 =
т • 2
-Jyz<P
= о,
= 0,
-УсФ2 -
- J ^
= 0.
= 0.
D)
E)
Равенства D) и E) можно рассматривать как однородные системы
линейных уравнений соответственно относительно хс, ус и Jxz, Jyz.
Определители этих систем одинаковы и равны величине ф2 + ф4. Если
тело вращается, то эта величина не может быть тождественно равной
нулю. Поэтому равенства D) и E) удовлетворяются только при выпол-
выполнении условий
хс =ус = 0, Jxz = Jyz = 0.
Таким образом, динамические реакции при вращении твердого те-
тела вокруг неподвижной оси равны статическим тогда и только тогда,
когда ось вращения является главной центральной осью инерции тела.
93. Уравнение движения физического маятника. Физичес-
Физическим маятником называется твердое тело, которое может вращаться
вокруг неподвижной горизонтальной оси под действием силы тяжес-
тяжести. Выберем неподвижную систему координат OXYZ так, чтобы ее
ось OZ совпадала с осью вращения маятника, а ось OY была направле-
направлена вертикально вниз. Связанную с маятником систему координат Oxyz
выберем так, чтобы центр масс маятника лежал на оси Оу, а оси Oz
и OZ совпадали. Тогда если а — расстояние от центра тяжести до оси
вращения, то Mz = —mgasinip, и из последнего уравнения системы C)
получим дифференциальное уравнение движения физического маятни-
маятника в виде
^+!^sin^ = o. F)
J z
Сравнивая это уравнение с уравнением движения плоского математи-
математического маятника, которое задается равенством F) п. 57, находим, что
физический маятник будет колебаться по такому же закону, что и ма-
математический маятник длиной
/ - — G)
1 ~ та- (')
Величину /, определяемую по формуле G), называют приведенной дли-
длиной физического маятника.
94. Фазовая плоскость для уравнения движения маятни-
маятника. Для выяснения общих свойств движения систем с одной степенью
§ 1. Вращение твердого тела вокруг неподвижной оси 181
свободы очень удобен метод фазовой плоскости. Рассмотрим его на при-
примере анализа дифференциального уравнения
х = f(x). (8)
Будем считать, что правая часть этого уравнения удовлетворяет усло-
условию существования и единственности его решения.
Можно считать, что уравнение (8) описывает движение в системе
с одной степенью свободы, в которой х играет роль обобщенной коор-
координаты, а кинетическая и потенциальная энергия определены равенст-
равенствами
Т = \х2, П = - [ f(x) dx.
Полная механическая энергия Е = Т + П постоянна во все время дви-
движения, т. е. уравнение (8) имеет первый интеграл
Е(х, х) = }zx2 + П(ж) = h = const. (9)
Уравнение (8) эквивалентно системе двух уравнений
х = у, y = f(x). A0)
Плоскость с координатами х, у называется фазовой плоскостью
уравнения (8). Точки фазовой плоскости называются фазовыми точ-
точками. В каждой точке плоскости, где определена функция /(ж), систе-
система A0) задает вектор с компонентами х, у; этот вектор называется фа-
фазовой скоростью. Решение системы A0) задает движение фазовой точки
по фазовой плоскости, причем скорость движения фазовой точки равна
фазовой скорости в том месте плоскости, где в данный момент нахо-
находится точка. Кривая, которую описывает фазовая точка, называется
фазовой кривой. В частных случаях фазовая кривая может состоять из
одной точки. Такие точки называются положениями равновесия. Вектор
фазовой скорости в положении равновесия равен нулю.
Интеграл (9) позволяет легко находить фазовые кривые. На каждой
фазовой кривой значение полной механической энергии Е постоянно,
поэтому каждая фазовая кривая целиком принадлежит одному уровню
энергии Е(х, х) = h.
Запишем интеграл (9) в виде
х2 = 2(h - Щх)). A1)
Совокупность фазовых кривых обладает следующими свойствами, ко-
которые полезно иметь в виду при анализе уравнения (8).
182
Глава VII
1. При данном h фазовые кривые могут располагаться только в той
части фазовой плоскости, где выполняется неравенство П(ж) ^ h. Эту
часть плоскости называют областью возможности движения. Неравен-
Неравенство П(ж) ^ h следует из того, что для реальных движений правая
часть формулы A1) не может быть отрицательной, так как ее левая
часть есть квадрат вещественной величины.
2. Как видно из системы A0), положения равновесия лежат на оси ж
фазовой плоскости, причем в положении равновесия ж = ж*, где ж» —
критическая точка потенциальной энергии, т. е. такая точка, в кото-
которой dH/dx = 0.
3. Если ж = ж* является точкой локального минимума функ-
функции П(ж), причем d2H/dx2 > 0 при х = ж*, то точка (ж», 0) на фа-
фазовой плоскости будет особой точкой типа центр для системы A0). Ес-
Если же ж = ж* — точка локального максимума и в ней d2H/dx2 < 0,
то (ж*, 0) — особая точка типа седло.
4. Совокупность фазовых кривых симметрична относительно оси ж.
Это свойство вытекает из формулы A1) ввиду четности входящих в нее
величин относительно ж.
5. В точках оси ж, отличных от положений равновесия, фазовые
кривые ортогональны оси ж. Это свойство сразу видно из системы A0),
так как в этих точках ж = 0, у = /(ж) ф 0.
Перечисленные свойства поз-
позволяют по виду графика функ-
функции П(ж) сразу делать выводы о
характере движения, описываемо-
описываемого уравнением (8). На рис. 93 для
примера показаны график потен-
потенциальной энергии и соответствую-
соответствующие фазовые кривые. Направления
движения фазовой точки показа-
показаны стрелками. При h = h\ есть
положение равновесия типа центр.
х Это положение равновесия окру-
окружено замкнутыми фазовыми кри-
кривыми. При h > hz фазовые кри-
кривые разомкнуты. На уровне энер-
ИС- гии h = Из есть положение равно-
равновесия типа седло. На уровне h = /13 расположена также фазовая кривая,
начинающаяся вблизи седловой точки и при t —> сю входящая в эту точ-
точку. Эта кривая отделяет область, где расположены замкнутые кривые,
окружающие точку типа центр, от разомкнутых фазовых кривых, со-
соответствующих значениям h, большим h%. Такие кривые, которые раз-
§ 1. Вращение твердого тела вокруг неподвижной оси
183
деляют области с различным характером поведения фазовых кривых,
называют сепаратрисами.
Построим фазовую плоскость для дифференциального уравне-
уравнения F), описывающего движение маятника. Для кинетической и по-
потенциальной энергии маятника имеем выражения
Т = -цЛъф2, П = —mgacosip.
Если положить ш\ = g/l, П* = — ш^сонср, то интеграл энергии
Т + П = const запишется в виде
^ф2 + П* = h = const.
A2)
h=a>.
h=-o),
Рис. 94
График функции П*(<^) и фазовые кривые представлены на рис. 94.
Картина фазовых кривых периодична по <р с периодом 2тг. При h < —oj2
движение невозможно. При h = —u>q маятник находится в положении
равновесия, когда его центр масс занимает самое низкое из возможных
положений. На фазовой плоскости <р, ф этому положению равновесия со-
соответствуют точки, в которых <р = 2ктт (к = 0, ±1, ±2, ...), а ф = 0.
Это точки типа центр. Они окружены замкнутыми фазовыми кривы-
кривыми, соответствующими колебаниям маятника. Колебательным движе-
движениям маятника соответствуют значения h, удовлетворяющие неравен-
неравенству —Шц < h < u>o-
При h = cOq возможны два типа движений. Один соответствует
положению равновесия маятника, когда его центр масс занимает наи-
наивысшее возможное положение. Этому равновесию на фазовой плоскости
соответствуют точки (р = тг + 2&тг (к = 0, ±1, ±2, ...), ф = 0. Это
точки типа седло. Для другого типа движений при h = ш% центр масс
184 Глава VII
маятника асимптотически при t —>¦ ос стремится занять наивысшее по-
положение. Асимптотическим движениям на фазовой плоскости соответ-
соответствуют кривые, соединяющие точки типа седло. Эти кривые являются
сепаратрисами.
При h > Wq движение маятника будет вращательным. Для это-
этого движения абсолютная величина угла ip монотонно возрастает. Этим
движениям на фазовой плоскости соответствуют незамкнутые кривые.
Сепаратрисы разделяют области колебательных и вращательных дви-
движений.
95. Некоторые сведения из теории эллиптических интегра-
интегралов и эллиптических функций Якоби. В этой главе и в некоторых
других разделах книги будут использоваться так называемые эллипти-
эллиптические интегралы и эллиптические функции. Дадим здесь необходимые
определения и понятия.
Интеграл
v
и = F{<p, к)= [ dx A3)
J V 1 — к2 sin х
называется эллиптическим интегралом первого рода. Величина к на-
называется модулем эллиптического интеграла. Обычно считается, что к
удовлетворяет неравенствам 0 ^ к < 1.
Интеграл
Е((р, к) = I v 1 — к2 sin2 х dx
A4)
называется эллиптическим интегралом второго рода.
Величина
2
K(k)=FU,k)=f dx A5)
У1 ' J \/\ - k2 sin2 x
называется полным эллиптическим интегралом первого рода, а величи-
величина
2
Е(к) = #(§, к) = /Vl - к2 sin2 х dx A6)
о
— полным эллиптическим интегралом второго рода.
§ 1. Вращение твердого тела вокруг неподвижной оси 185
При малых к интегралы A5), A6) представляются в виде сходя-
сходящихся рядов по степеням к:
Из A3) и A4) можно получить следующее выражение для произ-
производных эллиптических интегралов по модулю к:
dF((p, к) _ 1 (Е((р, к) - k'2F(p, к)
дк -~п*\ * _
дЕ{у, к) _ Е(<р, к) - F(p, к)
дк ~ к ' (^Uj
где к' = 1 — к2, к' — дополнительный модуль.
Если в равнствах A9) и B0) положить <р = ?-, то получим произ-
производные по к от полных эллиптических интегралов A5) и A6):
dK Е(к) - к'2К(к) dE Е(к) - К(к)
dk кк>2 ' dk к { >
Функция, являющаяся результатом обращения эллиптического ин-
интеграла первого рода, называется амплитудой и обозначается так:
<р = ати. B2)
Функции z = sn(u, к) (эллиптический синус) и z = сп(и, к) (эл-
(эллиптический косинус) определяются так:
z = sn(u, k) = sin<? = sin am и и z = сп(и, к) = cos<? = cos am и.
B3)
Так как simp и cos</5 имеют период 2тг по <р, то согласно A3) и A5),
эллиптические синус и косинус имеют по и период, равный АК(к).
Функция дельта амплитуды z = dn(u, к) определяется так:
_ _ (]„(„, h\ — ZJ_ — л/1 — k2 sin in — л/Л — k2 anVn k\ (9A\
A/ U.111 tfc. /II Z Д/ J- /v Olll UJ A/ J. /v Oil III. ft/1. 1^4:1
186
Глава VII
-1
и
Рис. 95
Функция дельта амплитуды
имеет период 2К(к) по и. Функ-
Функции <р = amu, z = sn(u, к),
z = сп(и, к), z = dn(n, к) анали-
тичны относительно к и при
к —> 0 стремятся соответствен-
соответственно к функциям (р = и, z = sin и,
z = cos и, z = 1.
Эллиптические функции Яко-
Якоби удовлетворяют следующим
легко проверяемым тождествам:
sn и + сп и = 1,
dn2
к2 sn2 и = 1.
B5)
Справедливы следующие формулы дифференцирования эллипти-
эллиптических функций:
А
du
А
du
sn и = сп и ¦ dn и,
спи = — snw • dnit,
B6)
-=- dn и = — fc2 sn и • сп и.
du
Графики эллиптических функций Якоби представлены на рис. 95.
96. Интегрирование уравнения движения маятника. Рас-
Рассмотрим три случая в соответствии с возможными значениями кон-
константы h в интеграле A2).
1. — о;2 < h < w2. В этом случае, как показано в п. 94, маятник
совершает колебания. Пусть /3 — максимальный угол, на который от-
отклоняется маятник от своего вертикального положения, соответствую-
соответствующего значению <р, равному нулю. Тогда h = —WqCos/З и интеграл A2)
запишется в виде
ф2 =
— cos/3).
Положим к\ = sin(/3/2) и сделаем замену переменных
= к\ sin^.
B7)
B8)
Тогда интеграл энергии B7) примет следующий вид:
B9)
§ 1. Вращение твердого тела вокруг неподвижной оси 187
Если принять, что при t = 0 <р = 0, то отсюда получаем
= f dx = F(i/,, h), C0)
о Jl — k\ sin2 x
sin2 x
т. е. ф = &v&(u)ot). Поэтому из B3) и B8) имеем окончательно
<р = 2arcsin(fci snu)ot). C1)
Функция (р периодична note периодом т, вычисляемым, согласно п. 95,
по формуле
т = Ш(кг)/ш0. C2)
Воспользовавшись разложением A7), получим, что при небольшом зна-
значении максимального угла отклонения /3 маятника от вертикали имеем
приближенное значение периода
т = 2iry/l/g, C3)
что совпадает с известным значением периода малых колебаний маят-
маятника. При учете двух первых членов разложения т в ряд по /3 получаем
более точное значение периода
Если /3 —> тт. то к\ —> 1 и период колебаний т неограниченно воз-
возрастает.
2. h > u>q. В этом случае маятник находится в режиме вращения.
Пусть при t = 0 ip = 0, ф = фо. Тогда h = xj^% ~ шо и интеграл A2)
запишется в виде
ф2 =Ф1(\- к2 sin2 |) , C5)
где введено обозначение
к\ = 4^|. C6)
Так как h > u>q, то ф\ > 4а;2, и, следовательно, Щ < 1. Из C5) имеем
?>/2
rfa; C7)
л • 2
ГЪ9 S111 X
188 Глава VII
Следовательно,
(р = 2am(ipot/2). C8)
Если начальная угловая скорость велика, т. е. ф\ ^> иJ,, то прибли-
приближенно (р = <pot и вращение маятника мало отличается от равномерного.
3. h = Wg. Этот случай соответствует асимптотическим движениям
маятника. Интеграл энергии A2) в этом случае дает соотношение
ф2 = 4uj2cos2(ip/2). C9)
Если при t = 0 (р = 0 и ф > 0, то отсюда после интегрирования
получаем
<y9 = -7r + 4arctg(eW0*). D0)
§ 2. Движение твердого тела вокруг неподвижной
точки
97. Дифференциальные уравнения движения твердого те-
тела вокруг неподвижной точки. Динамические уравнения Эй-
Эйлера. Пусть при движении тела одна из его точек О все время остается
неподвижной. Для получения уравнений движения тела воспользуемся
теоремой об изменении кинетического момента. Если Ко и Мо — ки-
кинетический момент тела и главный момент внешних сил относительно
неподвижной точки О, то, согласно п. 87,
dKo
dt
A)
Пусть Oxyz — подвижная система координат, жестко связанная с
телом, а р, q, г — проекции угловой скорости со тела на ее оси. Тогда
компоненты вектора Ко выражаются через величины р, q, r и элемен-
элементы тензора инерции тела для точки О — по формулам (8) п. 82.
Если абсолютную производную вектора Ко выразить через его
локальную производную, то уравнение A) запишется в виде
dKO , v „ „(е) ,„*
— +Ш*КО = МО . B)
Пусть Мх, Му, Mz — проекции вектора Мо на оси Ox, Oy, Oz.
§ 2. Движение твердого тела вокруг неподвижной точки 189
Тогда векторное уравнение B) запишется в виде следующих скалярных
уравнений:
JxP-Jxyq-JXzr+(Jz-Jy)qr+JyZ(r2-q2)+p(Jxyr-Jxzq) = Мх,
-JxyP+Jyq-Jyzr+(Jx-Jz)rp+Jxz(p2-r2)+q(JyZp-Jxyr) = Му, C)
-JXzp-Jyzq+Jzr+(Jy-Jx)pq+JXy(q2-p2)+r(Jxzq-Jyzp) = Mz.
Эти уравнения существенно упрощаются, если оси Ox, Оу, Oz —
главные оси инерции тела для точки О. В этом случае Jxy=Jxz=Jyz=0,
a Jx, Jy, Jz являются главными моментами инерции: Jx = A, Jy = В,
Jz = С. Уравнения C) примут вид
Ap + (C-B)qr = Mx,
Bq+(A- C)rp = Му, D)
Cr + (В - A)pq = Mz.
Уравнения D) называются динамическими уравнениями Эйлера. Ес-
Если Мх, My, Mz — функции р, q, r, t, то уравнения D) образуют замк-
замкнутую систему уравнений, интегрирование которой даст зависимость
величин р, q, г от времени t и начальных условий р0, qo, tq. После этого
из кинематических уравнений Эйлера (см. п. 36)
р = ф sin в sin (p + в cos (p,
q = ф sin 9 cos (р — в simp, E)
г = ipcosO + ф
можно найти углы ф, в, <р как функции времени и начальных условий.
Таким образом, в рассматриваемом случае решение задачи о дви-
движении твердого тела вокруг неподвижной точки распадается на две по-
последовательные задачи интегрирования систем трех уравнений первого
порядка. В общем же случае величины Мх, Му, Mz являются функция-
функциями времени, углов Эйлера и их производных. Тогда уравнения D) и E)
надо интегрировать совместно.
Наиболее простым и очень важным случаем является тот, когда
момент внешних сил относительно неподвижной точки равен нулю.
Тогда говорят, что имеет место случай Эйлера движения твердого те-
тела вокруг неподвижной точки. Этот случай, очевидно, возможен, когда
внешних сил нет совсем или тогда, когда внешние силы, приложенные
к телу, приводятся к равнодействующей, проходящей через неподвиж-
190 Глава VII
ную точку. В случае Эйлера уравнения D) принимают вид
Ар + (С - B)qr = 0,
Bq + (А - С)гр = 0, F)
Cr+(B - A)pq = 0.
Ниже мы рассмотрим движение тела в случае Эйлера подробно.
98. Первые интегралы. Так как в случае Эйлера главный мо-
момент внешних сил Mq относительно точки О равен нулю, то из урав-
уравнения A) следует, что
Ко = const, G)
т. е. кинетический момент Ко тела относительно точки О имеет не-
неизменное направление в неподвижной системе отсчета и величина его
постоянна.
Так как Ар, Bq, Cr — проекции вектора Ко на главные оси инер-
инерции тела Ox, Оу, Oz, а Ко — квадрат длины вектора Ко, то из G)
следует первый интеграл
K2O = A2P2+B2q2+C2r2= const. (8)
Из теоремы об изменении кинетической энергии можно получить,
что кинетическая энергия тела также постоянна. Действительно, так
как
dT = Мое) -udt + R(e) ¦ vo dt,
a vo = 0 и Mo = 0, то dT = 0. Поэтому существует первый интеграл
Т = i(V + Bq2 +Cr2) = const. (9)
Существование первых интегралов (8) и (9) можно установить и
непосредственно из системы уравнении F). Действительно, если пер-
первое уравнение системы F) умножить на Ар, второе — на Bq, а третье
— на Сг и результаты сложить, то получим А2рр + B2qq + C2rf = 0,
откуда следует первый интеграл (8). Если же первое, второе и третье
уравнения умножить соответственно на р, q, r, то после сложения по-
получим Арр + Bqq + Crr = 0, откуда вытекает первый интеграл (9).
99. Стационарные вращения твердого тела в случае Эйле-
Эйлера. Будем называть стационарным вращением такое движение твердо-
твердого тела, при котором его угловая скорость и> постоянна относительно
тела (а следовательно, и относительно неподвижной системы отсчета;
§ 2. Движение твердого тела вокруг неподвижной точки
191
см. п. 30). Для стационарного вращения величины р, q, r постоянны.
Для их определения из системы F) получим такие уравнения:
(С - B)qr = 0, (А - С)гр = 0, (В - A)pq = 0.
A0)
Y
Отсюда следует, что стационарное вращение тела может происхо-
происходить только вокруг главной оси инерции тела для точки О, причем
величина угловой скорости тела может быть произвольной.
В самом деле, если А = В = С, то уравнения A0) удовлетворяются
при любых р, q, r, т. е. вращение тела происходит вокруг оси, имеющей
произвольное направление. Но при А = В = С эллипсоид инерции для
точки О превращается в сферу, и поэтому любая ось, проходящая через
точку О, становится главной осью инерции тела.
Если два из моментов инер-
инерции равны, например А = В, то
уравнения A0) удовлетворяются при
р = q = 0 и любом г (вращение во-
вокруг главной оси инерции Oz), а так-
также при г = 0 и любых р и q (вращение
вокруг любой оси, проходящей через
точку О, лежащей в экваториальной
плоскости эллипсоида инерции и, сле-
следовательно, являющейся главной осью
инерции).
Если величины А, В и С различ-
различны, то уравнения A0) могут иметь
только такие решения, для которых две из величин р, q, r равны нулю,
а третья произвольна, т. е. снова вращение происходит вокруг главной
оси инерции.
100. Движение динамически симметричного тела в случае
Эйлера. Регулярная прецессия. Будем называть тело динамически
симметричным, если два его главных момента инерции для точки О
равны, например А = В. Ось Oz тогда будем называть осью динами-
динамической симметрии. Исследуем движение динамически симметричного
тела в случае Эйлера.
Неподвижную систему координат OXYZ выберем так, чтобы ее
ось OZ была направлена по вектору Ко (который в случае Эйлера по-
постоянен). Для проекций Ар, Aq, С г вектора Ко на оси связанной с те-
телом системы координат Oxyz, образованной главными осями инерции,
получаем такие выражения (рис. 96):
N
Рис. 96
Ар = Kos'm9s'm(p, Aq = Kosin.9 costp, С г = Kq cos в. A1)
192
Глава VII
Из последнего уравнения системы F) при А = В следует, что
г = го = const, A2)
т. е. проекция угловой скорости тела на ось его динамической симмет-
симметрии постоянна. Из A2) и третьего из равенств A1) получаем
cos# = Сг0 /Ко = const,
A3)
т. е. угол нутации постоянен.
При в = во = const, г = го = const кинематические уравнения
Эйлера E) запишутся в виде
р = ¦0sin^o simp, q = ф sin во cos <р, го = ф cos $о + Ф- A4)
Подставив выражение для р из A4) в первое из равенств A1), получим
ф = Ко/А = ш2 = const. A5)
Величина и>2 называется угловой скоростью прецессии.
Последнее из равенств A4) позволяет теперь найти ве-
величину ф. Получаем, воспользовавшись формулами A3)
и A5),
\а>
ф = го - ф cos во = г0 -j- cos во =
= г0 - -гго = —-т—го =Ш1= const.
A6)
Рис. 97
Величина u>i называется угловой скоростью собственно-
собственного вращения.
Движение твердого тела вокруг неподвижной точ-
точки, состоящее из его вращения вокруг оси, неизменно
связанной с телом, и движения, при котором эта ось
вращается вокруг пересекающей ее оси, неподвижной
в рассматриваемой системе отсчета, называют прецес-
прецессией. Прецессия называется регулярной, если вращение
тела вокруг неизменно связанной с ним оси и вращение самой этой оси
происходят с постоянными по модулю угловыми скоростями.
Таким образом, динамически симметричное тело в случае Эйле-
Эйлера совершает регулярную прецессию. В этой прецессии ось симметрии
тела описывает круговой конус с осью Ко и углом при вершине 2#о;
движение оси симметрии вокруг Ко происходит с постоянной угло-
угловой скоростью о»г; одновременно тело вращается с постоянной угловой
скоростью u>i вокруг оси симметрии.
§ 2. Движение твердого тела вокруг неподвижной точки 193
Пример 1. Покажем, что при движении твердого тела вокруг неподвиж-
неподвижной точки по инерции при условии А = В < С угол между образующей
и осью неподвижного аксоида не может быть больше 19°28'.
Из соотношений A3), A5) и A6) следует, что при А < С посто-
постоянный угол между угловыми скоростями собственного вращения и пре-
прецессии u>i и и>2 тупой (рис. 97).
Пусть а — угол между угловой скоростью тела ш и вектором ш^;
он равен углу между образующей и осью неподвижного аксоида. Буквой /3
обозначим угол между векторами ш и и>\. Из того, что при регулярной
прецессии угол нутации в и модули угловых скоростей ш\ и и>2 постоян-
постоянны, следует, что величины ш, а и C также постоянны. Имеют место
соотношения
<0;
cos/3=^<0, sin/3=Wl-4 =
, ы = <!-<% = Щ±?,
Kl Ко
tso = A^l<o.
Поэтому
Здесь 7 = С /А. По условию задачи С > А, и так как моменты инерции
всегда удовлетворяют неравенству А + В ^ С (см. п. 79), из которо-
которого при А = В следует, что 2А ^ С, то величина 7 удовлетворяет
условию 1 < 7 ^ 2. Теперь несложно получить следующую цепочку со-
соотношений:
Отсюда следует, что угол а между образующей и осью неподвижно-
неподвижного аксоида удовлетворяет неравенству а ^ arctg(\/2/4) = 19°28'.
101. Геометрическая интерпретация Пуансо. Пуансо дал за-
замечательную геометрическую интерпретацию движения твердого тела
в случае Эйлера. Эта интерпретация очень наглядна и позволяет доволь-
довольно просто выявить качественный характер движения твердого тела в
194
Глава VII
случае Эйлера. Поэтому само движение тела в этом случае называют
движением Эйлера-Пуансо.
Пусть Р — точка пересечения мгновенной оси вращения с поверх-
поверхностью эллипсоида инерции тела для точки О (рис. 98)
Ах2 + Ву2 + Cz2 = 1.
Обозначим тг плоскость, касательную к
эллипсоиду инерции в точке Р. Ее на-
называют плоскостью Пуансо. Отметим
следующие свойства (рис. 98) рассмат-
рассматриваемого движения.
1. Величина угловой скорости ш
пропорциональна длине радиуса-векто-
радиуса-вектора точки Р относительно О.
Действительно, так как векто-
векторы ОР и и> коллинеарны, то ОР = Хш,
и надо только показать, что Л — посто-
постоянная величина. Подставив координа-
координаты точки Р: хр = Хр, ур = Xq, zp = Xr
в уравнение эллипсоида инерции и вос-
К\
Рис. 98
пользовавшись интегралом (9), получим
X2(Ap2+Bq2+Cr2) = 1,
А =
1
= const.
2. Плоскость тг перпендикулярна кинетическому моменту Ко- Для
доказательства достаточно заметить, что вектор N, равный градиен-
градиенту функции Ах2 + By2 + Cz2, вычисленному в точке Р, направлен по
нормали к плоскости тг. Но
N =
2АхР
2ВуР
2CzP
= 2Л
Ар
Bq
Сг
= 2ХК,
о-
3. Проекция OQ радиуса-вектора ОР на направление кинетическо-
кинетического момента Ко есть величина постоянная.
В самом деле, воспользовавшись формулой A9) п. 84 и интегра-
интегралом (8), получим
OQ =
К°:ОР
^o
, 2Г \/2Г
= ХК~о = -Ко~ = C°nSt-
§ 2. Движение твердого тела вокруг неподвижной точки 195
Но кинетический момент Ко имеет неизменное направление и, со-
согласно второму свойству, перпендикулярен плоскости тг. Поэтому плос-
плоскость тг, ввиду постоянства ее расстояния от неподвижной точки О,
сохраняет неизменное положение в пространстве.
Таким образом, приходим к следующей, полученной Пуансо, гео-
геометрической интерпретации движения твердого тела в случае Эйлера:
эллипсоид инерции для неподвижной точки катится без скольжения по
плоскости, неподвижной в пространстве; эта плоскость перпендику-
перпендикулярна кинетическому моменту; угловая скорость тела пропорциональ-
пропорциональна длине радиуса-вектора точки касания, а по направлению с ним сов-
совпадает.
Движение эллипсоида по плоскости тг происходит без скольжения,
так как точка Р лежит на мгновенной оси вращения, и поэтому ее
скорость равна нулю.
При движении тела точка Р на эллипсоиде инерции вычерчива-
вычерчивает кривую, которая называется полодией. Соответствующая кривая на
плоскости тг называется герполодией. Так как точка Р лежит на мгно-
мгновенной оси вращения, то ясно, что полодия служит направляющей по-
подвижного аксоида, а герполодия — направляющей неподвижного аксо-
ида для движения твердого тела вокруг неподвижной точки (см. п. 26).
102. Интегрирование уравнений Эйлера. В п. 99 и 100 урав-
уравнения Эйлера F) рассматривались в частных предположениях о дви-
движении тела или его геометрии масс. Получим теперь аналитическое
решение уравнений F) в общем случае. Будем для определенности счи-
считать, что А > В > С.
Из первых интегралов (8) и (9) выразим величины р2 и г2 через
q2, А, В, С и постоянные Т, Ко-
р2 =
1 A(C - A)
A7)
r2 = c{(}_ A) [{K2o - 2TA) - B(B - A)q2] .
Определяемые отсюда значения риг подставим во второе уравнение
системы F). Получим дифференциальное уравнение для q с разделяю-
разделяющимися переменными
= ± 1 ,
Ву/АС'
A8)
iyj[{2TC - К2О) - В {С - В)?] [(К2О - 2ТА) - В (В - A)q2].
196
Глава VII
х
Если это уравнение проинтегрирова-
проинтегрировано, то функции риг найдутся из
равенств A7). При этом при извле-
извлечении квадратных корней перед ра-
радикалами возможны два знака: плюс
или минус. Конкретный выбор этих
знаков делается при помощи уравне-
уравнений F).
Рассмотрим три случая, соот-
соответствующих различным соотноше-
соотношениям между постоянными Т и Ко-
1. 2ТВ > Ко ^ 2ТС. В этом случае величина г всегда отлична
от нуля и полодии заключают в себе наибольшую ось Oz эллипсоида
инерции. Все полодии расположены на эллипсоиде инерции в областях,
обозначенных на рис. 99 цифрами I и П. Для интегрирования уравне-
уравнения A8) сделаем замену переменных
Рис. 99
= ±
К2О - 2ТС
(В-С)BТА-К2О)
ABC
и введем положительный параметр к2 < 1 согласно формуле
(А-В)(КО-2ТС)
(В-С)BТА-КО)-
В новых переменных уравнение A8) запишется в виде
ат
- Р sin2 Л.
A9)
Пусть при t = 0 q = 0. Тогда из A9), согласно п. 95, получаем Л = ашт.
Решение уравнений Эйлера F) в рассматриваемом случае записывается
через эллиптические функции Якоби в виде
Ko - 2ТС
А(А - С)
сп(т, к),
К2О - 2ТС
q = ±" B(B-c)sn{T'k)
9Т А — К2
B0)
§ 2. Движение твердого тела вокруг неподвижной точки 197
Здесь одновременно берутся либо только верхние, либо только нижние
знаки. Решение B0) соответствует полодиям, расположенным на рис. 99
в области I. Для получения решения, соответствующего полодиям, рас-
расположенным в области II, надо в формулах B0) величину q оставить
без изменения, а у р и г одновременно изменить знаки.
Направление движения по полодиям показано на рис. 99 стрелками.
Если Kq = 2ТС, то полодии вырождаются в две точки, совпадающие с
вершинами эллипсоида, лежащими на оси Oz. Они соответствуют ста-
стационарным вращениям твердого тела вокруг оси Oz.
2. 2ТА ^ Kq > 2ТВ. В этом случае величина р во все время
движения отлична от нуля. Полодии заключают в себе наименьшую
ось эллипсоида инерции Ох и расположены на эллипсоиде инерции в
областях, обозначенных на рис. 99 цифрами III и IV. Сделаем замену
переменных
2ТА-К2 (А-В)(К2-2ТС)
^sinA Т Гk
Тогда, если ввести параметр к2 < 1 по формуле
,2= (В-С)BТА-К2О)
(А-В)(К2О-2ТСУ
то уравнение A8) примет вид A9), и если принять, что при t = 0 q = 0,
то решение уравнений F), соответствующее полодиям из области III
на рис. 99, будет иметь вид
К2О-2ТС , ч 2ТА-К2О ,
^M ^' д = ±ЧЖА^Мт> fc)'
B1)
2ТА-К2О
Здесь одновременно берутся либо только верхние, либо только ниж-
нижние знаки. Чтобы получить решения уравнений F), соответствующие
полодиям, расположенным в области IV на рис. 99, нужно величину q
оставить такой же, как и в B1), ay риг одновременно изменить знаки.
Если Kq = 2TA, то полодии вырождаются в точки, лежащие на
оси Ох и отвечающие стационарным вращениям тела вокруг оси Ох.
Заметим, что в двух рассмотренных случаях величины р, q, r —
периодические функции времени, поэтому полодии представляют со-
собой замкнутые кривые. Отметим также, что картина расположения
198 Глава VII
полодий на эллипсоиде инерции симметрична относительно его глав-
главных плоскостей. Каждому движению твердого тела соответствует одна
вполне конкретная полодия. Какая именно, зависит от начальных зна-
значений величин р, q, r.
Рассмотрим еще третий случай, являющийся промежуточным
между двумя рассмотренными.
3. Kq = 2ТВ. Равенства A7) принимают вид
2 ^^ '^'Ъ B2)
Из B2) следует, что А(А — В)р2 = С{В — С)г2. Учитывая свойство 1
движения Эйлера-Пуансо (п. 101), получаем, что в рассматриваемом
случае полодии лежат в плоскостях
проходящих через среднюю ось эллипсоида инерции. Сечения эллип-
эллипсоида инерции плоскостями B3) будут эллипсами, на которых лежат
полодии двух типов. Во-первых, это полодии-точки, расположенные на
оси Оу и соответствующие стационарным вращениям тела вокруг сред-
средней оси эллипсоида инерции с произвольной угловой скоростью. А во-
вторых, есть четыре полодии, представляющие собой дуги эллипсов, со-
соединяющих упомянутые полодии-точки. Эти четыре полодии обозначе-
обозначены на рис. 99 цифрами 1, 2, 3 и 4. Они являются на эллипсоиде инерции
сепаратрисами, разделяющими области I, II, III, IV с отличающимся
характером поведения полодий. Если положить
T = \l ABC *'
то уравнение A8) в рассматриваемом случае примет следующий вид:
А" = ±-±=BТ - Bq2). B4)
Пусть при t = 0 q = 0. Тогда из уравнения B4) и равенств B2) с ис-
использованием известных соотношений между гиперболическими функ-
функциями
ch2r-sh2T = l, thr=4^
chr
§ 2. Движение твердого тела вокруг неподвижной точки
199
получим, что решение уравнений Эйлера F), соответствующее поло-
полодии 1 на рис. 99, имеет вид
Р =
\2Т{В-С) 1
А(А-С) chr'
2Т(А-В)
B5)
Решение уравнений F), соответствующее полодии 3, получается
из формул B5), если в них изменить знаки у величин р, г. Решения,
соответствующие полодиям 2 и 4, получаются из B5), если изменить
знаки соответственно у q, r и q, р.
Поведение гиперболических функций, входящих в формулы B5),
показано на рис. 100.
-1
1/chx
R
Рис. 100
Рис. 101
Пример 1. Однородная прямоугольная пластинка движется по инерции
вокруг неподвижной точки, совпадающей с ее центром масс. В началь-
начальный момент времени t = 0 пластинка приведена во вращение с угловой
скоростью и>о вокруг диагонали PQ (рис. 101). Обозначая а угол между
диагоналями, показать, что через промежуток времени t', равный
2if(sina)
где К — полный эллиптический интеграл первого рода, sin a — модуль
эллиптического интеграла, пластинка будет вращаться вокруг другой
диагонали RS.
Пусть QS = Ъ, QR = с и Ъ < с. Оси Оу и Oz системы коорди-
координат Oxyz перпендикулярны соответствующим сторонам пластинки,
а Ох перпендикулярна ее плоскости. Эти оси являются главными цен-
200 Глава VII
тральными осями инерции пластинки. Согласно п. 75 (пример 1), имеем
А = Jx = j^m(b2 + с2), В = Jy = j^r
Jy
C = Jz = ±mb.
Если диагональ пластинки равна d, то Ъ = dsina, с = dcos а и
A=j^md2, В = jrjmd2 cos2 а, С = -^md2 sin2 a.
При t = 0p = 0,q = ojo sin a, r = ojo cos а, поэтому
Т = \{Ар2 + Bq2 + Сг2) = jKind2 sin2 a cos2 a ¦ w2,
К2О = А2р2 + B2q2 + C2r2 = ^m2d4 sin2 acos2 a ¦ w2.
Так как при b < с угол а не превосходит тг/4, то, как нетруд-
нетрудно проверить непосредственным вычислением, справедливы неравенст-
неравенства А > В > С и 2ТВ > Kq > 2TC. Следовательно, мы имеем дело с
первым из рассмотренных выше случаев движения Эйлера-Пуансо.
Опираясь на проведенное выше исследование этого случая, после не-
несложных вычислений найдем:
p(t) = - sin ал/cos 2а • ш0 ¦ сп[т + К (к), к],
q(t) = sin а • loq ¦ sn[r + К (к), к],
r(t) =ojo-dn[T + K(k), к].
Здесь т = л/cos 2а ¦ и>о -t, к = sin а.
При получении выписанного решения p(t), q(t), r(t) динамических
уравнений Эйлера F) в формулах B0) взяты верхние знаки, а величи-
величина т заменена на т + К(к), что отвечает конкретным начальным усло-
условиям в рассматриваемой задаче о движении пластинки. Полодия, соот-
соответствующая выписанному решению, лежит на эллипсоиде инерции в
области I (рис. 99).
При t = t' имеем
т = Vcos 2а • ш0 ¦ t' = 2K(k);
поскольку (рис. 95) cn[3K(fc), k] = 0, sn[3K(fc), к] = -1, йп[Ш(к), к] =
= л/1 — к2, то
p(t') = 0, q(t') = —и>о sin а, r(t') = ojq cos а.
Отсюда следует, что при t = t' пластинка вращается вокруг диагона-
диагонали RS.
> 2. Движение твердого тела вокруг неподвижной точки
201
103. О герполодиях. Из рис. 98 видно, что QP = л/ОР2 - OQ2.
Так как, согласно п. 101, ОР = ш/у/2Т, OQ = \/2Т/Ко, то
QP =
B6)
Эта формула позволяет выявить некоторые общие свойства герпо-
лодий.
Для каждого из стационарных вращении ш = const, и герполодия
представляет собой точку, совпадающую с точкой Q.
Рассмотрим общий случай движения. Пусть А > В > С. Тогда
для движений тела, которым отвечают полодии, расположенные в об-
областях I-IV на рис. 99, величина ш = ур2 + q2 + г2 имеет минимум ш\
и максимум и>2- Согласно B6), величина QP также будет иметь мини-
минимум pi и максимум р2- Поэтому герполодия заключена между двумя
концентрическими окружностями с центром в точке Q (рис. 102 и 103).
Отметим без доказательства, что герполодия не имеет ни точек
перегиба, ни точек возврата и всегда обращена вогнутостью в сторо-
сторону точки Q, в которой вектор кинетического момента Ко пересекает
плоскость Пуансо тг.
Рис. 102
Рис. 103
В противоположность полодиям (из областей I-IV), которые явля-
являются замкнутыми кривыми, герполодии, хотя и состоят из симмет-
симметричных участков, представляют собой, вообще говоря, незамкнутые
кривые. Герполодия поочередно касается окружностей р\ = const и
р2 = const. Моменты касания соответствуют переходу вектора и> через
главные плоскости эллипсоида инерции. Дуга герполодии ab (рис. 102)
соответствует четверти дуги полодии. После того как точка Р придет
снова в то же положение на эллипсоиде и, следовательно, опишет пол-
полную полодию, радиус-вектор QP повернется на угол 4а, где а — угол,
202 Глава VII
образованный отрезками Qa и Qb на рис. 102. Если отношение а/тг —
рациональное число, то герполодия будет замкнутой, в противном слу-
случае она будет незамкнутой. Каждой из полодий 1-4 (рис. 99), сущест-
существующих в случае Ко = 2ТВ, соответствует герполодия, являющаяся
спиралью, навивающейся на точку Q (рис. 103). Эта спираль бесконеч-
бесконечно много раз обходит точку Q. Однако ее общая длина конечна, так как
она равна длине соответствующей дуги полодии.
Если эллипсоид инерции есть эллипсоид вращения, то как полодия,
так и герполодия представляют собой окружности.
104. Определение ориентации твердого тела в абсолютном
пространстве для движения Эйлера—Пуансо. После того как в
п. 102 величины р, д, r были определены как функции времени, мож-
можно из кинематических уравнений Эйлера E) найти углы ф,в,<р, опре-
определяющие ориентацию твердого тела относительно неподвижной сис-
системы координат OXYZ. Задача сильно упрощается, если, как и в
п. 100, ось OZ направить вдоль неизменного кинетического момен-
момента Ко (рис. 96). При таком выборе неподвижной системы координат
проекции Ар, Вд, Cr вектора Ко на оси связанной с телом системы
главных осей инерции Ox, Oy, Oz вычисляются, согласно рис. 96, по
формулам
Ар = Ко sinO simp, Bq = Ко sin в cos (р, Cr = Ko cos в. B7)
Эти соотношения позволяют сразу определить углы в и (р как функции
времени при известных функциях р, q, r:
cos0 = g, tgp=4P. B8)
Для нахождения угла -ф сначала получим величину ф из первых двух
уравнений E):
• _ р sin (р + q cos <p
Если затем в это выражение подставить величины sin<? и cos<?, полу-
полученные из первых двух равенств B7), то оно запишется в виде
• _ Ар2 + Вд2
Ко sin2 в '
Воспользовавшись теперь третьим из равенств B7) и формулой (8),
окончательно получим
2р2+
I 2. Движение твердого тела вокруг неподвижной точки
203
Отсюда угол ф найдется квадратурой. Так как правая часть форму-
формулы B9) положительна, то угол ф монотонно возрастает во всех трех
возможных случаях движения, рассмотренных в п. 102, т. е. при любой
возможной зависимости функций р, q, r от времени.
Если движение тела не является стационарным вращением или
асимптотическим движением, то, согласно п. 102, величины р, q, r пред-
представляют собой периодические функции времени. Когда значение t уве-
увеличивается на период, то синусы и косинусы углов в и (р принимают
свои первоначальные значения. Значения же sin^ и сонф через период,
вообще говоря, изменяются, так как за период угол ф увеличивается
на некоторую постоянную величину. Это следует из B1). Действитель-
Действительно, пусть т* — период по времени функций р и q. Тогда из B9) име-
имеем tp(t + т*) = ф{Ь) и, интегрируя, получим
Ф(г + т.) = ф(г) + с,
где с — постоянная интегрирования.
Если число с/Bтг) не рацио-
рационально, то твердое тело никогда
не возвратится к своей первона-
первоначальной ориентации в абсолютном
пространстве. Если же ф- = Щ-,
где т, п — целые числа (п ф 0),
то движение твердого тела перио-
периодическое, с периодом, равным пт*.
105. Уравнения движения
тяжелого твердого тела вокруг
неподвижной точки и их пер-
первые интегралы. Рассмотрим дви-
движение твердого тела вокруг непо-
неподвижной точки О в однородном по-
поле тяжести. Ось OZ неподвижной системы координат направим вер-
вертикально вверх. С движущимся телом жестко свяжем систему коор-
координат Oxyz, оси которой направим вдоль главных осей инерции тела
для неподвижной точки О. Координаты центра тяжести G в системе
координат Oxyz обозначим а, Ь, с. Ориентацию тела относительно не-
неподвижной системы координат будем определять при помощи углов Эй-
Эйлера ф, в, (р, которые вводятся обычным образом (рис. 104).
Моменты инерции тела относительно осей Ox, Oy, Oz обозначим
А, В, С, а силу тяжести Р.
Пусть единичный вектор п вертикальной оси OZ имеет в связан-
связанной с телом системе координат Oxyz компоненты 71, 12, 7з- Величи-
X
N
Рис. 104
204 Глава VII
ны 71, 72 и 7з равны множителям при ф в выражениях для р, q, и г в
кинематических уравнениях Эйлера E):
7i = sin Й sin 93, 72 = sin в cos <p,
C0)
73 = cos в.
Вектор п постоянен в неподвижной системе координат, поэтому его
абсолютная производная равна нулю: dn/dt = 0. Учитывая связь абсо-
абсолютной и локальной производных вектора (п. 30), последнее уравнение
можно записать в виде
^+шхп = 0, C1)
где и> — угловая скорость тела. Уравнение C1) называется уравнением
Пуассона. Обозначая, как обычно, р, q, г проекции и> на оси Ox, Oy, Oz,
векторное уравнение Пуассона можно записать в виде следующих трех
скалярных уравнений:
dji dj2 dj3 /QO4
—— = Г72 - gr73, —_ = p>y3 - r7b —— = gr7l - p72. C2)
dt dt dt
Внешними силами, действующими на тело, являются сила тяжес-
тяжести и реакция точки О. Последняя не создает момента относительно
точки О, а момент Мо силы тяжести Р относительно точки О ра-
равен OG х Р. Учитывая, что Р = —Рп, можно написать
= Рпх OG. C3)
Если Мх, Му, Mz — проекции Мо на оси Ox, Oy, Oz, то из C3) полу-
получим
), Mz=P{llb-l2a). C4)
Таким образом, динамические уравнения D) имеют вид
C5)
Уравнения C2), C5) образуют замкнутую систему шести диффе-
дифференциальных уравнений, описывающую движение тяжелого твердого
тела вокруг неподвижной точки.
§ 2. Движение твердого тела вокруг неподвижной точки 205
Если из системы уравнений C2), C5) величины р, q, г, 71;72;7з наи~
дены как функции времени, то функции 6(t), <p(t) находятся из C0), а
для нахождения функции фA) нужно воспользоваться любым из кине-
кинематических уравнений Эйлера E).
Таким образом, основная задача состоит в интегрировании систе-
системы уравнений C2), C5). Анализ этой системы и составляет главную
сложность задачи о движении тяжелого твердого тела вокруг неподвиж-
неподвижной точки.
Укажем три первых интеграла системы C2), C5). Один из них
следует из того, что модуль вектора п постоянен и равен единице:
712+72+7з2=1- C6)
Еще один интеграл следует из теоремы об изменении кинетичес-
кинетического момента. В самом деле, так как внешние силы — сила тяжести
и реакция точки О — не создают момента относительно вертикальной
оси, то (см. п. 87) проекция кинетического момента Ко тела на верти-
вертикаль постоянна, т. е. Ко • п = const. В подвижной системе координат
вектор Ко имеет компоненты Ар, Bq, Cr, поэтому последнее равенство
может быть записано в виде
Ap7i + В 572 + CV73 = const. C7)
Замечая далее, что работа реакции точки О равна нулю, сила тя-
тяжести является потенциальной и потенциал П не зависит от времени,
получим, что во время движения тела его полная механическая энер-
энергия Е = Т + П постоянна (см. п. 88).
Принимая, что потенциальная энергия равна нулю, когда центр
тяжести тела находится в горизонтальной плоскости OXY, получим,
что П = Ph, где h — взятое со знаком расстояние от центра тяжести
тела до плоскости OXY; h = OG ¦ п = ar/i + &7г + 073- И так как
Т = k{Ap2 + Bq2 + Cr2), то интеграл энергии запишется в виде
^ + Bq2 + Cr2) + P(a7i + 672 + Пз) = const. C8)
Если воспользоваться теорией множителя Якоби, то можно пока-
показать1, что для того, чтобы интегрирование системы C2), C5) можно
было свести к квадратурам при любых начальных условиях, достаточ-
достаточно помимо выписанных трех первых интегралов C6)-C8) найти еще
один независимый от них интеграл.
хСм. п. 162.
206 Глава VII
К настоящему времени показано, что четвертый алгебраический
первый интеграл относительно р, q, г, 71 > 72; 7з существует только
в следующих трех случаях, а именно: в случаях Эйлера, Лагранжа и
Ковалевской.
В случае Эйлера тело произвольно, но его центр тяжести находится
в неподвижной точке О, т. е. а = Ъ = с = 0. Этот случай подробно
изучен в п.98-104.
В случае Лагранжа эллипсоид инерции тела для неподвижной точ-
точки является эллипсоидом вращения, а центр тяжести находится на оси
вращения, т. е., например, выполняются равенства А = В, а = Ь = 0.
Как следует из последнего уравнения системы C5), в этом случае чет-
четвертым алгебраическим первым интегралом будет проекция угловой
скорости тела на ось динамической симметрии: г = const.
В случае Ковалевской эллипсоид инерции для точки О является эл-
эллипсоидом вращения, например вокруг оси Oz, моменты инерции удов-
удовлетворяют соотношению А = В = 2С, а центр тяжести тела лежит в
экваториальной плоскости эллипсоида инерции, т. е. в наших обозначе-
обозначениях с = 0.
Для эллипсоида инерции, являющегося эллипсоидом вращения, лю-
любая ось, проходящая через точку О и лежащая в экваториальной плос-
плоскости, служит главной осью инерции. Поэтому будем для простоты вы-
вычислений считать, что ось Ох проходит через центр тяжести, т. е. Ь = 0.
Тогда динамические уравнения Эйлера C5) в случае Ковалевской при-
принимают вид
2»^° 2 +"
и четвертый алгебраический первый интеграл, как нетрудно убедиться
непосредственным дифференцированием, опираясь на уравнения C2),
C9), имеет вид
(Р2 ~ Q2 ~ iJ + BPQ ~ 2J = const. D0)
Найдено и подробно исследовано также много случаев, когда су-
существуют частные алгебраические интегралы, позволяющие свести ин-
интегрирование системы C2), C5) к квадратурам. Но эти интегралы су-
существуют не для всех, а только для некоторых специфически выбран-
выбранных начальных условий1.
106. Основная формула гироскопии. Твердое тело, движущее-
движущееся вокруг фиксированной в нем точки, для которой эллипсоид инерции
1См.: Горр Г. В., Кудряшова Л. В., Степанова Л. А. Классические задачи динамики
твердого тела, Киев: Наукова думка, 1978.
§ 2. Движение твердого тела вокруг неподвижной точки 207
тела является эллипсоидом вращения, называют гироскопом. В п. 100
мы видели, что если момент внешних сил относительно неподвижной
точки О равен нулю, то гироскоп совершает регулярную прецессию
вокруг неизменного кинетического момента Ко-
Но для того, чтобы гироскоп совершал регулярную прецессию, во-
вовсе не обязательно, чтобы момент внешних сил относительно непо-
неподвижной точки был равен нулю. Рассмотрим этот вопрос подробно.
Пусть OXYZ — неподвижная система координат с началом в непо-
неподвижной точке О тела, a Oxyz — система координат, оси которой на-
направлены по главным осям инерции тела для точки О. Пусть А, В, С
— моменты инерции тела относительно осей Ox, Oy, Oz и А = В.
Динамические уравнения Эйлера D) в этом случае будут такими:
Aft+(C- A)qr = Мх,
А^-(С- А)гр = Му, D1)
Углы Эйлера -ф, в, (р вводим обычным образом; кинематические урав-
уравнения Эйлера имеют вид E).
Найдем условия, при выполнении которых гироскоп может совер-
совершать регулярную прецессию вокруг оси OZ с заданными постоянными
значениями угла нутации (в = во), угловой скорости собственного вра-
вращения (ф = ш{) и угловой скорости прецессии (ф = шг). Иными слова-
словами, надо найти, каким должен быть момент внешних сил Мо относи-
относительно точки О, чтобы была возможна регулярная прецессия гироскопа
с заданными величинами во, u>i, u>2.
Для заданных величин в, ф, ф кинематические уравнения Эйле-
Эйлера E) принимают вид
р = Ш2 sin#0 sin 93, q = Ш2 sm#0 costp, r = L02 cos #0 + ^1 ¦ D2)
Последнее из равенств D2) показывает, что г — постоянная вели-
величина. Поэтому третье из уравнений D1) дает
Mz = 0. D3)
Подставив величины р, q, r из формул D2) в первое из уравнений D1),
можно найти Мх. Имеем
Мх = Аи>2 sin#o cosip—rr + (С — A)u
ttv
208 Глава VII
Подставив сюда вместо производной dip/dt ее значение u>i, получим
Мх = ш2ш! sin в0 cos ip \(J + (С - А) ^| cos 0O] • D4)
Аналогично, из формул D2) и второго из уравнений D1) получим
Му = —lj2ui sin в0 sin (р \С + (С - А) -?¦ cos #0 . D5)
Замечая, что в системе координат Oxyz вектор из\ имеет компонен-
компоненты 0, 0, ш\, а вектор о>2 — компоненты w-i sin#o sin<?, W2 sin #o cos y>,
W2 cos^o; можно три формулы D3)-D5) записать в виде одного вектор-
векторного равенства
Мо=и>2 хил [С+(С-А)^ cos в0]. D6)
Отсюда видно, что вектор Мо постоянен по модулю и параллелен линии
узлов ON.
Формула D6) называется основной формулой гироскопии. Она поз-
позволяет по заданным моментам инерции А, С, углу нутации во и век-
векторам угловых скоростей и>\, и>2 найти момент Мо, необходимый для
осуществления регулярной прецессии.
Отметим, что, в отличие от случая Эйлера, рассмотренного в п. 100,
здесь кинетический момент Ко не остается постоянным; он движется
в соответствии с теоремой об изменении кинетического момента
w м°- D7)
Последней формуле можно дать весьма удобную и широко распро-
распространенную интерпретацию: скорость конца вектора Ко равна Мо
(теорема Резал я).
Пример 1. Центру основания однородного кругового конуса массой т,
высотой hue углом при вершине 2а, вершина О которого закреплена
и который может катиться без проскальзывания по неподвижной гори-
горизонтальной плоскости, сообщается горизонтальная скорость v. Найти
равнодействующую (величину, направление и точку приложения) реак-
реакции плоскости и реакции в неподвижной точке, возникающих во время
дальнейшего движения конуса.
Пусть (рис. 105) G — центр масс конуса, R — радиус его
основания, а С и А — его моменты инерции относительно оси
симметрии и оси, проходящей через вершину и перпендикулярной
оси симметрии. Тогда OG = |/i, С = ^miJ2, A = Jym(E2 + Ah2).
I 2. Движение твердого тела вокруг неподвижной точки
209
Ho R= 0\L = htga, поэтому С = -^mh2t
о
Кроме того, 0\К = Л, sin a, QG = jhcosa.
Пусть вектор скорости центра ос-
основания конуса перпендикулярен плос-
плоскости рис. 105 и направлен на чита-
читателя. Так как движение происходит без
скольжения, то мгновенная ось враще-
вращения конуса направлена вдоль его образую-
образующей OL. Величина угловой скорости най-
найдется из равенств vo1 = v = и) • О±К.
Получим
A =
tg2 a).
ю,1-
Рис. 105
Конус совершает регулярную прецессию;
угловые скорости u»i и и>2 собственного
вращения и прецессии направлены как показано на рисунке. Для их ве-
величин находим
cos а Л, sin а cos а'
hcosa'
Угол нутации в (угол между u>i и а^) равен тг/2 + а.
Прецессия совершается под действием силы тяжести, реакции
плоскости и реакции в неподвижной точке О. Момент Мо этих сил
может быть вычислен по основной формуле гироскопии D6). Исполь-
Используя найденные выше значения величин А, С, и>\, и>2 и в, найдем модуль
этого момента:
cosa[C-(C-
sin a | =
3 mv2 sin a
20
cos3 a
A +5 cos2 a).
Вектор Мо перпендикулярен плоскости рис. 105 и направлен на
читателя. Отсюда, с учетом того, что сила тяжести направлена вер-
вертикально, следует, что искомая равнодействующая реакций плоскости
и неподвижной точки О лежит в плоскости рисунка. Пусть равнодей-
равнодействующая приложена в точке S образующей конуса OL. Разложим ее
на вертикальную составляющую N и составляющую F, направленную
по образующей.
Величины N и F найдем, применяя теорему о движении центра
инерции (п. 86). Вертикальное ускорение центра тяжести равно нулю,
поэтому N = rag; сила же F вызывает нормальное ускорение центра
210 Глава VII
тяжести при его движении по окружности радиусом QG:
. 3 mv2
Далее, сумма моментов сил F, N и rag относительно оси, перпенди-
перпендикулярной плоскости рисунка и проходящей через точку О, должна рав-
равняться
N-OS-mg-QG = МО.
Отсюда получаем расстояние точки S от вершины конуса:
OS = %h cos a + |, ^Щ^A + 5 cos2 a).
4 iU
107. Об элементарной теории гироскопа. У гироскопов, при-
применяемых в современной технике, угловая скорость собственного вра-
вращения обычно значительно превосходит угловую скорость прецессии,
т. е. ш\ 3> (х>2- Если в этом случае пренебречь вторым членом в квад-
квадратных скобках в формуле D6), то получим
Мо = Си>2 х u>i. D8)
Эта формула лежит в основе элементарной, или приближенной, те-
теории гироскопа и называется приближенной формулой гироскопии1.
Формула D8) сразу следует из теоремы Резаля, если сделать ос-
основное допущение элементарной теории гироскопа, состоящее в том,
что у быстро вращающегося гироскопа в любой момент времени мгно-
мгновенная угловая скорость и кинетический момент направлены по оси
динамической симметрии, причем
Ко = Сшх. D9)
Отметим некоторые свойства быстро вращающегося гироскопа.
Пусть гироскоп закреплен так, что его центр тяжести совпадает с непо-
неподвижной точкой О. Такой гироскоп называют уравновешенным. Пусть
он вращается вокруг оси симметрии с угловой скоростью из\. Так как
в данном случае ось симметрии является главной центральной осью
инерции, то кинетический момент Ко гироскопа направлен по оси сим-
симметрии, причем Ко = Сш\. Последнее равенство является не прибли-
приближенным, а точным. Если момент внешних сил относительно центра тя-
тяжести равен нулю, то вектор Ко постоянен, и ось гироскопа сохраняет
свое начальное направление в неподвижной системе координат.
угол нутации во равен тг/2, то формула D8) дает не приближенное, а точное
значение для Mq независимо от того, выполняется неравенство wi 3> Ш2 или нет.
I 2. Движение твердого тела вокруг неподвижной точки
211
Предположим, что к оси гироскопа при-
приложена сила F, момент которой относитель- v
но точки О равен М (рис. 106). Согласно фор-
формуле D7), вектор Ко (а следовательно, и ось
симметрии гироскопа, так как их направле-
направления по предположению совпадают) будет от-
отклоняться, но не в сторону действия силы, а
в ту сторону, куда направлен вектор М (т. е.
перпендикулярно силе). В этом состоит одно
из интереснейших свойств быстро вращаю-
вращающегося гироскопа.
Если действие силы F прекращается, то
и ось гироскопа перестает отклоняться. Это
тоже очень интересное свойство, так как в
обычных условиях тело с прекращением действия силы продолжает
свое движение по инерции.
Пусть на быстро вращающийся гироскоп в течение малого про-
промежутка времени г действует сила F, причем величина Ft являет-
является конечной. Если плечо этой силы относительно точки О равно h,
то М = Fh. Конец а вектора Ко приобретает скорость va, модуль
которой, согласно теореме Резаля, равен Fh. Точка а за время г пере-
переместится на расстояние аа! = var = Fhr. Учитывая, что Оа равняет-
равняется Сш\, получаем, что ось гироскопа за время г повернется на малый
угол /3, определяемый равенством
Рис. 106
аа!_
Оа
Fhr
E0)
Так как Fhr — конечная величина, a Cui\ — большая, то угол C будет
малым.
Отсюда следует, что при кратковременном действии сил ось ги-
гироскопа практически сохраняет свое первоначальное положение в про-
пространстве.
При длительном воздействии силы F указанное свойство гироско-
гироскопа не будет сохраняться продолжительно. Увеличением кинетического
момента гироскопа Сш\ можно только увеличить промежуток времени,
по истечении которого отклонение оси гироскопа от ее первоначального
направления не будет превосходить определенного значения.
В технике характерным режимом работы гироскопа является рабо-
работа в условиях длительно действующих постоянных или медленно меня-
меняющихся моментов, которые при наличии достаточного кинетического
момента гироскопа сообщают ему весьма медленную прецессию. Это
медленное изменение положения оси гироскопа является важнейшим
212
Глава VII
(но не единственным) свойством гироскопа, широко используемым на
практике.
Рассмотрим гироскоп, вращающийся вокруг своей оси симметрии
с угловой скоростью u>i. Пусть гироскоп совершает прецессию за счет
того, что тело, на котором он установлен, вращается с угловой ско-
скоростью о»2- Необходимый для прецессии момент Мо создается силами
давления, действующими со стороны тела на гироскоп. Этот момент мо-
может быть вычислен по основной формуле гироскопии D6). По третьему
закону Ньютона гироскоп давит на тело, на котором он установлен, с та-
такими же по величине, но противоположно направленными силами. Эти
силы создают момент Мгир, воздействующий на тело, вынуждающее
гироскоп совершать прецессию. Этот момент называют гироскопичес-
гироскопическим моментом. Очевидно, что Мгир = — Мо- В рамках приближенной
теории гироскопа имеем
х и>2.
E1)
В заключение, опираясь на эле-
элементарную теорию гироскопа, рас-
рассмотрим задачу о движении тя-
тяжелого твердого тела вокруг непо-
неподвижной точки в случае Лагранжа
(см. п. 105). Пусть динамически сим-
симметричное твердое тело весом Р име-
имеет неподвижную точку О (рис. 107).
В начальный момент оно расположе-
расположено так, что ось симметрии Oz состав-
составляет угол в с вертикалью. Пусть те-
тело закручено вокруг оси симметрии с
угловой скоростью u>i, направленной
как показано на рис. 107. Момент Мо
силы тяжести Р при любом направлении оси Oz горизонтален. Следова-
Следовательно, вертикальная ось OZ является осью прецессии. Ось гироскопа
движется по поверхности конуса с углом при вершине, равным 26. На-
Направление движения указано на рис. 107 стрелками.
Угловую скорость прецессии найдем из формулы D8). Момент Мо
имеет величину Р ¦ OG ¦ sin#. Согласно D8), эта величина должна рав-
равняться Cu)iLO2 sin#. Приравняв эти два значения для Мо, получим
UJ2 =
P-OG
Сил "
E2)
Угловая скорость прецессии не зависит от угла в.
I 2. Движение твердого тела вокруг неподвижной точки
213
Таким образом, быстро вращающееся тяжелое твердое тело в слу-
случае Лагранжа совершает регулярную прецессию. Полученный вывод
является приближенным. Он получен в предположениях элементарной
теории гироскопов. В действительности движение гироскопа отлича-
отличается от регулярной прецессии. В частности, угол в не обязательно по-
постоянен, он может изменяться в некотором интервале; колебательное
движение оси симметрии гироскопа называется нутацией.
Рис. 108
Рис. 109
Пример 1. Гироскоп состоит из колеса радиусом R = 0,1 м, делающе-
делающего п = 100 оборотов в секунду. Рама гироскопа, не изображенная на
рис. 108, свободно вращается вокруг неподвижной точки О, расстоя-
расстояние которой ОО\ от колеса гироскопа равно 0,2 м. Считая колесо од-
однородным диском и пренебрегая массой рамы, определить направление
и угловую скорость прецессионного движения, которое начнет совер-
совершать гироскоп, если будет предоставлен самому себе при горизонталь-
горизонтальном положении плеча ОО\. Ускорение свободного падения принять рав-
равным 10 м/с .
Момент силы тяжести Мо горизонтален, перпендикулярен ОО\
и направлен как показано на рис. 108, его величина Мо = rag • ОО\,
где га — масса колеса. Согласно формуле D6), для указанного на ри-
рисунке направления вращения колеса момент Мо вызовет регулярную
прецессию гироскопа с угловой скоростью прецессии и>2, направленной
вертикально вверх.
Для подсчета величины угловой скорости прецессии можно восполь-
воспользоваться либо основной формулой гироскопии D6), либо формулой D8)
приближенной теории гироскопа (у нас в = тг/2, и поэтому эти формулы
совпадают). Получим
= mg ¦ ОО\.
214 Глава VII
Учитывая, что С = l/2mR2, находим отсюда
_ mg ¦ ООх _ mg ¦ ООх _ 2
1/2тД2-2тгп 7Г
В рамках приближенной теории гироскопа в = const и точка 0\ бу-
будет описывать горизонтальную окружность в направлении, указанном
2 1
стрелкой. При этом величина угловой скорости плеча 00\ равна ^^.
Пример 2. Модель аэроплана, летящая со скоростью v, совершает по-
поворот по горизонтальной окружности радиусом р. Момент инерции про-
пропеллера и мотора относительно их общей оси вращения равен С. Про-
Пропеллер и мотор вращаются с угловой скоростью Ы\. Найти момент
гироскопических давлений.
Угловая скорость прецессии вертикальна и по величине равна v/p,
угол нутации в равен тг/2. Согласно D6), находим
Mzuv = Сшх х и>2, Мгир =
Гироскопический момент МгиТ, горизонтален. Гироскопические же
давления вертикальны, и при направлении вращения пропеллера, ука-
указанном на рис. 109, гироскопические давления при повороте авиамодели
влево от курса стремятся поднять ее носовую часть вверх.
§ 3. Движение свободного твердого тела
108. Дифференциальные уравнения движения свободного
твердого тела. Пусть требуется найти движение свободного твердого
тела относительно неподвижной системы координат OaXYZ. Соглас-
Согласно теореме Шаля (п. 21), любое движение твердого тела можно рас-
рассматривать как совокупность поступательного движения, определяе-
определяемого движением произвольной точки тела (полюса), и движения тела
вокруг этой точки как неподвижной. При описании движения полюс
желательно выбрать так, чтобы его движение определялось наиболее
просто. Из основных теорем динамики следует, что за полюс удобно
взять центр масс. Действительно, согласно теореме о движении центра
масс, последний движется как материальная точка, к которой приложе-
приложены все внешние силы системы, а теоремы об изменении кинетического
момента и кинетической энергии для движения вокруг центра масс
(см. определение этого понятия в п. 81) формулируются точно так же,
как и для движения вокруг неподвижной точки.
§ 3. Движение свободного твердого тела 215
Пусть М — масса тела, vc — скорость центра масс, Кс — кине-
кинетический момент тела в его движении относительно центра масс, т. е.
(см. п. 81) относительно системы координат, которая имеет начало в
центре масс тела и движется поступательно. Если R^ и М^' — глав-
главный вектор и главный момент внешних сил относительно точки С, то
из теоремы о движении центра инерции (п. 86) и теоремы об изменении
кинетического момента (п. 87) имеем два векторных дифференциаль-
дифференциальных уравнения
dvG - R(e)
dt -R '
R М m
dt -R ' dt - c • A)
Если Xc, Yc, Zc — координаты центра масс тела в неподвижной сис-
системе координат OaXYZ, a Rx, Ry, Rz — проекции вектора R^ на
оси ОаХ, OaY, OaZ, то первое уравнение из A) запишется в виде сле-
следующих скалярных уравнений:
Md2Xc p Md2Yc р
M R m R
Пусть CXYZ — поступательно движущаяся кенигова система коорди-
координат, a Cxyz — система координат, жестко связанная с движущимся те-
телом. Если р, q, г — проекции угловой скорости тела на оси Сх, Су, Cz,
а Мх, Му, Mz — компоненты вектора Mq в системе координат Cxyz,
то второе уравнение из A) запишется в виде уравнений C) п. 97:
xVr ~ JxzQ) = Мх,
= му,
+r(Jxzq - JyZp) = Mz.
Здесь Jx, Jy, Jz, Jxy, Jxz, Jyz — компоненты тензора инерции тела
для центра масс в системе координат Cxyz. Если оси Сх, Су, Cz —
главные оси инерции тела для центра масс, то уравнения C) упроща-
упрощаются и принимают вид динамических уравнений Эйлера D) п. 97.
216 Глава VII
В уравнениях C) величины р, q, r можно заменить на их выраже-
выражения, задаваемые кинематическими уравнениями Эйлера
р = ф sin в sin (p + в cos (p,
q = ip sin в cos (p - в simp, D)
г = ipcosd + ф.
Углы Эйлера, задающие взаимную ориентацию систем координат Cxyz
и CXYZ, вводятся обычным образом.
Уравнения B)-D) образуют систему дифференциальных уравне-
уравнений, описывающую движение свободного твердого тела. В общем случае
правые части уравнений B), C) зависят от величин Хс, Yc, Zc, ф, О, ip,
их первых производных и времени, и в этом случае систему уравне-
уравнений B)-D) надо решать совместно.
Но в простых случаях возможно раздельное интегрирование сис-
систем B) и C)-D). Например, пусть свободное твердое тело движется в
однородном поле тяжести. Единственной внешней силой, действующей
на тело, является сила тяжести, приложенная в центре масс и направ-
направленная по вертикали вниз. Если ось OaZ направить по вертикали вверх,
то уравнения B) примут вид
d2XG „ d2Yc d2Zc
dt2 ' dt2 ' dt2 g'
где g — ускорение свободного падения. Отсюда следует, что при про-
произвольных начальных условиях центр масс тела будет двигаться по па-
параболе. А так как момент Мс силы тяжести относительно центра масс
равен нулю, то движение тела вокруг центра масс будет движением
Эйлера-Пуансо.
Если твердое тело несвободно, то величины Хс, Yc, Zc, ip, О, ip
и, может быть, их производные связаны некоторыми соотношениями.
Уравнения движения по-прежнему имеют вид B)-D), но в правые час-
части уравнений B) и C) войдут реакции связей.
Пример 1. В момент метания диска его плоскость занимает горизон-
горизонтальное положение, а центр диска находится на высоте h над поверх-
поверхностью Земли. Центру диска сообщена горизонтальная скорость vq, a
сам диск закручен с угловой скоростью и>о, составляющей угол S = тг/4
с его плоскостью. Векторы Vo и и>о лежат в неподвижной вертикальной
плоскости OaYZ (рис. 110). Считая диск тонкой однородной пластин-
пластинкой, найти его движение. Влиянием воздуха пренебречь.
В неподвижной системе координат OaXYZ, плоскость OaXY ко-
которой совпадает с горизонтальной поверхностью Земли, а ось OaZ вер-
j 3. Движение свободного твердого тела
217
Рис. 110 Рис. Ill
тикальна, центр масс диска С движется по параболе
Xc(t) = 0, Yc(t) = vot + YC(O), Zc{t) = h-
gt2
Движение диска относительно кениговой системы координат CXYZ,
оси которой параллельны соответствующим осям системы коорди-
координат OaXYZ, является регулярной прецессией. Оси жестко связанной
с диском системы координат Cxyz, образованной главными централь-
центральными осями инерции диска, направим так, чтобы в момент метания
диска t = 0 ось Сх совпадала с осью CY, ось Су совпадала с осью СХ,
а направление оси Cz было бы противоположно направлению оси CZ
кениговой системы координат (см. рис. 110 и 111).
Для главных центральных моментов инерции диска имеем: Jz =
= 2JX = 2Jy = l/2mR2 (m — масса диска, R — его радиус). Так
как Jz > Jx, то угол в между векторами и>\ и а»2, согласно п. 100,
тупой (рис. 111).
На рис. 111 показана ориентация вектора и> относительно диска
при t = 0/ имеем: р = ljqCOsS, q = 0, г = Го = —uiosinS. Поэтому
для неизменного модуля кинетического момента диска Кс получаем:
Кс =
J2yq2 + J2zr2 = J
218 Глава VII
Формулы A3), A5) и A6) п. 100 дают:
Шх = Го = Шо Sin О.
Jx
Вектор Ко задает ось прецессии. Он имеет неизменное направление в
пространстве: лежит в плоскости CY Z и составляет с горизонталь-
горизонтальной осью CY постоянный угол, равный в — тг/2. Для единичного векто-
вектора е, направленного вдоль Кс, получаем в системе координат CXYZ:
„г _ I n cos 5 2 sin 5
с — I и,
+ 3sin2 S Vl
Подставив в полученные выражения заданное значение угла S, рав-
равное 7г/4, получим, что в кениговой системе координат диск совершает
регулярную прецессию:
а 2 ; \/10 . \/2
в = тг - arccos—, ip = ш2 = —^-wo, Ч> = ui = ^"wo;
ось прецессии определяется вектором е' = @, 1/л/5, 2/л/5).
109. Плоское движение тела. Пусть все точки тела движутся
параллельно плоскости OaXY. Получим дифференциальные уравнения,
описывающие это плоское движение тела. Без ограничения общности
можно считать, что центр масс тела движется в плоскости OaXY', поэ-
поэтому Zc = 0. Также можно считать, что оси Сх, Су связанной с телом
системы координат Cxyz движутся в плоскости OaXY, т. е. ось Cz
перпендикулярна этой плоскости. Тогда, полагая в = 0, ф = 0, из кине-
кинематических уравнений Эйлера D) имеем
р = 0, g = 0, г = ф. E)
Подставив Zc = 0 в уравнения B), а выражения E) для р, q, r в урав-
уравнения C), получим
^ ^RY, Rz=0. F)
at at
§ 3. Движение свободного твердого тела
219
Последнее уравнение из F) и первые два уравнения из G) налагают
ограничения на геометрию масс тела, внешние силы и частично на
начальные условия, при выполнении которых плоское движение тела
возможно. Остальные три уравнения
dt1
= Кх,
w
at
'
§
(8)
являются дифференциальными уравнениями плоского движения твер-
твердого тела.
Пример 1. Тело совершает плоское движение под действием постоян-
постоянной во величине и направлению силы F. Линия действия силы лежит в
плоскости, проходящей через центр масс тела и параллельной плоскос-
плоскости его движения (рис. 112). Определить движение тела.
X
о.
X
У'
У/
а:
1
^__ А
\
mg'
i
\
Рис. 112
6V7/777777Ab7/7777/ x
Рис. 113
Пусть т — масса тела, а — расстояние от центра масс до точки
приложения силы, J — момент инерции тела относительно оси, прохо-
проходящей через центр масс тела и перпендикулярной плоскости движения.
Напишем уравнения движения тела (8). Направление оси ОаХ вы-
выберем так, чтобы оно совпадало с направлением силы F (рис. 112).
Тогда
тХс = F, т?с = 0, J(p = —
Из первых двух уравнений следует, что центр масс тела будет
(при 1G @) ф 0) двигаться по параболе
0 = ^r+^c(O)i + Xc(O), yo(t)=ic@)t-
220 Глава VII
если 1G @) = 0, то центр масс движется с постоянным ускорени-
ускорением F/m вдоль прямой, параллельной оси ОаХ, и за время t пройдет
путь a = =g| + XG(O)t.
Одновременно тело вращается относительно центра масс; это
вращение описывается третьим из написанных уравнений движения
тела. Сравнивая это уравнение с уравнением движения математи-
математического маятника (уравнение F) п. 57), видим, что относитель-
относительно центра масс тело движется как математический маятник дли-
длиной I = Jg/(Fd).
Пример 2. Тонкий однородный стержень приставлен одним концом к
гладкой вертикальной стене, а другим концом опирается на гладкий
горизонтальный пол (рис. 113). Стержень пришел в движение из со-
состояния покоя, когда он составлял угол а с вертикалью. Вычислить
начальные давления на стену и пол.
Движение стержня происходит под действием силы тяжести mg
и реакций Na и Nb стены и пола; Na имеет горизонтальное, а Nb
— вертикальное направления. Пусть а — длина стержня, а х, у —
координаты его центра тяжести С в показанной на рис. 113 системе
координат Оху. Дифференциальные уравнения движения стержня име-
имеют вид
тх = Na, mi) = Nb — mg, -^то?ф = — Naucosip +
Ho
x = 7rasin<?, у = ^
x = |(cos<y9 • ф - sin<^2), у = -1 (sin у; • ф + cos<? • ф2).
Поэтому из первых двух уравнений движения стержня имеем
Na = -кта(со$,ip • ф - smip-ф2), NB = mg- ^ma(sinip • ф + cos f -ф2)-
Подставив эти выражения для Na и Nb в третье из уравнений
движения стержня и учтя, что при t = 0 <р = а, ф = 0, получим, что
при t = О
Следовательно, искомые начальные значения величин Na и Nb будут
такими:
о
Na = -jmgsinacosa,
4
NB = mg (l - § sin2 a\ .
§^. Движение тяжелого твердого тела 221
Пример 3. Неоднородный диск ка- у
тится по неподвижной горизонталь-
горизонтальной плоскости так, что скольжение
отсутствует, а плоскость диска все
время остается в фиксированной вер-
вертикальной плоскости (см. пример 4
п. 87). Масса диска равна т, радиус a, q
центр масс С находится на расстоя-
нии Ь от геометрического центра, мо-
момент инерции относительно оси, пер- Рис- -Ч^
пендикулярной плоскости диска и проходящей через его центр масс, ра-
равен Jc- Используя теорию плоского движения, получим дифференциаль-
дифференциальные уравнения движения диска.
Движение диска происходит под действием силы тяжести и реак-
реакции плоскости, которая приложена в точке А* диска, в которой проис-
происходит его касание с плоскостью; разложим реакцию на две составляю-
составляющие: вертикальную N и горизонтальную F (рис. 114).
Уравнения (8) в рассматриваемой задаче будут иметь вид
тХс = F,
mYc = N — mg,
Лсф = F(a — Ь cos ф) — Nb sin <p.
Из условия отсутствия скольжения (скорость точки А* равна ну-
нулю) следует, что во все время движения должны выполняться равенст-
равенства
Хс = — (а — b cos (р)ф, Yc=bsinip^.
Следовательно,
Хс = —(а — bcos ip) • ф — bsin<p ¦ ф2, Yc = bsin<p ¦ ф + bcos <p • ф2.
Поэтому первые два из трех дифференциальных уравнений движения
диска дают зависимость составляющих реакции плоскости от ip, ф
и ф:
N = mg + mb(s'm (р ¦ ф + cos tp-ф2), F = —m[(a — b cos (р)ф + b sin tp-ф2].
Подставив эти выражения для N и F в третье из дифференци-
дифференциальных уравнений движения диска, придем к уравнению, описывающему
изменение угла ip во времени:
[Jc +m(a2 +b2 - 2ab cos (р)]ф + mab sin (p ¦ ф2 + mgb sin (p = 0.
В примере 4 п. 87 это уравнение было получено при помощи теоремы
об изменении кинетического момента.
222
Глава VII
Рис. 115
§ 4. Движение тяжелого твердого тела,
опирающегося на горизонтальную плоскость
110. Общие сведения. Поня-
Понятие о трении. Пусть жесткая по-
поверхность S движется, касаясь непо-
неподвижной поверхности Si (рис. 115).
Считаем, что поверхности S и Si вы-
выпуклы, а их касание происходит в од-
ной точке О. При движении поверх-
поверхности S точка О, вообще говоря, пере-
перемещается как по S, так и по Si. Пред-
Предполагается, что в каждый момент вре-
времени через точку О можно провес-
провести единственную касательную плос-
плоскость к S и Si. Очевидно, что ско-
скорость vo точки О, которой поверх-
поверхность S касается Si, лежит в общей касательной плоскости, проходящей
через О. Если vo = 0, то говорят о движении без скольжения. Если же
vo ф 0, то говорят о движении со скольжением, a vo называют скорос-
скоростью скольжения.
Примем точку О за полюс. Тогда движение поверхности S в каж-
каждый момент времени можно представить как совокупность поступа-
поступательного движения со скоростью vo и вращения с угловой скоростью и>
вокруг точки О. Разложим вектор и> на две составляющие и>в и и>к,
где вектор Шв перпендикулярен общей касательной плоскости, а Шк
лежит в ней; шв называют угловой скоростью верчения поверхности S,
а и>к — угловой скоростью качения.
Если vo = 0, то говорят, что поверхность S катится по поверхнос-
поверхности Si; если при этом и>в = 0, Шк ф 0, то имеет место чистое качение S
по Si, а если и>к = 0, и>в ф 0, то поверхность S совершает верчение.
Когда vo ф 0, а и>в = 0, и>к = 0, то говорят, что S скользит по Si. В
общем случае, когда vo ф 0, и>в ф 0, и>к ф 0, поверхность S скользит,
вертится и катится по Si.
Действие Si на S проявляется в следующем. 1) На поверхность S
действует сила N, перпендикулярная общей касательной плоскости и
направленная от Si к S; эта сила называется нормальной реакцией; для
реальных движений N ^ 0. 2) На S действует сила трения F, лежа-
лежащая в общей касательной плоскости. Согласно законам трения Кулона,
величина F не превосходит своего максимально возможного значения,
равного kN, где к — коэффициент трения. При этом если vo = 0,
то F < kN. Величину F в этом случае называют силой трения по-
§^. Движение тяжелого твердого тела 223
коя. При «о /0 имеет место равенство F = kN, a F называют силой
трения скольжения1.
Иногда приемлема такая идеализация, что поверхности можно счи-
считать абсолютно гладкими. Это означает, что величина к настолько ма-
мала, что величиной силы трения в рассматриваемой задаче можно пре-
пренебречь. Если поверхность S\ абсолютно гладкая, то ее воздействие
на S сводится к нормальной реакции N.
В действительности тела соприкасаются не в одной точке, а по
очень малой площадке. Тогда воздействие S на S\ уже нельзя считать
приводящимся к одной силе (являющейся геометрической суммой нор-
нормальной реакции и силы трения). Согласно теореме Пуансо (п. 71), сово-
совокупность сил, действующих на S в каждой точке площадки касания, в
общем случае будет приводиться к силе и паре. Упомянутая сила снова
может быть разложена на сумму нормальной реакции и силы трения, и
пару удобно представить также в виде совокупности двух пар. Одна из
них имеет момент, коллинеарный а»в, а другая — коллинеарный шк-
Первая пара является парой трения верчения, а вторая — парой трения
качения. Трение верчения и трение качения обычно малы по сравне-
сравнению с трением скольжения, и в прикладных задачах часто учитывается
только трение скольжения.
111. Волчок на абсолютно гладкой плоскости. Пусть эллип-
эллипсоид инерции твердого тела для его центра масс представляет собой
эллипсоид вращения. Задача о движении волчка по плоскости состоит
в исследовании движения этого тела в поле тяжести в предположении,
что одна из точек тела, лежащая на оси динамической симметрии, дви-
движется по горизонтальной плоскости. Будем считать, что волчок имеет
настолько острый конец, что его можно принять за острие, оканчиваю-
оканчивающееся точкой D. При движении волчка его точка D все время остается
на неподвижной горизонтальной плоскости (рис. 116).
Будем считать, что плоскость является абсолютно гладкой. Тогда
ее воздействие на волчок сводится к реакции N, имеющей вертикаль-
вертикальное направление. Так как активная сила — сила тяжести — также на-
направлена по вертикали, то на основании теоремы о движении центра
инерции (п. 86) получаем, что проекция центра масс G на горизонталь-
горизонтальную плоскость движется равномерно и прямолинейно. Без ограничения
общности будем считать ее неподвижной; тогда центр масс движется
по заданной вертикали.
Выберем неподвижную систему OXYZ так, чтобы ось OZ была
вертикальной и проходила через центр масс волчка, а плоскость OXY
1 Следует иметь в виду, что трение представляет собой весьма сложное явление,
поэтому законы Кулона имеют только приближенный характер.
224
Глава VII
совпадала с горизонтальной плоскостью, на которую при движении опи-
опирается волчок своей точкой D (рис. 116).
Ориентация волчка относительно
неподвижной системы координат зада-
задается углами Эйлера ф, в, ip.
Пусть т — масса волчка, I —
расстояние от центра масс G до точ-
точки D, которой волчок касается плос-
плоскости, С — момент инерции волчка
относительно оси динамической сим-
симметрии Gz, А и В (А = В) — мо-
моменты инерции волчка относительно
двух любых жестко связанных с волч-
волчком взаимно перпендикулярных и пер-
перпендикулярных Gz осей Gx и Gy. Для
расстояния h центра масс волчка от
опорной плоскости имеем выражение:
h = I cos в.
Так как А = В и внешние силы
X
Рис. 116
(реакция плоскости и сила тяжести) не создают момента относительно
оси Gz, то из третьего уравнения системы динамических уравнений
Эйлера (формулы D) п. 97) следует, что проекция г угловой скорости и>
волчка на ось его динамической симметрии является постоянной, т. е.
имеет место первый интеграл
г = го = const.
(9)
Пусть, как обычно, р и q — проекции и> на оси Gx и Gy. Так как
внешние силы направлены вертикально и, следовательно, не создают
момента относительно вертикальной оси OZ, то из теоремы об изме-
изменении кинетического момента (п. 87) вытекает постоянство проекции
кинетического момента волчка относительно центра масс на вертикаль:
Aqj2 + CV73 = const,
где величины 71, 72: 7з вычисляются по формулам C0) п. 105. Исполь-
Используя кинематические уравнения Эйлера (формулы E) п. 97) и соотно-
соотношение (9), последнее равенство можно записать в виде
A sin2 вф + Cro cos в = const.
A0)
Далее, поскольку связь, наложенная на волчок (h = Icos9), стационарна
и идеальна, а активные силы имеют потенциал П = mgh, не зависящий
§^. Движение тяжелого твердого тела 225
явно от времени, то полная механическая энергия постоянна (п. 88):
Е = Т + П = const.
Здесь Т — кинетическая энергия волчка, которая, согласно теореме
Кенига (п. 83), вычисляется по формуле
где vq = h — скорость центра масс волчка. Используя кинематические
уравнения Эйлера, соотношение (9) и равенство h = —lsin.ee, запишем
интеграл энергии в виде
(А + ml2 sin2 0H2 + A sin2 dip2 + 2mgl cos в = const. A1)
Интегралы (9)—A1) позволяют свести решение задачи о движении
волчка к квадратурам. Мы не будем исследовать движение во всей пол-
полноте, а рассмотрим только один частный случай. Пусть в начальный
момент волчок закручен вокруг оси симметрии и поставлен на плос-
плоскость без начальной скорости центра масс и пусть в начальный мо-
момент ось симметрии волчка наклонена к вертикали под углом во- Это
означает, что при t = 0 выполнены равенства
¦ф = 0, 0 = 0, в = 0О, ф = г0.
Кроме того, как мы предположили с самого начала, проекция цент-
центра масс на плоскость 0XY имеет скорость, равную нулю.
Для таких начальных данных интегралы A0) и A1) можно пере-
переписать в следующем виде:
Asm29ip = Cro(cos0o-cos0), A2)
(А + ml2 sin2 <9H2 + A sin2 0^2 = 2mgl(cos90 - cos в). A3)
Из A2) находим
• Cro(cos0o - cos0)
Ч> = ъ • A4)
Asin20 V '
Используя A4), интеграл A3) можно записать в виде
Asin2 в(А +ml2 sin2 в)в2 =/@), A5)
где
/@) = (cos 0О - cos0)[2Amg/sin2 0 - C2r\(cos 0O - cos0)]. A6)
226 Глава VII
Левая часть равенства A5) неотрицательна. Поэтому угол 0 может при-
принимать только такие значения, для которых /@) Js 0. Отсюда сле-
следует, что 0 Js во, так как при в < во функция f(9) представляет
собой произведение двух сомножителей, имеющих противоположные
знаки. Угол в колеблется между во и значением в\, являющимся бли-
ближайшим к во корнем уравнения /(в) = 0. Отметим, что #i < тг, так
как /(тг) = — (l+cos#oJC2fo < 0. Таким образом, при движении волчка
выполняются неравенства во ^ 0 ^ в\ < тг. Длина отрезка OD (рис. 116)
все время удовлетворяет неравенствам
/sinв0 ^ OD ^ /sin0i.
Поэтому траектория точки D на опорной плоскости заключена меж-
между двумя концентрическими окружностями радиусов / sin 0О и / sin 0i с
центром в точке О.
Из A4) следует, что когда в принимает во время движения свое
начальное значение во, то ф = 0. Отсюда вытекает, что траектория
точки D имеет на внутренней окружности радиуса Zsin#0 точки воз-
возврата (рис. 116).
Если начальная угловая скорость го вращения волчка вокруг оси
симметрии велика, то угол 9 мало отличается от своего начального зна-
значения. Действительно, приравняв нулю квадратную скобку в выраже-
выражении A6) для функции /@i), получим, что с погрешностью порядка 1/гд
угол 0i будет вычисляться по формуле
2Amgl sin 0O
0i — 0о
2 г2
Отсюда видно, что в\, а следовательно, и 0 сколь угодно близки к 0о,
если величина го достаточно велика.
112. Влияние трения на движение волчка. В действительнос-
действительности неподвижная плоскость, на которую опирается волчок, не является
абсолютно гладкой, а волчок заканчивается не острием, а поверхнос-
поверхностью вращения, более или менее заостренной, так что точка касания D
волчка и плоскости не лежит на оси симметрии. По этим причинам
движение волчка будет иным, нежели то движение, которое описано в
п. 111.
Один из самых интересных эффектов влияния силы трения состо-
состоит в том, что эта сила может приблизить ось симметрии волчка к вер-
вертикали. Рассмотрим этот эффект с качественной стороны, опираясь
на теорему об изменении кинетического момента. Пусть волчок быст-
быстро вращается вокруг оси симметрии и без начальной скорости центра
масс поставлен на плоскость так, что его ось симметрии составляет с
вертикалью некоторый ненулевой острый угол 0q.
^. Движение тяжелого твердого тела
227
Рис. 117
Кинетический момент К волчка отно-
относительно центра масс в начальный момент
направлен как показано на рис. 117. Пусть D
— точка ножки волчка, которой он касает-
касается опорной плоскости. Ножка теперь уже не
принимается за острие. Сила трения F на-
направлена в сторону, противоположную ско-
скорости точки D. Момент М силы трения
относительно центра масс направлен пер-
перпендикулярно плоскости, проходящей через
центр масс G и вектор F. Вектор М мож-
можно представить в виде суммы М\ + Мг,
где вектор Mi перпендикулярен К, а век-
вектор Мг коллинеарен вектору К, но (в ситу-
ситуации, представленной на рис. 117) направлен
противоположно К. По теореме об измене-
изменении кинетического момента скорость конца вектора К равна М. От-
Отсюда следует, что вектор К, уменьшаясь по величине (из-за наличия
составляющей Мг момента силы трения), стремится занять вертикаль-
вертикальное положение (из-за наличия составляющей М\ момента силы трения).
Таким образом, вектор К, а вместе с ним и ось симметрии волчка под
влиянием трения стремятся к вертикали. Если действие трения будет
достаточно продолжительным, то ось волчка может в конце концов за-
занять строго вертикальное положение и останется в этом положении
неподвижной. В этом случае говорят, что волчок «спит».
113. Движение однородного ша-
шара по плоскости при наличии тре-
трения. Пусть однородный шар массой т
и радиусом а движется по неподвиж-
неподвижной шероховатой горизонтальной плос-
плоскости. Введем две системы коорди-
координат: неподвижную OXYZ с вертикаль-
вертикальной осью OZ и началом О, совпада-
совпадающим с произвольной точкой опорной
плоскости, и поступательно движущую-
движущуюся GXYZ с началом в центре масс ша-
шара G и осями, параллельными соответ-
соответствующим осям неподвижной системы координат (рис. 118).
Реакцию плоскости R представим в виде суммы двух сил:
R = N + F, где N — нормальная реакция плоскости, a F — сила тре-
трения. Если ш — угловая скорость шара, а»с — скорость центра масс,
Рис. 118
228 Глава VII
то скорость vd точки D шара, которой он касается плоскости, вычис-
вычисляется но формуле
vD = vG + и> х GD. A7)
Сила трения скольжения определяется соотношением
F = -kNu, A8)
где к — коэффициент трения, и — единичный вектор, направленный
вдоль скорости точки D: vn = vr>u.
Из теоремы о движении центра инерции имеем
TO^-p =mg + R. A9)
Пусть Kg — кинетический момент шара относительно центра масс.
Тогда, учитывая, что момент инерции однородного шара радиусом а и
, 2 2
массой т относительно любого диаметра равен -=та, имеем
о
KG = \та2ш. B0)
о
Теорема об изменении кинетического момента для движения относи-
относительно центра масс дает уравнение
d? = -5-^GDxR. B1)
dt 2ma2
Пусть Х<з, Yg, Zg — координаты центра масс в системе OXYZ,
a Fx, Fy — проекции силы трения на оси ОХ и OY. Уравнения A1) в
скалярной форме запишутся в виде
=JL flo = ^ fZo=_g+±N B2)
dt2 m "' dt2
Так как Zq = a = const, то последнее из этих уравнений даст N = mg,
т. е. нормальная реакция плоскости равна весу шара, причем этот
вывод не зависит от того, скользит шар по плоскости (vd ф 0) или
нет (vD = 0).
Если wx, шу, uz — проекции вектора со на оси GX, GY, GZ, то
векторное уравнение B1) дает следующие три скалярных уравнения:
§^. Движение тяжелого твердого тела 229
Последнее из этих уравнений показывает, что при движении шара про-
проекция его угловой скорости на вертикаль остается постоянной. Это за-
заключение имеет место независимо от наличия или отсутствия сколь-
скольжения шара.
Пусть в начальный момент V?> ф О, т. е. имеется скольжение. Так
как N = mg, то из A8) получаем, что при наличии скольжения ша-
шара сила трения постоянна по величине: F = kmg. Покажем, что она
постоянна и по направлению. Для этого продифференцируем обе части
равенства A7) по времени и воспользуемся уравнениями A9), B1) и
равенствами R = — mg + F, GD = ^.g. Получим
о
B4)
=
dt 2т
Заменив здесь V?> на вди, a F — на правую часть равенства A8),
получим
Так как и — единичный вектор, то вектор du/dt перпендикулярен и.
Поэтому из B5) следует, что
Таким образом, вектор и имеет постоянное направление и, следова-
следовательно, сила трения постоянна:
F = -kmgu. B7)
Величина скорости точки D, согласно B6), изменяется во времени по
закону
vD(t) = vD@) - Ikgt. B8)
Если обозначить через а постоянный угол, который составляет ско-
скорость точки D с осью ОХ, то из первых двух уравнений B2), получим
XG(t) = -Ugcosa-12 + XG@)t + XG@),
: B9)
YG(t) = -ifcgsirm • t2 + YG@)t + YG@).
230
Глава VII
Первые два уравнения из B3) дают
п\ т\ 5% sin a
uY{t) =
5kgcosa
^1
C0)
Из B9) следует, что если в начальный момент скорость центра масс
и скорость точки касания не коллинеарны, то на стадии движения со
скольжением центр шара движется по параболе. Согласно B8), такое
движение происходит до момента t = t* где
и =
1kg •
C1)
Zi
При t = t» имеем vp = 0; скольжение прекращается и начинается
стадия качения шара (с верчением). Так как V?> = 0, то из B4) следует,
что на стадии качения сила трения равна нулю. Из B2) тогда получаем,
что центр масс движется по прямой. Согласно B3), угловая скорость ш
шара при качении постоянна по величине и направлению. Точка D на
плоскости движется по прямой, а на поверхности шара — по неизмен-
неизменной окружности, плоскость которой перпендикулярна вектору ш.
При переходе в режим качения центр шара движется по касатель-
касательной к параболе B9). Если эта касательная составляет тупой угол с на-
начальной скоростью центра шара, то шар может повернуть назад: явле-
явление, хорошо известное игрокам на бильярде.
114. Об уравнениях дви-
движения тяжелого тела произ-
произвольной выпуклой формы.
Пусть тело движется по непо-
неподвижной горизонтальной плоскос-
плоскости, опираясь на нее одной точкой
своей выпуклой поверхности, не
имеющей заострений и ребер. Дви-
Движение происходит в поле тяжести.
Движение тела будем изучать
по отношению к неподвижной сис-
системе координат OXYZ с началом
рис ]дд в некоторой точке опорной гори-
горизонтальной плоскости и осью OZ,
направленной вертикально вверх (рис. 119). Единичный вектор этой
оси обозначим п. С движущимся телом жестко свяжем систему ко-
координат Gxyz с началом в центре масс тела и осями, направленными
вдоль главных центральных осей инерции. Радиус-вектор р точки D,
которой тело касается плоскости, относительно центра масс имеет в
D(x,y,z)
§^. Движение тяжелого твердого тела 231
системе координат Gxyz компоненты х, у, z. Уравнение поверхности,
ограничивающей тело, в системе координат Gxyz запишем в виде
f(x, у, z) = 0, C2)
выбрав знак функции / так, чтобы совпадающий с п единичный век-
вектор внутренней нормали к поверхности C2) в точке D вычислялся по
формуле
gradj
п =
|grad/|
Пусть m — масса тела, g — ускорение свободного падения, v —
скорость центра масс, ш — угловая скорость тела, К — его кинети-
кинетический момент относительно центра масс, a R — реакция плоскости.
Уравнения движения тела можно записать в виде двух векторных урав-
уравнений:
v +ш х v = -gn + ^R C4)
K+u>xK = pxR, C5)
выражающих теоремы об изменении количества движения и кинети-
кинетического момента. В C4), C5) точкой обозначается дифференцирование
по времени в подвижной системе координат Gxyz.
Вектор п постоянен относительно неподвижной системы коорди-
координат OXYZ, поэтому он удовлетворяет уравнению Пуассона (см. п. 105)
п + и> х п = 0. C6)
Уравнения C4)-C6) справедливы и для движения без скольжения,
и для случая движения со скольжением при наличии трения, и для
абсолютно гладкой плоскости. Дополнительные к C4)-C6) уравнения,
отражающие характер взаимодействия тела и плоскости, для каждого
из этих случаев различны.
Пусть движение происходит без скольжения. Тогда скорость точ-
точки D касания тела и плоскости равна нулю. Это приводит к такому
векторному уравнению связи:
v + ш х р = 0. C7)
Уравнения C4)-C7) с учетом C2), C3) представляют собой полную
систему уравнений, позволяющую определить двенадцать неизвестных
232 Глава VII
величии: vx, vv, vz, p, q, r, x, y, z, Rx, Ry, Rz — компонент векто-
векторов v, ш, p, R в подвижной системе координат Gxyz.
Из теоремы об изменении кинетической энергии следует, что при
отсутствии скольжения полная механическая энергия тела постоянна,
т. е.
Е = Tjjnv2 + UК ¦ ш) - mg(p ¦ п) = const. C8)
Пусть теперь плоскость абсолютно гладкая. Тогда реакция R ор-
ортогональна плоскости:
R = Nn. C9)
Уравнение связи выражает условие того, что скорость точки D тела
направлена горизонтально и имеет вид
п ¦ {v + и> х р) = 0. D0)
Пусть Xq, Yq, Zq — координаты центра масс в неподвижной сис-
системе OXYZ. Соотношение D0) может быть также представлено в фор-
форме равенства
ZG = -n-(u>xp), D1)
которое, как нетрудно видеть, является следствием геометрической
связи Zg = —(р-п).
Уравнения C4), записанные в системе координат OXYZ, имеют
вид
XG = 0, YG=0, ZG = -g+^. D2)
Из первых двух уравнений следует, что в случае абсолютно гладкой
плоскости проекция центра масс тела на опорную плоскость движется
равномерно и прямолинейно. А третье уравнение с учетом соотноше-
соотношений D1) и C6) позволяет найти выражение для величины нормальной
реакции:
N = mg - run ¦ [ш х р + и) х р + и) х (и) х р)]. D3)
Уравнения C5), C6) с учетом C2), C3), C9), D3) образуют сис-
систему уравнений для нахождения шести неизвестных р, q, r, х, у, z.
Когда эти величины найдены, реакция и закон движения центра масс
тела по вертикали определяются из D3) и D2) .
§^. Движение тяжелого твердого тела 233
Отметим, что в случае абсолютно гладкой плоскости помимо ин-
интеграла энергии C8) и указанных выше интегралов, связанных с дви-
движением проекции центра масс на опорную плоскость, есть еще интег-
интеграл, выражающий постоянство проекции кинетического момента тела
на вертикаль:
К ¦ п = const. D4)
Этот интеграл следует из теоремы об изменении кинетического
момента, так как внешние силы, действующие на тело (сила тяжести
и реакция плоскости), направлены вертикально и не создают момента
относительно вертикальной оси, проходящей через центр масс тела.
Рассмотрим теперь случай движения тела со скольжением при на-
наличии трения, подчиняющегося законам Кулона. Пусть vp = v +ш х р
— скорость точки D шара и »д / 0. Тогда реакцию плоскости R можно
представить в виде
R = Nn + F, D5)
где Nn — нормальная реакция плоскости, a F — сила трения, которая
при заданном коэффициенте трения к определяется равенством
F = -fcJVjg. D6)
Уравнение связи, как и в случае абсолютно гладкой плоскости, за-
записывается в виде равенства D1), а величина нормальной реакции вы-
вычисляется по формуле D3).
При исследовании движения во всех трех рассмотренных случаях
следует иметь в виду, что величина нормальной реакции плоскости
должна быть неотрицательной. В противном случае возможен подскок
тела над плоскостью.
Глава VIII
Элементы небесной механики
§ 1. Задача двух тел
115. Уравнения движения. Небесная механика изучает движе-
движение небесных объектов, естественных и искусственных, под действием
сил гравитационного взаимодействия тел, сил сопротивлений, вызывае-
вызываемых наличием пылевых, газовых и других сред, сил светового давления
и т. п. Важнейшей для приложений задачей небесной механики являет-
является задача двух тел, а точнее — задача двух материальных точек.
Задача двух тел состоит в следующем. В пустом пространстве дви-
движутся две материальные точки, притягивающиеся одна к другой по
закону всемирного тяготения Ньютона. Заданы начальные положения
точек и их скорости. Требуется найти положения точек для любого
последующего момента времени.
Эта задача является основной в проб-
проблеме движения планет Солнечной системы
и искусственных спутников Земли, Луны и
планет, так как в большинстве случаев силы
взаимного притяжения планет, силы притя-
У жения спутника Земли планетами, силы со-
сопротивления космической среды, силы све-
светового давления и т. п. малы по сравнению
с силами гравитационного притяжения пла-
планеты и Солнца или спутника и Земли.
Замечательно то, что интегрирование
дифференциальных уравнений движения в
задаче двух тел сводится к квадратурам.
Для получения уравнений движения введем
инерциальную систему координат OaXYZ] ее начало совпадает, напри-
например, с центром масс Солнечной системы, а оси направлены на непо-
неподвижные звезды. Положения материальных точек Р и О задаются их
радиусами-векторами р и R соответственно (рис. 120). С точкой О свя-
свяжем поступательно движущуюся систему координат Oxyz, оси кото-
которой параллельны соответствующим осям системы OaXYZ. Положение
точки Р относительно точки О задается радиусом-вектором г.
х
/а
Рис. 120
; 1. Задача двух тел 235
Пусть Мит — массы точек О и Р соответственно, а 7 — универ-
универсальная гравитационная постоянная. Со стороны точки О на точку Р
действует сила F, определяемая законом всемирного тяготения:
Со стороны же точки Р на точку О действует сила — F. Радиусы-
векторы р и R удовлетворяют дифференциальным уравнениям
Так как г = р — R, то отсюда следует, что
at" r3 r3 r3
Если ввести обозначение к = j(m + М), то получим
A)
ш,- г"
Это уравнение определяет движение точки Р относительно точки О.
Если вектор-функция г = r(t) найдена, то определение движения от-
относительно системы координат OaXYZ не представляет труда. Дейст-
Действительно, пусть С — центр масс точек Р и О. Так как точки Р и О
образуют замкнутую систему, то, согласно теореме о движении центра
масс, точка С движется равномерно и прямолинейно; ее скорость пол-
полностью определяется начальными скоростями точек О и Р. Если Re
— радиус-вектор центра масс, то
71 /Г
= Rc-
p = Rc + ^^r, R = RC fr;r.
m + M m + M
116. Интеграл площадей. Второй закон Кеплера. Дифферен-
Дифференциальное уравнение A) описывает движение точки Р в подвижной сис-
системе координат Oxyz. Это уравнение можно (а для дальнейшего очень
удобно) интерпретировать как дифференциальное уравнение движения
точки Р относительно неподвижного притягивающего центра О под
действием центральной силы, равной —mkr/r3.
Согласно теореме об изменении кинетического момента, момент
количества движения точки Р относительно точки О остается посто-
постоянным. Отсюда следует, что
г х v = с. B)
236 Глава VIII
Это соотношение носит название интеграла площадей. В нем v = г —
скорость точки Р относительно точки О, с — векторная константа
интеграла площадей.
Проекции вектора с на оси системы координат Oxyz определяются
по формулам
сх = yz - yz, cy = zx - zx, cz = ху - ху, C)
в которых правые части вычисляются для любого (например, началь-
начального) момента времени.
Если сх = су = cz = О, то, очевидно, движение точки Р происхо-
происходит по прямой, проходящей через точку О. Если же хотя бы одна из
величин C) отлична от нуля, то вектор г во все время движения лежит
в одной и той же фиксированной плоскости, которая перпендикулярна
вектору с. Уравнение этой плоскости имеет вид
схх + Суу + czz = 0. D)
Таким образом, орбита точки Р является плоской кривой. Плоскость
орбиты однозначно определяется вектором с, или начальным положе-
положением Го и скоростью v0 точки Р относительно точки О.
Выясним геометрический смысл интеграла площадей. Введем сис-
систему координат Oxyz, совместив плоскость Оху с плоскостью орбиты.
Тогда с& = Су = 0, cz = ху - ху (с = ^с\ + с2у + с\ = \cz\j. Пусть в —
угол, который радиус-вектор г составляет с осью Ох. Тогда
x = rcos6, у = г sin в,
х = г cos В — Вт sin в, у = г sin в + вг cos в.
Отсюда и из выражения для cz получаем полярную форму интеграла
площадей:
^|=о, E)
Пусть теперь Р и Р' (рис. 121) — положения, которые занимает
точка Р в моменты t и t + At, где At — малая величина. Для площади
криволинейного треугольника ОРР' с точностью до величин первого
порядка малости включительно относительно Ав имеем выражение
AS = \г2Ав.
Разделив обе части этого равенства на At и устремив At к нулю, по-
получим
dt ~ 2 df ( '
; 1. Задача двух тел
237
Производная dS/dt в механике называется секторной скоростью. Из E)
и F) для нее получаем выражение
dS_lr_
dt ~ 2Cz-
Таким образом, секторная скорость точки Р постоянна. В этом состоит
геометрический смысл интеграла площадей.
Отсюда следует второй закон Кеплера:
площади, заметенные радиусом-вектором, иду- У
щим от Солнца к планете, пропорциональны про-
промежуткам времени, в которые они были замете-
заметены.
117. Интеграл энергии в задаче двух
тел. Кинетическая и потенциальная энергия точ-
точки Р в ее движении относительно притягивающе-
притягивающего центра О определяются равенствами
T=\mv\
П= -
тк
Рис. 121
Так как других сил, помимо потенциальных, нет и потенциал П не зави-
зависит от времени, то полная механическая энергия Е = Т + П постоянна.
Таким образом, в задаче двух тел существует интеграл энергии, кото-
который запишем в виде
= const).
G)
Константа энергии h определяется начальным положением и скоростью
точки Р:
Из интеграла G) следует, что при удалении точки Р от точки О
ее скорость убывает, а при приближении к точке О — возрастает. Ес-
Если h Js 0, то точка Р может уйти от точки О на сколь угодно большое
расстояние. Если же h < 0, то, как следует из G), расстояние г между
точками Р и О не может превзойти величину 2k/\h\, т. е. движение
точки Р происходит в ограниченной части пространства.
118. Интеграл Лапласа. Из A) и B) следует равенство
cx?,__i
(8)
Но так как
с х г = -у"(с х v)
(lib
238 Глава VIII
(г х г) х г = г(г ¦ г) - г (г ¦ г) = гг2 - rrr = г3 гг , гг = г34т (? ) >
г at V ' /
равенство (8) можно представить в виде
Отсюда следует, что
cxv + k^ = -f. (9)
Соотношение (9) называется интегралом Лапласа, а вектор / — век-
вектором Лапласа. Знак минус в правой части (9) введен для удобства
дальнейшего использования интеграла (9).
Из соотношения (9) сразу следует, что
с/ = 0, A0)
т.е. вектор Лапласа ортогонален векторной константе площадей и, сле-
следовательно, лежит в плоскости орбиты.
Модуль вектора Лапласа можно выразить через величину к и по-
постоянные h, с интегралов энергии и площадей. В самом деле, учитывая
ортогональность векторов с и v, из (9) имеем
f=kirl+c2v2 + f{cXv).r. A1)
Г2 '
Используя свойства смешанного произведения векторов и равенст-
равенство B), получаем
(с х v) ¦ г = —(г х v) • с = —с ¦ с = —с2.
Отсюда и из G) следует, что соотношение A1) может быть записано в
виде
f=k2+hc2. A2)
119. Уравнение орбиты. Первый закон Кеплера. При помощи
интеграла Лапласа и интеграла площадей можно получить уравнение
орбиты точки Р.
Из (9) сразу следует, что при с = 0 орбита точки будет прямолиней-
прямолинейной: г = — ?/. Пусть с /0. Умножим обе части интеграла Лапласа (9)
скалярно на г. Получим равенство
г-(схв) + |(гт) = ~{f -г).
; 1. Задача двух тел
239
Но, так как г ¦ (с х v) = —с , это равенство можно записать в виде
—с2 + кг = —fr cos v,
A3)
где v — угол между радиусом-вектором г точки Р и вектором Лапла-
Лапласа / (рис. 122). Угол v называется истинной аномалией.
Если ввести обозначения
A4)
Р =
fc'
то из A3) получим уравнение орбиты точки Р
в виде
Р
A5)
О
1 + е cos v'
Рис. 122
Соотношение A5) представляет собой уравнение конического сечения,
фокус которого находится в точке О. Величина р — параметр, е —
эксцентриситет орбиты. Орбита точки Р относительно точки О будет
либо эллипсом (е < 1), либо параболой (е = 1), либо гиперболой (е > 1).
При е = 0 орбита будет окружностью.
Для орбит планет справедлив первый закон Кеплера: пла-
планеты движутся по эллипсам, в одном из фокусов которых находится
Солнце.
120. Зависимость характера орбиты от величины началь-
начальной скорости. Первая и вторая космические скорости. Пусть
орбита точки Р не является прямолинейной, т. е. с ф 0. Если зада-
задано начальное расстояние го точки Р от точки О, то характер орбиты
точки Р вполне определяется величиной ее скорости vo- Рассмотрим
зависимость эксцентриситета орбиты от величины Vq.
Из A2) и A4) получаем выражение для эксцентриситета
Но константа энергии h равна Vq — 2k/r0. Отсюда следует, что ор-
орбита будет эллиптической (е < 1), если h < 0. Это означает, что
Vq < ^/2fc/ro. Скорости, удовлетворяющие этому неравенству, называ-
называются эллиптическими скоростями.
Если h = 0, т. е. vo = ^/2k/ro, то е = 1, и орбита будет парабо-
параболой. Скорость vq = ^/2k~frQ называется параболической. Она является
наименьшей скоростью, которую надо сообщить точке Р, находящей-
находящейся на расстоянии го от точки О, чтобы она удалилась на сколь угодно
большое расстояние от точки О.
240
Глава VIII
Орбита будет гиперболической (е > 1), если h > 0, т. е.
Такие скорости называются гиперболическими.
Первая космическая скорость vi — это круговая скорость у по-
поверхности Земли. Найдем ее величину. Пусть т — масса спутника, М
— масса Земли, j — универсальная гравитационная постоянная, g0 —
ускорение свободного падения у поверхности Земли. Тогда
mv,
A6)
Так как т <С М, то можно считать, что к = j(m + М) ~ jM. Поэтому
из A6) следует, что приближенно
Принимая радиус Земли г0 равным 6371 км, а величину g0 рав-
равной 9,82 м/с , получим, что vi ~ 7,91 км/с.
Вторая космическая скорость vu — это параболическая скорость
у поверхности Земли, т. е.
~ 11,2 км/с.
121. Третий закон Кеплера. Пусть орбита точки Р представ-
представляет собой эллипс с полуосями а и Ь. Из аналитической геометрии из-
известно, что величины аи 6 выражаются через параметр эллипса и его
эксцентриситет посредством формул
а =
Р
1-е2
Ь =
Р
A7)
Ближайшая к фокусу точка эллиптичес-
эллиптической орбиты называется перицентром, а
наиболее удаленная от фокуса — апо-
апоцентром. Перицентр и апоцентр обозна-
71 чены на рис. 123 буквами тг и а.
За время, равное периоду Т обраще-
обращения точки Р по орбите, радиус-вектор FP
заметет всю площадь эллипса. Учитывая,
что площадь эллипса равна жаЬ и что, со-
согласно интегралу площадей, секторная скорость точки Р постоянна и
равна с/2, получаем равенство
Рис. 123
ттаЬ = ±сТ.
A8)
; 1. Задача двух тел 241
Но из A4) и A7) следует, что с = у/рк и р = Ъ2/а. Поэтому из ра-
равенства A8) вытекает следующее выражение для периода обращения
точки Р:
Vk
Величина п = 2тг/Т является средней угловой скоростью вращения
радиуса-вектора FP, в астрономии ее называют средним движением.
Согласно A9),
п=%- B0)
3'2
Рассмотрим две точки Pi и Р^ массой nil и m-i- Если пренебречь вза-
взаимным притяжением этих точек, то каждая из них будет двигаться
вокруг точки О по коническому сечению. Пусть орбиты точек будут
эллиптическими. Тогда для периодов их обращения имеем выражения
ц + М)' ^i(m2 + М)
Отсюда следует, что
B1)
При nil <C M и ni2 <C M это соотношение переходит в следующее
приближенное равенство:
Т2 а3
-
Равенство B2) выражает трети й закон Кеплера: квадраты пери-
периодов обращения планет вокруг Солнца относятся как кубы их больших
полуосей.
122. Время в кеплеровском движении. Уравнение Кепле-
Кеплера. В предыдущих пунктах определен геометрический характер ор-
орбиты точки Р. Орбита является коническим сечением и находится в
плоскости, перпендикулярной векторной константе площадей с. Поло-
Положение самой орбиты в этой плоскости однозначно определяется векто-
вектором Лапласа /, который проходит через точку О, являющуюся фокусом
конического сечения, и направлен на перицентр тг.
242
Глава VIII
Чтобы закончить решение задачи двух тел, осталось найти закон
движения точки Р по ее орбите. Будем считать, что орбита являет-
является эллиптической. Из интеграла площадей имеем г2г> = с. Отсюда, из
уравнения орбиты A5) и равенств A4), A7) и B0) получаем
dv с с /л . \2 vk ,
л = 2 = -%(l + ecosi/) = ——(
at г р » '
A-е2K/2
A + ecosvf.
Пусть т — время прохождения точки Р через перицентр. Тогда из
последнего уравнения получаем неявную зависимость v = v{t):
V
I
dv
есозг/J A-е2K/2
(t - r).
B3)
Если отсюда найдена функция v = v(t), то закон движения точки по
орбите известен.
Найденное решение задачи двух тел зависит от шести произволь-
произвольных постоянных. За них могут быть приняты константа т и пять из се-
семи констант сх, cv, cz, h, fx, fv, fz, связанных двумя соотношениями A0)
и A2).
Нахождение зависимости v = v(t) из трансцендентного уравне-
уравнения B3) представляет собой довольно трудную задачу. Введем вмес-
вместо v новую переменную Е, через которую v выражается очень просто,
а зависимость Е = E(t) определяется уравнением, хотя тоже трансцен-
трансцендентным, но значительно более простым, нежели уравнение B3).
Рис. 124
; 1. Задача двух тел 243
Связь между Е и v зададим равенством
B4)
Величина Е называется эксцентрической аномалией. Можно показать,
что она имеет следующий геометрический смысл. Через точку Р про-
проведем (рис. 124) перпендикуляр к большой полуоси орбиты до его пере-
пересечения в точке Q с окружностью, построенной на большой оси как на
диаметре. Угол, который составляет отрезок, соединяющий центр эл-
эллипса и точку Q, с большой полуосью орбиты и будет эксцентрической
аномалией Е. Зависимость Е от v представлена на рис. 125. Из B4)
следует, что
7
аи =
1 — ecosE 1 — ecosE
Используя эти соотношения, получаем такое выражение для интег-
интеграла из левой части равенства B3):
v Е
^ 5- = - (l-ecosE)dE =
A + ecosisJ A-е2K/2 JK ' ,„..
о о B5)
= п \з^Е~еа]пЕ^
A - е2K'2
Введем обозначение n{t — r) = М; величину М в астрономии называют
средней аномалией. Тогда из B3) и B5) имеем следующее уравнение:
E-esinE = M. B6)
Оно называется уравнением Кеплера.
123. Кеплеровские элементы орбиты. Решение задачи двух
тел зависит от шести произвольных постоянных, определяемых началь-
начальными условиями движения. Их можно вводить по-разному и не обя-
обязательно именно так, как это было сделано в предыдущих пунктах в
процессе решения задачи двух тел. Рассмотрим произвольные постоян-
постоянные, которые носят название кеплеровских элементов орбиты и очень
широко используются в небесной механике. За кеплеровские элементы
принимаются следующие шесть величин, однозначно определяемых по
начальным условиям: п, г, р, е, ш, т.
244
Глава VIII
z,.
f
Рис. 126
Смысл величин р, е, т ясен из пре-
предыдущих пунктов: р — параметр орби-
орбиты, е — ее эксцентриситет, т — время
прохождения через перицентр. Величи-
Величина $7 — это угол, который составляет с
осью Ох линия пересечения плоскости
орбиты с плоскостью Оху (рис. 126); ве-
У личина п называется долготой восходя-
восходящего узла. Элемент г представляет собой
угол между плоскостью орбиты и плос-
плоскостью Оху; величину г называют на-
наклонением орбиты. Параметр ш опреде-
определяет положение орбиты в ее плоскости, он называется угловым рас-
расстоянием перицентра от узла и равен углу между направлением из
точки О на перицентр и линией пересечения плоскости орбиты с плос-
плоскостью Оху.
124. О задаче трех и более тел. Задача п тел (и ^ 2) состоит в
следующем. В пустоте находятся п материальных точек, взаимодейст-
взаимодействующих по закону всемирного тяготения Ньютона. Заданы начальные
положения и скорости точек. Требуется найти положения всех точек
как функции времени. Эта задача не решена до сих пор. Более того,
показано, что даже в случае трех тел помимо классических интегра-
интегралов, существование которых следует из общих теорем об изменении
количества движения, кинетического момента и кинетической энергии,
дифференциальные уравнения движения не имеют других интегралов,
которые выражались бы через алгебраические или через однозначные
трансцендентные функции координат и скоростей точек.
Для небесной механики и космодинамики наиболее важна так на-
называемая ограниченная задача трех тел. Она состоит в изучении дви-
движения точки малой массы под действием притяжения двух конечных
масс в предположении, что точка малой массы не влияет на движение
точек конечных масс. Тем самым в ограниченной задаче трех тел точ-
точки конечных масс движутся по орбитам, определяемым задачей двух
тел, так что движение этих двух точек известно. Таким образом, ана-
анализ ограниченной задачи трех тол сводится к исследованию движения
только одной точки малой массы. Конечно, эта задача значительно про-
проще общей (неограниченной) задачи трех тел. Но и она не интегрируется
(точнее, не проинтегрирована) в квадратурах.
i 2. Движение твердого тела в гравитационном поле
245
§ 2. Движение твердого тела в центральном
ньютоновском гравитационном поле
125. Главный вектор сил тяготения. Гравитационный мо-
момент. В обычных, «земных» задачах механики, связанных с ее приме-
применениями к устройствам, функционирующим вблизи или на поверхности
Земли, силы притяжения, приложенные к двум материальным точкам
равных масс, считаются равными и по величине, и по направлению.
Это приводит к известному положению о совпадении центра масс и
центра тяжести и, как следствие, к равенству нулю главного момента
сил тяготения (гравитационного момента) относительно центра масс.
В действительности силы притяжения различ-
различных точек тела Землей, как правило, не будут па-
раллельными, так как они направлены к ее центру1.
Кроме того, разные точки тела находятся, вообще,
на разных расстояниях от центра Земли. По этим
причинам силы тяготения не обязательно должны
приводиться к равнодействующей, проходящей че-
через центр масс тела: возможен еще и гравитацион-
гравитационный момент относительно центра масс. Появление
гравитационного момента можно пояснить очень
простым примером. Пусть две точки Pi и Р^ оди-
одинаковых масс соединены жестким стержнем прене-
пренебрежимо малой массы. Пусть О — середина стерж-
стержня (центр масс точек Pi и Рг)> а О, — притягива-
притягивающий центр (рис. 127). Пусть О*Р\ > О*Р2, тогда если hi — плечо
силы Fi, a hi — плечо силы F<i относительно точки О, то из сравнения
площадей треугольников O*PiO и О^Р^О получим
qj\
hi
hi
> i.
Отсюда и из неравенства F<i > i*i, справедливого при O*Pi > O*Pi,
следует, что F^hi > F\h\. Таким образом, появляется момент, стремя-
стремящийся расположить стержень PiPi вдоль прямой 0*0.
В обычных «земных» условиях гравитационные моменты малы по
сравнению с другими воздействиями. В задачах же небесной механики
'Мы предполагаем, что Земля представляет собой либо однородный, либо неод-
неоднородный шар, в каждой точке которого плотность зависит только от расстоянии
этой точки до центра шара. Можно показать, что в этом случае гравитационное по-
поле Земли такое же, какое создавалось бы материальной точкой, обладающей массой
Земли и помещенной в ее геометрическом центре.
246
Глава VIII
они часто играют решающую роль. Например, движение Луны относи-
относительно центра масс почти полностью определяется гравитационными
моментами, обусловленными притяжением Земли.
Орбита
центра масс
*о.
Рис. 128
Рассмотрим задачу о движении свободного твердого тела в цен-
центральном ньютоновском гравитационном поле. В соответствии с п. 108
для получения дифференциальных уравнений движения нужно знать
главный вектор сил тяготения и их гравитационный момент относи-
относительно центра масс тела.
Пусть OXYZ — система координат с началом в центре масс те-
тела и осью OZ, направленной по прямой, соединяющей притягивающий
центр О* и центр масс О тела (рис. 128). Ось OY направлена по би-
бинормали к траектории центра масс в ту сторону, откуда его движе-
движение видно совершающимся против часовой стрелки, ось ОХ дополняет
оси OY и OZ до правой прямоугольной системы координат. Систему
координат OXYZ обычно называют орбитальной.
Пусть R — радиус-вектор центра масс тела относительно притя-
притягивающего центра, а г — радиус-вектор выделенного в теле малого
элемента массой dm (рис. 129). Сила притяжения элемента dm опреде-
определяется по формуле
dr = —7 ъ г, A)
где 7 — универсальная гравитационная постоянная, а М — масса при-
§ 2. Движение твердого тела в гравитационном поле 247
тягивающего центра О*. Главный вектор F сил притяжения тела полу-
получается из A) путем интегрирования по всему объему тела. Произведем
вычисления, считая линейные размеры тела много меньшими расстоя-
расстояния от центра масс тела до притягивающего центра. Это предположение
вполне приемлемо для естественных и искусственных спутников пла-
планет.
Пусть р — радиус-вектор элемента dm, а X, Y, Z — его компо-
компоненты в орбитальной системе координат. Тогда
= R+p, r = R\ll + 2? + ?. B)
Если пренебречь величинами порядка (p/RJ и выше, то из B) получим
разложение величины 1/г3 в ряд Тейлора в виде
д3 { R)
Теперь надо величину г из B) и величину 1/г3 из C) подставить в
формулу A) и произвести интегрирование по всему объему тела. При
этом следует учесть, что так как центр масс тела находится в начале
координат, то
X dm= Y dm= / Z dm = 0.
Произведя интегрирование, получим, что с упомянутой точностью
главный вектор сил тяготения задается формулой
где т — масса тела. Отсюда следует, что если пренебречь величина-
величинами порядка (p/RJ и выше, то размеры тела не влияют на величину
и направление главного вектора сил тяготения. Следовательно, в рас-
рассматриваемом приближении можно считать, что центр масс движется
по коническому сечению. Это движение подробно изучено в предыду-
предыдущем параграфе.
Найдем теперь гравитационный момент. Пусть Oxyz — система
координат, жестко связанная с твердым телом; ее оси направлены по
главным центральным осям инерции тела (рис. 129). Ориентацию твер-
твердого тела относительно орбитальной системы координат будем опреде-
определять при помощи углов Эйлера ф, в, (р. Элементы ojj матрицы перехода
от системы координат Oxyz к системе OXYZ выражаются через углы
Эйлера по формулам C) п. 19.
248 Глава VIII
На основании формулы A) для главного момента Мо сил тяготе-
тяготения относительно центра масс получаем выражение
/f n X Г
р х dF = —jM I —j—dm, D)
где интегрирование производится по всему объему тела. Вычисление
интеграла D) проведем, используя систему координат Oxyz. В этой
системе
р = хг + yj + zk, R = R(a31i + a32j + a33k), E)
r = R + p=(x + Ra31)i + (y + Ra32)j + {z + Ra33)k, F)
p x r = R[(ya33 - za32)i + B:031 - xa33)j + {xa32 - ya31)k]. G)
Если в разложении величины 1/г3 в ряд Тейлора пренебречь величина-
величинами порядка (p/RJ и выше, то получим
уа32 + za33)\ . (8)
С той же точностью из G) и (8) получаем
уа32 + za33) [(уа33 - za32)i+
(9)
+ (za31 - xa33)j + (ха32 - уа31)к].
Подставим это выражение в формулу D) и произведем интегрирова-
интегрирование. Так как оси Ox, Oy, Oz являются главными центральными осями
инерции тела, то выполняются равенства
/ х dm = у dm = / z dm = О,
J J J AQ)
/ xy dm = J xz dm = J yz dm = 0.
Произведя интегрирование и учтя равенства A0), получим
ш ^М f 2 2 2 2
Мо = о / \\У ~ z )а32Язз* + (z - х )а3заз1,7 +
R J A1)
+ (ж2 - y2)a31a32k]dm.
§ 2. Движение твердого тела в гравитационном поле 249
Замечая, что
f(y2 -z2)dm = C-B, f(z2-x2)dm = A-C,
I\x2 - y2)dm = B-A,
где А, В и С — моменты инерции тела относительно осей Ох, Оу
и Oz соответственно, получаем из A1) такие выражения для проекций
Мх, Му, Mz гравитационного момента на оси Ох, Оу, Oz связанной с
телом системы координат:
M« = ~Ьг(С - в)а32п33, Му = -J^3-(A - С)а33а31,
Ьм A2)
Mz = —^~{В — ^4)аз1Яз2-
R6
Отметим, что выражения A2) являются приближенными. В них отбро-
отброшены величины, порядок которых не ниже (p/RJ.
126. Уравнения движения тела относительно центра масс.
Для получения уравнений движения тела относительно центра масс ис-
используем динамические уравнения Эйлера
А——\- (С — B)qr = Мх, В~Т + (^ ~ С)гр = Му,
A3)
С^- + {В- A)pq = Mz.
Величины Мх, Му, Mz вычисляются по формулам A2), в которых
величина R имеет вид
1 + ecosi/
где р' и е — параметр и эксцентриситет орбиты, v — истинная анома-
аномалия, представляющая собой угол между радиусом-вектором R центра
масс тела и линией, проходящей через притягивающий центр О* и пе-
перицентр орбиты. Согласно п. 122, величина v удовлетворяет уравнению
^ = ^(l + ecos*/J. A5)
v
Так как масса тела m много меньше массы притягивающего центра, то
можно считать, что к =
250 Глава VIII
Выразим проекции р, q, r абсолютной угловой скорости тела на
оси Ox, Oy, Oz через углы Эйлера, их производные и угловую ско-
скорость A5) движения центра масс по орбите. Для этого заметим, что
твердое тело участвует в сложном движении: оно вращается относи-
относительно орбитальной системы координат OXYZ, а орбитальная система
координат за счет движения центра масс по орбите вращается вокруг
оси OY. Проекции угловой скорости первого из указанных вращений
получаются из кинематических уравнений Эйлера, а угловая скорость
второго вращения направлена по оси OY и равна г>. Поэтому
р = tp sin в sin ip + в cos ip + vail,
q = ips'm6 costp — dsimp + va,22, A6)
p = 1p COS в + ф + i>U2Z,
где величины а^ определены равенствами C) п. 19.
Система семи уравнений A3), A5) и A6) с учетом равенств A2),
A4) и формул C) п. 19 является замкнутой системой дифференциаль-
дифференциальных уравнений, описывающей движение твердого тела относительно
центра масс. Эти уравнения или их модификации широко используют-
используются при изучении движения искусственных спутников Земли.
Если в A3) и A6), использовав A5), ввести вместо времени t но-
новую независимую переменную — истинную аномалию и, то получим
систему, состоящую из шести уравнений первого порядка. Если затем
величины р, q, r из A6) подставить в A3), то придем к трем уравнени-
уравнениям второго порядка относительно углов Эйлера ф, в, (р.
Отметим еще, что если орбита центра масс эллиптическая и a —
большая полуось орбиты, то согласно п. 120-122
и2 <л '-ecosi/K,
R3 A-е2K
где постоянная п есть среднее движение центра масс, п = л/jM/а3/2; на
круговой орбите (е = 0) п будет угловой скоростью вращения радиуса-
вектора R.
127. Относительное равновесие твердого тела на круговой
орбите. Если центр масс тела движется по круговой орбите, то сущест-
существуют движения, отвечающие положениям относительного равновесия.
Относительным равновесием тела мы называем такое его движение,
когда оно покоится в орбитальной системе координат, т. е. для таких
§ 2. Движение твердого тела в гравитационном поле 251
движений ф = const, в = const, <p = const. Одно из таких движений
определяется равенствами
¦ф = 0, в = 0, <р = 0. A8)
Длл этого движения оси Ох, Оу и Oz связанной с телом системы ко-
координат направлены вдоль осей OX, OY и OZ орбитальной системы
координат соответственно.
Чтобы убедиться в существовании решения A8), заметим, что из
уравнений A6) и формул C) п. 19 следует, что на круговой орбите
при <ф = в = <р = 0 имеем a,j = 6ij F,j — символ Кронекера),
р = 0, г = О, q = п = const. Отсюда следует, что для решения A8)
гравитационные моменты A2) обращаются в нуль и уравнения A3)
тождественно удовлетворяются.
Можно показать, что существуют двадцать четыре геометричес-
геометрически различных положения равновесия. Они соответствуют всевозмож-
всевозможным случаям совпадения главных центральных осей инерции спутника
с осями орбитальной системы координат. С механической точки зрения
(в рамках исследования задач динамики тела в гравитационном поле)
существенно лишь то, какая из главных центральных осей инерции тела
лежит вдоль данного направления. Очевидно, что из двадцати четырех
геометрически различных положений равновесия механически различ-
различных существует только шесть: для каждого из трех положений одной
из осей инерции (по радиусу-вектору центра масс, по касательной и по
нормали к орбите) существует два различных положения другой оси
инерции (что автоматически влечет два различных положения третьей
оси инерции).
Можно также показать, что если гравитационный момент опре-
определяется согласно приближенным выражениям A2), то не существует
положений относительного равновесия, для которых главные централь-
центральные оси инерции тела не совпадали бы с осями орбитальной системы
координат.
Для движений, соответствующих положениям относительного рав-
равновесия, вектор абсолютной угловой скорости тела направлен по нор-
нормали к плоскости орбиты, а величина абсолютной угловой скорости
тела равна величине угловой скорости п кругового движения центра
масс тела, т. е. период вращения тела равен периоду движения центра
масс. Отсюда следует, что тело все время обращено к притягивающе-
притягивающему центру одной и той же своей стороной. В природе примером такого
движения является движение Луны (она «смотрит» на Землю одной сто-
стороной) и многих спутников планет, в технике — большое количество
искусственных спутников Земли.
252
Глава VIII
128. Плоские движения. Дифферен-
Дифференциальные уравнения движения твердого те-
тела в центральном ньютоновском гравитаци-
гравитационном поле допускают решения, которые от-
отвечают плоским движениям тела. Для та-
таких движений одна из главных центральных
осей инерции тела все время перпендикуляр-
перпендикулярна плоскости орбиты центра масс.
Получим дифференциальное уравнение
плоских движений. Пусть для рассматривае-
рассматриваемых движений главная ось инерции Oz тела
перпендикулярна плоскости орбиты, т. е. во
все время движения
Рис. 130
7Г
2'
¦ф = 7Г.
Тогда формулы C) п. 19 переходят в следующие:
Оц = —
Я21 = 0,
а12 = simp,
aii = 0,
ai3 = 0,
Я23 = 1,
азз = 0.
A9)
B0)
Для движения A9) оси инерции тела Ох и Оу лежат в плоскости орби-
орбиты. Их расположение относительно осой ОХ и OZ орбитальной систе-
системы координат показано на рис. 130.
Из A2), A6) и A7) получаем, что при выполнении равенств A9)
имеют место соотношения
р = 0, 9 = 0, г = ф + г>,
Мх = 0, Му = 0,
Mz =
Зп2
A-е2)
г A + e cos vK (В — A) sin (p cos (p.
B1)
B2)
Подставив B1) и B2) в систему A3), получим, что первые два ее урав-
уравнения удовлетворяются тождественно, а третье запишется в виде
С(ф + i>) = 3-
ГA + е cos г/K (В - A)smipcosifi. B3)
A-е2K
Это уравнение вместе с первым из соотношений A7)
v =
п
A-е2K/2
A + ecosi/J
B4)
§ 2. Движение твердого тела в гравитационном поле 253
образует систему двух дифференциальных уравнений, описывающих
плоские движения твердого тела. Удобнее, однако, вместо двух уравне-
уравнений B3), B4) рассматривать одно дифференциальное уравнение, кото-
которое получается из уравнения B3), если в нем при помощи B4) ввести
вместо времени t новую независимую переменную — истинную ано-
аномалию v. Имеем соотношения
¦ _ dip . _ п dip
^ ~ dvV ~ (\ _ р2^3/2 dv
^~ A-е2K/2 Г*' с
= п , „ A + ecosi/K A + ecosi/)—% - 2esini/-^
A - е1N У dv1 dv
vfvf{l
dv A - e2K
Подставив ф и v в уравнение B3), получим
^ -2esini/l =
d J
Ct 94,(l + ecost/) [(l + ecosi/)| 2esini/^
A - e2K I dv2 dv
= 3 n 2 A + cos г/K (-В - Л) sin <p cos <y9.
Отсюда следует дифференциальное уравнение плоских движений твер-
твердого тела в центральном ньютоновском силовом поле1
A + ecosi/)—¦?¦ — 2esini/—— + 3—^— sin<^cos<^ = 2esini/. B5)
йг/ dv С
Пусть орбита центра масс тела является круговой. Если ввести обозна-
обозначение 2ip = а, то при е = 0 из B5) получим уравнение, описывающее
плоские движения тела на круговой орбите в виде
^^^ 0 (" = "*)• B6)
^f+ 3
dv <-/
Если А > В, то уравнение B6) будет уравнением движения физичес-
физического маятника. Его движение подробно исследовано в п. 93-96. Если
же А < В, то мы снова можем получить уравнение маятника, если
вместо замены переменной 2ip = а сделаем замену 2ip = а + ж. Ес-
ли А = В, то ф = 0, т. е. тело равномерно вращается вокруг нормали к
плоскости орбиты с произвольной угловой скоростью.
хЭто уравнение впервые получено в статье: Белецкий В. В. О либрации спутника.
В сб.: Искусственные спутники Земли, 1959, вып. 3, М.: Изд-во АН СССР, с. 13 - 31.
Глава IX
Динамика системы переменного состава
§ 1. Основные понятия и теоремы
129. Понятие о системе переменного состава. До сих пор мы
считали неизменными как массы т„ точек Р„ {у = 1, 2, ... , N), со-
составляющих систему, так и число N точек системы. Но в природе и
технике часто бывает так, что в некоторые моменты времени какие-
либо точки выходят из рассматриваемой материальной системы или
входят в нее. В результате этого состав системы, т. е. совокупность то-
точек, образующих данную систему, а значит, вообще говоря, и ее масса
будут со временем изменяться.
Будем говорить, что данная механическая система является систе-
системой переменного состава, если либо масса системы, либо материальные
точки, из которых она состоит, либо то и другое меняются со временем.
Случаи движения системы переменного состава можно встретить
во многих явлениях природы. Так, например, масса Земли возраста-
возрастает вследствие падения на нее метеоритов. Масса падающего метеорита
уменьшается, так как частицы метеорита отрываются от него, благода-
благодаря воздействию атмосферы, или сгорают. У плавающей льдины, вслед-
вследствие ее таяния, масса убывает и возрастает при замерзании льда или
из-за падения снежинок на ее поверхность. Примерами систем перемен-
переменного состава в технике могут служить: движущийся транспортер, на
который в некоторые моменты кладут (или с которого снимают) гру-
грузы; ракеты различных систем, масса которых изменяется в процессе
сгорания топлива; реактивный самолет, масса которого увеличивает-
увеличивается за счет воздуха, засасываемого в его двигатель, и уменьшается при
отбрасывании продуктов сгорающего топлива.
Почти все выводы, полученные в предыдущих главах, о движении
механических систем опирались на второй закон Ньютона, устанавли-
устанавливающий зависимость между ускорением точки и действующей на нее
силой. Однако второй закон Ньютона справедлив только для точки по-
постоянного состава. Динамика систем переменного состава требует осо-
особого рассмотрения.
Примем следующее предположение о математической модели сис-
системы переменного состава: малы и массы отделяющихся или присоеди-
присоединяющихся к системе точек, и промежутки времени между двумя их по-
§ 1. Основные понятия и теоремы 255
следовательными присоединениями или отделениями. Это предположе-
предположение дает возможность принять идеализацию, при которой масса Mi(t)
вышедших из системы точек и масса Мг(?) вошедших в систему то-
точек — непрерывные и дифференцируемые функции времени.
Если масса M(t) системы при t = О равнялась Mo, to с течением
времени она меняется по закону
M(t)=M0-M1(t)+M2(t),
где Mi, M2 — неубывающие неотрицательные функции времени и M(t)
непрерывна и дифференцируема.
Материальной точкой переменного состава мы будем называть
частицу переменного состава, настолько малую, что ее положение и
движение можно определить как для объекта, не имеющего размеров.
130. Теорема об изменении количества движения. Пусть
некоторая совокупность материальных точек движется относительно
инерциальной системы координат Oxyz. Рассмотрим замкнутую по-
поверхность S, которая перемещается относительно Oxyz и деформиру-
деформируется. Материальные точки при своем движении могут входить в об-
область пространства, ограниченную поверхностью 5, и могут выходить
из нее.
Обозначим G систему переменного состава, образованную матери-
материальными точками, находящимися внутри поверхности S. Количество
движения рассматриваемой системы обозначим Q.
Зафиксируем момент времени t = t' и обозначим G* систему по-
постоянного состава, образованную теми и только теми материальными
точками, которые в момент t' заполняли объем, ограниченный поверх-
поверхностью S. Количество движения системы G* обозначим Q*. Так как
при t = t' системы G и G* совпадают, то в этот момент
Q=Q*. A)
В момент времени t" = t' + At количества движения систем G и G* бу-
будут иметь соответственно значения Q + AQ и Q* + AQ*. На рис. 131
сплошной линией показано положение поверхности S в момент t", a
штриховой — положение поверхности, ограничивающей объем, запол-
заполненный в тот же момент t" теми материальными точками, которые
образуют систему G*. Очевидно, что
Q + AQ=Q* + AQ*-AQ1 + AQ2, B)
где AQi — сумма количеств движения в момент t" тех материальных
точек, которые за время At вышли из объема, ограниченного поверх-
поверхностью 5, a AQ2 — сумма количеств движения в момент t" точек,
256
Глава IX
вошедших за время At в объем, ограниченный этой поверхностью. На
рис. 131 эти точки заполняют соответственно объемы G\ и G2.
Из A) и B) получаем
Рис. 131
AQ = AQ* -
AQ2.
C)
Пусть i?(e) — главный вектор внешних сил, при-
приложенных к системе G (а следовательно, и к систе-
системе С*) в момент времени t'. Поскольку система G*
является системой постоянного состава, то к ней
применима теорема об изменении количества дви-
движения, т. е.
dQ*
dt
D)
Разделив обе части равенства C) на At и перейдя к пределу при At —>¦ О,
получим с учетом равенства D)
4
dt
где F = Fx + F2, a
= - lim
At-Ю At
F2 = lim
AQ2
дТАо At
E)
F)
Векторные величины F± и F2 имеют размерность силы. Условим-
Условимся называть эти величины реактивными силами. Реактивная сила F\
возникает за счет отделения материальных точек от рассматриваемой
системы, a F2 — за счет присоединения точек.
Таким образом, теорема об изменении количества движения сис-
системы переменного состава выглядит так же, как и в случае систем по-
постоянного состава; надо только в число внешних сил системы включить
еще добавочную (реактивную) силу F = F\ + F2.
131. Теорема об изменении кинетического момента. Пусть
А — неподвижная точка в инерциальной системе координат Oxyz,
— главный момент внешних сил и Ка — кинетический момент
системы G относительно точки А. Совершенно аналогично п. 130 можно
показать, что
_ м(е)
М
dt
М
(F)
G)
§ 2. Движение материальной точки переменного состава 257
где Мд ' = МА1' + Мд2' — дополнительный момент, возникающий за
счет того, что система G является системой переменного состава:
= lim
A1 д*-и) At ' Л2 At-ю At
Здесь AKai — сумма моментов количеств движения при t = t" тех
материальных точек, которые за время At вышли из объема, ограни-
ограниченного поверхностью S, а АКд2 — аналогичная величина для точек,
вошедших внутрь поверхности S.
§ 2. Движение материальной точки переменного
состава
132. Дифференциальное уравнение движения. Пусть мате-
материальная точка Р переменного состава движется относительно инерци-
альной системы отсчета Oxyz. Масса точки Р изменяется со временем
вследствие одновременного отделения и присоединения к ней малых
частиц материи, размерами которых можно пренебречь.
Пусть Mi — абсолютная скорость (скорость относительно Oxyz)
частицы, которая отделяется от точки Р в момент времени t', а и2
— абсолютная скорость частицы, которая присоединяется к Р в этот
момент. Пусть АМ\ и АМ2 — соответственно массы отделяющейся
и присоединяющейся частиц. Тогда, применяя обозначения предыду-
предыдущего пункта, имеем следующие равенства, справедливые с точностью
до членов первого порядка малости включительно относительно At
и AMi (i = 1, 2):
AQ2 = AM2u2,
и, следовательно, согласно формулам F) п. 130,
-, dM2
Здесь, как и в п. 129, Mi(t) и M2(t) представляют собой суммарную
массу всех частиц, отделившихся от точки Р и, соответственно, при-
присоединившихся к ней за время t, прошедшее от момента t = 0, когда
масса точки Р была равна Mq.
Пусть v — абсолютная скорость точки Р. Тогда ее количество
движения вычисляется по формуле
Q=Mv. B)
258 Глава IX
Подставив A) и B) в уравнение E) п. 130, получим
где R — равнодействующая сил, приложенных к точке Р. Используя
соотношение М = Mq — М\ + Mi, это равенство можно переписать в
виде
dt dt dt dt
^v Mg = R
dt dt dt dt dt
Перенеся первые два слагаемых левой части в правую часть равенства,
окончательно получим
Уравнение C) является дифференциальным уравнением движения точ-
точки переменного состава и называется обобщенным уравнением Мещер-
Мещерского.
Отметим, что щ — v = ulr — скорость отделяющихся частиц от-
относительно точки Р. Аналогично и^ — v = и2г — скорость присоединя-
присоединяющихся частиц относительно точки Р.
Пусть имеет место только отделение частиц. Тогда М2 = 0,
M(t) = Мо - M±(t) и dM/dt = —dMi/dt. В этом случае уравнение C)
принимает вид
Уравнение D) называется уравнением Мещерского. Из него видно,
что эффект отделения частиц эквивалентен действию на точку Р доба-
добавочной силы F± = —j—Uir (называемой реактивной силой). Аналогично
можно рассмотреть и эффект присоединения частиц к точке Р. Реак-
Реактивная сила численно равна произведению величины dM/dt (называе-
(называемой секундным расходом массы) на относительную скорость отделения
(или присоединения) частиц к точке переменного состава Р. В случае
отделения частиц реактивная сила направлена противоположно векто-
вектору Uir относительной скорости отделяющихся частиц, а в случае присо-
присоединения частиц реактивная сила и относительная скорость щг имеют
одинаковые направления.
Пусть имеет место только отделение частиц от точки Р перемен-
переменного состава. Если абсолютная скорость щ отделяющихся частиц равна
нулю, то уравнение Мещерского D) примет вид
^ = R
dt dt
§ 2. Движение материальной точки переменного состава 259
или
d(Mv)
= R,
dt
т. е. если абсолютная скорость отделяющихся частиц равна нулю, то
производная по времени от количества движения точки Р переменного
состава равна равнодействующей приложенных к ней сил. Если же от-
относительная скорость щг отделяющихся частиц равна нулю, то из D)
получаем
т. е. если относительная скорость отделяющихся частиц равна нулю, то
уравнение движения точки Р переменного состава записывается фор-
формально в том же виде, что и уравнения движения точки постоянного
состава.
133. Движение ракеты вне поля сил. Пусть точка Р перемен-
переменного состава движется в безвоздушном пространстве вне поля сил. Дви-
Движение точки моделирует, например, движение ракеты в космическом
пространстве, если ракету принять за точку и пренебречь силами со-
сопротивления космической среды, гравитационным притяжением, сила-
силами светового давления и т. п. Тогда R = 0 и из равенства D) получаем
векторное уравнение движения ракеты
где иг — относительная скорость отделения продуктов сгорания топ-
топлива. Будем считать, что скорость иТ постоянна и имеет направление,
противоположное скорости v ракеты. Тогда ракета будет двигаться по
прямой линии, имеющей направление вектора v. Примем эту прямую
за ось Ох (рис. 132). Проектируя обе части равенства E) на ось Ох,
получаем
где иг — величина относительной скорости иг. Полагая, что при t = О
масса ракеты равна Mq, а ее скорость равна Vq, и интегрируя F), по-
получаем
^ G)
260
Глава IX
Отсюда видно, что скорость ракеты
в данный момент времени зависит от от-
отношения начальной массы к текущему ее
значению. Пусть Мт — начальная мас-
масса топлива, а Мк — конечная масса ра-
ракеты после того, как израсходовано все
топливо (т. е. масса корпуса ракеты, по-
полезных грузов и оборудования). Тогда
Мо = Мк + Мт, и для скорости ракеты,
которую она приобретет в конце процес-
процесса сгорания топлива, получаем из G) сле-
следующее выражение, называемое формулой Циолковского:
Рис. 132
«к = Щ + ur In I 1 +
мЛ
(8)
Иэ этой формулы следует, что предельная скорость ракеты «к зависит
только от относительного запаса топлива и относительной скорости ис-
истечения продуктов его сгорания. От закона изменения массы ракеты
(режима работы двигателя) предельная скорость ракеты не зависит;
если задано отношение Мт/Мк = Z (называемое числом Циолковско-
Циолковского), то предельная скорость будет вполне определенной независимо от
того, быстро или медленно происходило сгорание топлива.
Путь, пройденный ракетой на активном участке траектории, зави-
зависит от закона сгорания топлива. Полагая, что х = 0 при t = 0, из G)
получаем
Мо
X =
"I
In
M(t)
dt.
(9)
134. Вертикальное движение ракеты в однородном поле тя-
тяжести. Пусть ракета движется вертикально вверх в однородном поле
тяжести при отсутствии сопротивления среды. Ракету принимаем за
материальную точку. Начальная скорость ракеты равна нулю, началь-
начальная масса Мо. Относительная скорость и,- отделения продуктов сго-
сгорания топлива постоянна и направлена вертикально вниз. Требуется
найти скорость ракеты и высоту ее подъема как функции времени,
считая, что закон изменения массы ракеты со временем задан.
На ракету действует внешняя сила — сила тяжести, направлен-
направленная вертикально вниз. Примем прямую, по которой движется ракета,
за ось Oz (рис. 133). Проектируя обе части уравнения D) на ось Oz,
получаем
§ 2. Движение материальной точки переменного состава 261
Интегрируя это уравнение, находим зависимость скорости ракеты от
времени
Если положить, что при t = 0 z = 0, то, проинтегрировав A0), найдем,
что зависимость высоты подъема ракеты от времени задается форму-
формулой
о
Пусть масса ракеты изменяется по экспоненциальному
закону: z•
М = Moe~at, A2)
v,
где а — постоянный положительный коэффициент, харак-
характеризующий быстроту сгорания топлива. Масса Mi отбро-
отброшенных продуктов сгорания возрастает по закону
Mi =M0(l-e
— at\
Мд
Для величины F\ реактивной силы, согласно первой из фор-
мул A) п. 132, получаем выражение
Fi = aMoe~atur = aurM,
ю
т. е. величина аиг есть ускорение, сообщаемое ракете за рис ^дд
счет реактивной силы.
Для закона изменения массы A2) из A0) и A1) получаем
v = (аиг - g)t, z = ^(aur - g)t2. A3)
Отсюда, в частности, следует, что вертикальный подъем ракеты воз-
возможен только при aur > g. Это означает, что ускорение ракеты за счет
реактивной силы должно быть больше ускорения свободного падения.
Пусть запас топлива Мт задан. Из A2) найдем время tn сгора-
сгорания топлива. Так как в конце процесса сгорания М = Мк, то из A2)
получаем
Мк = Moe~atK.
262 Глава IX
Учитывая, что Mq = Мк+Мт и вводя обозначение fi = 1пA+Мт/Мк),
получаем отсюда
tK = i- A4)
Из A3) следует, что скорость vk ракеты в конце процесса сгорания топ-
топлива и длина zk активного участка траектории ракеты определяются
формулами
После сгорания топлива, т. е. при t > Ьк, масса ракеты остается по-
постоянной, и, имея при t = Ьк скорость vk, она пройдет до наибольшей
высоты подъема расстояние
Для полной высоты подъема h = zk + s из A5) и A6) получаем выра-
выражение
Отсюда следует, что при возрастании а растет и наибольшая вы-
высота подъема ракеты. Наибольшая высота 7imax соответствует слу-
случаю а = оо, т. е. случаю мгновенного сгорания топлива. При этом
Л -
«max -
Найдем, при каком значении а длина zk активного участка будет наи-
наибольшей. Из A5) имеем
dzK _ п2 2g ~ aur d2zK _ n2 aur ~ 3ff цд,
да 2а3 да2 а4
Отсюда следует, что при а = 2g/ur, т. е когда ускорение, сообщаемое
ракете реактивной силой, вдвое больше ускорения свободного падения,
величина zk будет максимальной. Из A5) находим, что
§ 3. Уравнения движения тела переменного состава 263
При этом для высоты h подъема ракеты, согласно A7), получаем
h = л г 1
т. е. при наибольшей длине активного участка траектории ракеты пол-
полная высота ее подъема вдвое меньше наибольшей возможной высоты,
задаваемой равенством A8).
§ 3. Уравнения движения тела
переменного состава
135. Движение вокруг неподвижной точки. Твердым телом
переменного состава будем называть такую механическую систему, ко-
которая образована материальными точками Pv (у = 1, 2, ... , N), рас-
расстояние между которыми остается постоянным, причем хотя бы одна
из точек Pv является материальной точкой переменного состава.
Если mv(t) — масса точки Р„, то
mv{t) = т„@) - mvl{t) + mv2{t) (v = 1, 2, ... , N), A)
где mvi(t) (mV2(t)) — суммарная масса частиц, потерянных точкой Pv
за время t (соответственно присоединившихся к точке Pv). Неотрица-
Неотрицательные неубывающие функции mvi(t), mV2{t) считаем непрерывными
и дифференцируемыми.
Пусть твердое тело переменного состава имеет одну неподвижную
точку О. Для получения дифференциальных уравнений движения тела
воспользуемся теоремой об изменении кинетического момента системы
переменного состава. Пусть система координат Oxyz жестко связана
с телом, а Ко — кинетический момент тела относительно точки О.
Если со — угловая скорость тела, то из равенства G) п. 131 получаем
B)
где d/dt означает локальную (в системе Oxyz) производную, Мо —
главный момент внешних сил относительно точки О, Мо ' — дополни-
дополнительный момент, возникающий за счет того, что тело имеет перемен-
переменный состав.
Найдем вектор Мо . Пусть Amvi — масса частиц, отделившихся
от точки Р„, AmV2 — масса частиц, присоединившихся к точке Pv
за время At. Если uv\ и uV2 — абсолютные скорости отделяющихся
264 Глава IX
и присоединяющихся частиц в момент времени t, то с точностью до
членов первого порядка малости относительно Amvi, AmV2, At имеем
JV
Д.К01 = Е ^fnvlpv x uvl,
C)
AK02 = E Am^Pv x uv2,
v=l
где pv — радиус-вектор материальной точки Pv относительно непо-
неподвижной точки О тела. Из C) и формул (8) п. 131 получаем
N N
d
Пусть vu — скорость точки тела Ри, а и^ и uj2 — соответствен-
соответственно скорости присоединяющейся и отделяющейся частиц относительно
точки Pv. Тогда uvi = vv + и? (г = 1, 2), что позволяет записать
равенство D) в таком виде:
dt dt
При помощи соотношения A) это равенство приводится к виду
dmv ,_.
^tv- F)
Согласно уравнению C) п. 132, первая сумма в F) представляет
собой главный момент Мо реактивных сил относительно точки О.
Замечая, что vv = ш х pv и проводя преобразования, совершенно ана-
аналогичные преобразованиям, проведенным в п. 82, получим, что вторая
сумма в F) равна ^тт-t*;, где J — матрица тензора инерции тела для
точки О (которая является функцией времени). Таким образом, допол-
дополнительный момент Мо ', появляющийся за счет того, что рассматри-
рассматриваемое тело является системой переменного состава, может быть пред-
представлен в форме
§ 3. Уравнения движения тела переменного состава 265
Согласно формуле (9) п. 82, кинетический момент тела Ко может быть
записан в виде Ко = Зш. Отсюда и из равенств B), G) получаем
Ц-и + 3^ +и, х Ju> = Мое) + Мог) + §ги>,
at at u u at
или
J^ + u> х Ju> = Moe) + Мог). (8)
Если Jx, Jy, Jz и Jxy, Jxz, Jyz — осевые и центробежные моменты
инерции, ар, q, г — проекции угловой скорости тела на оси Ox, Oy, Oz,
то векторное уравнение (8) запишется в виде трех скалярных уравне-
уравнений C) п. 97, в правых частях которых появятся дополнительные слага-
слагаемые Мх , My , Mz , являющиеся проекциями момента реактивных
сил на оси Ox, Oy, Oz. В общем случае, когда момент внешних сил за-
зависит от ориентации тела в пространстве, при исследовании движения
тела вокруг неподвижной точки к этим уравнениям надо добавить еще
три кинематических уравнения Эйлера.
Если в процессе отбрасывания и присоединения частиц оси Ох,
Oy, Oz остаются главными осями инерции, то скалярная форма урав-
уравнения (8) примет форму динамических уравнений Эйлера:
В^ + (А- С)гр = Му + Му\г\ (9)
С^ + (В- A)pq = MZ+ М«,
где А, В, С — моменты инерции тела (зависящие от времени) относи-
относительно осей Ox, Oy, Oz, a Mx, My, Mz — проекции главного момента
внешних сил на эти оси.
136. Вращение вокруг неподвижной оси. Пусть Oz — не-
неподвижная ось, вокруг которой вращается тело переменного состава.
Тогда р = 0, q = 0, г = coz(t). Для получения уравнения движения тела
спроектируем обе части векторного уравнения (8) на ось Oz. Получим
Jz^=Mz+M^. A0)
Это и будет дифференциальным уравнением вращения твердого тела
вокруг неподвижной оси Oz. От соответствующего уравнения для тела
266 Глава IX
постоянного состава оно отличается наличием в правой части дополни-
дополнительного слагаемого Mz , являющегося проекцией момента реактив-
реактивных сил на ось Oz, и тем, что момент инерции Jz тела относительно
этой оси является переменной величиной.
Пример 1. Тело, имеющее форму кольца радиусом г, вращается под
действием постоянного момента М вокруг неподвижной вертикальной
оси, совпадающей с осью симметрии. Когда тело приобрело угловую ско-
скорость и>о, потребовалось затормозить его. Для таких целей на внеш-
внешнем ободе кольца на противоположных концах диаметра установлены
два реактивных двигателя. Относительная скорость истечения газов
в двигателях направлена по касательной к ободу кольца и равна и; се-
секундный расход топлива равен q, начальный момент инерции тела с
топливом равен Jq. Требуется найти расход топлива, необходимый для
полного торможения тела.
Согласно A0), дифференциальное уравнение, описывающее вращение
тела, будет таким:
(Jo - qr2t)^ = M - qur. A1)
Торможение вращения тела возможно, если величина реактивного мо-
момента достаточно велика (qur > М). Решив уравнение A1), получим
зависимость угловой скорости тела от времени:
, . qur -I, Л qr2
U)(t) = LJ0 Н In 1 ц— 1
qr \ Jo
Из уравнения и>(т) = 0 найдем время т торможения вращения тела, а
затем по формуле т = qr вычислим необходимый расход топлива. В
результате получим
j (
т = Ц 1 - е
Глава X
Дифференциальные уравнения
аналитической динамики
§ 1. Уравнения Лагранжа (второго рода)
137. Общее уравнение динамики в обобщенных коор-
координатах. Рассмотрим систему N материальных точек Pv (у =
= 1, 2, ... , N). Если система несвободна, то наложенные на нее связи
предполагаются удерживающими и идеальными. Пусть 5rv — вирту-
виртуальное перемещение точки Pv, mv — ее масса, wv — ускорение в инер-
циальной системе координат, a Fv — равнодействующая всех активных
сил, приложенных к точке Pv. Тогда имеет место общее уравнение ди-
динамики (п. 57)
N
-mvwv)-5rv = Q. A)
В том случае, когда все или некоторые из связей не идеальны, к ве-
величинам Fv следует добавить часть Gv равнодействующей реакций
связей, действующих на точку Р„, которая не удовлетворяет условию
идеальности. После этого изучаемую систему можно формально рас-
рассматривать как систему с идеальными связями.
Общее уравнение динамики A) мы принимаем за исходное при по-
получении основных дифференциальных уравнений аналитической дина-
динамики, которым посвящена данная глава. Фактически все изучаемые
ниже уравнения движения материальных систем являются только раз-
различными формами записи уравнения A), к которым оно приводится
при тех или иных предположениях о характере активных сил, действу-
действующих на систему, и о наложенных на нее связях.
Пусть на систему наложено г геометрических и s кинематических
неинтегрируемых связей. Пусть qi, #2; ••• , Чт — обобщенные коор-
координаты системы. Их число т равно 37V — г. Тогда радиусы-векторы vv
точек Ри относительно начала инерциальной системы координат запи-
записываются в виде функций аргументов qi, 52, • • • , Qm, t
rv = rv(qu q2, ... , qm, t), B)
268 Глава X
которые предполагаются дважды непрерывно дифференцируемыми. Ес-
Если система склерономна, то обобщенные координаты qi, 52, ••• , Qm
можно выбрать так, чтобы функции rv не зависели от t. Из B) получа-
получаем (см. п. 16)
щ^ + Ж (^ = 1,2, ...,7V), C)
М, = ]Г^<% (^ = 1,2, ...,7V). D)
j=i 3
Запишем общее уравнение динамики A) в обобщенных координа-
координатах. Для элементарной работы активных сил имеем выражение
N т
Y,Fv-5rv = Y,QM^ E)
где Qj — обобщенная сила, соответствующая обобщенной коор-
координате qj. Она в общем случае является функцией qi, щ и t
(/ = 1, 2, ... , т).
Преобразуем выражение для элементарной работы сил инерции на
виртуальном перемещении системы. Пользуясь формулой D) и меняя
порядок суммирования, получаем предварительно
F)
Но
N
2_j Tavwv ¦ 5rv
v=l
N
v=l
m
it"'
\u=l
m
3 = 1
drv
v dt
dVv5(
Qj
drv
dqj
N ,._ /N
* . r" _ a . ж ™ „ . -. » m r . ^
dt dqj dt\^ dqjj ^ dtd4j
(j = 1, 2, ... , m).
Последнее равенство при помощи формул B5) п. 16 можно записать в
виде
Д, drv drv d I v^ • drv \ sr^ ¦ drv
V mv—r- ¦ -^— = — > mvrv ¦ -7Г-Г- - > mvrv ¦ -^—
„=1 dt dqj dt\?[ dqj) ^ d1j G)
= l, 2, ... , m).
§ 1. Уравнения Лагранжа (второго рода) 269
Если использовать выражение для кинетической энергии системы
то равенство G) можно переписать в виде
m =
^—< v dt dqj dt dqj
Подставив (8) в формулу F), получим выражение для элементарной
работы сил инерции в виде
N
Подставим теперь выражения E) и (9) в соотношение A) и умножим
обе части получившегося равенства на —1. В результате получим общее
уравнение динамики в обобщенных координатах:
138. Уравнения Лагранжа. Пусть система голономна. Тогда ве-
величины 6qj (i = 1, 2, ... , то) независимы и число обобщенных коор-
координат равно числу степеней свободы системы (то = п). В силу неза-
независимости величин Sqj уравнение A0) удовлетворяется тогда и только
тогда, когда равны нулю коэффициенты при всех Sqj. Поэтому уравне-
уравнение A0) эквивалентно следующей системе п уравнений:
Уравнения A1) называются уравнениями Лагранжа второго рода1. Они
образуют систему п уравнений второго порядка относительно п функ-
функций qi{t). Порядок этой системы равен 2п. Заметим, что это наимень-
наименьший возможный порядок дифференциальных уравнений движения рас-
рассматриваемой системы, так как начальные значения величин q,, щ
(г = 1, 2, ... , п) могут быть произвольными.
1Уравнения A1) для краткости мы часто будем называть просто уравнениями
Лагранжа.
270 Глава X
Для получения уравнений Лагранжа надо выразить кинетическую
энергию Т системы через обобщенные координаты и скорости, найти
обобщенные силы и произвести указанные в A1) дифференцирования
функции Т {qj, qj, t) по обобщенным координатам, обобщенным ско-
скоростям и времени. Заметим, что форма уравнений Лагранжа не зависит
от выбора обобщенных координат q\, q-i, ... , qn. При другом их выбо-
выборе изменились бы только функции Т и Q,, а сама форма уравнений A1)
осталась бы той же. В связи с этим говорят, что уравнения Лагранжа
второго рода обладают свойством ковариантности.
В уравнениях Лагранжа не содержатся реакции идеальных связей.
Если же нужно найти реакции связей, то надо после интегрирования
уравнений Лагранжа подставить функции <&(?) в выражения B), и тог-
тогда равнодействующая Rv реакций связей, приложенных к точке Pv,
найдётся из соотношений
Rv = mvrv - Fu{ru, rv, t).
Пример 1 (Вращение твердого тела вокруг неподвижной оси и).
Здесь п = 1. За обобщенную координату примем угол <р поворота тела
вокруг оси и. Обобщенная сила Q^, равняется главному моменту Мие'
внешних сил относительно оси и {см. пример 2 п. 54). Кинетическая
энергия тела равна
Т=\.1иФ\
где Ju — момент инерции тела относительно оси и. Имеем
дТ т ¦ d дТ т ¦¦ дТ п.
аф dt аф oip
Уравнение Лагранжа
sLdT _ дТ _ п
dt дф dip 4ip
имеет вид
Ju<p = Мие).
Пример 2 (Уравнения движения сферического маятника). Сфе-
Сферический маятник представляет собой материальную точку, которая
движется в однородном поле тяжести, оставаясь на сфере постоян-
постоянного радиуса. Будем считать, что точка имеет массу т и закреп-
закреплена на одном из концов невесомого стрежня длиной I; другой конец
стержня при помощи шарнира прикреплен к неподвижной точке О так,
что стержень может иметь произвольное направление в пространстве
(рис. 134). Трением пренебрегаем.
; 1. Уравнения Лагранжа (второго рода)
271
Сферический маятник имеет две степе-
степени свободы. За обобщенные координаты примем
сферические координаты ip, в точки т. Так как
расстояние точки т до начала координат по-
постоянно и равно I, то, согласно формуле C0)
п. 9, для кинетической энергии имеем выраже-
выражение
Zlv
Т= ±
(в
в2
sin2
2).
A2)
У
Для нахождения обобщенной силы Qv дадим
точке виртуальное перемещение по параллели.
Тогда 8AV = 0 и, следовательно, Qv = 0. Что- "ИС- '¦^
бы найти обобщенную силу Qg, дадим точке виртуальное перемещение
по меридиану. Тогда 5Ag = mgs'me-16в = Qg56. Отсюда Qg = mglsinO.
Для координат в и ip [после деления обеих частей уравнений Ла-
гранжа на постоянные множители) получаем такие уравнения:
в -втвсоввф2 - jsinfl = 0, ^-(sin2 вф) = 0. A3)
I (lib
139. Анализ выражения для кинетической энергии. Рас-
Рассмотрим структуру выражения для кинетической энергии системы,
записанной через обобщенные координаты и скорости. Используя фор-
формулу C), кинетическую энергию можно представить в виде
A4)
' j,k=l
где введены обозначения
JV
drv drv
JV
' aj =
v=l
drv drv l
оси at I
JV
drv
A5)
Величины a.jk, aj, a0 — функции от q\, q2, ... , qm, t.
Формула A4) показывает, что кинетическая энергия является мно-
многочленом второй степени относительно обобщенных скоростей и пред-
ставима в виде
= Т2+Т1+Т0,
A6)
272 Глава X
где
т
Т =
j,k=l j=l
В случае склерономной системы drv/dt = 0 (у = 1, 2, ... , 7V) и
из A5) следует, что а,- = 0, ао = 0 (j = 1, 2, ... , то). Поэтому
m
\Y A7)
т. е. кинетическая энергия склерономной системы является квадратич-
квадратичной формой обобщенных скоростей, причем коэффициенты а^ в A7)
не зависят явно от времени.
Покажем, что квадратичная форма Тг является невырожденной.
Это означает, что определитель, составленный из ее коэффициентов,
отличен от нуля при любых qi, 52, ••• , Qm: t:
det
В самом деле, из того, что квадратичная форма Т^ может быть записана
в виде
JV
сразу следует, что она неотрицательна: Т2 ^ 0.
Докажем теперь, что она может обратиться в нуль только тогда,
когда все <jj (j = 1, 2, ... , то) равны нулю. Допустим, что это не
так, т. е. что Т^ может равняться нулю при некоторых значениях об-
обобщенных скоростей <7i, </!, ... , q^, среди которых есть отличные от
нуля. Тогда каждое выражение, заключенное в скобки в формуле A9),
должно обратиться в нуль, т. е.
^=° (" = 1, 2, ...,Л0.
3
В скалярной форме эти векторные равенства запишутся в виде
(и = 1,2, ...,7V).
§ 1. Уравнения Лагранжа (второго рода) 273
Равенства B0) показывают, что столбцы матрицы B2) п. 14 линей-
линейно зависимы, т. е. ранг этой матрицы меньше т. Согласно п. 14, это
невозможно, если величины qi, 52, ••• , Qm являются обобщенными
координатами.
Таким образом, квадратичная форма Т^ определенно-положитель-
определенно-положительна. Из критерия Сильвестра тогда следует, что определитель, состав-
составленный из ее коэффициентов, положителен. Следовательно, справедливо
неравенство A8).
Замечание 1. Если при данном выборе обобщенных координат
Qii Q21 ••• , Qm для некоторых положений системы неравенство A8) не
выполняется, то это означает, что при исследовании движения сис-
системы вблизи этих положений величины qi, 52, ••• , qm в качестве об-
обобщенных координат малопригодны. В окрестности таких положений
системы целесообразно вводить другие обобщенные координаты.
Комментарий 1. В качестве примера рассмотрим движение твердого
тела вокруг неподвижной точки О. Пусть А, В, С — главные момен-
моменты инерции, ар, q, r — проекции угловой скорости тела на его главные
оси инерции для точки О. Кинетическая энергия тела вычисляется по
формуле
T=±(Ap2+Bq2+Cr2). B1)
В качестве обобщенных координат примем углы Эйлера ф, в, <р, вводи-
вводимые обычным образом (п. 19). Найдем величину Т при значении угла в,
равном 0 или ж. Использовав кинематические уравнения Эйлера (п. 36),
получим из B1)
Т =\\{А cos2 tp + В sin2 ipN2 + С(ф ± фJ], B2)
^ L J
где знаки плюс и минус отвечают значениям в, равным 0 и ж соответ-
соответственно. Определитель квадратичной формы B2) равен нулю. Следова-
Следовательно, при значениях 9, близких 0 или ж, вводимые обычным образом
углы Эйлера неудобны для описания движения тела. Этот факт уже
отмечался в п. 19.
140. Разрешимость уравнений Лагранжа относительно об-
общеных ускорений. Используя структуру A6) выражения кинети-
кинетической энергии, уравнения Лагранжа A1) можно представить в виде
(г = 1, 2. ... , п), B3)
274 Глава X
где функции gi не зависят от обобщенных ускорений. Из предыдущего
пункта следует, что определитель линейной относительно щ системы
уравнений B3) отличен от нуля, поэтому она разрешима и имеет един-
единственное решение
4i = Gi(qk, qk,t). B4)
Как известно из теории дифференциальных уравнений, при некото-
некоторых ограничениях на G, (например, при существовании непрерыв-
непрерывных частных производных у функций Gi, которое в механике всегда
предполагается) система уравнений B4) имеет единственное решение
при произвольных начальных данных: ф = <$) Qi = Qii ПРИ t = to
(г = 1, 3, ... , п). Таким образом, уравнения Лагранжа удовлетворяют
условию детерминированности движения (см. п. 45).
141. Уравнения Лагранжа в случае потенциальных сил.
Функция Лагранжа. Пусть обобщенные силы Qi вычисляются по
формулам
<2г = -Р (» = 1, 2, ..., П),
где потенциал (потенциальная энергия) П есть функция qi,q2,.. .,qn,t.
Уравнения Лагранжа A1) в случае потенциальных сил имеют вид
d дТ дТ _ дП ,. , 2 ч
at oqi oqi oqi
Положим L = T — П, тогда эти уравнения примут вид
4#"# = 0 (t = l, 2, ..., п). B5)
dtdqi dqt v y y '
Функция L называется функцией Лагранжа (лагранжианом, кинетичес-
кинетическим потенциалом).
Используя выражение A6), функцию Лагранжа можно представить
в виде многочлена второй степени относительно обобщенных скоростей
L = L1+L2+L0, B6)
где
L2=T2, L1=T1, L0=T0-n. B7)
Замечание 2. Для получения дифференциальных уравнений движе-
движения B5) голономной системы в потенциальном поле сил надо знать
только одну функцию — функцию Лагранжа L. Уравнения Лагранжа не
§ 1. Уравнения Лагранжа (второго рода) 275
изменятся, если к функции L добавить полную производную по времени
от произвольной дважды непрерывно дифференцируемой функции f от
обобщенных координат и времени:
dt ^ dqr df
г=1
В самом деле, из последнего равенства имеем следующие два соотноше-
соотношения:
d ( д
A
dqi \dt
Правые части этих равенств одинаковы, так как f дважды непрерыв-
непрерывно дифференцируема, и поэтому возможно изменение порядка ее диф-
дифференцирования по (qi, qk, t). Поэтому если в B5) вместо L подста-
Т df d ( д df\ д (df\
вить L -\—=-, то величины -^ -^~г и ~^~ ~г взаимно цничто-
dt dt \ oqi dt J oqi \dt J
жатся, и уравнения Лагранжа останутся неизменными.
142. Теорема об изменении полной механической энергии
голономной системы. Пусть помимо потенциальных сил к систе-
системе приложены также некоторые непотенциальные силы. Часть обоб-
обобщенных сил, соответствующую непотенциальным силам, обозначим че-
через Q*. Тогда
и уравнения Лагранжа A1) примут вид
dt dqi dqt dqi ¦> i •••¦>)•
Найдем производную по времени от кинетической энергии
T{qk, ik, t). Имеем
dT_ _ у ((УЦ-. дТ Л дТ _
dt ?-*< \dqi l dqi 'J dt
1=1 / ч B9)
= A [ V^d I -^T (A9T - 9T) a. + 9T
dt [^ dqt 4~i \dt din dqi) * dt'
276 Глава X
Далее воспользуемся выражением A6) и теоремой Эйлера об од-
однородных функциях. Согласно этой теореме, для однородной функ-
функции f(x\, X2, ••• , хп) k-й степени справедливо равенство
Применяя эту теорему к функции A6), получаем
i=l
Используя еще уравнения B8), запишем равенство B9) в виде
п п
dT _ АBТ + Т ) + У^ —а - У^ О*а- + —
»=i »=i
или
lAi-M- lAi /i\f~T~i i OT"J i O^F \ t* /T^ i OT"J \ i
+ Д1 _ ОТ _ у^д*л. + (УГ
Так как 2Тг + 2Xi + 2То = 2Т, то отсюда вытекает следующее выра-
выражение для производной по времени от полной механической энергии
системы Е = Т + П:
(iijjj лг* _i_ (гтл i от1 ^ i t'-i.-i (JJ- / о л\
(ft t?f dt dt'
где
n
7V*=^Q*g.. C1)
г=1
Величина TV* называется мощностью непотенциальных сил.
Формула C0) выражает теорему об изменении полной механичес-
механической энергии голономной системы. Рассмотрим некоторые ее частные
случаи.
1. Пусть система склерономна. Тогда Xi = 0, То = 0, dT/dt = 0 и
~1Г = Я + ~яГ- У62)
§ 1. Уравнения Лагранжа (второго рода) 277
2. Пусть система склерономна и потенциал не зависит явно от вре-
времени. В этом случае дП/dt = 0 и из C2) получаем
3. Пусть система удовлетворяет следующим требованиям: а) она
склерономна, б) все силы системы потенциальны, в) потенциал не зави-
зависит явно от времени. Система, удовлетворяющая этим трем условиям,
называется консервативной. Для нее
f = °'
т. е. полная механическая энергия консервативной системы не изменя-
изменяется при движении системы; имеет место интеграл энергии
E = T + U = h = const.
143. Гироскопические силы. Непотенциальные силы называют-
называются гироскопическими, если их мощность равна нулю.
Из равенства C3) следует, что для склерономной системы, у ко-
которой потенциал П не зависит явно от времени, интеграл энергии су-
существует и при наличии гироскопических сил.
Пусть непотенциальные силы линейны относительно обобщенных
скоростей
п
Qi=J2^ikU (* = 1, 2, ... , п).
k=i
Матрицу, составленную из коэффициентов 7ifc, считаем кососимметри-
ческой, т. е. ¦уц. = —jki (* = 15 2, ... , п). Тогда силы Q* гироскопи-
гироскопические, а кососимметричность матрицы коэффициентов 7гй является
необходимым и достаточным условием гироскопичности сил Q*.
В самом деле, замечая, что у кососимметрической матрицы диаго-
диагональные элементы 7п (г = 1, 2,... , п) всегда равны нулю, получаем
г=1 i,k=l
Прежде чем переходить к рассмотрению примеров, обратим вни-
внимание на следующее. Имеет место равенство
N N
v=l
278 Глава X
Замечая, что
N
и что в случае склерономной системы drv/dt = 0, получаем отсюда
JV n
J^ JV • tv = ^ QiQi-
v=\ i=l
Поэтому в случае склерономной системы равенство N* = 0 выражает
условие гироскопичности
N
непотенциальных сил F*, приложенных к точкам материальной систе-
системы.
Пример 1. Покажем, что силы, приложенные к вращающемуся гироско-
гироскопу и обеспечивающие его регулярную прецессию, являются гироскопичес-
гироскопическими (отсюда и происходит термин «гироскопические силы»). Пусть О
— неподвижная точка гироскопа, u>i — его угловая скорость собствен-
собственного вращения, а и>2 — угловая скорость прецессии. Согласно п. 106,
главный момент Мо сил, приложенных к гироскопу, вычисляется по
формуле
Мо =и>2 x«i [С+{С -А)Щ cosво~\,
где С и А — моменты инерции гироскопа (относительно оси симмет-
симметрии и относительно перпендикулярной ей главной оси, проходящей через
неподвижную точку О гироскопа), во — постоянное значение угла ну-
нутации.
Для элементарной работы сил, приложенных к гироскопу (явля-
(являющемуся склерономной системой), имеем такое выражение:
SA = Mo -ojdt= Mo -u3\dt-\- Mo -u>2dt = 0.
Таким образом, силы, обеспечивающие регулярную прецессию гироскопа,
имеют мощность, равную нулю, и, следовательно, являются гироско-
гироскопическими.
Пример 2. Кориолисовы силы инерции в склерономной системе явля-
являются гироскопическими. В самом деле, пусть mv — масса точки Pv,
vv — ее скорость в неинерциальной системе координат, а ш — угловая
§ 1. Уравнения Лагранжа (второго рода) 279
скорость вращения этой системы координат относительно некоторой
инерциальной системы координат. Тогда кориолисова сила инерции jvc
для точки Pv вычисляется по формуле
jvc = -2ти(ш x vv).
Для склерономной системы действительное перемещение drv является
одним из виртуальных. Поэтому для элементарной работы кориолисо-
вых сил инерции имеем выражение
N N
М = 53 Jvc • <*rv = 53 jvc • drv =
v=l v=\
N N
= 53 J"c " vvdt = -2 53 «г„(а; х vv) ¦ vv dt.
v=\ v=\
Следовательно, мощность кориолисовых сил инерции равна нулю и они
являются гироскопическими.
144. Диссипативные силы. Функция Рэлея. Непотенциаль-
Непотенциальные силы называются диссипативными, если их мощность отрицатель-
отрицательна или равна нулю (N* ^ 0, причем N* ф 0).
Из равенства C3) следует, что для склерономной системы, у кото-
которой потенциал П не зависит явно от времени, при наличии диссипатив-
ных сил
dt ^U'
т. е. полная механическая энергия системы убывает во время движения.
Саму систему в этом случае называют диссипативной. Иногда говорят,
что происходит рассеивание, или диссипация, энергии. Отсюда и возник
термин «диссипативные силы».
Если мощность диссипативных сил N* будет определенно-отрица-
определенно-отрицательной функцией обобщенных скоростей щ (г = 1, 2, ... , п) 1, то
диссипация называется полной. Если же N* — знакопостоянная отри-
отрицательная функция2, то диссипация называется неполной или частич-
частичной.
Пусть задана положительная квадратичная форма
п
R = 2 53 bikUiUk (bik =Ьы),
i,k=l
хЭто означает, что при |д;| < е (i = 1, 2, ... , п), где е — достаточно малое
положительное число, JV* <J 0, причем JV* обращается в нуль только тогда, когда
все обобщенные скорости равны нулю.
2То есть в окрестности |д;| < е (г = 1, 2, ... , п) при сколь угодно малом е
справедливо неравенство N* <С 0 и N* может обращаться в нуль не только тогда,
когда все сц = 0 (i = 1, 2, ... , п).
280 Глава X
такая, что непотенциальные силы Q* задаются соотношениями
fc=l
Тогда для склерономной системы мощность N* непотенциальных сил
равна
JV n
^F*-vv = ^ Q*<ji = -2R <: 0. C6)
Функция R называется диссипативной функцией Рэлея. Из C3) и C6)
следует, что в случае склерономной системы с потенциалом, не завися-
зависящим явно от времени,
dE_ _ _О7?
dt
т. е. скорость убывания полной механической энергии системы равна
удвоенной функции Рэлея.
В качестве примера рассмотрим склерономную систему, к каждой
точке которой приложена сила сопротивления, пропорциональная ско-
скорости этой точки:
W — — I'm In — 1 9 ЛЛ f47"l
где к > 0. Мощность этих сил будет равна
N
N* = ^ Fv ¦ vv = -2R,
v=\
где
JV
2. C8)
145. Обобщенный потенциал. Пусть существует функция V от
обобщенных координат, обобщенных скоростей и времени такая, что
обобщенные силы Q, определяются по формулам
Тогда функция V называется обобщенным потенциалом.
§ 1. Уравнения Лагранжа (второго рода) 281
Если положить L = Т — V, то уравнения Лагранжа A1) запишутся
в той же форме B5), какую они имели в случае обычного потенциала
сил.
Из C9) следует, что
где функции fi не зависят от обобщенных ускорений. Но в теоретичес-
теоретической механике обычно рассматриваются только такие силы, которые не
зависят от ускорений. Поэтому обобщенный потенциал V должен быть
линейной функцией от обобщенных скоростей:
п
V = V1+V0, Vx=Y,Mi, D0)
i=l
где Vo, Ai (i = 1, 2, ... , n) — функции обобщенных координат и
времени.
Из C9) и D0) находим выражение для обобщенных сил:
D1)
Если dAf/dt = 0 (г = 1, 2, ... , п), т. е. линейная часть V\ обоб-
обобщенного потенциала не зависит явно от времени, то обобщенные силы
складываются из потенциальных сил —dVo/dqi (г = 1, 2, ... , п) и
гироскопических сил
п
Ф = $><*& (» = 1, 2, ..., п), D2)
k=i
где
Ък — 1кг — q^ q^ \г —,,..., nj. ^ J
Если к тому же система склерономна и часть Vo обобщенного потенци-
потенциала не зависит от времени, то, согласно п. 143, при движении системы
величина Т + Vo остается постоянной (однако Т + V ф const).
282 Глава X
Отметим, что в случае существования обобщенного потенциала
функция Лагранжа является многочленом второй степени относительно
обобщенных скоростей и представима в виде L = L<i + L\ + Lq, где
L2=T2, L1=T1-V1, L0=T0-V0. D4)
Квадратичная часть функции L совпадает с квадратичной частью ки-
кинетической энергии, и уравнения Лагранжа, как и в случае существо-
существования обычного потенциала П, разрешимы относительно обобщенных
ускорений.
Упражнение 1. Показать, что сумма переносных и кориолисовых сил
инерции всех точек системы всегда имеет обобщенный потенциал.
146. О составлении уравнений Лагранжа для описания дви-
движения в неинерциальной системе отсчета. При получении урав-
уравнений движения системы относительно неинерциальной системы коор-
координат можно применять различные способы. Укажем два из них.
Первый способ не связан с теорией относительного движения.
Здесь задача формулируется без введения сил инерции. Кинетическая
энергия абсолютного движения системы выражается через относитель-
относительные обобщенные координаты и относительные скорости точек системы.
Обобщенные силы вычисляются обычным способом (для заданных ак-
активных сил). В этом способе силы инерции учитываются автоматичес-
автоматически самой процедурой выписывания уравнений Лагранжа.
Второй способ основан на теории относительного движения. За-
Задачу формулируют, вводя переносные и кориолисовы силы инерции.
Кинетическую энергию здесь надо вычислять для относительного дви-
движения, а при подсчете обобщенных сил, помимо заданных активных
сил, учитываются и силы инерции.
Если в первом и втором из указанных способов за обобщенные ко-
координаты приняты одни и те же величины, то мы придем к одним и
тем же уравнениям движения. В конкретной задаче бывает ясно, какой
из способов предпочтительнее. Конечно, возможны и другие способы
получения уравнений Лагранжа, описывающих движение системы от-
относительно неинерциальной системы координат.
147. Натуральные и ненатуральные системы. Системы, в
которых силы имеют обычный П(%, t) или обобщенный V(qi, qi, t)
потенциал, называются натуральными. В таких системах функции Ла-
Лагранжа L вводится как разность Т — П или Т — V и является много-
многочленом второй степени относительно обобщенных скоростей, причем
i 2. Канонические уравнения Гамильтона
283
гессиан функции Лагранжа
det
dqidqk\\ik=1
= det
д2Т
i,k=l
= det||ojfc||"fc=1#0 D5)
и уравнения Лагранжа разрешимы относительно обобщенных ускоре-
ускорений.
В дальнейшем, если не будет оговорено особо, мы будем рассмат-
рассматривать более общие системы, в которых функция Лагранжа L не обяза-
обязательно определяется как разность кинетической энергии и потенциала
и в этом смысле является произвольной функцией L(qi, щ, t). Будем
лишь требовать, чтобы гессиан этой функции относительно обобщен-
обобщенных скоростей не был равен нулю:
det
д2ь
#0.
D6)
i,k=l
Такие системы будем называть ненатуральными. Требование D6) ана-
аналогично неравенству D5) и нужно для обеспечения разрешимости урав-
уравнений Лагранжа относительно обобщенных ускорений.
§ 2. Канонические уравнения Гамильтона
148. Преобразование Лежандра. Функция Гамильтона. В
уравнениях Лагранжа второго рода
d dL
dtdqt
9L
= 0
(г = 1, 2, ... , тг),
A)
описывающих движение голономной системы в потенциальном поле
сил, функция L зависит от переменных #,, g,, t (г = 1, 2, ... , п).
Эти переменные задают момент времени и кинематическое состоя-
состояние системы, т. е. положения и скорости ее точек. Переменные щ, щ, t
(г = 1, 2, ... , п) называют переменными Лагранжа.
Но состояние системы можно задавать и при помощи других
параметров. За такие параметры можно принять величины %, pi, t
(i = 1, 2, ... , п), где р, — обобщенные импульсы, определяемые ра-
равенствами
Pi =
дь
(t = l, 2, ... , п).
B)
Переменные gj, pi, t называют переменными Гамильтона.
284 Глава X
Гессиан функции L относительно переменных qi (г = 1, 2, ... , п)
отличен от нуля (см. неравенства D5), D6) п. 147). Замечая, что он
равен якобиану правых частей равенств B), на основании теоремы о
неявной функции получаем, что эти равенства разрешимы относитель-
относительно переменных д»:
Щ = <Pi(qi, • • • , qn, Pi, ¦¦¦, Рп, t) (г = 1, 2, ... , га). C)
Следовательно, переменные Лагранжа могут быть выражены через пе-
переменные Гамильтона и наоборот.
Гамильтон предложил записывать уравнения движения в перемен-
переменных Qj, pi, t. В этих переменных уравнения Лагранжа A) переходят
в разрешенную относительно производных систему 2п уравнений пер-
первого порядка, имеющую замечательно симметричную форму записи.
Эти уравнения называют уравнениями Гамильтона (или канонически-
каноническими уравнениями). Переменные д, и р, (г = 1, 2, ... , п) называются
канонически сопряженными.
Прежде чем получать уравнения Гамильтона, введем некоторые
вспомогательные определения. Пусть дана функция Х{х\, хг, ..., хп),
гессиан которой отличен от нуля:
det
д2х
dxidxk\\.k=l
Ф 0. D)
Перейдем от переменных х\, Х2, ••• , хп к новым переменным
2/1, 2/2, ••• , Уп по формулам
Уг = U (» = 1, 2, ...,п). E)
Преобразованием Лежандра функции Х{х\, жг, •••, хп) называется
функция новых переменных Y(yi, j/2, ••• , Уп), определяемая равен-
равенством
п
Y = ^yixi-X, F)
в правой части которого переменные Х{ выражены через новые пере-
переменные у» при помощи уравнений EI.
В курсах математического анализа показывается2, что преобразо-
преобразование Лежандра имеет обратное, причем если X при преобразовании
1Эти уравнения в силу условия D) разрешимы относительно ж, (г=1, 2, ... , п).
2См., например, гл. 6 книги: Фихтенгольц Г. М. Курс дифференциального и ин-
интегрального исчисления. Т. 1. - М.: Наука, 1966.
§ 2. Канонические уравнения Гамильтона 285
Лежандра переходит в Y, то преобразование Лежандра от Y будет сно-
снова X.
Преобразование Лежандра функции L (</j, qi, t) по перемен-
переменным щ (г = 1, 2, ... , п) есть функция
п
H{qt, pi, t) = ^Piqi - L{qj, qh t). G)
г=1
в которой величины g, выражены через qj, pj, t при помощи уравне-
уравнений B); при этом при проведении преобразования величины q,, t игра-
играют роль параметров. Функция Н называется функцией Гамильтона.
149. Уравнения Гамильтона. Полный дифференциал функции
Гамильтона вычисляется по формуле
g
С другой стороны, полный дифференциал правой части равенства G),
вычисленный при условиях B), будет таким:
Так как при переходе к новым переменным значение полного дифферен-
дифференциала не меняется, то правые части равенств (8) и (9) равны. Отсюда
следует, что
Ш&к Ша (V-1 2 п)
aqi
а также
at ~ df
Но согласно A) и B), р, = ^- (г = 1, 2, ... , п). Поэтому из A0)
получаем уравнения движения
и-г 2 п) П2)
Эти уравнения называются уравнениями Гамильтона (или каноничес-
каноническими уравнениями).
286 Глава X
Отметим, что попутно мы получили равенство A1), означающее,
что если функция Лагранжа не зависит явно от времени, то и функция
Гамильтона также не зависит от времени, и наоборот. Аналогично, из
равенств A0) следует, что если функция L не зависит от какой-либо из
обобщенных координат, то и функция Н от этой координаты не зависит,
и наоборот.
Пример 1. Получим гамильтонову форму уравнений движения матема-
математического маятника, рассмотренного в примере 2 п. 57. Для кинети-
кинетической и потенциалной энергии имеем выражения (см. рис. 55)
Поэтому
Из равенства
находим
Т = -^тпРф2, П = —mgl cos if.
L = Т - П = \т12ф2 + mgl cos if.
2
r ml21"
Используя формулу G), находим функцию Гамильтона
Н = ррф — L = -р2^ — mgl cos if.
Канонические уравнения A2) имеют вид
dpv
" ~df =
150. Физический смысл функции Гамильтона. Пусть система
натуральна. Тогда L = Li + L\ + Lq и, согласно формулам B) и G),
d(L2+L1 + L0)
п - 2_^ щ_ 4i - (L2 + L± + Lo),
г=1
но по теореме Эйлера об однородных функциях
г=1 г=1
§ 2. Канонические уравнения Гамильтона 287
поэтому
Я = BL2 + Ьг) - (L2 + LX+ Lo) = L2- Lo. A3)
Пусть T = T2 + Ti + To. Если силы имеют обычный потенциал П,
то Lo = То — П и, согласно A3),
Я = Т2 - То + П. A4)
Если же силы имеют обобщенный потенциал V = V\ + Vo, то Lo =
= Tq - Vo и
H = T2-T0 + V0. A5)
Пусть система натуральна и склерономна; тогда Т\ = 0, То = О
и Т = Т2. В том случае, когда силы имеют обычный потенциал,
Я = Т + П, A6)
т. е. для натуральной склерономной системы с обычным потенциалом
сил функция Гамильтона Н представляет собой полную механическую
энергию. В этом и состоит физический смысл функции Гамильтона.
Отметим также, что в случае склерономной натуральной системы
с обобщенным потенциалом сил
H = T + V0. A7)
151. Интеграл Якоби. Найдем полную производную функции
Гамильтона по времени. Используя уравнения A2), получим тождество
<Ш
EfdHdH дНдн\ | дН = дН
\ dqi dpi dpi dqi) dt dt '
т. е. полная производная функции Гамильтона по времени тождественно
равна ее частной производной:
<Ш дН
=
Система называется обобщенно консервативной, если ее функция
Гамильтона не зависит явно от времени. В этом случае dH/dt = 0 и в
силу тождества A8) dH/dt = 0, т. е. при движении системы
Я (и, Pi) = h, A9)
288 Глава X
где h — произвольная постоянная. Функцию Н называют обобщенной
полной энергией, а равенство A9) — обобщенным интегралом энергии.
В случае натуральной системы с обычным потенциалом сил функ-
функция Гамильтона вычисляется по формуле A4) и, если она не зависит от
времени,
Г2 - Го + П = h. B0)
Соотношение B0), где h — произвольная постоянная, называют интег-
интегралом Якоби.
Если система консервативна, т. е. она склерономна и силы имеют
потенциал, не зависящий от времени, то То = 0, Т\ = 0, Т = Т^ и
интеграл Якоби запишется в виде
Е = Т + П = Ь. B1)
Таким образом, консервативная систе-
система является частным случаем обобщен-
обобщенно консервативной и в рассматривае-
рассматриваемом частном случае обобщенный интег-
интеграл энергии переходит в обычный.
Пример 1. Гладкая трубка вращается
Рис. 135 в горизонтальной плоскости с заданной
постоянной угловой скоростью и). Внутри трубки движется шарик мас-
массой т.
Будем считать, что шарик можно принять за материальную точ-
точку. Угол <р, который составляет ось трубки с некоторым неизменным
направлением в горизонтальной плоскости, известен (<р = u)t). Поло-
Положение шарика будем задавать координатой г — расстоянием до оси
вращения трубки (рис. 135).
Потенциальная энергия шарика постоянна; примем, что П = 0.
Для кинетической энергии шарика имеем выражение
Т = \т{г2+и2г2),
т. е.
Т2 = \mr2, Ti =0, То = \mu?r2.
Имеет место интеграл Якоби B0), который в рассматриваемом при-
примере запишется в виде
Н = yinr2 — -~muJr2 = h = const.
§ 2. Канонические уравнения Гамильтона 289
Было бы ошибкой принять за интеграл полную механическую энер-
энергию Е = Т + П, так как рассматриваемая система (шарик во вращаю-
вращающейся трубке) не является консервативной.
152. Уравнения Уиттекера и Якоби. Пусть движение системы
описывается каноническими уравнениями A2). Если функция Гамиль-
Гамильтона не зависит явно от времени, то существует обобщенный интеграл
энергии
H(qi, ..., qn, pi, ..., рп) = h, B2)
где h — произвольная постоянная, определяемая начальными усло-
условиями, h = Н($, ... , 5°, pi, ... , р°п). В 2п-мерном простран-
пространстве qi, ... , qn, pi, ... , рп 1 уравнение B2) задает гиперповерх-
гиперповерхность. Будем рассматривать только такие движения, которые со-
соответствуют этой гиперповерхности. Иначе говоря, рассмотрим
движение системы на фиксированном изоэнергетическом уров-
уровне H(q±, ... , qn, pi, ... , рп) = h.
Покажем, что движение изучаемой системы на изоэнергетическом
уровне описывается системой дифференциальных уравнений, порядок
которой равен 2и — 2, причем эта система уравнений может быть за-
записана в виде канонических уравнений. Предположим, что в некоторой
области фазового пространства выполняется неравенство dH/dpi ф 0.
Тогда в этой области равенство B2) разрешимо относительно pi:
Pi = -K(qi, q2, ... , qn, p2, ••• , Pn, h). B3)
Перепишем систему уравнений A2), отделив два уравнения, соответ-
соответствующих значению г, равному единице, от остальных Bп — 2)-х урав-
уравнений
dt dpi' dt
dt apj dt dqj
Разделив почленно уравнения B5) на первое из уравнений B4), полу-
получим
dqi dpj dpi dqj
-г1 = , -г1 = 5 U = 2, 3, ... , п). B6)
dqi (Ш dqi Ш \J , , , J \ I
dpi dpi
хЭто пространство называют фазовым пространством.
290 Глава X
Подставив величину р\, задаваемую равенством B3), в левую часть
интеграла B2) и продифференцировав полученное тождество по пере-
переменной qj, получим
9Ж _ дЦ
Oqj dpt
Аналогично получим, что
Ж_ЖК г\ а о ч п\
dp, dPldPi
Преобразуя правые части уравнений B6) с использованием ра-
равенств B7) и B8), находим окончательно
^1_дК Ф1__дК и-2 3 п) B9)
dQl ~ дР/ dQl - dqj> (J ~2'd' •••' n)- {1Щ
Уравнения B9) описывают движение системы при Н = h = const и
называются уравнениями Уиттекера. Они имеют форму канонических
уравнений; роль функции Гамильтона играет функция К из B3), а роль
времени — координата ^i-
Интегрирование уравнений Уиттекера B9) дает
Чз = 4j(qi, h, а, ... , с2„-2),
Pj = РМи h, а, ... , c2n_2), (j = 2, 3, ... , и),
где ci, ... , C2n-2 — произвольные постоянные. Если эти выражения
для qj, pj подставить в равенство B3), то получим
Pi =Л(«ъ h, а, ... , с2„_2), C1)
Равенства C0), C1) задают геометрический характер движения: они
определяют уравнения траекторий в фазовом пространстве (точнее, на
гиперповерхности фазового пространства Н = К). Чтобы найти зави-
зависимость движения от времени, воспользуемся первым из двух урав-
уравнений B4). Если в его правую часть подставить величины pi, qj, pj
из C0) и C1), то получим
I, Ci, ... , C2n_2),
откуда
Г% + с2п-1. C2)
§ 2. Канонические уравнения Гамильтона 291
Разрешив уравнение C2) относительно qi, получим
Ч\ = Qi(t, h, a, ... , c2n_i). C3)
Уравнения Уиттекера B9) имеют структуру уравнений Гамильто-
Гамильтона. Их можно записать в виде уравнений типа Лагранжа. Пусть гессиан
функции К по переменным pj отличен от нуля:
det
д2к
C4)
Пусть Р — преобразование Лежандра функции К по перемен-
переменным pj (j = 2, 3, ... , п). Тогда
п
Р = P(q2, ...,qn, (&,..., q'n, Ql, h) = ^ q'jPj - K, C5)
где q'j = dqj/dqi. Величины pj в C5) выражаются через q'2, ... , q'n из
уравнений
т. е. из первых п — 1 уравнений системы B9).
При помощи функции Р уравнения B9) могут быть записаны в
следующей эквивалентной форме:
Щ-wr0 (i=2'3'•••'»>• C6)
Это уравнения типа Лагранжа. Они называются уравнениями Якоби.
Роль функции Лагранжа в уравнениях Якоби играет функция Р, а роль
времени, как и в уравнениях Уиттекера B9), — координата q\.
Преобразуем выражение C5) для функции Р, учитывая равенст-
равенства G), B3) и соотношение q[ = 1:
р = Ewi+й = Z>e* = f Z>* = f (x+H)- C7)
J=2 t=l 8 = 1
Пусть система консервативна. Тогда L = Т — П, Я = Г+П и из C7)
следует, что
Р=2?. C8)
292 Глава X
Но в консервативной системе
п
T=\Y, °«*g* = q\G(qi, ..., qn, q'2, ..., q'n), C9)
i,k=l
где
n
2
i,k=l
Из интеграла энергии Т + П = Л, и равенства C9) находим, что
И из C8), C9) получаем окончательное выражение для функции Р в
случае консервативной системы:
Р = 2^/(h-n)G. D0)
Пример 1. Найдем уравнения Уиттекера и Якоби, описывающие движе-
движение точки массой т в однородном поле тяжести. Пусть ось Oz непо-
неподвижной системы координат Oxyz направлена вертикально вверх. Тог-
Тогда
Т = ^m(x2 + y2 + z2), П = mgz,
L = ^m(x2 + у2 + z2) - mgz,
рх = mi, py = my, pz = mi,
Считая величину х положительной, из уравнения Н = h получа-
получаем рх = —К, где
К = -^J2m(h - mgz) - p\ - p\.
Уравнения Уиттекера B9) будут такими:
dy _ Py
dx
^2m(h - mgz) - p\ - p\
dz = Pz dpv =Q
dx /o /7 \ "Го ~о яж
y/2ra(/i - mgz) -p2y-p\
dpz
dx
- mgz) - p\ -
§ 3. Уравнения Рауса
293
Так как рассматриваемая система консервативна, то функция Р
может быть вычислена по формуле D0). Получаем
Тогда
Р = ^2m(h - mgz)(l + у'2 + z'2),
и уравнения Якоби C6) запишутся в виде
h - mgz j\ | mg
)
=Q
§ 3. Уравнения Рауса
153. Функция Рауса. Для описания состояния голономной систе-
системы в данный момент времени t Раус предложил комбинацию перемен-
переменных Лагранжа и Гамильтона. Переменными Рауса являются величины
Ча, Pa,
(г = 1, 2, ... , к; а = к + 1, ... , тг),
где к — произвольное фиксированное число, меньшее п. Пред-
Предположим, что гессиан функции Лагранжа по переменным qa
(а = к + 1, ... , п) отличен от нуля:
det
o2l
det
dqa dq/з
Для натуральной системы
d2L Г
#0.
A)
a,(i=k+l
dqadq/3
= det
д2Т2
= det
a,p=k + l
\a,/3=k
Последний определитель в равенстве B) отличен от нуля (положите-
(положителен), так как Тг — определенно-положительная квадратичная форма от
обобщенных скоростей и к ней применим критерий Сильвестра. Следо-
Следовательно, для натуральной системы неравенство A) всегда выполнено.
В случае ненатуральной системы это неравенство является дополни-
дополнительным к условию D6) п. 147 ограничением на функцию L.
294 Глава X
Обобщенные импульсы ра определяются обычным образом при по-
помощи равенств
Функцией Рауса R(q1, ... ,qk, qk+i, ... , qn, qi, • ¦ • , qk, Pk+i, ¦ • ¦ , Pn, t)
называется преобразование Лежандра функции L по переменным
qk+1, ¦¦¦ qn, т. е.
R = ^2 PaV"
а=к + 1
где qa (а = к + 1, ... , п) выражены через q,, qa, q,, pa, t из уравне-
уравнений C).
154. Уравнения Рауса. Полный дифференциал функции Рауса
вычисляется по формуле
E)
С другой стороны, вычислив полный дифференциал правой части ра-
равенства D) при условии C), получим
к / \ п / \
**¦=- Е (й%+id*j+аЕ+1 (*-*- - ?dfe j - fdL
Сравнение правых частей равенств E) и F) приводит к равенствам
8R _ 8L 8R _ 8L , ¦ 1 2 , ч /7ч
Но для нашей системы справедливы уравнения Лагранжа
lf-f=° U = l,2,...,n). A0)
§ 4- Уравнения движения неголономных систем 295
Из G) и A0) следует, что
lf-f=° (-1. 2'-.*). (И)
а равенства C), (8) и A0) дают:
dqa _ OR dpa _ QR
dt дра' dt dqa
(a = k+l, ... , n). A2)
Совокупность уравнений A1) и A2) образует систему уравнений
Рауса. Она состоит из к уравнений A1) второго порядка, имеющих
структуру уравнений Лагранжа второго рода, и 2(и — к) уравнений A2)
первого порядка, обладающих структурой уравнений Гамильтона.
Уравнения Рауса находят широкое применение при исследовании
движения систем с циклическими координатами (см. далее п. 165).
§ 4. Уравнения движения неголономных систем
155. Уравнения движения с множителями связей. Пусть на
систему наложено s дифференциальных неинтегрируемых связей, за-
заданных равенствами B6) п. 16:
т
^bpjiqi,... ,qm,t)qj + b(i(q1,... ,qm,t) = O ЦЗ = 1, 2, ... , s). A)
Тогда в общем уравнении динамики (см. п. 137)
величины Sqj не могут быть произвольными. Они связаны s независи-
независимыми соотношениями
т
Л = 0 (/3=1, 2, ... , s), C)
и число степеней свободы системы равно п = т — s.
Для вывода уравнений движения воспользуемся методом неопре-
неопределенных множителей Лагранжа. Каждое из s равенств C) умножим на
свой неопределенный скалярный множитель А/з и результаты вычтем
из B). Тогда получим
296 Глава X
В силу независимости равенств C) ранг матрицы, составленной из ко-
коэффициентов bpj (fi = 1, 2, ... , s; j = 1, 2, ... , то), равен s. Следо-
Следовательно, хотя бы один из ее миноров порядка s отличен от нуля. Для
определенности будем считать, что
=1^O. E)
Тогда величины Sqi, ... , Sqn можно принять за независимые, a 8qn+k
(к = 1, ... , s) однозначно выражаются через них из равенств C).
Выберем величины \р (/3 = 1, 2, ... , s) так, чтобы коэффициенты
при Sqn+i, ... , 6qm в выражении D) обратились в нуль. При усло-
условии E) это сделать можно, и притом единственным способом. При та-
таком выборе величин Л^ в выражении D) будут содержаться только
независимые вариации Sqi (г = 1, 2, ... , п), и, следовательно, коэффи-
коэффициенты при них должны равняться нулю.
Таким образом, приходим к следующим то уравнениям:
F)
К ним еще надо присоединить s уравнений связей A). Тогда по-
получим систему то + s уравнений для определения величин qj, \р
(j = 1, 2, ... , то; fi = 1, 2, ... , s). Величины Л^ называются множите-
S
лями связей. Слагаемые J^ ^fibfij в уравнениях F) представляют собой
/3=1
обобщенные реакции связей,
Пример 1. В качестве примера рассмотрим движение конька по гори-
горизонтальной поверхности льда (см. пример 5 из п. 10 и рис. 10) в пред-
предположении, что трение отсутствует. Пусть С — центр масс конька.
Положение конька зададим тремя обобщенными координатами х, у, <р,
смысл которых ясен из рис. 10. Неинтегрируемая связь задается урав-
уравнением
xtg<p-y = 0. G)
Если то — масса конька, a Jc — его момент инерции относитель-
относительно вертикальной оси, проходящей через центр масс, то кинетическая
энергия вычисляется по формуле
Т = \т{х2 + у2) + \3СФ2. (8)
§ 4- Уравнения движения неголономных систем 297
Уравнения F) принимают вид
d дТ дТ п
=Q
d дТ дТ
dt дф д<р Чч"
Так как трения нет, а потенциальная энергия П конька постоянна,
то обобщенные силы Qx, Qy, Qv равны нулю. Уравнения (9) с учетом
выражения (8) запишутся в виде
mii = Xtgip, ту = —А, ф = 0. A0)
Пусть в начальный момент центр масс конька находится в начале
координат и конек расположен вдоль оси Ох, т. е. при t = 0 имеем
х = 0, у = 0, <р = 0. Пусть, далее, в начальный момент скорость цент-
центра масс равна vq, а угловая скорость конька u)q, т. е. х = Vo, ф = ujq.
Из уравнения связи G) находим тогда, что при t = 0 у = 0. Третье
уравнение системы A0) при этих начальных условиях дает
ip = LJOt, A1)
т. е. конек движется, равномерно вращаясь вокруг вертикали.
Исключив теперь величину Л из первых двух уравнений систе-
системы A0), получим
x + tguioty = 0.
Используя уравнение связи G), исключаем отсюда величину у. Тогда с
учетом равенства A1) получим уравнение относительно х:
Х + U)OtgGJOtx = 0. A2)
Из G), A1) и A2) с учетом начальных условий найдем
V° -¦•-¦•* у = BUl -cosoj0t). A3)
Отсюда следует, что центр масс конька равномерно со скоростью Vo
движется по окружности радиусом vo/ljq, центр которой находится на
оси Оу (рис. 136).
298
Глава X
Множитель связи А можно найти теперь
из A3) и второго из уравнений системы A0):
Л = —
A4)
При известной величине Л можно найти реак-
реакцию R связи. Для ее проекций Rx, Ry из A0),
A1) получаем выражения
Rx =
Ry - -А.
Подставив в них значение Л из формулы A4),
получим
Ry =
Реакция R имеет постоянную величину mwoVo и направлена к центру
окружности, по которой движется центр масс конька.
156. Уравнения Воронца. Система уравнений A), F) помимо
функций qj (j = 1, 2, ... , то) содержит еще s дополнительных неиз-
неизвестных — множителей связей Л/э (fi = 1, 2, ... , s). Число уравнений
в системе A), F) равно то + s = п + 2s, т. е. превышает число степеней
свободы на удвоенное количество неинтегрируемых связей.
Большое количество уравнений в системе A), F) и наличие в
ней множителей связей ведет к значительным сложностям при ис-
исследовании движения. К тому же, когда целью исследования яв-
является только нахождение движения, т. е. определение зависимос-
зависимостей qjit) (j = 1, 2, ... , то), вычисление величин А^, позволяющих най-
найти реакции связей, является совершенно излишней процедурой.
Для неголономных систем со связями A) П. В. Воронец получил
уравнения, которые по форме близки к уравнениям Лагранжа второго
рода и свободны от упомянутых недостатков. Выведем эти уравнения,
предполагая, что система склерономна.
В случае склерономной системы величины Ър в уравнениях свя-
связей A) равны нулю, а коэффициенты bpj не зависят от времени. Сре-
Среди то обобщенных скоростей есть п независимых; пусть это будут об-
обобщенные скорости qi, G2, ... , qn- Тогда из A) находим
Чп+к =
* (fc = 1, 2, ... , s = то - п),
г=1
A5)
где aki — функции от qu q2, ... , qm.
§ 4- Уравнения движения неголономных систем 299
Когда система неголономна, то величины
не могут все одновременно быть тождественно равными нулю1. Урав-
Уравнения движения, содержащие множители связей, запишутся в виде
= 1,2,...,*).
Эти уравнения должны рассматриваться совместно с уравнениями свя-
связей A5).
Обозначим 0 функцию, получающуюся в результате исключения
при помощи равенств A5) величин qn+k (fc = 1, 2, ... , s) из выражения
для кинетической энергии Т:
T(qi, ¦¦¦ ,qm, qi, ¦¦¦ , qm, t) = Q(q1: ... ,qm, qi, ¦¦¦ , qn, t).
Согласно A5), справедливо равенство
д& _ от у- дт
r,--i 2 п)
К — 1
Следовательно,
d dQ d дТ
Ь dt dq
dt 3& + ^- Ь dt dqn+k f^dt dq
fci fc=i
n+k
Заменив здесь величины -т-тгт- и -т-тгт^— на их выражения из уравне-
(Й% dtdqn+k
ний A7), получим, что члены, содержащие множители связей, взаимно
уничтожаются, и равенство A8) запишется в виде
дв
A9)
1Если бы это было не так, то для всех к имели бы место равенства qn+h =
= Л(?Ъ 92> ¦¦¦ 5 ?m)i т. е. система не была бы неголономной. Действительно, усло-
условия А^ ¦ = 0 (г j = 1, 2, ... , п; к = 1, 2, ... , s) суть записанные с учетом ра-
п
венств A5) условия того, что величина dqn+k = Е akidqi является полным диффе-
i=l
ренциалом.
300
Глава X
Учитывая, что в соответствии с A5)
к=1 \з=1
из равенства A9) получаем
d dQ = dQ _ у^ дТ (у^
dqi
или
d dQ
dT
fct'i dqn
+k
dt
*-?
3=1
1п+к
B0)
B1)
Замечая, что выражение, заключенное в квадратные скобки в соотно-
соотношении B1), тождественно равно величине
>' = 1, 2, ... , n; fc = l, 2, ... , в),
где величины А], определены равенствами A6), и вводя для импульсов
обозначение
в = ?Г
получаем окончательно уравнения
s
(к = 1, 2, ... , s),
B2)
B3)
§ 4- Уравнения движения неголономных систем 301
Эти уравнения называются уравнениями Воронца. Они должны рассмат-
рассматриваться совместно с уравнениями связей A5). Полученная система
уравнений движения неголономной системы не содержит множителей
связей. Число уравнений равно n + s, т. е. совпадает с числом обобщен-
обобщенных координат.
157. Уравнения Чаплыгина. Пусть кинетическая энергия Г, ко-
коэффициенты aki (к = 1, 2, ... , s; г = 1, 2, ... , п) в уравнениях связей
и обобщенные силы Qi (I = 1, 2, ... , т) не зависят от обобщенных
координат qn+k (к = 1, 2, ... , s). Тогда уравнения B3) запишутся в
виде
=Qi + ^ kiQn+k + ^вк{^AV *) B4)
k=\ k=i S=i x >
(г = 1,2, ... ,n),
где
,(*) _ дам _
« " d
и j-i 2 n- к - 1 2 s)
Если в выражениях для обобщенных сил Qi (I = 1, 2, ... , т) и импуль-
импульсов вк (к = 1,2, ... , s) при помощи уравнений связей A5) исключить
обобщенные скорости qn+k (к = 1, 2, ... , s), то получим систему урав-
уравнений относительно <7; (г = 1, 2, ... , п), которую можно интегрировать
независимо от уравнений связей A5). Эти уравнения впервые были по-
получены Чаплыгиным и носят его имя.
После интегрирования уравнений B4) остальные координаты
qn+i, ¦ • ¦ , qm найдутся из A5) при помощи квадратур.
Если обобщенные силы потенциальны и потенциал П не зависит от
обобщенных координат qn+ki то уравнения B4) примут вид
d д® д® _ wi , x'd.lX1 л(")а,. 1 4 = 12... га). B6)
Пример 1 (Качение диска по неподвижной горизонтальной плос-
плоскости). Пусть однородный круговой диск катится без скольжения по
неподвижной горизонтальной плоскости, опираясь на нее одной точ-
точкой своего края. Движение отнесем к неподвижной системе коорди-
координат OXYZ с началом в некоторой точке О опорной плоскости; ось OZ
направлена вертикально вверх (рис. 137). Пусть GXYZ — посту-
поступательно движущаяся система координат, оси которой параллельны
соответствующим осям системы OXYX. Система координат Gxyz
302
Глава X
x
Рис. 137
жестко связана с диском: ее ось Gz перпендикулярна плоскости дис-
диска. За обобщенные координаты примем три угла Эйлера и две коор-
координаты х, у проекции Q центра тяжести G на опорную плоскость в
системе OXYZ. Третья координата z центра тяжести есть его рас-
расстояние до опорной плоскости. Из рис. 137 видно, что
z = psm(
B7)
где р — радиус диска.
Кинетическая и потенциальная энергия диска определяются выра-
выражениями
Т = \ш{х2 + у2 + i2) + 1
Bq2 + Cr2), H = mgpsm9,
где m — масса диска, g — ускорение свободного падения, р, q, r —
проекция угловой скорости ш диска на оси Gx, Gy, Gz, являющиеся его
главными центральными осями инерции, А, В, С — моменты инерции
диска относительно осей Gx, Gy, Gz, причем
а р, q, r задаются кинематическими уравнениями Эйлера
р = ф sin 9 sin ip + 9 cos <?>,
q = ф sin 9 cos (p — 9 sin (p,
r = ф cos 9 + ip.
B8)
§ 4- Уравнения движения неголономных систем 303
Принимая во внимание, что, согласно B7),
z = P6cose, B9)
выражение для кинетической энергии диска можно записать в виде
Т = \т{х2 + у2) + \mp2(l + 4 cos2 в)в2 +
2 8 . C0)
+ дmp2 sin2 9ф2 + jmp2(tpcos9 + фJ.
Уравнения связей получим из условия отсутствия скольжения. Если
скольжения нет, то скорость V?> точки диска, которой он касается
опорной плоскости, равна нулю. Поэтому
VG + Ш X Ш) = 0, C1)
где vg — скорость центра тяжести, GD — радиус-вектор точки D
относительно G.
На рис. 137 прямая DE является касательной к диску в точке D.
Она параллельна линии узлов GN. Прямая DG перпендикулярна DE, ле-
лежит в плоскости, проходящей через оси GZ и Gz, и составляет угол <р
с осью Gy. В системе координат OXYZ
v'G = (х, у, z),
GD ' = p(cos в sin ф, - cos в cos ф, - sin в), C2)
а/ = (всоъф + фътфътв, вътф - фсоъфътв, ф + фсоъв).
Третья компонента векторной правой части равенства C1) тождест-
тождественно равна нулю в силу равенства B9). Приравнивание нулю первых
компонент дает уравнения связей
х = р[в sin ф sin в — (ф cos в + ф) cos ф],
(оо)
у = —р[в cos ф sin в + (ф cos в + ф) sin ф].
Так как И, Т и уравнения связей не содержат обобщенных коорди-
координат х, у, то уравнения движения диска могут быть записаны в форме
уравнений Чаплыгина.
Для удобства вычислений введем временно обозначения
gi =9, q2 = (p, q3 = ф, q\ = x, q5 = y.
Тогда в обозначениях п. 156, 157 имеем
«и = psmq1s'mq3, a12 = -pcosq3,
3 = -/9cosgicosg3, 1 = -psinqx cosq3,
a.22 = -ps'mq3, a23 = -pcosqi s'mq3.
304 Глава X
Отсюда и из B5) следует, что
Щ ~^ = Psin(/3 ^ = ~^ =
Остальные величины Ai:j (i, j = 1, 2, 3; к = 1, 2) тождественно равны
нулю.
Для обобщенных импульсов в\, #2 имеем выражения
9\ = тх = m/9(sin<7i sinq^qi — cos G3^2 —
^2 = «У = —mp(smqi cosq3qi + sing3g2 + cosgi sing3g3).
Если теперь возвратиться к исходным обозначениям, то уравнения
Чаплыгина запишутся в виде
Здесь в есть кинетическая энергия C0), в которой величины х, у ис-
исключены при помощи уравнений связей C3):
6= \тр2в2 + Imp2 sin2 вф1 + ^тр2(ф cos в + фJ. C5)
о о 4
Подставив функцию в в C4), получим систему уравнений движения
в + sin в cos 0?А2 +f sin вф1р+ |f cos 0 = 0,
О О "
C6)
-f [(V> cos в + ф) cos в + i sin2 6>V>] = -1 si
Е'слы эта система проинтегрирована, то движение центра тяжести
диска найдется при помощи конечного соотношения B7) и двух квадра-
квадратур из C3).
Уравнения движения C6) допускают частные решения, для кото-
которых 9 = во = const. При этом
ф = u>i = const, ¦ф = и>2 = const, C7)
§ 4- Уравнения движения неголономных систем 305
а угол во удовлетворяет следующему соотношению, вытекающему из
первого уравнения системы C6):
COS #0 Sin #о<^2 + ^ S^n #0WlW2 + F п C0S ^0 = 0- C8)
О Or
Если во = тг/2, то это уравнение переходит в условие ш\Ш2 = 0. Отсюда
следует, что существуют следующие движения диска:
во = тг/2, ал =0, ш2 ф 0, C9)
6>о = 7г/2, Ш1 ^ О, w2 = 0, D0)
6»о = тг/2, ал =0, о;2 = 0, D1)
В движении C9) дыск вращается с произвольной постоянной угло-
угловой скоростью Ш2 вокруг одного из своих диаметров, который неподви-
неподвижен и занимает вертикальное положение. В движении D0) диск ка-
катится по прямой, при этом плоскость диска вертикальна, а центр
тяжести движется с произвольной постоянной скоростью |wip|. Дви-
Движение D1) соответствует покою диска в вертикальной плоскости.
В общем случае, когда во ф тг/2, величины и>\, и>2, во связаны между
собой соотношением C8), которое, следовательно, определяет двухпа-
раметрическое семейство движений диска. Для этих движений из урав-
уравнений связей C3) получаем
UJ COS #() + wl • / a W
где а и C — постоянные интегрирования, определяемые по начальным
условиям, а ф = u>2i + Фо- Отсюда и из B7) следует, что центр тя-
тяжести диска движется по окружности, расположенной в горизонталь-
горизонтальной плоскости и имеющей центр в точке (а,/3, psmdo); радиус этой
окружности
02 cos #о + w:
U>2
Отсюда и из рис. 137 следует, что точка D касания во время движения
диска описывает на опорной плоскости 0XY окружность с центром в
точке (а, /3) и радиусом, равным p\wi/wi\.
В самом общем случае аналитическое исследование движения дис-
диска приводится к интегрированию одного линейного дифференциального
уравнения второго порядка и квадратурам. Чтобы показать это, заме-
заметим, что фсозв + ф = г, и, рассматривая промежуток времени, на ко-
котором в ф 0, перейдем во втором и третьем уравнениях системы C6)
306 Глава X
к новой независимой переменной 9. Тогда получим
^ = |sin^, 4n (Vcos<9+ isin2<?vA = —§ sin6»(r — ф'со&в). D2)
aw о at? \ о / о
Исключив из этих уравнений величину ф, приходим к дифференциально-
дифференциальному уравнению
которое, если положить и = cos2 в, принимает вид
Это линейное дифференциальное уравнение второго порядка пред-
представляет собой известное из теории дифференциальных уравнении ги-
гипергеометрическое уравнение Гаусса. Его интегрирование дает величи-
величину г как функцию угла в. Из первого уравнения системы D2) и равенст-
равенства фсоъв + ф = г определяются затем фиф как функции угла в. Таким
образом, задача нахождения углов Эйлера сводится к нахождению в как
функции времени, так как ф(г) и ip(t) найдутся при известной функ-
функции 9(t) посредством квадратур.
Зависимость 9(t) также получается посредством квадратур. Дей-
Действительно, уравнения C4) имеют интеграл энергии
@ + U = h = const. D3)
Это следует из того (см. п. 143), что уравнения C4) можно рассмат-
рассматривать как уравнения движения склерономной системы под действием
гироскопических сил Qv = тр2 ътввф, Q^ = —тр2 ътввф и потенци-
потенциальной силы Qg = — mgp cos 9 с потенциалом, не зависящим от времени.
Подставив в равенство D3) величины ф, ф как функции угла в и
разрешив его относительно в, получим в как функцию в. Отсюда t вы-
выразится через в при помощи одной квадратуры, обратив которую най-
найдем в = d(t).
158. Уравнения Аппеля. Аппель предложил уравнения движе-
движения, которые не содержат множителей связей и применимы как к голо-
номным, так и к неголономным системам с неинтегрируемыми связя-
связями вида A). Получим эти уравнения в псевдокоординатах (см. п. 17).
Пусть псевдоскорости ttj определены по формулам B9) п. 17:
т
ТГг = ^CijiQl, 42, ¦ ¦ ¦ , Чт, t)Uj (г = 1, 2, . . . , и). D4)
§ 4- Уравнения движения неголономных систем 307
Для получения уравнений Аппеля выразим в псевдокоординатах
общее уравнение динамики
JV
^2{FV - mvwv) • Srv =0. D5)
v=\
Подставив в равенство
JV m
v=\ j=l
где Qj — обобщенная сила, соответствующая обобщенной координа-
координате щ, вместо величин Sqj их выражения через Swi по формулам C2)
п. 17, получим элементарную работу активных сил в виде
N т п п
v=\ j=l i=\ i=\
где
m
Пг = II;(gi, ... ,qm, -hi, ... , жп, t) = ^dijQj (г = 1, 2, ... , n).
D7)
Величины IIj называются обобщенными силами, соответствующими
псевдокоординатам тт, (г = 1, 2, ... , п).
Для получения элементарной работы сил инерции в псевдокоорди-
псевдокоординатах получим, при помощи равенств C5) п. 17, следующее выражение:
JV N п
^^ =
v=i i=i ( }
»=i V=i
Если ввести функцию S по формуле
N
v=l
то равенство D8) можно записать так:
N п
-Y,m,wv-Srv = -Y,§§-.^i- E0)
v=\ j=l l
308 Глава X
Функция S называется энергией ускорений. В общем случае она являет-
является функцией от дь ... , qm, тгх, ... , т:п, tti, ... , fcn, t.
Из равенств D6) и E0) следует, что общее уравнение динамики D5)
в псевдокоординатах имеет вид
Так как величины Swi могут принимать произвольные значения, то
отсюда следуют уравнения
9S _ тт. а — 1 9 п\ D9)
Эти уравнения называются уравнениями Аппеля. Они должны рассмат-
рассматриваться совместно с s уравнениями связей A) и п соотношения-
соотношениями D4), вводящими псевдоскорости.
Аналогично тому, как в п. 140 доказана разрешимость уравне-
уравнений Лагранжа относительно обобщенных ускорений q\, можно пока-
показать, что уравнения Аппеля E2) разрешимы относительно псевдоуско-
псевдоускорений ttj (г = 1, 2, ... , п). Кроме того, уравнения A) и D4), по самому
выбору псевдоскоростей, разрешимы относительно qj (j = 1, 2, ... , т)
(см. уравнения C0) п. 17). Таким образом, приходим к т + п
уравнениям, разрешенным относительно производных неизвестных
функций gi, ... , gm, tti, ... , тгга. Если заданы начальные значе-
значения gj, ... , g^, ttj1, ... , тг°, то, при не очень обременительных для ме-
механики условиях на силы, дальнейшее движение системы будет одно-
однозначно определено. Но по величинам q®, ... , g°(, -h®, ... , тт° из фор-
формул C0) п. 17 однозначно определяются совместимые со связями A)
начальные значения обобщенных скоростей gj, ... , g^. А по величи-
величинам g°, g° (j = 1, 2, ... , т) однозначно определяются совместимые со
связями начальные положения и начальные скорости точек системы
в декартовой системе координат. Отсюда следует, что если заданы не
противоречащие конечным и дифференциальным связям положения и
скорости точек системы, то дальнейшее их движение однозначно опре-
определено.
Если в качестве величин ttj приняты обобщенные скорости д,
(г = 1, 2, ... , и), то соответствующие обобщенные силы П, равны ве-
величинам Q't, вычисляемым по формулам A3) п. 63. Энергия уско-
ускорений S в этом случае будет функцией от gi, ... , gm,gi, ... , qn,
g'i, ... , qn, t, и уравнения Аппеля
oS _ qi (г = 1 2 n) E3)
§ 4- Уравнения движения неголономных систем 309
вместе с уравнениями связей A) образуют систему уравнений, опре-
определяющих движение рассматриваемой неголономной системы. Число
уравнений равно п + s = т, т. е., как и в случае уравнений Воронца,
совпадает с числом обобщенных координат. Если система голономна,
то т = п, Q'i = Qi, и уравнения E3) будут просто другой формой
записи уравнений Лагранжа второго рода.
Для получения уравнений Аппеля нужно вычислить функцию S
— энергию ускорений, определяемую по формуле D9). Это довольно
громоздкая процедура. Поэтому, как правило, выписывание уравнений
Аппеля является более трудоемкой процедурой по сравнению с получе-
получением уравнений Воронца и Чаплыгина, где вместо S надо вычислять
кинетическую энергию Т.
В качестве примера используем уравнения Аппеля для доказатель-
доказательства достаточности условий принципа виртуальных перемещений для
равновесия системы (п. 62).
Пусть условия C) и D) п. 62 выполнены и при t = to имеем
Tv = »Vo> vv = 0 {у = 1, 2, ... , N). Покажем, что тогда на всем проме-
промежутке времени to ^ t ^ t\ система находится в состоянии равновесия,
т. е. для этого промежутка времени rv = rvo (и = 1, 2, ... , N).
Из D4), D6) и условия D) п. 62 следует, что при rv = rvo
ПДдю, • • • , Что 0, ... , 0, ?) = 0 для t0 ^ t ^ t\ (здесь q10, ..., qm0 —
значения обобщенных координат, отвечающие положению равновесия,
задаваемому в декартовой системе координат радиусами-векторами г„о
точек системы). С другой стороны, величины
N
= 5>llv (, = 12n)
= 5>vllv (, = 1,2,...,n)
v=l
при rv = г,/о также равны нулю, так как тогда wv = 0. Следо-
Следовательно, уравнения Аппеля E2) имеют частное решение qj = q^
(j = 1, 2, ... , m), отвечающее положению равновесия rv = г„о
(^ = 1,2, ...,7V).
Достаточность условий принципа виртуальных перемещений сле-
следует теперь из принципа детерминированности движения Ньютона —
Лапласа (см. п. 45), так как, согласно этому принципу, принимаемому
в классической механике, движение системы однозначно определяется
положениями и скоростями ее точек в начальный момент времени.
159. Вычисление энергии ускорений. Аналог теоремы Ке-
нига. Пусть we — абсолютное ускорение центра масс, wv — абсолют-
абсолютное ускорение точки Pv системы, a wvr — ускорение этой точки в ее
движении относительно центра масс. Тогда для всех точек системы
wv = we + wvr. E4)
310 Глава X
Вычислим энергию ускорений
^m,^. E5)
Подставив E4) в формулу E5), получим
N
^ l E6)
v=\
N N
Так как J^ mv = М, a J^ mvwvr = Mwcr = 0, то из E6) получаем
N
S = ±Mu? + ± ?>„<., E7)
v=l
т. е. энергия ускорений системы равна сумме энергии ускорений, кото-
которую имела бы материальная точка, расположенная в центре масс сис-
системы и имеющая массу, равную массе системы, и энергии ускорений в
движении системы относительно центра масс.
Полученное утверждение является аналогом теоремы Кенига для
кинетической энергии (см. п. 83).
160. Энергия ускорений твердого тела, движущегося во-
вокруг неподвижной точки. Пусть Oxyz — жестко связанная с те-
телом система координат, начало которой совпадает с неподвижной точ-
точкой О тела. Оси Ox, Oy, Oz направлены по главным осям инерции тела
для точки О. Положение частицы mv тела определяется ее радиусом-
вектором rv, r'v = (ж„, yv, zv). Пусть ш — угловая скорость те-
тела, ш' = (р, q, r), a e — его угловое ускорение. Так как абсолютная
производная вектора ш совпадает с его относительной производной, то
е' = (р, q, r). E8)
Согласно п. 24, ускорение частицы mv определяется по формуле
Wv = ? X rv + Ш X (ш X Г„),
или
!с„ = ?Хг„ + ш(ш ¦ г„) — гиш2. E9)
§4- Уравнения движения неголономных систем 311
Отсюда получаем выражения для проекций ускорения wv на оси
Ox, Oy, Oz:
wvx = ~xv{q2 + г2) + yv(qp - f) + zv(pr + q),
wvy = -yv{r2 + p2) + zv(rq -p) + xv{qp + f), F0)
wvz = -zv(p2 + q2) + xv{pr -q) + yv(r
Если N — число частиц, на которые мы мысленно разбили тело, то
выражение для энергии ускорений имеет вид
JV
е-1Гга Г,,,2 о- vi2 4- it? *\
° — 2 2—1 mv\Wvx "г wvy "г wvz>-
v=\
Подставим сюда выражения F0) и произведем некоторые преобразова-
преобразования с учетом того, что Ох, Оу, Ох — главные оси инерции и, следова-
следовательно,
N N N
Jxy = 22 ГП^хиУи = 0, Jxz = 22 rnvXvZv = 0, Jyz = 22 rnvVvzi' = 0-
Если еще в S отбросить несущественные для уравнений Аппеля слага-
слагаемые, не зависящие от р, q, r, то получим
S = \ ( И т»х» ) (f2 + 2qpf +q2 ~ 2prq) +
(jv \
гл 2 \ / 2 2
> тиу,, (р + 2rqp + г — 2qpr) +
Н )
1 № Л, 2
+ ^ ) mvz,. \ (q + 2prq + р —
V=i /
или
i /~<„ ^ _|_ ^ _ jjjqrp -f- y^ — l, ji pq -f- yjj — _п.ур^
F1)
S = ±(Ap2 + Bq2 + Cf2) + (C - B)qrp +(A- C)rpq + (B - A)pqf,
где А, В, С — моменты инерции тела относительно осей Ox, Oy, Oz
соответственно.
Пример 1 (Вывод динамических уравнений Эйлера при помощи
уравнений Аппеля). Пусть Мх, Му, Mz — проекции момента Мо
внешних сил относительно точки О на оси Ox, Oy, Oz. В качестве
312 Глава X
псевдоскоростей примем величины ж\ = р, тгг = q, тгз = т- Для элемен-
элементарной работы внешних сил имеем выражение
5А = Мо ¦ шсИ = Мхрdt + Myqdt + Mzrdt = Мх5жх + Му5ж2 + Mz5ir3.
Поэтому обобщенные силы Hi, соответствующие псевдокоордина-
псевдокоординатам 7Г;, вычисляются по формулам
Щ = Мх, П2 = Ми, П3 = Mz. F2)
Уравнения E2) с учетом выражений F1) и F2) непосредственно при-
приводят к динамическим уравнениям Эйлера (см. уравнения D) п. 97).
Пример 2 (Качение шара по плоскости). Пусть однородный шар
движется по неподвижной горизонтальной плоскости без скольжения.
Движение шара отнесем к неподвижной системе координат OXYZ с
началом в некоторой точке О плоскости, ось OZ направим верти-
вертикально вверх. Пусть шх, шу, ^z — проекции угловой скорости ша-
шара на оси OX, OY, OZ, a p, q, r — проекции того же вектора на
оси Gx, Gy, Gz жестко связанной с шаром системы координат с нача-
началом в центре шара.
Пусть х, у, z — координаты центра шара в системе OXYZ; z = а,
где а — радиус шара. Условие отсутствия скольжения (равенство нулю
скорости точки D шара, которой он касается плоскости) приводит к
соотношениям
х = и;уа, У = —мха- F3)
Момент инерции шара относительно любого диаметра равен ^та2,
о
где т — масса шара. Из E7) и F1) получаем выражение для энергии
ускорений:
S=lm(x2+y2)+\ma2(p2 + q2 + r2). F4)
Введем псевдоскорости по формулам
iTi =wx, 7Г2 = шу, n3=toz- F5)
Из F3) тогда получим
х = аж2, у = —аж\. F6)
Пусть е — угловое ускорение шара. Тогда, замечая, что
• 9 •*> .*> 9 .*> .9 .*> ««*> ..9 ..9
р + q + rz = e1 = шх + Шу + ujz = тт( + ж2 + тгд
§ 4- Уравнения движения неголономных систем 313
и пользуясь равенствами F6), получаем из F4) такое окончательное
выражение для энергии ускорений:
S = г^та2[7(ж1 + тг|) + 2тг|].
Так как обобщенные силы Hi (г = 1, 2, 3) равны нулю, то из уравне-
уравнений Аппеля dS/diti = 0 (г = 1, 2, 3) следует, что щ = 0 (i = 1, 2, 3),
или и)х = const, шу = const, u>z = const. Таким образом, из уравнений
Аппеля сразу следует, что угловая скорость при движении остается
неизменной. Другим способом этот вывод получен в п. 113.
Глава XI
Интегрирование уравнений динамики
§ 1. Множитель Якоби
161. Множитель системы уравнений. Дифференциальное
уравнение для множителя. В данной главе будут получены неко-
некоторые общие утверждения, относящиеся к интегрированию уравнений
динамики. Сначала рассмотрим нужные в дальнейшем вспомогатель-
вспомогательные вопросы теории дифференциальных уравнений.
Пусть задана система дифференциальных уравнений
dxi _ dx2 _ _ dxk , .
Х Х Х
где Х( (г = 1, 2, ... , к) — заданные функции переменных
Xi, X2, ... , Хк.
Всякая функция f{x\, х2, ••• , Хк), которая постоянна при
х\, х2, ... , Хк, удовлетворяющих системе A), называется ее первым
интегралом. Если f(xi, х2, ... , Хк) — первый интеграл, то дифферен-
дифференциал df в силу A) тождественно равен нулю, т. е.
df = ^-dxx + -^dx2 + ...+ ^-dxk = О
дхг дх2 дхк
в силу уравнений A). Это означает, что необходимое и достаточное
условие того, что функция f(x\, x2, ... , хк) является первым интег-
интегралом, записывается в виде равенства
Обозначение X(f) введено для краткости записи. Очевидно, что если
Л) /2; ••• 5 fi {I ^ к — 1) — первые интегралы, то и любая функ-
функция F(/i, /2, ... , /j) тоже будет первым интегралом системы A).
Если известны / независимых первых интегралов
/i = ci, /2 = с2, ... , // = с/ (cj = const; j = 1, 2, ... , I), C)
1. Множитель Якоби
315
то их можно использовать для понижения порядка системы A) на I
единиц. В самом деле, если Д, Д., ... , /; независимы, то ранг матрицы
dfi_ dfi
dxi dx2
dh dh
dfi
dxk
df2
dxk
dfi
dfi
8X2
i
dxk
D)
равен /. Не ограничивая общности, будем тогда считать, что отличен
от нуля определитель 1-го порядка, составленный из первых / столб-
столбцов матрицы D), т. е. якобиан функций Д, Д., ... , /; по перемен-
переменным Х\, Х2, ••• , Х{\
d(fi, h, .-., fi)
d(xi, x2, ¦¦¦ , x{)
dfi dfi
dfi
dxi
dh
dx±
dfi
dx2
dh
dx2
dfi
dxi
dh
dxi
dfi
#0.
E)
При выполнении этого неравенства соотношения C) можно разрешить
относительно величин х\, жг, ... , ж/, в результате чего эти величины
выразятся через переменные xi+i, ... , хи и константы с\, сг, ... , с/.
Подставив их в функции Xj+i, ... , Xj, и обозначив получающие-
получающиеся в результате этой подстановка функции Х*+1, ... , Х?, где XJ
(j = I + 1, ... , к) — функции от ж;_|_1, ... , Хк и ci, C2, ... , Q, мы све-
дем систему A) к системе уравнений
dxk
Y* '
порядок которой на / единиц меньше порядка исходной системы A).
Система A) может иметь только к — 1 независимых первых интегралов.
Если они известны, то соотношения
Д = ci, /2 = с2, ... , fk-i = ск-1
F)
дают общий интеграл системы дифференциальных уравнений A). Вся-
Всякий же другой интеграл / будет функцией независимых интегра-
интегралов Д, /г, ..., fk-i- Для доказательства этого утверждения на-
316
Глава XI
до проверить, что якобиан функций /, /i, ... , fu-i по перемен-
переменным х\, Х2, ¦¦¦ 1 Xk равен нулю:
d(f, /1, ¦•¦ , fk-i) = 0 ,7,
д{х±, х2, ... , хк)
Действительно, если /, /i, ... , fu-i — первые интегралы, то
Эта система к линейных однородных уравнений относительно
Xi,X2,... ,Xk должна иметь нетривиальное решение. Следовательно,
выполняется равенство G). Что и требовалось доказать.
Разложив якобиан, стоящий в левой части равенства G), по эле-
элементам первой строки, представим это равенство в виде
(8)
где Д, (г = 1, 2, ... , к) есть алгебраическое дополнение г'-го элемента
первой строки якобиана.
Условие (8) означает, что / — функция первых интегралов
/i, /2, ... , fk-i- Если / — первый интеграл, то выполнено условие (8),
а если выполнено (8), то / — функция /i, /2, ... , fk-i и, следова-
следовательно, является первым интегралом. Поэтому равенство (8) является
необходимым и достаточным условием того, что (при известных пер-
первых интегралах Д, /г, ... , fu-i) / есть первый интеграл. Послед-
Последнее означает, что условия B) и (8) эквивалентны. Поэтому соответ-
соответствующие коэффициенты при производных df/dx, (г = 1, 2, ... , к)
в равенствах B) и (8) пропорциональны, т. е. существует функ-
функция М(х\, жг,... , Хк) такая, что
Д; =
г = 1, 2, ... , к).
(9)
Функция М называется множителем Якоби или просто множите-
множителем системы уравнений A).
i 1. Множитель Якоби 317
В равенство (9) входят интегралы /i, /2, ... , fk-i- Однако мож-
можно получить дифференциальное уравнение для М, которое не содержит
/i, /2, ... , fk-i- Покажем, что множитель М удовлетворяет линейно-
линейному уравнению в частных производных
д(МХг) + д{МХ2) + + d{MXk) = o
дхх дх2 ''' дхк
В самом деле, если в соответствии с (9) вместо величин MXi
(г = 1, 2,... , к) подставить в A0) их выражения Д,, то после про-
проведения содержащихся в A0) дифференцирований получим, что левая
часть равенства A0) представляет собой совокупность слагаемых, каж-
каждое из которых есть произведение производной второго порядка ви-
вида д2 fg/dxidxj (г ф j) на к — 2 частных производных первого порядка.
Поэтому, чтобы показать справедливость равенства A0), достаточно
убедиться в том, что его левая часть не содержит ни одной производ-
производной второго порядка. Возьмем, например, производную д2f\jdx\dx2.
Она содержится в двух слагаемых. В одном слагаемом при д2f\jdx\dx2
будет коэффициент при dfi/dx2 в Ai, т. е. определитель
d(f2, /з, ••• , fk-i)
д(х3, ж4, ... , хк)
а во втором — коэффициент при dfi/dxi в Дг, т. е. определитель A1),
взятый с противоположным знаком. Следовательно, сумма упомяну-
упомянутых слагаемых равна нулю. То же самое справедливо и для остальных
слагаемых.
Любое решение уравнения A0) принято называть множителем.
Справедливо следующее утверждение: частное двух множителей яв-
является первым интегралом системы A).
В самом деле, пусть М\ и М^ — множители, т. е. решения уравне-
уравнения A0). Тогда справедливы равенства
Л/ dXi
2- \Ml7h^
эм
4 «^ + *пЕЧ=о. A3)
i=l
Умножив первое из этих равенств на —М2, а второе на Mi и сложив
результаты, получим
к В ( М2
, дМ2 ,. дМ^ а
V ®Xi ®Xi J ^T
318 Глава XI
Следовательно, M2/Mi действительно является первым интегралом.
Верно и обратное: произведение какого-либо множителя на первый ин-
интеграл системы уравнений A) также является множителем. В этом
легко убедиться непосредственной проверкой.
Для дальнейшего приложения теории множителя к уравнениям ди-
k Qj?.
намики важно заметить, что из A0) следует, что если ^ -~—- = 0,
то М = 1 является множителем.
162. Инвариантность множителя. Последний множитель
Якоби. Сделаем в системе уравнений A) замену переменных, введя
вместо xi, х2, ... , хи переменные у\, у2, . ¦. , у и по формулам
Xi = Xi(yi, 2/2, ••• , Ук) (г = 1,2, ... , fc). A4)
Будем считать, что якобиан
д(хг, х2, ... , хк)
d(yi, 2/2, ••• , Ук)
A5)
отличен от нуля. Тогда замена переменных A4) является обратимой.
Для получения преобразованной системы уравнений введем вспомога-
вспомогательную переменную t так, чтобы каждое из отношений dxi/Xi равня-
равнялось ее дифференциалу dt. Тогда система A) запишется так:
—^ =Xi(x!, х2, ... , хк) (г = 1, 2,... , к). A6)
Рассматривая каждую из величин у» (г = 1, 2,... , fc) как сложную
функцию t: yi(xi(t), жг(*),... , Xk(t)), имеем
Выраженную через j/i, y2, ... , ук величину X(yi) обозначим Y,. Тогда
в новых переменных система уравнений A) будет такой:
dyi dy2 dyk . .
Отметим, что выражение X(f) инвариантно в том смысле, что
к
хЮ = Т,Ъш: = ПП- A8)
i 1. Множитель Якоби 319
В самом деле,
к
xm-Vx df -Vx
Равенство A8) показывает, в частности, что интеграл исходной систе-
системы уравнений A), будучи записанным в новых переменных, является
интегралом преобразованной системы A7).
Пусть /i, /2, ... , fk-i — независимые первые интегралы систе-
системы A) и / — произвольная функция, a Mq — какой-либо множитель,
удовлетворяющий тождеству1
M0X(f) = у» A'-»/*-i). A9)
д{хг, х2, ... , хк)
Умножив обе части этого тождества на определитель A5), получим
д(х1, х2, ... , хк) , . d(f, /1, ... , fk-i)d(xi, x2, ... , хк)
мх\1)
«9B/1, 2/2, ••• , Ук) д(хх, х2, ... , хк) d(yi, у2, ... , у к)
Если воспользоваться инвариантностью выражения Х(/) и правилом
умножения функциональных определителей2, то последнее равенство
можно записать так:
Ъ1Г д{хи х2, ... , xk)v... _ d(f, /i, ... , Л-i)
o{yi, 2/2, ••• , 2/a) c/(j/i, 2/2, ••• , Ы
Отсюда следует, что функция
о^1,Ж2,-,^)
9(j/i 2/2, ... , 2/fc)
является множителем преобразованной системы уравнений A7). Пусть
теперь М — произвольный множитель, т. е. какое-либо решение урав-
уравнения в частных производных A0), a Mq — множитель из тождест-
тождества A9). Согласно п. 160,
М = M0F,
1См. определение множителя системы уравнений A) при помощи равенств B),
G)-(9).
2См. гл. 3 книги: Гурса Э. Курс математического анализа. Т. 1, ч. 1, М.; Л.: ГТТИ,
1933.
320 Глава XI
где F — первый интеграл системы уравнений A) (а также и систе-
системы A7)). Умножив обе части этого равенства на определитель A5) и
воспользовавшись формулой B0), получим
Md(xlt ха, - , хк) = d(xlt ха, - , хк) = ^
<Л2/1, 2/2, ••• , Ы О(?/1, 2/2, ••• , Ук)
Но мы показали, что Мд — множитель для переменных
2/1, 2/2, ••• , Ук- А так как F — первый интеграл, то, согласно п. 161,
функция MqF также является множителем.
Таким образом, мы доказали теорему об инвариантности
множителя: если М — множитель для переменных х\, х2, ... , хк,
то его произведение на якобиан A5) есть множитель для новых пере-
переменных 2/1, 2/2, ••• , Ук-
Свойство инвариантности является основным для практического
применения теории множителя. Предположим, что известны к — 2 неза-
независимых первых интеграла системы дифференциальных уравнений A)
fj = ci (CJ = const; i = 1, 2, ... , k-2),
т. е. для получения общего интеграла недостает одного первого интег-
интеграла.
Введем новые переменные 2/i, 2/2, • • • , У к по формулам
2/1 = х±, у2=х2, 2/3 =Л,-.-, Ук = fk-2-
Тогда при г ^ 3 Yi = X(yi) и в новых переменных система уравне-
уравнений A) станет такой:
d№_ _ dy^ _ dy^ _ _ dyk
Yx ~ Y2 0 0 '
т. е. сводится к одному уравнению
Y2dyx - Yxdy2 = 0, B3)
в котором уз,... ,Ук рассматриваются как постоянные.
Если бы был известен множитель М для переменных хх,х2,... ,хк,
то, согласно теореме об инвариантности множителя, функция
М* = мдЫ,х2,...,хк)
о(Уг, 2/2, ••• , Ук)
была бы множителем для переменных 2/i, 2/2, ••• , У к, т. е. удовлетво-
удовлетворяла бы уравнению
~ — =0,
1. Множитель Якоби 321
которое с учетом того, что Y, = 0 при i ^ 3, имеет вид
d{M*Yj) | d(M*Y2) = Q
%i ду2
Последнее равенство означает, что функция М* является интег-
интегрирующим множителем Эйлера для уравнения B3), т. е. выражение
M*(Yzdyi —Y\dy2) будет полным дифференциалом. Следовательно, не-
недостающий первый интеграл может быть записан в виде
M*{J2dyx - Yxdy2) = const.
Функция М* носит название последнего множителя, или последнего
множителя Якоби.
Таким образом, если для системы A) известен какой-либо множи-
множитель, то ее интегрирование требует нахождения не к — 1, а лишь к — 2
независимых первых интегралов. Нахождение последнего недостающе-
недостающего интеграла сводится к квадратуре.
Пример 1 (Качение неоднородного шара по плоскости1). Рассмот-
Рассмотрим движение шара по неподвижной горизонтальной плоскости. Шар
считаем неоднородным, его центр масс совпадает с геометрическим
центром, движение происходит без скольжения.
Движение отнесем к системе Gxyz, образованной главными цен-
центральными осями инерции. Пусть а — радиус, А, В, С — момен-
моменты инерции относительно осей Gx, Gy, Gz, am — масса шара. Ес-
Если v' = (vx, vy, vz) — скорость центра шара, а из' = (р, q, r) —
угловая скорость, п' = G1, J2, 7з) — единичный вектор, направлен-
направленный вертикально вверх, то условие отсутствия скольжения (равенство
нулю абсолютной скорости точки D шара, которой он касается плос-
плоскости) запишется в виде
v = аи> х п. B6)
Уравнение движения шара получим в форме уравнений Аппеля. Энергия
ускорений вычисляется по формуле (см. п. 159, 160)
S =\mw + \ (Ap+Bg + c7r) +
+ (С - B)qrp + (A- C)rpq + (В - A)pqr,
1Эта задача решена С. А. Чаплыгиным в его работе «О катании шара по горизон-
горизонтальной плоскости» (см.: Чаплыгин С. А. Собр. соч. Т. 1, М.; Л.: Гостехиздат, 1948.—
С. 76-101).
322 Глава XI
где w' = (wx, wy, wz) — ускорение центра шара. Из B6) получаем
w = а[й хп + шхп+шх(шх п)]
или
wx = а[?7з - Н2 + 97з - П
wy = a[rj! - pj3 + r'ji - Р'уз + qvn ~ 72^2], B8)
wz = a[jyj2 - (Щ + P72 - 9 2
Здесь wn = p7i + 972 + Г7з — проекция вектора ш на вертикаль.
Принимая величиныр, q, г за псевдоскорости -к\, тгг, тгз и замечая,
что обобщенные силы ГЦ, П2, Пз равняются нулю, из уравнений Аппеля
получаем
Mi> + (А3 - A2)qr = ma27i(p7i + QI2 + Нз),
A2q+ (A± - A3)rp = ma272(P7i + ЧЪ + Пг), B9)
A3r + (A2 - A±)pq = ma2j3(jrfi + Tii + ^7з),
где А\ = A + ma2, A2 = В + ma2, A3 = С + ma2.
Уравнения B9) совместно с уравнениями Пуассона (см. п. 114)
7i = ^72 - 97з, 72 = Р7з - rji, 7з = 97i ~ PJ2 C0)
образуют замкнутую систему уравнений, описывающую движение шара
относительно его центра масс. Если она проинтегрирована, то траек-
траектория центра масс находится из уравнений B6) при помощи квадратур.
Покажем, что интегрирование системы уравнений B9), C0) сводится
к квадратурам.
Уравнения B9), C0) имеют интеграл энергии
A2q2 + A3r2) - ]^та2ш2п = h = const. C1)
Интегралами будут также величина вектора кинетического момента
шара относительно точки D касания его с плоскостью
(А\р - ma2jiujnJ + (A2q - ma2j2u>nJ + (A3r - ma2j3ujnJ = const
C2)
и проекция этого вектора на вертикаль
+ ^2972 + ^4з»з - та2шп = const. C3)
1. Множитель Якоби 323
Кроме того, существует очевидный геометрический интеграл
712+722+Тз2=1- C4)
Интеграл C1) следует из теоремы об изменении кинетической энер-
энергии (см. п. 88; левая часть C1) есть кинетическая энергия шара: она
постоянна, так как работа внешних сил, приложенных к шару, равна
нулю). Существование интегралов C2) и C3) следует из теоремы об
изменении кинетического момента в ее общей форме (см. формулу G)
п. 87). Действительно, момент внешних сил (силы тяжести и реакции
плоскости) относительно точки касания шара и плоскости равен нулю.
А так как скорость «геометрической точки», которая «вычерчивает
след» шара на плоскости, очевидно, равна скорости центра масс шара,
то из теоремы об изменении кинетического момента следует, что ки-
кинетический момент Kjj шара относительно точки касания остается
во все время движения неизменным. Но, воспользовавшись формулой D)
п. 81, легко получить, что
K'D = (Aip — ma27iwn, A2q — ma2j2un, A3r — m
Отсюда и следуют интегралы C2) и C3). В существовании упомяну-
упомянутых интегралов можно убедиться и непосредственно, вычислив полные
производные по времени от правых частей равенств C1)-C3) в силу
уравнений движения B9), C0) и убедившись, что эти производные тож-
тождественно равны нулю.
Указанных четырех интегралов достаточно, чтобы интегрирова-
интегрирование системы B9), C0) можно было свести к квадратурам. Чтобы в
этом убедиться, достаточно найти множитель Якоби М. Разрешив
уравнения B9) относительно производных, получим
Р = ^[Из- A3)qr +-угр],
q = 4-[(А3 - AJrp + у2<р], C5)
4
А-
-2
где
(
324 Глава XI
Множитель М удовлетворяет уравнению
Mr) + ?-(Мъ) + ^(МЪ) + ^тг) = О,
гдер, q, r, -yi, 72; 7з —правые части уравнений C5) мC0). Учитывая
C0), уравнение для множителя можно преобразовать к такой форме:
Подставив в выражение, стоящее в скобках, правые части уравне-
уравнений C5) и произведя необходимые дифференцирования, получим урав-
уравнение C8) в виде
fM + M C^*71 + ^^72 + ^^Тз) = 0.
Учитывая C0) м C7), имеем окончательно
2/М - М/ = 0.
Интегрирование этого уравнения дает такое выражение для множите-
множителя: М = C\/~f (с — произвольная постоянная). Из теории последнего
множителя Якоби следует теперь, что интегрирование систем диф-
дифференциальных уравнений B9), C0) сводится к квадратурам.
Упражнение 1. Показать, что для построения общего интеграла урав-
уравнений C2), C5) п. 105 помимо трех интегралов C6), C7) и C8) доста-
достаточно найти еще только один первый интеграл.
163. Приложение теории множителя к каноническим урав-
уравнениям. Пусть движение материальной системы описывается канони-
каноническими уравнениями Гамильтона:
dt - dpS dt ~ dQi ^*-х'л' ••• '"'•
В симметричной форме эта система уравнений запишется в виде
dqi dqn dp\ dpn di
'" dH_ _Ж' _ Ж
dpi dpn dqi dqn
D0)
5 1. Множитель Якоби
325
Так как
/ on \ , о I on \ ,
а
то для канонической системы уравнений существует множитель М = 1
(см. замечание в конце п. 161).
Так как для системы C9) множитель известен, то для построения
ее общего интеграла достаточно знать не 2п, а 2п—1 первых интегралов.
Построение 2п-го интеграла сводится к квадратуре.
Отметим еще одну возможность упрощения задачи интегрирова-
интегрирования канонической системы уравнений. Пусть функция Гамильтона Н
не зависит явно от времени. Тогда, отбрасывая в уравнениях D0) по-
последнюю дробь, содержащую dt, получим систему из 2п— 1 уравнений,
которая по-прежнему имеет множитель М = 1. Поэтому для постро-
построения ее общего интеграла достаточно знать 2п — 2 первых интеграла.
Но так как в рассматриваемом случае материальная система являет-
является обобщенно консервативной, то один интеграл нам известен заранее.
Это обобщенный интеграл энергии Н = h = const (см. п. 151). Поэтому
для построения общего интеграла достаточно знать еще 2п — 3 первых
интеграла. Если, например, п = 2, то кроме интеграла энергии Н = h
достаточно найти еще только один первый интеграл.
Пример 1 (Ограниченная задача
трех тел (см. п. 124)). Пусть точ-
точка Р малой массы движется под дей-
действием притяжения двух точек S и J
конечных масс, не оказывая влияния на
движение последних. Будем считать,
что точка J движется относительно
точки S по круговой орбите, а точ-
точка Р движется в плоскости этой ор-
орбиты (т. е. рассматривается так на- Рис- 138
зываемая плоская круговая ограниченная задача трех тел).
Выберем единицы измерения так, чтобы сумма масс точек S и J,
неизменное расстояние между ними и период их обращения по орбитам
равнялись единице. Пусть т — масса точки Р, а 1 — ^ и ^ — массы
точек S и J соответственно.
Движение точки Р будем рассматривать во вращающейся систе-
системе координат Оху с началом в центре масс точек S и J и осью Ох,
направленной на точку J (рис. 138). Обозначая х,у координаты точ-
х
326 Глава XI
ки Р и применяя теорему о сложении скоростей (п. 31), получаем для
проекций абсолютной скорости точки Р следующие выражения:
vx = х-у, vy =у + х.
Кинетическая энергия точки Р вычисляется по формуле
T=\m{v2x+v2y)=T2+T1+T0, D1)
где
Т2 = \т{х2+у2), Т1 = т(ху-ху), То = \т{х2 + у2). D2)
Потенциальная энергия точки Р определяется выражением
П=-т-^-т^, г\ = (х+цJ+у2, т\ = (х - 1 + цJ + у2.
D3)
Уравнения движения точки Р могут быть записаны в форме канони-
канонических уравнений Гамильтона. Функция Гамильтона явно от времени
не зависит, поэтому существует обобщенный интеграл энергии — ин-
интеграл Якоби:
Т2-Т0+П = Н = const. D4)
Так как число степеней свободы п = 2, то для построения общего ин-
интеграла недостает одного первого интеграла.
§ 2. Системы с циклическими координатами
164. Циклические координаты. Крайне важным источником
упрощения интегрирования дифференциальных уравнении движения
является наличие циклических координат. Рассмотрим этот вопрос для
голономных систем, движущихся в потенциальном поле сил. Пусть сис-
система имеет п степеней свободы, a q\, q2, ¦ ¦ ¦ , qn — ее обобщенные ко-
координаты. Координата qa называется циклической, если она не входит
в функцию Лагранжа, т. е. если dL/dqa = 0 г.
следует из п. 148, 153, -^— = — ^— = — „ , поэтому если координата
aqa aqa Oqa
циклическая, то она не входит также и в функции Гамильтона и Рауса; верно и
обратное.
§ 2. Системы с циклическими координатами 327
Теорема. Пусть qa — циклическая координата. Тогда соответству-
соответствующий ей импульс — первый интеграл: ра = са = const, при этом из-
изменение остальных координат со временем такое же, как в системе
с п — 1 степенью свободы, в которой са играет роль параметра.
Доказательство.
Доказательство проще всего провести, используя гамильтонову
форму уравнений движения
dqi _ дН dPi _ дН /,• _ 1 о _ч m
И12 ") A)
где Я = H(q1,... ,да_ьда+1,... ,qn,pi,... ,pa-i,Pa,Pa+i,-¦ ¦ ,Pn,t).
Если в A) i = а, то dH/dqa = 0 и dpa/dt = 0. Поэтому ра = са = const.
Положив в A) ра = са, придем к системе уравнений Bп —2)-го порядка
d*bL = dE_ Ф«__9Я /. = 1 2 п-гФа) B)
в которой Я = H(q±,.. .,qa-i,qa+i,.. .,qn,Pi, •¦ ;Pa-i,ca,pa+i,.. -,pn,t).
Интегрирование уравнений B) дает
q% = q,(t, ca, ci,... , c2n_2), pi = pi(t, ca, c±,... , c2n_2), C)
где ci,... , c2n_2 — произвольные постоянные. Зависимость цикли-
циклической координаты qa от времени определяется одним из уравнений
системы A)
dt дра' { '
в котором правая часть выражена через t и 2п — 1 постоянных
са, ci, ... , с2п_2 при помощи подстановки в нее функций C). Интег-
Интегрирование уравнения D) дает
dt + с,
дра
где с — 2п-я произвольная постоянная.
Аналогично, если не одна, а / обобщенных координат являются цик-
циклическими, то первыми интегралами будут / обобщенных импульсов и
порядок системы дифференциальных уравнений A) может быть пони-
понижен на 21 единиц.
165. Понижение порядка системы дифференциальных
уравнений движения при помощи уравнений Рауса. Пусть qa
328 Глава XI
(а = к + 1,... , п) — циклические координаты. Тогда имеем п — к пер-
первых интегралов
ра = -д-г- = са = const (а = к + 1,... , п). E)
Пусть гессиан функции Лагранжа по переменным qa отличен от нуля:
det
Ф о. F)
a,0=k+l
Составим функцию Рауса (п. 153)
СаЧа-L, G)
а=к+1
где qa выражены через q,, qt, са и t (г = 1, 2, ... , к; а = к + 1, ... , п)
из уравнений EI. Функция Рауса не содержит обобщенных скоростей,
отвечающих циклическим координатам:
R = R(qh qh ca, t) (i = 1, 2,... , к;, а = к + 1,... , п). (8)
Поэтому часть системы уравнений Рауса
d dR dR _ n /¦ • _ I о l,\ (n\
"Т7 7ГГ H — U U — 1, Z, . . . , ft, I 1У1
dt oqt oqt
описывает изменение нециклических координат со временем и может
интегрироваться независимо от другой ее части
соответствующей циклическим координатам.
Проинтегрировав систему уравнений (9), имеющую порядок 2к,
получим
q% = q,{t, ca, ci, с[,..., ck, c'k) (г = 1,2, ... , к), A1)
где Ci, с\ (г = 1, 2,... , к) — произвольные постоянные. Затем из пер-
первых п — к уравнений системы A0) находим зависимости циклических
координат от времени
OR ij. \ * ( у, I 1 \ (л с)\
1При выполнении условия F) уравнения E) разрешимы относительно q'a.
§ 2. Системы с циклическими координатами 329
где в функции dR/dca величины q^ заменены на их выражения A1).
Описанная в п. 164, 165 процедура понижения порядка системы
дифференциальных уравнений движения является одним из наибо-
наиболее эффективных и практически важных способов, применяемых при
интегрировании уравнений движения. Всякая симметрия задачи, до-
допускающая такой выбор обобщенных координат, чтобы некоторые из
них qa были циклическими, приводит к существованию первых ин-
интегралов ра = const и, как мы видели, позволяет свести исследование
движения к рассмотрению системы с меньшим числом обобщенных
координат. Для обобщенно консервативных систем с двумя степеня-
степенями свободы наличие одной циклической координаты позволяет свести
интегрирование уравнений движения к квадратурам (см. п. 164).
Пример 1 (Движение сферического маятника). Сферический маят-
маятник {см. пример 2 п. 138) имеет две степени свободы. Если за обобщен-
обобщенные координаты принять углы в и <р (рис. 134), то для кинетической
и потенциальной энергии будем иметь выражения
Т=^т12(в2 + sin2 вф2), n = mglcos0.
Так как функция Лагранжа
Ь = Т-П= ±т12(в2 + sin2 вф2)-тё1 cos в
не содержит <р, то эта обобщенная координата циклическая. Ей соот-
соответствует первый интеграл
pv = |^ = ml2 sin2 вф = ml2cooa, A3)
где а — произвольная безразмерная постоянная; обозначение ojq = s/g/l
введено для удобства.
Так как из A3) следует, что
Ф = -?h<*, A4)
sin в
то для функции Рауса
R = Ррф — L
получаем выражение
R = -\т1Ц1 + 1 ml2f2
1 l sin в
330 Глава XI
Уравнения
AdR _ OR =n
dt qq дв
отвечают системе с одной степенью свободы, которой соответствуют
кинетическая и потенциальная энергия, определяемые равенствами
Т* = =гт12в'2, П* = mgl cos# + i ^—.
^ ^ sin в
Эта система называется приведенной системой, а функция П* — при-
приведенным потенциалом, или потенциалом Рауса.
Приведенная система имеет интеграл энергии
=rml292 + mgl cos в + i ?— = =:т12ш1C, A6)
*• *• sin в *•
где C — безразмерная постоянная.
Введем обозначение и = cos#. Тогда й = — §швв и из A6) следует,
что
-\й2 = G(u), A7)
где G(u) — многочлен третьей степени,
G(u) = A - u2)(/3 - 2и) - а2, A8)
который можно также записать в форме
G(u)=2(u-u1)(u-u2)(u-u3), A9)
где т, U2, из — корни уравнения G(u) = 0.
Заметим, что С(+оо) = +оо, С(±1) = -а2 < 0 (если а ф 0),
G(—сю) = —сю. Так как G(u) — непрерывная функция, то хотя бы один
из корней, например из, должен быть не меньше единицы. Но на отрез-
отрезке —1 ^ и ^ +1 должны быть значения и, при которых функция G(u)
положительна или хотя бы обращается в нуль, так как в противном
случае равенство A7) невозможно для действительных значений и. Ве-
Величина же и обязятельно должна быть действительной, так как дви-
движение маятника,безусловно, физически существует. Отсюда следует,
что функция G(u) имеет ровно два вещественных корня и\, ui на от-
отрезке — 1 ^ и ^ +1 и один корень и% ^ 1. График функции G(u) должен
быть таким, как показано на рис. 139.
i 2. Системы с циклическими координатами
331
G(uh
и,
Рис. 139
Рис. 140
Так как для реального движения G{u) ^ 0, то интересующий нас
интервал изменения и определяется неравенством и\ ^ и ^ иг- Ему
соответствует область изменения угла в: 02 ^ в ^ в\, отвечающая
реальному движению маятника.
Рассмотрим движение, отвечающее различным значениям постоян-
постоянных а и ji. Сразу отметим, что из условий G(u) ^ 0 и — 1 ^ и ^ +1
следует, что величина /3 не может быть совсем произвольной, а должна
удовлетворять неравенству /3 ^ —2. Если /3 = —2, то постоянная а мо-
может быть только равной нулю, что соответствует положению равно-
равновесия маятника, когда он занимает вертикальное положение (и = —1,
т. е. в = тг).
Функция G(u) имеет максимум в точке
B0)
причем
где
i[
B1)
Для реального движения необходимо, чтобы выполнялось неравенст-
неравенство G(u*) ^ 0, т. е. чтобы
~2 " №¦ B2)
О ^ а2
На рис. 140 значения параметров а, A, удовлетворяющие неравенст-
неравенству B2), соответствуют точкам, лежащим в незаштрихованной об-
области плоскости или на ее границе. Верхняя граница области зада-
задается уравнением а2 = /(/3); она касается оси 0/3 в точке (—2, 0),
а при /3 —>¦ сю имеет асимптоту а2 = /3.
332
Глава XI
Для классификации движения маятника рассмотрим последова-
последовательно три возможных случая.
1) а = 0. Из A4) следует, что в этом случае ip = ip0 = const, и мы
приходим к задаче о движении математического маятника в плоскос-
плоскости ip = ipo- Эта задача подробно изучена в п. 93-96.
2) 0 < а2 < /(/3). В этом случае угол в изменяется в промежутке
02 ^ в ^ в\. На сфере радиусом I с центром в точке подвеса маятника
значения в = в\ и в = 02 выделяют два круга, лежащих в параллельных
плоскостях z = z\ = Icos6\ и z = Z2 = I cos 02- Материальная точка,
закрепленная на конце стержня, движется по сфере между плоскостя-
плоскостями z = z\ и z = Z2, попеременно касаясь этих плоскостей (рис. 141).
z=z.
Рис. 141
Рис. 142
При этом среднее положение точки всегда находится ниже гори-
горизонтальной плоскости, проходящей через точку О подвеса маятника
(рис. 134), т. е. их + 112 < 0. Чтобы убедиться в этом, приравняем
коэффициенты при первой степени и в тождестве A9). Получим
+
М2М3) = -2,
откуда
из = --
1 +
U2
Но так как «з > 0, a |uiU2| < 1, то отсюда сразу следует, что
Ui + U2 < 0.
Из уравнения A4) видно, что угол ip в рассматриваемом случае ли-
либо монотонно возрастает {если а > 0), либо монотонно убывает (ес-
(если а < 0). На рис. 142 показана проекция траектории материальной
точки на плоскость Оху для движения, соответствующего рис. 141,
когда обе плоскости z = z\ и z = Z2 лежат ниже точки подвеса маят-
маятника (принято, что а > 0). Эта проекция поочередно касается окруж-
окружностей радиусов pi = I sin в\ и р2 = I sin 62 и напоминает собой движе-
§ 2. Системы с циклическими координатами 333
ние по эллипсу, большая полуось которого вращается в горизонтальной
плоскости в направлении движения.
Для интегрирования уравнения A7) сделаем замену переменных
и = и\ + (иг — Mi) sin2 v. B3)
Отсюда и из A7), A9) получаем дифференциальное уравнение для новой
переменной v
v2 = ^2(u3-Ul)(l-k2sm2v), B4)
где
Если момент времени, когда и = и\, принять за начальный, то из B4)
получаем
V
т= I — doj = FUh h). B5)
•I v 1 — k2 sin u)
о
где F(v, k) — эллиптический интеграл первого рода (см. п. 95), а
/и3 -'
Тогда из B3) следует, что
и = ui + (г*2 — Ui)sn2T. B6)
Так как эллиптическая функция sn т имеет период 4К(к), где К(к) —
полный эллиптический интеграл первого рода, то sn2r имеет период,
вдвое меньший. Поэтому и = и\ для т = 2пК(к) и и = и^ для т =
= Bп + 1)К(к) (п = 1, 2,...). Следовательно, угол в периодически ко-
колеблется между значениями вх и в^- Период яг этих колебаний вычис-
вычисляется по формуле
B7)
Когда угол в найден как функция времени, зависимость <p(t) находится
из уравнения A4) при помощи одной квадратуры.
3) а2 = /(/3). В этом случае корни и\ и и^ многочлена G(u) сов-
совпадают, причем Mi = U2 = и%, и мы приходим к задаче о коническом
334 Глава XI
маятнике. Угол в при движении постоянен, 6 = 6*= arccosit* > ^.
Материальная точка движется по окружности радиусом Zsin^» в го-
горизонтальной плоскости z = z* = Icosd* < 0; время ее обращения по
/ К
окружности равно 2ттл — -^-. Стержень, на котором закреплена точка,
описывает поверхность конуса с осью симметрии Oz.
§ 3. Скобки Пуассона и первые интегралы
166. Скобка Пуассона. Пусть «и» — дважды непрерывно диф-
дифференцируемые функции от qi,... , qn, р\,... , рп, t. Выражение
называют скобкой Пуассона функций «ив.
Отметим основные свойства скобки Пуассона. Пусть и, v, w —
дважды непрерывно дифференцируемые функции переменных
Gi,... ,qn,p!,... , рп, t. Тогда
1) (и, v) = —(v, и),
2) (си, v) = c(u, v) (с = const),
3) (и + v, w) = (и, w) + (v, w),
5) {{и, v), w) + ((г;, го), и) + ((го, и), v) = 0.
Первые четыре свойства непосредственно вытекают из определения A)
скобки Пуассона. Пятое свойство, называемое тождеством Пуассона,
более громоздко для доказательства, хотя также несложно. Для сокра-
сокращения выкладок можно использовать то обстоятельство, что каждое
слагаемое в левой части тождества 5 есть произведение частной произ-
производной второго порядка на две частные производные первого порядка.
Поэтому, чтобы показать, что левая часть тождественно равна нулю,
достаточно убедиться в том, что она не содержит ни одной производ-
производной второго порядка, например, от функции и (так как и, v, w входят
в тождество 5 симметрично).
Вторые производные от и могут дать первое и третье слагаемые
в 5. Их сумму на основании свойств 1 и 2 можно записать в виде
((и, г>), го) + ((го, и), v) = (го, (г>, и)) - (г>, (го, и)).
§ 3. Скобки Пуассона и первые интегралы 335
Теперь уже нетрудно непосредственным вычислением проверить, что
правая часть этого равенства не содержит вторых производных от
функции и.
167. Теорема Якоби—Пуассона. Пусть переменные <^, pi удов-
удовлетворяют дифференциальным уравнениям Гамильтона
"•чг _ an щн _ an f — i 9 \ B)
dt dpi' dt dqi' 1111
Для того чтобы функция f(qi, pi, t) была первым интегралом, необхо-
необходимо и достаточно, чтобы ее полная производная по времени, в силу
уравнений B), тождественно равнялась нулю: df/dt = 0. Выразим это
условие через скобку Пуассона. В силу B) имеем
dt dt 2-d у dqi dt dpi dt ) dt 2-* \ dqi dpi dpi dqi) '
Применяя обозначение A) для скобки Пуассона, необходимое и доста-
достаточное условие того, что / — первый интеграл, можно записать в виде
равенства
^ + (/, Я) = 0. C)
Имеет место следующее замечательное утверждение.
Теорема (Якоби—Пуассона). Если /i м /г — первые интегралы сис-
системы B), то их скобка Пуассона (/i, /2) также будет первым интег-
интегралом этой системы.
Доказательство.
Пусть /i и /г — первые интегралы. Тогда, согласно C),
^ + (Л, Я) = 0, ^ + (/2, Я) = 0, D)
а нужно доказать, что
У^ + ((Л,Л),я) = о. E)
Преобразуем левую часть этого равенства. По свойству 4 скобок Пуас-
Пуассона имеем
336 Глава XI
Если теперь производные dfi/dt и dfz/dt заменить на их выражения
из равенства D) и затем воспользоваться свойствами 1 и 2 скобок Пу-
Пуассона, то получим
|(/ьЛ) = -((Л,я),/2) - (Л,(/2,я)) = ((я,д),/2) + ((/2,я),Л).
Подставляя это выражение в левую часть равенства E), получаем ее в
виде
Из свойства 5 скобок Пуассона следует, что последнее выражение
тождественно равно нулю, что и доказывает справедливость теоремы
Якоби-Пуассона.
Пример 1 (Движение материальной точки под действием притя-
притяжения К заданному центру О). Пусть Oqxq^qz — неподвижная пря-
прямоугольная декартова система координат, а П(г), где г2 = q\ + q\ + q\,
— потенциал силы притяжения. Если массу точки принять за единицу,
то для функции Гамильтона имеем выражение
Пусть
Д = Я2Рз ~ ЯзР2, h = q3Pi ~ ЯгРз-
Проверка показывает, что (Д, Н) = О и (/2, Я) = 0, т. е. Д и /2 —
первые интегралы. Они представляют собой проекции момента коли-
количества движения материальной точки относительно центра О {этот
момент постоянен, так как рассматриваемое силовое поле является
центральным) на оси Oq\ и Oqi- Согласно теореме Якоби-Пуассона,
функция (Д, /г) тоже должна быть первым интегралом. Имеем
Полученный интеграл есть проекция момента количества движения на
ось Oqz-
Может показаться, что теорема Якоби-Пуассона всегда позволяет
по двум известным первым интегралам найти еще один первый интег-
интеграл, затем еще один и так далее до тех пор, пока не будет получено
количество первых интегралов, необходимое для построения общего ин-
интеграла системы B). Это далеко не так. На практике скобка Пуассона
часто может быть либо константой, либо функцией известных первых
интегралов.
§^. Канонические преобразования 337
Для того чтобы можно было надеяться получить из двух первых
интегралов много или даже все первые интегралы, недостающие для по-
построения общего интеграла, надо, чтобы хотя бы один из двух извест-
известных исходных первых интегралов был характерен для рассматриваемой
частной задачи, чтобы он как можно полнее отражал физическую сущ-
сущность именно данной задачи. Если за исходные первые интегралы брать
интегралы, вытекающие из основных, общих для всех систем теорем
динамики, то вряд ли в общем случае можно надеяться на эффективное
применение теоремы Якоби-Пуассона.
§ 4. Канонические преобразования
168. Понятие канонического преобразования. Рассмотрим
гамильтонову систему дифференциальных уравнений в векторно-
матричной форме
Здесь z — 2п-мерный вектор-столбец, z' = (q',p'), q' = (qi, ¦¦¦ , qn),
P' = (Pb ••• ,Pn),
II f) Fj II
-E 0 ' *¦ '
II n II
En — единичная матрица n-го порядка. Н = H(z, t) — функция Га-
Гамильтона, Hz — матрица-строка размером 1 х 2п,
Hz = (Hq, Нр) = (Hqi,..., Hqrt, HPl,..., HPn).
Легко видеть, что
J' = J = -J, J2 = -E2n, det J = 1. C)
Получение решений системы уравнений A) часто оказывается
очень сложным делом. Поэтому надо искать какие-то пути, упрощаю-
упрощающие исследование движения. Например, в §2 показано, что наличие од-
одной циклической координаты позволяет понизить порядок системы A)
на две единицы. Это указывает на то, что удачный выбор обобщен-
обобщенных координат может существенно облегчить исследование движения,
а иногда позволяет провести его во всей необходимой полноте. С такой
ситуацией мы встретились в п. 165 при анализе движения сферического
маятника.
338
Глава XI
В некоторой области фазового пространства qi, q2, ... , qn,
Pi, P2, ••• , pn рассмотрим обратимую, дважды непрерывно дифферен-
дифференцируемую замену переменных q, р —>¦ Q, Р, содержащую время t в
качестве параметра:
Qi = Qi(q,P,t), Pi=Pi(q,P,t), (i = l, 2, ...,n), D)
или, если ввести обозначение C' = (Q', P'), Q' = (Qi, ••• , Qn), P' =
C = C(z,t). E)
Может случиться, что в новых переменных система уравнений A)
будет иметь более простую структуру и ее интегрирование будет про-
проще интегрирования исходной системы. В новых переменных уравнения
движения могут уже не быть гамильтоновыми. Мы, однако, будем далее
рассматривать только такие преобразования D), которые не нарушают
гамильтововой формы уравнений движения. Это будут канонические
преобразования. Ниже мы дадим определение канонических преобразо-
преобразований, получим критерии каноничности и укажем способ нахождения
функции Гамильтона, отвечающей преобразованным уравнениям.
Практический смысл канонических преобразований состоит в
упрощении уравнений движения, в выборе таких новых координат в
фазовом пространстве, которые более удобны для решения задачи о
движении системы, нежели исходные старые координаты. Метод ка-
канонических преобразований является широко распространенным и эф-
эффективным методом исследования гамильтоновых уравнений.
Пусть М — матрица Якоби преобразования D),
dQi dQi dQi dQi
dz
dQ
dq
dP
dq
dQ
dp
dP_
dp
dqi
dQn
dqi
dl\
dqi
dqn
dQn
dqn
dPi
dqn
dpi
dQn
dpi
dl\
dpi
dpn
dQn
• dpn
dl\
dpn
dqi
dPn dPn
dqn dpi
dPn
F)
Преобразование D) называется каноническим, если существует та-
такое постоянное число с ф 0, что матрица Якоби F) удовлетворяет тож-
тождеству
M'JM = cJ, G)
§^. Канонические преобразования 339
где матрица J определена равенством B). Число с называется валент-
валентностью канонического преобразования; если с = 1, то преобразование
называется унивалентным.
Замечание 1. Матрицы М, удовлетворяющие тождеству G) при с = 1,
называются симплектическими; если же в G) с ф 1, то матрица М
называется обобщенно симплектической (с валентностью с). Так как,
согласно C), det J = 1, то из равенства G) на основании теоремы об
умножении определителей получаем
detM = ±с",
т. е. обобщенно симплектические матрицы являются невырожденны-
невырожденными.
Замечание 2. Пусть в фазовом пространстве последовательно выпол-
выполнены два канонических преобразования: Сх = Ci(z> t) с валентностью с±
и ?2 = C2(Ci> t) c валентностью с2. Тогда результирующее преобразо-
преобразование С, = ?(z, t) = Сг(Ci(-^7 t)t t) тоже будет каноническим, и его
валентность с равна произведению
В самом деле, по условию
= ciJ, Mi = dC,i/dz
и
M2JM2 = c2J, M2 = dC.2ldC.x-
Поэтому
dz dCx dz '
а следовательно,
M'JM = (M2Mi)'J(M2Mi) = М^МзЛМг
= c2ciJ.
Отсюда, согласно определению G) канонического преобразования, сле-
следует доказываемое утверждение.
Пусть, далее, задано каноническое преобразование С, = C(z, t) с ва-
валентностью с. Тогда обратное преобразование z = z{C, t) также будет
каноническим, а его валентность равна 1/с.
Действительно, умножив обе части тождества G) слева на матрицу
(М'), а справа — на матрицу М, получим
(8)
340 Глава XI
Учитывая перестановочность операций транспонирования и взятия об-
обратной матрицы, приходим к равенству
(M-^'JM = \з. (9)
Так как матрицей Якоби обратного преобразования z = z(?, t) явля-
является матрица М, то отсюда следует, что это преобразование канони-
каноническое и имеет валентность 1/с.
Отметив еще, что тождественное преобразование Qi = qi, Pi = Pi
(i = 1,2,... , n), очевидно, будет каноническим, приходим к выводу,
что совокупность всех канонических преобразований образует группу.
Унивалентные преобразования составляют ее подгруппу.
169. Критерии каноничности преобразования. Равенство G)
позволяет легко проверить, является преобразование D) каноническим
или нет. Приведем еще некоторые критерии каноничности. Они экви-
эквивалентны условию G) и могли бы быть приняты за определение кано-
каноничности преобразования D).
Сначала введем понятие скобки Лагранжа и дадим критерий
каноничности в терминах этих скобок. Пусть заданы 2п функ-
функций (pj, xj)j (j = 1, 2,... , п) от двух переменных х, у и еще, может
быть, от некоторых других переменных. Тогда скобкой Лагранжа для
этих функций называется величина
Теорема. Если в качестве (pj, xj)j принять функции Qj, Pj из D), то
необходимое и достаточное условие каноничности преобразования D)
запишется в виде
[qi, qu] = 0, \pi, Ph] = 0, [qt, pk] = cSih (i, k = 1,2, ... , n). A1)
Здесь 5ik — символ Кронекера (8ц. = 1 при i = к и 8ik = 0 при i ф к),
ас — валентность канонического преобразования.
Доказательство.
Доказательство получается при помощи непосредственной провер-
проверки. В самом деле, левая часть равенства G) может быть записана в
виде следующей блочной матрицы:
(dQ\
_(др_Vм (д_о_удр__(др_
dq J dq \dq J dq \dq J dp \dq J dp
(dQ\ dP_ _ (dP\ dQ_ ('dQ_\ dP_ _ (dP_\ dQ_
M'JM =
\ dp J dq \dp ) dq \ dp J dp \ dp J dp
A2)
\4- Канонические преобразования
341
Вычисления, проведенные для левого верхнего блока этой матрицы с
учетом обозначения A0), дают
дО\' ЭР
)
dq ) dq \ dq ) dq
Е
j dPj dQj dPj
t dqk dqk dqt
i, k=l
\i, k=l'
Проведя аналогичные вычисления для остальных блоков матрицы A2),
убеждаемся, что равенство G) может быть записано в виде
\[Qi, Qk]
n
i, k=l
fa, pu]
lk=l ||[Pi> P*]
k=l
k=l
0 cE
-cE 0
A3)
Для доказательства теоремы теперь достаточно заметить, что равенст-
равенства A1) и A3) эквивалентны.
Получим теперь критерий каноничности преобразования D), ис-
использующий скобки Пуассона.
Теорема. Для того чтобы преобразование D) было каноническим, не-
необходимо и достаточно, чтобы скобки Пуассона функций Qj, Pj от
переменных q±,... , qn, pi,... , рп, t удовлетворяли равенствам
(Qu Qk) = 0, (Pis Рк) = 0,
i, Pk) = cSik (i, k = 1, 2,... , n).
A4)
Доказательство.
Доказательство проводится при помощи непосредственной про-
проверки эквивалентности равенств A4) и равенства G), положенного
в основу определения каноничности преобразования D). Возьмем от
обеих частей равенства (8) обратные матрицы и учтем, что, соглас-
согласно C), J = —J. Тогда придем к равенству
MJM' = cJ,
A5)
которое эквивалентно равенству G). Левая часть последнего равенства
может быть представлена в виде блочной матрицы
MJM' =
9Q_ f dQ\'_ 9Q_ f 9Q_\ 9R (дРV _ 9R {дР_
dq \др ) ^ dp \dq ) ^ dq \др ) ^ dp \dq )
^ ^ ^
дР_ (®Q\ _ дР_ f dQ\' дР (дР\' дР (дР\
dq\dp) dp \dq) dq \др ) dp \dq )
A6)
342
Глава XI
Непосредственные вычисления показывают, что левый верхний
блок этой матрицы может быть представлен в виде
dQ_
dq
_
др
_ (_\
dp \dq )
дРз дРз
\i, k=l
v*;iu, k=i-
Аналогичные вычисления для остальных блоков матрицы A6) позволя-
позволяют записать равенство A5) в следующей форме:
i, k=l
О
-сЕ
сЕ
О
A7)
РЛ\\п \\(P- РЛ\\п
Отсюда следует, что равенства A4) и G) эквивалентны, что и доказы-
доказывает теорему.
Приведенные критерии каноничности, как и само определение G),
позволяют по явно заданному преобразованию D) решить, является оно
каноническим или нет. Для дальнейшего построения теории каноничес-
канонических преобразований очень важен следующий критерий каноничности.
Теорема. Для каноничности преобразования D) необходимо и доста-
достаточно, чтобы существовала отличная от нуля постоянная с такая,
что выражение
п п
k=l k=l
является полным дифференциалом некоторой функции F(q, p, t).
При этом под полными дифференциалами 8F и 8Qu
(к = 1, 2,... ,п) понимаются дифференциалы, соответствующие изме-
изменению переменных q, p; величина t считается параметром.
Доказательство.
Для доказательства этой теоремы достаточно показать, что усло-
условия того, что выражение A8) есть полный дифференциал, эквивалентно
равенствам A1). Из D) имеем
Подставив эти дифференциалы в выражение A8) и изменив порядок
суммирования, получим это выражение в виде
A9)
г=1
§^. Канонические преобразования 343
где приняты обозначения
п „ „
' я^.. (,г — -L, ^,... , п). (М)
Условие того, что выражение A9) есть полный дифференциал, записы-
записывается в виде совокупности равенств
дХ, _ дХк д?{ _ dYk дХ{ _ dYk _
dqk ~ ддГ dpk-dPi> dpk~ % (^ fc-1, 2,-.., n). B1)
Непосредственное вычисление, использующее обозначения B0), пока-
показывает, что равенства B1) запишутся соответственно в виде
[ft, Чк] = 0, [Pi, рк\ = 0, [q,, рк] = cSik (г, к = 1, 2,... , п).
Так как эти равенства совпадают с равенствами A1), то отсюда следует
справедливость доказываемой теоремы.
170. Ковариантность уравнений Гамильтона при канони-
канонических преобразованиях. Если преобразование D) является кано-
каноническим, то в новых переменных система уравнений A) снова бу-
будет иметь гамильтонову форму. Более точно, имеет место следующее
утверждение.
Теорема. При каноническом преобразовании D) любая гамильтонова
система дифференциальных уравнений A) переходит снова в гамильто-
гамильтонову систему (вообще говоря, с другой функцией Гамильтона "Н(?, t))
%=ЗЩ. B2)
Доказательство.
Действительно, из E) и A) имеем
dt dz dt at z at
Ho
Поэтому, учитывая тождество A5), равенство B3) можно записать в
виде
344 Глава XI
Покажем, что если преобразование D) каноническое, то
|=ЛП, B5)
где W — некоторая функция переменных ?, t. В самом деле, опира-
опираясь на соотношения C) и F), получаем из B5) следующую цепочку
равенств:
т. е. соотношение B5) эквивалентно равенству
B6)
где W рассматривается как функция переменных q, p, t. В скалярной
форме равенство B6) запишется в виде 2п соотношений
dQl_dPidQl\ =
^ V "Pi * * P
где обозначения Ф;,, !?; для производных функции W введены для крат-
краткости записи. Величины Ф\~ и Ф[ являются производными по qp, и pi от
некоторой функции W в том и только в том случае, когда выполнены
условия
дФ„ дФ{ дФк д*{ дФк д*{
Эти условия, как показывают непосредственные вычисления, могут
быть записаны в виде
§-th, Qk] = 0, §~t[Pi, Рк] = 0, §-tWi,Pk] = 0 (i,k = l,2,...,n).
B7)
Так как преобразование D) каноническое, то имеют место равенст-
равенства A1), откуда вытекает справедливость равенств B7), а следователь-
следовательно, и равенства B5).
§^. Канонические преобразования 345
Таким образом, уравнение B4) может быть записано в виде
Если обозначить "Н функцию сН + W, то последнее уравнение примет
гамильтонову форму
Роль новой функции Гамильтона играет функция "Н. Теорема доказана.
Приведем некоторые простые, по практически важные примеры
канонических преобразований. Старую и новую функции Гамильтона
обозначим соответственно H(q, р, t) и 7i(Q, Р, t).
Пример 1. Тождественное преобразование
Qj = qj, Pj=Pj (j = l, 2,..., п). B8)
Это унивалентное каноническое преобразование; при этом
-H = H(Q,P,t).
Пример 2. Преобразование
Qj=Pi, Pj=qj (j = l, 2,..., п). B9)
Это каноническое преобразование с валентностью с = — 1. Оно меняет
ролями обобщенные координаты и обобщенные импульсы. При этом
U = -Н(Р, Q, t).
Пример 3. Преобразование
Qj = aqj, Pj = Cpj (j = 1,2,... ,n;a = const,/3 = const, aft Ф 0).
C0)
Это преобразование каноническое, и
Пример 4. Преобразование
lQ, ip, t\.
Qj = apj, Pj = [3qj (j = 1, 2,... , n; a = const, /3 = const, aft Ф 0).
C1)
Это преобразование также каноническое, а
346 Глава XI
Примеры 2 и 4 показывают, что при канонических преобразованиях
может исчезнуть различие между координатами и импульсами. Приме-
Применение названий «импульс» и «координата» может стать чисто услов-
условным. Поэтому для пары переменных Qi и Pi, очень удобно название «ка-
«канонически сопряженные переменные».
Пример 5. Перенос начала координат в фазовом пространстве
Q = q-f(t), P = p-g(t) C2)
представляет собой унивалентное каноническое преобразование. При
этом новые переменные Q, Р удовлетворяют системе дифференциаль-
дифференциальных уравнений с функцией Гамильтона
n = H(Q+f(t), P + g(t),t) + ^-Q-4?-P, C3)
где точкой обозначено скалярное произведение векторов.
Пример 6. Преобразование
Qj = V^rjsinipj, Pj = y/^Tj cos (pj (j = 1, 2,... , n) C4)
является унивалентным каноническим преобразованием. Оно осущест-
осуществляет переход от пары канонически сопряженных переменных qj, pj, иг-
играющих роль декартовых координат на плоскости, к паре канонически
сопряженных переменных (fj, tj (ipj — «координата», tj — «импульс»),
имеющих характер полярных координат.
Если старая функция Гамильтона имела вид
то уравнениям для переменных ipj, tj соответствует функция Гамиль-
Гамильтона
Пример 7. Преобразование
Qj = qj - Wj, Pj = qj + ipj (i = i, 2,..., n), C7)
где i — мнимая единица (г2 = —1), осуществляет переход к комплексно
сопряженным переменным. Оно является каноническим с валентнос-
валентностью 2 г и
§^. Канонические преобразования 347
Если, например, старая функция Гамильтона имеет вид C5), то
iQipr C9)
171. Канонические преобразования и процесс движе-
движения. Очень важным примером канонического преобразования служит
процесс движения, описываемого гамильтоновой системой дифферен-
дифференциальных уравнений.
Пусть для гамильтоновой системы A) при t = 0 z' = z<J = (q^, p'o).
Тогда вектор-функция С,' = СЧ^О; *) = (ч {Чо, Ро, t), p'(qo, Po, t)) удов-
удовлетворяет тождеству
§=Щ. D0)
Она задает преобразование фазового пространства q0, p0 —>¦ q, p.
Теорема. Преобразование фазового пространства, задаваемое движе-
движениями гамильтоновой системы, является унивалентным каноническим
преобразованием.
Доказательство.
Надо убедиться в том, что матрица Якоби М = д(,/дго удовлетво-
удовлетворяет тождеству G) при с = 1, т. е.
M'JM = J. D1)
Для этого найдем дифференциальные уравнения, которым удовлетво-
удовлетворяют матрицы М и М'. Продифференцировав обе части тождества D0)
по Zo, получим
или
^ = J#CCM. D2)
Транспонируя обе части этого равенства и учитывая соотношения C)
и симметричность матрицы Н^, получим
= М'Н'СС3' = -M'#CCJ. D3)
Учитывая D2) и D3), вычислим теперь производную по времени от
матрицы M'JM. Имеем
= ^jm + mj^ = -м'яссллм + m'jj#ccm.
(Ль (jAi (Ль
348 Глава XI
Если теперь заметить, что, согласно равенствам C), J2 = — Егп , то это
выражение можно представить и виде
Отсюда следует, что матрица M'JM постоянна. Но при t = 0 она, оче-
очевидно, равна J. Поэтому при всех t имеет место равенство D1). Теорема
доказана.
172. Теорема Лиувилля о сохранении фазового объема.
Пусть Go — некоторая область фазового пространства qi,...,qn,
Pi> • • • )Рп' Из каждой ее точки дю,... , дП(ъ Ркь • • • •, Рпо как из на~
чальной «выпустим» траекторию системы уравнений A). Пусть Gt —
совокупность точек q = q(qo, Ро, t), р = p(qo, Po, t) в момент време-
времени t, Vo — объем области Go, a Vt — объем области Gt.
Теорема (Лиувилля). При движении гамилътоновой системы фазо-
фазовый объем остается постоянным, т. е. Vt = Vo при любом t.
Доказательство.
Имеем равенства
Vo = / • • • / ^ю • • • dqnOdp10 ... dpn0,
, G° , D4)
Vt= / ... / dqi... dqndpi ... dpn.
В интеграле, входящем во второе из этих равенств, перейдем от пере-
переменных gi,... ,qn, pi,... ,рп к переменным q10,... ,qn0, p10,... ,рп0.
Тогда, как известно из курса математического анализа,
Vt = ... | det M| dq10 ... dqnOdplo ... dpn0, D5)
Go
где (в обозначениях предыдущего пункта) М = dC,/dzo. Матри-
Матрица М удовлетворяет равенству D1). Так как detJ = 1, то из не-
него следует, что detM = ±1. Но при t = 0, очевидно, М =
= Егп и detM = detE2n = +1. Отсюда, ввиду непрерывности М, полу-
получаем, что и при любых t detM = +1. Поэтому из D4) и D5) следует,
что Vt = Vo- Теорема доказана.
173. Свободное каноническое преобразование и его произ-
производящая функция. Пусть преобразование D) каноническое и в неко-
некоторой области фазового пространства удовлетворяет условию
det ^г-фО. D6)
др
§^. Канонические преобразования 349
Тогда преобразование D) называется свободным каноническим преобра-
преобразованием.
При выполнении условия D6) из первых п равенств D) можно вы-
выразить р через q, Q и t. Тогда выражение A8) может быть записано
в виде
п п
= SF(q, p(q, Q, t), t) = SS(q, Q, t), D7)
где S — функция F, в которой р заменено на p(q, Q, t).
Из равенства D7) вытекают соотношения
Функция S называется производящей функцией свободного каноническо-
канонического преобразования D).
Очевидно, что верно и обратное утверждение: если заданы дважды
непрерывно дифференцируемая функция S(q, Q, t) и число с ф 0, то
при условии
det
Ф 0 D9)
fe=i
формулы D8) задают свободное каноническое преобразование с валент-
валентностью с.
При условии D9) формулы D8) можно представить в виде D).
В самом деле, условие D9) означает, что первые п равенств из со-
соотношений D8) можно разрешить относительно Qi. Сделав это, полу-
получим Qi = Qi(q, p, t). Подставив эти функции в левые части послед-
последних п равенств из D8), получим Р, = Pi(q, p, t).
В п. 170 мы получили уравнение B4) и показали, что его можно
записать в гамильтоновой форме. Осуществим эту запись, используя
производящую функцию S. В B4) Н представляет собой старую функ-
функцию Гамильтона, выраженную через новые переменные, а
дС\' _ fdQ'(q,p,t) dP'jq, p, t)\
Tt) ~ \ Ш ' Ш ) ¦ E0)
В первых п равенствах соотношений D8) величину Q заменим на ее
выражение Q = Q(q, p, t). В результате эти равенства станут тож-
тождествами относительно старых переменных q, p, t. Продифференциро-
Продифференцировав их по t, получим
dq,dQk dt dq,
k=i
350 Глава XI
Меняя здесь порядок дифференцирования и пользуясь последними п
равенствами из D8), имеем
~
1^дГ dqi + dtdqi
k=l
Применяя векторно-матричные обозначения, запишем эти равенства в
виде
9Q' дР , d2S _n
или
{
дР dP\dt)'
Далее, последние п равенств из D8) дают
дР' = d2S Q(dS
= (
dt dQdt dQ\dt)'
Из E0) и E1), E2) получаем
1(
dt \дС dt
Следовательно, уравнение B4) имеет вид
и новая функция Гамильтона
Н = СН+^, E4)
где Н и S должны быть выражены через Q, P, t.
Таким образом, если заданы производящая функция S(q, Q, t) и
валентность с канонического преобразования, то связь старых и новых
переменных определяется из равенств D8), а функция Гамильтона, от-
отвечающая преобразованной к новым переменным Q, Р системе A),
вычисляется по формуле E4). Мы видим, что при преобразовании сис-
системы A) к новым переменным нужно все вычисления проводить не с 2п
функциями D), ас двумя функциями S и Н. Ясно, насколько это важ-
важно при рассмотрении конкретных задач, особенно при большом числе
степеней свободы п.
§^. Канонические преобразования 351
Можно заранее задать структуру новой функции Гамильтона
H(Q, P, t) и пытаться так подобрать производящую функцию S, что-
чтобы удовлетворялось равенство E4), которое, с учетом формул D8), за-
записывается в виде
Можно, например, потребовать, чтобы какие-то (или даже все) «коорди-
«координаты» Qi (г = 1, 2,... , п) не входили в новую функцию Гамильтона. И
если удастся так подобрать S, чтобы удовлетворялось уравнение E5),
то среди новых переменных в рассматриваемой задаче будут цикличес-
циклические «координаты», что позволяет (см. п. 164) понизить порядок системы
дифференциальных уравнений движения на величину 2fc (k — число
циклических координат). А если все координаты циклические, то зада-
задача сводится к элементарным квадратурам, так как тогда "Н = ti(P, t),
и уравнения движения в новых переменных имеют вид
*QdH dPd4-0 (i-i 2 n)
f(P t)
и, если Qi0, Pjo — начальные значения величин Qi, Pi, отсюда следует,
что
t
Qi= [ fi(Po,t)dt + QiO, Pi = Pi0 (* = 1, 2,... , n).
о
Таким образом, мы имеем вполне определенный метод упрощения урав-
уравнений движения, который приводит к новой постановке задачи интег-
интегрирования уравнений динамики A) — поиску функции S, удовлетво-
удовлетворяющей уравнению в частных производных E5).
Пример 1. Канонические преобразования примеров 1, 3, 5 п. 170 не яв-
являются свободными. В них переменные q, Q зависимы и свободно зада-
задаваться не могут.
Пример 2. Остальные канонические преобразования, рассмотренные в
примерах п. 170, являются свободными, причем для преобразования B9)
с=-1, S = -1?qjQj, E6)
для преобразования C1)
п
^ E7)
352 Глава XI
для преобразования C4)
п
с=1, S=i^>fctg^ E8)
и для преобразования C7)
п
c = 2i, S=Y,(Q2j-4Qj+lQ2j)- E9)
174. О других типах производящих функций. Мы видели,
что не все канонические преобразования являются свободными, и по-
поэтому не каждое каноническое преобразование можно задать при по-
помощи производящей функции вида S(q, Q, t). Однако можно перейти
к иным типам производящих функций. Пусть, например, преобразова-
преобразование D) таково, что
det ^ ф 0. F0)
ар
Тогда из последних п равенств D) можно выразить р через q, P и t и
можно получить производящую функцию Si канонического преобразо-
преобразования D), зависящую не от (q, Q, t), как это было в случае свободного
преобразования, а от переменных (q, P, t) 1. В самом деле, перепи-
перепишем A8) в виде
п
к=1 к=1 к=1 к=1
ИЛИ
k=l k=l \ k=l
Последнее равенство можно окончательно записать в виде
п п
c^PkSqk + ^QkSPk = SS^q, P, t), F1)
k=i k=i
1 Следует иметь в виду, что если каноническое преобразование свободное, то для
него производящая функция не обязательно есть функция S от (q, Q, t). Неравен-
Неравенства D6) и F0) могут, например, выполняться одновременно, и тогда для свободно-
свободного канонического преобразования в качестве производящей функции можно также
взять функцию Si от (q, P, t).
§^. Канонические преобразования 353
п
где через S\ обозначена функция F+ J^ QkPin в которой величины Qj,
k=i
заменены на их выражения из первых п равенств D), а переменная р
заменена затем на ее значение p(q, P, t), получающееся из послед-
последних п равенств D).
Из F1) следует, что
^=cPi, §p; = Qi (» = 1, 2,..., п). F2)
И в точности так же, как и для свободного канонического преобразо-
преобразования, можно получить выражение для функции Гамильтона преобра-
преобразованной системы A)
П = сН+^, F3)
где Н и dSi/dt должны быть записаны в новых переменных. Верно и
обратное: если заданы число с/Ои дважды непрерывно дифференци-
дифференцируемая функция Si(q, P, t), удовлетворяющая условию
deJ
Ф 0, F4)
k=l
то формулы F2) задают каноническое преобразование с валентностью,
равной с. При условии F4) формулы F2) можно записать в виде ра-
равенств D).
Мы рассмотрели два типа производящих функций S(q, Q, t) и
S\{q, P, t). Эти функции наиболее часто применяются при интегри-
интегрировании (точном или приближенном) уравнений динамики. Но q и Р
тоже не всегда можно принять за независимые переменные. Однако1
если заданы 2п независимых функций Q,, Р, от 2п независимых пере-
переменных qi, pi, то из An величин Qi, Pi, qi, pi (г = 1, 2,... , n) всегда
можно выбрать 2п независимых так, чтобы при соответствующей ну-
нумерации переменных производящая функция U зависела от величин
qx,...,qi, pi+1,...,pn, Qi,...,Qk, Pk+i,...,Pn (Z^0,fc^n),
F5)
и, быть может, от времени (в наборе 2п переменных F5) отсутствуют
пары канонически сопряженных переменных qi, pi или Qj, Pj). При
1См. § 29 книги: Гантмахер Ф. Р. Лекции по аналитической механике, М.: Наука,
1966.
354 Глава XI
этом каноническая замена переменных и новая функция Гамильтона
определяются по формулам
ди_ Ш1--с„ ML-_P. ML-Oh
U = cH+^j- (i = l,...,l;g=l + l,...,n;
dt F7)
j = 1,... ,к; h = к + 1,... ,п).
Пример 1. Тождественное преобразование B8)
Qj = 1h pj = Pi U = !' 2' • • • ' n)
задается производящей функцией
F8)
этом с = 1.
Пример 2. Для преобразования C0)
п
F9)
Пример 3. Для канонического преобразования C2), определяющего пе-
перенос начала координат в фазовом пространстве,
п п
с = 1, S1=Y,QjPj + Y, (Si (*K,- " /i (*)P,-) • G0)
Пример 4. Пусть задана произвольная дифференцируемая обратимая
замена обобщенных координат q —>¦ Q, определяемая формулами
Qi=fi(qi,..., qn, t) (г = 1, 2,... , n). G1)
Яри этом преобразовании новые координаты выражаются только через
старые координаты (но не импульсы). Оно является частным случаем
канонических преобразований. Действительно, если положить с = 1 и
п
Si = X)pi/i(9i» •••,?»,*), G2)
\4- Канонические преобразования
355
то, согласно формулам F2), новые и старые импульсы связаны соотно-
соотношениями
G3)
Пример 5. Рассмотрим важный частный случай предыдущего примера:
переход к вращающейся системе координат. Пусть
Q=Aq,
G4)
-1л
где А — ортогональная матрица (А' = А ), которая не обязательно
постоянна. Непосредственным вычислением нетрудно показать, что
формулы G4) вместе с заменой переменных
Р = Ар
G5)
определяют унивалентное каноническое преобразование. Согласно фор-
формуле G2), этому преобразованию соответствует производящая функ-
функция
Si = Р • Aq.
G6)
Примечательно, что обобщенные импульсы преобразуются по тем же
формулам, что и обобщенные координаты.
Новая функция Гамильтона 7i(Q, P,t) вычисляется по старой
H(q, p, t) в соответствии с равенством F3):
U(Q, P,t) = H(A'Q, АР, t) + ^.
G7)
Если матрица А постоянна, то dSi/dt = 0. Если же А не будет по-
постоянной матрицей, то
dA
dt
dAA-i
dtA
G8)
Так как А — ортогональная матрица, то произведение ^^А г (см.
п. 24) — кососимметрическая матрица. Пусть
dt
0
ш3
-ш2
-0J3
0
0J2
0
356 Глава XI
Если ввести вектор и> = (ш\, и>2, и>з), то
и формула G8) может быть записана в виде
Таким образом, окончательно получаем функцию Гамильтона, соот-
соответствующую движению во вращающейся системе координат:
U = H(A'Q, A'P, t)+u-[Qx P]. G9)
Пример 6 (Переход от декартовых координат к полярным). Пусть
х = г cosy, у = г simp. (80)
Если взять с = 1, а
Si = pxr cos (р + pyr sin (p,
то из равенств
Pr = -jj— = Pxcosip + PySimp, pv = -=— = —pxvsimp + pvr cos ip
находим
simp . cosip ,О1Ч
px=prcosip ijt^Pv, Py =prsimp+ —^рр. (81)
Формулы (80), (81) задают унивалентное каноническое преобразова-
преобразование х, у, рх, ру ->¦ г, (р, pr, pv. Если, например,
^ (82)
то
П=^(р2г+^р1) + Щг). (83)
Пример 7 (Переход от декартовых координат к сферическим).
Если
х = г sin в cos i-p, у = г sin й sin у, z = rcos#, (84)
§^. Канонические преобразования 357
то, положив с = 1, а
Si = pxf sin 0 cos <f + pyr sin 0 sin <p + pzr cos 0,
из соотношений
получим
. , sinw cos 0 cos w
ж = sin 0 cos yp,. - ^jP +
. . . cosw cos 0sinw (or.\
= sin 0 sin да, + y^gPv + f—~Pe, [!i0>
Равенства (84), (85) задают унивалентное каноническое преобразова-
преобразование х, у, z, рх, ру, pz -)• г, (р, 0, pr, pv, ре- Например, для
(86)
(87)
Пример 8. Пусть задана некоторая дифференцируемая обратимая за-
замена обобщенных импульсов:
Pi=gi(Pi,P2,...,Pn,t) (t = l, 2, ...,n), det|j#0. (88)
Формулы (88) задают связь старых и новых импульсов (но не коорди-
координат).
Положим с = 1, а
Y,P2,...,Pn,t). (89)
k=i
Тогда из формул F2) находим соотношения
(«- = 1,2,...,»»). (90)
358 Глава XI
Эти соотношения представляют собой линейную неоднородную сис-
систему уравнений относительно qi, G2,..., qn- Определитель систе-
системы — это транспонированный якобиан из (88). Так как он отличен
от нуля, то система уравнений (90) однозначно определяет величи-
величины qi, q2,..., qn как функции Q, Р и t:
qi = hi(Q1,Q2,...,Qn,Pi,P2,---,Pn,t) (t = l, 2, ... , n). (91)
Формулы (88) и (91) задают унивалентное каноническое преобразова-
преобразование.
§ 5. Метод Якоби интегрирования уравнений
движения
175. Уравнение Гамильтона-Якоби. Теория канонических пре-
преобразований приводит нас к методу Якоби интегрирования каноничес-
канонической системы уравнений движения
d*--M (,- = 1,2,...,»). A)
dt dpi dt dq
Если эту систему подвергнуть свободному унивалентному каноничес-
каноническому преобразованию, определяемому уравнениями
где производящая функция S имеет в качестве аргументов величины
Gi,... , GП, Qi,--- ,Qn, t, то, согласно п. 173, система уравнений A)
примет вид
где новая функция Гамильтона "Н определяется равенством
в правой части которого величины qi, pi (после вычисления частной
производной dS/dt) должны быть выражены через Qj, Pj на основании
уравнений B).
Если функция S выбрана так, что "Н = 0, то уравнения C) сразу
интегрируются:
Qi = ai Pi=pi (i = l, 2,... , п), E)
§ 5. Метод Якоби интегрирования уравнений движения 359
где a», pi — произвольные постоянные. Если функция S удовлетво-
удовлетворяет условию D9) п. 173, то из B) находится зависимость исходных
переменных от времени t и 2п произвольных постоянных сц, pi'.
qi = qi(t, aj: Pj), pt = pt(t, aj, Pj). F)
Функция S, согласно B) и D), должна при этом удовлетворять уравне-
уравнению
dS ,„(„ dS Л n m
Это уравнение в частных производных называется уравнением Гамилъ-
тона-Якоби. В нем S есть функция qi, q2,..., qn и t; величины
Qi, Qi,--- , Qn рассматриваются как параметры.
Общее решение уравнения в частных производных зависит от про-
произвольных функций. Такое решение называется общим интегралом это-
этого уравнения. Однако в приложениях к решению задач механики глав-
главную роль играет не общий, а полный интеграл уравнения G). Полным
интегралом уравнения G) называется его решение ?(<&, a», t), завися-
зависящее от п произвольных постоянных «1, «2? • • • , а„и удовлетворяющее
условию
det
Таким образом, мы получаем следующий способ интегрирования урав-
уравнений движения A), основанный на рассмотрении уравнения G).
Теорема (Якоби). Если S(qi, a», t) — полный интеграл уравне-
уравнения Гамилътона-Якоби G), содержащий п произвольных постоянных
«1, a-i,... , ап, то решение F) уравнений A) находится из соотноше-
соотношений
"Д — п. PJ — _я. (а — 1 о ri) (Q)
где pi — произвольные постоянные.
Теорема Якоби позволяет свести интегрирование системы обык-
обыкновенных дифференциальных уравнений A) к нахождению полного ин-
интеграла уравнения G) в частных производных. Вторая задача, конечно,
не проще первой, а даже более сложна. Но оказывается, что метод Якоби
является весьма эффективным среди существующих методов нахожде-
нахождения точных решений системы A). Он также является одним из наи-
наиболее мощных методов приближенного интегрирования канонических
уравнений.
360 Глава XI
Общего метода нахождения полного интеграла уравнения Гамиль-
тона-Якоби G) при произвольной функции Н не существует. Остано-
Остановимся только на некоторых частных способах нахождения полного ин-
интеграла.
176. Уравнение Гамильтона—Якоби для систем с цикличес-
циклическими координатами. Пусть координаты qp,+i,... , qn — цикличес-
циклические. Тогда
Н = H(q1,... , qk, pi,... , рк, Pk+i,.-. , Рп, t).
Полный интеграл уравнения G) ищем в виде
S = ah+1qk+1 + ... + anqn + S*(q1:..., qk, аь ... , а„, t). A0)
Подставив A0) в G), получим уравнение для S*
dSl+H(qi,...,qk, |^,..., f^, ak+1,..., On,t)=0. A1)
Таким образом, нахождение полного интеграла уравнения G) приво-
приводит к рассмотрению уравнения A1), в котором S* зависит уже не от
(п + 1)-й переменной, а от (п — к + 1)-й, т. е. число независимых пере-
переменных уменьшилось на число циклических координат.
177. Уравнение Гамильтона-Якоби для консервативных и
обобщенно консервативных систем. Пусть функция Гамильтона
не зависит явно от времени:
Н = H(q1,... , qn, pi,... , рп).
Тогда существует обобщенный интеграл энергии Н = h, где h — про-
произвольная постоянная. В уравнении G) положим
S = -ht + V, A2)
где функция V не зависит от t. Для нее получаем уравнение
H(qi,...,qn, W..W) = h. A3)
clqi aqn
Это уравнение и будет уравнением Гамильтона-Якоби для консер-
консервативных и обобщенно консервативных систем. Из A3) находим
V = V(qi,... , qn, «i,... , an-i, h), где «i,... , an-i — произвольные
постоянные, не зависящие от h. Из A2) имеем выражение для S:
S = -ht + V{qi,... , qn, ац,... , «„-i, h). A4)
§ 5. Метод Якоби интегрирования уравнений движения 361
Если функция S удовлетворяет условию (8) (ап = h), то A4) — пол-
полный интеграл уравнения Гамильтона-Якоби G) и равенства (9) дают
соотношения
||=Л(г = 1, 2,..., n), g = -ft(t = l, 2,..., п-1), A5)
где /?i,... , /?п — произвольные постоянные.
Последние п — 1 соотношений в A5) — геометрические: они дают
траектории в n-мерном координатном пространстве qi,... , qn. Вместе
с равенством A6) эти соотношения дают и закон движения по траек-
траекториям. Первые п соотношений в A5) служат для определения импуль-
импульсов pi (г = 1, 2,... , п).
178. Характеристическая функция Гамильтона. Функцию V,
входящую в правую часть равенства A4), называют характеристичес-
характеристической функцией Гамильтона. Она удовлетворяет уравнению A3) и бы-
была введена в п. 177 как не зависящая от времени часть производящей
функции S, задающей свободное каноническое преобразование, приво-
приводящее функцию Гамильтона H(qi,..., qn, pi,..., pn) консервативной
или обобщенно консервативной системы к функции % = 0.
Но функцию V(qi,..., qn, a\,..., an_i, h) можно рассмотреть
как производящую функцию некоторого канонического преобразова-
преобразования, свойства которого отличны от свойств преобразования, осущест-
осуществляемого функцией S. Рассмотрим унивалентное каноническое пре-
преобразование, при котором новые импульсы Pi будут постоянными cti
(г = 1, 2,..., п), причем ап = h. Пусть соответствующей производя-
производящей функцией будет V(qi,..., qn, Pi,..., Pn-i, Pn)- Согласно п. 174,
старые и новые переменные связаны соотношениями вида F2):
v.-dV О._Ж-Ж
Рг~ dqC Цг~ dP~ да{
Так как Н = h = an, то отсюда следует уравнение
n dV dV\-h
q Jh
которое совпадает с уравнением A3). Но функция V не зависит от t,
поэтому из равенства F3) п. 174 имеем такое выражение для новой
функции Гамильтона
U = Pn. A8)
362 Глава XI
Таким образом, характеристическая функция Гамильтона задает
каноническое преобразование, приводящее функцию H(qi,...,qn,
Pi,...,pn) к такой форме, когда все новые обобщенные координа-
координаты Qi (г = 1, 2, ..., п) являются циклическими.
В новых переменных
dQi _ дП _ r. Bfi)
где Sin — символ Кронекера.
Поэтому
Pi = а, = const, Qi = —fli = const (г = 1, 2,..., n — 1),
Pn = h = const, Qn-t = -f3n = const,
что, в силу A7), находится в соответствии с формулами A5), A6).
Замечание 3. Выбор величин а», входящих в характеристическую
функцию Гамильтона, в качестве новых импульсов является в неко-
некоторой степени произвольным. Постоянные а\, аг,..., an_i не имеют,
вообще говоря, определенного физического смысла, а просто представ-
представляют собой набор постоянных, появляющихся в процессе нахождения
полного интеграла уравнения Гамильтона-Якоби.
Применим к импульсам а.\,..., ап произвольное дифференцируемое
обратимое преобразование а.\,..., ап —> а\,..., ап:
«1 = gi(at,-.-, а*),...,а„ = gn(a\,..., а*). B1)
Замене импульсов B1) можно поставить в соответствие унивалент-
ное каноническое преобразование Qi, at —> Q*, а* всех канонически
сопряженных переменных (г = 1, 2,..., п). Для этого {см. пример 8
п. 174) достаточно взять производящую функцию в виде
В новых переменных функция Гамильтона будет иметь вид
U = gn(a*1,...,an). B2)
Преимущество новых импульсов а* состоит в том, что они могут
быть увязаны с физической сущностью задачи. Один частный случай
выбора новых импульсов вместо величин оц рассмотрен далее в §6.
§ 5. Метод Якоби интегрирования уравнений движения 363
179. Разделение переменных. Известны замечательные случаи,
когда полный интеграл уравнения Гамильтона-Якоби G) может быть
найден при помощи разделения переменных. Метод разделения пере-
переменных состоит в том, что решение уравнения G) ищется в виде сум-
суммы функций, каждая из которых зависит только от одной из перемен-
переменных (ft,... , qn и времени (и, конечно, произвольных постоянных):
S = S0{t) + Siiqu t) + S2(q2, t) + ... + Sn{qn, t). B3)
К сожалению, не существует простого критерия, позволяющего в общем
случае по структуре функции Гамильтона судить о возможности разде-
разделения переменных в уравнении G) х. Мы укажем только два простей-
простейших случая разделения переменных для консервативной или обобщенно
консервативной системы.
1°. Пусть
Я = Я(/1(д1, Р1),... , /„(<?„, рп)), B4)
т. е. функция Гамильтона зависит от п функций fi, каждая из кото-
которых зависит только от одной пары «своих» канонически сопряженных
переменных д,, р,. Будем предполагать, что
Й^° « = 1,2,-,»)- B5)
Уравнение Гамильтона-Якоби A3) имеет вид
Положим
При условии B5) равенства B7) можно разрешить относительно i
^=gi(qi, at). B8)
Тогда
i(qu Ц)="< (г = 1,2,..., п). B7)
п ,
»=i J
J
1 Исследование этого вопроса содержится в работе: Яров-Яровой М. С. Об интег-
интегрировании уравнения Гамильтона—Якоби методом разделения переменных // ПММ,
1963, Т. 27, вып. 6, С. 973-987.
364 Глава XI
а функция
п ,
Y, gi(Qi, оц) dqt B9)
г=1 J
является решением уравнения Гамильтона-Якоби G). Величина h в B9)
есть функции произвольных постоянных а\,... , ап:
h = H(ai,... , an). C0)
Так как
d2S _ dgi
дщдак~ дак (hk-1, 2,...,п),
а согласно B7) и B8)
то условие (8), записываемое в рассматриваемом случае в виде нера-
неравенства
t=l
очевидно, удовлетворяется. Следовательно, функция B9) будет полным
интегралом уравнения G).
2°. Пусть функция Н выражается последовательно «функцией от
функции», где каждая функция fi зависит от предыдущей функции /j_i
и «своей» пары канонически сопряженных переменных д,, р,:
Н = fn(fn-l, Qn, Рп), fn-1 = fn-l(fn-2, Qn-1, Pn-l)
и т. д., т. е. функция Гамильтона имеет такую структуру:
н = /п{-../з{/2[Л(91) Pi), i2, P2], q3, рз},.-., qn, Pn}- C2)
Будем считать, что
-— ^?0 (г = 1, 2,... , п). F6)
Для получения решения уравнения A3) положим
/n I an_i, qn, д— I = an = h.
\ oqn j
§ 5. Метод Якоби интегрирования уравнений движения 365
При условии C3) эти равенства можно разрешить относительно произ-
производных dV/dqi (г; = 1, 2,... , п). Получим
ОТ Т ОТ Т ОТ 7"
тр- = gi(gi, ai), тр- = g-2(g2, «i, a2), • • • , Jp- = gn(gn, an_i, an).
Функция
n .
»=i ^
будет решением уравнения G). Легко проверить, что неравенство (8)
при условии C3) выполнено, поэтому функция C4) будет полным ин-
интегралом уравнения G).
Мы рассмотрели весьма частные случаи, когда специальная струк-
структура функции Гамильтона позволяет дать общий конструктивный спо-
способ построения общего интеграла уравнения Гамильтона-Якоби. Следу-
Следует, однако, отметить, что указанные способы разделения переменных
применимы к таким важным задачам механики, как задача о гармони-
гармоническом осцилляторе, задача о движении физического маятника, задача
двух тел, задача о движении тяжелого твердого тела вокруг неподвиж-
неподвижной точки в случае Лагранжа и др.
Рассмотрим некоторые примеры.
Пример 1 (Свободное вертикальное падение материальной точки
у поверхности Земли). Пусть ось Oq направлена вертикально вниз.
Если т — масса точки, то
где р — импульс, соответствующий обобщенной координате q, g —
ускорение свободного падения.
Если
то
p = y/2m(a + mgq) C5)
и полный интеграл уравнения Гамилътона-Якоби
dt ' 2m\dq> -w^ = °
366 Глава XI
запишется в виде
S = —at + / \j2m{a + mgq) dq.
В соответствии с формулами (9) имеем
dS_= dS_ = -e.
dq ' да
Первое из этих соотношений дает равенство C5), а из второго полу-
получаем
или
Произвольные постоянные а и /3 находятся из начальных условий.
Пусть при t = О имеем q = О, q = 0. Тогда из C5), C6) м равенст-
равенства р = mq следует, что а = /3 = О и
gt2
g=", p = mgt.
Пример 2 (Движение стержня, опирающегося на горизонтальную
плоскость и вертикальную ось). Пусть в однородном поле тяжести
движется бесконечно тонкий однородный стержень длиной 21 и мас-
массой т. Нижний конец стержня перемещается по гладкой горизонталь-
горизонтальной плоскости, а верхний его конец на рассматриваемой стадии дви-
движения опирается на гладкую вертикальную ось OZ (рис. 143). Найдем
полный интеграл уравнения Гамилътона-Якоби в этой задаче.
Пусть qi — угол между проекцией стержня на плоскость OXY
и осью ОХ, а <7г — угол, который образует стержень с вертикалью.
Со стержнем жестко свяжем систему координат Gxyz, оси которой
направлены по его главным центральным осям инерции, причем ось Gy
лежит в плоскости, проходящей через стержень и вертикаль OZ. Для
кинетической и потенциальной энергии имеем выражения
Т = \{Ар2 + Bq2 + Cr2) + \mv2G,
П = mgl cos <7г,
где А, В, С — моменты инерции стержня относительно осей Gx, Gy,
Gz, a p, q, r — проекции его угловой скорости на эти оси, vq — ско-
скорость центра масс стержня, g — ускорение свободного падения.
§ 5. Метод Якоби интегрирования уравнений движения
367
Имеем А = В = ^ml2, а С = О ввиду
О
того, что стержень бесконечно тонкий. z
Далее,
v2G = I2(sin2
поэтому
T= ^
При помощи функции Лагранжа L = Т — П
находим обобщенные импульсы
Y
Рис. 143
Pi = -д-г- = ^ml2 sin2
dqi 3
* = If = I**2*
Гак как рассматриваемая система консервативна, то функция Га-
Гамильтона имеет вид Н = Т + П и для нее получаем следующее вы-
выражение:
/о \
3 / I
Н =
Положим
Pi=ai,
8m/2 \ sin2 q2
+ р2 I + mgl cos q2.
8ml2
—гч \-pl) + mgl cos q2 = a2.
sm2 q2 J
Тогда полный интеграл уравнения Гамильтона-Якоби будет иметь вид
/I 9
л ' (а2 - mgl cos 92) г^— dq2.
S = -
180. Теорема Лиувилля об интегрируемости гамильтоно-
вой системы в квадратурах. В п. 163 при помощи теории множи-
множителя показано, что для построения общего интеграла системы
dt ~ др{' dt ~ % l ' '••• ' h
C7)
где H = H(qi, pi, t), достаточно найти 2n — 1 первых интегралов.
Построение же 2п-го интеграла сводится к квадратурам. Изложенный
в п.п. 175-179 метод Якоби интегрирования системы C7) позволяет
368 Глава XI
получить существенно более сильный результат: во многих случаях
для сведения интегрирования системы C7) к квадратурам достаточно
знать только п ее первых интегралов.
ГОВОРЯТ, ЧТО фуНКЦИИ Ml, U2,... , Щ ОТ (ft.,... , qn, Pi,--- , Pn, t
находятся в инволюции друг к другу или что они образуют систему
в инволюции, если все скобки Пуассона (щ, ии) (г, к = 1, 2,... ,1)
тождественно равны нулю.
Теорема (Лиувилля). Пусть система уравнений C7) имеет п первых
интегралов
fi(qi,--- , Qn, Pi,--- , Pn, t) = cti = const (г = 1, 2,... , n), C8)
находящихся в инволюции, т. е.
(Л, Л)=0 (г, 8 = 1, 2,..., п), C9)
причем
' " ' ^п' ф 0. D0)
Тогда интегрирование системы C7) сводится к квадратурам.
Доказательство.
Заметим сначала, что при условии D0) уравнения C8) можно раз-
разрешить относительно обобщенных импульсов. В результате получим
Pi = <fi(qi,... , qn, "l,-.- , "и, t) (i = 1, 2,... , n). D1)
Покажем, что при выполнении условий теоремы имеют место равенства
!^Г = -^Г- (i,k = l,2,...,n). D2)
Заменив в равенствах C8) величины р, на их значения <?>, из D1)
и продифференцировав затем r-ое из получившихся тождеств по qt,
получим
dqt -^ дрк dqi
Умножив обе части этого тождества на производную д/8/др, и произ-
произведя затем суммирование по г, придем к соотношению
^{^дрдр dq
§ 5. Метод Якоби интегрирования уравнений движения 369
Аналогично, умножив на dfr/dpk обе части тождества, получающе-
получающегося в результате дифференцирования по g/. s-ro из равенств C8)
(при pi = ipi) и произведя затем суммирование по к, получим
*-~1 ори oqu *-*' *-*' ори opi oqu
Если здесь в первой сумме изменить индекс суммирования к на ин-
индекс г и поменять порядок суммирования в двойной сумме, то придем
к соотношению
/ ~t~ / / =0 (г, s = l, 2,..., п). D4)
t=i l г i=ik=i
Вычитая почленно равенства D3) и D4) и учитывая условия C9), по-
получаем
"~ ' ' =0 (г, s = l, 2,... , п). D5)
Возьмем п из этих соотношений, соответствующих какому-то фик-
фиксированному значению г, и запишем их в виде
п „ ,
^k "^ ^ J s j-\ / 1 О \ (Л ?\\
где
_
_ д<рк\
d)
Система уравнений D6) при условии D0) имеет только тривиальное
решение, т. е.
Ы(%И%*H (i,r = l,2,...,n). D7)
Взяв теперь п из этих соотношений, соответствующих фиксированно-
фиксированному значению г, совершенно аналогично покажем, что все выражения,
заключенные в круглые скобки в D7), равны нулю, т. е. справедливы
равенства D2).
Теперь обозначим Н* функцию Гамильтона Н из C7), в которой
величины pi заменены их значениями ip^ из D1). Покажем, что
(i-г 2 „)
370 Глава XI
Имеем из C7),D1) и D2)
dqt dt dt dt ^ dqj dt dt ^ dqt
Следовательно,
& ^Pi dH*
^ dqt dqt '
и справедливость равенства D8) доказана.
Равенства D2) и D8) являются необходимыми и достаточными
условиями существования такой функции S от qi, Q2,--- , qn, t и от
постоянных а\,... , ап, что
f=^ f = -я*-
Из математического анализа известно, что нахождение такой функ-
функции S требует только квадратур, т. е. вычисления интегралов от из-
известных функций.
Равенства D9) показывают, что функция S удовлетворяет урав-
уравнению Гамильтона-Якоби, соответствующему системе C7). Покажем,
что S будет полным интегралом этого уравнения. Для этого надо про-
проверить выполнимость неравенства (8), которое, в силу первых п ра-
равенств D9), приводится к виду
det
дак
ф 0. E0)
Эти неравенства представляют собой необходимые и достаточные усло-
условия разрешимости уравнений D1) относительно «i,... , an. Но урав-
уравнения D1) эквивалентны исходным интегралам C8), которые при по-
получении уравнений D1) уже разрешены относительно а\,... , ап. Сле-
Следовательно, неравенство E0) выполнено и S — полный интеграл.
При известном полном интеграле S интегрирование уравнений C7)
завершается рассмотрением соотношений (9).
Следует отметить, что далеко не каждая система C7) приводится
к квадратурам. Обычно нельзя найти необходимого количества пер-
первых интегралов. И не потому, что их нахождение технически сложно,
а потому, что существуют причины принципиального характера, пре-
препятствующие интегрируемости1.
1Подробное изложение этой проблемы можно найти в статье: Козлов В. В. Интег-
Интегрируемость и неинтегрируемость в гамильтоновой механике // УМН, 1983, Т. 38,
вып. 1, С. 3-67.
§ 6. Переменные действие-угол 371
§ 6. Переменные действие—угол
181. Случай одной степени свободы. Продолжим начатое в
п. п. 177-179 изучение некоторых вопросов, связанных с интегрирова-
интегрированием консервативных и обобщенно консервативных систем. Будем из-
изучать системы, движения которых обладают описанным ниже свойст-
свойством периодичности. Для таких систем Делонэ предложил специальный
выбор постоянных импульсов а* (г = 1, 2,..., п) в характеристической
функции Гамильтона п. 178. Эти новые импульсы представляют собой п
независимых функций от набора величин а», появляющихся при нахож-
нахождении полного интеграла уравнения Гамильтона-Якоби. Они называют-
называются действиями (точные определения см. далее) и ниже чаще всего бу-
будут обозначаться /,. Канонически сопряженные к ним координаты w,
называются угловыми переменными. Переменные действие-угол I,, w,
весьма удобны для описания движений, обладающих свойством перио-
периодичности. Они находят широкое применение в теории возмущений.
Чтобы понять сущность метода Делонэ, целесообразно сначала рас-
рассмотреть случай системы с одной степенью свободы. Фазовое простран-
пространство такой системы является двумерной плоскостью g, р, и периоди-
периодические движения могут быть двух различных типов.
В движениях первого типа функции q(t), p(t) являются периоди-
периодическими функциями с одним и тем же периодом. Точка, изображающая
движение в фазовой плоскости, описывает замкнутую кривую. В этом
случае говорят, что имеет место случай колебаний. Примером могут
служить колебания маятника, рассмотренные в п. п. 93-96. На рис. 94
им отвечают замкнутые фазовые кривые, окружающие особые точки
типа центр.
В движениях второго типа сама величина q(t) не является перио-
периодической функцией, но когда она увеличивается или уменьшается на
величину до, конфигурация системы не меняется. Здесь фазовые кри-
кривые р = p(q) незамкнуты и имеют период до по д. Периодические движе-
движения второго типа называют вращениями. Простейшим примером может
служить движение твердого тела, вращающегося вокруг неподвижной
оси. Координата g здесь является углом поворота тела, и ее изменение
на величину до = 2тг не изменяет положения тела. На рис. 94 случаю
вращений отвечают незамкнутые фазовые кривые, заполняющие части
плоскости, лежащие выше и ниже сепаратрис.
Пусть Н = H(q,p) — функция Гамильтона системы с одной степе-
нью свободы, причем Ц^- ф 0. Тогда, согласно п. 177-179, характерис-
характеристическая функция Гамильтона V = V(q, а), где а = h — постоянная
372 Глава XI
интеграла Н = h. Из формул A7) п. 178 имеем
Вместо а введем величину / по формуле
где интеграл берется по полному циклу изменения q (цикла колеба-
колебания или вращения, смотря по тому, какому случаю отвечает фазовая
кривая, определяемая уравнением H(q, p) = h). Величина / называет-
называется переменной действие. Из B) видно, что / — это поделенная на 2тг
площадь, ограниченная замкнутой фазовой кривой, в случае колебаний
или площадь, заключенная между фазовой кривой и отрезком оси q
длины q0, в случае вращений.
Подставив A) в B), получим
т. e. I = I(a). При условии — ф О из C) находим а = аA). И
CLGL
тогда (см. п. 178) получаем новую функцию Гамильтона Н = аA).
Производящая функция унивалентного канонического преобразова-
преобразования q,p —> w,I, вводящего переменные действие-угол, будет функци-
функцией q, I: V = V(q, «(/)). Угловая переменная w определяется равенст-
равенством
Таким образом, алгоритм введения переменных действие-угол в
гамильтоновой системе с одной степенью свободы выглядит так. Из
уравнения H(q, р) = h находим функцию р = p(q, h), а затем вычис-
вычисляем переменную / как функцию h:
I = ^ f P(q, h) dq.
E)
Обращение функции / = I(h) дает h = h(I). Производящая функ-
функция V(q, I), задающая замену q,p —> w,I, определяется равенством
V(q,I)=Jp(q,h(I))dq. F)
§ 6. Переменные действие-угол 373
Неявно замена q,p —iw,I задается формулами
> = %• ' = %¦ <7>
Новая функция Гамильтона
% = ПA) = Ц1). (8)
В переменных действие-угол уравнения движения будут такими:
§ = -§w=o, М = Ш=ш{1). (9)
dt ow dt ol
Отсюда следует, что
I = Iq = const, w = w(Io)t + Wq- A0)
Величина to называется частотой рассматриваемого периодическо-
периодического движения. Существенно то, что процедура получения величины ш не
потребовала ничего, кроме квадратур и разрешения уравнений относи-
относительно некоторых переменных.
Отметим, что когда координата q совершает полный цикл изме-
изменения (в случае колебаний или вращений), то угловая переменная w
возрастает на 2тг. В самом деле, обозначая через Aw приращение w за
цикл изменения q, имеем, с учетом D),
Вынеся производную по / за знак интеграла и приняв во внимание
формулу C), получим
Это поясняет название величины w угловой переменной. За один
цикл величина w изменяется на 2тг, и налицо полная аналогия с враще-
вращением тела вокруг оси (частота ш — аналог угловой скорости тела, w —
аналог угла его поворота вокруг оси).
Пример 1 (Твердое тело, вращающееся вокруг неподвижной оси).
Будем считать, что моменты внешних сил отсутствуют. Тогда, ес-
если А — момент инерции тела относительно оси вращения, a ip — угол
его поворота вокруг оси, то
2
Т=\Аф\ П = 0; pv=A<p, Я=||.
374
Глава XI
Считая, что ф > О, из уравнения Н = h находим pv = \/2Ah и, следо-
следовательно,
т
2тг
Р<р V =
2Ah
2тг
2тг
f ,
= J
v = J Pv ^ = I(p, w = m. = ^ Pv = ®l = i.
- I2 ,,-dH -
Пример 2 (Гармонический осциллятор частоты ш). Функцию Га-
Гамильтона возьмем в виде
Из уравнения Н = h имеем р =
равенства
/ Obi
^ — q2. Если в правой части
I =
1
'2h
сделать замену q = \j -^ sin ж, то получим
2тг
то есть
Для производящей функции замены q,p —iw,I имеем выражение
V = ±J^-q*dq=±J ^21 - q* dq.
Из формул G) находим замену, вводящую переменные действие-угол, в
виде
q = v2Ismw, p = v2Icosw. A1)
С заменой A1) мы уже встречались ранее в примере 6 п. 170.
§ 6. Переменные действие-угол
375
182. Переменные действие-угол в задаче о движении маят-
маятника. Задача о движении маятника подробно исследована
в п. п. 93-96. Несколько изменяя принятые там обозначения, напишем
дифференциальное уравнение, описыващее движения маятника, в виде
g + u;2sing = 0. A2)
Это уравнение второго порядка может быть представлено в виде систе-
системы двух гамильтоновых дифференциальных уравнений первого поряд-
порядка с функцией Гамильтона
Я = ^р2 -
cos q.
A3)
Для введения переменных действие-угол случай колебаний и вра-
вращений маятника надо рассмотреть отдельно.
В случае колебний константа интеграла энергии Н = h удовлетво-
удовлетворяет неравенствам — lJq < h < lJq. Пусть /3 — амплитуда колебаний.
Тогда, если к\ = sin тт, то
а действие / вычисляется по формуле
A4)
причем в последнем интеграле
Введя вместо g переменную ф по формуле
ф = arcsin I — sin -~ ) ,
выражение A5) можно переписать в виде
* { Jl - к\ sin2 ф
1 — к\ sin2 ф dip —
-A-kl
1I , ЛФ
{ Jl - fc2 sin2
A5)
A6)
A7)
A8)
376 Глава XI
т. е.
I=^L[E(h)-(l-kl)K(h)], A9)
где К и Е — полные эллиптические интегралы первого и второго рода
соответственно.
Равенство A9) определяет / как функцию к\. Продифференцировав
обе его части по h, получим, при учете формул B1) п. 95,
= ^klK(kl). B0)
Отсюда видно, что -^— /0 и, следовательно, на основании теоремы о
ок\
неявной функции, равенство A9) разрешимо относительно h, причем
для производной функции h по / имеем выражение
=
dl 8to0hK(h)'
Новая функция Гамильтона % зависит только от /, она определяет-
определяется из A4) и A9). Отбросив несущественную постоянную — ш^, получим,
что
U = 2w20kl B2)
где fci = к\{1) — обратная к 1{к\) функция, определяемая из A9).
Из B1), B2) находится частота колебаний
,, _дП _ дП dki _
Ш1 '
Ш1~ 01 ~ dh' dl ~ 2К{к1У
K - 2тг 4K(h)
Для периода колебании т = -p- получаем выражение г = —г. , сов-
падающее с выражением, полученным в п. 96.
Для производящей функции F) канонического преобразования
q, p —> w, I после замены переменных A7) получаем выражение
V(q, I) = 4u>o [Е(ф, h) - A - kl)F(ф, h)} , B4)
где F и Е — эллиптические интегралы первого и второго рода (см.
п. 95), ф определена равенством A7), а к\ = fci(J) — равенством A9).
Для угловой переменной w, согласно второй формуле из G), имеем
выражение
n-dV _ dV dh
оТ — FT,7ГГ-
ol oh ol
§ 6. Переменные действие-угол 2>11
Дифференцирование обеих частей формулы B4) по fci дает равен-
равенство
5K=4W \^E-+ д-^-^- + 2к F- A-к2) (—+ dZ^tX\ B6)
дк\ \_дк\ дф дк\ 1 \дк\ дфдк\)\
Но из A7) следует, что
дф si-аф ,
яГ~ = ~1 Г1 B7)
oki ki cos ф
Используя эту формулу и соотношения A3), A4), A9) и B0) из п. 95,
равенство B6) можно преобразовать к виду
^- = 4шок1Е(ф,к1). B8)
Учитывая B1) и B8), из формулы B5) находим, что
yjl-k\ sin2 ж
т. е.
w
^—. B9)
Теперь из A6), A7) и B9) получаем каноническое преобразова-
преобразование q, р, —> w, I, вводящее переменные действие-угол в случае колеба-
колебаний маятника
q = 2arcsin \k\ sn I ———w, k\
1 V /J C0)
BK(k1)
p = 2ix>ofci en ———w, i
V
Это каноническое преобразование унивалентно и 2тг-периодично по w.
Оно преобразует функцию Гамильтона A3) к виду B2).
Теперь рассмотрим случай вращений, когда переменная h интег-
интеграла энергии удовлетворяет неравенству h > u)q. Так как при замене р
на — р, a q на — q функция Гамильтона A3) не изменяется, то будем
рассматривать только случай вращений при положительных р. Пусть
при t = 0 имеем q = 0, р = ро > 0. Тогда
378 Глава XI
где
fc| = —г = , ° @ < fc2 < 1), C2)
Pa u? + h
а фазовая кривая р = p(q, h) задается уравнением
Для действия / имеем такое выражение:
или, если воспользоваться четностью подынтегрального выражения и
сделать замену q = 2ж,
о
т. е.
C4)
Принимая во внимание формулы B1) п. 95, из C4) находим
дк2
Так как -^f- ф 0, то равенство C4) разрешимо относительно к2, причем
ок2
для производной функции к2 по / имеем выражение
дк2
д!
C5)
Новая функция Гамильтона определяется из C1) и C4). Отбросив
несущественную постоянную — Wg, получим
It' C6)
§ 6. Переменные действие-угол 379
где к2 = к2A) — функция, обратная функции 1{к2) из C4).
Учитывая C5), для частоты ш2 вращений получим такое же выра-
выражение:
2 а/ а&2 а/ к2к(к2у [ '
За промежуток времени, равный -у-, величина q получает прираще-
ние 2тг.
Для производящей функции F) получаем выражение
V(q, I) = ^Е (|, к2) . C8)
Угловая переменная w вводится при помощи равенства
.„-&V- дУ дк2
01 дк2 01 '
которое, при учете формул C5) и выражения B0) п. 95, преобразуется
к виду
K(k2)w /q
Отсюда и из C3) находим
) ^(^^) C9)
Здесь к2 = к2A) из C4). Формулы C9) задают унивалентное каноничес-
каноническое преобразование q, р —>¦ w, I, приводящее функцию Гамильтона A3)
к виду C6).
183. О переменных действие—угол для системы с п степеня-
степенями свободы. Ограничимся лишь случаем, когда уравнение A3) п. 177,
определяющее характеристическую функцию Гамильтона V, является
уравнением с разделяющимися переменными. Тогда
п
V = Y,Vi(qi, «1, а2,...ап-ъ h). D0)
г=1
Отсюда и из формул A7) п. 178 получим
Pi = тг" = д-1 =Pi(qu "I, a2,...an_i, К) (г = 1, 2,..., п). D1)
380 Глава XI
Эти уравнения задают проекции траектории в 2п-мерном фазо-
фазовом пространстве qi, q2,..., qn,Pi, Pi-,----, Pn на плоскости qi, pi
(i = 1, 2,..., n). Будем предполагать, что движение в каждой из плос-
плоскостей обладает свойством периодичности, т. е. в плоскости д,, р^ кри-
кривая D1) замкнута или периодична по д, с некоторым периодом д,0-
Так как в случае D0) происходит полное разделение переменных,
то при фиксированных величинах а.\, а2,- ¦ .an-i, h движения в плос-
плоскостях qi, pi (г = 1, 2,..., п) независимы и каждое из них можно
исследовать, как это было сделано в п. 181 в случае одной степени сво-
свободы. Имеем
hj hj%idqi (« = 1» 2,..., n), D2)
где интеграл берется по полному циклу периодического движения (ко-
(колебания или вращения, смотря по тому, какой случай имеет место).
Равенства D2) определяют п функций /, = /,(ai, а2,- ¦ -an-i, h). Эти
функции независимы в силу независимости пар q,, Pi (г = 1, 2,..., п).
Величины Ii, I2,..., In можно принять за новые импульсы (вместо
а\, а2,.. .an-i, /г). Тогда
«1 = fi(h, h,---, In), «2 = /2СГ1, h,---, In),---,
an-i = fn-i(h, h,---, In), an = fn(h, h,---, In)-
Если эти величины подставить в D0), то получим
V = V(qi,..., qn, h,---, In)-
Соотношения
неявно задают унивалентное каноническое преобразование от исходных
переменных qi, pi к переменным действие-угол Ii, Wi. Новая функция
Гамильтона имеет вид
D4)
Все новые координаты (углы Wi) являются циклическими.
В новых переменных уравнения движения будут такими:
где Wi — частота периодического движения (в плоскости qi, pi)
§ 6. Переменные действие-угол 381
Как видим, метод Делонэ позволяет получить все частоты движе-
движения путем изучения функций Н и V, при этом не требуется полное
исследование движения системы.
Покажем, что г'-я угловая переменная w, за полный цикл измене-
изменения j-й координаты qj получает приращение
Aw, = 2wSij,
где Sij — символ Кронекера. Действительно, используя формулы D2)
и D3), находим
Замечание 4. Если координата qi циклическая, то соответствующий
ей импульс pi постоянен, и траектория в плоскости qi, pi будет пря-
прямой линией. Тогда движение в плоскости qi, pi можно считать перио-
периодическим (вращательного типа) с любым периодом д^0- Удобно принять
<7;о = 2тг. Тогда
2тг 2тг
1г = тг~ f Pi dqi = y~ / pi dqi = -^—pt / dqi = pi,
о о
т. е. переменная действие Jj в случае циклической координаты q, сов-
совпадает с импульсом pi.
184. Переменные действие—угол в задаче двух тел. Задача
двух тел изучалась в §1 гл. 8. Здесь будут рассмотрены переменные
действие-угол в этой задаче. Будем использовать обозначения из §1
гл. 8. Орбиту считаем эллиптической (или, в частности, круговой). Рас-
Расстояние г точки Р от притягивающего центра О удовлетворяет нера-
неравенствам п ^ г ^ гг, где п = аA — е), г2 = аA + е) (а — большая
полуось орбиты, е — ее эксцентриситет). Отсюда и из формул §1 гл. 8
следует, что
2
П + г2 = 2а, т\г2 = а A-е ) = ар = —,—, D5)
где р — параметр орбиты, с — константа интеграла площадей, величина
к определена в п. 115.
Уравнению A) п. 115 задачи двух тел соответствуют уравнения
Лагранжа второго рода с функцией Лагранжа L = Т — П, где Т = -~v2,
382 Глава XI
П = — j;. Для квадрата v2 скорости точки Р имеем в сферических
координатах (см. рис. 9) выражение C0) п. 9. Поэтому
L = \{г2 + г2 sin2 вф2+г2в2) + ?,
обобщенные импульсом вычисляются по формулам
Рг = г, Pip = r2 sin2 вф, рв = г2в, D6)
а функция Гамильтона Н = Т + П имеет вид
D7)
г sin в
Координата <р циклическая. Поэтому pv = av = const, а характе-
характеристическая функция Гамильтона имеет вид
V = av<p + рд d6 + pr dr, D8)
причем
2 о
2 + \ =а2 = const p2 + °^ Щ
+ -\- =а2в = const, p2r + °^r - Щ- = 2а3 = const. D9)
sin в г
Постоянная 2«з равна константе h интеграла энергии G) из п. 117 и
для эллиптической орбиты отрицательна.
Из D9) получаем выражение для величины р2:
г? 9 ,2к а1 _ 2а3(г - п)(г2 - г)
Рг = 2а3 + -5 J = о • E0)
Приравнивание коэффициентов при одинаковых степенях г в обеих
частях последнего тождества дает соотношения между постоянны-
постоянными ад, «з и величинами п, Г2-
E1)
Сравнивая первые формулы из D5) и E1), получаем соотношение
§ 6. Переменные действие-угол 383
Сравнение же вторых формул из D5) и E1) при учете соотношения E2)
приводит к равенству
ад = с, E3)
т. е. постоянная ад в D9) равна константе интеграла площадей.
Введем переменные действие Ir, Iv, Ig. Так как <р циклическая
координата, то, согласно замечанию предыдущего пункта, имеем
Величины Ig Ir определяются равенствами:
h = 2^ j> Рв сШ, !г = ^ <Р Pr dr. E5)
Для вычисления первого из интегралов E5) заметим1, что в сфе-
сферических координатах справедливо соотношение
2Т =ргг + р(рф + рдв. E6)
Если же в плоскости орбиты ввести полярные координаты г, v {у — ис-
истинная аномалия), то 2Т = г2 + г2г>2, рг = г, р„ = r2i>. Для импульсар„,
при учете интеграла площадей г2г> = с и формулы E3), имеем равенст-
равенства р„ = с = ад. Принимая это во внимание, выражение для удвоенной
кинетической энергии 2Т = prr + pvv можно записать в виде
2Т = prr + aev. E7)
Из сравнения правых частей формул E6) и E7), при учете ра-
равенств E4), следует, что
рдйв = agdv — Ivdip. E8)
За один оборот точки Р по орбите угол в совершает полный цикл его
колебания, а углы v и <р изменяются на 2тг. Поэтому, принимая в рас-
расчет формулу E8), для первого из интегралов E5) получаем выражение
1д = ад - Iv, т. е.
ад=1(р+1д. E9)
Величина рг во втором из интегралов E5) положительна, когда г
увеличивается от т\ до гг, и отрицательна при уменьшении г от гг до т\.
1См.: Голдстейн Г. Классическая механика. М.: Наука, 1975.
384
Глава XI
Принимая это во внимание и учитывая соотношения E0), выражение
для 1Г можно записать в виде
1т =
\/{г -п){г2 -г)
dr.
F0)
Для вычисления интеграла в правой части этой формулы введем вмес-
вместо г новую переменную х(г) по формуле
г =
Т\ + Г2Х
1 + х2
Тогда
(г2 - гг)х2 г2 - п ,
г-п = — —, г2-г=- ?", dr =
1 + 2 1 + 2
2(г2 - г\)х
— h-rh-
A + х2J
= 0, ж(гг) = +оо.
Поэтому
It =
оо
/
+ г2х2)A + х2)
2\2
dx.
F1)
Подынтегральное выражение в F1) можно представить в виде
+ г2х2)A + х
2J
г2 -
г±
Т2-ТХ
+
Но
оо оо оо
/dx _ 7Г j dx _ тг I
1 + ж2' J n+r2x2 ~ 2yrlr2"' J
dx
A + ж2J 4'
поэтому после интегрирования и несложных преобразований форму-
формулу F1) можно записать в виде
1т =
+Г2-
F2)
§ 6. Переменные действие-угол 385
Принимая во внимание выражения E1) для г\ + гг и т\Т2 и учитывая
равенство E9), формуле F2) можно придать следующую форму:
Но, согласно D7) и D9), Н = аз- Поэтому, учитывая унивалентность
канонического преобразования, вводящего переменные действие-угол,
из F3) получаем следующее выражение для функции Гамильтона, за-
записанной в переменных Ir, Iv, Ig:
к2—^- F4)
2(Ir
за за 3i~i
обозначим через wr, wv, wg. Так как ^^ = j^- = tjtS то соответству-
О1 Ol Ol
Угловые переменные, отвечающие переменным действие Ir, Iv, Ig,
за за 3i~i
О1Г Olv Olg
ющие им частоты u>r, ujv, ujg равны. Этого и следовало ожидать, так как
изучаемое движение материальной точки по эллиптической орбите яв-
является периодическим (см. п. 121).
185. Элементы Делонэ. Введем новые переменные I,, wt
(г = 1, 2, 3), имеющие более ясный геометрический и механический
смысл, нежели переменные Ir, Iv, Ig, wr, wv, wg. Для этого сделаем за-
замену переменных по формулам:
w\ = wv — wg, и>2 = wg — wr, W3 = wr, F5)
h = I<p, h=I<p + Ie, I3=Ir + Iv + Ie- F6)
При помощи какого-либо из критериев п. 169 можно проверить, что
равенства F5), F6) задают унивалентное каноническое преобразова-
преобразование. В новых переменных функция Гамильтона принимает вид:
н = -щ- F7)
Выясним смысл переменных I{, Wi (г = 1, 2, 3). Из E2) и F7) с
учетом того, что Н = аз, находим
h = Vka. F8)
Далее имеем
= Р_ = к = jvfc_ =
dlz II (kaf2 a3'2 '
386 Глава XI
где п — среднее движение (см. формулу B0) п. 121). То есть w3 —
это, с точностью до константы, средняя аномалия n(t — т) (см. п. 122;
т — это время прохождения точки Р через перицентр). Полагая эту
константу равной нулю, получаем, что
w3 = n(t - т). F9)
Теперь рассмотрим пару канонически сопряженных перемен-
переменных I2, W2- Из E3), E9) и F6) следут, что /г = с, т. е. /г — это
величина кинетического момента точки Р относительно притягиваю-
притягивающего центра. Но из D5) видно, что с = ^/fca(l — е2). Поэтому
h = у/ка{1 - е2). G0)
Так как —— = ^-у^ = 0, то W2 представляет собой некоторый постоян-
dt 0I2
ный угол, отсчитываемый в плоскости орбиты. Положим
w2 = ш, G1)
где (см. п. 123) и> — угловое расстояние перицентра от узла.
И, наконец, рассмотрим переменные Д, w\. Согласно E4) и F6),
1г = av, т. е. 1\ — это проекция кинетического момента точки Р на
ось Oz (см. рис. 9 и 126). Учитывая еще, что —^- = Ц^- = 0, получа-
dt oli
ем, что w\ — это некоторый постоянный угол, отсчитываемый в плос-
плоскости Оху. Примем, что w\ совпадает с долготой восходящего узла п.
Таким образом (см. рис. 126 и формулу G0)):
1г = с cos г = /г cos г = укаA — е2) cos г', u>i = п, G2)
где i — наклонение орбиты.
Введенные канонически сопряженные переменные 1\, /г, /з,
wi, vJ, W3 называются каноническими переменными Делонэ или, крат-
кратко, элементами Делонэ. Следуя Делонэ, для них часто используются
обозначения Н, G, L, h, g, I (не путать обозначения Н, L, h элементов Де-
Делонэ с обозначениями функций Гамильтона, Лагранжа и константы ин-
интеграла энергии!). Элементы Делонэ связаны с обычными элементами
орбиты п, г, а, е, ш, т следующими получаемыми из F8)-G2) соот-
соотношениями:
L = Vka, I = n(t — т),
G = ^/ka(l - е2), g=w, G3)
Н = v/fca(l-e2)cosi, h = п.
§ 6. Переменные действие-угол 387
В переменных Делонэ функция Гамильтона задачи двух тел запи-
записывается в виде
G4)
2L2
Две системы канонических элементов Пуанкаре. Для многих при-
приложений (например, связанных с исследованием движения планет) це-
целесообразно иметь канонически сопряженные переменные, среди кото-
которых есть такие, которые малы для малых значений эксцентриситетов и
наклонений орбит. Пуанкаре ввел две системы таких переменных. Их
называют элементами Пуанкаре.
Первая система элементов Пуанкаре Л, Г, Z, А, 'у, z связана с эле-
элементами Делонэ при помощи унивалентного канонического преобразо-
преобразования вида:
Л = L, Г = L - G, Z = G - Н,
X = l + g+h, j = -g-h, z =-h.
Отсюда и из G3) получаем выражения элементов Л, Г, Z, A, j, z через
обычные элементы кеплеровской орбиты:
А = n(t - т) + и> + п,
7 = -ш - О, G6)
Z = 1/fca(l-e2)(l-cosi), z =-SI.
Для орбиты малого эксцентриситета и наклонения элементы Г и Z бу-
будут величинами порядка е2 и г2 соответственно.
Во второй системе элементов Пуанкаре величины Л, А — те же ка-
канонически сопряженные переменные, что и в первой системе, а осталь-
остальные четыре элемента определяются формулами (?, р — импульсы, г], q
— координаты):
p
i— i—
= v 2Z cos z, q = V 2Z sin z.
Для орбиты малого эксцентриситета и наклонения величины ?, ц и р, q
имеет порядок е и i соответственно.
И для первой, и для второй систем канонических элементов Пуан-
Пуанкаре функция Гамильтона задачи двух тел имеет вид
& G8)
388 Глава XI
§ 7. Канонические преобразования в теории
возмущений
186. Предварительные замечания. Точное интегрирование
дифференциальных уравнений движения реальной механической сис-
системы возможно только в очень редких случаях. Эти случаи являются
скорее исключением, чем правилом. Поэтому разработано много мето-
методов, позволяющих проводить приближенное исследование систем, урав-
уравнения движения которых не могут быть решены точно, но в то же время
некоторая упрощенная задача, называемая невозмущенной задачей, до-
допускает точное решение. Совокупность этих методов образует теорию
возмущений, которая находит самое широкое применение во всех об-
областях науки и техники, где рассматриваются процессы, описываемые
дифференциальными уравнениями.
В теории возмущений предполагается, что различие между реаль-
реальной (возмущенной) системой и ее упрощенной (невозмущенной) мо-
моделью можно рассматривать как малые возмущения. Возмущения по-
появляются, например, за счет того, что к основным силам, приложенным
к точкам механической системы, добавляются некоторые другие силы,
являющиеся в определенном смысле малыми по сравнению с основными
силами. Например, если пренебречь влиянием Солнца и считать Землю
и Луну материальными точками, то невозмущенной задачей о движе-
движении Луны вокруг Земли будет задача двух тел (материальных точек).
Влияние притяжения Солнца и отличие Земли и Луны от точечных масс
можно считать малыми и отнести к возмущающим воздействиям, ко-
которые можно учесть методами теории возмущений.
Бывает и так, что уравнения движения механической системы
очень сложны и получить их точное решение нельзя, но можно подо-
подобрать другую систему, которая в определенном смысле почти такая же,
как и исходная, но ее уравнения движения могут быть проинтегриро-
проинтегрированы точно. Различие между исходной и таким образом подобранной
системой приводит к появлению малых возмущений.
В механике тщательно изучаются системы, уравнения движения
которых точно интегрируются. Это связано с тем, что интегрируемые
задачи часто используются в качестве невозмущенных в более слож-
сложных, но реальных и нужных задачах.
Методы теории возмущений позволяют исследовать движение ме-
механических систем, как правило, на конечном (хотя иногда и очень
большом) интервале времени.
В этом параграфе мы рассмотрим некоторые вопросы применения
канонических преобразований в теории возмущений систем, движение
которых описывается дифференциальными уравнениями Гамильтона.
§ 7. Канонические преобразования в теории возмущений 389
187. Вариация постоянных в задачах механики. Предполо-
Предположим, что в уравнениях движения механической системы
%_9Я dPi__dH_ (,_1 2 ч m
dt - dpi' dt - %' (|-х'2'---'n) A)
функция Гамильтона H(qi, pi, t) может быть представлена в виде сум-
суммы
Н = Щ + Н1, B)
причем дифференциальные уравнения A) с функцией Н = Но
dqi _ дНо dpi _ дН0
dt dpi ' dt dqi
(t = l, 2,..., n) C)
могут быть проинтегрированы в замкнутой форме. Пусть решение сис-
системы C) записано в виде
4i = qi(qio,--- , Чпо, Рю,--- , Pno, t),
Pi = Pi{qio, ••• , Qno, Рю, ••• , Pno, t),
где qio и pi0 — значения величин qi, pi в начальный момент t = 0. Для
интегрирования уравнений A) сделаем в них замену переменных по
формулам D), принимая величины д,о5 Pio за новые переменные. Так
мы приходим к проблеме вариации произвольных постоянных в задачах
механики, описываемых каноническими уравнениями Гамильтона A).
Формулы D) задают (см. п. 171) унивалентное каноническое пре-
преобразование. Это преобразование имеет обратное:
qio = qio(qi,-¦ ¦, qn, pi,---, pn, t),
Pio = p,o{qi,---, qn, pi,---, Pn, t),
которое также является унивалентным каноническим преобразовани-
преобразованием. Следовательно, скобки Пуассона функций E) удовлетворяют равен-
равенствам (см. п. 169)
(qio, Qko) = 0, (рм, Pko) = 0, (qi0, Pko) = Sik. F)
Кроме того, функции E), являясь интегралами системы C), удовле-
удовлетворяют, согласно п. 167, равенствам
^f + (<Ko, Ho) = 0, ?§f + (Pio, Яо) = 0. G)
390 Глава XI
Найдем производные по времени новых переменных д,о, Pio в силу
уравнений движения A). Дифференцируя выражения E) и учитывая
равенства G) и B), получаем
_ dqto ( . _
~ dt №o' ' ~
dt ~ dt + -^ \dqk dt + dPk dt ) ~ dt ()
= -(qi0, Ho) + (qi0, H) = (qi0, H - Ho) = (qi0, Hi),
dPio _ dPio \^ (dPiodqk, dPio dpA _ dPio , m =
dt dt +2-^\dqk dt dpk dt ) dt +1Ло' j (g)
= -(Pio, Ho) + (pi0, H) = (pi0, H - Ho) = (pi0, Hi).
Пусть HI — это функция Hi, в которой сделана замена переменных D).
Тогда
дНх = у (сЩдто + дЩ дрю
dqk дрю dqk J '
A0)
дрк T^i V dqi° дрк дрш дрк *
Используя эти равенства и соотношения F), имеем
dqk
дрк дрю дрк
^ J. Ill j ^ \ J_t/ V _!. f (г 1 w ZL ГЪ
П
1=1 1 = 1
Аналогично
дЩ
П fiff* П fiff*
Соотношения A1), A2) позволяют записать уравнения (8), (9) в виде
dqi0 дЩ dpio дЩ
dt дрм' dt dqi0
i = l,2,...,n). A3)
§ 7. Канонические преобразования в теории возмущений 391
Таким образом, если Н = Но, то величины дм, рм постоянны, а урав-
уравнения, описывающие их изменение, в системе с функцией Гамильто-
Гамильтона Но + Hi имеют каноническую форму, причем соответствующая
функция Гамильтона Н^ получается подстановкой в «возмущающую»
функцию Н\ величин д,, р, определяемых по формулам D), отвечаю-
отвечающим решению задачи Коши для «невозмущенной» задачи с функцией
Гамильтона До-
Задачу о вариации произвольных постоянных для системы A)
можно рассмотреть и иначе. Пусть решение «невозмущенной» систе-
системы C) найдено при помощи уравнения Гамильтона-Якоби
§ + Я0(и,Ц,*)=0. A4)
Пусть S = S(qi,... , qn, а.\,... , ап, t) — полный интеграл этого урав-
уравнения. Сделаем в уравнениях A) каноническую замену переменных по
формулам (9) п. 175, принимая полный интеграл S за производящую
функцию
g М д (i = i, 2,..., „). A5)
g=Pl, = д (i = i, 2,..., „).
При такой замене переменных роль новых координат играют величи-
величины «1,... , ап, а роль новых импульсов — величины /3i,... , /?„. Новая
функция Гамильтона %(ai,... , ап, /3i,... , /?„, t) вычисляется по фор-
формуле (см. п. 173)
Принимая во внимание уравнение A4), имеем отсюда % = Н{, где те-
теперь Н^ — это функция Hi, выраженная через переменные а», /%, t
согласно равенствам A5). Таким образом, новые переменные a», /3j
(г = 1, 2,... , и), которые постоянны, если Hi = 0, в «возмущенной»
системе удовлетворяют каноническим уравнениям
^ — L, 6, . . . , 11,1.
dt dpi dt да.
Для получения решения системы A) нужно из равенств A5) найти
функции
4i = q,(ai,... , ап, Pi,... , /3„, t), pt =pt(ai,... , an, /Зг,... , /3n, t)
и подставить в них величины а», /3,, являющиеся решениями диффе-
дифференциальных уравнений A6).
392 Глава XI
Следует отметить, что при получении уравнений A3) и A6) нигде
не предполагалась малость «возмущения» Hi. Однако изложенное выше
решение задачи вариации произвольных постоянных наиболее полезно,
когда величина Щ мала по сравнению с Щ, например, если функция Hi
имеет порядок малости е и требуется найти решение системы A) при
малых значениях е.
188. Классическая теория возмущений. Пусть функция Га-
Гамильтона Н в системе A) может быть представлена в виде ряда по
степеням малого параметра е:
ТТ ТТ _|_ ТТ _|_ (АЧ\
Будем считать, что при е = 0 система A) интегрируема (т. е. мы мо-
можем получить ее общий интеграл), а канонически сопряженные пере-
переменные qi, pi выбраны так, что функция Гамильтона Но, соответству-
соответствующая невозмущенной задаче, зависит только от импульсов, т. е.
Но = H0(pi,... , рп).
Так будет, например, в случае, когда невозмушенная система A) ин-
интегрируется методом Якоби при помощи разделения переменных, а ее
движения обладают свойством периодичности. Тогда pi это перемен-
переменная действие (см. п. 183), а возмущение Н — Но, записанное в перемен-
переменных действие-угол, будет 2тг-периодическим по угловым переменным
41,-¦¦ , Яп-
Невозмущенная система A)
dqi дН0 i \ dpi . .
-Ж = ^р-=^--->Р^ -dt=° A8)
сразу интегрируется:
Pi = Pio = const, qt = u>i(pi0,... , Pno)t + qio- A9)
Для приближенного исследования движения при малых, но отлич-
отличных от нуля значениях ? в механике разработан специальный аппа-
аппарат теории возмущений, основанный на применении канонических пре-
преобразований. Для простоты ограничимся здесь случаем консерватив-
консервативной или обобщенно консервативной системы с одной степенью свобо-
свободы (п = 1) х. Функция Гамильтона A7) имеет вид
Н = Щ(р) + eHi(q, р) + ... , B0)
1 Следует, однако, иметь в виду, что при п^2в теории возмущений возникают
принципиальные трудности, которых нет в случае одной степени свободы. См.: Ар-
Арнольд В. И. Малые знаменатели и проблемы устойчивости движения в классической
и небесной механике // УМН, 1963, Т. 18, вып. 6, С. 91-192.
§ 7. Канонические преобразования в теории возмущений 393
где Hi можно представить в виде ряда Фурье
оо
Hi = Hi(p) + ^(ал(р) cosfcg + bk(p) sinfcg). B1)
k=i
Здесь Hi(p) — среднее значение функции Н\:
2тг
Hi{p) = ± J Hi(q, p) dq.
о
Будем искать каноническое преобразование q, p —>¦ q*, p*, приводящее
функцию Гамильтона B0) к виду
U = H*(p*)+e2H*(q*,p*) + .... B2)
Искомое преобразование близко к тождественному и задается форму-
формулами (см. п. 174)
* = W' р = ^ B3)
где
Siili Р*) = ЧР* + е$1 (q, р*). B4)
Неизвестную пока функцию S[ подберем так, чтобы в новых пере-
переменных функция Гамильтона имела вид B2).
Подставив B4) в B3), получим соотношения
Отсюда с точностью до членов порядка е включительно находим замену
переменных q, p —>¦ q*, p* в явной форме:
q = q* — ?—1 „ ' , р = р* + ?—1 „ ' . B5)
op oq
Так как валентность преобразования равна единице, а функция Si не
зависит явно от t, то, согласно формуле F3) п. 174, новая функция
394 Глава XI
Гамильтона % получается из старой функции Н, если в последней ве-
величины q, p заменить их выражениями через новые переменные. Под-
Подставив q, p из B5) в функцию B0), получим
U = Н0(р*) + elfi(p') +
и(р*)—1 я »' Ь Y, (ak(p*) cos kq* + bh(p*)sinkq*)
O(l k=i
B6)
Здесь
и» = ^-
Чтобы "Н имела вид B2), нужно в функции B6) уничтожить зависимые
от q* члены порядка е. Для этого надо положить
q(i)( * „,ч_ 1 у^ Ьк{р*) cos kg* -ak{p*) sinfcg*
61 (9'р)-^J- fc ¦ B8)
При таком выборе функции S{ выражение, заключенное в квадрат-
квадратные скобки в формуле B6), тождественно равно нулю и новая функция
Гамильтона будет иметь вид B2), причем
Щ(р*) = Н0(р*)+еН1(р*). B9)
Если теперь в функции B2) отбросить члены выше первого порядка
малости по е, то соответствующая система уравнений
dq* = дЩ(р*) dp^ =
dt dp* ' dt
сразу же интегрируется. Подставив ее решение в формулы преобра-
преобразования B5), получим приближенное решение возмущенной системы
исходных переменных q, p.
Мы рассмотрели теорию возмущений в первом приближении по е.
Аналогично можно рассмотреть и более высокие приближения.
189. О линейных гамильтоновых системах дифференци-
дифференциальных уравнений. Пусть в системе A) функция Гамильтона не за-
зависит от времени и система допускает решение, для которого величи-
величины qi, pi(i = 1, 2,... , п) постоянны. Это решение отвечает положению
равновесия механической системы, имеющей уравнения движения A).
§ 7. Канонические преобразования в теории возмущений 395
Так как перенос начала координат является каноническим преобразо-
преобразованием (см. пример 5 п. 170), то, не ограничивая общности, можно
считать, что это положение равновесия отвечает началу координат в
фазовом пространстве q±,... , qn, Pi, • ¦ • , рп-
В следующем пункте мы покажем, как, используя канонические
преобразования, можно получить приближенное описание движения
рассматриваемой системы вблизи ее положения равновесия. Для это-
этого предварительно рассмотрим некоторые вопросы, связанные с линей-
линейными дифференциальными уравнениями Гамильтона с постоянными
коэффициентами.
Линейную гамильтонову систему дифференциальных уравнений
можно записать в виде
^-=Шх, х'={х1,...,хп,хп+1,...,х2п), C0)
где Хк, хп+и, {к = 1, 2,... , п) — канонически сопряженные пере-
переменные (xk — координаты, хп+и — импульсы). Как и в п. 168, здесь
принято обозначение
J =
О Е„
-Е„ О
(J' = J = -J, J2 = -Е2„, det J = 1).
В системе C0) Н — вещественная симметрическая матрица поряд-
порядка 2и. Будем предполагать ее постоянной.
Рассмотрим характеристическое уравнение
р(А) = det(JH - АЕ2„) = 0. C1)
Теорема. Характеристический многочлен р(\) — четная функция А.
Доказательство.
Доказательство вытекает из цепочки равенств:
р(Х) = det(JH - AE2n) = det(JH - AE2n)' = det(H'J' - АЕ2и) =
= det(-HJ - AE2n) = det(J2HJ + AJE2nJ) = det J(JH + AE2n)J =
= det J • det(JH + АЕ2и) det J = det(JH + AE2n) = p(-X).
Таким образом, уравнение C1) содержит только четные степени А.
Поэтому если у него есть корень А = а, то обязательно будет и ко-
корень А = —а. Будем рассматривать только тот случай, когда урав-
уравнение C1) имеет только простые чисто мнимые корни. Обозначим
396 Глава XI
их Xk = г'07,, Хп+и = —i^k (i — мнимая единица, к = 1, 2,... , и). Назо-
Назовем нормальной формой системы уравнений C0) такую систему кано-
канонических дифференциальных уравнений, которой соответствует функ-
функция Гамильтона1
\^ + у1+к). C2)
k=i
Найдем вещественное линейное унивалентное каноническое преобра-
преобразование Xj —>¦ yj (j = 1, 2,... , 2и), приводящее систему C0) к ее
нормальной форме:
A 'It
— =JH*y, у' =(yi,... , Уп, Уп+1,--- , У2п), C3)
где, в соответствии с C2), Н* — вещественная диагональная матри-
матрица, элементы которой определены равенствами h*kk = h*n+k n+k = 07,
(к = 1, 2,... , п) Пусть
х = Ау C4)
— искомое преобразование. Из C0), C3) и C4) следует, что постоянная
матрица А должна удовлетворять матричному уравнению
AJH* = JHA. C5)
Ввиду каноничности преобразования C4) матрица А должна быть сим-
плектической, т. е. она должна удовлетворять также и такому матрич-
матричному уравнению:
A'JA = J. C6)
Чтобы найти нормализующее преобразование C4), надо из бесчислен-
бесчисленного множества решений уравнения C5) выбрать хотя бы одно вещест-
вещественное, удовлетворяющее уравнению C6).
Решение уравнения C5) будем искать в виде А = ВС, где
С =
гЕ„ Е„
-*Е„ Е„
C7)
Тогда из C5) получаем уравнение для матрицы В:
BD = JHB, C8)
1Функция Гамильтона C2) отвечает механической системе, образованной п
не связанными один с другим гармоническими осцилляторами; их частоты рав-
равны |<rfc| (к = 1, 2,... , п).
§ 7. Канонические преобразования в теории возмущений 397
где D — диагональная форма матрицы JH. Для ее диагональ-
диагональных элементов имеют место равенства dkk = —dn+k, n+k = i&k
(fc = 1, 2,... , n). Таким образом, матрица В приводит матрицу JH
к диагональной форме. Она строится следующим образом1. Ее столб-
столбцами служат собственные векторы матрицы JH. Именно, пусть k-й
столбец матрицы В есть собственный нектор ей, соответствующий
собственному числу Ад, = гот-, а (и + к)-й столбец есть собствен-
собственный вектор еп+и, соответствующий собственному числу \п+и = —i&k
(fc = 1, 2,... , и).
Собственные векторы определяются с точностью до множителя.
Примем этот множитель вещественным и одинаковым для векторов е\~
и еп+и- Кроме того, соответствующие компоненты этих векторов вы-
выберем комплексно сопряженными. Такой выбор собственных векторов
обеспечивает вещественность матрицы А. Произвольные множители
собственных векторов определяются из условия их нормировки, кото-
которое получим из условия C6) каноничности преобразования C4).
Подставив А = ВС в уравнение C6), получим
C'B'JBC = J. C9)
Обозначим матрицу B'JB через F, ее элемент fmi равен скалярному
произведению векторов ет и Je/:
fmi = (em • Je;).
Так как для любых двух векторов а и 6 справедливо равенство
(а • J6) = — (Ja ¦ b), то матрица F кососимметрическая. Покажем еще,
что fmi = 0, если \т—1\ ф п. Для этого рассмотрим очевидное равенство
Преобразуя его левую и правую части, имеем последовательно
(ет ¦ JJHe;) = -(JHem • Je;),
(em • JA;e;) = -(Amem • Je;).
Последнее равенство можно переписать в виде
(Am + Xi)fmi = 0. D0)
Так как, согласно упорядочению собственных чисел, введенному при
построении матрицы В, Хт + А; = 0 только в случае \т — 1\ = и, то из
1См., например: Гантмахер Ф. Р. Теория матриц, М,: Наука, 1967.
398 Глава XI
равенства D0) следует, что fmi = 0, если \т — 1\ ф п. Таким образом,
матрица B'JB имеет такую структуру:
R'TR II ° G
BJB= -G 0
D1)
где G — диагональная матрица порядка п с элементами
gkk = (ek • Je»+A;)- Ни один из элементов gkk не равняется нулю, так
как в противном случае определитель матрицы D1) равнялся бы нулю,
а
det B'JB = detB' det J detB = (detBJ ф 0,
так как матрица В составлена из собственных векторов, соответству-
соответствующих различным собственным числам матрицы JH.
Пусть rkV.Sk — действительная и мнимая части собственного
вектора, соответствующего собственному числу Ад,. Тогда, учитывая
комплексную сопряженность соответствующих компонент векторов ek
и е„_|_/г, получим для элементов матрицы G выражения
ёкк = -2i(r% ¦ Jsk) (k = l, 2,... , n). D2)
Из равенств C7), C9) и D1) следует такое условие, обеспечивающее
симплектичность матрицы А:
А(гк-38к) = 1. D3)
Это равенство является, с одной стороны, условием нормировки собст-
собственного вектора е^, а с другой — условием выбора знака 07, в функции
Гамильтона C2), который до сих пор был не определен. Действитель-
Действительно, приравняв в обеих частях уравнения JHe;, = iukCu (e* = i\ + isk)
действительную и мнимую части, получим систему уравнений для Гк
и sk:
Шгк =
При одновременном изменении знаков 07, и компонент вектора г^ эта
система уравнений не изменяется. Знак же скалярного произведения
[vk ¦ Jsk) изменяется на противоположный. Поэтому равенству D3)
можно всегда удовлетворить выбором знака 07, в функции Гамильто-
Гамильтона C2) и соответствующей нормировкой собственного вектора ek-
Произведя некоторые вычисления, получим, что fc-м столбцом ис-
искомой матрицы А будет вектор —2s;,, а (и + fc)-M — вектор 2rv
190. Преобразование Биркгофа. Приближенное интегриро-
интегрирование гамильтоновой системы уравнений вблизи положения
равновесия. Пусть начало координат фазового пространства отвечает
§ 7. Канонические преобразования в теории возмущений 399
положению равновесия консервативной или обобщенно консервативной
системы с п степенями свободы. Предположим, что функция Гамильто-
Гамильтона является аналитической в некоторой окрестности начала координат
и ее разложение в ряд начинается с квадратичных членов:
Я = Я2 + Я3 + Я4 + • • • , D4)
где Нт — однородный многочлен (форма) степени т относительно ко-
координат и импульсов. Аддитивная постоянная (равная значению функ-
функции Гамильтона в положении равновесия) не влияет на уравнения дви-
движения и в разложении D4) отброшена.
Пусть характеристическое уравнение, соответствующее линеа-
линеаризованной системе уравнений движения, задаваемой функцией Га-
Гамильтона В.2-, имеет только простые чисто мнимые корни ±гсгк,
(к = 1, 2,... , и). Тогда, как показано в предыдущем пункте, подхо-
подходящим выбором канонически сопряженных переменных функцию Н^
можно представить в виде правой части равенства C2). Если еще сде-
сделать каноническую замену переменных1
Чк =Ук~ гУн+k, Рк=Ук + гуп+к (к = 1, 2,... , га), D5)
то квадратичная часть ряда D4) будет иметь вид
D6)
к=1
Движение линеаризованной системы представляет собой суперпози-
суперпозицию колебаний п гармонических осцилляторов с частотами \<тк\,
(к = 1, 2,... , п). Если в разложении D4) формы Нт при га ^ 3 не
равны тождественно нулю, то уравнения движения нелинейны. Чтобы
исследовать движение в этом случае, упростим функцию Гамильто-
Гамильтона D4) при помощи канонической замены переменных, носящей назва-
название преобразования Биркгофа.
Сделаем каноническую замену переменных qk, p/. —>¦ q'k, p'k, зада-
задаваемую формулами
i + f§ ' + (* 12)
где форму третьей степени ?з(<7а;, р'к) попытаемся подобрать так, чтобы
в новых переменных функция Гамильтона не содержала членов третьей
степени относительно q'k, р'к, (к = 1, 2,... , и).
1 Сравните с примером 7 п. 170.
400 Глава XI
Функция H%(qk, Pk) в D4) может быть записана в виде
Н3= Y, hVl,...,ltnq?...&"tf1...lC, D8)
где коэффициенты hVlt..., Рп постоянны. Величины v\,... , Цп — целые
неотрицательные числа. Функцию Бз ищем в виде, аналогичном D8):
So —
3 —
где постоянные коэффициенты s^lv..iMn подлежат выбору из условия
обращения в нуль членов третьей степени в новой функции Гамильтона.
Из D7) следует, что старые переменные qp,, Рк являются аналити-
аналитическими функциями в окрестности начала координат q'h = 0, р'к = 0 и
представляются рядами
где обозначенные многоточием члены имеют степени выше второй от-
относительно q'k, р'к, (к = 1, 2,... , и). Подставив эти выражения в функ-
функцию D4), получим новую функцию Гамильтона в виде
*=i
где многоточием обозначены члены выше третьей степени относитель-
относительно q'k, р'к.
Таким образом, квадратичная часть функции Гамильтона сохра-
сохранила свою форму, а члены третьей степени Н$ приняли вид
Положим Яд = 0. Принимая во внимание формулы D8), D9) и при-
приравнивая в этом тождестве нулю коэффициент при q[Vl ... q'nVn x
xpiW ...p'n^n, получим уравнения для нахождения Sj/lv..)Mn:
[<ti(i/i -//i) + ... + (Tn(i/n -//„)]sVl,...,pn = ihVu...,,,„. E1)
Справедливо соотношение
1^1 - Ml | + • • • + \vn - Mn | ^ V\ + Ml + ¦ • ¦ + Vn + Цп = 3.
§ 7. Канонические преобразования в теории возмущений 401
Отсюда и из E1) следует, что если величины а\,... , ап таковы, что
для целых чисел к\,... , кп, удовлетворяющих условию 0 < \к\\ + ... +
+ \кп\ ^ 3, выполняется неравенство1
... + knan ф 0, E2)
то выбрав величины s1/1,...,Mn согласно формулам
получим новую функцию Гамильтона Н' такой, что в ней будут отсут-
отсутствовать члены третьей степени по q'k, р'к.
Можно было бы попытаться аналогичным образом при помощи еще
одного канонического преобразования q'k, р'к —> q'^, p'? уничтожить чле-
члены четвертой степени if" в функции Гамильтона Н". Это, однако, не
удастся сделать, и в новой функции Гамильтона останутся некоторые
члены четвертой степени, имеющие вполне определенную структуру.
Если в системе нет резонанса до четвертого порядка включительно,
т. е. неравенство E2) удовлетворяется при 0 < \к\\ + ... + \кп\ ^ 4, то
в функции Гамильтона Н" можно уничтожить все члены четвертой
степени, кроме тех, которые содержат q? и р'^ в одинаковых степенях.
Действительно, уравнение E1) неразрешимо, если V]. = рь\. при всех
к = 1, 2,... , п. Тогда в Н'1 останется совокупность одночленов вида
И, вообще, методом математической индукции нетрудно показать, что
если в системе нет резонансов до порядка / включительно, т. е.
... + fcnO-n фО, 0 < |fci| + ...+ \кп
то существует каноническое преобразование q\. = q^ + ... , р\. = ^
задаваемое сходящимися в окрестности начала координат степенными
рядами, такое, что функция Гамильтона D4), выраженная через q%, p*k,
имеет вид
H* = H + H(ql,pl), E3)
где Н — многочлен степени не большей 1/2 от п произведений
5iPi,... , q*nP*n, а В. — сходящийся ряд по степеням q%, p*k, начинающий-
начинающийся с членов, степень которых не меньше / + 1. В этом случае говорят,
1В таких случаях говорят, что в системе нет резонансов до третьего порядка
включительно.
402 Глава XI
что функция Гамильтона приведена к нормальной форме Биркгофа с
точностью до членов степени / включительно.
Представление функции Гамильтона в виде E3) можно эффективно
использовать для приближенного интегрирования канонических диф-
дифференциальных уравнений движения. Для этого пренебрежем в E3)
членами Н, которые имеют более высокую степень относительно q%, p?,
нежели функция Н. Тогда Н* = Н. Замечательно, что система кано-
канонических уравнений с функцией Гамильтона Н* = H(qlpl,... ,д^Рп)
сразу интегрируется. Действительно, положим тк = q\p*k. Тогда урав-
уравнения с функцией Гамильтона Н запишутся в виде
Ч _ он * dpi _ дн ( _ , . .
Отсюда следует, что drk/dt = 0, т. е. тк = ск = const (к = 1, 2,... , п).
Подставив эти значения тк в уравнения E4), получим
g=iW, f =-Л* E5)
где Ак есть значение производной дН/дтк при тк = ск. Из E5) следует,
что
E6)
Приближенное решение исходных уравнений получится из равенств E6)
при помощи формул указанного выше канонического преобразования
Биркгофа, выражающих старые переменные через новые. Несложно
проверить, что в рассматриваемом случае чисто мнимых корней харак-
характеристического уравнения линеаризованной системы уравнений дви-
движения величины Ак (к = 1, 2,... , п) также будут чисто мнимы-
мнимыми, Ак = Шк (к = 1, 2,... , п), и, следовательно, старые переменные
будут рядами синусов и косинусов аргументов, кратных ilkt.
Если в системе вообще нет резонансов, то преобразование Бир-
Биркгофа можно применить для нормализации функции Гамильтона до
сколь угодно высокой степени (/ —> оо). Нормализованная во всех
степенях функция Гамильтона зависит только от переменных (qlpl)
(к = 1, 2,... , п). Тогда преобразованная система уравнений движения
может быть проинтегрирована, причем для этого не надо пренебрегать
в ее правых частях никакими членами. Казалось бы, что это должно
означать локальную (в окрестности положения равновесия) интегри-
интегрируемость уравнений движения. Однако это не так. Дело в том, что пре-
§ 7. Канонические преобразования в теории возмущений 403
образование Биркгофа, нормализующее функцию Гамильтона во всех
степенях, будет, как правило, расходящимся1.
В последние десятилетия разработаны новые способы применения
канонических преобразований в теории возмущений, например метод
Депри-Хори. С алгоритмической точки зрения он выгодно отличает-
отличается от изложенных классических методов. Например, его применение
не требует одной из самых громоздких процедур — обращения рядов,
а формулы метода задаются рекуррентно, и необходимые преобразо-
преобразования могут быть достаточно просто реализованы на вычислительной
машине1.
Пример 1 (Колебания математического маятника). Функция Га-
Гамильтона может быть {см. пример в п. 149) записана в виде
Н = -—^pl - mgl cos (p.
2ml
Для удобства введем безразмерные переменные <р', p'v, t' no формулам
E7)
Замена <р, pv —> <р', p'v — каноническое преобразование с валентнос-
валентностью с = — {см. пример Sen. 170). Учитывая еще, что введение
ml\/gl
вместо времени t новой независимой переменной t' приводит к делению
функции Гамильтона на \fg~fl, получим, что уравнениям движения в
безразмерных переменных E7) отвечает функция Гамильтона
н = ±v2-COfV- E8)
Рассмотрим движение маятника в окрестности его положения равно-
равновесия <р = 0. В этом случае <р' и р' — малые величины. Разлагая функ-
функцию E8) в ряд по степеням <р', p'v и отбрасывая несущественный для
уравнений движения постоянный член, получаем
H=±{Pv>2 + ip'2)-±[ip>4 + ..., E9)
1Изложение современного состояния задачи нормализации систем дифференци-
дифференциальных уравнений и подробную библиографию см. в исследовании: Брюно А. Д. Ана-
Аналитическая форма дифференциальных уравнении // Труды Московского математи-
математического общества. 1971, Т. 25, С. 119-262; 1972, Т. 26, С. 199-239.
1См., например: Джакалья Г. Е. О. Методы теории возмущений для нелинейных
систем, М.: Наука, 1979.
404 Глава XI
где многоточием обозначены члены выше четвертой степени относи-
относительно <р', pv'. Если в разложении E9) пренебречь всеми неквадратич-
неквадратичными членами, то уравнения движения станут линейными. В этом
линейном приближении движение маятника представляет собой гармо-
гармонические колебания. Чтобы выявить влияние нелинейностей в уравне-
уравнениях движения, учтем в разложении E9) член — A/24)у/ и для прибли-
приближенного исследования нелинейных колебаний используем преобразование
Биркгофа.
Сделав замену переменных (каноническую, с валентностью с = 2г)
q=tp' - ipv', p = ip' + ip'v, F0)
получим
где
Я2 = iqp, H4 = -j^(q4 + Aq3p + 6q2p2 + 4qp3 + p4).
Несложные вычисления показывают, что преобразование Биркгофа
q, р —> q*, р*, задаваемое производящей функцией qp* + Si{q, p*), где
Si = mq4 + kq3p* ~ kqp*3 ~ ткр*4>
приводит функцию Гамильтона к виду
H*=i{q*p*)-^(q*p*)\ F1)
причем переменные q, p выражаются через q*, p* по формулам
q = q*~ ^(V3 " 69>*2 -р*3), р = р* + jt-(q*3 + 6q*2p* - 2р*3).
F2)
В формулах F1), F2) отброшены члены, степень которых выше сте-
степени оставшихся членов.
Канонические уравнения с функцией Гамильтона F1) интегриру-
интегрируются. Если 5о; Ро — начальные значения величин q*, р*, то
q*=q*oeint', p* = p*e-im>, F3)
где введено обозначение
п = 1-^(<йр5)- F4)
§ 7. Канонические преобразования в теории возмущений 405
Приближенное решение задачи о нелинейных колебаниях маятника по-
получается теперь из формул E7), F0), F2), выражающих исходные вели-
величины <р, pv через новые переменные, в которых записано решение F3).
Пусть момент t = 0 соответствует максимальному углу отклоне-
отклонения /3 маятника от вертикали. Тогда из формул E7), F0), F2) следует,
что с точностью до квадратов величины C включительно
С той же точностью для периода т нелинейных колебаний маятника
получаем выражение
которое совпадает с выражением, полученным в п. 96 (формула
B8)) при помощи разложения в ряд точного значения периода коле-
колебаний маятника, записанного через полный эллиптический интеграл
первого рода.
Глава XII
Теория импульсивных движений
§ 1. Основные понятия и аксиомы
191. Ударные силы и импульсы. Рассмотрим механическую
систему, состоящую из N материальных точек Р„ {у = 1,2, ...,7V).
До сих пор мы изучали такие движения, в которых скорости точек Р„
изменялись непрерывно как по величине, так и по направлению. Но
на практике иногда приходится встречаться с явлениями, когда точки
материальной системы, начиная с некоторого момента t = to, в течение
очень малого промежутка времени т скачком изменяют скорости, а
система за тот же промежуток не меняет заметно своего положения.
В таких случаях говорят, что система испытывает удар. Примером
может служить движение брошенного в стену и отскочившего от нее
упругого мяча.
Явление удара вызывается силами большой величины, действую-
действующими на систему в течение столь малого промежутка времени т, что
точки системы не успевают переместиться сколь-нибудь заметным об-
образом. Такие силы называют ударными.
Движение системы под действием ударных сил называют импуль-
импульсивным движением. При аналитическом представлении импульсивного
движения промежуток времени т, в течение которого оно происходит,
считается бесконечно малым. При этом модуль импульса /„ ударной
силы Fv, приложенной к точке Р„ (он называется ударным импульсом),
Iv= I Fvdt (i/ = l, 2, ... ,N), A)
to
считается конечной величиной. Так как точки системы во все время
удара т имеют конечные скорости, то при т —> 0 их перемещениями
можно пренебречь. Ускорение же wv точки Р„ под действием ударной
силы бесконечно велико, и поэтому оно не может служить кинемати-
кинематической характеристикой импульсивного движения. С кинематической
точки зрения в импульсивных движениях, помимо момента to и поло-
положения точек Р„, нужно рассматривать лишь векторы скоростей точек
§ 1. Основные понятия и аксиомы 407
в момент, непосредственно предшествующий, и в момент, непосредст-
непосредственно следующий за t$. Эти скорости называют скоростью до удара и
скоростью после удара. Примем для них обозначения v~ и ю+.
192. Аксиомы. Пусть Fv — равнодействующая всех сил, дейст-
действующих на точку Р„, то„ — масса этой точки, предполагаемая посто-
постоянной, a wv — абсолютное ускорение точки. Из уравнения mvwv = Fv
посредством интегрирования по времени от to до to + t получим равен-
равенства
mv{v+-v-) = Iv (i/ = l,2,...,JV). B)
В правых частях этих равенств содержатся только импульсы удар-
ударных сил, так как обычные силы, т. е. силы, имеющие конечную величи-
величину, дают при т —> 0 пренебрежимо малые импульсы. Следовательно, на
скачкообразное изменение скоростей точек системы при ударах обыч-
обычные силы не влияют. Например, при ударе мяча о стену влиянием силы
тяжести на импульсивное движение мяча можно пренебречь.
Соотношения B) утверждают, что приращение количества движе-
движения точки за время удара равно ударному импульсу.
При действии ударных сил на несвободную систему возникают,
вообще говоря, ударные реакции связей. Поэтому изменение скорости
каждой точки системы определяется не только импульсами приложен-
приложенных к ней (активных) ударных сил, но также и ударными импульсами
реакций связей.
Соотношение B) является основным в теории импульсивных
движений. Оно заменяет основную аксиому динамики (второй за-
закон Ньютона). Роль ускорения в B) играет приращение скорости
Дю„ = ю+ — v~, а роль силы — ударный импульс /„.
В теории импульсивных движений принимается еще ряд аксиом,
аналогичных обычным аксиомам динамики: ударные импульсы, сооб-
сообщаемые друг другу двумя материальными точками, равны по величине
и направлены вдоль прямой, соединяющей эти точки, в противополож-
противоположные стороны; два ударных импульса, приложенных к точке, складыва-
складываются по правилу параллелограмма; полный ударный импульс для каж-
каждой точки системы складывается из ударных импульсов активных сил
и ударных импульсов реакций связей.
193. Главный вектор и главный момент ударных импуль-
импульсов. При исследовании импульсивных движений системы материаль-
материальных точек Р„ {у = 1,2, ...,7V) часто целесообразно подразделять удар-
ударные импульсы на внешние и внутренние. Внешние и внутренние удар-
ударные импульсы — это соответственно импульсы внешних и внутренних
ударных сил системы. При таком подразделении импульсов основное
408 Глава XII
уравнение B) импульсивного движения системы можно записать в сле-
следующем виде:
где Iv — сумма внешних ударных импульсов, a ii, — сумма внут-
внутренних ударных импульсов, действующих на точку Р„ системы.
Сумма всех ударных импульсов системы
JV
S = Tlu D)
называется главным вектором ударных импульсов.
Пусть г„ — радиус-вектор точки Р„ относительно точки О. Сумма
моментов ударных импульсов относительно точки О
N
v=l
называется главным моментом ударных импульсов относительно этой
точки.
Слагаемые, содержащие внутренние импульсы, входят в правые
части выражений D), E) попарно и взаимно уничтожаются. Поэтому
JV JV
S = 5(е) = Ё 7ie)' Lo = 4е) = Ё r» x 7ie)' F)
т. е. главный вектор и главный момент всех ударных импульсов сис-
системы равен соответственно главному вектору S^ и главному момен-
моменту Lq внешних ударных импульсов.
194. Задачи теории импульсивного движения. Цель исследо-
исследования импульсивного движения состоит в определении кинематическо-
кинематического состояния системы после удара, если известно ее состояние до удара.
При этом иногда целесообразно различать две основные задачи: 1) по
заданным ударным импульсам определить изменение скоростей точек
системы; 2) по заданному изменению скоростей точек системы опреде-
определить ударные импульсы. Иногда требуется также определить ударные
импульсы реакций связей.
§ 2. Теоремы об изменении основных динамических величин при импульсивном движении
§ 2. Теоремы об изменении основных
динамических величин при импульсивном
движении
195. Теорема об изменении количества движения. Сложив
уравнения C) п. 193 и учтя постоянство масс то„, получим равенство
N \ N N
0
„=1 „=1
или
дд = 5(е), (i)
т. е. изменение количества движения системы при ударе равно главному
вектору внешних ударных импульсов.
N
Так как Q = Mvc, где М — масса системы, М = Yl mv = const,
a vc — скорость центра инерции, то равенство A) можно переписать
в таком виде:
MAvc = 5(e), B)
т. е. импульсивное движение центра инерции системы происходит так
же, как импульсивное движение материальной точки, масса которой
равна массе системы и к которой приложены все внешние ударные им-
импульсы, действующие на систему.
Пример 1. Снаряд, летевший со скоростью v, разорвался в воздухе на
два осколка равных масс. Скорость первого осколка направлена под уг-
углом а к направлению первоначального движения и имеет величину 2v.
Найти скорость второго осколка.
Так как внешних ударных импуль-
импульсов нет, то вектор первоначального ко- mv
личества движения снаряда равен сумме
векторов количеств движения осколков.
Пусть т — масса снаряда, а C — угол
между вектором Vi скорости второго ос-
осколка и направлением движения снаряда.
Из рис. 144 легко получить, что v^ =
= 4v sin — в = — - — Рис' 144
Заметим, что при решении не потребовалось предположения об
отсутствии аэродинамических сил и силы тяжести, потому что эти
силы не являются ударными.
410
Глава XII
196. Теорема об изменении кинетического момента. Пусть
А — произвольная точка пространства, подвижная или неподвижная,
а /)„ — радиус-вектор точки Р„ системы относительно А. Умножим
обе части равенства C) п. 193 слева векторно на р„ и результаты про-
просуммируем. Тогда, учитывая постоянство то„ и тот факт, что р„ не
меняется во время удара, получаем соотношение
v=l
v=l
Сумма в левой части представляет собой абсолютный кинетический
момент Ка системы относительно центра А. Поэтому, учитывая ра-
равенства E) и F) из п. 193, последнее соотношение можно записать в
виде
C)
т. е. изменение кинетического момента системы относительно любого
центра равно главному моменту внешних ударных импульсов относи-
относительно этого центра.
Пример 1. Два шкива радиусов г\ и г2 вращаются вокруг параллельных
осей с угловыми скоростями u>i и и>2 (рис. 145), причем и>\Г\ > uJi'2-
На шкивы намотана ненатянутая лента. В некоторый момент лен-
лента натягивается, вследствие чего происходит удар. Требуется опре-
определить послеударные угловые скорости Hi и f^ шкивов и величину I
ударного импульса силы натяжения ленты, считая, что после удара
лента остается натянутой. Моменты инерции шкивов относительно
их осей вращения равны J\ и Ji-
Применяя формулу C) к враще-
-I __J-»-— нию первого шкива и учитывая, что
ударный импульс реакции оси вра-
вращения не создает момента относи-
относительно этой оси, имеем
Рис. 145
Для второго шкива получим
J2(fi2 - шг) = 1г2.
Но так как лента остается натянутой, то
D)
E)
F)
§ 2. Теоремы об изменении основных динамических величин 411
Из D)-F) находим
-102Г2)
- hr\ Tl ' Jir\ + J2r\
Если шкивы первоначально вращаются в противоположные стороны,
то в результате натяжения ленты возможно прекращение их враще-
вращения, причем одновременное. Это произойдет, если выполнено равенст-
равенство J\T2lO\ + J2T\W2 = 0
Пример 2. Находящемуся в покое тонкому однородному стержню мас-
массы т и длины I при помощи удара по одному из его концов сообщен им-
импульс I в перпендикулярном к стержню направлении (рис. 146). Найти
послеударное кинематическое состояние стержня.
Пусть vq — скорость центра масс стержня, а
ш — его угловая скорость после удара. Из формул B) О \
и C) получаем два уравнения U
Т 1 72 т1 РИГ 14fi
mvo = 1, Yo ш = ^о'
отсюда находим
„. _ I , . _ 6/ /<7\
Пример 3. Найти послеударное кинематическое состояние стерж-
стержня предыдущего примера, если один из его концов шарнирно закреплен
(рис. 147).
В этом случае после удара стержень
вращается вокруг точки А. Из формулы C)
получаем уравнение для нахождения угловой
скорости вращения и):
О
\т12ш = II,
О
отсюда Рис- 14?
ш = Ц. (8)
ml
Можно найти и неизвестный ударный импульс 1а шарнира. Из B) име-
имеем
mv0 = I + 1А,
но vq = uj^r = j^-. Поэтому I a = mvo — I = ±1.
412 Глава XII
197. Теорема об изменении кинетической энергии. Пусть Т
и Т+ — величины кинетической энергии системы до и после удара:
JV JV
,vv-\ T+ = \Y,mvv+\ (9)
l v=\
Имеет место следующая
Теорема. Иэменеие кинетической энергии при импульсивном движе-
движении равно сумме скалярных произведений каждого ударного импульса на
полусумму скоростей точки его приложения непосредственно перед уда-
ударом и после него:
т+-т- = ^^).^Ц^ + ?^).^±^. (Ю)
Доказательство.
Умножим каждое из уравнений C) п. 193 скалярно на ю+. Получим
равенства
mv{v+ - »") • v+ = Jje> • v+ + J« • v+ {v = 1, 2, ... , N).
Если в левых частях этих равенств сомножитель ю+ представить в виде
К = | \(К + v~) + (v+ - v~)\,
а затем произвести суммирование равенств по и, то после простых пре-
преобразований и учета обозначений (9) придем к соотношению
т" - Т+ = \flm^ - о2 - Е ^ ¦ < - Е & ¦ <¦
Теперь умножим уравнения C) п. 193 на vv , в левых частях получаю-
получающихся равенств представим сомножитель v~ в виде
и произведем суммирование по и. Тогда получим такое соотношение:
N N N
т+ - т~ = \ Е т^< - о2 + Е ^ -^
После вычитания равенства A1) из равенства A2) и деления на 2 при-
приходим к доказываемому соотношению A0).
§ 3. Импульсивное движение твердого тела 413
Пример 1. Найдем изменение кинетической энергии стержня в приме-
примерах 2 и 3 предыдущего параграфа.
Учитывая, что в твердом теле внутренние силы не соверша-
совершают работы и что перед ударом стержень покоился, из A0) получаем
Т+ = klv, где v — величина послеударной скорости той точки стерж-
ня, к которой приложена ударная сила.
В примере 2 получаем w = w0 + ш- = — -\ -- = — и Т+ = -^-.
от от о т2
В примере же 3 имеем v = wl = ^l = ^- и Т+ = ^т~.
ml m 2m
Замечание 1. Равенства A1) и A2) по существу представляют собой
еще две различные формы теоремы об изменении кинетической энергии
при импульсивном движении.
Дадим их словесное выражение.
Векторы v~ — ю+ и ю+ — v~ называют соответственно потерянной
и приобретенной скоростями, а величину
N N
t* = \y, ™л^ - о2 = \ Е т^< - ^? A3)
— кинетической энергией потерянных (или приобретенных) скоростей.
Приращение Т+—Т~ называют еще приобретенной, а величину Т~ —Т+
— потерянной кинетической энергией при импульсивном движении.
Используя эту терминологию, соотношение A1) можно прочитать сле-
следующим образом: потеря кинетической энергии равна кинетической
энергии потерянных скоростей, уменьшенной на сумму работ внешних
и внутренних ударных сил, если считать, что точки их приложения
имеют в течение всего времени удара постоянные скорости, равные их
послеударным скоростям.
А соотношение A2) означает, что приобретенная кинетическая
энергия равна кинетической энергии приобретенных скоростей, увели-
увеличенной на сумму работ внешних и внутренних ударных сил, если счи-
считать, что точки их приложения имеют в течение всего времени удара
постоянные скорости, равные их доударным скоростям.
§ 3. Импульсивное движение твердого тела
198. Удар по свободному твердому телу. Изучим влияние
заданных ударных импульсов на движение твердого тела. Так как ки-
кинематическое состояние тела вполне определяется вектором скорости
414 Глава XII
какой-либо его точки и вектором угловой скорости, то задача об им-
импульсивном движении свободного твердого тела сводится к нахожде-
нахождению изменений этих двух векторов за время удара.
Чтобы сделать вычисления наиболее простыми, возьмем за нача-
начало координат центр масс G тела, а за оси координат примем глав-
главные центральные оси инерции тела. Введем обозначения: Sx,Sy,Sz,
Lx,Ly,Lz ир, q, i проекции главного вектора S^e\ главного момента
Lq внешних ударных импульсов относительно центра масс и вектора
угловой скорости ш тела на указанные оси; т — масса; А, В, С —
главные центральные моменты инерции тела; величины Ар, Bq, Cr
будут проекциями вектора KG кинетического момента тела относи-
относительно центра масс.
Теоремы об изменении количества движения и кинетического мо-
момента, согласно равенствам B) и C) предыдущего параграфа, дают два
векторных уравнения
mAvG = 5(e), AKG = 1$. A)
Отсюда получаем выражения для проекций приращений вектора ско-
скорости центра масс AvG и вектора угловой скорости Да;:
m '
— Oz /г»\
-vGz =jfi, B)
r>+ - гГ - ^ „+ -„- -hi r+ _ r~ - hi C\\
P P — л 1 Ч Ч — r> 1 r r — r< - УА)
ABC
Если тело совершает плоское движение, например, параллельно
плоскости Оху, то из шести соотношений B), C) остаются только три:
Я Ч т
— m' Gy vGy — yy, , i i — ^-y • \^)
Упражнение 1. Показать, что первоначально покоящееся тело в его
импульсивном движении относительно центра масс начнет вращаться
вокруг радиуса-вектора той точки центрального эллипсоида инерции,
в которой плоскость, касательная к поверхности эллипсоида, перпенди-
перпендикулярна главному моменту ударных импульсов относительно центра
масс.
Найдем изменение кинетической энергии твердого тела под дейст-
действием заданных ударных импульсов. Согласно теореме Кёнига
(см. п. 83, 84), имеем такое выражение для кинетической энергии:
Г = \mv2G + \(Ар2 + Bq2 + Cr2).
§ 3. Импульсивное движение твердого тела
415
Подставив в это выражение сначала значения Vq, ш+ векторов
скорости центра масс и угловой скорости тела после удара, а затем их
значения Vq, ш~ до удара и вычтя почленно полученные равенства,
найдем, на основании уравнений B), C)
Т+ -
E)
q и ш+ можно отсюда исключить опять же при помощи
Величины
уравнений B), C). В результате получим следующее выражение для
изменения кинетической энергии тела через главный вектор S^ и
(е)
G
(е)
главный момент LG заданных ударных импульсов и через величи-
величины Vq, ш~, которые определяют доударное кинематическое состояние
твердого тела:
т+ _ т- = 1
si + si + si
m
¦ ш
F)
Упражнение 2. Неподвижное свободное твердое тело приводят к вра-
вращению относительно центра масс при помощи пары ударных сил. Ве-
Величина импульсивного момента пары равна L. Главные центральные
моменты инерции тела удовлетворяют неравенствам А > В > С.
Показать, что максимально возможное значение приобретаемой те-
телом кинетической энергии равно j^, а вектор момента пары должен
2G
быть при этом коллинеарен наибольшей оси центрального эллипсоида
инерции тела.
Пример 1. Горизонтальным кием уда-
ударяют бильярдный шар в его меридиан-
меридианной плоскости (рис. 148). На какой вы-
высоте h над центром шара следует сооб-
сообщить удар, чтобы после удара шар дви-
двигался без скольжения?
Пусть т — масса шара, R — его ра-
радиус, I — величина ударного импульса. Ес-
Если v — скорость центра, а и> — угловая
скорость шара после удара, то справедли-
справедливы уравнения
Рис. 148
mv = I, -^
о
= Ih.
G)
416 Глава XII
(Реакция плоскости конечна и не дает вклада в ударный импульс).
о
Из G) и условия v = ujR отсутствия скольжения находим h = jrR.
5
Пример 2. Твердое тело, имеющее форму плас-
пластинки, совершает произвольное движение в сво-
ей плоскости. Точку Р пластинки внезапно
останавливают (шарнирно закрепляют). Где
должна находиться точка Р, чтобы пластин-
v ка остановилась?
х Пусть v — скорость центра масс G,
"Р а ш — угловая скорость пластинки в момент,
Рис. 149 непосредственно предшествующий закреплению
точки Р. Для удобства вычислений ось Gx на-
направим вдоль вектора v, координаты точки Р обозначим через х, у
(рис. 149).
Так как Gz — главная центральная ось инерции, то для описания
импульсивного движения применимы уравнения D). В этих уравнениях
Lz = xSy — ySx, где Sx, Sy — компоненты ударного импульса, возника-
возникающего при закреплении точки Р.
Учитывая, что v~^x = v, v^ = Vqx = Vq = 0, r~ = u>,
r+ = 0, из уравнений D) находим Sx = —mv, Sy = 0, x — произволь-
произвольная величина, а у = —j^j- Следовательно, точка Р должна лежать в
полуплоскости у < 0 на прямой, параллельной направлению скорости
центра масс и отстоящей от него на расстоянии j^-
Пусть в точке Q покоящегося тела приложен ударный импульс J.
Из уравнений A), B) тогда получаем v^ = щ, Kq = GQ x I. Отсю-
Отсюда следует, что послеударное кинематическое состояние первоначально
покоящегося тела не вполне произвольно: скорость центра масс и кине-
кинетический момент относительно центра масс должны быть ортогональ-
ортогональными.
Упражнение 3. Из сказанного выше сразу следует, что если свободное
твердое тело движется так, что Kq ¦ vq ф 0, то его нельзя остановить
одним импульсом. Показать, что если Kq ¦ vq = О и vq ф 0, то тело
можно остановить, приложив к нему единственный импульс. Каковы
будут его величина и линия действия?
199. Удар по телу с одной неподвижной точкой. Неподвиж-
Неподвижную точку О примем за начало координат, а оси ж, у, z совместим
с главными осями инерции тела для точки О; через S и L обозначим
главный вектор и главный момент ударных импульсов активных сил.
§ 3. Импульсивное движение твердого тела 417
Задача состоит в нахождении приращения Да; вектора угловой скорос-
скорости тела и ударного импульса реакции, который может возникнуть в
точке О.
Проекции приращения вектора угловой скорости определяются
уравнениями C), в которых теперь А, В, С — главные моменты инер-
инерции тела относительно точки О.
Ударный импульс V реакции в точке О определяется первым из
уравнений A), которое в рассматриваемом случае принимает вид
mAvG = S + Г. (8)
Так как положение центра масс при ударе не меняется, то
Avg = Аш х OG. Поэтому на основании уравнения (8) заключаем, что
Г = тАш xOG- S. (9)
Рассмотрим частный случай, когда на тело действует единствен-
единственный активный ударный импульс I, приложенный в точке Р. Тогда
S = I, a L = ОР х J. Поставим следующий вопрос: возможно ли, и
при каких условиях, чтобы заданный активный импульс J не вызывал
ударной реакции связи. Этот вопрос требует ответа, когда, например,
необходимо посредством удара привести тело в движение вокруг непо-
неподвижной точки, но нет уверенности в достаточной прочности связи.
Пусть xg, yG-, zg — известные координаты центра масс, ах, у, z —
координаты точки Р приложения неизвестного импульса J. При J' = О
из (9) и C) получим три уравнения:
l - xl \ - ^
ix xizj - m.
Эти уравнения линейны и однородны относительно неизвестных про-
проекций импульса J, поэтому величина / этого импульса может быть
произвольной. Кроме того, J определяется еще с точностью до измене-
изменения его направления на противоположное.
Так как по смыслу задачи J ф 0, то определитель системы A0)
418
Глава XII
должен равняться нулю:
D =
УУс
С
ZZG
В
С
ZXQ
в
1
т
ZZG ,
А +
хуа
С
С
zyc
А
1
т
XXG
В
XZG
В
А
УУс
А
1
т
= 0.
A1)
Отсюда следует, что геометрическим местом возможного положе-
положения точек Р в общем случае является поверхность третьего порядка.
Импульс, приложенный в любой точке этой поверхности, не вызывает
ударной реакции связи. Линия действия импульса I определяется из
уравнений A0), если в них подставить координаты х, у, z выбранной
точки указанной поверхности.
В некоторых частных случаях поверхность A1) может вырождать-
вырождаться в более простые поверхности. Пусть, например, ось OG, проходящая
через неподвижную точку О и центр масс тела, будет главной осью
инерции. Если ее принять за ось Oz, то xq = ус = 0, и уравнение A1)
получит вид
т \ В
т
т ' и'
т. е. точка Р должна лежать на одной из двух плоскостей, перпендику-
перпендикулярных главной оси инерции Oz и расположенных по ту же сторону от
точки О, что и центр масс:
Z =
В
Z =
mzG-
A2)
Из уравнений A0) тогда следует, что (при А ф В) импульс J должен
быть параллелен оси Ох в первом случае и оси Оу во втором. Для ди-
динамически симметричного тела (А = В) плоскости A2) сливаются в
одну, а импульс J имеет произвольное направление в этой плоскости.
Пример 1. Твердое тело вращается вокруг неподвижной точки О. В
некоторый момент времени, когда угловая скорость тела равна ш~,
в нем внезапно закрепляется вторая точка О\, так, что после этого
тело может только вращаться вокруг оси и, проходящей через точки О
и О\. Найти угловую скорость тела в этом вращении.
Обозначим через а, C, j косинусы углов, ообразуемых осью и с ося-
осями Ох, Оу, Oz. Кинетический момент тела относительно оси и перед
j 3. Импульсивное движение твердого тела
419
закреплением точки 0\ равен Ар а + Bq /3 + Cr j, а после закрепле-
закрепления имеет (см. п. 77, 82) величину (Аа2 + ВC2 + Cj2) ui+. Но ударные
импульсы реакций в точках О иО\ не создают момента относительно
оси и. Следовательно, кинетический момент тела относительно этой
оси не изменяется во время удара. Поэтому
U! ' =
Ар а
Аа2 + ВC2 + Cj2
Г
200. Удар по телу с неподвижной
осью. Пусть твердое тело вращается вокруг
оси, проходящей через его неподвижные точ-
точки О и Oi (рис. 150). К телу прикладыва-
прикладывается ударная сила с импульсом I. Требуется
найти изменение угловой скорости вращения
тела, а также ударные импульсы реакций в
точках О и Oi.
Пусть Oxyz — система координат с на-
началом в точке О, ось Oz которой направлена
по оси вращения, а ось Ох перпендикуляр-
перпендикулярна направлению ударного импульса, так что Vuc. 150
вектор J задается компонентами 0, Iy, Iz. Центр масс G и точка Р»
приложения импульса имеют соответственно координаты xq, Vg-, %g
и ж*, у*, z*, вектор угловой скорости ш задается компонентами 0, 0, г.
Для компонентов ударных импульсов J' и J" реакций в точках О и О±
примем обозначения I'x, I'y, I'z и /", 1'у', I" соответственно. Матри-
Матрица J тензора инерции тела для точки О имеет вид D) п. 77. Расстояние
между точками О и О\ обозначим через h.
Из теорем об изменении кинетического момента и количества дви-
движения имеем
тАш xOG = 1+ Г + I", ЗАш = OP* x J + OOi x I".
В скалярной форме эти соотношения запишутся в виде следующих шес-
шести уравнений:
-myGAr = 1'х
mxGAr = 1У
I»,
-JxzAr = y*Iz - z*Iy - hly,
-jyzAr = -Xjz + hi1;,
JzAr = x*Iy.
A3)
A4)
A5)
A6)
A7)
A8)
420 Глава XII
Из последнего уравнения определяется изменение угловой скорости Дг.
Если ударный импульс I и ось вращения тела не лежат в одной плос-
плоскости, то величина Дг отлична от нуля. Остальные пять уравнений
A3)—A7) служат для нахождения шести проекций ударных импульсов
реакций в точках О и Oi. Эта задача является неопределенной: нель-
нельзя найти отдельно величины I'z и /", а можно определить только их
сумму.
Полагая, что Дг ф 0, рассмотрим задачу об определении условий,
при выполнении которых ударные импульсы реакций в точках О и О±
не возникают. При I' = I" = 0 из A5) следует, что Iz = 0, т. е. на-
направление ударного импульса параллельно оси Оу. А из A3) получаем,
что ус = 0. Следовательно, центр масс лежит в плоскости, проходя-
проходящей через ось вращения и перпендикулярную направлению импульса.
Если xq = 0, т. е. центр масс лежит на оси вращения, то (см. A4)) по-
поставленная задача не имеет решения: при I ф 0 всегда будут возникать
ударные реакции.
Пусть хс ф 0. Из A4) и A6) имеем Jxz — mxcz* = 0, или
N
^2 mvxv {zv - z*) = 0. A9)
А из A7) следует равенство Jyz = 0, что в сочетании с условием уа = 0
дает соотношение
N
Y,™»yAzv-z*) = 0- B0)
Равенства A9) и B0) означают (см. п. 78), что ось вращения является
главной осью инерции тела для своей точки с координатами 0, 0, z*.
Таким образом, произвольный по величине ударный импульс не
вызывает ударных импульсов реакций в точках О и О\ только тогда,
когда ось вращения является главной осью инерции тела. Если это усло-
условие выполнено, то импульс должен быть перпендикулярен плоскости,
проходящей через ось вращения и центр масс тела, причем он должен
лежать в плоскости, перпендикулярной оси и проходящей через ту ее
точку, для которой она является главной осью инерции.
Наконец из A4) и A8) находим
х* = mx~G' B1)
что окончательно определяет линию действия ударного импульса. Ее
называют осью удара, а точку, в которой она пересекает плоскость,
проходящую через ось вращения и центр масс — центром удара.
§ 3. Импульсивное движение твердого тела
421
Пример 1 (Случай пластинки). Рассмот-
Рассмотрим плоскую фигуру, которая может вра-
вращаться вокруг некоторой оси Oz, лежащей
в ее плоскости (рис. 151). Для любой оси Oz
можно найти центр удара. Это следует
из того, что ось Oz всегда является глав-
главной осью инерции для одной из своих точек.
Чтобы показать справедливость сказанно-
сказанного, перейдем к системе координат O'x'y'z,
смещенной относительно исходной систе-
системы Oxyz на вектор 00', имеющий в сис-
системе Oxyz компоненты О, О, z*. Ось Ох Рис. 151
(и ось О'х') лежит в плоскости пластинки.
Тогда Jyiz = О, так как для каждой частицы Pv тела имеем y'v = О.
Величина же Jx*z будет равна нулю, если z* выбрать в соответствии
с формулой A9): z* = m*j,z ¦
Теперь, если импульс I перпендикулярен плос-
плоскости пластинки и точка Q его приложения ле-
лежит на оси О'х', причем абсцисса х' точки Q
определяется (в соответствии с формулой B1))
равенством х' = * , то Q — центр удара.
" ' U
Например, для однородной двери ширины а центр
удара находится на середине высоты на расстоя-
расстоя\g\
\
\
h
7
А
нии =:а от оси.
о /
Пример 2. Тяжелый однородный параллелепипед с рис. 152
ребрами а, Ь, с скользит по гладкой горизонталь-
горизонтальной плоскости так, что ребро длины с вертикаль-
вертикально (рис. 152). Направление скоольжения перпендикулярно ребру длины Ь.
Внезапно это ребро задерживается препятствием и становится непо-
неподвижным. Найдем, при какой скорости движения v произойдет опроки-
опрокидывание параллелепипеда.
Послеударное движение параллелепипеда является вращением во-
вокруг оси и, содержащей остановленное ребро. Так как кинетический
момент относительно этой оси за время удара не изменяется, то
= Juu>,
B2)
где т — масса, и — послеударная угловая скорость параллелепипеда,
422 Глава XII
Ju — его момент инерции относительно оси и. Согласно п. 75, 76
Ju = 1 m (a2 + с2) . B3)
Для опрокидывания параллелепипеда необходимо и достаточно, что-
чтобы его центр тяжести при своем движении по окружности радиу-
радиуса yVa2 + с2 пересек вертикальную плоскость, проходящую через ось и.
При этом он поднимется над своим первоначальным положением на вы-
высоту
h = I (Vа2 + с2 - с) . B4)
Опрокидывание произойдет, если
±Juw2 > mgh. B5)
Из B2)-B5) находим
2 4g (a2 + с2)
2
Зс2
Пример 3. Стержень АВ шарнирно закреплен концом А, а вторым кон-
концом шарнирно соединен со стержнем ВС (рис. 153). Стержни покоят-
покоятся и составляют прямую линию. Определить характер послеударного
движения и ударные импульсы реакций в шарнирах А и В вследствие
импульса I, приложенного к стержню ВС под прямым углом на рас-
расстоянии а от шарнира В. Стержни считать тонкими и однородными,
масса каждого стержня равна т, длина I.
*| V2I
В
Рис. 153
Мысленно уберем шарнир В и рассмотрим импульсивное движение
каждого из стержней в отдельности под действием заданного импуль-
импульса I и ударных импульсов 1а и 1в реакций в шарнирах. Обозначим че-
через Vi и «2 послеударные скорости центров масс G± и Gi стержней АВ
и ВС соответственно, а через u>i и и>2 их угловые скорости. Так как
послеударное движение стержня АВ будет вращением вокруг точки А,
Соударение твердых тел 423
то вектор v\ перпендикулярен стержню, причем v\ = —k-. Упомянутые
векторные величины показаны на рис. 153 их компонентами в системе
координат Аху, ось Ах которой направлена вдоль стержней.
Из теорем об изменении количества движения и кинетического
момента, примененных к каждому из стержней, получаем следующие
шесть уравнений:
1ах - 1вх = 0, ^mujil = 1Ау - 1ву, ^тРол = -1ву1,
mv2x=I'Bx, mv2y=I + rBv, y^ml2uJ = -I f ^ - a j - I'By^.
B6)
Еще два уравнения получим, приравняв векторы послеударной скорости
шарнира, рассматривая его как точку, принадлежащую с одной стороны
стержню АВ, а с другой — стержню ВС:
О = v2x, u)\l = v2y - 2Ш*1- B7)
Но так как
^Вх = 1Вх, 1'ву = !ву, B8)
то имеем систему десяти уравнений B6)-B8) для нахождения десяти
неизвестных. Решив эту систему, получим
6/B/-За) 61 (8а-31) МBа + 1)
Lax = и, 1ау = —yi—' 1вх = 1вх = и' 1вУ = 1Ву =Yi¦
Отсюда, в частности, видно, что: 1) если а = -^1, то u>i = и>2 и в
послеударном движении стержни составляют прямую линию; 2) стер-
2/
жень АВ остается в покое, если а = -=-, т. е. если импульс I приложен
в центре удара стержня ВС, соответствующем оси вращения, прохо-
проходящей через шарнир В.
§ 4. Соударение твердых тел
201. Коэффициент восстановления. Пусть два движущихся те-
тела В\ и В2 в момент времени t = to соприкасаются точками О\ и О2
424 Глава XII
своих поверхностей (рис. 154) и в этот момент относительная скорость
точек О\ и 02 не лежит в общей касательной плоскости. Тогда про-
происходит соударение тел. В точке контакта возникают ударные силы,
приложенные к каждому из тел, они имеют одинаковые модули и про-
противоположное направление.
Рис. 154
Будем считать, что тела абсолютно гладкие. Тогда ударные силы
и их импульсы 1\ и 1г перпендикулярны общей касательной плоскости
к поверхностям соударяющихся тел В\ и ??2- Пусть п — единичный
вектор общей нормали к поверхностям тел в точке их контакта, на-
направленный внутрь второго тела, ani — единичная нормаль к телу В/.
в его точке Ok, направленная внутрь тела. Тогда очевидно, что
п = п2 = -щ, 1к = 1пк (к = 1, 2), A)
где / — модуль ударного импульса.
Величина / заранее неизвестна. Это отличает рассматриваемую за-
задачу о соударении двух тел от рассмотренной в предыдущем параграфе
задачи об импульсивном движении твердого тела под действием задан-
заданных ударных импульсов. Задача о соударении тел состоит в нахожде-
нахождении послеударного кинематического состояния тел и величины удар-
ударного импульса при известном доударном кинематическом состоянии
тел. Но, оказывается, что даже в простейших случаях соударения тел
число неизвестных превосходит число уравнений, выражающих общие
теоремы динамики. Поэтому необходимы дополнительные физические
предположения.
Гипотеза об абсолютной твердости тел здесь оказывается недоста-
недостаточной. Надо предположить, что тела претерпевают малые изменения
своей формы вблизи их точки соприкосновения. Сам процесс удара под-
подразделяется на две фазы. В течение первой фазы от t = to до t = to + т\
происходит сближение тел вдоль их общей нормали, причем модуль
проекции на нормаль относительной скорости точек О\ и 02 умень-
уменьшается до нуля, чем и определяется окончание первой фазы удара. В
конце первой фазы деформация тел максимальна. Затем начинается
Соударение твердых тел 425
вторая фаза. Проекция на нормаль относительной скорости точек О\
и 02 при t = to + п изменяет знак и при t > to + т\ возрастает по
модулю; тела, восстанавливая свою форму, удаляются друг от друга
вдоль общей нормали. При t = to + т\ + тг их соприкосновение будет
происходить в одной точке, тела отделяются друг от друга, чем и закан-
заканчивается вторая фаза удара, а вместе с ней и весь процесс соударения
тел.
Наблюдения показывают, что абсолютная величина проекции на
нормаль относительной скорости точек О\ и 02; вообще говоря, не
достигает своей исходной (доударной) величины. Полное исследование
описанного процесса соударения тел требует подробного рассмотрения
их физических свойств и весьма сложного математического анализа,
что выходит за рамки теоретической механики. Упрощая сложный ха-
характер явления, принимают следующее кинематическое предположе-
предположение, высказанное еще Ньютоном: отношение абсолютной величины про-
проекции на общую нормаль к поверхностям тел относительной скорости
точек контакта тел после удара к ее значению до удара есть некото-
некоторая постоянная величина, не зависящая ни от относительной скорос-
скорости, ни от размеров тел, а лишь от их материала.
Это отношение называется коэффициентом восстановления. В
дальнейшем оно будет обозначаться через ж. Пусть VqU и VqU — век-
векторы скоростей точки О*, до и после соударения (к = 1, 2). Тогда
Ы, ~ vo2) ¦ п =-^ Ыг ~ vo2) • п- B)
Учитывая соотношения A), равенство B) можно записать также в сле-
следующей форме:
®Oi " П1 + VO2 - ™2 = ~ж (vOt • nl + VO2 ' ) • C)
Коэффициент восстановления характеризует, насколько восстана-
восстанавливается нормальная составляющая относительной скорости после
удара. Как правило, полного восстановления не происходит. Поэтому
О ^ ж $С 1. Если ж = 0, то удар называется абсолютно неупругим. В
этом случае процесс соударения состоит только из первой фазы; когда
тела достигнут максимального сближения, восстановления их формы
не происходит и оба тела движутся как одно целое. При ж = 1 удар на-
называется абсолютно упругим. Здесь во второй фазе удара происходит
полное восстановление формы тел, нормальная составляющая относи-
относительной скорости точек контакта достигает доударной абсолютной ве-
величины. Промежуточные случаи 0 < ж < 1 , характерные для реальных
физических тел, называют неупругим ударом.
426 Глава XII
При использовании гипотезы B) следует иметь в виду, что она яв-
является первым (иногда очень грубым ) приближением к действитель-
действительным закономерностям, описывающим соударение реальных тел1.
Пример 1. В качестве примера использования ги-
J| потезы Ньютона B) рассмотрим задачу о соуда-
соударении материальной точки с неподвижной абсо-
абсолютно гладкой поверхностью.
" " Пусть перед соударением точка имеет ско-
скорость v~, образующую с внешной нормалью к по-
*" верхности угол падения а (см. рис. 155, где О —
точка, в которой происходит соударение, т —
единичный вектор касательной к кривой, явля-
являющейся пересечением поверхности и плоскости,
ис' проходящей через векторы нормали п и доударной
скорости v~). Масса т точки и коэффициент восстановления ае за-
заданы. Требуется найти модуль послеударной скорости точки v+, угол
отражения /3 и величину I ударного импульса.
Теорема об изменении количества движения дает два уравнения:
п
v+ sin/3 — v~ sin a = О,
D)
m(v+ cos/3 + v cos a) = I.
Из соотношения B) получаем недостающее третье уравнение:
v+ cos/3 = cE,v~ cos а. E)
Из D), E) находим
tg /3 = gg tg a, v+ = v~ v sin2 a + ae2 cos2 a, I = m(l + ae)w~ cos a.
F)
Из D)-F) следует, что: касательные составляющие скорости до и пос-
после удара равны между собой; при абсолютно неупругом ударе материаль-
материальная точка после удара имеет только касательную составляющую; при
абсолютно упругом ударе угол падения равен углу отражения, а модуль
скорости не изменяется (а = /3, v+ = v~); при неупругом ударе угол
падения меньше угла отражения (/3 > а); при абсолютно упругом ударе
ударный импульс в два раза больше импульса при абсолютно неупругом
ударе.
1 Обсуждение этого вопроса можно найти в книге: ПановкоЯ.Г. Введение в тео-
теорию механического удара.— М.: Наука, 1977. Современные математические модели
теории механического удара и их критический анализ содержатся в монографии:
Иванов А. П. Динамика систем с механическими соударениями. — М.: Международ-
Международная программа образования, 1997.
Соударение твердых тел 427
Пример 2. Однородный стержень, который может вращаться вокруг
горизонтальной оси, проходящей через его центр тяжести, находится
в равновесии. На один из концов стержня со скоростью v падает шар
массы т. Длина стержня 2а, масса М. Коэффициент восстановления
равен ж. Принимая шар за материальную точку, определим послеудар-
послеударное кинематическое состояние стержня и шара.
Пусть v+ — скорость шара, а и>+ — угловая скорость стержня
после удара. Из теоремы об изменении кинетического момента (отно-
(относительно центра тяжести стержня) следует равенство
mva = mv+a + -^Ма2ш+, G)
а из того, что удар абсолютно упругий, имеем
v+ — и>+а = —?EV. (8)
Из уравнений G), (8) находим:
+ Зго - аеМ + 3A + ге)ту
V V Ш
202. Общая задача о соударении двух абсолютно гладких
тел. С центром масс тела В), (к = 1, 2) свяжем систему коорди-
координат GkXkVkzki направив ее оси по главным центральным осям инер-
инерции тела (рис. 154). Через А)., В). Си обозначим соответствующие
главные моменты инерции тела, а через т\. — его массу. В систе-
системе координат GkXkVkzk точка Ok имеет координаты х/., Ук, z/., a
вектор нормали щ задается направляющими косинусами а/., Рк-, Ik-
Пусть и>к — вектор угловой скорости тела В^, a Vk — скорость его
центра масс Gk- Задача состоит в определении послеударных зна-
значений этих векторов, если известны их доударные значения. При-
Приращения Аи>к = сс>^~ — uifr и Avk = vk ~ vk заДаДим в системе
координат GkXkDkZk соответственно компонентами
и A.vXk, AvVk, AvZk. Момент Ми = GkOk x Ik ударного импульса
относительно центра масс Gk имеет в системе координат
компоненты МХк = 1?к, Мук = 1щ, MZk = 1(к, где ?к = ykjk ~
Vk = ZkOlk ~ XkJk, (к = Хфк ~ Ук^к-
Из теоремы об изменении кинетического момента и количества
движения имеем двенадцать уравнений
АкАрк = I&, BhAqh = Irik, ChArk = I (к,
mkAvXk = Iak, mkAvVk = Ij3k, mkAvZk = Ijk (к = 1, 2).
428 Глава XII
Отсюда находим послеударные значения кинематических величин те-
тела Вк:
лк ¦• nk
Bl „+ - „- . tK „+ - „-
Из A0), в частности, следует, что касательные составляющие скоростей
центров масс тел при ударе не изменяются.
В равенствах (9), A0) содержится неизвестная величина / ударного
импульса. Если найти ее через известные величины, а затем подставить
в (9), A0), то тем самым общая задача о соударении двух абсолютно
гладких тел будет решена.
Величину / найдем при помощи соотношения C). Для этого, заме-
заметив, что VQk = v? + w~l x GkOk, Vqu = vk~ + w^ x GkOk и воспользо-
воспользовавшись свойствами смешанного произведения векторов, находим ра-
равенство
(vok - vok) ¦ пк = &vk • пк + (GkOk x щ)
которое при помощи соотношений (9), A0) можно записать в виде
Отсюда после суммирования по к получаем равенство
Ыг " «oj • П1 + Ы2 ~ VO2) ¦ П2 = Ц21, (И)
где введено обозначение
/ B 2 а2 \
ifc U + Sl\ п 2)
сч'
Из уравнений A1) и C) находим
^A 2)
Заметим, что величина — {у~^ • Щ + Vq2 • щ) представляет собой до-
ударную проекцию скорости точки О\ контакта тела В\ относительно
точки контакта тела В^ на внутреннюю нормаль п тела _Е?2- Обозначим
Соударение твердых тел 429
ее через игп. Так как перед соударением оба тела стремились сблизить-
сблизиться, то эта величина положительна. Таким образом,
= -^~игп, A4)
причем все величины, входящие в правую часть этого равенства, из-
известны.
Подставив I из A4) в (9) и A0), получим полное решение рассмат-
рассматриваемой задачи о соударении двух абсолютно гладких тел.
Замечание 2 (Динамическое истолкование коэффициента восста-
восстановления). Пусть vj. , шк и VQk (к = 1, 2) — соответственно
векторы скоростей центров масс тел В)., их угловых скоростей и ско-
скоростей точек контакта Ои тел в момент t = to + т\ окончания первой
фазы удара. В этот момент выполняется равенство
v{? ¦ щ + «?> ¦ Щ = 0, A5)
означающее, что при t = to + т\ проекция скорости точки О\ отно-
относительно точки 02 на общую нормаль к поверхностям тел равняется
нулю.
Пусть /W и /B) — величины ударных импульсов, приложенных к
телам, за время первой и второй фаз удара соответственно. Тогда
и, кроме того, имеют место равенства (9), A0), в которых верхний
индекс + надо заменить на индекс A), а вместо I написать 1^.
Величина 1^ находится из соотношения A5). Проведя выкладки,
совершенно аналогичные выкладкам, проведенным выше при получении
формулы A4) из соотношения C), найдем
p?
и тогда из A4) и A6) получаем, что
гB) - _ае_
1 — _ 1
/"B)
Таким образом, ^—— = ж, т. е. при соударении двух абсолютно гладких
тел отношение величин импульсов ударных сил, возникающих между
телами во второй и первой фазах удара, равняется величине коэффици-
коэффициента восстановления.
430
Глава XII
Пример 1 (Удар о стенку (о неподвижную преграду)). Пусть непо-
неподвижной преградой будет тело ??2- Полагая v^ = 0, ш^ =0 к устрем-
устремляя величины т,2, ^4.2? ^2, Сг к бесконечности, из A2) находим {индекс
A) у величин, относящихся к телу В\, опускаем)
1 ~ m +
А
В
(^ - j/aJ
С
A7)
Величина иТп будет проекуией скорости точки контакта О\ тела В\
со стеной на внешнюю нормаль к телу в точке О\. Величина импуль-
импульса вычисляется по формулам A4), A7). Соотношения (9), A0) можно
переписать в виде
p+ =p
¦ — 2/3) , _ ГB;а-Ж7)
+ _ (x/3-ya) , _ г
Пример 2. Однородное колесо радиуса R катится без скольжения по
горизонтальной плоскости, оставаясь в вертикальной плоскости. Оно
ударяется некоторой точкой своего обода о неподвижное препятствие
высоты h < R. Удар происходит без трения, коэффициент восстанов-
ж
ления равен ж. Покажем, что если h >
R, то колесо
не преодолеет препятствие, как бы ни была велика до удара скорость
центра колеса.
Пусть а — угол между вертикалью и
радиусом колеса, соединяющим центр коле-
колеса G с наивысшей точкой препятствия О
(рис. 156), v — величина скорости центра ко-
колеса перед ударом, а г>+, г>+ — проекции его
скорости после удара. Приложенный к колесу
ударный импульс I, ввиду отсутствия тре-
трения, направлен по радиусу OG. Поэтому за вре-
время удара угловая скорость колеса не изменяет-
изменяется.
Рис. 156 Так как скольжение отсутствует, то не-
непосредственно перед ударом скорость точки контакта колеса с пре-
препятствием задается компонентами v (—vcosa, — v sin а). Из теоремы
об изменении количества движения при ударе и гипотезы Ньютона B)
имеем систему трех уравнений (т — масса колеса):
m(v? — v) = —I sin a,
mv
Z =
= I cos a, v^ sin a — Vy cos a = — zev sin a,
§^. Соударение твердых тел 431
решив которую, получим
I = m(l + x)vsina, v? = v[l — A + эе) sin2 a], v^ = (l + ae)i>sinacosa.
Колесо не преодолеет препятствие и отскочит назад, если г>+ < О
(если «+ = О, то колесо взлетит вверх вдоль оси Gy), т. е. если
„ . [R2 - (R - hJ]
A + as) sin а > 1. Но так как sin а — , то это озна-
R
чает, что должно выполняться условие
R J 1 + ав-
Отсюда и следует доказываемое неравенство.
203. Изменение кинетической энергии при соударении аб-
абсолютно гладких тел. Для каждого из тел В/, по формуле F) §3
имеем
1 / Т2 М2 М2 М2 \
^Tu = Tk -Tk = - уш + — + — + — j + (lk. Vk +Mk-uk).
Используя обозначения п. 202, это выражение можно переписать в виде
Замечая, что vk + и>к х GuOu = vok? производя суммирование и учи-
учитывая обозначение A2), находим изменение кинетической энергии сис-
системы двух тел
AT = АТг + ДТ2 = i/V + 1{ю~г ¦ щ + v~2 ¦ п2).
Принимая во внимание равенства A3) и A4), последнее выражение
можно записать в следующем окончательном виде:
A8)
Суммарная кинетическая энергия тела не изменяется только в случае
абсолютно упругого удара (зе = 1). В остальных случаях происходит
потеря кинетической энергии (ДТ < 0).
432 Глава XII
204. Прямой центральный удар двух абсолютно гладких
тел. Назовем линией удара прямую, проходящую через точку сопри-
соприкосновения тел при ударе перпендикулярно их общей касательной плос-
плоскости (на рис. 154 нормали пи к поверхносятм тел В^ лежат на линии
удара). Удар называется прямым, если скорости v^ центров масс до
удара направлены параллельно линии удара. Из упомянутой выше не-
неизменности касательной составляющей скоростей v^ следует, что при
прямом ударе скорости v? центров масс тел после удара будут парал-
параллельны линии удара.
Удар называется центральным, если центры масс тел перед
ударом лежат на линии удара. При центральном ударе моменты
Mjf = GfrOk x 1^ ударного импульса относительно центров масс G}. тел
равны нулю (величины ?^, щ, ^, в (9) обращаются в нуль). Поэтому,
согласно (9), при центральном ударе угловые скорости из\. обоих тел
остаются неизменными.
Рассмотрим задачу о соударении двух абсолютно гладких тел,
предполагая, что удар является прямым и центральным. В этом случае
центры масс тел лежат на линии удара, а их скорости направлены вдоль
этой линии как до, так и после удара. Так как еще и угловые скорости
тел при ударе не изменяются, то задача о прямом центральном ударе
сводится к нахождению изменений проекций скоростей центров масс
тел на линию удара. Простейшим примером задачи о прямом централь-
центральном ударе двух тел может служить задача о соударении двух одинако-
одинаковых шаров, центры масс которых движутся вдоль одной прямой.
За положительное направление на линии удара примем направле-
направление п = П2 внутренней нормали к поверхности тела В2. Пусть v^
и v? (к = 1, 2) — проекции на линию удара скоростей центров масс
тел В/, до и после удара. Для того, чтобы удар произошел, необходи-
необходимо, чтобы до удара относительная скорость центра масс одного из тел,
например, В\, была направлена к центру масс второго тела (v^ > v2).
Так как ?,и = Щ = Си = 0> то формула A2) принимает вид
р nix + т2
Подставляя это значение /х2 в выражение A4) и замечая, что в рассмат-
рассматриваемом случае
Urn = «Г - V2i B0)
получаем величину ударного импульса при прямом центральном ударе:
(V-, -¦у,). B1)
§^. Соударение твердых тел 433
Применяя теорему об изменении количества движения к каждому
из тел, получаем два равенства
Отсюда, принимая во внимание формулу B1), находим проекции пос-
послеударных скоростей центров масс тел на линию удара:
>i + т2A + эе)^2~
1+1112 ' B2)
+ (т2 -
1 nil + nii
Изменение кинетической энергии за время удара вычисляется по
формуле A8) при учете равенств A9) и B0):
1Aа;2) ПЦП12 {v-v~f
Рассмотрим частные случаи.
а) Абсолютно упругий удар (ж = 1). Из B3) следует, что в этом
случае нет потери кинетической энергии (AT = 0), а формулы B2), B1)
дают следующие выражения для послеударных скоростей центров масс
тел и ударного импульса:
+ _ (пц -m2)vi +2m2V2 + _ (mi - mi)«2" + 2roit>j~
Vl ~ nii+m2 ' V2 - m1+m2 ' [ >
1 = 2 miW2 (vi-v2-) B5)
nii + ni2 v г 2 ' x '
Если, кроме того, массы тел равны, то v\ = v^, v? = v^, т. е. центр
масс каждого из тел будет иметь послеударную скорость, какую имел
центр масс другого тела до удара. Таким путем происходит перенос
количеств движения при столкновении молекул идеального газа.
б) Абсолютно неупругий удар (ж = 0). Из B2) получаем
= = пну-+ш2у2
12 nii + то2 v '
т. е. скорости центров масс тел после удара становятся одинаковыми.
При этом происходит потеря кинетической энергии; по формуле B3)
находим
_ mirn2 2_
2(nii + m2)
434 Глава XII
Согласно B1), ударный импульс определяется выражением
nil + ТП2
т. е. он в два раза меньше, чем при абсолютно упругом ударе.
Пример 1 (Прямой центральный удар о неподвижную стенку).
Пусть стенка есть тело В2. Полагая v2 = О и устремляя т2 к беско-
бесконечности, находим из B1)-B3), что в этом случае:
v? = -аеиГ, vt = О, I = A + ai)niiv7, AT = -k(l - c?2)niiv7
Пример 2 (О некоторых практических приложениях формулы B3)).
Пусть тело В2 неподвижно (v^ = 0) и надо привести его в движение,
ударяя по нему телом В\. Кинетическая энергия тела Bi перед уда-
ударом приобретается за счет мускульных усилий человека и будет рав-
1 2
на ^niiv^ . Пусть это количество кинетической энергии Т задано. По-
(л ~2ч ГП2
ложим
I AT
ч т v- - 'mi+m2
При заданных величинах ж и т2 величина ц будет функцией от т\.
Если мы хотим придать телу В2 наибольшую возможную скорость,
то надо уменьшать потери \ AT \, т. е. увеличивать возможную массу
nil тела В\. Выгоднее, например, забивая гвоздь, пользоваться тяже-
тяжелым молотком, сообщая ему малую скорость, чем более легким при
большей скорости.
Совсем другая ситуация возникнет, когда надо будет разрушить
тело В2. Здесь надо увеличивать величину | ДГ \, т. е. увеличивать п.
Это означает, что надо уменьшать nil. Например, ковать лучше бо-
более легким молотком, сообщая ему (при заданной величине Т) большую
скорость.
Пример 3. Найдем необходимое и достаточное условие того, что при
прямом центральном ударе двух поступательно движущихся тел Bi
и В2 тело Bi после удара остановилось.
Из первой формулы B2) следует, что таким условием будет вы-
выполнение равенства
(nil — ?eni2)vi + т2A + ?e)v2 = 0.
Отсюда, в частности, следует: а) если v2 = 0, то ж = -щ-; б) если
до удара скорости тел были равны по модулю и противоположны по
направлению (v2 = —vt ), то -^ = 1 + 2ж.
§ 5. Дифференциальные вариационные принципы механики 435
Упражнение 4 (Косой удар двух шаров). При соударении двух ша-
шаров удар является центральным, но он не обязательно будет прямым,
так как скорости центров масс шаров могут не быть направлены по об-
общей линии центров. В общем случае это будет косой удар двух шаров.
Показать, что при косом соударении двух однородных абсолютно глад-
гладких шаров их угловые скорости и проекции скоростей центров масс на
общую касательную плоскость не изменяются, а проекции на линию
удара изменяются как при прямом центральном ударе.
§ 5. Дифференциальные вариационные принципы
механики в теории импульсивных движений
205. Общее уравнение динамики. Рассмотрим систему N ма-
материальных точек Pv {у = 1, 2,..., N). Состояние системы в некото-
некоторой неподвижной прямоугольной декартовой системе координат зада-
задается радиусами-векторами г„ и скоростями vv ее точек. Система пред-
предполагается свободной или несвободной со связями вида A), B) из §3
главы 1. Импульсивное движение возникает из-за того, что к точкам
системы прикладываются ударные импульсы /„, либо накладываются
новые связи, либо снимаются некоторые (или все) из старых связей,
либо из-за того, что и то, и другое, и третье осуществляется одновре-
одновременно.
Ограничения на скорости точек системы задаются (см. равенст-
равенства B), C) из §3 главы 1) равенствами вида
JV
Y, Я7„ • vv + 67 = 0 G = 1, 2,..., I). A)
Векторы B1V и скаляры &7 — заданные непрерывно дифференцируе-
дифференцируемые функции Гь гг,..., г„ и t. Через I в A) обозначено общее коли-
количество связей системы, голономных и неголономных. Если удар вызван
заданными ударными импульсами и при ударе структура системы не
изменяется, то / равно числу г + s голономных и неголономных связей
системы. Если же при ударе изменяется структура системы (изменя-
(изменяется количество связей), то число I отличается от величины г + s.
Если связи стационарные, то величины 67 в A) тождественно рав-
равны нулю, а вектор-функции B1V явно не зависят от t.
В дальнейшем также будут рассматриваться связи, для которых
величина 67 в A) тождественно равна нулю, но вектор-функции B1V
зависят явно от t. Эти связи линейны и однородны по компонентам
436 Глава XII
векторов скоростей точек системы. Наряду с движениями с возмож-
возможными скоростями v* они допускают движения, для которых скорости
всех точек системы имеют противоположные направления — v*. По этой
причине такие связи называют обратимыми1.
Пример 1. Связь, рассмотренная в примере п. 64, является обратимой
нестационарной связью.
Виртуальные перемещения 8rv точек системы определяются сле-
следующими уравнениями (см. уравнения A2), A3) из §3 главы 1):
JV
Y,BJV-Srv = 0(-y = l,2,...,l). B)
v=\
Ввиду кратковременности процесса удара вектор-функции B1V в урав-
уравнениях B) можно считать постоянными. Отсюда следует, что векторы
виртуальных перемещений 8rv могут считаться независящими от вре-
времени на промежутке времени удара от t = to до t = to + т.
Пусть Rv — равнодействующая реакций связей, приложенных к
точке Pv. Все связи системы будем предполагать идеальными во все
время удара, т. е считаем, что равенство A0) п. 55 справедливо для
любого момента времени из промежутка от to до to + т.
Обозначим через 1иц ударный импульс реакций связей, приложен-
приложенных к точке Р„,
(¦о-г'
*,= /
Тогда интегрирование по t от to Д° ^о + т обеих частей равенства A0)
п. 55, при учете постоянства величин Sru, приводит к соотношению
JV
v=l
Пусть Iv — ударный импульс активных сил, приложенных к точ-
точке Pv. Тогда равенства C) п. 192 можно записать в виде
Переписав равенства D) в виде Iv — mvlS.vv = —Ivr, умножив каждое
из них скалярно на 8rv и произведя суммирование по г/, получим при
1Эти связи называют также катастатическими. См., например: Парс Л. А. Ана-
Аналитическая динамика. М.: Наука, 1971.
§ 5. Дифференциальные вариационные принципы механики 437
учете равенства C) следующее соотношение:
N
y^(Iv - mvAvv) ¦ Srv = 0. E)
v=\
Это соотношение является общим уравнением динамики в теории им-
импульсивных движений.
Величины — mvAvv = —mv(vj~ — v~) можно назвать ударными им-
импульсами сил инерции. И уравнение E) может быть прочитано следую-
следующим образом: истинное послеударное состояние системы выделяется
из всех кинематически возможных тем, что для него и только для не-
него сумма работ активных ударных импульсов и ударных импульсов сил
инерции на любых виртуальных перемещениях равна нулю.
Остановимся подробнее на смыс-
смысле величин Sru, входящих в соотноше- У1
ние E). Если при ударе структура сис-
системы не меняется, то величины 8rv
сохраняют свой обычный смысл: они
удовлетворяют уравнениям A2), A3) §3
главы 1 (или эквивалентым им уравне-
уравнениям B) данного пункта). Если же при
ударе структура системы изменяется,
то ситуация несколько сложнее. Пояс-
Поясним это. Пусть Sr~ — совокупность виртуальных перемещений непо-
непосредственно перед ударом и пусть в момент времени t = to на систему
наложена новая идеальная связь, сохраняющаяся и после удара. В систе-
системе с изменившейся структурой будет новая совокупность виртуальных
перемещений SrJ~. Из-за наложения новой связи совокупность вирту-
виртуальных перемещений Sr~ будет, очевидно, шире совокупности Jr+. И
для того чтобы в соотношении E) иметь виртуальные перемещения,
пригодные во время всего ударного процесса от t = to до t = to + т,
надо в E) положить 8rv = SrJ~. Иное дело, когда идеальная связь во
время удара снимается. В этом случае совокупность виртульных пере-
перемещений Sr~ системы с доударной структурой уже совокупности Jr+,
и в E) следут принять 8rv = Sr~.
Пример 2. Дан ромб О ABC, образованный четырьмя шарнирно соеди-
соединенными невесомыми стержнями (см. рис. 157). Шарнир О неподвижно
закреплен. В шарнирах А и С помещены точечные массы величины т.
По направлению диагонали ВО к ромбу прикладывается ударный им-
импульс I. Считая угол а заданным, найдем послеударные скорости шар-
шарниров А и С.
438 Глава XII
Общее уравнение динамики E) записывается в виде
I ¦ бгв — mAvA ¦ Зга — mAvc • Src = 0. F)
Пусть I — длина каждого из стержней. Из рис. 157 имеем:
r'A = /(cos a, sin a), r'B = 2l(cosa, 0),
r'c = /(cosa, —sinа), I' = (—7, 0).
Поэтому
8r'A = I8a(— sin а, cos a),
Sr'B = -2lSa(sina, 0), (8)
8r'c = — I6a(s'ma, cos а).
Пусть v'A = (vAx, vAy), v'c = (vex, vCy). Тогда
'c = m(vCx, vCy)- (9)
Переписанное с учетом равенств G)-(9) соотношение F) после сокра-
сокращения на 18а приводит к уравнению
21 sin a + m(vAx + vCx) sin a ~ m(vAy — vCy) cos a = 0. A0)
Но из G) следует, что vax = — I sin ace, vav = / cos aa, vcx = —Is'maa,
vcv = —Icosaa. Отсюда вытекают еще три уравнения
VAx = VCx, VAx=4aVCy, VAy = -VGy A1)
Из системы A0), A1) получим искомые проекции векторов послеудар-
послеударных скоростей шарниров А и С:
/sin2 а I sin 2а
vax = vCx = т—, vAy = -vCy = 2т ¦
206. Принцип Журдена. Так как при ударе координаты точек
системы неизменны, а меняются лишь их скорости, то для решения за-
задач теории импульсивных движений более приемлем принцип Журдена
(см. §2 главы 3), а не общее уравнение динамики в форме E). Приняв
такую точку зрения, соотношение E) следует заменить равенством
JV
^2A„ - т„Д»„) ¦ Svv = 0, A2)
§ 5. Дифференциальные вариационные принципы механики 439
где по-прежнему Д»„ = »+ — v~, а конечные вариации скоростей Jtv
(в силу равенств B) п. 205 и A9) из §3 главы 1) удовлетворяют урав-
уравнениям
JV
Y,B-yu-Svv=0('y=l,2,...,l). A3)
v=l
Соотношение A2) выражает принцип Журдена в теории импульсивных
движений: послеударное состояние системы выделяется среди кинема-
кинематически возможных тем, что для него и только для него выполняется
соотношение A2).
Для дальнейшего использования принципа Журдена рассмотрим
подробнее вариации Svv, входящие в равенство A2). Ограничимся слу-
случаем, когда все связи системы являются обратимыми. Тогда величи-
величины 67 в A) тождественно равны нулю, а кинематически возможные
скорости точек системы определяются из уравнений:
JV
?)В71,-ц, = 0G = 1, 2,...,/). A4)
v=l
Если при ударе структура системы не изменяется, то уравнения A3),
определяющие вариации скоростей Svv, с точностью до обозначения не-
неизвестных совпадают с уравнениями A4), которым удовлетворяют са-
сами скорости vv точек системы. Поэтому в соотношении A2) вместо 8vv
можно написать vv, считая вектор vv любой кинематически возмож-
возможной скоростью. Соответственно принцип Журдена может быть записан
в виде соотношения
JV
^(Iv - mvi\vv) ¦ vv = 0, A5)
v=l
где Avv = v+ — v~, a vv — скорость точки Pv системы в любом состо-
состоянии движения, совместимом со связями.
Пусть во время удара на систему наложены новые идеальные об-
обратимые связи. Тогда в A5) vv — любой вектор скорости, допустимый
для системы с наложенными связями.
Если же во время удара происходит снятие идеальной обратимой
связи, то в A5) vv — любой вектор скорости, допустимый для системы
до снятия связи.
Упражнение 5. Рассмотрим покоящуюся систему с идеальными обра-
обратимыми связями. Пусть Vv и vv — скорости точек системы после
440 Глава XII
приложения ударных импульсов 1„ и 1„ соответственно. Показать,
что после приложения суммарного импульса Iv = 1„ + 1„ точки
системы приобретают скорости ад = ад + ад , т. е. суперпозиция им-
импульсов влечет за собой суперпозицию скоростей.
Пример 1. При помощи принципа Журдена найдем послеударную угловую
скорость и> стержня из примера 3 п. 196 (рис. 147).
Положив vv = w+ и учтя, что v~ = 0, а послеударная скорость
конца стержня, к которому приложен импульс, равна и>1, получим со-
N 2
отношение A5) в форме равенства IujI— ^ mvv~^ = 0. Это равенство
v=l
можно переписать в виде Iu>l = IT, где Т = „ • -цТпРиJ — послеударная
от
кинетическая энергия стержня. Отсюда получаем и> = -^-г.
207. Принцип Гаусса. Рассмотрим систему с идеальными свя-
связями. Возможные скорости ее точек определяются системой уравне-
уравнений A). Пусть к точкам Pv системы в момент t = to прилагаются
заданные активные ударные импульсы /„, или на систему накладыва-
накладываются новые идеальные связи вида A), или же осуществляется и то и
другое одновременно.
Пусть, как обычно, v~ и г>+ — векторы скоростей точек системы
непосредственно до и после удара, a vv — вектор любой кинематически
возможной скорости точки Pv в момент t = to + т окончания удара.
Пусть
v=\
Величина G = G(vu) является функцией от кинематичеки возможных
скоростей ад точек системы в ее послеударном состоянии.
Справедливо следующее утверждение.
Теорема (Робена). Состояние системы после удара будет таким, для
которого функция С?(ад) имеет наименьшее значение по сравнению с ее
значениями, отвечающими всем кинематически возможным послеудар-
послеударным скоростям системы.
Это утверждение аналогично принципу наименьшего принуждения
Гаусса в случае конечных сил (см. §3 главы 3), функция A6) является
аналогом принуждения Z.
Доказательство.
Положим vv = w+ + Svv и рассмотрим разность б?(ад) — G(v+).
§ 5. Дифференциальные вариационные принципы механики 441
Имеем
JV JV
G(vv) - G(»+) = ^2(mvAvv - Iv) -Svu + ^^2 mv(SvvJ, A7)
v=l v=l
где Avv = v+ - v~.
Так как vv и vj~ кинематически возможны после удара, то ва-
вариации скоростей 8vv удовлетворяют уравнениям A3) и справедливо
соотношение A2). Следовательно, первая сумма в правой части равен-
равенства A7) равна нулю. А так как не все величины 8vv равны нулю, то
из A7) следует, что G(vv) > G(v+). Это и требовалось доказать.
Упражнение 6 (Экстремальное свойство ударных импульсов ре-
реакций СЯЗЕй). Пусть /„д — ударные импульсы реакций связей. По-
Показать, что для действительного послеударного состояния системы ве-
величина
N Т2
имеет минимальное значение по сравнению с ее значениями для всех
кинематически возможных послеударных состояний системы.
Рассмотрим частный случай, когда активные ударные импульсы
отсутствуют. Положив в A6) /„ = 0, получим, что тогда функция
JV
mv{vv - v~J A8)
имеет минимум при действительных значениях послеударных скорос-
скоростей г>+ из совокупности скоростей vv, кинематически возможных для
системы с наложенными связями.
Пример 1. Два одинаковых тонких однород-
однородных стержня АВ и ВС массы т и длины I kVl j^2
каждый соединены шарниром В и находят- а | в \ с
ся в покое, составляя одну прямую. Опреде-
Определить послеударное кинематическое состоя-
состояние стержней вследствие ударного импуль-
импульса I, сообщенного точке С под прямым углом
к стержням (рис. 158).
Кинематическое состояние стержней АВ и ВС вполне определя-
определяется скоростями г>1 и г>2 их центров масс и угловыми скоростями u>i
и LJ2- Учитывая, что до удара стержни покоились (v~ = 0) и пренебре-
пренебрегая в A6) не зависящими от г>,, и>» (г = 1, 2) слагаемыми, выражение
I
442 Глава XII
для функции G можно записать в виде
N N
Пусть Т — суммарная кинетическая энергия стержней, аи — ско-
скорость точки С после удара. Тогда из A9) получаем
G = T -Iu=\m (v\ + «?) + ^mi1 {ш\ + w|) - Iu. B0)
Так как точка В принадлежит как стержню АВ, так и стержню ВС,
то имеет место кинематическое равенство:
Кроме того,
V! +Ш12 = V2 -Ш22- B1)
2L. B2)
С учетем равенств B1), B2) выражение B0) для функции G принимает
вид
G=\m
-' ~ B3)
¦ij-
Условия экстремума функции G дают три уравнения:
8G _п dG _п dG
системы четырех уравнений B1), B4) находим:
... _ I ... _ 3/ ... _ 5/ ... _ 91
"'- 4m' u/1" 2т/' "г " 4т' ^ " 2тГ
Отрицательные знаки у v\ и ш\ показывают, что действительные на-
направления скорости центра масс стержня АВ и направление его вра-
вращения противоположны направлениям, указанным на рис. 158.
Пример 2. Материальная точка массы т покоится на абсолютно глад-
гладкой поверхности, задаваемой уравнением /(ж, у, z) = 0. К точке при-
прикладывается ударный импульс I = (Ix, Iy, Iz). Найдем скорость точки
после удара.
j 5. Дифференциальные вариационные принципы механики
443
Для функции A6) имеем выражение
Уравнение связи f(x, у, z) = 0 дает соотношение
ox
oy
oz
B5)
B6)
Имеем задачу на условный экстремум: нужно найти точку экстремума
функции B5), если переменные х, у, z связаны соотношением B6).
Воспользуемся методом неопределенных множителей Лагранжа. Пусть
где А — неопределенный множитель. Условия экстремеума
ЯТр ftF f)T?
Цт-т = Чгт = Цгг = О дают три соотношения
ах oy oz
mx = Ix + X^—,
dx
Kjf-, mz = Iz+X1f-. B7)
dy dz y '
Вместе с соотношением B6) они образуют систему четырех уравнений
относительно четырех неизвестных х = х+, у = у+, z = z+ и X.
п .df .df .df
Отметим, что величины Х-^-, Х-^-, Х-^- являются проекциями
дх ду dz
ударного импульса реакции связи на соответствующие координатные
оси.
Пример 3. Тонкий однородный стержень дли-
длины I, занимающий горизонтальное положе-
положение, падает поступательно вниз. Он встре-
встречает точечное препятствие, отстоящее от
концов стержня на расстояниях ^1
4
и -т1
q.
U/
О
х
Рис. 159
(рис. 159). Скорость стержня перед ударом
равна v. Предполагая удар абсолютно неуп-
неупругим, найдем послеударное кинематическое
состояние стержня.
Кинематическое состояние стержня после удара полностью опре-
определяется его угловой скоростью и). Активных ударных импульсов нет.
444 Глава XII
Импульсивное движение возникает только из-за наложения новой свя-
связи, внезапной остановки точки О стержня. Так как для каждой точки
стержня v~ = v, то для функции G из A8) имеем такое выражение:
N
I ш . \ 1 / . . \
B8)
Пусть то — .масса стержня, vc — послеударная скорость его цент-
центра масс, а Jo — момент инерции стержня относительно точки О. Тог-
n n ^ N ^
да ^ fnv = то, 5^ mi/wi/ = mvc a h ^2 rnvvl = 4<7о^2 — кинетичес-
кая энергия стержня после удара, и функцию B8) можно представить
в виде
G = TjJoU2 — mvc ¦ v + „mv2.
Но Jo = га» , v' = @, —v), v'c = @, —w^). Поэтому имеем такое
окончательное выражение для функции G
Из условия ^^ = 0 находим и> = -=j-.
§ 6. Теоремы Карно
208. Первая теорема Карно. Рассмотрим движение системы,
связи которой идеальны и обратимы (в частности, стационарны). В
некоторый момент t = to на систему накладываются новые связи, ко-
которые также являются идеальными и обратимыми. Активных ударных
импульсов нет. Импульсивное движение возникает только за счет нало-
наложения новых связей. Найдем изменение кинетической энергии системы
за время удара.
Имеет место следующая (первая) теорема Карно:
Теорема. Если внезапно наложенные идеальные обратимые связи со-
сохраняются после удара вместе с ранее существовавшими идеальными
обратимыми связями, то потерянная в результате наложения новых
связей кинетическая энергия равна кинетической энергии потерянных
скоростей.
9. Теоремы Карно 445
Доказательство.
Можно было бы применить результаты п. 197, где рассмотре-
рассмотрена общая теорема об изменении кинетической энергии при импуль-
импульсивном движении, но удобнее воспользоваться принципом Журдена
(см. п. 206).
Так как /„ = 0, то соотношение A5) п. 206, справедливое для сис-
систем с идеальными обратимыми связями, можно записать в виде
N
Здесь vv — любой вектор скорости точки Р„, кинематически возмож-
возможный для системы с наложенными связями. Следовательно, vv = vj~, и
из соотношения A) следует, что
JV
Но так как (v~ - »+) • ю+ = ~ \v~ - v+2 - (v~ - v+J , то равенст-
^ L J
во B) можно переписать в виде
N N N
или, при обозначениях (9), A3) п. 197, Г" - Т+ - Т* = 0, т. е.
Т~ -Т+ = Г», C)
что и доказывает первую теорему Карно.
Эту теорему можно трактовать как теорему об изменении кинети-
кинетической энергии за время первой фазы удара. Как видно из C), за первую
фазу удара кинетическая энергия системы всегда уменьшается.
Пример 1. Два одинаковых шара движутся поступательно вдоль од-
одной прямой со скоростями Vi и v^. В некоторый момент времени ша-
шары соприкасаются и происходит абсолютно неупругий удар. После удара
шары образуют одно тело, движущееся вдоль исходной прямой со скорос-
скоростью v. Найдем величину v при помощи первой теоремы Карно. Пусть т
— масса каждого из шаров. Тогда
Т- = \m(v2 + v2), T+ = mv2, T* = \m(Vl - vJ + \m(v2 - vJ.
446 Глава XII
Из уравнения C) находим
Последнее равенство, очевидно, выражает неизменность количества
движения системы двух шаров при ударе. Оно могло быть также по-
получено из формул B2) п. 204 при я = 0 и т\ = тог.
209. Вторая теорема Карно. Пусть у системы с идеальными
обратимыми связями в некоторый момент t = to происходит внезапное
снятие связей (одной, нескольких или даже всех). Активных ударных
импульсов нет. Если моменту t = t0 предшествовала фаза деформации,
то при снятии связей возникают ударные импульсы реакций связей и
происходит увеличение кинетической энергии системы. Имеет место
следующая (вторая) теорема Карно:
Теорема. Кинетическая энергия, приобретенная при снятии связей,
равна кинетической энергии приобретенных скоростей.
Доказательство.
Как и в п. 208, используем принцип Журдена. Теперь в уравне-
уравнении A) vv = v~ — любой вектор скорости, кинематически возможный
для системы до снятия связей. Следовательно, справедливо соотноше-
соотношение
N
?>„(»+-»-)•»- =0. D)
Но имеет место тождество
Поэтому из D) следует равенство
N N N
1^т„и+2 - 1^т„и-2 - ^^2mv(v+ - v~f = 0.
v=l v=l v=l
Принимая во внимание обозначения (9), A3) п. 197, это равенство мож-
можно переписать в виде Т+ — Т~ — Г* = 0 или в виде
Т+ -Т~ =Т». E)
Отсюда и следует справедливость доказываемой теоремы.
Вторую теорему Карно можно трактовать как теорему об изме-
изменении кинетической энергии за время второй фазы удара (если она
существует). Из E) следует, что за вторую фазу удара кинетическая
энергия системы всегда увеличивается.
§ 6. Теоремы Карно 447
Пример 1. Снаряд, движущийся поступательно со скоростью v, раз-
разрывается на два осколка равных масс. После взрыва один из осколков
имеет скорость v\ и сохраняет направление первоначального движения
снаряда. При помощи второй теоремы Карно найдем скорость v<i вто-
второго осколка.
Пусть т — масса снаряда. Тогда
и из уравнения E) находим, что v<i = 2v — v\.
Величину г>2 можно было бы также найти из условия постоянства
количества движения: vnv = Щ-vi + Щ-vi-
Zi Zi
210. Кинетическая энергия потерянных скоростей в слу-
случае твердого тела. Получим формулу для вычисления кинетической
энергии потерянных скоростей в случае тела, совершающего произволь-
произвольные движения в пространстве. Пусть Gxyz — система координат, об-
образованная главными центральными осями инерции тела, А, В и С —
моменты инерции тела относительно осей Gx, Gy и Gz\ p, q, r — про-
проекции вектора ш угловой скорости тела на эти оси, т — масса тела,
vq — скорость центра масс. Радиус-вектор GPV точки тела Р„ в сис-
системе координат Gxyz задается компонентами ж„, у„, zv. Для скорости
vv точки Р„ имеем выражение vv = vq +ш х GPv. Поэтому для компо-
компонент вектора v~ — v+ потерянной скорости точки Р„ имеем следующие
выражения:
vvx - Vtx = (vGx ~ VGx) + (Ч~ ~ Q+)Zv ~ (г" " r+)Vv,
vvy ~ vty = (vGy ~ VGy) + (r~ ~ r+)Xv ~ (P~ ~ P+)zv, F)
vvz ~ Vtz = (VGz ~ VGz) + (P~ ~ Р+)У» ~ (<T " (t)xv.
Для кинетической энергии потерянных скоростей всех точек тела име-
имеем выражение
N
T* = \Y;m« [fc " <xf + (V~y ~ О2 + (V~z - «+ J] . G)
448 Глава XII
Но, согласно выбору системы координат Gxyz, имеют место равенства
N N N
ivVv = / mvzv = 0, (8)
N N N
N N N
"?тЛу1+4) = А, ^т„Й+^)=В, ^^(xl+yl) = С. A0)
v=l v=l v=l
Учитывая эти равенства и выражения F), получаем из G) следующую
окончательную формулу:
Т. = ±m(tfc " v+f + \ [А(р~ - p+Y + B(q- - q+f + C(r~ - r+J] .
(И)
В случае вращения твердого тела вокруг неподвижной точки О
совершенно аналогично можно получить формулу
Т. = \ [А(р~ - p+Y + B(q- - q+f + C(r~ - r+f] , A2)
где теперь А, В, С — главные моменты инерции тела для точки О, а
р, q, г — проекции вектора ш на соответствующие главные оси инер-
инерции Ox, Oy, Oz.
Рассмотрим еще случай вращения тела вокруг неподвижной оси и.
Пусть эта ось проходит через точку О тела, являющуюся неподвижной.
Косинусы углов, образуемых осью и и главными осями инерции Ох, Оу
и Oz, обозначим через а, /3 и 7 соответственно. Тогда р = ша, q = и>C,
г = W7 и формула A2) записывается в виде
Т* = \{Аа2 + В01 + С^2)(ш- - ш+J.
Но, согласно формуле A) п. 77, имеем Аа2 +Bf32 +C72 = Л, где Ju —
момент инерции тела относительно оси вращения. Поэтому
T* = \ju{u--u+J. A3)
Пример 1. При помощи первой теоремы Карно найдем угловую скорость
стержня после удара в задаче из примера 3 п. 207.
§ 6. Теоремы Карно 449
Для до и послеударной кинетической энергии стержня имеем сле-
следующие выражения:
T~ = \mv\ r+ = i.^cA A4)
Кинетическую энергию потерянных скоростей вычисляем по форму-
формуле A1):
Подстановка выражений A4), A5) в равенство C) дает уравнение от-
относительно и). Решив его, получим, что
Пример 2. При помощи теоремы Карно вычислим угловую скорость те-
тела и>+ в примере из п. 199.
Используя обозначения п. 199 и формулу A2), запишем уравнение C)
в виде
{Ар'2 + Bq~2 + Cr~2) - (Аа2 + Bf32 + C72 V+2 =
= А(р~ - аш+J + B(q~ - /3w+J + C(r~ - 7W"J.
Отсюда получаем
+ _ Ар~а + Bq~C + Cr~"f
U Аа2 + BC2 + C72 "
Пример 3. Найдем послеударные угловые скорости шкивов в приме-
примере 1 п. 196.
Имеем
Величину Т* находим по формуле A3):
Учитывая еще, что Qiri = О2Г2, из уравнения C) получаем
2 , т 2
450 Глава XII
211. Третья и обобщенная теоремы Карно. У систем с идеаль-
идеальными обратимыми связями кинетическая энергия за обе фазы удара,
как правило, уменьшается; исключением является случай только абсо-
абсолютно упругого удара, когда она остается без изменений. В этом состо-
состоит так называемая третья теорема Карно. Мы не останавливаемся на
ее доказательстве в общем случае. Отметим только, что в частном слу-
случае соударения двух абсолютно гладких тел эта теорема была получена
ранее в п. 203.
Формулу A8) п. 203 можно записать в несколько иной форме, выра-
выразив ее правую часть только через кинетическую энергию потерянных
скоростей Т* и коэффициент восстановления ж. С этой целью по фор-
формуле A1) п. 210 находим
Г. = \ ? mk{v- - <J + 1 j
k=l k=l
+ Bk(q--q+J+Ck(r^-r+J].
С учетом равенств (9), A0) и A2) из п. 202 это выражение преобразу-
преобразуется к виду
Т. = \„212. A6)
Учитывая равенство A4) п. 202, из формулы A8) п. 203 имеем
Т- т+ _1-эа2 ( 1ц2 \ _ 1-ае 2т2
2/? \1+ж) 2A + Ж)/' •
Отсюда, принимая во внимание равенство A6), окончательно находим,
что
т. е. потеря кинетической энергии за полное время удара равна
1 — 86
-т— ой доле кинетической энергии потерянных скоростей за это вре-
мя. Это утверждение называют обобщенной теоремой Карно.
Упражнение 7. Непосредственным вычислением убедиться в справед-
справедливости обобщенной теоремы Карно в задаче о соударении материаль-
материальной точки с неподвижной абсолютно гладкой поверхностью (пример 1
из п. 201) ив задаче о прямом центральном ударе двух тел (п. 204).
§ 7. Теоремы Делонэ-Бертрана и Томсона 451
§ 7. Теоремы Делонэ—Бертрана и Томсона
212. Теорема Делонэ—Бертрана. Рассмотрим систему матери-
материальных точек Р„ {у = 1, 2,..., N) с идеальными обратимыми свя-
связями. Первоначально она покоится, но в некоторый момент внезапно
приводится в движение заданной системой ударных импульсов /„. В
результате удара точка Р„ получает скорость ад , а система приобре-
приобретает кинетическую энергию Т^\ Наложим теперь на систему новые
дополнительные связи, также идеальные и обратимые. Тогда точки Р„
системы под действием тех же импульсов /„ приобретают, вообще го-
говоря, другие скорости ад , а система — кинетическую энергию Т^.
Новые скорости ад являются кинематически возможными как
для системы с увеличенным числом связей, так и для первоначальной
системы. Поэтому из принципа Журдена, согласно соотношению A5)
п. 206, следует справедливость следующих двух равенств:
Из этих равенств следует, что
или
JV JV
т. e.
Последнее соотношение означает, что для систем с идеальными об-
обратимыми связями имеет место следующее утверждение.
Теорема (Делонэ—Бертрана). Если точки материальной системы
получают заданные импульсы, то кинетическая энергия в возникающем
движении будет больше, чем кинетическая энергия, которую приобрела
бы система при тех же импульсах, если бы к первоначальным связям
системы были добавлены новые связи.
Иными словами, добавление новых связей при тех же импульсах
приводит к уменьшению послеударной величины кинетической энер-
энергии.
452 Глава XII
Пример 1. Иллюстрацией к теореме могут служить примеры 2 и 3 из
п. 196 (см. также п. 197). Для свободного стержня имеем Т^ = Ц^-
Если же один из концов стержня закрепить, то Т^ = w~- Поэтому
грA) Л
—— = -ц, т. е. (при заданном импульсе I) наложение связи (закрепле-
(закрепление конца стержня) уменьшило кинетическую энергию.
Содержание теоремы Делонэ-Бертрана можно выразить еще следу-
следующим образом. Рассмотрим кинематическое состояние системы после
действия заданных ударных импульсов как одно из кинематических
состояний системы с увеличенным числом связей. Тогда среди беско-
бесконечного множества таких состояний системы истинное послеударное
кинематическое состояние выделяется тем, что для него кинетическая
энергия имеет максимальное значение при тех же импульсах.
Пример 2. Определим при помощи теоремы Делонэ-Бертрана после-
послеударное кинематическое состояние стержня в примере 2 п. 196.
Кинематическое состояние стержня вполне определится, если
найти его послеударную угловую скорость и) и положение мгновенного
центра скоростей.
Мысленно наложим на стержень новую связь, шарнирно «закрепив»
его в точке, лежащей слева от центра масс стержня на расстоянии х
от него (рис. 146). Согласно теореме Делонэ-Бертрана, истинное поло-
положение мгновенного центра скоростей после удара найдется из условий
максимума кинетической энергии как функции х при заданной величине
импульса I.
Теорема об изменении кинетического момента дает следующее со-
соотношение между ш и х:
t\ J=j^ml2+mx2. A)
Для кинетической энергии стержня Т = !Щ— с учетом A) имеем вы-
выражение
S? {1 + 2XJ B)
Из условия ^f- = 0 находим х = j; и из A) получаем ш = ^Щ.
ах b ml
Пусть vv — кинематически возможные послеударные скорости то-
точек первоначально покоящейся системы. Согласно теореме об измене-
изменении кинетической энергии при импульсивном движении, величины vv
§ 7. Теоремы Делонэ-Бертрана и Томсона 453
и ударные импульсы /„ связаны равенством (см. формулу A0) п. 197):
N N
v=l v=l
Поэтому теореме Делонэ-Бертрана можно дать такую формулировку:
кинетическая энергия, сообщаемая системе с идеальными обратимыми
связями заданными импульсами Iv, есть максимум при условии C).
Пример 3 (См. также п. 198). К покоящемуся свободному твердому
телу приложены ударные импульсы с главным вектором S^ и главным
моментом L^ относительно центра масс тела. Определим кинема-
кинематическое состояние тела после удара при помощи теоремы Делонэ-
Бертрана.
Пусть т — масса тела, А, В, С — его главные центральные
моменты инерции, vG и ш — скорость центра масс тела и его уг-
угловая скорость после удара. В системе координат Gxyz, образованной
главными центральными осями инерции, имеем: S^ = (Sx, Sy, Sz),
?(e) = (Lx, Ly, Lz), vG' = (vGx, vGy, vGz), ш' = (p, q, г). В соответ-
соответствии с теоремой Делонэ-Бертрана, в послеударном состоянии тела
величина
Т = \m(vGx + vGy + vGz) + I(V + Bq2 + Cr2) D)
является максимальной при условии C), которое в рассматриваемом
случае, согласно формуле E) п. 198, может быть записано в виде
SxvGx + SyvGy + SzvGz + Lxp + Lyq + Lzr = 2Г. E)
Для решения задачи об условном экстремуме используем метод неопре-
неопределенных множителей Лагранжа. Составим функцию
F = Т - X(SxvGx + SyVGy + SzvGz + Lxp + Lvq + Lzr - 2Г) =
= A + 2A)T - X(SxvGx + SyVGy + SzvGz + Lxp + Lyq + Lzr).
Приравняв нулю частные производные функции F no vGx, vGy, vGz,
р, q, r, получаем следующие уравнения:
A + 2\)mvGx = XSX, (I + 2\)mvGy = XSy, A + 2X)mvGz = XSZ,
XLx, A + 2X)Bq = XLy, A + 2X)Cr = XLZ.
F)
454 Глава XII
Из E) и F) находим А = —1, а
что находится в соответствии с формулами B) и C) п. 198.
213. Теорема Томсона. Как мы видели в предыдущем пункте,
теорема Делонэ-Бертрана позволяет свести задачу об импульсивном
движении системы с идеальными обратимыми связями к задаче о на-
нахождении максимума некоторой функции. Теорема Томсона, изучае-
изучаемая ниже, сводит задачу об импульсивном движении к рассмотрению
некоторого минимума.
Пусть точки Р„ первоначально покоящейся системы под действием
ударных импульсов /„ приобретают скорости v'v. Если к системе при-
приложить другие ударные импульсы, то ее состояние после удара будет,
как правило, иным, нежели в первом случае: если v" — скорости точек
системы во втором случае, то, вообще говоря, равенство v'v = г>" не
будет выполняться для всех точек Р„. Пусть при этом новые импульсы
таковы, что новые скорости v" удовлетворяют равенству
JV JV
5>-<' = 1>-<- G)
v=l v=l
Напишем уравнение A5) п. 206 для системы импульсов /„ и двух систем
кинематически возможных скоростей v'v и v":
N N
I» - mvvi) 4 = 0, ^(/„ - mvv'v) ¦ v'J = 0.
v=l
Отсюда на основании условия G) получаем равенство
N
v=l
которое тождественными преобразованиями приводится к виду
N N N
т. е.
JV
2
v=l
§ 7. Теоремы Делонэ-Вертрана и Томсона 455
Это означает, что для рассматриваемой системы материальных точек
справедливо следующее утверждение.
Теорема (Томсона). Кинетическая
энергия, которую приобретает систе- >r-—^
ма в действительности от приложен- v
ных импульсов, будет наименьшей из д у vlx О
всех тех кинетических энергий, кото-
которые сообщили бы системе всевозмож-
всевозможные импульсы, удовлетворяющие усло-
условию G). <°2
Доказательство.
Предположим, что находящаяся в
v
В
покое система материальных точек Р„
(у = 1, 2, ..., N) приводится Рис.160
в движение неизвестными ударными
импульсами, приложенными к некоторым заданным точкам систе-
системы Pi, P2,..., Р„ (п < N), причем эти точки приобретают данные
скорости v'v (и = 1, 2,..., п). К остальным точкам системы не при-
приложено никаких активных ударных импульсов, их послеударные ско-
скорости обусловлены только наличием связей. В этом случае условию G)
можно удовлетворить, если новые импульсы подобрать так, чтобы вы-
выполнялись условия v'J = v'v для v = 1, 2,..., п. Теореме Томсона мож-
можно, следовательно, дать такую формулировку: если некоторые точки
системы внезапно приведены в движение с заданными скоростями, то
кинетическая энергия, приобретенная системой, меньше, чем кинети-
кинетическая энергия во всяком другом кинематически возможном состоянии,
при котором указанные точки системы имеют заданные скорости.
Пример 1. Два одинаковых тонких однородных стержня АО и ОВ мас-
массы т и длины I каждый шарнирно соединены в точке О и находятся
в покое перпендикулярно один другому. Концу В стержня ОВ внезап-
внезапно сообщается скорость v, параллельная направлению О А (рис. 160).
Определить кинематическое состояние стержней после удара.
При заданной скорости точки В послеударное кинематическое со-
состояние стержней АО и ОВ вполне определяется их угловыми скорос-
скоростями ш\ uui2- Пусть Vi и щ — скорости центров масс G\ и Gi стерж-
стержней после удара. Тогда
Т = \m(v\ + vl) + ^ml2{u;l + ш22).
Но из кинематических соотношений Vq = Vi+loi x G\O = v +Ш2Х ВО
456 Глава XII
и v2 = v + ш2 х BG2 следуют равенства
Vlx = —V — Ul2l, Щу = —^>ln, V2x = — V — 0J2y, V2y = 0,
поэтому
1 Г „ „ /2 7
T = -~m \(v + (jj2l) + LJi -г + (v + uJ g
Из уравнений
находим ш± = 0, ui2 = — ^7. Таким образом, непосредственно после уда-
ра стержень АО находится в состоянии мгновенного поступательного
движения, а стержень АО вращается по часовой стрелке с угловой ско-
ростью 4у.
8/
Пример 2. К заданной точке свободного твердого тела приложен им-
импульс, сообщающий этой точке данную скорость. Определить после-
послеударное состояние тела.
Как и в последнем примере п. 212, за начало координат примем
центр масс G тела, а за оси Gx, Gy, Gz — главные центральные
оси инерции. Кинетическая энергия Т тела после удара вычисляется
по формуле D) п. 212. Пусть а, Ь, с — координаты точки приложения
импульса, a vx, vy, vz — заданные проекции вектора ее скорости на
координатные оси. Тогда
vx = vgx + qc- rb, vy = vGy + ra- pc, vz = vGz + pb - qa. (8)
Нахождение величин vqx, vgv, vqzi P> 9? г, доставляющих минимум
функции Т при условиях (8), приводит к уравнениям
mvGx = Хх, mvGy = Ау, mvGz = Xz, (9)
Ар = b\z — cXy, Bq = cXx — aXz, Cr = aXy — bXx, A0)
где Xx, Xy, Xz — неопределенные множители Лагранжа, которые опре-
определяются вместе с величинами vGx, vGy, vGz, p, q, r из системы
девяти уравнений (8)-A0).
Отметим, что из формул B), C) п. 198 и уравнений (9), A0) сле-
следует, что Хх, Ху, Xz — проекции неизвестного вектора ударного им-
импульса на оси Gx, Gy, Gz.
§ 7. Теоремы Делонэ-Бертрана и Томсона 457
Теореме Томсона можно дать истолкование, близкое по форме
к данному в предыдущем пункте истолкованию теоремы Делонэ-
Бертрана. Будем рассматривать послеударное кинематическое состоя-
состояние системы, заданным точкам которой сообщены заданные скорости,
как одно из послеударных состояний системы с увеличенным числом
связей. Тогда среди бесконечного множества таких состояний истин-
истинное послеударное состояние выделяется тем, что оно дает наименьшую
кинетическую энергию при тех же скоростях заданных точек системы.
Иными словами, добавление новых связей при тех же скоростях
заданных точек системы приводит к увеличению ее послеударной кине-
кинетической энергии.
Сравнив теоремы Делонэ-Бертрана и Томсона, получим, что если
заданы ударные импульсы, приложенные в данных точках системы, то
послеударное состояние системы может быть найдено при решении за-
задачи максимума кинетической энергии, если же заданы скорости точек
приложения импульсов, то послеударное состояние находится как ре-
решение задачи минимума кинетической энергии при добавлении новых
связей.
Пример 3. Для иллюстрации рассмотрим два тонких однородных
стержня АВ и ВС, связанных шарнирно в точке В. Стержни поко-
покоятся и составляют одну прямую (рис. 158). Внезапно точке С сооб-
сообщается скорость v в направлении, перпендикулярном ВС. На основа-
основании вычислений, проведенных в примере 1 п. 207, можно получить, что
при этом система из двух стержней приобретет кинетическую энер-
энергию
Теперь мысленно проведем второй эксперимент. Закрепим шарнир-
шарнирно точку А и приведем точку С в движение с прежней скоростью v.
Использовав вычисления примера 3 п. 200, получим, что в этом случае
приобретенная кинетическая энергия Т^ = -fsrnv2.
4»
И, наконец, рассмотрим третий эксперимент. Кроме точки А за-
закрепим шарнирно еще и точку В, а точке С опять сообщим ту же
скорость v. Здесь после удара стержень АВ остается в покое, и приоб-
приобретенная кинетическая энергия Т^ равна послеударной кинетической
энергии стержня ВС. Согласно примеру из п. 197, имеем Т^ = |т«2.
Так как \ < -^ < \, то Т^ < Т^ < Т^, т. е., в соответ-
I 4о О
ствии с теоремой Томсона, наложение связей при неизменной скорости
точки С приводит к увеличению послеударной кинетической энергии.
Если же в трех рассмотренных экспериментах одинаковым будет
ортогональный ВС ударный импульс I, то приобретенная кинетичес-
458 Глава XII
кая энергия будет, соответственно, такой: Т^ = ^—, Т^ = -=—,
Т(з) = |Я_ Так шк 1 > Ц_ > 3 mo T(i) > тB) > Т(з)^ m е^ в со_
гласии с теоремой Делонэ-Бертрана, наложение новых связей привело
к уменьшению послеударной кинетической энергии.
Пример 4. При помощи теоремы Томсона найдем положение мгновен-
мгновенного центра скоростей тонкого однородного стержня, правому концу
которого сообщена скорость v перпендикулярно стержню (рис. 146).
Эта задача рассмотрена в предыдущем пункте при помощи теоре-
теоремы Делонэ-Бертрана. Здесь используем аналогичный подход. На стер-
стержень мысленно наложим связь, «закрепив» его при помощи шарнира в
точке, отстоящей от центра масс О на расстоянии х. Тогда после-
послеударная угловая скорость задается равенством ш = . Момент
инерции J относительно оси вращения вычисляется по формуле A).
Для кинетической энергии стержня в его послеударном состоянии по-
получим выражение
\ \ r±^ A1)
Согласно теореме Томсона, искомая величина х доставляет минимум
величине кинетической энергии. Это дает ж = 4, что совпадает с
результатом предыдущего пункта.
Сравнивая формулы B) и A1), видим, что g(x) = , т. е. тео-
J\x)
ремы Делонэ-Бертрана и Томсона привели к рассмотрению экстремума
одной и той же функции от х.
§ 8. Уравнения Лагранжа второго рода для
импульсивных движений
214. Обобщенные ударные импульсы. Рассмотрим голоном-
ную систему материальных точек Р„ (у = 1, 2,..., N) с идеальными
связями. Пусть она имеет п степеней свободы, a q±, q2,..., qn — ее
обобщенные координаты. В некоторый момент времени to к системе
прикладываются ударные силы, имеющие за время удара г ударные
импульсы /„ (у = 1, 2,..., N). Задача об импульсивном движении
системы в обобщенных координатах состоит в нахождении значений qf
обобщенных скоростей после удара по известным их значениям щ не-
непосредственно перед ударом. Для решения этой задачи могут быть ис-
использованы уравнения Лагранжа второго рода (см. п. 138).
§ 8. Уравнения Лагранжа второго рода для импульсивных движений 459
Введем понятие обобщенных ударных импульсов, аналогичное по-
понятию обобщенных сил (п. 54). Рассмотрим элементарную работу
N
SL = ^^ Iv ¦ Srv, A)
v=l
совершаемую ударными импульсами на любом виртуальном перемеще-
перемещении системы. Величины 8rv выражаются через вариации обобщенных
координат Sq, по формуле B7) п. 16. Поэтому выражению A) можно
придать такой вид:
Введя обозначение
N
/,-^(г = 1, 2,..., п), C)
равенство B) можно записать в виде
N
Величина Jj называется обобщенным ударным импульсом, соответству-
соответствующим обобщенной координате щ (г = 1, 2,..., п).
Принимая во внимание равенство A) п. 191, из формулы C) полу-
получаем такое выражение для обобщенного ударного импульса
to+т
дг to-t-т
to
Но величины -^- во время удара изменяются пренебрежимо мало и при
интегрировании их можно считать постоянными. Поэтому последнее
равенство можно переписать так
to+
460 Глава XII
Согласно формуле (9) п. 54, выражение в круглых скобках есть обоб-
обобщенная сила Qi, соответствующая обобщенной координате щ. Следова-
Следовательно,
to+т
Ji= I Qidt (i = l, 2,..., n). E)
to
215. Уравнения Лагранжа. Проинтегрируем обе части уравне-
уравнения A1) п. 138 по времени на промежутке, соответствующем продол-
продолжительности удара т. Тогда, учитывая формулы E) и тот факт, что
ВТ
интегралы от конечных величин ^— за время удара пренебрежимо ма-
малы, получаем соотношения:
где, как обычно, верхними индексами — и + обозначены значения со-
соответствующих величин до и после удара.
Соотношения F) образуют систему п уравнений Лагранжа второ-
второго рода для импульсивных движений. Неизвестными являются вели-
величины qf, q?,... ,g+. В отличие от уравнений Лагранжа A1) п. 138 для
движения под действием конечных сил, уравнения F) являются алгеб-
алгебраическими (причем линейными), а не дифференциальными.
Пример 1. Материальная точка массы т движется вдоль оси Ох со
скоростью v. К ней прикладывается ударный импульс I, направленный
вдоль оси Ох. Найдем послеударную скорость точки.
Результат сразу же следует из основного соотношения в теории
импульсивных движений (см. формулу B) п. 192). Но в иллюстративных
целях решим эту задачу при помощи уравнений Лагранжа F).
Из A) имеем SL = ISx, т. е. Jx = I. Но Т = ^пгх2, Цтт = тпх,
поэтому, согласно F), имеем уравнение (тх)+ — (тх)~ = Jx = I. Сле-
Следовательно, Х+ = V + щ.
Пример 2. Двойной маятник, образованный двумя тонкими однородны-
однородными стержнями длины I и массы т каждый, находится в покое, причем
центры тяжести стержней находятся на одной вертикали ниже точ-
точки А подвеса стержней (это значит, что на рис. 15 имеем <р = ф = 0).
Ему сообщается горизонтальный ударный импульс I, приложенный к
нижнему стержню на расстоянии а от шарнира, соединяющего стерж-
стержни. Найти угловые скорости каждого из стержней после удара.
§ 8. Уравнения Лагранжа второго рода для импульсивных движений 461
Сложив кинетические энергии стержней, образующих маятник, по-
получим
G)
В системе координат Аху, ось Ах которой направлена вертикаль-
вертикально вниз, а ось Ау горизонтальна и лежит в плоскости рис. 15, име-
имеем V = @, /), а радиус-вектор г' = (х, у) точки приложения им-
импульса имеет компоненты х = Icostp + асоёф, у = lsm<p + аътф.
Для элементарной работы A) импульса I на виртуальном перемеще-
перемещении 5r' = (Sx, 5y) получаем следующее выражение
5L = I ¦ 5г = 15у = II cos (р5(р + la cos ф5ф.
Следовательно,
Jv = II cos (р, Зф = 1асоиф. (8)
Уравнения Лагранжа F) будут такими:
дт\+-(—У=3 (&?] -(&?] =3 (9)
дф) \дф) *" удф) удф) ф'
Принимая во внимание формулы G), (8) и mom факт, что ф~ = ф = О,
а при ударе ф = ф = 0, уравнения (9) можно записать в следующем виде:
Отсюда получим искомые величины послеударных угловых скоростей
стержней:
., 61B1 -За) ., 6/(8а-3/)
V =^^^' Ф = 1ml2 ¦
В примере 3 п. 200 этот же результат получен при помощи теорем об
изменении количества движения и кинетического момента.
Пример 3. Тонкий однородный стержень АВ длины I и массы т дви-
движется в плоскости Оху (рис. 161). В некоторый момент времени он
ударяется об ось Ох своим концом А. Во время удара стержень со-
составляет с осью Ох угол а, компоненты скорости его центра масс
равны х~, у~, а угловая скорость равна ф~. Считая ось Ох абсолютно
гладкой, а удар абсолютно упругим, найти послеударное кинематичес-
кинематическое состояние стержня.
462 Глава XII
О
х
Если х, у — координаты центра масс
стержня, а ф — его угловая скорость, то
Т=\т(х2+у2) + ±т12ф2. A0)
Пусть I — неизвестный ударный импульс
оси Ох. Ввиду отсутствия трения он парал-
Рис. 161 лелен оси Оу. Для элементарной работы удар-
ударного импульса на виртуальном перемещении
стержня имеем следующее выражение:
8L = 15у — 1ц cos a Sip.
Отсюда следует, что
Jx=0, JV = I, Jv = -I-^ cos a. A1)
Уравнения Лагранжа F) имеют вид:
, ._ , ,_ 1 •>/•+¦ •—\ 1
ml qr.' qr. | —— (\ ffYj I i'i' >/i ) —— T yy) / I {}")' ('ft \ ^z — Tl CC\4 f\
\ Jb Jb I U, 11 v\U U I -t, jQ//fcb 1Ш UJ J ^ L I, ШВ Ll •
A2)
Они представляют собой систему трех уравнений относительно четы-
четырех неизвестных х+, у+, ф+, I. Недостающее уравнение получается
из условия того, что удар является абсолютно неупругим. Это условие
означает, что скорость точки А после удара не имеет составляющей
вдоль оси Оу, т. е.
у+ = ц1 cos аф+. A3)
Из системы A2), A3) находим, что
, _ , Aф~ + 6cosay~) cos a
х = х 1 У = и >
2A + 3COS а)
¦ + _ 1Ф~ + ^ cos аУ~ m(l cos аф~ - 2у~)
^ ~ /A+3 cos2 а) ' ~ 2A + 3 cos2 а)
216. Случай, когда ударные импульсы возникают только
из-за наложения новых связей. Правые части уравнений F) содер-
содержат как активные ударные импульсы, так и, вообще говоря, импульсы
ударных реакций новых идеальных связей, накладываемых на систему
§ 8. Уравнения Лагранжа второго рода для импульсивных движений 463
во время удара (если, конечно, такие связи есть). Но часто в задаче об
импульсивном движении систем надо узнать лишь послеударное кине-
кинематическое состояние системы и не требуется нахождение импульсов
ударных реакций связей. Рассмотрим алгоритм Аппеля, позволяющий
получать уравнения Лагранжа импульсивного движения, не содержа-
содержащие ударные импульсы новых связей, накладываемых на систему.
Рассмотрим голономную систему с п степенями свободы. Актив-
Активные ударные импульсы отсутствуют. Удар вызывается тем, что в не-
некоторый момент времени to на систему накладывается п — к новых
идеальных связей. Эти связи могут в момент t = to +т окончания уда-
удара сохраниться, а могут и исчезнуть. Первоначально существующие
связи тоже идеальны, они существуют во время удара и после него.
Обобщенные координаты qi, G2,..., qn всегда можно выбрать так,
чтобы новые связи задавались уравнениями
qk+i = О, qk+2 = 0,..., qn = 0. A5)
Эти уравнения выполняются во время удара. В послеударном состоя-
состоянии уравнения A5) выполняются, если только вновь наложенные связи
сохраняются после удара.
Принтегрируем обе части общего уравнения динамики (см. соот-
соотношение A0) п. 137, в котором m = п) по времени от t = to до t = to +r.
Учитывая формулы E) и тот факт, что во время удара величины 5qt
можно считать не зависящими от t, а интегралы от конечных вели-
чин Ц±- пренебрежимо малы, получаем следующее равенство:
oq
= 0. A6)
Так как активных ударных импульсов нет, а первоначальные свя-
связи сохраняются во время удара, то обобщенные ударные импуль-
импульсы Ji, J2,..., Jk равны нулю, a Jk+i, Jk+2, • • •, Jn определяются толь-
только ударными реакциями новых связей.
До удара вариации 5qi, 5q2,..., 5qn произвольны. Выберем их так,
чтобы они задавали виртуальное перемещение и для системы с нало-
наложенными на нее новыми связями. В соответствие с уравнениями A5)
тогда следует считать, что Sqk+i = Sqk+2 = ... = Sqn = 0, а величины
Sqi, 8q2,..., 5qk будут произвольными. При таком выборе вариаций из
соотношений A6) следуют уравнения
464
Глава XII
т. е. справедливо следующее утверждение.
Теорема (Аппеля). Производные от кинетической энергии по обоб-
обобщенным скоростям, отвечающим обобщенным координатам, не обра-
обращающимся в нуль во время удара, не изменяются во время удара.
В уравнениях A7) qu+i = qk+2 = • • • = Чп = 0, но соответствующие
обобщенные скорости qu+i, qk+2, ¦ ¦ ¦, Qn вовсе не обязаны быть равны-
равными нулю как до удара, так и после него. Они после удара равны нулю
лишь тогда, когда вновь наложенные связи сохраняются после удара,
в этом случае к неизвестных q^, q?,..., q^ находятся из к линей-
линейных уравнений A7). В других же случаях мы имеем к уравнений A7)
относительно п неизвестных q^, q^,..., q^ и, как и в случае удара,
не являющегося абсолютно неупругим, надо вводить дополнительные
предположения о поведении системы после удара.
Пример 1. Материальная точка Р
движется в вертикальной плоскос-
плоскости над циллиндрической поверхнос-
поверхностью, образующая которой горизон-
горизонтальна; на рис. 162 изображено се-
сечение у = <р(х) этой поверхности
плоскостью z = 0, перпендикуляр-
¦~у—(Р(х) ной образующей. В некоторый мо-
момент времени точка соударяется с
поверхностью. Перед ударом вектор
ее скорости v~ = (х~, у~). Счи-
fис. 1Ь2 тая поверхность абсолютно глад-
гладкой, а удар абсолютно упругим, найдем скорость v+ = (x+, у+) точ-
точки Р после удара.
За обобщенные координаты точки примем величины
qi=x, q2=y~ (p{x).
При ударе на точку накладывается новая связь дг = 0.
Из A8) имеем
A8)
x = qi, У = <p'qi+q2, A9)
где штрихом обозначено дифференцирование по х. Следовательно,
Т = \т{х2 + у2) = \т [A + y'2)q\ + 2<p>'ql42 + q2] . B0)
Из A7) имеем уравнение
дТ_\ = (дТ_\
d) \dqij '
§ 8. Уравнения Лагранжа второго рода для импульсивных движений 465
которое при учете формулы B0) записывается в виде
A + ф'2)(д+ - q~) + p'(q+ - q~) = 0.
B1)
Недостающее уравнение следует из предположения об абсолютной уп-
упругости удара:
it = ~
Решив систему уравнений B1), B2), получим
it = ii
Отсюда и из равенств A9) находим
it =
х' =
/2
- Ф .
Х~
1 + Ф
/2*
2ф' ._
^2~У '
1+ф'
У =
„/2"
1+Ф'
B2)
B3)
B4)
Если обозначить через а угол между каса-
касательной к кривой у = ф(х) в точке соуда-
соударения и осью Ох, то ф' = tga и равенст-
равенства B4) можно записать более компактно:
х+ = cos 2ax~ + sin 2ay~,
у+ = sin 2ax~ — cos 2ay~.
Пример 2. Две материальные точки
О
х
Рис. 163
масс nil и т,2, связанные невесомой не-
нерастяжимой нитью длины I, движутся
в плоскости Оху. В некоторый момент
нить натягивается. Зная состояние движения до удара, найти пос-
послеударное кинематическое состояние точек.
Пусть Xi, yi — координаты точки массы ггц (г = 1, 2), а ф, г —
полярные координаты, определяющие положение второй точки относи-
относительно первой (рис. 163). В качестве обобщенных координат примем
величины
ЧЪ=Ф,
B5)
При ударе на систему точек накладывается связь q± = 0.
Учтя, что х^ = Xi + rcostp, У2 = У\ + rsin<?, для кинетической
энергии системы
Т = \m1<yx\+yl)+'^m2{xl+yl)
466 Глава XII
можно получить следующее выражение
Т = \(пц + m2)(q21 + ql) + \m2 [(I - q4Jql + <&-
1 l B6)
-2A- q4)q3(qi sin q3 -q2cosq3) - 2qi(q1 cos q3 +q2s'mq3)].
Введя обозначение Ащ = qf — q[ (i = 1, 2, 3, 4) и выписав уравне-
уравнения A7) для г = 1, 2, 3, получим
(mi + m2)Aqi - m2(l — </4) s'mq3Aq3 — m2 cos(/3Ag4 = 0,
(mi + m2)Aq2 +m2(l - q±) cosq3Aq3 - m2 sin^A^ = 0, B7)
s'mq3Aqi - cosq3Aq2 - (I - q4)Aq3 = 0.
Уравнения B7) представляют собой систему трех уравнений относи-
относительно четырех неизвестных qf (i = 1, 2, 3, 4). Недостающее уравне-
уравнение получим, приняв гипотезу о том, что до и послеударные величины
г~ и г+ связаны соотношением г+ = — зег~, или, на основании послед-
последнего из равенств B5), q^ = —eeq^- Это приводит к уравнению
Aq4 = -(l + is)q^. B8)
Принимая во внимание обозначения B5) и считая, что во время удара
угол (р равен а, из системы уравнений B7), B8) находим
. + •- A + зе)тг cos a ._
т1+т2 B9)
, _ A + se)m2sma _ , _
У1 У1 ' nil +т2
Глава XIII
Интегральные вариационные принципы
механики
§ 1. Принцип Гамильтона-Остроградского
217. Прямой и окольный пути голономной системы. В гл. III
мы изучали дифференциальные вариационные принципы механики, ко-
которые дают критерий, позволяющий выделить истинное (действитель-
(действительное) движение механической системы среди других кинематически
возможных ее движений для данного момента времени. В этой главе
будут рассмотрены некоторые интегральные вариационные принципы.
В отличие от дифференциальных принципов, интегральные вариацион-
вариационные принципы механики дают критерий истинного движения системы
не для одного момента времени, а для некоторого конечного промежут-
промежутка to ^.t^.ti. Они характеризуют движение системы в целом, на всем
этом промежутке времени.
Как и в гл. III, будем предполагать, что рассматриваемая ме-
механическая система или свободна, или подчинена идеальным удер-
удерживающим связям, но ограничимся только голономными система-
системами1. Пусть а„ и Ь„ — возможные положения точки Р„ системы
[у = 1, 2, ... , N) в моменты времени t = to и t = t\ соответствен-
соответственно. Положение системы в момент t = to назовем ее начальным, а в
момент t = t\ — конечным положениями. Предположим, что в мо-
момент t = to можно так выбрать скорости точек системы, что при t = ti
точки Р„ займут их конечные положения. Совокупность траекторий,
которые будут описаны точками системы при их перемещении из на-
начальных положений а„ в их конечные положения Ь„, образуют истин-
истинный (действительный) путь системы. Его также называют прямым пу-
путем системы.
На прямом пути точка Р„ системы описывает кривую jv, соединя-
соединяющую точки а„ и &„. Совокупность соединяющих точки а„ и &„ кри-
кривых Yv, бесконечно близких к соответствующим кривым jv и таких,
1 Вопрос о применимости интегральных вариационных принципов механики к не-
голономным системам имеет длительную и непростую историю. Библиографию по
этому вопросу и основные результаты см. в статье: Румянцев В. В. Об интегральных
принципах для неголономных систем // ПММ, 1982, Т. 46, вып. 1, С. 3-12.
468
Глава XIII
что движение точки Pv по кривой Yv (v = 1, 2, ... , N) может про-
происходить без нарушения связей, называют окольным путем системы.
На рис. 164 сплошная линия соответствует прямому пути, а штрихо-
штриховые — окольным. Всюду в дальнейшем будем считать, что движение
всех точек Р„ по окольным путям начинается одновременно при t = to
и оканчивается при t = t\, т. е. движение системы по окольному пути
начинается и оканчивается в те же моменты времени, что и движение
но прямому пути.
t
Рис. 164
Рис. 165
Для голономной системы прямые и окольные пути удобно пред-
представлять в расширенном координатном пространстве, где координата-
координатами являются обобщенные координаты qi, q2, . . . , qn и время t. Пусть
точка Ао этого пространства отвечает начальному положению систе-
системы, a Ai — ее конечному положению. Движениям системы из ее на-
начального положения в конечное будут отвечать кривые, соединяющие
точки Ао и А\. На рис. 165 (для п = 2) сплошной линией показан прямой
путь системы, а штриховыми линиями — окольные пути. В расширен-
расширенном координатном пространстве за окольный путь может быть принята
любая бесконечно близкая к прямому пути кривая, соединяющая точ-
точки Ао и Aii любая такая кривая представляет собой кинематически
возможный путь, так как обобщенные координаты gi, G2, ... , qn всег-
всегда выбираются именно так, что геометрические связи, наложенные на
систему, удовлетворяются тождественно (п. 14), а других связей у го-
голономной системы нет.
Отметим, что задача о построении прямого пути, соединяющего
начальную и конечную точки Ао и А\, не является простой. Она при-
приводит к рассмотрению краевой задачи для системы дифференциальных
уравнений порядка 2п, описывающей движение изучаемой механичес-
механической системы. Если точка Ао соответствует значениям обобщенных ко-
координат </°, </°, • • • , 9°, а точка А\ — значениям q\, q\,... , q^, то ре-
§ 1. Принцип Гамилътона-Остроградского 469
шение qiit) дифференциальных уравнений движения должно удовлетво-
удовлетворять краевым условиям
qt(to) = Qi, qi(h) = q\ (* = 1, 2, ... , n).
Краевая задача может иметь единственное решение, а может не иметь
ни одного решения; она может иметь несколько или даже бесконечное
множество решений.
Если точки Aq и А\ достаточно близки, то решение упомянутой
задачи либо единственно, либо она имеет только конечное число реше-
решений. Для наших целей второй случай сводится к первому в том смысле,
что среди конечного числа прямых путей можно взять какой-то один
и рассмотреть его окрестность, достаточно малую, чтобы она не содер-
содержала точек других прямых путей, отвечающих значениям t из интер-
интервала to <t<t\. Окольные пути затем следует проводить именно в этой
малой окрестности выбранного прямого пути.
При достаточном удалении точки А\ от точки Ао может оказать-
оказаться, что краевая задача имеет решения, соответствующие бесконечно
близким прямым путям, проходимым механической системой за од-
одно и то же время ti — t0. В этом случае точки Ао и А\ расширенного
координатного пространства называют сопряженными кинетическими
фокусами.
Рассмотрим, например, одномерный гармонический осциллятор,
движение которого описывается дифференциальным уравнением
Через точки @, 0) и @, тг) расширенного координатного пространст-
пространства <7, t проходят бесконечно близкие один к другому прямые пути, за-
задаваемые равенством
q = csini,
где с — произвольная постоянная. Точки @, 0) и @, тг) — сопря-
сопряженные кинетические фокусы. Напротив, через точки @, 0) и (q1, t\)
при q1 > 0, ti < тг можно провести только один прямой путь.
Мы будем рассматривать не вполне произвольные окольные пути,
а те из них, которые получаются из прямого пути при помощи синхрон-
синхронного варьирования.
Пусть gv — положение, которое занимает в момент времени t точка Р„
системы при ее движении по прямому пути jv, соединяющему началь-
начальное и конечное положения а„ и &„ этой точки (рис. 166). В момент
времени t дадим точке Р„ произвольное виртуальное перемещение 8rv
из ее положения gv. Тогда точка Pv займет положение g^. Если эту
470
Глава XIII
процедуру проделать для всех положений gv точки Р„ на кривой jv
при to < t < t\ и через получающиеся при варьировании точки g[,
провести кривую, соединяющую положения а„ и Ь„, то эта кривая и
будет окольным путем. Соответствующие одна другой точки gv и g[,
на прямом и окольном путях проходятся в одни и те же моменты
времени. В декартовых координатах положение точки Р„ на прямом
пути задается радиусом-вектором rv(t), а на окольном — радиусом-
вектором rv(t)+Srv(t), где вектор-функции 5rv(t) удовлетворяют усло-
условию Srv(t0) = 0, 8rv(ti) = 0, (v = 1, 2, ... , N). Кроме того, будем пред-
предполагать, что 5rv(t) — дважды непрерывно дифференцируемая функ-
функция.
Нам потребуется сравнить между со-
собой не только прямой и окольный пути,
но и скорости г„ точек Р„ на прямом
пути с соответствующими их скоростя-
скоростями г„ + 8г„ на окольном пути для одно-
одного и того же момента времени. Покажем,
что операции синхронного варьирования и
дифференцирования по времени переста-
перестановочны, т. е.
Рис. 166
d
Ат> — —Ат>
6 v ~ dt6 v
(i/ = l, 2, ...,N).
В самом деле, по определению скорости, на окольном пути имеем
A)
Srv = j-t{
(v = 1, 2, ... , N),
откуда и следует равенство A). Аналогично, если в расширенном коор-
координатном пространстве прямой путь задается уравнениями
<ft = qi(t), <й(*о) = ??, qi(h) =q\ (* = 1, 2
, n),
B)
то окольные пути получаются из прямого при помощи виртуальных
перемещений 5qi(t) и задаются уравнениями
Ф = qi(t) + 5qi(t) (i = 1,2, ... , и),
где
Sqi(to)=0, Sqi(h)=O
(* = 1, 2, ... ,n).
C)
D)
Величины Sqi(t) предполагаются дважды непрерывно дифференцируе-
дифференцируемыми функциями /:. Они удовлетворяют равенствам, аналогичным A):
г = 1, 2, ...,
E)
§ 1. Принцип Гамильтона-Остроградского 471
218. Принцип Гамильтона—Остроградского. Итак, рассмот-
рассмотрим прямой путь голономнои системы и совокупность окольных путей,
получающихся из прямого пути при помощи синхронного варьирования
и совпадающих с ним в начальный и конечный моменты времени ?0 и t\.
Пусть т„ — масса точки Pv, a Fv — равнодействующая всех актив-
активных сил, приложенных к этой точке. Интегрирование общего уравнения
динамики
N
- mvwv) -5rv = 0 F)
дает равенство
JV JV
/ ^^ Fv ' Srv dt - ^^ mv I wv ' Srv dt = 0.
G)
Рассмотрим разность между значениями кинетической энергии систе-
системы в момент времени t на окольном и прямом путях
JV JV
IVm (r +,irJ-lVm r2
л / J г/ \l v \ " ' и) л / j ulv 11/ ¦
С точностью до величин первого порядка малости включительно отно-
относительно \8rv\ для этой разности получаем выражение
N
ST = ^^ mvrv • 5rv.
v=l
Отсюда
/ ST dt = 'Y^mv I tv- 8rv dt. (8)
/ v=\ •
to t0
Используя равенство A) и производя интегрирование по частям, пре-
преобразуем это соотношение к виду
N г N
JV
dt.
5T dt = ^2 тп„ rv ¦ dbrv = ^2 mv^v ¦ Srv - ^ mv \ wv ¦ 5rv
I v=1 to v=1 to »=1 I
Но так как 5rv(to) = 8rv(ti) = 0, то окончательно имеем
dt. (9)
<i jv
/ ST dt = - V mv I wv • 8rv
to to
472 Глава XIII
Это соотношение позволяет переписать равенство G) в следующем
окончательном виде:
dt = O. A0)
Равенство A0) является математическим выражением принципа
Гамильтона-Остроградского, который заключается в том, что
интеграл A0) равен нулю, если величины 8rv(t) соответствуют син-
синхронному варьированию прямого пути и 8rv(to) = 8rv(t\) = 0.
Таким образом, на прямом пути голономной системы интеграл A0)
равен нулю. Покажем, что, наоборот, если на каком-то кинематически
возможном пути интеграл A0) равен нулю, то этот путь — прямой.
Для этого достаточно убедиться в том, что из принципа Гамильтона-
Остроградского A0) вытекают уравнения Лагранжа второго рода.
Замечая, что
N N
^2 Fv ¦ 8rv = ^2 QiSqi,
v=l i=\
где Qi — обобщенная сила, соответствующая обобщенной координа-
координате <ft,и что
перепишем равенство A0) в виде
to l
Используя соотношения E), интегрируя по частям и учитывая,
что 8qi(t0) = Sqi(ti) = 0, имеем
1 dS* = ** ifM^dt = } i^8qidt.
to J dt dq{ J dt dqt
to to to to
Поэтому равенство A1) переходит в следующее:
§ 1. Принцип Гамилътона-Остроградского 473
Величины 5qt (г = 1, 2, ... , п) независимы и произвольны. Используя
это, покажем, что каждое из выражений в круглых скобках в форму-
формуле A2) равно нулю. Для этого положим, что 5qi = ... = 8qu-i = <5<ft+i =
= ... = 5qn = 0, a 5qk ф 0. Тогда равенство A2) сводится к равенству
/ | d дТ _ дТ _
Пусть1 выражение в круглых скобках в формуле A3) не равно
нулю при t = t* из интервала to < t < t\. Тогда в силу непре-
непрерывности существует окрестность — е + ?» < t < t* + e, лежащая в ин-
интервале to < t < ti, в которой круглая скобка из A3) сохраняет знак.
Произвольную функцию 8qu{t) выберем так, чтобы она вне окрестнос-
окрестности —е + t* < t < t* + г была равна нулю, а в самой этой окрестности
сохраняла знак. Тогда равенство A3) перепишется в виде
л /
U-e
Но так как при упомянутом выборе функции 8qk(t) подынтегральное
выражение сохраняет знак в окрестности — е + ?* < t < ?» + е, то по-
последнее равенство невозможно. Отсюда следует, что при всех t из ин-
интервала to < t < ti
d дТ дТ =q
dt dqk dqk k'
Проведенные рассуждения справедливы для любого к (к = 1, 2,... ,п).
Поэтому из принципа Гамильтона — Остроградского следуют уравне-
уравнения Лагранжа второго рода. Следовательно, этот принцип может быть
положен в основу динамики голономных систем.
219. Принцип Гамильтона—Остроградского для систем в
потенциальном поле сил. В потенциальном поле сил
N
^ Fv ¦ Srv = -m, A4)
1 Приводимое далее доказательство обращения в нуль выражения в круглых скоб-
скобках формулы A3) является стандартным. Оно лежит в основе доказательства так
называемой основной леммы вариационного исчисления (см. лемму 1 в §3 учебника:
Гельфанд И. М., Фомин С. В. Вариационное исчисление, М. : Физматгиз, 1961).
474 Глава XIII
где П = П (gi, ... , qn, t) — потенциальная энергия системы. Тогда фор-
формула A0) дает
- <Ш) dt = 0.
to
Так как функция Лагранжа имеет вид L = Т — П, то отсюда следует,
что
11
/¦
SLdt = O. A5)
to
Рассмотрим интеграл
5= Ldt. A6)
to
Этот интеграл называется действием по Гамильтону. Так как L —
функция qi, qi, t, то для вычисления величины S нужно задать функ-
функции qi(t) (г = 1, 2, ... , п) в промежутке to ^ t ^ ii, т. е. действие 5
является функционалом, зависящим от движения системы.
Используя обозначение A6) и учитывая неизменность to и t\ при
переходе от прямого пути к окольному и от окольного пути к другому
окольному, перепишем равенство A5) в виде
SS = 0. A7)
Это равенство выражает принцип Гамильтона-Остроград-
ского для голономной системы в случае существова-
существования потенциала сил: среди всех (сравниваемых) путей прямой
путь выделяется тем, что для него действие по Гамильтону имеет
стационарное значение (т. е. первая вариация 5S на прямом пути равна
нулю).
Будет ли действие принимать экстремальное значение на прямом
пути, т. е. будет ли значение интеграла A6), вычисленное на прямом
пути, наименьшим или наибольшим по сравнению с его значениями
на окольных путях? Ответ на этот вопрос будет получен в следующем
пункте, а сейчас рассмотрим пример, показывающий, что в некоторых
случаях действие по Гамильтону на прямом пути имеет меньшее зна-
значение, нежели на окольном.
§ 1. Принцип Гамильтона-Остроградского
475
Пример 1 (Движение материальной точки в однородном поле тя-
тяжести1). Пусть материальная точка массой т брошена под углом а
к горизонту с начальной скоростью v0. Пусть движение происходит в
плоскости Oxz. Траекторией точки будет парабола
1 ¦>
z = Vq sin at — ±gt , x = Vq cos at.
В момент времени
h =
sin a
g
A8)
A9)
где g — ускорение свободного паде-
падения, материальная точка пересечет
ось Ох в точке В (рис. 167), при-
причем пройденное ею расстояние вдоль
оси Ох
OB =
B0)
Рис. 167
Таким образом, в рассматриваемом
примере на прямом пути точка описывает в плоскости Oxz парабо-
параболу за время t\.
Это движение будем сравнивать с прямолинейным равномерным
движением точки из положения О в положение В. Окольный путь будет
отрезком ОВ оси Ох. Так как в принципе Гамильтона-Остроградского
время движения из начального положения системы в ее конечное по-
положение для прямого и окольного путей должно быть одинаковым, то
в рассматриваемом равномерном прямолинейном движении скорость v
должна быть равна «о cos a.
Для обоих движений
П = mgz.
Для параболического движения
Ь = Т -П = |т(ж2 +z2) -mgz = hm{vl - 4w0 sinagt
для прямолинейного движения
L = Т — П = yinv2 = -^rnvg cos2 a.
B1)
'См.: СлудскийФ. А. Заметка о начале наименьшего действия // Вариационные
принципы механики/Под ред. Л. С. Полака, М.; Физматгиз, 1959. С. 388-391.
476 Глава XIII
Для параболического движения
с f т ,и rnv^sina / 4 • 2 \ /oo^
S = / Lot = ^ A - ^ sin а ) , B2)
о
а для движения по прямой
5= ^ (l-sin2a). B3)
О
Лри любом а (в том числе и при достаточно малых а, когда прямой и
окольные пути могут быть сколь угодно близкими) величина B2) мень-
меньше величины B3), т. е. действие по Гамильтону на прямом пути мень-
меньше, чем на окольном.
220. Экстремальное свойство действия по Гамильтону. Рас-
Рассмотрим окрестность начального положения системы, достаточно ма-
малую, чтобы в ней отсутствовали сопряженные кинетические фокусы.
Тогда можно считать (п. 217), что за заданное время ti — to система
может перейти из своего начального положения в конечное положение,
расположенное в выбранной окрестности, только по одному прямому
пути. Покажем, что в этом случае действие по Гамильтону на прямом
пути будет наименьшим по сравнению с его значениями на окольных
путях системы.
Для доказательства воспользуемся гео-
геометрическим методом Жуковского1. Тра-
Траектории точек Р„ (v = 1,2,..., N) сис-
системы будем рассматривать в трехмерном
евклидовом пространстве. Пусть av — на-
начальное положение точки Pv, a fv и cv — ее
положения на каких-либо двух различных
кинематически возможных путях, по кото-
которым система за одно и то же время t — to
р ..„„ переходит из начального положения в по-
положение, отвечающее моменту времени t
(рис. 168). При этом to < t < t\, а промежуток времени t — to, во-
вообще говоря, мал, чтобы за время t — t0 система не могла выйти из
выбранной малой окрестности ее начального положения.
Пусть [af] и [ас] — действия по Гамильтону на этих путях системы,
хСм.: Жуковский Н. Е. О начале наименьшего действия // Собр. соч. Т. 1. М.; Л.:
Гостехизат,1948. С. 51-57.
т. е.
! 1. Принцип Гамилътона-Остроградского 477
t t
[af] = f(T-TL) dt, [ас] = Г(Т - П) dt, B4)
to to
причем первый и второй интегралы вычисляются на путях, по которым
точки Р„ переходят из положений а„ в положения fv и с„ соответствен-
соответственно. Для разности [ас] — [af] с точностью до величин первого порядка
включительно относительно \5rv\ и \8rv\ имеем выражение
[ас] - [af] = / V (mvvv ¦ 5rv - |2- • Srv ) dt,
f u=l V °rv '
to
где vv и dU/drv вычисляются на пути avfv. Учитывая, что
Fv = —dU/drv, интегрируя по частям и пользуясь тем, что 8rv(t0) = О,
имеем
JV * JV
[ас] - [af] = ^^ mvvv(t) ¦ 5rv(t) + / ^(-FV - mvwv) ¦ Srv dt.
Учитывая общее уравнение динамики F), это соотношение можно пе-
переписать окончательно в таком виде:
JV
[ас] - [af] = ^2lmvvv cos av8sv. B5)
v=\
Здесь vv — скорость точки Pv в момент времени t, когда она занимает
положение /„, av — угол между vv и 5rv, a 8sv — длина дуги fvcv.
Пусть bv — положение точки Pv, в конечный момент времени ti
движения системы, a jv и jl — кривые, по которым перемещается точ-
точка Р„ при движении системы соответственно по прямому и любому из
окольных путей (рис. 169). Сравним действие по Гамильтону на прямом
и окольном путях. Для этого возьмем на пути Yv точку с„, отвечаю-
отвечающую моменту времени t, где to < t < t\, а также бесконечно близкую
ей точку е„, отвечающую моменту t + dt. Проведем траектории avcv
для некоторого вспомогательного действительного движения точек Pv,
при котором они за время t — to приходят из начальных положений av в
их положения с„, расположенные на кривой jl, отвечающей окольному
пути. Аналогично, пусть кривые avcv будут траекториями еще одного
вспомогательного движения, при котором точки Р„ за время t + dt — t0
приходят из положений а„ в положения е„ на кривой Yv. И вообще про-
проведем траектории таких вспомогательных действительных движений
для всех положений точек Р„ на кривой jl (v = 1, 2, ... , N).
478
Глава XIII
ev
Пусть fv — положение, которое занимает
точка Р„ в момент времени t при ее движе-
движении по вспомогательной действительной траек-
траектории avev. Таким образом, дуги avfv и avcv
двух вспомогательных действительных траекто-
траекторий и дуга avcv, являющаяся частью кривой j'v,
отвечающей окольному пути, проходятся точ-
точкой Pv за одно и то же время t — to- Поэтому
дуга fvev на вспомогательной траектории и ду-
дуга cvev кривой jl проходятся также за одинако-
одинаковое время, причем это время равно dt.
Обозначим длины дуг /„е„ и cvev соответ-
соответственно dav и dlv. Из бесконечно малого тре-
треугольника cvfvev (рис. 169) получим
dlf, = da2, + 5s2, — 2d(j1/8sv
Рис. 169
Умножим обе части этого равенства на mv и просуммируем по всем
точкам системы. Замечая затем, что по предположению в рассматри-
рассматриваемой малой окрестности начального положения системы кинетичес-
кинетических фокусов нет и, следовательно, среди величин 8sv (v = 1, 2, ... , N)
хотя бы одна отлична от нуля, получаем неравенство
N
N N
у mvdcrv — 2 у mvd(iv cos av8sv.
B6)
Если X" — кинетическая энергия системы при ее движении по околь-
окольному пути, а Т — кинетическая энергия системы при движении ее
точек Р„ по дугам fvev, отвечающим вспомогательному действитель-
действительному движению, то
N
N
ll = 2T'dt
'dt2
= 2Tdt2.
B7)
Так как davjdt = vv, то, используя формулы B7), неравенство B6)
можно написать в виде
N
Т' dt > Т dt —
vVv cos av8sv.
B8)
Вычтем из обеих частей величину Ildt и воспользуемся равенст-
равенством B5). Получим
(Г' - Il)dt > (Т - n)dt + [af] - [ас].
B9)
§ 1. Принцип Гамилыпона-Остроградского 479
Так как
(Т - П) dt = [fe], [fe] + [af] - [ас] = [ae] -[ас],
то правая часть неравенства B9) равна дифференциалу dS действия
по Гамильтону при переходе от одной действительной траектории к
другой, когда время движения увеличивается на dt. Поэтому
(Г' -U)dt> dS. C0)
Интегрируя это неравенство от t = to до t = t\ и вводя обозначения Snv
и S0K для действия по Гамильтону на прямом и окольном путях систе-
системы, получим
Sm > Snv. C1)
Таким образом показано, что если начальное и конечное положения
системы достаточно близки, то действие по Гамильтону на прямом
пути имеет минимальное значение по сравнению с его значениями на
окольных путях, проходимых за то же время1.
Пусть точки Ао и А\ расширенного ко-
координатного пространства отвечают на-
начальному и конечному положениям сис-
системы (рис. 165). Если точки Ао и А\ до-
достаточно близки, то действие S на прямом
пути имеет минимум. Выясним, насколь-
насколько близкими должны быть точки Ао и А\,
чтобы на прямом пути действие оста-
валось минимальным2. На прямом пу-
пути AqAi первая вариация 5S действия по Гамильтону всегда равна
нулю. Если точка А\ близка к точке Ао, то в силу минимальности
действия вторая вариация 52S на прямом пути положительна3. Будем
удалять точку А\ от точки Ао.
Пусть t\ — то значение t\, при котором вариация S2S, вычисленная
на окольном пути A0HAi, в первый раз обращается в нуль (рис. 170).
Следовательно, действия по Гамильтону на путях A0HAi и A0BAi рав-
равны с точностью до членов второго порядка включительно относительно
величин \5qi\, \5qi\ (г = 1, 2, ... , п):
Sa0HA! = SA0BAf C2)
1По этой причине принцип Гамильтона-Остроградского часто называют принци-
принципом наименьшего действия.
2См. шестую лекцию в книге: Якоби К. Лекции по динамике. М.;Л.: ОНТИ, 1936,
а также гл. 12 книги: Лурье А. И. Аналитическая механика. М.: Физматгиз, 1960.
3Мы не рассматриваем те исключительные случаи, когда вопрос об экстремаль-
экстремальности 5 решается с привлечением вариаций более высокого порядка.
480 Глава XIII
Покажем, что на самом деле A0HAi — прямой путь, т. е. Ао и А\ —
сопряженные кинетические фокусы. Предположим, что это не так, т. е.
что путь AqHAi не является прямым. Тогда возьмем на нем точки С
и D и соединим их прямым путем CED. По доказанному выше для
достаточно близких точек С и D
ScED < ScHD- C3)
Отсюда и из C2) следует, что
C4)
Это неравенство противоречит предположению о том, что А\ есть пер-
первое положение на прямом пути A0BAi, при котором вторая вариа-
вариация 82S обращается в нуль при надлежащем выборе окольного пути,
проходящего через Ао и А\.
Проведенное рассуждение показывает, что если конечная точка А\
лежит перед кинетическим фокусом, сопряженным с начальной точ-
точкой Aq, то действие по Гамильтону на прямом пути A0Ai имеет ми-
минимум.
Пусть теперь А\ — сопряженный кинетический фокус для точ-
точки Ао, а конечная точка прямого пути F лежит за точкой А\ (рис. 170).
Здесь уже действие на прямом пути AqBAiF не будет минимальным.
Для доказательства укажем такой окольный путь, на котором действие
по Гамильтону меньше, чем на пути A0BA\F. Для этого на ранее по-
построенном прямом пути A0HAi возьмем точку G, настолько близкую
к F, чтобы действие на соединяющем эти точки прямом пути GKF
было минимальным. Тогда
Sgkf < Sga! + SAtF- C5)
Отсюда и из C2) получаем
= Saohg + Sgkf < Saohg
+ SAtF
т. е. действие на построенном окольном пути меньше, чем на прямом.
Поэтому действие на прямом пути не имеет минимума. Оно не может
иметь и максимума, так как на малых участках прямого пути A0BAiF
действие минимально. Таким образом, если фокус, сопряженный с на-
начальной точкой, лежит перед конечной точкой прямого пути, то дейст-
действие по Гамильтону не имеет на прямом пути ни минимума, ни макси-
максимума.
§ 1. Принцип Гамильтона-Остроградского 481
Пример 1 (Движение материальной точки по инерции на сфере).
Пусть точка движется, оставаясь все время на неподвижной сфере и
никакие активные силы на точку не действуют. Если т — масса точ-
точки, a R — радиус сферы, то в сферических координатах (рис. 134)
Т =^mR2(в2 + sin2 вф2), П = 0.
Li
На прямом пути выполняются уравнения Лагранжа
AdL_dL -о 9L -
at QQ об оф
((р — циклическая координата). Так как L = Т — П = Т, то отсюда
следует, что
2 = 0, sin2 вф = sin2 <9o<^o• C6)
Без ограничения общности можно считать, что на прямом пути век-
вектор v начальной скорости точки направлен по меридиану (<р = const),
т. е. фо = 0. Тогда из C6) следует, что во все время движения
ф = 0, в = const
и, следовательно, v2 = Д2^2 = const. Это означает, что прямой путь
представляет собой дугу большого круга, по которой точка движется с
постоянной скоростью v = vnv. При этом
L = =rmv2
*1 о 19
/пи)„ т1„„
Ldt=-r-^-to)=2(tl-toy C7)
to
где lnv — длина дуги, пройденной точкой на прямом пути за вре-
время t\ — to-
Кинетическим фокусом, сопряженным с произвольной начальной
точкой А, является диаметрально противоположная точка А* на сфе-
сфере, так как два больших круга, проходящих через А, пересекаются толь-
только в А*.
Пусть скорость движения по окольному пути, соединяющему две
точки А и В, постоянна и равна v0K. Тогда
SoK = W^i)' C8)
482 Глава XIII
Из C7), C8) и рассмотренного выше экстремального свойства дейст-
действия по Гамильтону следует, что проходящая через А и В дуга большо-
большого круга является кратчайшей среди кривых, соединяющих А и В, если
точка А* не лежит на этой дуге, т. е. если дуга меньше половины
окружности большого круга.
Упражнение 1. В примере п. 217 построить окольный путь, на котором
действие по Гамильтону меньше, чем на прямом пути.
§ 2. Принцип Мопертюи-Лагранжа
221. Изоэнергетическое варьирование. Рассмотрим голоном-
ную консервативную или обобщенно консервативную систему. Ее
функция Гамильтона не зависит от времени, и существует обобщенный
интеграл энергии
H(qx, ... ,qn, рх, ... , р„) = h. A)
Движение системы будем представлять в n-мерном координатном про-
пространстве gi, ... , qn 1. Пусть Aq и А\ — точки этого пространства, за-
задаваемые соответственно координатами q® и q] (г = 1, 2, ... , п). Пусть
в начальный момент времени t = to система занимает положение, отве-
отвечающее точке Ао, и обобщенные скорости д, (а, следовательно, и обоб-
обобщенные импульсы р^ могут быть выбраны так, что при t = t\ система
займет положение, отвечающее точке А\. Проходящую через точки Aq
и Ах кривую
qi = qi(t) (t = l, 2, ... , n), B)
вдоль которой удовлетворяются дифференциальные уравнения движе-
движения, назовем прямым путем системы (см. рис. 171, где п = 3). На пря-
прямом пути функция Гамильтона постоянна и равна h, где величина h
определяется начальными условиями.
Наряду с прямым путем рассмотрим другие кинематически воз-
возможные пути, бесконечно близкие к прямому. Эти пути будем называть
окольными путями, если они: 1) проходят через одни и те же начальные
и конечные положения Ао и Ах; 2) вдоль каждого окольного пути функ-
функция Гамильтона постоянна и равна величине h, отвечающей прямому
пути.
1А не в расширенном (п + 1)-мерном координатном пространстве, как это было
при изучения принципа Гамильтона-Остроградского в предыдущем параграфе.
§ 2. Принцип Мопертюи-Лагранжа
483
При таком изоэнергетическом варьиро-
варьировании время t\ — to перехода системы из
начального положения в конечное не обя-
обязательно одинаково для прямого и околь-
окольных путей. Пусть, например, материальная
точка массой т движется в отсутствие сил
в плоскости Оху. За движение по прямо-
прямому пути примем прямолинейное движение
вдоль оси Ох. В начальный момент време-
времени t = 0 точка находится в начале коорди-
нат О. Тогда на прямом пути х = у —t. Из
интеграла энергии Щ(х2 + у2) = h следует,
Рис. 171
tjt. Следователь-
lib
что на окольном пути выполняется неравенство х
но, по окольному пути невозможно прийти за одинаковое время t\ в то
же положение, что и на прямом пути, если постоянная h одинакова для
прямого и окольного путей.
Рассматриваемый в этом параграфе принцип Мопертюи-Лагранжа
дает критерий, позволяющий выделить прямой путь среди всех околь-
окольных, удовлетворяющих упомянутым выше свойствам 1 и 2.
222. Принцип Мопертюи—Лагранжа. При заданной константе
энергии h уравнения движения консервативной или обобщенно консер-
консервативной системы могут быть записаны в форме уравнений Якоби (см.
уравнения C6) п. 152). Эти уравнения имеют форму уравнений Ла-
Лагранжа второго рода, где в качестве функции Лагранжа L выступает
функция Якоби Р, а роль независимой переменной играет обобщенная
координата q\. По аналогии с действием S по Гамильтону введем1 дей-
действие по Лагранжу:
9l
W = / Pdqi.
C)
В предыдущем параграфе показано, что уравнения Лагранжа второ-
второго рода эквивалентны принципу Гамильтона-Остроградского, выража-
выражающемуся в стационарности действия по Гамильтону на прямом пути
системы (см. равенство A7) п. 219). Аналогично, уравнения Якоби эк-
1См. §20 книги: ГантмахерФ. Р. Лекции по аналитической механике. М.: Наука,
1966.
484 Глава XIII
вивалентны условию стационарности действия по Лагранжу
SW = 0. D)
Равенство D) выражает принцип Мопертюи-Лагранжа, за-
заключающийся в том, что среди всех кинематически возможных путей,
удовлетворяющих условиям, описанным в предыдущем пункте, прямой
путь выделяется тем, что для него действие по Лагранжу имеет ста-
стационарное значение.
Вопрос об экстремальных свойствах действия по Лагранжу реша-
решается точно так же, как и для принципа Гамильтона-Остроградского при
помощи рассмотрения сопряженных кинетических фокусов.
Отметим, что в интеграле C) полностью исключено время, и прин-
принцип D) содержит только геометрические элементы. В такой форме
принцип Мопертюи-Лагранжа впервые был представлен Якоби. Поэто-
Поэтому приведенную выше формулировку принципа Мопертюи-Лагранжа
часто называют принципом наименьшего действия Якоби.
Пусть система консервативна. Тогда функция Якоби Р вычисля-
вычисляется по формуле C8) п. 152 и действие по Лагранжу может быть пре-
преобразовано к виду
«1 *i
= I W-dqx = I'
W = I W-dqx = I2Tdt. E)
При применении принципа Мопертюи-Лагранжа в форме D), E) сле-
следует помнить, что в E) время ti не фиксируется, а может изменяться
при переходе от прямого пути к окольному и от одного окольного пути
к другому окольному. Кроме того, полная энергия Т + П одна и та же
на всех сравниваемых путях.
Выражение E) для действия по Лагранжу можно записать иначе:
Ч N N у
W = I \ m it2 fit = \ I m it Gs l(\\
to "~ "~ s0,
т. е. для консервативной системы действие по Лагранжу равно сумме
работ количеств движения точек системы на соответствующих их
перемещениях.
Пример 1 (Движение материальной точки по инерции на гладкой
ПОВЕРХНОСТИ1). Пусть материальная точка массой т движется по
гладкой неподвижной поверхности под влиянием начального толчка в
хСм. упомянутую книгу К. Якоби «Лекции по динамике».
§ 2. Принцип Мопертюи-Лагранжа 485
отсутствие поля сил (П = 0). Тогда v = vo = const и из F) получаем,
что
W = mvol,
где I — пройденный точкой путь. Из принципа Якоби следует, что
81 = 0, т. е. движение точки на поверхности происходит по геодези-
геодезической кривой1.
Если начальная и конечная точки Aq и А\ близки одна к другой, то
действие W минимально и геодезическая является кратчайшей кривой,
лежащей на поверхности и соединяющей точки Aq и А\.
Вопрос о минимальности действия решается в каждом конкрет-
конкретном случае при помощи привлечения кинетических фокусов. Если точ-
точка движется по развертывающейся поверхности (т. е. по поверхности,
которую после изгибания можно наложить на плоскость), например по
конусу или цилиндру, то действие W на прямом пути обязательно бу-
будет минимальным, так как на плоскости прямые, проходящие через
одну и ту же точку, никогда вновь не пересекаются (и, следовательно,
кинетические фокусы отсутствуют).
Пример 2 (Движение материальной точки в однородном поле тя-
тяжести2). Эта задача была рассмотрена в п. 219 для иллюстрация
принципа Гамилътона-Остроградского. Здесь мы ее применяем для ил-
иллюстрации принципа Мопертюи-Лагранжа, что поможет яснее пред-
представить разницу между этими принципами.
Прямой путь представляет собой параболу, задаваемую уравнени-
уравнением A8) п. 219. За окольный путь опять примем отрезок ОВ, лежащий
на оси Ох (рис. 167). Угол а считаем малым, так что прямой и околь-
окольный пути близки один к другому. Для обоих движений П = mgz.
Так как полная механическая энергия Т + П должна быть одинако-
одинаковой для прямого и окольного путей, то начальные скорости точки для
обоих движений одинаковы и равны vq. Но если на прямом пути время t\
движения точки определяется равенством A9) п. 219, то для окольного
пути оно будет иным и вычисляется по формуле
_ OB _ 2vosinacosa
fi ~ -щ- - g ¦ G)
Для параболического движения
Т = цгп(х + z ) = 7jTn(v0 — 2г>о sin agt + g^t ),
1 Геодезическая кривая характеризуется тем, что ее длина имеет стационарное
значение по сравнению с длинами других кривых, имеющих с геодезической одни
и те же концы.
2См. упомянутую работу Ф. В. Слудского «Заметка о начале наименьшего дейст-
действия».
486 Глава XIII
а для прямолинейного движения
Т = \mvl-
Действие по Лагранжу для движения по параболе
о
а для движения по прямой
2mv?.sma
zrnvn sin a ^rnv^sina / ~^
W = j} cos a = j} V1 — sin a =
(9)
A — ~ sin2 a — -q sin4 a — ...),
2itiVq sin a
g
где многоточием обозначены члены выше четвертой степени относи-
относительно sin а.
При достаточно малых значениях а величина (8) меньше величи-
величины (9), т. е. действие по Лагранжу на прямом пути меньше, чем на
окольном.
223. Принцип Якоби и геодезические линии в координат-
координатном пространстве. Рассмотрим консервативную систему с п степе-
степенями свободы. Ее кинетическая энергия — определенно положительная
квадратичная форма обобщенных скоростей
п
Т = ;г / Ягй((/1} • • • j Qn) Qi Qk- (Ю)
i,k=l
Пусть Р и Р' — две близкие точки координатного пространст-
пространства q-\_, ... , qn, задаваемые наборами координат qi, ... , qn и
<7i + dqi,... ,qn + dqn. Введем в координатном пространстве метрику,
определив квадрат расстояния ds2 между точками Р и Р' при помощи
удвоенной кинетической энергии
п
ds2 = 2Tdt2 = ^ aik(qi, ¦ ¦. , qn) dqi dqk. A1)
i,k=l
Отсюда следует, что
A2)
§ 2. Принцип Мопертюи-Лагранжа 487
т. е. в метрике A1) кинетическая энергия системы равна кинетичес-
кинетической энергии изображающей точки в координатном пространстве1, если
считать, что изображающая точка обладает массой, равной единице.
Пусть система движется по инерции, т. е. П = 0. Из интеграла
энергии Т + П = h = const и формулы A2) тогда следует, что
g A3)
т. е. в метрике A1) движению консервативной системы по инерции
отвечает равномерное движение изображающей точки в координатном
пространстве, причем скорость ее движения равна \f2~h.
Для этого движения действие по Лагранжу
W =
= 2 [Tdt = 2h(t1-t0) = V2hl, A4)
где I = \[2~h{t\ — to) — длина кривой, пройденной изображающей точкой
за время t\ —to- Из принципа Якоби следует, что 81 = 0, т. е. задача
о нахождении траектории свелась к задаче дифференциальной геомет-
геометрии о нахождении геодезической линии в координатном пространстве
с метрикой A1).
Пусть теперь движение системы происходит в потенциальном поле
(П ф 0). Тогда функция Якоби Р может быть вычислена по форму-
формуле D0) п. 152. Поэтому
ч\
W =
= f Pdq1=2 f y/(h - U)Gdqi = \/2 f
„0 „0 „0 \
(h
-П)
i
п
к=1
dqi dqk-
A5)
Область возможности движения в координатном пространстве опреде-
определяется неравенством П ^ h, которое получается из интеграла энер-
энергии Т + П = h и определенной положительности кинетической энергии.
При П ^ h вместо метрики A1) введем в координатном пространст-
пространстве другую метрику, определив квадрат расстояния da2 между двумя
близкими точками Р и Р' по формуле
п
da2 = (h - П) Y^ aik dqi dqk. A6)
i,k=l
1 Которое теперь является n-мерным римановым пространством с линейным эле-
элементом ds, определенным по формуле A1).
Глава XIII
На границе области возможности движения метрика A6) имеет осо-
особенность: чем ближе кривая к границе, тем меньше ее длина; в част-
частности, длина любой кривой, лежащей на самой границе, равна нулю.
Если П < h, то метрика A6) не имеет особенностей. Из A5) получаем
W = \/2t7,
где а — длина дуги, пройденной изображающей точкой в координатном
пространстве с метрикой A6). И нахождение траекторий снова свелось
к нахождению геодезических линий в координатном пространстве (те-
(теперь в метрике A6)).
Глава XIV
Малые колебания консервативной системы
около положения равновесия
§ 1. Теорема Лагранжа об устойчивости
положения равновесия
224. Устойчивость равновесия. Рассмотрим голономную кон-
консервативную систему, положение которой задается обобщенными ко-
координатами gi, ... , qn (n — число степеней свободы). Как показано в
п. 63, некоторое положение системы тогда и только тогда является ее
положением равновесия, когда в этом положении все обобщенные силы
равны нулю:
Qi = =0 (i = 12 п) A)
где П — потенциальная энергия системы, которая в случае консерва-
консервативной системы явно от времени не зависит. Без ограничения общности
будем считать, что в положении равновесия все обобщенные координа-
координаты равны нулю.
Если систему вывести из положения равновесия, сообщив ее точ-
точкам какие-то малые начальные отклонения от положений равновесия и
малые начальные скорости, то в последующем движении точки систе-
системы либо все время остаются вблизи положений равновесия, либо удаля-
удаляются от этих положений. В первом случае положение равновесия будет
устойчивым, а во втором — неустойчивым.
Дадим строгое определение устойчивого положения равновесия.
Положение равновесия q1 = q2 = ... = 0 называется устойчивым, ес-
если для любого е > 0 существует такое S = 5(е), что для всех t > to
выполняются неравенства
\qi(t)\<e, \qi(t)\<e (i = 1, 2, ... , п) B)
при условии, что в начальный момент t = to
\qi(to)\<S, \qi(to)\<6. C)
490
Глава XIV
\
Рис. 172
Это определение удобно геометричес-
геометрически интерпретировать в 2п-мерном про-
пространстве состояний <7,, <7;. На рис. 172 для
случая п = 1 изображены две окрестнос-
окрестности, задаваемые неравенствами B) и C). В
> случае устойчивости любое движение, на-
q чинающееся в момент t = to внутри квад-
квадрата со стороной 28, будет происходить все
время внутри квадрата со стороной 2е.
Устойчивость положения равновесия
можно исследовать, зная потенциальную
энергию системы.
225. Теорема Лагранжа. Достаточные условия устойчивости по-
положения равновесия консервативной системы дает теорема Лагранжа.
Теорема. Если в положении равновесия консервативной системы по-
потенциальная энергия имеет строгий локальный минимум, то это по-
положение равновесия устойчиво.
Доказательство.
Как уже отмечалось, без ограничения общности можно считать,
что в положении равновесия gi = дг = • • • = 9™ = 0. В силу того
что потенциальная энергия II(gi, ... , qn) определяется с точностью до
произвольной аддитивной постоянной, примем, что П@, ... , 0) = 0.
Так как в положении равновесия функция П имеет строгий локальный
минимум, то существует такое число ц > 0, что в окрестности
\qi\<r]
(t = l, 2, ... , п)
выполняется строгое неравенство
, ..., qn) >П@, ... , 0)=0,
D)
E)
если хотя бы одна из величин qi не равна нулю.
Будем предполагать также, что за обобщенные координаты
<7i,... , qn приняты такие независимые параметры, определяющие по-
положение системы, что определитель A8) п. 139 (при т = п) отличен
от нуля для всех д, из окрестности D), если т] — достаточно малая
величина. Тогда кинетическая энергия
т = Т2 = \
qn)
F)
г,к=1
§ 1. Теорема Лагранжа об устойчивости положения равновесия 491
является определленно положительной функцией обобщенных скорос-
скоростей, и, следовательно, полная механическая энергия системы
Е = Т + П G)
при выполнении неравенства D) строго положительна, если только
не все величины qi, щ (i = 1, 2, ... , п) равны нулю. А так как при
Qi = Qi = 0 (г; = 1, 2, ... , п) имеем Е = 0, то функция Е в начале коор-
координат 2п-мерного пространства состояний qi, <ji (г = 1, 2, ... , п) имеет
строгий локальный минимум, равный нулю.
Пусть е — любое число, удовлетворяющее ограничениям
О < ? < г]. Рассмотрим окрестность, задаваемую неравенствами B).
Граница этой окрестности является замкнутым множеством точек, и
непрерывная функция Е достигает на ней своей точной нижней гра-
грани а. Так как, кроме того, на границе окрестности B) все значения Е
положительны, то на ней
Е ^ а > 0.
В силу того что в начале координат qi = 0, qi = 0 (г = 1, 2, ... , п)
непрерывная функция Е имеет строгий локальный минимум, равный
нулю, можно найти такое 8 @ < 8 ^ г), что в окрестности
\qi\<6, Ш<8 (г = 1, 2, ... , п) (8)
будет выполняться неравенство
Е < а. (9)
Пусть теперь функции q, = qi(t) удовлетворяют дифференциаль-
дифференциальным уравнениям движения системы. Если начальные данные удовле-
удовлетворяют неравенствам C), то во все время движения выполняются
неравенства B). Действительно, при условии C) начальная полная
энергия Eq < а, а так как при движении консервативной системы
ее полная энергия постоянна, то при всех t ^ to имеем Е < а. Поэ-
Поэтому точка qi(t), щ{Ь), изображающая движение системы в простран-
пространстве qi, щ (i = 1, 2, ... , п), не может достигнуть границы окрест-
окрестности B), на которой Е ^ а, а поэтому всегда остается внутри этой
окрестности. Теорема доказана.
Отметим, что приведенные выше доказательства следуют сообра-
соображениям, содержащимся в первом строгом и полном доказательстве те-
теоремы Лагранжа, предложенном Дирихле. Эти соображения послужили
одним из основных источников для решения общей задачи об устойчи-
устойчивости движения1.
1 Ляпунов А. М. Общая задача об устойчивости движения // Собр. соч. Т. 2. М.;
Л.: Изд-во АН СССР, 1956. С. 7-263.
492 Глава XIV
Замечание 1. Предположим, что изучаемая механическая система не-
неконсервативна, но получается из консервативной добавлением гироско-
гироскопических или диссипативных сил или тех и других вместе. Пусть им
отвечают обобщенные силы Q*(qj, qj). Тогда мощность непотенциаль-
непотенциальных сил
Покажем, что обобщенные силы Q*, удовлетворяющие усло-
условию A0), обращаются в нуль, когда все обобщенные скорости равны ну-
нулю. Действительно, пусть при каких-либо значениях дм(г = 1, 2,... , п)
обобщенных координат хотя бы одна из обобщенных сил Q^ не равна
нулю, т. е. Ql(qio, 0) ф 0. Но тогда в силу непрерывности существовала
бы окрестность точки д, = q,o, щ = 0, в которой функция Ql(qj, qj) не
была бы равной нулю и, следовательно, ее значения имели бы один и
тот же знак. Но ввиду независимости величин qi и щ (г = 1, 2, ... , п)
их значения в указанной окрестности можно выбрать так, что
г=1
а это противоречит условию A0). Из сказанного, в частности, следу-
следует, что при наличии гироскопических и диссипативных сил положение
равновесия сохранится.
Так как интеграл энергии Е = Т + П = const существует и при
гироскопических силах (в отсутствие диссипативных сил; см. п. 142),
то приведенное выше доказательство теоремы Лагранжа остается без
изменений и при наличии гироскопических сил. Если же существуют
диссипативные силы (или диссипативные и гироскопические силы од-
одновременно), то, согласно п. 142,
f = N-<0,
т. е. при движении системы ее полная энергия Е не превосходит сво-
своего начального значения Eq. Но если Eq < а, то во все время движе-
движения Е < а и опять при всех t ^ to справедливы неравенства B).
Таким образом, при добавлении к консервативной системе гироско-
гироскопических и диссипативных сил теорема Лагранжа остается справедли-
справедливой.
226. Теоремы Ляпунова о неустойчивости положения рав-
равновесия консервативной системы. Теорема Лагранжа дает доста-
достаточные условия устойчивости положения равновесия. Вопрос о том,
§ 1. Теорема Лагранжа об устойчивости положения равновесия 493
будет ли неустойчивым положение равновесия консервативной систе-
системы, если в этом положении потенциальная энергия не имеет минимума,
является очень сложным, и до сих пор на него не получено исчерпы-
исчерпывающего ответа1. Первые строгие результаты в решении этого вопро-
вопроса получены Ляпуновым. Дадим без доказательства две его теоремы2.
Функцию П((/1, ... , qn) предполагаем аналитической в окрестности по-
положения равновесия.
Теорема 1. Если потенциальная энергия консервативной системы в
положении равновесия не имеет минимума и это узнается уже по чле-
членам второго порядка в разложении функции П в ряд в окрестности по-
положения равновесия без необходимости рассматривания членов высших
порядков, то положение равновесия неустойчиво.
Теорема 2. Если в положении равновесия потенциальная энергия име-
имеет максимум и это узнается по членам наименее высокого порядка,
которые действительно присутствуют в разложении этой функции в
ряд в окрестности положения равновесия, то это положение равновесия
неустойчиво^.
Пример 1 (Устойчивость равновесия тяжелого твердого тела на
абсолютно гладкой горизонтальной плоскости). Пусть тело огра-
ограничено произвольной выпуклой поверхностью а и общая нормаль {вер-
{вертикаль) к горизонтальной плоскости и к поверхности а в некоторой
ее точке D* содержит центр тяжести тела G. Тогда тело на плос-
плоскости может находиться в состоянии равновесия, причем в точке D*
поверхность тела соприкасается с плоскостью.
Обозначим Gxyz жестко связанную с телом систему координат,
ось Gz которой содержит отрезок прямой D*G, а оси Gx и Gy направ-
направлены параллельно линиям кривизны поверхности тела в точке D*. Тог-
Тогда уравнение поверхности тела в окрестности точки D* запишется в
виде
i( ?)- = °- (и)
1 Обзор полученных результатов содержится в монографии: Карапетян А. В., Ру-
Румянцев В. В. Устойчивость консервативных и диссипативпых систем. М.: ВИНИТИ,
1983. (Итоги науки и техники. Сер. Общая механика: Т. 6).
2 Доказательство можно найти в работе: Ляпунов A.M. О неустойчивости равно-
равновесия в некоторых случаях, когда функция сил не есть максимум // Собр. соч. Т. 2.
М.; Л.: Изд-во АН СССР, 1956. С. 391-400.
3Для применимости теоремы 2 в конкретных задачах необходимо, чтобы разло-
разложение функции П начиналось с однородной функции (формы) Щ, (qi, ... , qn) чет-
четной степени к, а функция IIj. должна быть отрицательной в некоторой окрестности
положения равновесия (исключая само эти положение).
494 Глава XIV
Здесь х, у, z — координаты точки D поверхности а, которой тело ка-
касается плоскости при малом его отклонении от положения равновесия
(рис. 119), h — расстояние центра тяжести тела от опорной горизон-
горизонтальной плоскости в положении равновесия (х = у = О, z = —h), r\
и Г2 — главные радиусы кривизны поверхности тела в точке D*; так
как поверхность а выпуклая и целиком находится выше опорной плос-
плоскости, то величины п, гг положительны. Многоточие в уравнении A1)
обозначает совокупность членов, порядок которых относительно х, у
выше порядка членов, выписанных явно.
Потенциальная энергия тела вычисляется по формуле
П = mgl, A2)
где I = — (п • GD) — расстояние от центра тяжести до касательной
плоскости к поверхности тела, an — единичная внутренняя нормаль
в точке D. Из уравнения A1) и формулы B5) п. 114 имеем следующие
выражения для компонент вектора п:
71 = -^ + -, Ъ = -% + -, 7* = 1-?D+4)+- A3)
Учитывая, что GD' = (х, у, z), и пренебрегая в выражении для П
несущественной аддитивной постоянной mgh, получаем из A1)—A3)
A4)
Отсюда и из теоремы Лагранжа следует, что если центр тяжести те-
тела находится ниже обоих главных центров кривизны поверхности тела
в точке его касания с опорной плоскостью, то положение равновесия
устойчиво. Если же центр тяжести лежит выше хотя бы одного из
главных центров кривизны, то, согласно теоремам 1 и 2 Ляпунова, име-
имеет место неустойчивость.
227. Стационарные движения консервативной системы
с циклическими координатами и их устойчивость. Пусть в
голономной системе с п степенями свободы обобщенные координа-
координаты qa (a = k + 1, ... , п) являются циклическими. Остальные обоб-
обобщенные координаты qi (г = 1, 2, ... , к) называются (при наличии цик-
циклических координат) позиционными. Потенциальная энергия П и коэф-
коэффициенты ац. кинетической энергии
§ 1. Теорема Лагранжа об устойчивости положения равновесия 495
будут функциями только от позиционных координат.
Согласно п. 164, существуют первые интегралы, отвечающие цик-
циклическим координатам:
|4 = §^ = са = const (a = k + l,...,n), A5)
"Ча <jqa
где L = Т — П — функция Лагранжа.
Считая, что гессиан F) п. 165 отличен от нуля, составим функцию
Рауса
п
R= Y, C«(l«-L A6)
a=k+l
и выразим ее через позиционные координаты д,, их производные д,
(г = 1, 2, ... , к) и постоянные са (а = к + 1, ... , п). Введем обозначе-
обозначение
R* = -R + I1. A7)
Тогда уравнения Рауса запишутся в виде
iWL-WL = -? (i = 1,2,...,*). A8)
dt dqt dqt dqi y ' y '
Функция R* может быть представлена в виде суммы
R* = R*2 + R\ + R*o, A9)
где i?J — квадратичная форма производных позиционных координат1,
к
и(<Ь' ¦ • ¦ ' Чк)№з- B0)
Функция R^ линейна относительно щ (г = 1, 2, ... , к) 2:
к
Ri=^2a*(q1, ... , qk,ca) = щ (а = к + 1, ... , п), B1)
1Можно показать, что Щ — определенно-положительная квадратичная форма
относительно qt (i = 1, 2, ... , к). См., например: Гантмахер Ф. Г. Лекции по анали-
аналитической механике. М.: Наука, 1966, гл. 7, а также: Меркин Д. Р. Гироскопические
системы. М.: Наука, 1974, гл. 1,
2Если выражение кинетической энергии не содержит произведений позицион-
позиционных скоростей qi на циклические скорости qa, т. е. если ajQ =0 (г = 1, 2, ... , к;
а = к + 1, ... , п), то функция Щ^ тождественно равна нулю. В этом случае рассмат-
рассматриваемая система называется гироскопически несвязанной.
496 Глава XIV
щ зависит только от позиционных координат и величин са.
Используя представление A9), запишем уравнения Рауса A8) в
виде
d оЩ ои2 _ сцп - щ) ( (I "Щ <JHi \ с_л п и\
at dqi dqi dqi \dt dqi dqi J
B2)
Из равенства B1) следует, что
где
т. е. выражение во второй круглой скобке правой части B2) приводит к
появлению гироскопических сил, линейных относительно позиционных
скоростей.
Итак, уравнения B2) можно рассматривать как дифференциаль-
дифференциальные уравнения движения некоторой приведенной системы с к степе-
степенями свободы, кинетическая энергия которой равна Л|, а обобщенные
силы состоят из гироскопических сил и потенциальных сил, производ-
производных от потенциала П* = П — Щ. Потенциал П* приведенной систе-
системы называют приведенным потенциалом (приведенной потенциальной
энергией), или потенциалом Рауса. Если исходная система является ги-
гироскопически несвязанной, то в приведенной системе гироскопические
силы отсутствуют.
Стационарными движениями исходной консервативной системы с
циклическими координатами называются такие ее движения, при ко-
которых позиционные координаты д, (г = 1, 2, ... , к) и циклические ско-
скорости qa (а = к + 1, ... , п) постоянны. Из A5) и B2) следует, что
стационарные движения существуют в том и только в том случае, ког-
когда отвечающие им значения позиционных координат удовлетворяют
уравнениям
^=0 (i = l,2,...,fc), B5)
т. е. стационарные движения исходной системы соответствуют положе-
положениям равновесия приведенной системы.
§ 1. Теорема Лагранжа об устойчивости положения равновесия 497
Пусть для каких-либо значений постоянных са = сао система урав-
уравнений B5) имеет решение q, = <7;о = const. Тогда в стационарном дви-
движении qi = qi0, qt = О (г = 1, 2, ... , к), са = са0 (а = к + 1, .. .п).
Допустим, что в начальный момент времени t = to величины qi, qi
мало отличаются от их значений, отвечающих стационарному движе-
движению. Будут ли тогда величины д, — qto,qi (г = 1, 2, ... , к) оставать-
оставаться малыми для всех t Js ?о? Иными словами, будет ли рассматри-
рассматриваемое стационарное движение устойчиво по отношению к перемен-
переменным qi, qi (i = 1, 2, ... , к)? Ответ на этот вопрос можно получить,
используя теорему Лагранжа.
Так как наличие гироскопических сил не нарушает закона сохра-
сохранения полной энергии, то для приведенной системы существует интег-
интеграл Е* = Щ + П*. Если теперь в п. 225 заменить Е на Е* и повто-
повторить рассуждения, проведенные при доказательстве теоремы Лагран-
Лагранжа, то придем к следующей теореме Рауса об устойчивости стационар-
стационарных движений голономной консервативной системы с циклическими
координатами.
Теорема. Если в стационарном движении потенциальная энергия
II*(gi, ... , g;,, cao) приведенной системы имеет строгий локальный
минимум, то это движение устойчиво по отношению к перемен-
переменным qi, щ (г = 1, 2, ... , к).
Замечание 2. Применяя теорему Лагранжа, мы фиксировали постоян-
постоянные са, оставляя их такими же, как и в самом стационарном дви-
движении. Ляпунову принадлежит существенное дополнение к теореме
Рауса, которое допускает малое изменении постоянных са. Именно,
если П* имеет минимум как при са = сао, так и при значениях
са = сао + А*а (|а*«| ^ 1> а = к + 1, ... , п), причем позиционные ко-
координаты qio(ca) в точке минимума П* непрерывны как функции са,
то стационарное движение устойчиво по отошению к возмущениям ве-
величин qi, щ (i = 1, 2, ... , k) 1.
Пример 1 (Устойчивость вращения диска вокруг вертикали).
Пусть круговой однородный диск рндиусом р и массой т движется в
однородном поле тяжести по абсолютно гладкой горизонтальной плос-
плоскости, касаясь ее одной точкой своего края. Как отмечалось в п. 114,
при движении твердого тела по абсолютно гладкой плоскости проек-
проекция его центра масс на плоскость движется равномерно и прямолиней-
прямолинейно. Без ограничения общности можно считать ее неподвижной; тогда
центр масс тела будет двигаться по заданной вертикали. Ориентацию
диска относительно неподвижной системы координат зададим при по-
1Подробности см. в упомянутой монографии А. В. Карапетяна и В. В. Румянцева.
498 Глава XIV
мощи углов Эйлера (рис. 137). Кинетическая и потенциальная энергия
диска определяются формулами (см. п. 157)
Т= Imp2 A + 4 cos2 9)92+ \mp2 sm2 9ф'2 + \mp2 (ф cos 9 + фJ,
о о 4
П = mgp sin 9.
Переменные ф и <р будут циклическими координатами. Им соответ-
соответствуют первые интегралы (L = Т — П) :
^—г = jmp2 sin2 9ф + -^mp2 (ф cos 9 + ф) cos 9 = Сф = const, B6)
дф 4 1
Цгт = -^тр2 (ф cos 9 + ф) = Сш = const. B7)
оф l
Приведенная система имеет одну степень свободы, а функция A9) име-
имеет вид
6
тр sin в mp
Если отбросить последнее слагаемое, несущественное для уравнений
движения, то для потенциальной энергии приведенной системы имеем
выражение
^-^°:°J B8)
тр sin 9
Существует такое движение, при котором один из диаметров диска
расположен вертикально, а сам диск вращается вокруг этого диаметра
с произвольной по величине постоянной угловой скоростью. Для этого
движения
9= |, ф = 0, ф'=ш = const, B9)
причем
Сф = ^mp2uj, cv = 0. C0)
Подставляя в функцию П* значения постоянных Сф и cv из C0), пола-
полагая 9 = Ц + q и разлагая П* в ряд по степеням q, получаем (несущест-
Li
венную постоянную в функции П* отбрасываем)
П* = \
- 4mgp)q2 + ±Bтр2ш2 + mgp)qA + ¦¦¦ C1)
S 2. Малые колебания 499
При выполнении неравенства
C2)
функция П* имеет строгий локальный минимум в точке q = 0. Поэ-
Поэтому, согласно теореме Рауса, при условии C2) стационарное движе-
движение диска B9) устойчиво. Если же неравенство C2) не выполняется,
то функция П* в точке q = 0 не имеет минимума, и это узнается
по членам второго порядка в разложении C1). Следовательно, согласно
теореме 1 Ляпунова (см. п. 226), при невыполнении неравенства C2)
имеет место неустойчивость1.
§ 2. Малые колебания
228. Линеаризация уравнений движения. Пусть консерватив-
консервативная система имеет положение равновесия, в котором все обобщенные
координаты qi (г = 1, 2, ... , п) равны нулю. Предполагая потенци-
потенциальную энергию системы H(qi, q2, ¦•¦ , qn) аналитической функцией в
окрестности положения равновесия, разложим ее в ряд Тейлора
где индексом 0 отмечены значения производных функции П в поло-
положении равновесия, т. е. при д, = 0 (i = 1, 2, ... , п). Без ограничения
общности можно считать, чтоП @, 0 ... , 0) = 0. Первая сумма в разло-
разложении A) равна нулю, так как в положении равновесия все обобщенные
силы равны нулю:
Oi = =° (* = 12n)
Таким образом, если ввести обозначения
д2П
hi dqk
1 Впрочем, для доказательства неустойчивости при выполнении неравенства C2)
применима и теорема 2 Ляпунова из п. 226, так как при этом функция П* в точ-
точке q = 0 имеет максимум, и это узнается по членам наинизшего (в нашем случае
— второго) порядка в разложении C1).
500 Глава XIV
то разложение потенциальной энергии в ряд будет начинаться с квад-
квадратичной формы, имеющей постоянные коэффициенты:
п
П = ? /2i с'к1'1к + • • • B)
i,k=l
Здесь многоточие обозначает совокупность членов, порядок которых
относительно величин qi (i = 1, 2, ... , п) больше второго. Будем пред-
предполагать, что квадратичная форма
п
2 2-~t Cik1i(lk ("*)
i,k=l
является определенно-положительной. Тогда точка q1 = q2 = ... =
= Qn = 0 будет точкой строгого локального минимума функции
П (Gi, G2, ¦•¦ , Чп) и; следовательно, согласно теореме Лагранжа, поло-
положение равновесия устойчиво.
В силу устойчивости положения равновесия величины qi, qi
(i = 1, 2,... , п) будут малыми во все время движения, если достаточно
малы их начальные значения. Используя малость величин g,, qi, можно
упростить дифференциальные уравнения движения системы вблизи ее
положения равновесия. Для этого можно заменить полные уравнения
движения приближенными, сохраняя в них только линейные члены от-
относительно qi, щ (i = 1, 2, ... , п) и отбрасывая все нелинейные члены.
Кинетическая энергия системы имеет вид
п
-L — 9 2.*/ a«*vGi> Ч2, • • • 1 qn) qi qu-
i,k=l
Будем считать, что функции ац- (qi, ... , qn) аналитические в окрест-
окрестности положения равновесия, и запишем их в виде рядов
a.ik(qi, 92, • • • , Qn) = a-ik + ¦ ¦ ¦
Здесь многоточие обозначает совокупность членов первого и более вы-
высоких порядков относительно д, (г = 1, 2, ... , п), ац. = a,k@, 0, ... , 0)
— постоянные коэффициенты. Функция Т запишется в виде ряда
п
Г=^а^ + ..., D)
i,k=l
где многоточие обозначает члены не ниже третьего порядка относи-
относительно qi, qi (I, 2, ... , п). Будем считать, что выбор обобщенных
S 2. Малые колебания 501
координат сделан так, что в положении равновесия определитель A8)
п. 139 (при т = п) отличен от нуля. Тогда квадратичная форма
п
\ X] а*.* 9iQk E)
i,k=l
будет определенно-положительной относительно qi (г = 1, 2, ... , п).
Уравнения движения запишем в виде уравнений Лагранжа второго
рода
Рассматривая эти уравнения при малых значениях величин (/,, щ, за-
заменим в функции Лагранжа L = Т — П величины Т и П их разложени-
разложениями D) и B). Тогда получим уравнения движения в виде
п
^2(aikqk + cikqk) +¦¦¦ = 0 (г = 1, 2, ... , n), G)
где многоточием обозначена совокупность членов второго и более вы-
высоких порядков. Если их отбросить, то придем к линейной системе с
постоянными коэффициентами:
п
^(aiktik + CikQk) = 0 (г = 1, 2, ... , п), (8)
k=i
Эти линейные уравнения получаются из уравнений F), если считать,
что в функции Лагранжа величины Т и П заменены их приближенны-
приближенными выражениями E) и C). Теория малых колебаний консервативной
системы вблизи устойчивого положения равновесия опирается на та-
такую линеаризацию и рассматривает приближенные выражения E) и C)
для Т и П как точные.
Когда говорят «малые колебания», то обычно имеют в виду движе-
движения, описываемые системой дифференциальных уравнений, полученной
в результате линеаризации полных (нелинейных) уравнений движения.
В случае движений в окрестности положения равновесия консерватив-
консервативной системы линеаризация сводится, как мы видим, к получению Т
и П в виде квадратичных форм E) и C).
Для упрощения записи уравнения (8) удобно представить в
502
Глава XIV
векторно-матричной форме. Пусть
Qi
42
Qn
, A =
c =
Cll
C21
Cnl
axl a12 ...
Й21 0,22
^tjI ^Ti2i • • •
Ci 9 * Ci
C22 • •• C2n
Cn2 ••• Cnn
aln
U2n
Onn
Тогда
Т=±(А«-«), n=i
и уравнения (8) запишутся в виде
(9)
A0)
229. Главные координаты и главные колебания. Выясним
структуру решений уравнений (8) (или A0)), описывающих малые ко-
колебания в окрестности положения равновесия. Для этого рассмотрим
пару квадратичных форм
(Aq ¦ q) =
aikqiqk,
(Cq ¦ q) =
cikqiqk.
A1)
i,k=l
i,k=l
Обе эти формы определенно-положительны. Из линейной алгебры из-
известно1, что если даже одна из форм A1) была бы определенно-
положительной (за такую форму мы будем принимать первую из квад-
квадратичных форм A1)), то существует вещественная неособенная замена
переменных
q = Ue (detU^O, e' = @i,02, ••• , 6n)), A2)
приводящая к сумме квадратов сразу обе квадратичные формы A1):
A3)
3=1
3=1
хСм., например, гл. VI книги: Мальцев А. И. Основы линейной алгебры. М.: Наука,
1975.
i 2. Малые колебания 503
При этом величины \j с точностью до порядка следования однознач-
однозначно определяются первоначальными квадратичными формами и не за-
зависят от выбора замены переменных A2). В нашем случае все Aj
(j = 1, 2, ... , п) положительны в силу того, что П определенно-поло-
определенно-положительна.
Отметим, что если в окрестности точки q\ = qi = ... = qn = 0
координатного пространства qi, q2, ¦ ¦ ¦ , qn ввести евклидову структу-
структуру при помощи удвоенной кинетической энергии 2Т, т. е. принять за
скалярное произведение векторов ми» величину (Aw- v), то преобра-
преобразование A2) можно выбрать ортогональным в смысле этой евклидовой
структуры. Это означает, что, если щ {j = 1, 2, ... , п) — j-ft столбец
матрицы U, т. е. замена переменных A2) имеет вид
то выполняется условие нормировки
(Аи; • Uj) = Sij, A5)
где S^ — символ Кронекера E^ = 1, если г = j и 8ц = 0, если г ф j).
Так как обобщенные скорости qi и 6j связаны теми же соотношениями,
что и обобщенные координаты (/, и в у.
то в первой из формул A3) можно величины qi заменить на qi, а ве-
величины 6j, на ву В новых переменных кинетическая и потенциальная
энергия имеют вид
Обобщенные координаты 6j называются главными, или нормальными
координатами. В главных координатах уравнения движения (8) запи-
запишутся в виде п не связанных одно с другим уравнений второго порядка
ej + \jej=O, (j = l, 2, ...,n). A7)
Так как все Л^ положительны, то каждое из этих уравнений описывает
колебания гармонического осциллятора:
6j = Cj sin(cjjt + Uj) (j = 1,2, ... , n). A8)
504 Глава XIV
Здесь ujj = i/Aj — частоты колебаний, Cj, ccj — произвольные посто-
постоянные.
Из A4) и A8) получаем общее решение уравнений (8) (или A0))
п
q = ^^ cjuj sin(ujjt + otj). A9)
Эта формула охватывает все решения системы (8). Пусть среди посто-
постоянных Cj (j = 1, 2, ... , п) отлична от нуля только одна постоянная си-
Тогда из A9) получаем
Чк = ckuk sin(ujkt + ак). B0)
Это решение описывает колебание системы, которое называют к-м глав-
главным, или нормальным колебанием. Вектор щ называют амплитудным
вектором к-го главного колебания . В fc-м главном колебании все обоб-
обобщенные координаты совершают гармонические колебания с одной и той
же частотой u>k, отношение амплитуд колебаний отдельных обобщен-
обобщенных координат определяется отношением соответствующих компонент
амплитудных векторов.
При практическом нахождении решения A9) можно поступать сле-
следующим образом. Ищем решение системы A0) в виде
q = usm(wt + a).
Подставив это выражение для q в уравнение A0) и сократив затем
на s'm(u>t + а), получим уравнение для амплитудного вектора и
(С-ЛА)и=0 (\ = ш2). B1)
Чтобы это уравнение имело нетривиальное решение относительно ком-
компонент амплитудного вектора и, надо потребовать, чтобы величина Л
удовлетворяла уравнению
det(C - ЛА) = 0. B2)
Это уравнение называется уравнением частот, или вековым уравне-
уравнением. Из предыдущего изложения теории главных колебаний следует,
что оно имеет только положительные решения; каждому корню Xj это-
этого уравнения соответствует амплитудный вектор щ (j = 1, 2, ... , п),
причем если какой-либо корень Ад, уравнения B2) будет кратным, то
всегда можно найти ровно столько соответствующих ему линейно неза-
независимых амплитудных векторов, какова его кратность. Амплитудные
векторы из уравнения B1) находятся с точностью до произвольного
постоянного множителя. Их нормировка (если она требуется) произво-
производится в соответствии с условием A5).
S 2. Малые колебания
505
Пример 1 (Малые колебания двойного маятника). Рассмотрим
двойной маятник, движущийся в вертикальной плоскости в поле тя-
тяжести (рис. 15). Потенциальная энергия маятника найдена в примере 3
п. 54:
П = -^mg-/Ccosiy9 + cos^).
Кинетическая энергия вычисляется по формуле (см. пример 2 п. 215)
Т = \ml2 [|
фф co
Существует положение равновесия маятника, когда оба стержня зани-
занимают вертикальное положение, а <р = ф = 0. В этом положении по-
потенциальная энергия маятника минимальна и равновесие устойчиво.
Исследуем малые колебания маятника вблизи этого положения равно-
равновесия.
Если отбросить несущественное постоянное слагаемое —2mgl
в разложении функции П в ряд в окрестности положения равнове-
равновесия <р = ф = 0 и сохранить только члены второго порядка малости, то
получим
U = \rngl (|^2 + \ф*) .
Аналогично, учитывая только члены второго порядка малости в разло-
разложении кинетической энергии в ряд, имеем
Если ввести обозначение q' = (ip, ф), то матрицы А и С в выражени-
выражениях (9) будут такими:
= ml2
4 1
3 2
1 1
2 3
, С = mgl
0 5
Уравнение частот B2) может быть записано в виде
7А2 - 42 ( | ) А + 27 ( f ) = 0.
Оно имеет корни
-И)*
Л2 - 3 ^1 -
Ч g
B3)
506
Глава XIV
Частоты loj главных колебаний вычисляются по формулам loj =
(j = 1, 2). Из уравнения B1) и условий нормировки A5) получаем сле-
следующие выражения для амплитудных векторов щ, отвечающих часто-
частотам u>j (j = 1, 2):
-1-77
5 + 77
-1 + 77
5-77
B4)
Таким образом, общее решение уравнений малых колебаний двойного ма-
маятника будет таким:
<р
-1-77
5 + 77
¦ai)
-1 + 77
5-77
a2),
B5)
где Cj, otj (j = 1, 2) — произвольные постоянные.
Первое и второе главные колебания отве-
отвечают значениям постоянных с\ ф 0, сг =0
м ci = 0, С2 ф 0 соответственно. Отношения
kj (j = 1, 2) амплитуд колебаний углов (рифе
первом и втором главных колебаниях и направ-
направления отклонений стержней от вертикали ха-
характеризуются величинами
77 _ 1 -277
9
1+277
б
5 + 77
1-77
5-77
9
~ -0,48,
~ 0,70,
Рис. 173
которые называются коэффициентами форм
главных колебаний. При первом главном колеба-
колебании (с большей частотой u>i) стержни в любой момент времени будут
отклонены от вертикали в разные стороны (рис. 173, а), а при втором
главном колебании (с меньшей частотой шъ) — в одну и ту же сторону
(рис. 173, б).
230. Колебания консервативной системы под влиянием
внешних периодических сил.
Пусть к точкам консервативной системы приложены внешние си-
силы, которым отвечают обобщенные силы Qi = Qi(t) (г = 1,2,... ,п).
Влияние этих сил на колебания системы вблизи устойчивого положе-
положения равновесия удобно исследовать, если воспользоваться главными
j 2. Малые колебания 507
координатами в\, #2; ... , 0п, введенными в предыдущем пункте. Си-
Силам Qi(t) в координатах <& (г = 1, 2, ... , п) отвечают обобщенные си-
силы @j(t) в главных координатах 6j(j = 1, 2, ... , п). Для нахождения
величин @j(t) приравняем выражение для элементарной работы сил в
координатах (/, и в у.
B6)
1=1
но согласно замене переменных A2)
Поэтому
п '«** = ?*? «л-= ?(?«*<
n n n I n
i=l i=l j=l j=l \г=1 /
Из равенств B6) и B7) следует, что
п
@j(t) = Y,uijQj(t) (j = 1, 2,... , n). B8)
г=1
В нормальных координатах малые колебания консервативной системы
с учетом внешних сил будут описываться уравнениями
0j+u;2jej = @j(t) (j = l, 2,..., n). B9)
Пусть внешние силы Qi{t) — периодические функции времени с перио-
периодом 2тт/Г2 и такие, что обобщенные силы B8) представимы в виде рядов
Фурье
оо
@j = Y bJk sin(kilt + ajk) (j = 1, 2,... , n) C0)
A:=0
Здесь bjk, ajk (j' = 1) 2,... , n; к = 0, 1, 2,...) — постоянные величи-
величины.
Общее решение уравнений B9) (при Ш ф ujj) имеет вид
6j = Cj sm(wjt + aj) + в*(t), C1)
508 Глава XIV
где Cj, aj — произвольные постоянные, а через #!•(?) обозначены сла-
слагаемые
^ sin(fcm + а^) (i = 1, 2,... , n), C2)
которые появились в общем решении из-за наличия внешних периоди-
периодических сил.
Из A4) и C1) получаем
аз)
Первая сумма в C3) представляет свободные колебания, а вторая — вы-
вынужденные колебания системы, возникающие из-за влияния внешних
периодических сил.
Если же при каком-либо значении числа к окажется, что Ш = Wj
для некоторого j, то при bjk ф 0 решение в форме C1), C2) непригодно,
так как в сумме C2) будет слагаемое с нулевым знаменателем. Говорят,
что в этом случае имеет место резонанс в вынужденных колебаниях
системы.
Каким будет решение уравнения B9) при резонансе? Для примера
рассмотрим одно уравнение вида
в + со2в = a smut. C4)
Общее решение этого уравнения имеет вид
в = csm(ut + a) +6*(t), C5)
где с, а — произвольные постоянные, а
e*(t) = -^tcosojt. C6)
Функция в* it) является неограниченной. Колебания, описываемые
уравнением C4), уже не будут малыми. А потому для описания дви-
движения вблизи положения равновесия уравнения C4) должны быть за-
заменены другими уравнениями, учитывающими отброшенные при ли-
линеаризации нелинейные члены в полных уравнениях движения. Так в
данном конкретном примере мы приходим к необходимости теории не-
нелинейных колебаний.
S 2. Малые колебания 509
Пример 1 (Плоские колебания твердого тела на эллиптической
орбите). Дифференциальное уравнение, описывающее плоские движе-
движения твердого тела в центральном ньютоновском гравитационном поле,
имеет вид (см. п. 128)
A + ecosi/)—tJ- — 2esini/—— + 3—-^— sin <^ cos <^ = 2esini/, C7)
dv dv С
где А и В — моменты инерции тела относительно его главных цен-
центральных осей инерции Ох и Оу, которые для плоских движений все
время расположены в плоскости орбиты, С — момент инерции те-
тела относительно оси, проходящей через центр масс перпендикулярно
плоскости орбиты; <р — угол между осью Оу и осью OZ, направленной
вдоль радиуса-вектора центра масс тела относительно притягиваю-
притягивающего центра, е — эксцентриситет орбиты, 0 ^ е < 1.
На круговой орбите существует положение равновесия твердого
тела в орбитальной системе координат, отвечающее решению <р = 0
уравнения C7) при е = 0. При условии А > В положение равновесия
устойчиво. Предполагая это условие выполненным, рассмотрим малые
плоские колебания твердого тела вблизи положения <р = 0, вызываемые
эллиптичностью орбиты. Эксцентриситет орбиты считаем малой ве-
величиной.
Линеаризуя уравнение C7), получаем
A + ecosi/)—tJ- — 2esini/-j^- + и?(р = 2esini/. C8)
dv dv
dv
A Г?
>% = 3
Здесь введено обозначение и>% = 3—^—. Так как моменты инерции
удовлетворяют неравенству треугольника А — В ^ С и по предположе-
предположению А > В, то
0 < w% ^ 3. C9)
Вынужденные колебания спутника, описываемые дифференциальным
уравнением C8), ищем в виде ряда по степеням е
V* =е(рх +e2ip2 + ... D0)
Подставив это разложение в уравнение C8) и приравняв коэффициенты
при одинаковых степенях е в его обеих частях, получим линейные не-
неоднородные дифференциальные уравнения для функций tpi, <p2,.... Для
функции ipi имеем уравнение
D1)
510 Глава XIV
Из D0), D1) находим решение, описывающее вынужденные колебания
тела, в виде
2 _ D2)
Щ -1
Эти колебания вызваны неравномерностью движения центра масс тела
по эллиптической орбите. В динамике спутников они носят название
эксцентриситетных колебаний.
Утверждение о существовании эксцентриситетных колебаний D2)
мы делаем здесь без обоснования. Можно, однако, строго показать1, что
при и>о ф 1 нелинейное уравнение C7) действительно имеет решение,
аналитическое по е при достаточно малых е и переходящее при е = 0
в положение равновесия <р = 0, причем разложение этого решения в ряд
начинается с члена первой степени по е, явно выписанного в форму-
формуле D2).
При и>о = 1 имеет место резонанс в вынужденных колебаниях.
Решение D2), полученное при помощи линеаризации, не имеет смыс-
смысла при резонансе, и для исследования движения тела вблизи положения
<р = 0 надо использовать нелинейное уравнение движения C7). Будем
считать, что ljq мало отличается от единицы:
ujo = 1+H (O^H<C1). D3)
В уравнении C7) сделаем2 замену переменных ip = е?, где е = е1/3.
Подставим это значение <р в уравнение C7) и представив обе его части
в виде рядов по степеням е, получим (после деления обеих частей на е)
такое уравнение:
(|)..., D4)
где многоточие обозначает члены выше второго порядка малости от-
относительно е.
1См.: СарычевВ.А. Вопросы ориентации искусственных спутников. М.: ВИНИ-
ВИНИТИ, 1978. — (Итоги науки и техники. Сер. «Исследование космического простран-
пространства»; Т. 11).
2Мы не даем здесь обоснования исследования колебаний при резонансе и в слу-
случае, близком к резонансному. О строгом обосновании излагаемой процедуры см.
статьи: Маркеев А. П., Чеховская Т. Н. О резонансных периодических решениях га-
мильтоновых систем, рождающихся из положения равновесия // ПММ. 1982. Т. 46,
вып. 1. С. 27-33.; Холостова О. В. О движении гамильтоновой системы с одной сте-
степенью свободы при резонансе в вынужденных колебаниях // Известия РАН. МТТ,
1996, №3, С. 167-175.
j 2. Малые колебания 511
Для приближенного исследования этого уравнения будем применять
теорию возмущений (см. § 7 гл. XI). Положим
^ § D5)
Тогда уравнение D4) может быть записано в эквивалентной форме в
виде канонических уравнений с функцией Гамильтона (q — координа-
координата, р — импульс)
U
D6)
Введем новые канонически сопряженные переменные Q, Р при помощи
унивалентного канонического преобразования (см. пример 6 п. 170)
p = V2PcosQ. D7)
Тогда
H = cj0P-?2 {ip2 C-4 cos 2Q +cos 4Q) +
1 D8)
Для упрощения уравнений движения введем переменные Q*, Р* при по-
помощи близкого к тождественному унивалентного канонического преоб-
преобразования Q, Р —>¦ Q*, Р*, задаваемого при помощи производящей функ-
функции
QP* +s2S2(Q, Р*,и) + ...
Новая функция Гамильтона Н* определяется по формуле (см. п. 174)
ТТ* _ ТТ : ^9S2
?1 — ?1 + ? —^ \- . . . ,
ov
в правой части которой старые переменные Q, Р должны быть заме-
заменены на их выражения через новые переменные Q*, Р*, получаемые из
равенств
Q*=Q + e2^ + ..., Р = Р*+?*Щ+... D9)
Вычисления показывают, что если функцию S2 взять в виде
512
Глава XIV
то
Н* =
cos(<2* - v)
E0)
Сделаем еще одну каноническую замену Q*, Р* —>¦ Ф, R по формулам
<2* = Ф + г/, P* = R. E1)
Тогда, учитывая равенство D3) и пренебрегая членами выше второго
порядка малости относительно е и ц, получаем приближенное выраже-
выражение для новой функции Гамильтона в виде
П = /iR-e2 (±Д2 + V2Rcos ф) .
E2)
Соответствующая приближенная система дифференциальных уравне-
уравнений второго порядка, описывающая плоское движение твердого тела при
резонансе или в случае, близком к резонансному, имеет вид
dv dR
In, 1
2
V2R / ^ »ф
E3)
Эта система уравнений имеет первый интеграл % = h = const и,
следовательно, интегрируется в квадратурах.
Если и>о = 1 (т. е. ц = 0), то при описании движения тела в
рамках линеаризованных уравнений движения мы получаем, что откло-
отклонение тела от его равновесного положения <р = 0 неограниченно воз-
возрастает со временем, так как уравнение D1) имеет частное решение
вида C6) {при ш = шо, а = 2). При нелинейной трактовке задачи о
движении твердого тела при резонансе ситуация иная. В самом деле,
пусть в начальный момент <р = 0, ф = 0. Тогда (с погрешностью, по-
порядок которой не ниже чем е3) и R = 0 при t = 0. Следовательно, в
интеграле % = h постоянная h равна нулю и во все время движения
Учитывая, что | cosФ| ^ 1, получаем отсюда, что R ^ Rmax =2^.
Если учесть цепочку замен переменных, при помощи которых исходное
уравнение движения C7) приведено к приближенной системе E3), то
получим, что отклонение угла <р от его равновесного значения <р = 0 не
превосходит величины \/2Rmaxe^ = 2\/2е.
j 2. Малые колебания 513
Решения R = Ro = const, Ф = Фо = const системы E3) отвеча-
отвечают 2тг -периодическим колебаниям спутника в исходных переменных. Из
E3) следует, что Фо может равняться только 0 или тг, а величина Rq
может быть найдена из уравнения третьей степени
и3+Зси2+2& = 0 (и = л/^соэФо). E4)
Здесь
^^ 6-2
Уравнение E4) имеет один или три вещественных корня в зависимости
от того, положителен или отрицателен дискриминант D = Ь2 + с3
этого уравнения1. Отсюда следует, что при выполнении неравенства
е > ^V2 E5)
существует одно, а при обратном знаке в неравенстве E5) — три пе-
периодических движения твердого тела, переходящих при е = 0 в его рав-
равновесное положение <р = 0 в орбитальной системе координат2.
Отметим, что при точном резонансе, когда ц = 0, существует
только одно 2тг-периодическое колебание тела и, согласно E4), ампли-
амплитуда этого колебания равна \/Жё.
хСм. гл. 9 книги: КурошА. Г. Курс высшей алгебры. М.: Наука,1975.
2Условие E5) иным путем получено в гл. 2 монография: Белецкий В. В. Движение
искусственного спутника относительно центра масс. М.: Наука, 1965.
Глава XV
Устойчивость движения
§ 1. Основные понятия и определения
231. Уравнения возмущенного движения. Определение
устойчивости. Пусть уравнения движения механической системы
представлены в виде системы дифференциальных уравнений
^=Yi(yi,y2,...,ym,t) (i = l,2,...,m), A)
правые части которых удовлетворяют условиям существования и един-
единственности решения.
Рассмотрим движение механической системы, которому отвечает
некоторое частное решение системы A)
Vi=fi(t) (* = 1, 2,..., т) B)
при начальных условиях
2/*о = /*(*о) (г = 1, 2,... , т). C)
Нас интересует вопрос о движении системы при отклонении начальных
условий ум от значений C). Решением этого вопроса занимается теория
устойчивости движения, элементы которой излагаются в этой главе.
Движение системы, описываемое функциями B), будем называть
невозмущенным движением. Все другие движения механической сис-
системы, возможные для нее при тех же силах, что и рассматриваемое
движение, описываемое формулами B), будем называть возмущенными
движениями. Разности
Xi = Vi-Mt) (г = 1,2,...,т) D)
значений у» для возмущенного и невозмущенного движений называют-
называются возмущениями.
Если в уравнениях A) сделать замену переменных по форму-
формулам D), то получим уравнения
dx-
—j^=Xi(xi,x2,...,xm,t) (i = 1, 2,... , m), E)
§ 1. Основные понятия и определения 515
которые называются дифференциальными уравнениями возмущенного
движения. Очевидно, что
Xi=Yi(x1+f1(t), x2 + f2(t),... , xm + fm{t), t)-
t), /2(t),..., fm(t),t).
Уравнения E) имеют частное решение ж» = 0 (г = 1, 2,... , т), отвеча-
отвечающее невозмущенному движению B). Если функции X, явно не зависят
от t, то невозмущенное движение будем называть установившимся, в
противном случае — неустановившимся.
Примем следующее определение Ляпунова. Невозмущенное движе-
движение называется устойчивым по отношению к переменным гц
(г = 1, 2,... , то), если для любого сколь угодно малого числа е > О
существует положительное число S = 8(е) такое, что для всех возму-
возмущенных движений, для которых в начальный момент времени to вы-
выполняются неравенства
\xi(to)\ <S (» = 1, 2,..., то), F)
при всех t > to выполняются неравенства
\Xi{t)\ <е (г = 1, 2,... , т). G)
Дадим еще определение асимптотической устойчивости в смыс-
смысле Ляпунова. Невозмущенное движение называется асимптотически
устойчивым по отношению к переменным у» (г = 1, 2,... , т), если
оно устойчиво и число 8 можно выбрать настолько малым, что для
всех возмущенных движений, удовлетворяющих неравенствам F), бу-
будут выполняться условия
Итж;(?) = 0 (г = 1, 2,... , т). (8)
t—»OG
232. Функции Ляпунова. Наиболее эффективным методом ис-
исследования устойчивости движения является прямой метод Ляпунова.
Этот метод не предполагает нахождения тех или иных решений уравне-
уравнений возмущенного движения, а связан с отысканием некоторых функ-
функций V переменных х\, жг,... , хт, t и изучением свойств самих этих
функций и их производных. Функции V будем в дальнейшем назы-
называть функциями Ляпунова. В основе прямого метода Ляпунова лежат
соображения, использованные Дирихле в его доказательстве теоремы
Лагранжа об устойчивости положения равновесия консервативной сис-
системы (см. п. 225).
516 Глава XV
Для простоты будем изучать только установившиеся движения.
Функции Xi(xi, X2,... , хт) в уравнениях возмущенного движения E)
считаем непрерывными в области
Xi\ <H (г = 1, 2,... , т), (9)
где Н — некоторая постоянная, и такими, что уравнения E) при на-
начальных значениях ж;о из области (9) допускают единственное решение.
В области \xi\ < h (i = 1, 2,... , m), где h — достаточно малое по-
положительное число, будем рассматривать функции V(x\, жг,... , хт),
предполагая их непрерывно дифференцируемыми, однозначными и об-
обращающимися в нуль в начале координат Х\ = Жг = ... = хт = 0.
Производной dV/dt функции V в силу уравнений возмущенного
движения E) называется выражение
г=1
Следовательно, dV/dt будет также функцией переменных
х\, жг,... , хт, которая непрерывна в области \xi\ < h и обращается в
НуЛЬ При Х\ = 2?2 = • • • = Хт = 0.
Кроме того, функции V могут обладать более специальными свой-
свойствами. Введем некоторые определения.
Функцию V(xi, a?2,... ) хт) назовем определенно-положительной
в области \xi\ < h, если всюду в этой области, кроме начала коор-
координат (где функция V равна нулю), выполняется неравенство V > 0.
Если же выполняется неравенство V < 0, то функция V называется
определенно-отрицательной. В том и другом случае функция V назы-
называется знакоопределенной.
Если в области |ж»| < h функция V может принимать значения
только одного знака (V ^ 0 или V ^ 0), но может обращаться в нуль
не только в начале координат, то она называется знакопостоянной (по-
(положительной или отрицательной).
Если в области |ж»| < h функция V может принимать как положи-
положительные, так и отрицательные значения, то она называется знакопере-
знакопеременной в этой области.
Например, при т = 2 функция V = х\ — х\ знакопеременна, а
функция V = х\ + х\ определенно-положительна; функция же V = х\
знакопостоянна, так как она обращается в нуль на оси 0x2, а вне этой
оси положительна.
Как узнать, будет функция V знакоопределенной или нет? Если V
представляет собой квадратичную форму, то знакоопределенность ее
§ 2. Основные теоремы прямого метода Ляпунова
517
можно установить при помощи известного критерия Сильвестра. Ес-
Если У — форма нечетной степени, то она, очевидно, будет знакоперемен-
знакопеременной функцией. В приложениях V часто бывает аналитической функци-
функцией в области \xi\ < h, если h — достаточно малая величина. В таких
случаях при решении вопроса о знакоопределенности функции бывает
полезно следующее легко доказываемое утверждение 1:
на h достаточно мала, то в области
если величи-
h знакоопределенность и
Рис. 174
знакопеременность формы сохраняются при добавлении к ней любой
совокупности членов более высокого порядка.
При достаточно малых значениях \с\ поверх-
поверхность V(xi, Х2, ¦ ¦ ¦ хт) = с, где V — знакоопре-
деленная функция, является замкнутой поверх-
поверхностью, содержащей внутри себя начало коорди-
координат. Для доказательства примем для определен-
определенности, что V определенно-положительна, и обо-
обозначим а точную нижнюю грань функции V на
границе области \xi\ < h. Так как функция V
определенно-положительна, то а > 0. Итак, на границе области \xi\ < h
V ^ а. Рассмотрим теперь значения функции V на непрерывной кри-
кривой, соединяющей начало координат с какой-либо точкой, лежащей на
границе области |ж,| < h. В начале этой кривой V = 0, а в конце кривой
значения функции не меньше чем а. В силу непрерывности функции V
в некоторой точке рассматриваемой кривой V обязательно принимает
значение с, если только с < а, что и будем предполагать. Это означает,
что выбранная кривая пересекает поверхность V = с. Так как рассмат-
рассматриваемая кривая может быть произвольной, то отсюда следует, что
поверхность V = с замкнута и окружает начало координат.
Если V — определенно-положительная функция и с\ > сг, то по-
поверхность V = С2 находится внутри поверхности V = с\, причем, в
силу однозначности функции V, эти поверхности не имеют общих то-
точек (рис. 174). Если с —>¦ 0, то семейство замкнутых поверхностей V = с
стягивается в точку, совпадающую с началом координат.
Отметим, что если V будет знакопостоянной или знакопеременной
функцией, то поверхности V = с при достаточно малых с разомкнуты.
§ 2. Основные теоремы прямого метода Ляпунова
233. Теорема Ляпунова об устойчивости движения . В этом
параграфе рассмотрены теоремы, составляющие основу прямого мето-
хСм., например, §7 книги; МалкинИ. Г. Теория устойчивости движения. М.: На-
Наука, 1966.
518 Глава XV
да Ляпунова в теории устойчивости движения. Будем изучать только
установившиеся движения. Сначала рассмотрим теорему Ляпунова об
устойчивости.
Теорема. Если дифференциальные уравнения возмущенного движения
таковы, что существует знакоопределенная функция V, производная
которой V в силу этих уравнений является или знакопостоянной функ-
функцией противоположного знака с V, или тождественно равной нулю, то
невозмущенное движение устойчиво.
Доказательство.
Пусть, например, V определенно-положительна. Тогда в окрестности
\Xi\ <h (i = 1, 2,... , т), A)
где h — достаточно малая величина, точка х\ = Х2 = ¦ ¦ ¦ = хт = 0 бу-
будет точкой строгого локального минимума функции V. Так как V sj О,
то на траекториях уравнений возмущенного движения в области A) V
будет невозрастающей функцией. Дальнейшее доказательство сводит-
сводится к почти дословному повторению рассуждений, проведенных в п. 225
при доказательстве теоремы Лагранжа.
Теорема Ляпунова дает достаточные условия устойчивости дви-
движения. Применение этой теоремы требует знания функции V, облада-
обладающей вполне определенными свойствами. Общих методов построения
таких функций нет. Однако во многих практически важных случаях
функцию V можно построить, если известны первые интегралы урав-
уравнений возмущенного движения. Например, при доказательстве теоре-
теоремы Лагранжа об устойчивости положения равновесия консервативной
системы в качестве функции V годилась полная механическая энергия
системы Е.
Пусть f/i, С/г,... 1 Uk — первые интегралы уравнений возмущен-
возмущенного движения. Без ограничения общности можно считать, что функ-
функции Uj(xi, a?2,... ) хт) (i = 1; 2,... , к) обращаются в нуль в начале
координат х\ = Х2 = • • • = хт = 0. Пусть ни одна из функций Uj не
является знакоопределенной. Будем искать1 функцию Ляпунова в виде
связки первых интегралов Uj (j = 1, 2,... , к):
v = \iUi + ... + \kuk + muf + ¦¦¦ + iikul
где Xj, \ij (j = 1, 2,... , fc) — неопределенные постоянные. Ясно,
что V будет первым интегралом уравнений возмущенного движения.
хСм.: ЧетаевН. Г. Устойчивость движения. Работы по аналитической механике.
М.: Изд-во АН СССР, 1962. По вопросу о методе интегральных связок Четаева см.
также работу: Пожарицкий Г. К. О построении функции Ляпунова из интегралов
уравнений возмущенного движения // ПММ. 1958. Т. 22, вып. 2. С. 145-154.
§ 2. Основные теоремы прямого метода Ляпунова 519
Если постоянные \j, /ij удастся выбрать так, чтобы функция V была
определенно-положительной, то она будет удовлетворять всем условиям
теоремы Ляпунова об устойчивости движения. При этом в тех случаях,
когда первые интегралы Uj (j = 1, 2,... , к) могут быть найдены из
каких-либо общих соображений (например, при помощи основных тео-
теорем динамики), отпадает необходимость составления самих уравнений
возмущенного движения, что существенно упрощает исследование.
Пример 1 (Устойчивость стационарных вращений твердого тела в
случае Эйлера). Как показано в п. 99, при стационарных вращениях
твердого тела в случае Эйлера вращение происходит с постоянной по
величине угловой скоростью вокруг любой из главных осей инерции тела
для неподвижной точки. Изучим устойчивость движения, в котором
р = со = const, q = О, г = 0. B)
Движение B) соответствует вращению вокруг оси, отвечающей мо-
моменту инерции А. Как показано в п. 98, динамические уравнения Эйлера
имеют два первых интеграла
U1=2T = Ap2+Bq2+Cr2, U2 = K2 = A2p2+B2q2+C2r2. C)
Введем возмущения х, у, z no формулам
p = w+x, q = y, r = z. D)
Уравнения возмущенного движения будут иметь первые интегралы
иг = Ах2 + By2 + Cz2 + 2Aljx, U2 = A2x2 + B2y2 + C2z2 + 2A2ljx,
E)
Последние выражения получены путем подстановки р, q, r из D) в
интегралы C) и отбрасыванием несущественных постоянных в полу-
получившихся выражениях для U\ и С/г-
Функцию V возьмем в виде
V = U2+Ul F)
Ясно, что значения функции V неотрицательны при любых х, у, z. По-
Покажем, что если А — наименьший или наибольший из моментов инер-
инерции, то функция V определенно-положительна. Для этого достаточно
показать, что при малых х, у, z система уравнений
U1 = 0, U2=0 G)
520 Глава XV
имеет единственное решение х = у = г = 0Из системы G) следует,
что
AUX -U2 = В (А - В)у2 + С (А - C)z2 = 0.
Если А — наименьший или наибольший из моментов инерции, то по-
последнее равенство возможно только когда у = z = 0. Из G) тогда следу-
следует, что х = 0 или х = — 2ш, и при достаточно малых х, у, z система
G) имеет единственное решение х = у = z = 0.
Следовательно, стационарные вращения твердого тела в случае
Эйлера вокруг оси наименьшего или наибольшего из моментов инер-
инерции устойчивы в смысле Ляпунова по отношению к возмущениям ве-
величин р, q, r. Этот факт хорошо иллюстрируется картиной располо-
расположения полодий на эллипсоиде инерции (см. рис. 99): вблизи осей Ох и Oz
эллипсоида инерции, отвечающих наибольшему и наименьшему момен-
моментам инерции, полодии являются замкнутыми кривыми, охватывающи-
охватывающими соответствующие оси. Напротив, вблизи оси Оу, отвечающей сред-
среднему по величине моменту инерции, полодии не охватывают этой оси,
и при малом возмущении стационарного вращения вокруг оси Оу век-
вектор угловой скорости с течением времени покидает окрестность этой
оси. Ниже в п. 235 мы строго докажем неустойчивость стационарного
вращения вокруг оси среднего по величине момента инерции тела.
Пример 2 (Устойчивость вращения тяжелого тела вокруг непо-
неподвижной точки в случае Лагранжа1). Движение тяжелого твердого
тела вокруг неподвижной точки описывается системой дифференциаль-
дифференциальных уравнений C2), C5) п. 105. В случае Лагранжа А = В, а = Ь = 0 и
уравнения движения имеют четыре первых интеграла
иг = А(р2 + q2) + С г2 + 2Рс7з = const,
U2 = A(p7i + QI2) + Crj3 = const,
U4 = r = const.
Уравнения движения имеют частное решение
р = 0, q = 0, г = r0 = const, 71 =0? 12 = 0, 7з = 1, (9)
которому отвечает вращение твердого тела вокруг вертикально рас-
расположенной оси Oz с постоянной угловой скоростью г$. Рассмотрим
устойчивость такого движения тела по отношению к возмущениям ве-
величин р, q, r, 7i 1 72? Тз- Положим
р = х±, q = х2, r = ro+x3, 7i = Ж4, 72 = Ж5, 7з = 1+жб-
хСм.: ЧетаевН. Г. Об устойчивости вращения твердого тела с одной неподвижной
точкой в случае Лагранжа // ПММ.—1954.—Т. 18, вып. 1. — С. 123-124.
§ 2. Основные теоремы прямого метода Ляпунова 521
Отсюда и из (8) получаем, что дифференциальные уравнения возмущен-
возмущенного движения имеют следующие первые интегралы:
Ui = А(х\ + х\) + С(х\ + 2г0х3) + 2Рсх6 = const,
U2 = А(х!Х4 + х2х5) + С(х3х6 + х3 + r0x6) = const,
U3 = х\ + х\ + х\ + 2жб = const,
U4 = Х3 = const.
Для получения условий устойчивости ищем функцию Ляпунова V в ви-
виде квадратичной связки первых интегралов A0) (Л — неопределенная
вещественная постоянная)
С (С — А)
V = UX+ 2XU2 - (Рс + Cro\)U3 + ——| -Ui - 2{r0 + X)CU4.
Функцию V можно представить в виде суммы трех квадратичных
форм:
V = /(ал, х4) + f(x2, хъ) + /(^Жз, а*), A1)
где
/(ж, у) = Ах2 + 2\Аху - (Рс + Сго\)у2. A2)
Из критерия Сильвестра получаем, что квадратичная форма A2)
определенно-положительна при выполнении неравенства
АХ2 + Сто А + Рс < 0, A3)
которое для вещественных А может удовлетворяться только тогда,
когда
С2г\ > 4АРс. A4)
При условии A4) постоянную А можно подобрать так, чтобы удов-
удовлетворялось неравенство A3). Тогда квадратичные формы в выраже-
выражении A1) будут определенно-положительными, каждая относительно
«своих» переменных, а функция V будет определенно-положительна
относительно всех переменных Х{ (г = 1, 2,..., 6). Таким обра-
образом, согласно теореме Ляпунова, условие A4) будет достаточным для
устойчивости движения (9) по отношению к возмущениям величин
Р, q, r, 7i, 72, 7з-
Условие A4) называют условием Маиевского-Четаева. Отметим,
что если с < 0 («висящее» твердое тело; центр масс расположен ниже
522 Глава XV
точки подвеса), то условие A4) всегда выполнено, а если с > О, то для
выполнения условия A4) требуется, чтобы угловая скорость вращения
flAPc
тела вокруг вертикали превосходила величину, равную
О
234. Теорема Ляпунова об асимптотической устойчивос-
устойчивости. Ляпунов получил следующую теорему, дающую достаточные усло-
условия асимптотической устойчивости движения.
Теорема. Если дифференциальные уравнения возмущенного движения
таковы, что существует знакоопределенная функцияУ(хх,Х2, •¦• ,хт),
производная которой V в силу этих уравнений есть знакоопределен-
ная функция противоположного знака с V, то невозмущенное движение
асимптотически устойчиво.
Прежде чем доказывать эту теорему, обратим внимание на до-
дополнительное, по сравнению с теоремой предыдущего пункта, условие,
которое обеспечивает асимптотическую устойчивость невозмущенного
движения. Это условие состоит в том, что производная V должна быть
знакоопределенной функцией противоположного с V знака. В предыду-
предыдущем же пункте функция V была лишь знакопостоянной.
Переходя к доказательству, заметим сначала, что если условия
сформулированной теоремы выполнены, то выполнены и условия теоре-
теоремы Ляпунова из предыдущего пункта, а значит, невозмущенное движе-
движение устойчиво. Согласно определению асимптотической устойчивости,
нам надо только доказать, что всякое возмущенное движение, для ко-
которого начальные возмущения достаточно малы, асимптотически при-
приближается к невозмущенному, т. е. что
lim xAt) = 0. A5)
t->oo
Без ограничения общности будем считать, что функция V определенно-
положительна; тогда в области A) V ^ 0, а V ^ 0, причем знаки ра-
равенства возможны только при х\ = Х2 = ¦ ¦ ¦ = хт = 0. Рассмотрим
какое-либо возмущенное движение, которому отвечают настолько ма-
малые начальные значения хщ = Xi(t0) (i = 1, 2,... , т), что поверх-
поверхность V = Vo, где Vo = V(x±0, x2o, ¦ • ¦ , хто), лежит в области
Ы<?, A6)
где е < h. Такой выбор величин хщ всегда возможен ввиду не-
непрерывности функции V. Покажем, что тогда возмущенные движе-
движения Xi{t) (i = 1, 2,... , т) удовлетворяют условиям A5), т. е. не-
невозмущенное движение асимптотически устойчиво.
§ 2. Основные теоремы прямого метода Ляпунова 523
Действительно, при е < h в области A6)
функция V(xi(t),X2(t),. ¦. ,xm(t)) остается от-
отрицательной, не обращаясь в нуль ни при ка-
каких значениях t. Это следует из того, что, в
силу единственности решения уравнений воз-
возмущенного движения при заданных начальных
условиях, функции Xi(t) (г = 1, 2,... , т) не
могут все одновременно обратиться в нуль при
каком-либо значении t = t*\ в противном слу-
случае было бы два разных решения с нулевыми
значениями при t = t*: рассматриваемое и тривиальное Х\ = х^ =
... = хт = 0. Так как V < 0, то функция V(xi(t), x2(t),... , xm(t))
монотонно убывает, оставаясь положительной. Но так как функция V
ограниченная, то существует предел
lim V(Xl(t), x2(t),... , xm(t)) = b^0.
t—юо
В m-мерном пространстве х\, жг,... , xm траектория уравнений воз-
возмущенного движения стремится к поверхности V = Ь, оставаясь вне ее
(рис. 175).
Покажем, что Ъ = 0, т. е. поверхность V = Ь вырождается в точку
х\ = Х2 = ¦ ¦ ¦ = хт = 0 и, следовательно, невозмущенное движение
асимптотически устойчиво. Предположим обратное, т. е. что Ъ ф 0.
Пусть — d — точная верхняя грань функции V в замкнутой области,
границами которой являются поверхности V = Ъ и V = Vo, т. е. в этой
области
V ^ -d. A7)
Отсюда следует, что
t
V(Xl(t), x2(t),... , xm(t))=V0+ I V dt^V0-d(t-t0), A8)
to
но это невозможно, так как при выполнении неравенства A8) опреде-
определенно-положительная функция V(xi(t), X2(t),... , xm(t)) для достаточ-
достаточно больших t должна была бы стать отрицательной. Противоречие до-
доказывает теорему.
Пример 1 (Асимптотическая устойчивость равновесия твердого
тела, имеющего неподвижную точку, в среде с сопротивлением).
Пусть тело вращается вокруг неподвижной точки О в среде, создающей
524 Глава XV
момент сопротивления
Мо = -/И • ш, A9)
где f(u>) > 0. Если существуют другие силы, приложенные к твердому
телу, то их главный момент относительно точки О считаем равным
нулю. Динамические уравнения Эйлера имеют вид
Л^ + (С- B)qr = -Пш)р,
^ -f(u)q, B0)
С^ + (В- A)pq = -/(Ш)г.
Уравнения B0) имеют частное решение р = q = г = 0, отвечающее
покою тела. Рассмотрим устойчивость этого частного движения тела
по отношению к переменным р, q, r.
Так как в невозмущенном движении р = q = г = 0, то уравне-
уравнения B0) будут дифференциальными уравнениями возмущенного движе-
движения. В качестве функции Ляпунова возьмем кинетическую энергию те-
тела
V = ±(Ap2+Bq2+Cr2). B1)
Для производной функции V получаем выражение
У = -/Н(р2+д2+г2). B2)
Так как V — определенно-положительная, aV — определенно-отрица-
определенно-отрицательная функции, то, согласно теореме Ляпунова, равновесие твердого
тела в среде, создающей момент сопротивления (9), асимптотически
устойчиво по отношению к переменным р, q, r.
235. Теоремы о неустойчивости. В этом пункте рассмотрены
три теоремы о неустойчивости движения, полученные Ляпуновым и Че-
таевым. Исторически сначала были получены две теоремы Ляпунова.
Эти теоремы были обобщены Четаевым, получившим теорему, кото-
которая нашла широкое применение при решении задачи об устойчивости в
конкретных задачах механики, а также в теоретических исследованиях
вопросов устойчивости. Мы сначала изложим теорему Четаева и затем
выведем из нее обе теоремы Ляпунова о неустойчивости движения.
Переходя к изложению теорем, заметим, что для обнаружения не-
неустойчивости невозмущенного движения достаточно установить су-
существование хотя бы одной траектории уравнений возмущенного дви-
движения, отвечающей сколь угодно малым значениям начальных возму-
возмущений и покидающей в некоторый момент времени окрестность начала
§ 2. Основные теоремы прямого метода Ляпунова
525
х.
h
координат, определяемую неравенствами A), в которых h — некоторая
заданная величина.
Введем определение. Областью V > 0 назовем какую-либо область
окрестности A), в которой V(xi, Ж2,... , хт) > 0. Поверхность V = 0
назовем границей области V > 0.
Теорема (Четаева о неустойчивости). Если дифференциальные
уравнения возмущенного движения таковы, что существует функ-
функция V(xi, Ж2,... , хт) такая, что в сколь угодно малой окрестнос-
окрестности A) существует область V > 0 и во всех точках области V > 0
производная V в силу этих уравнений принимает положительные зна-
значения, то невозмущенное движение неустойчиво.
Доказательство.
Зададимся окрестностью A) нача-
начала координат. Выберем начальную точ-
точку Жю, #20? • • • , Хто какой-либо тра-
траектории уравнений возмущенного дви-
движения в области V > 0. Так как гра-
граница области V > 0 проходит через
ТОЧКУ Х\ = Х2 = ¦ ¦ ¦ = Хт = 0, ТО
начальную точку можно взять сколь
угодно близко к началу координат (см.
рис. 176, где т = 2).
Так как по условию теоремы в об-
области V > 0 производная V положи-
положительна, то вдоль выбранной траектории рис ^6
функция V монотонно возрастает. Сле-
Следовательно, при t > to будем иметь
V(Xl(t), x2{t),... , xm{t)) > Vo > 0,
где Vq = V{x\q, Ж20, • • • , xmo). Поэтому траектория, начавшаяся в точ-
точке жю,Ж2о,.-. ,хто, не может выйти из области V > 0 через ее гра-
границу V = 0. Покажем, что с течением времени траектория выйдет
из окрестности A). Предположим обратное, т. е. что траектория при
всех t остается внутри окрестности A). Но тогда она должна находить-
находиться в области V > 0. Но это невозможно. Действительно, функция V,
как непрерывная и не зависящая явно от t, будет в области A) при
достаточно малых h ограничена, т. е.
О
h x.
V
B3)
где L — некоторое положительное число. В области G, являющейся
пересечением областей V > 0 и V > Vo, функция V положительна и
526 Глава XV
тоже ограничена. Пусть I — точная нижняя грань функции V в этой
области. Тогда при всех t > to
V ^ I > 0. B4)
Отсюда следует, что
V(Xl(t),
т. е. с течением времени функция V неограниченно возрастает, а это
противоречит неравенству B3). Противоречие доказывает теорему.
Функцию V, удовлетворяющую теореме Четаева о неустойчивости,
называют функцией Четаева.
Пример 1 (Неустойчивость стационарного вращения твердого те-
тела в случае Эйлера вокруг оси среднего по величине момента
ИНЕРЦИИ1). Рассмотрим устойчивость вращения B) твердого тела
в случае Эйлера, предполагая, что ось вращения отвечает среднему по
величине главному моменту инерции тела для неподвижной точки О.
Для определенности будем считать, что С > А > В и и> > 0.
Введя возмущения x,y,z no формулам D), из динамических уравне-
уравнении Эйлера получим дифференциальные уравнения возмущенного движе-
движения в виде
В-С . С-А, . ч . А-В, < , ,окч
х =—-|—yz, у= в (w + x)z, z= —?—(ш + х)у. B5)
Производная функции V = yz в силу уравнений B5) будет такой:
С-А 2 , А- В 2\ /ос\
zz + уг\ B6)
Если и> + х > 0, то в области V > 0, определяемой неравенства-
неравенствами у > 0, z > 0, производная V положительна. На основании теоре-
теоремы Четаева отсюда следует вывод о неустойчивости вращения тела
вокруг оси, отвечающей среднему по величине моменту инерции.
Теперь получим теоремы Ляпунова о неустойчивости.
Теорема (Первая теорема Ляпунова о неустойчивости движе-
движения). Если дифференциальные уравнения возмущенного движения та-
таковы, что существует функция V(x\, жг,... , хт) такая, что ее про-
производная V в силу этих уравнений есть функция знакоопределенная, а
сама функция V не является знакопостоянной, противоположного с V
знака, то невозмущенное движение неустойчиво.
хСм. уже упомянутую книгу Н. Г. Четаева «Устойчивость движения. Работы по
аналитической механике».
§ 3. Устойчивость по первому приближению 527
Доказательство.
Достаточно заметить, что при условиях теоремы 2 выполняют-
выполняются условия теоремы Четаева о неустойчивости. Действительно, пусть
функция V определенно-положительна. Тогда, в силу того, что V не
является знакопостоянной функцией, противоположного с V знака, су-
существует область V > О, расположенная сколь угодно близко к началу
координат, и в этой области V > 0.
Теорема (Вторая теорема Ляпунова о неустойчивости движе-
движения). Если дифференциальные уравнения возмущенного движения та-
таковы, что существует функция V такая, что ее производная, в силу
этих уравнений, в области A) может быть представлена в виде
V = asV + W, B7)
где зе — положительная постоянная, a W или тождественно обраща-
обращается в нуль, или представляет собой знакопостоянную функцию, и если
в последнем случае функция V не является знакопостоянной, противо-
противоположного с W знака, то невозмущенное движение неустойчиво.
Доказательство.
Как и в предыдущем случае, для доказательства теоремы 3 доста-
достаточно проверить, что при выполнении ее условий выполняются также
и условия теоремы Четаева о неустойчивости.
Если W тождественно равна нулю, то из B7) сразу следует, что
функция V положительна в области V > 0, которая обязательно су-
существует в сколь угодно малой окрестности начала координат (при не-
необходимости, когда, например, функция V определенно-отрицательна,
надо вместо V взять функцию —V). Следовательно, если W = 0, то
условия теоремы Четаева выполнены.
Пусть теперь W не равна тождественно нулю и для определеннос-
определенности будем ее считать знакопостоянной (положительной). Тогда, в силу
того, что V не является знакопостоянной, противоположного с W знака,
в любой сколь угодно малой окрестности начала координат существует
область V > 0. Но из B7) при W ^ 0 следует, что во всей окрестное-
тиA)
V^azV.
Следовательно, в области V > 0 производная V положительна. Поэтому
и в этом случае условия теоремы Четаева выполнены.
§ 3. Устойчивость по первому приближению
236. Постановка задачи. Будем рассматривать устойчивость
установившихся движений. Дифференциальные уравнения возмущен-
528 Глава XV
ного движения запишем в виде
^ = Ах+Щх), A)
где х — вектор-столбец, х' = (х\, ж2,..., хт); А — посто-
постоянная квадратная матрица то-го порядка; X — вектор-функция
от Ж1,ж2,... ,хт, X' = (ХЬХ2, • ¦ • ,Хт); функции Xt(i = 1, 2,... , т)
будем считать аналитическими в окрестности начала координат
х\ = Х2 = ... = хт = О, причем их разложения в ряды начинаются с
членов не ниже второго порядка малости относительно х\, жг,... , хт.
В приложениях вопрос об устойчивости движения очень часто ис-
исследуется при помощи уравнений первого приближения
которые получаются из полных уравнений возмущенного движения A),
если в последних отбросить нелинейные относительно х\, Ж2,... , хт
члены.
Рассмотрим уравнения B) подробнее. Пусть Ai, Лг,... , Хт —
корни характеристического уравнения1
det(A - ЛЕ) = 0, C)
a hj — собственный вектор матрицы А, отвечающий корню А^.
Если матрица А приводится к диагональной форме, то существу-
существуют т линейно независимых собственных векторов и общее решение
системы A) имеет вид2
D)
где cj — произвольные постоянные.
Если же матрица А к диагональной форме не приводится, то общее
решение системы B) будет записываться в виде
E)
1Среди величин Ai, Аг,--- , Ат могут быть и равные.
2См., например, гл. 2 учебника: Понтрягин Л. С. Обыкновенные дифференциаль-
дифференциальные уравнения. М.: Наука, 1970.
§ 3. Устойчивость по первому приближению
529
где компоненты векторов Щ являются многочленами относительно t.
Например, общее решение системы
Х\ = \х\ + Х2, Х2 =
имеет вид
Xl
x2
= Cl
1
0
At ,
e + C2
t
1
„At
Если бы уравнения возмущенного движения были линейными, то по
их общему решению, D) или E), вопрос об устойчивости невозмущен-
невозмущенного движения решался бы очень просто; в частности, необходимым
и достаточным условием асимптотической устойчивости была бы от-
отрицательность вещественных частей всех корней характеристического
уравнения; при наличии же хотя бы одного корня с положительной ве-
вещественной частью движение было бы неустойчивым.
Но, как правило, уравнения возмущенного движения нелинейны.
Поэтому возникает задача об определении условий, при которых вы-
выводы об устойчивости, полученные из анализа уравнений первого при-
приближения B), справедливы и для полных уравнений возмущенного дви-
движения A) при любых нелинейных членах Х\, Хг,... , Хт. Эта задача
была полностью решена Ляпуновым.
237. Теорема об устойчивости по первому приближе-
приближению. Один из основных результатов, полученных Ляпуновым при ре-
решении задачи об устойчивости по первому приближению, можно сфор-
сформулировать в виде следующей теоремы.
Теорема. Если все корни характеристического уравнения C) име-
имеют отрицательные вещественные части, то невозмущенное движение
асимптотически устойчиво независимо от нелинейных членов в A). Ес-
Если же среди корней характеристического уравнения есть хотя бы один
с положительной вещественной частью, то невозмущенное движение
неустойчиво — тоже независимо от нелинейных членов в A).
Доказательство.
Если в уравнениях A) сделать замену переменных по формуле
то они станут такими:
х = Су
dy
dt
Y(y),
F)
G)
где В = С 1АС, a Y(y) = С 1X(Cj/). Матрицу С (которая, вообще го-
говоря, комплексная) выберем так, чтобы матрица В была нормальной
530
Глава XV
жордановой формой матрицы А, т. е. чтобы матрица В состояла из од-
одной или нескольких жордановых клеток, расположенных по ее главной
диагонали, а все элементы, не входящие в жордановы клетки, равнялись
бы нулю1:
В =
хк
0
0
0
0
1
хк
0
0
0
0 ...
1 ...
хк ...
0 ...
0 ...
0
0
0
A,
0
0
0
0
1
A,
В уравнениях G) сделаем еще одну вспомогательную замену перемен-
переменных по формулам
Уз = M3Zj (j = 1, 2,... , т),
где ц — положительное, вообще говоря, малое число; условие для бо-
более конкретного его выбора будет видно из дальнейшего. В перемен-
переменных z\, z2, ¦ ¦ ¦ , zm система G) запишется в виде
Z±,
X2z2
Z2,
(8)
dzn
dt
~г
Здесь dj, равняется 0 или 1; Z\, Z2,.-. , Zm — нелинейные члены
относительно переменных z\, z2,... , zm, являющихся, вообще говоря,
комплексными.
Пусть Tj и Sj — действительная и мнимая части корня Xj характе-
характеристического уравнения C), т. е. Xj = r3- + isj (j = 1, 2,... , m); здесь
i — мнимая единица.
а) Пусть tj < 0 для всех j = 1, 2,... , m. Для доказательства
асимптотической устойчивости невозмущенного движения рассмотрим
функцию
(9)
1См. гл. 6 книги: ГантмахерФ. Р. Теория матриц. М.: Наука, 1967.
§ 3. Устойчивость по первому приближению 531
где чертой обозначена комплексно сопряженная величина. Функция (9)
является определенно-положительной функцией исходных перемен-
переменных х\, Х2, • • • , хт. Для ее производной в силу уравнений (8) получаем
выражение
т т
F = 2 ? rjzjzj +»F + YP&i + *&), A0)
3=1 3=1
где F — вещественная квадратичная форма, которая тождественно рав-
равна нулю, если все коэффициенты а3- в системе (8) равны нулю, т. е. если
матрица А приводится к диагональной форме.
Функция A0) является вещественной функцией исходных перемен-
переменных х\, Ж2,... , хт. Так как rj < 0 (j = 1, 2,... , m), то квадратич-
квадратичная часть функции V будет определенно-отрицательной функцией, если
число \х достаточно мало. А так как последняя сумма в правой части
выражения A0) содержит совокупность членов не ниже третьего по-
порядка, то и вся функция V при достаточно малых ц будет определенно-
отрицательной.
На основании теоремы Ляпунова об асимпотической устойчивос-
устойчивости получаем отсюда вывод об асимптотической устойчивости невозму-
невозмущенного движения, если вещественные части всех корней характерис-
характеристического уравнения отрицательны.
б) Пусть теперь п > 0, г2 > 0,... , гк > 0, гк+1 ^ 0,... , rm ^ 0.
Для доказательства неустойчивости невозмущенного движения вос-
воспользуемся второй теоремой Ляпунова о неустойчивости. Пусть
к т
V = -Y,zi*3+ Y, zi*3- (И)
3=1 j=k+l
Ее производную в силу уравнений (8)
к т
V = - 2 Y, riz^i + 2 12 riz^i +»G-
3=1 3=к+1
к т
-Ys(zizj + zjZ^+ Y, (zJzJ+zj^3)
3=1 i=k+l
можно записать в виде
V = asV + W, A2)
532 Глава XV
где зе — пока неопределенное положительное число, а
к т
W = ^(ээ - 2ri)zizi + Y^ Bгз ~ x)zi*i + № -
A3)
к т У '
~ YPiZi + ziZ^ + E $izi + z^i)'
3=1 j=k+l
Здесь G — квадратичная форма, появляющаяся в выражении для V
тогда, когда не все коэффициенты uj в системе (8) равны нулю.
Выберем число зе так, чтобы для j = 1, 2,... , к выполнялись нера-
неравенства 0 < зе < 2rj. Тогда при достаточно малых ц функция W будет
определенно-отрицательной. Но функция V, очевидно, знакопеременная
и, следовательно, не является знакопостоянной, противоположного с W
знака. На основании второй теоремы Ляпунова о неустойчивости полу-
получаем отсюда вывод о том, что при наличии хотя бы одного корня ха-
характеристического уравнения с положительной вещественной частью
невозмущенное движение неустойчиво. Теорема доказана.
Замечание 1. Ляпунов также показал1, что если у характеристичес-
характеристического уравнения C) нет ни одного корня с положительной вещественной
частью, но есть корни, у которых вещественная часть равна нулю,
то можно так подобрать нелинейные члены в уравнениях возмущенного
движения A), чтобы имела место устойчивость или неустойчивость,
по желанию.
Все случаи, которые могут представиться при решении задачи об
устойчивости, можно разбить на некритические и критические. В не-
некритических случаях вопрос об устойчивости решается рассмотрением
уравнений первого приближения B). В критических случаях уравнений
первого приближения недостаточно: для решения задачи об устойчивос-
устойчивости обязательно требуется привлечение нелинейных членов в уравнени-
уравнениях возмущенного движения A). Из доказанной выше теоремы следует,
что критическими будут те и только то случаи, когда характеристичес-
характеристическое уравнение B) не имеет корней с положительными вещественными
частями, но имеет корни с вещественными частями, равными нулю.
238. Критерий Рауса—Гурвица. Для практического использо-
использования теоремы об устойчивости по первому приближению важно опре-
определить знаки вещественных частей характеристического уравнения. В
частности, желательно иметь критерий, позволяющий по коэффициен-
1 Ляпунов А. М. К вопросу об устойчивости движения // Собр. соч. Т. 2, М.; Л.:
Изд-во АН СССР, 1956. С. 267-271.
j 3. Устойчивость по первому приближению
533
там характеристического уравнения определить, будут ли все его корни
иметь отрицательные вещественные части или нет.
Запишем характеристическое уравнение C) в виде
«о А71
= 0.
A4)
Коэффициенты а0, «i,... , ат, этого уравнения — вещественные чис-
числа. Не ограничивая общности, будем в дальнейшем считать, что стар-
старший коэффициент «о положителен.
Получим сначала одно очень простое необходимое условие отрица-
отрицательности вещественных частей всех корней Ai, Аг,... , Хт уравне-
уравнения A4): для того чтобы при «о > 0 все корни уравнения A4) имели
отрицательные вещественные части, необходимо, чтобы все его ко-
коэффициенты были положительны. Доказательство этого утверждения
непосредственно вытекает из формул Виета:
ц„ — \'Ч i /vl i • • • i 'Чп/:
0,2 л л л л
j7- = AiA2 + ... + Am_iAm,
A5)
ит _ ( -\\т\ \ \
"а^ — у1) Л1л2---Ат.
Но положительность всех коэффициентов уравнения A4) не являет-
является достаточным условием того, что его корни имеют отрицательные
вещественные части. Необходимое и достаточное условие дается кри-
критерием Рауса-Гурвица. Сформулируем соответствующую теорему, не
приводя ее доказательства1. Назовем матрицей Гурвица квадратную
матрицу то-го порядка
A6)
Эта матрица строится следующим образом: по ее главной диагонали
стоят коэффициенты а^ (г = 1, 2,... , т) в порядке возрастания значе-
значений индекса г; в каждом столбце элементы, стоящие выше главной диа-
диагонали, расположены так, что соответствующие им коэффициенты uj
«1
а0
0
0
«3
«2
«1
«о
а5 ..
й4 ..
а3 ¦¦
а2 ..
. 0
. 0
. 0
. 0
• ат
1 Доказательство см., например, в гл. 16 книги: ГантмахерФ. Р. Теория матриц.
М.; Наука, 1967.
534
Глава XV
идут в порядке последовательного возрастания индекса j на единицу,
а ниже главной диагонали — в порядке последовательного убывания
индекса j; те места матрицы, куда при таком правиле образования ее
элементов следовало бы вписать коэффициенты a,j для j < 0 или j > m,
заполняются нулями.
Составим главные миноры матрицы A6) (определители Гурвица)
= «1, Д2 =
«1 «3
а0 «2
«1 й3 й5
«о «2 «4
О «1 «з
,... , Ат =
_1. A7)
Теорема (Критерий Рауса—Гурвица). Для того чтобы все корни
уравнения A4) с вещественными коэффициентами и положительным
старшим коэффициентом а0 имели отрицательные вещественные час-
части, необходимо и достаточно, чтобы выполнялись неравенства
> О, А2 > 0,..., Ат > 0.
A8)
Отметим, также без доказательства, что если при а0 > 0 хотя
бы одно из неравенств A8) имеет противоположный смысл, то урав-
уравнение A4) имеет корни, вещественные части которых положительны.
Рассмотрим простейшие частные случаи (везде предполагается,
что а0 > 0).
Пример 1 (Уравнение первой степени (т = 1)).
Условия A8) сводятся к неравенству
«1 > 0.
Пример 2 (Уравнение второй степени (т = 2)).
«оЛ2 + «iA + «2=0.
Определители Гурвица A7) будут такими:
Ai = «1, Д2 = «i«2-
Условия A8) запишутся в виде неравенств
«1 > 0, «2 > 0.
Пример 3 (Уравнение третьей степени).
«оЛ3 + «iA2 + «2А + «3 = 0.
A9)
B0)
§ 4- Влияние диссипативных и гироскопических сил на устойчивость 535
Здесь
Ai = «1, Д2 = ai«2 - аоа3, Д3 = я3Д2,
и условия A8) означают, что
«1 > 0, «з > О, ai«2 - яоя3 > 0. B1)
Эти неравенства показывают, что при т > 2 положительности коэф-
коэффициентов уравнения A4) недостаточно для того, чтобы все его корни
имели отрицательные вещественные части: при т = 2> нужно еще по-
потребовать выполнения неравенства «i«2 > Я0Я3.
Пример 4 (Уравнение четвертой степени).
я0А4 + «iA3 + я2А2 + я3А + а4 = 0. B2)
Определители Гурвица имеют вид
Ах = (ц, Д2 = aia2 - а0а3, Дз = а3А2 - аАа\, Д4 = я4Д3.
Условия отрицательности вещественных корней уравнения B2) запи-
запишутся, как нетрудно проверить, в виде неравенств
«1 > О, аз > О, а4 > О, яз(й1Я2 — аоаз) — а±а\ > 0. B3)
§ 4. Влияние диссипативных и гироскопических
сил на устойчивость равновесия консервативной
системы
239. Влияние гироскопических сил и диссипативных сил
с полной диссипацией на устойчивое положение равновесия
голономнои системы. В п. 225 отмечалось, что при добавлении к
консервативной голономнои системе гироскопических и диссипатив-
диссипативных сил теорема Лагранжа об устойчивости положения равновесия
консервативной системы при наличии строгого локального минимума
потенциальной энергии остается справедливой, т. е. устойчивое при
одних потенциальных силах положение равновесия системы остается
устойчивым и при наличии гироскопических и диссипатипных сил. Это
утверждение содержит только часть результатов, полученных Томсо-
ном, Тэтом и Четаевым в задаче о влиянии гироскопических и дисси-
диссипативных сил на устойчивость положения равновесия голономнои кон-
консервативной системы. В данном параграфе рассмотрим другие теоремы
Томсона-Тэта-Четаева.
536 Глава XV
Теорема. Если в некотором изолированном положении равновесия по-
потенциальная энергия имеет строгий локальный минимум, то при до-
добавлении гироскопических сил и диссипативпых сил с полной диссипа-
диссипацией это положение равновесия становится асимптотически устойчи-
устойчивым.
Доказательство.
Без ограничения общности будем считать, что в положении рав-
равновесия все обобщенные координаты qi равны нулю. Для доказатель-
доказательства теоремы возьмем функцию V, совпадающую с полной механи-
механической энергией системы Е = Т + П. По условию теоремы она
будет определенно-положительной в окрестности начала координат
2п-мерного пространства состояний qi, qi (г = 1, 2,... , п). Из условия
теоремы следует, что
V = N*(qj, qj) = Y, Q*(Qj, Qi)Qi ^ °> (!)
i=l
где Q* — непотенциальная обобщенная сила, отвечающая обобщенной
координате щ (г = 1, 2,... , п), и знак равенства достигается только
при qi = 0 (г = 1, 2,... , п).
Из знакоопределенности функции V и неравенства A) на основа-
основании теоремы Ляпунова об устойчивости получаем, что положение рав-
равновесия устойчиво. Для доказательства асимптотической устойчивости
теперь достаточно убедиться в том, что если начальная точка траек-
траектории взята достаточно близко к началу координат qi = 0, qi = 0, то
при ? -»• оо имеем </,->¦ 0, щ ->• 0 для всех г = 1, 2,... , п.
Пусть движение происходит в столь малой окрестности начала ко-
координат, что последняя не содержит других положений равновесия,
кроме gi = G2 = ... = qn = 0, а мощность N* непотенциальных сил
является определенно-отрицательной функцией обобщенных скоростей.
Выбор такой окрестности всегда возможен в силу изолированности и
устойчивости положения равновесия qi = G2 = ... = qn = 0.
Приращение AV на любом конечном интервале времени At отри-
отрицательно, так как N* = 0 только при qi = q% = ... = qn = 0, и в
выбранной окрестности вне начала координат эти равенства не могут
иметь места в течение конечного времени At, так как начало координат
является изолированным положением равновесия. Действительно, если
бы на интервале At выполнялись равенства q\ = (/2 = ... = qn = 0,
но не все qi были бы равны 0, то, как показано в п. 225, все ги-
гироскопические и диссипативные силы Q*(qj, qj) были бы равны ну-
нулю и из уравнений Лагранжа второго рода B8) п. 142 следовало бы,
§ 4- Влияние диссипативных и гироскопических сил на устойчивость 537
что |!— = 0 (г = 1, 2,... , п) вне начала координат, т. е. изучаемое
положение равновесия не было бы изолированным. Таким образом, в
достаточно малой окрестности начала координат функция V монотонно
убывает. С возрастанием t она стремится к некоторому неотрицатель-
неотрицательному пределу Ъ. Аналогично п. 234 можно показать, что случай Ъ ф О
невозможен и, следовательно, V —> 0 при t —> оо. Но так как V — зна-
коопределенная функция величин qi, щ (i = 1, 2,... , п), то отсюда
следует, что qi —> О, <й —>• 0, при t —> оо. Теорема доказана.
240. Влияние гироскопических и диссипативных сил на
неустойчивое равновесие. Пусть положение равновесия консерва-
консервативной системы неустойчиво. Нельзя ли добавлением диссипативных
сил стабилизировать его, т. е. нельзя ли так подобрать диссипативные
силы, чтобы неустойчивое при наличии одних потенциальных сил по-
положение равновесия стало устойчивым или даже, может быть, асимп-
асимптотически устойчивым? Ответ на этот вопрос отрицательный.
Введем некоторые вспомогательные понятия. Как и в задаче о
малых колебаниях, будем считать, что кинетическая энергия кон-
консервативной системы в окрестности положения равновесия является
определенно-положительной квадратичной формой относительно обоб-
обобщенных скоростей:
п
Т = \ Y, «ikQiQk, B)
г, k=l
где ац. — постоянные коэффициенты. Пусть, далее, потенциальная
энергия в окрестности положения равновесия qi — q<i — ... — qn — 0
разлагается в ряд по степеням qi, G2, ... , qn и квадратичная часть
этого ряда не равна тождественно нулю. Тогда считаем, что
п
П = ^ XI cikQiQk, C)
г, k=l
где Cik — постоянные величины. Квадратичные формы B) и C) можно
одновременно привести к сумме квадратов при помощи вещественной
линейной замены переменных q —> в (см., например, п. 229, где рас-
рассматривались главные координаты и главные колебания консерватив-
консервативной системы в окрестности положения равновесия). В новых перемен-
переменных
е D)
г=1 г=1
538 Глава XV
Величины А, Пуанкаре предложил называть коэффициентами устой-
устойчивости. Если, как в п. 229, функция C) определенно-положительна,
то все величины Aj положительны и положение равновесия устойчи-
устойчиво. Если же хотя бы одна из величин А^ отрицательна, то положение
равновесия неустойчиво1. Число отрицательных коэффициентов устой-
устойчивости называется степенью неустойчивости. В дальнейшем важна
будет не сама степень неустойчивости, а ее четность или нечетность.
Пусть С — матрица квадратичной формы C). Тогда det С = Ai A2 ... А„.
Отсюда следует, что если det С > 0, то степень неустойчивости четная
(или равняется нулю), а если det С < 0, то степень неустойчивости
нечетная.
Теорема 1. Если среди коэффициентов устойчивости хотя бы один
является отрицательным, то изолированное положение равновесия не
может быть стабилизировано диссипативными силами с полной дисси-
диссипацией.
Доказательство.
Пусть V = -Е = -Т - П. Тогда
V = -2V* ^ 0, E)
где N* — мощность диссипативных сил, являющаяся по условию тео-
теоремы определенно-отрицательной функцией обобщенных скоростей.
Приращение AV на любом конечном интервале времени At поло-
положительно; это показывается совершенно аналогично тому, как показана
отрицательность AV в теореме предыдущего пункта. Далее, так как
среди величин А;, есть хотя бы одна отрицательная, то в любой сколь
угодно малой окрестности начала координат 2п-мерного пространства
состояний <7,, (ft (г = 1, 2,... , п) существует область V > 0. Дальней-
Дальнейшие рассуждения аналогичны проведенным в п. 235 при доказательстве
теоремы Четаева о неустойчивости.
Итак, диссипативными силами с полной диссипацией стабилизации
добиться невозможно. А нельзя ли стабилизировать положение равнове-
равновесия при помощи гироскопических сил? Частичный ответ на этот вопрос
содержится в следующей теореме. Будем рассматривать гироскопичес-
гироскопические силы, линейные относительно обобщенных скоростей.
ХИ не только в первом приближении, а для полных нелинейных уравнений воз-
возмущенного движения, что следует из теоремы об устойчивости по первому при-
приближению, так как при наличии отрицательных коэффициентов А; среди корней
характеристического уравнения есть и положительные корни. Заметим, что это яв-
является также доказательством сформулированной (но не доказанной) в п. 226 первой
теоремы Ляпунова о неустойчивости положения равновесия консервативной систе-
системы.
§ 4- Влияние диссипативных и гироскопических сил на устойчивость 539
Теорема 2. Если степень неустойчивости изолированного положения
равновесия консервативной системы нечетна, то стабилизация его до-
добавлением гироскопических сил невозможна, если же степень неустой-
неустойчивости четна, то гироскопическая стабилизация возможна.
Доказательство.
Для доказательства невозможности гироскопической стабилизации
при нечетной степени неустойчивости достаточно рассмотреть линеа-
линеаризованную систему уравнений возмущенного движения и показать,
что ее характеристическое уравнение и при наличии гироскопических
сил имеет хотя бы один положительный корень.
В переменных в{ (г = 1, 2,... , п) уравнения движения имеют вид
п
Oi+KOt = Y;"tikOk (* = 1, 2,... , п), F)
к = 1
где jo- = —jki — постоянные величины. Характеристическое уравне-
уравнение системы F) будет таким:
Д(Л) =
A2+Ai -712А
712А А2+А2
А2 + А„
= 0.
При А ->• +оо имеем А(А) ->• +оо. Но Д@) = Ai А2... А„ и в силу
нечетности степени неустойчивости Д@) < 0. Следовательно, харак-
характеристическое уравнение имеет хотя бы один положительный корень
и, согласно теореме п. 237 об устойчивости по первому приближению,
положение равновесия qi = G2 = ... = qn = 0 неустойчиво независимо
от нелинейных членов в уравнениях возмущенного движения, т. е. если
степень неустойчивости нечетна, то стабилизация гироскопическими
силами невозможна.
Чтобы показать возможность гироскопической стабилизации в
случае четной степени неустойчивости, рассмотрим простой пример.
Пусть движение системы с двумя степенями свободы описывается та-
такими дифференциальными уравнениями:
q\ + Аш -792 = 0, <72 +А2Ф2 + 7<?i = 0, G)
где Ai, A2, 7 — постоянные величины, А» < 0 (г = 1, 2). Последние сла-
слагаемые в уравнениях G) представляют собой гироскопические силы;
если они равны нулю, то положение равновесия gi = G2 = 0 неустойчи-
неустойчиво, а степень неустойчивости равна двум. Покажем, что гироскопичес-
гироскопические силы, т. е. величину 7 в G), можно подобрать так, что положение
равновесия станет устойчивым.
540 Глава XV
Характеристическое уравнение линейной системы G) имеет вид
*4 + (*i + *2+72)A2+A1A2 = 0. (8)
Нетрудно убедиться, что при выполнении неравенства
А2~+А2
(9)
корни уравнения (8) чисто мнимые и различны, и, следовательно, при
условии (9) положение равновесия <7i = <7г = 0 устойчиво.
Теорема 3. Если изолированное положение равновесия консервативной
системы имеет отличную от нуля степень неустойчивости, то оно
остается неустойчивым при добавлении гироскопических сил и дисси-
пативных сил с полной диссипацией.
Доказательство этой теоремы аналогично доказательству теоре-
теоремы 1.
Из рассмотренных в этом параграфе теорем следует, что: 1) добав-
добавление диссипативных сил не нарушает устойчивости или неустойчи-
неустойчивости изолированного положения равновесия консервативной системы;
2) добавление же гироскопических сил, не нарушая устойчивости поло-
положения равновесия, в некоторых случаях (при четной степени неустой-
неустойчивости) может стабилизировать неустойчивое положение равновесия;
3) однако если неустойчивое положение равновесия стабилизировано
гироскопическими силами, то при добавлении диссипативных сил с пол-
полной диссипацией положение равновесия снова будет неустойчивым.
Устойчивость, существующую при одних потенциальных силах,
называют вековой, а устойчивость, полученную с помощью гироско-
гироскопических сил,— временной.
Пример 1 (Устойчивость поступательного движения твердого те-
тела на круговой орбите). Пусть твердое тело обладает динамической
симметрией (А = В), а его центр масс движется по круговой орбите в
центральном ньютоновском гравитационном поле. Согласно п. 126 урав-
уравнения движения тела относительно центра масс могут быть записаны
в виде
А^+(С- A)qr = Зп2(С - А)а32а33,
^-(С-А)гр
dr -о
А^-(С-А)гр=-Зп2(С-А)а33а31, (Ю)
dt
§ 4- Влияние диссипативных и гироскопических сил на устойчивость 541
где
р = ф sin в sin (p + в cos (p + пп2\ ,
q = ф sin в cos <р> — в sin ip + na^i, A1)
Г = ф COS в + ф + Пп23 ¦
В уравнениях A0) ы A1) п — среднее движение центра масс тела по
орбите, а величины aij выражаются через углы Эйлера ф, в, (р по фор-
формулам C) п. 19.
Из третьего уравнения системы A0) следует, что имеет место
интеграл
г = го = const.
Уравнения движения имеют частное решение
6» = тг/2, ф = тт. A2)
Для этого частного решения
р = 0, q = 0, ф=-п + г0. A3)
Будем считать, что постоянная го равна нулю; тогда частное реше-
решение A2) отвечает поступательному движению твердого тела в аб-
абсолютном пространстве (в орбитальной же системе координат те-
тело вращается вокруг оси динамической симметрии с угловой скорос-
скоростью ф = —п).
Рассмотрим устойчивость этого движения тела по отношению к
переменным ф, в, ф, в. Пусть
8 = T>+qi, Ф = 'к + q2, 0 = qi, ф = qi-
Произведя линеаризацию первых двух уравнений системы A0) и разре-
разрешив их относительно старших производных, получим
q'; = D-3a)qi+2q2, q'2' = q2 - 2q[. A4)
Здесь штрихом обозначено дифференцирование по переменной v = nt и
введено обозначений а = С/А. Так как моменты инерции удовлетворя-
удовлетворяют неравенству треугольника А + В ^ С, то 0 ^ а ^ 2.
Первые слагаемые в правых частях уравнений A4) являются по-
потенциальными силами, порождаемыми потенциалом
I-igl, A5)
542 Глава XV
а последние слагаемые представляют собой гироскопические силы.
Если бы гироскопические силы отсутствовали, то положение рав-
равновесия qi = g2 = 0 (оно отвечает невозмущенному движению A2))
было бы неустойчивым, причем при а < 4/3 степень неустойчивости
четная, а при 4/3 < а ^ 2 нечетная. Поэтому из теоремы 2 следу-
следует, что при 4/3 < а ^ 2 гироскопическая стабилизация невозможна, и,
следовательно, в этом случае движение A2) неустойчиво по Ляпунову.
Из той же теоремы 2 следует, что при а < 4/3 гироскопическая
стабилизация в принципе возможна. Чтобы узнать, осуществляется
ли она в рассматриваемой задаче, при заданных конкретных гироскопи-
гироскопических силах, рассмотрим характеристическое уравнение системы A4)
Л4 + (За - 1)Л2 + D - За) = 0. A6)
При выполнении системы неравенств
За-1>0, 4-За>0, (За - IJ - 4D - За) > О A7)
корни уравнения A6) будут чисто мнимыми и, следовательно, движе-
движение A2) будет устойчиво в линейном приближении по отношению к пе-
переменным ф, в, ф, в. Если же хотя бы одно из неравенств A7) имеет
противоположный смысл, то у уравнения A6) будут корни с положи-
положительными вещественными частями и движение A2) неустойчиво по
Ляпунову.
Система неравенств A7), как нетрудно проверить, приводится к
виду
1<а<|. A8)
Следовательно, в нашей конкретной задаче в случае четной степени
неустойчивости при выполнении условия A8) гироскопическая стаби-
стабилизация осуществляется, а при а < 1 — нет.
Таким образом, показано, что поступательное движение твердого
тела на круговой орбите при а < 1 и а > 4/3 неустойчиво по Ляпу-
Ляпунову, а при 1 < а < 4/3 оно устойчиво в линейном приближении. Более
детальное исследование позволяет показать, что на самом деле при вы-
выполнении условия A8) движение будет устойчиво по Ляпунову не только
в линейном приближении, но и в рамках полных нелинейных уравнений
возмущенного движения1.
1См.: МаркеевА. П. Резонансные эффекты и устойчивость стационарных враще-
вращений спутника // Космические исследования. 1967. Т. 5, №3. С. 365-375.
§ 5. Об устойчивости гамилътоновых систем 543
§ 5. Об устойчивости гамильтоновых систем
241. Общие замечания. Пусть дифференциальные уравнения
возмущенного движения записываются и виде системы уравнений Га-
Гамильтона
! 2 п) ш
dt ~ dPj> dt ~ dQj U"i5 2'-'-' П)- Uj
Считаем, что функция Гамильтона аналитична в окрестности точки
qj = pj = 0 (j = 1, 2,... , п) и представима в виде ряда
Я = Я2 + Я3 + Щ + ... , B)
где ifm — формы степени т относительно qj, pj (j = 1, 2,... , п),
коэффициенты которых постоянны или 2тг-периодичны по t. К рассмот-
рассмотрению системы A) приводят многие задачи об устойчивости движения
в потенциальном поле сил.
Решение задачи об устойчивости невозмущенного движения (ему
отвечает решение qj = pj = 0 (j = 1, 2,... , п) системы A)) зависит
от свойств функции Гамильтона. Очень просто вопрос об устойчивос-
устойчивости решается в том случае, когда время t не содержится в уравнени-
уравнениях A), а функция Я является знакоопределенной в окрестности точ-
точки qj = pj = 0 (j = 1, 2,... , п). В этом случае функция Н будет
интегралом системы A) и невозмущенное движение устойчиво. Этот
вывод непосредственно следует из теоремы Ляпунова об устойчивости;
для применения этой теоремы в качестве функции Ляпунова V можно
принять функцию Н.
Если же функция Н не является знакоопределенной или зависит от
времени, то задача об устойчивости становится весьма сложной. Для
системы A) справедлива теорема Лиувилля о сохранении фазового объ-
объема, поэтому невозмущенное движение не может быть асимптотически
устойчивым; в системах, описываемых дифференциальными уравнени-
уравнениями Гамильтона, возможна либо устойчивость, либо неустойчивость.
Следовательно, если линеаризованные уравнения не дают строгого ре-
решения вопроса об устойчивости (как, например, в случае установив-
установившихся движений при наличии у характеристического уравнения хотя
бы одного корня с положительной вещественной частью), то возникает
необходимость рассмотрения нелинейных членов в уравнениях A), т. е.
мы имеем критический случай теории устойчивости.
В этом параграфе мы рассмотрим некоторые вопросы теории
устойчивости движения в системах, описываемых гамильтоновыми
дифференциальными уравнениями. При этом ограничимся случаем,
544 Глава XV
когда уравнения возмущенного движения A) линейные1. Часто вмес-
вместо термина «устойчивость невозмущенного движения» мы будем при-
применять термин «устойчивость системы A)» или просто «устойчивость
гамильтоновой системы».
242. Устойчивость линейных гамильтоновых систем с по-
постоянными коэффициентами. Запишем линейную гамильтонову
систему дифференциальных уравнений в матричной форме (см. п. 189)
-^=Шх, х'=(х±,... , хп, хп+1,... , х2п), C)
где Хк, хп+и (к = 1, 2,... , п) — канонически сопряженные перемен-
переменные (хк — координаты, хп+и — импульсы). Квадратная матрица J
порядка 2п имеет вид
J =
О Е„
-Е„ О
(J' = J 1 = -J, J2 = -E2n, det J = 1). D)
В системе C) Н — вещественная симметрическая матрица порядка 2п.
Она либо постоянна, либо является непрерывной 2тг-периодической по t.
Пусть матрица Н в системе C) постоянна. Рассмотрим характе-
характеристическое уравнение
р(А) = det(JH - АЕ2п) = 0. E)
Как показано в п. 189, многочлен р(А) — четная функция А. Поэтому ес-
если уравнение E) имеет корень А = а с отличной от нуля вещественной
частью, то система C) неустойчива, так как либо сам этот корень, либо
противоположный ему по знаку корень А = —а имеет положительную
вещественную часть. Согласно теореме об устойчивости по первому
приближению (п. 237), в этом случае неустойчива и полная нелинейная
система уравнений возмущенного движения A).
Таким образом, для устойчивости системы C) необходимо, чтобы
корни ее характеристического уравнения E) были чисто мнимыми. Это
условие будет и достаточным, если дополнительно потребовать, чтобы
матрица JH приводилась к диагональной форме.
243. О линейных системах с периодическими коэффициен-
коэффициентами. Рассмотрим линейную систему дифференциальных уравнений
4? = A(t)x, x' = (Xl,...,xm), F)
1Теория устойчивости нелинейных гамильтоновых систем изложена в работах:
Арнольд В. И. Малые знаменатели и проблемы устойчивости движения в классичес-
классической и небесной механике // УМН, 1963. Т. 18, вып. 6. С. 91-192; МозерЮ. Лекции о
гамильтоновых системах. М.: Мир, 1973; МаркеевА. П. Точки либрации в небесной
механике и космодинамике. М.: Наука, 1978.
§ 5. Об устойчивости гамилътоновых систем 545
где А(?) — непрерывная, 2тг-периодическая по t вещественная матри-
матрица. Структура решений системы F) описывается следующей теоремой
Флоке.
Теорема. Для системы F) фундаментальная матрица решений Х(?),
нормированная условием Х@) = Ет; представима в виде
X(t) = Y(t)em G)
где В — постоянная матрица, a Y(t) — непрерывно дифференцируе-
дифференцируемая, 2тг-периодическая по t матрица.
Доказательство.
Заметим прежде всего, что так как Х(?) — фундаментальная
матрица решений уравнений F), то, в силу 2тг-периодичности матри-
матрицы А(?), фундаментальной будет также матрица Х(? + 2тг). А это озна-
означает, что справедливо равенство
Х(? + 2тг) =Х(*)С, (8)
где С — постоянная матрица. Положив в равенстве (8) t = 0, получим,
что С = ХBтг). Таким образом,
Х(г + 2тг) = Х(*)ХBтг). (9)
Так как X(t) — фундаментальная матрица решений, то detXB7r) ф О,
и, следовательно, для матрицы ХBтг), как и для всякой невырожденной
матрицы, существует логарифм1 и поэтому она представима в виде:
ХBтг) = е27гВ. A0)
Теперь положим
Y(t) = X(t)e-m. A1)
Тогда
Y(t + 2тг) = X(t + 2тг)е-27гВ-ш =
Таким образом, матрица Y(t) 2тг-периодична, а из A1) следует, что она
непрерывно дифференцируема. Из A1) следует также, что фундамен-
фундаментальная матрица решений Х(?) представима в виде G). Теорема Флоке
доказана.
хСм. гл. 8 книги: ГантмахерФ. Р. Теория матриц. М.: Наука, 1967.
546 Глава XV
Для дальнейшего введем некоторые определения. Собственные чис-
числа \j матрицы В называются характеристическими показателями сис-
системы F). Собственные числа pj матрицы ХBтг) называются мульти-
мультипликаторами системы F). Из формулы A0) следует, что
Pi = e2irA'\ A2)
или
\j = ^(ln\pj\ + iavgpj + i2kTr) (fc = 0, ±1, ±2,...)- A3)
Характеристическое уравнение матрицы ХBтг), т. е. уравнение
det(XB7r) - pEm) = 0, A4)
называется характеристическим уравнением системы F). Отметим
без доказательства1 два утверждения о характеристическом уравне-
уравнении A4): 1) характеристическое уравнение не зависит от выбора фун-
фундаментальной матрицы решений; 2) характеристическое уравнение не
изменится, если систему F) подвергнуть невырожденному линейному
преобразованию с 2тг-периодической матрицей.
Система F) называется приводимой, если существует замена пере-
переменных
x = L(t)y, A5)
такая, что система F) преобразуется в систему с постоянными коэффи-
коэффициентами, а 2тг-периодическая матрица L(?) — непрерывно дифферен-
дифференцируемая, ограниченная при всех t, и такими же свойствами обладает
обратная матрица L-1(i). Имеет место следующая теорема Ляпунова.
Теорема. Линейная система F) с непрерывной периодической матри-
матрицей А(?) приводима.
Доказательство.
Примем за матрицу L(t) преобразования A5) матрицу Y(t), опре-
определенную равенством A1). Она непрерывно дифференцируема и огра-
ограничена при всех t вместе со своей обратной. Остается только показать,
что преобразованная система будет системой с постоянными коэффи-
коэффициентами. В этом легко убедиться, подставив
х = Х(г)е-Шу A6)
1 Доказательство можно найти, например, в гл. 5 книги: МалкинИ. Г. Теория
устойчивости движения. М.: Наука, 1966.
§ 5. Об устойчивости гамилътоновых систем 547
в систему F). Произведя выкладки, получим
? = »'¦ <">
Из формулы A7) видно, что характеристические показатели суть корни
характеристического уравнения преобразованной системы.
Ясно, что задачи об устойчивости систем F) и A7) эквивалент-
эквивалентны. Поэтому система F) устойчива тогда и только тогда, когда все ее
мультипликаторы принадлежат замкнутому единичному кругу \р\ ^ 1,
причем в случае существования кратных мультипликаторов, лежащих
на окружности \р\ = 1, матрица ХBтг) приводится к диагональной фор-
форме.
244. Устойчивость линейных гамильтоновых систем с пе-
периодическими коэффициентами. Пусть в системе C) матрица Н
является непрерывной 2тг-периодической по t, вещественной симмет-
симметрической матрицей. Задача об устойчивости линейных гамильтоновых
систем обладает рядом специфических особенностей по сравнению с за-
задачей об устойчивости общих линейных систем, рассмотренных в пре-
предыдущем пункте. Эти особенности вытекают из теоремы Ляпунова-
Пуанкаре о характеристическом уравнении гамильтоновых систем с
периодическими коэффициентами.
Прежде чем сформулировать теорему, введем определение. Урав-
Уравнение
f(z)=aozm + a1zm-1 + ... + am-1z + am=O {a0 ф 0) A8)
называется возвратным, если коэффициенты его, равноотстоящие от
крайних членов, равны между собой, т. е. если в A8) аи = ат-и- Для
возвратного уравнения имеет место тождество
/(*)= *m/(±) (гфО). A9)
И наоборот, если имеет место тождество A9), то уравнение A8) воз-
возвратное. Из тождества A9) следует, что возвратное уравнение нечет-
нечетной степени обязательно имеет своим корнем число z = — 1. Если т —
четное число, то при помощи подстановки
возвратное уравнение сводится к уравнению степени т/2 относитель-
относительно ш.
548 Глава XV
Имеют место следующие легко проверяемые свойства корней воз-
возвратного уравнения: если у него есть корень z = 1, то кратность это-
этого корня четная; если есть корень z = — 1, то его кратность четная
при четном т и нечетная при нечетном т; если уравнение имеет ко-
корень Zk ф ±1, то оно имеет и взаимно обратный корень zi = 1/zk той
же кратности.
Теорема (Ляпунова—Пуанкаре). Характеристическое уравне-
уравнение A4) линейной гамильтоновой системы C) с 2тг-периодической по t
матрицей Н(?) возвратное.
Доказательство.
Так как преобразование фазового пространства, задаваемое движе-
движениями гамильтоновой системы, является унивалентным каноническим
преобразованием, то (см. п. 171) матрица X(t) фундаментальных реше-
решений системы C) является симплектической, т. е. при всех t справедливо
равенство
X'JX = J. B0)
Так как Х@) = Е2п, то из B0) следует, что при всех t, в том числе и
при t = 2тг, det X = 1.
Рассмотрим следующую цепочку тождеств:
/(р) = det(XB7r) - pE2n) = detXB7r)(E2n -
= det(E2n - pJ-1X'BwK) = det J det(E2n - рХ'Bтг)) det J =
= det(E2n - pXBir))' = det(E2n - рХBтг)) =
= p2™det(xB7r)-iE2n) =P2nf(\).
Отсюда следует, что характеристическое уравнение A4) возвратное, и
теорема Ляпунова-Пуанкаре доказана.
Укажем важнейшие следствия этой теоремы.
Следствие 1. Линейная гамильтонова система C) устойчива тогда и
только тогда, когда все ее мультипликаторы pj расположены на еди-
единичной окружности \р\ = 1 и матрица ХBтг) приводится к диагональ-
диагональной форме.
Следствие 2. Мультипликаторы pj и 1/pj имеют одинаковую крат-
кратность.
Следствие 3. Если характеристическое уравнение A4) имеет ко-
корень р = 1 или р = — 1, то эти корни имеют четную кратность.
§ 5. Об устойчивости гамилътоновых систем 549
245. Алгоритм нормализации гамильтоновой системы ли-
линейных уравнений с периодическими коэффициентами. Снова
рассмотрим систему C), предполагая матрицу H(t) вещественной и
непрерывной 2тг-периодической по t. Согласно теореме Ляпунова, сис-
система C) приводима. Но матрица L(t) замены переменных A5), приво-
приводящей систему C) к системе с постоянными коэффициентами, опре-
определяется неоднозначно. Опишем алгоритм построения такой матри-
матрицы L(t), чтобы соответствующее ей преобразование A5) было вещест-
вещественным, каноническим, 2тг-периодическим по t и приводило бы сис-
систему C) к нормальной форме. Будем предполагать, что характерис-
характеристические показатели Ад, системы C) чисто мнимые (Ад, = г'07,, где
i — мнимая единица, ак — вещественные числа). Мультипликаторы
Pk = ехр(г2тго7г), pn+k = ex-p(—i2w(Tk) (к = 1, 2,... , п) считаем раз-
различными. Как и в п. 189 в случае линейной гамильтовой системы с
постоянными коэффициентами, нормальной формой 2тг-периодической
по t системы C) мы называем такую линейную систему, которой от-
отвечает функция Гамильтона
+ yl+k). B1)
к=1
Ограничимся только описанием алгоритмической части процедуры по-
построения матрицы L(t) г. Пусть Х(?) — фундаментальная матрица сис-
системы C), нормированная условием Х@) = Е2„, а гк и sk — действи-
действительная и мнимая части собственного вектора матрицы ХBтг), соот-
соответствующего мультипликатору рк. Векторы гк и su удовлетворяют
системе линейных уравнений
(ХBтг) - соз2тго-а;Е2П)га; + sm2iT(TkSk = 0,
(ХBтг) - cos2i:(TkE2n)sk = 0.
Из этой системы векторы гк и sk определяются с точностью до посто-
постоянного множителя. Нормируем их так, чтобы выполнялось равенство
4(rW«*) = l (fc = l, 2,..., п). B3)
Такая нормировка всегда возможна. При проведении нормировки в слу-
случае необходимости (как и в п. 188) следует соответствующим образом
выбирать знаки величин ак в функции Гамильтона B1) нормализован-
нормализованной системы.
1 Более подробное изложение можно найти в статье: МаркеевА. П. О нормализа-
нормализации гамильтоновой системы линейных дифференциальных уравнений с периодичес-
периодическими коэффициентами // ПММ. 1972. Т, 36, вып. 5. С. 805-810.
550
Глава XV
После нормировки векторов ги и Sk образуем постоянную квадрат-
квадратную матрицу Р порядка 2п. Ее к-м столбцом возьмем вектор —2su a
(п + к)-м — вектор 2ги-
Образуем, далее, квадратную матрицу Q(t) порядка 2п. Она имеет
такую структуру:
Q(*) =
Di(t) -
B4)
где Di(t) и
диагональные матрицы вида
COS (Tit
cos crnt
D2(t) =
B5)
Матрица L(t) искомого нормализующего преобразования A5) записы-
записывается в виде произведения трех матриц
= X(t)PQ(t).
B6)
Фактическое построение матрицы B6) возможно, как правило, только
на вычислительной машине.
246. Задача о параметрическом резонансе. Линейные га-
мильтоновы системы, содержащие малый параметр. В прило-
приложениях матрица H(t) системы C) обычно зависит от одного или не-
нескольких параметров. Задача о параметрическом резонансе дли систе-
системы C) состоит в определении тех значений параметров, при которых
ее характеристическое уравнение A4) имеет корни (мультипликаторы)
с модулями, большими единицы. Иными словами, эта задача состоит
в нахождении тех значений параметров, при которых система C) не-
неустойчива. Ограничимся рассмотрением того частного случая, когда
функция Гамильтона Н, соответствующая системе C), представляется
в виде сходящегося ряда по степеням малого параметра г:
Н = Н + еН + е Н + • • • , B7)
где Н(°\ Н^\ НB\... — квадратичные формы переменных
х\, жг,..., a?2n; причем коэффициенты формы if(°) постоянны,
а коэффициенты форм Н^\ Н^2\... — непрерывные веществен-
вещественные функции t с общим периодом 2тг. Кроме того, коэффициенты
форм if(°), i?W, H^2\... зависят от одного или нескольких парамет-
параметров.
§ 5. Об устойчивости гамилътоновых систем 551
Рассмотрим зависимость мультипликаторов системы C) (а следо-
следовательно, и ее характеристических показателей) от малого параметра е.
Так как правые части системы C) аналитичны по г, то и фундаменталь-
фундаментальная матрица решений X(t, e) также аналитична по е. Отсюда следует,
что коэффициенты характеристического уравнения A4) — аналити-
аналитические функции е. Но мультипликаторы (и характеристические пока-
показатели) не обязательно аналитичны. Они будут обязательно аналити-
аналитическими, если характеристическое уравнение при е = 0 имеет только
простые корни. Если же при е = О уравнение A4) имеет кратные корни,
то аналитичность его корней относительно е при е ф 0 может не иметь
места. Отметим, однако, что независимо от наличия при г = 0 кратных
корней корни уравнения A4) при е ф О, во всяком случае, непрерывны
по е.1
При е = 0 система уравнений C) имеет постоянные коэффициенты.
Как установлено в п. 242, при наличии хотя бы одного корня характе-
характеристического уравнения E) с отличной от нуля вещественной частью
система C) неустойчива. В этом случае уравнение A4) при г = 0 имеет
хотя бы один корень, модуль которого больше единицы. Ввиду непре-
непрерывности мультипликаторов относительно е характеристическое урав-
уравнение A4) при достаточно малых е также имеет корень, модуль которо-
которого превосходит единицу, и, следовательно, система C) при достаточно
малых е неустойчива. Как видим, в этом случае задача о параметри-
параметрическом резонансе проста и неинтересна.
Пусть теперь при е = О характеристическое уравнение E) систе-
системы C) имеет только чисто мнимые корни ±гот, (к = 1, 2,... , п). Тогда
уравнение A4) при е = 0 имеет только такие корни (мультипликаторы),
модули которых равны единице. Изучим поведение мультипликаторов
при малых е, отличных от нуля.
Сначала рассмотрим случай, когда при е = 0 нет кратных мульти-
мультипликаторов, т. е. когда, согласно A2), выполняются неравенства
ak±a^N (fc,/ = l, 2,... , щ TV = 0, ±1, ±2,...). B8)
В силу непрерывности мультипликаторов, они останутся некратными и
при достаточно малых г, отличных от нуля. Кроме того, при достаточно
малых ? мультипликаторы не могут иметь модулей, больших единицы.
Этот важный вывод является простым следствием теоремы Ляпунова-
Пуанкаре о характеристическом уравнении A4) системы C) (п. 244).
Согласно этой теореме, мультипликаторы расположены симметрично
относительно единичной окружности. При малых г мультипликаторы
не могут сойти с окружности, не нарушив указанной симметрии.
хСм. по этому поводу монографию: МалкинИ. Г. Некоторые задачи теории нели-
нелинейных колебаний. М.: Гостехиздат, 1956.
552
Глава XV
Рис. 177
Действительно, рассмотрим для наглядности случай п = 2. Харак-
Характеристическое уравнение A4) будет уравнением четвертого порядка.
Пусть pj (j = 1, 2, 3, 4) — его корни при е = 0. Будем изображать их
на комплексной плоскости р (рис. 177, а). Пусть при малых е один из
корней, например pi, сошел с окружности и стал по модулю больше еди-
единицы. Из-за вещественности коэффициентов уравнения A4) комплекс-
комплексно сопряженный корень р^1 с необходимостью сместился бы в точку,
симметричную относительно вещественной оси. А так как число всех
корней равно четырем и смещения корней р2, р^1 при малых е малы,
то у сместившегося корня р\ не оказалось бы обратного по величине,
что противоречит теореме Ляпунова-Пуанкаре.
Таким образом, если при г = 0 кратные мультипликаторы отсут-
отсутствуют или, что то же, выполняются условия B8), то система C) при
достаточно малых значениях е устойчива.
Если же при е = 0 существуют кратные мультипликаторы, распо-
расположенные в некоторой точке А единичной окруж ности, то при е ф 0
они могут, вообще говоря, сойти с окружности. При этом они могут
расположиться как изображено на рис. 177, б, и симметрия мульти-
мультипликаторов относительно единичной окружности не будет нарушена.
Но смещение мультипликаторов с единичной окружности происходит
не всегда, и, следовательно, в случае кратных мультипликаторов сис-
система не обязательно неустойчива при е ф 0. Рассмотрим этот вопрос
подробнее.
Предположим, что характеристические показатели iaj, при е = 0
таковы, что все величины аи (к = 1, 2,..., п) различны. Тогда, со-
согласно п. 189, при е = 0 систему C) при помощи линейной веществен-
вещественной канонической замены переменных можно привести к нормальпой
форме. В новых переменных функция Н^ приведется к форме B1) и
§ 5. Об устойчивости гамильтоновых систем 553
функция Гамильтона B7) запишется в виде
k=i
где Н^\ НB\... — квадратичные формы от новых переменных
2/1, г/2,... , 2/2п с непрерывными 2тг-периодическими по t коэффици-
коэффициентами. Задачи о параметрическом резонансе в старых и новых пере-
переменных эквивалентны. Но теперь существенно, что величины 07, в B9)
имеют вполне определенные знаки, полученные в процессе нормализа-
нормализации системы C) при е = 0.
Сформулируем без доказательства1 следующее утверждение.
Теорема. Для достаточно малых е линейная система с функцией Га-
Гамильтона B9) устойчива тогда и только тогда, когда величины aj не
связаны соотношениями
(Tk + (Ti=N (k,l = l, 2,... , щ 7V = 0, ±1, ±2,...). C0)
Иными словами, знак минус в соотношениях B8) можно опустить, а
при выполнении хотя бы одного из равенств C0) всегда можно так подо-
подобрать функции Н^\ Н^2\ ... в B9), что система будет неустойчива.
247. Нахождение областей параметрического резонан-
резонанса. Пусть величины 07, в функции Гамильтона B9) зависят от неко-
некоторого параметра а. И пусть при а = «о выполняется хотя бы одно из
соотношений
ah + al=N (k,1 = 1, 2,... , п; N = ±1, ±2,...). C1)
Когда равенство C1) выполняется при к = I, т. е. когда
2ак = N, C2)
то говорят, что имеет место простой резонанс. Параметрический резо-
резонанс, для которого в C1) к ф I, называется комбинационным. Покажем,
что при условии C1) для сколь угодно малых значений е может су-
существовать область неустойчивости, и найдем ее границы с точностью
до первой степени е включительно. Будем предполагать, что в = 2и
что при е = 0 выполняется одно из резонансных соотношений C1).
1 Доказательство можно найти в статье: J.Moser. New aspects in the theory of
stability of Hamiltonian system // Comm. Pure Appl. Math. 1958. V. 11, № 1. P. 81-114
и в монографии: Якубович В. А., Старжинский В. М. Линейные дифференциальные
уравнения с периодическими коэффициентами и их приложения.— М.: Наука, 1972.
554 Глава XV
Пусть в B9) квадратичная форма Н^> записана в виде
У?УгхУТ (" = + "й + /л + /х2). C3)
г/=2
Будем считать, что функции hVlV2/J/llJ/2(t) в их представлении в ви-
виде рядов Фурье не содержат нулевых гармоник; в противном случае
часть Н^\ не зависящую от t, мы включили бы в Н^°К Найдем об-
область изменения параметра а вблизи резонансного значения «о, для
которой линейная система дифференциальных уравнений, соответству-
соответствующая функции Гамильтона B9), неустойчива. Предполагаем, что при
а = ао выполнено неравенство
d((Tk + щ) , „
da
Будем применять методы теории возмущений, рассмотренные в §7
гл. XI. Нахождение областей неустойчивости основано на нескольких
следующих одно за другим канонических преобразованиях, приводя-
приводящих функцию Гамильтона B9) к некоторой простейшей форме, отра-
отражающей резонансный характер задачи и позволяющей весьма просто
построить искомые области неустойчивости.
Сначала введем комплексно сопряженные канонические перемен-
переменные qk, рк (к = 1, 2) по формулам
91 = 2/3+ «2/1, Ч2=У4+гу2,
Р1=УЗ~гу1, Р2=У4~гу2-
Новая функция Гамильтона равна 2гН. Разлагая стк(а) в ряд в окрест-
окрестности точки «о, получаем
2Ш = i<T1(a0)q1p1 + i(T2(a0)q2P2 +
+ i(a-a0) l^1qiPi + -^
\oaQ auo
_
C5)
Здесь многоточием обозначены члены не ниже второго порядка малости
относительно е и а — «о- Комплекснозначные коэффициенты aVlV2/J/llJ/2
линейным образом выражаются через hVlV2lilli2.
Сделаем замену переменных qk, рк —>¦ q'k, p'k согласно формулам
* = й> Рк = й (& = 1'2)' C6)
§ 5. Об устойчивости гамилътоновых систем 555
где производящая функция S имеет вид
S = qip'i + Я2Р'2 +eW = qxp\ + q2p'2 + s ^ w^^^^q^q^p'^p'^2.
C7)
Функции wVlV2fllfl2 подберем 2тг-периодическими по t и такими, чтобы
в новой функции Гамильтона
Н' = 2Ш+Щ C8)
члены порядка г приняли по возможности наиболее простой вид. Из C6)
и C7) получаем явный вид преобразования ф,, рр, —)¦ q'k, p'k с точностью
до членов порядка г включительно:
f Pk=p>k+ef^ (fc = l, 2), C9)
иРк U1k
где в функции W переменные qp, заменены на q'k. Из C5) и C7)-C9)
получаем выражение для коэффициента при первой степени е в Н'
где
Приравняв в тождестве D0) коэффициенты при q[Vl q^p'i^P^2 ^ полу-
получим дифференциальное уравнение для wvlV2tlltl2:
^mP2 + i[ff(i/ /x) + o-(^ ^)]w =
Если ввести обозначение
Ц\) + 02{V2 ~ &) D2)
и для простоты записи у функций, входящих в уравнение D1), не писать
индексы, то его общее решение может быть записано в виде
t
w(t) = w(G)e-ibt + е~т I eibx(a' - a) dx. D3)
556 Глава XV
Из D3) видно, что если число b не целое, то при любой функции a'(t)
решение w(t) уравнения D1) 2тг-периодическое при условии
= Ц-- [ eibtia-a') dt.
1 - ег27ГЙ J
Таким образом, если число b не целое, то в D0) можно положить
a'(t) = 0.
Если же число b целое, то при a'it) = 0 периодического решения
уравнения D1), вообще говоря, не существует. Для существования пе-
периодического решения следует функцию a'it) выбрать вполне опреде-
определенным образом, именно надо положить, что
„i(f\ — rp-ibt
где
2тг
¦iMa(t) dt, D4)
о
и периодическое решение уравнения D1) будет иметь вид
t
wit) = w@)e-ibt + е~т fic - aix)eibx) dx
о
при произвольном значении w@).
Пусть при а = «о имеет место комбинационный резонанс
<71 («о) + о-2 (а0) = N.
Согласно изложенному выше, полученная после преобразования C6)
функция Гамильтона C8) может быть приведена к виду
Я/ • ( \ i t * • ( \ t t * • ( \
— 20"! \(%0)QlPl ~г ^" v^O/Q2P2 ' 1{С{ — ^0/
+ eicllooe-iNiq[q'2 + coolleiNtp'lP'2) + ... D5)
Теперь введем вещественные переменные (р^, г и по формулам
<p\ р'к = Vb^e-^* (fe = 1, 2). D6)
§ 5. Об устойчивости гамилътоновых систем 557
Замена переменных q'k, p'k —> ipk, fk (tpk — координаты, r\~ — им-
импульсы), задаваемая этими формулами, является каноническим пре-
преобразованием с валентностью 1/Bг). В переменных ipk, i"k функция
Гамильтона примет вид
# * = ^Ып + а2(«0)г2 + (« - «о) (grx + g
cos(<^i + (р2 - Nt) + 7sin(<?i + <^2 - Nt)]
Постоянные величины /3, у, содержащиеся в D7), выражаются через
коэффициенты Фурье, отвечающие TV-й гармонике некоторой линей-
линейной комбинации функций hVlV2/J/llJ/2(t), входящих в функцию Гамильто-
Гамильтона B9). Вычисления, проведенные согласно каноническим преобразова-
преобразованиям C4), C9) и D6), дают следующие выражения для величин /3, -у:
2тг
Р=2^ K^ooii - uiioo) cos Nt + (ftiooi + h0110) sin Nt] dt,
7 = 2~ / [Cbiooi + Лоно) cos TV* - (/loon - /inoo) sin Nt] dt.
о
Сделаем еще одно каноническое преобразование ip^, r^ —>¦ Ф;,, i?;,
*2 + ^, ,,_ч
D9)
г2 = Д2,
где
Изменение переменных Ф;,, Ru со временем будет описываться диффе-
дифференциальными уравнениями, задаваемыми функцией Гамильтона
Н = (а - а0) ( -^-Ri + ~r^R2 ) + sS\/R1R2 sin(*i + Ф2) + • • • E0)
\da0 da0 )
Из соответствующей канонической системы дифференциальных урав-
уравнений с точностью до членов первого порядка относительно г и а — «о
включительно имеем
dR\ dR2
dt dt
E1)
dt ~ ^ "u^ da0
558
Глава XV
Ясно, что в первом приближении по е и а — «о задача об устойчивости
по отношению к переменным г/j (j = 1, 2, 3, 4) в исходной системе
с функцией Гамильтона B9) эквивалентна задаче об устойчивости по
отношению к переменным i?i, i?2 в системе E1). Покажем, что в пер-
первом приближении по е область параметрического резонанса (область
неустойчивости) задается неравенствами
еб
Q-2)
da0
¦ а0 < а < а0 +
еб
da0
E2)
и что при невыполнении этих неравенств имеет место устойчивость.
Действительно, второе утверждение следует из того, что функция
V = (Ri — R2J + Н2 является интегралом системы E1), который, как
нетрудно видеть, будет знакоопределенным по переменным R\ и i?2,
если неравенства E2) не выполняются. Следовательно, согласно теоре-
теореме Ляпунова об устойчивости, система E1) устойчива по отношению к
переменным Ri, R2. Утверждение о неустойчивости следует из сущест-
существования при выполнении неравенств E2) неограниченно растущего со
временем частного решения системы E1):
Ri(t) =
Ф2 =
arcsind,
а — ао d{a\ +
еб
da0
Случай простого параметрического резонанса, например 2cri = N,
рассматривается аналогично. Область неустойчивости задается
неравенствами
da0
+ a0 < a < ao +
da2
da0
E3)
где б =
fl = 2~ / [(^оого - /i2ooo) co&Nt + /11010 si
0
27Г
7 = 2тг / I'11010 C0S-^* ~ (^0020 - /12000) si
dt,
dt.
E4)
§ 5. Об устойчивости гамильтоновых систем 559
248. Уравнение Матье. Уравнением Матье называют дифферен-
дифференциальное уравнение второго порядка с периодическими коэффициента-
коэффициентами вида 2
^-f + (a + /3cost)x = 0, E5)
где а и /3 — постоянные величины. Это уравнение часто встречается
в различных задачах механики, например в теории движения Луны, в
задаче трех тел, в теории колебании упругих систем и т. п. Поэтому
уравнение Матье изучено очень подробно1.
Мы рассмотрим уравнение Матье для случая, когда оно мало отли-
отличается от дифференциального уравнения гармонического осциллятора:
^ a; = 0 @ «С е <С 1). E6)
При е = 0 уравнение описывает колебания с собственной частотой и>.
Согласно предыдущему пункту, при е/Ов плоскости параметров ш, е
могут возникать области неустойчивости, причем для малых значе-
значений е области неустойчивости исходят из тех точек оси е = О, которые
отвечают целым или полуцелым значениям частоты собственных коле-
колебаний:
2uj = N (N = 1, 2, 3,...). E7)
Например, если качели в процессе их раскачивания моделировать маят-
маятником с периодически изменяющейся длиной, то интенсивное раскачи-
раскачивание качелей (т. е. неустойчивость их вертикального положения рав-
равновесия) возникает, когда удвоенная частота собственных колебаний
маятника кратна частоте изменения его длины. На практике обычно
наблюдается случай, когда в формуле E7) N = 1, т. е. когда часто-
частота изменения длины маятника вдвое больше частоты его собственных
колебаний.
Используя общие формулы для областей параметрического резо-
резонанса, полученные в предыдущем пункте, найдем в первом приближе-
приближении по ? области неустойчивости, отвечающие резонансу
2ш = 1. E8)
Если ввести импульс рх, отвечающий координате ж, по формуле рх = ж,
то уравнение E6) будет эквивалентно канонической системе двух урав-
уравнений с функцией Гамильтона
Н = hpx2+w2x2)hcostx2. E9)
'См., например: Стокер Дж. Нелинейные колебания в механических и электричес-
электрических системах. М.: ИЛ, 1953; БейтменГ., ЭрдейиА. Высшие трансцендентные функ-
функции. Эллиптические и автоморфные функции. Функции Ламе и Матье. М.: Наука,
1967.
560 Глава XV
Введем новые переменные q и р при помощи канонического преобразо-
преобразования
Рх = \/пр, х = —q. F0)
Новая функция Гамильтона запишется в виде
H=^(p2 + q2) + ^}CoStq2. F1)
Из формул E3), E4), в которых N = 1, а
/l2000 = oZ;COS*' ^0020 = /llOlO = 0,
получаем область неустойчивости в первом приближении по е:
-\ш+\<ш< \ + \е. F2)
Пример 1 (Устойчивость эксцентриситетных колебаний твердого
тела НА эллиптической орбите). В п. 230 найдены плоские периоди-
периодические колебания твердого тела, вызванные эллиптичностью орбиты
его центра масс. В обозначениях п. 128, 230 эти колебания имеют вид
-... {иоф1), F3)
и? -1
где многоточием обозначены члены выше первого порядка относительно
эксцентриситета орбиты е.
Для исследования устойчивости движения F3) введем возмуще-
возмущение х по формуле
ip =ip* + х . F4)
1-he cos г/ у '
Подставив это значение <р в уравнение C7) п. 230 и произведя его лине-
линеаризацию относительно х, получим, что с точностью до первой сте-
степени е линейное уравнение возмущенного движения будет иметь вид
уравнения Матъе
сРх , г
dv2
¦ еA — и>1) cosi/Ja: = 0. F5)
При значении loq, близком У2, возникает область неустойчивости. В
соответствии с формулой F2) она задается неравенствами1
-|е+| <w0 < | + |е. F6)
1 Совершенно из других соображений область неустойчивости F6) получена в
гл. 2 книги: Белецкий В. В. Движение искусственного спутника относительно центра
масс. М.: Наука, 1965.
Список литературы
[1] Аппель П. Теоретическая механика: В 2-х т. М.: Физматгиз, 1960.
[2] Бухгольц Н. Н. Основной курс теоретической механики: В 2-х ч. М.:
Наука, 1972.
[3] Балле Пуссен Ш.Ж. Лекции по теоретической механике. М.: ИЛ,
т. 1, 1948; т. 2, 1949.
[4] Гантмахер Ф. Р. Лекции по аналитической механике. М.: Наука,
1966.
[5] Ламб Г. Теоретическая механика. Т. 2. М.: Гостехиздат, 1935.
[6] Леви-Чивита Т., Амальди У. Курс теоретической механики. Т. 2,
ч. 2. М.: ИЛ, 1951.
[7] Ляпунов А. М. Лекции по теоретической механике. Киев. Наукова
думка, 1982.
[8] Раус Э. Динамика системы твердых тел. Т. 1. М.: Наука, 1983.
[9] Суслов Г. К. Теоретическая механика. М.: Гостехиздат, 1946.
Предметный указатель
Аксиома взаимодействия 87
— динамики основная 86
— инерции 85, 86
— независимости действия сил 87,
88
Аксоид неподвижный 61
— подвижный 61
Амплитуда 185
Аномалия истинная 239
— средняя 243
— эксцентрическая 243
Апоцентр 240
Валентность канонического преоб-
преобразования 339
Вариация 38
Варьирование изоэнергетическое
482
— по Гауссу 40, 107
— по Журдену 40, 106
— синхронное 38
Вектор Лапласа 238
— амплитудный главного колеба-
колебания 504
— главный 90
сил тяготения 247
ударных импульсов 408
Верчение 222, 223
Винт динамический 136
левый 137
правый 137
— кинематический 70
левый 71
правый 71
Возмущение 514
Вращение 49
— мгновенное 57
— стационарное 190
Время абсолютное 19
Герполодия 195
Гироскоп 207
— уравновешенный 210
Движение Эйлера-Пуансо 194
— абсолютное 19, 72
— возмущенное 514
— замедленное 24
— импульсивное 406
— криволинейное 20
— круговое 20
— мгновенно винтовое 71
поступательное 57, 59
— механическое 15
— невозмущенное 514
неустановившееся 515
установившееся 515
устойчивое 515
ассимптотически 515
— относительно центра масс 151
— относительное 71
— переносное 71
— плоское 64
— поступательное 56
— прямолинейное 20
— равномерное 24
— сложное 71, 72
— среднее 241
— стационарное 496
— сферическое 52
— ускоренное 24
Действие по Гамильтону 474
— по Лагранжу 484
Предметный указатель
563
Дельта амплитуды 185
Динама 136
Динамика 16
Диссипация неполная 279
— полная 279
Длина приведенная физического
маятника 180
Долгота восходящего узла 244
Задача двух тел 234
— трех тел общая 244
ограниченная 244, 325
— динамики основная вторая 89
первая 89
Закон Кеплера второй 237
первый 239
третий 241
— Ньютона второй 87
первый 85
третий 87
— Паскаля 115
— сложения сил 87, 88
— сохранения количества движе-
движения 158
энергии 168
кинетического момента 161
— трения Кулона 222
Импульс внешних сил 157
— моментов внешних сил 161
— обобщенный 283
— ударный 406
обобщенный 459
сил инерции 437
Инвариант кинематический вто-
второй 69
первый 69
— статический второй 136
первый 136
Инертность 86
Интеграл Лапласа 237
— Якоби 288
— общий 359
— первый 156, 314
— площадей 236
— полный 359
— эллиптический второго рода
184
второго рода полный 184
первого рода 184
первого рода полный 184
— энергии в задаче двух тел 237
обобщенный 288
Качение 222
Килограмм 87
Кинематика 19
Ковариантность 270
Колебание главное 504
Колебания малые 501
— нормальные 504
— эксцентриситетные 510
Количество движения 150
Координаты главные 503
— криволинейные 27
ортогональные 28
— нормальные 503
— обобщенные 41
— позиционные 494
Косинус эллиптический 185
Коэффициент восстановления 425
— устойчивости 538
— форм главных колебаний 506
Коэффициенты Ламе 28
Кривая геодезическая 485
— фазовая 181
Критерий Рауса-Гурвица 534
Лагранжиан 274
Линия действия силы 91
— координатная 27
— узлов 50
Масса 86
Матрица Гурвица 533
564
Предметный указатель
— симплектическая 339
обобщенно 339
Маятник сферический 329
— физический 180
Мера принуждения 107
Метод Ляпунова прямой 517
Механика 15
— небесная 234
— опытная 15
— теоретическая 15
Множитель 316, 317
— последний 321
Якоби 321
— связи 296
— Якоби 316
Модуль эллиптического интеграла
184
— дополнительный 185
Момент гироскопический 212
— главный сил тяготения 245
системы сил относительно
оси 92
системы сил относительно
точки 92
ударных импульсов 408
— гравитационный 245, 246
— инерции главный центральный
146
осевой 145
относительно оси 140
полярный 140
центробежный 145
— инерции главный 146
— кинетический системы относи-
относительно оси 151
относительно точки 91
относительно центра 151
точки относительно оси 150
точки относительно центра
150
— количества движения системы
относительно оси главный 151
системы относительно
центра главный 151
точки относительно оси
150
— пары сил 134
— пары вращений 80
— силы относительно оси 91
Мощность непотенциальных сил
276
Мультипликатор 546
Наклонение орбиты 244
Нить идеальная 100
Нутация 213
Ньютон 85, 87
Область возможности движения
182
Определитель Гурвица 534
Ось винтовая мгновенная 70
— вращения 49
мгновенная 57, 61
— динамической симметрии 191
— инерции главная 146
центральная 146
— координатная 28
— удара 420
— центральная 137
Пара вращений 80
— сил 133
Параметр винта 70
Переменные Гамильтона 283
— Лагранжа 283
— Рауса 293
— действие-угол 371
для задачи двух тел 381
для маятника 375
— канонически сопряженные 284
Перемещение винтовое 49
— виртуальное 37, 38
— возможное 35
Предметный указатель
565
— действительное 37
— поступательное 49
Перицентр 240
Плечо пары вращений 80
сил 133
Плоскость Пуансо 194
— пары вращений 80
сил 133
— фазовая 181
Поверхность абсолютно гладкая
223
Показатели характеристические
546
Покой мгновенный 57
Поле силовое 94
потенциальное 95
нестационарное 95
стационарное 95
центральное 96
Полодия 195
Положение возможное 34
— конечное 467
— начальное 467
— равновесия 181, 489
неустойчивое 489
устойчивое 489
Полюс 49
Потенциал 95
— Рауса 330, 496
— кинетический 274
— обобщенный 280
— приведенный 330, 496
Преобразование Биркгофа 398, 399
— Лежандра 283, 284
— каноническое 338, 341
свободное 349
унивалентное 339
Прецессия 191, 192
— регулярная 192
Принуждение 107
Принцип Гамильтона-Остроград-
ского 467, 472, 474
— Гаусса 107, 108
в теории импульсивных дви-
движений 440
— Даламбера-Лагранжа 102, 104
— Журдена 106
в теории импульсивных дви-
движении 439
— Лагранжа 113
— Мопертюи-Лагранжа 482, 484
— вариационный 102
дифференциальный 102
интегральный 102
— виртуальных перемещений 113
— детерминированности Ньютона-
Лапласа 89
— наименьшего действия 479
Якоби 484
— наименьшего принуждения 108
— относительности Галилея 85
Производная абсолютная 72
— локальная 72
— относительная 72
Пространство абсолютное 19
— конфигураций 42
— координатное 42
— фазовое 289
Псевдокоординаты 46
Псевдоскорость 46
Псевдоускорение 46
Путь действительный 467
— истинный 467
— окольный 468, 482
— прямой 467, 482
Работа полная 93
— элементарная 93
Равновесие 89, 489
— тела на орбите относительное
250
Равнодействующая 88, 127
Радиус инерции 140
566
Предметный указатель
Расстояние угловое перицентра от
узла 244
Расход массы секундный 258
Реакция нормальная 222
Реакция связи 88
Резонанс 508
— параметрический комбинаци-
комбинационный 553
простой 553
Связь 31
— геометрическая 32
— голономная 32
— двусторонняя 32
— дифференциальная 32
— идеальная 98
— интегрируемая 32
— катастатическая 436
— кинематическая 32
— конечная 32
— неголономная 32
— неосвобождающая 32
— неудерживающая 32
— обратимая 436
— односторонняя 32
— освобождающая 32
— склерономная 34
— стационарная 34
— удерживающая 32
Сепаратриса 183
Сила 15, 85
— активная 88
— внешняя 89
— внутренняя 89
— гироскопическая 277
— диссипативная 279
— заданная 88
— инерции 103
кориолисова 171
переносная 171
— обобщенная 97
соответствующая псевдоко-
псевдокоординатам 307
— пассивная 89
— потенциальная 95
— реактивная 256, 258
— трения 222
покоя 223
скольжения 223
— ударная 406
Силы сходящиеся 128
Синус эллиптический 185
Система гироскопически несвя-
несвязанная 495
— голономная 33
— диссипативная 279
— замкнутая 86
— консервативная 277
— координат кенигова 151
неподвижная 19
орбитальная 246
— координат абсолютная 19
— материальных точек 20
— механическая 20
— натуральная 282
— неголономная 34
— ненатуральная 283
— несвободная 31
— обобщенно консервативная 287
— отсчета 19
абсолютная 19
инерциальная 85
неподвижная 19
— переменного состава 254
— приведенная 330
— приводимая 546
— реономная 34
— свободная 31
— сил 89
статически неопределимая
124
определимая 124
сходящихся 128
Предметный указатель
567
уравновешенная 121
эквивалентная нулю 121
— склерономная 34
Системы сил эквивалентные 121
Скобка Лагранжа 340
— Пуассона 334
Скольжение 195
Скорость 21
— абсолютная 72
— верчения 222
— возможная 35
— гиперболическая 240
— качения 222
— космическая вторая 240
первая 240
— обобщенная 44
— относительная 72
— параболическая 239
— переносная 72
— поступательного движения 57
— потерянная 413
— прецессии 192
— приобретенная 413
— радиальная 26
— секторная 237
— скольжения 222
— собственного вращения 192
— трансверсальная 26
— угловая 25
мгновенная 61
— фазовая 181
— эллиптическая 239
Спираль Архимеда 27
Статика 16, 89
Степени свободы системы 40
Степень неустойчивости 538
Сферический маятник 270
Тело абсолютно твердое 47
— твердое 47
динамически симметричное
191
переменного состава 263
свободное 48
Тензор инерции 144, 145
Теорема Аппеля 464
— Бернулли-Шаля 55
— Вариньона 127
— Гюйгенса-Штейнера 143
— Гюйгенса 24
— Делонэ-Бертрана 451
— Карно вторая 446
обобщенная 450
первая 444
третья 450
— Кенига 154
— Кориолиса 74
— Лагранжа 490
— Лиувилля 348, 368
— Ляпунова о неустойчивости
вторая 527
о неустойчивости первая 526
о приводимости 546
об устойчивости 517
асимптотической 522
по первому приближению
529
— Ляпунова-Пуанкаре 548
— Моцци 54
— Пуансо 135
— Рауса 497
— Резаля 208
— Робена 440
— Томсона 455
— Флоке 545
— Четаева о неустойчивости 525
— Шаля 53
— Эйлера 52
об однородных функциях 276
— Якоби 359
— Якоби-Пуассона 335
— о движении центра масс 157
— о сложении ускорений 74
— о трех моментах 131
568
Предметный указатель
— о трех силах 127
— об изменении кинетического
момента 159, 160
в неинерциальной системе
отсчета 171
при импульсивном движе-
движении 410
— об изменении кинетической
энергии 167
в неинерциальной системе
отсчета 172
при импульсивном движе-
движении 412
— об изменении количества дви-
движения 157
в неинерциальной системе
отсчета 171
при импульсивном движе-
движении 409
— об изменении полной механи-
механической энергии голономной сис-
системы 276
— об инвариантности множителя
320
Теоремы Ляпунова о неустойчи-
неустойчивости равновесия 492
— Томсона-Тэта-Четаева 535,
538, 540
Теория возмущений 388
— гироскопа элементарная 210
Тождество Пуассона 334
Точка изображающая 42
— материальная 20, 85
изолированная 86
переменного состава 255
— фазовая 181
Траектория точки 20
Трение 222
Углы Эйлера 50
Угол нутации 50
— прецессии 50
— собственного вращения 50
Удар 406
— абсолютно неупругий 425
— абсолютно упругий 425
— неупругий 425
— прямой 432
— центральный 432
Уравнение Гамильтона-Якоби 358
для консервативных и обоб-
обобщенно консервативных систем
360
для систем с циклическими
координатами 360
— Кеплера 243
— Матье 559
— Мещерского 258
обобщенное 258
— Пуассона 204
— вековое 504
— возвратное 547
— динамики общее 103
в обобщенных координа-
координатах 269
в теории импульсивных
движений 437
— статики общее 113
— характеристическое 546
— частот 504
Уравнения Воронца 301
— Гамильтона 284, 285
— Лагранжа второго рода 269
для импульсивных движе-
движений 460
— Рауса 293
— Уиттекера 290
— Чаплыгина 301
— Эйлера динамические 189
кинематические 79
— Якоби 291
— возмущенного движения 515
— канонические 284, 285
Уравнения Аппеля 308
Предметный указатель
569
Ускорение 21
— Кориолиса 74
— абсолютное 72
— возможное 35
— вращательное 59
— касательное 24
— нормальное 24
— обобщенное 44
— осестремительное 59
— относительное 72
— переносное 72
— поступательного движения 57
— тангенциальное 24
— угловое 25, 59
Условие Маиевского-Четаева 521
Устойчивость 515
— асимптотическая 515
— вековая 540
— временная 540
Фокусы кинетические сопряжен-
сопряженные 469
Форма нормальная уравнений Га-
Гамильтона 396
Формула Ривальса 59
— Циолковского 260
— Эйлера 58
— гироскопии основная 208
приближенная 210
Функция Гамильтона 285, 343, 353
характеристическая 361
— Лагранжа 274
— Ляпунова 515
— Рауса 293
— Рэлея диссипативная 280
— знакоопределенная 516
— знакопеременная 516
— знакопостоянная 516
— определенно-отрицательная 516
— определенно-положительная
516
— производящая свободного кано-
канонического преобразования 349
— силовая 95
Центр 150
— инерции 140
— конечного вращения 55
— масс 140
— скоростей мгновенный 65
— удара 420
— ускорений мгновенный 67
Центроида 66
— неподвижная 66
— подвижная 66
Число степеней свободы системы
40
— Циолковского 260
Эквивалентность систем сил 121,
124
Элементы орбиты Делонэ 385
кеплеровские 243
Пуанкаре 387
Эллипсоид инерции 146
— центральный 146
Энергия кинетическая 154
потерянных скоростей 413
приобретенных скоростей
413
— полная 168
обобщенная 288
— потенциальная 95
приведенная 496
— ускорений 308, 310